Целые функции. - Маркушевич А.И.

Глава вторая. Максимум модуля и порядок целой функции
Глава четвертая. Основная теорема высшей алгебры и малая теорема Пикара
Глава пятая. Алгебраические соотношения. Теоремы сложения
§ 2. Целые периодические функции. Теорема Вейерштрасса
Автор: Маркушевич А.И.
Теги: анализ математика целые функции
Год: 1975
Похожие
Асимптотические оценки и целые функции
Высшие трансцендентные функции. Гипергеометрическая функция. Функции Лежандра
Целые функции. Курс лекций
Целые функции многих комплексных переменных
Текст
                    А.И.МАРКУШЕВИЧ
лы
У
ц

А. И. МАРКУШЕВИЧ
ЦЕЛЫЕ
ФУНКЦИИ
ЭЛЕМЕНТАРНЫЙ
ОЧЕРК
Издание второе,
исправленное и дополненное
ш
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
Москва 1975

517.2
Μ 25
УДК 517.535.4
Главная редакция
20203—163 -- физико-математической литературы

ОГЛАВЛЕНИЕ
Предисловие. ..,,.,,«».».. 4
Глава первая. Понятие целой функции ... 7
Глава вторая. Максимум модуля и порядок
целой функции 22
Глава третья. Нули целой функции 45
Глава четвертая. Основная теорема высшей
алгебры и малая теорема Пикара 53
Глава пятая. Алгебраические соотношения.
Теоремы сложения 75
Приложение 96
§ 1. Малая теорема Пикара 96
§ 2. Целые периодические функции. Теорема
Вейерштрасса ПО

ПРЕДИСЛОВИЕ
Целые функции — самые простые и самые
распространенные функции. В курсе математики средней
школы рассматриваются либо целые функции (степень
с натуральным показателем, многочлен,
показательная функция, синус и косинус), либо функции
дробные (мероморфные), т. е. частные двух целых
функций (дробно-рациональные, тангенс, котангенс), либо,
наконец, обратные по отношению к целым и дробным
(корень с натуральным показателем, логарифмы,
обратные тригонометрические функции).
Целые функции обладают многими
замечательными свойствами. Но общая их теория, которой
посвящены специальные книги, требует для понимания
знания университетского курса теории аналитических
функций. Настоящая книжка не предполагает у
читателя подобных знаний. По сути дела, для чтения
основного текста нужны только знакомство с
комплексными числами и алгебраическими операциями над
ними и знание основ математического анализа
(дифференцирование и интегрирование, понятие
сходящегося ряда).
Конечно, эта книжка не дает и не может дать
развернутой теории целых функций — это дело
специальных монографий. Мы включили в нее главным
образом те сведения, которые помогают лучше и глубже
понять факты, относящиеся к школьному курсу. Здесь
4

выясняются сходство и различие между
алгебраическим и трансцендентным (с точки зрения анализа, но
не теории чисел). Выражаясь описательно,
трансцендентные целые функции — и по способу задания, и по
быстроте роста — это «многочлены бесконечно
высокой степени».
Например, «малая теорема Пикара»,
утверждающая, что уравнение вида f(x) = A, где
f(x)—трансцендентная целая функция и Л — данное комплексное
число, имеет, вообще говоря, бесконечное множество
корней, рассматривается как аналог основной теоремы
алгебры, в силу которой число корней уравнения
Р(х) = А, где Р(х)—многочлен, равно степени
многочлена. Малая теорема Пикара (точнее, некоторое
видоизменение ее, доказанное в § 1 Приложения)
позволяет установить, что уравнение 2х = Ах имеет
бесконечное множество корней, если А ф О, а уравнение
вида sin χ — Ах — бесконечное множество корней для
всех А без исключения. Указывается, как находить
асимптотические выражения этих корней.
Далее рассматриваются некоторые алгебраические
соотношения между целыми функциями (простейший
пример: sin2 χ + cos2 χ = 1), периодичность и
алгебраические теоремы сложения (пример: αΧ]α*2=αΧι+Χ2).
Книжка завершается теоремой Вейерштрасса
о том, что целые функции, обладающие теоремой
сложения, — это многочлены (алгебраические либо
тригонометрические) .
Для удобства читателей книжка разделена на две
части.
Основной текст, состоящий из первых пяти глав,
мы старались сделать наиболее доступным, исключив
из него доказательства сравнительно трудных теорем.
В основу этой части положены две лекции, читанные
автором весной 1962 г. на курсах усовершенствования
учителей при Московском университете.
5

Часть, выделенная в качестве Приложения,
содержит доказательство малой теоремы Пикара для целых
функций конечного порядка, разложение целой
периодической функции в тригонометрический ряд и
теорему Вейерштрасса (в ослабленном виде) о целых
функциях с алгебраической теоремой сложения.
В первой главе некоторые основные предложения
общей теории аналитических функций
сформулированы, но оставлены без доказательства. Тем, кто захочет
получить систематические сведения в этой области,
рекомендуем книги: В. Л. Гончаров, Теория
функций комплексного переменного, Москва, Учпедгиз,
1955; Б. Α. Φ у к с и Б. В. Ш а б а т, Функции
комплексного переменного и некоторые их приложения, изд. 3,
Москва, «Наука», 1964 или наш «Краткий курс
теории аналитических функций», Москва, Физматгиз,
1961, к которому приложен и список литературы для
дальнейшего чтения. К этому списку следует
присоединить еще содержательную книгу М. А. Евграфова
«Асимптотические оценки и целые функции», изд. 2,
переработанное, Москва, Физматгиз, 1962,
Автор

ГЛАВА ПЕРВАЯ
ПОНЯТИЕ ЦЕЛОЙ ФУНКЦИИ
1. Естественным обобщением понятия многочлена
являются всюду сходящиеся степенные ряды:
а0 + а1х + а2х2+ ... + апхп + ... (1)
Если здесь все коэффициенты, начиная с
некоторого (п + 1)-го, обращаются в нуль, то мы получаем
как частный случай такого ряда многочлен степени
не выше п:
Ρ (χ) = aQ + а{х+ ... + апхп. (2)
Простейший известный из курса средней школы
степенной ряд
1 + х + х2 + ... +хп+ ...
не является всюду сходящимся; он сходится только
при \х\ < 1. Сходиться при |x| ^5 1 ему мешают
слишком крупные коэффициенты (здесь ап = 1 при
любом п)._
Можно показать, что степенной ряд (1) будет
сходиться при любом χ тогда и только тогда, когда
limVl^j" = 0. (3)
П->оо
Ограничимся здесь доказательством достаточности
этого условия. При х = 0 ряд (1) сходится. Пусть
теперь χ φ 0. Тогда в силу условия (3) можно найти
такое Ν, что при п> N будет выполняться неравен-
.ство л/\ап\<-£щ, или | ап \\хп\< ψ-. Но это
означает, что все члены ряда (1) при η > Ν по
абсолютной величине меньше, чем члены геометрической
прогрессии со знаменателем у. Поэтому ряд (1)
сходится и притом абсолютно»
7

Мы будем считать в дальнейшем, что условие (3)
выполнено. Впрочем, иногда удобнее пользоваться
более простым достаточным (но не необходимым) уело-
вием сходимости ряда (1) всюду:
lim-^^-=0. (3r)
n-»oo an v '
Действительно, в этом случае предел отношения
последующего члена ряда (1) к предыдущему члену
ап+1хп+{: апхп = {ап+1: ап) χ
(предполагается, что апФ0 и хФО) будет также
равен нулю. Отсюда абсолютная сходимость ряда при
любом χ следует по известному признаку Даламбера.
Так, например, ряд
Х^ X X
всюду сходится, потому что
lim A/^=lim±e(
Точно так же ряд
Υ γ2 γΖ γΤΙ
1+7Г + 1Г + "зГ+ "· + ΊΪΓ +
всюду сходится, потому что
Jlmi7^w4]==0·
2. Сумма всюду сходящегося степенного ряда (1)
называется целой функцией.
Отсюда следует, что каждый многочлен является
целой функцией.
Другие примеры целых функций — это
показательная функция ах (0 < α, α Φ 1), cos#, sin x.
Действительно, в курсах анализа доказывается (с помощью
формулы Тейлора), что каждая из них изображается
суммой всюду сходящегося степенного ряда:
cos л: = 1 —|г "+* "Ϊ!— '•-, (5)
sin л: = я — ΊϊΓ + ΊΠ— ··· ^

В частном случае при а = е = 2,71828 ... (е — не-
перово число) получаем из формулы (4):
еХ=*+1Г + Ж+ .·.+-£+... (40
Отправляясь от этих формул, можно получить
множество других простых примеров целых функций:
^'-ΤΓ + ΐ-'·· +(-!)*-£+ ···'
3 ν6 χ3η
<"-ι+ΤΓ + ΊΓ +
1 /ι! ' ·"
ех —\ — χ J_ , _£_ ι _fl ι . χ""2 .
a:2 ~"2!t3!+4!+ ,,,+ nl +
sin λ; .. j^ , _**_
χ
cos У* = 1 ~ "2Γ *"*" ΤΓ ~~" Ίγ "^ "'''
sin λ/λ: . #_ . χ2
л]х~ ~ 3! +~δΓ "'
■ = * +"зГ + "5Г+ ···
и т. п.
Во всех этих примерах целые функции были
элементарными (показательная и
тригонометрические), либо простейшими комбинациями
элементарных функций.
Но, конечно, далеко не всегда целые функции
выражаются конечной комбинацией элементарных
функций. Таковы, например, целые функции
X2 X3 Хп
I \Х) = X + ~22" "Г "зГ Τ · · · ~Г ~^7Г *П « · · 9
ё ^ = -ζϊ^ψ + (in З)3 + · · · + (ln/г)* + · · ··
#2 JC3 ХП
и бесчисленное множество других, определяемых
рядами вида (1), при единственном условии (3),
наложенном на их коэффициенты.

3. До сих пор мы рассматривали целые функции,
молчаливо предполагая, что коэффициенты
степенного ряда — действительные числа и что переменное χ
также принимает действительные значения. Однако
ничто не мешает и те и другие считать любыми
комплексными числами, лишь бы по-прежнему
выполнялось условие (3), наложенное на коэффициенты ряда.
В самом деле, это условие обеспечивает абсолютную
сходимость ряда при любом значении модуля'
комплексного числа х. В дальнейшем во избежание
недоразумений мы сохраним букву χ для обозначения
действительного числа, а комплексное независимое
переменное будем обозначать буквой г, полагая z—x-\-iyy
где χ и у— действительные числа и / = д/—1.
Комплексное переменное г, как обычно, будет
геометрически представляться точкой плоскости с координатами
χ и у. В частности, ζ при у = 0 будет принимать
действительные значения ζ = χ. Любую целую функцию
можно будет рассматривать как функцию
комплексного переменного ζ, определенную во всей
комплексной плоскости. Сохраняя для показательной и
тригонометрических функций прежние наименования и
обозначения, будем иметь:
**=1 + ΊΓ + ΊΓ + ΊΓ + ΊΓ + ·'· +5+···· (7)
Ζ2 Ζ4 Ζ6 Ζ2η
cosz=l-ir + ir-gr+...+(-l)n(-Sjji + ...,(8)
г3 г5 η ι г2"-1
81пг = г-1Г + ж-...+(-1)- "(ΐ^ΓΤΓι + ··· (9)
4. Целые функции являются частным случаем
аналитических функций комплексного переменного. Если
каждой точке ζ какой-либо области G плоскости
комплексного переменного поставлено в соответствие
определенное комплексное число w, то говорят, что в
области G определена функция комплексного
переменного z\ при этом w называют значением функции
в точке ζ и пишут:
w = f(z);
вместо f могут быть использованы и другие буквы
латинского или греческого алфавита.
10

Функция комплексного переменного называется
аналитической в области G, если для каждой точки zo,
принадлежащей G, можно указать окрестность (т. е.
круг с центром в этой точке), в которой значения
функции представляются в виде суммы степенного
ряда, расположенного по степеням ζ — ζ0:
W = f(z) = C0 + Ci(2 — Z0) + C2 (Z — Zq)2 + ...
... +са(г-гая+ ... (Ю)
В частном случае, когда область G есть круг с
центром в точке го, для аналитичности f(z) в области G
достаточно потребовать, чтобы ряд (10) представлял
функцию f(z) во всем этом круге. В самом деле,
чтобы получить разложение f(z) в степенной ряд в
окрестности какой-либо Другой точки Ζι круга, достаточно
в формуле (10) представить ζ — ζ0 в виде
2 — Ζ0 = (Ζ — Zj) — (Ζ0— Ζι),
разложить каждый член ряда an(z — z0)n по степеням
разности ζ — Ζι, а затем собрать члены с одинаковыми
степенями ζ — zt (т. е. привести подобные члены).
То, что было сказано для случая круговой области,
применимо также и тогда, когда G есть вся
комплексная плоскость; ее можно рассматривать как круг
бесконечного радиуса с центром в любой точке, например
в начале координат.
В этом случае в формуле (10) можно положить
Zo = 0 и потребовать, чтобы ряд сходился во всей
плоскости (был всюду сходящимся степенным рядом, как
мы говорили выше).
Итак, целую функцию f(z) можно определить как
функцию комплексного переменного, аналитическую
во всей плоскости комплексного переменного ζ.
5. Производной функции комплексного переменного
f(z) в какой-либо точке z0 области, где функция
определена, называется предел (если он существует) отно-
шения ζ —ζ при 2ι,->ζ(ζ! Φ ζ), т. е.
ZX-*Z Zl Ζ
Из этого определения производной вытекает, что
правила дифференцирования, установленные для
И

функций действительного переменного, сохраняются
и для функций комплексного переменного. В
частности,
Можно показать, что сумма степенного ряда (10),
сходящегося в некотором круге с центром г0, обладает
в этом круге производными любого порядка. Каждая
из них получается путем, почленного
дифференцирования ряда (10), выполненного соответствующее
число раз:
f'(z) = cl + 2c2(z-Zo) + 3c3(z-z0)2+ ...
... +псп(г-го)п-1+ ...,
Г(г)=1.2с2 + 2.3са(г-2ь)+ ···
... +(п-1)псп(г-гаа~2+ ....
f'" (ζ) = 1 · 2 · Зс3 + 2 · 3 · 4с4 (ζ - г0) + ...
... +(п-2)(п-1)псп(г-го)я~*+ ....
Так, например, получим из формул (7), (8) и (9)
путем почленного дифференцирования
(ег)' = ег> (cos ζ)' = — sin z, (sin ζ)' = cos z.
Положим г=г0 в рядах для/(г), f'(z),f"(z), ...,/(/?)(г)> ···;
получим;
c, = f{z0), сх = ГЫ> C2 = ZWL^ •••^p = -^7TL. ·····
следовательно, коэффициенты степенного ряда
выражаются через значения в точке z0 производных от
суммы ряда. Поэтому ряд, представляющий функцию
f(z), можно записать в виде
f(z) = f(zo) + ^(z-z0)+f-^-{z-z0y+ ...
•. · Η -j (z zq) + .. ·
Ряд такого вида называется рядом Тейлора функции
f(z). Итак, степенной ряд, представляющий
аналитическую функцию f(z)t является для нее рядом
Тейлора.
12

Из полученных выражений для коэффициентов
степенного ряда следует, что если суммы двух степенных
рядов, расположенных по степеням ζ — ζ0, совпадают
в некотором круге с центром г0, то коэффициенты при
одинаковых степенях ζ — г0 должны быть попарно
равными.
В самом деле, если
а0 + ах {ζ — zQ) + .,. + ап (ζ — ζ0)η + ... =
= 6o + M*-?q)+ ··· +Μζ~ΖοΓ+...=/(ζ),
то
η _У(Я)Ы „ Λ _ f^to)
т. е. ап = Ьп при η = 0, 1, 2, 3, ... (Напомним, что
под f{0){z) подразумевается сама функция f(z), a 0!
принимается равным 1.)
Из того, что сумма степенного ряда имеет
производную, вытекает, что функция f(z)y аналитическая в
области G, обладает производной в каждой точке этой
области, г. е. дифференцируема в области G; поэтому
она и непрерывна в области G.
Замечательно, что имеет место и обратная теорема:
если функция f(z) комплексного переменного ζ
дифференцируема в некоторой области G, то она является
аналитической в этой области.
Вот почему определение аналитической функции
комплексного переменного может быть представлено
в следующей форме: функция f(z) комплексного
переменного ζ, определенная в некоторой области G,
называется аналитической в области, если она
дифференцируема в ней. Именно это определение обычно и
приводится в учебниках теории функций.
Следовательно, целую функцию можно определить
как функцию, дифференцируемую во всей плоскости.
Пусть f(z) и g(z)—какие-либо целые функции.
Тогда, в силу правил дифференцирования, будем
иметь:
[f(z)±g(z)Y = f'(z)±g'(z),
[f(z)-g(z)], = f(z)g(z) + f(z)g,(z),
Ш-Г(ж)ж(йГ^('),(,) <«»««*<».
{f[g(z)]}' = rig(z)]g'(z).
13

Из первых двух формул следует, что сумма,
разность и произведение целых функций — функции
целые.
Из третьей: частное двух целых функций есть
также целая функция, если только делитель нигде не
обращается в нуль.
Из четвертой, представляющей правило
дифференцирования сложной функции: целая функция от
целой функции есть также целая функция.
Например, целыми являются функции:
es{nz9 ee*, sin(e2), sin (cos ζ)
и т. д.
6. Благодаря своей сходимости (абсолютной)
всюду сходящиеся степенные ряды обладают многими
свойствами конечных сумм.
Во всяком случае, операции сложения, вычитания
и умножения выполняются над ними по тем же
правилам, как и одноименные операции над
многочленами, расположенными по возрастающим степеням ζ.
Так, если
/ (г) = α0 + αλζ + α2ζ2 + .. . + αηζη + ...,
g(z) = bQ + b{z + b2z* + ... +bnzn+ ...,
то
/ (z)±g (ζ) = (α0±60) + (αι±*ι) z+(a2±b2) ζ' + .
... +(an±bn)zn+ .
/ (ζ) g (z) = a0b0 + {αφχ + axb0) ζ +
+ (βΦι + α Α + a2b0) z2+ ...
... + (αΦη + я Α-1 + αΦη-2 + .. · + anb0) zn + .
(Π)
Если известно еще, что g(z) не обращается в нуль ни
при каком ζ, то можно утверждать (см. п. 5), что и
частное f(z):g(z) будет целой функцией;
соответствующий степенной ряд получится путем деления
ряда для f(z) на ряд для g(z) no правилам деления
многочленов.
14

Выполним несколько первых шагов этой операции:
а0+ ахг + a2z2 +...+дпгп+.. .| b0+blz+b2z2 + .. ,+Ьпгп+...
αι^ο —
bo
«ι&ο —
(й260 -
■ζ+ψ
г'+...
dob 1 , Й2&0 ~
г Η
• а0^г) ^о
— («ι^ο
»S
^-** + ...
T2 г + ···
σ0
— ЯоМ &ι
ζ2 +...
Итак,
Л^ = Со + С1г + ^г2+ ... +спгп+ ..., (12)
где коэффициенты с0, Сь с2, . ♦. имеют найденные выше
значения (см. первые члены частного). Можно
убедиться, что каждый коэффициент частного сп
выражается через предыдущие коэффициенты с0, си .. i
,.., cn-i по формуле
п an c0bn + сфп^1+ ... +grt-ifti /1Qv
€η — η^ Fq · (Ιό)
7. Вернемся к целым функциям (7), (8) и (9).
Положим в формуле (7) ζ = да, где w — снова
комплексное переменное. Найдем:
iW j , iw __ w2 /да3 , wi ,
Л м;2 , w{ \ , . / до3 . да5 \
"U-ir + ii— ···) + 'Г--ЗГ + -51— J*
откуда (сравните с формулами (8) и (9))
eiw = cos α; + / sin w. (14)
Это — знаменитая формула Эйлера, выражающая
показательную функцию через тригонометрические.
15

Замечаем в формулах (8) и (9), что разложение
косинуса содержит только четные степени переменного, а
разложение синуса — только нечетные; следовательно,
и для комплексных значений переменного косинус
является четной, а синус — нечетной функциями.
Поэтому формула (14) при замене w на —w перейдет
в следующую:
e~iw = cos w — i sin w. (15)
Складывая и вычитая почленно (14) и (15), найдем
еще две формулы Эйлера, выражающие
тригонометрические функции через показательную:
eiw + e-lw elw_e-iw
cosw — ~ » sin ay = 2/ · О6)
Из формул Эйлера следует, что показательная и
тригонометрические функции комплексного переменного
являются, так сказать, ближайшими родственниками
в мире целых функций.
В виде примера на умножение рядов образуем
произведение двух рядов для eZt и ег\ где zx и х2—
произвольные комплексные числа.
Так как
в*-1 + тг + #+4+··· +£+·■·.
2 У 2 2
е?, _ ι + _ + _ + _+ ... + ~^- + ...,
то
е*<** = 1 + ту (ζ, + z2) + 4" С2? + 2*1*2 + г|) +
+ 13 ι <з! о | «31 2 ι 3 1 ι
"зГ \ζι *~ "2ΪΤΓ *ι*2 ""г 7Ϊ2Γ г1г2 "г 22j "г · · ·
'··· +"лГ12? + (л-1)! И г?~122+ (я-2)! 2! *?"2*2+*··
• · · + n(n*l-l)ig!*g~l +«)+..· = ! + 7Τ(*ι + *2) +
+ ^fo+22)2+4-^+^)3+^.+i(^l + *2r +
Отсюда следует, что
β*ιβζ, _ gz,+*s, (17)
16

Это — так называемая теорема сложения для
показательной функции. Мы видим, что при умножении
двух значений этой функции соответствующие
показатели (комплексные числа zv и гг) складываются.
Положим здесь, в частности, Ζι = ζ и ζ2 = —ζ;
получим:
ez.e-z=eo==:it (i8)
Так как произведение чисел ez-e~zt в силу этой
формулы, не равно нулю, то отсюда следует прежде всего,
что показательная функция ег всегда отлична от нуля,
т. е. уравнение ег = 0 не имеет не только
действительных, но и мнимых корней. (Мы называем мнимым
всякое комплексное число, не являющееся
действительным; например, ι, (1 — i) —мнимые числа.)
Равенство (18) позволяет проверить на частном
примере, что частное двух целых функций есть целая
функция, если делитель нигде не обращается в нуль
(п. 5). Частное —г, очевидно, удовлетворяет этому
условию. Из формулы (18) следует, что
ег ~е l U "Г 2! 3! "^ 4! ##''
это действительно целая функция. (Мы заменили в
формуле (7) ζ на —г.)
Ниже будет доказано (п. 9), что любую целую
функцию g(z), нигде не обращающуюся в нуль,
можно представить в виде g(z) = ehw, где hiz)—также
f (ζ)
целая функция. Понятно, что частное ' ; ν можно
§ \Ζ)
представить в виде произведения f(z)e~hW9 откуда
снова видно, что это целая функция (как
произведение двух целых функций).
Перемножая почленно (14) и (15), получаем:
eiw . e-iw — (cos w _|_ ι sjn w} (cos w _ ι s}n w^
или, в силу равенства (18):
1 = cos2 до + sin2 до. (19)
Следовательно, сумма квадратов косинуса и
синуса равна 1 при любом комплексном значении
переменного.
17

Положим в равенстве (17) Z\ = z — любое
комплексное число и £2 = 2ш; получим:
Но по формуле Эйлера (14)
e2ni _ cos 2π + / sin 2π = 1;
следовательно,
e* = ez+2*', (20)
т. е. показательная функция является периодической с
чисто мнимым периодом 2ш\
Вычислим еще модуль и аргумент комплексного
числа ez. По формуле (17) получаем:
е2 = ex+iy = exeiy.
Но е*у = cos у + ί sin y\ следовательно,
ег = £* (cos у + ι sin у).
Мы получили представление £z в тригонометрической
форме: г (cos φ + i sin φ). Отсюда следует, что
\е'\=*ех, Avg(e*) = y + 2mt (я=*0, ±1, ±2, ...).
Первая из найденных формул показывает, что для
вычисления модуля ег достаточно в показателе
сохранить одну лишь действительную часть χ (а
слагаемое iy отбросить); например, \e]+i/y^~\ = e.
8. Рассмотрим уравнение
ez=A. (21)
Так как мы знаем, что при А = 0 это уравнение не
имеет ни одного корня, то будем считать, что А Ф 0.
Из равенства комплексных чисел ег и А вытекает, что
модули их равны, а значения аргументов могут
отличаться только на целые, кратные 2π. Но в п. 7
отмечалось, что если ζ = χ + iy, то модуль ez есть ех, а
одним из значений аргумента ег является #.
Поэтому из (21) должны следовать равенства:
6>* = |Л|, y = argA + 2nn (я = 0, ±1, ±2, ...).
Следовательно, х = ln| A | и
2 = χ + /у = 1п| Л | + i(arg Л + 2/ет), (22)
« = 0, ±1, ±2, ...
18

Итак, любой корень уравнения (21) должен
заключаться в формуле (22). Обратно, каждое число вида
(22) (а их бесконечно много!) является корнем этого
уравнения. Действительно,
ег —- е\п\А |-И (arg Α+2ηπ) == ^In | A \ei (arg A+ 2пл) =
= | А | [cos (arg A + 2ηπ) + i sin (arg A + 2nn)\ =
= I A | [cos (arg A) + i sin (arg A)] = A.
Итак, показано, что уравнение (21) имеет при
любом Л, кроме одного исключительного значения Л=0,
бесконечное множество корней (22). Иными словами,
уравнение бесконечно высокой степени
1+7Г + -2Г+ ... +"^г+ ··· =А
имеет бесконечное множество корней при любом ком*
плексном А Ф 0.
Естественно каждый корень уравнения (21) назьь
вать значением логарифма (натурального)
комплексного числа А. Обозначая вообще показатель степени,
в которую нужно возвести £, чтобы получить А у через
Ln/4, перепишем формулу (22) в следующем виде:
Ln Λ = In | Л | + / Arg Л = In I Л I + / (arg Л + 2nn)/ (22')
где л = 0, ±1, ±2, ...
Отсюда следует, что любое не равное нулю
комплексное число имеет бесконечное множество
значений логарифма, отличающихся друг от друга на
целые кратные числа 2ш. При η = 0 формула (22')
дает так называемое главное значение логарифма:
In Л = In | Л | + / arg Л. (22")
9. Будем рассматривать комплексное число А в
уравнении (21) как независимое переменное и
соответствующее ему значение ζ— корень уравнения—-
как функцию от А. Эта функция ζ = Ln А будет
обратной по отношению к показательной функции A=ezm-
Мы обнаружили в п. 8, что LnA является
многозначной функцией, определенной во всей комплексной
плоскости, кроме точки А = 0; она представляется
формулой (22г).
19

Из правила дифференцирования обратных
функций, котопое для функции комплексного переменного
в надлежащей формулировке сохраняет свою силу,
следует, что производная (LnA)' существует и равна
Будем вместо А пользоваться привычным
обозначением независимого комплексного переменного ζ.
Тогда получим:
Lnz = In|2|-W Argz,
(Lnz)' = y. (гФО).
Функция Ln ζ не является целой, во-первых, потому
что она не определена в точке ζ = 0 (в этой точке
она обращается в оо), а во-вторых, потому что она
многозначна — ее значения отличаются друг от друга
на целые кратные 2πί.
Однако если g(z)—какая-либо целая функция, не
обращающаяся в нуль ни в одной точке плоскости, то
f(z) = Ln g(z) является также целой функцией
(точнее говоря, Lng(z) представляет бесконечное
множество целых функций, отличающихся друг от друга на
константы, кратные 2ш).
Действительно, по общему правилу
дифференцирования функции от функции получаем
1Ьп*(*>]' = ^*Чг) = ·*$-.
т. е. функции Ln g(z) обладают производной в
каждой точке комплексной плоскости (вспомним, что
g(z)^O) и потому являются целыми функциями,
В виде примера положим g(z) = ez. Тогда
Ln(e*)==ln|e*H-*Argez;
но \е2\ = ех и Arg ег = у + 2пл (см. п. 5 основного
текста), поэтому
Ln(e2) = \п(ех) + i(y + 2ηπ) = .ν + iy+l · 2ητί=ζ+2πηΊ,
/ι = 0, ±1, ±2, ±:3, ...
Мы видим, что Ln(e2) представляет бесконечное
множество целых функций:
2, ζ + 2ш, ζ — 2ш, ζ + 4π/, ζ — 4л/, ...
20

Из изложенного вытекает теорема, которой мы
будем часто пользоваться: если f(z)—целая функция,
не обращающаяся в нуль ни в одной точке, то ее
можно представить в виде
f(z) = e**>,
где g (ζ) — некоторая целая функция.
В самом деле, по доказанному, Lnf(z)
представляет бесконечное множество целых функций, отличакь
щихся одна от другой на целые кратные 2ш.
Обозначим какую-либо из них через g{z)\ тогда
Lnf(z) = g(z) + 2nni (n = 0, ±1, ±2, ...)
и, следовательно,
j ^ή _ eLn f (г) _ eg (ζ)+2ηπί _ eg (г).
мы воспользовались тем, что 2πί — период
показательной функции (см, п. 7). Теорема доказана.

ГЛАВА ВТОРАЯ
МАКСИМУМ МОДУЛЯ
И ПОРЯДОК ЦЕЛОЙ ФУНКЦИИ
10. Замечательно, что коэффициенты степенного
ряда, представляющие целую функцию, можно
выразить в виде интегралов, под знаком которых стоит
данная функция.
Пусть ζ описывает в комплексной плоскости
окружность радиуса г > 0 с центром в начале координат.
Очевидно, что такую окружность можно
охарактеризовать уравнением |г| = г. Поэтому ζ можно
представить в виде
ζ = г (cos φ + i sin φ);
аргумент φ комплексного числа ζ меняется от 0 до 2π,
когда ζ описывает окружность однократно в
направлении против часовой стрелки.
Если w = F(z) —какая-либо функция
комплексного переменного, аналитическая в области,
содержащей окружность |^| = г, то в точках окружности
значения F(z) можно рассматривать как функцию
одного действительного переменного φ: каждому φ
(0 ^ φ ^Ξ 2π) соответствует определенное ζ и,
следовательно, комплексное число
w — и + iv = F (г)
(здесь а и υ — действительная и мнимая части w)
является функцией φ. Поэтому и и ν также являются
функциями φ:
tt = P(<p), i> = Q((p),
откуда
F{z) = P(<f) + iQ{<f).
Построим интегральную сумму для F(z)y
соответствующую какому-либо подразделению отрезка [0, 2π]
на части, посредством чисел
<Ро = 0 < φ{ < φ2 < ... < φΛ-ι < φη = 2π.
22

Каждому значению φ^ соответствует определенная
точка Zk на нашей окружности
zk = r(cosyk + ism(pk)
и значение функции
F(zk) = P(<pk) + iQ(q>k).
По определению, интегральная сумма для функции
F (ζ) есть выражение вида
η η
Σ F (zk) (φ* - <pft_,) = Σ [Ρ Ы + iQ (Фл)1 (Φα - Φα—ι> =
1 1
η η
= ΣΡ (Φα) (Φα ~ Φα—ι) + ι Σ Q Ы (Φα - Φα-ι).
1 1
Заметим, что аналитическая функция F(z), будучи
дифференцируема, непрерывна; отсюда можно
вывести, что непрерывны и ее действительные и мнимые
части Ρ (φ) и Q(cp) на отрезке [0, 2π]. При
бесконечном измельчении подразделения отрезка [0, 2π] таком,
что наибольшая из разностей
Φΐ — Φθ> Φ2 — Φΐ> · · . > φ/ι — Ф/г-1
стремится к нулю, суммы
η η
Σ Ρ (Φα) (Φα — Φα-ι) и Σ Q (Φα) (Φα ~ Φα—ι)
1 1
будут стремиться к пределам, а именно, к интегралам
2π 2π
J Ρ{φ)άφ и J <2(φ)Λρ,
о о
соответственно. Следовательно, комплексная
интегральная сумма
η
Σ^(ζα)(Φα-- Φα-ι)
ι
также будет иметь предел, который мы обозначим так:
2π
J F(z)d(f.
о
23

Из сказанного следует, что
2π
2π
2π
J F(z)dv=\P(V)d<t + i\Q(q>)d<p.
о о о
Итак, мы -определили в частном случае интеграл от
комплексной функции F(z) и выразили его через
интегралы от действительной и мнимой части этой
функции. Из неравенства
η Ι η
Σ F Ы (<Ра - φ*-ι) < Σ Ι F (zk) Ι (<pfc — <рк-х)
ι Ι ι
получаем путем предельного перехода:
12π Ι 2π
JWdp <$l/4z)ld<p,
т. е. модуль интеграла не превосходит интеграла от
модуля подынтегральной функции.
Вернемся к задаче выражения любого
коэффициента ар (ρ ^ 0) степенного ряда, представляющего
целую функцию, в виде интеграла. С этой целью
разделим все члены ряда на ζ? и проинтегрируем по
переменному φ в пределах от 0 до 2π. Сначала (после
деления) получим
t~^ = a0z-p + alzl-P+ ... +αρ + αρ+ιζ+ ...,
а затем
2π
2π
2rt
\1£Ld<v = a0\z-Pdq> + al\z-t>+4(f>+ ...
0 0 0
2π 2π
... +ap\ dq> + ap+l\zd({>+ ...,
о о
где ζ = r(cos φ + i sin φ) (г постоянно).
Мы не останавливаемся здесь на доказательстве
законности почленного интегрирования ряда
(доказательство это сводится к установлению равномерной
сходимости ряда относительно переменного φ при
постоянном г),
24

В правой· части интеграл с коэффициентом ар
равен 2π, так что соответствующий член равен 2пар. Что
касается остальных интегралов, под знаком которых
стоит степень ζ с целым, не равным 0 показателем, то
асе они равны нулю. Действительно, если т —
натуральное число, то по формуле Муавра
zm = rm (cos тер + / sin my).
Если m = — k и &>0, то
zk rk (cos kq> + / sin ky)
=r~k [cos (— Αφ) + i sin (— kq>)] = rm (cos m<p + / sin mcp).
Следовательно, при любом целом тф О
2π 2π
\ zm dtp = rm \ (cos mcp +1 sin Αηφ) d(p =
о о
_ гт Г sin mcp ι χ· cos тф "|2π _ Q
L m ~i~ m Jo
Поэтому
2π
J --^r ^φ = 2παρ,
о
2π
откуда
1 f fte)
^=1S J «^"d<P» где ^ = r(coscp + isinq>). (23)
о
Эта формула справедлива при ρ = О, 1, 2, 3, ..«
Обозначим максимум модуля функции f(z) в круге
радиуса г через Л1(г):
Af(r)= max|/(z)|*).
\z\<r
*) В Приложении (§ I) доказывается, что модуль целой
функции достигает своего максимума в круге не во внутренней
точке круга, а на окружности — в граничной точке круга.
Поэтому максимум модуля целой функции во всем круге совпадает
с максимумом модуля на окружности,
25

Из формулы (23) следует:
ι 2π Ι 2π
Ι ο Ι ϋ
Но при г = г (cos φ + / sin φ)
|г| = ги |f(z)|<Al(r).
Поэтому
2π
КК^-^Ф^^. Р-О, 1.2,... (24)
О
Это — неравенства Крши для коэффициентов
степенного ряда.
11. Встретившаяся в предыдущем пункте функция
Μ (г) играет весьма важную роль в теории целых
функций. Точное вычисление ее даже для простейших
целых функций может вызвать затруднения. Но часто
достаточно уметь оценивать ее, как говорят, сверху и
снизу (т. е. с избытком и с недостатком).
Рассмотрим сначала случай многочлена степени
п(п > 1)
Ρ (ζ) = а0 + а{г + ... + αηζη, αη φ 0.
Если ζ принадлежит кругу радиуса г с центром в
начале координат, то \z\ ^r и, следовательно,
\Р(г)\ = \а0 + а^ + ··· +*«*Ί<
<|flol + |flill-2|+...+|a„||2f,l|<|ael+...+|aJr«
или
li>WKI«bl'"[i+(Jfetif+-+i5l·»]·
При г ~> оо сумма в круглых скобках стремится к
нулю. Поэтому, как бы ни было мало положительное
число ε<1, можно указать такое г0(е), что при
τ > /Ό(ε) будет выполняться неравенство
ΚΙ г + ·'· + \ап\ г»< <ε· <25>
Следовательно, при г>г0(г) и |гКг
\P(z)K\an\rn(l+*). (26)
26

Рассмотрим значение 1Я(<г)| в произвольной точке г0,
лежащей на окружности \z\ = г. Для нее |z0| = г-
В этой точке также должно выполняться неравенство
(26) (при г > Го (ε)). С другой стороны,
\Ρ{ζο)\ = \αηΖο +{αη-χζΓι + ... + а0)\>
*>\anz*\ — \an-\*b~l+ ··· + ао\>
^IflJIzoPH^-illsoP'1-- ··· — Ι «ο 1 =
= 1^1^-1^-11^"1- ... -|ool =
При г > Го (ε) получим, в силу (25):
\P(zo)\>\an\rn(\~s). (27)
Итак, для любого ε > 0 и при всех достаточно
больших г модуль многочлена Я (-г) в точке -г0, |-г0| = г,
удовлетворяет неравенствам
|aJ^(l~e)<IP(e)|<|aJrrt(l+8). (28)
Это двойное неравенство будет использовано нами в
Приложении. Заметим, что оно, очевидно, справедливо
и для случая многочлена нулевой степени (п = 0).
Возвращаясь к (26), заключаем, что это неравенство
справедливо также и в той точке круга \z\ ^ г, в
которой |Я(2)| достигает своего максимума Μ (г).
Поэтому
Λί(Γ)<Κ|/·*(1+ε), если г>г0(е). (29)
С другой стороны, значение ^(г)! в точке -го,
лежащей на окружности \ζ\ = г, не может превзойти Μ (г):
следовательно, из неравенства (27) заключаем;
М(г)^\ап\гп(1-г)у если г>г0(г). (30)
Из (29) и (30) следует, что при г > г0(е)
и так как ε здесь произвольно мало, то
Пт1^7* = Ь (3D
27

Это соотношение можно формулировать так:
максимум модуля многочлена степени η асимптотически
равен модулю старшего члена многочлена (ведь
\ап\гп = \αηζη\, если \z\=r).
12. Вычислим функции Μ (г) для ez, cos z и sin г.
Чтобы их не смешивать, введем обозначения:
М{г\ ег)у Μ (г; cos г), Μ (г; sin z).
В каждом из этих случаев годится одно и то же
рассуждение, основанное на оценке модуля суммы
степенного ряда.
Из формулы
β*-Ι+ΤΓ+1Γ+ "■+£-+-
заключаем, что
2 УП
г t г* ш . ζ
ι*ζι=μ+-π-+-δτ+ ■■•+ir+
<
п\
В круге радиуса г с центром в начале координат
имеем |г|^ г; поэтому
η
1^1<1+тг + 1г+ ■■· +^г+ ··· при 1*К'·
Итак, \ez\ не превосходит ег в круге \ζ\ ^ г* Но в
точке ζ = г, лежащей на его границе, значение ez=er
и |ez| = er. Поэтому в этой точке модуль показатель*
ной функции достигает наибольшего возможного
значения и, следовательно,
М(г\ **)= тах|ег| = ег. (32)
1*|<г
Аналогично из формулы
%Ь χ\ %6
С08г=1-1г+-4Г--бГ+ ···
выводим, что
|cosz|<1+J|Ji + liJl+lit+...,
откуда
|cosz К 1+£ + -£ + -£+ ...
28

в круге радиуса г. Сумма ряда, стоящего в правой ча-
сти последнего неравенства, равна спг = -ζ (см.
формулы на стр. 9). Итак,
| cos ζ I ^ 2е—, если | ζ | ^ г.
Но в точке ζ = ir, лежащей на границе круга,
> cos ζ = cos {tr) = -^ = f— \
er 4-e~r
поэтому совпадает с максимумом модуля
косинуса в круге |г| ^ г, т. е.
Г ι —Г
Μ (г; cos z) = max | cos ζ \ = —~ . (33)
|z|<r Ζ
Наконец, из формулы
ζζ , ζ5 ζ7 .
smz = z-w + w-Jr+ ...
выводим, что
|sin2|<U|+^ + if. + ^f+ ...,
откуда
I sin г К г +-L. + -gf+7f + ···
в круге радиуса г. Сумма ряда, стоящего в правой
ег — е~г
части последнего неравенства равна shr = ^
(см. формулы на стр. 9). Итак,
| sinz I^ ~g—, если | ζ |^г.
Но в точке z = ir, лежащей на границе круга,
| sine | = | sin(/r)| =
0i(ir) ^p-i(ir)
2ί
*) Заметим, что в точке 2=—ir функция cos z принимает то
же самое значение (ведь это — четная функция).
**) То же значение |sin z\ имеет и в точке ζ ==■—ir (ведь
Bin z — нечетная функция).
29

Поэтому 2 совпадает с максимумом модуля
синуса в круге |г|^г, т. е.
ег — е~г
Μ (г; sins:) = max | sin ζ | = 5 · (3 0
lz|<r z
13. Легко понять, что во всех случаях максимум
модуля целой функции f(z) является неубывающей
функцией радиуса г. В самом деле, если /Ί > г, то
круг радиуса /ί с центром в начале координат
содержит круг с тем же центром и радиусом г. Поэтому
при отыскании максимума \f(z)\ в большем круге,
т. е. при отыскании числа Λί(/*ι), должны учитываться
все значения модуля функции f(z) в меньшем круге
1^1 ^ г, и среди них значение Ai(r), а также значения
модуля в круговом кольце г < \z\ ^ г\. Значит, М{г{)
будет либо больше Μ (г) (если в точках кольца
встретятся значения \f(z) | большие, чем Ai(r)), либо
равен Μ (г) (если в кольце больших значений не
встречается).
Итак,
Μ (г,) > Μ (г), если г, > г > 0. (35)
В виде примера убедимся в возрастании максимумов
модулей, вычисленных в предыдущем пункте.
Мы нашли, что
М(п ez) = e\
άλ / \ ег-\-е~г
M{r\ COS£) = 2 ·
%л / · \ ег — е~г
Μ (г; Sin ζ) = τ ·
Для первой из них возрастание является очевидным
фактом — это доказательная функция с основанием,
большим 1. Для последней Iе ~~е—J возрастание
вытекает из того, что ег возрастает, е~г убывает, а
следовательно, разность ег — е~г растет. Чтобы прове-
ег 4-е~г
рить, что функция 2 также возрастает (при
г >> 0), можно, например, вычислить ее производную*
30

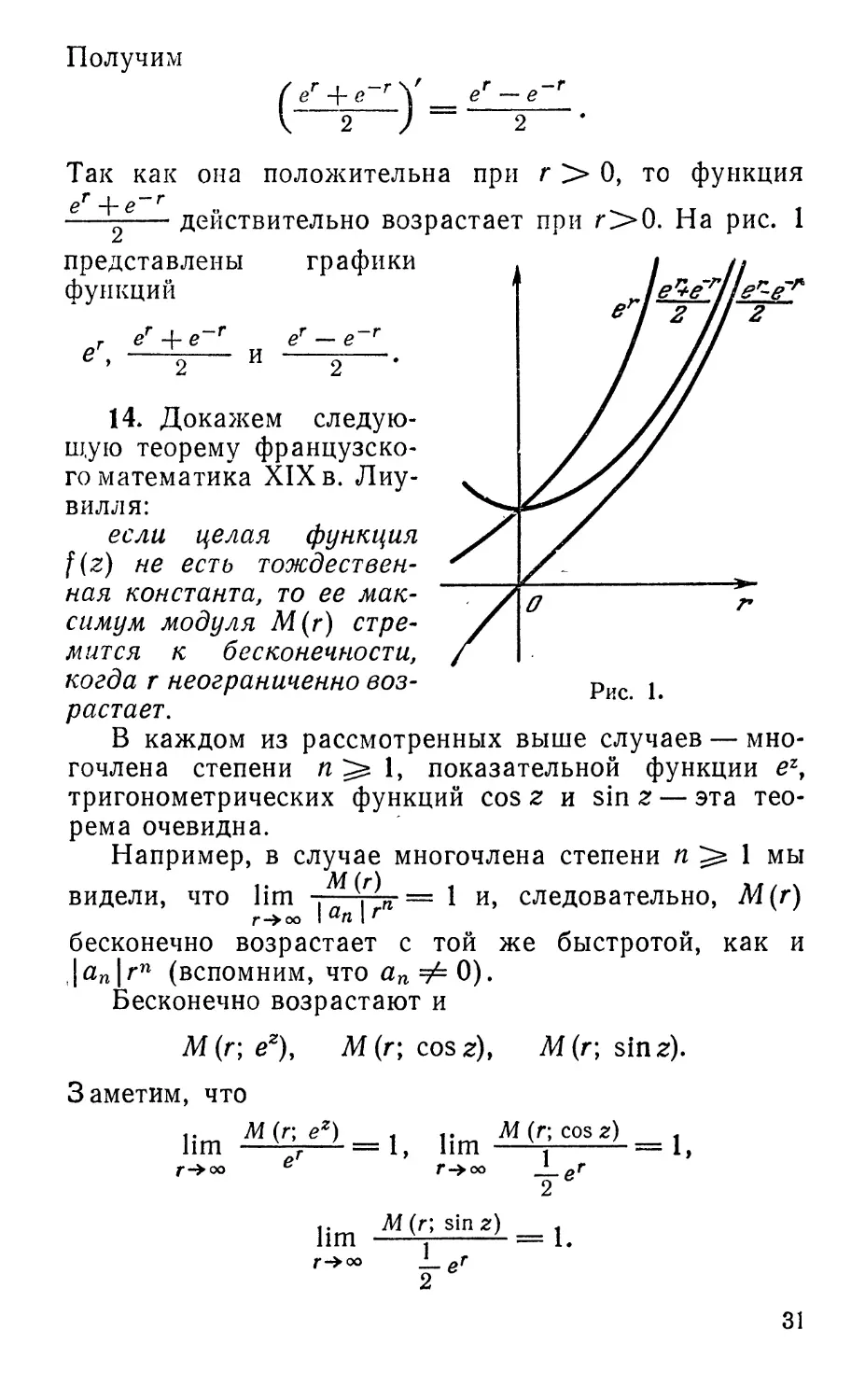
Получим
(i4^y=£-^.
Так как она положительна при г >> 0, то функция
е— действительно возрастает при г>0. На рис. 1
представлены
функций
г ег + е~г ег
графики
Рис. 1.
14* Докажем
следующую теорему
французского математика XIX в. Лиу-
вилля:
если целая функция
f(z) не есть
тождественная константа, то ее
максимум модуля Μ (г)
стремится к бесконечности,
когда г неограниченно
возрастает.
В каждом из рассмотренных выше случаев —
многочлена степени η ^ 1, показательной функции ezf
тригонометрических функций cos ζ и sin г — эта
теорема очевидна.
Например, в случае многочлена степени η ^ 1 мы
видели, что lim -.—т~= 1 и, следовательно, Μ (г)
Г->оо \аП\Г
бесконечно возрастает с той же быстротой, как и
Jan|rn (вспомним, что ап Φ 0).
Бесконечно возрастают и
Μ (г; е2), Μ (г; cos г),
Заметим, что
ι. Μ (г; ег)
lim —y-j—-
Г->оо & Г->оо
M{r\ sin г).
ι \\m M (r>cos *) ι
1, lim j = 1,
,. Μ (r; sin z) t
lim ——. L=l.
2
31

Иными словами, в каждом из этих случаев M[r\f(r)]
возрастает с быстротой а-ег (где а = 1 или α = γ],
т. е. бесконечно быстрее, чем любая степень г, ибо
гп
lim —г = 0, как бы ни было велико п. Последнее
Г->+со в
обстоятельство проще всего установить, заменив ет
соответствующим степенным рядом и отбросив в нем
все члены, кроме одного, содержащего rn+1, а именно:
гп гп η
: - < ==.·
е
г
1+ТГ+ ·
1! ^ "· ^ (л+DI ""' (п+ 1)!
= -— >0 при г->оо.
Но перейдем к доказательству теоремы Лиувилля.
Пусть
f(z) = a0 + alz+ ... +аагп+ ... (33)
В силу неравенств Коши (24),
I *. К ДМ
где Μ (г)—максимум модуля f(z) в круге |z|^>\
Так как Μ (г)—неубывающая функция г (см. п. 13),
то при возрастании г она либо будет оставаться
ограниченной, т. е.
М{г)^Су где С>0,
либо будет стремиться к оо.
Предположим, доказывая теорему от противного,
что последнее обстоятельство не имеет места. Тогда
С
|β/ζΙ^Ξ~тг при всех г>0 и п = 0, 1, 2, 3, ...
Каково бы ни было η ^ 1, правая часть неравенства
стремится к 0 при г->оо. Совершая этот предельный
переход и замечая, что левая часть от г не зависит,
найдем
|яя1^0, т. е. ап = 0 при я^1,
а это означает, что степенной ряд (36) сводится
только к свободному члену а0, т. е.
/ (ζ) = α0.
32

Мы видим, что предположение об ограниченности
М(г) (и, следовательно, об ограниченности |/(г)|)
приводит к выводу, что f(z) есгь константа. Если это
не так, то неубывающая функция Μ (г) не может быть
ограниченной, т. е. должна бесконечно возрастать.
15. В предыдущем пункте было замечено, что для
многочлена степени η максимум модуля стремится
к оо с быстротой гп (с некоторым положительным
коэффициентом), а для функций ez, cos г, sin г
максимум модуля стремится к оо быстрее, чем степень г со
сколь угодно большими показателями. Оказывается,
что справедлива следующая общая теорема, которую
можно рассматривать как усиление теоремы Лиу-
вилля:
если целая функция f(z) не является
многочленом, то ее максимум модуля растет бесконечно
быстрее, чем максимум модуля любого многочлена.
Иными словами, если ввести обозначения M(r\f) —
максимум модуля f(z) и М(г\Р)—максимум модуля
какого-либо многочлена P{z), то всегда
,. Μ (г; Ρ) Λ /0-ч
(напомним, что сама целая функция f(z) не является
многочленом).
Пусть
f(z) = a0 + alz+ ... +anzn+ ... (33)
Сказать, что f(z) не есть многочлен — это значит
сказать, что ряд (38) не обрывается ни на каком п,
т. е. что имеются отличные от нуля коэффициенты
ряда при сколь угодно высоких степенях zn. Пусть
степень многочлена Ρ (ζ) есть га и Ьт (ЬщфО) —
коэффициент старшего члена. Тогда для
фиксированного εο > 0 можно утверждать, что
Μ (г; Р)<| bm \rm (1 + во) при г > г0 (39)
(см. (29)); будем считать, кроме того, что г> 1.
Выберем среди тех членов ряда (36),
коэффициенты которых отличны от нуля, такой, степень
которого ρ будет больше чем га, т. е. ρ ^ m + 1 и ар φ 0.
В силу неравенства Коши (24)
33

откуда
M(r;f)^\ap\rp>\ap\rm+K (40)
Из (39) и (40) выводим при г > г0 и г > 1
Μ (г, Р) < \Ьт\гт(1+г0) \Ьт\ (1 + е0)_
M{nf) ^ \ар\гт+1 \а„\г
Поэтому
'™^Г7Г=°- <4,>
что и требовалось доказать. Так как при|г| —г
|P(z)|<M(r; P),
то
|Р(г)| ^ Λί(Γ, Ρ) .
Μ (г; /) ^ Μ (г; /) '
отсюда и из (41) следует, что
г1™Ш)=° (,г|=г)' (42)
каков бы ни был многочлен Ρ (ζ).
16. Применим результаты п. 15 к доказательству
трансцендентности функций ez, cos £, sin ζ и других
целых функций, не являющихся многочленами.
'Напомним, что функция f(z) называется
алгебраической, если она тождественно удовлетворяет
уравнению вида
Po(z) + Pi(z)f(z) + P2(z)[f(z)]2 + ...
•ν +Pamf(z)]a = 09 (43)
где Р0, Р\, ..., Ρ η — многочлены, п^ I и Ρη(ζ) Ф0.
(Такая запись означает, что Ρη(ζ) — либо многочлен
степени не ниже первой, либо константа, отличная от
нуля.)
Функции, не являющиеся алгебраическими*),
называются трансцендентными. Иными славами, сказать,
что f(z) есть трансцендентная функция, это значит
сказать, что не существует никакого уравнения вида
(43) (с указанными выше условиями, наложенными
*) При этом рассматриваются только аналитические функции.
34

на его коэффициенты), которому функция
удовлетворяла бы тождественно (при всех значениях
комплексного переменного ζ).
Докажем теорему:
если целая функция f(z) не есть многочлен, то она
трансцендентна.
Доказательство проводим от противного. Пусть
f(z) удовлетворяет некоторому уравнению вида (43).
Рассмотрим круги с центром в начале координат
радиусов 1, 2, 3, ... и в каждом круге радиуса k отметим
точку Zk, в которой модуль функции достигает своего
максимума в этом круге:
\f(zk)\ = M(k; f).
Так как limAi(fe; f) = oo (по теореме Лиувилля),
fc-»oo
то значения |/(zft)| бесконечно возрастают. Мы
можем поэтому считать, что f(zh)=£ О (по крайней мере,
для.достаточно больших k). Кроме того, модули \zk\
также стремятся к оо. (В каждом круге постоянного
радиуса R модуль функции ограничен, поэтому
точки zkf в которых значения |f(^)| неограниченно
возрастают, начиная с некоторого k, не будут
принадлежать этому кругу.) Положим теперь в уравнении (43)
2 = 2ft и разделим все члены на \f(zk)\n. Получим
Μ*,> + -^+...+τ^ = 0. (44)
При &->оо Pn(Zh) будет стремиться к оо (если это
многочлен степени не ниже первой) или оставаться
постоянным (если это многочлен нулевой степени, т. е.
константа). Но все другие члены левой части должны
стремиться к нулю в силу результата (42)
предыдущего пункта. В самом деле, например,
<Щь>рп-±
и вообще
1П*н)Г
M(k; f)
M(k'Pn-m) ^
м {kin [M(k-mm-1
(m>l).
В силу (42) все эти величины стремятся к нулю (не
забудем, что M(k; f) ->оо). Мы получили очевидное
35

противоречие: в равенстве (44) член Pn(Zk) не может
стремиться к нулю, тогда как из доказанного следует,
что он должен стремиться к нулю вместе с
остальными членами. Из этого противоречия и вытекает
справедливость теоремы. В частности, можно
утверждать, что ez, cos ζ, sin ζ — трансцендентные функции.
17. Из всего сказанного выше вытекает, что на
каждую целую трансцендентную функцию f(z) можно
смотреть как на своего рода «многочлен бесконечно
высокой степени».
Действительно, во-первых, в ряде
/ (ζ) = а0 + ахг + α2ζ2 + ... +αηζη+ ...
мы встречаем члены со сколь угодно высокими
степенями ζ и отличными от нуля коэффициентами.
Во-вторых, максимум модуля M(r;f) такой функции растет
быстрее, чем максимум модуля многочлена сколь
угодно высокой степени. К этой точке зрения на
трансцендентные функции мы еще будем возвращаться, а
сейчас отметим, что все целые трансцендентные
функции нельзя, так сказать, сваливать в одну и ту же
кучу, так как обнаруживается, что максимумы модуля
одних из них растут бесконечно быстрее, чем
максимумы модуля других.
В виде примера сравним максимумы модуля
функций ez, ez (k—натуральное число ^2) и ее . Для
первой максимум модуля равен ет\
Μ (г; ez)=er.
Вторую можно разложить в степенной ряд, заменяя
в разложении показательной функции (7) ζ через гК
Получим
ег=1+тг+^+---+^г+···.
откуда
Следовательно, в круге |г|^г
36

С другой стороны, в точке 2 = г значение ez сов-
к гк
падает с ет . Отсюда следует, что е и есть макси-
к
мум модуля ег в круге | ζ |<>:
М(г, ezk) = er\
Для вычисления ее можно в ряде (7) заменить ζ
через ez. Получим
»z ez e2z e z enz
(Этот ряд не является степенным, хотя его можно
было бы заменить степенным, если каждый член
разложить в ряд, пользуясь формулой (7), а затем
расположить все члены по возрастающим степеням ζ.)
Замечая, что |ez|s^£r в круге \z\^ r, находим
<1+ΤΓ+···+ΊΓΓ+···=*β·
С другой стороны, в точке z = r значение ее
совпадает с ее\ Отсюда следует, что ее и есть максимум
модуля функции ее в круге Izl^r:
Μ (г; eeZ) = ee\
Как и следовало ожидать, все найденные функции
Ai(r;ez), M(r\ ег ), М{г\ ее ) стремятся к оо при
г->оо (теорема Лиувилля). Но к оо они стремятся с
разными скоростями. Легко убедиться, например, в
том, что
г г2 rk
lim —г = 0, lim ~т = 0» · * · > lim —^ = 0, ...
г->оо ет г->оо ег г->оо ег
тк
..., lim ·£-?-= 0
г-»оо ее
(каково бы ни было натуральное число k). Отсюда
следует, что в последовательности целых
трансцендентных функций
2 22 23 2^ 2^+*
ν ) Ρ } ** > · · · I ** I ** > · · ·
37

максимум модуля каждой последующей растет
бесконечно быстрее предыдущей, а максимум модуля
функции ее растет бесконечно быстрее любой из них.
Покажем, как можно измерять конечными
числами рост максимума модуля каждой из этих функций
(кроме функции eeZ)t приняв за эталон роста
M(r\ez)—er. С этой целью перейдем к функциям,
растущим более медленно, взяв сначала вместо
максимумов модулей их логарифмы.
Получим последовательность
1пЛГ(г; ez) = r, In Μ (г; ez*) = r2, ...,
. . ., in Μ (η e*k) = r\ In Μ (η e2*+1) = r*+i ...
Но и здесь каждая последующая функция растет
бесконечно более быстро, чем предыдущая, поэтому мы
логарифмируем их еще один раз. Найдем
последовательность
1п1пАГ(г; ez)=\nr, In In AT (г; e*2) = 21nr, ...
. . . , In In Μ (г; ег ) = k In r, ...
Очевидно, что отношения последних функций
являются конечными числами. Образуем следующие
отношения:
In In Μ (г, ez2) ρ
In In M (r; ez)
In In Μ (г; ezZ) _ ? In In Μ (г; ez) ,
In In Μ (г; ez) °>'···> \n\nM(r,ez) *' " '"
Соответственно говорят, что порядок функции ег
равен 2,, порядок функции ez% равен 3, ..., вообще
порядок функции ег равен k (k = 1, 2, 3, ...)
(подразумевается порядок роста максимума модуля
функции по отношению к росту максимума модуля ez).
Порядок самой функции ez (эталона) естественно
получается равным 1.
В случае функции ее имеем
In In M (r; eeZ) In In (ееГ) г
—^j—^ = j-i—- — -. *oo при Г-*оо.
In In Μ (r; ez) In г In г r
Поэтому говорят, что порядок функции ее равен оо.
38

Вообще же порядком ρ целой функции f(z) называется
предел (если он существует) отношения повторного
логарифма M(r\f) к повторному логарифму M(r\ez)
при г —► оо:
,. lnlnAf(r; f) ,. lnInAf(r; f) ,,еч
Р =!Т~ ЫпМЬе» " ,1™ 1°г * (45)
~ - In In Af (r; f)
Если отношение ^—— не имеет предела ни
конечного, ни бесконечного при г—*оо, то берут так
называемый верхний предел этого отношения *) и его
называют порядком целой функции f(z):
г.— In In Μ (η f) /лх/\
P = lim ; (450
18. Формула (45) позволяет с помощью формул
(33) и (34) показать, что порядок каждой из функций
cos г и sin г равен 1. В самом деле,
Μ (г; cosz) =—-^ = е ^—.
Очевидно, что е-2г~>0 при г->со, и поэтому дробь в
правой части равенства стремится к пределу,
равному у Далее, логарифмируя, найдем
\+e~2r<
1 L Л-2Г I 1П
ΙηΛί (r^ cos ζ) = г + 1п
/ 1 1+е~2Г\
*) Пусть, вообще, φ (г) — какая-либо функция от г,
определенная на интервале 1 < г < оо и принимающая действительные
In In Μ (г; f) _
значения, в нашем случае φ (г) = :—-——. Если
существует lim φ (г) = α (конечный или бесконечный), то тогда и
Г-»оо
для любой последовательности значений {гп}, такой, что гп -> °°,
имеем lim qp(rrt) = a. Но если lim φ (г) не существует, то най-
«->оо Г->оо
дутся, по крайней мере, две последовательности {гя}, гп -> со, и
{гп}> гп ""** °°> такие, что lim φ (/) φ lim φ (r£). Рассматри-
вая все возможные последовательности {rn}, г η ->«>, для
которых {ф(гп)} имеет предел, можно показать, что среди всех
возможных пределов существует наибольший (конечный или
бесконечный). Он-то и называется верхним пределом φ (г) при г-»-оо
и обозначается так: Jim φ (г).
Г-»оо
39

где выражение в скобке стремится к 1 при г->оо.
Еще одно логарифмирование дает
1п1пЛ1(г; cos г);
■Гпг + ln^l + ^ J,
где второе слагаемое в правой части стремится к нулю
при г—*оо. Следовательно,
ι- In In Μ (г, cos z)
lim г-2 =
Г-»оо In Г
[ 4^)
= lim LI + — i—~ -
= 1.
Это и значит, что порядок cos г равен 1. Аналогично
с помощью формулы (34) найдем, что порядок sin z
также равен 1.
Во всех рассмотренных примерах порядок целой
функции оказывался члслом целым (или равнялся
бесконечности). Но существуют также целые функции
дробных порядков. Рассмотрим, например, функцию
ел/Т j_ е"^
f(z) = 2 · Эта функция является целой, так
как
л/Т ι ι У 2 ι ζ ι ζ Уζ ι я2 ,
е
- л/Т — ι _ У* ι JL _ 2У*
L n τ οι
1! ^2! 3! ^ 4!
и поэтому наша функция представляется следующим
всюду сходящимся степенным рядом:
еУ7 + а-УГ j_ £ ±
о ! Τ οι Τ 4| Τ с| Τ · · ·
2! ' 4! ' 6!
Рассуждая так же, как и в^п. 12,_найдем с помощью
этого ряда, что М\г\ ^ 1 = ^ .
Теперь уже сам читатель проверит, что порядок
ел/Т ι e~~^T* 1
целой функции -| равен у·
40

Рассмотрим вообще любое положительное рациональное число
-£- — не целое (наибольший общий делитель натуральных
чисел ρ и q равен 1, причем q ^ 2) и покажем, как можно
построить пример целой элементарной функции φ (г), порядок
которой равен — . С этой целью заметим сначала, что комплексное
число
2π , . . 2π
ε = cos h ι sin —
я я
я
представляет одно чэ значений VI; B самом деле, e^=cos2tt +
q /—
+ /sin 2π = 1. Остальные q — 1 значений VI можно получить,
возводя ε в степени с показателями 2, 3, ..., q:
2 3 α -ι
ε , ε , ..., &ч = 1.
я
На рис. 2 все q различных значений VI представлены
графически.
е**
2л
ез
2л/\
ц
2л\
* /
/ε*
/о\
я
ч 2η
\ g
} 2л
■ Я
\е*
ε?=τ
ттяш^^
·/
Ркс. 2.
Если т — какое-либо натуральное число, кратное qy т. е.
т = nq, то
<« + e2m+ _ +е^ = (е^)я + И2«+ ... +ИШ7 = <7· (46)
Если же m не является кратным q, то
е« + е2* + ... +8^ = ±_?_?__а (4?)
так как числитель здесь равен нулю, а знаменатель отличен от
нуля ί в самом деле, &д,п = 1, а вт = cos ί m J + / sin ( — m J
отлично от 1, поскольку — не является целым числом].
41

Рассмотрим теперь следующие q рядов ч):
1! ^ 2! </! ' (q + \)\
/^ , ■ ε2ζ* ε2"2/'
β _1+ I! ^ 21 +
"Τ
Я\ ^ (Я + W
Складывая их почленно, получим
"ΪΪ
и^«"+/^+... +/УЛ,«+»+«,+ --- + '%т+
, ε2 + ε2·2+·..+ε*·2,2Τ , , ε^ + ε"'2 + ... + β™ ρ,
t е"+' + е^+1)2+ ··■ + β»+'>« (9+I)f ,
+ fo + l)l 2 + —
В силу формулы (47) все коэффициенты при дробных степенях
обращаются в нуль, а в силу формулы (46) числитель каждой из
дробей, являющейся коэффициентом при целой степени 2,
равен q. Поэтому
ι,— ч,— ч
^г* + егЧ*Р+ _ ++4*,
Я+ q\Z + (2?)l* + (3^)! Z + ·"
*) В каждом из них угр — одно и то же (все равно какое)
значение корня.
42

Деля здесь обе части на q и обозначая полученную целую
функцию через φ (г), найдем
<p(2) = i ±£_ +·.·+· _
Я
г" . ζ2" , ζ3"
С помощью неоднократно использованного приема убедимся,
что
гр Г2Р ГЗР
Л(г,,)-,+_+_.+___+....
L· JL JL
я 2 я о я
Я
Замечая, что ε == 1, перепишем Μ (г; ф) в виде
ш ^ И1+^"-|)гЧ ■■■ +^г-')^ + е(е-')гТ
Μ (г; φ) = е —: — — -L ·
Я
(48)
Далее можно поступать так же, как и в случае вычисления
порядка функции cos -г, если только заметить, что каждое из
слагаемых вида
стремится к нулю, когда г->оо. Чтобы убедиться в этом,
вычислим модуль такого слагаемого. Для этого достаточно сохранить
в показателе его действительную часть (см. конец п, 7)t Но
Л ρ
U — \)гч = (cos Η sin — J — 1 rv =
ЧМжт)~0+/8|пНг)К=
= cos I ап—J — 1 г +*sin(m—J г
*) Заметим, что все выкладки с дробными показателями нам
понадобились для того, чтобы в показателях показательной
функции в левой части ζ фигурировало в дробной степени --, а
в правой части все степени ζ были целыми (иначе сама функция
не была бы целой),
43

(мы воспользовались формулой Муавра для возведения в
степень). Поэтому
Р
,(«"-!)r«l .[«»·(»■?■)-О'*
р_
= е\.-~\" я J 'У 9 (49)
Разность cosim—1 — 1, очевидно, отрицательна, так как
cos ί т — 1 при 1 ^ т ^ q — 1 строго меньше единицы. Из того,
что rq -> со при г-*оо, следует, что выражение (49) стремится
(вт-\)гя
к нулю при г->оо, что означает стремление к нулю и еу '
Установив это, получаем, что вся дробь в правой части (48)
стремится к пределу — Φ 0. Это и дает возможность проводить
дальше вычисления по образцу, указанному в начале этого
пункта.
В итоге найдем
v In In Μ (г; φ) _ ρ
r-»oo In r q

ГЛАВА ТРЕТЬЯ
НУЛИ ЦЕЛОЙ ФУНКЦИИ
19. Пусть
/ (ζ) = а0 + αχζ + α2ζ2 + ... +αηζη+ ... (50)
— целая функция.
Представляя ζ в виде ζ = α + (2— я), разложим
ζη по степеням ζ — а:
ζη = [α + (ζ-α)]η = αη + -γαη-*(ζ-α) +
+ "if^a*-*(z-af+ ... +(г-а)п,
и подставим в "(50). Собирая, наконец, члены с
одинаковыми степенями ζ — α, получим для f(z) всюду
сходящийся степенной ряд, расположенный по степеням
разности ζ — а:
f (ζ) = Со + с{ (ζ — а) + с2 (ζ — а)2 + ...
... +са(г-а)*+ ... (51)
В виде полезного упражнения советуем читателю проделать
эти выкладки для частного случая f(z) = ег. Он должен получить
тогда, что
а а а
е =е +-j]-(z-a)+ 7П~(*~ а) + ··· +-jjj-(* — а)я + ...
Конечно, этот результат можно было предвидеть: ведь,
ez = eaez~a =
-,[,+~+ь^г.+... +л-£+...].
Пусть /(,г)—целая функция, не равная
тождественно константе. Точка а комплексной плоскости
называется нулем функции f(z), если /(а)=0. Иными
45

словами, нуль целой функции это корень уравнения
Подставляя ζ = а в (51) и замечая, что по условию
/(а) = 0, найдем:
Итак, если а есть нуль функции f(z), то свободный
член в разложении (51) равен нулю. Может оказаться,
что еще несколько следующих за с0 коэффициентов
равны нулю (например, с1 = с2 = 0). Невозможно,
однако, чтобы все коэффициенты ряда (51) были
нулями. В противном случае функция f(z) тождественно
равнялась бы нулю, а мы с самого начала исключили
эту возможность. Итак, среди коэффициентов ряда
(51) должен встретиться первый отличный от нуля
коэффициент Ck, так что
скФ0, fe>l.
Номер k этого коэффициента (совпадающий с
показателем степени разности {ζ — a)h) называется крат*
ностью, а также порядком кратности или просто
порядком рассматриваемого нуля.
Итак, если порядок нуля а функции f(z) есть &, то
f (ζ) = ск(г- a)k + ck+l (ζ- α)*+ι + ..., (52)
скфО, fe>l.
Для примера возьмем функцию sin z:
ζζ , ζ5
Из разложения сразу видно, что начало координат
есть нуль первого порядка для sin z.
Рассмотрим теперь функцию ζ — sin z:
z_sinz = ^-----^+ ...
Очевидно, что для этой функции начало координат
есть нуль третьего порядка.
20. Если а есть нуль порядка k целой функции
f(z), то из формулы (52) следует, что f(z)
представляется в виде
/ (г) = (г - а)к [ск + Ск+1(г-а)+ ...], (52')
46

где Ck Φ Ο, k^\. Так как ряд (52') сходится при
Ёсех ζ, то и ряд, заключенный в квадратных скобках
в правой части (52'), сходится при любом ζ (при
ζ = а сходимость его очевидна; при ζ Φ а ряд
получается из сходящегося ряда (52) путем умножения
всех его членов на число (z — #)~ft). Поэтому сумма
последнего ряда есть целая функция; обозначим ее
через φ (-г):
4>(z) = ck + ck+l(z — a)+ ...
Так как φ(α) = Ch Φ О, то точка а не является нулем
функции φ (-г). Итак, получаем теорему:
если а нуль порядка k целой функции f(z), то f(z)
можно представить в виде
Пг) = {z -a)k φ (ζ), (53)
где φ (ζ)—также целая функция, для которой точка
ζ = а уже не является нулем.
Отметим случай, когда f(z) есть многочлен
степени η не ниже первой:
/ (г) = а0 + αχζ + α2ζ2 + ... + αηζη, αη Φ 0. (500
В этом случае, разлагая его по степеням ζ — а,
как было указано в начале п. 19, мы найдем, что
старшая степень ζ — а в выражении f(z) будет равна п9
причем коэффициент при ней совпадает с ап:
f(z) = c0 + c{(z-a)+ ... +сп(г-а)п, (510
сп = апфО.
Если а есть нуль f(z) и порядок нуля равен k
(1 ^ k ^ п), то эта формула примет вид
Г(г) = ск(г-а)* + см(г-а)™ + ... +cn(z- a)\
где скФ0 (K^k^n) и сп = апФ0; отсюда
?(г) = (г-а)к\ск + сш(г-а)+ ... + сп(г-а)п-*].
Сравнивая с общей формулой (53), видим, что в
случае, когда f(z) есть многочлен степени п, целая
функция φ (г) является также многочленом степени η — k9
О ^ η — k < п. Этот многочлен не обращается в нуль
при ζ = а\ коэффициент при старшей степени ζ — а
равен ап-
47

Из полученного результата вытекает известная
теорема Безу в следующей форме:
если f(z) —многочлен и z = a— его нуль
кратности kf то f(z) делится на (z — a)k.
Вернемся к общему случаю целой функции f(z),
которая в частном случае может быть и многочленом.
Пусть Ь Φ а нуль функции f(z) порядка /. Из
формулы (53) следует, что точка Ь будет нулем также и
для функции φ (ζ). В самом деле,
/(6) = (6-α)*φ(6) = 0,
и так как Ь — а Φ О, то φ(&) = 0.
Покажем, что Ь является нулем того же порядка /
и для функции φ (.г). Допустим, что это не так и что
порядок U точки Ь, рассматриваемой как нуль
функции φ (-г), не равен /, например, h < /. Тогда имеем
/(2) = (2-&)'ψ(ζ) и φ(*) = (*-&)'ιφι(*),
где ψ (-г) и φι(ζ) —целые функции, для которых точка
Ь не является нулем. Из формулы (53) заключаем, что
(г - ЬУ ψ (ζ) = (ζ - a)k (z - 6)'чр, (ζ),
откуда, сокращая на (г — Ь)1» (мы предположили, что
U < 0, получим
(ζ - b)l~1^ ψ (ζ) = (ζ- a)k φ, (ζ). (53')
Строго говоря, мы обосновали это соотношение только
для ζ φ Ь\ но так как слева и справа стоят функции,
непрерывные при ζ = b, то оно справедливо также и
при ζ = Ь. Полагая 2 = 6, получим слева нуль и
справа число (Ь — a)kq>\(b) φ 0. Из этого
противоречия вытекает, что предположение U < / неверно.
Точно так же убедимся, что неверно предположение о том,
что U > I- Итак, U = /.
Мы доказали, что каждый нуль функции f(z)f
отличный от а, является нулем того же порядка
функции φ (-г). Из формулы (53) следует также, что
каждый нуль φ (-г) должен быть нулем f(z). Поэтому
целая функция φ (-г) в формуле (53) имеет те же нули,
что и функция f(z), и притом тех же порядков, за
исключением лишь одной точки а, которая не является
нулем φ (-г).
48

Применяя к функции φ (г) и к одному из нулей
Ъ Φ а порядка / функции f (ζ) полученный результат,
найдем
φ (г) = (*-&)'χ (г). (54)
Здесь χ (г)—целая функция, имеющая те же нули,
что и функция φ (-г), и притом тех же порядков, за
исключением точки Ь, не являющейся нулем χ (-г). По
сравнению с f(z) функция χ (ζ) имеет, следовательно,
те же нули, за двумя исключениями точек а и Ь.
Из формул (53) и (54) следует:
Г(г) = (г-а)к(г-Ь)'х(г). (55)
Продолжая это рассуждение (его можно вести
далее по индукции), получаем следующий результат:
если а, b, :.., с не равные между собой нули f(z),
порядки которых соответственно равны k, I, ..., m, то
f(z) можно представить в виде
f(z) = (z-a)k(z-b)1 ...(г-с)та>(г)9 (56)
где ω (ζ)—целая функция, имеющая те же нули, что
и f(z), и притом тех же порядков, за исключением
точек а, Ь, . %., с, не являющихся нулями ω (ζ).
Весьма важен тот частный случай, когда точками
а, Ь, ..., с исчерпываются все нули f(z); это значит,
что f(z) имеет лишь конечное число нулей во всей
плоскости. Тогда целая функция ω (ζ) нигде не
обращается в нуль и по п. 9 может быть представлена
в виде
со(г) = ^<2),
где g(z)— целая функция.
Получаем следующую теорему:
если целая функция f(z) имеет лишь конечное
число нулей во всей плоскости а, Ь, ..., с и
натуральные числа k, /,..., m являются порядками этих нулей,
то f(z) можно представить в виде
f (ζ) = {ζ - af (z-b)1 ...(ζ- c)m eg <*>, (57)
где g(z) — целая функция.
Замечая, что (ζ — a)k(z — b)1... (ζ — c)m есть
многочлен степени k + / + ... + τη = η, заключаем,
49

что каждая целая функция, имеющая лишь конечное
число нулей во всей плоскости, равна произведению
некоторого многочлена на функцию вида e^z\ где
g(z)—целая функция.
В случае, когда функция f(z) сама является
многочленом степени п, функция ω (ζ) в формуле (56)
также является многочленом. Если а, &,..., с
исчерпывает все нули f(z), то ω (-г) есть многочлен, не
имеющий нулей. Из основной теоремы высшей
алгебры (которую мы докажем ниже, в п. 22) следует,
что ω (ζ) не может быть многочленом степени ^1,
так как любой такой многочлен имеет нули. Поэтому
степень ω (-г) равна нулю, т. е. ω (-г) есть константа.
Отсюда следует далее, что сумма порядков всех ну*
лей f(z) равна п:
k + / + ... + гп = п
и что
ω(ζ) = αη.
Поэтому разложение (57) для многочлена принимает
известный вид:
f(z) = an(z-a)k(z-b)1 ...(z-c)m.
21. Чтобы сделать некоторые заключения о нулях
целой функции в случае, когда их бесконечное
множество, докажем следующую лемму:
если f(z)—целая функция, не равная
тождественно нулю, то для каждой точки z0 плоскости можно
указать круг с центром в этой точке, в котором f(z)
не будет иметь нулей, за исключением быть может
самой точки Zq.
Пусть сначала f(z0) φ 0, тогда |/(£ο)| есть число
положительное. В силу непрерывности функции f(z)
(а непрерывность ее вытекает из дифференцируемое™
функции) для каждого ε > 0 существует круг с
центром 2ο, в котором выполняется неравенство
\f(z)-f(z0)\<e
и, в частности,
\f(z)\ = \f(zo) + [f(z0)-f(z0)}\>
>l/(z<))|-|/(z)-/(zo)l>l/(zo)l-e.
50

Примем ε=|/(2ο)|; тогда в соответствующем
круге
l/(2)|>lf(*0)|-|f(2o)| = 0, или |/(z)|>0,
Т· е' ϊ(ζ)Φ0.
Итак, в случае, когда f(zo) Φ О, существует круг с
центром 2о, в котором нет ни одного нуля функции.
Пусть теперь /(2ο)=0 и k — порядок точки z0;
тогда (см. п. 20)
f (г) = (г—го)* φ (г),
где φ (-г)—целая функция, для которой ζ0 уже не
является нулем. По только что доказанному существует
круг с центром 2о, в котором φ (ζ) не обращается в
нуль. Очевидно, что в этом круге f(z) не имеет других
нулей, кроме z0. Лемма доказана.
Из этого предложения вытекает теорема:
целая функция f(z), не равная нулю тождественно,
не может иметь бесконечного множества нулей ни в
каком круге конечного радиуса.
Допустим противное и пусть в круге \z\ ^ г
функция f(z) имеет бесконечное множество нулей. Тогда,
по известной теореме Больцано — Вейерштрасса (см.,
например, Г. М. Фихтенгольц, Основы
математического анализа, т. I, стр. 239), внутри или на границе
круга должна существовать точка Zo — предельная
для множества нулей. Это означает, что в любом
круге с центром Zo содержится бесконечное множество
нулей функции f(z), что, очевидно, противоречит
доказанной лемме.
Как следствие получаем теорему единственности
для целых функций:
если значения двух целых функций f(z) и g(z)
совпадают на бесконечном множестве точек,
принадлежащих какому-либо кругу К конечного радиуса, то
эти функции тождественно равны между собой:
f(z) = g(z).
В самом деле, разность f(z) — g(z) = ψ (ζ) есть
целая функция, обращающаяся в нуль в каждой точке,
в которой f(z) — g(z). Если допустить, что ψ (ζ) Φ 0t
то приходим к противоречию с доказанной теоремой.
Поэтому φ (ζ) = 0, т. е. f(z) = g(z).
51

В частности, если на бесконечном множестве точек
круга К функция f(z) принимает одно и то же
значение Л, то f(z) Ess А (достаточно применить доказанную
теорему к/(г) и к функции g(ζ) ξ= А).
Вернемся к случаю одной целой функции ί(ζ)Φ 0.
Ничто не мешает ей иметь бесконечное множество
нулей во всей комплексной плоскости. Например, нулем
sin z является каждое целое кратное π:
ля, п = 0, ±1, ±2, ...
Предположим, что f(z) имеет бесконечное
множество нулей во всей плоскости, и рассмотрим круги с
центром в начале координат и радиусами,
соответственно равными 1, 2, 3, ... По предыдущему в
каждом из этих кругов содержится только конечное число
нулей f(z). Это дает нам возможность перенумеровать
все без исключения нули /(-г), не допуская ни
пропусков, ни повторения. Вот как это можно сделать.
Сначала нумеруем в каком-либо порядке (например, в
порядке неубывающих модулей) все нули в круге
|-г| ^ 1. Пусть первое из неиспользованных при этом
чисел (номеров) будет ki ^ 1 (следовательно, в круге
\z\ ^ 1 находятся k\ — 1 различных между собой
нулей функции). Затем продолжаем нумерацию нулей,
принадлежащих круговому кольцу, заключенному
между окружностями | -г: j ===== 1 и \г\ —2 (точнее — в
кольце 1 < |^| ^ 2), начиная с ku и пусть к2 — первое
неиспользованное при этом число. Тогда переходим
к кольцу 2< \ζ\ ίζ 3, продолжая нумерацию
заключенных в нем нулей, начиная с номера fe, и повторяем
этот процесс до бесконечности. Из этого рассуждения
вытекает, что в случае, когда целая функция f(z)
имеет на плоскости бесконечное множество нулей, все
эти нули можно расположить в одну
последовательность
£\i ^-2» ^3> * * * У ^71» * * * »
перенумеровав их, например, в порядке неубывающих
модулей:
Uil<|z2l<...<UJ<|z*+il<...
Предел последовательности {zn} равен оо;
lim г„= оо.

ГЛАВА ЧЕТВЕРТАЯ
ОСНОВНАЯ ТЕОРЕМА ВЫСШЕЙ АЛГЕБРЫ
И МАЛАЯ ТЕОРЕМА ПИКАРА
22. Теорема Лиувилля, доказанная в п. 14,
позволяет сравнительно просто установить так называемую
основную теорему высшей алгебры:
Уравнение
tf0 + fll2+ ·.. +ап2П—®> г&е п ^1 и Я/г =7^0» (58)
имеет, по крайней мере, один комплексный корень.
Очевидно, что в этой теореме речь идет об общем
и весьма важном свойстве многочленов степени η ^ 1.
Полагая Рп (ζ) = а0 + <*\Ζ + - -. + ο,ηζη, будем
доказывать эту теорему от противного. Если она неверна,
то Ρη{ζ) нигде в комплексной плоскости не
обращается в нуль. Поэтому функция / (г) = р ( , долж-
на быть целой, как частное двух целых функций, в
случае, когда делитель не обращается в нуль (см.
п. 5). Очевидно, что она не является постоянной, так
как знаменатель ее изменяется и стремится к оо, когда
ζ -> оо (это следует, например, из формулы (27),
пригодной в любой точке Zq плоскости и для каждого
^многочлена степени п^1). По теореме Лиувилля
максимум модуля такой функции M(r;f) должен
стремиться к оо при г-> оо. Но это противоречит тому,
что сама функция стремится к нулю (так как
знаменатель дроби ρ, ν стремится к оо, тогда как
числитель остается постоянным). Из этого противоречия и
вытекает справедливость теоремы.
Считая каждый корень уравнения (58) столько
раз, какова его кратность, мы можем утверждать
теперь, что число всех корней уравнения (58) совпадает
со степенью многочлена f (z):
k + /+ ... +m = n
(см. конец п. 20).
53

23. В п. 17 мы настаивали на том, чтобы
рассматривать целую трансцендентную функцию
f(z) = a0 + alz + a2z2 + ... +anztl+ ... (59)
как своего рода многочлен бесконечно высокой
степени. Теперь наступило время проверить
основательность такой точки зрения. Ведь если аналогия
действительно имеет место, то уравнение «бесконечно
высокой степени»
во + a\Z + · · · + &nZn + · · · = 0 (60)
должно иметь бесконечное множество корней. На
первых порах нас ждет разочарование. Уравнение
1+Έ + ΊΪ+ ··· +1Г+...-0. (61)
т. е. ег = 0, не имеет ни одного корня, как это было
установлено в п. 7. Положение можно спасти ценой
небольшого компромисса. Вернемся к случаю
многочлена Ρη(ζ) степени я^1 и вместо уравнения (58)
рассмотрим уравнение более общего вида
α0 + α{ζ+ ... +αηζη = Α, (580
где А — любое комплексное число. Очевидно, что оно
также имеет η корней, так как сводится к уравнению
степени η уже рассмотренного типа
Qa(z) = 09 где Qn(z) = Pn(z)-A.
Итак, уравнение (58') при любом А имеет столько
же корней, какова степень уравнения, т. е. п.
В соответствии с переходом от (58) к (58')
рассмотрим вместо (61) более общее уравнение
1 +-Π" + ΐ+ '·· +5+ ··· =Лшше2 = Л, (610
где А — какое-либо комплексное число.
В п. 8 было установлено, что это уравнение имеет
бесконечное множество корней при любом А Ф О, т. е.
снова столько же корней, какова степень уравнения
(оо). Следовательно, аналогия между многочленами
и целой трансцендентной функцией (в данном
случае, ez) сохраняется для всех Л, кроме одного
исключительного значения.
54

Рассмотрим теперь вместо уравнения (6Г)
уравнение
cos ζ = Л. (62)
Заменяя cos z по формуле Эйлера (16), получим
или, замечая, что e-'z = —, и несколько преобразуя,
будем иметь
еш _ 2Ае*я + 1=0. (63)
Если положить здесь
eiz = w, (64)
то уравнение сведется к квадратному
w2 - 2Aw + 1 = 0,
откуда
w = А + ^Ж=Т = A+i У1~ Л2 (65)
(мы не пишем двойного знака перед корнем,
подразумевая, что должны рассматриваться оба значения
квадратного корня). Чтобы, отправляясь от w, найти
корни уравнения (62), нужно решить уравнение (64).
Мы уже знаем, что этому уравнению удовлетворяет
бесконечное множество значений показателя iz (и,
следовательно, бесконечное множество значений -г), если
только w Φ 0, а именно:
iz = Ln w и ζ = — i Ln w = — ι Ln (Л + / У1 — Л2). (66)
Но из формулы (65) вытекает, что если w = 0, то
/У 1 — Л2= — Л, откуда Л2 — 1 = Л2, что
невозможно. Итак, каково бы ни было Л, значение w,
определяемое по формуле (65), не равно нулю. Поэтому
уравнение (64), а следовательно, и уравнение (62)
имеют бесконечное множество корней при любом А
(без всяких исключений).
24. Оказывается, что закономерности,
обнаруженные на примерах уравнений
ez = A и cos z = Л,
55

имеют общее значение для всех целых
трансцендентных функций. А именно, французский математик Пи-
кар, еще в 1878 г. доказал следующее замечательное
предложение.
Малая теорема Пикара. Если f(ζ) — целая
трансцендентная функция, то уравнение
f(z) = A, (67)
где А — какое-либо комплексное число, имеет
бесконечное множество корней, за возможным исключением
одного значения А (зависящего от функции), для ко-
торого уравнение может иметь только конечное число
корней (и даже вовсе не иметь их).
Для функции ez таким исключительным значением
является А = 0; для функции cos z нет ни одного
исключительного значения. Можно проверить, что и
для функции sin z не существует исключительных
значений, т. е. что уравнение
sinz = A
имеет бесконечное множество корней, каково бы ни
было комплексное число А.
Мы видим теперь, на , какой компромисс нужно
пойти, чтобы восстановить утраченное право
рассматривать целые трансцендентные функции как
многочлены бесконечно высокой степени. Этот компромисс
заключается в допущении одного лишь возможного
исключения из общего правила для данной функции,
когда число корней уравнения (67) может и не
совпадать со «степенью» этого уравнения (равной
бесконечности).
Пикар получил также различные уточнения и
усиления предыдущей теоремы. Одно из них
формулируется следующим образом:
если порядок f(z) есть число конечное, не целое,
то уравнение (67) имеет бесконечное множество
корней при всех значениях А (без всяких исключений).
Так, например, _в п. 18 было отмечено, что порядок
е^г 4- е"^ 1
целой функции g равен у. Поэтому
можно утверждать, что уравнение
eV* +e-V
ι ζ
= Α (68)

имеет бесконечное множество корней, каково бы ни
было комплексное число Л. Впрочем, в данном случае
в этом можно убедиться без ссылок на общие
георемы, сведя уравнение к рассмотренному выше случаю
уравнения cos г = Л. В самом деле, введем вместо ζ
новое неизвестное ζ, положив
V'*=£.
Тогда уравнение (68) примет вид
2 = Л или cos ζ = Л.
Но последнее уравнение имеет бесконечное множество
корней при любом Л (см. п. 23). Каждому из этих
корней ζ соответствует корень ζ=(ίζ)2 =—ζ2
уравнения (68).
25. Среди примеров трансцендентных уравнений,
решаемых графически в курсе средней школы,
встречаются уравнения следующих типов:
ах = Ах, ах = Ах2, sin χ = Ах и т. п.
Здесь в левой части находится целая трансцендентная
функция, а в правой — многочлен (в данных
примерах он сводится к χ или л:2), умноженный на
некоторый коэффициент Л. Очевидно, что каждый из этих
случаев охватывается уравнением вида
f(z) = AP(z), (69)
где f(z) —целая трансцендентная функция, a P(z) —
многочлен.
Теоремы п. 24 не позволяют судить о числе корней
уравнения (69) для каждого данного Л. Записывая
это уравнение в форме
f(z)-AP{z) = 0,
видим, что задача заключается в отыскании нулей
целой функции f(z) — АР (z). Но может случиться, что
именно число 0, стоящее в правой части, является
исключительным значением функции f(z)—AP(z), и
тогда уравнение (69) будет иметь только конечное
число корней.
67

Следующая теорема показывает, как в
действительности обстоит дело с числом корней уравнений
вида (69):
если f(z)—целая трансцендентная функция и
Ρ (ζ)—многочлен, не равный тождественно нулю, то
уравнение (69) имеет бесконечное множество корней
для всех значений А, кроме, быть может, одного
исключительного значения (зависящего от f(z) и от Ρ (ζ)).
Из этой формулировки малая теорема Пикара (см.
п. 24) получается как частный случай, если положить
Ρ (ζ)==1. Поэтому справедливость теоремы Пикара
будет установлена, если доказать теорему этого
пункта. Такое доказательство дано в Приложении (§ 1),
однако при условии, что порядок функции f(z) есть
конечное число. Там же доказывается, что в случае,
когда порядок f(z) дробный, исключительного
значения А не существует.
Применим сформулированную здесь теорему к
частным случаям, указанным в начале этого пункта.
Заметим, что не ограничивая общности можно
считать основание а (а Ф \) показательной функции
равным е, В самом деле, если а Ф е, то, полагая
а = е1па, представим уравнение ах = Ах в виде
ех in а _ Αχ Введем новое неизвестное Χι = л: In a.
Тогда уравнение примет такой вид:
Например, уравнение 2*=2# преобразуется к виду
Итак, рассмотрим уравнение
ez = Az, (70)
причем сначала будем считать А действительным
числом и корни будем искать также только
действительные. Проведем из начала координат касательную к
кривой у = ех (рис. 3). Если (Хо, уо)—точка касания,
то уравнение касательной имеет вид
У — Уо = Уо(х — х0),
dex \
где у0 = ех* и у0 = -^- =ех*. Записывая, что ка-
\X=Xq
сательная проходит через начало координат (0,0),
58

найдем — у0 = — y'0xQi т. е. е** = е**х0, или х0=1, z/0—
= ^<» = β, т. е. угловой коэффициент касательной
равен е. С помощью рис. 3 убеждаемся, что при
О ig А <С е прямая у = Ах не имеет общих точек с
кривой у = ех, т. е. уравнение (70) не имеет
действительных корней. При А < 0 уравнение имеет один
действительный корень. Наконец, при А ^ е оно
имеет два (и только два)
действительных корня,
которые при А = е
(случай касательной)
сливаются в один кратный
корень*). Так обстоит
дело с действительными
корнями уравнения (70) при
А действительном.
Чтобы выяснить
наличие мнимых корней, не
будем больше требовать,
чтобы А было
действительным числом. При Л =
= 0 уравнение (70), как
мы знаем, совсем не имеет
корней. В силу теоремы
этого пункта, другого
исключительного значения быть не может и,
следовательно, при любом А Ф 0 уравнение (70) имеет
бесконечное множество комплексных корней.
В частности, если А — действительное число (=^0),
то действительных корней, как было только что
показано, не может быть больше двух. Поэтому уравнение
(70) имеет в этом случае бесконечное множество
мнимых корней.
Вопрос о числе корней уравнения
sin z = Az (71)
Рис. 3.
*) Что действительных корней не может быть больше двух,
следует из того, что кривая у = ех есть кривая выпуклая (книзу)
и, следовательно, прямая не может пересекать ее более чем в двух
точках. С другой стороны, прямая у = Ах (А > 0), встретив
кривую в первой точке, не может все время оставаться выше
кривой (так как ех растет быстрее, чем Ах)\ поэтому должна быть
и втсрая точка пересечения*
59

решается несколько сложнее потому, что в случае
уравнения (70) бросалось в глаза исключительное
значение Л = 0, а в данном случае неясно, существует
ли исключительное значение или нет.
Будем считать сначала А действительным числом.
При А = 0 уравнение принимает вид
sinz = 0;
оно имеет бесконечное множество действительных
корней ζ = птс (где η = 0, ±1, ±2, ...). Как можно
проверить, выражая sins: по формуле Эйлера (16),
уравнение это не имеет ни одного мнимого корня. Если
А Φ 0, то прямая у = Ах. пересекает синусоиду
у = sin χ только в конечном числе точек и во всех
случаях, по крайней мере, в одной точке — в начале
координат.
Следовательно, при действительном А, где А φ 0,
уравнение (71) имеет конечное число действительных
. корней (не меньше одного). Чтобы выяснить вопрос
об общем числе корней (и действительных и мнимых),
будем считать теперь А произвольным комплексным
числом. Перепишем уравнение (71) в виде
-^-Л. (7Г)
При этом мы можем потерять один (и только один)
корень уравнения (71), равный нулю. Функция ~—-
является целой трансцендентной функцией, ибо
sin z - ζ2 , ζ* ^ ζ6 .
Ζ ~1 3! + 5! 71 ■+" " " "
—■ всюду сходящийся степенной ряд. Можно без труда
убедиться, что порядок ее_ равен 1. Если сделать
замену переменного ζ = -\/ζ, то она перейдет в целую
функцию
л/ζ З! 51 71 9! '"'
порядок которой есть дробное число (γ).
Следовательно, к уравнению
60

можно применить усиление теоремы Пикара,
указанное в предыдущем пункте. Отсюда следует, что
уравнение (71") при любом А имеет бесконечное
множество корней, а поэтому и уравнение_(71') имеет
бесконечное множество корней (z = VO· Отсюда,
наконец, заключаем, что уравнение (71) имеет бесконечное
множество корней при любом-Л, т. е. исключительного
значения здесь не существует. При А Ф О все корни,
кроме конечного их числа, являются мнимыми.
26. В предыдущем пункте мы рассматривали
уравнение вида f(z) = AP(z), где f(z)—целая
трансцендентная функция, Ρ (ζ)—многочлен, А — комплексная
константа.
Рассмотрим, наконец, уравнение
f{z) = Ag(z), (72)
где f(z) и g(z)—различные целые трансцендентные
функции. Например; рассмотрим уравнение tgz = A,
которое можно переписать в виде sin z = A cos zt или
уравнение е1 = A sin ζ и т. п.
Справедлива следующая теорема:
если f(z) и g(z)—две трансцендентные целые
функции, отношение которых не есть рациональная
f(z) Ρ (ζ)
функция (т. е. если -~-γ Φ η) : , где Ρ (ζ) и Q(z) —
многочлены), то уравнение (72) имеет бесконечное
множество корней для каждого комплексного
значения Л, за возможным исключением двух значений, для
которых корни могут иметься лишь в конечном числе
(они могут и не существовать совсем).
Этот результат можно формулировать короче, если
воспользоваться важным самим по себе понятием
мероморфной функции. Функция φ (г) называется ме-
роморфной, если ее можно представить в виде
частного двух целых функций:
Самое название «мероморфная» можно было бы
перевести по-русски словом «дробная». Оно образовано от
греческих слов: мерос (дробь) и морфос (форма, вид).
Сюда относятся, в частности, рациональные
функции, т. е. функции, представляемые в виде частного
61

двух многочленов. Можно доказать, что каждая ме-
роморфная функция, не являющаяся рациональной, не
может быть и алгебраической и, следовательно, транс-
цендентна. Примерами трансцендентных мероморф-
•ных функций являются, например,
, sin ζ , cos ζ
& cos ζ ' ъ sin 2: '
1 1 1
sec ζ = , cosec ζ = -г—, ——г и τ· π·
cos ζ ' sin ζ * ez — 1
Из определения мероморфной функции следует, в
частности, что каждая целая функция f(z) также
является мероморфной, так как ее можно представить
в виде отношения
Ясно, что в основной теореме этого пункта речь идет
о корнях уравнения вида "
где φ (-г)—мероморфная функция (не являющаяся
рациональной).
Поэтому эту теорему можно сформулировать
следующим образом:
если φ (ζ)—трансцендентная мероморфная
функция, то уравнение
ψ(ζ) = Α
имеет бесконечное множество корней для каждого
комплексного значения А, за двумя возможными иск*
лючениями.
Покажем на примере простейшего уравнения
tgz = At (73)
что два исключительных значения действительно
возможны. В самом деле, tg zf по определению, равен
*в" . Переписывая уравнение в виде sin ζ = A cos z,
заменим sin г и cos г по формулам Эйлера (16).
Получим
eiz_ e-iz _ ^ eiz+e~iz
~ ' A n «
2/
62

откуда
(l-Ai)el2 = (l +Ai)e-1*.
Умножая обе части на eiz (число, не равное нулю),
приведем уравнение (73) к виду
{\-Ai)eliz = \+AL (730
Если А = ί, то уравнение принимает вид
2г21'2 = 0, или e2iz=0.
Мы знаем, что оно не имеет корней. Поэтому и
уравнение (73) не имеет корней при А = i.
Если А = —iy то уравнение (73') принимает вид
О · e0Jz = 2,
которое, очевидно, не имеет корней. Поэтому
уравнение (73) не имеет корней и при А = —и
Итак, мы нашли два исключительных значения +ί
и —i для уравнения (73). В силу теоремы этого
пункта никакое другое значение А не может быть
исключительным. В самом деле, пусть Α φ ±ί. Тогда
уравнение (73') можно представить в виде
е21г=В, (73")
1 4- Ai
где В = j _ д. фО. Переходя к логарифмам (см.
п. 8), находим
откуда
2iz = LnB,
z = -^rLnBt
или
В этой формуле объединено бесчисленное множество
корней уравнения (73).
Пусть например, А = 1 и, следовательно, речь
идет о решении простейшего уравнения
tgz=l.
По формуле (74) получаем
9—J_T n JL+jL- J_t n_H+J)L__
Ζ~ 2ί Ln 1-/ — 2/ П (l-i)(l+i) —
63

Но по формуле (220
Ln i = In I i | + i (arg i + 2azjt) =
= In 1 + /(γ + 2ηπ\ = i ίγ + 2nn),
/ι = 0,.± 1, ±2, ...
Окончательно получаем
ζ = ~2fi (τ + 2nnJ=-^- + ηπ, n = 0, ±1, ±2, ...
Все эти корни уравнения tgz = I известны из курса
элементарной математики. Однако из наших
выкладок вытекает нечто большее, а именно, что уравнение
это не имеет мнимых корней.
27. В нашу задачу не входит описание методов
практического вычисления корней уравнений. Эти
вопросы рассматриваются в руководствах по
приближенным вычислениям*). Ограничимся примером
вычислений асимптотических значений корней уравнения
ez = Az (АФО), (70)
т. е. выводом таких простых приближенных формул
для корней, которые становятся тем более точными,
чем больше модуль корня.
Мы уже отмечали в п. 25, что уравнение (70) имеет
бесконечное множество корней при любом А Ф 0.
Заметим еще, что для каждого А все эти корни можно
расположить в виде последовательности, стремящейся
к оо (п. 21). Будем для простоты считать А числом
действительным, положительным. Тогда из (70)
вытекает для любого его корня ζ = χ + iy
\ez\ = A\zl
или
^=Лд/^ + г/2. (700
Но модули корней стремятся к бесконечности
*) См., например, В. П. Д е м и д о в и ч и И. Α. Μ а р о н,
Основы вычислительной математики, «Наука», 1970, глава IV.
64

поэтому и £*->+оо, т. е. #->+оо. Переписывая
(700 в виДе
(ЯЧг-(*У <™">
и замечая, что—^-->0 при #->+оо, заключаем, что
| if I 1
'χ"~*"τ· τ· е· что Для действительных и мнимых
частей корней уравнения (70) справедливо
асимптотическое равенство
\у\*\е**).
Подставляя значение корня ζ = χ + iу в (70), будем
иметь
ex+iy = A(x~+iy),
или
exeiy = ex (cos у + i sin у) = А (х + iy),
откуда, сравнивая действительные и мнимые части,
находим
ех cosy = Ax, ex sin у = Ау. (70'")
Мы заменили уравнение (70) эквивалентной ему
системой (70"'). Выше было показано, что
действительные части корней стремятся к +°°· Поэтому для
достаточно удаленных от начала координат корней
можно считать, что χ > 0. Из уравнений (70'"), очевидно,
вытекает, что если^пара чисел (х, у) удовлетворяет
им, то (х, —у) также удовлетворяет. Это означает,
лто комплексные корни уравнения (70) расположены
симметрично относительно действительной оси, т. е.
попарно являются взаимно сопряженными числами.
Поэтому можно говорить о последовательности
корней, для которых у > 0, и о другой (симметричной),
для которых у < 0.
Начнем с рассмотрения корней, для которых у>0.
Для них — в силу доказанного выше асимптотического
равенства:
уъ\е\
*) Говорят, что переменные величины асимптотически равны,
если предел их отношения равен 1,
65

Поэтому второе из уравнений (70'") даст
sin у« 1,
а это означает, что
у = *+2пп-гП9 (70IV)
где гп -> 0 при η —► оо (я принимает целые
положительные значения). Подставляя это значение у в
первое из уравнений (70"'), получим
ех sin εΛ = Ах или sin ε^ = ——.
Так как sin εη ~ εη, то отсюда следует
асимптотическое равенство
Αχ Αχ χ \п(Ау)
Λ ex Ay у у
Но из формулы (70IV) вытекает, что у « 2пл и,
следовательно,
In (2Алп)
Итак,
тс . 0 In (2Апп)
уът + 2лп gS^—·
х«1п(^) = 1п[2Лл«+41-Л^^^] =
= i„(2^) + i„[i+i-J^]«
«In (2Ляп)+ -!■*),
Поэтому для корней уравнения (70) получаем
асимптотическую формулу
z = x + iy&\n (2Ann) + -^±i[2лп + γ - '" ^"w)],
*) Мы исходим из известной формулы
In (1 + ε) « ε при ε-> 0,
1 In (2Απη)
применяя ее при ε = η. 2 2— и затем отбрасывая сла-
1п (2Алп)
гаемое ' 0 .—, как бесконечно малое более высокого по-
1
рядка по сравнению с -j—.
66

где п принимает целые положительные значения (мы
представили в одной формуле обе последовательности
корней с положительными и отрицательными
мнимыми частями). Читатель может убедиться путем
подстановки, что уравнение (70) приближенно
удовлетворяется при найденных значениях ζ (с точностью до
in η w
величин порядка — бесконечно малых при η оес-
конечно большом).
Найденные формулы могут быть использованы и
для уравнения
sinz = Αζ (при Л>0). (71)
Здесь корни ζ = χ + iу располагаются попарно
симметрично относительно начала координат, причем \у\
бесконечно растет по мере удаления корней от начала
координат. Отсюда следует, что достаточно
рассмотреть, последовательность корней, для которых у < 0
(при достаточном удалении от начала, координат);
другая получится путем одновременной перемены
знаков при χ и у. Заменим sin г по формуле Эйлера;
тогда уравнение (71) запишется так:
е** — е-*г = 2А1г,
или, заменяя iz через новое неизвестное w,
ew — e~w=2Aw. (7 Г)
Здесь w = iz=—y + ix и \e~w\ = \ev~ix\ = еУ->0
при */-*—оо. Отбрасывая бесконечно малую
величину e~w, получим для приближенного вычисления
корней упрощенное уравнение
ew = 2Aw.
Сравнивая с уравнением (70), видим, что w можно
представить по асимптотической формуле вида
w = u + to ж In (4Апп) +-^±i\2nn + у 2π/Γ* ]'
Поэтому для ζ = -г w = — iw получаем
ΖΡύ ± [2jw +1 _ «-й£=>] _ f [,n (4Ля„) + ±.],
67

где п принимает целые положительные значения. Если
учесть-, что корни расположены симметрично
относительно начала координат, то двойные знаки следует
поставить и перед мнимой частью.
28. Аналогия между целыми функциями и
многочленами, которую мы неоднократно подчеркивали,
помогла в свое время Эйлеру найти разложение sin ζ в
бесконечное произведение. Прежде чем рассказывать
об этом, условимся записывать разложение
многочлена на множители в форме, несколько отличающейся
от привычной в алгебре. А именно, расположим все
нули многочлена Ρ (ζ) степени η в порядке
неубывающих модулей, повторяя каждый столько раз, какова
его кратность:
О, ..., О, а, ..., а, Ь, ..., 6, ..., с, ..., с. (*)
α k I m
Здесь a + k-\-l-\-... + m = n. Мы поместили на
первом месте нуль, расположенный в начале
координат. Если эта точка не является нулем многочлена,
то полагаем а = 0. Тогда во всех случаях будем
иметь разложение
Здесь С — коэффициент младшего члена P{z)\ его
можно вычислить по формуле
С = lim —^-L
2-»0 Ζ
(есля α = 0, то просто С = Р(0)).
В одной работе, посвященной вычислению сумм
оо оо оо
вида Σ~^' Σ"*"· Σ^· ··· (°пУблик°вана в
1 1 1
1740 г. в «Комментариях Императорской
Петербургской Академии наук»), Эйлер рассматривает
уравнение
sinz = z-^- + -g-- ...=0,
по аналогии с алгебраическими уравнениями, как
уравнение «бесконечно высокой степени». Оно имеет
бесконечно много корней: ζ = 0, ±π, ±2π, ±3π, ...
68

Не удивительно поэтому, что левая часть разлагается
в произведение бесконечного множества множителей
первой степени, среди которых нет равных: z, (l ·——-)»
(*+£)> 0--Й· 0+l9'··· Но это озна-
чает, что
-«-«О-£)(·+*)('-£)('+«) ·—
Здесь в правой части не выписан неопределенный
множитель С, потому что в данном случае он равен 1:
,. sin ζ -
hm —- = 1.
Конечно, с современной точки зрения, рассуждение
Эйлера нельзя считать доказательством. Это скорее
способ, позволяющий угадать нужное соотношение,
которое потом должно быть обосновано. К этому
вопросу мы еще вернемся. Однако полученный им
результат все же верен. В рассматриваемой работе
Эйлер довольствуется сказанным и спешит
сравнить между собой коэффициенты при ζ2 в ряде для
sin ζ ζ^ ζ^
—— = 1 ~ + -y^j- — ... и в произведении
~2
V1 пчУ 4π*)ν 9π0
Перемножая здесь двучлены по правилу
умножения многочленов, он получает в качестве
коэффициента при ζ2 сумму ряда
π2 [} + 22 "^ З2 "*" · · Vе
А так как коэффициент при ζ2 в степенном ряде для
sin z l
есть — -г\ то
ζ 6
14-J-4--J-4. — it
Это и есть один из результатов, которого Эйлер
добивался в этой статье.
69

Нетрудно, однако, указать пример, где подобный
способ рассуждения приводит к явной ошибке.
Рассмотрим вместо sin ζ другую столь же простую целую
функцию: ег—1. Здесь корнями соответствующего
уравнения «бесконечно высокой степени»
*ζ-1=*+ΐ+ΐ+···=°
служат все значения Ln 1 = In 1 + i(arg 1 + 2пл) =
= 2nnit т. е.
ζ = О, ± 2ш, ± 4ш, ± 6ш, ...
Следуя ходу идей Эйлера в предыдущем
рассуждении, заключаем, что ez—1 разлагается в
произведение множителей, среди которых нет равных: г,
1~ш· 1+ш· 1~ш- 1 + ш> ··· Это озна"
чает, что
«•-'-О -£■)(> +£·)(' -£)(' +£)■·-
==г(1+2&)(1+4&)··
В правой части не выписан неопределенный
множитель С, потому что и в данном случае
ez — 1
Iim—— =1.
Однако эта правая часть может быть представлена
в виде
что, согласно с разложением Эйлера для sin г, дает
— 2/ sin -γ. Легко видеть, что левая часть, т. е. ez— 1,
не совпадает с последней функцией. В самом деле,
ег - 1 = - 2ieT е 2~е* = <Д (- 2tsin-f-).
70

Поэтому верное разложение на множители для ег — 1
должно иметь вид
в»-1-Л(1 +^)(1 +^)(1 +"ё&) ...
Итак, для разложения целой функции на множители
мало знать все ее нули. Необходимо еще учесть
возможность множителя, не обязательно постоянного, но
не имеющего ни одного нуля. В нашем примере это е2.
При отыскании разложений на множители
функций sin ζ и ez— 1 мы до сих пор обходили молчанием
вопрос о сходимости получаемых бесконечных
произведений; в рассмотренных случаях они, как это можно
показать, действительно сходились. Однако в общем
случае целой функции f(z) с бесконечным
множеством нулей дело может обстоять иначе. Выпишем
последовательность нулей f(z) в порядке неубывающих
модулей:
мы знаем (стр! 52), что она стремится к оо. Если
формально составить соответствующее бесконечное
произведение, аналогичное разложению многочлена
на множители:
«■('~3Ό-τ)Ό-ί)'···.
то может оказаться, что оно расходится (при ζΦΟ, α,
b, с, ...) и, следовательно, не представляет собой ни
одну целую функцию. Чтобы преодолеть возникающую
здесь трудность, К. Вейерштрасс предложил в 1876 г.
ζ ζ ζ
вместо множителей 1 , 1 — у, 1 ,...,
каждый из которых имеет только по одному-единствен-
ному нулю, соответственно a, b, с, ..., пользоваться
более общими целыми функциями, обладающими тем
же свойством, а именно:
(1-£И<2\ (l-y>B<*>, (1~7>С(г)
71

где Α (ζ), Β (ζ), С (ζ), ... — некоторые целые функции.
Более того, он показал, что для произвольно заданной
последовательности комплексных чисел вида (**),
стремящейся к оо, можно подобрать такие много*
члены Α (ζ), Β (ζ), С (ζ), ..., что бесконечное
произведение
«■[(•-a'-no-fMto-T)""!"···
будет сходиться при любом ζ и представлять целую
функцию ψ {ζ), имеющую своими нулями все точки
заданной последовательности и только их. Чтобы
выписать подобную функцию в явном виде (их
существует бесконечное множество), будем обозначать по
порядку члены последовательности (**), отличные от
точки ζ = 0, через^ь ζ2, ζ3, ..., (например Ζι = ..,
... = Zh = a> zk+\ = ... = Zh+i = b, Zk+i+i = ..«
... = Zk+i+m = с и т. д.). Тогда по теореме Вейер-
штрасса одну из целых функций с требуемыми
свойствами представит формула
φ(ζ)-2·Π[θ-ΐ>^^+'"+·^Ί.
оо
Здесь Ц—знак бесконечного произведения (подоб-
1
оо
ный знаку Σ для бесконечного ряда).
Если функция φ (ζ) построена, то любую другую
целую функцию f(z) с той же последовательностью
нулей получим по формуле
где g(z) — целая функция, которую нужно найти, зная
φ(г) и f{z).
В случае целой функции конечного порядка общая
формула разложения на множители, как показали в
конце XIX в. французские математики Э. Борель и
Ж· Адамар, может быть упрощена. А именно,
предположим, что порядок целой функции f(z) есть р, и
пусть κ = [ρ] — целая часть р. Тогда разложение
72

функции f(z) на. множители можно представить в
виде
(если ρ < 1, так что κ = 0, то каждый показательный
множитель под знаком произведения заменяется
единицей). Преимущество этой формулы Бореля — Ада-
мара перед формулой Вейерщтрасса в том, что
неизвестная целая функция g(z) принимает здесь вид
многочлена степени κ и многочлены степени η под знаком
произведения также заменяются многочленами одной
и той же степени κ.
Применим последнюю формулу к разложению на
множители sin г. Здесь ρ = κ=1, α=1, ζ{ = π,
ζ2 = — π, ζζ = 2π, ζ4 = — 2π, ..., z2k-.{ = kn, z2k =
= —- &π, ... Получим, группируя попарно множители
для η = 2k — 1 и n = 2k:
оо
= ^+е"гП0-тЙг)·
Остается найти константы Со и с ι. Перепишем
полученную формулу в виде:
ОО
sin ζ ΊΓΤ / ζ2 \
Так как ^ и 11(1 -
- "д^т) — четные функции ζ,
то и eCo+Cl2 должна быть четной функцией. Поэтому
βέ?β+<?ι2 === gco-ci^ откуда e2ClSS=l и ^==0. Итак,
и, следовательно,
1 = lim -=ес\
2-»o г
73

Мы снова получаем разложение Эйлера:
sinz = *n(l~w)·
Рекомендуем читателю получить из общей
формулы Бореля — Адамара, независимо от разложения
для sin г, разложение
е*_1=Дщ1+_1у.
(Указание: воспользуйтесь тем, что ^ сг есть
четная функция.)
ге'
схг

ГЛАВА ПЯТАЯ
АЛГЕБРАИЧЕСКИЕ СООТНОШЕНИЯ
ТЕОРЕМЫ СЛОЖЕНИЯ
29. Мы видели, что целая функция f(z), отличная
от многочлена, не может удовлетворять никакому
алгебраическому уравнению (п, 16). Именно поэтому
такие функции и называются трансцендентными. Однако
две трансцендентные целые функции могут быть
связаны между собой алгебраическим уравнением.
Простейший пример — это sin ζ и cos ζ, удовлетворяющие
соотношению
sin2 z + cos2 z = 1. (75)
Рассмотрим более общее соотношение
[/(г)Г + [£(г)Г=1, (76)
где η — целое число, не меньшее двух, и поставим
задачу разыскать все целые функции, которые ему
удовлетворяют.
Начнем со случая η = 2. Имеются ли другие
целые функции, кроме sin z и cos z, которые связаны
между собой уравнением того же вида? Так как (75)
является тождеством относительно ζ, оно останется в
силе, если вместо ζ подставить любую целую
функцию. Так, например, мы можем писать:
sin2(I - ζ + 2Ζ3) + cos2(l - ζ + 2ζ?) = 1,
sin2 (ez) + cos2 (ez) = 1.
И вообще, если h(z)—какая-либо целая функция, то
sin2lft(z)] + cos2[A(z)]==l.
Так как целая функция от целой функции снова
является целой (п. 5), то мы получаем следующий
результат:
существует бесчисленное множество пар целых
функций
sin [А (г)] и cos [А (г)] (77)
75

(где h(z)—какая угодно целая функция), связанных
между собой алгебраическим соотношением (75).
Докажем теперь справедливость обратного
предложения:
если f(z) и g(z)— пара целых функций,
удовлетворяющих соотношению
U(z)]2 + [g(z)]2=L (78)
то существует такая целая функция h (ζ), что f (z) =
= cos [h (z)] и g (ζ) = sin [h (z)].
Для доказательства преобразуем уравнение (78)
к виду
[f(z) + ig(z)][f(z)-ig(z)]=l. (780
Отсюда видно, что f{z)+ig(z) есть целая функция,
не обращающаяся в нуль ни при каком ζ. Поэтому
(см. п. 9) существует некоторая целая функция —
представим ее в виде ih(z)— такая, что
f(z) + ig(2) = e*M, (79)
следовательно,
/(*)-'*(*>-,(,) + ,,(,)-«-ц<»· №
Из (79) и (80) следует:
f (z) = -2 γ cos [h (ζ)],
eih (г) _ e-ih (г)
g (ζ) = ^ = sin [h (г)],
что и нужно было показать.
30. Вернемся к общему уравнению
[/(г)Г + [£(г)Г=1, (76)
где η ^ 3, и докажем принадлежащую французскому
математику Монтелю теорему о том, что не суще-
ствует никакой пары целых функций, не равных
тождественно константам, которые удовлетворяли бы
этому уравнению.
Предварительно разложим двучлен вида хп + 1 на
линейные множители. Для этого достаточно найти
все η корней уравнения хп + 1 = 0, или хп = —1.
76

Корни эти таковы: #£ = cos—! (-isin—! ,
k = 0, 1, 2, ..., я — 1. В самом деле, все они попарно
различны и каждый удовлетворяет условию х% = — 1.
Полагая для краткости #o = cos—h ^ sin — ===== е,
будем иметь:
cos- + *sin — J =8-*+*, & = 0, 1, ..., я — 1.
Следовательно,
*я + 1 = (*— *ο) · · · (* — *«-ι) =
= (χ — ε) (λ: —· ε3) ... {χ — ε2η~!);
подставляя вместо # частное -Втг и умножая обе
части на [g{z)] , получим тождество
[f(z)r + [g(z)]n =
= If (z) - eg (z)) [f (ζ) - *?g (ζ)) [f (ζ) - tfg (ζ)} ...
...[f(2)-e*-'i(z)j. (81)
Из соотношения (76) вытекает, что ни один из
множителей в правой части (81) не может обратиться в
нуль ни при каком ζ. Так как каждый из них есть
целая функция, то замечаем (см. п. 9), что существуют
целые функции h0(z), hi(z), ,.., hn-i(z) такие, что
f(z)-Bg(z) = e»><*\ f(z)-e3g(z) = eft-<*>,
f (ζ) - e5g (ζ) = eh>(г) / («He*--'* (г) = Λ-(г).
Рассмотрим первые три из этих равенств (всего таких
равенств п, а мы предположили, что η ^ 3). Вычитая
почленно второе из первого, а третье из второго,
найдем
(83 _ 8) g φ _ eh, (ζ) _ eh, (г)9
(β5 — 83) g φ = eht (z) _ eh2 (г)л (83)
Заметим, что
e = cos—h ^ sin — ==«==0 и 8- = cos hi sin—ф±\
77

(так как п^ 3). Поэтому из тождеств (83) следует;
eh* iz) — ehi (z) ehx (ζ) __ eht (ζ)
ε (ε2- 1) = β3 (β2— 1) '
ИЛИ
eV»(2) + eh* (2> = (1 + ε2) eh> <2).
Представим последнее в виде
Г 8 Mz)~Mz)"|2 г ^ι(ζ)-Λι(ζ)Ί2
Lvt+72"^ 2 J +[νττ^* 2 J=1"
Так как функции в квадратных скобках целые, то по
теореме п. 29 должна существовать такая целая
функция h(z), что
fh(z)-hi(z)
е 2 = cos [h {z)]y
Vl +ε2
ι hi (ζ)-hi (ζ)
e 2 = sin [h (г)].
Vl +
(84)
Покажем, что h(z) есть тождественная константа.
Если допустить противное, то h (z) должна быть либо
многочленом степени не ниже первой, либо целой
трансцендентной функцией. В первом случае найдется
такое значение ζ = ζ0, что h (z) = γ (в силу основной
теоремы высшей алгебры). При ζ = ζ0 левая часть
первого из уравнений (84) отлична от нуля, а правая
равна нулю, что невозможно. Во втором случае, в
силу малой теоремы Пикара (п. 24), хотя бы одно из
двух уравнений h{z) = -j и h{z) = —~· будет иметь
корни (и даже бесконечное множество корней). Если
Zq — один из них, то, подставляя z0 в первое из
уравнений (84), снова получим противоречие.
Итак, доказано, что h(z) есть константа. Из
равенств (84) следует, что показатели в левых частях
также константы
h0 (ζ) — hi (ζ) _ h2(z) — hx(z) _ ,
2 ~a' 2 —
78

Но первое из равенств (83) дает
σ(ζ\ = £ 1 _ ehi (ζ) £ L —
8\ζ) ε(ε2~1) & ε(ε2-1)
2α ι
= *Λι (2) ! 2~ η = aehl (г)> (85)
ε (ε2 — 1) ' ν '
е2а—\
где α = —τ—2—гг есть константа. С другой стороны,
ε ^ε ι)
из второго из равенств (82) вытекает, что
/ (г) = e3g {ζ) + eh> <г) = (ε3α +l)eh*(2) = $eh> <2>, (86)
где β = ε3α+ Ι.
Подставляя в (76), найдем
т. е.
phi (ζ) _ — _ v
есть тождественная константа. Сопоставляя с (85) и
(86), убеждаемся в том, что f(z) и g(z)—также
тождественные константы. Теорема Монтеля доказана.
Подведем итоги двух последних пунктов: если
целые функции f(z) и g(z) удовлетворяют
алгебраическому соотношению вида
[f(z)]n + [g(z)]n=U
где п —целое число ^2, то при п = 2 они
необходимо имеют вид
f (z) = cos [h (г)], g (ζ) = sin [h (г)],
где h (ζ) — целая функция, а при η ^ 3 тождественно
равны константам.
Заметим, что приведенное выше доказательство
теоремы Монтеля можно почти без изменений
применить к доказательству следующей более общей
теоремы: не существует ни одной пары целых функций
f(z) и g(z), не равных тождественно константам,
которые удовлетворяли бы уравнению вида
a0[f(z)]n + al[f(z)]n-lg(z)+ ... +an[g{z)]n = by
где η ^ 3, Ь Φ 0, и уравнение а0хп + αχχη~χ + ...
... -\-ап = 0 имеет, по крайней мере, три не равных
79

между собой и отличных от нуля корня. В самом деле,
обозначая через λ:0, Хи ..., Χη-ι корни последнего
уравнения, мы можем переписать заданное
соотношение между целыми функциями в виде
χ I/ (*) - χο8 (*)] ί/ (*) - W Wl [/ («) - xtf Ш ■ ■ ■
...tf(z)-*„-iff(z)] = l
и далее применить к трем различным множителям
f (г) — Xog (г), f (г) — xxg (г), / (ζ) — x2g (ζ)
изложенные выше рассуждения, показывающие, что
f(z) и g(z)—тождественные константы.
31. Мы не будем рассматривать другие возможные
алгебраические соотношения между несколькими
различными целыми функциями.
Перейдем к алгебраическим соотношениям," связывающим
между собой значения одной и той же целой
функции, принимаемые ею в различных
точках.
Начнем с простейшего из них — условия
периодичности целой функции
/(ζ + ω) = /(ζ),
где ω — константа, называемая периодом функции
f(z). Примерами целых периодических функций
являются показательная функция ez (период 2ш),
тригонометрические функции cos -г и sin г (период 2π)
и др. Если ω — какое угодно комплексное число, не
равное нулю, то простейшим примером целой функции
с периодом ω может служить показательная функция
Се ω , где С Φ 0. Очевидно, что тождественную
константу можно рассматривать как периодическую
функцию, периодом которой является каждое
комплексное число. Покажем, что никакой многочлен, за
исключением константы, не может быть
периодической функцией. Действительно, Ρ(ζ)->-οο· при г—* оо.
Допустим, что ω ФЪ есть период многочлена. Если
Ζο — какая-либо точка, то
P(z0) = P(zo + <u)=P(zQ + 2to)=...=P(zo + n(u)=...
Очевидно, что z0 + ясо -* оо при η -* оо и,
следовательно, Ρ(ζο-\- ηω) -> оо при п—> оо. Но это
заключено

ние несовместимо с тем, что значение ^(ζο + Αίω)
остается равным константе Ρ(ζο). Таким образом,
целая функция /(г), не равная тождественно константе,
может быть периодической только в том случае, когда
она трансцендентна.
С помощью показательных функций можно
построить сколько угодно целых периодических функций.
Пусть, например, пи п2, ..., tik — какие-либо
различные между собой целые числа. Тогда каждая из целых
функций β ω ι , е ω 2 , ..., е ω k будет обладать
периодом ω. Помножая их на любые комплексные
числа Аи А2у ..., Ak (среди которых могут быть нули) .
и складывая, получим в сумме снова целую функцию
с периодом ω:
k 2πί
/=-1
Функции такого вида называются
тригонометрическими многочленами. Это название легко
оправдывается; заменяя показательную функцию
тригонометрическими по формуле
е ω / = cos (— ημ) +1 sin [— tijz),
представим f(z) в виде
k
/ (ζ) = £ [Aj cos (f. ημ) + iAi sin (£ n,z)].
Предположим, в частности, что щ = —ρ, η2 =
= — ρ + 1» · · ·> nk = ρ, где ρ — какое-либо целое
неотрицательное число (числа nlf п%, ..., пи идут,
возрастая на 1, от —ρ до р\ очевидно, что k = 2p+ 1),
Тогда тригонометрический многочлен примет вид
±р 2πι
tlsZ
-ρ
i(z)=fj[Aicos(fiz) + iAisin(fjz)].
-ρ
81

Используя четность косинуса и нечетность синуса,
последнюю сумму можно записать еще так:
/ (г) = А0 + £ [(Лу + Л-7) cos (-f- jz) +
+ (Μ, - /Л-,) sin (^ /г)].
Полагая Aj + /l_j = #j и *Л; — *71_j = bj,
запишем, наконец, тригонометрический многочлен в виде
f(z)=A0 + j][aicos^jz) + bIsm(fjz)l
Если здесь хотя бы одно из чисел ар и Ьр отлично
от нуля (а это значит, что хотя бы одно из чисел Ар
и А-р отлично от нуля), то ρ называется порядком
тригонометрического многочлена. При р=0 получаем
тождественную константу как частный случай
тригонометрического многочлена.
Следующая теорема выделяет тригонометрические
многочлены среди всех целых периодических функций:
если для целой периодической функции f(z) с
периодом ω φ 0 выполняется неравенство вида
\f(z)\<Ceyi«rz{
при некоторых С > 0, γ ^ 0 w всех достаточно
больших \z\ (\z\ > /?о), то f(z) есть тригонометрический
многочлен порядка не выше чем ρ = [у] ([у] — целая
часть у).
В частности, если 0 ^ у < 1, то ρ = [у] = 0;
поэтому при γ < 1 функция f(z) есть тождественное
постоянное.
Если целая периодическая функция с периодом ω
не является тригонометрическим многочленом, то она
изображается в виде суммы всюду сходящегося ряда
+оо 2л i
вида f(z)= Σ Апе ω , который можно представить
также в виде тригонометрического ряда
f (ζ) = α0 + [α, cos (^ ζ) + b{ sin(^- ζ)] + ...
... + [α„ cos {-^ nz) + bnsin (-£■ иг)] + ...; (87)
82

среди его коэффициентов имеется бесконечное
множество отличных от нуля.
Справедлива и обратная теорема: каждый всюду
сходящийся ряд такого вида представляет целую
периодическую функцию с периодом ω. При этом она,
наверное, будет отличаться от любого
тригонометрического многочлена, если среди коэффициентов ряда
найдется бесконечное множество не равных нулю.
Доказательства соответствующих фактов изложены
в § 2 Приложения.
32. Конечно, каждая функция, имеющая период ω,
имеет и другие периоды: —ω, 2ω, —2ω, ... ; вообще
периодом f(z) является любое целое кратное ω. Так,
например,
/ (г - Зсо) = / [(ζ - 3ω) + ω] = f (ζ — 2ω) =
= /[(«-2ω) + ω] = /(2-ω) = /[(2-ω)+ω] = /(ζ),
откуда и следует, что —Зсо также является
периодом f(z).
Если &со и Ζω — два каких-либо периода f(z), то
отношение их является числом рациональным (у)·
Спросим себя, однако, может ли случиться, что
для некоторой целой функции f(z) существуют два
периода coi и сог, отношение которых не есть
рациональное число? Оказывается, что если только f(z) не
равна тождественно константе, то ответ на этот
вопрос отрицательный. Иными словами, целая функция,
имеющая два периода, отношение которых не есть
рациональное число, тождественно равна постоянной.
Доказательство этого предложения подразделяется
на два случая.
Предположим сначала, что отношение -~ = а есть
число действительное иррациональное. Пусть η —
произвольное натуральное число и рп — целая часть
числа па. Тогда 0 < па — рп < 1, откуда \ηω2 — рпы\ \ =
= \па — рп\ |ωι|<|ωι|.
Очевидно, что если га Φ η, то гасог — Pm(Oi Φ
Ф ЯС02 — Рп(х)1 (еСЛИ ДОПУСТИТЬ, ЧТО гао)2 — /?mC0i =
Сйо Pm -~ Рп
=ясо2 — Pncoi, то получим а = —- = -£^—^— число
КО J ill "— ГЪ
рациональное, что противоречит условию). Поэтому
83

все точки бесконечного множества
со2 — Ριωί9 2ω2 — р2и>и ..., ηω2 — рп®ь · · ·
различны между собой и содержатся в круге
радиуса |coi| (с центром в точке 0). Но в каждой из них
периодическая функция f(z) принимает одно и то же
значение ϊ(ηω2— pn(u\) = f(Q) (ведь ог и coi —
периоды f(z)). Отсюда по п. 21 и следует, что f (г) = / (0),
т. е. f(z) есть константа.
Рассмотрим случай, когда — не является
действительным числом. Из этого предположения
вытекает, что векторы, изображающие он и сог и
проведенные из одной точки Zq (какой угодно), определяют
Рис. 4.
некоторый параллелограмм Ρ (рис. 4). Из
периодичности функции f(z) следует, что значение,
принимаемое ею в любой точке плоскости zf принимается
также в некоторой точке г' этого параллелограмма,
связанной с ζ соотношением вида
г = ζ' + Ш\®\ + пг2щ (т{ и пг2 — целые числа).
В самом деле,
f(z) = f (ζ' + тхщ + тзсоз) = / (г'),
так как ωι и сог являются периодами f(z). Поэтому,
если все значения \f(z) \ в параллелограмме Ρ не
превосходят некоторого положительного числа Μ (такое
число существует, так как функция f(z) непрерывна,
84

а следовательно, и ограничена по модулю в Я), то и в
любой точке плоскости будет выполняться
неравенство
IfUOKAf.
Иными словами, целая функция f(z) ограничена по
модулю во всей плоскости. Но по теореме Лиувилля
(п. 14) такая функция тождественно равна константе.
Этим и завершается доказательство нашего
предложения.
Вместо класса целых функций можно
рассматривать более широкий класс мероморфных функций
(см. п. 26). Оказывается, что среди мероморфных
периодических функций существуют отличные от
постоянных функции, обладающие периодами ωι и сог,
отношение которых есть мнимое число. Такие
функции называются двоякопериодическими или
эллиптическими функциями. Значения, которые они
принимают в параллелограмме периодов, построенном на
векторах ωι и сог, повторяются во всей плоскости*).
33. Некоторым обобщением соотношения
f(Z + «>) = f(z)
может служить соотношение вида
f(z + co) = af(z) (ω^Ο, αφΟ). (88)
Легко указать пример целой функции,
удовлетворяющей этому соотношению. Это — показательная функ-
In a
2
ция(р(г)=£ ω , где In α — главное значение
логарифма а (п. 8, формула (22")). Очевидно, что
In а . , . In а , , , In a In α
(г+ω) z+ln a In α г ζ
е ω =е ω —е е ω _ ае ω ?
т. е. функция φ (ζ) действительно, удовлетворяет (88):
φ (г + ω) = αφ (ζ). (88')
Разделим почленно (88) на (88'), получим
/ {ζ + ω) : φ (ζ + ω) = f (ζ) : φ (ζ).
*) См., например, А. И. Маркушевич, Замечательные
синусы, изд. 2, М., «Наука», 1974»
85

Отсюда следует, что частное }(ζ) :φ{ζ) есть функция
g(z) с периодом ω. При этом g(z) есть целая
функция, так как φ (г) не обращается в нуль. Итак,
In a
f{z) = q>{z)g(z) = e ω Zg{z\
т. е. каждая целая функция, удовлетворяющая (88),
есть произведение показательной функции е ω на
какую-либо целую функцию g(z) с периодом ω.
Введем обозначения
/ (ζ) = и, ϊ(ζ + ω) = ν.
Тогда уравнение (88) представится в виде
и — αυ = 0. (88")
Это линейное соотношение между и и υ. На первый
взгляд может показаться, что мы получим
значительное обобщение рассматриваемой задачи, если вместо
линейного уравнения (88") будем искать целые
функции, удовлетворяющие алгебраическому однородному
уравнению любой степени п:
a0un + alun-lv + a2un-2v2+ ... +αηυη = 0, /г>1, (88"0
где для определенности а0 Φ 0. Однако многочлен в
левой части уравнения всегда может быть разложен
на множители
а0 (и — χ0υ) (и — χχυ) ... {и — χη-\υ) = 0»
и, следовательно, все сведется к выполнению одного
из условий вида
u — xkv = 0 (u = f{z + (u), v = f {ζ)),
а этот случай уже был рассмотрен нами.
34. Интересный и важный тип алгебраических
соотношений между тремя значениями функции
представляют так называемые алгебраические теоремы
сложения.
Говорят, что функция f(z) (предполагается, что
это функция аналитическая, а в нашем изложении —
целая) обладает алгебраической теоремой сложения
86

(или подчиняется ей), если для любых Z\ и г2
значения функции f(Zi) = и, f(zz) = υ и f(Zi + 22) = w
связаны между собой алгебраическим соотношением
Ρ (и, υ, w) = 0 (89)
(Ρ (и, υ, w)—многочлен относительно трех
переменных и, υ, w).
Простейший пример целой функции, обладающей
теоремой сложения, — это линейная функция
f (ζ) = αζ.
Здесь и = azu υ = az%, w = α(ζι + ζζ)\ очевидно, что
w = u + u или w—-и— ϋ = 0.
Следовательно, в данном случае можно положить
Ρ (и, υ, w) = w — и — υ.
Другой пример — это функция
f(z) = az2.
Здесь и = αζ\, υ = az\, w = a(z{ + z2)2. Поэтому w =
— и + ό + 2 л/uv , или, освобождаясь от
иррациональности,
(w — и — υ)2 — Auv = 0.
Здесь Р(и, υ, w) = (w—и — α)2— Auv — многочлен
второй степени относительно и, υ, w.
Более общий случай — функция f (ζ) = αζη, где
/г —целое число, большее или равное 2. Здесь u = az'{,
η η η
ν = αζ%, w = a(zx+ ζ2)η, откуда л]т = У и + Vu ·
Здесь также можно было бы избавиться от
иррациональности и получить соответствующий многочлен
P(u,vfw). Однако нет необходимости фактически
приводить эти выкладки. Удобнее сохранить теорему
сложения для данного случая в этой простейшей
форме (с радикалами).
В случае показательной функции ez теорема
сложения, как известно (см. п. 7), имеет следующий вид:
или в наших обозначениях w — uv = 0. Здесь
P(u,vyw)=w — uv — многочлен второй степени.
87

Рассмотрим еще функции cos ζ и sin ζ. Так как
эти функции выражаются через показательные, то
теоремы сложения для них можно вывести из теоремы
сложения для показательной функции.
Проще всего это делается так. По формуле Эйлера
eiz = cos z + i sin ζ, поэтому
ei (Zl+Zl) = Cos (Z{ + z2) + i sin fa + z2). (90)
С другой стороны,
ei (zt+zi) _ eizxeiz2 _ (cos Zi _j_ ι sjn Zij (cos г2 _|_ j sjn 22j _
= (cos zj cos z2 — sin zi sin z2) H-
+ ι (sin]zi cos z2 + sin z2 cos z{). (91)
Сравнивая, получаем
cos (zj + z2) + ί sin (zi + 22) = cos z\ cos z2 —- sin zx sin z2+
+ i (sin zi cos z2 + sin z2 cos z{). (92)
Так как cos(zi + zz) и sin(zi + 22) в общем случае не
являются действительными числами, то у нас нет
возможности получить нужные формулы путем
«приравнивания» действительных и мнимых частей. Мы
придем к цели, используя четность cos z и нечетность sin z
(см. п. 7). Заменяя здесь Zi на —Zi и z2 на —z2,
найдем
cos (zi + z2) — ι" sin (ζχ + ζ2) = cos zx cos z2 — sin zx sin z2 —
— i (sin Zj cos z2 + sin z2 cos Zj). (93)
Наконец, путем почленного сложения,
соответственно вычитания, равенств (92) и (93) приходим к
формулам:
cos (ζχ + ζ2) = cos Ζχ cos z2 — sin Ζχ sin z2, (94)
sin (zj + £2) = sin Ζχ cos z2 + sin z2 cos z^ (95)
Первая из них при Ζχ = ζ и ζ2 = —ζ дает
l = cos2z + sin2z. (96)
Формулы (94) и (96) по внешнему виду отличны от
выше рассмотренных теорем сложения. В самом деле,
здесь значение cos(zi + z2), например, выражается не
только через cos Ζχ и cos z2, как должно бы быть, но
и через значения другой функции: sinzi и sinz2. На
88

помощь приходит формула (96). Полагая, как и
ранее, cos Z\ = w, cos Zi = υ, cos(2i + z2) = w, получаем
sinz! = дЛ — ^2» sin ,22 — Vl ~" ^2;
следовательно, формула (94) принимает вид
w = uo — V1 — и2 V1 ~~ ν2 ·
Достаточно избавиться от радикалов, чтобы
представить теорему сложения для cos z в виде,
непосредственно отвечающем определению алгебраической
теоремы сложения. Получим
(ад - uvf - (1 - и2) (1 - υ2) = 0,
или окончательно
ад? - 2иоад + и2 + у2 — 1 = 0. (97)
Итак, здесь Ρ (и, и, ад) = w2 — 2uvw -j- и2 -\- υ2 — 1 —
многочлен третьей степени.
Предоставляем читателю провести самостоятельно
выкладки для случая sin z.
35. Хорошо известна фундаментальная роль теорем
сложения в изучении и применении показательной и
тригонометрических функций. Все формулы
тригонометрии являются следствиями теорем сложения.
Мы вывели выше несколько теорем сложения для
соответствующих функций.
Покажем на примерах, как можно находить целые
функции, исходя из известных теорем сложения.
a) f(Zl + z2)=,f(zl)+f(z2).
Положим сначала Ζι = ζ и z2 = 0, получим f(z) =
= f(z)+ /(0), откуда /(0)=0.
Пусть теперь Ζι = ζ — фиксированная точка, а
ζ2 = ft Φ 0 — переменное число; получим
/(2Г + А) —f(2T) = /(*) —f(0).
Деля на ft и переходя к пределу при ft -> 0, получим
f (z) = F (0) = C = const.
Следовательно,
f(z) = Cz + b,
и так как /(0) = 0, то Ь = 0. Окончательно
Г(г) = Сг,
т. е. f{z)— линейная функция ζ.
89

Уравнение
f(zl+z2) = f(zl) + f(z2) + c,
где с — какое-либо комплексное число, сводится к
предыдущему, если положить f(z)=y(z)—с. В
самом деле, получим
Ψ (*ι + ζ2) = φ (ζχ) + φ (г2),
откуда φ(ζ) = αζ и, следовательно, /(г) = αζ — с.
Пусть читатель проверит, что уравнению
f(zi + z2) = j[f(zl) + f(z2)]
удовлетворяет только / (ζ) == const, а уравнению
f(z1+2r2) = |[f(2l) + f(22)] + l
вообще не удовлетворяет никакая функция (в обоих
случаях достаточно положить Ζι = ζ и ζ% = 0).
b) [f (ζ, + z2) - f (zt) - f (z2)f - 4/ (zx) f (z2) = 0.
Полагая zx = г и г2 = 0, получим
[/(0)]2-4/(0)/(z) = 0,
откуда либо /(0)=0, либо f (г) = -т/ (0) = const;
последнее приводит к f(z) г 0 (так как при г = 0
получаем /(0) = ^-/(0) и, следовательно, /(0) = 0).
Будем искать решение уравнения Ь), не равное
тождественно 0. Тогда для некоторого d Φ 0 мы
должны иметь f(d)=£0. Положим в Ь) Ζι = ζ и z2 = d.
Найдем
2 л/Шл/Ш = ± [f{z + di-fW-№].
В правой части здесь фигурирует целая функция (так
как f(z) и f(z-\-d)—целые функции). Поэтому и
левая часть, а следовательно и Vf(z)> есть целая
функция. Положим V/ (z) — Φ (ζ)-
Из b) вытекает
f (*ι + *2) - / (г.) - f (z2) = 2 Vffa) Vf^,
/(г,+г2) = (УП^+Уга)2>
90

откуда
или.
Мы нашли, что φ (г) удовлетворяет уравнению а).
Поэтому φ (г) = Cz, и так как f(z) = φ2 (г), то
/(г) = С222.
Здесь, при С = О вновь получается найденное выше
решение f(z) ==· 0.
с) f(zl + z2) = f(zl)f(z2).
Положим сначала Ζι = ζ и ζ% = 0; получим f(z) =
= /(2)/(0). Если f(0) = 1, то f(2)s=0. Это одно из
решений предложенного уравнения.
Пусть теперь 1(ζ)φ0; тогда /(0)= 1. Полагая
ζ{ = ζ и ζ2 = —г, получим
/(0)=1=/(гШ-г).
Отсюда вытекает, что f(z) ни при каком г не
обращается в нуль и, следовательно, Lnf(z) есть целая
функция (см. п. 9). Точнее говоря, существует такая
целая функция g(z)t что
Lnf(z) = g(z) + 2kni (& = 0, ±1, ±2, ...)·
Логарифмируя с), найдем
Ln / (ζ, + z2) = Ln / (гх) + Ln / (z2),
откуда
g iz\ + z2) = g {ζλ) + g (z2) + 2ηπί,
где η — некоторое целое число. Из этого уравнения
вытекает, что
п =~ы tefa + **> — g(zi) — еfe)J
— непрерывная функция от Ζι и z2 и, следовательно,
есть константа (будучи целым, η может меняться
только скачками). Поэтому
g {z) — az — 2пт,
где а — какое-либо комплексное число и
/ (ζ) = е*(2) = eaz-2nnl = еаг.
91

Итак, уравнению с) удовлетворяет f(z)=0 либо
f(z) = eazf где а — любая комплексная константа.
d) [f (z, +z2)-f (zdf ЫГ-[1 -Ϊ2 (z,)][l-f2(z2)]=0.
Полагая Ζ\ = ζ и ζ2 = 0, находим
f2(2)[l-f(0)]2-[l-f2(z)][l-f2 (0)1 = 0,
ИЛИ
[1 - Ϊ (0)] {2 [f (z)]2 -[l+f (0)]} = 0. (93)
Это соотношение удовлетворяется,, если [f(z)f =
= ^—- константа,, значение которой
определяется из уравнения
2[f(0)]2-f(0)-l = 0,
откуда
f (0) = 1 или f(0) = -l.
Непосредственная проверка показывает, что обе
константы / {z) ss 1 и f (z) s= — γ удовлетворяют
уравнению d). Будем искать другие решения уравнения d).
Для них, как показывает уравнение (98), должно
быть/(0)= 1.
Далее можно выбирать различные пути решения.
На первом из них мы сведем вопрос к
рассмотренному выше уравнению с), на втором получим
дифференциальное уравнение, которому должна
удовлетворять искомая функция.
Если /(0) = 1 и ϊ{ζ)Φ 1, то ϊ2(ζ)φ 1 и,
следовательно, найдется значение г2 = α такое, что !2{а)Ф 1.
Положим в d) Zi = ζ и Ζζ = а и перепишем
уравнение в виде
Vl-[f(z)]Vl-[f(«)]2=±tf(z + a)-f(z)/(«)].
Так как в правой части находится целая функция от ζ
(f{z)t а следовательно, и f(z + a)—целые функции),
то и дЛ -—[/ (г)]2— целая функция. Поэтому целой
должна быть функция f (z) -J- i Vl — [/ (ζ)]2 = φ (ζ)» Из
уравнения d) находим
f(zl+z2) = f(z1) f (z2) - Vl-[f(2,)]2 Vl~[ffe)J2 *),
*) Если перед произведением радикалов поставить знак +,
то при г\ = г2 =г получим: f(2z) = 1, откуда /(ζ) = 1, Эту
возможность мы теперь исключаем,
92

или после простых преобразований
Vl-[f(zi + z2)]2 =
= f (г,) Vl — [f (z2)]2 + f fe) У1 - [f (г,)]2.
Следовательно,
ψ(ζι + Ζ2) = ϊ(ζι + Ζ2) + ίΛ/ΐ-[ϊ(ζι+ζ2)]* =
= if (гг) f tel-Vl-Iffo)]2 Vl-[/(*2)]2} +
+ ί {f (*ι) Vl-[ffe)]2 + f (z2) Vl-tffa)]'}"
- {/ (21) + ί Vl - [/ (zi)]2} if (Z2) + i Vl-[/fe)]2} =
«= φ (21) φ (г2).
Мы нашли, что целая функция φ (г) удовлетворяет
уравнению с). Поэтому имеются две возможности:
во-первых, (р(г)=0, что следует исключить, так как
отсюда следовало бы, что [/(г)]2 = [f[z)f— 1, и, во-
вторых, φ (г) = eaz. Из f{z) + i^\ — [f (z)]2 = eaz
выводим, что
Ϊ (z)-i Vl - [/ (z)l2= 1 :if(z) + i Vl - If (z)]2] = «-"
и, следовательно,
/(z)==£_Ji£
или, полагая α = α/,
f & = 2 = C0S №-
При a s=s 0 снова получаем f{z)= 1.
Итак, уравнению d) удовлетворяют либо
тождественные константы—γ и 1, либо целые
трансцендентные функции вида cos(<*£), α φ 0.
Интересно рассмотреть и другой возможный
способ решения задачи. Будем снова искать ί(ζ)Φ const;
тогда, как мы видели выше, f(0)= 1. Подставляя в d),
£ι = —г2 = zt получим
[1 - f (z)f (- z)f - {1 - [f (ζ)}2) {1 - [f (- *)]*} = О,
или
ΙΪ(ζ)~ϊ{-ζ)Υ~0, откуда f{-z) = f(z).
93

Итак, функция f(z) должна быть четной. Отсюда
вытекает, что степенной ряд для f(z) должен содержать
только четные степени ζ:
f (ζ) = 1 + α2ζ2 + α4ζ4 + ...,
откуда, в частности, заключаем, что //(0)= 0.
Положим, наконец, B.d) z\ = ζ, ζ2 = h Φ 0 и
перепишем уравнение в виде
Ш {г + h) - f (ζ)] - f (ζ) [f (h) - l]}2 +
+ {!-[/ (г)}2} U (h) - 1] \f (h) + 1] = 0.
Замечая, что 1 = / (0), разделим обе части на А2;
получим
rf(2 + h)-f(z) _ f (г) f(h)-f (0)12 +
+ О - [/ (ζ)}2} 1Щр1 [f (А) +1] = о.
Переходя к пределу при /1->0и замечая, что
К« + »)-У(»)_»т iWzLiiO)_f(o)==0,
1ί^Ρ1->α2> f(h)->l,
найдем
[Π^]2 + 2α2{1-[/(ζ)]2} = 0
или, дифференцируя,
2Г(г)Г(г)-4а2/(з)Г(г) = 0.
Так как f {ζ) Φ 0 (f (г) # const), το
f'(z)~2a2f(z) = 0.
Это линейное дифференциальное уравнение второго
порядка с постоянными коэффициентами. Полагая
2а% = —а2 (а — комплексное число), представим его
общее решение в виде
f(z) = Cleal* + C2e-aiz.
Из условий / (0) = 1 и f (0) = 0 получаем Сх = С2 = -g*
Поэтому
ϊ\ζ) = -~ = coscf2.
94

36. В предыдущих пунктах мы встречались с
примерами функций, обладающих алгебраическими
теоремами сложения. Кроме тождественных констант, мы
рассматривали линейную функцию az, функции вида
αζη (η ^ 2), показательную функцию eaz, косинус и
синус- Возникает вопрос, каждая ли целая функция
обладает алгебраической теоремой сложения. Ответ
на этот вопрос, быть может несколько неожиданный,
дает следующая теорема Вейерштрасса:
если целая функция f(z) обладает какой-либо ал-
гебраической теоремой сложения, то она необходимо
является либо алгебраическим многочленом (в
частности, константой), либо тригонометрическим
многочленом.
Итак, любую такую функцию можно представить
либо в виде
f(z) = a0 + alz+ ... +anzn,
либо в виде
ϊ (ζ) = α0 + fai cos {az) + #1 sin (az)] -f [a2 cos (2az) +
+ b2 sin (2аг)] + ... + [aa cos (naz) + bn sin (naz)].
Конечно, все частные случаи, с которыми мы до сих
пор встречались, удовлетворяют этим требованиям.
Чтобы видеть, что показательную функцию eaz можно
рассматривать как тригонометрический многочлен,
достаточно представить ее по формуле Эйлера в виде
eaz _ cos (_ αιζ} _j_ ι sjn (— αιζ} _ cos (ai2) _ ι sjn (aiz).
Если искать функции, обладающие алгебраической
теоремой сложения, в классе мероморфных функций
(см. п. 26), более широком, чем класс целых функций,
то для этого случая получается следующий результат
(также принадлежащий Вейерштрассу):
алгебраической теоремой сложения обладают либо
рациональные функции, либо периодические функции,
представимые в виде частного двух
тригонометрических многочленов ( сюда попадают, в частности, функ-
sin ζ cos ζ \
ilHutgz = и ctgz = —:—1, либо, наконец, двоя-
cos ζ sin ζ /
копериодические, т. е. эллиптические, функции. Эти
рассмотрения выходят за рамки настоящей книжки.

ПРИЛОЖЕНИЕ
§ I. Малая теорема Пикара
1. Вначале нам потребуются дополнительные
сведения о максимуме модуля и порядке целой функции.
Докажем так называемый принцип максимума
модуля (он справедлив для любой аналитической
функции, однако для простоты изложения мы ограничимся
целыми функциями):
если целая функция f(z) Φ const, то ее модуль
\f(z) | не может иметь максимума ни в одной точке
плоскости.
В самом деле, пусть Zo — произвольная точка
плоскости. Если f(zo)=Ot то, как мы знаем, существует
круг с центром г0, в котором f(z) не имеет других
нулей, кроме точки ζ0 (π. 21). Это значит, что в этом
круге |/(г) | > |/(г0) | = 0, если ζ Φ z0i поэтому \f(z) \
в точке Zo не имеет максимума.
Пусть теперь ϊ(ζ0)Φ0. Разложим функцию в ряд
по степеням ζ — ζ0. Получим всюду сходящийся ряд
/(*) = /(2ο) + Μζ--*ο)+ ... +М*-*)Л+ .··
В этом ряде среди коэффициентов Ьп (п= 1, 2, ...)
должны иметься отличные от нуля (в противном
случае f(z) была бы тождественно равна константе /(го)).
Пусть bh — первый из числа отличных от нуля
коэффициентов ряда. Тогда
f(z) - / (*о) + bk {z-zQ)k + bk+l (ζ-ζ0)*+ι + ...(ЬкФ 0).
Перепишем (1) в виде
f(z) = f(zo) + bk(z-z0)k +
+ bk(z^z0)k[^(z^z0) + ^(z^zQY+ ...l(V)
96

Из точки Zq можно провести такой луч L, что для всех
точек ζ этого луча, отличных от z0, Arg[bk(z —z0)k]
будет совпадать с Arg f(z0)\ иными словами, векторы
bk(z — z0)h и f(z0) будут параллельны и направлены
в одну и ту же сторону (рис. 5, а и 6).
\
2п
Τ
I
у
V
Ь)
Рис, 5.
Достаточно заметить, что
Arg [bk (ζ - z0)k] = Arg bk + k Arg (z
Zq),
и следовательно, высказанное условие будет
удовлетворяться, если принять
т. е.
Arg bk + k Arg {ζ - z0) = Arg / (z0),
Arg(z
z \— Arg f(z0)--Arg ftfe
(читатель может убедиться, что этому условию
удовлетворяют k различных лучей, из которых в
качестве L достаточно взять какой-либо один; см. рис.5, а).
Очевидно, что при этом условии сумма f(z0) и
bk(z — zo)h по модулю больше, чем |/(г0)|9 на
величину \bk(z — z0)h\. Но формула (I7) показывает, что
для получения f(z) нужно к указанной сумме
добавить еще одно слагаемое
Так как
97

при ζ -> Ζο, то можно считать, что ζ столь близко к z0i
что —^^—г < — а это означает, что прибавле-
I bk(z-z0)k\. 2 » к
ние φ(ζ) к сумме /(г0) + bh(z — z0)h, если и может
уменьшить модуль этой суммы, то не более чем на
половину модуля второго слагаемого. Итак, в
точках ζ, лежащих, на L и достаточно близких к z0y будем
иметь
\f(z)\ = \f(zo) + bk(z-Zo)k + <t>(z)\>
>Ι/(*ο) + Μζ-2ο)*|--Ιφ(ζ)| =
= \f(zo)\ + \bk(z-z0)k\-\q)(z)\>
>\f(zo)\ + \bk(z-z0)k\--±\bk(z--z(J)k\>\f(zo)\. (2)
Из этого неравенства заключаем, что |/(г)| не
может иметь максимум в точке z0. Теорема доказана.
Из нее вытекает важное следствие:
если f(z)—целая функция, то для любого г>0
максимум модуля f(z) в круге \z\^r достигается
в точке, лежащей на окружности )z\ = г.
В самом деле, в случае, когда f(z)= const, ее
модуль есть также константа и, следовательно, максимум
модуля совпадает с его значением в любой точке
плоскости, в частности со значением в любой точке на
окружности | а: | ===== г.
Пусть теперь ί(ζ)Φ const. Так как \f(z) | есть
непрерывная функция ζ (что в свою очередь сразу
вытекает из непрерывности f(z)), то, по известной
теореме анализа, максимум \f(z)\ в круге |г|^г
должен достигаться в некоторой точке z0 этого круга. Но
эта точка, по доказанному, не может лежать внутри
круга (в противном случае |/(г)| имел бы максимум
в этой точке). Следовательно, z0 находится на
границе круга, т. е. |z0| = г·
Итак, значение Μ (г)—максимума модуля f(z) в
круге |г|^г — является одним из значений \f(z)\
в точках окружности |г| = г и, следовательно,
совпадает с максимумом модуля f(z) на окружности
\z\ = r
2. Установим неравенства для коэффициентов
степенного ряда, аналогичные неравенствам Коши (п. 10
основного текста), в которых, однако, вместо макси-
98

мума модуля функции будет фигурировать максимум
ее действительной части.
Пусть f(z)— целая функция
f (z) = a0 + alz + a2z2 + ... +anzn+ ... (3)
Обозначим через ап и βη соответственно
действительную и мнимую части ап, так что ап = ап + ίβη, и
представим ζ в тригонометрической форме
ζ = г (cos θ +1 sin θ) (г > 0).
Тогда получим
оо
/ (Ζ) = Σ (<** + 'W '* (COS ΑΖθ + i Sin /ΐθ).
о
Отсюда действительная часть f(z)—обозначим ее
через u(r, Q) — представится следующим рядом:
оо
и (г, θ) = α0 + Σ («л cos п® — β/г sin ηθ) rn. (4)
Считая г фиксированным и интегрируя обе части по θ
в пределах от 0 до 2π, найдем
2π
1
α°- 2π
J и(г, θ)έίθ. (5)
Аналогичным способом можно представить в виде
интегралов и остальные коэффициенты ряда (4). Чтобы
вычислить, например, ар (ρ ^ 1), умножим обе части
(4) на cos pQ и проинтегрируем в пределах от 0 до 2π.
2π
Тогда слева получим \ и (г, 0)cosp0rf9, а справа все
о
интегралы обратятся в нуль, кроме одного интеграла
\ cos2 /?θ dQ = π. Следовательно,
2π 2я
ί и (г, O)cos/?0rf9 = aprp \ cos2 ρθ dQ = яаргр,
99

откуда
2rt
aprp = ~J и (г, 9)cos/79rf9 (р=1, 2, 3, ...)· (6)
о
Аналогично, умножая обе части (4) на sin ρθ и
интегрируя, найдем
2π
far" = -±\ u(r,d) sin pQdQ (p =1,2, 3, ...)· (7)
О
Из формул (5), (6) и (7) выводим
2π
2a0 ± aprp = ~ J u (r, θ) (1 ± cos ρθ) dQ, (6')
о
2π
2α0 ± βρΓρ = 1 J μ (γ, θ) (1 τ sin ρθ) άθ. (70
ο
Преимущество последних формул перед формулами
(6) и (7) то, что теперь множители при и (г, Θ) под
янаками интегралов неотрицательны.
Обозначая max и (г, Θ) на окружности радиуса г
через μ(г):
μ(0= max и (г, Θ),
0<θ<2π
получим из формул (60 и (70:
2π
2сс0 ± аргр < ^ J (1 ± cos ρθ) dQ = 2μ (г),
о
2αο±βΡΓ*<2μ(Γ)
и, следовательно,
Ι„ , ^ 2 [μ (г) - α0] (ft ι ^ 2 [μ (г) - α0] , « 0 Q .
ΙαρΙ^ Ρ > ΙΡρΙ^ ^ (ρ=1,2,3, ...),
(8)
Теперь можно доказать следующую теорему,
являющуюся дальнейшим усилением теоремы Лиувилля
(п. 14 основного текста):
100

если действительная часть u(r,Q) целой функции
f(z) удовлетворяет неравенству
и (г, θ)<μ(Γ)<Οδ (δ>0) (9)
для всех достаточно больших значений г (г > г0), то
f (ζ). необходимо является многочленом степени не
выше, чем η = [δ] ([δ] — целая часть δ).
В самом деле, из неравенств (8) и (9) следует:
i«pi<2(Cf6f;tto). ^к2(Сг°Р~ао) (r>r0). (so
Если ρ > [δ], то, так как ρ — целое число, это значит,
что ρ ^ [δ] + 1 > δ, поэтому выражения в правых
частях неравенств (8') стремятся к нулю при г -> оо.
Следовательно, аР = βρ = 0, т. е. ар = аР + Фр = О,
если /? > [δ] = м. Поэтому формула (3) принимает
вид
ϊ(ζ) = α0 + αιζ + .♦. +αηζη, где я = [б],
что и доказывает теорему.
3. Докажем три леммы, относящиеся к
вычислению порядка целой функции.
Лемма 1. Если 'f(z)—целая трансцендентная
функция, ά Ρ (ζ) и Q(z)—многочлены степеней тип
соответственно, причем Ρ (ζ) Φ О, то порядок pi
функции P(z)f(z)-\- Q(z) совпадает с порядком ρ функции
f(z), т. е. pi = p.
Введем обозначения:
Μ (г) = max | f(z) |, Λί1 (r) = max \Ρ{ζ)ϊ{ζ) + Q(z) |. (10)
/*|<r |г|<г
По доказанному в п. 2 мы можем здесь не
рассматривать точек, лежащих внутри круга |2|^г, а
ограничиться только значениями модулей функций,
принимаемыми на окружности |2| = r.
Если amzm и bnzn — соответственно старшие члены
многочленов Ρ (ζ) и Q(z), то на основании неравенств
(28) основного текста, где мы положим ε = "2", можно
утверждать, что при \ζ\ = г > г0
^\ат\гт^\Р(г)\^^\ат\гт,
ъ\Ьа\гп<\Я(г)\<±\Ья\гя.
01)
101

Пусть z0 — точка окружности |z| = r, в которой
|/(г) | достигает значения Μ (г). Тогда
Αί, (г)>| Ρ(20) f (zo) + Q (26) \>\ Ρ (гь) || f (z0) |-1 Q (z0) >
>4-|а«ктМ(г)-||Ь„|Л (12)
С другой стороны, в точке гА той же окружности, в
которой \P(z)f(z) + Q(z) I достигает значения Ai^r),
имеем
Af, (r<HP(*i)f(zi) + Q(z,) 1<| Р(г,) II f (ζ,) | + | Q(z,) |<
<||ara|r'"Ai(r)+-|lM'·*. (13)
Следовательно,
l|am|r-M(r)[l-|/J^(r)]<Ml(r)<
<||ат|г-М(г)[1 + |а^пЛ"(г)]· (14)
Так как /(г)—целая трансцендентная функция, то
(см. п. 15 основного текста) Μ (г) растет быстрее, чем
максимум модуля любого многочлена, и,
следовательно, быстрее, чем любая степень г. Поэтому каждое из
выражений в квадратных скобках в неравенствах (14)
стремится к 1 при г—>оо. Следовательно, можно взять
г настолько большим, чтобы скобка справа была, на-
2
пример, меньше 2, а скобка слева — больше -j .
Получим
^\ат\гтМ(г)^МЛг)<3\ат\гтМ(гУ (15)
Напомним, что порядок целой функции /(г)—это
тт— In In Μ (г; f) / лт
|im —i—~ = p (п. 17 основного текста).
Г-»оо 1П Г
Логарифмируя (15), найдем
In (у I ат | rm) + In Af (г)< In Αί ,(г)<
< In (31 am | г1") + In Af (г).
102

или
1πΛί(Γ)[ΐ+ U 1ηΑ/(Γ) J<
<lnAi,(r)<lnAi(r)[l + ln(3|a|-^)ln^)]. (16)
Покажем, что выражения в квадратных скобках снова
стремятся к 1, когда г-* оо. Очевидно, достаточно для
\пС+\п(гт)
этого проверить, что выражения вида —\ м( ) *
С φ О, стремятся к нулю, когда г —> оо. Для слагае-
In С
мого . М( ν это очевидно (так как In Λί(/*)-> οο).
Пусть теперь ε !> О — любое положительное число.
Возьмем натуральное N столь большим, чтобы было
jr < ε, и выберем далее η > 1 так, чтобы при всех
mN
г > Го выполнялось неравенство _1 < ι (это
возлег)
можно вследствие того, что Μ (г) —максимум модуля
целой трансцендентной функции f(z)). Тогда
г*» < Μ (г), N In (rm) < 1η Λί (г) и £j^ < ^ < ε. Итак,
In (rm) л ~
in Λί (г)""* ПРИ Γ~*°°· Отсюда следует, что при
всех достаточно больших значениях г в неравенстве
(16) квадратная скобка справа будет меньше 2, а
квадратная скобка слева — больше у . Итак,
-jlnAf(r)<lnAf,(r)<21nAf(r).
Логарифмируя еще раз, получим
In γ + In In M (г) < In In Λί, (г) < In 2 + In In Λί (г).
Деля на Γη г и переходя к верхним пределам при
г-*оо, будем иметь
ш 1пЫЩг1< Ш InJnjMr) Ш ШпМ(г)
Г->оо 1П Г ,->«> ]ПГ Г-»оо In''
ИЛИ
Ρ<Ρι<Ρ>
103

откуда, наконец, ρ = pi. Мы доказали, следовательно,
что порядки функций f(z) и P(z)f(z)+Q(z) (Ρ (ζ) Φ
Φ 0) равны.
Лемма 2. Порядок целой трансцендентной функ*
ции вида
f(z) = P(z)e*& + Q(z),
где Ρ (z), Q(z) и g(z)—многочлены, причем Ρ (ζ) не
равен тождественно 0, а степень g(z) есть /г, равен п.
В силу леммы 1 порядок f(z) совпадает с порядком
функции φ (ζ) = e&z). Обозначим max | φ (ζ) | = Μ\ (γ).
\z\=r
Требуется доказать, что
77- In In Λί, (r) _ _
lim -—r— = «.
Положим g (z) = cQ + cxz + ·.. + cnzn,
Ck = 9k (cos ak + / sin ak) и ζ = r (cos θ + / sin θ);
по условию рп = | сп | Φ 0.
Тогда получим
η
g (z) = Σ pkrk (cos ak + / sin c^) (cos &Θ + / sin Щ —
η
= Σ Pkfk [cos (αΛ + fe9) + I sin (a* + &Θ)].
Чтобы получить модуль φ (г), достаточно сохранить в
показателе действительную часть последнего
выражения. Поэтому
η
Σ pkr* cos (α^+δθ)
|φ(*)| = **-°
Η
In I Φ (г) И Σ рАг*соз(а4 + *в).
ft=0
Очевидно, что мы получим In max | φ (ζ) 1, отыскивая
максимум последнего выражения при г постоянном и
0 < θ < 2π. Но
о
104

и, следовательно, для любого ε, О < ε < 1, и г >> г (ε)
будем иметь
1η|φ(ζ)|<Ρ//*(1+ε),
откуда
ΙηΛί,ίΓΧρ,/^Ι + β).
Пусть г0 — точка на окружности |z| = r, для ко·
торой cos (α,η + αζΘο) = 1 (таких точек найдется я; для
нашей цели достаточно взять одну из них). Имеем
п-\
1η Λί, (г) > In | ф (г0) I = pnrn + £ Pftr* cos (о* + k%) >
О
>р.г"-Е'1>И=р,г»[1-(^-!- + ... + а^)]>
О
> рпгп (1 — в) при г > г (ε).
Сопоставляя полученные оценки, заключаем, что
рУ (1 - β)< 1η Μ, (r)<Pnrn (1 + ε).
Логарифмируя еще раз, деля на In r и переходя к
пределу при г -* оо, находим
Следовательно, порядок φ (г) равен /г, а потому
равен η и порядок данной функции f(z).
Лемма 3. Если g(z)—целая функция и порядок
функции f(z)=e&z) конечен, то g(z) есть многочлен,
так что порядок f(z) необходимо является числом
целым.
Если ζ = г (cos θ + I sin θ) и и{ц, θ)—
действительная часть функции g(z), то \f(z) | = е*М>, откуда
ln|f(*)|«a(rfe).
Обозначим max | / (г) | = Μ (ζ) и max и (г, θ) = μ (г).
|г|=г 0<θ<2π
Тогда
1η Μ (г) = μ (г). (17)
Пусть δ —порядок /(г). Это означает, что
Г-»оо 1пГ
105

Для любого 8>0 существует г(е)> 1 такое, что при
г > г (в)
In In Μ (г) . А ,
т. е.
или
Ш NUT°'
lnlnAf(r)<ln(re+8)
In M (r)<r«+e.
(18)
Из (17) и (18) вытекает, что
μ (г) < гб+е, г>г (ε).
Из теоремы п. 2 этого параграфа следует, что g(z)
есть многочлен, степень которого η не превосходит
целой части δ + ε, т. е. η ^ [δ + ε]; так как ε
произвольно мало, отсюда следует, что η ^ [δ]. По лемме 2
порядок δ функций f(z) должен совпадать с п\
поэтому б — целое число:
6 = п.
Лемма 3 доказана.
4. Теперь легко доказать малую теорему Пикара
для случая целых функций конечного порядка. При
этом мы придадим ей более общую форму,
рассматривая вместо уравнения f(z) — A уравнение f(z) =
= ЛР(г), где Ρ (ζ)—многочлен. Пусть сначала
порядок целой функции не является целым числом.
Теорема 1. Если f (z) — целая трансцендентная
функция, порядок которой- Ь есть конечное, но не
целое число, и если Ρ (ζ) есть многочлен, не равный
тождественно нулю, то уравнение
f(z) = AP(z) (19)
имеет бесконечное множество корней при любом А
(без всяких исключений).
Будем вести доказательство от противного. Пусть
теорема неверна и существует такое А = А0, для
которого уравнение (19) имеет только конечное число
корней (и быть может, вовсе не имеет корней).
Тогда целая функция f(z) — A0P(z) имеет только
конечное число нулей. По пункту 20 основного текста
в этом случае f(z) — A0P(z) можно представить в.
виде
f(z)-A0P(z) = Q(z)e2(*\ (20)
106

откуда
f(z) = A0P(z) + Q(z)e*4 (21)
Здесь Q(z)—многочлен, не равный тождественно
нулю (его можно считать тождественно равным 1,
если уравнение f(z)—Α0Ρ(ζ)=0 совсем не имеет
корней), и g(z)—некоторая целая функция.
По лемме 1 предыдущего пункта порядок δ
функции f(z) должен совпадать с порядком функции e^W
и, следовательно, по лемме 3 является числом целым,
что противоречит условию теоремы. Итак, теорема 1
доказана.
Обратимся к целым функциям конечного целого
порядка. Здесь справедливо следующее предложение.
Теорема 2. Если f(z)—целая трансцендентная
функция, порядок которой конечное целое число п, и
Ρ (ζ)—многочлен, не равный тождественно нулю, то
уравнение
f(z) = AP(z) (22)
имеет бесконечное множество корней при любом А, за
исключением, быть может, одного значения А.
Допустим, что теорема не верна. Тогда должны
существовать по крайней мере, два значения а и ЬФа,
для каждого из которых уравнение (22) имеет только
конечное число корней. Это означает, что целые
функции f(z)—aP(z) и f(z)—bP(z) имеют конечное число
нулей. Можно утверждать, следовательно (см. п. 20
основного теста), что
f(z)-aP(z) = Ql(z)e^zK f(z)-bP(z) = Q2(z)e*^K (23)
где Qi(z) и Qz{z)—многочлены, не равные
тождественно нулю, a gi(z) и £2(2)—целые функции. Из
леммы 1 п. 3 следует, что порядки е*М и e&{z)
совпадают с порядком /(г), равным п.
На основании лемм 3 и 2 п. 3 заключаем, что
функции gi(z) и g2(z) должны быть многочленами
степени п. Отсюда следует, в частности, что можно
считать η ^ 1, так как при п==0 g\(z) и gz(z) являлись
бы константами и из формул (23) вытекало бы, что
f(z) есть многочлен (а не целая трансцендентная
функция). Вычтем равенства (23) почленно (второе
из первого), получим
Q, (ζ) е* <*> - Q2(z) e* <*> = (b - α) Ρ (ζ) = ρ (ζ), (24)
107

где многочлен p(z)=(b — α) Ρ (ζ) не есть
тождественный нуль (так как Ь Φ а и Ρ (ζ) Φ 0). Наша цель —
доказать, что такое тождество невозможно при
условии, что многочлены Qi(z), Q2(z) и ρ (ζ) не равны
нулю тождественно, a g\(z) и g2(z)— многочлены
степени ^1. Дифференцируя почленно (24), получим
[Q;W + Qi(2)firi(2)]^w-
- [QJ (ζ) + Q2 (ζ) & Щ е*м = р' (Ζ). (25)
Если рассматривать (24) и (25) как систему
уравнений с неизвестными eStiz) и*£#*(2), то определитель
A(z) системы будет таким:
Δ (ζ) = - Q1 (г) [QJ (г) + Q2 (ζ) g'2 (ζ)] +
+Q2W[Qi(2) + QI(z)ffI(z)]-Q2(«)Q;(z)-Q1(z)Q;(z)+
+ Ql(z)Q2(z)[g[(z)-g'2(z)l (26)
Покажем, что многочлен Δ(ζ)Φ0. В противном
случае, деля обе части тождества Δ(2)ξ=ξ0 на Qi(z)Q2(z),
получили бы
Интегрируя, находим
Ln-|^ + g, (ζ) - & (ζ) ^ const ==<:,, (27)
откуда
.filM eet м-g, w = ес, = с ф 0. (28)
Но из формул (23) следует;
<Ы*)е /(г)-бР(г)·
Поэтому формула (28) означает, что
f(z)-aP(z) _r
!(г)-ЬР(г) — °»
откуда
(l-C)f(z) = (a-bC)P(z).
103

Так как Ъ Φ а и Ρ (ζ) Φ 0, то С φ 1, следовательно,
д2)=-£^Р(г),
что противоречит условию (ведь f(z)—
трансцендентная функция!). Итак, Α(ζ)ψΟ, Решая систему
уравнений (24) и (25) относительно e8,iz) и е^г\ получим
- ρ (ζ) [Qi (ζ) + Q2(z) g', (ζ)] + ρ'(ζ)Q2 (г)
ееАг) = _ ,
/ (ζ) Q, (г) - ρ (ζ) [Qi (ζ) + Q, (г) β{ (z)]
«*w = д^ ·
Но равенства такого рода содержат противоречие, так
как слева стоят целые трансцендентные функции (их
порядок η не ниже 1), а справа — функции
рациональные (и, следовательно, многочлены). Этим и
завершается доказательство теоремы 2.
5. Если отвлечься от того обстоятельства, что при
условиях теоремы 1 п. 4 гарантировано отсутствие
исключительного значения, то обе теоремы 1 и 2
можно рассматривать как весьма частные случаи
следующей теоремы, которая, также принадлежит Пикару.
Теорема Π и к а р д. Пусть φ (ζ) —
трансцендентная мероморфная функция (в частности, целая
трансцендентная). Каково бы ни было комплексное число А,
конечное или бесконечное, за двумя возможными
исключениями, уравнение
ψ(ζ) = Α
имеет бесконечное множество корней.
Если ψ (ζ)—целая функция, то ни при каком ζ она
не обращается в оо. Поэтому одно исключительное
значение А = оо имеется для всякой целой функции.
Следовательно, в силу последней теоремы, в случае
целой трансцендентной функции может существовать
самое большее одно конечное исключительное значе-^
ние. Но об этом и говорит малая теорема Пикара.
Если f(z)— целая трансцендентная функция и
Ρ (ζ)—многочлен, не равный тождественно нулю, то
мероморфная функция 9te) = ^pW обращается в оо
только в конечном числе точек (в нулях многочлена
Ю9

Ρ (ζ)). Поэтому значение оо по-прежнему является
для нее исключительным и, в силу теоремы этого
пункта, возможно только еще одно исключительное
(конечное) значение. Следовательно, можно утверж-
f (ζ)
дать, что уравнение р' =А, или f(z) = АР (г), имеет
бесконечное множество корней для каждого
значения Л, кроме, быть может, одного конечного
значения А. Для случая, когда порядок f(z) конечен, мы
доказали это в п. 4 настоящего параграфа
(теоремы 1 и 2).
Пусть, наконец, f(z) и g(z)—две целые
трансцендентные функции, отношение которых не есть
рациональная функция. Это и означает, что *1 есть транс-
цендентная мероморфная функция. По теореме этого
пункта можно утверждать, что уравнение -ττΓΖ\~ А,
или f(z) = Ag(z), имеет бесконечное множество
корней при любом Л, за исключением самое большее двух
значений. Эта теорема упоминалась в п. 26 основного
текста.
§ 2. Целые периодические функции.
Теорема Вейерштрасса
6. В п. 31 основного текста функция е ω
приводилась в качестве простейшего примера функции с
периодом ω (ωφΟ). Полагая t = e ω , покажем,
что каждую целую периодическую функцию f(z) с
периодом ω можно рассматривать как однозначную
аналитическую функцию t во всех точках комплексной
плоскости t, исключая точку t = 0. В самом деле,
Ln t = —· ζ, откуда ζ = η^τLnt. При t φ 0 это
аналитическая (многозначная) функция от t. Так как все
значения Ln / при данном t отличаются одно от
другого на целые кратные 2ш, то все соответствующие
одному и тому же t значения ζ отличаются одно от
другого на целые кратные ω. Поэтому всем им
соответствует одно и то же значение периодической
функции f(z). Следовательно, f(z) —однозначная функ-
U0

ция t во всей плоскости, за исключением точки ί = О*
Обозначим ее через φ(0:
9(0-7(2)«=/(lsrLn/). (29)
По правилу дифференцирования сложной функции
т. е. производная q/(0 существует в любой точке ίφΟ.
Поэтому φ(ί) является аналитической функцией во
всех точках плоскости, отличных от начала координат.
Для таких функций справедлив следующий факт из
общей теории аналитических функций, являющийся
частным случаем теоремы Лорана:
если φ(ί)—функция однозначная и аналитическая
во всех точках плоскости, кроме, быть может, точки
t = 0, то ее можно представить в виде суммы всюду
сходящегося обобщенного степенного ряда (ряда
Лорана) вида
φ(0«Σ*ιΛ (зо)
— 00
содержащего, воооще говоря, степени t не только с
неотрицательными, но и с отрицательными целыми
показателями.
Если к ряду (30) применить прием для выражения
коэффициентов через интегралы, использованный в
п. 10 основного текста, то получим следующие
формулы:
2rt
/ о
где точка / = г (cos а + / sin α) описывает в
плоскости t в положительном направлении окружность с
центром в начале координат и радиусом г (г — любое
положительное число). Рассуждая и далее, как в п. 10,
выведем неравенства
ИК^, я = 0, ±1, ±2, ±3, ..., (32)
где
ц(г) = тах|<р(*)|. (33)
11 |=Г
111

В нашем случае
t = e» * и 4>(t) = f(-£rLnt) = f(z).
Поэтому из формулы (30) следует:
f(z)=Zane° nZ, (34)
— оо
т. е. любая целая периодическая функция f(z) с
периодом ω изображается в виде суммы всюду
сходящегося ряда (34), членами которого являются
простейшие периодические функции (показательные) с
2Ш „
пг
тем же периодом ω. Заменяя здесь е ω через
cos(— nzj +1 sin I — nz\ и группируя надлежащим
образом члены (что возможно в силу абсолютной
сходимости ряда), получим представление f(z) в виде
суммы тригонометрического ряда
оо
к*>=Σ [л«cos (ίγnz)+β»sin (■?■ «*)] · <35>
о
Докажем следующую основную теорему о
периодических функциях:
если целая периодическая функция f(z) с
периодом ω удовлетворяет неравенству вида
|/(z)|<Cevl«>i m (36)
для некоторых С > 0, ν > 0 и для всех достаточно
больших значений \z\ (|z|>#o), T0 f(z) необходимо
является тригонометрическим многочленом порядка
не выше чем ρ = [γ] (целая часть γ).
Для доказательства используем неравенства (32)
(аналогичные неравенствам Коши для коэффициентов
степенного ряда).
Заметим, что в нашем случае
ц(г) = тах|Ф(01 = тах|/(^Ьп/)|.
Чтобы оценить эту величину с помощью неравенства
(36), рассмотрим сначала значения -£-rLnt прл
112

|/| = г, т. е. при t = r(cos α + I sin α), где 0 s£! α < 2π.
Имеем
£iLnt = £.(\n\t\ + iArgt) = £i[\nr + i(a + 2kn)}==
Поэтому
= Κ-έω+1ΗΓΙηΓ)'
так как /ко—· период /(г). Следовательно,
»«-.ss.l'(*«+wta')l· <37>
Полагая 2 = -^ ω + "2^г'пг» заметим, что |г| =
= -1—-Ч 1пг + /сх | будет бесконечно возрастать не
только при г->оо, но ή при г—>0. Поэтому можно
считать, что |г|>#о либо при достаточно больших
г > /ί > 1, либо при достаточно малых г < гг < 1.
В каждом из этих случаев можно воспользоваться
неравенством (36) для оценки |f(z)|. Получим
так как 0 ^ α ^ 2π. Полагая Се2лч = Сь перепишем
это неравенство в виде
|/(z)|<CIeYlln4 (38)
Если, например, г> г{> 1, то| 1пг | = 1пг ne,vllnr, = rY.
Следовательно,
μ (г) «max |f (г) |< С!/*
и в силу (31)
Очевидно, что если η> ρ = [γ], то η>[γ] + 1 > γ, и
поэтому при г->оо правая часть неравенства
стремится к нулю. Следовательно,
ап=09 если я>/?,„т. е. αρ+1=αρ+2=αρ+3 = .,, =0. (39)
ИЗ

Пусть теперь г < г2 < 1. Тогда | In r f = In — и
неравенство (38) принимает вид: \f(z)\< C{r~v.
Следовательно, μ (г) = max |/ (z)\<C{r-v. В силу (31)
Будем придавать η отрицательные значения,
меньшие чем — р — — [γ]. Тогда л^~ р — 1, а так как
ρ + 1 = Μ + 1 > Υ, то — ρ — 1 < — γ, τ. е. п < — γ,
— λ — γ>0; поэтому γ~λ-υ->0 при г->0 и,
следовательно,
я„=0, если «<—-р, т. е. α_ρ_1=α_ρ-2=^ρ-3 = ··· = 0·
(40)
Учитывая (39) и (40), заключаем, что бесконечный
ряд (34) сводится к конечной сумме
+ Р 2Л(
/ω=Σ^~ . (340
-ρ
2πί
Заменяя здесь β ω пг через cos l·-— nz\+l sin ί-~/га;)
и группируя подобные члены (при этом используются
свойства четности косинуса и нечетности синуса),
получим окончательно
f(z) = aQ + [Aicos(^z) + Blsin(^z)] + ...
... +^C0s(^p2r) + 5psin(^p2)], (350
что и требовалось доказать.
Заметим, что обратная теорема также справедлива:
если f (ζ)—тригонометрический многочлен порядка р,
г. е. f (ζ) = Σ апе ω > T° существует такое положи·
-р
тельное число С, что
2л
|/(2)|<С/ТЙ|г1
для всех г.
114

В самом деле,
(40
Ρ
где C = 2|oJ.
-ρ
Поэтому периодическая функция, для которой не
выполняется условие основной теоремы, не может
быть тригонометрическим многочленом. Так как она
во всех случаях представляется в виде ряда
f(z)=Zane~nZ,
—оо
то в этом ряде бесконечное множество
коэффициентов ап должны быть отличными от нули.
7. Пусть f(z)—целая функция. Если она является
многочленом, то алгебраическая теорема сложения
для нее имеет место.
Действительно, из уравнений
f-f(22) = 0, [ (42)
w-f(zu+z2) = 0 J
переменные z4 и г2 могут быть исключены посредством
одного из приемов, указываемых в высшей алгебре*).
В результате получим алгебраическое соотношение
между α, ν и w:
Р(и, ι>, ш)=0
(Р(и, и, w)— многочлен).
Пусть теперь f(z)—целая трансцендентная
функция. Докажем,, что
если она обладает алгебраической теоремой ело*
жения, то функция эта необходимо является
периодической.
Это предложение составляет существенную часть
теоремы, первоначально доказанной Вейерштрассом.
Докажем сначала следующую лемму:
если р0(и, υ) Φ 0 — многочлен от и μ ν, то суще*
ствует бесчисленное множество значений и, для кото*
*) См., например, А. Г. Курош, Курс высшей алгебры,
изд, 10, стр. 340—343.
115

рых /?о(и, υ) не обращается в нуль тождественно
относительно V.
Пусть
Ро(и, υ) = q0 (и) vm + qx (и) vm~l + ... + qm (и),
где qo(u)9 ..., qm(u)— многочлены, причем q0(u) φ 0.
Если степень qo(u) равна 5, то существует не
более s различных значений и, при которых qo(u) = 0.
Для каждого из бесчисленного множества значений и,
отличных от этих 5 значений, qo(u)=f^O и,
следовательно, многочлен q0(и) vm + qi(u)α™-1 + ... + qm(и)
отличен от тождественного нуля. Лемма доказана.
Пусть теперь теорема сложения для f(z) имеет вид
Ρ (и, vt w) = wnpb(u, υ) + wn~lpi (u, υ) + ...
... +pn(u,v) = Q9 (43)
где ρ0(ιι,υ)φ 0, ρι(ιι, υ), ..., рп(и, υ)— многочлены.
В силу леммы можно найти бесконечное множество
различных значений и, для каждого из которых
р0(и, ν)Φ 0 относительно v. Если а и Ъ — два из таких
значений, то, в силу малой теоремы Пикара, по
крайней мере, одно из уравнений
/ (г) = а или f(z) = b (а Ф b)
имеет бесконечное множество корней. Допустим, что
это обстоятельство имеет место для уравнения
f(z) = a. (44)
Тогда можно указать η + 1 различных корней этого
уравнения: си с2, ..., cn+i. Итак, р0(а, u)#0h f(ci) =
= /(£2) = ... = f(cn+i) = я, где си с2, .. ♦, cn+i —
попарно не равные между собой числа.
Полагая в (43)
u = f{Ci) = a, v = f{z) и w = f(ci + z)9
получим
p0[a,f (ζ)] [f (с, + z)]n + ρ, [a, f (ζ)] [f (с, + ζ)Γ' + ...
... +рЛ«,/(г)] = 0 (/ = 1,2 n+l), (43')
Если ν = f(z) отлично от корней уравнения р0(а, υ)
(такое совпадение могло бы иметь место не более чем
116

для t значений функций f(z), где t — степень р0(а, ν)
относительно ν), то р0[а, f(z)] Φ 0 и уравнение
Po[aJ(z)]wn+p{[aJ(z)]w^+ ... + pn[a,№]=0 (43")
является уравнением степени η относительно w.
Поэтому оно имеет не более η различных корней. С
другой стороны, этому уравнению, в силу (43'), должно
удовлетворять каждое из η + 1 чисел
/ {с\ + z), f (c2 + ζ), ..., / (ся+1 + г)..
Отсюда следует, что, по крайней мере, два из этих
чисел должны быть равными между собой. Пусть,
например,
f(cj + z) = f(ck + z), ck¥=cj. (45)
Если взять другое значение ζ' φ ζ, то для него, быть
может, придется взять другую пару индексов /' и k\
и мы получим
f (с,> + ζ') = ϊ (сл* + г'), <V Φ с?.
Будем подставлять в качестве ζ любую точку из круга
\ζ\ ^ 1, следя лишь за тем, чтобы значение υ = f(z)
не совпадало ни с одним из t корней уравнения
ρ0(α, ϋ)=0. Таких исключений может быть только
конечное число;, поэтому получится бесконечное
множество различных ζ и для каждого своя пара
индексов /" и k в соотношении (45), причем 1 ^ / ^ η + 1
и 1^&^;я+1. Так как всех возможных пар
различных индексов существует только конечное число
/ (п+\)п\ _,
I именно, -—2 )» то хотя бы одна из паР» например
/о и ko> будет повторяться для бесконечно многих
точек ζ и£Г круга \ζ\^ 1. Следовательно, для
бесконечного множества точек ζ будет удовлетворяться
равенство
/ (ci. + z) = f (ck, + ζ), cko Φ с/о, (450
где индексы /о и k0 не меняются с изменением ζ. Так
как f (с/0 + z) и f (ck0 + ζ) — целые функции от ζ, то из
совпадения их значений на бесконечном множестве
117

точек, лежащих в круге |^| ^ 1, следует, что они
тождественно равны между собой (см. теорему
единственности для целых функций, п. 21 основного
текста).
Итак,
f (*/. + *)-/(<.,, +2) (45")
или, полагая с/0 + г = £ и, следовательно, 0^ + 2 =
= си, — е/о + ζ-
/ (0-f К+ (**-*/.)]. (46)
Мы видим отсюда, что ω = £*β —£/в=т^0 является
периодом f(z), т. е. f(z) есть периодическая функция.
8. Но не всякая целая трансцендентная
периодическая функция обладает алгебраической теоремой
сложения. Теорема Вейерштрасса утверждает далее,
что такая функция должна быть тригонометрическим
многочленом и, следовательно, подчиняться
неравенству вида (36). Доказательство этой части теоремы
может быть проведено на основании той же идеи,
что и доказанная часть, но требует более
углубленного знакомства с периодическими функциями и
опоры не на малую, а на так называемую большую
теорему Пикара. Заметим, что, в силу теоремы
Вейерштрасса в ее полном объеме, целая периодическая
функция ее (ее периодом является, очевидно, 2ni)
не подчиняется алгебраической теореме сложения
именно потому, что ее максимум модуля растет
слишком быстро (см. п. 17 основного текста).
Окончательно, теорема Вейерштрасса для целых
функций формулируется так:
Теорема Вейерштрасса. Если целая транс-
цендентная функция f(z) подчиняется алгебраической
теореме сложения, то она необходимо является
тригонометрическим многочленом.
Обратное утверждение также справедливо:
каждый тригонометрический многочлен подчиняется
алгебраической теореме сложения. В самом деле, пусть
р 2л1
ί^^Σαηβ—"2, (47)
-ρ
118

где ап — комплексные коэффициенты. Беря какие
угодно ζ^ и z2, можем писать
- (48)
-ρ
2πί 2nl
Положим для сокращения е ω 1==fi и е ω * = ί2·
Тогда соотношения (48) перепишутся в виде
α-Σ fluff = 0, ϋ-Σ^2 = 0, α>-Σ^2=0, (49)
-ρ . -Ρ -Ρ
или, освобождаясь от отрицательных степеней U и /г,
в виде
ut\— (a-p + a-p+ih+ ... +αρ*ιρ) = 0,
ttf? — (α-ρ + α-ρ+ι*2+ ... +αρίΙρ)β0.
^2ρ-(α-ρ + α-ρ+ι*ι*2 + ... +apt]pt22p) = 0.
(50)
Из этой системы трех алгебраических уравнений
относительно пяти переменных tu ί2, и, υ и w можно
исключить tx и h. В результате получится одно
алгебраическое уравнение между и, υ и w:
Ρ {и, υ, w) = 0.
Это и есть теорема сложения для
тригонометрического многочлена (47),

Алексей Иванович Маркушевич
ЦЕЛЫЕ ФУНКЦИИ
Элементарный очерк
М., 1975 г., 120 стр. с илл.
Редактор А. Ф. Лапко
Техн. редактор Н, В, Коше лев а
Корректор Л. С. Сомова
Сдано в набор 1/1V 1975 г. Подписано к печати 12/XI
1976 г. Бумага 84X1087** №3. Физ. печ. л. 3,75.Условн. печ.
л. 6,3. Уч.-изд. л. 5,47. Тираж 55 000 экз. Т-17374.
Цена книги 16 коп. Заказ № 768.
Издательство «Наука»
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени
Ленинградская типография № 2
имени Евгении Соколовой Союзполиграфпрома
при Государственном комитете Совета Министров СССР
по делам издательств, полиграфии и книжной торговли*
198052, Ленинградг Л-52, Измайловский проспект, 29л

Ι Ι целым функциям
относятся многочлены,
показательная функция,
тригонометрические (синус и косинус) и многие
другие функции, играющие
важную роль в математике и ее
приложениях. Замечательно, что те
целые функции, которые не
являются многочленами (они
называются трансцендентными), во
многих отношениях ведут себя
как своего рода «многочлены
бесконечно высокой степени».
Об основных свойствах целых
функций, об их нулях, скорости
роста, об алгебраических
соотношениях между их значениями и
т. п. рассказывает эта книжка. В
основу ее положены две лекции,
читанные автором на курсах
повышения квалификации учителей
при Московском университете.
От читателя требуется
знакомство с началами анализа
(дифференцирование и
интегрирование, понятие ряда) и
комплексными числами.