Автор: Стрелков С.П. Сивухин Д.В. Яковлев И.А. Угаров В.А.
Теги: физика механика задачи по физике
Год: 1977
Текст
СБОРНИК ЗАДАЧ
ПО ОБЩЕМУ КУРСУ
ФИЗИКИ
МЕХАНИКА
ИЗДАНИЕ ЧЕТВЕРТОЕ,
ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
Под редакцией
И. А. ЯКОВЛЕВА
Допущено Министерством
высшего и среднего специального обрагования СССР
в качестве учебного пособия для студентов физических специальностей
высших учебных заведений
ИЗДАТЕЛЬСТВО «НАУКА*
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
Москва 1977
530
С 23
УДК 530
АВТОРЫ!
С. П. СТРЕЛКОВ, Д. В. СИВУХИН, В. А. УГАРОВ,
И. А. ЯКОВЛЕВ
Сергей Павлович Стрелков,
Дмитрий Васильевич Сивухин,
Владимир Александрович Угаров,
Иван Алексеевич Яковлев
СБОРНИК ЗАДАЧ
ПО ОБЩЕМУ КУРСУ ФИЗИКИ
МЕХАНИКА
М., 1977 г., 288 стр. с илл.
Редактор Д. А. Миртова
Техн. редактор И. Ш. Аксельрод
Корректор Л. С. Сомова
Сдано в набор 26/VIII 1976 г. Подписано к печати 19/1 1977 г.
Бумага 84xlO8Vs2- физ. печ. л. 9. Условн. печ. л. 15,12.
Уч.-изд. л. 16,04. Тираж 90 000 экз. Цена Ш№И 67 коп.
Заказ № 659.
Издательство «Наука»
Главная редакция физико-математической литерашуры
117071, Москва, В-71, Ленинский проспект, 15
Ордена Октябрьской Революции
и ордена Трудового Красного Знамени
Первая Образцовая типография
имени А. А. Жданова
Союзполиграфпрома при Государственном комитете
Совета Министров СССР по делам издательств,
полиграфии и книжной торговли.
Москва, М-54, Валовая, 28
20401—022 © Главная редакция
С лео /ло\ 77 94-76 физико-математической литературы
{JOO[UZ)-// издательства «Наука», 1977 г., с изменениями
СОДЕРЖАНИЕ
Ответы
Задачи и решения
От издательства 4
Предисловие к четвертому изданию 5
§ 1. Кинематика 7 153
§ 2. Динамика прямолинейного движения мате-
материальной точки и простейших систем .... 19 160
§ 3. Статика 31 169
§ 4. Работа, мощность, энергия 36 172
§ 5. Законы сохранения количества движения и
энергии 40 174
§ 6. Динамика движения материальной точки
по окружности. Движение относительно вра-
вращающихся систем отсчета 52 187
§ 7. Динамика твердого тела. Динамика системы 63 200
§ 8. Тяготение 92 225
§ 9. Упругие деформации 105 242
§ 10. Колебания 112 249
§ 11. Гидростатика и аэростатика 125 257
§ 12. Гидродинамика и аэродинамика 129 260
§ 13. Акустика 139 267
§ 14. Специальная теория относительности ... 143 269
Приложение 284
ОТ ИЗДАТЕЛЬСТВА
Составление этого сборника задач было начато на фи-
физическом факультете МГУ по инициативе академика
С. И. Вавилова. Однако основная работа по составлению
Сборника и подготовке его к изданию выполнена под ру-
руководством С. Э. Хайкина. В 1949 г. вышло в свет первое
издание Сборника в двух частях: I. Механика. Электри-
Электричество и магнетизм, под редакцией С. Э. Хайкина; II. Оп-
Оптика. Молекулярная физика и термодинамика. Атомная
физика и физика ядра, под редакцией Д. В. Сивухина.
С тех пор Сборник переиздавался в 1960 и 1964 гг.
Предлагаемое, четвертое, издание Сборника существен-
существенно отличается от всех предшествующих прежде всего по
своему объему, так как число задач, включенных в Сбор-
Сборник, увеличено почти вдвое. Обогатилось содержание и по-
повысился уровень задач. По степени трудности, постановки
и решения задачи охватывают широкий диапазон: от самых
элементарных до задач, стоящих на уровне оригинальных
научных исследований, выполнение которых возможно на
основе углубленного знания общего курса физики.
В настоящем издании сборник выходит в пяти книгах,
каждая из которых может быть использована самостоя-
самостоятельно:
I. Механика. П. Термодинамика и молекулярная физи-
физика. III. Электричество. IV. Оптика. V. Атомная физика и
физика ядра.
ПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮ
Эта книга представляет собой значительно расширенное
издание раздела «Механика» первой часпг «Сборника задач
по общему курсу физики», выходившей в свет в 1949, 1960
и 1964 гг. под редакцией С. Э. Хайкина. В своей основе
эта часть сборника задач была результатом ведения семи-
семинарских занятий по общему курсу физики, читавшемуся
С. Э. Хайкиным в Московском университете в 1934—46 гг.1).
К сожалению, один из основных авторов задач по механике
С. П. Стрелков A905—1974) и редактор их формулировок и
решений С. Э. Хайкин A901—1968) уже не смогли принять
участия в подготовке четвертого издания Сборника.
В настоящем издании количество задач по механике уве-
увеличено приблизительно в полтора раза по сравнению с их
числом в последнем издании. При этом необходимо отметить,
что в подготовке Сборника к изданию был использован опыт
преподавания общего курса физики не только в МГУ, но и в
других вузах. Так, все параграфы этой книги в значительной
мере дополнены задачами, составленными Д. В. Сивухиным.
Эти задачи в течение многих лет предлагались для решения
студентам Московского физико-технического института.
В задачник включен новый § 14, содержащий задачи по ре-
релятивистской механике и написанный В. А. Угаровым на
основе опыта преподавания специальной теории относи-
относительности в Московском Государственном педагогическом
институте им. В. И. Ленина. Ряд новых задач, связанных,
в основном, с расчетами движения искусственных спутни-
спутников Земли, составлен А. А. Харламовым в ходе его педа-
педагогической работы на кафедре общей физики для механи-
механико-математического факультета МГУ, когда ею руководил
*) Содержание курса лекций С. Э. Хайкина по механике пол-
полностью вошло в книгу С. Э. Хайкин, Физические основы механики,
«Наука», 1971.
С. П. Стрелков. В задачник включены также новые задачи,
составленные сотрудником той же кафедры В. И. Шмаль-
гаузеном и сотрудником кафедры физики кристаллов МГУ
О. А. Шустиным.
Тщательное рецензирование рукописи книги было про-
произведено заведующими кафедрами физики твердого тела и
общей физики Киргизского государственного университета
Л. В. Тузовым и Д. И. Ибраимовым, а также сотрудником
кафедры физики твердого тела П. М. Козловым. Ряд ценных
замечаний сделал также заведующий кафедрой экспери-
экспериментальной физики Киргизского государственного универ-
университета Л. А. Спекторов. Авторы книги глубоко признатель-
признательны всем названным рецензентам за их внимание к рукописи
и ценные замечания. Авторы благодарны также В. К. Петер-
сону за доброжелательную и глубокую критику постанов-
постановки и решений ряда задач.
И. А. Яковлев
ЗАДАЧИ
§ 1. Кинематика
1. Лодка, идущая через реку на веслах, движется отно-
относительно воды со скоростью 2 м/с в направлении, перпенди-
перпендикулярном к течению. Течение реки имеет скорость 1 м/с.
Найти полную скорость v лодки и направление этого вектора
относительно берегов реки.
2. Две пристани перевоза расположены друг против
друга на противоположных берегах реки, скорость течения
которой составляет 0,5 м/с. Какой курс должна держать
лодка перевозчика, чтобы пересекать реку по прямой ли-
линии от одной пристани до другой? С какой скоростью v при
этом условии лодка будет двигаться поперек реки? Относи-
Относительно воды лодка развивает скорость 0,8 м/с.
3. На тележке, равномерно движущейся по горизон-
горизонтальной плоскости, установлена труба. Как должна быть
ориентирована на тележке эта труба, чтобы капли дождя,
падающие вертикально, пролетали через нее, не задевая
внутренних стенок? Движение капель считать равно-
равномерным.
4. Корабль идет на запад со скоростью 6,5 м/с. Ветер дует
с юго-запада со скоростью 3,5 м/с. Какую скорость v ветра
зарегистрируют приборы, расположенные на корабле? Ка-
Каково будет показываемое этими приборами направление
ветра относительно курса корабля?
5. Два самолета одновременно вылетают из одного места
по двум взаимно перпендикулярным направлениям. Один со
скоростью £>i=300 км/ч, другой со скоростью у2=400 км/ч.
Как возрастает со временем расстояние между самолетами?
Как велико это расстояние S в момент, когда первый само-
самолет пролетел путь Si=900 км?
6. Человек, находясь в точке В на расстоянии h от пря-
прямого участка дороги (рис. 1), видит, в точке А автобус, дви-
двигающийся по дороге с постоянной скоростью va. Расстояние
от человека до автобуса в этот момент АВ. В каком направ-
направлении следует бежать человеку, чтобы оказаться на дороге
в точке С с максимальным опережением по времени по от-
отношению к автобусу? Отношение расстояний h/AB=1/2',
А с отношение скоростей человека
' и автобуса vjva = ljV.
7. Два корабля движутся
параллельно друг другу в про-
противоположные стороны со ско-
скоростями Vx И V2. С ОДНОГО ИЗ
них стреляют в другой. Под
каким углом ф к курсу обстре-
обстреливаемого корабля надо направить орудие, чтобы попасть
в цель, если выстрел производится в момент, когда оба суд-
судна находятся на прямой, перпендикулярной к направлению
их движения? Скорость снаряда v0 считать постоянной.
8. Между двумя пунктами, расположенными на реке на
расстоянии L=100km один от другого, курсирует катер.
Катер проходит это расстояние по течению за время /i=4 ч,
а против течения за время /а^Ю ч. Определить скорость те-
течения реки Ui и скорость катера относительно воды v2.
9. Рыбак едет на лодке вверх по реке; проезжая под мо-
мостом, он роняет в воду багор. Через полчаса рыбак это об-
обнаруживает и, повернув назад,» нагоняет багор в 5 км ниже
моста. Какова скорость течения реки, если рыбак, двигаясь
вверх и вниз по реке, греб одинаково?
10. С одного из двух встречных поездов, имеющего ско-
скорость vu на платформу другого, имеющего скорость v2,
бросают некоторый предмет горизонтально и перпендику-
перпендикулярно к направлению движения со скоростью v0 (которую во
все время движения предмета можно считать постоянной).
1) Какой угол ф! с направлением рельсов образует след про-
проекции движущегося предмета на полотно? 2) Какой угол фа
с краем платформы другого поезда, параллельным движению
поезда, будет составлять след проекции движущегося пред-
предмета на платформе? 3) Каковы величины скорости предмета
относительно полотна железной дороги (v') и относительно
платформы (v")?
11. На листе бумаги начерчен прямой угол. Линейка,
оставаясь все время перпендикулярной к биссектрисе этого
угла, движется по бумаге со скоростью 10 см/с. Концы ли-
линейки пересекают стороны начерченного угла. С какой qKo-
ростью движутся по сторонам угла точки их пересечения с
линейкой?
k
a)
о
12. Фотограф, находящийся на расстоянии /от железно-
железнодорожного полотна, хочет сфотографировать поезд, идущий
со скоростью v, в тот момент, когда луч зрения, проверенный
от фотографа к поезду, со-
ставляет угол а с полотном
дороги. Какую максималь-
максимальную выдержку £макс мо-
может дать фотограф, если
допустимое размытие изо-
изображения на фотопластин-
фотопластинке не должно превышать
d, а фокусное расстояние
объектива фотокамеры рав-
равно /?
13. Тело, двигаясь с
постоянным ускорением,
проходит последовательно
два одинаковых отрезка
пути S по Юм каждый.
Найти ускорение тела а и
скорость v0 в начале пер-
первого отрезка, если первый
отрезок пройден телом за
время ^=1,06 с, а второй
за /2=2,2 с.
14. Начертить графики
зависимости от времени
скорости некоторых тел, если графики ускорения а этих
тел имеют вид, представленный на рис. 2 (начальная ско-
скорость тел во всех случаях равна нулю) 2).
6)
А А А
ц
в)
ЛЛ А А А
' И И Vs и
г)
Рис. 2.
6
Рис. 3.
10
15. Начертить графики зависимости от времени пути и
ускорения некоторого тела, если скорость этого тела как
функция времени представлена графиком на рис. 3 (см.
примечание к задаче 14).
*) На приведенных графиках зависимость ускорения от времени
схематизирована: предполагается, что ускорение в некоторые моменты
времени меняется скачком. Такой характер придан рисункам для упро-
16. Какова допустимая предельная скорость v приземле-
приземления парашютиста, если человек может безопасно прыгать с
высоты до h=2 м?
17. С вышки одновременно брошены два тела с одинако-
одинаковой начальной скоростью vQ: одно вертикально вверх, дру-
другое вертикально вниз. Как с течением времени будет менять-
меняться расстояние S между этими телами? Сопротивление воз-
воздуха движению тел не учитывать.
18. Какой начальной скоростью v0 должна обладать
сигнальная ракета, выпущенная из ракетницы под углом
45° к горизонту, чтобы она вспыхнула в наивысшей точке
своей траектории, если время горения запала ракеты 6 с?
Сопротивление воздуха движению ракеты не учитывать.
19. В какой точке траектории тела, брошенного под уг-
углом к горизонту, его нормальное к траектории ускорение
будет максимальным? Сопротивление воздуха движению те-
тела не учитывать.
20. Шарик, которому сообщена горизонтальная скорость
v, падает на горизонтальную плиту с высоты Л. При каждом
ударе о плиту вертикальная составляющая скорости умень-
уменьшается (отношение вертикальной составляющей скорости
после удара к ее значению до удара постоянно и равно а).
Определить, на каком расстоянии х от места бросания отско-
отскоки шарика прекратятся. Считать, что трение отсутствует,
так что горизонтальная составляющая скорости шарика v
не меняется.
21. Из артиллерийского орудия произведен выстрел под
углом ф к горизонту. Величина начальной скорости снаряда
v0. Исследовать аналитически движение снаряда, пренебре-
пренебрегая сопротивлением воздуха полету снаряда и кривизной
поверхности Земли. Найденные зависимости изобразить
графически. Найти: 1) вертикальную и горизонтальную
компоненты вектора скорости v и абсолютную величину
скорости как функцию времени; 2) время Т полета снаряда
от орудия до падения на землю; 3) зависимость от времени
угла а между вектором скорости снаряда и горизонтом;
4) декартовы координаты (ось X — горизонтальное направ-
направление, ось Y — вертикальное направление) снаряда как
функции времени; 5) уравнение траектории снаряда y=f(x)
щения дела. В действительности же ускорения могут изменяться очень
быстро, но все же не скачком — ускорения являются непрерывными
функциями времени. Предположение о скачкообразных изменениях
ускорений приводит к тому, что графики скорости имеют изломы. Ана-
Аналогичные соображения относятся и к задаче 15.
10
(построить согласно этому уравнению траекторию полета
снаряда); 6) максимальную высоту ЛмаКс полета снаряда над
землей; 7) горизонтальную дальность I полета снаряда как
функцию его начальной скорости и угла возвышения ору-
орудия. При каком угле возвышения ф* дальность будет мак-
максимальной при заданной начальной скорости снаряда?
22. Вычертить график линии, которую составят концы
векторов скорости снаряда, выпущенного из орудия под уг-
углом ф к горизонту, если все векторы, соответствующие ско-
скорости снаряда в каждый момент времени, построить из одной
точки. Искомый график называется годографом вектора ско-
скорости. Сопротивление воздуха полету снаряда не учитывать.
23. Из трех труб, расположенных на земле, с одинаковой
скоростью бьют струи воды: под углом в 60, 45 и 30° к гори-
горизонту. Найти отношение наибольших высот h подъема струй
воды» вытекающих из каждой трубы, и отношение дально-
дальностей падения I воды на землю. Сопротивление воздуха дви-
движению водяных струй не учитывать.
24. На какое максимальное расстояние I можно бросить
мяч в спортивном зале высотой 8 м, если мяч имеет началь-
начальную скорость 20 м/с? Какой угол ф с полом зала должен в
этом случае составлять вектор начальной скорости мяча?
Считать, что высота начальной точки траектории мяча над
полом мала по сравнению с высотой зала. Мяч во время по-
полета не должен ударяться о потолок зала. Сопротивлением
воздуха полету мяча пренебречь.
25. С палубы корабля, идущего со скоростью v^ выпу-
выпущен вертикально вверх снаряд с начальной скоростью v0.
Пренебрегая сопротивлением воздуха, найти величину и на-
направление вектора скорости v снаряда в зависимости от
времени и уравнение траектории снаряда в неподвижной сис-
системе отсчета. (Для упрощения решения можно воспользо-
воспользоваться результатами рассмотрения задачи 21.)
26. Следуя аналитическому методу исследования движе-
движения, примененному в задачах 21 и 25, найти траекторию,
скорость v и ускорение а некоторого тела, координаты кото-
которого следующим образом зависят от времени: x=ct2; y—bt*.
27. Точка движется в плоскости, причем ее прямоуголь-
прямоугольные координаты определяются уравнениями
х=А cos со/, у=В sin со/,
где Л, В, со — постоянные. Показать, что точка движется по
эллипсу. Определить его уравнение и радиусы кривизны в
точках пересечения эллипса с осями.
11
Рис. 4.
28. Точка движется в плоскости, причем ее прямоуголь-
прямоугольные координаты определяются уравнениями
х=А ch kt, y^B sh kt,
где Л, В, k — постоянные. По какой траектории движется
точка? Определить ее ускорение.
29. Концы твердого стержня MN могут свободно сколь-
скользить по сторонам прямого угла MON (рис. 4). Какую траек-
траекторию описывает точка Р стержня,
делящая его на части МР и PN, длины
которых соответственно равны Л и В?
30. Самолет летит на высоте h
горизонтально по прямой со скоро-
скоростью v. Летчик должен сбросить бом-
бомбу в цель, лежащую впереди само-
самолета. Под каким углом а к вертикали
он должен видеть цель в момент
выпуска бомбы? Каково в этот момент
расстояние / от цели до точки, над
которой находится самолет? Сопротивление воздуха дви-
движению бомбы не учитывать.
31. Скорость пули можно найти по понижению ее траек-
траектории Ыг на заданном расстоянии /при горизонтальном вы-
выстреле. Понижение траектории определяется по пробоинам,
сделанным пулей в двух верти- л о
кальных последовательно распо-
расположенных на пути пули щитах А
и В (рис. 5). Найти скорость пули,
считая Д/i и / известными и прене-
пренебрегая сопротивлением воздуха.
32. Цель, находящаяся на хол-
холме, видна с места расположения
орудия под углом а к горизонту. Рис. 5.
Дистанция (расстояние по горизон-
горизонтали от орудия до цели) равна /. Стрельба по цели произ-
производится при угле возвышения р. Определить начальную
скорость v0 снаряда, попадающего в цель. Сопротивление
воздуха не учитывать.
33. Из точки, лежащей на верхнем конце верти-
вертикального диаметра некоторой окружности, по желобам,
установленным вдоль различных хорд этой окружности,
одновременно начинают скользить без трения грузы.
Показать, что все грузы достигнут окружности одновре-
одновременно.
12
34. Материальная точка скользит без трения по произ-
произвольной наклонной кривой. Показать, что после того как
точка опустится на высоту Я, скорость ее будет такой же,
как и при свободном ее падении с той же высоты К.
35. С вышки одновременно с одинаковыми по величине
скоростями выбрасываются по всевозможным направлениям
шарики. Показать, что в отсутствие сопротивления воздуха
во всякий момент движения все шарики будут расположены
на сфере, центр которой опускается с ускорением свободно
падающего тела, а радиус равен vot, где v0 — начальная
скорость шариков, a t — время, прошедшее с момента их
выброса.
36. Вагонетка должна перевезти груз в кратчайший срок
с одного места на другое, находящееся на расстоянии /.
Она может разгоняться или замедлять свое движение только
с одинаковым по величине и постоянным во времени ускоре-
ускорением а, переходя затем или в равномерное движение или ос-
останавливаясь. Какой наибольшей скорости v должна дости-
достигать вагонетка, чтобы было выполнено указанное выше
требование?
37. Лодка, имеющая скорость vOt спускает парус в момент
времени tOy но продолжает двигаться. Во время этого движе-
движения произведены измерения скорости лодки, которые пока-
показали гиперболическую зависимость скорости от времени
(v~l/t). Показать, что ускорение а лодки было пропорцио-
пропорционально квадрату ее скорости.
38. Пользуясь условиями предыдущей задачи, найти за-
зависимости: 1) пути S, пройденного лодкой, от времени /;
2) скорости лодки v от пути, после того как на лодке был
спущен парус.
39. Снаряд выпущен горизонтально вперед со скоростью
vCH из орудия, находящегося на самолете, летящем горизон-
горизонтально со скоростью Усам. Пренебрегая сопротивлением воз-
воздуха, найти: 1) уравнение траектории снаряда относительно
земли; 2) уравнение траектории снаряда относительно само-
самолета; 3) уравнение траектории самолета относительно сна-
снаряда.
40. Лодка пересекает реку с постоянной относительно
воды скоростью v, перпендикулярной к течению. Скорость
течения реки, ширина которой d, равна нулю у берегов и
линейно возрастает по мере приближения к середине реки,
где она достигает значения и. Найти траекторию лодки, а
также снос лодки х0 вниз по течению, от пункта ее отправле-
отправления до места причала на противоположном берегу реки.
13
41. Провести решение предыдущей задачи в предпо-
предположении, что скорость течения реки нарастает от бе-
берегов к середине реки по параболическому закону
42. Точка движется равномерно по плоской траектории,
изображенной на рис. 6. В каком месте траектории уско-
ускорение точки будет макси-
максимальным?
43. Луна обращается во-
вокруг Земли с периодом Г=
b =27,3 сут относительно
у д Q/ звезд. Средний радиус орбиты
Луны #=3,8-10б км. Найти
линейную скорость v движе-
движения Луны вокруг Земли и ее
нормальное ускорение а.
л 44. Каковы будут графики
Рис- 6. зависимости от времени абсо-
абсолютных величин скорости и
ускорения при равномерном движении точки по кругу?
45. Найти среднюю угловую скорость искусственного
спутника Земли, если период обращения его по орбите во-
вокруг Земли составляет 105 мин.
46. Найти среднюю линейную скорость искусственного
спутника Земли, если период его обращения по орбите со-
составляет 111 мин, а средняя высота полета 1200 км.
47.. Пользуясь данными об искусственном спутнике Зем-
Земли, приведенными в предыдущей задаче, найти среднее зна-
значение его нормального ускорения на орбите.
48. Найти линейную скорость v точек земной поверхно-
поверхности на географической широте ф, вызванную суточным вра-
вращением Земли вокруг своей оси. Радиус земного шара R==
=6400 км.
49. Найти линейную скорость Земли, вызванную ее ор-
орбитальным движением. Средний радиус земной орбиты ра-
равен «1,5 -108 км.
50. Найти нормальное ускорение точек земной поверх-
поверхности, вызванное суточным вращением Земли. Найти значе-
значение проекции этого ускорения на направление земного ра-
радиуса в данной точке. Оценить значение искомых величин
для широты Москвы E5° северной широты). Радиус Земли
Я=6400 км.
51. Как показали радиолокационные измерения, Венера
вращается вокруг своей оси в направлении, обратном ее
14
орбитальному движению. Период осевого вращения Венеры
(относительно звезд) 7\=243 земных суток. Венера обращает-
обращается вокруг Солнца с периодом 712=225 земных суток. Опре-
Определить продолжительность солнечных суток на Венере, т. е.
время Т между двумя последовательными прохождениями
Солнца через один и тот же меридиан на этой планете (время
от полудня до полудня).
52. Определить скорость, с которой движется тень Луны
по земной поверхности во время полного солнечного затме-
затмения, если оно наблюдается на экваторе. Для простоты счи-
считать, что плоскости солнечной и лунной орбит (относительно
Земли) совпадают, а земная ось к ним перпендикулярна.
Скорость света считать бесконечно большой по сравнению
со всеми остальными скоростями, входящими в задачу.
Радиус лунной орбиты /?л=3,8-105 км.
53. В открытом море на экваторе возвышается высокая
вертикальная скала. Как будет двигаться по этой скале
тень, отбрасываемая сферической поверхностью Земли при
заходе Солнца? Найти ускорение такого движения. Радиус
Земли /?=6400 км. За какое время тень переместится от
основания до вершины скалы, если высота доследней
h=l км?
54. Якорь электромотора, вращавшегося с частотой N
оборотов в секунду, двигаясь после выключения тока равно-
замедленно, остановился, сделав п оборотов. Найти угловое
ускорение якоря после выключения тока.
55. Автомобиль движется со скоростью 60 км/ч. Сколько
оборотов в секунду делают его колеса, если они катятся по
шоссе без скольжения, а внешний диаметр покрышек колес
равен 60 см.
56. При условиях движения автомобиля, описанных
в предыдущей задаче, найти величину нормального
ускорения внешнего слоя резины на покрышках его
колес.
57. Разматывая веревку и вращая без скольжения вал
ворота, ведро опускается в колодец с ускорением 1 м/с2.
С каким угловым ускорением вращается вал ворота? Как
зависит от времени угол поворота вала? Радиус вала ворота
равен 25 см.
58. Автомобиль, движущийся со скоростью 40 км/ч, про-
проходит закругление шоссе с радиусом кривизны 200 м. На
повороте шофер тормозит машину, сообщая ей ускорение
0,3 м/с2. Найти нормальное и полное ускорение автомобиля
на повороте. Как направлен вектор полного ускорения
15
1 °
\ Yi
44JJ!
p/f\
/ Щ1
олн по отношению к радиусу кривизны R закругления
шоссе?
59. Колесо радиуса R катится без скольжения по гори-
горизонтальной дороге со скоростью v0 (рис. 7). Найти горизон-
горизонтальную компоненту vx линейной скорости движения произ-
произвольной точки на ободе колеса, вертикальную компоненту
vy этой скорости и модуль полной скорости для этой же точ-
точки. Найти значение угла а между вектором полной скорости
точек на ободе колеса и направ-
направлением поступательного движе-
движения его оси. Показать, что на-
направление вектора полной ско-
скорости произвольной точки А на
ободе колеса всегда перпенди-
перпендикулярно к прямой АВ и прохо-
дит через высшую точку катя-
Рис 7. щегося колеса. Показать, что
для точки A Vnom—BAiu. По-
Построить график распределения скоростей для всех точек
на вертикальном диаметре (в данный момент времени)
катящегося без скольжения колеса.
Выразить все искомые величины через vOt R и угол ф,
составленный верхним вертикальным радиусом колеса и ра-
радиусом, проведенным из центра колеса О в исследуемую точ-
точку его обода А.
Указание. Движение точек обода колеса можно
рассматривать как результат сложения двух движений:
поступательного движения со скоростью v0 оси колеса и
вращения вокруг этой оси. Для этих точек при отсутствии
скольжения колеса модули векторов скорости поступатель-
поступательного движения и линейной скорости, обусловленной враще-
вращением, равны друг другу.
60. Найти выражение для радиуса кривизны циклоиды
в ее вершине (см. задачу 63).
61. Пользуясь общими результатами, найденными в за-
задаче 59, найти величину и направление векторов скорости
г^для двух точек обода катящегося колеса, расположенных
в данный момент на противоположных концах горизонталь-
горизонтального диаметра колеса. Как будут направлены ускорения
этих двух точек?
62. Колесо радиуса R равномерно катится без скольже-
скольжения по горизонтальному пути со скоростью v. Найти коор-
координаты хну произвольной точки А на ободе колеса, выра-
выразив их как функции времени t или угла поворота колеса
16
Ф, полагая, что при /==0 ф=0, #=0, */=0 (рис. 8). По най-
найденным выражениям для х и у построить график траекто-
траектории точки на ободе колеса.
63. Пользуясь выражением для полной скорости точек,
лежащих на ободе катящегося колеса (см. задачи 59 и 62),
найти длину полного пути каж-
каждой точки обода колеса между
двумя ее последовательными ка-
касаниями полотна дороги.
64. Автомобиль с колесами
радиуса R движется со скоро-
скоростью v по горизонтальной дороге,
причем v2 > Rgt где g — ускоре-
ускорение свободного падения. На
какую максимальную высоту h
может быть заброшена вверх Рис. 8.
грязь, срывающаяся с колес
автомобиля? Указать положение той точки на покрышке
колеса, с которой при данной скорости движения автомо-
автомобиля грязь будет забрасываться всего выше. Сопротив-
Сопротивление воздуха движению отброшенной вверх грязи не
учитывать.
65. Используя условия качения колеса из задачи 59
и результаты ее решения, найти горизонтальную и верти-
вертикальную компоненты вектора ускорения произвольной
точки на ободе колеса. Указать величину и направление
вектора полного ускорения точек, лежащих на ободе
колеса.
66. Представление о величине и направлении вектора
полного ускорения при ускоренном вращательном движе-
движении (например, для точек якоря электромотора при его пу-
пуске) можно получить, рассмотрев следующую задачу.
Точка движется по окружности радиусом R с постоянным
тангенциальным ускорением аь но без начальной скорости.
Найти нормальное и полное ускорения точки, выразив их:
1) как функцию от времени / и ускорения at\ 2) как функцию
от углового ускорения а и угла1 поворота ф радиуса-вектора
точки из его начального положения. Найти угол р между
направлением вектора полного ускорения точки и ее ради-
радиусом-вектором.
67. Кинооператор, снимая через телеобъектив подни-
поднимающийся самолет, вращает свою камеру вокруг вертикаль-
вертикальной оси с угловой скоростью о)! и вокруг горизонтальной
оси с угловой скоростью 6J=W5. Вращению вокруг какой
17
одной мгновенной оси эквивалентны эти два движения ка-
камеры? Вращение с какой угловой скоростью вокруг этой
одной оси могло бы заменить указанные два вращения?
68. Некоторое твердое тело одновременно вращается с
угловыми скоростями о)ь (О2=2о)ь @3=3*0! вокруг трех вза-
взаимно перпендикулярных мгновенных осей, проходящих
через одну точку. Найти, как по отношению к названным
трем осям должна быть ориентирована одна ось , вращение
вокруг которой могло бы заменить сразу все три указанных
независимых вращения. С какой угловой скоростью тогда
должно вращаться тело вокруг найденной новой оси вра-
вращения?
69. Горизонтальный диск вращается с угловой ско-
скоростью coi вокруг вертикальной оси. В некоторой точке на
этом диске на расстоянии R от его оси установлен второй
диск, ось которого также вертикальна. Второй диск вра-
вращается вокруг своей оси в ту же сторону, что и первый диск,
но с угловой скоростью со2. Где располагается та мгновенная
ось вращения, движение вокруг которой второго диска бу-
будет эквивалентно его участию в двух описанных вращатель-
вращательных движениях с угловыми скоростями o)i и со2- С какой
угловой скоростью со должен вращаться второй диск вокруг
этой мгновенной оси?
70. Вращение от мотора автомобиля передается ведущим
колесам через дифференциал — устройство, благодаря ко-
которому каждое из ведущих колес может вращаться с разной
скоростью. Зачем нужен дифференциал? Почему нельзя оба
ведущих колеса закрепить жестко на одной оси, которой
передается вращение от мотора?
71. На основании общих соображений о движении авто-
автомобиля по криволинейному пути, развитых в предыдущей
задаче, рассчитать скорости колес автомобиля на закруг-
закруглении. Автомобиль с шириной колеи 1,2 м и радиусом колес
г=30 см движется по закруглению дороги с радиусом кри-
кривизны R=50 м. Скорость центра автомобиля 36 км/ч. Найти
линейные скорости vt- внутренних (по отношению к центру
кривизны дороги) и внешних va колес автомобиля.
72. Горизонтальный диск равномерно вращается с угло-
угловой скоростью со. На расстоянии R от центра диска постав-
поставлена вертикальная палочка. Найти закон движения тени па-
палочки на вертикальном экране, если весь прибор освещается
горизонтальным пучком параллельных лучей. По найден-
найденному закону движения построить график зависимости пути,
скорости и ускорения тени на экране от времени.
18
§ 2. Динамика прямолинейного движения
материальной точки и простейших систем
73. В лифте установлены пружинные весы, на которых
подвешено тело массы 1 кг. Что будут показывать весы, если
лифт: 1) движется вверх с ускорением 4,9 м/с2, .направ-
.направленным вниз; 2) движется вниз с ускорением 4,9 м/с2, на-
направленным вверх; 3) движется вниз, ускорение направлено
вниз и равно 1 м/с2?
74. На гладком горизонтальном столе лежат 6 одинако-
одинаковых кубиков с массой т= 1 кг каждый. Постоянная сила F=
= 1 кгс действует на первый кубик в направлении, указан-
указанном стрелкой (рис. 9). Найти результирующую силу /,
Рис. 9.
действующую на каждый кубик. Укажите на рисунке стрел-
стрелками силы, действующие на соприкасающихся гранях каж-
каждых двух кубиков. С какой силой Д четвертый кубик дейст-
действует на пятый?
75. На гладкий горизонтальный стол положена одно-
однородная палочка АС массы т и длины / (рис. 10). Постоянная
А В 0 р
М
Рис. 10.
сила F толкает правый конец палочки. С какой силой Ft
мысленно выделенный отрезок палочки Л5=4/6/ действует
на отрезок ВС той же палочки?
76. На гладкой горизон-
горизонтальной плоскости находится ,—
тело массы М (рис. 11). Дру- (
гое тело массы т подвешено на <
нити, перекинутой через блок *—
и привязанной к телу массы М.
Найти ускорения тел и натя-
натяжение нити. Трением тела
массы М о плоскость и трением
в блоке, а также массами блока Рис. П.
и нити пренебречь.
77. Вернемся к установке, описанной в предыдущей за-
задаче (рис. И). 1) Рассечем мысленно горизонтальной пло-
19
/77
м
Рис. 12.
скостью на половине высоты тело массы М. С какой силой
верхняя половина тела действует на нижнюю? 2) Рассечем
мысленно тело М на половине длины вертикальной пло-
плоскостью (перпендикулярной к плоскости рисунка). С какой
силой левая половина тела действует на правую?
78. На гладкую горизонтальную плоскость помещены
три массы ти т2 и т3, связанные нитями между собой и с
массой М, привязанной к
нити, перекинутой через
блок (рис. 12). 1) Найти
ускорение а системы;2) най-
найти натяжение всех нитей
при тех же предположе-
предположениях, что и в задаче 76.
79. По наклонной пло-
плоскости с углом наклона а
скользит тело. Сила трения
между телом и плоскостью
пропорциональна силе нор-
нормального давления тела на плоскость и не зависит от ско-
скорости тела. Коэффициент трения между трущимися поверх-
поверхностями тела и плоскости равен k. Найти ускорение а, с
которым скользит тело.
80. Два одинаковых тела связаны нитью и лежат на
идеально гладком горизонтальном столе, так что нить пред-
представляет собой прямую линию (рис. 13). Нить может выдер-
выдерживать натяжение с f
силой не более 2 кгс.
Какую горизонтальную
силу F следует прило-
приложить к одному из тел,
чтобы нить оборвалась?
81. Изменится ли сила, необходимая для разрыва нити
в условиях предыдущей задачи, если между телами и столом
есть трение и коэффициент трения одина-
одинаков для обоих тел?
82. Две пластинки с массами тх и т2
соединены пружиной (рис. 14). С какой
силой нужно надавить на верхнюю пла-
пластинку, чтобы после прекращения действия
этой силы верхняя пластинка, подпрыг-
подпрыг? Мй б
Рис. 13.
тг
Рис. 14.
р
нув, приподняла и нижнюю? Массой пружины пренебречь.
83. Доска лежит горизонтально на двух опорах, распо-
расположенных йод её концами. Посередине доски лежит покоя-
20
щееся тело. Какие силы действуют на это тело? Какие силц
действуют на доску и на опоры? (При рассмотрении этих
вопросов собственным весом доски можно пренебречь.)
84. На доске, описанной в предыдущей задаче, стоит
человек. Внезапно он приседает. Что произойдет в первый
момент: увеличится или уменьшится прогиб доски? Что
произойдет, если человек сидел на корточках и внезапно
выпрямился?
85. Лошадь равномерно тянет сани. Рассмотреть вза-
взаимодействие трех тел: лошади, саней и поверхности земли.
Начертить векторы сил, действующих на каждое из этих
тел в отдельности, и установить соотношение между ними.
86. Как изменятся соотношения между силами в приме-
примере, разобранном в предыдущей задаче, если лошадь и сани
движутся с ускорением а? Найти величину всех сил, если
а=20 см/с2. Масса саней с грузом М=0,5 т, масса лошада
т=0,35 т и коэффициент трения саней о снег 0,2.
87. Каков должен быть минимальный коэффициент трз-
ния k между шинами ведущих колес автомобиля и дорогой,
чтобы автомобиль массой в 2 т с грузом в 4 т двигался с уско-
ускорением а=0,2 м/с2? Рассмотреть задачу для двух случаев:
1) все колеса автомобиля ведущие, 2) только задние веду-
ведущие; считать, что центр масс автомобиля находится по-
посередине между осями его- колес, а центр масс груза — над
задней осью.
88. На горизонтальной доске лежит груз. Коэффициент
трения между доской и грузом 0,1. Какое ускорение в гори-
горизонтальном направлении следует сообщить доске, чтоб$>1
груз мог с нее соскользнуть?
89. На столе лежит доска массы Af=l кг, а на доске -г-
груз массы т==2 кг. Какую силу F нужно приложить к до-
доске, чтобы доска выскользнула из-под груза? Коэффициент
трения между грузом и доской 0,25, а между доской и ctq-
лом 0,5.
90. Воздушный шар массы М опускается с постоянной
скоростью. Какое количество балласта ДМ надо выбросить,
чтобы шар начал подниматься с той же скоростью? Подъем-
Подъемную силу Р шара считать постоянной.
91. Маятник массы т подвешен к подставке, укреплен-
укрепленной на тележке (рис. 15). Найти направление нити маятника,
т. е. угол а нити маятника с вертикалью, и ее натяжение Т
в следующих случаях: 1) тележка равномерно движется гго
горизонтальной плоскости; 2) тележка движется горизон-
горизонтально с ускорением а\ 3) тележка свободно скатывается с
21
наклонной плоскости, образующей угол q> с горизонтом;
4) тележка с некоторым ускорением &, направленным вдоль
наклонной плоскости, вка-
вкатывается на нее; 5) тележка
с тем же ускорением Ь ска-
скатывается с наклонной пло-
плоскости.
92. Камень брошен вер-
вертикально вверх. В каких
точках траектории камень
будет иметь максимальное
ускорение? Рассмотреть
два случая: 1) сопротивле-
сопротивление воздуха отсутствует; 2) сопротивление воздуха растет
с увеличением скорости камня.
93. Как направлено ускорение артиллерийского снаря-
снаряда после вылета из ствола орудия, если сопротивление воз-
воздуха отсутствует? Как изменится это направление при нали-
наличии сопротивления воздуха?
94. В снаряде, выпущенном вертикально вверх, на пру-
пружинах укреплен грузик А массы т (рис. 16). Чему будет
у//////////////////
'///////////////////////////////////7////////
Рис. 15.
Рис. 16.
сь
Рис. 17.
равняться сила, действующая на грузик со стороны пружи-
пружинок, при подъеме и спуске снаряда? Рассмотреть вопрос без
учета и с учетом сопротивления воздуха движению снаряда*
22
96. Простейшую машину Атвуда, служащую для про*
верки законов равноускоренного движения, можно схема-
схематически представить так: на нити, перекинутой через блок
Л, подвешены две неравные массы, mi и т2 (рис. 17). Найти
ускорение масс, натяжение нити Т и силу /, действующую на
ось блока этой машины. Блок и нить считать невесомыми,
трения в оси блока не учитывать.
96. На верхнем краю идеально гладкой наклонной пло-
плоскости укреплен блок, через который перекинута нить
(рис. 18). На одном ее конце
привязан груз с массой ть
лежащий на наклонной пло-
плоскости. На другом конце ви-
висит груз с массой т2. С каким
ускорением а движутся грузы
и каково натяжение Т нити?
Наклонная плоскость обра- Рис 18.
зует с горизонтом угол а.
97. Определить ускорение массы М в системе, изобра-
изображенной на рис. 19. Массой блоков и силами трения мож-
можно пренебречь. Клинья считать закрепленными жестко.
98. Система грузов находится на ма-
машине Атвуда (рис. 20). Грузы ш2 и т3
соединены пружиной. Систему удерживали
М
Рис. 19.
Рис. 20.
за груз ти а затем отпустили. Какие ускорения будут
у грузов пц и т8 в начальный момент движения?
99. На машине, описанной в задаче 95, массы тх и т2
движутся. Через промежуток времени / после начала движе-
движения масса Ш\ опустилась на я-ю часть того расстояния, кото-
которое она прошла бы за то же время при свободном падении.
Каково отношение масс тх и /л2?
100. Каждый из двух грузов на машине, описанной в за-
задаче 95, висящих по обе стороны блока, имеет массу т=
=250 г. На один из грузов положена дополнительно масса
(перегрузок) Дт=5 г. Определить время / от начала движе-
23
йия, за которое каждый груз пройдет путь s=l м, и ско-
скорость vt которую будут иметь грузы, пройдя это расстояние.
101. Определить по дан-
данным предыдущей задачи
силу давления р перегруз-
перегрузка на основной груз во вре-
время движения.
102. Машина, описан-
описанная в задаче 95, уравнове-
уравновешена на весах при затор-
заторможенном блоке (рис. 21I).
1) В какую сторону нару-
нарушится равновесие весов,
если освободить тормоз
блока? 2) Как уравновесить
Рис 21. весы при движущихся мас-
массах тх и т2?
103. Найти ускорения аг и а2 масс тг и т2 и натяжение
нити Т в системе, изображенной на рис. 22. Массой блоков
и нитей пренебречь. '//////////////////////л
(к
Рис. 22.
и
гпг
Рис. 23.
104. Найти ускорение массы тх ,и натяжения нитей Тг
й Т2 в системе, изображенной на рис. 23. Массой блоков и
нитей пренебречь, сил трения не учитывать.
Вследствие! этого массы тх и т% не движутся.
24
105. На рис. 24 изображен прибор для демонстрации за-
законов динамики. На коромысле весов укреплены два очень
легких блока а и с, один на конце, другой в центре коромыс-
коромысла; через блоки перекинута нить, на концах которой при-
прикреплены две одинаковые гирьки Л и В по 250 г. Средний
блок устроен так, что груз на нити находится под точкой
опоры коромысла. На другом конце коромысла подвешена
чашка с разновесом.
Пусть весы уравновешены при одинаковых грузах А и В
на нити. Как следует изменить груз на чашке весов для того,
чтобы восстановить равновесие весов при движущихся гру-
грузах в двух следующих случаях: 1) на гирьку, висящую на
конце коромысла, положен перегрузок в 25 г; 2) на гирьку
под серединой коромысла положен перегрузок в 25 г?
106. Система, изображенная на рис. 24 (см. предыдущую
задачу), уравновешена при наличии перегрузка в 50 г на
средней гирьке при заторможенном блоке. 1) Что следует
сделать для восстановления равновесия после того, как блок
будет освобожден и грузы начнут двигаться? 2) Ответить на
этот же вопрос, если вначале весы были уравновешены при
заторможенных блоках при наличии перегрузка в 50 г на
крайней гирьке.
107. Через блок, ось которого горизонтальна, перекину-
перекинута веревка длины / (устройство блока см. на рис. 17). За
концы веревки держатся две обезьяны, находящиеся на оди-
одинаковых расстояниях 1/2 от блока. Обезьяны начинают одно-
одновременно подниматься вверх, причем одна из них подни-
поднимается относительно веревки со скоростью vf а другая со
скоростью 2v. Через сколько времени каждая из обезьян
достигнет блока? Массой блока и веревки пренебречь; мас-
массы обезьян одинаковы.
108. Обезьяна, движущаяся с большей скоростью (см.
условие предыдущей задачи), обладает вдвое большей мас-
массой, чем другая. Которая обезьяна достигнет блока ракыие?
25
109. Обезьяна с массой т уравновешена противовесом
на подвижном блоке В (рис. 25). Блок В уравновешен гру-
грузом с массой 2т на неподвижном блоке С. Вначале система
была неподвижна. С какой скоростью будет подниматься
груз 2т, если обезьяна начнет выбирать
веревку с произвольной скоростью v (отно-
(относительно себя)? Массой обоих блоков можно
пренебречь.
110. Два шарика падают в воздухе. Ша-
Шарики (сплошные) сделаны из одного мате-
материала, но диаметр одного из шариков вдвое
больше другого. В каком соотношении будут
находиться скорости шариков при устано-
установившемся (равномерном) движении? Считать,
что сила сопротивления воздуха пропорцио-
пропорциональна площади поперечного сечения движу-
движущегося тела и квадрату его скорости.
111. Стальной шарик радиусом 0,05 мм
падает в широкий сосуд, наполненный глице-
Рис. 25. рином. Найти скорость v установившегося
(равномерного) движения шарика. Коэффи-
Коэффициент внутреннего трения в глицерине равен ц = 14 дин • с/см2,
плотность глицерина di= 1,26 г/см3, плотность стали
d2=7,8 г/см3.
Указание. Для решения задачи надо воспользо-
воспользоваться гидродинамической формулой Стокса, выражающей
силу сопротивления, испытываемую шариком, движущимся
в вязкой жидкости: /=6ягсл].
112. Как будет изменяться скорость тела, движущегося
вертикально вверх с начальной скоростью vOt если можно
считать, что сила сопротивления воздуха пропорциональна
скорости тела?
ИЗ. Тело бросают вертикально вверх в вязкой среде.
Сила вязкого трения пропорциональна скорости движения
тела. Вычислить время U подъема тела на максимальную
высоту его полета вверх и сравнить его со временем t0
подъема в отсутствие трения. Начальная скорость тела в
обоих случаях одинакова.
114. Из одного неподвижного облака через т секунд одна
за другой начинают падать две дождевые капли. Как будет
изменяться со временем расстояние между ними? Решить
задачу в двух случаях: 1) полагая, что сопротивление воз-
воздуха отсутствует; 2) полагая, что сопротивление воздуха
пропорционально скорости капель.
26
115. Лодка под парусом развила скорость v0. 1) Как бу-
будет убывать во времени скорость движения лодки по стоя-
стоячей воде после спуска паруса, если сопротивление воды дви-
движению лодки можно считать пропорциональным квадрату
скорости? 2) Как долго будет двигаться лодка? 3) Какой
путь она пройдет до полной остановки?
116. Рассмотреть вопросы, поставленные в предыдущей
задаче, в предположении, что сопротивление воды движению
лодки пропорционально первой степени ее скорости.
117. Пусть сила сопротивления воды движущейся лодки
пропорциональна скорости лодки (см. также условия двух
предыдущих задач). Как в таком случае скорость лодки,
после спуска паруса будет зависеть от пройденного лодкой
пути?
118. Парашютист совершает затяжной прыжок. До рас-
раскрытия парашюта он падает со скоростью 60 м/с, после рас-
раскрытия приземляется со скоростью 4 м/с. Подсчитать, како-
каково было бы максимальное натяжение Т строп парашюта,
если бы в конце затяжного прыжка он раскрывался мгно-
мгновенно. Масса парашютиста 80 кг, а силу сопротивления воз-
воздуха движущемуся парашюту можно считать пропорцио-
пропорциональной квадрату скорости (см. также следующую задачу).
Считать массу парашюта и его строп малой по сравнению с
массой парашютиста.
119. При затяжном прыжке, рассмотренном в предыду-
предыдущей задаче, парашют раскрывается не мгновенно, а посте-
постепенно. При этом натяжение Т строп все время вплоть до
полного раскрытия парашюта
остается примерно постоянным
и равным 720 кгс. Найти ско-
скорость падения v' к моменту пол-
полного раскрытия парашюта и вре-
время т, в течение которого пара-
парашют раскрывается.
120. По наклонной плоскости,
составляющей угол а с горйзон- Рис. 26.
том, ускоренно скользит доска
массы М (рис. 26). Коэффициент трения доски о наклонную
плоскость равен к. На доску кладут тело массы т, которое
скользит по доске без трения. Какова должна быть мини-
минимальная масса тела тмин, чтобы движение доски по наклон-
наклонной плоскости стало равномерным?
Ш. Через легкий вращающийся без трения блок пере-
перекинута нить. На одном ее конце привязан груз с массой тх.
27
По другому концу нити с постоянным относительно нее ус-
ускорением а2 скользит кольцо с массой т2 (рис. 27). Найти
ускорение ах массы Шг и силу трения R кольца о нить. Мас-
Массой нити можно пренебречь.
122; Обезьяны, о которых шла речь в задаче 107, начи-
начинают подниматься вверх с постоянным ускорением относи-
относительно веревки, причем одна из них поднимается с ускоре-
ускорением а, а другая с ускоре-
шеи 2а. Через какой проме-
промежуток времени каждая из
обезьян достигнет блока?
'///////////////////л
Рис. 27.
Рис. 28.
123. Для иллюстрации различных случаев зависимости
движения тяжелого маятника от ускорения его точки под-
подвеса могут служить известные опыты Н. А. Любимова
с маятником, подвешенным на падающем щитке (рис. 28).
Щиток, в верхней части которого укреплена ось вращения
маятника, вертикально падает вниз. Щиток скользит без
трения по направляющим проволокам. 1) Как будет дви-
двигаться относительно щитка маятник, если отклонить его от
вертикали, удерживая щиток йеподвижным, а затем осво-
освободить одновременно и щиток и маятник? 2) Как будет дви-
двигаться маятник относительно щитка, если сначала заста-
заставить его колебаться на неподвижном щитке, а затем осво-
освободить щиток в момент, когда скорость маятника не равна
нулю?
124. Каков будет период малых колебаний математиче-
математического маятника длины /, если маятник колеблется в вагоне,
движущемся в горизонтальном направлении с ускорением а?
28
125. Каков будет период малых колебаний маятника в
лифте, опускающемся с постоянным ускорением а? Каким
будет период маятника при a=g? Как будет вести себя ма-
маятник при a>g?
126. Каков будет период малых колебаний Т математи-
математического маятника длины /, подвешенного в вагоне, свободно
скатывающемся по наклонному пути с углом наклона а?
127. Тяжелое тело подвешено на пружине к потолку ка-
кабины лифта. Каково будет движение тяжелого тела относи-
относительно кабины, если кабина внезапно начинает свободно
падать под действием силы тяжести?
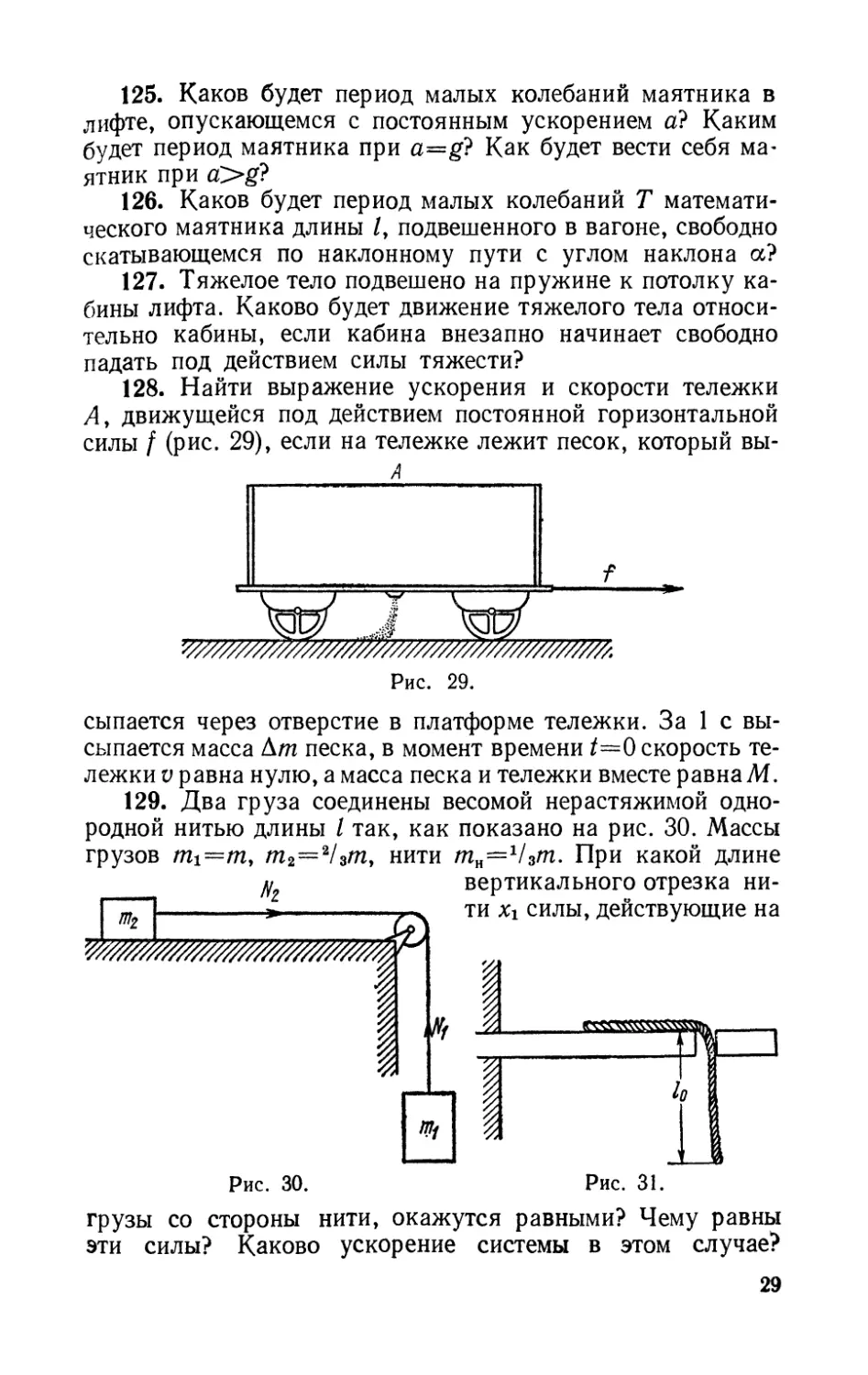
128. Найти выражение ускорения и скорости тележки
Л, движущейся под действием постоянной горизонтальной
силы / (рис. 29), если на тележке лежит песок, который вы-
А
Рис. 29.
сыпается через отверстие в платформе тележки. За 1 с вы-
высыпается масса Am песка, в момент времени /=0 скорость те-
тележки v равна нулю, а масса песка и тележки вместе равна М.
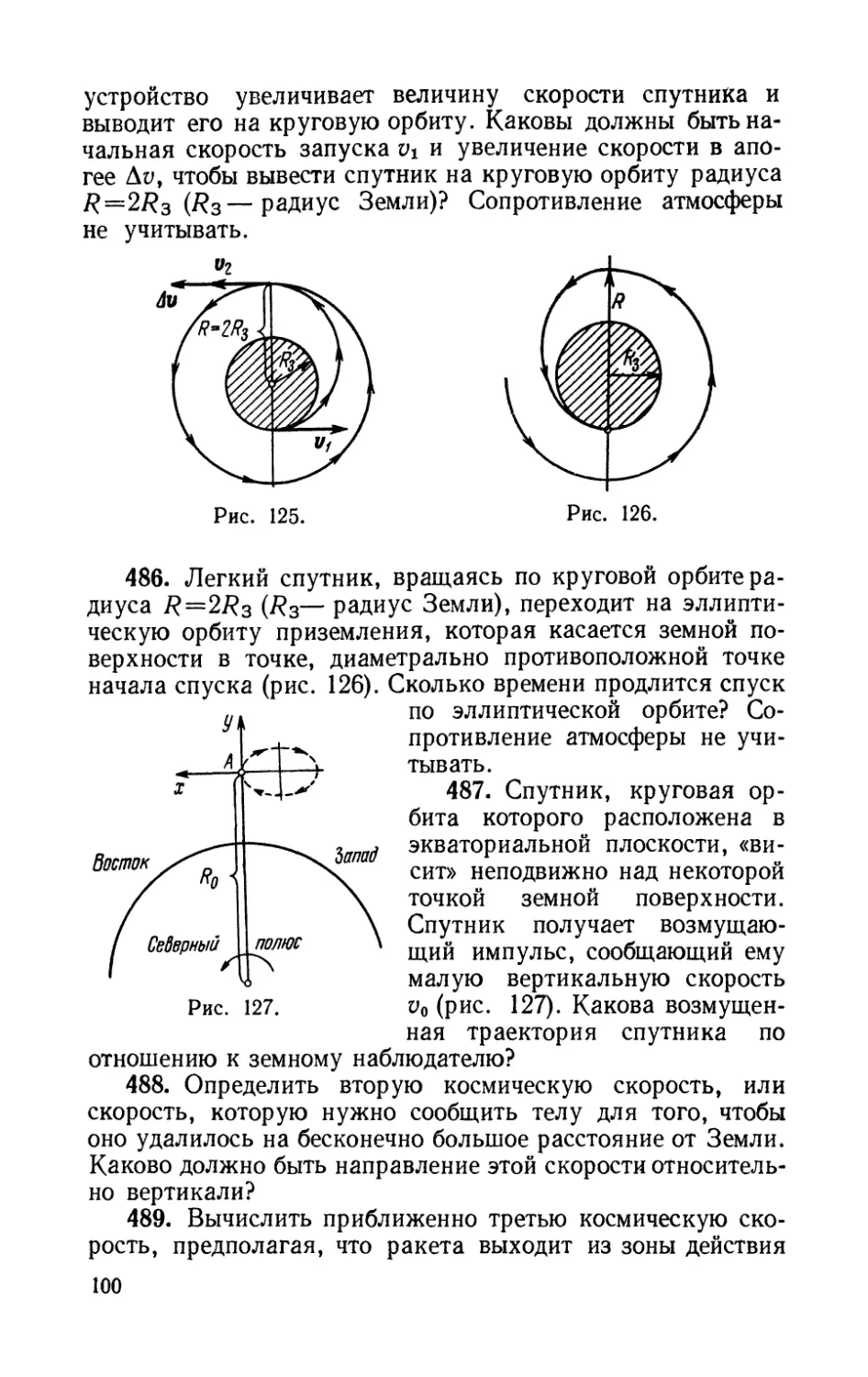
129. Два груза соединены весомой нерастяжимой одно-
однородной нитью длины / так, как показано на рис. 30. Массы
грузов т1=т, т2=2/зт> нити тн—1/3т. При какой длине
уу вертикального отрезка ни-
нити Хг силы, действующие на
Рис. 30.
Рис. 31.
грузы со стороны нити, окажутся равными? Чему равны
эти силы? Каково ускорение системы в этом случае?
29
U
Массой блока и трением во всех частях системы можно
пренебречь.
130. Шнур, положенный на доску, пропущен одним кон-
концом в отверстие, просверленное в доске (рис. 31). Найти, с
какой скоростью v соскользнет с доски конец шнура, если
известна длина всего шнура /и длина его конца /0, свешиваю-
свешивающегося в момент начала движения. Найти зависимость от
времени длины свисающего с доски отрезка шнура. Трение
между шнуром и столом не учитывать.
131. Три одинаковых шарика У, 2 и 3 подвешены на пру-
пружинах один под другим так, что расстояния между ними
у////////////////////, одинаковы (рис. 32). Следовательно, центр
масс этой системы совпадает с центром
второго шарика. Если обрезать нить,
удерживающую шарик 7, то система на-
начнет падать, причем ускорение центра
масс системы должно быть 3mg/3m=g
(по известному закону: ускорение центра
масс системы тел равно сумме внешних
сил, действующих на систему, деленной на
массу всей системы). Но пружина / тянет
шарик 2 вверх сильнее, чем пружина //
тянет этот шарик вниз (сила натяжения
пружины / в начальный момент f1=2mg,
а сила натяжения пружины // в начальный
момент/2=mg), следовательно, шарик 2 на-
начинает падать с ускорением, меньшим чем#.
Таким образом, мы пришли как будто к противоречию.
1) Объяснить кажущееся противоречие; 2) найти ускорения
всех шариков в начальный момент; 3) определить начальные
ускорения шариков, если мы перережем не нить, а пружину,
поддерживающую шарик 3.
I;
а
3(
Рис. 32.
/1
Рис. 33.
Рис. 34.
132. На горизонтальной плоскости лежит клин массы М
(рис. 33). На грань клина кладут тело массы т. Все поверх-
поверхности соприкасающихся тел гладкие. Найти горизонтальные
30
ускорения обоих тел и силы N и R, с которыми тело давит на
клин и клин давит на плоскость.
133. На наклонной плоскости лежит тело (рис. 34). Ко-
Коэффициент трения тела о плоскость fe=tg а, где а — угол
наклона плоскости к горизонту. Тело, толчком вдоль на-
наклонной плоскости, приводят в движение с начальной ско-
скоростью v0. Найти установившуюся скорость скольжения
тела в зависимости от величины v0 и направления толчка.
§ 3. Статика
134. На горизонтальной плоскости стоит человек веса Р,
который держит на весу с помощью неподвижного блока груз
веса Q (рис. 35). Определить, с какой
силой F человек давит на плоскость.
135. Фонарь массы т=10 кг под-
подвешен на канатике над серединой
улицы шириной /=10 м. Допустимое
натяжение канатика /?=50 кгс. Ка-
Какова должна быть высота крепления
концов канатика, если точка прикреп-
прикрепления фонаря к канатику должна
находиться на высоте /i=5 м?
136. Анализируя результат задачи
135, можно прийти к следующему
неожиданному выводу: любой канат
можно разорвать сколь угодно малой
силой. Действительно, представьте
канат натянутым и закрепленным на
концах; тогда достаточно приложить
к середине каната перпендикуляр-
перпендикулярную к нему небольшую силу, чтобы
создать сколь угодно большое натяжение каната. Почему же
все-таки канат нельзя разорвать сколь угодно малой силой?
137. Подвес фонаря устроен так, как показано на рис. 36.
Масса фонаря 5 кг. Определить силы, действующие на бру-
брусок АВ и проволоку СВ (размеры указаны на чертеже).
138. Веревка привязана к крючку А и перекинута через
блок С (рис. 37). К веревке в точке D прикреплен груз
20 кг, причем точка D не может смещаться по веревке. Ка-
Какой груз Q следует прикрепить к концу веревки,чтобы натя-
натяжение веревки на участке AD было в два раза больше, чем
в остальной ее части, и угол ADC=90°? Определить силу /\
вырывающую блок С.
31
139. Клин заколачивают в бревно. Каков должен быть
коэффициент трения, чтобы клин не выскакивал из
бревна? Угол клина при вер-
вершине равен 30°.
140. С какой силой / должен
человек тянуть веревку, чтобы
у////////////////////////////////////,
Рис. 36.
Рис. 37.
удержать платформу, на которой он стоит (рис. 38), если
масса человека mi=60 кг, а масса платформы т2=30 кг?
С какой силой F человек давит на платформу? Какова макси-
v/fr мальная масса платформы, которую
^ может удержать человек?
Рис. 38.
Рис. 39.
141. Конструкция и размеры крана указаны на рис. 39.
Определить силу натяжения F оттяжки АВ и силу Г, рас-
растягивающую стержень ВС, когда кран поднимает груз в 1 т.
Узлы В, С и D считать шарнирами.
32
в
Рис. 40.
142. Однородная палочка АВ, концы которой могут
скользить без трения по горизонтальной плоскости ОА и
вертикальной стенке ОВ, удерживается в положении рав-
равновесия натяжением нити ОС (рис. 40). Палочка наклонена
к горизонтальной плоскости под
углом а, а нить — под углом р.
Найти натяжение нити Г, если вес
палочки равен Р. При каких поло-
положениях точки С равновесие воз-
возможно и при каких невозможно?
143. Длина коромысла весов 2/=
=30см,масса коромысла тк=300г,
длина стрелки D=30 см. Перегру-
Перегрузок тк=0,01 г одной из чашек
отклоняет конец стрелки от верти-
вертикального положения на расстояние fe=0,3 см. Определить
расстояние d центра масс коромысла от ребра призмы.
144. Каков должен быть минимальный коэффициент тре-
трения k материала стенок куба о горизонтальную плоскость,
чтобы можно было его опрокинуть через ребро горизонталь-
горизонтальной силой Fy приложенной к верхней грани. Чему должна
быть равна приложенная сила?
145. Человек везет нагруженные сани с постоянной ско-
скоростью по горизонтальной дороге, натягивая веревку, при-
привязанную к саням, под углом ф к горизонту. Определить
силу натяжения веревки F, если масса саней с грузом равна
М, а коэффициент трения полозьев о
снег k. Направление веревки прохо-
проходит через центр масс системы. Найти
оптимальное значение угла ср. Как ме-
меняется оптимальный угол с изменением
k от 0 до 1?
146. Определить расстояние d центра
масс полуокружности радиуса R от
стягивающего ее диаметра.
147. Определить расстояние d центра
масс пластины, имеющей форму полу-
полукруга радиуса R, от ограничивающего
ее диаметра.
148. Однородная пластина ограни-
ограничена полуокружностью радиуса R и
равнобедренным треугольником с основанием и высотой,
равными 2R (рис. 41). Определить расстояние хс от центра
масс с этой фигуры до окружности.
2 Под ред. И. А. Яковлева 33
Рис. 41.
149. Определить положение центра масс пластины, вы-
вырезанной в виде кругового сегмента, дуга которого равна
2а, а радиус равен R.
150. Пластина вырезана в форме полукруга радиуса /?.
Четверо поднимают ее. Двое взялись за концы диаметра, ос-
остальные за окружность. На каком расстоянии d от диаметра
они должны взяться для того, чтобы каждый поддерживал
четверть веса пластины?
151. В вершинах правильного, горизонтально располо-
расположенного шестиугольника со стороной а (рис. 42) подвешены
грузы, веса которых равны: Ру 2Р, ЗР, 4Р, ЪР и 6Р. Опре-
Определить величину и точку М (х, у) приложения равнодейст-
равнодействующей. Координатные оси расположить так, как показано
на чертеже.
Рис. 43.
152. Однородный сплошной шар массы /л, разрезанный
вертикальной плоскостью пополам и скрепленный нитью
по большому горизонтальному кругу, лежит на столе. Най-
Найти натяжение Т нити.
153. Кронштейн, перспективный чертеж которого дан
на рис. 43, состоит из трех стержней АВ, АС и AD. Концы
стержней В, С и D укреплены с помощью шарниров в стене,
а другие концы сварены вместе в узел Л. Стержни АВ и АС
лежат в горизонтальной плоскости и образуют между собой
угол 2у. Вертикальная плоскость, проходящая через стер-
стержень AD, рассекает угол ВАС пополам. Стержень AD об-
образует со стеной угол р. На узел А действует сила F в пло-
плоскости, параллельной стене, образующая с вертикалью угол
а. 1) Найти силы, развиваемые в стержнях АВ, АС и AD.,
34
2) Найти условие, при котором в стержне АС не развивается
никаких усилий.
154. Может ли держаться ящик, висящий на веревке у
вертикальной стены так, как указано на рис. 44, в отсутствие
сил трения?
Рис. 44г.
Рис. 46.
155. Куб массой в 1 т опирается ребром D на выступ в
вертикальной стене, а за рббро В подвешен канатом АВ к
стене (рис. 45). Канат составляет угол 45° со стеной. Опре-
Определить силу F, с которой куб действует на выступ D.
156. Два одинаковых бруска опираются концами на опо-
опоры, как указано на рис. 46. Трение между брусками и сшо-
рами отсутствует. Между брусками зажат цилиндр Л, удер-
удерживаемый силами трения, а внизу бруски связаны верёвкой
Рис 46.
By привязанной к костылям, вбитым в бруски. Определить
силу натяжения Т веревки и давления F цилиндра на бру-
бруски, если известно расстояние h между осью цилиндра А и
веревкой, равное 20 см. Длина каждого бруска /»1,5м,
а масса М=220 кг, масса цилиндра га=20 кг.
157. Два куба с ребром 10 см спаяны гранями и образу-
образуют призму; масса одного куба 1 кг, масса другого 3 кг.
Призма стоит на шероховатой горизонтальной плоскости
2* 35
(рис. 47). Какую горизонтальную силу f нужно приложить
к верхнему основанию призмы перпендикулярно к ее ребру,
чтобы опрокинуть призму через ребро? Зависит ли эта сила
/ от того, находится наверху лег-
легкий куб или тяжелый?
158. Веревка, оба конца которой
свободны, обвита в один ряд вокруг
цилиндрического столба. К одному
из свободных концов веревки при-
приложена сила натяжения 7\. Какую
силу Т2 надо приложить к другому
концу веревки, чтобы она находи-
лась в равновесии? Коэффициент
^ й Л
р у р р
Рис. 47. ностью столба равен k, а число
витков веревки п.
159. На горизонтальной плоскости лежат три одинако-
одинаковых шара, соприкасающиеся между собой, так что их цент-
центры расположены в вершинах правильного треугольника.
Над центром этого треугольника положен четвертый такой
же шар. При каком минимальном значении коэффициента
трения k такие соприкасающиеся шары могут удерживаться
в равновесии, если коэффициенты трения шара о шар и ша-
шара о плоскость опоры одинаковы?
§ 4. Работа, мощность, энергия
160. Действуя постоянной силой в 20 кгс, поднимают
груз массой в 10 кг на высоту 10 м. Какая при этом совер-
совершается работа? Какой потенциальной энергией будет обла-
обладать поднятый груз?
161. Подсчитать работу, которую нужно совершить,
чтобы опрокинуть через ребро призму, описанную в задаче
157, для указанных в этой задаче случаев.
162. Коэффициент трения между некоторым телом и
плоскостью, наклоненной под углом 45° к горизонту, равен
0,2. На какую высоту поднимается это тело, скользя по на-
наклонной плоскости, если ему будет сообщена скорость
10 м/с, направленная вверх вдоль плоскости? Какова будет
скорость тела, когда оно вернется в нижнюю исходную точ-
точку своего движения?
163. Какую работу надо совершить, чтобы втащить (во-
(волоком) тело массы m на горку с длиной основания L и высо-
высотой Я, если коэффициент трения между телом и поверх-
36
ностью горки равен k? Угол наклона поверхности горки с
горизонтом может меняться вдоль горки, но его знак остает-
остается постоянным.
164. Какую полезную работу можно получить при со-
соскальзывании тела массы га с горки, длина основания кото-
которой равна L, а высота Я, если коэффициент трения между
телом и поверхностью горки равен k? Угол наклона поверх-
поверхности горки с горизонтом может меняться вдоль горки, но
его знак остается постоянным.
165. Показать, что если построить кривую, выражаю-
выражающую кинетическую энергию материальной точки как функ-
функцию пройденного пути, то сила, действующая в каждой точ-
точке в направлении перемещения, будет измеряться тангенсом
угла наклона касательной в данной точке кривой энергии
к оси абсцисс.
166. Из залитого подвала, площадь пола которого равна
50 м2, требуется выкачать воду на мостовую. Глубина воды
в подвале 1,5 м, а расстояние от уровня воды в подвале до
мостовой 5 м. Найти работу, которую необходимо затратить
для откачки воды.
167. В цилиндр сегнерова колеса налито 2 л воды; высо-
высота этого столба воды равна 60 см. Найти энергию U, запа-
запасенную в приборе.
168. Оконная штора массой в 1 кг и длиной 2 м сверты-
свертывается на тонкий валик наверху окна. Какая при этом со-
совершается работа? Трением пренебречь.
169. Горный ручей с сечением потока S м2 образует водо-
водопад высотой в h м. Скорость течения воды в ручье v м/с.
Найти мощность ручья W, выразив ее в лошадиных
силах.
170. Определить среднюю полезную мощность при вы-
выстреле из гладкоствольного ружья, если известно, что пуля
массы т вылетает из ствола со скоростью v0, а длина канала
ствола / (давление пороховых газов считать постоянным во
все время нахождения снаряда в канале ствола).
171. Отвес удерживают вертикально в вагоне, движу-
движущемся по горизонтальному пути с постоянным ускорением а,
а затем сразу отпускают. Найти: 1) выражение потенци-
потенциальной энергии U отвеса, отклоненного от вертикали на
угол а; 2) выражение работы А силы, отклонившей отвес на
угол а; 3) значение максимального угла отклонения отвеса
амакс в условиях опыта. 4) Показать, что этот угол макси-
максимального отклонения отвеса от вертикали вдвое больше угла,
образуемого с вертикалью направлением установившегося
37
отвеса в ускоренно движущемся вагоне (см. также за-
задачу 91). 5) Описать движение отвеса, после того как он был
освобожден из вертикального положения.
172. Отвес в железнодорожном вагоне остается в верти-
вертикальном положении, пока поезд идет с постоянной ско-
скоростью. При торможении поезда отвес начинает качаться,
причем его максимальное отклонение от вертикали состав-
составляет 3°. Какой путь S пройдет поезд до полной остановки,
если считать, что его ускорение все время остается постоян-
постоянным, а скорость поезда в момент начала торможения была
47 км/ч?
173. На поверхность Земли с очень большого расстояния
падает метеорит. С какой скоростью метеорит упал бы на
Землю, если бы атмосфера не тормозила его движения?
Считать, что начальная скорость метеорита вдали от Земли
равна нулю.
174. Дают ли возможность результаты решения преды-
предыдущей задачи ответить на вопрос: какой должна быть мини-
минимальная скорость ракеты, запущенной с поверхности Зем-
Земли, для Того чтобы она преодолела силу земного тяготения и
ушла в межпланетное пространство?
175. На Землю с очень большого расстояния падает ме-
метеорит массой т—\ т. Найти кинетическую энергию Т ме-
метеорита на расстоянии /i=200 щ от поверхности Земли. Счи-
Считать, что начальная скорость метеорита вдали от Земли рав-
равна нулю.
176. Какую мощность W затрачивает лошадь на движе-
движение садей, если она тянет их в гору равномерно со ско-
скоростью v? Масса саней га и трение между санями и поверх-
поверхностью горы постоянно, коэффициент трения k. Угол
наклона горы а.
177. Показать (для условий задачи 115), что полная ра-
работа силы трения лодки о воду будет равна начальной кине-
кинетической энергии лодки.
178. Определить потенциальную энергию U сжатой
пружины как функцию ее деформации, считая, что сила де-
деформации пропорциональна третьей степени величины
деформации с коэффициентом пропорциональности р.
179. Определить отношение потенциальных энергий де-
деформации Ui и U2 двух пружин с коэффициентами упруго-
упругости ki и k2 в двух случаях: 1) пружины соединены последо-
последовательно и растягиваются грузом Р (рис. 48, а)\ 2) пружины
висят параллельно, причем груз Р подвешен в такой точке,
что обе пружины растягиваются на одну и ту же величину
38
(рис. 48, б). Деформацией пружин под действием собствен-
собственного веса пренебречь.
180. Под действием подвешенного груза спиральная
пружина удлинилась от /0 до /. Потянув рукой за середину
пружины, удлинение верхней половины ее довели до /—/0.
у////////////////////////,
SJ
Рис. 48.
После этого руку отняли. В пружине возникли быстрые
колебания. Какое количество тепла выделится в пружине
после того, как колебания затухнут? Коэффициент упруго-
упругости пружины равен к.
181. Маховик радиуса R и делает п оборотов в минуту,
передавая ремнем приводу мощность Я^л.с, Найти натя-
натяжение Т кгс ремня, идущего без скольжения.
182. Для определения мощности двигателя его вал А
сжимают между двух колодок 1 и 2 (рис. 49). Этот зажим
Рис. 49.
снабжш рычагом, перпендикулярным к валу, на который
подвешивается такей груз, чтобы рычаг сохранял свое го-
горизонтальное положение, когда двигатель развивает пол-
полную мощность, вращаясь в направлении стрелки. Какова
мощность двигателя, если при п оборотах вала в минуту на
расстоянии R см от оси вала находится груз массы m кг?
39
183. Два шкива, находящиеся на одном уровне, соеди-
соединены ремнем; первый шкив — ведущий (рис. 50). В каком
случае предельная мощность, которую можно передать
ремнем при определенном числе оборотов, будет больше:
когда шкивы вращаются
по часовой стрелке или
против?
184. Через неподвиж-
неподвижный блок, массой кото-
~~ ' рого можно пренебречь,
Рис. 50. перекинута замкнутая
тяжелая веревка массы
М. В начальный момент времени за точку веревки, располо-
расположенную между блоком и нижним заворотом ее, цепляется
обезьяна массы т и начинает карабкаться вверх так, чтобы
удержаться на неизменной высоте. Какую мощность W
должна для этого развивать обезьяна? Через сколько вре-
времени она перестанет справляться со своей затеей, если мак-
максимальная мощность, которую она может развивать, равна
^макс?
185. Два протона с энергией £=0,5 МэВ каждый летят
навстречу друг другу и испытывают лобовое столкновение.
Как близко могут сойтись они, если учитывать только элек-
электростатическое взаимодействие между ними?
186. Идеально упругий шарик движется вверх и вниз в
однородном поле тяжести, отражаясь от пола по законам
упругого удара. Найти связь между средними по време-
времени значениями его кинетической К и потенциальной U
энергий.
§ 5. Законы сохранения количества движения
и энергии
187. С какой скоростью v после горизонтального выстре-
выстрела из винтовки стал двигаться стрелок, стоящий на весьма
гладком льду? Масса стрелка с винтовкой и снаряжением
составляет 70 кг, а масса пули 10 г и ее начальная ско-
скорость 700 м/с.
188. Определить силу, с которой винтовка действует
на плечо стрелка при выстреле, если считать, что со стороны
винтовки действует постоянная сила и смещает плечо стрел-
стрелка на 5=1,5 см, а пуля покидает ствол мгновенно. Масса
винтовки 5 кг, масса пули 10 г, и скорость ее при вылете
равна 0=500 м/с.
40
189. Из пушки, свободно соскальзывающей по наклон-
наклонной плоскости и прошедшей уже путь /, производится выст-
выстрел в горизонтальном направлении. Какова должна быть
скорость v снаряда для того, чтобы пушка остановилась пос-
после выстрела? Выразить искомую скорость v снаряда через
его массу т, массу пушки М и угол а наклона плоскости к
горизонту. Учесть, что т<^М.
190. Снаряд разрывается в верхней точке траектории на
высоте /i=19,6m на две одинаковые части. Через секунду
после взрыва одна часть падает на Землю под тем местом,
где произошел взрыв. На каком расстоянии S2 от места вы-
выстрела упадет вторая часть снаряда, если первая упала на
расстоянии 51=1000 м от места выстрела? Сил сопротивле-
сопротивления воздуха при решении задачи не учитывать.
191. Три лодки одинаковой массы т идут в кильватер
(друг за другом) с одинаковой скоростью v. Из средней лодки
одновременно в переднюю и заднюю лодки бросают со ско-
скоростью и относительно лодки грузы массы тх. Каковы будут
скорости лодок после переброски грузов?
192. Человек, стоящий в лодке, подтягивает вторую
лодку за веревку до их соприкосновения и далее удерживает
их вместе (рис. 51). Где будут находиться обе лодки, когда
их движение в результате трения о воду прекратится? Тре-
Трение лодок о воду считать пропорциональным их скорости
и одинаковым для обеих лодок, массы лодок mt и ш2, началь-
начальное расстояние между центрами их масс /.
193. Две лодки идут навстречу параллельным курсом,
Когда лодки находятся друг против друга, с каждой лодки
во встречную перебрасывается мешок массой в 50 кг, в ре-
результате чего первая лодка останавливается, а вторая идет
со скоростью 8,5 м/с в прежнем направлении. Каковы были
скорости лодок до обмена мешками, если массы лодок с гру*
зом равны 500 кг и 1 т соответственно?
194. В шар массы ти движущийся со скоростью vu
ударяется другой шар массы т2, догоняющий первый в
том же направлении со скоростью v%. Считая удар вполне
41
неупругим, найти скорости шаров после удара и их кинети-
кинетическую энергию.
195. Два идеально упругих шарика с массами Шх и т2
движутся вдоль одной и той же прямой со скоростями Vi и v2.
Во время столкновения шарики начинают деформироваться,
и часть кинетической энергии переходит в потенциальную
энергию деформации. Затем деформация уменьшается, и
запасенная потенциальная энергия вновь переходит в ки-
кинетическую. Найти значение потенциальной энергии дефор-
деформации в момент, когда она максимальна.
196. На гладком горизонтальном столе лежит шар массы
/Ль соединенный с пружиной жесткости k. Второй конец
щ / пружины закреплен (рис.
v (Г~\. * р 52)- Происходит лобовое
* #"ААЛАЛг—р упругое соударение этого
^^^^^^ шара с другим шаром, мас-
Рис. 52. са которого т2 меньше ти
а скорость равна v. В ка-
какую сторону будет двигаться второй шар после удара? Опре-
Определить амплитуду колебаний первого шара после соуда-
соударения.
197. Система состоит из двух шариков с массами m и М,
соединенных между собой невесомой пружиной с коэффи-
коэффициентом упругости k (рис. 53). Третий шарик с массой т,
движущийся вдоль оси ^ /^"х
пружины со скоростью v, Q, > f\~Aj\/\/\r-f \
претерпевает упругое Ч^
столкновение с шариком т т II
ш, как указано на рис. Рис. 53.
53. Считая шарики абсо-
абсолютно жесткими, найти после столкновения: 1) кинетиче-
кинетическую энергию К движения системы как целого; 2) внутрен-
внутреннюю энергию системы Еш\ 3) амплитуду колебаний одного
шарика относительно другого Л. До удара система покои-
покоилась, а пружина не была деформирована. Какие шарики
могут рассматриваться как абсолютно жесткие?
198. Навстречу друг другу летят два шара;с массами тх и
т2. Между шарами происходит неупругий удар. Известно,
что кинетическая энергия одного шара в 20 раз больше ки-
кинетической энергии другого. При каких условиях шары по-
после удара будут двигаться в сторону движения шара^ обла-
обладавшего меньшей энергией?
199. С какой скоростью v должен лететь снаряд массы
ш=10 кг, чтобы при ударе о судно массы УИ = 100 тпослед-
42
нее получило скорость ^=0,1 м/с? Удар считать не-
неупругим.
200. Ледокол, ударяясь о льдину массы М, отбрасы-
отбрасывает ее, сообщив ей скорость v м/с. Положим, что давление
ледокола на льдину нарастает равномерно во времени при
сближении ледокола со льдиной и также равномерно убыва-
убывает, когда они расходятся. Найти при этих условиях макси-
максимальную силу давления льдины на борт корабля, если удар
продолжался т с.
201. В одном изобретении предлагается на ходу напол-
наполнять платформы поезда углем, падающим вертикально на
платформу из соответствующим образом устроенного бун-
бункера. Какова должна быть приложенная к платформе сила
тяги, если на нее погружают 10 т угля за 2 с, и за это время
она проходит равномерно 10 м? Трением при движении
платформы можно пренебречь.
202. Подсчитать работу, совершенную паровозом за вре-
время погрузки на платформу некоторой массы угля Am (см.
предыдущую задачу), и сравнить ее с кинетической энерги-
энергией, которую получила погруженная масса угля.
203. Кусок однородного каната висит вертикально, при*
чем нижний конец каната доходит до горизонтального стола.
Показать, что если верхний конец каната освободить, то в
любой момент падения каната сила его давления на стол
будет в три раза больше веса части каната, уже лежащей на
столе.
204. На клин, составляющий угол в 45° с горизонтом,
вертикально падает шарик. Какова будет траектория шари-
шарика после удара о клин? Поверхность клина гладкая, удар
вполне упругий.
205. Найти количество движения р, получаемое стенкой
при упругом ударе о нее тела массы т, скорость v которого
составляет угол а с нормалью к стенке.
206. Движущаяся частица претерпевает упругое столк-
столкновение с покоящейся частицей такой же массы. Доказать,
что после столкновения, если оно не было лобовым, частицы
разлетятся под прямым углом друг к другу. Как будут дви-
двигаться частицы после лобового столкновения?
207. Найти изменение кинетической энергии А/С и им-
импульса Ар тела, движущегося со скоростью и, при упругом
ударе его о стенку, движущуюся в том же направлении рав-
равномерно со скоростью u<Cv. При каком соотношении между
скоростью тела v и скоростью стенки и ударившееся о нее
тело остановится?
43
208. Ядра дейтерия D и трития Т могут вступать в ре-
реакцию
D+T->He4+n+17,6 ДОэВ,
в результате которой образуются нейтроны п и а-частицы,
т. е. ядра гелия Не4. При каждой реакции выделяется энер-
энергия 17,6 МэВ. Определить, какую энергию уносит нейтрон
и какую а-частица. Кинетические энергии, которыми обла-
обладали частицы до реакции, пренебрежимо малы.
(Дейтерий — изотоп водорода с атомным весом 2, три-
тритий — изотоп водорода с атомным весом 3, Не4 — гелий с
атомным весом 4).
209. Ядра дейтерия D могут вступать друг с другом в ре-
реакцию, в результате которой образуется протон и ядро три-
трития Т. Каждый протон уносит кинетическую энергию
ЗМэВ. Какую кинетическую энергию уносит ядро атома
трития и каков общий энергетический выход реакции? Кине-
Кинетические энергии, которыми обладали частицы до реакции,
пренебрежимо малы.
210. Ядра дейтерия могут вступать также в реакцию
D+D->He3+n+3,25 МэВ.
Какую энергию уносит нейтрон и какую ядро гелия Не3 с
атомным весом 3? Кинетические энергии, которыми облада-
обладали частицы до реакции, пренебрежимо малы.
211. В реакции
получаются протоны с энергией 14,6 МэВ. Какую энергию
уносит ядро гелия (Не4) и какой общий энергетический вы-
выход реакции? Кинетические энергии, которыми обладали
частицы до реакции, пренебрежимо малы.
212. При бомбардировке гелия а-частицами с энергией
1 МэВ найдено, что налетающая частица отклонилась на 60°
по отношению к первоначальному направлению полета.
Считая удар упругим, определить ее энергию и энергию ядра
отдачи.
213. Определить долю энергии, теряемую частицей мас-
массы mi при упругом столкновении ее с неподвижной частицей
массы т2, если после столкновения частица продолжает
двигаться в прежнем (когда т1>т2) или прямо противопо-
противоположном (когда т1<т2) направлениях. Показать, что доля
теряемой энергии не зависит от того, какая частица движет-
движется, а какая покоится. При каком соотношении масс т1/т2
44
потеря энергии максимальна? Используя полученные ре-
результаты, объяснить, почему в ядерных реакторах для за-
замедления нейтронов используется рассеяние их на ядрах
легких (дейтерий, углерод), а не тяжелых атомов.
214. Определить долю энергии а, теряемую протоном
при упругом рассеянии под углом 180° на протоне, дейтро-
дейтроне, ядре гелия и ядре углерода.
215. Каков максимальный угол # рассеяния а-частицы
и дейтрона при упругом рассеянии на водороде?
216. Альфа-частица, летящая со скоростью v0, испыты-
испытывает упругое столкновение с неподвижным ядром и летит под
углом 90° к первоначальному направлению движения. При
каком соотношении масс а-частицы т и ядра М это возмож-
но? Определить скорость а-частицы v и ядра V после столк-
столкновения. Определить также угол Ф между направлением ско«
рости вылетающего ядра и первоначальным направлением
движения а-частицы.
217. Протон, летящий горизонтально со скоростью V,
сталкивается с невозбужденным неподвижным атомом массы
М, после чего он отскакивает и летит в прямо противополож*
нем направлении с половинной скоростью V72, а атом пере*
ходит в возбужденное состояние, т. е. в состояние с более
высокой внутренней энергией. Определить скорость атома v
после столкновения и энергию Е, которая пошла на возбуж-
возбуждение атома. Для каких невозбужденных атомов описанный
процесс невозможен?
218. Атомное ядро с массой т и кинетической энергией Е
сталкивается с другим ядром, которое до столкновения по-
коилесь. Происходит ядерная реакция, в результате которой
образуются две частицы с массами тг и га2, причем на реак-
реакцию затрачивается энергия Q. При каких условиях скорости
образовавшихся частиц будут направлены вдоль или против
скорости падающей частицы?
219. Первая искусственная ядерная реакция
N14+He4=O17+p
наблюдалась Резерфордом в 1919 г. Она идет с поглощением
энергии Е=\х\3 Мэв. Какую минимальную энергию Ео
надо сообщить в лабораторной системе а-частице (т. е. ядру
атома гелия), чтобы при бомбардировке неподвижной мише-
мишени из N14 указанная реакция могла пойти?
220. Ядерная реакция Li7+p->Be7+n (литий неподви-
неподвижен) имеет порог £"лор=1,88 МэВ, т. е. может идти только
тогда, когда энергия протона равна или превосходит вели-
45
чину £пор. При каких энергиях бомбардирующих протонов
£р нейтроны в такой реакции могут лететь назад от литие-
литиевой мишени?
221. При столкновении протонов высоких энергией мо-
могут образовываться антипротоны р согласно реакции
р + р—*Р+Р + Р+Р-
Какой минимальной (пороговой) кинетической анергией
должен обладать протон, чтобы при столкновении с покоя-
покоящимся протоном была возможна такая реакция?
222. Какой минимальной кинетической энергией должен
обладать протон, чтобы при столкновении с покоящимся ней-
нейтроном была возможна реаади-я
р+п-+ р+п + Л + Л?
Массы покоя частиц, участвующих в реакции: mp=1836me,
гап = 1838гае, тл=тл=2183те. Различием масс протона и
нейтрона можно пренебречь.
223. Тело массы* nil ударяется неупруго о тело массы ш2.
Найти долю q потерянной при этом кинетической энергии,
если тело т% было до удара в покое.
224. Лифт опускается с постоянной, скоростью. Каково
будет натяжение троса, на котором висит кабина, в момент
внезапной полной остановки барабана, с которого сматывает-
сматывается трос? Как будет изменяться натяжение троса после проис-
происшедшей задержки?
225. Подсчитать максимальную силу Т натяжения кана-
каната и* его удлинение (см. предыдущую задачу), если коэффи-
коэффициент упругости каната для той его длины, при которой про-
произошла остановка барабана, равен 1 тс/см. Масса лифта 3 т,
его скорость 10 м/с.
226. На нити длиной / подвешен груз массы т. Опреде-
Определить, на какую минимальную высоту надо поднять груз пг9
чтобы он, падая, разорвал нить, если минимальный покоя-
покоящийся груз Mf разрывающий нить, растягивает ее перед
разрывом на 1 %. Считать, что сила, с которой нить действует
на груз, пропорциональна растяжению нити вплоть до ее
разрыва.
227. Баллистический маятник — это маятник, употреб-
употребляющийся для определения скорости снаряда. Принцип его
действия заключается в том, что снаряд, скорость которого
следует измерить, ударяется в тело маятника (рис. 54). Если
известны условия удара и массы снаряда и маятника, то по
углу отклонения маятника а можно вычислить скорость v
46
снаряда до удара. Показать, как это сделать для следующих
различных случаев: 1) снаряд после удара застревает в маят-
маятнике; 2) снаряд отскакивает после удара со скоростью v' на-
назад; 3) снаряд падает вниз, потеряв свою скорость. Масса
маятника М кг и масса снаряда т кг известны; маятник
можно рассматривать как математический длины /.
/У/////////////////,
V
м
Рис. 54.
Рис. 55.
228. Механическая система, показанная на рис. 55,
находится в положении равновесия в поле силы тяжести.
Расстояние между осями блоков равно /, а отношение масс
грузов равно m1/m2=yr2. Размерами и массахми блоков и
трением можно пренебречь. Нить следует считать невесомой и
нерастяжимой. Среднему грузу толчком сообщают скорость,
направленную вниз, после чего он опускается, а затем начи-
начинает подниматься вверх. Какую скорость следует сообщить
среднему грузу, чтобы при последующем движении он
мог подняться до высоты уровня осей блоков? На сколько
в результате толчка должен опуститься средний груз?
22£. Два маятника в виде шариков разных масс тх и т2
свободно подвешены на нитях разной длины U и /2 так, что
шарики соприкасаются. Первый маятник отводят в плоско-
плоскости нитей на угол а оп первоначального положения и отпу-
отпускают. Происходит центральный удар шариков. На какие
углы ах и а2 относительно отвесной линии отклонятся маят-
маятники после удара (углы считать малыми, удар считать уп-
упругим)?
230. С гладкой наклонной плоскости, составляющей угол
45° с горизонтом, соскальзывает с высоты h небольшое тело.
Как будет двигаться тело, если оно в конце наклонной пло-
плоскости встречает 1) вполне упругую горизонтальную
плоскость, 2) горизонтальную плоскость неупругую, но
гладкую?
47
231. На наклонной плоскости стоит ящик с песком;
коэффициент трения ящика k о плоскость равен тангенсу уг-
угла а наклона плоскости. В ящик вертикально падает неко-
некоторое тело и остается в нем. Будет ли двигаться ящик после
падения в него тела?
232. От поезда, идущего с постоянной скоростью, отры-
отрывается последний вагон, который проходит путь /. и останав-
останавливается. На каком расстоянии от вагона в момент его ос-
остановки будет находиться поезд, если тяга паровоза посто-
постоянна, а трение каждой части поезда не зависит от скорости и
пропорционально ее весу?
233. Лодка массы М с находящимся в ней человеком
массы т неподвижно стоит на спокойной воде. Человек
начинает идти вдоль по лодке со скоростью и относительно
лодки. С какой скоростью w будет двигаться человек отно-
относительно воды? С какой скоростью v будет при этом дви-
двигаться лодка относительно воды? Сопротивление воды дви-
движению лодки не учитывать х).
234. Пусть человек прошел вдоль по лодке, описанной
в предыдущей задаче, путь /. Каковы будут при этом смеще-
смещения лодки Si и человека S2 относительно воды?
235. Пусть человек, находящийся в лодке (см. задачи
233 и 234), начинает бежать вдоль по лодке с ускорением а
относительно лодки. С какими ускорениями аг и а2 будут
при этом двигаться, соответственно, человек и лодка отно-
относительно воды? С какой силой F бегущий человек будет дей-
действовать на лодку в горизонтальном направлении?
236. На противоположных концах лодки, описанной в
задаче 233, стоят два человека одинаковой массы т и пере-
перебрасываются мячом массы Am. Скорость брошенного мяча
относительно воды и. Найти: 1) скорость движения лодки v
в течение времени перелета мяча с одного конца лодки на
другой; 2) смещения лодки Si и мяча S2 относительно воды
после каждого перелета мяча вдоль лодки, если длина пути
мяча вдоль лодки равна /.
237. На носу лодки длиной / стоит человек, держа на вы-
высоте h ядро массы т. Масса лодки вместе с человеком равна
М. Человек бросает горизонтально ядро вдоль лодки. Какую
скорость по горизонтали должен сообщить человек ядру,
чтобы попасть в корму лодки? Сопротивление воды движе-
движению лодки можно не учитывать.
*) При решении задач 233—236 и 240 закон сохранения количества
движения надо применять в векторной форме.
48
238. На дне маленькой запаянной пробирки, подвешен-
подвешенной над столом на нити, сидит муха, масса которой равна
массе пробирки, а расстояние от дна до поверхности стола
равно длине пробирки /. Нить пережигают, и за время паде-
падения муха перелетает со дна в самый верхний конец пробир-
пробирки. Определить время, по истечении которого нижний конец
пробирки стукнется о стол.
239. На прямоугольный трехгранный клин ABC массы
Л4, лежащий на абсолютно гладкой горизонтальной плоско-
плоскости, положен подобный же, но
меньший клин BED массы т (рис. в
5C). Определить, на какое расстоя-
расстояние х сместится влево большой
клин, когда малый клин сосколь-
соскользнет вниз и займет такое положе-
положение, что точка D совместится с С.
Длины катетов АС и BE равны
соответственно а и Ь.
240. Вопрос о движении тела с переменной массой был
впервые исследован И. В. Мещерским. Частную форму урав-
уравнения Мещерского можно вывести из рассмотрения одного
простого случая движения ракеты. Пусть для получения
ускорения ракета выпускает непрерывную струю газа, вы-
вылетающую из ракеты с относительной скоростью #. Масса
газа, вылетающая в единицу времени, ji, масса ракеты в дан-
данный момент времени М. Найти уравнение движения ракеты.
241. Теория ракет для межпланетных сообщений была
разработана К. Э". Циолковским. Им было найдено соот-
соотношение, связывающее скорость и, достигнутую ракетой,
с ее массой М в один и тот же момент времени. Поль-
Пользуясь результатами решения предыдущей задачи, найти
это соотношение, если масса ракеты на старте равна Мо,
а скорость газовой струи и относительно ракеты посто-
постоянна и направлена против ее движения.
242. Реактивный корабль массы М приводится в движе-
движение насосом, который забирает воду из реки и выбрасывает
ее назад с кормы корабля. Скорость струи воды относитель-
относительно корабля постоянна и равна #, а масса ежесекундно вы-
выбрасываемой насосом воды также постоянна и равна р.
Найти: 1) модуль скорости корабля v как функцию времени;
2) коэффициент полезного действия системы ц как функцию
величин UKV. Исследовать выражение коэффициента полез-
полезного действия на максимум. Силы трения в насосе и сопротив-
сопротивление воды движению корабля не учитывать.
49
243. В ускорителях на встречных пучках исследуемые
частицы, разогнанные до одинаковых релятивистских энер-
энергий, движутся навстречу друг другу и реагируют при столк-
столкновении. Суммарный импульс таких частиц, а с ним и кине-
кинетическая энергия, связанная с движением центра масс,
равны нулю как до, так и после столкновения. Поэтому вся
кинетическая энергия частиц может быть использована для
получения исследуемой реакции. Разобрать выгоду исполь-
использования ускорителей на встречных пучках на следующем
примере. Два протона с одной и той же кинетической энер-
энергией /чГ= 10 ГэВ движутся навстречу друг другу. До какрй
кинетической энергии К надо ускорить только один протон,
оставляя второй (мишень) неподвижным, чтобы эта энергия
была эквивалентна энергии К (в смысле возможности пре-
превращения сталкивающихся частиц)?
244. Для лучшего уяснения закономерностей движения
ракеты полезно рассмотреть модель ракеты, когда она выбра-
выбрасывает вещество не непрерывно, а конечными дискретными
порциями одной и той же массы Am. Пусть иря каждом вы-
выбрасывании порция вещества Am получает одну и ту же
скорость 1>отя относительно ракеты, направленную назад.
Определить скорость ракеты vNf которую она достигнет пос-
после N выбрасываний, если начальная масса ракеты равна т0.
Показать, что в предельном случае, когда Am~^0, N-+oo,
но произведение iVAm остается постоянным, выражение для
vN переходит в формулу Циолковского.
245. Найти связь между массой ракеты m(f), достигну-
достигнутой ею скоростью v(t) и временем /, если ракета движется
вертикально вверх в поле тяжести Земли. Скорость газовой
струи относительно ракеты и считать постоянной. Сопротив-
Сопротивление воздуха и изменение ускорения свободного падения g
с высотой не учитывать. Какую массу газов \i(t) должна
ежесекундно выбрасывать ракета, чтобы оставаться не-
неподвижной относительно Земли?
246. Космический корабль движется с постоянной по ве-
величине скоростью v. Для изменения направления его полета
включается двигатель, выбрасывающий струю газа со
скоростью и относительно корабля в направлении, перпен-
перпендикулярном к его траектории. Определить угол а, на кото-
который повернется вектор скорости корабля, если начальная
масса его т0, конечная т, а скорость и постоянна.
247. Космический корабль, движущийся в пространстве,
свободном от поля тяготения, должен изменить направление
своего движения на противоположное, сохранив скорость
50
по величине. Для этого предлагаются два способа: ^снача-
^сначала затормозить корабль, а затем разогнать его до прежней
скорости; 2) повернуть, заставив корабль двигаться по дуге
окружности, сообщая ему ускорение в поперечном направ-
направлении. В каком из этих двух способов потребуется меньшая
затрата топлива? Скорость истечения газов относительно
корабля считать постоянной и одинаковой в обоих случаях.
248. Определить коэффициент полезного действия раке-
ракеты, т. е. отношение кинетической энергии /С, приобретенной
ракетой, к энергии сгоревшего топлива Q. Скорость, достиг-
достигнутая ракетой, и=9 км/с. Теплота сгорания топлива q=*
=4000 ккал/кг, скорость выбрасываемых продуктов сгора-
сгорания относительно ракеты а=3 км/с.
249. В ракете продукты сгорания (газы) выбрасываются
со скоростью а—3 км/с (относительно ракеты). Найти от-
отношение т] ее кинетической энергии /fpaK к кинетической
энергии продуктов сгорания Ктаз в момент достижения ра-
ракетой скорости Укон—12 км/с.
250. С поверхности Луны стартует двухступенчатая ра-
ракета. При каком отношении масс первой (mi) и второй (т2)
ступеней скорость контейнера с полезным грузом (массы т)
получится максимальной? Скорость истечения газов и в дви-
двигателях обеих ступеней постоянна и одинакова. Отношения
массы топлива к массе ступени равны соответственно ах и
а2 для первой и второй ступеней. Отделение ступеней и кон-
контейнера производится без сообщения добавочных импульсов.
251. Обобщить формулу Циолковского B41.1) *) на слу-
случай релятивистских движений ракеты. Считать, что ско-
скорости ракеты и газовой струи направлены вдоль одной
прямой.
252* Показать, что при р<^1 релятивистская формула
B51.4) переходит в формулу Циолковского B41.1).
253. Для путешествий к звездам требуются скорости,
сравнимые со скоростью света. Оцените перспективы ис-
использования ракет на химическом топливе для достижения
звездных миров. Допустите, что скорость истечения газа
и=\0 км/с (что для химического топлива сильно завышено)
и ракета должна достигнуть скорости v^c/4. Определите
отношение стартовой массы ракеты т0 к ее массе т после
достижения указанной скорости.
*) В книге принята сквозная нумерация формул для каждой зада-
задачи, причем начало нумерации может быть дано в условии задачи, а
продолжение — в ответе.
51
254. Для межзвездных полетов идеальной была бы фо-
фотонная ракета, в которой вещество превращается в электро-
электромагнитное излучение. Роль газовой струи играет пучок фо-
фотонов, излучаемых ракетой в определенном направлении.
Определить мощность фотонной ракеты, движущейся за
пределами Солнечной системы с нерелятивистской скоростью
и постоянным ускорением g=lO м/с2. Масса ракеты т=\ т.
255. Человек поддерживается в воздухе на постоянной
высоте с помощью небольшого реактивного двигателя за
спиной. Двигатель выбрасывает струю газов вертикально
вниз со скоростью (относительно человека) и=1000 м/с.
Расход топлива автоматически поддерживается таким, что-
чтобы в любой момент, пока работает двигатель, реактивная
сила уравновешивала вес человека с грузом. Сколько вре-
времени человек может продержаться на постоянной высоте,
если его масса mi=70 кг, масса двигателя без топлива /п2=
= 10 кг, начальная масса топлива то=2О кг? Какое рас-
расстояние / в горизонтальном направлении может пролететь
человек, если он разбежался по земле, приобрел гори-
горизонтальную скорость у=10 м/с, а затем включил дви-
двигатель, поддерживающий его в воздухе на постоянной
высоте?
256. Сферическая капля воды свободно падает в атмо-
атмосфере пересыщенного водяного пара. Считая, что скорость
возрастания массы капли dm/dt пропорциональна ее поверх-
поверхности и пренебрегая силой сопротивления среды, опреде-
определить движение капли. Предполагается, что в момент зарож-
зарождения капли (/=0) скорость ее падения равна нулю.
§ 6. Динамика движения материальной точки
по окружности. Движение относительно вращающихся
систем отсчета
257. Найти силу F> с которой тележка массы т, дви-
движущаяся со скоростью vy давит на мост в одном из следую-
следующих случаев: 1) горизонтальный мост; 2) выпуклый мост
(рис. 57); 3) вогнутый мост. (Для случаев 2) и 3) силу F
определить для наивысшей и наинизшей точек моста.)
258. Тело движется прямолинейно с постоянной ско-
скоростью v0 по горизонтальной поверхности стола, которая
имеет закругленный край с постоянным радиусом закруг-
закругления, равным R (рис. 58). Каково должно быть минималь-
минимальное значение скорости vOt чтобы тело, падая со стола, не
касалось закругления?
52
259. По гладкой внутренней поверхности чаши, имеющей
форму параболоида вращения с вертикальной осью z, с
высоты h соскальзывает шарик массы га. Уравнение пара-
параболоида: z=k(x2+y2). Найти ускорение а шарика и силу
его давления F на дно чаши в ее нижней точке.
Рис. 57.
260. С какой начальной скоростью v0 должен вылететь
снаряд из орудия в горизонтальном направлении, чтобы
двигаться вокруг Земли, не падая на нее?Каким ускорением
будет обладать снаряд при этом? (Радиус Земли 7? = 6,4х
X 103 км.)
Щ
Рис. 58.
261. Пусть выстрел из орудия произведен под некоторым
углом к горизонту, а начальная скорость снаряда меньше
найденной при решении предыдущей задачи. По какой тра-
траектории будет двигаться в этом случае снаряд и каково бу-
будет его ускорение? Сопротивлением воздуха движению сна-
снаряда пренебречь.
262. Тележка массы т скатывается без трения по изо-
изогнутым рельсам, имеющим форму, изображенную на рис. 59.
1) С какой минимальной высоты h должна скатиться тележ-
тележка для того, чтобы она не покинула рельсов по всей их дли-
длине? 2) Какие силы действуют на тележку в наивысшей точке
53
В петли? 3) Каково будет движение тележки, если она ска-
скатывается с высоты, меньшей Я? При решении задачи считать
колеса тележки малого размера и малой массы и их враща-
вращательного движения не рассматривать.
Рис. 59.
263. Каков должен быть минимальный коэффициент
трения скольжения k между шинами автомобиля и асфаль-
асфальтом, чтобы автомобиль мог пройти закругление с радиусом
#=200 м при скорости t;=100 км/ч?
264. На внутренней поверхности конической воронки
с углом 2а при вершине (рис. 60) на высоте h от вершины
находится малое тело. Коэффициент
трения между телом и поверхно-
поверхностью воронки равен k. Найти мини-
минимальную угловую скорость вра-
вращения конуса вокруг вертикаль-
вертикальной оси, при которой тело будет
неподвижно в воронке.
265. Велосипедист при повороте
по кругу с радиусом R наклоняется
внутрь закругления так, что угол
между плоскостью велосипеда и
землей равен а. Найти скорость v
велосипедиста.
266. К Г-образной подставке, установленной на оси цент-
центробежной машины, привязана нить длины / с грузом т на
конце (рис. 61). 1) На какой угол а отклонится от вертикали
нить, если центробежная машина вращается с угловой ско-
скоростью со? 2) Каково будет при этом натяжение нити 7?
54
Рис. 60.
3) Будет ли у нити излом при вращении машины, если к се-
пелине нити прикрепить небольшую массу?
V Рассмотрение вопросов 1) и 2) провести для двух случа-
рв- 1) для малых углов отклонения нити от вертикали, соот-
соответствующих малой угловой скорости вращения центро-
центробежной машины, 2) для произвольной угловой скорости вра-
вращения машины. Решение получившегося во втором случае
тригонометрического уравнения для угла а провести гра-
графическим методом.
Рис. 61.
Рис 02.
267 Шарик радиуса R висит на нити длиной I и каса-
касается вертикального цилиндра радиусом г, установленного
на оси центробежной машины (рис. 62). При какой угловой
скорости со вращения центробежной машины шарик пере-
перестанет давить на стенку цилиндра?
26& В вагоне поезда, идущего по закруглению желез-
железнодорожного пути, сделанному, как обычно, с уклоном
внутрь, на пружинных весах подвешено тело. Весы показы-
показывают увеличение веса тела на п% по сравнению с весом того
же тела, измеренным в поезде, идущем прямолинейно с по-
постоянной скоростью. Весы могут свободно поворачиваться
около точки подвеса и на закруглении остаются висеть пер-
перпендикулярно к полу Еагона. Найти радиус кривизны пути
R, если поезд идет со скоростью о.
269 Шофер едущий на автомобиле по горизонтальной
площади в тумане, внезапно заметил недалеко впереди
себя стену, перпендикулярную к направлению движения.
Что выгоднее: затормозить или повернуть в сторону, чтооы
предотвратить аварию?
55
270. Автомобиль движется с постоянной скоростью вдоль
извилистой горизонтальной дороги. Принимая дорогу за
синусоиду, найти максимальную скорость, которую может
развивать автомобиль, чтобы не было заноса.
271. Решить ту же задачу, предполагая, что автомобиль
движется с постоянной скоростью по эллипсу с полуосями
А и В. В каких точках траектории нормальное ускорение
автомобиля достигает максимального и минимального зна-
значений? Найти эти значения.
272. При выполнении самолетом «мертвой петли», осу-
осуществленной впервые русским летчиком П. Н. Нестеровым,
сила, действующая на крылья самолета, изменяется по срав-
сравнению с их нагрузкой при горизонтальном полете.
Пусть самолет Нестерова массой в 3/4 т делает «мертвую
петлю» радиуса R=125 м и движется по ней со скоростью
120 км/ч. Найти максимальное значение нагрузки на крылья
самолета. Указать, в каком месте траектории эта нагрузка
будет максимальной.
273. Самолет делает «мертвую петлю» радиуса R =
= 100 м и движется по ней со скоростью у=280 км/ч. С ка-
какой силой тело летчика массой в 80 кг будет давить на сиденье
самолета в верхней и нижней точках петли?
274. На самолете, делающем «мертвую петлю», подвешен
отвес. Указать направление отвеса в различных точках
п «мертвой петли» при различ-
_f |_ a ных значениях скорости само-
самому—1 г лета v и радиуса Петли R.
Z) 275. Самолет совершает
вираж, двигаясь по окружно-
^ сти с постоянной скоростью v
* на одной и той же высоте.
Определить радиус г этой
~j окружности, если плоскость
крыла самолета наклонена к
горизонтальной плоскости под
постоянным углом а.
276. Груз массы М может
скользить без трения по
L-J'" стержню а, укрепленному пер-
Рис. 63. пендикулярно к оси враща-
вращающейся центробежной маши-
машины (рис. 63). Ось машины вертикальна, и сквозь нее прохо-
проходит нить, на которой висит груз массы т\ нить перекинута
через блок с и другой ее конец прикреплен к грузу массы М.
56
Найти положение груза массы М на стержне а,
когда центробежная машина вращается с угловой скоро-
скоростью со.
277. В предыдущей задаче ось вращения центробежной
машины пересекает горизонтальный стержень а. Каков бу-
будет ответ, если они не пересекаются?
278. В каком положении будет находиться груз массы М
на стержне, если всему прибору, описанному в задаче 276
(рис. 63), сообщить вращение с угловой скоростью со, а
затем отсоединить прибор от привода центробежной маши-
машины? Будет ли у груза устойчивое положение на стержне?
Моментом инерции прибора по сравнению с моментом инер-
инерции груза массы М можно пренебречь. Трения в подшипни-
подшипниках прибора не учитывать.
279. Каково может быть положение груза массы М в
предыдущей задаче, если моментом инерции /0 самого при-
прибора нельзя пренебрегать?
280. В приборе, аналогичном описанному в задаче 276,
на стержень насажены по одну сторону от оси вращения
два груза с массами т1 и т2, соединенные нитью длины /.
Ближайший к оси груз массы тх соединен нитью длины R
с осью вращения. Определить натяжение нитей, если угло-
угловая скорость со вращения машины известна.
281. На приборе, описанном в задаче 276, вместо тела
массы т к нити прикреплена пружина, другой конец которой
закреплен неподвижно. Каковы должны быть свойства пру-
пружины, чтобы тело массы М при вращении машины с угловой
скоростью со могло находиться в равновесии на любом рас-
расстоянии от оси вращения? Когда тело массы М находится у
оси вращения, пружина не натянута.
282. На приборе, описанном в задаче 276, груз массы
Af = 100 г, находящийся на стержне, соединен пружиной с
осью. Каков коэффициент упругости k
пружины, если известно, что при угловой
скорости вращения о>= 120 об/мин она
растянулась на 50% первоначальной
длины?
283. Шарик массы т подвешен на иде-
идеальной пружине жесткости k и начальной
длины / над центром платформы центро-
центробежной машины (рис. 64). Затем шарик
начинает вращаться вместе с машиной с
угловой скоростью со. Какой угол а образует при этом
пружина с вертикалью?
57
284. В приборе, изображенном на рис. 65, треугольник
CDE вращается вокруг вертикальной оси АВ с углшой
скоростью со. По стержню CD, представляющему гипотенузу
треугольника, может скользить без трения муфточка К-
R каком положении будет нахо-
находиться муфточка?
2S5. Металлическое кольцо,
подвешенное н& нити к оси цен-
центробежной машины, как указано
Рис. 65.
на рис. 66, равномерно вращается с угловой скоростью со.
Нить составляет угол а с осью. Найти расстояние от
центра кольца до оси вращения.
286. Однородный стержень длины / равномерно враща-
вращается вокруг свободной оси, перпендикулярной к стержню и
проходящей через его центр. Какова
должна быть угловая скорость вра-
вращения со, при которой стержень еще
не разрывается под действием внутрен-
внутренних напряжений, возникающих в нем
при вращении? Максимальная сила
натяжения, отнесенная к единице
площади поперечного сечения стерж-
стержня, равыа 7\ Объемная плотность
материала стержня равна р.
287. Жесткие стержни образуют
равнобедренный прямоугольный тре-
треугольник, который вращается с по-
постоянной угловой скоростью со вокруг
вертикального катета АВ (рис. 67). На стержень АС надета
и скользит без трения муфта массы т. Муфта связана пру-
пружиной, с жесткостью k, с вершиной А треугольника, имею-
имеющей в нерастянутом состоянии длину /. Определить, при
58
Рис. 67.
каком значении са муфта будет в равновесии при недефор-
мированной пружине? Будет ли это равновесие устойчивым?
288. Доска качелей с сидящими на ней людьми весит Р.
Какое наибольшее натяжение Т будут испытывать веревки,
если отвести качели на 45° от положения равновесия и
предоставить им качаться?
289. На закруглениях железнодорожного пути наруж-
наружный рельс делают немного приподнятым по сравнению с
внутренним. Объяснить, для чего это делается, и дать рас-
расчет необходимого угла наклона полотна.
290. Иногда устраивают в качестве аттракциона комна-
комнату, вращающуюся вокруг вертикальной оси. Пол такой ком-
комнаты имеет вогнутую форму. Во время вращения все нахо-
находящиеся там предметы и люди стоят на этом полу, как на
плоском, устойчиво и нормально к его поверхности. Опре-
Определить форму пола, если угловая скорость вращения ком-
комнаты равна со.
291. На нити длиной L, привязанной одним концом к
штифту в точке О, подвешен как отвес маленький шарик
(рис. 68). Отвес отводит
вправо, в горизонтальное
положение 1 и затем отпу-
отпускают. В точке В, располо-
расположенной на расстоянии L/2
от точки О, имеется гвоздь,
за который задевает нить
возвратившегося в верти-
вертикальное положение 2 от-
отвеса. Найти: 1) какой угол
а с вертикалью будет со-
составлять направление нити
отвеса в положении 3 в тот
момент, когда ее натяжение Рис. 68.
обратится в нуль; 2) какой
будет скорость шарика v отвеса в этой точке его траектории;
3) какой геометрической кривой будет траектория шарика
после того, как сила натяжения нити обратится в нуль?
292. Суточное вращение Земли приводит к отклонению
артиллерийских снарядов и ружейных пуль от начального
направления выстрела, заданного в горизонтальной пло-
плоскости по земным ориентирам. Рассчитать величину попе-
поперечного смещения х пули, выпущенной в плоскости мери-
меридиана по горизонтальному направлению, за первую секунду
ее полета. Выстрел произведен на широте Москвы E5°45')э
59
начальная скорость пули 1000 м/с. Указать, в какую сто-
сторону отклонится пуля, если в момент выстрела ствол ружья
был направлен на юг. Силу сопротивления воздуха полету
пули не учитывать. Решить задачу в системе отсчета, свя-
связанной с Землей.
293. Из орудия, установленного в точке земной поверх-
поверхности с географической широтой ф=30°, производится вы-
выстрел в направлении на восток. Начальная скорость сна-
ряДа у0—500 м/с, угол вылета снаряда (т. е. угол наклона
касательной в начальной точке траектории к плоскости го-
горизонта) а=60°. Пренебрегая сопротивлением воздуха и
учитывая вращение Земли, определить приближенно откло-
отклонение у точки падения снаряда от плоскости стрельбы. Ка-
Какое это будет отклонение: к югу или к северу? (Плоскостью
стрельбы называется плоскость, проходящая через направ-
направление касательной в начальной точке траектории и направ-
направление отвеса в той же точке.)
294. На 60° с. ш. паровоз массой в 100 т идет с юга на
север со скоростью у=72 км/ч по железнодорожному пути,
проложенному по меридиану. Найти величину и направле-
направление той силы, с которой паровоз действует на рельсы в на-
направлении, перпендикулярном к ходу поезда.
295. На 60° с. ш. паровоз массой в 100 т идет с запада на
восток со скоростью v=72 км/ч по железнодорожному пути,
проложенному вдоль географической параллели данной
местности. Найти величину и направление вертикальной и
горизонтальной компонент кориолисовой силы, действую-
действующей на паровоз.
296. Пароход движется на восток вдоль параллели с гео-
географической широтой ф=60°. Скорость парохода v== 10 м/с.
Определить вес тела Р на пароходе, если взвешивание про-
производится на пружинных весах. Вес того же тела, неподвиж-
неподвижного относительно Земли, в той же точке земной поверхно-
поверхности равен Ро.
297. На экваторе на рельсах стоит пушка. Рельсы на-
направлены с запада на восток, и пушка может двигаться по
ним без трения. Пушка стреляет вертикально вверх. Ка-
Какую скорость v0 будет иметь пушка после выстрела? Куда
будет направлена эта скорость? Масса пушки М, масса ска-
ряда /я, длина ствола /. Считать, что снаряд движется в
стволе с постоянным ускорением а.
298. На сколько будут отличаться конечные скорости
разбега самолета, если самолет взлетает на экваторе, причем
один раз его разбег производится с запада на восток, а вто-
60
рой раз с востока на запад. Подъемная сила, действующая
на крылья самолета, пропорциональна квадрату его ско-
скорости относительно Земли. Необходимая конечная ско-
скорость разбега самолета вдоль меридиана равна v0.
299. Методом последовательных приближений получить
законы свободного падения тел в поле тяжести Земли с уче-
учетом ее вращения. Движение рассматривать в системе отсче-
отсчета, в которой Земля неподвижна.
300. Вращение Земли приводит к отклонению свободно
падающих тел (без начальной скорости) от направления от-
отвеса. В какую сторону направлено это отклонение и чему
равна его величина? Провести решение задачи в системе
отсчета, связанной с Землей.
301. Вычислить восточное и экваториальное отклонения
свободно падающего тела (без начальной скорости) для
широты Москвы (ф=56°), если высота падения /i = 100 м,
500 м, 1000 м, 2000 м.
302. Провести решение предыдущей задачи в системе от-
отсчета, связанной не с вращающейся Землей, а с Солнцем и
звездами. Рекомендуется воспользоваться двумя методами:
1) непосредственным применением к падающему телу зако-
законов Ньютона, 2) применением к падающему телу закона со-
сохранения момента количества движения.
303. Из ружья произведен выстрел строго вверх (т. е.
параллельно линии отвеса). Начальная скорость пули vo=
= 100 м/с, географическая широта места ф=60°. Учитывая
осевое вращение Земли, определить приближенно, на-
насколько восточнее или западнее от места выстрела упадет
пуля. Сопротивление воздуха движению пули не принимать
во внимание.
304. Под каким углом а к вертикали надо произвести
выстрел вверх, чтобы пуля упала обратно в точку, из кото-
которой был произведен выстрел? Использовать данные преды-
предыдущей задачи.
305. Вращение Земли вызывает отклонение поверхности
воды в реках от горизонтального положения. Рассчитать
наклон поверхности воды в реке к горизонту на широте ф.
Река течет с севера на юг.
306. В чем ошибочность следующего рассуждения;
пусть А и В — две неподвижные материальные точки, рас*
стояние между которыми равно г. Состояние покоя точки
В можно рассматривать как результат сложения двух вра-
вращений с одинаковыми, но противоположно направленны-
направленными постоянными угловыми скоростями: +<о и —ю. При
61
первом вращении возникает центростремительное ускорение
^=0)^, при втором — центростремительное ускорение
а2=(—(oJr=(o2r=ai. Результирующее устарение точки В
равно a=ai+a2=2a>ar. Следовательно, точка А действует
на точку В с силой притяжения F=2mco2r, где т — масса
точки В. Поскольку со — величина произвольная, полу-
получается абсурдный результат, что точки А и В притягива-
притягиваются друг к другу с произвольной, наперед заданной
силой.
307. Стрелок и мишень находятся в диаметрально про-
противоположных точках карусели радиуса R=5 м, равномерно
вращающейся вокруг вертикальной оси. Период вращения
карусели Т=10 с, скорость пули у=300 м/с. Пренебрегая
максимальной линейной скоростью вращающейся карусели
со/? по сравнению со скоростью пули, определить прибли-
приближенно, под каким углом а к диаметру карусели должен це-
целиться стрелок, чтобы поразить мишень. Задачу рассмотреть
как с точки зрения вращающейся, так и с точки зрения
неподвижной системы, и сравнить результаты.
308. В диаметрально противоположных точках карусе-
карусели диаметра D=20 м, вращающейся с постоянным угловым
ускорением со, расположены стрелок в точке С и мишень М.
Стрелок целится в мишень, не вводя поправки на вращение
карусели. Каково должно быть угловое ускорение карусели
со, чтобы при этих условиях пуля попала в цель, если в
момент выстрела угловая скорость карусели была щ=
= 1 рад/мин, а скорость пули и0=200 м/с. Стрелок и условия
стрельбы предполагаются идеальными. Влиянием центро-
центробежной силы пренебречь.
309. Представим себе, ~что в земном шаре просверлен
канал по диаметру в плоскости экватора. Вычислить силу
F, с которой будет давить на стенку канала тело, падаю-
падающее по нему с поверхности Земли, в тот момент, когда оно
достигнет центра Земли. Считать, что трения нет, а плот-
плотность Земли однородна.
310. Велосипедное колесо радиуса R вращается в гори-
горизонтальной плоскости вокруг своего центра. По спице ко-
колеса без трения может двигаться шарик. В начальный мо-
момент времени шарик находился у обода колеса. Какую
начальную скорость v0 следует сообщить шарику в ра-
радиальном направлении, чтобы он мог достигнуть оси вра-
вращения? Угловая скорость вращения <о поддерживается по-
постоянной.
62
311. Один из маятников Фуко установлен в Ленинграде
в Исаакиевском соборе. Длина маятника /=98 м, линейная
амплитуда колебаний шара маятника (т. е. наибольшее от-
отклонение его из положения равновесия) #0=5 м. Маятник
отпускался из крайнего положения без начального толчка.
Определить боковое отклонение шара маятника от положе-
положения равновесия в момент прохождения его через среднее
положение. Географическая широта Ленинграда ср = 60°.
312. Для создания искусственной тяжести на космиче-
космическом корабле, обращающемся вокруг Земли по круговой
орбите, было предложено ускорять корабль до скорости vf
превышающей первую космическую скорость. Для удер-
удержания корабля на круговой орбите при такой скорости
включается двигатель, сообщающий кораблю ускорение,
нормальное к траектории корабля. При какой скорости v
космонавт на корабле будет испытывать такую же «тяжесть»,
что и на Земле? Подсчитать расход топлива, который тре-
требуется для выведения корабля на круговую орбиту и после-
последующего (однократного) облета по ней вокруг земного шара
в этих условиях. Скорость газовой струи (относительно ко-
корабля) «=3 км/с. Считать, что орбита проходит недалеко
от поверхности Земли, и пренебречь изменением ускорения
свободного падения g с высотой.
§ 7. Динамика твердого тела. Динамика системы
313. Найти ускорение грузов и натяжение нитей на ма-
машине, изображенной на рис. 69, учитывая момент инерции /
вращающегося блока, при условии, что нить не скользит
по блоку. Определить усилие в подвеске Л, если масса бло-
блока равна М.
314. Однородный цилиндр массы М и радиуса R
(рис. 70) вращается без трения вокруг горизонтальной оси
под действием веса груза Р, прикрепленного к легкой нити,
намотанной на цилиндр. Найти угол ср поворота цилиндра
в зависимости от времени, если при /=0 ср=О.
315. Представьте себе, что груз Р (см. предыдущую за-
задачу) состоит из двух одинаковых частей, связанных нитью.
Определить натяжение этой нити Т.
316. На ступенчатый цилиндрический блок намотаны
в противоположных направлениях две легкие нити, на-
нагруженные массами тг и т2 (рис. 71). Найти угловое ускоре-
ускорение блока и натяжения Тх и Т2 нитей, учитывая момент
инерции / блока.
63
317. Модель ворота укреплена на одной чашке весов
(рис. 72). На ворот с моментом инерции / намотана нить с
У///////У/////А
О*
о*
Рис G9.
Р
Рис. 70.
грузиком массы т. Весы уравновешены, когда ворот затор-
заторможен, и нить не разматывается. Насколько следует изме-
изменить вес гирь на другой чашке весов для того, чтобы вос-
восстановить равновесие, когда ворот вращается под действием
опускающегося вниз грузика?
Рис. 72.
318. При каких условиях наступит равновесие весов
прибора, описанного в предыдущей задаче, в том случае,
когда грузик на модели ворота поднимается вверх вследствие
инерции раскрутившегося маховичка?
64
319. Схема демонстрационного прибора (диск Максвел-
Максвелла) изображена на рис. 73. На валик радиусом г наглухо
насажен сплошной диск радиуса R и массы М. Валик и диск
сделаны из одного материала, причем выступающие из диска
части оси имеют массу т. К валику прикреплены нити оди-
одинаковой длины, при помощи которых прибор подвешивается
к штативу. На валик симметрично наматываются нити в один
ряд, благодаря чему диск поднимается, а затем предоставля-
предоставляют диску свободно опускаться. Найти ускорение, с которым
опускается диск.
'///////////у////////////////////////.
У////////////,
У///////////////Л
Рис. 73.
Рис. 74.
320. Подсчитать ускорение а, с которым будет опускать-
опускаться диск, описанный в предыдущей задаче, если к стержню,
свободно (без трения) проходящему через отверстие внутри
валика, на нитях подвешено тело массы т=314 г (рис. 74).
Размеры диска указаны на рисунке, диск и валик сде-
сделаны из стали (плотность 8 г/см3). Весом нитей и оси пре-
пренебречь.
321. На горизонтальную неподвижную ось насажен блок,
представляющий собой сплошной цилиндр массы М. Через
него перекинута невесомая веревка, на концах которой
висят две обезьяны массой т каждая. Первая обезьяна на-
начинает подниматься с ускорением а относительно веревки.
Определить, с каким ускорением относительно неподвиж-
неподвижной системы координат будет двигаться вторая обе-
обезьяна.
322. Автомобиль трогается с места с постоянным уско-
ускорением а. Одна из дверок автомобиля открыта и ее плоскость
3 Под ред, И. А, Яковлева 65
составляет угол 90° с кузовом автомобиля (рис. 75). За ка-
какой промежуток времени Т дверка закроется? Центр масс
дверки находится на рас-
расстоянии d от петель дверки
автомобиля.
323. С каким ускоре-
ускорением а будет опускаться
катушка с массой М и мо-
моментом инерции / относи-
относительно оси симметрии, если
она подвешена аналогично
диску с валиком в задаче
319 (рис. 76). На катушку
намотаны еще две нити, к которым подвешен груз массы т.
Определить натяжения нитей. у/////////////////////////////л
324. Найти ускорения, с ко-
которыми будут опускаться центры
двух одинаковых дисков прибо-
прибора, описанного в задаче 319,
если один подвешен к другому
а2
Рис. 75.
Рис. 76.
Рис. 77.
так, как указано на рис. 77. Момент инерции диска и ва-
валика относительно оси диска равен /, масса диска и вали-
валика т, радиус валика, на который намотана нить, г.
326. По наклонной плоскости, образующей угол а с го-
горизонтом, скатывается без скольжения сплошной однород-
однородный диск, Найти линейное ускорение а центра диска.
326. Найти ускорение а центра однородного шара, ска-
скатывающегося без скольжения по наклонной плоскости, об-
образующей угол а с горизонтом. Чему равна сила трения
сцепления шара и плоскости?
66
327. Найти кинетическую энергию К катящегося без
скольжения рбруча массы jW, толщину которого можно
считать очень малой по сравнению с его радиусом.
328. По наклонной плоскости, составляющей с горизон-
горизонтом угол а«=30°, скатывается без скольжения сплошной
однородный цилиндр, масса которого равна 300 г. Найти
величину силы трения цилиндра о плоскость.
329. Какова должна быть величина коэффициента тре-
трения k, чтобы однородный цилиндр скатывался без скольже-
скольжения с наклонной плоскости, образующей угол а с горизон-
горизонтом?
330. С одного уровня наклонной плоскости одновременно
начинают скатываться сплошные цилиндр и шар одинако-
одинаковых радиусов. 1) Какое тело будет иметь большую скорость
на данном уровне? 2) Во сколько раз? 3) Во сколько раз
скорость одного будет больше скорости другого в данный
момент времени?
331. Какая из форм конца вала, изображенных на рис. 78,
выгоднее (при равных силах давления на опору и скоростях
%
а) Я
Рис. 78.
вращения) с точки зрения уменьшения потерь на трение
при вращении вала в опорном подшипнике. Трением о бо-
боковые стенки можно пренебречь.
332. К тележке, стоящей на горизонтальной плоскости,
привязана нить, перекинутая через блок, укрепленный у
края стола; к концу нити прикреплен груз массы тз^бОО г.
Определить ускорение тележки а, если известно, что масса
платформы тележки mi=l,4 кг, масса каждого колеса
т2=*=400 г и колеса представляют собой сплошные диски.
Колеса катятся по поверхности стола без скольжения, а
трение качения отсутствует.
333. На горизонтальной плоскости лежит катушка ни-
ниток. С каким ускорением а будет двигаться ось катушки,
3* 67
если тянуть за нитку с силой F (рис. 79)? Каким образом
надо тянуть за нитку для того, чтобы катушка двигалась в
сторону натянутой нитки? Катушка движется по поверхно-
поверхности стола без скольжения. Найти силу трения между ка-
катушкой и столом.
dv
dt
Рис. 79.
334. На шероховатой доске на расстоянии / от ее право-
правого конца находится сплошной цилиндр (рис. 80). Доску
начинают двигать с ускорением а0 влево. С какой скоростью
относительно доски будет двигаться центр цилиндра в тот
момент, когда он будет находиться над краем доски? Дви-
Движение цилиндра относительно
доски происходит без сколь-
скольжения.
335. Каток состоит из
сплошного цилиндра радиуса
Рис. 80.
Рис. 81.
R массы Мг и рамы массы М2 (рис. 81). К раме катка нитью
привязана масса М3. Всю эту систему пускают с наклонной
плоскости, образующей угол а с горизонтом. Найти уско-
ускорение системы а, если известен коэффициент трения k тела
Af3 о плоскость. (Каток скатывается без скольжения,) Как
следует расположить всю систему — массу М3 впереди и
каток позади (как указано на рисунке), или наоборот, что-
чтобы при движении нить была натянута?
336. Какое максимальное ускорение может развить ав-
автомобиль с задней ведущей осью, если коэффициент сцепле-
68
ния (трения покоя) колес с дорогой /г, расстояние между ося-
осями автомобиля /, высота центра массы автомобиля над доро-
дорогой — /г, и он расположен
посередине колесной базы
(рис. 82)?
337. Однородный тон-
тонкий тяжелый стержень дли-
длины / висит на горизонталь-
горизонтальной оси, проходящей через
один из его концов. Какую рис. 82.
начальную угловую ско-
скорость со надо сообщить стержню, чтобы он повернулся на 90°?
338. Найти момент количества движения Земли L отно-
относительно ее полярной оси. Считать Землю правильным ша-
шаром радиус* #=6000 км, имеющим плотность d=5,5 г/см3.
339. Какой момент сил следует приложить к Земле,
чтобы ее вращение остановилось через 100 000 000 лет
(год — 366,25 «звездных» суток)?
340. На краю свободно вращающегося достаточно боль-
большого горизонтального диска, имеющего радиус R и момент
инерции /, стоит человек массы т. Диск совершает п об/минв
Как изменится скорость вращения диска, если человек пе-
перейдет от края диска к центру? Как изменится при этом
энергия системы? Размерами человека по
сравнению с радиусом диска можно пре-
пренебречь.
341. На покоящемся однородном го-
горизонтальном диске массы М и радиуса
R находится человек массы т. Диск
может вращаться без трения вокруг
вертикальной оси, проходящей через его
центр. В некоторый момент человек
начал двигаться. С какой угловой ско-
скоростью со вращается диск, когда человек
идет по окружности радиуса г, концен-
концентричной диску, со скоростью v относи-
относительно диска?
342. Экспериментатор стоит на спе-
специальной табуретке и держит в руках
вертикальную ось свободно вращающе-
вращающегося колеса, имеющего момент инерции 1г относительно
этой оси АА (рис. 83). Колесо вращается в горизонтальной
плоскости с угловой скоростью о>1. Табуретка устроена так,
что она может свободно вращаться вокруг вертикальной оси,
Рис. 83.
т. е. представляет собой так называемую скамью Дуков-
ского. Момент инерции табуретки и экспериментатора во-
вокруг вертикальной оси равен /2. Ось колеса и ось табуретки
лежат на одной прямой. На какую величину Д£к изменится
кинетическая энергия £к всей системы табуретки и колеса,
если экспериментатор повернет ось колеса на 180°, на 90°?
343. Монета массы т и радиуса г, вращаясь в горизон-
горизонтальной плоскости вокруг своей геометрической оси с уг-
угловой скоростью со, вертикально падает на горизонтальный
диск и «прилипает» к нему. В результате диск приходит во
вращение вокруг своей оси. Возникающий при этом момент
сил трения в оси диска постоянен и равен Мо. Через какое
время вращение диска прекратится? Сколько оборотов N
сделает чиск до полной остановки? Момент инерции диска
относительно его геометрической оси /0. Расстояние между
осями диска и монеты равно d.
344. Сплошной однородный короткий цилиндр радиуса
г, вращающийся вокруг своей геометрической оси со ско-
скоростью п об/с, ставят в вертикальном положении на гори-
горизонтальную поверхность. Сколько оборотов N сделает ци-
цилиндр, прежде чем вращение его полностью прекратится?
Коэффициент трения скольжения между основанием ци-
цилиндра и поверхностью, на которую он поставлен, не зави-
зависит от скорости вращения и равен k.
345. На горизонтальный диск, вращающийся вокруг гео-
геометрической оси с угловой скоростью (оь падает другой
диск, вращающийся вокруг той же оси с угловой скоростью
со2. Моменты инерции дисков относительно указанной оси
равны соответственно h и /2. Оба диска при ударе сцепля-
сцепляются друг с другом (при помощи острых шипов на их по-
поверхностях). На сколько изменится общая кинетическая
энергия вращения системы после падения второго диска?
Чем объясняется изменение энергии? Геометрические оси
обоих дисков являются продолжением одна другой.
346. Шкивы двух маховиков соединены ремнем (рис. 84).
Радиусы шкивов равны Rt и R2. Моменты инерции махови-
маховиков относительно их геометрических осей равны /i и /2.
Удерживая второй маховик и ремень неподвижными,
раскручивают первый маховик до угловой скорости со0,
вследствие чего между осью первого маховика и ремнем воз-
возникает скольжение. Затем ремень и второй маховик отпу-
отпускают. Пренебрегая всеми силами трения, за исключением
сил трения скольжения между ремнем и осями маховиков,
найти установившиеся скорости вращения маховиков щ и
70
со2, т. e. скорости после прекращения скольжения. Найти
также потерю АК кинетической энергии на трение скольже-
скольжения. Массой ремня пренебречь.
Рис. 85.
Рис. 84.
347. Почему в предыдущей задаче полный момент коли-
количества движения системы не сохраняется?
348. Однородный диск А массы Мх и радиуса г± (рис. 85)
раскручен до угловой скорости щ и приведен в контакт с
диском В, ось вращения кото-
которого перпендикулярна к оси
диска Л. Масса диска В равна
М 2, а расстояние между точкой
соприкосновения и осью диска
А равно а. Найти установив-
установившиеся угловые скорости дисков
coi и со2 и потерю энергии в про-
процессе установления. Трением в
осях, а также трением качения
пренебречь.
349. Метеорит массы т== Юь т,
двигавшийся со скоростью
у*=50 км/с, ударился о Землю на широте ф=60°. Вся его
кинетическая энергия перешла в тепловую (внутреннюю)
энергию, а сам он испарился. Какое максимальное влияние
мог оказать удар такого метеорита на продолжительность
суток?
350. Оценить, с какой минимальной скоростью v нужно
выпустить на экваторе Земли снаряд массы т=1000 т, что-
чтобы изменить продолжительность земных суток на AT=
= 1 мин?
351. Пульсарами называются небесные объекты, посы-
посылающие импульсы радиоизлучения, следующие друг за
другом с высокостабильными периодами, которые для из-
известных к настоящему времени пульсаров лежат в пределах
примерно от 3-Ю до 4 с. Согласно современным пред*
ставлениям пульсары представляют собой вращающиеся
71
нейтронные звезды, образовавшиеся в результате гравита-
гравитационного сжатия. Нейтронные звезды подобны гигантским
атомным ядрам, построенным из одних только нейтронов.
Плотность вещества р в нейтронной звезде не однородна,
но при грубых оценках ее можно считать одной и той же по
всему объему звезды и по порядку величины равной
1014 г/см3. Оценить период вращения Г, с каким стало бы
вращаться Солнце, если бы оно превратилось в нейтронную
звезду. Плотность вещества Солнца возрастает к его центру,
а различные слои его вращаются с различными скоростями.
При оценке этими обстоятельствами пренебречь и считать,
что средняя плотность солнечного вещества ро=1,41 г/см3,
а период вращения Солнца Т0=2,2-10в с.
352. Тонкий стержень длины 2/ и массы т подвешен
за середину к нижнему концу длинной вертикально ви-
висящей проволоки, верхний конец которой закреплен. На
стержне укреплены два одинаковых сплошных шара ра-
радиуса R и массы М, каждый таким образом, что центры
шаров оказались на концах стержня. Система закручена
на некоторый угол и предоставлена самой себе. Предпо-
Предполагая, что возникающий при этом вращающий момент
пропорционален углу кручения а, выразить угловое уско-
ускорение dto/dt в зависимости от угла а и параметров системы.
353. Тонкий стержень массы т и длины L (рис. 86)
подвешен за один конец и может вращаться без трения во-
вокруг горизонтальной оси. К той же оси подвешен на нити
ft
Рис. 86.
Рис. 87.
длины / шарик такой же массы т. Шарик отклоняется на
некоторый угол и отпускается. При какой длине нити ша-
шарик после удара о стержень остановится? Считать удар аб-
абсолютно упругим,
72
Qm
Рис. 88.
354. Математический маятник массы т и стержень мас-
массы М (рис. 87) подвешены к одной и той же точке Л, вокруг
которой они могут свободно колебаться. Длина нити ма-
маятника равна длине стержня. Шарик маятника отклоняют
в сторону, так что он приподнимается на высоту h относи-
относительно своего нижнего положения. Затем шарик отпуска-
отпускают, и он сталкивается неупруго со А ^
стержнем. Как будут двигаться ша-
шарик и нижний конец стержня после
удара и на какие высоты они подни-
поднимутся?
355. Решить предыдущую задачу
в предположении, что до удара был
отклонен стержень (нижний конец его
был поднят на высоту /i).
356. Твердый стержень длины / и
массы М может вращаться вокруг го-
горизонтальной оси А, проходящей через
его конец (рис. 88). К той же оси А подвешен математический
маятник такой же длины / и массы т. Первоначально стер-
стержень занимает горизонтальное положение, а затем отпу-
отпускается. В нижнем положении происходит идеально упругий
удар, в результате которого шарик и стержень дефор-
деформируются, и часть кинетической энергии переходит в по-
потенциальную энергию деформации. Затем деформация умень-
уменьшается, и запасенная потенциальная энергия вновь перехо-
ходит в кинетическую. Найти значение потенциальной
энергии деформации U в момент, когда она максимальна,
357. Вертикально висящая однородная доска длины
L=l,5 м и массы М = \0 кг может вращаться вокруг гори-
зонтальной оси, проходящей через ее верх-
ний конец. В нижний конец доски ударяет
пуля, летящая горизонтально с начальной
скоростью V0=600 м/с. Пуля пробивает
доску и летит далее со скоростью V. Опре-
Определить скорость V, если после выстрела
доска стала колебаться с угловой амплиту-
амплитудой а=0,1 рад. Масса пули т==10 г.
358. В общей точке подвеса А (рис. 89)
подвешены шарик на нити длины / и одно-
однородный стержень длины L, отклоненный
в сторону на некоторый угол. При возвращении стержня
в положение равновесия происходит упругий удар. При
каком соотношении между массами стержня М и шарика
73
/77
Рис. 89.
т шарик и точка удара стержня будут двигаться после
удара с равными скоростями в противоположных направле-
направлениях? При каком соотношении между массами Мит опи-
описанный процесс невозможен?
359. Каким участком сабли следует рубить лозу, чтобы
рука не чувствовала удара? Саблю считать однородной
пластинкой.
360. Однородная тонкая квадратная пластинка массы
т0 может свободно вращаться вокруг вертикальной оси
(рис. 90). В точку Л, находящуюся на расстоянии 2/3а от
оси, нормально к пластинке ударяется шар с массой /л,
летевший со скоростью v. Как будут двигаться пластинка
и шар после соударения, которое происходит по закону уп-
упругого удара?
361. Однородный сосновый брус с массой М (плотность
0,5 г/см3)„ размеры которого указаны на рис. 91, может
свободно вращаться около оси АВ. В точку О бруса ударяет
горизонтально летящее ядро массы т=10 кг. Какова ско-
скорость ядра v, если брус отклонился на угол ср=28°, а ядро
упало на месте удара?
362. Стержень массы М и длины /, который может
свободно вращаться вокруг неподвижной горизонтальной
оси, проходящей через один из его концов, под действием
силы тяжести переходит из горизонтального положения в
74
вертикальное (рис. 92). Проходя через вертикальное поло-
положение, нижний конец стержня упруго ударяет о малое
тело массы т, лежащее на гладком горизонтальном столе.
Определить скорость тела т после .
удара. Г
363. Воспользовавшись условием jj
задачи 362, определить, на какое и
расстояние S переместится тело т пос- jj
ле удара, если коэффициент трения N
между телом и столом равен k и не ji
зависит от скорости. Стержень после
удара остановился. Тело скользит по
столу без вращения. Рис. 92.
364. На гладком горизонтальном
стержне, вращающемся вокруг вертикальной оси с посто-
постоянной угловой скоростью (о=40я с, около оси находится
закрепленная неподвижно муфта массы т=100 г.
В некоторый момент муфту отпускают, и она скользит
без трения вдоль стержня. Какой момент сил М должен
быть приложен к стержню для того, чтобы он продолжал
равномерное вращение? Найти расстояние х муфты от
оси в любой момент времени t. В начальный момент центр
тяжести муфты находится на расстоянии ао==2 см от
оси.
365. На полюсе установлена пушка, ствол которой на-
направлен горизонтально вдоль меридиана и может свободно
вращаться вокруг вертикальной оси, проходящей через
замок орудия. С какой угловой скоростью относительно
Земли будет вращаться ствол пушки после выстрела? Счи-
Считать, что в начальный момент времени снаряд находится на
оси вращения и движется внутри ствола при выстреле с
постоянным ускорением а. Масса пушки (Л4 = 1000 кг) зна-
значительно больше массы снаряда (т=10 кг). Длина ствола
значительно больше его диаметра.
366. Вертикальный столб высотой I подпиливается у
основания и падает на землю, поворачиваясь вокруг ниж-
нижнего основания. Определить линейную скорость его верхне-
верхнего конца в момент удара о землю. Какая точка столба будет
в этот момент иметь ту же скорость, какую имело бы тело,
падая с той же высоты, как и данная точка?
367. Однородный стержень массы т и длины I (рис. 93)
падает без начальной скорости из положения 1, вращаясь
без трения вокруг неподвижной горизонтальной оси О.
Найти горизонтальную Fr09 и вертикальную FBepT составля-
75
ющие силы, с которыми ось О действует на стержень в го-
горизонтальном положении 2.
368. Абсолютно твердая однородная балка веса Р и дли-
длины L лежит на двух абсолютно твердых симметрично распо-
расположенных опорах, расстояние между которыми равно /
(рис. 94). Одну из опор выбивают. Найти начальное значение
'берт
О
Рис. 93.
1
f
и
\
Рис
1
Р
. 94.
1
I»-
f
силы давления F, действующей на оставшуюся опору. Рас-
Рассмотреть частный случай, когда Z=L. Почему при выбива-
выбивании опоры сила F меняется скачком?
369. Гимнаст на перекладине выполняет большой оборот
из стойки на руках, т. е. вращается, не сгибаясь, вокруг пе-
перекладины под действием собственного веса. Оценить при-
приближенно наибольшую нагрузку F на его руки, пренебрегая
трением ладоней о перекладину.
370. Человек на аттракционе «гигантские шаги» движет-
движется по замкнутой траектории таким образом, что достигае-
достигаемая им высота относительно положения
равновесия меняется в пределах от/*мин
Д° ^макс- Определить максимальную и
минимальную скорости человека при
таком движении, если длина веревки, на
которой он удерживается, равна /.
371. Uo внутренней поверхности ко-
конической воронки, стоящей вертикаль-
вертикально, без трения скользит маленький ша-
шарик (рис. 95). В начальный момент шарик
находился на высоте /г0, а скорость его
v0 была горизонтальна. Найти v0, если
известно, что при дальнейшем движении шарик поднимает-
поднимается до высоты h, а затем начинает опускаться. Найти также
скорость шарика в наивысшем положении v.
372. Тяжелая веревка (линейная плотность р) длины L
перекинута через блок с моментом инерции / и радиусом г.
76
Рис. 95.
В начальный момент блок неподвижен, а больший из свеши-
свешивающихся концов веревки имеет длину /. Найти угловую ско-
скорость вращения блока со, когда веревка соскользнет с него.
Веревка движется по блоку без скольжения, трение в оси
блока не учитывать.
373. На двух параллельных горизонтальных брусьях
лежит сплошной цилиндр радиуса R и массы т, на который
намотана веревка. К опущенно-
опущенному вниз концу веревки прило-
приложена вертикальная сила F,
равная половине веса цилинд-
цилиндра (рис. 96). Найти горизонталь-
горизонтальное ускорение цилиндра и мини-
минимальное значение коэффициента
трения между цилиндром и
брусьями, при котором будет
происходить качение без сколь-
скольжения. Ось цилиндра перпенди-
перпендикулярна к брусьям, центр его
масс и сила F лежат в вертикальной плоскости, прохо-
проходящей посередине между брусьями.
374. К концу веревки, намотанной на цилиндр (см. ус-
условие задачи 373) привязан груз массы Л4. Веревка перебро-
переброшена через блок, как показано на рис. 97. Определить уско-
ускорение груза М. Выяснить условия, при которых качение
Рис. 96.
Рис. 97.
цилиндра будет происходить со скольжением. Весом ве-
веревки и блока, а также силами трения на оси блока можно
пренебречь. Считать, что во всех случаях движение цилинд-
цилиндра будет плоскопараллельным.
375. Обруч радиуса г свободно скатывается с вершины
неподвижной цилиндрической поверхности радиуса R>r
(рис. 98). В какой точке поверхности начнется скольжение
обруча? Коэффициент трения между обручем и поверхно-
поверхностью &=0,5.
77
376. Два катка, связанные штангой S, скатываются без
скольжения с наклонной плоскости, образующей угол в
30° с горизонтом (рис. 99). Катки имеют одинаковые массы
т=5 кг и одинаковые радиусы #=5 см, момент инерции
первого /i=80 кг-см2, второго /2=40 кг. см2. Массами рам
Рис. 98.
Рис. 99.
катков и штанги можно пренебречь. Подсчитать угловое ус-
ускорение, с которым катки скатываются без скольжения с на-
наклонной плоскости. Определить силу, передаваемую штан-
штангой, если каток с большим моментом инерции движется впе-
впереди, и наоборот.
377. На подставке, имеющей массу ти укреплена ось,
на которой может свободно вращаться цилиндр радиуса R
и массы т3. Нить, намотанная на цилиндр, прикреплена к
F
Рис. 100.
телу массы т2. Определить ускорения масс Шг и т2 и ци-
цилиндра при следующих условиях. 1) К массе т2 приложена
горизонтальная сила F (рис. 100) и сил трения нет. 2) Те же
условия, но при наличии сил трения между плоскостью и
телами масс тх и т2. Трением в оси цилиндра пренебречь.
3) К веревке в точке А приложена горизонтальная сила F,
масса т2 убрана; определить ускорения массы mi и цилинд-
цилиндра. Движение всех тел считать плоским.
378. Когда диск Максвелла достигает нижнего положе-
положения, он начинает подниматься вверх, сообщая «рывок»
78
Рис. 101.
нитям. С каким ускорением поднимается диск? Найти на-
натяжение нити во время опускания и поднятия диска, а так-
также оценить приближенно натяжение нити во время рывка.
Масса диска М = 1 кг, его радиус /?==10 см, радиус валика
г=0,5 см. Массой валика, а также растяжением нити во
время рывка пренебречь. Предполагается, что вначале диск
был подвешен на длинных нитях, при-
причем длина намотанной части каждой
нити равна /=50 см.
379. К шкиву креста Обербека
(рис. 101) прикреплена нить, к кото-
которой подвешен груз массы Л1 = 1 кг.
Груз опускается с высоты h==l м до
нижнего положения, а затем начинает
подниматься вверх. В это время
происходит «рывок», т. е. увеличение
натяжения нити. Найти натяжение
нити Т при опускании или поднятии
груза, а также оценить приближенно
натяжение во время рывка Туыв. Ра-
Радиус шкива г=3 см. На кресте укреп-
укреплены четыре груза с массой т=250 г каждый на расстоя-
расстоянии R=30 см от его оси. Моментом инерции самого креста
и шкива пренебречь по сравнению с моментом инерции
грузов. Растяжение нити во время рывка не учиты-
учитывать.
380. Определить ускорение а центра шарика, скатываю-
скатывающегося без скольжения по наклонному желобу, образу-
образующему угол а с горизонтом.
Форма поперечных сечений же-
желоба изображена на рис. 102.
381. С какой высоты Я дол-
должен скатиться по наклонному
желобу шарик с радиусом инер-
инерции р, для того чтобы он смог
без скольжения описать мерт-
мертвую петлю по желобу радиуса
R? Радиусом шарика г по срав-
сравнению с R пренебречь.
382. Цилиндр или шар радиуса г катится по плоскости,
наклоненной под углом а к горизонту. Определить, при
каком значении угла а начинается качение со скольжением,
если коэффициент трения скольжения между катящимся
телом и плоскостью равен к.
79
5)
Рис. 102.
383. Шарик радиуса г скатывается без начальной ско-
скорости и без скольжения по поверхности сферы из самого
верхнего положения А (рис. 103). Определить точку, в ко-
которой он оторвется от сферы и начнет свободно двигаться
под действием силы тяжести.
Рис. 103.
Рис. 104.
384. По наклонной плоскости, образующей угол а с го-
горизонтом, скатывается массивный полый цилиндр массы т-
и радиуса г (рис. 104). По поверхности цилиндра бежит
собака таким образом, что она все время занимает наивыс-
наивысшее положение на поверхности цилиндра. Определить, с
каким ускорением а скатывается цилиндр, если масса со-
собаки тг.
385. По поверхности большого полого цилинДра, лежа-
лежащего на горизонтальной плоскости, начинает бежать собака
массы т в направлении к наивыс-
наивысшей точке А и притом так, что она
все время находится на одном и том
же расстоянии от этой точки (рис.
105). В результате цилиндр начи-
начинает катиться по горизонтальной
плоскости без скольжения. Масса
цилиндра Му а угол АОВ равен
а. Определить: 1) ускорение оси
цилиндра а; 2) силу трения между
цилиндром и плоскостью во время
качения Flv; 3) время /, р течение которого собака способ-
способна оставаться на указанном расстоянии от точки Л, если
максимальная полезная мощность, которую она способна
развить, равна Ямакс. Какая при этом будет достигнута
максимальная скорость имакс поступательного движения
цилиндра? (Полезной мощностью здесь называется мощ-
ьи
Рис. 105.
ность, которая затрачивается собакой на увеличение кине-
кинетической энергии системы.)
386. Определить ускорение а, с которым цилиндриче-
цилиндрическая бочка, целиком заполненная жидкостью, скатывается
без скольжения с наклонной плоскости, образующей угол а
с горизонтом (рис. 106). Трение
между жидкостью и стенками боч-
бочки считать пренебрежимо малым.
387. Полый цилиндр массы М
скатывается без скольжения с нак-
наклонной плоскости, образующей угол
а с горизонтом. В цилиндре нахо-
находится гладкий шарик, который мо-
может скользить по внутренней по- Рис. 1С6.
верхности цилиндра без трения.
Существует ли такое положение шарика, при котором он
будет двигаться параллельно наклонной плоскости, т. е.
с тем же ускорением а, с каким движется ось цилиндра?
Найти это положение, если оно существует. Что будет в
предельном случае: т<^М и а<^1 (угол а мал).
388. Известно, что для того чтобы отличить сырое яйцо
от сваренного вкрутую, достаточно попытаться закрутить
его на столе. Вареное яйцо крутится долго. Сырое же
раскрутить не удается. Объяснить, на чем основан этот
способ.
389. Величина трения между осью и смазанным подшип-
подшипником в основном определяется движением и внутренним
трением жидкости в смазывающем слое.
В гидродинамической теории смазки Н. П. Петрова да-
дается следующее выражение для момента сил трения, дей-
действующего на единицу длийы вращающейся оси:
где |х — вязкость смазывающей жидкости, а — радиус оси,
(о — ее угловая скорость и б — толщина слоя. Пользуясь
этим выражением, найти закон вращения ротора, ось кото-
которого укреплена в подшипниках; другие внешние моменты
сил на ротор не действуют.
390. Сплошному цилиндру радиуса R = IO см и весаР
сообщено вращение вокруг его оси с угловой скоростью
со= 10 об/с. Вращающийся цилиндр кладут на горизонталь-
горизонтальную плоскость и предоставляют самому себе. Он начинает
двигаться по плоскости, причем коэффициент трения сколь-
81
жения между цилиндром и плоскостью равен 0,1. Опреде-
Определить, через какое время Т движение цилиндра перейдет в
чистое качение без скольжения. Сила трения скольжения
предполагается не зависящей от скорости, а трение каче-
качения отсутствует. Какое ускорение будет иметь цилиндр при
ОТ?
391. Сплошной цилиндр, ось которого горизонтальна,
движется без вращения по гладкой горизонтальной плоско-
плоскости в направлении, перпендикулярном к его оси. В некото-
некоторый момент цилиндр достигает границы, где поверхность
становится шероховатой и возникает постоянная (не за-
зависящая от скорости) сила трения скольжения, а трение
качения отсутствует. Каково будет движение цилиндра после
перехода границы? Как распределится кинетическая энер-
энергия поступательного движения цилиндра?
392. Сплошному однородному шару радиуса г, лежащему
на горизонтальной плоскости, сообщается в начальный
момент времени поступательная скорость v0 без вращения.
Учитывая трение скольжения, но пренебрегая трением ка-
качения, найти угловую скорость шара, когда его движение
перейдет в чистое качение. Определить потерю кинетиче-
кинетической энергии на трение.
393. Сплошной однородный шар радиуса г, вращающий-
вращающийся вокруг горизонтального диаметра с угловой скоростью
(о0, ставится на горизонтальную плоскость без сообщения
ему поступательного движения. Учитывая трение скольже-
скольжения, но пренебрегая трением качения, найти линейную ско-
скорость v центра шара, когда его движение перейдет в чистое
качение. Определить потерю кинетической энергии на
трение.
394. На внутренней стороне тонкого обруча массы М
и радиуса /?=0,5 м прикреплено тело массы m=1/10 M,
размеры которого значительно меньше R. Обруч катится
без скольжения по горизонтальной плоскости. Какой долж-
должна быть скорость центра обруча v0, когда тело находится в
нижнем положении, чтобы обруч «подпрыгнул»?
395. Бильярдный шар катится без скольжения по го-
горизонтальной плоскости со скоростью v и ударяется в покоя-
покоящийся такой же бильярдный шар, причем линия центров
параллельна скорости движения. Определить скорости
обоих шаров после того, как их движения перейдут в чистые
качения. Какая доля первоначальной кинетической энер-
энергии перейдет в тепло? Считать, что при столкновении
шаров передачи вращательного движения не происходит.
82
Потерей энергии на трение при чистом качении пренеб-
пренебречь.
396. Как надо ударить кием по бильярдному шару, что-
чтобы сила трения шара о сукно бильярдного стола заставляла
его двигаться: а) ускоренно, б) замедленно, в) равномерно?
Предполагается, что удар наносится горизонтально в вер-
вертикальной плоскости, проходящей через центр шара и точку
касания его с плоскостью бильярдного стола.
397. Как надо ударить кием по бильярдному шару, что-
чтобы при столкновении с другим (неподвижным) шаром 1) оба
шара стали двигаться вперед (удар с накатом), 2) первый
шар остановился, а второй двигался вперед, 3) второй шар
двигался вперед, а первый откатился назад (удар с оттяж-
оттяжкой)? Относительно направления и плоскости удара ввести
те же предположения, что и в предыдущей задаче.
398. Вращающийся с угловой скоростью со0 сплошной
однородный цилиндр радиуса г ставится без начальной по-
поступательной скорости у основания наклонной плоскости,
образующей угол а с горизонтальной плоскостью, и начи-
начинает вкатываться вверх. Определить время, в течение кото-
которого цилиндр достигает наивысшего положения на наклон-
наклонной плоскости.
399. Считая в предыдущей задаче коэффициент трения
скольжения k цилиндра о наклонную плоскость заданным и
постоянным, определить: 1) ускорение цилиндра аи когда
качение происходит со скольжением; 2) время tu по истече-
истечении которого наступает чистое качение; 3) высоту Ни ко-
которой достигает цилиндр, прежде чем начинается чистое ка-
качение; 4) ускорение а2 при чистом качении; 5) дополнитель-
дополнительную высоту Н2, на которую поднимается цилиндр при
чистом качении; 6) полную высоту поднятия Н\ 7) время
обратного скатывания цилиндра вниз /. Предполагается,
что /O>tg a.
400. Вращающийся с угловой скоростью со0 сплошной
однородный цилиндр массы тх ставится без начальной посту-
поступательной скорости на длинную доску массы т2, лежащую
на гладкой горизонтальной плоскости. Начальная скорость
доски равна нулю. Пренебрегая силой трения качения, но
учитывая трение скольжения между доской и цилиндром,
найти угловую скорость вращения цилиндра после того,
как его движение перейдет в чистое качение. Доска предпо-
предполагается настолько длинной, что чистое качение успевает
установиться до того, как цилиндр скатится с доски,
83
401. Большой однородный свинцовый шар массы М
лежит на плоской горизонтальной поверхности. Небольшая
пуля массы т выпущена из ружья горизонтально со ско-
скоростью V в направлении к центру шара. После выстрела
пуля застревает внутри шара. Определить линейную ско-
скорость шара v после того, как его движение перейдет в чи-
чистое качение. При рассмотрении движения шара после
удара считать его однородным, пренебрегая массой застряв-
застрявшей пули. Трением качения пренебречь.
402. Шар массы М= 1000 г, лежащий на горизонтальной
плоскости, пробивается по диаметру пулей, летящей го-
горизонтально с начальной скоростью Vo—500 м/с. После
удара шар начинает скользить по плоскости. Спустя не-
некоторое время его движение переходит в чистое качение с
постоянной скоростью у=3 м/с. Опреде-
^ лить скорость пули V после вылета ее
LH3 шара, если масса пули т=10 г. Тре-
^ s*\ нием качения пренебречь.
^ 403. На гладком горизонтальном сто-
Го q ле лежит однородный стержень длины /,
который может двигаться по столу без
трения (рис. 107). В начальный момент,
когда скорость стержня равна нулю,
в него ударяется шарик, движущийся
по столу перпендикулярно к стержню.
Рис 107. На каком расстоянии х от центра
стержня С ударился шарик, если не-
непосредственно после удара концы стержня А и В начали
двигаться со скоростями vA и vB соответственно? (Ско-
(Скорости vA и vB считаются положительными, когда они на-
направлены в ту же сторону, что и скорость шарика до удара,
и отрицательными в противоположном случае.)
404. На идеально гладкой горизонтальной поверхности
лежит стержень длины / и массы М, который может
скользить по этой поверхности без трения (см. рис. 107).
В одну из точек стержня ударяет шарик массы т, движущий-
движущийся перпендикулярно к стержню. На каком расстоянии х
от середины стержня должен произойти удар, чтобы шарик
передал стержню всю свою кинетическую энергию? Удар
считать абсолютно упругим. При каком соотношении масс
Мит это возможно?
405. В конец стержня массы М, лежащего на гладком
горизонтальном столе, попадает шарик, летевший перпен-
перпендикулярно к стержню и параллельно плоскости стола со
84
скоростью v0. Считая массу шарика т пренебрежимо малой
по сравнению с массой стержня, определить кинетическую
энергию К стержня после удара, если удар был абсолютно
упругий.
406. В доску массы М, лежащую на горизонтальном
столе, попадает пуля массы т, летевшая перпендикулярно
к доске и параллельно плоскости стола со скоростью v0.
Определить кинетическую энергию /С, перешедшую во вну-
внутреннюю энергию (тепло) системы, если точка попадания
пули находится от конца доски на расстоянии 1/4 ее длины.
Массу пули по сравнению с массой доски считать пренебре-
пренебрежимо малой, шириной доски пренебречь.
407. На гладком горизонтальном столе лежит однород-
однородный упругий стержень массы М. В конец стержня ударяет
упругий шарик массы т, движущийся со скоростью v пер-
перпендикулярно к стержню. Найти значение энергии дефор-
деформации системы в момент, когда она максимальна. Трением
между стержнем и столом пренебречь.
408. На гладком горизонтальном столе лежит однород-
однородный твердый стержень длины / и массы Л4, в край которого
ударяет твердый шарик массы т, движущийся со скоростью
у0, перпендикулярной к стержню. Считая удар идеально
упругим и предполагая, что силы трения между поверхно-
поверхностью стола и лежащими на ней телами пренебрежимо малы,
вычислить угловую скорость вращения стержня после
удара.
409. По гладкой горизонтальной поверхности стола по-
поступательно движется твердый стержень длины / и массы М
со скоростью Уо, перпендикулярной к его продольной оси.
Навстречу стержню перпендикулярно к той же оси движется
твердый шарик массы т. Шарик ударяется в конец стержня,
а затем отскакивает от него. Считая удар абсолютно упру-
упругим и предполагая, что трение между поверхностью стола
и движущимися по ней телами пренебрежимо мало, опреде-
определить, с какой скоростью v0 должен двигаться шарик, чтобы
после удара центр масс стержня остановился. Найти также
угловую скорость вращения стержня вокруг центра масс
после удара.
410. Легкая штанга длины / может свободно вращаться
вокруг горизонтальной оси О, проходящей через один из ее
концов (рис. 108). На втором конце штанги укреплена дру-
другая ось А, на которую насажен однородный диск радиуса
г. Закрепив диск на оси Л, штангу поднимают до горизон-
горизонтального положения, а затем отпускают. Когда штанга
85
I
I
\s)
проходит через положение равновесия, диск мгновенно
освобождают, так что он в дальнейшем может свободно вра-
вращаться вокруг оси Л. Определить высоту подъема ди-
диска, х при последующем движении си-
системы.
411. Гладкий твердый стержень
длины /0 и массы М равномерно
вращается с угловой скоростью со0
вокруг неподвижной оси, проходя-
проходящей через один из концов стержня
перпендикулярно к его продольной
оси. На стержень надет шарик массы
т. Вначале шарик находится на сво-
свободном конце стержня и вращается
вместе с ним (упор, имеющийся на
конце стержня, не позволяет шарику
соскользнуть со стержня). В некоторый момент шарику
сообщается скорость v, направленная вдоль стержня к
оси вращения. Определить наименьшее расстояние /, до
которого приблизится шарик к оси вращения, и угловую
скорость системы со в этом положении. В какую сторону
будет изогнут стержень, когда шарик движется по направ-
направлению к оси вращения? Как изменится изгиб стержня,
когда шарик, достигнув наименьшего удаления до оси,
начнет двигаться в обратном направлении?
412. На тело Л, находящееся на горизонтальной по-
поверхности стола, положено сверху тело В (рис. 109). Какую
Т
\
Рис. 108.
Рис. 109.
нужно приложить горизонтальную силу F к телу Л, чтобы
тело В соскользнуло с поверхности тела Л. Коэффициент
трения между столом и телом Л равен kl9 между телами Л и
В равен k2. Массы тел шА и пгв.
413. Определить горизонтальную составляющую уско-
ускорения тела а2 и ускорение клина ах (задача 132, рис. 33)
при следующих условиях: 1) Если между телом и клином
имеется трение (коэффициент трения k)y я между клином и
плоскостью трения нет. 2) Если между телом и клином тре-
86
V
Рис. ПО.
ния нет, а между плоскостью и клином есть трение с коэф-
коэффициентом k. 3) Указать максимальные значения коэффи-
коэффициентов трения, при которых движения клина и тела будут
иметь место.
414. Прямоугольная призма стоит на шероховатой доске,
лежащей на горизонтальном столе (рис. ПО). С каким ми-
минимальным ускорением амин надо начать двигать доску по
столу, чтобы призма опрокинулась назад (по отношению к
направлению движения дос-
доски) через свое нижнее заднее
ребро? Найти силу нормаль-
нормального давления N и коорди-
координату х ее точки приложе-
приложения, с которой доска дейст-
действует на призму при движении
доски с ускорением а.
Провести решения задачи
в системах отсчета, связанных
с доской и со столом.
415. Автомобиль с шири-
шириной колеи 2Ь и высотой h цент-
центра массы над землей проходит
горизонтальное закругление дороги радиуса R. 1) Пока-
Показать, что при скорости автомобиля v >VbRg/ti он опроки-
опрокинется, если не возникнет скольжения колес в направлении,
перпендикулярном к движению автомобиля. 2) Предпола-
Предполагая, что скорость автомобиля достаточна для того, чтобы
он мог опрокинуться, найти, при каком минимальном зна-
значении коэффициента трения
k между колесами автомо-
автомобиля и покрытием дороги
это может произойти?
416. На горизонталь-
горизонтальном вращающемся диске
стоит цилиндр. При какой
угловой скорости со ци-
цилиндр свалится с диска,
если расстояние между ося-
осями диска и цилиндра R, а коэффициент трения k>D/h9 где
D—диаметр цилиндра, a h — его высота (рис. 111).
417. Физический маятник, состоящий из шарика, йа-
саженного на конец тонкого жесткого стержня, может сво-
свободно колебаться вокруг горизонтальной оси Л, проходя-
87
Рис. 111.
щей через верхний конец стержня. Ось А неподвижно за-
закреплена на геометрической оси горизонтального диска,
равномерно вращающегося вокруг этой (вертикальной)
геометрической оси с угловой скоростью со. Таким образом,
плоскость колебаний маятника вращается вместе с диском
с той же угловой скоростью со. Найти период малых колеба-
колебаний маятника, если масса стержня пренебрежимо мала по
сравнению с массой шарика. При каком условии нижнее
вертикальное положение стержня станет неустойчивым по-
положением равновесия?
418. Легкий желоб свернут в виде вертикальной цилин-
цилиндрической спирали радиуса /?, которая может свободно
вращаться около вертикальной оси симметрии. Витки спи-
спирали наклонены к горизонту под углом <р=л;/4. По желобу
скользит без трения тело массы т. Какую скорость приобре-
приобретет тело в конце спирального спуска, опустившись с высо-
высоты ft, если скольжение началось без на-
начальной скорости. Считать массу желоба
равной массе тела. Какова будет угловая
скорость вращения желоба?
Рис. 112.
У////////////////////////////Л
Рис. ИЗ.
419. А просит В разъяснить следующее недоразуме-
недоразумение.
Л.— Как сообщается ускорение велосипеду, я понимаю,
а как оно сообщается паровозу,— не понимаю. Возникно-
Возникновение силы, действующей на раму велосипеда, мне пред-
представляется так: действие ведущей цепи на заднее колесо
можно изобразить силой, направленной вперед и приложен-
приложенной к колесу в некоторой точке над осью (рис. 113). Эта сила
вращает колесо вокруг мгновенной оси, проходящей через
точку С, т. е. точку соприкосновения шины с дорогой, так
что колесо толкает ось вперед и сообщает движение всей
машине. Ведь это правильно?
88
В.— Верно. Но вы не все учли.
Л.— Так же можно рассматривать паровоз, но у паровоза
нет ведущей цепи, а есть водило, и это радикально меняет
дело. Действительно, когда точка приложения силы со сто-
стороны водила к колесу находится над осью, сила поршня тя-
тянет колесо вперед, и здесь, так же как и у велосипеда, колесо
толкает паровоз вперед. Но ведь через пол-оборота точка
приложения силы к колесу будет под осью и сила будет на-
направлена назад. Рассуждая так же, как и раньше, приходим
к выводу: колесо толкает паровоз назад. Почему же паровоз
идет вперед?
В.— Все наши рассуждения о силах, действующих на
колесо, правильны, но ...
Выясните Вопрос.
420. Определить силу /, действующую со стороны рельса
на колесо (см. ответ задачи 419), в те моменты, когда место
соединения его с водилом (шип) находится над (или под)
осью колеса. Известны: сила давления
на поршень Q, радиус колеса R и рас-
расстояние от оси колеса до оси шипа г.
421. Тонкий стержень длиной а+Ь
шарнирно закреплен в точке, отстоящей
на расстояние Ь от одного из его концов,
и вращается с угловой скоростью со
вокруг вертикальной оси, описывая кру-
круговой конус (рис. 114). Определить угол
отклонения стержня от вертикали.
422. Найти угловую скорость прецес-
прецессии наклоненного волчка, прецессирую-
щего под действием силы тяжести. Вол-
Волчок имеет момент инерции /, угловую ско-
скорость вращения со, расстояние от точки
опоры до центра массы волчка равно L
В каком направлении будет прецессиро-
вать волчок?
423. Подсчитайте момент М гироскопических сил< дей-
действующих на вал со стороны пропеллера, если самолет при
скорости «=300 км/ч делает поворот радиуса /? = 100 м.
Пропеллер с моментом инерции /=7 кг-м2 делает N=
= 1000 об/мин.
424. Оценить, с какой минимальной скоростью v надо
выпустить на полюсе Земли снаряд массы /л=1000 т, чтобы
повернуть земную ось относительно системы «неподвижных
звезд» на угол а=1°. Масса Земли Af=6-1023iT. Длина
89
Рис. 114.
Рис. 115.
градуса земного меридиана /=111 км. Землю считать одно-
однородным шаром.
425. Симметричный волчок, ось фигуры которого нак-
наклонена под углом а к вертикали (рис. 115), совершает ре-
регулярную прецессию под действием силы тяжести. Точка
опоры волчка О неподвижна.
Определить, под каким углом р
к вертикали направлена сила, с
которой волчок действует на
плоскость опоры.
426. Гироскопический маят-
маятник, используемый в качестве
авиагоризонта, характеризуется
следующими параметрами: масса
маховичка гироскопа т=5 • 103 г,
момент инерции маховичка
относительно оси фигуры /ц ==
=8 • 104 г -см2, расстояние между
точкой подвеса и центром массы
маховичка а=0,25см. Гироскоп делает 20000 об/мин. Когда
самолет, на котором был установлен прибор, двигался равно-
равномерно, ось фигуры маятника была вертикальна. Затем в те-
течение времени т=10 с самолет двигался с горизонтальным
ускорением уо=1 м/с2. Определить угол а, на который от-
отклонится от вертикали ось фигуры гироскопического маят-
маятника за время ускорения.
427. Однородный гладкий сплошной шар, находящийся
на горизонтальном столе, быстро вертится вокруг своего
вертикального диаметра с угловой скоростью со0 (рис. 116)»
В него ударяет второй, в точнос-
точности такой же шар. Происходит
абсолютно упругий удар без пе-
передачи вращения. Ударяемый
шар начинает двигаться по сто-
столу со скольжением. Коэффициент
трения скольжения k считается
не зависящим от скорости. Найти
угол а между мгновенной осью
вращения ударяемого шара и вертикальной линией для лю-
любого момента времени /, когда еще не прекратилось сколь-
скольжение. Найти также значение этого угла в момент, когда
движение переходит в чистое качение. Трением верчения и
трением качения пренебречь. Рассмотреть частный случай,
когда величины v0 и соо связаны соотношением vo=(dor.
90
Рис. 116.
У////////////
Рис. 117.
428. Гироскопические эффекты используются в дисковых
мельницах. Массивный цилиндрический каток (бегун),
могущий вращаться вокруг своей геометрической оси, при-
приводится во вращение вокруг вертикальной оси (с угловой
скоростью Q) и катится по горизонтальной опорной плите
(рис. 117). Такое вращение можно рассматривать как вы-
вынужденную прецессию гироскопа, ка-
каковым является бегун. При вынуж-
вынужденной прецессии возрастает сила
давления бегуна на горизонтальную
плиту, по которой он катится. Эта
сила растирает и измельчает мате-
материал, подсыпаемый под каток на
плиту. Вычислить полную силу дав-
давления катка на опорную плиту, если радиус бегуна
г=50 см, а рабочая скорость 1 об/с.
429. Диск радиуса г, вращающийся вокруг собственной
оси с угловой скоростью со, катится без скольжения в на-
наклонном положении по горизонтальной плоскости, описы-
описывая окружность за время Т. Определить Т и радиус окруж-
окружности R, если i?^>r, а угол между
горизонтальной плоскостью и плос-
плоскостью диска равен а.
430. Условие, при котором сим-
симметричный гироскоп может совер-
совершать регулярную прецессию, мож-
можно получить, применяя теорему
Кориолиса. Рассмотреть тонкое
кольцо, равномерно вращающееся
в своей плоскости с угловой ско-
скоростью <о и прецессирующее вок-
вокруг одного из диаметров с постоян-
постоянной угловой скоростью Q (рис. 118). Какие силы надо прило-
приложить к кольцу для поддержания такой регулярной пре-
прецессии?
431. Планета движется вокруг Солнца по эллипсу, в
одном из фокусов которого находится Солнце. Доказать,
что момент количества движения планеты относительно
Солнца есть величина постоянная.
432. Доказать, что момент количества движения пла-
планеты относительно Солнца может быть представлен в виде
L=[r mv]=2ma=const,
где m — масса, а а — секториальная скорость планеты.
91
Рис. 118.
(Секториальной скоростью планеты называется площадь,
описываемая радиусом-вектором планеты за единицу вре-
времени.)
433. Найти производную по времени момента импульса
системы материальных точек L относительно начала коор-
координат О, движущегося с произвольной скоростью v0. Все
скорости материальных точек относить к «неподвижной»
(инерциальной) системе отсчета. В каких случаях результат
переходит в обычное соотношение L = Af?
434. Найти параметры эллипсоида инерции для точки Л,
лежащей в вершине однородного куба массы М с длиной
ребра I (рис. 119).
Ч.
Рис.
120.
Р*
\
Рис. 119.
435. Для прямоугольного однородного параллелепипеда
массы М и длиной ребер /, m, n (рис. 120) определить момент
инерции относительно его диагонали.
§ 8. Тяготение
436. Определить ускорение свободного падения g на по-
поверхности Земли по следующим данным: средний радиус
Земли /?»6400 км; средняя плотность Земли d=5,4 г/см8,
гравитационная постоянная G=6,7-10~8 дин*см2/г2.
437. Определить ускорение свободного падения g на
высоте 20 км над Землей, принимая ускорение свободного
падения на поверхности Земли go=981 см/с2, а радиус Земли
#«6400 км.
438. Найти ускорение свободного падения £л на Луне,
если ее радиус равен 1738 км, а средняя плотность составляет
0,6 плотности Земли.
439. Подсчитать ускорение свободного падения а на по-
поверхности Солнца, если известны #«150-10е км — радиус
земной орбиты, г«7-10б км — радиус Солнца и Т — время
обращения Земли вокруг Солнца.
440. Какое ускорение а сообщает Солнце телам, находя-
находящимся на Земле?
92
441. Тело на экваторе взвешивается на пружинных весах
в полдень, когда гравитационные силы Земли и Солнца тя-
тянут его в противоположные стороны. Одновременно такое же
тело взвешивается в полночь в диаметрально противополож-
противоположной точке земного шара, когда обе эти силы направлены в
одну сторону. Вес какого тела будет больше? Неоднород-
Неоднородностью гравитационного поля Солнца в окрестности Земли
пренебречь.
442. Решить предыдущую задачу с учетом неоднородно-
неоднородности гравитационного поля Солнца, считая, что, кроме Земли
и Солнца, никаких других небесных тел нет.
443. Найти разность между весами одинаковых тел в ди-
диаметрально противоположных точках земного шара, обу-
обусловленную неоднородностью гравитационного поля Луны,
Считать, что центры Луны, Земли и обе рассматриваемые
точки 1 и 2 лежат на одной прямой (см. задачу 441). От гра-
гравитационного поля Солнца и прочих астрономических тел
отвлечься.
444. Маятник, который делает в Ленинграде 3601,4
колебаний за час, за это же время и при той же температуре
делает в Москве 3600,0 колебаний. Каково отношение уско-
ускорений свободного падения для этих двух городов?
445. Как изменился бы ход маятниковых часов на Луне
по сравнению с их ходом на Земле?
446. Время обращения Юпитера вокруг Солнца в 12 раз
больше времени обращения Земли. Сколько километров от
Юпитера до Солнца, если расстояние от Земли до Солнца
равно 150-10е км. Считать орбиты планет круговыми.
447. Определить отношение массы Солнца М к массе
Земли /л, если среднее расстояние R от Земли до Солнца в
390 раз больше среднего расстояния г от Земли до Луны, а
время обращения Т Земли вокруг Солнца больше времени
обращения t Луны вокруг Земли в 13,4 раза.
448. Найти ускорение свободного падения gc на поверх-
поверхности Солнца, если известны: продолжительность земного
года Т, расстояние от Земли до Солнца R (^8,3 световых ми-
минуты) и угол а, под которым виден диаметр Солнца (^32').
449. Найти расстояние d планеты от Солнца, если даны:
масса Солнца М> период обращения планеты вокруг Солнца
Т и гравитационная постоянная G.
450. Луна делает полный оборот вокруг Земли за время
Т=27 сут 7 ч. Радиус ее орбиты равен 60 радиусам Земли.
Найти ускорение свободного падения g на Земле. Радиус
Земли /?^6400 км.
93
451. Силы приливного трения, вызываемые лунными
приливами, замедляют вращение Земли вокруг своей оси.
Этот процесс будет продолжаться до тех пор, пока угловая
скорость вращения Земли вокруг своей оси не станет равной
угловой скорости орбитального движения Луны вокруг
Земли. Определить общую угловую скорость вращения Зем-
Земли и орбитального вращения Луны со, продолжительность
земных суток Т и радиус лунной орбиты а, после того как
это произойдет. Использовать следующие данные: в настоя-
настоящее время угловая скорость вращения Земли вокруг своей
оси (о3 равна 7,29-Ю" рад/с, момент количества движения
Земли относительно своей оси /,3=5,91 -1040 г-см2/с, радиус
лунной орбиты ао=3,84-1О10 см, время обращения Луны
вокруг Земли (относительно звезд) Гл=27,3 сут, масса Луны
т=7,35-1026 г, момент инерции Земли относительно оси
вращения /3=8,11-1044 г-см2. Для простоты считать, что
земная ось перпендикулярна к плоскости лунной орбиты.
452. Найти потенциальную энергию тела (точки) массы
m на различных расстояниях R от центра Земли. Величину
потенциальной энергии на бесконечно большом расстоянии
считать равной нулю.
453. Согласно третьему закону Кеплера отношение куба
большой полуоси эллиптической орбиты а к квадрату пери-
периода обращения планеты Т есть величина, одинаковая для
всех планет Солнечной системы. Она называется постоянной
Кеплера и обозначается К- Третий закон Кеплера строго
справедлив, когда масса планеты пренебрежимо мала по
сравнению с массой Солнца. Найти выражение для постоян-
постоянной Кеплера.
454. Как изменится третий закон Кеплера, если не пре-
пренебрегать массой планеты тп по сравнению с массой Солн-
Солнца М?
455. Найти расстояние R между компонентами двойной
звезды, если их общая масса Мг+М2 равна удвоенной массе
Солнца Мо и звезды обращаются по круговым орбитам во-
вокруг их центра масс с периодом Т=2Т0, где То—продолжи-
То—продолжительность земного года. Расстояние от Земли до Солнца
#о=1,5-108 км.
456. Минимальное расстояние между компонентами
двойной звезды, обращающимися один относительно дру-
другого, равно гг. Относительная скорость их в этом положении
равна vx. Сумма масс обоих компонентов равна М. Найти
расстояние между компонентами г2 и их относительную ско-
скорость v2 при максимальном удалении относительно друг
94
друга. При каком минимальном значении относительной
скорости Vi двойная звезда распадается?
457. Показать, что если высота над земной поверхностью
мала по сравнению с радиусом Земли R, то зависимость
ускорения свободного падения от высоты определяется
приближенной формулой
g « g0 A -2 4") «ft A-0,00314/1),
где go— значение g на земной поверхности. Предполагает-
Предполагается, что высота h измеряется в километрах.
458. Для вычисления средней плотности Земли р Эйри
предложил и осуществил следующий метод. Измеряются
ускорения свободного падения g0 на поверхности Земли и g в
шахте глубины h. Принимается, что плотность Земли в по-
поверхностном слое толщины /г однородна и равна ро=з2,5 г/см3.
(Это предположение плохо соответствует действительности.)
В опытах Эйри было g—go=*0,000052 gQ, #//i=16 000
(R — радиус Земли). Пользуясь этими данными, вычислить
среднюю плотность Земли. (Обратите внимание, что g
вблизи поверхности Земли возрастает с глубиной! Чем
это объяснить?)
459. При каких условиях движение планеты вокруг
Солнца будет финитным и при каких — инфинитным?
(Финитным называется движение, при котором планета ос-
остается в ограниченной области пространства и не может ухо-
уходить в бесконечность. Если же область, в которой может
двигаться планета, неограничена, т. е. планета может ухо-
уходить в бесконечность, то движение называется инфинитным.)
460. Как показывает интегрирование уравнений движе-
движения, планета вокруг Солнца движется по коническим сече-
сечениям. Когда траектория планеты будет эллиптической, ги-
гиперболической и параболической?
461. Допустим, что в результате взрыва астероид, дви-
двигавшийся по круговой орбите вокруг Солнца, распался на
два осколка одинаковой массы. Один осколок непосредствен-
непосредственно после взрыва остановился, другой продолжал движение.
По какой траектории будет двигаться второй осколок: эл-
эллиптической, гиперболической или параболической?
462. В условиях предыдущей задачи оба осколка разле-
разлетаются в перпендикулярных направлениях с одинаковыми
скоростями. По каким орбитам они будут двигаться?
463. Снаряду с массой покоя то=ЮОО т сообщена ско-
скорость V в направлении касательной к земной орбите. Какова
95
должна быть разность между скоростью света с и скоростью
снаряда V, чтобы Земля стала двигаться относительно Солн-
Солнца по параболической траектории? Масса Земли М=6 «1021 т,
скорость ее орбитального движения у=29,8 км/с. Сравнить
кинетическую энергию снаряда с кинетической энергией ор-
орбитального движения Земли.
464. Планета движется вокруг Солнца па эллипсу. Не
интегрируя уравнений движения, а пользуясь только за-
законами сохранения энергии и момента импульса, найти вы-
выражение для длины большой оси 2а этого эллипса.
465. Комета движется вокруг Солнца по ветви гипербо-
гиперболы. Не интегрируя уравнений движения, а пользуясь только
законами сохранения энергии и момента импульса, найти
расстояние 2а между вершинами рассматриваемой и сопря-
сопряженной с ней ветвей гиперболы.
466. Какую скорость на поверхности Земли надо сооб-
сообщить искусственному спутнику, чтобы вывести его на эллип-
эллиптическую орбиту с расстояниями от центра Земли: в перигее
^1=31/зо R, в апогее г2=33/3о R (R — радиус Земли)?
467. Искусственный спутник Земли был выведен на ор-
орбиту с максимальным удалением от поверхности Земли
/!макс=1300 км и минимальным /гмип = 292 км. Через некото-
некоторое время период обращения спутника уменьшился на ДГ=
=3 мин. Какая часть начальной полной энергии спутника
была израсходована к этому моменту на работу против сил
трения? Радиус Земли /? = 6370 км.
468. Показать, что если планета движется по эллипсу,
то средние по времени значения ее полной и кинетической
энергий связаны соотношением
469. Показать, что если планета движется по кругу, то
ее полная и кинетическая энергии связаны соотношением
470. Пусть от поверхности Земли до ее центра прорыта
узкая шахта и некоторое тело падает из бесконечности в эту
шахту, достигая центра Земли. Какую скорость будет иметь
тело в этот момент, если Землю считать однородным
шаром?
471. Найти скорость v движения искусственного спут-
спутника Земли по круговой орбите радиуса R. Выразить зна-
значение v через /?, радиус Земли Ro и ускорение свободного
падения g на поверхности Земли.
96
472. Найти радиус R орбиты «стационарного» спутника
Земли. (Стационарным называют спутник, движущийся по
круговой орбите вокруг Земли так, что время его оборота
равно 24 часам.) Стационарный спутник, движущийся в
плоскости экватора в сторону вращения Земли, будет оста-
оставаться неподвижным относительно нее. Выразить R через
радиус Земли Ro, угловую скорость со вращения Земли и
ускорение свободного падения g на ее поверхности.
473. С воображаемой возвышенности, расположенной на
полюсе Земли, посылаются с одинаковой скоростью v0 два
снаряда. Начальная скорость первого снаряда направлена
так, что он движется по направлению радиуса Земли; на-
начальная скорость второго перпендикулярна к радиусу
Земли, и он движется по эллиптической траектории. 1) Ко-
Который снаряд достигнет максимального удаления от Земли?
2) Найти отношение RJR2 максимальных возможных рас-
расстояний от центра Земли соответственно первого и второго
снарядов. Скорость v0 > VgR0 = vKl>, где vKV есть скорость
движения спутника Земли по круговой орбите (теоретиче-
(теоретической) с радиусом Земли Ro. Сопротивление воздуха дви-
движению снарядов не учитывать и полагать, что на снаряд
действует только поле тяготения Земли.
474. С некоторой площадки на экваторе посылаются два
спутника по эллиптическим орбитам: первый в направлении
вращения Земли, второй против. Каково будет наибольшее
удаление Ri и R2 каждого из спутников от центра Земли,
если известно, что начальные горизонтальные скорости их
относительно Земли одинаковы по величине и равны уо=
= 10 км/с? Расстояния выразить через радиус Земли Ro.
475. Показать, что период спутника, обращающегося
вокруг планеты (или любого другого тела со сферически
симметричным распределением масс) в непосредственной
близости от ее поверхности зависит только от средней плот-
плотности планеты р. Вычислить период такого спутника для
нейтронной звезды, считая, что плотность вещества ней-
нейтронной звезды такая же, что и плотность вещества внутри
атомных ядер (р^Ю14 г/см3).
476. Как связаны между собой период Тг спутника, об-
обращающегося вокруг планеты в непосредственной близости
от ее поверхности, и период колебаний тела Т2 внутри пря-
прямолинейного канала, проходящего от одного полюса пла-
планеты к другому, если плотность вещества планеты р по-
постоянна? Качественно описать, как изменится соотношение
4 Под ред. И. А. Яковлева 97
между периодами., если плотность планеты при сохране-
сохранении ее массы будет возрастать к центру.
477. Вычислить массу Земли, используя параметры ор-
орбиты советского искусственного спутника «Космос-380». Пе-
Период обращения спутника (относительно звезд) Т= 102,2мин,
расстояние до поверхности Земли в перигее 210 км, в
апогее 1548 км. Землю считать шаром с радиусом 6371 км.
478. Среднее время обращения советского корабля-спут-
корабля-спутника «Восток», на котором Ю. А. Гагарин 12 апреля 1961 г.
впервые облетел вокруг земного шара, 7\=89,2 мин при
средней высоте полета над земной поверхностью h=
=254 км. Ближайший спутник Марса — Фобос — обра-
обращается вокруг планеты за время Т2=7 ч 39 мин, находясь
от центра Марса в среднем на расстоянии /?2=9350 км.
Определить отношение массы Марса М2 к массе Земли Л4Ь
если средний радиус земного шара # = 6371 км.
479. Искусственный спутник, имеющий форму шара ра-
радиуса г=0,5 м, обращается вокруг Земли по круговой орби-
орбите на такой высоте (я^200 км), где плотность атмосферы
р= 10"3 г/см8. Оценить, на сколько будет снижаться спут-
спутник за один оборот вокруг планеты. Плотность вещества
спутника, усредненная по его объему, ро=1 г/см8.
480. Спутник поднят ракетой-носителем вертикально
до максимальной высоты, равной /? = 1,25 /?з (#з — радиус
Земли), отсчитываемой от центра Земли. В верхней точке
подъема ракетное устройство сообщило спутнику азиму-
азимутальную (горизонтальную) скорость, равную по величине
первой космической скорости: v0—vu и вывело его на эллип-
эллиптическую орбиту (рис. 121). Каково максимальное и мини-
минимальное удаление спутника от центра Земли?
Рис 121.
Рис. 122,
481. Легкий спутник Земли вращается по круговой ор-
орбите с линейной скоростью Vq. Ракетное устройство увеличи-
98
вает абсолютную величину этой скорости в |/"l,5 раза, и
спутник переходит па эллиптическую орбиту (рис. 122).
С какой скоростью спутник пройдет наиболее удаленную от
центра Земли точку Л (апогей) своей орбиты? Сопротивление
атмосферы не учитывать.
482. Спутник Земли, вращаясь по круговой орбите ради-
радиуса R^Rs (низкий спутник), перешел на эллиптическую
орбиту с большой осью 2a=4i?3 (%з— радиус Земли).
Определить, во сколько раз увеличится время обращения
спутника? Сопротивление атмосферы не учитывать.
483. Спутник, вращаясь по круговой орбите радиуса
^=3/2^з (#з— радиус Земли), получает радиальный им-
импульс, который сообщает ему дополнительную скорость vp>
направленную от центра Земли по радиусу (рис. 123). Ка-
Каково должно быть минимальное значение дополнительной
скорости, чтобы спутник мог покинуть область земного
притяжения?
Рис. 123.
Рис. 124.
484. Спутник, вращаясь по круговой траектории радиуса
R = 2R3 (R3— радиус Земли), получает радиальный импульс,
сообщающий ему дополнительную скорость ур в направле-
направлении центра Земли, равную по величине скорости иф движе-
движения по круговой орбите (рис. 124). На какое минимальное
расстояние рмин приблизится спутник к центру Земли и
какова будет его скорость в этой точке? Сопротивление ат-
атмосферы не учитывать.
485. Спутник запускается на круговую орбиту в два эта-
этапа: сначала на поверхности Земли ему сообщают горизон-
горизонтальную скорость и выводят на эллиптическую орбиту,
перигей которой совпадает с точкой запуска (рис. 125),
а апогей — с точкой на круговой орбите. В апогее ракетное
4* 99
устройство увеличивает величину скорости спутника и
выводит его на круговую орбиту. Каковы должны быть на-
начальная скорость запуска Vi и увеличение скорости в апо-
апогее Аи, чтобы вывести спутник на круговую орбиту радиуса
R=2R3 (R3—радиус Земли)? Сопротивление атмосферы
не учитывать.
Рис. 125.
Рис. 126.
Восток
Ъаппд
486. Легкий спутник, вращаясь по круговой орбите ра-
радиуса R=2R3 (R3— радиус Земли), переходит на эллипти-
эллиптическую орбиту приземления, которая касается земной по-
поверхности в точке, диаметрально противоположной точке
начала спуска (рис. 126). Сколько времени продлится спуск
по эллиптической орбите? Со-
Сопротивление атмосферы не учи-
учитывать.
487. Спутник, круговая ор-
орбита которого расположена в
экваториальной плоскости, «ви-
«висит» неподвижно над некоторой
точкой земной поверхности.
Спутник получает возмущаю-
возмущающий импульс, сообщающий ему
малую вертикальную скорость
v0 (рис. 127). Какова возмущен-
возмущенная траектория спутника по
отношению к земному наблюдателю?
488. Определить вторую космическую скорость, или
скорость, которую нужно сообщить телу для того, чтобы
оно удалилось на бесконечно большое расстояние от Земли.
Каково должно быть направление этой скорости относитель-
относительно вертикали?
489. Вычислить приближенно третью космическую ско-
скорость, предполагая, что ракета выходит из зоны действия
100
Рис. 127.
земного тяготения под углом Ф к направлению орби-
орбитального движения Земли вокруг Солнца. Считать, что,
кроме Земли и Солнца, на ракету никакие другие тела
не действуют. (Третьей космической скоростью называется
минимальная скорость, которую надо сообщить ракете от-
относительно Земли, чтобы ракета навсегда покинула пре-
пределы Солнечной системы (ушла в бесконечность).)
490. Вычислить приближенно четвертую космическую
скорость, т. е. минимальную скорость, которую надо сооб-
сообщить ракете на поверхности Земли, чтобы ракета
могла упасть в заданную точку Солнца. Средний угловой
радиус Солнца а=4,65-10~3 рад. Предполагается, что
Земля движется вокруг Солнца по круговой орбите со ско-
скоростью Ук=29,8 км/с. Вычислить, в частности, значение
четвертой космической скорости при дополнительном усло-
условии, чтобы ракета падала на Солнце радиально (т. е. чтобы
продолжение ее прямолинейной траектории проходило через
центр Солнца).
491. Искусственный спутник Земли вращается по кру-
круговой орбите радиуса R с периодом 7\. В некоторый момент
на очень короткое время был включен реактивный двигатель,
увеличивший скорость спутника в а раз, и спутник стал вра-
вращаться по эллиптической орбите. Двигатель сообщал уско-
ускорение спутнику все время в направлении движения. Опре-
Определить максимальное расстояние спутника от центра Зем-
Земли, которого он достигнет после выключения двигателя.
Найти также период Т2 обращения спутника по новой
(эллиптической) орбите.
492. Космический корабль вращается вокруг Луны по
эллиптической орбите с максимальным удалением от по-
поверхности Луны (в апоселении) 312 км и минимальным уда-
удалением (в периселении) 112 км. На сколько надо изменить
скорость корабля, чтобы перевести его на круговую орбиту
с высотой полета над поверхностью Луны 112 км, если дви-
двигатель включается на короткое время, когда корабль нахо-
находится в периселении? (Средний радиус Луны # = 1378 км,
ускорение свободного падения на ее поверхности g=
= 162 см/с2.)
493. Космический корабль подходит к Луне по парабо-
параболической траектории, почти касающейся поверхности Луны.
Чтобы перейти на стелющуюся круговую орбиту, в мо-
момент наибольшего сближения включают тормозной двига-
двигатель, выбрасывающий газы со скоростью и=4 км/с отно-
относительно корабля в направлении его движения. Какую
101
часть общей массы системы будет составлять горючее, ис-
использованное для торможения корабля? (Данные, относя-
относящиеся к Луне, см. в предыдущей задаче.)
494. Вычислить вторую космическую скорость при старте
ракеты с поверхности Юпитера, используя следующие дан-
данные. Третий спутник Юпитера — Ганимед — вращается
вокруг планеты практически по круговой орбите радиуса
/?=1,07-106 км с периодом обращения Т=7,15 сут. Радиус
планеты г=7-104 км.
495. Искусственный спутник запущен вокруг Земли по
круговой орбите. Из-за наличия разреженной атмосферы
траектория спутника переходит в медленно свертываю-
свертывающуюся спираль. Как влияет сила сопротивления среды на
величину скорости спутника и момент количества движения
его относительно центра Земли? Спутник с массой /п=1 т
снижается за сутки на 100 м. Найти тангенциальную со-
составляющую ускорения спутника и силу сопротивления сре-
среды, которую он испытывает.
496. Космический корабль без начальной скорости сво-
свободно падает на Землю из удаленной точки. В каком месте
следует повернуть направление движения корабля на 90°
(без изменения величины его скорости), чтобы он стал дви-
двигаться вокруг Земли по круговой траектории?
497. Космический корабль движется вокруг Земли по
эллиптической орбите. В какой точке орбиты и на какой
угол следует изменить направление скорости корабля (без
изменения ее величины), чтобы корабль стал двигаться по
круговой орбите?
498. Космический корабль движется вокруг Земли по
эллиптической орбите. В точке пересечения эллипса с его
малой осью включается двигатель. Как надо изменить ско-
скорость корабля в этой точке, чтобы он перешел на параболи-
параболическую орбиту?
499. Наибольшее расстояние кометы Галлея от Солнца
/i=35,4, наименьшее /=0,59 (за единицу принято расстояние
Земли от Солнца). Линейная скорость движения кометы
^1=0,91 км/с в точке наибольшего удаления ее от Солнца в
афелии. Как велика линейная скорость v2 кометы, когда она
ближе всего подходит к Солнцу в перигелии?
500. Определить начальную скорость метеоритов v^,
"если максимальное прицельное расстояние, при котором они
еще падают на Землю, равно / (/>/?, R—радиус земного
шара). Получить численный ответ при /=27?. (Прицельным
расстоянием называется длина перпендикуляра, опущенно-
102
го из центра Земли на исходное направление касательной к
траектории метеорита, когда он находился в бесконечности.)
501. Найти отношение силы гравитационного притйже-
ния между двумя электронами (и двумя протонами) к силе
их электростатического отталкивания.
502. Найти потенциальную энергию и силу гравитацион-
гравитационного притяжения между однородной полой сферой массы М
и материальной точкой массы т.
503. Доказать, что две однородные полые сферы притя-
притягиваются друг к другу так, как если бы их массы были сосре-
сосредоточены в их центрах.
504. Доказать, что два однородных шара притягиваются
друг к другу так, как если бы масса каждого шара была
сосредоточена в его центре. Доказать также, что если вну-
внутри однородного шара имеется сферическая полость, центр
которой совпадает с центром шара, то гравитационное поле
внутри такой сферы равно нулю. Показать, что эти резуль-
результаты справедливы и для шаров с концентрически слоистым
распределением масс, т. е. таким, когда плотность вещества
р в каждом шаре зависит только от расстояния до его
центра.
505. Рассчитать напряженность гравитационного поля,
т. е. силу, действующую на единицу массы, внутри и вне
шара радиуса /?, заполненного веществом с постоянной объ-
объемной плотностью р.
506. Подсчитать гравитационную энергию U шара ра-
радиуса /?, равномерно заполненного веществом с объемной
плотностью р.
507. В прошлом столетии Г. Гельмгольц и В. Томсон
выдвинули гипотезу, согласно которой излучение Солнца
поддерживается за счет гравитационной энергии, освобожда-
освобождающейся при его сжатии. Оценить возраст Солнца / по такой
гипотезе, предполагая, что в начальном состоянии вещество
Солнца было равномерно распределено по всему бесконеч-
бесконечному пространству, а в конечном состоянии плотность сол-
солнечного вещества одинакова по всему объему Солнца. Масса
Солнца Л1=2-1033 г, радиус /? = 7-1010 см. Считать, что мощ-
мощность излучения Солнца за все время его образования оста-
оставалась постоянной и равнялась современному значению Р—
=3,86 -1033 эрг/с. Обсудить правдоподобность гипотезы
Гельмгольца — Томсона, приняв во внимание, что по гео-
геологическим данным возраст Земли составляет 4—4,5 -109 лет.
508. В сплошном однородном шаре с плотностью веще-
вещества р сделана сферическая полость, центр которой Ог
103
смещен относительно центра шара О (рис. 128). Найти гра-
гравитационное поле в такой полости.
509. Определить величину потенциальной энергии тела
(материальной точки), находящегося в воображаемой верти-
вертикальной шахте, проходящей через
центр Земли. Массу Земли считать
равномерно распределенной по все-
всему объему земного шара.
510. Тело падает с уровня по-
поверхности Земли в воображаемую
вертикальную шахту, проходящую
через центр Земли. Определить
скорость тела, когда оно будет про-
пролетать вблизи центра Земли. Тре-
Трение о стенки шахты и сопротивле-
Рис. 128. ние воздуха движению тела не
учитывать.
511. Представьте себе снаряд такого размера, что в нем
могут находиться люди вместе с приборами. Пусть этот сна-
снаряд летит в межпланетном пространстве с некоторым уско-
ускорением, обусловленным существующим в этой области про-
пространства полем тяготения. Что будут показывать нагружен-
нагруженные еще на Земле пружинные весы в снаряде? Каким спо-
способом можно измерять массу тел в снаряде во время полета?
512. Что будут показывать пружинные весы предыдущей
задачи при взвешивании тела массы т, если снаряд попадает
в атмосферу планеты и получает, кроме ускорения в поле
тяжести, ускорение а вследствие сопротивления атмос-
атмосферы движению снаряда?
513. В одной книге описывается, что в некоторый момент
времени обитатели снаряда, пущенного на Луну, перестали
ощущать наличие силы тяжести. Когда это может про-
произойти?
514. Простой анализ механических движений позволя-
позволяет выяснить, являются ли кольца планеты Сатурн сплош-
сплошным образованием или скоплением мелких спутников. Для
этого нужно лишь знать, какой край кольца, внутренний или
внешний, движется быстрее. Какие закономерности можно
положить в основу такого анализа?
515. Четыре тела А, В, С и D (рис. 129), которые можно
считать материальными точками, вращаясь вокруг некото-
некоторого центра, остаются все время на одной прямой и сохраня-
сохраняют неизменным расстояние друг от друга. Между всеми те-
телами действуют силы притяжения по закону всемирного тя-
104
готения Ньютона. Массы С и D равны и ничтожно малы по
сравнению с массами А и Б, а расстояние г очень мало по
сравнению с R. Какие еще силы должны действовать со
стороны тела В на С и D, чтобы расстояния между всеми
телами оставались неизменными?
R
Рис. 129.
516. Солнце притягивает тела, находящиеся на Земле,
с некоторой силой, которая ночью направлена в ту же сто-
сторону, что и силы притяжения этих тел Землей, а днем на-
направлена в обратную сторону. Вызывает ли это изменение
направления силы притяжения Солнца изменение веса тел
в течение суток? (См. задачи 441—443).
517. Анализируя результат предыдущих задач, объяс-
объясните происхождение приливов, вызываемых притяжением
Луны. Вычислите приливообразующую силу, или уменьше-
уменьшение силы веса тела, когда оно находится вблизи линии, сое-
соединяющей центры Земли и Луны.
518. Найти ту точку на прямой линии, соединяющей
Землю и Луну, в которой напряженность g результирующе-
результирующего поля тяготения Земли и Луны равна нулю. Масса Земли
приблизительно в 81 раз больше массы Луны, среднее рас-
расстояние между этими планетами 384 000 км.
519. Пренебрегая сопротивлением атмосферы, найти
минимальную работу,4 которую надо затратить, чтобы до-
доставить массу в 1 кг с поверхности Земли на поверхность
Луны. Радиус Земли 6400 км, радиус Луны 1740 км; уско-
ускорение свободного падения на Луне, вызванное ее собствен-
собственным притяжением, составляется=0,16 £з> где#3=9,8м/с2—
ускорение свободного падения на поверхности Земли.
Влияние Солнца и других планет не учитывать.
§ 9. Упругие деформации
520. Коэффициент линейного теплового расширения ста-
стали равен 12 -Ю" ОС~Х, модуль Юнга £=2 -1012 дин/см2.
Какое давление р необходимо приложить к торцам стального
цилиндра, чтобы длина его оставалась неизменной при по-
повышении температуры на 100 °С?
105
521. Можно ли использовать кабель из тонкой медной
проволоки в свинцовой броне для телефонной связи с привяз-
привязным аэростатом, находящимся на высоте 300 м? Предел
прочности свинца 2 кгс/мм2. Плотность свинца 11,4 г/см3.
522. При укладке рельсов трамвая их сваривают между
собой в стыках. Как велики напряжения /?, появляющиеся
в них при колебаниях температуры от /2=—25 °С зимой до
/2=30°С летом, если укладка произведена при /t = 15 °С?
Для железа модуль Юнга £=2-106 кгс/см2, а линейный ко-
коэффициент теплового расширения а=1,25 -10~б °С"Х.
523. Стальной канат, могущий выдержать вес неподвиж-
неподвижной кабины лифта, имеет диаметр 9 мм. Какой диаметр
должен иметь канат, если кабина лифта может иметь уско-
ускорение до 8 g!
524. Насколько изменится объем упругого однородного
стержня длины / под влиянием силы Р, сжимающей или ра-
растягивающей стержень по его длине?
525. Какую равномерно распределенную нагрузку Q
может выдержать гранитная плита, представляющая собой
правильный шестиугольник со стороной а=10 см, если до-
допускаемое напряжение на сжатие гранита равно р=
=45 кгс/см2?
526. Насколько вытягивается стержень из железа, под-
подвешенный за один конец, под влиянием собственного веса?
Насколько при этом меняется его объем?
527. Стержень поперечного сечения S растягивается
силой F, параллельной его оси. Под каким углом а к оси
наклонено сечение, в котором тангенциальное напряжение т
максимально? Найти это напряжение.
528. Резиновый цилиндр с высотой ft, весом Р и пло-
площадью основания S поставлен на горизонтальную плоскость.
Найти энергию упругой деформации цилиндра, возникаю-
возникающей под действием его собственного веса. Во сколько раз
изменится энергия упругой деформации рассматриваемого
цилиндра, если на верхнее основание его поставить второй
такой же цилиндр.?
529. Определить относительное изменение объема поло-
полого латунного шара радиуса #=5 см, в который накачан
воздух до давления 11 атм (наружное давление 1 атм).
Толщина сферической оболочки d=\ мм. Модуль Юнга ла-
латуни £=1012 дин/см2, коэффициент Пуассона |ut=0,3.
530. Прямоугольная пластинка зажата между верти-
вертикальными плоскостями, перпендикулярными к оси X, так
что в направлении этой оси частицы пластинки смещаться
106
не могут (рис. 130). В направлении оси Z пластинка подвер-
подвергается равномерному одностороннему давлению Р. Опреде-
Определить давление РХУ которому подвергается пластинка со
стороны плоскостей, между которыми она зажата. Найти
выражение для плотности упругой энергии и, а также отно-
относительное сжатие пластинки в направлении оси Z и относи-
относительное расширение в направлении оси Y.
У////////////////////////////У/Л
Рис. 131.
531. Стержень длины / шарнирно закреплен на одном
конце и подвешен на двух пружинах (рис. 131); коэффициент
жесткости пружины, прикрепленной к концу, равен ku
а прикрепленной к середине — &2. Определить удлинение
пружин и силы натяжения их под действием нагрузки Р,
приложенной к концу стержня. Стержень считать абсолют-
абсолютно жестким и невесомым, а пру-
пружины нерастянутыми в отсутствие
внешней нагрузки.
532. Груз подвешен на трех
тросах, как указано на рис. 132.
Тросы сделаны из одного материа-
материала, причем два крайних троса оди-
одинаковой длины. Найти соотношение
между напряжениями в материале
тросов, если деформации при на-
нагрузке очень малы.
533. Груз весом Р подвешен на
трех тросах, как сказано в условии предыдущей задачи
(см. рис. 132). Найти усилия в тросах, если все они имеют
одинаковые сечения и сделаны из одного материала.
534. На трех тягах одинаковой длины подвешена аб-
абсолютно жесткая балка, к которой привязан груз Р
(рис. 133). Тяги сделаны из одного материала и имеют се-
сечения Si, S2 и S3. Определить усилия в тягах Рь Р2, Рз,
107
если они расположены на одинаковых расстояниях, а груз
подвешен посередине между двумя тягами. Определить ус-
ловие, при котором все три
тяги будут растянуты.Весом
балки можно пренебречь.
Рис. 133.
Рис. 134.
Рис. 135.
535. Стальной стержень с прямоугольным сечением
(рис. 134) заделан одним концом в стену. Отношение высоты
стержня к его ширине равно 3:1. Для стержня выбран пя-
пятикратный запас прочности. 1) Какая нагрузка Р допустима
на конце стержня, если длина его 15 см, а ширина 5 мм?
Разрушающее напряжение в материале равно 100 кгс/мм2.
2) Рассчитать стрелу прогиба \
стержня при допустимой на-
нагрузке. Модуль Юнга равен Е=
= 20 000 кгс/мм2.
536. Балка закреплена кон-
концами на шарнирах (рис. 135)
причем один из шарниров под-
подвижен. Определить стрелу про-
прогиба X балки под действием силы Р, приложенной к середи-
середине балки. Известны длина балки /, модуль Юнга мате-
материала Е и момент инерции поперечного сечения /. Балку
считать невесомой и прогибы очень малыми.
537. Решить задачу 531, считая стержень упругим
(рис. 131). Модуль Юнга материала стержня равен Е и мо-
момент инерции поперечного сечения равен /.
538. Коромысло весов имеет прямоугольное сечение со
сторонами а==8 мм (горизонтальная) и Ь=10мм (вертикаль-
(вертикальная). Длина коромысла /=250 мм. Какова наибольшая
стрела прогиба коромысла Я, если весы рассчитаны на мак-
максимальную нагрузку Р=500 гс, а модуль Юнга материала
коромысла равен 15 000 кгс/мм2?
539. Деревянная балка длины 1=4 м и квадратного се-
сечения со стороной а=40 см покоится своими концами на двух
108
опорах и несет посередине груз Р==2 тс. Как велика стрела
прогиба А,, если модуль Юнга данного сорта дерева равен
1000 кгс/мм2?
540. Медная трубка, внешний и внутренний диаметры
которой D = 20 мм и d=10 мм, концами опирается на под-
подставки, расстояние между которыми /=400 мм. Посередине
трубка несет груз Р=90 кгс. Модуль Юнга для меди Е=
= 104 кгс/мм2. Определить стрелу прогиба X трубки посере-
посередине между опорами.
541. Круглый металлический стержень радиуса R=
= 10 мм закреплен одним концом в горизонтальном положе-
положении, а на другом его конце висит груз Р=1 кгс. Длина стер-
стержня 1-Х м. Стержень под влиянием груза прогибается,
стрела прогиба А,=4 мм. Чему равен модуль Юнга£ матери-
материала стержня?
542. Как изменилось бы выражение для расчета модуля
Юнга Е в предыдущей задаче, если бы стержень был укреп-
укреплен обоими концами, а груз помещен посередине?
543. Стержень круглого сечения расположен вертикаль-
вертикально и закреплен верхним концом. К нижнему концу прикреп-
прикреплен горизонтально блок радиуса /?=50 мм. Ось стержня про-
проходит через центр блока. От концов диаметра блока идут по
касательной две нити, на которые действуют равные силы
Р=Ъ кгс, закручивающие блок в одном направлении. На
какой угол ф закрутится стержень? Модуль сдвига материа-
материала стержня N=8000 кгс/мм2, радиус стержня г=Ъ мм, длина
его 1=1 м.
544. На тонкий вертикальный вал насажен эксцентрично
диск массы т\ расстояние между центром диска и осью
вала равной. Известно, что горизонтальная сила, приложен-
приложенная к валу в месте закрепления диска, вызывает смещение,
пропорциональное силе. Коэффициент пропорционально-
пропорциональности k. Найти прогиб вала £ при угловой частоте вращения
вала со. Массой вала по сравнению с массой диска можно
пренебречь.
545. Как показывает опыт, скорость v распространения
импульса поперечных деформаций вдоль натянутой одно-
однородной струны зависит от силы ее натяжения F и от массы р,
приходящейся на единицу длины струны. Пользуясь мето-
методом размерностей, найти выражения зависимости скорости
v от указанных параметров струны.
546. Рамку чувствительного гальванометра, вращаю-
вращающуюся между полюсами магнита, подвешивают на тонкой
платиновой нити. Найти максимальный допустимый вес
109
рамки гальванометра, если предел прочности, платины
^30 кгс/мм2, а для подвеса использована нить диаметром в
4 мкм.
547. Как показывает опыт, скорость v распространения
продольных деформаций в сплошной среде зависит от мо-
модуля упругости среды £ и от ее плотности р. Пользуясь ме-
методом размерностей, найти выражения для зависимости v
от указанных параметров среды.
548. В упругом стержне создана такая начальная дефор-
деформация сжатия, что скорости всех частиц в деформированной
области направлены в одну сторону (например, вправо),
причем в каждой точке плотность потенциальной энергии
в а раз превосходит плотность кинетической энергии. Опре-
Определить, какая доля первоначальной энергии будет унесена
возмущением, распространяющимся вправо, а какая доля-
возмущением, распространяющимся влево.
Указание. В бегущем возмущении плотность потен-
потенциальной энергии равна плотности кинетической.
г
Рис 136.
649. Проволоку натягивают между двумя зажимами А и
В, находящимися на расстоянии / (рис. 136). На середине
проволоки подвешивают груз весом Р, вследствие чего воз-
возникает прогиб X. Определить зависимость прогиба X от Р,
если известны модуль Юнга
Е, диаметр проволоки d ц
выполнено условие -у<^1.
550. Какую максимальную
скорость может приобрести
стрела массы т при стрельбе
21
-W
Хп«1
р р рбе
из лука? Считать, что концы
Рис. 137. лУка при выстреле движутся
по прямой, а натяжение тети-
тетивы линейно зависит от смещения ее центра: Т=Т0+%х,
где Го— предварительное натяжение тетивы, а х — по-
постоянный коэффициент (рис. 137).
ПО
551. Стальная проволока диаметром d=l мм огибает ба-
барабан диаметром D=2 м. Определить дополнительные на-
напряжения, возникающие в материале проволоки, если мо-
модуль Юнга стали £=2-106 кгс/см2.
552. На гладкую горизонтальную плоскость положен
брусок АВ из однородного материала массы т, сечения S
и длины L, упирающийся одним концом в выступ (рис. 138).
F * '
У////////////////////////////////Л
Рис. 138.
На другой конец бруска действует постоянная сила F, рав-
равномерно распределенная по всему сечению бруска. Тогда,
как известно, длина бруска уменьшится на величинуА1=
AL =« ~g- -дг F, где Е —модуль Юнга. Спрашивается, насколь-
насколько сожмется брусок и как в нем будет распределено сжатие,
если он не будет упираться в выступ, а все прочие условия
останутся неизменными?
553. Упругий стержень массы т, длины / и площади
поперечного сечения S движется в продольном направлении
с ускорением а (одинаковым для всех точек стержня). Найти
упругую энергию деформации, воз-
возникающую вследствие ускоренного
движения.
554. Из задачи 552 вытекает, что
в ускоренно движущемся бруске
существует напряжение. Будет ли
существовать напряжение в сво-
свободно падающем бруске?
555. Однородный диск массы М
и радиуса R вращается вокруг сво- рИс. 139.
ей оси с угловым ускорением |$
(рис. 139). Силы, ускоряющие диск, равномерно, распреде-
распределены по ободу диска. Найти касательную силу F, дейст-
действующую на единицу длины окружности, ограничивающей
мысленно выделенную часть диска радиуса г (заштрихован-
(заштрихованную на рисунке).
556. Тонкий однородный упругий стержень, длина ко-
которого L, масса М и модуль Юнга £, равномерно вращается
с угловой скоростью со вокруг оси, перепендикулярной к
стержню и проходящей через один из его концов. Найти
111
распределение усилий Т в стержне и полное его удлине-
удлинение AL. При подсчете линейной деформации и усилий
считать поперечное сечение неизменным и удлинение
малым.
§ 10. Колебания
557. Построить графики зависимости от времени сме-
смещения, скорости и ускорения при простом гармоническом
колебании. Построить графики зависимости скорости и ус-
ускорения от смещения. Найти соотношения между ампли-
амплитудами смещения, скорости и ускорения.
558. Найти выражения для потенциальной, кинетиче-
кинетической и полной энергии материальной точки массы /л, со-
совершающей гармоническое колебание по закону Acosa>t.
559. Два одинаковых груза массы m связаны пружиной
(рис. 140). Как изменится частота собственных колебаний
системы, если один из грузов за-
закрепить?
560. Ареометр с цилиндрической
трубкой диаметра D (рис. 141),
Г~ТЛЛЛЛ/Ч~~1
Рис. 140.
Рис. 141.
плавающий в жидкости плотности р, получает небольшой
вертикальный толчок. Найти период колебаний Т ареомет-
ареометра, если масса его m известна. Движение жидкости и ее со-
сопротивление движению ареометра не учитывать.
561. На ракете, взлетающей вертикально вверх с уско-
ускорением а, установлены маятниковые часы. Какой промежу-
промежуток времени Тг измерят часы с
момента старта ракеты до па-
падения ее на Землю, если дви-
двигатель работал время Т во
время подъема ракеты, изме-
измеренное по часам на Земле?
562. Жидкость налита в
изогнутую трубку {рис. 142),
колена которой составляют с
горизонтом углы аир, длина столба жидкости I. Если жид-
жидкость выведена из положения равновесия, то начинаются
112
Рис. 142.
колебания уровня в трубках. Найти период колебаний*
Капиллярными силами и вязкостью жидкости пренебречь.
563. Вертикальный цилиндр, имеющий поперечное сече-
сечение 3=80 см2, закрывается поршнем массы т=1 кг. Объем
цилиндра под поршнем vo=5 л. В начальный момент дав-
давление /?о воздуха в цилиндре равнялось атмосферному. Ка-
Каково будет движение поршня, если его сразу отпустить?
Трение между поршнем и цилиндром отсутствует. Считать
процесс сжатия и расширения воздуха адиабатным (у=
=^=1,4).
564. Что изменится в предыдущей задаче, если вместо
воздуха в цилиндре будет: 1) водород; 2) гелий? Остальные
условия те же.
565. Представьте себе шахту, пронизывающую земной
шар по одному из его диаметров. Найти закон движения
тела, упавшего в эту шахту, учитывая изменения значения
ускорения свободного падения внутри Земли. Трение о
стенки шахты и сопротивление воздуха не учитывать.
566. Как изменится период малых колебаний маятника,
подвешенного вблизи поверхности Земли, если под маят-
маятником в Земле сделана сферическая полость радиуса г=8 м,
а расстояние между центром полости и точкой подвеса ма-
маятника /г=20 м? Длина маятника пренебрежимо мала по
сравнению с h. Средняя плотность Земли ро=5,5 г/см3,
плотность грунта у поверхности Земли в окрестности поло-
полости р=2,75 г/см3. Радиус Земли # = 6400 км.
567. Рассмотреть движение поезда под действием силы
тяжести в отсутствие трения и сопротивления воздуха в ги-
гипотетическом туннеле длиной /=6400 км, прорытом вдоль
одной из хорд земного шара. Влияние осевого вращения
Земли не учитывать. Как будет направлена линия отвеса
в движущемся поезде? Какое время будут показывать маят-
маятниковые часы, установленные на поезде, когда он достигнет
противоположного конца хорды, если на поверхности Зем-
Земли они шли точно? Землю считать однородным шаром радиу-
радиуса # = 6400 км.
568. Самолет летит с постоянной скоростью, описывая
окружность на постоянной высоте. Какое направление будет
указывать нить отвеса, подвешенного в салоне самолета?
Найти период малых колебаний математического маятника
внутри самолета, если длина маятника равна /, корпус са-
самолета наклонен к направлению горизонта под углом а.
569. Самолет летает на постоянной высоте по окружно-
окружности радиуса #=25 км с постоянной скоростью у=250 м/с.
из
m
В кабине самолета установлены пружинные и маятниковые
часы. Какое время полета f покажут маятниковые часы,
если это время, измеренное пружинными часами, равно
/=1 ч? Часы считать идеальными. Силу Кориолиса, ввиду
ее малости, не учитывать.
570. На тележке укреплен горизонтальный стержень, по
которому может скользить без трения муфта массы т=1 кг
а ^ (рис. 143). К муфте
*" прикреплены две пру-
пружины, общий коэффи-
коэффициент жесткости кото-
которых &=0,1 кгс/см. Как
будет двигаться груз
относительно системы
отсчета, связанной с те-
тележкой? Рассмотреть
два случая: 1) тележка
получает ускорение,
очень медленно нарастающее от нуля до а=0,98 м/с2;
2) тележка в момент t=0 внезапно получает ускорение а,
остающееся затем неизменным. Трение считать очень малым.
571. В состоянии равновесия центры масс муфты и те-
тележки, описанные в условии предыдущей задачи, находи-
находились на одной вертикали (см. рис. 143). Какое возникает
движение, если муфту сместить от положения равновесия
на величину 1=6 см и прикрепить нитью к тележке, а
затем нить пережечь? Масса тележки без муфты равна
М—5 кг, массой пружины можно пренебречь. Силу трения не
учитывать.
Ш7Ш/////////уШ^
Рис. 143.
т
-о
Рис 144.
572. Найти период свободных малых колебаний грузика
массы т, укрепленного на середине тонкой струны длины
L (рис. 144). Массой струны можно пренебречь; натяжение
струны постоянно и равно Р.
114
673. Материальная точка в поле тяжести скользит по
хорде круга А В без начальной скорости (рис. 145). Пока-
Показать, что время ее движения из точки А в точку В не зави-
зависит от положения точки А на окружности. (Этот факт был
использован Галилеем для установления законов малых ко-
колебаний "математического маятника.
Для нахождения периода колебаний
маятника Галилей заменил малую
дугу окружности ADB, по которой
движется материальная точка, хордой
А В.) Вычислить период колебаний
маятника в этом приближении и убе-
убедиться, что оно приводит к правиль-
правильной зависимости периода колебаний от
длины маятника I и ускорения сво-
свободного падения g. Сравнить резуль-
результат с правильной формулой.
574. Через неподвижный блок с
моментом инерции / (рис. 146) и радиусом г перекинута
нить, к одному концу которой подвешен груз массы /п.
Другой конец нити привязан к пружине с закрепленным
нижним концом. Вычислить период колебаний груза, если
коэффициент упругости пружины равен &, а
нить не может скользить по поверхности блока.
575. К пружине, один конец которой за-
закреплен, подвешен груз веса Р, лежащий на
подставке так, что пружина не растянута
(рис. 147). Без толчка под-
подставка убирается. Найти дви-
движение груза и максимальное
натяжение пружины. Коэф-
Коэффициент жесткости k пружи-
пружины известен.
576. Найти частоту малых | \р
собственных колебаний около
положения устойчивого равновесия для
системы, показанной на рис. 148. Нить
невесома и нерастяжима, блоки невесомы
и не имеют трения в осях.
677. На доске лежит груз весом
Р=1 кгс. Доска совершает гармоническое
колебание в вертикальном направлении с периодом Г=*1/2с
и амплитудой а~2 см. Определить величину силы давле-
давления F груза на доску.
115
Рис. 146
Рис. 147.
578. С какой амплитудой А должна колебаться доска с
грузом в предыдущей задаче, чтобы груз начал отскакивать
от доски?
Рис. 148.
Рис. 149.
у/////////////////.
579. На массивной чашке пружинных весов лежит ма-
маленький грузик (рис. 149). Масса чашки равна т, масса
грузика пренебрежимо мала. Ко дну чашки подвешен груз
массы М. Вся система находится в равновесии. При каком
соотношении между массами Мит грузик на чашке начнет
подскакивать, если быстро снять груз М?
580. Горизонтальная мембрана совершает синусоидаль-
синусоидальные колебания с круговой частотой со и амплитудой А. На
мембране лежит маленький грузик. При каком условии
грузик будет колебаться вместе с мембраной и при каком он
начнет подскакивать?
581. Доска совершает гармоническое колебание в гори-
горизонтальном направлении с периодом Г=5 с. Лежащее на
ней тело начинает скользить, когда ам-
амплитуда колебания достигает величины
А =0,6 м. Каков коэффициент трения покоя
k между грузом и доской?
582. На чашку весов, подвешенную на
пружине, падает с высоты h груз массы т
и остается на чашке (рис. 150), не подпры-
подпрыгивая относительно нее. Чашка начинает
колебаться. Коэффициент жесткости пру-
пружины k. Определить амплитуду А колеба-
колебаний (массой чашки и пружины по сравнению
с массой груза можно пренебречь).
583. К пружине прикреплена нить, на которой висит
груз массы т=1 кг (рис. 151). Оттягивая груз вниз и от-
отпуская, приводят его в колебания. На какое расстояние х
116
Рис. 150.
можно оттянуть вниз груз, чтобы при колебаниях нить все
время была натянута? Коэффициент жесткости пружины
k=0,05 кгс/см.
{//////////////////л
Рис. 151.
Рис. 152.
584. Материальная точка (например, шарик на пружи-
пружине) под действием квазиупругой силы F=—kx совершает
колебания вдоль оси X вокруг положения равновесия. По-
Показать, что средние по времени значения кинетической и
потенциальной энергий при таких колебаниях одинаковы.
585. Тело подвешено на пружине и имеет собственный
период колебаний 1/2 с (рис. 152). На тело действует направ-
направленная вертикально синусоидальная сила с амплитудой F=
= 100 дин и некоторая сила трения. Определить амплитуду
FTp силы трения и коэффициент трения (сила трения про-
пропорциональна скорости движения), если амплитуда коле-
колебаний при резонансе Лр составляет 5 см.
586. Система совершает вынужденные колебания под
действием внешней силы, изменяющейся по гармоническо-
гармоническому закону. Показать, что при резонансе при прочих рав-
равных условиях работа внешней силы за период будет макси-
максимальной.
587. Однородная палочка подвешена за оба конца на
двух одинаковых нитях длины L. В состоянии равновесия
обе нити параллельны. Найти период Т малых колебаний,
возникающих после некоторого поворота палочки вокруг
вертикальной оси, проходящей через середину палочки.
588. Тело вращения радиуса а с моментом инерции /
(относительно геометрической оси) и массой m катается без
скольжения по внутренней поверхности цилиндра радиуса
117
/?, совершая малые колебания около положения равнове-
равновесия (рис. 153). Найти период этих колебаний.
589. Решить предыдущую задачу в предположении, что
тело катается по внутренней поверхности эллиптического
Рис. 153.
Рис. 154.
цилиндра. Одна из главных осей соответствующего эллип-
эллипса 2А расположена горизонтально, а другая 2В (ось симмет-
симметрии) — вертикально (рис. 154).
590. Достаточно тонкая пластинка из однородного ма-
материала имеет форму равностороннего треугольника высо-
////у у//у ты h (рис. 155). Она может вра-
вращаться вокруг горизонтальной оси,
совпадающей с одной из сторон
пластинки. Найти период малых
колебаний Т этого физического
маятника.
591. Кольцо из тонкой проволо-
проволоки совершает малые колебания, как
маятник около горизонтальной оси
(рис. 156). В одном случае ось
лежит в плоскости кольца (рис. 156, а), в другом пер-
перпендикулярна к ней (рис. 156, б). Определить отношение
Рис. 155.
а)
Рис. 156.
периодов малых колебаний 7\ и Т2 при этих двух видах
колебаний кольца.
118
592. Сплошной однородный диск с радиусом г-=10 см
колеблется около оси, перпендикулярной к плоскости диска
и проходящей через край диска. Какой длины / должен быть
математический маятник, имеющий тот же период колеба-
колебаний, что и диск?
593. Диск состоит из двух половин одинаковой толщи-
толщины: одна половина алюминиевая (плотность 2,5 г/см3), вто-
вторая — свинцовая (плотность 10 г/см3). Каково будет от-
отношение периодов колебаний этого диска вокруг осей, пер-
перпендикулярных к плоскости диска? В од-
одном случае ось проходит через точку Л, в
другом — через точку В (рис. 157).
Рис. 157.
Рис. 158.
594. Физический маятник состоит из стержня квадрат-
квадратного сечения, подвешенного за конец, и груза, прикреплен-
прикрепленного на другом конце (рис. 158). Груз имеет форму куба с
ребром а=40 мм, а стержень длину /=400 мм и сторону се-
сечения 6=4 мм; груз и стержень сделаны из одного материа-
материала. Найти приближенное значение периода колебаний Т
такого маятника (при расчете можно полагать стержень до-
достаточно тонким).
595. При колебаниях маятника, описанного в предыду-
предыдущей задаче, с амплитудой ао= 10°, груз отрывается от стерж-
стержня в тот момент, когда маятник проходит положение равно-
равновесия. Каковы будут амплитуда а'о и период колебаний Т
стержня после отрыва груза?
596. Ответить на вопросы, поставленные в предыдущей
задаче, если груз отрывается при наибольшем отклонении
маятника от положения равновесия.
597. Тонкий однородный стержень длины / качается
около оси, проходящей через конец стержня перпейдику-
119
Рис. 159.
Рис. 160.
лярно к нему. Есть ли такое место на стержне, прикрепив
к которому небольшое по размерам тело значительной мас-
массы, мы не изменим периода колебаний стержня?
598. Маятник метронома представляет собой груз М,
качающийся около оси О, с прикрепленной к нему спицей,
по которой может перемещаться малый груз т (рис. 159).
Как зависит период колебаний
маятника от координаты х грузи-
грузика? Массу т считать точечной.
599. В какой точке следует под-
подвесить однородный стержень длины
/ (рис. 160), чтобы частота его ко-
колебаний, как физического маятни-
маятника, была максимальна? Чему равна
эта частота?
600. На тонкий стержень дли-
длины / надето с трением небольшое
кольцо массы т. Какая сила дейст-
действует со стороны стержня на коль-
кольцо, когда стержень, подвешенный за конец, колеблется, как
маятник с малой угловой амплитудой а0? Расстояние коль-
кольца от оси маятника равно d. Массой кольца при вычислении
периода колебаний можно пренебречь.
601. Однородная пластинка, имеющая форму равносто-
равностороннего треугольника, подвешена за вершины тремя нитя-
нитями, имеющими одинаковую длину L. В состоянии равнове-
равновесия пластинка горизонтальна и нити вертикальны. Найти
период крутильных колебаний
пластинки вокруг вертикальной
оси (считать, что каждая нить^
отклоняется на малый угол от
вертикали).
602. На горизонтальной плос-
плоскости находится цилиндр с мо-
моментом инерции / (относительно
продольной геометрической оси),
массой т и радиусом /*. К оси
цилиндра прикреплены две оди-
одинаковые горизонтально расположенные спиральные пру-
пружины, другие концы которых закреплены в стене (рис. 161,
вид сверху). Коэффициент упругости каждой пружины
равен k\ пружины могут работать как на растяжение, так
и на сжатие. Найти период малых колебаний цилиндра,
которые возникнут, если вывести его из положения равно-
120
Рис. 161.
весия и дать возможность кататься без скольжения по
горизонтальной плоскости.
603. Однородная квадратная плита подвешена за свои
углы к потолку зала на четырех параллельных веревках,
длина каждой из которых равна /. Определить период ма-
малых крутильных колебаний плиты, которые возникнут,
если повернуть ее на малый угол вокруг вертикальной оси.
604. Три однородных стержня длины / каждый соеди-
соединены короткими нитями, образуя фигуру в виде перевер-
перевернутой буквы П. Горизонтальный стержень этой системы
поворачивают на малый угол вокруг вертикальной оси,
проходящей через центр системы, и отпускают. Найти
период возникших при этом малых колебаний, если массы
стержней одинаковы.
Рис. 162.
Рис. 163.
Рис. 164.
605. Шарик массы т подвешен на двух последовательно
соединенных пружинках с коэффициентами упругости kx и k2
(рис. 162). Определить период его вертикальных колебаний.
606. Найти период крутильных колебаний диска, плот-
плотно насаженного на составной стержень, состоящий из двух
различных последовательно соединенных стержней (рис.
163). Верхний конец А стержня неподвижно закреплен.
Если бы диск был насажен только на первый стержень, то
период колебаний был бы равен 7\. Если бы он был насажен
только на второй стержень, то период колебаний оказался
бы равным Г2.
607. Найти период малых колебаний физического маят-
маятника массы т, к центру масс С которого прикреплена гори-
горизонтальная спиральная пружина с коэффициентом упруго-
упругости k. Другой конец пружины закреплен в неподвижной
стенке (рис. 164). Момент инерции маятника относительно
121
точки подвеса равен /, расстояние между точкой подвеса р
центром масс маятника равно а. В положении равновесия
пружина не деформирована.
608. Колебательная система состоит из однородного
стержня длины / и массы /я, который может вращаться во-
вокруг горизонтальной оси О, проходящей через его конец и
перпендикулярной к продольной оси стержня (рис. 165).
Другой конец стержня подвешен на пружине с коэффициен-
коэффициентом упругости k. Расстояние между серединой стержня и
осью вращения С0=а. Момент инерции стержня относи-
относительно оси О равен /. Найти удлинение пружины х0 (по
сравнению с ее длиной в недеформированном состоянии)
в положении равновесия, если в этом положении стержень
горизонтален. Определить также период малых колебаний
стержня около положения равновесия.
Рис. 165.
Рис. 166.
609. К концу однородного стержня длины / и массы т
прикреплена короткая упругая пластинка. Пластинку зажи-
зажимают в тисках один раз так, что стержень оказывается вни-
внизу, а другой раз — вверху (рис. 166). Определить отноше-
отношение периодов малых колебаний стержня в этих случаях.
Момент упругих сил пластинки пропорционален углу от-
отклонения стержня от положения равновесия, причем коэф-
коэффициент пропорциональности равен k.
610. Два незакрепленных шарика с массами т\ и т2
соединены друг с другом спиральной пружинкой с коэффи-
коэффициентом упругости k. Определить период колебаний шари-
шариков относительно центра масс системы, которые возникнут
при растяжении пружинки.
611. Два диска с моментами инерции 1г и /2 насажены
на общую ось, проходящую через их центры. Осью является
стержень с модулем кручения /. Определить период крутиль-
122
ных колебаний одного диска относительно другого в пред-
предположении, что система свободна. Массой стержня пренеб-
пренебречь.
612. Как изменится ход карманных часов, если их поло-
положить на горизонтальный абсолютно гладкий стол? Считать,
что ось крутильного маятника часов проходит через их
центр, а момент инерции часов /0 в 500 раз больше момента
инерции маятника /♦
613. Два сплошных однородных цилиндра одинакового
радиуса R с массами тх и т2 лежат на горизонтальном сто-
столе и соединены между собой
двумя одинаковыми пружина-
пружинами с коэффициентом упруго-
упругости k каждая, как показано на
рис. 167 (вид сверху). Опреде-
Определить период малых колебаний,
которые возникнут, если рас-
растянуть пружины и предоста- Рис- 167.
вить систему самой себе, не
сообщая ей дополнительной скорости. Цилиндры катаются
по столу без проскальзывания около неподвижного центра
масс системы. Пружины могут работать как на растяже-
растяжение, так и на сжатие.
614. На тележке, стоящей на горизонтальных рельсах,
подвешен маятник длины /, масса которого М сравнима с
массой тележки т. Тележка может кататься по рельсам
практически без трения. Найти период малых колебаний
маятника. Массой колес пренебречь.
615. На конце тонкого однородного стержня длины /
проделано малое отверстие, через которое продета горизон-
горизонтально натянутая непрогибаемая проволока. Найти перио-
периоды малых колебаний такого физического маятника в двух
случаях: 1) когда маятник колеблется в вертикальной плос-
плоскости, перпендикулярной к проволоке; 2) когда колебания
происходят в вертикальной плоскости, параллельной про-
проволоке. Во втором случае точка подвеса маятника может
скользить по проволоке без трения. Найти также отноше-
отношение этих периодов.
616. В сплошном однородном цилиндре радиуса R сдела-
сделана цилиндрическая полость радиуса R/2 с осью, проходя-
проходящей через середину радиуса цилиндра (см. рис. 247). Опре-
Определить период малых колебаний Г, которые возникнут, ес-
если положить цилиндр на горизонатальную плоскость и дать
ему возможность кататься по ней без скольжения.
123
617. Физический маятник состоит из двух одинаковых
массивных шаров радиуса г=5 см на невесомом стержне
(рис. 168). Ось маятника расположена на расстоянии Ь==
= 10 см ниже центра верхнего шара. При каком расстоянии
х между центрами шаров период маятника Т будет наимень-
наименьшим? Найти этот период, приведенную длину маятника / и
расстояние а между осью и центром масс маятника С.
618. По штанге, вращающейся в горизонтальной плос-
плоскости с постоянной угловой скоростью (о, может скользить
без трения груз массы т, удерживаемый
на некотором расстоянии от оси вращения
пружиной с коэффициентом упругости k и
начальной длиной г0. Найти движение гру-
груза, которое возникнет, если штангу мгно-
веннно остановить.
|ЛЛЛ/У-|
^—О
Рис. 168.
Рис. 169
619. На горизонтальной пружине укреплено тело мас-
массы Л1 = 10 кг, лежащее на гладком столе, по которому оно
может скользить без трения (рис. 169). В это тело попадает
и застревает в нем пуля массы т=10 г, летящая с горизон-
горизонтальной скоростью и=500 м/с, направленной вдоль оси пру-
пружины. Тело вместе с застрявшей в нем пулей отклоняется
от положения равновесия и начинает колебаться относи-
относительно него с амплитудой а=10 см. Найти период колеба-
колебаний тела.
тЧОг
т-п
Рис. 170.
620. На струне с постоянным натяжением в 4 кгс укреп-
укреплены две массы по 10 г, как показано на рис. 170. Какие
124
следует задать начальные условия грузикам, чтобы они со-
совершали гармоническое колебательное движение с одина-
одинаковым периодом? Вычислить частоту этих колебаний (их
называют нормальными). Отклонения при колебаниях счи-
считать очень малыми по сравнению с /.
621. Н. Е. Жуковским было предложено устройство
совершенного (без потерь) подвеса маятника, схемати-
схематически показанное на рис. 171. Муф-
Муфта Л, насаженная на вал С, состав- С^у~^Л
ляет одно целое с маятником В. Вал
расположен горизонтально и равно-
равномерно вращается с угловой скоростью
со, маятник совершает колебания в
плоскости, перпендикулярной к валу.
Показать, что если угловая ско-
скорость вала достаточно велика и сила
трения муфты о вал не зависит от
скорости скольжения, то потери энер-
энергии колебаний в подвесе не будет. Как
велика должна быть угловая скорость
вращения вала?
622. Каким образом изменится ха-
характер колебаний маятника, если
сила трения муфты овал (см. рис. 171)
будет зависеть от скорости скольже-
скольжения муфты по валу, при сохранении
остальных условий предыдущей задачи? Рассмотреть два
случая: 1) сила трения возрастает с увеличением скорости
скольжения; 2) сила трения уменьшается с увеличением
скорости скольжения.
623. Определить положение равновесия, около которо-
которого совершает колебания маятник, описанный в предыду-
предыдущей задаче. Известно, что сила трения вала о муфту равна
\iP, где [г — постоянная величина, Р — величина давле-
давления муфты на вал; расстояние от оси вращения до центра
массы маятника равно а и радиус вала R.
§ 11. Гидростатика и аэростатика
624. Два сплошных тела из одного и того же вещества
подвешены к концам неравноплечего рычага и уравнове-
уравновешивают друг друга в воздухе. 1) Сохранится ли равновесие,
если погрузить эти тела в сосуд с водой? 2) Изменится ли
равновесие, если вещество тел различно?
125
Рис
625. Из какого материала надо сделать гири, чтобы при
точном взвешивании можно было не вводить поправки на по-
потерю веса в воздухе?
626. Полый металлический шар, внешний и внутренний
диаметры которого dx и d2, плавает на поверхности жидко-
жидкости. Плотность металла рь плотность жидкости р2. Какой
груз р нужно добавить внутрь шара, чтобы он плавал внут-
внутри жидкости? Сжимаемостью шара можно пренебречь.
627. Найти условие устойчивости однородного прямо-
прямоугольного параллелепипеда, плавающего на поверхности
жидкости в положении, когда одно из оснований его гори-
горизонтально. Длины сторон горизонтального основания А и В,
высота С(А>В). Плотность материала тела относительно
жидкости р<1.
628. Та же задача для однородного цилиндра радиуса г
и высоты /, плавающего в вертикальном положении.
629. Та же задача для однородного цилиндра радиуса г
и длины /, плавающего в горизонтальном положении.
630. Какова подъемная сила F 1 м3 гелия, идущего на
наполнение дирижаблей, если плотность гелия относитель-
относительно воздуха равна 0,137 и 1 м3 воздуха весит 1,3 кгс?
631. Баллон сферического аэростата имеет объем
700 м3. Баллон наполнен водородом, 1 м3 которого при дав-
давлении в 1 атм весит 90 гс. Вес корзины, оболочки, всех при-
принадлежностей и двух пассажиров 447 кгс. 1) Сколько надо
добавить балласта AXQ, чтобы аэростат уравновешивался
вблизи поверхности Земли при нормальном давлении?
2) Сколько надо затем сбросить балласта A 2Q, чтобы поднять-
подняться на высоту 2 км, если на этой высоте 1 м3 воздуха весит
1 кгс? У поверхности Земли 1 м8 воздуха весит 1,3 кгс.
632. На дне сосуда с жидкостью (или газом) лежит тело,
плотность которого немного больше плотности жидкости
(или газа). Можно ли, повышая давление на жидкость
(или газ), заставить тело подняться
вверх.
633. Каково давление Р воздуха
в кессоне, опущенном в воду и пред-
предназначенном для подводных работ на
дне реки на глубине h м, если атмо-
атмосферное давление равно Н мм рт. ст.?
Рис. 172. Плотность ртути р.
634. Тонкая палочка одним концом
прикреплена к стенке сосуда, а другим погружена в воду
(рис. 172). Палочка может свободно вращаться относитель-
126
но горизонтальной оси шарнира Л, находящегося над уров-
уровнем жидкости. Найти плотность р материала палочки, если
при равновесии в воду не погружена \1п часть палочки.
Капиллярные силы не учитывать.
635. Найти силу давления F воды на квадратную стенку
аквариума (сторона равна а). На какой высоте h от дна на-
находится точка приложения равнодействующей сил давле-
давления на стенку?
636. Желоб имеет сечение, указанное на рис. 173. Желоб
наполнен до краев водой. Определить силу давления Р на
1 м длины боковой стенки и момент этой силы М относитель-
относительно ребра А дна.
L1
Рис. 173.
Рис. 174.
637. Сечение желоба дано на рис. 174. Желоб наполнен
водой. Ответить на вопросы, поставленные в предыдущей
задаче.
638. Найти результирующую силу давления Р воды на
речную плотину, имеющую форму трапеции (рис. 175),
если h = 5м, й=10м,с=15м.
639. Специальным щитом j
закрывают воду в канале, по-
подающем воду на мельничное
колесо. Определить момент
сил, действующих на щит
относительно горизонтальной
оси, лежащей в плоскости
щита на высоте 0,25 м над
уровнем воды, если ширина
канала 1 м и высота уровня запертой в канале воды
0,75 м.
640. Подсчитать усилие, разрывающее вертикальный
шов на высоте Н= 1 м в цилиндрическом сосуде, наполнен-
наполненном водой до краев (рис. 176).
127
Рис. 175.
641. Баллоны из ткани, которая выдерживает на раз-
разрыв 850 кгс на погонный метр, наполнены газом х). Балло-
Баллоны с газом представляют собой шары радиуса 10 м. Какое
превышение давления Ар над атмосфер-
атмосферным допустимо в баллонах?
642. На какой высоте h плотность воз-
воздуха в земной атмосфере уменьшается
вдвое (предполагается, что температура
атмосферы неизменна по всей ее высоте)?
У поверхности Земли считать давление
е р0 = 10 330 кгс/м2 и плотность воздуха
Ро===1, 293 кг/м3.
643. Найти распределение давления
внутри земного шара, считая его состоя-
состоящим из однородной несжимаемой жидкос-
жидкости и пренебрегая осевым вращением Земли.
Вычислить в том же приближении давле-
давление в центре Земли Рц (см. задачу 505).
644. На тележке стоит сосуд с водой.
Тележка движется в горизонтальном на-
направлении с ускорением 0,29 g. Какой угол а с горизонтом
составляет поверхность воды?
645. Цилиндрический замкнутый сосуд, наполненный
водой, закрыт сверху пробкой (рис. 177). Какое ускорение
а в горизонтальном на-
направлении вдоль оси сосуда
нужно сообщить сосуду для
того, чтобы пробка вылете-
вылетела, если она может выдер-
выдержать давление 0,05 атм, а
расстояние отверстия от
одного днища сосуда 1 м
и от другого 0,1 м?
646. Как изменился бы ответ к предыдущей задаче, ес-
если бы сосуд был не цилиндрическим, а имел вид усеченного
конуса, но расстояния отверстия до днищ оставались бы
теми же самыми?
Рис. 176
Рис. 177.
*) Упругие напряжения, действующие во всякого рода оболочках,
пленках и т. п., удобно характеризовать силой, отнесенной к единице
длины поперечного сечения оболочки. Приведенная в условиях задачи
прочность ткани на разрыв означает, что полоса этой ткани шириной
в 1 м может, не разрываясь, выдержать равномерно распределенную по
ширине полосы силу в 850 кгс.
128
647. Поезд, в составе которого имеется закрытая цис-
цистерна с нефтью, двигался со скоростью vOy а затем в резуль-
результате торможения начал двигаться равномерно замедленно и,
пройдя отрезок пути s, остановился. Найти силы давления
нефти на заднюю и переднюю стенки цистерны во время тор-
торможения поезда. Цистерну считать прямоугольным парал-
параллелепипедом с длиной /, шириной а и высотой h\ плотность
нефти равна р.
648. Оценить сплюснутость Земли, обусловленную ее
осевым вращением, считая Землю однородным несжимае-
несжимаемым жидким шаром.
§ 12. Гидродинамика и аэродинамика
649. Какова скорость v истечения жидкости из отверстия
в стенке сосуда, если высота h уровня жидкости над отвер-
отверстием 4,9 м? Вязкость жидкости не учитывать.
650. Цистерна наполнена водой и нефтью (плотность
0,9 г/см3). Какова будет вначале скорость v истечения воды
из отверстия в дне, если высота слоя воды /ij = l м, а слоя
нефти /i2=4 м? Вязкостью пренебречь.
651. Подсчитать максимальное давление ветра, имею-
имеющего скорость 20 м/с, на горизонтальную стену, если ветер
дует перпендикулярно к стене. Величину давления выра-
выразить в сантиметрах водяного столба. Плотность воздуха
считать равной V« кгс-с2/м4.
652. В цилиндрическом сосуде, стоящем на подставке,
расположены два отверстия на расстоянии 25 см одно над
другим. Струи, вытекающие из отверстий, пересекаются.
Найти точку пересечения струй, если известно, что уро-
уровень воды выше верхнего отверстия на 25 см.
1_
Рис. 178.
653. На рис. 178 представлена схема водомера: по го-
горизонтальной трубе переменного сечения протекает вода.
5 Под ред. И. А. Яковлева 129
Определить расход воды Q по разности уровней воды Ah в
двух манометрических трубках, если сечения трубы у осно-
оснований трубок известны.
654. Схема устройства, позволяющего паровозу на ходу
пополнять запас воды, изображена на рис. 179. Вдоль
рельсов устроен канал, наполненный водой. К паровозу
приделана изогнутая тру-
труба, опускающаяся в канал
так, что ее отверстие на-
направлено вперед. Подсчи-
Подсчитайте, на какую высоту h
поднимется вода, если
скорость v поезда равна
36 км/ч. Вязкостью воды
пренебречь.
655. Когда один моряк
пытался в трюме судна зак-
закрыть доской небольшое
отверстие, через которое
врывалась струя воды, то это ему не удавалось, струя
отбрасывала доску. Когда же с помощью товарища ему
удалось прижать доску плотно к отверстию, то он мог затем
держать ее один. Объяснить, почему давление на доску в
обоих случаях разное?
656. В аэродинамических трубах с помощью вентиля-
вентилятора создается поток воздуха. Контур закрытой аэродина-
аэродинамической трубы круглого сечения имеет форму, показан-
показанную на рис. 180. В начале трубы находится раструб, через
Рис. 179.
-2м 1м
1,6м
Рис. 180.
который засасывается воздух из окружающей среды, затем
идет цилиндрическая часть, в которую помещают модель.
Далее — расширяющаяся труба и за ней опять цилиндри-
цилиндрическая, в которой и располагается вентилятор. 1) Рассчи-
Рассчитать давление Ар снаружи на стенку средней цилиндри-
цилиндрической части трубы при скорости потока и=100 м/с.
2) Как изменится результат, если учесть взякость воздуха?
130
657. Схема устройства пульверизатора изображена на
рис. 181. Определить максимальную высоту А, на которую
он может засасывать жидкость из резервуара, если давле-
давление перед входом в трубку Л,
где скорость очень мала, рав-
равно р0. Вязкостью пренебречь.
Рис. 181.
Рис. 182.
658. Подсчитайте, какая сила F вырывает из бака слив-
сливную трубку, если поперечное сечение струи S=4 см2, а
расход воды Q=24 л/мин? Трубка имеет форму, показан-
показанную на рис. 182.
659. Найти зависимость от времени силы F, действую-
действующей на дно цилиндрического стакана площади S, в который
наливают воду из чайника
(рис. 183). Известно, что
за секунду в стакан нали-
наливают постоянное количест-
количество Q см3 воды.
660. В вертикально
стоящий цилиндрический
сосуд налита идеальная
жидкость до уровня Н (от-
(относительно дна сосуда).
Площадь дна сосуда равна
S. Определить время /, за
которое уровень жидкости
в сосуде опустится до вы-
высоты А (относительно дна сосуда), если в дне сосуда сде-
сделано малое отверстие площади а. Определить также время
Т, за которое из сосуда выльется вся жидкость.
661. Прямоугольная коробка плавает на поверхности
воды, погружаясь под действием собственного веса на глу-
глубину А. Площадь дна коробки равна 5, высота Н. Через
Рис. 183.
5*
131
какое время коробка утонет, если в центре дна ее проде-
проделать малое отверстие площади а и с помощью боковых
направляющих сохранять неизменной ориентацию ко-
коробки?
662. Через какое время наполнится водой шаровая кол-
колба радиуса R, если в центре ее нижнего основания сделано
малое отверстие площади а? Колба погружена в воду до
нижнего основания ее горлышка.
663. На горизонтальной поверхности стола стоит ци-
цилиндрический сосуд, в который налита вода до уровня Н
(относительно поверхности стола). На какой высоте h (от-
(относительно поверхности стола) надо сделать малое отвер-
отверстие в боковой стенке сосуда, чтобы струя воды встречала
поверхность стола на максимальном расстоянии от сосуда?
Вычислить это расстояние.
664. Определить форму сосуда, чтобы уровень жидкости
в нем опускался с постоянной скоростью, если в централь-
центральной точке дна проделать малое отвер-
отверстие.
665. В широкий сосуд с плоским
дном налита идеальная жидкость. В
дне сосуда сделана длинная и узкая
щель, в которую вставлена насадка,
образованная двумя плоскостями, на-
наклоненными друг к другу под малым
углом (рис. 184). Расстояние между
ними в нижней части насадки равно
11у а в верхней— /2. Определить рас-
распределение давления жидкости в на-
насадке, если атмосферное давление рав-
равно Ро- Длина насадки равна Л, расстояние между нижним
концом насадки и уровнем жидкости в сосуде равно Я.
666. Вода вытекает из широкого резервуара через вер-
вертикальную коническую трубу, вставленную в его дно. Дли-
Длина трубы равна /, диаметр верхнего основания du нижнего
основания d2(di>d2). При каком уровне Н воды в резервуа-
резервуаре давление в верхнем сечении трубы будет равно Р, если
атмосферное давление равно Ро?
667. Определить скорость v стационарного истечения
через малое отверстие струи идеальной несжимаемой жид-
жидкости, находящейся под давлением Р в закрытом сосуде
(рис. 185).
668. Для того чтобы струя жидкости вытекала из сосуда
с постоянной скоростью, применяют устройство, изобра-
132
-
—-
p
к
h
ИС.
ll .
184.
женное на рис. 186. Определить скорость истечения струи v
в этом случае.
669. Определить скорость стационарного течения вдоль
оси и расход несжимаемой жидкости между двумя коакси-
коаксиальными цилиндрами с внутренним радиусом Ri, внешним R2
и длиной /. (Расходом жидкости называется масса ее, еже-
ежесекундно протекающая через поперечное сечение трубы.)
Рис. 185.
Рис. 186.
670. Показать, что при ламинарном стационарном тече-
течении несжимаемой жидкости вдоль прямолинейной трубы
произвольного поперечного сечения S и длины / скорость
жидкости v удовлетворяет уравнению
ду*'гдг*'1г
lx\
F70.1)
(Координатная плоскость YZ перпендикулярна к оси трубы,
оси Y и Z взаимно перпендикулярны и ориентированы про-
произвольно.)
671. Определить скорость течения и расход жидкости в
трубе эллиптического сечения.
672. Пользуясь соображениями размерности, найти вид
формулы, определяющей раеход несжимаемой жидкости
при стационарном ламинарном течении вдоль прямолиней-
прямолинейной трубы произвольного поперечного сечения.
673. На тележке стоит цилиндрический сосуд, напол-
наполненный водой. Высота воды в сосуде 1 м. В сосуде с противо-
противоположных сторон по ходу тележки сделано два крана с от-
отверстиями площадью 10 см2 каждое, одно на высоте /ii=
=25 см над дном сосуда, а другое на высоте /i2==50 см. Ка-
Какую горизонтальную силу F нужно приложить к тележке,
чтобы она осталась в покое при открытых кранах?
133
674. На весах для демонстрации давления жидкости
на дно сосуда (рис. 187) установлен прямой цилиндр с во-
водой. Высота столба воды в нем h=25 см. Как изменится на-
нагрузка, уравновешивающая давление на дно, если через от-
отверстие в дне цилиндра вытекает струя воды с сечением
5=1/4 см2? Понижение уровня воды в цилиндре можно не
учитывать.
Рис. 187.
675. Как изменится сила давления воды на щит (см. за-
задачу 639), если поднять его над дном канала так, что из-под
щита будет вытекать струя воды высотой 5 см, а уровень воды
перед щитом останется прежним? Скорость по высоте струи
считать одинаковой.
676. Дать приближенный расчет максимальной мощно-
мощности и определить наивыгоднейшую скорость вращения ниж-
небойного колеса (рис. 188),
если известны: высота на-
напора воды /i=5m, попереч-
поперечное сечение струи S =
=0,06 м2, радиус колеса
/? = 1,5 м. Вода струи не-
непрерывно бьет в лопасти и
после удара падает вниз.
677. Вода, вытекающая
из насадки пожарного на-
насоса, имеет скорость, дос-
достаточную для того, чтобы
струя достигала высоты
20 м. Насколько поднимет-
поднимется температура воды, если направить эту струю в закрьГтый
неподвижный бак? Считать, что выделяющееся тепло пойдет
только на нагревание.воды. Трением воздуха пренебречь.
134
Рис. 188.
678. При обсуждении проекта гидроледореза — маши-
машины для резания льда струей воды, выбрасываемой под дав-
давлением около 60 атм, высказывалось предположение, что
резание льда происходит за счет того, что при ударе о лед
вода нагревается и лед под ней тает. Обсудите справедли-
справедливость такого предположения.
679. Определить форму свободной поверхности жидко-
жидкости, равномерно вращающейся с угловой скоростью со во-
вокруг вертикальной оси Z в цилиндрическом сосуде.
680. 1) Найти распределение давления р на дне сосуда
вдоль радиуса в условиях предыдущей задачи. 2) Определить
величину давления у стенок сосуда вблизи его дна, если со-
сосуд вращается со скоростью 4 об/с. Высота столба воды на
оси цилиндра равна 10 см. Радиус цилиндра равен также
10 см.
681. Цилиндр, наполненный водой, закрыт со всех сто-
сторон; в нем находятся: пробка, кусочек свинца и некоторое
тело А, плотность которого равна плотности воды. Цилин-
линдр приводят в быстрое вращение вокруг его оси. Как
будут расположены тела в цилиндре, если ось вращения
вертикальна?
682. Цилиндр, наполненный водой, равномерно враща-
вращается со скоростью 1 об/с вокруг вертикальной оси, увле-
увлекая за собой и воду. К гладкому горизонтальному стержню,
расположенному по диаметру цилиндра и погруженному
в воду, прикреплен кубик с ребром в 2 см, сделанный из
материала с плотностью р=2 г/см3. Кубик прикреплен
так, что может скользить по стержню и удерживаться пру-
пружинкой на расстоянии 50 см от оси цилиндра. Найти на-
натяжение пружинки Т.
683. Во вращающемся сосуде давление на дно у стен-
стенки сосуда (см. задачу 680) больше, чем в центре. Поче-
Почему же при вращении сосуда вода не течет от стенки к его
центру?
684. Можно ли измерить распределение давления
жидкости во вращающемся сосуде следующими спосо-
способами.
1) Манометрическая трубочка В вращается вместе с со-
сосудом и заполняется той же жидкостью, что и сосуд, как
указано на рис. 189. Капиллярные давления в трубоч-
трубочках можно не учитывать.
2) Манометрическая трубочка состоит из двух частей,
соединенных через муфту С, как показано на рис. 190.
Часть трубочки АС закреплена неподвижно относительно
135
сосуда, вторая часть CD неподвижна относительно земли.
Муфта С обеспечивает герметичное соединение этих частей
и находится на оси цилиндра.
3) Манометрическая трубочка имеет такой же вид, как
показано на рис. 190, но обе части трубочки у муфты С скре-
скреплены друг с другом. Следовательно, и часть АС неподвиж-
неподвижна относительно земли. Трубочка АС, находящаяся в сосу-
сосуде, достаточно тонка и не влияет на движение жидкости.
Край отверстия А расположен горизонтально.
Л
Рис. 189.
Рис. 190.
685. В сосуде, изображенном на рис. 189, над водой на-
находится масло, так что высота слоя масла в центре равна
2 см. Какую форму принимает теперь поверхность воды при
вращении сосуда около вертикальной оси и как изменится
высота уровня в трубочке, если плот-
плотность масла 0,8 г/см3?
686. Вращающаяся в сосуде вода
приняла форму, изображенную на
15см рис. 191. Высота воды у стенки сосуда
h= 15 см. Найти силу F, действующую
на вертикальную полоску стенки со-
сосуда шириной в 1 см.
687. Цилиндрический сосуд ра-
радиуса R с налитой в него идеальной
Рис 191. несжимаемой жидкостью вращается
вокруг своей геометрической оси,
направленной вертикально, с угловой скоростью со. Оп-
Определить скорость истечения струи жидкости через малое
отверстие в боковой стенке сосуда при установившемся
движении жидкости (относительно сосуда).
688. Некто предложил следующий проект вечного дви-
двигателя. Сосуд А (рис. 192) плотно окружен кольцевым же-
136
лобом С с трубкой В; стенки сосуда имеют отверстия Е,
через которые жидкость из сосуда проходит в желоб С и
трубку В. Сосуд А может вращаться, а желоб С остается
при этом в покое. Легко видеть, что при вращении возни-
возникает движение жидкости по трубке В, если она предвари-
предварительно вся была заполнена жидкостью. При равномерном
Л
вращении сосуда А жидкость будет переливаться через
трубку В, и струю жидкости можно использовать для при-
приведения во вращение водяного колеса D. Автор проекта
предлагал часть работы водяного колеса, через специаль-
специальную передачу (на рисунке не показана), использовать на
преодоление трения при рав-
равномерном вращении сосуда. По-
Почему не будет работать такой
двигатель?
689. В боковой стенке сосуда
имеется отверстие, нижний край
которого находится на высоте h
(рис. 193). При каком горизон-
горизонтальном ускорении а сосуда налитая в него жидкость не
будет выливаться из отверстия, если в покоящемся сосуде
(при закрытом отверстии) жидкость была налита до высо-
высоты Я?
690. Сосуд прямоугольной формы, наполненный водой,
может без трения перемещаться вдоль горизонтальных рель-
137
Рис. 193.
сов (рис. 194). В боковой стенке сосуда вблизи его дна сде-
сделано малое отверстие, закрытое пробкой. Если вынуть
пробку, то под действием силы реакции вытекающей струи
сосуд придет в движение. Определить скорость этого дви-
движения, когда вся жидкость вытечет из сосуда. Массу сосуда
в течение всего времени движения считать пренебрежимо
малой по сравнению с массой воды. (В конце движения это
условие перестанет выполняться. Обсудить, как это обстоя-
обстоятельство повлияет на точность окончательного результата.)
Негоризонтальностью поверхности жидкости во время дви-
движения пренебречь.
Рис. 194.
Рис. 195.
691. Решить предыдущую задачу в предположении, что
сосуд имеет коническую форму (рис. 195).
692. На рис. 196 изображен известный опыт с течением
вязкой жидкости по трубе, показывающий падение давления
—
н
'-15с
] \
■-1
-■10 см
: ♦
\;]5ш
Г~~ -"■> ' ■*"*'" ' ■ "^
* 1[)см ♦<♦ tgCM +U-1
Рис. 196.
вдоль трубы. Как на основании данных, указанных на
рисунке, определить скорость вытекающей жидкости, если
плотность ее равна 1 г/см3?.
138
693. Для определения подъемной силы крыла важно
знать, что при плоском безотрывном обтекании г) тела
идеальной жидкостью сила, действующая вверх со стороны
потока на любой мысленно вырезанный вертикальный ци-
цилиндрик сечения dS> выражается так:
VtPivl-vl) dS,
где Vi— скорость у верхней поверхности цилиндрика, v2—
—у нижней, р — плотность жидкости. Вывести приведен-
приведенную формулу.
694. Модель корабля длиной /2=5 м приводится в дви-
движение мотором с мощностью Рг=5 л. с. со скоростью V!=
= 15 км/ч. Какой мощности Р требуется мотор для приведе-
приведения в движение корабля длиной /=80 м, геометрически по-
подобного модели, если его движение гидродинамически по-
подобно движению модели? Определить скорость корабля v
при таких условиях.
695. Во сколько раз следует изменить угловую скорость
вращения вертикального винта вертолета и мощность его
двигателя, чтобы подъемная сила осталась неизменной
при замене винта и самого корпуса вертолета геометрически
подобными им, но с линейными размерами, увеличенными в
а раз?
§ 13. Акустика
696. Пуля пролетела со скоростью 660 м/с на расстоя-
расстоянии 5 м от человека. На каком расстоянии от человека была
пуля, когда он услышал ее свист?
697. Эхолот измеряет глубину моря по отражению зву-
звука от морского дна. Какова должна быть минимальная точ-
точность в определении времени отправления и возврата сиг-
сигнала, если прибор рассчитывается на измерение глубин
более 30 м с точностью до 5%? Скорость звука в воде
1500 м/с.
698. Паровоз подходит к наблюдателю со скоростью
20 м/с. Какую частоту основного тона гудка он услышит,
если машинист слышит тон в 300 Гц? Насколько изменится
частота гармоник гудка?
г) При плоском течении каждая трубка тока лежит в плоскости,
параллельной некоторой заданной плоскости. Безотрывное течение —
такое, при котором жидкость плавно обтекает тело без образования за-
завихрений за телом.
139
699. Два камертона дают 20 биений за 10 с. Частота ко-
колебаний одного камертона 256. Чему равна частота колеба-
колебаний другого?
700. Камертон, излучающий звук частоты v0, прибли-
приближается к удаленной стене со скоростью и по нормали к ней.
Неподвижный приемник звука помещается на линии дви-
движения камертона. Пусть: 1) камертон находится между
стеной и приемником; 2) приемник находится между камер-
камертоном и стеной. Будет ли приемник звука регистрировать
акустические биения, если скорость и много меньше скоро-
скорости звука с? Какова будет частота этих биений?
Стержень
J/\ Тиски
Рис. 197.
701. При измерении скорости звука методом пыльных
фигур Кундта (рис. 197) длина полуволны звука в воздухе
оказалась равной 6 см. Чему равна скорость v звука в
стержне, если длина стержня равна 60 см и закреплен он в
середине?
702. Длина закрытой с концов трубы равна 1,7 м. Под-
Подсчитать собственные частоты Nk этой трубы.
703. Найти частоты Nkf на которые будет резонировать
труба длиной 1,7 м, закрытая с одного конца.
704. В цилиндрической, открытой с концов трубе воз-
возбуждаются колебания, соответствующие второй гармонике.
Изобразить графически распределение амплитуды смещения
частиц вдоль трубы, распределение амплитуд скорости и
амплитуд давления. Указать места, в которых потенциаль-
потенциальная и кинетическая энергия имеют наибольшее значение.
705. Какова длина L струны, если при укорочении ее
на 10 см частота колебаний повышается в полтора раза?
Натяжение струны остается неизменным.
706. Две синусоидальные волны излучаются двумя ис-
источниками. Как найти движение частицы, находящейся
на расстояниях di и d2 от этих источников, если распрост-
распространение волн подчиняется принципу суперпозиции,
источники колеблются в одинаковой фазе и с одинаковой
частотой и если направления колебаний в рассматриваемой
точке совпадают?
707. Определить адиабатическую сжимаемость воды,
если скорость звука в воде примерно равна 1500 м/с. (Коэф-
140
фициент сжимаемости вещества равен относительному
уменьшению его объема при увеличении давления на I атм.)
708. В жидком гелии, обладающем при Г=4,2 К плот-
плотностью 0,15 г/см3, скорость звука равна 220 м/с. Найти ади-
адиабатическую сжимаемость р жидкого гелия.
709. Стержень с закрепленными концами имеет длину
1=1 м. При трении стержень издает звук, основная частота
которого vo=700 Гц. Какова скорость звука с в стрежне?
Какие обертоны может иметь звук, издаваемый стержнем?
710. Две струны имеют одинаковую длину и натяжение.
Как относятся периоды их собственных колебаний, если
диаметр одной струны в два раза больше диаметра другой?
Струны сделаны из одного материала.
711. Как следует изменить натяжение струны, чтобы она
давала тон в три раза более низкий?
712. Почему скорость звука в идеальном газе не зависит
от давления, а зависит только от температуры?
713. Подсчитать максимальное ускорение и максималь-
максимальную скорость частицы воздуха в ультразвуковой волне с
частотой 50 000 Гц и амплитудой смещения частицы 0,1 мкм.
(Законы распространения ультразвуковых волн в воздухе
впервые были исследованы Н. П. Неклепаевым в лаборато-
лаборатории П. Н. Лебедева.)
714. Струна звучит с частотой 400 Гц. В каком месте и
как следует задержать движение струны, чтобы она звучала
с частотой: 1) 800 Гц; 2) 1200 Гц? Можно ли, зажимая стру-
струну, понизить частоту ее звучания?
715. Показать, что для любой бегущей акустической
волны относительное изменение давления dplp в данной точ-
точке равно отношению скорости частицы к скорости звука,
умноженному на y=cp/cv, где ср и cv— теплоемкости веще-
вещества среды соответственно при постоянном давлении и по-
постоянном объеме.
716. Плоская бегущая акустическая волна может быть
представлена следующим уравнением:
у=0,05 sin A980/-6л;),
где у — смещение частицы в направлении распространения
волны в сантиметрах, /— время в секундах, х — расстоя-
расстояние в метрах по оси, вдоль которой распространяется волна.
Найти: 1) частоту колебаний v в секунду; 2) скорость с рас-
распространения волны; 3) длину волны Я; 4) амплитуду коле-
колебаний скорости и каждой частицы и 5) амплитуду колебаний
141
давления Др, если давление р и объем v связаны законом
адиабаты /wb4=const.
717. По одному направлению бегут две синусоидальные
плоские волны со скоростями распространения vx и v2
и длинами волн Кг и Я2 соответственно. Найти скорость и
перемещения в пространстве тех точек, где колебания, со-
соответствующие каждой волне, имеют одинаковую фазу.
Найти расстояние Л между двумя подобными точками.
718. Понятие групповой скорости можно весьма нагляд-
наглядно иллюстрировать, разобрав следующий пример. Пусть
идут рядом две команды спортсменов: мужская и жен-
женская. В каждой команде спортсмены идут цепочкой, один
за другим, с интервалами в женской команде dly в муж-
мужской d2- Женская команда движется со скоростью vu муж-
мужская со скоростью и2. Через определенные промежутки време-
времени мимо неподвижного наблюдателя проходит пара идущих
рядом спортсменов. Если наблюдатель сам начнет дви-
двигаться, то он может эти промежутки времени уменьшить.
С какой скоростью и должен двигаться наблюдатель, что-
чтобы мимо него спортсмены проходили только парами?
719. Амплитуда колебаний давления звуковой волны
Др=100 дин/см2 (громкий звук). Найти поток энергии У,
попадающей за 1 с в ухо человека. Считать площадь S уха
равной 4 см2 и ухо перпендикулярным к направлению рас-
распространения волны. Плотность воздуха р = 1,3 -10~ г/см3,
скорость звука 334 м/с.
720. Человек с хорошим слухом может еще слышать
звук с колебанием давления до 0,001 дин/см2 при частоте
2000 Гц. Подсчитать амплитуду
А смещения частиц воздуха в
такой волне.
721. Акустический резонатор
представляет собой обычно ша-
шарообразную полость с неширо-
нешироким горлом и отростком с очень
малым отверстием на противопо-
противоположной стороне (рис. 198). Акус-
Рис* 198t тическая волна приводит в ко-
колебание воздух в горле разона-
тора. Масса этого воздуха колеблется вдоль горла при-
примерно как твердое тело, а воздух в полости по отношению
к этой массе играет роль пружины, так как скорость час-
частиц воздуха при колебаниях в горле велика по сравне-
сравнению с их скоростью в шарообразной полости.
142
Найти период собственных колебаний воздуха в резона-
резонаторе, считая известными площадь сечения горла 5, его дли-
длину /, объем шаровой полости V и скорость звука в воздухе с.
Воспользоваться аналогией с задачей 563 о колебаниях
поршня, закрывающего цилиндр с газом.
722. Как изменится частота, на которую будет резони-
резонировать акустический резонатор, если его наполнить водо-
водородом вместо воздуха? (Плотность водорода относительно
воздуха 0,069.)
§ 14. Специальная теория относительности *)
723. Вдоль оси X инерциальной системы отсчета К дви-
движется ракета со скоростью У=0,9 с (с— скорость света),
проходящая начало координат О в момент времени ^=0.
В момент tx = 9 с вслед за ракетой посылается световой сиг-
сигнал из точки О, а с ракеты — световой сигнал в точку
О. Предполагая, что ракета движется в вакууме, найти:
1) момент времени t2, когда световой сигнал, посланный из
точки О, достигнет ракеты; 2) момент времени t3t когда сиг-
сигнал, посланный с ракеты, придет в точку О; 3) на каком
расстоянии х2 от точки О будет ракета, когда к ней придет
сигнал из точки О; 4) когда вернется в точку О посланный из
нее сигнал, если он отражается от зеркала, установленного
на ракете (момент времени £4)?
724. Найти связь между промежутком собственного вре-
времени между двумя событиями (т. е. в инерциальной системе
отсчета, в которой рассматриваемые события наступают в
одной точке) и промежутком времени между этими же дву-
двумя событиями в другой инерциальной системе отсчета, в
которой эти два события наступают уже в разных точках
(и где отсчитывается уже координатное время), с помощью
следующего мысленного эксперимента.
В системе К на оси г1 на расстоянии z'o от начала отсчета
О' закреплено зеркало (рис. 199). Из источника, находяще-
находящегося в О', вдоль г' направляют световой сигнал, посылка и
х) Поскольку разделу «Специальная теория относительности» лишь
в последнее время стали уделять заметное внимание в курсе общей фи-
физики, а в этот задачник впервые вводятся задачи, связанные с СТО,
было сочтено целесообразным привести в виде Приложения основные
предположения и определения, принятые в СТО (см. стр. 284), Как
в условиях, так и в решениях задач данного параграфа приводятся
ссылки на формулы этого Приложения.
143
обратный приход которого фиксируются по часам, покоя-
покоящимся в О'. Эти часы отсчитывают промежуток собственно-
собственного времени Ат0. Эти же два события (посылку и прием сиг-
сигнала) рассмотрите в системе К (рис. 200) и найдите промежу-
промежуток времени между двумя этими событиями в этой системе.
Считая, что в момент посылки сигнала начала отсчета О
и О' совпадают, а часы в этот момент в обеих системах в
точке, где совпадают начала О и О', отсчитывают моменты
К'
К
0'
Рис. 199.
О Ш В Ж 0'
г г
Рис. 200.
времени /=0 и £' = 0, найти показания часов из систем К
и К для события «возвращение сигнала». Расстояния по на-
направлениям, перпендикулярным скорости относительного
движения, определенные во всех системах, одинаковы.
725. Космический корабль с постоянной скоростью
V= B4/25)с движется по направлению к центру Земли. Ка-
Какое расстояние в системе отсчета, связанной с Землей, прой-
пройдет корабль за промежуток времени At'= 7 с, отсчитанный
по корабельным часам? Вращение Земли и ее орбитальное
движение не учитывать.
726. Найти связь между собственной длиной стержня
/0 и его длиной, измеренной в системе отсчета /С, относи-
Рис. 201.
Рис. 202.
тельно которой он движется со скоростью У, на основе сле-
следующего мысленного эксперимента. В системе К' покоящий-
144
ся стержень расположен на оси х\ так что один его конец
находится в О' (х[=0), а другой в точке х'2=10 (рис. 201).
Из О' вдоль стержня посылается световой сигнал, который,
отражаясь от зеркала, установленного в точке х'2у возвра-
возвращается обратно. В О' есть часы, отмечающие моменты по-
посылки и возвращения сигнала; разность показаний этих
часов определяет интервал собственного времени Ат0.
Длина стержня /0 равна сДто/2. Рассмотрите эти же два со-
события (посылку и приход светового сигнала) в системе К
и, пользуясь постулатом об инвариантности скорости света
в вакууме во всех системах отсчета, найдите длину стержня
/ в системе К (рис. 202) и связь между / и /0.
727. Космонавт находится в неосвещенном космическом
корабле, движущемся относительно Земли со скоростью,
очень близкой к скорости света с. На небольшом расстоя-
расстоянии от космонавта расположено зеркало так, что линия, сое-
соединяющая космонавта и зеркало, параллельна скорости
корабля. Увидит ли космонавт
свое изображение в зеркале пос-
после включения источника света,
расположенного рядом с космо-
космонавтом? (Загадка Эйнштейна.) А ^^ В
728. 1) Фронт плоской све-
тобой волны, идущей в вакууме, Рис* 203*
падает под углом а на плоскую
поверхность АВ фотолюминесцирующего вещества. Найти
скорость v перемещения границы свечения Ф вдоль пря-
прямой АВ. Можно ли считать эту скорость v скоростью рас-
распространения некоторого сигнала вдоль прямой АВ
(рис. 203)?
2) Световой «зайчик» от пульсара NP-0532 в Крабовид-
ной туманности перемещается по поверхности Земли со
скоростью и~1024 см/с (угловая скорость вращения пульса-
пульсара ~200 с, а расстояние до пульсара порядка 1021 см).
Можно ли скорость v перемещения «зайчика» пульсара
рассматривать как скорость распространения светового
сигнала?
729. Из начала отсчета системы К вдоль оси х через ин-
интервал времени Т (по часам К) посылаются кратковремен-
кратковременные световые импульсы. Найти интервал времени, через
который эти импульсы будут приходить к наблюдателю в
системе /(', учитывая также относительность промежутков
времени между событиями (см. задачу 724). Рассмотреть
случаи удаления и сближения наблюдателя и источника.
145
Переходя от периодов к частотам, получить релятивистские
формулы для продольного эффекта Доплера.
730. Используя преобразования Лоренца, показать, что:
1) два события, одновременно наступившие в одной системе
отсчета /С, во всех других системах отсчета наступают в
разные моменты времени (если только они не наступили в
одной и той же точке системы /С); 2) два события, наступив-
наступившие в одной и той же точке системы /С, во всех других систе-
системах отсчета наступают в точках, имеющих различные коор-
координаты (если только в системе К они не были одновремен-
одновременны).
731. Неподвижный в системе К наблюдатель может из-
измерить длину движущегося стержня следующим образом.
Пусть стержень ориентирован вдоль общей оси х, х' и поко-
покоится в К' - Наблюдателю из К известна (он может ее изме-
измерить) скорость системы К (и стержня) V. В руках наблю-
наблюдателя часы, по которым он отмечает моменты прохождения
мимо него начала и конца стержня U и t2\ пусть At=t2—U.
Тогда он считает длиной стержня величину V (tx—t2). По-
Показать, что и при таком определении длины справедлива
формула / = /0 j/*l — V2/c2, где /0 — собственная длина
стержня.
732. Получить формулу, связывающую промежуток
собственного времени между двумя событиями Дт0 с проме-
промежутком времени между теми же двумя событиями At\
отсчитанными в любой другой системе отсчета (/('):
Если два события происходят в системе К в одной и той
же точке, но в разные моменты времени U и t2y то Дт0—
= t2—ti. Наблюдатель любой другой системы, определив ко-
координаты этих же событий, установит расстояние между
точками, в которых они наступили, и, разделив его на из-
известную ему относительную скорость систем отсчета, по-
получит величину At'.
733. Стержень, собственная длина которого равна /0|
покоится в системе отсчета /('; он расположен так, что со-
составляет с осью х' угол ф\ Какой угол составляет этот
стержень с осью х другой системы отсчета /С? Чему равна
длина этого стержня в системе /С?
734. Пользуясь формулами преобразования Лоренца,
показать, что в момент /=0 (в системе К) все часы системы
К\ находящиеся на положительной оси х> отстают от часов
146
системы /С, а все часы из К на отрицательной оси х опере-
опережают часы системы /С. Разница показаний часов возрастает
по мере удаления от начала координат О по закону
с2
Аналогично в момент Г=0 (в системе К) все часы системы
/С, находящиеся в точках л/>0 оси л;', опережают часы из
системы К\ а находящиеся в точках л;'<0— отстают. Раз-
Разница показаний часов возрастает по мере удаления от на-
начала координат О' по закону
В чем причина различия в знаках в полученных формулах?
Не нарушается ли этим равноправие систем К и /С'? Что
нужно сделать, чтобы добиться симметрии в формулах?
735. Стержень, собственная длина которого равна /0,
расположен параллельно оси х и движется в положительном
направлении оси у. Скорость его в системе К равна w.
В системе К этот же стержень оказывается несколько на-
наклоненным относительно положительного направления оси
х . Объясните этот результат, не пользуясь преобразова-
преобразованиями Лоренца. Пусть центр стержня проходит через точку
*=0, f/=0, /==0, у'=0 в момент времени t=t'=O. Вычисли-
Вычислите угол ф', образованный стержнем и осью х' в системе /('.
736. Метровый стержень, расположенный параллельно
оси х системы /С, движется вдоль оси х со скоростью V.
Тонкая пластинка, параллельная плоскости xz системы /С,
движется вверх вдоль оси у со скоростью w. В пластинке
проделано круглое отверстие диаметром в 1 м, центр кото-
которого лежит на оси у. Середина метрового стержня оказыва-
оказывается в начале координат системы К в тот самый момент, ког-
когда движущаяся вверх пластинка достигает плоскости у=0.
Но метровый стержень относительно К испытал лоренцево
сокращение и, следовательно, свободно проходит через от-
отверстие. Соударения между стержнем и пластинкой по этим
соображениям не произойдет.
Однако рассмотрим это «столкновение» с точки зрения
системы /(', связанной со стержнем. В системе К стержень
не подвержен сокращению, поскольку он покоится, зато
лоренцево сокращение испытывает отверстие в пластине.
Следовательно, по этим соображениям соударение между
метровым стержнем и отверстием будто бы неизбежно.
147
Произойдет ли соударение стержня с пластинкой в действи-
действительности? (Парадокс метрового стержня.)
737. Имеются три инерциальные системы отсчета /С, К\
К", все* оси координат которых параллельны друг другу.
Система К' движется равномерно и прямолинейно со ско-
скоростью Vi относительно системы /С, причем вектор ее ско-
скорости параллелен осям х. Система К" движется с постоян-
постоянной скоростью V2, параллельной Vu относительно систе-
системы /('. В начальный момент времени начала координат всех
трех систем совпадают между собой.
Показать, что результат последовательно выполненных
преобразований Лоренца для координат и времени при
переходе от системы К к системе К' и затем от системы К к
системе' К" эквивалентен преобразованию Лоренца, осу-
осуществляемому непосредственно при переходе от системы К
к системе К", с соответствующим значением их относи-
относительной скорости.
Показать, что результат двойного преобразования Ло-
Лоренца в этом случае коммутативен относительно скоростей
Vi и V2 систем координат К и /(".
738. Пусть система К движется относительно системы
К так, как описано в условии предыдущей задачи, но сис-
система К" движется равномерно относительно системы К со
скоростью V2t параллельно осям у. Выразить координаты х",
у\ г" и время Г, измеряемые в системе /(", через х, у, z и t
в системе /С. Заметьте, что в этом случае окончательный ре-
результат преобразования времени t"-+t и координат х\ у\
z" -+■ х, у, z не коммутативен относительно скоростей Vi и
V2 (ср. предыдущую задачу).
739. Пусть в системе К движение частицы задано выра-
выражениями: x=x(t), y=y(f), z=z(f). Определяя скорость обыч-
обычными формулами, например, vx=dx/dt и т. д., и применяя
преобразования Лоренца, найти формулы преобразования
компонент скоростей при переходе от системы отсчета К
к системе /С', где соответственно v'x=dx'/dt' и т. д.
740. 1) Используя формулы преобразования компонент
скорости, полученные в предыдущей задаче, рассмотреть
случай, когда в системе К частица движется вдоль оси х,
так что vx=v. Найти формулу преобразования величины
скорости для этого случая.
2) Для случая движения частицы вдоль оси х, рассмот-
рассмотренного в п. A), доказать следующую теорему. Если ско-
скорость движения частицы v в системе К меньше с, то в любой
другой системе отсчета ее скорость также меньше с. При
148
этом предполагается, что относительная скорость систем
отсчета также всегда меньше с.
741. С помощью формулы преобразования скоростей
(см. задачу 740) получить результат опыта Физо. В этом
опыте в лабораторной системе отсчета определялась ско-
скорость света в воде, текущей со скоростью V. В результате
опыта Физо получил для скорости света значение
с ( 1 \
v==z [_]/ I 1 _j f где п—показатель преломления воды.
Какого порядка члены относительно Vic отброшены при
выводе теоретической формулы?
742. Пусть в системе /С две частицы движутся вдоль оси
х навстречу друг другу со скоростями Vi—axc и v2=ot2p,
где аг и а2 больше 1/2, но меньше 1. Найти скорость сближе-
сближения этих частиц в системе /С. Эта скорость превосходит с,
что, однако, не противоречит основам теории относительно-
относительности. Почему? Найти относительную скорость частиц сог-
согласно формуле преобразования скоростей и убедиться, что
эта скорость всегда меньше с.
743. 1) В системе К частица движется в плоскости
(х\ у') со скоростью v' под углом & к оси х'. Найти абсолют-
абсолютную величину скорости v в системе К и угол д, который со-
составляет скорость частицы с осью х.
2) Пусть в системе К' луч света распространяется в
вакууме вдоль оси у''. Найти угол, который образует этот
луч света с осью у системы К (угол аберрации), применяя
формулы, полученные в предыдущей задаче. Оси у и у* на-
направить вниз. Найти выражение для угла аберрации клас-
классической теории, т. е. применяя преобразования Галилея
и классическую формулу «сложения» скоростей. На какой
порядок относительно величины Vic отличаются классичес-
классическая и релятивистская формулы?
744. Проверить, что преобразования Лоренца оставляют
инвариантным интервал между событиями.
745. Имея в виду, что положение частицы в данный мо-
момент времени является событием, записать интервал между
двумя такими событиями в системе /С, относительно которой
она движется, и в системе К\ относительно которой она по-
покоится. В силу инвариантности интервала еще раз получить
связь между промежутком собственного времени между
двумя событиями и промежутком координатного (лабора-
(лабораторного) времени между теми же событиями.
746. Найти условие того, что можно подобрать такую
систему /С', в которой два события, происходящие в системе
149
отсчета К в разных точках пространства и в разные моменты
времени, происходили бы: 1) в одной точке системы К'\
2) одновременно в системе К'\ 3) наступали бы в системе К'
в одной точке и в один и тот же момент времени.
747. Исходя из классического и релятивистского урав-
уравнений движения, вывести выражения для энергии частицы.
748. Найти зависимость координаты и скорости части-
частицы от времени, если движение одномерное, сила постоян-
постоянна, а уравнение движения — релятивистское. Сравнить
полученное решение с решением для того же случая, но для
классического уравнения. Убедиться, что при решении ре-
релятивистского уравнения — в соответствии с основными
принципами теории относительности — скорость частицы в
любой момент времени остается меньше с.
749. Сравнить величину релятивистского и классичес-
классического импульсов электрона при скорости v—B4/25) с =0,96 с.
750. Найти выражение для трехмерного ускорения час-
частицы из релятивистского уравнения движения (9).
751. Рассмотреть движение электрона в плоском кон-
конденсаторе (напряженность электрического поля Е) на ос-
основе классического и релятивистского уравнений динамики.
Начальные условия: в момент £=0 электрон влетает в кон-
конденсатор со скоростью v0, параллельной пластинам. Найти
скорость и координаты электрона как функцию времени и
траекторию электрона. Сравнить классический и реляти-
релятивистский случаи и убедиться, что при условии (v/c)<^\
релятивистские результаты переходят в классические. По-
Почему проекция скорости электрона на направление, парал-
параллельное пластинам конденсатора, остается постоянной в
классическом случае и убывает в релятивистском?
752. Найти скорость частицы (заряде, масса т), прошед-
прошедшей разность потенциалов V без начальной скорости. Най-
Найти предельные выражения для скорости: 1) для классичес-
классического случая (v<<Zc) и 2) для ультрарелятивистского (v&c).
753. Две одинаковые частицы движутся в лабораторной
системе отсчета К навстречу друг другу с одинаковыми ре-
релятивистскими скоростями. Система/С является для них си-
системой центра масс и их энергия в этой системе равна
2<£ (<§ — энергия каждой частицы). Найти суммарную
энергию частиц в системе отсчета, где одна из частиц поко-
покоится. Найти выигрыш в энергии столкновения, если две
частицы, каждая с энергией <§, идут навстречу друг другу,
по сравнению с тем случаем, когда одна частица с энергией
<£ падает на неподвижную.
150
754. Показать, что релятивистское уравнение движения
заряженной частицы в постоянном магнитном поле совпа-
совпадает с классическим уравнением движения при тех же ус-
условиях, но с некоторым другим значением массы.
755. Найти пробег I релятивистской заряженной части-
частицы с зарядом е и массой т при начальной полной энергии <£0
в тормозящем однородном электрическом поле, параллель-
параллельном начальной скорости частицы.
756. Какую часть энергии покоя частицы должна со-
составлять релятивистская кинетическая энергия, чтобы от-
относительная ошибка, полученная при использовании нере-
нерелятивистского выражения для кинетической энергии, со-
составляла бы 1%? Найти соответствующую энергию для
протона и электрона.
757. Выразить в мегаэлектроновольтах энергию покоя
электрона и протона.
758. На 1 м2 поверхности, перпендикулярной направле-
направлению солнечных лучей, около Земли вне ее атмосферы при-
приходит примерно 1,4 кВт световой энергии от Солнца. (Зна-
(Значение 1,4 кВт/м2 называется солнечной постоянной.)
Какое количество массы теряет Солнце в секунду за
счет излучения света? На какое время хватит 0,1 массы Солн-
Солнца, чтобы поддерживать его излучение? Расстояние от
Солнца до Земли составляет около 150 -106 км. Масса Солн-
Солнца 2-Ю30 кг.
759. Доказать с помощью преобразований A7) справед-
справедливость соотношения A8), т. е. инвариантность модуля
4-вектора.
760. Показать, что из формул преобразования компо-
компонент 4-скорости получаются формулы преобразования 3-ско-
рости, выведенные из преобразований Лоренца в задаче 739.
761. Найти компоненты 4-вектора ускорения W^
Найти формулы преобразования 3-ускорения при пере-
переходе от системы К к системе К двумя способами: 1) спосо-
способом, использованным в задаче 739, т. е. составив выраже-
выражения dvx и т. д. из E) и деля их на dt из C); 2) преобразуя
компоненты 4-ускорения согласно A7). Объяснить, почему
равноускоренное движение в одной системе отсчета — уже
не равноускоренное во всех остальных.
762. Найти преобразование компонент 4-импульса час-
частицы при переходе от собственной системы К0 к любой дру-
другой системе отсчета. (Собственной системой отсчета части-
частицы называется система, где частица покоится.)
151
763. Доказать, что квадрат модуля 4-вектора энергии —
импульса Р — определяет массу покоя частицы. Найти
формулу, связывающую релятивистские энергию и импульс
частицы с ее массой; найти выражение энергии релятивист-
релятивистской частицы через ее импульс.
764. В собственной системе отсчета К0 на частицу дей-
действует трехмерная сила F. Преобразуя компоненты 4-силы,
найти компоненты 3-силы в произвольной системе отсче-
отсчета к.
765. Записать формулы преобразований Лоренца,
3-скоростей и 3-ускорений для случая произвольного на-
направления относительной скорости систем отсчета К и /£'.
766. Выразить релятивистский импульс частицы, мас-
масса которой равна т, через ее релятивистскую кинетичес-
кинетическую энергию.
767. Найти выражение 3-скорости частицы через ее
релятивистский импульс.
768. По заданной релятивистской энергии <£ и массе
частицы т найти 3-скорость частицы. Рассмотреть отдель-
отдельно нерелятивистский (v<^c) и ультрарелятивистский (vzzc)
пределы.
769. На покоящуюся частицу массы Шг налетает частица
массы т2, кинетическая энергия которой равна Г2. После
столкновения частицы слипаются и движутся как целое.
Найти массу образовавшейся частицы. При каких условиях
эта масса приблизительно равна сумме масс исходных час-
частиц? Найти скорость образовавшейся частицы.
770. При распаде некоторой частицы появляются две
частицы с массами тх и т2. Из опыта известны абсолютные
величины импульсов рг и р2 этих частиц и угол д между
направлениями их разлета. Найти массу распавшейся ча-
тицы.
771. Покоящееся тело массы М распадается на две час-
части с массами тх и т2. Вычислить кинетические энергии 7\
и Т2 продуктов распада.
772. Частица массы m испытывает упругое соударение
с неподвижной частицей такой же массы. Найти кинети-
кинетическую энергию Тг рассеянной частицы по кинетической
энергии Го налетающей частицы и углу рассеяния Фх.
ОТВЕТЫ И РЕШЕНИЯ
§ 1. Кинематика
1. |у|= У~Ь м/с; вектор скорости составляет с берегом реки, от кото-
которого удаляется лодка, угол а=63°30'.
2. Курс лодки должен составлять угол в 39° с прямой, соединяющей
пристани; а=0,62 м/с.
3. Труба должна быть наклонена от вертикали вперед, по ходу те-
тележки, на угол a = arqtg (vT/vK).
4. v = 9,3 м/с; угол 165Q относительно курса корабля.
5. Расстояние между самолетами возрастает каждый час на ве-
величину 500 км; 5=1500 км.
6. фОпт = 105° (ф — Угол между прямыми АВ и ВС).
7. Под углом ф = агссоэ l(Vi~\-v2)/v0].
2. txt2
8. ^i = 4-TT
2 tt2
9. v = 5 км/ч.
10. Qq^arctgfoo/P!), 2) <pa=arctgr [vo/fa+vj], 3) v'=V v\+v% ,
«2 = 4^=^ = 17,5 км/ч.
I11
11. 14,1 см/с.
12. ^aKC
Указание. Поезд находится от фотографа на расстоянииv
//sin a. Составляющая скорости поезда в направлении, перпендикуляр-
перпендикулярном к лучу зрения (только она вызывает размытие изображения), есть
v sin a. Скорость движения изображения поезда на фотопластинке
Ииа = (tf Sin2 a)//, *„акс = <*Мга-
13. S1=y0^i+a^i/2, S2=(y0+a'i) ^2+«^/2. Так как S1=S2=Si то
14. См. рис. 204.
К рис. 204, а. Зависимость скорости от времени описывается
соотношением v=at.
153
К рис. 204, б. График составлен из чередующихся отрезков го-
горизонтальных (y=const при а=0) и наклонных (v=at при a=const=^0)
прямых.
К рис. 204, в. График составлен из отрезков горизонтальных прямых
,м/с
8
D
к
8
а)
+ "■ ' ■
1 '
1Z
С
' h 8
6}
1
1Z
'
1 Г
0}
и отрезков парабол, описываемых
уравнением вида v=kt2l2 (при а—
~kt), если при построении этих
парабол принимать за начало коор-
координат точки /, 3, 5.
К рис. 204, г. График составлен
из отрезков парабол. От точек 0, 2,
4, 6 построены параболы, удовлет-
удовлетворяющие уравнению вида v=kt2l2.
В пределах участков оси времени
1—2, 3—4, 5—6 расположены от-
отрезки парабол, удовлетворяющие
уравнению v=vMZKC —kt2i2 l).
15. См. рис. 205 и 206.
К рис. 205. На участке 0—1 за-
зависимость S от / описывается урав-
уравнением S=at2/2, на участках 1—3,
3—4, 4—6 — уравнениями
z и
г)
Рис. 204.
Btfi
S= const и т. д.
К рис. 206. На участке 0—1
dvldt — а = Qonst > 0. На участках
1—3 и 3—4—соответственно а=0 и a=const<0 (см. примечание к
ответу задачи 14).
16. i>==J/&/i«6,2m/c.
17. S=2v0t.
18. уо=82 м/с.
19. В наивысшей точке траектории нормальное ускорение будет
максимальным и равным ускорению g свободного падения; во всех ос-
остальных точках траектории оно равно проекции g на нормаль к траекто-
траектории в этой точке.
20. x = v\T2h/g (l + a)/(l — a).
21. 1) vx=v0 cos ф, vy=v0 sin ф—gt, v=V vl-tg2t2 — 2vQ sin y-gt\
2v0 sin ф o. , . gl
-»х- 3) 1да = 1дф
2) T = -
g
3)
f
v0 cos
4) x =
cos
x) Функциональные зависимости кинематических величин от вре-
времени, приводимые здесь и в решении задачи 15, отыскиваются путем
графического или аналитического дифференцирования и интегрирования.
154
7) /=
Рис. 206.
22. См. рис. 207.
24. / да 40 м, ф да 38°40'.
25. | v |2 = У1 +Уо — 2gtvo-\-g2t2y tga = (y0—gt)/vlt где a—угол
вектора v с горизонтом; уравнение траектории снаряда будет
y~vtx 5^|*'
если совместить начало координат с той точкой пространства, в ко-
которой был выпущен снаряд.
X* У"
27. Точка движется по эллипсу "ТГ+'Бг"^ ' с ускорением
а — @2Г) где г — радиус-вектор движущейся точки, направленный
от центра эллипса.
Решение. В точках пересечения большой оси с эллипсом
скорость v=\ У \ — \соВ cos cot J = соВ, ускорение нормальное и равно
155
a = |"i| = G>4. To же ускорение можно выразить через радиус кри-
кривизны эллипса: a = v2/R=(u2B2/R. Сравнивая результаты, получим
R=B2/A. В точках пересечения эллипса
с малой осью R = A2/B.
28. По гиперболе (х2/А2)—(у2/В2)=\
с ускорением a = k2r.
29. Эллипс
где g— ускоре-
ускореlg cos a
Рис. 207.
30.
31. v =
ние свободного падения.
33. Грузы, двигаясь по желобам с ус-
ускорением g sin a, должны пройти до встре-
встречи с окружностью пути l=2R sin a, где
a — угол желоба с горизонтом, а R — радиус окружности. Поэтому
они достигают окружности через промежуток времени т= \r4R/gi не
зависящий от угла наклона желоба.
36. v= Via.
38. 1) S = voto ln( j- ) для / > /0; 2) v=voexp I — гу) Для ^ > 0.
Решение. v — dSjdt —voto/t> следовательно,
s
\dS = voto \ у,
о ^
или S =
откуда можно получить и ответ на второй вопрос.
39. 1) у=7
8
■гх2у начало системы координат в точке
выстрела; 2) y=gx2/2vcnapy начало системы координат на самолете;
3) у — — #л;2/2сснар» начало системы координат на снаряде. Ось X
всюду направлена горизонтально по курсу самолета, ось Y направ-
направлена вертикально вниз.
40. Траектория состоит из ветвей двух парабол (рис. 208):
У ~ V и ~ V ~2~ и ' °~2v '
Решение. Написанные уравнения находим для первой пара-
параболы из условий:
при / = 0 х = 0 и # = 0, D0.1)
и уравнений
t/y = u = const или y = vt9 D0.2)
dx 2u Qx
Vx^ — ^ky^-j-y. D0.3)
at a
156
Интегрирование уравнения D0.3) при учете D0.1) и D0.2) дает
х=~ t2. Исключая время /, находим уравнение ветви первой пара-
d
болы. Подставляя в него
половине ее пути.^ Урав-
нение ветви второй пара-
болы легко получить еле-
дующим образом. Выберем
новое начало координат
Х'0'Y' в той точке О' на
середине реки, которой до-
стигнет лодка, пройдя пер-
вую половину пути. Те-
перь начальные условия
движения запишутся так:
при /=0 *'=0 и у'=0.
y = d/2f находим снос лодки на первой
п
Далее, yr =vt9
j-
но vx = u—j-y'. Решая
, d
эти уравнения, как и в первом случае, находим у =~к —
— у —
Возвращаясь к прежним координатам, при помощи
соотношений у = у' + -х-
= х'+^- , находим уравнение ветви
второй параболы в прежних координатах. Очевидно, что эта ветвь
второй параболы будет перевернутым повторением ветви первой
параболы.
41. Первая половина траектории лодки будет описываться уравне-
уравнением у= Y~3vx/k, вторая половина траектории будет, как и в преды-
предыдущем случае, обращенным повторением первой ветви. Величина сноса
лодки %=Ы3/12у.
42. Там, где кривизна траектории наибольшая, т. е. около точки Л.
43. v=2nR/T=3 650 км/ч; a=4n*R/T2=35 км/ч2.
44. Прямые, параллельные оси времени.
45. @=0,00093 с-1^0,001 с-1.
46. у«7,2 км/с.
47. aN~0Jg.
48. v= 1670 cos ф км/ч.
49. i/«30 км/с.
50. 0^=0,03 cos ф м/с2 и ад=0,03 cos2 <p м2/с, где ф —географи-
—географическая широта точки; соответственно для Москвы имеем а^=0,017 м/с2
и ад «0,01 м/с2.
51. Г=Г1712/(Г1+Г2)=116 земных суток.
52. Тень движется с запада на восток со скоростью
т) ~ 0,5 км/с,
157
где Гсут — продолжительность суток, Гмес — продолжительность
месяца.
53. Тень будет двигаться вверх с постоянным ускорением
= 3,4 см/с2, /=
= 4 мин.
54. а
55. /х«9 об/с.
56. а_
57. а=4 рад/с2, ф=2/2 рад.
58. о#=0,6 м/с2, лполн=0,67 м/с2. Угол между аПолн и /?составля-
/?составляет 153°.
59. 1;* = 1;о A +cos <р) = 2y0cos2-|-, vy = — v0 sin q>, уполн =
ф
ф
60. Решение. Ускорение движущейся точки направлено к цен-
центру катящегося круга и равно v2/R. В вершине циклоиды скорость точки
равна 2у, ускорение нормальное и может быть представлено в виде
BуJ/р. Отсюда р=4#. __
61. Для обеих точек колеса IflJHtH У 2, где V— скорость качения
колеса; вектор скорости передней точки будет наклонен вперед и вниз
под углом 45° к горизонтальному диаметру. Для задней точки — соот-
соответственно вверх и вперед под тем же углом. Вектор ускорения передней
точки будет горизонтален и направлен против хода движения колеса.
Вектор ускорения задней точки — горизонтален и направлен по ходу
движения колеса.
Рис. 209.
62. *=/?(ф—sin ф)=#(со*—sin со/), #=/?A— cos ф)=/?A— cos cof),
где ф=со/ и со=у//? есть угловая скорость вращения колеса. Траекто-
Траекторией точек, находящихся на ободе движущегося колеса, будет простая
циклоида, уравнения которой в параметрической форме и получены
(рис. 209).
63. S=8R.
158
Решение.
Ф__ ш _ dtp _ ф
^полн = 2у0 cos f = 2cd/? cos -| =r 2 ^ /? cos f,
dS = оиол„Л - 2 ^- /? cos |- d/ = 2/? cos | dq>.
Таким образом, для подсчета пройденного точкой пути интегрирование
по времени можно свести к интегрированию по углу поворота ф колеса.
Очевидно, что угол поворота колеса ф между двумя последовательными
касаниями дороги одной и той же точкой на ободе колеса изменяется в
пределах от 0 до +2л. Таким образом, находим
64. /1максва/?+|^+^ <64Л)
[^фЬмакс^-^/^2» F4.2)
где ф — угловая координата искомой точки на ободе колеса (см. рис. 8
к задаче 62).
Решение. Координата у произвольной точки на ободе колеса
может быть записана выражением
F4.3)
откуда
y — vsin — t. F4.4)
Величины у, у и h связаны соотношением
Подставляя выражения F4.3) и F4.4) в F4.5), находим F4.2) из усло-
условия dh/dq>=0. После этого из F4.5) при учете F4.2), F4.3) и F4.4) полу-
получаем F4.1).
v2 v2
65. агориз —"Ъ~ si" Ф» аверт =-гГ с°5ф- При равномерном вра-
вращении полное ускорение всегда направлено к центру колеса.
, |аимв1 =£*■
67. Искомая ось вращения должна была бы составить с верти-
вертикалью угол ф = агс!дО,2. Угловая скорость вращения вокруг этой
оси должна быть (l^ J^l,04.
158
68. Косинусы углов между новой осью вращения и тремя прежними
осями определяются выражениями
12 3
COSP CO
yr=r , COSP =
/14
Угловая скорость вращения вокруг новой оси будет сох /Ti.
69. Искомая мгновенная ось вращения будет описывать окружность
с радиусом /-=(о2/?/(со1+(о2) вокруг оси первого диска. Угловая скорость
вращения вокруг этой мгновенной оси будет (o=(d1+cu2.
70. При повороте автомобиля его внешние и внутренние (по отно-
отношению к центру закругления дороги) колеса описывают разные окруж-
окружности, т. е. проходят разные пути, и угловая скорость вращения колес,
если они не скользят по дороге, должна быть различной. Это условие для
задних ведущих колес обеспечивает дифференциал в заднем мосте авто-
автомобиля. Колеса, не имеющие привода от мотора, могут вращаться неза-
независимо друг от друга с различной угловой скоростью, так как они уста-
установлены на подшипниках.
71. 1>/=9,88м/с, fle= 10,12 м/с.
72. Если х есть смещение в горизонтальном направлении тени па-
палочки на экране, то x=R cos (со/ ± ф). Здесь ф—угол между пло-
плоскостью экрана и вертикальной плоскостью, проведенной через палочку
и центр диска в момент времени /=0. Величина х измеряется от той
точки экрана, в которую падает световой луч, прошедший через центр ди-
диска. Очевидно, что колебания тени палочки будут симметричны относи-
относительно этой точки экрана. Зависимости от времени величин скорости v
тени палочки и ее ускорения а запишутся соотношениями
у == —=— /?со sin (со/ ± ф)= /?со cos (со/ ± ф + -л"
d2x
a = -Tfi=— R®2 cos (со/ ± ф) = /?со2 cos (со/ ± ф+ я).
Графически зависимости величин дг, v и а от времени представятся сину-
синусоидами, смещенными относительно друг друга по фазе.
§ 2. Динамика прямолинейного движения материальной точки
и простейших систем
73. 1) Г=0,5 кгс; 2) Г= 1,5 кгс; 3) Г=0,9 кгс.
Указание. Показания весов можно найти из уравнения движе-
движения тела, подвешенного на весах, ma=mg—Т, где пг — масса тела, g —
ускорение свободного падения, Т — сила натяжения пружины (ею оп-
определяются показания весов), а — ускорение тела массы т.
74. / = 7в кгс, /1 = 7з кгс.
75. F^-'/bF.
т _ Mm
Ж 2 Т 8
160
Решение. Так как длина нити не меняется во время движения
грузов, то оба тела движутся с одинаковым по величине ускорением а.
На тело М действует по направлению движения только сила натяжения
нити Т, откуда
Т=-Ма. G6.1)
На тело массы пг вдоль направления движения (по вертикали) действуют
две силы сила притяжения Земли mg и сила натяжения нити Т. Следо-
Следовательно, mg—T=ma\ принимая во внимание уравнение A), находим
искомые величины.
77. 1) Верхняя половина тела действует на нижнюю с силой, вер-
вертикальная составляющая которой равна Mg/2, а горизонтальная —Ма/2;
2) левая половина действует на правую с направленной горизонтальной
силой —Ма/2, где а — ускорение, с которым движется тело.
М
Ж a T^
79. a =g (sin a — k cos a).
80. F ^ 4 кгс.
81. Сила натяжения нити, связывающей два тела, определяется
только величиной приложенной к ним силы F и не зависит от коэффици-
коэффициента трения между телами и столом, если он одинаков для обоих тел.
82. F>(m1+m2)g.
Указание. Для того чтобы нижняя масса т2 приподнялась
над столом, верхняя тх должна подпрыгнуть настолько, чтобы пружина
растянулась на величину x>m2g/k относительно своего недеформиро-
ванного положения, где k — коэф- *
фициент упругости пружины. Под- |
прыгнет же масса тг на такое же рас-
расстояние вверх от деформированного
ее весом положения пружины, на
какое она опустилась вниз от этого
положения под действием внешней
силы F.
83. См. рис. 210. U 2 и 3 — си-
силы, приложенные к доске. Силы 1 и
2 действуют со стороны опоры,
«противодействующая» каждой из
них приложена к опоре и направле- Рис. 210.
на вниз. Сила 3 действует со стороны
тела на доску, «противодействующая» ей сила приложена к телу. («Про-
(«Противодействующие» силы обозначены пунктирными стрелками.)
84. Прогиб доски уменьшится при приседании, увеличится при вы-
выпрямлении человека.
6 Под ред. И. А. Яковлева 161
'1
1 4 <
1
3.
л
1
* 1
I
t
85. Пусть Ау Bt С схематически изображают лошадь, сани и
землю соответственно (рис. 211). Тогда силы F2 и / приложены
Рис. 211.
к лошади со стороны саней и земли, силы Fx и /'— к саням, fx и
/i — к земле. На основании третьего закона Ньютона
l^iM^il. l/l-l/il. \f'\ = \fi\-
Так как движение равномерное, то на основании второго закона
Ньютона
1/1 = 1 Л I. \Fi\ = \f'\, \fi\ = \/i\-
86. При тех же обозначениях, что и в предыдущей задаче, по-
получим следующие новые соотношения:
/—F2 = ma, F1—ff = May f =0,2Mg\
l^^l» имеем f = M @,2g+a) +
^ 0,02. В этом случав
учитывая, что по-прежнему l^il^^
+ та « 117 кгс.
87. 1) Если все колеса ведущие, то
необходимый минимальный коэффициент трения от веса автомобиля не
зависит, так как сила трения пропорциональна давлению колес.
2) Если только задние колеса ведущие, то fc^a/(ng), где п — доля
общего веса, приходящаяся на задние колеса автомобиля; в рассматри-
рассматриваемом случае л=5/6 и £>0,2/E/6g)« 0,024.
88. Ускорение доски должно быть больше, чем 0,98 м/с2.
89. Больше 2,25 кгс.
Решение. Уравнение движения доски F—0,5(m+M)g-—f=Ma
и, соответственно, уравнение для груза /=та, где / — сила трения ме-
между грузом и доской, а — ускорение. Максимальное значение /=
=0,25mg; следовательно, максимальное ускорение груза 0,25g, и мак-
максимальна я сила Fy при которой еще будет происходить движение груза
и доски как целого, должна сообщать доске и грузу ускорение 0,25g.
А для этого должно быть
/7=0,25(M+m)^+0,5(M+m)^=2,25 кгс.
90. АМ=2(М—Pig).
Указание. Для опускающегося шара Mg—Р—/?=0, для под-
поднимающегося шара (М—AM)g—Р+/?=0, где R — сила сопротивления
воздуха.
162
01. 1) a = 0, T^mg\
2) a = arctg-^, T = m V^+J2\
о
3) a — —ф, т. е. нить нормальна к наклонной плоскости;
Т = mg cos ф;
Ь
— СОЭф
4) tga = —%-. , T=m Vg2+ b2 + 2bg sin (p;
\-\ sin ф
b
СОЭф
5) lga = 1 , T = m Vg2 + 02—2bgs\nq>.
1 sin ф
Здесь a — угол между нитью маятника и вертикалью; этот угол счи-
считается положительным при отклонении нити маятника от вертикали в
направлении хода часовой стрелки; положительное направление верти-
вертикали совпадает с направлением ускорения свободного падения.
92. 1) Ускорение всюду одинаково и равно g. 2) Ускорение камня
максимально в начале движения в нижней точке его траектории.
93. В отсутствие сопротивления воздуха ускорение направлено
вертикально вниз. При наличии сопротивления ускорение отклонено от
вертикали в направлении, противоположном движению снаряда.
94. В результате выстрела возникнут колебания грузика А; когда
они затухнут, результирующая сила со стороны пружинок будет равна
нулю, если сопротивление воздуха отсутствует. Если на снаряд действует
сила сопротивления воздуха, то результирующая сила пружинок равна
т(а—g), причем как ускорение снаряда а, так и натяжение пружинок
считается положительным, когда они направлены вниз. При подъеме
эта сила направлена вниз, при спуске — вверх, т. е. навстречу дви-
движению.
95. a=^J-I^ r = 2-^l^_g, f = 2r =
tn\m- m1-\-m2
__M (m1-{-m2) — 4m1m2 sin a
' a ~ M (mx + m2)+ ^m^^ *"
_L
-]-
Решение. Натяжение пружины Т в начальный момент будет
= mdg, поэтому as — 0, а1= ; (mxg—m2g—/
/72j -j— ГП2
99. ЛЬ±~П~* , Этот результат легко получить из ответа за-
m2 n— 1
дачи 95, положив a=g/n.
6* 163
100. /~4,5с; и»44 см/с.
=4,95 re.
n/tn'
102. 1) Весы наклонятся вправо, так как при движущихся мас-
массах т1 и т2 сила давления на ось блока будет равна удвоенной
силе натяжения нити 2Т = ~—^~ g < (тг + m2) g (см. ответ за-
nii -\- tu2
дачи 95).
2) Для сохранения равновесия весов надо в этом случае снять
с правой чашки груз (tn^m^g—2Т =
m1-\-m2
Указание. Условие, связывающее ускорения аг и а2, можно
получить, обозначив через хг и х2 расстояния масс М1 и М2 от горизон-
горизонтальной плоскости; тогда х1-\-2х2 есть величина постоянная. Дифферен-
Дифференцируя это равенство два раза, получаем искомое условие %=—2а2.
104 а = m* ^m% ^m^ кт*т* о
1 m(m + m) + 4m/n
1 4m2m3 + m1(m2 + m3)' 2 Am2m3 + m1(rn2 + m3)'
Указание. Обозначив через хъ хъ х3 расстояния масс тъ т2,
т3 от плоскости, к которой прикреплен блок, можно написать следую-
следующее равенство: л:2+л;3+2*1= /2+2/j+const, где /х и /2 — длины нитей.
Дифференцируя его два раза, получаем необходимое для решения задачи
соотношение между ускорениями всех трех масс: а2+я3+2а1=0.
105. В обоих случаях необходимо добавить на чашку одинако-
одинаковый груз Ар == , .—;—Amg да 12 гс.
fj r 2 + Ат/т б
106. 1) Добавить на чашку весов груз Ар=- да 22,7 гс.
Л. ^ А 1 + Ат/т А
2) Снять с чашки весов груз Ар= ' .—-—Amj? = 27,3 гс.
/ fj г 2 _|_ Ат/т &
107. Обе обезьяны достигнут блока одновременно через промежуток
времени t=//3i>. Действительно, натяжение веревки по обе стороны от
блока одинаково. Значит, одинаковы ускорения и скорости обезьян отно-
относительно блока. Так как они приближаются друг к другу со скоростью
3vt то весь путь / они пройдут за время H3v.
108. Блока достигнет раньше более легкая обезьяна, потому что ее
ускорение относительно блока будет направлено вверх, а ускорение
тяжелой обезьяны — вниз.
109. Груз будет двигаться вверх со скоростью у/4, независимо от
того, постоянна она или нет.
164
110. Скорость большего шарика будет в |/*2 раз больше скорости
меньшего.
Ш. у 2 ill^g^^o^ см/с.
У Г)
112. v = — \( v0 — +1 J е т — 1 , где т — масса тела, г —
коэффициент сопротивления воздуха.
Решение. Уравнение движения имеет вид т dv/dt=—mg—го.
Полученный выше результат найден интегрированием этого уравнения
с начальным условием v=v0 при /=0.
113. /! = /<>— ln ( ! + —) «/<>/1.73, где vo=\J3 v* (^ —ско-
vo \ V*/
рость установившегося движения тела в вязкой среде), to=vo/g.
114. l)AS=() [ ^-^
где v0 — скорость установившегося движения капель, г — коэффициент
сопротивления при падении капель в воздухе. Время / отсчитывается
от начала падения первой капли.
115. 1) Изменение скорости лодки v со временем будет происхо-
дить по закону v = — , где т — масса лодки, г — коэффициент
/72 -f- TV^t
сопротивления воды. При сделанном предположении о зависимости
силы сопротивления от скорости лодка должна двигаться бесконечно
долго, и пройденный ею путь также будет стремиться к бесконеч-
бесконечности: S=—In I \-\ t) . Но это предположение о силе сопро-
сопротивления перестает быть справедливым при малых скоростях движе-
движения лодки, когда сила сопротивления становится пропорциональной
первой степени скорости (см. следующую задачу).
-— /
116. v = voe m и очевидно, что прр.,сделанном предположении
движение лодки будет продолжаться неограниченно долго. Однако
для пути S, пройденного лодкой после спуска паруса, будет иметь
место условие lim S — vom/r (ср. с результатом предыдущей задачи).
117. v — Vq S, где обозначения те же, что и в предыдущей
/72
задаче.
V2
П8. TMaKC = mg 2 пад =18 000 кгс.
приземл
Примечание. Такого натяжения не выдержали бы ни стропы
парашюта, ни парашютист, на которого стропы действовали бы с такой
165
силой. В действительности парашют раскрывается не мгновенно, и на-
натяжение строп оказывается гораздо меньше.
120. mMMH^Mtga~fe.
k
Решение. Уравнение движения доски при условии, что тело
скользит по ней без трения, имеет вид
Ma—Mg sin a— (M+m)£g cos a.
Полагая а = 0, находим тмин = М-^-т . При т> тмин доска
остановится.
121 а ^т^~^2(g—oa) ^^mim2Bg-g2)
1 mY-\-m2 * тх-\-т2
122. Обе обезьяны достигнут блока одновременно через промежу-
промежуток времени т= /2//За. В самом деле, сила натяжения веревки вдоль
всей ее длины одинакова, значит, и ускорения обезьян относительно
Земли одинаковы. Движение они начинают одновременно, приближаясь
друг к другу с ускорением За; чтобы достичь блока, они обе вместе долж-
должны пройти путь /.
123. 1) Маятник будет падать вместе со щитком, сохраняя на нем
неизменное положение.
2) С момента начала падения щитка скорость маятника относитель-
относительно щитка перестанет изменяться, и с этой скоростью он начнет вращать-
вращаться вокруг точки подвеса.
124. Т = 2
125. 7 = 2я Т/ . При a—g период становится бесконеч-
g ~~~ ^
ным, т. е. маятник качаться не будет. При а > g маятник перевер-
перевернется и будет колебаться около своего наивысшего положения с пе-
периодом Т = 2я ///(a—g).
126. T = 2jt Vlj{g cos a).
127. Тело будет совершать колебания на пружине. Амплитуда коле-
колебаний будет равна той длине, на которую груз растягивал пружину в
неподвижной кабине.
128. Ускорение тележки -jr— ал__\ Интегрируя это урав-
/ М
нение и учитывая, что i> = 0 при ? = 0, получаем v = -~— In ^_ .
129. Силы становятся равными, когда длина свешивающейся
части нити принимает значение х1 = 3/ъ lt N — 2/bmg, x1=B/bg.
Решение. Уравнения динамики для нити и масс тх и т2 за-
запишутся: plx1 = px1g + N1 — N2i m1i1 = m1g— Nlt
166
где #! — длина свешивающейся части нити, p=mjl — масса нити на
единицу длины. Определяя отсюда хъ Ni, N2 и приравнивая значения
Nx и N2, получаем приведенные ответы.
130. v = l/-S-a» —/J). * =/о <
Указание. Решение получается интегрированием уравнения
tnx= -j- gx, где т — масса всей веревки, а х —длина ее части, свеши-
свешивающейся в данный момент времени со стола. Начальные условия: v=0
при /=/0.
131. Для того чтобы расстояние между шариками было одинаковым,
пружины в нерастянутом состоянии должны иметь несколько различную
длину (или иметь различную упругость), так как на пружину / действует
вес двух шариков, а на пружину // — вес одного шарика. Поэтому:
1) при свободном падении всей системы шариков центр шарика 2
уже не является центром масс системы, а ускорение массы шарика 2
не является ускорением центра масс системы, так как при движении
расстояние между шариками меняется под действием пружинок. Центр
масс системы имеет постоянное ускорение g\
2) fl1=3^I a2=a3=0;
3) fl!=0, a2=— g, <h=g.
Решение. Исходные условия равновесия рассматриваемой сис-
системы шариков будут иметь вид
mg-TH+7\=0, mg— 7yf7\,=0, mg—T2=0,
где Тъ Т2 и Гн — натяжения соответственно пружин / и // и нити. Из
этих уравнений могут быть найдены значения Тъ Т2 и Гн. При
мгновенном перерезывании нити или пружины обращаются в нуль
силы Тн или Т2. В этот момент времени уравнения второго закона дина-
динамики для шариков в первом случае примут вид
mg+Tl=malt mg—T1+T2=ma29 mg—T2=ma8t
а во втором
tng—Тц+Т^таь /ng—Г1+712=/яа8» mg=ma3.
Решая для каждого случая соответствующую ему систему уравнений,
находим искомые значения ускорений шариков в начальный момент
времени.
132. Ускорения клина и тела, соответственно:
mg sin 2d _ Mg sin 2a
ai==2(M + msin2a)' a* ~~2 (M + m sin2a) >
сила давления тела на клин W и сила давления клина на горизон-
горизонтальную плоскость R определяются выражениями
.т Mm cos a n __M (^ + M)g
~yw+msin2a®' ~M + m sin2 a'
167
Решение. Начертим силы, действующие на каждое тело
(рис. 212). Только сила N может сообщить клину ускорение в направле-
направлении оси X (горизонтальной оси). Обозначим ускорение клина М через
%, горизонтальную составляющую ускорения тела т через а2 и верти-
вертикальную через а3. Тогда уравнения динамики дают:
N ъта=
mg—N'cosa=ma3, N's\na=ma2, \N\ = \
Между ускорениями аъ аъ а3 существует еще кинематическая связь,
выражающая условие скольжения тела т по грани клина. Эту связь
можно получить так: обозначим координаты какой-либо точки тела т на
Рис. 212.
поверхности, соприкасающейся с клином М, через х и у\ эта точкаилежит
на линии t/=tg а(х—Ь). Принимая во внимание, что при движении х и b
изменяются, а а остается постоянным, продифференцируем это равенст-
равенство два раза: y=tg а (л:—£); легко видеть, что у=—а3, х==—а2 и Ь=аг;
тогда равенство as= tg a(a2+%) и есть искомое соотношение. Совмест-
Совместное решение уравнений динамики при использовании найденного соот-
соотношения между ускорениями даст приведенные выше ответы на постав-
поставленные вопросы.
133. vcx> = 1/2v0{\— sincpo).
Решение. Составляя уравнения динамики для движущегося
тела в проекции на ось К и в проекции на касательную, находим:
y = dv/dt. Отсюда y = v-\-c, где v—абсолютная величина скорости
тела. При / = 0
Полагая при
168
v@)=vOt c = — vo A — sin ф0).
оо у (t) —^—v^t и v (t) ~^Уда, получаем ответ.
§ 3. Статика
134. F=P—Q (Q должно быть <Р).
136. Если бы канат был нерастяжимым и опоры абсолютно жестки-
жесткими, то тогда, действительно, канат можно было бы разорвать сколь угод-
угодно малой силой; однако наличие даже небольших растяжений каната и
деформаций опоры существенно ограничивает величину вызываемых ма-
малой силой натяжений каната.
137. На брусок А В действует сила сжатия 5 кгс; на проволоку
СВ — сила растяжения «7,1 кгс.
138. m = 4 Vb кг, F = 4(l/*5 + 2l/+^5—2 |/*5) кгс и на-
клонена к вертикали под углом а = arctg-*■—^ в сторону
крючка А.
139. fc^tg 15° = 0,176.
140. / = 22,5 кгс; F = 37,5 кгс; (т2)макс = 180 кг.
Указание. Обозначим через fa натяжение участка а веревки,
через ft, — натяжение участка Ь и т. д. Тогда fa = fb = f и fc = fd —
= 2/. Условия равновесия: mlg+m2g = fa + fb-{-fd = Af.
141. F=200Krc, Г=1000 кгс.
142. Т — гг—.—; зт • Равновесие возможно, если а > |3, т. е.
2 sin (а — р)
когда точка С лежит ниже центра масс палочки. В противном слу-
случае равновесие невозможно.
143. d = ^4 VD2—k2 « 0,05 см.
tnk
J44. &мин = 1/2> F > mg/2, где т — масса куба.
= 0 Фопт = 0; при
146. d = —
л
147. d = *
т
2 /?sin3a
149. хс=— :— , где хс — расстояние от центра круга.
150. d = 8
151. Я=
152. r=3
Указание. Можно считать, что на каждое из полушарий дейст-
действуют две силы, по величине равные Т и приложенные в точках, где нить
169
переходит с одного полушария на другое; так как расстояние центра
масс полушария от центра шара равно 3/&R, то уравнение моментов дает
? 4 r
153. 1) ТЛВ
F /cos a tg p , sin a\
~~2 \ cosy 'sin у/ '
JL /cosatgP sina>
2 \ cos у sin '
F cos a
cos C
2) tga=tg p tg у, при этом сила F лежит в плоскости, образован-
образованной стержнями А В и ЛО.
154. Нет, так как нет силы, которая уравновесила бы момент силы
тяжести относительно ребра Б.
155. F= ]A0/4 тс, причем слагающая, направленная вниз,
равна 3Д тс> а направленная к стене — ХД тс-
156. T = F = -~
= 900 кгс.
Указание. Так как трения в опорах нет, то F=T; эти силы об-
образуют пару, момент которой Г'/i и уравновешивает моменты сил
тяжести относительно опоры.
157. /=1 кгс в обоих случаях.
158. Решение. Рассмотрим бесконечно малый участок веревки
А В (рис. 213). Сила нормального давления его на поверхность столба
будет Т da. Разность натяжений на концах веревки dT—-r- da должна
быть уравновешена силой трения kT da. Это приводит к уравнению
dTlda—kT, интегрирование которого дает Т2=Т1е-2лкп (формула
Эйлера).
Л
T(a;+doc)
В
Рис. 213.
Рис. 214.
159. Решение. Пусть Л, Б, С, D — центры шаров (рис. 214).
По условию они должны находиться в вершинах правильного тетра-
тетраэдра. Возьмем единичные векторы £ь е2, еЗУ исходящие из вершины D
170
вдоль ребер тетраэдра. Силы Flt F2, F3, с которыми шары А, В, С давят
на шар D, можно представить в виде
F1^= — aeli F2=—ae2, F3^-—aebi
где а — положительный численный коэффициент.
Сила трения flt с которой шар А действует на шар D, лежит
в плоскости ADE, где Е — середина ребра СБ. Вдоль прямой DE
направлен вектор (e2 + es). Таким образом, векторы ег и (е2 + еь)
лежат также в плоскости ADE, а потому по ним можно разложить
силу flt т. е. /i = P (^2 + ^з) + Т^1- Так как сила/х перпендикулярна
к ёъ то скалярным умножением на ег отсюда получаем
(Мы воспользовались соотношениями ef = e^e^ = lt е1
= eg^r^cos 60° = 1/2.) Следовательно, /i = P(e2 + 03—ei)- Коэффи-
Коэффициент р -отрицателен, так как сила /х должна быть направлена
наружу тетраэдра. Возведением в квадрат и последующим извлече-
извлечением квадратного корня из последнего равенства находим /х = —р У~2 .
С другой стороны, величина силы трения /х может быть представ-
представлена в виде f1=zkF1 = ka. Это дает р = —kajY^* Аналогичные рас-
рассуждения применимы и к силам трения f2 и /3» с которыми на шар D
действуют шары В и С. В результате получается
/1» yj
ka
/2 = ^=
ka
/s=—f=-
Результирующая сил давления и трения, действующих на шар D,
будет — а A +&/]/" 2) (tfi + 02 + ^з)* Она должна быть уравновешена
весом шара mg. Это дает
Отсюда а = —
Найдем, наконец, силы трения xlt т2, т3, действующие на шары
А, Б, С со стороны горизонтальной плоскости, на которой они ле-
лежат. (Чтобы не усложнять рисунок, мы приложили эти силы к цен-
центрам шаров, хотя на самом деле они приложены в точках касания
шаров с упомянутой плоскостью.) Для наших целей достаточно найти
одну из этих сил, например тх. Эта сила направлена вдоль биссек-
биссектрисы АЕ угла ВАС. Туда же направлен вектор (е2 + е3)/2 —ег.
Поэтому можно положить Ti = e(e2 + e3 — 2^), где е—численный
коэффициент. Возведя в квадрат, а затем извлекая квадратный ко-
171
рень, получим т/1 = е/3. С другой стороны, давление на плоскость
всех четырех шаров равно Amg, а давление в точке касания шара
Л = 4/3 mg. Поэтому 'Xi = 4/3kmgJ а следовательно,
4 4
k
Остается только написать условие равновесия шара А. (Усло-
(Условия равновесия шаров Б и С не дают ничего нового.) Оно имеет вид
/ri+/i + Ti + N = 0, где F[ = — Flt /i = — /i—силы давления и тре-
трения, действующие на шар А со стороны шара D, а через N обо-
обозначена сила, нормальная к плоскости опоры. Для исключения N
умножаем написанное условие скалярно на вектор (е2 + е3— 2^),
нормальный к N. После простых преобразований приходим к квад-
квадратному уравнению 4&2 + 31^ 2/г—1=0, из которого находим
k= (/34 — 3/19/8 = 0,198.
Это и есть минимальное значение коэффициента трения, при котором рав-
равновесие возможно.
§ 4. Работа, мощность, энергия
160. Работа Л=200кгс-м. Потенциальная энергия £/=100кгс-м.
Половина работы идет на увеличение кинетической энергии поднимае-
поднимаемого тела.
161. 0,06кгс-м; 0,038 кгс-м.
162. 4,25 м; «8,16 м/с.
163. A=mg(H+kL).
164. A=mg(H—kL). Необходимо, чтобы в любом положении тела
соблюдалось условие h—&х>0, где h — высота, с которой спустилось
тело к рассматриваемому моменту, ах — пройденный им путь в гори-
горизонтальном направлении к тому же моменту. В противном случае тело
скатиться с горки не сможет.
,„_ d fmv2\ dv dt dv _
ds V 2 ) dt ds dt
166. Л«4,3-105 кгс-м.
167. (/=0,6 кгс-м.
168. 1 кгс-м.
,70. W=^
4/
a
171. 1) U=mgl(\— cos a). 2) A— \mal cos a da=mal sin a.
0
172
3) Приравнивая работу силы инерции потенциальной энергии
отвеса, отклоненного на угол а, находим g A — cos амакс)=а sin осмакс,
откуда легко получаем tg м^кс — — или aMaKC = 2arctg—.
4) Сравнивая найденный результат с результатами задачи 91,
получаем, что, действительно, амакс = 2а0, так как ao = arctg —.
о
5) После освобождения отвеса он сначала отклонится на угол
амакс, а затем начнет колебаться от направления, определяемого этим
углом, до вертикали, т. е. около направления, определяемого значением
угла а0. Постепенно колебания затухнут и отвес остановится в положе-
положении, задаваемом этим углом. В этом положении сумма действующих на
отвес сил будет равна та, и отвес будет двигаться вместе с вагоном.
172. 330 м.
Решение. При торможении с ускорением а возникнут колеба-
колебания (см. решение предыдущей задачи), и отвес отклонится на наиболь-
наибольший угол 2a/g= Зл/180 =0,052, следовательно, 2а=0,51 м/с и S=v2/2a.
173. v~ }Л>£/?= 11,2 км/с, где R — радиус земного шара.
174. Ввиду того, что поле тяготения является потенциальным полем
и все механические процессы в нем обратимы, очевидно, что ракета, на-
начальная скорость которой превышает значение, найденное в предыдущей
задаче, преодолеет силу земного тяготения и уйдет в межпланетное про-
пространство.
175. Т « ' m,^m ~ 6,2.109кгс-м, R — радиус Земли и g— ускоре-
ние свободного падения у поверхности Земли.
176. W=mgv(k cos a+sin a).
177. Решение. Уравнение движения лодки будет иметь вид
mdv/dt=—/г»2. Умножая обе части уравнения на элемент пути dS, полу-
получаем справа элементарную работу dA силы сопротивления на отрезке
пути dS:
do ,о 0 ,о v%m2dS JA
dt
или
, ,, ,»«.w . ~и...— Votn9dt
mvdv = d[ —jp l— —
Интегрируя последнее уравнение при условиях, что v=Vq при /=0
и у=о при /—их>, находим, что правая часть равенства также равна
ту2/2, что и требуется доказать.
178. £/=P*4/4, где х — деформация пружины.
179. 1) Ui/U2=k2^i* 2) Ui/U2=zk1/k2. Когда одна из пружин —
очень жесткая по сравнению с другой, практически вся потенциальная
энергия будет запасена в случае а) в более мягкой, а в случае б) — в бо-
более жесткой пружине.
173
180. Q=
181. T=2250W/(nRn) кгс.
182. W=nnRmg/2>000 кгс-м/с.
183. По часовой стрелке, так как при этом работающий участок рем-
ремня будет меньше провисать и охватывать большую часть окружности
шкивов, чем при вращении против часовой стрелки, и сцепление ремня
со шкивом будет больно.
185. г=е2/2Е, где е—заряд протона. Для вычислений формулу целе-
целесообразно преобразовать, положив E=eV. Тогда r=e/2V= 1,4- Ю-13 см
BУ=106В). Опыты по рассеянию ядерных частиц показали, что радиус
действия ядерных сил по порядку величины равен 10~*13 см. Поэтому при
расчете столкновения протонов, энергии которых превосходят примерно
0,5 МэВ, помимо электростатических сил, надо учитывать также ядерные
силы.
186. Поместив начало координат в одной из точек пола и направив
ось X вертикально вверх, получаем
—- (щхх) = тх2 — mgx = 2К— U,
где К—кинетическая, a U=mgx—потенциальная энергии шарика.
Проинтегрируем это соотношение от ^=0 до t=T, а затем устремим Т к
бесконечности. В результате найдем 2K=U.
§ 5. Законы сохранения количества движения и энергии
187. v= 10 см/с.
/72У
188. F== оом = 17 кг «с, где М и m — массы винтовки и пули.
189. у=М.
m
m cos a
Указание. Приведенное выражение для v легко получить,
применив закон сохранения количества движения к слагающим импуль-
импульса пушки и снаряда, направленным вдоль наклонной плоскости, непо-
непосредственно до и после момента выстрела. Импульс силы тяжести (дейст-
(действующей на оба тела) за короткий промежуток времени At выстрела пре-
пренебрежимо мал.
190. S2= 5000 м.
Решение. Падение одной половины снаряда под местом разры-
разрыва показывает, что все количество движения, которое имел снаряд в верх-
верхней точке, передано второй половине снаряда. Падение за 1 с с высоты
в 19,6 м говорит за то, что падающая часть получила при разрыве на-
начальную скорость vQ вниз, следовательно, и вторая половина получила
174
такое же количество движения вверх. Поэтому вторая часть снаряда
после разрыва имеет начальную скорость 2vrop в горизонтальном на-
направлении (где угор есть горизонтальная составляющая скорости снаря-
снаряда при выстреле), а в вертикальном направлении v0. Скорость v0 опреде-
лится из равенства h =
где т—время падения первого
осколка. Горизонтальная составляющая скорости агор определится
из равенства S1 = vropt и h
Расстояние места падения второго осколка от места разрыва по гори-
горизонтальному направлению можно определить по формулам, описываю-
описывающим полет снаряда в безвоздушном пространстве:
h т ,
Заменяя игор на У g/2h Sb получаем ответ:
m1(u—u)-\-mv
182. ^ = //2.
Решение. В рассматриваемом случае центр масс системы будет
смещаться за счет действия внешней силы (сил трения). Обозначим силу
натяжения веревки между лодками Т. Тогда:
равенство справедливо и после того момента, когда лодки
столкнутся и будут двигаться совместно до остановки. Проинтегрируем
его по времени от 0 до ос:
т1х1
+ т2х2
так как х\ @)=i2 @)=^ (оо) = л:2 (оо) = 0, ^@)=
д;1(оо) = д;2(оо) = ^оо, получим: 2хоо — / = 0, хж = 1/2.
193. 9 м/с и 1 м/с.
104 .. —
т1+т2
к
195. У
196. После соударения второй шар отскочит назад. Л =
2m2v --/ пц__
т2 f k
175
+ т2
Mnu2 -,/" Mm
6)A~V V k(M+m) *
198. При условии, что m1lm2>20t где mj — масса шара, имевшего
меньшую энергию. Ответ легко найти из следующих соотношений:
ОЛ 2 2 fll\Vi — tTl2V2 _
/Hi -f- т2
где г — скорость шаров после удара, v± и v2 — их скорости до удара.
199. v= 1000 м/с (из равенства mv=Mv1).
200. F=2Mv/t.
201. /г=Ат1у/А/^2500 кгс, где А/^ — масса угля и At — время,
за которое эта масса погружена на платформу.
202. Работа FASf= -г— vAS'= Am «у2, кинетическая же энергия
угля равна Am-v2/2, т. е. вдвое меньше. При соприкосновении с плат-
платформой куски угля сначала скользят по полу платформы (в сторону,
противоположную движению платформы), и работа паровоза идет также
на преодоление возникающих при этом сил трения. Эта работа (превра-
(превращающаяся в тепло) равна Am-v2/2.
203. Дополнительное давление на стол (сверх веса части каната,
уже лежащей на столе) вызвано потерей импульса падающими элемен-
элементами каната при их ударе о стол. Пусть за элемент времени dt на стол
падает элемент каната с массой dm=\i dx, где jn — масса, приходящаяся
на единицу длины каната, a dx — элемент длины каната. Сила, действую-
действующая со стороны этого элемента на стол, будет
AF = dm- v/dt = \idx- v/dt = \iv2,
• скорость, с которой элемент dm достигает стола. Но, как
нетрудно заметить v2=2gx, где х —
длина части каната, лежащей на сто-
столе. Отсюда AF=2[igx. Таким об-
образом, полная сила, действующая
на стол, будет равна 3\igx.
204. Шарик отразится от клина
в горизонтальном направлении и
полетит дальше по параболе (рис.
215).
205. p=2mv cos a.
Рис.215. 206. Решение. Пусть V—
скорость первой частицы до столк-
столкновения, vt и v2 — скорости частиц после столкновения. Законы
сохранения импульса и энергии дают
Возводя первое соотношение в квадрат и вычитая из него второе,
176
получим (flitf2) = 0. Если оба вектора Vi и v2 не равны нулю, что
будет при нелобовом ударе, то угол между ними будет равен 90е.
При лобовом столкновении t?x = 0, V2 = v, т. е. частицы просто обме-
обмениваются скоростями.
207. AK=2m(v—и)и\ Др=—2т(v—и); тело после удара остано-
остановится, если u=v/2.
Указание. Законы упругого удара о движущуюся стенку легко
получить, если в формулах для скоростей, имеющих место после удара
двух упругих тел, перейти к пределу, полагая массу одного тела (стен-
(стенки) бесконечно большой.
208. а-частица уносит 3,5 МэВ, нейтрон— 14,1 МэВ.
209. Ядро трития уносит энергию 1 МэВ; общий энергетический
выход реакции 4 МэВ.
210. Нейтрон уносит энергию 2,44 МэВ, ядро Не3 — 0,81 МэВ.
211. Ядро Не4 уносит энергию 3,7 МэВ; общий энергетический вы-
выход реакции 18,3 МэВ.
212. 74МэВ и 3/4МэВ.
213 ^L=4
Е
,. Потеря энергии максимальна при тх—т2.
214. а = 4Л/A +ЛJ, где Л — атомная масса частицы, с которой
сталкивается протон.
Л
а
1
1
2
0,89
4
0,64
12
0,284
215. Решение. Пусть тг — масса рассеиваемой частицы (а-
частицы или дейтрона), v — ее скорость до рассеяния; т2 — масса рас-
рассеивающей частицы (атома водорода); vx и v2 — v
скорости частиц после рассеяния (рис. 216). За-
коны сохранения импульса и энергии дают
mip = m\i\ cos a -(- m2v2 cos P,
m^sin a = m2y2 sin p, t i' ^>V
Исключив отсюда угол C и скорость v2t получим
для v1 квадратное уравнение
(m1+m2)u2—2m1w1cos a+ (m1—m2)v2=0.
Условие вещественности корней его, как легко
видеть, имеет вид sin a<m2/m1. Максимальный угол а, удовлетворя-
удовлетворяющий этому условию, и будет равен углу О. Таким образом,
177
sin$=m2!mi. Отсюда находим для а-частицы Ф=14°30', для дейтрона
ft=30°.
216. Масса а-частицы должна быть меньше массы ядра: т < М\
— m T/ mvo-./ 2M x_a n / M — m
о|_ 3 тУ _ ЗтУ2 Л Зт \
217. и=——— , ^==—5— 1 тт~ » гДе m—масса прото-
Z /И о \ М ]
на. Процесс невозможен, если М < 2>т.
218. Решение. Пусть р—импульс падающей частицы, /?х и
р2—импульсы образовавшихся частиц. Если все импульсы колли-
неарны, то
Р-Р1+А. fc=4
Исключив р2, получим квадратное уравнение для рг. Потребовав, чтобы
его корни были вещественными, найдем искомое условие:
т
В случае равенства оба корня квадратного уравнения совпадают, в слу-
случае неравенства они различны.
219. Решение. Импульс а-частицы до столкновения Ро^^Не^о-
После столкновения импульс сохранится. С ним связана кинетическая
энергия движения центра масс:
К = Р" = тНе Е
Дц'м 2(m + m) m + m °>
которая не затрачивается на ядерные превращения. Искомая энер-
энергия Ео найдется из условия
откуда
Е Не
220. Решение. Минимальное значение искомой энергии про-
протона £р соответствует лобовому столкновению, когда все частицы до и
после столкновения движутся вдоль одной и той же прямой. Поэтому
можно ограничиться только такими столкновениями.
Допустим сначала, что энергия бомбардирующего протона равна
пороговой £Пор- Тогда получающиеся в результате реакции ядро
Be и нейтрон должны двигаться вперед с одинаковыми скоростями
и уносить кинетическую энергию Е0=Р^ор/[2 (mBQ + mn)], гдеРпор —
178
импульс протона, соответствующий пороговой энергии £пор =»
= Р2 Д2тр). Разность этих двух энергий
£"°р-£°= тве+тп Р Е"°* <220Л>
затрачивается на ядерную реакцию.
Найдем теперь энергию бомбардирующего протона £р, при ко-
которой получаются нейтроны в состоянии покоя, а ядра бериллия
летят вперед. Если Рр —импульс протона до реакции, то £р=Рр/Bтр),
а кинетическая энергия образовавшегося ядра бериллия ^gg5^
= P2/BmBe). Разность этих энергий
идет на ядерную реакцию, а потому равна величине B20.1). При-
Приравнивая выражения B20.1) и B20.2), находим
или, пренебрегая различием масс протона и нейтрона,
Be p
При больших энергиях появятся нейтроны, летящие назад.
221. Решение. Условие, при котором рассматриваемая реакция
происходит с минимальной затратой энергии, легко найти, рассмотрев
процесс в системе центра масс. Затраченная энергия будет минимальна,
если в этой системе все четыре образовавшихся частицы покоятся. В ла-
лабораторной системе они будут двигаться с одинаковыми скоростями, как
если бы образовалась одна частица с массой покоя М=4тр или энергией
покоя 4трс2. Эту энергию удобно обозначить 2Е. Таким образом, 2£=
=4трс2=4£0, где Ео — энергия покоя протона. Полная энергия движу-
движущегося протона (с импульсом р) до реакции будет ]/г£2+(рсJ. Посколь-
Поскольку при столкновении импульс сохраняется, полная энергия образовав-
образовавшихся частиц представится выражением уBЕJ-\-(рсJ. Закон сохране-
сохранения энергии дает
Ve\ + (рс)« + Ео = 1/
отсюда
Чтобы найти исходную кинетическую энергию протона, надо из полной
энергии его вычесть энергию покоя. Это дает
В рассматриваемом случае Е=2Е0, так что /С=6£о=5,62 ГэВ»
179
222. 7,08 ГэВ.
223. q=
224. В момент остановки барабана, как и при движении лифта, си-
сила натяжения будет равна весу лифта, а дальше трос будет растягивать-
растягиваться и сила натяжения будет постепенно возрастать, пока кабина не оста-
остановится. В момент остановки кабины сила натяжения будет наиболь-
наибольшая — больше веса кабины. (Отсюда видно, что в таком положении лифт
не может оставаться неподвижным; он начнет подниматься кверху —
возникнут колебания кабины.) Быстрота нарастания натяжения во вре-
времени и его величина зависят от упругих свойств троса и массы кабины.
225. Удлинение «55 см, Г«55тс.
М
226. h = 0,005—/.
т
227. 1) , = 2^+^sin (а/2); 2) p=2Af Kfgrin (а/2)-/т>'
/72 /72
3) 1
т
Решение задачи о соударении баллистического маятника и пули
проведено путем применения закона сохранения количества движения к
системе маятник — пуля. Этот способ решения, очевидно, справедлив
только в том случае, если удар пули не передается оси вращения маят-
маятника. Дело обстоит именно так в том случае, когда пуля ударяется в так
называемый центр качания маятника, находящийся на расстоянии при-
приведенной длины физического маятника от его оси вращения, и скорость
пули перпендикулярна к прямой, соединяющей точку подвеса маятника
с его центром качания. При ударе же пули в произвольную точку маят-
маятника для решения задачи необходимо воспользоваться законом сохра-
сохранения момента количества движения в системе маятник — пуля. В пер-
первом же случае применение закона сохранения момента количества
движения будет эквивалентно применению закона сохранения количест-
количества движения. Аналогичных вопросов об ударе в твердое тело, закреплен-
закрепленное на оси, касаются задачи 359—361. Подробности о таких случаях см.,
например, В. Л. Кирпичев, Беседы о механике, Гостехиздат, 1957.
228. i1 = o0 = V
Решение. Отсчитывая координаты грузов от уровня осей бло-
блоков, запишем для положения равновесия:
cos фо=/7г1/2т2= /2/2, фо=я/4, х?=//2.
Из условия нерастяжимости нити следует кинематическая связь:
где L — полудлина нити.
180
Записывая полную энергию E = K+U для трех положений
системы хх = 0, х1 = х1= 1/2, х1—-х1макс:
l/ WJ+ (^-
= ?£ A + со52Фо) vl - mlgx\ + 2m2g
= —migxl макс
получим два уравнения, из которых следуют значения, приведенные
в ответе.
у x\ макс + ( yj ,
229. а1=—*-■—-а, а2 = -^—а 1/ -г1-.
/Hi -j- tTl-t ы ТПл -4- /По г /о
230. 1) Опишет над плоскостью параболу, вершина которой будет
на высоте hl2\ 2) будет равномерно скользить по плоскости со скоростью
V
231. Ящик не будет двигаться, потому что сообщаемые ему нор-
нормальная рдг и тангенциальная pf (по отношению к наклонной пло-
плоскости) слагающие импульса р вертикально падающего тела будут
удовлетворять соотношению p^/Pf = tga, которому удовлетворяют
слагающие веса ящика mg^//mgf = tga = kt а в результате действия
последних ящик не приходит в движение. После полной остановки
падающего тела в ящике увеличение веса ящика по той же причине
не приведет его в движение.
М
232. На расстоянии — /, где М — масса поезда до момента
отрыва вагона, а т — масса вагона.
233 w= MU v= mU
М + т* М + т'
234. Sl=~^'
Ма —та тМа
- -гг.—; , uo — ~rz , / — -r-j—; •
М + т М + т М + т
-Ami c (М + 2тI
т
I
237. 1/ =
A + т/М)
Решение. Из закона сохранения количества движения имеем
Ми = — mv, где и — скорость лодки с человеком после броска, v —
скорость ядра. Скорость ядра иОтн относительно лодки vOTH — u4-v —
=v (I + m/M). Для того чтобы ядро попало в корму лодки, необхо-
необходимо, чтобы смещение ядра по горизонтали относительно лодки за
время его падения (t= yr2h/g) было равно длине лодки: v0Tnt — l,
181
238.
239. x^-jj^— (a — b).
240.
Решение. Уравнение движения легко получить из условия со-
сохранения количества движения в системе ракета — газ. Приравнивая
количество движения системы в момент времени t количеству движения
системы в момент времени t-\-dtt получаем
Mv=(M—dM) (v+dv)+dM (v+u).
Отбрасывая члены второго порядка малости и учитывая, что dM=\idt,
получаем искомое уравнение.
оуМ n , —iiudt —dMudt dM
241. Решение. dv=—^—=—п ir=— W"XT-
М dt M M
Интегрируя это уравнение при условии v = Q при Л4 = Л40, находим:
t; = « In (Mo/M) или
ev/u = M0/M. B41.1)
Полученное соотношение называется формулой К. Э. Циолковского.
при и = «/2.
Решение. Приравнивая количества движения системы в момент
времени t и t-\-dt, получаем уравнение
Mv=M (v+dv)—(u—v)\i dt B42.1)
Интегрируя его, находим зависимость модуля скорости корабля от вре-
времени. Для получения к. п. д. системы надо составить отношение вели-
величины полезной работы (в данном случае это будет приращение кинетиче-
кинетической энергии корабля d{Mv2>l2)—Mvdv) к величине работы насоса
(\idt*u2/2) за одинаковые промежутки времени: r[=2Mvdv/\iu2dt; поль-
пользуясь уравнением B42.1), можно написать:
\]=2(и—v)v/u2.
Отыскивая максимум этого выражения как функцию v/u> находим
?1макс=1/2 при v=ul2.
243. Решение. Рассмотрим сначала движение частицы в сис-
системе центра масс. В этой системе протоны движутся навстречу друг другу
с одинаковыми скоростями. Обозначим через Е полную энергию каждого
из них в этой системе. Поскольку суммарный импульс протонов равен
нулю, они вместе могут рассматриваться как одна частица (как до, так
и после столкновения) с массой покоя М> определяемой соотношением
2ЕМс.
Перейдем теперь в лабораторную систему отсчета, в которой один
из протонов (мишень) покоится, а другой движется. Такой переход, оче-
182
видно, никак не скажется на внутренних превращениях, которые могут
претерпеть частицы. Обозначим через Е1 полную энергию движущегося
протона, а через Р — его импульс в лабораторной системе отсчета. За»
дача состоит в том, чтобы найти связь между энергиями Е и £'. Суммар-
Суммарный импульс обоих протонов в той же системе отсчета будет, очевидно,
Р, а энергия Е'-\-Ео. В релятивистской механике энергия связана с
импульсом соотношением
£' + £0 = V(Mc2J+(PcJ^ VBEJ + (Pc)*,
откуда
(РсJ=(Е'+Е0J-BЕJ.
С другой стороны, если написать соотношение между энергией и импуль-
импульсом только для движущегося протона, то получится
откуда (РсJ = Е'2—Е1
Сравнивая оба выражения для (РсJ, получим
Е2
Чтобы получить кинетическую энергию протона Кг в лабораторной
системе, надо вычесть отсюда энергию покоя Ео. Это дает
K" = 2(^--£„
Если, как в разбираемом случае, £0<^£, то
Для протона Ео= 0,937 ГэВ, а поэтому К' — 250 ГэВ.
244. Решение. Пусть vlt v2i ...— скорости ракеты после 1-го,
2-го, ... выбрасываний. По закону сохранения импульса (т0—Ат)их+
+ Ат»^=0, где w — скорость выброшенной массы Am после первого вы-
выбрасывания. Очевидно «=£>!—w. Исключая w, получим
vx—u. B44.1)
Найдем теперь v2- В системе отсчета, движущейся со скоростью v2, ра-
ракета перед вторым выбрасыванием неподвижна, а после второго выбрасы-
выбрасывания приобретает скорость v2—v±. Поэтому можно воспользоваться
формулой B44.1), сделав в ней замену то-+то—Am, v-^-^v^—vv Это дает
Am
2 1~~m0—Am
Комбинируя это соотношение с B44.1), находим v2. Продолжая этот про-
процесс дальше, нетрудно получить
ГАт , Am , , Am "j
[^Щ— Ат+ '# # +m0- (N — 1) AmJ "'
183
В пределе, когда Дт->0, Л^-уоо, т0—(N—l)Am->m, сумма, стоящая в
квадратных скобках, переходит в интеграл, и мы получаем
С dm*
т
где т — конечная масса ракеты. После взятия интеграла получается
формула Циолковского.
245. ^-^.
г dt и
Решение. Уравнение движения ракеты
dv dm
mir^-uit-m8
перепишем в форме
d dm d (v + g t) и
dt v ' б ; dt dm m
Это дает
m m б
Величина \i, очевидно, равна —dmldt и находится из условия, что для
неподвижной ракеты dv/dt—O.
246. а = ±1„В>.
v m
Решение. Ускорение корабля по абсолютной величине равно
G)V=cou, причем V— const. Поэтому уравнение движения т dvldt=u dmldt
переходит в mvcodt——и dm. Замечая, что da= со dt есть угол поворота
за время dtt и интегрируя, получим ответ.
247. Первый способ требует меньшей затраты топлива.
249. Решение. Приращение скорости ракеты v связано с из-
изменением ее массы т соотношением mdv — — и dm, причем dmra3 =
5= — dm, где тгаз — масса выброшенных газов. Приращение кинети-
кинетической энергии газов:
dK
Подставив сюда игаз = и—и и воспользовавшись формулой Циолков-
ского т = тое V/Ut получим
или после интегрирования
184
где для краткости введено обозначение x = vK0H/u. Кинетическая
энергия ракеты:
/Срак =4- mvloH = 4" fnQu44"^
В результате находим
При *=4 г)=45%.
250. Решение. Если бы не было притяжения Луны, то задача
свелась бы к нахождению наивыгоднейшего отношения tnjtni для дости-
достижения заданной скорости ракеты. Поэтому от действия силы тяжести
можно отвлечься и считать, что ракета движется в пространстве, сво-
свободном от тяготения. Примем за единицу массы полную массу ракеты в
момент старта. Тогда
mH-ma+m^l. B50.1)
После выгорания топлива в первой ступени масса системы уменьшится
на а^тх. Если при этом будет достигнута скорость vlt то по соотношению
Циолковского
evt/u_.!
!
A—aj т1 + т2 + m
Масса A—<х1)т1 отделяется, и включается двигатель второй ступени. По-
После выгорания топлива во второй ступени скорость ракеты возрастает
еще на величину v2i причем
ev2/u __ Щ + т
A—аа) т2 + т'
В этом можно убедиться, если перейти в систему отсчета, в которой ра-
ракета в момент отделения первой ступени покоится. Полная достигнутая
скорость найдется перемножением двух предыдущих соотношений и по-
последующим логарифмированием. Исключая еще при этом массу т2 с по-
помощью соотношения B50.1), получим
—=1п A—т{) — In A—ajmi) — In [A—a2) A—m{)-\-a2m\.
Здесь т и и играют роль постоянных параметров, а тх — аргумента, от
которого зависит скорость у. Дифференцируя по тх и приравнивая про-
производную нулю, получим условие максимума
——г + о-^ 1 '— = 0. B50.2)
тх—\ ' р — тх ' у — т1 v '
где введены обозначения
Р = 1, Y=l+T-^-m.
r ax r ' 1— а2
185
Условие B50.2) приводит к квадратному уравнению относительно тъ
решая которое, найдем
P —?)•
Перед корнем взят минус, так как по смыслу задачи 0<т!<1. С помощью
B50.1) находим массу т2, а затем искомое отношение тг1тх. Возвра-
Возвращаясь при этом к прежним параметрам аг и а2, получим
t — m
аг 1—a2
Решение имеет смысл при выполнении условия
5ГТ=?т<1>
В реальных условиях, когда т<^1, а параметры аг и а2 отличаются не
очень сильно, это условие соблюдается. При ax=a2 получается простая
формула
ш2/т1= Ym. B50.4)
251. Пусть т и v — масса покоя и скорость ракеты в произволь-
произвольный момент времени t, а тгаз и vra3 — те же величины для газов,
образовавшихся из топлива ракеты к этому моменту времени. Так
как газы, уже покинувшие ракету, не оказывают влияния на ее
движение, то можно принять я?газ = 0. Однако газы непрерывно
образуются, так что dmTa3 Ф 0. На основании закона сохранения
импульса и энергии (релятивистской массы)
JtV +^grgagrg3__==ri,nst B51.I)
V 1—i
tn . i
Дифференцируя уравнение B51.1) с учетом B51.2) и полагая в окон-
окончательном результате тгаз = 0, получим
dn-\- (v — ^газ) Q' г — Q*
По релятивистскому закону сложения скоростей
где w — скорость газовой струи относительно ракеты. Исключая угаз,
после несложных преобразований находим
dv и dm
v2—c2 ~~"c*~m'
186
Предполагая скорость и постоянной и интегрируя, получим
mP_f -нг"" B51.4)
253. По формуле B51.4) то/т= 5 -103327. Для ориентировки заметим,
что масса Галактики —3-1044 г, Метагалактики ~1066 г. Таким обра-
образом, даже масса Метагалактики невообразимо мала по сравнению с мас-
массой космического корабля. Было бы неосторожно применять к столь ги-
гигантским «кораблям» обычные законы физики и, в частности, формулу
B51.4). Наш пример показывает лишь абсолютную непригодность ракет
на химическом топливе в качестве звездолетов.
254. Решение. Если v — скорость ракеты, то mv=P—Elc,
где Р — полный импульс, а Е — энергия излученного света. Дифферен-
Дифференцируя по времени и пренебрегая изменением массы ракеты, находим ис-
искомую мощность — = mcg=3-1012 Вт = 3-109 кВт, что превосходит
мощность крупной электростанции примерно в 1000 раз.
255. t=—In { 1 —I -^—j =22с. Приближенно ввиду малости
m° —=25 с, / = irf = 220 м.
g
g
256. Решение. Уравнение движения капли
d (tnv) dv . v dm
—-—~=mg, или ==Z8'
dt dt m dt
Так как m~r3 и, по предположению, dm/dt~r2, то drldt—C—const. От-
Отсюда с учетом начальных условий получаем r=Ct. Уравнение движения
приводится к виду
dv v
Решая его и учитывая, что при ^=0 и=0, получаем v=1l^gt. Падение
капли будет равноускоренным с ускорением a=g/4.
§ 6. Динамика движения материальной точки по окружности.
Движение относительно вращающихся систем отсчета
257. 1) F = mgt 2) F = mg—^t 3) F = mg+^t где/? —
радиус кривизны моста.
258. иомин = V"Rg-
187
Решение. Радиус кривизны траектории, нормальное ускорение
тела и его скорость связаны соотношением p—v2/an. Для начала закруг-
закругления нормальное ускорение максимально и равно an=g, следователь-
следовательно» Рмнн—уУё- Условие р># дает для скорости vl^Rg, откуда и следует
приведенный ответ.
259. F=(\+4kh)mgt a=4kgh.
Решение. В нижней точке траектории шарик будет иметь
ускорение ауу, направленное вверх. Поэтому давление шарика на
дно чаши можно записать так: F = m{g-\-aN). Ускорение а^ можно
найти следующим образом. Дифференцируя уравнение параболоида
два раза по времени, имеем: z — 2k (*2 + #2) + 2& (хх + у'у). Поэтому
искомое ускорение шарика а в нижней точке траектории, где
х — у — 0, будет иметь значение
a = z0 = aN = 2k (x20 + yl) = 2kui где vo = 2gh. B59.1)
Следовательно, zQ~a^ — ^kgh. Заметим, что в изложенном приеме реше-
решения обойдено вычисление радиуса кривизны параболы в ее нижней точке,
который обычно бывает необходимо знать для вычисления нормального
ускорения
ajv=vVpt B59.2)
где р — радиус кривизны траектории. Зная уравнение параболы, мож-
можно было бы методами дифференциальной геометрии найти значение
р= 1/2Л. B59.3)
Тогда, используя выражения B59.1) — B59.3), можно найти значение
a/sr иначе, чем это_было сделано выше.
260. vo= Y^gR^S км/с; ускорение снаряда равно g и нормально к
траектории; v0 принято называть первой космической скоростью.
261. Траекторией снаряда будет дуга
эллипса. Эта кривая изображена на рис.
217 сплошной линией. Остальная часть эл-
эллипса изображена пунктиром. Один из
фокусов этого эллипса будет совпадать с
центром Земли. Ускорение а снаряда бу-
будет направлено всегда к этому фокусу
эллипса, причем a=GM/R2t где G — пос-
постоянная тяготения, М—масса Земли и
R — расстояние до центра Земли.
262. 1) h=5R/2. 2) На тележку дейст-
действуют сила притяжения Земли mg и сила
рис 217 давления рельсов mv2/R—mgtrj\ev — ско-
скорость тележки в этой точке. 3) Не доходя
до верхней точки, тележка отделится от рельсов [и будет двигаться
по параболе до встречи с рельсами в нижней части петли.
188
263. k
264. со2 =
g (cos a — k sin a)
/itga(sina + fc cos a)'
Решение. Так как в рассматриваемом случае сила трения имеет
максимальное значение kN (N — сила нормального давления тела на
стенку воронки) и направлена вдоль образующей конуса вверх, то урав-
уравнение вращательного движения
тела (массы т) вокруг верти-
вертикальной оси и условие отсутст-
отсутствия ускорения тела по вертика-
вертикали можно записать в виде
mco2/i tg cl-=N cos a—kN sin a,
mg—N sin a-\-kN cos a,
откуда и следует искомый ре-
результат.
265. 0 =
266. 1) sin a=G)V0/(g—со2/).
2) Тригонометрическое уравне-
уравнение a>2/sina+a>2r0=gtga ре-
решаем, пользуясь рис. 218. 3) На
нити будет излом в месте при-
прикрепления к ней дополнитель-
дополнительной массы, так как направление нити, определяемое углом а, зави-
зависит от величины /, вдвое большей для одного из грузов.
267. со2 ==-т= g
Рис. 218
268. R -^ уп £ + 0,01/1)'
269. Затормозить.
270. При движении по синусоиде нормальное ускорение максималь-
максимально в ее вершинах, где кривизна кривой максимальна. Если у—у(х) —
уравнение синусоиды, то в вершинах */'=0, и радиус кривизны в этих
точках можно вычислить по формуле \/R=\y"\. Записав уравнение сину-
синусоиды в виде у=А sin 2n-x/l (амплитуда А и пространственный период /
постоянны), нетрудно получить условие, при котором заноса не будет:
у< 1 1/ М , где и, — коэффициент трения, g — ускорение свободного
2л г А
Заноса не будет при усло-
услопадения.
271. макс
вии v < в У\щ/А-
272. Самолет во время совершения петли будет иметь ускорение
a=i;2/#=:9 м/с2, направленное к центру петли. В нижней точке петли на
189
крылья будет действовать давление воздуха
—) » 1.92 mg « 1,4 тс,
т. е. нагрузка на крылья будет почти вдвое больше, чем при горизон-
горизонтальном полете. Отсюда видна необходимость запаса прочности в конст-
конструкции самолета для выполнения им фигур высшего пилотажа.
273. В нижней точке петли летчика будет прижимать к сиденью с
80
силой ц-х F0,5+9,8)кгс« 563 кгс, соответственно в верхней точке —
с силой«403 кгс.
274. При v2/R>g в точке Л «отвес» будет направлен вверх, при
v2/R < g—вниз (рис. 219). На этом же рисунке указано расположе-
расположение отвеса в других точках при v2/R<g.
А
Рис. 219.
275. r=v2/(gtga).
Указание. Когда самолет летел прямолинейно, плоскость кры-
крыла была горизонтальна. Подъемная сила в этом случае направлена вер-
вертикально вверх, т. е. перпендикулярна к плоскости крыла. При поворо-
повороте корпуса самолета вокруг продольной оси подъемная сила поворачи-
поворачивается на тот же угол, т. е. продолжает оставаться перпендикулярной
к плоскости крыла, так как силы взаимодействия самолета с окружаю-
окружающей средой зависят лишь от относительного движения самолета и среды.
276. Груз массы М займет либо ближайшее возможное положение
к оси, либо наиболее удаленное. Положение на расстоянии R=mg/(MaJ)
от оси соответствует равновесию, но оно неустойчиво, так как даже при
небольшом увеличении радиуса R веса mg будет недостаточно, чтобы
удерживать массу М на окружности, и она уйдет в наиболее удаленное
положение от оси. Наоборот, при небольшом уменьшении радиуса R
190
вес mg будет больше силы, необходимой для того, чтобы удерживать мас-
массу на расстоянии R, и она будет приближаться к оси.
277. Тот же, что и в задаче 276.
278. Решение. Груз массы М будет совершать движение по
кругу радиуса RQ—mg/(MaJ). Так как момент количества движения
массы М должен оставаться постоянным, то M(dR2=L== const. Отсюда
следует, что центробежная сила может быть представлена в виде
f=M(iJR=L2/(MR*).
График зависимости центробежной силы от R изображен на рис. 220.
Постоянная сила натяжения нити F=mgi действующая на массу М в
противоположную сторону, изобразится на этом же рисунке в виде
прямой, параллельной оси абсцисс. Устойчивому положению массы М
на вращающемся стержне соответствует точка пересечения этой прямой с
кривой центробежной силы. Отклонение груза массы М от положения
RQi независимо от направления этого отклонения, вызывает силу, воз-
возвращающую массу М в положение RQ. Это и означает, что положение
массы М на расстоянии Rq от оси вращения будет устойчивым. Различие
в полученных результатах по сравнению с результатами предыдущей
задачи объясняется постоянством момента количества движения систе-
системы, заданным в условиях задачи. Все это рассмотрение имеет смысл, если
выбраны условия, при которых RQ не мало. Иначе нельзя было бы пре-
пренебречь моментом инерции прибора по сравнению с моментом инерции
массы М.
Центробежная сила
\
-Вес массы т
Центробежная
сила
Bug массы т
Рис. 220.
Roz
Рис. 221.
Я
279. Возможны (при не слишком большой массе т) два положения
равновесия: устойчивое R02 и неустойчивое Rolt если не считать устойчи-
устойчивого положения равновесия R=0 (рис. 221). Так как в этом случае по-
постоянный момент количества движения есть (Л1/?2+/0)со«*а, то центро-
центробежная сила равна Ma2R/(/Q+MR2J. Пользуясь графиком сил так же,
как и в ответе предыдущей задачи, можно решить вопрос об устойчиво-
устойчивости равновесия.
191
Наличие двух положений равновесия тела на стержне в этом случае
непосредственно вытекает из того, что величина центробежной силы
должна обращаться в нуль не только при R-+oo, как в условии предыду-
предыдущей задачи, но также и при #->0. Действительно, существование у сис-
системы момента инерции /0 приводит к тому, что при приближении массы
М к оси вращения угловая скбрость вращения остается конечной вели-
величиной и выражение M(D2R при #->0 обращается в нуль. Между двумя
равными нулю значениями непрерывной функции должен иметь место
максимум этой функции и, следовательно, кривая функции должна
дважды пересечь всякую прямую, параллельную оси абсцисс и проходя-
проходящую ниже максимальной ординаты функции. В данном случае наш гра-
график дважды пересечет прямую, соответствующую значению силы mg.
Знаки производной функции в местах ее пересечения с прямой f=fng
и определяют устойчивость и неустойчивость положений равновесия
массы М.
280. Нить, привязанная к оси, натянута силой (.o2[m1RJrm2(RJr I)]',
нить, связывающая массы, натянута силой со2т2(#+/).
281. Сила натяжения пружины должна быть пропорциональна ее
удлинению. Коэффициент упругости пружины должен быть равен УИсо2.
282. £«48гс/см.
kg k — mco2
283.^0, если ц- < mlo{g/l*+k/my иначе cosa^-^-
(a> < V~kjm).
Решение. Пусть Т — натяжение пружины. Тогда
T=k(l-lQ), l=lo+T/kt
Т cos a=mg, T—mg/cos a, T sin a=mco2r,
где r=/sina. Если a=£0, то имеем:
m@2\ O| Ql Д со2
=maW0 cos a, cosa=--2- 1 — —3
w \ 2
где Qi=g/lo, Ql = k/m. Зто справедливо, если —-====r < co< Q2»
V Qi+Qi
Если со < x 2 , то a = 0; при со -> Q2 ^ ~* °°» т- е« пружина
обрывается.
284. В зависимости от значения со либо внизу, либо вверху, так как
положение равновесия, соответствующее расстоянию от оси R=
—gCE/itfED), неустойчиво. См. ответ к задаче 276.
285. x=(g/co2) tga.
286. р/2со2<87\
287. со2=-у-1^2. Равновесие устойчиво, если kl>mg cosa=—j=. mg,
192
Решение. Запишем уравнение динамики для системы коорди-
координат, вращающейся вместе с треугольником:
Здесь N—сила нормальной реакции, /?к—сила Кориолиса, F^ —
центробежная сила инерции. В проекции на гипотенузу АС полу-
получим
mR == — mg cos a—k (R — /) + mco2/? sin2 a,
или
k — mco2 sin2 a \ D kl — mg cos a
fc — mco2 sin2(
cc J '
где /? — расстояние груза (координата) от точки А на гипотенузе.
Полагая /? = 0, определяем положение равновесия муфты:
kl-mgzos* ш2
fe — mco2 sin2 a '
приравнивая /?*=/, находим угловую скорость:
/ sin2 a /
Если ввести смещение из положения равновесия \ — R—R*t то
получим
v fe — mco2 sin2 a ?
что для k > mco2 sin2 a соответствует гармоническим колебаниям
муфты около положения равновесия с частотой
m
и означает устойчивость положения равновесия.
288. Г«1,6Р.
289. Наклон делается для того, чтобы давление поезда на полотно
железной дороги было нормально к плоскости полотна и чтобы реборды
колес не срывали рельсы со шпал в сторону.
где a — угол наклона полотна к горизонту, v — скорость поезда и R —
радиус закругления.
290. Пол комнаты представляет собой параболоид вращения г=
ОJ
=^— (*2+#2); ось Z направлена по оси вращения, начало координат
"о
находится в нижней точке, а оси X и Y лежат в горизонтальной пло-
плоскости.
291. 1) Сила натяжения нити обратится в нуль, когда она займет
положение, определенное углом а (см. рис. 68), для которого cos a=2/3.
7 Под ред. И. А. Яковлева 193
2) В этой точке траектории шарика v= y~gLl3.
3) Дальнейшее движение шарика будет происходить по параболе
до тех пор, пока нить не будет вновь натянута в результате перемещения
шарика.
292. Решение. Пуля вылетает из ружья, имея скорость, на-
направленную на юг. Следовательно, на нее будет действовать направлен-
направленное на запад кориолисово ускорение
d2x/dt2=2vto sin ф,
где со — угловая скорость вращения Земли и ф — географическая широ-
широта местности, в которой произведен выстрел. Считая в первом приближе-
приближении вектор скорости пули постоянным, получаем (путем двукратного
интегрирования по времени выражения для кориолисова ускорения)
величину западного отклонения пули от первоначального направления
выстрела x=vt2to sin ф=5,8 см.
оло лг 4@^0 sin ш cos a sin2 а _,
293. К югу, */= -*—2 «71 м.
о
294. Паровоз действует на правый (по ходу поезда) рельс железно-
железнодорожного пути с силой (ход решения задачи ясен из рис. 222)
F—2mv(D sin ф=2б кгс,
где со — угловая скорость вращения Земли вокруг своей оси.
Рис. 222.
Рис. 223.
295. Расположение нужных для решения векторов угловых скоро-
скоростей и сил показано на рис. 223. Вектор скорости поезда перпендикуля-
перпендикулярен к плоскости чертежа и направлен за чертеж. Направленная верти-
вертикально компонента кориолисовои силы F^=2mv(a cos ф= 14,9 кгс. На-
Направленная на юг горизонтальная компонента кориолисовои силы Ff=
~2mv(u sin ф= 25,3 кгс, где ф — географическая широта места.
296. Р = Р
S
| »i-0 i 1—2— cos <
— 7,5-10-£) (/? — радиус Земли).
194
297. v0—2m/co0/(M+/n). Скорость пушки направлена на запад.
Решение. В системе отсчета, связанной с Землей, уравнение
движения пушки со снарядом во время движения снаряда внутри ее ство-
ствола можно записать в виде
(М + т) — = 2m(o0v — 2m(a0at)
где v — мгновенное значение скорости снаряда, аH — угловая скорость
вращения Земли вокруг ее оси. Следовательно,
1ч
о о
Шш- ™*-^
298. Av^2(o0vl/gy где соо—угловая скорость вращения Земли во-
вокруг своей оси.
Решение (в системе координат, связанной с Землей). С учетом
действия центробежной силы инерции и кориолисовой силы условия
отрыва самолета от Земли можно записать в виде:
1) при разбеге с запада на восток
mg—
2) при разбеге с востока на запад
mg-\-2tn(u0v2
3) при разбеге вдоль меридиана
mg—m(ulR=kvl>
где i>i и v2 — окончательные скорости разбега, R — радиус Земли.
Решение этой системы дает
Учитывая, что g^> alR, находим Ai>.
299. Решение. Уравнение движения:
Отбрасывая малый член 2[фсо], находим ускорение и скорость
в нулевом приближении: a = g, v = Vo-\-gt. Подставляя полученное
значение v в правую часть уравнения движения, находим ускорение,
а его интегрированием—скорость в первом приближении:
Аналогично находятся второе и высшие приближения. Во втором
7* 195
приближении
r=
В частности, если тело падает без начальной скорости, то для его
смещения из начального положения s = r—г0 получим
300. К востоку:
COS ф = 2/з ®'Л COS ф,
4g Sin 2ф = V2W/ Sin ф
к экватору:
где ф — географическая широта рассматриваемого места,
h — высота падения.
301.
— время.
Л, м
sB0CT, см
58кв> СМ
100
1,2
5,3-Ю-6
500
13,8
1,3-Ю-3
1000
38,7
5,3-Ю-3
£000
ПО
2,1-Ю-2
302. 1) В неподвижной системе отсчета отклонение падающего тела
к востоку (от вертикали, проведенной через точку первоначального поло-
положения тела) объясняется различием в тангенциальных скоростях точек
земной поверхности и тела, находившегося над Землей на высоте h.
Вызванная суточным вращением Земли линейная скорость точки С
(рис. 224, a) vc—Rto, где R — радиус Земли и со — угловая скорость ее
вращения. Соответственно для тела, находящегося на высоте h в точке
Л, vT— (R-{-h)(o. Следовательно,
hm. C02.1)
Согласно закону инерции падающее тело должно сохранять свою тан-
тангенциальную скорость неизменной. Поэтому в процессе падения тело
сместится на восток дальше, чем точка С. Это обстоятельство было впер-
впервые указано* Ньютоном в 1679 г. При h<^R различие в скоростях точек
196
Аи С C02.1) в течение времени падения тела /= у S2hlg должно привести
к смещению тела на восток от точки С на расстояние *=/ico Y2h/g.
Однако приведенный расчет является лишь приближенным. Мы
предполагали, что в тангенциальном по отношению к Земле направлении
падающее тело движется по инерции равномерно. Между тем, сила
тяжести будет нормальна к первоначальной скорости тела только в
А
h
X. д\
Дуга
эллипса
й)
Рис. 224.
6)
точке А. В последующих точках эллиптической траектории падающего
тела (см. задачу 261) сила тяжести, направленная всегда к центру Земли,
уже не будет перпендикулярна к скорости падающего тела и будет из-
изменять не только ее направление, но и абсолютную величину. Произве-
Произведем расчет, учитывая это обстоятельство. На рис. 224, б легко видеть,
что ускорение падающего тела вдоль направления X будет
= --gsina« — g—»— g
« — gat.
После интегрирования этого уравнения при начальных условиях
при f = 0 получим для ртела следующее уточненное выражение:
Следующее интегрирование (выполненное при начальных условиях
х = 0 при t =0) даст уточненное значение *тела = —1/в&оэ*3 +
_^ (R-^-h) со/. За время падения тела точка С на поверхности Земли
сместится на отрезок xc=R®t (при h<^.R). В результате смещение упав-
упавшего тела на восток относительно точки С окажется равным
2 / 2 /*8/*со
197
Разумеется, полученное выражение совпадает с результатом реше-
решения задачи 300, выполненным во вращающейся системе отсчета, связан-
связанной с Землей.
2) Применение к падающему телу закона сохранения момента коли-
количества движс шя основано на следующих соображениях. На падающее
тело действует центральная сила притяжения Земли. Поэтому момент
количества движения тела относительно земной оси должен оставаться
неизменным. Следовательно (рассматривается падение тела на экваторе)
т(/? + /iJco = m(R + y)* (fi>-|_ij—) , C02.2)
где М — масса тела, R — радиус Земли, h — первоначальная высота
тела над Землей, у — расстояние тела до поверхности Земли, со — угло-
угловая скорость вращения Земли, v — тангенциальная скорость тела отно-
относительно Земли. Полагая h и y<^R$ находим из C02.2) v=2co(h—у).
С другой стороны, h—y—gt2/2. Поэтому v=(ugt2. Смещение х упавшего
тела от основания перпендикуляра, проведенного с поверхности Земли
в точку первоначального положения тела, будет
о о
Последнее изящное решение задачи принадлежит К. А. Туманову. Если
опыт производится на географической широте ф, то в выражение для х
войдет множитель cos ф.
303. Пуля отклонится к западу на расстояние
#зап ===~о" п— COS ф Л/ 01 СМ.
Результат может показаться неожиданным. При движении вверх корио-
лисова сила направлена на запад, а при движении вниз на восток. На
первый взгляд кажется, что отклонение к западу должно компенсиро-
компенсироваться последующим отклонением к востоку. На самом деле это не так.
Когда тело движется вверх, его боковая начальная скорость равна ну-
нулю. В наивысшую точку тело приходит, однако, с западной составляю-
составляющей скорости, которую оно приобретает под действием кориолисовой
силы. Поэтому обратное падение тела начинается с начальной скоростью,
направленной на запад. Следовательно, скорость все время направлена
на запад и перед ударом о землю обращается в нуль.
304. Ствол ружья надо наклонить к востоку под углом
а=-| — cos ф » 2,45-10~4 рад « 0,85' » 51*.
305. Поверхность воды образует с горизонтом угол а, определяемый
формулой tg а = Bvw/g) sin ф, где и— скорость течения реки, со —угло-
198
вая скорость вращения Земли, g — ускорение свободного падения. Ре-
Результат находится из условия, что поверхность жидкости должна быть
нормальна к равнодействующей приложенных к ней сил, т. е. силы
тяжести и кориолисовой силы.
306. Решение. Не учтено кориолисово ускорение. Введем
систему отсчета 5, равномерно вращающуюся вокруг точки А с уг-
углевой скоростью +со. Пусть точка В вращается относительно этой
системы с угловой скоростью —со. Обозначая вектор АВ через г,
имеем для скорости и ускорений точки В:
*отн = — [юг], аотн = апер = — со2г, акор = 2 [й>г>отн] = 2со2г.
Следовательно, аабс = аотн + «кор + «пер = 0.
307. a = 4nR/(vT) = 0,0209 рад =1,2°.
308. Решение. В системе отсчета, связанной с вращающейся
каруселью, боковое ускорение пули а^ок — 2 [г>отнсо] + [гсо], или
в скалярной форме Ябок^—2t'0co + /-(o. Отклонения вправо считаются
положительными, влево — отрицательными
(рис. 225). Радиус г считается положи- ^
тельным выше центра О и отрицательным— ^/
ниже. Учитывая начальные условия г —
= —D/2, со = соо при tf = 0, получим
r = v0t — D/2t со
Интегрируя последнее уравнение, находим
боковое отклонение. При t — D/v0 оно долж-
должно обращаться в нуль. Это дает со = 4y0co0/D=
= 2/3 рад/с2. Линейное ускорение на пе- Рис. 225.
риферии карусели будет 6,67 м/с2.
309. F=-y~ у —Р «0.12Я, где Р — вес тела на поверхности
Земли, Т — продолжительность звездных суток, R — радиус Земли.
310. 1>о>со#.
311. Решение. Задача решается проще, если движение рас-
рассматривать в неподвижной системе отсчета (точнее, в системе отсчета,
вращающейся относительно Земли вокруг вертикали рассматриваемого
места с угловой скоростью —сов, где сов — вертикальная составляющая
угловой скорости осевого вращения Земли). В этой системе уравнение
малых колебаний математического маятника имеет вид г+&2г=0, где
Q2=g/l, а г — смещение маятника из положения равновесия. В началь-
начальный момент маятник, вращаясь вместе с Землей, имеет боковую ско-
скорость сов#о. Поместим начало координат О в положение равновесия
маятника. Ось X направим из точки 0 к точке (х=х0, у=0), в которой
199
маятник находился в начальный момент. Для движения вдоль оси Y
имеем i/+Q2y=0. Решая это уравнение при начальных условиях yt=<r=
3=10, £f=o=toBA:o, получим
В среднем положении Ш=л/2, и для бокового отклонения в этом поло-
положении наша формула дает
у=-^=-^. sin ф * 1 мм.
312. Решение. Если корабль движется по круговой орбите с
постоянной скоростью v, то на тело массы \х в корабле действует центро-
центробежная сила инерции \iv2/Rt направленная от Земли. «Вес» тела на ко-
корабле получится вычитанием из нее силы гравитационного притяжения
[ig: \i(v2/R—g). По условию эта величина должна равняться \ig. Отсюда
находим i>= Y~2gRj т. е. корабль должен двигаться по круговой орбите с
параболической (второй космической) скоростью vn= y~2gR— 11,2 км/с.
Если Мо — стартовая масса корабля, а т0 — масса, с которой он выво-
выводится на круговую орбиту, то
Molmo=exp(vn/u). C12.1)
Найдем теперь расход массы при облете корабля вокруг земного
шара. Уравнение движения имеет вид
таабс= — и dmldt-\-mgy
где скорость газовой струи и направлена радиально от центра Земли.
2
Так как при обращении корабля аабс=аНорм = ~ = %?» то Щ~
= — и dm/dty или в скалярной форме dmlm——g dtlu. Отсюда
m=moexp (—gt/u).
Если t — период обращения, то gt = 2nRg/va = nva. Следова-
Следовательно, для конечной массы ткон получаем
или на основании C12.1)
mK0H и
§ 7. Динамика твердого тела. Динамика системы
313. а2 = — ax= - ^~]~~&- Натяжение нитей:
ttl2 -\~ fill -\ о*
Г
)т~т rt _L_ m . rt I It
200
усилие:
Решение. Натяжение нити будет различным для правого (Г2)
и левого (Тх) отрезков нити. Уравнения поступательного движения под-
подвешенных грузов:
C13.1)
C13.2)
Уравнение вращения блока вокруг его геометрической оси
(Т2—Тл) r=I dmldt, C13.3)
где dtoldt — угловое ускорение блока. Учитывая отсутствие скольжения
нити по блоку и нерастяжимость нити, получаем уравнения
а»=—ai=r daldt. C13.4)
Решение пяти уравнений C13.1) — C13.4), содержащих пять неизвест-
неизвестных, ах, а2, со, Тх и ?2, дает ответ на задачу.
гт/2
314. Ф=2£1
3,5. T ^
4A+Mg/2P)*
flfco m2R—mxr
~!F~~ т.Г" ^
fits
317. С чашки весов надо снять груз ..—§-.
318. Если с чашки весов снят тот же груз, что и в предыдущей
задаче, потому что при подъеме и при спуске грузика ускорение его одно
и то же как по величине, так и по направлению.
320. Д=м , "V// 2^^ 196 см/с2, где /—момент инерции
диска и валика, а М — их масса.
321 а 2та
6Zl a
Решение. Уравнения движения обеих обезьян по вертикали от-
относительно неподвижной системы координат, уравнение вращательного
движения блока и уравнение кинематической связи можно записать в
виде
тах = Тх—mg, ma2 — Т2—mg,
1/2MR^ = (T1-T2) R, ах = а-аъ,
где ах и а2 — ускорение первой и второй обезьян, Р — угловое ускоре-
201
иие блока, равное $—a2lRy Тг и Т2 — соответствующие натяжения ве-
веревки, R — радиус блока. Отсюда и получаем а2.
я/2
f
J
о
322. Г= тДЛг f г— =1.855
J
о
где / — момент инерции дверки, m — ее масса. Интегрирование вы-
выполнено численно.
323. Решение. Пусть 7\/2 и Т2/2 — натяжение верхней и ниж-
нижней нитей. Тогда ускорение центра масс катушки а= (Mg-\-T2—T^lM;
угловое ускорение катушки d(aldt~{T2-\-T^)rll\ ускорение груза а2=
— (mg—T2)lm. Из кинематических условий следует: a=r da>/dt=ai/2.
Отсюда:
324. Ускорения центра нижнего и верхнего дисков
1+-^- 14-
8 a
Решение. Обозначив через # координату центра нижнего диска,
через х — координату центра верхнего диска, через щ и со2 — угловые
скорости нижнего и верхнего дисков, черкез 7\ катяжение нижней пары
нитей и через Т2 — натяжение верхней пары нитей, можно написать
следующие уравнения движения и кинематические соотношения (кине-
(кинематические соотношения вытекают из условия нерастяжимости нитей):
mg-{-T1—T2 — tna2, a2=^<d2rt mg—T1 = mali
ai—#2==a)ir» T2r = I(d2, Tir~l(uv
Решая совместно эти уравнения, получаем значения ускорений.
325. a=2/sgs\na (рис. 226).
Решение. Уравнение движения
щ since центра массы диска параллельно наклон-
наклонной плоскости
mg sin a—/Tp=ma. C25.1)
Уравнение вращательного движения дне-
Рис. 226. ка вокруг геометрической оси диска
/ da>/dt=fTVRt C25.2)
где dmldt — угловое ускорение диска, / — момент инерции и R — ради-
радиус диска. Вследствие отсутствия скольжения
a=Rda>/dL C25.3)
Из уравнений C25.1) — C25.3) находим a, dau'dt и /тр. Так как диск
202
сплошной и однородный, то /=т#2/2. Подставляя значение / в выраже-
выражение для а, получаем результат, приведенный в ответе.
326. а=б/7& s*n а» Сила трения равна 2/7mgsina, где т -«-масса
шара.
327. K=Mv2, где v — скорость движения центра обруча.
328. f=llzmg sin а=50 гс.
329. *>78tg а.
330. 1) Шар. 2) В /5/14 раз в данном месте. 3) В 15/14 раз.
331. Выгоднее ось, сточенная на конце. Сила трения остается неиз-
неизменной, но момент силы трения относительно оси пропорционален
радиусу поверхности опоры. Если kN — сила трения, N — сила давле-
давления на опору, то при равномерном распределении силы трения по поверх-
поверхности опоры на единицу площади ее момент будет равен 2l$kNR% где R —
радиус круга опоры.
332. а= -^- =115 см/с2.
тг-\-Ьт-\-тг
000 F(Rcosa—r)R .
333. а=— —г™ » гДе ' и /я — момент инерции и масса
катушки соответственно; а > 0, если cos а > г//?; сила трения
f=F cos a—та.
334. у = 2 У 1ао/3.
Решение. В системе координат, связанной с доской, уравнения
поступательного и вращательного движения цилиндра имеют вид
та = та0—FTpt /а/г — Flprt
где та0 — сила инерции, Flp — сила трения, действующая на цилиндр
со стороны доски, / — момент инерции цилиндра иг — его радиус. Ре-
Решение этой системы уравнений дает а = 2/3а0. Учитывая, что v== \^2la,
находим окончательный результат.
335. Обозначим натяжение нити через Т и силу взаимодействия ме-
между рамой и катком — через V'. Если каток идет сзади, то можно напи-
написать уравнения движения так:
для катка,
sin а—Т'+Т для рамы,
Mza=^Mzg(s\na—kcosa)—Т для тела массы М3.
Из этих уравнений получим
(Mi-\-M2 + M3) sin a—kMz cos a
1/2М1 sin a—k C/2Mi+M2) cos a
Если tg а > k C -f- 2M2/Mi), то Т > 0. Чтобы нить была натянута в этом
203
случае, каток следует пускать сзади. Если tg a < k C+2М2Шг), то
каток следует пускать впереди.
336- А
Р г ш е н и е. Условия равновесия сил и моментов (в неинерциаль-
ной системе отсчета):
для критического случая T — kP2
. (mg , mah\ f. kh\ , mg kg
Это справедливо, если kh/l^ 1/2. В противном случае (Рх < 0) авто-
автомобиль опрокидывается; поэтому всегда a^kg.
337. @= Vbgfl.
Указание. По закону сохранения энергии
1 , « 1 / 9 mgl
т/й2=ттш=т-
338. L = Ve^*(o«52.1010 г.см2/с.
339. 1,67'1011 тс »км. Величину момента количества движения см.
в ответе предыдущей задачи.
340. Скорость вращения возрастет в A+т/?2//) раз. Кинетическая
энергия вращения возрастет во столько же раз. Увеличение энергии
произойдет за счет работы, произведенной человеком при перемеще-
перемещении его по диску.
tnrv
342. 1) А£к = 2/2со2//2; 2) Д£к = /2со2/2/2.
344. N = 3nrn2/Dkg).
345. Кинетическая энергия вращения уменьшится на
346. Решение. Благодаря трению скольжения натяжения рем-
ремня сверху Ti и снизу Т2 будут разными. Записывая для маховиков урав-
уравнения движения, получим
204
Поделим эти уравнения соответственно на Ri и R^ сложим и проинтег-
проинтегрируем. Тогда получим
Входящая сюда постоянная равна /1co0/^i, так как в начальны^ момент
сэ1=соо, соа=0. Когда скольжение прекратится, то ш1^1=соа/?а. Решая
полученную систему уравнений, найдем угловые скорости сох и 0J после
прекращения скольжения:
URt I1R1R2
(Oj = -i G)o, С02 = — @0
Потеря кинетической энергии на трение равна
Д/( = — L_2_J— ,л*
2
348. % = s-5-^ ЮО» ^2 = r-i-i @0 =
Потеря энергии
&к= /-7"' .,<
349. Максимальное изменение продолжительности суток ДГ, выз-
вызванное ударом метеорита, определяется формулой
ДГ mvR cos ф _
где Г=86 164 с — продолжительность суток, #=6400 км — радиус»
М=6*1021 т — масса Земли» / — ее момент инерции. Если считать Зем-
Землю однородным шаром, то /=2/5 MR2 (на самом деле из-за возрастания
плотности к центру Земли момент инерции ее несколько меньше и состав-
составляет приблизительно I=4SMR\ В результате получится ДГ/Г^
-2-10~15, ДГ~2.10-10с.
350. Наивыгоднейшим является выстрел в горизонтальном направ-
направлении в плоскости экватора. В этом случае
с—v 5 т*с*Т* 25 mW4 . 1П м
<//-^/^ 9.10""**
,</
с ~ 18 пЧМ (ДГJ ~ 36 я2М2/?2 (ДГ)
где с — скорость света в вакууме. Остальные обозначения такие же, как
в предыдущей задаче.
351. Т «Го(Ро/р)г/а=1.3.1О-3 с.
352- —~
353. / = Z
205
354. Решение. Скорость шарика в нижнем положении до удара
ио= Vr2gH. Так как удар неупругий, то непосредственно после удара
шарик и нижний конец стержня в нижнем положении будут иметь одну
и ту же скорость v. Она найдется из закона сохранения момента им-
импульса относительно оси Л
где 1—1/9М12 — момент инерции стержня относительно той же оси. Так
как у=/со, то написанное уравнение дает
ml2 3m
v Г^
Теперь надо решить, будут ли шарик и стержень после столкновения
двигаться вместе или при дальнейшем движении они разойдутся. С этой
целью вычислим скорость шарика v± и нижнего конца стержня v2 при
поднятии на какую-то одну и ту же высоту hlt если бы при этом они дви-
двигались независимо друг от друга. Эти скорости найдутся из уравнений
сохранения энергии
*-x$ = 2ghlt ±-L(v*-vl) = Mg!±.
Преобразовав второе уравнение к виду
v2—vl=3ghlt
видим, что t»i>y2. Поэтому в любом положении шарик будет стремиться
обогнать стержень. А так как шарик движется позади стержня, то он
все время будет прижиматься к стержню. Отсюда следует, что после
удара шарик и стержень будут подниматься как единое тело. Высоту
поднятия h легко определить из закона сохранения энергии. Она равна
/ + т/ 6т2
(M+2m)gl*xr (М + 2т)(М + Зт)
355. После удара шарик поднимается на высоту h1~
3 ( М \2L/ . и
~ ~¥ \ 'м ' ) • нижний конец стержня — на высоту п2 =
2
п
пгт„ .. 1 ml2 ЖА , 3 Mm f .
356. U=~2 ix-ml2 Mgl = ~2 M + 3m g ' ГДе момент
стержня.
357. K=V0--~ У y^siny = 444 м/с.
358. ML2=ml2. Так как L>/, то для возможности процесса необхо-
необходимо М<.т. При М>т процесс невозможен.
359. Лозу следует рубить участком сабли, отстоящим на 2/3 длины
от ручки сабли.
206
Решение. Пусть удар с силой F пришелся на расстоянии г
от середины сабли, которую будем считать однородной пластинкой
(рис. 227). Под действием этой силы пластинка начнет двигаться поступа-
поступательно и вращаться; если при этом точка О останется в покое, то рука
не будет чувствовать удара. Напишем уравнение движе-
ния центра тяжести С пластинки:
т
где dvldt — ускорение центра тяжести. Для вращения
пластинки относительно оси, проходящей через центр
тяжести С,
ml2 da
2" 1Г~/Т'
где dco/dt — угловое ускорение пластинки, т — мас-
масса пластинки, т/2/12— момент инерции пластинки
относительно центра тяжести С. Точка О будет в по-
покое, если скорость поступательного движения v и ли- О
нейная скорость точки 0, обусловленная вращением Рис. 227.
пластинки вокруг точки С с угловой скоростью со, бу-
будут равны по величине и противоположны по направлению, или если
dv I dw „
---=-— —-. Подставляя это условие в уравнения движения, полу-
dt 2i ut
чаем /•=1/в/, откуда уже легко найти ответ.
Искомая точка на пластинке (сабле) есть так называемый центр
удара, совпадающий с центром качаний физического маятника той же
пластинки, подвешенной в точке 0. Разгрузка оси вращения от действия
удара особенно необходима в случае баллистического маятника (см.
также задачу 227).
360. Пластинка будет вращаться с угловой скоростью со =
12m v Зт0—4т
, а шар полетит назад со скоростью t>i=-|—~-т>— v.
a v v x 4m+3m0
361. i/ = -
362. v =
\
Решение. Применяя закон сохранения энергии к стержню до
удара и законы сохранения момента количества движения и энергии к
системе стержень — тело во время удара, получим
Mgl/2 = М2со2/6, 7зМ/2со = 73М/2со'' + mvU
Ve^/2co2 = 7eM/2co'2'+ mi>2/2,
где со и со' — угловые скорости вращения стержня при его вертикальном
положении до и после удара соответственно, v — скорость тела после
удара. Из решения этой системы уравнений получаем значение v.
207
363. 5=Ve M2ll(m2k).
Решение. Применяя закон сохранения энергии к стержню до
удара и закон сохранения момента количества движения к системе стер-
стержень — тело во время удара получим
.. / 1 ml2®2 1 Алп
Mg -j^-^ -у-» "з м 1 ш = mvl'
где со — угловая скорость вращения стержня в момент удара, v — ско-
скорость тела т сразу после удара. Перемещение 5 тела можно найти из
условия mv2l2—kmgS. Из написанных уравнений следует ответ.
364. Движение муфты вдоль стержня будет происходить по закону
x=aoch со/=2сЬDОя/) см,
М= 2х -^- ©о« 64 • 105 sh (80я/) дин -см.
Решение. Движение муфты удобно рассматривать во вращаю-
вращающейся системе координат. Тогда уравнение движения вдоль стержня под
действием центробежной силы будет иметь вид т d2x/dt2=m(a2x. Общее
решение этого уравнения х=Ае®*-\-Ве-®*. Подставляя х@)—а01
i@)=0, получаем решение. Момент количества движения муфты отно-
относительно оси вращения стержня L—m(ax2\ он растет со временем. Для
его увеличения необходимо приложить внешний момент сил M=dL/dt=
i
365. (о=Зтсо0Ш=2,2-10-в рад/с, где шо= 7,3 Л0-$ рад/с — угло-
угловая скорость вращения Земли вокруг своей оси.
Решение. В системе координат, связанной с Землей, на движу-
движущийся внутри ствола снаряд (а, следовательно, и на систему пушка —
снаряд) будет действовать сила Кориолиса, направленная на запад и
равная F—2mv(iHt где v — мгновенное значение скорости снаряда и соо —
угловая скорость вращения Земли вокруг своей оси.
Уравнение движения пушки со снарядом, имеет вид
где / — момент инерции пушки (моментом инерции снаряда можно пре-
пренебречь ввиду условия M^>m)t r — расстояние снаряда от оси вращения
в данный момент времени, со — мгновенное значение угловой скорости
вращения ствола пушки. Полагая v = at, получим
о /0
где t0— У21/а—время движения снаряда внутри ствола. Интегрируя
это уравнение, находим со.
366. V— У 3gl. Искомая точка находится на расстоянии х = 2/31
от основания столба.
208
367. Решение. Кинетическая энергия стержня в горизонталь-
горизонтальном положении 1/2/оJ==1/2/й^/. Центростремительное ускорение центра
масс стержня в том же положении йJ//2. Отсюда по теореме о движении
центра масс
п I ml2 3
Применив к вращению стержня в положении 2 уравнение I d(o/dt==Mt
получим / --jj=mg —. Отсюда находим вертикальную составляющую
ускорения центра масс в том же положении:
I doa mgl2 3
Далее, ma = mg—FBepT. В результате получится
369. F=(\-\-4a2mlI)mgt где т — масса, / — момент инерции чело-
человека относительно перекладины, а — расстояние между осью вращения
и центром масс человека. Если при оценке момента инерции моделиро-
моделировать человека однородным стержнем, вращающимся вокруг одного из его
концов, то получится F=4mg.
370. Решение. На основании закона сохранения энергии
y2+2g/i=const. C70.1)
Момент силы тяжести относительно точки подвеса не имеет вертикаль-
вертикальной составляющей. Момент силы натяжения веревки равен нулю. По-
Поэтому при движении человека вертикаль-
вертикальная составляющая его момента количества
движения остается неизменной. В положе-
положениях, где высота h максимальна или ми-
минимальна, скорость человека v горизон-
горизонтальна, а момент количества движения
равен mvrt где г — расстояние до верти-
вертикальной оси, вокруг которой вращается
человек. Значит, в этих положениях вели-
величина vr одна и та же. В момент, когда вы-
высота h максимальна или минимальна, опи-
опишем в вертикальной плоскости окружность
с центром в точке подвеса О, проходящую
через точку нахождения человека М
(рис.228). По известной геометрической теореме г2=АВ*ВС, или г2=
= B/—h)h. Поэтому в положениях, где h максимальна и минимальна,
B/—h)hv2= const. C70.2)
209
Запишем соотношения C70.1) и C70.2) для этих положений, имея в виду,
что максимуму h соответствует минимум и, и наоборот. Получим:
^ + 2gfr = у
B1 —Лмин) ЛМину2макс = B/—/1Макс)
Решая эти уравнения, получим
макс B1 — ^макс) /Q7n Оч
C70'3>
2g/tMHHB/~/tMHH)
7—t Г Г
При этом учтено, что в реальных условиях h < /, так что величина
C70.3) действительно максимальна, а C70.4)—действительно мини-
минимальна. Если /iMaKC и /iMHH пренебрежимо малы по сравнению с /,
то Умакс=2^/1макс, уМин = 2£/:мин.
371. vl =
372. (о2х= Pf 2[L2 + 4r2 —/2 —(L—/—ягJ].
Указание. Воспользоваться законом сохранения энергии.
373. Решение. Уравнение моментов вращения цилиндра около
оси, лежащей на плоскости качения, будет
где R — радиус цилиндра. При качении без скольжения центр масс
цилиндра получает горизонтальное ускорение dv/dt—R dca/dt, которое
сообщает сила трения; следовательно,
k( F \ > R d(° = F
где k — искомый коэффициент трения. По условию задачи F/m=g/2.
Таким образом, dv/dt=g/3 и fc>2/9.
374. Решение. Качение без скольжения. Силы, действующие на
цилиндр, показаны на рис. 229. Сила натяжения веревки F, сила трения
/, ускорение груза а. Уравнения поступатель-
поступательного движения: цилиндра F-\-f=1/2ma, груза
•** \искорение^а Mg—F=Ma и уравнение вращения ци-
цилиндра (F—f)R=1/2mR2a/2R. Отсюда полу*
^ чаем
F = */Sma9
с-
Скольжения не будет, если \f\<kmg или ЛХв+Зт/Л!)-1, гдеk — коэф-
коэффициент трения.
Качение со скольжением. Угловое ускорение цилиндра E, ускорение
оси цилиндра Ь. Теперь уравнения движения будут
210
Ускорения связаны условием a=b-\-$R и сила трения f=kmg. Отсюда
получаем а=(\—1/3km/M)(l-{-1/3m/M)-1gi при условии &<(8+Зт/Л!)-*.
Замечание. Полезно рассмотреть движение при /=0 в отсут-
отсутствие сил трения.
375. Скольжение начнется в точке с угловой координатой ф*=
= arccos 0,8 или на высоте 0,8# от горизонтального диаметра цилиндри-
цилиндрической поверхности.
Решение. Записываем уравнения динамики для скатывающего-
скатывающегося обруча:
тап = mg cos ф — N, max== mg sin ф—Flt
где an — v2/(R-\-r)t ax=^dv/dt> FT — сила сухого трения, N—сила
нормального давления,/0 — момент инерции обруча. Отсюда определя-
_ mg .
ем силу трения FT = —^- sin ф и силу нормального давления обруча
V2
на цилиндр N = mg cos ф —mn_i • Закон сохранения энергии дает
и2
=g(l—cos ф), следовательно,
R + r
N=mg B cos ф— 1).
Условие начала скольжения
Приравнивая соответствующие величины при 6=0,5, получаем: cos ф=
=0,8; или высота от горизонта, на которой начинается скольжение,
376. Обозначив силу, действующую на катки со стороны штанги,
через /, можно записать уравнения движения катков (линейные и угло-
угловые ускорения обоих катков одинаковы): для первого
для второго
I 2» 2 dt — 2^>
где Ft и F2 — силы трения, возникающие между катками и плоскостью.
Кроме того, так как скольжение отсутствует, то dv/dt—R dw/dt. Отсюда
dco 2Rgs\na сс 9 ? h — 12 dm п о„
—=—-Л ^66 с-2, / = -l_J_-^0,27 кгс.
at /1 + /2 . nno Zi< at
т
Положительное значение / при выбранных нами знаках в уравнени-
уравнениях движения соответствует тому, что штанга сжата и толкает катки. Сле-
Следовательно, если каток с большим моментом инерции внизу, штанга сжи-
сжимается; если он вверху, штанга растягивается.
211
377. Решение. Обозначим ускорение груза тп\ через а, ускоре-
ускорение подставки Ьу угловое ускорение цилиндра Р, натяжение нити 7\
коэффициент трения к.
1) Уравнения движения:
Условие, связывающее ускорения, a=b-\-$R. Отсюда определяем а—
Н2)-1/7, где
2) Первые два уравнения движения:
F—Т—km^g—m^a, T—
третье такое же, как и в случае 1), и такая же связь между ускорениями,
Отсюда получаем:
mzj ~"*т3' г- R •
3) a=(mi-\-tn3)~1F в отсутствие трения; a=(ml-\-m3)~1F—kg —
при наличии трения, $=2F/(msR).
378. Пока движение совершается без рывка, диск опускается и под-
поднимается с одним и тем же ускорением, направленным вниз:
2г2
Натяжение нити при опускании и поднятии диска также одно и то же
и равно
Для оценки среднего натяжения нити во время рывка Грыв обозначим
через v максимальную скорость диска в нижнем положении. За время
полоборота диска At—nr/v количество движения диска изменяется на
2Mv. Это изменение равно импульсу силы, действующей на диск, за то
же время, т. е. BГрЬ1В—Mg)At. Вычисления дают
Во время рывка нить испытывает дополнительное натяжение
Д7 « —^ Mgx3t\4 H.
nr g s
Полное натяжение нити во время рывка 71=710+АГ«8,0 Н.
212
-\ щ-Т & 1,427*0, где / — момент инерции системы, То — натяже-
натяжение нити при неподвижном грузе.
380. а) а= 2 I l/D2_/l24gsina> где р —радиус инерции шарика,
R2
2h —ширина желоба; б) а= D2gsina.
4р -f-K
381. Я= Т 2Р R. Для сплошного шара H = 27/10Rt для полого
г2 А-о2
382. tga>—^fc, где р —радиус инерции катящегося тела.
Для сплошного шара tga > 7/2k, для полого tga > ?/2k. Для сплош-
сплошного цилиндра tga > 3k, для полого tga > 2k.
383. Положение точки Б, в которой шарик отрывается от сферы и
начинает свободно двигаться под действием силы тяжести, определяется
углом а, косинус которого равен
cos a=2r2/Cr2+p2),
где р — радиус инерции шарика. Результат не зависит от радиуса сферы.
Для сплошного шарика cos a=10/17, для полого cos a=6/u.
384. Будем рассматривать все движения в системе отсчета, в кото-
которой наклонная плоскость неподвижна. Так как центр масс системы и
мгновенная ось вращения А (см. рис. 104) движутся параллельно, то
уравнение моментов относительно этой движущейся оси имеет вид
/ dmldt—M (см. задачу 433). Момент количества движения системы L
слагается из момента количества движения цилиндра /со и момента ко-
количества движения собаки m^vh, где /i=r(l-f-cos a) —длина перпенди-
перпендикуляра, опущенного на наклонную плоскость из точки «S. Итак,
L=I(a-\-mlrv A+cos a),
причем под / следует понимать момент инерции цилиндра относительно
мгновенной оси, т. е. величину 2шг2. Из-за отсутствия скольжения v=
= сог, а потому
<x)]rv.
Так как центр масс системы и мгновенная ось А движутся параллельно,
то производная L по времени должна равняться моменту внешних сил
относительно мгновенной оси Л, т. е. (m+tnjgr sin a. Приравнивая оба
выражения, получим
2m
£ sin a.
6
213
886. a =
mg sin a
fl2 '
i 386. Решение. При отсутствии трения между жидкостью и
стенками бочки вращение бочки не передается жидкости. Жидкость дви-
движется поступательно как целое со скоростью v, равной скорости движе-
движения центра масс. Момент количества движения системы относительно
мгновенной оси А равен L^/^co+mi^y, где R — внешний радиус боч-
бочки, Iд — момент инерции ее относительно мгновенной оси Л, т — масса
жидкости. Из-за отсутствия скольжения v=coRt так что
Центр масс бочки движется параллельно мгновенной оси, а потому
где М — масса бочки (см. решение задачи 433). Отсюда
(M+m)R2
а=
При этом мы не учитывали моменты инерции днищ бочки, считая их
пренебрежимо малыми. Можно решить ту же задачу с помощью уравне-
уравнения моментов относительно центра
масс, а также с помощью уравнения
сохранения энергии.
387. Решение. Допустим, что
требуемое положение шарика сущест-
существует. На основании теоремы о движе-
движении центра масс
(M-\-m)a=(M-\-tn)g sin a—FTp,
где FTp— сила трения, с которой нак-
наклонная плоскость действует на цилиндр
(рис. 230). Уравнение вращения ци-
цилиндра (без шарика) будет
/ da>/dt=FTpr,
где 1=Мг2 — момент инерции цилиндра относительно его геометриче-
геометрической оси. Сила давления шарика на цилиндр в это уравнение не входит,
так как она нормальна к поверхности цилиндра и не дает момента отно-
относительно его оси. Ввиду отсутствия скольжения a==r dmldt, Из написан-
написанных уравнений находим
М + т
тд
Рис. 230.
214
Найдем теперь то же ускорение из уравнения движения шарика
та = mg sin a—FRaB sin ф, FRaB cos q> = mg cos а,
где ^дав — сила, действующая со стороны цилиндра на шарик. Отсюда
a=g(sin a—cos a tg ф). Путем сравнения с ранее найденным выражени-
выражением получаем
М
Из полученного результата следует, что требуемое положение шарика
существует, причем ф<а. Если m<^.Mt то tgф«1/2tga. Если сверх
того а<^1, то ф»1^.
388. Яйцо, сваренное вкрутую, вращается как твердое тело, сы-
сырое — как сосуд, наполненный жидкостью; сообщая скорлупе вращение,
мы еще не сообщаем вращения всем частицам жидкости.
389. I dtojdt = — 2л[ха3/со/6, где / — момент инерции ротора и / —
длина подшипников. Отсюда со = со0ехр ( ~-—1 , где со0 — на-
начальная скорость.
390. Решение. На цилиндр, имеющий вначале момент количе-
количества движения /со0, действует сила F=Q, I P. Эта сила сообщает цилиндру
угловое и линейное ускорения:
таким образом, со = со0—0,2 -~ t и v = 0tl gt. Время Т определится
К
из условия v = (aR или со0# — 0,2^Г==0,1^Г. Отсюда Т « 2,14 с. При
t > Т ускорение равно нулю.
391. Движение после перехода границы будет сначала равнозамед-
ленное, а затем с постоянной скоростью; 1/3 энергии превратится в теп-
тепло, 2/9 — во вращательную энергию и 4/9 останется в виде энергии по-
поступательного движения.
Решение. Пусть масса цилиндра т, момент инерции /, сила
трения / и начальная скорость v0. Тогда
т dv/dt=—/, /г= / dto!dt%
откуда
После перехода границы шероховатости скорость скольжения будет
vCK=zv—(ur=v0 — aft, где a= 1—j-=— (так как / = тг2/2).
Через время T = vo/af скорость скольжения обратится в нуль,
и дальше начнется чистое качение без скольжения. Скорость
215
поступательного движения при чистом качении будет
Угловая скорость качения (ок = ~-у=с/о-^-. Следовательно,
«пост—у ^ —J. Чф^—ПйЫ*
в тепло превращается энергия
П mv2° П П mvo 1
Чтепл = ~2 «пост — v вращ= -у — •
Можно также независимо подсчитать работу сил трения и показать,
ть1 1
что она равна —=
z ша
392. Решение. Напишем уравнение движения центра масс и
уравнение моментов (относительно центра шара):
т dvldt=—Ft I du/dt= rF,
где F — сила трения, действующая в точке касания шара с плоскостью.
Исключая почленным делением силу F, находим dvld(a=—I/(mr). Инте-
Интегрирование этого уравнения дает v=—/со/тл+С Постоянная интегри-
интегрирования С найдется из условия, чтпри v~v0 шар не вращается (о)=0).
Это приводит к соотношению
vQ—и==—со.
0 тг
Когда наступит чистое качение, должно выполняться второе соотноше-
соотношение у==сог. Из этих двух соотношений находим
тг 5 v0
Вычислив кинетические энергии в начале и в конце, найдем потерю ки*
нетической энергии на трение:
Ir 2 к1, 1 тг2 . 2 t
393. р = ——ц0 = 7гц0, AK = J1—-I . /со^-7
394. vo> Y (M/m-\-4m/M + 3)gR=8,l м/с.
395. Скорость первого шара v1 = 2/7v, второго v2 = &/1v. Потеря
кинетической энергии на трение составляет 20/49 начального значения
кинетической энергии.
396. Шар будет двигаться равномерно, если точка удара лежит вы-
выше его центра на расстоянии 2/5 радиуса. Такие удары называются нор-
216
мальными. Если она лежит еще выше, то движение шара будет ускорен-
ускоренным. Если же точка удара лежит ниже, то шар будет двигаться,замед-
двигаться,замедленно. Соответствующие удары называют высокими и низкими. Решение
получено в предположении, что сила трения шара о плоскость стола пре-
пренебрежимо мала по сравнению с силой, с которой
на шар действует кий во время удара.
397. Случай 1) реализуется при высоких
ударах, случай 2) — при нормальных, случай
3) — при низких.
398. Решение. Пусть F — сила трения,
действующая на цилиндр, в месте соприкосно-
вения его с наклонной плоскостью (рис. 231).
Она заставляет цилиндр подниматься по наклон-
наклонной плоскости. Сначала, пока не установилось ^ис- 231.
чистое качение, F является силой трения сколь-
скольжения. После перехода движения в чистое качение F становится силой
трения покоя (сцепления). Однако, независимо от характера движения,
оно всегда подчиняется уравнению движения центра масс т dvldt—
—F—mgsina и уравнению моментов (относительно геометрической оси
цилиндра) / d(uldt=—Fr. Исключая F, получим
dv . dco
mr-jr=— / —г;—mgr sin a.
dt dt
Интегрирование этого уравнения с учетом начального условия (о)=соо
при /=0) дает
/ягу=/ (со0—со)—mgrt sin a.
Это соотношение справедливо в течение всего времени движения, неза-
независимо от того, происходит ли оно со скольжением или является чистым
качением. В наивысшей точке должно быть v=0. Отсюда следует, что
в той же точке со=0. В противном случае цилиндр продолжал бы вкаты-
вкатываться, и рассматриваемая точка не была бы наивысшей. Поэтому время
подъема / найдется, если в предыдущем уравнении положить i/=co=O.
Это дает
,_ /сор _ г(оо
~~~ mgr sin a ~~2g sin a'
Любопытно, что время поднятия t не зависит от коэффициента тре-
трения между цилиндром и наклонной плоскостью. Результат не изменился
бы даже тогда, когда коэффициент трения стал переменным. Решение
предполагает, однако, что трение достаточно велико, чтобы цилиндр мог
вкатываться на наклонную плоскость. При недостаточном трении будет
происходить лишь замедление скорости вращения цилиндра. Нетрудно
подсчитать, что время замедления определяется прежней формулой.
Напротив, время обратного скатывания цилиндра вниз, а также наи-
наибольшая высота поднятия его зависят от коэффициента трения. Такое
217
различие объясняется тем, что скатывание цилиндра все время является
чистым качением. Поднятие же его вверх сначала происходит со сколь-
скольжением, а затем переходит в чистое качение.
399. ai==g{k cos a—sin а), направлено вверх;
/СОрГ ЩГ __ 1 о .
1"" (/ + тг2) ах + mr2g sin а~ (Зк cos a —sin a)g' Л] ~~Y ulh S1" а>
-r-4gCftcosa-sina)W0' •
Г l ^oro -|/~3 (/? cos a—sin a)
ia"~2firsina У '<
a2 sin a"~ 2^ sin a r 3^cosa — sin a
400. (o=^ , 0 2 <D0-
mL-(- 3m2
402. V=V0~if — 0 = 80 м/с.
403. * = ——4—-^-. Результат не зависит от характера удара.
404. х — —- 1/ 1 . Для возможности описанного про-
2 уз г т
цесса необходимо М^т. Условие х^1/2 дает еще
M. A7tt^
407. U =--n—7 к— .Впредельных случаях l)Af = 0 и 2) Л4 = оо
получаем 1) G = 0 и 2) U—1/2mv2.
408. Решение. Если Z7 — сила, действующая на шарик во
время удара, то уравнение движения шарика будет т dv/dt=—F. Урав-
Уравнение движения центра масс стержня: М dV/dt—F. Уравнение моментов
для стержня относительно центра масс: / rfco/d/=/7//2. Почленным деле-
делением исключаем F и получаем
/ doa / * / dco /
Интегрируя в пределах от начального значения угловой скорости со=0
до конечного, найдем
- — — у- 2 7
°~~ lm* I M *
218
причем в этих уравнениях v> V и со означают величины соответствующих
скоростей после удара. Угловая скорость со найдется из уравнения со-
сохранения энергии. Если в него подставить значения v и V, то для со
получится квадратное уравнение
т ' М
Один из корней этого уравнения (со =0) дает угловую скорость стержня
до удара, второй — после удара. По условию задачи надо взять вто-
второй корень. С учетом соотношения /=-ргЛ4/2 для него получаем
l2mvQ
@ =
Dт + М) Г
Ml _.
—Уо
/3
410. *==
411. со = соо-| 5— » l = h 1/ — • При приближе
(ЧМ + I2 ° К со
= h 1/ — •
° К со
яии шарика к оси вращения стержень будет изгибаться в сторону,
противоположную вращению. При удалении шарика изгиб стержня
изменится в обратную сторону.
412. F>FOt rjieFQ = (kl + k2)(mA + mB)g.
Решение. Максимальное горизонтальное ускорение, которое
может иметь тело В, равно a — k2g. Сила FOi сообщающая ускорение а,
определится из условия
подставляя сюда значение а, находим ответ.
.<о 1Ч .. М (sin a—k cos a) cos а
413. 1) Ускорение тела а2= .. , . . г . . д, кли-
' v * М + т (sin a — fccosa) sin a6
на «! =
пч ,. М sin a (cosa + fc sin a)
2) Ускорение тела я2 = т7-1 :—^—r-.—! z —г8> клина
1 v а М + т sin a (sin a — /г cos aN
_m sin a cos a—k (M + tn cos2 a)
1 M + m sin a (sin a—k cos a)
3) В первом случаев < tga, во втором — условие движения клина
т sin a cos a
cos2a'
414. amiH — gb/ht где g — ускорение свободного падения; N = mg\
= ah/2g.
219
415. &мин > b/h\ если k < kMHnt то автомобиль при v = YbgRjh со-
соскользнет с дороги на ее закруглении.
416. Цилиндр опрокинется и свалится с диска при угловой скорости
вращения диска
со= У Dg/(Rh).
417. Т = 2л У l/(g—/со2), если /со2 < g. При /<о2 > g положение
равновесия неустойчиво.
■'- /4<
418. v= 1/ —gh, a) = -n^ у з
Решение. Закон сохранения момента количества движения для
системы желоб — тело
cos
где и — скорость тела относительно желоба, со — угловая скорость вра-
вращения желоба, /0 — момент инерции желоба. Закон сохранения энер-
энергии для этой системы дает /со2+т [(и cos +#J+22]2/
Отсюда:
1>2 = (w COS ф _|_ /^@J _j_ U2 ,sj П2 ф _ БД gft w I ^7 gh.
419. Нельзя ограничиться анализом сил, действующих только на
колеса, нужно учитывать и силы, действующие на остальные части па-
паровоза.
'//////////////^^^^
Рис. 232.
Рассмотрим силы, действующие на колесо и паровоз, в отдельности
(рис. 232, а). Для простоты считаем у паровоза одно ведущее колесо. При
220
положении водила выше оси колеса к паровозу приложены силы Q' со
стороны водила и F' со стороны колеса. К колесу приложены силы / со
стороны рельсов, F со стороны паровоза и Q со стороны водила. Для про-
простоты рассуждений предположим равномерное движение паровоза. По
второму закону динамики F—f-\-Qt по третьему Q^Q' и F=F'. К паро-
паровозу приложена сила f=F'—Q't направленная вперед. Для положения
водила ниже оси (рис. 232, б) распределение сил следующее: силы, при-
приложенные к колесу,— /, Q и F, f-\rF=Q (по второму закону динамики),
а силы, приложенные к паровозу, — F' и Q' (F'=F и Q'=Q (по третьему
закону)), и потому к паровозу приложена равнодействующая Q'—/7/=/,
т. е. сила, направленная вперед.
Итак, во втором случае ось колеса толкает паровоз назад (сила F')
но, кроме этого, большая сила (сила Q') толкает его вперед.
420. f=(r/R)Q.
421.
Решение. В системе координат, вращающейся вокруг верти-
вертикальной оси с угловой скоростью со, условие равновесия стержня можно
записать в виде Muc=AfCiT, где ЖЦ-С— момент центробежной
силы и МСг т— момент силы тяжести относительно точки закрепления
стержня.
Центробежная сила инерции, действующая на элемент стержня дли-
длиной dxt находящийся на расстоянии х от точки закрепления, будет равна
. _ mdx
dF
Соответствующий момент силы можно записать в виде
бШц> с — dF^ с • х cos a.
Отсюда для полного момента центробежной силы инерции имеем
а
1 /ясо2 sin a cos a,
{
mco2sinacosa С 9. 1
*ц.с = 5+6 3 x dx=T
b
a + b v
-ь
a—b
Приравнивая эту величину моменту силы тяжести Л4с>т = т^—^—sin a,
получим ответ.
422. Угловая скорость прецессии
Q_mgl sin a mgl
/со sin a /to '
где a — угол, образованный осью волчка с вертикалью. Направление
прецессии совпадает с направлением вращения волчка.
■=612Н-м2
221
424. Решение. Максимальный поворот получится, когда ско-
скорость снаряда v перпендикулярна к земной оси. Снаряд уносит мо-
момент импульса L = m[rv]/V^l—v2/c2, перпендикулярный к скорости
v. Земля получает такой же момент в обратном направлении. При
этом вектор угловой скорости вращения Земли со отклоняется вбок
на угол a = L/(/co). Подставив сюда / — 2/б Mr2 и учтя, что разность
с—v очень мала, получим
с—v 2Бт2с2
' 8Л42/2со2
1,9- Ю-22.
Заметим, что приведенная оценка годится для поворота земной оси
«в пространстве», т. е. относительно системы «неподвижных звезд».
Для исследования поворотов оси вращения «в теле», т. е. относительно
самой Земли, надо учесть сплюснутость земного шара. Это связано с тем,
что вращение шара вокруг фиксированного в нем диаметра неустойчиво.
425. tg $=azm2g sin a/^co2), где 7ц — момент инерции волчка от-
относительно оси фигуры, т — масса волчка, а — расстояние от точки
опоры волчка до его центра массы.
428. а^тау0т/(/цсо)«0,43°«25/.
427. Решение. После удара центр ударяемого шара начнет
двигаться с начальной скоростью v0. По теореме о движении центра
масс его скорость в момент времени t будет v = v0—kgt. Пусть ш —
мгновенное значение вектора углевой скорости. Момент силы трения
относительно центра шара будет kmgri, где i—единичный вектор,
направленный за плоскость рисунка и перпендикулярный к ней. Из
уравнения моментов / dtojdt — kmgri получаем 2/5 г da/dt = kgi. Отсюда
ю = fc>o~b-<f— ** Мгновенная ось вращения всегда лежит в плоскости,
перпендикулярной к плоскости рисунка. Угол а определяется урав-
уравнением tg а = бД fc&V(rc°o)-
Определим теперь момент начала чистого качения. Скорость поступа-
поступательного движения шара зависит только от горизонтальной составляю-
составляющей вектора со. Момент начала чистого качения найдется из условий
bUkgt—v^—kgt. С этого момента угол а становится и продолжает оста-
оставаться постоянным, причем tg а—ь/^0/гщ. В частном случае, когда %=
~c«v\ tga=6/7, a=35°32'. Заметим, что найденное решение определяет
поворот оси вращения относительно внешнего пространства, а не внутри
самого шара.
428. FRaB=P+I\\u2/r-=P+ ~mQV, где Р —вес бегуна, а /я —его
масса. При г=50см и рабочей скорости 1 об/с (Q=2k рад/с) получаем
1/2tnQ2r^mg=P. Следовательно, /7дав^2Р. Заметим, что полный мо-
момент импульса L не направлен вдоль оси фигуры бегуна, так как имеется
еще момент, возникающий из-за вращения вокруг вертикальной сси.
-222
Однако последний момент остается неизменным при вращении катка, а
потому при решении задачи его можно не принимать во внимание.
3 !^!
о о
430. Решение. Разделим мысленно кольцо на бесконечно ма-
малые элементы—материальные точки с массами dm. Рассмотрим дви-
движение одной из таких материальных точек. Так как tf0TH = [w]» то
по теореме Кориолиса действующая на точку сила
df= — dm ©V + dm [Й [Qr]]+2dm [Й [©г]].
Это выражение меняет знак при изменении знака г, а потому при
интегрировании по всему кольцу дает нуль. Отсюда следует, что ре-
результирующая сила, действующая на кольцо, должна равняться нулю.
Для вычисления момента dM силы df введем прямоугольную систему
координат с ортами itjt k, направив ось X вдоль со, а ось Y—вдоль Q.
После простых вычислений получим
dM = 2 [Йсо] y*dm + Q BcoJ—Qi) yz.
При интегрировании по всему кольцу последнее слагаемое дает нуль,
а потому
где lz и 1Х — моменты инерции кольца относительно осей ZnX соот-
соответственно. Таким образом, искомый момент М должен быть перпен-
перпендикулярен как к со, так и к Й. .Результат верен и в том случае,
когда векторы со и Й не взаимно перпендикулярны.
431. Согласно закону динамики, dL/dt—M, где L — вектор мо-
момента количества движения, а М—момент силы, действующей на
тело. В рассматриваемом случае момент силы, действующей на пла-
планету (рассчитанный относительно Солнца), Al = [rF], где г—радиус-
вектор планеты, a F—сила тяготения, действующая со стороны
Солнца на планету. Так как векторы г и F направлены по одной
прямой, то И# = 0 и, следовательно, L — const. Это утверждение спра-
справедливо для всех движений под действием центральных сил.
432. Решение. Для доказательства можно воспользоваться
следующими соотношениями:
где (d = da/dt — угловая скорость планеты, а а—угол поворота ее
радиуса-вектора. Учитывая, что
o ds
получаем искомое равенство. В самом деле, по правилам векторной
алгебры, последнее векторное произведение может быть представлено
223
так: [г [wr]] = cor2—г (гсо) = cor2, так как г_]_со. Но (or2dt =
есть удвоенная площадь, описываемая радиус-вектором г за время dt.
Из ранее доказанного (см. предыдущую задачу) следует, что а = const.
Последнее соотношение представляет содержание второго закона
Кеплера.
433. Решение. В случае одной материальной точки L =
= [(г— Л))/*], где г—радиус-вектор материальной точки относительно
неподвижного начала, г0—радиус-вектор движущейся точки О отно-
относительно того же неподвижного начала, p — mv—количество движе-
движения материальной точки. Дифференцированием по времени получаем
L — [(r—ro)p]-\-[(v—vo)p]. Первое слагаемое в правой части есть
момент М силы F=p относительно движущегося начала. Слагаемое
[vp] обращается в нуль ввиду коллинеарности векторов v и р.
В результате получается L = M-\-[pvo] = M+m [vv0].
Для обобщения полученного результата на случай системы мате-
материальных точек напишем последнее соотношение для каждой мате-
материальной точки, а затем такие соотношения сложим. Введя при этом
скорость движения центра масс системы Vc — 2j niiVi/m, найдем
L — M-\-m [Vc*o]> гДе т, L и М теперь означают массу, момент
количества движения и момент внешних сил для всей системы
материальных точек. Если скорости Vc и v0 коллинеарны, то L = M.
В частности, это имеет место, когда начало О помещено в центре
масс системы.
434. Главная полуось эллипсоида инерции направлена по диаго-
диагонали, соединяющей противоположные вершины куба, и равнаа=\/ Y~Tq\
две другие полуоси равны между собой: Ь — с = а/У 5,5, где /0 =
=х/в т12—момент инерции для любой оси, проходящей через центр
масс куба.
Решение. Эллипсоид инерции для центра куба — шар радиуса
а=\/ Y~Tq. Для точки А ось, совпадающая с диагональю куба, остается
главной с моментом инерции /0. Для любой оси, перпендикулярной к диа-
диагонали в точке Л, момент инерции определяется по теореме Штейнера
где d=-y Y%—диагональ куба. Отсюда следует приведенный выше
ответ.
435. I—~е «2 1—2jT—2 •
Решение. Главные моменты инерции для центра масс:
, М
224
направляющие косинусы для оси вращения относительно системы коор-
координат, связанной с главными направлениями и с началом в центре масс,
равны
cos a— l/d, cos p=m/<3, cosy=n/d,
где d2—l2+m2-\-n2 (d — диагональ параллелепипеда). Момент инерции
для оси любого направления представляется через главные моменты
инерции следующей формулой.
/= /tcos2a+ /2cos2p+/3cos2v
Подстановка в эту формулу значений величин приводит к данному
ответу.
§ 8. Тяготение
436. g=4nRGd/3~ 974 см/с2.
437. g = g0 (щ^У « 975 см/с2.
438. #л « 162 см/с2.
439. a—4n2R3/(T2r2)tt28g, где g — ускорение свободного падения
на поверхности Земли.
440. Такое же, как и самой Земле (если пренебречь размерами Земли
по сравнению с расстоянием до Солнца), т. е. ускорение a=4n2R/T*a*
«0,6 см/с2, где R — радиус земной орбиты, в Т — период обращения
Земли вокруг Солнца.
441. Веса обоих тел одинаковы.
442. Решение. Веса тел в диаметрально противоположных
точках земного шара / (день) и 2 (ночь) будут соответственно равны
Рх = f3— FQ (R — r) — mm2r + mwOi
P2 = F3+ Fc (R-\-r)—muPr — mw0
(рис. 233). Здесь F$ и Fc — силы гравитацион-
гравитационного притяжения Земли и Солнца соответствен-
соответственно, R — расстояние между их центрами, г — ра-
радиус Земли, w0 — ускорение центра Земли под
действием гравитационного притяжения Солнца.
Очевидно, mwo—F(R). Вычитая, находим
Р2-Рх = [FQ(R + r)-Fc (/?)] +
— г) — /
= mg (M — масса
т — масса тела).
225
Разлагая обе разности в квадратных скобках
по формуле Тейлора и ограничиваясь квадра-
квадратичными членами по г, получим Р2—Pt =
== r2d2Fc/dR2. Преобразуем это выражение, ис-
используя соотношения Fc — GMm/R2 = 4n2R/T2mt P
Солнца, Г—-период обращения Земли вокруг Солнца,
8 Под ред. И. А. Яковлева
После несложных преобразований найдем
Я2—Р1_24я2 Л2__12я2г2
~Р ~ gT2 R~" sR *
Здесь s—1/2gTz означает расстояние, которое проходила бы Земля в те-
течение года, если бы она двигалась равноускоренно с ускорением g. Вы-
Вычисляя это расстояние, получим s^5»1012km и далее (Р2—P^lP^
«6,5-10-*2.
443. ^i=^2-g^^8.1O^o, где Ms и Л*л-массы
Земли и Луны, R — расстояние между их центрами, Т — период обра-
обращения Луны вокруг Земли, г—радиус Земли. Таким образом, влия-
влияние Луны на разность весов Р2—Р1 примерно на два порядка больше,
чем Солнца.
444. gJl =gM (\+2AT/T)=gM A+0,0008), где АГ — разность зна-
значений периодов Т колебаний маятника в Москве и Ленинграде.
445. Часы шли бы медленнее примерно в 2,5 раза, так как £л /g3 «
^0,16 (см. задачу 438).
446. R^ 785-106 км.
4я/? / 2 \
448. gQ ~ -yg- ^~ J „ МЪ М/С .
449. ^=^
450. g = 4n260*R/T* » 985 см/с2.
451. Решение. Используя приведенные данные, находим: мо-
момент инерции Луны относительно оси вращения Земли /л~пга2 =
— 1,08-1047 г -см2 (моментом инерции Луны относительно ее собст-
собственной оси пренебрегаем), угловую скорость вращения Луны по ор-
орбите сол—2,67-10~6 рад/с, момент количества движения Луны 1,л =
=/лсол = 28,9-1040 г-см2/с, полный момент количества движения
системы Земля — Луна L — L3-\~ 1^=34,8-1040 г-см2/с. По закону
сохранения момента количества движения (/3 + ma2) co = L. По за-
закону Кеплера я3со2 = я^л* ^3 ЭТИХ ДВУХ уравнений можно получить
неизвестные а и со. Пренебрегая моментом инерции /3, пишем пш2(й=Ь
и находим
со/сол = (ао/аK/* = 0,573, Г = 27,3/0,573 = 47,7 сут.
226
452. U(R)=—mgRl/R) где Ro — радиус Земли.
Решение. Сила тяготения, действующая на тело, находящееся
на расстоянии г от центра Земли, равна f=mgRl/r2. Тогда потенциаль-
потенциальная энергия на расстоянии R будет
R
U \*\j—- | / м-f р
mgRl
453. /<5за3/Га=(Ш/4я2, О — гравитационная постоянная.
Указание. Рассмотреть круговое движение планеты.
454. Решение. Когда масса планеты пренебрежимо мала,
Солнце можно считать неподвижным и написать tnr — F. С учетом
движения Солнца это уравнение заменится на n'r = F, где pi=*
= Мт/(М-\-т) — приведенная масса. Переписав его в форме тг =*
= —^—F, видим, что учет движения Солнца формально эквива-
эквивалентен увеличению гравитационной постоянной в (М-\-т)/М раз*
Поэтому
_оЗ М + т М а3 _ G
Г2""" М 4д2' или
456, г2=( г-—1)гъ Vz^—Vx. Звезда распадается,
\2GM- rxv\ ) Г2
2GM/rv
^—— «6,5 г/см3,
о g—go "
go h
459. Кинетическая энергия планеты /C=mt/r/2+^2/B/), где первый
член представляет энергию радиального, а второй — вращательного
движения, причем момент импульса планеты L относительно Солнца со-
сохраняется. Так как момент инерции планеты относительно Солнца /»
=тг2, то уравнение сохранения энергии запишется в виде
l
2
где М — масса Солнца, am — масса планеты. При r=oo E=mvf/2, Это
равенство может выполняться только при £>0. При £<0 оно выпол-
выполняться не может. Отсюда следует, что при £<0 движение будет финит-
финитным, а при £>0 — инфинитным.
460. Если £<0, то траектория планеты — эллипс, если £>0 —
гипербола. В промежуточном случае £=0 траектория — парабола.
8* 227
Эллипс может вырождаться в отрезок прямой, а гипербола — в пря-
прямую, уходящую в бесконечность.
461. По гиперболической.
462. Оба осколка будут двигаться по параболам.
463. с— V»
0-17 см/с;
2(/3— 2/ 2)M2v2
/Ссн//С3 « 2 ( У~2 — l) c/v « 8,3-103.
464. Решение. В перигелии Р и в афелии А (рис. 234) радиаль-
радиальная скорость планеты равна нулю. Поэтому момент количества движения
И
планеты в этих точках можно записать
в виде mvr. Учтя уравнения сохране-
сохранения момента количества движения и
энергии, получим для этих точек
L2
2тЕ
=0.
D64.1)
При Е<0 это квадратное уравнение
имеет два вещественных положитель-
Рис. 234. ных КОРНЯ ri и Г2- Один из корней со-
соответствует перигелию Р, другой —
афелию А. Сумма корней rl-\-r2 дает длину большой оси эллипса:
Mm r M
.__ _____ __.,
D64.2)
где е= Elm — полная энергия, приходящаяся на единицу массы плане-
планеты. Так как для движения по эллипсу в<0, то выражение D64.2) сущест-
существенно положительно, как это и должно быть.
Рис. 235.
465. Решение. Пусть комета движется по правой ветви гипер-
гиперболы (рис. 235). В ее вершине справедливо уравнение
2тЕ
3
Е
228
Вообразим, что по сопряженной ветви гиперболы движется вспомога-
вспомогательная частица с той же массой т и энергией £, но на эту частицу
действует сила отталкивания, исходящая из фокуса Flt величина кото-
которой совпадает с силой притяжения, действующей на комету. Для
такой частицы в вершине гиперболы
2 rMm L2 Л
Е 2тЕ
Разность положительных корней написанных уравнений и дает искомую
длину
где г — Ejm — полная энергия, приходящаяся на единицу массы пла-
планеты.
466. v=vu Vl— Л/2а = 8,1 км/с, где vu= V~2gR = Ui2 км/с —
вторая космическая скорость, 2а—длина большой оси эллиптической
орбиты.
467. ^
468. Решение. Если р — импульс, а г — радиус-вектор плане-
планеты относительно Солнца, то
При периодическом движении среднее по времени значение -?- (рг),
очевидно, равно нулю, откуда и вытекает результат: £ + /С = 0.
470. и= 1^3g#0> где Ro — радиус Земли.
471. v — v0V~R0/R, где vQ= V~gR0 « 7,9 км/с — скорость движе-
движения спутника по круговой орбите (теоретической) с радиусом Земли Ro.
Указание. Сила тяготения, действующая со стороны Земли
на спутник массы т, равна mgR2jR2.
з / s
472- *" К 5ЧГ.*° * 6>61/?0> где ^г
5ЧГ.
Указание. Центростремительное ускорение спутника со2У?
должно быть равно ускорению, сообщаемому спутнику силой тяготения,
l
473. 1) Первый. 2) /?1//?2
Решение. Для первого снаряда, по закону сохранения энергии,
имеем
» «! ZgRl
О S'^U— S Г) > """ 'U— _ .. 2
2 ^1 2^o—0o
229
так как его скорость в верхней точке равна нулю. (См. также задачу 452
и ее решение.)
Для второго снаряда, по закону сохранения энергии,
где Vi— скорость в наиболее удаленной точке; кроме того, по закону
сохранения момента количества движения, v0RQ=ViR2. Отсюда получаем
474- R^
со — угловая скорость и RQ— радиус Земли.
Указание. См. решение задачи 473.
475. Г= V 3n/(Gp) « 1,2-Ю-3 с.
476. Если р= const, то Г1 = 712. Если р возрастает к центру
планеты, то Тг > Г2.
4л2 я3
477. М~-~- =^ « 6-1027 г, где а—большая полуось эллиптиче-
эллиптической орбиты спутника.
478. ^=^y^y«O,U, где /?,=/?+ Л = 6625 км -сред-
нее расстояние корабля-спутника от центра Земли.
479. ДЯ/#~Зя/ф/(фо)==1,2-1О-6, А/?—8 м, где R — радиус зем-
земного шара. (При решении использовано выражение для силы сопротив-
сопротивления F~pv2S, где S=nr2 — площадь поперечного сечения спутника )
Почему снижение спутника не зависит от значения гравитационной по-
постоянной?
480. Минимальное удаление р^ 1,25 #з; максимальное удаление
Решение. Энергия спутника в полярных координатах равна:
E = ^-[?2 + (p\n—j (C=GmM3).
Момент количества движения относительно центра сил равен:
L=mp(p(p). Исключая из уравнения энергии <р и учитывая, что
в точках максимального и минимального удаления спутника от цент-
центра Земли р = 0, уравнение энергии можно записать в следующем
виде:
9 \Е\ p
Здесь учтено, что полная энергия спутника Е на эллиптических орбитах
всегда отрицательна. Два корня этого уравнения дают расстояние до
230
перигея рх и апогея р2 эллиптической орбиты. Согласно теореме Виета:
где а — главная полуось эллиптической орбиты. Используя уравнение
эллипса в полярных координатах, записанное для перигея и апогея:
Р1»2=р/0 i£)> можно представить все геометрические параметры орбиты
через механические константы движения.
В данной задаче полная энергия спутника:
С mvl_ С
где vl = v\=— квадрат первой космической скорости. Большая
С С
ось орбиты 2а =-у—=р1+р2, отсюда р1=1,25/?з>Р2=Тр1—
481. va=-
о о*
Q
Решение. Для круговой орбиты v2 = —5- , R0—9i—радиус кру-
круговой* орбиты, С = бтМз, т — масса спутника, G-— гравитационная
постоянная. Для эллиптической орбиты: ух = у0- 1^1,5 — vP. Полная
энергия спутника
^"~ 2
Большая ось орбиты
Q
g4/?0 = 4p1, отсюда p2==4p1~-pI =3pt = 3i?0.
Для концов большой оси орбиты имеет место равенство L=
mp2VA (^ — момент количества движения), отсюда
482. 7y:rK = 2/1^2,82.
Решение (см. решение задачи 480). Выражая момент количест-
количества движения через секториальную скорость для эллиптической ор-
орбиты: L—2m ds/dt, получаем для периода
Тэ = —т- S = 2л -г- аи,
L2
Поскольку Ь2 = а—р, то
~-а3 (C = GmM3).
231
Для круговой орбиты:
Отсюда, с учетом данных задачи, получим
483. Vp= У2/зёЯз = У\\/У 3, Уц —вторая космическая скорость.
Решение. Условие преодоления спутником земного притяже-
притяжения — — = £' = 0, где С = GmM3, E—полная энергия спутника;
2 /\
2С С
отсюда v2=v^ + ^ф = —б • На круговой орбите v^ =—-, поэтому
VP = n^~~mR~~~~tnR~~~bg 3==~3 '
_mv%R*_ R __п _ R _ •■/" 2С __ ( _
вторая космическая скорость.
Решение. Момент количества движения спутника массы т на
новой орбите определяется из условия:
L = mvq)R — mvpMim = const. D84.1)
Квадрат скорости движения спутника на круговой орбите равен:
у^— (С=бтМз). D84.2)
Полная энергия спутника на новой орбите:
2 С tn С
у*, ITLU w ГГЬ . п . rtv w -^
Из D84.1) — D84.3) следует ответ.
485. Скорость запуска с Земли v1—{2l yr~3 ) ui«1,16ui , где v\ —
первая космическая скорость. Добавочная скорость в апогее Ди=
Решение (см. решение задачи 480). Для эллиптической орбиты
большая ось равна
2а = 2R3 + Яз = З^з = С/1 Е | (С =
Энергия спутника
С __ С mi>i_ С mvt
1 ' ~/? /? ""/? 2 '
• 4 с 4 о
откуда скорость запуска спутника ^ = — —^-=—^, скорость в апо-
О ttl /\3 «5 *
232
1 С 1 1
гее vl==-J-^nr==-3v\> скорость на круговой орбите у* = —^; от-
отсюда добавочная скорость
3 /* 3 /?ч
486. Время снижения т = -гп 1/ ——- .
Решение. Большая ось орбиты снижения 2а = j
Время обращения по эллиптической орбите
Время снижения
(у
GmM3 V 2 У 3
487. Спутник будет описывать малый эллипс:
х (t) = — ?Й A — cos 0H» У @=— sin 0^,
О) СО
вершина которого лежит в точке равновесного положения спутника, а
центр смещен на запад на расстояние 2ио/со, со — угловая скорость вра-
вращения Земли.
Решение. Исходим из уравнения динамики: та0 — Р— [2m(ov0l,
где Р—«вес» тела, который для точки, равновесия спутника А равен
нулю:
Для возмущенного движения
С 2С
В проекциях на оси координатной системы X, К, Z с началом в точ-
точке А уравнения динамики записываются в виде:
Отсюда i = —2соу, у-\-(й2у = 0, что при начальных условиях у @) = 0,
y@) = vo дает
у @=5 sin со/.
Для координаты х при *@) = 0 получаем:
= — — A— coscoO-
CD
233
488. vii=V2gRQf**ll92 км/с. Скорость может составлять любой
угол с вертикалью.
2
Решение. По закону сохранения энергии -—■ mgR0=0.
Потенциальная энергия на поверхности Земли (см. задачу 452) —mgROt
а на бесконечном расстоянии кинетическая и потенциальная энергии
равны нулю.
489. Решение. Все скорости относительно Земли условимся
обозначать малыми, а относительно Солнца — большими буквами. Раз-
Разделим движение ракеты на два этапа. На первом этапе движение будем
рассматривать в системе отсчета, в которой Земля неподвижна, прене-
пренебрегая при этом полностью неоднородностью поля солнечного тяготе-
тяготения. В этом приближении сила гравитационного притяжения Солнца
полностью компенсируется силой инерции, связанной с ускоренным
движением центра Земли. Считая массу Земли М бесконечно большой
по сравнению с массой корабля т, запишем уравнение энергии в виде
то2 r Mm mvl,
где Vn— скорость ракеты в тот момент, когда она практически выходит
из зоны действия земного тяготения. Вводя круговую скорость и2 =
—GMlr, получим v2qo=v2—2у2. После того как ракета выйдет из зоны
действия земного тяготения, будем относить ее движение к системе
отсчета, в которой неподвижно Солнце. Скорость ракеты в этой сис-
системе отсчета векторно складывается из скорости v<x> и скорости кругового
движения Земли VK: V= Vk+v,», Возведя в квадрат, получим
Чтобы найти третью космическую скорость, надо в этом соотношении
положить V—Vn— }^2 VKi где Vn— параболическая, а Кк=29,8км/с—
круговая скорости движения ракеты относительно Солнца. Это приводит
к уравнению
из которого находим
Уео = ( / +COS2 О —COS О) VK-
(Положительный знак перед квадратным корнем выбран потому, что
величина и«, по своему смыслу существенно положительна.) После этого
получаем
Наименьшее значение третьей космической скорости получается при
0=0 (ракета выпущена в направлении орбитального движения Земли),
наибольшее при 0==^ (ракета выпущена в направлении против
234
орбитального движения Земли):
* 16,7 км/с,
«макс = V( Г~2 + 1) V» + 2о« я 72,7 «м/с
490. Решение. Ракета на старте движется вокруг Солнца вмес-
вместе с Землей со скоростью VK. Чтобы ракета упала на Солнце, надо ее
движение затормозить. Как и в
предыдущей задаче, находим, что
по выходе из поля земного тяготе-
тяготения ракета будет иметь скорость V=
= ^к+^оо (относительно Солнца).
Наименьшая для замедления раке-
ракеты затрата энергии соответствует
случаю, когда скорости VK и я то на- ^ис# 236.
правлены противоположно. В соот-
соответствии с этим полагаем К= VK—v» (все скорости положительны) и
находим энергию, приходящуюся на единицу массы ракеты:
(R—CA — расстояние ракеты до центра Солнца, рио. 236). Если эта
величина отрицательна, то ракета будет описывать вокруг Солнца
эллипс с большой осью
9 GM
в ""
Один из фокусов эллипса находится в центре Солнца. Пусть х=СР —
расстояние от центра Солнца до ближайшей вершины этого эллипса,
тогда 2a=R+x, Это приводит к квадратному уравнению, меньший ко-
корень которого
Заданием расстояния х на поверхности Солнца определяется линия, на
которой должна лежать заданная точка. Таким образом, искомая ско-
скорость v определяется выражением
При *=0 (прямолинейное движение по направлению к центру Солнца)
скорость v максимальна и равна
31,8км/с.
Ракета упадет в передней точке Солнца. При х=г (г — радиус Солнца)
235
скорость минимальна:
« 29,2 км/с.
Ракета упадет в задней точке Солнца, двигаясь по касательной к его
поверхности.
491. Решение. Обозначим через Ек полную энергию спутника
при движении по круговой орбите, тогда
£к=-/(, У=—2/С.
После того как отработал двигатель, скорость спутника возросла
в а раз, а кинетическая энергия К — в а2 раз. Потенциальная энергия
не изменилась, так как за время работы двигателя спутник переместился
пренебрежимо мало. Таким образом, полная энергия спутника на эллип-
эллиптической орбите будет
= (а2—2) К = B-а2) £к.
Большие оси эллиптических орбит обратно пропорциональны полным
энергиям (см. решение задачи 464). Поэтому
a/R= 1/B—а2), а== R B—а2).
Орбита будет эллиптической, если ос2<:2. Максимальное расстояние
спутника от центра Земли (в апогее)
#макс = 2а—R = a2R/B —a2).
Период обращения Т2 найдется из третьего закона Кеплера и равен
Г2 = 7\/B — а2)з/2.
492. Решение. Изменением потенциальной энергии корабля во
время кратковременной работы двигателя в периселении (или апоселе-
апоселении) можно пренебречь. Поэтому Де= A(v2/2)—vAv. С другой стороны,
_,,, . GM . 1 ,. ,
так как 2а=—GM/e, Де= —^ Аа= -^ g Aa, где g — ускорение сво-
свободного падения на Луне в периселении. Приравнивая оба выражения,
после некоторых преобразований получим
Ay==oi 1/ 4-Да = — 42 м/с.
493. 20=^A^2-1)-^ «0,17.
т и
494. и =
495. Решение. Движение спутника почти круговое, а потому
К=—Е (см. задачу 469). Сопротивление среды уменьшает полную энер-
энергию спутника, а следовательно, увеличивает кинетическую энергию
236
его. Момент количества движения спутника уменьшаете^. Перепишем
предыдущее соотношение в виде mv2=—U и дифференцируем по времени:
2mvdv/dt=—dU/dt. Подставив сюда U=mgR2/r (R — радиус Земли) и
введя скорость снижения спутника w=—drldt, получим
d"fB.wx£w~8-\0-*m/c\
dt 2v r2 2v
Здесь можно считать, что v«8 км/с (первая космическая скорость).
Тангенциальное ускорение направлено по движению спутника. Сила
сопротивления среды может быть найдена из уравнения энергии и равна
F=mdv/dt^ 80 дин.
496. Посередине между центром Земли и начальным положением
корабля.
497. Решение. Так как энергия корабля зависит только от
длины 2а большой оси его орбиты, то переход на круговую орбиту про-
произойдет на расстоянии а, т. е. в точке пересечения эллипса с его малой
осью. Направление скорости корабля надо повернуть на такой угол,
чтобы оно оказалось перпендикулярным к линии, соединяющей корабль
с центром Земли.
498. Увеличить в У 2 раз.
499. v2 = vih/l = 54,6 км/с.
500. voo = R
: 6,5 КМ/С.
501. Frp/F3Jl = Gm2/e2, где е = 4,8-10-10 СГСЭ—элементарный
заряд. Подставляя в формулу массу электрона т^ = 9,1Ы0~28 г и
массу протона mjP= 1,67-Ю-24 г, получим для электрона FTp/F93l=
=2,4-10~43, для протона Frp/F9JI = 8.10~37.
502. Решение. Соединим центр сферы О с точкой Л, в которой
помещена точечная масса т (рис. 237). Из точки О, как из вершины,
Рис. 237.
-опишем два круговых конуса с общей осью О А, образующие которых
наклонены к этой оси под углами О ид+сКК Они вырежут на поверхности
<сферы элементарный поясок с площадьюdS=2nr2 sin ft dft, где г —радиус
237
сферы. Масса этого пояска dM—M -—^—М sin Odd. Так как точки пояс-
пояска равноудалены отточки Л, то потенциальная энергия гравитационного
взаимодействия пояска и точечной массы т равна
Перейдем к новой переменной р —расстоянию между точечной массой т
и какой-либо точкой пояска. Эта переменная связана с О соотношением
p2=#2+r2—2Rr cosd, где # —расстояние О А между центром сферы
и точечной массой т. При перемещении вдоль поверхности сферы вели-
величины R и г остаются постоянными, поэтому
pdp=Rr sin Odd,
а, следовательно,
Р макс
Л Mm , г> „ Mm Г
Рмин
Если точка Л лежит вне сферы (рис. 237, а), то максимальное
и минимальное значения р равны соответственно Рмакс =/?+''
и Рмин = /? — г. В этом случае интегрирование дает
U=—GMm/R. E02.1)
Потенциальная энергия такая же, как если бы вся масса сферы была со-
сосредоточена в одной точке, а именно в центре сферы. То же справедливо
и для силы взаимодействия F=—dU/dR——GMm/R2. Можно сказать,
что сфера притягивает материальную точку так, как если бы вся ее
масса была сосредоточена в ее центре. Можно сказать и иначе: точечная
масса притягивает сферу так, как если бы вся масса последней была
сосредоточена в ее центре.
Если же точка Л лежит внутри сферической полости (рис. 237,6),
то Рмакс = г + ^» Рмин = г — Я» и интегрирование дает
U=—GMm/r. E02.2)
На границе полости выражения E02.1) и E02.2) совпадают. Согласно
E02.2) потенциальная энергия материальной точки внутри полости не
зависит от R, она постоянна. Сила F, действующая на материальную
точку в этом случае, равна нулю, так как £/=const, а потому F==
503. Доказательство. Как показано в предыдущей задаче,
гравитационное поле первой сферы не изменится, если всю массу этой
сферы сосредоточить в ее центре. Поэтому не изменится и сила, с кото-
которой это поле действует на вторую сферу. Задача свелась к нахождению
силы, с которой точечная масса действует на сферу. Но в предыдущей
238
задаче показано, что эта сила не изменится, если и массу второй сферы
сконцентрировать в ее центре. Этим и завершается доказательство.
505. Решение. Поле вне шара равно g—GMlr2, где М — масса
шара. Для вычисления поля в точке А (рис. 238), лежащей внутри шара
на расстоянии г от центра, проведем через эту точку вспомогатель-
вспомогательную сферу с центром в точке О. Вещество шара, расположенное вне
вспомогательной сферы, не влияет на поле внутри нее. В частности,
оно не влияет на поле в точке А. Гравитационное поле в точке Л соз-
создается только веществом, сосредоточенным вну-
внутри вспомогательной сферы. Оно равно Gmlr2y
где т — масса вещества, ограниченного вспо-
вспомогательной сферой. Таким образом,
М 4:rtG №
-^-=-y- —Р, если r^R>
m
— =о 9Г> если
4 T Рис. 238.
При r=R оба выражения совпадают.
506. Решение. Гравитационная энергия шара есть потенциаль-
потенциальная энергия, обусловленная силами тяготения, действующими между
материальными точками, на которые можно мысленно разбить шар.
Она равна взятой с противоположным знаком работе, которую должны
затратить внешние силы, чтобы привести вещество шара в бесконечно
разрозненное состояние, когда каждая частица вещества удалена в
бесконечность. Эта работа не зависит от способа, каким шар переводится
из начального состояния в конечное. Поэтому при вычислении можно
поступить следующим образом. Разделим мысленно весь шар на беско-
бесконечно тонкие концентрические слои и будем последовательно удалять в
бесконечность каждый из таких слоев, начиная с самого крайнего. На-
Напряженность поля тяготения в любой точке выделенного слоя, создавае-
создаваемая веществом, внешним по отношению к этому слою, равна нулю. Поле
создается только веществом, которое окружено рассматриваемым слоем.
Если m — масса этого вещества, a dm — масса слоя, то работа, затрачи-
затрачиваемая на удаление слоя в бесконечность, равна dA=Gmdm/r. Но для
однородного шара m=M(r/RK, где М — масса всего шара. Поэтому
М2
dA=3G-^Q г4 dr. Учитывая, что dA=—dU и интегрируя, получим
о
За нуль потенциальной энергии мы приняли энергию шара в бесконечно
разрозненном состоянии.
239
607. г«~^£-«5,9.1014с« 1,9-10? лет.
508. Решение. Вообразим, что полость заполнена веществом,
плотность которого равна плотности шара. Тогда искомое гравита-
гравитационное поле g представится разностью гравитационных полей двух
сплошных шаров с центрами в О и Oi соответственно. Точка наблюде-
наблюдения А расположена внутри каждого из этих шаров. Поэтому можно вос-
воспользоваться формулой E05.1) и написать
4л / 4я
где R — радиус-вектор, проведенный из центра шара О к центру поло-
полости Ov Поле однородно, т. е. во всех точках полости одинаково по ве-
величине и направлению.
509. U (г)=тЩ£ --. mgROt где пг—масса тела и г — расстоя-
ZHq 2.
ние его от центра Земли.
Решение. Внутри шахты (см. задачу 505) сила тяготения
f = mg~—t поэтому
АО
или
Можно выбрать величину 1/@) так, чтобы значение потенциальной энер-
энергии по формуле, приведенной в задаче 452, совпадало с полученным на
поверхности Земли при ^—Rq; тогда
U(R0)=:U@) + ^^-=-mgR0t или U @) = —j mgRo.
510. о= ]/^ = 7,2 км/с.
Указание. См. задачу 509.
511. Все тела в снаряде, находясь в том же поле тяготения, что и
снаряд, испытывают такое же, как снаряд, ускорение, поэтому тело,
подвешенное к неподвижным относительно снаряда пружинным весам,
не вызовет их растяжения. Массу тела можно измерить, например, так.
С помощью пружины можно сообщить телу некоторое ускорение отно-
относительно снаряда, и по отношению силы (отсчитываемой по растяжению
пружины) к ускорению можно найти массу тела (предполагается, что
масса снаряда много больше измеряемой массы).
512. Весы покажут «вес» р—та. Подвешенные в снаряде пружин-
чые весы будут в этом случае растягиваться в направлении, противо-
противоположном ускорению снаряда (вызванному сопротивлением атмосферы
планеты).
240
513. Если бы не было сопротивления воздуха, то приборы в снаряде
перестали бы регистрировать наличие силы тяжести при выходе снаряда
из жерла орудия. Вследствие сопротивления воздуха снаряд получает
дополнительное отрицательное ускорение, а приборы, находящиеся в
снаряде, регистрируют силу «тяжести», направленную в сторону, про-
противоположную испытываемому снарядом ускорению, т. е. в сторону
движения снаряда.
514. Линейная скорость движения любого спутника по орбите
обратно пропорциональна квадратному корню из расстояния спутника
от центрального тела. Линейная же скорость элементов сплошного
кольца, наоборот, прямо пропорциональна их расстоянию от цент-
центрального тела.
R
At
515. Решение. Пусть центр масс тел Л и В находится в
точке О (рис. 239). Неизменное расстояние между телами Л и В
будет сохраняться только при вращении их с угловой скоростью
о =-н- Л/ ——^зг— вокруг точки О. Условия равновесия тел
НУ Н
С и D во вращающейся (связанной с телами А и В) системе коор-
координат запишутся так:
где положительное направление выбрано от Л к В, Fc и F'/>— искомые
силы, G — постоянная тяготения. Исключая о, принимая во внимание
соотношение асо2= GMq/R2 и пренебрегая членами высших порядков
относительно r/Rt получаем окончательно:
т. е. при Мс—Мр обе силы меньше силы притяжения этих масс телом
В на одинаковую величину.
516. Решение. В задаче 515 можно рассматривать Л как центр
Солнца иМ^ как его массу, В — как центр Земли и Mr— как ее массу,
С и D — как два положения одного и того же тела массы Mq—Md на
241
поверхности Земли (С — днем, D — ночью) (см. рис. 239). Из решения
этой задачи следует, что все тела будут в полночь и в полдень весить не-
немного меньше, чем утром и вечером. Но эта разница в весе, как легко ви-
видеть, гораздо меньше, чем сила притяжения Солнца, так как сила при-
притяжения Солнца GMcMj\lR2 умножается на очень малую величину 3r/R.
(Массой Земли Мд по сравнению с ЗМ^, где Мд — масса Солнца, при
оценке изменений веса, конечно, можно пренебречь.)
517. Схему задачи 515 можно применить к объяснению происхож-
происхождения приливов, вызываемых Луной. Луна А и Земля В вращаются
вокруг общего центра масс О (см. рис. 239). В точках С и D на по-
поверхности Земли, где вода «весит» меньше, чем во всех других точках,
образуются водяные «горбы». Для расчета приливообразующей силы
подставим вместо Мд и Mr соответственно массы Луны и Земли. Тогда
из формул, полученных в задаче 515 (так как массой Луны по сравнению
с массой Земли можно пренебречь), найдем приближенно вес тела массы
М в ближайшей к Луне и в наиболее удаленной от нее точках земной
поверхности
где go— ускорение, сообщаемое Землей, г — радиус Земли, R — рас-
расстояние от центра Земли до центра Луны.
518. Точка, в которой g= 0, делит отрезок прямой линии между
центрами этих планет в отношении 9 : 1 и, следовательно, лежит на рас-
расстоянии ^36,7-103 км от поверхности Луны.
519. Л»6,12-106 кгс-м.
Решение. Минимальная работа по перемещению массы т с
Земли на Луну может быть записана следующим образом: A&mR3g3—
~~mRji£ji' где ^3 и ^Л —" РаДиУсы Земли и Луны, g3 и £л, соответст-
соответственно, ускорения свободного падения на поверхности этих планет, выз-
вызванные силами тяготения самих планет (см. решение задачи 473).
§ 9. Упругие деформации
520. /7=2450 кгс/см2.
521. Нет. Длина цилиндра, который не выдержит собственного
веса, равна l—p/pg, где р — напряжение разрыва, ар — плотность
материала; /=175 м.
522'. р — Еа (t1 — t2); рзим « + 1000 кгс/см2 (растяжение) и
Рлет ~ —375 кгс/см2 (сжатие).
523. D=27 мм.
524. AV = —=-^-/Р, где Е—модуль Юнга, jx—коэффициент
Пуассона. AV < 0 при сжатии, AV > 0 при растяжении.
626. M=pglV2E, где Р_плотн«сть рещества стержня,,1-его
длина, Е—модуль Юнга; объем увеличивается на АVп= ]"" 2>t K»oc
где 1/0 —первоначальный объем, pi—коэффициент Пуассона 5 — по*
перечное сечение. '
52jr. a=45°, x=F/2S.
528. U=P2hfFES). Упругая энергия увеличится в 7 раз.
529. Решение. В силу симметрии касательное напряжение т,
действующее в оболочке,одно и то же и одинаково во всех направлениях.
Возьмем малый элемент оболочки, имеющий форму прямоугольника.
При вычислении относительного изменения площади этого элемента под
действием касательных напряжений т можно отвлечься от кривизны эле-
элемента, приняв его за плоскую прямоугольную пластинку. Тогда вычи-
вычисление дает AS/S=2A—|л)т/£ (изменением площади, вызванным нор-
нормальным давлением, пренебрегаем). Поскольку площадь S пропорцио-
пропорциональна V2/3, относительное изменение объема будет AWl/=3/2 AS/5.
Так как поверхность искривлена, то натяжение т создаст разность нор-
нормальных давлений. Для нее нетрудно получить 2id/R (см. формулу Ла-
Лапласа в учении о поверхностном натяжении). Эта разность должна
быть уравновешена разностью давлений газа АР по разные стороны
оболочки. В результате получим
530.
4Р
р2
=='2E(l~li2)'
Аг
z
— рг A [X ),
■Р'Р* = ТГ*Г1ПГР-
531. А/1==2А/2
532. Деформации (удлинения) тросов показаны на рис. 240 в уве-
увеличенном виде. Если длина среднего троса L, то относительные удли-
Д/i AJ2
нения первого и третьего тросов ех = 83=-т-
— х Напряжение о = Ег для
- cos а, второго е2 = —r^s
= _. i—
L cos а
каждого троса
Е — модуль Юнга ма-
материала. Поэтому о1~о3 —
533. Силы натяжения
троса Р2, бокового троса Рх:
Р cos2 a
x~l+2cos3aJ
Р
г2 cos2 a.
среднего
Рис. 240.
2 l+2cos3a'
Замечание. Полезно рассмотреть случай, когда сечение сред-
среднего троса в два раза меньше, чем крайних.
243
534. Силы натяжения: Рх = -
2а2-ах
где а, = 1
a2=l/Sa>
растянуты при Sx > S2/2.
Решение. Если удлинение первой тяги
то можно составить следующие уравнения:
_Р_
~ 2
i3 = \/Ss. Все тяги
х, а третьей — Дх3,
где А — определенная постоянная величина. Добавим еще два уравне-
уравнения: Pi+Рг+^з— Р — уравнение равновесия сил и Pi=P2+3P3—
следствие уравнения моментов. Решая эти пять уравнений, найдем ответ.
535. Р=125 кгс, Я=5 мм.
Указание. 1) Если максимальное напряжение в поперечном
сечении стержня у места заделки будет равно а, то распределение нор-
га
мальных напряжении в этом сечении описывается выражением — z,
где а — высота поперечного сечения иг — расстояние от середины се-
сечения. Тогда равенство мо-
моментов внешних сил Р/ и
внутренних сил в сечении
заделки можно записать так:
а/2
а
z2dz =
aba2
Рис. 241.
2) Кривая прогибов консольно
где Ь — ширина сечения
стержня,
закрепленного стержня
У(х)
(рис. 241) определяется дифференциальным уравнением х)
Р(/_х)=Е/d2y/dx2,
где Р(/—х) — момент внешних сил относительно сечения балки, имею-
имеющего координату х, I — момент инерции площади поперечного сечения
стержня относительно горизонтальной оси, проходящей через центр
масс сечения. Для прямоугольника высотой а и шириной Ь 1=а?Ы 12.
Уравнение, определяющее прогибы, можно два раза проинтегрировать,
dy
и учесть, "-л """ —
х) См., например, С. П. Стрелков, Механика, «Наука», 1975,
§§ 88, 89.
244
Тогда
-£ j (•-*)«-■!&• (*•-?)■
отсюда Я,= «/(/)=Р/3/C£7); подставляя значение /, получаем для стре-
стрелы прогиба к=4Р1*/ (с?ЬЕ)=Ь мм.
536. %=РР/D8Е1).
Указание. Стрелу прогиба можно подсчитать по формуле,
указанной в ответе предыдущей задачи, если учесть, что поперечное
сечение в середине балки не кр
повернулось при деформа- g* I I
ции. Поэтому прогиб будет |jp°' —j^«^^^———-
такой же, как и прогиб кон- ^ """"""^^^as
сольно закрепленной полови-
половины балки под действием ре-
реакции опоры конца балки,
равной Р/2.
537. Решение. Пусть Рис. 242.
смещение конца стержня
А/. Под действием силы Р2 средней пружины стержень выгнется вверх
и стрела прогиба будет б. Тогда стержень будет находиться в равнове-
равновесии под действием сил, показанных на рис. 242, где Рх = &XA/, P2 =
Считая А/ очень малым, можно определить 6 по
М
-р ° ) •
формуле, указанной в ответе предыдущей задачи, или б
Условие равенства моментов сил: Ргк
ний находим
Д/ =
= -— —
этих уравне-
уравне4 + 2а Р
где а
k2l3 f
жесткость средней пружины
^«жесткость» половины стержня на изгиб
Исключая А/ и б, получим ответ:
р
2
2
Проверьте случай абсолютно жесткого стержня (а=0) и случай иде-
идеального гибкого стержня (а=оо).
538. Х=РР/BаЬ3Е)&0,03 мм (см. указание к задаче 536).
539. ^=Р/3/Dа4£)«1,25 мм.
245
540. Так как момент инерции сечения трубки /*=я(О4—d4)/64,
4Р/8
^ «''6 мм.
4Р/з
541. Е = 3 р4л « 104 кгс/мм2 (см. момент инерции в ответе пре-
предыдущей задачи).
1 Р/3
542. Е= 1
I
Рис. 243.
Указание. Стрелу прогиба и в этом случае можно подсчитать
по формуле задачи 536, если учесть, что вследствие симметрии каждую
четвертую часть длины балки можно
рассматривать как консольно закреп-
закрепленную (рис. 243)
Это возможно потому, что изгиба-
изгибающий момент равен нулю в тех мес-
местах, где мы мысленно рассекли балку.
Вследствие симметрии кривизна в этих
местах равна нулю, а следовательно, и
изгибающий момент равен нулю.
543. Решение. Считаем, что
при закручивании поперечное сечение
стержня, находящееся на расстоянии dl
от другого сечения, поворачивается на
угол dcp относительно него. Кольцо,
вырезанное между этими сечениями,
имеющее радиус р и толщину ф, сдви-
сдвинется на угол (рис. 244) da=pdyldl. Касательное напряжение в се-
сечении на расстоянии р от оси будет T=Npdq>/dl. Момент сил, дейст-
действующих на поверхность кольца радиуса р и толщины dp,
dM =2лр dptp =2nN -^-
Рис. 244.
246
Момент сил в сечении
г
о л/ ^Ч> Г зл _тг;/^2. г*
= 2nN^- С p»dp =
где г —радиус стержня. Момент М равен моменту внешних сил;
отсюда M = 2PR. Подставляя это в предыдущее выражение, полу-
dcp APR APRl 1
чаем —п~=—mr t следовательно, ф =—тт-т , Ф = т— ~ а,6 .
а/ яЛ/г4 яЛ/r4 5я
544. Центр масс диска описывает при вращении окружность ра-
радиуса d+£, где £ — прогиб вала, зависящий от числа его оборотов.
Упругая сила &£ сообщает центру масс центростремительное ускорение.
Поэтому можно написать mco2 (d+£)=k£>y откуда прогиб (в мм)
d E44.1)
— 1
(Угловую частоту со= У k/m, при которой ?-^оо, называют критической
частотой и, очевидно, стараются так подобрать условия работы вала,
чтобы он не работал при критических частотах. Вал может работать и
при частоте выше критической. Для этого надо, ускоряя вращение вала,
достаточно быстро пройти через критическое значение угловой частоты.
Амплитуда колебаний вала не успевает заметно возрасти.)
545. v~k YFlpy где k — безразмерный коэффициент, значение ко-
которого не может быть найдено примененным методом решения задачи.
Решение. [F]~MLT~2, [p]~ML~ly [v] — LT~l, гдеМ — масса,
L — длина и Т — время. Имеем v = f(Fy р), или [v\ =[Fmpn], LT-1 =
= (MLT)m-(ML-'1)n1 откуда для степеней Г, L и М в выражении
для размерности скорости получаем соответственно уравнения:
m— /i=l, 2m = 1, m-\-n = 0, из которых находим /n = -f- 1/2, л= —1/2.
546. 0,4 гс.
547. v = kYT?]p.
Указание. См. решение задачи 545.
548. Решение. Для простоты введем такие единицы, чтобы
плотности кинетической и потенциальной энергий выражались фор-
формулами wK]in— у2, wnoT—P2. Представим начальное возмущение P,v(P —
давление, v — скорость частиц стержня) в виде суммы двух возмущений:
Рь 1>! и Р2, v2. Тогда P^Pi+^2» v=vlJrv2. Величины Plt vx и Р2, v2 под-
подберем так, чтобы каждое из начальных возмущений Ръ vx и Р2, v2 по-
порождало возмущение, бегущее в одном направлении. Тогда P\—v\t
P\~v\. Если первое возмущение бежит вправо, а второе — влево, то
P2v2<0. Учитывая это, получаем Pi~vXy Р2=—v2 и далее
- v)/29 Р2= — У2= {P—v)/2.
247
Отношение энергий, уносимых возмущениями, равно
P-v
ИЛИ
/
549. Х=т
550. , = 2*0 |/1
ml
тетивы.
Решение. Сила, действующая на стрелу,
-, где т — масса стрелы, /—длина
Приравнивая энергию деформации лука кинетической энергии стрелы,
находим ее скорость.
551. Из подобия треугольников (рис. 245)
А/
2/
d/2 D+d
при
I,
М d u
откуда —= пл_и • Напряжения, возникающие при удлинении верх-
верхнего волокна, равны
Нейтрипьная
тния =2.104.^=10 кгс/мм2.
552. Укорочение бруска будет в два
раза меньше.
Решение. В отсутствие упора бру-
брусок будет ускоренно двигаться. Сила сжа-
сжатия в сечении стержня на расстоянии х от
А будет T~F(\~x/L)t так как предшест-
предшествующие элементы бруска должны сооб-
сообщать ускорение последующим. Измене-
Изменение длины элемента стержня dx, удаленного на х от Л, будет
5 Центр барабана
Рис. 245.
Общее изменение длины5 следовательно, будет
248
553. U=ma2l/FES).
554. Никакого напряжения не будет, так как в этом случае сила
притяжения Земли действует на все элементы бруска, сообщая им оди-
одинаковое ускорение. В задаче 552 сила была приложена к одному концу
бруска, и последующие элементы бруска получили ускорение только
вследствие сжатия предшествующих.
Р
М.
*kr т Мсо2 п Жсо2
556. У = 0. ■ {Lz—xl)y Д£г=__/д где *-—расстояние рас-
^ь OJCO
сматриваемого сечения от оси вращения.
§ 10. Колебания
557. Графики зависимости от времени — синусоиды, смещенные
относительно друг друга по фазе (на рис. 246 эти графики изображены
для колебания х—х0 cos со/). Графики зависимости скорости от смеще-
смещения — эллипс, ускорения от смещения — прямая. Если амплитуда
Смещение
Скорость
Ускорение \ i
Рис. 246
-смещения х0, то амплитуда скорости v~(x>x0 и амплитуда ускорения
^о=02а:о, где со — угловая частота колебаний.
558. £K1IH=-±^L(l_cos2o)/), Епот=^~- A + cos 2g>/),
v -X
559. Уменьшится в ^2 раз.
560. r=4-l/"—.
561. Тг =
Решение. Во время взлета ракеты с ускорением чясы будут
«дти быстрее в V~l+a/g раз, чем в обычных условиях. После вы-
249
ключения двигателя часы остановятся. Таким образом они покажут
время Тх = Т V\+a/g.
562. r = 2
563. Движение поршня будет происходить по закону
A
Ро L V У rnvQ
т. е. возникнут колебания с периодом
Т = *?]/™^ о,15 с.
S У уро
564. 1) Не изменится ничего; 2) частота уменьшится, а амплитуда
увеличится. (Для двухатомных молекул N2, O2 и Н2 y = cp/cv = 7/5.
Для одноатомного газа Не у = 5/3.)
565. Гармоническое колебание с периодом 7==2я У RolgOy где
Ro— радиус земного шара, gQ— ускорение свободного падения на по-
поверхности Земли.
Решение. Ускорение в точке, находящейся на расстоянии г
от центра земного шара, если r<RQy есть g0 r/RQ, т. е. ускорение пропор-
пропорционально смещению. Значит, тело будет совершать гармонические ко-
колебания около центра земного шара с амплитудой Ro и периодом Т=
=2лУ R0/g0 (см. задачу 509).
566. Если То— период колебаний маятника при отсутствии поло-
полости, то при наличии полости период будет
567. Поезд будет совершать гармонические колебания с периодом
Т = 2п VR/g « 84 мин, не зависящим от длины хорды /. Линия
отвеса будет перпендикулярна к хорде, вдоль которой движется поезд.
Часы в поезде будут идти медленнее, чем на Земле, в У 1/cos ф раз,
где 2ф —центральный угол, опирающийся на хорду длины /. По при-
прибытии в противоположную точку земного шара часы покажут время
t' = t У cos ф =0,933/, где t — время, отсчитываемое по неподвиж-
неподвижным часам. Таким образом, часы отстанут на 2,8 мин.
568. Нить отвеса установится перпендикулярно к полу салона
самолета. Г = 2я Vl cos a/g.
569. Г = ^1+^)=:1 ч5бс.
570. 1) Муфта будет постепенно (по мере роста ускорения) смещать-
смещаться в направлении, обратном ускорению; максимальное смещение £ =
=maiktt\ см. 2) Муфта начнет совершать колебания по закону
250
х= —г A—cosco^), где х—координата муфты относительно тележки, от-
отсчитываемая от начального положения муфты, причем х считается по-
положительным в направлении, противоположном ускорению тележки;
0)= |^/г//п«9,9 с*1. Вследствие наличия трения и сопротивления возду-
воздуха эти колебания постепенно будут затухать.
Замечание. При вычислении величин смещения | и частоты
со необходимо соответствующие величины, указанные в условии задачи,
перевести в одну систему единиц (СИ, СГС и т. п.). Это замечание следует
иметь в виду и при решении других задач.
571. Если отклонение муфты от общего центра масс будет хъ а от-
отклонение тележки — х2, то тх1=Мх2. Уравнение движения тележки
Мх2——&(*2+*i)» заменяя Xi из предыдущего равенства, получаем
Аналогично для муфты
Следовательно, будут происходить гармонические колебания тележки
и муфты с частотой со= 1/ ——~—- « 10,8 с. Амплитуды коле-
бании муфты 1-Г7-.— = 5 см, тележки I тг->—=1 см.
J^ М + т М-\-т
572. Т = к
573. Т =8
574. Г = 2л
575. jc = -t- f I — cos Л/ -~ t ) . Максимальное натяжение пру-
пружины равно 2Р.
,1R * g Bm2/m1)sin390 g ^^
576. cdo= -щ 1 + с08ф =T V 3*
Решение. Для малых колебаний около положения равновесия
кинетическая энергия системы равна
а потенциальная энергия
ц 1 d2U
" 2 дх\
здесь, %—Xi—х\—малое отклонение среднего груза от положения
равновесия. Полагая £ (t) = A cos (®ot-\-a) и ^Макс = ^макс» нахо-
находим искомый ответ.
251
577. Если сила, действующая на груз со стороны доски, F'=-— /v
то уравнение движения груза Р—F'=m d2x/dt2. Значение ускорения
груза находим из закона его колебаний: х—а cos со/; тогда получаем^
—F'=F=— Р—таен2 cos со/=—A+0,32 cos 4л/) кгс.
Рекомендуем начертить график изменения силы F со временем.
578. А > —-=М-==Т±-- м. При предельной амплитуде Ло«6,2 см*
тон* о*5 шя4
сила давления груза в верхней точке становится равной нулю.
579. Решение. При снятии груза М положение равновесия^
сместится вверх на величину xo=Mg/k. Возникнут колебания чашки от-
относительно нового положения равновесия: х—х0 cos со/. Когда чашка
начнет подниматься вверх, то вместе с ней будет подниматься и грузик т.
В верхнем положении ускорение чашки достигает максимального зна-
значения awaKC=(u2xo—kxo/m=Mg/m и направлено вниз. Если амшс<£,„
т. е. Л1<т, то при обратном движении чашки вниз грузик будет про-
продолжать лежать на ней, и подскакивания не возникнут. Если яМакс>£>~
т. е. Л1>т, то грузик отстанет от чашки и появятся подскакивания.
580. При G)M>g грузик будет подскакивать, при соМ<£ — коле-
колебаться вместе с мембраной.
581. k =
583. x^mg/k = 20 см.
585. При резонансе сила трения равна внешней силе: FTp =г
= 100 дин. Амплитуда скорости v0 = Арсо = 20л см/с, k=FTV/v0—5/n г/с.
586. При резонансе фаза скорости совпадает с фазой внешней
силы и амплитуда скорости наибольшая, поэтому работа внешней силы
Т
за период А = \ fds— \ fvdt будет наибольшей,
о
587. Г = 2л VTj3g.
588. Решение. Рассматривая движение тела как вращение во-
вокруг мгновенной оси с угловой скоростью со, напишем для скорости
его центра v — oaa. Ту же скорость можно представить в виде у =
= (R—а) ф. Приравнивая оба выражения, находим со = ф. Ки-
Кинетическая энергия по теореме Кёнига
K»+f<*)V
Потенциальная же энергия
U=mg(R-a)(\- cos <p) « 2£ (R -а) Ф2.
252
Применяя общий метод, находим
В частности, для сплошного цилиндра и сплошного шара
589. Т — 2л у [ 1-]—^ j —- . В частности, для сплошного
цилиндра и сплошного шара
590. Т = 2я V~h/2g, где Л —высота треугольника.
591. 7y7V=2//3~.
592. /=15 см.
593. Гл/Гд «0,9.
Решение. Пусть х — расстояние центра масс полудиска от
центра диска, у — расстояние центра масс всего диска от центра
диска. Тогда, по теореме Гюйгенса — Штейнера момент инерции полу-
полудиска относительно оси, проходящей через его центр масс, /0=
= m(R2/2—x2)t где m — масса полудиска и R — радиус диска. Момент
инерции относительно оси, проходящей через точку А, равен
Момент инерции относительно точки В:
fB-R[rncB^YR-
Периоды колебаний будут:
= 2пу (nhM + mJlR+y)g' Тв = 2пу
Учитывая, что у= св ,——х и —££-=-—- = 4, получаем у=*/ьх. Так
* т + т тал 2,5 у у 1Ъ
как x = *UR/n9 то ТА/ТВ « 0,9.
594 Т 2
594. Г-2
Решение. Т = 2п Y^IftMgh), где / — момент инерции колеблю-
колеблющейся системы, М — ее масса, h — расстояние от точки подвеса до
253
центра масс. В данном случае
!) я»],
где р—плотность материала.
595. a0 = arocos (l —/со2ао/C^)) « 8°, где со —частота колебаний
маятника до отрыва груза; Т = 2я \f2l/3g я 1,04 с.
Указание. В момент отрыва груза стержень обладает угловой '
скоростью о^Оо©, кинетической энергией £кин=/ст(о2а2/2, где /ст—
момент инерции стержня. Приравнивая эту энергию работе по подъему
центра масс стержня до его полной остановки Mg-^ (I—cos aj),
находим новую амплитуду.
596* Период будет таким же, как и в предыдущей задаче. Амплитуда
будет равна начальному отклонению маятника, г. е. 10°.
597. Да, это место — центр качаний, находящийся на расстоянии
2/з / от подвеса. Подвеска груза в центре качания любого физического
маятника не изменит его периода, однако размеры груза должны быть
значительно меньше расстояния от центра качания до точки
подвеса.
598. Г = 2д l/T±«*L.
V Ma—mx
Решение. Уравнение малых колебаний системы грузов будет
(/ + т*2)ф + (Ma—mx) gy = 0,
откуда и получаем ответ (/ — момент инерции маятника без грузика
относительно оси качания.)
расстояние точки подвеса от середины стержня.
Решение. Для физического маятника: со* = —-2-=-—-£—-
f/0==_—-/?j. Максимум частоты находим из условия: d(o2/ds = Qt
откуда и получаем ответ.
600. Решение. Движение маятника происходит по закону
a==a0cos y~3g/2l t. Второй закон Ньютона для кольца дает:
F—mgsin a = mad, где F—нормальная составляющая искомой силы
(нормальное давление стержня). Так как sin a « а, то F = m(ad-\-ga);
подставляя вместо а и a их значения из закона движения стержня,
находим
F = aomg (I — 3d/2l) cos Vbgftl t.
Касательную к стержню компоненту искомой силы (силу трения)
Q определим из следующего уравнения: Q — mg cos a = m(aJ d\ За-
254
меняя cos а через 1—а2/2, получим Q=m[g(l—a2/2) + (aJ4J или,
окончательно,
■ т
601. 7 = я
602. Г =— 1/ ^— . Для сплошного цилиндра Т =я Y3m/k.
603. Г = 2я V~l/3g В более общем случае, когда плита не одно-
родна, но центр масс ее совпадает с геометрическим центром плиты,
Т = 2я ]//l/(MgcP), где / — момент инерции плиты относительно верти-
вертикальной оси, проходящей через ее центр, а—длина одной из сторон
плиты.
604. Г«2я
605. Г
где Т — период колебаний
неподвижных часов, а Г'—часов, лежащих на абсолютно гладком
горизонтальном столе. Ход часов ускорится на 0,1%.
О1«5. У =Я I/ 7Г7 i \'
/ ш~
614. Г=2
M-\-m g
615. Г! = 2я V2l/3g, Г2 = 2
616. Решение. Задача сводится к нахождению выражений для
потенциальной и кинетической энергий системы. С этой целью мысленно
заполним полость тем же веществом, из которого сделан цилиндр- Обра-
Образовавшийся таким образом сплошной однородный цилиндр назовем
цилиндром 7, а цилиндр вдвое меньшего радиуса, заполняющий
255
полость,— цилиндром 2. Массы цилиндров обозначим соответственно
тг и т2. Энергия системы, как потенциальная, так и кинетическая,
будет равна разности энергий цилиндров 1 и 2. При повороте системы
из положения равновесия на угол ф (рис. 247) центр масс цилиндра /
остается на прежней высоте, его
потенциальная энергия Ui не
изменяется. Потенциальная же
энергия цилиндра 2 становится
равной U2=m2gh2, где /i2=
D
= #+ — cos ф — высота центра
Рис. 247. масс этого цилиндра над гори-
горизонтальной плоскостью, на кото-
которой находится система. Полная потенциальная энергия всей системы
U = U1 — U2 = const — m2gR A +1/2 cos ф).
Единственное переменное слагаемое, которое она содержит, есть
— V2 тчМ^ cos ф. Поэтому при надлежащем выборе аддитивной по-
постоянной величину U всегда можно представить в виде
£/ = const+ 1/2m2g/? (I—cos ф) = const + m2gR sin2 (ф/2),
или для малых углов ф U « const + 1/4 /я^Яф2. Кинетическая энер-
энергия системы /С = 1/2(/1 — /2) ф2, где /г и /2 — моменты инерции ци-
цилиндров относительно мгновенной оси. При изменении угла ф вели-
величины /г и /2 изменяются. Но для малых колебаний этими измене-
изменениями можно пренебречь и отнести 1Х и /2 к тому моменту, когда
система находится в положении равновесия. В этом положении
с помощью теоремы Гюйгенса —Штейнера нетрудно получить 1Х =
= 3/г щК2у ^2 = 19/впг2^2- Приняв еще во внимание, что m1 — 4m2i
найдем /С = 29/16 т2/?2ф2. На основании полученных выражений для
U и К заключаем, что малые колебания системы будут гармониче-
гармоническими с периодом Г —л J/ 29R/g.
617. а= |/1/2(^ + 2/бГ2)==7,42 см, /=а+ J =49,6 см,
618. r — ro( H о cos соом , где щ— Vk/m. При этом
\ coo—со2 /
должно быть со < соо. В противном случае груз на вращающейся
штанге неограниченно удалялся бы от оси вращения, и равновесие,
вопреки условию задачи, было бы невозможно.
619. Г = 2л^±^а« 1,26 с.
то
620. 1) Если отвести оба грузика в одну сторону в плоскости,
проходящей через точки крепления струны, на одинаковое расстояние,
256
то период колебаний 7\ = 2я У ml/F « 0,05 с. 2) Если отвести оба
грузика на одинаковые расстояния в разные стороны, то период Т2 =
= 2л |/ ml/2F « 0,035 с. См. замечание к ответу задачи 570.
Указание. В первом случае средняя часть струны (между гру-
грузиками) будет всегда параллельна первоначальному положению, и ус-
ускорение массам будут сообщать натяжения только крайних отрезков
струны. Следовательно, массы будут двигаться так, как вдвое большая
масса, находящаяся на середине укороченной в два раза струны при
том же натяжении. Во втором случае средняя точка струны находится
в покое; следовательно, каждый грузик колеблется так, как если бы
он находился в середине струны, укороченной в два раза.
621. Если при колебаниях маятника его максимальная угловая
скорость (d<p/dt)MaKC меньше угловой скорости вала со, или со—dy/dt>0
для любого момента времени, то момент силы трения, действующей со
стороны вала на маятник, всегда направлен в одну сторону. Так как
этот момент постоянен, а маятник при колебаниях проходит по направ-
направлению вращения и против вращения один и тот же путь, то работа мо-
момента сил трения за период равна нулю.
622. При колебаниях сила трения, действующая на муфту со сто-
стороны вращающегося вала за одну половину периода, направлена по
движению маятника, когда вал и муфта вращаются в одну сторону, а в
другом полупериоде эта сила направлена против движения маятника.
1) Если сила трения увеличивается со скоростью скольжения, то
она больше в ту половину периода, когда муфта и вал вращаются в про-
противоположные стороны. Следовательно, работа силы трения маятника
о вал за целый период положительна, затухание маятника возрастает
из-за трения между муфтой и валом.
2) Если сила трения уменьшается со скоростью скольжения, то
по тем же причинам, наоборот, работа силы трения маятника о вал за
весь период отрицательна, вал сообщает энергию маятнику и затухание
колебаний уменьшается. В том случае, когда работа силы трения о вал
больше, чем потери энергии на трение других частей маятника, энергия
колебаний маятника будет увеличиваться, амплитуда будет возрастать,
а маятник может совершать автоколебания.
623. Положение равновесия смещено в сторону вращения вала на
угол (po=arctg ([iR/a).
§ 11. Гидростатика и аэростатика
624. 1) Да. 2) Равновесие может нарушиться, если объем тел раз-
различно изменяется при погружении в воду вследствие того, что сжимае-
сжимаемость их различна. Сжимаемостью называется величина — AV7(Ap V),
где AV •— изменение объема V, вызванное изменением давления Др.
9 Под ред. И, А, Яковлева 257
625. Гири должны быть из того же вещества, что и взвешиваемое
тело.
626. р—JWtp.-pO + dWef.
627. Б2>6рA— р) С2.
628. г2>2рA—р)/2.
629. 1/г > {2 sin (a/2)}2, где угол а определяется из трансцендент-
трансцендентного уравнения a—sina = 2np. Например, при p = V2 из него по-
получаем а — Пу и условие устойчивости принимает вид / > 4г. При
других значениях р равновесие может быть устойчивым и при мень-
меньших значениях /. Так, при а — п/2 и а = Зя/2 получаем соответ-
соответственно р= 1/4 — 1/2д да 0,091 и р = 3/4 + 1/2я да 0,841. При таких
значениях р равновесие устойчиво, если / > 2г. При / > 4г равно-
равновесие устойчиво, каково бы ни было р < 1.
630. F«l,12 кгс.
631. 1) AxQ«400 кгс, 2) A2Q=196 кгс.
Указание. Давление водорода в баллоне аэростата практиче-
практически будет равно внешнему атмосферному давлению и на высоте 2 км.
Часть водорода уйдет из баллона через клапан. Зная вес 1 м3 воздуха
на высоте 2 км, можно найти вес 1 м8 водорода при новом давлении из
пропорции 1/1,3=*/90.
632. Если сжимаемость жидкости (или газа) больше сжимаемости
тела, то принципиально можно.
633. P=:# + iL-^MM рт. ст.
634. р= 1—1//г2.
635. F — 1l2cPpg, где р — плотность воды, h=1/Jta.
636. Р = 8,64 кгс, Ж = 41,6 кгс-см.
637. Р = 34,56 кгс, М = 332,8 кгс-см,
638. p=ft2£+^==146Tc.
о
639. Л1=210 кгс-м.
640. Решение. Выделим в стенке сосуда пояс шириной 1 см,
расположенный на высоте 1 м. Силы со стороны соседних к поясу ча-
частей стенки не действуют на пояс в горизонтальном направлении, и
поэтому силы давления жидкости уравновешиваются только упруги-
упругими силами пояса. Выделим элемент этого пояса длиною R d<pf где R —
радиус цилиндра и dtp — угол. К концам этого элемента приложены со
стороны соседних элементов силы, уравновешивающие силу давления
pRdy на элемент, т. е. 2F d<p/2=pR d<p. F представляет искомое уси-
усилие. Подставляя р=0,4 кгс/см£, #=1 м, получаем F=40 кгс/см.
641. Ар=0,017 кгс/см2.
Указание. Для решения задачи можно воспользоваться следу-
следующими соображениями. Рассечем мысленно баллон произвольной диа-
268
метральной плоскостью. На каждую полусферу будет действовать сила
ApnR2. Полусфера будет удерживаться в равновесии силами натяжения
ткани Т, приложенными на окружности большого круга (в сечении бал-
баллона диаметральной плоскостью). Это значит, что Лря/?а==Т2я/^, откуда
Ap=2T/R. Подставляя для Т его предельное значение 850 кгс/м, на-
находим максимально допустимое превышение давления газа в баллоне
над внешним атмосферным давлением.
642. Л» 5,4 км.
Указание. Изменение давления dp с изменением высоты dh
связано равенством dp=—pgdh, где pg—плотность воздуха. При
постоянной температуре plpg—pjpg^ Подставляя это в предыдущее
равенство и интегрируя, получаем р=рое~р^в^/\
643. Р=-^-(/?2 —г2), Pll = 1/2pgR, где г —расстояние от центра
Земли, /? —радиус Земли. Если бы земной шар состоял из несжи-
несжимаемой воды, то было бы Рц = 1/20/? (Рц — в атмосферах, R—в мет-
метрах). С учетом плотности Земли (р^=5,5) Рц = 0,275Я « 1,75- 10е атм.
644. a=arctg 0,29=16°10\
645. а=0,5 g при ускорении в направлении удаленного днища,
a—§g— в обратном направлении.
646. Не изменится.
647. Сила давления на переднюю и заднюю стенки цистерны
Р Pak ( ah Л- V*°l
648. Решение. Так как фигура Земли мало отличается от ша-
шаровой, то ускорение свободного падения внутри земного шара можно
считать направленным к центру Земли и пропорциональным расстоя-
расстоянию до ее центра. В этом приближении с учетом центробежной силы
уравнения гидростатики принимают вид
дР х , , дР у , 2 дР г
где #о— радиус Земли, со — угловая скорость ее вращения. Начало
координат мы поместили в центре Земли, а ось Z направили вдоль оси
ее вращения. Интегрируя эти уравнения, получим
где С — постоянная интегрирования, определяющаяся значением дав-
давления Р на земной поверхности (его можно считать равным нулю, так
как атмосферное давление пренебрежимо мало). Сплюснутость Земли
определится из требования постоянства давления на земной поверхности.
Выбрав сначала точку на экваторе, а затем на полюсе, пишем
9* 259
P(R9, О, 0)=Р@, 0, Rn)y где R9 и Rn — экваториальный и полярный
радиусы Земли. С учетом явного вида давления отсюда получаем
(о>2—£-) #э = §-Ri и далее
\ АО / АО
Следовательно, для сплюснутости е земного шара получается
р _^
#„ ~ 2g ~580*
Действительное сжатие Земли заметно больше, а именно 1/297. Рас-
Расхождение объясняется грубостью модели, положенной в основу рас-
рассуждений, а также несовершенством метода расчета. При строгой по-
постановке задачи надо учитывать, что поле тяготения сплюснутого шара
не является центральным 1). Тем самым задача сильно усложняется,
так как само гравитационное поле заранее неизвестно, а зависит от не-
неизвестной формы поверхности Земли. Подробное исследование пока-
показывает, что задача, сформулированная таким образом, не имеет одно-
однозначного решения. Возможно несколько различных форм равновесной
поверхности, в том числе и эллипсоид вращения с определенной степенью
сжатия.
§ 12. Гидродинамика и аэродинамика
649. i/=/l>iS = 9,8 м/с.
650. v = V 2g(h1 + 019h2) « 9,5 м/с.
651. р=2,5 см вод. ст.
652. Точка пересечения струй лежит ниже второго отверстия на
25 см.
653. Q = S1S2V2gAh/(Sl-S21).
654. h = v2/2g=5,\ м.
655. Когда моряк подносил доску к отверстию, то врывающаяся
струя воды действовала на доску с силой pu2S=2pg/tS, где h — высота
столба воды над отверстием к S — площадь отверстия. Когда доска
закрыла отверстие, на нее действовала сила pg/iS, т. е. в два раза мень-
меньшая.
656. 1) Др=ру2/2«0,06 атм (р — плотность воздуха). Вентилятор
создает разрежение, и воздух под действием разности давления Ар по-
получает в трубе скорость v. 2) Из-за вязкости давление увеличится, ибо
часть перепада давления уравновесится силами трения.
657. h=po/(pg)y где р — плотность жидкости.
х) С учетом этого обстоятельства расчет дает е=б/4 со2аУ#« 1/232.
260
668. F=pQ2AS«40 re.
669. Решение. Вертикальная скорость струи на уровне воды в
стакане v~ yr2g(H—h). За 1 с уровень воды поднимается на величину
A/i*=Q/S. Сила давления на дно от падающей воды: MipSv, где р —
плотность воды. Все давление равно F~hgSp-\-&hSvp. Через время t
после начала h = Aht = (Q/S) t и F = MipS[gt + y~2g(H—h)].
Окончательно
660. * = — 1/ —
661. * = —
a
* 15a
663. Л = ///2, хмакс=хН.
664. Площадь горизонтального поперечного сечения сосуда должна
быть пропорциональна квадратному корню из расстояния этого сечения
от отверстия. Если сосуд обладает осевой симметрией, то он должен иметь
форму параболоида вращения четвертого порядка.
665. P=P0-p^+P^{l-M~|=7^T}, где *-рас-
стояние по вертикали от нижнего конца насадки.
fififi И (^0
666- Я==
667. i/= Yi (Р —Р0)/р + 2gh, где Ро—атмосферное давление.
668. Пока уровень жидкости в сосуде выше нижнего конца
трубки АВ, скорость истечения постоянна и равна у= У~2gh. После
этого скорость истечения начнет уменьшаться.
669. Решение. Рассмотрим кольцевой слой жидкости с внут-
внутренним радиусом г и внешним r+dr. Сила внутреннего трения, действу-
действующая на него в направлении течения, равна
1
(Индексы г и r+dr обозначают, что величины, заключенные в круглые
скобки, должны быть вычислены при значениях радиусов г и r-\~dr
соответственно.) В том же направлении действует сила разности давле-
давлений (Pi—P2Jnr dr. При стационарном течении сумма обеих сил обра-
обращается в нуль. Это приводит к уравнению
d(dv\_ Рг-Р.
dr\dr)~~~ lr\ '
261
Г/ dv\ ( dv\ I o , d ( dv\ .
LV drjr+dr V rfr/d rfr V ^/
Решение его, обращающееся в нуль при r=Ri и г=/?2» есть
С 2 в \
А1ш\ I • I ]♦-, /Г) /D \ D | "
Расход жидкости:
670. Решение. Возьмем прямоугольную систему координат
X, К, Z с осью X, направленной вдоль трубы (рис. 248). Выделим столб
жидкости, имеющий форму прямо-
угольного параллелепипеда с ребра-
ми, параллельными координатным
осям. На боковую грань этого па-
раллелепипеда, перпендикулярную
к оси у^ действует сила внутреннего
трения — r\ldz (dv/dy)y, на противо-
противоположную — сила 4\ldz(dv/dy)y+d)n
где / — длина параллелепипеда. Сумма этих сил:
Рис.
—
248.
Аналогично находится результирующая сил внутреннего трения, дей-
действующих на остальные две грани. Полная сила внутреннего трения
будет Tj/dS ("TT+^t ) * ^на Должна быть уравновешена силой
разности давлений (Р2—^i) dS. Отсюда и следует искомый результат.
671. Эта задача относится к типу задач, решаемых методом угады-
угадывания. Угадывается вид решения дифференциального уравнения F70.1),
а затем коэффициенты в этом решении подбираются так, чтобы удов-
удовлетворить граничному условию на стенке трубы: t;=0. Направим коор-
координатные оси Y и Z вдоль главных осей нормального эллиптического
поперечного сечения трубы и будем искать решение в виде и=Лг/2+
+Вг2+% Это выражение удовлетворяет уравнению F70.1), если
р р
2Л+2В== -.—- . На внутренней поверхности эллиптической трубы
1у\
у=0, т. е. /4«/2+Бг2+ав=0. Это уравнение должно переходить в урав-
W2 22
нение эллиптического сечения трубы -^-\"rz — 1, а потому А——vofa%t
В——vo/b2. Для определения постоянных А, В, v0 получилось три ли-
линейных уравнения. Решая их, находим
Р р
Постоянная v0 есть, очевидно, скорость течения на оси трубы.
262
Вычислим теперь расход жидкости. Поверхности, на которых
и2 г2
скорость v постоянна, суть эллиптические цилиндры -^2"+-гт2"= 1,
полуоси которых определяются соотношениями
6'2 = £2 J> # Возьмем два таких эллиптических цилиндра с беско-
бесконечно близкими значениями параметра v. Площадь нормального се-
сечения между ними dS = d (na'b')~—я — dv. Расход жидкости:
, или Q =
672. Решение. При стационарном ламинарном течении силы
вязкости уравновешиваются градиентами давлений. В уравнения дви-
движения давления входят только через градиенты. Поэтому разность дав-
давлений Pi~P2 на концах трубы и длина последней / могут войти только
в комбинации (Pi—P^ll. А так как жидкость движется без ускорения,
то характер течения не может зависеть от плотности жидкости р. Поэто-
Поэтому плотность р и расход жидкости Q могут войти лишь в комбинации
Q/p. Принимая все это во внимание, методом размерностей нетрудно
получить
где S — площадь поперечного сечения трубы, а С — постоянный чи-
численный коэффициент, значение которого зависит от формы этого по-
поперечного сечения. В полученной формуле содержатся все законы, эк-
экспериментально установленные Пуазейлем.
673. Нужно приложить силу F—2Spg(h1—/i2)=0l5 кгс, толкающую
тележку со стороны отверстия, расположенного выше.
674. Показания весов уменьшаются на 12,5 кгс.
Решение, Вытекающая из отверстия вода приобретает ежесе-
ежесекундно количество движения pv2S=2pghS. Следовательно, с такой силой
вода в цилиндре действует на воду в струе. Значит, струя действует
вверх на воду в цилиндре с силой 2pghS. Поэтому со стороны сосуда,
стоящего на весах, к покоящейся воде в цилиндре должна быть прило-
приложена сила, меньшая веса воды на эту величину. Таким образом, умень-
уменьшение давления воды в цилиндре на его дно будет в два раза больше
прежнего давления pghS столбика покоящейся жидкости на ту же пло-
площадку S.
675. Сила давления воды на щит уменьшится на 72,5 кгс.
Указание. Вытекающая под щитом вода будет ежесекундно
получать количество движения pSv2=2pghS=72,b kic-c, т. е. вода
263
перед щитом будет действовать на вытекающую струю с силой 75 кгс.
По третьему закону динамики струя с равной и обратной по направ-
направлению силой будет действовать на воду в канале (реакция струи).
676. Полагаем, что струя после удара о лопасть продолжает
движение со скоростью лопасти v. Тогда ежесекундно масса воды
S(V~2gh — v) p теряет скорость ( У 2gh — v). Поэтому на колесо дей-
действует сила F = S ( V^2gh — vJ р, работа которой за секунду равна
5р {V 2gh—vJ v. Максимум будет при v = 1/9 }/r2gh. Следовательно,
максимальная мощность будет */27 Bgh)s^2 Sp « 8,75 кгс-м/с и оп-
оптимальная угловая скорость вращения 1/8 V2gh/R « 2,2 с*1.
677. На 0,047 °С.
678. Если бы кинетическая энергия струи, составляющая около
6 Дж на 1 см8 воды («1,5 кал/см8), полностью превращалась в тепло,
то температура струи в результате удара о лед повышалась бы всего на
1,5 °С; этого явно недостаточно для объяснения эффекта.
со2
679. Параболоид вращения; образующая парабола г = —х2,
где х—расстояние от оси вращения, z — повышение уровня поверхно-
поверхности по сравнению с уровнем ее в центре сосуда.
ООJ/?2
680. 1) р*=Ро+ о • где Ро—Давление в центре дна, р—-плот-
р—-плотность воды и R — расстояние от центра дна; 2) р « 42,3 гс/см2.
681. Пробка — у оси вверху, свинец — у стенки цилиндра внизу,
тело А — в любом положении (если его сжимаемость равна сжимаемо-
сжимаемости воды).
682. Т«16 гс.
683. Разность давлений сообщает каждой частице жидкости цен-
центростремительное ускорение как раз такое, которое необходимо, чтобы
частицы двигались по окружности и не приближались к оси вращения.
684. 1) Жидкость в трубочке В поднимается до того уровня, где про-
продолжение поверхности параболоида вращения, образованного поверх-
поверхностью вращающейся жидкости, пересечется-со стенками трубочки.
Следовательно, высота жидкости в трубочке не покажет давления у
измерительного отверстия трубочки.
2) При любом положении отверстия А жидкость в трубочке D под-
поднимается только до уровня жидкости на оси цилиндра, так как жид-
жидкость в трубочке С А находится во вращательном движении. Поэтому в
горизонтальном колене трубочки СА будет перепад давления, измеряе-
измеряемый разностью высоты над точкой А и центром. Следовательно, и этот
способ непригоден.
3) Высота столба в трубочке D будет равна высоте уровня жидко-
жидкости над отверстием Л. Таким способом можно измерить распределение
давления.
264
685. Наличие масла не изменяет формы поверхности воды. Высота
уровня будет ниже того уровня, о котором шла речь в предыдущей за-
задаче, на 4 мм.
686. /?«112,5 гс.
687. Решение. Перейдем в систему отсчета, в которой жидкость
покоится. В ней добавятся две силы инерции: центробежная и кориолисо-
ва. Кориолисова сила не совершает работы. Она лишь искривляет
линии тока, но не сказывается на справедливос-
справедливости и форме общего уравнения Бернулли. Цент-
Центробежная сила добавляет новый член к потен-
потенциальной энергии. Полная потенциальная энер-
энергия единицы массы жидкости будет u=gz—1/2®2г2>
так что уравнение Бернулли запишется в виде
где v—относительная скорость жидкости (т. е. скорость относительно
вращающейся системы отсчета). Постоянная Бернулли В одна и та
же для всех линий тока, поскольку все они начинаются вблизи по-
поверхности жидкости, где скорость v пренебрежимо мала. Применим
уравнение F87.1) к линии тока АВ, начинающейся на поверхности
жидкости в точке А (рис. 249). Если начало координат поместить
в точке Л, то zA= гд=уа=0, /?i4=P^=Po, vb=v, zB = — h, rB=Rt и мы
получим v= У2(gh-\-со2/?2). Здесь h означает высоту наиболее низ-
низкой (центральной) точки А уровня жидкости относительно отверстия.
Переход к неподвижной системе отсчета не представляет затруднений.
688. Потому, что для равномерного вращения сосуда к нему необ-
необходимо приложить момент сил М, больший момента сил трения Мтр,
Работа момента М—Мтр идет на увеличение энергии воды, переходя-
переходящей при переливании от центра к периферии сосуда Л, и энергия пада-
падающей воды не может быть больше этой работы. Следовательно, работа
водяного колеса недостаточна для поддержания равномерного вращения
сосуда.
689. Сосуд должен иметь ускорение a<2g(H—h)llt направленное
вправо на рис. 193.
690. t> =
691. 0 =
692. Падение давления на трение на участке трубы между сосудом
и первой манометрической трубкой должно быть тоже 5 см; следова-
следовательно напор в 3 см сообщает кинетическую энергию жидкости, теку-
текущей в трубке. Эта энергия на 1см3 жидкости равна pgh= 2940 эрг/см3,
откуда скорость жидкости «77 см/с.
693. Решение. На рис. 250 показано сечение бесконечно длин-
длинного цилиндрического тела, образующая которого перпендикулярна
265
к рисунку. Там же показаны трубки тока, прилегающие к телу, и ука-
указаны давления р и скорости v вблизи трех сечений трубок тока, отме-
отмеченных индексами 0, 1,2. Сечение 0 достаточно удалено от тела. Тогда,
по уравнению Бернулли,
Сила, действующая вверх на цилиндрик, вырезанный из тела, будет
равна
(P2-Pi) dS = l/2p(vl-vl) dS.
При выводе учитывается, что dSt cos 0Ly=dS и rf52cos a2=d$, где dSt—
площадь верхней поверхности цилиндра, а аг— угол, который образует
нормаль к этой поверхности с вертикалью; так же й-для нижней поверх-
поверхности.
604. Решение. Кинематическая вязкость воды v=0,010 см2/с.
Вычисляя числа Рейнольдса и Фруда для модели, получаем
2
Re = -^ = 2,blO7, F = -2- = 0,022.
Определяющую роль играет число Фруда, влияние числа Рейнольдса
не очень существенно. Из равенства чисел Фруда получаем v—vx (UltfU—
= 60 км/ч. Далее из соображений размерности находим
р ^£,2/5/2^1/2дКе^ p) = pF/7/2^3/2/(Re, F).
Отсюда, если пренебречь влиянием числа Рейнольдса, P=Pj (//у7'*»
«80 000 л. с.
695. Решение. Из соображений размерности следует, что подъ-
подъемная сила и мощность должны выражаться формулами
Поскольку плотность воздуха и его вязкость в обоих случаях одина-
одинаковы, подъемная сила не изменится, если не изменятся значения функ-
функции /х и коэффициента при ней. Условием этого является /?оI
откуда aJ/co1=(/1//2J=l/a2 и далее
/2@2
h
266
§ 13. Акустика
696. jc«9,6m.
Решение. Звук, вышедший из точки Л, через время т достигнет
уха человека D (рис. 251); в это время пуля будет в точке С. Учитывая,
что угол ADC — прямой, а
/Ш=340т, ЛС=660т, получим
ответ.
697. Ю-3 с.
698. Высота тона повышает-
повышается приблизительно на 1# Гц,
высота гармоник — на пЛ8 Гц,
где п — номер гармоники. Рис. 251.
699. 254 или 258.
700. Биения с частотой 2v0 и/с будут зарегистрированы приемником
только в первом случае.
701. v = 3400 м/с.
702. Nk=k c/BL), где с — скорость звука в газе, заполняющем тру-
трубу, L — длина трубы, *=1, 2, 3, . . . Основной тон, если труба заполне-
заполнена воздухом, соответствует #1=100 Гц.
„лл xr 2k+\ с
703. /Vfc + i=—-—у-; обозначения те же, что и в предыдущей
задаче. Основной тон соответствует частоте Л^ = 50 Гц,
Рис. 252.
704. См. рис. 252. Точки 2 и 4—узлы смещений и скорости,
пучности давления, места наибольших значений потенциальной энер-
энергии (при /=0, t = 1/zT). Точки /, 3 и 5—узлы давлений, пучности
скоростей и смещений, места наибольших значений кинетической
энергии (при t — 1/^, t=3/^T)t Г — период колебаний.
267
705. L = 30cm.
Указание. Частота колебаний v=7rrl/ —, где Т—натя-
У j'
жение струны, р —масса струны на единицу длины и L—длина
струны. Пользуясь этим соотношением, находим первоначальную
длину.
706. Если
— колебание рассматриваемой частицы, вызываемое первой системой
волн, а
-=-—-£ j
=a2sin (Ш—<p2)
— колебание, вызываемое второй системой волн, то суммарное колебание
У=У1+Уг=А sin
где
707. Скорость звука и связана с адиабатической сжимаемостью
psE соотношением и— V^l/pp, где р — плотность среды, v—ее
объем и р—давление. Для воды находим р « 4,35-10 см2/кгс.
708. Р«1,35»10 см2/кгс. Жидкий гелий выделяется среди других
жидкостей, в частности, своей большой сжимаемостью.
709. c=2vo/=14OO м/с. Обертоны v =kv0, где k=2, 3 и т. д.
710. Период колебаний тонкой струны меньше в два раза.
711. Уменьшить в девять раз.
712. Скорость звука в газе зависит от отношения давления к плот-
плотности. Так как это отношение при постоянной температуре — величина
постоянная, то скорость звука от давления не зависит.
713. Ускорение а=0,1 BяJ-52-108 мкм/с2«1000#, скорость и =
=0,Ь2я-5'104 мкм/сл;3,14 см/с.
714. 1) Зажать струну на очень коротком участке в середине;
2) так же зажать на расстоянии 1/3 от конца. Понизить тон звучания
струны такими способами нельзя.
715. Решение. Из уравнения адиабаты следует dp/p = ydp/p.
Если у — смещение частицы в волне, то относительное сжатие есть
— ду/дх и dp/p = —dy/dx. Следовательно, dp/p = —ydy/dx. С другой
стороны, если смещение в бегущей волне у = A sin Г со/ «— j ,
то
2ш\
268
а скорость частицы
Отсюда
дУ л
чг = Ло) cos
f 4 2пх\
Г—г)-
и Лео ( 2ядр\ 2пА ( . 2пх\ ду
-=— cos Ы—rj=-T-cos (erf—x-J—з*.
а значит,
716. 1) v = 990/n « 315 с-1, 2) с = ЗЗО м/с, 3) А, = я/3 « 1,05 м,
4) w =t 99 см/с, 5) Ар = y^w/c ^ 3,2 мм рт. ст.
717. ц =
а
Решение. Ищем точки *х и х2, в которых в момент / фазы обеих
волн совпадают. Координаты точек должны удовлетворять уравнениям:
где ^х и k2 — волновые числа, равные 2л/Кх и 2я/Я2 соответственно.
Отсюда Л = *2—*1=т—М- . Точка, в которой фазы совпадают,
Ai— А2
в момент времени f будет иметь координату x'v т. е.
откуда скорость перемещения этой точки
i—й)а
*'— / ^ — k^ Я2—Я,. #
2
719. 7=^1— « 460 эрг/с = 4,6-10-5 Вт.
Указание. Поток энергии J ==^~-cSy из решения задачи 715
и/с = Ар/(ур)', учтя, что скорость звука с= У~ур/р, получаем ответ.
720. А =—=г -— «2-10-9см (см. решение задачи 715, ат-
© у р со \г
мосферное давление считать равным 1013• 103 дин/см2).
т. r-i /f. __
722. Частота колебаний увеличится в 1/^0,069^3,8 раз.
§ 14. Специальная теория относительности
723. /2=10 с, /3=9,9 с, /4=11 с.
В момент времени t± ракета будет находиться на расстоянии xx—Vh
от начала координат О. Момент времени /а можно найти двумя эквива-
эквивалентными способами:
269
1) Скорость, с которой световой сигнал догоняет ракету, равна
х V
с—V. Поэтому t2 — t1 ——~= у/х. Определяя отсюда t2t полу-
получим t*=l__'Vjct1.
2) В момент времени tt расстояние между ракетой и началом
координат О равно хх. Пусть световой сигнал догонит ракету в точке
x2 = Vt2. Ясно, что x2z=x1-\-(V/c)x2, откуда хг = (\—V/с)х2. Но
x1 = Vti, a x2 = Vt2f и мы снова получаем t2 = ?—ттт-t^
* — VIс
Скорость сигнала, идущего от ракеты к точке О, равна с, поэто-
поэтому h—t1 = x1/c = (V/c) tly откуда ts = (l-\-V/c) tv
В момент времени t2 ракета находится на расстоянии x2—Vt2 от
точки О, и отраженный сигнал придет в точку О в момент /4 та"
кой, что /4—h — (V/c) /2» откуда /4 = ' ^ /1#
724. Очевидно, что Дто=22:о/с. Но в системе К источник и зеркало
движутся, так что путь светового луча —ломаная ОАО'. Длина этой
ломаной больше, чем го» поэтому промежуток времени Д^ между той же
парой событий больше Дт0 (скорость света с во всех системах одинакова!):
Из рис. 199 ясно, что 0Л= V OB2+z20, а Д/=2-ОЛ/с. Но OB=V Д//2,
и комбинируя два последних равенства с учетом того, что 2о=2о, мы
найдем, что Д/=ГДт0, где Г определяется согласно B).
Показание часов из К' в точке О' равно /А=0+Дт0=Дт0. Показание
часов из К в точке О' равно /=0+Д/=ГДт0.
725. Если на корабле отсчитан промежуток собственного времени
Д/',то по земным часам будет отсчитан промежуток Д/=ГД/', где Г=
=25/7, поэтому
24 25
S=VAt= — с~ Д*'=24ст (Д/'=7т, т=1 с).
726. Обозначим длину стержня в системе К через /. Тогда промежу-
промежуток времени Д^ между посылкой и приходом светового сигнала в 0f
можно сосчитать так. Время, необходимое свету, чтобы дойти до зерка-
зеркала Si, равно /i=//(c—V), а чтобы после отражения вернуться к источ-
источнику /а=//(с+ V). Ясно, что Д/=/1+/а=B//с)Г*. Но Д/=ГДто=
= ГB/0/с). Из двух последних равенств следует искомая формула
727. Да, увидит; если пренебречь временем реакции глаза, мгно-
мгновенно!
728. v—cls\n а. В обоих случаях скорости v не соответствуют рас-
распространению какого-либо физического объекта, а потому не являются
скоростями распространения сигнала.
270
729. Пусть источник покоится в К, а наблюдатель — в /С'. Если ис-
источник посылает импульсы с интервалом Т, то удаляющийся наблюда-
наблюдатель в К' получает эти сигналы через промежуток времени
71' ________ т
(по часам /С). Чтобы получить промежуток времени по часам наблю-
наблюдателя К\ следует перейти к собственному времени наблюдателя Ц
для которого Tq = (\/T)T\ и мы получим 7о
ходя к частотам, получим
(Сд°=
Аналогично, при сближении источника и наблюдателя
730. 1) Используя формулу C), получим при Д/=0
&t'=—T(V/c2)&X?<:0.
2) Используя формулу C), получим при Д*=-0
731. Очевидно, 10 = х'2—х[. Однако по формуле C) Д*г = ~TVM =
= Г/ (Д^ = 0), поскольку Д/=/2 — tv
732. Д/=Дт0. Согласно C) Ах'= —ГУДт0, а наблюдатель из /С'
должен считать Д/' =—(Д*'/КК отсюда Д/'' = ГЛт0.
733. В системе # проекции стержня на оси х и у будут равны
Д*=Дл;7Г, Ьу=Ау\ Очевидно, /в = (Д^'
Таким образом, в системе К:
так как Ддс'=?0 созф". Что касается угла ф, то он определится из
соотношения
734. Из формул A) и (Г), положив f=0 и /'=0, получим искомые
формулы. Различие в знаках обусловлено тем, что для К направление
относительной скорости совпадает с положительным направлением оси х,
а для системы К' эти направления противоположны.
271
735. В системе К все точки стержня пересекают ось х, х' одновре-
одновременно, однако этого нет в системе /С'. В момент времени ?=0 (по часам
К) часы из К вдоль положительной части оси х отстают от часов системы
/С, а вдоль отрицательной части их опережают (см. задачу 734). Значит,
по часам системы /С' в момент /'=0 правый конец стержня уже пересе-
пересечет ось х\ а левый будет только к ней приближаться, но середина стерж-
стержня в момент /'=0 будет находиться на оси х (в начале координат). Следо-
Следовательно, в системе К стержень несколько наклоцен по отношению к
оси xt х'.
В системе К правый конец пересекает ось х в точке х1 = 10/2
в момент / = 0. Координаты этого же события в системе К' (см. A)):
*'=Г70/2, Г = — Г (/0/2) (V/c2). Но нам нужно положение правого
конца в момент /'=0, т. е. на время 6/' = Г (/0/2) (V/c2) позже.
Чтобы определить положение правого конца в этот момент времени,
нужно знать компоненту скорости стержня по оси у в системе /('.
Она найдется по формуле F): ш'=ш/Г, тогда как о£=—V. В мо-
момент /'=0 правый конец окажется в точке с координатами
У о = wybt' = <Ш/Г> Г Л/2) (W
х'о = Г A,12) = w'x6t' = Г/о/2- VT A,12) (Vic2) =
Имея в виду, что в этот момент времени середина стержня находится
в начале координат, получим для угла q/' значение:
736. Соударения не произойдет и в системе /С'. В системе К стер-
стержень не подвергается лоренцеву сокращению, но плоскость движущейся
пластинки наклоняется (ср. решение задачи 735). В итоге метровый
стержень с полностью «сохранившейся» длиной проскальзывает через
сократившееся отверстие, но расположенное уже под углом к стержню.
При этом колцы стержня в системе К проходят через плоскость пластин-
пластинки не одновременно.
737. Запишем последовательно выполняемые преобразования Ло-
Лоренца, при переходе от системы К к системе К' и от системы К к системе
Путем простого пересчета можно показать, что выражения для f
х" могут быть приведены к виду
t-Wx/c2 х„_ x-Wt
Y\—(wjc)% ' Vi-OW f
272
V 4-V
где W = . **/%, 2y 2—относительная скорость систем /("и /С. Послед-
нее выражение не изменяется при перестановке в нем величин V\
и V2f что и требовалось доказать.
738. Запишем последовательно выполняемые преобразования Ло-
Лоренца при переходе от системы К к системе К' и от системы К' к систе-
системе К":
, *— Vxt
f\(Vl)i
г= ££££_
Из написанных формул легко получить:
УI - (К2/с)» ' f I- I
г"
откуда очевидна некоммутативность окончательного результата отно-
относительно скоростей Vx и V2 систем отсчета К' и К".
739. Если движение частицы в К задано, то через преобразова-
преобразование Лоренца можно найти: *'=**(/'), y''—y'(t')t 2* = z'(/'), по-
поскольку t' ~V (t). Пусть в К время изменилось на dt. Тогда непо-
непосредственно найдем dx, dy, dz, а согласно A) и dx' = T(dx—Vdt)t
dy'— dy, dz"~dz, dt'==rldt г"^). Разделив почленно первые
три равенства на четвертое, получим формулы F).
2) Решение. Согласно предыдущему результату нетрудно по-
получить
откуда и следует нужный результат.
741. Пусть К'— система отсчета, где вода покоится. В этой системе
скорость света i/ равна с/п. Переходя к системе /С, относительно кото-
которой Кг движется со скоростью V, имеем
273
Для скорости воды V/c<^i знаменатель можно принять равным единице
с точностью до V*/c2. Тогда
опять же с точностью до V2/c2.
742. Пусть vt направлено в положительном направлении оси х
(t>i>0), а v2— в отрицательном (р2<0). Скорость их сближения в сис-
системе К равна
Однако это не есть реальная скорость распространения чего бы то ни
было физического. Относительная скорость частиц в теории относитель-
относительности — это скорость одной частицы в, системе отсчета, где другая ча-
частица покоится. Воспользуемся формулой преобразования скоростей,
полученной в задаче 740. Чтобы Vi было равно нулю, необходимо, чтобы
V=Vl=a1c (это очевидно, так как система К связана с частицей). Но
тогда
Остается только доказать, что при заданных условиях коэффициент
при с всегда меньше единицы, но это сразу же следует из неравен-
неравенства (<*!—1H— Оа) <0.
743. 1) Используя формулы E), легко обнаружить, что vz—0$
т. е. что и в К частица движется в плоскости (х, у). Вводя углы §
и -б1', образуемые скоростью частицы соответственно с (совпадаю-
(совпадающими) осями jc, **, запишем: yx = ycosd, vy — vsin^t v'x = vf cos d',
Подставляя значения компонент в E), получим:
u'cosft' + V . a и'sin
а разделив вторую формулу на первую,—
v» у 1— в2 sin О*
Возводя в квадрат эти же формулы и складывая, получим
n2ft* _^+yrJ~^ [9'V\
274
2) В случае распространения света (для фотона*) v = v*=c.
Пусть свет падает вдоль оси у". Тогда <И = л/2 (свет идет сверху
вниз), и из формулы для tg# предыдущей задачи имеем
/ / j/2" / V \
11/ 1 г/~"/• Угол аберрации (^-—дополнительный к уг-
лу д(а/. + # = я/2); tgar = ctg #=( — / Л/ \ — —s-). По класси-
ческим формулам с* = 0, v'y~c, Vz~0, и так как t> = t>'-fV, то
г* = Vt vy =с» v2 = 0; отсюда tgar = K/c. Классическая и реляти-
релятивистская формулы совпадают с точностью до У3/^3.
745. ds2 = c2dt2—dx2—dy2 — dz*=c* (И'* — Aх'*-Aу'*—Aг">. В
системе /(': dx1 =dy'=dz'= 0, a dt'^dx. Отсюда
и окончательно d%— У l—v2/c2dt.
746. s2 = s'2 т. е. с2/2 /2 ~c2t'2 /'2
1) Если /i2 = 0, то
2) если ^2 = 0, то
3) если ^2 = 0 и t'12 = 0, то это означает (за исключением слу-
случая, когда распространяется световой сигнал), что /12 = 0 и /12=0.
747. В обоих случаях применяем один и тот же прием. Обе части
уравнения движения
dpldt=F
скалярно умножаются на скорость v. Справа получим работу силы
над частнцей в единицу времени (мощность). Следовательно, по за-
закону сохранения энергии, слева должно стоять изменение энергии
в единицу времени. Преобразование левой части для классического
и релятивистского уравнений различно. Из уравнения Ньютона:
dv
т -гг'О
причем То приравниваем нулю. Из релятивистского уравнения, имея
в виду, что y= Y3PP (P =^/с)» получим:
d ....
v — (myv) — vmyv + mv2y = с2 {myfifi + m$2ysfifi) =
d
— myftfic2 A +Y2P2) —tnc2y = -jj-(mc2y).
Мы воспользовались также соотношением w = vv, вытекающим из
равенства v2=v2. Таким образом, получается:
d
dt
275
где А — некоторая постоянная. Нужно показать, что она равна нулю.
Для этого рассматривается предельный нерелятивистский случай vfc-+Ot
V/c-+Q. Из B9) имеем для преобразования импульса
у
Следствием этой формулы должен быть классический закон сложения
скоростей. Однако он получается только при условии Л=0.
_._ d ( то \ _ __
748. -тг [ — - )—F. Интегрируя, получим
(считаем, что при /=0 скорость v=0). Из последнего выражения нахо-
находится зависимость скорости от времени:
Film vc
v =ж — ■ ■ — = с с < с,
V\ + (Ftlmc)* Vvl + c*
где vc = Ft/m.
749. Так как pr*=*myv, a pc~mv, то их отличие определяется
множителем у = 25/7.
Указание. Раскрыть левую часть A1), произведя дифферен-
дифференцирование, и учесть B8).
751. Выберем ось у параллельно начальной скорости электрона,
а ось х—в направлении, противоположном полю Е. Движение про-
происходит в плоскости jc, у. Уравнение движения запишется в виде
поскольку сила, действующая со стороны электрического поля на за-
заряд, равна еЕ. Импульс —релятивистский—p~myv. Уравнение
движения в компонентах рх = еЕ, Ру = 0, откуда px = eEt-\-pox,
Ру=Роу Так как, исходя из начальных условий, po* = 0> apOl/ = po, то
Пользуясь связью между энергией и импульсом f=скр?-)-'/п2 с2,
найдем <£= V$* + №*)*> где <§l =
С2
Согласно C0) v = -^-pt откуда
_ dx pxc2 ft _dy_
276
Подставляя полученные выше выражения для pXt py и $ и инте-
интегрируя, с учетом начальных условий найдем
Исключив t из этой системы, получим траекторию
jc = ^(ch—- — 1] (цепная линия).
Btl \ ^Ро J
Для сравнения с классическим результатом (он предполагается из-
известным) полагают v/c<^.l. Тогда у « 1, po = mvQ, a (^>0 = mc2.
Кроме этого, нужно использовать формулу, годную для а<^1:
-1 а*
752. Кинетическая энергия равна работе поля, так что
еу
еу г
откуда у = 1 Н 2~, а следовательно, v = c у 1 — (\/уJ. Оконча-
Окончательно:
Если бУ<^тс2, то
если еК^>тс2, то
В последних двух случаях используется разложение подкоренного
выражения основной формулы в ряд по малому параметру.
753. В лабораторной системе К $1 = $2 = гпс2У = $; импульсы
-» i
частиц р1 — —myv, p2 — myv\ 4-векторы частиц: Рх (—ру —^),
~Р2[Ру --<§)• в системе /(', где частица 2 покоится (^=0),
^ = 0. Согласно B9)
последние преобразования выполнены для ультрарелятивистских
частиц, когда, согласно C0), для v & с имеем р = $/с. а V/c-^l.
277
Этот же результат легко получается из общей формулы A3)
где уг относится к скорости частицы 1 в системе /С". Согласно F)
Но в системе К Т — у, и следовательно, $i = 2y2mci, т. е. $[ «
Отсюда видно, что ту же «полезную» энергию столкновения можно
получить при покоящейся частице 2, разгоняя частицу / до энергии
в Г раз большей, чем для «встречных» пучков.
754. Релятивистское уравнение движения имеет вид
Так как магнитное поле не меняет энергии частицы и у — const, то
уравнение движения принимает вид
%=—
dt my с
где множитель перед векторным произведением — постоянная величина.
Это уравнение движения отличается от нерелятивистского только тем,
что вместо массы тела m стоит масса ту.
755. По закону сохранения энергии кинетическая энергия Тг
полностью расходуется на работу против сил поля: Trzs$—tnc2~eEl,
откуда и можно определить /.
Другой способ использует соотношение
о
где т—время полной остановки частицы.
Из формулы C0) v~c2p/$, а из A1) dp = eEdt, поэтому
т о о
dp с С pdp
о р0 р*
BlL BE*
756. Воспользовавшись разложением бинома:
1/2 , , 1 V2 , 3 У4 ,
получим для (v/c) <^ 1:
278
Составив отношение второго члена Тг к первому, приравняем это отно-
отношение одной сотой:
•§■£=0.01, откуда iU
В этом же приближении:
Гг _у*/с*^ 1
me2 ~ 2 150*
757. Энергия покоя электрона 0,51 МэВ, протона — 938,2 МэВ.
758. Если пренебречь потерями при распространении света, полная
энергия, излучаемая Солнцем в секунду, равна солнечной постоянной,
умноженной на площадь сферы, проведенной из центра Солнца радиусом,
равным расстоянию от Солнца до Земли. Эта площадь равна «З'Ю23 м2,
а энергия
A,4 Дж/(см2))-C-1023 м2) » 4-1023 Дж/с.
Таким образом, Солнце за счет излучения света теряет в секунду массу:
4-1023 Дж/с . 1ЛЙ ,
п f^1ft—отт « 4-106 кг/с.
9-1016 м2/с2 '
Десятая часть массы Солнца составляет 2 • 1029 кг. Она будет израсходо-
израсходована за 2• 1029/4• 106=5• 1022 c^IG15 лет.
760. Пусть в К задана 4-скорость V (yv, icy). Компоненты 4-ско-
рости V в системе /С* выразятся уже через новые переменные:
V (у'ч>\ icy'), так как абсолютная величина скорости меняется:
у ф у'1. Используя формулы A7) и A9), запишем
()
подставляя значения компонент, имеем
y'v'x = T {yox — yV)9 y'vy = yv
icyu = T(icy-iByvx).
Из последнего равенства вытекает, что
С помощью этого соотношения три первых равенства G60.1) сво-
сводятся к F).
761. 1) Воспользуемся соотношениями E), связывающими значе-
значения vXt Vy, vz и vx, Vy, vz, для того, чтобы найти связь между бес-
бесконечно малыми приращениями скоростей dvx и dvx (и остальных).
Имеем
1 —
279
Разделим обе части этого равенства почленно на dt =*
=3 Г ( Л* + т й*') (см* @)). Левая часть полученного равенства
dvx/dt даст значение ускорения тела vx в системе /С, а отношение
dv'x/df'*=Ь'Х—ускорение тела в системе /С'. Окончательно имеем:
v*
y T*(\+Vv'xl*)% "
Формула для Ьг записывается аналогично формуле для vy. Движе-
Движение тела в системе К не будет равноускоренным даже в том случае,
если оно равноускоренно в К\ так как vx, vyi vz зависят от vx.
2) В формулы A7) подставляют значения компонент 4-вектора
W и W':
W (y2v-\-yffyt icyy), W (y'2vf -f- y'v'y', icy'y').
I - V л,\
Из соотношения Д1==Г( Аг — i — Л4 J следует, например,
. . / ., ,. V
V u*t-\-yvхУ ==:Г ( V fjp—}- V VxY"~—i — icy1 ^
\ ^
Или
М" • G61.1)
Из соотношения Л4 = Г f Л4+1 — А[\ следует
Т=Г^(у'+^-(т'^+тЧ)). G61.2)
Используя соотношение
гх:= l_
Y \+Vvx/c*
и G61.2), найдем выражение для Ьх из G61.1), совпадающее с выра-
выражением, найденным способом A). Для нахождения формул преобра-
преобразования vy и ve нужно воспользоваться соотношениями Л2 = Л2,
762. В системе /С0 4-импульс: Р° @, i^0/c), где <§0 = тс2 — энер-
энергия покоя. Переход к К'1 производим по формулам A7):
280
т.е. Р;=-Г-^^0 = --^^' = -^К, так как £'
= Рг = О.
763. Р*
764. В системе К0: F = F(F, 0). Используя A7), получим
y'F'x=TFx, y'F'y=Fv, y'F't = Fz,
/(^) (^^). G64.1)
откуда (так как у'1— Y)
Физический смысл равенства G64.1) предоставляем выяснить
читателям.
765. *■ = *',+•
i. 1 • (
где s=l—
Решение. В векторной записи необходимо различать преобразо-
преобразование векторов, параллельных направлению относительной скорости
и перпендикулярных к ней. Если есть два вектора а и Ь, то слагающи-
слагающими вектора а, параллельными и перпендикулярными вектору Ъ% будут
векторы
3-ради ус -вектор можно представить, следовательно, так;
Помня о том, что пространство изотропно и что ось х в наших обычных
формулах A) направлена по V, можно переписать A) следующим об-
образом:
Г1=ГХ; гн =Г(гп_ к/),
281
Аналогично для преобразования скорости и ускорения нужно
воспользоваться формулами F) и формулами, полученными в за-
задаче 761. Формула для v' может быть получена дифференцироваиием
формулы для г1' по dt1 = Г ( dt ^ dx J . Аналогичным образом из
формулы для v' можно получить выражение для v'.
766. Воспользуемся соотношениями р2 = ^~— т2с2, $=тс2-\-Т.
с
Подставляя ^, выраженное через Т, в выражение для импульса,
непосредственно находим
767. Исходя из C0) и результата задачи 763, имеем
S Vm2c2 + t
768. Исходим из соотношения £ — *
v/c= V^ — iSo/SJ* где ^0 = me2. Для перехода к нерелятивистскому
случаю нужно учесть, что $ = Т-\-тс2у причем по условию задачи
Т<^.тс2. Тогда:
Ультрарелятивистский случай соответствует неравенству
откуда v/c^l-t/tigo/SJ.
769. Запишем законы сохранения энергии и импульса:
=Е, где Е1 = т1с2, E2 = m2c2 + T2t
2z=P> гДе pi = Qy Ръ задан.
Масса М образовавшейся системы определяется из соотношения
М2с2 = ^-Р2 = с2(т1 + т2J + 2T2mv
Суммарная масса примерно равна сумме масс исходных частиц, если
(Т2гпх/с2) <^ (mi + ЩJ' Скорость образовавшейся частицы
Е (тх -\- т2) с2
770.
гР% E
с
P=Pi-\-p2j где индексы 1 и 2 относятся к частицам, возникшим
после распада,
_ (
= (mj+ml) с* + 2 (У(р\ + mfc2) (pi + m22ca) - Plp2 cos d).
282
771. Запишем законы сохранения энергии и импульса в системе,
где покоится исходное тело:
0, G71.1)
Разделив это на G71.1), получим
A-& = c*(m;--mS)/Af. G71.2)
Из G71.1) и G71 2) найдем ^ и ^2:
^-[УИ^ + с2 (т*-т22)]/2М,
Отсюда
772. Запишем законы сохранения энергии и импульса для про-
процесса соударения:
21 7*2 = То—7*i,
{Po—PiJ = Pt* pi—P\—Po = —2poPi cos #f.
Ho p2c2 = T(T + 2mc2), поэтому
, 2 2 2Tt(T0+2mc*)
P2— Pi— Po= £2 • G72.1)
С другой стороны:
—2роЛ cosOi= -2c0^dl VГоГИГо + гтс*) (Г! + 2тс2). G72.2)
с
Приравнивая G72.1) и G72.2), получим после некоторых алгебраиче-
алгебраических преобразований:
Го cos2 #!
/i = —\ fT0\ *
%)
ПРИЛОЖЕНИЕ
В специальной теории относительности (СТО) под событием пони-
понимают все то, что происходит в данной точке пространства в данный мо-
момент времени. В СТО рассматриваются только инерциальные системы
отсчета, которые определяются как системы отсчета, в которых спра-
справедливы все три закона Ньютона. Все инерциальные системы отсчета
движутся друг относительно друга равномерно и поступательно (с раз-
различными скоростями). В задачах предполагается, что во всех системах
отсчета оси у, у' и г, г' соответственно параллельны друг другу, а отно-
относительная скорость любых двух систем отсчета направлена по общей
оси xf х'. Скорость системы К относительно К обозначается через V
(скорость системы К относительно К' равна —V). Система отсчета
всегда связана с материальными телами, и поэтому ее скорость V
всегда меньше с. Здесь и всюду через с обозначена скорость электро-
электромагнитных волн (света) в вакууме. В каждой системе отсчета можно
определить координаты любого события (в «координаты» включается
также и время наступления события). Преобразования Лоренца — это
преобразование координат события при переходе от одной системы к
другой. Эти преобразования при переходе от К к К и от К' к К имеют
следующий вид:
y' = y, z' = zt Г = г(*-^*). A)
у = у\ г = г\ * = Г (*'+.£*•), (Г)
где
Г=1// — V2/c2. B)
В B) входит постоянная скорость относительного движения двух систем
отсчета, поэтому Г — постоянная величина. Ниже вводится величина
в которую входит переменная скорость частицы v.
Преобразования Лоренца A) и (Г) подразумевают, что наборы ча-
часов, покоящихся в каждой системе отсчета, синхронизованы по Эйн-
Эйнштейну, а в момент совпадения начал отсчета О и О' часы из систем К и
К\ находящиеся в точке О,. О'', показывают соответственно /=0 и /'=0.
Если рассмотреть два события с координатами (xlt ylt zx, ti) и (x2,#2>"
г2. '2I то» записав для каждого из них преобразования A) и составив
284
разности лг2—*1=Дл:', у'2—У1=&уУ г2—z'i=&z't t'%—/1=Д/', х2—Ху=&х
и т. д., мы получим удобные формулы для преобразования пространст-
пространственных расстояний и промежутков времени между событиями:
C')
Промежутком собственного времени между двумя событиями назы-
называется промежуток времени, отсчитываемый в той системе отсчета, в
которой эти два события наступают в одной точке; промежуток соб-
собственного времени отсчитывается одними часами; здесь мы его будем обо-
значать через Дт. Промежуток собственного времени для двух данных
событий можно отсчитать лишь в одной системе отсчета. Во всех других
системах отсчета эти события наступают уже в разных точках, и проме-
промежуток времени между их наступлением отсчитывается уже двумя ча-
часами, находившимися в точках, где наступили события. Отсчитанный
промежуток времени будет промежутком координатного времени Д/.
Промежутки координатного и собственного времени пропорциональны
друг другу:
Д/=ГДт. D)
При переходе от одной системы отсчета к другой компоненты скоро-
скорости преобразуются следующим образом: для перехода от /С' к К
„
для перехода от К к К'.
Сигналом в СТО называется любой способ передачи энергии и
импульса из одной точки пространства в другую, так что, передав
сигнал, можно инициировать (прекратить) некоторое явление или
включить (или выключить) какой-либо прибор. СТО учит, что всякая
передача энергии связана с передачей импульса. Скорость передачи
сигнала не может превышать с.
Интервалом между двумя событиями 1 и 2 называется выражение
где (*i, yl9 zlf tx) и (х2, уз, z2, t2) — координаты первого и второго
событий. Удобно ввести обозначения
'ia= h-h** Д/,
(8)
285
Тогда
Основное свойство интервала — его инвариантность по отношению к
преобразованиям Лоренца:
s\2^c4\2-ll2 = s[l^c4[l-l[l A0)
Релятивистское уравнение движения частицы имеет вид
F, A1)
где
y(t)= , 1 A2)
v= @ — скорость частицы.
Полная энергия частицы
Кинетическая энергия в релятивистской механике Тг опреде-
определяется как разность
Tr = £-go=rnc*(y-l)t A4)
гДе So~mc2 — энергия покоя частицы. В формулах A1) — A4) через
m обозначена масса покоя. Никакой другой массы ни в формулировках
задач, ни в решениях не встречается.
Очень плодотворной оказалась четырехмерная интерпретация тео-
теории относительности. В 4-пространстве-времени («мир Минковского»)
в каждой точке с координатами (*, yt z, t) может наступать событие. Су-
Существенное упрощение в выкладках достигается введением четвертой
мнимой координаты х) id и симметризацией обозначений Xi=xf х2:==:у,
лг3=г, x4—ict (i'2=—1). Таким образом, вводится 4-радиус-вектор R
D-векторы обозначаются стрелочкой над буквой) с компонентами:
;/*! Х2 *3 *4 V
\х у г id)'
.(г, id). A5)
Преобразования Лоренца — это преобразование компонент 4-век-
—>•
тора R:
—xAi х'2 = х2, *з = *з> xl = r(x4—i — xAt A6)
— xA, x2 = x2t x3 = x3, Xt = r(xl + i — x'A. A6')
х) Необходимо подчеркнуть, что появление мнимой координаты
связано исключительно с тем, что мы хотим сохранить тот вид основных
геометрических формул, к которому привыкли в трехмерном евклидовом
пространстве. Можно избежать введения мнимой координаты, но тогда
появляется необходимость введения метрического тензора и разделения
ко- и контравариантных координат; введение этих понятий едва ли оп-
оправдано в курсе общей физики»
286
(С помощью A5) нетрудно проверить, что эти формулы совпадают с A)
и (Г).)
Все 4-векторы преобразуются по правилам преобразования 4-ра-
диуса-вектора. Если заданы компоненты 4-вектора А(АЪ А2у А9, АА) в
системе /С, то компоненты этого же вектора в К найдутся по формулам
(мы приводим также и формулы обратного перехода):
A7)
Квадрат модуля 4-вектора является инвариантом и определяется по
формуле
A8)
В механике СТО вводят 4-векторы:
4-асорости
где dx=dt/y — собственное время частицы. Компонентами 4-скорости
являются (приводим обычные и симметричные обозначения в фигурных
скобках, а также сокращенное обозначение с использованием трехмер-
трехмерных векторных величин)
«1 «. «з иЛ
yvx yvy yv2 icy f 4 Yh v ;
4-um пульса
P = mv9 B0)
где m — инвариантная масса покоя, с компонентами
(Pi Р* Рз Р
?(
В B1) р—релятивистский импульс частицы:
p = myv, B2)
а £—релятивистская энергия частицы A3);
4-силы Минковского F с компонентами
где F—обычная трехмерная сила;
287
4-ускорения
W = dv/dT B4)
с компонентами
*{Ul 2W: ■ щ М. B5)
Запишем четырехмерное уравнение движения
в компонентах (первые три компоненты сведены в одно трехмерное век-
векторное уравнение):
щ \,,4vj—m , B7)
d
Л (тс2у) = Fv. B8)
Уравнения B7) и B8) легко получаются из B4), если воспользоваться
B1), B3) и учесть, что dx=dt/y.
Используя A7) и определение B1), получим закон преобразования
импульса и энергии частицы:
B9)
Из определения релятивистской энергии частицы и релятивист-
релятивистского импульса следует полезное соотношение
. '£•• C0)
Для системы невзаимодействующих частиц масса М системы опре-
определяется соотношением
" C1)
где суммирование ведется по всем частицам, а ^/ и рг определяются
согласно A3) и B2).
Для системы невзаимодействующих частиц можно определить
также скорость центра масс системы. Из B9) видно, что для того,
чтобы Рх=0, необходимо скорость V принять равной
V=c*px/£. C2)
Обобщение этого результата на систему частиц очевидно: