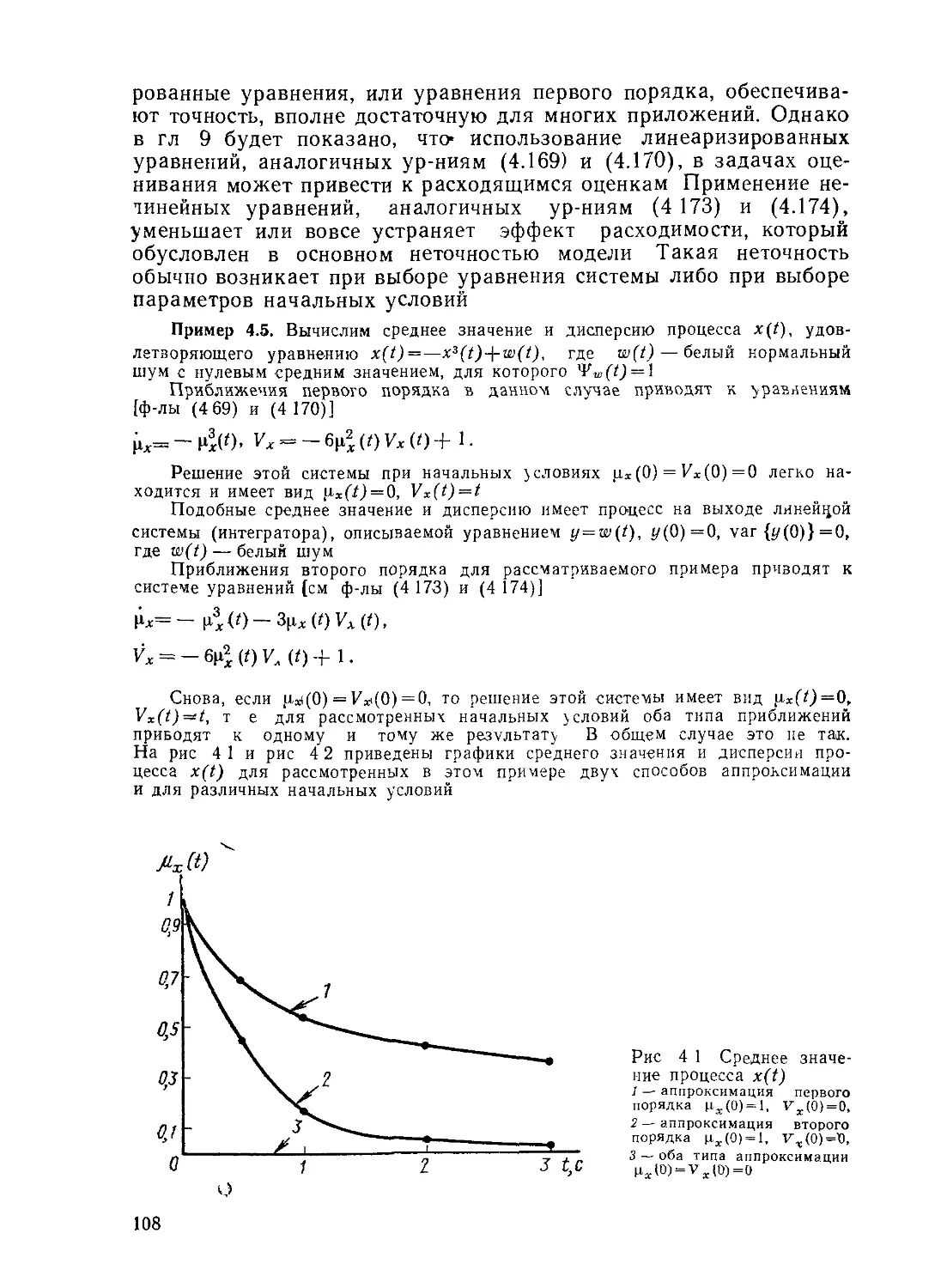
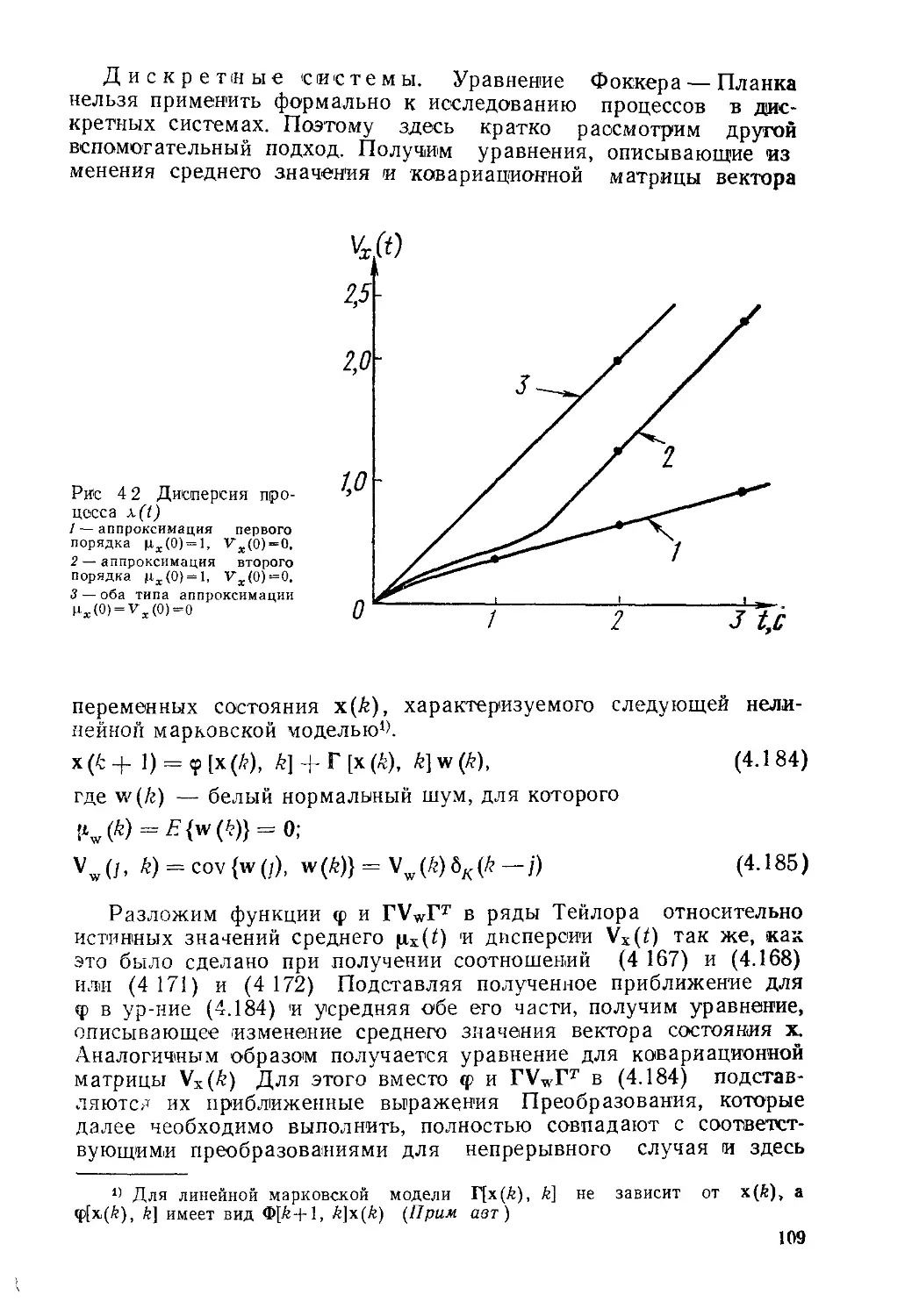
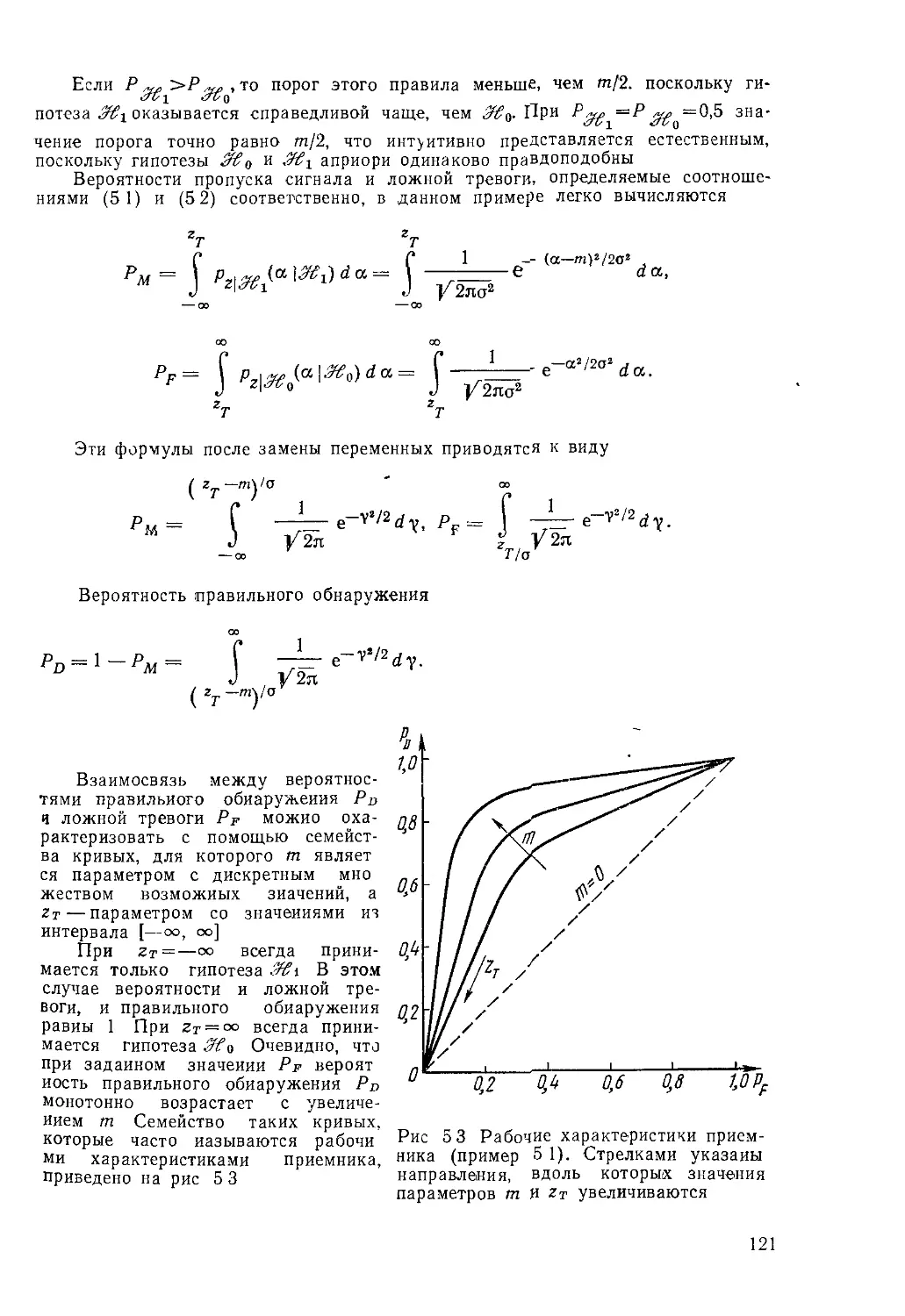
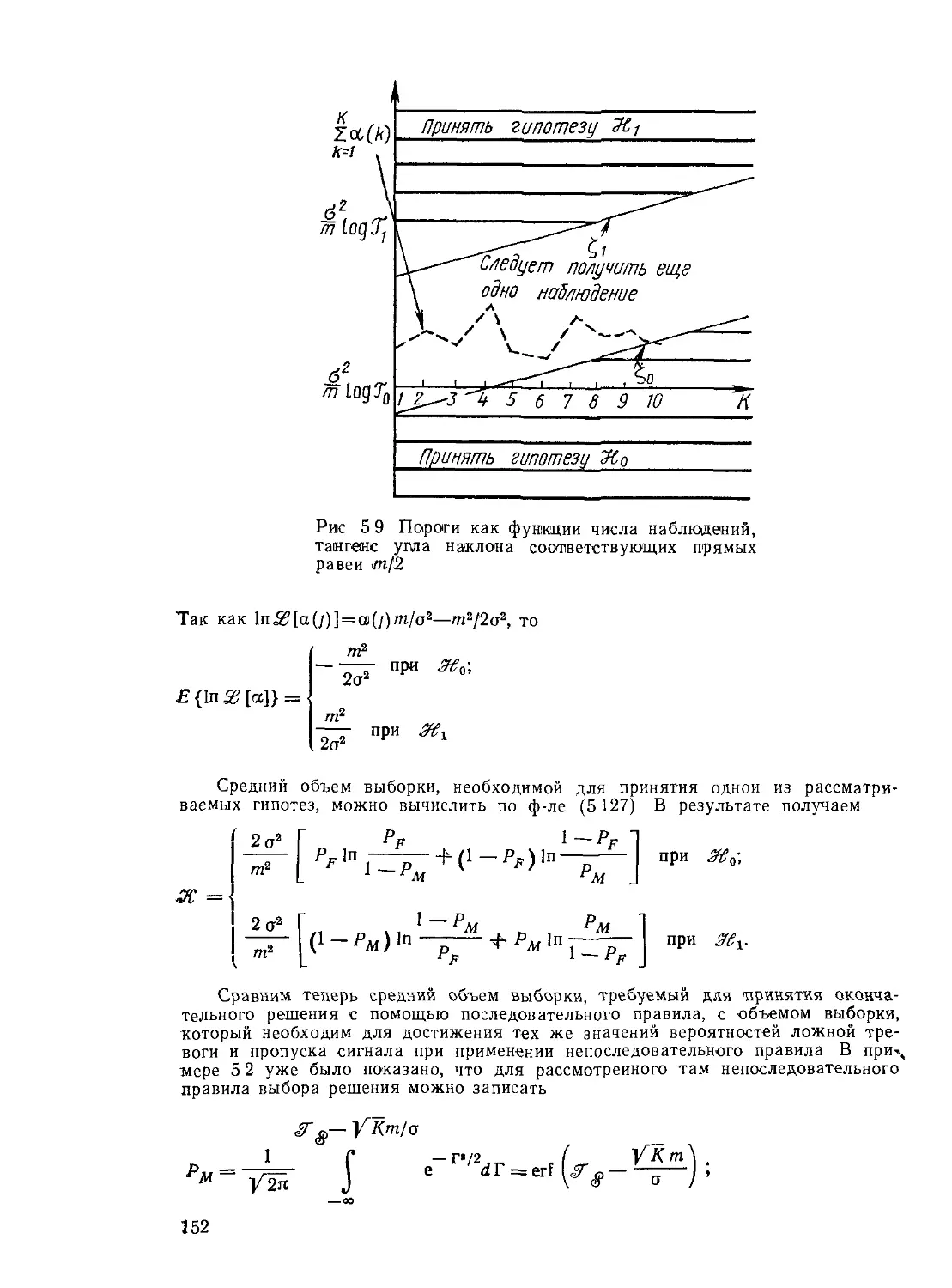
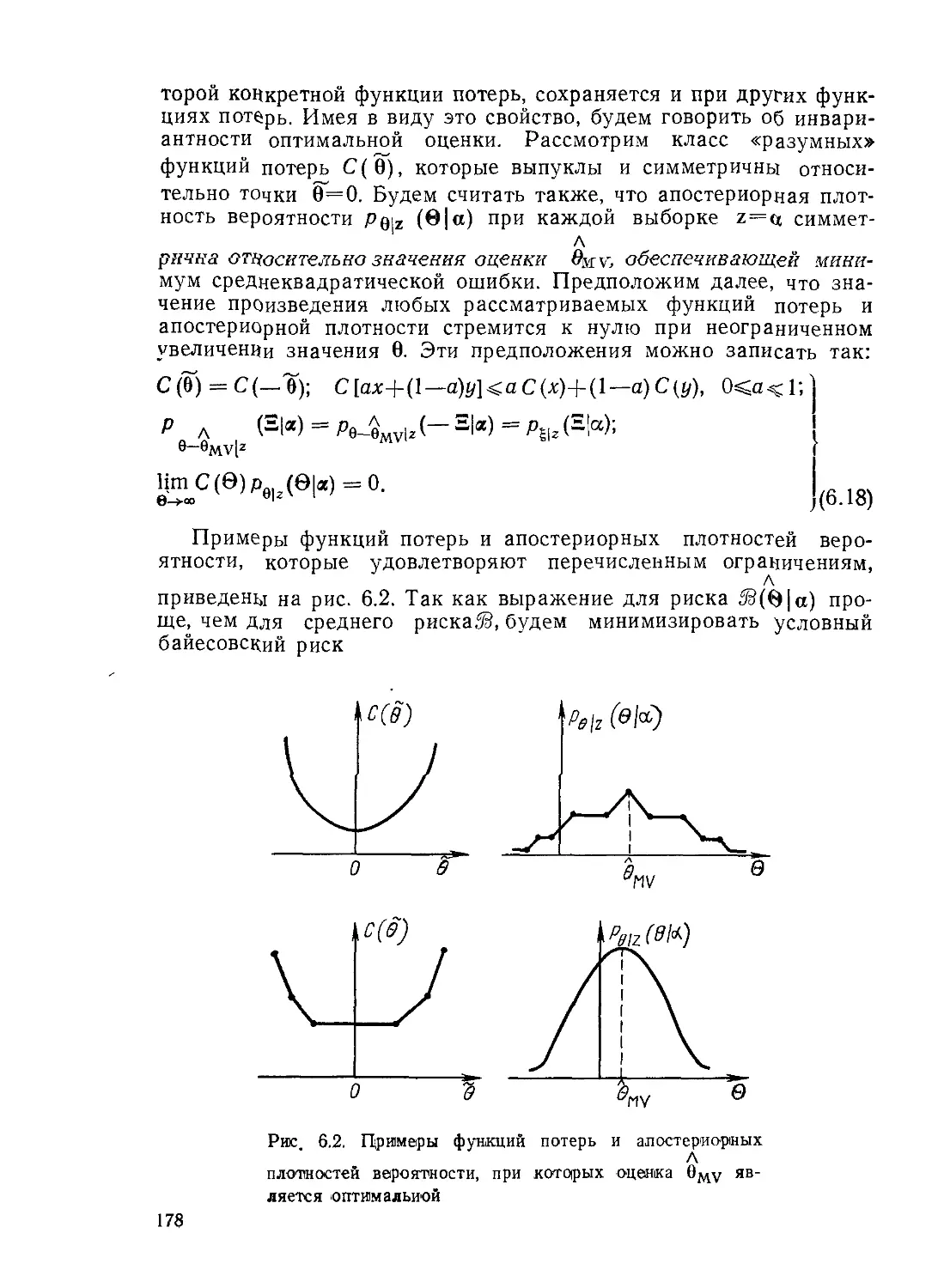
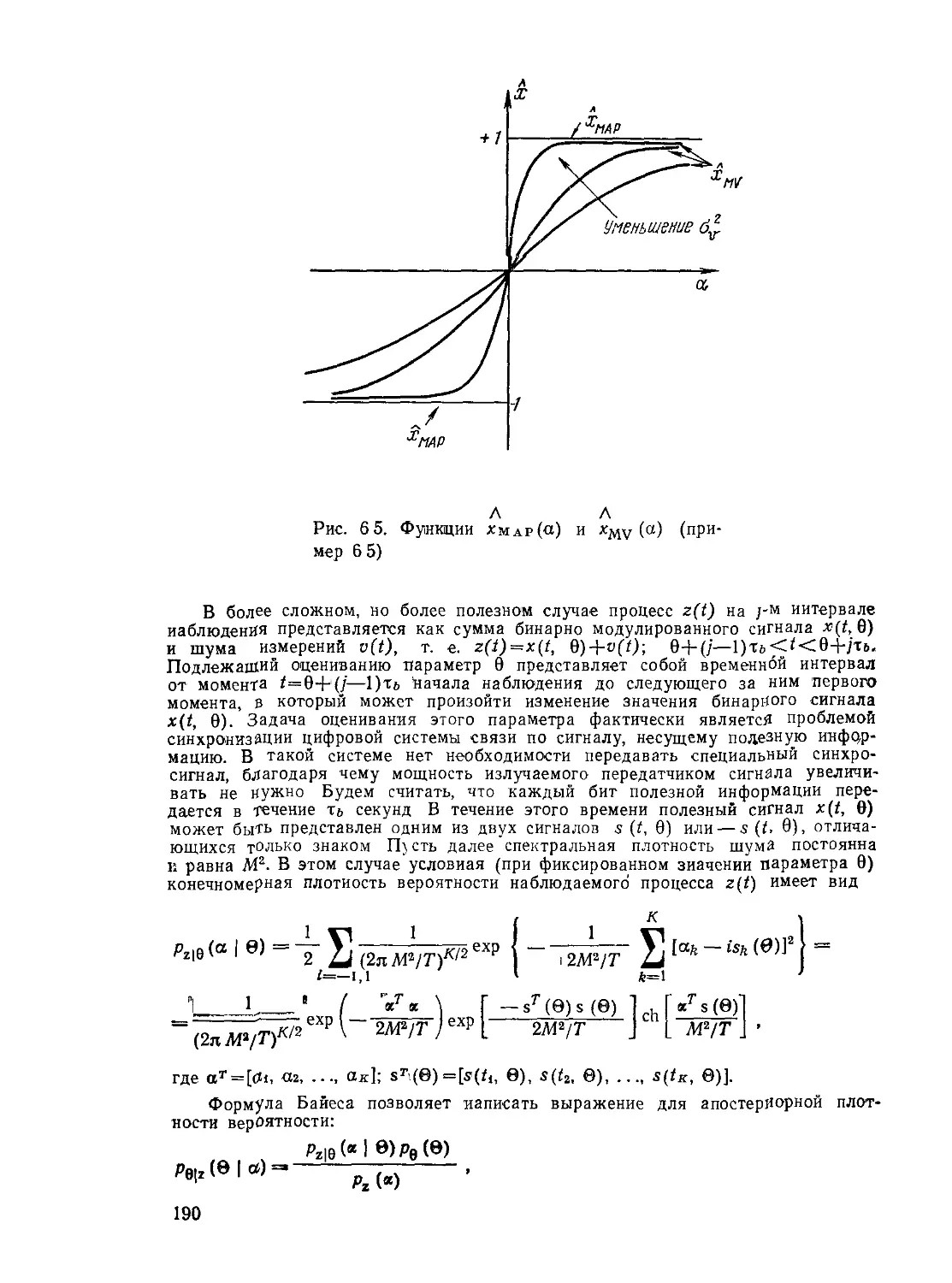
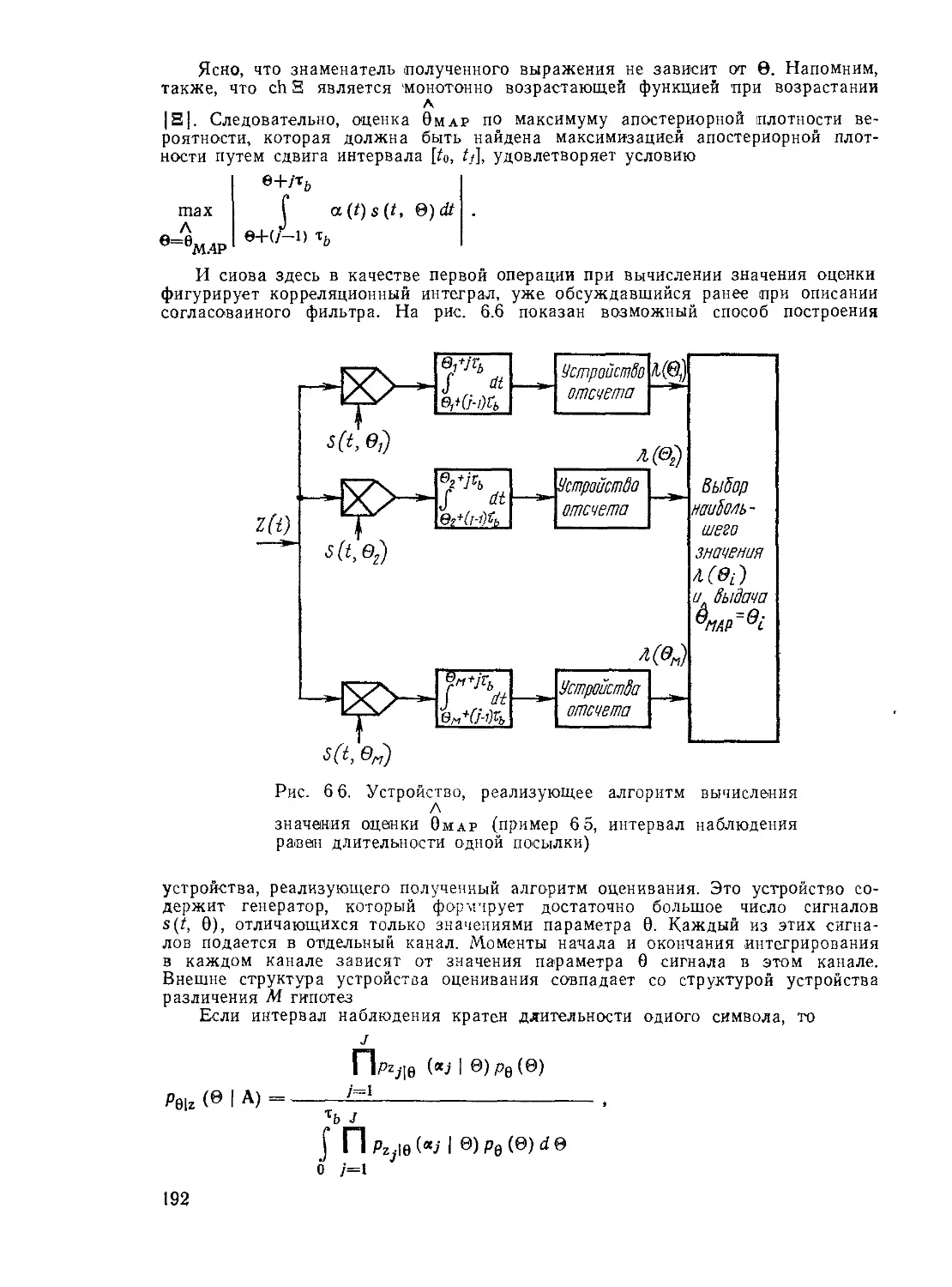
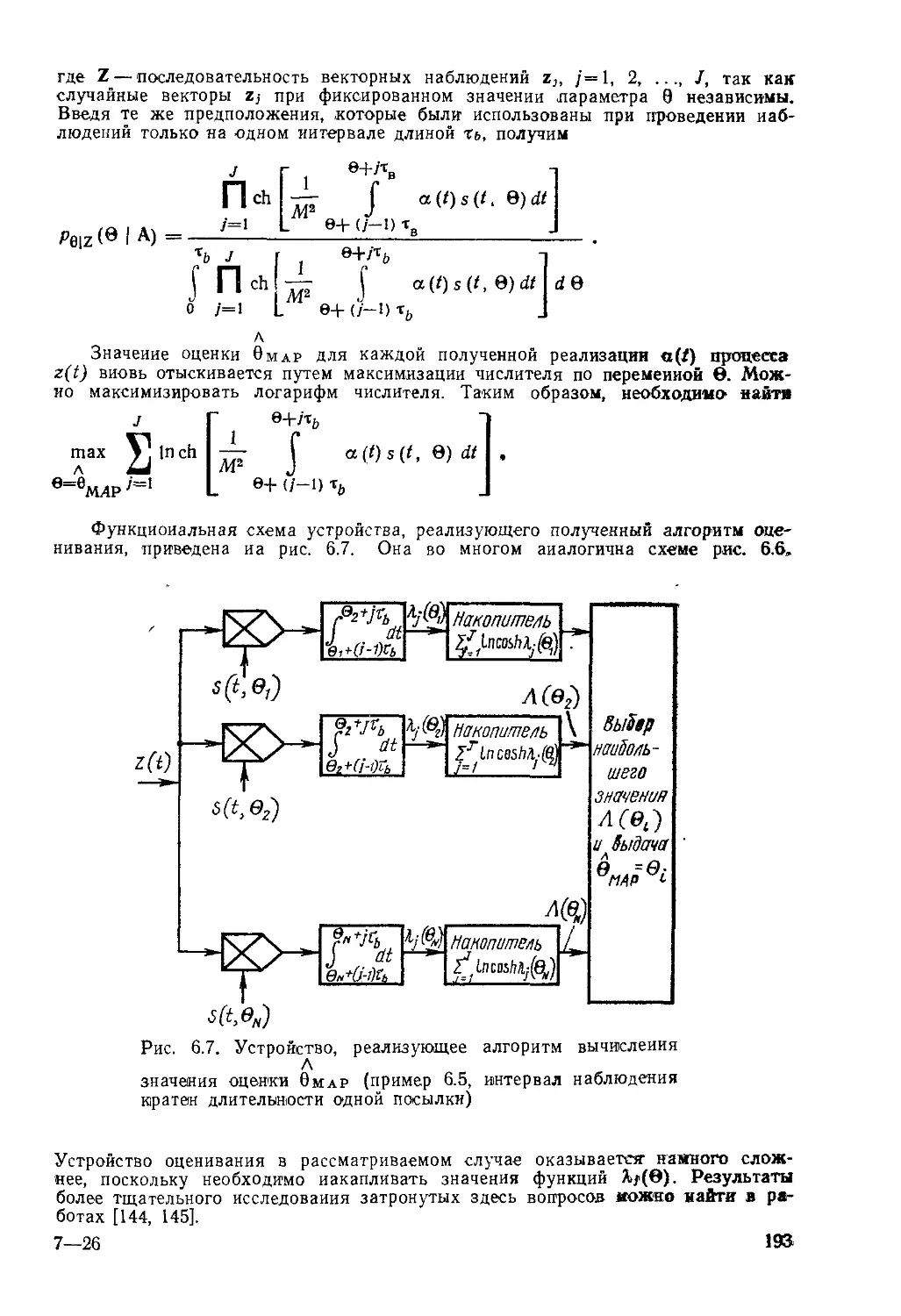
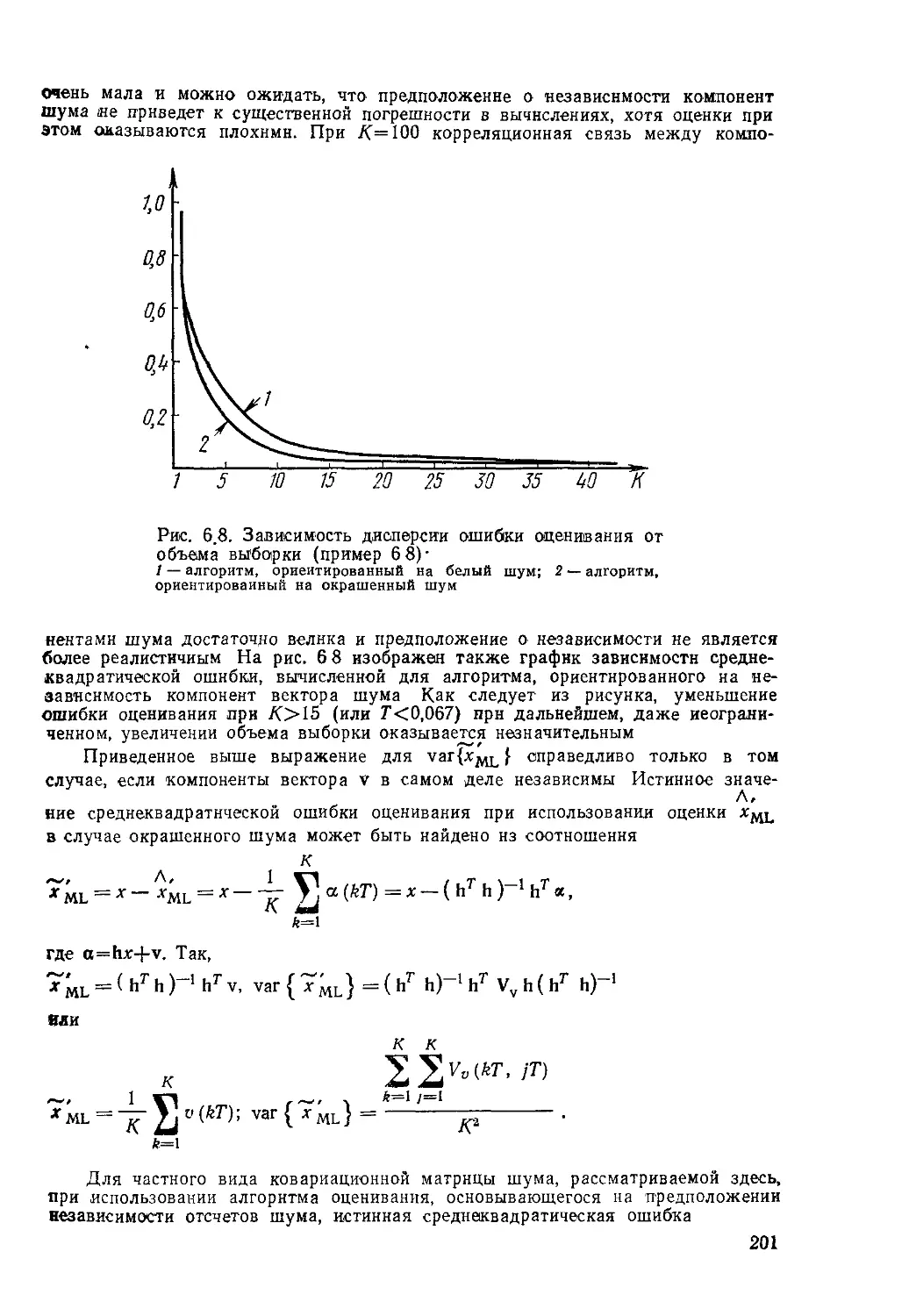
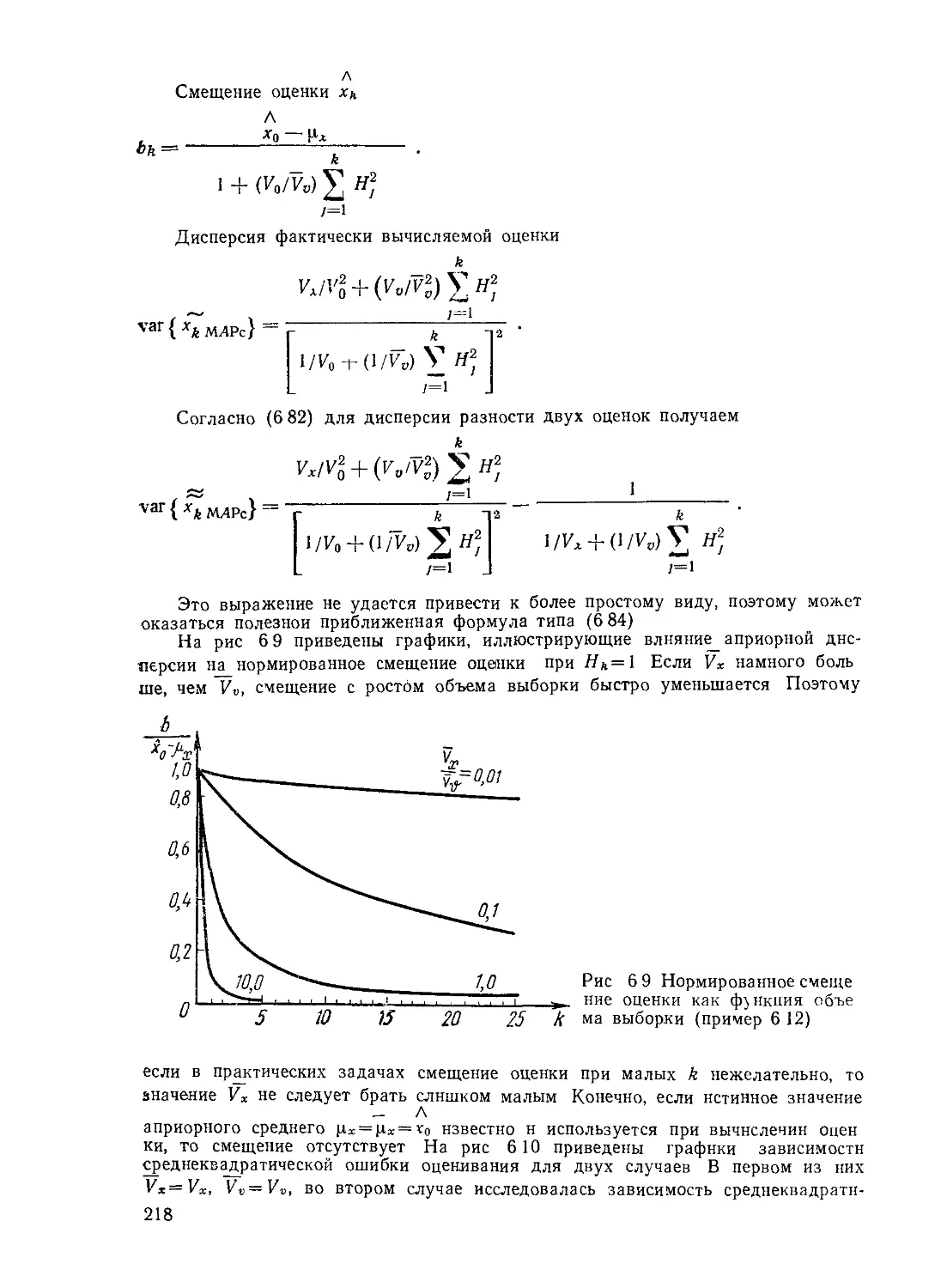
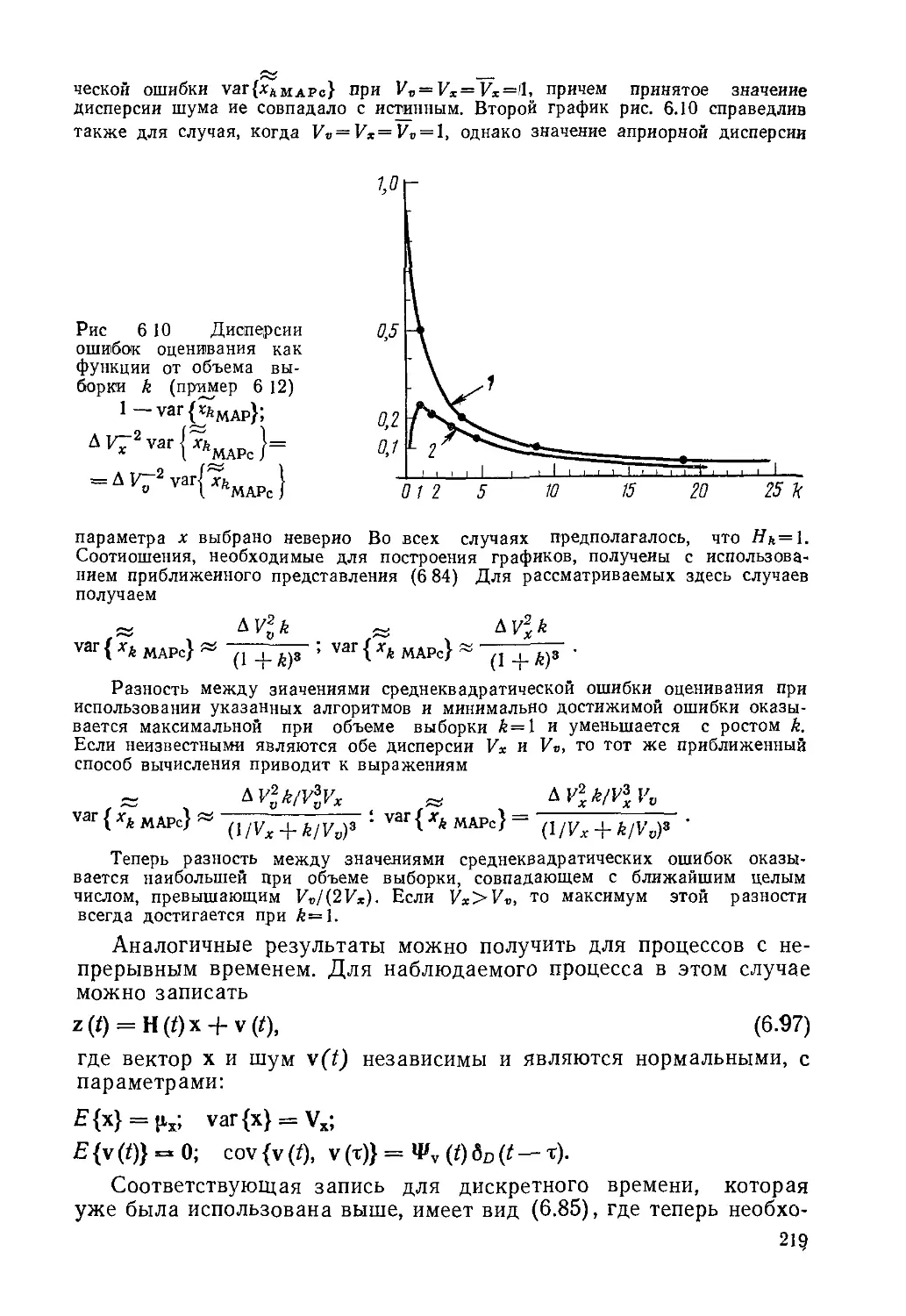
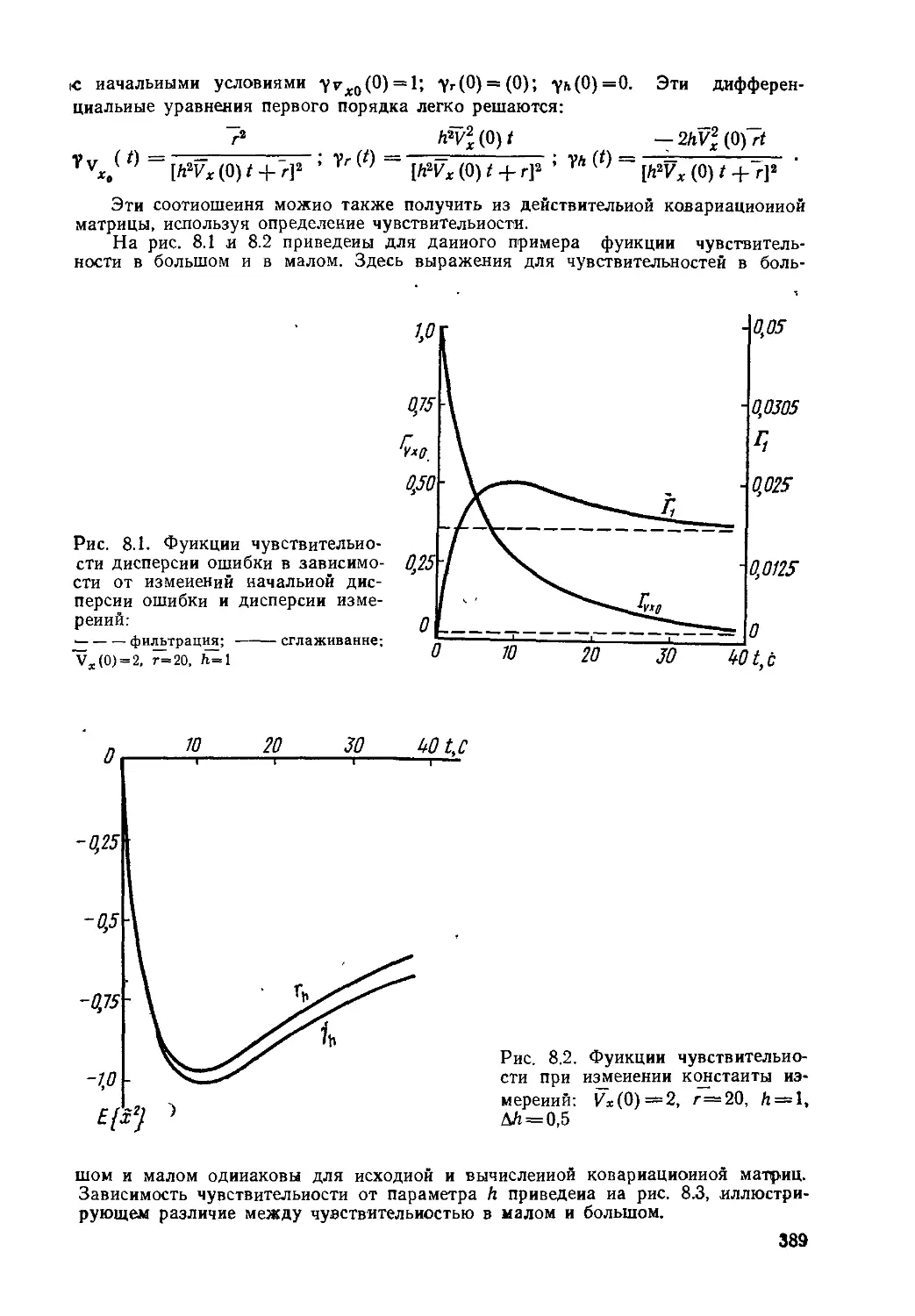
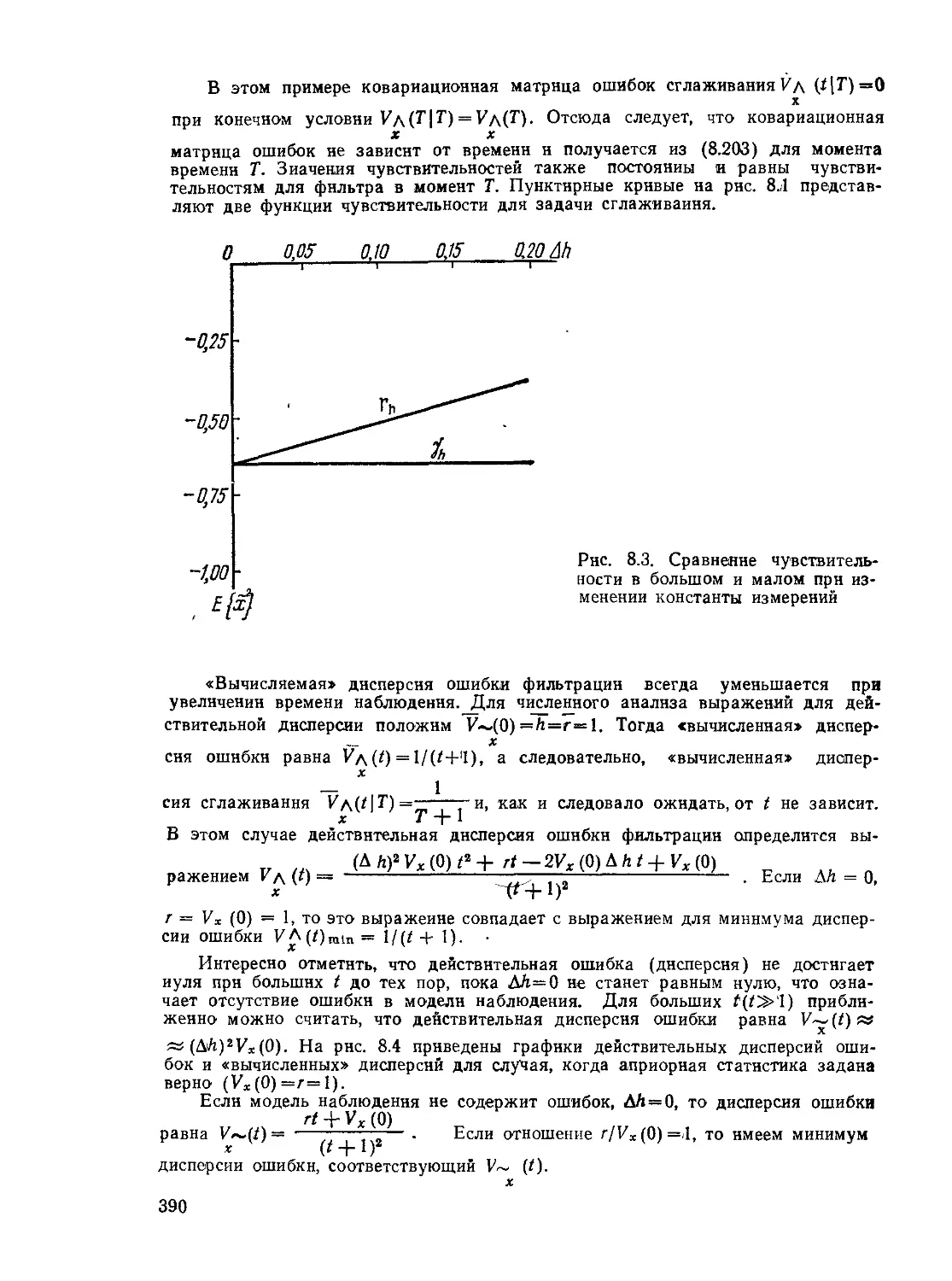
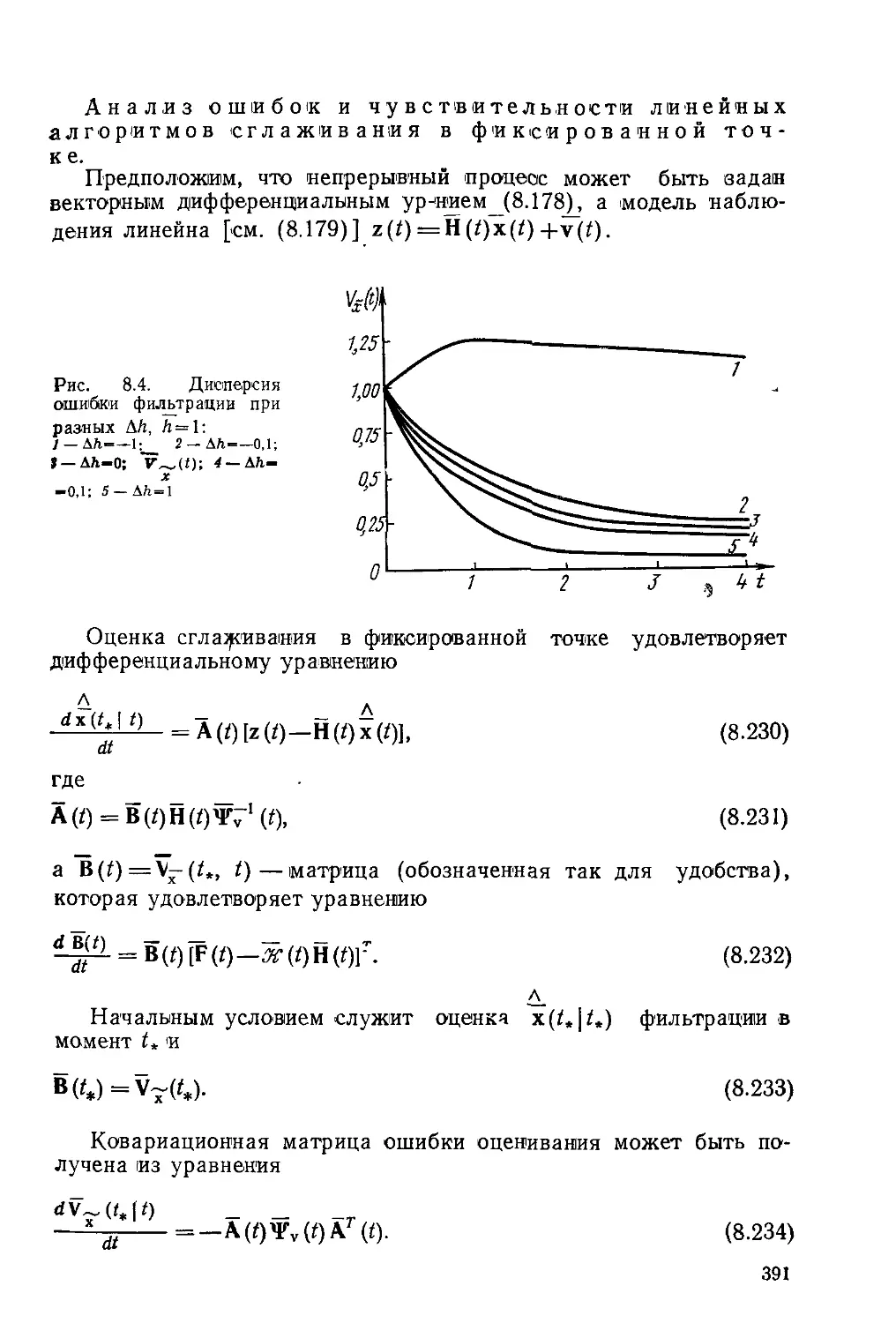
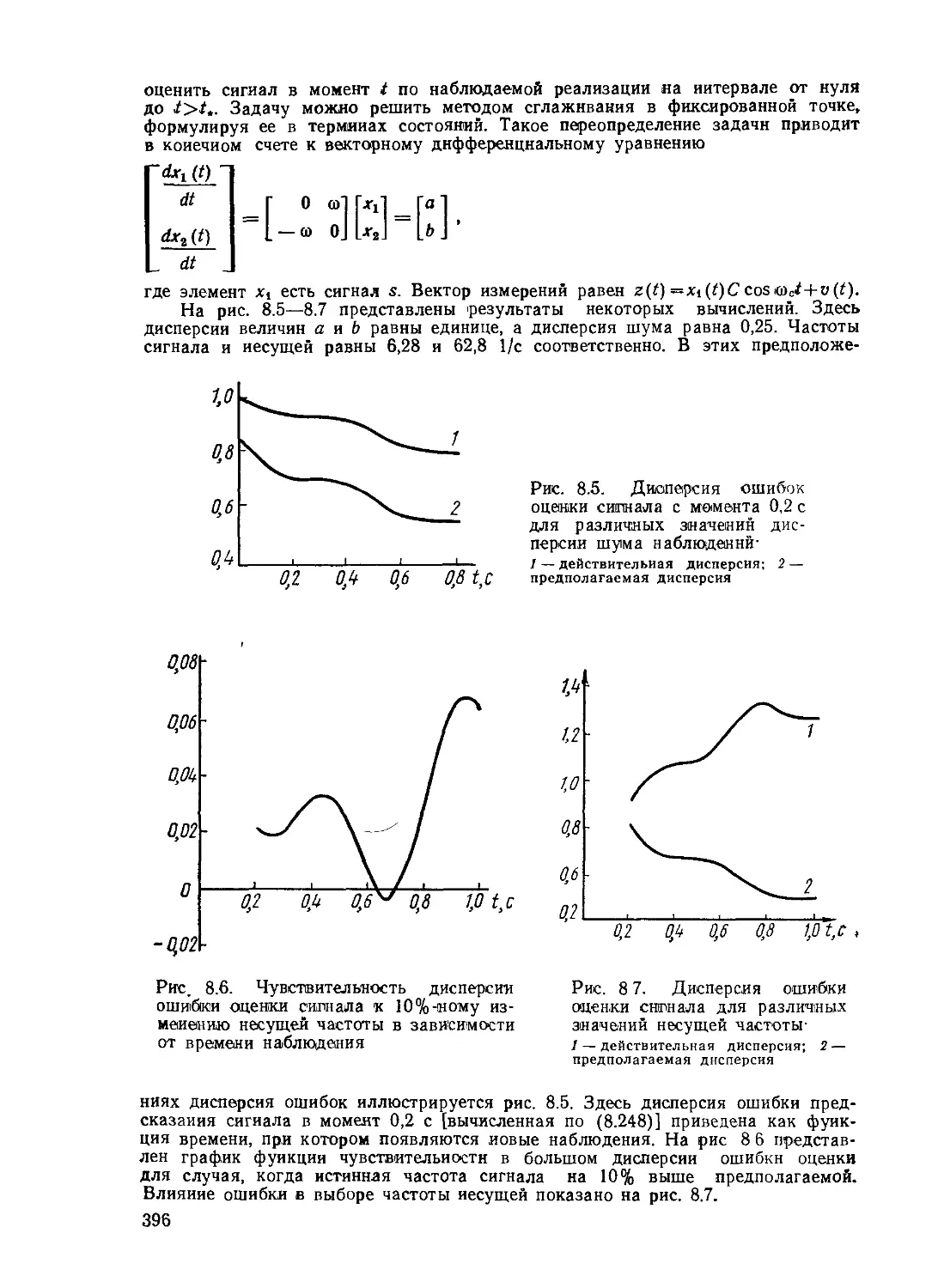
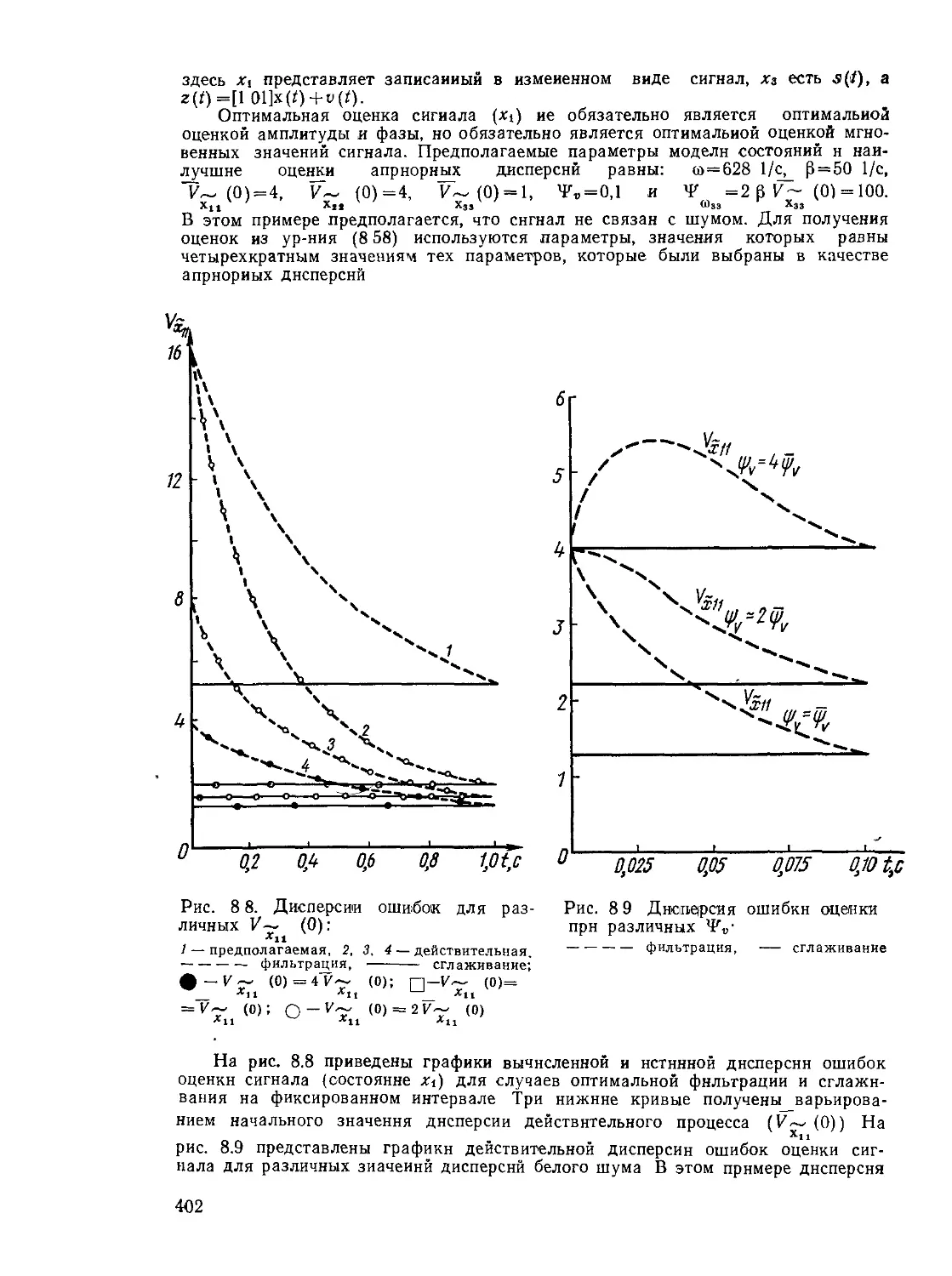
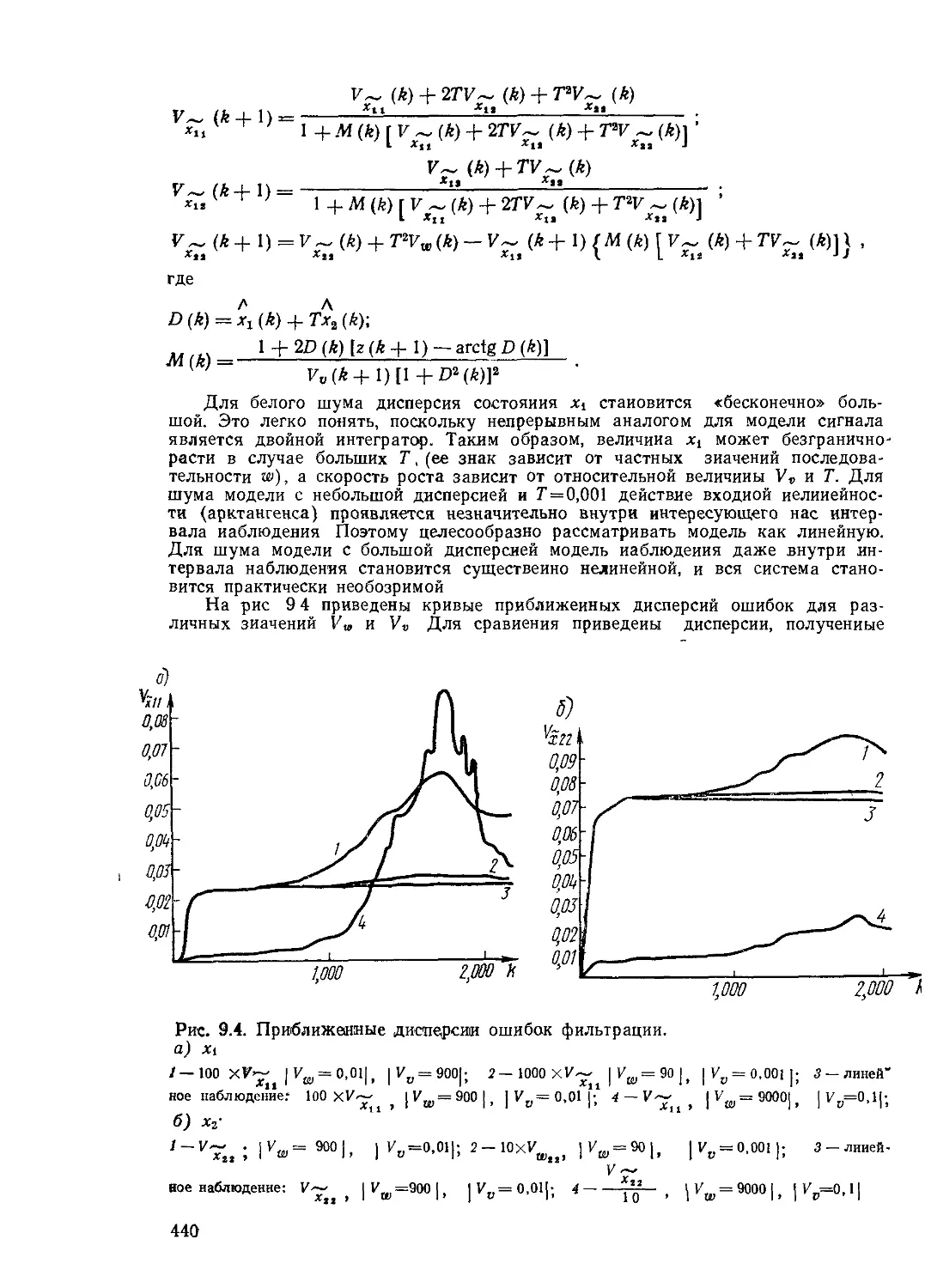
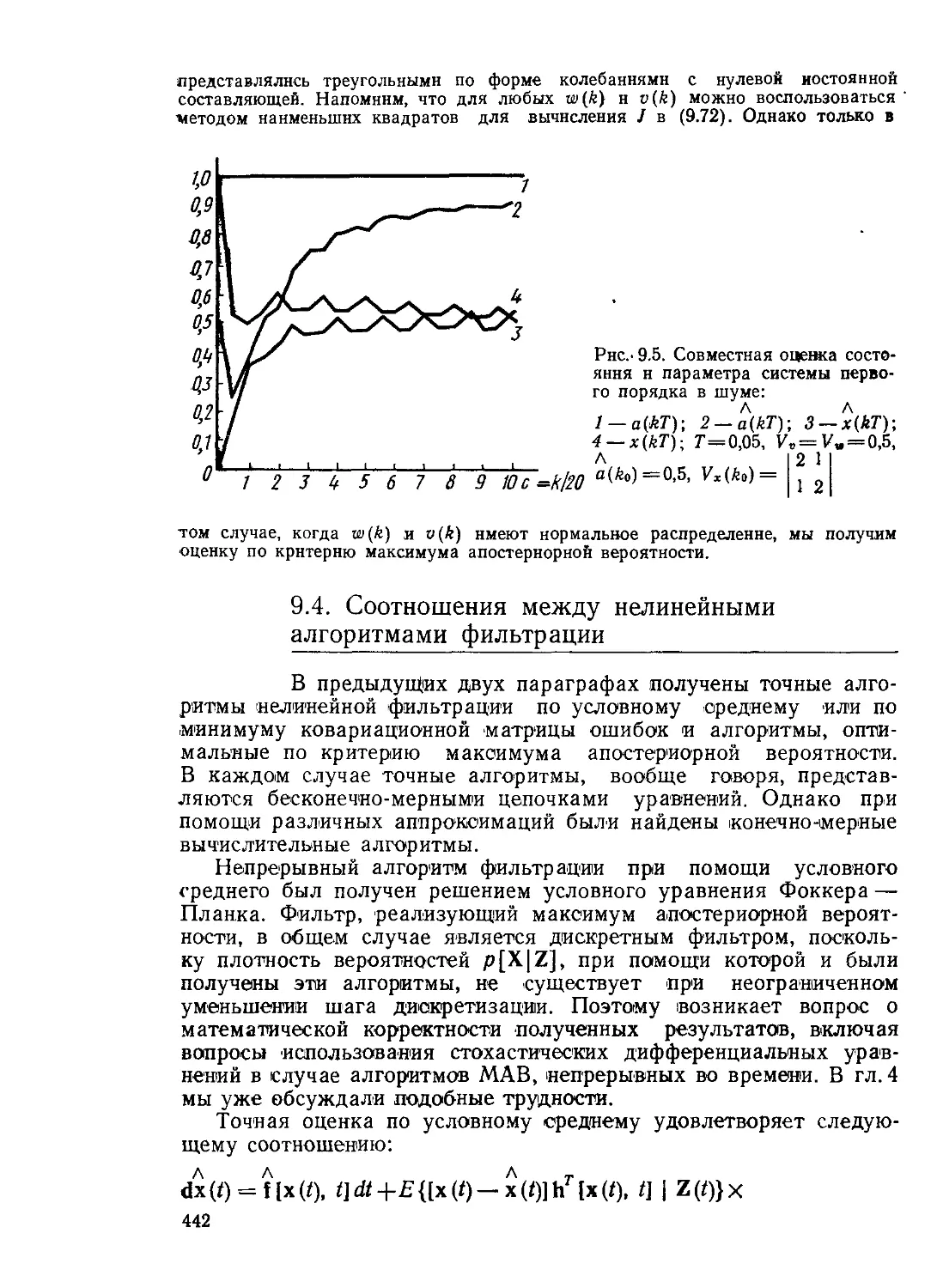
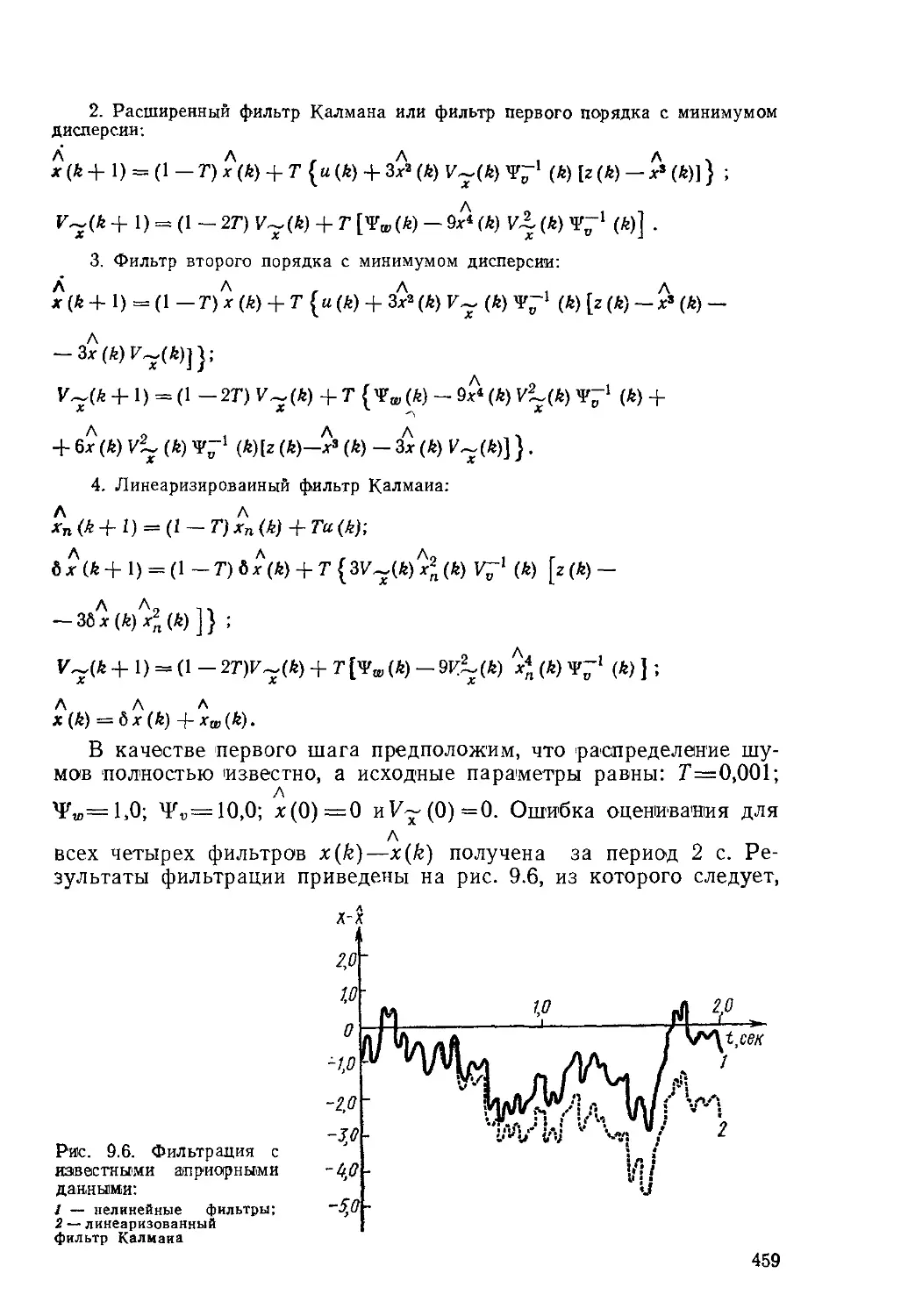
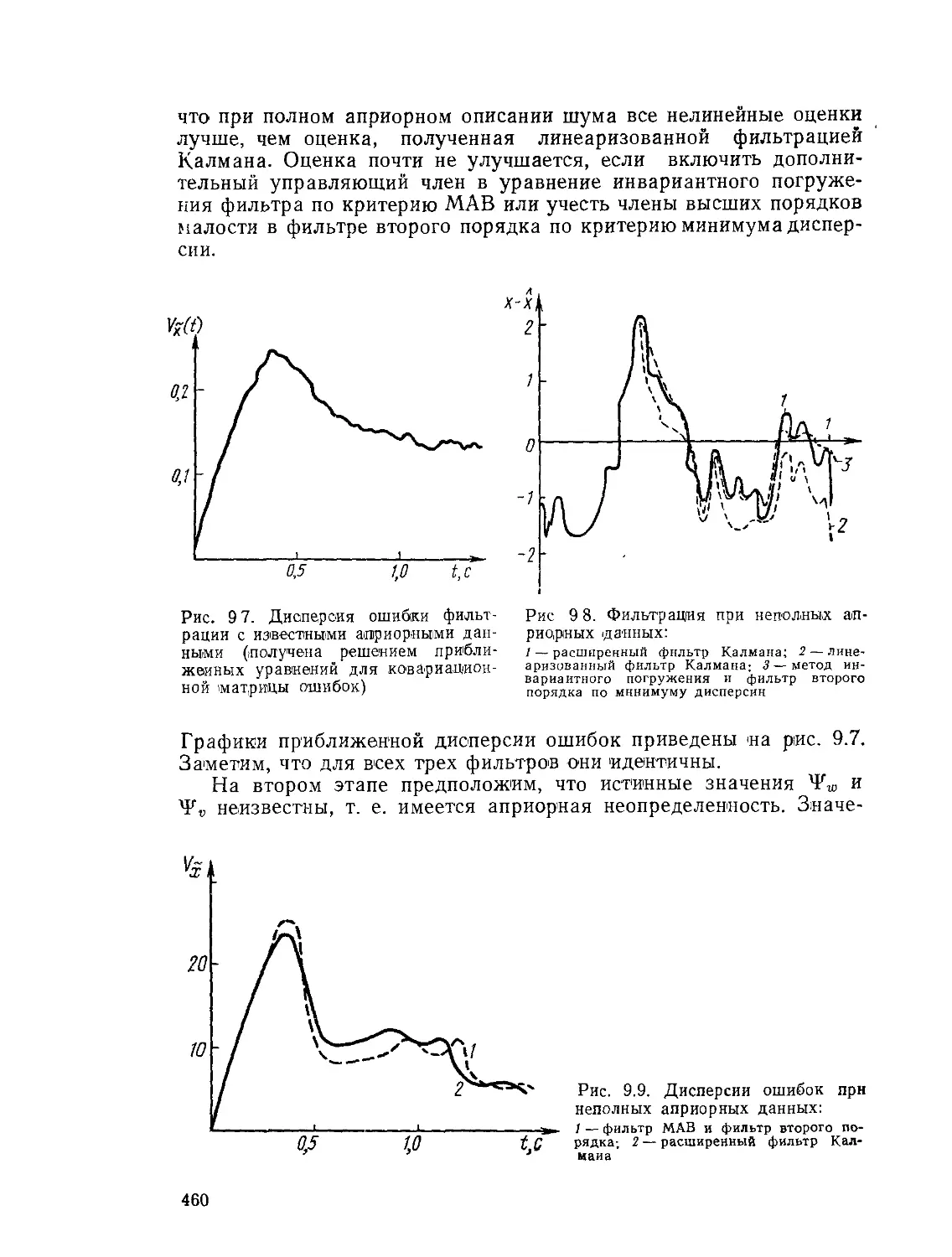
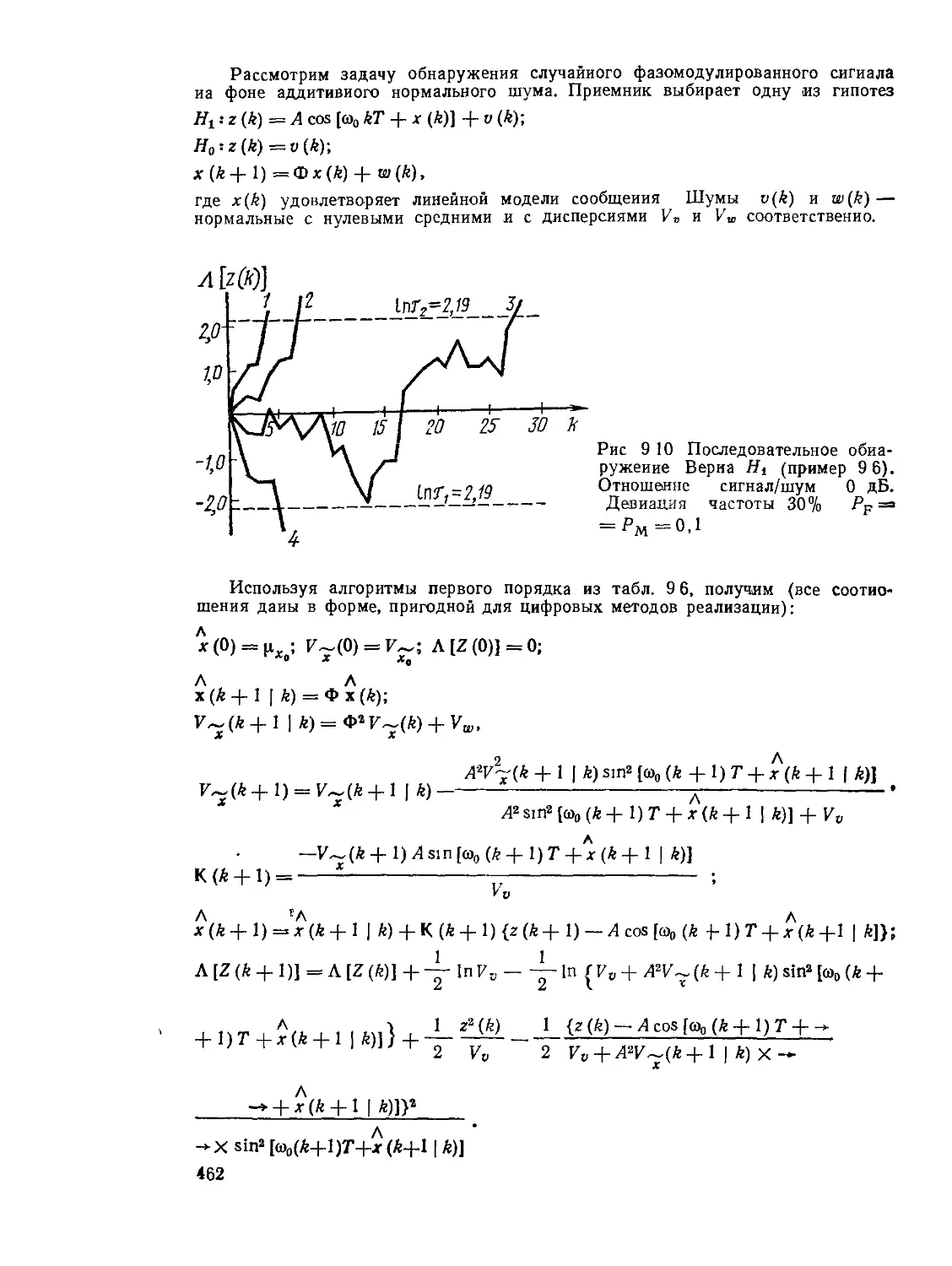
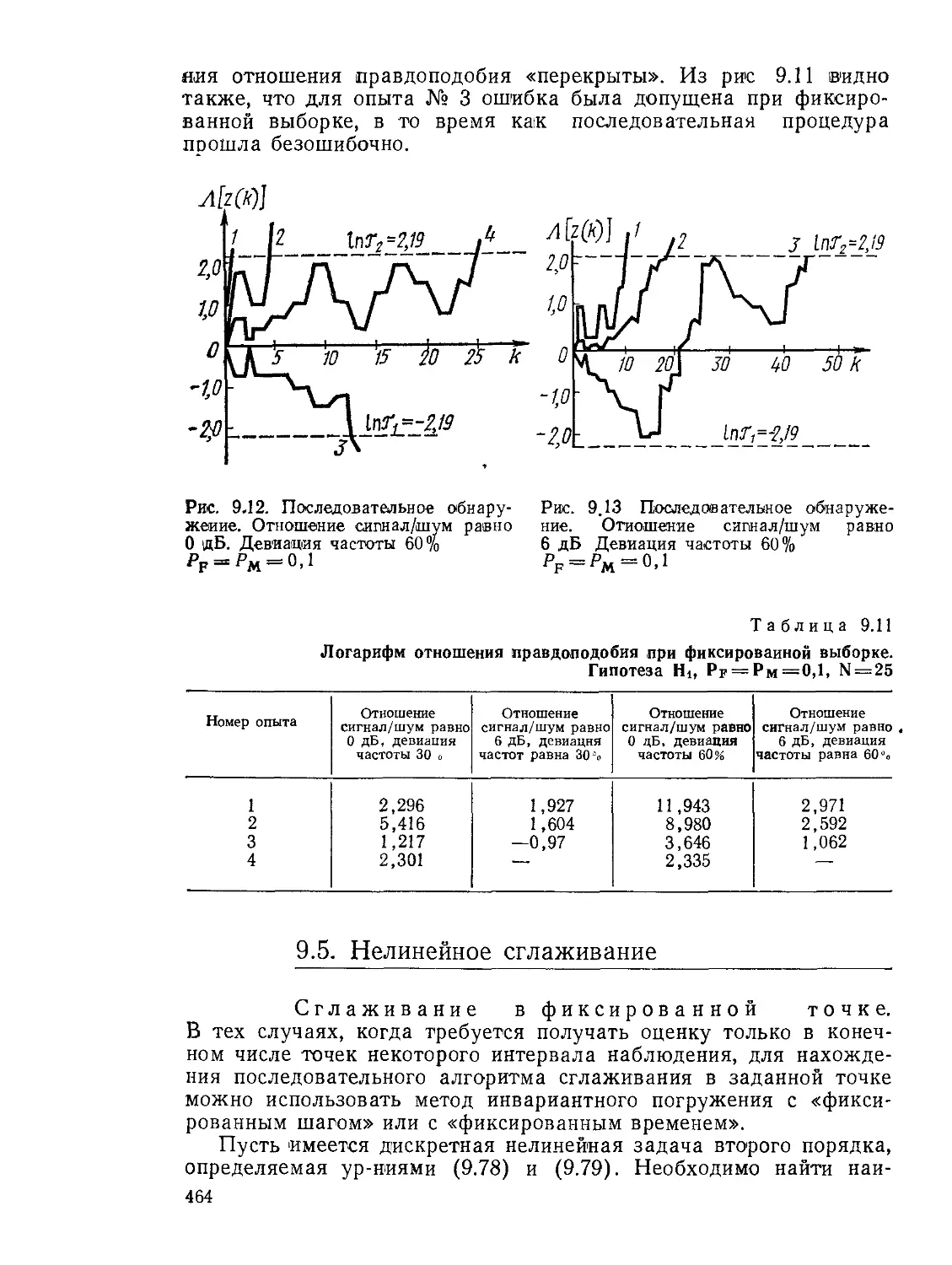
Текст
Э. СЕЙДЖ, ДЖ. МЕЛС
Теория оценивания
и ее применение
в связи
и управлении
Перевод с английского
под редакцией проф. Б. Р. Левина
Выпуск 6
ИЗДАТЕЛЬСТВО «СВЯЗЬ*
МОСКВА 1976
6Ф0.1
С28
УДК 621.39: 519.25(075.8)
Редакционная коллегия:
Б. Р. ЛЕВИН (ответственный редактор серии), А. Г. ЗЮКО,
Е. Н. САЛЬНИКОВ, Л. М. ФИНК, Б. С. ЦЫБАКОВ, В. В. ШАХ-
ГИЛЬДЯН, Ю. С. ШИНАКОВ.
Сейдж Э., Меле Дж.
С28 Теория оценивания и ее применение в связи и управ-
лении. Пер с англ, под ред. проф. Б. Р. Левина. М,
«Связь», 1976.
496 с. с ил., табл. (Статистическая теория связи, вып. 6).
Книга посвящена теории оптимальной линейной н нелинейной фильтра-
ции сигналов и приложениям этой теории к задачам связи н управления
Кинга не требует от читателя специальной математической подготовки. Она
отличается высокими методическими качествами изложения н обилием фак-
тического материала, не содержащегося в аналогичных монографиях
Книга рассчитана на научных работников, аспирантов н студентов стар-
ших курсов Она будет полезна широкому кругу инженеров
30401 — 125
С ------------ 10—76
045(01)—76
6Ф0.1
А. Р. S a g е and J. L. М е 1 s е. Estimation Theory with Ap-
plication to Communication and Control. N.-Y.
McGraw-Hill, 1972.
© Перевод на русский язык. Издательство «Связь», 1976 г.
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Представляемая книга относится к области теории оце-
нивания. Но основное внимание авторы книги уделяют система-
тическому изложению вопросов фильтрации, экстраполяции и
интерполяции случайных сигналов на фоне случайных помех.
Хотя в Советском Союзе и за рубежом издано немало моногра-
фий, посвященных этим вопросам, некоторые особенности книги
Сейджа и Мелса побудили нас включить ее перевод в серию
«Статистическая теория связи». Это, во-первых, высокие методи-
ческие качества изложения и обилие фактического материала, не
содержащегося в аналогичных 'монографиях, по крайней мере, на
русском языке. Далее, как подчеркивают авторы в предисловии,
книга написана инженерами для инженеров и поэтому не требует
от читателя специальной математической подготовки. Для освое-
ния представленного материала необходимы прочное знание ву-
зовских курсов теории вероятностей и математической статистики
и, конечно, терпение при анализе довольно громоздких .алгорит-
мов, а также настойчивое повторение, если понимание не прихо-
дит сразу. Наконец, для практического использования в задачах
связи и управления читатель получает детально разработанные
(и сведенные в таблицы) алгоритмы линейной и нелинейной
фильтрации (а также экстраполяции и интерполяции) сигналов
на фоне белых и небелых шумов в непрерывном и дискретном
(для реализации на ЦВМ) вариантах.
Первая половина книги искусно подготавливает необходимый
математический аппарат, но хорошо подготовленному читателю
следует познакомиться с этой частью книги лишь для освоения
часто необычных обозначений и терминов, используемых автора-
ми. Редактор не решился на изменения многих обозначений и не-
скольких терминов, хотя по ряду причин некоторые замены оказа-
лись неизбежными. Следует, например, иметь в виду, что случай-
ный (полезный) сигнал представляется авторами как исходное
сообщение (детерминированное), искаженное шумами. Кроме
того, шумы возникают и при наблюдении (измерении). Неологизм
«innovation process» переведен здесь как «обновляющий процесс»
(ранее в работе [300*] использовался термин «порождающий
процесс»). Было признано целесообразным в некоторых местах
сократить оригинальный текст, особенно за счет длиннот и повто-
рений 1>.
Перевод выполнили Е. Б. Левина (гл. 1—3), Ю. С. Шинаков
(гл. 4—6), В. И. Журавлев (гл. 7 и первая половина гл. 8),
С. Д. Свет (вторая половина гл. 8 и гл. 9).
Проф. Б. Р. Левин
По предложению издательства в перевод не включены задачи для само-
стоятельного решения, которые содержатся в оригинале.
3
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
( —.......................................—----------—
Для меня весьма приятной оказалась возможность дать
несколько кратких комментариев к русскому изданию «Теории
оценивания и ее применениям в связи и управлении». Летом
1975 года в течение чуть больше двух недель я находился в Со-
ветском Союзе В этот период я посетил несколько советских
городов, встречался со многими советскими учеными и обсуждал
с ними научные вопросы, представляющие взаимный интерес.
После такого путешествия особенно волнующим оказалось для
меня известие о том, что книга, которую написали мы с доктором
Сэйджем, станет более доступной советским ученым благодаря
ее переводу на русский язык
Эта книга была задумана как попытка собрать воедино и в
одинаковых обозначениях огромное количество результатов ис-
следований, которые были посвящены такой широкой теме, как
теория оценивания с особым упором на методы последователь-
ного оценивания и их приложение к связи и управлению В двух
или трех местах приведены несколько способов получения резуль-
татов, с тем чтобы показать различные пути подхода к частному
алгоритму и его использованию Мы считаем, что такой подход
будет особенно полезен изучающим теорию, и мы уже получили
положительные отзывы относительно такой методологии. Боль-
шинство алгоритмов, для облегчения ссылок на них, сведены в
таблицы.
Книга может быть разбита на три основные части. В главах
2, 3 и 4 приведен обзор теории случайных величин и случайных
процессов, детально рассмотрено общее представление марков-
ских процессов в виде динамической системы и, в частности, нор-
мальных марковских процессов В главах 5 и 6 излагаются осно-
вы теории обнаружения и параметрической теории оценивания.
В главах 7 и 8, составляющих основную часть этой книги, при-
водится полное изложение теории линейного фильтра Калмана —
Бьюси в его различных видах Глава 9 представляет собой введе-
ние в теорию нелинейной фильтрации Отличительной особен-
ностью этой главы является подробный вывод некоторых прибли-
женных алгоритмов фильтрации по критериям условного среднего
и максимального правдоподобия и сравнение этих алгоритмов
Джеймс Л Меле
Университет Нотр Дам
Индиана, 1975 г
Глава 1
ОБЗОР СОДЕРЖАНИЯ книги
Одна из основных задач, с которой приходится сталки-
ваться инженерам (а также и большей части человечества), за-
ключается в том, чтобы наилучшим образом извлечь из наблю-
дений данные, необходимые для принятия решения. В этой книге
изложены математические процедуры нахождения оптимальных
решений в условиях, когда на эти решения оказывают влияние
все имеющиеся в наличии данные. Эту процедуру мы называем
оцениванием. Последнее, по существу, связано с понятием инфор-
мация, которое мы определим как совокупность сведений, полу-
ченных в результате принятия решения
Задача оценивания далеко не нова и относится, по крайней
мере, к временам Лежандра [135] и Гаусса [75]. Гауссу приписы-
вают первое употребление понятия оценивания (в приложении
к расчету орбит) на основе его высказывания о том, что наиболее
вероятным значением оцениваемого параметра является такое,
при котором минимизируется сумма квадратов разностей между
действительно наблюдаемыми и вычисленными значениями, умно-
женная на весовой коэффициент, отражающий относительное до-
верие к наблюдениям Это принцип минимальной среднеквадра-
тичной оценки, который будет подробно обсуждаться в гл 6 и 9.
Будем рассматривать теорию оценивания в приложении ко
многим различным областям Так, в теории связи чаще всего оп-
ределяют характеристики передаваемых сообщений по информа-
ции, извлеченной из принимаемых сигналов, которые представ-
ляют собой искаженные шумом модулированные передаваемые
сообщения Теория управления используется при разработке
автоматических систем, которые управляют установками на осно-
вании наблюдений за окружающей средой (или за действиями
противника) При исследовании операций или техническом проек-
тировании решаются задачи распределения ресурсов, товарного
учета, программирования и т. и
Для использования методов теории оценивания в конкретной
инженерной задаче эта задача должна быть сформулирована ма-
тематически на языке теории вероятностей и случайных процес-
сов После изложения основных положений этих теорий рассмот-
рим методы теории оценивания и их приложения к задачам связи
и управления. В заключение будут приведены эффективные алго-
ритмы решения упомянутых задач. Материал в книге распределен
по главам следующим образом.
5
Глава 2. Основы теории вероятностей. Теория вероятностей
изучает усредненные характеристики эмпирических событий. Эти
характеристики образуют совокупность утверждений, имеющих
различную степень уверенности относительно их справедливости.
Хотя и предполагается, что читатель имеет предварительное
представление о вероятности, в гл. 2 дается краткий обзор основ-
ных положений теории вероятностей. Основное внимание уделяет-
ся усреднению, поскольку (как будет показано) средние от функ-
ции случайных величин постоянно используются при определении
оптимальных оценок Подчеркивается различие между априорны-
ми и апостериорными (или условными) плотностями вероят-
ностей
Глава 3. Случайные процессы. Здесь рассматриваются случай-
ные процессы, являющиеся функциями времени. Вводятся такие
важные понятия, как корреляция и ковариация, которые являют-
ся мерой временной связи случайных процессов Наконец, значи-
тельное внимание уделено реакции линейных непрерывных и
дискретных систем на входной сигнал, представляющий собой
случайный процесс.
Глава 4. Нормальные марковские процессы и стохастические
дифференциальные уравнения. Разработка эффективных алгорит-
мов оценивания часто бывает возможна только в тех случаях,
когда статистика нормальная. Вследствие того, что процессы с
нормальным распределением в дальнейшем изложении будут
играть весьма важную роль, в гл. 4 дается детальное рассмотре-
ние нормальных процессов. Приводится центральная предельная
теорема, использование которой позволяет (к счастью) аппрокси-
мировать нормальным процессом многие случайные процессы.
Допущение марковости, означающее, что знание настоящего
отделяет прошедшее от будущего, также справедливо для широ-
кого класса задач и будет использовано в дальнейшем изложе-
нии. Эго допущение придает особую важность понятию условного
среднего, введенному в гл 2 Сначала более детально рассматри-
ваются нормальные марковские процессы в линейных системах.
При исследовании нелинейных систем выявляется, что обычные
правила дифференциального и интегрального исчисления не
всегда применимы Рассматривается стохастическое исчисление
Ито, позволяющее решать многие фундаментальные задачи,
включающие в себя преобразования случайных процессов в не-
линейных системах Решение уравнения Фоккера — Планка в
частных производных и его приближенное решение дают возмож-
ность получить закон изменения среднего и дисперсии в непрерыв-
ных нелинейных системах Использование теоремы об условном
среднем для нормальных случайных процессов позволяет найти
среднее и дисперсию процессов в дискретных нелинейных систе-
мах
Глава 5. Теория решений. Часто теорию решений считают от-
личной от теории оценивания и эти два предмета рассматривают-
ся как два основных раздела в статистике. Здесь, напротив, упор
6
делается на сходство теорий оценивания и обнаружения. До гл. 4
включительно в основном рассматриваются случайные сигналы и
их прохождение через линейные и нелинейные системы. В гл. 5
рассматривается вопрос: присутствует ли сигнал в смеси с шу-
мом?
Возможно, наиболее важной областью приложения теории ре-
шений является оптимальное обнаружение сигналов на фоне по-
мех и шумов. Задаваясь величиной потерь, связанных с принятием
различных решений, можно определить порог, с которым над-
лежит сравнивать наблюдения. В главе рассматриваются как де-
терминированные, так и случайные сигналы в шуме, двоичные и
М-ичные процессы принятия решения, а также проверки гипотез
при фиксированном размере выборки и при последовательном
анализе. Наконец, задача теории решений формулируется в тер-
минах переменных состояния, что дает возможность установить
связь между теорией решений и теорией оценивания.
Глава 6. Основы теории оценивания. Эта глава посвящена не-
которым основным аспектам оценивания состояний и парамет-
ров — второй основной области статистических решений Основ-
ные результаты относятся к так называемым точечным оценкам.
Сначала рассматривается байесовская теория оценивания как
логическое продолжение байесовской теории решений, представ-
ленной в гл 5 При недостатке априорной информации об оцени-
ваемых параметрах используется классическая оценка макси-
мального правдоподобия. Будет сформулирован ряд свойств оце-
нок, а также будет дано понятие псевдо байесовских оценок и про-
веден анализ ошибок
Затем в предположении, что известны лишь два первых момен-
та распределения сигнала и шума, вводится ограничение линей-
ности оценки. Используя лемму ортогонального проектирования
и уравнение Винера — Хопфа, которые являются двумя наиболее
существенными в теории решений и теории оценивания, опреде-
ляется оптимальная линейная оценка.
И, наконец, для случая, когда полностью отсутствуют априор-
ные данные о сигнале и шуме, вводится оценка по методу наи-
меньших квадратов Если соответствующим образом выбрать ве-
совые матрицы и модели оценок, то можно показать, что такая
оценка эквивалентна оценке максимального правдоподобия или
байесовской оценке
Глава 7. Оптимальный линейный фильтр. Большинство оценок,
приведенных в гл 6, не являются ни последовательными, ни ре-
куррентными в том смысле, что .наблюдения не обрабатываются
по мере их получения и оценка не корректируется по мере того,
как поступает новая информация Для получения оптимальной
оценки при помощи методов гл. 6 все наблюдения обрабатывают-
ся одновременно Если же наблюдения обрабатываются по мере
их поступления, то может быть получена значительная экономия
объема вычислений. Часто такая последовательная обработка
следует из самой природы оценки.
7
В гл. 7 рассматривается решение задачи о последовательной
нестационарной линейной оценке с минимальной дисперсией ошиб-
ки, данное Калманом, Бьюси и другими, как развитие основной
работы Винера. Вначале рассматривается дискретный вариант
задачи, при этом для решения используется лемма ортогонального
проектирования. Затем для того, чтобы можно было использовать
байесовский метод, вводится предположение о нормальном зако-
не распределения сигнала и шума. При этом будет показано, что
линейная оценка с минимальной дисперсией ошибки совпадает с
байесовской оценкой.
Алгоритмы непрерывного во времени оценивания получаются,
если предположить, что выборки производятся достаточно часто.
Приводятся результаты для классического фильтра Винера и Об-
суждаются вопросы, связанные с устойчивостью алгоритмов и их
асимптотическими характеристиками.
Глава 8. Обобщение результатов теории оптимальной линей-
ной фильтрации. Основное предположение, используемое в гл. 7,
состоит в том, что шумы объекта и шумы измерения — белые.
Для учета коррелированное™ шумов объекта достаточно три-
виальное расширение вектора переменных состояния. Значительно
сложнее определить оптимальный фильтр, если коррелированы
шумы, присутствующие в наблюдении или измерении В связи
с этим предлагается несколько методов обработки сигналов для
различных подклассов задачи измерения коррелированного шума.
Последовательные процедуры, приведенные в гл 7, не при-
способлены для Оценок, учитывающих наблюдения, поступающие
в более позднее время. Однако во многих задачах учет таких на-
блюдений, так называемое сглаживание, весьма желателен.
В гл 8 дается новый метод синтеза алгоритмов сглаживания для
фиксированного интервала, фиксированного запаздывания и фик-
сированной Т0”КИ
Далее обсуждается влияние некорректного выбора априорных
дисперсий параметров и моделей сообщения и наблюдений, а так-
же излагаются процедуры анализа ошибок и устойчивости при
фильтрации и сглаживании Глава заканчивается рассмотрением
понятия расходимости, определяющего различие между оценкой
состояния и самим состоянием, которое возрастает во времени.
Глава 9. Нелинейное оценивание. Заключительная глава по-
священа задачам нелинейного оценивания Вновь рассматривают-
ся стохастические дифференциальные уравнения, приведенные <
в гл 4 Для случая, когда оцениваемый вектор переменных состоя-
ния зависит от наблюдения, выведено уравнение Фоккера— План-
ка Приближенные решения этого уравнения в частных производ-
ных для нелинейной фильтрации в непрерывных системах приво-
дят к физически реализуемым алгоритмам вычислений Затем по-
казано, в каких случаях дискретная оценка максимальной апос-
териорной вероятности эквивалентна оценке, полученной по методу
наименьших квадратов
8
Обобщенные алгоритмы нелинейной фильтрации для дискрет-
ного и непрерывного случаев получаются с помощью линеариза-
ции нелинейных моделей сообщений и наблюдений и применения
теории линейной фильтрации. С помощью теорем об условных
средних нормальных случайных величин получены псевдобайесов-
ские алгоритмы нелинейной дискретной фильтрации. Приведен
пример, иллюстрирующий сходство и различие некоторых алго-
ритмов нелинейной фильтрации. Наконец, представлены байесов-
ские алгоритмы сглаживания и предсказания.
Библиография. В библиографии дан в алфавитном порядке
список многих ранее опубликованных работ, относящихся к тео-
рии оценок и ее приложениям в связи и управлении. Список снаб-
жен примечаниями, в которых указано, к какому разделу(ам)
или главе(ам) больше всего относится данная ссылка, для того
чтобы ориентировать читателя при выборе работ, подходящих к
данному разделу1).
*) Работы, включенные в библиографию редактором перевода, отмечены
звездочками (Прим отв ред)
Глава 2
ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
2.L Введение
В любой системе связи или управления некоторые
характеристики сигналов априори неизвестны, так как передача
априори известной информации не имеет смысла. В этой главе
дан обзор тех математических методов теории вероятностей, кото-
рые имеют наибольшее применение в теории оценивания и приня-
тия решений в области связи и управления *>.
2.2. Теория вероятностей
Теория вероятностей изучает усредненные характерис-
тики событий или экспериментов, которые могут быть описаны
математически. Основное положение теории заключается в том,
что некоторые из этих средних величин приближаются к детер-
минированным величинам, когда число испытаний или наблюде-
ний возрастает. Например, при бросании монеты герб выпадает
примерно в половине случаев, если бросать монету достаточно
большое число раз.
Для того чтобы четко определить область применения теории
вероятностей, необходимо быть точным при описании экспери-
ментов, содержащих элемент случайности. Будем называть ре-
зультат эксперимента просто исходом. Набор всех возможных
исходов данного эксперимента представляет собой выборочное
пространство Q. События могут быть простыми или неразлагае-
мыми, а также составными, т. е. разлагаемыми. Например, выпа-
дение четного числа при бросании кости является составным собы-
тием, так как его можно разложить на три простых события: по-
явление двойки, четверки и шестерки.
Отношение числа случаев, когда появляется событие, к обще-
му числу испытаний называется относительной частотой появле-
ния события. Когда число испытаний неограниченно возрастает,
мы говорим об относительной частоте как о вероятности появле-
*> Для более детального ознакомления с теорией вероятностей и случайных
процессов читателю следует обратиться к работам, указанным в библиографии
в конце этой книги (Прим авт.).
10
ния этого события. Таким образом, запишем вероятность Рх(а)
появления события Ч х=а в виде * 2>
Р (a)Al™
х N-ы, N
(2.1)
где «х(а)—число случаев появления события х-ад N — общее
число испытаний. Здесь х относится к событию, а а — к значению
этого события. Для простоты изложения предположим, что собы-
тия аг независимы, так что никакие два события а; и а3 не могут
появиться одновременно.
Если выборочное пространство состоит из М независимых со-
м
бытий di, <Х2,
, ам, то
N='£nx(al)
i=i
так что
м
2 Пх (“г) и
l = 2L=|im-‘A----------= УПт
N N-+CO N N-±a, N
1=1
Z=1
(2.2)
Другими словами, сумма вероятностей независимых событий, ко-
торые составляют выборочное пространство, равна единице. Кро-
ме того, отметим, что вероятность любого события всегда неотри-
цательна.
Иногда два эксперимента проводятся одновременно и необхо-
димо определить вероятность появления события х=а в первом
эксперименте и события у—^ во втором. Из ур-ния (2.1) непо-
средственно следует:
Рх (а) = lim ; Рв ф) = lim . (2.3)
./V—>оо N N—><x> N
Но эти две вероятности не полностью описывают возможные исхо-
ды эксперимента, так как представляет интерес также вероят-
ность совместного появления событий х=а и у=$. Если пред-
положить, что события появляются совместно пХ:У(а, р) раз, то
вероятность того, что х = а и г/= р, равна 3 * S))
рх. у (а, £) A lim ——
(2.4)
*; Часто вероятность события обозначают PfAJ. ЭтоАюжет привести к
путанице, в то время как мы бы хотели провести четкое различие между функ-
циональной зависимостью и значением функции. (Прим авт.).
2) Символ Д означает равенство по определению. Здесь автор использует
определение вероятности по Мизесу. Переход к пределу не имеет строгого обос-
нования и лишен практического смысла. Частотная интерпретация понятия
вероятности означает, что в достаточно длинных сериях экспериментов частота
появления события приблизительно постоянна и близка к величине вероятности.
Аксиоматическое определение вероятности принадлежит А. Н. Колмогорову
[291*]. (Прим. ред. перевода).
S) Утверждение «вероятность того, что х=а» означает вероятность появления
события х = а (Прим, авт ).
11
' • Пусть в ф-ле (2.4) представляет интерес только одна величи-
на, например, х. Тогда число появлений события х=а равно
му
nAa')==Ynx-y(a’ <2-5)
1=1
где Му — число независимых событий, связанных с Q, т. е. fh,
Р2, , &му. Объединяя ф-лы (2.1) и (2.4), получим
му
Рх(а) (“’₽.)• (2.6)
Х = 1
Подобным же образом находим
РйФ) = уРх.й(а1, Р), (2.7)
4ми>
1=1
где Мх — число независимых событий в пространстве О, т. е. ои,
аг, ..., ам х Функции Рж(а) и Рй(р) в ф-лах (2.6) и (2.7) назы-
ваются маргинальными (индивидуальными) вероятностями.
Нас может интересовать вероятность появления как события
х—а или события у—$, так и обоих событий. При N испытаниях
событие х=а появляется пж(а) раз, событие у=$ появляется
нй(Р) раз, события х=а и у=р совместно появляются пж,у(а, р)
раз. Число появления любого из событий х—а и у=$ равно чис-
лу появлений события х = а плюс число появлений события у=р
минус число совместных появлений этих событий. Таким образом,
Рх у(х = а или у = р) = lim
ЛГ->00
nx (а) + (Р) — пх у (а, Р)
N
= Рх(а) + Ру(₽)-/\й(а, ₽).
(2-8)
Член пх,у(а, р) надо вычитать, так как его учли дважды, один
раз в пж(а) и один раз в ну(р). Когда появление одного из собы-
тий исключает появление другого, события называются взаимно
несовместными и пЖ;1/(а, р)=0.
Типичной задачей теории связи является определение оценки
передаваемого сообщения по известному принятому сигналу.
Для решения этой задачи необходимо знать или иметь возмож-
ность вычислить Вероятность того, что передаваемое сообщение
присутствует в принятом сигнале. Таким образом, желательно
иметь возможность определить вероятность появления события
р=р при условии, что событие х=а наступило. В серии из N
испытаний событие х=а появляется пж(а) раз, а события х=а,
у=р совместно появляются пх,у(а, р) раз. При определении ус-
ловной вероятности, т. е. вероятности того, что у=^ при условии,
что х=а, необходимо рассматривать только те события, в кото-
рых х—а, так как мы знаем, что событие х=а наступило. Если
число совместных появлений событий поделить на число появле-
12
ний события х=а W перейти к пределу, получим условную вероят-
ность появления события при условии, что событие х=а
наступило. Это утверждение известно как теорема о совместной
вероятности. Аналитически оно записывается в виде
. . п (а, Р) ”>-«(“> PW Рг „(а, ₽)
Ри\х Ф а) = Нт —— = Нт х’у ’— = (2.9)
#-><» пх (а) jV—Nx (a.)/N Рх (а) ’
где Рх\у (р|а) называется условной вероятностью появления собы-
тия у=р, при условии, что событие х=а наступило. Аналогично
имеем
рх|Доф) = Рх,И<х. Р)/^(Р). (2.10)
Если совместная вероятность Рж,у(а, р) является простым
произведением индивидуальных вероятностей Рх(<х} и /\(Р),
т. е.
Рж.Да,₽) = Рх(«)^Ф), (2.П)
для всех возможных а и р, то события х и у называются незави-
симыми. Из ф-лы (2 10) легко получить, что если х и у независи-
мы, то вероятность события х~а при условии у— р не зависит
от а, так что
Ру\* (₽|а) = Ру (р) (2.12)
и аналогично
Рж|Д<х|Р) = Рх(<х). (2.13)
Представляет интерес скомбинировать ф-лы (2 10) и (2 9) так,
чтобы исключить вероятность совместного появления. В результа-
те получим формулу Байеса
Р*\у (<*!₽) = Рух (₽|а) Рх (а)/Ру Ф). (2.14)
Формула или теорема Байеса широко используется в теории
оптимальных оценок. Часто известна условная вероятность при-
нятого сообщения и требуется определить условную вероятность
переданного сообщения при данном принятом сообщении. Тео-
рема Байеса дает метод получения этой вероятности.
В этом разделе были изложены основные понятия теории ве-
роятностей, базирующиеся на понятии относительной частоты
появления события Мы оставили в стороне более строгий аксио-
матический подход к теории вероятностей с тем, чтобы подчерк-
нуть физическую природу вероятности и ее связь с эксперимен-
тальными результатами.
2.3. Случайные величины
Случайная величина х(со) представляет собой действи-
тельную функцию, значение которой определяется результатом
<й произвольного эксперимента. Иначе говоря, случайная величи-
на присваивает вещественное значение каждой точке выборочного
13
пространства. В предыдущем разделе мы определяли вероятности
конечных совокупностей событий, вычисляя относительную часто-
ту появления каждого события. Для определения плотности ве-
роятности и функции распределения непрерывных случайных ве-
личин, определенных на бесконечных множествах событий, ис-
пользуется предельный переход. Важными для дальнейшего
изложения будут понятия вероятности по времени и вероятности
по ансамблю, которые непосредственно приводят к определению
случайного процесса как выборочного пространства, состоящего
из событий, являющихся функциями времени. Таким образом,
случайный процесс можно представить как совокупность функций
времени. В гл. 3 будет дан обзор теории случайных процессов.
В этой главе ограничимся только случайными величинами.
Когда выборочное пространство для случайного эксперимента
состоит из непрерывного, а значит, из бесконечного множества
значений, вероятность получения одного определенного значения
или элемента множества равна нулю. Однако сумма вероятностей
по бесконечному числу элементов во всем выборочном простран-
стве должна равняться единице В этих случаях удобно опреде-
лить функцию распределения вероятностей Fx(a) следующим об-
разом:
Fx(a)APx.[—оо<х<;а], (2.15)
где Рх(а) представляет собой вероятность того, что х меньше
или равен а. Чтобы связать это с полученной ранее дискретной
вероятностью, следует лишь отметить, что мы просто определяем
событие А, как то, что —оо<х^а, или, выражаясь более строго,
что событие А является совокупностью исходов а, принадлежа-
щих выборочному пространству Q, таких, что х(а)^‘а, т. е.
А = {а: —оо < х (а) < a); Fx (а) А Рх (Л). ; ч (2.16)
Если В представляет собой (событие
В = {а: ад < х (а) а^}, (2.17)
то, используя ф-лу (2.16), получим, что вероятность события В
P^B^FM-F^). (2.18)
Если а2=<Х1+Да, то из предыдущего выражения находим
Рх (В) __ Fх (tti 4- A tt) Fx (Од) ^2 ] g\
Да Да'
Предел в ф-ле (2.19) при Да->0, если он существует, называют
функцией плотности вероятности рх(сц):
рх(ccj) = lim + . (2.20)
да->0 Да d at
Из определения рх(В) согласно (2.18) и события В согласно
(2.17) следует, что
P-Ja: Од <х(а) < ад + Д а}] = рх (ад) Д а. (2.21
14
Таким образом, вероятность того, что событие х больше ai, но
меньше или равно ои+Ла, равно значению функции плотности
вероятности Px(ai), умноженной на Да. Из ур-ния (2.20) следует,
что функцию распределения вероятностей можно получить ин-
тегрированием функции плотности вероятности
Fx(a) = Jpx(a)da. (2.22)
— оо
Некоторые свойства плотностей вероятностей и функций распре-
деления, на которые следует обратить внимание, приведены
ниже:
fx (— °0) = 0; ^(оо) = 1; Fx < Fx (а2) для всех аг < а2; рх (а) >0 для всех а; Jpx(a)da-= 1. — оо (2.23а) (2.236) (2.23в) (2.23г) (2.23д)
Приведем некоторые примеры часто используемых непрерывных
распределений (ниже во всех случаях а>0, <т>0):
Равномерное:
Рх (а) = 1 а sC a Ci о; Ь — а 0 в остальных случаях; 0 a <a;
Fx (“) = V/ в V/ V В <2 а । а Ч 1 - 8 1 <5
Экспоненциальное:
М«) = — ё~а/а 0 < a; а
Fx(a) = 0 в остальных случаях; 0 а<0; 1_е-“/а 0<а.
Импульсное:
6
Рх(а)=4- (а~г);
1=1
6
^(«)= о-
1=1
15
Релеевское:
Рх(“)==
О
сь е~а’/2а
а
Рх (а) — 11 е—а'/2а
а<0;
а > О;
а<0;
а > 0.
Гауссовское (нормальное):
рх (а) = yJ-— exp Г — -С-—Hl
х ' /2 л a L 2 а2
Fx(a) = erf
’ \/2сг /
Здесь 6d(t)—дельта-функция; p_i — единичная ступенчатая
функция, начинающаяся при т=0; erf — табулированный интег-
рал Ч
erf а =
Графики приведенных выше функций даны >на рис. 2.1. Импульс-
ное распределение показывает, что дискретные распределения
Рис. 2.1. Примеры непрерывных распределений вероятности:
а) равномерное; б) экспоненциальное; в) импульсное; г) релеевское;
д) гауссовское
*) Существует большое количество определений функций ошибок (erf), име-
ющих, по существу, одинаковый смысл. (Прим. авт.).
16
могут быть представлены как непрерывные с плотностями в виде
дельта-функций. Нормальное распределение является весьма важ-
ным, в чем мы сможем убедиться в дальнейшем.
Если имеются две случайные величины xt и х2, можно опреде-
лить двумерную функцию распределения вероятностей:
FXl, ж, (ai> а2) А.^х,. х, [ оо<хх<ах, —оо<^х2^а2], (2.24)
которая представляет собой вероятность того, что Xi меньше или
равно cxi и х2 меньше или равно а2. Чтобы связать эту функцию
с двумерной дискретной функцией распределения вероятностей,
следует лишь заметить, как и в одномерном случае, что мы опре-
деляем событие А, как событие, при котором —oo<xj^ai,
—оо<х2-^'сс2; другими (словами,
А = {®: — оо < хх (®) ах, — оо <z х2 (®) < а2};
РХ1, хг (ai, Pxt, х, (Л). (2.25)
Определим теперь событие Е следующим образом:
Е = {®: ax <zхх (®) ax + A «1. a2 <x2 (®) < a2 + A «2}; (2.26)
тогда вероятность наступления события Е
Pxlt х, (В) — Pxt, xs (-<4) PXl, х, (В) — РЖ1, Хг (С) PXt, Х,(Р), (2.27)
где события А, В, С и D определены как
А = {®: хх (®) < ах, х2 (®) < а2};
В — {®: хх (®) < ах, х2 (®) < а2 -ф Д а2};
С = {со: хх (со) <:ах + Д ах, х2(®)<а2}; (2.28)
D = {®: хх (®) < ах + Д ах, х2 (®) < а2 + Д а2}.
Обе части ф-лы (2.25) можно разделить на Да1Да2 и записать
через функции распределения:
pXl, xs (£) __ Fxt, X, (Ki + А «1. «2 + А «2) — FXi' Х1 (eg + A gx, a2) _
A ax A a2 A ax A a2
— a2 + Aa2)-FXi ^(ax, a2)
A ax A a2 ’ V • /
Переходя к пределу при Даг-И), получим
lim Р^- (£) = 1 Г ^^„^.(«i + Agn «2)
да^о A ax A а2 A ах L д а2
dFxt, х, (ai, аг)~
да2
• (2.30)
Если теперь определить предел при Даг->0, получим ^следующий
важный результат:
Рх^хЛ*1!’ a2)Alim
Да,->0
Aas->0
Рх'.хДЕ)
A ax A a2
dax <3a2
(2.31)
Выражение Px,. x, (ai, 02) представляет собой совместную функ-
цию плотности вероятности двух случайных величин. Из опреде-
ления события Е видно, что
17
PXl, x, [{и (и) < &L + Д а1( а2 < х2 (а) < а2 + Д а2}] =
= Д а± Д а2 pXl. х, (ар а2). (2.32)
Это выражение является другим определением плотности вероят-
ности двух случайных величин. Вероятность того, что Xi и х2
лежат в прямоугольной области, образованной приращениями
Да1Да2, равна значению функции плотности вероятности, умно-
женному на площадь прямоугольника, образованного прираще-
ниями.
Функцию распределения вероятности можно записать, проин-
тегрировав выражение (2.31):
a2
FXt.xAai> a2) = j J Pxt,xAai> a2)da2dav
(2.33)
Некоторые свойства двумерных плотностей и функций рас-
пределения, на которые следует обратить внимание, приведены
ниже:
FXi, х, (“1, — оо) = Г Х1, Хг (— оо.а2) = FXlt Х2 (— оо, —оо) = 0; (2.34а)
Fxt.xA°°> оо)=1; (2.346)
х,(“1, ОгХ^.хЛар а2 + Д) для всех Д > 0; (2.34в)
Fx^xA^i, аа) ^Fxt, Хг («1 + д, а2) для всех Д > 0; (2.34г)
FXi,xAai> °o) = fXi(a1); (2.34д)
Fxl,xA<x< “2) = Лг(а2)’. (2.34е)
хг («1, «2) > 0 для всех aj и а2; (2.34ж)
00
j J pXl, Хг (an Oj) d d аг = 1. (2.34з)
--00
Если имеются больше чем две случайные величины, система
обозначений, которой мы до сих пор пользовались, становится
громоздкой. Гораздо выгоднее использовать векторную запись.
Поэтому удобно определить М-мерный вектор-столбец как
хг = [Xi х2 х3 ... х^, (2.35)
где символ Т означает транспонирование Нам понадобится также
приращение Димерного вектора х, которое будем определять как
d х = dxr dx2 dx3... dxN . (2.36)
Здесь dx является скалярным элементом. Следует быть вни-
мательными и отличать его от дифференциального вектора dx,
который будем определять как
dxr = [dxjdx2dx3... dxNJ. (2.37)
Для удобства будем говорить, что один вектор меньше друго-
го, когда каждая составляющая первого меньше соответствующей
18
составляющей 'второго. Таким образом, следующие записи экви-
валентны:
х z/j, x2<II/2>-"> ViV <~-^.v • (2.38)
В векторной форме:
Рх (®) = Рх1, хг, , (СТ1* СТ2>-"> “jV )> (2.39)
^х(«)А JPx(a)da; (2.40)
---00
р(Л) = = - ; (2.41)
и да дх1да2...дау
рх(а) d а = Fx(a -f- b а) — F„ («) = Р [а < х < а + Ь а], (2.42)
где интеграл с векторными пределами является М-мерным интег-
ралом Мы сможем неоднократно убедиться в том, что векторное
представление случайных величин значительно проще для их по-
нимания и операций над ними, чем эквивалентное скалярное пред-
ставление.
Часто представляет интерес возможность получения распреде-
ления или плотности только одной величины по совместному рас-
пределению или плотности. Для двух случайных величин из ф-л
(2 33) и (2 34д) следует
^x,(ai) = *.(«!. о°) = J a^darda2. (2.43)
Таким образом, индивидуальная плотность вероятности
э °0
Рх, (<Ч) = - = f Рх„ X, (<Ч> d аг. (2.44)
О CCj J
—оо
Для М-мерного случая индивидуальная плотность вероятности
одной величины хг (/-й компоненты вектора х) может быть легко
выражена, если определить (п—1)-(мерный вектор хг как исход-
ный вектор х, в котором исключена i-я компонента, т. е.
х—i — (х^ х2... х(—1 х1+1... Ху ]. (2.45)
Так как функция плотности вероятности случайного вектора
является функцией совместной плотности, то индивидуальная
плотность вероятности может быть представлена в виде
3F (a,)
P*A<*i)=—;--------= px(a)da_,. (2.46)
‘ <?at J
Этот результат легко распространяется на случай, когда нуж-
но получить совместную плотность для более чем одной случай-
ной величины из совместной плотности для N (случайных величин.
19
Во многих случаях для определения непрерывных случайных
величин нужно знать условные функции распределения и плот-
ности. Начнем с двух случайных скалярных величин х и у, а за-
тем распространим результат на векторные случайные величины
X и у.
Определим два события Л и В:
Л = {ю:— оо<х(й)<а}, В = {со : Р1 <у (®) < Р2}. (2-47)
Тогда согласно (2.10) вероятность того, что х больше, чем —оо,
но меньше или равен а при условии, что значение у лежит в ин-
тервале от —Pi до р2, равна
(Л/В) = Рх,у (Л, В)/Р, (В). (2.48)
Используя функции плотностей вероятности, можно это выра-
жение представить в виде
а р2
[ [ Рх j/ 46 da
Рх\и (Л|В) = . (2.49)
[ Ру (6) 46
Pt
Так'как вероятность/Того, что —оо<х.^’а при условии, что
Р1<г/^Р2, уже получена, то теперь нужно получить функцию рас-
пределения х при условии, что у задано. Действительно, при
Pi=p2=p мы должны получить функцию распределения. Однако
возникают некоторые трудности, так как знаменатель в правой
части (2.49) будет равен нулю почти во всех случаях, когда
Рг— Pi. Если положить р2—pi=Ap, то
а ₽4-Д р а
f рх,у{а, b)dbda ж Др у(а, $)da\
— ОО р — <»
Р+ДР
[ М^ЛжДррДр).
3
Таким образом, при р2—>-pi=p условная функция распределе-
ния вероятности для х при условии £/= р имеет вид
Exit,(а|Р) = limРХ|ДЛ|В) = ( f Px.yifl, $)da |/рД₽). (2.50)
др—>0 \ * /
\—оо /
Условная плотность вероятности определяется как производ-
ная от условной функции распределения:
0 . (а I— аГл/и|Р) - р^(а’ р) (2 51)
PxiMcqp)- да - • (2.01)
20
Интересно отметить, что это выражение имеет тот же вид, что
и (2.48). Точно также .можно показать, что
3
Fvl * (₽1“) = j Ру\* (6|а) db, (2.52)
-00
где условная плотность вероятности
Ру\х (₽|а) = рх,у (а$урх (а). (2.53)
Выражения, подобные (2.51) и (2.53), весьма часто исполь-
зуются при оценке и обнаружении сигналов. Например, если х
представляет собой переданное, а у — принятое сообщение, то
условная средняя оценка включает определение рх\у (ст|р). По-
этому при изложении вопросов обнаружения и оценки сигналов
будут широко использоваться условные плотности вероятности.
Когда условные плотности или распределения не зависят от слу-
чайных величин, две случайные величины независимы, т. е. для
независимых случайных величин
Fx\y (а|Р) = Fx (а); рх[у (а|р) = рх (а) (2.54)
или
Fу\* (₽|а) = Fy (₽); Pylr (₽|а) = Ру (₽)• (2.55)
Из (2.51) следует, что если две случайные величины независимы,
то
Fx.y(a$) = «Ж Рх, у (а, Р) =рх(а)рДР). (2.56)
Объединяя ф-лы (2.51) и (2.53) так, чтобы исключить рх,у(а, р),
получим формулу Байеса для плотностей вероятностей
Рх\у (а'Р) = Ру\х ф|а) рх (а)/ру (₽). (2.57)
Это выражение аналогично формуле Байеса для дискретных со-
бытий (2.15):
р , (А\В} - Р^(ВИ)РИЛ)
^Х\у И|В) pv
Понятия условной плотности остаются справедливыми и для
векторного случая, для которого имеем следующие выражения
для условных плотностей вероятностей через совместные:
Рх\у(«|Р) = рх,у(«> ₽)/ру(₽); (2.58)
Ру,'х (Р|«) = Рх.у (Я, ₽)/Рх («) (2‘59)
и для индивидуальных плотностей:
Рх (а) = ( Рх.у (а, Р) d Р; (2.60)
--ОО
РУ(Р) = jpx,y(a, ₽)d«. . (2.61)
21
Для двух независимых случайных векторов хну имеем:
^х|у (я|₽) = Fx (я); Рх|У («|₽) = Рх («); (2.62)
Fy|x (Р|я) = F? (Р); ру|х (Р|Я) = Ру (Р); (2.63)
Fx.y(a,p) = Fx(«)Fy(P); рх.у(я, ₽) = рх (я) ру (₽). (2.64)
Формулу Байеса можно также непосредственно применить к
векторному случаю, и она имеет такой же вид, как и (2.57):
Рх|у (я|₽) = ру,х (Р|я) рх (я)/ру (Р). (2.65)
Во многих случаях в теории оценивания и ее применении в связи
и управлении необходимо вычислить плотность вероятности функ-
ции случайных величин Обратим теперь внимание на эту важ-
ную задачу.
2.4. Алгебраические действия над случайными
величинами
Задачи теории оценивания довольно часто приводят
к необходимости вычисления результатов комбинации двух или
более случайных величин, а также линейных или нелинейных
операций над одной или более случайными величинами. В этом
параграфе последуют комбинации двух или более случайных ве-
личин и результаты алгебраических действий над ними.
Начнем с простого случая линейного преобразования скаляр-
ной случайной величины х:
у = ах -\-Ь, 'а > 0, (2.66)
где а я b известные постоянные величины. Известна также плот-
ность вероятности рх(а) и требуется получить плотность вероят-
ности ру(а). Определим событие Л = {со: x(<o)'^ai} и событие
В = {ico : z/((o)-^'a.ai + b}. Поскольку оба события относятся к од-
ному и тому же исходу, ясно, что
РДЛ) = РДВ) и Fx(a1) = Fv(aa1 + 6). (2.67)
Если обозначить y—aat + b , то
F,(y) = Fx(^). (2.68)
Искомая функция плотности вероятности новой величины у полу-
чается при дифференцировании этого выражения по у:
Ру (у) = — Рх для а > 0. (2.69)
Если а отрицательна, то необходимо переопределить события
А и В так, чтобы А = {<в : x(<o)-^‘ai} и В = {со : у (со) ^аа1+Ь}.
Так же, как было получено выражение (2.68), находим
рДу) =-----Для а<0. (2.70)
а \ а /
22
Объединяя (2.69) и (2.70), получим ру (у) = уу-рх
Несколько более сложное преобразование получается при про-
хождении случайной величины х с известной функцией плотности
вероятности через устройство с квадратичной характеристикой.
Пусть
У = х2. (2.71)
Преобразование от данного х к значению у однозначное. Однако
обратное преобразование неоднозначно. -
соответствуют два значения х= ±Уу.
Таким образом, для случайной
Данному значению у
величины у событие
В= {и : г/(со) р} при р>0 соответствует событию Л = : — р2 С
<х((о)С02), так что имеем РХ(А)=РУ(В) Это означает, что
^(Р) = М+Г )-РД-ГГ (2.72)
Дифференцируя предыдущее распределение по р, получим плот-
ность вероятности для преобразования у=х2
ЛДР) =
рДР2//2р2 +рД-У)12У р:
0 в остальных случаях.
Если функция плотностей вероятности рх(а) симметрична отно-
сительно а=0, то из ф-лы (2 73) следует
(2.73)
Л/(Р) =
(2.74)
0 в остальных случаях.
Теперь исследуем общий случай нелинейного безынерционного
преобразования скалярной случайной величины (рис. 2 2):
У=Цх). (2.75)
Событие В определим как В = {<о : р<г/(<о)’^’р+Др}. Как по-
казано на рис. 2 2, может существовать некоторое число интер-
валов на оси х, соответствующих одному и тому же интервалу на
оси у. Таким образом, определим событие для х как A =JJ{<o : a,sC
^х(со) ^щ + Да,}, так что РХ(А) = РУ(В) При малых Др имеем
Р«Ф) |д РI = £ Рх (аг) IД «г 1> (2.76)
где взяты абсолютные значения Др и Даг, так как плотности ве-
роятности должны быть неотрицательны. Поделив это выражение
23
на |Др | и перейдя к пределу при Др и Даг, стремящихся к нулю,
получим плотность вероятности для случайной величины у
Ру($>} = У.РЛЪ) тН(2.77)
dpi
Рис 2 2 Общий вид не-
линейного безынерцион-
ного преобразования
где i распространяется на все значения х=аг, которые соответ-
ствуют у=$ Значения аир связаны между собой ур-нием
(2 75). Если множество решений ур-ния (2.75) имеет вид
₽ = f(a,)> «Ч = &(₽), (2-7 8)
то окончательно имеем
(2.79)
Этот результат является наиболее общим выражением для
плотности вероятности скалярной случайной величины у, полу-
ченной с помощью алгебраического преобразования скалярной
случайной величины х
Во многих задачах теории оценивания две или более случай-
ные величины комбинируются для формирования скалярной или
векторной случайной величины. Например, одной из важных за-
дач, которая будет изложена ниже, является оценка сигнального
вектора х по наблюдаемому процессу z, который является адди-
тивной смесью шума v и нелинейного преобразования сигнала
z = h [х] + у. (2.80)
Вначале рассмотрим несколько простых вариантов комбина-
ций случайных величин, а затем перейдем к более сложным. Од-
ной из самых простых комбинаций является сумма двух скаляр-
ных случайных входных сигналов
г = х-{-у. (2.81)
Предположим, что известна совместная плотность вероятнос-
ти х и у и необходимо определить плотность z. Если обозначить
события В = {и : г(и) Оу, х(<в) —а} иЛ = {<в : у(й)’О'у—<х,х(<в) =
= а}, то PZ(B) =РУ(А) и
Fz\x (у|а) = Fyix(y — а|а). (2.82)
24
Дифференцируя это выражение по у, получим
Рг\х (у|а) == Ру\х (у — а|а). (2.83)
Но согласно (2.51) совместные плотности вероятности являются
произведениями условных и индивидуальных плотностей, т. е.
Рг,х(у. а) = р2|х(у|а) рх(а); (2.84)
Рх.у (а. У — «) = Ру\х (у — а|а) рх (а).
Умножая обе части (2.83) на рж(а), получим
(2.85)
Рг,х (у, а) = рХ:у (а, у — а). (2.86)
Так как индивидуальные плотности можно получить интегриро-
ванием совместной плотности, то искомая плотность вероятностей
Pz(y)= ^Pz.xiy, a)da = JРх,у(а’ У—a)da.
(2.87)
Формула (2 87) выражает функцию плотности вероятностей z
через совместную плотность вероятностей х и у.
Возможен и иной метод получения этого результата при дру-
гом подходе к решению таких задач Вероятность того, что z
меньше некоторой величины у, эквивалентна тому, что все значе-
ния х и у лежат слева от линии х+у—у, как это показано на
рис 2 3. Для определения этой вероятности рассмотрим вероят-
ность попадания в полосу шириной da всех значений у от г/=—оо
до у—у—а.
V—a
J Рх.у (a, b)db
da.
25
Для получения искомой функции распределения Fz(y) следует
проинтегрировать последнее выражение по а от —оо до оо:
Ft(y) = [ J Рх,и(а< tydbda. (2.88)
—-со -00
Дифференцируя (2.89), получим функцию плотности вероят-
ности
Рх (у) = [ Рх.и (а, у — а) d а. (2.89)
— 00
Это же выражение может быть записано иначе:
Pz(y) = 1 Рх.у (У — ₽- PW- (2-90)
—<ээ
Если случайные величины х и у статистически независимы, из
ф-лы (2.90) получаем
оо оо
рг(у) = px(Y — JPx(a)P^(Y — a)da, (2-91)
-00 -00
т. e. Pz(y) представляет собой свертку двух функций плотности
вероятности.
Если z=x+y, где х и у независимы, то с помощью ур-ния
(2.91) можно вычислить рх(у)- Аналогично, если u=iz + w, где z
и w независимы, можно получить, используя (2.91) следующее
выражение для плотности вероятности случайной величины
V = w + x + y.
pv(v)= J pw(.y)pz(v— y)dy = JJ pw(y)pv$)px(y — Y — 0)d0dy.
— 00 —00
(2.92)
Рассмотрим теперь общий метод определения плотностей ве-
роятности для комбинаций случайных величин. Рассмотрим век-
торную A-мерную случайную величину у, полученную из вектор-
ной А-мерной случайной величины х с помощью векторного пре-
образования
y = f(x), (2.93)
которое является обратимым в том смысле, что обратное преоб-
разование существует и оно единственное, т. е.
x = g(y) = gH(x)]. (2.94)
Определим событие В= {<о : у(<о) ^р} и соответствующее со-
бытие А={® : f[x(<o)] ^р}=={(о : х(ш) sC*g(P)}. Вероятностные
26
связи величин х и у определяются из равенства Ру(В)=Рх(А),
которое можно записать через функции распределения Fy (₽) = Fx [g (₽)] или через интегралы от плотностей: (2.95)
₽ g (₽) Jpy(b)db= J px(a)da. — 00 Со (2.96)
Если продифференцировать кратные интегралы по каждой из
компонент р, то, как легко убедиться, получим
ру(₽)= |det[^]|px[g(P)J. (2.97)
Здесь dg(p)/dp представляет матрицу размера NXN, элемент
которой равен dgi Таким образом,
dgi J>gL_ dgl
д Pi д р2 ’ ’ ’ д Pw
dg (Р)
. Зр .
dg2 dg2 dg2
api ap2 ” apw
(2.98)
dgN dgN dgN
_a₽i ap2 apw
и det[dg(P)/dp]—определитель матрицы (его часто называют
якобианом преобразования/). Символ |det[dg(P)/dp]| обозна-
чает абсолютную величину якобиана преобразования.
Другой метод доказательства ф-лы (2.97) получим путем за-
мены переменной в (2.96):
a = g(r); da =
detp^>
L д'г
d у.
(2.99)
Тогда ф-ла (2.96) принимает вид
В В
\py(b)db= C detMpil px[g(Y)]dy.
J JI L d X JI
--00 00
Дифференцирование этого кратного интеграла по каждой состав-
ляющей р непосредственно приводит к ф-ле (2.97). Эту формулу
будем часто использовать в дальнейшем.
2.5. Средние значения
В предыдущих разделах рассматривались понятия ве-
роятности, плотности вероятностей и функции распределения ве-
роятностей для одной и более чем одной случайной величины. Мы
видели, что вероятности соответствуют относительным частотам
появления событий и не удивительно поэтому, что средние значе-
ния (математические ожидания) случайных величин или векто-
27
ров могут быть определены из функции распределения вероят-
ностей случайных величин.
Рассмотрим дискретную случайную величину х, которая при-
нимает М возможных значений: ai.'cte, ..., От- Если, как и раньше,
обозначим через пх(а) число случаев появления события х=а и
положим, что общее число событий равно N, то найдем среднее
значение дискретной случайной величины х в виде
М >
Е{х} = Ит-^-У]аг^(аг)Д (2.101)
w->oo V Xj
г=1
Вероятность наступления события х=аг определялась нами
из предельного соотношения
px(ai)= Ит/гх(аг)Ж (2.102)
>-О0
Объединяя (2.101) и (2.102), получим выражение среднего
значения через вероятность наступления событий
м
Е{х}= £агРх(аг). (2-103)
г=1
При возрастании М число дискретных событий увеличивается
и, наконец, для очень больших М можно рассматривать а как
непрерывную величину, которая аппроксимирует дискретную ве-
личину, принимающую значения аг с вероятностью Рх(аг} —
=Рх(аг)Ааг. Таким образом, (2.103) преобразуется к виду
м
Е W = 2 Рх А а'1' (2.104)
<=1
При Даг->4), Л4->-оо сумма в ф-ле (2.104) может быть замене-
на интегралом, который определяет среднее значение непрерыв-
ной случайной величины
Е {х} = J а рх (a) d а. (2.105)
-00
Когда распределение дискретное
м
Px(a) = X/’x(az)6D(a —aj), (2.106)
подстановка (2.106) в (2.105) непосредственно приводит к ф-ле
(2.103) для среднего значения дискретной случайной величины.
С помощью рассуждений, аналогичных тем, которые использо-
вались при выводе ф-лы (2.105), получим выражение для сред-
него значения случайного вектора
00
Е{х} = J а px(a) d я = рх. (2.107)
28
'Понятие среднего может быть распространено и на случайный
вектор х, полученный преобразованием случайного вектора у:
x = g(y) (2.108)
при помощи основной теоремы о среднем значении
оо со
Е{х}= J «рх(я) d х = Jg(₽)py(₽)d₽. (2.109)
--00 —00
ч С помощью этой теоремы можно получить математические
ожидания значений степеней случайного вектора. Таким образом,
определяют различные статистические моменты. Величина
£{xn}= ^anpx(a)da (2.110)
-—со
называется п-м моментом случайной величины х Первый мо-
мент Е{х} называется средним значением или математическим
ожиданием и обозначается рж- Центральные моменты случайной
величины определяются как
00
£{(* —Их)"}= J(a—Hx)"Px(“)da- (2.111)
— со
Особенно важными являются среднее значение средне-
квадратическое значение Фж и дисперсия Vx случайной величины:
ржД£{х} = Japx(a)da; (2.112)
--00
ФхД£{х2} = ^a2px(a)da; (2.113)
—•со
00
VxJ^E{(x — рх)3} = J(a — ц,х)2 px(a)da= Фя — р2 (2.114)
— 00
Эти понятия можно без каких-либо изменений применять и
для векторного случая, когда вводятся понятия среднего значения
вектора, матрицы среднеквадратических значений и 'ковариацион-
ной матрицы вектора х. Эти величины определяются следующим
образом:
НхД£{х}= У«рх(«)^зс; (2.115)
— оо
Фх Д Е {х хг } = ^ххт px(x)dx; (2.116)
— со
00 <
УхД£{(х —рхцх —pxf} = J(« — Ь)(« — у.х)т px(x)dx, (2.117)
-----------------------------00
29
где ххт— симметричная матрица размера jVxM:
ххх2
х2
Л2
•X1XN ~
X2XN
(2.118)
~ XN Х1 XN Х2 • • • XN
Отсюда следует, что члены главной диагонали ковариацион-
ной матрицы представляют собой дисперсию случайных величин,
образующих случайный вектор. Можно определить моменты не-
посредственно из характеристических функций, которые полу-
чаются, если положить в (2.108) g(y)=e~sTy, так что
[ —ST?) “ — sTa
My(s)^E\e J = I ру(зс)е da. (2.119)
-QO
Тогда
(2.120)
(2.121)
Для скалярной случайной величины n-й момент
E{tf } = (— 1)" — Му (s)—
dsn
s—Q
Используя приведенные результаты, легко показать, что сред-
нее значение суммы случайных величин равно сумме средних
значений слагаемых. Важно отметить, что при этом нет необхо-
димости в специальной оговорке относительно статистической
независимости.
В большинстве задач, которые рассматриваются в дальней-
шем, появляются случайные величины, зависящие от других слу-
чайных величин. Поэтому закончим главу определением моментов
случайных величин, зависящих от других случайных величин.
Условное среднее значение случайной величины х, когда зави-
симая от нее случайная величина приняла определенное значение,
равна
00
|1х|у (₽) = Е {х|у = 0} = apx\y(a\$)da. (2.122)
— 00
Безусловное среднее значение случайной величины х
00
|лх = Е {х} = Jac рх (зс) da.
—оо
(2.123)
30
Так как индивидуальная плотность вероятности рх(а). может
|ыть получена из совместной плотности рх,у(а, р), рх(а) =
= J Рх,у(а> ₽)^Р> то совместная, условная и Индивидуальная плот-
ности связаны соотношением рХгУ(а, P)=pxU, (а|Р)ру(р). Тогда
можно записать эквивалентное (2.123). выражение в виде
Е {х} = J Рау («!₽) Ру (ftdad р.
— 00
В этом выражении легко выделить условное математическое ожи-
дание (2.122). Таким образом, получим соотношение между услов-
ным и безусловным средними значениями
£{х}= j£{xjy = p}py(P)dp (2.124)
—со
или Ех{х} = Еу{ЕХ|У{х|у}}, (2.125)
где индексация используется для выделения случайной величины,
для которой находится среднее. Как правило, мы не будем ис-
пользовать индексацию моментов распределения, если только это
не будет необходимо для ясности.
Условная дисперсия х, если задан у, будет обозначаться как
var{x|y=p} или vX|y (р). Имеем
var {х|у = р} = Е {(х — Е {х| у = р}) (х — Е {х|у = р})Т |у = р} =
= J(« — £{*|У = р})(а—Е{х|у= pfpX|y (a|P)da. (2.126)
— 00
Для условных дисперсий .можно получить выражения, анало-
гичные ф-лам (2.124) и (2.125). Легко показать, что
Е {(х — Е {х}) (х — Е {х})7' |у = р} = Е {(х — Е {х| у = р}) (х —
- Е {х|у = p}f |у = р} + (Е{х| у = р} - Е{х}) (Е {х|у — р} — Е {х}Г,
(2.127)
где все символы усреднения относятся к х или к х, зависящему
от у. Если теперь рассмотреть усреднение п<) у в ур-ниях (2.127),
то получим:
Еу {Ех {(Ех {(х - Ех {х}) (х - Ех {x}f |у = Р} = varx {х};
ЕУ {Ex {(х — ЕХ|У {х|у = р}) (х — ЕХ|У {х|у = р})г }|у = Р) =
= Еу {varX|y {х|у = р}}; (2.128)
Еу{(Ех|у{х|у = р} —Ех{х})(Ех {х|у = р} — Ех{х})г } = vary {Ех,у {х|у = р}},
где введены индексы для дисперсий, чтобы Исключить возможную
путаницу. Объединив полученные результаты (с 2.127), увидим,
31
что дисперсия случайной величины х эквивалентна среднему по у
условной дисперсии х плюс дисперсия по у условного математи-
ческого ожидания х. Это утверждение можно записать следую-
щим образом:
varx{x} = Ey{varx|y{x|y= £}} + vary {£х|у{х|у = £}}. (2.129)
Определяя условную характеристическую функцию
Мс|У(^)Д£х1у{е^к|у = 0}= ^e~sTapx]y^)da, (2.130)
--00
можно использовать ее для получения различных моментов.
В частности, имеем
ОО
Mx(s) = £y{Mxly(s|₽)}=jMx|y(s|₽)py(₽)d₽. (2.131) •
Глава 3
СЛУЧАЙНЫЕ ПРОЦЕССЫ
3.1. Введение
В гл. 2 символ х(а>) использовался вместо символа х
чтобы отразить тот факт, что х является случайным вектором
значение которого зависит от эксперимента со. Рассмотрение слу
чайных величин, являющихся
функциями времени, приводит
нас к изучению случайных про-
цессов. Если каждому исходу
эксперимента со поставить в
соответствие временную функ-
цию x(t, со), получим то, что в
дальнейшем будем называть
случайным процессом. На
рис. 3.1 представлена графиче-
ская иллюстрация случайного
процесса. Случайный процесс
является функцией двух пере-
менных— времени / и исхода
эксперимента со. Обычно для
представления случайного про-
цесса используется только сим-
вол х(/). Для любого фиксиро-
ванного значения t случайный
процесс является случайной ве-
личиной.
Рассуждения, которые при-
водились в предыдущей главе,
должны быть лишь слегка мо-
Рис. 3 I. Реализации случайного про-
цесса
дифицированы, чтобы их можно было применить для случайных
процессов. Рассмотрим ковариационную, автокорреляционную и
взаимную корреляционную функцию, ортогональные и спектраль-
ные представления случайных процессов, стационарные и эргоди-
ческие случайные процессы и реакцию линейной системы на слу-
чайный процесс. ;
3.2. Вероятностные характеристики
Выражения для вероятностных характеристик случай-
ных процессов в основном такие же, как и для случайных вели-
2—26 33
чин. Для фиксированных t можно определить событие как группу
исходов, для которой случайный JV-мерный вектор х(/) меньше
или равен некоторой постоянной а (а не является функцией вре-
мени) :
А = {<в: х (I, а) < а}. (3.1)
Функция распределения вероятностей х(/) определяется, как
и раньше, следующим образом:
(О («) Д Рх (Л) = Рх [X (/) < «]. (3.2)
Функция плотности вероятности Px(t)(a) и функция распреде-
ления Рх(()(й) связаны между собой соотношениями 1):
.Рх (#) («) =
д а
а
Л (<)(«)= [
— ОО
(3.3)
(3.4)
Результаты § 2.5 могут быть непосредственно распростране-
ны на случайные процессы. Так, ф-лы (2.108) и (2.109) можно
применить к случайным процессам, если быть внимательным при
обозначении временной завиоимости случайных величин. Напри-
мер, если y(J) — функция случайного процесса x(t)
y(O = g[x(O. О»
то
00
£{У(0}(= J g(«. t)pxW(a)da.
— 00
(3-5)
(3.6)
Более детальное исследование средних значений случайных
процессов представлено в следующем параграфе.
3.3. Средние значения
Как было указано в предыдущем разделе, общие мето-
ды исследования средних значений, изложенные в § 2.5, могут
быть непосредственно применены к случайным процессам. Однако
из-за введения временного аргумента некоторые средние случай-
ных процессов не имеют прямого аналога в теории случайных
величин. В частности, отметим связь между понятиями усредне-
ния по времени и по ансамблю и понятиями стационарности и
эргодичности.
О Часто используются другие выражения типа fx(a, t) и px(a, /). (Прим,
авт.).
34
Среднее значение. Вектор математического ожидания
случайного векторного процесса определяется как
Нх(0Д5{х(0}Д У «Рх(0 (я) da.
(3.7)
Если рх(0 не зависит от времени, то говорят, что процесс стацио-
нарный по среднему значениюДостаточным условием незави-
симости Цх(0 от времени является то, что рх(ц(а) не зависит от
времени. Это условие, однако, не необходимо.
Когда случайный процесс стационарен по среднему значению,
среднее по времени этого процесса
х Д lim -Д- С х (/) dt. (3.8)
2tf J
'‘I
Если среднее по времени х стационарного по среднему значе-
нию случайного процесса [см. (3.8)] равно (с вероятностью 1)
постоянному среднему по ансамблю [см. (3.7)], то процесс эрго-
дичен по среднему значению, или просто в среднем.
Вместо оценки вектора средних путем усреднения по непре-
рывному времени можно ввести оценку, полученную усреднением
по дискретному времени. Для эргодического в среднем процесса
вектор среднего по дискретному времени имеет вид
*) Общие вопросы стационарности и эргодичности будут изложены в этой
главе дальше. (Прим авт.).
2> Последовательность случайных величин х* 1, Z=l, 2,... называется сходя-
щейся по вероятности к х, если вероятность того, что случайная величина х*
не достигнет х, равна нулю Аналитически это можно записать как
limPx[||x'—х||>е]=0.
i->to
Более сильной, чем сходимость по вероятности, является сходимость с вероят-
ностью единица. Последовательность случайных величин х1 сходится с вероят-
ностью единица к пределу х, если вероятность, относящаяся к совокупности не-
сходящихся последовательностей реализаций х", равна нулю. Аналитически это
выражается следующим образом: /)ж[Нт||х*—х|| = 0]=1.
Еще более сильной сходимостью является сходимость в среднем. Последова-
тельность случайных величин х* сходится в среднем к пределу х (LIM — предел
в среднем), если
Е {|x!il2}<°° для всех (;
Е{|[х||2} <оо;
limEfllx1—х||2} =0
Важно отметить, что сходимость в среднем не означает сходимости с вероят-
ностью единица.
2*
35
к
•х Л lim ---J----- V, x(feT),
= К_>со 2Я+1 Li
k=-K
(3-9)
где T — интервал квантования во времени. В реальных измере-
ниях невозможно использовать ф-лы (3.7) и (3.8) с бесконечными
пределами. Поэтому усреднение осуществляется по конечному
числу выборок.
С р е д н е кв а д р а ти ч ес к о е значение и дисперсия.
Матрица среднеквадратических значений векторного случайного
процесса имеет вид
00
Фх(О Д Е{х(0 хг (/)} = Ja ат рх{Г) (a) da.
— 00
(3.10)
Это выражение в точности соответствует (2.116). Если средне-
квадратическое значение не является функцией времени, должно
быть выполнено другое необходимое условие стационарности
случайного процесса. Если процесс и стационарен и эргодичен,
то среднеквадратическое значение, вычисленное путем усреднения
по ансамблю реализаций, равно (с вероятностью 1) среднему по
времени от произведения ххт:
_____ i Ь
Фх = хх7'ДНт------ I x(f)xr(t)dt. (З.И)
Нетрудно записать дискретный аналог ф-лы (3.11). Матрица
среднеквадратических значений эргодического процесса, получен-
ная усреднением по дискретному времени, равна
к
^=lim У] х(6Т)хг(£Т). (3.12)
Л—>00 Z Д -ф" *
k=-K
Матрица дисперсий векторного случайного процесса имеет вид
Vx (t) Д var {х (0) = Е {[х (0 — рх (0] [х (0 — рх (0]г } =
₽ Jl« ——Рх(01гРх(о(«И«- (3.13)
—со
Отсюда непосредственно следует, что
Ух(0 = Фх(0-рх(0^(0. (3.14)
Будем опускать индекс х в обозначении матрицы дисперсий V
в тех случаях, когда это не вызовет путаницы.
36
Корреляционные и ковариационные функции.
Рассмотрим матрицу средних произведения двух значений вектор-
ного случайного процесса с временным сдвигом
Фх(*1. Х2)ДЕ{х(Х1)хг(Х2)}, (3.15)
которую называют матрицей автокорреляционных функций. Ис-
пользуя результаты § 2.5, нетрудно получить следующее выраже-
ние для Фх (Xi, л2):
Фх(Хр Л.2)=Л«₽грх(М)> Х(х2)(«, $)dad$. (3.16)
— <30
Введем также матрицу взаимных корреляционных функций
двух векторных случайных процессов:
Фху(/, т)Л Е{х(ПуЧт)}. (3.17)
Подобным же образом вводятся матрицы ковариационных и
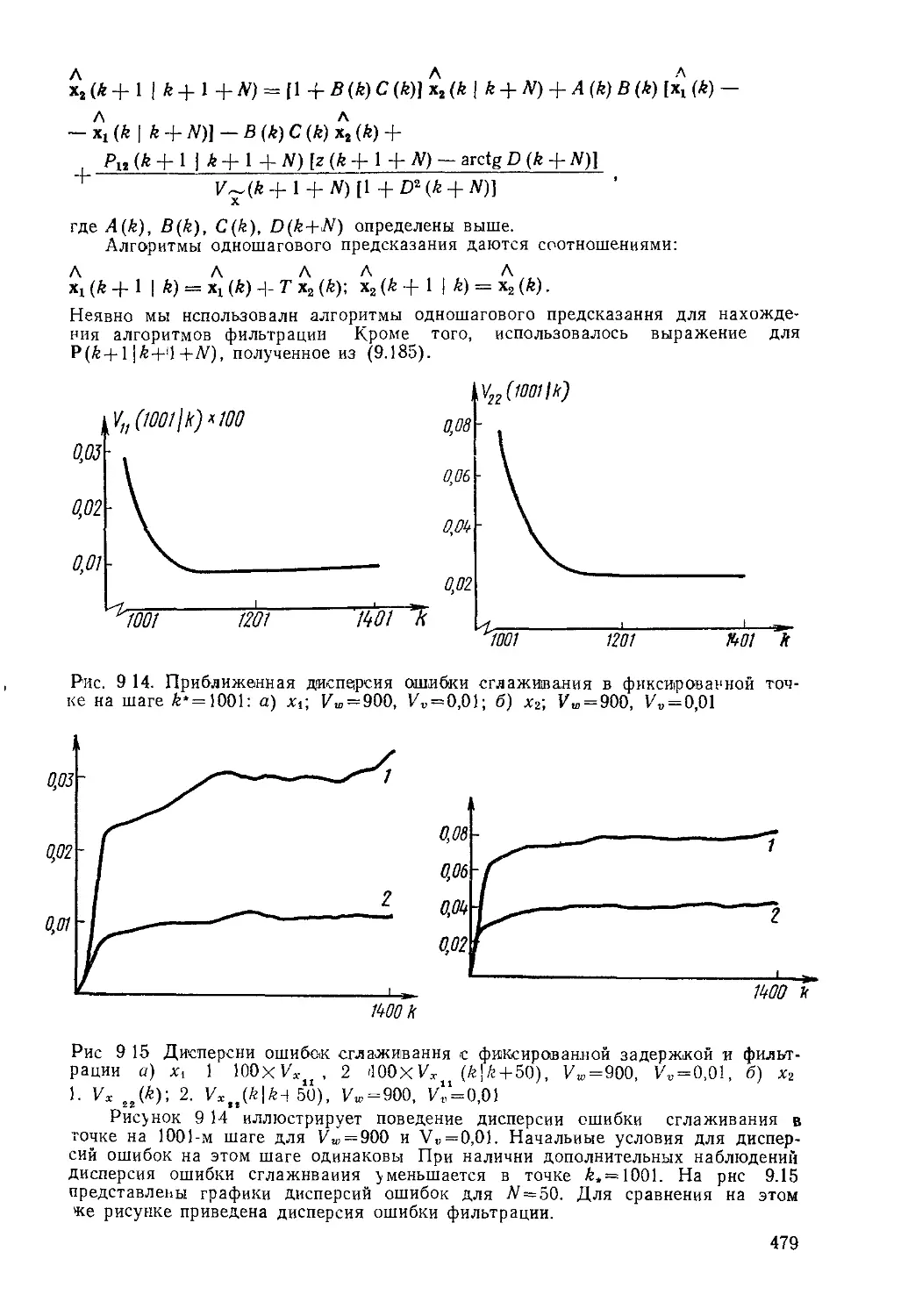
взаимных ковариационных функций. Матрица 'ковариационных
функций (называемая также ядром ковариации) определяется
следующим образом:
Vx (t, т) = cov {х (/), X (т)} Д Е {[х (t) - рх (/)] [х (т) - (т)Г }, (3.18)
т. е. представляет собой среднее произведения центрированных
случайных процессов в моменты времени t и т. Ясно, что
Vx (0 = var {х (/)} = cov (х (0, х (/)} = Vxx (/, /). (3.19)
Матрица взаимных ковариационных функций равна
Vxy (t, т) = cov {х (/), у (т)} =
== £{[х (?) — рх (01 [у (т) - ру (т)Г }. (3.20)
Легко показать, что матрицы средних дисперсий и ковариацион-
ных функций связаны соотношением
Vx(/, т) = фх(/, т)-рх(0рхЧт), (3.21)
а матрицы соответствующих смешанных моментов •— соотноше-
нием
vxy (t, т) = Фху (/, т) - рх (0 р£ (т). (3.22)
Важность первых двух статистических моментов, которые опре-
деляют среднее значение, среднеквадратическое значение, диспер-
сию, корреляционную и ковариационную функции случайного
процесса, обусловлена двумя факторами. Во-первых, обычно на-
много легче найти среднее значение или ковариационную функ-
цию случайного процесса, чем закон распределения. Во-вторых,
многие важные фундаментальные задачи, связанные со случайны-
ми процессами, могут быть решены на основе знания вектора
среднеквадратического значения и матрицы ковариационных
функций. В частности, задачи «линейной оценки» могут быть
37
легко решены, если основываться на знании этих вероятностных
характеристик.
Однако важно не переоценить надежды, возлагаемые на ис-
пользование векторов средних и матрицы ковариационных функ-
ций Можно показать, например, что для определения ошибок
при оценивании диопераии случайного сигнала по его реализации
конечной длительности потребуется четвертый момент распреде-
ления. Таким образом, с помощью только первых двух моментов
можно решить хотя и большое число задач, но не все.
Стационарность и эргодичность Случайные про-
цессы делятся на два широких класса—стационарные и неста-
ционарные (называемые также эволюционными). Стационарным
называется процесс, в котором совместное распределение или
плотность вероятности инвариантны во времени. Случайный про-
цесс является строго стационарным k-vo порядка, если совместное
распределение или плотность k-ro порядка не зависят от времен-
ного сдвига, так что
Px(f,), . x(tk) («, Р...х) =
= Px(f,+T)), x(/.+T)), , «Й-И) («> ₽.х) Для любого Т). (3.23)
Процесс является строго стационарным, если он строго стациона-
рен k-ro порядка при любом k
Можно указать поистине фантастическое число работ по опре-
делению стационарности в строгом смысле Поэтому нас обычно
будет удовлетворять определение стационарности в широком
смысле, для которой требуется независимость от выбора начала
отсчета времени только первых двух моментов. Если процесс
строго стационарный второго порядка, он стационарен в широком
смысле, обратное не справедливо Для стационарности в широ-
ком смысле требуется, чтобы вектор среднего значения не зави-
сел от времени, так что
ОО
Рх (0 = Е {х (0} = J « Рх(0 («) d а = рх, (3.24)
—со
и чтобы матрица корреляционных функций была функцией только
временного сдвига:
Фх(^, т) = £{х(0х^(т)} =
со
= Ja^pxp), х(т)(«, $)dad$ = Сх(/ — т). (3.25)
— 00
Матрица корреляционных функций стационарного в широком
смысле процесса может быть записана в виде
Фх(^ + т) = Сх(т). (3.26)
Более слабым, чем стационарность в широком смысле, но все
же очень полезным для дальнейшего изложения является поня-
тие ковариационной стационарности. Случайный процесс является
38
ковариационно стационарным, если матрица ковариационных
функций зависит только от временного сдвига t—т, так что
V,(Z, T) = Rx(f-T)
или
VXU / + t) = Rx(t).
(3.27)
(3.28)
Можно легко связать понятия стационарности в широком
смысле и ковариационной стационарности. Так как
Vx (t, т) = Фх(/, т) - рх(0у* (т), (3.29)
то для ковариационно стационарного случайного процесса из
ф-лы (3 27) находим
Фх(/, t) = Rx(^-t) + px(0^(t)=Cx(^-t). (3.30)
Таким образом, 'случайный процесс стационарен в широком
смысле (или является стационарным второго порядка), если он
ковариационно стационарен и если он стационарен в среднем.
При этом px(t) в (3.30) можно заменить на цх-
Как отмечалось выше, в некоторых случаях усреднение по
ансамблю можно заменить усреднением по времени. Строго
стационарный процесс x(f) является эргодическим, если для лю-
бой функции f[x(0] средние от этой функции по времени на ко-
нечном интервале времени или по выборке конечного размера
сходятся (с вероятностью 1) к среднему по ансамблю [56].
Таким образом, для эргодического процесса при произволь-
ной f [х]
к
,im ттгУf [х^г)] = £{f
К—>с° Л 1
k=Q
с вероятностью 1.
(3.31)
1 н
hm — \ f [х (ЭД dt = Е {f [х (0]}
t f->00 J
' о
Случайный процесс называется эргодическим в среднем, если
средние по времени на конечном интервале и по выборке конеч-
ного размера
t, _ к
= х(КП = ^7?2хт (3’32)
1 О k=0
сходятся к константе при увеличении длины реализации. Другими
словами, если
[ IjrnjV—(ЭД = 0; lim V-(ДТ) = 0,
11—>оо
(3.33)
s»
так что средние от реализации конечной длительности стремятся
к средним по ансамблю, то процесс эргодичен в среднем. Можно
показать [182], что необходимым и достаточным условием эрго-
дичности в среднем является_сходимость к нулю ковариации слу-
чайных величин х (КТ) [или х (£/)] и х (t):
Vx 7 (t, КТ) = cov {X (О, X (КТ)} (3.34)
при ДТ=^->оо, т. е.
lim V-(/, ДТ) = 0.
KT=t-+<° * х
(3.35)
Необходимым условием эргодичности является строгая ста-
ционарность. Таким образом, все эргодические процессы стацио-
нарны, но не все стационарные процессы эргодические.
3.4. Спектральные и ортогональные
представления
В этом разделе будут рассмотрены два метода характе-
ризации случайных процессов, которые связаны с разложением
сигнала на простые элементарные составляющие.
Спектральное представление. Средняя мощность
i-й реализации случайного скалярного эргодического процесса
хг (i) D
Т/2
PaV = lim — f[xf(t)]2dt. (3.36)
т->® Т J
—Т/2
Для того чтобы ввести преобразование Фурье сигнала x*’(f),
который может иметь бесконечную энергию, рассмотрим сначала
усеченный сигнал с нулевым средним
х£ (0 — р,ж
О
x‘T(t)= {
М>Т/2.
(3.37)
Преобразование Фурье усеченного сигнала имеет вид
оо Т/2
XlT (s) = J Ху (0 e~s< dt = J [х‘ (t) — е~s z dt.
— оо —T/2
(3.38)
о Обозначение х*(() используется как сокращенная запись х (i, <ог). (Прим,
авт.).
49
Средняя мощность усеченного сигнала или исходного сигнала
на интервале от —TJ2 до Т/2 в соответствии с теоремой Парсе-
г.аля
со i со
(0/2(0^=^ J (3.39)
—СО — 1 во
равна
1 С Г I /Л12 Г [ ХТ W]2 .. 1 f ХТ Is) ХТ s) J /Ч ДСП
Y J dt= J—-—^=—— j --------------------------ds. (3.40)
—Т)2 —со — ioo
Назовем величину XlT (s)XlT (—s)/T спектральной плотностью
мощности i-й реализации x{(t) на интервале времени —Г/2^
^7^Т/2 и обозначим ее через Rlx (Т, s). Определим спектраль-
ную плотность случайного сигнала x(t) как предел (при Г—>-<х>)
среднего по ансамблю спектральной плотности мощности реали-
зации
/?_(&) = lim — Е(Х (s)X (— s)l = limE{flx(T, s)}, (3.41)
Г—>с» Т 1 ’ Т-><х
где
Rx (Т- s) A (s) Хт (- s)/T. (3.42)
Для того чтобы этот результат был справедлив, мы должны
ввести ограничение, состоящее в том, что Xt(s)—сходящаяся
несмещенная оценка X(s) в том смысле, что
lim E[RX(T, $)} = Rx(s) и limvar {RX(T, s)] = 0.
r "tf? ,
Для выяснения условий, при которых выполняется первое тре-
бование, рассмотрим выражение
г Г/2
ч)=£!4 И
—T/2
Ц JJr, - у е- = " е' Si X, d Ч.
—7/2
(3.43)
которое заменой переменных т=А,1—Ла, t]=Xi+X2 приводится к
виду
т
Е{/?Х(Г, S)}= J[l-M)/4(T)e-STdt =
—т
т т
= j>x(r)e-sx dx - у^Дж(т)е-5Х^т.
—Г —т
(3.44)
41
Первый интеграл в этой формуле представляет собой искомый
результат. Второе слагаемое должно стремиться к нулю при
Т—>оо. Для этого необходимо потребовать, чтобы
J |тДх(т) | dr <2 оо. (3.45)
—оо
Это и есть то ограничение, 'которое необходимо при определении
(3.41). Если это ограничение выполняется, то из (3 44) следует
соотношение
оо
ед = 1 im4- Е (хт (S) XT(-S)}= Г Rx (т) е"s т d т; (3.46)
Т—>оо I J
—оо
отсюда видно, что спектральная плотность (для эргодического
процесса) является преобразованием Фурье от ковариационной
функции.
Следует заметить, что мы могли бы определить спектральную
плотность просто как преобразование Фурье от ковариационной
функции стационарного случайного процесса Продолжая, как и
раньше, наши рассуждения и используя понятие средней по вре-
мени мощности, мы ограничимся эргодическими процессами. Пре-
имущество получения спектральной плотности с помощью преоб-
разования ковариационной функции случайного процесса по сравг-
нению с ее определением из преобразования Фурье или двойного
преобразования Лапласа заключается в том, что можно избежать
трудностей, связанных со сходимостью (3 41). В теории гармони-
ческого анализа случайных процессов тот факт, что корреляцион-
ная функция и спектральная плотность составляют пару преобра-
зований Фурье, известен под названием теоремы Винера — Хин-
чина [274] (ом также [296*]. Прим. отв. ред):
оо
flx(s)= ^Rx(-t)e-sxdv, (3.47)
—оо
i оо
— 1 оо
Формулу Винера — Хинчина можно также выразить через ко-
синус-преобразование Фурье. Легко показать, что ковариацион-
ная функция и спектральная плотность симметричны, т. е. Rx(t) —
*> В работе Винера спектральная плотность определяется как преобразова-
оо
ине корреляционной функции Cx(s) = J Cx(t)e~sTdx
— со
Очевидно соотношение между определениями: Rx(s)=Cx(s)—|12x6d(s).
(Прим авт )
42
==Rx(—т) и Rx(s) =iRx(—$)• Используя формулу Эйлера, полу-
чим из (3.47) (где s = ko):
Rx(s) = J Rx (т) cos co т d x = 2 J Rx (?) cos co т d t; (3.48)
—оо 0
Rk(t) — jRx(a>) coscor d co = — Jrx(co) coscoxdco. (3.49)
— 00 0
Можно также определить спектральные плотности для стацио-
нарных случайных последовательностей (случайных процессов с
дискретным временем). Для скалярной случайной величины в
стационарном случае можно определить
Rx (пТ)— Фх(кТ, IT") = Rx(k~iT) = E{x(kT)x (i Т)}, (3.50)
где п принимает только целые значения.
Дискретную спектральную плотность определим как дискрет-
ное преобразование Фурье или двойное Z-преобразование кова-
риационной функции случайной последовательности. Таким обра-
зом, имеем дискретный вариант теоремы Винера — Хинчина:
R„(z) = R У Rx(nT)z~n-, (3.51)
П=—00
Понятие дискретной спектральной плотности в дальнейшем
используется редко, но случайные последовательности будут рас-
сматриваться часто.
Результаты этого раздела непосредственно обобщаются на
векторный случай Матричная спектральная плотность опреде-
ляется следующим образом:
Rx(s)= hm4-£{Xr(s)X£(-s)}. (3.52)
Г—>со 1
Теорема Винера — Хинчина в векторном случае записывается
в виде
Rx (s) = J Rx (т) e~s T d x; (3.53)
— 00
1 00
Rx(t)=—— [ Rx(s)eSTds.
2 Я1 J
—100
Переход к векторным дискретным последовательностям осуще-
ствляется непосредственно и, следовательно, нет необходимости
приводить здесь отдельно соотношения для этого случая.
43
Ортогональные представления. Рассмотрим усе-
ченный во времени сигнал, энергия которого конечна:
772 «>
J x*tf)dt = § х* (f) dt <Z °о. (3.54)
—772 — оо
Выясним, можно ли записать хт(/) в виде бесконечного ряда
= £ аг фг (0, (3.55)
t=i
где i|h(0 — совокупность ортонормальных функций. Простым
примером совокупности ортонормальных функций служат функ-
ции фг(О = ^2/Т cos 2л it/T. Совокупность этих функций ортонор-
мальна на интервале —7/2</<Г/2, так как согласно определе-
нию ортонормальности функций
Г/2
[ (О ’I’/ (0 dt = бА- (« — /)- (3-56)
—т/2
где &к(1—/) — символ Кронекера. Ясно, что временной интервал
ортогональности может быть произвольным; чаще всего исполь-
зуется интервал (О, Т).
Коэффициенты аг в разложении по ортогональным функциям
выбираются так, чтобы величина
Т/2_
J (f) dt
—Т/2
Т/2 Г К "12
У X(t) — £акфь(0 dt
—Т/2 L
(3-57)
А=1
интегральной квадратичной ошибки аппроксимации x(t) конеч-
ной суммой была минимальна для каждого К. Положив
dJlda.i = Q и используя ортонормальность совокупности фг, полу-
чим величины
Т/2
di = j" х (t) фг (0 dt,
—Т/2
(3.58)
которые, как нетрудно показать, минимизируют J в ф-ле (3.57).
Можно также показать, что /->-0 при К-э-оо, что указывает на
среднеквадратичную сходимость, так как lim Е{7}=0.
К—>со
Коэффициенты аг в (3.58) могут принимать те или иные зна-
чения в зависимости от выбора системы ортогональных функций
фг(0- Целесообразно выбрать ф, так, чтобы а, имели нулевое
среднее значение и были некоррелированны:
Е {czj = 0; Е {аг а,} = (z — /). (3.59)
Если подставить а, из (3.58) в (3.59), получим
Т/2
Е {а{ а,} = у у ф4 (0 <ря (t, т) фу (т) dt d х = (z — j).
(3.60)
—Т/2
44
Это соотношение выполняется при условии
Т/2
J Фх(*> т)ф/(т)йт. (3.61)
—Т/2
Неотрицательные числа Хг называют собственными значения-
ми, а фг(0—собственными функциями интегрального ур-ния
(3.61). Разложение (3.55) при выполнении условия (3.59) из-
вестно как разложение Карунена— Лоева [50].
Пример 3.1. В гл 6 рассматривается задача оценки параметра неизвестного
постоянного параметра х по наблюдению за известной функцией, зависящей
от х Наблюдение z(t) искажается аддитивным шумом, так что z(t)~h(x, /)4-
-\-v(t) Если используется ортогональное представление модели наблюдения,
так что
ak = [ z (0 Фй (/) dt; bk (x) = J h(x, t) фй (t) dt;
*0 ^0
Ck= [ (t)dt = J [?(/) — h(x, t)]^k(t)dt,
t0 h
то находим ak=bk(x)-{-Ck Случайные величины at представляют собой функ-
ционалы наблюдаемого процесса z(t) и иногда их называют наблюдаемыми
координатами Можно оценить х на основании первых k значений аь а затем,
при необходимости, устремить k к бесконечности Как будет показано, это
представление позволяет получить достаточную статистику при затрате отно-
сительно небольших усилий и, таким образом, оно весьма полезно при решении
задач теории решений и оценок Теперь приведем пример, физически более
мотивированный
Пример 3.2. Одним из фундаментальных случайных процессов является ви-
неровский процесс x(t), который получается при прохождении белого шума
w(t) через интегратор
t
x = w (0; X (0) = 0; RW (т) = a2dD (т); х (t) = [ w (rj) dт).
6
Корреляционная функция винеровского процесса
t т t т
ФИО т) = Е {х (/) X (т)} = Е {ш (T]1) W (»)2)} rf Т]1 d Пг = (тц —
6о оо
, ( a21 t
— т)2)</т)2^т)1 = й niin{/, т}= { ,
(сгт т
Для этого процесса на интервале 0<7' ур-ние (3 61) приводится к виду
т t т
Хуф/ (/) = <Рх (О т) фу (т) d х = о2 J тфу (t) dт ф- о2 р фу (т) d)x.
6 6 i
Решение приведенного интегрального уравнения может быть получено с
помощью ортогональных рядов Эффективным методом решения является преоб-
разование интегрального уравнения в дифференциальное Другие методы приве-
дены в работах [39], [269] Если дважды продифференцировать интегральное
о2
уравнение по времени,
получим
Фз+ » ФЛО —0
л/
Решение этого уравнения
45
(так как а2 и А,- положительны) имеет вид фД/) =go cos &/+£1 sin b3t, b,=
= Y c2lf.}. Подставляя это решение в интегральное уравнение, получим
_ / 1 1 t \
Л/go cos bjt + sin bjt = o2g0 ( — cos bjt — — + — sin bjT + o2gi X
\ b, b2 bi /
/ 1 t
X I — sin bjt----cos bjT \ .
\ 6/ b} J
Для того чтобы последнее уравнение было справедливым при любых t и Т,
необходимо положить £о = О, чтобы член о2£о/63, который не зависит от вре-
мени t и Т, был равен нулю. Полагая £о=О, получим А/ sin bjt — о2 I ——sinfey/—
— — cos6jT'Y Это равенство выполняется при любых t, если А,
bj /
= о2Т2/(у— л2. Так как {др (0} —совокупность ортонормальных функций, то
£4= У 2/Т и, следовательно, ортогональное представление винеровского про-
цесса имеет вид
г-’ оо
x(t) = S ai ФИО;
/=1
т
aj= j x(t)tyj (/) dt,
о ___
т/2 Г/ 1 \ я <
где ф;(0= У у Sin I у — у) у .
На рис. 3 2 показана структурная
фициентов На первый взгляд может
Рис. 3 2 Структурная схема гене-
ратора случайных функционалов
для ортогонального разложения
х(7)
схема генератора ортогональных коэф-
показаться, что мы сильно усложняем
любую задачу, вводя разложение по
ортогональным функциям. На самом
деле это не так Как будет показано
в гл 5 первые несколько коэффици-
ентов а, (чаще всего первый) дают
уже всю необходимую информацию
для того чтобы принять оптимальное
решение или получить оптимальную
оценку. Эти несколько коэффициен-
тов будем называть достаточной ста-
тистикой. Такая простая трактовка
термина, конечно, удачна для частно-
го примера, но не при любом ортого-
нальном представлении случайных
процессов.
3.5. Реакция линейных систем
В § 2.4 были рассмотрены алгебраические действия над
случайными величинами. Основной результат был представлен
46
ф-лои (2 97) Необходимо распространить этот результат на
случайные процессы Однако для случайных процессов из-за
временной зависимости необходимо рассматривать динамические
преобразования, т. е преобразования, которые описываются диф-
ференциальными илн разностными уравнениями Поскольку ре-
зультат динамического преобразования зависит как от предыду-
щей, так и от текущей информации, процесс, полученный таким
преобразованием, должен быть «более коррелированным» и в
этом смысле менее случайным, чем входное воздействие «Сглажи-
вание» случайных данных в результате динамического преобра-
зования является, как мы увидим дальше, одним из основных
принципов теории оценивания
К сожалению, имеется мало общих формул динамических пре-
образований и операции, требуемые для их выполнения, в неко-
торых специальных случаях могут быть чрезвычайно сложными.
Мы ограничимся линейными системами и будем иметь дело
только со средними значениями и моментами второго порядка.
В § 4 5 будет дано обобщение на довольно широкий класс нели-
нейных систем.
Хотя рассмотрение ограничивается только средним и момен-
тами второго порядка выходного процесса, для нормальных рас-
пределений такое рассмотрение эквивалентно полному статисти-
ческому описанию процесса В § 4 2 показано, что результатом
любой линейной операции над нормальным распределением будет
также нормальное распределение Следовательно, если входное
воздействие на линейную инерционную систему нормальное и если
можно определить среднее и второй момент процесса на выходе,
то тем самым полностью определяется выходное распределение.
Наше изложение содержит две части’ непрерывные процессы и
дискретные процессы Начнем с непрерывных процессов
Класс непрерывных динамических преобразований, который
нам предстоит рассмотреть, задан векторным дифференциальным
уравнением первого порядка с меняющимися во времени коэффи-
циентами
<(0 = F(0x(0 + G(0w(Q. (3.62)
Положим, что исходные средние и вторые моменты w(£) и х(£«)
известны:
(0 = Е {w (0); Vw (tv tz) = cov {w (tj, w (3.63)
Hx (U = E {x Vx (Q = var {x (Q).
Мы не предполагаем, что w(^) стационарный случайный про-
цесс Задача состоит в определении среднего цх(0 и второго мо-
мента Vz(/i, t2), а также взаимной ковариационной функции
Vwx(^, t2) процессов x(t) и w(£).
Решение ур-ния (3 62) имеет вид
х(0 = Ф(^, t0)х(t0) + [ Ф(t, г) G (т) w (т)с?т, (3.64)
^0
47
где переходная матрица состояния системы Ф((, to) является
решением однородного линейного дифференциального уравнения
«И, *о) = ~£-ф(^ Q = F(t^(t, t0) (3.65)
с граничным условием
ф(4» Q=I.
(3.66)
Это решение, которое очень легко проверить, получено путем
элементарных преобразований переменных состояния [223].
Среднее значение x(t) легко определяется из ф-лы (3.64):
МО Д Е {х (0) = Е {Ф It, t0) х (t0)} + Е [Ф (t, т) G (т) w (г) d х =
= Ф(£, t0)(t0) + Е j^(t, -r)G(T)w(T)d-rl,
где —среднее значение процесса x(t) в начальный момент
to Переставляя операторы усреднения и интегрирования, полу-
чаем искомый результат
М0=ф(0 ^o)MA>) + f ф(0 T)G(t)liw(T)dT. (3.67)
^0
Заметим, что выражение для fix(t) состоит из двух частей:
«свободной», которая зависит от рх (to), и «вынужденной», кото-
рая представляет собой интеграл свертки, следовательно, реше-
ние для Цх(0 аналогично решению для x(t), за исключением того,
что в выражении для px(t) случайные величины заменяются их
средними
Интегральное представление (3 67) для juix(t) трудно исполь-
зовать из-за наличия в нем интеграла свертки и необходимости
определения переходной матрицы состояния Вычисление интегра-
ла свертки встречает большие трудности и при машинном и при
ручном способах Поэтому желательно записать выражение для
ju.x(t) в другом виде Продифференцируем обе части (3 67), при-
меняя правило Лейбница* 2’ к интегралу свертки.
*> Использование символа Ф как для переходной матрицы состояния, так и
для корреляционной функции общепринято и не должно вызывать путаницу,
так как корреляционная функция всегда имеет индекс, а переходная матрица
состояния — нет (Прим авт )
2> Правило Лейбница, которое доказывается в большинстве книг по
современной вычислительной математике, утверждает, что если f(t, т), a(t) и
$(t) —непрерывны и дифференцируемы по t, то
PU) Р (О
a (О a(f)
при условии, что интеграл существует (Прим авт)
48
Йх (0 = Ф (t, t0) m (Q + J Ф (t, t) G (t) pw (t) d T + Ф (t, f) G (0 pw (0 =
= F(f)
Ф (t, t0) Их (t0) + J Ф (t, r) G (r) |iw (r) d r
+ Ф(/, fl G (9 MO,
где используется (3.65) для замены Ф(^, f0) во втором выраже-
нии. Заметив, что выражение в скобках есть просто цх(0 и что
Ф(0 0=1, получим
M0 = F(OMO + G(OHw(O- (3.68)
Последнее соотношение можно также получить усреднением (3.62).
Можно получить Цх(0, решив ур-ние (3.68) с учетом началь-
ного условия ц.х(О). Конечно, общим решением ур-ния (3.68) яв-
ляется выражение (3.67). Однако если для нахождения цх(0 ис-
пользуются численные методы, которые необходимы при решении
всех задач, кроме самых тривиальных, то вычисления с помощью
непосредственного интегрирования ур-ния (3.68) существенно
проще, чем те, которые потребовались бы при вычислении (3.67).
Перейдем теперь к определению ковариационной функции
VXw(^i, tz) для ti, tz>to, которая имеет вид [см. ф-лу (3.64)]
Vx W (tlr t2) Дcov {х &), w (У) = Ф (f1( Q cov {x (Q, w (f2)} +
+ cov
Произведя еще раз перестановку операций интегрирования и
усреднения и используя предположение, что х(/0) и w(f) для
t~>t0 некоррелированны, получим
VxwKi, £ф(д T)G(T)Vw(r, /2)dr, Д t2>t0. (3.69)
При этом опять появляется интеграл свертки. Прежде чем про-
изводить дальнейшее преобразование этого выражения, рассмот-
рим выражение для Vx(^i, t2).
Используя, как и раньше, решение (3.64), находим, что для
tl, t2^>to
Ф(У т) G (т) W (т) d т, w(Q .
vx(*i, УД cov {х (У, х(У} =
= Ф(У f0)cov{x(f0), х(ЦФт(/2, у +
+ Ф (У U cov j x (Zo), f Ф (4, t) G (t) w (t) d т I +
+ cov ( f Ф (tlt t) G (t) w (t) d т, Ф (t2, t0) x (Q +
+ cov
G (TJ w (tj, ртаФ(/2, G (т2) w (tJ
49
После несложных преобразований получим
Vx (h, t2) = ф (G, Q Vx (U Фг (4, Q +
G
+ Ф&, ^o) J COV{X(Q, w(t)} Gr(x) Фг(£2, T)d? +
t0
+ J ф (h, T) G (t) cov {w (t), x (f0)J Фг (t2, t0) d t+
to
tl ti
+ J d тх p т2 Ф (tlt tx) G (rx) Vw (tx, t2) Gr (т2) Фг (t2, t2).
^0 ^0
Так как w(t) для t>^0 некоррелированно с x(^0), окончатель-
ное выражение при ti, имеет вид
Vx&, /2)=Ф(^ *оПх(*о)ФГ(^ *о) +
+ Jd J d т2 Ф (tl, тх) G (Ti) Vw (т1; т2) GT (т2) Фг (t2, т2).
(3.70)
Формулы (3.69) и (3.70) представляют собой наиболее общие
из полученных нами выражений для вторых моментов Vxw(£i, /2)
и Vx(^, /2). К сожалению, эти выражения, особенно (3.70), не так
просто использовать. Для упрощения выражения, с тем чтобы
использовать его в более удобной форме, необходимо наложить
ограничение на входной сигнал. Чтобы быть более точными, пред-
положим, что w(t) являемся белым шумом, так что
Vw (tr, t2) = (Q 6D (ty - (3.71)
Заметим, что мы не требуем, чтобы w(^) был стационарным
процессом. Кроме того, преобразуя переменную состояния х(0,
легко перейти ко входному воздействию в виде небелого шума.
Поэтому мы предполагаем, что переменная состояния преобразо-
вана, так что w(^)—белый шум. Тогда из (3.69) получаем
Vx w (ti, t2) = J Ф (tt, т) G (т) Tw (т) 6p (т — t2)dx
и, используя свойство дельта-функции *), находим
*> Используется симметричная дельта-функция, для которой
f ь
J f(T)6D(T—/)dr =
а
0,
f (а)/2,
ttb)/2.
f(t).
если t < а или t > b\
если t = а;
если t = b;
если а < t < гь
где f(t)—любая функция, непрерывная на интервале [а, Ь] Для случая, когда
/(т) не непрерывна. Обоснования использования этого частного вида
дельта-функцин, а также причины, по которым следует весьма осторожно обра-
щаться со стохастическим интегралом, будут изложены в § 4.4. (Прим, авт.)
50
Vxw (^1> ^2) -------
' 0
G(4)Tw(Q/2,
Ф&, Z2)G(/2)VW(Q,
если
если
если
(3.72)
^0 <-- t-2>
^0 ~ ^2>
^0
Отсюда следует, что в точке ti=t2 функция VXW(Z<, fe) терпит
разрыв.
Используя ф-лы (3.70) и (3.71), находим выражение для
Vx(f!, t2):
Vx &, t2) = Ф Q Vx(f0) Фг&, t0) +
G t,
+ P Tt J d т2 Ф (tt, Tj G (rx)Tw (tx)Gt (t2) Фт (t2, T2) 8d (tx - T2).
te
Следует внимательно отнестись к порядку интегрирования.
Для того чтобы гарантировать попадание точки, в которой наблю-
дается всплеск дельта-функции, в область интегрирования, необ-
ходимо вначале интегрировать по переменной, имеющей больший
диапазон. Другими словами, если '/i>Z2> то необходимо вначале
интегрировать по ть Окончательное выражение для Vx(tlt t2)
имеет вид
vx(4, *2) = ф&, QVX(^4> /0) +
min t,y
+ f Ф(4,т)С(т)ЧМт)Ст(т)Фг(/2, x)dx. (3.73)
^0
Хотя эта формула проще, чем (3.70), однако из-за наличия
интеграла свертки пользоваться ею не просто. Для упрощения
этого выражения удобно вначале ограничиться случаем, когда
ti = t2=t, так что Vx(^, t2)=Vx(t), и тогда
ад = Ф(*, дух(/0)Фг(/, у +
t
+ JФ (t, т) G (t)Tw (т) Gr (т) Фг (t, т) d X, (3.74)
^0
где Vx(^o) —дисперсия процесса x(t) в начальный момент време-
ни. Может получиться так, что это последнее выражение в дейст-
вительности не проще, чем (3.73). Однако интегральное выраже-
ние в такой форме можно преобразовать в дифференциальное
уравнение. Это преобразование может быть выполнено путем
дифференцирования обеих частей (3.74). Используя еще раз пра-
вило Лейбница, получим
51
Vx(0 = Ф(Л /0)¥х(/0)ФГа. и+Ф(^> /о)¥х(/о)Фг(/, Q +
t
+ |ф(Л т)С(т)^(т)Сг(т)Фг(0 r)dr +
^0
t
+ J Ф (t, т) G (r)Tw (r) Gr (т) Фг (t, т) d т +
to
+ Ф (t, f) G (0TW (0 GT (0 Ф (t, 0 = F (0 Ф (t, t0) Vx (Q Фт (t, t0) +
+ j Ф (t, t) G (t)Tw (t) Gr (г) Фг (t, r) d r + Ф (t, t0) Vx (t0) Фт (t, t0) +
to - -
+ J Ф (t, T) G (0TW (t) Gr (г) Фг (t, r) d TI F7 (0 + G (0TW (t) GT (t).
to J
При получении второго выражения мы использовали тот факт, что
Ф(0 т)=Р(0Ф(0 т) и Ф(0 0 = 1. Сравнивая предыдущее урав-
нение с (3.74), заметим, что выражение в скобках равно ¥х(0,
так что его можно записать в виде
Vx (0 = F (0 ¥ (0+ ¥х (0 Fr (0 + G(0 (0 Gr (0. (3.75)
Уравнение (3.75) представляет собой искомый результат и дает
возможность определить ¥х(0 путем решения простого линейного
дифференциального уравнения с начальным условием ¥х(0). За-
метим, что для решения ур-ния (3 75) не требуется знание пере-
ходной матрицы. Подстановкой (3.75) и (3.74) в (3.73) легко по-
казать, что для белого шума
|¥Х(0)ФГ(0, 0), 0<0.
Формулу (3.75) также легко получить непосредственно путем
дифференцирования выражения для ¥х(0:
Vx (0 = -±- (Е {х(0 хг (0}) = Е {х (0хг (0 + х (0 хг (0),
at
где для удобства полагаем, что цх(0=О. Теперь, подставляя
х(0 из ф-лы (3 62), получим
¥х (0 = Е { F (0 х (0 хг (0 + G (0 w (0 хг (0 } +
+ Е { х (0 хг (0 Fr (0 + х (0 wr (0 Gr (0 } =
= F (0 Vx (t) + ¥x (0 Fr (0 + G (0 ¥wx (0 + ¥xw (0 Gr (0. (3.77)
Искомые ковариационные функции ¥wx(0 и ¥xw(0 можно
определить из (3.72), положив ti=t2=t, так что ¥xw(0 А,
A¥xw(0 0 = G(0Tw(0/2 и ¥wx(0 A¥txw(0=T^ (0GT(0/2.
52
С учетом последних выражений ф-ла (3.77) переходит в (3.75).
Следует иметь в виду, что ф-лы (3.72)—(3.75) справедливы
только, если w(£) —белый шум, причем с ненулевым средним.
Если w(Q — небелый шум, то можно рассматривать w(f) как
выходной процесс динамической системы вида (3.62), на которую
воздействует белый шум. Объединяя уравнения, описывающие эту
динамическую модель, с уравнениями исходной системы, получим
преобразованную динамическую систему, на которую воздействует
белый шум и для которой справедливо выражение (3.20). Такой
метод представления небелого (коррелированного) шума более
подробно будет рассмотрен ниже.
Пример 3.3. Для иллюстрации полученного выражения рассмотрим простой
скалярный случай Динамическая модел_ задается уравнением x(t) =—х(/) +
+w(t)
Предположим, что состояние системы при t=0 известно, х(0)=0 и, таким
образом, начальные среднее и дисперсия Цх(0) =£{xi(0)}=0 и Vx(0) =
=var{x(0)}=0 Входной шум — белый с единичным средним и дисперсией, изме-
няющейся по гармоническому закону pw(/) = l и фю(0 = 1 + cos t
Дифференциальное уравнение для среднего значения имеет вид [ур-ние (3 68)]
Цх(0=—Цх(0+1 с начальным условием Цх(0)=0 Решение этого уравнения,
как легко видеть, имеет вид [i,x(t) = \—е_(
Уравнение для дисперсии Vx(t) =—2Vxf/)4-14-cos t, 1Д(0)=0 Легко пока-
зать, что его решение имеет вид
Vx (t) = (4cos t 4- 2sin t — 9e~2< 4. 5)/l0.
Читателю рекомендуется получить эти результаты, используя интегральные
ур-ния (3 67) и (3 74)
В то время как дисперсия входного шума Чгш(/) = l+cos t является функ-
цией времени, дисперсия выходного шума Vx(t) достигает установившегося
значения лишь через 3 или 4 секунды
F4cos 14- 2sin /4-5 1 1
Vx (0 =------= — -E sin U + 63,43).
’ 10 2 /10 ’
Выходная дисперсия изменяется по синусоидальному закону, но никогда не
обращается в нуль, как дисперсия входного воздействия
Пример 3.4. Рассмотрим следующую «модель сообщения»'
х = F (/) х + G (/) w (/),
где w(/) —небелый шум, так что его модель можно в общем случае предста-
вить в виде
Т = Е (0 т (04^ S (0 и (0;
w(f) = H(/)Y(0+v(0.
где и(?) и v(7) — белые и некоррелированные шумы Можно преобразовать
Гх (01
переменную состояния, вводя вектор состояния х(7) Л_ , который удовлет-
LY (OJ
воряет дифференциальному уравнению x=F(f)x(/) +G(/)w(f), где
FF(O G (0 Н (/)
[о s (0
G(0 =
G(/)
0
w(0 =
v(01
U (0 J ’
0 1
E(0 J
53
которое имеет тот же вид, что и ур-ние (3 62), при белом шуме Следовательно,
в рассматриваемом случае можно использовать ф-лы ,(3 75) и (3 76) для опре-
деления Vx(7) и Vx(7i, i2), а ф-лу (368)—для определения fix(t). Начальные
условия запишутся в виде
J4 (to) =
Их (^о)
. (?o).
Vx (to) =
ГМ*о)
о
vv (to)
о
Таким образом, полученные выше выражения для вторых мо-
ментов действительно являются весьма общими
Очень важный подкласс задач охватывает стационарные (по
крайней мере, в широком смысле) процессы, для которых средние
значения постоянны, а вторые моменты зависят только от разнос-
ти y=ti—12. Матрица коэффициентов системы F(t) и матрица
распределения G(t) не зависят в этом случае от времени, так
что ур-ние (3.62) принимает вид
x = Fx(0 + Gw(O, (3.78)
где F и G — постоянные матрицы. Так как средние значения по-
стоянные, ур-ние (3.68) упрощается: px~0=Fpx+Gjiw или цх=
= F'Guw.
Если F сингулярна, то, вообще говоря, цх не будет иметь
стационарного значения, хотя для того, чтобы цх было неограни-
ченным, это необходимо. Сингулярность F означает, что система
имеет один или более полюсов в исходном состоянии и что по-
стоянное входное воздействие вызывает неограниченный выход-
ной сигнал.
В стационарном случйе выражение для взаимной ковариацион-
ной функции между входным и выходным сигналами имеет вид 9
[см ф-лу (3 69)]
i+v
Rxw(t)AVxw(( + 7, 0= J ф(^+ y,r)GRw(T — t)dx,
*0
где Rw(t—Z)=Vw(t, t). Так как динамическая система стацио-
нарна, переходная матрица становится функцией разности времен-
ных аргументов, так что
Ф(^, (3.79)
Для получения стационарного решения достаточно, чтобы
входное воздействие было приложено с момента t0=oo, так что
*+v
Rxw(y)= J 2(f+ т — t)GRw(t — t)dx.
(3.80)
Здесь для стационарного случайного процесса по определению RXw (А—t2) A
ZyVxw(A, t2) Эквивалентное определение j?Xw (it—fe) = Vx»(fi, t2). (Прим авт.)
54
Может показаться, что Rxw является функцией времени t, что
должно указывать на нестационарное решение. Но этот вывод
неверен. Я®ная зависимость от t исчезает после замены перемен-
ной интегрирования Х=т—t'.
X
Rxw (l) = ( 2 (у — X) GRW (X) d X.
— ОО
Из условия физической осуществимости системы следует, что
О (у—К) должно равняться нулю при Х>у. Таким образом,
результат не изменится, если верхний предел интегрирования уве-
личить от у до оо, так что получим
оо
Rxw(y) = [Q(y-X)GRw(X)dX. (3.81)
— 00
Полученный результат снова имеет вид интеграла свертки,
который, хотя и является более простым, чем в общем нестацио-
нарном случае, все же неудобен для вычислений. Следует пом-
нить, что при выводе (3 81) мы не ограничиваемся случаем бело-
го шума
Формулу (3 81) можно записать иначе, положив £=у—X:
—оо 00
RxwCr) = -f 2 (£) GRW (у — £) d £ = J 2 (В) GRW (у(3.82)
00 — 00
Поскольку выражение (3 81) аналогично стандартному интег-
ралу свертки для детерминированных систем, целесообразно про-
вести преобразование Фурье ф-лы (3 81), что даст возможность
получить выражение для взаимной спектральной плотности
00 ОО
Rxw (s)A F {Rx. (у)} Д J e“s {d у f 2 (у - X) GRW (X) d X,
— oo —oo
где .F — оператор преобразования Фурье
Меняя порядок интегрирования, получим
RXw(s)= [ ^2(у —X)Ge“s?dy Rw(X)dX.
(3.83)
Представим теперь e~sv как тогда ф-лу (3 83) мож-
но записать в виде
FsXdX.
Rkw(s)= J jQ(y-X)Ge-sMdy Rw(X)e
Выражение в скобках является
Тогда
преобразованием Фурье от 0(0-
*> Преобразование Фурье от Q(Z)
татель при этом не должен забывать,
функции (Прим авт)
обозначается просто заменой t на s Чи-
что Q (t) и Q (s) — совершенно разные
55
00
Rxw ($) = Q (s) GJ Rw (X) e"s x d X
— 00
или
Rxw (s) = Q (s) G Rw (s).
Ясно, что взаимная спектральная плотность
Rwx (s) = RL (— s) = Rw (s) GT QT (— s).
(3.85)
Как известно из теории переменных состояния, резольвента
J}(s) матрицы F равна:
й (s) = (s I — F)-1
и может быть легко определена с помощью алгоритма Леверье.
Формулами (3.84) и (3.85) легко пользоваться, так как они вклю-
чают в себя только алгебраические действия.
Выражение (3.70) для второго момента выходного процесса
принимает в стационарном случае следующий вид:
Rx (У) Д Vx(f + у, t) = Й (t + у -tQ) Rxfa) QT(t-tQ) +
4- J d Ti J d t2 Й (t + у — тх) GRw fa — r2) G Й (t — r2).
Если снова положить t0=—оо и Rxfa)=0, то получим
<+v
Rx (у) = J d^i
-----------00
t
Jdr2Q(£ + y —rJGRwfa —r2)Gr QT (t—x^.
—co
(3.86)
Теперь сделаем подстановку Xi=^+y—ту и Хг—t—тг. Тогда из
ф-лы (3.86) находим
R* (у) = j d \ Jd Х2 Й fa) GRW fa + у - XJ Gr Йг fa)
о 0
или
Rx’(y) = f JQ (X^GRw fa + у - M cfa GrQr fa) d X,.
о 0
Здесь нижние пределы в обоих интегралах можно без измене-
ния результата положить равными — оо, так как fifa=O при
t<0. Если сделать такую замену, Rx(y) будет иметь вид
Rx(y)=J jQfa)GRwfa + y —X1)dX1 GrQr(X2)dX.
'2-
(3.87)
Объединяя ф-лы (3.87) и (3.82), замечаем, что выражение в
скобках есть просто Rxwfa+y), следовательно,
Rx (Т) = J RxW fa + у) Gr fa) d X,. (3.88)
— оо
56
С помощью замены переменных легко показать, что RK(y)
можно также записать в виде
Rx (у) = JQ (XJ GRwx (у — (3.89)
—oo
Выражение для спектральной плотности RK(s) можно полу-
чить, взяв преобразование Фурье либо от (3.88), либо от (3.89)
и выполнив действия, аналогичные тем, которые проводились при
выводе (3.84). В результате получим
Rx (s) = a (s) GRW (s) Gr QT (— s). (3.90)
Формулы для спектральной плотности (3.84) и (3.90) могут
быть также получены более простым путем. Предположим, что
v/(t) и х(/)—центрированные стационарные сигналы, для кото-
рых существуют обычные преобразования Фурье W(s) и X(s).
(Чтобы быть более точными, мы можем рассматривать преобра-
зование Фурье от одной реализации и, если это необходимо, ис-
пользовать ограничения § 3.4 в применении к финитным сигна-
лам). Спектральные плотности Rxw(s) и RK(s) можно записать
в виде
RXw(s)A£{X(s)Wr(-s)} (3.91)
и
Rx (S) Д Е {X (s) Хг (— S)}. (3.92)
Выражение для X(s) можно получить, подвергнув формально
преобразованию Фурье ур-ние (3.78):
sX(s) = FX(s) + GW(s)
или
X(s) = ($I — F)~’GW(s) = Q(s)GW(s). (3.93)
Поэтому Rxw(s), как следует из (3.91), будет иметь вид
RxW (s) = Е {Й (s)G W (s) Wr (- s)} = Q (s) GRW (s)
и
Rx (s) = Е { a (s) GW (s) [a (-S) GW (- s)f } =
= a (s) g e {w (s) wr (— s)} Gr ar (— s) = a (s) g rw (s) gt ar (— S),
что совпадает с результатом, полученным выше при строгом вы-
воде. Хотя приведенный способ формальный и нужно поэтому
быть осторожным при его применении к нестандартным случаям,
он тем не менее часто используется.
Пример 3.5. Используем ф-лы (3.85) и (3.90) для определения спектраль-
ных плотностей i/?rw и Ry($) в случае простой стационарной системы с одним
входом, которая описывается уравнениями:
х (/) = Fx (/) ♦ gw (/); У (t) = hx (/).
57
Предположим, что спектральная плотность Rw(s) процесса w(t) известна.
Формулы (3 84) и (3 90) могут быть непосредственно использованы для
получения спектральных плотностей Rxw и Rxi(s):
Rxw (s)SRw (s) и Rx (s) = (s) S Rw 4) 2 ( s)>
где fi(s) = (sl—F)-‘. Искомую спектральную плотность Ryw (s) получим из
Rxw указанным выше формальным способом:
Ryw 4) = Е У 4) (s)} = h Е {X (s) W (s)} = hRxw (s) = h О (s) gRw (s).
Заметим, что hQ(s)g — переходная функция, связывающая у и ш, или
Y(s)/W(s) =H(s) =hfi(s)g Тогда tRxw(s) можно записать в виде
Ryw 4) = 4) Rw (s) •
Аналогично получаем выражения для Ry(s)- Ry(s)=H(s)H(—s)Rw(s). Можно
было бы использовать и формальный способ:
tfY(s) = £ {Y (s)Y (—s)} = Е {И (s) W (s) W (—s) И (—s)} = Н (s) Rw Н s).
Дополнительные примеры читатель найдет в библиографических ссылках, при-
веденных в конце этой главы.
Перейдем к рассмотрению дискретных систем. Изложение
вопросов, относящихся к дискретным системам, в этом разделе
точно соответствует приведенному выше изложению, относяще-
муся к непрерывным системам. По этой причине многие доказа-
тельства значительно сокращены.
Переход к дискретным системам осуществляется с помощью
векторного разностного уравнения первого порядка:
«4+0 = Ф (4+ь 4) х (4) + г,(4) w (4),
где 4-м—4—k-fi интервал квантования во времени. Исключая слу-
чаи переменного интервала квантования, запишем .просто 4+1—4 =
= Т; 4+1 = (& +1) Т, так что
х (£ + 1) = Ф (k 4- 1, Л) х (£) -(- Г (£) w (Л). (3.94)
Запишем среднее значение и второй момент в виде
(k)AE{w(k)}-, Vw (#, /)Дсоу{иг(А!), w(j)}. (3.95)
Получим результирующее и разностное уравнения для сред-
него и второго моментов x(k) и для ковариации x(k) и w(j). Лег-
ко убедиться, что решение ур-ния (3.94) имеет вид
/—1
х(/) = Ф(/> 0)х(0) + Уф(/, i+ l)r(t)w(j). (3.96)
Если усреднить обе части (3.96), то получим
Их (/) = Фа(/, 0) (0) + £ Ф (/, i + 1) Г (/) |iw (Z). (3.97)
1 — 0
Разностное уравнение для цх можно получить значительно проще
путем непосредственного усреднения (3.94):
М/ + 1) = ф(/+ 1, 4-Г(j)tbr(j). (3.98)
Si
Результирующие выражения для Vxw(j, k) и Vx(j, k) следуют
из определений этих величин и ф-лы (3.98)
Vxw (j, k) = V Ф (j, i + 1) Г (0 Vw (i, k); (3.99)
i=0
Vx(j, k) = Q(j, 0)Ух(0)Фг(6, 0) +
+ ££ф(/, i+ l)r(OVw(Z, p)VT(p)QT(k, p+1), (3.100)
1=0 p=0
где Vx(0) _A Vx(0, 0) A var{x(0)}. Читателю предлагается само-
стоятельно получить эти выражения.
Если выборки случайного процесса некРррелированны или если
он «белый», так что Vw(j, k) = Vw(j)8ik, то
7-1
Vxw (/, k) = £ Ф (/, i + 1) Г (0 Vw (0 6K(i-&).
i=0
Это выражение можно записать а виде
( 0 при k ~> i — 1;
VXw(j,^) = |ф(/.f ^+1)r(^)Vw(^) при ( ’101)
Для случая, когда выборки w(k) некоррелированны, выраже-
ние для Vx(j, k) имеет вид
Vx(z, А) = ф(/, 0)Ух(0)Фг(^, 0) +
1-1 k~l
+S 2 ф (/> 1 +г (/) Vw (/) (Z -р) г (/?) ф р +1}’
i=0 р=0
откуда с учетом определения символа Кронекера 6к (i — р) следует
vx(j, *) = Ф(/, 0)Vx(0) Фг(£, 0) +
+ ’фо, <+ 1)F(0VW (0Гг(0Фг(£, i+ 1). (3.102)
i=0
Чтобы вывести разностное уравнение для Vx(/)AVx(j, /), ана-
логичное ур-нию (3.75), можно использовать определение Vx(j)
и ф-лу (3.94):
vx О’ + 1) = COV {х 0 + 1), X (/ + 1)} = COV {[Ф (/ + 1, /) X 0)’+
+ Г (/) W (/)], [Ф 0 + 1, /) X (/) + Г (/) W (/)]}.
Это уравнение после некоторых алгебраических преобразований
можно привести к виду
^(/ + 1) = ф (/ + 1, /) vx (/) фг о + 1. /) +
+ Г (/) cov {w (/), х 0’)} фг (/ + 1, /) +
+ ф О + 1, j) COV {х (/), w (/)} Гг (/) + Г (j);vw (/) Гг 0). (3. ЮЗ)
59
Из (3.101) или непосредственно из физических 'соображений
ясно, что VXW(/) = VWX(/) = 0, так как х(/) зависит только от w(i),
i<j, и w(/) не коррелирован с w(i), i^j. Тогда ф-ла (3.103) при-
водится к виду
Vx(/+1) =Ф(/ + 1, /)¥х(/)Фг(/ + 1, /) + r(/)Vw(/)rr(/). (3.104)
Легко показать, что когда w(k) — белый,
vx(&, л-/Ф(А’ k>}’ (3.105)
1У#)Фг0\ k), k<j.
Читателю рекомендуется самостоятельно доказать, что выра-
жение (3.102) для j—k является решением ур-ния (3.104). Сле-
дует помнить, что соотношения (3.101) — (3.104) справедливы,
если w(/e)—белый. Случай, когда w(k)—небелый, может быть
представлен, как и в непрерывном случае, введением вектора
переменных состояния.
Пример 3.6. Для того чтобы показать, как использовать выражения (3 98)
и (3 104) для и Vx(j), рассмотрим простую скалярную задачу. Динами-
ческая система задается скалярным нестационарным разностным уравнением
*(/^1) = (/^ 1)*(/)4^(/).
Шум на входе—белый с нулевым средним Vw(j)=j2. Начальные условия
ц«(0) = 1 и V=?(0) = 1.
Среднее значение выходного процесса можно найти из (3 98), которое для
этого примера имеет вид
М/ 4-1) = (/ 1) Цх (/) 0, рх (0) = 1.
Легко убедиться, что решение этого уравнения имеет вид Цх (/)=/!- Запи-
шем разностное уравнение для дисперсии Vx(j):
^(/^i) = (/>i)2vx(/)>72
с начальным условием Р»(0)=1. Хотя простого решения этого уравнения в
замкнутой форме не существует, все же легко вычислить Vx(i) непосредствен-
но Например,
Vx (1) = (1)2 (1) > (О)2 = 1; Vx (2) = (2)2 (1) ♦ (I)2 = 5;
Vx (3) = (3)2(5)^ (2)« = 49.
Интересно отметить, что здесь Vx(l) = Vx(0).
Это вполне приемлемый и корректный ответ, если вспомнить, что Vw(0)=0.
Таким образом, здесь нет (среднеквадратической) неопределенности входа в
нулевом СОСТОЯНИИ, И МЫ ПРИХОДИМ К ВЫВОДУ, ЧТО Vx(l) = Vx(0).
Рассмотрим теперь стационарный случай для дискретных сис-
тем. Для инвариантных во времени систем выражение (3.94) мож-
но заменить уравнением
х (/г + 1) = Qx(A) 4- rw(&), (3.106)
где Q = Q (Г) =Ф (k+ 1, k) = Ф[(&+1)Т, kT] и Q (/) = £Р = Ф (k + j,
Т, kT). Если w(k)— стационарен в широком смысле, то вто-
рой момент Vw(/, k) зависит только от разности времен, т. е. от
i=j—k, так что Rw(t)= Vw(&+i, k) для всех k.
60
Среднее значение выходного процесса можно легко опреде-
лить усреднением обеих частей ур-ния (3.105):
V-x(k + 1) = + rMw-
Если входной процесс стационарен в среднем, выходной процесс
также стационарен (по крайней мере, в широком смысле), цх(&+
+1) = Цх (k) = Цх ‘и имеем
?х=а1*х+1Х
или
|*х = (1-аг1г1Ч. (З.Ю7)
Решение ур-ния (3.106) имеет вид
х(/)= S a(/--i-^)rw(^).
k=— «О
Здесь для простоты и без потери общности мы предположили, что
в начальной точке система находится в состоянии покоя х=0 при
k ——оо. Взаимная ковариационная функция
Ж-i
Rxw (г) Л cov {х (/ + г). w (/)} = cov 2 2 О’ + <’ — 1 — ^)Г w (k),
k~—со
/4-г—1
w(j) = V Q(J +z- 1 - £)FRW(A! - /).
k——co
Для того чтобы исключить явную зависимость ОТ }, положим
m=k — j. Тогда получим
Rxw(0= S Q0’— 1 — m)rRw(m). (3.108)
m=—оо
Из условия физической осуществимости системы следует, что
D(fe)=0 при fe<0 и, следовательно, верхний предел суммирования
может быть распространен до бесконечности, т. е.
ОО
Rxw (i) — й (i — 1 — т) Г Rw (m).
m=—oo
(3.109)
Теперь можно получить выражение для спектральной плотно-
сти с помощью ^-преобразования обеих частей (3.109):
со оо со
Rxw (2) Д т £ г-1 Rxw (z) = Т 2 £ Q (i - 1 - m) Г Rw (tn),
i——co i=—oo m——«
Меняя порядок суммирования и записан z—‘ как z-(t-i-m)
получим
со Г оо
Rxw (z) = 2 2
m=—оо |_i =•—«
FRw(m)2-'n .
Выражение в скобках представляет собой Sl(z) и, следова-
тельно,
Rxw(z)= 2—1 Q(z)T V 1Х(ф”"
m——
ИЛИ
Rxw (z) = Q (z) Г Rw (z). (3.1 10)
Подобным же образом можно показать, что второй момент на
выходе Rxfi) определяется выражением
2 2(/)r«M*+‘-j) гГй7>)
/. *=о
или
= T 2 Rxw(* + /+ 1)Гй^), (3.111)
k=!—00
а спектральная плотность — выражением
Rx (г) = Й (г) Г Rw (г) ГГ Йг (г~*). (3.112)
Соотношения между дискретными и непре-
рывными процессами. Связь между непрерывным и дискрет-
ным белым шумом устанавливается предельным переходом от ко-
вариационной функции дискретного белого шума:
cov{w (kT), w (jT)} = Vw (k) 8K (k-j) (3.113)
к ковариационной функции непрерывного белого шума w(7), когда
выборки берутся достаточно часто:
cov{w$, w (т)} = lim cov {w (kT), w(/7)}= VW(£)6D(£ —т), (3.114)
k, /->«>
feT->t
/T->T
T->0
где
4f„(kT) = TV„(k). (3.115)
Строгое изложение этих результатов представлено в гл. 4. По-
кажем, что выражение (3.104) переходит в (3.75). Прежде всего,
заметим, что уравнение системы
х(£+"1Т) ==Ф(Т^Г1Т, kT)*(kT) + V(kT)w(kT) (3.116)
переходит в пределе в непрерывное уравнение
k=F(0x(0 + G(0w(0, (3.117)
62
когда выборки берутся часто. Матрицы в предыдущих двух выра-
жениях связаны между собой следующим образом:
F (0 = lira (/г + 1Л kT)~ , (3.118)
г->о Т
kT-¥t
G(0 = hm^?-. (3.119)
т->о Т
kT-+t
Также просто показать, что этот предельный переход дает воз-
можность перейти от дискретного уравнения
Vx(&+ 1) = Ф(Й + 1, й)Ух(/г)Ф7’(й +1, k) 1Г(/г)У#(0Гг(/г)
(3.120)
к непрерывному
Vx == F (0 Vx (0 + Vx (0 F7 (0 + G (0 (0 Gr (0, (3.121)
как это видно при подстановке ф-л (3.118) и (3 119) в (3.120) 0.
*> Для углубления знаний по теории случайных процессов рекомендуются
следующие монографии [48], [56], [129], [134], [182] (см также [289*], [290*],
[292*] Прим, ред перевода).
Глава 4
НОРМАЛЬНЫЕ МАРКОВСКИЕ ПРОЦЕССЫ
И СТОХАСТИЧЕСКИЕ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
4.1. Введение
В двух предыдущих главах уже было дано определение
нормальной случайной величины и нормального процесса. Тем не
менее, так как понятие нормального процесса чрезвычайно важно
для дальнейшего изложения, в данной главе будут приведены до-
полнительные сведения о таких процессах. Обсуждение начнем с
векторных (многомерных) нормальных процессов. Затем будет
сформулирована центральная предельная теорема, из которой вы-
текает, что многие процессы можно считать, по крайней мере при-
ближенно, нормальными.
Решение многих задач оценивания и обнаружения существенно
упрощается в случае марковских процессов. Для таких процессов
знание значений процесса в настоящем приводит к независимости
будущего процесса от его прошлого, в связи с чем понятие услов-
ной плотности вероятности оказывается очень важным. В преды-
дущих двух главах этому понятию уже было уделено достаточно
много внимания.
В § 4.4 исследуются случайные процессы в нелинейных систе-
мах. Указано, что обычные правила дифференцирования и интег-
рирования не всегда применимы к случайным процессам. Напри-
мер, интегрирование произведения двух случайных процессов
нельзя осуществить с помощью обычных правил интегрального ис-
числения. Поэтому введено понятие стохастического интеграла Ито,
благодаря которому окажется возможным решить многие фунда-
ментальные проблемы, возникающие при исследовании случайных
процессов в нелинейных системах. Затем выводится дифференци-
альное уравнение Фоккера — Планка, решение которого характе-
ризует эволюцию плотности вероятности вектора переменных со-
стояния широкого класса нелинейных систем с белым нормальным
шумом на входе. Примененный при этом подход используется в
гл. 9 для вывода модифицированного уравнения Фоккера — План-
ка. Это уравнение позволяет находить условную плотность вероят-
ности вектора состояния при известном значении вектора наблю-
дений. Предполагается, что вектор наблюдений является нелиней-
ной функцией вектора переменных состояния, значения которой из-
меряются с ошибкой. Названное уравнение является отправной
точкой при введении аппроксимации нелинейных алгоритмов
фильтрации. Читатели, интересующиеся теорией линейной филь-
трации, могут опустить при чтении § 4.4 и 4.5, так как подобные
64
вопросы, относящиеся к стохастическим дифференциальным урав-
нениям для нелинейных систем, в случае линейных систем не воз-
никают вообще или легко разрешаются.
4.2. Нормальные случайные процессы
В этом параграфе рассматриваются многомерный нор-
мальный случайный процесс и его наиболее важные характеристи-
ки. В гл. 2 уже приводились основные сведения об одномерном и
двумерном нормальных процессах. Теперь же желательно обсу-
дить некоторые свойства общего многомерного нормального рас-
пределения. Рассмотрение начнем с центральной предельной тео-
ремы. Эта теорема позволяет ожидать, что многие реальные про-
цессы будут нормальными. Затем обсуждаются неравенство Чебы-
шева и другие важные соотношения, в том числе и условные нор-
мальные плотности вероятности. Понятие условной плотности
вероятности вообще очень важно, а в теории оценивания оно явля-
ется одним из основных.
Многомерные нормальные случайные процес-
сы. Наиболее важной для данного раздела является многомер-
ная нормальная плотность вероятности, которая для вектора х с N
компонентами имеет вид
Рх (₽) = ------------ль- ехр [--— (В — u./ V-1 (В — и, ) , (4.1)
vr7 (2л)Л-2 (det Vx)1/2 L 2 r 7 x 7 J ' 7
где
14 = E {x}; Vx = var{x}. (4.2)
Характеристическая функция, соответствующая нормальной
плотности вероятности, определяется соотношением
Mx(s) = J Рх(₽)е-/₽й₽.
(4-3)
При подстановке p=Vx2 т] + цх получаем
СО 1
< = Г------ехР V ехР [“ s? (vx2 + Их)] d =
(2л)"-'2 \ 2 ) L \ J
—!----ехр [------— (т/ « -j- 2sr V 2 d тп.
(2л)^2 L 2 1 1 х "] ‘
/ т
= ехр (— s
Дополнив до полного квадрата выражение в квадратных скоб-
ках последнего выражения, можно записать
Mx(s) = exp(—s7'«ix+^-s7'Vxsj f------~-ехр[-----Hij + Vx2s) Х
/ _1\]
х + Vx2/J d у-
3—26
65
Поскольку интеграл здесь оказывается равным единице, то для
характеристической функции, соответствующей нормальной плот-
ности, получаем окончательно
Мх(s) = exp sr jix + -у sr Vxsj . (4.4)
Центральная предельная теорема. В теории вероят-
ностей и математической статистике сформулировано много пре-
дельных теорем. Под центральной предельной теоремой понимают
целую совокупность теорем с одним и тем же утверждением, от-
личающимся друг от ^руга лишь исходными предположениями
[57]; здесь будет приведена только одна формулировка. Пусть
х* есть произвольный элемент совокупности из К. одинаково рас-
пределенных независимых векторных случайных величин со сред-
ними значениями, равными нулю, и конечными дисперсиями. Вве-
дем величину
к
ъ----х'. (4 5)
В центральной предельной теореме утверждается, что распре-
деление случайной величины z при неограниченном увеличении К
стремится к нормальному, т. е. (более точно) для любого а
J pz («) d а = J -------J------- ехр ---V?1 а) d а, (4.6)
(2n)^(detVzf2
где Vz =уаг{х*} при любом I. Часто, но далеко не всегда это
означает, что
Pz («) =-------!-----у ехр (---ягУ7‘ a "J. (4 7)
(2n)w/2 (det Vz ) 2
Подходящую форму доказательства этого результата можно най-
ти в [57].
Центральная предельная теорема полезна при аппроксимации
вероятностей событий, связанных с суммами случайных величин,
не являющихся нормальными. Так, при конечном значении К для
/-Й компоненты вектора х можно воспользоваться следующим при-
ближением:
г- К 1 “
Р —«С----------------------!---e~a‘/2VH da= \—erf (—\ , (4.8)
У к Я J \VVjj)
L- 1—1 J aj
где [УХ]„ = УП.
66
Такое приближение, однако, может оказаться плохим. Напри-
мер, если компонента х}- имеет равномерное распределение на ин-
тервале [—1, +1], то
X -1
Р =0
/К Li
для любого aj, которое больше, чем ]/К. Использование равенст-
ва (4.8) в этом случае приводит к серьезным ошибкам. Для
а}< ]/К подобная аппроксимация будет полезной, однако, только
для достаточно больших значений К. Часто оказывается, что при-
ближения, построенные с помощью центральной предельной тео-
ремы, нельзя использовать на «хвостах» распределения суммы, в
то время как они вполне приемлемы для конечных интервалов, не
слишком удаленных от центра распределения.
Неравенство Чебышева. Это неравенство фактически
можно рассматривать как простейшую предельную теорему. Со-
гласно этому неравенству вероятность того, что модуль случайной
величины, среднее значение которой равно нулю, окажется боль-
ше некоторого положительного числа
дисперсии этой случайной величины к
8, меньше, чем отношение
е2, т. е.
(4.9)
нетрудно проверить [57].
от
Справедливость неравенства (4.9)
Для случайной величины, среднее значение которой отлично
нуля и равно Цх, неравенство Чебышева принимает вид
Р[|х-ИД>8]^7х/82. / (4.10)
Одна из форм слабого закона больших чисел является прос-
тым следствием этого неравенства. Рассмотрим сумму из К неза-
висимых одинаково распределенных
наковыми средними значениями цх
случайную величину
случайных величин xi с оди-
и дисперсиями Vx и введем
(4.11)
легко вычисляются: |1У=|1Ж,
Первые два момента величины у
Vy=Vx/K, так что неравенство Чебышева записывается следую-
щим образом:
^[|у-Рх|>8]^=да. (4.12)
Отсюда следует справедливость утверждения слабого закона
больших чисел. Введенную с помощью соотношения (4.11) случай-
ную величину у в дальнейшем будем называть выборочным сред-
ним. Согласно (4.12) вероятность того, что выборочное среднее у
будет отличаться от истинного среднего значения цх более чем на
величину 8, близка к нулю при достаточно больших К-
3*
67
Линейные преобразования. Линейные преобразования
нормальных случайных величин вновь приводят к нормальным
случайным величинам. Например, пусть
у = Ах + Ь, (4.13)
где А — неслучайная матрица; b — неслучайный вектор; у — век-
тор с М компонентами. Можно попытаться применить централь-
ную предельную теорему для того, чтобы установить, что случай-
ный вектор у является, по крайней мере, приближенно нормаль-
ным. Поскольку среднее значение и ковариационная матрица это-
го вектора равны соответственно:
£{у} = AE{x} + b = A[ix + b; (4.14)
var {у} = var {Ах} = AVxAr, (4.15)
то для плотности вектора у можно записать
РУ (Г) =---------------j exp [-(у — А р,х — bf (AVxAr)-1 x
(2n)M/2[det(AVxA7’)] 2
Х(т-АИх-Ь)]. (4.16)
Если у обратимое преобразование х, так что А является несин-
гулярной матрицей размера NxN, то можно определить два собы-
тия:
Е1! = {(В: х (<в) < Р); Е2 = {<в: у (<в) < А 0 + Ь}. (4.17)
Очевидно, должно быть справедливым равенство
PJJEJ = Py(EJ, (4.18)
которое можно переписать следующим образом (положив
у=Ар+Ь):
ЗД) = рх [А-1 (т-Ь)]. (4.19)
Из ф-лы (4.18) также очевидна необходимость существования об-
ратного преобразования. Дифференцируя обе части последнего
равенства по у, приходим к следующему соотношению для плот-
ностей:
Ру= dv LF7M d— = (def А-1)Рх A~* (Т — ’ (4-20)
• • -“Tv
Если х является нормальным случайным вектором, то
Ру (Y) =----—-------у ехР [---y А”' Y — A-1 b — X
(2n)w/2 (det Vx) 2
X(A *T-A ' b - Hx)] = (2n)W2 [det Vx д)[1/2 exp [ 1-(Y-
— А щ — bf (AVXAT* (у - А ;ix - b)l , (4.21)
68
т. е, является плотностью вероятности вектора у, выписанной ра-
нее для более общего случая [см. (4.16)]. Здесь уже нет необхо-
димости в использовании центральной предельной теоремы. Ана-
логично можно доказать справедливость такой записи в более
общем случае, когда М не равно N.
Часто при анализе точности измерений случайных процессов или
при решении задач нелинейной фильтрации необходимо знать чет-
вертый момент нормальной случайной величины с нулевым сред-
ним значением. Для этого момента справедливо представлено
Е {ххх2х3хД = Е {ххх2) Е {х3хД -I- Е {ххх3} Е {-Ч-Ч} "Ь Е {-Ч-Ч} Е {-Ч-Ч}*
(4.22)
Это равенство несложно получить, если воспользоваться понятием
характеристической функции. Если случайные величины имеют
средние значения, отличные от нуля, то вместо (4.22) имеем
£ {xix2x3x4} = £ {ххх2} £ {х3хД + £ {ххх3} £ {х2х4} + £ {ххх4) £ {х2х3) —
— 2£ {хх} £ {х2} £ {х3} £ {х4}.
Условно нормальные случайные векторы. Боль-
шая часть рассуждений в последующих главах книги будет осно-
вываться на понятии условных нормальных случайных величин.
В данном разделе приведено несколько теорем относительно услов-
ных нормальных случайных векторов.
Рассмотрим два совместно нормальных случайных вектора Х[
и х2 размерности и У2 соответственно, которые могут быть
зависимыми. Для первых двух моментов составного вектора мож-
но записать:
(4.23)
Vx2l
var{х}=
var
V
VX„.
(4.24)
Условные плотности вероятности в данном случае также явля-
ются нормальными, что можно показать, воспользовавшись извест-
ной формулой для условной плотности:
£х,|х2 (011102) —
^х2|х2 (02 I 01) =
Рх„ х2 (?1> ^з)
Рх, (М
Рх,, х2(?1’ ^з)
Рх, (₽1)
(4.25)
69
Плотность вероятности рассматриваемого составного вектора
Рх„ х, (Pi. ₽а) = -------!--------- ехР [--(₽ — Нх)Г V71 (₽—Их)] .
(2n)^‘+^)/2(def Vx) 2
в то время как плотности вероятности каждого вектора имеют вид
Р.,(» -------------!-----— ех₽[-ф (₽»-1‘..)гуЙ(Ь-1и]
(2n)w*/2 (def VXjj ) 2
Рх, (₽1) =---------!-----у ехР [- Y (₽1 - Нх,)г (₽1 - Их,)]
(2n)w‘/2 (det VXij) 2
Используя теперь ф-лы (4.25), можно установить следующие
очень важные соотношения:
F{хх | х2} = Их1 + VXis V-i (х2 - Их>), var {хх | х2} = - Vx„V~'VXi;
E {x21 xx} = Их1 + VXji V-; (xx - Их1), var {x21 xx} = Vx> - VXt< X
X Vx"i Vx„- (4.26)
Эти соотношения позволяют записать условные плотности вероят-
ности векторов х1 и Хг.
Заметим, что условные математические ожидания Е{Х[ |х2} и
£{х2|х1} являются линейными функциями от величин, стоящих в
условии. При изучении теории оценивания будет показано, что
упомянутые выше соотношения определяют оптимальные линей-
ные оценки для нормальных случайных величин. Полезно сформу-
лировать ограничения на функцию плотности вероятности, при ко-
торых условное математическое ожидание оказывается линейной
функцией. Можно показать [54], что если и только если
дМ „ (sx, s2) I дМ„ (s2)
_ Х„Х,Ч. 2) = _ д X, I 2) ,
osx |S1=o " <3s2 ' ’
то условное математическое ожидание двух случайных векторов
имеет линейную форму
£{хх|х2}=а + Ах2. (4.28)
Нормальная плотность вероятности удовлетворяет этому условию.
Известно большое число интересных результатов, справедливых
для условных нормальных плотностей вероятности. Например,
можно показать, что вектор
хх = хх—Е {хх | х2} (4.29)
70
статистически не зависит от вектора х2, стоящего в условии. Это
утверждение можно проверить непосредственно, показав, что х2
ортогонален к xt. Из равенств (4.23), (4.26) и (4.29) следует, что
cov{x1( x2} = FXi XJ(^-Fx Xj{x7})(x2-EXi Xi{x2})^ = Ехх.
- 4 - VX1, V-> (x2 - Их>)] (x2 - Иху} = vx - VX1 V-1VX1 =0.
(4.30)
Далее можно показать, что Xj ортогонален к EfxJxJ, т. е.
cov {х1; Е{Xj/xJ} = 0. (4.31)
Каждое из этих равенств представляет собой утверждение леммы
об ортогональном проецировании, которая существенно будет ис-
пользоваться в дальнейшем (см. § 6.6).
4.3. Марковские случайные процессы
Чтобы дать полное статистическое описание случайной
последовательности хт=[х1х2х3 ... Хк], необходимо задать совмест-
ную плотность вероятности рх($)=рХ1, х2, ..., х (₽1, ₽2, ..., ₽к),что
может оказаться просто невозможным при больших значениях К.
В предыдущем параграфе было указано, что если случайные вели-
чины являются нормальными, то знания двух моментов EfxJ и
cov{xt, х}} для всех значений индексов i и / от 1 до К (т. е. для
всех i, /е[1, К]) достаточно для полного определения плотности
вероятности рх(₽). В этом параграфе будет рассматриваться про-
цесс, для которого проблема отыскания алгоритмов оптимального
оценивания или оптимального решения так же, как и для нор-
мального процесса, существенно упрощается.
Марковский процесс может быть процессом с дискретным или
непрерывным временем. Процесс с дискретным временем (последо-
вательность) {х(^)}, tt>to, или процесс с непрерывным временем
х(^), t>to, называется марковским, если для каждого
р1|(им If Ю1В«1 = ₽«,„«,, If WlfWb - (4-32>
где X(t) = {x(s) :В дискретном случае t и т прини-
мают только дискретные значения. Таким образом, для марковско-
го процесса условная плотность вероятности его значений в мо-
мент времени t при заданном значении Х(т) зависит только от зна-
чения х(т) и не зависит от значений процесса до момента т.
Простое, но важнейшее свойство марковского процесса состоит
в том, что его совместные плотности вероятности могут быть пред-
ставлены в виде произведений переходных плотностей вероятно-
сти Переходная плотность вероятности
= (Ш-О-
71
Любую совместную плотность вероятности можно представить
с помощью условных плотностей следующим образом:
PXft A Pxk, XA_J....X, (₽*’ • • •> ?1) = Pxk I Ха_1 (₽К I BA_j) X
X P^k-i (B4-1) = Pxft| ХА_! (?* I ВА_1} Pxft_1|Xft_2 ( । ВА_2) X
k
х Рх^, (Вм) - Р„ (₽1) П । в,-,)• (4-34)
7=2
Здесь для последовательностей х, и 0, при /=1, 2, k введены
обозначения Xft и В* соответственно. Если x(t) является марков-
ским процессом, то
(fb I В,^, ) - РХ;В;_1 (?> I - Р„. ?,->) (4-35)
и для совместной плотности вероятности получаем
k k
Pxh (В«) = Рх. (₽1) П РхЛх.^ I ?7-1) = Рх. (W П Рх. X , ?,_,)>
Г1- J J L J 1
7=2 7=2 1
(4.36)
т. е. начальная одномерная плотность вероятности рх. (Pi) и пе-
реходная плотность вероятности в этом случае полностью опреде-
ляют совместную плотность pxk (Bft).
Пример 4Ц. Приведем полезное представление для совместной плотности
вероятности рх* (Вк) ^мерного марковского процесса хл, если *>
xA-pi = Фа-pi, k Га wfc, й=1, 2, . . ., К,
где W), «белый» нормальный процесс, для которого
E{wh}—0, cov{wfe, w;} = Qfe6K(ft —/);
Е <Xi> = P-i, var{x1}=V1, covfXi, wft} = 0.
Будем предполагать также, что Xi является нормальной величиной В этом слу-
чае Хл+! как линейная комбинация нормальных случайных величин также яв-
ляется нормальной Из § 2 4 и 4 2 следует, что для условных моментов вели-
чины Хй+1 можно записать
Е{ xa+i I ХЧ = ф*+1. k var { xa+i I Ч = га Qa Г( .
Таким образом, на основании ф-лы (4 36) получаем
*> Вместо x(th) будем использовать более простые обозначения Хл и x(fe).
(Прим, авт)
72
exp [ — -у- (gx — рУ УГ> (gj — th) I
Рхл(вк)= J x
(2n)v/2(detV1) 2
K exP [ ~ "y (₽* ~ Ф4 ,4-1 &k-if ( r4-i Qa-i r£_j) 1
ХП (2n)V/2
k=2 ’
(gft — ФА> *-i ₽4-i)j
[det ( Гл_, Qft_j Г£_,)] 2
Подобные представления являются чрезвычайно важными для последующе-
го изложения Во многих случаях оказывается желательной несколько иная
форма записи совместной плотности вероятности:
Рх (Вк) ~
Л
&l)-NK/2
~ Ф4, 4-1 &4-1)Г ( Г4-1 °4-1 Г4-1) ' (&й ~ Ф4, 4-1 &4-1)
J. К _1
<det VJ 2 П [det ( rA_j Q4_1 Г[_,)] 2
4—2
Отсюда, в частности, очевидно, что нельзя получить аналог этого представ-
ления для процесса с .непрерывным временем, неограниченно уплотняя моменты
отсчетов Действительно, при неограниченном увеличении К приведенные выра-
жения теряют смысл Однако в дальнейшем будут рассматриваться отношения
плотностей вероятности, для которых при увеличении К оказывается возмож-
ным получение полезных и имеющих смысл результатов .
Марковский процесс — однородный, если pXfe) Xfe_j (pft, pft_i)
не зависит от k. Говорят также, что такой процесс имеет ста-
ционарный механизм перехода. Для однородного марковского
процесса pXfc> Xj (Ph, Р3) зависит только от разности k — j ('или
th—1}). Механизм перехода из состояния х3 = Р3 в состояние xft = pft
за k—j шагов для (однородного) марковского процесса характе-
ризуется условной плотностью вероятности pXft; (Ph, Pj) • От-
метим, что однородный марковский процесс не обязательно ста-
ционарный, даже если он имеет стационарный механизм перехода.
Так как pXftj Xfe_j (Ра, Pa-j) является условной плотностью вели-
чины хй при условии, что фиксировано значение х^-ь то должно
выполняться равенство
р,„. (fe. ?.= !• (4.37)
•С н «—1
73
Полезное соотношение для марковских необязательно однород-
ных процессов может быть получено следующим образом. Извест-
но, что
J Рхь- xk-r V-2 = Рх*- хА_2 ^-2)’ (4.38)
— оо
Кроме того, для марковского процесса из (4.36) имеем
Py.h, х х (Р*’ Pft-1’ Pft-2) = Pxftlx.
X ^’xfe_1j xft_2 ( Pfe-2) ^xft-2 ( Pft-г)- (4.39)
Поскольку pxki Xft_2(₽ft, PA_2) = Pxft|xfe-2(Mfe_2) Pxft_2(₽fc-2),
то, объединяя три последних равенства, получаем уравнение
J Pxkx/!_1(^> Pfe-1) PXft_p xfe_2( Pft-p Pfe-2)^Pfe-l = Pxft, xA_2(Pft> Р/г-2)’
(4.40)
которое известно как уравнение Колмогорова — Чепмена.
Полезно рассмотреть эволюцию плотности pXfc (Р/0 как функ-
ции от k. К сожалению, на основании ур-ния (4.40) это сделать
нелегко. Если бы оказалось возможным найти уравнение, описы-
вающее эту эволюцию, то тем самым был бы решен вопрос об
определении этой плотности вероятности для большого класса не-
линейных систем со случайным входом. Известно, что
Pxk, х (Pb P*-l) = Pxftlx (PfelPfe-1) Рх (Pft-l)’ (4-41)
« ft—1 «I ft—1 ft—1
В этом выражении для простоты дальнейших рассуждений при-
нято, что х — скалярная величина. Интегрируя обе части равенст-
ва (4.41), получим
Pxft(Pft)== J ^ftl*ft_1(Pft^*-i)^*ft_1(^-i)^P*-r
— СО ’
Введем теперь следующие обозначения: th—t, —А/, Xk=x(t),
Xk-i=x(t—At). Тогда
Px(/)[p(oi= J Px(oix(<_AOiP(0ipa-A0ipx(<_AO[pa-A0ix
Xd$(t — At). (4.42)
Воспользуемся теперь характеристической функцией условной
плотности рХ({-д /)[₽ (t) | р (f — At)]:
Мх (01Х (/-д/) (s) = J e~S [₽ <о~₽ </-Д,] Рх (/)|х (<_д<) IP (О IР а - Д 01 d р (О,
(4-43)
74
которая является прямым преобразованием Фурье функции
p[x(t) |x(V— АО]/ умноженной на es₽(<-A<> . Так как справедливо
и обратное преобразование
Р, и№ „-до 1₽ (') I ₽ « - Л 01 = 24j J « '*•
(4.44)
то можно записать
₽. <0 1₽ (01 = ~ j j’ е’18 „_д„ (s) р, X
X$(t — M)\dsd$(t — Af). (4.45)
Но характеристическую функцию можно представить в виде сле-
дующего разложения по моментам относительно значения
О)|х «-до = 1 + S (0 — ₽ (^ — А 01. (4.46)
1=1
где m‘[x(t)~ x(t — A/)] = Е {[%(£) — x(t — Af)]'|x(f — A/)j. (4.47)
Следовательно,
Wf>«l“S7 J ? e’«(1 + jm'[₽(0 -
— OO —/00 I 1=1
-₽ (t - A 01 (,_д<) [₽ (t - A 01 dsd ₽ (t - A t). (4.48)
Заметим, что плотность вероятности pX(t)[0(f)] может (а в об-
щем случае и будет) зависеть явно от времени, так что здесь более
точным было бы обозначение РхщЕРГО» И- Однако ради простоты
здесь будет использоваться обозначение Px(t)[₽(Z)]', ПРИ этом надо
помнить, что pX(t)[^(t)] может явно зависеть от времени.
Далее, так как
1 С° /_ suesip to-р «-до] ds = / —P(z~
231 [Ж0Г
i= 0, 1, 2, • • •, (4.49)
то из (4.48) имеем
pxW [₽(0]-Рх(<-д/)1Р(^-Л01 =
Е” (-!/ ——AQJ) { рХ(^А<) [р(< —AQ1})
‘1 [ар(оР
<=1 н ’ ы=о
75
Наконец, разделив обе части этого равенства на А£ и устремив Л/
к нулю, получим
ё>Рх(О[Р(0] у, (- 1/ [р (0 — p(Q]} {Рх(о[р (<)]})
dt М [5₽(01‘
(4.51)
Это уравнение в частных производных называется стохастиче-
ским или кинетическим уравнением. Его решение необходимо
отыскать при следующем начальном условии:
Px(<=u[₽a=Q] = Po[₽0- (4.52)
которое представляет собой известную плотность случайной вели-
чины х в начальный момент.
Величина тг[₽ГО—₽-ГО] есть предел при Л^->0 отношения
i-го статистического момента процесса x(t)—x(t—АО при условии,
что x(t—А0 = ₽(£—At), к приращению аргумента At. Таким обра-
зом, если положить p_(^=lim ₽(^—то выражение
Л^О
т{ Гр (t) — р (0] = lim ^L(O-P(<-A.O] = lim — х
д(^о д< д^оД*
X J [Р(0 — И- A0N₽(O (4.53)
—оо
можно записать в следующей удобной форме:
оо
т1 [р (0 - р_ (/)] = lim -i- f (АР)' (<_д<) [Ар | р (t - А 01 d Ар =
Л I J 1
— со
= lim , (4.54)
д/->о Л t
где использовано обозначение Ax=x(t)—x(t—At).
Очень интересным и важным является случай, когда процесс
x(t) удовлетворяет дифференциальному уравнению
= /[х(0] + ^(0- (4.55)
в котором w(t) — «белый» нормальный случайный процесс с нуле-
вым средним значением и
cov {ш (0, w (т)} = (/) (t — т). (4.56)
Можно показать, что в этом случае
^1Р(0-Р_(0] = /1Р(0];
[Р(О-Р_(О] = 41,(0];
т1 [Р(О - р_(0] = 0, г->2.
76
(4.57)
Следовательно, ур-ние (4.51) принимает вид
9рх </) (₽ (01 _ э {f (₽ (01 Рх w (₽ (0]} 1 ф э*рх (0 [₽ (ci
dt ~ dW) г 2 [Эр(OF ' ?
Это уравнение известно как уравнение Фоккера — Планка. Оно
решается при граничном условии Ро[₽(^о)]- Если в качестве
граничного условия используется Px(t„) [ ₽ (to) ] = 6d[ ₽ (М—₽о], то
очевидно, что функция плотности вероятности с таким граничным
условием является функцией переходной плотности вероятности
\ (0 IP (0] = рх W]x (,о) IP (t) P(Q] 4px w, x (M IP (0- P (Ш (4-59)
В этом случае уравнение Фоккера — Планка можно переписать
следующим образом:
х </„)!₽ W. ₽(-'»)] д {ИР х(^ [₽ (О’ ₽('»)!}
dt " Фр (г) ф
| 1 ЦГ /А д2рх (б. *(1,) [Р (О’ Р(0)] М gQx
+ 2 Та,(О [д р (<)]2 • '
Это уравнение часто называют прямым уравнением Колмогорова.
Если выписать сопряженное ему уравнение, то получим обратное
уравнение Колмогорова
d7xW. Х(/О)[Р(О. РО (.o<^dPXW, Х(/О)1₽(0, Р(0)]
dto ~ ~ dp(f„)
____L v (П ^x(f).xu0)[P(Q’ РО ,4 6П
2 [ЭР(0)]2 * * * * * В ’ ' '
которое оказывается очень полезным для теории стохастического
управления. Обратное уравнение можно вывести точно так же, как
и прямое. Оба уравнения иногда называют также диффузионными
уравнениями. Они подробно обсуждаются в монографиях по теории
случайных процессов [28], [56], [257].
В дальнейшем в основном будут рассматриваться векторные
случайные процессы. Прямое и обратное уравнения, только что
полученные, можно модифицировать таким образом, чтобы они
оказались справедливыми и для векторных процессов. Это будет
сделано в следующем параграфе, где будет получено модифициро-
ванное уравнение Фоккера — Планка для условной плотности
вероятности вектора переменных состояния х при фиксированных
наблюдениях Z ,
Пример 4.2. Рассмотрим решение уравнения Фоккера—Планка для очень
простого случая Пусть модель «сообщения» является линейной, т е.
х =— ах (t) -|- w (t), E{w(t)}=0; cov {w(t), w (t)} = 4fH,6D (t — t).
Уравнение Фоккера—Планка в этом случае имеет вид
dpxW. x(/o)t₽(o. PW1 з{₽(о7х(/), я(М[₽(0> ₽№)]} ,
dt ~а арсо +
2 [Э₽(/)]2
77
Это уравнение можно записать в следующей более простой форме, если
опустить обозначения 0 и Zo
fr[x(0J _ а {Л- (Ор [%(/)]} 1 d2p[x(t)]
dt дх (/) 2 w [дх (О]2
Предположим теперь, что нормальное распределение с дисперсией Vx(t) =
= <J2‘x(t) н плотностью
1
р к (01 = ——--------ехР
/2лоА(0
£ к (0~Нх(0121
2 <?х (() I
является решением этого уравнения После подстановки этой плотности в урав-
нение н сокращения экспоненциального множителя получим *>
_ 1 dqx(Z) + у(0-^ (0 dpx(t) + k(0~tu (Q]2 d°xW
2/2ла^(0 dt /2лоЗ(0 dt 2/2n<rJ(f) di
_ a _ ay(0 k (0 —Hx (01 1 f — 1
У2л <jx (t) у2л аз 2 j у2л <j* (t)
k(n-Hx(oq
/2Наз(0 11 •
Выделим в обеих частях уравнения слагаемые, содержащие x(t) и pxfO и
ие содержащие x(t) и ЦхС^), и запишем
- ---- = — 2а <?х (t) Yw;
di
dfixtf) , г(0-Цх(0 daxW h ^kW-Hxtt)]
. tt" ' = — uX (i I .
dd 2o£ (/) dt 2q* (t)
Если теперь первое выражение подставить во второе и вспомнить, что
Ех = о2х, то придем к следующим уравнениям
«ДМП du,x(t)
=-20^(0^^; -й^_ = -аих(().
at at
Первое из этих уравнений уже встречалось ранее в одной частной задаче и яв-
ляется уравнением для дисперсии Второе уравнение описывает изменение во
времени среднего значения Их решения легко находятся, например, так, как
это было сделано в § 3 5
Попутно при рассмотрении данного примера еще раз доказано утвержде-
ние о том, что случайный процесс на выходе линейной системы, на вход кото-
рол воздействует нормальный ппоцесс, также является нормальным Можно
было бы теперь решить обратно” диффузионное уравнение с тем, чтобы полу-
чить результаты, чрезвычайно полезные при решении задач теории стохасти-
ческого управления [258] Однако этот вопрос не будет здесь исследоваться.
Отхметим только, что решение обратного уравнения находится в основном тем
же способом, как и решение прямого уравнения
Чтобы продолжить обсуждение вопросов преобразований мар-
ковских процессов в нелинейных системах, необходимо уметь с
*> Напомним снова, что p[xfOJ зависит от времени, т. е. p[x(t), f], поскольку
Их и о2х — функции времени. (Прим авт )
78
величайшей осторожностью обращаться с непрерывными процесса-
ми. Здесь очень легко можно совершить ошибки, которые приве-
дут к совершенно неверным результатам. Чтобы избежать этих
ошибок в следующем специально выделенном параграфе, рассмот-
рим стохастические дифференциальные уравнения и их примене-
ние для получения дифференциальных уравнений для условных
плотностей вероятности.
4.4. Стохастические дифференциальные
уравнения
В этом параграфе исследуются многие фундаментальные
вопросы, касающиеся случайных процессов, в частности преобра-
зования процессов в нелинейных системах Вновь обсуждено поня-
тие белого шума и выявлена связь этого шума с вьнеровским про-
цессом Обсуждаются трудности, возникающие при отыскании
уравнения для дисперсии в случае непрерывной системы, возбуж-
даемой белым шумом Здесь эти трудности преодолеваются путем
введения стохастического исчисления и стохастических дифферен-
циальных уравнений.
Белый шум. Многие реальные случайные процессы явля-
ются приближенно нормальными и приближенно стационарными.
Часто они имеют энергетический спектр, мало отличающийся от
равномерного в полосе частот, намного большей, чем полоса про-
пускания исследуемой системы. Вместо таких процессов с матема-
тической точки зрения удобно использовать белый шум, даже
несмотря на то, что такой процесс лишен физического смысла, по-
скольку для его генерирования требуется бесконечно большая
мощность. Понятие белого шума можно отнести к той же совокуп-
ности категорий, которой принадлежит и понятие импульсного от-
клика линейной системы. Важную роль играют импульсные функ-
ции — дельта-функции Дирака, которые часто определяются как
пределы некоторых последовательностей функций. Аналогичным
образом можно рассматривать и белый шум.
Будем говорить, что непрерывный нормальный процесс являет-
ся белым шумом с нулевым средним значением, если
£{w(f)}=0; cov{w(0, w(т)} = (<)SD(t — т). (4.62)
Это определение не является строгим, так как дельта-функция
Дирака может быть строго определена только в терминах интег-
ральных выражений, таких, как
* т+|е|
f f>D(t — x)dt--= 1; lim i 6D(t — x)dt — 1. (4.63)
4 e- ^0 ', ,
t—|e|
79
Дельта-функцию Дирака можно рассматривать как предел обыч-
ных функций времени, которые являются, например, симметричны-
ми при сколь угодно малом положительном значении е:
6ьа-т) =
—, т------<t<_X---- ,
е 2 2
О в противном случае.
(4.64)
При малых значениях Т можно также ввести процесс w(feT) с
дискретным временем, обладающий основными свойствами белого
шума:
£{w(feT)}= 0;
cov {w (kT)} ,w (/Т)} = Vw (kT) (k - jT) = (k _ /7).(4.65)
При e->0 или при Г->0 в пределе получаем импульсную функцию и
непрерывный белый шум соответственно.
В предыдущей главе для системы, описываемой уравнением
k = F(f)x(0 + G(/)w(0;£{x(fo)} = O; (4.66)
var{x(Q} = VX(Q
и возбуждаемой некоррелированным с x(t0) белым нормальным
шумом с нулевым средним значением, путем дифференцирования
выражения
Vx(f) = var{х(0} = Е {х(0хт(0) (4.67)
было получено следующее уравнение для ковариационной мат-
рицы:
Vx (0 = Е {х (0 хт (0) + Е {х (/) хг (f)} = F(t)E{x (t) хт (f)} +
+ G (/) E {w (0 xT(0) + E {x (0 xT (t)} FT(f)-\-E{x (t) w7' (0} GT (t).
Воспользовавшись теперь обозначением ковариационной мат-
рицы, запишем
Vx (0 = F (/) Vx (0 + Vx (0 Fr (/) + G (0 E {w (0 xr (0} +
+ £ix(/)wr(0}Gr (0- (4.68)
Так как E {x (to) w7' (/)} =0 для t~^t0, то слагаемые, характе-
ризующие взаимную корреляцию, могут быть записаны в следую-
щей форме:
t
Е {x(t)wT (t)} = J<t>(f, t)G(t)£ {w(t) wT(t)} dx =
^0
t
= $<P(t, x)G(T)4^(t)8D(x-t)dx. (4.69)
Так как 6-функция здесь располагается на конце интервала
интегрирования, то значение этого интеграла зависит от использу-
80
емого типа дельта-функции. В данной главе используется симмет-
ричная дельта-функция, интеграл от которой по области, лежа-
щей справа от точки т=0 равен 1/2 и равен интегралу по области
слева от этой точки. В этом случае равенство (4.69) принимает
вид
Е ( х (0 wr (0} = -L G (0 Ф. (0. (4.70)
Аналогичные рассуждения приводят также к равенству
Е { w(0 хт (0 } = у 4»w (0 GT (0. (4.71)
Таким образом, получаем уже известный результат:
Vx (0 = F (0 Vx (0 + Vx (0 F7" (0 + G (0 (0 GT (0 (4.72)
с начальным условием Vx(^o)-
Если дельта-функцию определить как несимметричную функ-
цию, для которой
х 0
J 8D(t)dt = 1 — a; J 8D(f)dt = a, (4.73)
О —=0
ТО
Е { w (0 хт (0 } = (1 - a) Ф. (0 GT (0 (4.74)
и
E{x(t)wT (0}=oG(0Vw(0. (4.75)
Следовательно, снова получаем уравнение
Vx (0 = F (0 Vx (0 + Vx (0 Fr (0 + G (0 (0 GT (0. (4.76)
Правильный ответ для ковариационной матрицы Vx получается
даже при различных представлениях матриц: E{x(t)wT (t)} и
E{w(t)xT(t)}.
Можно было бы привести разумные соображения в пользу ис-
пользования симметричной дельта-функции. Например, дельта-
функция часто используется в качестве ковариационной функции,
которая обязательно должна быть симметричной. Такой подход
при аккуратном обращении может быть использован без особых
затруднений при исследовании линейных систем Однако в случае
нелинейных систем необходимо развить новый способ решения
этой проблемы.
Полезно также повторить приведенный выше вывод, начав с
дискретного времени, и перейти затем к пределу, увеличивая чис-
ло отсчетов на интервале наблюдения с тем, чтобы проверить воз-
никает ли при этом уже отмеченная трудность неоднозначности.
Рассмотрим дискретный аналог уравнения системы (4.66) в фор-
ме (см. § 3.5):
х (МИТ) = Ф (Г=ЛТ, kT) х (kT) + Г (kT) w (kT), (4.77)
81
где
Ф(Г+~1Т, kT)=l + TF(kT); Г (kT) = ТG(kT). (4.78)
Так как E{x(kT)wT(kT)} =0, то уравнение для ковариацион-
ной матрицы, соответствующей ур-нию (4.77), на основании ре-
зультатов § 3.5 примет вид
Vx (F+~IT) = Ф (МЙГ, kT) Vx (kT) Фт(k+TT, kT) +
+ Г (kT) Vw (kT) Гт (kT). (4.79)
Теперь при увеличении числа отсчетов получаем уравнение
vx = ДД = Нт= F (t) Vx (t) + Vx (t) Fr (t) +
al k->a> 1
T~>0
kT->t
+ G(04M)Gr (t), (4.80)
которое является уравнением для ковариационной матрицы при
непрерывном времени. При выводе этого. уравнения трудность,
имевшая место при выводе аналогичного соотношения сразу для
непрерывного времени, не возникла благодаря тому, что
Е {х(£Т) wT (kT)} = 0 Если положить t = kT, dt = Т и2)
dx (t) = х (k + IT) — x (kT) = x (t + dt) — x (t), (4.81)
то ур-ние (4.66) можно записать следующим образом:
dx (f) = F (t) x (t) dt 4- G (t) w (t) dt
или
dx(t) = F(t)x(t)dt + G(t)du(t), (4.82)
*> Указанное представление не является, конечно, единственным Можно
было бы использовать для Ф(й+1Т, kT) матрицу переходов, получаемую из
уравнения
ЙФ(/, Т)
----*-^-=Р(/)Ф(/, т), Ф(/о. 4>) = 1
ш
при /=(А+1)Т и х—JzT. Кроме того, для Г(6Г) можно было бы использовать
соотношение
(A+D т
V(kT) = J Ф(Й4- IT, T)G(T)dT.
kT
В обоих случаях пределы ур-ний (3 118) и (3 119) остаются справедливыми
(Прим, авт.)
2> Здесь используется обозначение х= (d/dt)x(f) =dx/dt для производной по
времени вектора x(t). Скалярная величина dx(t) обозначает М-мерный объем
dx = dxtdx2 ..dxN, а вектор dx(t) с П компонентами — дифференциал х (Прим,
авт )
82
где
du (f) = w (t) dt. (4.83)
Хотя ф-лу (4.82) можно получить формальным умножением ур-ния
(4.66) на dt, в дальнейшем будет показано, что это слабое разли-
чие оказывается чрезвычайно важным. Стохастический процесс
u(t), определяемый соотношением
t
u (t) = J w (т) d т, (4.84)
о
называется винерОвским процессом, свойства которого достаточно
подробно обсуждаются в дальнейшем.
В и н ер о в с к и й' пр оцесс. В дальнейшем изложении вине-
ровский процесс играет очень важную роль. Этот процесс был вве-
ден Н. Винером в качестве простой модели броуновского движе-
ния. Пусть u(t) обозначает положение некоторой частицы в момент
времени t, которая при t=0 находилась в начале координат. Бро-
уновская частица передвигается под воздействием соударений с
аналогичными частицами. Смещение некоторой частицы в течение
интервала времени (s, t), намного превышающего среднее время
между двумя следующими друг за другом столкновениями, можно
рассматривать как сумму большого числа малых смещений. Следо-
вательно, здесь имеется возможность применить центральную пре-
дельную теорему, что позволит функцию распределения прираще-
ния u(s)—u(t) аппроксимировать нормальным распределением.
Винеровский процесс u(t) определяется как интеграл от стаци-
онарного нормального белого шума w(t), имеющего нулевое сред-
нее значение, т. е.
t
u(t) — j* w (X) dk, и (0) = 0,
6
где
cov {w (0, w (т)} = (t — t).
(4.85)
(4.86)
Легко показать, что
1*^(0 = ^{«(O) = 0;
cov {и (t), и ($)} = E
t s
w (Xx) w (X2) d Xx d X2
о о
— Y^minfs, t}.
Кроме того, для приращения u(s)—u(t) можно записать
83
Отсюда следует, что приращение винеровского процесса имеет
среднее значение, равное нулю, и дисперсию
var {и (s) —и (/)} = Е С С (к2) d k-^d к2\ = | s — 1|. (4.90)
Винеровский процесс часто называют также процессом броу-
новского движения или процессом Винера — Леви [56, 182]. Этот
процесс имеет много интересных свойств, из которых здесь отме-
тим лишь следующие:
1. Винеровский процесс является процессом с независимыми
приращениями, т. е. если принять и(0)=0, то случайные величины
u(tt)—u(tQ), u(tz)—u(th)—u(th-t) независимы для
tk>th-\> ... >to^O. Так как случайно величина ы(^+т)—«(^-iT-t)
имеет ту же функцию распределения, что и приращение
u(tk)—u(th^), то винеровский процесс можно назвать процессом
со стационарными независимыми приращениями.
2. Винеровский процесс является марковским процессом, так
как
Ри (ts)i(u (/,). и (t2) (Тз I Yi> Тг) Ри (<3)]u (t2) (Тз I Ya)>
< ^2 ^з-
(4.91)
Это соотношение легко доказывается, если записать
ы (t3) - С w (к) d к — Г w (к) d к + (' w (к) d к = «. (t2) + f w (к) d к.
Отсюда получаем
Е {и (t3) | и (Z2)} = и (f2); var {и (t3) | и (Q) = (t3 — Q
Точно такие же значения имеют E{u(t3) |u(Z2), и
var{n(f3) |«(^),
3. Винеровский процесс является мартингальным процессом, т. е. •
его условное математическое ожидание в момент времени th при
фиксированных значениях u(t0), и (tx), .... u(th-i) равно последне-
му наблюдаемому значению u(th-i), где tk>tk-i>...>t0. Таким
образом,
(4.92)
Отметим здесь, что марковский процесс не обязательно является
мартингальным процессом.
4. Винеровский процесс обладает свойством осцилляции Леви,
т. е. если r=t0, ..., th — разбиение интервала [О, Г] такое, что
/о=О, th=T, то [56]
Ит S [«(6г)--м(^-1)]2 = ГФ-
"“( **
(4.93)
84
где сходимость суммы понимается в среднеквадратическом смысле.
Приведенные соотношения будут использоваться в дальнейшем
при обсуждении преобразований случайных процессов в нелиней-
ных системах.
Стохастический интеграл и стохастические
дифференциальные уравнения.
Винеровский процесс был определен выше как интеграл от
белого шума w(t), а именно, u(t) = § w(K)dk, ы(0)=0. Дж. Дуб
о
показал [56], что реализации винеровского процесса являются не-
прерывными функциями, но не имеют ограниченной вариации и
почти нигде не дифференцируемы. Причину недифференцируемо-
сти реализаций частично поясняет соотношение (4.90), из которо-
го следует, что var{u(/+r) — u(t)} =Чгют, т^О, так что среднеквад-
ратическое значение приращения ы(/+т)—u(t) имеет порядок
Тогда производная приращения имеет в среднем порядок
отношения V т/т, которое стремится к бесконечности, если т стре-
мится к нулю.
Таким образом, если u(t) — винеровский процесс, то производ-
ной du(t) трудно придать какой-либо разумный смысл. Можно
dt
попытаться также ответить на вопрос, определен ли для произ-
вольной непрерывной функции т}(/, X) следующий интеграл Ри-
мана:
t
(t, А.) d X. (4.94)
J d A
о
Интегралы такого типа уже встречались ранее, когда исследо-
вался отклик линейной системы на воздействие в виде белого
шума. Если система описывается уравнением x=F(t)x(t) +
+ g(t)w(t), х(0)=0, то
t t
х (/) = у ф (t, A.) g (X) w (1) d 1 (t,
о b
где т, (t, A) = Ф (/, X) g (A)
Смысл последнего интеграла неясен, так как пока что отсутст-
вовало строгое определение для производной du(A)/dA.
Один из возможных способов преодоления этой трудности со-
стоит в том, чтобы попытаться использовать понятие интеграла
Лебега — Стилтьеса, записав
t t
!(/)= СтЗ(/, A)^^-dA= Сч(/, l)d«(A). (4.96)*
J d A J
о о
A)^MrfA, (4.95)
d A
85
Однако этот способ не устраняет трудности, так как u(t) не
является функцией с ограниченной вариацией, и следовательно,
интеграл Лебега — Стилтьеса оказывается неопределенным.
Естественным статистическим обобщением интеграла Лебега—
Стилтьеса является стохастический интеграл, при определении ко-
торого последовательность интегральных сумм сходится к значе-
нию интеграла по вероятности *). Именно замена сходимости в
обычном нестатистическом смысле сходимостью по вероятности
позволяет преодолеть отмеченную выше трудность.
Пусть |(0 —векторный случайный процесс с М компонентами,
a X) —произвольная матричная функция, кусочно-непрерывная
при всех Хе [0, I] и зависящая, самое большее, от настоящего и
прошлых значения процесса |, т.е. от |(т), Os^tsCX. Это ограниче-
ние можно записать следующим образом:
cov{i](f, Xi), |(Х2)}=0 для X2>Xi.
Обозначим через В множество функций X), на котором
может быть определена вероятностная мера. В множестве В выде-
лим следующие три подмножества:
1. Е° — множество функций из Е, кусочно-постоянных по X на
интервале [0, 0.
2. В1— множество функций из В, интегрируемых в квадрате по
X на интервале [0, 0.
3. В2 — множество функций из В, интегрируемых в квадрате по
X на интервале [0, 0 с вероятностью 1.
Для любой функции из В0 существуют точки /2, ..., 0, ...,
такие, чтот](£, Х)=т](Е 0) при i0^X<0+i; множество {0} являет-
ся множеством точек, в которых функция т] (t, X) имеет скачки.
Стохастический интеграл или интеграл Ито для таких функций
можно определить следующим образом:
1(0= [ч(0 ^)d§(A) = S’3(0 0) [5(0+1)-5(0)]- (4-97)
6 I
Если i)(£, Х)еЗ, но не принадлежит подмножеству В0, для
обобщения определения (4.97) используется традиционный пре-
дельный переход [56]
t 4-1
!(0 = ^(0 X) d § (X) = L.LM S 4(0 0) [5 (0+1)-5(0)]. (4-98)
0 б-»о '=>
1де L. ЕМ обозначает предел в среднем (при &->оо и б->0), и
> 0-1 0-2 -> ' ' •> 0 — 9;
6 = max [ O+i — 0 }> для всех I-
*> Последовательность случайных величин Г)лг сходится по вероятности к
случайной величине т], если при Л/->оо вероятность того, что |т]лг—ч | >е, стре-
мится к нулю для любого е>0, т. е, если lim />[|т]ЛГ—т]| >е>0]=0. (Прим.
N—co
авт.)
8G
Следует отметить, что стохастический интеграл может быть,
определен и несколько иными способами. Например,
I (0 = L.LM. (t, Q (t.+1) - § ft)], (4.99>
б->о ‘=1
где или при произвольно малом положительном е
Г(0 - U.M.21,(11 ',+1 -,) + ’i(l' '<> (5 (f,.+1)- Jft)]. (4.100)
б-»0 1=1
В общем случае определения (’4,99) и (4.100) не эквивалентны
определению (4.98). Если т) принадлежит множеству В0, то нетруд-
но видеть, что три указанных определения приводят к одному и
тому же результату, это же можно сказать и относительно других
возможных определений. Однако, если т] не является элементом
подмножества 3°, то эти определения не являются, вообще говоря,
эквивалентными из-за свойства осцилляции Леви. Хотя определе-
ния (4.99) и (4.100) и имеют некоторые преимущества, далее бу-
дет показано, что определение (4,98) обычно является более под-
ходящим. Связь между различными определениями стохастическо-
го интеграла и обычным нестатистическим определением более под-
робно будет обсуждаться позднее.
Интеграл, определенный с помощью соотношения (4.98), будем
называть интегралом Ито [241]. Его можно рассматривать каю
линейное преобразование ц, т. е.
t t t
paTjft M + kft *)]«5ft) = a J 4ft X)dg(X) + ₽ JTft X)d§(X),
0 0 0
для каждой пары допустимых функций ц и у и для любых дейст-
вительных матриц аир.
Если т] принадлежит подмножеству В1, а |ft) является вине-
ровским процессом uft), то интеграл Ито обладает следующими-
двумя свойствами, полезными для последующего изложения:
7] (t, к) du (X)
(4.101>
р г t
Е И 7] (t, к) du (X) J т] ft т) du (т)
(о [о
= j£{T3ft X)Vwijrft^)}^-
0
(4.102>
Доказательства этих свойств основываются на том факте, что
приращение [uft,+i)—uft,)] статистически не зависит от T]ft, t,)
для j<i по условию и от [u(ft+i)—uftft], j=/=i согласно свойст-
ву винеровского процесса о независимости приращений на непересе-
кающихся интервалах. Для простоты здесь приведем доказатель-
ство лишь для случая, когда t]eS°; доказательства для более об-
щих случаев проводятся аналогично.
87
Рассмотрим сначала равенство (4.101). Используя (4.97), за
пишем
-.Е J" (t, X) du (X)
6
ДЕ ^(f, у [up.+1)_u(Q]
= О[и(^.+1)-и(^)]}.
Так как т](7, \ti) и [и(Тг+1)—u(fj] статистически независимы,
то среднее значение произведения можно записать как произведе-
ние средних значений. Тогда
t
J 7] (t, X) du (X)
о
= S£0i(U/)}£{u(^)-i*(O}-
Так как среднее значение приращений винеровского процесса
равно нулю, то правая часть последнего равенства также оказыва-
ется равной нулю, что доказывает справедливость равенст-
ва (4.101).
Аналогичным образом проводится доказательство справедливо-
сти соотношения (4.102). Воспользовавшись сначала определени-
ем (4.97), запишем
t
Л (f) = Е J 7] (t, X) du (X) J т] (t, т) du (т)
J
X [U (ti+l) — u (0] [u (ti+l) — U (^)f 71? (t, tj) .
В силу независимости приращений имеем
Вновь, используя независимость приращений и равенство
(4.90), можно записать
^{[u ( ^+i) — u &)] [u ( ^ч-i) — u ipw> i _ у
Таким образом, для A(f) получаем
Л(0 = £Е{^, 04W(f, Q)(Z.+1_Q.
I '
Так как т](£, X) является элементом подмножества S0, то пра-
вая часть последнего равенства может быть записана как обычный
интеграл A(^)=J E{t](f, X)TwT]t(^ X)} dX, что завершает доказа-
о
зельство.
88
Если т) не принадлежит подмножеству Е° и используется отлич-
ное от (4.98) правило интегрирования, то равенства (4.101) и
(4.102) могут оказаться несправедливыми. Это одна из главных
причин, из-за которых в данной книге выбирается определение
(4.98), поскольку соотношения (4.101) и (4.102) будут довольно
часто использоваться в дальнейшем. Необходимо также, чтобы
функция т) принадлежала подмножествам S1 или Е2, так как в
противном случае интегральные суммы не будут, вообще говоря,
сходиться по вероятности или с вероятностью 1 соответственно.
В дальнейшем потребуется выражение для дисперсии диффе-
ренциального приращения du. На основании (4.90) можно запи-
сать var {u(s)—u(7)}=Tw|s—ф Если теперь положить s = t+dt,
то приращение u(s)—u(t) можно записать как du(Z). Тогда при
dt^O получаем представление
var{du(0} = (4.103)
где cov {w(T), w(t)} =Tw6d(^—т).
Этот результат еще раз подтверждает, что приращение du
имеет порядок У dt, вследствие чего производная du/dt не суще-
ствует.
Нетрудно показать, что для величины [du(^)duT(Z)] все момен-
ты, начиная со второго, имеют больший порядок малости по срав-
нению с dt. Следовательно, при достаточно малых значениях dt
получаем, что E{du(^)duT (t)})dt = y¥^ и E’{[du(0duT(Q]ft}/W = 0
для k = 2, 3.........Отсюда следует, что величина Au(t) Аит (t)/dt
фактически является детерминированной и' равной Tw для беско-
нечно малых значений dt. Тем самым установлено следующее важ-
ное соотношение:
Р (du (t) dur (t) 1 _du (<) dur (t) _ш
£ I dt) J ~ dt ~ w’
из которого следует
E {du(0 dur (0) = du (0 dur (0 = dt. (4.104)
Таким образом, винеровский процесс действительно является
необычным процессом. Будучи всюду непрерывным, он почти ни-
где не дифференцируем; дисперсия приращения значений этого
процесса на бесконечно малом интервале совпадает с квадратом
приращения. Аналогичным образом можно показать также, чго
dt du (0 = 0- (4-105)
Интересно также следующее свойство винеровского процесса.
Если функция т| (t, %) не зависит от t, то интеграл Ито, определен-
ный соотношением (4.98), является мартингалом, т. е.
£{1(0|и(т), 0^x^s<Z} = I(s). (4.106)
89
Это свойство становится очевидным, если рассмотреть
во (4.101). Действительно, так как
i s t
1 (0 = J 7] (ty du (X) = J 7] (X) du (X) + 7] (X) du (X),
0 0 ’s
равенст-
то условное среднее величины I(Q, стоящее в левой части равенст-
ва (4.106), можно записать в виде
S
£ {I (t) | и (т), 0 < т
С $ < /} = Е. J (X) du (X) | и (т),
О <1 т < s <Л
t
+ Е J т] (X) du (X) | и (т), 0
S
т < s< t
В первом интеграле функция и полностью известна на всем
интервале интегрирования, так как она входит в условие. Поэтому
этот интеграл не является стохастическим. В то же время во вто-
ром интеграле условие не играет уже подобной роли в силу неза-
висимости приращений процесса и на непересекающихся интерва-
лах. Поэтому на основании ф-лы (4.101) второе слагаемое в пра-
вой части последнего равенства равно нулю. В результате полу-
чаем
Е {I (t) | и (т), 0 < s < t} = J 7} (X) du (X) = I (s).
о
Еще одно полезное свойство интеграла Ито состоит в том, что
его конструкция допускает определение интеграла
t k—i
J П *) d h (*) d h (X) = L.I M. £ л (t, ti) ( f,.+1) - b (t) ] X
о <=0
Х[1,(^+1)-^(ОЬ (4.107)’
где т](^, X) —произвольная непрерывная функция, а |(0 —М-мер-
ный непрерывный случайный процесс. Из этого определения сле-
дует, в частности, что если |(7)—.M-мерный нестационарный ви-
неровский процесс и(^), для которого f{u(^)}=0; var{du(^)} =
то справедливо (в среднеквадратическом смысле, с ве-
воятностью 1) равенство
I t t
Jn(^, X) dut (f) du} (0 = |t](^ X)[Vw(0]o^ (4.108)
о 0
(cm. [56]).
Обратимся теперь к изучению процесса на выходе нелинейной
системы, описываемой уравнением
= Т[Х(О) + Glx(0, flw(0,
(4.109)
90
если на ее входе действует /^-мерный векторный нормальный бе-
лый шум w(7), для которого
£ {w (/)} = 0; cov {w (0, w (т)} = Vw (0 bD (t — x).
Здесь x(t)—JV-мерный случайный вектор состояния; f[x(7), —
JV-мерная нелинейная векторная функция от x(t) и t; G[x(7), J] —
матричная функция размерности JVx/?.
Формальным интегрированием ур-ния (4.109) можно найти сле-
дующее неявное выражение для отклика или вектора состояния
системы
t t
x(f) — x(t^ = f f[x(%), jG[x(%), %]du(2i), (4.110)
^0 ^9
где du(7) — винеровский процесс; du(7)=^w(7)dt для которого
£'{du(Z)}=0; var {du(7)J =4pw(7)dj. Заметим, что первый интеграл
в ф-ле (4.110) является обычным, в то время как второй — стоха-
стическим. Если случайный векторный процесс x(t) с вероятностью
1 удовлетворяет полученному стохастическому интегральному ура-
внению, то ур-ние (4.110) можно записать в следующей символи-
ческой форме:
dx(0=f[x(0, 0<ft + G[x(O, 0du(0. (4.111}
Это уравнение в дальнейшем будем называть стохастическим
дифференциальным уравнением. Это равенство можно рассматри-
вать как удобный способ записи ур-ния (4.110) в случае, когда
функции f[x(7), J] и G[x(f), /], определенные при всех допустимых
значениях x(t), принадлежат подмножеству S2 9
В дальнейшем будет указано, что при преобразованиях интег-
рала Ито необходимо использовать правила, отличающиеся от
правил преобразований обычных интегралов. Будем считать, что
х(/) является процессом Ито2); предположим далее, что
<р[х(7), J]—функция от x(t) и t, имеющая непрерывные частные
производные второго порядка по x(t) и t. Используя правило диф-
Условия существования и единственности решений ур-ний (4 110) и
(4.111) обсуждались Скороходом в [2 411 Если x(t0) не зависит от и(7), а
flx(0> fl и G[x(Z), fl определены на рассматриваемом временном интервале для
всех х(/), являются измеримыми и удовлетворяют двум условиям:
— для каждого <£>0 существует такое, что при ||х||^ и [|y||=g<#
справедливо неравенство (Т—to)||f[x(i/), fl—f[y(O> fllP+tr{G[x(/), flGT[x(7), fl) si
||x(7)-y(OII2,
— существует X такое, что (T—/oHffxffl), fll^+trfGIxfO, flGT[x('Z), fl} si
<^(l + l|x(OH2), то уравнение (4 110) с вероятностью 1 имеет единственное не
прерывное решение Первое условие является условием Липшица; второе —
условием «квазилинейности» (Прим авт)
2) Пусть u(Z)—винеровский процесс. Случайный процесс х(/), связанный с
с помощью функций f и G, является процессом Ито, если x(t) удовлет-
воряет ур-нию (4 110) (Прим авт)
91
ференцирования Ито, получаем, что <р[х(7), /] также является про-
цессом Ито и удовлетворяет уравнению
‘,’>=[^+fa- + Vtr(srFT»)l<"+(4£Pd?’ <4-112)
L ох 2 \ дх2 Ц ' \д х J
в котором ради простоты записи использованы следующие сокра-
щенные обозначения
Ф = ф[х(/), /]; f=f[x(Z), /];
3 = G[x(0, x = x(0; du=4»7^du(0-
Это уравнение играет очень важную роль при получении мно-
гих результатов теории случайных процессов; оно, например,
используется при отыскании характеристических функций случай-
ных процессов.
Стохастическое дифференциальное ур-ние (4 111) можно пере-
писать в несколько ином виде, если воспользоваться введенными
выше обозначениями & и du:
<dx (f) = f [x (f), t]dt [x (f), /] du (/). (4.113)
Здесь винеровский процесс имеет среднее значение, равное нулю,
и ковариационную матрицу
var [du (01 = I dt. (4.114)
Подробное и удобное по форме доказательство правила диф-
ференцирования Ито для скалярного случая дано в работе [241].
Обобщение этого доказательства на векторный случай не встреча-
ет принципиальных трудностей. Здесь приведем лишь упрощенные
нестрогие рассуждения. Интегрирование (4.112) приводит к урав-
нению (для t>t0)
Ф[х(0, л-ф[х(4), (’[y+rl? + _Ltrfg7'^g')l^ +
J L dt д х 2 \ дх2 /I
*0
t
(4Л15)
^0
которое также является полезным.
Разложим функцию ф[х(7)?/] в ряд Тейлора относительно точ-
ки x(t)=x(tQ) и /=/0:
Ф[х(о, Л =ф[х(*о), и + [х(0 —x(QJ +
\дх) |х=х(<0)
+ _L[x(0_x(Zo)f!^M [Х(0__хО + у-| [Z-ZJ + Q,
2 д х2 |х=х (<0> dt [<=<„
где слагаемое £2 содержит члены порядка dt2 или (dx)r(dx) и бо-
лее высокого порядка Используя теперь ф-лу (4.110) для
x(t)—x(t0) и учитывая, что dt — бесконечно малая величина,
92
вследствие чего в разложении из-за свойства осцилляции Леви
появляются слагаемые типа
-L (д2 <р/с/х2) 3? dt и
dt du (0 = 0; dx (t)dt = 0; [dTi (ЭД [du (t)\T = I dt, (4.116)
получаем ур-ние (4 115), которое эквивалентно ур-нию (4.112).
Иногда удобнее правило дифференцирования Ито записывать в
виде
Лф[х(ЭД Л = --1 + ^{ф[Х(0, +
\ at ) ( д х (t) J
XW f]du(O, (4.117)
где Z обычно называется обратным дифференциальным операто-
ром;
2{.} = №W, Ч^ + ф1г {srU(0. Ч 9IX((, /]} .
(4.118)
Таким образом, % {ф[х((), (]} является дифференциальным ге-
нератором процесса ф[х(ф), £].
Пример 4.3. Исследуем процесс на выходе нелинейной системы, описывае-
мой уравнениями
х1 = х2(/)и>(/), хх(0)=0; x2 = w(f), (0) = 0,
на вход которой воздействует нормальный белый шум w(t) с ковариационной
матрицей var {w(t), w(-t)} ='¥w8D(t—т)
Используя обычное правило интегрирования, получаем
t t
x2(t) = w(K) d \ = § du(K) = и (t),
о о
т е процесс x2(t) является винеровским процессом, что и следовало ожидать
Для вычисления xi(t) необходимо использовать интеграл Ито, так как
t t
jq (f) = J x2 (X) w (X) d /. = J и (X) du (X).
о о
Использование обычного правила интегрирования привело бы к результату
t
(/) = J u (z.) d« (X) = u2 (Z)/2. (4.119)
о
Однако рассматриваемый интеграл является стохастическим, и здесь необхо-
димо воспользоваться определением (4 98) Поэтому следует писать
А—1
(0 = L I .М у и (/,) [и ( /(+1) — и (/,)].
д->0 1=0
93
Последнее равенство с помощью простых алгебраических преобразований
приводится к виду
xL (t) = L.I ,М.
4->=о
б->0
W+1)-“W
1=0
Первая сумма легко вычисляется, давая в результате и2(/)/2—и2(0)/2 Так
как и(0) =0, то
4-1
Хх (0 = и2 (0/2 - L. I ,М. 4“ V [« ( /(+i) - « (О)]2.
Л—>со Z
д-> ( /=0
Второе слагаемое можно легко вычислить, если воспользоваться свойством
осцилляции Леви [см. равенство (4 93)] Так как 6->0, то
для Xi(t) получаем
t
xr(o = ^(o/2-yJ [d“(x)i2-
О
Используя (4 104), это выражение можно переписать в виде
t
хг(0 = «2(0/2--^-]*тю</А,.
о
Обычный интеграл в правой части этого равенства легко вычисляется, так
что для Xi(t) окончательно получаем Xi(0=u2(0/2—Yw//2.
Чтобы показать, что определение (4 99) в общем случае неэквивалентно
определению (4 98), вычислим теперь Xi(t), воспользовавшись правилом (4 98)
Для этого положим t\ = y/1+i-|-(1—у)/г, где 0<у<1 Тогда значение u(t',)
можно приближенно положить равным 0,5[£и(/г) + (1—£)w(fl+1)] и записать
4-1
Xi (0 = LЛМ ~ [£ и (/,) ->(! — £)«( /(+1)] [и ( /(+1) - и (/,)].
б->0 1=о
Дальнейшие вычисления, проводимые так же, как выше, приводят к еле
дующему результату
Xi (0 = «2 (0/2-^(£-1/2)/.
Этот результат совпадает с решением, получаемым при обычном исчисл-
нии при £=4/2, и совпадает с решением, основанном на использовании интегра-
ла Ито, при £= 1.
Другой способ получения корректного выражения для Xi(t) основывается
на использовании правила дифференцирования Ито Так как уже известно, что
решение содержит слагаемое вида u2(t), где u(t) — винеровский процесс, то
появляется возможность рассмотреть линейную систему
dy/dt = w(t), у (0) = 0, (4 119а)
где w(t) — белый нормальный шум с нулевым средним значением Соответству-
ющий процесс Ито удовлетворяет стохастическому уравнению dy(t) = du(t),
4/(0) =0.
94
Положим <р[х(/), /]=у2(/). Так как правило дифференцирования Ито [см.
(4.112)] записывается в виде
13 <р [и(/), Л dip [а (Л, /1 1
лрк(о. n= 1г/(о. и-^j J^Tg4y(o. ох
з2фЕр(0. '11 о<р[1/(0, О г ,А л . ...
х' dy(tf Г4-’ дуц} ' ё[у^’ t]du{i}'
где для рассматриваемой задачи <р=р2; /=0; g=ylrlw'2, так что d<p/dt=O, а
d<p/dy=2y, то в данном случае
d<р [у (/), 0 = dt + 2Ч^2 y(t)du = Ww dt +2y(t) dy (t)
(поскольку du.= W ~r'2 du и du=dy). Интегрированием получаем
t t
Ф [У (0, 0 = У2 (i) = f w dt + 2 J у (t) dy (I).
о о
Если теперь учесть, что у ft)— винеровский процесс u(t), то последнее урав-
нение можно переписать следующим образом:
f 1
J u(t)du(t) = — u*(t)-Vwt/2.
о
Таким образом, вновь получено решение для переменной состояния Xi(t)
исходной нелинейной задачи, рассматриваемой в этом примере.
Пример 4.4. Рассмотрим другую (билинейную) систему
dx (/)
—У- = -0,5х(/)-Ь x(t)w(t), х(0) = 1,
dt
которая описывается следующим стохастическим дифференциальным уравне-
нием:
dx(t) = — 0,5x(/)d/-f- x(t)du(t), х(0) = 1, 4^=1.
Легко проверить, что решение этого уравнения, найденное методами обычного
исчисления, имеет вид х(/) = ехр[—0,5/+«(7)]. Однако, если положить <р[х(Т), /] =
= In x(t), то правило дифференцирования Ито приводит к уравнению
d<p[x(/), /]= — dt^duft).
Отсюда ф[х(7), /]=—t+u(t) — ln x(t), так что корректное решение имеет вид
x(t) =ехр {—t 4- u(t)}.
Здесь снова результаты, полученные с помощью обычного исчисления и сто-
хастического исчисления, не совпадают. Причиной этого несовпадения, конечно,
является то, что для вычисления стохастического интеграла J x(t)du(t) обыч-
0
ные методы, вообще говоря, применять нельзя.
Для того чтобы получить алгоритмы оценивания в любой физи-
ческой задаче оценивания, приходится выполнять два наиболее важ-
ных этапа исследований. На первом из них решается задача моде-
лирования или выбора стохастического дифференциального урав-
нения, которое описывало бы рассматриваемый физический
процесс. Эта модель, которая в конечном счете представляет неко-
торый процесс, является в общем случае компромиссом между ма-
тематической точностью и простотой вычислений.
95
Цель второго этапа — найти алгоритмы оценивания. Этот этап
выполняется лишь после того, как выбрана математическая модель
процесса. Ниже рассматриваются некоторые аспекты второго
этапа.
Ранее уже было отмечено, что стохастический интеграл (интег-
рал, содержащий произведение двух случайных процессов),
нельзя во всех случаях рассматривать как обычный интеграл. При-
веденные выше два примера достаточно ясно иллюстрируют раз-
личия между этими интегралами. Если для моделирования алго-
ритмов оценивания используются цифровые вычислительные ма-
шины, то подходящая интерпретация стохастического интеграла не
является тривиальной. Здесь возможны два подхода. Один из них
основывается на обычном исчислении, другой — на стохастическом
исчислении. Специальное рассмотрение этих двух подходов будет
проведено в гл. 9. Здесь же приведем только некоторые рекомен-
дации для выбора одного из них [77]:
1. Если функция %[x(t), t} не зависит от х, то обычное и сто-
хастическое исчисления приводят к одним и тем же результатам и
необходимость специального исследования стохастических интегра-
лов просто отпадает. Подобный факт уже упоминался ранее. Этот
же случай встретится при исследовании проблемы построения ли-
нейных оценок, для которой окажутся возможными существенные
упрощения.
2. Если проблема оценивания должна быть сформулирована
строго в математическом отношении, то следует использовать сто-
хастическое исчисление.
3. Если ур-ние (4.111) рассматривается как аппроксимация со-
ответствующего дискретного уравнения или как предел уравнения
X ( t. , ) — X (ti)
= f [х ft), tt] + G [х ft), w ft) (4.120)
4+1 — 4
при неограниченном увеличении числа отсчетов на любом конеч-
ном интервале, то необходимо использовать стохастическое исчис-
ление.
4. Если в равенстве (4.109) входной белый шум используется
вместо шума с малым интервалом корреляции, то следует приме-
нять методы обычного исчисления.
Различие между этими двумя подходами с вычислительной
точки зрения также нетрудно выявить (см. [281]). Если использо-
вать понятия обычного исчисления при отыскании решения x(t)
ур-ния (4.111), то фактически будет получено решение уравнения
dxft = f[х(t), t]dt + (—!sT[x(t), t} —f $[x(0, fl/dt +
\ 2 ( d x) }
+ S[xft, flduft. (4.121)
В большом числе случаев решение ур-ния (4.121), полученное
методами обычного исчисления, с достаточно высокой точностью
будет совпадать с решением стохастического дифференциального
Э6
ур-ния (4.111) (заметим, что если %) не зависит от х, то, как
уже отмечалось выше, методы обычного исчисления приводят к
точному решению).
С помощью правила дифференцирования Ито можно получить
прямое диффузионное уравнение или уравнение Фоккера — План-
ка. Рассмотрим для этого нелинейную систему dx(^) =f[x(/),
+ $ [x(Z), i]du(0 и положим
<р[х(t), t\ = ехр {—sr[x(Z)— x(i0)l}. (4.122)
Применение правила дифференцирования Ито [равенство (4.112)]
дает
dq> = ( — fs + -±-sTggTs}([)dt~ srS<pdu(0. (4.123)
Интегрируя обе части полученного равенства на интервале от
t0 до t и учитывая, что <р[х(/0), /0] = 1, получим
<p[x(0, 1 + С<₽[х(Х), Х]( —f[x(X), X]s Д- — sr$[x(X), Х]Х
J I 2
^0
t
x [X (X), %] s j d % — sT J $ [x (%), %] ф [x (X), X] du (X). (4.124)
Заметим, что условное среднее значение функции <р[х(7), /] при
заданном значении x(t0) есть условная характеристическая функ-
ция случайного вектора x(t) при заданном x(to):
fl|x(f0)} = Mx(0|x(M(s). (4.125)
Для условного математического ожидания правой части равен-
ства (4.124) можно записать
Мх(0(х(Л,)(S) = 1 + X] {-fr[x(X), X]s + y S7':Дх(Х),Х]Х
to
X$T[x(X),X]sj x(f0)jdX. (4.126)
Здесь учтено, что условное среднее последнего интеграла в
£4.124) равно нулю, как это следует из (4.101), поскольку процесс
u (t) имеет нулевое среднее значение и не зависит от х (t0). Но ус-
ловная характеристическая функция есть преобразование
Фурье относительно x(t) от условной плотности вероятности
Рх(«)|х(«„) (₽|₽о) • Дифференцируя равенство (4.126) по t, получаем
[х (0, i] {- И [х (/), t\ S + 2- sT $ [X (i), i] x
X/[x(iM]s) x(f0)l. (4.127)
4—26
97
дМх Щ|х «,> (s)
dt
Раскрывая теперь содержание оператора математического ожи-
дания, запишем
<p[x(f), f{x(0, Hs +-^sr^[x(0, t\ х
х & [X (t), n s| px(()|x IP = x (t) I Po = XО d X (/).
Вычисляя, наконец, обратное преобразование Фурье от обеих
частей последнего равенства, приходим к уравнению Фоккера —
Планка *> для векторного процесса [определяемого ур-нием
(4.1П)]:
,^..[.x(9l2L«g)L = _tr(-A-{flx(t), Пр[х(0|х(Шк
dt \дъ(1) )
+ ^wWG'lxW. Пр[х(0 |Х(/О)]П ,
(4.128)
где .3?T = G4fwGT, так как правило дифференцирования Ито по-
лучено для винеровского процесса du(7) с единичной матрицей не-
зависимых приращений, а этот процесс связан с исходным винеров-
ским процессом с помощью соотношения duff) = ЧГ~1/2 duff).
Таким образом, вновь получено уравнение в частных производ-
ных Фоккера — Планка. Это уравнение может быть использовано
для отыскания плотности вероятности переменной состояния не-
линейной системы, описываемой ур-нием (4.111) и возбуждаемой
нормальным белым шумом. Вектор переменных состояния такой
системы является марковским процессом. В основе этого вывода
лежит правило дифференцирования Ито. К сожалению, не сущест-
вует прямого способа выбора функции <p[xff), f], Во многих слу-
чаях полезной оказывается такая функция <р, которая получается
при использовании обычного интеграла Римана.
Одно из неудобств, связанных со стохастическими интегралами
и стохастическими дифференциальными уравнениями, состоит в
том, что для последних могут оказаться несправедливыми прави-
ла преобразований обычного исчисления. Конечно, стохастический
интеграл можно было бы определить и таким образом, чтобы обыч-
ные правила вычислений, как, например, интегрирование по час-
тям, остались справедливыми. На первый взгляд такой подход мо-
жет показаться привлекательным и более естественным, чем опре-
деление Ито. Однако, как будет здесь показано, на самом деле это
не так. Ради простоты ограничимся рассмотрением лишь скаляр-
Отм«тим снова, что плотность вероятности p[x(t) |х(/0)] может, а в об-
щем случае и будет явно зависеть от времени, т е. запись РХ(щХ((о)Ф, ^о)
была бы более правильной. Ради простоты обозначений эта явная зависимость
от времени не всегда будет выделяться, однако всюду будет предполагаться,
что функция р[х(7)|х(7о}] может зависеть от времени. (Прим., авт.)
98
ного случая. Исследование многомерного случая проводится ана-
логично и не встречает принципиально новых трудностей.
Рассмотрим подробнее свойства интеграла (4.96) I(t) —
= J т](6 h)du(h), который при более общих обозначениях молено
о
записать в форме
t
l[t} = ^L[u{K со), t]du(k, со). (4.129)
о
Здесь м(Л, со)—реализация винеровского процесса, а
L[u(Z, со), /]— функция от и(к, со). Такой интеграл не может
быть определен как интеграл Римана. Можно предложить следу-
ющее определение для интеграла (4.128), которое является незна-
чительным обобщением определения (4.97):
i-1
I (0 = L.I.M. S С1 [и ( 0 со) - и (tt, со) ], (4.130 )
-о
где C‘ = Z.[u(Z', со), 0] (4.131)
и t'x — некоторая точка из интервала [0, А+i]. Однако из-за нали-
чия свойства осцилляции Леви [см. (4.93)] значение интеграла
может зависеть от выбора точки t1Такая зависимость уже была
проиллюстрирована в примерах 4.3 и 4.4. В первом из них при
использовании определения Ито было принято = и
С = L[u(ti, a), tt], (4.132)
Стохастическое исчисление Ито и обычное исчисление часто
приводят к разным результатам. Например, при использовании для
стохастического интеграла определения Ито легко проверить, что
t
J [и (к) - и О du (X) = 2- [Ы (0 - «(/„)]*-(t -10) Ww.
^0
Обычное правило интегрирования вообще приводит к другому
значению этого интеграла. Точно такое же значение можно полу-
чить только в том случае, если в разложении в ряд Тейлора подын-
тегральной функции ограничиться членами второго порядка и
использовать запись [du(t)'\z = y¥wdt [см. (4.104)]. То есть для
скалярной функции Л[м(0], зависящей только от и, должно быть
справедливо равенство
dL [и (0] = dL [и (/)1 du (0 + — d~L [du (0]2 = dL lu (Z)1 du (0 +
du (0 V 2 [du (01* V П du(t) V
42L[u(0] dL
2 w [du (0]2
(4.133)
4*
99
Аналогично должно выполняться соотношение
d{Lx[u(t), t]L2[u(t), t]} = [и^’ tl-L*[и ' t]-dt ^Lx [и(t), t] X
dt
XdL2 [и (t), t] + L2 [u (t), t] dLx [u(0, t] + 4W dL11^' -1- X
du (t)
X~?[u^’ t]-dt (4.134)
d«(Q v ’
для обычного исчисления, чтобы правила вычисления обычного и
стохастического исчислений приводили к одним и тем же резуль-
татам.
Если стохастический интеграл определить так, чтобы получаю-
щиеся при этом результаты оказались совместимыми с результата-
ми обычного исчисления, то равенства (4.101) и (4.102) нарушатся,
что очень нежелательно. Действительно, эти два равенства чрез-
вычайно полезны в том отношении, что они позволяют существен-
но упростить вычисления математических ожиданий.
Стратонович в работе [258] ввел «симметризованный» стоха-
стический интеграл, в котором
С1 = L [0,5u( ^+1, со) 4-0,5u(/(, со), (4.135)
Подобное определение стохастического интеграла дано также
в работе [77], где было принято
C‘ = 0,5(L[«(fl+1, со), ti+[]-rL[u(tL, ffl), ZJ}. (4.136)
В работе [148] предложена аппроксимирующая формула
'*+1
С‘ =------!--- f E{L[u(t, со), • • -,u(tn)}dt, (4.137)
в которой tv, t[, ..., tn — выделенная совокупность точек на интер-
вале интегрирования. Можно было бы также рассмотреть аппрок-
симацию вида
С‘ = L {и (Zt, со), tt\ + dL[“^ [«( *,+1. со) - и (/., со)]. (4.138)
Хотя каждое из перечисленных четырех определений приводит
к некоторым полезным свойствам стохастического интеграла, все
они имеют серьезный недостаток: равенства (4.101) и (4.102) ока-
зываются несправедливыми. Следовательно, многие последующие
соотношения должны быть модифицированы. Например, если в
определении стохастического интеграла используется равенство
(4.136), то уравнение Фоккера — Планка (4.128) оказывается не-
справедливым, а среднее значение последнего интеграла в правой
части равенства (4.124) не равно нулю, поскольку при новом опре-
делении величины Сг равенство (4 101) нарушается. Можно пока-
зать, что «новое» уравнение Фоккера — Планка, которое соответ-
ствует соотношению (4 136), имеет вид
100
X (g [x (/), t] [“]Г {^v (V GT [X (0, t\ p [X (0 I X .
(4.139)
Изменение уравнения Фоккера — Планка при таком переходе
намного существенней, чем это можно было ожидать вначале.
Вычислять моменты теперь намного труднее. Стохастические диф-
ференциальные уравнения, которые получаются при использовании
любого из соотношений (4.135) — (4.138), приводят к случайным
процессам, не являющимся более марковскими. Поэтому в даль-
нейшем в данной главе и в гл. 9 без особых оговорок будем ис-
пользовать исчисление Ито, основанное на определении (4.98).
4.5. Среднее значение и дисперсия процесса
на выходе нелинейной системы
Системы с непрерывным временем. Найти
решение уравнения Фоккера — Планка часто оказывается невоз-
можным. Но для целей данной книги обычно достаточно знать
лишь вектор средних значений и ковариационную матрицу процес-
са x.(t) на выходе системы. К счастью, эти характеристики, в край-
нем случае приближенно, могут быть получены из уравнений Фок-
кера — Планка.
Рассмотрение начнем с нелинейной системы, возбуждаемой ви-
неровским процессом и описываемой уравнением
dx (0 = f [X (i), t] dt + G [X (0, t] du (t),
где jiu (t) = 0; var {du (0} = *₽»(0 dt.
Как и ранее, введем обозначения:
2? [х(0, t] = G[x(0, 0Ч\Д0;
du (t) = 2 (t) du (t)
и запишем уравнение системы в виде
dx (0 = f [х (0, t] dt + $ [x (0, t] du (0,
(4.140)
(4.141)
(4.142)
(4.143)
где du(i) теперь является винеровским процессом с независимыми
приращениями, для которого
var|{du (t)} = I dt.
(4.144)
101
В принципе, переходную плотность вероятности процесса мож-
но получить как решение уравнения Фоккера — Планка (4.128),
которое при введенных обозначениях записывается следующим об-
разом:
адущ = _ fr /{f [х(/)> Z]р [х(/) j х(,о)]}\ +
д/ \д х (0 /
+ №T[*(t), Ар[х(0|х(/о)]П. (4.145)
2 \д х (/) [д х (/) J J/
Практически же решить это уравнение удается лишь в том
случае, когда функция f линейна по х, a $ вообще от х не зави-
сит. Вектор средних значений и ковариационная матрица процесса
x(t) определяются путем интегрирования переходной плотности ве-
роятности. Так,
£{х(П}= J₽px(0lx(/o)(₽l₽o)d₽ (4-146)
—со
или, в несколько иных обозначениях,
р.х(0 = £{х(0}= J x(/)p[x(/)|x(/0)]dx(i). (4.147)
—со
Аналогично
var {х (t)} = Vx (/) = J [x (0 - E {x (/)}] [x (/) - E {x (/)}]r X
Xp[x(0|x(/o)]dx(/). (4.148)
Преобразуем уравнение Фоккера — Планка(4.145) в стохасти-
ческое дифференциальное уравнение [имея в виду, что dy(i) =
=7(i+dO-T(O]
dp [х (t) | x (Q] = p [x (/), t + dt | x (t0), t + dt, /0] — p [x (/), 11 x (Q, t, /0]=
=-tr (Л {f [x /] p[x ® i * (*o)]}) +4tr frW X
'ax j 2 \d x (t) l_a x (t) J
X{S[x(i), /] У[х(/), i]p[x(f)|x(y]})df. (4.149)
Умножая обе части этого уравнения на x(t) и интегрируя по
х(0 в пределах от —оо до +оо, получаем
dpx(0 = M* + ^)-M0 = £{f[x(0> t]}dt, (4.150)
где интеграл от правой части равенства (4.149) вычислялся по
частям при следующих граничных условиях:
Х{ (t) ft [X (0, Л Р [X (/) I х (Q] = xt (t) ([-М7" S [X (/), t\ [x (0, t] x
IL o x (t)j
Xp[x(O|x(Ql) ={S[x(0, Orlx(0, /] p[x(0 |x (/0)]}{/ - 0
J i
102
для всех i и j при х(0 =—00 и х(0 = оо. Слагаемое nx(t + dt) не-
посредственно получаем из основного определения
^(t + dt)= J ₽Рх(<)|х(<о)[₽. * + &, tQ]d$.
—МО
Для приближенного вычисления величины £{f[x(Q, t]}dt разло-
жим функцию f[x(7)> в ряд Тейлора относительно среднего зна-
чения E{x(t)} =fix(i) процесса х(7). Ограничившись в разложении
слагаемыми второго порядка, запишем
f [X (0, 0 « f [Их (0, 0 + Л - [X (0 - Их (0] +
+ V : Iх (О - (01 [X (0 - Их (Of > [(4.151)
2 [дЦх(01
где
..: [х (0 “Их (01 [ х (0 ~ ®]Т = ([[х (01 х
= У К(0-РхД0][хД0-рхЛ0]/----[^У’ • (4.152)
д цХ1 (0 д ‘1Х1 (t)
i, /=1
Для последнего слагаемого в выражении (4.151) удобно ис-
пользовать также и другое обозначение
гсР.ж- ,,1 , /а2[Ж]г; ,,\ .. 1CQ.
] ----: Jf\ = tr —-—— J . (4.153)
t d x2 J(7- ( d x2 / v '
которое впредь будет использоваться для любой матрицы N и
квадратной симметричной матрицы М. Подставляя в (4.150) ап-
проксимирующую функцию (4.151) вместо f[x(0), 0], получаем
приближенное соотношение
d Их (0 = f Н-Ч (0, t] dt + 4- ; ® dt’ (4-154)
2 [<3|ix(0]2
в котором
Vx(0 = £{[x(0-px(0][x(0-px(0f} = var{x(0}. (4.155)
Из этого соотношения следует, что для вычисления среднего
значения процесса x(t) необходимо знать ковариационную матри-
цу этого процесса. Если система линейна, то df/dx=F и среднее
значение процесса х не зависит от его ковариационной матрицы,
как это уже было показано в § 3 5.
Если в разложении функции f[x(Q, t] ограничиться только ли-
нейным членом, т. е. принять аппроксимацию
f [X (0, 0 « f [|1х (0, 0 + [X (0 _ ,1х (0],
д х (/)
(4.156)
103
то стохастическое дифференциальное уравнение для среднего зна-
чения процесса x(t) примет вид
dpx(0 = f[px(0X]<#. (4.157)
Его можно записать как «обычное» дифференциальное урав-
нение
d рх (/)/d/ = f [рх (/), /]. (4.158)
Во многих случаях оказывается, что абсолютное значение про-
изводной d2f/dx2 достаточно мало. Для линейной системы, когда
f=Fx, оно просто равно нулю. В таких случаях последнее уравне-
ние практически будет обеспечивать ту же точность вычисления
вектора средних значений, что и ур-ние (4.154).
Получим теперь выражение для ковариационной матрицы
(4.155) процесса x(t). Еще раз подчеркнем, что правильные ре-
зультаты в общем случае могут быть получены лишь при исполь-
зовании методов стохастического исчисления. Воспользуемся лег-
ко проверяемым тождеством
[х (0 — рх (/)] [х (0 — px(/)F = [х (/) — рх (/ + d/)J X
X [X (0 - рх (/ + dt)]T + [рх (t + dt) - рх (/)] [рх (/ + dt) - рх (t)]T +
+ Iх (0 — Рх (t + dt)] [рх (t + dt) — px (/)f 4- [px (t + dt) — px (/)] X
X [x (/) — px (/4-d/)f, (4.159)
которое перепишем следующим образом:
[X (t) - рх (/)] [X (t) - px (Of = [X (0 - {lx (/ + [X (0 - Px (t + dt)]T +
+ d Px (0 d pj (t) + [x (0 — Px (t + dt)] d p£ (/) + d px (0 [X (0—p.x(t+dt)]r.
(4.160)
Умножая обе части уравнения Фоккера — Планка (4.149) на
эквивалентные выражения матрицы [x(i)—Цх(0] [х(0—Цх(0]т и
интегрйруя их по всем возможным значениям x(t), получим сле-
дующее точное соотношение F
dvx (0 + d Рх (0 d pj (t) = E {f [x (/), /] [x (0 - px (OF + [x (0 - Px (01X
ХИ[х(0, 0}^ + £{S[x(0. fl£rlx(0. t]}dt. (4.161)
К сожалению, решить для общего случая это уравнение не уда-
ется. Поэтому снова воспользуемся аппроксимациями функций
f[x(7), /] и $ [х(7)л /] &T[x(t), ?] с помощью рядов Тейлора
относительно точки fix(t). Ограничиваясь в этих разложениях та-
кими членами, что в ф-ле (4.161) получаются моменты процесса
x(t), порядок которых не более дяух, и учитывая, что нечетные
*> Здесо левая часть (4 149) умножается на правую часть (4 160), а правая
часть (4 149)—на левую часть (4 160) и используется интегрирование по час-
тям Следует проявлять большую осторожность при интерпретации получен-
ного уравнения (Прим авт)
104
степени разности x(t)fix(t) имеют нулевое среднее значение Ч,
получим приближенное уравнение
dV, (fl + d ь (0 d fl (0 = а-a П V-W dt + V"И dt +
+ S [f, (fl. fl [fx(fl. fldl + 4-a,S?— 11 :V-w*
(4.162)
основывающееся на разложении функций f[x(7), t] и S (x(4), Л X
X $T[x(T/ /]. Здесь использовано обозначение ф-лы (4.153). Для
того чтобы полностью определить это уравнение для ковариацион-
ной матрицы вектора состояния х нелинейной системы, описывае-
мой ур-нием (4.143), необходимо изучить слагаемое d|mx(T)d|uixT (0.
Из ур-ния (4,154) следует, что это слагаемое будет включать чле-
ны, содержащие величину dt только во второй степени. На основа-
нии рассуждений, которые были использованы при выводе соотно-
шения (4.115), можно считать, что (di)2 = 0 (напомним, что вели-
чина dt бесконечно мала). Следовательно, слагаемое djuuf^)d|mTx(^
можно положить равным нулю. Таким образом, приближенное
уравнение для ковариационной матрицы вектора переменных со-
стояния принимает вид
dVx(0 = v«(fl<« + V,(fl 11 dl +
+ 9(1". (fl. flSrlfx(fl. fl d< + 4 g lllf Vk ‘1 f4lfa W • A : V, (0 dfl
' ",( >l (4.163)
Разделив обе части этого уравнения на dt и положив
S? = GT»1’2^), получим следующее «обычное» дифференциальное
уравнение:
dVx(f) df[ux(f), fl g fT r„ (t\
-r “ v'« + v’ ® 4,4) + G (MO. fl ЧЩ9 X
T 1 d2 G [px (fl, f] (f) GT [|1X (f), fl ' v
X GT [px (0, +-2- ................................. • V< (0- (4-164)
[<W0J2
Часто последнее слагаемое в этом уравнении оказывается
малым и его можно опустить; получающееся при этом уравнение
по точности сравнимо с ур-нием (4.158).
Таким образом, для нелинейной системы, описываемой диффе-
ренциальным уравнением
= f[х(0, fl + G[x(0, flw(0,
(4.165)
*> Это утверждение, конечно, справедливо для нормального распределения
Будем также считать, что оно приближенно справедливо для распределений,
близких к нормальным (Прим авт)
105
где w(7) —нормальный белый шум с нулевым средним значени-
ем и ковариационной матрицей
cov{w(0, w(t)} = 4*w(06d(/-t), (4.166)
получены две системы приближенных уравнений, позволяющих оп-
ределить эволюцию вектора средних значений и ковариационной
матрицы вектора переменных состояния х. При выводе первой сис-
темы уравнений использовались приближения
f [х (0, q «f [Их (0. fl + Iх (О - Их (01; (4.167)
G[x(0, fl~G[{ix(0> fl, (4-168)
при которых
= /]; (4.169)
dVx(t) dt [px(fl, fl д tT fu, (t)
XG^PxCO- tl (4-170)
Если же используется аппроксимация с учетом членов разложе-
ния второго порядка, т. е.
f [х (0, fl «f [{ix (/), fl + [х (fl — рх (01 + — .
: [x (0 — fix (/)] [x (fl — {ix (fl]r; (4.171)
E [x (0, fl as E [Hx (0- fl + Iх (0 ~ (Of H (Hx (0, fl +
d Px (fl
+ т : [x W (01 Iх (0 - Hx (Of >
2 [dPx(0I2
где B[x(7), /] = G[x(7), /]Tw(Z)GT[x(O, t], то рассматриваемая
система приближенных уравнений принимает вид
lM0- = f[{lx(o, /] + - -d2ftit^)’ ^••Ух(0;
_ Vxf) = 0 V (А 4- V (A Л . gr
dt d^t) vxW+vxW dv.x(t)
x оЧм(), л +
2 [d!ix(0I2
Для решения систем ур-ний (4.169) и (4.170) или
(4.174) необходимо указать начальные условия
(4.172)
(4.173)
(4.174)
(4.173) и
р,х(/0) и
Vx(70>), которые можно рассматривать как априорные среднее зна-
вида G[x(7), ZlYwf/JGlxf/J, fl = G[^x(/X flx
d F
----— G[pz('(M]4rw(0Gr[pxW’ fl приводит
d Rx (0J
о Приближение для G[x(^), t
XYw(0G4nx(a fl+lx(O-Цх(0]
к тем же результатам. (Прим авт )
106
чение и ковариационную матрицу вектора переменных состояния х.
По определению,
(Q = Е {х О = р (и (₽) d ₽; (4.175)
—со
Vx(i0) = var{x(Q} = (4-176)
•—оо
Уравнения (4.169) и (4.170), найденные при использовании при-
ближений первого порядка, можно получить также путем линеари-
зации системы, описываемой дифференциальным ур-нием (4.165).
Используя разложения слагаемых в ф-ле (4.165) относительно
среднего значения процесса x(t), запишем
-рр = f [Нх (О, fl + q [X (0 - Их (fl] + g [{1х (fl, fl W (0
(4.177)
или
^- = F(flx(O + ®(0, (4.178)
где F (fl = д f [{ix (fl, t]/d Их (fl (4.179)
— матричный коэффициент линеаризованной системы, а
<o(i) = f[{ix(i), fl-^P^’ Л M) + G[M0> flw(0 (4.180)
д Hx (0
— шум на входе линеаризированной системы, для которого
Е {<» (0} = f [ {1х (0, п - Их (0 = (0;
cov {(О (0, <о (т)} = G [их (0, fl (0 G7 [-Лх (fl, fl bD (t - т) = Фш (fl X
X6d(/-t). (4.181)
Используем теперь полученные ранее соотношения, определяю-
щие эволюцию среднего значения и ковариационной матрицы век-
тора состояния линейной системы. Такими соотношениями являют-
ся ур-ния (3.146) и (3.153):
^х(О = РС0Их(0Н-Иш(О; (4.182)
Vx (t) = F (0 Vx (fl + Vx (0 F7" (0 Ф Фш (t). (4.183)
Подставляя в эти уравнения выражения для F(T) из (4.179)
и |Ши(Т) и ’Fm(7) из (4.181), приходим к ур-ниям (4.169) и (4.170).
Конечно, ур-ния (4.173) и (4.174), при выводе которых исполь-
зовались приближения второго порядка, нельзя получить из линей-
ной теории, изложенной в гл. 3. Часто оказывается, что линеаризи-
107
рованные уравнения, или уравнения первого порядка, обеспечива-
ют точность, вполне достаточную для многих приложений. Однако
в гл 9 будет показано, что использование линеаризированных
уравнений, аналогичных ур-ниям (4.169) и (4.170), в задачах оце-
нивания может привести к расходящимся оценкам Применение не-
чинейных уравнений, аналогичных ур-ниям (4 173) и (4.174),
уменьшает или вовсе устраняет эффект расходимости, который
обусловлен в основном неточностью модели Такая неточность
обычно возникает при выборе уравнения системы либо при выборе
параметров начальных условий
Пример 4.5. Вычислим среднее значение и дисперсию процесса x(t), удов-
летворяющего уравнению x(t)=—x3(t)-\-w(t), где w(t) — белый нормальный
шум с нулевым средним значением, для которого = 1
Приближения первого порядка в данном случае приводят к уравнениям
[ф-лы (4 69) и (4 170)]
(О, = - 6р2х (/) Vx (0 + 1.
Решение этой системы при начальных условиях цх(0) = Vx(0) =0 легко на-
ходится и имеет вид р.х(7) = 0,
Подобные среднее значение и дисперсию имеет процесс на выходе линейной
системы (интегратора), описываемой уравнением y=w(t), i/(0)=0, var {у(0)} =0,
где w(t) — белый шум
Приближения второго порядка для рассматриваемого примера приводят к
системе уравнений (см ф-лы (4 173) и (4 174)]
Vx = -6nJ(0K (0+1.
Снова, если ух(0) = Vx(0) = 0. то решение этой системы имеет вид р,х(7)=0,
Vx(t) — t, т е для рассмотренных начальных условий оба типа приближений
приводят к одному и тому же результату В общем случае это не так.
На рис 4 1 и рис 4 2 приведены графики среднего значения и дисперсии про-
цесса x(t) для рассмотренных в этом примере двух способов аппроксимации
и для различных начальных условий
Рис 4 1 Среднее значе-
ние процесса x(t)
1 — аппроксимация первого
порядка ц.ж(0) = 1, Va.(0) = 0,
2 — аппроксимация второго
порядка цх(0) = 1, Тх(0)=10,
3 — оба типа аппроксимации
Hx(°) = vx(0)=0
108
Дискретные системы. Уравнение Фоккера — Планка
нельзя применить формально к исследованию процессов в дис-
кретных системах. Поэтому здесь кратко рассмотрим другой
вспомогательный подход. Получим уравнения, описывающие из
менения среднего значения и ковариационной матрицы вектора
Рис 4 2 Дисперсия про-
цесса x.(t)
1 — аппроксимация первого
порядка цх(0) = 1, Гж(0) = 0.
2 — аппроксимация второго
порядка цж(0) = 1, Тж(0)=0,
3 — оба типа аппроксимации
переменных состояния x(k), характеризуемого следующей нели-
нейной марковской моделью1).
x(t-J-1) = ср [x(Z>), k} + F [х(k), k]-w(k), (4.184)
где w(/e) — белый нормальный шум, для которого
!lw(£) = £{w(b)} = 0;
Vw(j, 6) = cov{w(j), W(&)} = Vw(/j)6K(£—j) (4.185)
Разложим функции ср и FVwrT в ряды Тейлора относительно
истинных значений среднего p,x(i) и дисперсии Vx(i) так же, как
это было сделано при получении соотношений (4 167) и (4.168)
или (4 171) и (4 172) Подставляя полученное приближение для
ф в ур-ние (4.184) и усредняя обе его части, получим уравнение,
описывающее изменение среднего значения вектора состояния х.
Аналогичным образом получается уравнение для ковариационной
матрицы Vx(&) Для этого вместо ф и FVwrT в (4.184) подстав-
ляются их приближенные выражения Преобразования, которые
далее необходимо выполнить, полностью совпадают с соответст-
вующими преобразованиями для непрерывного случая и здесь
*> Для линейной марковской модели Г[х(/г), k] не зависит от x(fe), а
ф[х(А), А] имеет вид Ф[/г+1, А]х(А) (Прим авт)
109
опускаются. Искомые уравнения, основанные на аппроксимации
первого порядка, имеют вид
М* + 0 = *1; (4.186)
vx0+ 1) vx(/o *]+ПМ^ *1Х
х' ’ д jix (k) х' ' djix(fc)
XVw(^)rr[|ix(A), k\. (4.187)
Аналогичные уравнения, полученные при использовании ап-
проксимации второго порядка, записываются следующим обра-
зом:
М*+ !) = ? + :Vx(&); <4Л88)
Z [О Их (к)J
1 v«<*> aX;:w'"'+г им*,, я х
Vx(^) + S(^), (4.189)
где слагаемое
1 N
s (*) = у S ЩЬ)]ц + [Vx[Vx(Ш X
i, /\ I ,m—l
„ дЧ[^(Ю, k] fel
Aa[Hx(fe)]fa[Hx(fe)]/ ^[i»xW]zd[gx(A)]m < '
получено из
£ f xxs?1 i’ (ч - мч и * w-л <} (=
U [d Hx (*)12 J I PlM*)]
:[x(Z?) — px( k}\ — рх(/г)]т) (4.191;
после применения формулы разложения момента четвертого по-
рядка нормальной случайной величины и учета того факта, что
центральные моменты третьего порядка нормальных случайных
величин равны нулю.
Часто оказывается возможным пренебречь слагаемым 3(й),
поскольку оно содержит произведения малых величин типа
(д2ф/д|ш2х)2. Начальными условиями, которые необходимы для
решения полученных систем уравнений при аппроксимациях пер-
вого и второго порядка, являются априорные среднее значение и
ковариационная матрица:
рх(0) = £{х(0)}; Vx(0) = var{x(0)}. (4.192)
Полезно рассмотреть случай, когда в этих приближенных вы-
ражениях частота отсчетов неограниченно увеличивается. Пред-
110
положим, что справедливы следующие предельные соотношения,
связывающие свойства белого шума при дискретном и непрерыв-
ном времени:
Vx (0 = lim Vx (k); Ч\ (0 = lim T Vw (k)
k-b-tt k—>oo
kT-+t kT-+t
T-+0 T->0
и пусть также
f[x(0, t] = lim [x (k), k\~ x(4)};
k—>OO 1
kT-+t
T-tO
G[x(0, 0 = lim — {Г [x (k), ^]}.
T
kT-+t
r->o
В этом случае при увеличении частоты отсчетов в ур-ниях
(4.186) и (4.187) приходим к ур-ниям (4.169) и (4.170). Анало-
гичным образом можно показать, что при -некоторых условиях
ур-ния (4.188) и (4.189) при увеличении частоты отсчетов пере-
ходят в ур-ния (4.173) и (4.174), полученные при аппроксимации
второго порядка для непрерывного времени. Здесь важно отме-
тить, что слагаемое В (k) при таком, предельном переходе стре-
мится к нулю.
Глава 5
ТЕОРИЯ РЕШЕНИЙ
5.1. Введение
Проверка статистических гипотез и оценивание вектора
переменных состояния систем или параметров наблюдаемых про-
цессов являются двумя важнейшими разделами общей теории
статистических выводов В данной главе излагаются основные
результаты теории проверки гипотез или теории решений. Кроме
освещения некоторых аспектов классической теории решений,
здесь обсуждаются также вопросы применения результатов этой
теории к задачам связи и управления.
Можно привести много примеров задач, при решении которых
существенную роль играют методы теории решений (в техниче-
ской литературе по вопросам связи теория решений часто назы-
вается теорией обнаружения) В локации на основе принимаемого
сигнала необходимо решить вопрос о наличии или отсутствии цели,
по результатам анализа среза ткани какого-либо органа человека
можно пытаться определить наличие или отсутствие раковой
опухоли.
В каждом из указанных случаев необходимо выбрать лишь
один ответ из двух возможных — да, нет, — которым удобно по-
ставить в соответствие гипотезы и Довольно часто
встречаются задачи, в которых число гипотез больше двух, в та-
ких случаях требуется решить, какую одну из N возможных ги-
потез следует принять.
В каждом рассматриваемом случае удобно считать, что вы-
бор одной из возможных гипотез осуществляется некоторым ис-
точником, выходной сигнал которого однозначно определяет вид
гипотезы Однако выходной сигнал этого источника недоступен
непосредственному наблюдению, так как в противном случае
проблема выбора решения просто не существовала бы. Наблюде-
нию доступен только результат преобразования выходного сигна-
ла источника; можно считать, что это преобразование осуществ-
ляется устройством, между выходным и входным сигналом кото-
рого существует только вероятностная связь — вероятностный
механизм перехода. При каждом фиксированном сигнале на
входе этого устройства выходной сигнал, который можно рассмат-
ривать как точку из пространства наблюдений, выбирается соглас-
но некоторой вероятностной мере, заданной на этом пространст-
ве. По полученным наблюдениям с помощью правила выбора
решения выбирается одно из возможных решений, указывающее,
какую гипотезу следует принять.
112
Правило выбора решения должно учитывать не только ре-
зультаты наблюдений, но и априорные вероятности различных
гипотез, а также условные вероятности, характеризующие вероят-
ностный механизм перехода. Если априорные вероятности гипотез
и обозначить соответственно как P#g иР^.то Р^о4-
+ Р Ж — 1, поскольку одна из этих гипотез обязательно должна
быть справедливой После получения одного наблюдения z, пред-
ставляющего собой искаженный помехой сигнал, необходимо вы-
нести решение о справедливости одной из гипотез 0: z=v0;
: z— 1 -f- Vt.
Статистические характеристики помехи v в общем случае могут
зависеть от того, какая из гипотез является справедливой. Знание
вероятностного механизма перехода эквивалентно знанию плот-
ностей вероятности помех и0 и щ; как правило, эти помехи в
дальнейшем будем называть шумом измерения. Схема, приведен-
ная на рис. 5.1, иллюстрирует последовательность преобразова-
ний, выполняемых при вынесении решения в бинарном случае.
В бинарной задаче выбора решения возможны ошибки двух
типов Можно ошибочно принять гипотезу когда она на са-
мом деле неверна, либо принять гипотезу <£/{\, когда в действи-
тельности верна гипотеза <Sft0. В локации, где гипотеза <$ 0 соот-
ветствует отсутствию, a^'j—наличию цели и, следовательно,
отраженного от нее сигнала, принятие гипотезы когда на
самом деле она неверна, называют пропуском сигнала, а вероят-
ность принятия такого решения—вероятностью пропуска Рм-
Величина Рр=1—Рм называется вероятностью правильного об-
наружения. Принятие гипотезыт. е. решения о том, что цель
присутствует, когда эта гипотеза несправедлива и цели в дейст-
вительности нет, называется ложной тревогой, а вероятность
такого решения — вероятностью ложной тревоги Ру.
Рис 5Л Элементы бинарной задачи теории решений
/ — источник 2 — вероятностный механизм перехода, 3 — пространство на-
блюдений, 4 — правило выбора решения
Смысл этих величин можно пояснить графически. Для этого
рассматриваемую задачу выбора решения сформулируем следую-
щим образом Будем считать, что при гипотезе 4*0 на пространст-
ве наблюдений задано распределение с плотностью вероятности
Pz(a) =pz^yg (а | е/?о), а при — распределение с плотностью
вероятности pz(a)=pz|^ (а| ^i).
Цель принятия решения теперь состоит в том, чтобы при по-
лученном наблюдении z выбрать одну из двух указанных плот-
113
костей: Р г\,^а или Pz]^x > как наиболее правильно характеризую-
щую вероятностное распределение на пространстве наблюдений.
Если наблюдение z является скалярной величиной, то рассмат-
риваемые плотности можно изобразить, например, так, как на
рис. 5.2. Предположим, что правило выбора решения состоит в
том, чтобы получаемый результат наблюдения z сравнивать с ие-
Рис 5 2 Плотности вероятности н
пространстве наблюдений и ввроят
нооти пропуска сигнала и ложно
тревоги
^Рг^^ 2-р^(а\^х)
которым пороговым значением a = zT, причем, если z = a1>zT, то
принимается гипотеза <§{х, если же выполняется обратное нера-
венство, то принимается гипотеза зй?0. В действительности вели-
чина z обычно определяется как достаточная статистика, значение
которой вычисляется не по одному единственному наблюдению,
а по нескольким. Однако здесь удобно предположить, что z —
скалярная величина.
В этой главе сначала рассматривается задача обнаружения
известного сигнала, наблюдаемого на фоне шума, а затем обсуж-
дается обнаружение случайного сигнала в шуме.
В § 5.2 задача обнаружения решается в предположении, что
решение о наличии или отсутствии сигнала должно выноситься
по одному единственному наблюдению. Эти результаты обобщают-
ся на случай многократных наблюдений в § 5 3. Задача разли-
чения нескольких гипотез (больше двух) обсуждается в § 5.4.
Исследование проблемы проверки гипотез по выборкам фиксиро-
ванного объема завершается рассмотрением сложных параметри-
ческих гипотез. Объем выборки, требуемый для вынесения реше-
ния, часто можно существенно уменьшить, если использовать по-
следовательные правила выбора решения, которые рассматри-
ваются в § 5.6. Такие правила позволяют выносить решения
после каждого наблюдения. В заключение главы задачи после-
довательного анализа изучаются для важного случая нормальных
шумов измерений и марковских моделей сигналов. Приводимые
здесь результаты получены >с использованием метода переменных
состояния.
5.2. Выбор решения при однократном
наблюдении
Обсуждение проблемы выбора решения на основе одно-
го наблюдения начнем с определения вероятностей ложной трево-
114
ги и пропуска сигнала. Согласно предположению, введенному в
конце предыдущего параграфа, для вероятности пропуска сигна-
ла можно записать (см. рис. 5.2)
гт
Рм= J Pz|^(a|^i)da. (5.1)
--ОО
Аналогично для вероятности ложной тревоги получаем
00
PF= J Pz|^(a|5?0)da. • (5.2)
гт
Из этих формул следует, что, например, вероятность пропуска
можно получить сколь угодно малой, если только не обращать
внимания на вероятность ложной тревоги. В практических прило-
жениях обычно вероятность ложной тревоги PF выбирается рав-
ной некоторой допустимой величине, а правило решения (т. е.
порог гт) выбирается так, чтобы обеспечить минимально возмож-
ное значение вероятности пропуска Рм. Этот критерий, известный
как критерий Неймана — Пирсона, в рассматриваемом здесь слу-
чае оказывается тривиальным. Действительно, для обеспечения
заданного значения вероятности ложной тревоги здесь необходи-
мо соответствующим образом выбрать и зафиксировать значение
порога, что приведет к вполне определенному значению вероят-
ности пропуска сигнала.
В более реальных случаях, когда имеется несколько наблю-
дений, оказывается возможным, используя метод множителей
Лагранжа, наложить ограничение на вероятность ложной тревоги,
не фиксируя одновременно значение вероятности пропуска сигна-
ла. Следовательно, в этом случае можно найти минимум выра-
жения
(5-3)
в котором А—неопределенный множитель Лагранжа, а у — тре-
буемое значение вероятности ложной тревоги. Используя теперь
равенства (5.1) и (5.2) и дифференцируя (5.3) по zT, запишем
= 0 = pz^ (zT | ^) — A pz^ (zT | $f0).
Отсюда получаем правило выбора решения
Pz| yg (a I ^i)
основывающееся на отношении правдоподобия, при наблюдении
z=a. Согласно этому правилу гипотеза принимается в том
случае, если это отношение больше А, а гипотеза принимается,
если отношение правдоподобия меньше Л. Параметр А (множи-
тель Лагранжа) выбирается из условия PF—у.
115
Если ложное обнаружение и пропуск сигнала имеют одинако-
вые последствия, то можно минимизировать сумму вероятностей
пропуска сигнала и ложной тревоги
2т »
PF+M = Рм + Pf = J f Pzi^Aa\^o)da (5.5)
~°° Zj.
путем выбора порога zT Дифференцируя правую часть послед-
него равенства по zT и приравнивая производную нулю, по-
лучим
d^T = 0 = Pz\ ( zt I ~ Pz\Jf ( zt I ^o)«
Таким образом, значение порога zT совпадает с тем значе-
нием переменной се, при котором оказываются равными значения
плотностей вероятности Если для полученного значения z=a.
оказывается, что Pz\^^>Pz\ffe0-, то принимается гипотеза Пра-
вило выбора решения в рассматриваемом случае также основы-
вается на отношении правдоподобия и записывается в виде
(«I ^?i)
g 1.
pz\ж ।
(5.6)
Реальные проблемы выбора решения вообще намного слож-
нее, чем рассматриваемая здесь задача при простом скалярном
наблюдении Часто, например, представляется неестественным
предположение, что ложная тревога и пропуск сигнала приводят
к одинаковым последствиям В общем случае с этими ошибками
могут быть связаны различные потери, кроме того, потери могут
быть приписаны и правильным решениям. При рассмотрении за-
дач подобного типа используется критерий байесовского риска, а
соответствующие правила называются байесовскими правилами
выбора решения
При проверке гипотезы против одной единственной альтерна-
тивы возможны четыре ситуации и следующие связанные с ними
потери’
Соо — потери при принятии гипотезы когда на самом деле
справедлива гипотеза
Coi — потери при принятии гипотезы 0, когда на самом деле
справедлива гипотеза St х,
С10 — потери при принятии гипотезы St i, когда на самом деле
справедлива гипотеза
Сц — потери при принятии гипотезы St\, когда на самом деле
справедлива гипотеза e%Jx.
Соо и Сц характеризуют потери при принятии правильных реше-
ний, в то время как См и С10 — потери при ошибочных решениях.
116
Определим байесовский риск S3 как -среднее значение потерь
в указанных выше четырех -ситуациях. Тогда можно записать
S3 = С00Р (принять 3?0, 3%0 справедлива) 4- С01Р (принять 3%0, 3¥г
справедлива) 4- С10Р (принять ,%’1, 3?п справедлива) + СПР (принять
справедлива). (5.7)
Воспользовавшись правилом умножения вероятностей
Р(А,В) =Р(А\В)Р(В), выражение для риска S3 можно перепи-
сать следующим образом:
33 = С00Р Р (принять | ЗКй справедлива) + coip^p (принять
3^01 3¥-l справедлива) 4- С10Р Р (принять 3^х 13%0 справедлива) 4-
+ Р (принять З^х | 3^г справедлива).
Если теперь правило выбора решения представляет собой
простое сравнение результата наблюдения с порогом, т. е. соглас-
но этому правилу принимается гипотеза если полученное зна-
чение а наблюдаемой величины больше порогового значения zT,
и принимается гипотезаесли a<zr, то риск S3 можно запи-
сать -в виде следующего выражения:
zt zt
®=С™РЖ„ J Pz|^(al'^o)da + Coi% J Pz^(*\^')da +
-------------00 —oo
+ C10P^0 J p^tamda + C^P^ J pz^(<*mda. (5.8)
zt гт
Значение порога zT теперь -необходимо выбрать так, чтобы
минимизировать значение байесовского -риска (5.8) Естественно
предположить, что потери при неправильных решениях будут
больше, чем потери при правильных решениях (часто потери при
правильных решениях принимают равными нулю), т. е. СОо<Сю
и Сц<С01. Будем считать также, что потери при любых решениях
неотрицательны.
Так как
” р
.[ Рх\у (a IY) dа = 1 — f Рх\и («I у) dа, (5.9)
Р —оо
то вместо (5 8) можно записать
53 = С^Рж0 + + J [(С°°— С1°) Pw0 pz\^e+
--ОО
+ (Co1-C11)P^iPz|^(a|.^1)]da. (5.10)
117
От порога zT в последнем выражении зависит только значе-
ние интеграла. Дифференцируя риск ЗВ по zT и приравнивая произ-
водную нулю, получим равенство
( £<ю) P#g0 Рг\.9ё ( гт । = (С®1 (^11^ Pz\tfe ( Zt I(5.11)
являющееся необходимым условием, которому должен удовлетво-
рять порог zt. Эквивалентной является следующая форма записи
этого условия:
Рг| yg ( гт I 1) (С1<> с«о) Р
Рг| gg ( ZT । ^о) (С,1 Си) Р
(5.12)
В действительности значение наблюдения z может оказаться
меньшим или равным порогу zT. Из ф-лы (5.10) и рис. 5.2 сле-
дует, что если z окажется меньше, чем zt, то условная плотность
вероятности z при еЖ’о возрастет, в то время как условная плот-
ность вероятности z при уменьшится.
То есть, в этом случае отношение уменьшится. Сле-
довательно, правило выбора решения можно определить следую-
щим образом:
Рг| («I ^i) (Сю — Соо)
yg (а I ^о) (См Cu) Рi
Отношение двух рассматриваемых плотностей
называется отношением правдоподобия
I —
pz\M (a| -^о)
Порог данного правила выбора решения имеет вид
s — р$g0 (£io £00)/^^ (£<*! £ц)*
вероятностей
(5.14)
(5.15)
Используя эти обозначения, правило выбора решения, наи-
лучшее в смысле критерия среднего риска, можно записать
в виде
£(a)s^. (5.16)
Часто полезно преобразовать соотношение (5.16), взяв, напри-
мер, натуральный логарифм от его обеих частей. В этом случае
получаем
In S: (a) yS 1п У. (5.17)
Такое преобразование особенно удобно в том случае, когда
обе рассматриваемые плотности вероятности являются нормаль-
ными. В последующем анализе предполагается, что имеется вся
информация, необходимая для вычисления значения порога S
данного правила. В действительности значения потерь и априор-
ных вероятностей обычно неизвестны и должны быть определены
из каких-либо дополнительных соображений или на основе резуль-
418
татов дополнительной обработки реальных наблюдений, что при-
водит к адаптивным правилам выбора решения.
Иногда потери известны, а неизвестными остаются только
априорные вероятности Р## и Рда. В этом случае можно ис-
пользовать минимаксное правило выбора решения, являющееся
байесовским для наихудших значений априорных вероятностей.
Это означает, что минимаксный риск
= max min ® ( гмм) (5-18>
равен 'минимально возможному значению среднего риска при та-
ком значении Р$ей, которое максимизирует этот риск. Минимакс-
ный критерий имеет некоторые преимущества по сравнению с
критерием среднего риска. Однако следует иметь в виду, что он
может привести к чрезмерно осторожным правилам выбора ре-
шения.
Воспользовавшись формулами для вероятностей пропуска сиг-
нала и ложной тревоги, выражение (5.10) для байесовского риска
можно переписать следующим образом:
33 = СиР+ С^Р^ + (Со1 Сх1) Р^РМ (Qo Qo) Р^я (1
Но так как Р^о + Р = 1, то
•?3 = (С01 — CJ Рм СХ1 [Соо — СХ1 — (Со1 — Сп) Рм 4-
+ (C10-C00)PF]P^a. (5.19)
Если желательно получить минимаксное правило, то порог
нужно выбрать так, чтобы байесовский риск не зависел от значе-
ния Р Следовательно, коэффициент при в ф-ле (5.19)
должен быть равен нулю и для минимаксного правила получаем
G>o — Qi'— (^oi Qi) Рм “Ь (Сю — Соо) PF = 0. (5.20)
Отсюда для особенно важного случая, когда С0о=Сц=0,
имеем
ColPM = CwPF. (5.21)
Последнее равенство можно рассматривать как соотношение, оп-
ределяющее минимаксное правило.
Отношение правдоподобия -£ (а) играет очень важную роль
при изучении вопросов, рассматриваемых в данной книге. Все
правила выбора решения, рассмотренные до сих пор, основывают-
ся на отношении правдоподобия.
Байесовское правило выбора решения минимизирует апосте-
риорный риск. Это становится очевидным, если воспользоваться
Если коэффициент при Р
можно увеличить путем увеличения
(Прим авт )
не равен нулю, то значение риска <59 всегда
Р после того, как выбрано значение Zun.
<?£ о
119
формулой Байеса и записать отношение правдоподобия (5.14) в
виде
X (а) = ^Iz^11 pjg|z^i|a) р$ей 22.
р &e\z ।а)рг (а)/^^о рж\г 'а) р.'/е1
Первый сомножитель правой части этого выражения пред-
ставляет собой отношение апостериорных вероятностей рассмат-
риваемых гипотез. Отметим здесь, что в данной книге апостериор-
ные распределения постоянно будут служить предметом внима-
тельного изучения.
Пример 5.1. Простейшей задачей, относящейся к рассматриваемой в дан-
ном разделе проблеме построения правила выбора решения, является обнару
жение постоянного сигнала на фоне аддитивного нормального шума, среднее
значение которого равно нулю Здесь гипотезе Жо соответствует отсутствие сиг-
нала, согласно гипотезе ./гД сигнал со значением т>0 присутствует на всем
интервале наблюдения, т е можно записать .-Ж) z=v, z=m-\-v, где
'’"'“’-тЪ'
е—а!/2а* 2
Задача проверки гипотез возникает, например, тогда, когда необходимо
проверить, какому из двух возможных значений — 0 или т — равно среднее
значение нормальной случайной величины Для вычисления отношения правдо
подобия необходимо знать плотности вероятности, соответствующие разным
гипотезам Для рассматриваемого примера имеем
Рг|^(а|Ж)-
рг1^(а|^1) = у=
е-а2/2а2 .
е— (а—т)2/202
Логарифм отношения правдоподобия
2сг
m (а — т/2)
о2
Байесовское правило выбора решения принимает вид
т(сх—т/2) P>/£a (Cw ~~
о2 Р (Он 01)
ИЛ -I
т а2 , (С1° ~ Со°) л
а г: — + —-In — ------------Л г_
2 т Р^01 £ц)
Согласно этому правилу решение выносится после сравнения полученного
значения а наблюдаемой величины со значением порога z-v Это выражение
для правила получено непосредственно из соотношения (5 17)
Если потери при правильных решениях принять равными нулю, т е поло
жить Соо = Сц = О, а потери при ошибках обоих видов — отличными от нуля и
равными, то правило проверки рассматриваемых гипотез записывается в виде
m о2
а : — 4- —
2 ' m
Р
1
120
Если Рyg >Рyg , то порог этого правила меньше, чем т/2. поскольку ги-
потеза Жх оказывается справедливой чаще, чем При ^^,^ = ^^>^ = 0,5 зна-
чение порога точно равно т/2, что интуитивно представляется естественным,
поскольку гипотезы и априори одинаково правдоподобны
Вероятности пропуска сигнала и ложной тревоги, определяемые соотноше-
ниями (5 1) и (5 2) соответственно, в данном примере легко вычисляются
гТ гТ
Г Г 1 (а—т)2/2с2 ,
— со —со
PF~ J рг|^о(а|^о)^а- J а/2° da-
Z„ Z„ *
Эти формулы после замены переменных приводятся к виду
-V2/2dVi PF =
Вероятность правильного обнаружения
е ^^dy.
Взаимосвязь между вероятнос-
тями правильного обнаружения Ра
ч ложной тревоги Ру можно оха-
рактеризовать с помощью семейст-
ва кривых, для которого m являет
ся параметром с дискретным мно
жеством возможных значений, а
Zt — параметром со значениями из
интервала [—оо, оо]
При zT=—оо всегда прини-
мается только гипотеза Ж’] В этом
случае вероятности и ложной тре-
воги, и правильного обнаружения
равны 1 При Zr = oo всегда прини-
мается гипотеза -vA Очевидно, что
при заданном значении Ру вероят
иость правильного обнаружения Рт>
монотонно возрастает с увеличе-
нием m Семейство таких кривых,
которые часто называются рабочи
ми характеристиками приемника,
приведено на рис 5 3
Рис 5 3 Рабочие характеристики прием-
ника (пример 5 1). Стрелками указаны
направления, вдоль которых значения
параметров tn и zT увеличиваются
121
5.3. Выбор решения при многократных
наблюдениях
В большей части задач теории решений однократное
наблюдение не позволяет обеспечить нужное для практических
целей достаточно малое значение минимума байесовского риска.
Это приводит к необходимости многократного проведения наблю-
дений Введем пространство наблюдений, которое удобно рас-
сматривать как пространство векторов zT=[zt, z2, Крите-
рий байесовского риска легко обобщается на случай векторного
наблюдения. Вместо выражения (5 8) для байесовского риска
теперь получаем
= f Рг। at + CoiP^1 j Pz I л +
Of Of
+Cio^o f Pz\W& +б’цР%’1 J (5.23)
Of Of
тде и называются областями принятия решений. Если
вектор наблюдений принадлежит области , то принимается
гипотеза Если же этот вектор попадает в область , то
принимается гипотеза S^'o Задача теперь состоит в том, чтобы
минимизировать значение байесовского риска путем подбора об-
ластей и^; при этом объединение этих областей
должно совпадать со всем пространством наблюдений
Как и в случае однократного наблюдения, равенство (5 23)
можно записать так, чтобы в его правую часть входила только
область
= ^10 — С<ю) Pz ’У (® I
^.УУ\ (Со1 Сц) pz|^>(at | ^i)] d а. (5.24)
Поскольку потери и априорные вероятности предполагаются из-
вестными, то первые два слагаемых в правой части этого ра-
венства не зависят от формы области Далее будем считать,
что Сю>Соо и Со1>Сц, так что Р (Cio—Соо)р/|.%(«|.%’о) >0 и
P^^Coi—Cii)pz|^ (а| ) ^0. Минимальное значение риска S3
обеспечивается в том случае, если к области отнести все зна-
чения а такие, что Р(Сщ—Сц)р z|j^(a | 3^) >Р (С10—
—Соо) pz|^(a| е^0) > так как при этих значениях а подынтеграль-
ная функция в равенстве (5 24) отрицательна; в свою очередь, все
значения а, для которых
(^oi— Си) Pz\ УС (® I ^1) Coo) Pz| УС I ^о)>
следует отнести к области 3£0 . Для таких значений а подынтег-
ральная функция в (5 24) положительна, так что риск увеличил-
122
ся бы, если бы эти значения были отнесены к области . Таким
образом, байесовское правило выбора решения принимает вид
X (ас) 3S ST, (5.25>
где X (а) обозначает отношение правдоподобия
X (ас)Д
pz|j^ (а | Ж)
а 3~ — порог данного правила
(6jo Cqq) Р
& .
(Col Сц) Р ус
(5.26)
(5.27)
Если для полученного вектора наблюдений значение отноше-
ния правдоподобия больше значения порога, то принимается гипо-
теза Жь в противнсхм случае принимается гипотеза е%?0.
Последние три формулы, справедливые для случая векторного
наблюдения, являются очевидными аналогами ф-л (5 14) — (5 16),
полученных ранее для скалярного случая
Для рассматриваемых двух гипотез можно указать скаляр-
ную достаточную статистику S (z) и соответствующий этой ста-
тистике порог y^(z). Нестрого говоря, под достаточной здесь
будет пониматься статистика, которая содержит всю ииФорма-
цию! необходимую для вынесения решения. Условная плотность
вероятности рг|х (а|0) наблюдаемого вектора z=h(x)+v при фик-
сированном значении вектора состояния или параметра х являет-
ся такой статистикой S(z), представляющей собой линейное или
нелинейное преобразование наблюдаемой случайной величины.
у
Выборочное среднее у= [1/(У+ 1)]^х(&Т) также является статис-
А=0
такой Так, если статистика является настолько «хорошей», что
знание ее значения эквивалентно знанию значения вектора на-
блюдений г, то при данном параметре х для достаточной статис-
тики должно быть справедливым следующее соотношение:
p<S>[x (S | а)«—> (S | а, ₽).
(5.28)
Следовательно, некоторая статистика S (z) может быть доста-
точной только в том случае, если
Pz|5> (ас IS) *pz|#>x(«|S, Р).
(5.29)
Таким образом, условные плотности вероятности, стоящие в
левых частях последних двух соотношений, не зависят от х, если
§ является достаточной статистикой. Конечно, здесь имеется в
виду независимость алгебраическая, в то время как некоторая за-
висимость от х в статистическом смысле имеет место. Используя
формулу Байеса и соотношения (5 28) и (5.29), можно получить
123
другое определение достаточной статистики, основывающееся на
соотношении
Рф(₽1*)*—PxiHIW (5.30)
т е если статистика § является достаточной, то получение зна-
чений z и ® не увеличивает знания о векторе х, содержащегося
только в статистике $ Ясно, что для справедливости соотноше-
ния (5 30) необходимо, чтобы
P$|x(s)₽)’<—>-Pz|x (я1₽) (5-31)
Можно допустить, что вектор х определяет гипотезы Дг?0 и
Тогда на основании (5 31) для достаточной статистики® (а)
получаем
Р8\Ж (Sl <^о) «—>Pz|^(«l^o). (5.32)
P&\dt (SI ^i) Рг\Ж (* I ^i)- (5-33)
Из этих соотношений следует, что отношение правдоподобия
(5 26) можно заменить отношением правдоподобия
£s (S) = ---- (5 34)
p8\d£
длч достаточной статистики, которое может быть использовано
для построения правила выбора решения типа (5 25)
Используя распределения достаточной статистики при рас
сматриваемых гипотезах, запишем байесовский риск в виде
= СооР^о J Pts'll (“51 ^о)^ + C01Pj^i J yg (SI 7CJ dS 4-
— QO —00
+ ciop^o f Ps^WdS + CJ3^ [ (5.35)
~rS
Порог J g здесь следует выбрать таким образом, чтобы полу-
чить минимально возможное значение риска S3 Этому условию
удовлетворяет значение порога, являющееся решением уравнения
(^01 Qi) Р8\Ж (^8 | ^”1) " Соо) (j g j ^f0) (5.36)
или
p8\ W (7 8 I ^0
p#| (7 8 1 ^°)
P'(610 600)
P (601 бц)
(5.37)
J 8,
что совпадает co значением порога (5 27)
Для правила выбора решения, основывающегося на достаточ-
ной статистике, можно вычислить вероятности ложной тревоги и
прописка сигнала
124
д
Pf = J‘ PS\ Ж (SI ^o) dS, PM - J (S | 3^^dS
/ о —00
(5 38)
Можно найти также правила выбора решений, удовлетворяю-
щие критерию Неймана — Пирсона и минимаксному критерию
Для большей части задач невозможно указать явное выраже-
ние для достаточной статистики, если не получено выражение для
отношения правдоподобия X (а) Если же достаточную статисти-
ку указать удается, то можно получить отношение правдоподобия
(£(§) , которое и используется для построения правила выбора ре-
шения В противном случае следует 1начинать с отношения
правдоподобия
PX| w I -^i)
X («) = ------—
(5 39)
Воспользовавшись понятием у словной плотности вероятности,
запишем
Pz| А (* I ^i) = ,у| (S, YI ^i) = к (S | 7^) py]S< ж (Y | S, ^),
(5 40)
Pz|% (« I ^o) =P$ у|ж ($> Y I ^0) =
= Pg (Y|S, 7?0)
(5.41)
В этих выражениях $ —скалярная величина, z — /(-мерный,
а у—(/(—1)-мерный векторы Тогда для отношения правдоподо
бия получаем
Py|S ^(V|S
I tf0) Pyj^ | S,
(5 42)
Если статистика *? является достаточной, то отношение
правдоподобия X (а) не должно зависеть от у, т е должно быть
справедливым равенство
Ру Id?, V (Y I s, Я\) = py[S< (YIS, ^0) (5.43)
Стедоватетьно, в этом стуч^е плотность вероятности векто
ра у оавис it от того, какая из двух рассматриваемых гипотез
справедшва Этот фак> разъясняет смысл сформулиооваиного
выше твсрждечия о том, что достаточная статистика аккумули-
рует в~ю информацию, содержащуюся в наблюдениях и необхо
димую для вынесения решения Полезна следующая интерпрета
ция д'1 та‘-очной статистики Echi суп ествует достатошая статис-
тика, то можно указать таксе преобразование координат, при
котор^ v’ од ia из новых координат будет содержать гею информа-
цию, необходим ю для вынесениз реше шя о справедливости
12з
одной из двух рассматривающихся гипотез. Остальные координа-
ты, число которых равно (К—1), не содержат совсем информации,
полезной с точки зрения вынесения решения. Понятие достаточ-
ной статистики является очень важным и часто будет использо-
ваться в последующем изложении.
Пример 5.2. Вновь рассмотрим пример 5 1, приняв теперь, что имеется К
наблюдений, полученных при одной из двух возможных гипотез В этом случае
можно записать
zk — vh\ | __j ?
Будем предполагать, что случайные величины vk и v} статистически неза-
висимы при 'kУ=1 и одинаково распределены Их совместная плотность вероят-
ности
/ К ч
где vT = [£>!, t>21..., =[а1( а2...... ай].
Условные плотности вероятности наблюдаемого вектора
тезах имеют вид
при разных гипо-
/ К ч
' k=l '
1
Pz(^(al^)=7^K72exp
1 К
— J(aft-m)2
fc=l
Отношение правдоподобия вычисляется как отношение этих плотностей В ре
зультате имеем
х (а) = ехр
К
k=i
Правило выбора решения, основывающееся на отношении правдоподобия, запи-
сывается теперь согласно (5 25) следующим образом
К
(2 ак т — ш2) =е 1п <У
fe=i
или
К
т
а2
Кт
~2~
Таким образом, достаточная статистика в рассматриваемом случае пред-
ставляет собой просто сумму наблюдаемых величин Удобнее достаточную ста-
тистику нормировать и решение выносить на основе статистики
126
£ •
Правило выбора решення_прн этом записывается в виде
о У Кгг
Я (z) _ In
т УК 2а
Найдем плотности вероятности нормированной статистики при обеих гипо-
тезах Непосредственно из определения статистики получаем
оУК Я
a
Е да (z) - Е {<g> (z)J2} = l.
Поэтому
(S|^o)= e-S2/2 ;
„ ,____1 _ - "Ч о)72
P&\&e(S№i)- у^у
Графики этих функций изображены на рис 5 4
Если условные плотности вероятности достаточной статистики известны то
можно вычислить значения байесовского риска и вероятностей ложной тревоги
и пропуска сигнала для правила Неймана—Пирсона или минимаксного правила
Причем эпи вычисления оказываются проще, чем подобные вычисления, основы
вающиеся на совместном распределении выборки Полезно также вычислить
среднюю вероятность ошибки и рабочую характеристику приемника, реализую-
щего анализируемое правило выбора решения
Рис 5 4 Условные плотности вероятности достаточной ста
тистики
Согласно определениям для вероятностей пропуска сигнала и ложной тре-
воги можно записать соответственно
7Г ур & $ У Ktnjo
Рм = J S J
dT,
127
Здесь при вычислении вероятности_пропуска сигнала использована замена
переменной интегрирования Г=(5—/Л’т)/о.
Если предположить, что Р~Р gg = Соо = Си = О; Coi = Cio, так что
на основании ф-лы (5J15) имеем 0 = il, то средняя вероятность ошибки
Выделив из отношения правдоподобия достаточную статистику и определив
новое значение порога т/2о, последнюю формулу можно переписать
следующим образом
(+ /к т/2 а \ со
с 1 —Г1 2/2 1 С 1 — Г2/2
1— ---— е ' dr = I ---------е </Г= 1 — erf (0/2).
J /2л / J 2л
—Укт/2а J S)/2
Здесь разность между средними значениями статистики $ при гипотезах
и определяет расстояние 0 = Iff —Е'{<?|0?о}|='// m/о. Напом-
ним, что для функции erf Л в гл. 2 было дано следующее определение:
А
erf Л = f —е— “а/2 а
J /2л
В этом случае, если вероятности ложной тревоги Pf и правильного обна-
ружения Рп заданы, то необходимые значения порога <0 и расстояния 0 мож-
но вычислить с помощью соотношений:
PF = 1 — erf (In 0/0 ф- 0/2); PD = 1 — erf (In 0/0— 0/2).
Так как расстояние 0 при фиксированных значениях параметров тио
можно увеличивать путем увеличения объема выборки К, то можно вычислить
объем выборки, необходимый для обеспечения заданных значений Pf и Рп
Точки рабочей характеристики минимаксного приемника для частного слу-
чая, когда Соо = Сц = 0, определяются из соотношения (5 21)
Он — Он (1 Р и ) = Он Рf •
Рабочая характеристика минимаксного приемника описывается уравнением
PD=l--^-P„
D /-> г •
СО1
Ранее уже отмечалось, что достаточную статистику можно рассматривать
как результат преобразования координат пространства наблюдений Например,
при К = 2 введем преобразование:
1 1
<S,(z) = -T7=’(zi + z2); у (z) =-~т=-(Zi — ?2).
а У 2 а у 2
Тогда
Р<8\Ж ^<>) = e-S /2-
1 -У2/2
Ж = (ylS’ -Жо) = /1^е
128
Таким образом, в этом 'примере условная плотность вероятности новой пе-
ременной у не зависит от того, какая из двух гипотез справедлива. Этот факт
ь общем случае устанавливается соотношением (5.43).
Рассмотрим теперь более общую задачу, связанную с нор-
мальными случайными величинами. Различные частные случаи
этой задачи охватывают многие проблемы теории обнаружения
сигналов Будем рассматривать модель наблюдений
zR = mh + vk, k= 1, 2, . . ., К, (5.44)
где zh и vh — нормальные случайные величины, a mk — известные
числа. Введем векторные обозначения:
Z = 1 1 rd CJ , . . N N N 1 1 ; т = тг т2 JnK _ ; v - _ VK _ (5.45)
и будем предполагать, что при гипотезе E{m|,^0} = m°; £{v|^o) = O; £{z|.^u /УТ? о } = m°;
var{m|^0} = 0; var {v | %" о} = к°. var{z ^0} = R°, (5.46)
а при гипотезе Е (т | = т1; Е {v | = 0; £{21.5^} = т1;
var {т | .7^} = 0; var{v|.%'l} = R1; var {z (5.47)
Таким имеют вид образом, условные плотности наблюдаемых величин
Pz|.^ (ai ^о)=----------—2П ехр [~ Т ~ (R°) *(а — m°)J:
[ (2л)к det Ro]2 (5.48)
(а I Ж) =--------------Т ехР [— V (а — ml)r («—т1)].
[ (2л)к det R1] 2
Отношение правдоподобия и правило выбора решения, осно-
вывающееся на отношении правдоподобия, теперь можно записать
следующим образом:
2(«) = (Su2 ехр[~~+
+ _1_ (а _ mo)T (RO)-1 (я _ т0)
•2 (а) У; У
(Оо Оо)
(Он 01)
(5.49)
р
1
Вычислив логарифмы обеих частей неравенства, для байесов-
ского правила выбора решения получим (при практическом ис-
5—26
12»
пользовании этого правила вместо а необходимо подставлять ре-
зультат наблюдения — выборку z)
---7 (я — ml)T (я — т1) + -|- (а — т0)7 X
х (R0)-1 (а — т°) =S In Т —in det R°-рIn det R1. (5.50)
Левую часть этого неравенства можно рассматривать как до-
статочную статистику
§ (а) = (а — m0)7 (R0)'1 (я — т°) — — (а — т1)7 (R1)-1 (а — т1).
(5.51)
Из (5 50) следует, что вычисление таких важных характерис-
тик полученного правила, как вероятности ложной тревоги и про-
пуска сигнала, по распределениям этой достаточной статистики
при различных гипотезах сопряжено со значительными труднос-
тями Это обусловлено тем, что рассматриваемая статистика яв-
ляется нелинейной функцией нормальных случайных величин,
вследствие чего ее распределения отличны от нормальных
В более простом, но все еще полезном для приложений слу-
чае, когда ковариационные матрицы вектора v при обеих гипо-
тезах одинаковы, т е. R°=R1 = R, правило выбора решения (5 50)
принимает вид
(гл1 — m0)7 R1 а . ; 1п У + — [(m1)7 Rm1 — (m0)7 Rm0]. (5.52)
Правило (5 50) намного сложнее, чем правило (5 52), посколь-
ку согласно второму с порогом следует сравнивать взвешенную
сумму результатов наблюдений, в то время как при использова-
нии первого правила необходимо вычислять значения и разность
двух квадратичных форм от результатов наблюдений Удобно
ввести вектор разности средних значений
Д m = ш1 — т° (5 53)
и нормированную скалярную достаточную статистику
1
8(a) = A m7R-1 a/(A m7R-1 А т)2 . (5.54)
Нетрудно показать, что
e{w\ ^о} = -А т~-1 т-Ч
(Д т7 R-1 Д т) 2
Д т7 R1 mi
Е{8(а) |^i} =
(m7 R-1 Д т) 2
var{S (а) | Жо} = var{§ (а) | = 1.
(5.55)
130
При рассмотрении примера 5.2 было показано, что пара-
метр 3), названный расстоянием или мерой различия рассматри-
ваемых гипотез, при фиксированном значении порога опреде-
ляет качество (т. е. значение байесовского риска) правила вы-
бора решения. В этом примере достаточная статистика также
была нормирована таким образом, чтобы ее дисперсия была рав-
на единице. Теперь параметр Ж удобно определить как разность
найденных средних значений достаточной статистики, деленную
на среднеквадратичеокое отклонение. В этом случае для ®2 мож-
но записать
Ж2 = [£{^(«)|.^1}-£{^(«)|.^0}]2
(5.56)
var {d? (а) | .У/Д
а параметр ® интерпретировать как отношение сигнал/шум. Для
общей задачи, связанной с гауссовскими случайными величинами
с одинаковыми ковариационными матрицами при разных гипо-
тезах, имеем
®2 = AmrR J Am.
Приведенные соотношения дополнительно упрощаются, если
компоненты вектора шума измерений статистически независимы,
т. е. если
R = о21. (5.58)
Статистика § (а) и параметр ®2 при этом принимают вид
к
^mkak
k=i
(5.57)
© / ч д т' а
®(«) = ----------
(Д тт Д т) 2
к
2
(5.59)
mJ
Л
. \k=\
т к
др = А mA m 1 уч
а2 ' а2 U
*=1
Эти результаты справедливы в случае векторных наблюдений
zfe = mh + vft, k = 1, 2, . . ., К, (5.60)
когда zfe имеет размерность N. Для того чтобы выписанные ранее
соотношения
наблюдений
z = m-ф v
остались справедливыми, достаточно ввести вектор
(5.61)
(5.62)
5*
131
Часто оказывается, что не только шум измерений, но и само
сообщение является случайным. Пусть zft—V-мерный элемент вы-
борки объема К- Эту выборку представим как выборку объема
Л/Д' со скалярными элементами [см. ф-лу (5.61)]. Пусть далее
возможны две гипотезы:
^0:z = v; ,%’1:z = m + v. (5.63)
Будем предполагать, что m и v—нормальные независимые
случайные векторы, средние значения которых равны нулю, а ко-
вариационные матрицы
Vm = var {m} = Е {mmr };
Vo = var {v} = E {vvr } (5.64)
известны. Очевидно, что рассматриваемые гипотезы можно опреде-
лить также и следующим образом:
।
^1:var(z|‘^1}_R> = Vm+V„. f
Правило выбора решения для проверки этих гипотез совпа-
дает с правилом (5.49). Отношение правдоподобия при этом имеет
вид
X («) = Г_detv^ 1 Техр [_ J_ g,T+ v )-’я+± я _
[det (Vm+Vo)J f [ 2 m 2
(5.66)
Достаточная статистика
§(«) = _ -L ят(ут + Vp)-i я + ±_ f v-i я (5.67)
здесь аналогична статистике (5.51). Как уже отмечалось ранее,
эта достаточная статистика не является такой простой, как в
случае одинаковых ковариационных матриц при разных гипоте-
зах Поэтому для нее желательно найти другие представления.
В простейшем случае независимых наблюдений, когда каждый
элемент выборки zfe является скалярной величиной, имеем Vm=
— Vml и V„=KrI. Так что достаточная статистика
§(я) =--------!----У а2 + -1- V а2 =------------У а2 .
2(Vm + Vv) U k 2VvU k 2Vu(Vm+Vv)U k
k=l k=l k-\
Найдем теперь условное математическое ожидание вектора m
при фиксированной выборке z, предполагая, что справедлива ги-
потеза Согласно определению математического ожидания
m = E{m|z}= J у рт}2 (у |«)d у. (5.68)
— ОО
Л
Вычислить m можно относительно просто, поскольку известно,
что условная плотность вероятности рт | г является нормальной.
132
Действительно, на основании формулы Байеса можно записать
Pm I 2 (у | га) —pz\ т (га | у) рт (у)/рг(га). Все три плотности вероятности
в правой части этой формулы являются нормальными со следую-
щими параметрами:
Е {z | m} = m, var {z | m} =
E {m} =- 0, var {m} = Vm;
£{z} = 0, var{z) = Vm+ ¥0.
Следовательно,
exp {“ 4~ — Y)T V“"' ~ T) v7't “ “] }
Рт!г(Г|Я)“ (2.т)Л'к/2 [det (VmV„)/det (Vm + V,,)]1/2
Приведя это выражение к стандартной форме, в которой обыч-
но записывается нормальная плотность вероятности, получим
(предполагая, что справедлива гипотеза
Рт^ 1 Я) = (2:7)^' ^de^J1' -' “Р [-~ ’ (5‘69)
где
m = E{m|z = «}=-- ¥„,(¥„+¥,)-’«= (¥^ + ¥71)“1 V71 (5.70)
Vmi2= var{m|z} = (¥~1 + V71r1 .
В следующих двух главах будет подробно описана интерпре-
л
тация математического ожидания m как оценки сообщения т.
Воспользуемся теперь леммой об обращении матриц, на осно-
вании которой для рассматриваемого примера можно записать
(¥п>+¥0)-1 =¥7’ -V71 (¥"’ + ¥71)-1 V71 .
Подставляя это представление для обратной матрицы в ф-лу
(5.67), получим выражение для достаточной статистики:
§(«) = -!- ят ¥7' (¥7' + ¥7') ¥7’ «. (5.71)
Используя, наконец, формулу для условного математического
л
ожидания m вектора m при фиксированной выборке z, получаем
S(«) =-i-«г¥71т. (5.72)
Это выражение можно интерпретировать как дискретную кор-
реляционную обработку. В частном случае, когда Vv=Vvl,
к
1 А 1 т А
статистика S принимает вид § (я) = — V aftmh= — я m ,
2Vv лял 21 v
k=l
133
1. е. действительно может рассматриваться как выборочный кор-
реляционный момент между наблюдаемыми величи-
л л
нами и оценкой m Заметим, что значение оценки m вычисляется
по всей имеющейся выборке. В простейшем случае, когда Vm=
Л V £
=Vml и Vt= V„I, оценка m = ” V <xh.
Vm + Vv CJ
*=i
Во многих интересных для приложений случаях шум измере-
ний можно считать белым и при вычислениях принять, что
Vr=VrI. Однако подобное предположение относительно сигна-
ла m обычно недопустимо. Важным для практических приложе-
ний является случай, когда сигнал является решением линейного
разностного уравнения nift+i=<I>ftmft+rfeWft, где wft — независимые
случайные векторы, каждый из которых распределен по нормаль-
ному закону с ковариационной матрицей VWft. В гл. 3 и 4 уже
были описаны способы вычисления ковариационных матриц Vmh
и Vm такого сигнала.
Из полученных для достаточной статистики выражений
S («) = -L ят [V71 - (Vm + Vc)-1] 4- + vr1)-1 V71] «
z z
или $(«)=-|'*TV71m
следует, что каждый элемент выборки умножается на другие эле-
менты выборки и соответствующий весовой коэффициент Кроме
того, при вычислении значения достаточной статистики необходи-
мо обращать несколько матриц. Однако можно ввести специаль-
ное обозначение V^1 и положить
V# = V71 Vm(Vm + VcT1 = V (Vm1 + vr1)-1 v0-’.
Эта матрица может быть вычислена заранее
Таким образом, в общем случае вычислению подлежит статис-
тика §(«) = —<xrV^’«. Эти вычисления далеко не всегда яв-
ляются простыми, особенно при больших объемах выборки К й.
*> Другой способ вычисления значений достаточной '’татисти' и основывается
на дискретном аналоге разложения Карунена—Лоэва Пусть Q — матрица раз-
мера NKxNK, столбцы которой являются собственными векторами матрицы
V$ Тогда матрица D = QTV^,Q является диагональной Элементы этой мат-
рицы dtt являются собственными значениями матрицы V^, Если ввести обозна-
чение ad = Qa, то достаточную статистику можно записать следующим образом.
(Прим авт)
134
Полезно рассмотреть случай непрерывного времени, к которо-
му можно перейти, увеличивая неограниченно число отсчетов на
конечном временном интервале наблюдения. Использованный
ранее подход к задаче различения гипотез, основанный на увели-
чении размерности вектора наблюдений, в случае непрерывного
времени неприменим, поскольку объем выборки К оказывается
неограниченным; он неудобен также при отыскании последова-
тельных правил выбора решения (см. § 5 6). Поэтому задачу
сформулируем таким образом, чтобы ее решение можно было
получить и для непрерывного случая. Предположим, что шум
измерений — белый нормальный, имеет нулевое среднее значение
и одну и ту же ковариационную матрицу при обеих гипотезах.
Кроме того, здесь будем рассматривать только случай полностью
известного сигнала. Более общий вариант этой задачи будет рас-
смотрен в рамках теории последовательного обнаружения в § 5.7.
Таким образом, рассматриваются следующие гипотезы:
^o:zft = mO + vft;
= m’ +vft,
где m® и m ’ — известные сигналы и
Е {vft} -= 0, cov {vm, vn} = Vvm t>K (m — n).
Для этих гипотез отношение правдоподобия
Pz( %? I ^"1)
= --------------=
П 1-----------ехр — ----(xk--- т*)Г 'Ts.1 (“А — т1)]
1 1 /2n(det Vv*) 2 ' W vi \ " WJ
_ fe=l________________________________________________
~ К
—==—--------гтх ехр [— -—' (а* — т?)г — т2)
У 2л (det Vv*)1/2 L 2 V k’ vkV
*=!
(5.73)
(5.74)
Его можно переписать следующим образом:
к
2’(Л)=ехр i
k=i
где A mh = m* — m®.
[2A ml Vva1 «ft — (mi)r VVk mi + (mj)r Vvk m£] ,
(5.75)
(5.76)
Эта форма записи особенно удобна для отыскания отношения
правдоподобия при непрерывном времени
Правило выбора решения, основывающееся на использовании
логарифма отношения правдоподобия, теперь можно записать в
виде
135
К К
A mJ Vv* mk—(m*)T VvJ m”]- (5.77)
*=i ft=i
Правая часть соотношения (5.77), для которой введем обозна-
чение £, может быть вычислена заранее и ее значение может
храниться в запоминающем устройстве, t, является просто поро-
гом, значение которого известно, если известны векторы сигналов
т° и т*, и ковариационные матрицы Vva, а также заданы ап-
риорные вероятности Pyf, 1И ?:%i 'и потери Соо, Он, С1о, С1Ь
Следовательно, вместо (5.77) можно записать
S AmJV^S^. (5.78)
Й=1
На рис. 5.5 изображена структурная схема устройства, реали-
зующего правило (5.78). Это устройство можно интерпретировать
как дискретный согласованный фильтр. Поступающие значения
выборки Zft=afe умножаются на значения сигнала AmJ Vvk. Полу-
ченные произведения AmJ XVv*aft, fe=l, 2, ..., А являются ска-
лярными величинами, которые накапливаются в сумматоре. После
А-го шага число, полученное в сумматоре, сравнивается со значе-
нием порога В зависимости от результата сравнения выносится
решение принять гипотезу или В обычном согласованном
фильтре каждый элеменД выборки z^ является скалярной величи-
ной, а диспепсия шума постоянна. Основное назначение со-
Рис. 5 5 Дискретный сог-
ласованный фильтр (вектор-
ые сигналы)
гласованного фильтра — формирование достаточной статистики
К
X AmJV~* afti которая используется в байесовском правиле выбора
k=i
решения.
При построении правила выбора решения для непрерывного
времени будем использовать следующую модель наблюдаемого
процесса:
^’1:z(0 = m1(0+ v(t),
136
to<Zt <Z if',
t0<t< th
(5.79)
где m°(Z) и ml(t)—известные функции времени, a v(^)—нор-
мальный белый шум, среднее значение которого равно нулю, а
ковариационная функция
cov {v ft), v ft)} = £{v (О vr ft)} = Vv (0) 6D ft -t2). (5.80)
При замене этой непрерывной модели наблюдаемого процесса
соответствующей ей дискретной моделью вместо (5.79) получим
W0:z(kT) = + vftn
: z (kT) = m1 (kT) + v (kT). (5.81)
При этом положим, что ковариационная матрица шума
cov {v (тТ), v (пТ)} Sx (т^пГ) (5.82)
и при 7А>-0, m->oo, п-^оо, nT-+t2 переходит в ковариацион-
ную матрицу
cov {v ft), v ft)} = Vv(^i)SDft —12) (5.83)
шума v(/) с непрерывным временем. Воспользовавшись пред-
ставлением (5.82), запишем сначала для дискретного случая от-
ношение правдоподобия:
S’(A) = ехр
_1_
2
— miftr)] — [я ft?) —
{[я (kT) — m1 (kT)]T Ф?’ (kT) [я (kT) —
m°(kT)f^ (kT) [я (kT) — m° (kffl}T I
(5.84)
Если теперь объем выборки увеличивать так, что Т->-0, k-^-oo,
то в пределе получим
/
^(А)=ехр у J (2Д тг(0Ф71(0я(0 —[m1ftIrV71(0m1ft +
t О
+ [т° ftf Ф?1 (t) т° (t)} dt^ . (5.85)
Следовательно, правило выбора решения, основанное на ис-
пользовании логарифма отношения правдоподобия, можно запи-
сать в виде
if
J Amrft4f71(0«(0^sS,
to
(5.86)
где теперь порог
if
SA 1п^ +yj {[irfftf ФГ’фтЧО — (m°ftf (5.87)
to
137
На рис. 5 6 'изображена структурная схема байесовского обна-
ружителя, основной составной частью которого является согла-
сованный фильтр корреляционного типа, аналогичный дискрет-
ному согласованному фильтру (см рис 5 5)
Возможен и другой способ реализации полученного правила
выбора решения. Напомним, что отклик линейной системы с по-
AmT(t)¥v-'(t)
Рис 5 6 Согласован? ый
фильтр корреляции ного ти
па при непрерывном вре-
мени
стоянными параметрами и векторной импульсной характеристикой
h(^) на воздействие a(t) можно записать в виде свертки
jJh7> —Х)«(Х)<П. (5 88)
<0
Сравним теперь этот интеграл с интегралом в левой части
ф-лы (5 87) Очевидно, что для реализации обнаружите чя с ис-
пользованием простого фильтра достаточно положить
h7 (tf -4) = Am7 (X) Ф71 (ft, hr (т)= Am7 (tf — т) ФГ1 (if — т). (5.89)
Рис 5 7 Возможные способы реализа
ции байесовского обнаружителя с сог
л ас «в энными фильтрами
/ — фильтр, согласованный с сигналом m'(t)
т), 2 — фильтр, согла
сованный с сигналом m°(f), h0(T)=m0(/y—
—Т)ЧГ71 (tf—r)
Структурная схема обна-
ружителя с подобным фильт-
ром изображена на рис. 5 7.
В более простом, но часто
встречающемся случае наблю-
даемый процесс является одно-
мерным, а дисперсия шума из-
мерений Фу (0 не зависит от
времени и равна N2. В таких
условиях байесовское правило
выбора решения принимает
вид
б
A m(t)a (t) dt №£ (5 90)
io
При реализации этого прави-
ла, следовательно, можно ис-
пользовать согласованный
фильтр с импульсной характе-
ристикой
Л(т) = Дщ(^ — т). (5.91)
138
Сигналыная компонента на выходе такого фильтра определяет-
ся выражением
G б
£{§}= J — K)dK = J Am2(^)<i X, (5.92)
to to
т e совпадает co средним значением достаточной статистики.
Дисперсия шумовой компоненты на (выходе согласованного фильт-
ра равна дисперсии достаточной статистики
var {§} = N2 A m2(X) d X. (5.93)
«о
Таким образом, для скалярного случая отношение сипнал/шум
1 ef
$а = ^|Ат2(Ш (5.94)
^0
Может показаться, что соотношения (5.89) и (5.91) приводят
к двум различным определениям согласованного фильтра Однако
представление (5 91) является частным случаем более общего
выражения (5 89) для импульсной характеристики фильтра. Если
исходным является представление (5.89), то сигнальная компо-
нента на выходе согласованного фильтра, которая является ска-
лярной величиной, определяется выражением
G if
£(§) = j hT(^— Х)Ат(^)Д = j Дтг(Х)Ф71(Х)Дт(Х)й!^ (5.95)
to t0
в то ®ремя как дисперсия шумовой компоненты
tc
var{S} = j Д тт (X) Ф71 (М А т (k)d X. (5.96)
«о
Таким образом, в общем случае отношение сигнал/шум
tj
Ж2== j Д тг(Х)ФГ1(Х)Дт(^)й!^. (5.97)
f о
Из этой формулы, как частный случай, получается выражение
(5 94)
Снова подчеркнем, что в левой части неравенства (5 86) или
неравенства (5 90) записано выражение достаточной статистики.
Эта статистика является нормальной случайной величиной, так
как представляет собой линейный функционал от нормального
случайного процесса a(t) Поэтому вычисление вероятностей лож-
ной тревоги и пропуска сигнала, а также определение рабочей
характеристики байесовского приемника и минимаксного правила
выбора решения оказываются достаточно простыми.
Другой способ построения байесовского обнаружителя извест-
ных сигналов основан на ортогональном разложении наблюдаемо-
139
бия:
£(«) =
или
3» =
го процесса, например, на разложении Карунена — Лоэва Такой
подход был использован Ван Триссом [269] и Миддлтоном [163].
Разложение Карунена — Лоэва в данной книге будет использова-
но при отыскании оптимальных оценок параметров известных
сигналов в гл 6 Перейдем теперь к изучению проблемы проверки
сложных гипотез, к которой сводятся задачи обнаружения при
наличии неизвестных параметров.
5.4. Проверка сложных гипотез
Часто задача проверки гипотез намного усложняется
вследствие того, что условные плотности вероятности выборки при
рассматриваемых гипотезах зависят от параметра 0, значение
которого при получении выборки неизвестно. Если неизвестный
параметр 0 является случайной величиной, то будем считать, что
заданы плотности вероятности pZ;0|^ («, 0| ^i) и pZj0|j^(«, 0| ^о)-
В этом случае, воспользовавшись безусловными плотностями
вероятности выборки, можно вычислить отношение праРдоподо-
ОО
4>| —СО
(« I J?o) »
J pz,o| 61 ^°)
—СО
Оо
J pz|6, ж ।91 ^i) 1
. (5.99)
оо
J ^z|6,J^ I 9’ (9 I ^о)
—со
Отношение правдоподобия здесь вычисляется после интегриро-
вания по 0 . Далее задача проверки сложных гипотез решается
так же, как и задача проверки простых гипотез.
Если 0 является случайной величиной, но плотность вероят-
ности этой величины неизвестна, или если этот параметр вообще
не является случайным, то воспользоваться ф-лой (5 99) не
удается Один из возможных подходов к задаче проверки слож-
ных гипотез в подобных случаях состоит в следующем. Вместо
неизвестного значения параметра 0 используются оценки, вычис-
ленные по той же выборке. Одна оценка вычисляется в предполо-
жении, что справедлива гипотеза , другая — в предположении,
что справедлива гипотеза Подходящими для этого являются
оценки максимального правдоподобия, которые позволяют ввести
обобщенное отношение правдоподобия
m6axpz|6,^(al6' -^1)
%6 (а) ~ тах Рг\ь, Ж । ’
% 1
140
Это отношение может быть использовано для построения правила
выбора решения В следующей главе будет дано обоснование це-
лесообразности использования именно оценки максимального
правдоподобия.
При проверке сложных гипотез желательно использовать рав-
номерно наиболее мощные правила [118] Наиболее мощное пра-
вило проверки простой гипотезы против простой альтернати-
вы обеспечивает максимально возможное значение вероятности
отвержения гипотезы ^0, когда она на самом деле не справедли-
ва (мощность правила равна 1—Рм), при заданном значении
вероятности неправильного выбора гипотезы (уровень значи-
мости IS = PF) Равномерно наиболее мощное правило обеспечи-
вает наибольшую мощность относительно каждой допустимой
альтернативной гипотезы ‘??’1 Для того чтобы правило выбора
решения было равномерно наиболее мощным, необходимо, чтобы
отношение правдоподобия не зависело от значения параметра 0;
такие правила существуют не всегда
Если отношение правдоподобия зависит от параметра 0 , то
правило выбора решения, основывающееся на отношении правдо-
подобия, использовать невозможно Такое правило (в том числе
и правило, в котором используется оценка максимального правдо-
подобия параметра '0 ) не может быть равномерно наиболее мощ-
ным
Рассмотрим простой пример, который позволит проиллюстри-
ровать основные понятия, используемые при анализе проблемы
проверки сложных гипотез.
Пример 5.3. Рассмотрим задачу проверки гипотез
Жв z — v и z — m-^-v
] — /2(7^
Шум v будем считать нормальным, так что pt, (у) = тт~-е
f 2л сг^
Если параметр т — случайная величина с нулевым средним значением и
1 —М2/2 а2
I т
нормальной плотностью вероятности Рт(-М) =—т==---е » то отношение
V 2л <зт
правдоподобия (5 99) принимает вид
» J - M>/2oZm J —(a—Af)2/2a2
I —т=-----е —— е dM
J 'КЗл ат /2л 6„
У 2л сг0
Выполнив интегрирование и вычислив логарифм обеих частей этого равен-
ства, можно записать следующее выражение для правила выбора решения,
основанного на отношении правдоподобия при одном наблюдении г=а:
2<y2v(o2v+<y2m) ( 1 +
a2 ==---------------- In ST -Е ~ 1п-------------
(Г \ * о*
141
Рассмотренная задача эквивалентна задаче проверки простой гипотезы про-
тив простой альтернативы Ее можно описать следующим образом
1 -
Рг[~( (а|^0) - е ;
•^1 = Рг]ж («1^)
1 е-“’/2 ( < + ста)
/2SF о2 4- а2т
Здесь можно воспользоваться результатами, полученными для более об-
щего случая [см ф-лу (5 50)]
Рассмотрим теперь случай, когда параметр т либо не является случайной
величиной, либо случаен, но его плотность вероятности неизвестна Восполь-
зуемся отношением правдоподобия (5 100) с очевидной заменой 0=zn
Поскольку параметр т входит только в числитель дроби, стоящей в правой
части ф-лы (5 100), то оценка максимального правдоподобия для 0 должна
вычисляться только в предположении справедливости гипотезы . Это озна-
чает, что в качестве оценки для параметра 0 при наблюденном значении г=а
должно выбираться то значение переменной 0, при котором достигается
। -(а-в)«/2ц2
тахр .д ~Ла\&, J^) = max-77=—е
0 г|о, .it е у 2л
Очевидно, что значение оценки 0i = a Обобщенное отношение правдоподо-
бия и правило выбора решения при этом принимают вид
1//2лоп a*/2a2
<gg(a)== Л
(l/fftiaje °
Ранее уже отмечалось, что наиболее мощное правило проверки гипоте-
зы против альтернативы максимизирует вероятность правильного обна-
ружения PD=1—Рц при фиксированном значении уровня значимости 1а=Рр
Правило будет равномерно наиболее мощным, если оно является наиболее мощ-
ным относительно каждой допустимой гипотезы х Если параметр т не яв-
ляется случайным и его значение неизвестно, но больше нуля, то можно попы
таться применить правило вида z=a^t,t
Аналогично, если т принимает только отрицательные значения, то представ-
ляется вполне разумным применить правило типа z =
Е<-ли известно, что паэамсгр м принимает только положительные значе-
ния, то
“ , -а’,2СТ2
( 1 о
Рр — /о — I —т=-е da;
F s J /2л a0
€1
« ! -(a-M)./2a2
Л) = 1 -/и = 1 - I ---e d«-
J /2л aB
Если задать уровень значимости то тем самым будет задано и значение
порога gi Вероятность правильного обнаружения PD при этом оказывается
максимально возможной при любом значении М Таким образом, если т при-
нимает только положительные значения, то рассматриваемое правило выбора
решения является равномерно наиболее мощным Аналогичным образом можно
показать, что правило выбора решения z = a^^ является равномерно наиболее
мощным, если параметр т принимает только отрицательные значения Для это-
го правила
142
р 1 ““/2ст,
Рр =/о= --——е
+® — (а-М)‘/2а^
pd =1-Рм=1— ( -----------е da.
<> у 2л о0
Если же знак параметра т неизвестен, т е если т при получении наблю-
дений может принимать как отрицательные, так и положительные значения, то
равиомеоно наиболее мощного правила не существует
Таким образом, в данном примере рассмотрены три различных подхода при
построении правила выбора решения При первом подходе предполагалось, ч-о
параметр т — случайный и его плотность вероятности известна При втором
подходе ^тот параметр считается неслучайным и используется обобщенное от-
ношение правдоподобия Наконец, если известно, что параметр т принимает
только положительные или только о-эицательные значения, то можно указать
равномерно наиболее мощное правило
Нельзя, конечно, ожидать что рассмотренные правила обеспечат достаточ-
но малые вероятности ошибок различения гипотез, поскольку решение выно-
сится всего лишь по одному единственному наблюдению Если имеется воз-
можность использовать выборку объема К. с независимыми элементами, а зна-
чение параметра т неизвестно, то условные плотности выборки при разных
гипотезах имеют вид
(X х
^) = -^7^7Гехр
Значение переменной М, при котором последнее выражение принимает наиболь-
шее значение, совпадает с выборочным средним
Правило выбора решения, основывающееся на
шения правдоподобия (5 100), принимает вид
статистике обобщенного отно-
In (а) = —-—
S 2а^
In^-.
Это правило можно записать несколько иначе, используя достаточную статис-
тику
(«) = -^=-
Ук
к
Е“*
К=1
^ = /2а2щ^ .
(Так как статистика У К на Л4 — нормальная со средним р. У К и дис-
персией сг20 при гипотезе .ЙП и с нулевым средним и дисперсией а2^ при гипо-
тезе Ж. то в рассматриваемом случае
143
PF = 2[1—erf (^/ao)I;
/ &s+ v^VK A / +
PM = 2 — erf ---------------- I — erf ------------
\ av / \ ®O
-Прим отв. ped.)
Мсяно построить рабочие характеристики этого правила. Основываясь ".а
полученной достаточной статистике, можно найти байесовское правило проверки
рассматриваемых сложных гипотез, которое в данном случае будет аналогично
правилу проверки двух простых гипотез.
5.5. Проверка многих гипотез
Результаты, полученные при решении задачи проверки двух
гипотез, в этом разделе будут обобщены на случай проверки М.
гипотез. Как и ранее, в качестве критерия оптимальности здесь
будет использован минимум среднего риска. Выражение для
среднего риска (5.23) при М гипотезах принимает вид
М-1 М— 1
S 2 \5.101)
1=0 %.
где Сг; — потери при принятии гипотезы когда на самом
деле справедлива гипотеза.^-; Pggj— априорная вероятность
гипотезы \ р —плотность вероятности выборки при
/-й гипотезе; — выборочное пространство при гипотезе Жр,
М— 1
% = — выборочное пространство
/=0
Повторив рассуждения, проведенные для бинарного случая,
можно переписать выражение (5.101) и получить правило выбора
одной из М гипотез, основанное на использовании отношения
правдоподобия [163]. Согласно этому правилу принимается та
гипотеза Wj, для которой справедливо неравенство
М— 1 М—1
Сл ржк Pz\ ж («I < Z C,nftP^fe (а | ,^h) (5.102)
*=0 k=0
для всех m^j. Рассмотрим здесь более подробно следующий
частный случай. Пусть потери при правильных решениях равны
нулю, а при ошибочных — одинаковы; предположим также, что
все рассматриваемые гипотезы равновероятны. На основании
•ф-лы (5.102) гипотеза Жк принимается, если
pWk Pz|(х I > pwm Pz|(х I (5.103)
для всех m^=k. Воспользовавшись формулой Байеса, неравенст-
во (5.103) можно записать следующим образом:
(5.Ю4)
144
Таким образом, следует вычислить апостериорные вероятности
М рассматриваемых гипотез и принять ту'гипотезу, апостериорная
вероятность которой максимальна
Можно рассмотреть также задачу проверки М сложных гипо-
тез В частности, оказывается, что при назначении потерь таким
образом, как это было сделано выше, для принятия решения не-
обходимо вычислять интегралы
оо
J O)p6|z(0|a)d0, г — О, 1, 2, . . ., М-1. (5.105)
Принимается гипотеза Жг с таким индексом i, для которого
интеграл (5 105) оказывается наибольшим
Пример 5 4. Рассмотрим задачу проверки М. следующих гипотез (7И = 5)
z = — 2а-j-v, z = — а 4-и, z = о; z=a^-v,
z = 2a 4- v,
где v — нормальный шум с нулевым средним значением и дисперсией о2 Зна-
чение параметра а будем считать известным и положительным, а все рассмат
риваемые гипотезы — равновероятными Примем также что потери при правиль-
ных решениях равны нулю, а при любых неправильных—единице
После проведения наблюдений будем принимать tv гипотезу , апосте-
риорная вероятность которой при полученной выборке наибольшая
Согласно формуле Байеса
Р
PW\Z 1 = pz|J^ Pz (aj
Так как P=0,2 для любой рассматриваемой гипотезы, то отыскание
гипотезы, апостериорная вероятность которой максимальна, сводится к отыска-
нию гипотезы при которой значение плотности
1 —(ct-M)2/2CT*
Р = ----е
у 2п а
при полученном единственном наблюдении оказывается наибольшим Здесь Mt
обозначает возможные значения сигнала —2a, —a, 0, а 2а Этот способ при-
нятия решения приводит к выбору гипотезы с наименьшим значением мо-
дуля |а—М,\ Границы областей принятия отдельных гипотез определяются
просто как проекции точек пересечения функций плотности вероятности наблю-
даемой величины при эт ix гипотезах (см рис 5 8)
Рис 5 8 Области принятия отдельных гипотез (пример
5 4)
145
: — оо а < —
За
2 ‘
Значение байесовского риска для этого примера совпадает с вероятностью
ошибки и может быть г- и-глено по формуле
- Раш - 2_
/=0
1— [ pz|^ (a|.^?()da
Из рис
5 7 следует, что вероятность ошибки определяется выражением
Р_______
* ОШ — г—
2л a
—За/2 со
f Г — (а + «)2 1 , , f Г — (а + 2а)
I ехР ----------:---- «« + I ехР — /гд-------------
J И L 2а2 ] J L 2а2
—оо —За/2
da +
d а
(а — 2а)2
~ 2а2
За/2
— (а —а)2
2а2
Путем введения новой переменной интегрирования все инте,ралы этого вы-
ражения можно выразить через интеграл от стандартной нормальной плот-
8 Г J а \1
ности вероятности В результате получимР0ш=—I—еГЧ— I • Как и следовало
5 L \2а ) ]
ожидать, вероятность ошибки уменьшается с ростом а и уменьшением а По-
лученные в этом примере соотношения можно без труда обобщить на случай
выборки объема К
5.6. Последовательный анализ
В предыдущих разделах данной главы предполагалось,
что объем выборки, на основе которой выносится решение, фик-
сирован. В § 5.3 уже отмечалось, что значение риска, связанного
с принятием решений, уменьшается при увеличении числа наблю-
дений. Вообще механизм вынесения решений может быть выбран
таким образом, чтобы, кроме основных решений, он позволял
определять и необходимый объем выборки. Можно ожидать, что
в этом случае удалось бы сократить время от начала наблюдения
до принятия решения при том же самом значении риска. Тем са-
146
мым было бы построено правило выбора решения, которое следо-
вало бы признать лучше правила, основанного на выборке фикси-
рованного объема. В данном параграфе будут изучены два таких
последовательных правила выбора решения для простого бинар-
ного случая. Одно из них называется байесовским, а другое — по-
следовательным правилом Вальда [86, 88, 166, 272].
Напомним, что при проверке гипотез по выборке фиксирован-
ного объема отношение правдоподобия X сравнивается с поро-
гом У. При последовательном анализе используются два порога
S'o(k) и 3\(k), которые могут- изменяться с изменением числа
наблюдений k. Если на k-м. шаге отношение правдоподобия боль-
ше порога (k), то принимается гипотеза ,%’1. Если оно меньше,
чем (k), то принимается гипотеза Ж(). Если же значение
отношения правдоподобия лежит между этими порогами, то не-
обходимо произвести очередное наблюдение.
Отношение правдоподобия
X [A (fe)] = ----------д
д pz(^„)z(^).............» (О). • • • * (О I ^11
~ Pl(ka),Z(kl).ilk) \Ж ' X W 1
где рг(к} |J^i—совместная плотность вероятности выборки Z при
гипотезе , полученной за первые k шагов. Для вычисления
порога непоследовательного правила выбора решения необходимо
знать априорные вероятности гипотез Жо и • Аналогично для
определения порогов последовательного правила на £-м шаге не-
обходимо знать априорные вероятности $
этих гипотез перед k-м шагом. Эти априорные вероятности
можно рассматривать как апостериорные, вычисляемые после
первых (k—1) шагов. Их можно определить из соотношений:
f1) — 1) 0] =
__________PM,k—l ^0’ pz(k—l)\ ж 1°е^~О1-^’о1___________
PW,k— 1 Pz(k~l)\^X^~Ol^ol+^j^ 0* х
x pz(k—01 ’ (5.107)
Pw,k— 1 ^t,k~ OPZ(A—1)|J^ I® (-k~ *) I k~ Ox
x Ol^ol • (5-108)
Поделив обе части последнего выражения на соответствующие
части предыдущего, получим простое выражение для отношения
априорных вероятностей на k-м шаге:
147
(5.109)
В качестве начального значения в этом соотношении следует
выбрать отношение }Р которое использовалось бы при
построении непоследовательного правила. На каждом шаге отно-
шение априорных вероятностей подстраивается путем умножения
на отношение правдоподобия X[a(k—1)]:
Рг(к_Bid’ll . .
- 1)] = ( f — • (5-110)
зависящее только от результатов наблюдений на предшествующих
шагах. Если элементы выборки независимы, то отношение правдо-
подобия для всей выборки можно записать как произведение от-
ношений правдоподобия для наблюдений на разных шагах:
И-1
Х[А (k — 1)J = П [«(/)] = Ж fa (А — 1)] Ж [А (£— 2)].
Так как
PM,k— 1 k~ P.££,k-i (‘^1’ *~2)
p#e,k~i k~ p#e,k—2k~
(5.111)
(5.112)
------=- X [A(k — 1)] .
р£££0
Определить среднее значение
продолжении наблюдений (что
байесовского последовательного
то рекуррентное соотношение (5.109) можно записать в следую-
щей полезной форме:
Р w h Р&
(5.113)
потерь при наличии решений о
необходимо при рассмотрении
правила) довольно трудно. По-
этому обратимся к более простому подходу, предложенному
Вальдом [272]. Это правило, называемое обычно последователь-
ным правилом Вальда, является модификацией непоследователь-
ного правила Неймана — Пирсона.
Покажем, что пороги (£) и<$70 (£) последовательного пра-
вила Вальда связаны простыми соотношениями с вероятностями
ложной тревоги и пропуска сигнала. Предположим, что при k = K
отношение правдоподобия оказалось равным порогу 1 (^) 1'- * В
*> В общем случае при дискретной выборке может оказаться, что 2? .
Однако если объем выборки велик, то превышение порога достаточно мало.
В случае непрерывного времени гипотеза ,££х принимается, как только дости-
гается равенство ££=£Хт. е. отношение правдоподобия не может быть боль-
ше порога (Прим авт.)
148
Следовательно, на этом шаге принимается гипотеза и
Ж(Ю1 =
1А Wl^ol
(5.114)
Умножая обе части последнего равенства на величину
Pz(^.) [А(Ю | 9?° ] и интегрируя в области принятия гипотезы
SK 1, получим
J А = ^х(/0 J [Al^oJdA. (5.115)
ЗД) W)
Это равенство можно записать следующим образом:
PD(K)= 1 - РМ(К) = J(K)PF(K). (5.116)
Если отношение правдоподобия равно значению порога То (k),
то принимается гипотеза ,3^0. Поскольку при этом
5₽[А(К)] = ^0(Ю> (5.117)
то нетрудно установить равенство, аналогичное равенству (5.116)
/Mtf) = ^o(W-JW)L (5.И8)
Из равенств (5.116) и (5.118) следует, что для обеспечения
заданных значений вероятностей ложной тревоги и пропуска сиг-
нала следует выбрать следующие значения порогов:
'-РуМ
PFM
Рм^)
1-PF(K) ’
(5.119)
Из этих выражений, в частности, следует, что значения порогов
последовательного правила Вальда не зависят от номера наблю-
дения k, если вероятности Рм и PF не зависят от k.
При использовании последовательного правила объем выбор-
ки, при котором принимается одна из рассмотренных гипотез,
оказывается случайным (можно показать, что одна из гипотез
всегда принимается в результате конечного числа шагов). Поэто-
му желательно определить хотя бы среднее значение необходимого
числа наблюдений. Предположим, что пересечение порогов невоз-
можно Тогда существуют всего две возможности при завершении
проверки: достигается либо порог х , либо порог . Поскольку
при этом может быть справедливой либо гипотеза SVlt либо ги-
потеза , то возможны следующие четыре комбинации при окон-
чании проверки на /f-м шаге:
£ [А (К)] = <Т0 при
X [А (К)] = при
[А (К)] = при ^Го,
[А (/<)] = ^Гх при ^Гх>
Р«[А(7()]|j? №о I ^о) = 1 — PF ;
р£[ л(ю\\ж № о I >^1) == рм;
Р%[А(К)ЦЖ ($~ 11 ^о) = Pf ’
PS[A(K)]\W (^"11 1 •“ Рм •
(5.120)
149
Среднее значение отношения правдоподобия при окончании на-
блюдений (при объеме 'выборки К)
Е{£[А(К)]} = — + при ^о;
' XS'oPm + SW-Pm) при 9tv ( }
Вычислим теперь отношение правдоподобия X [A(7V)] для
У>7С, предположив для простоты, что элементы выборки незави-
симы и одинаково распределены. В этом случае справедливо пред-
ставление (5 111) при Ло=1- Поэтому можно записать
2 [А (У)] = П 5? [«(/)]= П («(*)] П [«(7)1 =
!=\ 4=1 /=К+1
= ЛЛ(К)1 П [«(/)]• (5.122)
/=К+1
Правую часть этого равенства можно рассматривать как произ-
ведение двух независимых случайных величин. Вычисляя нату-
ральный логарифм от обеих частей этого равенства, получим
N N
1п^[А(А)] = £ 1п 2 [«(/)] = In £ [А (/()] + 2 1п5?[«(/)]. (5.123)
/=1 /=К+1
Найдем теперь математические ожидания обеих частей полу-
ченного равенства:
Е{In X [А (У)]} = NE {In X [а]} = Е {In X [А (К)]}+(У— £{£}) £{1п X [а]}.
(5.124)
Здесь предполагается, что математическое ожидание £{1п S? [«(/)]}
не зависит от номера наблюдения j Равенство (5 124) записано
с учетом того, что
Е {In X [А (/()]} = Е {/<} Е {In X [а]}. (5.125)
Формулу (5.121) можно записать в несколько ином виде:
Е {In X [А (А)]} =
(1 — Рр) In <У0 + PF In при
рм1п + (1 — Рм) 1п <^1 При 5^1-
(5.126)
Учитывая теперь равенство (5.125), для математического ожида-
ния <У —Е{К} объема выборки получаем
= (1 - ln^i при Жо;
Е{1п£?[<х]}
Рм In У'о + (1 — Рм) In У1
£{1п^[а]} при Ж
(5.127)
Интересно сравнить последовательное правило с аналогичным
правилом, использующим выборку фиксированного объема. Та-
кое сравнение для задачи с нормальными случайными величина-
ми, дисперсии которых известны и одинаковы при рассматривае-
150
мых гипотезах, проведено в примере 5.5. Результаты сравнения
для случая непрерывного времени будут приведены позже.
Пример 5 5. Снова рассмотрим простую задачу различения двух гипотез:
zl = vl, i = l,2,. ;
J^! z, = т 4- vt, i = l, 2,.. ,
где положительный параметр т известен, т е гипотеза о среднем значении
нормальной случайной величины с известной дисперсией проверяется
против простои альтеэ (ативы Как уже отмечалось ранее, при отыскании пра
вила различения этих гипотез можно использовать различные подходы Найдем
теперь последовательное правило выбора решения Ради простоты будем пред-
полагать, что элементы выборки независимы (иногда в таком случае говорят,,
что шум измерения б°лый)
Согласно ф ле (5 106) отношение правдоподобия
X
Г~| -{Га(А)-т?/2<г2}
"г(К\\Ж ._.
$е [(л (Ю1 .
(Ю1Ж1 |q| е~{[а (*)]2/202}
*=1
Значения порогов последовательного правила можно вычислить по ф-ле-
(5 119), если задать и считать постоянными вероятности ложной тревоги и:
пропуска сигнала, так что
&г = (1 '> &0 = М1 Рр )
Таким образом, последовательное правило выбора решения можно записать,
следующим образом
X
LmK а2
а (k) > ?! = —- + — log „У 1,
2 т
*=1
то принимается гип01еза
К
а2 тК VX . тК о2
если --log J . « (*) + — l°g i
т 2 2 т
*=1
то следует провести еще одно наблюдение,
если
X
пК а2
71 “(*) &> = — log^o,
м 2 т
*=1
то принимается гипотеза -ТА •
К
Как и при выборке фиксированного объема, функцию от выборки , a (k)
*=1
можно рассматривать как достаточную статистику Пороги построенного таким
образом последовательного правила изменяются с ростом номера наблюдения
(см рис 5 9) Разница между значениями порогов постоянна и равна
<т2 , ST 1 а2 , С ~~ (1 ~ Рр)
-— In----= — In ----------5-------
w т Рм PF
— Si So
Рис 5 9 Пороги как функции числа наблюдений,
тангенс угла наклона соответствующих прямых
равен т/2
Так как 1п<2?[а(/)] = со(/)т/а2—т2/2а2, то
£{1п^[а]} =
т2
— при ,^0;
2а2
т2
ТТ ПРИ
2а2
Средний объем выборки, необходимой для принятия одной из рассматри-
ваемых гипотез, можно вычислить по ф-ле (5 127) В результате получаем
при
2 а2 Г ' Рм
при
Сравним теперь средний объем выборки, требуемый для принятия оконча-
тельного решения с помощью последовательного правила, с объемом выборки,
который необходим для достижения тех же значений вероятностей ложной тре-
воги и пропуска сигнала при применении непоследовательного правила В при^
мере 5 2 уже было показано, что для рассмотренного там непоследовательного
правила выбора решения можно записать
ST Кт! а
1 С — Г’/2 ( VК т\
^ = 7^ J е dr = erfks>- а Р
— 00
152
7 s
где порог $i"& при использовании достаточной статистики определяется соотно-
шением ST а =———-In^" -ф- YJSJIL ' а ,?Г —порог этого правила. Зададим
тУК 2а
теперь некоторые значения вероятностей ложной тревоги и пропуска сигнала для
этого непоследовательного правила Неймана — Пирсона и найдем требуемый
объем выборки Из трех предыдущих равенств получаем
erf-1 Р
о
тУК
1п<£Г—
УКт
2а
м —
„ 1 о
erf-1 (1 — РР) =
' F' mV К
1п,Г +
УКт
2о
Отсюда объем выборки, необходимый для обеспечения заданных вероятностей
ошибок при использовании правила Неймана—Пирсона,
*NP = [erf-1 (1 - PF) - erf-1 Рмр.
Это выражение получено из двух предыдущих равенств путем исключения пе-
ременной SP . Таким образом, для обоих рассматриваемых правил необходимое
число наблюдений растет с увеличением дисперсии а2 и уменьшается с рос-
том т.
Интересно отметить, что объем выборки явно не зависит от порога прави-
ла ef , как это следовало бы ожидать, поскольку порог должен выбираться
так, чтобы обеспечить заданные значения вероятностей Рр и Рм Особенно
важным является отношение KnpI^ Значение этого отношения при заданных
вероятностях Рг и Рм зависит от того, какая из гипотез справедлива На
рис 5 10 приведены графики изменения этого отношения при гипотезе Ока-
Рис 5 10 Отношение
объема выборки непо
следовательного правила
к среднему объему вы
борки последовательного
правила при вероятно-
стях ложной тревоги и
пропуска сигнала, оди-
наковых для обоих пра-
вил, справедлива гипоте
за
153
зывается что при использовании последовательного правила требуется в сред-
нем меньший объем выборки, чем для непоследовательного И эта экономия
среднего числа наблюдений становится существенной при малых значениях ве-
роят-остей Pf и Рм-
Пример 5.6. Рассмотрим теперь задачу предыдущего примера, предположив,
однако, чго число отсчетов значений наблюдаемого процесса на конечном интер-
вале времени может быть неограниченно увеличено. Это позволит построить
последовательное правило выбора решения при непрерывном времени Рассмат-
риваемые гипотезы 'Можно описать следующим образом:
: z(t) : z(<) =/п-J-о (0. t0 < t,
где значение параметра т известно, a v(t)— стационарный белый нормальный
шум, среднее значение которого равно нулю, а ковариационная функция
cov {о (<0, v О = Е {v (/0 V (t2)} = 6D (<! — t2).
Начнем с отсчетов непрерывного наблюдаемого процесса в дискретные мо-
менты времени и примем, что
иг
cov{o(Z>, Т), v(jT)} = -^-6K(k~i) = Vv6K(k— i),
т. е при любом Т элементы выборки предполагаются независимыми. Для этого
частного случая отношение правдоподобия, рассматривавшееся в предыдущем
примере, примет вид
<2? [А (К Т)] = ехр
х v z.
k=k„
Положим теперь, что число отсчетов на конечном интервале наблюдения не-
ограниченно увеличивается, т. е. Т->0, А—>-°о и kT-a-t. Нетрудно выписать пре-
дел отношения правдоподобия
5? [А (0)] —ехр
где /0 — известный момент начала наблюдения, a tf — неизвестный момент пре-
кращения наблюдения, который определяется последовательным правилом. По-
роги, с которыми сравнивается значение отношения правдоподобия при непре-
рывном времени, остаются такими же, как и в предыдущем примере. После-
довательное правило можно записать следующим образом:
f' tn w*.
а(0 Л > = — (tf — t0) 4- —- log^t,
^0
то принимается гипотеза
если £0 С j а (0 d t <
то интервал наблюдения следует увеличить;
t,
то принимается гипотеза
Пороги данного правила являются функциями времени наблюдения. ’Ложно
вычислить среднее время от момента начала наблюдения до принятия оконча-
154
тельного решения и оценить выигрыш, обеспечиваемый последовательным пра-
вилом по сравнению с непоследовательным при фиксированных вероятностях
ложной тревоги и пропуска сигнала. Полученные здесь результаты аналогичны
результатам, приведенным в предыдущем примере.
Полученные в этом разделе соотношения можно легко моди-
фицировать с тем, чтобы охватить задачи проверки сложных ги-
потез с помощью последовательных правил. Последовательность
рассуждений при этом полностью совпадает с той, которая под-
робно описана в § 5.4.
Здесь следует использовать отношение правдоподобия
УС ^А 1
Ж [А (К)1= - ----------,
которое при наличии случайного параметра 6 можно записать
следующим образом:
00
У рг(К),0|.ж[А(К)’01-^11d0
X [А (К)] = —-------------------------=
оо
J ₽ZW,0|^[AW-
—оо
оо
J ^Z(K)[A I ] pQ| (0 | d 6
= —--------. (5.128)
00
J ^Z(/()|0 [А (Ю I ^ol I -^o) d 0
— 00
Последовательное правило проверки сложных гипотез после этого
строится, как последовательное правило проверки соответствую-
щих простых гипотез.
Вероятности ложной тревоги и пропуска сигнала в этом случае
зависят от значения параметра, так как
(0) = f PZ(/O|0,.^[AI0-ЖИА; (5.129)
^i(K)
%(0)= J PZ(K)|o,.^[Al°> (5.130)
^о(Ю
Средние значения вероятностей ложной тревоги и пропуска
сигнала могут быть определены с помощью соотношений:
оо
Pf= J ^е(0) Ре1^(01ЖМ0;
-----00
J ^e|(0)pe|^(0|^1)dO.
— 00
(5.131)
(5.132)
155
Значения порогов для рассматриваемых последовательных
правил вычисляются по формулам: = —Pm)/Pf', У о =
= РМ(\—Рр). Как и ранее, эти вероятности и пороги иногда могут
зависеть от номера наблюдения К-
Если векторный параметр 6 не случаен и его значение неиз-
вестно, то можно воспользоваться обобщенным отношением
правдоподобия [см. также ф-лу (5.100)]
mftax PZ(^|O,J^ [А (ЛГ)10, JT’d
X 1А (All = —____________________________
е max pz,^|0 [А (К) | 6, ^о] ’
(5.133)
в котором оценки максимального правдоподобия неизвестного
параметра 6 отыскиваются путем максимизации соответствующих
условных плотностей вероятности по допустимым областям значе-
ний 6 при фиксированной выборке Z.
Можно рассмотреть также задачу проверки нескольких гипо-
тез с помощью последовательного правила. При этом необходимо
ввести вероятности нескольких ошибок, которые служат аналога-
ми вероятностей ложного обнаружения и пропуска сигнала. Соот-
ношения, получающиеся при решении этой задачи, полностью
аналогичны тем, которые были получены для бинарного случая.
Поскольку объем К выборки, используемой для вынесения
окончательного решения с помощью последовательного правила,
является случайной величиной с 'математическим ожиданием СК
то может оказаться необходимым ограничить максимально допус-
тимое число наблюдений или время наблюдения. То есть, если
после получения К наблюдений окончательное решение с по-
мощью последовательного правила не принято, то для выбора
одной из рассматривающихся гипотез используется другое пра-
вило:
еП X [А (Amax)] '. '-2'lA (Ашах)]-О О’
Вальд [272] указал границы для вероятностей ложной тревоги
и пропуска сигнала подобных усеченных последовательных пра-
вил.
В примерах данного раздела были рассмотрены простые за-
дачи последовательного анализа для нормальных случайных ве-
личин. Теперь перейдем к анализу более полезного варианта этой
задачи, который будет играть очень важную роль при изложении
в гл. 7 результатов, полученных Калманом при решении задач
фильтрации.
5.7. Последовательное обнаружение марковских
сигналов в нормальном шуме
Проблема обнаружения нормальных сигналов в нор-
мальном шуме уже обсуждалась в § 5.3. Там же были отмечены
трудности решения этой проблемы. В данном параграфе будет
156
описан метод вычисления отношения правдоподобия или, что
эквивалентно, достаточной статистики для бинарной задачи обна-
ружения нормальных сигналов в нормальном шуме. Здесь будут
использоваться некоторые понятия теории марковских процессов
и аппарат разностных и дифференциальных уравнений Ч. Изложе-
ние начнем с решения задачи обнаружения для процессов с дис-
кретным временем. Аналогичные результаты для процессов с не-
прерывным временем будут получены с помощью предельного
перехода, когда число отсчетов на конечном интервале времени
неограниченно 'возрастает. В заключение укажем некоторые воз-
можные обобщения рассматриваемых методов, которые позволят
охватить задачи с сигналами, отличными от нормальных.
Итак, будем рассматривать гипотезы:
^0:z(^)-- v(£);
= H(^)x(A)+v(/e), k= 1, 2, . . .
(5.134)
Здесь нормальный шум v(£) является белым, имеет среднее
значение, равное нулю, и статистически не связан с сигналом или
вектором переменных состояния х(£). Будем предполагать, что
для сигнала справедлива линейная марковская модель, т. е. сиг-
нал является решением разностного уравнения
х(£ + 1) = ф(А + 1, k)x(k) + r(k)w(k). k = 0, 1, . . ., (5.135)
где w(&) — нормальный белый шум, среднее значение которого
равно нулю.
Таким образом, имеем:
cov {v (£), v (/)} = Vv (£) (k — j);
cov{w(£), w(/)} = Vw(£) (£ — j); (5.136)
£{x(0)} = 0; var {x (0)} = Vx (0).
Отношение правдоподобия для рассматриваемых гипотез
имеет вид
Pzik)\ "/£ ।
X [А (А)] = - ( )| У--------------------
(5.137)
Воспользовавшись правилом умножения вероятностей, запишем
Pz(k) (£)1 = Pz(k)\Z(k-l) № I А (Р 01 Pz (4-1) (Р 1)1 =
= Pz(k)\Z(k~ 1) I 1)1 Pz(k— 1)1Z (4—2) (P 1) I A (p 2)] X
XPz(k-2)^(k — 2)1 == PZ(I) [«(!)] П PZ(O12:(,-1)1 A(I — !)]. (5.138)
О При чтении этого параграфа желательно уже иметь некоторые сведения
о линейном и нелинейном оценивании, приведенные в гл 7 и 9 Читатель может
повторно детально изучить данный параграф после того, как будут прочитаны
гл. 7 и 9 (Прим, авт.)
157
Отношение правдоподобия (5.137) представляет собой отно-
шение двух нормальных плотностей вероятностей. Следовательно,
оно полностью определяется первыми двумя моментами соответ-
ствующих плотностей. Пусть
x(A) = E{x(A)|Z(^), ад V~(^)^var{x^)|Z(A), ад
x(£) = x(£) — х(£), V~(Aj£ — 1) = var{x(^)|Z(A — 1), ад
*(k\k— l) = E{x(A)|Z(A — 1), ад (5.139)
х (k | k — 1) = x(/?) — x(k | k — 1).
Заметим, что при гипотезе
Е {z (г)} = 0;
var {z (г)} = var {H (г) х (г) + v (г)} = Н (г) Vx (г) НГ (г) + Vv (г);
Е {х (г) | Z (г — 1)} = Е{Ф (г, i — 1) х (i — 1)+Г (г — 1) w (г— 1) | Z (г— 1)}=
— Ф (г, г — 1) х(г — 1) = х (г | г — 1);
var {х (г) | Z (г — 1)} = Ф (г, i - 1) V~ (i - 1) фГ (г, i - 1) +
+ Г (г —. 1) Vw (г - 1) Г7 (г - 1) A V- (г | i - 1);
Е {z (01Z (: - 1)} = £{Н (0 х (г) + v (/) | Z (г - 1)} =
= Е{Н(г) [Ф(г, г — 1)х(г—1) + Г (г — l)w(i- 1)]+
+ v (г) | Z (г — 1)} = Н (г) Ф (г, i — 1) X (г — 1);
var {z (i) | Z (г — 1)} = Н (г) V- (г (г - 1) НГ (г) + Vv (г). (5.140)
При гипотезе .^f0 требуемые моменты вычисляются совсем
просто. Так,
E{z(j)|Z(j—1)} = 0; var{z(i)|Z(i —1)} = Уг(1)- (5.141)
л
Для х(й) и Vд (/г//г) можно получить рекуррентные записи. Для
этого достаточно воспользоваться представлением (5.135) и обо-
значениями (5.139) и
хА(/> + 1) - Е{х (k + 1) | Z (А + 1), <};
V~ (k + 1) = var {х (k + 1) | Z (k + 1), (5.142)
а также учесть соотношения (5.140). В результате приходим к
уравнениям фильтрации Калмана (см. табл. 7.2):
х(^+ 1) = Ф(А+ 1, £)х(£) + К(£Ч- 1) [z(^+ 1) —
— Н^+ 1)Ф($+ 1, ^)х(Л)];
158
К(А+ 1) = V~(^+ 1)Нг(/г+ 1) УГ1 (*+ ');
V~ (k 4- 11 k) = Ф (k + 1 ,k) V~ (k) Фг (k + 1, k) + Г (*) Vw (k) Гт (k)',
V~(£+ 1) = V~(£ + 1|£)-V~(6+ l|£)Hr(£+l)[H(£+ 1) X
X V~(^+ (k + 1) + V. (k + I)]’1 H (k + 1) V~ (k + 116) (5.143)
с начальными условиями, задаваемыми при формулировке задачи.
Такими условиями могут быть, например, следующие:
(х) = 0; V~(0) = Vx(0). (5.144)
Ковариационная матрица ошибок оценивания V— (/г) =
л
= уаг{х(й)—х(&)} определяется с помощью соотношения
V~(6) = Ут(Ш-1)-К(£)Н(£)У~(Ш-1). (5.145)
Отношение правдоподобия (5.137) теперь можно записать
следующим образом:
ехР {- ~ [«(z) - Н (О Ф (z, i - 1) х (z)f [Н (z) V~ (z | i - 1)Х->
k -X Нг(0+ Vv (i)]~> [a (j) — Н (j) Ф (I, Z— 1) £(/)]}
(2л)Л'/2 (det [Н (i)V~ (i | i - 1) Нг (i)+ Vv (0] }1/2
^[А(й)] =
b
* exp
£
k
i==i (2л)"/2 {det[ Vv(I)]}1/2
[ det Vv (i)]1/2
ехр {$[ А (&)]}, (5.146)
где достаточная статистика
k л
§[А(^)] = -lJ{[«(j)-H(i)*(i, Z — 1) х (г) ]Г X
XlH^v-^-DH^O + v^)]-1 х
[« (i) — Н (г) Ф (z, i — 1) х (г)] — лт (i) V?1 (г) л (г)}.
(5.147)
Следовательно, правило выбора решения, основанное на отно-
шении правдоподобия, при фиксированном объеме выборки К
принимает вид
{det [ Vv (г)]}1/2
§[А(К)]
1п,7
{det [Н (i) VT(t | i- 1) Hr(6+Vv(i)] }"2
(5.148)
159
Чтобы воспользоваться полученным правилом, необходимо
предварительно вычислить значение правой части неравенства
(5.148). В выражении для достаточной статистики (5.147) почти
л
все слагаемые, за исключением а (/г) и х(&), также можно вычис-
лить заранее. Однако значение этой статистики может быть вы-
числено лишь после того, как решены уравнения фильтрации
л
Калмана для оценки х(&). Эта оценка является наилучшей и вы-
числяется по результатам наблюдений z(&) =а(&) при всех зна-
чениях k от &=1 до k—K.
Из ф-л (5.147) и (5.148) следует, что значения достаточной
статистики можно вычислять последовательно по мере поступле-
ния результатов наблюдений. Это означает, что на основе этой
статистики можно построить последовательное правило, введя
два порога £Г0 и и модифицировав правило (5.148).
Полезно рассмотреть другой способ получения этих же ре-
зультатов. В предыдущем разделе уже было показано, что если
сигнал является известной функцией времени, зависящей воз-
можно от случайного или неизвестного неслучайного векторного
параметра 6 , а шум измерений является белым, то отношение
правдоподобия может достаточно просто вычисляться последова-
тельно по мере поступления наблюдений. Из ф-лы (5.111) для
случая известного сигнала имеем In X [А(&)] =1п 5фА(/е—1)] +
+1п55[а(й)]. Это равенство можно рассматривать как простое
скалярное разностное уравнение. Введем новое обозначение
1п^?=Л и перепишем Предыдущее соотношение следующим об-
разом:
Рт1Ъ\\ Vf ' '^’il
Л [А (А)] = Л [A (k - 1)] + In - (5-149)
pz{k)\ К
К сожалению, ур-ние (5.149) нельзя использовать в случае, ко-
торый рассматривается в данном параграфе, когда сигнал или
вектор состояния х(/) является случайным процессом. Объясняет-
ся это тем, что теперь используется представление (5.138), т. е.
равенство pzp) । z(i-i)=pZ(i), которое было использовано в предыду-
щем разделе, теперь несправедливо, поскольку ковариационная
матрица сигнала не является диагональной. Однако на основании
(5.138) отношение правдоподобия (5.137) можно записать следую-
щим образом:
X [А (/г)] = Z(fe—1), (fe) 1 A(fe~
Pz(k) I Z(k— 1),Ж Iя I A (^ — 1)> ^ol
pZ(k~ 1)| Ж A l^ol
160
Следовательно,
In X = Л [А(А>)1 = Л [A (k— 1)] + In - 7(fe№
pz(k)\Z(k-
-1), &е 0- -^il
1} [а (^) 1А (Л—1), Ж,] ’
(5.150)
Равенство (5.150) представляет собой требуемое рекуррентное
выражение для отношения правдоподобия в задаче обнаружения
случайного сигнала. Его следует использовать с начальным значе-
нием Л[А(0)]=0. Ранее уже были получены выражения (5.140)
и (5.141) для моментов плотностей вероятностей, входящих в
(5.150). Воспользовавшись этими выражениями, для отношения
правдоподобия можно записать рекуррентную формулу
Л[А(£)] = Л[А(£—1)]+ — lndetVv(Ai) —
----In det [Н (k) V~ (k | * — 1) H7 (k) + Vv (£)] +
+ у aT (k) V71 (k) a (fi) — -у- [Я ^) _ н (k) Ф (k, k — 1) x (Aj)]r X
X [H (k) V~ (k \k ~ 1) H' (£)+ Vv (б)]"1 [«(Л) — H (4) Ф (Л, k - 1) x (£)].
(5.151)
По этой формуле отношение правдоподобия может вычислять-
ся после получения каждого очередного наблюдения. В случае не-
последовательного правила вычисленное на /(-м шаге значение
отношения сравнивается с порогом зГ . Значение Л[А(Л)] можно
также сравнивать с двумя порогами и 0 на каждом шаге,
если необходимо использовать последовательное правило Вальда
для проверки гипотез и . Таким образом, теперь становит-
ся очевидным, что только что рассмотренный подход (который
был предложен в работе [230]), полностью эквивалентен тради-
ционному методу решения задачи обнаружения, приведшему к
правилу (5.148).
Получим аналогичные результаты для случая непрерывного
времени при следующих моделях полезного сигнала и наблюдае-
мого процесса:
x = F(0x(0 + G(0w(0; (5.152)
^o:z(0 = v(O;
^f1:z(0 = H(0x(0 + v(0. (5.153)
Здесь w(^) и v(Q —нормальные случайные процессы, матема-
тические ожидания которых равны нулю, а ковариационные мат-
рицы
cov {v (0, v (т)} = Фу (0 бд (г — т);
cov{w(0, w(T)}== Фте(т)бп(/ —т). (5.154)
Соответствующие модели при дискретном времени имеют вид
6—26 161
(5.155)
(5.156)
xft + 1Т)=-Ф(Л+ 1, 4)x(/&T) + r(4T)w (kT); '
ffl0:z(kT) = у (kT);
3VX z (kT) = H (kT) x (kT) + v (kT),
где Ф(£ + 1, k) = I +TF(kT); Г (kT) = TG(kT);
cov{vm v(jT)}= (k^T);
Cov {w (kT), w (jT)} = (k=-jT).
Воспользуемся теперь результатами, полученными ранее для
процессов с дискретным временем, и найдем соответствующие
предельные соотношения, приняв, что Т->0 и k-+-<x> так, что
kT-^t и KT-^tf. Уравнения фильтрации Калмана (5.143) при этом
переходят в уравнения фильтрации при непрерывном времени
(см. также табл. 7.4):
i = F (t) х (t) + К (t) [z (t) - H (0 x (OJ;
K(0 = vr ftlfftMV'ft;
v~ = F(0 V~ (t) + V~ft Fr (t) - v~ ft X
X H (t) V7* 1 (t) H (t) V~ (t) + G (t) vw (t) GT(t) , (5.157)
где xft = £{xft|Zft}, V~(O = var{xft} = var{xft|Zft};
V~(°)=Vx(0), x(0)=0. (5.158)
Вместо достаточной статистики (5.147) при непрерывном вре-
мени получаем
§ [ A ft)] ---L jf {[зс ft - Н (t) х ftf V71 (t) [«(t) - H (t) x ft]-
0
— aT(t) (t)a(t)}dt. (5-159)
Правило выбора решения, основывающееся на отношении
правдоподобия, в соответствии с (5.148) принимает вид1)
о Последнее слагаемое в правой части ф лы (5 160) является пределом
1
* {det [4% (Z)]} 2
lim 1п । ।-------------------------------------------- ,
T^° i=l {det [TH (i) V~(Z | i - 1) Hr (0 Vv (/)}T
что нетрудно установить, если воспользоваться следующими приближениями:
det (I-pTS) l-j-T tr S, 1п(1+Га) xTa, справедливыми при малых значениях Т.
(Прим. авт.).
162
* f
$ [A to)] == In У + -j- J tr [H (/) V~ (0 HHr (f) Ф?1 (0 dt. (5.160)
о
Последовательность вычислений значения используемой здесь
достаточной статистики такая же, как и при дискретном времени.
Сначала полученная реализация наблюдаемого процесса исполь-
зуется при решении уравнения фильтрации. Затем эта же реали-
зация и полученное решение используются при вычислении значе-
ния достаточной статистики. Финальный момент времени <tf может
быть задан заранее; в этом случае получаем непоследовательное
правило выбора решения. Для последовательного правила tf яв-
ляется текущим временем.
Тот же результат можно получить, если воспользоваться пред-
ставлением (5.151). В обоих случаях функция правдоподобия или
достаточная статистика рассматривается как вектор состояния,
и задача состоит в том, чтобы получить разностное или диффе-
ренциальное уравнения, описывающие эволюцию этого вектора
во времени. Именно процессу получения подобных уравнений бу-
дет постоянно уделяться основное внимание в этой книге.
Пример 5.7. Выпишем явное выражение для отношения правдоподобия при
гипотезах:
: z (t) = v (0; : z(t)=x (t) -f- о (/)
и скалярной модели источника сигнала х= Fx(t)+w(t), где var{x(0)} = Vo;
cov {»(/), о(т)} = E{v (t)o(x)} = 4MD (/ — т);
cov {w (/), w (%)} = E {w (/) w (t)} = 4rtB (t — t) .
Уравнения фильтрации Калмана (5157) и (5158) принимают вид
А А VT(0 А Л
х = F х (04s----Щ---- 1г (0 — х (/)] > х (0) =0;
V~= 2 FV~(t) 4- Vw~ V2~(t)/4v, У~(0) = VXo,
а для достаточной статистики (5 159) получаем
G Л it
1 Г'.а (/) —xtol2—a2to If' Л Л
1А to)] = - — U dt = - [2a (/) x(0 - x2 (0) dt,
J * J
0 0
Непоследовательное правило в соответствии с ф-лой (5.160) для рассматри-
ваемого случая записывается следующим образом.
1
[A to)] 1п Г 4- V -----------•
£ J I v
0
Для последовательного правила в выражении для достаточной статистики
параметр tf следует заменить на переменную t. Последовательное правило при
этом можно записать следующим образом:
6* 163
1 Г V'xW dt
если |A (0) > >n^i т Y I--------------7---> то принимается гипотеза
2 . J T t)
0
1 f V~(t)dt i /. V^(t)dt
если In <^о + — I —----------- < $ [A (/)] < In + — I ——------------- , то провер-
<7 * Z' ~ J * U
о 0
«у следует продолжать,
i / V~(t)dt
«если S’ [A (/)] In 4- — I —---------> то принимается гипотеза
2 J xo
о
Функция V~(t) может быть вычислена заранее или вычисляться в реальном
времени Структурная схема последовательного обнаружителя, осуществляющего
вычисление значения достаточной статистики, изображена на рис 5.11. Во мно-
Рис. 5 11. Структурная схема последовательного обнаружителя (при-
мер 5.7)
тих примерах длительность проверки гипотез настолько велика, что фактически
имеется стационарный режим В этих случаях можно положить V~=0h пос-
тоянную Vx найти как положительный корень получившегося квадратного урав-
нения Передаточная функция, определяемая как отношение значения оценки к
значению наблюдаемого процесса z(t), при этом имеет вид
z(s) S-P+V~rv9
Перейдем теперь к изучению более сложной проблемы обнару-
жения случайного сигнала, не являющегося нормальным процес-
сом, на фоне аддитивного нормального шума. Для этого случая
получим алгоритмы последовательного вычисления отношения
правдоподобия. Как будет показано, такие алгоритмы оказывают-
ся нелинейными. Рассмотрим гипотезы:
^0:z(^) = v(k)\ = h[x(&), &] + v(&), (5.161)
« 164
где v(k) —нормальный шум, имеющий нулевое среднее значение
и положительно определенную ковариационную матрицу
cov {v (k), v (/)} = Vv (k) 6* (/> — /), (5.162)
a x(k) —случайный процесс, не обязательно нормальный, для ко-
торого справедлива следующая .марковская модель:
х (k 4- 1) = Ф [х (k), Л] 4- Г [х (k), A] w (k). (5.163)
Здесь v/(k) —нормальный белый шум с нулевым средним значе-
нием и положительно полуопределенной ковариационной матри-
цей
cov {w (k), w(j)} = Vw(k)dK(k — j)- " (5.164)
Будем предполагать, что случайные величины v(/‘) и ’w(k) взаим-
но некоррелированны друг с другом и со случайной величиной
х(0) при всех j, k^O.
Для вычисления отношения правдоподобия воспользуемся со-
отношением (5.106). На основании правила умножения вероят-
ностей, которое применимо также и для плотностей вероятностей,
функцию Pz(k)\№ [A(fe)|^i] запишем в виде
р [Z (£)'| = р [z (k) | Z (k - 1), р [Z (k - 1) | =
= p[z(£)|Z(&—1), $Qp\z(k — 1)|Z(4 — 2), .^l/HZ^ — 2)J5TX] =
k
= p[z(l)[ n p[z(7)lZ(/S—1), .ад (5.165)
/=2
Нижние индексы здесь опущены. Так как при гипотезе спра-
ведливо представление z(/)=h[x(j), f]+v(/), то
р [z (/) | Z (/— 1), ад = р{Ь[х(у), /] 4-v(j)|Z(/—1),ад. (5.166)
Первые два момента этой плотности вероятности запишем сле-
дующим образом:
£{h[x(j), jl+v(/)|Z(/ -1), ад =
— ^{h[x(j),/] |Z(/—1), аддь[х(7), Л; (5.167)
var {h [х(/), Л 4- v (j) | Z (j - 1), = W~(i | 1)4- Vv (j)5A Vz (/ | j-1),
(5.168)
где
V~(jI /~ 1) = var{h [x(j), j] | Z(j- 1), «
= var{h[x(/), Л—h[x(J), /[|Z(/— 1), .ад (5.169)
В общем случае плотность вероятности (5.165) не является
нормальной. Тем не менее обычно полезно ввести «пвсевдобайе-
совскую» плотность вероятности 1>, которую можно получить, пред-
О Понятия, относящиеся к псевдобайесовскому оцениванию, будут разъяс-
нены в следующей главе. (Прим. авт.).
165
положив, что плотности вероятности (5.166) являются нормальны-
ми, т. е.
р [Z (j) I Z (j - 1), = {(2}l)Ardet[^T(/|/_ [ИУу(/)])>/2 X
X ехр (— {z (/) — h fx (j), }]}т V?1 (i I j — 1) {z (/) — h [х (j), j]). (5.170)
Введя это предположение и учитывая, что
Р Iz О') IZ (/ — 1), = 7-------------П72 Х
1 и 1 и ° { (2nf det [Vv (/)]}1/2
X ехр J— у zTt(j) V71 0) zT (j) J , (5.171)
отношение правдоподобия (5.106) запишем в виде
k
П Р [*(/) I Z (/- 1),^]
£ [Z (£)] = р tZ(fe) 1 = —-------------------- =
‘ P[Z(*)|^O] *
п рМ) |Z (7-1),
/=i
_ Г] {det[Vv(/)]}1/2___________________ <8>[Z(£)] .
'J 7-1)+ vv(/)}1/2 • }
Здесь использовано представление (5.165), а достаточная ста-
тистика
S IZ (£)]=—у £ ({z (j) - h [x (j), j]f V71 (j | j — 1) X
/=i
X {z(j)-h[x(j), /]}-zr (j) V71 (j)z(j)). (5.173)
Таким образом, правило выбора решения, основанное на отно-
шении правдоподобия, принимает вид
S [Z (*)] S In 3~— In П —<det.LVL.O)D1/2-. (5 Л 74)
{det [Vz (j | 7-1)]}1/2
С другой стороны, можно вычислить логарифм отношения
правдоподобия A[Z(^)] = ln3 fZ(&)] и воспользоваться рекур-
рентной ф-лой (5.150). В рассматриваемом здесь случае
A[ Z (£)] = Л IZ (k — 1)] + у In’det [Vv (£)]-In det [Vz (Ш — 1)] +
+ 4-z? (k> (k) z(^~ 4- (z ~ h Ix (k), k]}T x
X V71 (k | k — 1) (z (k) — h Ix (k), k}. (5.175)
166
Эта формула может быть использована для вычисления отно-
шения правдоподобия на каждом шаге k по мере поступления
результатов новых наблюдений. Для получения последовательно-
го правила Вальда теперь достаточно сравнивать значения этого
отношения с двумя порогами In и 1п^2. К сожалению, полу-
ченное правило не так просто использовать практически. Это
л
объясняется тем, что необходимо знать значения h[x(j), j] и
—1), которые в общем случае невозможно вычислить точ-
но. В гл. 9 будет показано, что для функции h[x(j), j] часто ока-
зывается допустимой аппроксимация рядом Тейлора относительно
точки х(/)=х(/|/—1), которая является апостериорным средним,
т. е.
x(j|j-1) = E{x(j)|Z(j-1)}. (5.176)
Если при этом в разложении функции h[x(/), j] ограничиться
слагаемыми, порядок которых не выше первого, то получим
h [X (/), j] « h [X (j I j — 1), j] + дНх(/ I /- 1). /1 [x x (/ | j — 1)].
dx(/ | / — 1)
Тогда, согласно соотношениям (5.167) — (5.169) и (5.176), можно
записать:
h[x(/),/] л;h[x(j|j—1), /]; (5.177)
(/1 / — 1)» dh[x(/1 / —1), /] v~ (j । j _ j) д 0 । /-1)’ /)1
Зх(/|/—1) <Эх(/|/~ 1)
(5.178)
где V~(/|j — 1) = var{x(/|j — 1)|Z(j — 1)} = var{х (j)]Z(j — 1)}.
(5.179)
Л
Если бы алгоритмы для вычисления x(/|j—1) и V~(j|j—1)
были найдены, то можно было бы воспользоваться последова-
тельным правилом (5.174) или использовать при вынесении реше-
ний рекуррентную ф-лу (5.175). Приближенные алгоритмы вы-
числения условного среднего значения будут приведены в § 9.4,
где решается задача фильтрации при дискретном времени. Отме-
тим также, что при исследовании проблемы фильтрации будет по-
лучено довольно большое число алгоритмов, полезных при реше-
нии задач нелинейного последовательного обнаружения. Чтобы
воспользоваться полученной формой правила, уже сейчас можно
обратиться к таблице алгоритмов 9 7, описывающих дискретный
обобщенный фильтр Калмана (или дискретный фильтр первого
порядка для вычисления условного среднего). Для этих же целей
можно использовать также алгоритмы табл. 9.9, которые описы-
167
вают дискретный итерационный фильтр первого порядка для вы-
числения условного среднего. Эти алгоритмы следует применять
совместно со скалярным разностным уравнением для логарифма
отношения правдоподобия, записываемым в форме
Л [Z(Ar)J = Л [ Z (k — 1)]+ -i-In det Vv (*) — ~ In х
X det (Vv (k) +
A _ Л
dh [x(fe | fe— 1), k] k | kd hT [x (fe I fe—1), k\
d x (k 1 k—1) d x (k | k—1)
x (Vv (k) + v~ (k | £ - 1) :
\ dx(k[k — 1) dx(k]k~ 1) J
X {z (k) — h [x (k | k — 1), £]}
(5.180)
с начальным условием
A[Z(0)] = ln£[Z(0)]= 1. (5.181)
Можно использовать также аппроксимацию второго порядка
функции h[x(6), 6] с помощью ряда Тейлора. В этом случае
h [х (А>), 6] = h [х(6 | k — 1), /г] + -h [Х(6)—х(6| 6—1)]+
д х (k | k — 1)
+ — d2 h [х (* I & ~ О, 6]. . x (6 16 — 1) xT (6| k — 1), (5.182)
2 [dx(k | k — 1), Й]2
где введено обозначение (:), чтобы избежать тензорных выраже-
ний, которое было приведено в гл 4. При аппроксимации второ-
го порядка имеем:
h [X (/), /] « h [х (/1 / - 1), J] + -L •_ V~ (j I j- 1); (5.183)
[dx(/ | j— I)]2
1^ДИШДИ1,т(/|(_ 1) ah + i;-i>l fl+s(f).
dx(/|/—1) dx(/|/~ 1) (5.184)
Выражение ппч слагаемого S(/) можно найти в табл. 9.8.
Полученные соотношения позволяют ввести аппроксимацию
второго порядка для отношения правдоподобия, а также записать
дискретные алгоритмы фильтрации, приведенные в табл. 9.8. Та-
кие алгоритмы применяются для вычисления апостериорного сред-
него значения сигнальной составляющей наблюдаемого процес-
са, которое затем используется в приведенном ранее правиле вы-
168
бора решения. Заметим также, что для вычисления отношения
правдоподобия на k-м шаге необходимо знать значение оценки
л
х(&]&—1), с помощью которой осуществляется экстраполяция
сигнальной составляющей на один шаг.
Аналогичные результаты для непрерывного времени нестрого
можно получить с помощью следующих предельных переходов:
f [х </), /] = lira --1-
т->о Т
>со
kT-+t
G [х (0, t] = lira --[x-(feb --I.
т->о Т ’
kT-+t
h[x(0, /] = limhfx (%), &];
т->о
kT-+t
(0 - lim TVw (A);
T->0
k—>00
kT-*t
Vv (/) = lim T Vv (£).
r->o
fe-> =o
kT->t
Нетрудно показать, что
lim V1„___________{.^|Ууад)'я_________________
К.",-0 {«[VT(,J,--1) + V, Wl}"2
*т->т
lim 1) = Vv(£).
т->о
kT->t
(5.185)
(5.186)
(5.187)
(5.188)
r(5.189)
- Jtr[V~® v7'(g)]rfg;
0 (5.190)
(5.191)
Таким образом, отношение правдоподобия оказывается зави-
сящим только от достаточной статистики. Согласно представле-
ниям (5.172) и (5.173) получаем [102, 147, 209]:
55 [Z(01 = exp{S[Z(O]}; (5.192)
t
8 [Z (/)] = pd z (k) Ф71 (X) h [x (X), %] + hr [x (X), X] V?1 (X)dz (X))—
0
f Л Л
----f hr [x (X), А,] ФГ1 (X) h [x (X), X] d X, (5.193)
0
где h[x(O, = £{h[x(O> t]l Z(t)}.
Один из интегралов в последнем выражении является стоха-
стическим. Полезно заметить, что даже, несмотря на то, что плот-
169
ность вероятности (5.165) отлична от нормальной при дискретном
времени, она оказывается таковой в непрерывном случае; в ре-
зультате полученные выше приближенные выражения будут точ-
ными при непрерывном времени [102]. Подробное обсуждение
проблем нелинейной фильтрации будет проведено в § 9.2. Полу-
ченные там результаты и приведенные здесь последние два соот-
ношения позволяют достаточно просто решать многие важные в
теоретическом отношении задачи построения правил выбора реше-
ний при непрерывном времени. Однако с точки зрения практиче-
ских приложений эти результаты оказываются мало пригодными,
поскольку часто невозможно вычислить точно не только значение
Л Л
функции h[x(/), /], но даже и оценки х(/), являющейся условным
средним £{х(/) |Z(tf)}.
Для получения приближенного решения задачи последователь-
ного обнаружения при непрерывном времени можно воспользо-
ваться линеаризацией соотношений (5.182) и (5.183) с последую-
щим применением приближенных алгоритмов, приведенных в
табл. 9.1 и 9.2.
Полезно указать другой способ получения уже найденных для
непрерывного времени соотношений, не опирающийся на псевдо-
байесовское предположение. Это предположение было необходи-
мо для введения аппроксимации (5.170). Можно показать [48],
что точное выражение для условной плотности вероятности
p[z(j)\Z(j—l),^i], где z(j)—скалярная переменная, записы-
вается в виде ряда Грама — Шарлье
р [г (j) ]Z(j — 1), .^] = -]гехр (- ± /]}2\ х
/2л 2 Рф2(/|/-1) у
X
00
5]Сг (/)7Л
г=о
z (/) — h [х (/), /]
V’/2(/ | /— 1)
(5.194)
где Нг(-) —полином Эрмита i-ro порядка и коэффициенты Сг(/)
являются функциями условных центральных моментов случайной
величины z(j). Первые пять коэффициентов определяются с по-
мощью соотношений:
Со (j) = -1/9 1----; Сг == 0; С2 = 0;
' гф2(/|/-1) 1 2
Сз(1) —
1 Уз (/)
3! г®/2(/|/-1)
G (!) = —
4!
(?)
гдеуп(/)Л£'({г(/)—Л[х(/), /]}п| Z(/—1)). Представление (5.194)
является точным. Однако его трудно применять из-за того, что
оно содержит бесконечный ряд. Используя (5.194) и представле-
ние (5.171) для плотности p[z(j) |Z(/—1), ] из (5.106) и
(5.165), получаем следующее точное выражение для отношения
170
правдоподобия в случае последовательности скалярных наблю-
дений:
= п ад»
/=1 ч=1
2(/) —Д[Х(/), /]
- О
/ К
хехр—гЕ
\ /=1
{z(/)-ft[x(/), ДР
Уг(И /-1)
(5.195)
Учитывая соотношения (5.168) и (5.189) и переходя к пределу
при Т-Ч), можно показать, что при конечном ЧД
lim VW (j) Со (/) = 1, lim VW (j) Cn (j) = 0, n #= 0.
T->0 T->0
Определим теперь случайную величину z(j) с помощью вине-
ровского процесса, положив z(jT)T=u(j+lT)—u(jT), где для
процесса u(jT) справедливы равенства:
£{«(/Т)}=0;
£{[«(ГНT)-u(jT)] [и(ГП T)-u(lT)]}^Vz(j+^\jT)TdK(j=kTy
Дж. Дуб [56] показал, что при этих предположениях допус-
тим предельный переход при Т-+-0 в выражениях, подобных
(5.195), причем соответствующие пределы существуют в средне-
квадратическом смысле. Таким образом, получаем
k л ____
X [ Z(t)] = lim X [Z (£Т)] = lim V h [ - iT]-[u (/+ 1 Г) ~ “(/T)]-
*-><» *-><» ’V0(jT)
T->0 T->0 /=1
*T->f kT-^t
* Л
— lim yi (5.196)
*^eo ZJ Vo(/T)
T->0 /=1
kT-^t
Если теперь в это выражение ввести обозначение стохастиче-
ского интеграла, то придем к скалярному варианту статистики
(5.193). Тем самым более строго доказана справедливость равен-
ства (5.193). Тот факт, что это равенство справедливо, в то время
как (5.132) является лишь приближением, может привести к за-
ключению, что последовательное обнаружение случайного сигна-
ла, не являющегося нормальным, на фоне нормального шума при
непрерывном времени в каком-то смысле «лучше», чем при диск-
ретном. Это действительно было бы возможно, если бы удалось
точно реализовать требуемые алгоритмы и вычислить стохастиче-
ские интегралы. Однако это невозможно, так что приближенные
алгоритмы должны использоваться как при непрерывном, так и
при дискретном времени.
Глава 6
ОСНОВЫ ТЕОРИИ ОЦЕНИВАНИЯ
6.1. Введение
В этой главе будут рассмотрены основные аспекты
второй обширной области теории статистических выводов — теории
оценивания векторов состояния и параметров систем. Сначала из-
лагается байесовская теория оценивания как обобщение теории
выбора решений, развитой в гл. 5, затем метод максимального-
правдоподобия, применяемый обычно для построения оценок при
отсутствии априорной информации относительно вероятностных
характеристик оцениваемых параметров.
Далее обсуждаются некоторые желаемые свойства оценок, во-
просы анализа ошибок при оценивании и псевдобайесовские оцен-
ки. Будет показано, что псевдобайесовские оценки являются линей-
ными оценками с минимальной дисперсией. Уравнение Винера —
Хопфа и лемма об ортогональном проецировании выводятся в про-
цессе обсуждения проблемы линейного оценивания с минимальной
дисперсией. При обсуждении связи метода наименьших квадратов
с другими методами построения оценок будет охарактеризована
взаимосвязь между различными методами оценивания, рассмотрен-
ными в данной главе.
6.2. Байесовские оценки
Большая часть результатов предыдущей главы относи-
лась к байесовской теории решений, в которой при выборе одной
из М возможных гипотез необходимо было обеспечить минималь-
ное значение байесовского риска S3 [ф-ла (5.101)]:
М-1
^=1 ZQdx. (6.1>
ь /=0
Этот риск представляет собой среднее значение потерь при при-
нятии Одной из гипотез, рассматривающихся в задаче выбора ре-
шения. Здесь Сг] — потери при принятии гипотезы когда на са-
мом деле справедлива гипотеза.^, а рг, yg.— совместная плот-
ность вероятности вектора наблюдений z и гипотезы.?/;. Часть вы-
борочного пространства, в которой принимается гипотезат/, обо-
значена буквой 2бг.
В этой главе рассматривается более общая проблема определе-
ния или оценивания значений параметров систем, которая назы-
172
вается задачей оценивания параметров. Пусть 0 —параметр, под-
л
лежащий оценке, а0— оценка для 0. Параметр 0 в задаче оцени-
вания является аналогом номера гипотезы в проблеме выбора ре-
шения, рассмотренной в предыдущей главе. Однако 0 теперь явля-
ется непрерывной величиной и принимает значения из некоторого
интервала. Аналогом потерь в задаче выбора решения, обусловлен-
ных принятием гипотезы,^, когда на самом деле справедлива ги-
потеза гКв задаче оценивания являются потери при оценивании
величиной 0г неизвестного значения параметра, когда на самом
деле его истинное значение равно 0. В задаче оценивания 0, явля-
ется непрерывной случайной величиной, а ошибка оценивания *>
определяется следующим образом:
~ Л1
0 = 0 — 0. (6.2)
Функция потерь Сг] в проблеме выбора одного из М возможных
решений заменяется в задаче оценивания функцией С( 0). Вследст-
вие этого байесовский риск* 2) (6.1) теперь принимает вид
®=Jj"C(6)pz 0(а, Q)dxdQ, (6.3)
— СО
где z также является вектором наблюдений. Пределы интегрирова-
ния в обоих интегралах здесь равны —оо и +оо, так как теперь не
выделяется частная область выборочного пространства, соответст-
вующая какому-либо частному значению непрерывного параметра.
Из ф-лы (6 3) и фундаментальной теоремы о среднем значении
функции от случайных величин следует, что байесовский риск для
л
некоторой оценки 0 может быть записан так:
®Д£{С(0)} = £{С(0 —0)}. (6.4)
Следовательно, байесовский риск является средним значением не-
которой функции от ошибки оценивания. Основная задача теперь
состоит в том, чтобы минимизировать этот риск или среднее значе-
Л
ние потерь путем соответствующего выбора оценки 0. Оценку,
О После приведенных рассуждений может показаться, что в качестве ошиб-
~ Л
ки оценивания можно было бы принять величину 0=0—0 В большей части
классических работ по статистике используется именно это определение Но так
как почти во всех работах, на которые в дальнейшем будут приведены ссылки,
Л
ошибка определяется как 0 — 0 и это определение авторам представляется бо-
лее естественным, то оно и используется в дальнейшем Ошибка равна разности
между истинным значением параметра и значением оценки (Прим авт)
2> Можно было бы рассмотреть даже более общую задачу оценивания, в
которой имеется неопределенность относительно наличия сигнала Это проблема
совместного выбора решения и оценивания параметра, копда решающее устрой-
ство должно не только принять гипотезу .7Д или .ЗД, но и вычислить значение
оценки для параметра 0 Здесь эта довольно сложная проблема обсуждаться
не будет (см [164]) (Прим авт)
173
удовлетворяющую этому требованию, в дальнейшем будем назы-
л
вать оптимальной оценкой Так как 0 является функцией наблюде-
Л
ний z=a, то необходимо было бы писать 0(z). Однако в дальней-
д л
шем будем использовать в основном обозначение 0, а 0 (z) будет
применяться только в том случае, если возможны недоразумения.
л
Естественно, что оптимальная оценка 0 (г) будет зависеть от
выбранного вида функции потерь Наиболее часто используются
следующие три типа этой функции:
С(0) = (0)2; С(0) = |0|; С(0) =
1
е
в задачах оценивания скалярного параметра и
С(6) = ||в|Ц;
С(О) =
С(0) =
о,
1
е
(6-5)
при оценивании векторного параметра Здесь S — неотрицательно
определенная матрица, которую без потери общности можно счи-
тать симметричной. В обоих случаях первая функция называется
квадратичной, вторая — модульной, третья — простой функцией по-
терь При выборе третьей функции предполагается, что потери
равны нулю при малых ошибках и равны 1 /е, если модуль ошибки
превышает величину s На рис 6 1 приведены графики этих функ-
О в
Рис 6 1 Функции потерь, применяемые при оценивании скалярного
параметра
а) квадратичная, б) модульная, в) простая
ций потерь для случая скалярного параметра Часто выбор кон-
кретного вида функции потерь представляет собой компромисс
между практической полезностью такой функции и простотой ана-
литического решения задачи отыскания оптимальной оценки.
К счастью, для большого класса задач оценивания оценки, опти-
174
мальные для одного вида функции потерь, сохраняют свойство оп-
тимальности для целого класса практически полезных функций
потерь. Найдем теперь выражения для оценок, оптимальных при
квадратичной и простой функциях потерь.
Построение оценок с минимальной среднеквад-
л
ратической ошибкой. Оценка 0mv(z) с минимальной сред-
неквадратической ошибкой должна обеспечивать минимально воз-
можное значение среднего риска (6 3) при квадратичной функции
потерь
(6.6)
тде матрица S выбирается симметричной и неотрицательно опреде-
ленной. Следовательно, оценку необходимо выбрать таким обра-
зом, чтобы минимизировать риск
®mv = [[(© — e)7'S(0 — 0)ре z(0, x)dQdx,
—со
для которого справедлива также следующая запись:
СО Г СО д Д
= f if(0- e)ZS(0-O)pe|2(0«)d0}pz(a)da. (6.7)
— 00 ‘ — Oo
A
- Так как 0 не является переменной интегрирования во внешнем
интеграле, а плотность вероятности pz(a) всегда положительна, то
минимизация риска 53mv соответствующим подбором функции
л
0 (а) может быть осуществлена путем минимизации значения внут-
реннего интеграла для каждого значения а соответствующим под-
А
бором значения переменной 0.
Таким образом, минимизация байесовского риска 33, представ-
ляющего собой среднее значение потерь из-за ошибок оценивания
параметра 0, полностью эквивалентна минимизации условного
среднего значения потерь при данной выборке z. Это означает, что
вместо минимизации риска 33 достаточно ограничиться миними-
зацией условного байесовского риска
53(0|a)=£’{C(0)[z = a}= Jc(0)p01z(0|a) d&. (6.8)
— со
При квадратичной функции потерь условный байесовский риск
%v$l«)= f(0 - 6)rS (0 - 0)peiz (0|a) d 0. (6.9)
—oo
Значение оценки, обеспечивающей минимальную среднеквадра-
тическую ошибку, при данной выборке z=a можно найти, прирав-
175
л л
няв нулю градиент риска ®mv(0 |а) по переменной 0 и решив
получившееся уравнение
Л оо
—’ = 0 — 2 S(0 — 0)peu (0|a)J0 (6.10)
d 6 0 = Одоу —®
Л
относительно 6. Равенство (6.10) будет выполняться, если
6MV J Рщг (ela) d е= J ©Р0|г(©Ж0-
-----СО -оо
Учитывая теперь, что функция р0|2 является обычной плотно-
стью вероятности, получаем представление для оптимальной
оценки
<Lv(a) = J0 Рщг (01аИ 0- (6.1!)
Нетрудно показать, что рассмотренная процедура минимизации
в самом деле приводит к минимально возможному значению рис-
ка. Действительно, матрица вторых производных риска ®mv по
Л Л
компонентам вектора 0 d? S3mvId 02 = 2S, т. е. является неотрица-
тельно определенной, поскольку матрица S неотрицательно опре-
делена. В правой части равенства (6.11) стоит выражение для ус-
ловного среднего значения параметра 0, вычисляемого при фикси-
рованной выборке z. Следовательно, оценкой с минимальной сред-
неквадратической ошибкой является условное среднее значение
6МУ («) = % (Я) = J0 Р9|г (9I«) d 0- (6-12)
Подставив оценку (6 12) в выражение (6 8), получим мини-
л л
’мально возможное значение риска S3 му для оценки 0=0mv- Во
многих задачах достаточно рассматривать лишь ковариационную
~ л
матрицу вектора ошибок оценивания var { 0mv} =var {0—0mv},
которая и будет в основном использоваться в дальнейшем для ха-
рактеризации точности оценок.
Оценки по максимуму апостериорной плотно-
сти вероятности. При простой функции стоимости байесов-
ский риск
UCF —
Л
eUCF +Е/2
-Т J
Л
0UCF —г/2
Pe|z(0ia)d0 Pz(a)da.
(6.13)
176
Часто рассматривают случай, когда значение параметра е стре-
мится к нулю (е^О). При этом в пределе простая функция потерь
л л
записывается как дельта-функция, т. е. С( 0) =6р(||0—0||). Тогда
для обеспечения минимально возможного значения риска .©иск в
качестве значения оптимальной оценки при каждой выборке z=a
следует выбирать то значение параметра 0, при котором апостери-
орная плотность вероятности р012(0|а) принимает максимально
возможное значение. Такую оценку будем называть оценкой по
максимуму апостериорной плотности вероятности; для нее введем
л
обозначение 0 мар. При каждой выборке z = a значение этой оцен-
ки обычно является корнем уравнения
dpo|_(0|a) I у
- --|z Л =0. (6.14)
д 0 <э=6мар <“)
л
Значение оценки 0мар можно найти также путем максимиза-
ции относительно 0 функции In р®\ z (0|a). Если воспользоваться
формулой Байеса и вычислить логарифм от апостериорной плотно-
сти вероятности, то можно записать
1п р0|г (0|«) = In р2|0 (а|0) + 1п ре (0) — In рг (а). (6.15)
Так как безусловная плотность вероятности pz(a) не зависит от пе-
ременной 0, то максимизация плотности p0|z (0|a) сводится к
отысканию положения максимума совместной плотности вероят-
Л
ности pz е (а, 0). Следовательно, значение оценки 0мар можно
найти как корень уравнения
д 1П Pzfi (“I0)
д&
dlnpg (О) ’
dQ
|0=6MAP (“)
или уравнения
аРг, е(*- °) I Л
д 0 |®=9мар (“)
аРг|9(*10)Р9(0) | д
д 0 |®=9мар (“)
(6.16)
(6.17)
+
= 0
Максимизация плотности вероятности рг\е (а|0) путем подбо-
ра значения 0 позволяет находить значение оценки максимального
правдоподобия (см. § 6.3). Оценка максимального правдоподобия,
значение которой »при выборке z = a совпадает со значением пере-
менной 0, максимизирующим плотность pz|0 (a|0), в некоторых
работах называется условной оценкой максимального правдоподо-
бия [86, 163]. Оценка же, которая максимизирует значение безус-
ловной плотности вероятности pz 0(а, 0) [а значит, и апостериор-
ной плотности p0|Z(0|a)], называется безусловной оценкой мак-
симального правдоподобия [86, 163] или байесовской оценкой мак-
симального правдоподобия [94, 133, 202]. В этой книге такая тер-
минология использоваться не будет.
Инвариантность оптимальных оценок. Во многих
случаях оптимальность байесовской оценки, построенной для неко-
177
торой конкретной функции потерь, сохраняется и при других функ-
циях потерь. Имея в виду это свойство, будем говорить об инвари-
антности оптимальной оценки. Рассмотрим класс «разумных»
функций потерь С(0), которые выпуклы и симметричны относи-
тельно точки 0=0. Будем считать также, что апостериорная плот-
ность вероятности (0|а) при каждой выборке z=q симмет-
л
рична относительно значения оценки fhtv, обеспечивающей мини-
мум. среднеквадратической ошибки. Предположим далее, что зна-
чение произведения любых рассматриваемых функций потерь и
апостериорной плотности стремится к нулю при неограниченном
увеличении значения 0. Эти предположения можно записать так:
С(0) = С(— 0); С[ах+(1— a)t/]<aC(x)+(l— a)C(y), 0<а<1;
р Л (S|a) = Pe4MV|z (- = h\z
9~0mv[z
limC(O)p,|i(e|«) = 0. |(618)
Примеры функций потерь и апостериорных плотностей веро-
ятности, которые удовлетворяют перечисленным ограничениям,
приведены на рис. 6.2. Так как выражение для риска ®(0|а) про-
ще, чем для среднего риска®, будем минимизировать условный
байесовский риск
Рис. 6.2. Примеры функций потерь и апостериорных
Л
плотностей вероятности, при которых оценка 0MV яв"
ляется оптимальной
178
53(0|a) = £{C(0)|z = а} = JC(0)p0|2 (0|а) d 0 (6.19)
— со
при ограничениях (6.18). Используя соотношения (6.18) и введя
обозначение S = 0—0mv, запишем
Я(Ш) = Е{С(е-0) |z = а} = Е{С(Е +%,-0/z = а} =
= Jc(S + 0mv-0%|Z (Hk)dS =
—оо
= JC (H - »MV + ®) PSI- (HW d s- (6-20)
—oo
Этот риск можно записать также в виде полусуммы последних
двух интегралов равенства (6.20). Так как рассматриваемые функ-
ции потерь выпуклы, то для них справедливо неравенство
~ [С (Г.) + с (Г2)] > С [-1- (Г, + Г2)]. (6.21)
Следовательно, для условного риска можно записать
^(0 [«) =^-£’{(С(Н + 0MV —в) + С(Н —4-0)]]z = «} >
>E{C(=)|z = a}. (6.22)
Чтобы в этом неравенстве можно было поставить знак равенства,
т. е. обеспечить минимально возможное значение условного риска,
необходимо положить
л л
0=0MV. (6.23)
Витерби показал [270], что последнее ограничение в (6.18) до-
статочно для того, чтобы включить простую функцию потерь в рас-
сматриваемый класс функций потерь, даже хотя эта функция не
является выпуклой. Приведенные здесь результаты являются чрез-
вычайно важными. Они указывают на то, что байесовская оценка,
оптимальная при квадратичной функции потерь, остается опти-
мальной даже при изменении условий задачи оценивания.
Пример 6й. Рассмотрим задачу оценивания параметра х при наличии шу-
ма v. Будем предполагать, что векторы х и v статистически независимы и
имеют нормальные распределения с параметрами:
£{х}=рх; var{x}=Vx; £{v}=0; var{v}=Vv .
Для наблюдаемого вектора z примем линейную модель z=Hx-f-v, где х являет-
ся ./V-мерным, a z и v — М-мерными векторами Н — модуляционная
матрица размера M%N. Как будет показано в дальнейшем, к этой задаче сво-
дятся многие практические проблемы.
Чтобы найти оценку с минимальной среднеквадратической ошибкой или
оценку по максимуму апостериорной плотности вероятности, необходимо знать
179
апостериорную плотность px|z (₽|а) Воспользовавшись формулой Байеса, по-
лучаем
Р?|Х (« I ₽) Рх (₽)
PX|Z (₽!“)= Pz(e)
Все плотности в правой части этого равенства являются нормальными с па-
раметрами
Е {z | х} = Н х; var {z | х} = Vv ;
Е {х} = |ЛХ; var {х} = Vx;
Е {г} = И Их; var {z} = HVXH7 + Vv.
Поэтому их нетрудно выписать
р=|- <•" - ^(Lv, У-" “Р [ - т '* ~ "”Г " ”];
’ ' v;1 <р -
1 Г 1
Pz (“) =---;---------г----гтгт ехР — (а — н Рх) х
(2n)A1/2[det(HVxHr + Vv)]1/2 L 2
X (HVxHr d- Vv)-’ (a-Hpx)] .
В результате апостериорная плотность вероятности
PX|Z(₽ I «) =
[det (НУХНГ + Vv)]1/2
(2n)N/2 (det VX)I/2 (det Vv )1/2
exp — (p — ?)Z S'
где введены обозначения
g = (Vx-1 + Hz v?1 H)~' (Hr v7*« + VT1 Px) = 2 (Hz v1« + vr1 Ях);
s-1 = v~l + hz vv 1 н.
Оценка с минимальной среднеквадратической ошибкой является условным
средним или средним значением апостериорной плотности вероятности, т е
оо
xmv = J ₽Px|z(₽ I а) =
________со
Значение оценки по максимуму апостериорной плотности вероятности при каж-
дой выборке z = a совпадает с тем значением переменной 3, при котором апо-
Л
стериорная плотность pX|z (01а) максимальна. То есть снова получаем хмар =
Л
? xmv-
Оптимальная оценка при модульной функции потерь, обеспечивающая ми-
нимум среднего значения абсолютной ошибки, также имеет вид xABS = ? При-
веденные результаты иллюстрируют инвариантность указанной здесь оптималь-
ной оценки для рассмотренного частного примера, а именно,
ХМЛР = XMV = X/BS = ( У?' + НГ У?' Н)~' (НГ Vv ' a + Vx ' M •
Можно показать, что Е является ковариационной матрицей вектора ошибок
~ Л
оценивания Vx =var{x|z} = var{x—х} и что отношение детерминантов являющее-
180
ся множителем перед экспонентой в выражении для условной плотности px|z
равно det V~. Поэтому эту условную плотность вероятности можно записать в
виде
/ 1 Г 1 . Л т — 1 Л 1
P(X|Z)= [(2^detV~]i/2 eXp[~TvX~X) V3T (x-x)J.
Ei ли воспользоваться леммой об обращении матриц, то можно получить другое
полезное выражение для ковариационной матрицы вектора ошибок
V~ = Vx - VxHr ( V, + HVxHr)~1 HVX,
при использовании которого требуется обращать матрицу более низкого поряд-
ка Статистику § можно назвать достаточной, поскольку она удовлетворяет
всем требованиям к достаточной статистике, сформулированным в предыдущей
главе
Заметим, что оптимальная оценка в рассмотренном примере является ли-
нейной, поскольку она представляет собой линейную комбинацию элементов
выборки Оценки такого типа часто будут рассматриваться в дальнейшем
В часто встречающемся частном случае этого примера наблюдается после-
довательность скалярных величин zn=x-\-vn, п=1, 2, , N При этом также
Здесь Vx=Vx и является скалярной величиной Оптимальная оценка дл®
этого частного случая принимает вид
!'W + £ (V^.a,
ЛАЛ it у=1
ХМЛР = XMV = ХЛВ5 = N
W.+ 2 Ми
I, /=1
Если элементы выборки независимы и одинаково распределены, то Vv =
= о2„1 и с введением обозначения Vx — o2x для оптимальной оценки получаем
выражение
Вх/°х + (Wo) S Пл + ( S аз
Л_______________ц=1______________/=1
Mv 1 /о* + N/ol 1 + N ох/о„
Как следует из (6 9), условный байесовский риск в этом случае совпадает
со среднеквадратической ошибкой Из общего выражения для ковариационной
матрицы вектора ошибок S можно получить, что дисперсия оценки при незави-
симых наблюдениях в скалярном случае
var { xmv}
1 + №>*
Л
Это же выражение для дисперсии оптимальной оценки xMV в этом примере
181
можно получить прямым вычислением момента var{x—xMV}.
Интересно рассмотреть случай, когда уже после того, как вычислено зна-
чение оптимальной оценки по выборке объема К, получено еще одно новое
наблюдение. Новое значение оценки может быть вычислено с помощью пов-
торного использования выражений, полученных в этом примере Однако с вы-
числительной точки зрения этот путь не является наилучшнм Если восполь-
зоваться леммой об обращении матриц, то можно предложить последователь-
ный алгоритм вычисления значения оценки, в котором «новое» наблюдение
Л
учитывается в форме некоторой поправки к «старому» значению оценки х. При
этом нет необходимости полностью повторять все вычислительные операции со
старыми наблюдениями. Более подробно проблема последовательного оцени-
вания будет изучаться позднее.
Пример 6.2. Предположим, что проведены независимые наблюдения и по-
лучена выборка zn=x^+vn, п=1, 2, ..., N, оде нормальные случайные вели-
чины х и vn независимы, имеют нулевые средние' значения н дисперсии
var{x}=o2x, var{on} = о2„. Найдем оценку по максимуму апостериорной плот-
ности вероятности для х. Снова выписываем плотность вероятности
1 V* 1 / ₽а \
ехр — — У (а/ — ₽3)2 ехр--------------
_ Pzix(HP)pHP) _ L __________________________L ____V 2о* /
X|Z Pz (2л)^2 Pz (а) (2л)1/2 <зх
Чтобы получить значение оценки Хмар при данной выборке, необходимо
минимизировать эксиоиеиты путем подбора значения переменной (к В резуль-
тате получаем
д Гу(«/-Р3)2 Р2
Л
Р^МАР
Л
Таким образом, значение оценки является решением алгебраического уравнения
пятого порядка.
Для каждой полученной выборки все коэффициенты этого уравнения являются
Л.
известными числами. Поэтому для отыскания значения оценки Хмар теперь
достаточно воспользоваться любым подходящим алгоритмом вычисления корней
этого уравнения
Намного сложнее оказывается задача отыскания оценки х^у, так как для
этого необходимо вычислить условное среднее, т. е. среднее значение апосте-
риорной плотности вероятности Px|z(Pla)- Последняя же задача в данном при-
мере представляется совсем трудной, поскольку эта плотность не является нор-
мальной.
Пример 6.3. Рассмотрим теперь пример дискретной адресной системы с
произвольным порядком доступа, по которой передается модулированная по
амплитуде последовательность сигналов Qnh(t). Здесь h(t) — известная функ-
ция времени с энергией Е2 на временном интервале от 0 до //. Каждый из па-
182
раметров 0„ представляет собой дискретные отсчеты сообщения, подлежащего'
передаче. Так что 0„ является случайной величиной, которую будем считать,
нормальной с нулевым средним значением. Будем предполагать далее, что зна-
чения 0„ получаются в результате отсчетов с периодом T=l/(4nW) значений
ограниченного по полосе белого шума, ширина энергетического спектра которого
равна И7 1/с. Это означает, что случайные величины 0„ независимы и имеют
одну и ту же нормальную плотность вероятности. Принимаемый сигнал иска-
жается аддитивным нормальным белым шумом, для которого
Е {Чп (0) = °; cov {°п (о. t>m (т)} = М2 ък (п — т) 6D (t — т).
Задача состоит в том, чтобы указать оптимальные оценки для параметров 0П>.
вычисляемые по результатам наблюдений процессов
zn(t) = Qnh(t) + vn(t), 0<i <tf, n=l, 2...........N.
Модель наблюдаемого процесса можно записать в векторной форме:
z (/) = 0 /г (/) + v (0, 0 < t < tj,
где z(Z), 0 и v (^) — векторы с N компонентами, которые можно записать в виде-
Е {v (/)} = 0; cov {v (/), v (т)} = М2 6D (t — т) I.
Здесь М2— спектральная плотность белого шума измерений При решении этой
задачи поступим следующим образом. Сначала рассмотрим эквивалентную дис-
кретную задачу, а в полученном ее решении осуществим предельный переход,,
неограниченно увеличивая число отсчетов на интервале наблюдения. При дис-
кретном времени будем считать, что получена выборка объема К, для элементов^
которой справедливо представление
z(kT) = eh(kT) + v(kT), k=l, 2, . . ., К,
М2
где cov {v (kT), v (jT)} = — (й — /) 1 = (* ~ /) 1 •
Если ввести составной вектор наблюдений
Тг = [ zT (Т) zT (2Т) . . .zT (КТ)],
то можно было бы непосредственно воспользоваться результатами примера 6.1.
Однако очевидные неудобства, связанные с предельным переходом, вынуждают
отказаться от этого подхода. Для сформулированной задачи оценка, обеспечи-
вающая минимальное значение среднеквадратической ошибки, и оценка по мак-
симуму апостериорной плотности вероятности совпадают. При отыскании обеих
оценок предварительно необходимо найти апостериорную плотность вероятности
Peiz (® I А) —
Pzie (А ! Q) Ре (Q)
Pz (А)
Оценка 0 мар определяется путем максимизации плотности
Pz, е (А> = Pzie (А I ®) Ре
поскольку безусловная плотность рг (А) не зависит от частных значений па-
раметра 0. Согласно условиям задачи имеем
183
К J
pzie (A I в) = fl------Г7ехР
(2nM2lT)NIZ I
у [a (kT)~Qh(kT)]r [x(kT)-
-6W)]^= (2nW)^2 eXP
1 T 2
1 e/’e
к
J] iiam-6ftmi|2
*=i
Следовательно, совместная плотность вероятности
Pz, е (А* ®)
Г к
II a(kT)~ eh(kT) ||2 4—^ 116Ц2
Zj=1
(2n)w/2 (2л)ж/2 (M21T )NK/Z
Положение максимума этой плотности по переменной 0 при фиксирован-
ном значении А можно найти путем минимизации значения показателя экспо-
ненты т е необходимо минимизировать величину
подбирая значение переменной 0 Вычислив градиент функции J относительно 0
и положив его равным нулю, получим следующее уравнение для оптимальной
оценки
dj |
т- л =o=
5© s=e .n
1 MAP
1
К
Sh(kT)ieh(kT)-»(kT)]+^-\ л
°e 4v
Решение этого уравнения легко находится так что оптимальная оценка имеет
вид
•Л Л
®MAP — ®MV =
К
(l/о*) Цй(йТ)а(ЙТ)
k=l
К
1/о2е + (1/о2)£й2(йТ)
*=i
Полученное выражение для оценки в этом примере можно интерпретировать как
оптимальный дискретный фильтр или дискретное устройство оценивания пара
метра
Выражение для оптимальной оценки при непрерывном времени можно по
лучить с помощью предельного перехода, когда o2B=M2/T, а Т->-0 и й—>-оо так,
что kT-+t и КТ—rtf В результате имеем
(1/Л42) \h(t)a(t)dt
АЛ 0
«млр-Omv» ^ + ei№
184
где ^h2(t)dt='E2— энергия сигнала h(t) Значение этой оценки можно полу-
о
чить как значение сигнала в момент времени t=tf на выходе оптимального
фильтра, один из возможных способов реализации которого показан на рис 6 3.
Рис 63 Один канал Мканалыно
го оптимального фильтра (при
мер 6 3)
h(t)
Ковариационная матрица вектора ошибок имеет существенное значение при
анализе качества функционирования приемника В данном примере эта матрица
легко вычисляется и имеет вид
~ л Af2
var {©> = var {0 - 0MV} =---------- I.
1 J M2/c2e + E2
Дисперсия ошибки оценивания во всех каналах одна и та же Эта дисперсия
возрастает с уменьшением отношения сигнала/шум Е2/Л12
Полезно рассмотреть и другой способ получения тех же результатов в
данном примере, основанный на разложении Карунена—Лоэва Наблюдаемый
процесс x(t) при этом следует представить в виде ряда в форме (3 55) и (3 58)
^-добно ввести обозначение фц (/) =h (t) 'Е В этом случае
5 1 5
ах= J г(О’ЫО‘й = Е0 + — J v(f)h(t)dt.
о
В соответствии с рассуждениями приведенными в предыдущей главе, коэффи-
циент ai можно рассматривать как векторную достаточную статистику# =а8
с условными моментами
Е {# | 0} = Е 0, var {# | 0} = М2 I.
Найдем теперь условную плотность вероятности
р0|# I ^) = е I в) Ре (°)/р# >
где
р#|0I в) = (2я^2)Ж-ехР [ (<*-Ев)г-Ев)];
1 Г 1 т
р„ (#) =-----------------ехр —--------~------S1 #
' [2л (Е2 о20 + М2)]^2 [ 2(Е2о|+Л12)
Таким образом
(Е2а| + М)^2 г 1 / #Е \Т
Р0|# (в I ^) = {2n)N/2^2&M2^/2 еХр 2 у “ е2 + ) Х
X\Afa + <re/\ Е24-Л42/00 )
185
Отсюда сразу получаем, что оптимальная оценка и ковариационная матрица
вектора ошибок оценивания определяются с помощью выражений:
Л Л <8>Е ~
вмлр —®mv~ о ; var{в} =
Е2 + M2/Og Е2/М2 -f- 1/Og
которые совпадают с полученными ранее.
Может показаться, что дисперсии оценок var{0} должны уменьшаться при
увеличении времени наблюдения Однако это не так, поскольку в данной задаче
введено ограничение
‘f
j Л2(/)е# = Е2.
о
При увеличении значения параметра // здесь приходится уменьшать мощность
сигнала h(t). Именно это требование приводит к тому, что точность оценива-
ния не увеличивается с увеличением времени наблюдения //. Если же мощность
сигнала остается постоянной, то увеличение tf приводит к увеличению энергии
Е2 и, следовательно, к уменьшению дисперсий ошибок оценивания.
Пример 6.4. Рассмотрим несколько измененную задачу примера 6 3 А имен-
но, предположим, что параметр 0П входит нелинейно в модель наблюдаемого
процесса.
Пусть zn (/) =hn (0n, /)+on(Z), G<t<tf, n=l, где h — известная
функция Все остальные обозначения имеют тот же смысл, что и в предыду-
щем примере. Такая модель наблюдаемого процесса может быть использована
для описания дискретной адресной системы передачи данных с многостанцион-
иым доступом, в которой применяются частотные или фазомодулированные сиг-
налы.
Если имеются N наблюдаемых процессов, то можно ввести векторные обоз-
начения z(<)=h[0, Z] + v(Z), Q<t<tf, где
Статистические характеристики параметров 0 и v будем считать такими
же, как и в предыдущем примере При дискретном времени совместная плот-
ность вероятности оцениваемого параметра и выборки
______________1____________ _j
Pz. е (А. 6) - (2я)ЛГ/2 (2я)„к/2 е ,
где «функция потерь» 4
К
4- у. u«(*T)-h(6, Ann2 +4
<%> LS °е
lieil3
о
Значение этой функции необходимо минимизировать путем подбора значения 0.
При непрерывном времени соответствующая функция потерь имеет вид
(f)-h(e, 01м + 4 иеца
1
ЛР
I II «
О
Наилучшая оценка 0млр Для параметра 0 может быть найдена после диффе-
ренцирования' и отыскания корня уравнения:
186
3J_|
3вИдАР
G
1 r dhr(6, t)
м2 J de
0
[ h (6, t) — a (/)] dt -+Д- 6
a8
л
в=0МАР
В соответствии с определением функции h(0, t) имеем
~ ЭМбг, О 0
5©!
3hT(0, t) dh2(e2, Q
де ~~ де2
0 MN(eN , t)
так что можно записать:
Г аьт(е, t) 1 3М0/. t)
L 50 Jv~ det
dhT(8. t) . Г dhi(0Z, t) 1
3 0 -diag[ dQ[ J,
Уравнения для оптимальных оценок, таким образом, принимают вид
1 с'аме.. О . .. .. , _1_ с'амег, О а ... м
лр] det hl^* l’t}dt+ ^=м2} det at{t}dt-
о 6 о
Решения этих уравнений снова можно интерпретировать как N несвязанных
фильтров так же, как это было сделано в предыдущем примере для линейной
модели
Особенно интересным для техники связи оказывается случай, когда пара-
метр является фазой полезного сигнала При этом
dh, (е{, t)
hl(Qi, t) =asin(<o£t + 0f); --—------= a cos (co, t + 0J,
d e£
Уравнение для оптимальной оценки в этом случае принимает вид
tf
а2 С 0; а С
— J cos (Ш; t + 0f) sin (co, * + e{) dt + — = — j az (/) cos (co, 0Z) dt.
0 °e 0
Л
Приняв, что @i = 0t map, перепишем это уравнение следующим образом:
Л ДОд Р Л Л
0/ МАР = (0 ~ а Sin (“i + 0/ MAP)1COS < + 0< MAP) dt-
Такая запись является типичной при решении задач фазовой автоподстройки
частоты [270]. Используя теперь тригонометрическое тождество sin Д cos/1 =
= 0,5 sin 2А, получим
Л аав С ai л
0/ МАР = J а1 (0 cos (“»+ 0/ мар) — J sin (2®/ { +120/ мар) М •
о
187
Если несущая частота со. достаточно велика, то последний интеграл в этом
уравнении можно опустить. В результате' получаем приближенное уравнение
для-'оптимальной оценки:
я
Л са0 f Л
МАР J ai (0COS (®i t + МАР) dt-
О
Решение этого уравнения уже следует считать приближенно оптимальной оцен-
кой параметра. Возможный способ построения устройства, осуществляющего
вычисления такой оценки на основе принципа фазовой автоподстройки частоты,
показан на рис. 6 4а.
а)
Рис. 6.4. Оптимальный
демодулятор при фазо-
вой модуляции:
а) нелинейная модель;
б) линеаризованная мо-
дель
Среднеквадратическую ошибку оценивания с помощью подобного демоду-
лятора вычислить довольно трудно из-за того, что оценка является нелинейной.
Поэтому оказывается полезным даже какой-либо приближенный способ анализа
точности полученных здесь оценок. Напомним, что для наблюдаемого процесса
справедливо представление
= ht (0t, t) + Vi (t) = a sin (ait + 0Z) + ot- (t).
Если воспользоваться формулами для тригонометрических функций двой-
ного угла, то можно записать: sin A cos В=0,5 sin (А—В) -f-0,5 sin (Л+<8) Теперь
слагаемое с двойной частотой опустим и введем аппроксимацию sin (А—В) х
«Л—В при мало отличающихся друг от друга значениях А и В. Тогда для
Л
оценки 0! млр можно получить приближенное соотношение
9
Л а Оа С л л
МАР J [ °>5а (0< — 0( мар) + vi (0 cos (®i * + 0j map)] dt-
0
A
Введем далее модифицированный шум =2nt(Z)cos(wt<+0! мар)/«, для ко-
торого
Е{ °((0}=0; c°v{ Мт)} =-j М*~г)-
Это позволяет для линеаризованной оценки написать равенство
188
л 0,5а2 о| р л
0Z МАР = J ~ °! МАР + vi (0] dt
0
Возможный способ реализации такой оценки показан на рис. 6 46. Для этой
оценки уже возможно вычислить среднеквадратическую ошибку оценивания,
если воспользоваться одним из методов, рассмотренных в гл. 4. Такие вычис-
ления здесь пока проводить не будем, отложив их до решения аналогичной
более общей задачи.
Пример 6.5. В этом последнем примере параграфа рассмотрим задачу оце-
нивания бинарного сигнала, наблюдаемого на фоне шума. В результате реше-
ния этой задачи должны быть построены оценка по максимуму апостериорной
плотности вероятности и оценка, обеспечивающая минимум среднеквадратиче-
ской ошибки. К подобной задаче сводятся, например, проблемы посимвольной
синхронизации в цифровых системах связи. Будем считать, что для одного ска-
лярного наблюдения справедливо представление z=x-f-v, где х и v — незави-
симые величины; v является нормальной случайной величиной с параметрами:
£{а}=0; var{o} = o20; плотность вероятности случайной величины х рх(р) =
=0,5бо(Р—1)+0,5боф+1).
При вычислении апостериорной плотности pxlz(P|a) — pzix (a| Р)рх(Р)/рг(а)
следует принять, что
1
Рлх (а I Р) = --------ехр
У 2л ов
(a~P)2 I .
2о„
Pz (а) = i Рл (Р) Pz|x (а I Р) d Р =-7=— I ехР
J 2/2лов (
+ ехр
_ («+1)2
2о2
(а-1)3
2ов2
При отыскании оценки плотность pxlz(P|a) следует максимизировать на
множестве значений переменной Р, содержащем всего две точки, Р = ±1, так
как только в этих точках априорная плотность р»(р) отлична от нуля. Какое
из двух значений +1 или —1 выбрать, определяется тем, при каком из них
апостериорная плотность pxtz(P|a) максимальна. Очевидно, что это будет то
значение р, которое оказывается ближайшим к полученному наблюдению а.
Таким образом, получаем 0MAP = sign{a}.
Оценка, обеспечивающая минимум среднеквадратической ошибки, является
средним значением найденной условной плотности вероятности pX|Z(|3|a). После
простого интегрирования и некоторых алгебраических преобразований получаем
09
0MV = f Р РХ\г (р I a) d Р = th — .
А °*
Следовательно, оценка по максимуму апостериорной плотности вероятности
отлична от оценки с минимальной среднеквадратической ошибкой. Соответству-
ющие этим оценкам функциональные преобразования наблюдаемых величин
изображены на рис. 6.5 Из этого рисунка очевидно, что найденные оценки ста-
новятся фактически одинаковыми при больших отношениях сигнал/шум (при
малых значениях дисперсии шума о2в). Подобная эквивалентность рассмотрен-
ных здесь оценок при достаточно больших значениях отношения сигнал/шум
вообще часто имеет место в самых различных задачах оценивания.
189
Рис. 65. Функции хмдр(а) и xMV (а) (при-
мер 6 5)
В более сложном, но более полезном случае процесс z(t) на ;-м интервале
наблюдения представляется как сумма бинарно модулированного сигнала x(t, 0)
и шума измерений v(t), т. е. z(t)=x(f, O)+v(f); 0+(j—1)ть<<<0-Нть.
Подлежащий оцениванию параметр 0 представляет собой временной интервал
от момента £=0-р(/—1)ть Начала наблюдения до следующего за ним первого
момента, в который может произойти изменение значения бинарного сигнала
x(t, 0). Задача оценивания этого параметра фактически является проблемой
синхронизации цифровой системы связи по сигналу, несущему полезную инфор-
мацию. В такой системе нет необходимости передавать специальный синхро-
сигнал, благодаря чему мощность излучаемого передатчиком сигнала увеличи-
вать не нужно Будем считать, что каждый бит полезной информации пере-
дается в течение Ть секунд В течение этого времени полезный сигнал x(t, 0)
может быть представлен одним из двух сигналов s (t, 0) или — s (t, 0), отлича-
ющихся только знаком Пусть далее спектральная плотность шума постоянна
к равна Л12. В этом случае условная (при фиксированном значении параметра 0)
конечномерная плотность вероятности наблюдаемого процесса z(f) имеет вид
{К
*=1
1__1._’ _( "аТ а \ [ — sr (0) s (0) ] pIi [ аг s (0)1
= (2л Ю/Т)™ МР ' 2М2!Т ' МР L 2М2!Т J L М2/Т -1 ’
где aT=[<Ji, «2, ..., Ок]; sri(0) =[s(£i, 0), s(tz, 0), ..., 0)].
Формула Байеса позволяет написать выражение для апостериорной плот-
ности вероятности:
Pejz (в | «) =
Pzie (* I 6) Ре <в)
Pz <«)
190
если предварительно вычислить безусловную плотность
со
Рг(«) = J Pz[0<“ I 0)p9(®)d0-
—оо
Подставив выражение для условной плотности Pzg(a|@) в формулу Байеса и
проведя некоторые сокращения, получим
Г sT(0)S(0)] Г «rs(0) 1
ехр — 2М1!Т ch МЧТ
(0 I “) = —----
J еХР
sT (0) s (0)
ZMt/T
ch
aT s (0) I
—------- | (0) d Q
ЛР/Т 0 '
Если теперь число отсчетов на интервале наблюдения неограниченно уве-
личивать и при этом воспользоваться соотношениями типа
т к , Ч
аг s(0) Т 1 £
S е,<"'
/к~*Ч *iC*4
то придем к следующему выражению:
ехр
1
2Л12
~ j a(t)s(t, Q)di р0(0)
Jexp ~i.fs4t’&)di
-» L <o
1 г
ch TfT aC)sC> 0)Л
/И J
-* X pQ (0) d 0
где ?/=0+/ть; <0=0+(J— 1)Ть. Длина интервала наблюдения здесь действи-
тельно равна длительности одного передаваемого символа. Предположим далее,
что энергия полезного сигнала на любом интервале времени длиной хъ равна Е2,
а параметр 0 является случайным и имеет равномерное распределение на ин-
тервале (0, ть), т. е.
Ч
J s2 (/, 0) di = Е2;
<»•
( 1/хь,
/’e(0) = jo>
о < 0 < ХЬ;
0^0, 0 > хь.
При таких дополнительных предположениях апостериорная плотность ве-
роятности
Pq\z (0 I *)
1
Л42
Ч
j a(t)s(i, G)dt
t.
191
Ясно, что знаменатель полученного выражения не зависит от О. Напомним,
также, что ch В является 'монотонно возрастающей функцией при возрастании
л
|В|. Следовательно, оценка 0мар по максимуму апостериорной плотности ве-
роятности, которая должна быть найдена максимизацией апостериорной плот-
ности путем сдвига интервала [£0> if], удовлетворяет условию
®+/тЬ
max J <d)dt
e=w e+(/-1)T"
И снова здесь в качестве первой операции при вычислении значения оценки
фигурирует корреляционный интеграл, уже обсуждавшийся ранее при описании
согласованного фильтра. На рис. 6.6 показан возможный способ построения
Рис. 6 6. Устройство, реализующее алгоритм вычисления
Л
значения оценки 0мар (пример 6 5, интервал наблюдения
равен длительности одной посылки)
устройства, реализующего полученный алгоритм оценивания. Это устройство со-
держит генератор, который формирует достаточно большое число сигналов
s(t, 0), отличающихся только значениями параметра 0. Каждый из этих сигна-
лов подается в отдельный канал. Моменты начала и окончания интегрирования
в каждом канале зависят от значения параметра 0 сигнала в этом канале.
Внешне структура устройства оценивания совпадает со структурой устройства
различения М гипотез
Если интервал наблюдения кратен длительности одного символа, то
j
Прг;|е (aj | ©)ре(0)
Peiz (0 I А) =-----Ь»------------------------ ,
ТЬ J
J П Pz>ie(“J I 0)p0(0)<i0
192
где Z — последовательность векторных наблюдений Z;, /=1, 2, ..., J, так как
случайные векторы Zj при фиксированном значении параметра 9 независимы.
Введя те же предположения, которые были использованы при проведении наб-
людений только на одном интервале длиной Хь, получим
Peiz I А)
J г »+Лв
□ ch f a(t)s(t.Q)dt
/=1 е+ (л-p тв
о /=1
сЬ[м2
л
Значение оценки 0мдр для каждой полученной реализации а(/) процесса
z(t) вновь отыскивается путем максимизации числителя по переменной 0. Мож-
но максимизировать логарифм числителя. Таким образом, необходимо» найти
J Г 0+Ль
max Inch J 0) dt ,
в=ем4Р'=1 L 0+</-1)ть
Функциональная схема устройства, реализующего полученный алгоритм оце-
нивания, приведена на рис. 6.7. Она во многом аналогична схеме рис. 6.6.
Рис. 6.7. Устройство, реализующее алгоритм вычисления
Л
значения оценки 0млр (пример 6.5, интервал наблюдения
кратен длительности одной посылки)
Устройство оценивания в рассматриваемом случае оказывается намного слож-
нее, поскольку необходимо накапливать значения функций Хг(0). Результаты
более тщательного исследования затронутых здесь вопросов можно найти в ра-
ботах [144, 145].
7—26 19®
6.3. Оценки максимального правдоподобия
В предыдущем разделе рассматривалась байесовская те-
ория оценивания. Одной из наиболее полезных оценок, полученных
там, является оценка по максимуму апостериорной плотности ве-
роятности. Значения этой оценки определяются путем максимиза-
ции условной плотности
1 Ре (“)
относительно переменной 0. Для этой оценки было введено специ-
л
альное обозначение Омар. Так как безусловная плотность /?г(а) не
л
зависит от параметра 0, то значения оценки 0Мар могут отыски-
ваться путем максимизации совместной плотности
(6.25)
относительно 0 Можно также максимизировать значение натураль-
ного логарифма от этой плотности. В этом случае значение оценки
л
0МАр ПРИ каждой выборке z = a является корнем уравнения
dlnPz,e(“- е)
де
Л _____ л __.
0=6... „ = и =
МАР
51nPz|e (“Iе) 31пРе (е)
де + де
РмАР ' (6‘26>
Предположим теперь, что никаких априорных сведений о пара-
метре 0 нет. Если бы параметр 0 был случайным и имел нормаль-
ную плотность вероятности
Ре(9) =--------------5------р ехР----------(© - Ре/ Ve 1 (0 - |i0)],
(2л)*/2 (det Ve) 2
то рассматриваемый здесь случай можно было бы получить пре-
дельным переходом при неограниченном увеличении дисперсий
всех компонент вектора 0. Так как при этом
ln(,e(e)--ln[(2«)K'!(detVe)2
"'"‘У ° -V?’ (6 — fe),
то при Vg->oo имеем V-'-H). Таким образом, при отсутствии апри-
орных сведений о параметре можно положить
д In рв (в)
Эе
194
(6.27)
Получающаяся при этом из ур-ния (6.26) оценка называется оцен-
кой максимального правдоподобия. Она является корнем уравне-
ния
4ie (“ Ie) | л _ п
д е |0=емь " 0
(6.28)
или, что эквивалентно,
д In pz|0 («|6) I Л
(6.29 )
Оценка максимального правдоподобия была предложена рань-
ше, чем была развита байесовская теория оценивания [166].
Она определялась как значение параметра 0, при котором функ-
ция правдоподобия pz|0(a|0) принимает наибольшее значение. Из
приведенных выше рассуждений должно быть очевидным, что точ-
ность оценки максимального правдоподобия будет хуже, чем байе-
совской оценки. Несмотря на это, существуют достаточно веские
причины, из-за которых использование этой оценки оказывается
разумным. Так, довольно часто встречаются задачи оценивания, в
которых
— параметр 0 не является случайным, а его значение неиз-
вестно;
— параметр 0 является случайным, однако его априорная плот-
ность вероятности неизвестна;
— выражение для апостериорной плотности p0z (0|а) [или
для pq z (0, а)] оказывается настолько сложным, что его трудно
использовать для вычислений, в то время как функция правдопо-
добия pz|0 (а|0) имеет относительно простой вид.
В первом случае вообще нет возможности найти байесовскую
оценку, поскольку о плотности вероятности pq (0) вообще нельзя
говорить. Один из возможных путей преодоления этой трудности
состоит в том, чтобы использовать псевдобайесовские оценки. Та-
кие оценки будут рассмотрены в § 6 5.
Пример 6.6. Рассмотрим одну из классических задач оценивания, которая
была решена с использованием оценок максимального правдоподобия. Пусть
требуется оценить среднее значение и дисперсию нормальной случайной вели-
чины по выборке из К. независимых наблюдений этой величины Для наблю-
даемой величины при этом имеем
Zk = Xk', k=l, 2, . . ., Д’, где
В силу независимости наблюдений можно записать
К
Рг\цх, (“ । °2) = Гкй |цж Vx (аЛ I °2) =
k=l
г к 1
_ 1 _V (ад - И)2
(2ла2)к/2 еХР 2аа
7
195
В этой задаче подлежащие оцениванию параметры р. и <т2 ие являются случай-
ными, так что байесовские оценки найти нельзя.
Случай 1. Будем считать, что значение параметра а2 известно В этом
случае оценка максимального правдоподобия для среднего значения р является
корнем уравнения
^гцхд, °2)
Л =0.
W=,XML
К
-X Л 1 П
Это уравнение имеет единственный корень pML =“ V а;г,который и следует
*=1
принять в качестве оценки максимального правдоподобия для среднего значе-
ния. Так как математическое ожидание этой оценки совпадает со зна-
К
чением оцениваемого параметра, т. е Е { pML} = — = р,
то эту оценку называют несмещенной *>
Случай 2. Предположим теперь, что значение параметра р известно. Оцен-
ка максимального правдоподобия для дисперсии в этом случае является корнем
уравнения
<Ч|М,. у(а1?< ст2) I
----*---f---------- Л2 =0.
О СТ |о=аМЬ
Решив это уравнеине, получаем
К
S(—)2-
*=1
Эта оценка также является несмещенной, поскольку E{o2KL} —°2-
Рассмотрим теперь задачу оценивания стандартного отклонения а Можно
предположить, что эта оценка представляется как корень квадратный из оценки
для дисперсии. Это действительно так, поскольку оценка
Л
^ML =
К
у («А-И)2
2
2
является корнем уравнения
I р. ст2) I
——— -------------=0.
до ia=alAL
Случай 3. Значения обоих параметров р и а2 неизвестны В этом случае
оцениваться должны два параметра 0( = ц и 02 = о2 Вычисляя производные
функция правдоподобия по переменным ц и а2, приравнивая их нулю и решая
найденную систему из двух уравнений, получаем
К К
л 1 V3 Л? 1 VI л
.mml=Ъ “ft; Oml=т ~
a=i *=i
*> Определение понятия несмещенности будет дано в разделе 6 4. (Прим,
авт.)
196
сред-
оцеяи-
Мож-
Оценка среднего значения здесь вновь является несмещенной, а
, Л, т А"—1
нее значение оценки дисперсии ел <tMl }= —~ о2 не равно значению
л К
2
ваемого inapanerpas т е aML в указанных условиях является смещенной
Л
ио было бы, введя поправку, получить несмещенную оценку —1), ко-
торая не является, однако, более оценкой максимального правдоподобия
Л
Часто полезно иметь алгоритмы последовательного вычисления оценок цк
и а2л Здесь нижние индексы оценок максимального правдоподобия заменены
индексом К, который указывает объем используемой для оценивания выборки.
л 1 V
При объеме выборки, равном (К—1), оценка 1 ~ TfTLT / Поэтому ал-
*=1
последовательного вычисления этой оценки имеет
Л
Л
ВИД Цк =
Л
оценки а2к
горитм
1
==— [(К— 1) +ак]. Алгоритм последовательного вычисления
отыскивается несколько сложнее Воспользуемся уже полученным
жением для оценки
ранее выра-
Л9 1
Ок — —
к К
г Л-1
^(«й-Рк)2 + («к-£к)2
-k=l
Л
и выпишем аналогичное выражение для оценки <t2k-i'
К-1
Л„ 1 «П л
4-1 = (aft ~ ^К-1 )2-
k=l
Л
Оценку цк теперь представим в рекуррентном виде Тогда из двух выписанных
раве —: после немногочисленных алгебраических преобразований получаем
Л„ 1 Г , Л9 К л
° К ~ ~~ 1 ) стК-1 + __ 1 ( ак ~ Нк )2 j
л Л
Рекуррент1ые алгоритмы вычисления оценок цк н <т2к должны использоваться
совме^п о
Л
Пример 6 7. Найдем оценку максимального правдоподобия xML для пара-
метра х рассмат пинавшегося в примере 6 1 Теперь плотность вероятности
Pz|x (“ I Р) = (2п)Л1/2 ((jet Vv )1/2- ехР j ~ И Р)Г (“ Н Р) j •
Оценка максимального правдоподобия определяется как корень уравнения
<Ч|х<«1Р) | Л
H1L
и имеет вид
В рассматриваемом случае можно найти и байесовскую оценку
xMV = Е {х | г = = { V71 + Нг V71 И)”1 (Нг V71 а + V71 Их) .
197
Если принять, что VXJ= 0, Цх=0> то оценка, обеспечивающая минимум средне-
квадратической ошибки, совпадает' с оценкой максимального правдоподобия.
Интересно отметить, что в этом случае оценка с минимальной дисперсией, ко-
торая совпадает также с байесовской оценкой при модульной функции стои-
мости и с оценкой по максимуму апостериорной плотности вероятности, так же,
как и оценка максимального правдоподобия, является несмещенной
Чрезвычайно полезно вычислить корреляционные матрицы вектора ошибок
этих двух оценок. Для байесовской оценки такая матрица уже была вычислена
и было показано, что
var {*mv} = var {х - xmv} = (V?1 + Нг V71 н)-1.
Для оценки максимального правдоподобия получаем
var{^Ml} == var {х—xML} = var{x—(H^V'H)-1 HrV~'aj.
Если теперь воспользоваться представлением a=Hx+v, то
var {^ML} = var { (Hr V71 H)"1 Нг V71 v} = (Нг V71 Н)“*.
Корреляционная матрица вектора ошибок при использовании оценки макси-
мального правдоподобия всегда больше, чем корреляционная матрица вектора
ошибок для оценки с минимальной среднеквадратической ошибкой. Эти матри-
цы совпадают только в том случае, когда V”1 =0
Полезно рассмотреть также случай, когда матрица Н является единичной,
т. е Н = 1. При этом z=x+v.
Оценка максимального правдоподобия, байесовская оценка и их корреляцион-
ные матрицы в этом случае принимают вид
л ~
XML = «; var { xML) = Vv;
xmv = (v?1 + v?1)-1 № «5 var { xmv} = (v?‘ + v?1)-1 •
Здесь нельзя ожидать, что оценка максимального правдоподобия окажется
достаточно точной, поскольку ее значения просто совпадают со значениями по-
лучаемой выборки.
Если объем выборки намного больше размерности оцениваемого парамет-
ра х, то оценка максимального правдоподобия может оказаться достаточно хо-
рошей. Например, пусть z=Hx+v, где х — скалярный параметр, а векторы z
и v имеют размерность К Предположим также, что
£{х}=р.Л; var{x} = a2;
Е {v} = 0; var {v} == о? I
и Н=[Л1, Ла, ..., hx]. Рассматривающиеся здесь оценки и их среднеквадрати-
ческие ошибки при этом определяются соотношениями
К
XX «А
Л *=1 ~ %
XML — Л > var {xMLJ —
£ hl s
4=1 4=1
К
АЛ®й+Нх/<4 _2
л 4=1 вг
*MV =-----------к----------: var { *mv} = —к----------------•
(1/Ov) S Ай + 1/а* ХХа + ^М
a=i 4=1
198
Часто оказывается, что для достаточно больших значений К. выполняется
К
неравенство Оу/ох< h?k . В этом случае среднеквадратические ошибки
k=i
обеих оценок будут фактически одинаковы
Аналогичные результаты можно получить при непрерывном времени для
примера 6 3 Если модель наблюдений в последнем примере с дискретным вре-
менем трактовать как дискретный аналог следующей модели наблюдаемого
процесса
z (t) = h (0 х + V (0, 0 < t < tf,
где v(t) — нормальный белый шум с нулевым средним значением, то, используя
обозначения примера 6 3, можно получить
tf
С h (t) а (0 dt
Л о ~ ч М2
xml- tf • var { xml} - tf
^htttjdt h2 (t) dt
о 6
Отсюда следует, что если вид функции h(t) не изменяется при изменении
t!t то среднеквадратическая ошибка оценивания уменьшается с ростом tf. Если
же энергия сигнала h(t), определяемая какЕ2= I №(t)dt, должна оставаться
о
постоянной при любом значении параметра tf, то значение среднеквадратической
ошибки не зависит ни от длительности \tf, ни от формы сигнала h(t) Если
Л
Л12/о2х<Е2, то среднеквадратическая ошибка байесовской оценки х Mv факти-
чески будет такой же, как и у оценки максимального правдоподобия Если же
это не так и справедливо обратное неравенство Af2/<J2X<E2, то это означает,
что либо имеется достаточно интенсивный шум (Л42 велико), либо имеется
хорошая априорная оценка для х, с которой можно начать (о2х мало) Значе-
ния оценки с минимальной среднеквадратической ошибкой и среднеквадратиче-
ская ошибка этой оценки при этом мало отличаются от соответствующих па-
раметров априорного распределения и можно записать
tf
(1/Л12) [й +
Л 6
xmv— t ~ 9х’
(1/М2) й2 (t) dt + 1 /о*
6
Л-Р
var { *mv} = —--------------»°; •
J № (t) dt + M2/o2x
о
Так что в этом случае среднее значение априорного распределения прини-
мается в качестве наилучшей оценки для параметра х В примере 6 5 уже от-
мечалось, что при больших отношениях сигнал/шум среднеквадратические ошиб-
ки оценивания при использовании оценки по максимуму апостериорной плот-
ности и оценки с минимальной среднеквадратической ошибкой практически
одинаковы. Из результатов этого примера следует, что при больших значениях
199
отношения сигиал/шум (здесь при E2a2x/M2>l) точность оценок xvm и Хмар
практически такай же, как и у оценки максимального правдоподобия
Пример 6.8. Приведем теперь подробный анализ простой задачи оценивания
по методу максимального правдоподобия при наличии окрашенного шума В про-
цессе решения этой задачи будут проиллюстрированы соображения, которыми
можно будет пользоваться при практическом выборе интервала дискретизации.
Пусть наблюдению доступны реализации скалярного процесса z(t) = x-{-v(t),
0</<1, где х — постоянный скалярный параметр, и
E{p(/)} = 0; cov {»(/). о(т)}==е~501 *“’1 =^(z> *)
Для решения задачи оценивания параметра х поступим следующим обра-
зом Введем соответствующую модель наблюдений при дискретном времени
z(kT)=x-(-v(kT), 0<ЛТ<1, где период отсчетов Т выбирается так,
чтобы изменения процесса z(t) на таком интервале были хорошо заметны. Для
этой модели имеем
Е {о (kT)} = 0; cov (v (kT), v (jT)} = e-50r 1 k~‘1.
Наблюдаемый процесс можно теперь записать в векторной форме:
V = (hrv71h)-1 hrV7‘a,
тле ковариационная матрица шума Vv = var{v} имеет элементы:
IVv]У = е~50Г11~’1 . 1
Если объем выборки К достаточно велик, то обращение матрицы Vv является
достаточно сложной с вычислительной точки зрения задачей
Среднеквадратическая ошибка оценивания при использовании оценки мак-
симального правдоподобия
var{*ML} = (h7’v71 h)~ *•
Вычисление этой ошибки при больших значениях К также сопряжено со зна-
чительными трудностями обращения матрицы VT большого размера На рис. 6.8
приведен график зависимости среднеквадратической ошибки от объема выбор-
ки К (нли от периода отсчетов Т—1/К.)
Если период отсчетов выбран достаточно большим, то компоненты вектора
шума V можно считать независимыми случайными величинами Если принять,
что var{v}=I, то выражения для оценки и среднеквадратической ошибки при-
мут вид
К
* ml = Y var = VK.
Л=1
Отсюда видно, что среднеквадратическая ошибка оценивания уменьшается
обратно пропорционально объему выборки К. Может показаться, что при /С->оо
ошибка стремится к нулю Однако это не так, поскольку здесь в примере рас-
сматривается окрашенный шум При больших значениях К компоненты векто-
ра z нельзя считать независимыми. Если объем выборки ^=10, то коэффициент
корреляции между соседними компонентами шума равен ехр{—50(0,1)} ~0,0067.
При /(=100 он равен ехр{—50(0,01)} «0,606 В обоих случаях имеет место
корреляционная связь между компонентами шума. Однако при К—2 эта связь. 200
200
очень мала и можно ожидать, что предположение о независимости компонент
шума не приведет к существенной погрешности в вычислениях, хотя оценки при
этом оказываются плохими. При К.= 100 корреляционная связь между компо-
Рис. 6.8. Зависимость дисперсии ошибки оценивания от
объема выборки (пример 6 8)-
1 — алгоритм, ориентированный на белый шум; 2 — алгоритм,
ориентированный на окрашенный шум
нентамн шума достаточно велика и предположение о независимости не является
более реалистичным На рис. 6 8 изображен также график зависимости средне-
квадратической ошибки, вычисленной для алгоритма, ориентированного на не-
зависимость компонент вектора шума Как следует из рисунка, уменьшение
ошибки оценивания при К>15 (или Т<0,067) прн дальнейшем, даже неограни-
ченном, увеличении объема выборки оказывается незначительным
Приведенное выше выражение для var{xML} справедливо только в том
случае, если компоненты вектора V в самом деле независимы Истинное значе-
Л,
ние среднеквадратнческой ошибки оценивания при использовании оценки
в случае окрашенного шума может быть найдено нз соотношения
К
* ML = *-*ML = X- V У a(^)=x-(hTh)-1 hTa,
Л w
А=1
где a=hx+v. Так,
* ML = ( hrh )-1 hr v, var { = ( hr h)-1 hT Vv h( hr h)-1
или
к к
1 fl г~' 1 *=!/=!
*ML = /j v №)', var { •rML} = ^2
Для частного вида ковариационной матрицы шума, рассматриваемой здесь,
при использовании алгоритма оценивания, основывающегося на предположении
независимости отсчетов шума, истинная среднеквадратическая ошибка
201
к
var {^ml} = (K—k) exp (- 50Tk).
k=i
Зависимость этой ошибки оценивания от объема выборки приведена на
рис. 6 8 Из рисунка видно, что при объеме выборки К>40 (или Г< 0,025)
алгоритм, ориентированный на белый шум, обеспечивает значение среднеквад-
ратической ошибки, лишь незначительно превышающее значение ошибки для
алгоритма, ориентированного на окрашенный шум Поскольку алгоритмы для
белого шума намного проще, чем алгоритмы для окрашенного шума, то в прак-
тических приложениях можно поступить следующим образом, объем выборки К
принять равным 40 и использовать простые алгоритмы оценивания, ориентиро-
ванные на белый шум, если такая высокая частота отсчетов допустима Средне-
квадратическая ошибка оценивания по выборке объема Л=15 при использова-
нии алгоритма для окрашенного шума (когда шум на самом деле окрашен)
равна среднеквадратической ошибке оценивания по выборке объема Л=40 при
использовании алгоритма для белого шума Отношение этих среднеквадрэтиче-
ских ошибок при Л=15 равно примерно двум
6.4. Свойства оценок
До настоящего раздела уже неоднократно использова-
лись такие термины, как оценивание, оценка и устройство, реали-
зующее алгоритм вычисления значения оценки. Под оценкой здесь
будем понимать некоторое правило, согласно которому вычисля-
л
ются частные значения 0, соответствующие частным выборкам
z = a. Другими словами, оценка есть некоторая случайная величи-
на. Под оцениванием здесь будем понимать процесс получения
частных значений оценрк.
Понятие достаточности статистики было введено в предыдущей
главе. Здесь отметим только, что под достаточной будем понимать
такую статистику, которая содержит всю информацию, необходи-
мую для построения либо оптимального правила выбора решения,
либо оптимальной оценки. В данной главе уже рассмотрено не-
сколько примеров получения достаточной статистики.
Из желаемых свойств оценок можно выделить следующие
четыре:
1. Несмещенность оценки.
2. Минимум дисперсии в классе несмещенных оценок.
3. Состоятельность или сходимость оценки (состоятельность и
сходимость в среднем квадратичном).
4. Эффективность, асимптотическая эффективность, оптималь-
ность в классе асимптотически нормальных оценок.
Оценка называется несмещенной, если ее математическое ожи-
дание равно математическому ожиданию оцениваемой величины,
л л
Так, если £{0}=£{0}, то говорят, что оценка 0 безусловно не-
смещена. Это равенство можно записать несколько иначе:
Д {0 (z = «)} = р0 = Е {0} = J© р0 (0) dQ. (6.30)
— оо
202
Можно также воспользоваться эквивалентным выражением
£{0 («)} = Ez 1е{0(«)}=jJ6(«)рг 0(«, Q)dxdQ^ J0(«)pz (я) de,
— оо —оо
(6.31)
из которого уже совсем очевидно, что вычисляется безусловное ма-
тематическое ожидание оценки. Если математическое ожидание
оценки вычисляется при условии, что значение оцениваемого пара-
метра фиксировано, то для условно несмещенной оценки должно
выполняться равенство б
Е{0(«)|0}=0 (6.32)
для всех 0. Если оценка является смещенной, то эти два условия
нарушаются, так что для безусловного и условного математических
ожиданий получаем:
Е{0(«)} = {ie + b; Е{0(«)|0} = 0 + Ь, (6.33)
если оценка имеет известное смещение, которое можно исключить,
или
Е{0(«)} = Е{0} + Е{6(0)}; Е{0 («) | 0} = 0 + b (0), (6.34)
если смещение оценки зависит от значения 0 оцениваемого пара-
метра и, следовательно, неизвестно; в этом случае смещение оцен-
ки устранить невозможно.
Для любой оценки можно вычислить корреляционную матрицу
вектора ошибок оценивания
Е {(0 — 0) (0 — 0/ } = var {0} + (Е {0} — Е {0}) (Е {0} — Е {0}г . (6.35)
Таким образом, эта матрица равна сумме ковариационной матри-
цы вектора ошибок и матрицы, обусловленной смещением оценки
л
Е{0}—Е{0}. Аналогичное представление для корреляционной
матрицы вектора ошибок можно получить с применением операто-
ра усреднения при фиксированном значении параметра 0.
л
Оценка 0 называется несмещенной оценкой с минимальной дис-
персией (условно минимальной или безусловно), если она несме-
щена [т. е. если для нее справедливо равенство (6.30) или (6.32)],
и, кроме того, соответствующая ей ковариационная матрица
*> Более аккуратно это равенство следовало бы записать так-
рЛ
'6 («)|0
{0|0}=0, указав явно усредняемую величину и переменную в условии,
при фиксированном значении которой вычисляется математическое ожидание.
В дальнейшем подобный ннжннй индекс прн операторах усреднения н кова-
риационных матрицах будет использоваться только в тех случаях, когда воз-
можны недоразумения. (Прим, авт.)
203
var{0 } меньше ковариационной матрицы вектора ошибок любой
другой несмещенной оценки.
Говорят, что оценка сходится к оцениваемой величине, если ее
точность возрастает с увеличением объема выборки. Введем обо-
л
значение 0К для оценки параметра по выборке объема К. Оценка
называется состоятельной, если для любого е>0
lim Р(0 — е<0К< 0 + е) = 1. (6.36)
К—
Говорят, что оценка состоятельна в среднем квадратичном или
сходится в среднем квадратичном, если
limE{(0)K —0)(0К —0)г}= 0. (6.37)
К—>оо
Как следует из ф-лы (6.35), ковариационная матрица вектора оши-
бок и смещение этой оценки сходятся к нулю. Состоятельность
оценок можно также определить, используя оператор условного
математического ожидания, когда усреднение осуществляется при
фиксированном значении параметра 0.
л
Оценка 0К, состоятельная в среднем квадратичном, называ-
Л
ется эффективной, если для любой другой оценки 0K.s справедли-
вы неравенства:
£{(0К)(0К)г} < £{(0* )(0К)Т) (6.38)
— при использовании оператора безусловного математического
ожидания и
Е{(0К)(0*)Г|0}<£ {(0£)(0* )W (6.39)
— при использовании оператора условного математического ожи-
дания. Здесь 0К=0К—9; 0Kg=0Kg—0
л
Наконец, оценка вк называется наилучшей в классе асимпто-
тически нормальных оценок, если распределение случайного век-
л
тора у К( 0К—0) при К->-оо стремится к нормальному со сред-
ним значением, равным нулю, и ковариационной матрицей Vq и
л /- Л
не существует другой оценки 0Ks, такой, что вектор у K(^Ks—0)
при К->-оо асимптотически нормален со средним значением 0 и ко-
вариационной матрицей VS0, такой, что V0>VS0.
Очень важное неравенство для дисперсии произвольной ска-
л
лярной оценки 0 параметра 0 установлено Крамером [48] и Рао
[190] (неравенство Крамера — Рао). Они показали, что для лю-
бой несмещенной оценки
204
var{0 —0|в)>——-
E де I
(6.40}
или, что эквивалентно,
л —1
var {9 — 010} >--чтт------, 1оЛ-- . (6.41 '
1 1 52lnpzl0 (а|0) ) J
Е ( д 02 J
Для смещенной оценки неравенство Крамера — Рао принимает вид
L t ^(0)7
Д{9-0)2|0}>----------1----d& . (6.42 >
i52 In pZ|6 (а|0) | F
Е\ 9 02 )
Если же применить оператор безусловного математического ожи-
дания, то для смещенной оценки получаем
£ (Г, | ^(0) 121
Е {(9 — 0)2} >-------1----. /6.43)
р р[1прме(«, 0)1 I2 ( 1
Ег\в I д0 )
Для знаменателей дробей, стоящих в правых частях этих не-
равенств, справедливы также следующие выражения:
™(Г д InPzie (“I®) 12I p(52inpz(e (а|0) 1
£>IL 5 0 ] J ~ Д I д 02 J
F (Р1пРг>0(*> 0) ТМ F (53 inpz,e («, 0) (
z,0 90 J I ~~ 1 9 02 |
(6.44}
4'".. e(>. 8» 1- 0)rf^0 =
(7 0 I r ^[v 4 '
- Пpz’9Je- -](6.45>
— oo
При анализе точности оценок максимального правдоподобия
используют обычно неравенства с оператором условного математи-
ческого ожидания, в то время как при анализе байесовских оце-
нок применяют неравенства с операторами безусловного матема-
тического ожидания.
Аналогичные неравенства могут быть получены для векторного
параметра. Соответствующие выкладки полностью повторяются.
Так, вместо неравенства (6.40) теперь для ковариационной матри-
цы несмещенной оценки получаем
205>
var {6 (z) — 0[0) > — E ||O) | • (6.46)
Из этого выражения, в частности, следует, что равенство здесь до-
стигается только в том случае, если
'^^±L = S(e)iS(z)-ei. (в.47)
Если эффективная оценка не существует, то вместо неравенст-
ва Крамера — Рао лучше использовать более точную границу
Бхаттачария. Возможность использования этой границы для ошиб-
ки оценивания обсуждалась Возенкрафтом и Джекобсом [284].
Однако практическое применение этой границы наталкивается на
значительно большие трудности, чем при использовании неравен-
ства Крамера—Рао. Поэтому здесь будет приведено доказатель-
ство лишь неравенства (6.40) для скалярного параметра и услов-
ной дисперсии оценки, вычисляемой при фиксированном значении
этого параметра.
Начнем с выражения для условного математического ожида-
л
«ия оценки в(г=а)
£{0(«)|0} = j0(«)pz|e(«|0)d«
—оо
и отметим, что £{0 | 0}= 0. Запишем
£{©(«) —0|0} = J[0(«)-0]pz|0(«|0)d* = 6(0)- (6.48)
—оо
Продифференцировав обе части этого равенства по 0, получим
fieAW-eis^?L = । + ^1.. (6.49)
J д 6 а®
Так как
dlnpz(e (»|0) = 1 дргЩ (»|0)_
d 0 pzjQ (а|0) д 0
то равенство (6.49) можно записать следующим образом:
(16 («) - в) [Р„е We)F ^Ув>- !р,|в («Р)Г d . -1 + .
J 1 и ЧУ * U ЧУ
(6.51)
Используя теперь для оценки интеграла в левой части этого ра-
венства неравенство Шварца, получаем *)
оо оо со
*> Если J a(x)b(x.)dx = 1, то j az(x)dx J &2(у)4у^1, где равенство дости-
—оо —оо —оо
гается только в том случае, когда а(х) — СЬ(х) и С не зависит от х. (Прим,
авт.)
206
« л ?.г а 1пр„й (bi©) 12
Jm-0Fpz|e(«i0)d« м₽т>
Ul + ЁМШ2. (6.52)
[ d 0 J
Отсюда уже легко получается неравенство Крамера — Рао, ко-
торое, таким образом, доказано для этого частного случая. Равен-
ство в (6.52) достигается, если
-^^L = S(e)(Ae(.)-01. (6.53
Если для некоторой оценки неравенство Крамера — Рао переходит
в равенство и, следовательно, справедливо представление (6.53),
то можно показать, что эта оценка является эффективной. Если
плотности вероятности (а|0) или Рв|г (0|а) являются нор-
мальными, то эффективные оценки существуют.
Пример 6.9. Рассмотрим случай скалярного параметра, когда
z (/) = h (0) v (t), 0 < t < tf,
где случайный параметр 0 статистически не связан с процессом h — из-
вестная функция и
Е {0} = 0; var {0} = , E{v (/)} = 0; cov {v (t), v (т)} = Л-Р (t — т).
Если перейти к модели с дискретным временем и выписать соответствую-
щие плотности вероятности, то можно найти байесовскую оценку и оценку мак-
симального правдоподобия для параметра 0 Поэтому, приняв, что (flv—fWIT
является дисперсией шума при дискретном времени, запишем:
Pzie (“]©) =-----hr к ехр ! 1“ ~h (®)1г Iя —h (0)Й ;
(2л)К/2о* I 2о2 j
Pz, 0) =
__________1__________
(2л) а*
Рассмотрим сначала неравенство для среднеквадратической ошибки оценки
максимального правдоподобия. В общем случае эта оценка будет смещенной,
так что необходимо использовать ф-лу (6 42). Вычисления оказываются прос-
тыми, и в результате для условной среднеквадратической ошибки получаем сле-
дующую ннжнюю границу.
л [1 + db(e)/de]2
Е {[0 (а) — 0]2 I 0} >--—------'-+!--i-- ,
(К/о2) [dh(&)/d 0]2
где 6(0) —смещение оценки максимального правдоподобия
Выражение для числителя [14-d&(0)[d&\ может быть найдено из (6.48) или
нз (6 49). Однако в общем случае эта задача может оказаться довольно труд-
ной, особенно тогда, когда смещение оценки зависит от значения оцениваемого
параметра. Неравенством (6.43) можно воспользоваться для отыскания ннжней
границы значений безусловной срещнеквадратнческой ошибки Соответствующие
неравенства для непрерывного времени можно получить с помощью предельного
207
перехода, неограниченно увеличивая чясло отсчетов на интервале наблюдения.
При этом Kpflr, следует заменить на tjlMz. Для условной среднеквадратической
ошибки при непрерывном времени получаем
л [1+d6(0)/d0]2
« <[0 («) ~ вР I 6} > ZjIrJroLL ’
(tf/M.2) [an (0)/d 0]2
6.5. Точность оценок и априорная информация
Исследуем теперь точность оценок максимального прав-
доподобия и байесовских оценок в условиях, когда априорные зна-
чения математических ожиданий и дисперсий известны неточно.
Будут рассмотрены два случая. В первом из них будет предпола-
гаться, что априорная плотность вероятности р$ (0) параметра 0
неизвестна, хотя значения ее первых двух моментов заданы; при
этом также считается известной условная плотность вероятности
Pz|0 (а1®)- Для этого случая можно найти оценку максимального
л
правдоподобия 0мь- Но поскольку среднеквадратическая ошибка
байесовской оценки меньше, чем оценки максимального правдопо-
добия (см. пример 6.7), то вполне можно считать оправданными
попытки использования псевдобайесовской оценки, при построении
которой вместо недостающей априорной плотности вероятности
оцениваемого параметра вводится какая-либо другая плотность.
При анализе первого случая такой вводимой функцией служит нор-
мальная плотность вероятности. При этом будет показано, что по-
лучающаяся псевдобайесовская оценка имеет меньшую средне-
квадратическую ошибку, чем оценка максимального правдоподо-
бия. Во втором случае будем считать, что неизвестными являются
также и среднее значение, и дисперсия оцениваемого параметра.
В подобных условиях будет предложено использовать эмпириче-
ские псевдобайесовские оценки, основывающиеся на априорных
-оценках неизвестных значений математического ожидания и дис-
персии.
Анализ точности: оценки м а к с и м а л ь н о го п р а в-
доподобия. Рассмотрим линейную модель наблюдений:
zh = Hfe х -f- vfe, k = 1, 2,..., A, (6.54)
где Zfe и Vfe — векторы с M компонентами, представляющие собой
выборку и вектор шума; х — постоянный А-мерный параметр, под-
лежащий оцениванию; Hfe —• модуляционная матрица размера
MXN. Будем предполагать, что V& является нормальным случай-
ным вектором с нулевым средним значением и ковариационной
матрицей
cov{vy, vj = Vvft 6К (/ — k). (6.55)
Оценка максимального правдоподобия для параметра х опре-
деляется максимизацией по р плотности вероятности
Р2)х (А1₽) = ------1----— еХР [- ~ (А - Н ₽)Г V^' (А - Н ₽)] =
(2л)км/2 det (Vo)2
208
--------------Г ехр
(2л)^2П (det Vvft) 2
А=1
Нетрудно показать, что
xML = (HrV71H)-’Hr V?1 А =
у £(«ft-Hft₽)rV^(«fc-Hft₽) .
*=i , J
(6 56)
О “
Vv2
О V
_ VK _
К \-1 к
VhIv^'hJ Ун1¥7*Ч. (6.57)
А=1 / k=\
В действительности часто оказывается, что ковариационные
матрицы шума V,;/i известны лишь приближенно. Поэтому при-
мем, что вместо точных матриц VVk или Vv в алгоритме оценива-
ния используются несколько отличающиеся матрицы Vv или Vv.
Так что фактически будет вычисляться оценка
л / к \-1 к
xMLc = (НГ V71 Н)‘ 1 Нг ¥и 1 А == yHIVvftHfel VhJV^X, (6.58)
\А=1 / k= 1
которая является несмещенной при каждом фиксированном значе-
нии оцениваемого параметра (условно несмещенной).
Рассмотрим теперь следующие ошибки:
XML Х XML ’ XMLc Х XMLo ’ XMLc = XML XMLc‘
(6.59)
Здесь xml является ошибкой, которая получается при использова-
нии алгоритма для вычисления значений оценки максимального
правдоподобия, ориентированного на точную ковариационную мат-
рицу Vyi; (такую оценку назовем идеальной); хМьс — ошибка оце-
нивания, когда используемый алгоритм ориентирован на предпо-
_ ЛА
лагаемую матрицу VVk; разность xml—хмьс между значениями
действительной оценки максимального правдоподобия и вычисля-
емой обозначена символом хмьс.
Из ф-лы (6.25) для безусловной среднеквадратической ошибки
получаем
~ /к \-i
var{xML}=(HrV71H)-1= VhIv^'hJ , (6.60)
\fci /
209
если для оценивания используется идеальная оценка максимально-
го правдоподобия. С другой стороны, для оценки хмьс имеем:
xMLc = х - Xmlc = Х - (НГ V71 Н)-1 Н7 V/ А =
= х (Нг¥7'н)-1 HrV7'(Hx + v)= — (H^Vr'H)1 HTY7'v; (6.61)
var { xmiJ = (H7" V»' И)"1 H V~l ¥„¥„"’ H (Hr ¥7* H)', (6.62)
или с использованием обозначений, принятых в (6 54),
к _ _ _ _
var { xMLc } = J (Hl ¥7*’ Hj-1 Hl ¥Д’ Vv& H,_ (h( ¥Д’ H J"1 . (6.63)
k=i
Можно показать (см. § 6.7), что
var { XML } <var {XMLC} • _ (6-64)
Полезно рассмотреть разность xMLc двух анализируемых оценок,
поскольку она характеризует точность вычисления значений иде-
альной оценки максимального правдоподобия. Для ковариацион-
ной матрицы вектора xMLc получаем
var {xMLc} - (нг ¥7' н)-1 н7 vr1 vo v;' н (нг V;' н)-1 — (нг у~' нг1.
(6.65)
Рассмотрим теперь случай, когда предполагаемая ковариаци-
онная матрица шума «близка» к истинной, т. е. можно положить
¥0 = ¥0 + Д Vo, (6.66)
где AVt, «мало». Тогда
¥0 = Vo (I + V71 AVO) (6.67)
или
V = (vo+ Д ¥„)“’ « V71 — V71 д ¥о¥7’ -№ Д¥„¥7‘ Д¥о¥7’ .
(6.68)
Используя это приближение и учитывая также, что
(Нг V71 н)-1 w (Нг V71 н — Н7 ¥7’ Д¥о¥7' н +
+ Нг ¥?' Д ¥0¥Г' Д ¥о ¥7' Н)~’ « (Нг ¥7’ Н)-1 +
+ (Нг ¥7’ Н)-1 Нг ¥7' Д ¥о ¥7’ Н (Нг ¥7’ Н)'1 —
— 2 (Нг ¥7' Н)-1 Нг ¥7' Д ¥г ¥7‘ Д ¥о ¥7’ Н (Нг ¥7’ Н)"1,
получаем
var (xMLc ) (Нг ¥7’ Н)-’ Нг ¥7’ Д ¥0 [v~' -
— ¥7’ Н (Нг ¥7' Н)-1 Нг ¥7‘] Д Nv ¥7' Н (Нг ¥7’ Н)~*. (6.69)
210
Пример 6.10. В скалярном стационарном случае, когда
VV4 = <£ ДУуЛ=До^; Hft = l,
приходим к следующим выражениям для оценок и их дисперсий:
К 2 2
Л 1 V л 1 V > °v
JrML — 2jak> УаГ{Хм1-}— ’ •rMLc — X а^> var{*MLc}= д ’
4=1 4=1
Х MLc — °; var { *MLc } — 0 •
Интересным оказывается тот факт, что для этого частного случая не нуж-
но знать дисперсию шума при вычислении оценки максимального правдоподобия
И это справедливо всякий раз, когда выборка является скалярной, а ее эле-
менты независимы и одинаково распределены
Пример 6.11, Допустим теперь, что предполагаемая ковариационная матри-
ца шума отличается от истинной, причем
Д = V0 = (I + й!)У0.
Выражения для рассматриваемых оценок и их ковариационных матриц при
этом имеют вад
XML = (нг A; var { 7ml} = (Hr V71 н)->;
*MLC = (Hr VpH)-1 Hr Vo-> A; var { ^Lc } = (HrV^1 H)"1;
'xmlc =°; var{£^Lc } = 0,
так что вновь оценка максимального правдоподобия оказывается нечувстви-
тельной к подобным ошибкам в определении ковариационной матрицы шума
Пример 6.7 позволил показать, что оценка максимального
правдоподобия хуже, чем байесовская оценка. Она приводит к
большей среднеквадратической ошибке оценивания, поскольку при
построении оценки максимального правдоподобия совсем не учи-
тывается априорная плотность вероятности оцениваемого пара-
метра. Перейдем теперь к анализу точности байесовских оценок.
Анализ точности: байесовские оценки. Снова
рассмотрим линейную модель наблюдаемого процесса
zfe = Hfex-j-vfe, k = 1,2,..., К, (6.70)
где случайный параметр х является А-мерным вектором, выбороч-
ное значение которого одно и то же для всех элементов выборки;
векторы zfe и Vfe имеют размерность М, а модуляционная матрица
наблюдений Hh— размер M\N. Будем предполагать, что xnvfl —
независимые нормальные векторы с параметрами:
Е{х} = рх; var{x} = Vx;
£{vfe} = 0; cov{vfe, v;} = Vv,6x(^-/). (6.71)
Как и в примере 6.1, для оценки по максимуму апостериорной
плотности вероятности получаем
Хмар = (H? Н + V^’ (нГ А + (6-72)
211
или
Л f к \-1 ( К
хмар = (yHlv^Hb+vr1 * * * * * I VhIv;;4 +vx-'b)- (6.73)
\ft=i / \*=1
Ковариационная матрица вектора ошибок при использовании
этой оценки
'Ч» = игл {₽ -’мар} = (Нг V7’ Н + vr’)-’ =
МАР х хМАр
(К А-1
£ н! V?; Hfe + vr1 . (6.74)
4=1 /
Предположим теперь, что вместо истинных математических ожи-
даний и ковариационных матриц в ф-ле (6.73) используются дру-
гие матрицы Vx и Vvfe или V„ для составного вектора. Так что
фактически вычисляется оценка
*марс == (НГ vr’ Н + Vx-1)-1 (Нг vr1 А + Vx-1 Рх ), (6.75)
которая не является уже безусловно несмещенной, так как
Е (*марс) = (НГ V н + Vx-1)-1 (Нг V^H Рх + Vx-1 Рх ) =
= Рх + (нг V71 Н + vr1)-1 vr1 (рх - Их) • (6.76)
Л
Оценка хмарс будет несмещенной только в том случае, когда-
либо рх=рх, либо V-'x=0. Корреляционная матрица вектора оши-
бок при использовании этой оценки вычисляется обычным образом
с использованием (674) Так как
х - хмарс = х - (НГ V н + V71)-1 (Нг V Нх + Н vr1 V 4- vr1 Рх) =
= X - (Нг V н + vr1)-’ [(Нг V71 Н + V?1) X - vr1 X '-
+ Нг V71 v V71 Рх ] = (Нг V Н + V?1)-1 [Vr1 (х - рх ) ~ Нг V~l v] ,
то (6.77)
Е { (Х ХМАРс) (Х ’ ХМАРс)7' ) ~
= (Нг V?1 Н + V?1)-1 { V?1 [Vx + (рх - рх) (рх - рх)г] V71 +
+ Нг V?1 V71 V71 Н} (Нг V71 Н+Vr1)-1 • (6.78)
Эта матрица зависит от величины смещения оценки [см. второе
слагаемое в ф-ле (6.76)] Ковариационная матрица вектора оши-
л
бок Для оценки Хмарс
var (хМАрс) = (Нг V71 Н + V?1)-1 (V?1 Vx V71 +
212
+ HrVr1V0Vr1H)(HrV71H +V?1)-1 . (6.79)
Если ковариационные матрицы, используемые при вычислении
оценки Хмарс, оказываются равными истинным, то ф-ла (6.79) пе-
реходит в (6.74). Во всех же других случаях
var {*МАРс} > var {*МАр}> (6-80>
и равенство достигается тогда, когда VX=VX; = Разница
между знаменателями двух рассматриваемых оценок хмарс =
л
= хМАр—хМарс получается путем вычитания (6.75) из (6.73). Кова-
риационную матрицу этого вектора, var{хмарс}, можно вычислить
с помощью соотношения
var { *МАР - *МАРс } = var {*МАР - *МАРс } =
= var {хМАр} -j- var {хМАРс} cov {ХМАР. xMAPcj cov {хМАРс, xMApjr
(6.81)
где cov (хмАР, хМАРс} = cov (хМАрс, 7мдр} = (Нг V?1 Н + Vr')-1 .
Так что окончательно имеем
var {хМАРс} = (Нг V71 Н + V?1)-1 (V?1 Vx V?1 +
+ HrV7’ V0Vr1H)(HrVr‘H + V?1)-1 — (НгУГ‘Н+ Vr‘)~‘ • (6.82)
Эта матрица равна нулю, если моменты, используемые при вы-
д
числении оценки хмарс, совпадают с истинными. Формулы (6 76)
и (6 82) позволяют провести анализ точности оценки по максиму-
му апостериорной плотности вероятности при неточно известных
ковариационных матрицах оцениваемого параметра и шума.
Полезные приближения для полученных выражений можно ука-
зать для случая, когда
VvA = VvA + AVvA; Vo—V0-f-AV0; VX = VX + AVX, (6.83)
где AV„ и AVX малы Для этого достаточно воспользоваться следу-
ющими приближенными представлениями:
V?1 Vx V?1 « V?1 - 2V?1 A Vx V?1 + V71 AVX Vx~‘ A Vx V?1;
Hr vr1 V71 V71 H « Hr vr1 н — 2 Hr V71 A V71 H+
+ Hr V.71 A Nv V71 A Vo vr1 H.
При этом
var {*mapc} « (Hr H + V^r’ [Vx-1 A Vx vr1 A Vx vr* +
+ Hr V7‘ A Vo V?1 A Vo V71 H — (Hr V71 A Vo V~l H +
213
+ vr1 л vx vr1) (HV71 H + vr1)-1 (Hr V71 A Vo V H +
+ V?1 A Vx VZ1)] (Hr V~l H + VrT1 . (6.84)
Если ошибки в определении априорных ковариационных матриц
малы, то использовать это выражение несколько проще, чем
(6.82). Однако более важным следствием, вытекающим из ф-лы
л Л
(6.84) и касающимся точности оценок Хмар и Хмарс, является то,
что согласно (6.84) ковариационная матрица вектора разности
этих оценок пропорциональна (AV„)2, (AVX)2 и (AVxAVv). То есть,
если при вычислении оценки используются ковариационные матри-
цы, отличающиеся от истинных на то это приводит к увеличению
на £2 дисперсий ошибок оценивания. Аналогичное замечание сле-
дует сделать относительно ф-лы (6.69), определяющей ковариаци-
онную матрицу вектора разности двух оценок максимального прав-
доподобия.
Приведенные выше соотношения позволяют оценить ухудшение
точности оценок максимального правдоподобия и байесовских оце-
нок при неправильном выборе априорных средних значений и ко-
вариационных матриц. Показано, что оценка максимального прав-
доподобия всегда остается несмещенной. Однако байесовская оцен-
ка оказывается смещенной, если априорное среднее значение ог-
лично_от истинного либо выбранная обратная ковариационная мат-
рица V-1x не равна нулю. Если же V-1x принимается равной нулю,
то байесовская оценка переходит в оценку максимального правдо-
подобия.
Исследуем теперь смещение последовательных оценок, возника-
ющее из-за неточного знания априорных данных. Снова примем,
что
zh = Hhx-(-Vfc, (6.85)
где случайные векторы х и V& будем считать независимыми и нор-
мальными с параметрами:
£{*} = SV. var{x) = Vx; Е {vft} = 0; cov {vft, vj = VvA 8K (k — j).
A
Однако при построении последовательной оценки х^ для пара-
метра х, вычисляемой на каждом шаге k, k=\, 2, ..., было принято,
что априорное среднее значение и ковариационная матрица этого
параметра равны соответственно рх и Vx.
Сначала будем предполагать, что ковариационная матрица
шума_ Уть_уже выбрана и может считаться заданной, в то время
как рх и Vx неизвестны и вместо них будут использоваться оценки
л
Хо и Vo.
В соответствии с (6.73) имеем
л ( к _ 1 / к _ \
xh = V Hl V^1 Hfe + V?1 V Hl V^1 + V?1 px , (6.86)
\*=i J \k=i /
214
л
где xfe — оценка по максимуму апостериорной плотности вероятно-
сти (или байесовская оценка при симметричной функции потерь)
для параметра х, вычисляемая по выборке zb Z2,zK.
При /<=1 эта оптимальная оценка ймеет вид
хх = (Н[ V?/ Нх + Vr!)-! (Hf V?/ + VZ1 Рх )• (6.87)
л
Если теперь использовать предложенные оценки Vo и х0 вместо
Vx и р,х и воспользоваться леммой об обращении матриц, то пос-
леднее выражение можно переписать следующим образом:
хх = х0 + КХ(Я1 - HjXq); Кх = V0H[ (Нх Vo Hf + Vvi f1 .
При 7(=2 получаем
х2 = (нГ V^1 Нх + н2г v?2! н 4- Vo'-1)-’ (Hf Vx! «х + Н2Г Vv2 «2 + V х0).
(6.88)
Это выражение можно переписать следующим образом:
Л Л Л
х2 = Xj + К2(«2 — Н2хх),
где K! = V1Hj(H2V1H2T + Vv2)-1; Vx = (I —К^) Vo.
Здесь снова использована лемма об обращении матриц. Повторяя
подобные рассуждения для К=’3У 4, ..., можно установить следую-
щее рекуррентное соотношение:
Л Л л л _ )
х4+1 = + Kfc-p; («4+1 — Н4+1 xfe), x0 = px;
K*+i = V/jH^+i (H*+i Vfe h£+i + Vv (н-i)) (6.89)
Vfe = (I - Kfe Hft) V4-1 = ( V Hj V?; H, + vr! 1 1,
\l=t / J
где Vfe = var{x|«n «2,..., aj = var{x|Afe). (6.90)
Это и есть искомые алгоритмы последовательного оценивания.
Полученные выражения являются частным случаем алгоритмов,
описывающих фильтры Калмана и Винера, которые будут обсуж-
даться в следующей главе. Эти соотношения можно получить так-
л
же непосредственно из общего выражения для оценки хк, если
учесть, что
V4+1 Х4+1 — H(+i Vv (4+d я^+1 + V4 ! xfe;
_ (k+l _ \-1
V4+1 = (V?1 + Н4+1 Vv (4+1) Н4+1Г1 = У Hj V71 Н; + vr1
\/=1 J
(6.91)
Эти оба набора соотношений можно использовать для построе-
ния алгоритма последовательного вычисления оценки. Если раз-
215
мерность векторов z или v меньше размерности вектора х, то набор
соотношений (6.89) намного предпочтительнее с вычислительной
точки зрения. Это объясняется тем, что в этом случае при вычис-
лении значений оценки хк требуется обращать матрицы более низ-
кого размера. Очевидно также, что оба набора соотношений при-
водят к более сложным вычислениям, чем исходное выражение для
•оценки'
Л /4
= у
к
V/ «7 + Vq Хо
(6.92)
7=1
Поэтому это выражение и следует использовать при практиче-
ских вычислениях, если нет необходимости в последовательном
получении значений оценок. Если же требуются последовательные
алгоритмы, то необходимо использовать соотношения (6.89). Сле-
дует, однако, иметь в виду, что подобными рекомендациями мож-
но руководствоваться не всегда. Обычно последовательные алго-
ритмы более предпочтительны с точки зрения их реализации по
сравнению с непоследовательными.
Найдем теперь смещение оценки при использовании последова-
тельного алгоритма. Пусть рх — истинное среднее значение оцени-
ваемого параметра. Тогда смещение
bh = E{xh}-px= I+Vo^hJv-’hJ (х0 —рх). (6.93)
\ /=1 J
Отсюда следует, что смещение оценки стремится к нулю при
k—>-оо, так что эта оценка асимптотически несмещена. Смещение
уменьшается также с ростом априорной ковариационной матрицы
Vo- Кроме того,
lim xh = ( V Hf V--1 Н А ’ У Hf У-’яд
\ /=1 / /=1
lim Vh = О,
(6.94)
так что при достаточно большом числе наблюдений априорное сред-
нее значение и ковариационная матрица вектора х не оказывают
существенного влияния на вычисляемые значения оценок. Однако
при малых значениях k смещение оценки по максимуму апостери-
орной плотности вероятности, обусловленное неточностью априор-
ных оценок среднего значения и ковариационной матрицы векто-
ра х, может быть существенным. Если выбранная матрица от-
личается от истинной матрицы шума VVfe, то ковариационная мат-
рица фактически вычисляемой оценки может быть найдена по ф-ле
(6.78). Так что для ковариационной матрицы ошибки xfeMAPc =
Л
=х—xh получаем
516
/ k _ _ \-1
var ft МЛР.) = V "Г И/ + v’~' X
\/=t !
/ _ _ ft _ _ \ / * _ _ \— 1
X vr‘vxvr‘+VHfV^Vv/V-^H^ V Hf V^Hj + vr1 , (6.95)
\_ _ /=i 7 \/=i /
где Vx и VVj — предполагаемые, a Vx и Vvj — истинные ковариа-
ционные матрицы. Выражение для смещения bfe было приведено
выше. Заметим, что только в том случае, когда предполагаемые
матрицы оказываются равными истинным, выражение для ко-
вариационной матрицы var {xfeMApc} совпадает с приведенным ра-
нее выражением для матрицы V&. В гл. 8 будет показано, что най-
денное здесь соотношение для ковариационной матрицы ошибок
можно записать в форме разностного уравнения. Здесь же приве-
дем выражение для ковариационной матрицы ошибок при исполь-
л
зовании оценки х^марс после достаточно большого числа шагов.
Имеем
(* _ \—1 ft _ _ / * _ \—i
У И/ н; 2 н[ V?’ Vv/ V-1 ну у н; V-1 Н7) .
/=1 J /=1 ' /=1 /
(6.96)
При >оо смещение и ковариационная матрица этой оценки стре-
мятся к нулю, даже если ковариационная матрица шума неизвест-
на. Подчеркнем, однако, что эти выводы остаются справедливыми
только для этого частного примера, в котором оцениваемый пара-
метр не меняет своего значения от наблюдения к наблюдению. В
общем случае, когда значения оцениваемого параметра изменя-
ются во времени, и смещение оценки, и ковариационная матрица
вектора ошибок не стремятся к нулю с ростом времени наблюдения
или объема выборки k.
Пример 6.12. Если предположить, что х и являются скалярными вели-
чинами и дисперсия шума v& не зависит от номера наблюдения, то полученные
выше соотношения существенно упрощаются. Действительно, в этом случае
совокупность алгоритмов последовательного оценивания (6.89) принимает вид.
Л Л ^ft+1 Hi Л Л _____
Xft-H = Xh + ( aft+1 - Hk+l Xky, x0 =
Непоследовательная оценка и предполагаемая дисперсия этой оценки могут
быть найдены в результате решения этих разностных уравнений. Так что
ft Л
l/^o + (l/V0) V Ео + (1/Е0)у^
/=1
217
bk =
Смещение оценки хА
Л
Хр—Рх
k
1 + (Vo/Va) X я2
Дисперсия фактически вычисляемой оценки
var{ xk МДРс} — f- k 12
i/v0 -r (i/FL) V я2
Согласно (6 82) для дисперсии разности двух оценок получаем
Это выражение не удается привести к более простому виду, поэтому может
оказаться полезной приближенная формула типа (6 84)
На рис 6 9 приведены графики, иллюстрирующие влняние_ априорной дис-
персии на нормированное смещение оценки при Нк=\ Если Vx намного боль
ше, чем ~Vv, смещение с ростдм объема выборки быстро уменьшается Поэтому
Рис 6 9 Нормированное смеще
ние оценки как функция объе
ма выборки (пример 6 12)
если в практических задачах смещение оценки при малых k нежелательно, то
значение Vx не следует брать слишком малым Конечно, если истинное значение
_ Л
априорного среднего рх = Их=то известно и используется при вычислении оцен
ки, то смещение отсутствует На рис 610 приведены графики зависимости
среднеквадратической ошибки оценивания для двух случаев В первом из них
Vx=Vx, Vv = Vv, во втором случае исследовалась зависимость среднеквадратн-
218
ческой ошибки var{xiMAPe} при V„ = Vx = Ух —1, причем принятое значение
дисперсии шума ие совпадало с истинным. Второй график рис. 6.10 справедлив
также для случая, когда Vv—Vx=Vt> = l, однако значение априорной дисперсии
Рис 6 10 Дисперсии
ошибок оценивания как
функции от объема вы-
борки k (пример 6 12)
1 — var {’•ймдр};
ДУ^2 varix's 1=
* I МАРс)
= д У?2 varix's |
и I МАРс)
параметра х выбрано неверно Во всех случаях предполагалось, что Я*=1.
Соотношения, необходимые для построения графиков, получены с использова-
нием приближенного представления (6 84) Для рассматриваемых здесь случаев
получаем
~ Д У2 k ~ Д У2 k
var { xk марс} » () + й)3 ! var { xk МАРс} ss (1 •
Разность между значениями среднеквадратической ошибки оценивания при
использовании указанных алгоритмов и минимально достижимой ошибки оказы-
вается максимальной при объеме выборки k=\ и уменьшается с ростом k.
Если неизвестными являются обе дисперсии Vx и У®, то тот же приближенный
способ вычисления приводит к выражениям
~ ДУ02^Рх « ДР^/УЗУО
var{^MAPc}« (1/Vx + */Vo)3 ‘ var{хА МАРс}- (1/Vx + W, •
Теперь разность между значениями среднеквадратических ошибок оказы-
вается наибольшей при объеме выборки, совпадающем с ближайшим целым
числом, превышающим У„/(2УХ). Если Vx>Vv, то максимум этой разности
всегда достигается при й=1.
Аналогичные результаты можно получить для процессов с не-
прерывным временем. Для наблюдаемого процесса в этом случае
можно записать
z(0 = H(0x + v(0, (6.97)
где вектор х и шум v(t) независимы и являются нормальными, с
параметрами:
£'{x} = t*x; var{x} = Vx;
£ {v (/)} « 0; cov {v (0, v (r)} = 4\ (0 6D (t — t).
Соответствующая запись для дискретного времени, которая
уже была использована выше, имеет вид (6.85), где теперь необхо-
2ig
димо положить Vvfe=4fv('&7')/7'. Вновь предположим, что при оп-
ределении алгоритмов оце_нивания неизвестная априорная диспер-
сия шума принята равной VVft = ''Fv(&7’)/7’. Будем считать также, что
возможны ошибки при выборе значений £{х} и var {х}. Воспользо-
вавшись уже известным предельным переходом, из (6.89) получаем
следующие последовательные алгоритмы фильтрации при непре-
рывном времени:
x = K(0Iz(0-H(0x(0], х(0) = рх;
К(0 = V(0Hr(Z)V^(Z);
v (0 = - v (0 нг (0 ф-‘ (0 н (/) v (О, V (0) = vx.
(6.98)
Явное выражение для оценки имеет вид
о
(6.99)
Смещение этой оценки
а матрица вектора ошибок
var(x(0MAPc} =
нг(офг’ (0Н(0 л + уг!
(6.100)
vr! vxv;' +
+ J нг (0 ф?! (0 ч\ (0 Ф7! (0 Н (t) dt
о
(6.101)
Теперь нетрудно выписать аналогичные выражения для только
что рассмотренного скалярного случая при непрерывном времени.
Необходимые для этого рассуждения полезно провести читателю
самостоятельно.
До сих пор при анализе ошибок оценивания не предпринима-
лись попытки уточнить значение дисперсии шума. Теперь попыта-
емся это сделать. Будем рассматривать последовательность на-
блюдаемых случайных величин
zfe = Hfex + vfe, Z>=1, 2,..., (6.102)
где случайные величины V& независимы, нормальны, имеют нуле-
вое среднее значение и одну и ту же дисперсию Vv. Будем иссле-
довать байесовскую оценку для параметра х, который является
520
нормальным случайным вектором с известными моментами
£{х}=рх; var {x}=Vx. В соответствии с (6.73) байесовская оценка
*кмар= +' (^нГу^Ч + уг’А (6.ЮЗ)
\*=i / \s=i /
Отсюда ясно, что для того, чтобы воспользоваться этим выра-
л
жением для вычисления значений оценки xft, необходимо знать дис-
персию шума. Поскольку для построения байесовской оценки дис-
персии шума потребовалось бы вводить плотность вероятности этой
дисперсии, то здесь в качестве оценки для ковариационной матри-
цы V® используем оценку максимального правдоподобия. Такой
выбор будет более обоснованным, если относительно параметра У®
предположить, что он неслучаен и его значение неизвестно, а не
считать его случайным. Подобные логические рассуждения приво-
дят к выбору из двух возможных оценок оценки максимального
правдоподобия. В примере 6.6 уже было показано, что в рассмат-
ривающихся здесь условиях оценки максимального правдоподобия
для параметров V® и х имеют вид
(6.104)
Сразу же становится очевидным, что при попытке решать эту
систему уравнений относительно оценок для параметров V® или х
неизбежно возникнут значительные трудности. Их можно обойти,
если задачу оценивания сформулировать несколько иначе. А именно,
от К Al-мерных векторных наблюдений zp /=1, 2, ..., К перейдем к
МК скалярным наблюдениям zh, k=\,
Если предположить, что V® = diag(o2®, о2®, ..., о2®), то рассмат-
риваемые оценки максимального правдоподобия примут вид
(6.105)
^MKML MKLi\ak
k=\
Д /Л4Л \ — 1 Мк
I Н, I \ НЛ сс^.
\й=1 / А=1
Теперь для вычисления значений
значение оценки о-ъ mkml В то же
(6.106)
л
оценки хМкМЛ не нужно знать
Л
время значения оценки xmkml
л
используются при вычислении оценки о2® mkml
Если необходимо указать последовательные алгоритмы оцени-
вания, то можно (воспользоваться подходом, который уже был
221
применен ранее для получения последовательных оценок [242].
/мк \-1
Введем сначала обозначение = I У Н* Нй .Заметим, что
\Л=1 /
МК-1
Влд = У, + НлхН^ = Влд-i +Нлд Нд^.
*=1
Используя лемму об обращении матриц, получим
Влд = Влд-i — Влк-i Нлд (1 + Нлд Влд-i Нлх) 1 Нлд Вмд-ь
Для оценки максимального правдоподобия вектора состояния
можно записать
л т л т
Хлдмь = Влд У Н* afe; Хлд-1мь = Влд-i X Н* ak.
й=1
Объединяя эти два равенства, получаем
А —1 А г
хлгдМь = Вид Влд-i хлд—iML + Влд Нлд алд •
Снова используя лемму об обращении матриц применительно
к матрице Влд, имеем окончательно
A A н£ А
Хл*Дмь = xmk-1ml Н “ ту [лмк Иид xmk-iml ) -(6-107)
Аналогичным образом можно найти последовательный алго-
л
ритм для оценки о2„мкML. В результате получаем
л 1
о2 = ——
° МК
(МК— 1)о2 к ,
' ’ » МД—1ML
( алд~ НЛД Х MK-1ML )2
1 + НЛДВЛД-1 нлд
Эти последние два алгоритма могут быть использованы для по-
следовательного адаптивного оценивания. Алгоритмы для более
сложных случаев можно найти в работах [97, 208].
Псевдобайесовские оценки. Покажем, что при оце-
нивании случайного параметра среднеквадратическая ошибка оце-
нивания при использовании оценки максимального правдоподобия
больше, чем при использовании байесовской оценки. Именно это
имея в виду, будем говорить, что оценка максимального правдо-
подобия хуже байесовской. Основная причина такого соотношения
оценок состоит в том, что при построении байесовской оценки учи-
тываются некоторые априорные сведения об оцениваемом пара-
метре, в то время как при отыскании оценок максимального прав-
доподобия подобные сведения игнорируются. Правда, к сожале-
нию, неправильный выбор значений параметров априорных рас-
пределений приводит к появлению смещения байесовской оценки.
Вычисление смещения в таких условиях может оказаться трудно
разрешимой проблемой. Таким образом, желательно использовать
222
байесовские оценки с тем, чтобы обеспечить минимально возмож-
ное значение среднеквадратической ошибки. Однако при этом не-
обходимо предусмотреть подстройку значений параметров априор-
ного распределения с целью уменьшения смещения оценки.
Рассмотрим линейную модель при дискретном времени, когда
zfe = Hfex + vfe, &=1,2,..., (6.109)
а х и Vfe независимы и
Е {Vfe} = 0; cov {Vy, vfe} = Vv* <5K (k — j). I
Ранее уже было найдено выражение для оценки максимально-
го правдоподобия для этого случая при дополнительном предполо-
жении, что шум vk является нормальным. Чтобы найти оценку
максимального правдоподобия, основывающуюся на одном един-
ственном наблюдении, необходимо максимизировать значение
плотности р2/|х(«;|3). Это приводит к следующему выражению:
VML = WV’“'H')“,HP««r <6.1И)
Условные математическое ожидание и ковариационная матри-
ца этой оценки равны соответственно:
£{х/мь I х = ₽} = 0;
1 л J (6.112)
var{%ML|x = p} = (HrV->H7)->.
Таким образом, эта оценка является несмещенной, а ее кова-
риационная матрица
var (Vml ) = ’ar (l> ~ £«.} = WК' HV' <6'113>
и совпадает с условной ковариационной матрицей.
Чтобы найти оценку максимального правдоподобия, основыва-
ющуюся на выборке объема К, необходимо максимизировать зна-
чение плотности вероятности рг К|Х(Ак| 3), где 7-к— выборка
объема К. В соответствии с (6.57) имеем
/к \-1 к
VHrv-'a». (6.114)
L \Л=1 J *=1
Эта оценка не смещена, так как
£{х„ |х=0}=0, (6.Н5)
а ее ковариационная матрица
~ л
var 1 х„ 1 = var 1 х | х = 0
t kmlJ 1 *ML
1 / rib
k \’k R
(6.1 Гб)
223
Ранее было получено также выражение для -оценки по макси-
муму апостериорной плотности вероятности для случая, когда па-
раметр х являлся нормальной случайной величиной. Если оценка
должна основываться на одном наблюдении z,-, то ее значения
отыскиваются путем максимизации апостериорной плотности ве-
роятности px\Zj (P|aJ. В соответствии с (6.73) имеем
Х'МАР = (Н/ V-1 ну + V-’)-« (н; V-J + V-> Мх). (6.117)
Л
Эта оценка является несмещенной, так как E{xjmap } =цх. Сог-
ласно (6.74) ее ковариационная матрица
Var {%АР } = Var {₽ - *'МАР } = (НГ Н/ + V)-'- (6. 1 18)
Если же оценка по максимуму апостериорной плотности ве-
роятности должна основываться на выборке объема К., то для ее
отыскания необходимо максимизировать значение апостериорной
плотности вектора х при условии, что значение выборки ZK фик-
сировано. Эта процедура максимизации приводит к следующему
выражению для оценки:
л 7 * /Л \
’ь.л 2ТО+’Г' У HJV-'(6.119)
МАР \*=1 J \*=1 /
Можно также показать, что
/ к \-1
Сравнивая матрицы (6.116) и (6.120), нетрудно заметить, что
var{xxMAP } можно записать в виде
таг {4U=Kvar {4JF'+v< Г (6-12l)
Используя теперь лемму об обращении матриц, получаем
var 1 х^ 1 = var 1 xL 1 — var 1 х„ 1 /Vx + var 1 x„ 1 )-* X
I лмар/ I ml/ I ml/\ 1. ml/J
X varix,, 1. (6.122)
I ml/
Заметим, что вторая матрица в правой части этого равенства
неотрицательно определена. Это означает, что среднеквадратиче-
окая ошибка оценивания при использовании оценки по максимуму
апостериорной плотности вероятности всегда меньше или, в край-
нем случае, равна ошибке- оценивания при применении оценки
максимального правдоподобия.
Если среднее значение -и ковариационная матрица параметра х
известны, но функциональный вид плотности вероятности этого
224
параметра неизвестен, то оценку по максимуму апостериорной
л
плотности вероятности найти нельзя. Поскольку оценка Хмар при
нормальных оцениваемом параметре и шуме зависит только от
среднего значения и ковариационных матриц этого параметра и
шума, то можно попытаться использовать оценку Хмар в указан-
ных выше условиях даже при неизвестной плотности вероятности
параметра х. Эту оценку будем называть псевдобайесовской. Как
будет показано в следующем разделе, подобная псевдобайесов-
ская оценка эквивалентна линейной оценке с минимальной сред-
неквадратической ошибкой.
Среднеквадратические ошибки оценивания при использовании
псевдобайесовской оценки и оценки по максимуму апостериорной
плотности вероятности одинаковы. Это следует из того, что алго-
ритмы этих оценок одинаковы, а при вычислении соответствую-
щих им среднеквадратических ошибок используются только мо-
менты второго порядка. Если распределения оцениваемого пара-
метра и шума являются нормальными, то наилучшей будет оцен-
ка по максимуму апостериорной плотности вероятности. Если же
распределение вектора х отлично от нормального, то наилучшей
линейной оценкой оказывается псевдобайесовокая оценка. В этом
случае, вообще говоря, могут существовать нелинейные алгоритмы
оценивания, обеспечивающие меньшую среднеквадратическую
ошибку.
Предположим теперь, что среднее значение цх и ковариацион-
ная матрица Vx априорного распределения неизвестны. Можно
найти оценки этих параметров, основывающиеся на выборке объе-
ма J, и использовать эти оценки при построении псевдобайесов-
ской оценки для параметра х. Оценки параметров априорного рас-
пределения обозначим соответственно р/х и VJX. Если эти оценки
используются при построении псевдобайесовской оценки, то ее
будем называть эмпирической псевдобайесовской оценкой. Усло-
вия оценивания при этом оказываются точно такими же, как и
при построении оценки (6.75), т. е. для эмпирической псевдобайе-
совской оценки, основывающейся на выборке объема К, можно
записать
Л Л
2 HI vvT н„ + (VI)-'
+ (Vx) 1 Нх .
(6.123)
Соответствующая корреляционная матрица вектора ошибок оп-
ределяется тем же выражением, что и матрица (6.79), т. е.
г к 1
var I Чр J = var < *млрс = S Н* Ч + (v*)~’
1 L*=i
8—2G
225
(V')“* Vx (vO"‘ + V H[ V-> H,1 Гу Hl V7A* Hft + (Vx)-1
4=1 J L*=i
(6.124)
Построенная таким образом псевдобайесовская оценка смещена.
Ее смещение можно найти с помощью соотношения (6.76). Так что
Можно показать, что если оценки ц7х и VJX являются выбороч-
ным средним и выборочной ковариационной матрицей соответст-
венно и вычисляются по результатам J априорных наблюдений,
то эмпирическая псевдобайесовская оценка параметра х асимпто-
тически не смещена. Это является следствием несмещенности вы-
борочного среднего
Если среднее значение и ковариационная матрица параметра х
неизвестны, то в качестве оценок jiJx и VJX будем использовать
оценки максимального правдоподобия. К сожалению, в том слу-
чае, когда априорная плотность вероятности вектора х не являет-
ся нормальной, выборочное среднее и выборочная ковариационная
матрица J априорных оценок параметра х не являются статисти-
чески независимыми оценками. Наличие статистической зависимо-
сти между этими оценками существенно усложняет вычисление
корреляционной матрицы вектора ошибок при использовании эм-
пирической псевдобайесовской оценки. Поэтому здесь будем пред-
полагать, что случайные векторы х и v являются нормальными.
Предположим далее, что можно осуществить J наблюдений.
Пусть в течение каждого наблюдения записывается выборка объе-
мом I. Будем считать также, что значение параметра х случай-
ным образом и независимо изменяется от наблюдения к наблю-
дению. Вычислим I значений оценки максимального правдоподо-
бия
л / 1 \-i 1
й = Унгу-'НЛ j = 1, 2, • • •, J, (6.126)
'ml 1 Vl / ‘ ‘ ‘
v=i / <=1
л
где x’/ML — оценка значения параметра х при у'-м наблюдении, ос-
новывающаяся на выборке объема I. Очевидно, что
£1х/ 1=Их; var/xj 1 = Vx + (V Hf . (6.127)
1 ZMLJ I ML) у
Л
Таким образом, при конечном объеме выборки / оценка x3iML
сама является нормальной случайной величиной. Так как для лю-
л л л . л
бых двух оценок x3'lML и xfe/ML cov{x^ML, x*/ML}=0, то эти оцен-
226
ки статистически независимы. Напомним здесь, что если взаимная
ковариационная матрица двух нормальных случайных векторов
равна нулю, то эти векторы независимы.
В качестве среднего значения и ковариационной матрицы ап-
риорной плотности вероятности вектора х используем выборочное
среднее и выборочную ковариационную матрицу случайных век-
Л
торов x’\ML, / = 1, ..., J. Эти оценки в рассматриваемых здесь ус-
ловиях являются оценками максимального правдоподобия, по-
л
скольку случайные величины x’iML, /=1, ..., J нормальны и не-
зависимы. Совсем необязательно, чтобы все выборки имели один
и тот же объем. Однако здесь, ради простоты, будем предпола-
гать, что такое равенство имеет место. Поэтому, опустив нижний
индекс 1, запишем
Оценки и VJX являются случайными величинами. Посколь-
л
ку уУх представляет собой линейную комбинацию нормальных
случайных величин, то она тоже является нормальной величиной.
Первые два момента этой оценки при одинаковых объемах выбо-
ров в разных наблюдениях определяются соотношениями:
X HF Vw Н'
1=1
J
Л Л 1 7 мт
Е { = рх; var { ц'} = var--у—2-
(6.129)
В простейшем скалярном случае, когда дисперсия шума не за-
висит от номера наблюдения и Яг=1, последние два равенства
принимают вид
Е { Нх} = Н/ var { р'} = —----. (6.130)
Здесь величины о2ж и являются скалярными аналогами мат-
риц Vx и Vv.
Оценка VJX также является случайной. Элементы нормирован-
л л
ной случайной матрицы SC = (7—IMvarlx^JJ-'V^x имеют %2-рас-
8* 227
пределение с (J—2) степенями свободы Плотность
л
диагональных элементов матрицы VJX имеет вид
J 1 I Т_/9 / J 1 \
вероятности
Р л (Y) =
[
y(Z 3),/2 ехр
хмь)дд 2иг{хж/М
Г[(7—1)/2]
О,
у > 0;
у <Z 0,
(6.131)
л
VJX и сред-
где Г(т])—гамма-функция. Среднее значение оценки
неквадратические ошибки при ее использовании определяются со-
отношениями:
£{^}=vx+(2h<7’v-1 н'
Л 2 Л
(6.132)
Л.
Отметим, что так как случайные величины хДь нормальны и
Л Л
независимы, то выборочные моменты рД и VJX также независи-
мы [48].
Можно показать [119], что если при построении эмпирических
псевдобайесовских алгоритмов оценивания используются оценки
Л Л
pJx и VJX, то получающиеся при этом оценки оказываются несме-
щенными, т. е. математическое ожидание таким образом построен-
ной эмпирической псевдобайесовской оценки, имеющей вид (6 123),
равно среднему значению оцениваемого параметра
л
Е I х. 1 = рх.
[ ZEP<®[ ‘
Среднеквадратическая ошибка этой оценки
~ л ~
var/x, l=var[x — х. 1 — 9?рр<л var 1 х. 1.
[ ZEP-»J 1 ZEP^J tKZZ ) zmlJ
Для множителя$ в случае скалярного параметра
дено следующее выражение:
_ 1 ру2 + 0,25(7 —1)2(1 —^>,^)(.^t<g+l/J)
П(/—1)/2]J "
о
[y + U-1)(1-^^)/2]2
где ^=Vx^H{(HftVxH[ + VvA)-'Hfe
МАР
1> См работы [48] или [182] (Прим авт)
(6.133)
(6.134)
в [119] най-
(6.135)
var 1 х
(6.136)
228
Интеграл в этом выражении вычислить точно не удается. Од-
нако при больших объемах выборок J возможно приближенное
вычисление. В результате получаем
1 +(1 — .%.#)(%,# + 1//) 2 (1 — й?^)(— 1 + 2.%.yr|-3/V)
(2-^)2 + 7 —1 (2-^^ ’
(6.137)
Ошибка вычисления при этом составляет менее 4% при 7^5 и
менее 1,5% при 7^10.
На рис. 6.11 приведены результаты численных расчетов значе-
ний множителя J?Ep gj для различных значенийи 7. Заметим,
что параметр Яg фактически является отношением мощности сиг-
нала к общей мощности при-
нятого колебания. Таким обра-
зом, если объем выборки J
больше десяти, то эмпиричес-
кая псевдобайесовская оценка
намного лучше, чем оценка
максимального правдоподобия
если критерием сравнения яв-
ляется величина среднеквадра-
тической ошибки оценивания
Причем выигрыш в точности
увеличивается с уменьшением
значения параметра,/’^» . Дру-
гими словами, при малых от-
ношениях сигнал/шум эмпири-
ческие псевдобайесовскиеоцен-
ки могут обеспечить значитель-
но более высокую точность
оценивания по сравнению с
оценками максимального прав-
доподобия (или с байесовски-
ми оценками при неправильно
установленных значениях па-
раметров априорных распреде-
Ленин, когда нет возможности Рис '^ЕР-'й как Ф>икция от
оценить эти параметры) Если объема выборки J
объем выборки J неограничен-
но возрастает, то эмпирическая псевдобайесовская оценка почти
эквивалентна байесовской оценке, использующей точные значения
параметров априорного распределения вектора х Это объясняется
тем, что при больших объемах выборки значения оценок макси-
мального правдоподобия мало отклоняются от истинных значений
оцениваемых параметров При больших объемах выборки 7 для вы-
числения можно воспользоваться следующим приближен-
ным выражением'
229
,GJ38)
л
Если бы оценка VJX была несмещенной, то рассмотренная вы-
ше эмпирическая псевдобайесовская оценка обеспечивала бы то
же значение среднеквадратической ошибки, что и байесовская
л
оценка. Однако, как это следует из (6.132), оценка VJX является
смещенной. Если объем выборки J неограниченно увеличивается,
л
то смещение оценки VJX стремится к нулю. Если при этом еще
и J неограниченно увеличивается, то можно показать, что „<g> =
Пример 6.13. Снова рассмотрим скалярный (одноканальный) вариант диск-
ретной адресной системы с произвольным порядком доступа, рассмотренной
ранее в примере 6.3. Принимаемый сигнал, модулированный по амплитуде,
искажается аддитивным нормальным шумом с моментами:
Е {vn (/)} = 0; cov {vn (f); vn (т)} = Af2 6D (t — t) .
Обсудим возможность использования псевдобайесовской оценки для оцени-
вания скалярного параметра 0П по результатам наблюдений, полученным за
время п-й записи:
z " (0 = 0" h (t) + vn (t), 0 < t < tf.
Здесь верхний индекс указывает на то, что обработке доступен целый набор
подобных записей.
Будем предполагать, что 0П является нормальной случайной величиной,
а в" и ek независимы при любых неравных значениях индексов п и k. На
рис. 6.3 приведена структурная схема оптимального приемника, найденная в
примере 6.3. Будем считать, чт;о отношение сигнал/шум по мощности на входе
этого приемника намного меньше единицы. Этот случай является типичным для
многих задач техники связи. Пусть 2?{£)} = р,е; var {0} = Og = Vg являются истин-
ными значениями параметров априорного распределения величины 0. Перейдем
к модели с дискретным временем и запишем гпк = 0^hi, + unk, где
М2
Е {vfe} = 0; cov {vs, Vj} = — ёк (k—j) = VvdK(k — j).
Снова предположим, что
К
( h2 (t) dt = Е2; Т X' ^=£2.
о А--1
Легко показать, что если 2ь = йьХь, то дисперсия выходного сигнала байесовско-
го приемника и приемника максимального правдоподобия равна о| Следова-
тельно, отношение сигнал/шум на выходе такого приемника можно определить
как отношение дисперсии Од к дисперсии ошибки оценивания. Для приемника
максимального правдоподобия дисперсия ошибки оценивания определяется вы-
ражением (6 106). Поэтому для отношения сигиал/шум (на К-м шаге) на вы-
ходе приемника максимального правдоподобия можно записать
'_£\
Ж /ML
£2о| £2 о|
~TV^ = М2
230
Эта формула справедлива для обеих моделей наблюдаемого процесса с дис-
кретным и непрерывным временем.
Для байесовского приемника на основании ф-лы (6.119) получаем
°е £2о2е + ЛР
-------— =-----------;— °е .
/млр
к
Л12а|
\*=1 7
Эта формула остается справедливой и для псевдобайесовского приемника, по-
скольку оцениваемый параметр в является нормальной случайной величиной.
В правой части этой формулы можно выделить сомножитель, являющийся от-
ношением сигнал/шум на
В результате получаем
выходе приемника
максимального правдоподобия.
\JY / МЛР \JV /ML
£2 а| + /И2
где Ж =
М‘2
£2 Од ЕН д^
Здесь .3?^ определяется ф-лой (6.136). Можно
(6.134) и выписать выражение для отношения
воспользоваться соотношением
сигнал/шум на выходе прием-
' 8_ \ _
Ж /ЕР® ~
ника, реализующего эмпирическую псевдобайесовскую оценку
1 / # \
— ® П- • Коэффициент определяется ф-лой (6.135). При боль-
•/7EP-®,,..t/ml иг
ших объемах выборки 7 можно получить приближенное аналитическое выпя-
жение, характеризующее выигрыш в точности оценивания при применении
псевдобайесовской оценки по сравнению с оценкой максимального правдоподо-
бия. Для этого достаточно воспользоваться приближенным соотношением
(6 137).
Для рассмотренного здесь примера значение отношения сигнал/шум на вы-
ходе байесовского приемника превышает отношение сигнал/шум на выходе
приемника максимального правдоподобия ровно в раз, причем обозначе-
ние ?Н gj ранее было введено для отношения среднеквадратических ошибок
двух оценок
var { ^Кдолр }
ЕН®=---------~-------•
var{°/<ML}
Выигрыш в точности оценивания при использовании эмпирической псевдобайе-
совской оценки обратно пропорционален величине , которая представ-
ляет собой отношение среднеквадратических ошибок двух оценок ®ЕР-® =
Var{%P.®l
= -----------L----, причем lim .39г-.ПеЯ=.3? ж, При малых отношениях сиг-
var 7 (К. j
t «ML J
ьал/шум на входе, т е. при Л42/(Е2Од )»1, уменьшение среднеквадратической
ошибки оценивания при использовании байесовской или эмпирической псевдо-
байесовской оценки вместо оценки максимального правдоподобия оказывается
значительным. Это следует из выражения для коэффициента.®и графиков
для приведенных на рис. 6.10.
231
6.6. Линейные оценки с минимальной
среднеквадратической ошибкой
В данном параграфе будет изложен способ оценивания,
не требующий знания полных вероятностных характеристик наб-
людаемого процесса и оцениваемого параметра. Однако это будет
достигнуто путем введения следующего ограничения: оптимальная
оценка должна быть найдена в классе оценок, являющихся взве-
шенными линейными комбинациями элементов выборки. В следу-
ющем параграфе будет обсуждаться еще один метод оценивания,
для применения которого вообще не требуется знать вероятност-
ные характеристики ни шума, ни оцениваемого параметра.
Сначала рассмотрим следующую модель наблюдаемого про-
цесса:
z(0 = H(0x(0 + v(0, о (6.139)
Здесь процессы z(t) и v(t) являются векторами с М компонента-
ми; Н(7)—• модуляционная матрица размера MxN; x(t)—вектор-
ный случайный параметр, значения которого необходимо оценить.
Пока будем предполагать, что шум v(t) имеет среднее значение,
равное нулю, и ковариационную матрицу
cov{v(0, v(t)} = ¥v(0 6dG-t) (6.140)
и не обязательно является нормальным. Предположим далее, что
функция распределения векторного параметра х неизвестна; од-
нако первые два момейта этого распределения
£{х(0} = Нх(0; var{x(0) = Vx(0 (6.141)
всегда будем считать известными.
Наилучшая оценка параметра x(t) должна быть найдена в
классе несмещенных линейных оценок, для которых справедливо
представление
А *
xL(0 = ?(6+ A)z(A)dA. (6.142)
о
Оптимальной в этом классе будем называть оценку, для которой
след ковариационной матрицы вектора ошибок
Е {||xL(0||2 } =tr(varpJ0}) = tr(var{x(/) —xJO}) (6.143)
минимален. Такую оценку в дальнейшем будем называть линей-
ной оценкой с минимальной дисперсией и обозначать символом
л
xLmv(0- Можно также показать, что алгоритм вычисления значе-
л
ний оценки Xlmv(0> которая обеспечивает минимально возможное
значение для E{\\xL(t) H2s}, не зависит от неотрицательно-опреде-
ленной весовой матрицы S. Сначала здесь будет решена задача
232
оценивания для модели с непрерывным временем, а затем будут
приведены результаты для дискретного времени. Важнейшим ре-
зультатом данного параграфа является лемма об ортогональном
проецировании, которая служит отправной точкой многих иссле-
дований в следующих двух главах О.
Простейшее требование, которое должно быть выполнено, со-
стоит в том, чтобы искомая оптимальная оценка была несмещен-
ной. Вычисляя математические ожидания от левой и правой час-
тей равенства (6.142), получим
Е{х£(0}=§(0+ Х)Н(Х)р.х(Х)й% = ИхG). (6.144)
6
Отсюда следует, что для несмещенной оценки должно выпол-
t
няться равенство ?(0=Их(0— %) Н (A,)jlxx(Л,)cfA.. Подставляя
о
полученное выражение для 5j(^) в (6.142), получаем новую запись
для линейной несмещенной оценки:
xL(0 = Hx(0 + jE(t %) [Z (X) — Н (X) р.х (%)] d % (6.145)
6
Чтобы найти линейную оценку с минимальной дисперсией, не-
обходимо минимизировать значение следа
tr(var [ х£(/)]) = tr I var
х (0 — (t) — f Е (t, Л) [z (А) —
6
— H(Z)px (A)]dA
Для решения этой задачи используем методы вариационного ис-
числения [202, 223]. Пусть
Е(/, А) = Е(/, A) + Л),
(6.146)
л
где B(t, X)—оптимальная весовая функция, а (£, X)—произ-
вольная функция. Очевидно, что если
Str(var { х£(Ч})
де
= 0.
е=0
(6.147)
Для линейной оценки можно получить также следующее представление:
t
*l (0 = S' (0 + У S' (4 *) [z (M - H (X) XL (X)] d X,
6
~ Л
в котором процесс /(X) =z(X) =z(X)—H(X)Xt(X) обычно называют обновляю-
щим Этот подход к проблеме линейного оценивания будет обсуждаться в гл. 7
и 8. (Прим, авт.)
233
то это равенство будет справедливо при любой функции i]s • То
есть для любой функции ijs должно быть справедливым равенство
tr Е П J 713 (/, ^) [z (^) - Н (^) рх (Ml d
11о
* Л
- J [ zr (Z2) - pl (Л2) Нг (ХОНГ (/, ^) d Z2]
[х(о —Нх(0]г—
(6.148)
= 0.
Это будет действительно так, если
{( t
Iz (^) - Н (^) рх (^)l lx (0 - px (t)]T — J [ Zr (X2) -
I 0
-|ф(МНгИ]2^
или, что эквивалентно, для любого ?ч, такого, что OsOi<T
cov{z(\t), х(/)} = cov Jz^), х, (t)\, (6.149)
I mv /
или
covlz^), x (t)\ = 0, (6.150)
I MV J
A
где Xlmv (0 — оптимальная оценка, имеющая вид (6 145) при
л
S(f, K)=3(t, X). Уравнение (6.150) легко выводится из (6.149),
если раскрыть выражение для cov{z(Xi), x(t)}, воспользовавшись
Л ~
представлением х(7) =xLmv(0+хьму(0 Действительно, в этом
случае
cov {z (^), х (t)} = cov Iz (AJ, x (0 + x (t)\ =
I MV MV I
A ~
^covlz(X1), XL (f)\ +covlz(A,1), x (t)\ .
I MV J I MV J
Следовательно, если справедливо равенство (6149), то необходи-
мо справедливо и равенство (6 150).
Уравнение (6.149) часто записывается в интегральной форме.
Эту запись можно получить, если в (6.149) изменить порядок сле-
дования символов под знаками ковариации, а затем в получившее-
ся уравнение подставить выражение (6.145), положив S(£, Z.) =
л
= S(t, К) В результате приходим к уравнению
? А
cov{x(f), z(^)} = j S(Z, t)cov{z(t), z(Z1)}Jt, (6 151)
6
где 0<Xi<£. Уравнения (6.149) и (6.151) известны как уравнения
Винера—Хопфа. Таким образом, чтобы отыскать оптимальную ве-
234
совую функцию, необходимо решить эти интегральные уравнения.
Подобная задача обычно чрезвычайно трудна почти для всех слу-
чаев, за исключением лишь некоторых тривиальных.
Если обе части ур-ния (6.149) умножить на Ё((, А,) и проинте-
грировать по переменной 2ц в пределах от 0 до t, то получим ос-
новное равенство леммы об ортогональном проецировании:
cov 1 х, (t), x(t)\ = cov 1 х (t), x (t)\ , (6.152)
l MV I I MV MV J
которое чаще записывается в виде
covlx. (t), х = 0. (6.153)
I MV MV )
Согласно этой чрезвычайно важной лемме оптимальная линей-
ная оценка с минимальной дисперсией ортогональна вектору оши-
л
бок оценивания. Заметим, что явных выражений для Е здесь пока
не получено. Главная цель проводимых здесь рассуждений состоя-
ла в том, чтобы сформулировать утверждение леммы об ортого-
нальном проецировании, которое записано в форме равенств
(6.152) и (6.153).
А
Способы получения явных выражений для весовой функции Е
будут описаны в гл. 7.
Пример 6.14. Линейные задачи § 6 2, 63 и 65 можно теперь решить с ис-
пользованием леммы об ортогональном проецировании или уравнения Винера —
Хопфа Нелинейные модели, рассматривавшиеся в § 6 2 и 6 3, такими способами
проанализировать нельзя Проблема нелинейного оценивания с минимальной
среднеквадратической ошибкой будет основательно изучена в гл 9
Здесь приведем решение задачи, уже рассмотренной в примере 6 1 Усло-
А
вия этого примера сохраним неизменными и предположим, что xz, Mv = px +
А
+ S(z—Нрх) Такая оценка является частным случаем оценки (6 145) Далее
А
матрицу 3 необходимо подобрать так, чтобы математическое ожидание проек-
ции оценки на вектор ошибок оценивания было равно нулю Равенство (6 153)
А А
для рассматриваемого здесь случая принимает вид cov {xtMV , х—Хьму }=0.
Раскрывая обозначение, стоящее в левой части этого равенства, получаем
А А
cov {рх + 3 (z — Н рх), х} = var {рх + 3 (z — Н рх)}
ИЛИ
Е {[3 (Нх + v - Н рх)] хг } = Е {[3 (Нх + v - Н рх)] [ 3 (Нх + v - Н рх)]г }.
А
Таким образом, в условиях примера 6 1 для матрицы 3 имеем уравнение
А А л А А_
3 HVX = SHVxHr Ет + 3 V, Зг .
Решение этого уравнения имеет вид
3 =VxHr(HVxHr+ Vv)-'
235
Итак, оптимальная оценка с минимальной диспепсией
xLmv = ^ + v*hT (HvxHT + Vv)-’ (z - н fe) = (v-’+ HT V71 H)-’ X
X (HrV71z + V71 gx).
Это выражение для оценки получено в результате прямого применения леммы
об обращении матриц. Ойо совпадает с выражением, полученным в примере 6.1.
Эти же результаты могут быть получены в несколько иной фррме Будем
считать, что случайные векторы х и у имеют нулевые средние значения, но
могут быть коррелированными. Согласно лемме об ортогональном проецирова-
Л
нии для оптимальной оценки должно выполняться равенство £{xx^mv } =
( Л Л- , л
X/-MV X/-MV >и если оценка XlMV =Sz- то получаем
a = £{xzr}(£ {zzT
Таким образом,
xL = 2 z = £{xzT }(£ {zzr })~'z.
Если средние значения рассматривающихся здесь случайных векторов не равны
нулю, то нетрудно показать, что
Л
XLMV =fix + cov{x, zT}(cov{z, zr}-‘fz—Jlv—Hjlx).
Вернемся .снова к исходной модели наблюдаемого процесса
z (t) = Н (/) х (f) + v (/). (6.154)
Попытаемся теперь оценить значение процесса x(t) в момент вре-
мени t\ по реализации процесса z(t), полученной для всех
Ze[0, t2]- При этом моменты времени t, и t2 будем считать либо
фиксированными, либо текущими. Для этого выберем несмещен-
ную линейную оценку
*L (fl I 4) = Рх (Q + f Y (tl, I У (z Р-) — (X) — н (Л) р.х (Л)] d к
6
(6.155)
л
где Xl(^|^) обозначает линейную оценку для значения х в мо-
мент времени t\ по результатам наблюдений «плоть до момента t2.
Будем предполагать, что х(7) и v(t)— случайные процессы, ко-
торые в общем случае могут быть зависимыми. Задача состоит
в том, чтобы минимизировать значение следа
tr[var { xj/x | i2)}] = trfvar { x^) —хд(/2 | /2)}]. (6.156)
Эту задачу минимизации можно решить тем же способом, кото-
рый уже привел .к ур-ниям .(6.150) — (6.153). В результате при-
ходим еще к одному варианту записи утверждения леммы об
236
ортогональном проецировании: для любого Л, такого, что
cov{z(Л), х^)} = cov lz(A), х (/j J t2)} (6.157)
I MV J
или cov|z(A), x£ (i. | /2)| == 0, (6.158)
где x (/j | у = px(/j) + 1у(/1; Л ] i2) [z (A) — ji — H (Л) цх (A)l d Л.
MV J J
Выписанное здесь уравнение является уравнением Винера—
Хопфа. Другой вариант записи этой же леммы
cov / х. (^ I /,), X (t1 I /2)1 =0. (6.159)
I MV MV J
Равенство должно иметь место для всех значений и t2. Здесь
хл Vi I U — х (О xz. Vi I У
MV MV
(6.160)
обозначает ошибку оценивания. Именно эта формулировка леммы
об ортогональном проецировании является достаточно общей и
постоянно будет использоваться в дальнейшем при обсуждении
проблем предсказания, фильтрации и некоторых задач сглажива-
ния. Отметим также, что не является принципиальным тот факт,
что лемма сформулирована для случая с непрерывным временем.
Точно также можно было бы рассмотреть задачу фильтрации про-
цесса с дискретным временем. В этом случае задача оптимизации
сводится к решению уравнения
cov{z(j), x(^)} = covlz(/),
Л
х£ (*11 ш
MV )
(6.161)
где ko^js^k2, которое является дискретным аналогом уравнения
Винера—Хопфа. Здесь
л к*
(ki I ki) = Рх (^i) + V у (^, / | k2) [z (j) — pv (!) — H (j) px (/)] •
MV =1
1 (6.162)
Лемма об ортогональном проецировании при дискретном вре-
мени записывается в виде
covlx (&J | #„), х (/?i |О = 0. (6.163)
I MV " MV J
Интересно и важно отметить также, что ошибка оценивания здесь
снова ортогональна наблюдаемому процессу, поскольку из ур-ния
(6.161) следу ет, что
cov{x(^ I k2), z(j)} == 0, k0^j < k2. . (6.164)
Подчеркнем в заключение, что, хотя уравнение Винера—Хоп-
фа и лемма об ортогональном проецировании для общего случая
237
получены легко, решение этих уравнений не является столь же
простой задачей. Возможные способы решения таких уравнений
достаточно подробно будут обсуждаться в следующих двух гла-
вах.
6.7. Оценки наименьших квадратов
Подход к задаче оценивания, излагаемый в данном па-
раграфе, существенно отличается от подходов, уже обсуждавшихся
в предыдущих параграфах этой главы. Здесь не требуется знание
вероятностных характеристик рассматриваемых случайных величин
или процессов. Фактически описываемый здесь метод в этом смыс-
ле является другим крайним случаем по сравнению с байесовским
подходом, при котором необходимо иметь не только полное ве-
роятностное описание наблюдаемого процесса, но и знать функ-
цию потерь. Метод максимального правдоподобия при этом мож-
но рассматривать как промежуточный, поскольку для его приме-
нения нет необходимости знать априорную плотность вероятности
оцениваемого параметра. При построении линейных оценок с ми-
нимальной дисперсией требуется еще меньше априорной инфор-
мации. Здесь достаточно знать лишь первые два момента иссле-
дуемых процессов.
Возможно, следует дополнительно разъяснить утверждение о
том, что здесь не используются сведения ни о вероятностных, ни
о статистических характеристиках исследуемых процессов. Все
же и теперь необходимо выбирать меру качества оценок. А эго
может рассматриваться как неявное предположение о вероятно-
стной структуре наблюдаемого и оцениваемого процессов. Будет
показано также, что если выбрать соответствующим образом
функцию потерь, то оценка наименьших квадратов оказывается
оптимальной байесовской оценкой при некоторых вероятностных
характеристиках исследуемых процессов. С другой стороны, для
некоторой иной функции потерь по-прежнему можно найти и ис-
пользовать оценку наименьших квадратов, даже хотя она более не
является оптимальной байесовской оценкой в этих новых усло-
виях.
Начнем с задачи непоследовательного оценивания постоянно-
го вектора х. Затем укажем последовательные алгоритмы вычис-
ления значений таких оценок, которые во многих случаях могут
привести к существенным упрощениям вычислений. В заключение
рассмотрим задачу оценивания меняющегося векторного парамет-
ра, которая уже непосредственно примыкает к общей проблеме
последовательного оценивания вектора состояния, подробно изу-
чаемой в последующих трех главах.
В задаче оценивания A-мерного постоянного параметра х при-
мем следующую модель наблюдаемых величин:
zl = Hlx4-vJ, (6.165)
где шум v имеет среднее значение, равное нулю. Предположим,
238
что имеется выборка объема k, которую удобно представить в
виде
z* = Н*хv*. (6.166)
Здесь Zft ТИ-мерный составной вектор, который можно записать
следующим образом:
zk -----
Zi
Z2
Acol(zp z2, • • -, zft);
Н" и vh— матрицы размера MxN и МХ1 соответственно, опреде-
Заметим, что размерность M вектора z может быть больше k (чис-
ла наблюдений), так как результат каждого наблюдения может
представляться вектором. Будем требовать, чтобы M^N, хотя
обычно требуется, чтобы М было намного больше N; это необхо-
димо для получения более высокой точности оценок.
Теперь задача состоит в том, чтобы выбрать такое значение
л
оценки Хй вектора х, при котором значение квадратичной формы
J (xfe) = 4- (Z* - Н%)т Я-l № - НЧ)
(6.167)
оказывается минимальным. Оптимальную оценку, которая мини-
мизирует форму (6 167), будем называть оценкой наименьших
л
квадратов и обозначать символом XsLS. Для этой оценки
л л л
/(хй LS) ^JfXfe), где Хй — произвольная другая оценка. Нижний
л
индекс k в обозначении xft введен для того, чтобы подчеркнуть,
что при вычислении значения этой оценки используется k вектор-
ных наблюдений. Вообще здесь этот индекс является излишним,
но он будет необходим при построении алгоритма последователь-
ного вычисления значений оценки наименьших квадратов.
Матрицу весов размера МХМ будем считать положитель-
но определенной и симметричной, хотя такие ограничения вовсе не
обязательны Д Позже будет показано, каким образом выбор Ий
может быть связан с вероятностными характеристиками шума Vk',
*> Даже если исходная матрица весов несимметрична, квадратичную функ-
цию потерь (6 167) всегда можно записать в терминах симметричной матрицы
R^1 (Прим авт)
239
будет также пояснено, почему в качестве матрицы весов исполь-
зуется обратная матрица J?-’, а не матрица
Пока це будем ориентироваться на то, что результаты наблю-
дений могут поступать в определенном порядке. Результаты k
наблюдений могут быть получены последовательно во времени
один за другим или могут быть зарегистрированы сразу все в
один и тот же момент времени, либо для их получения исполь-
зуется какая-либо другая процедура. При решении задачи оцени-
вания сейчас исходным является следующее предположение: име-
ется конкретная выборка объема k, на основе которой должно
быть указано такое значение оценки для вектора х, при котором
л
значение формы /(хк) оказывается минимально возможным. Пос-
л
кольку минимизация формы J(xk) представляет собой обычную
детерминистскую проблему минимизации, то значение оценки наи-
меньших квадратов (если оно существует) является корнем урав-
нения
д/ (хь)
Л
дхь
л л =0. (6.168)
4s
Л
Подставляя (6.167) в выражение для J(х-ь) и выполняя операции
вычисления частных производных, получим
Л л = H<W J?-1 (zft - h4ls) = 0.
Xft~4s
искомая оценка наименьших квадратов для вектора х
xhLS - (6.169)
д/ (хь)
Л
дх;.
Отсюда
Отметим, что использование этой оценки предполагает обращение
матрицы Н& размера Лгх№>. Для сокращения записи
введем обозначение
Р^Н^^Н*)-’ (6.170)
или
р-1 = Н(*>Т j^-1 н*. (6.171)
Л
Оценку XhLS тогда можно записать в виде
^LS = pArRrIzft- (б-172)
Предположим теперь, что произведено новое очередное изме-
рение вектора х, а результат измерения Zfe+1 — Нй+1х+уй+1. Этот
*> По существу это требование доступности наблюдению См §75 или ра-
боту [202]. (Прим, авт.)
240
новый результат можно присоединить к предыдущим и записать
= Н*+[ х + vk+\ (6.173)
где
z*+J =
zfe
. ZH-1.
Hfc
Hfe
v';
(6.174)
; Н*+> =
• —
Теперь, воспользовавшись уже полученной формулой, можно
сразу выписать выражение для новой оценки, основывающейся на
результатах (^+1)-наблюдения. Таким образом, получаем
Н*+>)-> , z*+', (6.175)
где Я~^л— новая матрица весов для задачи оценивания по выбор-
л
ке объема (&+1). Используя обозначение (6.170), оценку xft+1LS
запишем в виде
\+1LS = PA+1H(ft+1)r^>^+1>
где Рж * (Н<*+Ог н^1)-1 .
(6.176)
(6.177)
Заметим, что снова необходимо обращать матрицу размера
МХЛ/ и ни один из промежуточных результатов, полученных при
Л
вычислении значения оценки xftLS, здесь не может быть исполь-
зован.
Другими словами, добавление одного результата нового наб-
людения приводит к необходимости заново повторить все вычис-
ления. Этот факт оказался отправной точкой для новых исследо-
ваний, цель которых — отыскание способов построения последо-
вательных алгоритмов вычисления значений оценки наименьших
квадратов. В таких алгоритмах результаты новых наблюдений
учитываются только путем внесения поправки в значение уже
имеющейся оценки, причем полностью повторять все вычисления
заново не нужно. Такие последовательные алгоритмы можно най-
ти, если ввести одно простое предположение относитель ю матри-
цы весов R^.j . А именно, будем предполагать, что матрица
имеет вид
М о '
(6.178)
Введение такой формы матрицы означает отказ от необходи-
мости взвешивать произведения ошибок между результатами ста-
рых и нового наблюдений. Более подробно целесообразность вве-
дения такого ограничения будет обсуждаться позднее.
241
= н^7^-1 Н* +
Если матрица имеет форму (6.178), то произведение мат-
риц Rft+* Hft+1 можно представить в виде
н*+* = [H<*)q Hf. .1
«-Н L I о ]|
+ Hf,1R-'H....
1 Л-т-i Л-f-i Л*т1
Если теперь сравнить (6 171) и (6.177), то можно записать
РЙ^РГ'+НЦ.КЙ.Н,,., (6.179)
«•™ р,+, = (Р-‘, + нц, r-д н,+1)-'. (6.180)
Применяя лемму об обращении матриц, получаем
Р^, =Pft — P*Hf.. (R. , +Hk.1P*hLi)-1 Н. .,Pft. (6.181)
Л-f-l к к «-f-l \ «-f*l 1 я-f-i Л-f* к v '
Если размерность наблюдаемого вектора z^+1 меньше размер-
ности N вектора х, то это последнее представление может привес-
ти к существенному сокращению объема вычислений. Так, если
zft+1 — скалярная величина, то матрица (Rh+i+ Hft+1PftHrft+1)
также оказывается скалярной величиной, так что ее обращение
сводится к обычному делению Отметим также, что «старые» сла-
гаемые типа H(ft)rR->Hft не нужны более в явном виде для вычис-
ления Pfe+i.
л
Подставляя (6 181) в (6 176) для оценки Xk+ils, получим но-
вую запись:
л
Ън, - [Р.- P.HI,, (Rw, + Н,+, РЛ4Г+,)-' ни, Р4] н»'г.+.,
(6.182)
Вследствие специально выбранной формы матрицы R^ [см. ф-лу
(6.178)] для произведения матриц zA+1 имеем х
X ^н-i г*+'= zk 4- H(+i R-^j zft+1 Поэтому оценка (6.182)
принимает вид = [Р, — РД1Ц, ( R,+, + Н1+, Р»НЦ,)*' Ht+I Р4] X
X (Н« г- + НЦ, РЦ, х,+,). (6.183)
Перепишем это выражение следующим образом:
’•+'ls “ !' -Р,НХ <”•+' + Нч ' Н»+,] (Р.Н<-+
+ Р»НН4 - (»«..~ Н.-н ₽»НЦ,)-' Н,+, Р,НЦ, Rjl J г,+|. (6.184)
(В соответствии с (6 172) вектор zft в правой части
л
этого выражения есть оценка xvLs Кроме того,’ введем обозна-
чение
242
к*4-1 — pьЩ+i (p*+i + ^*4.1 1 • (6.185)
Теперь вместо (6.184) можно записать
X*+1ls = — К*-м H*+i) XftLS + PftH*+i [P*+i (Ph-i ~ Hfe±i х
X Р&Н|+1) 1 Нл+, PhH£+1 R^J zft+1. (6.186)
Это выражение, в свою очередь, можно переписать так:
Xfe+ILS = K*+l Hfe+1) XfeLS + PhHA+1 (Rft+I + HA+1 PhHJ+j)-1 X
X [(Rfc+I + HA+I PftHr+I) R?_i, _ Hft+I PhHr+1 R-^] Zfc+I
или с использованием обозначения (6.185)
X*-MLS ~ КйНй+1) xh^ 4- Kft+i (I + Hft+I PfcHJ+j R^j
^fe4-l PA+l)Z4+r
Так что окончательно имеем
л л л
= xh + кь., (Z.,. — Н.,. xh ). (6.187)
«-HLS LS «+1 I «-Н «+* ”LS I ' '
Это и есть искомый последовательный алгоритм вычисления
значений оценки наименьших квадратов. Здесь матрица Кь+i оп-
ределяется соотношением (6 185). Отметим, что в соответствии с
ф-лой (6.187) новое значение оценки вычисляется путем прибав-
л
ления к старому значению оценки x&LS поправки, зависящей от
разности между новым значением z&+1 и ожидаемым значением
л
Hft+1xftLS полезного слагаемого.
л
Можно получить несколько иное выражение для оценки Xh+iLS>
если учесть, что матрица Кй+i может быть записана в виде
^,=i,w«u.Rdr <6188>
Справедливость такой записи легко проверить путем прямой под-
становки правой части ф-лы (6.181) в это выражение. Для оцен-
л
ки xft+iLS при этом получаем
**+lLS = XfeLS + РМ-1 Н*+1 ( Z*+l — Н*+> XftLs) ‘ (6‘1 89)
Рассмотрим два примера, иллюстрирующих полезность полу-
ченных соотношений. После этого будет охарактеризована взаи-
мосвязь оценки наименьших квадратов с другими оценками, об-
суждавшимися ранее.
243
Пример 6.15. Пусть неизвестный параметр х является скалярной величи-
ной х и имеется выборка объема k скалярных величин z,=x+v,. Следователь-
но, в данном примере
Н<*>г=(1, 1,..., 1).
В качестве матрицы весов Л выберем единичную матрицу.
В соответствии с ф-лой (6 169) оценка наименьших квадратов величины х
имеет вид
т. е. совпадает с выборочным средним.
Если бы был получен результат следующего наблюдения, то прн 7?^^ = I
нетрудно показать, что для рассматриваемой простой задачи новое значение
4+1
л 1 in
оценки -4+lLS = ^j-i2jZ-
£==1
Найдем теперь частный вид последовательного алгоритма (6 189) для этой
задачи. Из (6.470) следует, что
Г 1'
1
Ph =
[1. 1...........И ।
= (*)
1
к ’
так что для ps+i на основании (6.181) получаем
1 1 / 1 \-1 1 1
Pk-X-\— . - , 0) Н + ь . — . . , •
я • 1 к k \ k ) k /г1
Л
Следовательно, последовательный алгоритм для оценки хь-hls записывается
так:
Л Л 1 Л
*4+1 = *4 + , . 7 ( г^и-1 xh. q) •
+ LS LS fe+l\ LS/
Легко проверить, что эта запись полностью согласуется с ранее полученной не-
последовательной формой оценки
Если результаты отдельных наблюдений поступают последовательно во вре-
мени один за другим, то использовать последовательный алгоритм можно с мо-
мента начала наблюдений, приняв, что
Л Л 1 Л
Xi = v. j +— (Zi~x , \ , i = 2, 3..............
LS LS i V LS'
A
где *iLS = zj.
В данном простом примере использование последовательного алгоритма не
приводит к заметному уменьшению объема вычислений Однако и здесь при
применении последовательного алгоритма нет необходимости хранить результа-
ты отдельных наблюдений после их обработки. Это также может оказаться важ-
ным, особенно в том случае, когда объем выборки k достаточно велик Кроме
того, последовательный способ вычислений дает возможность иметь текущее
значение оценки после каждого очередного наблюдения, что позволяет иногда
принять решение о прекращении наблюдений, если значение оценки практически
перестает изменяться
244
Пример 6Л6. Рассмотрим задачу оценивания постоянного параметра х по
результатам двух наблюдений
Г21 Г1 1]
zi4iHo i]x+vi;
z2 = 4= [1 2] х + v2,
используя для этого как последовательный, так и непоследовательный алгорит-
мы обработки данных Примем, что R^"1 =1, так что представление (6.178)
справедливо и R]-1 =1, R2=l.
Для построения непоследовательного алгоритма
блюденин сведем в составной вектор z<2> = Н<2>х + v<2>,
имеющиеся результаты иа-
где
z(2) =
Н,
н2
Z1
?2
" 1
О
1 1
2
Подставляя эти соотношения в ф-лу (6 169)
х(2) = /’н(2,гН(2))~1 H(w2>=
LS v >
= 1, получим
и полагая
Построение последовательного алгоритма начнем с вычисления значения
Л
оценки Xi Ls , основывающейся на результате только первого наблюдения. Вы-
ражение (6 169) здесь принимает вид xiLS= (Н[ НО-’Н т Zi, так что
Л /[1 °] Р Pv1 Г1 °1 [2 1 Р 1
X1LS= J [о 1Д [1 1J [1 | [1 1 '
т Г 2 —п
Матрица Pi=(H1Hi)~1, т е Pi= I Теперь в соответствии с (6 181)
находим, что
(1 + 1121[-1
Г 2
[ — 1 2/3 ] ’
Следовательно, согласно (6 189) для оценки x2LS
получаем
Л л т л [1 1 Г 2 — Ч Г1 1 / Г
4s = 4s + ₽2 н2 & - H24s) = | 1 ] + [ _ I 2/з] 12 ](4 -11 21 [ 11) =
- Г1
[4/3] ’
что, конечно, совпадает с предыдущим результатом
Для того чтобы обсудить взаимосвязь между оценкой наимень-
ших квадратов и линейной оценкой с минимальной дисперсией,
желательно несколько упростить используемые обозначения. В
частности, опустим нижний индекс k и индекс, написанный кур-
сивом, в соотношениях для оценок наименьших квадратов. В этом
245
случае для наблюдаемой величины справедливо более простое
представление
z=^Hx + v, (6.190)
а оценка наименьших .квадратов вектора х принимает вид
xLS = (Нг R-1 Н)-1 Нг R-1 z, (6.191)
где R-1 — матрица весов квадратичной функции потерь.
Чтобы подчеркнуть линейность этой оценки и дополнительно
упростить последующее изложение, будем писать
xLS = Kz, (6.192)
где матрица
К= (Нг R1 Н)1 HR1, (6.193)
или, если воспользоваться определением матрицы Р,
K^PHR1 , (6.194)
поскольку
P = (HrR”‘H)-1. (6.195)
Из (6.193) следует, что КН = 1. Это равенство фактически оз-
начает несмещенность оценки наименьших квадратов (в предпо-
ложении, что шум v имеет среднее значение, равное нулю). Что-
бы показать это, достаточно выписать выражение для ошибки оце-
нивания:
~ л
XLS - Х — XLS = Х — KZ.
Но для z справедливо представление (6.190), так что
?LS = x — K(Hx + v) = Kv, (6.196)
поскольку КН = 1. Следовательно, математическое ожидание ошиб-
ки
£{xls} =KE{v} = °. (6.197)
л
Таким образом, если gT=0, то оценка xls является несмещен-
ной. Ковариационная матрица вектора ошибок оценивания при
использовании этой оценки
Е хи Е {™т} = KVv КС
Подставив сюда (6.193), получим
V~ s = (Нг R-* Н)~‘ Н7 R-1 Vv R1 Н (Нг R~‘ Н)-1 . (6.198)
Линейная оценка с минимальной среднеквадратической ошиб-
кой для вектора х, основывающаяся на выборочных значениях
246
наблюдаемого вектора (6.190), была найдена в § 6.6. Для частно-
го случая, когда gx = 0 и V~’=0, эта оценка имеет вид
х = (Hr V7> Н)-> Нг V7> z (6.199)
и является, таким образом, несмещенной. Ковариационная матри-5
ца вектора ошибок оценивания при использовании этой оценки
V-, = £/х~ х£ 1 = (fFV-'H)-1. (6.200)
х MV I mv Mv/ v v '
Простым сравнением выражений (6.191) и (6.199) легко обна-
ружить, что если при построении оценки наименьших квадратов
в качестве матрицы весов R выбрать ковариационную матрицу
шума Vv, то оценка наименьших квадратов и линейная оценка
с минимальной дисперсией совпадают. Тан им образом, если R=Vv,
то ковариационная матрица вектора ошибок оценивания при ис-
пользовании оценки наименьших квадратов
V— I = (Нг V”1 Н)-> Нг V-1 Vv V'1 Н (Нг V-1 Н)-‘ =
LS R=V V v/ vvv \ v/
I v
= (Hrv-H)-1=v~w
что и следовало ожидать. '
Поскольку оценка наименьших квадратов является линейной,
а линейная оценка с минимальной дисперсией обеспечивает ми-
нимально возможную среднеквадрати'ческую ошибку оценивания,
то справедливость неравенства
V~ > V~£ (6.201)
LS MV
очевидна. При R=Vv в данном неравенстве достигается равен-
ство. Вообще для установления справедливости неравенства
(6.201) не обязательно использовать оптимальность оценки (6.199).
Можно показать, что матрица (6.200) всегда меньше или, в край-
нем случае, равна ковариационной матрице вектора ошибок
(6.198). Для доказательства этого утверждения достаточно вос-
пользоваться матричным неравенством [79], являющимся анало-
гом неравенства Шварца для функций. Если А и В две произ-
вольные матрицы размера ky.N, k^N и матрица В имеет ранг
N, то
Аг А> (вг A)r (ВГВ)~’ (Вг А), (6.202)
где равенство достигается тогда, когда существуют два 77-мер-
ных вектора 1 и у, такие, что ВХ+Ау=0.
Чтобы доказать это неравенство, рассмотрим следующее по-
ложительно полуопределенное скалярное произведение
(В X-f-А у)г (ВХ-f-А у) > 0, (6.203)
где X и у — два произвольных A-мерных вектора. После выполнения
247
операций умножения неравенство (6.203) принимает вид
ХГВГВХ4-ХГВГАТ + угАгВМ ГГАгАу > 0.
Теперь, учитывая, что матрица В имеет полный ранг и, следова-
тельно, обратная матрица (ВТВ)-1 существует, последнее выра-
жение запишем следующим образом:
[1 + (Вг В)-1 Вг А у]г Вг В [X + (вг В)-1 Вг А у] -|- уг [Аг А —
— (Вг А)г (Вг В)”1 (Вг А)] у > 0. (6.204)
Справедливость такой записи можно легко проверить путем
выполнения операций умножения в левой части этого неравенства.
Неравенство (6.204) должно быть справедливым для любых век-
торов 1 и у. Если 1 выбрать так. чтобы 1 = — (ВтВ^’Ау, то вмес-
то (6.204) получаем
/ [дт а — (Вг А)г (Вг В)-1 (Вг А)] у > 0. (6.205)
Поскольку вектор у здесь еще является произвольным, то эта
квадратичная форма может быть неотрицательной только в том
случае, если матрица (АТА— (К1 А)т (К1 К)-> (ВтА)] неотрицатель-
но определена, т. е. неравенство (6.202) действительно справед-
ливо.
Неравенство (6.202) можно использовать для доказательства
справедливости соотношения (6.201). Для этого положим А =
= Vv 2КТ; B = Vv 2 Н. Вместо (6.202) теперь имеем
KVKr>\HrV 2 V 2 кг (Нг VJ Н)-1 IН7 V 2V2KH
или KVvKr > (Нг К7/(НгV71 Н)-1 (Нгкг). Так как КН = 1,
НТКТ = 1, то предыдущее неравенство принимает вид V~ls=
= KVvK7'^(HtV;.-1H)-1=VxTm , т. е. доказательство завершено.
Рассмотрим теперь случай, когда значение вектора х не явля-
ется постоянным, а меняется от наблюдения к наблюдению. При
этом примем, что х — решение линейного разностного уравнения
х(/+1) = Ф()+1 j)x(j). (6.206)
Будем считать, что выборочные значения наблюдаемого про-
цесса
z(J) =H(/)x(J) + v(j) (6.207)
поступают последовательно во времени одно за другим. Найдем
оценку для текущего значения вектора x(j), основывающуюся на
результатах Z(j) = {z(l), z(2), ..z(])} последнего и всех пред-
шествующих наблюдений и минимизирующую «потери»
V[z(0-H(i)x(f I /)fR-i (г) [z(z) — H(i) x (1 I /)]. (6.208)
1=1
248
Здесь x(i\j)—оценка вектора x(t), основывающаяся «а выборке
Z(]). После получения первого элемента выборки z(l) = Н(1)х(1)+
+v(l) для оценки вектора х(1) получаем
х(1 | 1) = [Нг(1) R1 (l)H(l)]-1 Hr(l)R-’ (1) z(l) = Р(1)НГ(1 )Х
X R"1 (l)z(l);
где Р(1)А[НГ(1) R-1 (l)H(l)]-1.
Теперь предположим, что произведено следующее измерение,
результат которого z(2) =Н(2)х(2) +v(2). Оценивать значение
х(2) необходимо по результатам обоих измерений: z(l) и z(2).
л
Так как интерес представляет оценка х(2|2), то, используя пред-
ставление (6.206) для z(l), запишем z(l) =Н(1)Ф(1,2)х(2)+v(l).
Далее можно найти оценку для х(2), основывающуюся на резуль-
тате первого измерения z(l). Эту оценку обозначим символом
Л
х(2|1). Выражение для этой оценки нетрудно получить путем диф-
л
ференцирования правой части равенства (6.208) по х(2|1). При-
равняв найденную производную нулю и решив это уравнение, по-
лучим
х(2 | 1)= Ф (2,1) [Нт(1) R-1 (1)Н(1)]-1 HT(1)R~'(l)z(l). (6.209)
Используя теперь найденное ранее выражение для оценки
л
х(111), можно записать
х(2 | 1) =< Ф(2,1)х(1 | 1). (6.210)
Если ввести обозначение
Р(2 ] 1) = Ф (2,1) Р(1) Фг (2,1), (6.211)
то для этой оценки получаем следующее стандартное представ-
ление:
х(2 | 1) = Р(2 | 1)[Н(1) Ф(1,2)]гR1 (1)z(1), (6.212)
л
т. е. x=PHR-iz, поскольку Н в этом случае представляет собой
матрицу Н(1)Ф(1,2). Получить такую стандартную форму записи
для оценки необходимо, так как это позволяет сразу же исполь-
зовать последовательный алгоритм.
Теперь учтем следующее наблюдение z(2). Используя (6.189),
запишем
х(2 | 2) = х(2 | l)+P(2)Hr(2)R-1 (2)[z(2)— Н(2)х(2 | 1)]. (6.213)
Может оказаться, что необходимо произвести некоторое конечное число
измерений до преобразования, указанного в (6 207) Здесь основной целью яв-
ляется построение последовательного алгоритма оценивания общего вида Если
такой алгоритм будет найден, то процедура начала вычислений легко устанав-
ливается (Прим авт )
249
Подставляя сюда (6.209), получаем
х(2 | 2) = Ф(2,1)х(1 | 1)+ P(2)Hr(2)R-I(2)[z(2) —Н(2)Ф(2,1) X
Хх(1| 1)], (6.214)
где согласно (6.181) Р(2)=Р(2| 1)—Р(2| 1)Нг(2) [R(2)+Н(2)Р(2| 1) X
ХНГ(2)]-1 Н(2)Р(2 | 1). (6.215)
Если описанную процедуру повторять для каждого нового наб-
людения, то тем самым будет построен последовательный алго-
ритм оценивания вектора x(j) по результатам всех предыдущих
наблюдений Z(/) = {z(l), z(2), ..., z(j)}. Если (ввести обозначение
л л
*(/)_ х(/|/), то ЭТОТ алгоритм записывается следующим образом:
х (/) = Ф (Л /• - 1) х (/ - 1) + Р (/) Нг (j) R-1 (/) [z (/) - Н (/) х
ХФ (/, /—1)х(/—1)]. (6.216)
Здесь Р (j) = Р (/ | / - 1) - Р (j | / - 1) Нг (/) [R (/) + Н (/) Р (/ | / - 1)Х
X Нг(/)]-* Н(/)Р(/|/—1); (6.217)
Р(/ I/— 1) = Ф(Л J— 1)Р(7— 1)ФГ(/, /-1). (6.218)
Более подробно проблема оценивания вектора состояния будет
обсуждаться в следующих трех главах. Однако одно заключитель-
ное замечание здесь следует сделать. Если матрицу весов R(/)
принять равной матрице Vv(j), то приведенный выше алгоритм
будет совпадать с последовательным алгоритмом вычисления зна-
чений линейной оценки с минимальной дисперсией. Матрица Р(])
при этом будет представлять собой ковариационную матрицу
V~(/) вектора ошибок оценивания. Отметим также следующий
важный момент: полученная оценка не определена для нулевого
шага, т. е. ничего нельзя сказать о начальных значениях оценки
л
x(j) и матрицы Р(]) в ф-лах (6.216) и (6 217). Считается, что
наблюдения начинаются на первом шаге, т. е. z(l) есть результат
первого наблюдения. Обычно предполагается, что априорные све-
дения о вероятностных свойствах вектора х отсутствуют и что
|iix=0; V-‘ = 0. Если подобные предположения нежелательны, то
вместо (6.208) следует использовать функцию потерь
J = Н х(0) — V-xllp-i + £ jiz(z)—H(z)x(z | /) — (6-219)
При такой функции потерь, как и ранее, получается байесов-
ская оценка, если матрицы весов выбираются на основе априор-
ных вероятностных характеристик оцениваемого вектора и шума,
а именно, PO=VX; R(i) = Vv(i). Легко показать, что при p,v = 0 в
этом случае приходим к алгоритму (6.216) со следующими началь-
л
ными условиями: х(0)=|*х; Р(О)=Ро.
•
Глава 7
ОПТИМАЛЬНЫЙ ЛИНЕЙНЫЙ ФИЛЬТР
7.1. Введение
В этой главе будут рассмотрены решения некоторого
класса задач оценивания, впервые сформулированных и развитых
Калманом и Бьюси (105, 111] как обобщения классической работы
Винера [275]. Нас будет интересовать класс линейных последова-
тельных алгоритмов оценивания состояния, обеспечивающих мини-
мальную среднеквадратическую ошибку. Эти алгоритмы получили
название «фильтров Винера—Калмана», «фильтров Калмана» по
имени авторов, чьи работы послужили началом теоретических ис-
следований в этой бурно развивающейся области. Алгоритмы
фильтра Калмана или одного из многочисленных его обобщений
и модификаций уже применяются при решении многих практиче-
ских задач, включающих в себя управление движением в косми-
ческом пространстве и определение параметров орбиты. Рассмот-
рение фильтра Калмана разделено на две части: в первой дан вы-
вод основных результатов, во второй приведены обобщения.
В этой главе будет дан вывод алгоритма фильтрации Калма-
иа и исследованы его асимптотические характеристики.
Рассмотрение фильтра Калмана начнем с дискретного вариан-
та задачи, т. е со случая дискретных во времени наблюдений дис-
кретной динамической системы. Дискретная задача выбрана для
первоначального рассмотрения до некоторой степени произволь-
но. Но такова историческая последовательность, и, кроме того,
дискретный вариант имеет некоторые методические и теоретиче-
ские преимущества. Для простых задач дискретные алгоритмы
могут быть реализованы и вручную проверены и могут быть про-
ще объяснены. Последовательная обработка информации приводит
к более простым выкладкам. Кроме того, некоторые теоретические
особенности задачи легче объяснить для дискретного варианта,
чем для непрерывного. Как мы убедимся в дальнейшем, это, од-
нако, справедливо не для всех аспектов задачи. Введение такого
важного понятия, как «обновляющий» процесс, оказывается осо-
бенно полезным лишь для непрерывного случая.
При выводе дискретного алгоритма будут использованы два
различных подхода. Сначала будут получены линейные, оптималь-
ные в смысле минимума среднеквадратической ошибки алгоритмы
с помощью метода ортогонального проецирования. Затем будет
рассмотрен подход, связанный с оцениванием по максимуму апо-
стериорной вероятности (см. § 6.2). Непрерывный алгоритм сна-
251
чала выводится из дискретного путем увеличения частоты отсче-
тов и предельного перехода. Затем результаты, соответствующие
непрерывному случаю, непосредственно выводятся из интегрально-
го уравнения Винера—Хопфа [см. ур-ние (6.151)], а также путем
прямого использования вариационного метода решения задачи оп-
тимизации.
Подобные подходы к выводу алгоритма фильтрации Калмана
служат не только иллюстрацией различных возможностей; некото-
рые вспомогательные результаты могут быть использованы при
решении задач нелинейной (и линейной) фильтрации, рассмотрен-
ных в гл. 9. Стремление показать, что данную задачу оценивания
можно рассматривать с различных точек зрения, служит оправда-
нием для изложения нескольких различных способов решения, хо-
тя одного было бы вполне достаточно, поскольку основные резуль-
таты аналогичны. Можно надеяться, что рассмотрение задачи с
различных точек зрения будет способствовать более глубокому
пониманию физических и статистических особенностей полученных
результатов.
Если время наблюдения неограниченно увеличивается или, по
крайней мере, становится достаточно большим по сравнению с
длительностью переходных процессов в системе и если параметры
системы инвариантны во времени и априорное распределение ста-
ционарно, по крайней мере, в широком смысле, тогда получается
стационарная асимптотическая форма фильтра Калмана. Этот
стационарный фильтр Калмана аналогичен фильтру Колмогоро-
ва—Винера, хотя для большинства задач подход Калмана дает
значительные вычислительные преимущества. Соотношение подхо-
дов Калмана и Винера обсуждается в § 7.4.
Устойчивость асимптотических характеристик фильтра Калма-
на исследуется в § 7.5. Устойчивость алгоритма особенно важна,
так как она обеспечивает стабильность ошибки оценивания при
увеличении интервала наблюдения. Показано, что при слабых
ограничениях алгоритм является асимптотически стабильным в
большом, что позволяет применять этот алгоритм с малой вероят-
ностью нежелательного режима, даже несмотря на незнание ап-
риорного распределения.
7.2. Оптимальный линейный дискретный фильтр
В данном параграфе мы рассмотрим дискретную форму
линейного несмещенного алгоритма, обеспечивающего минималь-
ную среднеквадратическую ошибку, предполагая, что модель со-
общения задана.линейным векторным разностным уравнением1)
х(/г + 1) = Ф (k + 1, k)x(k') + Г(k)w(k), (7.1)
где входной шум (или шум объекта) w представляет собой белый *
*) Ради простоты обозначения явная зависимость от величины интервала
между выборками здесь не указана Заметим, однако, что дискретизация во вре-
мени не обязательно должна быть равномерной (Прим авт )
252
шум с нулевым средним и ковариационной матрицей
cov {w (4), w (/)} = Vw (k) (k - /). (7.2)
Модель наблюдения или измерения задается линейным алгеб-
раическим соотношением
2(A) = H(ft)x(4) + v(^ (7.3)
где шум измерения v представляет собой белый шум с нулевым
средним и
cov {v (k), V (/)} = VV (k) (k — j). (7.4)
Ради простоты первоначальных выкладок предположим, что w
и v некоррелированны, т. е.
cov{w(A), v(/)} = 0 для всех j, k. (7.5)
Начальное значение х представляет случайную величину со сред-
ним значением рх(0) и дисперсией VB(0), иначе говоря,
Е {х (0)} = рх (0); var {х (0)} = Vx (0). (7.6)
Будем также полагать, что cov{x(0), w(^)}=0 для всех /г 2^0.
Найдем оценку величины х(]) по совокупности последователь-
ных наблюдений Z(k) = {z(1), z(2), ..., z(k)}. Обозначим эту оцен-
л
ку через x(7j^), а ошибку оценивания — через
М/ I *) = х(/)-х(/ I *) (7.7)
В зависимости от соотношения между величинами j и k оцени-
вание называется предсказанием или экстраполяцией (/>&), филь-
трацией или сглаживанием (/=Л) и, наконец, интерполяцией
(/'<&). Подобное деление интуитивно вполне понятно, поскольку,
например, предсказание (/>&) означает оценку состояния в /-Й мо-
мент, основанную на всех наблюдениях вплоть до й-го момента.
В этой главе в основном будем рассматривать задачу фильтра-
ции *>, а предсказание и интерполяция будут исследованы в сле-
дующей главе.
Оценка будет условно и безусловно несмещенной, т. е.
£{х(/|/г) | Z(/e)} =£{х(/) |Z(£)} и £{х(/1/г)} =£{х(/)}, а также бу-
дет линейной функцией последовательности наблюдений. Из мно-
жества возможных линейных несмещенных алгоритмов оценива-
ния выберем лишь тот, который дает минимальную дисперсию
ошибки, 1. е. тот, для которого V~ (/|/г) = var{х(/1/г)} или
var{x(j\k) |Z(k)} минимальны.
В предыдущей главе мы установили, что оценка х по критерию
минимума среднеквадратической ошибки совпадает с условным
о Решение задачи одношагового предсказания будет получено как проме-
жуточный результат при выводе алгоритма фильтрации Калмана методом орто
тонального проецирования (Прим авт )
253
средним значением величины х при заданной совокупности наб-
людений Z. Однако в общем случае, даже если модели сообщения
и наблюдения являются линейными' (а для сформулированной
здесь задачи они являются именно такими), условное среднее не
является линейной функцией наблюдений, следовательно, алго-
ритм оценивания не обладает желательным свойством линейности.
Чтобы получить линейный алгоритм оценивания, обеспечиваю-
щий минимальную дисперсию ошибки, мы должны использовать
один из двух подходов. Один из них состоит в том, чтобы опреде-
лить условное среднее, представляющее линейную форму, а затем
найти наилучший вариант такой формы. Этот подход основан на
использовании ортогонального проецирования. Другой подход ос-
нован на предположении, что случайные величины х, w и v сов-
местно нормальны. В силу доказанного в гл. 4 свойства линейных
систем не изменять нормальный закон распределения точное ус-
ловное среднее в этом случае будет линейной формой. Линейная
оценка с минимальной дисперсией должна быть равна оценке с
минимальной дисперсией, если последняя действительно является
линейной. Это имеет место, если предполагать нормальные зако-
ны распределения^
Заметим, что если мы требуем, чтобы алгоритм оценивания
был линейным, то фактический закон распределения величин х,
w и v не имеет значения. Однако, если распределения действи-
тельно являются нормальными, как это часто бывает, тогда услов-
ное среднее фактически является линейной формой. Иначе гово-
ря, фильтр Калмана представляет собой наилучший (в смысле
минимума дисперсии ошибки) линейный фильтр независимо от
вида распределения и наилучшии алгоритм из всех возможных ли-
нейных и нелинейных алгоритмов оценивания, если шумы объекта
и измерения, а также начальное состояние имеют нормальные за-
коны распределения.
При выводе уравнения для фильтра Калмана будем предпола-
гать и требовать, чтобы наблюдения обрабатывались последова-
тельно. Независимо от того, является ли алгоритм оценивания по-
следовательным или нет, значения полученных оценок состояния
не корректируются. Однако существенное значение имеет вычис-
лительная реализуемость метода. Вероятно, наиболее значитель-
ный вклад Калмана и Бьюси состоит в том, что они впервые полу-
чили линейный алгоритм оценивания «по критерию минимума дис-
персии в последовательной форме, используя понятие переменных
состояния. Проблема линейной последовательной фильтрации по
критерию минимума дисперсии ошибки была давно уже решена
Винером и другими авторами применительно к системам с одним
входом и одним выходом. Главная заслуга Калмана состоит в
том, что он обобщил теорию фильтрации Винера на случай неста-
ционарных многомерных систем с нестационарными шумовыми
реализациями конечной длительности и получил решение задачи
фильтрации в рекуррентном виде.
254
Так как изложение существа проблемы несколько затянулось,
перед тем, как непосредственно приступить к ее решению, подве-
дем итоги. Мы хотим получить оптимальную по критерию миниму-
ма дисперсии ошибки линейную несмещенную оценку состояния
линейной нестационарной динамической системы, на которую воз-
действует белый шум с нулевым средним и известной дисперсией.
Для получения оценки мы наблюдаем изменяющуюся во вре-
мени линейную функцию состояния на фоне аддитивного белого
шума с нулевым средним и известной дисперсией. Начальное со-
стояние процесса представляет собой случайную величину с изве-
стными средним значением и дисперсией. Корреляция между вход-
ным шумом и шумом измерения отсутствует и требуется найти ал-
горитм оценивания в рекуррентном виде. Алгоритм фильтрации
Калмана представляет собой решение этой задачи. Применительно
к дискретным системам рассмотрим два различных подхода к вы-
воду уравнения фильтра Калмана, которые являются иллюстра-
цией двух идей, изложенных выше. В первом случае, когда ис-
пользуется подход, основанный на ортогональном проецировании,
мы заранее выберем линейную форму алгоритма оценивания, а
затем найдем наилучший алгоритм. Во втором случае, когда оце-
нивание производится по максимуму апостериорной вероятности,
будем предполагать, что случайные величины имеют нормальные
законы распределения и найдем оптимальный алгоритм оценива-
ния, который действительно окажется линейным. При выводе
уравнения фильтрации Калманом использовался подход, основан-
ный на методе ортогонального проецирования, поэтому изложение
начнем с этого метода.
Ортогональное проецирование. Теория ортогональ-
ного проецирования вкратце была рассмотрена в § 6.6. Здесь без
доказательства ’> будут представлены некоторые обобщения приве-
денных там результатов; они нам понадобятся в дальнейшем. Ли-
нейная оценка величины х по критерию минимума дисперсии ошиб-
ки при заданном линейном пространстве наблюдений Z задается
л л
ортогональной проекцией х на Z, т. е. x=E{x|Z}.
л
Здесь использован символ Е вместо Е, поскольку линейная
оценка с минимальной дисперсией не совпадает в общем случае с
условным математическим ожиданием. Если бы мы заранее пред-
положили, что случайные величины имеют нормальные распреде-
А
ления, то E{x|Z} просто совпало бы с £{x|Z}; однако мы созна-
тельно выбрали другой подход, чтобы подчеркнуть, что предполо-
жение о нормальных распределениях не является необходимым,
если помнить, что полученный при этом алгоритм оценивания мо-
жет оказаться не абсолютно наилучшим, а наилучшим лишь в
классе линейных алгоритмов. Если ортогональная последователь-
11 Теория ортогонального проецирования подробно изложена в книге Деча
(1965) {Прим авт)
255
ность {«j, аг, ..am} образует базис для Z, то х может быть пред-
ставлена следующим образом
л л т
х = £{х | Z}= 2£{х< <7-8>
! = 1
Для получения решения в рекуррентной форме нам понадобит-
ся следующий результат. Если р— вектор, ортогональный Z, т. е.
£{Ртаг}=0, для i=l, 2, ..т, где {си, аг, ..., ат}—ортогональ-
ный базис для Z, тогда
Д{х | Z, р}=Е{х | Z}+E{x | Р}. (7.9)
Этот результат и представляет собой лемму об ортогональном
проецировании. Хотя нас будет интересовать фильтрация х, т. е.
л А
x(j\j) & Е{x(j)\Z(j)}, рассмотрим сначала одношаговое предска-
Л л
зание, т. е. x(/ + l]j) Д Е{х(/ + 1) jZ(/)}. Для того чтобы получить
решение в требуемой рекуррентной форме, воспользуемся принци-
л
пом математической индукции. Предположим, что х(/|/—1) из-
Л л
вестна и представим х(/ + 1|/) через х(/|/—1) и новое наблюдение
z(j). Однако z(j), вообще говоря, не ортогонально Z(/‘—1) и преж-
де, чем воспользоваться ур-нием (7.9), необходимо найти состав-
ляющую наблюдения z(j), ортогональную Z(j—1). По существу,
это сводится к выделению новой информации, содержащейся в
2(1).
Легко показать, что вектор
Д(/| }-1) = Г(/|/—1)= z(/)-H(/)x(/| /-1) (7.10)
ортогонален Z(/'—1). Заметим, что z(/J/—1) представляет собой
«новую информацию», содержащуюся в z(j), так как для получе-
ния z(f|/—1) наилучшая оценка величины х(/[/—1) при условии,
Л
что задан Z(/—1), а именно Н(/)х(/|/—1), вычитается из z(j).
Это другая форма утверждения о том, что z(/1 j—1) ортогонален
Z(j—1). Случайная величина .7 известна под названием «обнов-
л
ляющей». Используя ур-ние (7.10), можно выразить х(/ + 1|/) че-
рез обновляющую случайную величину следующим образом:
х(/+ 1 | /)1Е{х(/ + 1) 1 Z(/ —1), z(/)} = Е{х (/+ 1) [ Z(j— 1),
2(J I i— !)}•
11 Для удобства обозначения в дальнейшем будем опускать индекс
Т Л
. *-MV для х’ так как в этоа и последующих главах будут рассматриваться лишь
Л Л
линейные алгоритмы оценивания, а Х1Муи хмар в этом случае будут совпа-
дать (Прим авт.)
256
Эти два выражения эквивалентны, так как z(/)—z(j|j—1) со-
держится в пространстве наблюдений Z(/—1) и, следовательно,
не добавляется никакой дополнительной информации по сравне-
нию с той, которая содержится в Z(/—1). Поскольку Z(j—1) и
z(/|j—1) ортогональны, можно воспользоваться ур-нием (7.9) и
записать х(/+1|/) как х(/ +11/) = Е{х(/ +1) |Z(j—1)} + £{х(/ +
+ 1) |z(;|/~ 1)}. Так как E{x(j + 1) | Z(/— l)}^x(/ + 11/— 1), то
это выражение можно представить в следующем виде:
х(/+ I | /) = х(/ + I I j -1) + Е{х(/ + 1) |^(J | /— 1)}. (7.11)
л
Отсюда следует, что х(/ + 1|/‘) получается путем предсказания
значения случайной величины х(/ + 1) по предыдущим наблюде-
ниям Z(/—1) с последующей коррекцией предсказанного значения
в соответствии с новой информацией z(/|j—1), содержащейся в
текущем выборочном значении случайной величины z(j). Концеп-
ция предсказания и коррекции является очень плодотворной и
позволяет наглядно интерпретировать алгоритм Калмана. Поэто-
му при выводе алгоритма фильтрации будем использовать подход,
опирающийся на идею предсказания и коррекции. Проанализи-
руем в отдельности каждый из двух членов, стоящих в правой
части ур-ния (7.11). Согласно выражению (7.1) х(/+1) задается
л
как х(/ +1) =Ф(/ +1, j)x(j) +r(/)w(j). Поэтому х(/ + 1|/—1), ко-
Л
торая по определению равна Е{х(/+1) |Z(j—1)}, теперь становит-
ся равной
х(/ + 1 | /-1) = £{Ф(/ + 1, /)x(j) + r(j)w(j) | Z(j-1)} =
= Ф(/+ 1, j)F{x(j) | Z(/-l)} + F{r(/)w(j) | Z(/-l)}.
Л Л
Согласно определению E{x(j)|Z(j—1)}=х(/|/—1) и мы имеем
*(/ + 1 | j- 1) = ф(/ + 1, /)х(/ | /- 1) + E{r(j)w(/) I Z(j- 1)}.
Так как Z(j—1) зависит только от w(j) для —1 и w представ-
ляет собой белый шум, то математическое ожидание величины
xv(j) при заданном Z(j—1) просто совпадает с безусловным мате-
матическим ожиданием £'{w(/)}=0. Таким образом, приведенный
выше результат преобразуется в следующий:
*(/ + 1 | /-1) = ф(/ + 1, /)Х(/ I /-1). (7.12)
Мы видим, что предсказанное значение х(/-М), основанное на
л
наблюдении Z(/—1), получается из х(/|/—I) как результат не-
возмущенного перехода на один шаг вперед, т. е. при w(j)=Q.
Этот вывод не является неожиданным, поскольку наилучшая оцен-
9—26 257
ка vr(j), основанная на наблюдении Z(/—1), как было показано
выше, тождественно равна нулю. Из этого также следует
w(/]^ = E{w(/)]Z(^)} = 0, (7.13)
Это означает, что и при фильтрации, и при предсказании наи-
лучшая оценка белого шума с нулевым средним тождественно рав-
на нулю. Этот вывод жрайне важен и будет весьма полезен, осо-
бенно при обсуждении понятия «обновляющего» процесса. Ниже
л
аналогичным образом будет показано, что х(/|/—1) определяет-
л л
ся как х(/|/—1) =Ф(/,/—1)х(/—11/—1) и что в действительности
х(/ I &) = Ф(/> H)*(k | k), k < /. (7.14)
Если подставить ур-ние (7.12) в (7.11), то получим
»(/ +1 I /) = Ф(/ + 1, /) х(/ | /—1) + £{х(/ + 1) | Г(/ | / — 1)}.
(7.15)
Рассмотрим второе слагаемое в правой части этого уравнения,
л ~
Используя ур-ние (7.8), Е{х(/ +1) ]z(/'|/—1)} можно записать в
следующем виде:
£{х(/ + 1) [7(/ | j- 1)} = £{х(/+ 1)Т(/ | / - 1)}[Е{7(/ | j- 1)Х
xV(/1 j-l)}]z~(/ I/- 1). (7.16)
Теперь исследуем отдельно каждый член, стоящий в правой
часта этого уравнения. Подставив (7.1) для х(/ +1), получаем для
первого члена уравнения
Е { х (/ + l)z г(/ | / - 1)} = Е {[Ф (/ + 1, j) х (/) + Г (/) w (/)] X
XV(/|J-1)}. (7.17)
Теперь, используя определения величин z(j) и z(/1 j—1) [см. ур-ния
(7.3) и (7.10)], z(/|/—1) (можно записать в следующем виде:
®(/ I /— I) = z(/) — Н(/)х(/ [ /—l) = H(/)x(/) + v(/) —
- Н (j) х (f | j - 1) = H (/) x (/ | / - 1) + v (/),
~ A
где х(/|/—l)=x(/)—x(/'|/'—1). Поэтому ур-ние (7.17) принимает
вид
Е{х(/+ 1)Т(/ | /-1)} = £{[Ф(/+ 1, /) х (j) + Г (/) w (/)] х
Х[Н(/)х~(/ | /_ 1) + у(/)]гЬ
а после перемножения соответствующих членов преобразуется к
виду
258
Е {х (j + 1)Т и | j - 1)} = ф (/ + 1, /) Е (j I j - 1)} X
ХНг(/) + Ф(/+ I, /) E{x(/)vr(/)} +r(/)F{w(/) хг(/[/-1)}х
XHT(j) + F(j)£H)vT (/)}.
Так как x(j) зависит только от w(j—1) .и х(/—1), a w и v ие
коррелированы, то E{x(/)vT(/)} =0. Поскольку w представляет
собой белый шум, а 1) зависит от w(i) только при —1,
то E{w(j)x(j\j—1)} = 0 и третий член в правой части приведенного
выше уравнения должен быть равен нулю. Последний член в пра-
вой части уравнения также равен нулю, так как w и v — не кор-
релированы. Поэтому остается только первый член и в результате
имеем
Е{х(/+ 1)V(/ I /-1)} =ф(/+ 1, /)Е{х(/)Т(; I /-1)}нг(/).
(7.18)
Полученное выражение можно еще более упростить, если учесть,
л ~ ~ ~
что x(j)=x(j]j—1) +х(/|/—1). При этом Е{х(/)хт(Л/—1)} стано-
вится равным
£{х(/)хГ(/ | /—1)} =Е{[х(/ ] j — l) + x(i | j— 1)]T(/| / — 1)}=
= E {x(J | j— 1) хг(/ | j— 1)} +E{x(j ] /— l)V(j | j — 1)} .
Но первый член согласно лемме об ортогональном проецировании
равен нулю. Поэтому ур-ние (7.18) можно записать в виде:
Е{х(/ + -1)Т(/|/-1)} = Ф(/ + 1, j)V~(j J (7.19)
где V~(/|/—1)Аvar{x(/|/—1)}. Аналогичным образом можно по-
казать, что
Е{1(/ | /- 1)Т(/ | / — 1)} = Н(/) ¥~(/ ] /—1)НГ(/) + Vv(/). (7.20)
Если подставить ур-ния (7.19), (7.20) и (7.10) в (7.16), то
Е{х(/ +1) | 7(/ | j-1)} = Ф (/ + 1, /) ¥~ (/ | - 1) Нг(/) X
X [Н (/) ¥~(/ | / -1)Нг(/) + Vv(/) J’1 [z(/) - Н(/) х(/ | / - 1)]. (7.21)
А
Поэтому выражение для х(/ +1 |/) принимает вид
х(/+ 1 I /) = Ф(/+ 1. /)х(1 I /— 1) +Ф(/+ 1. /)v~(/ I /— ОХ
X Нг[(/) [Н (/) ¥~ (/ ] / — W (/) + Vv (у)]-1 [z (/) — Н (/) х(j | / — 1)].
L (7.22)
9* 259
Этот результат можно представить в более удобной форме, если
ввести обозначение
К (/ + 1, /) = Ф (/ + 1, /) ¥~(/ | / - 1) PF (/) [Н (/) ¥~ (/ | / - 1) X
ХНГ(/) + ¥у (/)]->, (7.23)
так что получаем окончательно
х(/ + 1 I j) = Ф(/ 4- 1, /)х(/ I /— 1) + К(/ + 1- /)[z(/) —
Л
~Н(/)х(/|/-1)]. (7.24)
Величина К(/ + 1,/) называется коэффициентом усиления од-
ношагового экстраполятора Калмана. Форма решения, представ-
ленного ур-ниями '(7-23) и (7.24), очень интересна и удобна с
вычислительной точки зрения. Мы получили последовательный ал-
л л
горитм вычисления х(/ + 1|/) по известной величине х(/|/—1), вы-
численной на предыдущем шаге, и новому наблюдению z(j). Но-
вая оценка здесь формируется как результат экстраполяции ста-
рой оценки и последующей коррекции при помощи взвешенного
____________________________ л
сигнала ошибки наблюдения z(j|/—l)=z(j)—H(j)x(/|j—1).
Структурная схема экстраполятора Калмана показана на рис.
7.16; для сравнения исходные модели сообщения и наблюдений
Наблюдение Обновляющий процесс
и
Текущая оценка
---------ЛсДЙ
^^Предсказание •
Коррекция г
Задержка
на такт
_______
Предсказанное
наблюдение
Нф
Предыдущая оценка
Wlj-o
Рис 7.1. Структурные схемы задачи одношагового предска-
зания
а) модели сообщения и наблюдений, б) устройство одноша-
гового предсказания
показаны на рис. ТЛа Прежде чем воспользоваться полученным
выше результатом, необходимо сначала найти выражение для
260
О, чтобы вычислить К(/-Н1,/). Можно поступить иначе
и найти V~(/+l|j). Для того чтобы определить V-(/+1 |j), «ай-
дем сначала рекуррентное выражение для х(/+1|/). Объединяя
ур-ния (7.1) и (7.24), получаем
*(/ + 1 I /) = х(/.+ О—х(/+ 1 I /)-=Ф(/+ 1, /)x(/) + F(/)w(/) —
-Ф(/+ 1. /)*(/ I /-1)-К(/ + 1, /)[г(/) —Н(/)х(/ | /- 1)].
Если теперь подставить выражение (7.3) для z(j) и выполнить
ряд простых алгебраических преобразований, то поиведенное вы-
ше выражение приводится к виду
?(/ + 1 [ /) = [Ф (/ + 1, /) - К(/ + 1, /)Н(/)]х(/ | j - 1) + Г (/) X
Xw(/)-K(/+I,/)v(j). (7.25)
Кроме того, что ур-ние (7.25) может быть использовано при
вычислении V~(j +11/), оно представляет также самостоятельный
интерес жак закон изменения ошибки оценивания.
Так как среднее значение величины х(/ + 11/) равно нулю (по-
скольку оценка является несмещенной), а величины х()|/—1),
w(j) и v(/) —не коррелированы, то выражение для V~(j +11/) мо-
жет быть получено непосредственно, исходя из определения этой
величины и ур-ния (7.25), в виде
V~(/ + 1 | /)^г{х(/ + 1 | /)} = var{x(j + 1) | Z(j)} = [Ф(/ +
+ 1, /)-К(/+ 1, /)Н(/)J¥~(/ | /-1)[Ф(/+ 1, /)-К(/ + 1, /)Х
XH(/)]r + r(/)Vw(/)rr(/) + K(/+ 1, j)Vv(/)Kr(/ + l, /)
V~(/+1 I/) = Ф(/+1, /)V~(/|—1)ФГ(/+ 1. /) + К(/+1,/)Х
x [H (/) V~ (/ I j - 1) Hr (/) + Vv (/)] Kr (/ +1, j) - к (/ + 1, /) X
XH(/)V~(/1 /-1)ФЧ/ + 1, /)-Ф(/+ 1, /)V~(/1 J-I)x
X Hr (/) Kr (/ + 1, /) + г (j) vw (/) Гг (/).
Если теперь подставить (7.23) для К(/+1, j) и упростить по-
лученный результат, то получим следующее выражение для дис-
персии ошибки:
V~(/ + 1 | /) = ф(/ + 1, /)¥~(/ I / - 1)ФЧ/ + 1. /) + И/) Vw(/) X
ХР(/)-Ф(/ + 1, /)¥~(/ | / — 1)Нг(/)[Н(/)¥~(/ I /-1)НЧ/) +
+ Vv(/)]-’ H(i)V~(j I/- 1)ФЧ/+ 1. /). (7.26)
Уравнение (7.26) совместно с (7 23) и (7.24) полностью опре-
деляют линейный последовательный одношаговый экстраполятор
с минимальной дисперсией ошибки.
261
Прежде чем воспользоваться полученным выше результатом,
л
необходимо в уравнениях для х hV~ задать соответствующие на-
чальные условия. Очевидно, что наилучшей оценкой величины х(0)
при условии, что не было произведено наблюдений, является
£{х(0)} и, следовательно1), х(1|0)=Ф(1, 0)х(0|0) =Ф(1, 0)gx(0).
Поэтому
V~(l | 0) = var{x(l)—х(1 | 0)}^уаг{х(1)-Ф(1, 0)Их(0)}==
= Ф(1, 0)V~(0 | 0)Фг(1, 0)-|-Г (0) Vw (0) Гг (0).
Итак, в качестве начальных условий для алгоритмов одношагово-
Л’
ю предсказания выбираем х(0|0) =gx(0); V~(0|0) =V~(0).
Все алгоритмы одношагового предсказания сведены в табл. 7.1.
Уравнение (7.26) можно переписать также в следующем виде:
V~(y + 11 /) = [ф (/• + 1, /)-К(/ +1, /) н (/)] V~(j | / — 1) Фг (/• +
+ 1, j) + r(j)Vw(j)r^j).
Если задать начальные условия в ур-ниях (7.24) и (7.26), то
можно последовательно использовать алгоритмы одношагового
предсказания. Например, ур-ние (7.23) с начальным условием
v~(i|O) может быть использовано для нахождения К(2,1) , кото-
Л
рое затем необходимо подставить в (7.24) для вычисления х(2| 1)
по первому наблюдению z(l). Уравнение дисперсии (7.26) исполь-
зуется на следующем этапе при пересчетеV~ в V~(2|l). Получен-
ное значение величины V~ (211) затем используется для вычисле-
ния К(3,2) и т. д. Обработка данных согласно уравнениям пред-
сказания схематически показана на рис. 7.2. Внимательный ана-
лиз ур-ний (7.23) и (7.26) показывает, что вычисление величин
К(/+1, j) hV~(j+1|/) фактически выполняется без обращения к
последовательности наблюдений z(l), z(2), ..., z(/). Можно зара-
нее вычислить и запомнить матрицы коэффициентов усиления К.
Вероятно, мы могли бы не принимать этот метод предварительно-
*) Будем использовать символ х(1]0) для обозначения оценки величины х,
как результата экстраполяции при отсутствии априорной информации. Это обо-
Л
значение означает, что x(li|O) есть оценка х(1) по наблюдению с номером k = 0.
Так как наблюдения начинаются только при k=i, то этот случай соответствует
Л
отсутствию наблюдения и, следовательно, х(110) есть не что иное, как априор-
л л Л
ное значение х(110) = Ф(1, 0)х(010). Конечно, если заданы х(1|0) иУ~(1|0)
Л
вместо х(0|0) и V-—(0 ] 0), то они непосредственно могут быть использованы в
качестве начальных условий при решении этой задачи. {Прим, авт.)
262
Таблица 7.1
Дискретные алгоритмы одношагового предсказания
Модель сообщения
х(/+1) = Ф(/ + 1, j)x(j) +r(f)w(/). (7.1)
Модель наблюдений
z(/) = H(/)x(7) +v(/). (7.3)
Априорные данные
£{w(/)} = 0; E{v(/)} = 0; Е {х (0)} = рх (0);
cov{w(/), w(£)} = Vw (/)6К (/— k);
cov{v(j), v (Л)} = Vv (j) (j — k);
cov{w(/), v(k)} = cov {x(0), v (&)} = cov {x (0), w (Jfe)} = 0;
var {x (0)} = V~(0) = Vx (0).
Алгоритм предсказания
х(/ -H |/) = Ф(/-H, /)х(/|у —1)+К(/+1, /)[z(/)—Н(/)х(/| j —1)]. (7.24)
Вычисление коэффициента усиления
КП-Ы, /) = ф(/+1, /)v~(n/-i)H4/)[H(/)V~(ni-i)Hr(/) +
+vv (/)]-‘. (7.23)
Вычисление априорной дисперсии
v~() +11 /) = ф (7 +1, 7) V~(j 17-1) фг (j 4-1, 7) +
+Г (7) Vw (7) гг (7) - ф (7 +1, 7) v~ (/17 -
-1) нг (7) [Н (7) v~(/17 -1) Нг (7) + Vv (/)]-' Н (/) V~(/1 / -1) Фг (7 +1, j).
(7.26)
Начальные условия
х (1[| 0) = Ф (1, 0)х(0) = Ф(1, 0)Е{х(0)};
VA (1 |0) = Ф(1, 0) V- (0 1 0) Фг (1, 0) + Г (0) Vw (0) Гт (0).
го вычисления матриц К, если бы скорость поступления наблюде-
ний на вход процессора не была такой высокой и не препятство-
вала бы выполнению вычислений согласно ур-ниям (7.23) и (7.26)
в реальном масштабе времени или если бы возможность запоми-
нания не являлась более доступной и дешевой по сравнению с воз-
можностью вычислений в реальном времени.
263
Главное 'преимущество алгоритмов фильтрации Калмана зак-
лючается не столько в том, что они дают решение задачи фильт-
рации (решение другими способами было получено гораздо рань-
ше), 'Сколько в том, что решение непосредственно определяет прак-
тическую реализацию результатов. При решении многих практи-
Рис. 7.2. Структурная схема вычислений по алгоритмам пред-
сказания
ческих задач можно обеспечить реализуемость вычислений по
ур-ниям (7.23) и (7.26) в реальном масштабе времени и, следова-
тельно, реализовать последовательные алгоритмы фильтрации в
реальном масштабе времени. Еще одна характерная особенность
рассмотренного подхода заключается в том, что дисперсия ошибки
VST (J+11/) вычисляется как составная часть оценки и поэтому
может быть использована для контроля точности процедуры оце-
нивания. Это основано на предположении о том, что модели сооб-
щения и наблюдений, а также априорное распределение извест-
ны полностью.
Пример 7Л. Пусть модели сообщения и наблюдений заданы скалярными
уравнениями:
х (k + 1) = 0,5х (k) + ш (k); z(k) = х (k) -|- v (k),
причем Vw{k, j)=6K(k—j) и V„(k, ])=26K(k—]) или yw(fe)=il, Vv(k)=2.
Здесь мы предполагаем, что шум является стационарным и белым, хотя,
вообще говоря, не обязательно, чтобы он был стационарным. Предположим
также, что начальное значение х имеет нулевое среднее и единичную диспер-
сию, так что pi(0)=0 и Уж(0) = 1.
264
Для этого примера уравнение оценивания (7.24) принимает вид
х (j + 1 I /) = 0,5 х (j | j — 1) + К (j + 1, j) [г (/) — х (/ [ / — 1)]
с коэффициентом усиления К(/+1, /), определяемым из уравнения
К(/ + В /) =0,5 V~(J | j~ 1) [ V~(j i/-!)+ 2]-l.
Уравнение дисперсии имеет вид
V~ti +1 I i)=0,25Г~(/ | j - 1) + 1 -0,25 [ V~(j | / - I)]2 [ V~(j | j - 1) +
+ 2]-i .
Л Л
Вычислим x(2| 1) и x(3|2) в предположении, что у нас имеются наблюдения
2(1) =4, z(2) =2. Вычисляем сначала коэффициент усиления /<(2, 1), используя
начальное условие Цх(0) = 1:
V~(l | 0) = (0,5)2 (1) + 1 = 1,25; К (2,1) = (0 ,5) (1,25) (1,25 + 2)—1 =5/18.
Л Л
Используя начальное условие цх(0)=0, получаем х(110) = (0,5) (0) =0 и х(2|1) =
5 10
= (0,5) (0) + "^"(4—0) = . Дисперсию погрешности этой оценки определим из
/ 5 \
уравнения дисперсии следующим образом: У~(2|11) = (0,5)2 (— +1—
х \ 18 /
/ 5 W 5 \-i
— (0'5)21ТД) ГХ+2 -0,9948. Теперь необходимо повторить все этапы вычис-
\ 1 О / \1 О /
лений, чтобы найти /<(3,2), оценку х (3|2) и, наконец, дисперсию V~ (3|2).
Хотя рассмотренный пример является чрезвычайно простым, но он достаточно
наглядно иллюстрирует все этапы вычислений, которые необходимо выполнить
в процессе применения алгоритмов одиошагового предсказания Калмана.
Одной из практически важных задач, возникающих три исполь-
зовании (Приведенных выше результатов и даже более трудной,
чем нахождение среднего значения и дисперсии начального со-
стояния, является определение дисперсии входного шума и шума
измерения. Значения дисперсий Vw и Vv часто могут быть полу-
чены либо из анализа физической сущности задачи, либо (путем
непосредственного измерения с разумной точностью. Аналогичные
замечания можно сделать относительно априорных моментов век-
тора состояния. Величина цх(0) выбрана как наилучшая оценка
среднего значения вектора состояния на нулевом шаге, т. е. до
того, как были произведены наблюдения, a Vx(0) как характерис-
тика степени неопределенности при выборе gx(0).
В чисто качественном смысле можно утверждать, что чем зна-
чительнее неопределенность относительно истинного значения
цх(0), тем большие значения Vx(0) мы задаем.
Теперь обратимся к задаче фильтрации. Одношаговый зкстра-
полятор использовался как удобный этап решения этой основной
задачи, .и он часто имеет практическое значение. Мы убедимся,
что решение проблемы фильтрации включает в себя одношаговое
предсказание, результаты которого затем корректируются в соот-
ветствии с текущей информацией. Часто, но не всегда, решение
265
проблемы фильтрации следует предпочесть решению проблемы од-
ношаговой фильтрации.
Если оценка x(k), полученная как результат фильтрации, а
л л
именно x(i£|ifc), известна, то х(&+1|^) может быть получена как
л л
х(*+ 1 I А) = Ф(^+ 1, k)x(k I k). (7.27)
Так как x(k) и, следовательно, z(k) зависят от w(7) только
для i<&, то пространство наблюдений Z(k) не содержит инфор-
мации относительно vf(k), где — дискретный белый шум.
Следовательно, для предсказания значения х(&+1) по наблюде-
л
ниям Z(k) достаточно предсказать значения x(k\>k) на один шаг
л
вперед, полагая w(^|£)=0. Такой подход позволил получить
ур-ние (7.27), которое будет использовано в дальнейшем. Умыш-
ленно допуская нестрогую запись ради простоты обозначения, за-
л л
пишем х(7|/) как x(j). За исключением специально оговаривае-
л
мых случаев, как в х(/|/—1), будем предполагать, что условия
задаются пространством Z(j). В этих обозначениях ур-ние (7.27)
перепишется в виде
х(£ + 1 | k) = Ф (k + 1, k) x(k). (7.28)
Очевидно, что две оценки х(/+'1), основанные на наблюдении Z(j),
должны быть эквивалентны. Следовательно, можно использовать
ур-ние (7.28) для получения последовательного алгоритма оцени-
л
вания x(j) из ур-ний (7.23), (7.24) и (7.26). Сначала подставим
ур-ние (7.28) при &=/, /—1 в (7.24). В результате получим
Ф(/+1, /)х(/) = Ф(/+ 1, /)Ф(/, /_1)х(/-1)+К(/+1, /)Х
X [z (/) — Н (/) Ф (/, у— 1) х(7— 1)].
Если умножить обе части этого уравнения на Ф(/,/+1), кото-
рая в силу свойств переходной матрицы состояний равна
Ф-1 (/ +1, /), то получим
х(/) = Ф(/, /— 1)х(7— 1)4-Ф(7, /X 1)К(7+ I, /)[z(7) —
-Н(/)Ф(7, /-i)x(j-i)].
Чтобы упростить полученное выражение, введем К(7), опреде-
ляемую как К(/) 1 Ф(/, / + 1)К(/+1,/) , или
K(/) = V~(/ I 7— 1)H^(7)[H(7)V~(7 I /- 1)НГ (j) + Vv(/•)]->, (7.29)
если использовать для определения К(/+1,/) ур-ние (7.23). По-
266
этому x(j) записывается в виде
X (/) = ф (/, / - 1) X(/ - 1) + K(j) [z (j) - Н (/) Ф (j, j - 1) - 1)].
(7.30)
Хотя ур-иие (7.30) представляет собой, вероятно, наиболее
удобную форму записи уравнения оцеиива1иия для фильтра Кал-
маиа, в принципе можно получить несколько других форм записи.
Две из них оказываются особенно полезными. Если воспользо-
л л
ваться соотношением х(/|/—1) =Ф(/+1, j)x(j), то ур-иие (7.30)
можно переписать в следующем виде:
х(/)= Х(/ I /- 1)K(/)[z(/) —Н(/)х(/ I /- 1)]. (7.31)
Это выражение можно еще более упростить, если ввести «обиов-
~ л
ляющую» величину z(j|/—l)=z(/)—H(j)x(/|j—1), чтобы полу-
чить
х(/) = х(/ I /_1) + К(/)1(/ I /-1). (7.32)
Уравнения (7.29)—(7.31) или (7.32) совместно с ур-нием (7.26)
полностью дают решение проблемы линейной фильтрации по кри-
терию минимума средиеквадратической ошибки. Заданные началь-
ные условия по х, а именно |1х(0) и Vx(0), используются для фор-
А
мирования начальных условий соответственно для х(/|/) и V~(j| j)
так же, как и в одношаговом экстраполяторе.
Алгоритмы фильтрации Калмана могут быть представлены в
более удобной форме, если найти выражения для дисперсии ошиб-
ки фильтрации V~ (/)^var{x(j)}. К тому же дисперсия V~(j) мо-
жет быть использована как критерий качества процедуры оцени-
вания. Дисперсию V—(/1/—1) часто называют априорной диспер-
сией, так как она представляет собой дисперсию оценки x(j) до
момента наблюдения z(/), а дисперсию V~(j) называют апо-
стериорной дисперсией. Для того чтобы определить¥~(/), сначала
найдем выражение для х(/). Опять возможно несколько форм пред-
ставления х (/) Одной из наиболее удобных для нашего случая
является представление x(j) с помощью ур-ния (7.32). В этом
случае x(j) определяется следующим образом:
х(/)Дх(7) —x(j) = x(/) —х(/ | у— 1) —K(/)z(/ | / — 1)= х(/ | / —
-1)-К(/)7(/ | /-1).
Поэтому
¥r(/) = VT(/| i~ 1) + К(/)Е{Г(/|/-1)Т(/ | /- 1)}КГ(Д-
267
-К(/)Е {!(/ I j- 1)хгЛ I /- !)} — ^{ X(/ I /- l)zr(/ I /- 1)} x
X Kr(/).
Если теперь подставить ур-ния (7.29) для К(/) и (7.19) и (7.20) для
£{^(/|/—I)Z^(/|/—1)}=£-{х(/)^(/|/—1)} и £-{Z(;|/—1)Z^(/|/—1)}
в это выражение, то получим
vT(/) = vr(/1 i-1)-v~(/1 /- 1)H4/)[H (/)¥-(/1 /-1) НЧ/) +
4- Vv(/)]-i H(/)V~(/ | /-1).
Если воспользоваться ур-нием (7.29) для Kf/), то последнее
выражение может быть переписано в 'виде
VT(/) = H-K(/)H(/)]Vr(/| /-1). (7.33)
Согласно этому уравнению дисперсия ошибки фильтрации до-
статочно просто выражается через дисперсию ошибки одношаго-
вого предсказания. Использование величиныV~f/) позволяет так-
же значительно упростить ур-ние (7.26). Перепишем его в виде
v~(/+ 1 | /) = Ф(/+ 1, /){¥-(/ I /-1)-¥~(/ I /—1)НГ(/)Х
Х[Н (/)¥-(/ I /-l)H4/) + Vv(/)]-’ Н(/)¥-(/ I /- 1)}ФЧЖ,/)+
-ь r(/)Vw(Z)rr (/).
Воспользовавшись ф-лой (7.29) для К(7)> можно записать это
выражение как
V~(/ + 1 | /) = Ф (/ + 1, /) [¥~(/ j j - 1) - К(/)Н(j) ¥T(j | j - 1)] X
X Фг(/ + Е/)+r(/)Vw(j)rr(j) = Ф(/+ 1, I /-
-1)}Фг(/ + 1, /) + r(7)¥w(/)rr(/).
Легко заметить, что величина, стоящая в фигурных скобках,
представляет не что иное, как ¥~ (j). Поэтому имеем
v~(/ + i | /) = Ф(/ + 1, /)¥-(/)ФЧ/ + С /) + r(/)Vw(/)rr(/)-
(7.34)
Это выражение могло быть получено обычным способом путем
вычисления дисперсии случайной величины, задаваемой ур-нием
(7.1) при заданном Z(k).
Уравнения (7.29), (7.30), (7.33) и (7.34) полностью опреде-
ляют окончательный вариант дискретного фильтра Калмана. Эти
уравнения сведены в табл. 7.2. Структурная схема вычислений
согласно полученным алгоритмам приведена на рис. 7.3, а струк-
турная схема дискретного фильтра Калмана — на рис. 7.4.
Обращаем еще раз внимание на то, что в уравнение для дис-
персии и коэффициента усиления не входит последовательность
наблюдений, поэтому при необходимости эти величины могут быть
вычислены заранее. Эта возможность условно показана на рис. 7.3
пунктирной линией.
268
Таблица 72
Сводка дискретных алгоритмов фильтрации Калмана
Модель сообщения
х(/ +1) = Ф (/ +1, /) х (/) +r(/)w(/). (7 1)
Модель наблюдений
z (/) = Н (/) х (/) +v(/) (7.3)
Априорны’' данные
£{w(/)}=0, £{v(/)}-0, Г{х(0)}=рх(0),
cov {w (/), w (£)} = Vft (/) 6K (j — k),
cov(v(/), v(6)}=Vv (/)6,4 (/ — k),
cov{w(/), v (k)} = cov {x (0), w (k)} = cov {x (0), v (£)} = 0,
var{x(0)} =V~ (0)
Алгоритмы фильтрации
x(7) = Ф (b / — 1) х(/ — f) + К(7) fz(j) — ff(7) Ф (/, j — I) x(j — I)f (7 30)
Вычисление коэффициента усиления
К G) = v~(/1 / — 1) н7" (/) [H G) v~(/ I i -1) HT G) +vv (у)Г1 =
= V~G)H7’G)Vv“,G) (7 29)
Вычисление априорной дисперсии
(/ + 1 I/) = Ф (/ +1, /)v~G)*r(/ + h /) + r (/) vw (/) гг 0). (7 34)
Уравнение для -постериорной дисперсии
V~ G) = [I -K(/) H G)] v~ GI/-1)
(7 33)
Начальные условия
x (0 | 0)= x (0) = (0), V~ (0 | 0)= V~(0) = Vx (0)
Анализ структурной схемы рис. 7 4 показывает, что в фильтре
Калмана реализуется идея предсказания — коррекции Предыду-
д
щая оценка х(/ — 1) экстраполируется на один шаг вперед и затем
используется Атя получения наилучшей оценки нового наблюде-
ния z(j), основанной на всех предыдущих наблюдениях. Ошибка
между «чаилучшей оценкой» текущего наблюдения и фактическим
наблюдением а именно J (/1/—1) или z(/|j—1), представляет со-
бой новую информацию [компоненту z(/), ортогональную Z(/—1)].
Ошибка взьешх1зас"-еч с весом Kf/), учитывающим значение дис-
персий входного процесса, измерения и ошибки оценивания для
269
Рис 73. Структурная схема вычислений по алго-
ритму фильтрации Калмана
Наблюдение
Обновляющий процесс
K(j)
Коррекция
Првдсказа-
~~1 нов
— x(j\j-i)
Текущая оценка
x(j).
'{Задержка
такт
*(Н)
Предыдущая
оценка
Рис. 7.4. Структурная схема дискретного фильтра Калмана
формирования сигнала коррекции. Сигнал коррекции складывает-
ся с предсказанной оценкой и в результате получается .новая
оценка.
Заметим, что структура фильтра Калмана, соответствующая
ур-1нию (7.30) и изображенная на рис. 7.4, очень напоминает струк-
туру исходной модели сообщения, заданной ур-нием (7.1) и при-
веденной на рис. 7.1а. Алгоритм фильтрации строится на исполь-
270
зовании '«обновляющей» компоненты, которая содержит новую ин-
формацию, полученную в результате наблюдения.
Пример 7.2.
Для иллюстрации применения алгоритма фильтрации Калмана рассмотрим
двумерную модель сообщения, задаваемую уравнением
х (&+!)= Г Jjx (&) + »(&)•
V~(0) =
Наблюдение осуществляется согласно скалярной модели z(k) =Xi(k) +v(k).
[° ° 1
Входной шум является стационарным с Vw(/)= , а шум измерения —
нестационарным с VB(/)=2+(—I)3 Другими словами, измерения для четных
индексов j осуществляются менее точно, чем для нечетных Предположим, что
дисперсия начальных ошибок (или начального состояния) задается матрицей
10 01
0 10 Требуется вычислить значение К(у) для всех j от 1 до 10.
Используя ур ния (7 29) и (7 34), а также начальное условие Vx(0), можно
легко вычислить V~ (110) и К(1), которые соответственно равны
V~(l
X
0) =
120
[10
10 I
И J
к (1)
[0,951
L -I •
10,4»J
Теперь с помощью ур-ния (7 23) можно вычислить апостериорнхю дис-
персию
[0,95 0,481
V~(l) =
’ [0,48 0,24]
а также априорную дисперсию, которая изменяется для следующего шага
согласно ур нию (7 34) и становится равной
V~(2
х
8,14
6,71
6,711
7,23] '
Теперь можно вычислить К(2) и т д Компоненты вектора К(/), при изме-
нении j от 1 до 10, показаны на рис 7 5 Отметим характерное увеличение
коэффициента усиления для нечетных значений ], в результате которого усили-
ваются относительно точные изме-
рения Можно заметить, что коэф-
фициент усиления достигает свое-
го установившегося периодически
изменяющегося значения за не-
сколько выборок Вероятно, полез-
но вкратце и чисто качественно
обсудить влияние соотношения
величин Vw и Vv на K(j), даже
если трудно получить общие коли-
чественные результаты Во-первых,
здесь важны относительные зна-
чения, а не абсолютные В част-
ности, легко показать, что в том
случае, когда Vw(/), Vv(/) л
Vx(0) умножаются на одну и ту
же положительную скалярную по-
стоянную, то К(у) не изменяется.
Весьма приближенно можно лишь
утверждать, что коэффициент уси-
ления зависит от отношения сиг-
Рис 7 5 Изменение коэффициентов уси-
ления фильтра Калмана, рассмотренно-
го в примере 7.2
271
нала [Vw (/)] к шуму (Vv(/)] Элементы матрицы коэффициентов уменьшаются
по мере уменьшения значений элементов матриц Vw(j) н Vx(0) [или только в
Vx(0)J или увеличения значений элементов матрицы Vv(j). Этот результат
представляется интуитивно вполне понятным, поскольку по мере уменьшения
Vn(/) следует ожидать все меньших изменений в состоянии х, а поэтому иет
необходимости «отслеживать» наблюдения так точно. Аналогичным образом,
если Vx(0) уменьшается, то повышается точность начальной оценки х и по-
требность в информации, содержащейся в наблюдениях, снижается и, следова-
тельно, коэффициент усиления уменьшается. С другой стороны, если Vv будет
возрастать, то коэффициент усиления снова уменьшается, препятствуя добавле-
нию к оценке чрезмерного шума измерения. В пределе, когда Vw(y) стремится
к нулю, как нетрудно показать, К(/) асимптотически приближается к нулю для
больших значений у. Когда К стремится к нулю, дисперсии ошибок также стре-
мятся к нулю и процедура оценивания становится не зависящей от наблюдения
и входит в режим, известный под названием насыщения по входным данным.
Этот режим может привести к серьезным проблемам расходимости. Методы кор-
рекции расходимости подробно обсудим в разд. 8 5.
Оценивание по критерию максимума апосте-
риорной вероятности. Получим линейный алгоритм оцени-
вания, предположив, что w, v и х(0) имеют нормальные законы
распределения. В этом случае нетрудно показать (см. § 4.2), что
х и z — случайные величины с нормальным законом .распределения
для всех k^Q. Поэтому E{x(k)\1(tk)} представляет собой линей-
ную функцию наблюдения. Иначе говоря, линейный алгоритм оце-
нивания по критерию минимума дисперсии ошибки является алго-
ритмом оценивания с минимальной дисперсией ошибки, причем
дисперсия ошибки меньше или равна дисперсии ошибки любого
другого линейного либо нелинейного алгоритма оценивания.
Чтобы получить алгоритм оценивания по критерию максимума
апостериорной вероятности, требуется лишь определить условную
плотность вероятности величины -x.(k) при заданном а затем
найти ее математическое ожидание. Так как условное распреде-
ление ~x.(k) при заданном Z(k) нормальное, то, как известно (см.
§ 6.2), алгоритм оценивания, вычисляющий условное математиче-
ское ожидание, минимизирует не только средний квадрат ошибки,
но также среднее значение абсолютной ошибки при простой и
многих других функциях потерь.
Таким образом, можно подучить алгоритм оценивания с мини-
мальной дисперсией, рассмотрев оценивание при любых других
функциях потерь, например, оценивание по критерию максимума
апостериорной вероятности (сокращенно МАВ-оценивание), когда
функция потерь выбирается простой, а сценка совпадает с модой
условной плотности.
Воспользуемся этим приемом [94] и построим алгоритм
МАВ-оценивания. Так как некоторые выражения, с которыми при-
дется оперировать, могут оказаться слишком длинными, в процес-
се изложения иногда будем пользоваться упрощенной формой за-
писи. Допуская незначительную нестрогость, откажемся от индекс-
ного обозначения для плотностей вероятности, а рассматриваемые
случайные величины будем обозначать как аргументы этих плот-
ностей. Например, значение плотности вероятности случайной ве-
личины х в точке а, р*(а) записывается в этом случае как р(х.)',
272
аналогично px|z(a]₽) записывается как p(x|z). И не надо пытать-
ся трактовать эту упрощенную форму записи как вероятность то-
го, что х=х (это явная бессмыслица), (вернее, плотность вероят-
ности р(х) следует рассматривать как функцию, а не как значе-
ние этой функции, которое она принимает для конкретного наблю-
дения. К сожалению, в нестрогой математике, которой пользуются
инженеры, часто недостаточно четко подчеркивается различие
между функцией, как отображением одного множества в другое,
и конкретным значением этой функции.
Функция плотности вероятности, рассматриваемая при оцени-
вании на основе критерия максимума апостериорной вероятности
либо на основе условного математического ожидания, представ-
ляет собой функцию случайной (величины х(1г) при заданной по-
следовательности наблюдений Z(&) и обозначается как
p[x(k) | Z(\k)J. Алгоритм оценивания, основанный на условном ма-
тематическом ожидании, определяется как
х (k) = J х (Л) р [х (k) | Z (A)] d х (k). (7.35)
--00
Оценка по критерию максимума апостериорной вероятности, кото-
л
рую будем обозначать как хмар(^), находится как решение урав-
нения
^pfxffl J Z (fe)J
д x(k)
л =0
х (А)=хмар <ft)
(7.36)
при условии, что
д Гдр[х(*)|2(ЭД
д х (А) [ д х (k)
л <0.
х <А)=хмар («
(7.37)
Если выполняется условие (7.37), которое требует, чтобы мат-
рица вторых производных была отрицательно определенной, то ре-
шение ур-ния (7.36) соответствует максимуму условной плотности.
Чтобы найти выражение для p[x(k) ]Z(<k)], воспользуемся тео-
ремой умножения и запишем p[x(k) |Z(A)] как
р[х(£) | Z(Z>)] = р[х(/г), Z(£)]/p[Z(A)]. (7.38)
Если рассматривать Z(k) как объединение нового наблюдения
и Z(k—1) предыдущих наблюдений, то ур-ние (7.38) перепишется
в виде
р[х(*) | Z(£)] =
p[x(fe), z (fe), Z(k — 1)]
p[z(k), Z(k~l)]
(7.39)
Рассмотрим числитель этого выражения. Применяя теорему
умножения, можем записать
273
p[x(£), z(k), Z(k—1)] = p\z(k) | x(£), Z(k—1)]р[х(й), Z(k—1)]
и далее
p[x(A), z(k), Z(k— 1)] = p\z(k) | x(^), Z(k— 1)]p[x(Z’) | Z(£— 1)] X
Xp[Z(.%— i)j
или
p[x(k), z{k), Z(k-\)]=p\z(k) I x(£)]p[x(£) I Z{k- l)]p[Z(t-l)],
(7-40)
так как знание x(k) несомненно исключает необходимость сохра-
нения Z(k—1). Если x(k) задана, то в z(k) случайной величиной
является только v(£) и поскольку v — белый шум, то
никакой информации о v(k) не содержится ни в x(k), ни в Z(k—1).
Если подставить'выражение (7.40) в (7.39), то получим
p[z(k) )х(Ь)]р[х (k) fZ(k~l)}plZ(k-l)]
p[z(k), Z(k~l)J
p[x(k\ I Z(£)] =
Применяя теорему умножения к знаменателю, полученное вы-
ражение запишем в виде
гх(-м | Z Ofe)I = p[z(^ 1 х(*)1 I Z(fe—l)]p[Z (fe —1)1
P p[z(k) I Z(k-l)lp[Z(k-1)]
После сокращения на общую скалярную функцию вероятности
p[Z(k—1)] получаем
p[x(k) I Z6H1 = -р[^ l-£(4I_p[xWIZ(fe-l)l
11 p[z(*)|Z(*-l)]
(7.41>
Теперь можно определить условную плотность вероятности слу-
чайной величины x(k) при заданном Z(k) путем вычисления каж-
дого выражения для вероятности, стоящего в правой части ур-ния
(7.41). Рассмотрим каждый член в отдельности, доказывая, что
каждая плотность вероятности, входящая в (7.41), нормальная, и
определяя первые два момента, характеризующие нормальное рас-
пределение. Исследуем сначала p[z(k) (х(й)]. Так как z(k) задает-
ся уравнением z(k) = Н(7г)х(£) + v(A), a v—нормальный случай-
ный процесс, то плотность вероятности p[z(k)|х(^)] несомненно
является нормальной, поскольку z(k) есть сумма нормального слу-
чайного процесса и постоянной величины H(k)x(k). Среднее зна-
чение процесса равно
Е {z (k) | х (k)} = E {H (k) x (k) + v (k) | x (4)} = H (Л) x (k), (7.42)
поскольку v — случайный процесс с нулевым средним значением.
Дисперсия случайного процесса равна по определению
var{z(£) | x(^)}AE{[z(^) — Н(й)х(А)] [z(£) —-Н(£)х(£)]г}, (7.43')
а в данном случае
var{z(&) | х (Л)} = var{v(6)} = Vv(£). (7.44)
274
Отсюда плотность вероятности p[z(i£) |х(7г)] можно записать в сле-
дующем виде:
_ 2
р [z (k) I X (*)] = {(2п)м det [ Vv (£)]} 2 ехр j- [z (k) - H (*) X
X x (6)И V ($) [z (k) - Н (k) х (A)]j . (7.45)
Теперь рассмотрим знаменатель выражения (7.41), точнее,
плотность вероятности величины z(k) при заданном Z(&—1). Ис-
пользуя уравнение для модели наблюдений, pfz(A)|Z(&—1)] мож-
но записать как
p[z(k) | Z(4-l)] = p[H(A)x(A) + v(4) | Z(£— 1)J.
Согласно исходной постановке задачи известно, что v(k) имеет
нормальный закон распределения и не зависит от Z(>fe—1). Если
предположить, что р[х(£) |Z(ife—1)] — нормальная, то несомненно
p[z(£)|Z(&—1)] также является нормальной, так как z(k) пред-
ставляет собой линейную функцию (сумму) двух случайных вели-
чин, имеющих нормальный закон распределения. Плотность ве-
роятности случайной величины x(k) при заданном Z(&—1) и не-
нормальная, так как она в этом случае просто совпадает с р[х(0)],
которая согласно исходному предположению — нормальная. Ниже
будет показана справедливость допущения о том, что
p[x(fe)|Z(A—1)], а следовательно, и p[z(fe) |Z(ife—4)] являются нор-
мальными для всех Среднее значение г(1г) с плотностью
p[z(ife) | Z(Л— 1)] равно
E{z(k) | Z(£-l)} = H(£)E{x($) | Z(^-l)} + E{v(A) | Z(A-1)} =
= H(A)x(A | k— 1), (7.46)
Л
где использовано ранее введенное обозначение x(fe|<fe—1) =
— E{x(k) |Z(A—1)}; Е{у (k)\Z(k—1)} равно нулю, так как v — бе-
лый шум с нулевым средним. Дисперсия процесса i(k) по опреде-
лению равна
var{z(Z>) | Z(k — l)}Af{[z(/e)— Н(А)х(А | k— l)][z(A) — Н(А)Х
Хх(^ | k— l)f}.
Подставляя выражение для z(k) и используя обозначения
х(£|£—1) =,х(А)—x(k\\k—1), получим var{z(£)|Z(£—1)} =
=<H(£)var{x(fe|i£— l)}HT(fe) +var{v(£)} или
var{z(A) | Z(fe—1)) = H(A)V~(A | k- l)Hr(Z:) +Vv(£)- (7.47)
Здесь мы воспользовались тем, что x(fe|i&—1) и v(k) независи-
мы (v — белый шум), и исключили член, представляющий собой
275
cov{x(ifc|i£—1), v(ife)}. Поэтому условная плотность вероятности
величины z(k) при заданном Z(k—1)
__1
р [z (k) I Z— 1)1 = {(2n)M det [H (k) V~(k I k - 1) Hr (£) + Vv (A)]| 2x
Xexpl-----‘ [z(A)-H(ft)x(A | £-l)f [H(fe)V~(fc | k— 1)HT(£) +
+ Vv (6)]-1 [z(A)-H(A)x(fe | k- 1)]} . (7.48)
Если предположить, что p[x(ife)|Z(&—1)] — нормальная, то не-
обходимо найти только среднее значение и дисперсию. Среднее
значение определяется ур-нием (7.28)
E{x(k) | Z(k — 1)} = Ф (A?, k — 1)х(А — 1) = х(% | k — 1). (7.49)
Из предыдущих результатов также известно, что дисперсия
xfife) при заданном Z(ife—1) просто совпадает с априорной диспер-
сией ошибкиУ~(&|£—1). Таким образом, из ур-ния (7.34) имеем
var{x(/?) | Z(k — 1)) = Ф(/?, k — \)V (k — 1)ФГ(А, £—1) +
+ Г (A- 1) Vw(*- 1)R(*_ 1). (7.50)
Теперь плотность вероятности f{x(k)\Z(k—1)] можно записать
в виде
__1
p[x(k) I Z(k- 1)] = {(2л/det[VT(6|Z!- 1)]} 2exp{-----J-[x(£)-
— x(A | k— l)]rV^! (k\k — 1)[x(A) — x(k | k— 1)]} . (7.51)
Итак, <все члены, стоящие в правой части выражения (7.41), опре-
делены и 'Можно записать условную плотность вероятности вели-
чины x(k) при заданном Z(k). Подстановка ф-л (7.45), (7.48) и
(7.51) в (7.41) приводит к следующему результату:
р [х (A) I Z (А)] = {(2л/ det [Vv (£)] {det [Н (k) V~ (k | k — 1) H7 (k)
__i
+ Vv (£)]}“’ det[v~(Z! | k— 1)]) 2exp(— у {[z (Л?) — H(4)x(^)f <
X V7> (k) [z (k) - H (*) x (£)] + [x (k) - x (k | k - 1)F V~> (£ | k - 1) X
X[x(fc)-x(* | 1)] - [z (6)-H (*)£(* I k-l)f[H(A)V~(£ I k-
— l)Hr + Vv(fe)]-1 [z(fe)-H(fc)x(£ I k~ 1)]}) . (7.52)
276
Это выражение может быть записано в более компактном виде:
р [к (k) | Z (ft)] = А ехр [- -1- [х (k) - х (k}? y-i (/г) [х (k) - х (ft)]| ,
(7.53)
где А —постоянная;
x(ft)A£{x(ft) | Z(ft)} = x(ft | k— 1) + K(ft)[z(ft) — H(ft)x(ft | k— 1)];
(7-54)
К (k) = V~(k | k — 1) H7 (ft) [H (k) V~(ft | k — 1) H7 (ft) + Vv (ft)]-» =
= VT(ft)H4ft)V7'(ft); (7.55)
Vr(ft)^var{x(ft)} = [I —K(ft)H(ft)] V_(ft j ft— 1) = V~(ft | ft— !) —
— V~(ft | ft — 1) H7 (ft) [H (ft) V~(ft I % — 1) Hr (ft) + Vv (ft)]-» x
X н(ft) V~(ft I ft — 1) = [IF (ft) Vy1 (ft) H (ft) + V~»(ft 1 ft — l)]-> . (7.56)
Здесь дисперсия величины x(k) при заданном Zfft), а именно
Vxfftjft), обозначена через так как дисперсия величины x(k)
при заданном Zfft) определяется V~(ft).
Доказательство эквивалентности выражений (7.52) и (7.53),
хотя, в принципе, и не трудно, требует достаточно большого числа
алгебраических преобразований. Равенство экспонент в этих двух
выражениях можно доказать, если выписать соответствующие вы-
ражения, используя ф-лы (7.54) и (7 56), и применить леммы об
обращении матриц. (Коэффициент А легко найти, если вспомнить,
что плотность p[x(&)\Z(&)]— нормальная с дисперсией V~(ft) От-
сюда имеем следующее выражение для коэффициента А:
___1
Д = {^nfdetlV^ft)]} 2 =
___1
( (2n)Jvdet[Vv(ft)]det|‘V-r(ft | k-I)] | 2
= ( det[H(ft)V~(ft|ft-l)H7(ft)+Vv(ft)] j
Теперь можно проверить предположение о том, что плотное;ь
pfx(ft) Z(ft—1)] — нормальная. Мы показали, что если плотность
p[x(ft) Z(ft—1)] является нормальной, то плотность ppcfift) ]Z(ft)]
также нормальная. Используя ур-ние (7.1) и тот факт, что w —
белый шум, можно показать, что плотность p[x(ft+1) |Z(ft)] так-
же нормальная. Итак, имеем цепь утверждений, причем известно,
что плотности р[х(0)] и р[х(0) |Z(0)], рассматриваемые в каче-
стве начальных в этой цепи, являются нормальными. Следователь-
но, подтверждается предположение, что плотность p[x(ft)[Z(ft—1)]
нормальная.
277
Оценка состояния x(k) при заданном Z(k), основанная на ус-
ловном математическом ожидании (оценка по критерию миниму-
ма дисперсии ошибки), определяется ур-нием (7.54) и согласуется
с ранее полученными результатами [см. (7.30)]. Однако в этом
Л
случае оценка х(А) точно равна условному математическому ожи-
данию (поскольку здесь предполагалось нормальное распределе-
ние), а не является наилучшей только в классе линейных оценок.
Конечно, для нормального распределения обе оценки совпадают,
так как условное математическое ожидание — линейная функция
наблюдения.
Чтобы определить МАВ-оценку, необходимо найти значение
х(&), которое максимизирует p[x(k) | Z(ik)] >). Воспользуемся извест-
ным приемом и будем искать максимум не самой плотности
р[х(^|2(Ж а ее логарифма. В этом случае МАВ-оценка опреде-
ляется выражением
(7.57)
После подстановки выражения (7.53) в это уравнение получаем
___________________1
-(In {(2^)"det [V~ (£)]) 2 [х^)-х(<¥^!(й)Х
X[x(fe) — x (/?)])
л =0.
х ХМАР
Так как первый член не содержит x(k), имеем
- vi*^) [ хмлр (£) - х (*)] = 0. (7.58)
Таким образом, получаем окончательный результат, который
представляется совершенно очевидным при рассмотрении ур-ния
(7.53):
*мар (*) = *<*)• (7-59)
Достаточное условие максимума, выражаемое неравенством
(7.37), теперь имеет вид
д (д Ш р [х (fe) I Z (fe)] )Т
д х (k) ( д х (fe) /
и в данном случае соблюдается в силу физических свойств мат-
рицы дисперсий ошибок. Следовательно, МАВ-оценка совпадает
с оценкой условного математического ожидания и оценкой по
критерию минимума дисперсии ошибки. Совокупность величин
л = -V~(fc)<0 (7.60)
х ХМДР Х
О По аналогии с предыдущими выводами можно было бы сразу заметить,
Л Л
что XMAP(fe)=x(fe) Здесь же все выкладки повторяются для того, чтобы при-
дать изложению самостоятельный характер. (Прим авт.)
278
{¥~(А). x(X)} является достаточной статистикой для оценивания
в том смысле, что полностью определяют условную плотность
p{x(k)\Z(k)]^p{x(k)\V~ (k),x(k)].
Следует отметить, что можно было бы непосредственно вос-
пользоваться исходной формой записи плотности p{x(k)\Z(k)]
[выражением (7.52)], а не компактной формой (7.53). Такой под-
ход представляется более привлекательным, так как в этом слу-
чае не требуется знание более компактной формы, которая не яв-
ляется достаточно простой и очевидной. Если воспользоваться вы-
ражением (7.52) для p{x(k)\Z(k)], то в результате преобразования
ур-ния (7.57) имеем
Нг(^¥?Ч*)[2(^-Н(^)хмлр(А)] ~V^(k | 1)[хМЛР(*)-
— x(k | k— 1)] =0. (7.61)
л
Если теперь сгруппировать члены, включающие в себя хмар(&)>
то получим
[Нт (k) (k) H (k) + Vx1 (k | k - 1) ]ЛХмЛР (k) = ¥X (k | £ - 1) X
Xx(& | k— 1) + IF(A>) ¥“*(&) z(&), (7.62)
л
решение которого относительно хмар(^) приводит к следующему
результату:
хмлр (k) = [IF (k) V7i (k) H (k) + V^k | k - 1)]-' [¥x> (k | k - 1) x
X x (k ] k — 1) + IF (k) V^i (k) z (£)]. (7.63)
Хотя это решение для оптимальной оценки представлено не в
такой удобной форме, как предыдущее, оно легко может быть при-
ведено к (7.62), если воспользоваться леммой об обращении мат-
риц либо непосредственно выражениями (7.55) и (7.56).
Из алгоритмов фильтрации Калмана можно получить ряд инте-
ресных и полезных выражений для дисперсии. Вот некоторые из
наиболее полезных, связанные с понятием «обновляющего про-
цесса»:
var{z(£) — H(A)x(yfe I k— 1)} = H(£)¥_(£ | k— 1) IF (£) + V v k\
(7.64)
var {K (k) [z (k) — H (k) x (k I k — 1)]} = var {x (k) — x (k | k — 1)} =
= ¥~ (Л I k — 1) — ¥~ (k). (7.65)
279
До сих пор мы предполагали, что w и v — случайные процессы
с нулевым средним. Теперь рассмотрим случай, когда среднее зна-
чение процесса w не равно нулю:
£{*(/)} = Pbw(j). (7.66)
Определим те поправки, которые необходимо внести в уравне-
ние фильтрации Калмана для того, чтобы оценка по-прежнему
оставалась несмещенной. Из результатов, полученных в гл. 6, сле-
дует, что известное среднее должно быть включено в уравнение
фильтрации.
Уравнение, определяющее закон изменения среднего значения
вектора состояния, было выведено в гл. 3 [ур-ние (3.98)] и приме-
нительно к ур-нию (7.1) записывается в следующем виде:
М1+ 1) = Ф(/ + 1, /) Их (/) ч- Г (/) ^ (/), (7.67)
где р,х(0) =-Е{х(0)}. Если вычесть это уравнение из (7.1) и ввести
центрированные величины х°(У) =х(/)—цх(У) и w°(/) =w(/)— p,w(j),
то получим
х°(/+1) = Ф(/+1, /)x»(j)4-r(j)wo(/), (7.68)
где Е{х°(0)} =Е{х(0)—Цх(0)}=0. Заметим, что w° и х° являются
случайными процессами с нулевым средним. Аналогично можно за-
писать уравнение для модели наблюдения:
z»(/) = H(/)x0(j) + v(j), (7.69)
где z° (/) = z (/) — Н (/) рх (/).
Теперь уравнение фцльтра Калмана может быть непосредствен-
но применено к модифицированным моделям (с нулевым средним)
сообщения и наблюдения, так что выражение для оценки запишет-
ся в виде
* ° (/) = ф (У, у - о х° (/ - в + к (/) [z« о) - н (/) ф (/, i -1) х
Xx»(/-l)J. (7.70)
Так как Цх(7) известно, то наилучшая (линейная по критерию
минимума дисперсии ошибки) оценка вектора состояния x(j) при
л
заданном Z(j) должна быть равна х°(/) +цх(/). Поэтому, комби-
нируя уравнение для среднего значения р,х(У) =Ф(У, /—1)р,х(У—1) +
+Г(/—l)nw()—1) с ур-нием (7.70), получаем
х (/) = Ф (/, / — 1) х (/ — 1) + Г (/ — 1) p,w (/ — 1) + К (У) [z° (У) -
— Н (У) Ф (У, У — 1) х°(У — 1)]. (7.71)
Если теперь подставить выражение для z°(/), то результат за-
пишется в виде
х(У) = ф(/, у— 1)х(/— 1) + Г(У— l){iw(y— 1) + К(/‘)[z(/) —
- Н (У) щ (У) - Н (У) Ф (У, У — 1) х° (У - 1)1.
280
После подстановки 'выражения для Цх(/) имеем
х (/) = * О’ I / - 1) + К (/) [z (/) - Н (/) х (/ | / - 1)], (7.72)
где предсказанное значение оценки теперь равно
х(/ [/—1) = Ф(Л /-l)x(/-l) + r(/-l)pw(/-l). (7.73)
Уравнение (7.73) представляется естественным, так как х(/[/—I)
л
по-прежнему формируется путем экстраполяции х(/—1) на один
шаг нперед с использованием наиболее вероятного значения
w(j—1) [которое представляет собой также оптимальную оценку
л
W(/—1)], а именно, |xw(/—1).
Изложенный подход может быть также использован, когда на
систему воздействует известная функция дискретного времени, т. е.
когда модель сообщения имеет вид
х(/+1) = Ф(/+1, j)x(j) + r(j)w(/)+B(/)u(/), (7.74)
где u(j)—известная детерминированная функция дискретного
л
времени. В этом случае предсказанное значение х(/|/—1) запи-
сывается в виде
х(/ I /-1) = Ф(/, j- 1)х(/ — 1) -f-В (/—l)u(/- 1) +
+ F(/)pw(/-l). (7.75)
Это уравнение представляется особенно важным при решении
задач стохастического управления. Аналогичным образом можно
рассмотреть случай, когда v—случайный процесс с ненулевым
средним или когда известная детерминированная функция дис-
кретного времени у действует на выходе системы, т. е. когда мо-
дель наблюдения имеет следующий вид:
z 0) — H(/)x(j) + v(j) + у (/), (7.76)
где E{v(j)} =jiv(j). Применительно к этой задаче уравнение филь-
трации (7.72) записывается в виде
х (/) = х (/ | / — 1) + К (j) [z (/) — pv (/) — у (/) — Н (/) х (/ | / — 1).
(7.77)
Можно получить еще одно обобщение, если предположить, что
w и v коррелированны и имеют ковариационную функцию вида
cov{w(j), v(A)} = Vwv(j)6K(/— k). (7.78)
Поскольку вывод уравнений оценивания в этом случае анало-
гичен предыдущим, но гораздо длиннее, здесь он не приводится.
Алгоритм для сличая коррелированного шума может быть полу-
чен из алгоритма, выведенного для некоррелированного шума, ес-
281
ли «декоррелировать» сообщение и шумы. Это легко сделать, за-
писав уравнение для модели сообщения как
х(/+ 1) = Ф(/+ 1, j)x(j) + r(j)w(j) + S(/)[z(j)-H(j)x(j)-v(/)]
(7.79)
или
х(7 + 1) = Ф*(/ + 1, j)x(j) + w*(/) + S(/)u(/), (7.80)
где Ф *(/ +1, /) = Ф (/ +1, /) — S (/) Н (/); w* (7) = Г(7) w (7) —а (7) V(7);
«(/)=z(7).
Теперь модель сообщения, задаваемая ур-нием (7.80), содер-
жит известную функцию на нходе u(j), связанную с z(j). Выберем
3(7) такой, чтобы шумы объекта и измерений были некоррели-
рованны. Из соотношения z(j) = H(j)x(j) +v(j) получаем
cov {w* (7), v (7)} = cov {Г (7) w (7) — 3 (7) v (7), w (j)} = г (j) vwv (j) —
—S(/) Vv(7).
Ковариационная функция будет равна нулю, если выполняется
условие
S(D = Г(7) Vwv(7)V->(7). (7.81)
Таким образом, используя модель сообщения (7.80), мы реа-
лизуем алгоритмы фильтрации Калмана ,в стандартной форме.
Поэтому легко получить алгоритмы, приведенные в табл. 7.3.
Таблица 7.3
Обобщенный дискретный фильтр Калмана
Модель сообщения
« (/ + О = $ О' + 1. /) х О') + Г (/) w (/) + В (/) и (/).
Модель наблюдений
«О') = Н (/) х (7) + v (7) + у (/).
Априорные данные
е {w (7)} = pw o'); S{v0')} = pv0); £{х(0)}=рх(0);
cov {w О'), w (k)} = Vw (/) 6Л (j — k); cov {v (/), v (k)} = Vv (7) 6^ (j — k)-,
cov {w (7), v (k)} = Vwv O') (j — k); var {x (0)} = Vx (0).
Алгоритм одношагового предсказания
Л Л
X О' +11 /) == Ф 0 +1 > /) х 0) 4-ГО) Hw О') 4- в О') и 0)4-
4-Кр 0) Iz О') — Pv О') — У О') — Н (/) х 0)1
.282
Продолжение
Алгоритм фильтрации
+1) = х(/ + 1 |/)+K(/+l)[z(/ +l)-pv(/ + l)_
— У (/ + !)— Н(/4-1)х(/+ 1 [/)]•
Вычисление коэффициента усиления при одношаговом предсказании
Вычисление коэффициента усиления при фильтрации
К (/ + 0 = V- (/ +11/) Нг (/ +1) [Н (/ + 1) V- (/• +
+ 1 |/)Н7’(/ + 1)+ Vv(/ +1)]-\
Вычисление априорной дисперсии
V~(/ + 11 /) = (ф (/ +1, /) - Кр (/•) н (/)] v~ (/) [Ф (/+1,7)-
- Кр (1) н (fi]T + г (/•) vw (/) г7" (/) - Кр (7) vv (7) к£ U).
Вычисление апостериорной дисперсии
v~(/ +i) = [i—К(/ + 1)Н(/+i)]V~(/+11/).
Начальные условия
х (0) = х (0 | 0) = Рх (0) = Е {х (0)}; V-(0) = V~(0 | 0) = var {х (0)} = Vx (0).
Они дают решение задачи линейной дискретной фильтрации в
наиболее общей формулировке. В заключение отметим, что из об-
щих результатов следуют, как частные, результаты, приведенные
в табл. 7.2, если положить jiw, цт, и, у и Vwv равными нулю.
7.3. Оптимальный линейный непрерывный фильтр
В этом параграфе алгоритм фильтрации Калмана дис-
кретных процессов обобщается применительно к обработке непре-
рывных процессов. Основные результаты получены с помощью
трех различных, но взаимно дополняющих друг друга методов.
Сначала рассматривается предельный случай дискретной задачи,
когда интервал между выборками стремится к нулю. Во втором
случае для минимизации дисперсии ошибки оценивания непосред-
ственно используется матричный принцип минимума. В третьем
случае показывается, как интегральное уравнение Винера—Хопфа
может быть преобразовано в дифференциальное уравнение фильт-
ра Калмана в рекуррентной форме.
283
Модель сообщения 'записывается в форме векторного диффе-
ренциального уравнения первого порядка
ж(0 = F(0x(0 + G(0w(0, (7.82)
где w(t) — белый шум с нулевым средним и дисперсией
-cov {w (0, w (т)} A Vw (t, т) = 4»w (0 6D (t - т). (7.83)
Известны также начальные среднее значение и дисперсия состоя-
ния x(t):
(0) = Е {х (0)}; Vx (0) = var {х (0)}. (7.84)
Предположим также, что cov{x(0), w(0}=O для всех t>0.
Модель наблюдений аналогична модели, используемой при реше-
нии дискретной задачи, т. е.
з(0 = Н(0х(0 + у(0. (7.85)
Однако здесь измерения выполняются непрерывно. Шум измере-
ний также предполагается белым с нулевым средним и ковариа-
цией
cov {v (0, V (т)} A Vv (t, т) = 4»v (0 6D (t ~ T). (7.86)
Предполагается, что шум измерений и входной шум не коррелиро-
ваны, так что
•cov {w (0, V (т)} A Vwv (/, т) = 0. (7.87)
Найдем линейный последовательный алгоритм оценивания состоя-
ния x(t) с минимальной дисперсией ошибки при заданных на ин-
тервале измерениях z(r), т. е. Z(0.
Предельный случай. Один из первых выводов алгоритма
фильтрации Калмана для непрерывных процессов был основан на
предельном переходе от алгоритма, полученного для дискретных
процессов, при уменьшении интервала дискретизации.
Рассмотрим следующую дискретную модель сообщения 6
х(Г+ГТ) = Ф(Г+-17’, kT)x(kT) + r(kT)w(kT), (7.88)
где w — дискретный белый шум с нулевым средним значением и
дисперсией
VW(AT, /Т) = ^JkT)\(k-j). (7.89)
При kT = t получаем:
Т (0 = lim — [Ф (FH Т, kT) ~ I]; (7.90)
т->-о Т
G(f) = \\m — V(kT)^ (7.91)
т->о Т
’> Интервал между выборками Т введен в дискретные уравнения, рассмат-
риваемые в данном разделе, чтобы подчеркнуть, что он является переменной ве-
личйной. (Прим, авт )
284
В справедливости этих выражений легко убедиться, если учесть,
что ®(t+T,t)=l + TF(t)+O(T2) и r(/)=TG(/)+O(F).
Используя приведенные выражения, можно показать, что дис-
кретная модель сообщения переходит в непрерывную, задаваемую
ур-нием (7.82), при Т-Ч):
х (0 = lim -*.<£+= iim _L [ф (t + т, t) х (t) + Г (t) w (t) —
т->о T т-^-о Т
-x(0] = F(0x(0 + G(0w(C.
Модель наблюдений для дискретного случая при переходе к
пределу также совпадает с непрерывной моделью наблюдений, за-
даваемой ур-нием (7.85). Дисперсия шума измерений
vv (kT, jT) = у ¥v (kT) (k - j). (7.92)
Уравнения (7.85), (7.88), (7.89) и (7.92) полностью опреде-
ляют дискретный аналог сформулированной непрерывной задачи
оценивания.
Если дискретный фильтр Калмана, уравнения которого приве-
дены в табл. 7.2, применить для решения представленной выше
дискретной задачи фильтрации, то получим
х(0 = Ф(^, t — T)x(t — T) + K(t)[z(t) — Н(/)Ф(*, t — T)x(t — T)],
(7.93)
где коэффициент усиления
К (0 = V ~ (t 11 - Т) нг (0 Гн (0 v~ (t \t - Т) ндо + -у Yv (0 ]-1.
(7.94)
Уравнение для априорной дисперсии (7.34) имеет вид
v~(t + Т I 0 = Ф (t + Т, t) V~(0 Фт (t + T,t) + у Г (t) (t) П (t),
(7.95)
а уравнение для апостериорной дисперсии (7.33) теперь записы-'
ьается как
V~(0 = [I — K(0H(0)V^ I t — T). (7.96)
Здесь для простоты введено обозначение kT — t.
Для того чтобы получить алгоритм фильтрации для непрерыв-
ного случая, перепишем (7.94) в виде
К(0 = TV~(t I t — T)W(t)[T\l(t)N~(t I t — T)W(t) + 4»v(0]-1 ,
(7.97)
где множитель 1/T просто вынесен из-под знака обратной опера-
ции. Это выражение может быть записано в компактной форме
K(t) = TKT(t), (7-98)
285
где
кг (0 = vT(M t - T) нг (О [т н (О v~(M t - Т) нг (О + tv (Oj->.
(7.99)
Здесь использован индекс Т для того, чтобы подчеркнуть, что
рассматривается интервал между выборками. Если теперь перей-
ти к пределу при Т-Ч), то получим
lim Кг (0 = V~(0 IF (О Т-1 (0 = СК (t). (7.100)
T-+0 х
Заметим, что априорная дисперсия ошибки стремится к V~(t),
т. е. к фактической дисперсии, когда Т->-0.
Этот результат можно доказать, если воспользоваться другой
формой записи уравнения для коэффициента усиления (7.55), из
которого получаем К(0 = (0- Если подставить
ур-ние (7.98) в (7.93), то получим
АЛ Л
х(0 = Ф(1, t — T)x(t— T) + TKT(t)[z(t)~ Н(0Ф(*, t— T)x(t — T)J,
(7.101)
откуда следует
x(0*lim ——T) = lim—{Ф(^, t — T)x(t — T) +
~T-+o T t-+o T 1
+ T Kr (0 [z (0 - H (0 x (t - T)1 - T Kr (t) H (t) [Ф (t, t - T) -1J X
Л A
X x (t — T) — x (t — T).
После несложных алгебраических преобразований это выражение
приводится к следующему:
Л ( 1 Л А
х (0 = limМф (t, t - Т) - I] х (t - Т) + кг (0 [Z (0 - Н (0 х (t - Т)] -
т-ицт
— Кг(0Н(0[Ф(^, t-Т)_ IJx(f — Г)} .
Предел может быть легко вычислен, если использовать ур-ния
(7.90) и (7.100). В результате получаем
х (0 = F (0 х (0 + СК (t) (z (t) - Н (t) х (01. (7.102)
Следовательно, уравнение фильтрации есть дифференциальное
л
уравнение (с начальным условием х(0)=Е{х(0)} , решение кото-
рого может быть получено, если известен коэффициент усиления
CK(t). Для того чтобы определить Ж (t), необходимо найти выра-
жение для дисперсии ошибки V~(7). Можно было бы ввести выра-
жение для дисперсии ошибки непосредственно из ур-ний (7.82) и
(7.102) точно таким же способом, как это было сделано в гл. 3
286
г,ри рассмотрении непрерывного случая. Однако воспользуемся
иным подходом и получим уравнение перехода для V~(0 из ре-
зультатов, справедливых для дискретного случая, путем вычисле-
ния предела.
Мы не можем использовать отдельно как ур-ние (7.95), так и
ур-ние (7.96) для отыскания выражения для дисперсии в непре-
рывном случае, поскольку, вычисляя предел в любом уравнении,
получаем совершенно очевидный результат lim V-- (t\t—Т) —
т->о х
= limV~(7). Кроме того, невозможно составить выражение типа
T-M)
производной, используя лишь одно из этих уравнений, так как
VT(0^=lim-^-[Vr(/ | t — Т) — V~(t — Т)]¥=0. (7-103)
Поэтому для получения выражения, определяющего истинный
закон изменения дисперсии во времениУ~ (t), необходимо исполь-
зовать эти уравнения совместно. Подставляя (7.96) в (7.95), по-
лучим
V^ + T | 0 = ФЦ + Т, 0(1 —K(0H(0]V~(f j t — Т)Ф(« + Т, о +
+ Г(0Ч^(0П(0/7\
Если воспользоваться ур-ниями (7.90) и (7.98) и выполнить ряд
несложных алгебраических преобразований, то получим
N~(t + T | 0 = V (f | t — T) + TF(0Vr(f | t — T) + TV~(t | t —
— | t-T) + r(0Yw(0F(0/7 + O(7!),
(7.104)
где lim (1/7’)О(Г2) =0. Из ур-ния (7.104) можно получить диффе-
ренциальное уравнение для дисперсии ошибки:
[v7 (' +т I '> - VX I ‘ = St [v? (/1 ‘ -
— T) + TF(0VT(f | t— T) + TN~(t [ / — 7)^(0 —7^(011(0 x
xv~(i I t~T)+ 2-r(0Tw(0r4O-vT(f | f-T) + 0(r).
Переходя к пределу в правой части этого выражения и используя
ур-ние (7.100), получаем
V~(0 = F (0 V~(0 + V~(0 Fr (0 - V~(0 Hr (0 Ф71 (0 H (0 V~(t) +
+ G (0 (0 Gr (0. (7Л05>
Уравнение (7.105) представляет собой искомый результат, из
которого следует, что закон изменения дисперсии ошибки во вре-
мени V~ (0 описывается матричным уравнением Риккати. За-
287
метим также, что в данное выражение входят только вторые мо-
менты процессов -w(t) и v(t) и не входят наблюдения z(t). Сле-
довательно, ур-ние (7.105) может быть решено предварительно до
получения каких-либо результатов наблюдений, хотя это и не
совсем обычный прием. Начальным значением для V~ (t) служит
V~(0) =уаг{х(0)} =VX(0). Можно было бы также получить ур-ние
(7.105), определив V~(7), ,какУ~(/) = lim^- [V~ (t+T)— V~ (t)], и
затем использовать ур-ния (7.96), (7.98) и (7.100).
ЕслиУ~(7) известна, то может быть вычислен коэффициент
усиления, а из ур-ния (7.102) может быть определена оценка со-
стояния x(t). Для удобства все результаты решения задачи фильт-
рации с помощью непрерывного фильтра Калмана сведены в
табл. 7.4.
Таблица 74
Уравиеиие непрерывного фильтра Калмана
Модель сообщения х (t) = F (t) х (/) 4- G (/) w (t). (7 82)
Модель наблюдения z(O = H(0x(f)+v(O- (7 85)
Априорные данные
Е {w (0) = Е {v (/)} = О; £ {х (0)} = рх (0); cov (w (0, w(r)}='Fw (f)6D (t —т); cov{v(0, v (т)} = Yv (f) 6D (t cov{w(f), v (t)} = cov {x (0), w (/)} = cov {x (0), v(/)}=O; var { x (0)} = Vx (0). — T),
Алюритм фильтрации x (0 = F (0 X (/) +Ж (0 [z (0 — H (0 x (01 (7.102)
Вычисление коэффициента усиления ^(0=v~ (/)Hr(oV(O. (7.100)
Вычисление дисперсии ошибки v~ (0 = F (i) V~ (0 +V~ (0 F7 (0 - - V~ (f) Hr (t) V (t) H (t) V~ (0 + G (/) 4'w (0 GT (i) (7 105)
Начальные условия
х (0) = Е {х (0)} = рх (0); V- (0) = var{x (0)} = Vx (0)
288
Структурные схемы модели сообщения и фильтра приведены
на рис. 7.6. Следует отметить, что фильтр включает в себя, как
составную часть, модель сообщения, на вход которой поступает
S)
Рис 7 б Структурные схемы непрерывного фильтра Кал-
мана
а) модель сообщения; б) фильтр
сигнал ошибки, пропорциональный разности между наблюдением
л л
z(t) и ожидаемым условным наблюдением z(t) = H(t)x(t) при за-
данном Z(Q, с коэффициентом веса, рапным коэффициенту уси-
л
ления Следует запомнить, что x(t) на самом деле есть
х(7| t) = E{x(t) |Z(7)}, a z(t)—z(t)=E{z(t)\7.(t)}. Выражение
Л
z(t)—H(t)x(t) определяет «обновляющий» процесс.
Пример 7.3. В качестве иллюстрации применения непрерывного фильтра
Калмана рассмотрим простую скалярную задачу. Пусть модель сообщения за-
дается уравнением x(t)=0, где F(f) и w(t) приняты равными нулю Модель
наблюдений определяется как z(t) =x(t) +v(t), где v(t)—белый шум с нуле-
вым средним и единичной дисперсией Начальное состояние х(0) имеет сред-
нее значение, равное нулю, и дисперсию, равную 10
Если уравнения для моделей сообщения и наблюдений, а также значения
параметров подставить в ур-ние (7 105) то получается следующий результат;
v~(0 = -[v~(0}2, v~(O) = io.
Решение этого уравнения имеет видУ~(/) = 10/(101+1) Так как H(t) н Y.fO
равны единице, то коэффициент усиления<X(t) просто совпадает с V~(/). По-
этому алгоритм оценивания состояния x(t) определяется следующим образом:
Л Ю Л Л
х(1) = [?(0—х(О)> гДе начальное значение x(t) равно нулю.
2»
10—26
Перед тем как приступить к выводу алгоритма непрерывного
фильтра Калмана путем непосредственного применения матрич-
ного принципа минимума, получим дифференциальное уравнение
для x(t).
~ . Л
По определению, x(t)=x(t)—x(t). Подставляя ур-ния (7.82) и
л
(7.102) соответственно для x(t) и *(t), получаем
х(0 = F (t) х (0 + G (0 w (0 - {F (0 х (0 + Ж (0 [z (0 - Н (0 х (01} =
= F (0 х (0 + G (0 w (0 — Ж (0 [z (0 — Н (0 х (0]. (7.106)
Если использовать ур-ние (7.85), то получим два эквивалент-
ных представления «обновляющего» процесса:
л л
J(0 = z(0 —H(0x(0 = H(0x(0 + v(0 —Н(0х(0;
J (0 = Г(0 = z (0 — Н (0 х (0 = Н (0 х (0 + v (0. (7.107)
Используя последнее уравнение, получим дифференциальное урав-
нение
х (0 = [F (0 — Ж (t) Н (0] х (0 + G (0 w (0 — Ж (0 v (0, (7.108)
которое аналогично ур-нию (7.36), полученному для дискретного
случая. Уравнение для дисперсии ошибки теперь может быть лег-
ко получено одним из разобранных выше способов.
Вывод уравнений фильтра методами вариаци-
онного исчисления. Существуют два подхода, опирающие-
ся на методы вариационного исчисления, которыми можно вос-
пользоваться при решении задачи оценивания с минимальной дис-
персией ошибки. Один из них состоит в использовании метода,
аналогичного методу ортогонального проецирования, изложенно-
му в § 6.6. Этим методом получено уравнение Винера—Хопфа
[202]. Методы вариационного исчисления могут быть использованы
также непосредственно в задаче минимизации дисперсии ошибки,
решение которой приводит к алгоритму фильтрации Калмана.
Здесь будем следовать второму методу, впервые опубликованному
в работе [12].
Предположим, что алгоритм фильтрации задается обобщенным
линейным дифференциальным уравнением
х(0 = А (0 х(0 + B(0z(0. (7.109)
Здесь, как раньше, будем обозначать оценку состояния x(t) как
fyt), хотя этим и не подчеркиваем какую-либо связь (по крайней
мёре, первоначально) этой оценки с результатами, полученными
в 'предедидущих разделах. Конечно, в конце концов, будет пока-
зана эквивалентность этих двух оценок и, следовательно, введен-
ное обозначение окажется вполне логичным. Задача состоит в
290
том, чтобы найти такие матрицы A(t) и B(t), чтобы оценка x(t)
была несмещенной и имела минимальную дисперсию ошибки.
Сначала рассмотрим задачу построения условно и безусловно
несмещенной оценки. Производная по времени уравнения ошибки
оценивания определяется следующим образом:
. х(0 Д х (0 — х (0 = F (0 х (0 + G (0 w (0 - [А (0 х (0 -И В (0 z (0].
Если подставить модель наблюдений z(t) из ур-ния (7.85), то
получим
х(0 = F (0 х (0 + G (0 w (0 - А (0 х (0 — В (0 н (0 х (0 — В (0 V (0.
(7.110)
Учитывая, что x(t)=x(t)—x(t), можно записать ур-ние (7.110)
как
х (0 - [F (0 - А (0 - В (0 Н (0J х (0 + А (0 Г(0 + G (0 w (0 - В (0 v (0.
(7.111)
л
Если x(t) является условно несмещенной оценкой состояния
х(0 для всех t>G, то условное среднее какх(0,таких(0 при фик-
сированном Z(t) должно быть равно нулю. Если бы среднее я: (0
для некоторого t не было равно нулю, то из этого следовало бы,
что среднее x(t) также должно быть не равным нулю. Следова-
тельно, если вычислить условное среднее обеих частей ур-ния
(7.111) при фиксированном Z(t), то имеем
О = [F(0 —А(0 —В (0H(0]E{x(0 I Z(0}, (7.112)
так как E{w(t)} и E{v(t)} также равны нулю. Так как мы не
можем предположить, что E{x(t)\Z(t)} равно нулю для всех t,
то условие (7.112), вообще говоря, может соблюдаться только,
если
F(0 —А(0—-В(0Н(0 = 0 для всех / > 0. (7.113)
Поэтому ур-ние (7.109) принимает вид
х (0 = [F (0 — В (0 Н (0] х (0 + В (0 г (0.
Этот результат может быть представлен в форме, очень сход-
ной с уравнением фильтра Калмана:
x(0 = F(0x(0 + B(0(z(0-Hx(0). (7.114)
Следовательно, удовлетворение требования условной несмещен-
ности оценки приводит к структуре фильтра, аналогичного фильт-
ру Калмана, за исключением пока еще неизвестных коэффициен-
тов усиления B(t) в ур-нии (7.114) и X'(t) в ур-нии (7.102). На-
10* 291
л
чальное состояние х(0) может быть также определено, исходя из
л
требования условной несмещенности оценки. Так как Е{х.(Е)}
должно быть равно E{x(t)} для всех /^0, то тем более это долж-
но соблюдаться при £ = 0. Поэтому
х(0) = Е{х(0)} = рх(0). (7.115)
Теперь задача состоит в отыскании такой матрицы B(t) пере-
менных коэффициентов усиления, при которой дисперсия ошибки
оценивания была бы минимальна. Очевидно, достаточно было бы
просто сопоставить ур-ния (7.114) и (7.102), чтобы убедиться, что
при B(t), равной M(t), где M(t) определяется ф-лой (7.100), по-
лучается линейный алгоритм оценивания с минимальной диспер-
сией. Поступим иначе и покажем, что независимо от полученных
ранее результатов уравнение фильтра Калмана может быть вы-
ведено непосредственно с привлечением методов вариационного
исчисления. Еще раз напоминаем читателю, что наша задача зак-
лючается не в получении новых результатов, а в изложении и
иллюстрации возможных точек зрения и нескольких различных
способов вывода уравнений фильтра Калмана. Необходимо выб-
рать матрицу B(t) на интервале наблюдения 0^/^т, которая ми-
нимизировала бы скалярную функцию риска 7 (т) = Е {хг (т) S (т) X
Хх(т)}.
Как было показано в предыдущей главе, решение не зависит от S
и, следовательно, для простоты предположим, что 3 = 1. Рассмотрим
функцию риска 7(т) =Е{хт(т)х(т)}. Ее можно представить в бо-
лее удобной форме, учитывая соотношение 7(т) =Е{хт(т)х(т)} =
=Е{1г[х(т)хт(т)]}. Так как операторы следа матрицы и усредне-
ния линейны, то можно изменить порядок выполнения операторов
и записать
J (т) = tr (Е {х(т)хг (т)}) = tr [Vt(t)]. (7.116)
Матричное дифференциальное уравнение дляУ~(7) может быть
получено из (7.111) с помощью методов, представленных в § 3.5,
в виде
v~(0 = [F (0 - в (0 н (01 vT (0 + v~(0 [F (0 - в (/) H(t)]T +
+ G(0Yw(/)G’-(0 + B(0^v(0Br(0 (7-H7)
с начальным условием
V д,(0) = var {x (0)} = E {[x (0) - x (0)] [x (0) - x (0)]T }=E{[x(0)-
- (0)1 [x(0)-tix (0)f} Vx(0). (7.118)
Здесь, как и в предыдущих выкладках, использован тот же са-
мый символ для обозначения ковариации ошибки оценивания. Од-
наке и здесь этим мы не хотим подчеркивать какую-либо связь
292
между двумя ковариациями. Ниже, когда будет показано, что
В(7) совпадает с Ж(1)— коэффициентом усиления фильтра Кал-
мана, использованное обозначение окажется вполне логичным.
Задача оценивания теперь сводится к задаче оптималь-
ного управления, в которой необходимо найти матрицу В(7) на
интервале наблюдения которая минимизировала бы функ-
цию риска 7(T)=tr[V~(T)] при ограничении, заданном дифферен-
циальным ур-нием (7.117) и при начальном условии (7.118). От-
метим, что здесь мы сталкиваемся с задачей, которая совершенно
не зависит от фактической оценки и наблюдения, и имеем дело
исключительно с вероятностными характеристиками задачи оце-
нивания. В частности, с дисперсиями. Согласно терминологии,
принятой в теории управления, элементы матрицыV~ (t) являют-
ся «переменными состояния», а элементы матрицы B(t)— «пере-
менными управления». Сформулированная задача представляет
собой простую линейную задачу управления с заданным началь-
ным значением, произвольным конечным значением и фиксирован-
ным временем управления и относится к типу вариационных задач
Мейера. Оптимальная матрица В(£), 0<Л^т может быть найдена
при помощи принципа максимума Л. С. Понтрягина. Поскольку
’Bt(t) является матрицей, то необходимо использовать принцип мак-
симума в матричной форме [8].
Чтобы применить принцип максимума к решению этой задачи,
введем присоединенную матрицу или матрицу множителей Лаг-
ранжа А(0 размера NxN и скалярную функцию И, определяе-
мую как
ЯД tr[V~(0Ar(0]. (7.П9)
Используя (7.117), получим
Н = tr [(F — ВН) V~Ar + V~(F — ВН) Аг + G GT Аг +
4-В Вг Аг j . (7.120)
Здесь для сокращения записи временной аргумент опущен.
Если ввести понятие матрицы градиентов [10], то необходимые
условия, которым должна удовлетворять оптимальная матрица
коэффициентов усиления В(/), записываются в виде
А (/) = — dH/dV~(fy, V~(t) — д Н/д l\.(fy, (7.121)
dH/db(t) = 0 (7.122)
с граничными условиями:
д tr Г V~(T)1
л (т) = аУМт)~ '; v *(0)=Vx (0)- (7’123)
Если теперь подставить Н из ур-ния (7.120) и использовать прин-
293
цип максимума, то можно убедиться, что ур-ние (7.121) перехо-
дит в (7.117):
л (о = - [F (0 - В (О Н (01г л (0 - Л (О [F (0 — В (0 Н (01, (7.124)
а (7.122) переходит в
- л (о v~(0 нг (О - лг (о v~(o нг (О + л (о в (о yv (о +
+ Ar(i)B(04rv(0 = 0 (7.125)
и, наконец, граничные условия (7.123) становятся
Л(т) = 1; V~(0) = Vx(0).
(7.126)
Из (7.124) следует, что если Л(/) —симметричная матрица для
некоторого значения t, 0^7/^т, то она является симметричной для
всех значений t, Так как согласно ур-нию (7.126) Л(/) —
матрица симметричная при t = т, можно заключить, что Л (/) —
симметричная матрица. Кроме того, из линейности ур-ния (7.124)
и граничного условия (7.126) следует, что Л(/) является несингу-
лярной матрицей для всех t, Следовательно, Л(£) —сим-
метричная несингулярная матрица для всех t, 0^/^т.
Так как Л(/)—симметричная несингулярная матрица, то
ур-ние (7.125) можно умножить слева на Л-1 (0 и, воспользовав-
шись тем, что Yv(0 также симметрична, получить
В (0 = V~(i) Нг (О Y71 (0- (7.127)
Если теперь сравнить ур-ния (7.127) и (7.100), то можно за-
метить, что R(t) совпадает с M(t), еслнУ~(1) в (7.127) удовлет-
воряет ур-нию (7.105). Чтобы убедиться в справедливости этого
утверждения, подставим (7.127) для B(i) в (7.117). В результа-
те получим
v~(0 = [F (0 - V- (П нг (0 Y71 (0 н (0] v~(0 +
+ V~(0 [ F (0 — V~(0 Hr (0 Y71 (0 н (0]T +
+ G (0 (0 Gr (0 + V~ (0 Hr (0 T7’ (0 Yv (0 T7’ (0 H (0 V~ (0 =
=F (0 v~(0 + v~(0 Fr(0-v~(0 нг (0Y7'(0H(0V~(0+G(0Yw(0 Gr(i).
Можно заметить, что уравнение для В(7) совершенно не зави-
сит от Л (Q и конечного момента т. Следовательно, можно считать
т=оо, и полученный результат, который совпадает с алгоритмом
непрерывного фильтра Калмана, справедлив для всех
В ы в о д у р а в н е н и й ф и л ь т р а К а л м а н а с помощью
уравнения Винера — Хопфа. Вывод уравнений непрерыв-
ного фильтра Калмана начнем с анализа уравнения Винера — Хоп-
294
фа, которое было получено в § 6.6. Было показано, что если оценка
х(/) состояния x(i) определяется интегралом свертки1)
л '
х (0 = JS (t, т) z (т) d т, (7.128)
о
то B(t, т) удовлетворяет уравнению Винера—Хопфа
t
Vxz(^ о) = J S(/, t)Vz (t, a)dx при (7.129)
о
В § 6.6 упоминалось, что решение уравнения Винера—Хопфа в
общем случае получить трудно. Здесь будет показано, как инте-
гральное уравнение Винера—Хопфа может быть преобразовано в
эквивалентное дифференциальное уравнение, которое, как мы убе-
димся, аналогично алгоритму фильтрации Калмана.
Начнем с того, что вычислим частную производную по t левой
части ур-ния (7.129). В результате получим
-^-Vxz(i, a) = -^-cov{x(0, z (a)} = cov {х (i), z(o)}.
dt dt
Если использовать подстановку x=Fx + Gw, то это выражение
можно записать в виде
Vxz (t, о) = F (О VX2 (t, а) + G (О Vwz (t, а). (7.130)
Однако w(t) и z(a) независимы при a<t, поскольку z(a) за-
висит от w(t) только при т^о, а w — белый шум. Поэтому
Vwz(i, о) равна нулю и ур-ние (7.130) принимает более простой
вид:
Vxz (t, о) = F (t) Vxz (t, о) при a < t.
Используя уравнение Винера—Хопфа, это уравнение можно
записать как
t
— Vxz(i, о) = jF(i)S(i, t)Vz(t, 0)dr при a<L (7.131)
__________ о
*) Линейный алгоритм оценивания более общего вида может быть пред-
Л р
ставлен как x(Z)=g(f)+ I Е(/, т)г(т)</т. Однако g(Z) =0, если р.х=0 (см. § 6.6),
6
что н предполагалось с самого начала. Еще один вывод уравнения может быть
получен, если использовать «обновляющий» процесс как возмущающую функцию
в интеграле и записать линейный алгоритм оценивания в виде
Ар Л
х(о= X)[z(X) —н(X)х(Х)]<a.
о
Вывод уравнений в этом случае получается действительно проще, чем данный
вывод Вывод алгоритмов оценивания на основе этого подхода представлен
в § 8 3 (Прим авт)
295
Теперь вычислим частную производную по t правой части урав-
нения Винера—Хопфа (7.129). Согласно правилу дифференциро-
вания (см. §3 5) получаем
t t
f S (i, -v) Vz (t, o) d т = f d SJ_Z;-T) Vz (t, oj d x + S (t, t) Vz (t. o).
dt J J [5/
о 0
(7.132)
По определению, Vz(0 о) представляет собой cov{z(0, z(o)}
и, если использовать уравнение модели наблюдений z(t), то по-
лучим
Vz (t, о) = cov {Н (0 х (t) + v (/), z(o)} = Н (0cov{x(0, z(o)} +
4-cov{v(0, z(o)}. (7.133)
Так как v — белый шум, a v и w не коррелированы, причем
t>c, то cov{v(i), z(o)}=0 и ур-ние (7.133) записывается как
Vz(0 o) = H(0Vxz(0 о). (7.134)
Используя уравнение Винера — Хопфа для замены VXz(zt, о),
имеем
t
vz(t, о)= jH(0E(0 t)Vz(t, a)dx. (7.135)
о
Воспользовавшись этим уравнением при замене Vz(0 о) во
втором слагаемом ур-ния (7.132), получаем
Js (0 т) Vz (т, о) d х = J [-d S^--T) Vz (т, о) +
о о
4-5(0 0H(0S(0 t)Vz(t, о)рт. (7.136)
Так как (7.131) и (7.136) представляют собой соответственно
частные производные обеих частей уравнения Винера—Хопфа, то,
приравнивая друг другу эти два выражения, получаем
t -
J[F(0E(0 т)-^р--Е(0 0Н(ОЕ(0 T)]vz(T, o)dT = 0.
о
(7.137)
Очевидно, это интегральное уравнение будет удовлетворяться,
если
F(0S(0 т)——5(0 0Н(0Е(0 т) = 0. (7.138)
Калман и Бьюси [111] также показали, что если — положи-
тельно определенная матрица, что и предполагалось, то ур-ние
(7.138) является необходимым условием справедливости ур-ния
л
(7.137). Если учесть, что х (/) задается ур-нием (7Л28), то не-
296
трудно выяснить, как следует использовать (7.138), чтобы
л
получить искомый алгоритм фильтрации. Запишем x(t) в виде
х(0=-^- j*S(C r)z(r)dr= pBgfT) 2(T)dt-t-E(t, t)z(t). (7.139)
b b
Из ур-ния (7.138) следует, что d~(t' =F(t)S(t, т)—В(/, /) X
dt
ХН(1)2(г, т). Следовательно, (7.139) можно записать как
л '
х (t) = [F (f) — В (t, t) H (£)] f E (t, t) z (t) d т 4- В (t, t) z (t).
о
Замечая, что интеграл в этом выражении представляет собой
л
просто x(t), находим
x(0 = [F(^) — Е(С 0H(0]x(0 —S(/, t)z(t). (7.140)
Это выражение по форме совпадает с уравнением фильтра Кал-
л л
мана х(/) = F(/)x(/) ->-.%'(/) [z(/)— H(^)x(^)J, если определить
JT(0=-S(t 0- (7-141)
Теперь остается только наши выражение для B(t, t). Запишем
Vz(t, о) в виде
Vz (т, а) Д cov {z (т), z (а)} = cov {z (т), Н (а) х (а) + v (а)} =
= Vzx(t, о)Нг(а) + Vzv (т, а).
Так как v — белый шум, который не зависит от w, то Vzv(t, а) =
= Vv(t, о) =Тгу(т)бо(т—а). Поэтому
Vz (т, а) = Vzx (т, а) Н7 (а) + ’К. (т) 6D (г - о). (7.142)
Если подставить этот результат в уравнение Винера—Хопфа,
то получим
t
VX7 (t, о) = Е (t, т) [vzx (т, а) Нг (а) + ТС (т) 6р (т — а)] d т или
о
t
Vxz(t, = t)Vzx(t, а) Нг (а) d т + В (/, а)Ч\(а). (7.143)
о
Используя определение величины Vzx(t, а), это выражение можно
записать в виде
t
У™ (t, а) — JE (t, т) cov {z (т), x (a)} Hr (a) d т + E (/, a) ’lrv (a),
о
297
Меняя порядок выполнения операций интегрирования и вы-
числения ковариации, получаем
{/
JB(t, т)z(т)dт, х(о)
о
Hr(o) + B(i, o)Tv(o).
Интеграл в фигурных скобках представляет собой просто х(Т),
поэтому
VX2 (/, о) = cov {х (0, х (о)} Нг (о) + В (/, о) 'Tv (о). (7.144)
Согласно определению левая часть '(7.144) есть
Vxz(i, a)Acov{x(0» z(o)} = cov{x(i), H (о) х (о) + v (о)} =
= cov {х (/), х (о)} Нг (о) + cov {х (i), v (о)}.
Предположим, что cov{x(i), v(o)} = 0, так что это выражение
упрощается и принимает вид
vxz (i, о) = cov {х (i), X (о)} Нг (о). (7.145)
Подставляя этот результат в ур-ние (7.144), находим
cov {х (/), х (о)} Нг (о) = cov {х (/), х (о)} Нг (о) + В (/, о) 4% (о).
Сгруппировав два оператора вычисления ковариации, полу-
чаем
cov{x(i)— x(i), x(o)}Hr(o) = cov{x(i), х(о)}Нг(о) = В(t, o)Wv(a).
Из этого выражения можно найти S(t, о), умножив справа обе
части равенства на Чг71('а)- В результате получим
B(i, а) = V~X(Z, a)Hr(o)WI(o)- ‘ (7-146)
Так как это выражение является непрерывной функцией отно-
сительно аргумента о, то B(i, t) можно найти, вычислив предел,
к которому стремятся обе части уравнения (7.146) при
В (t, t) = lim E (t, o) = lim V~x (t, о) Hr (о) T71 (o)
a->t a->t
ИЛИ
В (*. О = VTx (t> О НГ (0 ’J’V1 (a). (7.147)
Это выражение для B(t, t) отличается от полученного выра-
жения для ^C(t), поскольку здесь мы рассматривали V~ (t, t)
вместо ранее использованной V~(7). Чтобы убедиться, что эти вы-
ражения эквивалентны, достаточно только записать
V~x (t, 0Дсоу{х(0, х(0) = cov{x (i), x(i) + x(0} =
= cov {x (i), x (/)} + cov {x (i), x (/)}.
298
Согласно лемме об ортогональном проецировании cov{x(7), х(7)} =
=0, поэтому t) — V~(t). Уравнение (7.147) для E(i, t) =Ж(/)
теперь имеет вид
Я? (0 А Е (/, 0 = V~(0 Нг (О Y71 (0- (7-148)
Этот результат, как и следовало ожидать, совпадает с (7.100).
И, наконец, чтобы завершить вывод, необходимо получить диф-
ференциальное уравнение для V~(7). Так как оно уже было вы-
ведено дважды: в § 3.5 и в самом начале данного параграфа [см.
(7.105)], то вывод этого уравнения повторять не будем.
Пример 7.4. [7]. Предположим, что в задаче фильтрации заданы следующие
модели сообщения и наблюдений:
(1)
z = Н1Х1 -|e-v. (2)
Матрицы Fi, Gi, Hi, вообще говоря, состоят из переменных во времени эле-
ментов, но для удобства обозначения временные аргументы здесь опущены. Если
произвести линейное преобразование переменных в виде
Xi(Z) = P(Z)x2(Z) (3)
или х2(<) = Р~“' (ZjxJZ), (4)
где Р (0 —несингулярная матрица, составленная из переменных во времени эле-
мейтов для всех Z^sZo, то модели сообщения и наблюдений могут быть выра-
жены через x2(Z):
х2 = F2x2 + G2w; (5)
z = H2x2 + v. (6)
Хорошо известно, что эти два представления моделей связаны между собой
следующими выражениями
F2 = Р~' FjP — Р~‘ р; (7)
G2=P~1G1; (8)
H2 = HiP. (9)
Заметим, что как в одном, так и в другом представлениях моделей входной и
выходной шумы w и v, а также наблюдение z идентичны.
Наша задача — показать, как связаны между собой линейные по критерию
минимума среднеквадратической ошибки оценки состояний Xi и х2. В частности,
будет показано, что
х2(0 = Р(0 x2(Z); (10)
v~(Z) = P(Z) (11)
Очевидно, эти соотношения справедливы и при t=to, так как Xi(Z0) —случайная
величина, a P(Z0) —матрица, составленная из постоянных величин. Сначала рас-
смотрим соотношение между дисперсиями ошибки, определяемое ур-нием (11).
Если под V(Z) подразумевать V(Z) = P(Z) V ~ (Z) Рг (Z), то необходимо показать,
что V(Z)=V~(Z). Производная по времени равна V=PV~PT + PV~ Рт +
Xj Xg Xj
+ PV —Рг. При подстановке ур-ния дисперсии (7.105) в V~ получаем
Xg х$
V = PV Рг + PV~ Pr + Р / F2 V~ + V~ F[ + G2 Vw G2r -
Xg Xg \ Xg X g
— Pr.
X, 2 v 2 X, )
299
Теперь, если воспользоваться ур-ниями (7)—(9) для замены F2, G2 и Н2,
то после ряда алгебраических преобразований имеем
V = £,PV~ Pr -J- PV~ Pr Fl 4- Gi Ч» G? — PV~ Рг Il'[ ФТ1 H.PV~ Рг
1 xt х, 1 х w 1 х, 1 v 1 Xj
Так как V=PV~PT, то это выражение записывается в виде
Х3
V = FXV + VFf + Gj G[ - vnf Ф71 H1V,
причем оно совпадает с уравнением дисперсии V~ (/). Начальные условия для
V н V~ также совпадают, поскольку V(£) = Р(£) V~ (£) Рт (/0) = V ~ (/о).
Аналогичным способом можно доказать справедливость соотношения (10).
Л ..АЛЛ
Пусть x(t) определяется как х(/) =Р(?)х2(?), так что x=Px2+Px2=Pxj -f-
+ P[F2x2+V~ H’W-iy (z—H2x2)].
Теперь воспользуемся ур-ннями (7), (9) и запишем
х = Рх2 + Р [( Р-1 FjP - Р-1 Р) х2 + VXj Рг Н[ Ф71 (z - Hi Рха)] =
= FiP £ + Р¥~РГ Н[ ф~’ (z — HjPxa).
Согласно определению состояния х и ранее доказанному соотношению (11)
получаем x=F4x+ У£^'Н{ф^‘1(г—Hix).
Л
Таким образом, уравнение для х(/) совпадает с уравнением для х±(/), причем
Л
начальные условия также равны. Следовательно, для всех t^to.
Этот пример показывает, что любое эквивалентное множество переменных со-
стояния может быть использовано при описании моделей сообщения и наблю-
дений, поскольку оценки любого множества состояний могут быть получены из
оценок некоторого другого множества. Это, в свою очередь, означает, что вы-
бором переменных состояния можно сократить объем вычислений, связанных с
реализацией фильтра. Однако до сих пор еще не найдена методика определения
наилучшего представления переменных состояния.
Пример 7.5 [167]. Рассмотрим применение фильтра Калмана для получения
производной линейной функции состояния, определяемого моделью сообщения.
Иначе говоря, задана функция у(/) =С(0х(/), где х(/) определяется уравнением
модели сообщения (7.82), а модель наблюдений — ур-нием (7.85). Необходимо
определить линейную по критерию минимума среднеквадратической ошибки
оценку состояния у. Если предположить, что С(/) существует, то y(Q опреде-
ляется как у(0 = С(/)х(0+С(0х(0. Воспользовавшись уравнением модели
сообщения, это выражение можно записать в виде
У (0 = [С (f) + С (0 F (0J X (0 + С (0 G (0 w (t).
Определим наилучшую оценку случайной величины, как условное среднее
Л
этой величины при заданных наблюдениях Таким образом, имеем у(0 =
= £ {у (^|Z (0} Так как £ {w (^ ] Z (£)} = 0, то
у(0 = [С (i)+C(/)F(i)]x(0.
Пример 7.6. Теперь покажем, как идея фильтра Калмана может быть легко
применена в задаче определения структуры оптимального AM демодулятора в
300
системах передачи непрепывиых сообщений. Рассмотрим модели сообщения и
наблюдения, представлен1 ые на рис. 7.7 и описываемые уравиениими: х—Fx(/) +
Gaw(Z), z(t) =x,(t)H sin i(Z), в которых w(t) и v(tj — независимые случай-
HsinQc t
Двухполосная амплитуд-
ная модуляция с подав-
ленной несущей
Рис. 7.7. Модель сигнала с амплитудной модуляцией
и модель наблюдений
ные процессы с нулевым средним и коэффициентами дисперсии Чги(/) и Чгс(/).
Матрицы F и G соответственно имеют вид
С1
С2
С3
CN.
Уравнения фильтра Калмана (7.J02) и (7.105) записываются в виде
л л
х = Fx (/) +
Н sin toc t
4v(t)
[z (t) — H xt (t) sin toc ij;
, _ T №sin2 a>ct
v~= FV^ + <f) F + G 4P№ (i) G ~ x
А А А ’Г V [L)
- (t) V~ (t) (t) (f) . . .v~ (t) v~ (t)
*tl Хц Xji Л12 А11 А
(t) v~ (t) v~ (/) v~ (t) . . .V~ (t) y~ (0
Xja Xn Xj2 Xj2 *12 X
xw 11
w w .
Теперь заметим, что компоненты V~ меняются во времени медленно, особен
но по сравнению с несущей частотой Поэтому можно исключить составляющие
двойной частоты в уравнениях фильтрации и дисперсии, полагая sin2®),^
= 0,5—0,5 cos 2 W» 0,5 Это приближение упрощает уравнение фильтрации и
уравнение дисперсии и, кроме того, позволяет, если это необходимо, заранее по-
лучить решение уравнения дисперсии
Если для реализации фильтра воспользоваться стационарным решением
уравнения дисперсии ошибки, то в результате получим фильтр, структурная
схема которого изображена на рис 7 8
301
Рис. 7.8 Квазиоптимальный приемник сигналов с ам-
плитудной модуляцией и модель наблюдений
Интересно вычислить стационарную дисперсию ошибки для случая, когда х
представляет скалярную величину Установившееся значение дисперсии ошибки
в этом случае равно
Дисперсия сигнала x(t) легко может быть вычислена, она равна Vx = Ct2XVw/2di
Если величину H2Vxl4v рассматривать как отношение сигнал/шум S'/N, то дис-
Персию ошибки можно выразить в виде V~=-------~~
х 8Ц\Г
Как
и следовало ожидать, дисцерсия ошибки уменьшается с увеличением отношения
сигиал/шум.
В заключение рассмотрим задачу непрерывной линейной филь-
трации в общем виде, когда шумовые процессы w и v коррелиро-
ганы и имеют ненулевые средние значения, а модели сообщения
и наблюдений также включают в себя известные функции време-
ни. В этом случае модели сообщения и наблюдения имеют вид
k(0 = F(0x(0+G(0w(0 + 5(0u(0; (7.149)
z0 = H(Ox(O + v(f) + y(O, (7.150)
где u(t) и y(t)—известные функции времени, a w(t) и v(t) —
взаимно коррелированные процессы. Алгоритм фильтрации для
этого случая приведен в табл. 7.5.
Таблица 75
Обобщенный непрерывный фильтр Калмана
Модель сообщения
*х (0 = F (t) х (t) + G (t) w (t) +E(t)u (t). (7.149)
Модель наблюдений z(O = H(/)x(t) -j-v(f) +y(0- (7.150)
302
Продолжение
Априорные данные
E{w(t)} = pw (ty, £{v(t)} = !iv(0; E {x (0)} = (0);
cov {w (Z), w (t)} = (Z) 6O (t — t), cov {v (Z), v(T)} = Tv (Z) 6д (t — r);
cov{w(Z), v(T)} = Vwv(i)6D (Z-т), var{x(0)}=Vx (0)=Vx (0);
cov{x(0), v(Z)} =cov{x(0), w(Z)}=0.
Алгоритм фильтрации
x (Z) = F (t) x (t) +G (Z) pw (Z) + E (Z) u (/) +
4- К (Z) [z (t) - |iv (Z) — у (Z) — H (Z) x(Z)J.
Вычисление коэффициента усиления
(0 = [V~ (Z) Hr (z) + G (Z) Twv (014V1 (0 •
Вычисление дисперсии ошибки
v~ (0 = F (Z) v~ (Z) + V~ (Z)Fr(Z) +
+G (Z) Tv (Z) GT (t) - Ж (t ЖТ (t).
Начальные условия
x (0) = E {x (0)} = (0); V~ (0) = var {7(0)} = Vx (0).
7.4. Стационарные процессы и фильтр Винера
Здесь рассмотрим частный случай задачи, разобранной
в предыдущем параграфе, и назовем его фильтром Винера. Для
простоты ограничимся исследованием только непрерывного слу-
чая. Все выкладки, представленные в этом параграфе, являются
частным случаем общей теории фильтра Калмана—Винера. Метод
вычислений, основанный на алгоритме фильтра Калмана, вообще
говоря, ближе к практическому осуществлению, чем метод, рас-
сматриваемый здесь. С другой стороны, многие практически важ-
ные задачи оценивания можно отнести, по крайней мере с доста-
точным приближением, к стационарным, и методы, излагаемые в
этом параграфе и разработанные раньше общей теории Калмана,
уже нашли успешное применение в многочисленных практических
задачах.
В 1949 г. была опубликована работа Винера «Экстраполя-
ция, интерполяция и сглаживание стационарных временных после-
довательностей». Ее публикация явилась важной вехой не только
потому, что результаты были новыми и вызвали к себе повышен-
ный интерес, но и (что более важно) они возводили частную за-
303
дачу в ранг теории, которая в то время нашла широкое примене-
ние, в частности, теории частотных фильтров. К сожалению, из-за
того, что основные результаты были сформулированы на «частот-
ном языке», они непосредственно не могли быть обобщены на не-
стационарные задачи. Хотя нестационарная задача и была сфор-
мулирована в общем виде, т. е. записано уравнение Винера—Хоп-
фа, но было получено очень мало практических результатов, за
исключением только работ Бутона [31], Заде и Рагазини [287],
[288]. До тех пор, пока не был разработан алгоритм фильтра Кал-
мана, вычислительные трудности не были преодолены в общем
нестационарном случае.
Стационарный фильтр Калмана. В стационарном
варианте общей задачи оценивания состояния должны выполнять-
ся следующие три условия:
1. Модели сообщения и наблюдения не изменяются во време-
ни, т. е. они описываются уравнениями с постоянными коэффи-
циентами:
x(t) = Fx(f) + Gw(r); (7.151)
z(f) =Hx(0 + v(0, (7.152)
где F, G, H — матрицы постоянных коэффициентов.
2. Входной шум и шум измерений стационарны, по крайней
мере, в широком смысле, т. е.
cov{w (f-b т), w(f)} = Vw (f + т, t) = Rw (т) = 6D (т); (7.153)
cov {v (t + t), v (f)} = Vv (f +1, t) = Rv (т) = 4rv (t), (7.154)
где Yw и 'Ey — матрицы постоянных коэффициентов. Кроме того,
предполагается, что w и v — некоррелированные белые шумы с
нулевым средним.
3. Интервал наблюдений начинается при t =—оо. Очевидно,
что это условие никогда не может выполняться на практике. Од-
нако, поскольку момент начала наблюдений расположен доста-
точно далеко в прошлом, так что все переходные процессы успе-
вают закончиться, то это допущение можно считать справедливым.
Если эти три допущения выполняются, то, очевидно, задача
оценивания уже не зависит от выбора начала отсчета времени в
том смысле, что допустимо любое конечное перемещение шкалы
времени без изменения условий задачи. Поэтому коэффициент
усиления фильтра Калмана должен быть постоянным для конеч-
ных значений времени t, поскольку не существует причины его
изменения между двумя конечными моментами времени t Кроме
л ~
того, случайный процесс x(t) и, следовательно, процесс x(t) ста-
ционарны, так что V~(7) = V~(0) =const, а уравнение дисперсии
(7.105) записывается в виде
0 = FV~(0) + V~(0) F — V~(0) H 4V‘ H V~(0) + G 'lH GT. (7.155)
304
Постоянный коэффициент усиления Калмана в этом случае
определяется как
<Ж-(0) = V~(0) НГТ7’,
(7 156)
и, наконец, уравнение фильтрации имеет вид
x(/) = Fx(0 + Jr(0)[z(0 —Нх(ЭД, х(— оо)=0. (7.157)
Заметим, что в стационарном случае уравнение дисперсии
превращается в вырожденное матричное уравнение Риккати
Один И'- часто используемых способов решения ур-ния (7.155)
(обычно с помощью ЦВМ) заключается в решении нестационар-
ного уравнения дисперсии (7 105) с соответствующими постоян-
ными значениями коэффициентов, из которых составлены матри-
цы F, Н, 'Irw и 'Ey, и произвольной неотрицательно определенной
матрицей начальных условий для V~ в текущем времени до тех
пор, пока полученное решение не достигнет постоянного устано-
вившегося значения. Это окончательное значение V~ принимается
за искомое решение ур-ния (7.155). Здесь алгебраическое урав-
нение преобразуется в дифференциальное, так как алгоритмы ре-
шения дифференциальных уравнений на цифровых (или аналого-
вых) вычислительных машинах, как правило, эффективнее алго-
ритмов решения нелинейных алгебраических уравнений. Другой
подход, который может быть использован для отыскания решения
ур-ния (7.155), связан с реализацией на ЦВМ поисковой проце-
дуры, например, градиентного метода [202].
Пример 7 7 Определим стационарный фильтр, обеспечивающий минимальною
дисперсию ошибки, для системы
Г 0 11 ГО]
*(')=[_, о]х(0 + 1 I (0’ г(/) = [1 °] х (#)-4-" (0.
ГО 0]
где ЧЦ = |0 J и Ч\, = 3
Вырожденное уравнение Риккати (7 155) для
и виде
этого примера записывается
— 1 '
0 ~
0] _
1! ’
Если перемножить все сказанные матрицы, го получим следующие три урав-
нения
1 9 1
21/-----— V- = 0, V~ — V- — —V— V— =0, — 2V— —
Хи з х„ Х2, X,, 3 Х,2 X,, X,,
1 2
— — vL 4-1=0
3 х„
305
Решение последнего уравнения относительно / р имеет вид
— 6 ±/36+ 12 г- п
V~ =----------2----=—3±2У 3=0,464—6,464.Если выбрать в качестве реше-
ния положительный корень этого уравнения, то получим V~ =±1,67 и соответ-
ственно V~= ±2,59 Для того чтобы V—(0) была положительно определенной,
Xg# X
необходимо выбрать положительные значения для V— и V.— так, что в ре-
Хц Xgj
[1,67 0,4641
зультате имеем V~(0) = .
? х ' ' [0,464 2,59 J
Таким образом, мы нашли, как и требовалось, действительные положительно
определенные корни вырожденного уравнения Риккати.
Чтобы найти постоянный коэффициент усиления фильтра Калмана ^(0),
0,5571
[о,155 ’
достаточно подставить найденную матрицу V~(0) в ур-ние (7.156). В результа-
те получаем Ж (0) =
На рис. 7.9а показана «каноническая» реализация фильтра Винера. Если
нас интересуют, как это часто бывает, только оценки состояния х4 или х2, то
*—Модель сообщения-----*- *------Каноническая реализация фильтрат’-
$ в)
Рис. 7.9. Структурные схемы фильтров, рассмотренных в примере 7.7
могут быть использованы фильтры, реализованные по структурным схемам
рис. 7.96, 7.9в. Эти фильтры могут оказаться проще фильтра, изображенного на
рис. 7 9а. Однако фильтр, структурная схема которого представлена на рис. 7.9а,
’А А
одновременно формирует оценки хД1) и x2(t), которые в общем случае не свя-
А А
заны соотношением Xt = x2. Теперь рассмотрим классическую форму решения
уравнения фильтра Винера, которое лежит в основе реализации фильтров, изо-
браженных на рис. 7.96, 7.9в.
Фильтр Винера. Выше результаты решения стационарной
задачи оценивания были получены путем введения дополнитель-
ных предположений, связанных со стационарностью задачи и поз-
воливших упростить обобщенный алгоритм фильтрации Калмана.
В частности, было установлено, что фильтр Калмана становится
стационарным. Теперь сформулируем стационарную задачу оце-
306
нивания в другой форме, достаточно близкой к первоначальной
работе Винера. Сформулируем задачу на «частотном языке» с
использованием таких понятий, как передаточные функции, спек-
тральные плотности. На первый взгляд может показаться, что су-
ществует лишь незначительная связь между задачами Калмана и
Винера. Однако ниже будет показано, что эти две задачи эквива-
лентны, хотя решение, полученное в форме фильтра Калмана, с
точки зрения вычислений часто оказывается предпочтительнее.
Задачу можно представить в виде структурной схемы, изображен-
ной на рис 7.10. Сигнал y(t) искажается аддитивным шумом v(t),
Рж 7 J0 Представление мно-
гомерной задачи фильтоации
Винера
причем y(t) и v(t) взаимно некоррелированные стационарные
случайные процессы с нулевым средним и со спектральными плот-
ностями Ry(s), Rv(s). Наблюдение z(t)-y(t) +v(0 пропускается
через линейный фильтр с постоянными параметрами и передаточ-
ной функцией W(s). Сигнал на выходе фильтра обозначен как
л
y(t). Задача состоит в выборе такого фильтра W(s), на выходе
которого формировалась бы наилучшая, в смысле минимума дис-
персии, оценка исходного сигнала уг(7), который получается при
действии идеального оператора I(s) на сигнал y(t) Часто под
идеальным оператором понимают тождественный (единичный)
оператор, поэтому yt(t) представляет собой неискаженный сигнал
y(t). Короче говоря, необходимо выбрать передаточную функцию
фильтра Wfs), которая обеспечивала бы минимальное средне-
квадратическое значение ошибки *> (СКО)
СКО == Е { уг (0 у (t)} = tr [£ { у (0~ут (0}] = tr [var {7(0}]. (7-158)
где у(0 = У>(0 —У(0-
Согласно теореме Парсеваля среднеквадратическая ошибка мо-
жет быть выражена через матрицу спектральных плотностей ошиб-
ки Ry (s):
СКО = —tr
2 л 1
Rr (s) d s
(7.159)
*> Предполагается, что все случайные процессы имеют нулевые средние зна
чения, так что среднеквадратическая ошибка и дисперсия ошибки в этом случае
совпадают (Прим авт)
307
Это выражение, которое определяет среднеквадратическую
ошибку как интеграл спектральной плотности ошибки, заданной
в области комплексных частот, позволяет выполнить вывод урав-
нения фильтра в частотной области, оперируя лишь со спектраль-
ными плотностями. Этот частотный подход позволяет значительно
упростить выкладки, но, очевидно, его применение ограничено
лишь стационарными задачами
Спектральная плотность ошибки, которая может быть найде-
на методами, рассмотренными в § 3.5, равна
Ry(s) = [I (s) - W (s)] Ry (s) [I (- s) - W (- s)]r -4-
+ W (s) Rv (s) Wr (- s). (7.160)
Подставляя это выражение в ур-иие (7.159), получаем
/ i оо
CKO=-L-tr( С{[1 (s) — W(s)] RY(s) [I (—s) —W(—s)]r +
Л 1 I J
i oo
+ W(s)Rv(s)Wr(—s)}dsj. (7.161)
Задача состоит в том, чтобы выбрать матричную передаточ-
ную функцию W(s), минимизирующую среднеквадратическую
ошибку. Для решения этой задачи представим W(s) как
W(s) = W0(s)+8T](s), (7.162)
1Де Wo (з)—оптимальная передаточная функция, q (з)—произ-
вольная матричная передаточная функция; е — скалярная вели-
чина. Передаточная функция оптимального фильтра получается
как решение уравнения
ЭСКО I == 0
(7.163)
д е |е=0
При ПРОИЗВОЛЬНОЙ q (s)
Воспользуемся этим методом для решения сформулированной за-
дачи оценивания Если считать, что W(s) = W0(s) + eq (s), то сред-
неквадратическая ошибка выражается следующим образом-
СКО(е, ^) = —1— tr J {[1 (s) — Wo (з) — в q (s)lRy (з) [I (-s) -
— 1 00
- Wo(- S) - 8 4 (- S)f +[W0 (s) + 8 7] (S)l /?v (s)[W0(-S)+e 1J(-S)f }ds.
(7.164)
Здесь мы ввели два аргумента е и q, чтобы подчеркнуть, что
СКО зависит как от 8, так и q Уравнение (7 163) теперь записы-
вается в виде
308
(I 00 \
[ {Wo (s) [Ry (S) + Rv (s)l - I (s) RY (s)} / (- s) d И +
— 1 00 /
(1 00
J (s) {[Ry (s) + RV (s)l Wj (-s) - ry (S) IT (- s)} ds |.
- 1 00 /
(7.165)
Если воспользоваться свойством симметрии матриц спектраль-
ной плотности и тождеством tn(xyT) = tr(yxT), то ур-ние (7.165)
можно записать в виде
/ 1 00 \
tr f {W0(s)[Ry(s) + Rv(s)] — I(s)RY(8)Hr(— s)ds 1=0. (7.166)
\— * 00 /
Уравнение (7.166) будет удовлетворяться при произвольной ^(s),
если
Wo (s) = I (s) Ry (S) [Ry (s) + Rv (S)!"1 .
(7.167)
Это решение соответствует физически нереализуемому фильт-
ру Винера, поскольку W0(s), вообще говоря, имеет полюса в пра-
вой полуплоскости комплексной переменной 8. Напоминаем, что
наличие полюсов в правой полуплоскости свидетельствует не о
неустойчивости системы, а скорее о физической нереализуемости
системы, так как в такой системе отклик опережает воздействие.
Для того чтобы W(s) =W0(s)+eT](s) представляла собой до-
пустимое решение, W (5), Wo (s) и q (s) должны быть физически
реализуемыми или, другими словами, должны иметь все полюса
в левой полуплоскости комплексной переменной 5. Используя это
ограничение на q(s), можно выбрать Wo(s), которая удовлетво-
ряла бы ур-нию (7.166) и была физически реализуемой.
Допустим, что матрица спектральной плотности RvfsJ+Rvfs)
представляет собой спектр, который допускает факторизацию в
виде
Rz(s) = Ry(s) + Rv(8) = Д(8)Дг(-з), (7.168)
где Д(8)—матрица, для которой detfA(s)] имеет все нули и по-
люса в левой полуплоскости комплексной переменной s Выпол-
нение этого условия гарантирует, что A(s) и обратная матрица
Д-1(х) будут аналитическими функциями в правой полуплоскости
комплексной переменной s Процедура нахождения A(s) представ-
ляет собой, вообще говоря, трудную вычислительную задачу, ко-
торую можно обычно довести до конца только численным мето-
дом при помощи достаточно сложных алгоритмов [2] Уравнение
(7 166) теперь можно записать в виде
tr I * J [Wo (s) Д (s) — I (8) Ry (8) Д~г (- s)] ДT (- s) s) ds
’ — lx
= 0.
(7.169)
309
Представим I(s)Ry (s) A~T(—s) в виде двух слагаемых
I (s) Ry (s) Д“г (— s) = A (s) + В (— s), (7.170)
где A(s) объединяет все члены, имеющие полюса в левой полу-
плоскости, а В(—s)—все члены, имеющие полюса в правой по-
луплоскости.
Матрицу Afs), которую можно также рассматривать как пре-
образование Лапласа части отклика фильтра, существующей при
положительном времени, назовем физически реализуемой частью
фильтра и обозначим А(з) = [I (s) RY (s) А-т(—s) ]pr. При этом пол-
ный импульсный отклик фильтра определяется как преобразова-
ние Лапласа для величины, стоящей в правой части ур-ния (7.170).
Если подставить ур-ние (7.170) в (7.169), то необходимое ус-
ловие оптимальности запишется в виде
{! оо
J [Wo (s) A (s) - A (s)l Аг (- s) fiT (- s) ds +
— I 00
1 GO
+ J В (— s) Аг (— s) (— s) d s
-- 1 OO J
= 0.
(7.171)
Однако второй интеграл здесь равен нулю, так как все полюса
В(—s)AT(—s)t]t(—^) лежат в правой полуплоскости. Если контур
интегрирования заканчивается слева и ни один полюс не распо-
ложен внутри контура, то значение интеграла равно нулю, так
что ур-ние (7.171) принимает вид
{1 00
j [Wo (з) Д (s) — A (s)] Дг (-s)/ (~s)ds
— 1 00
= 0.
(7.172)
Поэтому оптимальный физически реализуемый фильтр имеет
передаточную функцию
W0(s) = A (s) A"1 (з),
(7.173)
которую можно также выразить через исходные величины
Wo (з) = [I (з) Ry (s) Д-г (- s)]PR A”1 (s). (7.174)
Итак, мы получили окончательное решение многомерной ста-
ционарной задачи оценивания в форме матричного фильтра Ви-
нера. Матричный фильтр Винера как решение многомерной ста-
ционарной задачи оценивания был получен Дарлингтоном [49],
Янгом и Томасом [279], а также Девисом [51]. Однако этот резуль-
тат не нашел широкого применения в инженерной практике из-за
достаточно трудных проблем вычислительного характера, связан-
ных с необходимостью факторизации спектра, заданного в виде
матрицы. Хотя в работах [2], [90], [198] приведены вычислитель-
ные процедуры для факторизации спектра, которые основаны на
решении матричных уравнений Риккати, широкое использование
алгоритмов фильтрации Калмана вытеснило многих сторонников
использования матричного фильтра Винера
310
В том случае, когда сигнал y(t) и шум v(t) — некоррелирова-
ны, оптимальный фильтр имеет передаточную функцию
Wo (s) = [I (s) Rzy (s) Д~г (- s)]pr A"’ ($). (7.175}
где
Д (s) Д“г (- s) = Rz (s) = RY (s) + Rv (s) + Ryv (s) + Rvy (s); (7.176}
Rzy (s) = Ry (s)+ Rvy (s). (7.177)
В одномерном случае
Го (8) = [/ (8) /?ZY (8)/Д (- eJlPR/Д (S) (7.178}
и, наконец, когда сигнал y(t) и аддитивный шум v(t) некоррели-
рованы, -передаточная функция оптимального линейного фильтра
имеет вид
Wo (s) = [/ (s) RY (з)/Д (- s)]pR/Д (s).
(7.179}
Пример 7.8. Рассмотрим простую одномерную задачу. Спектральная плот-
п 3600
ность сигнала равна RY (s) = —77,----г • Шум белый со спектральной плот-
—s2(169—зц
ностью 7?y(s) = l, причем сигнал и шум — некоррелированы. Необходимо оце-
нить сигнал y(t), причем 7(s) = 1. В рассматриваемом случае
Rz (s) — RY (* s) + Ry (s)
3600 — s2 (169 — s2) 3600 — 169s2 + s*
“ — s2(169 —s2) “ — s2(169 — s2)
Факторизацию спектра легко выполнить, и в результате имеем:
6Q+17s + s2 60- 17s + s2
(S) s(13+s) ’ ( S) — s(13— ’
Отметим, что два полюса, расположенные в начале координат, были разде-
лены так, что один из них был отнесен к правой полуплоскости, а другой — к
левой полуплоскости. Используя ур-ние (7.179), иолучаем:
(s) =
r3600/[-s2(13 + s)( 13 —S)] |
(60 - 17s+ s2)/[-s(13-s)]Ipr
(60 + 17s + s2)/[s (13 + s)]
Г_________3600_________1
I s(60— 17s+ s2) (s + 13) Jpr
(60 + 17s + s2)/(13 + s)
Рассмотрим числитель этого выражения. Разложение на элементарные дроби
имеет вид
________3600_________
s(s + 13) (s2 — 17s+ 60)
60 8
13 13 __jv_(s)__
s —s+ 13 + s2 — 17s + 60
Функция N (s) не имеет существенного значения, так как в нее входит s в пер-
вой степени, а нас интересует только та часть разложения на элементарные
дроби, которая имеет полюса только в левой полуплоскости. Так как s3—17s+60
стоит в числителе А(—s), то эта функция должна иметь и'орни только в правой
полуплоскости комплексной переменной s Следовательно, получаем
60 8
_________3600__________1 13 13 _ 4s+ 60
. s(s + 13)(s2— 17s+ 60) Jpr= s ~ s + 13 ~ s (s + 13)
311
и передаточная функция оптимального фильтра
(4s + 60)/[s (s + 13)] = 4s+ 60
o(S) (s3 + 17s + 60)/[s (s + 13)] s2 + 17s + 60’
Минимальная величина дисперсии ошибки вычисляется путем
подстановки выражения для U7o(s) в ф-лу (7.159) и последующего
интегрирования по контуру. Эта часть работы значительно облег-
чается тем, что интегралы вида
4- i «
Z„ = -L [ An(s) Ап(—s)ds, (7.180)
2л 1 J
где
. . . Со + Сх S + С3 S2 + . . . + С ] sn 1
Ап ($) ----------------------------------—
do + d-i s + d2 s2 +... + dn s
(7.181)
табулированы для всех значений l^n^lO [172]. При /1=1, 2, 3
значения интегралов 1п соответственно равны:
/ — с° • j _ со + с‘ .
1 “* idod^ ’ 2 “ idod^do ’
tj + A + ( 2 с0 cs) do df + Cq ds d3
=-------------------------------------. (1.1 oz)
2 dg d3 (— do do + dl d2)
Однако сведение выражений к табличным интегралам часто
требует выполнения громоздких алгебраических преобразований.
Если сигнал и шум некоррелированны, то
Ry(s) = [I (s) - W (s)l RY (5) [1 (- s) - W (- s)f +
+ W(s)Rv(s) Wr(-s).
(7.183)
Анализируя отдельно каждый член, входящий в это выраже-
ние, можно заметить, что разложение на множители, которое не-
обходимо для сведения интегралов к табличным, легко выполняет-
ся просто разложением на множители спектральных плотностей
Ry (s) и Rvf-s), которые очень часто уже заданы в факторизован-
ном виде.
Полезным свойством этого метода является то, что он сразу
дает возможность разделить среднеквадратическую ошибку на со-
ставляющую сигнала и составляющую шума. Если соответствен-
но обозначить эти составляющие как СКОу и СКОу, то получим
СКО = СКОу + СКОу, (7.184)
где
{4-1«
С [I (s) — W ($)] Ry (s) [I (— S) — W (—s)f ds
J
—i co
(7.185)
312
CKOV =
tr
W(s)Rv(s)
----Ico
Wr (— s)ds
(7.1 $6)
1
2 л i
Пример 7.9. Воспользуемся представленным выше методом для определения
минимальной величины среднеквадратической ошибки оптимального фильтра, син-
тезированного в примере 7.8 Так как сигнал и шум некоррелированны, то вос-
пользуемся упрощенными ур-ниями (7.184) — (7.186). Среднеквадратическая
ошибка определяется выражением
-4-1 оо
„ ~ 1 f / 4s + 60 \l — 4s + 60 \
CKOY =------ 1 —------------!------ 1 — —--------—------ x
Y 2л I J ( s3 +17s 4-60 Д s2— 17s 4-60 J
— ico
3600 _L+C° 60 60
X — s2(169— s2) 2л i J s2 4-17s 4-60 s"—17s 4-60 ^S'
Это выражение записано в таком виде, который позволяет непосредственно
использовать для вычислений табличный интеграл (7Л82) с параметрами
Ct = 0, с»=do=60, dt= 17 и d2=H. В результате получаем
CKOY =
(60)2(1)
2 (60) (17) (1)
60
34
= 1,765.
Согласно выражению (7.186)
ошибки
шумовая составляющая среднеквадратической
CKOV = ~т
v 2л 1
4s 4- 60
s2 4- 17s 4- 60
— 4s 4~ 60
s2 — 17s 4-60
И в этом случае воспользуемся табличным интегралом с параметрами: Сп=60,
Ci=4, do=6O, di=il7, d2=l. В результате получаем
rvn (60)2(1) 4-(4)2 (60)
v 2 (60) (17) (1)
76
34
= 2,235.
Наконец, находим суммарную среднеквадратическую ошибку:
СКО= 1,765 4-2,235 = 4,00. '
Более полное исследование фильтра Винера, в том числе и ряд
обобщений основной теории, интересующийся читатель может най-
ти в литературе (см например, [171], [202], [299*]). Дискретный ва-
риант фильтра Винера подробно изучен в [123].
Соотношение между стационарными фильтра-
ми Калмана и Винера. В предыдущих пунктах этого па-
раграфа были исследованы два различных метода решения ста-
ционарной задачи оценивания. Уравнение стационарного фильтра
Калмана, или вырожденной формы обобщенного фильтра Калма-
на, было получено во временной области и выражено через пере-
менные состояния. Уравнение фильтра Винера, напротив, было по-
лучено в частотной области и выражено через частотную харак-
теристику. В обоих случаях вывод уравнения базировался на не-
посредственном использовании методов вариационного исчисле-
ния. При неглубоком анализе может показаться, что эти два под-
313
хода имеют мало общего. Однако это не так, и существует тес-
ная связь между этими двумя подходами.
Основное отличие между задачами, сформулированными для
фильтров Калмана и Винера, состоит в способе задания модели
сообщения. При рассмотрении фильтра Калмана модель сообще-
ния задается векторным дифференциальным уравнением первого
порядка (7.151), а связанная с ней модель наблюдений — ур-нием
(7.152). При рассмотрении фильтра Винера модель сообщения
задается через спектральную плотность RyCs) сигнала y(t). Оче-
видно, что эти два подхода эквивалентны, так как можно найти
спектральную плотность процесса, который связан с моделью со-
общения, используемой при рассмотрении фильтра Калмана, как
Ry(s)=H(sI — F)-1 (— si — Fr)~‘ Hr. (7.187)
Точно также, если задана спектральная плотность сообщения,
то можно всегда определить связанные с ней векторные диффе-
ренциальные уравнения первого порядка, формирующие процесс
с заданной спектральной плотностью. В частности, для скаляр-
ного наблюдения можно разложить Ry(s) на два сомножителя:
Ry(s) =(Ry(s)]+[Ry(s)]~, где [Ry(s)]+ имеет все полюса и нули в
левой полуплоскости, a имеет все полюса и нули в пра-
вой полуплоскости. Если записать [7? уfs)]+ в виде
[М]+ =
«О+ «!$+ •+«»! s'”
₽0 + Pl S + • • • + Pra s”
m<Zn,
(7.188)
то можно построить модель сообщения с переменной фазой в ви-
де [см. (7.151) и (7.152)]
Т 0 ... О fl-
00 ... о о
о о ... о о
_0 О . . . О 1_
Чтобы установить эквивалентность стационарных фильтров
Калмана и Винера, выберем модели сообщения и наблюдений в
постановке задачи Калмана и найдем их эквивалентное спектраль-
ное представление, которое необходимо при использовании под-
314
хода Винера. Затем решим эти две задачи оценивания и сравним
полученные результаты.
Предположим, что модели сообщения и наблюдений при реше-
нии задачи методом Калмана заданы уравнениями:
x(0 = Fx(0+Gw(0; (7.190)
z(0 = Hx(0+v(0, (7.191)
где v и w — белые шумы с нулевым средним значением и кова-
риациями cov{w(7), w(t)}=TW'6d(Z—т); cov{v(7), v(t)} =
= Tv6d(/—t).
Предположим, что система, описываемая ур-нием (7.190),
асимптотически устойчива и управляема. Эквивалентная спек-
тральная плотность сигнала y(t) в постановке задачи Винера оп-
ределяется как
Ry(s) = H2(s)G'FwGr2r(— s)Hr, (7.192)
где й(х) —резольвентная матрица;
G(S) = (SI-F)-*, (7.193)
а спектральная плотность шума v(t) равна
RV(S)=TV. (7.194)
Матрица Tv предполагается положительно определенной, так
что она допускает представление
TV = NN, (7.195)
где N — положительно определенная симметричная матрица. Тре-
бование, чтобы матрица Tv была положительно определенной,
физически означает, что в каждом канале наблюдения присутст-
вует шум.
Стационарная задача фильтрации Калмана теперь сформули-
рована как многомерная задача фильтрации Винера и могут быть
применены результаты решения, полученные в предыдущем пунк-
те. На первом этапе матрица спектральной плотности Rz(s), опре-
деляемая как
Rz (s) = Ry (S) + Rv (s) = N2 + н e (s) G Gr 2r (— 5) Hr, (7.196)
должна быть разложена согласно (7.168). Спектр факторизуется,
если в качестве A(s) рассматривать матрицу
A ($) = N + Н 2 (s) KN, (7.197)
где K = RHrT7' (7.198)
и R — положительно определенная симметричная матрица, пред-
ставляющая собой решение вырожденного матричного уравнения
Риккати:
FR+RFr — KTvKr+GTwGr = 0. (7.199)
Существование такого решения гарантируется устойчивостью
ур-ния (7.190) (см. § 7.5). Приведенное выше разложение спектра
315
может быть проведено непосредственной подстановкой. Произве-
дение Д($)ДТ(—$) равно
Д (s) Дг (—s) = N2 + Н 2 (s) KN2 + N2 Кг 2Г (— s) Нг +
H-H2(s)KN2Kr2r(— s) Нг. (7.200)
Так как К определяется ур-нием (7.198) KN2 = K4rv==RH7, то
ур-ние (7.200) принимает вид
Д(8)ДГ(—s) = N2 +H2(s)RHr+ HR2r (—s)Hr +
+ H 2(s)KTvKr2r(—s)Hr
или
Д (s) Дг(—s) = N2 + H 2 ($) [R (—s I — Fr) +
+ (s I - F) R + К Tv Kr] 2 (— s) Hr.
После исключения членов —sR и + sR и подстановки ф-лы (7.199)
получим окончательно
Д(5)ДГ(— s) = N2 + H2(s)GTwGr2r(— s)Hr. ч (7.201)
Итак, мы показали, что Rzfs) может быть представлена в виде
(7.170), причем Д ($) определяется из ур-ния (7.197). Остается те-
перь показать, что все полюса и нули det[A(s)] лежат в левой по-
луплоскости комплексной переменной s'. Используя специальное
матричное тождество [214], получим
•det [Д (s)] = det [N + Н 2 (s) К N] = det [N det [I + Н 2 (s) К] =
= det N det [2 (s) КН + I].
Так как й($) —несингулярная матрица, то 2(s) также может
быть разложена на множители. В результате получаем
det [Д (s)J = det N det [2 (s)] det (s I — F + KH),
так что
det [Д (s)] = det N F ~^KH) • (7.202)
Используя теорию линейного регулирования [108] и принцип дуаль-
ности, можно показать, что все корни полиномов det (si—F+KH)
и det (si—F) расположены в левой полуплоскости. Следовательно,
Д(«) удовлетворяет всем требованиям и может быть выполнена
Факторизация матрицы Rz(s).
Если матрицу A(s), определяемую ур-нием (7.197), подставить
в ф-лу (7.177), то Wofs) будет иметь вид
Wo (s) = { Н Q’(s) G Gr Qr (— s) Hr [N +
+ N К 7 2T (— s) H7-]-1 }pR [N + H Q (s) KN]"1 . (7.203)
Теперь необходимо выполнить разложение на простые дроби и
выделить физически реализуемую часть фильтра A(s). Чтобы по-
316
лучить правильный результат, перепишем Нйр) GTWGTO7'(—s) Нг,
используя ур-ние (7.199), в следующем виде:
Н Й (s) GTW Gr Йг (— s) Нг = Г (s) =
= Н Й (s) (К Tv Kr — FR — RFr) й7 (— $) Нг. (7.204)
Добавляя ±sR к величине, стоящей в круглых скобках, и ис-
пользуя (7.193), ур-ние (7.204) можно записать как
Г (s) = Н й ($) [tf Tv Кг + Й“‘ (s) R 4- R Й“г (— $)] Йг (—s) Нг
или
Г (s) = Н Й ($) К Tv КГ Йг (— s) Hr + HR^ (— s) Hr + Н Й (s) RHr. (7.205)
Так как RHr = KTv и Tv = №, то (7.205) можно записать в
виде
Г (s) = Н Й (s) KN [NKr Йг (— s) Hr + N] + Tv Кг Йг (— $) Нг,
так что
Г($) = НЙ($)КМДГ(—s) +ТуКгЙг(— $)Нг. (7.206)
Если это уравнение теперь подставить в ф-лу (7.203), то пере-
даточная функция W0(s) будет иметь вид
Wo ($) = [НЙ (s) KN + Tv Кг Йг (— s) Нг Д~г (— s)]pr A-1 (s). (7.207)
Согласно лемме об обращении матриц А~т(—s) можно запи-
сать:
Д-г (— s) = N-1 — Кг (— s I — Frj+ Нг tf г)“’ Нг N-1 , (7.208)
так что
W0(s) = { НЙ (s) KN + Tv Кг Йг (— s) Hr [N-1 — Кг(— s I — Fr +
+ Нг К7)-1 Нг N-1 ] }pR А-1 ($). (7.209)
После разложения йгк(—s)HTN-1 на множители, где
«k(s) = (sl — F + КН)-1 , (7.210)
и выполнения ряда алгебраических преобразований W0(s) запи-
шется в виде
Wo (s) = [НЙ (s) KN + Tv Kr Як (- s) HT N~’ ]PR A"1 (s). (7.211)
Используя те же самые доводы, что и при анализе Д(х), мож-
но заключить, что йгк(—$) имеет все полюса в правой полуплос-
кости, а й(«)—в левой. Поэтому передаточную функцию W0(s)
фильтра можно записать в виде
Wo (s) = Н й (s) KN А-1 (.5) = НЙ(х)КМ[М + НЙ(5)КМГ1 . (7.212)
Если еще раз применить лемму об обращении матриц и ис-
пользовать ур-ния (7.193) и (7.210), то получим
W0(s) = Hfi(s)K[l — H(sl— F + КН)-1 К] =
= НЙ($)(*1—F— KH + KN) йк(5)К
317
или
W0(s) = Н J2K(s)K = H(s I — F + KHp'K. (7.213)
Стационарный фильтр Калмана, обеспечивающий решение рас-
сматриваемой задачи, определяется ур-ниями (7.155) — (7.157),
причем y(t) = Нх(Т). Сравнение этих результатов с ур-ниями
(7.198) и (7.199) показывает, что К=^(0) и R=V~(0). Легко по-
казать, что передаточная функция фильтра Калмана определяет-
ся ур-нием (7.213), что свидетельствует о полной эквивалентности
алгоритмов Калмана и Винера для решения стационарных задач
фильтрации.
Вообще говоря, алгоритм Калмана в вычислительном отноше-
нии обладает преимуществом перед алгоритмом Винера главным
образом благодаря тому, что он лучше приспособлен для вычис-
лений на ЦВМ, особенно при решении многомерных стационар-
ных задач или уравнений высокого порядка, в которых наблюде-
ние является вектором, а также нестационарных задач. С другой
стороны, имеется ряд задач, в которых факторизация спектра мо-
жет,быть выполнена в общем виде, и это позволяет глубже вник-
нуть в сущность полученного решения. Методом Винера могут
быть также исследованы случаи небелого шума наблюдений,
идеальные операции предсказания и задержки, а также учтены
ограничения, связанные с насыщением и ограниченной полосой
пропускания системы [172], [202]. Заметим, однако, что после того,
цак найден оптимальный фильтр Wofs), для получения требуемой
частотной характеристики необходимо еще определить его физи-
чески реализуемую часть, а это далеко не всегда простая задача.
7.5. Асимптотические свойства
В этом параграфе мы обсудим некоторые асимптотиче-
ские свойства фильтра Калмана. Так как этот вопрос очень мало
изучен, изложение будет кратким и будет состоять, главным об-
разом, из формулировок отдельных положений, доказательство
которых не будет приводиться вообще, либо будет приводиться в
сокращенном виде. Доказательства этих свойств, хотя и не очень
трудные, опираются на теоремы устойчивости по Ляпунову [223],
[85], [107], [111]. Из-за непреодолимых трудностей, которые возни-
кают при изучении асимптотического поведения случайного про-
л
цесса x(t), основное внимание здесь будет уделено изучению
ур-ний (7.33) и (7.34) для дискретного случая и (7.24) для непре-
рывного случая.
При изучении случайного процесса обычно можно сделать ряд
утверждений относительно свойств процесса, таких, как непрерыв-
ность, ограниченность, используя понятие сходимости почти на-
верно или с вероятностью единица. При анализе поведения дис-
318
Персии ошибки оценивания можно избежать этих тонкостей, так
как уравнение для дисперсии ошибки — детерминированное.
Существуют два связанных друг с другом вопроса, касающие-
ся асимптотического поведения алгоритма фильтрации Калмана,
которые будут рассмотрены в данном параграфе. Во-первых, оп-
ределим условия существования стационарного решения уравнения
дисперсии. Ответ на этот вопрос полезен тем, что он позволяет
определить, когда существует решение стационарной задачи оце-
нивания (задачи Винера), и указывает условия, выполнение кото-
рых необходимо для того, чтобы процесс оценивания оставался
эффективным при увеличении интервала наблюдения.
Второй и несомненно более важный вопрос касается устойчи-
вости алгоритма фильтрации. Если фильтр устойчив, то влияние
любой небольшой ошибки в априорных данных о начальном
состоянии при увеличении времени будет постепенно ослабе-
вать. Практическое значение устойчивого в вычислительном отно-
шении алгоритма фильтрации трудно переоценить, поскольку очень
редко имеются точные сведения о начальном распределении со-
стояния x.(t). Перед тем как приступить к обсуждению каждого
из этих вопросов, необходимо ввести понятия управляемости и
наблюдаемости.
Понятия управляемости и наблюдаемости были использованы
Калманом [105], [106] для описания совокупности условий, кото-
рые были связаны с существованием решений некоторых линей-
ных задач управления.
Подробное изложение этого вопроса можно найти в литерату-
ре [42], [105]—[108], [114], [120], [202], [223].
Чтобы облегчить обсуждение понятий управляемости и наблю-
даемости, удобно рассматривать входной шум 'w(t) в модели со-
общения как входной сигнал управления, который может быть
выбран произвольно. Кроме того, предположим, что шум измере-
ний v(t) отсутствует.
Управляемость, грубо говоря, означает, как можно было до-
гадаться по названию термина, способность каждой переменной
изменяться под действием входного сигнала управления. С другой
стороны, под наблюдаемостью подразумевается способность каж-
дой переменной состояния влиять на выходной сигнал системы.
Определим каждое из этих понятий более точно.
Модели сообщения, описываемые ур-ниями (7.1) или (7.82),
называются управляемыми в момент времени t0, если существуют
такие момент времени tf>t0 и управление w(£), заданные на ин-
тервале [^о, tf], которые, вообще говоря, зависят от to, и х(/0) та-
кое, что х (tf) = 0 Если может быть найдено управление для каж-
дого состояния x(to), то говорят, что модель сообщения является
вполне управляемой в момент времени to и если это справедливо
при любом t0, то модель сообщения является вполне управляемой.
В ходе последующих рассуждений будут особенно важны свой-
ства абсолютной и равномерно абсолютной управляемости. Для
непрерывного случая легко показать, что модель сообщения, оп-
319
ределяемая ур-нием (7.82), является вполне управляемой тогда и
только тогда, когда для любого t0 существует такое tf>t0, что
симметричная матрица Грама [74]
if
lff(to> Ф(^о, t) G (t) GT (t) Фт (tg, t)dt (7.214)
to
положительно определена. Здесь Ф(£, т) — переходная матрица
состояний, которая определяется уравнением
= F(O<P(f, т), Ф(т, т) = 1. (7.215)
Если для некоторого А>0 и всех t0 матрицы °lff (to, f0+A) и
Ф(^о+А, ta)Jtff(to, г‘о + А)Фт(г1о-гА, t0)—положительно определен-
ные и ограниченные независимо от to, то модель сообщения явля-
ется равномерно вполне управляемой.
При изучении закона изменения дисперсии в линейных систе-
мах в § 3.5 отмечалось, что удобно преобразовать интегральное
уравнение, которое по форме совпадает с ур-нием (7.214), в диф-
ференциальное. Этот же прием может быть использован и здесь.
Вычислим частную производную:
--Iй: tf) = - ф (to, to) G (to) GT (to) ФТ (to, to) +
+ ff а-фЛ0,?) G ® gT ® фТ dt+
to
+ f Ф (Zo, t) G (t) GT (t)
^0
Так как Ф(г“,’ т)—переходная матрица, которая удовлетворяет
ур-нию (7.215), то это выражение можно представить в виде
<f) = — G (t0) GT (to) + F (t0) [ф (t0, t) G (t) GT (t) Фт (t0, t) dt +
dto J
- * 1
+ J Ф (to, t) G (t) GT (t) фт (to, t) dt FT (to).
- t0
Отсюда следует [см. (7.214)], что
—tf) = — G(to) GT (to) + F (to) Iff (to, tf) + Iff (to, tf) Fr (to). (7.216)
Так как ‘W' (tf, tf)=Q, to "Iff (to, tf) однозначно определяется для
всех to, tf>to решением обыкновенного дифференциального ур-ния
(7.216) в обратном времени. Одно из главных достоинств этого
метода заключается в том, что здесь нет необходимости вычис-
лять переходную матрицу Ф(1, т).
320
Для непрерывных систем с постоянными коэффициентами, в
которых F и G — матрицы постоянных коэффициентов, свойство
равномерности вс'егда соблюдается, и модель является (равномер-
но) вполне управляемой тогда и только тогда, когда удовлетво-
ряется условие
rank[GlFG!F2G’_ . . . !Fn-1g] = N. (7.217)
Легко показать, используя теорему Дели—Гамильтона, что это
условие является прямым следствием условия, сформулированно-
го выше в терминах Ж(/о, tf)- Достаточное условие полной управ-
ляемости, аналогичное ур-нию (7.217), существует также и для
систем с переменными параметрами [42].
В дискретном случае модель сообщения [см. (7.1)] является
полностью управляемой тогда и только тогда, когда для любого k0
существует такое kf>ka, что симметричная матрица Грама, опре-
деляемая как
kt
W (k0, kf) = £ Ф (k0, k) Г (k) Гт (k) Фт fa, k), (7.218)
k=ka
положительно определена. Условия для равномерной полной
управляемости записываются точно так же, как и в непрерывном
случае, за исключением разве того, что k в этом случае может
принимать только целые значения. Для дискретной системы с
постоянными параметрами необходимое и достаточное условие
равномерно полной управляемости модели сообщения записывает-
ся в виде
rank [ГТФГТФ2Г! . . . 1 Ф^1 Г] = N. (7.219
Можно также получить разностное уравнение для Iff fa, kf), экви-
валентное ур-нию (7.216) для непрерывного случая.
Как можно будет убедиться в дальнейшем, понятие наблюдае-
мости по сравнению с понятием управляемости в задаче оценива-
ния является до некоторой степени более фундаментальным. Кал-
ман [105] впервые ввел понятие наблюдаемости и исследовал
его, рассматривая систему, дуальную исходной. Дуальная система
оказывалась управляемой, когда исходная система была наблю-
даемой. Подход, развитый Калманом, здесь использоваться не бу-
дет, хотя он имеет определенные преимущества. Вместо этого рас-
смотрим непосредственно проблему наблюдаемости. При обсуж-
дении этой проблемы необходимо рассматривать модели наблюде-
ния и сообщения совместно, так что под системой в широком'
смысле будем понимать комбинацию этих моделей. Будем также
полагать, что w и v тождественно равны нулю.
Невозмущенная система называется вполне наблюдаемой на
[£о, 1/], если для данного t0 и tff>t0 любое состояние х(/0) может
быть однозначно определено по известному наблюдению z(t) =
= H(t)x(t) на интервале [/0, //]. Если для любого t0 существует
tf>t0, которое может зависеть от t0, так что система является
11—26 321
вполне наблюдаемой на [Аъ А1> то систему принято называть впол-
не наблюдаемой. Так же, как и в случае управляемости, наблю-
даемость системы может быть установлена при анализе матрицы
Грама. Можно непосредственно показать, что непрерывная систе-
ма является вполне наблюдаемой на [A, AL если симметричная
матрица Грама, определяемая как
А
= А) Нг (t) Н (/) Ф (t, t0) dt, (7.220)
t а
.есть положительно определенная или несингулярная матрица. Ес-
ля для некоторого А>0 и для всех tQ матрицы (/0, А+А) и
/о+А).//’(А, А + А)Ф(/0, ^о+А)—положительно определен-
1ЯЫЕЯ юифаниченные независимо от 10, то модель сообщения равно-
мерно вполне наблюдаема. Для дискретной системы (to, tf) опре-
деляется дискретным аналогом ур-ния (7.220), определяемым как
= 2 ФГ(*. *о)Нг(<0Н(*)Ф(Л, k0). (7.221)
Эти же-условия должны быть соблюдены для различных форм
наблюдаемости. В частном случае, когда w(7) = 0, v(t) — нормаль-
ный случайный процесс с нулевым средним значением и единич-
ной дисперсией, матрица >-M(t0, tf) совпадает с известной в мате-
матической статистике информационной матрицей Фишера. В этом
А
случае дисперсия любой несмещенной оценки 0 (t) состояния
удовлетворяет неравенству Крамера—Рао (6 43):
£{ie(Q-E{0(O}f [0(0-Е{0(/)}]}> QT(f)^~l (to, 06(0- (7-222)
где'BIx(f)] — любая действительная линейная функция x(t) Кал-
ман назвал 0(0 смежным состоянием, поскольку оно связано с
введенным им понятием дуальной системы и понятием дуально-
сти в линейной алгебре. Для любого смежного состояния 0 суще-
ствует несмещенная оценка с минимальной дисперсией, для кото-
рой в выражении (7.222) выполняется знак равенства тогда и
только тогда, когда .Л положительно определенная матрица.
Для систем с постоянными параметрами свойство равномер-
•чости всегда соблюдается, и можно показать [105], что непрерыв-
ная система с постоянными параметрами является (равномерно)
вполне наблюдаемой тогда и только тогда, когда
»апк^т(ГтНг} (Fr)2fl?i . . =N. (7.223)
В дискретном случае необходимо выполнение следующего усло-
вия:
танк [НТ:Ф7Н7 j (Ф7)2 Н7, . f (Ф7)^1 Н7] = N. (7.224)
Опираясь на введенные понятия управляемости и наблюдаемо-
сти, можно приступить к анализу уравнения дисперсии. Для про-
.322
стоты ограничимся рассмотрением непрерывного случая; обобще-
ние результатов применительно к дискретному случаю выполняет-
ся достаточно просто. Рассмотрим сначала вопрос о существования
решения уравнения дисперсии (7.105):
v~ (0 = F (0 у~ (0 + v~ (0 Fr (0 - v~ (0 нг (0 ч’т* н (0 v~ (0 4-
+ G(0Yw(0Gr(O. (7.225)
Для любого заданного фиксированного начального момента
времени t0 и неотрицательно определенной симметричной матрицы
V~Go) = V°r ур-ние (7.105) имеет единственное решение
V~(0 =V~(/|V°~, t0) (7.225)
для всех t, таких, что р—/0| является достаточно малой. Для тоге
чтобы подчеркнуть, что решение ур-ния (7.105) зависит от началь-
ных условий, в ф-лу (7.226) введены аргументы, указывающие ус-
ловия. Существование и единственность решения для достаточно»
малых значений р—£0| прямо следуют из того факта, что урщие
(7.105) удовлетворяет условию Липшица [НО].
Так как ур-ние (7.105) нелинейное, то существование решения
для достаточно малых значений |г! — /0| еще не гарантирует суще-
ствования решения уравнения для всех t. Однако Кал мац показал.'’
[107], что решение этого уравнения существует для всех.
^о>—00 и однозначно определяется выбором V~. Следователь-
но, для всех задач, в которых интервал наблюдения конечен, суще-
ствование и единственность решения уравнения дисперсии, а зна-’
чит, и уравнения для коэффициента усиления гарантируются выбо-
ром V~. Заметим, что до сих пор никакие ограничения на накла-
дывались на модели сообщения и наблюдений, которые первона-
чально были введены в § 7.3. Чтобы исследовать задачу с беско-
нечным интервалом наблюдений, т. е. при t0=—оо, необходимо
ввести не очень сильное ограничение либо на модель сообщения,
либо на модель наблюдений. Например, если то V~(7J =
= VX(Q для всех t и если модель является неустойчивой, то Vx(?)
и, следовательно, V~(0 будут неограниченно возрастать прн
—оо.
Решение задачи с бесконечным интервалом наблюдений будет,
существовать в том смысле, что
limV~(f | 0, t0)=V~(t)
tr+- "°
существует для всех t и является решением ур-ния (7.105), когда
либо модель сообщения является равномерно асимптотически ус-
тойчивой, либо система является вполне наблюдаемой [85].
Если система является вполне наблюдаемой, то всегда можно
оценить х(7) с конечной ошибкой и, следовательно, V~ (О будет
оставаться конечной. Как мы убедимся в дальнейшем, решение
И* 323
V~(0), определяемое ур-нием (7.226), можно рассматривать как
«движущуюся» точку равновесия уравнения дисперсии.
*
В стационарной задаче оценивания V~(7), определяемое ур-нием
(7.226), представляет собой матрицу постоянных коэффициентов.
Следовательно, введенные выше условия устойчивости или наблю-
даемости гарантируют существование решения задачи фильтрации
Винера. Таким образом, необязательно, чтобы модель сообщения
была устойчивой, важно, чтобы система была наблюдаемой.
Существование стационарного решения на бесконечном интер-
вале наблюдений, определяемого выражением (7.226), выражает
одну из форм устойчивости алгоритма фильтрации. Мы уверены в
том, что если при tQ=—оо наблюдение начинается с V~ = 0, то урав-
нение дисперсии имеет решение для всех t. Гораздо более важным
является ответ на следующий вопрос: если решение уравнения
дисперсии на конечном интервале выполняется при неправильном
значении начальной дисперсии, то будет ли это решение стремить-
ся к решению, которое получалось бы при правильном выборе на-
чальной дисперсии? Правильное решение в действительности опре-
*
деляется выражением (7.226) дляУ~(7/ но, разумеется, начинать
вычисления при t0——оо совершенно нереально.
Чтобы установить, что стационарное решение V~ (t), определя-
емое выражением (7.226), представляет устойчивую траекторию в
том смысле, что некоторое возмущение траектории полностью за-
тухает при £->оо, необходимо ввести достаточно жесткое ограниче-
ние на модели сообщения и наблюдений. Если модели сообщения
и наблюдений являются равномерно вполне управляемыми и рав-
номерно вполне наблюдаемыми, если матрицы lv(t) и ЧЧ (О,
G(f) 4fw(0 GT(Z) соответственно положительно определенные и
положительно полуопределенные, а также ограниченные для всех
t, и, кроме того, ограниченной для всех t является матрица F(t),
то оптимальный фильтр равномерно асимптотически устойчив.
Кроме того, решение V~ (/) =V~(f| V~,f0) сходится к стационарно-
*
му решению¥~ (t), определяемому согласно (7.227) при К->-оо, для
любой симметричной неотрицательной определенной матрицы V~
Значение устойчивости алгоритма фильтрации Калмана труд-
но переоценить. Если алгоритм устойчив, то любая ошибка в вы-
боре начального значения дисперсии ошибки [а ошибка весьма
вероятна, поскольку часто мы выбираем V~(70) до некоторой степе-
ни произвольно] будет стремиться к нулю при ^->оо и в конечном
счете будут обеспечиваться оптимальные качественные показатели.
Оценка скорости сходимости, которая часто оказывается достаточ-
но высокой, может быть выполнена с помощью второго метода Ля-
пунова [107]. Чувствительность алгоритма фильтрации к ошибкам
в выборе значений статистических моментов, а также моделей со-
324
общения и наблюдений будет проанализирована в следующей гла-
ве. Кроме того, там будет показано, что при практической реали-
зации алгоритма фильтрации часто можно наблюдать расходи-
мость или неустойчивость даже в тех случаях, когда алгоритм
в вычислительном отношении является устойчивым.
В заключение главы интересно, хотя бы вкратце, рассмотреть
один из способов аналитического решения нелинейного уравнения
дисперсии путем решения системы линейных матричных дифферен-
циальных уравнений. В вычислительном отношении этот метод не
представляет большой ценности, поскольку, за исключением слу-
чая стационарных моделей сообщения и наблюдений, получающие-
ся при этом уравнения не могут быть достаточно легко решены. С
другой стороны, этот метод часто оказывается весьма полезным
при формулировке общих выводов о характере решения уравне-
ния дисперсии.
Пусть 0(7, t0)—переходная матрица размера 2WX2N для
2Л^-мерного векторного дифференциального уравнения
§(0 = S(0§(0, (7.228)
где &(t0, £0)=1 и S(t) матрица размера 2NX2N, определяемая в
структурной форме как
з(0_Г—рг(0 НГ(0Ч^‘(ПН(О
[G(OTw(nGr(0 F(0
Если Q(t, t0) записать в виде
„ ©И (^> 4>) Ф12 ^о)
“ (ь ‘о/ =
. А)) ®2а(^> QJ
где каждый элемент /0) —матрица размера NXN, то полу-
чим решение уравнения дисперсии (7.105) для произвольной неот-
рицательно определенной матрицы V~:
Vx~(O = V~(Z|Zo, V°~) = [021(f, t0) +
'о) V°~] [0п(/, t0) + 012(f, t0) V!L]-1 (7.231)
Доказательство этого результата, которое сводится к подста-
новке (7.230) в ур-ние (7.105), предоставляется читателю. Непре-
одолимые трудности, которые возникают при попытке получить
аналитически решение уравнения дисперсии даже для системы
первого порядка [202], не позволяют рассматривать этот метод в
качестве реального метода решения уравнения дисперсии.
(7.229)
(7.230)
Глава 8
ОБОБЩЕНИЕ АЛГОРИТМА
ОПТИМАЛЬНОЙ ЛИНЕЙНОЙ ФИЛЬТРАЦИИ
8.1. Введение
Основной целью данной главы является обобщение алго-
ритмов фильтрации, рассмотренных в предыдущей главе, для ре-
шения нескольких новых задач. В первую очередь будет исследо-
вана задача фильтрации для случая небелого шума измерений как
для дискретных, так и для непрерывных процессов.
В § 8.3 алгоритмы фильтрации Калмана распространены на
задачи предсказания и сглаживания.
При выводе алгоритмов сглаживания для непрерывного случая
используется подход, основанный на теории «обновляющих» про-
цессов, а для дискретного случая применяется метод максимума
апостериорной вероятности.
Во многих практических случаях невозможно точно описать мо-
дели сообщения и наблюдения, а также их априорные характери-
стики. Влияние ошибок при выборе модели и априорных данных
рассматривается в § 8.4.
В некоторых практических задачах оценивания оценки расхо-
дятся с действительными значениями, и ошибка между действи-
тельными и оцененными состояниями увеличивается со временем.
Это явление, а также несколько методов, позволяющих контроли-
ровать его, обсуждаются в § 8.5.
8.2. Небелый шум
В этом параграфе будет исследована задача оценива-
ния состояния в линейных системах с небелым шумом. Под #гбе-
лым шумом» мы понимаем случайный процесс, ковариационная
функция которого не равняется нулю для несовпадающих моментов
времени. Другими словами, рассматривается случайный процесс
а(/), такой, что cov {«(£), а(т)}=/=0 для т=/=/. В частности, небе-
лый шум будет рассматриваться как процесс на выходе линейной
динамической системы, на вход которой воздействует белый шум.
Кроме того, может также присутствовать или отсутствовать бе-
лый шум. Хотя такое представление небелого шума и не являет-
ся наиболее общим, но во всяком случае оно таково с практиче-
ской точки зрения. Даже при определении параметров этой прос-
той модели встречаются значительные трудности, так что использо-
вать более общую форму представления небелого шума еще более
трудно.
326
Небелый шум на входе, или шум объекта, не создает никаких
трудностей, так как динамическая система, формирующая такой
шум, может быть просто включена в модель сообщения точно так,
как это было сделано в § 3.5. Поэтому основной задачей, представ-
ляющей интерес, является исследование небелого шума измере-
ний. Одним из первых и во многих отношениях наиболее полным
исследованием небелого шума в непрерывных системах является
работа [36]. Исследование небелого шума в дискретных системах
было проведено в работе [34] и распространено на задачу сгла-
живания, [159]. Оценивание в непрерывных системах, в которых
каждое наблюдение содержало только небелый шум, рассматрива-
лось в работах [253, 259].
В наиболее общей постановке задачи каждое наблюдение мо-
жет содержать белый шум, небелый шум марковского типа, не со-
держать шума вообще или быть некоторой комбинацией трех рас-
смотренных возможностей. Поэтому в дальнейшем под термином
«небелый шум» понимается наличие шума марковского типа или
отсутствие шума вообще в одном или нескольких измерениях.
Прежде чем непосредственно заняться рассмотрением такой об-
щей задачи, исследуем сначала более простые задачи, а затем по-
кажем, как методы, использованные при решении этих задач, мо-
гут быть применены к исследованию общей задачи. В первую
очередь рассмотрим случай, когда каждое наблюдение содержит
только шум марковского типа, а затем задачи оценивания при
отсутствии шума.
Применительно к случаю чисто марковского шума, когда каж-
дая составляющая является только небелым шумом, подробно
будут выведены алгоритмы для непрерывных систем, а распростра-
нение этих алгоритмов на дискретные системы будет рассмотре-
но очень кратко. Модели сообщения и наблюдения записываются
в обычной форме
х(0 =F(/)x(0 + G(0w(0, (8.1)
где v,’(t) — белый шум с нулевым средним и cov {w(7), w(r)} =
= 4fw(t)6D(t~ т),
и z(0 = H(0x(0 4-v(/). (8.2)
Однако в данном случае мы предполагаем, что, в свою очередь,
v(t) образуется на выходе линейной динамической системы вида
v(o = A(ov(o + ;(o, (8-3)
на которую воздействует также белый шум с нулевым средним
и cov {£(0, £(t)}=’F5 —т); cov{w(^), £(т) }==(). Предполо-
жим, что среднее цх(М и дисперсия Vx(70) начального состояния
x(t0) известны и дополнительно к этому начальное значение пере-
менной состояния v, т. е. v(t0), является случайной величиной с
нулевым средним значением и известной дисперсией Vv(^o). Мо-
жет показаться, что предположение о том, что Vv(^o) известна, яв-
ляется чрезмерно ограничивающим по сравнению с предыдущими
327
предположениями относительно шума, однако, как будет показа-
но ниже, это не так. Начальная дисперсия необходима для опре-
деления дисперсии Vv(7) по уравнению модели шума (8.3) и
Vs (t, т).
Ставится задачу оценивания состояния x(t) на основании на-
блюдения Z(7) = {z(r), которое содержит небелый шум.
Наш подход будет строиться на преобразовании данной задачи в
связанную с ней задачу оценивания, которую можно решить с по-
мощью стандартного алгоритма фильтрации Калмана для случая
белого шума измерений. Для осуществления такого преобразова-
ния рассмотрим наблюдение z*(t), которое получается из исход-
ного в результате преобразования
z* (0 = z (0 — А (0 z (0 (8.4)
и после подстановки z(t) из ур-ния (8.2) принимает вид
z* (0 = [Н (0 + Н (0 F (0 — А (0 Н (0] х (0 +
+ H(0G(0w (0+5(0. (8.5)
Подставляя в приведенное выше выражение x(t) из ур-ния
(8.1) и v(t) из (8.3), получаем для z*(t)
z* (0 = Н (0 х (0 + Н (0 х (0 + v (0 - А (0 Н (0 х (0 - А (0 v (0
или, иначе,
Z*(0 = H(0X(0 + H(0F(0X(0+H(0G(0W(0 +
+ А (0 V (0 + 5 (0 — А (0 Н (0 х (0 - А (0 V (0.
Этот результат может быть представлен в виде обычной моде-
ли наблюдения для случая белого шума измерений
z*(0 = H*(0x(0 +v*(0, (8.6)
где введены следующие очевидные обозначения:
Н* (0 = Н (0 + H(0F(0 —А (0Н(0; (8.7)
v*(0 = H(0G(0w (0 + 5(0. (8.8)
Очевидно, что преобразованный шум измерений v*(0 —белый,
с ковариационной функцией
Vv. (0 т) = [Н (0 G (0 (0 GT (0 Нг (0 + 40 (0] (t - т). (8.9)
Шум измерений уже не является независимым от 'w(t), так как
Vwv<(0 t) = 4^w (0Gr (0^(060 0 — 0. (8.10)
Поэтому следует использовать алгоритм фильтрации Калмана
из табл. 7.5, в котором 'Fwv не предполагается равной нулю.
Исходное наблюдение z(t) может быть полностью восстановле-
но по z*(t) и z(t0) с помощью ур-ния (8.4), решение которого
328
можно записать в виде ,
t
= /0)z(/0) +уфл(/, T)z*(T)dT, (8.11)
^0
где z*(7) рассматривается как известный процесс на входе. Здесь
Фа (0 to) является переходной матрицей состояния, связанной с
Л(0, так что ~ <S>A(t, t0) =А(7)Фа(/, ^о);Фа(/о, А))=1. Поэтому
оценка состояния х(0, основанная на z(t), должна быть
идентична оценке состояния х(/), основанной на z*(0, и
z(to), т. е.
х(0 = E{x(0|Z(0) = E{x(0|Z*(0. z(Q), (8.12)
где, каки раньше, Z(t) — {z(x), Z*(7) = {z* (т),
л
Если бы 1*(t) и z(t0) были ортогональны, то оценку х(7) можно
было бы записать в виде
х (0 = Е{х (0 I Z* (0) + Е {х (01 z (Q). (8.13)
Однако, как нетрудно показать, Z*(7) и z(70) не являются ор--
тогональными. Поэтому такое решение не может быть использова-
но и, прежде чем получить оценку, необходимо ортогонализиро-
вать информацию, связанную с наблюдением. Если обозначить
z*(t) как компоненту z*(t), которая ортогональна z(t0), т. е.
cov {z*(7), z(70)}=0, то оценка состояния х(7) может быть запи-
сана в виде
х (0 = Е {х (0 | г (f0)} + Е {х (0 | Z* (0), (8.14)
где Z*f^) = {z* (т),
Рассмотрим в первую очередь оценку, основанную на z (t0).
Эта задача была решена ранее в примере 6.14, где было получено:
Е {х (t0) | z (Q) = цх (0>) + Vx (t0) Нг (t0) [Vv (t0) +
4- H (t0) Vx (t0) Hr (у]"1 [z (Q - H (Q gx (QJ. (8.15)
Л
Для простоты обозначений определим x[/|z(70) ] как
x[^|z(/0)] AE{x(0|z(/o)J. (8.16)
о Здесь используется линейный метод оценивания на основе критерия мини-
мума дисперсии ошибки для того, чтобы подчеркнуть общность полученного
решения с точки зрения наилучшей (в смысле минимума дисперсии ошибки)
линейной оценки вообще или наилучшей оценки в частном случае ноомальиого
распределения. С другой стороны, можно сделать соответствующие предполо-
А
жения о нормальном законе распределений, и тогда х(0 будет как условным
средним (оптимальной оценкой по критерию минимума дисперсии), так и
оценкой по критерию максимума апостериорной вероятности. (Прим, авт.)
329
Так как w(T) не зависит от v(t0) и имеет нулевое среднее значе-
ние, то
x[Z|z(/0)] = Ф (0 Z0)ltf0|Z(/0)L (8.17)
где Ф(1, t0) — переходная матрица состояния, связанная с F(7),
следовательно,
х [f| z (f0)l = F (0 х [/1 z (Q], (8.18)
Л
где x[/o|z(^o)] определяется на ур-ния (8.15).
Введем величину
7*(0 Az*(0 —H*(0x[f|z(fo)J, (8.19)
которая, как легко показать, ортогональна z(T0). Теперь можно
л _
получить алгоритм фильтрации для x[/|Z* (/)] непосредственным
применением обобщенного алгоритма фильтрации Калмана, при-
веденного в табл. 7.5. Находим, что
х [/1Z* (0] = Г (0 х [f | Z*(0] + СК (0 {z* (0 — Н*(0 х 1 Z* (/)]}, (8.20)
где СК (0 = [V~(0 Н*г (0 + G (0 4^wv. (0] Ч^.1 (0,
и после подстановок соответствующих выражений из ур-ний (8 9)
и (8.10) получаем
(0 = [ V~(0 Н*г (0 + G (0 ЧХ (0 Gr (0 Нг (0] X
X [H(0G(0^w (0G7’(0H7’(0 + ^s(0]-1 • (8-21)
Алгоритм вычисления дисперсии ошибки определяется как
V- (0 = F (0 V~(0 + V~ (t) Fr (0 + G (0 ЧХ (0 GT (0 -
— СК (0 [H (0 G (0 ЧХ (0 Gr (0 Hr (0 + 40 (0] CKr (0. (8.22)
Л Л ~
После определения x[0z(0)] и x[/|Z*(0] можно, используя
Л
ур-ние (8.14), записать х(Т) в виде
х (0 = х 1 z (Q) + х [/1Z* (0), (8.23)
так что
x(0 = xf/|z(Q] + x[0iZ*(0]. (8.24)
Используя (8.18) и (8.20), получаем
х (0 = F (0 х 1 z (0)] + F (0 х [/1 Z* (0) +
+ СК (0 {7* (0 — Н* (0 х [q Z* (01) (8.25)
330
или x(t) = F(i)x(i) + M0{z* (i)—H*(i)x[i]Z* (i) ]}.
Если воспользоваться определением z*(t), приведенным в ф-ле
<8.19), то x(t) = F(t)x(t)+M(t)[z*(t)—VL*(t)x(t)]. Подставляя
z*(t), выраженное в виде (8.4), получаем окончательную форму
алгоритма
х (0 = F (0 х (0 + :к (i) [z (0 — А (0 z (0 — Н* (0 х (0]. (8.26)
л
Начальное условие для x(t) получается из ф-лы (8.15):
х (i0) = Их (io) + Vx (i0) Hr (i0) ]Vv (i0) +
+ H (i0) Vx (i0) Hr (io)]-* 1 * * * [z (i0) - H (i0) Mx (i0)]. (8.27)
Начальное значение N~(tQ), необходимое для решения ур-ния
(8.22), представляет собой дисперсию ошибки после приема z(i0).
Эта дисперсия также была определена в примере 6 14 как
V~ (i0) == Vx (i0) -Vx (i0) Hr(i0) ]H (i0) Vx (i0) Hr (i0) +
+ Vv(io)r1H(io)Vx(io). (8.28)
Уравнения (8.26), (8.21) и (8.22) совместно с начальными ус-
ловиями (8 27) и (8 28) представляет собой полный алгоритм
оценки состояния в ситуации, где каждое измерение содержит
только небелый шум. Для того чтобы ими было легко воспользо-
ваться, все уравнения сведены в табл. 8.1. Можно избежать ис-
Таблица 81
Алгоритм фильтрации в случае небелого шума измерений
в непрерывных системах
Модель сообщения
i(0 = F(0x(0+G(0w(0. (8.1)
Модель наблюдения
z(l)=H(f)x(f)+v(i). (8.2)
v(0 = A(0v(0+£(0 (8 3)
Априорные данные
Е {w (0) = Е К (0} = Е {v (0)} = 0; Е {х (0)} = рх (0),
cov{w(0, w(t)} = 'Fw (t)8D (t — T), cov{£(0, ь(т)) = (0so (i ~T):
•cov{w(0, g(T)} =0;
var{x(/o)} = Vx(0); cov {x (0), v (0} =0, t > 0;
var {v (0)} = Vv (0); cov {x (0), J (0} = 0, t > 0.
331
Продолжение
Алгоритм фильтрации х (0 = F (/) х (f) + Ж (0 [z (t) - A (t) z (t) - Н’ (0х (0]. (8.26)
Вычисление коэффициента усиления Ж (0 = [V- (0 н’г (0 + G (!) 'Fw (0 GT (t)Hr (t)J X X [H (t) G (i) Yw (0 GT (/) Hr (0 +'Fg (0Г1 . (8.21)
где H* *(0 = H(/) +H(0F(0-A(0H(/). (8.7)
Вычисление дисперсии ошибки v~ (0 = F (0 V~ (0 + V~ (0 Fr (0 + G (0 Tw (0 GT (0 - -Л-(0 [H (0G(0Yw (/) GT (0 Hr(0+Ys (t)]XT(t). (8.22)
Начальные условия
x (to) = (tx (0) + Vx W Hr (/„) [Vv (O) + H (/„) Vx (/„) Hr (UP1 [z (0) - -H(0) px (0)]; v~(0) = Vx (0) - Vx (0) Hr (0) [H (0) Vx (0) (Zo) + vv (О)]-1 н (t0) Vx (8 27) (ta). (8.28)
пользования z(t) в уравнении, но в этом случае необходимо опре-
делить ^следующим образом.
Предположим, что Ж (t) кусочно-непрерывна и рас-
смотрим ~[W(t)z(t)] = X‘(t)z(t) +№(t)z(t) так, что W(t)z(t) =
dt
= (t)z(t)]—W(t)z(t). Тогда из ур-ния (8.26) получим
dt
л л я
х (0 = F (О X (0 + 4 \Ж (0 z (01 - Ж (t) z (i) -
at
AJA Л
- Ж (0 [А (0] Z (0 + Н* (0 х (01 или w [х (/) - Ж (/) г (/)] = F (i) х (0 -
* - Ж (t) [А (0 г (t) + Н*Х0 х (0] - &(t)z(t).
Добавлением величины W(t)z(t) из этого дифференциального
л
уравнения может быть получено уравнение для х(7). Данный под-
ход при решении аналогичной задачи применительно к дискрет-
ным системам использовался в работе [34]. Общая сводка урав-
нений алгоритма представлена в табл. 8.2; вывод алгоритма
фильтрации для дискретного случая предоставляется читателю в
332
Таблица 8.2
Алгоритм фильтрации в случае небелого шума измерений
в дискретных системах
Модель сообщения
x(i +1) = Ф(» + 1, I) x(i)+T(i) w(i).
Модель наблюдения
z(i) = H(i) x(i) 4-v(i); v (i +1) = Фл (i + 1, i) v (i) + £ (i).
Априорные данные
E {w (i)} = E {l (i)} = E{v (>•„)} =0; E {x (i0)} = ;ix (i0);
cov w(/)} =VW (‘—/); cov « (/)}=Vg (i)sx (»—/);
cov{w(i), U/)}= 0;
var{x(i0)} = Vx(i0), cov{x(i0), v(/)} = 0; 1
var{v(i0)}=Vv(i0), cov{x(i0), £(/)} =0; Г
Алгоритм фильтрации
x (i) = Ф (i, i — 1) x(i — 1 | i) + KC (i) [z (i) —
A
— Фл (i, i — l)z(i — 1)— H*(i — 1) x(i — 1)],
где
H*(i — 1) =H (i) Ф (i, j—1) —Фл(1, i ——1).
Алгоритм одношагового сглаживания
x(i — 1 11) = x (i — 1) 4- Ks (£ — 1) [z (i) — Фл (i, i — l)z(i — l) —
— H*(i —l)x(i —1)].
Вычисление коэффициента усиления при сглаживании
Ks (i - 1) =V~ (i - 1) H*r (i - 1) [H* (i - 1) V~ (i - 1) H*r (i - 1) +
+ VJi - 1) +H (i) Г (i - 1) Vw (i - 1) Г (i - 1) Hr (i)]-1 .
Вычисление коэффициента усиления при фильтрации
Кс (i) = Г (i - 1) Vw (i - 1) rT(i - 1) Hr (i) [H* (i - 1) V~ (i - 1) H*r (I’ - 1) +
+ vji -1) + н (i) г (i -1) vw (i -1) rr (i -1) нг G)]-1.
Вычисление дисперсии ошибки фильтрации
У~(1) = Ф((, i — — 1 |i) фг(1, i — 1) +
+ r(i-l)Vw +
+ v5 (i-1) +H(i)F(i-l)Vw (i - 1) rT(i - 1) Hr (i)] КГ (i)_
333
П родолжение
— Ф(С i — 1) К, (i - 1) Н (i) Г(г — 1) Vw (i — 1) Гг (i — 1) —
— Г(1 -1) vw (i -1) гг (i -1) нг (i) Kf (i -1) Фг (i, i -1).
Вычисление дисперсии ошибки сглаживания
V^i — l 1i) = [I —Ks (i - 1) H* (i - 1)] V~ (i -
— +ks (i -1) [ve (f-i)+
+И(<)Г{1 - 1) vw (i - 1) Гг (i - 1) Hr (0] Ksr(i - 1).
Начальные условия
— P-x (io) + Vx (io) (i0) [Vv (i0) +
+H(i0) vx (i0) Hr (io)]-1 [z(i0) — н (i0) px (io)];
v~(io) = Vx(i0) - Vx (io) Hr(i„) [H (i0) Vx(io) Hr (io) +Vv (io)]'1 H (i0) Vx (i0).
качестве упражнения. В этом случае
z*(x) =z(i + 1) — Фл (i + 1, i)z(i) (8.29)
«« оценка состояния х(0, основанная на z*(i), фактически являет-
ся оценкой одношагового сглаживания, так как z*(i) зависит от
Поэтому, как показано в табл. 8,2, алгоритм фильтрации
включает в себя одношаговое предсказание оценки, полученной
как результат сглаживания.
Таблицы 8.1 и 8.2 представляют собой полную сводку алгорит-
мов оценивания состояния в том случае, когда каждое измерение
содержит только небелый шум. Рассмотрим теперь задачу в усло-
виях, когда шум измерений отсутствует. Может показаться, что
подобная задача достаточно проста и для дискретного случая это
.действительно так. Напротив, для непрерывного случая эта задача
сказывается настолько сложной, что некоторые ее аспекты полно-
стью не разрешены до сих пор 1>. Сначала обсудим дискретный слу-
чай, а затем кратко рассмотрим возможный способ решения зада-
чи для непрерывного случая.
Модель -сообщения, как и раньше, задается в виде
ж(*4-1) = Ф(£+ 1, k)x(k) + r(k)w(k), (8.30)
модель наблюдения не содержит шума измерений и задается в
виде
я(4) = Н (£) х (А), (8.31)
где шум объекта w(k)— белый с нулевым средним и
<£СЯГ {*(&), -wGj}=Vw(fej6K(^—/).
•» В том случае, когда отсутствует и шум объекта, метод, развитый Люне-
берпфом (141, 142], является одним из возможных подходов к оешению этой
задачи. (Прим, авт.)
Л34
Необходимо найти оценку x(k) по заданной последовательно-
сти наблюдений Z(k). Будем предполагать, что соответствующие'
распределения нормальные, и определим МАВ-оценку состояния!
х(й). Запишем апостериорную плотность вероятности, используя
формулу Байеса (см. § 7.2) в виде
Р [х (й) | Z (£)] =
p[z (k)\x(k)]p[x(k)\Z(k-l)]
p[z(k)]Z(k—l)]
(S.32%
Необходимо найти значение х(й), которое максимизирует
р[х(й) |Z(&)]. Может показаться, что результаты § 7.2 непосредст-
венно применимы к этой задаче, и это действительно так. Однако
читатель должен иметь в виду, что некоторые из выражений § 7-2.'
справедливы только при условии, что V-'v существует. В частно-
сти, выражение К(/) = V~(/) Нг(/) V—*v (/) из табл. 7.2 использовать
уже нельзя. Вывод алгоритма оценивания по критерию максимума
апостериорной вероятности из § 7.2 также неправомерен, если не
существует V-'v. Рассмотрим вывод алгоритма МАВ-оценивание
для случая, когда V-1v не существует.
Задача подобного типа рассматривалась ранее в § 6.2 и 7.2 Я
поэтому можно записать условные плотности вероятности
p[x(k)\Z(k—1)] и p[z(k)\Z(k—1)] непосредственно как
р [х (k) | Z(k — 1)] = Aj ехр {-- [х (k) — х (k | k — l)f X
X V~(A | A — 1) [x (4) — x (/fe ) Л — 1)]; (8.33)
p [z (k) | Z (k — 1)] = A2exp |-[z (k) —H(#)x(&}& —
— l)lr[H(£)V~(£|&- 1)Нг(£)Г' [z (Л>) — H (£) £(& | £— 1 )U- W
~ Л Л
Здесь V~ (k | /г— 1) = var {x(k | k— 1) }; x(k | k— 1) = Ф (k, k—1 )хМЛ(. (k):„
А; и A — копировочные константы, конкретные значения которых!
не так важны.
Однако получить обычное решение для p[z(&) |х(й)] невозмож-
но, так как отсутствует ш\ м измерений. Действительно, при дан-
ном x(k) z(k) полностью известно, так что z(k) в данном случае
является неслучайной величиной. Следовательно, р[z(k)|х(й)}
становится просто дельта-функцией при z(k) = H(k)x(k) или
р [z (А) | х (Л)] = ]z (£) - Н (6) х (£)]. (8.35))
Теперь, объединяя ур-ния (8.33), (8 34) и (8.35), получим сле-
дующее выражение для апостериорной плотности вероятности:
р [х (й) | Z (/;)] = A [z (k) — Н (й) х (/г)] ехр J— -j- [х (й) —
— x(k\k — l)]TV~'(k\k- l)[x(k) — x(k \k — 1)] 4-
33S>
+ 2- [z (fe) - Н (k) x(k)k- l)]r [H (fe) N~(k I k -
— 1)Нг(£)Г* [z (fe) — H(fe)x(fe|fe — 1)]}. (8.36)
Для максимизации p[x(fe)|Z(fe)] по x(fe) необходимо решить
уравнение
z (fe) — H(fe) xMAp (fe) = 0. (8.37)
В остальных случаях p[x(k) [Z(k)] будет равняться нулю. Фи-
зически это условие означает, что оценку состояния x(k) следует
просто выбирать такой, чтобы оценка наблюдения была равной са-
мому наблюдению, которое в данном случае свободно от шумов.
л
Однако ур-ние (8.37) не определяет хмар(^) однозначно, кроме
того случая, когда H(k) является неособенной и задача становит-
ся тривиальной. Если H(k)—особенная матрица, что обычно и
имеет место, то XMAp(fe) не только должно быть решением ур-ния
(8.37), но также и максимизировать оставшуюся часть плотности
p\x(k)\Z(k)\, а именно, p\x(k) |Z(fe— l)]/p[z(fe) |Z(fe— 1)]. Может
показаться, что бессмысленно говорить о максимизации
p[x(k)\Z(k)}, если решение ур-ния (8.37) обращает плотность ве-
роятности в бесконечность. Однако, если внимательно проследить
вывод процедуры байесовской оценки (см. § 6.2), то можно заме-
тить, что p[x(k)|Z(fe)] находится под знаком интеграла и поэто-
му необходимо максимизировать «вес» или «площадь» дельта-
функции для того, чтобы получить точную МАВ-оценку.
Л
Можно рассматривать задачу как выбор такого хмар(^), кото-
рое максимизирует p[x(fe)|Z(fe—l)]/p[z(fe) |Z(fe—1)] при условии
(8.31). Такой подход обычен в задаче оптимизации при ограниче-
ниях, которая может быть решена методом неопределенных мно-
жителей Лагранжа. Рассмотрим задачу максимизации выражения
7 [х = + ехр {V [z - н w х №
г Lz W I * Л
которое может быть записано в виде
/[x(fe)] = /<ехр^---2~[х (fe) — x(k\k— l)]rV~(fe | k —
— l)[x(fe)-x(fe|fe- 1)] + ~ [z (fe) —H (fe)x(fe | fe —
-1 )Г [H (fe) V~(k | k - 1) Hr (fe)]-1 [z (fe) — H (fe) x (fe |fe — 1 )][+
+ exp {Xr (fe) [z (fe) — H (fe) x (fe)]. (8.38)
Здесь множитель Лагранжа введен в достаточно необычной
форме для того, чтобы упростить алгебраические преобразования
в процессе решения задачи.
336
До максимизации 7[х(7>)] удобно прологарифмировать это вы-
ражение. В результате имеем
1п/[х(Д>)] = 1п/С— 4-[х(А)— 1)]гУ~(£|А —
— ])[х(А)-х(*|А- 1)] -|_ -1_ fz(£) —Н(Аг)х(*1 А ~
— 1)]Г[Н(£)У~(Ш- 1)Нг(*)Г' [г(6)-Н(4)£(Ш- 1)] +
+ Xr(£)[z(£) —Н(&)х(&)]. (8.39)
Оценка хмар(^) может быть получена как
д In J [х (&)] . л
—- л = 0 = — V~(& |&—1)[х . (&) —
о X (k) X (Л) = хМАр (*) х V 1 ' L MAP V /
— *(k\k— 1)] + Нг(£)Х(£).
При решении этого уравнения Хмар(й) получается в виде
W) = x(^~ 1)+У~(*|£-1)Нг(£)Х(£). (8-40)
Множитель Х(&) определяется путем подстановки ур-ния
(8.40) в (8.37). В результате получаем
z ($) — Н (k) [х (k | k — 1) + V~(k | k — 1) Hr (k) X (.<>)] = 0, (8.41)
откуда
1(&) = [H(£)V~(£|& — 1)Нг(А>)Г* [z(A)—H(A)x(A|A—1)]. (8.42)
Если этот результат подставить в ур-ние (8.40), то МАВ-оценка
состояния х(7г) приобретает вид
*мар (*) = х (Ш - 1) + I k - 1) Нг (k) X
X [Н(£)У~(/гЦ— l)tf (A)]'1 [z(A) - Н(Л) х (k | k — 1)]. (8.43)
Легко проверить, что оценка хмар(^), полученная из (8.43),
удовлетворяет также ур-нию (8.37). Если определить матрицу ко-
эффициентов усиления как
S (k) = V~(k I k - 1) Hr (k) [H (k) V~(& \k - 1) Нг(б)Г1 , (8.44)
то этот алгоритм ’) принимает стандартную форму
XMAP (k) = х (k \k - 1) + S (k) [z (k) - H (£) x (k | k - 1)]. (8.45)
n Следует соблюдать осторожность при применении этого алгоритма, так
как при этом возможно потребуется выполнить обращение плохо обусловлен-
ных или особенных матриц (см. задачу 8.29). Один из возможных способов
избежать это затруднение заключается в использовании наблюдений без шума,
для того чтобы уменьшить мерность пространства состояний, как это поел-
лагается ниже для непрерывных систем. (Прим, авт.)
337
Выполняя обычные преобразования, сходные с теми, которые
применялись в § 7.2, получаем разностное уравнение для дисперсии
ошибки в виде
V~(A +Ш) =Ф(*+ 1, #)¥—(£) Фг(& + 1> 4)+Г(4)У«(4)Гг(А),
(8.46)
где V~(6) = [I-S(£)H(*)]V~(£|£-1). (8.47)
Начальные условия определяются как
Хмар (»’о) = Их(4); V~(Z0) = Vx (г0). (8.48)
Исходя из ур-ний (8.44) и (8.47), легко показать, что
Н(й)¥~ (А)НЧ^) =0. Это соотношение непосредственно следует из
того факта, что полностью известно, так как шум изме-
рений отсутствует. Алгоритмы фильтрации при отсутствии шума
измерений совпадают с алгоритмами, приведенными в табл. 7.2.
Хотя и может показаться, что при отсутствии шумов измерений
возможно идеальное оценивание, результаты приведенного анали-
за достаточно ясно показывают, что это далеко не всегда так. К
сожалению, приведенная выше методика не может быть примене-
на к непрерывным системам вследствие трудностей выполнения ог-
раничения, задаваемого ур-нием (8.31) в случае непрерывного вре-
мени.
Брайсон и Йохансен [36] развили иной подход к задаче оцени-
вания для непрерывных систем в случае наблюдений без шума.
Этот подход основывается на последовательном дифференцирова-
нии наблюдений без шума до тех пор, пока не получатся измере-
ния, которые содержат белый шум. Свободные от шума измерения
(как исходные, так и производные) используются для сокращения
размерности пространства состояний, и наблюдения на фоне бело-
го шума используются для оценивания оставшейся части вектора
состояния. Основываясь на приведенном описании идеи метода,
рассмотрим данную задачу более подробно.
Модель сообщения в непрерывном случае имеет вид х(7) =
= F(/)x(f) +,G(iJ) w(Z); наблюдение не содержит шума измерений и
определяется соотношением
z(t) = Н(/)х(/). (8.49)
Предположим, что Н(7)— матрица полного ранга, так что из-
мерения линейно независимы. Если это не так, то любые линейно
зависимые строки могут быть устранены, так как они не несут ни-
какой новой информации, и может быть найдено наблюдение экви-
валентное z(t), но меньшей мерности.
Продифференцируем z(Z); это всегда можно сделать, так как
z(t) не содержит белого шума. Поскольку требуется, чтобы
G(i‘)4rw(/)GI’(Z) была только неотрицательно определенной, то
гполне возможно, что некоторые элементы z(t) не содержат бело-
го шума. Продолжим дифференцирование этих элементов до тех
338
пор, пока каждый из них или не будет содержать белый шум, или
измерение не станет линейно зависимым от других измерений.
Иначе говоря, производные от каждого элемента z(t) берутся до
получения белого шума или до того момента, когда элемент стано-
вится линейно зависимым, после чего дифференцирование прекра-
щается.
Сигналы, полученные из z(t), и производные разбиваются на
два множества. Первое из них содержит свободные от шума ис-
ходные измерения и часть линейно независимых, свободных от
шума производных в виде
z°(0 = H»(0x(0. (8.50)
Второе множество включает в себя все производные измерения,
которые содержат белый шум в виде
z* (?) = Н* (/) х (0 + v* (0, (8.51)
где v *(7) =M(7)w(Q— белый шум, коррелированный с w(7), так
как он образуется из w(t). Величина z*(t) содержит 7? измерений,
где 7? — ранг матрицы TwfO, если дифференцирование прекраща-
ется (как это было отмечено выше), когда все измерения становят-
ся линейно зависимыми. Таким образом, матрица дисперсий Tv-fQ
будет неособенной, что и требуется для алгоритма фильтрации
Калмана. Дисперсии Vv*(/, т) и Vwv*(£, т) равны:
Vv. (t, т) = М (t} ЧД (0 Мг(0 6д it — т);
Vwv.(i, x) = Tw(0Mr(06D(/ —т).
Используем М-мерный, свободный от шума, вектор измерений
z°(t) для уменьшения размерности пространства состояний путем
линейного преобразования переменных состояния в новый вектор
состояния в виде
Х*(0 = P(t) х(0,
(8.52)
где х*(7) —новый вектор состояния. Матрица P(t) размера NxN
предполагается неособенной и имеет вид
Р(0 =
PJ0’
н°“(0.
(8 53)
Следовательно, последние М элементов x.*(t) соответствуют из-
мерениям без шума, а первые N—М элементов линейно независи-
мы. Матрица размера N—MXN может быть выбрана произволь-
но, лишь бы матрица Р(7) была неособенной. Исходный вектор со-
стояния x(t) может быть восстановлен по x.*(t) следующим обра-
зом:
х(7) = Р"1 (;)x*(Z) = Р-1
Г хГ(01
(0
.z°(0.
(8.54)
где x*i(Z)—N—М-мерный вектор, содержащий первые N—М элемен-
339
тов Поэтому, как только получена оценка состояния х *!(£),
оценка состояния x(t) известна, поскольку известно z°(£).
Если исходную модель сообщения выразить через x*(i), то из
ур-ния (8.1) находим
х* (0 = [Р (О Р 1 (0 + Р (О F (О Р 1 (/)] х* (/) + Р (О G (0 w (0- (8.55)
Так как z°(£) уже известно, то необходимо рассмотреть только
первые (N—М) уравнений, которые могут быть записаны в виде
xj (0 = Fl! (t) X1 (0 + F*2 (0 z° (0 + G* (0 w (0- (8.56)
Эта модель сообщения выражена уже почти в стандартной
форме, за исключением добавочного члена, содержащего извест-
ную входную величину z°(£), поэтому алгоритмы табл. 7 5 могут
быть использованы непосредственно
Если выразить уравнение наблюдения с шумом (8.51) через
х*(/), то получим
z* (t) = Н* Р-1 (0 х* (t) + v* (/). (8.57)
Чтобы подчеркнуть, что в это наблюдение включена известная
функция z°(0, перепишем (8.57) в виде
z* (о = н;* (о х; (о + н** (о z° (о + v* (/). (8.58)
Теперь для нахождения оценки состояния x*i(Z) и, следовательно,
x(t) можно применить алгоритм фильтрации Калмана (см. табл.
75).
После того как была разработана методика решения задачи
для наблюдений без шума, можно рассмотреть еще один подход к
решению задачи в случае, когда каждое измерение содержит толь-
ко небелый шум Для того чтобы пояснить этот подход, рассмот-
рим снова модели сообщения, шума и наблюдения для случая не-
белого шума (для непрерывных систем), которые описываются
ур-ниями (8.1) — (8 3). Определим расширенный вектор состояния
у(0 как
(8.59)
так что
У(0 =
Модель наблюдения определяется в этом случае как
z(0 = [H(0,i]y(0,
(8.60)
(8.61)
и такие наблюдения оказываются свободными от шумов. Следова-
тельно, для решения этой задачи можно применить полученный
выше алгоритм. Основная трудность использования такого подхо-
да заключается в увеличении порядка системы и, следовательно,
объема вычислений, который растет приблизительно как квадрат
340
числа переменных и может оказаться чрезмерно большим при ус-
ловии, что число наблюдений велико. Однако возможно осущест-
вить алгоритм, описанный в начале данного параграфа, используя
подход, основанный на расширении вектора состояния, и в этом
смысле оба подхода эквивалентны. Дополнительно следует отме-
тить, что расширение вектора состояния можно использовать и
тогда, когда измерения содержат небелый и белый шум, так как
наблюдения с белым шумом дифференцировать нельзя.
8.3. Сглаживание и предсказание
В вводных замечаниях относительно задачи оценивания,
приведенных в § 7.2, упоминалось, что задачи оценивания состоя-
ния разделяются на три класса: предсказание, фильтрацию и сгла-
живание В задаче предсказания требуется оценить x(t) по данным
наблюдения, полученным до момента времени т<£; при фильтра-
ции оценивается x(t) при заданном Z(7); в задаче сглаживания
известно наблюдение Z(7J при T>t. В гл. 7 рассматривалась толь-
ко задача фильтрации, так как она наиболее часто встречается на
практике и, как будет видно из дальнейших выкладок, является
основой для исследования задач предсказания и сглаживания.
Для простоты ограничимся в данном параграфе рассмотрением
случая, когда шум наблюдения белый. Методы, представленные в
предыдущем параграфе, применительно к небелому шуму могут
быть распространены (с небольшими изменениями) и на задачу
сглаживания. Уже опубликованы результаты, полученные в этом
направлении [343, 159]
Предсказание. В основополагающих работах Калмана и
Бьюси решение задачи предсказания (прогнозирования) было-
представлено в виде простого обобщения алгоритмов фильтрации.
Алгоритм одношагового предсказания был получен в качестве про-
межуточного результата при выводе алгоритма дискретной фильт-
рации, основанном на методе ортогонального проецирования (см.
§ 7.2). Предположим, что необходимо оценить x(t2) при заданном
множестве наблюдений Z(^), где ti<t2. Используя обычную форму
записи модели сообщения, получим
^2
х(^2) = Ф (t2, G)x(Q Ц- Ф(/2, г) G (т) w (т) d т. (8.62)
Здесь Ф(^ т) —переходная матрица состояния, связанная с невоз-
мущенной моделью сообщения и удовлетворяющая уравнению
~Ф(1, т) =Р(0Ф& т), Ф(т, т)=1. (8.63)
dt
В дальнейших рассуждениях более удобно рассматривать диф-
ференциальное уравнение для Ф(/, т) при условии, что т — пере-
менная, a t — фиксирована. Это можно получить, вычислив произ-
341
годную от выражения Ф(^, т)Ф(т, t) [которое равно единичной мат-
рице, так как Ф(т, ^)=Ф“1(2‘, т)]:
—[Ф (t, т) Ф (т, 0] = [ — Ф (t, т)1 Ф (т, t) +
dt [д х J
Н- Ф (t, т) — Ф (т, А = 0. (8.64)
д х
Из ур-ний (8.63) и (8.64) получаем
Г-— Ф (t, т)1 Ф (т, t) = — Ф (t, т) F (т) Ф (т, t)
L дх J
или
± ф (;, Т) = _ ф (Т; t) F (т). (8.65)
дх
Если вычислить условное среднее1) от левой и правой час-
тей ур-ния (8.62) при заданном Z(/t), то получим
Е {х (^ | Z (G)} = Ф (t2, Е {х (Q | Z (у} +
Н-уФ(^2, t)G(t)E{w(t)| Z(^)}dt. (8.66)
<> Л
Теперь, используя обычные определения x(^pi) =E{x(Z2) |ZX
л
X^i)} и х(Л) =E{x(^i) |Z(^)}, ур-ние (8.66) можно записать в
виде
х(^Ю = Ф(^, *i)x(G)+ [Ф(^2, T)G(T)E{w(T)|Z(Q}dT. (8.67)
i,
Так как w(t)— белый шум, то никакая информация о его прош-
лом, содержащаяся в Z(7i), не может быть использована для пред-
сказания w(t) при т>^1. Поэтому
E{w(t) | Z(/j)} = £'{w(t)} = 0 для т > tr (8.68)
и из ур-ния (8.67) следует
х (t2 И1) = Ф (t2, У X (4) для (8.69)
Это уравнение представляет собой искомый алгоритм предсказа-
ния.
Хотя при выводе алгоритма за основу была принята непрерыв-
ная модель сообщения, аналогичный подход может быть исполь-
зован и для дискретного случая. Конечно, окончательное выраже-
ние (8.69) справедливо как для непрерывного, так и для дискрет-
ного случаев — для этого достаточно рассматривать tx и t2 как
непрерывные или как дискретные моменты времени. Фактически,
если данные поступают в дискретные моменты времени, ур-ние
(8.69) может быть использовано для непрерывного предсказания
4> Можно использовать метод ортогонального проецирования, оговорив ус-
ловия оптимальности полученного алгоритма. {Прим авт )
342
до момента поступления следующей выборки. Таким образом, дан-
ный алгоритм действует как устройство восстановления сообще-
ния.
В задаче последовательного предсказания состояния либо tx,
либо либо оба вместе возрастают с течением времени. В зави-
симости от характера изменения tx и различаются три вида пред-
сказания:
— предсказание с фиксированным интервалом: t2=t и t\ —
фиксировано;
— предсказание с фиксированной точкой: фиксировано t2 и
— предсказание с фиксированным упреждением tx = t и t2 =
= t + T, где Т — фиксированное время упреждения.
Алгоритм (8.69) применим для всех этих типов предсказания,
хотя процедура вычислений все же должна быть незначительно ви-
доизменена.
Наиболее простым случаем является предсказание с фиксиро-
ванным интервалом. Здесь требуется оценить текущее состояние по
данным фиксированного множества наблюдений в прошлом, т. е.
при фиксированном t\. Практическим примером служит оценива-
ние орбитальных параметров космического корабля в предположе-
нии того, что данные телеметрии и визуального наблюдения из-
вестны до некоторого определенного момента времени в прошлом.
Уравнение (8.69) для предсказания с фиксированным интервалом
принимает вид
харо = Фа, му, t>tr, (8.70)
л
где фиксировано. Оценка х(^) получается с помощью алгоритма
фильтрации. Поэтому единственное, что требуется определить в
ходе вычислений, — это вычислить элементы переходной матрицы
состояния Ф(^, ^) путем решения матричного дифференциального
уравнения
G) = F(O<I>(f, у (8.71)
с начальным условием Ф(^1, ^i) = I-
В задаче предсказания с фиксированной точкой требуется оце-
нить состояние в фиксированный момент времени в будущем как
функцию текущего момента времени. Например, в начальных ста-
диях запуска искусственного спутника Земли желательно предска-
зать состояние в момент выхода на орбиту (в момент выклю-
чения маршевых двигателей) как функцию текущего времени.
В этом случае ур-ние (8 69) принимает вид 9
хО) = Ф(г2, 0*(0 (8-72)
*> Так как t2 фиксировано, a t возрастает, очевидно, что t, в конце концов,
превзойдет t2 Если следует сохранить информацию о состоянии x(f2), то в
этом случае следует использовать алгоритм сглаживания с фиксированной точ-
кой, который обсуждается ниже (Прим авт)
343
Так как в данной задаче второй аргумент переходной матрицы со-
стояния является переменной величиной, то можно использовать
ур-ние (8.65) и записать
0 = -Ф(4. 0F(0- (8-73)
Используя граничное условие Ф(^2, М=1. следует решить ур-
ние (8.73) в направлении прошлого. Можно или запомнить реше-
ние ур-ния (8.73) и обращаться к нему по мере необходимости или
получить начальное условие ®(fe, 0) (0 — время начала наблю-
дения) путем обратного прохода в начальное состояние, а затем
интегрировать уравнение в прямом направлении для нахождения
искомой матрицы Ф(Д О-
Предсказание с фиксированным упреждением является, очевид-
но, тем случаем, который обычно и описывается как собственно
предсказание. В этой задаче требуется предсказать состояние на
время Т вперед относительно текущего момента времени t. При
этом уравнение оценивания принимает вид
х (t + Т U) = Ф (t + Т, /) х (/). (8.74)
Так как оба аргумента переходной матрицы состояния являют-
ся в данном случае функциями текущего времени, то ни одно из
стандартных ур-ний (8.63), (8.65) не описывает полностью эволю-
цию Ф(/ + Д t). Для получения необходимого уравнения определим
производную по времени Ф(£ + Т, t), как
4Ф</ + 7’’ 0 = Oil +[4-ф(т-0] • (8-75)
аг [ от J|x=r+r [ ot J x=t+T
Необычная форма записи этого уравнения выбрана для того,
чтобы подчеркнуть истинную переменную для операции дифферен-
цирования. После подстановки выражений (8.63) и (8.65) для со-
ответствующих производных получаем уравнение Ф(/ ф- Т, t) =
= [F(r) Ф(т, 0)|T=f+7. — [Ф(т, О F (Z)]|T=f+7., которое после ряда
преобразований имеет вид
— Ф^ + Л t) = F(Z + 7Тф(^ + Т, t) — Ф(^+ Т, (8.76)
dt
Необходимое граничное условие Ф(^о + Д Д) может быть полу-
чено путем решения ур-ния (8.63) в направлении от t0 к /о+ Т. Пред-
сказанная оценка состояния может оказаться очень неточной, если
интервал предсказания и (или) коэффициент дисперсии шума объ-
екта не являются достаточно малыми, а модели сообщения и на-
блюдения построены недостаточно точно Д Для того чтобы быть
уверенным в правильности полученных результатов при необходи-
Методы устранения погрешностей при выборе моделей сообщения и на-
блюдения, а также неточности априорных данных рассматриваются в § 8.4
(Прим, авт.)
344
мости использования предсказанных оценок, крайне важно контро-
лировать дисперсию ошибки предсказания. Даже если алгоритм
гарантирует получение несмещенной оценки и, следовательно, ма-
тематическое ожидание оценки совпадает с истинным состоянием,
дисперсия может быть значительной. Уравнение для дисперсии
ошибки может быть получено следующим образом.
Ошибка предсказания записывается в виде
х(^О==х('2)-х(Ш)- (8.77)
Используя ур-ния (8.62) и (8.69), находим
х(^1) = ф(^> G)X(G) + ^Ф(^> Т) G (т) w (т) d т для (2>(х, (8.78)
ц
так что дисперсия ошибки равна
V- (^21 ti) = var {х (t21 = Ф (t2, tj V~ (G) Фг (t2, Q +
+ Jj4((2, т)О(т)Чг«(т)О7'(Л)Ф7'(Л, A)6d(t —A)dAdr. (8.79)
При выводе ур-ния (8.79) использовалось то обстоятельство,
что w(r) и х(7Д некоррелированны при Выполняя интегри-
рование по переменной Л в ур-нии (8.79), получаем
v~((2 1G) = Ф ((2, (х) v~(G) Фг {t2, у +
+ J ф ((2, т) G (т) (т) Gr(T) Фт(t2, т) dт. (8.80)
Так как подынтегральное выражение в ур-нии (8.80) является
неотрицательно определенным, дисперсияУ~ ((г|(1) может в общем
случае безгранично расти по мере увеличения разности между
и и h. Кроме того, если система неустойчива, первое слагаемое в
правой части ур-ния (8.80) также будет увеличиваться по мере
увеличения t2—ty
Пример 8.1. Рассмотрим три приведенных выше вида предсказания для
моделей сообщения и наблюдения:
0
[0 1
x(0 + L г (t) = x1(t) + v (t),
которые имеют переходную матрицу состояния
(Го 11
Ф((2, М = ехр 11 0 (12—й)
Г1
L0
1
Тогда алгоритм предсказания записывается в виде
Л Г1
х (/21 4) = К
/2 — (1
1
или же как система уравнений
х 01)> Ч t
Л Л Л Л Л
Х Ог I (1) — Х1 ((1) + 0г-------- (1)-*2 ((1); Х Ог I 6) = Х2 01) •
345
Алгоритм предсказания с фиксированным интервалом записывается в виде
АЛ Л Л А
М =X1 (Б) + —ti)x2(tr); х2(/| Zi) — x2(/i).
Л Л
Алгоритм предсказания с фиксированной точкой имеет вид лч</2|Л =*i(/) +
• ЛА л
+ (/2—t)x2(t)-, х2(/2|П=х2(0-
Л
Наконец, алгоритм с фиксированным упреждением записывается как х1(/+Т|/) =
АЛЛ Л
= Xi(/) Ч-^Хг(/); х2(/Ч-Т|/) =х2(/).
При постоянной Yw алгоритм вычисления дисперсии ошибки предсказания
согласно ур-нию (8 80) принимает вид
xjr
«2 I h) = (0 + 2 ]t2 - tr] v~ (tr) + [t2 ~ tr]2 (tr) + ]t2 - /JS ;
А11 Л.Ц Хц Л22 О
If
v~ (h1 4) = v~ (4) + [/2 - tr] v~ (tr) + [/2 - 4I2 ~
Xjg Л-12 Xgj /.
V~ (t2 I tr) = V~ (tr) + (t2~ tr)
x22 x22
Как и следовало ожидать, дисперсия ошибки предсказания с фиксирован-
ным интервалом неограниченно возрастает, так как t2=t, it фиксировано, a t
неограниченно возрастает. Дисперсия ошибки в случае предсказания с фиксиро-
ванным упреждением зависит от величины времени прогнозирования Т = t2—tr.
Дисперсия ошибки предсказания с фиксированной точкой равна дисперсии
ошибки фильтрации, так как /2 фиксировано, Л = /, a t в конечном счете рав-
но t2. “
Сглаживание. В задаче сглаживания необходимо получить
оценку состояния х(^) при заданном наблюдении Z(^2) =
= {z(t), где t2>ti. Иными словами, оценивается состо-
яние в момент времени, который предшествовал текущему момен-
ту времени в последовательности наблюдений. Так же, как и в слу-
чае предсказания, задача сглаживания может быть разделена на
три вида:
— сглаживание с фиксированным интервалом: интервал на-
блюдения фиксирован, так что /2 — постоянная величина, а изме-
няется от t0 до /2;
— сглаживание с фиксированной точкой: фиксирован момент
времени tr, когда должна быть получена оценка, и t2 = —
текущее время;
— сглаживание с фиксированной задержкой: в этом случае
ни ti, ни t2 не фиксируются, но их разность остается постоянной.
В этом случае ^=/и t2~t+T, где Т — постоянное время задержки.
К сожалению, в отличие от задачи предсказания, три вида
сглаживания требуют для своего осуществления трех различных
алгоритмов, хотя, как будет показано ниже, некоторые алгорит-
мы следуют непосредственно из других. Брайсон и Фрэзер опубли-
ковали одну из первых работ по последовательным алгоритмам
сглаживания [33]. Они показали, что сглаживание (так же, как
и фильтрация) может рассматриваться как задача оптимизации и
решаться с использованием обычных методов вариационного ис-
числения.
Аналогичные алгоритмы сглаживания, а также некоторые их
обобщения были предложены в работах [192], [195], в которых
346
были получены алгоритмы для дискретного времени с помощью
оценивания по максимуму апостериорной вероятности и алгоритмы
для непрерывного времени путем использования предельного пере-
хода (см. § 7.3).
Медич, опубликовавший ряд фундаментальных статей по сгла-
живанию [151]—[156], первый четко определил три вида задач
сглаживания. Он распространил предельный переход, применен-
ный в работе [195], на сглаживание с фиксированной точкой и
сглаживание с фиксированной задержкой, а также дал для непре-
рывного случая непосредственный вывод уравнения сглаживания
с фиксированной точкой из уравнения Винера — Хопфа. При вы-
воде алгоритмов дискретного сглаживания Медичем был развит
метод ортогонального проецирования, впервые использованный
Калманом [109].
В недавних работах [70], [158] обсуждалась новая форма ал-
горитмов сглаживания, которые используют комбинацию двух оце-
нок, полученных при фильтрации с помощью прямого и обратного
фильтров Калмана. Как было указано выше, Мера и Брайсон
[160] и Брайсон и Хенриксон [34] распространили алгоритмы сгла-
живания на случай небелого шума соответственно для непрерыв-
ных и дискретных процессов. Один из подходов к задаче сглажи-
вания и фильтрации, предложенный Кайлатцом [101] и Кайлат-
цом и Фростом [103, 104], основан на теории «обновляющих» про-
цессов. Этот подход позволяет существенно упростить вывод алго-
ритмов фильтрации и сглаживания и будет использован в настоя-
щем разделе при выводе алгоритмов сглаживания для случая не-
прерывного времени. В первую очередь будет рассмотрен случай
непрерывного времени, а затем будут получены алгоритмы для ди-
скретного времени.
Подход, основанный на теории «обновляющих» процессов и
впервые использованный Волдом и Колмогоровым в задаче линей-
ного оценивания по критерию наименьших квадратов, заключает-
ся в «обелении» последовательности наблюдений и переходе к бо-
лее простой задаче для белого шума. Боде и Шеннон [29] успешно
применили этот подход к выводу уравнения классического стацио-
нарного фильтра Винера. Другим преимуществом такого подхода
являются более общая постановка задачи оценивания и его воз-
можное применение к некоторым нелинейным задачам. Для про-
стоты изложения ограничимся рассмотрением линейных систем с
сосредоточенными параметрами; интересующиеся могут познако-
миться с другими применениями этого подхода в статьях [101],
[103], [104].
Основной задачей при использовании подхода, основанного на
теории «обновляющих» процессов, является получение при помо-
щи физически реализуемой и обратимой линейной операции из на-
блюдаемого процесса z(t) процесса типа белого шума, который
называется обновляющим и обозначается как «7 (t). В общей по-
становке задачи определение подходящего преобразования может
оказаться настолько сложным, что лишит возможности использо-
347
вать данный подход. Однако для линейных систем с сосредоточен-
ными параметрами нетрудно показать, что для некоррелирован-
ных процессов w(t) и v(t) с нулевыми средними процесс
.J(f) =z(^) = z(Q —Н^)х(^) (8.81)
является белым шумом. Так как z(t) может быть получено из
У (/) как
z(0 = J(0+HG)x(0. (8.82)
то очевидно, что .7 (t) и z(t) связаны физически реализуемым, об-
ратимым линейным преобразованием, и поэтому .7 (t) является
«обновляющим» процессом. Иными словами, оценка, основанная
на z(t), может быть выражена также через У (t), так что У (t) и
z(t) «эквивалентны» в том смысле, что они содержат одинаковую
статистическую информацию. Таким образом, если необходимо, ал-
горитм фильтрации может быть выражен через У (t), а не через
z(t). Такой алгоритм может оказаться значительно проще, чем
вывод при непосредственном использовании наблюдения z(t).
Как указывалось в § 7.2 и 7.3, «обновляющий» процесс У (t)
можно рассматривать как новую информацию, содержащуюся в на-
блюдении z(t). Кроме того, можно показать, что ’>
cov {У (О, У (т)} = 4% (0 йо (t — т). (8.83)
Интересным и очень полезным дополнительным свойством У(()
является то, что он является нормальным процессом, если v(t) —
нормальный процесс. Таким образом, можно рассматривать У (t)
и v(t) как две различные формы представления одного и того же
случайного процесса [ЮЗ].
Как отмечалось (см. § 6.6), ошибка оценивания х(^р2) =
л
=x(^i)—х(^р2) и последовательность наблюдений z(t) ортого-
нальны при ^о=Ст<^2. Так как z(Q и У (t) эквивалентны, то оче-
видно, что х(^р2) и У (т) при ^о^т<^2 также должны быть орто-
гональны. Запишем оценку в виде линейной функции от У (/):
л
х (^ I г2) = ( S ft, т) у (т) d т. (8.84)
^0
Так как
cov{x(^| t2), J(^)}=0, t0^K<zt2, (8.85)
то из ур-ния (8.84) следует уравнение Винера — Хопфа
cov{xft|Q, .7 ft)} = cov {х ft) — xftft2), Jft)} =
G
= cov{x(^), J (A.)}—fHft, t)cov{J(t), Jft)}dr = 0,
t,
*' Можно показать, что в дискретном случае процесс ,7(/), определяемый
ур-нием (8 81), является белым шумом, но ковариация J(f) уже не равна
коварнацни v(/). (Прим. авт.)
348
так что
cov{x(0), J(A)}=jE(O, t)cov{J(t), J (A)} dr, f0<A<f2. (8.86)
^0
Это обычная форма записи уравнения Винера — Хопфа. Однако
вследствие того, что «обновляющий» процесс является белым шу-
мом [см. (8.83)],
cov {х (У, J (А)} = [ Е (О, т) 'Fv (т) <5о (т -- A) d т, t0 < А < t2. (8.87)
^0
Благодаря фильтрующему свойству дельта-функции это уравне-
ние преобразуется в
cov {х (Q, J (А)} = Е (tb A) 'Ey (A), t0 < А < t2. (8.88)
Следовательно, интегральное уравнение Винера — Хопфа для
Е(0, т) превращается в простое алгебраическое выражение, из ко-
торого
S (^ т) = cov {х (0), J (т)} Y7i (т). (8.89)
Поэтому
а (^ 1tj = j cov {х (0), J (т)} 'Ey1 (т) J (т) d т. (8.90)
io
Этот результат имеет принципиально важное значение и пред-
ставляет собой решение задач сглаживания (0>0)> фильтрации
(0=0) и предсказания (0<0)- Остается только определить
cov{x(0), J (т)}.
Хотя основным предметом нашего рассмотрения является не
фильтрация, а сглаживание, оказывается, что решение задачи
фильтрации играет большую роль при выводе алгоритмов сглажи-
вания. Поэтому необходимо кратко остановиться на решении зада-
чи фильтрации в терминах «обновляющего» процесса, прежде чем
перейти к выводу алгоритмов сглаживания.
Для задачи фильтрации из ур-ния (8.90) при 0 = 0=^ следует
х (t) = х (t |0 = J cov {x (0, J (г)} 'Ey1 (t) J (t) d t. (8.91)
^0
Если продифференцировать обе части ур-ния (8.91) по t, то
получим
x(0 = cov{x(0, +
t
+ J-^-cov{x(0, J(T)}'F71(T)J(T)dT. (8.92)
‘‘о
349
Используя уравнение модели сообщения, можно записать
— cov{x(0, J (т)} = cov {х (t), .7 (т)} = cov{ F(0x(0 + G(0w(0, J(r)},
dt
но w(t) и J (т) при О=Ст<^ некоррелированны, так что
^-cov{x(0, .7 (т)} = F(0cov{x(0> J(t)}, tg^rCt. (8.93)
Поэтому ур-ние (8.92) принимает вид
x(0 = cov{x(0> J(0} Ч’Т1 (О 3 (t) + F (0 J cov {x (0,
^0
(У(т)}Т7*(т)(У(т)йт. (8.94)
A
Интеграл просто равен x(t), поэтому получаем
x(/) = F(0x(0+cov{x(0, J (ОПТ1 (t)Cf (t). (8.95)
Далее cov {x(0, J (0} = cov {[x(0+x(0], [H (t)x(t) +v(t) ]}.
Так как x(0 и x(Q ортогональны, то cov{x(0, J (t)} = coV{x(0,
H(0x(0} + cov{[x(Q + x(0], v(0) = V~(0 HT(0+cov{x(0, v(0}.
Ho x(Q зависит только от w(t), 0=sSt<7 и х(0), причем каждая
из этих величин независима от v(f). Поэтому
cov{x(0, y(t)} = V~(t)HT(t). (8.96)
л
Подставляя этот результат в ур-ние (8.95), получим x(t) =
= F (О X (0 + V- (О Нг (О 'F?1 (0,7 (0 или х (0 = F (t) х (t) +
+V~(OHr(O'FT1 (О[z(0 — Н(Ох(01- (8.97)
Это уравнение может быть приведено к стандартной форме, ес-
ли использовать соотношение
(0 = V~(t) Нг (0 'F?1 (0- , (8.98)
Теперь обратимся к алгоритму сглаживания. Уравнение (8.90)
может быть записано в виде
х Vi 112) = J cov {x (0), J (t)} 'FT' (r) J (t) d т +
+ J cov {x (0), J (t)} 'FT1 (T) J (t) d r.
ti
350
л
Так как первый интеграл в этом выражении равен xf/J,
х & | /2) = X (/J + f cov {х (У, J (т)} Т71 (Т) J (т) d т. (8.99)
Аналогично можно показать, что
cov{x(/1)J(t)}=V~(f1, т)Нг(т), (8.100)
Ковариационная матрица V~ (ti, т) может быть записана в виде
¥-(/,. т) = V~(G) ф! (т, tj, т > tv (8.101)
•где Фе(т, ^) переходная матрица состояния [см. (7.88)]
х (f) = [F (0 — СК (/) Н (/)] х (0 +G (0 w (/) — СК (0 v (0- (8.102)
Иными словами, Фе(т, h) удовлетворяет дифференциальному
уравнению
-^Фе(т, /у) — [F(t) — 5^(т)Н(т)] Фе(т, tj (8.103)
д т
с Фр(Т1, ^i)=I. Уравнение (8.101) может быть легко получено,
•если т) записать в виде
Vsr(<i, T) = cov{x(Q, x(t)}=cov х(^), Фе(т, (G)+
+ [фе(т, Л) [G (Л) w (Л) — JT(A,)v(A)]dJ. (8.104)
it J
Так как x(^), w(Z) и v(X) независимы для X>ti, ур-ние (8.104)
упрощается и получаем
V-^i’ t) = cov{x(/1), Фе(т, G)x(Q} = У~(^)ФГ(т, tj). (8.105)
Если подставить ур-ния (8.101) и (8.100) в (8.99), то для
Л
х(/||^2) получаем
x^J^^x^+V-^) (ф;(т, ^)Нт(т)ТТ' (t)J(t)^t (8.106)
или
х(^|/2)-= x^+V-^X^, t2), (8.107) .
где
X (tlt t2) = jФе (T, ix) Нг (т) TV1 (Т) J (Т) d т. (8.108)
351
Оценка состояния xf/J как результат сглаживания при задан-
ном Z(t2) состоит из оценки, полученной в результате фильтрации
Л
x(7J, и сигнала коррекции, который зависит от информации, полу-
ченной на временном интервале [/ь t2].
Дисперсия оценки, как результат сглаживания, может быть
найдена из ур-ния (8.106) как функция дисперсии оценки, полу-
ченной в результате фильтрации V~(ij).
В соответствии с определением ошибки имеем
хО2) = х(^) — х(/1|/2) =
(8.109)
Поэтому дисперсия ошибки сглаживания
V~(^!^)Avar{x (^1^)} =
= V~ ft) - V~&) } ФГ(т, у Нг (т) 4V1 (т) cov {J (т), х &)} d т -
ц
G *1
J cov {х &), J (т)} Т?1 (т) Н (т) Фе (т, 0 d Т V- (У +
Vt (4).
+Vr(fx)
(8.110)
Ковариация х(^) и .7 (т) записывается в виде cov{x(ij), J(t)} =
=cov{x(i]), [Н (т)х(т)+v(t) ]}, но так как v(t) и х(^) при т>/1
некоррелированны, то cov{x(tj)(t)}=V~(/ь t) Ht(t),t>£. Если
теперь подставить выражение дляУ~ (/ь т) из ур-ния (8.105), то
получим
cov{£(4), ^(т)) = Уг(/1)Ф1(т, уНг(т). (8.111)
При подстановке (8.111) в ур-ние (8.110) после очевидных ал-
гебраических преобразований имеем
v~O2) = v~ (M-v~(G)
фГ(т, ^)НГ(т) X
ХЧГГ’(т) Н (т) Фе (т, tt)dr V~(y.
(8.112)
Это очень интересный результат, так как из него ясно видно,
насколько уменьшается дисперсия ошибки оценки состояния
x(ii), полученной в результате фильтрации, за счет сглаживания
данных, которые поступят в будущем.
352
Рассмотрим каждый из трех видов сглаживания отдельно. В
первую очередь рассмотрим сглаживание с фиксированным интер-
валом, для которого = t и ti=T, где Т — постоянная величина.
При этом ур-ния (8.107) и (8.108) принимают вид
х (t\ Т) = х (0 +V~(0 к (Л Т), /<Г; (8.113)
т
1 (t, Т) = J ф! (т, t) Нт (т) Т?' (т) J (т)d х. (8.114)
t
Если продифференцировать последнее выражение по текущему
времени t, то получим
4 k (t, Т) = - ФГ (t, t) нг (0 т?1 (0 j (0 +
at
Т
^4феГ(т> 0Нг(т)Чг71(т) V(x)dx. (8.115)
t
Так как Фе(т, f) удовлетворяет ур-нию (8.103), частная произ-
водная Фте(т, t) по t
4®I(t, 0 = -(F(0-^(0H(0f ФГ(т, 0- (8.116)
Используя этот результат и то, что Фе(£, 0 = 4, запишем (8.115)
в виде
4 k У, Т) = - нг (0 4V1 (0 3 (0 - [F (0 -
т
— X (t) Н (Of Jф! (т, О Нг (т) 4'V1 (т) .7 (т) d х.
t
Интеграл в правой части уравнения равен Г), поэтому
^к(Л Т) = —Нг(0ЧГ71(0^(0 —[F(0 —JT(0H(0f к(Л Т). (8.117)
Теперь вернемся к началу и продифференцируем ур-ние (8.113)
по t *>:
д Л Л а
— x(;|T)=x(0+V~(0k(Z, T)+V~(n4-k(0 T). (8.118)
at dt
Л
В результате подстановки ур-ний (7.82) и (7.85) для х(/) и
y^(t), а также (8.117) для 6к(/, 7)/dt и выполнения ряда алгебра-
ических преобразований получаем
д л л
5rx(/\T)-F(t)x(t|7’) + G(t)^w(t)Gr(t)k(t, Т). (8.119)
о Так как Т — постоянная величина, можно было бы использовать обыч-
ные производные вместо частных. Однако во избежание недоразумений будем
использовать частные производные. (Прим, авт.)
12—26 353
Выражение для k(t, Т) может быть получено из (8.113):
T) = V~1(0[x(^7’)-x(0L (8.120)
так что ур-ние (8.119) принимает вид
д л л , д л
х (f | Т) = F (0 х (П Т) + G (0 (t) G (0 V~ (/) [х (t | Т) - х (/)]. (8.121)
Для компактной записи этого выражения введем матрицу коэф-
фициентов усиления при сглаживании
H(Z|T)==G(0*Fw(0Gr (0V-1 (0 (8.122)
и запишем ур-ние (8.121) в виде
х (И Т) = F (0 х (f | Т) + П (f | Т) [х (/1 Т) - х (/)]. (8.123)
Форма записи ур-ния (8.123) очень сходна с формой записи
уравнения исходного фильтра Калмана, за исключением того, что
ошибка здесь представляет собой разность между оценкой как ре-
зультатом сглаживания и оценкой как результатом фильтрации, а
не между действительным и ожидаемым наблюдениями.
Начальное условие для ур-ния (8.123) определяется при t—T
Л Л
как х(У| Т) =х(Т) и получается при применении алгоритма фильт-
рации. Уравнение сглаживания с фиксированным интервалом
(8.123) решается по времени в обратном направлении до момента
t=t0. Полная процедура вычислений для получения решения зада-
чи сглаживания включает в себя применение алгоритма фильтра-
ции в прямом по времени направлении с t0 и до Т с последующим
интегрированием ур-ния (8.123) в обратном направлении, начиная
с t=T. Так как оценка как результат фильтрации используется в
л
ур-нии (8.123), то х(т), должна храниться в памяти в
течение всего времени фильтрации. Алгоритм сглаживания с фик-
сированным интервалом является процедурой, выполняемой не в
реальном масштабе времени, так как обратный ход должен произ-
водиться после получения решения задачи фильтрации, которая
выполняется в реальном масштабе времени.
Используя обычные определения и обозначения, запишем ошиб-
ку сглаживания в виде
x(f|T) = x(f) —x(f|T), (8.124)
~ Л
так что х(^|Т)=х(£)—х(£|Т). После подстановки модели сообще-
ния и ур-ния (8.123) в последнее выражение получаем
х (/ {Т) = F (0 х (0 + G (0 w (0 -{F(0x(dD +
+ n(f| T)[i(f|T)-x(f)]}
354
или
X (f [ Г) = F (О X (t IT) 4- n (f | T) [x (f | T) - X (01 + G (0 w (t). (8.125)
Следует обратить внимание на сходство полученного выраже-
ния с ур-нием сглаживания (8.123). Данное выражение может
быть получено из (8.109), если воспользоваться теми же рассуж-
дениями, что и при выводе алгоритма сглаживания (8.123). Урав-
нение (8.125) решается в обратном направлении по времени при
начальном условии х(Т\Т)=х(Т).
Дисперсия ошибки сглаживания с фиксированным интервалом
может быть получена из ур-ния (8.112) при t\ = t и t% = T в виде
v~(/ I Т) = VA (0 - V- (0 [ф! (т, о Нг (т) X
х ь
X Ч'Т1(т)Н(т)ф(!(т, t)dr (8.126)
В такой форме это выражение неудобно с той точки зрения, что
сначала необходимо вычислить Фе(т, /), а затем выполнить интег-
рирование. Для получения более удобного с вычислительной точки
зрения решения возьмем частную производную по t от обеих час-
тей ур-ния (8.126). В результате получим
ХНГ (т)Ч'?1 (т)Н(т)Фе(т, t)dx V~(0-
- т
-V~(0 £фГ(т, /)Нг(т)^7!(т)Н(т)Фе(т, t)dr V~(0-
-t
, т
- V~ (01 - нт (O^-1 (0 H(0 + J JA ф[ (т, t) X
XHr(T)W‘(T)H(T)®{(T, t)dr +
+]'ф1(т, /)dT|v~(0.
t ‘
(8.127)
Используя ур-ния (7.85) и (8.116), после несложных алгебраи-
ческих преобразований получим
V~ (f | Т) = [F (0 + п (t I Т)] V- (И Т) + V~(t I Т) [F (0 +П (И Т)]т ~
~G(/)^w(0Gr(0. (8-128)
12* 356
Это уравнение также решается в обратном направлении по вре-
мени страничным условиемV~(Г|Г) =V~(7’), которое получается
из решения задачи фильтрации. Полный алгоритм сглаживания с
фиксированным интервалом для непрерывного времени приведен в
табл. 8.3.
Таблица 83
Непрерывные алгоритмы сглаживания с фиксированным интервалом
Алгоритмы сглаживания с фиксированным интервалом
xa|T) = F(0x(HT) +п (0 |Т)[х(/1 Т) —£(<)]; (8 123)
П(/|Т) = б(ОЧ\, (OGT(OVZJ(O- (8-122)
Вычисление дисперсии ошибки сглаживания с фиксированным интервалом
V~ (t IT) = [F (/) +П (t | Г)] V~ (t | Т) +V^(t | T) [F (t) + П (/ | T)f -
-G(t)Ww (t)GT(t). (8.128)
Начальные условия
x(T|T) = x(T); V~(T\T) = V~(T).
Примечание Предварительно должны быть выполнены вычисления со-
гласно алгоритмам фильтрации, приведенным в табл 7 4.
При сглаживании с фиксированной точкой фиксируется момент
времени, в который необходимо получить оценку, а далее увеличи-
вается время наблюдения. Следовательно, в ур-нии (8.106) ti = t„—
константа и t^—t, поэтому получаем
£(U0 = ^)+v~(uf<tf(T. инг(т)Т7'(тр(т)бЬ, t>t*.
(8.129)
Если взять производные по t от обеих частей ур-ния (8.129), го
получаем
1(М0 = |мМ0=Уг(МФ"(^ инт (0W1 (0^(0- (8-130)
Используя (8.105), этот результат можно записать в виде
x(M0 = v~(^, (8-131)
Л Л
Начальное условие x(t„\tt) =x(tt) получается из алгоритма
фильтрации.
Желательно выразить¥~ (t,, t) как решение дифференциально-
го уравнения с тем, чтобы избежать вычисления <be(t, it) Конечно,
для нахождения ®e(t, t»} можно было бы просто решить ур-ние
356
(8.116). Однако если продифференцировать уравнение (8.105), то
получим
vr(^, 0 = Ml =
=v~ aj of (t, zj [F (о - х (о н
или
V~a*, 0 = V~a#> t) [F(8.132)
Решая ур-ние (8.132) с граничным условиемV~(7„
которое получается из алгоритма фильтрации, получаем V~(7„ t).
Итак, алгоритм сглаживания с фиксированной точкой полностью
определен.
л
Следует заметить что для получения x(t) фильтрация должна
выполняться одновременно со сглаживанием. Если момент начала
наблюдений t0 меньше tt, то можно использовать предсказание с
фиксированной точкой при t<t„, а затем, когда t станет больше
t„, перейти к сглаживанию.
Дифференцируя выражение х(£»|£) =x(f.)—x(f,|f), получаем
уравнение ошибки для сглаживания с фиксированной точкой
X (И tj = - X (^ 10 = V~ (f*, t) н7 (0 т?1 (0 [Z (0 - н (0 X (f)].
Так как J (/) = z (f) — Н (t) х (t) — Н (/) х (/) 4- v (t), то
х (f* |f)= —V~ (f#,
(8.133)
Уравнение дисперсии ошибки для сглаживания с фиксирован-
ной точкой легко получается из (8.112):
t
v~(M0=v~(u-v~(^ |ф*(т> UX
. tf,
ХНг(т)^7‘(т)Н(т)Фе(т, tjdx VT(Q. (8.134)
Вычисляя производные по t, получаем V~(£»|£) =—V~ (t„) X
ХФет(^, £*) HT(i)4f-1v(0 Н(/)Фе(£, Z,)V~ (f„). Используя ур-ние
(8 105), находим
vr(Mo=-vTa*, oHr(ow‘KOH(ov^a*, о (8.135)
с начальным условием Правая часть ур-ния
(8.135) отрицательна и, следовательно,V~(7,| t) монотонно убыва-
ет. Сводка уравнений алгоритма сглаживания для непрерывных
процессов с фиксированной точкой приведена в табл. 8.4.
357
Таблица 8.4
Непрерывные алгоритмы сглаживания с фиксированной точкой
Алгоритм сглаживания с фиксированной точкой x(M0=v~(^, (0[z(f)-H(0x(0L (8.131)
Вычисление второго момента V~(^, f) = V~(f., 0[F(0-^(/)H(/)f . (8.132)
Вычисление дисперсии ошибки сглаживания v~0J0 = -v~(C. t). (8.135)
Начальные условия
х(М« = х(М: V~(^, /*)=У~(^|/„) = V~ (/„).
Примечание Для получения решения задачи сглаживания с фиксиро-
ванной точкой необходимо предварительно выполнить вычисления согласно алго-
ритмам фильтрации, приведенным в табл. 7.4
Медич [157] предложил непрерывный алгоритм сглаживания с
фиксированной точкой несколько в ином виде:
£(ЛИО = В(*. UW)[z(0-H(0x(0L t>t*, (8.136)
где 3£(t) — коэффициент усиления обычного фильтра Калмана и
В(7, /.)[F(0 + G(0Tw(0Gr(0V^(0]. причем
B(/», f*) = I. Доказательство эквивалентности этих двух алгоритмов
предлагается читателю в качестве самостоятельного упражнения.
Непрерывный алгоритм сглаживания с фиксированной задерж-
кой был получен Медичем из дискретного алгоритма Рауха [192]
путем довольно сложного предельного перехода.
Для сглаживания с фиксированной задержкой (ti = t и t2—t+T,
где Т — положительная константа) вывод алгоритма сходен с вы-
водом аглоритма сглаживания с фиксированным интервалом.
Сначала запишем ур-ние (8.107), которое в этом случае прини-
мает вид
+ = t + T), (8Л37)
и ур-ние (8.108)
t+T
l(t, t + T)= JoI(t, 0Нг(т)Чг?1(т)J(r)dr. (8.138)
t
Так же, как и при выводе ур-ния (8.117), вычисляем производную
X(t t + T) в виде
358
i(t, t+T) =Oer(f4-T, t)HT(t + T)^\t + T)Cf(t + T) —
— Нг(0Т7’(0^(0- lF(0 — ^(OH(Of X(f, t + T). (8.139)
Это уравнение имеет такой же вид, что и (8.117), за исключением
первого члена, который обусловлен наличием переменной t в верх-
нем пределе интегрирования.
Вычисляя, как и в предыдущем случае, производную от
(8.137),получим x(t\t + T)=x(t) + V~(Z)X(t t+T) + N~(t)i(t, t+T).
Л
Подставляя в это выражение ур-ние (7.102) и (7.105) для x(t)
nV~ (t), а также (8.139) для h(t, t + T), после некоторых алгеб-
раических преобразований получаем
x(f| t + T) = F(t)x(t\t + T)+G(t)^ (t) GT(t)X(t, t +
+ Т)+У~Ч)фТ(?+Т, t)HT(t + T)^(t + T)ff(t + T). (8.140)
Из ур-ния (8.137) следует, что t + T) выражается следую-
щим образом: 1(7, t + T) = V~ (t) [х(7| t + T)—x(7)], так что (8.140)
принимает вид
л л _ . л
х (t 114-Т) = F (t) х (t 11 + T) + G (t)4^ (t) GT(t) V~ (t)[x(t\t + T)~
- x (01 + V~(0 Of (t + T, t) fF (t + T) (t + T) [z (t + T) —
-H(t + T)x(t+T)]. (8.141)
A
Граничное условие x(t0\t0 + T) получается из алгоритма сгла-
живания с фиксированной точкой от t0 до t^ + T.
Чтобы завершить вывод данного алгоритма, обратим внимание
на то, что дифференциальное уравнение
ФЛ+Т, t) = [F(t+Т) — СК(t+ T)H(t+ Т)] Фе^+Т, t)-
- Фе (t + Т, t) [F (0 - СК (О Н (01 (8.142)
получается тем же способом, который использовался при выводе
уравнения предсказания с фиксированным упреждением (3.76).
Граничное условие <be(t0 + T, to), необходимое для решения ур-ния
(8.142), получается при решении ур-ния (8.103) в прямом направ-
лении от tQ до to + T. Можно было бы также заметить, что
V~(t)<beT (t+T, t) = N~(t+T, t) и вывести уравнение для V~(^+Г, О
точно так же, как это было сделано в случае сглаживания с фикси-
рованной точкой.
Уравнение ошибки сглаживания с фиксированной задержкой
определяется путем дифференцирования выражения x(t\t+T) =
=x(t)—x(t\t+T). В результате получаем х(7|/+Т)=х(7)—
359
—После подстановки уравнения модели сообщения и
(8.141) имеем
x(t114-Т) = F(0х(t\t + Т) +G (О(0Gr(ОХ
XV- (0 [x(t R + Т) -х (01 - Vr(0 Ф? (t +
+ Т, t)Нт(t +T)^(t + T)H(t+T)x(t + T)~
-У-^Ф^+Л t)HT(t + T)W-l(t + T)v(t+T)+G(t)w(t). (8.143)
Начальное условие x(Z0|iZ0+7’) получается из ур-ния (8.133) ошиб-
ки для сглаживания с фиксированной точкой.
Дисперсия ошибки сглаживания с фиксированной задержкой,
как и в предыдущем случае, получается из ур-ния (8.112). После
несложных алгебраических преобразований получаем
v~ (t \t + Т) = [F (0 + G (0 (0 GT (О V-1 (f)] V- (ф + Т) +
+V~(f| t + T) [F (0 + G(OYw (0 G?(0 V~ (Of -
- V~ (0 Ф1 (t+T, t) Hr {t+T) +T) H (t+
+ T) Ф, (t + T, t) V~(0 - G (0 Tw (0 Gr (0- (8.144)
Здесь граничное условие V ~ (0 ро+Г), как и раньше, получается
согласно алгоритму сглаживания с фиксированной точкой. Урав-
нения непрерывного алгоритма сглаживания с фиксированной за-
держкой сведены в табл. 8.5.
Таблица 8.5
Непрерывные алгоритмы сглаживания с фиксированной задержкой о
Алгоритм сглаживания с фиксированной задержкой
x(t\t+T) = F(t)x(t\t + T) +G(/)TW (t)GT(t) V-1 (/)[£(/]/ +Т)-х(/)] +
+V~ (0 (t +T, 0 Hr (t +T) Y71 (t + T) [z (t + T) - H (t +7) x (t + T)].
(8.141)
Вычисление переходной матрицы ошибок
Фе(/ +т, 0 = [F(/ +Т)-<ЗГ(/ + Т)Н(< +Т)]фе(^ +Т, t)~
— Qe(t+T, t) [F(0— 5Г(/)Н(/)1. (8.142)
Вычисление дисперсии ошибки сглаживания
V- (/1 / + Т) = [F (/) + G (0 (/) GT (0 V-1 (/)] V~ (t И +D +
360
Продолжение
+ V- (И t +Г) [F (t) 4- G (t) Tw (f) GT (t) VX* (Of - V~ (0 фег (t +
+ r, f)HT(/ +т)чг7’(<+ Г)Н(/ +Т)Фе(«+г, ov~(o —
-G(t)V„(t)GT(t). (8.144)
Начальные условия
Фе(0+?’> «о)—получается из ур-иия (8.103);
Л 1
х (<о I 0 + Т) I — получаются из решения задачи сглаживания
V__(t0 | ta + Т) I с фиксированной точкой
’) Алгоритмы фильтрации из табл 7.4 должны быть реализованы совместно
с алгоритмами сглаживания с фиксированной задержкой. Алгоритмы сглажива-
ния с фиксированной точкой из табл. 8 4 должны быть использованы для полу-
чения начальных условий.
Подход, основанный на теории «обновляющих» процессов, мо-
жет быть также использован для вывода алгоритмов сглаживания
для дискретных процессов. В дискретном случае «обновляющий»
процесс хотя и является белым шумом, но уже не имеет ту же
самую дисперсию, что и v(0. Поэтому получать необходимые ре-
зультаты несколько сложнее.
Для того чтобы подчеркнуть многообразие подходов, которые
могут использоваться при решении задач оценивания, при выводе
дискретных алгоритмов сглаживания используем подход, основан-
ный на критерии максимальной апостериорной вероятности. Как
уже было отмечено ранее, такой подход первоначально был пред-
ложен в работе [195].
Модели сообщения и наблюдения записываются, как обычно, в
виде
х(А>4-1) = Ф(А>4-1, k)x(k)+r(k)v/(k); (8.145)
г(Л) = Н(Л)х(6)+у(£), (8.146)
где v/(h) и v(k) — нормальные белые шумы с нулевыми средними
и с E{w(k) vT(i)} = ^(k)f>K(k-i)\E{v(k)vT(j)} =Vv(k)t>K(k-j).
Дополнительно предполагается, что начальное условие x(k0) име-
ет нормальный закон распределения со средним цх(&о) и дисперси-
ей Vxf&o). Поэтому все плотности вероятности, рассматриваемые
при решении этой задачи, нормальные, полностью определяемые
средними и дисперсиями.
В качестве оценки состояния х(/г) по методу максимальной апо-
стериорной вероятности при заданном множестве наблюдений
Z(W), N>k принимается значение x(k), которое максимизирует
условную плотность вероятности p[x(k) |Z(W)]. Аналогичным об-
391
л л
разом определяются x(£|(V) и х(£ +1 |(V) как величины, одновре-
менно удовлетворяющие двум уравнениям ,
dp[x(k), х (&-|-1) | Z (У)] Л = 0- х (*)=x(i/AT) v’ Л x(*4-l)=x(*+l|W) (8.147)
dx(k)
др[х(&), х (ft -у 1) | Z QV)] л
ax(£-H) х(«=хда
х(*-Н)=х(4+1|Л0
Как будет показано ниже, необходимо, чтобы удовлетворялось
только ур-ние (8.147).
Согласно формуле Байеса условная плотность вероятности
p[x(k), х(£+1) |Z((V)] может быть записана в виде
р [х(£), х(k + 1) IZ(N)] = -Р-^),/[^)]1),--У)]
Воспользовавшись теоремой умножения, получим
р[х(Ч x(k+ l)IZ(AT)] =
P[*(k), x(fe-)- 1), z(fe + l). z(TV)|Z(fe)}p[Z(fe)}
P[Z(*+ 1).....Z(V) | z(£))P [Z(A)]
p[x(k), x(^ + l)|Z(^] =
— PfxW- x(^-l-l), z(At -|- 1)....z (TV) |Z (£)]
p[z(* + l).... Z(A7)|Z(fc)]
Еще раз применяя теорему умножения, находим
p[x(k), x(fe + l)|Z(^] =
_ p[x(fe-K 1), Z(fe-bl).... z(N)\x(k), Z (>fe)] p [x (fe) [ Z (fe)J
P[z(£-J-1)...«(A^)|Z(^)1
Если известно x(k), то множество наблюдений 2(k) не содер-
жит новой информации, следовательно, аргумент, фиксирующий
условие в первом множителе числителя, может быть просто заме-
нен на x(k). Поэтому
p[x(fe), x(*+l)|Z(A0J =
= p[x(feH- 1), z(&4-l).z ((V) | х (&)] р [х (&) | Z (fe))
p[z(* + l)..z(7V) |Z (£)]
*> Читатель может задать уместный вопрос, почему используются
оценки по максимуму апостериорной вероятиостн, получаемые из ур-ния (8 147)
dp[x(k) | Z (Л7)]Г
или (8.148), а не оценка, получаемая из уравиеиня----г---—---- л =
dx(k) /х(*)=х(* | ЛГ)
= 0.
Это объясняется простотой дифференцирования н тем, что в оригинальных работах
алгоритмы сглаживания получены именно таким образом. Отметим, что предыду-
др [X (k) | Z (Л)] /
щне ур-ння (8 97) и (8.98), а также уравнение --—~.------/ л =0
dX(k) /х (*)=Х (* | АГ)
для рассматриваемых задач приводит к одному и тому же результату. (Прим,
авт.)
362
Еще раз применим теорему умножения, и исключая аргумент
x(k), получим
р[х(Ч x(fc + l)|Z(2V)] =
__ p[z(*+l).....Z (TV) I X (fe-Ь 1)] р [х (fe 4- 1) I X (^)] р [х (fe) [ Z (fe)] ,g j4Q
p[z(£-Hl)....z(^|Z(A)] ’ '
Уравнение (8.149) представляет собой удобную форму записи
условной вероятности, так как только две плотности вероятности в
данном выражении включают в себя x(k), а именно,
p[x(fe+1) ]х(Л)] и p[x(k) |Z(7>)], а эти плотности могут быть лег-
ко найдены. Так как оба распределения нормальные, то требуется
найти только соответствующие средние и дисперсии.
Для распределения р[х(7*+ 1) |x(7Q] находим:
E{x(k+ 1)| х(Л)} = Ф(& + 1, k)x(k);
var {х (k + 1) | х (k)} = Г (k) Vw Гг (k).
Поэтому
р[х^ + 1)(х(Л)] =Д1ехр Jy [х($ +1) — Ф(Л + 1, Л)х(£)]гХ
Xfr(*)Vw Ж7^)]-1 [Х(Л + 1)- ф(£ + 1, Л) х (*)]}, (8.150)
где предполагается, что [rVwrT]-1 существует.
Для плотности p[x(k)^Z(k)J оказывается, что среднее пред-
ставляет собой оценку, полученную в результате фильтрации
E{x(k) |Z(&)} =x(k), а дисперсия равна дисперсии ошибки фильт-
рации var{x(£) |Z(£)} = V~(&). Обе эти величины могут быть по-
лучены в результате фильтрации. Функция плотности вероятности
p[x(k) [Z(k)J записывается в виде
р [х (£) | Z(Л)] = ехр {- -1- [х (Л) - х (k)]T V-1 (b) [х (k) - х (А)]}-
(8.151)
где К2 — нормирующая константа.
Если подставить ур-ния (8.150) и (8.151) в (8.149), то получим
р [ х (k), х (k + 1) | Z (У)] = К ехр (- 4~ {х (%) - х (£)f V-1 (k) [x(k) -
-х (£)] + [х(Л + 1)-Ф(^ + 1, £) х(6)]г[Г (£) Vw (&) Гг (£)Г’ [х(* + 1) —
Ф($ + 1, fe)x(fe)]}) p[z(fe+1). z(V)U(fe+l)]_ (8,152)
Чтобы упростить это выражение, прологарифмируем обе его
части. В результате получим
1п р [х (k), х (k + 1) IZ (N)] - 4- {[X (*) - X U)]r V~’ (A) [X (k) - X (Л)] +
363
+ [X (k + 1) - Ф (k + 1, k) x (/г)]г [Г (£) Vw (k) Гт (k)]-' [x (k + 1) -
— Ф(£-)-1, k) x(&)]} 4-(члены, которые не включают х(&). (8.153)
Следовательно, оценки, как результат сглаживания, должны
удовлетворять уравнению
c>lnp[x(fe), xU + i)|ZGV)J _ n
л_/м xU)=x(A|AT) U
' ’ х(4+1)=Ш+11А0
=V^ (k) [x (k I N) —x (A)] - Фг(й + 1, .4) X
Х[Г(^(й)Гг(*)Г' [x(fe + l)|V)-O(^+l, k)x(k\N)]. (8.154)
л
Если решить это уравнение относительно х(й| V), то получим
х (k | N) = {I + V~(k) Фт (Л + 1, k) [Г (£) Vw (k) X
хГг(й)Г'Ф(^ + 1, £)}~‘{x(A!)+VT(fc)Or(A + l, fc)[r(*)Vw(fc)X
х Гг(&)]-1 х(&-)-1 |V)}.
Используя лемму об обращении матрицы и выполняя некото-
рые алгебраические преобразования, получаем
x(ife|V) = x(fe)+A(jfe)[x(* + l|V) — Ф(^+1, Л)х(4)], (8.155)
где коэффициент усиления
А (Л) = V~(fc) Фг (k + 1, k) [Г (k) Vw (k) Гг (k) +
+Ф(6 + 1, £)У~(А)Фг(А+1, *)]“'.
Используя соотношение для априорной дисперсии
V~(£-f-l |£) = Ф(£+1, Л)У~(А)ФЧ^4-1, ^) + r(^)Vw(A)r’’(fe),
выражение для Affc) можно переписать в виде
А(А) = V~(£)®r(£ + 1, A)V~ (Л-f-1 |Л). (8.156)
л
Выражение (8.155) представляет собой уравнение для x(£|V) в
конечных разностях с обращенным временем при данных
х(&+1 |V) и x(k). Здесь значение n(k) получается в результате
предварительных вычислений согласно алгоритму фильтрации, а
л
x(k+1 |V) получается из (8.156) с использованием граничного ус-
л л
ловия для конечного момента времени x(Af|./V) =х(Л/), которое
также получается из алгоритма фильтрации. Поэтому для того,
л
чтобы получить x(k+11V), необходимо решить ур-ние (8.148).
364
л
Так как x(k) используется в ур-нии (8.155), то решение задачи
фильтрации предварительно должно быть получено и сохранено в
памяти для использования при сглаживании. Возможно также по-
лучение алгоритма в такой форме, когда запоминаются данные
наблюдений, а не оценка, полученная в процессе фильтрации
[195]. Так как решение задачи фильтрации необходимо для полу-
чения граничных условий ур-ния (8.155), то ни один из этих алго-
ритмов не обладает существенным преимуществом с точки зрения
простоты вычислений.
Уравнение в конечных разностях для ошибки сглаживания по-
~ Л
лучается непосредственно из x(k\N)=x(k)—х(£|У). Оно имеет
следующий вид:
x(k\N) =х(&) + А (&) [х (£ -]- 1 | У) — Ф(& -f-1, k)x(k)]—
— A(£)r(6)w(6) (8.157)
с начальным условием x(N\N)=x(N) при k=N, которое получает-
ся из решения задачи фильтрации.
Уравнение для дисперсии ошибки сглаживания с фиксирован-
ным интервалом может быть получено, если вычесть x(k) из обеих
частей ур-ния (8.155)
—x(k | N) = — х(6) — А(&) [х(&+ 11N) — Ф(&+ 1, k) x(#)J.
После перегруппировки членов это уравнение принимает вид
х(£|У)— А (Л)x(k + 11У) = x(k)—А(А)ф(& + 1, k)x(k). (8.158)
Если определить ковариации обеих частей ур-ния (8.158), учи-
тывая, что
соу{х(й|У), х (k + 11N)} = cov {x (k), x(&)} —0;
cov{x(£ + 1|У)} = Vx (# + 1)—V~(£-]- 1 |У);
cov{x(6)} = Vx(£) —V~(6);
Vx(fc-|-1) =Ф(#4-1, £)Ух(6)Фг(6 + 1, fc)+r(£)Vw(fc)rr (k),
то получается рекуррентное уравнение для V~
V~ (k | N) = V~(£) + A (k) [V~(fc + 11N)- V~(k + 11 ft)] A^). (8.159)
Это уравнение также решается в обратном направлении по време-
ни с граничным условием У~(У|У) = У~ (У).
Вычисление дисперсии ошибки сглаживания с фиксированным
интервалом также требует знания дисперсии ошибки фильтрации.
Так как ур-ние (8.159) требуется решить в обратном направлении
по времени, то обычно необходимо предварительно вычислить и
запомнить дисперсииV-(fe) и V~(k\k—1). Однако можно показать
365
(см. задачу 8.14), что дисперсии ошибок фильтрации могут быть
вычислены в обратном направлении по времени с помощью урав-
нений:
V~(* | k - 1) = V~(£) + ¥Г(Л) Нг (k) [Н (Л) V~(k) нч*)-
-Vv(£)J-W)V~(*);
¥~(Л-1) = Ф(Л-1, Л)[У~(^|Л—1)—
—Г(4 — l)Vw(fc — 1)Гг(&— 1)]ФГ(6 — 1, k).
Эти два уравнения должны использоваться с большой осто-
рожностью, так как они являются матричными уравнениями и
обычно нестабильны. Сводка уравнений дискретного алгоритма
сглаживания с фиксированным интервалом приведена в табл. 8.6.
Таблица 86
Дискретный алгоритм сглаживания с фиксированным интервалом ’>
Алгоритм сглаживания с фиксированным интервалом
х(Ш) = х(/г)+А(Щх(/г-Ь1 ;Л0—Ф(/г + 1, k)x(k)]. (8.155)
A (k) = V~(k) Фг (k + 1, k)V~l (k 4- 1 I k). (8.156)
Вычисление дисперсии ошибки сглаживания
V~ (k | N) = V~ (fe) +A(fe)[V~(fc +1 | A)— V~(fe +1 |fe)]Ar(fe). (8.159)
Начальные условия
- x(jV|A7) = x(A); V~ (N ( Л7) = V~ (N).
’> Предварительно должны быть выполнены вычисления согласно алгоритмам
фильтрации из табл. 7.2.
(8.160)
Вывод алгоритма сглаживания с фиксированной точкой начнем
с алгоритма сглаживания с фиксированным интервалом, описыва-
емого ур-нием (8.155). Но теперь конечный момент времени N яв-
ляется переменным, поэтому алгоритм следует записать в виде
х(£|/) = х(£) + А(£)[х(£ + 1 (у)—Ф(£-ф1, Л)х(£)], />£•
Если заменить / на j — 1 и затем вычесть полученный резуль-
тат из приведенного выше выражения, то получим
х(Лг|Л—х(^|/ —1) = А(Л)[х(Л + 1|/)-х(Л + 1|/-1)]. (8.161)
Можно получить алгоритм сглаживания с фиксированной точкой,
полагая k—k» (где k — константа),
X (^ I /)—х (k* I i-1) = А (%,) [ X (k* + 11 /)-х (.^ +1 I j-1)]. (8.162)
366
Если теперь в ур-нии (8.161) считать k = k)t + l и подставить по-
лученный результат в (8.162), то получим
х(^|/)—х(^|/—1) = А(^)А(.^ + 1)[х(^+2|;)—хЛ(^+2|/~ 1)].
(8.168)
Продолжая увеличивать k в ур-нии (8.161) и подставляя ре-
зультаты в уравнение сглаживания до тех пор, пока k не станет
разным /, получим в итоге
х (** I /)-х(£* | /— 1) = П А (/) [х (/)— х (/1 /— 1)].
г—Л
Этот результат может бьгь записан в виде
X (&* I /) = X (^ I 1) + В (^ I /) [X (/)—х(/| / — 1)], (8.164)
где
В(М/) = П А(/) = В(^;/-1)А(/-1) (8.165)
i=k,
и В (£*!£*) = I Уравнения (8.164) и (8.165) представляют собой
рекуррентный алгоритм сглаживания с фиксированной точкой.
Так как х(/)=х(/|/—1)+К(/) [z(/)—H(/)x(/|/—l)], то ур-ние
(8.164) можно записать в виде
х (Лг# | /) == х (Л-# | / — 1) 4- В (Л# J /) К (/) [z (j)—Н (/) х (/1 / — 1)]. (8.166)
Используя простые преобразования матриц получим
X (^ I/) =х(^ I j-1) + W(^ I /) Hr(j) V71 (/) [2(7)—Н (/) х(/1 /-1)],
(8.167)
где W(£*|/) удовлетворяет рекуррентному соотношению
w (^ I /) = W (^ I /-1) фГ (/, / — 1) [I — Нг(/) Vv- (/) Н (/) V- (/)]. (8.168)
Преимуществом такой формы записи является то, что теперь
не надо вычислять матрицу, обратнуюVa (£|£—1), хотя и необхо-
димо знать Vv-1(j)- Следует учитывать, что в большинстве случа-
ев размерность х больше, чем v, и это приводит к значительному
сокращению вычислительных операций.
л л
Начальное условие х(£*|£*) =х(£*) для ур-ния (8.164) получа-
ется из решения задачи фильтрации. Уравнение ошибки сглажива-
ния с фиксированной точкой получается непосредственно из
367
x(^.|j) =x(&.)—x(fe.|j). Если подставить ур-ние (8.164) в это вы-
ражение, то получаем
| /) = х| j— 1) + В(£# |/)[х(/)—х(/1/— 1)].
Для вычисления дисперсии ошибки применяется тот же ход
рассуждений, что и для случая сглаживания с фиксированным ин-
тервалом, что приводит к выражению
v~(** | /) = VT(^ I /— 1)—В I j) К (/) H (/) VT(j|j-1) Br (k* I j).
(8.169)
Сводка уравнений алгоритма сглаживания с фиксированной
точкой для дискретных процессов приведена в табл. 8.7.
Таблица 8.7
Дискретный алгоритм сглаживания с фиксированной задержкой О
Алгоритм сглаживания
х I k) = | k- 1) +B | k) [x (k) — х(Л| Л — 1)]. (8.164)
Вычисление коэффициентов усиления при сглаживании
= —1)А(& —1); (8.165)
A (k) = V~(k) Фг (k + 1, k) V—1 (Л 4-1 |£)- (8.156)
Вычисление дисперсии ошибки сглаживания
V- (^ I k) = V- (^ I k - 1) -В (*J k)X
X К (k) Н (k) V~ (k I k — 1) Br (kt I k). (8.169)
Начальные условия
x (k* I kJ = X (&*); V~ (kt I kJ = V~ (£*); В (^ I £*)=!.
Альтернативный вариант алгоритма сглаживания
X(^I/) = X(^|/-1) +W(^|/)Hr(/)V71 (/') [z (/) — Н (/) х (/’| / — 1)]. (8.167)
Вычисление коэффициента усиления при альтернативном варианте алгоритма
сглаживания
W(M /) = W(^|J- 1) Фг(/, j- 1) [I - Hr(/)V71 (/)H(/)V~ (/)]. (8.168)
-----------------------------------------------------------------*----.
’) Для получения решения задачи сглаживания с фиксированной точкой дол-
жны быть также реализованы алгоритмы фильтрации из табл. 7.2а.
Алгоритм сглаживания с фиксированной задержкой для дис-
кретных процессов получается в виде комбинации алгоритмов с
фиксированным интервалом и фиксированной точкой. Начнем с ре-
шения ур-ния (8.155) для сглаживания с фиксированным интерва-
368
лом х^+1И)=Ф^+1, k)x(k) + (k) [x(A|V)—xp)]. Добавим
и вычтем Фр+l, k)x(k\N) в правой части этого уравнения. Тогда
х(6+1|Л/)=ф(А4-1, k)x(k\N)— [Ф(^ + 1, &)—А~1(6)][х(6|Л0—
—x(A)J. (8.170)
Заменяя N на &4-J, где I — время фиксированной задержки, полу-
чаем
x(6-f- 1 | k J) = Ф(А + 1, k)x(k\k + J)—
—[Ф(&4-1, /г)—К~' (Хг)][х(Хг| jfe +J)—х(£)]. (8.171)
Перепишем алгоритм сглаживания с фиксированной точкой, оп-
ределяемый ур-нием (8.166) при kt = k+l н j—k+i+J. В резуль-
тате получаем
х ('- + 1 |^-f-l+J) = x(fe-f-l|fe+J) +
+ В(* + 11 k + 1 + J) К(Л+ 1+ J)[z(A + l+J) +
_рН(^ +1+У)х(А +1+У | Аг + У)]. (8.172)
Подставляя теперь ур-ние (8.171) и (8.172) для того, чтобы за-
л
менять x(k + 11& + 7), получаем
x(k +1 |А 4-1 + J) = ф (k 4- 1, k) х (k | k J) —
-[Ф(Л4-1, fe)-A~' (fe)][x(A|A4-J)-x(^)]4-
4-В (Л 4-11 -f-1 4- 7) К (4 4-1 4-7) [z (4 4- 1 4-7) —
—H (& 4-1 4-7)x(& 4-1 4-71 £-f-7)J. (8.173)
Можно упростить выражение (8.173), учитывая, что
Ф(Л4-1, £)—А-1 (А) = Ф(А 4-1, k)—[r(k)Vv/(k)rT(k) +
4-Ф(&4-1, 6)У~(£)Фг(б4-1, 6)]Ф-г(*4-1, *)V~'(fc) =
= - Г (6) Vw (k) Гт (k) ф-г (k 4-1, k) V-1 (k).
Если подставить это выражение в ур-ние (8.173), то получим
х(^4-11 k-\-1 4- J) = Ф(А-}-1, А)х(&| k 4-7)4-
4- Г (k) Vw (А) П (*) Ф-^ 4-1, Л) V-1 (k) [х №4-7)-
— х(£)]4-В(&4-1 A4-14-7)K(^4-14-7)[z(A4-14-7)—
—Н(А?4-1 4-7)х(^4-1 4-7 | А 4-7)]. (8.174)
369
Для завершения вывода алгоритма необходимо получить ре-
куррентное соотношение для В (&+1/&+1 + /). Его легко вывести
из ур-ния (8.165):
В (k + 11 k + 1 + J) = A-' (k) В (k | k + J) A (k + J). (8.175>
Л
Начальные условия для to(k/k + J) и x(k/k + J) получаются из
алгоритма сглаживания с фиксированной точкой
Алгоритм вычисления ошибки сглаживания получается непо-
средственно из определения ошибки для сглаживания с фиксиро-
ванной точкой и алгоритма сглаживания, описываемого уо-нчем
(8 174), как
|£+1+J) = ф(£+1, k)x(k\k+J) +
+ Г (k) Vw (£) Гг (k) Ф~т (k + 1, k) V-1 (k) [x(k | k + J) 4-
+ x(^)]-B(jfe + l |^ + l+J)K(ife + l+J) [H(^ +
+ 1 +J)x(£+1 + J | jfe -p J) +V(£ +1 +/)]. (8.176)
Можно показать, что дисперсия ошибки сглаживания опреде-
ляется уравнением
V~(k I k + J) = V(k I k— 1)—B(& + J)K(fc +J)H(*!4-J)V~(k I & —
-1)B4^|k + J)-A-' (fc—-1)[V~(&—1)—V~(&—
— 11 fc — l +j)jA-r(&— 1). (8.177)
Начальное условиеV~ (&o|k0 + J) получается из алгоритма сглажи-
вания с фиксированной точкой. Все уравнения алгоритма сглажи-
вания с фиксированной задержкой приведены в табл. 8 8.
Таблица 88
Дискретный алгоритм сглаживания с фиксированной задержкой ’>
Алгоритм сглаживания с фиксированной задержкой
л Л
х (k + 1 | k +1 + J) = Ф (k +1, k) x (k \k +J) +
+ Г (k) Vw (k) Гт (k) Ф~т (k + 1, k) V~ (k) [x (k | k + J) — x (A)] +
+ B(£ +1 |£ +1 +7) К (6 +1 +J)[z(A + l +/)-
— H(£ +1 +J)x(k +1 +J|£ +7)]. (8 174>
В (k + 1 \k +1 +Z) = A~1 (£)B (k | k +J)A(k +J). (8 175)-
Вычисление дисперсии ошибки сглаживания
V~ (Л | k -pj)=V~ (£| k — 1)— В (Л | k -f-J) K(£ +J)H(& —
— 1) BT (& I & +J) — A~‘ (k — 1)[V~ (k — 1)V~ (k — 1 Ik— 1 + J)] A~T (k — 1).
(8 177y
370
Продолжение
Начальные условия
Л
х I + 7), V~ (£0 | ka + J), В (£0 | kQ +•/)—получаются из алгоритмов
х сглаживания с фиксированной
точкой
*> Совместно с алгоритмом сглаживания с фиксированной задержкой долж-
ны выполняться алгоритмы фильтрации из табл 7 2, а для получения начальных
условий должны быть использованы алгоритмы сглаживания с фиксированной
точкой из табл 8 7
8.4. Анализ ошибок и априорные данные
В течение последних лет методы нестационарной (во
времени) фильтрации и сглаживания широко использовались в
различных задачах. Задачи фильтрации и сглаживания подразу-
мевают оценивание сигнала по наблюдениям, состоящим из ад-
дитивной смеси сигнала и шума. Различие этих двух задач со-
стоит в моментах времени оценки сигнала и в интервалах време-
ни наблюдения. В задачах фильтрации оценку получают в конце
интервала наблюдения, при сглаживании сигнал оценивается в
некоторые моменты внутри интервала наблюдения. В гл. 7 и
§ 8.2, 8 3 эти проблемы основательно обсуждены.
Две трудности препятствуют практическому использованию
уравнений фильтрации и сглаживания- это выбор математической
модели вектора состояний оцениваемого сигнала и выбор соот-
ветствующих ковариационных матриц сигнала и наблюдения, ис-
пользуемых при решении этих задач. Желательно, чтобы модель
сигнала описывала его достаточно полно и в то же время была
проста настолько, чтобы алгоритмы фильтрации поддавались чис-
ленному решению Матрицы ковариаций для сигнала и шума
измерений также желательно иметь такие, чтобы они соответст-
вовали реальным процессам К сожалению, полное статистиче-
ское описание подобных процессов, как правило, невозможно.
Основным показателем расхождения модели и сигнала и мат-
риц ковариаций является анализ чувствительности ковариацион-
ной матрицы ошибок оценивания. Анализ чувствительности в за-
дачах фильтрации при больших ошибках был рассмотрен для
случая дискретных наблюдений в [60], [87], [173], [174], а для
непрерывного времени в [175] Детальный анализ чувствитель-
ности в задачах сглаживания дан в [82], [84] В этом разделе
построим алгоритмы, необходимые для анализа чувствительности
в задачах сглаживания и фильтрации. Эти алгоритмы будут по-
лучены для задач сглаживания в фиксированной точке и сглажи-
вания на временном фиксированном интервале. Отсюда как част-
ные случаи будут получены алгоритмы чувствительности задач
фильтрации.
371
Анализ ошибок и чувствительности уравнений
фильтрации и сглаживания на фиксированном
интервале при непрерывном времени Рассмотрим
несколько примеров, иллюстрирующих применение разработан-
ных ранее алгоритмов вычисления ковариационных матриц оши-
бок оценивания и дифференциальных матричных функций чувст-
вительности в малом и большом.
Предположим, что процесс описывается моделью
x = F(0x(0+G(0w(0 (8.178)
и предположим, что измерения (наблюдения) могут быть пред-
ставлены в линейной форме
z(0 = H(0x(04-v(0. (8.179)
Будем считать также, что шумы нормальные белые с нулевыми
средними и матрицами интенсивностей 4rw(0 и Чгт(/) соответст-
венно. Как и в гл. 6, черта сверху указывает, что эти величины
предполагаемые и могут не быть равными их действительным
значениям. Оптимальный фильтр, минимизирующий среднеквадра-
цическую ошибку
J(t\t) = E{\\x(t)-х«}, (8.180)
может быть описан уравнениями, содержа щи млея в табл 7 4.
л _ д _ _ л
х - F (0 X (0 + Ж (t) [Z (0—Н (0 X (01; (8.181)
Я- (0 = V- (0 Нг (0 Т?1 (0; (8.182)
=f (0 v~(0+v~(0 Р (0 -VT(0 X
X Нг (0 Y71 (0 Н (0 V~(0 + G (0 Tw (0 GT (0, (8.182а)
л
где х(0—оптимальная оценка вектора состояний в момент t
при предполагаемых параметрах F, G, Н, Ту.
Дифференциальное уравнение для оценки сглаживания на фик-
сированном интервале, полученное минимизацией выражения
J(t\T) = Е{||х(0—^|Т)|12}, (8.183)
дано в табл. 8.3. Оценка вектора состояний удовлетворяет урав-
нению
л _ л _ _
х (t |Т) = F (07 (/1Т) + G (0 Т» (0 х
_ _ л л
X Gr (0V~ (0 [X (i IТ) - X (01. (8.184}
Ковариационная матрица ошибок также удовлетворяет неко-
торому дифференциальному уравнению, но только в том случае,
372
когда модель процесса и априорные данные достоверны. Это диф-
ференциальное уравнение имеет вид
а I Г) = [F (0 + G (О (0 Gr(0 V~ (01 v~ (t\ T) +
+V~(/1 T)[F(0+G(0Vw (0Gr(0 V~' (0]r-G(0^w (0Gr(O- (8.185);
Начальные условия для (8.185) вытекают из решения задачи
фильтрации. Как уже известно, ур-ния (8.184) и (8 185) решают-
ся в обратном времени для всех /е[0, Г] и решением является
оценка сглаживания, а также соответствующая ковариационная
матрица ошибок Важно отметить, что для того чтобы найти оцен-
ку сглаживания, нет необходимости вычислять ковариационную-
матрицу ошибок.
Указанные алгоритмы оптимальной фильтрации и сглаживания
обеспечивают минимальный риск только в том случае, если мо-
дель совпадает с реальным процессом. Если же этого не проис-
ходит, то матрица ковариаций ошибок оценивания уже не являет-
ся истинной ковариационной матрицей ошибок Таким образом,
действительная ковариационная матрица ошибок может выявлять
ошибки, возникающие в результате использования некорректной
модели. Поэтому эта матрица играет первостепенную роль в лю-
бом анализе ошибок и исследовании чувствительности алгоритмов
фильтрации и сглаживания Как сейчас будет показано, для дей-
ствительной матрицы ковариаций можно получить специальное
дифференциальное уравнение
Сначала предположим, что реальный физический процесс точ-
но описывается уравнением
х = F(Ox(0+G(i)w(O, (8.187)
а вектор измерений равен
z(O = H(0x(O+v(O (8.188)-
и величины Чг(0 и 4*4(0 являются точными Теперь найдем урав-
нения для действительной ошибки фильтрации
~ 2)
x(i) = x(i)—х(() (8.189)
и ошибки сглаживания
~ Л
= (8.190)
Используя введенные соотношения, можно получить дифферен-
циальные уравнения, которым должны удовлетворять ошибки оце-
нивания. В случае фильтрации имеем
x(i) = (AF—Ж AH)x(Z)-f-(F—Ж Н)х (i) + Gw (Z)—^’v(i), (8.191)
а для сглаживания
i(i|T) = AFx(O + iF+G^wGrVT(i)]x(i|n-
—GVwGrVi;1(0x(0 + Gw(i), (8.192)
373
где
AF = F—F; АН = Н—Н. (8.193)
В ур-ниях (8 191) и (8.192) для упрощения записи у некоторых
функций не указан аргумент (время) Образовывая новый вектор
состояний, можно векторные дифференциальные уравнения для
действительной ошибки фильтрации сглаживания и ошибки моде-
ли свести в одно дифференциальное уравнение
но определить как
“x(d т)~
Х(0
* (0 _
а новый входной вектор
W(o = rw(^ .
Lv(O J
Тогда новое уравнение для
как
1^1=F(0X(0+G(0W(0;
Этот вектор мож-
х(о =
(8.194)
(8.195)
вектора состояний
можно
записать
(8.196)
F(0 =
F + G¥w GrV~ (0
0
О
- GTW GTV~l(t)
F — >Н
О
AF
AF—Ж АН
F
(8.197)
G
G(0 = G
G
Теперь,
ного оператора, можно найти уравнение для ковариационной мат-
рицы процесса Х(0
Дифференциальное уравнение для Х(0 имеет следующее ре-
шение.
О’
—я-
0_
внося операцию
(8.198)
усреднения под знак дифференциаль-
т
X(0 = S(0 Т’)Х(Т)—jE(0 т) G (т) W (т) d т,
t
(8.199)
где 3(0 т)—переходная матрица состояний (8.199). Используя
о Действительно, мы имеем выражение для среднего квадрата Если
ДЕ = ДН=0 или р,х(0)=0, то оценки несмещенные, а ковариация есть
просто среднеквадратическая ошибка В нашем случае результирующее выра-
жение описывает поведение любой среднеквадратической величины или кова-
риации в зависимости от используемого начального условия (Прим авт)
374
(8.196) и (8.199), а также свойство дельта-функции, имеем
4 £ {X (0 Хг (()} = F (0 Е {X (0 хг (0} +
at
+Е {X (0 Хг (i)} Fr (i)—G (i) S (0 GT (t) +
+ E(i, T) E {X(T)Wr (t)}GT (i) + G(i) E {W (i)Xr (T)}Sr (t T),
(8.200)
(8.201}
Для того чтобы двигаться дальше, следует вычислить взаим-
ные ковариационные члены в (8 200). В следующем ниже приме-
ре, который читатель, интересующийся только конечным резуль-
татом, может пропустить, показано, как вычисляются взаимные
ковариации.
Пример 8.2. Взаимная ковариационная матрица S(/, 7’)£[X(7’)WT(/)] в
(8 200) может быть выражена в такой форме, что для ее нахождения можно
использовать только одно дифференциальное уравнение Такая форма позво-
ляет найти выражение для S(Z, Т) и упрощает вычисление ковариационной
матрицы действительных ошибок оценивания Матрица £{Х (7) WT (/)} может
быть разбита на подматрицы, поскольку х (Т/Т) =х(Т)
£{X(T)Wr (t)} = a 3(t, Т) может бь ’E{7(T)wr(0} £{7(Т) wr (0) _£ {х (Т) wr (/)} 1ть представлена Г) Е12(Л Т) £{7(T)vr (/)}' E{^(T)vT(t)} . £{х(7) vr (/)}_ (1)
следующим Sis(t Т)- образом
(t,
S(Z, Т) = 0 — 22 (£ F) Е2з(/, Т) » (2)
0 0 —зз (^> F)_
1де 3„— подматрица размером NxN
Подматрицы ур ния (1) определяются из векторного дифференциального
уравнения
—^- = D(0Y(0 + C(0U(0, (3>
где
Y(n = [xW]-mn = rF~^H 4F~«Afll- (4)
[х (о J ’ L 0 f J ’
и (t) = [w Wl G (t) = [G — X] . (5>
Lv (0 Lg OJ
Решение ур-ния (3) может быть записано в виде
Т
У(Т)=в(Т, 0) Y (0) + j е (Г, т)С(т) U(T)dT, (6)
о
d&(t, 0) Гх(0П
где ---' - D(/)0(f,O), 0(0,0)=! и Y(°)=[x 0 ] •
Выражение для £{Y(T)UT (/)} можно найти, усредняя произведение в правой
375
части ур-ння (6) и UT(/) и учитывая то, что при начальном условии Y(0) сиг-
нал и шум наблюдения независимы. Тогда имеем
£{Vi(T) Ur (/)} = Е
в(Т, т) С (т) И (т) Ur (/) dx
(7)
Можно упростить это выражение, если, поменяв местами операции интегриро-
вания и усреднения, выполнить интегрирование с учетом соотношения
. т , r4’w(06D(<-х) о т
Е {U (т) Ur (/)} = 40 (/) бп (t — т) =
1 и ' D [ 0 4v(t)6D(t — t)J
и свойств дельта-функции Результирующее уравнение можно представить
£ {Y?T) U (t)} = в (Т, /)С(/)Чги(О. (8)
Поскольку Y(Z) есть компонента вектора Х(£), то, следовательно, соотношения
6и(7, 0 = 322(7, 0,012(7, /)=В23(7, 0; 022(7, 0=3зз(7, 0; 021(7, 0 =
= В32(7, t) верны
Далее
£{7(Т) Wr (0} = [S22 (Т, о+ з23 (7, 0]G4»W(0; £{7(T)vr(o} = -
-S22(T, /)Згч»у(О;
£{x(7)wr (0} = З33 (7, 0G«»w(0; £{x(T)vr(0} = 0.
Если эти выражения подставить в правую часть (1) и результирующую матои-
цу умножить слева на правую часть ур-ния (2), то получим
S(t, T)£{X(T)Wr(0} = M, (9)
где
MU = {[SU(O 7) + S12(0 7)][322(Т, 0+S2S(7, 0] + Sia 7) X
X S33 (7, 0} G 4*w (/); (10)
m12 = -[2u(0 7) + s12(0 7)]S22(t, 0^4»v(0;
M21 = [S22(O 7) S22 (T, 0+322(Л 7)E23(7, t)+B23(C 7)B33(T, 1)]G4>„ (0;
A422 = E22(/, T)B22(T, t)M4v(t);
М31 = Езз(£ 7)E33(7, 0G4»w(0;
M32 “ 0 »
здесь M,,— подматрнцаМ Если матрицу перехода обозначить через Ф(+ to), то,
как известно, Ф_1(/о, Л)=Ф(О, М- Это свойство может быть использовано для
редукции М21, М22 и М31 к выражениям следующего вида-
М21 = (1+Е22(О 7)323(Т, О + Е23(О 7) Е33 (Т, 01G4»w(0; (11)
М22 = - ж vv (0; М31 = G 4»w (0.
Если уравнение 8(0 7)3(7, 0=1 записано в составной форме, то, как легко
видеть, уравнение
В22(Л 7) Е23 (7, 0 + В23(Л 7) Е33 (Т, f) = 0. (12)
Следовательно, M2i = G,Irw(l)
Два выражения из (10) еще содержат компоненты 3. Эти компоненты равны:
А = [Еи(С 7) + Е12П, 7)] 322(Т, /); (13)
•Д=[3П(/, 7)+Е12(/, 7)]В23(Т, t) +E13(t, 7)388(7, t). (14)
376
Их можно вычислить, если определить матрицу S. Последнюю можно найти,
однако, только в случае, когда найдены дифференциальные уравнения для Л
и й. Сначала возьмем производную от ур-иия (14). Это дает
<ЭЛ ( d )
T) + Si2(Z- Л! S22(T, 0 + [Eu(t П + Е22(/, Т)]Х
at { at )
dZ22(T, t)
X----aa — - . (15)
Как было показано выше, 3(/, Т) удовлетворяет дифференциальному уравнению
d.S =F(/)8(/, Т), S(T, Т) = 1
dt
Следовательно,
-^-[Eu(t, T) + a12(t, T)]=(F + G¥wGrV~,)[311(f, Т) +
at
+ B22tf, T)]-G4»wGrV^S22(t, Т). (16)
„ dE (Т, t)
Но В (г, t) должно удовлетворять дифференциальному уравнению------ =
dt
= — В (Г, t) F(t), откуда видно, что
dS22(T, t) ___
-----—S22(T, O(F-^H). (17)
dt
Следовательно, если (16) и (17) подставить в (15), то получим
A = [F у G Tw Gr V—1 (t)J Л — G V~ — Л (F — X H). (18)
Аналогично можно иайти дифференциальное уравнение и для й, если сначала
взять производную от ур-ния (15) и проделать все указанные процедуры. Тогда
Q = [F + G Tw Gr V-1 (О] Q — Q F + Д F — Л (Д F — X Д Н). (19)
Начальные условия для этих уравнений имеют вид В(Т, Т) = 1
Тогда Л(Т)=1, Q(T)=0. Теперь все компоненты уравнения определены через
известные величины или величины, которые могут быть найдены решением
ур ний (15) и (19)
Расширяя матрицу ковариаций для Х((), получим
var{X(()}= Vd(0
ve(0
Vdr(0 V[(i) ~
vT(0 vj(()
vc(0 vx(0
(8.202).
где Vc(() =cov{x((), x(()}; Vd(() =cov{x((), x(i) |T)} и Ve(() =
= cov{x((), x((|7’)}. В алгоритмах фильтрации действительная
ковариационная матрица ошибок оценивания определяется реше-
нием дифференциального матричного уравнения
V~(t) =(F-^H)Vr(i)+V~(()(F - ^Н)г +
+(Д F—Ж Д H),v; (() + Vc (() (Д F—Ж Д Н)г +
+ G/Fw (0 Gr + Ж (0~жт, (8.203>
377
где Vc удовлетворяет условию
ve (0 = F V до+V. (0 (F - Hf +
+ Vx (t) (A F—УС А Н)г + G (0 Gr, (8.204)
a Vs(0 условию
Vx (0 = F vx (0 +Vx(о Fr+G Tw (0 Gr. (8.205)
Эти соотношения легко получить методами, развитыми в § 3.5.
Начальными условиями для предыдущих уравнений являются
VT(0) = Vc(0) = Vx(0). (8.206)
Если матрицы F и Н одинаковы для модели и действительного
физического процесса, то ур-ние (8.203) приобретает такой вид,
что для его решения не нужны ур-ния (8.204) и (8.205). Наконец,
если 4/’w=4/’w и 4rv=4rv, то (8.203) переходит в (8.183), являю-
щееся строгим уравнением для ковариационной матрицы ошибок,
если модель и априорные данные верны.
Дополнительные дифференциальные уравнения:
V~(* | Т) = [F+ G Gr V-1 (i)] V~ (t | T) +
4- v~ (/1 T) [F+G G^V-1 (0f-
— [GTW Gr V~ (/)] V, (t | 71)—vj (t | T) [G¥w GT V~' (0)r+
+ (A+Q)GTwGr+Ve(i|T)AFr + AFVe(i|T)-
—GTwGr + GTwGr(A+Q)r; (8.207)
v7(< IT) = [F-jr H] Vd (t IT) + [A F-JfA H] Ve (i |T)+
+Vd (i| T) [F+Gt GrV~’ (Of -
—V~(i|T)GTw GrV~ (Of+Ver (i)AFr + GTwGr(A+Qf ф
+ Z7fTv ^rAr;” [[(8.208)
<(i | T) = F Ne (t | T) + Ve (i | T)*[F+G Tw Gr V~' (t)]T-
—Vc (0 [G Gr V~' (Of +V~(0 A Fr + G Gr (Л + Й)г; (8.209)
A=[F+GVW GrV~ (0) A —A(F—3fH)—G GrV~ (0; (8.210)
Й = [F + GVwGrV~ (0)2 — GF+AF—A(AF—ЙЛН) (8.211)
с начальными условиями:
Vr(r|T) = V~(0; Vd(0-V~(T);
Ve(T|T) = Vc(T); A(T) = I; G(T) = 0 (8.212)
должны быть решены в том случае, если в задаче сглаживания
необходимо найти ковариационную матрицу действительных оши-
378
бак ^сглаживания. Вычисление по этим соотношениям следует не-
посредственно и предоставляется читателю в качестве упражне-
ния.
Два из предыдущих дифференциальных уравнений могут быть
исключены. Это можно сделать путем следующего определения
матриц:
Ve(t I Л = Vx (0 (0 + ve (0 ЛГ (0; (8.213)
Vd (t\T) = V~(0 КГ (0 +vr (0 йг (Г). (8.214)
Поскольку правые части этих тождеств удовлетворяют дифферен-
циальным уравнениям и начальным условиям левой части, то
указанные тождества справедливы. Использование этих тождеств
в ур-нии (8.207) дает
V—(7IТ) = [F + GTW GTV~ (0] V~ (0 T) +
+v~ (t IT) [F + G Tw GT V-' (0]r-
-G Tw GT V-1 (0 [V-(0 Ar + VTC (t) Йг] -
_ [Л V~(0 + ®vc (0] [G Gr V-1 (0]r + A F [Vx (t) Й7 + Vc (0 A7] +
+ [Й Vx (0 + AV[(0] AF^+(A + S)GTWG’’ +
+ GTwGr(A + 2)r— GTwGr, (8-215)
что является эквивалентным выражением для полученных ранее
соотношений (8.207) — (8.209). Для нахождения ковариационной
матрицы сглаживания ур-ния (8 210), (8.211) и (8.215) должны
решаться в обратном времени для всех t^[T, 0]. Если модель
действительно отражает реальный физический процесс, то ур-ние
(8.215) переходит в (8.186).
Если ковариационная матрица действительной ошибки найде-
на, то матричные функции чувствительности в большом опреде-
ляются соотношениями:
гм(0 =
V- (0 Т) - V~ (t I T)
r>.s(0= X
Л Dt
(8.216)
v— W~VT(/)
Л0
для случаев фильтрации и сглаживания соответственно; ЛЬ, — раз-
ность между значением параметра модели, используемой для
оценивания, и параметра действительного процесса. Величины
V—(0 и вычисляются при действительном значении пара-
метра Ьг, а V—(0 nV—(070—при предполагаемом его значе-
нии Ьг.
Действительный риск как для фильтрации, так и для сглажи-
Л л
ванпя может быть записан в виде J = £{(х—х)г (х—х)} —
л л л
=’tr(£'{(x—х)(х—х)т}), где х — оценка сигнала в случае фильтра-
ции или сглаживания. Таким образом, по матрице ковариаций
379
•функции чувствительности в большом мы можем определить чув-
ствительность в большом функции риска из соотношений:
4# = Ь-[ГЛ,(0]; 4г- = tr[n.s(0]. (8.127)
Д&г М>1
Если различия между моделью и действительным процессом
невелики, то полезным оказывается анализ чувствительности
дифференциального типа или чувствительности в малом. Матрица
чувствительности в малом для алгоритмов фильтрации опреде-
ляется как
av~ (О
дЬг
ь=ь
(8.218)
где b — истинный параметр, а b — предполагаемое его значение.
Прямое вычисление полученного выше выражения в задачах, свя-
занных с чувствительностью в большом, может оказаться затруд-
нительным, поскольку аналитические выражения для ковариа-
ционных матриц обычно не существуют. Однако можно найти
матричное дифференциальное уравнение для матричной функции
чувствительности, пригодное для изменений первого порядка.
Если взять частную производную от обеих частей ур-ния
(8.203), поменять порядок дифференцирования и множество пара-
метров действительного процесса заменить на множество пара-
метров модели фильтрации, то получим дифференциальное урав-
нение для чувствительности в малом, (которое имеет вид
= (F-3?H)YlJ(0 + Kf(0(F-^Hf+Iu(0, (8.219)
где
lu(0
а(р-л’н) I v - р(р-л’Н)
db( |ь=ь v х dbt
a(G TwGr)
db{
(8.220)
Начальным условием для этого выражения является соотноше-
ние
(0)
av~ (0)
dbt
(8.221)
Подобное начальное условие позволит нам вычислить чувстви-
тельность действительной ковариационной матрицы и разности
начальных дисперсий модели и действительного процесса. Заме-
тим, что матричная функция чувствительности в малом может
быть вычислена легче, чем чувствительность в большом. Однако
последняя более полезна.
Матричная функция чувствительности в малом позволяет най-
ти еще две величины, представляющие интерес. Можно найти мат-
рицу разности между действительной ковариационной матрицей
,380
и ковариационной матрицей 'модели
(=1
(8.222)
где ,р — число компонент вектора b, a dbt — дифференциальный
оператор. Матрицу чувствительности в малом можно использо-
вать также для нахождения чувствительности в малом функции
риска тем же методом, который использовался при анализе чув-
ствительности в большом. В результате чувствительность функции
риска равна
_ = tr[7(J(01. (8.223)
dbt 1ь=_ь
Полученное выше выражение для чувствительности функции рис-
ка имеет такой же вид, который использовался в [202].
Для задач сглаживания также можно определить матричную
функцию чувствительности
5V~ (t\T)
b=b
(8.224)
Так же, как и в случае фильтрации, можно получить для этой
функции следующие дифференциальные уравнения:
Yi.s(0 = [F+G^w G7V~' (0] Y,-.sr(0 +
+Гм(0 [F + GTW G7V~ (0]т+ li.s(0; (8-225)
I,.S(O = -GTw GrV~' (0[Гм(0ЛГ +v~(nru(0] -
-[Ar^(0 + rU0V~(0][GTwGrV~(0f +Л —w— _ +
L 00^ Ь—ь
^ИЛ)
+ dbt
_ Ar + Yt-,d (0 GTw GT + G Tw GT -tld (0-
b=b
^G^G7-)
dbt
b=b
dF
dbt
I df
_v~(OAr+AV~(o(7T
b=b
(8.226)
где
r.,d(0 = [iWw GrV~ (01 Tir<<(0-Ti.d(0F. (8-227)
Кроме того,
<8-228»
Начальными условиями являются:
Ks(n = T«.f(n Т«.ДП = 0. (8.229)
Аналогичные результаты для анализа чувствительности в малом
можно получить и для алгоритмов сглаживания на фикгаирован-
381
ном интервале. В табл. 8.9 и 8.10 приведены алгоритмы анализа
ошибок и чувствительности для задач фильтрации и сглаживания
на фиксированном интервале в непрерывном времени. Используя
Таблица 8.9
Алгоритм анализа ошибок и чувствительности
для фильтрации в непрерывном времени
Предполагаемая модель сообщения x = F(0F(0 +Gp)w(0. (8.178)
Предполагаемая модель наблюдения z(0=H(0x(0+vp). (8.179)
Алгоритм фильтрации Л Л _ Л 7= F (0 Г(0 +я- (0 [z (0 - н р)7(01 (8.180)
Вычисление коэффициента усиления X (i)... V~ р) Нг (0 У71 (t). (8.181)
Вычисление предполагаемой ковариационной матрицы ошибок V- = F (0 vr(0 +VT (t) Fr (0 - V~ (0 Hr (t) ¥7! (t) H (tfV- (t) + X X X X X + G(f)¥w(/)Gr(/). (8.182)
Предполагаемые априорные данные Vx(0); VW(Z); 4v(t); £x(0), (8.183)
Действительные априорные данные V~(0); Yw(0; ’Fv (t); px(0). (8.184)
Действительная ошибка фильтрации Л 7(0 = х(0 — «(О- (8.189)
Вычисление действительной ковариационной матрицы ошибок фильтрации V~P) = (F — ЖН) V~ (t) +V~ P)(F—5ГН)г + (A F — X A H) Vc (t) + + VC(/)(AF-^AH)T +0^(0+^^ (/)Z (8.203)
Вычисление моментов Vc(0 = FVc (i) +Vc(/)(F-5fH)r +V~ (0(AF-5TAH)r + + GVW (t)Gr. vx (t) = F Vx (i) + Vx (0 Fr +G p) aT (8.204) (8.205)
382
Продолжение
Начальные условия
Л _ _ _
7(0) = их (0); Vr(0) = Vx(0); V~ (0) = Vc (0) = Vx (0).
Вычислительные чувствительности в большом
vT(/)-vT(0
(8.216а)
(8.217а)
Вычисление чувствительности в малом [см. также (8.219), (8.221)] для вспо-
могательных результатов
5у~(/) I
-ft f = —77— -
•' д Ь( [ь=ь
(8.218)
"Таблица 8.10
Анализ ошибок и чувствительности алгоритмов сглаживания
иа фиксированном интервале в непрерывном времени
(алгоритмы фильтрации табл. 8.9 составляют общую часть алгоритмов
этой таблицы)
Алгоритм сглаживания
Л _ _Л _ ____ Л л
x(l|T)=F(/)x (t\T) +G(Z) 4»w (0 GT (t) VZ1 (/)[x(/|T)-7(/)]. (8.185)
Предполагаемая ковариационная матрица ошибок
V ~ (t I T) = [F (/) +G (0 <FW GT (t) VZ1 (01 V~(Z|T) +
+ VT(/iT)[F(0+G(0^w(OGr(OV~1(/)]r -G(t)Vv(t)GT (/). (8.186)
Действительная ошибка сглаживания
Л
х (/1 Г) = х (0 — (190)
Действительная ковариационная матрица ошибок
V ~ (t [Г) = [F - G <FW GT VZ1 (/)] V~ (/ | T) +
+ V~ (t I T) [F + G GT VZ1 (Of -
- G gt vz1 (t) [V~ (0 Ar + vcr (0 aT ] -
- [A v~ (Z) + q vc (01 [G ¥w GT VZ,1 (Of + A F [Vx (t) QT +
+ Vc(f)Ar] +[OVX(0 +Af(0]AFT ^(A + O)G<FwGr +
+ G<FW Gr(A +Gf -G>Fw Gt. (8.207)
383
П родолжение
Вычисление моментов
Л= [F+ GTW GrVZ.‘ (0J Л — A(F — 5Г Н) —GVW Gr VX1 (t). (8.210)
Q =[F + GTW GrV~ (f)J Q — OF 4-AF — A(AF — Ж AH) (8.211)
Граничные условия
Л Л _ _
7(Т|Т)=7(Т); V~ (Т | Т) = V~ (Т);
V~ (Т|7) = (Т); Л(Т)=1; О(Т)=0.
Вычисление чувствительности в большом
V~ (t I Т) — V~ (t I T)
Гм(/)=-2---------------------- (8 2166)
A/s
—~ = tr [Г( s (/)]. (8 2176)
zA h s ’
Вычисление чувствительности в малом [см также (8 225)—(8.229) для про-
межуточных результатов]
д V~ (t | Г) I
Tf,sW =------------- _• (8-224)
о bi |ь=ь
ту же методику, можно получить и дискретный аналог выведен-
ных алгоритмов. Без вывода они даны в табл. 8.11 и 8.12.
Таблица 811
Дискретные алгоритмы анализа ошибок и чувствительности
фильтрации
Предполагаемая модель сообщения
7(A) = Ф (А, А — 1)7(А — 1) -f-Г (А — 1) w (А — 1).
Предполагаемая модель наблюдения ,
z(A) = Н (A) 7(A) +?(А). \
Алгоритм фильтрации
Л Л _ _ Л.
х (А) = х (А | А — 1) — К (A) [z (А) — Н (А) х (А | А — 1)].
Алгоритм одношагового предсказания
Л _ Л
7 (А | А — 1) = Ф (А, А —1)7 (А —1).
384
Продолжение
Вычисление коэффициента усиления
K(*) = V~(*. й-1)Нг(й)Н(А)У~(А|А-1)Нг(А)4-Уу(й)Г1 •
Предполагаемая априорная матрица ковариаций ошибок
V — (й| А— 1)= Ф (Лг, k — 1)V~(A- 1)Ф(А, k — 1)4-
+ Г (k — 1) Vw (й-1) Гг(А-1).
Предполагаемая ковариационная матрица ошибки
V ~ (k) = [I — К (k) Н (k) V~ (k | k — 1)
Вычисление ошибок
~ ~ A,
x (k) = x (k) — "xfk'). x (k I k — 1) = x (k) — x (k | k — 1);
A H (k) = H (k) — H (k\, Дф(/г, k — 1) = Ф(/г, fe —1) —Ф(/г, k — 1).
Предполагаемые данные
V x(0); йх(0); Vw (Й); Vv(A>).
Действительные данные
V x(0); Hx(0); Vw (fe); Vv(fe)
Вычисление действительной ковариационной матрицы ошибок
V ~ (k) = К (k) A Н (k) Vx (k) A Hr (fe) Kr (k) +
+ [1-К(/г)Н(/г)] V~(ft| A —1)[I - К (A) H (A)]r -
— К (k) Д H (k) Vc (k | k — 1) [I — К (k) H (k)]T -
- [I - К (k) H (A)] VTC (k | k - 1) A Hr (k) Kr (k) + К (k) Vv (k) Kr (k),
Вычисление априорной действительной ковариационной матрицы ошибок
V- (А-| k- 1) = ДФ (k, fe —1) VX(A —1) ДФГ(Й, k — 1)+Ф(/г, k —
— 1)V~ (k — 1)ФГ(А, k — 1)4- ДФ(А, k — 1) Vc(k — 1)ФГ(/г, k — 1) 4-
4-Ф(А, k — 1) V^(k— 1 | A-l) ДФГ(£, A-l) 4-Г(А) Vw (k)rT(k).
Вычисление априорной взаимной ковариационной матрицы
Vc (i |/) == cov {х (i); x(i | /)};
V e(A| k — 1) = Ф(А, k — 1)VC (k — 1) ДФГ(£, k — 1) 4-
4-Ф(А, (k, k-l) 4-Г(А) Vw (k) rT(k).
13—26
385
Продолжение
Вычисление взаимной ковариационной матрицы
Ve(A) = Vc(A|A-l)[I -KWH (А)]г -VxWAH7’WKtW.
Вычисление действительной матрицы ошибок
УХ(А) = Ф(А, A-l)Vx(A-l^r(A, k-V) + T(A)VW (А)ГТ(А).
Начальные условия
х(0) = цх(0); V~ (0) == VT (0);
'V-(O) = Vx (0) = Vc (0) = var {x (0)}.
Вычисление чувствительности в большом
V~ (*) - V~ (k)
Вычисление чувствительности в малом (дифференциальное уравнение для
у,,/(А) можно найти в [84])
Таблица 812
Дискретные алгоритмы анализа ошибок и чувствительности
для сглаживания на фиксированном интервале
(алгоритмы фильтрации табл. 8 11 составляют общую часть алгоритмов
этой таблицы)
Алгоритм сглаживания
АЛ, Л _ Л
"x.(k\N) = x(k) + А(А) f£(k +1 ]A) —Ф(А +1, k)*(k\А)].
Вычисление коэффициента усиления
Х\А) = V~ (А) Фг (А + 1, A) V~ (А 4-1 | А).
Вычисление предполагаемой ковариационной матрицы ошибок
V- (А | N) = V~ (А) + A(A)[V~ (А + 11 А) —V~ (А + 1 I А)]"ХГ (А).
Вычисление ошибки
А
'х (»] /} = х(0 — 7(i I /).
Вычисление действительной ковариационной матрицы ошибок сглаживания
V~(A|jV)=V^(A)+X(A)[V~(A +1 |А)—Ф(А + 1, A) V~ (А) Фг (А 4-
х X X к
386
Продолжение.
+ 1, k) +rpyvw (k)TT(k) +Дф(А + 1, 4)Л(4)АФг(Н1.*)-
— ДФ(А4-1, k) Vx (k) AT (k) — Л (k) Vx (k) Д Фг (k + 1, A) +
_|_Дф(А+1, k) Vc(k)*T (k +1. k) QT (k) + 0 (k) Ф (k +
+ 1, *П^)ДФГ(Н1, k)+r(k)Vv(k)rT(k)lT(k) +
+ l(k)r(k)Vv (А) Гг (A)fAr (A) — [I — X(A) Ф (A +1, A)]X
X V~ (k) Фт (k + 1, k) 0T (k) A T (k) — A (k) О (k) Ф (k +
+ 1, A) V~ (A) [I—А (А) Ф (A 4-1, А)]г — у£(А)Д’Фг(А-|-1. А)АГ(А) —
-Г(4)ДФ(4 + 1. А)¥е(А)+[I—Г(А)Ф(А+1, А)]х
ху£(А)Лг(А)'А7’(А)-|- Г(А)Л(А)УС(А)[1—А(А)Ф.(А4-1, А)],
Вычисление моментов
й(А) = А(А-|-1)О(А4-1)Ф(А +2,^А 4-1)[1—К(А4-1)Н(А-|-1)]4-
+ К(А + Г)Н(А +1);
Л(А) = [1 — Х"(А 4-1) Q (А + 1) Ф (А 4-2, k + 1)] {Д Ф (А + 1, А) —
— К(А Ч-1) [Н (А +1) Ф (А +1, А) —Н (А+1) Ф (А + 1, А)]}+
+Г(А+ 1)[Л(А+1)—ДФ(А+2, А + 1)] Ф (А 4-1, А);
g(A) = ff(A +1) О (k + 1) Ф (А + 2, А +1) [I — К(А + 1)Н(А+ 1)] +
+ К (А +1) Н (А + 1) — + 1) [Л (А +1)—ДФ(А +2, А +1)].
Начальные условия
Л Л _ _
7(У|Л0=?(У); V~ (У | N) = V~ (У); У~ (У) У) = V—(У);
Q (У — 1) = К(У) н (У); Л(У —1)= ДФ(У, У — 1) —
— К(У)[Н(У)Ф(У, У—1)—Н (У)Ф(У, у — 1)];
5(У-1) = К(У)Н(У).
Чувствительность в большом
У~ (А|У)-У~ (А 1 У)
Чувствительность в малом (уравнение для ?1,з(А|У) можно найти в [84])
Поскольку получение предыдущих результатов заняло много места и вре-
мени, мы рассмотрим один простой пример, чтобы продемонстрировать разра*
ботанные идеи. Более сложные примеры можно найти в [82, 84].
13* 387
Пример 8.3. Рассмотрим простой пример, в котором предположим, что мо-
дель процесса описывается соотношениями:
Г(0=0; г (0 =/17(0 +^(0.
где предполагаемая дисперсия шума равна 'Ft)=r, а начальная диспепсия со-
стояния есть Ух(0). Эта модель может описывать движение объекта на по-
стоянной высоте, данные о которой снимаются с альтиметра и нскажеиы белым
шумом.
Уравнение для ковариационной матрицы ошибок фильтрации имеет вид
, ft2VF(/) - 7Vx(0)
У—(/) =——~—.Решение этого уравнения У5Г(/) =--------------— н, следо-
х г _ h2 Vx (0) t + г
й Vx (0)
вательно, коэффициент усиления Ж (t) =-—------— .
h2 Vx (0) < + т
Если предположить, что параметры h, г и Ух(0) являются действительными,
то ур-нне (8.203) для действительной ковариационной матрицы ошибок примет
внд
йУх(О)
. й2ул(0)/ + 7 .
2
1
— 2й2Ух(0) 2ДййУх(0) ,
v-V)=—-— _ v~(o - —=—Ус (/) +
х й2 Ух (0) t + г х ft2 Vx (0) t + г
где Ус удовлетворяет уравнению
— й2Ух (0) Wx (0) Д h
Ус (/) = —Z---Ус (0 - ~ Vx W
h2Vx (0) t + г К1 Vx (0) t + r
и t±h=h—h. Но Ух есть дисперсия состояния и Ух(0=0. Начальные условия
V- (0) = Ус(0) = Ух(0). Решение приведенных уравнений дает:
Vx (/) = Ух (0); Ус (0 = ft2Vx(o)Z+r~ I” Vx (0) д ht + Vx (0)1?;
г-(/) = [ft2- (0)/+^ <Vx (0) V*(0) + (0) r ~ 2Vx (0) 7д h Pz(0) x
X h] t + Vx (0) 7}.
Непосредственное использование (8.216) дает выражение для чувствитель-
ности в большом алгоритмов фильтрации:
7 /12 У2 (0)z
Г\(t) = [й2ух (0) t +7]2 ’ Гг (Z) = [Wx (0HJ-7]2 ’
/I2 Д /1У® (0) /2 — 2V2 (0) /171
Га (/) = [й2Ух(0)/ + 7]2
Дифференциальные уравнения матричных функций чувствительности в малом
можно получить нз (8.219) н (8.220) в виде
2й2Ух(0)
Yi (0 = —-----Z — Yz +
й2Ух(0)/ + г
где i соответствует Ух(0), г или /1, прн этом
Г /1 Ух (0) Т
/„ = 0; 1Г = —----------
Ч L й2 Vx(0) t + г .
2/1 V2 (0) г
I h := -_——.
[*Й2УЖ (0) + г]2
388
tc начальными условиями Vvx0(0) = l; уг(0) = (0); уЛ(0)=0. Эти дифферен-
циальные уравнения первого порядка легко решаются:
72 — 2ЛУ*(0)7/
Y VX.( ° ’ [Wx(0)/ + r]2 : Yr (0 = [W, (0) < + г]2 ; YA (/) = [ft2Vx (0) t +7р ’
Эти соотиошеиня можно также получить из действительной ковариационной
матрицы, используя определение чувствительности.
На рис. 8.1 и 8.2 приведены для данного примера функции чувствитель-
ности в большом и в малом. Здесь выражения для чувствительностей в боль-
Рис. 8.1. Функции чувствительно-
сти дисперсии ошибки в зависимо-
сти от изменений начальной дис-
персии ошибки и дисперсии изме-
рений:
------фильтрация;------сглаживание;
"vx(0) = 2, r=20, h=l
Рис. 8.2. Функции чувствительно-
сти при изменении константы из-
мерений: Их(0)=2, r=20, /г = 1,
АЛ = 0,5
шом и малом одинаковы для исходной и вычисленной ковариационной матриц.
Зависимость чувствительности от параметра h приведена на рис. 8.3, иллюстри-
рующем различие между чувствительностью в малом и большом.
389
В этом примере ковариационная матрица ошибок сглаживания Уд (1[Г)=0
X
при конечном условии Уд(Г|Г) = Уд(Г). Отсюда следует, что ковариационная
X X
матрица ошибок не зависит от времени и получается из (8.203) для момента
времени Т. Значения чувствительностей также постоянны и равны чувстви-
тельностям для фильтра в момент Т. Пунктирные кривые на рнс. 8.1 представ-
ляют две функции чувствительности для задачи сглаживания.
Рнс. 8.3. Сравнение чувствитель-
ности в большом и малом прн из-
менении константы измерений
«Вычисляемая» дисперсия ошибки фильтрации всегда уменьшается при
увеличении времени наблюдения. Для численного анализа выражений для дей-
ствительной дисперсии положим У~(0)=й=г=1. Тогда «вычисленная» днспер-
_ х
сня ошибки равна Уд(/) = 1/(/+'1), а следовательно, «вычисленная» диспер-
X
— 1
сия сглаживания Уд(/|Г) и, как и следовало ожидать, от t не зависит.
х Т +1
В этом случае действительная дисперсия ошибки фильтрации определится вы-
„ ... (Д/г)2Ух(0)^+г,-2Ух(0)Д^ + УЯ0) .. _
ражением Ид(г)= ---------------------------------------- . Если ДА = 0,
х У + 1)
г = Vx (0) = 1, то это выражение совпадает с выражением для минимума диспер-
сии Ошибки VA(/)mln = 1/(/ + 1). •
Интересно отметить, что действительная ошибка (дисперсия) не достигает
нуля прн больших t до тех пор, пока ДЛ=0 не станет равным нулю, что озна-
чает отсутствие ошибки в модели наблюдения. Для больших f(/3>l) прибли-
женно можно считать, что действительная дисперсия ошибки равна V~(t)&s
~(ДЛ)2Ух(0). На рнс. 8.4 приведены графики действительных дисперсий оши-
бок и «вычисленных» дисперсий для случая, когда априорная статистика задана
верно (Ух(0) =/•= 1).
Если модель наблюдения не содержит ошибок, Дй=0, то дисперсия ошибки
rt + Vк (0)
равна У~(/) = — ---—— - Если отношение г/Ух (0) =1, то имеем минимум
х (« + *)
дисперсии ошибки, соответствующий V~ (t).
X
390
Анализ ошибок и чувствительности линейных
алгоритмов сглаживания в фиксированной т о ч -
к е.
Предположим, что непрерывный процесс может быть задан
векторным дифференциальным ур-нием_(8.178), а модель наблю-
дения линейна [см. (8.179)] z(£) = Н (/)х(/)+v(f).
Рис. 8.4. Дисперсия
ошибки фильтрации при
разных ДЛ, /1=1:
1 — bh--1;__ 2 —ДЛ----0,1;
» —ДЛ-0; У~(/); 4 — \h-
х
-0,1; 5 — ДЛ-1
Оценка сглаживания в фиксированной точке удовлетворяет
дифференциальному уравнению
л Л
= А (/) [z (/)—Н (0 х (/)], (8.230)
где
A(0 = B(0H(0Y7* (0,
(8.231)
a B(f)=V-(/„ t)—матрица (обозначенная так для удобства),
которая удовлетворяет уравнению
^ = B(0[F(0-jr(0H(0f.
(8.232)
л
Начальным условием служит оценка х(/, р.) фильтрации в
момент и
B(U=v~(q.
(8.233)
Ковариационная матрица ошибки оценивания может быть по-
лучена из уравнения
dV~(L[O _ _ _
—---------= - А (0 Yv (0 Ar (/).
(8.234)
391
Эта матрица ошибок удовлетворяет ур-нию (8.234) только в
том случае, если модель и ее априорные характеристики совпа-
дают с действительным процессом и его характеристиками. На
практике обычно это условие <не выполняется. Поскольку действи-
тельная ковариационная матрица ошибок оценивания позволяет
выявить ошибки при использовании неадэкватной модели, она
играет основную роль в анализе ошибок и чувствительности ал-
горитмов сглаживания.
В непрерывном времени действительная ковариационная мат-
рица вычисляется следующим образом. Сначала постулируем мо-
дель для действительного процесса в том же виде, что и в ур-ниях
(8.178), (8.179), за исключением того, что не ставим черты сверху.
Далее находим дифференциальное уравнение для действительной
ошибки оценивания подстановкой соотношений:
л л
х(0 = х(0-Г(0; х(/#|0 = х(/#)-х(^|0 (8.235)
в (8.230), где действительные ошибки оценок фильтрации и сгла-
живания определены выражениями:
~ л _ Л
x(/)=x(0-x(0; х(/#|/) = х(/#)-х(/#|/). (8.236)
Тогда результирующее дифференциальное уравнение для
ошибки оценивания имеет вид
-АЦМ-О = —А [Д Н х (0+v (0+H X (0J. (8.237)
Для простоты обозначений зависимость матриц от временного
параметра не указана; ДН определяется как разность между Н
и Н. Следующий шаг состоит в образовании нового дифферен-
циального уравнения для вектора приращений с использованием
предыдущего уравнения, уравнения для действительной ошибки
оценивания в случае фильтрации, которую мы рассмотрели в пре-
дыдущем параграфе, и дифференциального уравнения для дей-
ствительного процесса:
lZ£L = Cy(0+Du(0, (8.238)
at
где
392
Матрицы AF и К были определены в предыдущем параграфе.
Далее выпишем решение ур-ния (8.238):
У(0 = a (t, tj у (Q + J В (t, т) D (т) и (т) d х, (8.240)
t,
где В(Л t») удовлетворяет матричному дифференциальному урав-
нению
-3(*; 4)- = СS(t f#); 3(f, 0 = 1. (8.241)
at
Затем необходимо усреднить произведение вектора y(t) на
транспонированный вектор yT(t). Тогда получим
£{y(0yr(0} = S(^ Q£{y(Uyr(U}Sr(f, Q +
+ ув& т) D (т) Е {и (т) ут (tj} Вт (t,
t.
+ [В (f, Е {у &) иг (т)} Dr (т) Ег (t, т) d т+
t.
+ j J В (t, т) D (т) Е {и (т) иг (т)} Dr (ст) Вт (t, <j)dudx. (8.242)
t.
В последнем выражении два средних (внутренних) интеграла
равны нулю, так как среднее в подынтегральных выражениях для
всех х, больших t», равно нулю. Среднее в последнем члене
(8.242) можно представить в виде
Е {и (т) иг (ст)} = J (ст) dD (т—ст);
J(CT) = [1Fw(a) ° 1. (8.243)
L 0 Yv(ct)J '
Если взять внутренний интеграл в последнем слагаемом
(8.242), то, используя свойства дельта-функции, можно получить
Е {у (0 Уг (0} = а (/. U Е {у (/*) ут О ВТ (t, Q +
t
+ J В (/, т) D (т) J (т) D?- (т) ВТ (/, Т) d х. (8.244)
t.
Члены этого уравнения содержат искомые ковариационные
матрицы. Однако численное решение этого уравнения затрудни-
тельно. Эти трудности можно обойти, если найти дифференциаль-
ное уравнение для Е{у(t)yT(/)}. Его можно получить следующим
образом. Сначала берется производная от обеих частей ур-ния
(8.244). Далее в полученное уравнение подставляется ур-ние
393
(8.241). Наконец, используя (8.240), находим
х)}- = с (0 Е {у (0 Уг (0}+£{у (О уг (0) (о+D (0 J (/) Dr (0.
(8.245)
По определению имеем
rvT(^l0 v/ЧО
E{y(t)yT(t)} = V f(t) V~(t)
v]M
Vf (0
vx(0_
1_ад vc(o
где
Vf (/) = E{x (/)xr & I /)}; Vg (0 = E{x (t) xT (t* | /)},
(8.246)
(8.247)
a Vc определено соотношением (8.204). Дифференциальное урав-
нение для действительной ковариационной матрицы ошибки сгла-
живания имеет вид
------= — А [н V/ (/) + A HVg (0] + A Аг-
at
— [HVf(/) + AHVg(/)]rAr, (8.248)
где Vf и Vg удовлетворяют уравнениям:
- dV^(0 = (F—Ж Н) V{ (0 + (A F—Ж A Н) Vg (t) —
— lV~(f) Нг + Vi (0 А Нг] Аг + Ж Tv Аг; (8.249)
- dV^t} =^Vg(/) — [V(.(0Нг+ Vx(0JAНг] Аг. (8.250)
Начальными условиями являются:
vr& I U2=.v х (U; vf &) = v~(/#);
Vg(Q = Vc(/J. (8.251)
Дифференциальные уравнения для V~(f), VC(Z) и VX(Z) даны
в предыдущем разделе совместно с результатами фильтрации.
Как только действительные ковариационные матрицы ошибок
найдены, матричные функции чувствительности в большом можно
определить из соотношения
П (/* 10 = —----' (8.252)
По определению ЛЬг есть разность между параметрами дейст-
вительного процесса и параметрами модели, используемой для
нахождения оценки сглаживания. Так же, как и в случае сглажи-
вания на фиксированном интервале, функции чувствительности
могут быть использованы для нахождения чувствительности в
большом функции риска.
394
Дифференциальная матричная функция чувствительности
(чувствительность в малом) находится из выражения
д bi
ъ=ъ
(8.253)
Символом b обозначено множество параметров действительно-
го процесса; b — соответствующее множество параметров модели
оценивания; bt—i-й элемент множества Ь. Если разности между
истинными параметрами и параметрами модели малы, то функции
чувствительности в малом могут быть использованы для нахож-
дения матрицы разностей между ковариационными матрицами
модели и процесса. Эта матрица определяется как V~(^*|^) —
_ р _
—V~(^*|£) =2тг(^*Ю^^1, гДе Р — число параметров множества Ь,
i=i _
a dbz — дифференциал i-ro параметра множества Ь.
Прямое вычисление (8.254) если не невозможно, то затрудни-
тельно, потому что почти не существует аналитических решений
для действительных матриц ковариаций. Если взять частную
производную от обеих частей ур-ния (8.248), то можно найти
дифференциальные уравнения, решением которых является иско-
мая функция чувствительности. Если после этого поменять поря-
док дифференцирования, то получим
— — A ^НТм (0 + — Ng |ь=т ] -
(— д Н I — т — ( д \ —т
А +АЬг- ь=ь)А ’ <* 8-254)
где Yi,d и Уй|ь=ь удовлетворяют уравнениям
dy .(Л ---------- г _т - / ЭН I \1 _ т
= (f-jth)Ym(0- tuf(0Hr+V7(0(-^|ь=ь)] А +
— Wv I т д? I — I dH | \1
+#hr- - A + -яг- - VJ. b; (8.255)
1 \ dbt |b=b / L dbt lb=b \ dbt |b=b /] glb=b v '
L = FlV* (01 |b=b -V~ (0Hr Ar. (8.256)
ui lb=b
В ур-нии (8 255) член уг, f появляется в результате анализа
чувствительности в малом задачи фильтрации, а ур-ние (8.219)
представляет алгоритм для его вычисления. Для указанных трех
уравнений начальными условиями являются:
Tt(t* IU = ъ.г(Q; Гм (U = YM(Q; Ng(U|b=b = v~(U- (8.257)
Пример 8.4. Рассмотрим упрощенную модель, в которой принимаемый амп-
литудно модулированный сигнал аддитивно взаимодействует с белым шумом.
Пусть полезный сигнал имеет вид л(/) =а cos at+b sin <о t, где а и b — нор-
мальные случайные величины с нулевыми средними и дисперсиями Va и Уь
соответственно Этот сигнал модулирует несущую, так что наблюдаемое коле-
бание имеет вид tf(t) =s(t) С cos Шер) + о(/). Здесь предполагается, что v(t) —
белый нормальный шум с нулевым средним и иитеисивиостью 4%. Необходимо
395
оценить сигнал в момент t по наблюдаемой реализации на интервале от нуля
до i>t„ Задачу можно решить методом сглаживания в фиксированной точке,
формулируя ее в терминах состояний. Такое переопределение задачи приводит
в конечном счете к векторному дифференциальному уравнению
-
г ° ®1 РЧ Г°1
dxt(i) L-® о] U2J Ы ’
_ <и _
где элемент Xi есть сигнал s. Вектор измерений равен z(t) =xt(t)C cosia)ct+v(t).
На рис. 8.5—8.7 представлены результаты некоторых вычислений. Здесь
дисперсии величин а и b равны единице, а дисперсия шума равна 0,25. Частоты
сигнала и несущей равны 6,28 и 62,8 1/с соответственно. В этих предположе-
Рис. 8.5. Дисперсия ошибок
оценки сигнала с момента 0,2 с
для различных значений дис-
персии шума наблюдений-
/ — действительная дисперсия; 2—
предполагаемая дисперсия
Рис. 8 7. Дисперсия ошибки
оценки сигнала для различных
значений несущей частоты-
1 — действительная дисперсия; 2 —
предполагаемая дисперсия
Рис, 8.6. Чувствительность дисперсии
ошибки оценки сигнала к 10%-ному из-
менению несущей частоты в зависимости
от времени наблюдения
ниях дисперсия ошибок иллюстрируется рис. 8.5. Здесь дисперсия ошибки пред-
сказания сигнала в момент 0,2 с [вычисленная по (8.248)] приведена как функ-
ция времени, при котором появляются новые наблюдения. На рис 8 6 представ-
лен график функции чувствительности в большом дисперсии ошибки оценки
для случая, когда истинная частота сигнала на 10% выше предполагаемой.
Влияние ошибки в выборе частоты несущей показано на рис. 8.7.
396
Алгоритмы анализа для сглаживания в фиксированной точке в непрерыв-
ном времени сведены в табл. 8ЛЗ, а для дискретного случая в табл. 8.14.
Таблица 8 13
Алгоритмы анализа ошибок и чувствительности для сглаживания
в фиксированной точке в непрерывном времени
(алгоритмы фильтрации табл 8 9 составляют общую часть алгоритмов
этой таблицы}
Алгоритмы сглаживания Л d x (t If) — _ Л .? -A(f)[z(f)-H(f)x(f)]. at (8.230)
Вычисление моментов A(/)=B(f) Hr (f)HV1 (f). (8.231)
dB(t) _ _ — _ _ Л - в (/) if (о - ус (о н (/)f. (8.232)
Вычисление предполагаемой ковариационной матрицы ошибок dV~(f,|f) dt --Mt)^v(t)hT(t). (8.234)
Действительная ошибка сглаживания — x'(f11|/) = x(f,) — x(f,|f). (8.2366)
Действительная ковариационная матрица ошибок сглаживания
----------- = - А [Н Vf (/)+ Д Н Vg (f)] +А Vv Аг -
— [Н Vf (/) +Д Н Vg (7)У А7-. (8.248)
Вычисление моментов
= [F — 5fH)Vf (f) + (AF — XAH)Vg(f) —
— [V~ (/)iF +V7(0AHrl Ar (8.249)
= F Vg (0 — [Vc (t) HT + Vx (f) Д Hr] Ar . (8.250)
at
Начальные условия
Л Л _ _
х (f. | /*) = х (f,); В (f,)= V~ (f, |«,) = V- («,);
V- (<* I = V~ (f,); Vf (f.) = VT (Q,
Ve(t*)=Vc (/,).
397
Продолжение
Чувствительность в большом vT(M0-v~(MC (8.252)
Чувствительность в малом -П(М0 = -^Т7 _ д bi ь=ь [см (8 254)—^(8 257) для получения промежуточных результатов] (8.253)
Таблица 8 14
Алгоритмы анализа ошибок и чувствительности алгоритмов сглаживания
в фиксированной точке в дискретном времени
(алгоритмы фильтрации табл 8 11 составляют общую часть алгоритмов
этой таблицы)
Алгоритм сглаживания
Л Л _ Л Л
X I k) = х (£, [ k — 1) +В (£, | k) [х (k) — х (k\k — 1)].
Вычисление коэффициента усиления
В(^|А) = В(£,|Й —1) А(А—1);
A (k) = V~ (k) Фг (k + 1, k) V~l (k + 1 | k)
Вычисление предполагаемой ковариационной матрицы сглаживания
V- (^ I k) = V~ (£, I k - 1) +В (й.| k) [V~ (k) - v~ (k | k - 1)1 В T I k)
Вычисление ошибки
_ . Л
X (£* I k) = X (£*) — X (&* I k)
Вычисление действительной ковариационной матрицы ошибок сглаживания
V-(M*) = V~ 0-1) +В (й,| k) К(й) [АН (Л) Ух(й) х
•хд Нг (k) — Н (k) V~ (k, k — 1) Нг (й) +Д Н (k) Vc (k I k — 1) Hr (k) +
-+ Vv (й) + H (k) vcr (k I k - 1) А Нг (£)] Kr (k) В (k, Ik) +
4- [V[ (k, \k - 1) A Hr (k) + vj (kt I k - 1) Hr (£)] Kr (k) Br (^ I k) -
— B"(A, | k) К (k) [A H (Й) Vc (k, | k - 1) +H (k) Vd (k, I k - 1)],
Вычисление моментов
4d(k*\k — 1) =>cov{x(fc| k — 1) x(kt | k — 1)};
Vrf (k* I k — 1) = [А Ф (k, k — 1) — Ф (k, k — 1) К (k — 1) A H (k —
398
Продолжение
— 1)1 {Vc (kJ k —2) — [Vx (k — 1) А Нг (k — 1) +
4-vc(А — 1 \k — 2)Hr(k — 1)1 Кг (6 — 1) Br(k,|k-1)} +
4-Ф(£, k-1) [I -K(k-l)H(k-l)]{Vd(kJk-2)-
-[Vf(k-l|k-2)AHr(k-l) +
+ V~ _ 1 \ k — 2)НГ (k-l)[Kr(k —l)Br(k,.|k—2)} +
+ Ф (k, k — 1) К (k - 1) Vv (k - 1) Kr (k - 1 )V (k, \k - 2);
Vc(k— 1 |k.) = cov{x(k), xjk* | k — 1)};
vc(fe — 1 Р,) = Ф(Й, k - 1){VC (k-2 1 k,) - [Vx {k - 1) AHr (k - 1) +
+ Nc (k - 1 | k - 2) Hr (A — 1)] Kr (k - 1)V (kJk-2)}.
Начальные условия
Л Л _
x(kjkj = x(kj, V~ (kJ kJ = V~ (kJ;
V~(kJIkJ = V~ (*J;
У4(^|у = ДФ(4, + 1, kjvjkjkj+^ + i, wv~(V.
Vc (k* [ kJ = Ф (k, + 1, kJVJkJkJ; B(kJkJ = J.
Чувствительность в большом
V~(M*)-V~(kJk)
Г. (k. I k) = ---------------•
Чувствительность в малом
5V~ (kjk)
Ti (k, I k) =--—------ _ •
d bi b=b
Дифференциальное уравнение для у, (k, |k) дано в [82]
Вычисление соответствующих алгоритмов для сглаживания с
фиксированной задержкой мы оставляем в качестве упражнения
для заинтересованного читателя. Теперь основное внимание будет
уделено вычислению границ ошибок для ковариационных матриц
ошибок фильтрации и сглаживания.
Границы ошибок. Нишимурой [175] были найдены
границы дисперсии ошибок при использовании алгоритма фильт-
рации Калмана — Бьюси. Основной результат содержится в сле-
дующей теореме:
если V7 (f0)— V~(*o) (т)(т) >0 и (т) — Ч\ (т) >0 для
всех т из интервала [Zo, (], то
(8.258)
39»
для всех Элементы (Л|0 и V~ (f*|f) являются диаго-
нальными элементами матриц V~ (Л |0 иУ~(Л|0 'Соответственно.
Знак ^0 означает, что матрица левее этого знака положительно
полуопределена.
Следовательно, если приведенные выше соотношения выполня-
ются, то существует верхняя грань дисперсии ошибки сглажива-
ния в точке даже в том случае, если дисперсия истинного процес-
са неизвестна. Теорема, данная выше, применима только к непре-
рывным уравнениям сглаживания в точке. Однако, поскольку
время t„ произвольно и может принимать любые значения внутри
интервала [Лэ, /], то результат этой теоремы оказывается спра-
ведливым и для уравнений сглаживания на заданном интервале
и с фиксированной задержкой. Конечно, можно установить соот-
ветствующие условия и для дискретных алгоритмов сглаживания.
Проверить указанную теорему можно, выписав дифферен-
циальные уравнения, которым должны удовлетворять действи-
тельные ковариационные матрицы. Для алгоритмов фильтра-
ции— это ур-ние (8.203) при условии, что ДР=ДН = 0:
- = [F(0- W) Н(Щ V~(0 +V~(f) [F(0—H (0f +
+X (f) Tv (0 (t) + G (0 (f) GT (t), (8.259)
где F(£) и G(0 —матрицы размера NxN и NxR, определяемые
моделью (8.178), a m-мерный вектор измерения z(f)=H (0х(0 +
4-v(0, где H(f) — матрица размера MxN, a JT(f)—матрица
коэффициентов усиления фильтра Калмана размера NxM. Пред-
полагается, что реальный процесс представляется той же самой
моделью, за исключением того, что процессы w(f) и v(t) заме-
няются на w(t) и v(/).
В такой ситуации, когда единственным отличием модели
оценки от реального процесса является различие в ковариацион-
ных матрицах, (8 248) сводится к уравнению
<dV~(M0 - - т -- т
---5------= - А (0 Н (0 Vf (f) - vj(t) Нг (0 Аг (0 + А (0 4% (0 Аг (f),
dt
(8.260)
где A(f) =В(0 Нт(г')Ч,71 (0- Матрицы Vf (t) и В (t) удовлетво-
ряют ур-ниям (8.249) и (8.232). Поскольку модели сообщения и
наблюдения не содержат ошибок, то Vg(f) из (8.250) равно нулю.
Определим
*v~O) v^(0’
vf(0 v~(0_
(8.261)
400
а затем для Y(0 найдем дифференциальное уравнение
= С (0 Y (0 + Y (0 Ст (0+D (0 S (0 Dr (0,
at
где
D(0 =
О А(0
G(0 z¥(0
(8.262)
(8.263)
Далее, если Y определено как Y, то 4fv->'Fv, 'Fw->4fw,V~-»-V~
и можно найти уравнение для матрицы Y, представляющей раз-
ность между матрицами Y и Y:
= С (0 Y (0 + Y (0 Сг (0 + D (0 [S (0-S (0] Dr (0. (8.264)
Решение этого уравнения можно записать в виде
Y (0 = S(0 ^)Y(QBr(f, t*) +
t _
4-JS(£, t)D(t)[S(t)—S(t)]D7’(t)S7’(0 T)dx, (8.265)
t.
где = C(0S(t, tj, 3(0., = I.
Теперь, если Тт(т)—^(rJ^O и Yw(t)—4fw(r):2s0 для всех
г из интервала наблюдения [Zo, t], то S(t)—S(x)^O и, следова-
тельно, матрица, представляющая интегральный член ур-ния
(8.265), должна быть положительно полуопре делена. Если
v~(M-v~ (М>0, tov~(M>v~(M, и тогда первый член в
правой части (8.265) тоже положительно полуопределенная матрица.
Отсюда следует, что матрица Y(0 тоже положительно полуопре-
делена. Но верхние диагональные элементы
откуда следуют ур-ние (8.178)
хи
указанной теоремы.
Y(0=v-(M0-
ли
и справедливость
Пример 8.5. Предположим, что необходимо передать сигнал известной час-
тоты с неизвестной амплитудой и фазой. Принимаемый сигнал может быть
записан в виде A sin(w f+fl) +s(f) +u(f), где s(£)—экспоненциально-коррелиро-
ванный шум, a n(t)—белый шум. Шум s(f) моделирует случайный процесс,
возникающий при передаче, a v(t)—шум приемника. Мы хотим оценить сигнал
иа некотором интервале времени. Запишем сигнал в виде a sin ® t+b cos <в t.
Модель состояний для такого сигнала и аддитивного шума можно оппеделить
следующим образом:
м’
*2
Лз.
0 <й
— о О
О О
О
О
О
*2
-*3_
О
о
401
здесь х( представляет записанный в измененном виде сигнал, хз есть s(t), а
2(0 =[1 01]х (0 +v(0-
Оптимальная оценка сигнала (Xi) ие обязательно является оптимальной
оценкой амплитуды и фазы, но обязательно является оптимальной оценкой мгно-
венных значений сигнала. Предполагаемые параметры модели состояний н наи-
лучшне оценки априорных дисперсий равны: w=628 1/с^ 0 = 50 1/с,
(0)=4, V~ (0)=4, V~(0) = l, Чг»=0,1 и 'Р = 2 0 V- (0) = 100.
Хц Xjj Х33 СО33 Х33
В этом примере предполагается, что сигнал не связан с шумом. Для получения
оценок из ур-ния (8 58) используются параметры, значения которых равны
четырехкратным значениям тех параметров, которые были выбраны в качестве
априорных дисперсий
Рис. 8 8. Дисперсии ошибок для раз-
личных V~ (0):
/ — предполагаемая, 2, 3, 4— действительная.
-------. фильтрация,------ сглаживание;
• (0)==4V% (0): (0)=
=TZi<0); o-v^ii <0) = 2^~11 <0)
0,025 0,05 0,075 0,10 tfi
Рис. 8 9 Дисперсия ошибки оцеики
прн различных 4V
--------фильтрация, — сглаживание
На рис. 8.8 приведены графики вычисленной и истинной дисперсии ошибок
оценки сигнала (состояние Xi) для случаев оптимальной фильтрации и сглажи-
вания на фиксированном интервале Три нижние кривые получены варьирова-
нием начального значения дисперсии действительного процесса (V—— (0)) На
рис. 8.9 представлены графики действительной дисперсии ошибок оценки сиг-
нала для различных значений дисперсий белого шума В этом примере дисперсия
402
ошибки оценки сигнала почти не зависит от изменений действительной дис-
персии процесса s(t), поэтому мы не приводим эту зависимость. Значительные
ошибки при выборе априорных дисперсий V~ (0) и ’Р® вызывают существен-
ные увеличения дисперсий ошибки оценивания реального сигнала, которые на-
много больше оптимального значения дисперсии. Но в силу сформулированной
выше теоремы действительные дисперсии все равно находятся ниже уровня,
определяемого верхней гранью вычисленных дисперсий ошибок оценивания.
8.5. Расходимость
В некоторых приложениях можно обнаружить, что ис-
тинные ошибки оценивания во много раз превышают теоретиче-
ски предсказанные ошибки, характеризуемые дисперсией V—(/).
Действительно, реальная ошибка может увеличиваться безгранич-
но, даже если теоретическая ошибка калмановской фильтрации
пренебрежимо мала. Это явление, называемое расходимостью
(неустойчивостью) или насыщением информации, может вызвать
серьезные возражения по поводу целесообразности применения
фильтра Калмана. Впервые возможность нестабильного поведения
фильтра была проанализирована самим Калманом [105] и позд-
нее в работах Кнолла и Эдельштейна [117] и других, посвящен-
ных применению алгоритмов калмановской фильтрации в задачах
пространственной навигации и определения орбит.
Может показаться, что утверждение о расходимости резко
противоречит результатам по устойчивости, полученным в § 7.5.
Однако на самом деле это не так, поскольку расходимость вызы-
вается такими ошибками, которые учтены в этом параграфе не
были. Одними из главных причин расходимости являются: неточ-
ность задания процесса, моделирующего сообщение и наблюдение,
линеаризация уравнений, отсутствие полной информации о реаль-
ной физической задаче, а также всякого рода упрощающие пред-
положения, позволяющие дать математическое описание задачи.
Кроме того, неустойчивость могут вызывать ошибки, связанные с
моделированием вероятностных характеристик шума и неизвест-
ных входных сигналов. Неустойчивость могут вызвать также ошиб-
ки округления, неизбежно возникающие при цифровом моделиро-
вании алгоритмов фильтрации и которые могут привести к потере
положительной определенности и симметрии ковариационной
матрицы ошибок.
Для того чтобы выяснить, каким образом возникает расходи-
мость и как ее можно проконтролировать с помощью простой мо-
дификации алгоритма фильтрации, рассмотрим простой пример,
в котором расходимость возникает в результате неточного зада-
ния модели сообщения.
Допустим, что необходимо оценить состояние дискретного про-
цесса
х(А) = х(А—l)-|-ct, (8.266)
где а — постоянная. Однако модель сообщения, которую мы ис-
403
пользуем, задана в виде
x(k}=x(k— 1). (8.267)
Модель наблюдения
z (k) = х (k) + v (k), (8.268)
где v(k)—последовательность случайных независимых нормаль-
ных величин с нулевыми средними и одинаковой единичной дис-
л
Персией. Положим, что х(0)=0 и¥-^(0)—¥ж(0)=оо, иными слова-
ми, у нас нет информации о начальном состоянии.
Используя алгоритмы табл. 7.2, легко показать, что оценка
после N наблюдений определится соотношением
л N
x(N) = x (0) + а + А- £ и (f), (8.269)
(=1
а дисперсия ошибки, согласно фильтрации по Калману, равна
¥-(¥)= 1/М (8.270)
Следовательно, при увеличении N дисперсия будет стремиться
к нулю, и оценка будет очень точной. Однако легко убедиться,
что это неверно, если вычислить действительную дисперсию
ошибки.
Действительное состояние после N наблюдений равно
x(¥) = x(0)+ aN. (8.271)
Поэтому действительная ошибка оценивания раина разности
между (8.271) и (8.269):
JV,
x(N) = а_ J_ £ v(i}. (8.272)
z=i
Следовательно, действительная среднеквадратическая ошибка
равна
фт(¥)= -fcAT. а2 + ± = у~(¥) + [£{4]г, (8.273)
откуда видно, что при увеличении N ошибка 'неограниченно воз-
растает и оценка расходится.
Может показаться, что подобная задача тривиальна, посколь-
ку мы просто игнорируем константу, которую должны были бы
учесть. Однако даже если и включить константу в модель сооб-
щения, то оценка все равно могла бы разойтись, до тех пор пока
два входных сигнала не станут абсолютно равными, что, к сожа-
лению, практически трудно сделать. Если, например, модель сооб-
щения задать в виде
x(k) = x(k— 1)+P, (8.274)
404
то очень просто показать, что действительная среднеквадратиче-
ская ошибка равна
Фу W = («-Р)2 + ^- (8.275)
и оценка снова будет расходиться до тех пор, пока а будет не
равна р.
Основная причина, вызывающая расходимость в фильтре Кал-
мана, состоит в том, что коэффициент передачи (усиления) K(k)
фильтра очень быстро стремиться к нулю. Поэтому оценка пере-
стает быть зависимой от последовательности наблюдений и расту-
щая ошибка наблюдений на нее не влияет.
Эта трудность может быть преодолена одной из простых мо-
дификаций алгоритма фильтрации. Можно, например, просто
ограничить снизу коэффициент передачи K(k) так, чтобы он не
становился меньше некоторого значения, скажем, l/М. Другими
словами, после М наблюдений считаем К постоянной величиной
для всех будущих наблюдений. Для того чтобы продемонстри-
ровать этот прием, найдем среднее значение действительной
ошибки оценивания. В случае немодифицировэнных уравнений —
это линейная оценка по минимуму дисперсии и поэтому из ур-ния
(8.272) получим следующий результат (поскольку £{и(/)} = 0’
для всех /):
= (8.276}
Так как, с другой стороны, мы ограничили К снизу величиной
l/М, то легко показать (см. задачу 8.24), что
(N)} = (1 - ^±1 а. (8.277)
Тогда при N->-oo ошибка стремится к нулю и фильтр не воз-
буждается. Можно возразить, что при этом фильтр перестает
быть оптимальным, и это на самом деле правильно. Однако
немодифицированный фильтр также не является оптимальным,
поскольку моделью входной сигнал не учитывается. Если а равно
нулю, то можно показать, что дисперсия модифицированного
фильтра будет больше немодифицировэнного. Однако, если нет
оснований считать а равной нулю, то можно пойти на такое
ухудшение качества, являющееся платой за сохранение устой-
чивости.
Другой подход к устранению расходимости в указанной выше
задаче возникает в случае, когда в рассматриваемой модели а
есть неизвестное состояние некоторой динамической системы, уп-
равляемой белым шумом Ч Хотя эта процедура часто дает хоро-
шие результаты, она имеет неприятную особенность, связанную с
повышением порядка рассматриваемой задачи. Так как порядок
•> Превосходное описание этого подхода дано в работе {71]. (Прим, авт.)
405
фильтра и алгоритма вычисления дисперсии для //-мерной моде-
ли сообщения равен JV(JV+3)/2, то даже небольшое увеличение N
может привести к значительному усложнению вычислительных
процедур. К примеру, если сначала Д1=5 и просто добавить одно
новое состояние в модели в качестве неизвестного входного сиг-
нала, то порядок уравнений (число их) увеличится с 20 до 27.
Если увеличить N с 5 до 7, то придется добавить еще 15 новых
уравнений. Даже если не обращать внимания на вычислитель-
ный аспект задачи, все равно нужно помнить, что эффективное
решение можно получить в случае, если требования к вычисле-
ниям не являются основной проблемой и если «природа» неизвест-
ного сигнала такова, что его можно представить эффективной мо-
делью.
Выводы, полученные при рассмотрении этой простой задачи,
имеют фундаментальное значение и в общем случае. Расходи-
мость может возникнуть из-за слишком малого веса новой инфор-
мации или, наоборот, из-за слишком большого веса прошлых на-
блюдений. Поэтому расходимость (насыщение информацией) —
явление противоречивое. Как уже известно из гл. 7, в том случае,
когда входной шум мал по сравнению с наблюдениями, дисперсия
ошибки калмановской фильтрации и, следовательно, коэффи-
циент усиления имеют тенденцию быстро уменьшаться при увели-
чении времени. В том случае, когда модель сообщения вообще
не содержит управляющего шума, коэффициент усиления асимп-
тотически стремится к нулю. Эта особенность, которая в общем не
является неожиданной, поскольку каждый отсчет (в среднем)
содержит гораздо больше нежелаемого шума наблюдения, чем
информации об управляющем шуме, имеет тенденцию «отклю-
чать» фильтр от последовательности наблюдений и таким образом
вызывать неустойчивость. Итак, мы приходим к тому, что ситуа-
ции, в которых управляющий шум слабо сравним с шумом наблю-
дения, приводят к проблемам неустойчивости. Насколько сильно
проявляется расходимость и в каких случаях она возникнет
вообще, все это зависит от длины интервала наблюдения и от
точности моделирования реального процесса.
Основываясь на предыдущих рассуждениях, можно предло-
жить определенные модификации фильтра Калмана, устраняющие
расходимость. В работе (221] рассматриваются несколько прос-
тых методов устранения неустойчивости в специфических задачах
•определения орбит. Основная идея этих подходов связана с огра-
ничением коэффициента усиления для того, чтобы избежать «не-
чувствительности» к наблюдениям. Эти методы можно разбить на
три широких класса:
— уменьшение матричных коэффициентов усиления;
— ограничение дисперсии ошибок;
— искусственное увеличение мощности управляющего шума
сигнала.
Рассмотрим каждый из этих методов.
406
Существует 'несколько способов непосредственного уменьшения
матричных коэффициентов усиления. Так, можно использовать
процедуру, развитую в рассмотренном /выше примере, и ограни-
чить элементы матрицы снизу некоторой заранее выбранной вели-
чиной. Можно просто добавить к элементам матрицы некоторую
величину или использовать менее очевидные способы для увели-
чения усиления Например, в работе [222] матрица коэффициен-
тов усиления представлена в виде
К (£) = [V- I k - 1) + в I] 1Г (*) [Н (fc) V~ (k I k- 1) Hr (Z>) + Vv (*)]->.
(8.278}
Подобно тому, как можно ограничивать снизу элементы мат-
рицы коэффициентов усиления, аналогичная методика может
быть применена для ограничения элементов матрицы дисперсий-
ошибок. Легко видеть, что из-за неизбежной неопределенности в
формулировке начальных условий физически невозможно иметь
ошибку, равную нулю. Однако точную нижнюю границу диспер-
сии ошибки также трудно найти, если не использовать экспери-
мент. Можно показать, что, имея минимальное значение дисперсии
ошибок, можно избавиться от расходимости.
Поскольку основная причина, из-за которой матричные коэф-
фициенты становятся малыми и возникает неустойчивость, со-
стоит в том, что управляющий шум модели значительно слабее,,
чем шум наблюдения, то очевидное решение задачи состоит в ис-
кусственном увеличении дисперсии управляющего шума. Несмотря
на то, что можно вычислить величину необходимой добавки к
дисперсии управляющего шума, точная ее величина должна на-
ходиться экспериментально.
Нетрудно видеть, что при использовании перечисленных выше
методов дисперсия ошибки будет большей, если модель сообщения
на самом деле точная. Другими словами, контроль расходимости
может быть осуществлен только за счет увеличения дисперсии
ошибки свыше «теоретического» минимума. Конечно, если опти-
мальный фильтр неустойчив, то модифицированный неоптималь-
ный фильтр будет иметь дисперсию ошибки, меньшую, чем дейст-
вительная дисперсия ошибки «оптимальной» фильтрации.
Другой подход, позволяющий контролировать расходимость,
состоит в вычислении квадратного корня из матрицы ковариаций
ошибок оценивания. Подобный способ был развит в работах [21],
[23], [5]. Эта процедура полезна в случаях, когда неустойчи-
вость вызывают ошибки округления. Тогда лучше вычислять
квадратный корень из дисперсии, чем саму дисперсию, потому
что число необходимых операций при счете сокращается в два
раза. Рассматривая этот способ, предположим, что шум модели
равен нулю; мы уже видели, что неустойчивость возникает чаще
всего при малом шуме модели, поэтому наше предположение не
является ограничительным. В случае ненулевого шума можно
воспользоваться алгоритмом, разработанным в [58].
407
В дискретном времени уравнения для ковариационной матри-
цы ошибок оценивания при Vw(fe)=0 записываются в виде
V~(£|£—1) = Ф(£, * — 1)¥~(6)Ф(£, Л —1); (8.279)
V~(k) = [I — ВДН(Л)] V- (Ш — 1). (8.280)
Легко показать прямой подстановкой, что корень из матрицы
ковариаций равен
[V~ (k | k-1)] Ф (* \k -1) [V~ (А)]^; (8.281)
JV~ (£)] = [V~ (k | k- 1)]^(I -{[V~ (k | k-l)]^f x
xH(fe)^[Vv(fe)+Hr’(fe)V~(fe|fe — 1)ВД}2 j X
X {vv(fe)+H4fe)V~(fe|A-l)H(^ +
+ [Vv(*)p-} 1 W) [v~ (fe|fe- l)pj, (8.282)
где используется нижняя треугольная матрица корней из дис-
персий. Аналогичные выражения для случая непрерывного време-
ни были получены .в [5].
Другой подход [96] 'состоит в том, что оценку получают
только по прошлым М-наблюденмям, где М — некоторое фикси-
рованное число отсчетов, достаточно большое, чтобы его еще
можно было бы наблюдать в системе. К сожалению, этот метод
требует одновременного использования алгоритмов фильтрации и
предсказания и, следовательно, становится практически непри-
годным, если алгоритм фильтрации расходится, что и является
его основным ограничением. Однако в [96] была предложена
подоптимальная процедура, позволяющая снять это ограничение
и исключить тем самым проблему неустойчивости.
Для устранения неустойчивости можно воспользоваться адап-
тивными алгоритмами фильтрации [97], [208], [243]. Примене-
ние этих алгоритмов может оказаться более целесообразным, по-
скольку при этом ошибка из-за расходимости становится большой,
а значит, и большее количество информации можно использовать
для адаптации.
Глава 9
НЕЛИНЕЙНОЕ ОЦЕНИВАНИЕ
9.1. Введение
В завершение изучения теории оценивания подробно
обсудим проблемы, связанные с нелинейным оцениванием. При
использовании многих методов 'модуляции, таких, как частотные
или фазовые, 'модели наблюдаемых сигналов обладают существен-
но нелинейной структурой. Кроме того, модели сообщений в
реальных динамических системах управления и контроля также
существенно нелинейны. В этой главе мы рассмотрим как методы
линеаризации около заданной траектории, так и непосредственно
методы нелинейного оценивания.
Используемые источники даны в общем списке литературы. Час-
тичное отношение к этой главе имеют работы Кушнера [124],
[127], Уонхэма [285], Бьюси [37], Снайдера [246], Сэйджа и
Эвинга [205], [206], Сэйджа [203], Кайлатца и Фроста [103]. и
Фроста [73].
9.2. Оценивание при помощи условного
среднего
В этом параграфе рассматриваются алгоритмы услов-
ного среднего или, другими словами, алгоритмы фильтрации с
минимальной дисперсией ошибки для непрерывных во времени
нелинейных систем1). Оценка по наблюдению Z(/) = {z(t),
CJt^’I} определяется соотношением
x(0 = £{x(0|Z(0}= J x(Z) р [х (/) | Z (/)] d х(/). (9.1)
—oo
Рассмотрим класс нелинейных систем, управляемых белым
шумом. Само наблюдение представляет собой аддитивную смесь
сигнала и белого шума2). Таким образом,
X = f [X (0, fl + G [х (fl, fl w (0; (9.2)
z(fl = h[x(fl, fl + v(fl, (9.3)
*> Здесь мы отступаем от способа обозначений, принятого в гл. 6, н не ис-
пользуем индексы для указания критерия для различных оценок. (Прим, авт.)
2> Вся информация о входных сигналах заложена в f. Если w(/) и v(f)
имеют известные ненулевые средние, то их можно учесть с помощью f и h.
(Прим, авт.)
409
тде w(t) и v(Z)—статистически независимые нормальные белые
шумы с нулевыми средними и, кроме того, х(0) выбрано так, что
для t>t0
(0 = 0; cov {w (0, w (т)} = Tw (t) 8d (t — t);
Hv (0 = 0; cov {v (0, v (т)} = Уv (0 (t - t);
cov {w (0, v (t)} = cov {w (0, x (t0)} = cov {v (0, x(r)} = 0. (9.4)
План построения алгоритмов оценивания следующий. Сначала
выразим уравнения для исходного сигнала и наблюдения в фор-
ме Ито, которая дана в § 4.4, а затем выпишем условное уравне-
ние Фоккера — Планка в частных производных, решением кото-
рого является условная плотность вероятности вектора х(0 при
известном Z(0. Далее найдем два приближенных уравнения для
л
оценки х(0 с помощью разложения f[x(0, /], G[x(0, /] и
Л
h[x(0, 0 в ряд Тейлора около точки х(0. Наконец, дадим при-
ближенные выражения для ковариационной матрицы ошибок и
приведем несколько иллюстративных примеров, представляющих
интерес для связи и управления.
Модель оценки. Выясним сначала, что представляют
собой стохастические дифференциальные уравнения. Используем
определение винеровокого процесса и определяем новое наблюде-
ние так, что d©(0=w(0d/; dv(0 —N(t)dt-, dy(t)=z(t)dt, где
dy(Z) есть dy(0 =y(t+dt)—y(t), и поэтому стохастические диф-
ференциальные уравнения, описывающие нашу модель, можно
записать в вйде
dx(0 = f [х(0, 0 dt + G[x(0, t] d w (t); (9.5)
dy (0 = h [x (0, /] dt + d v (0, (9.6)
причем
Mw(0 = 0; cov {to (0, w(t)} = Tw(0min{0 r};
M'v (0 == °! cov (v (0> v (>)} = niin T}' (9.7)
Здесь <в(0 и v(0—независимые винеровские процессы 9, не
коррелированные с х(/0). Как отмечалось в § 4.4, ур-ние (9.5)
определяет непрерывный марковский векторный процесс.
Найдем некоторые характеристики моделей сообщения и на-
блюдения, которые понадобятся нам ниже, отметив, что их вы-
числение непосредственно следует из результатов § 4.4:
^{dy(01x(0}= h[x(0, t\dt-
var {dy (01 x (0) = Tv (0 dt. (9.8)
*> Строго говоря, <£>(^) н v(f) не являются вннеровскнмн процессами, по-
скольку они не обладают стационарными приращениями. Однако, используя
методы § 4.4, легко преодолеть эту трудность. (Прим, авт.)
410
Поскольку dy(Z) определяется как винеровский процесс с не-
нулевым средним, то плотность вероятности dy(Z) при условии
х(£) нормальна. Нам также потребуется ковариационная матрица
случайного процесса dy(/):
var {dy (/)} = Yv (fl dt - pg (t), (9.9)
где
§(O = dy(fldyr(fl. (9.10)
Таким образом, для очень малых dt отношение ^(t)ldt детерми-
нировано в том смысле, что
!ю=1гш_тио (911)
Кроме того,
Е {dx (t)} = f [х (t), fl dt\
E {dx (fl dxr (fl) = G [x (fl, fl Tw (fl Gr [x (t), t]dt. (9.12)
Для упрощения обозначений целесообразно ввести операторы
условного среднего:
f [x(fl, fl = E{f[x(fl, fl | Z(fl) = £{f[x(fl, fl | Y(fl};
h [x (t), fl = E {h [x (fl, fl | Z (fl) = E {h [x (fl, fl | Y (fl). (9.13)
Условное уравнение Фоккера — Планка. Теперь
перейдем к определению условного или модифицированного урав-
нения Фоккера — Планка, решением которого является условная
плотность вероятностей p[x(t), £]Z(£)]„ по которой и находится
условное среднее (9.1). Мы явно включаем параметр t в выраже-
ние для плотности, чтобы подчеркнуть зависимость этой функции
от времени.
Прежде чем рассмотреть какой-либо из двух подходов опреде-
ления уравнения Фоккера — Планка, приведем один вспомога-
тельный результат, полученный Кушнером [124]. Сначала рас-
смотрим поведение условной плотности p[x(t), Z|Z(fl] в зависи-
мости от дифференциала наблюдения dy(fl, а затем поведение
этой функции в зависимости от изменений x(fl.
Определим условную плотность как
Р [х (fl, #| Z(t + dt)] = p[x(t), t\Z(t), dy(fl]. (9.14)
Этот результат следует из марковского свойства процесса. Так
как p[x(fl, f|Z(fl]=p[x(fl, ИY(fl], то, определяя dy(/) =z(t)dt,
получаем ,&?
У (fl — У (А>)= fz(X)dX,
откуда следует, что в 4(t), представляемым у(Х) для t0^J^t
относительно x(t), содержится не больше информации, чем в
411
Z(Z), представляемым z(ih) для tQ^).^t. Поскольку
P [X (0, q Y (t + dt)] = p [x (t), t I Y (t), у (t + dt)]=p[x(/), t I N(t), dy(/)],
(9.15)
то получаем'соотношение (9.14). Уравнение (9.15) можно перепи-
сать следующим образом:
Р[х(t), t\\(t + dt)] = p [х (t), t I Y(t), dy (01 =
_ p[dy(Q | x(Q, Q Y(Q]p[x(Q, q Y(Q]
P[dy(0|Y(/)l
= P[dy(Q|x(Q. t, Y(Q]p[x(Q, / | Y(Q](g
j p [dy (/) | x (0. t, Y (01 p [x (0, t I Y (01 d x (0
—co
По причинам, которые станут понятными далее, целесообразно
внести отношение
S [dy (/), dt, 0= /?[Х(0’ + . (9.17)
р[х(о. qY(01 7
Из (9.6) следует: р[dy (Z) |х(Z), t, Y(/)] =p[dy(/) |х(/), /], т. е.
условная плотность вероятностей процесса dy(Z) действительно
не зависит от Y(/). Подстановка двух последних соотношений в
(9 16) с учетом (9.8) дает
ехр fc1 {dy (t) - h [х (/), dt}T «Р71 (/) {dy (0->
S [dy(O, dtf]= ------------------------j----------------------
[ ₽[x (0, t | Y (OJexp f— -J- {dy(O—h[x(0, 0 dt}T-*
v \ леи
— oo
— — h[x(/),
- T71 (0{dy (/)- h[x (f), n <#})d x(0
Сокращая члены, не содержащие х(/) в числителе и знаменателе,
получим
S(dy(0. Л, fl = <1-0.31/х~
J р [X (t), t I Y (01 exp { dy7" (0¥v-‘ (0 h X —>
—oo
—»X[x(Q, 0W71(Qh[x(0, t]dt }___________
-»X[x(0, o— o,5hr[x(/), О ЧТ4 (0h[x(0.0<«}dx(0 ‘
Для того чтобы упростить S[dy(/), dt, f], желательно выра-
зить p[x(Z), 11Y(t+dt)] через p[x(£), <|Y(f)]. Это можно сделать,
412
раскладывая предыдущее соотношение в ряд Тейлора около точки
dy=O и dt—O. Удерживая члены порядка dt, получаем
S[dy(0, dt, t] = s [о, o, q + |^ +
1 3 V ’ J 1 I d [dt] dy(/)=oj
dt=O
dB[dy(Z), dt, Z]
d [dy (01
fdy(Q +
dy(Z)=O( v
dt=o )
( ^ВМу(О. dt, t]
2 У ( ( P[dy (OJ}2
dy(Z) —0
dt=O
(9.19)
Если теперь подставить
учесть (9 18), то можно
искомого ряда:
S [О, О, Z] = 1;
dB[dy(Z), dt, Z]
d[dZ]
вычисленные производные
получить коэффициенты
в (9.19) и
разложения
dy(<)=o = ” °’5hr [X (Z)’ П (Z) h [X (Z)’ Z1 +
dZ=O
dy(0=o = Tv-' h [X (0. Л ~ ^7* (0E{h [x (t), Z] I Y (*)};
dt-0
dy(0=o = {T7I(0h[x(Z), П) {Y7'(/)h[x(0, f]}7-
+ 0.5E { hr [X (Z), Z] Tv-' (f) h [X (t), Z] 1 Y (Z) } ;
dB[dy(Z), dt, Z]
d [dy (Z)]
^B[dy (Z), dt, Z]
P [dy (OJ}2
-2;{Y7'(/)h[x(/), Z]}(Yv-'(Z)E{h[x(Z), t] | Y(Z)}/ + 2(Y7'(Z) X
xE{h[x(Z), Z] | Y(l)))(Y;40E{h[x(Z), t] | N(t)}y-E{^(t) x
Xh[x(Z), Л {T7'(Z)h[x(Z), Л}г| Y(Z) } .
Теперь займемся довольно утомительной процедурой подста-
новки полученных трех соотношений в (9.19), а затем упроще-
нием результирующего выражения. Очевидное упрощение дают
члены второго порядка d2S{<?[dy(t) ]}2. Например, первый член
c)2S {<?[dy (t) ]}2, подставленный в выражение (9.19), дает
-l-dy’’(O{^-»(Oh [х(0, П) {V (0h[x(0, П}г dy(O,
что с учетом, того что dyrY7’ h — скаляр, легко может быть пере-
писано в виде
~ hr [х (t), /] (0 dy (0 dyr (/) V/ (t) h [x (Z), f].
Теперь, учитывая, что для бесконечно малого dt производная
dy(Z)dyr(Z)/dZ детерминирована, что dy(Z)dyr(Q ='FT(Z)dZ, полу-
чим — hr [х (/), П Т7' (Z) h [х (Z), Z] dt.
•i
413
Подобная процедура может быть проделана со всеми осталь-
ными членами разложения Тейлора, и тогда окончательно нахо-
дим
S[dy(0, dt, = 1 -f- {dy (0 — h [х (0, (0{h[x(0,0—h[x(0,0}.
(9.20)
Подстановка этого соотношения в (9.17) дает
p[x(0, t | Y(/ + p[x(0, t | Y(OJ =
= p[x(0, 11 Y(0]{dy(0 —h [x(0, Л -h’[x(0, 4}.
(9.21)
Теперь приступим ко второй части вывода, которая идентична
выводу уравнения Фоккера — Планка в гл. 4. Удобно в целях со-
кращения обозначений член в правой части (9.21) обозначить
через v. Тогда
p[x(0, t | Y + dt)] - р [х (/), t | Y(0, dy (0] = p[x(Z), t | Y(Z)l + v.
(9.22)
Первая половина нашего вывода касалась выяснения влияния
на условную плотность вероятностей изменений dy(f). Сейчас мы
рассмотрим, как влияют на поведение этой функции бесконечно
малые приращения dx(Z). Используя теорему умножения вероят-
ностей, получаем
р [х (t -\-jji), t -j- dt | Y (t “I- dt)] =
— J P Iх (^ + dt), t + dt, x (t), t | Y (t + dt)] d x(/) —
----OO
= f p[*(t + dt), t + dt \ x(t), t, N(t+dt)]p[*(t), 4 (t-\-dt)]dx(t).
Л (9.23)
Далее применяем марковское свойство модели сообщения [см.
(9.5)]:
dx (t) = x(t + dt) — x (t) = f [x (t), dt + G [x (t), d w (t)
и видим, что
p [x {t + dt), t + dt | x (/), t, Y (t + dt)] =
= p [x (t + dt), t + dt | x (t), t, Y (t), dy (0] = p [x(f + dt), t+dt | x (t), f],
поскольку при известном x(t) в N(t+dt), Y(/) или dy(/) никакой
информации относительно x(t + dt) не содержится. Y(Z) зависит
только от прошлых и настоящих значений x(t). A dy(£) или, что
эквивалентно, h[x(£), /] dt + dv(t) также не несет дополнитель-
ной информации по сравнению с той, что содержится в x(t), так
414
как мы предположили, что dat(/) и dv(fl независимы. Таким об-
разом, имеем
р [х (t + dt), t+ dt | Y (t + dfl] = j p [x (t + dt),
t-ydt | x(fl, flp[x(fl, t | Y (t. + dt)} d x (t). (9.24)
Теперь разложим произвольную скалярную функцию Л[х(£+
Ydt) ] в ряд Тейлора около точки x(t + dt) =x(t):
A[xa+dO] = A[x(OJ+{-^^±^)L fdx(0 +
l Эх(/ + «) х(Г+<»)= x (/)!
+ — dx7 (t) (+ I I dx (t). (9.25)
Из уравнений для модели сообщения имеем с учетом (9.12) и
(9.13)
£{dx(fl} = f[x(fl, t}dt- E{dx(t)dxT (t)} = G[x(fl, fl GT [x (t), t] dt.
Всеми моментами dx(fl более высокого порядка можно пренеб-
речь, поскольку порядок всех их выше порядка dt. Таким обра-
зом, мы производим усечение ряда до Л-го члена, ибо порядок
всех остальных членов разложения выше порядка dt.
Умножая ур-ние (9.24) на Ли интегрируя по x(t+dt), получим
J Л[х(/ + Л)] p[x(t 4- dt), 14- dt | Y(f + dt)]dx(t 4- dt) —
— 00
= j J Л [x (t 4- dt)} p [x (t 4- dt), t -\-dt | x (t), fl p [x (fl,
t | Y(t 4- dt)} dx(t)dx(t dt).
Окончательно интегрируем по частям x(fl и x(t+dt), перенося
два последних члена в правую часть равенства. Предполагаем,
что граничные условия на A[x(^4-dfl] заданы на бесконечности,
X(fl = ± оо;
Л= fpA=GYwG7> — = GYwGrA — = GYwGrA— = 0.
дх дх дх
Тогда, меняя порядок интегрирования, имеем
j Л [х (/ 4- dt)} р [х (t 4- dt), t-\-dt \ Y (t 4- dfl] d x (t 4- dt) —
— 00
— j A[x(^4-dfl] [p[x(f + dt), t\N(t + dt)} —
. tr/g{Ux(f + fl, flp[x(f + dQ, /|Y(/ + dfl]}\ 1
\ d x (t 4- dt) / ]
415
+ 4 trI-- (Г д * К{G[X(t + dt), t] Tw Gr[x (t + dt)t]x
2 [ d x (t 4- dt) \ d x (t 4- dt) J
X p[*(t + dt), t I N(t + dt)]})dx(t + dt).
Поскольку Л — произвольная функция, предыдущее соотношение
должно быть верным для любого Л, поэтому
p[x(t + dt), t + dt | Y (£ 4- cf£)] = p[x(t + dt), t\ Y (£ +dt)] —
_ tr / дЩх«4-&). Цр[х(/4-<й). /| Y(/ + d/)]} \ dt
\ d x (t 4- dt) J
+ — tr Г-----------f [----------? {G [x (t 4- dt), t] Tw (t) GT x
2 L д X (t 4- dt) k L д X (t 4- dt) ] v 1 v '* J 7
X [X (t 4- dt), fl p [X (t 4- dt), f I Y (t 4- dfl]})] dt. (9.26)
Теперь можем заменить x(t+dt) на x(fl, так как ур-ние (9.26) не
содержит члена x(fl. Полученное уравнение будет совершенно
эквивалентно уравнению Фоккера — Планка [(4.128), гл. 4], если
отбросить условие \(t+dt). Подстановка выражения для
p[x(fl, flY(/4-dfl] из (9.22) в предыдущее соотношение дает мо-
дифицированное уравнение Фоккера — Планка
р [х(0, 14- dt | Y (t 4- dt)]-p [x(fl, t | Y (fl] =
= _ tr ( d{f flP[x(Q. | Y(Q1> \dt ,
\ d x (t) J
+4 44г ([ -4лГ <G Tw GT t]p tx v>’11Y x
2 [dx (t) \|_ d x (/)]
X dt 4- p [x (t), t I Y (fl] {dy (t) — h [X (t), t] dt}T x
X T?1 (fl {h [x (t), fl — h [x (fl, fl}, (9.27)
в котором опущены члены, такие, как dy(t)dt и (dt)2, поскольку
они на порядок выше члена dt Последний член в правой части
уравнения отражает влияние наблюдаемой реализации dy(fl.
л
Если h[x(fl, fl не зависит от x(fl, то h[x(fl, fl—h[x(fl, fl равно
л
нулю, так как в этом случае h(fl =£'{h[x(fl, fl | Y(fl} равно прос-
то h(fl. Тогда модифицированное уравнение переходит в обычное
уравнение Фоккера^—Планка (4.123).
В некоторых случаях целесообразно представлять модифици-
рованное стохастическое дифференциальное уравнение Фоккера —
Планка в ином виде:
dp[x(fl, 11 Y (/)] _ _ / <Э {f [х (Z), /]р[х(/), 11 Y(Z)]} \
dt k d x (/) J
+ V tr ItAtTtxW- fl4MflGr[x(fl, flp[x(fl, t I Y(fl]})]4-
2 |_d x (t) \L d x (Z)J
4-p[x(fl, t | Y(fl]{z(fl-h[x(fl, A/T71 (fl{h[x(fl, fl-h[x(fl, fl}
(9.28)
416
Если исключить условную переменную Y((), то последние члены
в правых частях ур-ний (9.28) и (9.27) станут равными нулю, и
тогда мы придем к исходному уравнению Фоккера — Планка, рас-
смотренному в гл 4.
Представляет интерес применить правило дифференцирования
Ито для получения модифицированного уравнения Фоккера —
Планка. Введем следующую функцию случайного процесса:
<р [х (t), f] = ехр [— sr х (f)]. (9.29)
Тогда условная характеристическая функция этого процесса равна
Mx(/)|Y(o (s) =Е{<р[х(0, G | Y(0).
Применение правила Ито [см. (4.108)] дает результат, эквива-
лентный соотношению (4.123):
d <р [х (t), /] = {— Г [х (0. (] s + у sr G [х(0, fl (0 GT [х (t), /] s| x
Хф[х(1), f]df-s7'G[x(f), f](p[x(f), f]d(o(f). (9.30)
Обратным преобразованием Фурье находим
dp [х(t), t | Y(01 = — tr |df[*(0. UpM- z 1 Y(z)1 jdt +
+1Ч^й(МйГ<0|х<')’ <lx
X p[x(0, t I Y(/)]})] dt + p [x(0, t I Y (01 --^-У-Г (t)~ h?J/0’1 x(0} X
x T71 (0 {dy (0 — h [x (0 0 dt}, (9.31)
что эквивалентно модифицированному уравнению Фоккера —
Планка, полученному выше довольно сложными вычислениями.
Многие авторы используют для произвольного скаляра обозначе-
ние прямого дифференциального оператора [37], [39]:
х [7^([^rG|xW' ЧЧ'-ЙбЧхИ. /)( )] .
В этом случае можно показать, что модифицированное уравнение
Фоккера — Планка может быть записано в виде
dp [х (t), t | Y (/)] = %+ {p [x (/), t | Y (()] dt} + .%• dt,
где
CK = p (x(/). t | Y (/)] — [x(7), t]di | x(Q} x
' dt
X ЧТ1 (/){z(f)-h[x(0, /]}.
14—26 417
Оценка с минимумом ковариационной матри-
цы ошибок. Теперь займемся решением уравнения Фоккера —
Планка для того, чтобы получить оценку x(t) с минимальной ко-
вариационной матрицей ошибок вектора состояний х(/). Будем
считать, что сообщение и наблюдаемый сигнал заданы ур-ниями
(9.2) и (9.3) [или (9.5) и (9.6)] с априорными данными (9.4)
или (9.7).
Условная ковариационная матрица ошибок и оптимальная
оценка определяются следующими соотношениями:
Vr(0 = var{x(0 —х(0 | Z(0}= j [х(0 —х(0Пх(0 —x(Olrj»fx(O,
qZ(0]dx(0; (9.32)
х(0 = £{х(0 | Z(0}= ? x(t)p[x(t),t\Z(t)]dx(t), (9.33)
I’ -00
в которых можно заменить Y(Z) на Z(t), поскольку в Y(t) со-
держится вся информация о Z(t).
Если умножить обе части модифицированного уравнения Фок-
кера— Планка (9.27) на х(Л и проинтегрировать в бесконечных
пределах по x(t), то получим7
х (t + dt) — х (t) = dx (t) = f [x (t), t]dt -P £ {[x (t) — x (f)] h7 x
X [x (0, t] | Y (0) Y71 (t) {dy (0- h [x (О, fl dt}. (9.34)
Это соотношение является точным выражением для оптимальной
оценки.
В процессе получения этого результата мы попутно доказали
теорему о нелинейном проецировании
Е {х (0 hr [х (t), fl) = Е {х (\) 2Т (A«j)} =Е x(Xx)Zr (А,2) = 0. (9.35)
В данном случае полагаем Л1<Лг и используем приведенное выше
л
определение «обновляющего» процесса 3(t)=z(t)—h[x(fl, £] =
=7(0-
Выведем теперь уравнение для ковариационной матрицы оши-
бок. Легко установить следующее тождество [см. (4.60)]:
[X (0 - х (/)] [X (fl - X (Of = [X (0 -x(t + dt)] [X (0 - X {t + dt)]T +
4- dx (fl dxr (0 + [x (0— x (t + dt)] d xT (t) + dx (fl [x (t) — x (t + dt)]T .
(9.36)
Для того чтобы получить уравнение для ковариационной матрицы
ошибок, умножим это тождество на р[х(£), £]Y(£)] и проинтегри-
руем в бесконечных пределах по х(£). Если члены равных знаков
правой части (9.36) умножить на члены с равными знаками левой
418
части ур-ния (9.27), а члены левой части (9.36) с равными знака-
ми умножить на члены правой части (9.27), то после интегриро-
вания по частям можно получить
dV~ (0 + dx (0 dxr (0 = Е {f [ х (0, О [х (0 - х (ЭД71 Y (0} dt -f- £([х (0 -
— Г(0Лг[х(0, о | Y(0}^ + £{G[x(0, п^(0Сг[х(0. О I У(0)Л +
+ £{[х(0-х(01 [х(0— х(0]г {h [х (0, Л — h[x(0, 0}гТ7*(0 X
X {dy (0 - h [х (0, 0 dt} | Y (0). (9.37)
Уравнения (9.34) и (9.37) определяют оценку (условное сред-
нее) с минимумом ковариационной матрицы ошибок. В общем
случае эти два уравнения связаны между собой. В линейном слу-
чае этой связи не существует.
Теперь найдем два приближенных решения этих уравнений.
Пр иближение первого порядка. Разложим
и h[x(£), t] в ряд по оптимальной оценке и ограничимся линей-
ными членами. Тогда имеем
д л л
f [х (0, 0 « f [х (0, 0 + df[xA(0' ---1- [х (0 - х (01; (9.38)
Зх (О
А Л л
h [х(0, 0 « h [х(0, о +'?МхА(0’ [Х(0 - х (ОК (9.39)
д х (t)
Положим также
G [х(0, 0Yw(0Gr[x(0, 0«G[x(0, 0Yw(0Gr[x(0, 0.+
+ [х(0 - х(0]
д
л
Зх(/)
?G[x(0, 0Yw(0Gr[x(0,^]
(9.40)
Подставляя эти выражения в (9.34) и (9.37) и усредняя, получим:
dx (0= f[x (0, 0 dt + V~(0 - h^x(<)’^ Y71 (0 {dy (0 - h[x(0, fl<tt>;(9.41)
5x(O
dV~(0 + dx(0 dxr(0 = { af[x(0, d V~(0 +
1 5x(0
+V~ (t) + G [x (0, 0 'Fw (0Gr [x(0, 01. dt. (9.42)
a x (Г)
*> Это можно получить, разлагая G[x(/), i] в ряд ио условному среднему.
(Прим авт)
М* 419
л
Здесь предполагается, что среднее вектора x(fl—x(fl равно нулю,
л
Подставляя выражение для dx(fl из (9.41) в (9.42) и опуская
члены второго порядка малости, получаем уравнение фильтрации
первого порядка:
Л Л а ь7 /1 Л
dx (fl = f [х (fl, fl dt + V~ (fl чг-1 (0 {dy (fl _ h[x(0> fl dt}.
dx(t) (9.43)
dv~ (fl= I V~ (fl + V~ (fl afr[*(a-fl + G [x (t), t] X
I 3x(Z) dx(Z)
X Yw(flGr[x(fl, fl—V~(fla h? [AX (Z)’ Z] У71 d-[x(Z)’ fl v~ (fl Lfl (9.44)
d x (i) dx(t) J
где нужно учесть, что (dfl2=0; dy(fld£=z(fl (dfl2=0; dy(fldyr(fl =
=^YT(fld/.
Уравнения (9.43) и (9.44) являются приближенными (перво-
го порядка) нелинейными алгоритмами фильтрации. В линейном
случае эти алгоритмы сводятся к уравнениям фильтрации Калма-
на и представляют одцу из форм «линеаризованного» фильтра
Калмана для нелинейного случая. Мы должны ясно представлять,
л л
что уравнение для x(fl нелинейно по x(fl, как и должно быть в
случае действительно линеаризованного фильтра. Иногда целе-
сообразно представить эти алгоритмы в виде
д-^~ = f [X (fl, fl + V~(fl (fl _ h [x (0> fl}; (9.45)
d x (t)
1^12 = (0, t] + v_ + G * x
d x (/) dx (/)
X Tw (fl Gr [x (fl, fl — V~ (fl аьГ[лХ(0' t} 4V1 (fl j9 h^x(Z)’ t] I V~ (fl.
d x (Z) I 3x(Z) )
(9.46)
Тогда их можно интерпретировать как стохастические диффе-
ренциальные уравнения. Отметим, что ур-ния (9.33) и (9.34) были
получены при начальных условиях в момент t0 до наблюдения
с априорно известными средним и дисперсией процесса:
х(А) = £{^(АЯ Z(/o)} =/Т{х(/0)}; (9.47)
V~Ko)= var{x(fl) I ZK0)} = var{x(fl)} = var{x(fl) | Z(fl)}. (9.48)
Рассмотренные алгоритмы сведены в табл. 9.1.
420
Таблица 9.1
Уравнения фильтрации первого порядка в непрерывном времени
Модель сигнала
x=.f[x(Z), Л +G(x(Z), i]w(i). (9.2)
Модель наблюдения
z(Z) = h[x(Z), H+v(0. (9.3)
Априорные данные
HWJO = O; cov{w(0, w(T)) = »yw (t)6D (t~т);
Hv~(0=0; cov{v(0, v(t)} = Tv(0 6o(Z—t);
cov{w(Z), v(-c)} = cov{w(Z), x(Z0)} = cov {v(0> x(t)}=0. (9-4)
Уравнение фильтрации
dx(t) Л dhT[x(t\, Z] , л
—=»[х(0. Н +V~ (Z)---------- ,U 4V1 (0 {^(0— h [x(Z), Z}. (9.45)
U4 х _ 'х
Вычисление ковариационной матрицы ошибок
5.v~(0 df[x(Z), Z] <3fr[x(Z), Z]
~7Г~ = vr +vt (0------------------------------+
d x (Z) dx (Z)
Л т Л dhTIx(Z), Z]
+ G[x(0, t]Tw (0Gr[x(0, z]-v~(z)------------ —-X
dx(Z)
,Л
, Jd h [x(Z), Z] „ ,
x«V <0--------— v~ w• (9-46>
d x (t)
Начальные условия
7 (Z.) = E {x (<0) | Z (/0)} = E {x (/„)}. (9.47)
V~ (Z.) = var (x(Z0) | Z (Zo)} = var {x^)}. (9.48)
Приближение второго порядка. Уравнения (9.34)
и (9.37) являются точными уравнениями для оценки при помощи
условного среднего и ковариационной матрицы ошибок; выше мы
получили приближенные уравнения, используя разложение в ряд
ур-ния (9.38) и подстановкой его в (9.40). Таким же образом
могут быть найдены приближенные алгоритмы фильтрации более
высоких порядков точности. Так, можно получить:
t [X (0, t]« f [X (О, П + at [x^^-7 (0 + -- ; [X (Z)V (01;
dx(t) px(Z)]’ (9.49)
421
h[х(/), «ь[х(t), t\x(() + — 2L221121;[x(/)xr(01;
2 -’Л..... (9.50)
A 2 A
dx(t) [dx(Z)]2
G[x(Z), t] (Z) Gr [x (Z), Z]« G[x(Z), Z] (Z) GT [x (Z), Z] 4-
+ x (t)
rG[x(Z), t] Yw (Z) GT [x (Z), Z]>4-
д 1
A
Ldx(Z) J
4- 2 d^A/), Z]Y: (Z) Gr [x (Z), Z] . ~(0~r (0L
где
(9.51)
[Л (or
что следует из (4.153). Теперь подставим полученные выражения
л
для f, h и GTwG1, в точные соотношения для x(Z) hV~(Z), про-
делаем все указанные операции, опуская члены порядка (dt)z и
выше. В результате полученное уравнение для оценки х будет
таким же, как и в предыдущем (случае. Однако уравнение для
ковариационной матрицы ошибок получить значительно сложнее
из-за вычисления одного члена. Поскольку эта операция довольно
сложна, то без потери общности продемонстрируем ее на при-
мере.
Пример 9Л
Исследуем выражение
Ski = fi{7(Z)^(Z)(h (x(Z), Z] — h[x (Z), Z])r}^71 (t) (dy (Z) — h [x(Z), t]dt),
которое является одним из членов ур-ния (9 37) Используя разложение (9 50)
для h[x(£), t] и предполагая, что моменты третьего порядка равны нулю
=0, получим
г N
S*z = £' {*л(0 *t (Z)
A
d2h[x(Z), z]
dx, (Z) dxj (Z)
т
V~(0 4V1 (Z) dy (t) - h Iх (0 . Z] dt -
л
1 d2h[x(Z), Z]
~ 2 A
(dx(Z)]2
A
d®h (x(Z), Z] .
_------L_L21_L . v_ (a dt
[dx(Z)]2 J
Моменты четвертого порядка (в предположении нормальности плотностей) рав-
ны (см. (4 22)]
E{^(Z)x7(Z)^(Z)7nz)} = [vT(Z)M]{VT(Z)j//4-[vT(Z)U[vT(Z)]w4.
422
Тогда
Sm =
+s4~v~
2
N
S[V~ (Z)v~ (0 + v.
L ik * ij
s
,/=l dxi^dxjit)
dati [x(Q, Z]
Л
[dx(Z)]2
Х'ГГ’К) dy(Z)-h[x(Z), i] dt—
~ «V- (Z)»^ +
* a; " t 1 A A
kl 4 dXi(t)dXij(t)
_J-V_ wnr
it * ь/ I Л X
ы I Px(01»
2
2
•.V~(t)di ,
X
Sh/ =
откуда с учетом (4.13) получаем
i N Л xT
v~ (z)v~ (z)+v~ (Z)v~ (Z)i?*h tx(^’ X
tk ч li М(оД-(о J
x.
, ash[x(z), zi
xT7](z) dy(Z)-h[x(Z), t\dt- — A - =vA(Z)dz .
[dx(Z)p x
Это и есть тот единственный член, который отличает алгоритм решения второ-
го порядка от полученного выше приближения первого порядка.
Используя этот пример, можно было бы найти алгоритм
фильтрации второго порядка аналогично алгоритму фильтрации
первого порядка. Дадим лишь окончательные результаты (см.
табл. 9.2).
Таблица 9.2
Уравнения фильтрации второго порядка в непрерывном времени
(модели сообщения и наблюдения и априорные данные те же,
что и в табл. 9.1)
Уравнение фильтрации
Л Л
dx(t) Л 1 d2f[x(Z), zj
-^2- = f[x(Z), d + v - - --
at 2
dhr [x(Z), Z]
: V~(Z) + V~(Z)-------- - -
x v ' x ' ' Л
(Z) z(Z) - h [x(Z),
[д х (Z)]2
1 d2h[x(Z), Z]
z]__ -^-J.-V-P) .
[dx(Z)]’
5x(Z)
(9.52)
Вычисление ковариационной матрицы ошибок
оУ~(0 at[x(Q, <] „ ... dfr [x(Q, <1
dt ~ Л
Jx(0
dhr [x (t), Z] ,
X -----Л ’ - ~ T71 (Z)
<3x(Z)
v~(Z) + v~(0
3 x(t)
-v~(z)x
v~(Z) + s(v~(Z), x(Z), z] 4-
Л X A
M)
dhHM/), Z]
л
423
Продолжение
Л т Л 1 d2G|x(/), л ‘Pw (0 Gr [х (/), И
+ G [х(О, Л (О GT [х(О, Н + ----------L А ------------L ^’'- =
[5х(0]2
:VT(/). (9.53)
Вычисление тензора l N Л т „ 1 Г d2h[x (/),/] Sft|- 9 7j W+v~ (OV~ (t) J 12 XJ 1 xih lj * kl li ,Л ... Л 1 i, j=i dxt (t) dxj (0 < A i i d2 h [x (И, П xV(0 dy(O-h[x(t), t]dt- lAV’’ ':VT(f)dA. 1 ' [dx(t)l2 ) 1 r 1 X (9.54)
Начальные условия
Л
x(M = £{x(/o)|Z(y} = £{x(/o)}. (9.47)
V~(^o) = var {x(/0) 1 Z(?o)} = var{jT(/0)}. (9.48)
Пример 9.2. Найдем алгоритмы фильтрации для следующей простой нели-
нейной задачи. Пусть сигнал и наблюдение задаются соотношениями:
х——х3(0 +'ю(/); z(t) =x(t) +v(t), где w(t) и v(t)—нормальные белые шумы
с нулевыми средними. Применение соотношений (9.45) и (9.46) дает следующий
результат:
х = — х3 (0 + V~(t) [z (t) -х (0J Yyl (t).
v~= - 6x2(0 vr(Z)-vL(0V (0 + ^(0 •
Уравнения фильтрации второго порядка следуют из (9.52) и (9 53):
х = - х3 (/) + v~ (0 Т71 (0 [г (0 -х (/)] - зх (о vT(0;
v~ = - бх2 (0 v~(t) - v2~ (0 ту1 (0 + (0.
В каждом случае начальные условия задаются в виде известных априори сред-
него значения и дисперсии. Так как модель наблюдения линейна по х(0, то,
как и следовало ожидать, уравнения в обоих случаях одинаковы.
Пример 9.3. Теперь рассмотрим линейную модель сигнала и нелинейную мо-
дель наблюдаемого процесса: х=—x(t) +u(f) +w(t); z(t)=x3(f)+v(t), где u(t)—
известный сигнал на входе. Даже если мы предположим, что шум имеет нуле-
вое среднее, то известный (контрольный) сигнал или ненулевое среднее входно-
го сообщения можно просто рассматривать как составляющую члена
f[x(f), fl, который входит в модель сообщения. Использование обычным образом
приближенных уравнений фильтрации дает следующие соотношения:
х = - х (0 + и (0 4- Зх2 (t) V~(t) 47’ (t) [z (t) - x3 (/)];
424
V~=- 2Г~(0 + (О - Эх4 (О V2~(t) V (О.
представляющие фильтр первого порядка, н уравнения:
X = - х (0 + и (0 + Зх’ (0 V~(0 V (0 [г (0 - х3 (0 -Зх (0 V ~(0];
V~= - 2V~(0 + (0 - 9х* (0 VL(0 Ч71 (0 + 6x(f) vL(0 Y-1 (0 [z (0 _
— x®(0—3x(0 V~(0],
являющиеся приближением второго порядка. Заметим, что наблюдение z(0
входит в уравнение для ошибки. Это происходит в том случае, когда модель
наблюдения нелинейна.
Пример 9.4. Рассмотрим систему с фазовой модуляцией £246]. Здесь типич-
ная для многих систем связи модель сообщения является линейной системой,
управляемой скалярным белым нормальным шумом с параметрами: р.и(0=О;
8{w(t), a>(T)}=4rw(0dD((—т); x=Fx(0+Gw, где
.0“ — Ci ~
.0 с2
<0 1 0 0 . .
— d2 0 1 0 . .
— d3 0 0 1 . .
................1 :
— 0 9 ... .0 cN
Модель наблюдения нелинейна и описывается соотношением z(0=/7sin[<W+
+mxi(0]+v(0, где Н и т— постоянные, а <ос— несущая частота; v(t)—нор-
мальный шум с нулевым средним и интенсивностью 44(0. Модели сообщения
и наблюдения показаны на рис. 94.
C1SN'1+CzSn~2+...+CN
5N^d1sN'^... + dN
'Разовый
модулятор
/01п [щ.1 +тх1 (t)]
Рис. 9.1. Модели фазомодулированного сигнала и наблю-
дения
Рассмотрим уравнения первого порядка для условного среднего. Из (9.45) и
(9.46) находим:
X - (0 “ 11
A A x -F x (0 X - (0 12 H tn д 41 v (0 cos [<oc t mxj (0] {г(0 — H sin [coc t +
w
— X
4-тгх (0]}:
Н2т2
V~= FV~(0 + V~(0 FT (0 + G GT - 5рД0 X
425
v~ (0V~ (0 АЦ A Jj v~ (0V~ (0 . *11 *11 . .Vr (0V~ (0 -
V~(0Vr (t) *1» *11 v~ (OV~ (0 • *11 *11 . .V~(0V~ (0 X*1 xlN
v~ (0 v~ (t) . . . V~ (0V~ (0
x w 11 1W IN _
л
X cos2 [сос t + mxY (0].
В выражении для ковариационной матрицы дисперсий ошибок естественно
оставить только члены, которые медленно меняются по сравнению с несущей
Л 1
частотой. Это ведет к следующей аппроксимации: соз2(шс/ + mxi (f) = —+
1 Л 1
+ — cos[2o)c^+2mxj(i)]« —, нз которой следует, что уравнение для ошибки
2 2 л
может решаться независимо от наблюдения и оценки xi.
Если шум, порождающий сигнал, и шум наблюдения стационарны, то дис-
персия ошибки довольно быстро достигает своего постоянного значения. Соот-
ветствующая структурная схема субоптнмального фазового детектора показана
на рнс. 9.2. Членами с двойной частотой пренебрегаем. Этот демодулятор ока-
Рнс. 9.2. Структурная схема подоптнмального прием-
ника фазомодулированного сигнала
зывается простой системой фазовой автоподстройки.
Для случая, когда х — скаляр, уравнения фильтрации первого порядка при
стационарном шуме запишутся в виде
A A mH А
х = — а х (t) + — V~(t) { z (0 cos [сос t + тх (/)]},
Тр х
где F=—a; G= У2a, а члены с двойной несущей отброшены. Кроме того,
К~ = - 2a V~ (t) + 2афда - —— vL(0 .
х х 2Тр х
Это уравнение имеет стационарное решение
х L2 +V+ аФ0 / J ‘
где отношение HWwIaMv можно трактовать как отношение снгнал/шум S/N,
поэтому
2
rrPS/N
426
_s \2
N J
Пример 9.5. Рассмотрим снова прием одного сообщения в системе с фазовой
модуляцией [246] и моделью сигнала такой же, как и в предыдущем примере.
Однако модель наблюдения в такой системе будет обладать «памятью». Для
того чтобы ввести эту память в уравнение для состояний, мы можем «нарас-
тить» вектор состояний. Таким образом, полагая yo=xt(t) и определяя вектор
размерностью N+1
yT(t) = [л-о (0......xN (/)]г,
можно построить новую модель
y = Fy (0 + Gw (О,
сообщения
Модель наблюдения определяется соотношением
t
сос t -|- т J (Л) d Л
О
z (t) = H sin
+ v (t) = Н sin [<ос t + zny0 (01 + v (t).
Уравнения фильтрации первого порядка можно записать в виде
“ V- (0 -
yoo ' '
„ V- (0
ЛА Нт г/01 ' ' Л
У = Fy (0 + Tv (0 • cos [сос/+ zny0 (/)] {г (0—Н Sin [шс / +
_ W>_
+ "1^о (01);
v~= FVT(0 + F? + G (Z) G? - x
~v~ (0 v~ (0 i7~ (0 v ~ (0 . . (0 „(t) -
yOO'1 У 00 ' z/00' ' z/01 ' ' Z/00V ' // 0/Д '
V~ (0V~ (0 V- (t)V— (0 . . +~ (/)F~ ,(/)
Z/ОГ' у 00V ' z/ОГ ' Z/ОГ ' у or ' yON
''„-«(’’WL
A
X cos2 [шс t + my0 (/)].
Л 1
Используя аппроксимацию cos2[o)<7 + /ny»(Z)]~~, уравнение для дисперсии ошиб-
ки можно сделать независимым от уравнения для оценки.
Если теперь предположить, что шумы стационарны, то тогда существует
стационарное решение уравнения для дисперсии ошибки, а подоптимальную
427
структуру приемника можно представить структурной схемой, изображенной на
рис. 9.3, на котором представлена также модель сигнала с фазовой модуля-
цией.
V(t)
Рис. 9 3. Структурные схемы модели с частотной модуляц-тэи
и подоптималБного приемника
9.3. Оценивание по максимуму
апостериорной вероятности
В предыдущем параграфе рассмотрены оптимальные и
подоптимальные алгоритмы фильтрации с минимумом ковариа-
ционной матрицы дисперсий ошибок Здесь мы изучим методы
оценивания по критерию максимума апостериорной вероятности.
Основное внимание в этом параграфе уделено дискретной модели
оценки. Для непрерывного времени результаты получены в тер-
минах переопределенной модели оценки.
Дискретные модели сообщения и наблюдения определяются
следующими соотношениями б;
х(&+1)'= Ф[х(&), £Ц-Г[х(Л), #]w(£); (9.55)
z (Л) = h [х (k), k] +v (k), (9.56)
где x(k)—JV-мерный вектор состояний; Ф[х(6), k]—JV-мерная
векторнозначная функция: Г[х(6), &]—матрица размером
JVXJW; w(6)—ТИ-мерный вектор шума, входящий в мо-
дель сообщения; z(k)—-7?-мерный вектор наблюдения; h[x(6), k\ —
—7?-мерная векторнозначная функция; v(6)—7?-мерный вектор
шума наблюдения. В случае дискретного времени w(6) и v(6)
являются независимыми нормальными (марковскими) случайны-
о Заметим, что Ф[х(й), А] — нелинейная функция х(£) Если задача линей-
на, то Ф(х(й), А}=Ф(й+1, й)х(й). (Прим, авт.)
428
ми последовательностями типа белого шума с параметрами:
Е {w (k) wT (j)} = Vw (ft) 6/C (k- j); (9.57)
£{v(*)vr(/)) = Vv(£)6/C(*-j), (9.58)
где —j) —дельта-функция, a Vw(6) и Vv (k) —положительно
определенные матрицы ковариаций размерами МхМ и кХк
соответственно
Соотношения для непрерывного времени часто определяют с
помощью нестрогого предельного перехода в дискретной модели,
устремляя шаг дискретизации tk+i—tk к нулю и 4—>-/. Тогда не- прерывная модель определится следующим образом:
x(/) = f[x(/), Z]+<J,[x(Z), /] w (/); (9.59)
z(0 = hl/), fl+v(0. (9.60)
Здесь w(/) и v(/) —статистически независимые белые нормаль-
ные шумы с нулевыми средними и
Е {w (/) wT (т)} = Vw (0 6D (/- х); (9.61)
£{v (/)vr(T)} = Tv(06o(/-T). (9.62)
Коэффициенты в этих уравнениях можно получить с помощью еле-
дующего нестрогого предельного перехода:
f [х (/), t] = lim — {Ф [х (Л), k] — х (&)}; т_^л Т (9.63)
1 —л tlr~t
G [х (/), = lim ~ {Г [х (£), А]}; (9.64)
Т->0 Т
h [х (if), /] = limh[x(£), £]; Т->0 (9.65)
(0 = lim£Vw (6); T->0 (9.66)
Vv (/) = lim T Vv (*). Г->0 (9.67)
tk-^t
Дифференциальное ур-ние (9.59) можно записать в виде сто-
хастического дифференциального уравнения
dx(/) = f [х(/), t] dt -фG [х (t), t] du (/),
где du(^)—винеровский процесс. Соотношения (9.63)—(9.67)
можно получить строго с помощью соответствующих вероятност-
ных операций, подобно тому, как это сделано в гл. 4 и в преды-
дущем параграфе.
Обозначим последовательности х(60), x(£i),...,х(Л/) и z(£i),
z(62),..., z(6r) через Х(^) и Z(fy) соответственно. Аналогично
множество непрерывных значений х(/) и z(t) в интервале [f0, tf]
429
обозначим через Х(//) и Z(7f). Соответствующие условные плот-
ности вероятностей К при условии Z обозначим через
p[X(kf) |Z(kf)] и p[X(tf) |Z(//)]. Далее предположим, что извест-
ны плотности вероятностей р[х(&0)] и р[х(^0)], а именно,
р[Х(^)] и р[Х(/в)] обладают нормальными распределениями со
средними р.х и Vx .
Наилучшая оценка х внутри интервала наблюдения, вообще
говоря, будет зависеть от выбранного критерия качества. Здесь
термин «наилучшая» оценка определяет оценку по максимуму
условной плотности вероятностей р[Х|Z] по функции х, заданной
на интервале наблюдения. Такая оценка называется оценкой
максимума апостериорной плотности вероятностей.
По формуле Байеса
р (X(fy) I Z(b)J = Iх (fyl . (9.68)
p [z (fy)]
Из ур-ния (9.55) следует,что еслих(б) известно,тор[z(&) |х(&)] —
нормальная плотность вероятностей, так как v(k) — нормальный
случайный процесс. Если Х(6/) задано, то
p[Z(.4-,))X(A>f))=^
X ехр[‘~ 4"(z № — h Iх fe)]r№ W (z (fe) — h [X (k), *))|
= П —J----------------------------------T----------------(9-69)
*=*•+> (2л)л/2 det [Vv (k)]2
По правилу умножения вероятностей р[а, р] =р[а| ₽]р[р] полу-
чим, что
p[X(Az)] = p[x(^)|X(V1)]p[x(^-1)|X(^_2)] . . .
. . . р [х (A-J I х(£0)]р[х(£0)].
Так как w(&)—последовательность независимых нормальных,
марковских случайных величин, то х(й) — марковский процесс и
р1х(Аг) | Х(^_1)] = p[x(kr) | x(^_i)].
Таким образом,
/>(Х(М = р[х(У П р[х(/г) | х(^-1)], (9.70)
где р[х(&) [х(6—1)] —нормальная условная плотность вероятнос-
тей с параметрами: средним Ф[х(&—1), k—1] и ковариационной
матрицей Г[х(&—1), k—1]VW(&—1)Гг[х(&—1), k—1].
Поскольку p[Z(kf)] от x(k) не зависит, то ее можно рассмат-
ривать просто как нормировочный множитель при максимизации
условной плотности. После некоторых преобразований выражение
(9.68) может быть записано с учетом (9.69) и (9.70):
p(X(fy | Z(.fy)] = Дехр
1 *f
~Т X И*)-Мх(*)’ <V71(4) -
430
kf
—[ j II**4)-W-ПЛ-ilIlV',.-,,--’
*=*°+1 (9.71)
где А от х(й) не зависит и Q(£) =Г[х(й), £]Vw(£)rr[x(£), fe].
Ясно, что нахождение максимума (9.71) по Х(£/) эквивалентно
минимизации
kf~i
J = + t S llz<4+')-
k=k0
-l,[x(4+lM+l)||2v7i„+1,+-r j] l|»(<v-(ls, <9-72)
с учетом (9.55) и соответствующего начального условия для реше-
ния задачи фильтрации
л г
х(*0) = ИХ(М = J x(«0)p[x(^0)]rfx(^0). (9.73)
--<30
Аналогично максимизация р [X/) | Z (tf) ] эквивалентна миними-
зации
г - у II’ «•> - <« IIV- ‘ + т.( {IIг W - h |х(,)'(| т +
+ 11"(<-‘т}‘" (9.74)
Л
при условии (9.59) и начальном условии х(/о) = fix(t0) из (9.73).
Уравнение (9.72) записано в такой форме, что можно (Приме-
нить дискретный принцип максимума [202]. Гамильтониан опре-
деляется в виде
Н[х (k), v/(k), X (k + 1), k] = -|-||z(£4-1) — I[x(k), w(&),
*+'lirv-,«+o+vliwWllv;'<» 4+
+ Хг(& + 1)Г[х(&), k]'w(k),
где l[x(k), w(£), & + 1] АЬ_{Ф[х(А’), £]-|-Г[х(&), k]'w(k), ^4-1).
Канонические уравнения и граничные условия задаются соотноше-
ниями:
л дН . л
X^ + J l*/)= w+T): M = v~4p(*o)-x(M; (9.75)
431
X(ft | kf) =
' 1 " dx(k)
A »
x(*)=x(fe) I (k})
Х(А/|Л0=О; -^- = 0.
dw (k)
Эти канонические уравнения и соответствующие граничные усло-
вия определяют специфическую граничную нелинейную задачу
второго порядка, решением которой является оценка сглаживания
на заданном интервале. Заметим, что (9.73) не является гранич-
ным условием для задачи сглаживания
В результате алгебраических преобразований получаем окон-
чательно следующие канонические уравнения:
x(ft+ 1 | ft7) = O[x(ft | kt), 6] — Г [ х(& | kf), k]Vw(k) Гг х
X[x(ft | kf), \kf\, (9.76)
X{k 1 | kf) =4>-1 X(k | kf) + ahlLxC* + W’ (k +1) x
dx(fe-f- 1 | kf)
X {z(ft-]-l) — 1 1 kf), ft+1]}, (9.77)
где
ф = d4>r[x(fe|fef), k] + <?[Г[х(б | kf), k]w(k)]T .
d x (k | kf) d x (k | kf)
w(k) = -Vw(k)VT[x(k | kf), 4] | kf).
Л
Решение канонических уравнений для x(ft|ft/) может быть по-
лучено различными способами. Точное решение задачи в нереаль-
ном времени может быть получено способом градиента или квази-
линеаризации [156, 202, 213]
Для того чтобы получить несколько уравнений, которые можно
решать в текущем реальном времени, рассмотрим метод инва-
риантного погружения в текущем дискретном времени [202] и
используем его для нахождения приближенных рекуррентных
уравнений фильтрации.
Будем предполагать, что нелинейная граничная задача второ-
го порядка может быть определена в следующем виде:
x(ft+ 1)= f(x(k), l(k), ft]; (9.78)
X(ft+ l) = g[x(ft)X(ft), ft] (9.79)
с граничными условиями X (ft0) =а, X(ftJ =0
Процесс начинается в точке ft0 и кончается в точке kf. Оценка век-
л
тора состояний определяется так, что x(ft/)=r(C, kf) и отражает
л
зависимость х от конечного шага и от конечного добавочного век-
432
тора. Граничные условия выбираются такими, что Х(А/)=С, где
СЕ(—оо, оо); г(С, kf) теперь обозначают граничное условие, на-
л
ложенное на оценку х(&) для процесса, развивающегося от точки
k0 и заканчивающегося в точке kf и удовлетворяющего условиям
1 (k0) = a; Z, (kf) = 0; г (С + AC, kf + 1) может быть выражена как
г(С + АС, ^+1) = г(С,^) + ^ДС+|1+--^-ДС, (9.80)
О V О kf О V О kf
где 6 г/6 С интерпретируется как матрица первых частных произ-
водных с компонентами, определяемыми следующими соотноше-
ниями:
/б г \ г((С4-ДС;, kf)—г, (С, kf)
\бСЛ/— ’
где АС^ = [0 0 ... ACjO .. 0]. Аналогично <5г/<5£/ есть первая част-
ная производная
/11 'j — r‘^C’ fef+ 1) —fy)
Из (9.79) следует
AC-k(^+l)-X(^)= g[r(C, kf), С, kf]-С, <9.81)
а из (9 78) имеем
r(C+AC, fy + 1) — г(С, ^) = /[г(С, kf), С, — r(C, kf). (9.82)
Подстановка (9 81) и (9 82) в (9 80) и заканчивает процедуру
дискретного инвариантного погружения в дискретном времени
+ + С> ^-с} =
о kf L № о V/ о kf J
= /[г(С, kf), С, ^]-г(С, kf). (9.83)
Эквивалентное уравнение инвариантного погружения в непре-
рывном текущем времени, использованное в [53] и полученное в
более ранней работе [25], определяется и виде
~(ДС.’ Г [г (С, tf), С, ^] = г} [г (С, tf), С, tf],
Otf о с
где соответствующая непрерывная нелинейная граничная задача
второго порядка задается в виде
*(t) = -q[x(t), l(t), Л; *(Л=гЙ)> W), Л
с граничными условиями Х(^о)=а, Х(Л)=0. Процедура погруже-
л
ния определяется так, что х(Л)=г(С, tf) и k(tf)—C. Этот резуль-
тат можно получить прямо из (9.78) и (9.79), уменьшая шаг дис-
кретизации на интервале [&о, kf] и определяя
1} [х (t), X (t), Л = lim {f [х (k), X (k), k] —x (&)} =
T->0 1
tk->0
433
= f [x (t), t]—G[x (t), /] (0Gr [x (О, fl x (0;
Y[x(fl, l(t), fl = lim {g [x (k), K(k)f k — l(k)} =
T-+0 1
tk-^t
= dfr[x(O- <1 x (/) + dhT[x(<). <1 T71 |Z _ h[x (t), fl}+ S,
d x (t) d x (t)
где S — квадратичная форма в X и поэтому в окончательных
уравнениях может быть опущена-
„ _ 1 д S (t) G [х (t). t] 'F-1 (t) GT [x (/), /] 1 (t)
“2 Л
M)
Подробное исследование уравнений инвариантного погружения в
непрерывном времени в различных его формах дано в [202]
Если предположить, что решение ур-ния (9 83) должно быть
получено в виде
г (С, k) = х (6) — Р (А) С, (9.84)
где kj заменено на k, чтобы подчеркнуть тот факт, что kf есть
текущее время, уравнение инвариантного погружения определит-
ся следующим образом
х(£+1) —P(* + l)g[x(4) —Р(й)С, С, Аг] = /[х(^)— Р(£)С, С, k] (9 85)
Поскольку на конечном шаге добавочная переменная равна нулю,
л л
то целесообразно разложить g[x(A)—Р(£)С, С, &] и f[x(£)—
—Р(£)С, С, &] в ряд Тейлора около точки С—0 для того, чтобы
получить следующие соотношения
g[x(£)-P(£)C, С, ^] = g[xp), 0, с- ^[с=С+. ;
/[х(^)-Р(/?)С, С, k\ = f[x(k), 0, fe]+a/[xW Д(*)С’С *1 с=С+ ..
Если предыдущие два соотношения подставить в (9 85) и вычис-
лить С, то получим приближенные рекуррентные уравнения
фильтрации, вытекающие из решения соответствующей граничной
задачи второго порядка
х(^ + 1) —P(^ + l)g[x(ft), O,£] = f[x(fc), 0, k}\ (9.86)
Р (/>+!)
fdg[x(6)-P(6), С, С, k]
д С
с=о
[х — р Gfe) с,с fe]
— ас
с==о
(9 87)
Теперь мы можем решать совместно ур-ния (9 86) и (9 87) при
434
начальных условиях, определяемых соотношениями (9 73), (9 75)
и (9 84)
х (k0) = (*0), Р (k0) = V~ (k0) = Vx (Z>0) (9.88)
и таким образом, получать приближенное решение задачи фильт-
рации Итак, выражения (9 55) и (9 56) определяют нашу дис-
кретную модель, а ур-ния (9 76), (9 77) и (9 86) — (9 88) опреде-
ляют приближенно оптимальный фильтр
Хотя основное внимание в этой главе уделяется исследованию
различных дискретных алгоритмов решения задачи нелинейной
фильтрации, оптимальных по критерию максимума апостериорной
вероятности (М.АВ), целесообразно рассмотреть сейчас прибли-
женный нелинейный алгоритм одношагового предсказания, что в
дальнейшем упростит рассмотрение алгоритмов фильтрации
Рассмотрим задачу максимизации апостериорной плотности
вероятности p[X(kf+ 1) |Z(A)] Мы уже отмечали, что эта задача
эквивалентна задаче минимизации
Л 'Л
J'= X||X(£O)-MMIV-,U)+v Е llz(^-hIx^^Hv7’w +
k; Л
или j'= -h||w(^) ||2v-i(fe/)+J,
где из ур-ния (9 55) следует, что
л л л
r(fe/)w(fe/) =x(kf+ 1)—Ф[х(й/), kf], a J определяется соотноше-
нием (9 72) Если последовательность Х(&/), минимизирующая J,
задана, то J' является минимумом в предположении, что остаточ-
ный член равен нулю В результате имеем уравнение
х (kf + 1) — Ф [х (kf), kf] = 0, (9.89)
л
где х(йг) означает оценку фильтрации на шаге kf. Если положить
теперь, что kf—текущая переменная, то получим приближенный
алгоритм предсказания на один шаг
х(й+1 | &) = ф[х(£), k], . (9 90)
Для того чтобы получить алгоритмы фильтрации, необходимо
вычислить f и g в (9 86) и (9 87) Из (9 76) и (9 77) после алгеб-
раических преобразований следует, что
f(*(k), 0, k] = f[x(kf | kf), 0, Af]| *г* = Ф[х(£), k]= x(k+ 1 | k)-,
g[x(k), 0, £] = g[x(fy | kf), 0, fy]| =
435
=------ghrtx(fe+l I fe),..l+.l.LV71 (k + 1 ){z(k + 1) — h[x(^ + 11k),k +1 ]}.
d x (k + 1 I k)
Это позволяет нам найти уравнение фильтрации
х(^ + 1) = х(й + 1 | £)4-K(6 + l){z(£+1)—h[x(£ + l I k),k+ 1]}, (9 91)
где
К (k + 1) = Р (k + 1) ghrtx(fe+lp). fe+Jl v_ 1 (£ +1
d x (fe+1 I k)
(9.92)
а уравнение для одношагового предсказания дается соотношением
(9 90) Чтобы получить выражение для Р(&+1), заметим, что
л
а/[х (fe) — Р (fe) С, С, fe]
д С
л
д Ф [х (k), k]
P(*)~
— Г[х(&), &]VW (£)Гг[х(£), k]
д х (А)
Л
д Ф [х (A), k]
—Т
Л
d x (A)
N—N (£ + 1)
Л л-Т
д Ф fx (k), k] J
(9 93)
д х (fe) 1
причем N(&+1) мы определим
rfgft(fe)-P(fe)C, С, fe]
д С
несколько позже Имеем также
dhr[x(M-l I fe) fe+1] y_!
d x(fe+ 1 I fe)
I----------------------
Л
д х (k 4- 1 I k)
Л 1-T
ЭФ [x(fe), fe] I
Л I
d x (fe) 1
Определим симметричную матрицу в виде
ahr[x(fe+ 1 I fe) fe+1]
d x(fe +1 I fe)
—h[x(fe4-l | k), k+1
N(£ + l)
Hr(^+ 1)V7‘ (k+ 1)H(*+ 1)= ----
d x(k+ 1 I k)
X Vv'^ + l) jz(* + l) —h[x(£+ 1 I k), /г + 1
Тогда
₽(*+!)= N-'^+l)
д
Л
д x(k 4-1 | k)
hr [x (fe 4- 1 I k), fe + 1]
d x(k +1 I k)
(9 94)
436
X V71 (^+1) z(^+1) —h[x(^ +1 \k, £4- I)j}j .
Применяя лемму об обращении матрицы, из этого уравнения
получим
Р(£ +1) = N(64-1) — N(^+1)H7'(^+1)[H^+ 1)N(£ 4 1)Нг(й 41)4
4-Vv (*4-I)}-1 Н(*4- 1)N(44-1). (9.95)
В подобном виде это выражение предпочтительнее, поскольку об-
ращенная матрица имеет невысокий порядок, вообще говоря, ниже
того порядка, которым обладала матрица в ранее полученном
выражении для Р(&+1) В общем случае Н(£)—функция от
z(&), поэтому операции с этой матрицей не тривиальны
Мы сразу замечаем по аналогии с линейным фильтром Калма-
на и по виду функции риска, что Р(&41) есть (приближенное)
выражение для ковариационной матрицы ошибок V~(#+l) Легко
видеть также, что N(&+1) есть (приближенное) соотношение для
ковариационной матрицы ошибок предсказания V~ (&41|&)
Дискретный алгоритм фильтрации, оптимальный по критерию
максимума апостериорной вероятности, приведен в табл 9 3
Таблица 93
Дискретные алгоритмы фильтрации по критерию МАВ
Модель сообщения
х (k + 1) = Ф [х (k), k] +Г[х(А), 4w(A) (9 55)
Модель наблюдения
z(£) = h[x(£), A] -|-v(A). (9 56)
Алгоритм фильтрации
х(А 4-1) = х(Л41 | k) +К(й+ 1) {z(A 41) — h[x(A + 1 | k), k 4-1]} (9 91)
Априорные моменты
Рх(М=Рх/ Vx(^o) = Vxo’
(А) =0, cov{w(A), w(/)} = Vw(A)6K(A— j),
jxv(A) = O, cov{v(A), v(/)}= Vv(A)6K(A —/),
cov{v(A), w (/)} = cov {v (k), x (A)} = cov {w (k), x(&o)}=O, k > ka
Алгоритм одношагового предсказания
x (A 4-1 [ A) = Ф [x(A), A] (9 90)
Вычисление коэффициента усиления
K(*41) = V~(6 4 1) а [Х (д+ 1 1 :-Л +— V71 (fe 4 1) (9 92)
д х (k 41 I Л)
437
Продолжение
Вычисление априорной матрицы ковариаций ошибок
дФГх(й), k\ д Фт [х [(А), А] т
V~(k + 1 I k) =-----—L + Г (k) V (k) VT (k).
X A X /\
<3 x (k) dx (k)
(9 93)
Вычисление ковариационной матрицы ошибок
V~(A + 1) = N~(k +1 | k) — V~(A + 1 | k)HT (k +1) [H (k +1) X
XV^(/i +1 | fe)Hr(A +1) +Vv(A +1) H(fe+l)Vr (A + l | k) (9 95)
Вычисление матрицы наблюдений
/ т Л
т , —д /дЬг[х(й-|-1 | k), А + 1]
нг (k +1) V71 (k +j7H (k +1) = —------------ ----~ ~ х
д х (k +1 | k) \ д х (k + 1 I k)
X V71 (k + 1) {z (k +1) - h [x (k +1 P), k +1J} j . (9 94)
Начальные условия
х№) = Их0; v~№) = vXo. (9 96)
Интерпретация этих алгоритмов аналогична калмановским
дискретным алгоритмам фильтрации (см. табл 7 2).
Алгоритмы фильтрации в непрерывном времени, оптимальные
по критерию МАВ, даны в табл. 9 4 Они получаются из дискрет-
Непрерывные алгоритмы фильтрации Таблица 94 по критерию MAB
Модель сообщения x = f[x(0, tj +G[x(Z), <}w(t). (9 59)
Модель наблюдения x(0 = h[x(Z), Z] +v(Z). (9 60)
Априорные моменты Их Ро) = Рх7 Vx (Zo) = VXo; Pw (f) = °- co' <w (() • w (T)} = (() — pv(0 = 0; cov{v(Z), V(T)}= 4»v (Z)6D (t—t), cov{v(Z), w p)} = co< {v p) , X P)} = COV {w P), Xpo)} = 0
438
Продолжение
Алгоритм фильтрации
Л Л dhr[x (П, tl Л
х (t) = f [х (/),/] + Vr(t)---1 U’ 1 4V1 (t) {z (t) - h [x (t), m. (9.97>
A A
dx(Z)
Вычисление ковариационной матрицы ошибок
df [х(П, /1 dtT [х (t), /1
V~(t) = л ------л + x
dx(t) dx(t)
(9.98}
Начальные условия
v^(«=vx„-
(9.99}
ных соотношений путем устремления шага дискретизации к нулю
или же с помощью непрерывного принципа максимума с использо-
ванием (9.74), (9.59) и (9.60) [53, 202]. Оба алгоритма фильтра-
ции как дискретный, так и непрерывный являются точными толь-
ко в том случае, если модели сигналов и наблюдений линейны.
Пример 9.6. Рассмотрим простую для целей численного расчета дискретную,
модель оценки второго порядка Положим, что модель описывается следующи-
ми соотношениями
х’х (^ “Ь О — xi (£) Тх2 (k)', х2 (k -j- 1) — х2 (k) -f- Tw (k)',
z(k+l) = arctg [Xi (k + 1)] + v (k + 1),
где 7=0,001 Применяя дискретный принцип максимума, получим
вариант нелинейной граничной задачи второго порядка-
следующий
Х1 (^ + О = xi W + ?х2 (к);
х 2 (k + 1) = х2 (k) + T2VW (k) [Т At (k) - Л2 (A)];
A 2 (k -f- 1) — A2 (k) T Aj (k).
Уравнения фильтрации определятся соотношениями
х1(А+1) = О(А) +
V- (k + 1) {г (k + 1) - arctg (D (А)]}
M*+l)[l +W)1
Л Л V- (А+ 1) {г (А+1)-arctg [О (А)]}
х2 (k + 1) = х2 (k) + yo(k+l)[l+D^(k)]
439
V~ (k) + 27V~ (fe) + (k)
v (bj_l) =----------—-----------—-----------—--------- •
1+.M(fe)p~(fe) + 27V~ (fe)-j-T’V —(fe)]’
(k) + TV~(k)
R~ (fe+ 1) =----------------—----------—-------------------- '
**• ’ ’ 1 + M (fe) [7 ~ (fe) + 27V~ (fe) + T27~(fe)] ’
V~ (k + 1) = V~ (fe) + T27w (fe) - V~ (k + 1) fM (fe) Г V (fe) + 7V~ (fe)] } ,
xti xn xit I L xis x*i
где
P (fe) — л"1 (fe) + Tx2 (fe);
1 + 20 (fe) [z (fe + 1) — arctgO(fe)]
Jvi (ft) =---------------------------------- .
70(fe+l)[l+P*(fe)]2
Для белого шума дисперсия состояния Xi становится «бесконечно» боль-
шой. Это легко понять, поскольку непрерывным аналогом для модели сигнала
является двойной интегратор. Таким образом, величина xt может безгранично-
расти в случае больших Т, (ее знак зависит от частных значений последова-
тельности ш), а скорость роста зависит от относительной величины V® и Т. Для
шума модели с небольшой дисперсией и 7=0,001 действие входной нелинейнос-
ти (арктангенса) проявляется незначительно внутри интересующего нас интер-
вала наблюдения Поэтому целесообразно рассматривать модель как линейную.
Для шума модели с большой дисперсией модель наблюдения даже внутри ин-
тервала наблюдения становится существенно нелинейной, и вся система стано-
вится практически необозримой
На рис 9 4 приведены кривые приближенных дисперсий ошибок для раз-
личных значений Vu и Vv Для сравнения приведены дисперсии, полученные
Рис. 9.4. Приближенные дисперсии ошибок фильтрации.
a) Xi
/ —100 J 1"^ = 0,0|[, |Vo = 900|; 2 — 1000 XV~ 1^=90], |Vp = 0.001 |; 3 - линей'
ное наблюдение.* 100 XV~ |1/[и = 900|, | Vv= 0,01 |; 4 — V ~ | V& = 9000|, | ур=0,1|;
б) х2-
'-v722; 1^= “N- I 2-10хЧ,> 1^=901- Ич=0'0011; з-лиией-
V ~
ное наблюдение: |va)=900|, | Уо= 0.01|; <----уу~ , \v,u, = 9000|) | Ур=0.11
440
при замене arctgxj на Xi при Уш=900 и У®=0,01. Значения дисперсии ошибки
при линейной фильтрации достаточно близки к десятикратным значениям дис-
персий ошибок для нелинейной модели, в которой шумы модели сигнала и на-
блюдения в десять раз меньше, чем в линейной. При больших значениях V»
и Vv ошибки фильтрации в нелинейной модели становятся больше ошибок в
линейной системе, полученной заменой arctg Xi на xt В нелинейной системе дис-
персия ошибки не достигает какого-то постоянного установившегося уровня. По
мере увеличения амплитуды xi способность модели отражать изменения Xi па-
дает и, следовательно, возрастает ошибка фильтрации
Пример 9.7. Теперь рассмотрим задачу оценки постоянного параметра а
в модели x(4+l)=ax(4)+tia(4). При этом наблюдение z(k) =x(k) +v(k). Мо-
дель сообщения можно переопределить, полагая a(k+l)=a(k). Это соотноше-
ние описывает эволюцию постоянного параметра а и определяет дополнитель-
ный вектор состояний параметра, который должен быть оценен. Таким обра-
зом, имеем [x(k)=Xi(k), a(k) =Xi(k)];
х1(4+1) = х2(4)х1(4) + ш(4); х2(4 +1) = х2(4); z(k)=x1(k) + v(k).
Тогда
Гх2 (k) х, (4)"| - Г1 1
Ф (лг(Л), 4] = 2 7 7 ; Г[х(4), 4] = ; h[x(k), 4] = хх(4).
L *i (я/ J u J
Используя табл 9 3, найдем следующие алгоритмы фильтрации
Л Л Л
A (k + 1 | k) = х2 (k) xt (k);
*2 (4 + 1 | 4) = x2 (k);
x1(4 + l) = x1(4 + l I £) + V~ (* + DlT (k + 1) [z(k + 1) - xt (k + 1 I 4)];
x2(4+l) = x2(4+1 I k) + V^ (k + l)V~l (4 + 1) [z (4 + 1) — x^(4 + 1 I 4)];
И- (4+1) = xl (4) V~ (4) + 2x^(4) V~ (4) + x* (4) V~ (4) + Vw (4);
*11 *11 *12 *22
v~t (k +11k}=(k) vxt (k) + **(k) (k)i
(4 + 1 I 4) = V~ (4),
*2 2 *2 2
(4+l)=V~ (4+1 I 4) — Y (4 + 1) (4 + 1 | 4);
(4 + 1) = Г~ (4 + 1 | 4)-T(4 + l)V~ (4+1 | 4) V~ (4+1 | 4);
(4 + l) = V~ (4 + 1 | 4)-Y(4 + l)V~ (4 + 1 | 4),
где
V~(4+l |4) + YP(4 + I)’
Л Л
Решением этих уравнений служит оценка параметра [х2(4)=а(4)] и вектора
состояний На рис 9 5 представлены типичные экспериментальные зависимости,
полученные в результате использования этих уравнений Для того чтобы под-
черкнуть, что нормальное распределение не необходимо для того, чтобы можно
было пользоваться методом наименьших квадратов, в качестве шума в экспери-
менте были взяты «неизвестные» по форме функции, которые на самом деле
441
представлялись треугольными по форме колебаниями с нулевой постоянной
составляющей. Напомним, что для любых w (k) и v(k) можно воспользоваться
методом наименьших квадратов для вычисления J в (9.72). Однако только в
Рнс.' 9.5. Совместная оценка состо-
яния н параметра системы перво-
го порядка в шуме:
1 — a(kT)\ 2 — a(kT); 3 — x(kT)-,
4 — x(kT) -, T=0,05, V„=Va = 0,5,
Л I 2 1 I
а(йо)=0,5, Vx(*o)= . J
том случае, когда w(k) и v(k) имеют нормальное распределение, мы получим
оценку по критерию максимума апостериорной вероятности.
9.4. Соотношения между нелинейными
алгоритмами фильтрации
В предыдущих двух параграфах получены точные алго-
ритмы нелинейной фильтрации по условному среднему или по
минимуму ковариационной матрицы ошибок и алгоритмы, опти-
мальные по критерию максимума апостериорной вероятности.
В каждом случае точные алгоритмы, вообще говоря, представ-
ляются бесконечно-мерными цепочками уравнений. Однако при
помощи различных аппроксимаций были найдены конечно-мерные
вычислительные алгоритмы.
Непрерывный алгоритм фильтрации при помощи условного
среднего был получен решением условного уравнения Фоккера —
Планка. Фильтр, реализующий максимум апостериорной вероят-
ности, в общем случае является дискретным фильтром, посколь-
ку плотность вероятностей p[X|Z], при помощи которой и были
получены эти алгоритмы, не существует при неограниченном
уменьшении шага дискретизации. Поэтому возникает вопрос о
математической корректности полученных результатов, включая
вопросы использования стохастических дифференциальных урав-
нений в случае алгоритмов МАВ, непрерывных во времени. В гл. 4
мы уже обсуждали подобные трудности.
Точная оценка по условному среднему удовлетворяет следую-
щему соотношению:
<1х(0 = Пх(0, /]Л+£{[х(0— х (/)] hr [х (/), /] I Z(/)}X
442
X VTJ(O{dy(O — h[x(fl, t]dt}, (9.100)
которое было получено из уравнения Фоккера-Планка или эквива-
лентного ему соотношения
л л л л
dx(fl=f[x(fl, fl^+K[x(fl, fl{dy(fl — h[x(fl, t]dt}, (9.101),
где
K[x(fl, fl = £{[x(fl-x(/)](hr[x(a fl-hr[x(fl, fl} | ZfflJHV1 (fl.
Эти два соотношения объединяются теоремой проецирования для-
нелинейных непрерывных процессов (x(Z)—оценка условного,
среднего)
л
£{x(flhr[x(fl, fl} = 0 (9.102}
или эквивалентными соотношениями:
Е {х(XJ гт (Х2)} =0, Xj > Х2;
£{x(X1)Zr(X2)}-0, (9.1031
где введенный выше оператор условного среднего равен
h[x(fl, fl = £{h[x(fl, fl | Z(fl}.
Линеаризованный фильтр Калмана. Линеаризо-
ванный фильтр Калмана является эвристическим обобщением ре-
зультатов ранней* работы Калмана и Бьюси [111], рассмотренной
в гл. 7, и представляет собой фильтр с минимумом ковариацион-
ной матрицы ошибок, основанный на линеаризации по заданной
траектории. Предположим, что дифференциальное уравнение за-
данной траектории xn(t) описывается соотношением (9.1), в кото-
ром положено w(fl=0. Если отклонения вдоль заданного наблю-
л
дения 6z(fl=z(fl—zn(i), где zn(t) =h[xn(fl], и отклонения от
заданной траектории 6x(fl достаточно малы, то оценка 6х(/)
определяется следующими соотношениями:
л л т 1 л
б х (fl = F (fl 6 х (fl + v6~ (fl Нг (t) Y?1 (t) [6 z (fl - H (fl б к (fl]; (9.104)
V67 (fl = F (fl V6~ (fl + Ve~ (fl Fr (fl - V6~x (fl Hr (fl Y71 (fl H (fl VeT(fl +
+G [xn (fl, fl (fl GT [xn (fl, fl (9.105}
с начальными условиями 6x(/o)=O и Ve x(fl) = Vx< . F(Z) и H(fl
определяются соотношениями:
л л
F(fl = H (fl= 9 h (Xn W’. (9.106}
d *n(t) d xn (fl
443.
Полная оценка состояний равна
Л Л Л
х(0 = хп(0 + 8х(0, (9.107)
’Л
где хп(/о) =Цх(^о) —есть априорное среднее процесса х(/).
Для удобства сведем алгоритмы линеаризованной фильтрации
Калмана в табл. 9.5. Аналогичным образом полученные соответ-
ствующие линеаризованные дискретные уравнения фильтрации
представлены в табл. 9.6.
Таблица 9.5
Линеаризованный фильтр Калмана в непрерывном времени
(модели наблюдения и сигнала и априорные данные те же, что и в табл. 9.4)
Заданная траектория
АЛ Л
Xn = f[*n(0> Л’. *п Оо) = Оо) •
Заданное наблюдение
Zn0) = h[xn0), /]•
Линеаризованная модель сигнала
Л
df[xn(O,/] Л
8.x = г х (/) _]_ G [xn (t), /] w (/).
3 xn (/)
Линеаризованная модель наблюдения
Л
д h [хп (/), Л
« Z (о =--- д (0 + v 0) •
дхп(0
Линеаризованный алгоритм фильтрации Калмана
• Л / \
Л И[хп(П, /1 Л / дЬ[хп(Л, f] Л ।
8х = x(Z)-^O) 8z(f)-— Л 8 х (0 .
дхп(/) \ 5хп(0 /
Линеаризованный алгоритм вычисления коэффициента усиления
т Л
X М = v6 Т (/) д Ь-[дП-(-—--1- 4V1 (0.
Зхп(0
Линеаризованный алгоритм вычисления ковариационной матрицы ошибок
фильтрации
Л т Л
<х Л б X ' ’ “ б X ' ' Л
dxn(t) 3xn(t)
444
П родолжение
- _(()ю v „ +
dxn(t) d*n(J)
+ G[xn(t), /].
Начальные условия
8x(/o) = O; Vg T(Q = VXo.
Полная линеаризованная оценка вектора состояний
Л Л „Л
x(Q = xn(f)+6x(/).
Таблица 9.6
Дискретный линеаризованный фильтр Калмана
(модели сигнала и наблюдения и априорные моменты те же, что н в табл. 9 3)
Заданная траектория
х»* (Л-J- 1) ==Ф[хп(£)> &]>’ хп (М = ^х0-
Заданное наблюдение
zn(£) = h [хл (k), k].
Линеаризованная модель сообщения
дф [ xn (k), k] Л
5х(*+1) =-------- - 8x(fe) +Г[хп(й), t]w(4).
д хп (k)
Линеаризованная модель наблюдения
Л
д h ]xn (A), k]
8z(*)=-----' 8х(А) +v(fc).
6 хл (k)
Линеаризованный алгоритм одношагового предсказания
Л
Л дФ[хп(й), fe] Л
« х (k + 1 | k) =-L^-~ 8 х(й).
д хп (й)
Линеаризованный алгоритм фильтрации
8>(* + l) = 8x(* + l I k) +К(Л +l)(8z(fe +1) - dh[Xn^- +-1)’ *+И х
dxn(* + 1)
Х8х(Н1 I ^))-
445
Продолжение
Линеаризованный алгоритм вычисления коэффициента усиления фильтра
" 1 ’ б х' 1 ’ Л V ' > >
dxn(k + 1)
Линеаризованный алгоритм для априорной матрицы ковариаций
Л т Л
дф[хп(£), kl d(Jr[xn (£), &1 Л
ve +1 । k) = ’’ 1 v6 ~ (k)----+ Г [Хп (А)> k]
д xn (k) д хп (k)
X Vw (fe) Г [х„ (k), fe].
Линеаризованный алгоритм вычисления матрицы ковариаций ошибок
т Л
, dhr[xn (£4-1), k +11
|fe)------ л -----------L
Ол и л ил f\
5xn (k + 1)
f 3hr[xn (A 4-i), fe +1} v . 5hr[xn (fe + 1), k +1)
X ----------------------V 4-1 I k)-------------------------- +
\ dxn(*4-l) dxn(*4-l)
\ A
+ V, (t + 1Г' + Ve _+11 *).
/ dxrt(fe4-l)
Начальные условия
8x(feo)=O; V6~(^)=VXo.
Полная линеаризованная оценка вектора состояний
Л Л Л
х(0 = хп (0 4-8 х (0.
Расширенный фильтр Калмана. Предполагая, что
оценка по условному среднему известна, можно .получить различ-
ные алгоритмы фильтрации в непрерывном времени. Разлагая
функции модели сообщения и модели наблюдения в ряд Тейлора
л
около точки х(0=х(0, можно получить ряд линейных уравнений
относительно х(0:
« f [х(0, 04- -дПхл(<)'-1 [х (0 - х(0] 4-G [х (0, 0 w (0; (9.108)
Си А
д х(0
Л Л Л
z(0 = h[x(0, 0 +£М1Ш1[х(0-х(0)4-у(0. (9.109)
д х(0
446
Сравнивая эти модели сообщения и наблюдения, видим, что в ос-
новной модели
= F (О X (О + G (О W' (0 + U (0; (9.110)
z(0 = H(0x(0+v(0 + y(0- (9.111)
Теперь известны входной сигнал и возмущение:
и (о == f [X (0, /] - g f Z1 X (0; (9.112)
У (0 = — д ь (ХЛ(0’ П • X (0 (9.113)
3 х(<)
и линеаризованные матричные коэффициенты:
F (Z) = df(x(<). 01. G(0 — G[x (t), 0;
d x(/)
Л
H (/)= dh[x(<), <]
M),
Определение фильтра Калмана тривиально. Используем просто
соотношения:
л
= f (/)х (0+ж (0 [Z (0 - н (0 X (01 - УЙ01 + 11(0; (9-114)
dV~(0
= F (0 v~ (0+V- (0 Fr (0 - v~ (0 нг (0 У7* н (0 v~ (0+
+ G(0 ЧМ0°Т(О, (9.115)
учитывая предыдущее определение величин F, G, Н. В результа-
те оказывается, что расширенный фильтр Калмана в непрерывном
времени совпадает в точности с фильтром первого порядка, при-
веденным в табл. 9.1.
Дискретный расширенный фильтр Калмана может быть полу-
чен точно так же, как и аналогичный фильтр в непрерывном вре-
мени. Он представлен в табл. 9.7.
Таблица 9.7
Расширенный дискретный фильтр Калмаиа
(модели сообщения и наблюдения те же, что и в табл. 9.3)
Алгоритм фильтрации
Л Л Л
х (fe + 1) = х (fe + 1 | k) + K(fe +0{z(fe + l)-h[x(A + l |fe), fe + 1]}.
447
Продолжение
Алгоритм одношагового предсказания
х(4 + 1 I k) = Ф[х(4), *}.
Алгоритм для априорной ковариационной матрицы ошибок
Л _ Л
ЗФ[х(4), 4] ЗФг[х(4), 4] Л
V~(k + 1 | k) =----Л V~(k)--------------.......+ Г[х (k), 4] Vw (k) X
d x (k) d x (k)
X Гг[х(4), 4].
Алгоритм вычисления ковариационной матрицы ошибок
т Л
д 1г [х (k + 1 | k), k 4-1]
V~(4 + 1) = V~(4 +1 I k)-V~(k +1 I k)----1 .X
dx(4 + l | k)
/ A „ A
ah[x(* + i I k), й+i] 3hr[x (Л + 1 I *), 4 + 1]
X ---------- V~(4 + 1 | 4) - +
\ dx(4 +1 | 4) 3x(4 +1 | 4)
+v,lt + 1)-yi'|.A<» + .|».t+.lvr(t + 1, t).
/ d x (4 + 1 | 4)
Вычисление коэффициента усиления
К (4 + 1) = V~(4 + 1)"| ——+ 1 1 ’ * + 1]- VX- (4 + I).
/ dx(4 +1 I 4)
Начальные условия
x(40)=gx,; V~(4o) = VXe.
Однако дискретный аналог непрерывного во времени нелиней-
ного фильтра первого порядка получить нельзя. Причиной этого
является то обстоятельство, что для дискретных систем не доказа-
на теорема нелинейного проецирования и поэтому нельзя ис-
пользовать подход с помощью уравнения Фоккера — Планка. Все
же при некоторых ограничениях можно получить приближенные
конечно-мерные вычислительные алгоритмы, используя уравнение
Фоккера — Планка (9.109) или теорему проецирования (9.101).
Приближенная дискретная фильтрация при
помощи условного среднего. Используя теоремы об ус-
ловном среднем и условной дисперсии, приведенные в гл. 4, мож-
но получить несколько приближенных алгоритмов фильтрации.
448
Из (4.26) для нормальных 'случайных величин аир следует, что
Е {« I 0} = Ца + Vaf5 V₽-' (0 - J*p) ; (9.116)
var{a|P) = Va-Va3Vp-’Vpa. (9.117)
Из (9.116) и
р [х (А) | Z (£)] = р [х (&) | z (£), Z(k — 1)] (9.118)
находим условное среднее
х(#) = £{х(/г) | Z(^)) = £{x(^) | Z(%— 1), z(£)} =
— £{х(й) | Z(£— l))+cov{x(&), z(£) | Z(£— 1)} x
X var-1{z(£) | Z(£— 1)} fz(£) —£{z(£) ] Z(£— 1)}].
Учитывая определение моделей сигнала и наблюдения и замечая,
что
h[x(£), .£] = E{h[x(£), k]Z(k — l)) = E{z(£) | Z(A— 1)};
A
x(A | k— l) = £{x(£) | Z(£ — 1)},
оценку по условному среднему можно выразить следующим соот-
ношением:
л л
х(£) = х(& | k — l)4~cov{х(£), z(&) | Z(k — 1)} х
X var-1{z(£) | Z(k — 1)} {z (£) —h[x(£), £]}. (9.119)
Легко видеть, что член, управляющий процедурой оценивания,
представляет «обновляющий» процесс. Однако нужно заметить,
что (9.119) есть только приближение в нелинейном случае, так
1 ак соотношение (9.116) верно только для нормальных процессов.
Используя аналогичную теорему об условной дисперсии [см.
(9.117)] и учитывая (9.118), можно получить
var{x(£) | Z(6)} = var{x(£) | Z(k — 1)) — cov{x(£).
z(£) j Z(fe—1)}var""1 {z(£) | Z(k—l)}cov{z(£), x(fe) | Z(k—1)}.
Так же как и в предыдущем случае, это выражение верно только
для нормальных случайных процессов. В гл. 7 отмечалось, что
V~(£) = var {х(£) — х(&) | Z(fe)}= var{x(&) j Z(b)}t
поэтому оценка по условному среднему—несмещенная. Кроме того,
V~(& ] k — 1) — var {х(&)— х(/г | k — 1) | Z(k — 1)) =
= var(x(£) [ Z(k—1)),
откуда следует приближенное соотношение для ковариационной
матрицы ошибок фильтрации:
V~(A) — | i— 1) — cov{x(&), z(%) ] Z(k— 1)} x
15—26 449
X var-1{z(A) I Z(k — l))cov{z(£), x(k) | Z{k — 1)}. (9.120)
Итак, ур-ния (9.119) и (9.120) являются приближенными урав-
нениями дискретной нелинейной фильтрации по условному сред-
нему и соответствующей ковариационной матрицы ошибок. Для
того чтобы этими алгоритмами можно было пользоваться, необхо-
димо найти выражения для cov{x(£), z(£)|Z(£—1)},
var(z(£) |Z(£—1)}. Поскольку задача в общем случае нелинейная,
точные выражения найти трудно и поэтому приходится использо-
вать приближенные соотношения.
Приближение первого порядка для ковариационных матриц
может быть получено разложением в ряд Тейлора функций Ф и
h в окрестности оценки фильтрации и отбрасыванием членов по-
рядка малости больше первого
Ф [х (Л), k\ « Ф [х(A), k\ + d<t>[x(Z;)’ [х (6) — x’(t)h (9.121)
д х (k)
h [X (Л), k]« h [X (k I k — 1), A] + [x(k)—x (k I k— 1)].
d*(k\k-1) 1(9.122)
Теперь используем приближение первого порядка для rvwrr в
л
окрестности оценки х(£):
Г[х(£), &]VW (£)Гг[х(£), 6]«Г[х(£), £]VW(А-)Г^х(Л), k] +
+ [x(^)-x(^)i
Л _ Л
Г[х(А), £]¥„(£) Гг[х(£), k\.
(9.123)
Это дает возможность приближенно вычислить ковариационные
матрицы:
cov{x(£), z(k) | Z(k — 1)} = cov{x(£ | Л — 1), h [x(£), A1] | Z(t — 1)} «
т Л
« V~ (k I k— 1)dh ; (9.124)
d x (k | k—1)
var{z(£) | Z(k — 1)} = var{h(x(£), k] | Z(k — 1)} +
A T A
, r z,,, d h [x (k | k — 1), k],, i , ,. 5h' [x (k | k— 1),k 1 , ,,.
+ var{v(£)} ==----| k— 1)------------------------!—1—!----’—+\lv(k).
dx(k\k — 1) 5x(*| As — 1) (9.125)
Для того чтобы закончить вычисление фильтра первого порядка,
необходимо получить выражение для априорной матрицы ошибок,
что легко сделать, используя разложение в ряд
(k | k — 1) = var {x(£) | Z(k — 1)} = var{x(£) | Z(k — 1)} —
= var{®lx(£— 1), k— 1] + Г[х(Л— 1), k— l]w(£— 1) | Z(k— 1)}=
450
л -Л
_ ЭФ[х(А-1), А-1] „ ,, 1Ч дФг[х(Е-1, А— 1] ,
Л х Л '
д х (А — 1) д x(k— 1)
4-Г[х(А—1), k — 1] Vw(6 — 1)Гг[х(А — 1), 6—1]. (9.126)
В табл 9 3 приведены алгоритмы фильтрации первого поряд-
ка, которые полностью эквивалентны дискретным алгоритмам рас-
ширенного фильтра Калмана Интересно, что использование
\р ния (9 120) устраняет необходимость применения леммы об
обращении матрицы для нахождения эффективной вычислитель-
I ой формы уравнений для дисперсий При уменьшении шага дис-
кретизации эти алгоритмы переходят в алгоритмы расширенной
фильтрации Калмана в непрерывном времени или в аналогичные
алгоритмы фильтрации первого порядка по условному среднему
[см табл 9 1] Заметим также, что эти алгоритмы очень близки
к алгоритмам дискретной фильтрации по критерию МАВ (см.
табл. 9.3).
Аналогичным образом можно получить приближение второго
порядка, удерживая в разложении Ф, h, rVwrT члены второго по-
рядка малости:
Ф [х (6), 6] = Ф [х (6), 6] + х (6) +
д х (А)
Л
+ 2-Э2ф^х^’?1 х(£)хг(6); (9.127)
2 Рх(А)]2
h[x(6), A] =h[x(6 | k— 1), A] + ah[^(fe|fe~1),fe]x(fe | k —1)4-
dx(k | k— 1)
4- — d2Hx(A|A-l), A] । k_^~T(k । k_ (9.128)
[3 x(A | k — I)]2
Г[х(А), k]Vw (А)Гг[x(A), А] = Г[х(А), A]Vw (А)Гг[x(A), £]-]-
. Г 3 у л т л
+ hrTTj Их (A), A]Vw(A)rr[x(A), A] 4-
fA T A
4- — ^Пх(А), A] Vw (А) Гг [x(A), A] ~(*~r (9,129)
2 (dx(A)]2
Выражения для ковариационных матриц ошибок получаются в
предположении, что все третьи моменты равны нулю н, кроме
того, используются четвертые моменты нормальной случайной
величины. В примере 9.1 рассмотрена процедура вычисления этой
величины для непрерывного случая. Однако непосредственное ее
15* 451
Таблица 9.8
Дискретные алгоритмы фильтрации второго порядка по условному среднему
(модели сообщения и наблюдения и априорные моменты те же, что и в табл. 9.3)
Алгоритм фильтрации
х(А н- 1) = х(Аг +1 I k) + K(fe +1) z(fe + l) — h[x(fe + 1 I k), fe + 1] —
Алгоритм одношагового предсказания
Л Л 1 32®[x(fe), fe]
x(fe + l |fe)=<D[x(fe), fe] +----Ш------:V~(fe).
i+w
Вычисление коэффициента усиления
, dhr[x(fe+ 1 | fe), fe + 1] ,
К(fe +1)= V~(fe + 1)------1 V7l (k +1).
d x (fe +1 | fe)
Вычисление априорной ковариационной матрицы
d®[x(fe), fe] 5®r[x(fe), fe] Л
V~(fe + 1 | fe) = —— - V~(fe)----------- ; ; + Г [X (fe), fe] vw (fe)X
3 x (fe) d x (fe)
>|+ 1 gn+). +S(t).
2
Вычисление ковариационной матрицы ошибок
dhr [х (fe +1 |fe), fe + 1]
V~(fe + 1) = V~(fe + 1 I fe) — V~ (fe + 1 I fe)-----1 X
d x (k + 1 | fe)
( dh[x(k + l |fe), fe + 1] 5hr[x(fe + l |fe), fe+1]
X | --------;---------------- V~(fe +1 1 л г
d x (fe +1 | fe)
dx(fe +1 | fe)
\ dh [x(fe + 1 |fe), fe+1]
+ Vv(fe + 1)+S(fe+1 |fe) —Л—-—^V7(fe + 1 |fe).
ax(fe +i | fe)
Вычисление тензора
S(^ + H^)=V J] {[ vt(*+1 I VT(fe + l I fe)]// +
452
П родолжение
+ v7(, +11 Ч.г[v~(ft +1 ] %}-^htX(fe+1|^fe + 11 X
d [х (ft 1 I &)]> д [х (ft + 1 | k)]j
d2hr[x(fe +1 I ft), fe + 1]
<?[x(ft + l | ft)]ftd[x(ft+ 1 I k)]t
N
B<«-T X ([V7<‘>MVr»]<, +[VT'‘»t;l',T?<»l,I)x
Z, /, I, m=l
^O[x(ft), ft] d2(pr[x(ft), ft]
d [x (ft)]z d [2(ft)]; d [x (ft)], d [x (ft)]m
Начальные условия
x(*o I ko) = м~; vr(ft01 ft0) = v
xo X X(
использование представляется довольно сложным Поэтому мы
даем в табл 9.8 лишь результирующие дискретные алгоритмы
фильтрации второго порядка по условному среднему. Заметим,
что эти уравнения при увеличении частоты дискретизации не пере-
ходят в непрерывные алгоритмы табл. 9.2, хотя разница между
ними невелика.
Хотя теорема об условном среднем, примененная к ур-нию
(9.119), несправедлива в случае дискретного времени, для нели-
нейной задачи в непрерывном времени она справедлива. Исполь-
зуем результат одношагового предсказания
x(k | k — 1) = Е{х(&) | Z(£ — 1)} = Ф[х(£), k] (9.130)
и соотношение между дискретной и непрерывной системами [см.
(9.63)]:
f [х(0> fl = Ит-1-{Ф[х(А), k] — х(«)}.
Tk-+0 Тk
tk~+ t
Тогда при увеличении частоты дискретизации имеем
д х (6= f [x(fl, fl + lim =-cov{x((), z(t +) | Z(t —)} x
dt Tk-^‘k
tk-^t
X var-1 {za + ) [ Z(M}{z(0~ h[x(0, fl},
где символы t— и t+ поясняют, каким образом Z(k—1) и z(k)
достигают своих значений в момент t. Мы видели из (9.124) и
453
(9.125), что при уменьшении шага дискретизации ур-ние (9.119)
переходит в дифференциальное уравнение
= f[x(0, п+^[х(0, и {z(0- h[x(0, 0}. <9-131)
где ^[x(Q, £], как легко видеть, равно
^[х(0, /] = £{х(0 hr[x(0. Л I гдаг1 (0,
что легко получить и с помощью теоремы проецирования, вводя
эквивалентное определение.
Аналогичным образом можно показать, что соотношение для
условной 'ковариационной матрицы в дискретном времени (9.120),
по существу, переходит в выражение для ковариационной матри-
цы из (9.37). Заинтересованный читатель может проделать этот
переход в качестве упражнения; действительно, просто показать,
что при увеличении частоты дискретизации (9.120) переходит в
уравнение
d V~ (t) ~
—= E{f[x(0, Л хг(0 I Z(0)+E{x(0fr[x(0, q I Z(0)+
+ E{G[x(0, f]¥w(0 Gr[x(0. Л}-£{х(0Ьг[х(0.Л Z(0}x
X Y71 (0 £ {h [X (0, f] xr (0 | z (0), (9.132)
которое аналогично (9.37) Отличие этих двух соотношений со-
держится в последних членах каждого из них
Можно задать вопрос, почему для нахождения дискретного
расширенного фильтра Калмана мы выбрали метод линеаризации.
Ответ состоит в том, что, разлагая Ф в ряд, мы получаем нужную
л
текущую оценку х(£—1) в момент А—1. Затем при поступлении
л
нового наблюдения z(£) на основе z(&)—h[x(£|k—1), вычис-
л л
ляем оценку x(k). Мы надеемся, что оценка x(k—1|£) лучше,
л
чем оценка x(k—1), и поэтому желательно линеаризировать
л
функцию Ф[х(£—1), k—1] в точке x(k—l|ft). Аналогично счи-
л л
таем, что оценка x(k) «вероятно» лучше, чем оценка х(£|£—1).
Таким образом, мы приходим к дискретному итерационному
л
фильтру, который пересчитывает новую оценку x(k) на основе
линеаризированных значений Ф и h. Эта итерационная процедура
может повторяться любое желаемое число раз. В [277] делается
вывод о том, что для большого числа задач вполне достаточно
одной итерации.
Однако необходимо еще получить соотношения для нахожде-
л
ния x(k—11£). Из (9.116) следует, что
454
x(fe—1 I £) = E{x(fe — 1) I Z(fc)) = E{x(% — 1) ] z(fc), Z(fe —1)}=
A
= x(k— l)+cov{x(A— 1), z(k) I Z(k — l)}var_1{z(£) | Z(k — 1)} x
X {z(£) —h[x(&), Л]}. . (9 133)
Легко показать также, что
cov{x(Z> — 1), z(&) [ Z(k — 1)} = cov{x(& — 1), h [x(&), £] | Z(k — 1)}
(9.134)
Подставляя Ф[х(&—1), k—>1] + Г[х(^—1), k—l]w (k) вместо
x(k) И используя те же соображения, что и при выводе (9.124),
получим
cov{x(Z>—1), z(k) | Z(k — 1)} = V~(* — 1) x
X ЭФг1х(/г-1), fe-l]ahrtx(fe| fe-1), k] (9 135)
d x (k—1) dz(k\k—1)
A
Теперь желательно получить выражение для оценки x(k—1|А), не
содержащее в себе наблюдения. Подстановка (9.125) и (9.135) в
л
(9.79) дает алгоритм для x(k—1|£) с задержкой на один шаг, .
объединение которого с (9.119) дает
х(& — 1 | Л) = х(£ — 1) + V~(^- 1) ^1). х
д x(k — 1)
XVr (k \ k — 1)[х(#) —х(6 | k— 1)].
л
Вычисленная по этому алгоритму оценка x(fe—l|fe) используется
затем для линеаризации членов Ф и rVwrT. Это позволяет нам
определять итеративную дисперсию на предыдущем шаге с по-
мощью ур-ния (9.126) и пересчитанной оценки. Эту предшест-
вующую оценку обозначим через V~(fe|fe—1). Далее находим ите-
л
ративную оценку x*(fe|fe—1), полученную линеаризацией Ф в точ-
ке x(fe—l|ft). Легко показать, что эта оценка удовлетворяет
соотношению
х*(k [ k — 1) = Ф[х(k — 1 I k), k — 1] + I x
<?X (k — 1 I k)
X [x(6—1) —x(£ —1 [ &)],
которое можно получить линеаризацией уравнения для модели
л
сообщения около точки x(fe—l|fe) и затем операцией усреднения
455
обеих частей линеаризованного уравнения при наличии L(k—1).
л
Оценка **(k\k—1) используется для линеаризации выражения
для h и затем определяется итеративная предыдущая оценка
л
сигнала х*(&). Подобная итерационная процедура может повто-
ряться любое число раз. В табл. 9.9 приведены сводные алгорит-
Таблица 9.9
Дискретные итеративные алгоритмы фильтрации по условному среднему
Итеративный алгоритм одношагового предсказания
Л,
Л, л. д Ф[х£ (k I k +1), ft]
xz (ft 4-1 | k) = Ф[х* (k I Jfe 4- ---X
dx1 (k | A4-1)
Л Л.
X [X (k) — x1 (k I jfe 4-1)1-
Итеративный алгоритм вычисления ковариационной матрицы
д Ф[х1 (k I k + 1), k} дФт [ xz (k | k +1), ft]
vri. (ft +i |ft) = - Л—J ’ V~(k) —+
ax1’ (ft | ft +1) axz (ft | ft4-1)
4- Г [xz (ft|ft+l), ft] Vw (ft) Гг [ хЛ/ (ft | ft +1). ft].
итеративный алгоритм вычисления ковариационной матрицы ошибок
_ А,
а им х (ft +1), ft +i]
v~z (ft +1) = v~i (ft +1 I ft)-v~i (ft + lift)---- :
dx1 (ft 4-1)
( ah[xz (ft 4-1), ft4-1] , ahr[xz (ft 4-1), ft-|-i]
X ------- vsrz (* +1 I ft)------------------------- A - 4
\ aXz (ft 4-1) * X dx1 (ft 4-1)
\-1 Л,
\ ah [ xz (ft 4-1), ft 4-1]
+ vv (ft + 1) ----- Л ------------— V3TZ (k +1 1 *)•
dx1 (ft 4-1)
Итеративный алгоритм вычисления коэффициента усиления
, ahr[xz (ft4-i), ft4-1] .
Kz (ft +1) = V^i (ft +1)-------- J- ---------V71 (ft 4- 1)
A,
dx1 (ft 4-1)
Итеративный алгоритм фильтрации
Xz+*(ft + l) =XZ (ft 4-1 I ft) 4-K{ (ft 4-1) {Z(ft 4-l)-h[xl (ft 4-1), ft-Не-
456
Продолжение
Л,
5h [xf (6 + 1), 6 + 1]
л,
д х1 (6 + 1)
[х' (6 + 1 |6)- х' (6 + 1)]
Алгоритм оценки с задержкой на один шаг
Л£.. , Л <?Фг[хг (6 1 6+1), 6] х1+’(6 | 6 + 1) — х (6) + V~(6) 1Л г /> J rv~t(6 + l|6) дх1 (6|б + 1) г’ *
X [х‘+1 (6 + 1)- х‘ (6+1 | Аг)].
Итерационные начальные условия
Л Л х1 (6 | 6 + 1) — х (6);
Л Л х1(6+1) = х(6 + 1 I 6),
Соотношения на шаге пересчитывания
Л. Л х (6 + 1), х1 (6|6 + 1), V~f (6 + 1) Финальные (т. е. к которым сходи-
лись) значения используются как фиксированные значения на следующем шаге.
Начальные условия
Л x'i(60) = рХо; v~ (б0) = vXi.
мы итеративной дискретной фильтрации. Модель сообщения и на-
блюдения, априорные данные те же, что и в расширенном фильт-
ре Калмана табл. 9.5 (после каждого наблюдения итеративные
алгоритмы могут использоваться для любого на каждом шаге).
Для удобства алгоритмы проиндексированы в том порядке, в ко-
тором происходят вычисления (i=l, 2, 3,...). Заметим, что каж-
дая итерация требует столько же времени на вычисление, что и
обработка нового наблюдения в расширенном фильтре Калмана.
Пример 9.8. Рассмотрим значимость дополнительного управляющего члена
уравнения для ковариационной матрицы ошибок и влияние высших порядков
малости иа фильтр второго порядка с минимальной дисперсией ошибок. Полу-
ченные результаты сравним с аналогичными результатами для линеаризованной
фильтрации Калмана.
Предположим, что модель оценки описывается уравнениями.
X (0 = — л- (0 + ы (0 + w(0; х(0) = -1;
z(t} = x^t) +v(t),
где z(t) и x(t)—скаляры, a u(t)—детерминированная постоянная составляю-
щая на входе, равная u(t)=5. Кроме того, предположим, что шум стационарен
и Чги(/) и Фм(0 постоянны в интересующем нас интервале
Рассмотрим четыре случая: линеаризованный фильтр Калмана, фильтр вто-
рого порядка с минимумом дисперснн, расширенный фильтр Калмана и фильтр,
457
оптимальный по критерию максимума апостериорной вероятности. Соответст-
вующие этим случаям уравнения имеют следующий вид:
1. Фильтр по критерию МАВ, основанный на методе инвариантного погру-
жения:
Л Л Л . Л
лг (0 = — лг (0 + «(0 + Зх2 (0 v~(f) Ч~1 (0 [г (t) - х» (01;
л , л
V~(0 = - 27^(0 + Ч'да (0 - 9х' (0 К~(0 Т7* (0 + 6х (0 V~(t) X
, Л
х V (0([z(0-xs(0].
2. Расширенный фильтр Калмана нли фильтр первого порядка с минимумом
дисперсии:
АЛЛ Л
х (0 = - х (0 + и (0 + Зх2 (0 7~(0 т-1 (0 [2 (0 - х3 (01;
V ~(0 = - 2V-(0 + Тж (0 -9^(0К2^(0 Т71 (0.
3. Фильтр второго порядка по минимуму дисперсии:
Л Л Л . АЛ
х (0 = - X (0 + и (0 + 3х2(0 V~(t) V (0 [2 (0 - X» (0 - Зх (0 7~(0];
V ~(0 = - 2К~(t) + Та, (0 - 9х* (0 К2~(0 Т^1 (0 + 6хЛ(0 7^(0 Та~' (0 [г (0-
А Л
— x3(t) — 3x(t) 7~(0].
4. Линеаризованный фильтр Калмана:
хп (0 = — хп (0 + и (fy
А х (0 = - б х (0 + 3V~(0 х2 (0 Т^1 (0 [г (0 - 36 х (0 х2 (0];
V~(0 = - 27~(0 + Тю (0 - 9kL (0 х* (0 Т71 (0;
АЛЛ
х(0 = бх(0 + хп (0.
Если алгоритмы фильтрации в непрерывном времени реализовываются на
ЭВМ, то должна быть проведена дискретная аппроксимация. Не оставляя в
стороне стохастическую интерпретацию, которая должна быть дана приближен-
ным уравнением фильтрации, можно показать, что вполне приемлемой является
ступенчатая аппроксимация непрерывных функций. Если в рассматриваемом
примере применить этот способ, то получаются следующие дискретные алгорит-
мы фильтрации:
1. Фильтр инвариантного погружения по критерию МАВ:
Л Л г Л , Л ,
X + 1) = (1 _ Т) х (k) + Т {и (k) + Зх* (k) V~(k) TJ-1 (k) [z (k) - г’ (Й)]};
V~(k 4- 1) = (1 - 2T) V~(k) 4- T (4W (k) - эА (k) X
X V2~(k) T-l {k) + fix(k) vL(k) T-l (k) [z {k) .
458
2. Расширенный фильтр Калмана или фильтр первого порядка с минимумом
дисперсии-.
Л Л , Л . Л ,
х (k + 1) = (1 - Г) х (k) + Т {и (k) + Зха (k) V~(k) (*) [Z (k) - х» (*)]} ;
+ 1) = (1 -2Г) У~(Й) + Т [Тж (А) - 9х* (k) (k) Т-1 (А)] .
3. Фильтр второго порядка с минимумом дисперсии:
X (k + 1) = (1 - Г) X (k) + Т { и (k) + Зх2 (k) V~ (k) V (k) [г (k) - х2 (k) -
~3x(k) r~(*)]};
V~(k + 1) = (1 -2T) V~(k) + T (4w(k) ~ 9x* (k) V2~(k) T”1 (k) +
+ 6x (k) vL (k) T“ (*)[z (й)-х2 (k) - 3x (k) .
4. Линеаризированный фильтр Калмана;
xn (k + 1) = (1 - T) xn (k) + Tu (k);
S x (k + 1) = (1 - T) S x (k} + T (ЗУ~(Й) x* (k) V71 (k) [z (k) -
Л A
-36x(A)x£(*)]} ;
V^(k + 1) = (1 - 2T)V^(k) + T [Ta, (k) - 9V2~(k) x^ (k) T71 (k) ] ;
АЛЛ
x (k) = бх (Й) + xw(k).
В качестве первого шага предположим, что распределение шу-
мов полностью'известно, а исходные параметры равны: Т=0,001;
л
4^= 1,0; Ч%=10,0; х(0)=0 иУ~(0)=0. Ошибка оценивания для
л
всех четырех фильтров x(fe)—x(fe) получена за период 2 с. Ре-
зультаты фильтрации приведены на рис. 9.6, из которого следует,
Рис. 9.6. Фильтрация с
известными априорными
данными:
I — нелинейные фильтры;
2 — линеаризованный
фильтр Калиаиа
459
что при полном априорном описании шума все нелинейные оценки
лучше, чем оценка, полученная линеаризованной фильтрацией
Калмана. Оценка почти не улучшается, если включить дополни-
тельный управляющий член в уравнение инвариантного погруже-
ния фильтра по критерию МАВ или учесть члены высших порядков
малости в фильтре второго порядка по критерию минимума диспер-
сии.
Рис. 9 7. Дисперсия ошибки фильт-
рации с известными априорными дан-
ными (получена решением прибли-
женных уравнений для ковариацион-
ной матрицы ошибок)
Рис 9 8. Фильтрация при неполных ап-
риорных данных:
1— расширенный фильтр Калмана; 2 — лине-
аризованный фильтр Калмана; 3—метод ин-
вариантного погружения и фильтр второго
порядка по минимуму дисперсии
Графики приближенной дисперсии ошибок приведены на рис. 9.7.
Заметим, что для всех трех фильтров они идентичны.
На втором этапе предположим, что истинные значения и
4% неизвестны, т. е. имеется априорная неопределенность. Значе-
Рис. 9.9. Дисперсии ошибок при
неполных априорных данных:
1 — фильтр МАВ и фильтр второго по-
рядка; 2 — расширенный фильтр Кал-
маиа
460
ния параметров: 7=0,001; Yu, (действ.) =0,1; 4% (действ.) = 10;
т. , л
Чго (предполаг.) =1; ЧЛ, (предполаг.) = 100; х(0)=0 иК~ (0) =0.
Ошибка оценивания определяется экспериментально для данной
выборки шума. Результаты приведены на рис. 9.8.
Снова видно, что нелинейные оценки существенно лучше оце-
нок, даваемых линеаризованным фильтром Калмана. Более того,
в случае априорной неопределенности поучителен тот факт, что
добавочный управляющий член в фильтре инвариантного погруже-
ния по критерию МАВ и использование членов высших порядков
малости в уравнениях фильтрации по минимуму дисперсии обес-
печивают лучшую чувствительность в слежении за траекторией
на отрезке быстрого изменения переменной состояния. Прибли-
женные дисперсии ошибок представлены на рис. 9.9.
Таблица 9.10
z Алгоритмы первого поридка вычисления отношения правдоподобия
(используются все алгоритмы табл. 9.7 и даваемые ниже)
Алгоритм вычисления отношения правдоподобия
A [Z (k + 1)] = A [Z (Л)] +y In {det [ Vv (k +1)]} - ~ In
det ( Vv (k + 1) +
dh[x(^ + l Ц), Ar + l] dhr[x(^ + l | k), *+l] ’ ,
+--------------------V~ (k +1 R)---------------------- +
d x (k 4-1 | k) d x (k +1 | k)
+ Vzr(^ + l)V71(^+l)z(^ + l)-^-(z(^ + l)-h[x%+l p), k + l]}r X
2 2
/ A
/ ,, ,, dh[x(^ + 1 I k), Л + 1]
X Vv (k + 1) + -1 —V~(k + 1 | k) X
i — A x
\ d x (k + 1 | k)
5hr[x(£-|-l | k), k +1]
X Л
d x (k + 1 | k)
{z(k + 1) -h [x(Ar + 1 | k), Л -f-1]}.
Начальные условия
x(°) = t40; v3K°) = vx0; Afz(O)]=o.
Пример 9.9. Для того чтобы показать, как дискретные алгоритмы фильтра-
ции по условному среднему можно применить для построения последователь-
ных алгоритмов отношения правдоподобия, необходимо вернуться к некоторым
выводам § 5.7. Если объединить дискретные алгоритмы из табл. 9.7 с ур-ниями
(5.180) и (5.181), то получим алгоритмы, приведенные в табл. 9.110, для прибли-
женного (первого порядка) отношения правдоподобия. Конечно, в случае необ-
ходимости можно использовать алгоритмы второго порядка или алгоритмы одно-
шаговой итерационной фильтрации для получения отношения правдоподобия
(209].
461
Рассмотрим задачу обнаружения случайного фазомодулированного сигнала
на фоне аддитивного нормального шума. Приемник выбирает одну из гипотез
Нг: г (k) = A cos [<й0 kT + х (й)] + v (й);
Но: г (й) = v (й);
X (Й+ 1) = Фх(Й) + ш(й),
где х(й) удовлетворяет линейной модели сообщения Шумы о(й) и ш(й)—
нормальные с нулевыми средними и с дисперсиями Vv и Vw соответственно.
Рис 910 Последовательное обна-
ружение Верна Hi (пример 9 6).
Отношение сигнал/шум 0 дБ.
Девиация частоты 30% Рр =*
= P^^QA
Используя алгоритмы первого порядка из табл. 9 6, получим (все соотно-
шения даиы в форме, пригодной для цифровых методов реализации):
х (0) = п ; 7 (0) = V~; A [Z (0)] = 0;
и Л Xq
А А
х (й + 1 | й) = Ф х (й);
Р~(й + 1 |й)=Ф2Р~(й) + Уа),
2 А
А2Р~(й + 1 | й) sm2 (<в0 (й + 1) Т + х (й + 1 | й)]
И~(й + 1) = Кт(й + 1 | й) -----х-------------------д------------------- •
A2 sm2 [<й0 (й + 1) Т + х (й + 1 | й)] + К0
—У~(й + 1) A sin [<й0 (й + 1) Т +х (й + 1 | й)]
К(й + 1) =-----х----------------------------------- ;
Ку
А ГА д
лг(А + 1) = х (А + 1 I Л) + К (А + 1) {2 (А+ 1) — Л cos (А + 1) Т +х(АН-1 I £]};
А[2(й + 1)1=Л[2(й)Ц-4-1пРа- 4~1п rvu+AW~(k+l | й)sin2[<й0(й +
Z Z х. х
+1) т + ?(t +1 | t)l} + -i- ци - <* + > r + -
1 2 Vv 2 Vv + А2И~(й + 1 | й) X -*
-^ + х(й + 1 I й)]}2
-*X sin2 [<й0(й-|-1)Т-|-х (Й4-11 Й)]
462
Для того чтобы осуществить последовательную процедуру обнаружения,
логарифм отношения правдоподобия A[Z(fe)] сравнивается при каждом k с по-
рогами In^Tj н In^j, где
-г
Рм — вероятность пропуска, а Рр — вероятность ложной тревоги.
Если A[Z(£)]^sln-S'г, то принимается гипотеза Hi; если
A[Z(£)]==sln S'i, то принимается гипотеза Но. При In S'
^A[Z(fc)]^ln S'2 наблюдения продолжаются. При фиксирован-
ном объеме выборки N обнаружение по критерию минимума ве-
роятности ошибки производится сравнением A[Z(A)] с нулевым
порогом.
Приведенные алгоритмы проще всего реализовывать на ЭВМ,
при этом как последовательное обнаружение, так и обнаружение
при фиксированном объеме выборки могут быть проведены для
различных наборов параметров. Результаты для некоторых слу-
чаев приведены на рис. 9.10—9.13. Здесь A2/Vw — отношение сиг-
Рис 9 11. Последовательное
обнаружение Отношение сиг-
иал/шум равно 6 дБ Девиация
частоты 30% Рр^= = 0,1
нал/шум, а девиация частоты определяется отношением 1/4 части
ширины спектра мощности сигнала к частоте несущей.
В табл. 9.11 представлены различные варианты значений пара-
метров, при которых решалась задача обнаружения, а на рисун-
ках представлены выборочные значения логарифма отношения
правдоподобия для различных случаев. Таблица 9.11 содержит
также значения отношений правдоподобия для проверки гипотез
при фиксированном объеме выборки, равном 25. Номера на кри-
вых совпадают с номерами в соответствующей колонке таблицы.
Из приведенных данных видно, что во всех случаях, когда после-
довательное обнаружение происходит неверно, обнаружение при
фиксированном объеме выборки происходит безошибочно: значе-
463
ния отношения правдоподобия «перекрыты». Из рис 9.11 видно
также, что для опыта № 3 ошибка была допущена при фиксиро-
ванной выборке, в то время как последовательная процедура
прошла безошибочно.
Рис. 9.12. Последовательное обнару-
жение. Отношение сипнал/шум равно
О дБ. Девиация частоты 60%
pf = pm = o,i
Рис. 9.13 Последовательное обнаруже-
ние. Отношение сигиал/шум равно
6 дБ Девиация частоты 60%
PF = PM = 0,l
Таблица 9.11
Логарифм отношения правдоподобия при фиксированной выборке.
Гипотеза Н4, Рр = Рм=0,1, N = 25
Номер опыта Отношение сигнал/шум равно 0 дБ, девиация частоты 30 о Отношение сигнал/шум равно 6 дБ, девиация частот равна 30% Отношение сигнал/шум равно 0 дБ, девиация частоты 60% Отношение сигнал/шум равно 6 дБ, девиация частоты равна 60%
1 2,296 1,927 11,943 2,971
2 5,416 1,604 8,980 2,592
3 1,217 —0,97 3,646 1,062
4 2,301 — 2,335 —
9.5. Нелинейное сглаживание
Сглаживание в фиксированной точке.
В тех случаях, когда требуется получать оценку только в конеч-
ном числе точек некоторого интервала наблюдения, для нахожде-
ния последовательного алгоритма сглаживания в заданной точке
можно использовать метод инвариантного погружения с «фикси-
рованным шагом» или с «фиксированным временем».
Пусть имеется дискретная нелинейная задача второго порядка,
определяемая ур-ниями (9.78) и (9.79). Необходимо найти наи-
464
лучшую -оценку вектора состояний на некотором фиксированном
шаге, скажем, шаге kt, где В дальнейшем kf станет
текущей переменной и поэтому целесообразно обозначить наи-
лучшую оценку через x(k*\kf). Эту оценку определим так, что
£(** | £,) =г(Л*, kh С), (9.136)
л
где отражена зависимость оценки х(&*|&/) от шага оценивания, от
текущего времени и от значения добавочной переменной-1 (&),
которая на шаге kf определяется так, что
1(^) = С. (9.137)
Далее, разлагая (9.79) в ряд в окрестности точки С=0, имеем
AC=g[r(fy, kf, С), С, fy] —С. (9.138)
Для того чтобы АС удовлетворяло (9.138), полагаем
r(^, ^+1, C + AC) = r(^, kh С). (9.139)
Левая часть предыдущего уравнения может быть выражена в виде
r(k*, kf+\, C + AC) = r(^, kf, C)+^AC+^-+-^-AC,
cl 0 kt OCoAf
(9.140)
где бг/бС и бг/б^г — первые частные производные. Подстановка
’(9.138) и (9.139) в (9.140) приводит к уравнению инвариантного
погружения с фиксированным шагом:
С>’ с>^-с} = °- (9.141)
О fef • \О I О С О kj )
где г(&*, kf, С) —решение этого уравнения. Решение на текущем
л
шаге kf определяет оптимальную оценку x(kt\kf) на шаге k„ с
использованием информации Z(&/). Определив
r(kf, kf, С) As (С, kf), (9.142)
можно воспользоваться уравнением инвариантного погружения
для s(C, kt), полученным в § 9.3, которое удовлетворяет уравне-
нию, аналогичному (9 83) Таким образом, необходимо, чтобы
6 s (С, kf)
Skf
Гб s (С, kf)
L 6С
d2s(C, kf) '
bCbkf
{g[s(C, kf), C, kf] — C} =
= /[s(C, kf), C, fy-s(C, kf),
(9.143)
где
s(C, O) = PoC + MU (9-144>
Решение ур-ний (9 143) и (9 144) определяет начальные значе-
ния, которые должны быть получены к моменту k*. На шаге kt
начальное условие
r(^, k, C) = s(C, k*) (9.145)
16—26 465
налагается ур-нием (9.141), а ур-ния (9.141) и (9.142) должны
одновременно решаться на шаге kt. Нетрудно видеть, что s(C, kf)
представляет решение задачи фильтрации по 'критерию МАВ.
При увеличении частоты дискретизации (9.141) и (9.145) пере-
ходят в уравнения инвариантного погружения в непрерывном вре-
мени. Легко показать, что при этом уравнение инвариантного по-
гружения с фиксированным временем будет иметь вид
с) +C)Y[S(C, tf), С, ЭД = 0, (9.146)
off д С
где s(C, tf) —решение задачи фильтрации, полученное из уравне-
ния инвариантного погружения в текущем времени с граничным
условием
1%, ЭД, C) = s(C,/Д (9.147)
причем
^^- + ^^r[s(C, tf)C, tf] = 7J[S(C, tf), C, ЭД. (9.148)
Уравнения инвариантного погружения с фиксированным вре-
менем в непрерывном случае были получены также другим спосо-
бом в работе [99].
Переходя к приближенным алгоритмам сглаживания в фикси-
рованной точке, предположим, что решение ур-ний (9.141) и
(9.142) можно представить в виде
г((ЭД, k, С) = х(ЭД, | £) — ₽(&* | &)С; (9.149)
s(C, £) = х(ЭД—P(fc)C; (9.150)
используя разложение в ряд Тейлора, получаем
| k + 1) = х((ЭД | £)+₽(£* | fe + l)g[x(ft), 0, £]; (9-151)
Р(^ | k+ 1) Р (*), С- С. । ч (9.152)
где Р(ЭД, | kJ = Р(^); х(ЭД, | х(ЭД,). (9.153)
Эти соотношения представляют приближенные уравнения сглажи-
вания в фиксированной точке. Для того чтобы их можно было
использовать, необходимо одновременно решать приближенные
уравнения фильтрации, приведенные в табл. 9.3.
Пример 9.10. Рассмотрим линейное оценивание по методу наименьших квад-
ратов для модели, определяемой следующими соотношениями:
х (k + 1) = Ф (й + 1, k) х (k) + Г (k) w (й);
z(* + 1) = Н (й + 1) х (й + 1) + v (й + 1).
Для такой модели граничная задача второго порядка удовлетворяет ур-ниям
(9.76) и (9.77):
466
* (k + 1) = Ф (й + 1, k) х (й) — Г (й) Q (й) Гг (й) Ф~т (й + 1, й) X (й);
X (й + 1) = [I + Нг (й + 1) R-1 (й + 1) Н (й + 1) Г (й) Q (й) Гг (й)] Ф~г (й +
+ 1, й)Л(й) + Нг (й + 1) R-1 (й + 1) [г(й + 1) — Н (й+1) Ф (й+1, й)х(й)].
Используя алгоритм приближенного нелинейного сглаживания в точке, получен-
ный выше, уравнения оценки в фиксированной точке можно записать в виде
х (й, I й + 1) = х(й, ( й) + Р (й, I й + 1) Нг (й + 1) R-1 (й + 1) [г(й + 1) -
Л
— Н(й + 1) Ф (й+ 1, й)х(й)];
Р (й, | й + 1) = Р (Й, | й) {Ф-1 (й + 1, й) [I + Г (й) Q (й) Гг (й) Нг (й + 1) X
XR~‘ (Й+ 1)Н(й+1)] + Р(й)Ф7’(й+1, Й)НГ(Й+ 1)R—1 (й+ 1) Н (й-+-1)}—1 .
Последнее уравнение преобразуется следующим образом:
k
Р (й, I й +1)= Р(Й.)П {Ф-1 (‘’ + 1 > О 11 + Г (О Q (О Гг (i) Нг (1 + 1) х
i=k,
X R-‘(i+l) Н (/+1)1 + Р («) ФГ О’ + 1 > О Нг (/ + 1) R-1 (/ + 1) Н («+1)}-1 =
k
- Р (*») П (Ф-1 (‘ + 1. <){1 + [г (9 Q (9 Гг (9 + ф (/ + I, <•) Р (/) Фг X
/=й.
k
х (/ +1, о1 нг («+1) r-1 (/ +1) н а + ц}-1 = р (й*) п <ф~' (< +1. о х
i=k,
k
X [I + р (i + 1 | i)HT(i+ 1) R-1 (f + 1) H (I + 1)1}-» =P(^) П «₽ («'+1 I OX
i=k,
x [p-1 (i+ 1 | 0 + Hr (/ + 1) R-1 (t + 1) H (/ + l)!}-1 Ф (« + 1, /)) =
k k
= Р(йж)П P(/+1)P-1 (/+ i I 0Ф0 + 1. O = P(A*) П Фг(» +1, ox
<=*. 1=Л.
k
x p-1 (/ + i | о p (/ + о = П Ip (0 Ф7” (‘ +1 > 0 p~ ’ G + i I 0] p (й + i).
i=kt
k
Введя функцию В(й*|й+1)= fl A(i), где A(z) =P (/)ФТ (i+1, i)P-*(i + 1 | i)
можно алгоритм оценки в фиксированной точке записать в виде
х(й* | й + 1) = х (й* | й) + В (й„| й + 1) К (й + 1) [z (й + 1) - Н (й + 1) X
Л
X х(й + 1 | й)],
где К(й + 1) = Р(й +1) Нг (й + 1)R-'(й+1).
Если R=Vv и Q = VW, то приведенные выше алгоритмы оценки идентичны
алгоритмам для линейной модели оценивания, полученным в гл. 8. Таким обра-
зом, в линейном случае приближенные алгоритмы сглаживания переходят в
точные алгоритмы сглаживания в фиксированной точке.
16* 467
В табл. 9.12 приведены алгоритмы для дискретного сглажива-
ния в фиксированной точке. К 'ним необходимо присоединить ал-
горитмы фильтрации из табл. 9.3. До шага k используются толь-
ко алгоритмы фильтрации. Далее используются все вместе взятые
Таблица 9 12
Дискретные нелинейные алгоритмы сглаживания по критерию МАВ
в фиксированной точке
(модели сигнала и наблюдения и алгоритмы фильтрации те же, что и табл. 9 3)
Алгоритм сглаживания в фиксированной точке
т Л
Л, , Л <9Ь~[х(/г +1 I k), k + 11 i
*(ft* |ft-|-l) = x(ft, | *) — P (** | k +1)-—7---------J-V^tf + l) X
d x (k + 1 | k)
-X {z(ft+ 1) — h[x(ft +1 | k), ft + 1]}. (9.154)
Алгоритм для вычисления квазиковариационной матрицы на данном шаге
Р (ft* I k + 1) = Р (ft* | k) fe]- VZ1 (k + 1 I k) v~(k +1) =
= p(ft* I k) дфТ[^’к] li-Hr(fe + i)V71(fe + i)H(^ + i) v~(ft +1 I ft)]-1
Л L x j
Начальные условия
x(ft* | ft*) = x(ft*); P(ft* | ft*) = V~(ft*);
V~(ft* | ft*) = V~(ft*); В (ft* | ft*) = I.
Алгоритм для вычисления ковариационной матрицы ошибок при сглаживании
в фиксированной точке
V (ft* I ft + 1) = V~(ft* I ft) +B (ft* | ft +1) [ V (ft +1) - V~(ft + 1 | ft)] X
X Br (ft* | ft + 1). (9.156)
B(ft* | ft +0 = В (ft* | ft)A(ft);
д Фт [x (ft), ft] <
A (ft) = V~(ft)-------L V-1 (ft + 1 | ft).
d x(ft)
алгоритмы. Заметим, что для решения задачи сглаживания не
обязательно иметь уравнения для ковариационной матрицы оши-
бок, которые мы получим несколько позже. Отметим также, что
путем преобразований уравнений для ковариационных матриц
ошибок можно получить различные формы обращения матриц.
Частным примером этого служит ур-ние (9.155).
468
Из дискретных уравнений инвариантного вложения можно по-
лучить несколько уравнений сглаживания в точке в непрерывном
времени путем увеличения частоты дискретизации или использова-
нием ур-ния (9.146) так, что
х(^ | 0 = Р(^ I О, /]; (9.157)
Р(^ I 0 = ~Р(^ I 0 pz[x(0~-^(Z)C’ С’ q )| (9.158)
( о С J | с=о
где | /*) = х(^); Р(^ | ^) = Р(^)
и
х(0 = Р(0т[х(0, 0, t] +-q [х(0, О, /]; (9.159)
Р(0=— Р (0f dr[x(Q-P(f)C, С, <] 11 _
I д С I |с=о
дч [Х(О — Р (f), С, с, /1 I , (9160
. д С |с=о
причем
х(М = МА>); Р(А>) = Р0; P(O = v~(o. (9.161)
Для того чтобы получить непрерывные алгоритмы сглажива-
ния в точке, мы используем определения у и т), которые следуют
из граничной задачи второго порядка для сглаживания в непре-
рывном времени-
Ч[х(0, 0, t] = f [х(0, /]; (9.162)
Y[x(0, 0, t] = a-hT (0{z(0-h [ х(0, t]}; (9.163)
д х (f)
dq[x(Q—P(QC, C,
dC
с=о
— G[x(0, t] 'Fw (t) Gr [x (О, /];
== _ Ix(Z), p^_
d x(0
(9.164)
ат[х(о-Р(рс, c, <]
dC
с=о
_ d ( д ьг[*(0- Л
Л Л
-3 x (f) \ d x (t)
p(/) dfrl*(0. <1.
d x (f)
(9.165)
Если подставить эти соотношения в (9.156) и (9.161), то получим
искомые уравнения Из (9 160) и (9 161) следуют алгоритмы
469
фильтрации в непрерывном времени (табл. 9 4), которые при
решении задачи сглаживания должны быть присоединены к урав-
нениям табл 9 13
Таблица 9 13
Непрерывные нелинейные алгоритмы сглаживания в точке по критерию МАВ
(для решенйя к этим алгоритмам должны быть присоединены алгоритмы
фильтрации из табл 9 4)
Алгоритм сглаживания в точке
A dhr[x(O, Л 1 А
х (М 0 = р (/* | 0 —(0 {z (0 - h [х (0, ф
ахр)
Алгоритм для вычисления квазиковариационной матрицы
P(f, I 0 = Р(<* I о
д ( дhT [х(0, Л 1 А
— ---------л— <7* (О (х (Л - h [X (0, Л}
;(0 \ Зх(О
a fr [х (0 л
+ р(Л 10—
ах (л
(9 166)
(9.167)
Начальные условия
х (Л | Q = х\), Р (Л | О) =? V~(C | Q = V~(C)
Алгоритм для вычисления ковариационной матрицы ошибок сглаживания
аьг[х(о,л 1 аь[х(л, л
v~(f, | л = - р (0 I 0--^7 (0 — - р (О I О
а х (л а х (л
(9 168)
Сглаживание на фиксированном интервале.
При выводе уравнений фильтрации мы получили приближенное
решение граничной задачи второго порядка, описываемое ур-ния-
ми (9 76) и (9 77) только для фиксированного шага kf Задача
сглаживания на заданном интервале нами еще не решалась При
использовании наблюдений в заданном интервале дисперсия
ошибки оценивания должна быть уменьшена или, по крайней
мере, не увеличена при оценивании состояния на некотором шаге
внутри интервала наблюдения Это можно сделать, используя
процедуру сглаживания в заданной точке, и получить набор по-
следовательных алгоритмов оценки Однако возможно и сглажи-
вание только в одной точке (или более чем в одной, если фильтр
используется для каждой точки k„) Если обработка происходит
не в реальном масштабе времени, то можно использовать про-
цедуру сглаживания на заданном интервале Ошибки при сглажи-
вании в точке и на заданном интервале будут одинаковы, по-
470
скольку в каждый момент оценивания используется одно и то же
количество наблюдаемой информации Таким образом, если тре-
буется сглаживание на интервале и имеется возможность обра-
ботки не в реальном времени, то для вычислений сглаживание на
фиксированном интервале будет более предпочтительным
Рассмотрим граничную нелинейную задачу второго порядка в
форме ур-ний (9 76) и (9 77) Если алгоритмы фильтрации ис-
пользуются для оценки вектора х(й) от начального шага ko до
л
конечного шага kf, то оценка х(й/) может быть получена обработ-
кой по всей наблюдаемой выборке, заданной на интервале
л л
[ko, kf] В силу этого оценка фильтрации x(kT) и оценка x(kf\kf)
сглаживания на фиксированном интервале в точке kf одинаковы
л
При фиксированном шаге kf оценка фильтрации x(kf) и дополни-
1ельный член 1(йт)=0 составляют набор граничных условий на
конечном шаге, превращая тем самым граничную задачу второго
порядка в задачу на начальные значения, которая и дает в ка-
честве своего решения сглаживание на фиксированном интервале
Для того чтобы избежать вопросов устойчивости, возникающих
при решении канонических уравнений в обратном времени^, жела-
тельно применить линейное приближение для 1(й), которое связы-
вает оценки сглаживания на фиксированном интервале с оценками
последовательного сглаживания (фильтрации) В случае линей-
ных систем это эквивалентно преобразованию Риккати для доба
вочной переменной Из ур-ния (9 75) видно, что в этом случае
X (k | kf) = Р-1 (k) [х (k)- х (k | kf)], (9 169)
A
где через l(fe|&/) и x(k\kf) обозначены решения ур-ний (9 166) и
л
(9 167), a x(k) и P(k) (что эквивалентно V~(&)) —оценка и соот-
ветствующая ковариационная матрица ошибок задачи фильтра-
ции Заметим, что (9 169) не является единственной аппроксима-
цией, которая может быть сделана, но именно это приближение
переходит в точное решение в случае линейной модели оценива-
ния Используя указанное приближение, алгоритм сглаживания
на заданном интервале можно записать в виде
х(4 + 1 | kf) = f{x(k | kf), Р~’ (£)[х(£)—x(k | kf)],k),
x(kf | kf) = x(kf). (9.170)
Таким образом, до конечного шага используются алгоритмы
фильтрации в прямом времени Далее значения x(k) и P(k) ис-
пользуются для решения (9 170) в обратном времени в качестве
начальных условий, что и приводит к оценкам сглаживания на
фиксированном интервале.
471
Алгоритмы в непрерывном времени можно получить либо пре-
л
дельным переходом, либо полагая, что X 11/±) = Р—1 (/) [х(/)—•
—х(Ф/)].
Имеем:
х(М tf) p-i(t)[x(t)-x(t\tf)],t}-, (9.171)
x(tt | tf) = x(if), (9.172)
причем необходимо использовать данные табл. 9.4, чтобы полу-
чить алгоритмы фильтрации. Окончательные алгоритмы, которые
получаются при использовании соотношений для f и т), даны в
табл. 9.14 и 9.15.
Таблица 9.14
Дискретные алгоритмы сглаживания на фиксированном интервале
(предварительно должны быть использованы алгоритмы фильтрации
из табл. 9.‘3)
Алгоритм сглаживания на фиксированном интервале
*(k +1 | fe/) = 4>[x(fe | kf) k] - T[x\fe I kf), fe]Vw (k) Гт [*(k | kf), fe] X
d<bT[x(k I kf), fe] , Л Л
X------ 1 VZ-1 (fe) [x (fe) — x(fe|fe/)]. (9.173)
A x
d x (fe | kf)
Приближенный алгоритм сглаживания на фиксированном интервале
АЛЛ Л
х (fe | fe/) = x(fe) +A(fe) [x(fe + 1 | kf)— x (fe +1 | fe)]. (9.174)
Алгоритм для вычисления ковариационной матрицы ошибок
V_(fe | kf) = V~(k) +А (fe) г V~(fe + 1 | kf)~ V~(fe +1 | fe)] x Ar(fe). (9.175)
X x LX X J
d0r[x(fe), fe] .
A(fe)=V~(fe)------LaV VzJ (fe + 1 | fe). (9.176)
d x (fe)
Начальные условия
x(fe/ | fe/) = x(fe/); V~(kf | kf) = V~(fe/).
Таблица 9.15
Непрерывные алгоритмы сглаживания на фиксированном интервале
(предварительно должны быть использованы алгоритмы фильтрации
из табл. 9.4)
Алгоритм сглаживания на фиксированном интервале
^(/|/f)=f(x(/pf), /] +n(/|/f)[x(^f)-x(/)] (9.177)
472
Продолжение
Вычисление ковариационной матрицы ошибок сглаживания иа фиксирован-
ном интервале
Г Л 1
• dt [х (t I tf), tl I
v~ (t Pf) = —4 ' J - П (^f) vr(/1 tf) +
I dx(f]ff) J
г Л л
+ -П(ф,)У~(ф (9.178)
I 5x(H<f) '
n(/pf) = G[x(H<f), f]¥w (t) Gr[x(<| tf), q V-1 (t).
Начальные условия
x^f|Q) = x(/f); V~(t{\tf)=V~(tf),
Часто начальные условия для задачи сглаживания в дискрет-
ном времени вычислить затруднительно. Трудность состоит в том,
л
«то r(k*, kf, С) вычисляется по оценке x(k + 1 \kf). В свою очередь
х(й|Л/) нелинейно входит в Ф и поэтому, вообще говоря, на каж-
дом шаге необходимо решать нелинейное алгебраическое (или
матричное) уравнение.
В некоторых частных случаях удобно выразить (9.173) приб-
лиженным уравнением. Когда нелинейность содержится только в
А Л
наблюдаемой модели Ф[х(й|й/), k] =Ф(&+1, k)x(k\kf), ур-ние
(9.173) может быть заменено на
x(k | kf) = x(k) 4~А(й) [x(&4~ 1 | kf)—х(&4~ 1 I $)L (9.174)
где А(й) определяется из (9.139) [см. табл. 9.14].
Конечно, это соотношение может быть использовано и для не-
линейной модели сообщения со следующим приближением:
Ф(^4-1, fe)=dg±y)- k]x(k | kf).
d x (k)
Сглаживание с фиксированной задержкой. Мы
получили алгоритм сглаживания на заданном интервале в виде
приближенного решения граничной задачи второго порядка, опи-
сываемой ур-ниями (9.76) и (9.77). С точки зрения вычислений
этот алгоритм обладает двумя недостатками. Его необходимо
реализовать не в реальном времени и, кроме того, нужно запом-
нить оценку фильтрации и ее ковариационную матрицу ошибок.
Как альтернативный подход,к решению задачи оценивания на
фиксированном интервале можно рассмотреть сглаживание с фик-
сированной задержкой. При этом алгоритм реализуется в реаль-
473
ном масштабе времени и требования к памяти существенно мень-
ше, чем при сглаживании на фиксированном интервале. При оце-
нивании состояния х(й) на шаге k используются наблюдения
вплоть до шага k+<N, где Д1>0 и k + N^iki. Таким образом,
вообще говоря, оценка состояния в заданном интервале будет
хуже, чем оценка сглаживания на фиксированном интервале, но
лучше оценок последовательной фильтрации из-за использования
дополнительных наблюдений. Если алгоритмы оценки точные, то
ковариационная матрица ошибок сглаживания с фиксированной
задержкой будет лежать между матрицей ковариаций ошибок
фильтрации и сглаживания на фиксированном интервале.
Замена й» на й+1 и &+1 на & + 1+Л1 в (9.151) и (9.152) при-
водит к следующим соотношениям:
x(fc+l I k+ 1+ЛГ) = x(k+ 1 I А+Л0+Р(& + 1 | HI+^gX
x [x(k+N), О, (9.179)
Р(Л.+ 1 [ =
l д С I c=o
= P(£+ 1 | * + N). (9.180)
л
Заменяя в (9.170) kt на k+N, находим х(/г+1 |/г + У) —
=/{x(£|&+A7j, Р-‘(й)[х(й)—х(й|й+Д1)], k}.
Подставляя это соотношение в (9.179), получаем приближенный
алгоритм сглаживания с фиксированной задержкой:
х(^+1 | .^ + 1+Л1) = /{х(й | k+N), Р-'^Й^-х^ | &+Л7)], £}+
+ Р(& + 1 | * + 1 +N)g{*(k + N), 0, &+ЛП. (9.181)
Соотношение для Р(^-Ь1 |+ I 4-Л^) дается ур-нием (9.180), а
л
начальное условие задается оценкой x.(ko\ko + N), получаемой ре-
шением задачи сглаживания в фиксированной точке. Алгоритмы
фильтрации и сглаживания в фиксированной точке используются
от шага k(! до шага k0+N, определяя тем самым начальное усло-
вие для рассматриваемого алгоритма сглаживания. Далее сгла-
живание с фиксированной задержкой и фильтрация происходят
одновременно, что дает требуемую оценку вектора состояний. По-
л
скольку вычисление х(& +11 k+1 +JV) требует вычисления
л
х(й + А), то эти вычисления разнесены на N шагов.
Уравнения сглаживания в непрерывном времени можно полу-
чить, если воспользоваться упомянутым выше предельным пере-
ходом
х(/| Г+Т) = Ч{х(Г| t + T), Р-'(0[х(0-х(/ | / + ")], о +
474
+ Р(/ | / + Т)Т[х(/ + Т), 0, f+T]; (9.182)
P(t | t+T) = — P(t | t + T) (Эу[х(< +7')-P« + 7')C. c. <+71.]l 4-
l д C J c=o
[ ‘‘i 1 x I t + T), P 1 (/) [x(/) x (< I < 4~ 7*)], Л pj j 7^ (g 183)
5 x(q/+ T)
Для того чтобы P(& + 1 |й + 1 +N) можно было находить рекур-
рентно, ур-ние (9.180) необходимо переписать с учетом соотно-
шения
Р(&+ 1 | k + N} = A-!(Z?)P(£ I k + N),
которое можно получить из (9.174) и (9.175) в случае сглажива-
ния на фиксированном интервале. Здесь начальное условие за-
л
дается оценкой х (fo| t0 4- Т), получаемой сглаживанием в фикси-
рованной точке to, а использующийся алгоритм фильтрации
такой же, как и в табл. 9.4. Если в эти соотношения подставить
соответствующие выражения для f, g, tj, у, то получим ка'к дис-
кретные, так и непрерывные алгоритмы сглаживания с фиксиро-
ванной задержкой, которые сведены в табл. 9.16 и 9.17.
Таблица 9 16
Дискретные алгоритмы сглаживания с фиксированной задержкой
(к данным алгоритмам должны быть присоединены алгоритмы фильтрации
из табл 9 3 и алгоритмы сглаживания в фиксированной точке из табл 9j12)
Алгоритмы сглаживания с фиксированной задержкой
Л Л
х(А- + 1|й + 1 +А) = Ф[х(й|^ + А), k] —
— r[^(k\k + N), fc]Vw (k) Гг [x(&) k +A), k\X
!d<t>[x(k\k +N), k]
A
d x (k\k 4-A’)
—т
V-1 (k) [x(k)-x(k\k 4-A)] 4-
dhr[x(£ 4-1 4-А|й +N), k+ N 4-1]
4- P (k 4-1 I k 4-1 4- N)-— L-----------------22---
d x(k+ 1 + N I k+ N)
, A
XV7'(^ + 1 +A){z(^ + 1 4-A) — h[x(£ 4-1 4-ЛШ4-Л/), k 4-A-f-l]}.
(9.184)
Вычисление квазимоментов
. , д Ф т [х(& N), k 4- IV]
Р (k 4-1 | k + 1 4- N) = A-1 (k) Р (k Ik 4- N)x - — —-----!----X
d x (k 4- N)
XV—1 (k +N 4-1 H4-W)V~ (Л4-А4-1). (9.185)
475
Продолжение
Вычисление ковариационной матрицы ошибок сглаживания с фиксированной
задержкой
V ~ (k + 1 | k + 1 + tf)J= V~ (k + 1 Ik) + A'1 (k) [V~ (k) -
- V^ (felfe + N)] A~r(k) +B(k +llk +1 + A) [V~ (k +1 + A)-
- V~ (k + 1 +Af|fc +A)J BT (k +1 | й + 1 +A);
* Л LX
d x (k)
В (k + 1 | k + 1 +A)=A~1 (k)B(k\k +N) A(k + N). (9.186)
Начальные условия (определяются алгоритмом сглаживания в фиксирован-
ной точке)
x^l^o+A); V^^l^+A); Р (k +1 | k + 1 + N).
Таблица 9 17
Непрерывные алгоритмы сглаживания с фиксированным интервалом
(к этим уравнениям должны быть присоединены уравнения фильтрации
и сглаживания в точке из табл 9.4 и 9.18)
Алгоритм сглаживания с фиксированной задержкой
Х(Ш +7-)=f[x(qz +7-), П + П(;|/+Г)[Х(;|#+П-Х(О] +
<3hr[x(Z +7"), t -4-7'] . Л
+ Р (< \t + Т)- Л --------“ ^7 У + T){z (t +7') - h [х (t+T), U7|}.
dx(t +T)
(9.187)
Вычисление квазимоментов
П (t | t + Т) = G [х (t \t + Т) (t) GT X
X [х (< I < + 7")] V~ (t).
(9.188)
p'(t]t +t) = -p(/|; +T)
d
dx(t +T)
f dhr[x(t +T), t +7"] . a \
----L-aT 47'(Z +7){z(< +7-)-h[x(/ + 7-), t +7]} X
\ d x (~+ T) J
x Ex (Z + 7'), <+Г]1 + Г gtr[x(Z+T), /] +
dx(t+T) _ - 5x(Z|/4-7’)
476
П родолжение
+ G[x(t\t+T), Л'У-1 (0Ог[х(ф -f-Г),
РО +П
(9.189)
Вычисление ковариационной матрицы ошибок сглаживания с фиксирован-
ной задержкой
(df [х(0, И 1
V~ (t 11+Т) = ; L—- +П (t 11+D v~ (t\ t +T) +
I dx(t) J
I т Л X
_ d tr [x (t), л T I
+v~(d<+n -----------J +пг(/п +П}-п(; 1t 4T)x
x I Л I
l d x (t) J
d hT [xft+T), t + T] ,
xv~ (0 - p (/1; +n —[ -I / 7 J 4V tt + D x
X dx^+T)
d h [x(; +T), t 4-T] r
X ' Л —’^_L" рГ (Ф + Л • (9.190)
дх(/ +T)
Начальные условия (находятся решением задали сглаживания в точке при
непрерывном времени)
хСо^о+П; V- ((о По + П; Р(/оПо +П-
Приближенные выражения для ковариацион-
ных матриц ошибок. Часто необходимо оценить увеличе-
ние точности при применении различных алгоритмов сглажива-
ния в зависимости от времени, которое тратится на решение при
использовании алгоритмов фильтрации. Для одного класса нели-
нейных систем, рассматриваемых ниже, можно найти приближен-
ные соотношения для ковариационных матриц ошибок. Эти соот-
ношения переходят в точные в случае идентично определенных
линейных систем.
Как для дискретного, так и для непрерывного времени прибли-
женные выражения для ковариационных матриц ошибок пред-
ставлены в табл. 9.3 и 9.4. Выше было показано, что линеаризация
граничной задачи второго порядка приводит к возможности ис-
пользования расширенных уравнений для ковариационной мат-
рицы ошибок для оценки ковариационной матрицы ошибок нели-
нейного сглаживания. Представленные ниже приближенные урав-
нения для вычисления ковариационной матрицы ошибок сглажи-
вания используют этот результат В случае сглаживания в фикси-
рованной точке приближенный алгоритм определяется ур-нием
(9.156) для¥~(й*|й) в табл. 9.12. Аналогичные результаты пред-
ставлены в табл 9.13—9.17 для других алгоритмов сглаживания.
Приближенные алгоритмы нелинейного оценивания для слу-
чаев: фильтрации, сглаживания на интервале, в заданной точке,
477
с фиксированной задержкой и одношагового предсказания были
получены на основе байесовской теории оценок, а выбранная функ-
ция риска соответствовала критерию максимума апостериорной
вероятности. Был использован дискретный принцип максимума
и получена граничная нелинейная задача второго порядка, кото-
рая была решена методом инвариантного погружения в «текущем
и фиксированном времени», что позволило определить соответст-
вующие уравнения фильтрации и сглаживания. Был получен так-
же алгоритм одношагового предсказания. Линеаризацией нели-
нейной граничной задачи второго порядка были представлены
соответствующие алгоритмы для ковариационных матриц ошибок.
Полученные уравнения оценивания являются приближенными, но
они важны в том смысле, что для аналогично определенной линей-
ной модели они переходят в найденные ранее алгоритмы для ли-
нейной системы с линейной моделью наблюдений. В некоторых
случаях члены высших порядков, отсутствующие в линейных
уравнениях, часто улучшают качество оценивания вектора со-
стояний системы.
Пример 9.11. Продолжим исследование задачи 9.10. Все предположения и
модель сообщения остаются неизменными. Алгоритмы сглаживания в точке:
л .. . . , ,, л . Pu(k„ ] А: + 1) [z (* + 1) — arctg Д (*)1
Xi (k, | k + 1) = Xj | k) J-----------------------------------
Л /<, i h , n _Л /ь i м i P12<k* । + ]) [?(£+ ]) ~ arctg Д(А)]
x,^ |*+l)-xHM*)+ + +H«(*)1
p (k ,, , I) =____Pn(Mk)±T^\k)__________
t ) \+M(k)\V- (k)+2TV-(k)+T2V- (b)\ ’
Pi2 (k, | k) + 77>22 (k* | k)
] + M j- w _|_ 2TV- (k) + T*V~ (A)] ’
P№ (k, | k + 1) = P22 {k, I k) ~M (k) г V ~ (k) + TV — (*)1 P12 (kt j k + 1).
Алгоритм сглаживания на фиксированном интервале
х^+1 | kf) =xx (k \kf)+T x2 (k | kf)-,
i (k + 1 | kf) = [1 + В (k) C (k)] X, (k | kf) + A (k) В (k) [£(k) - xt (k I Ml -
— B(k) C (k) n2(k).
T2V (k}
™ + B(k) = V^k)V-{k)-v£W''
C(k) = { v- (k) + TV- (k)y, D {k} = A (k) +
1 +^D(k) [г(й+ 1) — arctg
1)11+£>г(Мг
Алгоритм сглаживания с фиксированной задержкой принимает вид
(k + 1 I k + 1 + N) = x, (k | k + N) + T x2 (k I k + N) +
Pu (fe + 1 | + 1 + A) [z (fe + 1 + A) — arctg Д (A + A)]
+ 1 +Ж1 + W + ^)l
478
X,(*+1 I *4-1 = HAHWWIM*)-
-xi(* | k + N)]~B(k)C(k)xt(k) +
P12(fe + 1 | *+ 1 Ч-ЛГ) [z(fe+ 1 + Л9 ~arctg£>(fe + JV)l
+ V~(k + 1 + N) [1+ D2(* + 2V)J
где Л(&), B(k), C(k), D(k+N) определены выше.
Алгоритмы одношагового предсказания даются соотношениями:
Xj (k + 1 | k) = Xj (k) + T x2 (k); x2 (k + 1 | k) = x2 (k).
Неявно мы использовали алгоритмы одношагового предсказания для нахожде-
ния алгоритмов фильтрации Кроме того, использовалось выражение для
Р(£+1 |£-Н1+У), полученное из (9.185).
Рис. 9 14. Приближенная дисперсия ошибки сглаживания в фиксированной точ-
ке на шаге £*=1001: a) xt; Уш = 900, У„=0,01; б) х2, Кш = 900, V„ = 0,01
Рис 9 15 Дисперсии ошибок сглаживания с фиксированной задержкой и фильт-
рации a) Xi 1 100xVxlt, 2 dOOxVx^ (й|Л + 50), V'„ = 900, Vv = 0,01, б) x2
1- Vx 22(й); 2. Vx„(£|ZH 50), V»=900, v“=0,01
Рисунок 9 14 иллюстрирует поведение дисперсии ошибки сглаживания в
точке на 1001-м шаге для Vw = 900 и У„=0,01. Начальные условия для диспер-
сий ошибок на этом шаге одинаковы При наличии дополнительных наблюдений
дисперсия ошибки сглаживания уменьшается в точке £,= 1001. На рнс 9.15
представлены графики дисперсий ошибок для N — 50. Для сравнения на этом
«е рисунке приведена дисперсия ошибки фильтрации.
479
СПИСОК ЛИТЕРАТУРЫ
При изложении теории оценивания и ее применений к задачам связи и уп-
равления были приведены многочисленные ссылки на работы, имеющие отноше-
ние к проблемам, обсуждаемым в различных разделах Некоторые интересные
приложения изучаемой теории не были затронуты К ним можно отнести про-
блемы распознавания образов, теории игр, стохастической аппроксимации, сто-
хастического управления и теории синтеза сигналов Изучение этих вопросов
здесь часто уводило бы далеко от главного предмета книги Например, для
достаточно полного освещения проблемы синтеза сигналов потребовалось бы
привести много сведений из теории оптимизации я т д Однако в книге приве-
дены фундаментальные результаты, необходимые для систематического изуче-
ния названных проблем
Все работы, на которые имеются ссылки в тексте книги, в списке литерату-
ры, приведены в алфавитном порядке После названия каждой работы в скоб-
ках указаны номера параграфов, в которых имеются ссылки на нее Если рабо-
та имеет отношение к содержанию всей главы, то в скобках указывается только
номер соответствующей главы В том случае, если в работе рассматриваются
вопросы, не изучаемые специально в данной книге, то после библиографического
описания работы в скобках указывается также и область применения ее основ
ных результатов Буквы П и Т являются признаками дополнительной классифи-
кации буквой П обозначены работы, ориентированные, главным образом, на при-
ложения рассматриваемых в ннх вопросов, буквой Т — работы, в которых рас-
сматриваются в основном вопросы теории Конечно, приведенная в книге клас-
сификация не является единственно возможной
Даже несмотря на то, что список литературы содержит довольно много на
званий, перечислить все работы, известные авторам и имеющие отношение к
изучаемым в книге вопросам, просто невозможно В список литературы включе-
на лишь незначительная часть таких работ
1 Albert A., Sittier R W. A Method for Computing Least Squares Estima-
tors That Keep Up with the Data —«J SIAM Control», 1965, ser A, v 3,
p 384—417 (7, T)
2 Anderson B. D. O. An Algebraic Solution to the Spectral Factorization
Problem —«IEEE Trans Autom Control» 1967, v AC 12, N 4, p 410—414
(7 4, T)
3 Anderson B. D. O., Moore J. B. State Estimation via the Whitening Fil-
ter — Proc Joint Autom Control Conf, June, 1968, p 123—129, Ann Arbor,
Mich (7, П)
4 Anderson T. W. An Introduction to Multivariate Statistical Analysis, John
Wiley & Sons, Inc, New York, 1958 (2, 3, T)
Рус пер Андерсон T Введение в многомерный статистический анализ Пер
с англ под ред Б В Гнеденко М, Физматгиз, 1961
5 Andrews A. A. Square Root Formulation of the Kalman Covariance Equa-
tions— , AIAA J», 1968, v 6, N 6 p 1165—1166 (8 5, T)
6 Aoki M._ Huddle J. R. Estimation of the State Vector of a Linear Stochas-
tic System with a Constrained Estimator —«IEEE Trans Autom Control», 1967,
v AC 12 N 4, p 432—433 (7, Оценивание при ограничениях)
7 Athans M. The Relationship of Alternate State — Space Representations in
Linear Filtering Problems —«IEEE Trans Autom Control», Dec 1967, v AC 12,
N 6 p 775—776 (7 3, T)
8 Athans M. The Matrix Minimum Principle —«Inform Control», 1968, v 11,
p 592—606 (Оптимизация, T)
9 Athans M., Falb P. L. Optimal Control An Introduction to the Theory and
Its Applications, McGraw Hill Book Company, New-York, 1966 (T)
480
10 Athans M., Schweppe F. C. Gradien Matrices and Matrix Calculations»,
MIT Lincoln Lab Tech Note, 1965—53 Lexington, Mass , 1965 (7 3, T)
11 Athans M., Schweppe F. C. Optimal Waveform Design via Control Theo-
retic Concepts —«Inform Control», 1967, v. 10, N 4, p. 335—377 (7, Синтез сиг-
налов, T)
12 Athans M., Tse E. A Direct Derivation of the Optimal Linear Filter Using
the Maximum Principle—«IEEE Trans Autom Control», 1967, v AC-12, N 6,
p 690—698 (7 3, T)
13 Athans M., Wishner R. P., Bertolini A. Suboptimal State Estimation for
Continuous time Nonlinear Systems from Discrete Noisy Measurements — «IEEE
Trans Autom Control», 1968, v AC-13, N 5, p 504—514 (9 4, T)
14 Baggeroer A. B. Maximum a Posteriori Interval Estimation, presented at
WESCON, Aug 1966, session 7, The Application of State-variable Techniques to
Communication and Radar Problems (6 2, 9 3, T)
15 Baghdady E. J., Kruse К W. Signal Design for Space Communication
and Tracking Systems —«IEEE Trans Commun Technol», 1965, v COM-13, N 4,
p. 484—498 (6 Синтез сигналов, П)
16 Balakrishnan A. V. A General Theory of Nonlinear Estimation Problems
in Control Systems —«J Math Anal Appl », 1964, v 8, N 1, p 4—30 (9, T).
17 Balakrishnan A. V. On a Class of Nonlinear Estimation Problems —«IEEE
Trans Inform Theory», 1964, v IT-10, N 4, p 314—320 (9, T)
18 Balakrishnan A. V. Communication Theory, McGraw-Hill Book Company.
New York, 1968 (Общее руководство, T)
Рус пер Балакоишнан А В Теория связи Пер с англ под ред Б Р Ле-
вина М, «Связь» 1972
19 Bass R. W., Norum V. D., Schwartz L. Optimal Multichannel Nonlinear
Filtering —«J Math Anal Appl», 1966, v 16, p 152—164 (9 2, T)
20 Battin R. H. A Statistical Optimizing Navigation Procedure for Space
Flight — «ARS J», 1962, v 32, p 1681—1996 (7, T)
21 Battin R. H. Astronautical Guidance. McGraw-Hill Book Company New-
York, 1964 (8 5, T)
22 Beckmann P. Probability in Communication Engineering, Harcourt, Brace
& World, Inc, New-York, 1967 (2,3,4 2, T)
23 Bellantoni J. F., Dodge K. W. A Square Root Formulation of the. Kalman-
Schmidt Filter — «AIAAJ», 1967, v 5, N 7, p 1309—1314 (8 5, П)
24 Bellman R. E., Kagiwada H. H., Kalaba R. E., Sridhar R. Invariant Im-
bedding and Nonlinear Filtering Theory —«J Astron Sci», 1966 v 13, p 110—
115 (9 3 T)
25 Bellman R. F., Kalaba R. On the Fundamental Equations of Invariant Im
bedding 1 —«Proc National Academy of Sciences», USA, 1961, v 47, p 336—
338 (9 3 T)
26 Bendat J. S. Principles and Application of Random Noise Theory» John
W’lley & Sons, Inc, New York, 1958 (Общее руководство, T)
P\c пер Бендат Дж Основы теории случайных шумов и ее применения
Пер с англ под ред В С Пугачева М, «Наука», 1965
27 Bendat J. S., Pierson A. G. Measurement and Analysis of Random Data»,
John Wiley & Sons, Inc, New-York, 1966 (3, 4, T)
28 Bharucha-Reid A. T. Elements of the Theory of Markov Processes and
Their Applications McGraw Hill Book Company, New York, 1960 (4 2, 4 3 T)
Рус nep Баруча Рид A T Элементы теории марковских процессов и их
приложения Пер с англ под ред А Н Ширяева М, «Наука», 1969
29 Bode Н. W., Shannon С. Е. A Simplified Derivation of Linear Least-squa-
res Smoothing and Prediction Theory —«Proc IRE», 1950, v 38, p 417—425
(7 4,T)
30 Bongiorno J. J., JR., Youla D. C. On Observers in Multi-variable Control
Systems —«Intern J Control», 1968, v 8, N 3, p 221—243 (7)
31 Booton R. C. An Optimization Theory for Time varying Linear Systems
with Nonstationary statistical Inputs —«Proc IRE», 1952, v 40, p 977—981
481
32 . Bryson A. E., Jr. Applications of Optimal Control Theory in Aerospace
Engineering. — «J. Spacecraft Rockets», 1967, v. 4, p. 545—553 (7, П).
33 . Bryson A. E., Frazier M. Smoothing for Linear and , Nonlinear Dynamic
Systems.— «Proc. Optimum System Synthesis Conf.», 11962, Sept., p. 11—13,
Wright-Patterson AFB, Ohio (8. 3, T).
34 . Bryson A. E., Henrikson L. J. Estimation Using Sampled-data Containing
Sequentially Correlated Noise, Harvard ’ University, Div. Eng. Appl. Phys., Tech.
Rept. 533, Cambridge, Mass, June, 1967 (8. 2, T).
35 . Bryson A. E., Ho Y. C. Applied Optimal Control, Blaisdell Publishing
Company, Waltham, Mass., 1969 (7, 8, 9, T).
36 . Bryson A. E., Johansen D. E. Linear Filtering for Time-varying Systems
Using Measurements Containing Colored Noise. — «IEEE Trans. Autom. Control»,
1965, v. AC-10, N 1, p. 4—10 (8.2, T).
37 . Bucy R. S. Nonlinear Filtering Theory. — «IEEE Trans. Autom. Control»,
1965, v. AC-10, N 2, p. 198—199 (9. 2, T).
38 . Bucy R. S. Optimal Filtering for Correlated Noise. — «J. Math. Anal.
Appl.», 1967, v. 20, p. 1—8 (8. 2, T).
39 . Bucy R. S., Joseph P. D. Filtering for Stochastic Processes with Applica-
tions to Guidance, John Wiley & Sons, Inc., New-York, 1968 (7, 8, 9. 2, Т,П).
40 . Carney T. M., Coldwyn R. M. Numerical Experiments with Various Opti-
mal Estimators.— «J. Opt. Theory Appl.», 1967, v. 1, N 2, p. 113—130 (8,9, П).
41 . Chang S. S. L. Synthesis of Optimum Control Systems, McGraw-Hill
Book Company, New-Work, 1961 (Общее руководство, T).
Рус. пер.: Чанг Ш. С. Л. Синтез оптимальных систем автоматического уп-
равления. Пер. с англ, под ред. В. В. Солодовникова. М., «Машиностроение»,
1964.
42 . Choate W. С., Sage А. Р. Operator Algebra for Differential Systems. —
«IEEE Trans. System Sci. and Cybernetics», 1967, v. SSC-3, N 3, p. 137—147
(7. 5, T).
43 . Collins L. D. Realizable Whitening Filters and State-variable Realiza-
tions.— «Proc. IEEE», 1968, v. 56, N 1, p. 100—101 (7, П).
44 . Collmeyer A. J., Cupta S. C. Linear Filtering with Constraints, Proc. Joint
Autom Control Conf., June 1968, p. 137—144, Ann Arbor, Mich. (7, П).
45 . Cox D. R., Miller H. D. Theory of Stochastic Processes, John Wiley &
Sons, Inc., New-York, 1965 (2 3, 4. 2, T).
46 Gox H. On the Estimation of State Variables and Parameters for Noisy
Dynamic Systems. — «IEEE Trans. Autom. Control», 1964, v. AC-9, N 1, p. 5—12
(9. 3, T).
47 . Cox H. Estimation of State Variables via Dynamic Programming, Proc.
Joint Autom. Control Conf., June 1964, p. 376—381, Stanford University, Leland-
Stanford, Calif (9. 3, T).
48 . Cramer H. Mathematical Methods of Statistics. Princeton University
Piess, Princeton, New-York, 1946 (2, 3, 4, T).
Русс inep.: Крамер Г. Математические методы статистики. Пер с англ, под
ред. А. Н. Колмогорова. М, «ИЛ», 1948.
49 . Darlington S. Linear Least Squares Smoothing and Prediction, with Ap-
plications.— «Bell System Tech. J.», 1958, v. 37, p. 1221—1294 (7.4, T).
50 . Davenport W. B., Root W. L. Introduction to Random Signals and
Noise, McGraw-Hill Book Company, New-York, 1958 (2, 3, 4, Общее руководст-
во, T).
Русс, пер Давенпорт В. Б., Рут В. Л. Введение в теорию случайных сиг-
налов и шумов Пер с англ, под ред. Р. Л Добрушина. М., «ИЛ», 1960
51 . Davis М. С. Factoring the Spectral Matrix. — «IEEE Trans. Autom. Cont-
rol», 1963, v. AC-8, N 4, p. 296—305 (7. 4, T).
52 . Danham W. F., Pines S. Sequential Estimation When Measurement Func-
tion Nonlinearity Is Comparable to Measurement Error. — «AIAAJ» 1966, v. 4.
N 6, p. 1071—1076 (9.4,T).
53 . Detchmendy D. M., Sridhar R. Sequential Estimation of States and Para-
meters in Noisy Nonlinear Dynamical Systems. — «Trans. ASME, J. Basic Eng.»,
1966, v. 88D, p. 362—366, April (9. 3, T).
482
54 . Deutsh R. .Estimation Theory, Prentice-Hall, Inc., Englewood Cliffs, New-
York, 1965 (Общее руководство, T).
55 . DiToro D. M., Steiglitz K. Application of the Maximum Principle to the
Design of Minimum Bandwidth Pulses. — «IEEE Trans. Commun. Technol.», 1965,
v. COM-13, N 4, p. 433—438 (Синтез сигналов, T).
56 . Doob J. L. Stochastic Processes. John Wiley & Sons, Inc., New-York, 1953.
(3, 4, T).
Рус пер.: Дуб Дж. Вероятностные процессы. Пер. с англ, под ред.
А. М. Яглома, М., «ИЛ», 1956.
57 . Dubes R. С. The Theory of Applied Probability, Prentice-Hall, Inc., Engle-
wood Cliffs, New-York, 1968 (2, 3,4. 2, T).
58 . Dyer P., McReynolds S. Extension of Square — Root Filtering to Include
Process Noise. — «J. Opt. Theory Appl.», 1969, v. 3, N 6, p. 444—458 (8. 5, T).
59 . Esposito R. On a Relation between Detection and Estimation in Decision
Theory. — «Inform. Control», 1968, v. 12, p. 116—120 (3. 7, T).
60 . Fagin S. L. Recursive Linear Regression Theory, Optimal Filter Theory,
and Error Analyses of Optimal Systems, 1964. IEEE Intern. Conv. Record,
New-York, Mar. 23—26, 1964, p. 216—240 (8. 4, T).
61 . Fagin S. L. Feedback Realization of a Continuous time Optimal Filter.—
«IEEE Trans. Aerospace Electron Syst.», 1967, v. AES-3, N 3, p. 494—509 (7, П).
62 . Fagin S. L. The weighting Function Form of the Continuous Optimal Fil-
ter. Proc. Joint Autom. Control Conf., June, 1968, p. 619—625, Ann Arbor,
Mich. (7, .П).
63 . Fagin S. L., Grinoch E., Graefe A. Continuous Time — varying Optimal
Feedback Applied to the Augmentation and Rapid Alignment of Inertia Sys-
tems. IEEE Aerospace Systems Conf., July 11—15, 1966, p. 661—678, Seattle,
Wash. (7, П).
64 . Fang В. T. Kalman-Bucy Filter for Optimum Radio-inertial Navigation.—
«IEEE Trans. Autom. Control», 1967, v. AC-12, N 4, p. 43-431 (7, П).
65 . Feller W. «An Introduction to Probability Theory and Its Applications»,
John Wiley & Sons, Inc., New-York, 1950, 1957, v. 1, (2, T).
Рус. nep : Феллер В. Введение в теорию вероятностей и ее приложения,
т. 1. Пер. с англ, под ред. Е. Б. Дынкина. М., «Мир», 4952, 1967.
66 . Feller W. An Introduction to Probability Theory and Its Applications,
John Wiley & Sons, Inc., New-York, 1966 (2, T).
Рус. nep.: Феллер В. Введение в теорию вероятностей и ее приложения. Т. 2.
Пер. с англ. Ю. В. (Прохорова. М., «Мир», (1967.
67 . Fisher J. R. Optimal Nonlinear Filtering, Advan. Control Systems, 1967,
v. 5, p. 197—300 (9. 2,T).
68 Fisher J. R., Stear E. B. Optimal Nonlinear Filtering for Independent
Increment Processes Parts I and II. — «IEEE Trans. Inform. Theory», 1967,
v. IT-13, N 4, p. 558—578 (9.2, T).
69 . Fisher R. A. Theory of Statistical Estimation. — «Proc. Cambridge Phil.
Soc.», 1925, v. 22, p. 700 (6, T).
70 . Fraser Donald C. On the Application of Optimal Linear Smoothing Tech-
niques to Linear and Nonlinear Dynamic Systems. Ph. D. Thesis, Massachusetts
Institute of Technology, January, 1967.
71 . Friedland B. Treatment of Bias in Recursive Filtering.— «IEEE Trans.
Autom Control», 1969, v. AC-14, N 4, p. 359—367 (7. 5, T).
72 . Friedland B., Bernstein I. Estimation of the State of a Nonlinear Process
in the Presence of Nongaussian Noise and Disturbances. — «J. Franklin Inst.»,
1966, v 281, N 6, p. 455—480 (9. 4, T).
73 . Frost P. A. Nonlinear Estimation in Continuous Time Systems, Stanford
Univ., Systems Theory Lab., Tech. Rept. 6304—4, U. S. Air Force Contract
F33615—67—C—1245, May 1968 (4.4,9. 2, T).
74 . Гантмахер Ф. P. Теория матриц. M., «Наука», 1966.
75 . Gauss К. F. Theory of the Motion of the Heavenly Bodies Moving about
the Sun in Conic Sections, 1809 Dover Publications, Inc., New-York, 1963. Reprint
(6, T).
483
76 Golomb S. W. et al Digital Communications with Space Applications,
Prentice-Hall, Inc, Englewood Cliffs, New-York, 1964 {Общее руководство, П, T).
Рус пер Голомб С В и др Цифровые методы в космической связи Пер
с англ под ред В И Шляпоберского М, «Связь», 1969
77 Gray А. Н., Caugney Т. К. A Controversy in Problems Involving Ran-
dom Parametric Excitation —«J Math Phys», September 1965, v 44, p 288—296
(4 4, T)
78 Graybill F. A. An Introduction to Linear Statistical Models McGraw-Hill
Book Company, New-York, 1961, v 1 (2,3,4 2, T)
79 Grenander U., Rosenblatt M. Statistical Analysis of Stationary Time Se-
ries, John Wiley & Sons, Inc, New-York, 1957 (2, 3, 4 2, T)
80 Griffin R. E., Sage A. P. Large and Small Scale Sensitivity Analysis of
Optimum Estimation Algorithms —«IEEE Trans Autom Control», 1968, v.
AC-13, N 4, p 320—329 (8 4, T)
81 Griffin R. E., Sage A. P. Error Bounds for Optimum Smoothing Algo-
rithms — «Proc Matl Electron Conf», December 1968, p 58—63 (8 4, T)
82 Griffin R. E., Sage A. P. Sensitivity Analysis of Fixed Point Linear
Smoothing Algorithms —«Intern J Control», 1968, v 8, N 4, p 321—337
(8 4, T)
83 Griffin R. E., Sage A. P. Error Bounds in Optimum Smoothing — «Proc
IEEE», 1969, v 57, N 4, p 725—726 (8 4, T)
84 Griffin R. E., Sage A. P. Sensitivity Analysis of Discrete Filtering and
Smoothing Algorithms —«А1АА J», 1969, v 7, N 10, p 1890—1897 (8 4, T).
85 Hahn W. Theory and Application of Liapunow’s Direct Method Prentice-
Hall, Inc, Englewood Cliffs, New York, 1963 (7 5, T)
86 Hancock J. C., Wintz P. A. Signal Detection Theory McGraw-Hill Book
Company, New-York, 1966 (5, T)
87 Heffes H. The Effect of Erroneous Models on the Kalman Filter Respon-
se — «IEEE Trans Autom Control», 1966, v AC-11, N 3, p 541—543 (8 4, T)
88 Helstrom C. W. Statistical Theory of Signal Detection Pergamon Press,
Inc, London, 1960 (5, T)
Рус пер Хелстром К Статистическая теория обнаружения сигналов Пер
с англ под ред Ю Б Кобзарева М, «ИЛ», 1963
89 Hildebrand F. В. Methods of Applied Methematics Prentice Hall,, Inc
Englewood Cliffs, New York, 1965 (Общее руководство, T)
90 Но В. L., Kalman R. Е. Spectral Factorization Using the Riccati Equation,
Aerospace Corp Rept TR 1001 (2307)il, November, 1966 (7 4, T)
91 Ho Y. C. On the Stochastic Approximation Method and Optimal Filter
Theory —«J Math Anal Appl», 1962 v 6, p 152—154 (Стохастически аппрок-
симация 6, 7, T)
92 Ho Y. C. The Method of Least Squares and Optimal Filtering Theory,
RAND corp RM-3329-PR, October, 1963 (6 7, T)
93 Ho Y. C., Agrawala A. K- On Pattern Classification Algorithms, Introduc-
tion and Survey —«Proc IEEE», 1968, v 56, N 12, p 2101—2114 t Распознав ыие
образов, T)
94 Но Y. С., Lee R. С. К- A Bayesian Approach to Problems in Stochastic
Estimation and Control —«IEEE Trans Autom Control», 1964, v AC 9, N 4,
p 333—339 (7 2, T)
95 Holtzman J. AL Signal — Noise Ratio Maximization Using the Pontryagin
Maximum Principle —«Bell System Tech J», 1966, v 45, N 3, p 433—488
(Синтез сигналов, T)
96 Jazwinski A. H. Limited Memory Optimal Filtering — «IEEE Trans Au-
tom Control», 1968, v AC-13, N 5, p 558—563 (7, П)
97 Jazwinski A. H. Adaptive Filtering —«Automatical 1969 v 5, N 4,
p 475—485 (8 4, T)
98 Johansen D. E. Solution of a Linear Mean Square Estimation Problem
When Process Statistics Are Undefined — «IEEE Trans Autom Control», 1966,
x AC II, N 1, p 20—30 (8 4, T)
484
99 Kagiwada H. H., Kalaba R. E., Schumitzky A., Sridhar R. Invariant Im-
bedding and Sequential Interpolating Filters for Nonlinear Processes, — «Trans
ASME J Basic Eng», 1969, v 91D, N 2, p 195—200 (9 5, T)
TOO Kailath T. Adaptive Matched Filters, Proc Symp Math Optimization
Tech, University of California Press, Berkeley, 1963 (5, T)
101 Kailath T. An Innovations Approach to Least Squares Estimation-Part 1
Linear Filtering in Additive White Noise —«IEEE Trans Autom Control», 1968,
\ AC-13, N 6, p 646—655 (7 3, T)
102 Kailath T. A General Likelihood Ratio Formula for Random Signals in
Guussian Noise—«IEEE Trans Inform Theory», 1969, v IT-15, N 3, p 350—
361 (5 7, T)
103 Kailath T., Frost P. Mathematical Modeling for Stochastic Process,
Stochastic Problems in Control Proc of Symposium of AACC, published by
ASME, June, 1968, Ann Arbor, Mich , (4 4, 9 2, T)
104 Kailath T., Frost P. An Innovations Approach to Least Squares Estima-
tion , Part II Linear Smoothing in Additive White Noise —«IEEE Trans Autom
Control», 1968, v AC 13, N 6, p 655—660 (8 3, T)
105 Kalman R. E. A New Approach to Linear Filtering and Prediction Prob-
lems — «Trans ASME, J Basic Eng», 1960, v 82D, p 34—45 (7, T)
106 Kalman R. E. On the General Theory of Control Systems Proc IFAC
Moscow Congress, 1960, v 1, p 481—492 Butterworth Inc, Washington, D C
(7 5, T)
107 Kalman R. E. New Methods in Wiener Filtering Theory Proc First
Symp Eng AppI Random Functions Theory Probability, 1963, John Wdey &
Sons, Inc , New-York (7, T)
108 Kalman R. E. When is Linear Control System Optimal’ — «Trans ASME,
J Basic Eng», March 1964, v 86D, p 51—60 (7 4, T)
1109 Kalman R. E. Linear Stochastis Filtering Theory Proc Symp System
Theory, 1965, p 197—205, Polytechnic Press, Brooklyn, New-Work (7, T)
110 Kalman R. E., Bertram J. E. Control System Analysis and Design via
the «Second Method» of Liapunov, 1, Continuous — time Systems —«Trans.
ASME, J Basic Eng», 1960, v 82D, p 371—393
111 Kalman R. E., Bucy R. New Results in Linear Filtering and Prediction
Theory —«Trans ASME, J Basic Eng», March 1961, v 83D, p 95—108 (7, T)
112 Kalman R. E., Englar T. S., Bucy R. S. Fundamental Study of Adaptive
Control System, Wright Patterson Air Force Base, Ohio, ASD-TR 61—27, 1961
(7, T)
113 Kalman R. E., Falb P. L., Arbib M. A. Topics in Mathematical System
Theory, McGraw Hill Book Company, New-York, 1969 (7 5, T)
114 Kalman R. E., Ho Y. C., Nahendra K- S. Controllability of Linear Dyna-
mical Systems —«Contributions to Differential Equations», 1962, v 1, N 2,
p 189—213 (7 5, T)
115 Klein P. I. Application of the Concept of Referenced Radio Navigation —
«IEEE Trans Aerospace Electron Systems», 1968, v AES-4, N 4, p 494—498
(7, П)
116 Klinger A. Prior Information and Bias in Sequential Estimation —
«IEEE Trans Autom Control», February 1968, p 102—105 (6 5)
117 Knoll A., Edelstein M. Estimation of Local Vertical and Orbital Parame-
*ers for an Earth Satellite Using Horizon Sensor Measurements —«А1АА J»,
1965, v 3, N 2, p 338—345 (8 5, П)
118 Korn G. A., Korn T. M. Mathematical Handbook for Engineers and
Scientists McGraw-Hill Book Company, New-York, 1961
Рус пер Корч Г , Корн T Справочник по математике для научных работ-
ников и инженеров Пер с англ под ред И Г Арамановнча М, «Наука», 1970
119 Kozin С. Н, Cooper G. R. The Use of Prior Estimates in Successive
Point Estimations of a Random Signal —«J SIAM Appl Math», 1966, v 14,
N I, P H2—130 (6 5, T)
120 Kreindler E., Sarachik P. E. On the Concepts of Controllability and Ob-
servability of Linear Systems —«IEEE Trans Autom Control», 1964, v AC-9,
N 2, p 129—136 (7 5, T)
485
121 Kroy W. H., Stubberud A. R. Identification via Nonlinear Filtering —
«Intern J Control», 1967, v 6, N 6, p 499—522 (9 4, T)
122 Kullback S. Information Theory and Statistics, John Wiley & Sons, Inc,
New-York, 1959 (7 5, T)
Рус пер Кульбак С Теория информации и статистика Пер с англ под
ред А Н Колмогорова М, «Наука», 1967
123 Кио В. С. Analysis and Synthesis of Sampled-Data Control Systems
Prentice-Hall, Inc, Englewood Cliffs, New-York, 1963 (7 4, T)
124 Kushner H. J. On the Differential Equations Satisfied by Conditional
Probability Densities of Markov Processes, with Applications —«J SIAM Cont-
rol, ser А», 1962, v 2, N 1, p 106—119 (9 2, T)
125 Kushner H. J. Dynamical Equations for Optimal Nonlinear Filtering —
«J Differential Equations», 1967, v 3, p 179—190 (9 2, T)
126, Kushner H. J. Nonlinear Filtering The exact Dynamic Equations Satisfied
by the Conditional Mode —«IEEE Trans Autom Control», 1967, v AC 12, N 3,
p 262—267 (9 2, T)
127 Kushner H. J. Approximations to Optimal Nonlinear Filters —«IEEE
Trans Autom Control», 1967, v AC-12, N 5, p 546—556 (9 2, T)
128 Kwakernaak H. Optimal Filtering in Linear Systems with Time Delays —
«IEEE Trans Autom Control», 1967, v AC 12, N 2, p 169—173 (7, T)
129 Laning J. H., Jr., Battin R. H. Random Processes in Automatic Control
McGraw-Hill Book Company, New-York, 1956 >(2,3,4.2, Общее руководство, T)
Рус пер Лэиинг Дж X, Бэттин Р Г Случайные процессы в задачах
автоматического регулирования Пер с англ под ред В С Пугачева М, «ИЛ»,
1958
130 Larson R. Е., Peschon J. A Dinamic Programming Approach to Trajecto-
ry Estimation —«IEEE Trans Autom Control», 1966, v AC-11, N 3, p 537—540
(9, T)
131 Lawson J. L., Uhlenbeck G. E. Threchold Signals, McGraw-Hill Book
Company, New-York, 1950 (2,3,4 2, T)
Рус пер Пороговые сигналы Пер с англ под ред А П Сиверса, М, «Со
ветское радио», 1952
132 Lee В. The improvement of a Low — cost Inertial Navigator through Con-
ditional Feedback — «IEEE Trans Aerospace Electron Systems», 1968, v AES-4,
no, p 627—634 (7, П)
133 Lee R. С. K. Optimal Estimation, Identification and Control M I T Res
Monograph 28, Cambridge, Mass, 1964 (7, 8, 9, T)
Рус пер Ли РСК Оптимальные оценки, определение характеристик и
управление Пер с англ под ред Я 3 Цыпкина М, «Наука», 1966
134 Lee Y. W. Statistical Theory of Communication John Wiley & Sons, Inc,
New-York, 1960 (2,3,4 2,7 4, T)
135 Legendre A. M. Nouvelles methodes pour la determination des orbites des
cometes Paris, 1806 (6, T)
136 Lehman E. L. Testing Statistical Hypotheses John Wiley & Sons, Inc,
New York, 1959 (5, T)
Рус nep Леман Э Проверка статистических гипотез Пер с англ Ю В Про-
хорова М, «Наука», 1964
137 Leondes С. Т., Peller J. В., Stear Е. В. Nonlinear Smoothing Theory —
«IEEE Trans System Sci Cybernetics», 1970, v SSC-6, N 1 (9, T)
138 Liebelt P. B. An Introduction to Optimal Estimation Addison-Wesley
Publishing Company, Inc, Reading, Mass, 1967 (2,3,4 2, 7, T)
139 Loeve M. Probability Theory D Van Nosirand Company, Inc, Princeton,
New York, 1955 (2, 3, 4 2, T)
Рус пер Лоэв M Теория вероятностей Пер с англ под ред Ю В Про-
хорова М, «ИЛ», 1962
140 Lucky R. W., Saiz J., Weldon E. J. Jr. Principles of Data Communica-
tion McGraw-Hill Book Company, New-York, 1968 (Общее руководство, П)
141 Luenberger D. G. Observing the State of a Linear System — IEEE
Trans Mil Electron», 1964, April, v MIL-8, p 74—80 (7, T).
486
142 Luenberger D. G. Observers for Multivariable Systems. — «IEEE Trans
Autom Control», 1966, v AC-11, N 2, p 190—197 (7, T)
143 McAulary R. J. Numarical Optimization Techniques Applied to PPM Sig-
nal Design —«IEEE Trans^ Inform Theory», 1968, v IT-14, N 5, p. 708—716
(Синтез сиг галов, T)
144 McBride A. L., Sage A. R. Optimum Estimation of Bit Synchronization —
«IEEE Trans Aerospace Electron Systems», 1969, v 5, N 3, p 525—536 (6, П)
145 McBride A. L., Sage A. P. On Discrete Sequential Estimation of Bit
Synchronization —«IEEE Trans Comm Technology», 1970, v 18, N 1, p 48—68
(6, П)
146 McGhee R. B., Walford R. B. A Monte Carlo Approach to the Evaluation
of Condition Expectation Parameter Estimates for Nonlinear Dynamic Systems —
«IEEE Trans Autom Control», 1968, v AC-13, N 1, p 29—36 (9 2,9 4, П)
147 McLendon J. R., Sage A. P. Computational Algorithms for Discrete De-
tection and Likelihood Ratio Computation —«Information Sciences», 1970, v 2,
N 3 (5 9, T)
148 McReynolds S. R. A New Approach to Stochastic Calculus, presented at
the Seminar on Guidance Theory and Trajectory Analysis, May 31, 1967, NASA
Electronics Research Center, Cambridge, Mass (4 4, T)
149 Magil D. T. Optimal Adaptive Estimation of Sampled Stochastic Proces-
ses — «IEEE Trans Autom Control», 1965, v AC-10, N 4, p 434—439
(8 4, Распознавание образов)
150 Mayne D. Q. A Solution of the Smoothing Problem for Linear Dynamic
Systems —«Automatics», 1966, v 4, p 73—92 (8 3, T)
151 Meditch J. S. Orthogonal Projection and Discrete Optimal Linear Smoot-
hing — «SIAM J Control», 1967, v 5, N 1, p 74—80 (8 3, T)
152 Meditch J. S. Optimal Fixed Point Continuous Linear Smoothing —
Proc Joint Autom Control Conf, June 1967, p 249—257 (8 3, T)
153 Meditch J. S. The Wiener — Hopf Solution and the Optimal Fixed Point
Smoothing Problem Inform processing Control Systems Lab Tech Rept 67—11,
June 1967 (8 3, T)
154 Meditch J. S. On Optimal Fixed Point Linear Smoothing, Boeing Sci
Res Lab Inform Sci Rept 1, August 1967 (8 3, T)
155 Meditch J. S. On Optimal Linear Smoothing Theory —«Inform Control»,
1967, v 10, p 598—615 (8 3, T)
156 Meditch J. S. A Successive Approximation Procedure for Nonlinear Data
Smoothing, Proc Symp Inform Processing, April 1969, p 555—568, Purdue
L’niversity, Lafayette, Ind
157 Meditch J. S. Stochastic Optimal Linear Estimation and Control McGraw-
Hill Book Company, New-York, 1969 (2, 3, 4, 7, 8, T)
158 Mehra R. K. On Optimal and Suboptimal Linear Smoothing, Proc 1968,
Nat Electron Conf, 1968, p 119—124 (8 4, T)
159 Mehra R. K-, Bryson A. E. Jr. Linear Smoothing Using Measurements
Containing Correlated Noise with an Applicatoin to Inertial Navigation — «IEEE
Trans Autom Control», 1968, v AC-13, N 5, p 496—503 (8 2,8 3, T)
160 Mehra R. K-, Bryson A. E. Ir. Smoothing for Time varying Systems Using
Measurements Containing Colored Noise, Proc Joint Autom Control Conf, 1968,
p 871—883, Ann Arbor, Mich (8 2,8 3, T)
161 Melsa J. L. Frequency Domain Derivation of the Stationary Kalman Fil-
ter Proc First Ann Hounston Conf Circuits Systems Computers, 11969,
p 323—332 (7 4, T)
162 Melsa J. L., Schultz D. Linear Control Systems McGraw Hill Book Com-
pany, New-York, 1969 (Общее руководство, T)
163 Middleton D. Introduction to Statistical Communication Theory McGraw-
Hill Book Company, New York, 1960 (2 3, 4, 5, 6, общее руководство, T)
Рус пер Миддлтон Д Введение в стохастическую теорию связи Пер с англ
под ред Б Р Левина М, «Советское радио», т 1, 1961 т 2, 1962
164 Middleton D., Esposito R. Simultaneous Optimum Detection and Estima-
tion of Signals in Noise —«IEEE Trans Inform Theory», 1968, v IT-14, N 3,
p 434—444 (5 7,T)
487
165 Middleton D., Van Meter D. Detection and Extraction of Signals in Noi-
se from the Point of View of Statistical Decision Theory — «J Soc Ind. Appl
Math», 1955, v 3, p 192, 1956, v 4, p 86 (5, T)
166 Mood A. M., Graybill F. A. Introduction to the Theory of Statistics, 2d
ed , McGraw-Hill Book Company, New-York, 1963 (2 3, 4 2, 5, 6, T)
167 Moore J. B. Optimum Differntiation Using Kalman Filter Theory —
«Proc. IEEE», 1968, v 56, N 5, p 871 (7, П)
168 Nash R. A. The Estimation and Control of Terrestrial Inertial Naviga-
tion System Errors Due to Vertical Deffections —«IEEE Trans Autom Control»,
1968, v. AC-13, N 4, p 329—338 (7, Стохастическое управление, П)
169 Nash R. A., Tuteur F. B. The Effect of Uncertainties in the Covariance
Matrices on the Maximum Likelihood Estimate of a Vector —«IEEE Trans Au-
tom Control», 1968, v 13, № 1, p 86—88 (8 4, T)
170 Neal S. R. Linear Estimation in the Presence of Errors in Assumed Plant
Dynamics —«IEEE Trans Autom Control», 1967, v AC-12, N 5, p 592—594
(8 4 T)
171 Newbold P. M., Ho Y. C. Detection of Changes in Characteristics of a
Gauss-Markov Process —«IEEE Trans Aerospace Electron Systems», 1968,
v AES 4, N 5, p 707—718 (5 7, T)
172 Newton G. C. et al. Analytical Desing of Linear Feedback Controls John
Wiley & Sons, Inc, New-York, 1957 (7 4,T)
173 Nishimura T. On the Apriori Information in Sequential Estimation
Problems —«IEEE Trans Autom. Control», 1966, v AC-11, N 2, p 197—204
(8 4 T)
174 Nishimura T. Correction to and Extension of «On the Apriori Informa-
tion in Sequential Estimation Problems» — «IEEE Trans Autom Control», Feb-
ruarj 1967, v AC-12, p 123 (8 4, T)
175 Nishimura T. Error Bounds of Continuous Kalman Filters and the Appli-
cation to Orbit Determination Problems — «IEEE Trans Autom Control», 1967,
v AC-12, N 3, p 268—275 (8 4, T)
176 North D. O. Analysis of the Factors Which Determine Signal/Noise Dis-
crimination in Pulse Carrier Systems —«Proc IRE», 1963, v 51, p 1016—1028
(5, 6, T)
177 Ohap R. F., Stubberud A. R. A Technique for Estimating the State of
a Nonlinear System —«IEEE Trans Autom Control», 1965, v AC-10, N 2,
p 150—155 (9 4, T)
178 Omura J. K. Signal Optimization for Additive Noise Channels with
Feedback, presented at WESCON, August, 1966, session 7, The Application of
State — variable Techniques to Communication and Radar Problems (7, Синтез
сигналов, T)
179 Oppenheim A. V., Schafer R. W., Stockham T. G. Jr Nonlinear Filtering
of Multiplied and Convolved Signals —«Proc IEEE», 1968, v 56, N 8, p 1264—
1291 (9 4, T)
180 Papoulis A. Probability, Random Variables and Stochastic Processes,
McGraw-Hill Book Company, New York, 1965 (2, 3, 4 2, 4 3, T)
181 Parzen E. Modern Probability Theory and Its Applications, John Wiley
& Sons, Inc, New-York, I960 (2 3,4 2, T).
182 Parzen E. Stochastic Processes, Holden-Day, Inc, Publisher, San-Fran-
cisco, 1962 (2,3,4 2,4 3, T)
183 Pearson J. B. On Nonlinear Least-squares Filtering—«Automatica»,
1967, v 4, p 97—105 (9 3, T)
184 Pentecost E. E., Stubberud A. R. Synthesis of Computationally Efficient
Sequential Linear Estimators — «IEEE Trans Aerospace Electron Systems», 1967,
v AES-3, N 2, p 242—249 (7, T)
185 Peterson W. W., Birdsall T. G., Fox W. C. The Theory of Signal Detecta-
bility— «IRE Trans Inform Theory», 1954, v PGIT-4, p 171 (5, T)
186 Pickholtz R. L., Boorstyn R. R. A Recursive Approach to Signal Detec-
tion — «IEEE Trans Inform Theory», 1968, v IT-14, N 3, p 445—450 (5 7, T)
187 Potter J. E., Fraser D. C. A Formula for Updating the Determinant of
the Covariance Matrix —«А1АА J», 1967, v 5, N 7, p 1352—1354 (7.T).
488
188 Пугачев В. С. Теория случайных функций М, Физматгиз, 1960
189 Raiffa Н., Schlaifer R. Applied Statistical Decision Theory, Graduate
School of Business Administration, Harvard University, Boston, 1961 (5, 6, T)
190 Rao C. R. Information Accuracy Attainable in the Estimation of Statisti-
cal Parameters —«Bull Calcutta Math Soc», 1945, v 37, p. 81—91 (6 4, T).
191 Rao C. R. Linear Statistical Inference and Applications Johns Wiley &
Sons Inc, New-York, 1965 (общее руководство, T)
Рус пер Р а о С Р Линейные статистические методы и их применения Пер
с англ под ред Ю В Линника М, «Наука», 1968
192 Rauch Н. Е. Solutions to the Linear Smoothing Problem —«IEEE Trans
Autom Control», 1963, v AC 8, N 4, p 371—372 (8 3, T)
193 Rauch H. E. Optimum Estimation of Satellite Trajectories Including Ran-
dom Fluctuations in Drag —«А1АА J», 1965, v 3, N 4, p 717—722 (7, П).
194 Rauch H. E. Least Squares Estimation with a Large Number of Para-
meters — «Proc Joint Autom Control Conf», 1967, p 241—2487 (8 5,11)
195 Rauch. H. E., Tung F., Striebel С. T. Maximum Likelihood Estimates of
Linear Dynamic Systems —«А1АА J», 1965, v 3, N 8, p 1445—1450 (7, 8 3)
196 Rice S. O. Mathematical Analysis of Random Noise —«Bell System
Tech J», 1944, v 23, p 282—332 (2,3,4 2, T)
197 Richman J., Friedland B. Design of Optimum Mixer-Filter for Aircraft
Navigation Systems, Natl Aerospace Electron Conf Proc, May 1967, p 429—
438, Dayton, Ohio (7, П)
198 Riddle A. C., Anderson B. D. O. Spectral Factorization Computational As-
pects — «IEEE Trans Autom Control», 1966, v AC-11, N 4, p 764—765 (7 4, T).
199 Roberts A. P. Optimal Linear Filtering and Lagging Filtering of Colou-
red Noise —«Intern J Control», 1968, v 8, N 4, p 401—416 (8 3, T)
200 Rose R. E., Lance G. M. Analysis of the Behavior of Continuous Parame-
ter Estimation Methods Proc Joint Autom Control Conf, June 1968, p 109—
115, Ann Arbor, Mich (7, T)
201 Rosenblatt M. Random Processes Oxford University Press, New-York,
1962 (2, 3, 4 2, 4 3, общее руководство, T)
202 Sage A. P. Optimum Systems Control Prentice-Hall, Inc, Englewood
Cliffs, New-York, 1968 (7,8,9, Оптимизация, T)
203 Sage A. P. Quasihnear Techniques for Filtering in Discrete Nonlinear
Systems Proc Third Ann Princeton Conf Inform Sci Systems, March 1969,
p 452—456 (9 4, T)
204 Sage A. P. Maximum Apostenon Filtering and Smoothing Algorithms —
«Intern J Control», 1970, v 11, N 3 (9 3,9 5, T)
205 Sage A. P., Ewing W. S. Approximate Solution Algorithms for Nonlinear
Filter Problems Proc Second Ann Princeton Conf Inform Sci Systems,
March 1968, p 323—327 (9 4, T)
206 Sage A. P., Ewing W. S On Smoothing Algorithms for Nonlinear State
and Parameter Estimation Proc Second Hawaii Intern Conf System Sci,
Jun 1969, p 373—376 (9 5, T)
207 Sage A. P., Ewing W. S. On Filtering and Smoothing Algorithms Non-
linear State Estimation —«Intern J Control», 1970, v 11, N 1, p 1 —18 (9 5, T)
208 Sage A. P., Husa G. W. Adaptive Filtering with Unknown Prior Sta-
tistics, Proc 1969 (8, 4, T)
209 Sage A. P., McLendon J. R. Discrete Sequential Detection and Likelihood
Ratio Computation for Non — Gaussian Signals in Gaussian Noise, Proc Symp
Inform Processing, Apr 1969, p 589—598, Purdue University, Lafayette, Ind
(5, T)
210 Sage A. P., Masters G. W. On-line Estimation of States and Parameters
for Discrete Nonlinear Dynamic Systems Proc Natl Electron Conf, 1966,
D 677—682 (9 3, T)
211 Sage A. P, Masters G. W. Identification and Modeling of States and
Parameters of Nuclear Reactor Systems — «IEEE Trans Nuclear Systems» 1967,
v NS-14, N 1, p 279—285 (9 3, T)
212 Sage A. P., Masters G. W. Least Squares Curve Fitting and Discrete
Optimal Filtering —«IEEE Trans Educ», 1967, v. E-10, N 1, p 29—36 (7, T).
489
213. Sage A. P., Melsa J. 1. System Identification. Academic Press Inc.,
New-York, 1970 (9, Стохастическая аппроксимация, T).
Рус. пер.: Сейдж Э. П., Мелса Дж. Л. Идентификация систем управления.
Пер. с англ, иод ред. Н. С. Райбмана. М., «Наука», 1974.
214. Sain М. К- On the Control Applications of a Determinant Equality Rela-
ted to Eigenvalue Computation. — «IEEE Trans. Autom Control», 1966, v. AC-11,
N 1, p. 109—111 (7. 4, T).
215. Sakrison D. The Use of Stochastic Approximation to Solve the System
Identification Problem. — «IEEE Trans. Autom. Control», 1967, v. AC-12, N 5,
p. 563—567 (Стохастическая аппроксимация, T).
216. Sakrison D. Communication Theory: Transmission of Wave Forms and
Digital Information. John Wiley & Sons, Inc., New-York, 11968 ( 2, 3, 4.2,
Общее руководство, T).
217. Saridis G. N. Learning Applied to Successive Aproximation Algorithms,—
Proc. Joint Autom. Control Conf., June 1968, p. 1007—1013, Ann Arbor, Mich.
(Распознавание образов, T).
218. Saridis G. N., Stein G. Stochastic Approximation Algorithms for Linear
Discrete Time Svstem Identification. — «IEEE Trans. Autom. Control», 1968,
v. AC-13, N 5, p. 515—523 (9, T).
219. Sarma V. V. S., Deeksnatulu B. L. Optimal Control When Some of the
State Variables Are Not Measurable. — «Intern. J. Control», 1968, v. 7, N 3 (7, П).
220. Sawaragi Y., Sunahara Y., Nakamizo T. Statistical Decision Theory in
Adaptive Control Systems. Academic Press. Inc., New-York, 1967 (5, T).
221. Shlee F. H., Standish C. J., Toda N. F. Divergence in the Kalman Fil-
ter. — «А1АА J.», 1967, v. 5, N 6, p. 1114—1120 (8. 5, T).
222. Schmidt S. F. et al. Case Study of Kalman Filtering in the C-5 Aircraft
Navigation System. Case Studies in System Control, sponsored by IEEE Group
on Autom. Control, 1968, Joint Autom. Control Conf., Ann Arbor, Mich., 1968
(7,8, T).
223. Schultz D. G., Melsa J. L. State Functions and Linear Control Systems,
McGraw-Hill Book Company, New-York, 1967 (Общее руководство, T).
224. Schwartz L., Bass R. W. Extensions to Optimal Multi-channel Nonlinear
Filtering, Hughes Aircraft Co., Space Systems Div., Rept. SSD 60220R, Feb. 21,
1966 (9. 2, T).
225. Schwartz L., Stear E. B. A Valid Mathematical Model for Approximate
Nonlinear Minimalvariance Filtering. — «J. Math. Anal. Appl.», January 1968,
v. 21, p. 1—6 (9 2, T).
226. Schwartz L., Stear E. B. A Computational Comparison of Several» Nonli-
near Filters. — «IEEE Trans. Autom. Control», 1968, v. 13, N 1 (9. 4, T).
227. Schwartz M. Abstract Vector Spaces Applied to Problems in Detection
and Estimation Theory.—«IEEE Trans. Inform. Theory», 1966, v. IT-12, N 3,
p. 327—336 (5, T).
228. Schwartz M., Bennett W. R., Stein S. Communication Systems and Tech-
niques, McGraw-Hill Book Company, New-York, 1966 (Общее руководство, П, T).
229. Schweppe F. C. Optimizataion of Signals, M. I. T. Group Rept. 1964—4,
Jan. 16, 1964 (Синтез сигналов, T).
230. Schweppe F. C. Evaluation of Likelihood Functions for Gaussian Sig-
nals.— «IEEE Trans. Inform. Theory», 1965, v. IT-11, N 1, p. 61—70 (5. 7, T).
231. Schweppe F. C. Radar Frequency Modulations for Accelerating Targets
under a Band-width Constraint. — «IEEE Trans. Mil. Electron.», 1965, v. MIL-9,
N 1, p. 25—32 (Синтез сигналов, П).
232. Schweppe F. C. Recursive State Estimation Unknown but Bounded Erroes
and System Inputs. — «IEEE Trans. Autom. Control», 1968, v. AC-13, N 1,
p. 22—28 (7, П).
233. Schweppe F. C. Sensor-array Data Processing for Multiple-signal Sour-
ces.—«IEEE Trans. Inform. Theory», 1968, v. IT-14, N 2, p. 294—305 (5, П).
234. Schweppe F. C., Gray D. L. Radar Signal Design Subject to Simultaneo-
us Peak and Average Power Constraints.—«IEEE Trans. Inform. Theory», 1966,
v. IT-12, N 1, p. 13—26 (Синтез сигналов, T).
490
235. Seidman L. P. An Upper Bound on Average Estimation on Error in
Nonlinear Systems. — «IEEE Trans. Inform. Theory», 1968, v. IT-14, N 2,
p. 243—249 (9, T).
236. Selin I. The Sequential Estimation and Detection of Signals in Normal
Noise, I. — «Inform. Control», 1964, v. 7, p. 512—534 (5, T).
237. Selin I. The Sequential Estimation and Detection of Signals in Normal
Noise, II. — «Inform. Control», 1965, v. 8, p. 1—35 (5, T).
238. Selin I. Detection Theory. Princeton University Press, Princeton,
New-Jersey, 1965 (5, T).
239. Sherman S. Non-mean-square Error Criteria. — «IRE Trans. Inform.
Theory», 1958, v. IT-4, N 3, p. 125—126 (6.2,T).
240. Sims C. S., Melsa J. L. Specific Optimal Estimation.—«IEEE Trans.
Autom. Control», 1969, v. AC-14, N 2, p. 183—186 (7. 3, T). •
241. Скороход А. В. Исследования no теории случайных процессов. Изд-во
Киевского ун-та, 1961.
242. Smith G. L. On the Theory and Methods of Statistical Inference, NASA
Tech. Rept. NASA TR R-251, April, 1967 (6. 7,T).
243. Smith G. L. Sequential Estimation of Observation Error Variances in a
Trajectory Estimation Problem. — «А1АА J.», 1967, v. 5, N 11, p. 1964—1970
(8.4, T).
244. Smith G. L., Schmidt S. F., McGree L. A. Application of Statistical Filter
Theory to the Optimal Estimation of Position and Velocity on Board a Circumlu-
nar Vehicle». NASA Tech. Rept. NASA-TR R-135, 1962 (7, 8, П).
245. Snyder D. L. The State — variable Approach to Analog Communication
Theory. — «IEEE Trans. Inform. Theory», 1968, v. IT-14, N 1, p. 94—104 (9. 2, T).
246. Snyder D. L. The State-Variable Approach to Continuous Estimation with
Applications to Analog Communication Theory. M. I.T. Res. Monograph 51, Camb-
ridge, Mass., 1969 (7, 9, П).
247. Солодовников В. В. Введение в статистическую динамику систем авто-
матического управления. М.—-Л. Изд-во технико-теоретической литературы, 1952
(2,3,4 2, Общее руководство, Т).
248. Soong Т. Т. On Apriori Statistics in Minimum — variance Estimation
Problems. — «J. Basic Eng.», March, 1965, p. 109—112 (8. 4, T).
249. Sorenson H. W. Kalman Filtering Techniques. — «Advan. Control Sys-
tems», 1966, v. 3, p. 219—292 (7, T).
250. Sorenson H. W. On the Error Behavior in Linear Minimum Variance
Estimation Problems. — «IEEE Trans. Autom. Control», 1967, v. AC-12, N 5,
p. 557—562 (8. 4,T).
251. Sorenson H. W., Stubberud A. R. Recursive Filtering for Systems with
Small but Non-negligible Non-linearities —«Intern. J. Control», 1968, v. 7, N 3,
p. 271—280 (9. 4, T).
252. Sorenson H. W., Stubberud A. R. Non-linear -iltering by Approximation
of the Aposteriori Density. — «Intern. J. Control», 1968, v. 8, N 1, p. 33—51
(9 4, T).
253. Stear E. B., Stubberud A. R. Optimal Filtering for Gauss-Markov Noi-
se.— «Intern J. Control», v. 8, N 2, p. 123—130, 1264—1268 (8. 3, T).
254. Stein S., Jones J. J. Modern Communication Principles with Application
to Digital Signaling. McGraw-Hill Book Company, New-York, 1967 (Общее руко-
водство, П, T).
Рус. пер : Стейн С., Джонс Дж. Принципы современной теории связи и их
применение к передаче дискретных сообщений. Пер. с англ, под ред. Л. М. Фин-
ка. М., «Связь», 1971.
255 Steinway W. J., Melsa J. L. Discrete Estimation Algorithm for Randomly
Sapled Stochastic Signals. — «IEEE Trans. Autom. Control», 1970, v. AC-15, N 3
(8, T).
256. Stoep D. R. V. Trajectory Shaping for the Minimization of State Variab-
le. Estimation Errors. Proc. Joint Autom. Control Conf., 1968, June, p. 884—
891, Ann Arbor, Mich. (7, П).
257. Стратонович P. Л. Избранные вопросы теории флуктуаций в радиотех-
нике. М., «Советское радио», 1961 (2, 3, 4, Т).
491
258. Стратонович Р. Л. Условные марковские процессы и их применение к
теории оптимального управления. М., изд. МГУ, 1966 ’(4.4, 9.2).
259. Stubberud A. R. Optimal Filtering for Gauss-Markov Noise. Aerospace
Rept. N. TR-0158 (3307-01)-10, December, 1967 (8. 2, T).
260. Swerling P. Note on a New Computational Data Smoothing Procedure
Suggested by Minimum Mean Square Estimation. — «IEEE Trans. Inform. Theo-
ry», 1966, v. 12, N 1, p. 9—12 (7, T).
261. Thau F. E. On Optimum Filtering for a Class of Linear Distributed-para-
meter Systems. Proc. Joint Autom. Control Conf., June 1968, p. 610—618,
Ann Arbor, Mich. (7, T).
262. Thompson J. S., Titlebaum E. L. The Design of Optimal Radar Wave-
forms for Clutter Rejection Using the Maximum Principle. — «Suppl. IEEE Trans.
Aerospace Electron Systems», 1967, v. AES-3, N 6, p. 581—589 ’(Синтез сигна-
лов, T).
263. Tinkleman M., Pearson J. D. A Decomposition Approach to the Optimal
Smoothing Problem. JACC Preprints, 1967, p. 646—654 (8.3, T).
264. Titlebaum E. L. Optimization Methods for Signal and Processing.—
«Suppl. IEEE Trans. Aerospace Electron. Systems», 1967, v. AES-3, N 6,
p. 543—551 (Синтез сигналов, T).
265. Toda N. F., Schlee F. H., Obsharsky P. The Region of Kalman Filter
Convergence for Several Autonomous Navigation Modes. — «А1АА J.», 1969, v. 7,
N 4, p. 622—627 (8. 5, T).
266. Tufts D. W., Shnidmal D. A. Optimum Waveforms Subject to Both Ener-
gy and Peak-value Constraints. — «Proc. IEEE», 1964, v. 52, N 9, p. 1002—1107
(Синтез сигналов, T).
267. Tung F. Linear Control Theory Applied to Interplanetary Guidance. —
«IEEE Trans. Autom. Control», 1964, v. AC-9, N 1, p. 82—89 (7, Совместные
операции оценивания и управления, П).
268. Turin G. L. An Introduction to Matched Filters. — «IRE Trans. Inform
Theory», June 1960, v. IT-6, p. 311—329 (5, 6, T).
269. Van Trees H. L. Detection Estimation, and Modulation Theory. Part I,
John Wiiey & Sons, Inc., New-York, 1968 (5, 6, 7, T).
Рус. nep.: Ван Трисс Г. Теория обнаружения, оценок и модуляции. Т. 1. Пер.
. англ, под ред. В. И. Тихонова. М., «Советское радио», 1972.
270. Viterbi A. J. Principles of Coherent Communication, McGraw-Hill Book
Company, New-York, 1966 (5, 6, Общее руководство, П, T).
Рус. пер.: Витерби А. Дж. Принципы когерентной связи. Пер. с англ, под
ред. Б. Р. Левина. М., «Советское радио», >1970.
271. Вайштейн Л. А., Зубаков В. Д. Выделение сигналов на фоне случайных
помех. М., «Советское радио», 1960.
272. Wald A. Sequential Analysis, John Wiley & Sons, Inc., New-York, 1947
(5, T).
Рус. nep.: Вальд А. Последовательный анализ. Пер. с англ, под ред Б. А. Се-
вастьянова. М., Физматгиз, 1960.
273. Wald A. Statistical Decision Theory. John Wiley & Sons, Inc., New-York,
1949 (5, T).
См. также Вальд А. Статистические решающие функции. Пер. с англ, под
ред. Н. Н. Воробьева и И. Н. Врублевской. В кн.: Позиционные игры. М, «Нау-
ка», 1967.
274. Winer N. Generalized Harmonic Analysis. — «Acta Math.», 1930, v. 55,
p. 117 (3.4,T).
275. Winer N. The Extrapolation, Interpolation, and Smoothing of Stationary
Time Series with Engineering Applications», John Wiley & Sons, Inc., New-York,
1949 (3,4, 7.4, T).
276. Wilks S. S. Mathematical Statistics. John Wiley & Sons, Inc., New-York,
1962 (2, 3,4. 2,5, 6, T).
Рус. nep.: Уилкс С. С. Математическая статистика. Пер. с аигл. под ред.
Ю. В. Линника. М., «Наука», 1967.
277. Wishner R. Р., Tabaczynski J. A., Athans М. A Comparison of Three
Nonlinear Filters. — «Automatica», 1969, v. 5, N 4, p. 487—496 (9. 4, T).
492
278. Wolowich W. A. On State Estimation of Observable Systems. Proc.
Joint Autom. Control Conf., June 1968, p. 210—220. Ann Arbor, Mich. (7, П).
279. Wong E., Thomas J. B. On the Multidimensional Prediction and Filtering
Problem and the Factorization of Spectral Matrices. — «J. Franklin Inst.», 1961,
v. 272, N 2, p. 87—99 (7 4, T).
280. Wong E., Zakai M. On Convergence of the Solutions of Differential
Equations Involving Brownian Motion. Univ, of California Electron. Res. Lab.
Rept. Rept. 65—5, Berkeley, Calif., January, 1965 (4.4, T).
281. Wong E., Zakai M. On the Relation between Ordinary and Stochastic
Differential Equations. — «Intern. J. Eng. Sci.», 1965, v. 3, p. 213—229 (4. 4, T).
282. Wonham W. M. Some Applications of Stochastic Differential Equations
to Optimal Nonlinear Filtering. — «J. SIAM Control, ser. А», 1965, v. 2, N 3,
p. 347—369 (9. 2, T)
283. Woodward P. M. Probability and Information Theory with Applications
to Radar. McGraw-Hill Book Company, New-York, 1957 (2, 3, 4. 2, 5, 6, T).
Рус. пер.: Вудворт Ф. M. Теория вероятностей и теория информации с при-
менениями в радиолокации. Пер. с англ, под ред. Г. С. Горелика. М., «Советское
радио», 1955.
284. Wozencraft J. М., Jacobs I. М. Principles of Communication Engineering.
John Wiley & Sons, Inc., New-York, 1965 (2,3,4.2, Общее руководство, T).
Рус. пер.: Возенкрафт Дж. М., Джекобс И. М. Теоретические основы техники
связи. Пер. с англ, под ред. Р. Л. Добрушина. М., «Мир», 1969.
285. Youla D. С. On the Factorization of Rational Matrices. — «IEEE Trans.
Inform. Theory», 1961, v. IT-7, N 3, p. 172—189 (5. 6, T).
286. Zadeh L. A., Desoer C. A. Linear System Theory: The State Space Ap-
proach. McGraw-Hill Book Company, New-York, 1963 (Общее руководство, T).
Рус пер.: Заде Л., Дезоер Ч. Теория линейных систем. Пер. с аигл. под ред.
Г. С. Поспелова. М., «Наука», 1970.
287. Zadeh L. A., Ragazzini J. R. An Extension of Wiener’s Theory of Predic-
tion.— «J. Appl. Phys. Applied Physics», July 1950, v. 21, p. 645—655 (7. 4, T).
288. Zadeh L. A., Ragazzini J. R. Optimum Filters for the Detection of Sig-
nals in Noise. — «Proc. IRE», 1952, v. 40, p. 1223—1231 (5, 6, T).
289* . Большаков И. А., Гуткнн Л. С., Левин Б. Р., Стратонович Р. Л. Мате-
матические основы современной радиоэлектроники. М., «Советское радио», 1968.
290* . Гихман И. И., Скороход А. В. Теория случайных процессов. М., «Нау-
ка», т. 1, 1971; т. 2, 1973.
291* . Колмогоров А. Н. Основные понятия теории вероятностей. Изд. 2-е. М.,
«Наука», 1974.
292* . Левин Б. Р. Теоретические основы статистической радиотехники. Изд.
2-е. М, «Советское радио», кн. первая, 1974; кн вторая, 1975
293* . Лиииик Ю. В. Статистические задачи с мешающими параметрами. М.,
«Наука», 1966.
294* . Липцер Р. Ш.,- Ширяев А. Н. Статистика случайных процессов. М.,
«Наука», 1974.
295* Невельсои М. Б., Хасминский Р. 3. Стохастическая аппроксимация и
рекуррентное оценивание. М., «Наука», 1972.
296* . Фалькович С. Е. Оценка параметров сигнала. М., «Советское радио»,
1970.
297* . Хазен Э. М. Методы оптимальных статистических решений и задачи оп-
тимального управления. М., «Советское радио», 1968.
298* Цыпкин Я. 3. Основы теории обучающихся систем. М., «Наука», 1970.
299. Kailath Т. A. View of Three Decades of Linear Filtering Theory.— «IEEE
Trans», 1974, v. IT-20, N 2.
300*. Теория обнаружения сигналов и ее применение.— «ТИИЭР», 1970, № 5,
пер. с англ, под ред. Б. Р. Левина. М., «Мир», 1970.
ОГЛАВЛЕНИЕ
Стр.
Предисловие редактора перевода .............................. , . 3
Предисловие автора к русскому изданию................................. 4
Глава 1
Обзор содержания книги . .............................. 5
Г лава 2
Основы теории вероятностен . . . .......................10
2.1. Введение..........................................................Ю
2.2. Теория вероятностей..............................................10
2.3. Случайные величины...............................................I?
2.4. Алгебраические действия над случайными величинами................22
2.5. Средние значения.................................................27
Глава 3
Случайные процессы . ..............................33
3.1. Введение.........................................................33
3.2. Вероятностные характеристики.....................................33
3.3. Средние значения.................................................34
3.4. Спектральные и ортогональные представления.......................40
3.5. Реакция линейных систем..........................................46
Глава 4
Нормальные марковские процессы
и стохастические дифференциальные уравнения . .... 64
4.1. Введение....................................................... 64
4.2. Нормальные случайные процессы....................................65
4.3. Марковские случайные процессы....................................71
4.4. Стохастические дифференциальные уравнения........................79
4.5. Среднее значение и дисперсия процесса на выходе нелинейной системы 101
Глава 5
Теория решений ..............................112
5.1. Введение........................................................112
5.2. Выбор решения лрн однократном наблюдении....................... 114
5 3. Выбор решения при многократных наблюдениях......................122
5 4. Проверка сложных гипотез...................................... 140
5.5. Проверка многих гипотез .............................144
5.6. Последовательный анализ........................................ 146
5.7. Последовательное обнаружение марковских сигналов в иормальчом
шуме..................................................................156
Глава 6
Основы теории оценивания ..................................... 172
6.1. Введение ..................................................... 172
6.2. Байесовские оценки......................... .... 172
6.3 Оценки максимального правдоподобия.............................. 194
6 4 Свойства оценок.............................................202
6.5. Точность оценок и априорная информация....................... 208
494
Стр.
6.6. Линейные оценки с минимальной среднеквадратической ошибкой . 232
6.7. Оценки наименьших квадратов..................................7 238
Глава 7
Оптимальный линейный фильтр..........................................251
7.1. Введение........................................................251
7.2. Оптимальный линейный дискретный фильтр....................252
7.3. Оптимальный линейный непрерывный фильтр....................283
7.4. Стационарные Процессы и фильтр Винера...........................303
7.5. Асимптотические свойства........................................318
Глава 8
Обобщение алгоритма оптимальной линейной фильтрации .... 326
8.1. Введение...................................................... 326
8.2. Небелый шум . . 326
8.3. Сглаживание и предсказание.....................................341
8.4. Анализ ошибок и априорные данные . 371
8.5. Расходимость . . 403
Глава 9
Нелинейное оценивание .............................................. 409
9.1. Введение........................................................409
9.2. Оценивание при помощи условного среднего...................' . 409
9.3. Оценивание по максимуму апостериорной вероятности .... 428
9.4. Соотношения между нелинейными алгоритмами фильтрации . . . 442
9.5. Нелинейное сглаживание..........................................464
Список литературы....................................................480
Э Сейдж, Дж Меле
ТЕОРИЯ ОЦЕНИВАНИЯ И ЕЕ ПРИМЕНЕНИЕ
В СВЯЗИ И УПРАВЛЕНИИ
Ответственный редактор Б Р Левин
Редактор С Т Симонова
Технические редакторы К Г Марко ч, Е Р Черепова
Корректор Л Н Лещева
Сдано в набор 26/1 1976 г Подп в печ 14/IX 1976 г
Формат 60X90/16 Бумага тип No 2 31 0 усл печ л 34 06 уч изд л
Тираж 7000 экз Изд № 16911 Зак № 26 Цена 2 р 89 к
Издательство «Связь» Москва 101000 Чистопрудный бульвар, д 2
Типография издательства «Связь» Госкомиздата СССР
Москва 101000, ул Кирова, д 40