Автор: Вентцель Е.С. Овчаров Л.А.
Теги: теория вероятностей и математическая статистика теория вероятностей математическая статистика комбинаторный анализ теория графов математика
ISBN: 5-06-003830-0
Год: 2000
Текст
Е.С.Вентцель ЛАОвчаров
Теория
вероятностей
и ее инженерные
приложения
ИЗДАНИЕ ВТОРОЕ, СТЕРЕОТИПНОЕ
Рекомендовано
Министерством образования Российской Федерации
в качестве учебного пособия
для студентов высших технических
учебных заведений
Москва
«Высшая школа» 2000
УДК 519.21
ББК 22.171
В 29
Рецензент, директор Института проблем передачи информации РАН
академик НА. Кузнецов
Вентцель Е.С., Овчаров Л.А.
В 29 Теория вероятностей и ее инженерные приложения.
Учеб. пособие для втузов.— 2-е изд., стер.— М.: Высш.
шк., 2000.—480 с: ил.
ISBN 5-06-003830-0
В книге дано систематическое изложение основ теории
вероятностей под углом зрения их практических приложений по
специальностям: кибернетика, прикладная математика, ЭВМ,
автоматизированные системы управления, теория механизмов, радиотехника,
теория надежности, транспорт, связь и т. д. Несмотря на
разнообразие областей, к которым относятся приложения, все они
пронизаны единой методической основой.
Первое издание вышло в 1988 г.
Для студентое высших технических учебных заведений. Может
быть полезна преподавателям, инженерам и научным работникам
разных профилей, которые в своей практической деятельности
сталкиваются с необходимостью ставить и решать задачи, связанные
с анализом случайных процессов.
УДК 519.21
ББК 22.171
Учебное издание
Вентцель Елена Сергеевна
Овчаров Лев Александрович
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И ЕЕ ИНЖЕНЕРНЫЕ ПРИЛОЖЕНИЯ
Редактор ТА. Рыкова
Художественный редактор Ю.Э. Иванова
ЛР № 010146 от 25.12.96. Изд. № ФМ-204. Подп. в печать 27 01.2000
Формат 60x88 1/16 Бум. газеты Гарнитура «Обыкновенная» Печать офсетная
Объем 29,40 усл.-печ. л , 29,40 усл. кр.-oiT., 25,21 уч -изд. л
Тираж 10000 экз. Заказ № 461
ГУП издательство «Высшая школа», 101430, Москва, Неглинная ул , д 29/14
Отпечатано в ГУП ИПК «Ульяновский Дом печати»,
432601, г Ульяновск, ул. Гончарова, д 14
ISBN 5-06-003830-0 © ГУП издательство «Высшая школа», 2000
Оригинал-макет данного издания является собственностью издательства
«Высшая школа» и его репродуцирование (воспроизведение) любым
способом без согласия издательства запрещено
ПРЕДИСЛОВИЕ
Книга представляет собой систематическое изложение
основ теории вероятностей под углом зрения их
практических инженерных приложений. Интересы этих
приложений определяют и отбор материала, и стиль
изложения, и его методическую основу. Книга изобилует
примерами решения практических задач, требующих
применения вероятностных методов и относящихся к
самым различным специальностям: кибернетика,
прикладная математика, ЭВМ, автоматизированные системы
управления, теория механизмов, радиотехника, теория
надежности, транспорт, связь и т. п. Несмотря на
разнообразие областей, к которым относятся приложения, все
они пронизаны единой методической основой, единой
системой подходов.
Эта книга относительно небольшого объема написана
на базе лекций по теории вероятностей, читанных
авторами в различных втузах на протяжении последних
десятилетий. Она предназначена для инженеров и научных
работников разных профилей, которые в своей
практической деятельности сталкиваются с необходимостью
ставить и решать задачи, связанные со случайными
явлениями и требующие вероятностного подхода. Книга
адресована широкому кругу читателей, она может быть
использована и в учебном процессе студентами и
преподавателями втузов, и как пособие для самообразования.
Изложение ведется на уровне, доступном читателю,
знакомому с математикой в объеме обычного втузовского
курса. Там, где по ходу дела приходится пользоваться
более сложными понятиями, они поясняются. Главный
упор делается не на тонкости математического аппарата,
а на методическую сторону вопроса и на
непосредственные практические приложения. Многолетний опыт
авторов в преподавании теории вероятностей п смежных с
нею дисциплин во втузах, а также обширный опыт приме-
4 ПРЕДИСЛОВИЕ
нения вероятностных методов в самых различных
областях инженерной практики показывает, что именно такой,
а не формальный подход к изложению теории
вероятностей больше всего пригоден тем, для кого изучение
теории вероятностей не самоцель, а средство решения
конкретных инженерных задач и примеров. Окончание
решепия примера или задачи отмечается знаком >•
Вместе с тем, авторы стремились нигде не
поступаться точностью формулировок и должной математической
строгостью и изложить материал в соответствии с
современным уровнем развития науки о случайных явлениях.
В книгу не вошли теория случайных процессов,
теория массового обслуживания, специальные главы
математической статистики и их инженерные приложения.
Ограниченный отбор материала в данную книгу
определялся тем, что авторы предполагают по каждому из
указанных выше разделов написать отдельное руководство,
где, так же как и здесь, основное внимание будет уделено
инженерным приложениям.
Авторы приносят глубокую благодарность академику
АН СССР В. С. Пугачеву и профессору В. Н, Тутубалину
за ценные советы и поддержку, которую они оказали при
составлении проекта книги; члену-корреспонденту АН
СССР Н. А. Кузнецову, любезно согласившемуся
отрецензировать рукопись и сделавшему ряд полезных
замечаний; доценту Г. В. Данилову, оказавшему авторам
большую помощь при подготовке кнпги и изданию, а
также доктору физико-математических, наук А. Д. Вентцелю
за ряд ценных предложений.
Е.С. Вентцель,
ЛА. Овчаров
— Вы можете,—
продолжал Гермаин,— составить
счастие моей жизни, и оно ничего
не будет вам стоить: я знаю,
что вы можете угадать три
карты сряду...
А. С. Пушкин «Пиковая дама»
ВВЕДЕНИЕ
Теорией вероятностей называется математическая
наука, изучающая закономерности в случайных явлениях'.
Условимся, что мы будем понимать под «случайным
явлением».
При научном изучении и описании окружающего
мира часто приходится встречайся с особого типа
явлениями, которые принято называть случайными.
Характерна для них большая, по сравнению с другими, степень
неопределенности, непредсказуемости. Случайное
явление — это такое явление, которое при неоднократном
воспроизведении одного и того же опыта (испытания,
эксперимента) протекает каждый раз несколько по-
иному.
Приведем несколько примеров случайных явлений.
1. Одно и то же тело несколько раз взвешивается на
точных (аналитических) весах; результаты повторных
взвешивании несколько отличаются друг от друга. За счет
чего это происходит? За счет влияния многих мелких,
второстепенных факторов, сопровождающих взвешивание,
таких, например, как положение тела и разновесок на
чашках весов; вибрации аппаратуры; смещение головы
и глаза наблюдателя п т. п.
2. Производится ряд испытаний заводских изделии
определенного типа, например реле, на длительность
безотказной работы. Результат испытания от раза к разу
не остается постоянным, меняется. Эти изменения
обусловлены влиянием ряда малозначительных,
трудноуловимых факторов, таких, например, как микродефекты в
металле; разные температурные условия; разные условия
хранения и транспортировки изделии; отклонения
напряжения от номинала и т. д.
3. Производится ряд выстрелов из одного и того же
орудия по одной и той же цели. Условия стрельбы (вид
снаряда, угол установки орудия) одни и те же. Тем не
б ВВЕДЕНИЙ
менее точки попадания снарядов обнаруживают разброс
(так пазываемое «рассеивание»). Теоретически
траектории снарядов совпадают; практически они разнятся за
счет таких малозначительных, трудноуловимых факторов,
как-то: ошибки изготовления снарядов; отклонения веса
заряда от номинала; неоднородность его структуры, уже
не говоря о метеоусловиях, которые от выстрела к
выстрелу могут меняться.
4. Самолет определенного типа совершает полет на
заданной высоте; теоретически он должен летать
горизонтально, равномерно и прямолинейно. Фактически
полет сопровождается отклонениями центра массы самолета
от горизонтальной прямой и колебаниями самолета около
центра массы. Эти отклонения и колебания являются
случайными и связаны с турбулентностью атмосферы и
ошибками пилотирования.
5. Круглая, правильной формы монета щелчком
подбрасывается, вращается в воздухе и падает па стол,
открывая одиу из сторон: «герб» или «решку». Опыт
повторяется несколько раз. Как бы ни стараться соблюдать
одинаковыми его условия (высоту подбрасывания,
начальную скорость и момент вращения), результат
варьируется от раза к разу: иногда выпадает «герб», иногда —
«решка». Исход опыта — «герб» или «решка» —
обусловлен множеством мелких, трудноуловимых причин, в
числе которых, например, неровности поверхности стола.
6. Рассматривается непрерывная работа ЭВМ между
двумя очередными сбоями в решении задачи. Все
контролируемые условия работы ЭВМ: температура,
влажность, напряжение, характер решаемой задачи остаются
неизменными. Повторяя такой опыт несколько раз, мы
убеждаемся, что время работы ЭВМ между двумя
очередными сбоями будет разным (случайным). Это
объясняется тем, что различные элементы ЭВМ подвергаются
незначительным, неконтролируемым изменениям.
Все приведенные примеры рассмотрены здесь под
одним и тем же углом зрения: подчеркнуты случайные
вариации, неодинаковые результаты ряда опытов,
основные условия которых остаются неизменными. Эти
вариации всегда связаны с наличием каких-то второстепенных
факторов, влияющих на исход опыта, но не заданпых
в числе его основных условий. Основные условия опыта,
определяющие в общих и грубых чертах его
протекание, сохраняются неизменными; второстепенные — меня-»
ВВЕДЕНИЕ 7
ются от опыта к опыту и вносят случайные различия
в их результаты.
Совершенно очевидно, что в природе,нет ни одного
явления, в котором не присутствовали бы в той или
иной мере элементы случайности. Как бы точно ц
подробно ни были фиксированы условия опыта,
невозможно достигнуть того, чтобы при его повторении
результаты полностью и в точности совпадали. Случайные
отклонения неизбежно сопутствуют каждому
закономерному явлению. Тем не менее в ряде практических задач
этими случайными элементами можно пренебречь,
рассматривая вместо реального явления его упрощенную
схему, «модель», и предполагая, что в данных условиях
опыта явление протекат вполне определенным образом.
При этом из бесчисленного множества фактов,
влияющих на явление, выделяются самые главные, основные,
решающие; влиянием остальных, второстепенных,
факторов просто пренебрегают. Такая схема изучения
явлений (которую будем называть «детерминистской»)
постоянно применяется в физике, механике, технике.
Согласно этой схеме при решении любой задачи прежде
всего выделяется основной круг учитываемых условий и
выясняется, на какие параметры задачи он влияет; затем
применяется тот или иной Математический аппарат
(например, составляются и решаются дифференциальные
уравнения, описывающие явление); таким образом
выявляется основная закономерность, свойственная данному
явлению и дающая возможность предсказать результат
опыта по его заданным условиям. По мере развития
науки число учитываемых факторов становится все
больше, научный прогноз — все точнее. Это — классическая
схема так называемых «точных наук» — от условий опыта
к его однозначному результату.
Однако для решения ряда задач такая схема
оказывается плохо приспособленной. Это — те задачи, где
интересующий нас результат опыта существенно зависит
от стоЛь большого числа факторов, что практически
невозможно зарегистрировать и учесть их все. В этих
задачах многочисленные тесно переплетающиеся
второстепенные факторы так тесно связаны с результатом опыта,
что ничтожное, на первый взгляд, их изменение может
сыграть решающую роль, обусловить «успех» или
«неуспех» опыта. В таких случаях классическая схема точных
наук — детерминистская — оказывается непригодной,
8 ВВЕДЕНИЕ
Вернемся к вышеприведенным примерам случайных
явлений, в частности, к примеру 3 (стрельба из орудия).
Если мы конструируем прицельное приспособление, то
классическая, «детерминистская», схема вполне
достаточна. Проинтегрировав уравнения движения снаряда, мы
можем определить его траекторию, точку попадания.
Но предположим, что стрельба ведется по цели, размеры
которой меньше зоны рассеивания снарядов, и нас
интересуют вопросы: какой процент выпущенных снарядов
в среднем попадет в цель? Сколько нужно потратить
снарядов для того, чтобы с достаточной надежностью
поразить цель? Какие следует принять меры для
уменьшения расхода снарядов? И т. д.
Чтобы ответить на такие (и подобные им) вопросы,
обычная схема точных наук оказывается недостаточной.
Эти вопросы органически связаны со случайной природой
явления; для того чтобы на них ответить, очевидно,
нельзя просто пренебречь случайностью, надо изучить
явление рассеивания снарядов со стороны
закономерностей, присущих ему именно как случайному явлению.
Надо исследовать закон, по которому распределяются
точки попадания снарядов; выявить случайные причины,
вызывающие рассеивание, сравнить их между собой по
степени важности и т. д.
Рассмотрим другой пример. Некоторое техническое
устройство (скажем, система автоматического
управления) решает определенную задачу в условиях, когда на
нее непрерывно воздействуют случайные помехи. В
результате система решает задачу с некоторой ошибкой,
иногда выходящей за пределы допустимой. Возникают
вопросы: как часто будут появляться такие ошибки?
Какие меры надо принять для того, чтобы практически
исключить их возможность? И т. д.
Чтобы ответить на такие вопросы, необходимо
исследовать природу и структуру случайных возмущений,
воздействующих на систему, изучить реакцию системы на
эти возмущения, выяснить влияние конструктивных
параметров системы на вид реакции.
Подобные задачи, число которых в физике, технике
и инженерном деле чрезвычайно велико, требуют
изучения не только основных, главных закономерностей,
определяющих явление в общих чертах, но и
анализа случайных возмущений и искажений, связанных
с наличием второстепенных факторов и придающих
ВВЕДЕНИЕ 9
исходу опыта при заданных условиях элемент
неопределенности.
Какие же существуют пути и методы для
исследования случайных явлений?
С чисто теоретичесгсоп точки аренпя те факторы,
которые мы условно назвали «случайными», в принципе
ничем не отличаются от тех, которые мы выделили в
качестве «основных». Теоретически можно неограниченно
повышать точность решения задачи, учитывая все новые
и новые факторы. Однако на практике попытка
одинаково подробно и тщательно проанализировать влияние
всех факторов, от которых зависит явление, привела бы
только к тому, что решение, в силу непомерной
громоздкости и сложности, оказалось бы практически
неосуществимым и к тому же не имело бы никакой
познавательной ценности, относясь только к узкому кругу плохо
контролируемых условий.
Должна существовать принципиальная разница в
методах учета основных факторов, определяющих в
главных чертах ход и исход явления, и вторичных,
второстепенных факторов, влияющих на него в качестве
«погрешностей» или «возмущений». Племент
неопределенности, сложности и многопричинности, присущий
случайным явлениям, требует специальны? методов для
их изучения. Такие методы и разрабатываются в
теории вероятностей. Ее предметом являются специфические
закономерности, наблюдаемые в случайных явлениях.
Практика показывает, что, наблюдая в совокупности
массы однородных случайных явлений, мы часто
обнаруживаем в них своего рода устойчивости. Напри1
мер, если много раз подряд бросать монету, частота
появления герба (отношение числа выпавших гербов
к общему числу бросаний) постепенно выравнивается,
стабилизируется, приближаясь ко вполне определенному
числу, а именно к 1/2. Такое же свойство устойчивости
частот наблюдается и при многократном повторении
ряда других опытов с заранее неизвестным,
неопределенным исходом. Так, например, в хорошо налаженном
производстве устойчивым оказывается процент
доброкачественных изделий. Многолетние наблюдения показывают,
что частота рождения мальчиков для самых разных
географических и климатических условий весьма
устойчива (приблизительно равна 0,51). Устойчивость частот
наблюдается даже в таких сугубо непредсказуемых яв-
40 ВВЕДЕНИЕ
лениях, как уличный травматизм (именно эта
устойчивость позволяет планировать работу лечебных
учреждений и службы скорой помощи).
Устойчивость частот наблюдается в тех случаях,
когда мы имеем дело с массой однородных опытов, для
которых механизм воздействия случайных факторов
сходен. Не обладают свойством устойчивости частот те
явления с неопределенным исходом, где условия явно
неоднородны и даже несопоставимы. Например,
бессмысленно говорить об устойчивой «частоте возникновения
войн» (историческому процессу свойственны черты
неповторимости, направленности развития). Также
бессмысленно говорить об устойчивой частоте, скажем,
правильно решенных научных проблем или появления
гениальных произведений искусства.
Теория вероятностей занимается только темп
явлениями с неопределенным исходом, для которых
предполагается наличие устойчивости частот. Для таких
явлений она устанавливает определенные закономерности,
характерные для массы случайных явлений. Одно,
отдельное случайное явление остается в своем результате
неопределенным, непредсказуемым; только в массе
случайных явлений проявляются специфические
закономерности, которые выполняются тем точнее и строже, чем
обширнее массив изучаемых явлений. При очень
большом числе таких явлений случайность, непредсказуемость
практически исчезает.
Поясним это примером. В сосуде заключен некпй
объем газа, состоящий па большого числа молекул.
Каждая из них за секунду испытывает множество
столкновений с другими молекулами, многократно меняет скорость
и направление движения; траектория каждой отдельной
молекулы случайна. Известно, что давленР1е газа на
стенку сосуда обусловлено совокупностью ударов
молекул об эту стенку. Казалось бы, если траектория
каждой отдельной молекулы случайна, если неизвестно,
в какой точке и с какой скоростью она ударится о
стенку, то и давление на стенку должно было бы изменяться
случайным и непредсказуемым образом. Однако это не
так. Если число молекул достаточно велико, то давление
газа практически не зависит от траекторий отдельных
молекул и подчиняется вполне определенно]! и очень
простой физической закономерности. Случайные
особенности, свойственные движению каждой отдельной моле-
ВВЕДЕНИЕ 11
кулы, в массе взаимно погашаются, компенсируются.
В результате, несмотря на сложность и запутанность
отдельного случайного явления, возникает простая
закономерность, справедливая для массы случайных
явлений. Отметим, что именно массовость случайных
явлений обеспечивает выполнение этой закономерности
(при ограниченном числе молекул в объеме начинают
сказываться случайные отклонения от закономерности,
так называемые флуктуации).
Рассмотрим другой пример: производится ряд
взвешиваний одного и того же тела на аналитических весах;
каждый раз результат взвешивания записывается.
Вначале, пока число взвешиваний невелико, набор
результатов представляется хаотичным, беспорядочным. Однако
по мере увеличения числа взвешиваний в совокупности
результатов начинает обнаруживаться вполне
определенная закономерность; она проявляется тем отчетливее,
чем большее число взвешиваний произведено. Становится
ясно, что результаты группируются практически
симметрично около некоторого среднего значения; в
центральной области они расположены гуще, чем по краям,
причем густота их с удалением от центра убывает по вполне
определенному закону (так называемому «нормальному»,
которому большое внимание будет уделено в
дальнейшем).
Подобного рода закономерности (их называют
«статистическими») возникают, когда мы наблюдаем в
совокупности массивы однородных случайных явлений. Они
оказываются практически независимыми от
индивидуальных особенностей отдельных случайных явлении,
входящих в массив; эти особенности как бы взаимно
погашаются, нивелируются; выражаясь образно, «из
множества беспорядков возникает порядок». Средний, массовый
результат множества случайных явлений оказывается
практически уже не случайным, предсказуемым. Это н
является базой для практического применения
вероятностных (статистических) методов исследования.
Методы теории вероятностей не отменяют и не
упраздняют случайности, непредсказуемости исхода
отдельного опыта, но дают возможность предсказать, с каким-
то приближением, средний суммарный результат массы
однородных случайных явлений. Чем большее количество
однородных случайных явлений фигурирует в задаче,
тем отчетливее выявляются присущие им специфические
12 ВВЕДЕНИЕ
законы, тем с большей уверенностью и точное!ью
можно осуществлять научный прогноз.
Цель вероятностных (статистических) методов —
в том, чтобы, минуя слишком сложное (и зачастую
практически невозможное) исследование отдельного
случайного явления, обратиться непосредственно к законам,
управляющим массами таких явлений. Изучение этих
законов позволяет не только осуществлять прогноз в
области случайных явлений, но и целенаправленно влиять
на ход этих явлений, контролировать их, ограничивать
сФеРУ действия случайности, сужать ее влияние на
практику.
Приступая к изучению теории вероятностей с ее
специфическим объектом исследования (случайные, т. е.
непредсказуемые явления), надо отдавать себе отчет
в том, что прогнозы, даваемые методами этой науки,
несколько отличаются по своему характеру от привычных
нам прогнозов «точных наук». Не давая точного
указания, что именно произойдет при таких-то условиях,
вероятностный прогноз является приближенным; он
указывает только границ ы, в которых, с достаточно
высокой степенью достоверности, будут заключены
интересующие нас параметры. Чем обширнее изучаемый массив
случайных явлений, тем уже эти границы, тем точнее
и определеннее становится вероятностный прогноз.
Характерным для сегодняшнего этапа развития
науки является все более широкое применение
вероятностных методов во всех ее областях. Это связано с двумя
причинами. Во-первых, изучение явлений окружающего
мира, становясь более глубоким, требует выявления не
только основных закономерностей, но и возможных
случайных отклонений от них. Во-вторых, наука все больше
внедряется в такие области практики, где наличие и
большое влияние именно случайности не подлежит
сомнению, а иногда даже является определяющим.
В настоящее время нет практически ни одной
области науки, в которой в той или иной степени не
применялись бы вероятностные методы. В одних науках, в
силу специфики предмета и исторических условий, эти
методы находят применение раньше, в других — позднее.
Исторически первые пачаткп вероятностных методов
с соответствующим, еще довольно примитивным
математическим аппаратом возникли в XVIT веке, при
разработке теории азартных игр с целью дать рекомендации
ВВЕДЕНИЕ 13
игрокам. Затем эти методы стали применяться в
практике страховых компаний для установления разумных
размеров страховых премий. Постепенно область
применения вероятностных методов расширялась. Сегодня эти
методы распространяются все шире и шире. Целые
разделы современной физики (в частности, ядерная физика)
базируются на математическом аппарате теории
вероятностей. Широко применяются вероятностные методы
в современных электротехнике, радиотехнике, теории
связи, теории автоматического регулирования,
кибернетике, вычислительной технике, теории АСУ
(автоматизированных систем управления). Это и естественно, так как
работа современных автоматизированных систем
протекает в условиях случайных воздействий, без учета
которых невозможно разумное проектирование подобных
систем, выбор их конструктивных параметров.
Любая процедура управления чем бы то ни было
(техническим устройством, группой устройств, человеко-
машинным комплексом) протекает в заранее
неизвестных, случайных условиях, неизбежно сопровождается
случайными ошибками измерения тех или других
параметров, ошибками выполнения команд и т. д.; анализ
работы такой системы практически невозможен без
учета случайных факторов. Столь важные в народном
хозяйстве метеорологические прогнозы не могут строиться
без учета случайности процессов, протекающих в
атмосфере.
Знакомство с методами теории вероятностей
необходимо сегодня каждому грамотному инженеру. И не
только инженеру. Биология, физиология, медицина,
социология все шире применяют вероятностные методы. Не
чуждаются их и такие «исконно гуманитарные» науки,
как психология, лингвистика, литературоведение, даже
эстетика.
Как бы ни был обширен перечень научных
дисциплин, где сегодня применяются вероятностные методы, он
все же неизбежно страдает неполнотой. Короче будет
сказать, что нет области знаний, где не могли бы сказать
свое слово эти методы исследования.
Считать ли теорию вероятностей специальным
разделом математики или одной из естественных наук? И то
и другое. Математические законы теории вероятностей —
это отражение реальных статистических законов,
объективно существующих закономерностей в массовых слу-
14 ВВЕДЕНИЕ
чайных явлениях природы. К изучению этих явлений
теория вероятностей применяет математический метод и
по своему методу является одним из разделов
математики, столь же точным и строгим, как другие
математические науки.
Для инженера, применяющего теорию вероятностей
в своей практической деятельности, всего важнее не
математические тонкости этой теории, а умение распознать
в реальной задаче ее вероятностные черты, поставить,
если нужно, эксперимент, разумно обработать его
результаты и выработать рекомендации, как поступать, чтобы
добиться желаемого результата с минимальной затратой
сил и средств. Лучше всего такое умение приобретается
при рассмотрении конкретных примеров из области
инженерной практики. Таких примеров в нашей книге
будет много.
ГЛАВА 1
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
1,1. Случайное событие. Его вероятность
Любая наука, развивающая общую теорию какого-
либо круга явлений, содержит ряд основных понятии, на
которых она базируется. Таковы, например, в геометрии
понятия точки, прямой, линии; в механике — понятия
силы, массы, скорости, ускорения. Естественно, что не
все основные понятия могут быть строго определены,
ибо «определить» понятие — это значит свести его к
другим, более известным. Очевидно, процесс определения
одних понятий через другие должен где-то кончаться,
дойдя до самых первичных понятий, к которым сводятся
все остальные и которые сами не определяются, а только
поясняются. Такие понятия существуют и в теории
вероятностей. Здесь мы рассмотрим некоторые из них.
Под опытом (экспериментом, испытанием) мы будем
понимать некоторую воспроизводимую совокупность
условий, в которых наблюдается то или другое явление,
фиксируется тот или другой результат. Заметим, что
«опыт» не обязательно должен быть поставлен
человеком; он может протекать независимо от него; при этом
человек выступает в роли наблюдателя или фиксатора
происходящего. От него зависит только решение: что
именно наблюдать и какие параметры фиксировать.
Если результат опыта варьируется при его
повторении, говорят об опыте со случайным исходом. Именно
такие опыты мы будем здесь рассматривать и добавление
«со случайным исходом» для краткости опускать. Тот
факт, что при повторении опыта его основные условия
сохраняются, и, значит, мы вправе ожидать устойчивости
частот, тоже не будем каждый раз оговаривать.
Случайным событием (или, короче, просто событием)
называется всякий факт, который в опыте со случайным
исходом может произойти или не произойти. События мы
будем обозначать большими буквами латинского
алфавита.
16 ГЛ. 1, ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Рассмотрим несколько примеров событий.
1. Опыт — бросание монеты; событие А — появление
герба.
2. Опыт — бросание трех монет; событие В —
появление трех гербов.
3. Опыт — передача группы из п сигналов по каналу
связи; событие С—искажение хотя бы одного из них.
4. Опыт —выстрел по мишени; событие Z)
—попадание.
5. Опыт — вынимание наугад одной карты из колоды;
событие Е — появление туза.
6. Тот же опыт, что в примере 5; событие F —
появление карты червонной масти.
7. Опыт (наблюдение)—измерение количества
осадков, выпадающих в данном географическом пункте за
определенный месяц; событие G — выпадение более
N миллиметров осадков.
8. Опыт — лечение группы больных определенным
препаратом; событие Я — существенное улучшение более
чем у половины из них.
Все приведенные примеры начинались с описания
опыта, в котором появляется или не появляется событие.
В общем случае это необязательно; опыт может
упоминаться после формулировки события; например:
А — появление герба при бросании монеты;
В — появление трех гербов при бросании трех
монет и т. д.
Рассматривая перечисленные в наших примерах
события А, В, ..., Я, мы видим, что каждое из них обладает
какой-то степенью возможности — одни большей,
а другие меньшей, причем для некоторых из них мы
сразу можем решить, какое из них более, а какое менее
возможно. Например, сразу видно, что событие А более
возможно (вероятно), чем В1 а событие F более
возможно, чем Е. Относительно других событий нашего списка
таких выводов сразу сделать нельзя; для этого условия
опыта описаны недостаточно подробно. Так пли иначе,
любое случайное событие обладает какой-то степенью
возможности, которую в принципе можно измерить
численно. Чтобы сравнивать между собой события по
степени их возможности, нужно связать с каждым из
них какое-то число, которое тем больше, чем более
возможно событие. Это число мы и назовем
вероятностью события.
1.1. СЛУЧАЙНОЕ СОБЫТИЕ. ЕГО ВЕРОЯТНОСТЬ 17
Отметим, что сравнивая между собой по степени
возможности различные события, мы склонны считать более
вероятными те события, которые происходят чаще, менее
вероятными — те, которые происходят реже;
маловероятными—те, которые почти никогда не происходят.
Например, событие «выпадение дождя в Москве 1-го июня
предстоящего года» более вероятно, чем «выпадение
снега в Москве в тот же день», а событие «землетрясение
в Москве, превышающее по интенсивности 3 балла, в
течение предстоящего года» крайне маловероятно (хотя
такое землетрясение и наблюдалось в 1977 г., и
статистика говорит, что подобные события происходят примерно
раз в 100 лет). Таким образом, понятие вероятности
события с самого начала тесно увязывается с понятием его
частоты (подробнее это основное понятие будет
освещено ниже, см. п. 1.3).
Характеризуя вероятности событий числами, нужно
установить какую-то единицу измерения. В
качестве такой единицы естественно взять вероятность
достоверного события, т. е. такого, которое в результате
опыта неизбежно должно произойти. Пример
достоверного события — выпадение не более шести очков при
бросании игральной кости*). Другой пример
достоверного события: «камень, брошенный вверх рукой, вернется
на Землю, а не станет ее искусственным спутником».
Противоположностью достоверного события является
невозможное событие — то, которое в данном опыте
вообще не может произойти. Пример: «выпадение 12 очков
при бросании одной игральной кости». Невозможному
событию естественно приписать вероятность, равную
нулю.
Если приписать достоверному событию вероятность,
равную единице, а невозможному — равную нулю, то все
другие события — возможные, но не достоверные, будут
характеризоваться вероятностями, лежащими между
нулем и единицей, составляющими какую-то долю
единицы.
Таким образом, установлены единица измерения
вероятности — вероятность достоверного события и диапазон
изменения вероятностей — числа от нуля до единицы.
Какое бы событие А мы ни взяли, его вероятность Р(А)
*) «Игральной костью» называется кубпк, на шести гранях
которого нанесены 1, 2, 3, 4, 5, 6 точек (очков),
18 гл i. оснопные понятия теории перогттноглтп
удовлетворяет условию:
0<Р(Л)<1. A.1.1)
Очень большую роль в применении вероятностных
методов играют практически достоверные и
практически невозможные события.
Событие А называется практически невозможным,
если его вероятность не в точности равна нулю, но очень
близка к нулю:
Р {А)« 0.
Пример. Опыт: 32 буквы разрезной азбуки
смешаны между собой; наугад вынимается одна карточка,
стоящая на ней буква записывается, карточка возвращается
обратно и смешивается с другими. Такой опыт
производится 25 раз. Событие А состоит в том, что после 25
выниманий мы запишем первую строчку «Евгения Онегина»:
«Мой дядя самых честных правил».
Событие А не является физически невозможным;
в дальнейшем (см. п. 2.3) мы даже подсчитаем его
вероятность, которая равна (&) ". Она настолько мала,
что событие с такой вероятностью смело можно считать
практически невозможным. >
Аналогично, практически достоверным называется
событие, вероятность которого не в точности равна
единице, но очень близка к единице:
Введем новое важное понятие: противоположное
событие. Противоположным событию А называемся событие
JJ, состоящее в непоявлении события А.
Пример. Опыт: один выстрел по мишени.
Событие А — попадание в десятку. Противоположное событие
А — непопадание в десятку. >
Вернемся к практически невозможным и практически
достоверным событиям. Если какое-то событие А
практически невозможно, то противоположное ему А
практически достоверно, и наоборот.
Практически невозможные (п сопутствующие им
практически достоверные) события играют большую роль
в теории вероятностей: на них основана вся ее
познавательная ценность. Ни один прогноз в области случайных
явлений не является и не может являться полностью
1.1. СЛУЧАЙНОЕ СОБЫТИЕ ЕГО ВЕРОЯТНОСТЬ 19
достоверным; он может быть только практпческ и
достоверным, т. е. осуществляться с очень большой
вероятностью.
В основе применения всех выводов и рекомендаций,
добываемых с помощью теории вероятностей, лежит
принцип практической уверенности, который может быть
сформулирован следующим образом:
Если вероятность события А в данном опыте весьма
мала, то (при однократном выполнении опыта) можно
вести себя так, как будто событие А вообще невозможно,
г. е. не рассчитывать на его появление.
В повседневной жизни мы постоянно (хотя и
бессознательно) пользуемся этим принципом. Например,
выезжая куда-то на такси, мы не рассчитываем на
возможность погибнуть в дорожной катастрофе, хотя некоторая
(весьма малая) вероятность такого события все же
имеется. Отправляясь летом на Кавказ или в Крым, мы но
захватываем с собой зимней верхней одежды, хотя
какая-то (очень малая) вероятность того, что нас
настигнет мороз, все-таки не равна нулю.
Обратим внимание на слова «при однократном
выполнении опыта» в формулировке принципа практической
уверенности. Дело в том, что производя много опытов,
в каждом из которых вероятность события А ничтожно
мала, мы повышаем вероятность того, что событие А
произойдет хотя бы один раз в массе опытов.
В самом деле, представьте себе лотерею, в которой на
миллион билетов всего один выигрыш. Некто покупает
одип билет. Вероятность выигрыша для него 0,000001,
т. е. ничтожно мала, и можно считать выигрыш
практически невозможным. А теперь представьте себе, что
распроданы все 1000000 билетов. Кто-то из купивших
получит выигрыш, т. е. для него произойдет
практически невозможное событие. За счет чего? За счет того,
что опыт (покупка билета) произведен очень много раз.
Аналогично обстоит дело с надежностью сложных
агрегатов. Пусть агрегат состоит из большого числа N
элементов. Каждый из них отказывает (выходит из строя)
с ничтожно малой вероятностью. Но за счет того, что
элементов очень много, вероятность того, что откажет
хотя бы один из них, перестает быть близкой к нулю
(см. пример 16 п. 2.4).
Переходим к самому тонкому и трудному вопросу:
насколько мала должна быть вероятность
20 гл. i. основные понятия теории вероятностей
события, чтобы его можно было считать
практически невозможным?
Ответ на этот вопрос выходит за рамки
математической теории и в каждом отдельном случае решается из
практических соображений, в соответствии с той
важностью, которую имеет для нас желаемый результат
опыта. Чем опаснее возможная ошибка
предсказания, тем ближе к нулю должна быть
вероятность события, чтобы его считать
практически невозможным.
Например, когда мы, на основе вероятностных
расчетов, предсказываем, что средний результат N
взвешиваний не отклонится от истинного веса тела больше, чем па
заданную величину е, а вероятность того, что
отклонение будет больше е, равна 0,01, мы еще можем
примириться с этим и считать событие А — «ошибка
больше е» — практически невозможным. Чем мы в данном
случае рискуем? Легкой неправильностью предсказания.
Совершенно другое дело — если вероятность взрыва
космической ракеты при ее запуске равна тем же 0,01.
Риск велик, велика ответственность; в таких условиях
во что бы то ни стало надо добиваться «вероятности
неудачи», на несколько порядков меньшей.
Размер допустимой «вероятности риска» всегда
назначается исследователем, исходя из степени опасности
риска. Выбирается он более или менее произвольно.
Поэтому на всех прогнозах, осуществляемых методами
теории вероятностей, всегда лежит отпечаток «начального
произвола», связанного с выбором достаточно малой
«вероятности риска»,— вероятности того, что прогноз не
оправдается. Это обстоятельство отнюдь не снижает
ценности вероятностных методов исследования.
«Ориентировочный прогноз» все же лучше, чем «никакой прогноз»,
который вытекал бы из требования, чтобы «вероятность
риска» была в точности равна нулю.
Чтобы убедиться в полезности вероятностных методов
предсказания, предлагаем читателю (если он не ленив
и любопытен) проделать элементарный опыт: бросить
монету любого достоинства N = 1000 раз (для простоты
можно бросать сразу по 10 штук, тщательно
перетряхнув их в коробке) и подсчитать число появившихся
гербов. На основе вероятностных методов можно утверждать
с практической достоверностью (в данном случае с
вероятностью приблизительно 0,997), что число выпавших
1.2. НЕПОСРЕДСТВЕННЫЙ ПОДСЧЕТ ВЕРОЯТНОСТЕЙ 21
гербов не выйдет за пределы D53-5-547)*). Не слишком
точное предсказание, не правда ли? Но ведь не
пользуясь вероятностными методами, мы могли бы дать
только одно, строго достоверное, но зато тривиальное
предсказание: число выпавших гербов будет заключено в
пределах @-М000).
1.2. Непосредственный подсчет
вероятностей
Существует класс опытов, для которых вероятности
их возможных исходов можно вычислить, исходя
непосредственно из самих условий опыта. Для этого нужно,
чтобы различные исходы опыта обладали симметрией и
в силу этого были объективно одинаково возможными.
Рассмотрим, например, опыт, состоящий в бросании
игральной кости. Если кубик выполнен симметрично,
«правильно» (центр тяжести не смещен ни к одной из
граней), естественно предположить, что любая из шести
граней будет выпадать так же часто, как каждая из
остальных. Так как достоверное событие «выпадет какая-
то из граней» имеет вероятность, равную единице, и
распадается на шесть одинаково возможных вариантов A,
2, 3, 4, 5 или 6 очков), то естественно приписать
каждому из них вероятность, равную 1/6.
Для всякого опыта, обладающего симметрией
возможных исходов, можно применить аналогичный прием,
который называется непосредственным подсчетом
вероятностей.
Симметрия возможных исходов чаще всего
наблюдается в искусственно организованных опытах, где
приняты специальные меры для ее обеспечения (например,
тасовка карт или костей домино, которая для того и
производится, чтобы каждая из них могла быть выбрана с
одинаковой вероятностью; или же приемы случайного
выбора группы изделий для контроля качества в
заводской практике). В таких опытах подсчет вероятностей
событий выполняется всего проще. Не случайно
первоначальное свое развитие (еще в XVII веке) теория
вероятностей получила на материале азартных игр,
которые поколениями вырабатывались именно так, чтобы
*) О том, как делаются такие предсказания, можно узнать в
гл. 10, п. 10.2, пример 12.
22 ГЛ. 1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
результат опыта не зависел от поддающихся контролю
его условий (рулетка, кости, карточные игры). Прием
непосредственного подсчета вероятностей, исторически
возникший вместе с математической теорией случайных
явлений, был положен в основу так называемой
«классической» теории вероятностей и долгое время считался
универсальным. Опыты, не обладающие симметрией
возможных исходов, искусственно сводились к
«классической» схеме.
Несмотря на ограниченную сферу практического
применения этой схемы, она все же представляет известный
интерес, так как именно на ней легче всего
познакомиться со свойствами вероятностей.
Перед тем как дать способы непосредственного
подсчета вероятностей, введем некоторые вспомогательные
понятия.
1. Полная группа событий. Говорят, что
несколько событий в данном опыте образуют полную
группу, если в результате опыта неизбежно должно
появиться хотя бы одно из них.
Примеры событий, образующих полную группу:
1) «выпадение герба» и «выпадение решки» при
бросании монеты*);
2) появление «1», «2», «3», «4», «5», «6» очков при
бросании игральной кости;
3) «два попадания», «два промаха» и «одпо
попадание, один промах» при двух выстрелах по
мишени;
4) «появление белого шара» и «появление черного
шара» при вынимании одного шара пз урны, в которой
2 белых и 3 черных шара **);
5) «появление хотя бы одного белого» и «появление
хотя бы одного черного шара» при вынимании двух
шаров из той же урны.
Специально обратим внимание на последний пример.
В нем даны два события, которые не исключают друг
друга: в самом деле, если вынуть 1 белый и 1 черный
шар, появляется и то и другое. Но не зря же при
определении полной группы событий мы сказали «неизбеж-
¦) Исход «монета встанет на ребро» мы отбрасываем, как
ничтожно маловероятный (практически невозможный).
•*) Во всех задачах «па урпы» здесь и в дальнейшем мы
будем предполагать, что шары тщательно перемешаны.
1.2. НЕПОСРЕДСТВЕННЫЙ ПОДСЧЕТ ВЕРОЯТНОСТЕЙ 23
но должно появиться хотя бы одно из них»
(«хотя бы одно» значит «одно или больше»). Если события
образуют полную группу, то опыт не может
кончиться помимо ни х. К полной группе событий
можно прибавлять еще какие угодно события, любые
исходы опыта; от этого полнота группы событий не
утрачивается.
2. Несовместные события. Несколько
событии в данном опыте называются несовместными, если
никакие два из них не могут появиться вместе.
Примеры несовместных событии:
1) «выпадение герба» и «выпадение решки» при
бросании монеты;
2) «два попадания» и «два промаха» при двух
выстрелах;
3) «выпаденпе двух», «выпадепие трех» п
«выпадение пяти» очков при однократном бросашш игральной
кости;
4) «появление туза», «появление десятки» и
«появление карты с картинкой» (короля, дамы или валета)
при вынимании одной карты из колоды;
5) «появление трех» и «появление более трех»
очков при бросанпп игральной кости;
6) искажение «ровно пяти», «ровно двух» п «не
менее шести» символов при передаче сообщения,
состоящего пз 10 символов.
Вспомним, что к полной группе событии можно
было добавлять любые другие события, не нарушая
полноты. Что касается несовместных событий, то из них
можно выбрасывать любые (пока остаются хотя бы два),
не нарушая свойства несовместности.
3. Равновозможные события. Несколько
событий в данном опыте называются равновозможными,
если по условиям симметрии есть основание считать, что
ни одно пз них не является объективно более
возможным, чем другое.
Заметим, что равновозможные события не могут
появляться иначе, чем в опытах, обладающих симметрией
воЗхМожных исходов; наше незнание о том, какое пз
них вероятнее, не есть основание для того, чтобы
считать события равновозможнымп.
Примеры равновозможных событий:
1) «выпадение герба» и «выпадение решки» прп
бросании симметричной, «правильной» монеты;
24 гл. i. основные понятия теории вероятностей
2) выпадение «трех», «четырех», «пяти» и «шести»
очков при бросании симметричной, «правильной»
игральной кости;
3) появление шара с номером «1», «2», «4» и «5»
при вынимании наугад шара из урны, в которой 10
перенумерованных шаров;
4) появление шаров с номерами «2 и 3», «3 и 4»,
«5 и 8» при вынимании двух шаров из той же урны;
5) появление карточки «с буквой а», «с буквой ф»
и «с буквой щ» при вынимании одной из тщательно
перемешанных карточек детской азбуки;
6) появление карты «червонной», «бубновой»,
«трефовой» или «пиковой» масти при вынимании карты из
колоды.
Заметим, что равновозможность событий в каждом из
этих опытов обеспечивается специальными мерами
(симметричное изготовление костп; тасовка карт;
тщательное перемешивание шаров в урие и т. п.).
Из группы, содержащей более двух равновозможных
событий можно исключать любые (кроме последних
двух), не нарушая их равновозможности.
С опытами, обладающими симметрией возможных
исходов, связываются особые группы событий, обладающие
всеми тремя свойствами: они образуют полную группу,
несовместны и равновозможны.
События, образующие такую группу, называются
случаями (иначе «шансами»).
Примеры случаев:
1) появление «герба» и «решки» при бросанип
монеты;
2) появление «1», «2», «3», «4», «5» и «6» очков
при бросании игральной костп;
3) появление шара с номером «1», «2», ... при
вынимании одного шара из урны, в которой п
перенумерованных шаров;
4) появление карты «червонной», «бубновой»,
«трефовой» и «пиковой» масти при вынимании одной карты
из колоды в 36 листов.
Если опыт обладает симметрией возможных исходов,
то случаи представляют собой исчерпывающий набор
его равновозможных и исключающих друг друга исходов.
Про такой опыт говорят, что он сводится к схеме
случаев (иначе —к «схеме урн», ибо любую
вероятностную задачу для такого опыта можно заменить экви-
1.2. НЕПОСРЕДСТВЕННЫЙ ПОДСЧЕТ ВЕРОЯТНОСТЕЙ 25
валентной ей задачей, где фигурируют урны, содержащие
шары тех или других цветов). Для таких опытов
возможен непосредственный подсчет вероятностей, основанный
на подсчете доли так называемых благоприятных
случаев в общем их числе.
Случай называется благоприятным (или
«благоприятствующим») событию Л, если появление этого случая
влечет за собой появление данного события.
Например, при бросании игральной кости из шести
случаев («1», «2», «3», «4», «5», «6» очков) событию А —
«появление четного числа очков» благоприятны три
случая: «2», «4», «6» и не благоприятны остальные три.
Событию В — «появление не менее 5 очков»
благоприятны случаи «5», «6», и не благоприятны остальные
четыре.
Если опыт сводится к схеме случаев, то вероятность
события А в данном опыте можно вычислить как долю
благоприятных случаев в общем их числе:
m А
РD)--^, A.2.1)
где wA —число случаев, благоприятных событию А; п —
общее число случаев.
Формула A.2.1), так называемая «классическая
формула» для вычисления вероятностей, предложенная еще
в XVII веке, когда главным полем приложения теории
вероятностей были азартные игры (в которых симметрия
возможных исходов обеспечивается специальными
мерами), долгое время (вплоть до XIX века) фигурировала в
литературе как «определение вероятности»; те задачи,
в которых схема случаев отсутствует, искусственными
приемами сводились к ней. В настоящее время
формального определения вероятности не дается (это понятие
считается «первичным» и не определяется), а при его
пояснении исходят из других принципов, непосредственно
связывая его с понятием частоты события (см. п. 1.3).
Применяется также аксиоматическое,
теоретико-множественное построение теории вероятностей на основе
общих положений теории множеств и небольшого числа
аксиом (см. пп. 1.4, 1.5).
Что касается формулы A.2.1), то она сохраняется
ныне лишь для подсчета вероятностей событий в опытах,
обладающих симметрией возможных исходов. Приведем
несколько примеров ее применения.
26 ГЛ. 1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Пример 1. В урне находится 5 шаров, из которых
2 белых и 3 черных. Из урны наугад вынимается один
шар. Найти вероятность того, что этот шар будет белым.
Решение. Обозначим А интересующее нас событие:
А = (появление белого шара) *).
Общее число случаев п = 5; из них два благоприятны
событию А: тА = 2. По формуле A.2.1) Р(^) = 2/5. >
Пример 2. В урне 7 шаров: 4 белых и 3 черных.
Из нее вынимаются (одновременно или последовательно)
два шара. Найти вероятность того, что оба они будут
белыми:
В = {оба шара белые).
При решении этой задачи и других ей подобных мы
будем пользоваться элементарными формулами
комбинаторики, в частности, формулой для числа с о ч е т а н и it.
Число сочетаний из к элементов по / — это число
способов, какими можно выбрать / различных элементов из
к\ обозначается оно Ck и вычисляется по формуле:
ri *(*-1) ¦•.(/;- /-!- 1)
Или, пользуясь знаком факториала (!)
, Л: (Л- — 1) ...(*— /+ 1) *I
Число сочетаний обладает следующими свойствами:
Пользуясь формулой A.2.2), решим пример 2.
Решение. Общее число случаев в примере 2 равно
числу способов, какими можно выбрать 2 шара из 7:
а число случаев, благоприятных событию 5,— это число
способов, какими можно выбрать 2 белых шара из 4:
*) Здесь и в дальпейшем мы будем пользоваться подобпым
обозначением событий, ставя о фигурные скобки их словесное
описание.
1.2. НЕПОСРЕДСТВЕННЫЙ ПОДСЧЕТ ВЕРОЯТНОСТЕЙ 27
Отсюда
Р(В)-±- 2 ь
Пример 3. В партии из К изделий М дефектных.
Пз партии выбирается для контроля к изделий (к<К).
Найти вероятность того, что среди них будет ровно т
дефектных (т ^ к).
Решение. Общее число случаев п = Ск* Найдем
mD — число случаев, благоприятных событию
D = {ровно т дефектных изделий в контрольной партии).
Найдем сперва число способов, какими из М
дефектных изделий можно выбрать т для контрольной партии;
оно равно C™i- Но ото еще не все: к каждой комбинации
дефектных изделий пужно присоединить комбинацию из
fe — m доброкачественных; это можно сделать CjfJlj
способами. Каждая комбинация из т дефектных изделий
может сочетаться с каждой комбинацией пз k — m
доброкачественных; число тех и других комбинаций надо
перемножить. Поэтому число благоприятных событию D
случаев равно nip = C^'CkIIm и
Р(В)-СТгСкК--УСкК. > A,2.3)
Пример 4. Некто выбирает наугад 6 клеток
«Спортлото» F пз 49). Найти вероятность того, что он
правильно угадает пз числа выигравших 6 номеров:
А = {ровно три},
В =» {ровно четыре},
С== {ровно пять},
D = {все шесть}.
Решение. Нетрудно убедиться, что задача по
структуре полностью совпадает с предыдущей, если считать
«дефектными» выигравшие номера, а
«доброкачественными»—не выигравшие. Применяя формулу A.2.3),
полагая в ней ЛГ = 49, М = 6, а т — последовательно
равным 3, 4, 5, 6, получим:
с. С ^
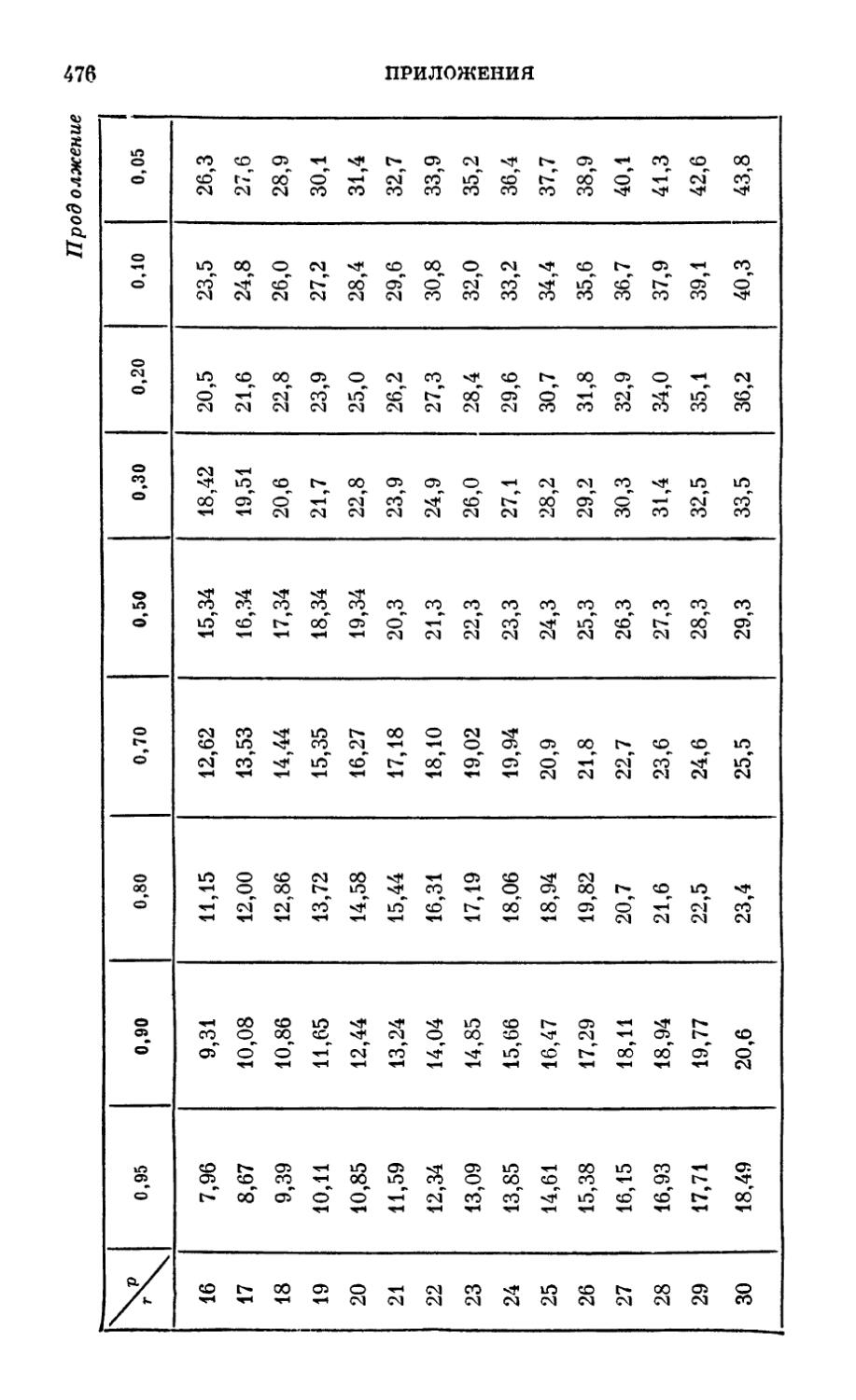
р (А) - -±^ » 1,765.1(Гг, Р (Я) - -5-12 « 9,686- Ю~\
С С4»
~8' >
28 ГЛ. 1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Пример 5. Опыт состоит в одновременном (или
последовательном) бросании двух монет. Найти вероятность
события
А = {хотя бы на одной монете выпадет герб}.
Решение. С первого взгляда легкомысленному и
торопливому читателю может показаться, что в данной
задаче три случая:
Л! = {два герба); Лг^дпе решки};
Аг = {герб и регака}.
Однако это неверно: эти события неравновозможны;
последнее вдвое вероятнее каждого из остальных.
Составим схему случаев; для этого назовем монеты: первая
и вторая (если они бросаются последовательно, первой
будет первая по времени; если одновременно, то,
например, та, центр которой ляжет севернее). Случаями будут
следующие события:
2?i = {на первой монете герб, на второй герб},
В2 =» {на первой монете решка, на второй решка),
Bz * {на первой монете герб, на второй решка),
^ — {на первой монете решка, на второй герб).
Найдем Р(А). Из четырех случаев событию А
благоприятны все, кроме В2; значит, тА = 3 и РD) = 3/4.
Событию As = {герб и решка) благоприятны два
последних случая В3 и /?4, откуда Р (^3) = 2/4 «* 1/2, т. е.
событие А3 вдвое вероятнее каждого из событий Av и А2. >
1.3. Частота пли статистическая
вероятность события
Как уже знаем, формула A.2.1) для
непосредственного подсчета вероятностей применима только тогда,
когда опыт, в результате которого может появиться
интересующее нас событие, обладает симметрией возможных
исходов. Очевидно, это далеко не всегда так, и
существует огромный класс событий, вероятности которых нельзя
вычислять по «классической» формуле.
Возьмем, к примеру, неправильно сделанпую
игральную кость (со смещенным центром тяжести). Событие
А «{выпадение 5 очков) уже не будет обладать
вероятностью 1/6. Но какой же? И как ее найти? Ответ
интуитивно ясен: надо «попробовать» побросать кость доста-
i.3. частота или статистическая вероятность 29
точно много раз и посмотреть, насколько часто будет
появляться событие А,
Очевидно, что вероятности таких событий, как
В = (попадание в цель при выстреле},
С = {выход из строя интегральной схемы в течение
одного часа работы),
D = {при контроле изделий будет выявлено за день
ровно т дефектных),
также не могут быть пайдены по формуле
A.2.1)—соответствующие опыты к схеме случаев не сводятся. Тем не
менее, естественно предположить, что каждое из них
обладает какой-то степенью объективной возможности,
которая при многократном повторении соответствующих
опытов будет отражаться в относительной частоте
событий.
Мы будем исходить из предположения, что каждое из
случайных событии (сводится опыт к схеме случаев или
нет, лишь бы он был неограниченно воспроизводим)
обладает какой-то вероятностью,
заключенной между нулем и единицей. Для
опытов, сводящихся к схеме случаев, подсчет вероятностей
производится (прямо или косвенно) по формуле A.2.1).
С теми же опытами, которые к схеме случаев не
сводятся, дело обстоит сложнее: прямое или косвенное
нахождение вероятностей событий корнями своими уходит
в сбор данных, статистику, массовый эксперимент.
Введем одно из важнейших понятий теории
вероятностей — понятие частоты случайного события.
Если производится серия из п опытов, в каждом из
которых может появиться или не появиться событие А,
то частотой события А в данной серии опытов
называется отношение числа опытов, в которых появилось
событие Л, к общему числу п произведенных опытов.
Частоту события часто называют его
статистической вероятностью (в отличие от ранее введенной
«математической» вероятности).
ч Подчеркнем, что для вычисления частоты события
недостаточно знать условия опыта, нужно еще располагать
каким-то массивом статистических данных. Частота —
характеристика опытная, экспериментальная.
Условимся обозначать частоту (статистическую
вероятность) события А знаком Р*(-4) (здесь и в дальней-
30 ГЛ. 1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
шем звездочка у буквы будет указывать на
статистический характер соответствующего параметра). Согласно
определению, частота события А вычисляется по
формуле:
м
р*(Л) = -^г A.3.1)
где п — число произведенных опытов (не путать с
числом случаев в «классической схеме»!), МА — число
опытов, в которых событие А появилось.
При небольшом п частота события носит в
значительной мере случайный характер. Пусть, например,
опыт — бросание монеты, событие А = (появление герба}.
Вероятность этого события, по формуле A.2.1), Р(Л) =
— 1/2. Что касается частоты Р* {А), то она вовсе не
обязана равняться 1/2 и даже быть близкой к ней.
Например, при пяти бросаниях (п = 5) вполне возможно,
что герб появится только один раз: Р* (А) =* 1/5; менее
вероятно, но тоже возможно, что он не появится вообще
ни разу: Р* (А) = 0, или все пять раз: Р*(А) = 1.
Одним словом, при малом числе опытов частота события
непредсказуема, случайна. Однако при большом числе
опытов п частота все больше теряет свой случайный
характер: она проявляет тенденцию
стабилизироваться, приближаясь, с незначительными колебаниями,
к некоторой средней постоянной величине*). Например,
при многократном бросании монеты частота появления
герба будет лишь незначительно уклоняться от 1/2 — 0,5.
Для иллюстрации в табл. 1.3.1 приведены результаты
серии из п = G00 бросаний монеты (для простоты опыт
подразделен на 60 «подсерпй», в каждой из которых
бросались одновременно 10 тщательно встряхнутых монет
и подсчитывалось число выпавших гербов).
Для иллюстрации на рис. 1.3.1 изображена
зависимость частоты Р*(Л) появления герба от числа
опытов л.
Из этого графика видно, что по мере увеличения п
частота проявляет тенденцию стабилизироваться,
приближаясь сквозь ряд случайных отклонений к постоян-
*) Естественно, это справедливо только для тех случайных
явлений, которые обладают свойством устойчивости частот (см.
введение), но только такими явлениями и занимается теория ьэ-
роятяостей.
1.3. ЧАСТОТА ИЛИ СТАТИСТИЧЕСКАЯ ВЕРОЯТНОСТЬ
31
ной величине, которую мы положим равной 0,5 (это —
как раз вероятность Р (А) появления герба в одном
опыте).
Из рассмотрения табл. 1.3.1 и графика рис. 1.3.1 мы
можем сделать ряд поучительных выводов.
1. По мере увеличения числа опытов п частота
события имеет тенденцию приближаться к его вероятности.
Т а б л и ц а 1.3.1
Число
ОПЫТОВ ?1
10
20
30
40
50
60
70
80
90 -
100
110
120
130
140
150
100
170
180
190
200
Р* (А)
0,600
0,650
0,600
0,575
0,540
0,550
0,528
0,512
0,588
0,490
0,550
0,492
0,523
0,500
0,493
0,475
0,471
0,472
0,463
0,465
п
210
220
230
240
250
260
270
280
290
300
310
320
330
340
350
360
370
380
390
400
Р* U)
0,462
0,472
0,470
0,479
0,484
0,477
0,489
0,482
0,493
0,497
0,500
0,503
0,497
0,506
0,497
0,497
0,495
0,492
0,500
0,498
п
410
420
430
440
450
460
470
480
490
500
510
520
530
540
550
560
570
580
590
600
Р* U)
0,502
0,512
0,512
0,514
0,519
0,515
0.515
0,510
0,508
0,510
0,506
0,516
0,513
0,515
0,513
0,511
0,512
0,509
0,507
0,505
2. Это приближение идет довольпо медленно (гораздо
медленнее, чем хотелось бы!), но явно прослеживается
на экспериментальном материале.
3. Колебания частоты около вероятности носят
случайный, незакономерный характер. Если бы мы повторили
тот же массовый опыт (произвели бы другие 600
бросаний монеты), то кривая зависимости частоты Р* (А) от
числа опытов п имела бы другой конкретный вид, но,
по-видимому, общая тенденция приближаться к 0,5
сохранилась бы.
Теперь спросим себя: можно ли сказать, что при
увеличении п частота Р* (^4) стремится к вероятности
Р (А) в обычном математическом смысле слова? Нет,
этого сказать нельзя, именно в связи со случаи-
32
ГЛ 1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
н о с т ь ю процесса приближения. В самом деле,
теоретически, например, могло ли бы случиться, что все
600 раз выпал герб и Р* (А) оказалось равным единице?
Теоретически могло бы, а на практике — нет. Вероятность
того, что все 600 раз выпадет герб, настолько мала
(в дальнейшем (см. гл. 2, п. 2.4) мы вычислим ее и
убедимся, что она равна A/2N00), что можно пренебречь
возможностью такого совпадения. Подсчеты показывают,
0,650
0,500
0,550-
100
200 300
Рис. 1.3.1
Ц-00
500
600 л
что даже значительно меньшие отклонения частоты от
вероятности при п = 600 практически не встречаются.
Забегая вперед (см. гл. И), сообщим читателю, что при
шестистах бросаниях монеты частота появления герба
почти наверное не отклонится от 0,5 больше, чем 0,06
(в дальнейшем вы научитесь самостоятельно находить
такие границы, за которые практически наверняка не
выйдут отклонения численного результата опыта от
заранее предсказанного или искомого значения (см.
гл. 11)).
Подмеченная нами на конкретном примере
закономерность имеет более общий смысл. А именно, если
воспроизводить достаточное число раз один и тот же опыт
со случайным исходом, в котором может появиться или
не появиться событие Л, частота Р*(Л) этого события
1.3. ЧАСТОТА ИЛИ СТАТИСТИЧЕСКАЯ ВЕРОЯТНОСТЬ 33
имеет тенденцию стабилизироваться, приближаясь сквозь
ряд случайных отклонений к некоторому постоянному
числу; естественно предположить, что это число и есть
вероятность события. Проверить такое предположение
мы, естественно, можем только для событий, вероятности
которых могут быть вычислены непосредственно, по
формуле A.2.1), т. е. для опытов, относящихся к схеме
случаев. Многочисленные массовые эксперименты,
проводившиеся разными лицами со времен возникновения теории
вероятностей, подтверждают это предположение: частота
события при увеличении числа опытов действительно
приближается к его вероятности. Естественно допустить,
что и для опытов, не сводящихся к схеме случаев, тот
же закон остается в силе и что постоянное значение,
к которому при увеличении числа опытов приближается
частота события, и есть не что иное, как вероятность
события. Тогда частоту события при достаточно
большом числе опытов можно принять за приближенное
значение вероятности. Знание законов теории
вероятностей позволяет оценить ошибку этого
приближенного равенства, а также найти число опытов /г, при
котором можно с достаточной степенью достоверности
ожидать, что ошибка не превзойдет данной величины.
Специально отметим, что характер приближения
частоты к вероятности при увеличении числа опытов
существенно отличается от «стремления к пределу» в
математическом смысле слова. Когда в математике мы
говорим, что переменная хп с возрастанием п стремится
к постоянному пределу а, это значит, что разность
\хп — а\ становится меньше любого положительного е для
всех значений п, начиная с некоторого. Относительно
частоты и вероятности такого категорического
утверждения сделать нельзя. Нет ничего физически
невозможного в том, что частота события при большом
числе опытов сильно отклонится от его вероятности, но
такое отклонение оказывается практически
невозможным—настолько маловероятным, что можно не
принимать его в расчет.
Таким образом, при увеличении числа опытов п
частота события приближается к его вероятности, но не
с полной достоверностью, а с большой вероятностью, тем
большей, чем большее число опытов произведено.
Такой способ приближения одних величин к другим
очень часто встречается в теории вероятностей, лежит
2 Теория вероятностей и ее
инженерные приложения
34 гл. i. основные понятия теории вероятностей
в основе большинства ее выводов и рекомендации и
носит специальное название: «сходимость по вероятности».
Говорят, что величина А'п сходится по вероятности
к величипе а, если при сколь угодио малом е
вероятность неравенства \Хп — а\ < г с увеличением п
неограниченно приближается к единице.
Применяя этот термин, можно сказать, что при
увеличении числа опытов п частота события не «стремится»
к его вероятности, а «сходится к ней по вероятности».
Таким образом, вводя поиятие частоты события и
пользуясь связью между нею и вероятностью, мы
получаем возможность приписать определенные вероятности,
заключенные между нулем и единицей, не только
событиям, для которых применима схема случаев, но и тем
событиям, которые к этой схеме не сводятся; достаточно,
чтобы опыт обладал свойством устойчивости частот,
иными словами, мог быть неограниченно воспроизводим в
практически одинаковых условиях. Тогда можпо,
производя достаточно большое число опытов, приближенно
положить искомую вероятность события равной его
частоте.
В дальнейшем мы увидим, что для определения
вероятности события в опыте, не сводящемся к схеме
случаев, сравнительно редко надо непосредственно
находить из серии опытов его частоту. Теория вероятностей
располагает способами, позволяющими находить
вероятности событий не прямо, а косвенно, через
вероятности других событий, с ними связанных. В сущности,
такие косвенпые способы и составляют главное содержание
теории вероятностей. Но и при пользовании косвенными
способами (если опыт не сводится к схеме случаев)
в копечном итоге все же приходится обращаться к
экспериментальным данным.
Выведем некоторые свойства частот, справедливые не
только при большом, по и при любом число опытов гс.
1. Правило сложения часют. Если два
события А и Б несовместны, то частота события С,
состоящего в том, что появится А или В (безразлично, какое
имепно), равна сумме частот этих событий:
Р* (С) - Р* {А или В} - Р* (А) + Р* (В). A.3.2)
Действительно, если число опытов, в которых
появилось событие А, равно МА, а число опытов, в которых
1.3. ЧАСТОТА ИЛИ СТАТИСТИЧЕСКАЯ ВЕРОЯТНОСТЬ 35
появилось событие В, равно Мв и события А и В
несовместны, то
Р* (С) = Л^4^ = ^ + ^ = Р* (Л) + Р*(Я).
2. Правило умножения частот. Для любых
двух событий А и В частота события Д состоящего в том,
что появятся оба события:
D = U и В)
равна частоте одного из них, умноженной на «условную
частоту» другого, вычисленную в предположении, что
первое имело место:
Р*(?>) = Р*{Л и В)-Р*(А)-Р*(В\А)% A.3.3)
где Р* (В | А) — частота события #, вычисленная
только для тех опытов, в которых
произошло событие А (предполагается, что МАФЪ).
Действительно, пусть в МА опытах произошло
событие А; в MD опытах оно сопровождалось появлением
события В, т. е. происходило событие D = {А и В). Тогда
частота события D
Но второй сомножитель в формуле A.3.4) есть не что
иное, как частота события В, вычисленная только
для тех опытов, в которых произошло
событие А (назовем «условной частотой события В при
наличии А» и обозначим Р*(В\А)).
Заметим, что условную частоту события В при
наличии А можно вычислить и исходя из P*(D) по
формуле:
P*{B\A)-P*(D)/P*(A), A.3.5)
т. е. условная частота события В при наличии А может
быть получена делением частоты события D = {А и В] на
частоту события А.
В дальнейшем мы увидим, что аналогичные правила
сложения и умножения справедливы и для вероятностей
событий.
Понятие частоты события является кардинально
важным в теории вероятностей. Можно построить все ее
здание, исходя из основного понятия частоты и постуди-
36 ГЛ. 1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
руя свойства не вероятностей, а частот (такое
построение теории вероятностей было еще в начале XX века
предложено Р. Мизесом; да и в настоящее время
некоторые авторы предпочитают излагать теорию вероятпо-
стей на частотной основе). С нашей точки зрения
наиболее современным (и, что немаловажно, соответствующим
традициям изложения теории вероятностей в
университетах) является аксиоматический теоретико-
множественный подход, связанный с идеями
А. Н. Колмогорова; этого подхода мы и будем
придерживаться в дальнейшем.
ГЛАВА 2
АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ.
ПРАВИЛА СЛОЖЕНИЯ И УМНОЖЕНИЯ
ВЕРОЯТНОСТЕЙ И ИХ СЛЕДСТВИЯ
2.1. Элементарные сведения
из теории множеств
Напомним тому, кто их знает, и сообщим тому, кто
впервые с ними встречается, основные понятия этой
математической науки.
Множеством называется любая совокупность
объектов произвольной природы, каждый из которых
называется элементом множества.
Примеры множеств: 1) множество студентов,
обучающихся в данном вузе; 2) множество натуральных чисел,
не превосходящих 100; 3) множество точек на плоскости,
лежащих внутри или на границе круга радиуса г с
центром в начале координат; 4) множество точек на
числовой оси, расстояние от которых до точки с абсциссой а
не превышает d.
Множества мы будем обозначать по-разному: или
одной большой буквой, или перечислением его элементов,
данным в фигурных скобках; или указанием (в тех же
фигурных скобках) правила, по которому элемент
относится к множеству. Например, множество М
натуральных чисел от 1 до 100 может быть записано в виде:
М = И, 2, ..., 100) - U- целое; 1<К 100} -
-{f-1, ..., 100}.
Множество точек на числовой оси, расстояние от
которых до точки с абсциссой а не превосходит d, может
быть записано в виде
S = {\z-a\^d) или S = {x: |*.-a| <d),
где х — абсцисса точки.
Множество С точек на плоскости, лежащих внутри
или на границе круга радиуса г с центром в начале
координат, может быть записано в виде
С = {хг + уг<г*) или ? = {(*, у): х2 + у2^г*},
38 ГЛ. 2. АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
где х, у — декартовы координаты точки, или же
С = {р < г},
где р — одна из полярных координат точки.
По числу элементов множества делятся на конечные
и бесконечные. Множество М = {1, 2, ..., 100} конечно
и состоит из 100 элементов. В частности, конечное
множество может состоять из одного элемента.
Множество всех натуральных чисел Nt = {1, 2, ...
..., /г, ...} бесконечно; так же бесконечно и множество
четных чисел: /V2 = {2, 4, ..., 2и, ...}. Бесконечное
множество называется счетным, если все его члены можно
расположить в какой-то последовательности,
перенумеровать (оба множества Л^ и N2 являются счетными).
Вышеупомянутые множества S и С оба бесконечны и
несчетны (их элементы нельзя перенумеровать).
Два множества А и В совпадают (или равны), если
они состоят из одних и тех же элементов. Например,
множество корней уравнения х2 — Ъх + 4 = 0 совпадает с
множеством И, 4), а также с множеством {4, 1).
Совпадение множеств обозначается знаком равенства: А=В.
Запись а^А означает: объект а является элементом
множества А; другими словами, а принадлежит А. Запись
а&А означает: а не принадлежит А.
Пустым множеством называется множество, не
содержащее ни одного элемента; оно обозначается символом 0.
Пример: множество точек плоскости, координаты
которых ху у удовлетворяют неравенству х2 + у2^— 1:
Все пустые множества равны между собой.
Множество В называется подмножеством (частью)
множества Л, если все элементы В содержатся также и
в А; обозначение В^А или А эВ.
Примеры: {1, 2, 3}е{1, 2, 3, ..., 100); {г + 2
1)У + Ч2)
Подмножество может быть равно самому множеству:
{1, 2, 3, 4} = {1, 2, 3, 4}. >
Отношения подмножества и множества можно на*
глядно изображать с помощью геометрической
интерпретации (рис. 2.1.1), где элементами множеств являются
точки на плоскости; каждая точка фигуры В принадле-
2.1. СВЕДЕНИЯ ИЗ ТЕОРИИ МНОЖЕСТВ 39
жит также и фигуре А;
Объединением (суммой) множеств А и В называется
множество С = А + В, состоящее из всех элементов А и
всех элементов В (в том числе и тех, которые
принадлежат и А и В). Короче: объединение двух множеств —это
Рис. 2.1.1
совокупность элементов, принадлежащих хотя бы
одному из них.
Объединение множеств А и В часто обозначают A U Вх.
Так как мы будем обычно называть объединение
событий их суммой, нам удобнее обозначать эту
операцию знаком «+». Очевидно, что если В^4, то А +
А.
Примеры: 1) {1, 2, ..., 100} + {50, 51, ..., 200)
-{1, 2, ..., 200); 2) A, 2, ..., 100) + {1, 2 1000}
~<1, 2, ..., 1000}; 3) {х2 + у2<2) + {х2 + у2<4}{2
+ У2<4).
Геометрическая интерпретация объединения двух
множеств А и В дана на рис. 2.1.2, где А и В —
множества точек, входящих соответственно в фигуры А и 5.
Аналогично объединению двух множеств
определяется объединение (сумма) нескольких мпожеств, а именно
п
Ах + А2+ ... + Лп - 2 Аг
есть множество всех элементов, входящих хотя бы в
одно из множеств Аи А2, ..., Ап- Рассматриваются
также объединения бесконечного (счетного) числа
множеств, например:
A, 2} + {2, 3} + C, 4) + ... + {п - 1, и) + ... -
«{1,2,3,...,/г, ...}.
40 ГЛ 2. АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
Пересечением (произведением) множеств А и В
называется множество D = А В, состоящее из элементов,
входящих одновременно и в А и в В.
Пересечение множеств А и В часто обозначают А Л В,
но мы (опять-таки в целях удобства) будем обозначать
эту операцию знаком произведения «•» или «X», а иногда,
как принято в алгебре, и совсем
опуская этот знак. Очевидно, что
если Bs^, то АВ = В.
Примеры: {1, 2, ..., 100) X
Х{50, 51, ..., 200) -E0, 51, ...
..., 100}; A, 2 100} -И, 2, ...
Рис. 2^.3 ^ •••' 50} = {1, 2, ..., 50}.
Геометрическая интерпретация
пересечения (произведения) двух множеств А и В дана на
рис. 2.1.3.
Аналогично определяется пересечение нескольких
п
множеств; множество A1»AZ-... -Ап= JJ Ах состоит из
i = l
элементов, входящих одновременно во все множества
Аи Л2, ..., Ап. Определение распространяется и на беско-
ОО
нечное (счетное) число множеств: Д Аг есть множество,
г=1
состоящее из элементов, входящих одновременно во все
множества Аи Аг, ..., Л„, ...
Операции объединения (сложения) и пересечения
(умножения) множеств обладают рядом свойств,
аналогичных свойствам обычных сложения и умножения чисел:
1. Переместительное свойство:
А+В = В + А\ А В = ВА.
2. Сочетательное свойство:
(А+В) + С = А +(В + С)\ (АВ)С = А (ВС).
3. Распределительное свойство:
А (В + С)
Операции прибавления пустого множества и
умножения на пустое множество также аналогичны
соответствующим операциям над числами, если считать нуль за
пустое множество:
Л + 0-Л; А .0-0.
2.2. АКСИОМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ 41
Однако некоторые операции над множествами не
имеют аналогов в обычных операциях над числами; в
частности для множеств
А+А =А; А А=А.
Пользуясь вышеизложенными элементарными
сведениями по теории множеств, дадим
теоретико-множественную схему построения теории вероятностей и ее
аксиоматику.
2.2. Аксиомы теории вероятностей и их следствия.
Правило сложения вероятностей
В этом пункте мы изложим теоретико-множественный
подход к основным понятиям теории вероятностей и
сформулируем ее аксиомы.
Пусть производится некоторый опыт (эксперимент,
испытание) со случайным исходом (см. п. 1.1).
Рассмотрим множество Q всех возможных исходов опыта;
каждый его элемент со ^ Q будем называть элементарным
событием, а все множество Q — пространством
элементарных событий. Любое событие А в
теоретико-множественной трактовке есть некоторое подмножество
множества Q: A s Q. Если множество А распадается на
несколько непересекающихся
подмножеств А = A t + А2 + ...
... + Аа {Ах-А^0 при *¦*/),
то будем называть события
Аь А2у ..., Ап «вариантами»
события А (на рис. 2.2.1
событие А распадается на три
варианта: Аи А21 А3).
Примеры. 1) Опыт
—бросание игральной кости; прост- Рпс. 2.2.1
ранство элементарных событий
?2 = {1, 2, 3, 4, 5, 6). Каждое из указанных чисел
очков — элементарное событие. Событие А = {выпадение
четного числа очков)={2, 4, 6); варианты события А:
4,-Ш, Л2 = {4); А3 = Ш; А^А, + А2 + А3.
2) Опыт — выстрел по мишени, представляющей
собой круг радиуса г с центром в начале координат
(рис. 2.2.2). Элементарное событие со — попадание в
любую точку с координатами (х, у)\ пространство элемен-
42
ГЛ. 2. АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
тарных событий — вся плоскость хОу. Событие А =
(попадание в мишень} «¦ {х2 + уг< г] есть подмножество
пространства Q: A s Q.
Варианты события Л: Л! = (попадание в правую
половину мишени}; Л2 = (попадание в левую половину};
А, = {х2 + у2 < г2; х > 0}; Л2 - (я2 + </2 ^ г2; х < 0}.
3) Опыт —приход поезда к определенной станции; в
расписании стоит время прибытия t0. Фактически поезд
может опоздать (прибытие eh) раньше tQ будем считать
X
( А
о tn
Рис. 2.2.2
Рис. 2.2.3
практически невозможным). Событие А состоит в том,
что поезд опоздает не более чем на т минут.
Пространство элементарных событий —половипа числовой оси Of
(рис. 2.2.3), лежащая правее точки U (f —момент
прибытия поезда).
Событие А — множество точек на числовой оси,
отмеченное штриховкой на рис. 2.2.3:
Варианты события А можно построить, если
разделить участок от *<> до U + x на несколько
непересекающихся участков, например, на два:
);
Среди событий, являющихся подмножествами
множества Q, можно рассмотреть п само Q (водь каждое
множество есть свое собственное подмножество); оно называется
достоверным событием (см. определение достоверного
события в п. 1.2). Ко всему пространству Q
элементарных событий добавляется еще и пустое мпожество 0;
2.2. АКСИОМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ 43
это множество тоже рассматривается как событие и
называется невозможным событием (см. п. 1.2).
Заметим, что элементарные события со в одном и
том же опыте можно задавать по-разному; например, при
случайном бросании точки на плоскость положение
точки можно задавать как парой декартовых координат
(х, у), так и парой полярных (р, ср).
Дадим теоретико-множественное истолкование тем
свойствам событий, которые мы рассматривали в п. 1.2.
Несколько событий Аи А2, ..., Ап образуют полную
п
группу, если 2 ^ = 2. т. е. их сумма (объединение)
есть достоверное событие.
Два события Л, В называют несовместными, если
соответствующие множества не пересекаются, т. е. АВ = 0.
Несколько событий Аи А2, ..., Ап называются
попарно несовместными (или просто несовместными), если
появление любого из них исключает появление каждого из
остальных: A\Ai ^ 0 (при i Ф /).
Так как события представляют собой множества, то
для них точно так же определяются операции сложения
(объединения) и умножения (пересечения), как и для
множеств вообще, и сами операции обладают теми же
свойствами. Ввиду важности этих операций над
событиями дадим их определения:
Суммой двух событий А и В называется событие С,
состоящее в выполнении события А или события 5, или
обоих событий вместе (см. рис. 2.1.2).
Суммой нескольких событий называется событие,
состоящее в выполнении хотя бы одного из этих событий.
Произведением двух событий А
и В называется событие D,
состоящее в совместном выполнении
события А и события В (рис. 2.1.3).
Произведением нескольких
событий называется событие, состоящее
в совместном выполнении всех этих
событий. Рис. 2.2.4
Противоположным по отношению
к событию А называется событие Л, состоящее в
непоявлении А и, значит, дополняющее его до Q
(рис. 2.2.4).
На основе вышеизложенной трактовки событий как
множеств сформулируем аксиомы теории вероят-
44 ГЛ. 2. АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
но с те й. Пусть каждому событию А ставится в
соответствие некоторое число, называемое вероятностью
события. Вероятность события А мы будем обозначать
Р(А)*). Так как любое событие есть множество, то
вероятность события есть функция множества.
Потребуем, чтобы вероятности событий удовлетворяли
следующим аксиомам:
1. Вероятность любого события заключена между
нулем и единицей:
2. Если А и В несовместные события (АВ — 0), то
B.2.1)
Аксиома B.2.1) легко обобщается (с помощью
сочетательного свойства сложения) на любое число событий:
если AiAi*=0 при гФ], то
PI V A. I V р/1\ /о о о\
т. е. вероятность суммы несовместных событий равна
сумме вероятностей этих событий.
Аксиому сложения вероятностей B.2.2) иногда
называют «теоремой сложения» (для опытов, сводящихся
к схеме случаев, она может быть доказана), а также
правилом сложения вероятностей (мы будем
предпочтительно пользоваться последним термином).**)
3. Если имеется счетное множество несовместных
событий Ai, Аи ..., Ап, ... (AiAj = 0 при iФ]), то
РУ 1 У D/l\ /OO Q\
Третью аксиому приходится вводить отдельно, так как
она не выводится из второй.
Вернемся к понятиям «полная группа событий»,
«несовместные события», «равновозможные события», о ко-
¦) Если событие (множество) обозначается не буквой, а его
словесным описанием, или формулой, или просто перечислением
элементов множества, мы будем при записи вероятности
пользоваться не круглыми, а фигурными скобками, например
•¦) Напомним, что частоты событий (п. 1.3) также
подчиняются этому правилу.
2.2 АКСИОМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ 45
торых мы говорили в п. 1.2 и дадим им
теоретико-множественную формулировку.
Понятие «несовместные события» мы уже
рассмотрели: события Аи Л2, ..., Ап несовместны, если А{А}=*0
при i Ф /.
События Лi, А2, ..., Ап образуют полную группу, если
2 Аг = а. B.2.4)
События Aiy A2i ..., Ап равно возможны, если
...-P(^). B.2.5)
Если группа событий обладает всеми тремя
свойствами — полноты, несовместности и равновозможности, то
их называют случаями.
Выведем из аксиомы сложения B.2.2)
«классическую» формулу A.2.1) для непосредственного подсчета
вероятностей. Пусть результаты опыта могут быть
представлены в впде п случаев Л„ Аг% ..., Ап. Случай А{
благоприятен событию А, если он представляет собой
подмножество А (А,^А), иначе — вариант события А.
Так как случаи Ац Аг, ..., Ап образуют полную
группу, то
2 Л, - Q.
Так как случаи Аи Аг, ..., Ап несовместны, то к ним
применимо правило сложения вероятностей:
Так как случаи Аи А2, ..., АЛ равновозможны, то
Р(АХ)-Р(А%)~ ... -РDп)-1/п.
Благоприятпые событию А случаи образуют тА его
вариантов; так как вероятность каждого из них равна
1/и, то, по правилу сложения,
раз
а это и есть уже знакомая нам «классическая формула»
A.2.1).
46 ГЛ. 2. АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
Аксиомы теории вероятностей позволяют вычислять
вероятности любых событий (подмножеств
пространства Q) через вероятности элементарных событий (если их
конечное или счетное число). Вопрос о том, откуда
берутся вероятности элементарных событий, при этом не
рассматривается. На практике они определяются либо
непосредственно по условиям опыта (если он обладает
симметрией возможных исходов), либо на основе
экспериментальных статистических данных (если он такой
симметрией не обладает, что бывает значительно чаще).
Правило сложения вероятностей имеет ряд важных
следствий. В качестве одного из них докажем, что сумма
вероятностей полной группы несовместных событий
равна единице, т. е. если
п
2 Ai = Q; AiAj= 0 при i ф /,
то
п
2Р (АЛ — \ /о ofi\
Действительно, так как события Аи А2, ..., Ап
несовместны, то к ним применимо правило сложения:
/ п \ п
24 -2
U-l I i=l
В частпости, если два события А и А
противоположны, то они образуют полпую группу несовместпых
событий и
т. е. сумма вероятностей противоположных событий
равна единице.
Это свойство противоположных событий очень
широко применяется в теории вероятностей. Часто бывает
проще вычислить вероятность противоположного
события А% чем вероятность интересующего нас события А.
Тогда вычисляют Р{А), вычитают ее из единицы и
находят:
Р(Л)-1-Р(Л). B.2.7);
Таким приемом мы очень часто будем пользоваться
в дальнейшем.
2 2. АКСИОМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
47
Выведем еще одио следствие правила сложения. Если
события А и В совместны (АВФ 0), то
Р (А + В) = Р (А) + Р (В) - Р (АВ). B.2.8)
Докажем его. Представим событие А + В как сумму
трех несовместных вариантов (см. рис. 2.2.5)
А + В = {А, но не В) + {В, но не А) + АВ =»
По правилу сложения
Р {А + В) - Р {АВ) + Р (В А) + Р (АВ). B.2.9)
Но
А = АЪ~+АВ; Р(А) = Р(АВ) +Р(АВ);
В = ВА + АВ; Р(В) = Р(ВА) +Р(АВ);
откуда А
. B.2.10)
Рис. 2.2.5
Подставляя выражения B.2.10)
в B.29), нолучим Р(Л + Я) =
- Р (А) -Р(АВ) + Р(В) - Р (ЛВ) +
+ Р (АВ) - Р (Л) + Р (В) - Р (Л?),
что и требовалось доказать.
Формулы типа B.2.9) можно вывести и для более
чем двух совместных событий, но мы на этом не будем
останавливаться.
Предложим читателю самостоятельно вывести
формулу для вероятности суммы трех совместных событий Л,
В и С (рис. 2.2.6):
+ Р (В) + Р (С) - Р (АВ) - Р (АС) - Р (ВС) + Р (ABC).
Заметим, что прием непосредственного подсчета
вероятностей A.2.1) допускает иногда распространение и
на случай, когда множество элементарных событий
несчетно, например, представляет собой совокупность точек
на плоскости внутри некоторой области Й (рис. 2.2.7).
Опыт состоит в том, что в пределы области Q
«случайным образом» бросается точка U. Выражение «случай-
ГЛ. 2. АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
ным образом» в данном случае означает, что все точки
области Q «равноправны» в отношении попадания туда
случайной точки U — она бросается «наугад», без
какого-либо предпочтения одному положению перед другим.
Тогда естественно считать, что вероятность попадания
Рис. 2.2.7
точки JJ в какую-то область А (подмножество Q)
пропорциональна площади этой области:
Р (А) - Р {U е А} - SA/SQf B.2,11)
где 5А —площадь области A, «So —площадь всей
фигуры Q.
На этом основан подсчет вероятностей в некоторых
задачах (иногда его называют «геометрическим»).
Приведем некоторые примеры.
Пример 1. Два лица-4 и В-условились
встретиться в определенном месте, договорившись только о
том, что каждый является туда в любой момент времени
между 13 ч. и 13 ч. 30 мин. и ждет в течение 15
минут. Если партнер к этому времени еще не пришел или
уже успел покинуть условленное место, встреча не
состоится. Найти вероятность того, что встреча состоится.
Решение. Элементарное событие со
характеризуется двумя параметрами: х — момент прихода Any —
момент прихода В. Будем изображать это событие точкой
с координатами (х, у) на плоскости хОу. Выберем за
начало отсчета 13 часов, а за единицу измерения — 1 час
и построим на плоскости хОу пространство
элементарных событий Q. Это есть квадрат со стороной 0,5
(рис, 2.2.8),
2.2. АКСИОМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
49
Событие С =(встреча) произойдет, если разность
между х и у по абсолютной величине не превзойдет 0,25
часа A5 мин.). Область С, «благоприятная» этому
событию, на рис. 2.2.8 заштрихована. Ее площадь равна
площади всего квадрата SQ — 0,52 ¦= 0,25 без суммы
площадей двух угловых треугольников,
не заштрихованных на рис. 2.2.8:
So - SQ - 2 .A/2) • 0,252 - 0,1875.
Отсюда
0,25 0,5 X
Рис. 2.2.8
что из этих частей можно составить
Пример 2. Стержень
единичной длины произвольным
образом разламывается на три части
х, у и z (рис. 2.2.9). Найти
вероятность того,
треугольник.
Решение. Элементарное событие со
характеризуется двумя параметрами хну, ибо z ¦¦ 1 — (х + у).
На них наложены ограничения: я > 0, у > 0, х + у<
< 1. Пространство элементарных событий Q есть
внутренняя часть прямоугольного треугольника с катетами,
равными единице (рис. 2.2.10).
Его площадь Sq ¦-1/2. Условие
А, чтобы из отрезков х, у, 1 —
— {х + у) можно было составить
треугольник, сводится к следую-
X
У
Рис. 2.2.9
0,6 1 а?
Рис. 2.2.10
щим: 1) сумма любых двух сторон больше третьей; 2)
разность любых двух сторон меньше третьей. Этим условиям
соответствует треугольная область А, заштрихованная на
рис. 2.2.10 с площадью 5А — A/2) • A/4); отсюда Р(А)=*
-Sa/Sq-Щ. >
Пример 3. Задача Бюффона. Плоскость разграфле*
на параллельными прямыми на расстоянии L друг от
друга (рис. 2.2.11). На плоскость произвольным образом
бросается игла длины I < L. Найти вероятность того, что
игла пересечет одну из прямых,
50
ГЛ 2 АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
Решение. Исход опыта (положепие иглы на
плоскости) будем описывать двумя координатами:
я—абсцисса центра иглы относительно ближайшей прямой
слева и ф —угол, который составляет игла с прямыми
(рис. 2.2.12). Очевидно, что все значения х и ф равно-
возможны (в этом и проявляется бросание иглы
«наугад»). Очевидно, можно (не теряя общности) ограничить
V 1/2
Л/2
L
L
L
Рис. 2.2.11
X L
Рис. 2.2.12
1/2 ос
Рис. 2.2.13
возможные значения х участком от 0 до L/2, а ф-от
О до я/2, рассматривая возможность пересечения только
с одной (ближайшей левой) прямой. Прямоугольник па
плоскости хОу со сторонами LI2 и я/2 (рис. 2.2.13)
представляет пространство элементарных событий Й; SQ =*
= Zji/4. Если абсцисса х центра иглы будет меньше, чем
-7j- sin ф, то игла пересечет прямую, интересующее нас
Л Л f ^ * ' \ , *
событие A = j?<-7psin ф| (см. заштрихованную область
на рис. 2.2.13). Площадь этой области
л/а
I . / 21
-тр sin yd ф = -?-; Р (А) «» S^/S^ = ^у. >
о
-I
2.3. Условная вероятность события.
Правило умножения вероятностей
Пусть производится опыт со случайным исходом, в
результате которого могут произойти (или пе произойти)
какие-то события А и В.
Условной вероятностью события В при наличии А
называется величина
Р(В\А) = Р(АВ)/Р{А) B.3.1)
(прп этом предполагается, что
2 3 УСЛОВНАЯ ВЕРОЯТНОСТЬ СОБЫТИЯ 51
Вспомним, как мы определяли в п. 1.3 условную
частоту события В при наличии А; один из способов
ее определения состоял в том, что мы делили частоту
события АВ на частоту события А, Условная частота
имеет и другой смысл: это —частота события В,
вычисленная при условии, что событие А
произошло. Точно так же и условную вероятность Р{В\А )
можно трактовать, как вероятность события 5,
вычисленную при условии (в предположении), что
событие А произошло.
На практике формулу B.3.1) обычно читают «в
обратном порядке», для чего записывают ее в виде:
Р\АВ) = Р{А).Р{В\А), B.3.2)
т. е. вероятность произведения (пересечения,
совмещения) двух событий равна вероятности одного из них,
умноженной на условную вероятность второго при
наличии первого.
Сформулированное правило мы будем называть
правилом умножения вероятностей*). Его статистический
аналог — правило умножения частот — мы уже
рассматривали в п. 1.3.
Совершенно очевидно, что неважно, какое событие
выбрать первым, а какое —- вторым. Поэтому правило
умножения вероятностей можно записать и в виде
Р(В).Р(А\В) B.3.3)
(при этом предполагается, что Р(В)фО).
Очевидно, что если событие А достоверно (Л=й),
то Q >В = В и P(Q.?) = PB?).
Пример 1. Из урны, содержащей 4 белых и 3
черных шара вынимаются (одновременно или
последовательно) два шара. Найти вероятность того, что оба шара
будут белыми.
Решение. Представим событие
С = {оба шара белые)
как произведение двух событий:
где
А = {первый шар белый},
В = {второй шар белый}.
*) Иногда это правило называют теоремой умножения
вероятностей.
52 ГЛ 2 АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
Найдем вероятность события С по формуле B.3.2):
Очевидно Р (-А) = 4/7. Найдем Р (В \ А). Для этого
предположим, что событие А уже произошло, т. е.
первый шар был белым. После этого в урне осталось 6
шаров, из которых 3 — белые:
р (jS | Л) — 3/6 — 1/2.
Отсюда
Р(О-D/7)-A/2)-2/7.
Кстати, точно такую же вероятность появлепия двух
белых шаров мы получили другим способом в примере 2
п. 1.2. >
Пример 2. В урпе 5 белых шаров и 2 черных. Из
нее вынимаются один за другим два шара. Найти
вероятность того, что они будут разных цветов.
Решение: Событие С = {шары разных цветов}
распадается на сумму двух несовместпых вариантов:
C-d + d,
где
Сг = {первый шар белый, второй черный},
Сг = {первый шар черный, второй белый}.
Вероятность каждого из вариантов найдем по
правилу умножения. Не вводя специальных буквенных
обозначений для событий, произведением которых образован
вариант Си вычислим его вероятность сразу по правилу
умножения: умпожим вероятность того, что первый шар
белый, на условную вероятность того, что второй шар
черный, при условии, что первый — белый:
Р(С1)-E/7).B/6)-5/21.
Так же вычислим и вероятность второго варианта:
Р(С1)-B/7).E/б)-5/21.
Отсюда, по правилу сложения вероятностей,
¦) Мы уже говорили о том, что безразлично, вынимаются ли
шары последовательно или одновременно; во втором случае
можно их перенумеровать любым способом.
2.3 УСЛОВНАЯ ВЕРОЯТНОСТЬ СОБЫТИЯ 53
Правило умножения вероятностей B.3.2) легко
обобщается на случай произвольного числа событий:
Р{АхА2...Ап) =
- Р{АХ) Р(А%\А1)Р(Аг\А1А%)... Р(Ап\АхА2... An_x), B.3.4)
т. е. вероятность произведения нескольких событий
равна произведению вероятностей этих событий, причем
вероятность каждого последующего события вычисляется
при условии, что все предыдущие имели место.
Пример 3. В урне 5 перенумерованных шаров с
номерами 1, 2, 3, 4, 5. Из урны один за другим
вынимаются все 5 шаров. Найти вероятность того, что их
номера будут идти в возрастающем порядке.
Решение. Событие А = {1, 2, 3, 4, 5). По
формуле B.3.4)
Р(А) - A/5).A/4).A/3).A/2) - 1/120. >
Особенно простой вид получает правило умножения
вероятностей в случае, когда события, образующие
произведение, независимы.
Событие А называется независимым от события В,
если его вероятность не зависит от того, произошло В
или нет, т. е. Р (А \ В) = Р {А),
В противном случае, если Р(А\В)ФР(А)У
событие А зависит от В.
Зависимость и независимость событий всегда
взаимны: если А зависит от В, то и В зависит от Л, и
наоборот.
Докажем это. Пусть событие А не зависит от
В: Р (А | В) » Р (А). Запишем правило умножения в двух
формах:
р (АВ) - Р (А) Р (В | А) « Р (В) Р (А | В). B.3.5)
Отсюда, заменяя в последнем выражении условную
вероятность Р(А\В) на «безусловную» Р(А), имеем:
Р(А)Р(В\А) = Р(В)Р(А).
Или, предполагая, что Р (А)фО, и деля обе части
равенства на Р (А),
т. е. событие В не зависит от Л, что и требовалось
доказать.
54 ГЛ 2. АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
В связи с этим можно дать новое определение
независимых событий:
Два события называются независимыми, если
появление одного из них не меняет вероятности появления
другого.
Пример 4. Опыт состоит в последовательном
бросании двух монет; рассматриваются события:
А = (появление герба на первой монете),
В = {появление герба на второй монете).
Из физических соображений ясно, что появление
герба на одной из монет никак не влияет на вероятность
появления герба на другой:
Р(А); Р(В\А) = Р(В).
События А и В независимы. >
Пример 5. В урне 2 белых шара и 3 черных; два
лица вынимают из урны по одному шару.
Рассматриваются события:
А = {появление белого шара у первого лица),
В = {появление белого шара у второго лица),
события А и В зависимы. >
Для независимых событий правило умножения
вероятностей принимает особенно простой вид:
Р(АВ) = Р(А)Р(В), B.3.6)
т. е. вероятность произведения двух независимых
событий равна произведению вероятностей этих событий.
Из формулы B.3.6) легко вывести следствие: если
события А и_В_ независимы^ то независимы также и
события А и В, А и В, А и В. Докажем, например, что А
и В независимы (для остальных пар доказательство
будет аналогичным).
Представим событие А как сумму двух вариантов:
По правилу сложения:
2.3. УСЛОВНАЯ ВЕРОЯТНОСТЬ СОБЫТИЯ 55
В
Р(АВ) = Р (А) - Р (АВ) = Р(А) - Р (А).Р(В) =
= Р(А)Ц-Р(В)] = Р(А).Р(В),
откуда видно, что события А и В независимы.
Несколько событий А{, A2j ..., Ап называются
независимыми, если любое из них не зависит от любой
комбинации (произведения) любого числа других. Для
независимых событий правило умножения принимает вид:
Р{АГА%.... -Ап) -Р{Аг).Р(А2).... -Р(Ап) B.3.7)
или, короче, пользуясь знаком произведения:
т. е. вероятность произведения нескольких независимых
событий равна произведению вероятностей этих событий.
Заметим, что если имеется несколько событий Аи
А2, ..., Л,и то их попарная независимость (т. е.
независимость любых двух событий Ai и А) с разными
индексами) еще не означает их независимости в
совокупности. Убедимся в этом па конкретном при»
мере.
Пример 6. Пусть имеется ЭВМ, в которой
информация хранится в виде нулей и едипиц; эту информацию
время от времени приходится пересылать с одного места
на другое. При пересылке, хотя и редко, возникают
ошибки. Чтобы бороться с ними, поступают так:
пересылают не по одному знаку 0 или 1 (биту), а сразу по
три: #о, Х\у Хг. Из них хи хг — это те знаки, которые нас
интересуют и которые мы должны переслать, а х0 —
добавочный знак, который служит целям контроля и
автоматически создается машиной так, чтобы сумма хо +
+ Xi + x2 была четной. После каждой пересылки сумма
эта проверяется на четность; если опа оказывается
нечетной, подается сигнал ошибки.
Предположим, что знаки хи х2, которые мы хотим
переслать, припимают значение 0 пли 1 с вероятностью
1/2, причем независимо друг от друга. Рассмотрим
события:
56 ГЛ. 2. АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
Найдем вероятности этих событий, их попарных
произведений A0Al1 AQA2, AtA2, а также произведения всех
трех: А0А{А2. По условию Р (Лх) = Р (А2) =* 1/2,
Р (АгА2) - Р (Л J.Р (А2) «. 1/4. Найдем Р (Ао).
Событие Ло происходит, когда ^i = x2 = 0 или X! = ^2 = 1, т. е.
распадается на два варианта:
Ло = AiA2 + ЯДг,
откуда
12) + Р(ЛХЛ2) - A/2)-A/2) + A/2).A/2) - 1/2.
Что же касается событий А*Аи А0А2, А0АхАг, то это —
одно и то же событие, совпадающее с АХА2: каждое из
них происходит тогда и только тогда, когда хх = хг = 0.
Их вероятности:
Отсюда видно, что события Ло и Аг независимы, так
как вероятность их произведения равна произведению
вероятностей:
Р (АОАХ) - 1/4 - A/2) .A/2) - Р (Ло) Р (Лх).
Ясно, что по той же причине независимы и события
Л о и Л 2. Следовательно, события Ло, Aif Аг попарно
независимы.
Теперь посмотрим, независимы ли они в своей
совокупности? Очевидно нет, так как вероятность их
произведения не равна произведению вероятностей:
Р (А0АхА2) - 1/4 Ф Р (Ло) Р (Лх) Р (Л2) - 1/8.
Таким образом, мы убедились, что попарная
независимость событий еще не означает их
независимости в совокупности.
Рассмотренный пример намеренно упрощен по
сравнению с действительностью: в реальных ЭВМ биты
пересылаются не тройками, а большими порциями
(«байтами»). >
В основе независимости событий лежит их
физическая независимость, сводящаяся к тому, что
множества случайных факторов, приводящих к тому или
другому исходу опыта, не пересекаются (или почти не
пересекаются). Например, если опыт состоит в том, что
два лица в двух разных городах бросают по монете, то
события Л = {выпадение герба у первого лица) и В =»
2.3. УСЛОВНАЯ ВЕРОЯТНОСТЬ СОБЫТИЯ 57
«= {выпадение герба у второго} смело можно считать
независимыми. Если опыт состоит в том, что некто
стреляет п раз по мишени, каждый раз прицеливаясь заново
и не вводя поправку на ранее допущенную ошибку, то
события Аи А2, ..., Ап, где Лг= {попадание при i-u
выстреле} можно считать независимыми. Если же стрельба
ведется очередью из автоматического оружия и
прицеливание производится однажды перед всей очередью, те же
события будут уже зависимыми, так как ошибка
прицеливания будет общим случайным фактором, влияющим
на все выстрелы.
Мы знаем, что в природе нет абсолютно независимых
явлений, но есть практически независимые. Так же
обстоит дело и с событиями: у некоторых из них
зависимость настолько слаба, что их можно в расчетах полагать
независимыми и, вычисляя вероятность их произведения,
просто перемножать вероятности этих событий.
С понятием «независимых событий» тесно связано
понятие «независимых опытов». Несколько опытов
называются независимыми, если их исходы представляют
собой независимые события. Пример независимых опытов:
п бросаний монеты, в каждом из которых может
появиться «герб» или «решка». Пример зависимых опытов:
п дней подряд измеряется температура воздуха t° в
одном и том же пункте в одно и то же время дня; в
результате каждого опыта могут появиться или не
появиться события
А = U° < 0}; В = {0 < Г < 10°С} и С = {*° > 10°С}.
Совершенно очевидно, что опыты являются зависимыми.
Пример 7. Возвращаясь к п. 1.1, подсчитать
вероятность того, что в результате описанных 25 опытов мы
запишем первую строку «Евгения Онегина».
Решение. 25 опытов в примере п. 1.1 независимы;
применяя правило умножения для независимых событий,
получим:
т. е. вероятность события А настолько мала, что его
можно смело считать практически невозможным. >
Пример 8. Вычислить вероятность события В =
*= {при N = 600 бросаниях монеты все 600 раз появится
герб}.
58 ГЛ 2. АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
Решение. По правилу умножения для независимых
событий
Р(Я)==A/2N00«2,4(М(Гш,
что еще значительно меньше, чем вероятность события А
в предыдущем примере. >
2.4. Примеры применения основных
правил теории вероятностей
Правило сложения и правило умножения вероятностей
редко применяются порознь; обычно они применяются
вместе. Наиболее типична следующая схема: событие Л,
вероятность которого требуется найти, представляется
в виде суммы нескольких вариантов
Каждый из вариантов представляется в виде
произведения каких-то событий. Вероятность каждого варианта
вычисляется по правилу умножения, затем вероятности
вариантов складываются. Бывают и более сложные
схемы, где вероятность каждого из событий, произведением
которых образован вариант, в свою очередь вычисляется
по правилу сложения, и т. д.
Ниже мы приводим ряд примеров на применение
основных правил теории вероятностей.
Пример 1. Имеется две урны, в первой 2 белых и
3 черных шара, во второй — 4 белых и 2 черных. Из
каждой урны вынимается по одному шару. Найти
вероятность того, что они будут одного и того же цвета.
Реше н и е. Событие А = {оба шара одного цвета)
можно представить в виде суммы двух вариантов:
шара белые); Аг = {оЪъ шара черные);
Каждый из вариантов есть произведение двух
событий:
ili-Bi-Д,; Л,-С,-С„
где
2?i« {из первой урны вынут белый шар),
2?2 = {из второй урны вынут белый шар},
С, «=* {из первой урны вьшут черный шар},
Сг «¦ {из второй урны вьшут черный шар},
2 4. ПРИМЕНЕНИЯ ПРАВИЛ ТЕОРИИ ВЕРОЯТНОСТЕЙ 59
События Ви В2 между собой независимы; также и
события С,, С2. Применяя правило умножения для
независимых событий B.3.7), получим:
Р (А,) - Р (Вг) Р (В2) - B/5).D/6) - 4/15;
р (А2) = Р (Сх) Р (С2) - C/5). B/6) = 1/5.
Так как варианты At и Аг несовместны, то по
правилу сложения
р (А) ~ Р (Аг) + Р (А2) = 4/15 + 1/5 - 7/15. >
Пример 2. В условиях предыдущего примера найти
вероятность того, что шары будут разных цветов:
D = (шары разных цветов).
Решение: Можно было бы, конечно, как в
предыдущем примере, представить D в виде суммы двух
вариантов:
Dx = {из первой урны вынут белый шар,
из второй—черный),
Z>2 = (из первой урны вынут черный шар,
из второй — белый),
но гораздо проще будет решить задачу, воспользовавшись
результатами предыдущего примера; действительно,
событие D противоположно событию А предыдущего
примера: D = А, откуда Р (D) « 1 — Р (А) = 8/15. >
Пример 3. Производятся три независимых
выстрела по мишени; вероятности попадания в мишень при
первом, втором, третьем выстреле равны соответственно
Ри Рг, Рз. Найти вероятность того, что в мишень
произойдет ровно два попадания.
Решение. Событие А = {ровно два попадания)
представим в виде суммы трех несовместных вариантов:
А = {попадание при первом, попадание при втором
и промах при третьем выстреле) +
+ {попадание при первом, промах при втором
и попадание при третьем выстреле) +
+ {промах при первом, попадание при втором
и попадание при третьем выстреле).
Вероятности промаха при первом, втором и третьем
выстрелах равны соответственно 1 — ри 1 — /?2, 1 — р3.
60 ГЛ. 2. АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
Применяя правило умножения для независимых событий
и складывая вероятности вариантов, получим
Plp2(l — р3) + Pi(l — Рг)Рз + A — Pi)
Пример 4. В условиях предыдущего примера
найти вероятность хотя бы одного попадания.
Решение. Можно было бы событие С = {хотя бы
одно попадание} представить в виде суммы трех
вариантов: Ct = {ровно одно попадание); С2 = {ровно два
попадания} и С8 = {все три попадания} и найти
вероятность каждого из них подобно тому, как это было
сделано выше.
Но гораздо проще будет от события С перейти к
противоположному событию: С = {ни одного попадания}.
Событие С есть произведение трех независимых
событий:
С »{промах при первом выстреле} • {промах при
втором выстреле} • {промах при третьем выстреле}.
По правилу умножения для независимых событий
имеем
откуда
Почему в данном примере оказалось выгодным
перейти к противоположному событию С? Потому что оно
представляет собой только один вариант (все три
промаха) вместо трех вариантов Си С2, С3. >
В связи с этим можно сформулировать одну
практическую рекомендацию: если в данной задаче
противоположное событие А распадается на меньшее число
вариантов, чем интересующее нас Л, то имеет смысл при
вычислении вероятности переходить к противоположному
событию.
Пример 5. Из колоды карт, содержащей 32 листа,
вынимается наугад 4 карты. Найти вероятность того, что
среди них будет хотя бы один туз.
Решение. При нахождении вероятности события
А » {хотя бы один туз} _явно выгоднее перейти к проти-
воположйому событию А = {ни одного туза} =» А\ • А2 X
X Аг • А4,
2.4. ПРИМЕНЕНИЯ ПРАВИЛ ТЕОРИИ ВЕРОЯТНОСТЕЙ 61
где
А{ = {первая карта не туз},
Л2 = {вторая карта не туз},
Л*={третья карта не туз},
Л4={четвертая карта не туз}.
События АХч А2, Л3, А4 зависимы. По правилу
умножения вероятностей B.3.7) имеем:
Тузов в колоде 4; не тузов 32-4 = 28. Учитывая
это, имеем:
Р (Л) - B8/32) • B7/31). B6/30) • B5/29)« 0,568,
откуда Р (Л) - 1 - Р (Л)« 0,432. »>
Пример 6. В шкафу находятся девять однотипных
приборов. В начале опыта они все новые (ни разу не
бывшие в эксплуатации). Для временной эксплуатации
берут наугад три прибора; после эксплуатации их
возвращают в шкаф. На вид прибор, бывший в
эксплуатации, ничем не отличается от нового. Такого рода
операция производится три раза. Найти вероятность того, что
в результате трехкратного выбора и эксплуатации
в шкафу останется хотя бы один новый прибор.
Решение. От события Л = {хотя бы один новый
прибор} выгоднее перейти к противоположному: А =»
¦- {ни одного нового прибора}. Событие Л может
произойти одним-единственным способом: и первый раз, и
второй, и третий из шкафа будут взяты новые приборы.
Первый раз это обеспечено; поэтому
Р (Л) - 1. F/9). E/8). D/7). C/9) • B/8). A/7) * 0,0028,
Откуда Р (Л) & 1 - 0,0028 & 0,997.
Итак, событие Л имеет высокую вероятность 0,997 и
может, пожалуй, считаться практически достоверным
(предсказывая его, мы будем ошибаться примерно
в 0,3% случаев). >
Пример 7. Завод изготовляет изделия, каждое из
которых с вероятностью г (независимо от других)
является дефектным. Для контроля из продукции завода
выбирается наугад п изделий. При осмотре дефект, если он
существует, обнаруживается с вероятностью р. Найти
62 ГЛ. 2. АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
вероятности следующих событий:
А = {ни в одном из изделий не обнаружено дефекта);
5 = {среди п изделий ровно в двух обнаружен дефект);
С = {среди п изделий не менее чем в двух обнаружен
дефект).
Решение. Вероятность того, что в одном наугад
взятом изделии обнаружен дефект, равна гр
(г—вероятность того, что дефект есть, р — условная вероятность
того, что дефект будет обнаружен при условии, что он
есть); вероятность того, что дефект не обнаружен, равна
1 — гр. По правилу умножения для независимых событий
Найдем вероятность события В. Оно распадается на
столько вариантов, сколькими способами можно из п
изделий выбрать два, в которых обнаружен дефект, т. е.
^2 П (И — 1) _>
на Сп = ^ вариантов. Вероятность каждого из них
равна {грJA — гр)п~2\ эти варианты несовместны; по
правилу сложения
Чтобы найти вероятность события С, перейдем к
противоположному событию:
С — {менее чем в двух изделиях обнаружен дефект),
которое распадается на два варианта:
Со = {ни в одном изделии не обнаружено дефекта),
(?i = {ровно в одном изделии обнаружен дефект).
С-
По правилу умножения
По правилам умножения и сложения:
Р {CJ = Cirp A - rpf-1 = nrp A - rp)n~\
Отсюда
P (С) = P (Co) + P (CO - A - rp)" (nrp +l-rp)
P(C) = 1 - P(C) - 1 - A - rpf-1 \{n-\)rp + 1].
2 4 ПРИМЕНЕНИЯ ПРАВИЛ ТЕОРИИ ВЕРОЯТНОСТЕЙ 63
Пример 8. Прибор состоит из п блоков, каждый
из которых (независимо от других) за время t
эксплуатации прибора может отказать (вьппи из строя).
Надежность (вероятность безотказной работы за время t)
каждого блока равна р. Безотказная работа всех без
исключения блоков необходима для безотказной работы
прибора в целом. Найти вероятность того, что в течение
времени t прибор будет работать безотказно.
Решение. Событие А = {безотказная работа
прибора) есть произведение п независимых событий АХу А2, ...
..., Ап, где At = {безотказная работа 1-го блока).
По правилу умножения для независимых событий
Р{А)-р". >
Пример 9. Прибор, обладающий падежпостыо
(вероятностью безотказной работы за время /), равной р1
представляется недостаточно надежным. Для повышения
надежности он дублируется еще одним точно таким же
работающим прибором. Если первый прибор за время t
отказал, происходит автоматическое (и безотказное)
переключение на дублирующий. Приборы отказывают
независимо друг от друга. Найти вероятность того, что
система из двух приборов проработает безотказно время t.
Решение. От события
В = {система будет работать время i)
перейдем к противоположному:
В ~ {система не будет работать).
Для того чтобы система не работала, нужно, чтобы
отказали (вышли из строя) за время Jo б а прибора:
и основной, и дублирующий. Событие В есть
произведение двух событий:
В = {основной прибор отказал за время t) X
X {дублирующий прибор отказал за время t).
По правилу умпожепия для независимых событий:
Пример 10. Сколько нужно поставить дублирую-
Щих приборов с той же надежностью р, что и основной,
64 ГЛ. 2. АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
чтобы надежность системы приборов была не ниже
заданной величины ^?
Решение. Если система состоит из п приборов
(один основной и (ai — 1) дублирующих), то ее
надежность (вероятность безотказной работы) равна
Мы хотим, чтобы эта надежность была не меньше
заданной 9>\
Преобразуем неравенство к виду
A-р)п^1
Откуда, логарифмируя, имеем
Деля левую и правую часть на отрицательную
величину lg(l — />), получим
p). B.4.1)
Таково общее число приборов в системе (один
основной плюс (п— 1) дублеров), гарантирующее ее
надежность не менее заданной 5^. >
Пример 11. Прибор (см. пример 9) имеет
надежность р; для ее повышения он дублируется еще таким
же прибором, но не с полной достоверностью:
переключающее устройство имеет надежность ра. Надежность
системы:
РЛ >
Пример 12. По каналу связи передается 5
сообщений. Каждое из них (независимо от других) с
вероятностью 0,2 искажается. Найти вероятности следующих
событий:
А = {все сообщения будут переданы без искажений);
2? = {все сообщения будут искажены);
С «= {не менее двух сообщений будет искажено).
Решение. Вероятность того, что отдельное
сообщение будет передано без искажений, равна 1 — 0,2 = 0,8.
По правилу умножения вероятностей для независимых
событий
Р {А) - 0й8б ^ 0,328; Р (В) - 0,28 & 0,00032
2.4. ПРИМЕНЕНИЯ ПРАВИЛ ТЕОРИИ ВЕРОЯТНОСТЕЙ 65
(событие В можно считать практически невозможным).
Чтобы найти Р(С), перейдем к противоположному
событию:
С «¦ {мепее двух сообщений будет искажено) = CQ + Си
где
Со — {ни одно сообщение не будет искажено),
€t « {ровно одно сообщение будет искажено).
Так как Со - 4, Р (Со) « 0,328.
Событие <?i распадается на 5 несовместных вариантов
(искажено может быть любое из 5 сообщений);
вероятность каждого варианта по правилу умножения равна
0,2-0,8*; отсюда
Р (CJ-5.0,2.0,8* «0,410.
Находим Р (С) « 0,328 + 0,410 - 0,738.
Откуда Р (С)« 1 — 0,738 - 0,262, >
Пример 13. Происходит воздушный бой между
истребителем и бомбардировщиком. Начинает стрельбу
истребитель; он дает по бомбардировщику один выстрел
и сбивает его с вероятностью 0,2. Если бомбардировщик
не сбит, он отвечает истребителю огнем и сбивает его
с вероятностью 0,3. Если истребитель не сбит, он
продолжает атаку, подходит к бомбардировщику ближе и
сбивает его с вероятностью 0,4. Найти вероятности
следующих исходов воздушного боя:
А — {сбит бомбардировщик);
В ={сбит истребитель),
С = {ни один из самолетов не сбитК
Решение. Событие А распадается на два
несовместных вариалта:
AA
где
Ах — {бомбардировщик сбит первым выстрелом
истребителя);
Аг = {бомбардировщик сбит вторым выстрелом
истребителя).
По правилу сложения Р (А) = Р (Ах) + Р (А2). По
условиям задачи PDi) — 0,2. Найдем РD2). Для того
чтобы событие А2 произошло, нужно, во-первых, чтобы
3 Теория вероятностей и ее
инженерные приложения
66 ГЛ. 2. АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
второй выстрел истребителя состоялся (а для этого
нужно, чтобы первым выстрелом бомбардировщик не был
сбит и сам истребитель не был сбит ответным
выстрелом бомбардировщика), и, во-вторых, чтобы вторым
выстрелом истребитель сбил бомбардировщик.
Р(А2) найдем по правилу умножения вероятностен,
представив Аг как произведение трех зависимых событий:
At-D-E-F,
где
D = {первым выстрелом истребителя бомбардировщик
не сбит};
Е «¦ {ответным выстрелом бомбардировщика истребитель
не сбит};
F = {вторым выстрелом истребителя бомбардировщик
сбит}.
По правилу умножения вероятностей для зависимых
событий:
P(At)-P{D)-P(E\D)-P(F\DE)-
- A - 0,2).A - 0,3)-0,4 - 0,224.
Применяя правило сложения, имеем:
Р (А) _ Р (Аг) + Р (Л2) - 0,2 + 0,224 - 0,424.
Теперь (это будет нам проще) найдем вероятность
события С:
С — {пи один самолет не сбит} =»
= (первым выстрелом истребителя бомбардировщик
не сбит) * {ответным выстрелом бомбардировщика
истребитель не сбит} • {вторым выстрелом истребителя
бомбардировщик не сбит} ==»
«A-0,2) «A-0,3) A-0,4) -0,8 0,7 0,6 -0,336.
Итак, Р(С) —0ft336, Так как события Л, В, С
несовместны и образуют полную группу,
откуда
РE) « 1 _ [Р(Л) + Р (С)] « 1 - 0,76 - 0,24. >
Пример 14. При одном цикле обзора
радиолокационной станции объект обнаруживается с вероятностью
2.4. ПРИМЕНЕНИЯ ПРАВИЛ ТЕОРИИ ВЕРОЯТНОСТЕЙ 67
р; при следующем цикле обзора он теряется с
вероятностью г; если при следующем цикле обзора он не
потерян, то слежение за объектом продолжается. Сколько
потребуется циклов обзора для того, чтобы с
вероятностью не менее $Р установить устойчивое слежение за
объектом?
Решение: Условия задачи сходны с условиями
примера 10, с той разницей, что устойчивое слежение за
объектом может быть установлено только за два
последовательных цикла: в первом объект должен быть
обнаружен, во втором — не потерян; вероятность этого
равна рA — г). По формуле B.4.1) получим число
необходимых пар циклов:
n>ig(i-mii-p(i-r)]. >
В данном пункте нам неоднократно встречались
задачи одного и того же типа, а именно, независимые
опыты повторялись несколько раз и требовалось либо найти
вероятность того, что какое-то событие А появится хотя
бы один раз, либо найти число опытов п,
достаточное для того, чтобы с заданной вероятностью Ф
гарантировать появление события Л. Подобные задачи часто
встречаются на практике. Чтобы избежать каждый раз
таких подробностей, как переход к противоположному
событию, логарифмирование и т. п., решим здесь эти
задачи в самом общем виде.
Задача 1. Производится п независимых опытов,
в каждом из которых событие А может появиться с
какой-то вероятностью; для i-vo опыта эта вероятность
равна Pi (i = l, 2, ..., п). Задан ряд вероятностей:
Ри Рг, .. ¦, Рп*
Найти вероятность Rt того, что событие А появится
хотя бы один раз.
Решение. Переходя к противоположному событию
!Я«» (событие А не появится ни разу}, применяя правило
умножения для независимых событий и вычитая
произведение из единицы, получим
или, пользуясь энаком произведения П,
= 1-11A-/>,)• B,4,2)
68 ГЛ. 2. АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
В частности, когда все вероятности Pi — p одинаковы:
Л4 —1 —A —р)*. > B.4.3)
Этими формулами мы в дальнейшем будем
пользоваться в готовом виде, не выводя их для каждого част*
ного случая.
Задача 2. Производится п независимых опытов,
в каждом из которых событие А появляется с
вероятностью р. Сколько нужно сделать опытов для того, чтобы
с вероятностью & гарантировать хотя бы одно появление
события А?
Решение. Рассуждая точно так же, как в
примере 10, получим:
n>lg(l-nig (*-/>)• > B.4.4)
Пример 15. По цели производится 5 независимых
выстрелов; вероятности попадания соответственно равны:
Pi -0,1; р2 = 0,2; />8 = 0,3; />4 = 0,4; р5~0,5.
Найти вероятность Нг хотя бы одного попадания.
Решение. По формуле B.4.2) имеем:
flt-1-0,9.0,8-0,7-0,6-0,5-0,8488. >
Пример 16. Прибор состоит из элементов,
надежность каждого из которых равна р = 0,98. Выход из
строя каждого из элементов равносилен выходу из строя
прибора в целом. Не больше какого числа л элементов
1 должно быть в приборе для того, чтобы надежность
прибора не стала меньше, чем 0,9?
Решение. Рассмотрим п элементов как п
независимых опытов, в каждом из которых событие А — (отказ)
происходит с вероятностью 0,02. Подставляя в формулу
B.4.4) 0,02 вместо р и 0,1 вместо ^, найдем то число
элементов Я, при котором вероятность отказа хотя бы
одного элемента станет не меньше 0,1; получим:
«5,20.
Переходя от Я к числу элементов п, при котором не
должна достигаться такая вероятность отказа, получим
п < 5,20,
т. е. число элементов не должно превосходить пяти. >
2.5. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ 69
2.5. Формула полной вероятности
Следствием обоих основных правил теории
вероятностей—правила сложения и правила умножения —
является формула полной вероятности.
Допустим, что предполагается провести опыт, об уело*
виях которого можно сделать п исключающих друг друга
предположений (гипотез):
# и #2, ..., Нп (ВД - 0 при IФ /). B.5.1)
Каждая гипотеза осуществляется случайным образом
и представляет собой некоторое событие. Вероятности
гипотез известны и равны
Рассматривается некоторое событие А% которое может
появиться только вместе с одной из гипотез B.5.1). За*
даны условные вероятности события А при каждой из
гипотез:
Р(А\Н& Р(А\Н2), ...>Р(А\Нп).
Требуется найти вероятность события А. Для этого
представим А как сумму п несовместных вариантов:
А - НгА + Н^А + ... + IIпА = 2 HiA-
По правилу сложения вероятностей
По правилу умножения
Р{НгА)-Р(Н{).Р{А\Нй.
Откуда
Р(А)=%Р(Нг)Р(А\Нг), B.5.2)
т. е. безусловная вероятность события А в опыте с
гипотетическими условиями вычисляется как сумма
произведений вероятности каждой гипотезы
на условную вероятность события при этой
гипотезе.
Формула B.5.2) называется формулой полной
вероятности. Она применяется во всех случаях, когда опыт со
70 ГЛ. 2. АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
случайным исходом распадается на два этапа: в первом
как бы «разыгрываются» условия опыта, во втором —
его результат.
Пример 1. Имеются три одинаковые на вид урны;
в первой 2 белых шара и 3 черных, во второй — 4 белых
и 1 черный, в третьей — 3 белых шара. Некто подходит
наугад к одной из урн и вынимает из нее один шар.
Найти вероятность того, что этот шар будет белым:
А — {появление белого шара),
Решение. Выдвигаем три гипотезы:
Нх = {выбрана первая урна);
Нг=* {выбрана вторая урна);
Ih = {выбрана третья урна).
Р {А 1//Л-2/5; Р{А\Н2) = Ц5; Р(Л|#8) = 1.
По формуле B.5.2)
Р(Л) - A/3).B/5) + A/3).D/5) + A/3). 1 =
- A/3).B/5 + 4/5 + 5/5) - A/3).A1/5) - 11/15. >
Пример 2. Прибор может работать в трех
режимах: 1) нормальном, 2) форсированном и 3)
недогруженном. Нормальный режим наблюдается в 60% случаев
работы прибора, форсированный — в 30% и
недогруженный—в 10%. Надежность прибора (вероятность
безотказной работы в течение заданного времени t) для
нормального режима равна 0,8, для форсированного 0,5, для
недогруженного 0,9. Найти полную (с учетом
случайности условий) надежность прибора.
Решение. Гипотезы: /У\ — нормальный режим,
#а — форсированный режим, Н9 — недогруженный режим,
-0,6; Р(Я,)-0,3;
А = {безотказная работа прибора).
По формуле B.5.2)
Р(А) - 0,6-0,8 + 0,3-0,5 + 0,Ь0,9 - 0,72. >
Пример 3. Имеется две партии однородных
изделий; первая состоит из N изделий, среди которых п де-
2.5. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ 71
фектных; вторая — из М изделий, среди которых т
дефектных. Из первой партии берут случайным образом к
изделий, из второй I изделий (k<N\ KM) и
смешивают между собой. Из полученной партии к +1 изделий
берут наугад одно. Найти вероятность того, что взятое
изделие будет дефектным.
Решение. Л = {взятое изделие дефектно).
Гипотезы:
Я1 = {изделие принадлежит первой партии),
#2 = {изделие принадлежит второй партии),
Р (Нг) - к/(к + I); Р (Я,) - 1/(к + I).
Условные вероятности события А:
По формуле B.5.2)
Р (А) - [к/(к + I)] • (n/N) + [Щк + 1)\. (т/М). >
Пример 4. Завод изготовляет изделия, каждое из
которых независимо от других с вероятностью р имеет
дефект. В цехе имеется три контролера; изделие
осматривается только одним из них (с одинаковой
вероятностью первым, вторым или третьим). Вероятность
обнаружения дефекта, если он имеется, для 1-го, 2-го и 3-го
контролеров равпа соответственно ри р2, р*- При
обнаружении дефекта изделие бракуется. Если изделие не было
забраковано в цехе, то оно отправляется на ОТК завода,
где дефект, если он имеется, обнаруживается с
вероятностью р0; изделие, дефект которого обнаружен,
бракуется. Найти вероятность того, что изделие будет
забраковано.
Решение. Событие А = {изделие будет
забраковано). Здесь удобно перейти к противоположному событию
Л = {изделие не будет забраковано).
Представим событие Л как сумму двух несовместных
вариантов:
Л e At + Лгу
где
Л, = {изделие не имеет дефекта),
Л% = {изделие имеет дефект, но он не обнаружен
ни в цехе, ни в ОТК завода).
72 ГЛ. 2. АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
Найдем Р(А2). Для этого надо умножить
вероятность того, что изделие имеет дефект, на вероятность
того, что этот дефект не будет обнаружен ни в цехе, ни
в ОТК. Вероятность того, что имеющийся дефект не
будет обнаружен в цехе, по формуле полной вероятности
равна A/3)[A — Pi) + A — Рг) + A — Рз)]. Вероятность того,
что имеющийся дефект после цехового осмотра не будет
обнаружен в ОТК, равна 1 — р0. По правилу умножения:
Р(А2) - р [1 - A/3) (Pl + Р2 + ps)l(l - Ро);
Пример 5. Цех завода производит определенного
вида изделия; любое из них, независимо от других, с
вероятностью р имеет дефект. Каждое изделие
осматривается контролером, который обнаруживает дефект, если
он имеется, с вероятностью р{ и не обнаруживает с
вероятностью 1 — рх. Изделие с обнаруженным дефектом
бракуется. Кроме того, иногда контролер допускает
ошибку и бракует доброкачественное изделие; это происходит
с вероятностью рг. За смену контролер осматривает
N изделий. Найти вероятность того, что хотя бы одно из
них будет квалифицировано им неправильно: или,
будучи дефектным, отнесено к доброкачественным, или
наоборот (считается, что результаты осмотров отдельных
изделий независимы).
Решение. Сначала найдем вероятность события А —
= (неправильная квалификация одного отдельного
изделия} по формуле полной вероятности. Гипотезы:
Hi ¦= {изделие имеет дефект},
7/2 = {изделие не имеет дефекта}.
Условные вероятности события А при этих гипотезах
равны:
По формуле B.5.2)
Теперь найдем вероятность события В = {хотя бы
одно из N изделий будет квалифицировано неправильно}.
2.5. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ 73
Гораздо проще будет найти вероятность
противоположного события:
2? = (все N изделий будут квалифицированы правильно}.
Событие В есть произведение N независимых
событий, каждое из которых состоит в том, что отдельное
изделие квалифицировано правильно. Вероятность этого
равна 1 — Р {А) = 1 — [р A — рх)+ р2 A — р)]. По правилу
умножения вероятностей для независимых событий
Р (В) = {1 —[рA — Pl) + ft (I f
Откуда
РР >
Пример 6. Прибор состоит из двух дублирующих
друг друга узлов и может работать в одном из двух
режимов: нормальном и неблагоприятном. Нормальный
режим наблюдается в 80% случаев эксплуатации прибора;
неблагоприятный — в 20% случаев. Надежность
(вероятность безотказной работы) каждого из узлов в
нормальном режиме равна 0,9, в неблагоприятном — 0,6. При
выходе из строя (отказе) узла происходит автоматическое
и безотказное переключение на дублера. Найти полную
вероятность Р(А) безотказной работы прибора.
Решение. Гипотезы:
Нх — {прибор работает в нормальном режиме};
#2 = (прибор работает в неблагоприятном режиме};
Р (#0-0,8; Р (#,)-0,2.
В нормальном режиме вероятность безотказной
работы прибора
Рнор - 1 - A ~ 0,9J - 0,99;
в неблагоприятном
Рнеб=1-A-0,6J = 0;84.
Полная вероятность безотказной работы прибора
Р (А) - 0,8-0,99 + 0,2-0,84 - 0,792 + 0,168 - 0,960. *
Пример 7. Сообщение может передаваться по
одному из каналов связи, находящихся в различных
состояниях; из них nt каналов в отличном состоянии, пг —
в хорошем, щ — в посредственном и гс4 — в плохом (л, +
+ п2 + п3 + л4 = /г). Вероятность правильной передачи.
74 ГЛ. 2. АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
сообщения для разного вида каналов равна,
соответственно, ри /?2, /?з, р^ Для повышения его достоверности
сообщение передается два раза по одному и тому же каналу,
который выбирается наугад. Найти вероятность того, что
хотя бы один раз оно будет передано правильно.
Решение.
А = {хотя бы один раз сообщение передано правильно).
Переходим к противоположному событию:
А = {оба раза сообщение передано неправильно).
Сделаем ряд гипотез о том, по какому типу канала
были переданы сообщения:
Hi = {по каналу в отличном состоянии),
Нг =¦ {по каналу в хорошем состоянии),
#з = {по каналу в посредственном состоянии),
Нк = {по каналу в плохом состоянии).
Полная вероятность события Ж
Р (А) - A/п) [п, A - Plf
Пример 8. Производится посадка самолета на
аэродром. Если позволяет погода, летчик сажает самолет,
пользуясь, помимо приборов, еще и визуальным
наблюдением. В этом случае вероятность благополучной
посадки равна р{. Если аэродром затянут низкой
облачностью, то летчик сажает самолет, ориентируясь только
по приборам. В этом случае вероятность благополучной
посадки равна рг\ рг < Ри Приборы, обеспечивающие
слепую посадку, имеют надежность (вероятность
безотказной работы) #*. При наличии низкой облачности и
отказавших приборах слепой посадки вероятность
благополучной посадки равна р3; р$<р2- Статистика
показывает, что в к% случаев посадки аэродром затянут
низкой облачностью. Найти полную вероятность события
А = {благополучная посадка самолета).
2.5. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ 75
Решение. Гипотезы:
//i = {низкой облачности нет},
//2 = (низкая облачность естьУ.
Условную вероятность Р (^41Я2) снова найдем по
формуле полной вероятности с гипотезами
Н[ = (приборы слепой посадки действуют),
Н2 = (приборы слеиой посадки отказали)г
По формуле полной вероятности
Р(А\Н2) = ?р2 + A-
Откуда
Пример 9. По объекту производится три
одиночных (независимых) выстрела. Вероятность попадания при
первом выстреле равна 0,4, при втором 0,5, при третьем
0,7. Для вывода объекта из строя заведомо достаточно
трех попаданий; при двух попаданиях он выходит из
строя с вероятностью 0,6; при одном — с вероятностью
0,2. Найти вероятность того, что в результате трех
выстрелов объект будет выведен из строя.
Решение. 4 — {объект выведен из строя).
Гипотезы:
Я, = {в объект попал один снаряд},
#2 = {в объект попало два снаряда},
//3 = {в объект попало три снаряда}.
Находим вероятности гипотез. Событие Ht
представим в виде суммы трех несовместных вариантов:
{первый выстрел попал,] (второй выстрел попал,]
второй и третий не > + {первый и третий но \ -f
попали J [попали J
(третий выстрел попал,]
-j- (второй и первый не >.
(попали I
76 ГЛ. 2. АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
Применяя правила сложения и умножения
вероятностей, имеем:
Р(Нг) - ОД.0,5-0,3 + 0,6-0,5.0,3 + 0,6-0,5.0,7 « 0,36.
Аналогично,
Р(#а) - 0,6-0,5.0,7 + 0,4-0,5-0,7 + 0,4-0,5-0,3 - 0,41;
Р(#3) = 0,4-0,5.0,7 «0,14.
Условные вероятности события А при этих
гипотезах равны
Р D1*0-0,2; Р (A IJEg-0,6; Р (А \ И3) = 1,0,
По формуле B.5.2):
РD) - 0,36-0,2 + 0,41-0,6 + 0,14-1,0 = 0,458. *
2.6. Теорема гипотез (формула Бейеса)
Следствием правила умножения и формулы полной
вероятности является теорема гипотез или формула
Бейеса.
Представим себе следующую ситуацию. До опыта о
его условиях можно было сделать ряд гипотез Ни /72, ...
,.., /7ft, несовместных и образующих полную группу:
Вероятности гипотез до опыта (так называемые
«априорные вероятности») заданы и равны:
Р (#i), Р (Я,), ... t Р (//„); 2 Р (Я«) - 1.
Теперь предположим, что опыт произведен, и в
его результате появилось событие А. Спрашивается, как
нужно пересмотреть вероятности гипотез с учетом этого
факта? Другими словами, найти «апостериорные»
вероятности гипотез при условии, что опыт дал
результат А:
г\А); Р(ПШ\А); ...; Р(Я
Решим эту задачу, пользуясь правилом умножения
и формулой полной вероятности.
2.6. ТЕОРЕМА ГИПОТЕЗ (ФОРМУЛА БЕЙЕСА) 77
Возьмем любую гипотезу Я* и вычислим вероятность
произведения НА по правилу умножения в двух формах:
Р (НгА) - Р (Нг) Р(А\Нг) = Р (А) Р (?Г41 А).
Теперь отбросим левую часть:
P(HiyP(A\Hi)^P(A)P(Hi\A) B.6.1)
и разделим обе части равенства B.6.1) на Р(А)
(предполагается, что она не равна нулю); получим
Р (Я, \Л) - [Р (Я,) Р (А | #0]/Р (А). B.6.2)
Наконец, заменим Р {А) его выражением по формуле
полной вероятности:
(/^1,2, ,..,и). B.6.3)
Формула B.6.3) называется формулой Бейеса.
Она позволяет пересчитывать вероятности гипотез в
свете новой информации, состоящей в том, что опыт дал
результат А.
Пример 1. Имеется 3 урны; в первой 3 белых
шара и 1 черный; во второй — 2 белых шара и 3 черных;
в третьей — 3 белых шара. Некто подходит наугад к
одной из урн и выпимает из нее 1 шар. Этот шар
оказался белым. Найти послеопытные (апостериорные)
вероятности того, что шар вынут из 1-й, 2-й, 3-й урны.
Решение. Гипотезы:
Hi = {выбрана первая урна),
Нг в (выбрана вторая урна),
Нг *= {выбрапа третья ypnah
Так как урна выбирается наугад, то априорные ве-
роятпости гипотез равны:
В результате опыта появилось событие
А в {из выбранной урпы вынут белый шар).
Условные вероятности события А при гипотезах tflt
г, Я,:
W; Р(Л[Я,)-2/5; Р(Л|Я8) = 1.
78 ГЛ. 2. АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
Применяя формулу Бейеса B.6.3), находим
апостериорные вероятности гипотез:
А\ A/3) C/4) {Ъ_.
") A/3) (з/4) + A/3) B/5) + A/3) -1 43 '
Р(Я2|Л)«|-; Р(//зИ = §/)
Таким образом, в свете информации о появлении
события А вероятности гипотез изменились: самой
вероятной стала гипотеза #3, наименее вероятной —
гипотеза Нг. >
Пример 2. В партии изделий смешаны изделия трех
заводов: Nt изделий первого, Nt изделий второго и N3
изделий третьего вавода. Известно, что вероятность
дефекта для изделий 1-го, 2-го, 3-го завода равна
соответственно pi, ргУ Рз* Бели изделие дефектно, то оно не
проходит испытания. Взято наугад одно изделие из
смешанной партии; оно не прошло испытания. Найти
вероятности того, что оно изготовлено 1-м, 2-м, 3-м
заводом.
Решение. Л «={изделие не прошло испытания}.
Гипотезы:
tfi = {изделие изготовлено 1-м заводом};
Иг = {^изделие изготовлено 2-м заводом};
Н^ = {изделие изготовлено 3-м заводом}.
Априорные вероятности гипотез:
р (Щ) - Ni/(Nt + NU + Nz) (i - 1, 2, 3).
Условные вероятности события А:
По формуле Бейеса апостериорные вероятности
гипотез:
Р(я,И),
NiPi - («- 1, 2, 3). >
¦) Заметим, что так как гипотезы несовместны и образуют
полную группу, Р (Я3 | А) можно было бы не вычислять, а найти
по формуле
2.6. ТЕОРЕМА ГИПОТЕЗ (ФОРМУЛА БЕЙЕСА) 79
Пример 3. До опыта об его условиях можно было
сделать четыре гипотезы: Ни Я2, Я3, ЯА с
вероятностями, равными, соответственно,
-ОИ; Р(Я3) = 0,5; Р(Я4) = 0,2.
В результате опыта появилось событие Л, которое
невозможно при гипотезах #i, Я2 и достоверно при
гипотезах #з, Я4. Найти апостериорные вероятности гипотез.
Решение.
По формуле Бейеса:
Р (Я, |4)-0,5/@,5+ 0,2)-5/7;
Р(Я4|Л)-2/7. >
Пример 4. Расследуются причины авиационной
катастрофы, о которых можно сделать четыре гипотезы:
Ии Я2, Я3, #4. Согласно статистике Р (Ях) - 0,2; Р(Я2) =-
«=0,4; Р(Я3)=0,3;Р(Я4)=0,1. Осмотр места катастрофы
выявляет, что в ее ходе произошло событие А «=*
{воспламенение горючего). Условные вероятности события А
при гипотезах Ни Я*. Я8, Я4, согласно той же
статистике, равны: Р (А \ II\) - 0,9; Р (А \ Н2) - 0; Р (А \ Я3) - 0,2;
Р(-4|Я4)=* 0,3. Найти апостериорные вероятности гипотез.
Решение. По формуле Бейеса имеем:
0,2-0,9 2_9
0,2.0,9 + 0,4.0 + 0,3.0,2 + 0,1-0,3 e 3f
0; Р(Я8|Л)-2/9; Р(Я41А)- 1/9. >
Пример 5. Объект, за которым ведется
наблюдение, может быть в одном из двух состояний:
Hi «* {функционирует) и Н2 в {не функционирует).
Априорные вероятности этих состояний Р (Я^ — 0,7,
Р(Я1)-0Д
Имеется два источника информации, которые
приносят разноречивые сведения о состоянии объекта; первый
источник сообщает, что объект не функционирует,
второй — что функционирует. Первый источник вообще дает
правильные сведения с вероятностью 0,9, а с
вероятностью ОД — ошибочные. Второй источник менее
надежен: он дает правильные сведения с вероятностью 0,7,
80 ГЛ. 2. АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
а с вероятностью 0,3 — ошибочные. На основе анализа
донесений найти новые (апостериорные) вероятности
гипотез.
Решение. Наблюдено событие
А = {первый источник сообщил Я2, второй #J.
Условные вероятности этого события при гипотезах
Я, и #2 равны:
Р (А | Нг) = Р {первый источник дал неверные
сведения, второй — верные) — 0,1 • 0,7 — 0,07;
Р (А | Н2) в Р {первый источник дал верные сведения,
второй — неверные) = 0,9 • 0,3 = 0,27,
По формуле Бейеса
Итак, в результате апализа стала значительно более
вероятной вторая гипотеза: объект не функционирует. >
Пример 6. Испытывается прибор, состоящий из
двух узлов: 1 и 2. Надежности (вероятности
безотказной работы за время т) узлов 1 и 2 известны и равны
рг » 0,8; рг = 0,9. Узлы отказывают независимо друг от
друга. По истечении времени т выяснилось, что прибор
неисправен. Найти с учетом этого вероятности гипотез:
Н{ ¦¦ {неисправен только первый узел);
II г «¦ {неисправен только второй узел);
Я, — {неисправны оба узла).
Решение. До опыта возможны были не три, а
четыре гипотезы, включая Яв = {исправны оба узла). Опыт
показал, что имеет место одна из гипотез Hh Я2, Я3,
причем наблюденное событие А есть сумма этих гп-
потез:
Априорные вероятности гипотез:
Р (//,)« 0,2-0,9 «0,18;
Р(Я2) = 0,8-0,1 «0,08;
Р(Я3)« 0,2.0,1-0,02.
Условные вероятности
2.6. ТЕОРЕМА ГИПОТЕЗ (ФОРМУЛА БЕЙЕСА) 81
По формуле Бейеса находим апостериорные
вероятности:
ш
Р(Я3|Л)«0,071. »>
Пример 7. Два стрелка независимо друг от друга
стреляют по одной и той же мишени, делая каждый по
одному выстрелу. Вероятность попадания в мишень для
первого стрелка равна 0,8, для второго — 0,4, После
стрельбы в мишени обнаружена одна пробоина. Найти
вероятность того, что эта пробоина принадлежит
первому стрелку ¦).
Решение. До опыта возможны следующие
гипотезы:
Hi — {'ни первый, ни второй стрелки не попадут),
#2 = (оба стрелка попадут),
Hi — {Первый стрелок попадет, а второй — нет),
Я4 — {первый стрелок не попадет, а второй попадет).
Априорные вероятности гипотез:
Р(Нг) - 0,2-0,6 - 0,12; Р(Я2) = 0,8-0,4 - 0,32;
Р(#3) - 0,8-0,6 - 0,48; Р(Я4) = 0,2-0,4 - 0,08.
Условные вероятности наблюденного события А =
= {в мишени одна пробоина) при этих гипотезах равны:
Р(Ах\Н,)-0; Р(Л|Я2)«0;
Р(Л|Я3)«1;
После опыта гипотезы Ht и Н2 становятся
невозможными, а апостериорные вероятности гипотез Я» и Я4 по
формуле Бейеса будут:
Р1Н \л\ - °-48'1 - 6-
Г\Л*\А)— 0,48-1 + 0,08.1"" 7»
1-6/7-1/7. >
*) Исход {обе пробоины совпали} отбрасываем, как ничтожно
маловероятный.
ГЛАВА 3
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ИХ ЗАКОНЫ
РАСПРЕДЕЛЕНИЯ
3.1. Понятие случайной величины.
Закон распределения.
Ряд распределения дискретной случайной величины
Одним из важнейших понятий теории вероятностей
является понятие случайной величины. Под
случайной величиной понимается величина, которая в
результате опыта со случайным исходом принимает то
или иное значение. Возможные значения случайной
величины образуют множество S, которое мы будем
называть множеством возможных значений случайной
величины.
Примеры случайных величин.
1) Опыт — бросание игральной кости; случайная
величина X — число выпавших очков. Множество
возможных значений: Е = И, 2, 3, 4, 5, 6).
2) Опыт — бросание трех монет; случайная
величина R — частота появления герба; множество возможных
значений 2«|0, -g-, -g-t lj.
3) Опыт — работа ЭВМ после очередного ремонта;
случайная величина Т — время наработки ЭВМ до
первого отказа (сбоя). Множество возможных значений
В — теоретически вся правая половина оси абсцисс 01,
включая 0: it > 0}; практически этот участок ограничен
справа, но граница расплывчата, неопределенна.
Множество возможных значений S в данном случае несчетно.
4) Опыт — дважды измеряется емкость конденсатора
с помощью точных электронных приборов. Случайная
величина Z — разность между результатами первого и
второго измерений. Множество возможных значений S
(опять-таки теоретически)—все точки на оси Оя, как
z < 0, так и z > 0.
5) Опыт — ведется тестирование изделий до
появления первого исправного изделия. Случайная величина
3.1. ПОНЯТИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 83
Y — число тестов, которое будет произведено. Множество
возможных значений S = {1, 2, ..., п, ...} — бесконечно,
но счетно.
6) Опыт — измерение сопротивления линии (с
помощью прибора с грубыми делениями); результат
округляется до ближайшего целого значения. Случайная
величина X — ошибка от округления. Множество
возможных значений S — участок числовой оси от —1 до
+1, включая концы, т. е. S = {[— 1, +1]}; оно несчетно.
Условимся в дальнейшем, как правило, случайные
величины обозначать большими буквами, а их возможные
значения — маленькими. Например: случайная величина
X, ее возможные значения х. Вместо слов «случайная
величина» часто будем пользоваться сокращением с. в.
Уже из приведенных примеров видно, что случайные
величины бывают двух типов: у одних множество
значений S конечно или счетно (их можно перенумеровать
в каком-то порядке; примеры 1), 2) и 5)); у других это
множество сплошь занимает какой-то участок числовой
оси, границы которого могут быть как
зафиксированными (пример 6)), так и неопределенными (примеры 3),
4)), а множество возможных значений несчетно.
Условимся случайные величны первого типа называть
дискретными, а второго — недискретными (в дальнейшем
недискретные случайные величины мы тоже разделим на
два типа).
В принятой нами теоретико-множественной трактовке
основных понятий теории вероятностей случайная
величина X есть функция элементарного события: Х = ф((о),
где о) — элементарпое событие, принадлежащее
пространству Q (о е fi). При этом множество S возможных
значений с. в. X состоит из всех значений, которые
принимает функция ф(со). Если множество S конечно или
счетно, с. в. X называется дискретной, если несчетно —
недискретной.
Задумаемся немного над тем, существуют ли в
реальности недискретные случайные величины. Ведь измеряя
какое-то значение с. в., полученное в результате опыта,
мы всегда выражаем его в каких-то единицах
(сантиметрах, тоннах, вольтах); учитывая это обстоятельство,
можно было бы стать на такую точку зрения, что в
реальности мы имеем дело только с дискретпыми
случайными величинами, значения которых разделены
расстоянием, равным единице измерения. Но, во-первых, эта
84 ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
единица не всегда уточнена (имеется потенциальная воз*
можность повысить точность измерения). Кроме того,
в случаях, когда возможные значения с. в. очень
многочисленны и расположены очень тесно на числовой оси,
проще рассматривать ее как недискретпую, а множество
возможных значений —• как сплошь занимающее какой-
то участок числовой оси.
Введем новое, очень важное понятие теории
вероятностей — закон распределения. Законом
распределения случайной величины называется любое правило
(таблица, функция), позволяющее находить вероятности
всевозможных событий, связанных со случайной
величиной (например, вероятность того, что она примет какое-
то значение или попадет на какой-то интервал). Если
св. X имеет данный закон распределения, то про нее
говорят, что она «распределена» по этому закону (или
же «подчинена» этому закону распределения).
Наиболее простую форму можно придать закону
распределения дискретной случайной величипы. Для этого
достаточно перечислить возможпые зпачения с. в. X:
#it Яг, ¦.., &п, ... и соответствующие им вероятности.
Рядом распределения дискретной с. в. X называется
таблица, в верхней строке которой перечислены в
порядке возрастания все возможные значения с. в. X: хи х2, ...
..., Хщ •.., а в нижней — вероятности этих значений:
Ри Рь • • м />п, ..., где Pi « Р {X = Хг) — вероятность
того, что в результате опыта с. в. X примет значение хг
(«-1,2, ..., и, ...).
Ряд распределения с. в. X мы будем записывать в
виде таблицы:
*х
р<
2
Рп
C-1.1)
Так как события {X «= art>, {X -¦ х2), ... несовместны
и образуют полную группу, то сумма всех вероятностей,
стоящих в нижней строке ряда C.1.1), равна единице:
Spi-1. C.1.2)
i
Эта единица как-то распределена между
значениями св. (отсюда и термин «распределение»).
Пример 1. Рассматривается работа трех
независимо работающих технических устройств (ТУ); вероятность
нормальной работы первого ТУ равна 0,2, второго — 0,4,
8.1. ПОНЯТИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 85
третьего — 0,5; с. в. X —число работающих ТУ.
Построить ряд распределения с. в. X.
Решение. Возможные значения св. X: 0, 1, 2, 3.
Соответствующие им вероятности найдем, пользуясь
правилами сложения и умножения. Для краткости будем
обозначать нормальную работу знаком «+», а отказ —
знаком «—».
Pl _ Р{Х - 0} - Р { } - 0,8.0,6-0,5 - 24.
0,2-0,6.0,5 + 0,8-0,4-0,5 + 0,8-0,6.0,5 -
«0,06 + 0,16 + 0,24-0,46.
- 0,8.0,4-0,5 + 0,2-0,6-0,5 + 0,2-0,4-0,5 -
-0,16+ 0,06+ 0,04 «0,26,
р4« Р{Х - 3} - Р{+ + +} - 0,2-0,4-0,5 - 0,04.
Как и следовало ожидать, 2 Pie 1- (Кстати, этим
свойством можно было воспользоваться и не вычислять
одну из вероятностей /?<, а просто дополнить сумму
остальных до единицы.)
Ряд распределения с. в. X имеет вид:
0
0,24
1
0,46
2
0,26
3
0,04
Пример 2. Производятся независимые тестирования
больших интегральных схем (БИС) до тех пор, пока
не будет обнаружена первая исправная БИС, после чего
тестирование прекращается. Вероятность того, что
тестирование произвольной БИС закончится успешно, равна р.
Построить ряд распределения св. У — число тестов,
которое придется произвести.
Решение, св. Y дискретпа и имеет бесконечное
(счетное) множество возможных зпачений: {1, 2, ...
..., I, ...). Найдем их вероятности, начиная с pt:
Условимся энаком «+» обозначать успешное
тестирование, знаком «—-» — неуспешное.
Для того чтобы достаточно было произвести одно
тестирование, нужно, чтобы первый же тест закончился
ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
успешно:
Найдем р2 = Р {Y — 2}. Чтобы тестирование
прекратилось после второго теста, нужно, чтобы первый тест
был неуспешным, второй — успешным:
р2 = Р{_+} = Р{Г = 2} = A-/>)/>,
или, обозначая вероятность неуспешного тестирования
1 - Р - Я,
Р* - ЯР-
Аналогично найдем
(г-1)раз
Ряд распределения с. в. Y имеет вид:
Y :
Убедимся, что
1
р
2
...
C.1.3)
1. Действительно,
«- — ^9*г и? суммируя бесконечную геометрическую
q i=i
прогрессию с первым членом q и знаменателем q < 1,
имеем
Графическое изображепие ряда распределенпя
называется многоугольником распределения. Строится он так:
для каждого возможного значения с. в. восстанавливается
перпендикуляр к оси абсцисс, на котором откладывается
вероятность данного зпачения с. в. Полученные точки для
наглядности (и только для паглядпости!) соединяются
отрезками прямых (рис. 3.1.1).
Для с. в. X, рассмотренной в примере 1,
многоугольник распределения показан на рис. 3.1.2.
Для с. в. У, рассмотренной в примере 2, при р = 0,6,
q = 0,4 ряд распределения имеет вид:
1
0,0
2
0,24
3
0,096
4
0,0384
5
0,01536
3.2. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
87
Первые несколько ординат многоугольника
распределения показаны на рис. 3.1.3 (продолжение памечено
пунктиром).
Кроме геометрической интерпретации распределения
дискретной с. в., часто оказывается полезной и ее
Pi
1 2 3 ось
Рис. 3.1.2
механическая интерпретация. Это — ряд
материальных точек на оси абсцисс, имеющих абсциссы хи
%2, ..., Xif ... и, соответственно, массы ри р2, ..., р<, ...,
0,5
о,и
0,2
РЧ
1-1
К
\
Р1
Pi Pi
2 3 Ц- 5
Рис. 3.1.3
х1 о хг
Рис. 3.1.4
в сумме образующие единицу (рис. 3.1.4). В дальнейшем
мы убедимся в полезности такой механической
интерпретации*
3.2. Функция распределения
случайной величины. Ее свойства
Ряд распределения (и, соответственно, многоугольник
распределения) могут быть построены только для
дискретной случайной величины (для
недискретной они не могут быть построены хотя бы
потому, что множество возможных значений такой случай-
вой величины несчетно, и их нельзя перечислить в верх-
83 ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
ней строке таблицы). Наиболее общей формой закона
распределения, пригодной для всех случайных величин
(как дискретных, так и недискретных), является
функция распределения.
Функцией распределения случайной величины X
называется вероятность того, что она примет значение
меньшее, чем заданное х:
C.2.1)
Геометрически функция распределения
интерпретируется как вероятность того, что случайная точка X
попадет левее заданной точки х (на рис. 3.2.1
соответствующая часть оси абсцисс, т. е. множество точек,
представляющее событие {Х<х), отмечена штриховкой).
X
в
•X
Iх г
С
Рис. 3.2.1 Рис. 3.2.2
Из геометрической интерпретации очень наглядно
(хотя и не вполне строго) можно вывести основные
свойства функции распределения:
1) F(x)— неубывающая функция своего аргумента,
т. е. при z2>zl F(xz)>F(xt).
2) F(-oo)=0.
3) F(+oo)~i.
Действительно, рассмотрим на оси абсцисс две точки
хг и х2, причем x2>xt (рис. 3.2.2).
Представим событие С = {X < х2) как сумму двух
несовместных событий: С = А +В, где А = {X < xj, В =
«= {#! < X < х2).
По правилу сложения
т.е. Р{Х<х2} = Р{Х<х1} + Р{х1^Х<х2), или
C.2.1')
Но Р {#! ^ X < #2}' как и всякая вероятность, не может
быть отрицательной; следовательно, F(z2)>F(ar1).
Для обоснования второго свойства будем отодвигать
точку х на рис. 3.2.1 все левее и левее (до —<»). Оче-
3.2. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ 89
видно, в пределе событие {X < я), состоящее в том, что
случайная точка X попадет левее х, становится
невозможным, а его вероятность — равной нулю, и
F(-oo)-0.
Аналогично, перемещая точку х по оси абсцисс
направо до +оо, убедимся, что F(+oo)= 1 (событие {Х<х)
в пределе становится до-
стоверным).
Итак, функция
распределения F(x)
любой случайной
величины есть
неубывающая функция
своего аргумента, зна- ^
чения которой за- О х
ключейы между 0 и рис 323
1: Q^F(x)<\, причем
F(—oo) = 0, F(+oo)=:l. в отдельных точках эта функция
может иметь скачки (разрывы первого рода), на
некоторых участках она может быть постоянной, на других —
монотонно возрастать (см., например, рис. 3.2.3).
В дальнейшем вместо слов «функция распределения»
будем иногда писать сокращенно ф. р.
Если в задаче фигурирует не одна случайная
величина, а несколько (например X, У, Z), нужно
по-разному обозначать их функции распределения, например,
^х(х), Fv(y), Ft(z) или же Ft(x), F2(y), F,(z).
Совершенно все равно, какой буквой
%ш*м»'шмм//#^ обозначать аргумент функции
О а р х распределения; мы его
обозначили малой буквой х, соответствую-
Рис. 3.2.4 щей большой букве X,
обозначающей случайную величину, но
это вовсе необязательно; например, можно обозначить
ее q и определить функцию распределения случайной
величины Z как
Зная функцию распределения F(x) случайной
величины X, можно вычислять вероятности любых событий,
с нею связанных.
Выражение вероятности попадания на
участок через ф. р. Рассмотрим на оси абсцисс
участок от а до р (рис. 3.2.4). Для определенности левый
90 ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
конец участка будем включать в него, а правый — нет.
Пусть известна функция распределения F(x) случайной
величины X. Найдем вероятность того, что с. в. X в
результате опыта примет значение, лежащее на участке
от а до ? (включая его левый конец). Полагая в
формуле C.2.Г) a=*a;it $ = хг, получим:
Откуда
Р {а < X < Р} - F (р) - F (а), C.2.2)
т, е. вероятность того, что с. в. X в
результате опыта попадет на участок от а до р
(включая а) равна приращению функции
распределения на этом участке.
В других обозначениях формулу C.2.2) можно
записать в виде:
где квадратная скобка обозначает, что дапный конец
включается в участок, а круглая — что не включается.
Формула C.2.2) справедлива для любых случайных
величин — как дискретных, так и недискретных.
Выражение для вероятности отдельного
значения с. в. через ф. р. Возьмем любую точку
а на оси абсцисс и примыкающий к ней участок [a, fi).
Имеем:
Будем неограниченно приближать точку р к точке a
(см, рис, 3.2.4). В пределе получим:
Р {X - а} - lim [F (р) - F (а)], C.2.3)
6-кх
Значение этого предела зависит от того, непрерывна
ли функция F(x) в точке а или терпит разрыв. Если
функция F(х) в данной точке а непрерывна, то
предел C.2.3) равен нулю. Если же функция F(x) в
точке а совершает скачок, то предел C.2.3) равен
величине этого скачка. В любом случае веро-
ятпость события {X = а} равна величине скачка
ф.р. случайной величины X в точке а (равен
этот скачок нулю или нет).
3.2. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ 91
В частности, если функция F(x) везде
непрерывна, то вероятность каждого
отдельного значения с. в. X равна нулю.
С первого взгляда этот вывод может показаться
парадоксальным. Мы до сих пор встречались с
событиями, вероятности которых равнялись нулю, но то были
невозможные события. Событие {Х = а} для с. в. X с
непрерывной функцией распределения F(x)
возможно, но его вероятность равна нулю. Более
того, в результате опыта непременно произойдет
одно из таких событий, т. е. случайная величина X
примет одно из своих возможных значений; а вероятность
каждого из них равна пулю! Как же быть с правилом
сложепия вероятностей? Ведь сколько нулей ни
складывай, ничего отличного от нуля не получится!
Рассеем это недоумение (если оно возникло).
Вспомним, что аксиому сложения мы ввели только для
конечного и для счетного бесконечного множества
событий; для несчетного она попросту несправедлива.
Вероятность попадания св. на участок от а до ? равпа
сумме вероятностей попадания на элементарные участки,
образующие его, как бы малы эти участки ни были,
но не равна сумме вероятностей попадания в отдельные
точки (каждая из этих вероятностей может быть и
равна нулю).
Представление о событии, имеющем отличную от
нуля вероятность, но складывающемся из событий с
нулевой вероятностью, не более парадоксально, чем
представление о фигуре, имеющей определенную площадь,
тогда как ни одна точка внутри фигуры отличной от
нуля площадью не обладает. Фигура состоит из
таких точек, но ее площадь не равна сумме их
площадей. Сколь угодно малый элемент, выделенный из
фигуры, имеет площадь; она приближается к нулю при
уменьшении размеров элемента и в пределе равна нулю
для точки.
Если событие А в данном опыте возможно, но имеет
нулевую вероятность, то противоположное ему событие
А не достоверно, но вероятность его равна единице
(например, событие {X Ф а} для с. в. X, функция
распределения которой в точке а непрерывна).
Из того, что событие {X = а) имеет вероятность,
равную нулю, вовсе не следует, что это событие не будет
появляться, т. е, частота его равна нулю. Мы знаем,
92
ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
что частота события при большом числе опытов не
равна, а только приближается к вероятности. Из того,
что вероятность события {X = а} равна нулю, следует
только, что при неограниченном повторении опыта оно
будет появляться сколь угодно редко.
3.3. Функция распределения дискретной
случайной величины. Индикатор события
Зная ряд распределения дискретной случайной
величины, легко построить ее функцию распределения, и
обратно.
Продемонстрируем как это делается, на примере 1 из
п. 3.1. Ряд распределения св. X —числа попаданий
имеет вид:
X:
0
0,24
1
0,46
2
0,26
3
0,04
Будем задаваться различными значениями х и
находить для них F (х) — Р {X < х}.
7) Пусть х < 0; так как число попаданий
отрицательным быть не может, то для любого х < 0 (включая 0)
F(*)-0.
2) Пусть 0 < х < 1 (например, х — 1/2); F (х) —
р(Х0} 024
3) Пусть 1<ж
Р {Х<х} - Р{Х
FCx)
2 (например, x = 1,75); F(*)=»
0} + P {X = 1} - 0,24 + 0,46 =0,70.
Опевидпо, что и F B) — 0,70.
4) Пусть 2<z<3; F(x)=*
= P {X = 0} + P {X = 1} +
+ P {X = 2} = 0,24 + 0,46 +
+ 0,26 = 0,96.
5) Пусть ar>3; F (x)
X
{> + {}
Изобразим функцию F(x)
на графике (рис. 3.3.1).
Функция F(x) показана
жирной линией; жирными
точками отмечены значения
F(x) в точках разрыва (функция F(x) при подходе к
точке разрыва слева сохраняет свое значение; про такую
функцию говорят, что она «непрерывна слева»).
Мы видим, что в нашем примере функция
распределения имеет четыре скачка; эти скачки происходят в
3.3. ДИСКРЕТНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА
03
точках, отвечающих четырем возможным значениям с. в.,
и по величине равны вероятностям этих значений.
Между скачками функция F(x) сохраняет постоянное
значение.
Эти особенности характерны не только для нашего
примера, во имеют и более общее значение, а именно:
функция распределения любой дискретной
случайной
велика;)
1
2/6
5 6 х
чины есть
разрывная ступенчатая
функция, скачки
которой
происходят в точках,
соответствующих
возможным
значениям случайной
величины, и
равны вероятностям
этих вначений. Сумма всех скачков функции F(x)
равна единице.
Пример 1. Дискретная св. X — число очков, вы-
павших при бросании игральной кости. Построить ее
функцию распределения.
Решение. Ряд распределения св. X имеет вид:
2 J 4
Рис. 3.3.2
1
1/6
2
1/6
3
1/6
4
1/6
5
1/6
в
1/в
Функция распределения F(x) имеет в скачков,
равных по величине 1/6 (рис. 3.3.2). >
Таким образом, зная ряд распределения дискретной
с. в. X, легко построить ее функцию распределения, и
наоборот: если задана функция распределения со
скачками рг, р2, ...,/>«,•.., рп в точках xif a?tt ..., х,, ..., я„,
п
причем 2 Pi ¦¦ 1» то ряд распределения имеет вид:
X :
Введем новое важное понятие индикатор
события; оно очень пригодится нам в дальнейшем.
Индикатором события А называется случайная
величина U, равная единице, если в результате опыта
*1
Pi
^2
...
...
• • «
. . .
*п
Рп
94 ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
событие А произошло, и нулю — если не произошло:
A, если А произошло,
U — '
(О, если А но произошло.
Ряд распределения с. в. V имеет вид:
U :
Где р — вероятность события А в данном опыте.
Многоугольник распределения св. U имеет вид,
показанный на рис. 3.3.3.
Fix) .
0
1-р
1
р
0
Pi
Рис.
1
3.3.3
I
p
1
1-p
I
3
Рис.
I
I
1 a?
3.3.4
Функция распределения индикатора события А имеет
два скачка: равный A-р) в точке 0 и равный р в
точке 1 (рис. 3.3.4).
В дальнейшем мы убедимся, как пользование
индикаторами событий упрощает решение многих задач
теории вероятностей.
3.4. Непрерывная случайная величина.
Плотность распределения
Рассмотрим дискретную случайную величину X,
имеющую очень много возможных значений,
расположенных очень близко друг к другу на числовой оси, и
построим ее функцию распределения (рис. 3.4.1). По мере
увеличения числа возможных значений и уменьшения
интервалов между ними число скачков становится все
больше, а сами скачки — все меньше. Ступенчатая
линия приближается к плавной, непрерывной (см.
пунктирную линию на рис. 3.4.1). Естественной
идеализацией такого положения является случай, когда функция
F(x) непрерывна.
3.4. НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА 95
Условимся называть случайную величину X
непрерывной, если ее функция распределения не только
непрерывна в любой точке, но и дифференцируема всюду,
кроме, может быть, отдельных точек, где она терпит
излом (рис. 3.4.2)*).
Fte)
X
Рис. 3.4.1 Рис. 3.4.2
Так как для таких случайных величин функция F(x)
нигде не имеет скачков, то вероятность любого
отдельного значения непрерывной случайной величины равна
нулю:
Р {X = а} = 0 для любого а.
Таким образом, для непрерывной случайной величины
бессмысленно говорить о распределении вероятностей
между ее значениями: каждое из них имеет пулевую
вероятность. И все же в каком-то смысле среди
значений непрерывной с. в. есть «более и менее вероятпые».
Например, вряд ли у кого-либо возникнет сомнение, что
зпачепие случайной величины У—рост наугад взятого
человека 170 см — более вероятно, чем 220 см, хотя и
то и другое значение могут встретиться на практике.
В качестве закона распределения, имеющего смысл
только для непрерывных случайных величин, введем
попятив плотности распределения или
плотности вероятности.
Подойдем к нему, исходя из механической
интерпретации распределения вероятностей. Для дискретной с. в.
X эта интерпретация сводится к тому, что в точках хи
¦) Из «непрерывности» необязательно следует «дифференци-
руемость» (можно построить искусственные примеры функций
непрерывных, но не дифференцируемых; по мы в эти тонкости
вдаваться не будем).
96 ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
#2, ..., х{, ... сосредоточены массы ри р2, ..., /?,, ...,
причем сумма всех масс равна 1,
Обобщим эту интерпретацию на случай непрерывной
с. в. Представим себе, что масса, равная 1, не
сосредоточена в отдельных точках, а непрерывно «размазапа»
по оси абсцисс Ох (рис. 3.4.3) с какой-то, в общем
случае, неравномерной плотностью.
Вероятность попадания с. в. X на
любой участок Ах будет интер-
Рис. 3.4.3 претироваться как масса,
приходящаяся на этот участок, а
средняя плотность на этом участке — как отношение массы
к длине; на участке [х, х + Ах) средняя плотность будет
равна:
Р{х^Х<х + Ах}/Ах.
Вероятность попадания с. в. X па участок [х, х + Ах)
равна приращению функции распределения на этом
участке; поэтому средняя плотность на участке от х до
х + Ах будет равна
F(x + Ax)-F(x)
Переходя к пределу при Ах -> 0, получим плотность
в точке х:
lim *(«+Ах)-Г(*) == р' (*), C.4.1)
а это — не что иное, как производная функции
распределения (вот для чего нам понадобилось, чтобы
функция F(x) была дифференцируема!).
Таким образом, мы ввели в рассмотрение новое и
очень важное понятие теории вероятностей: плотность
распределения.
Плотностью распределения (или плотностью
вероятности^ иногда просто плотностью) непрерывной
случайной величины X в точке х называется производная ее
функции распределения в этой точке. Обозначим ее j(x\:
f(x) = F'(x) = ^LF(x). C.4.2)
Про случайную величину X будем говорить, что она
имеет распределение с плотностью f(x) или,
проще, распределена с плотностью f(x) на
таком-то участке оси абсцисс.
3.4. НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА
97
Далее (см. п. 11.3) мы дадим понятие о том, из
каких соображений может быть найдена (прямо или
косвенно) плотпость распределения (п.р.).
Если в задаче фигурирует не одна случайная
величина, а несколько (X, Г, Z), то их плотпость
распределения будем различать соответственными индексами у
буквы /: А (я), ДМ, /з(г) пли /*(*), fv(y), U(z). Так же
как и аргумент функции распределения, аргумепт
плотности может быть обозначен любой буквой; f(x) и f(y) —
одна и та же функция, только с по-разному
обозначенным аргумептом.
Плотпость распределения j(x), как и функция
распределения F(z)> является одной из форм закона
распределения; в отличив от функции распределения, эта
форма не универсальна: она существует только
для непрерывных св.
График плотпости распределения f(x) называется
кривой распределения (рис. 3.4.4).
Введем новое важное понятие: элемент
вероятности. Рассмотрим непрерывную с. в. X с плотностью
}{х) и элементарный участок их, примыкающий к точке
х (рис. 3.4.4). Вероятность попадания с. в. X на этот
fix)
участок dx (с точностью до бесконечно малых высших
порядков) равна f(x)dx. Величина f(x)dx называется
элементом вероятности для точки х. Геометрически
элемент вероятности приближенно равен площади
элементарного прямоугольника, опирающегося на отрезок dx%
примыкающий к точке х (заштрихована на рис. 3.4.4).
Выразим вероятность попадания с. в. X на участок
от а до р (рис. 3.4.5). (Оговорку «включая а»
отбросим, так как для непрерывной с. в. событие {X — а)
имеет нулевую вероятность.) Очевидно, вероятность
попадания с. в. X на участок (a, (J) равна сумме элементов
4 Теория вероятностей и ее
инженерные приложения
98 гл. з. случайные величины
вероятности на всем этом участке, т. е. интегралу:
Р {ос < X < р} - J /(х) их. C.4.3)
а
В геометрической интерпретации эта вероятность
равна площади, ограниченной сверху кривой распределения
и опирающойся на участок (а, Р) (заштрихована на
рис. 3.4.5).
Формула C.4.3) сразу же дает возможность
выразить функцию распределения F(x) через плотность
распределения f(x). Действительно,
х
F(x)-P{X<x)-P{-oo<X<x}= J f{x)dx. C.4.4)
— оо
В геометрической интерпретации ф. р. равна площади,
ограниченной сверху кривой распределения и лежащей
f(x) левее точки х (на
рис. 3.4.6 эта площадь
заштрихована) .
- Укажем осповные
свойства плотности
распределения }(х):
Рис- 3**6 1. Плотность
распределения — неотрицательная функция:
f{x)>0. C.4.5)
Это свойство вытекает из определения f(x);
производная пеубывающей функции отрицательной быть не
может.
2. Интеграл в бесконечных пределах от плотности
распределения равен едипице:
f(x)dz-l. C.4.6)
Это свойство следует из формулы C.4.4J, если
положить в ней х*=<х> и учесть, что F(+«>)— 1.
Геометрически основные свойства C.4.5) и C.4.6)
плотности /(х) интерпретируются как:
1) вся кривая распределения лежит не ниже оси
абсцисс;
2) полная площадь, ограниченная кривой
распределения и осью абсцисс, равна единице.
3.4. НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА 99
Выясним размерности функции распределения F(x)
и плотности f(x). Функция распределения
как всякая вероятность, размерности не имеет.
Размерность плотности распределения, как следует из
формулы C.4.1), обратна размерности с. в. X.
В схеме непрерывных случайных величин можно
вывести аналоги формулы полной вероятности и формулы
Бейеса, знакомых нам по схеме событий.
Пусть вероятность какого-то события А зависит от
того, какое значение х приняла непрерывная с. в. X с
плотностью f(x).
Сделаем гипотезу, состоящую в том, что с. в. X
приняла значение, лежащее на элементарном участке dx,
примыкающем к точке х (рис. 3.4.4). В пределе при
dx -* 0 это условие превращается в X = х.
Обозначим Р(Л|т) условную вероятность события А
при условии Х — х. Замепяя в формуле полной
вероятности B.5.2) вероятность гипотезы элементом
вероятности, а сумму — интегралом, получим полную вероятность
события А:
00
Р(А)= j P(A\x)f(x)dx. C.4.7)
— оо
Формула C.4.7) называется интегральной формулой
полной вероятности.
Соответствующий аналог в схеме непрерывных
случайных величин имеет и формула Бейеса. Пусть до
опыта с. в. X имела плотность распределения 1(х).
Произведен опыт, в результате которого появилось событие А.
Условную вероятность события А при X — х обозначим
Р {А | х). Найдем условную плотность распределения
с. в. X при условии, что появилось событие А;
обозначим ее /а(х). Заменяя в формуле Бейеса B.6.3)
вероятности гипотез элементом вероятности f(x)dx,
сумму — интегралом, получим:
fA{x)-f(*)P{A\x)l] Р(А\х)Пх)*хх C.4.8)
где в знаменателе стоит не что иное, как полная
вероятность события А (см. формулу C.4.7)):
C.4.9)
100
ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Формулу C.4.9) будем называть интегральной
формулой Бейеса.
Рассмотрим ряд примеров, связанных с
распределениями непрерывных случайных величин.
Пример 1. Функция распределения непрерывной
с. в. X задана выражением:
0 при я<0,
F(x) = a^ при 0<д:<11 C.4Л0)
1 при х > 1
(рис. 3.4.7). 1) Найти коэффициент а; 2) найти
плотность распределения /(х) с. в. X и построить ее график;
fix)
Рис. 3.4.7
0.95 0,5 1
Рис. 3.4.8
х
3) найти вероятность того, что св. X в результате
опыта примет значение между 0,25 и 0,5.
Решение. 1) Так как функция F(x) непрерывна,
то F(l) — 1, т. е. orjSt-4—1, откуда а — 1.
2) Плотность распределения JW^F'fa) выражается
формулой:
10 при
2х при
0 при х>1
пли, короче:
f(x) = 2x при 0<х<1.
В дальнейшем мы будем записывать выражение
плотности распределения только на участках, где она
отлична от нуля, подразумевая, что повсюду вне этих
участков она равна нулю.
График плотности (кривая распределения) дан на
рис. 3.4.8.
3) Можно было бы вычислить вероятность попадания
с. в. X на участок @,25; 0,5) по формуле C.4.3), но мы
этого делать не будем; воспользуемся тем, что нам уже
известна ф. p. F(x) = ax2=t^2, и вычислим ее приращение
3.4. НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА
101
на участке @,25; 0,5):
Р {0,25 < X < 0,5} = F @,5) - F @,25) = 0,52 - 0,252 -
-0,1875. +
Пример 2. Плотность распределения f(x) св. X
задана формулой:
1{х) = ае-°* (при х>0) C.4.11)
(а — положительный коэффициент)
Это — так называемое показательное распределение,
которое не раз встретится нам в дальнейшем.
а а
Рис. 3.4.9
1) Построить кривую распределения; 2) найти и
построить функцию распределения с. в. X; 3) найти
вероятность того, что с. в. X примет значение, лежащее между
1 и 2.
Решение. 1) Кривая распределения с. в. X
показана на рис. 3.4.9.
2) По формуле C.4.4)
f(x)dx,
3
X
При х < 0 / (я) = О, значит J / (x) dx — 0. При я > О
F(x)= J /(я) Дс = J f(x)dx + J /(x)dx. Первый интеграл
»—oo — oo 0
X
равен нулю; второй F(x) — j ae"axdx — 1 — е""азс. Итак,
о
ф. р. случайной величины X, имеющей показательное
распределение C.4.11), имеет вид:
*<*>-!« °« ПРИ Х<°Л C-4.12)
> / М — о—ах при "•"^" '
— е
График функции C.4.12) показан на рис. 3.4.10.
102
ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
3) Вероятность попадапия с. в. X па участок A, 2)
вычислим как приращение ф. р. на этом участке:
— A _ е~*а) — A — е-а) = е~а — е~2а.
Например, при а = 1 получим е~1 — е~г « 0,3679 —
-0,1353 = 0,2326. >
Пример 3. Непрерывная с. в. X имеет плотность
j(x) = a cos х при — я/2 < х < я/2.
1) Найти коэффициент а; 2) построить кривую
распределения с. в. X; 3) найти вероятность попадания с. в.
-7t/2
Q 7t/2 X
Рис. 3.4.11
Fix)
7Г/2
Рис. 3.4.12
X на участок от 0 до я/4; 4) пайти и построить функцию
распределения F(x) с. в. X.
Решение. 1) Определим коэффициент а из свойст-
Л/2
ва C,4.6) плотности: J / (х) dx=* J a cos x dx — 2а — 1 >
-Я/2
отсюда а = 1/2.
2) Кривая распределения показана па рис. 3.4.11.
3) По формуле C.4.3)
я/4
J
4) По формуле C.4.4) находим ф. р,
0 при х < — я/2;
F(x)
(sin x + 1)/2 при — я/2 < х < я/2;
1 при х>п/29
Графпк ф. р. дап па рис. 3.4.12. >
3.4. НЕПРЕРЫВНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА
103
Пример 4. Плотность распределения св. X задана
формулой:
1) Построить кривую распределения; 2) найти
вероятность того, что с. в. X попадет на участок (—1, +1).
-4 -3 -2 -/ 0 1 2 3
Рис. 3/1.13
х
1
0
fix)
ш
ш
1
ш..
1
X
Рис. 3.4.14
Решение. 1) Кривая распределения дана на
рис. 3.4.13.
2) Р{- КХ< 1} - Jdx/[n(l + х*)] -
— —arctgtfJLi « 1/2
(соответствующая площадь на рис. 3.4.13
заштрихована). >
Пример 5. Вероятность события А зависит от
случайной величины X, распределенной с постоянной
плотностью /(#)= 1 на участке от 0 до 1 (рис. 3.4.14):
/(ж)=1 при 0<#<1.
Условная вероятность события А при X = х равна
Найти полную вероятность события Л.
Решение. По интегральной формуле полной
вероятности C.4.7)
¦) Так называемый закон Коши в простейшей (канонической)
форме,
104
ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Пример 6. Линейный размер изделия L есть
непрерывная случайная величина с плотностью j(x)
(рис. 3.4.15). При контроле бракуются все изделия,
линейные размеры которых выходят за пределы интервала
Aи 12). Найти условную
плотность распределения
размера V изделия, если
известно, что оно при контроле
не забраковано.
Р е ш е н и е. По
интегральной формуле Бейеса C.4.9)
f(x),fA(x)
X
Рис. 3.4.15 Ja \x) = / (я) I
В результате опыта наблюдено событие
А = {изделие не забраковано) = {lt < L < /2),
Эта вероятность равна площади, заштрихованной на
рис. 3.4.15.
При L = хе(/„ Z2) P(A\x) = i.
При L = x>h P(A\x) = 0.
Условная плотность /д(х) при условии, что появилось
событие А вне участка (lt, h) равна нулю, а в пределах
этого участка равна
П(х) - f(x)/P(A) ~f(x)JHf{x)dx\
(на рис. 3.4.15 условная плотность /а(#) показана
жирной линией; внутри интервала (Zt, l2) ее ординаты
пропорциональны ординатам f{x)). >
3.5. Смешанная случайная величина
Помимо дискретных случайных величин, имеющих
конечное или счетное множество возможных значений,
и непрерывных случайных величин, функция
распределения которых непрерывна, существуют (и на практике
3 5. СМЕШАННАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА
105
Fix)
довольно часто встречаются) случайные величины,
которые называются смешанными. Это как бы
промежуточная разновидность между дискретными п
непрерывными случайными величинами.
Случайная величина X называется смешанной, если
ее функция распределения F(x) на некоторых участках
непрерывна, а в отдельных точках имеет разрывы
(скачки)—см. рис. 3.5.1. На участках, где F(x) непрерывна,
вероятность каждого отдельного
значения равна нулю; вероятности тех
значений, где функция F(x)
совершает скачки, отличны от нуля и
равны каждая величине
соответствующего скачка. Кроме того, ф. р.
F(x) смешанной с. в. X должна
быть дифференцируема всюду,
кроме отдельных точек, где она либо
терпит излом, либо имеет скачок.
Общая формула C.2.2) для вероятности попадания
на участок [а, {})
х
Рис. 3.5.1
Fit)
справедлива и для смешанных случайных величин. Как
и для дискретных случайных величин, функция F(x)
непрерывна слева (жирные точки на рис. 3.5.1).
Приведем ряд примеров смешанных случайных
величин.
Пример 1. Поезд должен прибыть на станцию по
расписанию, но иногда, по случайным причинам,
задерживается (прибытие раньше
_ назначенного срока
исключено). Случайная величина Т —
время опоздания поезда —
представляет собой смешанную
случайную величину. В начале
координат ее функция распреде-
— ления F(t) имеет скачок, вели-
* чина которого равна
вероятности того, что поезд не опоздает
ро = Р{Т = О) (рис. 3.5.2). >
Пример 2. Некоторый прибор испытывается в
течение ограниченного времени т. Случайная величина Т —
время безотказной работы прибора. В случае, если
прибор некондиционен, он отказывает мгновенно в момент
Рис. 3.5.2
406
ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
включения (вероятность этого Р {Т = 0} = р0). Может
оказаться, что прибор проработает безотказно все время
испытания т; вероятность этого Р{Т = т} = рх. Функция
распределения F(t) случайной величины Т имеет два
скачка: в точках J=0 и ? = т (рис. 3.5.3). >
Пример 3. Заработок рабочего Z в течение месяца
зависит от его выработки V; величина V случайна
(будем считать ее непрерывной) и имеет функцию
распределения Fv(x). Заработок рабочего вообще
пропорционален его выработке: Z = aV, но не может быть меньше
гарантированного zt и максимального z2.
Найти и построить функцию распределения Ft(x)
случайной величины Z:
C.5.1)
zx при
aV при zx<x<z2\
z2 при
Решение. Случайная величина Z —смешанная, на
участке (zu z2) ее функция распределения непрерывна
Fix)
Рис. 3.5.3
Рис. 3.5.4
и вероятность каждого значения равна нулю: крайние жо
значения zt и z2 имеют отличные от нуля вероятности:
№) ()
Между Zx и z2 случайная величина Z равна аУиее
функция распределения
График функции Fz(x) показан на рис. 3.5.4. >
В дальнейшем изложении мы встретимся с рядом
других примеров смешанных случайных величин.
ГЛАВА 4
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
СЛУЧАЙНЫХ ВЕЛИЧИН
4.1. Роль и назначения числовых характеристик.
Математическое ожидание случайной величины
Выше мы познакомились с рядом полных,
исчерпывающих характеристик случайных величин — а именно
законов распределения. Каждый закон
распределения исчерпывающим образом описывает
распределение вероятностей и дает возможность вычислять
вероятности любых событий, связанных со случайной
величиной. Универсальным видом закона распределения,
пригодным для любой случайной величины — дискретной,
непрерывной или смешанной, является функция
распределения
Кроме этого универсального, существуют еще и
частные виды законов распределения: ряд распределения
(только для дискретных случайных величин) Pi =
= Р {X = tfi}, i = 1, ..., /г, ... и плотность распределения
f{x)^=Ff(x) (только для непрерывных случайных
величин) .
Каждый закон распределения представляет собой
некоторую функцию, указание которой полностью
описывает случайную величину с вероятностной точки
зрения.
Однако во многих вопросах приктики нет надобности
в таком полном описании; зачастую достаточно бывает
указать только отдельные числовые параметры,
характеризующие существенные черты распределения; папример,
какое-то среднее, вокруг которого разбросаны
значения случайной величины; какое-то число,
характеризующее величину этого разброса (так сказать, «степень
случайности» случайной величины), и т. п. Пользуясь
108 ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
такими характеристиками, мы хотим существенные
особенности случайной величины охарактеризовать сжато и
лаконично, с помощью небольшого набора чисел. Эти
числа, призванные выразить в сжатой форме наиболее
существенные черты распределения, называются числовыми
характеристиками случайной величины.
В теории вероятностей числовые характеристики
играют огромную роль. С их помощью существенно
облегчается решение многих задач (многочисленные примеры
мы увидим в дальнейшем). Часто удается решить
задачу до конца, вовсе оставляя в стороне законы
распределения и оперируя одними числовыми характеристиками.
Например, когда в задаче фигурирует большое
количество случайных величин, каждая из которых оказывает
известное влияние на численный результат опыта,
сравнимое с влиянием каждой из остальных, то закон
распределения этого результата зачастую практически но
зависит от законов распределения отдельных случайных
величин (возникает так называемый «нормальный закон»,
которому в дальнейшем будет уделено много внимания).
В таких случаях для решения задачи, связанной с
конечным результатом опыта, нет надобности в
знании законов распределения отдельных
случайных величин: достаточно знать их числовые
характеристики.
Не преувеличивая, можно сказать, что умение
применять теорию вероятностей для решения практических
задач в значительной мере определяется искусством
пользоваться числовыми характеристиками случайных
величин, оставляя в стороне законы распределения.
Среди числовых характеристик случайных величин
прежде всего рассмотрим характеристики
положения, фиксирующие положение случайной
величины на числовой оси, т. е. некоторое среднее,
ориентировочное значение с. в., около которого группируются ее
возможные значения.
Среднее значение с. в. является как бы ее
«представителем» и заменяет ее при грубых, ориентировочных
расчетах. Когда мы говорим «средняя дневная
температура июля в данпой местности равна 20°С» или «средняя
точка попадания смещена относительно цели на 2 м
вправо», мы этим указываем определенную числовую
характеристику с. в., описывающую ее положение на
числовой осид т. е, характеристику положения.
4.1. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ 109
Из характеристик положения в теории вероятностей
наибольшую роль играет математическое ожидание,
которое иногда называют просто средним значением
случайной величины.
Подойдем к понятию математического ожидания,
исходя из механической интерпретации распределения
дискретной с. в. Пусть единичная масса распределена
между точками оси абсцисс хи х2, .. ., хпу причем
материальная точка Xi имеет массу р{ (i«l, 2, ..., п).
Нам требуется выбрать одну точку на оси абсцисс,
характеризующую положение всей системы
материальных точек, с учетом их масс. Естественно в качестве
такой точки взять центр массы системы материальных
точек. Обозначим абсциссу центра массы М [X]. Имеем
Х\Р\ + хгРг + • • • + хпРп
n
или, учитывая, что 2 Рг =
1=1
Это есть среднее взвешенное значение с. в. X,
в которое абсцисса каждой точки xt входит с «весом»,
равным соответствующей вероятности.
Полученное таким образом среднее значение
случайной величины X называется ее математическим
ожиданием. Это — одно из важнейших понятий
теории вероятностей. Дадпм ему словесную формулировку.
Математическим ожиданием дискретной случайной
величины называется сумма произведений всех возможных
ее значений на вероятности этих значений.
Теперь рассмотрим случай, когда число возможных
значений дискретной с. в. X не конечно, а бесконечно
(образует счетное множество). Формула для
математического ожидания остается той же, только в верхнем
пределе суммы п заменяется на бесконечность:
f D.1.2)
по
ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
2
1/2
22
1/22
23
1/23
...
2*
1/2'
Некоторая сложность заключается в том, что
бесконечная сумма D.1.2) может и расходиться, т. е.
соответствующая с. в. X — не иметь математического ожидания.
Например, для X с рядом распределения
X :
числовой ряд, дающий математическое ожидание
М [X] = 2 2721 = 2 U
расходится (сумма его равна <»), и, значит, у такой с. в.
математического ожидания не существует. Такую
возможность всегда надо иметь в виду, рассматривая
случайные величины с бесконечным числом возможных
значений. На практике, как правило, множество
возможных значений с. в. распространяется лишь на
ограниченный участок оси абсцисс и, значит, математическое
ожидание существует.
Перейдем от дискретной с. в. X к непрерывной с
плотностью f(x). Механическая интерпретация
математического ожидания сохранит тот же смысл: центр массы
для единичной массы, распределенной непрерывно на
оси абсцисс с плотностью f(x). Заменяя в формуле D.1.2)
«скачущий» аргумент Х\ непрерывно меняющимся х, а
вероятность р< —элементом вероятности f(x)dx, получим,
= J xf(x)dx.
D.1.3)
Разумеется, те значения х, для которых f(x) = O, можно
выбросить из области интегрирования. Так же, как и
сумма D.1.2), интеграл D.1.3) может расходиться, и
математическое ожидание — не существовать, но на
практике обычно область значений с. в., для которых f{x)?=
^0, ограничена и математическое ожидание существует.
Несколько сложнее определяется математическое
ожидание смешанной случайной величины; оно состоит из
двух слагаемых, суммы и интеграла:
М [X]
2
+
( xF (x
(Н)
) dz,
D.1.4)
где сумма распространяется на все значения а\, имею-
4.1. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
Ш
щие отличные от нуля вероятности, а интеграл — на всо
участки оси абсцисс, где функция распределения F(x)
непрерывна; множество участков непрерывности
функции F(x) обозначим Н.
В дальнейшем для краткости вместо слов
«математическое ожидание» будем иногда сокращенно писать м. о.
Пользуясь интегралом Стилтьеса, можно выразить
оо
м. о. любой св. X через ее ф. р.: М [Х\ = J xdF(x).
— 00
Эта формула для математического ожидания
случайной величины имеет скорее теоретическое
значение; в конкретных случаях вычисления проводятся по
формулам D.1.2), D.1.3), D.1.4).
Математическое ожидание с. в. связапо тесной
зависимостью со средним арифметическим ее наблюденных
значений при большом числе опытов. Действительно,
пусть имеется дискретная с. в. X с рядом распределения
и к значениями:
X :
где pi — Р{Х = .г*}. Пусть производится п независимых
опытов, в каждом из которых с. в. X принимает
определенное значение из множества {хи х2, ..., хк).
Предположим, что значение хх появилось щ раз, значение хг —
h
пг раз и т. д.; 2 п% = п* Среднее арифметическое на-
блюденных значений с. в. X обозначим М* [X]. Имеем
к
М* [X] =* (х1п1 + х2п2 + ... + хкпкIп — 2 *гП\1п.
Но njn есть не что иное, как частота (или
статистичеPi.
*2
P-i
...
...
Pi
...
Xh
Ph
ская вероятность) события {Х =
итак,
обозначим ее
D.1.5)
т. е. среднее арифметическое наблюденных значений с. в.
равно сумме произведений ее возможных значений на
соответствующие им частоты.
112
ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
Мы знаем, что при увеличении числа опытов п
частота события р* будет приближаться (сходиться по
вероятности) к вероятности р< этого события. Значит, и
среднее арифметическое М* [X] будет приближаться
(сходиться по вероятности) к математическому
ожиданию М [X] случайной величины X. Это значит, что п р п
достаточно большом числе опытов можно
среднее арифметическое наблюденных
значений с. в. X принимать приближенно
равным ее м. о.
Указанная выше связь между м. о. и средним
арифметическим составляет содержание одной из предельных
теорем теории вероятностей (так называемого закона,
больших чисел; строгое доказательство этой теоремы, а
также оценка ошибки приближенного равенства М* [X] «
» М [X] будут даны далее, в гл. 10 и И).
Выше мы ввели обозначение М [X] для
математического ожидания с, в. X. Иногда бывает удобнее
обозначить его одной буквой тж, где индекс х у буквы т
напоминает о той случайной величине Xt м. о. которой
рассматривается. Иногда, когда яспо, о какой случайной
величине идет речь, мы будем этот индекс опускать и
обозначать математическое ожидание просто т.
Математическое ожидание —не единственная
характеристика положения, применяемая в теории
вероятностей; иногда применяются и другие: мода и медиана
случайной величины.
Модой случайной величины называется ее наиболее
вероятное значение (то, для которого вероятность р{ или
плотность распределения f(z) достигает максимума).
Условимся моду случайной величины X обозначать Мх.
На рис. 4.1.1 показан многоугольник распределения
дискретной с. в. X с рядом распределения
X :
для которой Мх = 1. На рис. 4.1.2 показана кривая
распределения непрерывной с. в. X; точка, в которой
плотность f(x) достигает максимума, и есть мода М».
Экспериментальные (статистические) аналоги моды: для
дискретной с. в. X — то значение, которое в данной серии
опытов встречалось чаще всего; для непрерывной с. в.—
центр того элементарного интервала, для которого «плот-
0
0,2
1
0,4
2
0,25
3
0,1
4
0,05
4.1. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
113
ность частоты» (отношение частоты попадания в эют
интервал к его длине) достигает максимума.
Если вероятность пли плотность вероятности
достигают максимума не в одной, а в нескольких точках,
распределение называется полимодальным (рис. 4.1.3 и
4.1.4). Наличие более чем одной
моды часто указывает на
разнородность статистического
материала, легшего в основу исследования.
1 2 3 Ц. х
Рис. 4.1.1
х
Иногда применяется еще одна характеристика
положения—медиана случайной величины X, которую мы
обозначим хт. Эта характеристика применяется, как
правило, только для непрерывных св. Медианой
непрерывной случайной величины X называется такое ее значение
хт, для которого
т. е. одинаково вероятно, окажется ли с. в. X меньше хт
или больше хт. Геометрически медиана — это абсцисса
Pi
f(X)
///¦
Ряс. 4.1.3
Рис. 4.1.4
той точки на оси Ох (рис. 4.1.5), для которой площади,
лежащие слева и справа от нее, одинаковы и равны 1/2
(рис. 4,1.5).
В случае симметричного распределения (имеющего
моду) математическое ожидание (если оно существует),
мода и медиана совпадают.
114
ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
Пример 1. Найти математическое ожидание и
моду для дискретной случайной величины X, имеющей ряд
распределения
X :
(многоугольник распределения показан на рис. 4.1.6).
0
0,1
1
0,3
2
0,5
3
0,1
X
Решение. По формуле D.1.1)
М [X] = тх - 0-0,1 + 1-0,3 + 2-0,5 + 3-0,1 - 1,6.
Мода св. X — ее самое вероятное значение: Мх =*
~=2. >
Пример 2. Непрерывная с. в. X имеет плотность
f(x) = (sin х)/2 при х е @, я)
(рис. 4.1.7). Найти математическое ожидание тх, моду
М* и медиану хт случайной
величины X,
Решение. Исходя из
симметрии распределения, находим
абсциссу центра массы:
т* — я/2.
51ПХ
Я/2 Tt Так как в этой точке }(х) дости-
Рис. 4.1.7 гает максимума, мода М* — я/2.
Очевидно, медиана хт также
равна я/2 (площади по правую и левую стороны от линии,
проходящей через точку я/2, равны). >
Пример 3. Непрерывная с. в. X распределена по
«закону прямоугольного треугольника» на участке @, 2)
и(рис. 4,1.8):
}(х) = ах при *е=@, 2).
4.2. МОМЕНТЫ. ДИСПЕРСИЯ
115
Найти коэффициент а, м. о., моду и медиану с. в. X.
Решение. Коэффициент а найдем из условия, что
площадь треугольника равна единице: 5д=-я~« 2 *2а] =1,
откуда а = 1/2. Математическое ожидание с. в. X найдем
из механической интерпретации: абсцисса центра массы
треугольника тх = B/3) • 2 - 4/3 « 1,33.
Мода с. в. X, очевидно, есть абсцисса точки, где /(#)
достигает максимума, т. е. Мх — 2.
Медиана хт — абсцисса точки, где площадь, ограничеп-
ная кривой распределения, делится пополам (рис. 4.1.9),
f(x> «*>
2а 1
О
х
Рис. 4.1.8
Рис. 4.1.9
т. е. площадь треугольника, опирающегося на отрезок хт
(заштрихована дважды на рис. 4.1.9), равна 1/2: -тр X
1 *т 1
X -f-«m --?--?-, откуда *m - V2 ж 1,41.
На рис. 4.1.9 показано взаимное расположение точек
тх, хт и Мж в порядке возрастания абсцисс. >
4.2. Моменты. Дисперсия. Среднее
квадратическое отклонение
Кроме характеристик положения, в теории
вероятностей употребляется еще ряд числовых характеристик
различного назначения; каждая из них характеризует
случайную величину с точки зрения тех или иных
особенностей ее распределения. Среди* них особое значение
имеют моменты — начальные и центральные.
Начальным моментом s-ro порядка случайной
величины X называется математическое ожидание 5-й степени
этой величины:
а,[Х]-М[Хв]. D.2.1)
Для дискретной с. в. X начальный момент 5-го порядка
116 ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
выражается суммой:
2 \ D.2.2)
где х{ — значения с. в. X, р{ — соответствующие
вероятности; для непрерывной — интегралом:
оо
J *«/(*)<**, D.2.3)
где /(ж) —плотность распределения; для смешанной —
суммой плюс интегралом:
а8 [X] - 2 x\Pi + f *F (x) dz, D.2.4)
4 (Н)
где сумма распространяется на все значения #<,
обладающие ненулевыми вероятностями, а интеграл — на все
участки, где функция распределения непрерывна
(формула D.1.4) для м. о. смешанной с. в.).
Выражения D.2.2) и D.2.3) и их обобщение D.2.4)
мы здесь записали без специального доказательства,
считая их естественными; сомневающиеся могут найти
вывод выражения для м. о. любой функции случайной
величины в п. 8.1.
Ранее введенная характеристика положения —
математическое ожидание с. в.-*- есть не что иное, как ее
первый начальный момент
^-М [X] - аг [X]. D.2.5)
Перед тем как дать определение центральных
моментов, введем новое понятие «центрированной случайной
величины». Центрированной случайной величиной
называется отклонение случайной величины от ее
математического ожидания:
X = X-mx. D.2.6J
Условимся отличать центрированную св. значком °
наверху. Нетрудно убедиться, что м. о. центрированной
с. в. равно нулю:
п п п
= 2 (xi — тх) Pi — 2 хгРг — тх 2 Pi =
аналогично и для непрерывной и для смешанной с. в.
4.2. МОМЕНТЫ. ДИСПЕРСИЯ Ц7
Центрирование случайной величины, очевидно,
равносильно переносу начала отсчета в точку тх (центр
распределения).
Моменты центрированной случайной величины
называются центральными моментами. Они аналогичны
моментам относительно центра массы в механике.
Центральным моментом порядка s с. в. X называется
м. о. з-й степени центрированной с. в.:
щ [X] - М [х8] - М [(X - mx)% D.2.7)
Для дискретной с. в. центральный момент
выражается суммой:
п
^ = 2 (хг-ггьхУп; D.2.8)
для непрерывной — интегралом:
00
ц.- J (x-mxyf(x)dx; D.2.9)
— 00
для смешанной
!*• - 2 («1 - w*)s pi + J (ж - m*)8 F' (ж) cfe.
* (Н)
В дальнейшем, в тех случаях, когда не возникает
сомнений, о какой с. в. идет речь, мы будем для краткости
вместо а8 [X] и [ia [X] писать просто а« и \ia.
Очевидно, для любой с. в. X центральный момент 1-го
порядка равен нулю:
щ - М [&] - М [X — тпх] - 0. D.2.10)
Между центральными и начальными моментами
существует связь: одни выражаются через другие. Выведем
соответствующие формулы для дискретной случайной
величины (для непрерывных вывод будет аналогичным при
замене х{ на х, pt на f(x)dx, сумм на интегралы). Второй
центральный момент:
- *Hx2 Pie
а2 — 2m? + mi = а2 •
118 ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
Аналогично, пользуясь формулой для куба разности,
найдем:
Из — аз — За2/пл + 2ml.
Точно таким же способом могут быть получены
выражения для jju, Ц* (мы на этом не будем
останавливаться). Итак, центральные моменты выражаются через
начальные формулами:
1X1== 0; |х2 = «2 — тпг\ Цз¦ а3 — 3/7za2 + 2т3, ..« D.2И)
Особое значение для практики имеет второй
центральный момент |л2. Он называется дисперсией с. в.
Ввиду крайней важности этой характеристики среди
других, введем для нее специальное обозначение D[X], или
кратко Dx:
Согласно определению центрального момента:
D [X] - Dx - М [Ь] - М [(X - mxf\y D.2.12)
т. е. дисперсия случайной величины есть математическое
ожидание квадрата соответствующей центрированной
величины.
Для непосредственного вычисления дисперсии служат
формулы
i D.2.13)
А
и, наконец,
DX = D[X]
(для
(для
дискретной с. в
00
]= j (x-mxf
непрерывной с.
-mxfPi+ J (
(Н)
.);
f(x) dx
в.)
х-тх)Ч
D.2.
D.2.
14)
.15)
(для смешанной св.);
сумма распространяется на все значения хи где
функция распределения F(x) терпит разрыв, а интеграл —
на все участки, где она непрерывна)
4.2. МОМЕНТЫ. ДИСПЕРСИЯ Ц9
На практике часто бывает проще вычислить второй
начальный момент, чем дисперсию; тогда пользуются
выражением последней через аг (вторая из формул
D.2.11)):
Dx = a2-ml D.2.16)
или, в других обозначениях:
т. е. дисперсия случайной величины равна
математическому ожиданию ее квадрата минус квадрат
математического ожидания. Эту формулировку полезно запомнить.
При вычислении дисперсии по формуле D.2.17) часто
бывает удобно произвести предварительно «грубое
центрирование» с. в. X, для чего перенести начало отсчета в
какое-либо круглое значение аргумента, поближе к
математическому ожиданию тх.
Дисперсия с. в. есть характеристика рассеивания,
разбросанности св. около ее математического ожидания.
Само слово «дисперсия» означает «рассеивание».
Если обратиться к механической интерпретации
распределения, то дисперсия есть не что иное, как момент
инерции распределения масс относительно центра масс
(математического ожидания).
Дисперсия имеет размерность квадрата случайной
величины, что не всегда удобно; для наглядности в
качестве характеристики рассеивания удобнее пользоваться
числом, размерность которого совпадает с размерностью
с. в. Для этого из дисперсии извлекают квадратный
корень. Полученная величина называется средним квадра-
тическим отклонением (иначе «стандартом» или
«стандартным отклонением») случайной величины. Будем
обозначать его о [X] (или ох):
а[X] = ах- УОЩ - УХ. D.2.18)
Корень берется его арифметическим, т. е.
положительным значением.
Для упрощения записей мы часто будем пользоваться
сокращением о* для среднего квадратического
отклонения (или просто а, если ясно, о какой с. в. идет речь).
Вместо слов «среднее квадратическое отклонение» будем
иногда писать с. к. о.
Для неотрицательной случайной величины X в
качестве характеристики «степени ее случайности» иногда
120 ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
применяется коэффициент вариации, равный отношению
с. к. о. к м. о.:
v = o/m. D.2.19)'
Зная м. о. и с. к. о. случайной величины X, можно
составить себе приближенное представление о диапазоне
ее возможных значений. А. именно, значения случайной
величины X только изредка выходят за пределы
интервала
т±3с, D.2.20)
и в большинстве случаев можно считать, что они
укладываются в этот интервал. Это правило (оно более
строго будет обосновано в дальнейшем, п. 10.2 гл. 10) носит
пазвание «правила трех сигма». Согласно этому правилу
для того, чтобы приближенно представить себе размах
случайных отклонений с. в. X от ее м. о., достаточно
отложить от точки m вправо и влево по отрезку, равному
За (рис. 4.2.1).
Математическое ожидание тм, дисперсия D (или
с. к. о. о) — чаще всего применяемые числовые
характеристики с. в. Они характеризуют самые важные черты
распределения: его положение и степень
разбросанности. Для более подробного описания
распределения служат моменты высших порядков. Третий
центральный момент ц,3 служит
Для характеристики асиммет-
рИИ («скошенности») распре-
0 m ее деления. Если распределение
Рис. 4.2.1 симметрично относительно м. о.
(или, в механической
интерпретации, относительно центра массы), то все
центральные моменты нечетного порядка (если они существуют)
равны нулю. Действительно, при симметричном
распределении и нечетном s в сумме
h
На — 2 (*i — ™>YPl
каждому положительному слагаемому соответствует
равное ему по абсолютной величине отрицательное
слагаемое, так что они взаимно уничтожаются и сумма равна
нулю (то же справедливо и относительно интеграла,
выражающего ц, для нечетного s, который равен нулю как
интеграл в симметричных пределах от нечетноц
функции), Естественно поэтому в качестве характеристики
4.2. МОМЕНТЫ. ДИСПЕРСИЯ
121
асимметрии распределения выбрать какой-либо из
нечетных моментов — проще всего \i3. Он имеет размерность
куба случайной величины; чтобы получить
безразмерную характеристику, делят ее на куб с. к. о. Полученная
величина носит название «коэффициента асимметрии»
или просто «асимметрии» (иначе — «скошенности»); ее
обозначают Sk (от английского skew—«косой»):
5А: = |ы3/а3. D.2.21)
На рис. 4.2.2 изображены две асимметричных кривых
распределения /4(#), U(x)\ °Дна
из них (I) имеет положительную
асимметрию (Sk > 0), вторая
(II)— отрицательную (Sk < 0).
Четвертый центральный
момент ц4 служит для
характеристики так называемой «крутости»,
т. е. островершинности или пло-
сковершинности распределения
(применяется в основном к непрерывным с. в.)\ Это
свойство характеризуется с помощью так называемого
эксцесса:
ех = ц4/04~3. D.2.22)
Число 3 вычитается из отношения (х4/а* потому, что
для весьма распространенного и часто встречающегося
fAx)
Рис. 4.2.2
х
Рис. 4.2.3
нормального распределения (о нем будет идти речь в гл. 6
и далее) отношение |14/04 = 3. Для нормального
распределения гх =* 0; кривые, более островершинные, чем
нормальная, обладают положительным эксцессом, более
плосковершинные — отрицательным (рис, 4.2.3), Характери-
122 ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
стикой ех пользуются главным образом для
симметричных распределений.
Кроме рассмотренных выше начальных и
центральных моментов, иногда применяются также абсолютные
моменты (начальные и центральные), определяемые
формулами:
Очевидно, абсолютные моменты четных порядков
совпадают с ранее введенными моментами а, и \i$. Из
абсолютных моментов для характеристики рассеивания
иногда применяется первый абсолютный центральный
момент:
v1-Ml\X\]-M[\X — m\], D.2.23)
называемый также средним арифметическим
отклонением. На практике пользование им не так удобно, как
дисперсией (или с. к. о.), так как оперировать с формулами,
содержащими знак модуля, не очень удобно.
Математическое ожидание, начальные и центральные
моменты (в частности, дисперсия и с. к. о., асимметрия
и эксцесс) — наиболее употребительные числовые
характеристики. Во многих задачах практики полная,
исчерпывающая характеристика с. в.— закон распределения —
пли не может быть получена, или вообще не нужна.
В этих случаях ограничиваются приблизительным
описанием с. в. с помощью числовых характеристик. Часто
числовыми характеристиками пользуются для
приближенной замены одного распределения другим, причем
обычно стремятся произвести эту замену так, чтобы
сохранились неизменными несколько важнейших моментов.
Из определения м. о. и дисперсии следуют некоторые
простейшие и достаточно очевидные свойства этих
числовых характеристик.
1) Математическое ожидание неслучайной величины
с равно самой величине с:
М [с] - с.
(Действительно, если с. в. X имеет только одно
значение с с вероятностью 1, М [с] = с Л — с).
2) Дисперсия неслучайной величины с равна нулю:
D [с] - 0.
4.2. МОМЕНТЫ. ДИСПЕРСИЯ 123
3) При прибавлении к с. в. X неслучайной
величины с к ее м. о. прибавляется та же величина:
М [X + с] - М [X] + с
(это свойство достаточно наглядно следует из
механической интерпретации м. о. как центра массы).
4) При прибавлении к с. в. X неслучайной
величины с ее дисперсия не меняется:
D[X + c) = D[X].
Действительно, при прибавлении к с. в. X
неслучайной величины та же неслучайная величина с
прибавляется к ее м. о., а центрированная с. в. не меняется
(это же наглядно следует из механической
интерпретации дисперсии как момента инерции относительного
центра массы).
В частности, из свойства 4 следует, что при
центрировании случайной величины ее
дисперсия не меняется.
5) При умножении св. X на неслучайную величину
с на ту же величину с умножается ее м. о.:
М [сХ] - сМ [X]
(это свойство достаточно наглядно следует из того, что
при умножении на с масштаб по оси Ох также
множится на с).
6) При умножении с. в. X на неслучайную величину
с ее дисперсия множится на с2:
Действительно, каждое значение св. множится на с,
на то же с множится ее м. о. и каждое значение цент-
о о
рированной с. в. X; ее квадрат Хг множится на с*, на то
же с1 множится и дисперсия:
D [сХ] = М [с*Х2] « с2М [I2] - сЮ [X].
7) Извлекая корень, получим:
т. е. о р и умножении с. в. X на неслучайную
величину с ее с. к. о. множится на модуль
этой неслучайной величины.
124 ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
В п. 3.3 мы ввели в рассмотрение очень важную и
удобную для практических применений св. U — инди-
катор события. Пусть вероятность события А в данном
опыте равна р; вероятность непоявления А равна # =
в 1 — р. Ряд распределения индикатора события А:
U
Найдем важнейшие числовые характеристики
индикатора U: м. о., дисперсию и с. к. о. по его ряду
распределения; имеем
0
я
1
р
Дисперсию найдем через второй начальный момент:
а2 [U] - О2-? + 12-р - р; D [U] - а2 [U] - (М [С/]J -
откуда о [U] = а« pg
Итак, м. о. индикатора события А равно
его вероятности; дисперсия равна
произведению вероятности его появления на
вероятность непоявления. Это полезно запомнить
для дальнейшего.
В ряде случаев при определении важпейших числовых
характеристик дискретных с. в. может помочь аппарат
так называемых производящих функций.
Пусть имеется дискретная с. в. X, принимающая
неотрицательные целочисленные значения 0, 1, 2, ..., Л, .. •
с вероятностями р0, pi9 /?2, ..., Рь ...; Л в РИГ ¦¦ к).
Производящей функцией для с. в. X называется
функция вида:
ф(*)- 2/>***> D-2.24)
ft=0
где z — произвольный параметр @ < z < 1).
Коэффициенты при zh в производящей функции
равны вероятностям того, что с. в. X примет значение ft.
В случае, когда число возможных значений X конечно
(ft = 0, 1, ..., п), выражение D.2.24) сохраняет силу, так
как при к>п все вероятности рк обращаются в нуль.
Очевидно, при z = 1
2й-1. D.2.25)
4.2. МОМЕНТЫ. ДИСПЕРСИЯ 125
Возьмем первую производную по z от производящей
функции:
и положим в ней z *== 1:
а это есть не чю иное, как ы. о. с. в. X. Итак, мы
пришли к выводу: м. о. неотрицательной целочисленной с. в.
равно первой производной ее производящей функции
(f(z) при z — 1;
М [X] - m _ q/ A). D.2.26)
Возьмем вторую производную функции ф"(я):
Полагая в ней г «¦ 1, получим
Ч>"<1)- 2 (#-*)Л- S *«Р*- 2 *Л- D.2.27)
Первая из двух сумм в выражении D.2.27) есть не что
иное, как второй начальный момент оса с. в. X, вторая —
ее м. о. т\ откуда получаем выражение второго
начального момента:
а2т = а2«ф''A) + ф'A), D.2.28)
т. е. второй начальный момент с. в. равен сумме второй
производной от производящей функции при z = 1 плюс
ее м. о.
Аналогично, беря третью производную
ф"' (*) - 2 * (* - 1) (к - 2) Л**
и полагая в ней z«— 1, получим:
И так далее, что позволяет, в случае надобности, выразить
начальные моменты более высокого порядка через
моменты более низкого.
126 ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
Рассмотрим ряд примеров на определение числовых
характеристик различных с. в.
Пример 1. В техническом устройстве работают
независимо два блока. Вероятность безотказной работы
первого блока равна pi = 0,4, второго р2 = 0,7. Св. X —
число работающих блоков. Найти ее м. о., дисперсию
и с. к. о.
Решение. X — дискретная случайная величина с
тремя значениями: 0, 1 и 2. Вероятности этих значений:
Ро - Р{Х = 0} = 0,6-0,3 - 0,18;
р2 _ р (X = 2} - 0,4-0,7 - 0,28.
Вероятность рг = Р {X = 1} найдем, дополняя до
единицы сумму двух других вероятностей:
pt = l-@,18+ 0,28) = 0,54.
Ряд распределения с. в. X:
X :
Непосредственно из ряда распределения с. в. X
получим
тх - 0 • 0,18 + 1 • 0,54 + 2 • 0,28 -1,1.
Тот же результат получим, вводя производящую
функцию
Ф {z) = 0,18 + 0,542 + 0,28z2,
дифференцируя ее
ф'B)-0,54 + 0,562
и полагая 2 — 1:
Обратим внимание на то, что тх ** pt + рг в 0,4 + 0,7;
это не случайно; в дальнейшем (п. 8.3) мы докажем, что
м.о. числа появлений события в п независимых опытах,
в 2-м из которых вероятность появления события равна/?*
п
(г — lf ¦.., га), равно 2 Ри т. е. м. о. числа появлений
события в нескольких опытах равно сумме вероятностей
его появления в отдельных опытах.
0
0,18
1
0,54
2
0,28
¦) 6 данном случае производящая функция сравнительно
мало нам помогла; дальше вам встретятся примеры, где ее введение
сильно облегчает задачу.
4.2. МОМЕНТЫ. ДИСПЕРСИЯ 127
Дисперсию с. в. X найдем, как и выше, через второй
начальный момент:
а2 - О2 • 0,18 + I2 • 0,54 + 22 • 0,28 - 1,66;
ml - 1,12 « 1,21; Dx - 1,66 - 1,21 = 0,45.
(Опять-таки не случайно 0,45 = 0,4 • 0,6 + 0,7 • 0,3 —
д2 = 1- р2\ в гл. 8 мы
докажем это в общем виде.)
Извлекая корень из
дисперсии, получим
ох - ГО^Г« 0,67. ~~ о\ х
Третий центральный
момент с. в. X вычисляем непосредственно по формуле
2
Из = 2 (xi — Wx)sPie @ — 1,1K-0,18 +
'~° + A - l,lK-0,54 + B - 1,1K-0,28 = 0,15948. ^
Пример 2. Непрерывная с. в. X распределена по
так называемому закону Лапласа (рис. 4.2.4):
Найти коэффициент Ь, м. о., дисперсию, с. к. о.,
асимметрию, эксцесс с. в. X.
Решение. Для нахождения Ь воспользуемся
свойством плотности:
ОО 00
J f(x) dx - 2ft J e-*dx - 26 - 1,
-оо О
откуда b = 1/2.
Так как фупкция Ъхе~ы нечетная, то
Это так же следует из симметрии п. р.
Дисперсия и с. к. о. равны соответственно:
оо оо
Dx = J A/2) j*erMdx = 2 A/2) J a*e—dx = 2;
—оо О
Ох= УК- У I,
128 ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
Так как распределение симметрично относительно
м. о., то Sk = 0.
Для вычисления эксцесса находим р,4:
1
0,75
0у25
0
Fix)
{
1
Рис.
2 07
4.2.5
откуда
т. е. эксцесс распределения положителен, чего и
следовало ожидать, исходя из
островершинности кривой }(х). >
Пример 3. Смешанная с. в.
X имеет функцию распределения,
задапную графически на рис. 4.2.5.
Значения 1 и 2 имеют отличные
от нуля вероятности:
P<jr-l>-0f25;
р {X « 2} - 0,25.
(=0; при х> 2 F(#)=l.
На участке 1<#<2 F(x) изменяется по
линейному закону. Найти числовые характеристики с. в. X:
М[Х] и D [X].
Решение: Проводя прямую через точки с
координатами A; 0,25) и B; 0,75), получим F(x)*-x/2 - 0,25,
По формуле D.1.4) для м. о. смешанной св., имеем:
М[Х] = 1-0,25+ 2-0,25 +
2 2
+ jxF' (х) dx - 0,25 + 0,5 + J|- dx - 1,5,
<z2[X] = 1^0,25+ 2*-0,25 +
2 3
+ \x*F' (x)dx - 0,25 + 1 + f ^-dx - ~t
г г
D [X] = a2 [X] - (M [X]J - 11/4 - C/2J - 0,5;
T\ - Vofi. >
ГЛАВА 5
НЕКОТОРЫЕ ВАЖНЫЕ ДЛЯ ПРАКТИКИ
РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СЛУЧАЙНЫХ
ВЕЛИЧИН
5.1. Биномиальное распределение
Говорят, что дискретная с. в. X имеет биномиальное
распределение, если ее возможные значения: 0, 1, .,.
•.., J», ..., л, а соответствующие вероятности:
Рт - Р {X - т) = Om3n-m* E.1.1)
где
0<р<1; g = l-p; го = 0, 1, *.., л.
Распределение E.1.1) зависит от двух параметров
п vi р.
На практике биномиальное распределение возникает
при следующих условиях. Пусть производится п
независимых опытов*), в каждом из которых событие А
(условно можно его назвать «успехом» опыта)
появляется с вероятностью р; св. X — число «успехов» при
п опытах.
Покажем, что с. в. X имеет биномиальное
распределение. Действительно, событие В — {X «¦ т) распадается
на ряд вариантов, в каждом из которых «успех»
достигается в т опытах, а «неуспех» (событие Л) в п — т
опытах. Обозначая «успех» знаком +, а «неуспех»
знаком —, запишем одип из таких вариантов:
тпраз (n—m) раз
По правилу умножения вероятностей
или, обозначая q — 1 - р, Р (Вх) — pmqn~me
Очевидно, точно такую же вероятность будет иметь
вариант, в котором т «успехов» и (п — т) «не-
*) Опыты называются независимыми, если вероятность
какого-либо исхода каждого из них не зависит от того, какие исхода
имели другие опыты.
5 Теория вероятностей и ее
инженерные приложения
130 ГЛ. 5. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
успехов»
{+ + + — + + — + ..-—}.
«-Итпраз, «—»(п—т)раз
Подсчитаем число таких вариантов. Оно равно С™,
т. е. числу способов, какими можно из п опытов
выбрать т «успешных». Отсюда, по правилу сложения,
складывая вероятности всех С™ вариантов события В =*
¦- {X « w), получим
т. е. св. X имеет биномиальное распределение. В
частности,
р0 - Р{х - 0} -р{ •••--} - л
праз
что также вытекает из формулы E.1.1), учитывая, что
Равным образом формула E.1.1) справедлива и для
т «в п:
Рп вР(+ + + ;-> + +} ^ Рп в Оп*
праз
На практике часто приходится вычислять вероятности
«не менее т успехов в п опытах»; будем их
обозначать Rmi
или
Дт- 2 С„рУ-'. E.1.2)
Иногда бывает удобнее вычислять Rm через
вероятность противоположного события:
т. в,
^m-l-l^pV1-'. E.1,3)
i—О
Какой из формул E.1.2)у E.1.3) пользоваться,
зависит от того, в какой из аих сумма содержит меньше
членов.
5.1. БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 131
Найдем важнейшие числовые характеристики с. в. X,
распределенной по биномиальному закону. Для этого
напишем ее производящую функцию:
ф(*)- 2 PmZm= 2 C
но мы знаем, что именно так выглядит п-я степень
бинома
ф(*)-(? + Р*)в E.1.5)
(отсюда и термин «биномиальное распределен
н и е»).
Пользуясь производящей функцией, найдем числовые
характеристики с. в. X: м. о. и дисперсию.
Дифференцируя E.1.5) по z, имеем:
Полагая здесь z — 1, получим
<р'A)= n(q + р)п~1 • р = п • 1П"! • р — пр.
Итак, математическое ожидание с. в. X,
распределенной по биномиальному закону с параметрами пир,
равно
тх = пр. E.1.6)'
Заметим, что получить этот результат
непосредственно из ряда распределения без производящей функции
было бы несравненно труднее.
Аналогично находим второй начальный момент по
формуле D.2.28):
а2 = ф
Имеем
Второй начальный момент
а2 - ф" A)+ тх = п{п- \)рг + пр. E.1.7)
Дисперсию св. X найдем, вычитая из E.1.7) т? — и2р2:
Дев п {п — 1)р2 + пр — пгрг = /г2рг — /гр2 + пр — л2/?2 «
— яр — пр2 — wpg.
Таким образом, дисперсия с. в. X, имеющей
биномиальное распределение с параметрами /г, р, равна
(g = l-p), E.1.8)
132 ГЛ. 5. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Извлекая квадратный корень из дисперсии,
получим с. к. о.:
Ох _ уох - 1/npq. E.1.9)
Итак, для с. в. X, распределенной по биномиальному
закону с параметрами /г, р,
тпх^пр, Dx = npq, ox = l/npq. E.1.10)
Эти выражения полезно запомнить.
Пример 1. Передается и = 5 сообщений по каналу
связи. Каждое сообщение с вероятностью р = 0,3
независимо от других искажается. Случайная величина X —
число искаженных сообщений. Построить ее ряд
распределения. Найти ее м. о., дисперсию и с. к. о.
непосредственно по ряду распределения и сравнить с теми,
которые дают формулы E.1.10). Найти вероятность того, что
будет искажено не менее двух сообщений.
Решение, св. X — число искаженных сообщений —
распределена по биномиальному закону (под «опытом»
разумеется передача сообщения, а под «успехом» — его
искажение).
По формуле E.1.1) находим:
P0 = qb = 0,75 = 0,16807;
Рг = Clp.q* « 5-0,3-0,74 - 0,36015;
- !^-0,32-0,73 = 0,30870;
= 0,13230;
4 q = 0,02835; Рь = ръ = 0,00243.
Или, приближенно, с точностью до 0,001:
Ро = 0,168; Р4-0,360; Р2 = 0,309;
Ps = 0,133; Р4 = 0,028; Р5 = 0,002
(значение Р3 округлено в большую сторону, чтобы
сумма всех вероятностей Рт была не 0,999, а ровно 1).
Приближенно ряд распределения будет иметь вид:
0
0,168
1
0,360
2
0,309
3
0,133
4
0,028
5
0,002
Пользуясь приближенным рядом распределения,
находим м. о. случайной величины X:
т« - 0 • 0,168 + 1 • 0,360 + 2 • 0,309 + 3 -0,133 +
+ 4.0,028 + 5-0,002=1,499.
5.1. БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 133
Первая из формул E.1.10) дает для тх более точное
значение:
т* = 5 0,3=1,5.
Имея в виду возможность ошибок, хоть и
незначительных, дисперсию Z)x вычисляем, пользуясь не
приближенными, а точными значениями /\». Второй начальный
момент
аг - О2 • 0,16807 + I2 • 0,30015 + 22 • 0,30870 +
+ З2 • 0,13230 + 42 • 0,02835 + 52 • 0,00243 « 3,30.
Вычитая из а2 точное зпачение гп% = 2,25, получим
Дс = 1,05, что совпадает с результатом, даваемым второй
формулой E.1.10):
ох=Г1ДM« 1,03.
Найдем вероятность /?2 того, что будет искажено не
менее двух сообщений:
Пример 2. Игральная кость бросается четыре раза.
Найти вероятности того, что шестерка появится а)
ровно один раз; б) хотя бы один раз.
Решение: св. X — число появлений шестерки —
имеет биномиальное распределение с параметрами п =
= 4; р - 1/6.
а) Р {X - 1} - С\р A - pf - 4 • A/6) E/6K » 0,386.
б) Вероятность Rx - Р{Х^ 1} - 1 - Р{Х< 1} - 1 -
- Ро= 1 - E/6L & 1 - 0,483 - 0,517. »>
В ряде задач практики приходится иметь дело не с
биномиальным распределением, а с его обобщением на
случай, когда вероятность «успеха» в п независимых
опытах не постоянна, а меняется от опыта к опыту:
в i-м опыте она равна р< (*", 2, ..., л). Будем
называть это распределение обобщенным
биномиальным.
Производящая функция с. в. X, распределенной по
обобщенному биномиальному закону, имеет вид:
ф1*1-1?1 + Л*1 («а + Ра*). . •(?» + PnZ\ J5.1.11)
134 ГЛ. 5. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
или, короче,
п
Ф (z) === И (?i + Piz)x E.1.12)
1=1
где 9» = 1 — Р*.
Нетрудно убедиться, что, перемножая биномы E.1.12)
и приводя подобные члены с одинаковыми степенями z,
мы получим
фB)= 2 PmZm1 E.1.13)
где Рт — сумма всех возможных произведений, в
которые входят т букв р, с разными индексами и {п — т)
букв д< с разными индексами. Но точно по такому же
алгоритму составляются и коэффициенты при zm в
разложении производящей функции E.1.12) по степеням г.
При вычислении вероятностей Рт в обобщенном
биномиальном распределении часто бывает удобнее не
перебирать все возможные комбинации произведений, а
перемножать биномы производящей функции.
Важнейшие числовые характеристики с. в. X,
имеющей обобщенное биномиальное распределение, равны:
тх « 2 PD Ас - 2 PiQu E.1.14)
Формулы E.1.14) можно было бы вывести, исходя
из производящей функции E.1.12), по в дальнейшем
(п. 8.3) мы получим их гораздо более простым путем.
Пример 3. По каналу связи передаются четыре
сообщения. Каждое из пих, независимо от других, может
быть искажено. Первое сообщение искажается с
вероятностью pt =» 0,1, второе — с вероятностью р2 = 0,2,
третье — с вероятностью р3 = 0,3, четвертое — с
вероятностью рк = 0,4, св. X — число искаженных сообщений.
Пользуясь производящей функцией, построить ряд
распределения с. в. X. Найти вероятность того, что будет
искажено: а) хотя бы одно сообщение, б) не менее двух
сообщений. Найти — непосредственно и по формулам
E.1.14)—ее числовые характеристики: тХ1 Dx и о».
Решение. Производящая функция:
Ф (z) = (gi + PiZ) (g2 + Pzz) (?з + Psz) (g4 + PkZ) =*
- @,9 + 0,lz) @,8 + 0,22) @,7 + 0,3z) @,6 + 0,4z) -
- 0,3024 + 0,4404z + 0,2144z2 + 0,0404s3 + 0f0024z\
5.2. РАСПРЕДЕЛЕНИЕ ПУАССОНА
Ряд распределения с. в. X имеет вид:
X :
135
0
0,3024
1
0,4404
2
0,2144
3
0,0404
4
0,0024
/и, = 0 • 0,3024 + 1 • 0,4404 + 2 • 0,2144 + 3 • 0,0404 +
+ 4 • 0,0024 = 1,000.
Тот же результат даст первая формула E.1.14):
тх = 0,1 + 0,2 + 0,3 + 0,4=1.
Дисперсию вычислим не через второй центральный
момент, а непосредственно:
D» = @- IJ • 0,3024+ A - 1)г • 0,4404 +
+ B-1J • 0,2144+ C-1J -0,0404 +
+ D- 1)*- 0,0024 = 0,7.
Тот же результат получим по второй формуле
E.1.14):
Dx = 0,9 • 0,1 + 0,8 • 0,2 + 0,7 • 0,3 + 0,6 • 0,4 = 0,7.
Извлекая корепь из DXJ получим
Ох« у 6/7 » 0,837.
Вероятность того, что будет искажено хотя бы одно
сообщение и не менее двух сообщений:
д, = 1 - р0 в 0,6976; R2 - 1 - (Ро + Л) = 0,2572. >
5.2. Распределение Пуассона
Говорят, что с. в. X имеет распределение Пуассона,
если ее возможпые значепия: 0, 1, 2, ..., т, ...
(бесконечное, но счетное множество значений), а
соответствующие вероятности выражаются формулой
Рт = ?L е~а (т = 0, 1, 2, .. .)• E.2.1)
Распределение Пуассона играет большую роль в
практическом применении теории вероятностей: многие
физические явления приводят именно к такому
распределению вероятностей.
Закон Пуассона E.2.1) зависит от одного параметра
а, смысл которого в следующем: од является одновре-
136 ГЛ. 5. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
меино математическим ожиданием и дисперсией св. X,
распределенной по закону Пуассона. Докажем это.
Воспользуемся для этого производящей функцией (p(z)
случайной величины X:
Sf6 z
Сумма в последнем выражении есть не что иное, как
еагу поэтому
фСО-е-.в"-^'-". E.2.2)
Чтобы найти м. о. величины X, продифференцируем
производящую функцию E.2.2) по z:
ж положим в ней z = 1; получим тх = а.
Дифференцируя второй раз, найдем
cp"B) = aV<*-1); <p"(l) = a2. E.2.3)
Найдем второй начальный момент:
Дисперсию с. в. X выразим через а2 и тх:
Dx = a2 — m% = а2 + а —а2 = а.
Итак, параметр а пуассоновского распределения
равен одновременно математическому ожиданию и
дисперсии св. X, имеющей это распределение. Найдем с.клк:
ах = уд:=У^ E.2.4);
Коэффициент вариации для с в. X, распределенной по
закону Пуассона, равен
v = Gjmx e U/a = ilia E.2.5);
и стремится к нулю при увеличении а.
Многоугольники распределения для св. X,
распределенной по закону Пуассона с параметрами а = 0,5; а =
= 1,0; а = 2; а = 3,5 показаны на рис 5.2.1.
Рассмотрим условия, при которых возникает пуассо-
новское распределение.
Прежде всего покажем, что оно является
предельным для биномиального, когда число опытов п
неограниченно увеличивается (п ->• «>) и одновременно
5.2. РАСПРЕДЕЛЕНИЕ ПУАССОНА
137
параметр р (вероятность «успеха» в одном опыте) пе-
ограниченно уменьшается (р-*0), но так, что их
произведение пр сохраняется в пределе постоянным и
равным а:
lim пр = а.
Из предыдущего пункта мы знаем, что м. о.
случайной величины X, распределенной по биномиальному
закону с параметрами пир, равно пр. Мы обозначили
0123Ц-5д7т
Рис. 5.2.1
/гр==а. Для случайной величины X, имеющей
биномиальное распределение с параметрами п и а/п,
Посмотрим, каков будет предел этого выражения нря
Преобразуем выражение, стоящее под знаком
предела в формуле E.2.6):
l~m = n(n-D •<-(n-m + l) am_
Первая дробь и знаменатель последней дроби при
постоянном т и п -*¦ оо стремятся к единице. Преобразуем
138 ГЛ. 6. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
числитель последней дроби к виду
В пределе при п -* <» это выражение, как мы знаем
из курса математики, стремится к е~а. Следовательно,
предельное значение в формуле E.2.6) равно
а это и есть распределение Пуассона.
Из доказанного предельпого свойства следует, что
распределение Пуассона с параметром а = пр можно
приближенно применять вместо биномиального, когда число
опытов п очень велико, а вероятность р очень мала, т. е.
в каждом отдельном опыте событие А появляется крайне
редко. Отсюда происходит применяющееся еще иногда
для закона Пуассона название «закон редких явлений».
В свое время «классическим» примером случайной
величины X, распределенной по закону Пуассона,
приводившимся во многих учебниках, было «число солдат-
кавалеристов, убитых за год ударом копыта лошади».
Число опытов п здесь — число встреч
солдат-кавалеристов с лошадью, ар — вероятность того, что встреча за-
копчится столь плачевно. Статистические данпые
показали хорошее совпадение распределения с. в. X с пуас-
ооновским. В настоящее время этот пример, по
понятным причинам, потерял свою актуальность. Однако и в
наше время есть задачи, где распределением Пуассона
можно пользоваться вместо биномиального. Например,
если речь идет о многократном применении технического
устройства высокой надежности, такой, что вероятность
отказа при одном применении очень мала.
Для контроля возможности замены биномиального
распределения пуассоновским можно па всякий случай
подсчитать одну-две ординаты точного, биномиального,
распределения и сравнить с теми, которые получаются
по приближенному, пуассоновскому.
Помимо этого «предельпого» случая возникновения
пуассоновского распределения, па практике встречается
ряд ситуаций, где это распределение имеет место.
Рассмотрим, например, такую задачу. Пусть па оси
времени Qt случайным образом возникают точки — мо-
5.2. РАСПРЕДЕЛЕНИЕ ПУАССОНА 139
менты появления каких-то однородных событий
(например, вызовов на телефонной станции, приходов
посетителей в магазин, поступлений информации в АСУ
и т. п.). Последовательность таких моментов обычно
называют «потоком событий». Предположим, что поток
обладает следующими свойствами.
1. Стационарность, Это свойство означает, что
вероятность попадания того или иного числа событий на
участок времени длины т не зависит от того, где на оси Ot
расположен этот участок, а зависит только от его
длины т. Из этого следует, что среднее число событий,
появляющихся в единицу времени, постоянно. Обозначим
его X и будем называть интенсивностью потока.
2. Ординарность. Грубо говоря, это свойство означает,
что события возпикают поодиночке, а не группами по
два, по три и т. д. Точнее, ординарность потока
выражается в том, что вероятность попадания на малый
участок At двух или более событий пренебрежимо мала по
сравнению с вероятностью попадания на него одного
события (при At -*¦ 0 вероятность попадания на участок At
более чем одного события — бесконечно малая более
высокого порядка малости, чем вероятность попадания на
него же ровно одного события).
3. Отсутствие последействия. Это свойство означает,
что вероятность попадания того или другого числа
событий на заданный участок оси Ot не зависит от того,
сколько событий попало на любой другой не
пересекающийся с ним участок (в частности, «будущее» потока
не зависит от его прошлого; отсюда и термин
«отсутствие последействия»). Эта пезависимость физически
сводится к тому, что события появляются на оси времени
в силу случайных причин, индивидуальных для каждого
из них.
Поток событий, обладающий этими тремя
свойствами — стационарностью, ординарностью и отсутствием
последействия, называется простейшим (или стационарпым
пуассоновским) потоком.
Простейший поток тесно связан с распределением
Пуассона. Действительно, возьмем на оси Ot участок
времени длиной т (рис. 5.2.2) и докажем, что случайная
величина X —число событий, попадающих на этот
участок, имеет распределение Пуассона. Разделим мысленно
участок т на п равных частей длины At = т//г.
Математическое ожидание числа событий, попадающих на эло-
140 ГЛ. 5. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
ментарный участок Д?, очевидно, равно XAt, где X —
интенсивность потока. Согласно свойству 2 (ординарности)
потока можно пренебречь вероятностью попадания на
элементарный участок Д* двух и более событий.
Назовем элементарный участок Д* «занятым», если
на нем появилось событие из потока, и «свободным» —
At
Гис. 5.2.2
если не появилось, и введем индикатор U события
«участок At занят» (см. п. 3.3):
{1, если участок At занят,
О, если участок At свободен.
Математическое ожидание индикатора события
«участок At занят» равно вероятности этого события:
М [U] = рЫ9
где рм — вероятность того, что участок At будет занят.
Среднее число — математическое ожидание — числа
событий, попадающих на участок Д*, очевидпо, равно
откуда находим
Теперь рассмотрим п участков оси 0*, как п
независимых опытов (независимость следует из свойства 3
потока), в каждом из которых может появиться событие
А — {участок занят) с вероятностью К At. Число занятых
элементарных участков — это число X событий на всем
участке т (если ни на каком из элементарных участков
не может появиться более одного события; в пределе при
Д*-*0 это будет именно так). Случайная величина X
имеет биномиальное распределение
Хт
с параметрами пи -,
С (?/ (!-?
5.2. РАСПРЕДЕЛЕНИЕ ПУАССОНА
141
Теперь будем неограниченно увеличивать число
элементарных участков At и найдем в пределе (при п -> «>)
вероятность того, что на участок т попадет ровно т
событий:
Но мы только что доказали, что при условии п ->• оо?
^1)и постоянном значении произведения п—= Ат
биномиальное распределение стремится к пуассоновско-
му с параметром Кт:
Таблицы значений функции Р (т, а) = ^ е а
приведены в приложении 1.
Таким образом, мы выяснили еще один тип условий,
в которых возникает распределение Пуассона.
Отметим (мы сделаем это без специального
доказательства), что условие 1 (стационарность потока) не
является обязательным для
того, чтобы число событий,
попадающих на участок
длины т, распределялось по
закону Пуассона (достаточно,
чтобы выполнялись условия
Рис. 5.2.3
Рис. 5.2.4
2 и 3). Если интенсивность потока событий Я не постоянна,
а зависит от времени Л=:А,(?), то вероятность попадания
ровно т событий на участок длины т, начинающийся
в точке tQ и кончающийся в точке to + r (рис. 5.2.3),
т
имеет тоже распределение Пуассона:
-0,1, 2,...), где
а —
j^-e (то
X{t)dt.
142 ГЛ. 5. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Добавим к этому, что ось 0*, на которой случайным
образом появляются точки, вовсе не обязательно должна
быть осью времени, а точки на ней — моментами
появления событий. Картина может иметь другой
физический смысл (например, точки причаливания к берегу
лодок, действующих независимо друг от друга).
Более того, закон Пуассона может возникать в
результате появления случайных точек не только на оси,
а на плоскости или в пространстве. В таких случаях
говорят не о «потоке событий», а о поле точек на
плоскости (см. рис. 5.2.4) или в пространстве.
Три условия, обеспечивающие простейший характер
потока для поля точек, формулируются в виде:
1. Однородность поля — это значит, что вероятность
попадания того или иного числа точек в какую-то
фигуру S (см. рис. 5.2.4) (объем) не зависит от того, где
&та фигура (объем) находится, а зависит только от ее
площади (объема).
2. Ординарность поля — это значит, что точки на
плоскости (в пространстве) появляются поодиночке, а не по
две, по три и т. д. Точнее, что вероятность попадания
в элементарный участок плоскости (пространства) двух
или более точек пренебрежимо мала по сравнению с
вероятностью попадания одной точки.
3. Отсутствие взаимодействия в поле —это означает,
что вероятность попадания того или иного числа точек
в плоскую (или пространственную) фигуру не зависит
от того, сколько точек попало в любую другую
непересекающуюся с ней фигуру.
Роль интенсивности К потока событий в случае поля
точек играет его плотность X — среднее число точек,
попадающих в единицу площади (объема). Для
однородного поля точек Я = const; для неоднородного К зависит
от координат точки (я, у) на плоскости; (я, у, z) —
в пространстве.
Можно доказать (мы этого делать не будем), что для
поля, обладающего всеми тремя свойствами, число тд»чек,
попадающих в заданную плоскую (пространственную)
фигуру, распределено по закону Пуассона с параметром
а, равным Х$, где s — площадь фигуры (или %v, где и —
объем фигуры).
Для того чтобы возникало распределение Пуассона,
не обязательно соблюдение всех трех условий,
достаточно соблюдения двух последних (ординарности и отсутст-
5.2. РАСПРЕДЕЛЕНИЕ ПУАССОНА 143
вия взаимодействия). Если такое поле неоднородно, то
число точек, попадающих в плоскую (пространственную)
фигуру, вычисляется по формулам
а — \ \ X (хх у) dx dy (для плоскости)
(8)
a -a J f j X (х, у, z) dx dy dz (для пространства).
(S)
или
(V)
Двойной интеграл распространяется на всю плоскую
фигуру 5, а тройной — на всю пространственпую
фигуру V.
Для вычисления различных вероятностей, связанных
с закопом Пуассона, полезно пользоваться функцией
Я(т, а):
m m
R (mf a) - 1 - 2 w e~* - 1 - 2 P ^ ^ E-2'8>
таблицы которой приведены в [4].
Обозначим
Я (m, а) - 1 — Б (да, а) - 2 ^ (*, л). E-2.9)
С помощью этой функции можно подсчитать вероятности
событий, связанных со с. в. Х9 распределенной по закону
Пуассона с параметром а:
где [х] — целая часть числа х (например, [0,5] ¦- 0;
[2,7] — 2). Следовательно,
P{X<*}-l-J([x]fa), E.2.10)
откуда
P{X>*}-l-P{X<*}-E(Mfa). E.2.11)
Пример 1. На автоматическую телефонную станцию
поступает простейший поток вызовов с интенсивностью
Я, — 0,8 (вызов/мин). Найти вероятность того, что за две
минуты: а) не придет ни одного вызова; б) придет ровно
один вызов; в) придет хотя бы один вызов.
144 ГЛ. 5. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Решение. Св. X — число вызовов за 2 минуты —
распределено по закону Пуассона с параметром а =
— К • т — 0,8 • 2 — 1,6. Имеем:
J *~1
а) Ро - Jj *~1>в; так как 0! = 1,
Р, _*-<.'« 0,202,
б) Р2 = 5-в-1« 1,6-0,202 « 0,323,
в) fljL-PIX^ll-l-PIX-OI-l-Po^Ojee. >
Пример 2. Поток грузовых железнодорожных
составов, прибывающих на сортировочную горку, можно
считать простейшим с интенсивностью А, —4 (состав/ч).
Найти вероятности того, что эа полчаса на горку
прибудет: а) ровно один состав; б) хотя бы один состав; в) не
менее трех составов.
Решение, т — 0,5; а — 4 • 0,5 -¦ 2,
а) Л - 2 ¦ в'2 « 2 • 0,135 - 0,270.
б) А«-1-Р9*> 0,865.
в) Д,«1--(Р0 + Р1 + р,)-1-ДB, а)-ЛB, а)-
«ЛB,2)« 0,325. >
Пример 3. На оси абсцисс Ох (рис. 5.2.5) случайным
образом расположены наблюдательные посты; их
плотность (среднее число постов на единицу длины)
К (пост/км). Объект, пересекающий ось абсцисс в точке
с заданной абсциссой |, обнаруживается с
наблюдательного поста, если он проходит от него на расстоянии не
0 I ее
Рис. 5.2.5
более г км, причем обнаруживается не с полной
достоверностью, а с вероятностью р. Посты обнаруживают объект
независимо один от другого. Найти вероятность того, что
объект будет обнаружен.
Решение. Перейдем от последовательности постов
на оси к последовательности «обнаруживающих постов»,
линейная плотность которой X' = Хр. Вероятность того,
что объект будет обнаружен, равна вероятности того, что
на участок длиной 2г с центром в точке ? попадет хотя
бы один «обнаруживающий пост». Св. X — число
«обнаруживающих постов» на участке длиной Ъг —
распределена по закону Пуассона с параметром а = 2rk' =*2гкр9
5.2. РАСПРЕДЕЛЕНИЕ ПУАССОНА 145
Вероятность Rt — 1 — Ро появления хотя бы одного
«обнаруживающего поста» на участке 2г равна /?t = 1 —
— е-™*. >
Пример 4. Космические частицы, попадающие в
спутник, образуют поле с плотностью X (частица/м2).
Агрегат спутника, находящийся в поле частиц, занимает
площадь S (м2). Для выхода из строя агрегата заведомо
достаточно попадания в него двух частиц; при попадании
одной частицы он выходит из строя с вероятностью р.
Найти вероятность события А = {выход агрегата из
строя).
Решение. Находим среднее число попадающих в
агрегат частиц:
Найдем вероятность выхода агрегата из строя по
формуле полной вероятности с гипотезами:
7/i = (в агрегат попала одна частица},
Hz ¦* (в агрегат попало не менее двух частиц}.
По закону Пуассона
; Р(Н2) - Д, - 1 - Р, - Л - Я A, 315) -
. P(A\Ht)-p;
по формуле полной вероятности
Р(А) - XSpe~K8+ 1 - e~xs(i + XS). >
Пример 5. Поток вызовов на АТС — пуассоновский
нестационарный с интенсивностью k{t), зависящей от
времени. На участке времени от 0 ч до 6 ч 40 мин
интенсивность X(t) возрастает по линейному закону:
причем к 0 ч она равна 0,2 (вызовам в минуту); а в
6 ч 40 мин — 0,4 (вызов/минуту). Найти вероятность Р
того, что за 10 минут, от 3 ч 15 мин до 3 ч 25 мин,
придет не менее трех вызовов.
Решение. Найдем постоянные Ъ и с: Х@) = 0,2; с==
-=0,2 [вызов/мин]; X F ч 40 мин) —А. D00 мин) = 6 400+.
+ 0,2 = 0,4 [вызов/мин], откуда b = 0,2/400 [вызов/мин2] =»
¦= 1/2000 [вызов/мин2]. Среднее число вызовов а в интер-
146 ГЛ. 5. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
вале от 3 ч 15 мин -* 195 мин до 3 ч 25 мин — 205 мин
205 205
будет о - f (Ы + с) dt = [b % + ct) - гхяг* B052 —
195 195
- 1952) + 0,2 B05 - 195) - 420254^(K8025 + 2-3. Искомая
вероятность Р будет
Р - # Ц2], 3) - 2? B, 3) - 0,57681 » 0,577. »>
5.3. Геометрическое распределение
Говорят, что случайная величина X имеет геометри*
ческое распределение, если ее возможные значения 0, 1,
2, ..., т, ..., а вероятности этих значений:
Pm~qmp, E.3.1)
где 0<р<1; g = l —p; m —0, 1, 2, ...
Вероятности Pw для последовательных значений m
образуют геометрическую прогрессию с первым членом р
и знаменателем q (отсюда и название «геометрическое
распределение»):
На практике геометрическое распределение
появляется в следующих условиях. Пусть производится ряд
независимых опытов, с целью получения какого-то
результата («успеха») А; при каждой попытке (опыте) «успех»
достигается с вероятностью р. Случайная величипа X —
число «безуспешных» попыток (до первой попытки, в
которой появляется результат 4). Нетрудно убедиться, что
св. X имеет геометрическое распределение E.3.2).
Действительно,
Р {X — 0} = Р {первая же попытка успешна) « р,
Р {X ш- 1} =* Р {первая попытка безуспешна,
вторая успешпа) =* q * р,
Р {X «* т) » Р {первые тга попыток безуспешные,
(т +1) -я успешна) ~ gm • р.
Ряд распределения с. в. X имеет вид:
01 1 I 2 | 3
б.З. ГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ 147
Первые четыре ординаты геометрического
распределения для р = 0,4; <7 = О,6 показаны на рис. 5.3.1.
Найдем числовые характеристики с. в. X,
распределенной по геометрическому закону. Для этого запишем ее
производящую функцию: .Рт
00 '
m~° ? # 0.2h
Суммируя бесконечно убы- 01_
вающую геометрическую про- ' __
грессию со знаменателем qz< q\ ^ ^ j j-—--
< 1, получим
ф(г) = ?A- gz)~\ E.3.3) Рис. 5.3.1
Дифференцируя выражение E.3.3) по z, найдем:
ф' (z) = /?g(l — qz)~z. E.3.4)]
Откуда находим и.о.:
Сокращая на р — 1 — q, находим:
«,-g/p. E.3.5J
Дифференцируя еще раз E.3.4), имеем
Отсюда находим второй начальный момент с. в. X:
аг _ ф" A) + тх = 2д7р* + g/р = gBg + р)/?1.
Но 2q + p = q + p + q = i + q (так как р + q = 1); отсюда
а.-«A + «)/р\ E.3.6);
Вычитая из E.3.6) т* = ?*//>*, находим дисперсию
с.в.Х
Dx = q/p* E.3.7):
и, наконец, с. к. о.
o« = Vg7? = V?7p. E.3.8):
На практике чаще приходится рассматривать не с. в. X,
имеющую геометрическое распределение, а другую св.:
E.3.9J
148
ГЛ. 5. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
(число попыток до первого «успеха», включая
удавшуюся).
Ряд распределения с. в. У имеет вид:
112 | 3 l...| m 1...
У :
Будем называть такое распределение «геометрическим,
сдвинутым на единицу» или «геометрическим + 1».
Многоугольник распределения с. в. Y при р = 0,4 имеет тот
же вид, что и на рис. 5.3.1, но сдвинут вправо на одну
единицу (рис. 5.3.2).
Найдем м. о. и дисперсию с. в. X. Пользуясь
свойствами числовых характеристик, приведенными в п. 4.2,
получим
М [X + 1] = тх + 1 = q/p + 1 = 1/р,
ту
By = D [X + 1] = Dx
= ах
E.3.10)
E.3.11)
E.3.12)
Пример 1. При каждом цикле обзора
радиолокатора объект (независимо от других циклов)
обнаруживается с вероятностью р = 0,2.
Найти м. о. и дисперсию
числа X циклов обзора,
которое придется
произвести без обнаружения
объекта и числа Y
циклов обзора, которое
придется произвести вплоть
до обнаружения объекта
(включая тот, при кото-
5 т
1 2 3 А
Рис. 5.3.2
ром объект будет
обнаружен). Найти м. о., дисперсию и с к. о. каждой из св. X,
Y. Пользуясь правилом трех сигма, найти максимальное
практическое возможное число циклов, за которое объект
еще не будет обнаружен. Найти вероятность того, что
фактическое число «безуспешных» циклов превзойдет его
м. о. больше, чем на За.
Решение: св. X имеет геометрическое
распределение с параметром р = 0,2; по формулам E.3.5), E.3.7)
и E.3.8) имеем:
тх = A-0,2)/0,2 = 4; Дс = 0,8/0,04 = 20; ох= V20 « 4,46;
св. У имеет «геометрическое + 1» распределение; ее м. о.
с. в. X:
Найдем
5.3. ГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ 149
5; ее дисперсия такова же, как дисперсия
Dv — 20; оу * 4,46.
m-=0
g18
0,818« 0,0180144.
Таким образом, вероятность того, что с. в. X
превзойдет свое м. о. больше, чем на Зо, довольно мала (меньше
2%; отклонения в меньшую сторону не рассматриваем,
так как они приводят к отрицательным значениям X, что
вообще невозможно). >
Пример 2. В нашем распоряжении имеется п
лампочек; каждая из них с вероятностью р имеет дефект.
Лампочка ввинчивается в патрон и в сеть включается
ток; при включении тока дефектная лампочка сразу же
перегорает и заменяется другой. Рассматривается
случайная величина Z — число лампочек, которое будет
испробовано. Построить ряд распределения с. в. Z и
найти ее м. о.
Решение. Распределение св. Z для всех значений
т<п есть «геометрическое +1» распределение с
параметром q — 1 — р. Найдем Р {Z = п). Это есть
вероятность того, что будут испробованы все п лампочек, а
значит, первые п — 1 лампочек окажутся дефектными.
Следовательно, P{Z = п} = рп~*.
Ряд распределения с. в. Z имеет вид:
где q = 1 - р.
Производящая функция с. в. Z равна
Бе производная:
-p"-1^"-1) a-pz)+p (z - Pn-hn)
^r-
150 ГЛ. 5. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Полагая в ней z = 1, получим:
„n-i
i - РП
(В дальнейшем — см. гл. 8 — мы вернемся к этой задаче
и найдем тг другим способом, как м. о. минимума из
двух величин: св. У, распределенной по
геометрическому закону с параметром р, и неслучайной
величины п.) >
5.4. Гипергеометрическое распределение
Говорят, что случайная величина X имеет
гипергеометрическое распределение с параметрами а, Ь, п, если ее
возможные значения 0, 1, ..., т, ..., а имеют вероятности:
Рп = Р {X = тп) = (ССГЖ)/Сь (ш - 0, .... а).
E.4.1)*)
Гипергеометрическое распределение возникает при
следующих условиях: имеется урна, в которой Ь белых
и а черных шаров; из нее вынимается п шаров.
Случайная величина X — число белых шаров среди вынутых.
В п. 1.2 мы уже сталкивались с такой задачей и
убедились, что формула E.4.1) справедлива.
Важнейшие числовые характеристики случайной
величины X, имеющей гипергеометрическое распределение,
равны соответственно:
mx e па/(а + Ь)% E.4.2)
E.4.3)
Выводить эти выражения непосредственно из
распределения E.4.1) или его производящей функции
<pw- is
тп=0
¦) При пользовании формулой E.4.1) надо полагать 67^ = 0,
если г > kt
S.4. ГИПЕРГЕОМЕТРЙЧЁСКОЕ РАСПРЕДЕЛЕНИЕ 151
было бы сложно; в дальнейшем (п. 8.3) мы выведем эти
формулы гораздо более простым путем (пользуясь
теоремами о числовых характеристиках), а пока предложим
читателю Припять их па веру.
Пример 1. В шкафу находятся 9 приборов; из них
5 новых и 4 бывших в употреблении. Из шкафа наугад
вынимается 4 прибора; св. X — число новых приборов
среди вынутых. Построить ряд распределения с. в. X.
Вычислить м. о., дисперсию и с. к. о. с. в. X двумя
способами: непосредственно по ряду распределения и по
формулам E.4.2), E.4.3).
Решение. Вероятности Pm = P{X=:m}, m = 0, I,
2, 3, 4 находим по формуле E.4.1), полагая в ней а = 5;
Q Я 7 А
Ъ = 4; а + Ь = 9; знаменатель С\ ^'
Имеем:
= «0476 *-?*0,317;
J^« 0,040.
Ряд распределения с. в. X:
v.
0,008| 0,159 10,476 10,317 10,040Г
По ряду распределения находим тх:
тх = 0 -0,008 + 1 -0,159 + 2 -0,476 + 3 -0,317 +
+ 4.0,040 = 2,222,
То же значение тх = 2,222 получим по формуле
E.4.2):
ш х = -я- = 2,222 *)•
Для нахождения дисперсии сначала «грубо
центрируем» с. в. X, перенося начало отсчета в точку с
абсциссой 2, близкую к тх\ при этом, как мы знаем, дисперсия
¦) Точного совпадения могло и во быть, так как вероятности
в нижней строке ряда распределения округлены до 0,001.
152 ГЛ. 5. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
не меняется. Получим ряд распределения св. Y = X — 2:
-2 I —1 I о I 1 I 2
0,008 | 0,159 | 0,476 | 0,317 10,040
Второй начальный момент с. в. Y:
а2 [у] = (-2J ¦ 0,008 + (-1J • 0,159 + О2 - 0,476 +
+ I2 • 0,317 + 22 • 0,040 » 0,668,
откуда дисперсия
D [Y] _ D [X] - а2 [Y] — roj « 0,668 - (тх — 2f&0fil9.
По формуле E.4.3) получим более точное, чем это,
значение дисперсии: Dx = 0,617.
Небольшое расхождение в последнем знаке с ранее
вычисленной дисперсией объясняется погрешностями
округления вероятностей в ряде распределения. >
В заключение заметим, что при а -*• «>t Ь -+ «>,
а/(а+Ь) — р гипергеометрическое распределение
приближается к биномиальному с параметрами п и р. В этих
условиях п зависимых опытов, состоящих в вынимании
п шаров из урны, содержащих а белых и Ъ черных
шаров, становятся практически независимыми, а вероятность
появления белого шара от опыта к опыту не меняется
и остается равной р = а/(а + Ь).
Гипергеометрическое распределение применяется на
практике при решении задач, связанных с контролем
продукции (пример 3 п. 1.2),
ГЛАВА 6
НЕКОТОРЫЕ ВАЖНЫЕ ДЛЯ ПРАКТИКИ
РАСПРЕДЕЛЕНИЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ
ВЕЛИЧИН
6.1. Равномерное распределение
Говорят, что с. в. X имеет равномерное распределение
на участке от а до Ь, если ее плотность f(x) на этом
участке постоянна:
|т при х е (а, Ь), )
ь-а р . F.1.1)
О при х ф. (a, b) J
Говоря о непрерывных случайных величинах, мы
будем, как уже условились, в целях простоты записывать
выражение для плотности f(x) только на тех
участках, где она отлична от нуля; при этом будет
подразумеваться, что на всех остальных участках она
равна нулю. В частности, плотность равномерного
распределения будем записывать в виде:
или же совсем коротко
F.1.2)
F.1.3)
1
Ъ-п
fix)
Значения f(x) в крайних точках а и Ъ участка (а, Ь)
не указываются, так как вероятность попадания в любую
из этих точек для
непрерывной с. в. равна нулю.
Кривая равномерного
распределения (рис. 6.1.1)
имеет вид прямоугольника,
опирающегося на участок (а,Ь);
в связи с этим равномерное
распределение иногда
называют «прямоугольным».
Математическое ожидание с. в. X, имеющей
равномерное распределение на участке (а, Ь), как видно из меха-
шзческой интерпретации (центр массы), равно абсциссе
а /пх
Рис. 6.1.1
х
154 ГЛ. 6. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
середины участка:
««-Ц^. F.1.4)
Тот же результат можно получить и вычисляя
интеграл:
ь
xdx a-
~ J
~-
Дисперсию с. в. X также можно найти, исходя из
механической интерпретации (момент инерции
распределения относительно центра массы):
Тот же результат можно получить, вычисляя
интеграл:
ь
¦ b2dx (Ъ — аJ
2 ) b — a 12
а
Из F.1.5) следует выражение для с. к. о.
равномерного распределения:
F.1.6)
Моды равномерное распределение не имеет; его
медиана, из соображений симметрии, равна тх = (а + Ь)/2.
Из тех же соображений симметрии третий центральный
момент с. в. X равен нулю:
Для определения эксцесса найдем четвертый
центральный момент:
\
откуда эксцесс с. в. X равен
8х = И4/^-3--.1,2. F.1.7)
Как и следовало ожидать, эксцесс отрицателен.
e.i. равномерное распределение
155
Найдем вероятность попадания с. в. X, равномерно
распределенной на участке (а, Ь), на любую часть (а, Р)
участка (а, Ь) (рис. 6.1.2). Геометрически эта вероятность
представляет собой площадь, дважды заштрихованную на
рис. 6.1.2
Р{а<Х<Р} = ^. F.1.8)
Функция распределения F(x) для св. X,
распределенной равномерно на участке (a, b), геометрически
представляет собой площадь, ограниченную кривой
распределения и лежащую левее точки х (рис. 6.1.3):
0 при х<.а,
(х — а)/(Ь - а) при а < х < Ь,
1 при х > Ъ
F (х)
F.1.9)
Ъ-а
График функции распределения дан на рис. 6.1.4.
Рассмотрим несколько
типов физических условий,
при которых возникает рав-
номерное распределение.
1. Производится
измерение какой-то величины с
помощью прибора с грубыми
делениями; в качестве при-
ближепного значения
измеряемой величины берется: а) ближайшее целое; б)
ближайшее меньшее целое и в) ближайшее большее целое.
Рассматривается св. X — ошибка измерения. Так как
ни одно из значений с. в. ничем не предпочтительнее
а ос fib
рис g | 2
Ъ-а
Пх)
I
а х Ь
Рис. 6.1.3
F(oi)
а Ъ
Рис. 6.1.4
других, естественно, что с в. X распределена равномерно:
в случае а) на участке (—1/2; 1/2), в случае б) на
участке @; 1), в случае в) на участке (—1; 0) (в качество 1
берется цена деления).
156 ГЛ. 6. ЙЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Очевидно, такое равномерное распределение имеют и
ошибки, возникающие от округления даниых при
расчетах (в частности, на ЭВМ).
' 2. На оси абсцисс имеется последовательность точек,
разделенных строго постоянным интервалом I (рис. 6.1.5).
На ось абсцисс «бросается» случайная точка ®,
занимающая то или другое положение безотносительно к
последовательности точек
X Y 1у 21, ..., ml, ... Случай-
gT^* ная величина X — рас-
Q I 21 31 kl ^ стояние от случайной точ-
Рис. 6.1.5 ки © до ближайшей
левой из точек 2, 2/, ...
..., ml, ..., очевидно, имеет равномерное распределение
на участке (О, I):
/(я)=1Л при 0<х<1 F.1.10)
(совершенно такое же распределение имеет и
расстояние У до ближайшей правой точки).
3. Вертикально поставленное симметричное колесо
радиуса г (рйс. 6.1.6) приводится во вращепие и затем
останавливается вследствие трения. Случайная величина
6 —угол, который после остановки
будет составлять с горизонтом / — /
фиксированный радиус О А.
Очевидно, величина 0 имеет
равномерное распределение на участке
@, 2я).
Такое распределение случайных
углов поворота деталей механизмов Рис. 6.1.6
нередко встречается на практике.
4. В современной вычислительной технике при
моделировании случайных процессов часто приходится
пользоваться случайной величиной X, имеющей равномерное
распределение в пределах от 0 до 1:
/(*)=1 @<*<1). F.1.11)
Эта величина, которую коротко называют «случайным
числом от 0 до 1», служит исходным материалом, из
которого путем соответствующих преобразований
получаются случайные величины с любым заданным
распределением (о том, как это делается, будет рассказано
в п. 9.2).
Пример 1. Длина комнаты измеряется с помощью
рулетки с грубыми делениями, отделенными расстояния-
6.1. РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ
157
ми 10 (см). Округление производится до ближайшего
деления; св. X —ошибка измерения. Найти и построить
ее п.р. /(#), ее ф.p. F(x)y найти ее м.о., дисперсию
и с. к. о.
Решение. Плотность f(x) показана на рис. 6.1.7,
ф.р. FJx)-ua рис. 6.1.8; mx = 0; Z)x = 10712 «8,333;
gx ~VAc« 2,887. >
Пример 2. Поезда метрополитена идут регулярно с
интервалом 2 (мин). Пассажир выходит на платформу в
F(x)t
х
случайный момент времени, никак не связанный с
расписанием поездов. Найти п. p. j(x) случайной
величины Т — времени, в течение которого ему придется ждать
поезда, ее м. о., дисперсию и с. к. о. Найти вероятность
того, что ждать придется не больше полминуты.
1/2
1
Ъ-а
'Л I X
1/2 1 2 х
Рис. 6.1.9
а Ь
Рис. 6.1.10
1/2 @<я<2)
= 2712 = 1/3;
(рис. 6.1.9);
mt
Решение. /(#) =
р{г<|} = 1/4; Dt
ot - У1/3. >
Пример 3. С. в. X распределена равномерно на
участке (а, 6). Найти вероятность того, что в результате
опыта она отклонится от своего м. о. больше, _чем на Зох.
Решение. Находим а» = F — а)/BУЗ); 3ax = 3(b —
— а)/BУЗ)»= УЗ(Ь — а)/2. Но при равномерном
распределении на участке (а, Ь) крайние точки а и Ь, ограничи-
158
ГЛ. 6. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
вающие участок возможных значений с. в., отстоят от ее
м.о. тож = (а + Ь)/2 на расстояние (Ь — а)/2 (рис. 6.1.10),
которое меньше, чем УЗ(Ь — а)/2; следовательно, Р{|Х —
|З} 0
6.2. Показательное распределение
Говорят, что непрерывная с. в. X имеет показательное
(или «экспоненциальное») распределение, если
?"~х* при #>0,
О при х ^ О
или, короче,
}(х) = \е~** (.г>0). F.2.1)
Положительная величина X называется параметром
показательного распределения. График показательного
х
Рис. 6.2.1
Рис. 6,2.2
распределения показан на рис. 6.2.1. Его функция
распределения:
X
X
F (х) - J b-**dx - 1 -
(х > 0).
График ф. р. показательного распределения показан
на рис. 6.2.2.
Найдем числовые характеристики показательного
распределения:
00 ОО
о о
Производя интегрирование по частям и учитывая, что
при х -*• <» е~* стремится к пулю быстрее, чем возрастает
любая степень х, находим
1
6.2. ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ 15$
т. е. м. о. случайной величины, имеющей показательное
распределение, обратно его параметру X (который имеет
размерность, обратную размерности с. в. X).
Вычислим дисперсию с. в. X по формуле:
оо
Dx - а2 — ш\ _ X J A~**d* — j% - ji- F.2.3)
о
Отсюда с, к. о.
0,-1/Х, F.2.4)
т. е. с. к. о. с. в. X, имеющей показательное
распределение, равно ее м. о.:
ох = шх = 1 Д.
Коэффициент вариации св. X, имеющей показатель*
ное распределение F.2.1), равен единице:
р —o,/jni —1. F.2.5)
Коэффициент вариации, показывающий, какую долю
математического ожидания составит с. к. о., служит своего
рода характеристикой «степени случайности»
неотрицательной случайной величины и в ряде случаев
применяется для ее оценки. Случайные величины, имеющие v < I,
так сказать, «менее случайны» по сравнению с
имеющими показательное распределение; имеющие v > 1 — «более
случайны».
Чтобы найти асимметрию показательного
распределения, найдем его третий центральный момент:
00
^3 « X J (я - 1/Я)" e~**dx - 2/X\
о
Откуда коэффициент асимметрии
Как и следовало ожидать, асимметрия показательного
распределения положительна.
Показательное распределение тесно связано с
простейшим (стадионарпым пуассоновским) потоком событий*
Покажем, что интервал времени Т между двумя
соседними событиями в простейшем потоке имеет
показательное распределение с параметром, равным интенсивности
потока:
**-" {*> оь 16.2,61
160 ГЛ. 6. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Для этого найдем сначала ф.p. F(t):
Рассмотрим на оси 0* интервал времени Т между
двумя соседними событиями потока (рис. 6.2.3). Для того
чтобы выполнялось неравенство Т < t, нужно, чтобы
хотя бы одно событие потока попало па участок
длины t\ вероятность этого
t откуда
F(t)= 1 — e~u (f >0)\
F.2.7)
Дифференцируя, получим плотность:
-%e-u (t>0), F.2.8)
а это есть не что иное, как показательное распределение
F.21).
Показательное распределение играет большую роль в
теории марковских случайных процессов, теории
массового обслуживания и теории надежности — существенных
разделах прикладной теории вероятностей.
Пример 1. С. в. X имеет показательное
распределение с параметром X = 2. Найти вероятность события
{1Х2>
Решение. Имеем F(.r) = 1 — е* (х>0).
Вероятность попадания на участок A, 2) равна приращению
ф. р. на этом участке:
-е —e"s« 0,368 — 0,135 = 0,233. >
Пример 2. Время безотказной работы ЭВМ —
случайная величина Г, имеющая показательное
распределение с параметром X (физический смысл величины Я —
среднее число отказов в единицу времени, если не считать
простоев ЭВМ для ремонта). Известно, что ЭВМ уже
проработала без отказов время т. Найти при этом условии
плотность распределения fx(t) времени Гт, которое
проработает ЭВМ после момента т до ближайшего отказа.
Решение. Так как простейший поток отказов не
имеет последействия, вероятность появления хотя бы
одного отказа на участке от т до т +J не зависит от того,
6.3. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 161
появлялись ли отказы ранее момента т (рис. 6.2.4):
F, @ » Р {Тх < t) - 1 - е~и (t > 0),
откуда
т. е. распределение времени, оставшегося до следующего
отказа, не зависит от
того, сколько време- ^V
ни ЭВМ уже
проработала безотказно.
Заметим, что этот вы-
,
вод точен только при про- If t
стейшем потоке отказов, рис q.2.4
но приближенно
справедлив и при потоке отказов, мало отличающемся от
простейшего, а такие потоки нередко встречаются на
практике. >
6.3. Нормальное распределение
Нормальный закон распределения (иногда
называемый законом Гаусса) играет исключительно важную
роль в теории вероятностей и занимает среди других
законов распределения особое положение. Говорят, что
с. в. X распределена по нормальному закону с
параметрами пг, о, если ее плотность распределения имеет вид:
(r-mJ
<6-ЗЛ)
или, пользуясь весьма удобным способом записи
показательной функции ехр {х) = е*
(она позволяет избегать
«многоэтажных» формул),
Кривая нормального
распределения имеет симметричный,
холмообразный вид (рис. 6.3.1).
Максимальная ордината кривой, равная 1/(оУ2л),
достигается при х «= т (мода Мх = т); из соображений
симметрии мы вправе ожидать, что она совпадает с м, о, слу-
6 Теория вероятности к с
инженерные приложен»! i
162 ГЛ. 6. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
чайной величины X, если оно существует (ниже мы
непосредственно в этом убедимся). По мере удаления от
точки т плотность j(x) падает, и при х-+ «> кривая
распределения асимптотически приближается к оси абсцисс.
Вычислим основные характеристики с. в. X,
распределенной по нормальному закону F.3.1),—-м.о., дисперсию
и с. к. о. Имеем:
оо оо (х—т)а
М [X] - J */<*) dx - -±== J xe 2o1 dx. F.3.2)
Применяя замену переменной
*«(z-m)/@-y2)f F.3.3)
получим
00
М [X] - X* f (о /2 / + m) «-'"Л -
Первый из интегралов в формуле F.3.4) равен нулю, как
интеграл в симметричных пределах от нечетной функции;
второй представляет собой известный интеграл Эйлера —
Пуассона:
00 ОО
J e"t%dt - 2 J tf-''л = /я, F.3.5)
-оо О
Следовательно, м. о, величины X существует и, как мы и
ожидали, равно т:
М [X] « т. F.3.6)
Величина т — м. о. нормально распределенной с. в, X,
называется ее «центром рассеивания».
Вычислим дисперсию с. в. X:
Применим снова замену перемониой F.3.3):
оо
6 3 НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Интегрируя по частям, получим:
163
о
V
ос
2 Г о **
Первое слагаемое в фигурных скобках равно нулю (так
как е~* при t -> <» убывает быстрее, чем возрастает любая
степень *)> второе слагаемое, согласно F.3.5), равно Уя,
откуда
D [X] = о\ F.3.7)
т. е. дисперсия с. в. X, распределенной по нормальному
закону с параметрами т, о, равна о2. Значит, параметр а
есть не что ппое, как
отклонение св. X:
среднее квадратическое
/D[XJ
с.
F.3.8)
Размерности как м. о.~ /га, так и с. к. о.~ о совпадают
с размерностью с. в. X.
Посмотрим, как будет меняться кривая распределения
при изменении параметров ш, о. При изменепии m
кривая /(x)t не изменяя своей формы, просто будет смещаться
вдоль оси абсцисс. Изменепие о равносильно изменению
масштаба кривой по обеим осям; например, при
удвоений о масштаб по оси абсцисс удвоится, а по оси
ординат — уменьшится в два раза. Для иллюстрации на
рис. 6.3.2 показаны три нормальные кривые
распределений; для всех трех т=*»0; для кривой (I) 0 — 1, для
кривой (II) 0 = 2,5, для кривой (III) ов 1/2 (при построе-
164 ГЛ. 6. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
нии кривых мы пользовались таблицей значений функции
— нормальная плотность для т » О, о = 1, приведенной в
приложении [4]). Как видно из рис. 6.3.2, при
увеличении о кривая распределения становится более плоской,
растягивается вдоль оси абсцисс; при уменьшении о —
вытягивается вверх, одновременно сжимаясь с боков
(в обоих случаях ограничивая единичную площадь).
Вычислим для нормальной св. X F.3.1) ее
центральные моменты любого порядка \i, [X]. Имеем
00 °° (х—тJ
Р.[Х]~ f (*-mO(*)<**-—L= f (x-m)'e~ w* dx.
Снова делая замену переменной F.3.3), получим:
f.-1"*. F.3.9)
Естественно, при любом нечетном s |л, = 0 (интеграл
в симметричных пределах от нечетной функции равен
нулю); предположим, что s четно, и применим к F.3.9)
интегрирование по частям:
Имея в виду, что первый член внутри фигурных
скобок равен нулю, получим:
2 Л/ п J
—оо
Теперь подставим в формулу F.3.9) s —2 вместо s:
",-••*. F.3Л1)
6.3. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 165
Сравнивая между собой правые части формул F.3.10)
и F.3.11), видим, что они отличаются только
множителем E — 1) о2. Следовательно,
\x. = {s-l)o2iis-2. F.3.12)
Формула F.3.12) представляет собой простое
рекуррентное соотношение, позволяющее выражать
центральные моменты более высоких четных порядков через
центральные моменты более низких. В частности, учитывая,
что для любой св. m.q — 1, получим: и* —а2; щ — За4;
|д,6 в 3 • 5о8 = 15ов и т. д.
Из выражения для ц4 получим
ц4/о4 - Зо7о4 - 3.
Следовательно, эксцесс нормального распределения
равен нулю:
8ж = jx4/0* — 3 = 0 F.3.13)
(мы об этом уже упоминали в п. 4.2).
Вычислим для нормальной с. в. X вероятность
попадания на участок от а до р:
0 (x-m)a
Р 20* dx. F.3.14)
а w а
Сделав в интеграле F.3.14) замену переменной t=*
*=*(х — т)/о и соответственно изменяя пределы
интегрирования, получим
Г — *2/2
Как известно, неопределенный интеграл J e dt
не выражается через элементарные функции, но его
можно выразить через специальную функцию
'2/2^ F'3-15)
называемую функцией Лапласа (или «интегралом вероят-
156
гл- в- НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
ностей»), для которой составлены таблицы
(приложение 2)*).
С помощью этой функции вероятность попадания
нормально распределенной с. в. X на участок от а до ?
выражается простой формулой:
Функция Лапласа Ф{х) обладает следующими
свойствами: 1) Ф@) = 0; 2) Ф(-х) = -Ф(х) (нечетная
функция); 3) Ф(+оо)«0,5 (и, значит, Ф(-»)--0,5].
Действительно, первое свой-
ffic) ство очевидно:
-о.
Докажем второе:
рис. б.з.з
х
делая замену переменной 4
получим
Третье свойство следует из того, что, согласно F.3.5),
Наиболее просто выражается через функцию Лапласа
вероятность попадания нормально распределенной с. в.
X на участок длиной 21, симметричный относительно
центра рассеивания (рис. 6.3.3). А нменпо,
¦) В некоторых руководствах по теории вероятностей
«функцией Лапласа» называют не функцию F.3.15), а другую,
отличающуюся от нее постоянным множителем, в чем нетрудно в
случае надобности разобраться.
6 3 НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 167
или, принимая во внимание нечетность функции
Лапласа,
Р {| X - т | < 1} - 2Ф (Z/j). F.3.17)
Через функцию Лапласа выражается и ф. p. F(x)
нормально распределенной св. X. По формуле @.3.16),
полагая а = — <», ? = я и учитывая, что Ф(—«>)=: —1/2,
получим:
F.3.18)
Теперь несколько слов об условиях возникновения
нормального распределения и о причинах его широкой
распространенности в случайных явлениях природы. Опо
возникает в тех случаях, когда складывается много
независимых (или слабо зависимых) случайных величин
Xi, Х1у ..., Хп
Х« %Х{ F.3.19)
i
(причем эти величины сравпимы по порядку своего
влияния на рассеивание суммы). Тогда, каковы бы ни были
законы распределения отдельных величин Х„ Хг, .,., Хп,
закон распределения их суммы X будет близок к
нормальному (причем тем ближе, чем больше число
слагаемых п).
Высказанное выше положение, которое мы пока
никак не обосновываем, представляет собой, в грубых
чертах, содержание центральной предельной те о*
ремы теории вероятностей, с различными
формами которой мы познакомимся в гл. 10. Ограничение,
налагаемое на складываемые случайные величины («чтобы они
были сравнимы по порядку своего влияния на
рассеивание суммы») становится попятным, если представить себе,
что, скажем, одна из случайных величин Хи Хг, ..., Хп
обладает очень большим рассеиванием, резко
превалирующим над рассеиванием всех остальных; ясно, что
закон распределения именно этой случайной величины на-
тожит свой отпечаток па закон распределения суммы,
[ никакой «нормализации» не произойдет. Это условие
гримерной «равноправности» слагаемых будет выражено
а математической форме для различных форм
центральной предельной теоремы в гл. 10.
168 ГЛ. 6. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Очерь часто встречающиеся на практике случайные
величины образуются именно в результате суммирования
многих случайных слагаемых, сравнимых по степени
своего влияния на рассеивание суммы. В частности, в
очень многих случаях практики ошибки
измерения распределяются по закону, близкому к
нормальному. Действительно, пусть, например, мы взвешиваем
тело на точных (аналитических) весах. Обозначим X
ошибку взвешивания и представим ее в виде суммы
большого числа малых погрешностей, каждая из которых
вызвана действием одной, отдельной, не зависимой от
других причины:
г=1
где, например, X, — ошибка, возникающая из-за
положения тела на чашке весов; Х2 — ошибка от неточности
зрительного совмещения стрелки весов с определенной
отметкой шкалы; Х3 — ошибка, связанная с вибрацией
стола, на котором установлены весы, и т. д. Ясно, что
число п таких «элементарных» ошибок весьма велико;
мы вправе ожидать, что с. в. X будет иметь нормальное
У (или близкое к нормальному) распре-
(X у; деление. Это и подтверждается опытом:
I __j как Правило? ошибки «точных измере-
| ний» имеют распределение, близкое
| к нормальному*).
I Ошибки стрельбы (координаты точ-
i~~^ ки попадания X, Y в системе коорди-
* й
" л нат, связанных с точкой прицелива-
Рис. 6.3.4 ния 0 (рис. 6.3.4)) по тем же
причинам имеют нормальное (или близкое
к нему) распределение: каждая из величин X, У
представляет собой сумму большого числа слагаемых
(элементарных ошибок), связанных с отдельными причинами,
вызывающими отклонение снарядов от точки прицеливания.
Ошибки выполнения команд автоматизированным
устройством; ошибки вывода космического корабля в за-
*) Ранее мы показали, что ошибка «грубого измерения»
имеет равномерное распределение. «Грубое измерение» отличается от
«точного» тем, что его повторение дает всегда одно и то же
значение измеряемой величины; при «точном» же измерении
результат от раза к разу меняется.
6.3. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
169
данную точку пространства; ошибки параметров
элементов вычислительной техники, а также множество других
«ошибок», сопровождающих целенаправленную
деятельность человека, в очень большой доле случаев имеют
нормальное или близкое к нормальному распределение.
В дальнейшем (пп. 9.5, 9.8) мы встретимся с
примерами случайных величин, образованных суммированием
большого числа случайных слагаемых и поэтому
распределенных практически нормально. Заметим, что при
увеличении числа слагаемых закон распределения их суммы
довольно быстро «нормализуется». Продемонстрируем это
2 со
А
и-
"о
(X)
'Л
1 1
1 1,
Рис.
5
6.
i
2
3.5
3 oc
(пока без доказательства) на примере суммирования
независимых случайных величин, имеющих равномерное
распределение на участке @,1). Кривая распределения
U{x) одной такой случайной величины показана на
рис. 6.3.5, а. На рис. 6.3.5, б показана плотность
распределения fz(x) суммы двух таких случайных величин; на
рис. 6.3.5, в —плотность распределения /3(х) суммы
трех таких величин (кривая составлена из трех отрезков
параболы и по виду уже напоминает нормальную,
подробнее см. пример 2 п. 9.5)* Если же сложить шесть та-
170 ГЛ. 6. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
кпх случайных величин, то получится случайная
величина с плотностью распределения, практически не
отличимой от нормальной*).
Решим несколько примеров, связанных с нормальным
распределением.
Пример 1. Найти абсциссы точек перегиба кривой
распределения f(x) нормального закона (рис. 6.3.6).
Решение. Точки переги-
f(X) ба — это такие точки, в кото-
**. рых вторая производная функ-
/ \ ции f(x) обращается в нуль.
Дифференцируя функцию f(x) =
о у 2л
раза' пмеем
два
Г(*)^(*)[1(*тOоЧ/о\
Рнс 6.3.6 F.3.20)
Выражение F.3.20) обращается в нуль в точках т±
±а; таким образом, точки перегиба кривой
распределения нормального закона отстоят па расстояние а в ту
и другую сторону от центра рассеивания т, как и
показано на рис. 6.3.6. >
Пример 2. Имеется с. в. X, распределенная нор-
мальпо с параметрами w, а. Найти вероятиость того, что
с. в. X отклонится от своего математического ожидания
т больше, чем на За.
Р
{||>} {|
по формуле F.3.17), полагая J = 3o, паходим:
По таблицам функции Лапласа (приложение 2)
паходим
ФC)« 0,49865; 2ФC)« 0,9973;
Р{|Х-ml >3о) «0,0027.
Это — действительно малая вероятность. >
*) При моделировании случайных явлений на ЭВМ часто
пользуются вместо нормального распределения суммой шести, в
крайнем случае десяти независимых с. в., имеющих равномерное
распределение на участке @,1) (см. п. 6.1).
6.3. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 171
Заметим, что само «правило трех сигма» ведет свое
начало именно от нормального распределения, которое
очень часто встречается в случайных явлениях природы.
Для нормального закона это правило выполняется с
очень высокой точностью; применяя его, мы будем
ошибаться приблизительно в трех случаях из 1000. Если
такая точность нас не устраивает, можно увеличить
диапазон возможных значений с. в., распределенной
нормально, до т ± 4а:
Р{|Х- /п|>4а} = 1- 2ФD)« 1-2-0,499968 -
= 0,000064,
т. е. с. в. с нормальным распределением будет отходить
от своего математического ожидания т больше, чем на
4о, только примерно в 6 случаях на 100000 опытов.
Пример 3. Откладывая от математического
ожидания т последовательно, один за другим, отрезки длиной
о, найти (с точностью до 0,001) вероятности попадания
с. в. X, распределенной нормально, на эти отрезки.
Решение. По формуле F.3.16):
Р{т<Х<т + о} = ф(-1) -Ф@) - ФA)&0,341;
+ о<Х<т +2а} =ф(^)-ф(-^)« 0,136;
За}-ф(^) — ф(-^)« 0,021.
Суммируя эти вероятности, вычисленные с
погрешностью не более 0,01, найдем вероятность попадания с. в,
X правее точки т: она равна 0,5. Числа 0,34, 0,14 и 0,02
полезно запомнить для ориентировочной «прикидки»
вероятностей попадания нормально распределенной с. в.
на какие-то участки. >
Пример 4. Завод изготовляет шарики для
подшипников, номинальный диаметр которых равен 10 (мм),
а фактический диаметр случаен и распределен по
нормальному закону с м. о. т — 10 (мм) и с. к. о. о =
¦=0,4 (мм). При контроле бракуются все шарики, не
проходящие через круглое отверствие с диаметром dt —
¦-10,7 (мм) и все, проходящие через круглое отверстие
с диаметром di —9,3 (мм). Найти процент шариков,
которые будут браковаться,
172 ГЛ. 6. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Решение. Вероятность того, что шарик будет
забракован:
Р{\Х-т\>0,Т}-1-Р{\Х-т\<0,1).
По формуле F,3,17)
Р {| X - т | < 0,7} = 2Ф (-J4) « 2 • 0,459 - 0,918,
Р{|Х-иг|> 0,7} = 0,082.
Таким образом, браковаться будет около 8,2%
шариков. >
Пример 5. Номинальное напряжение в схеме
равно и0; фактическое напряжение U случайно и имеет
нормальное распределение с параметрами
q(u) щ и ом. В схему включается
радиолампа. Вероятность q(u) того, что лампа
перегорит в момент включения,
зависит от напряжения U и возрастает
линейно от 0 при C/ = u0 до 1 при
U = Ui (рис. 6.3.7). Найти полную
вероятность того, что радиолампа
перегорит в момент включения.
Решение. Функция q(u) имеет вид:
q{u)
0 при и < и0,
(и — поУ^ — ио) при ио<и<ии
1 при и > их.
По интегральной формуле полной вероятности (п. 3.4)
находим:
J q{u)j{u)du%
где q(и) — вероятность отказа радиолампы при U = и;
f(u)—плотность распределения напряжения С/,
нормальная с параметрами и0 и о«:
6.4. ГАММА-РАСПРЕДЕЛЕНИЕ 173
Следовательно,
Последняя вероятность
P{U>ul}-P{ul<U <*>}¦.
Вычислим интеграл:
Функция под знаком интеграла есть не что иное, как
\ (м-«о)М
производная от функции exp s — -f—) по и, следо-
l u J
вательно,
6.4. Гамма*распределение и распределение Эрлапга
Неотрицательная с. в. X имеет гамма-распределение\
если ее п. р. выражается формулой:
Ft4tl)
174 ГЛ. 6. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
где К > О и к > О, Г (к) — гамма-функция:
-У-1^, F.4.2)
Гамма-распределение довольно часто встречается в
приложениях теории вероятностей, особенно в
математической статистике.
Гамма-функция обладает свойствами:
Г(А+1) = /сГ(*), ГA)-1, F.4.3)
откуда следует, что если к целое неотрицательное число,
то
Г(* + 1)"-*!-1-2-...-Л. F.4.4)
Кроме того, нам в последующем потребуется еще
одно свойство гамма-функции:
F.4.5)
Найдем числовые характеристики с. в. Ху подчинен*
ной гамма-распределению:
о
о
В соответствии с равенством F.4.3) получим:
тх - М [X] - к/К. F.4.6)
Второй начальный момент найдем по формуле
00 00
»+a*iK Г (к + 2) _ к (к + 1)
f
J
О О
откуда
Г (к) -J Я2Г(А) - xtr(A)
Ас - D [X] - а2 [X] - mj - 4-. F.4.7)
л
При к — i гамма-распределение превращается в
показательное с параметром Я, рассмотренное в п. 6.2, так как
¦) Например, при к — 4 имеем: BЛ — 1}!! = B4— 1)!! —.
. 711— 1-8-5-7 — 105.
6.4. ГАММА-РАСПРЕДЕЛЕНИЕ 175
При целом к > 1 гамма-распределение превращается в
распределение Эрланга к-то порядка:
0; А = I- 2, 3, .. .)• F.4.8)
Подробнее об инженерных условиях возникновения
закона Эрланга Аг-го порядка говорится в п. 9.5. Здесь
достаточно лишь указать, что закону Эрланга Аг-го порядка
подчинена сумма независимых с. в. Х{ + Х2 + ... + Хк1
каждая из которых распределена по показательному
закону с параметром Л. Закон Эрланга А:-го порядка тесно
Рис. 6.4.1
связан со стационарным пуассоновским (простейшим)
потоком с интенсивностью К.
Действительно, пусть имеется такой поток событий
во времени (рис. 6.4.1). Рассмотрим интервал времени Г,
состоящий из суммы к интервалов между событиями в
таком потоке. Можно доказать, что с. в. Т будет
подчинена закону Эрланга А-го порядка. В п. 9.5 это
утверждение будет доказано.
Плотность распределения с. в. X, распределенной по
закону Эрланга Л-го порядка, может быть выражена
через табличную функцию распределения Пуассона E.2.7):
(Л>0; *>0; к-1,2, ...), F.4.9)
где
Можно доказать, что ф. р. с. в. X
X X
о
1 - R (к - 1, JLr) = Я (к -1, he), F.4.10)
176 ГЛ. 6. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
где Я (ft, tar)— I ~i?(ft, Kx) определяются выражениями
E.2.8) и E.2.9). Следовательно, имеют место равенства,
которые нам в дальнейшем пригодятся:
-P(k,a); R (к, а)^^Р (к, х) dx. F.4.11)
Пример. Поток производимых на конвейере
изделий является простейшим с параметром К. Все
производимые изделия контролируются, бракованные
укладываются в специальный ящик, в котором помещается не
более к изделий, вероятность брака равна р. Определить
закон распределения времени Т заполнения ящика
бракованными изделиями и величину к исходя из того,
чтобы ящик с вероятностью ^ = 0,99 не переполнялся в
течение смепы.
Решение. Интенсивность простейшего потока
бракованных изделий будет Хр. Очевидно, что время Т
заполнения ящика бракованными изделиями распределено
по закону Эрланга с параметрами к и Хр:
следовательно (см. F.4.6) и F.4.7)):
Число бракованных изделий за время / будет
распределено по закону Пуассона с параметром Xpt.
Следовательно, искомое число к нужно находить из условия
0,99 - ^ - Р (Т < t) - Fh (t) = R {к - 1, kpt). F.4.12)
Например, про Х=а20 [изделие/ч]: р = 0,1; * = 8 [ч]
из уравнения
0,99 = /? (ft, 16)
по таблицам приложения 2, помещенным в [4]. получаем:
при ft - 26 (ft - 1 - 25)
^ « 1 — 0,0131 да 0,9869 да 0,99. >
ГЛАВА 7
СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
(СЛУЧАЙНЫЕ ВЕКТОРЫ)
7.1. Понятие о системе случайных величин
В гл. 3 и следующих за нею главах мы
рассматривали отдельные случайные величины (дискретные и не-
дискретные), их законы распределения и числовые
характеристики. В принятой нами теоретико-множественной
трактовке любая случайная величина X есть функция
элементарного события со, входящего в пространство
элементарных событий Q:
каждому элементарному событию со s Q ставится в
соответствие некоторое действительное число a;sS, где
S — множество возможных значений случайной
величины X.
В данной главе мы будем рассматривать не
отдельные случайные величины, а системы (совокупности)
нескольких случайных величин — двух или более.
Примеры систем случайных величин.
1. Точка приземления космического летательного
аппарата может быть охарактеризована системой двух
случайных величин: X—географическая широта и У —
географическая долгота точки; совокупность двух
случайных величин {X, Y) является системой случайных
величин.
2. Успеваемость студента, окончившего курс обучения
в вузе, характеризуется системой п случайных величин
Xi, Х2у ..., Хп —¦ оценками, проставленными в его
дипломе по пятибалльной системе.
3. Состояние вычислительной машины в момент
времени t характеризуется системой многих случайных
величин, среди которых: время наработки после последнего
отказа ЭВМ; количество ячеек оперативной памяти,
занятых обработкой информации; положение магнитных
178 ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
лент и накопителей; число отказавших элементов ЭВМ;
общее число отказов ЭВМ с момента ввода ее в
эксплуатацию и т. д. Конкретный набор случайных величин,
вводимых в рассмотрение, зависит от того, какая задача
решается и с какой целью.
Аналогично этому, состояние любого технического
устройства в заданный момент t характеризуется
системой (набором) нескольких случайных величин.
Условимся систему нескольких случайных величин
X, У, ..., W обозначать (X, У, ..., W). Система
случайных величин (как и каждая из ее составляющих) есть
функция элехментарного события
(X, У, ..., ^)-ф(ш);
каждому элементарному событию со ставится в
соответствие несколько действительных чисел: значения,
принятые случайными величинами X, F, ..., W в
результате опыта.
Пример. Опыт состоит в том, что вынимается
наугад одна кость из полного набора костей домино; с. в.
X—сумма чисел очков, стоящих на половинах кости;
случайная величина У — их произведение. Пространство
элементарных событий состоит из 28 элементов,
соответственно 28 костям домино:
Й = {0/0; 0/1; 0/2; ...; 1/1; 1/2; ...
...; 1/6; ...; 5/5; 5/6; 6/6}.
Если в результате опыта появилось какое-то из этих
элементарных событий, то случайные величины X, У
получают вполне определенные значения; например, если
вынута кость 3/4, то X —7; У =12. Совокупность этих
значений — функция элементарного события ю. >
Случайные величины (X, У, ..., W), входящие в
систему, могут быть как дискретными, так и
недискретными (непрерывными или смешанными; в вышерассмот-
ренном примере обе с. в. X и У дискретны).
Для наглядности рассмотрения и исследования
системы случайных величин удобно пользоваться
геометрической интерпретацией. Так, систему двух случайных
величин (X, У) можно изобразить случайной гонкой на
плоскости с координатами X и У (рис. 7.1.1), или, что
равносильно, случайным вектором, направленным из
начала координат в точку (X, У) (рис. 7.1.2); случайные
величины X, У представляют собой составляющие
7.2. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СИСТЕМЫ 179
этого вектора (рис. 7.1.2). Аналогично, систему трех
случайных величин (X, У, Z) можно изобразить как
случайную точку в трехмерном пространстве с
координатами X, У, Z или, что равносильно, как случайный
вектор, направленный из начала координат в эту точку, с
составляющими X, У, Z.
I T(X,Y)
I a: ^
"^ X х
Ряс. 7.1.1 Рис. 7.1.2
При числе измерений больше трех геометрическая
интерпретация теряет наглядность, но пользование
геометрической терминологией остается удобным. Так, мы
будем говорить о системе случайных величин (Хи Хг, ...
..., Хп), как о случайной точке в пространстве п
измерений или о случайном векторе в том же пространстве
и пользоваться для него обозначением
Xе {Xif Xiy #,., Хп).
Очевидно, свойства системы случайных величин не
исчерпываются свойствами отдельных величин, входящих
в систему; существенны также связи (зависимости)
между величинами. Полной характеристикой системы
случайных величин является ее закон распределе-
н и я, который, как и для отдельных случайных величин,
может иметь разные формы (функция распределения;
плотность распределения; таблица вероятностей
отдельных значений случайного вектора и т. д.). Кроме вако-
нов распределения, мы будем рассматривать также и
числовые характеристики системы случайных величин.
7.2, Функция распределения системы
двух случайных величин
Функцией распределения (или «совместной»
функцией распределения) системы двух случайных величин
(X, У) называется вероятность совместного выполнения
двух неравепств: X <х\ Y <у:
Р (*, У) - Р {* < Ъ У < У}* G.2.1)
180 гл. 7. системы случайных величин
Стоящее в фигурных скобках событие означает
произведение событий {Х<х) и {Y<y):
{Х<х; Y<y} = {X<xHY<y}*).
Пользуясь геометрической интерпретацией системы
(X, Y) как случайной точки иа плоскости, можно
дать геометрическое истолкование
функции распределения F(x, у):
это есть не что иное, как
вероятность попадания случайной точки
(X, У) в бесконечный квадрант с
~5Г вершиной в точке (х, у),
лежащий левее и ниже ее (заштри-
Рис 721 хован на рис. 7.2.1). Правая и
и ' * ' верхняя границы квадранта в
него не включаются.
Пользуясь геометрической интерпретацией, выведем
основные свойства функции распределения системы двух
случайных величин.
1. Функция распределения F(x, у) есть
неубывающая функция обоих своих аргументов, т. е.
при х2>хг F(х2У y)^F(xv у); |
при у2 > у, F (х, у2) > F (х, у,) Г [ '
Это свойство следует из того, что при увеличении
какого-нибудь из аргументов (я, у) (или обоих сразу)
квадрант, заштрихованный на рис. 7.2.1, увеличивается;
естественно, вероятность попадания в него случайной
точки (X, Y) уменьшиться не может.
2. Если хотя бы один из аргументов обращается в
—оо, функция распределения равна нулю:
F(Xt -oo) = F(-oo, y)-F(-oof _oo)«o G.2.3)
или, короче, повсюду на минус
бесконечности функция распределения равна нулю.
Это свойство следует из того, что при х -* — <», или
у -+ _«>, или х -> — оо, у -> —оо квадрант с вершиной в
точке {х, у) будет «уходить» с плоскости хОу;
естественно, вероятность попадания в него случайной точки будет
стремиться к нулю. Это свойство вытекает также из
определения G.2.1) функции F(x, у), так как события Х<
•) К такой упрощсппой форме записи мы прибегаем, чтобы
избежать фигурных скобок внутри фигурных.
7.2. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СИСТЕМЫ
181
-«>, а также и их произведение
невозможны.
3. Если оба аргумента равны +©о?
функция распределения равна единице:
/г(+оо, +оо)-1. G.2.4)
Это следует из того, что при х ->- +<», у -+¦ +<»
квадрант с вершиной в точке (я, у) заполняет всю плоскость,
а попадание случайной точки (X, Y) на эту плоскость —
событие достоверное.
4. Если один из аргументов обращается в +<»,
функция распределения F(x, у) становится равной
функции распределения случайной величины,
соответствующей другому аргументу:
F(x, + оо)
F(+oo,y)
(У)
G.2.5)
где F{(x), F2{y) — фупкции распределения случайных
величин X и Y соответственно:
Fx(x)
F2(y)
Действительно, F(x, + оо) == Р {Х<?х, У < + оо}. Но
{У<+оо} — событие достоверное; а любое событие,
Рис. 7.2.2
Рис. 7.2.3
будучи умноженным на достоверное событие Q, не
меняется (см. п. 2.3); отсюда
F(x, + oo) = P{X<x} = Fx(x).
Точно так же доказывается, что
F(+oo,y)-P{Y<y}-F2{y).
Последнее свойство функции распределения F{x, у)
наглядно можно проиллюстрировать, смещая ту или
иную границу квадранта, изображенного на рис. 7.2.1,
на +«> (рис. 7.2.2 и 7.2.3). В этом случае квадрант пре-
182
ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
1 ^
вращается в полуплоскость, вероятность попадания в
которую есть ф. р. с. в., соответствующей тому
аргументу, который не равен +<».
5. Из определения G.2.1) следует, что функция
распределения F(x, у) (как и функция распределения
любой случайной величины) непрерывна слева по
любому аргументу. Из этого видно, что в геометрической
интерпретации F(x, у) как
вероятности попадания в
квадрант с вершиной (х, у)
правая и верхняя границы
квадранта в него не включа-
ются.
В геометрической интер-
претации функция распреде-
ления F(x, у) есть некоторая
поверхность,
обладающая указанными свойствами. Вид этой поверхности
зависит от того, дискретны, непрерывны или смешанны
входящие в систему св. (X, Y).
Зная функцию распределения F(x, у), можно найти
вероятность попадания случайной точки (X, Y) в
пределы прямоугольника R со сторонами, параллельными осям
координат, ограниченного абсциссами (а, [}) и
ординатами (*f, б) (левая и нижняя границы включаются в /?,
а правая и верхняя — не включаются; см. рис. 7.2.4, где
жирными линиями обозначены включаемые в R
границы). Докажем, что
р х
Рис. 7.2.4
G.2.6)
Действительно, вероятность попадания в
прямоугольник R равна вероятности попадания в квадрант с
вершиной в точке (Р, б), минус вероятность попадапия в
квадрант с вершиной в точке (а, б), минус вероятность
попадания в квадрант с вершиной в точке ((J, *у), плюс
вероятность попадания в квадрант с вершиной в точке
(a, if)» которую мы вычли дважды.
Функция распределения F(x> у)— наиболее
универсальная форма закона распределения, пригодная для
системы любых двух случайных величин — дискретных и
педискретных.
7.3. СИСТЕМА ДВУХ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН 183
7.3. Система двух дискретных случайных
величин. Матрица распределения
Рассмотрим случай двух дискретных случайных
величин (X, У). Для простоты будем считать, что
множество возможных значении каждой из них конечно; для
св. X это Е = {хи х2, ..., хп), а для св. У — Н =
= {г/t, у2, ..., ут]. Обозначим рц вероятность того, что
с. в. X примет значение хи а с. в. У — значение у^.
G.3.1)
Событие
-х,; Y-Vj\.
есть произведение событий
{ х y3
Аналогом ряда распределения одной дискретной
случайной величины X для двух дискретных случайных
величин (X, Y) является матрица распределения —
прямоугольная таблица, в которой записаны все вероятности
Ра A-1, ..., п\ / = 1, ..., т). Матрицу распределения
системы двух дискретных с. в. (X, Y) будем записывать
в виде:
(X,Y) :
Х2
Х\
хп
V,
Рп
'21
Рп\
У*
Р\г
Р22
Pit
Рп2
Pi)
Рю
Pi)
Рп}
Vm
Pim
Р*т
Pim
Рпт
G.3.2)
Сумма всех вероятностей pih стоящих в матрице
G.3.2), равна единице как сумма вероятностей полной
группы несовместных событий:
1.
184
ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИИ
Если известна матрица распределения G.3.2)
системы двух дискретных случайных величин (X, У), то ее
функция распределения находится суммированием всех
вероятностей рц, для которых хг<х, Уз<у:
(См. выделенный «левый верхний угол» матрицы 7.3.2').
Множество возможных значений дискретных
случайных величин X и У может быть не только конечным, но
и бесконечным (счетным).
(X ,У):
\
*2
Х\
V,
Рп
Рп
Рп
V.
Pl2
Рц
Рц
хп
Рщ
Р-пг
щ
р2)
Pi)
Рп}
Ут
Р\т
Р^т
Ргт
Рпт
G.3.2')
В этом случае матрица распределения имеет
бесконечные размеры, но ее свойства сохраняются теми же, что
при конечных п и т.
Ниже мы для простоты будем считать пит
конечными; в случае, когда множество возможных значений
одной из с. в. (X, Y) (или обеих) бесконечно (счетно),
соответствующие пределы п и т в суммах нужно
заменить на бесконечные.
Зная матрицу распределения системы двух
дискретных случайных величин (X, У), легко можно найти
законы (ряды) распределения отдельных случайных
величин X и У, входящих в систему. Обозначим
7.3. СИСТЕМА ДВУХ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН 185
Найдем Р {X = xfy, для этого события {Х = хг}
представим как сумму несовместных вариантов:
По правилу сложения вероятностей
/^-Р{*-*>-Дру G.3.3)
и, аналогично,
т. е. для того, чтобы найти вероятность
того, что отдельная случайная величина,
входящая в систему, примет определенное
значение, надо просуммировать вероятности
ри, стоящие в соответствующей этому
значению строке (столбце) матрицы
распределения.
Пример 1. Два стрелка, независимо друг от друга,
делают по два одиночных (независимых) выстрела
каждый по своей мишени. Случайная величина X — число
попаданий первого стрелка, Y -— число попаданий
второго стрелка. Вероятность попадания при одном выстреле
для первого стрелка pt = 0,7, для второго р2 = 0,4.
Построить матрицу распределения \\pi}\\ системы случайных
величин (X, У) и законы (ряды) распределения
отдельных случайных величин X и У. Найти функцию
распределения F(x, у).
Решение. Возможные значения случайных
величин X и У:
*i = 0; хг = 1; яз = 2; #1 = 0; j/2 = l; j/3 = 2.
Возможные пары значений системы случайных
величин (X, У):
@,0), @,1), @,2), A,0), A,1), A,2);
B, 0), B, 1), B, 2).
Соответствующие этим парам вероятности вычисляем,
пользуясь правилами сложения и умножения вероятностей,
186 ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
Имеем:
ри = Р {Х = О, У = 0} = Р {первый стрелок оба раза
промахнулся и второй стрелок оба раза промахнулся}=
= A-/>,)гA-/>*)' = 0,0324.
р12 = Р{Х = 0; У - 1} - 0,3^2-0,4-0,6 = 0,0132;
р13 = р {X = 0, У = 2} = 0,0144;
Рп _ р {* = 1; У = 0} = 0,1512;
р22 *= р {X = 1, У - 1} - 0,2016;
ргз = Р{Х = 1; У-2} = 0,0672;
/>31 = Р {X = 2; У = 0} = 0,1764;
Рз2 = Р {^ = 2; У = 1} = 0,2352;
Рзз - Р {* - 2; У = 2} = 0,0784.
Матрица распределения системы случайных величин
(X, Y) имеет вид:
Y):
*i \
0
1
2
0
0,0324
0,1512
0,1764
1
0,0432
0,2016
0,2352
2
0,0144
0,0672
0,0784
G.3.5)
На основании матрицы G,3.5) находим значения
функции распределения F(x, у) (см. G.3.6)).
N. У
0<х
Кх
х>
\
0
<
2
ч
1
2
0
0
0
0
0<1/<1
0
0,0324
0,1836
0,3600
0
0,0756
0,4284
0,8400
у>2
0
0,0900
0,5100
1,000
G.3.6)
7.3. СИСТЕМА ДВУХ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН 187
Законы распределения отдельных случайных величин
X и У получим, суммируя вероятности, стоящие
соответственно в строках (столбцах) матрицы G.3.5):
р - Р {X = 0} = 0,0324 + 0,0432 + 0,0144 = 0,09;
Р*2 = Р <* = !> = 0,42;
р„ -Р<У-1}-0,48;
(Эти значения мы могли бы получить непосредственно
из условий задачи, не пользуясь матрицей G.3.5).)
Ряды распределения случайных величин X и Y име«
ют вид:
X ;
0
0,09
1
0,42
2
0,49
; У i
0
0,36
\
0,48
2
0,16
G.3.7)
Пример 2. Для условий примера 1 построить
матрицу распределения двух других случайных величин:
(сумма п разность чисел попадания первого и второго
стрелков). По этой матрице найти законы (ряды)
распределения случайных величин U и V по отдельности.
Решение. Возможные значения случайной
величины U:
Mi = 0; и2 = 1; м3 в 2; ик = 3; и5 — 4.
Возможные значения св. V (в порядке возрастания):
^ = -2; 0, —-1; г,-0; У4 = 1; i>»*=2.
Найдем все вероятности
188
ГЛ. 7. СИСТЕМЫ СЛУЧАЙПЫХ ВЕЛИЧИН
Для этого составим таблицу значений случайных
величин U и V при заданных значениях X и Y (см.
G.3.8)); значение величины U записано в верхней левой
половине клетки, величины V — в нижней правой:
0
1
2
0
X
х
х
1
X
X
X
2
X
X
X
G.3.8)
Пользуясь этой таблицей и матрицей распределения
G.3.5), найдем:
Рп = р {U = 0; V 2} = 0
(так как клетки с такой парой значений в таблице
G.3.8) нет); аналогично
i3
=0; F=-l)=0
pi3=P{?/=0; F=0} =0,0324
=О; F=l}=0
=0; V--2}=0
—1; г—2}=о
-*5 И—1^0,0432
1; F=l}=0,1512
=Р{?/:=:2; F=-2}=0,0144
413; !-'=—2}=0
p42=P{f/=3; F=-l) =0,0672
3=Plf=3; F=0}=0
4=P{f/=3; F=l}=0,2352
4; F=-2}=0
ч=Р{?/=4; F=0}=0,0784
4; F=2}=0
^55
Матрица распределения системы случайных величин
7.3. СИСТЕМА ДВУХ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН 189
(?/, V) имеет вид:
ui \^
их=0
аа=2
«4 — 3
и.-4
р.—2
0
0
0,0144
. 0
0
0
0,0432
0
0,0672
0
«3 = 0
0,0324
0
0,2016
0
0,0784
0
0,1512
0
0,2352
0
0
0
0,1764
0
0
G.3.9)
Суммируя вероятности, стоящие в строках и столбцах
матрицы G.3.9), получим:
р^-Р^-О}-0,0324;
р {и - 1} = 0,1512 + 0,0432 - 0,1944;
р {U = 2} = 0,2016 + 0,0144 + 0,1764
р {U = 3} = 0,0672 + 0,2352 = 0,3024;
1} = 0,1104;
PVi = P{V=i} = 0,3864;
р,в-Р{К-2}-0,1764.
Ряды распределения случайных величин U и F:
F :
0
0,0324
i о
0,0144
1
0,1944
— 1
0,1104
2
0,3924
0
0,3124
3
0,3024
1
0,3364
4
0,0784
2
0,1764
G.3.10)
190 ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
Зная матрицу распределения 11/?011 системы двух
дискретных случайных величин (С/, V), можно найти ее
функцию распределения F(u, и):
F{u,v)- 2 2/V G.3.11)
где первая сумма распространяется на все значения pih
для которых и{ < и; вторая — на все значения />„, для
которых vt<v. >
7.4. Система двух непрерывных
случайных величин. Совместная
плотность распределения
Система двух с. в. (X, Y) называется непрерывной,
если ее ф. p. F(x, у) есть непрерывная функция,
дифференцируемая по каждому из аргументов, у которой су-
02F (*, у) **
ществует вторая смешанная производная &Хди ' е
составляющие системы X и Y представляют собой
непрерывные с. в.
Аналогично тому, как мы определяли п. p. j(x) для
одной св. X, определим п. p. f(x1 у) (иначе —
совместную плотность) для системы двух непрерывных с. в.
(X, F). Это есть не что иное, как предел отношения
вероятности попадания случайной точки (X, Y) в
элементарный прямоугольник, примыкающий к точке (#, у),
к площади этого прямоугольника, когда оба его размера
стремятся к нулю.
Рассмотрим на плоскости хОу малый прямоугольник
Д/?ху, примыкающий к точке (х, у), с размерами Ах, Ду
(рис. 7.4.1), п найдем вероятность попадания в него
случайной точки (X, Y). Согласно формуле G.2.6) эта
вероятность равна:
« F (х + Ах, у + Ду) — F (х, у + by)—F (х+Ах, у) + F(x, у).
Будем неограпичепно уменьшать оба размера
прямоугольника: Ах -+¦ 0, Ау -** 0 и вычислим предел:
lim **(* + **»? + А^) ~Г(**У + А,У) ~ F (x + Ах, у) + F (*, у)
Ах Ьу '
G.4.1)
7.4 СИСТЕМА ДВУХ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН 194
Если функция F(x, у), как мы условились считать,
непрерывна и дифференцируема по каждому аргументу,
то предел G.4.1) есть не что иное, как вторая
смешанная частная производная функции F(x, у):
J^fay). G.4.2)
Функция /(#, у) называется плотностью
распределения (иначе — совместной плотностью) системы двух
непрерывных с. в. (X, Y).
Плотность /(#, у) обладает следующими свойствами:
оо
i) f(x, у)> 0; 2) J J /(*, y)dxdy=i. G.4.3)
— ОО
Первое свойство следует из того, что F(x,
у)—неубывающая функция по каждому из аргументов; второе
свойство будет доказано ниже (см. G.4.8)).
У
0
Рис.
X
ТАЛ
***
ш
/X
Рис. 7.4.2
Геометрически совместная плотность /(я, у) системы
двух св. (X, Y) изображается поверхностью
распределения (рис. 7.4.2). Так как )(х, у)>0, то вся
поверхность распределения лежит не ниже плоскости хОу. Так
00
как J J /(#,y)dxdy — 1, то полный объем, огра-
— 00
ничейный поверхностью распределения и
плоскостью хОу, равен единице.
Аналогично тому, как мы ввели понятие «элемент
вероятности» f(z)dx для одной случайной величины X,
введем понятие элемента вероятности для системы двух
192
ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
непрерывных случайных величин:
/(я, y)dxdy.
G.4.4)'
V
С точностью до бесконечно малых величин высших
порядков элемент вероятности /(#, y)dxdy равен
вероятности попадания случайной точки (X, Y) в
элементарный прямоугольник dRxy с размерами dx и dy,
примыкающий к точке (х, у) (рис. 7.4.3). Эта вероятность
приближенно равна объему эле-
ментарного параллелепипеда с
высотой f(x, у), опирающегося
иа ^д^ ^рцс^ 7.4.4).
Аналогично тому, как
вероятность попадания одной с. в. X в
пределы участка (а, р)
геометрически изображалась площадью,
ограниченной сверху кривой распределения,
опирающейся на этот участок, вероятность попадания случайной
точки (X, У) в область D на плоскость хОу
геометрически изображается объемом тела, ограниченного сверху
X X
их
Рис. 7.4.3
Рис. 7.4.5
поверхностью распределения f(x, у) и опирающегося на
область D (рис. 7.4.5). Эта вероятность определяется по
формуле
Р {(X, Y) €= В) = J [ / (х, у) dx dy. G.4.5)
Если область D представляет собой прямоугольник Й
со сторонами, параллельными координатным осям,
ограниченный абсциссами а, () и ординатами f, б (рис. 7.4.6),
7.4. СИСТЕМА ДВУХ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН 193
то вероятность попадания в нее случайной точки (X, Y):
P{(X,Y) R}-$$f(x,y)dxdy. G.4.6)
a v
Выражение функции распределения
системы (X, Y) через совместную плотность
/(*. У)-
Функция распределения F(x, у) системы двух
случайных величин (X, Y) равна вероятности попадания
случайной точки в бесконечный квадрант с вершиной
в точке (я, у), лежащей левее и ниже этой точки
(рис. 7.2.1). Рассматривая этот
квадрант как прямоугольник, у
ограниченный абсциссами — °°, (Г
х и ординатами —оо, у, по
формуле G.4.6) получим:
х у
г
F(x,y)~ f j f(x,y)dxdy.
ее р х
Рис. 7.4.6
G.4.7)
Полагая в формуле G.4.7) х = у = +°°, получим:
оо,
G.4.8)
и второе свойство плотности доказано.
Выражение законов распределения
отдельных случайных величин, входящих
в систему, через закон распределения
систем ы.
Зная закон распределения системы случайных
величин (случайного вектора) (X, У), можно найти закон
распределения каждой из величин, входящей в систему,
в любой удобной для нас форме: функция распределения,
плотность (для непрерывных св.), ряд распределения
(для дискретных св.).
Рассмотрим сначала случай системы двух
непрерывных случайных величин, более часто встречающийся
в инженерной практике.
В п. 7.2 мы показали, что F(x, +°°) =Fi(x);
F{+°°> y)=sc^T2(y), т. е. для того, чтобы полу-
7 Теория вероятностей и ее
инженерные приложения
194 гл. 7 системы случайных величин
ч и т ь функцию распределения одной из
величин, входящих в систему, достаточно
положить в функции распределения системы
аргумент, соответствующий второй
случайной величине, равным +«\
Учитывая формулу G.4.7), выражающую функцию
распределения F(x, у) системы двух непрерывных
случайных величии через их совместную плотность, и
заменяя в ней аргументы х, а затем у на +«>, получим:
X оо оо у
FA*)- j j f[x,v)dxdy, F2(y)= j J f(x,y)dxdy.
— ЭО —ОС —СЮ — JO
G.4.P)
Чтобы найти плотности /j (x) и /2A/),
продифференцируем выражение G.4.9) соответственно но х и по у:
Применяя известное правило дифференцирования
интеграла по переменной, входящей в его предел,
получим:
оо оо
Ш- J fi*,V)dy; U(У)- j f{z,y)dxi G.4.10)
т. е. для того чтобы получить плотность
распределения одной из величин, входящих в
систему, надо проинтегрировать
совместную плотность в бесконечных пределах по
аргументу, соответствующему другой
случайной величине.
7.5. Зависимые и независимые случайные величины.
Условные законы распределения
В предыдущих пунктах мы показали, как, зная закон
распределения системы двух (дискретных или
непрерывных) случайных величин, найти законы распределения
отдельных величин, входящих в систему (X, У).
Возникает естественный вопрос: а яелыш ли, зная
законы распределения отдельных с. в. X и У, входящих
в систему, найти закон распределения системы?
7.5. ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 195
Нет, оказывается, в общем виде этого сделать
нельзя: знание законов распределения отдельных св. X и
У еще не дает возможности найти закон распределения
системы. Это можно сделать только в одном частном
случае: когда св. X и У, образующие систему, неза-
в и с и м ы.
Две с. в. X и У называются независимыми, если
независимы все связанные с ними события: например,
{Х<х} и {Y<y}\ {X = Zi) и 1У=*&У и т. д. Так как
зависимость и независимость событий всегда
взаимны (если Л не зависит от 2?, то и Б ке зависит от А),
то зависимость и независимость случайных величин
также всегда взаимны; если св. X не зависит от св. У, то
и с. в. У не зависит от с в. X.
В терминах законов распределения независимость с в.
можно определить так: две случайные величины
называются независимыми, если закон распределения
каждой из них не зависит от того, какое значение приняла
другая.
Понятие независимых с. в. очень важно в
практических применениях теории вероятностей. Вводя в
рассмотрение систему с. в., надо стараться по возможности
обеспечить их независимость.
Если с. в. X и У, образующие систему, пезависимы,
то ф. р. системы выражается через ф, р. отдельных
величин, входящих в систему. В самом деле,
F(x,y) = P{X<x\ Y<y}.
Но события {Х<х) и {Y < у} независимы; по правилу
умножения вероятностей для независимых событий
ИЛИ
F(r, j/) = F,(z) Ft(y)*), G.5.1)'
т. е. ф. р. системы двух независимых св. р а в-
на произведению ф. р. величин, входящих
в систему.
Это правило справедливо для любых случайных ве-
личип — дискретных, непрерывных и смешанных.
Если X и У—две независимые дискретные с. в,
с матрицей распределепия Иру11 (*' = 1, 2, ..., п; / — 1,
*) Формулу G.5.1) иногда называют теоремой умпожепчя
законов распределения.
196 ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
2, ..., т), то элементы этой матрицы очень просто
выражаются через законы (ряды) распределения отдельных
с. в. X и У. А именно,
р.. = Р {X = Xi\ Y = у.}\
но события {X == хх) и (У —у,-} независимы; отсюда
или, пользуясь обозначениями рх. = Р{Х = Zj}; ру. ==
^" **Л/ . G-5-2)
т. е. каждый элемент ри матрицы
распределения двух независимых св. равен
произведению соответствующих им (i-ro и /-го)
элементов рядов распределения св. X и У.
Условие G.5.2) есть необходимое и достаточное
условие независимости двух дискретных случайных величин
X и Г. Если оно выполняется, с в. X и Y независимы,
если не выполняется — зависимы.
Вернемся к примеру 1 п. 7.3 и посмотрим, зависимы
или независимы приведенные там случайные
величины (X, Y).
Рассматривая матрицу распределения системы
дискретных с в. (X, У) в примере 1 п. 7.3 и ряды
распределения G.3.7), убеждаемся, что
0.09-0,48-0,0432
^зз^ Рх,-Ру, = 0,49.0,16 = 0,0784,
т. е. условие G.5.2) выполнено, а с в. X, У независимы.
Составить заключение о независимости можно было
бы и не строя матрицы распределения системы и рядов
распределения отдельных величин, входящих в систему:
ведь стрелки стреляют независимо друг от друга, и число
попаданий первого никак не влияет на число попаданий
второго; т. е. множества причин, обусловливающих
значения, принятые в опыте случайной величиной X и
случайной величиной У, не пересекаются.
Теперь обратимся к примеру 2 п. 7.3. Рассматривая
матрицу распределения G.3.9) системы случайных ве-
7.5. ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 197
личин (?/, F) — сумма и разность чисел попадания 1-го
и 2-го стрелков, убеждаемся в том, что вероятности /?4j
в матрице G.3.9) не равны произведениям вероятностей
Ри. и Рг.> стоящих в рядах G.3.10)t ц поэтому
случайные величины U и V зависимы.
Так проверяется зависимость и независимость
дискретных с. в.
Рассмотрим теперь более важный для инженерной
практики случай двух непрерывных св. (X, У). Пусть
эти величины независимы. Дважды дифференцируя
формулу G.5.1) (спачала по х, потом по */), получим
совместную плотность 1(х, у):
(хч у)
дхду
dx
dF2 (у)
dy
или
fix, у)
f(x, у) = Д (x)-f2 (*/), G.5.3)
т. е. совместная плотность двух
независимых непрерывных св. равна произведению
плотностей распределения отдельных
величин, входящих в систему.
Выполнение равенства G.5.3) —необходимое и
достаточное условие независимости двух непрерывных с. в.
Хи У.
Пример 1. Система двух непрерывных св. (X, У)
распределена с постоянной плотностью /(#, i/) = cb
пределах прямоугольника Л,
ограниченного абсциссами
(а, Р) и ординатами (¦у, б)
(рис 7.4.6). Найти
константу с. Определить, зависимы
или независимы с. в. X и У.
Найти ф.p. Fix, у) системы
(X, Y).
Решение. Поверхность
распределения системы
(X, У) вне прямоугольника
R совпадает с плоскостью
хОу {f(x, j/) = 0), а для его
внутренних точек параллельна плоскости хОу и отстоит
от нее на с (рис 7.5.1). Объем, ограниченный этой
поверхностью и плоскостью хОу, должен быть равен
единице:
Рпс. 7.5.1
198 гл 7 системы случ ишых вкличгнт
откуда с = 1/(р — а) F — if);
— а) (б — у) при (дг, у) €
О при (х,у)$
G.5.4)
Примепяя формулы G.4.10) для отдельных величин,
входящих в систему, получим:
при д-ge (а, р),
при д:^ (а, Р) '°*
/i W - f / U, ff) ^ - J [1/(P - a) F - Y)J <fo =
^l' о
i-V)
п, аналогично,
0 при у ^ (Yf 6).
G.5.6)
Из G.5.4), G.5.5) п G.5.С) видно, что /(*, у)«
¦* f\{x)U{y) и случайные величины X, У независимы.
Теперь найдем функцию расиределония системы
F(x, у). Так как X и Y независимы, то, согласно
формуле G.5.1),
F(x4y)-Fl(x)F1(y).
Найдем Ft(x) и F2{y).
В п. 6.1 мы нашли ф. р. (см. F.1.9)) для
равномерного распределения на участке. Получим:
0 при аг^сс,
(x — a)/((J — а) при a < a: < P,
1 при ar;
G.5.7)
Аналогично
0 при !/
(U — T)/(s — V) при У
1 при у
:«,
G.5.8)
Перемножая G.5.7) и G.5.8) при (я, y)^R и
учитывая, что F(xt +*>)*»Л(*)т /4+^) У)~Рг{у)) получим
7 5. ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ СЛУЧАЙНЫЙ ВЕЛИЧИНЫ 199
таблицу значений функции распределения для
различных значений аргументов (х, у):
X
%<
X
< а
х< р
0
0
0
1мТу
(у-
v<
0
!:)/(,f
S-Y)
X
)J
0 ч
(•г - а)/(Р
1
-а)
Поверхность, изображающая функцию распределения
F(x, у), дана на рис. 7.5.2. >
Пример 2. Система св. (X, Y) распределена с
постоянной плотностью f(x, y)~c внутри квадрата R со
стороной а, стороны которого составляют углы 45°
с осями координат (рис. 7.5.3). Найти константу с.
Найти плотности j^{x) и /2(#) отдельных величин X и К,
Рис. 7.5.2
Рис. 7.5.3
входящих в систему. Определить, зависимы или
независимы св. (X, Y), входящие в систему.
Решение. Поверхность распределения вне квадрата
R совпадает с плоскостью хОуу а внутри его —
параллельна ей в проходит па высоте с. Из того, что объем тела,
показаппого на рис. 7.5.4, равен единице, следует, что
аг • с в 1, откуда с -¦ 1/а2 и
A/а2 при (х,у)<=ПЛ
О при (x1y)<?R.j
G.5.9)
200
ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
х) найдем по формуле
Плотность распределения
G.4.10):
х (*) = j / (*, у) dy =
прп | х | > а/У %
+x
-L Г dy = 2 («/"[/Г + х)/а2 при -а/1/2<д:<0,
I a" J
при
G.5.10)
Аналогично
G-5.11)
f(x,y)dx
при
при -
2(a/V2-y)/a* при
Кривая распределения /i(^) имеет вид, показанный
на рис. 7.5.5 (совершенно такой же вид имеет и кривая
распределения fz(y)). Такой за-
кон распределения называется
законом Симпсоиа (или «законом
равнобедренного треугольника»).
Так как /(.г, у)Ф fi(x)f2(y), то
случайные величины X, У
зависим ы. >
f(x .
Рис. 7.5.5
Если случайные величины, образующие систему,
зависимы, то для нахождения закона распределения
системы недостаточно знать законы распределения отдельных
величин, входящих в систему: требуется еще знать так
7 5. ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 201
называемый условный закон распределения
одной из них.
Условным законом распределения одной из величин
(X, У), входящих в систему, называется ее закон рас-
пределепия, вычисленный при условии, что другая
случайная величина приняла определенное значение (или
попала в какой-то интервал).
В случае произвольного типа случайных величин
(дискретных, непрерывных или смешанных) функция
распределения F(z, у) системы зависимых случайных
величин (X, У) может быть записана в виде:
F(x,y) = P{X<z; Y<y} = P{X<x}'P{Y<y\X<x}~
-Fi(x)-P{Y<y\X<z].
Условная вероятность Р {У <С у \ X < х) — вероятность
события {Y<y} при условии, что величина X приняла
значение меньшее, чем х1 может быть названа
условной функцией распределения св. У при
условии {X < х)\ обозначим ее
Тогда
F(x, y) = Fi(x)F2(y\X<x). G.5.12)
Аналогично, беря в качестве «первой» случайную
величину У, получим:
F{x, y) = F2(y)Fl(x\Y<y). G.5.13)
На практике чаще всего применяют другой вид
условного закона: закон распределения одной из случайных
величин при условии, что другая приняла вполне
определенное значение. Вычислим такие условные
законы распределения для случая системы двух
дискретных случайных величин. Они образованы условными
вероятностями, представляющими собой вероятность
того, что с. в. X примет значение Х\ при условии, что У = yj
(или, наоборот, вероятность того, что с. в. У примет
значение yj при условии, что X = х^.
Найдем эти условные вероятности. Вспомним, как
в п. 2.3 мы определяли условную вероятность события В
при наличии А:
Р(В\А)-Р{АВ)/Р{А).
202 ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИИ
Применяя эту формулу, найдем условную вероятность
того, что случайная величина Y примет значение у} при
условии, что Х~зсг:
Pvj\xi = PijiPxi (г — 1, 2, ..., и; 7 = 1,2,..., то)
G.5.14)
п, аналогично,
Рх'\у\ === Pij'Pvi v === ? ' • • •» ^» 7 == ' * • • •» ТО).
G.5.15)
Совокупность вероятностей G.5.14) для 7 = 1» 2, ...
..., то представляет собой условный ряд
распределения св. У при условии X = х{\ этот ряд
распределения обладает свойством обычного ряда
распределения: сумма образующих его вероятностей равна
единице.
Действительно,
Аналогично и
п
Пример 3. Найти условные ряды распределения
JPtj|«i и Рщ\*} (* = 1, 2, 3, 4, 5; /«1, 2, 3, 4, 5) для
зависимых дискретных случайных величин С/, У,
приведенных в примере 2 п. 7.3.
Решение. Применяя формулы G.5.14) и G.5.15),
а также учитывая ряды распределения G.3.10), получим
для всех клеток табл. G.3.9), где стоят нули, условные
вероятности равными нулю; отличными от нуля
оказываются только:
- 0,0324/0,0324 = 1; pv^u2 -
= P2*JPu2 « 0,2222;
.* °'7778; *\|«, ^ °'0367; J4ltts ^ °>5138'
p/Iii"« 0,4495; р« |w «0,2222; р„ N «0,7778; pv ,u ==1#
51 8 *| 4 41 4 3> 5
Предлагаем читателю самостоятельно найти все
отличные от нуля условные вероятности Pu{\vj и сравнить
7 5. ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 203
с нижеперечисленнььми:
Pu.it. «0,6453; Ри „ да 0,2510; ри „ «0,3913;
31 3 51 3 2| 4
/^«0,6087; Pu3|V{. = 1. >
Теорема умножения плотностей.
Рассмотрим систему двух зависимых непрерывных с. в. (X, Y)
и докажем, что их совместная плотность
равна произведению плотности одной из них
на условную плотность другой при
заданном значении первой:
/(*• y)~hHh(y\x) G.5.16)
или, что равпосилыю,
/(*, У) = f2(y)f\{x I у), G.5.17)
где f2(y ! х)-~ условная плотность случайной величины Y
при условии, что с. в. X приняла значение г; /i(#ly) —
аналогично.
Это правило называется теоремой умножения
плотностей; в схеме непрерывных случайных вели*
чин она аналогична правилу умножения вероятностей
в схеме событий и может быть
из него выведена.
Рассмотрим элемент
вероятности /(#, y)dxdy,
приближенно (с точностью до
бесконечно малых высших порядков)
равный вероятности попадания Р"<>. 7.5.6
случайной точки (X, Y) в
элементарный прямоугольник dRxy со сторонами dx и dy,
примыкающий к точке (#, у) (рис. 7.5.6). Попадание
точка (X, Y) в него представим как произведение двух
событий:
Ах = {Х^(х, x + dx))\ A2 = {Y<=(yy y + dy)},
откуда, по правилу умножения, элемент вероятности
равен:
f{x,y)dxdy-P(Al)-P(Ai\Al) =
= P(.Vg (х, х + dx)} ¦ Р {Y <= (у + dy) | X <= (х 4- Жг)}.
G.5.18)
I i
204 гл. 7. системы случайных величин
Теперь устремим к нулю dx и dy; в пределе условие
Хе(а;, x + dx) в формуле G.5.18) превратится к X = х\
формула G.5.18) примет вид:
откуда, деля обе части на dxdy^Q, получим формулу
G.5.16) (формула G.5.17) выводится аналогично).
Из G.5.16) и G.5.17) вытекают формулы,
выражающие условные плотности распределения:
Му\х)=Н*,уШ*); fi(*\y)-f{*,v)'h(y), G-5.19)
т. е. чтобы получить условную плотность
распределения одной из св., входящих
в систему, надо разделить совместную
плотность на плотность распределения
другой св.
Учитывая формулы G.4.10), выражающие плотности
распределения одной из с. в., входящих в систему, через
совместную плотность, можно записать формулы G.5.19)
в виде:
G.5.20)
Формулы G.5.19), G.5.20) выражают условные
плотности через совместную плотность /(.г, у).
Условные плотности распределения ji{y\x). /i(#lff)
обладают свойствами обычных плотностей:
G-5.21)
f1(x\y)dx=l.
Из формул G.5.20) для условных плотностей
распределения вытекает их полезная геометрическая
интерпретация, а именно: кривая условной плотности ji{x\y)
подобна сечению поверхности распределения плоскостью,
параллельной координатной плоскости jOx, отсекающей
на оси Оу отрезок у (рис. 7.5.7), и получается из нее
7.5. ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 205
f(x,y)
делением всех ординат на площадь данного сечения.
(На рис. 7.5.7 величина а{ — коэффициент
пропорциональности.)
Пример 4. Время безотказной работы Г,
электронного устройства (ЭУ) распределено по показательному
закону с параметром к>
>0; время
восстановления ЭУ после его отказа
Т2 также подчинено
показательному закону, но его
параметр \х
пропорционален времени безотказной
работы ЭУ: \i = atx (а>0).
Найти совместную п. р.
системы св. G\, T2)y
а также п.р. св. 7\ и Т2
и их характеристики.
Решение. По условию
*2>0).
По формуле G.4.10) находлм:
/а('.)
Рис. 7.5.7
Можно убедиться в том, что п. р. с. в. Тг обладает все-
ми необходимыми свойствами: /2(^)^0; J /2(^2)^2"" ^ф
Следовательно,
(X + at2f tf
(tv t, > 0),
Отметим, что условная п. р. с. в. Тх при
фиксированном значении Т2 = t% является законом Эрланга 2-го
порядка с параметром (% + at2).
ГЛ 7 СИСТЕМА СЛУЧАЙНЫХ ВЕЛИЧИН
Найдем числовые характеристики с. в. Tt и Т2:
оо
М [7\] « U.e~ui dt = ^; D [7\] = 1Д2;
м. о. и дисперсия с. в. Т2 не существуют, так как
соответствующие интегралы расходятся. >
На практике нам далеко не всегда бывает известна
совместная плотность распределения /(#, у) системы
двух с. в.; может возникнуть необходимость непосред-
ственнного определения условной плотности по
результатам опытов. Сразу же оговоримся, что для этого
экспериментальный материал должен быть достаточно
обширным (порядка уже не сотен, а тысяч опытов). Покажем
на конкретном примере, как это можно выполнить.
Пусть случайная величина X — рост наугад взятого
человека, У —его вес. Ясно, что случайные величины X
и У зависимы; в среднем более высокие люди имеют и
больший вес, хотя в конкретных случаях от этого
правила могут быть и отступления. Предположим, что мы
хотим приближенно найти по опытным данным условную
плотность распределения f2(y I 180), т. е. плотность
распределения веса человека, имеющего рост 180 (см). Как
это сделать?
Надо из всего массива опытных данных отобрать те,
для которых рост приближенно равен х « 180 (см), и для
этой группы данных
приближенно построить плотность
распределения веса (о том, как это
делается, подробнее мы будем
говорить в гл. И).
Пример 5. Пользуясь
геометрической интерпретацией
условной п.р., найти 1г(у\%) и
/i(#i#) Для пары случайных
величии (X, У), рассмотренных в
примере 2 данного пункта, и сравнить с теми
результатами, которые получаются по формулам G.5.20).
Решение. Поверхность распределения /(я, у)
имеет вид, показанный на рис. 7.5.4. Сечение этой
поверхности плоскостью, параллельной плоскости fOx и
отстоящей от нее на расстоянии у, имеет вид прямоугольника,
показанного на рис, 7,5,8; подобная ой фигура представ-
Рис. 7.5.8
7.5 ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 207
ляет собой кривую равномерного распределения.
Следовательно, условная п. p. fi(x\y) является постоянной на
участке (—(а/У2 — It/I; + (а/У2 — \у\)) (условное
распределение равномерно). Исходя из условия равенства
единице площади, ограниченной кривой распределения,
получим выражение для условной плотности распределения:
@ _ при \х\>а//2-\у\;
-\i/[2(a/V2-\y\)] при -(а/У2-\у\)<
\ <х<(а/]/2-\у\).
Аналогичное выражение можно записать и для другой
условной п. р.:
0 оря \y\>a/V2-\x\;
-|*0] при -(я//2-И)<
<0<(а//2-|*|). >
Пример 6. Точка (X, У), изображающая объект яа
круглом экране радиолокатора, распределена с
постоянной плотностью в пределах круга К радиуса г с центром
Рис. 7.5.9
Рис. 7.5.10
в начале коордипат (рис. 7.5.9). Записать выражение
совместной плотности /(#, у). Найти плотности /t(x),
U(У) отдельных величии, входящих в систему (X, У),
а также условные плотности fi(x \ у), fz(y I x), построить
ях графики. Определить, зависимы или независимы
случайные величины X и У. Найти вероятность того, что
расстояние от точки (X, У) до центра экрана будет
меньше г1#
208
гл. 7. системы случайных величин
Решение.
С при (я, у) е К,
0 ири (х,у)<?К.
Поверхность распределения показана на рис. 7.5.10;
она имеет вид прямого кругового цилиндра радиуса г,
стоящего на плоскости хОу, центр основания которого
совпадает с началом координат. Так как объем цилиндра
должен быть равен единице, то его высота Л = 1/(яг2).
Следовательно,
1B) при *2 + i/
при х2 + у
) по формуле:
Найдем плотность
со
г —х-
1 ?*-
/г8-.
при
| < г.
График плотности /i(#) показан на рис. 7.5.11.
Аналогично получим выражение для
плотности U(y):
Рис. 7.5.11
Аналогично:
y2/{nr2) при \у\<г.
Условную плотность fi(x\y)
находим по формуле G.5.19), имея
в виду, что MiO^O:
при
при
Условная плотность распределения )i{x\y) при
определенном значении y(yz<rz) будет представлять
собой плотность равномерного распределения па участке
(—1/г2 — х2; 1/г2 — х2). График условной плотности fi(x\y)
при у = г/2 показан на рис. 7.5.12.
Так как ji{x)?* fi(x\y), то случайные величины X и
У зависимы.
7.5. ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 20$
Вероятность того, что точка (X, У) на экране
радиолокатора будет находиться не более чем на расстоянии
г, от центра экрана, равна вероятности того, что
произойдет событие {X2 + Y2 < г\}, т. е. случайная точка
(X, У) будет принадлежать области Dt — кругу радиуса
ги центр которого совпадает с центром экрана
(рис. 7.5.13). Эту вероятность проще всего подсчитать,
пользуясь понятием «геометрической вероятности»,
введенной в п. 2.2: искомая вероятность
Р {(X, Y)
{X2 + У2
Пример 7. Рассматривается совместная работа двух
ЭВМ. Случайные величины Ти Тг представляют собой,
соответственно, время безотказной работы первой ЭВМ
Рис. 7.5.13
и время безотказной работы второй; обе ЭВМ выходят
из строя независимо друг от друга. Каждая из
случайных величин Ти Тг имеет показательное распределение
с параметрами \и Хг соответственно. Написать
выражение совместной плотности /(flf t2). В начальный момент
t = 0 обе ЭВМ работают.
Найти вероятности следующих событий:
А = {в течение времени т после начала работы обе ЭВМ
будут продолжать работу};
В = {в течение времени т после начала работы первая
ЭВМ будет продолжать работу, а вторая выйдет
из строя};
С = {вторая ЭВМ выйдет из строя раньше, чем первая}.
Решение. Так как величины Ти Т2 независимы, их
совместная плотность f(th t2) = fi{ti)f2(t2), где
/,(*«) =
240
ГЛ 7 СИСТЕМА СЛУЧ\ПИЫХ ВЕЛИЧИИ
Это выражение обращается в нуль в области, где хотя
бы один из аргументов ?,, t2 отрицателен, т. е. вне
первого квадранта К плоскости tfit2 плотность f{th t2) равна
нулю, а внутри его выражается формулой:
/('и Q = ККе~К'гЧ2 ('i > 0, /2> 0).
Находим Р (А) = Р {Тг > т; Т2 > т}.
Так как события {7\>т}, {Г2>т} независимы, то
Р (А) = Р G\
Аналогично
т} • Р {Т2 > т}
Найдем Р(С) = Pjr, > Г2}; для этого выделим
область С, соответствующую неравенству 7\ > 7'2
(абсцисса случайной точки (ThT2)
больше ординаты). На рис.
7.5.14 эта область С
заштрихована. Имеем:
Рис. 7.5.14 Расставляя пределы в этом
двойном интеграле и
записывая его как повторный, получим:
Этот результат можно объяснить достаточно
наглядно. Представим себе на оси 0/ совмещенпыми
(наложенными друг на друга) два простейших потока событий;
первый — поток отказов 1-й ЭВМ с интенсивностью Х{
(кружочки) и второй — поток отказов 2-й ЭВМ с ип-
тенсивностью Кг (крестики) (см. рис. 7.5.15). Вероят-
7 5 ЗАВИСИМЫЕ И НЕЗАВИСИМЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 211
иость того, что первое после t = О событие из «потока
крестиков» придет раньше, чем первое из «потока
кружков», с достаточной очевидностью равна доле, которую
составляет интенсивность к2 «потока кружков» в общей
интенсивности Ki + А,2 обоих потоков. >
Вернемся к вопросу о зависимости и независимости
случайных величин. Мы знаем, что для независимых
случайных величин
а отсюда следует, что условная плотность распределения
1г{у\х) случайной величины Y равна «безусловной»
плотности /2(у). На практике заключение о зависимости или
независимости случайных величии делается, как правило,
не путем сравнения условных законов распределения с
«безусловными», а исходя из других, по большей части
Рис 7.5.15
физических соображений, касающихся множеств
факторов, обусловливающих появление тех или иных значений
случайных величин. Если множества этих факторов для
двух случайных величин X и Y не пересекаются (или
практически пе пересекаются), можно допустить, что
случайные величины X и Y независимы. Если же эти
множества имеют существенную общую часть, то
случайные величины X, Y зависимы; только тогда возникает
вопрос об условных законах распределения.
Остановимся более подробно на понятии
зависимости случайных величин. Не следует ее путать
с привычной для пас в математике функциональной
зависимостью. Если две величины зависимы
функционал ь и о, то, зная значение одной из них, можно
совершенно точно указать значение другой. Если же мы
имеем дело с зависимыми случайными величипами, то,
в общем случае, зная значение одной, можно только
указать закон распределения другой. Такая
зависимость называется вероятностной (или
стохастической). Зависимость между случайными величипами
может быть более или менее теспой: от полного ее
отсутствия, через разные степени вероятностной зависимости,
вплоть до жесткой, функциональной зависимости, когда,
212 ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
зная значение одной с. в., можно в точности указать
значение другой.
Рассмотрим несколько примеров.
Пример независимых случайных
величин. Опыт состоит в том, что два стрелка, не
сговариваясь, стреляют каждый по своей мишени. Случайная
величина Xt — абсцисса точки попадания первого
стрелка; с. в. Хг — абсцисса точки попадания второго; эти
случайные величины можно считать независимыми, так как
причины, обусловливающие появление того или иного
значения каждой из них, различны.
Пример функционально зависимых
случайных величии. Опыт состоит в том, что
техническое устройство работает в течение какого-то времени
т; время от времени в нем могут возникать
неисправности. Устранение одной неисправности обходится в
определенную сумму (а рублей). Случайная величина X —
число возникших неисправностей; случайная величина
У — сумма, затраченная на их устранение. Между
случайными величинами X и У существует функциональная
зависимость У = аХ.
Примеры случайных величин, связанных
вероятностной зависимостью.
1. ЭВМ работает в течение одного года; св. X —
число отказов ЭВМ за этот период; св. У — стоимость
затрат, связанных с поддержанием ЭВМ в
работоспособном состоянии в тот же период. Очевидно, что
случайные величины X и У зависимы; при увеличении X
случайная величина У также проявляет тенденцию к
увеличению, но связь между X и У не жесткая, не
функциональная.
2. Св. X — число действующих скважип на
месторождении нефти; У — количество нефти, добываемой в
единицу времени на этом месторождении. Зная значение
одной из этих случайных величин, нельзя указать
точного значения другой; можно лишь утверждать, что чем
больше будет действующих скважин, тем вероятнее, что
будет добыто большее количество нефти.
3. Ранее рассмотренные нами случайные величины:
X — рост человека и У — его вес — также связаны
вероятностной зависимостью. Эта зависимость не является
функциональной, хотя и существует всем известная
эмпирическая формула, связывающая вес человека У (кг)
с его ростом X (см): У = X—100.
7.6. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СИСТЕМЫ 213
Эта зависимость, как нетрудно убедиться,
справедлива лишь в среднем, а в конкретных случаях от нее
наблюдаются более или менее значительные отклонения.
Величины X и У связаны вероятностной
зависимостью.
Не следует думать, что зависимость между
случайными величинами может быть только «положительная»,
когда при увеличении одной другая имеет тенденцию
тоже увеличиваться. Например, две случайные величины
X — средний балл школьника па выпускных экзаменах
и У — число часов, проведенных им же у телевизора в
период подготовки, несомненно, зависимы, но при
увеличении одной другая имеет тенденцию уменьшаться.
Существуют и такие виды зависимости случайных
величии, когда при увеличении одной другая не
проявляет тенденции ни увеличиваться, ни уменьшаться;
меняется только ее закон распределения; для пары
зависимых случайных величин (X, У), рассмотренных в
примере 6, это именно так.
7.6. Числовые характеристики системы
двух случайных величин. Ковариация
и коэффициент корреляции
В качестве числовых характеристик системы двух с. в.
(X, У) обычно рассматриваются начальные и
центральные моменты различных порядков.
Начальным моментом порядка к, s
системы двух с. в. (X, У) называется математическое
ожидание произведения ХА па У3:
Центральным моментом порядка /с, $
системы двух с. в. (X, У) называется математическое ожи-
0 О
дание произведения Хк на У8
цм = м[х*Н G.6.2)
о о
где X = X — тх\ Y = Y — ту — центрированные с. в.
Для системы дискретных св. (X, У) получим:
п т
«М = 2 S Лу)рц, G-6.3)
214 гл 7. системы апуччгшых псличтш
п m
\^к,в = S 2 (xi — т*) (У) — mvf Pi) '• G.0/0
Для системы непрерывных с. в. (X, Y)
hy*f(x,ij)dxdy, G.6.5)
с — тх)к (у — niy)s / (,r, у) clx dy. G.6.6)
Порядком начального (или центрального) момента
называется сумма его индексов к + $.
В инженерных приложениях чаще всего встречаются
моменты первого и второго порядков.
Начальные моменты первого порядка:
= М [X] - тх; а0|1 - М
G.6.7)
представляют собой математические ожидания с. в. X п К.
Точка (тх, ту) на плоскости хОу представляет собой
характеристику положения случайной точки (X, У): ее
рассеивание (разброс) происходит вокруг точки (тх, mv).
Центральные моменты первого порядка, естественно,
равны нулю:
Начальные моменты второго порядка:
^2,о ~ "* \X~Y \ =¦= М [X ] =и сх2 [X]j
Оо'8 = М [Х°Г2] - М [Г2] = а2 [У]; п б 8)
«1Д = М [Х1^1] = М [XY].
Последний из этих моментов — математическое
ожидание произведения двух с. в. X и F, довольно часто
встречается в приложениях.
7.6 ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СИСТЕМЫ 215
Центральные моменты второго порядка:
G.6.9)
Первые два из них представляют собой уже
известные нам дисперсии с. в., а третий заслуживает
отдельного рассмотрения. Он называется ковариацией (иначе —
корреляционным моментом) случайных величин (X, У);
мы будем обозначать его К^:
Кху - М [xy] = М [(X - тх) (Y - ту)]. G.6.10)
В механической интерпретации, когда распределение
вероятностей на плоскости хОу трактуется как
распределение единичной массы на этой плоскости, точка (тх,
ту) есть не что иное, как центр массы распределения;
дисперсии Dx, Dv — моменты инерции распределения масс
относительно точки (тх, ту) в направлении осей Ох и
Оу. Что касается ковариации G.6.10), то в
механической интерпретации это — не что иное, как
центробежный момент инерции распределения масс.
По определению ковариации
?*-*,., G.6.11)
т. е. при перемепе индексов местами коварпация не
меняется.
Дисперсию с. в. можно рассматривать как частный
случай ковариации:
Dx - М й - М [хх] = Кхх; Dy = M [y2] = Kyyi
G.6.12)
т. е. дисперсия с. в. есть не что иное, как «ковариация
ее с самой собой».
Для независимых с. в. ковариация равна нулю;
докажем это. По определению G.6.10)
Кху = Щд - М [Xy\ = j J {x — mx) (у — my)f(x1 у) dx dy.
— oo
Для независимых св. доказано, что 1{x,y)=^ji{x)j2{y)}
210 ГЛ 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
следовательно,
оо оо
Кху=* ) (x—mx)fl(x)dx* j (y — my)f2(y)dy.
— ОО —ОС
Но каждый из полученных интегралов представляет
собой первый центральный момент, который равен пулю:
оо
J (х — тх) Д (х) dx = |ix [X] = 0;
— 00
оо
Таким образом, ковариация двух независимых с. в. равна
нулю.
Ковариация двух с. в. (X, У) характеризует не только
степень зависимости случайных величин, но также их
рассеивание вокруг точки (тх, ту).
Ковариацию Кху часто удобно выражать через
начальные моменты низших порядков: Кху = а1Л — ам • cco,i или
Кху = М [Х-У] - М [XJ-M [Г]» G.6.13)
(доказательство — в п. 8.2). Полезно запомнить словесную
формулировку этой формулы: ковариация двух
случайных величин равна математическому ожиданию их
произведения минус произведение математических ожиданий.
Размерность ковариации Кху равна произведению
размерностей с. в. X и Y. Чтобы получить безразмерную
величину, к тому же характеризующую только
зависимость, а не разброс, ковариацию делят на произведение
с. к. о. охоу:
г^Ях/ta)- G.6.14)
Величина гху называется коэффициентом корреляции
с. в. X и У; он характеризует степень зависимости этих
величин, причем не любой зависимости, а только л и-
нейной, проявляющейся в том, что при возрастании
одной с. в. другая проявляет тенденцию также возрастать
(или убывать). В первом случае гху>0, и говорят, что
с. в. X и У связаны положительной
корреляцией, во втором гху<0, и корреляция
отрицательна. Далее (п. 8.3) мы докажем, что для любых
двух случайных величин X, У
-1^г^<1. G.6.15)
7.6 ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СИСТЕМЫ
217
Модуль коэффициента корреляции случайных
величин X, Y характеризует степень тесноты
линейной зависимости между ними. Если линейной
зависимости нет, гху = 0. Если между случайными
величинами существует жесткая функциональная линейная
зависимость:
то гху = + 1 при а > 0 и гху — —1 при а < 0 (это мы
также докажем в п. 8.3).
Если ковариация Кху двух с. в. (а значит и их
коэффициент корреляции) равна нулю, с. в. X и Y
называются некоррелированными; если не равна нулю —
коррелированными. Из независимости с. в. следует их
некоррелированность; но из некоррелированности
св. (гху = 0) еще не вытекает их
независимость. Если гху = 0, это означает только отсутствие
линейной связи между св.; любой другой вид
связи может при этом присутствовать.
Пример 1. Матрица распределения системы двух
дискретных с. в. (X, Y) задана таблицей
(X, У) :
1
2
4
0
0,1
0
0,1
2
0
0,3
0,3
5
0,2
0
0
. G.6.16)
Найти числовые характеристики системы (X, Г):
м. о. ~ тху ту, дисперсии Dx, Dy, с к, о. ох, оу, ковариа-
цию Кху и коэффициент корреляции г^.
Решение. Прежде всего найдем ряды
распределения отдельных величин, входящих в систему: суммируя
вероятности pih стоящие в первой, второй и третьей
строках G.6.16), получим:
/7,1 = Р {X « 1} = 0,1 + 0 + 0,2 = 0,3;
рх[ = Р {X = 2} - 0 + 0,3 + 0 - 0,3;
Рх = р {X = 4} - 0,1 + 0,3 - 0,4.
1
0,3
2
0,3
4
0,4
218 гл. 7 системы случайных величин
Ряд распределения с. в. X имеет вид
X :
Ее м. о.
тх = 1 • 0,3 + 2 • 0,3 + 4 • 0,4 - 2,5.
Дисперсию Dx находим через второй начальный
момент:
а2[Х]- 12-0,3 + 22-0,3 + 4-0,4-7,9;
Dx - а2 [XI -ml- 7,9 - B,5)» - J ,65.
Среднее квадратическое отклонение
ох=Ш~ 1,285.
Аналогично находим ряд распределения с. в. F,
суммируя вероятности p(j по столбцам табл. G.6.10):
Ру, - P{Y = 0} - 0,1 + 0,1 - 0,2; рч - Р{Г « 2} = 0,6;
//J/ === 1^ | X === О/ === U)U«
3
Ряд распределения св. Y имеет вид:
Y :
ту = 0-0,2 + 2- 0,6 + 5- 0,2 = 2,2;
Dy = a2 [FJ - wij = О2-0,2 + 22-0,6 + 52-0,2 - B,2J=2,56;
Находим м. о. произведения с. в. X и К:
М[Х.У] = ЬО-ОД + 1-2-0+ 1-5.0,2 + 2.0.0 +
+ 2-2.0,3 + 2-5^0 + 4-0.0,1 + 4-2-0,3 + 4-5-0 - 4,6.
Ковариацию Кху вычисляем по формуле G.6.13):
?„-4,6-2,5 -2,2—0,90. .
Деля Кху па oxov, получим коэффициент корреляции:
что показывает, что между с. в. X и Y существует
отрицательная линейная зависимость, т. е. при увеличении
0
0,2
2
0,6
5
0,2
7 0 ЧИСЛОПЫЕ ХЛРЛКТЬРИСТНКИ СИСТЕМЫ
219
однон из них другая имеет некоторую тенденцию
уменьшаться. >
Пример 2. Для системы св., приведенной в
примере 2 п. 7.5, распределенной равномерно в квадрате R
со стороной, равной а и составляющей угол 45° с осью
Ох (рис. 7.6.1), найти ковариацию и коэффициент
корреляции св. X, У.
Р е ш е н н е. Из соображений симметрии
распределения, его «центр массы» лежит в начале координат: тх =
= /и„ = 0.
Находим м. о. произведения величин X и Y (каждая
из которых совпадает со своей центрированной):
к,
(R)
Пли, учитывая, что /(х, г/)=1/а2, в квадрате R
у = -V1 i f .вд <ь <ty +
« I («о
+ J J згу dx dy + J j xy dx du + J j ^z/ dx dy ,
где fli, /?2, /?3, /?4 — четыре треугольника, на которые оси
координат делят квадрат R у
(рис. 7.6.1). В первом из них fl/^
(/?,) х>0, j/>0; во втором
(R2) x<Q, y>0\ интегралы
по обеим областям равны по
модулю и противоположны по
знаку; при суммировании они
взаимно уничтожаются. То же
относится и к интегралам по
областям R3 и /?4; в первой
из них х < 0, у < 0, во второй
х>0, у < 0; суммирование интегралов дает нуль.
Отсюда
т. е. с. в. X и У некоррелированны. Из примера 5 п. 7.5
мы знаем, что эти величины зависимы; таким образом
мы паглядно убеждаемся, что из некоррелированности
еще не вытекает их независимость.
Для коррелированных с в. характерно, что среднее
значение каждой из них зависит от того, какое значение
приняла другая» >
220 ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
7.7. Условные числовые характеристики
системы случайных величин (X, У).
Регрессия
Условным математическим ожиданием одной из с. в.,
входящих в систему (X, У), называется ее м. о.,
вычисленное при условии, что другая с. в. приняла
определенное значение, т. е. найденное на основе условного
закона распределения. Для двух дискретных
с. в. (X, У) условные м. о. вычисляются по формулам:
m
М [Y\Xi] = Шущ = _2 У>Рч)\Н'
М [Х\у.) = шх\у. = 2 *iP*,|vjf
где
РуЛч = Р {Y = yj | X = a-j};
— условные вероятности значений с. в. У и X
соответственно при условии, что другая с. в. приняла
определенное значение. Для двух непрерывных с. в. X и У
00
М [У | х] = шу]х - J yf2 {у | х) dy;
"Г G-7.2)
]-i»Klv- J ^(
где ji{y\x), /,(о:Iу) — условные плотности распределения
случайных величин У при X == х и X при У = у
соответственно.
Условное математическое ожидание с. в. У при
заданном X = х\ М [У | х] == ту\х называется регрессией У на
х\ аналогично М [X | у] = тх\у называется регрессией
X на у. Графики этих зависимостей от х и у
называются линиями регрессии или «кривыми регрессии» У на
х и X на у соответственно (рис. 7.7.1 и 7.7.2).
Пример 1. Построить линии регрессии У на х и
X на у для пары св. (X, У), приведенных в примере 1
п. 7.6.
7.7. УСЛОВНЫЕ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
221
Решение. По данным матрицы G.6.1G) находим
условные ряды распределения с. в. У при хх = 1, х2 = 2,
Рис. 7.7.1
О У
Рис. 7.7.2
= 4. По формулам G.7.1) находим: ру |, =P{F =
0|Х = 1> = 0,1/0,3 = 1/3; РуЛ - Р {Y - 21! X - 1} =* 0;
/3К = Р {^ = 51 X = 1} = 0,2/0,3=2/3. Откуда
0• 0,333 + 2 • 0 + 5.0,6667 » 3,333.
Аналогично
Р«*\*г = Р {Г = 21X = 2} = 0,3/0,3 = 1;
Наконец
0,1/0,4 = 0,25;
ту]х - 0-0,25 + 2-0,75 + 5-0 - 1,5.
Аналогично находим
Р*м. = 0.1 А2 = 0,5; рж,9 = 0; рх,« - 0,5;
II 1 Л 1 ill 1
га»,, = 1 -0,5 + 2-0 + 4-0,5 = 2,5.
Далее
РхдУг « 0; рда|У8 = 0,3/0,6 = 0,5;
рх , = 0,5; т„„ - 1-0 + 2-0,5 + 4-0,5 = 3
31 2 'л
и, наконец,
^xily3 ^ 0»2/0,2 = 1; Р*2;у3 = Рх3\у3 == О
и
тХ|Уз= 1-1 + 2-0 + 4-0= 1.
Линия регрессии X на у показана на рис. 7.7.3. >
222
ГЛ 7 СИСТЕМА СЛУЧЧЙНЫХ ВЕЛИЧИН
Для независимых с. в. линии регрессии Y на х и X
на у параллельны координатным осям, так как м. о.
каждой из них не зависит от того, какое значение
приняла другая.
Линии регрессии могут быть параллельны
координатным осям и для зависимых с. в., если только м. о.
каждой из них не зависит от того, какое значение приняла
/ 2 3 , U 5 yL
Pjjc. 7.7,3
другая. Например, для двух зависимых случайных
величин А' и У из примера 2 п. 7.5 условное м.о. каждой
из с. в. равно нулю, независимо от того, какое значение
приняла другая; линии регрессии Y на х и X на у
совпадают с координатными осями Ох и 0#. Если сместить
квадрат R так, чтобы его центр находился в точке
(тх, ту), то линии регрессии будут параллельными осям
координат прямыми х = тх\ у = ту.
Так как все моменты — начальные и центральные —
любых порядков представляют собой
математические ожидания, то можно говорить об условных
моментах (условных дисперсиях D [У | г], D [X | у],
условных начальных и центральных моментах любых
порядков).
Пример 2. Для системы случайных величин (X, 7),
распределенной с постоянной плотностью в пределах
круга с радиусом г и центром в начале координат (пример 6,
75) й D[F|] и D[^|]
п. 7.5), найти условные дисперсии D[y|x]
Решение. Условная плотность распределения св. F
при Лг = х постояппа и равна ]г{у\х)~ const на участке
}г2-
(-Уг2--^
х2<у
т.
и
е.
-}'r2-x2<y<l/r*-x2
Условная дисперсия D [У|х]
.@1х)-1/[2У^-*Ч при
O^O вне этого участка,
для равномерного распре-
7 8 ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОГО ВЕКТОРА 223
деления на участке (а, $) равна (р-аO12, откуда:
Dy]x = B //"^^702/12 - (г2 - х*)/3
@<я<г). G.7.3)
При я = г эта дисперсия обращается в нуль, так как
значение св. Y становится вполне определенным: Y = r.
При х = 0 св. У распределена равномерно на участке
(—г, +г) и ее дисперсия Dv*x-0 равна BгO12 = г73, что
и следует из формулы G.7.3) при х = 0.
Аналогично Dylx определяем условную дисперсию Dx]y:
D[X\y] = Dx]y = (>•* - у*)/3 @ < у < г). > G.7.4)
7.8. Закон распределения и числовые
характеристики га-мерного
случайного вектора
Закон распределения системы п с. в. — /г-мерного
случайного вектора с составляющими Xh Х2, ..., Хп:
X = (Xh Хг, ..., Хп)
в самом общем случае может быть задан в виде ф. р.
F (xv х2У ..., хп) = Р {Xl < хх% Х2 < х2, ..., Хп < хп} =
{ №<*!}}- G.8Л)
Свойства ф. р. G.8.1):
1. F(xh #2, ..., #п) есть неубывающая функция
каждого из своих аргументов.
2. Если хотя бы один из аргументов xif хг, »»., хп
обращается в — «>, функция распределения равна нулю.
3. Ф.р. любой подсистемы (подмножества) (Хи Х2, ...
..., Xk) системы (Хи Хг, ..., Хку ..., Хп) определится,
если положить аргументы, соответствующие остальным
случайным величинам ХМ1, ..., Хп, равным +<»:
^1,2 н(хи ..., xk)-F(xh ..., хк% +оо, ..., +ooj G.8.2)
(нумерация аргументов — в произвольном порядке).
В частности, ф. p. Fh(xh) одной из случайных величин,
входящих в систему, получится, если положить в
функции F(xu , ¦», хп) все аргументы, кроме хк} равными +<»:
o, +оо, . . ., Хк) +оо +оо). G.8.3)
224 ГЛ 7. СИСТЕМА СЛУЧАЙНЫХ ВЕЛИЧИН
4. Функция F{xu ..., хп) непрерывна слева по
каждому из аргументов.
Доказательства этих свойств проводятся так же, как
и для ф.р. двух с. в, (п. 7.2), и поэтому мы их не
приводим.
Если с. в. Х1у Х2, ..., Хп независимы (т. е. закон
распределения каждой из них не зависит от того, какие
значения приняли другие), то
F (xv *„..., хп) = F, (а-,) • F2 (х,) ...Fn (xn) = E>i (ъ).
G.8.4)
Для инженерной практики преимущественное
значение имеет случай системы непрерывных случайных
величин; для такой системы ф.р. F(xu ..., хп) непрерывна
и дифференцируема по каждому из аргументов, а
также существует п-п смешанная частная производная
F( )/(d)
Плотностью распределения (или совместной
плотностью) системы п непрерывных с. в. (Хи Х21 ..., Х„)
называется м-я смешаппая частная производпая
функции распределения, взятая один раз по каждому
аргументу:
Совместная плотность обладает свойствами:
оо оо
2) J (n) J /fo, т2, . . ., т,г) с?^• dx2. . .dxu =
— оо —-оо
Доказываются эти свойства так же, как и для двух
св. Функция распределения F{xu x2, ...» хп)
выражается через плотность га-кратным интегралом:
F(xv х2, ..., хп) = f <я> J /(хх, ..., xn)dxx.. .б/хп. G.8.7)
— оо —оо
•) Так обозначается л-кратный интеграл.
7.8 ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОГО ВЕКТОРА 225
Элементом вероятности для системы (Хг1 X2j • • *, Хп)
в точке (хи х2у ..., хп) называется величина
/(*i, *2, ..., хп) dXidxt... dxn, G.8.8)
приближенно (с точпостью до бесконечно малых высших
порядков) равная вероятности попадания в
элементарную область га-мерного пространства с размерами
dxi • dx2... dxny примыкающую к точке (xlt х2, •¦•* хп):
f(xv . ,м Xn)dxx...dxn»
« Р {Хг € (xt f *x + Асх), ..., Хп е (хя, *п + ^п)}* G.8.9)
Вероятность попадания случайной точки \XU X2i •«.
..., Хп) в произвольную область D тг-мерного
пространства выражается /z-кратным интегралом по области D:
Р {(Хи f. fi Xn) s ?} - J (n) J/(*if ,. .j ^n) Л?1.. Лхп.
{D) G.8.10)
Чтобы найти п. р. любой подсистемы (Xt| X2t .. *, XJ,
входящей в систему (Хи ..., Xfc, ..., Хя) (нумерация
произвольна), надо проинтегрировать совместную
плотность i(xu *»., хп) (п — к) раз по аргументам (xfc+f, ..*
..., хп), относящимся к остальным случайным величинам:
00 ОО
G,8,11)
В частпости, плотность распределения одной св. Xk,
входящей в систему, равна
ОО 00
/*(**)- J <n~1) J /(*lf f •.1«п)АР1.|.Лг*-1«4г*+Х.»|4Р|и
G.8,12)
Условной плотностью распределения любой
подсистемы (Xlf Х2, •.., Xfc), входящей в систему (Хи Хг, •.*, Xn)t
'(нумерация произвольная), называется плотность
распределения этой подсистемы, вычисленная при условии, что
остальные с. в. приняли определенные значения: Xh+l =*
Х*+а«х»+2; •..; X» —xft. Условная плотность под-
8 Теория вероятностей и ее
инженерные приложения
226 ГЛ. 7* СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
системы вычисляется по формуле
G.8.13)
Плотность распределения системы и с. в. может быть
представлена в виде
/(*t, *,., ^n)e/i(x1)-/2,1(a:2ki)-/s|i,2(^3Ui, я2)...
• ../nii,if8 n-i(«nUti «if , ¦., *n-i), G.8.14)
где все плотпости, кроме первой, являются условными
Л вычисляются при условии, что предыдущие с. в.
приняли определенные значения.
Зная условные п. р. системы с. в. (Xt> ..., Х„),
можно найти условные ф. р. этой системы по формулам:
^2|1 (#2 I Xl) e 1 /2|1 (^2 I Xl) dxV
-? G.8.14')
^зц,2 (ж, | xv х2) - J
Законы распределения системы п зависимых с. в.,
являющиеся функциями многих аргументов, чаще всего
неудобны в практическом применении и к тому же
для своего определения (хотя бы приближенного)
требуют огромпого объема экспериментальных данных.
В большинстве инженерных приложений вместо законов
распределения (иолной, исчерпывающей характеристики
системы п с. в.) рассматриваются ее важнейшие
числовые характеристики.
1. п математических ожиданий:
2. п дисперсий:
Ох - D [Хг]; Д, - D [XJ; ...; Д„
3. п{л—1) ковариаций:
] G.8.15)
7.8. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОГО ВЕКТОРА 22?
Снова отметим, что дисперсия с, в. X есть не что
иное, как ковариация Кп:
DlXil-Mfijl-MlWil-ATu (/ = 1, ...fn). G.8.16)
Ковариации Ki} (вместе с дисперсиями Dt — Kti)
образуют матрицу ковариации (иначе «ковариационную
матрицу»; иногда ее называют «корреляционной матрицей»),
т. е. таблицу, состоящую из п строчек и п столбцов:
К
П
к
m
КЩ КП2
G.8.17)
Так как Кц»Kiu матрица G.8.17) симметрична
относительно главной диагонали. По главной диагонали,
матрицы G.8.17) стоят дисперсии св.: Di — Kti (i =¦
-1, 2, ..., п).
Ввиду симметричности матрицы G.8.17) ее часто
заполняют только наполовину и представляют в виде:
К
П
G.8.18)
где по главной диагонали стоят п дисперсий.
Если случаппые величины (Хи Х2, ¦.., Хп) попарно
некоррелировапы, т. е. /?у = 0 при i5^/, то матрица
G.8.18) имеет вид:
п 0 0 ... О
К22 0 ... о
К О
G.8.19)
Такая матрица называется диагональной. Часто
вместо матрицы ковариации пользуются матрицей
коэффициентов корреляции:
ги Г1з
'и
Чп
где
G.8.20)
G.8.21)
228
ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
По главной диагонали такой матрицы стоят единицы,
так как
Ки _ Д; щ « Di/QiOi)~ Di/Di - 1. G.8.22);
Бели св. Хи Хи ..., Хп попарно некоррелированы,
т. е. Гц-*0 при i?*/, матрица коэффициентов
корреляции принимает вид:
1 0 0
1 0
1
G.8.23)
Такая матрица называется единичной.
Зная закон распределения системы величин (Xlf Х2, ¦ ¦ •
• .., Хп), можно найти все ее числовые характеристики,
например:
G.8,24)
G.8.25)
G,8.26)
J м
— 00
oo
1<-
••00
oo
»j
— 00
oo
> J
— 00
00
— J (n) J (л:< —
но по уже упомянутым выше причинам в нашем
распоряжении сравнительно редко бывает совместная
плотность распределения системы нескольких с. в. На
практике обычно числовые характеристики системы
определяются помимо эаконов распределения,
непосредственно по опытным данным. Каждая из них есть
математическое ожидание той или другой св. и может
быть приближенно найдепа как среднее арифметическое
наблюденных значений этой с. в. или иным способом
|(подробнее об оценках числовых характеристик но опыт*
ным данным см. гл. 11).
Помимо упомянутых выше числовых характеристик
случайного вектора (Хи Х%, . ¦., ХА) — математических
ожиданий ти тг> .. Фу тп и матрицы ковариаций 11Я<,11 —
нередко рассматривается условное математическое
ожидание одной из св., например Xit при условии, что все
7.8, ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОГО ВЕКТОРА 229
остальные величины Х2, ..., Хп приняли определенные
значения: xz, ..., хп:
G.8.27)
Это условное м. о. называется регрессией Xt на
#г, ».., #». Геометрически регрессия интерпретируется
как поверхность в n-мерном пространстве (xif • •»
..., #я) и называется поверхностью регрессии Хг на
^2, • .., хп- Регрессия называется линейной, если
поверхность регрессии описывается линейной функцией:
п
1*. »„ - Yio + 2 Yi««it G-8.28)
где Yio, Чи ('в2, .,., п)'— постоянные коэффициенты^
В двумерном случае линия регрессии — прямая; в
трехмерном—плоскость, в общем случае (л-мерном)—
гиперплоскость в пространстве п измерений.
В п. 7.10 мы покажем, что для системы случайных
величин (Xlf Х2у ..., Хп), имеющей нормальное
распределение (а этот случай очень важен для практики),
регрессия всегда линейна.
Кроме числовых характеристик, относящихся к
одному случайному вектору, в теории вероятностей
применяются также числовые характеристики, относящиеся к
двум случайным векторам одинаковой размерности пик:
Пусть случайные векторы ХЦ) и ХB> имеют числовые
характеристики: математические ожидания тп^^ш^% •••
.. м^пХ); J»i*\ ш^\..._, тд2); и ковариационные матрицы
порядков пик:
по главным диагоналям которых стоят дисперсии
(i** U •. .| w); D$2) (/ « 1, ..., /с). Помимо этих
числовых характеристик, относящихся к каждому случайному
вектору в отдельности, рассматривается их взаимная
ковариационная матрица% элементами которой являются ко-
230 ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН '
вариации
Я<]><2> - М [X\1]Xf] (i - 1, .. м я; ; - 1, ..., А). G.8.29)
Взаимная ковариационная матрица двух случай-
пых векторов ||/П]д2)|| — прямоугольная матрица порядка
п X к; но даже в том случае, когда п =* к и эта матрица
квадратная, она совершенно ие обязательно должна быть
симметричной относительно главной диагонали.
Два случайных вектора X{i) и ХB) называются
независимыми, если все составляющие одного из них не
зависят ни от одной из составляющих другого.
Для независимых случайных векторов их совместная
плотность распределения равна произведению совместных
плотностей отдельных векторов:
- Г D1\ ..., rf}) 1Л) W\ ..., 42)). G.8.30)
Векторы АтA) и ХB) называются некоррелированными,
если все элементы их взаимпой ковариационной
матрицы, определяемые по формуле G.8.29), равны нулю:
- М [X\»Xf] «0 A-1д..#1 и; / - 1, . ..,*).
G.8.31)
Можно показать, что если случайные векторы
независимы, то они и некоррелированы.
7.9. Двумерное нормальное
распределение
В инженерных приложениях теории вероятностей из
систем случайных величин чаще всего встречаются пе-
прерывные системы, имеющие нормальное распределение.
О причинах широкой распространенности нормального
распределения в случайных явлениях природы мы уже
говорили в п. 6.3.
Нормальное распределение случайного вектора имеет
ряд преимуществ перед другими. Немаловажное из пих
состоит в том, что задание числовых характеристик си-
7.9. ДВУМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 231
стемы: ть т2, ..., тп\ Du ZJ, . ¦., Dn и матрицы кова-
риации \\Кц\\ равносильно заданию закона
распределения системы.
Естественно начать рассмотрение нормального
распределения случайного вектора с самого простого случая —
системы двух случайных величин.
Говорят, что непрерывная система с. в. (X, Y)
распределена но нормальному закону, если ее
совместная плотность
G.9,,
где exp(z) = e* — показательная функция.
Распределение G.9.1) называется двумерным
нормальным распределением (или нормальным законом на
плоскости). Двумерное нормальное распределение часто
встречается на ирактике. Например, совокупность
ошибок (X, Y) в двух измерениях какой-то величины (или
выполпепия каких-то команд), как правило, имеет
двумерное нормальное распределение. Координаты точки
приземления (или приводнения) космического
летательного аппарата также распределены по двумерному
нормальному закону.
Выяснил! смысл параметров тх, пгу, ох, ауу гху,
входящих в формулу G.9.1). Как нетрудно догадаться, они
представляют собой не что иное, как математические
ожидания св. (X, Г), их с. к. о. и коэффициент
корреляции. Докажем это.
Действительно, по формулам G.6.5) и G.6.7)
оо
М [X] - J J xj (x, у) dx dy. G.9.2)
—оо
Сделаем замену переменных
G.9.3)
232 ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
откуда
х — оху 2хх + тх\ у —ОуУъУ 2A — гху) + оугху у 2хх + шу0
G.9.4)
Для нахождения якобиана / преобразования
координат G.9.3) вычислим производные:
а,г„/2; Д-а,
Следовательно,
|.=а,г„
dxjdx1
ду/дхх
дх ду дх ду 9 л г. -у"
&Г ду ду дх л v г *>ут
G.9.5)
С учетом G.9.1), G.9.3)—G.9.5) выражение G.9.2)
примет вид:
Ы
1 — ^х У 2 ххе ldxx \ е ldyx
I
Интеграл
} -4
\ ххе dxt
+
«1-т
G.9.6)
так как выражение в фигурных скобках представляет
собой математическое ожидание случайной величины Z,
имеющей нормальное распределение с параметрами
М [Z] » 0; D [Z] = 1 (см. F.3.2)).
Интеграл
J e'^dx,
— 00
G.9.7)
7.9. ДВУМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
233
а все выражение в фигурных скобках равно единице,
так как оно представляет собой интеграл в бесконечных
пределах от нормальной плотности распределения с. в. Z,
у которой М [Z] = 0; D (Z) = 1. Следовательно, М [X] = тХг
что и требовалось доказать.
Аналогично доказывается, что М [Y] = ту. Для
вычисления дисперсии Z?x найдем сначала второй
начальный момент случайной величины X:
G-9.8)
Применяя замену переменпых G.9.3) с учетом
G.9.4), G.9.5), получим
М [X2] -
+ ml) e^xdx1 JI J e'VldyX
G.9.9)
2/2
Вычислим интеграл:
3/2
J v^e d
G.9.10)
Выражение в фигурных скобках равно единице, так как
оно представляет собой дисперсию нормальной с. в. Z
с параметрами М [Z] =0; D [Z] = 1.
С учетом G.9.6), G.9.7) и G.9.10) получим
M[X*]=ol + m2Xi G.9.11)
откуда
что и требовалось доказать. Аналогично D [Y] *= aj.
Покажем, что г*у есть не что иное, как коэффициент
корреляции случайных величин (X, Y):
г„-**/(<**), G.9.12);
где Кк, — ковариация (X, У), По формуле G.6.10),
У)dx dV< G'9ЛЗ)
234 ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
Примопяя замепу переменных G.9.3) с учетом
G.9.6), G.9.7) и G.9.10), получим:
J Xle idxA\ J yie yidyi
Деля ковариацию на охву, получим коэффициент
корреляции величин X и У, который равен r*v, что и
требовалось доказать,
Таким образом, закон двумерного
нормального распределения полностью
определяется заданием его числовых
характеристик, что очень удобно в практических применениях.
Действительно, для того чтобы записать (пусть
приближенно) совместную плотпость /(#, у) двух нормально
распределенных случайных величин (X, У), достаточно
определить из опыта приближенные значения числовых
характеристик системы (X, У) (как это делается,
подробно рассказывается в гл. 11).
Условные законы распределения с. в. X и У найдем
по формуле G.5.19):
x — тл у —
ехр-
G.9.14)
Нетрудно убедиться, что каждый из условных
законов распределения является тоже нормальным с условным
математическим ожиданием и условной дисперсией,
определяемыми по формулам:
¦ тх + гхуах {у — ШуIоу\ Dxw = al (l — rly),)
7.9. ДВУМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 235
Из формулы G.9.15) видпо, что для системы
нормально распределенных с. в. X и У линии регрессии тх|у
и ту\х представляют собой прямые линии, т. е.
регрессия для нормально распределенной системы (X, У)
всегда линейна.
Таким образом, для полного описания системы двух
нормально распределенных с. в. (X, У) нужно знать пять
параметров: координаты центра рассеивания (пгх, тпи) и
матрицу ковариаций, состоящую из четырех элементов:
d\ у
УХ "и II
Если случайпые величины X и У пекоррелированы
У~ 0), то выражение G.9.1) прамет вид:
-ШШ, G.9.17)
где /,(.г) — нормальный закон распределения св. X
с параметрами тх, о» и /2(//)—нормальный закон
распределения с. в. У с параметрами mv, oy (см. F,3.1)).
Отсюда следует, что если две нормально распределенные
с, в. X и У некоррелированы, то они и независимы, так
как их совместная плотность равна произведению
плотностей отдельных с. в. Для нормально
распределенных случайпых величин термины
«независимость» и «некоррелированность»
эквивалентны.
В геометрической интерпретации совместная
двумерная нормальная плотность f(x, у) представляет собой
холмообразную поверхность (рис. 7.9.1), вершина
которой находится над точкой (mx, my) плоскости хОу.
Аппликата этой вершины равна
f{mx, my) « \\[2noxovYl-rly\ G.9.18)
Сечение поверхности /(#, у) плоскостью, параллельной
плоскости хОу, представляет собой эллипс, уравнение
проекции которого на плоскость хОу имеет вид:
(х — mxf/ol — 2гху {х — тх) (у — ту)/{охоу) + (у—туJ/о1=а\
G.9.19)
где а2 - [in [Ь2похоу У 1 — гху)\. (— 2) A — r%y)% b — рас-
236
ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
стояние плоскости сечения от плоскости хОу
@<b<f(mx, my)).
Оси симметрии эллипса, центр которого находится в
точке (тХ1 ту), образуют с осью Ох углы а и а + я/2
У
1 .
Г
-^
' V
)
X'
Рис. 7.9.1
'(рис. 7.9.2}, определяемые из условия
tg 2а — 2rxipxov/{ol — ol).
G.9.20)
Оси симметрии эллипса называются главными осями
рассеивания, сам эллипс — эллипсом рассеивания
(эллипсом равной плотности), а центр эллипса — точка
{Щх, щ\— центром рассеивания.
U w
Рис. 7.9.2
Если координатные оси совпадают с осями симмет*
рии эллипса рассеивания, то уравнение эллипса рассей-
7.9. ДВУМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 237
вания будет иметь простейший («канонический») вид.
В соответствии с рис. 7.9.2 для приведения уравнения
эллипса к каноническому виду достаточно перенести
начало координат в точку (тх, ту), а координатные оси
повернуть на угол а. В преобразованной системе
координат х'О'у' система случайных величин (Х\ У) будет
выражаться через составляющие исходной системы
случайных величин (X, У) формулами:
X' шт (X — тх) cos а + (У — ту) sin af
Y' — — (X — тх) sin а + (У —- ту) cos а
} G,9,21)
В новых осях х'О'у' каноническая форма нормального
закона системы с. в. (X', У) имеет вид:
где ох и ov называются главными средними квадрат*
ческими отклонениями,
(о'хУ — о\ cos2 a + rxlflxOy sin 2a + ol sin2 a 1
(<fyJ = a» sin2 а — гХ1рхоу sin 2а + a2, cos2 а. j ^ '
При этом
М [X'] - М [Г] - 0.
Нормальное распределение называется круговым
с центром в точке (mXi my), если случайные величины X
и У некоррелированы (^ = 0) и ох=*оу — о. В этом
случае эллипс рассеивания превращается в круг и
случайные величины остаются независимыми при любом
выборе системы декартовых координат, т. е. при любом
повороте координатных осей. Это облегчает решение
многих прикладных инженерных задач.
Найдем вероятность попадания случайной точки
(X, У), распределенной по нормальному закону с
параметрами m*«mtf = 0; о*; оу в эллипс рассеивания Bkf
центр которого совпадает с началом координат, а
полуоси ах и пу пропорциональны средним квадратическим
отклонениям ах и ау {ах = ках; ау~коу) и направлены
по координатным осям. Уравнение эллипса Вк будет
иметь вид
238
ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
ехр {- т [?+ •?
По общей формуле G.4.5) находим:
Р {(X, Y) €= В*}-J§
Проведя замену переменных и = х/(У2ох); y(v)
мы преобразуем эллипс Вк с полуосями ах == ках и ау_== коу
в кругjCk с безразмерным радиусом к/1/2 = аж/(У2ох) =
= а„/ (У2а„). Следовательно,
Р {(X, У)
J J
Этот интеграл проще найти, перейдя от декартовой
системы координат к полярным координатам г, ср:
u = rcoscp; v = rsinq) @<г</с/У2; 0<ф<2я).
Якобиан У такого преобразования равен:
j I ди/дг ди/ду I
J ~~ I dv/dr dv/dq> \
Следовательно,
oos <р — г sin
sin
г cos
-г.
re
о о
2я Г 1 _r8,
1Г J Iе d
i-e~
G.9.24)
Рассмотрим случайную точку (X, F),
рассеивающуюся вокруг начала координат 0 по круговому нормальному
закону: mx = my = 0; ох =
у
Введем в рассмотрение
величину Rz = УХ2 + Y2 —
расстояние от случайной точки (X, Y)
до центра рассеивания
(рис. 7.9.3). Найдем ф.р. св.
Д2: ^(г)-Р{Да<г},т. е. ф.р.
св. i?2 равна вероятности того,
что случайная точка (X, Y)
попадает внутрь круга Ск с
радиусом г (рис. 7.9.3). Эта
вероятность определяется по
/
Рис. 7.9.3
формуле G.9.24) при к-
G.9,25)
7.9. ДВУМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 239
Следовательно, плотность распределения с. в. Rz будет
/ (г) - F' (г) - ? <Гг2/B(у2) (г > 0). G.9.26)
Закон распределения св. R2 (см. G.9.25), G,9.26))
называется законом Рэлея, зависящим от одного
параметра о. Найдем его числовые характеристики:
ОО 7* ОО q
.2 ~Т
Последний интеграл представляет собой гамма-функцию
(см. F,4.2)). Следовательно (см. F.4.5)):
G.9.27)
Найдем второй начальный момент:
ОО
¦J
г\ го*
г
2?
G.9.28)
так как последний интеграл равен м. о. с. в.,
распределенной по показательному закону с параметром X — 1 (см.
F.2.2)). Следовательно,
D [R2] - a2 [Rz] - (М [Д2]J - 2a2 - яа2/2 = D - я) а2/2 ^
«0,429а2, G.9.29)
а [Д2] = (D [R2]f2 - о [D - я)/2]1/2« 0,655а. G.9.30)
Можно доказать следующее утверждение: если
расстояние Rz от начала координат до точки (X, Y) (рис. 7.9.3)'
подчинено закону Рэлея с параметром о, а угол Ф
распределен равномерно и интервале от 0 до 2л и не
зависит от с. в. /?2, то система с. в. (X, Y) имеет
нормальное круговое рассеивание:
•• ту =» 0; Ох =
тпх •
о.
Если случайная точка (X, У) распределена нормально
по закону G.9.17), то вероятность ее попадания в пре-
240
ГЛ. 7, СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
делы прямоугольника R со сторонами, параллельными
главным осям рассеивания (рис. 7.9.4), равна
б 0 6
а V
Так как область интегрирования — прямоугольник со
сторонами, параллельными координатным осям, то
G,9.31)
где Ф(г) — функция Лапласа.
Чтобы приближенно найти вероятность попадания
случайной точки {X, Y), распределенной по двумерному
нормальному закону, в произвольную
область D на плоскости хОу
(рис. 7.9.5), можно приближенно
заменить область D областью,
составленной из прямоугольников. На этой
идее основано применение так на-
J.
ос fix зываемых сеток рассеивания, состав-
Рис. 7.9.4 ленных из квадратов, вероятности
попадания в которые вычислены
заранее. Сетка рассеивания, отвечающая случаю кругового
рассеивания (о* ~Оу = о), выполняется на прозрачной
бумаге и накладывается на изображение области D%
У
X
X
Ряс. 7.9.5
Рис. 7.9.6
перестроенное в соответствующем масштабе. Если область
D выпукла и невелика по сравнению с эллипсом
рассеивания (ее размеры в направлениях осей Ох и Оу не
превышают а«, оу)} то удовлетворительную точность можно
7.9. ДВУМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
241
получить, заменяя область D одним прямоугольником
примерно той же площади (рис. 7.9.6) и вычисляя
вероятность попадания точки (X, У) в этот прямоугольник.
Пример 1. На станке-автомате изготавливается
деталь цилиндрической формы. Полученные в результате
обработки длина L и радиус Н детали являются
независимыми с. в., распределенными по нормальным законам
с характеристиками: М [L] = 100 мм; a [L] = Oi «= 0,1 мм;
М [Н] = 10 мм; а [Я] = oh = 0,01 мм. Определить процент
бракованных деталей, если деталь считается годной,
когда ее размеры
определяются условиями A00—0,1) мм <
<L<A00 + 0,05) мм; A0-
-0,005) мм < Ж A0 +
+ 0,007) мм.
Решение. Вероятность р
того, что деталь не будет
забракована, определяется
вероятностью попадания системы
независимых нормально распределенных
угольник Л, изображенный на рис.
G.9.31) получаем:
10+0,07
10-0,05
wo-o,i
Рис, 7.9.7
700+0,5"
с. в. в прямо-
7.9.7. По формуле
р-
( 100 + 0,05 — 100
\ о,1
л /
Ю0 - 0,1 — 100
X
ф /Ю + 0,007 - 1(Л ф АО - 0,005 -
0,01
« 0,239.
Следовательно, вероятность брака равна 1 — р &>
«0,761. >
Пример 2. Приземление космического летательного
аппарата (KJIA) проводится с помощью парашютной
системы. Рассеивание точки (X, У) приземления КЛА
является нормальным круговым с характеристиками: тх =
= ту = 0, Ох = оу = о. Найти радиус круга г, в который
с вероятностью д* приземлится КЛА.
Решение. Искомый радиус г найдем из равенства
3> - Р {Rа < г} - 1 - ехр {- г2/Bа2)},
откуда
(
Так, например, при о =
г = 2(— 2 InО
и^ = 0,95
»4,89 км. >
242
ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
й •
б\
V \
0 'I х
— ехр {— пгЩ (г > 0).
Откуда
/(г). -= F' (г) - 2пкг ехр {-
Пример 3. Место посадки КЛА па планете
представляет собой поверхность, па которой в случайном
порядке находятся кратеры. Считая, что центры кратеров
на поверхности планеты представляют собой пуассонов-
ское поле точек с интенсивностью X, найти закон
распределения расстояния /?2 от места посадки КЛА до
центра ближайшего кратера.
Решение. Найдем функцию распределения св. Я2,
для чего проведем вокруг точки П посадки КЛА
окружность радиуса г (рис. 7.9.8). На рис. 7.9.8 центры
кратеров изображены в виде точек.
Для того чтобы расстояние Rz от
точки П до ближайшего к ней
центра кратера Б было меньше
г, надо, чтобы в круг радиуса г
попал хотя бы один центр
кратера. Следовательно,
Рис. 7.9.8
Таким образом, с. в. R2 подчипена закону Рэлея с
параметром а = 1/BяХI/2. Напомним, что в данном
примере величина X представляет собой среднее число центров
кратеров, находящихся на определенной площади
планеты.
Если в точке П поместцть начало декартовой
системы координат хОу с произвольной ориентацией осей,
то точка Б будет иметь координаты (X, У),
распределенные по нормальному закону с параметрами тх = ту»
«0; ох = ау = о = i/BnX)u\ >
Пример 4. По небольшой (точечной) цели ведется
стрельба снарядами, радиус поражения которых равен гп,
т. е. цель поражается, если снаряд разорвался на
расстоянии от цели, не превышающем величину гп, в
противном случае цель остается непораженной. Рассеивание
при стрельбе нормальное круговое, систематические
ошибки отсутствуют.
Определить вероятность поражения цели Р при п
независимых выстрелах.
Решение. Вероятность Р будет определяться как
вероятность того, что хотя бы один снаряд попадет в
7.10. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 243
круг СГп с радиусом гп, в центре которого находится
цель. Вероятность р того, что один снаряд попадет
в круг СГп, будет
Следовательно,
р _ 1 _ A _ Pl)«.1 _ ехр (-
7.10. Многомерное нормальное распределение
Перейдем к рассмотрению нормального распределения
—>
для системы произвольного числа п с. в.—вектора Х =
» (Xiy Х2, ..., Хп) в л-мерном пространстве. Его
плотность записывается в виде:
|п п
- т 2 2 Мг1} to -
G.10.1)
где Wi — математическое ожидание величины Х< (i = 1,
2, ..., /г); а А представляет собой определитель
ковариационной матрицы Шц\\ системы св. (Хи Х2, ¦.., X»):
к1г к12 ... л:
МГ^"" элементы матрицы, обратной по отношению к
ковариационной матрице \\Ktj\\ системы св. (Хи Х2, ,.., Хп):
^ G.10.3)
Л ^ — алгебраическое дополнение элемента Кц матрицы
ковариаций.
В силу симметрии ковариационной матрицы (Кц —
« Кц), обратная ковариационная матрица также обладает
свойством симметрии:
Таким образом, для описания нормального закона
распределения системы п случайных величин нужно знать
следующие величины:
244
ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
п математических ожиданий: mlt m2, ..., тп;
n(n+i)/2 элементов ковариационной матрицы (из
которых п дисперсий):
К-" G.10.3)
К
22
Напомним, что по главной диагонали ковариационной
матрицы G.10.3) стоят дисперсии случайных величин
Xi (*-l, 2, ..., п): Kii**Di.
Если нормально распределенные с. в. (Хи Х2, . •., Хп)
некоррелированны, то ковариационная матрица
превращается в диагональную:
,. 0
ох о
G.10.4)
В этом случае определитель А будет равен
произведению диагональных элементов:
п
а обратная ковариационная матрица также является
диагональной:
i/Dt о ... О
1/#й «.. 0
G.10.5)
Следовательно, для нормально распределенной
системы некоррелированных с. в. совместная плотность G.10.1)
имеет вид:
a,
7Л0. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 245
Мы показали, что нормально распределенная система
некоррелированных случайных величин (Хи Х2, ...t Xn)
представляет собой нормально распределенную систему
независимых случайных величин, так как совместная
плотность системы (Хи ..., Хп) равна произведению
плотностей отдельных величин (Хи ..., Хя), входящих
в систему. Таким образом, для нормально
распределенной системы п св. из
некоррелированности отдельных величин следует их
независимость.
Нетрудно доказать (мы этого делать не будем), что
любая подсистема случайных величин (Хи Х2, ..., Хк),
входящая в нормально распределенную систему {Хи
Х2, ..., Jfft_t, X*, Xft+1, ..., Хп) (нумерация произвольная),
также распределена по нормальному закону, зависящему
от следующих параметров: к математических ожиданий:
к (к +1)
77ii, M21 . •., rnk] —g— элементов ковариационной
матрицы, составленной из соответствующих элементов
ковариационной матрицы системы G.10,3):
К
12
22
4*
^2А
G.10.7)
Кь
Следовательно, подсистема
случайных величин (Xlt X2,
нормальную плотность:
нормально распределенных
•*., Хк) имеет совместную
k k
I
G.10.8)
где величина Д(М равна определителю ковариационной
матрицы G.10.7) подсистемы (Xlt X2, #.#f Xk):
*П Я1
V2A
— элементы матрицы, обратной по отношению к
ковариационной матрице Itfiil G.10#7)#
246 гл, 7. системы случайных величин
По формуле G.8.13) можно определить условную
плотность распределения подсистемы св. (Xft+,, ХА+2, ...
..•, X»), вычисляемую при условии, что остальные
случайные величины Хи Х2, ..., Хку входящие в систему,
приняли определенные значения: xi} х2, ..., хк:
, ..., xn)/h k(xu ..., хк), G.10.9)
где f(xu ..., хп)'— нормальная плотность распределения
системы случайных величин (Хи Хг, .•., Хл),
определяемая по формуле G.10.1); /t *(#!, ..., хк)— нормальная
плотность распределения подсистемы случайных величин
(Хи Х2, ..., Хк), определяемая по формуле G.10.8).
Нетрудно доказать (мы этого делать не будем), что
условный закон распределения G.10.9) будет тоже
нормальным.
В инженерных приложениях чаще всего имеют дело
с условным законом распределения случайной величины
Х<, вычисленным при условии, что остальпые случайные
величины, входящие в систему, приняли определенные
значения: Xt = #,; ...; Х^х^=х^х\ Xt+1~xi+1; ...; Хп =
= хп. Этот условный закон будет нормальным с
характеристиками
п
тх$г = т>- 2 МГ1}(*>- т})/к\тг) (< —1, 2 л),
G.10.10)*)
D*i\*i *i-u ^i.....*» - DXi\xt - ^ (t - 1, ..., n).
G.10.11)
Условное математическое ожидапие ^х.|-.
представляет собой линейную функцию (/г —1) переменных xj
(/ — 1, 2, ..., п; /=^0» поэтому поверхность регрессии Х<
на #t, ..,, Zi-U xi+u ..., жта представляет собой
гиперплоскость в л-мерном пространстве.
*) Введенное для сокращения обозначение m .- эквивалент»
яо ваппси и»^ х,_г*1+1 *„•
7.10. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
247
Условная плотность распределения с. в. Хи при
условии, что Xi «» #!, ,.., Xi-i =¦ Xi-i, Xi+\ = Xi+i} ..., Хп == хП1
равна
GЛОЛ2)
Вероятность попадания случайной точки '(Xlf XZj ...
•.., Хп) в произвольную область D я-мерного
пространства будет определяться по
формуле G.8.10). В случае,
если нормально распределенные
с. в. независимы, а область D
представляет собой «-мерный
прямоугольный
параллелепипед /?« со сторонами,
параллельными координатным осям,
то вероятность попадания
случайной точки (Х|, Хг, ..., Xrt)
в эту область выражается
через функцию Лапласа:
Рис. 7.10.1
р «х„ х , хп)
П [ф (Ц=)- *?=?)}<
G.10ЛЗ)
где а<, Pi — координаты границ прямоугольного
параллелепипеда Rn в направлении оси 0xt (а< < р<); т<, о< —
м. о. и с. к. о. случайной величины Хи Ф(г)—функция
Лапласа. Для гс = 3 область /73 показана на рис. 7.10.1,
Если нормально распределенные с. в. независимы (не-
коррелированы) и при этом т< = 0 (*в1, 2, .,., п), то
их п. р. может быть записана в таком виде:
• ехр
G.10.14)
которая называется канонической (простейшей) формой
нормального закона системы п св. (Хи ..., Хп).
Найдем вероятность Рп попадания случайной точки
1Хи ..., Хп) в п-мерной гиперэллипсоид равной плотно-
248 гл, 7, системы случайных величин
сти Вк, уравнение которого можно получить из условия:
/ \ 1> • ¦ •> *"п) *""" const,
откуда
G.10.15)
При п = 2 получаем уравнение эллипса равной
плотности в декартовой прямоугольной системе координат на
плоскости х$хг (рис. 7.10.2):
Центр этого эллипса находится в начале координат,
его полуоси равны: at = кои а2 = ко2. Вероятность Р% =
= Р {(Х1? Х2) е Вь) попадания случайной точки (Хи Х2)
в такой эллипс была найдена в п. 7.9.
а2
%\ а?
Рис. 7,10.2
Рис. 7.10.3
При п = 3 получим уравнение эллипсоида, равной
плотности Вк в декартовой прямоугольной системе
координат в пространстве трех измерений
ХЛ \ — ТА
Центр этого эллипсоида находится в начале
координат, его полуоси равны а4 = 0А&; аг = огк\ а9 — o8ft
{рис. 7.10.3).
Найдем вероятность попадания случайной точки
'(Xi, X2, Xs), распределенной нормально с параметрами
m? = m2 = т3 = 0; о4| а2, а4, в эллипсоид равной
плотности Вк по формуле:
7.10. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 249
В этом интеграле перейдем от декартовых координат хи
#2, #s к полярным г, ф|, ф2:
xi-rVi(<Pu <pi)V2at (t=l, 2, 3), G.10.16)
где
G.10.17)
vi (фи Фг) — cos Ф1 cos Фг>
v2 (ф!» Ф2) == cos (pjSin ф2| v3 (фц" Ф2) == sit
Этим преобразованием координат эллипсоид Bh
превращается в сферу С с радиусом к/У2 (ft = ai/a<; i=*
= 1, 2, 3). В дальнейшем мы увидим, что конкретный
вид функций У»(ф1, Фг) (* = 1, 2, 3) нам не потребуется.
Якобиан преобразования равен
T/2Vl
*^(91. Фа), G.10.18)
где и>'(ф!, ф2) —некоторая функция углов поворота; в
нашем случае м?(ф4, ф2) = совф1.
Следовательно,
123
-ш
« J e~r r2dr X J j ^(ф1, ф2) d^Q
о (Ар)
где />ф — область изменения углов q
значение
Г f
щ) О
nKs G.10.19)
и ф2. Введем
обоG.10s20)
250
ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
Следовательно,
При неограниченном увеличении эллипсоида равной
плотности (/с-^оо) Р8 = 1, откуда (см. F.4.2) и F.4.5))
/00 \ —1 / °° Я \ ~1
AT'V
v? G10-21>
где Г (ж)—гамма-функция. Этот прием позволил нам
вычислить интеграл G.10.20), чем мы воспользуемся в
дальнейшем.
Таким образом,
к/Г2
= JL [t -«"/? JL
dt — du;
G.10.22)
где Ф(х)— фупкция Лапласа.
Найдем функцию распределения с. в. R3 —
= у Хг + XI + Х\—* расстояние от лачала координат 0
до случайной точки (Хи Хг, Х*). Система св. (Xh X2i
Ха) распределена нормально с параметрами тх^гпг^
=* тг «¦ 0; Gi = о2 «¦ Оз в о. Для этого достаточно в
выражении G.10.22) положить величину к =* г/о:
(г)
г) - 2Ф (^) - Щ
е~™
(r>0),
G,10,23)
7.10. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 251
Дифференцируя G.10.23), найдем плотность
распределения с. в. /?3:
/8(г) - F;(г)
(а3 /S) (г> 0). G.10,24)
Полученный закон распределения носит название закона.
Максвелла, Найдем его характеристики:
Mi
/2 j^gj - а2 /2/ /я « 1,64а;
G.10.25)
D[Я,] - а,№J- (М [Д3]J»0,371о2;
а [Л,]- /D[fl3]« 0,606а.
Перейдем к системе п нормально распределенных
независимых случайных величин и найдем вероятность
попадания случайной точки (Хи Х2, ,,., Хп) в /г-мерный
гиперэллипсоид Bk (тг = 0; i = 1, 2, .,., п):
}
J<n)J /(^l» ^a» • * •' *») da:ida;a •' • d*n»
(B)
Введем в и-мерном пространстве (xit х2} ..., хп)
преобразование координат вида
фп-0, G.10.26);
L/a
G.10827)
где
Г = \ -7Г
— «расстояние» от начала координат до точки (xi, . •., хп)
в га-мерном пространстве, ^(фь ..., фп-i) некоторая
функция углов поворота <pi, ф2, ..., фп-i координатных
осей O^i, 0х2} ..., 0хп.
Этим преобразованием /г-мерный гиперэллипсоид
превращается в я-мерную гиперсферу. Якобиан преобра-
252 ГЛ. 7, СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
зования
/ = г*1-1 ( /2)ПП arw(ffl9 Фа, ,.., фп-Oi G.10.28)
где w((fu ,.., фп-,)—некоторая функция углов ф4| ...
Таким образом, мы свели задачу нахождения
вероятности попадания случайной точки (Хи Х2, ,,,Д„) в
гиперэллипсоид Bk, к задаче нахождения вероятности попа-
/ n \i/a
дания конца случайного радиуса вектора #п ¦¦ 2 X?
в пределы гиперсферы:
^Pff г - » 1
e J исл-х>3 гп"(Уг2)лЦог«м'(ф11 -.Фп)йф1..»йфй X
[
где D« — область изменения углов поворота
координатных осей;
Ъп = J(n-i) f ( VI)п П W (фц .. •! фп-i
Если неограниченно увеличивать гиперэллипсоид (к
ро), то
Следовательно,
откуда
7,10. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЙ 253
В этом интеграле проведем замену переменных; г* — *;
VF; dr-f*dt/2i
j j
0 0 О
Полученный интеграл представляет собой
гамма-функцию (см. F.4,2)), следовательно,
На основании свойств гамма-фупкции F.4.4) в F.4.5)
получаем
21 (-j — lj! при п —> четном (п > 2),|
ntm[VT*lJ[V] при п-нечетном (и>3),|
G.10,29)
где (»-2)!1«1-3-5-7"-(»-2), (п/2 —1)! —1 • 2 ¦ 3
..-(n/2-l).
При г» > 2 —четном имеем (см. F.4.11))
hlYl
J
- 1)! - 1 - Л (n/2 - 1
G.10.30)
m
где Д(л1А а) жт 2 а1етЛ1\\^ функция, описывающая рас-
пределение вероятностей случайной величины Х9
распределенной по эакону Пуассона с параметром а (п. 5.2).
При п>3 нечетном вероятность попадания в
гиперэллипсоид Bh равна:
G40.31)
254 гл. 7. системы случайных величин
где сумма определяется только для нечетных индексов
т = 1, 3, 5, ..., (тг-2), (п>3); Ф(х)—функция
Лапласа.
Напомним, что в формулах G.10.30) и G.10.31)
величина к представляет собой отношение полуосей тг-мер-
ного гиперэллипсоида к соответствующим средпим квад-
ратическим отклонениям:
При нормальном тг-мерном «круговом» рассеивании все
с. к. о. равны: Oi=* о2 = Оз — *'. = Оп — о. В этом случае
гиперэллипсоид Bh превращается в гиперсферу Cki а
вероятность того, что радиус-вектор Rn = (Х\ + Х% +
+ Х\ + ... +Х'пУ/2 не выйдет за пределы гиперсферы
с радиусом г, будет определяться выражением, которое
получится, если в формулы G.10.30) и G.10.31) вместо
величины к подставить г/о {г>0\
1 — R(n/2 — 1; г2/Bа2)) при п > 2 (четном);
*
11 при п>
G.10.33)
Дифференцируя выражение G.10.33) по г найдем
плотность распределения случайной величипы Rn
». G.10.34)
где величина Ъп определяется по формулам G.10.29) для
различных тг. При п»2 получаем закон Рэлея, при п =»
=» 3 — закон Максвелла.
С помощью гамма-функции выражение G.10.34)
может быть записано в виде
G1аз5)
7.10. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 255
Можно убедиться в том, что
00
М [Rn] = J rfn (r) dr = a /2Г ((л + 1)/2)/Г (и/2), G.10.36)
О
«а [Rn] = М [RI] - М [ | X? 1 = 2 ММ- по»,
G.10.37)
D [Д„] = а2 [Яп] - (М [R,,]f. G.10.38)
Пример 1. Рассматривается производство больших
интегральных схем (БИС). БИС проходит контроль, если
ее входные параметры L — индуктивность, С — емкость и
Т — быстродействие не превышают величин Z, с и t
соответственно. Величины L, С, Т независимы, распределены
нормально с характеристиками mh о*; mc, oc; mt, Ot.
Найти вероятность р того, что БИС пройдет контроль.
Решение. Вероятность р найдем из условия
Так как с. в. L, С и Т независимы, то
р = Р {L<l}.P {С <с}Р {Т <t}.
По формуле G.10.13) получим
Пример 2. Рассматривается вывод межпланетной
станции (МС) в заданную область космического
пространства (КП) в заданное время t. Область КП, куда
должна быть выведена МС, представляет собой
эллипсоид BSi подобный эллипсоиду рассеивапия, полуоси
которого равны двум с. к. о. по соответствующим
координатам рассеивания МС в КП; координаты МС (X,, Х2, Х3)
относительно центра области Въ в момент t представляют
систему независимых, нормально распределенных с. в. с
характеристиками шг = т2 == ть = 0; ои о2, о3. Ошибка
во времени Т распределена нормально с характеристика-
256
ГЛ. 7. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
ми ntt = 0; о, и не зависит от с. в. Xi, Х2, Xs.
Определить вероятность Р того, что MG будет выведена в об*
ласть В г КП в интервале времени t ± 2ot.
Решение. Искомую вероятность находим из условия
Р - Р {(*!, Х2, Х3) еВ3}'Р {- 2а, < Т< 2а«).-
По формуле G.10.33) для га = 3 и к = 2 находим
2Ф B) - Й *-«''i 2IS, « 0t739.
По формуле F.3.17);
Р {- 2at < Т < 2at} = 2Ф (^Ч « 0,955,
Окончательно получим
Р& 0,739.0,955^0,706. >
Пример 3. Условия предыдущего примера
остаются теми же, за исключением того, что рассматривается
д.
2б1
Рис. 7.10.4
четырехмерное пространство не-
зависимых нормально
распределенных св. (Хи Х2, Х3, Г)'.
Требуется найти вероятность Р
попадания этих с. в. в
четырехмерный гиперэллипсоид i?4,
подобный гиперэллипсоиду
рассеивания указанных с. в., по*
луоси которого равны двум
с. к. о. по соответствующим координатным осям.
Решение. По формуле G.10.33) при гс
находим
4; ft —2
- 1 - Д D/2 - 1; 22/2) = 1 - Д A, 2) = R A, 2).
По таблице приложения 2 в [4] имеем Р « 0,594. >
Пример 4. Условия примера 2 остаются такими же,
за исключением того, что область КП, куда должна
попасть МС, представляет собой прямоугольный
четырехмерный гиперпараллелепипед Д4, центр которого
совпадает с центром рассеивания св. Хи Х2, Х8, Г, а стороны
равны четырем соответствующим с. к. о, и параллельны
координатным осям,
7.10. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 257
Решение. По формуле G.10.13) для п = 4
получаем
Эта вероятность получалась большей, чем в примере 3.
Объясняется это тем, что область /?4 больше, чем область
В4. Наглядно это можно изобразить для двумерного
случая: прямоугольник /?2 со сторонами 4а4 и 4о2 больше
эллипса Вг с полуосями 2а, и 2а2 (рис. 7.10.4). По этой
же причине вероятность Р« 0,706 в примере 2 больше
вероятности Р = 0,594 в примере 3. >
9 Теория вероятностей и ее
инженерные приложения
ГЛАВА 8
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
СЛУЧАЙНЫХ ВЕЛИЧИН
8.1. Математическое ожидание
и дисперсия функции
В круге практических, в частности, инженерных,
применений теории вероятностей большое место занимают
задачи, требующие нахождения числовых характеристик
функций с. в. В простейшем случае задача ставится так:
на вход технического устройства (ТУ) поступает
случайное воздействие X (рис. 8.1.1). ТУ подвергает
воздействие X некоторому функциональному преобразованию ср
и дает на выходе с. в.
(8.1.1)
Нам известен закон распределения с. в. X (в
некоторых случаях — только его числовые характеристики).
Требуется найти числовые характеристики с. в. Y,
Рис, 8,1.1 Рис. 8.1.2
В более сложном случае на вход преобразователя <р
подается не одно, а несколько случайных воздействий
(Хь Х2, ..., Хп), а на выходе снимается несколько
случайных величин (Ки YZi ¦.., Yk) (в общем случае к?*п)}
рнс. 8.1.2.
Требуется, здая закоп распределения (в некоторых
случаях — только числовые характеристики) входной
системы (Xt, Х2, ..., Хп), найти числовые
характеристики выходной системы (Yu У2, ..., Yk).
Преобразователем ф может быть не только
техническое устройство. Например, в его роли может выступать
некоторое производство, входами которого могут быть
всякого рода ресурсы: Х4 — сырье, Х2 — топливо, Х3 —
энергия, Х4 — вода, Х5 — фондовооруженность и т. п.,
а выходами — различного рода продукции (Yu F2,..., Yh).
8.1. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И ДИСПЕРСИЯ ФУНКЦИИ 25Э
Здесь в общем случае могут возникнуть три
задачи.
1. Зная закон распределения случайного воздействия
X (или системы случайных воздействий (ХЬХ2,..., Хп)),
найти закоп распределения выходной случайной
величины У==ф(Х) (или системы случайных величин У, =
~Vj(XuXlt ..., Хя); (у = 1, ..., к)).
Это — задача сравнительно сложная, и ее мы в
данной главе касаться не будем (ей будет посвящена
глава 9).
2. Зная закон распределения случайного воздействия
X (или системы (Х1у Хг, ..., Хп)), найти числовые
характеристики выхода У (или системы (У^ У2, ..., Yk)).
Оказывается, для того, чтобы их найти, вовсе не
обязательно знать закон распределения
выхода У (или системы (У1? У2, ¦.., Ук)).
3. В некоторых случаях (при особом виде
преобразования ф) для пахождения числовых характеристик
выхода не требуется даже знать закон распределения входа,
а достаточно знать только его числовые
характеристики.
В данной главе мы рассмотрим вторую и третью
задачи — определение числовых характеристик выхода без
пахождения его закона распределения.
Мы уже упоминали о том, что во многих
практических задачах удается находить числовые характеристики
интересующих нас случайных величип, вовсе не зная их
законов распределения. В данной главе мы в этом
убедимся. Добавим, что искусство применения теории
вероятностей в прикладных задачах в значительной мере
сводится к умению обходиться числовыми
характеристиками, минуя 8 а коны распределения. Чем
искуснее в споем деле специалист по прикладной теории
вероятностей, тем свободнее он пользуется аппаратом
числовых характеристик и тем реже прибегает к
законам распределения.
Рассмотрим, одну за другой, несколько задач па
нахождение числовых характеристик функции случайных
величип.
Задача 1. Числовые характеристики
функции одного случайного аргумента.
Рассмотрим с. в. У, зависящую функционально от с. в. X:
У-Ф(ДГ). (8.1.2)
260
ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
Предположим, что с. в. X дискретна и мы знаем ее
ряд распределения:
X :
Pi
*2
...
...
*i
Pi
...
хп
Рп
где
i, 2, ...,и);
, (8.1.3)
(8.1.4)
"К*.)
Pi
ф(*2)
p2
...
ft
ФЫ
Pn
При X = #, У = <р(#<); вероятность этого события равна
р{. Может показаться, что мы уже нашли ряд
распределения с. в. У:
(8.1.5)
Но это не совсем так: в ряде распределения с. в. У
значения верхней строки должны идти в возрастающем
порядке; кроме того, некоторые из <р(#,) могут совпадать,
и при построении ряда распределения с. в. У
соответствующие вероятности должны складываться. Но для того,
чтобы найти числовые характеристики с. в. У, такого
«упорядочения» вовсе не нужно, достаточно ряда
распределения с. в. У в форме (8.1.5). Действительно, находя
сумму произведений возможных значений с. в. У на их
вероятности, получим,
Шу - М [Y] - М [<р (X)] = S Ф fa) Л- (8.L6)
Таким образом, зная закон распределения
аргумента X, можно сразу найти
математическое ожидание его функции (8.1.2).
Аналогично находится дисперсия с. в. У:
где Y = Y — my.
Действительно, (Y — mv)г есть некоторая функция
с. в. X:
а ее математическое ожидание, согласно (8.1.6), равно
D, = D [Y] - 2 [ф fa) - %]^j. (8-1.7)
8.J. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И ДИСПЕРСИЯ ФУНКЦИИ 261
Аналогично определяются и начальные и
центральные моменты любых порядков с в. Y:
п
<*/ [У] = 2 l<p(*i)]lPi, (8.1.8)
^-тИ'л. (8.19)
Если с, в. X непрерывна и имеет плотность j{x), то,
заменяя в формулах (8.1.6), (8.1.7), (8.1.8), (8.1.9)
вероятности р{ элементом вероятности f(x)dx, а суммы —
интегралами, получим:
00
щ = М [У] = М [ф (X)} - J ф (ж) /(*) Лг, (8.1.10)
— 00
оо
Dy-D [У] -М [У*] = j (ф (*) - т,J/ (*) dxx (8.1.11)
— 00
00
а/[У] -М[У'] - J 1ф(*)]'/(*) Ас. (8-1.12)
^/W^. (8.1.13)
Мы видим, что для нахождения числовых
характеристик функции У==ф(Х) вовсе не
нужно знать ее закон распределения, а
достаточно знать закон
распределения аргу-
мент a.
Пример 1. Непрерывная
св. X распределена с плот-
А
, , v COS X ¦¦¦¦— I и
ностью / (х) = —j- при х е ji О
€=(—?;+ -j) (рис 8.1.3). Рис. 8.1.3
Найти м. о., дисперсию св. Y = 2 — 3 sin X = ф (X).
Решение.
Л/2 Л/2
М[У]- f ф(*)/(х)&-
-Л/2 -Л/2
262
ГЛ 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
JT/2
j
я/2
j
j j B - 3 sin x |
-Я/2 -Я/2
D [Y] - a2 [У] - (M [Y]J = 1 - A/2J = 3/4. >
Задача 2. Числовые характеристики
функции нескольких случайных
аргументов. Если с. в. Y (выход преобразователя ср) есть
функция не одного аргумента, а нескольких: У = ф(Хь Аг2, ...
..., Хп),\\ известна совместная плотность f(xu x2, ..., хп)
системы аргументов, то м. о., дисперсия, начальные и
центральные моменты с. в. У определяются формулами:
.. ,2 xn)j{xv
— OO —00
— C» — 00
00 00
J (n) J [ф^-.^
—00
00
— 00 —00
00 00
(8.1.14)
... dxn}
(8.1.15)
(8.1.16)
— 00 —00
(8.1.17)
Пример 2. Точка С/, изображающая объект на
круглом экране радиолокатора, распределена равномерно в
пределах круга радиуса г (рис. 8.1.4).
Найти п. о., дисперсию и третий
цептральпый момент расстояния L
от точки U до центра экрана.
Решение. В примере 6 п. 7.5
было показано, что координаты
точки U внутри круга радиуса г
имеют плотность распределения
f{ )(* + 1/2<г2).Расстся*
координаты X, Y
М [L] —
Рис. 8.1.4
пие L
точки
выражается
U так: L
через
* (*
декартовы
Следовательно,
VX*+Y\
s)j Vx* + y2 —i dx dyr где область К
nr*
круг радиуса г.
8.1. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И ДИСПЕРСИЯ ФУНКЦИИ 263
Перейдем к полярным координатам х » р cos ф, у «=¦
- р sin ф. Якобиан преобразования равен р. Тогда
Аналогично найдем:
а2 [L] = М [L2] =
/ г «4
О ^ О '
Следовательно,
Третий центральный момент определяем по формуле
г 2Я
J J \ 3/ дГ2 135'
о о
Вернемся к числовым характеристикам св. Y =»
= ф(Х1, ..., Х„) и запишем их в несколько другом виде,
чем (8.1.14)—(8.1.17). Плотность распределения системы
с. в. №,...,Хп) может быть записана так: f(xh.. .,#„) =
/t Л(х1, ..., хк\хк+1, ..., хп)—условная п. р. системы св.
(Хи Хг, ..., ХА), вычисленная при условии, что с в.
(Хк+и ..., Хп) приняли определенные значения лгЛ+1, ...
• .., Хп, /*+1..пО*л+1, ..., хп)—п. р. системы с в. (Xh+U ...
..., Хя).
Тогда формула (8.1.14) может быть записана в виде:
00 СО
J (") J q>(xv ...2
— 00 —00
264 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
^d d
OO f OO 00
— 00 —OO I —OO —OO
X/i fcfo, .. .,**|**+i» .^,xn)dx1... dxk\x
... Arn. (8.1.18)
«Внутренний» fc-кратный интеграл, стоящий в
фигурных скобках, представляет собой условное
математическое ожидание M[F| xh+1, ..., хп] с л у ч а й-
ной величины У, вычисляемое при условии, что
случайные величины Хк+и • • •> %п приняли определенные
значения
оо оо
J (ft) J (p(xv ..., arn)/i л(яц..м**|
...d^. (8.1.19)
— 00 — OO
Следовательно, безусловное м. о. М [У] будет
определяться через условное М[У|.г/,+1, t..j^n] по формуле:
X Л+1§|..,п (^fc+н . • м *n) Arft+i * • * dxn, (8.1.20)
которая носит название интегральной формулы полного
математического ожидания.
По формуле, аналогичной (8.1.19), можно найти
условный начальный момент Z-ro порядка М [у'|яа+1, ...
,.., хп] с. в. У, вычисляемый при условии, что с. в. Xh+i,...
•.., Хп приняли определенные значения xk+u ..., хп:
, ..., хп] =»
00
J
(fc)
— ОО —00
хЛг!... dxk, (8.1.21)
а безусловный начальный момент 1-го порядка с. в. Y,
8.1. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И ДИСПЕРСИЯ ФУНКЦИИ 265
будет определяться по формуле
00 ОО
«([У]= J(n-A) J a,[Y\xh+l, ...,xn) X
— 00 —ОО
X/hi п(я*+1, •.., ^я)йлгй+1 ... Й2?п. (8.1.22)
Обратим особое внимание на способ вычисления
дисперсии случайной величины Y через второй начальный
момент:
D [Y] - а2 [У] - ml (8.1.23)
где величины a2[Y] и ту определяются по формулам
(8.1,22) и (8.1.20) соответственно.
В различных инженерных приложениях бывает
удобно выражать индикатор U события А (см. формулу
C.3.1) п. 3.3) как функцию нескольких с. в. Хи Х2,..., Хп:
A — если событие А имело место;
•••» п) — |q __ в противном случае.
Например, событие А состоит в том, что техническое
устройство работает нормально; при появлении события
А его индикатор равен единице: U = %(XU ..., Х„)=1,
где Xi, ..., Хп — случайные параметры, связанные с
работой устройства (температура, давление, влажность и
т. п.). Мы знаем (п. 3.3), что индикатор события А есть
дискретная случайная величина, имеющая ряд
распределения
0
1
Р(А)
Откуда (в соответствии с формулой (8.1.14)) получим
Р(Л) - М [U] = М [%(XV Хг, ..., Хп) -
90 00
- J <"> J X(*i. • • м *«)/(*!. • • •• xn)dXl ... dxn, (8.1.24)
— оо —оо
т. е. вероятность события А равна
математическому ожиданию индикатора этого
события Л.
Аналогично тому, как было определено условное
математическое ожидание (8.1.19), определяем условную
вероятность события А: Р D1 хк+ъ • • •» хп), вычисляемую
при условии, что случайные величины X^i, ,.., Хп
206 ГЛ 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
приняли определенные значения #А+1, ..., хп\
оо оо
1 ^R' 1 A \**li * • •» ^я/ /l.....fc V^ii • • *» «^ft ••'A+l» • • •» **^n/ л
...Лск. (8.1.25)
— ОО —00
Тогда безусловная вероятность события А вычислит-
ся по формуле, аналогичной (8.1.20):
(n-fc) J Р (Л | ЯГА + 1, ,.*,
..Лс„, (8.1.26)
— 00 —00
которая носит название интегральной формулы
полной вероятности.
Частным случаем этой формулы является ранее
выведенная формула C.4.7).
Пример 3. Выпуск предприятием продукции Y
может бы!ъ приближенно определен по
«производственной функции» вида
У - diXi + d2X2,
где du йг — не случайные параметры, с. в. Х{ —
трудовые ресурсы, св. Хг — основные фонды; св. Хг
распределена равномерно в интервале (а, Ь); с в. Х2
распределена равномерно на участке 2А, центр которого равен
cXi. Найти математическое ожидание с в. Y.
Решение. По условию примера
*) foe (в, 6));
U fo I *i) - s (** G ^ "" А; сд>1 + А^-
По формуле (8.1.19) найдем условное математическое
ожидание с. в. Y при условии, что с в. Xt *= xt:
J
8.2 ТЕОРЕМЫ О ЧИСЛОВЫХ ХАРАКТЕРИСТИКАХ 267
По формуле (8.1.20) найдем
8.2. Теоремы о числовых характеристиках функций
случайных величин
Во многих задачах инженерной практики числовые
характеристики с. в. F = cp(Xi, ..., Хп) могут быть
определены как некоторые функции числовых характеристик
системы с. в. (Xi, ..., Хп). В этом случае не требуется
знать закон распределения системы аргументов j(xu ...
..., Хп), а достаточно зпать лишь числовые
характеристики этой системы.
В данном пункте мы докажем ряд теорем о числовых
характеристиках функций с. в., которые могут быть
использованы в инженерных приложениях.
Некоторые из них были уже доказаны ранее (см.
п. 4.2), здесь мы их повторим для полноты.
1. Математическое ожидание неслучайной величины
с равно с:
М[с]=с. (8.2.1)
2. Дисперсия неслучайной величины с равна нулю:
D [с] - 0. (8.2.2)
3. Математическое ожидание произведения неслучай*
ной величины с на с. в. X равно произведению этой
неслучайной величины на м. о. с. в. Х\
М [сХ] - сМ [X], (8.2.3)
т. е. неслучайную величину с можно выносить за знак
математического ожидания.
4. Дисперсия произведения неслучайной величины с
на с. в. X равна произведению квадрата этой
неслучайной величины на дисперсию с. в. X:
Dlc-X]=c*D[X]; (8.2.4)
D [сХ] - М 1(еХ - М [cX]f] = М [(сХ - сМ [X]J] -
= м [с2{Х - М [X]f] - с2М [(X ~ М [X]f] = c2-D [Xj,
268 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
т. е. неслучайную величину можно выносить из-под
знака дисперсии, возведя ее в квадрат.
Извлекая квадратный корень из (8.2.4) и беря его
арифметическое (положительное) значение, получим
о[сХ\ = \с\о[Х1 (8.2.5)
т. е. неслучайную величину можно выносить из-под
знака среднего квадратичного отклонения ее абсолютным
значением.
5. Теперь мы докажем одну из важнейших теорем
теории вероятностей: теорему сложения математических
ожиданий. Сначала докажем ее для двух случайных
величин Х% и Хг:
М [X, + Х2] - М [Хг] + М [Х2], (8.2.6)
т. е. математическое ожидание суммы двух случайных
величин равно сумме их математических ожиданий.
Начнем со случая непрерывной системы с. в. (Хч Х2)
с плотностью f(xu хг) (это проще по записи, чем
случай дискретных). Сумма Xi + X1 есть функция
случайных величин Хи Х2\ согласно (8.1.14) ее м. о. равно:
00
М [Хх + Х2] - j J (х, + х2) f (xlt za) dxidx, -
— 00
00 OO
— j J *i/(a?i, x2) dxYdx2 + j j x2f (xv x2) dxxdx2. (8.2.7)
—.oo — oo
Но первый из двойных интегралов в правой части (8.2.7)
есть не что иное, как М [Хх], второй — М[Х2], и теорема
(8.2.6) доказана.
В случае двух дискретных случайных величин,
заменяя в (8.2.7) двойные интегралы — двойными суммами,
по i и по ;, непрерывные аргументы х4, х2 —
отдельными значениями х\г\ хB\ а элемент вероятности
/(#!, x1)dxidx1 — вероятностью Р {Х1 о» а/Д Х2 = x[j)) и
применяя почленно суммирование, докажем ту же
теорему. Предлагаем читателю проделать это
самостоятельно *).
Специально подчеркнем, что теорема сложения
математических ожиданий справедлива для любых случайных
¦) Можно доказать, что теорема сложения математических
ожиданий справедлива и для смешанных случайных величин,
8.2. ТЕОРЕМЫ О ЧИСЛОВЫХ ХАРАКТЕРИСТИКАХ 269
величин: зависимых и независимых,
коррелированных и некоррелированных.
Применяя метод математической индукции (переход
от п к п+ 1), нетрудно доказать, что теорема сложения
математических ожиданий справедлива и для суммы
любого (счетного) числа случайных величин:
Г п 1 п
i 2** -2
I i-l J i-l
MlJUiJ-gMlXi], (8.2.8)
т. е. математическое ожидание суммы случайных
величин равно сумме их математических ожиданий. Иначе
говоря, знак суммы 2 и зыак математического ожидания
М можно менять местами.
6. Математическое ожидание линейной функции с. в.
Xt, ..., Хп равно той же линейной функции от
математических ожиданий этих с. в.:
М L + 2 aXi] = ао + 2 «iM [Xih (8.2.9)
где а{ (/ = 0, 1, ..., п) неслучайные величины.
Доказательство. Применяя последовательно
формулы (8.2.6), (8.2.3) и (8.2.1), получим:
[71 "| Г П 1
Mi "X1 V I IV Л Г 1 i Hil i "VI V 1
a0 + jj aiAi s= ivi [ao\ t M ^ a{A{ =
t=i J L i=i J
n n
^j IVI [fljA j] «g До + x^
Эта теорема также справедлива для любых с. в.— как
зависимых, так и независимых.
7. Дисперсия суммы с. в. равна сумме всех элементов
ковариационной матрицы Н/?У11 эпг.г св.:
*i. (8-2.10)
Так как ковариациопная матрица IIAyi симметрична
относительно главной диагонали, на которой находятся
дисперсии отдельных величин, то формулу (8.2.10)
можно переписать в виде:
d[ 2 хЛ - S D[XfJ + 2 2 К их (8.2.И)
Li=l J i=l «<j
270 ГЛ. 8 ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКГИЙ
где суммирование во втором слагаемом распространяется
на все те элементы ковариационной матрицы, которые
стоят правее и выше ее главной диагонали. Число таких
элементов равно п (п — 1)/2 = (пг — п)/2.
Доказательство. Выразим дисперсию суммы
через ее второй начальный момент:
Применяя формулу (8.2.6), получим:
m[(Ix'-m[JH)]-m
-"Hi,!*-1
/ n П \2]
[ V ^ V jy| ry.1 I
что и требовалось доказать.
Следствие. Если св. Хи ..., Хп
некоррелированны, то справедлива теорема сложения дисперсий:
2 DI-YJ, (8.2.12)
т. е. дисперсия суммы некоррелированных с. в. равна
сумме дисперсий слагаемых. Теорема сложения
дисперсий, разумеется, справедлива и в случае, когда
случайные величины независимы, так как из независимости
с. в. следует их некоррелированность.
8. Дисперсия линейной функции случайных величин
определяется по формуле:
D L + S пгхЛ - 2 *iD [Хг] + 2 2 e^ffy, (8.2.
13)
где aOt ai, ..., an — неслучайные величины, Кц —
элемент ковариационной матрицы \\К^\ системы с. в.
(Xi, ..., лп).
Формула (8.2.13) может быть записана также в виде:
+ 2 ^х} = 22 а^Кф (8.2.14)
8 2. ТЕОРЕМЫ О ЧИСЛОВЫХ ХАРАКТЕРИСТИКАХ 271
Доказательство. Найдем дисперсию случайной
п
величины а0 + 2 а^ь так как при прибавлении к слу-
чайной величине неслучайной ее дисперсия не меняется,
получим
D L + 2 пгХг] - D [ 2 «а1 - D [ 2 гХ (8.2.
.15)
где Yi^uiXt (/=1, ..., ri). Применяя к правой части
(8.2.15) теорему о дисперсии суммы (8.2.10), получим:
.16)
D L + 2 агх\ = 2 D [Y{] + 23 2 К$, (8.2.
L «-1 J i=l i-U-1
где AT^ — корреляционный момент случайных величин
Yu Yj. По определению,
о о
Ktf = M IYM - М [(Г, - «П (Г, - шП], (8-2.17)
ПО
m\v) - М [У«] - М [а{Хг] - ajM [X,];
mJV> - М [У;] - М [п,Х,] - Й;М [^]
и формула (8.2.17) дает
из (8.2.16) следует, что
D f a0 + 2 «Л1 - D [2 «i^il - 2D MJ +22 щвД«
или, окончательно, вынося аг за знак дисперсии,
получаем
? ?
+ ?
1-1
и формула (8.2.13) доказана.
Из формулы (8.2.13) следует, что если случайные
величины Хи ..., Хп пекоррел и ров аны (А^ = 0 при
z^/), то дисперсия их линейной функции вычисляется
272 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
по формуле
D L + 2 агХг] = 2 *iD [Хг]. (8.2.18)
9. Математическое ожидание произведения двух
случайных величин равно произведению их математических
ожиданий плюс их ковариация:
М [ХХ.Х2] - М [Хх] М [Х2] + КХ2. (8.2.19)
Доказательство. Будем исходить из определения
ковариации:
КХ2 - М [ХХХ2] - М [(Хх - тг) (Х2 - т2)] -
= М [ХХХ2 — mtX2 — щХ1 + тхт2]у (8.2.20)
щетг^М[Х1]; т2= М [Х2].Применяя теорему сложения
математических ожиданий и вынося пе случайные
величины ти т2 из-под знака м, о., получим
-MIX^X.I-MIXJ.MI^], (8.2.21)
откуда следует доказываемая формула (8.2.19).
Формулу (8.2.21) часто применяют для вычисления
ковариации. Полезно запомнить ее словесную
формулировку: ковариация двух случайных величин равна
математическому ожиданию их произведения минус
произведение математических ожиданий.
Следствием этого правила является широко
применяемая формула, выражающая дисперсию одной случайной
величины Х{ через ее второй начальный момент:
D[X11-M[X*]-(M[X1])«. (8.2.22)
Действительно, D[Xj = Кп\ применяя формулу (8.2.21),
получим (8.2.22).
Если случайные величины Х{, Хг некоррелированы
(К12 = 0), то формула (8.2.19) дает:
М [ХгХ2] - М [Xг] .М [Х2], (8.2.23)
то есть математическое ожидание произведения двух
некоррелированных случайных величин равно
произведению их математических ожиданий.
Это положение называют теоремой умножения
математических ожиданий.
8.2. ТЕОРЕМЫ О ЧИСЛОВЫХ ХАРАКТЕРИСТИКАХ 273
Теорема умножения м, о. обобщается и на
произвольное число сомножителей, но в этом случае для ее
применения недостаточно, чтобы величины, образующие
произведение, были некоррелированы: требуется, чтобы
обращались в нуль и некоторые высшие центральные
смешанные моменты, число которых зависит от числа
сомножителей. Не останавливаясь на подробностях,
сообщим, что эти условия заведомо выполнены при
независимости сомножителей. В этом случае:
(8.2.24)
т. е. математическое ожидание произведения
независимых случайных величин равно произведению их
математических ожиданий. Формула (8.2.24) легко выводится
из (8.2.20) методом полной индукции.
Формула (8.2.24) означает, что для независимых
случайных сомножителей знак математического ожидания
М и знак произведения П можно менять местами.
10. Дисперсия произведения независимых случайных
величин Хь Х2, .ш.,Хп выражается формулой
где
Доказательство. По определенно дисперсии:
Возводя в квадрат и применяя формулу (8.2.24),
получим:
К этому выражению применим формулы (8.2.9) п
(8.2.24):
274 ГЛ. 8 ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
Так как ( ТТ X, | = JJ X] и М
i=l
i=l
П М
1=1
+ II mi) » что и требовалось доказать.
Формулу (8.2.25) можно записать через вторые
начальные моменты:
п
i-1
где a2[X<] -*- второй начальный момент с. в. X*. При
п = 2 имеем
D
при п
D [ХД
D2m\,
DJ)zm\ + D2Djn\
Dxm\m\ + D2m\m\
Если с. в. Хь Х2, ..., Xn независимы и центрированы
(т^ = 0? i=l, ..., я), то
(8.2.20)
11. Числовые характеристики векторной суммы слу~
чайных величин. Рассмотрим два я-мерных вектора:
ХA) с составляющими Х^\
Х( l) V(l) \ZG.\
2 , ..., лп и лкч с
составляющими Х^\ ХB2), ..., X(n2)f
Векторной суммой двух п-
мерных случайных векторов
и ХB) называется п-мер-
x1
^2
G)
л
vB) v(i; о?. иьтй случайный вектор
=XA) + XB) tя составля
ри g9J
XA) + XB), t-я составляющая
которого равна сумме i-x
составляющих случайных векторов ХA) и ХB):
Yi - X[l) + Х{с} (I - 1, 2, ..., и). (8.2.27)
На рис. 8.2.1 дана геометрическая интерпретация вектор-
8 2 ТЕОРЕМЫ О ЧИСЛОВЫХ ХАРАКТЕРИСТИКАХ 275
ной суммы двух случайных двумерных векторов на
плоскости Х{0х2.
Числовые характеристики гс-мерного случайного
вектора Y равны:
т\у) = М [У,] = М [Х\1) + Х|2)] = т\1) + т{?\ (8.2.28)
где т\1) = М [Х'\1)], т^ = М [Х^] (I = 1, 2, ..., /г).
Элементы ковариационной матрицы | К$ || случайного
вектора У определяются следующим образом:
Aij =!VI[^ri — mi )\Yj — fUj )\ = IVI [/ iijj =
-Ml
= М [-Y'i1^0] + М [X^Xf J + M [XPX^>J + M [Z^Xf ] =
= K\f + A'(ijK2) + Kf(l) + K$. (8.2.29)
Применяя свойства ковариации К$ = X^f, получим:
*<]><*> + jfJjXD _ ^i)B) + ^(|)(De (8.2.29')
В соответствии с определением дисперсии и с учетом
теоремы о дисперсии суммы получим выражение для
дисперспи i-ii составляющей случайного вектора Y:
= D\l) + Df + 2K\\*2\ (8.2.30)
12. Числовые характеристики случайного вектора У,
равного сумме двух некоррелированных n-мерных
случайных векторов Х(!) (с составляющими Х[1\ ХB]\ ...
V(l)\ Vr2^ / VB) vB)
..^An'j и ли) (с составляющими Aj ,A2 , ...,
определяются по формулам:
™(У) *>^d) I v^B)
(8.2.31)
т. е. математическое ожидание У< —- г-й составляющей
о, ч о, . о, о.
[Л i Ai J —I— Wl .
276 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
вектора У — равно сумме математических ожиданий со-
ответствующих составляющих векторов Х{1) и Х{г);
дисперсия случайной величины У, равна сумме дисперсий
этих составляющих, а ковариация составляющих У< и Yt
случайного вектора У равна сумме ковариаций
составляющих Х\г) и Х(/* вектора ХA) и составляющих Х^ и
X<j2) вектора X™.
Доказательство формул (8.2.31) следует
непосредственно из формул (8.2.28) и (8.2.29), так как для
некоррелированных векторов ХA> и ХB) К§*2) « 0 (*, j -
-1,2, .... и).
Так как сумма двух квадратных матриц порядка п
равна квадратной матрице того же порядка п, у которой
элемент матрицы равен сумме соответствующих
элементов суммируемых матриц, то имеет место равенство
(8.2.32)
Это равенство называется теоремой сложения
ковариационных матриц: ковариационная
матрица суммы двух некоррелированных случайных
векторов равна сумме ковариационных матриц слагаемых.
8.3. Применение теорем о числовых
характеристиках к решению
инженерных задач
Зная свойства числовых характеристик, мы можем
решить ряд общих задач, о которых уже упоминалось
ранее.
Задача 1. Коэффициент корреляции
линейно зависимых случайных величин.
Случайная величина У связана со с. в. X линейной
зависимостью
у = аХ+Ъ, (8.3.1)
где а и Ъ — неслучайные величины. Найти коэффициент
корреляции г^ с. в. X и У.
Решение. По определению
гху = Кху/ (охоу),
где /Cry — ковариация св. X и У, аХ1 оу — ях с.к.о. Най-
8.3. ПРИМЕНЕНИЕ ТЕОРЕМ О ХАРАКТЕРИСТИКАХ
277
0 0 0
дем ковариацию: Кху = М [XY]; св. Y = Y — ту = аХ +
о
+ Ъ — М [аХ + Ь] = аХ + Ь — атх — Ъ = а (X — тх) = аХ.
Отсюда
Кху = М [ХаХ] - аМ [X2] - а/?х.
Дисперсия св. Y равна:
D [аХ + Ъ) = D [аХ] « a2Z)r = Z)y; ay = | а | ох.
Находим коэффициент корреляции rxv:
aot
'ху
то есть
'ху ¦
°XQV
-1
0
1
1a Iе
при
при
при
а
а
а
-\
<
=
>
о,
о,
0.
(8.3.2)
Функция, обладающая такими свойствами (быть
равной 1 при положительном аргументе; —1 при
отрицательном и нулю при нулевом) в математике обозначается
«signer» («сигнум икс»):
(8.3.2')
f— 1 при
sign х = { 0 при х = О,
1 при х > 0.
Таким образом,
г*, = sign а. (8.3.3)
Мы доказали, что коэффициент корреляции св. X и
У, связанных линейной зависимостью (8.3.1) равен +1
при а > 0 (то есть, когда при возрастании X величина Y
тоже возрастает); равен —1, когда а<0 (при
возрастании X величина Y убывает) и обращается в нуль, когда
а = 0, т. е. линейной зависимости между X и У не
существует. >
Задача 2. Границы изменения
коэффициента корреляции. Доказать, что для любых с.в. X
и У коэффициент корреляции по модулю не превосходит
единицы:
lrj<l. (8.3.4)
278 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
Решение. Рассмотрим св. Z = ауХ ±oxY, где
0«, оу — с. к. о. случайных величии X и. Y:
Определим дисперсию св. Z. По формуле (8.2.13) для
дисперсии линейной функции св. X и Y найдем:
D [Z] = o2yDx + olDy ± 2охоуКху = 2olo2y ± 2ахауК
ху
Так как дисперсия случайной величины
отрицательной быть не может, то
или охоу±Кху>0, откуда \Кху\ <охсу, а следовательно,
кУ1<1. >
Задача 3. Математическое ожидание
числа появлений события в серии опытов.
Производится серия из п опытов, в каждом из которые
может появиться или не появиться событие Л;
вероятность появления события А в i-ы опыте равна pi (I ~
= 1, 2, ..., п)\ св. X — общее число появлений события
А в серии из п опытов. Найти М. о. случайной
величины X.
Решение. Представим св. X в виде суммы п
слагаемых:
где ЕЛ — индикатор события А в г-м опыте:
A, если событие А в i-u опыте появилось,
1 ~~ @, если А не появилось.
По теореме сложения математических ожиданий:
Но в п. 4.2 мы показали, что м. о. индикатора события
равно его вероятности в данном опыте, т. е. М [Ui] = pi •
откуда
п
Mr Vi V^ /О О сг\
[AJ == 2^ Ри (О.О.О)
т. е. математическое ожидание числа появлений события
8 3 ПРИМЕНЕНИЕ ТЕОРЕМ О ХАРАКТЕРИСТИКАХ 279
в п опытах равно сумме всех вероятностей его появления
в отдельных опытах.
Специально отметим, что формула (8.3.5) для м. о.
числа появлений события применима к любым
опытам—как зависимым, так и независимым. >
Задача 4. Математическое ожидание и
дисперсия числа появлений события в
серии независимых опытов. Проводится п
независимых опытов, в каждом из которых может появиться
или не появиться событие А\ вероятность его появления
в 1-м опыте равна pit Найти м.о. и дисперсию св. X —
числа появлений события А,
Решение. Снова представим св. X как сумму
индикаторов события А в отдельных опытах:
X - 2 С/*, (8.3.6)
где
1, если в г-м опыте событие А появилось,
М, если в г-м опыте соб
4 в [0, если А пе появилось.
Так как опыты независимы, то независимы и все
случайные величины Uи ?/2, ¦.., Un. Формула (8.3.5)
сохраняет силу:
М [X] - ? Pi. (8.3.7)
Найдем дисперсию св. X, выраженной суммой
(8.3.6), по теореме сложения дисперсии:
Но мы в п. 4.2 показали, что дисперсия индикатора
события А в i-м опыте равна /><?<, где j<=1-pu отсюда
i=l
Итак, в серии независимых опытов математическое
ожидание числа появлений события равно сумме
вероятностей его появления в отдельных опытах, а дисперсия
числа появлений события равна сумме произведений
вероятности появления на вероятность непоявления
события в отдельных опытах.
280 гл. 8. числовые характеристики функций
В частности, когда вероятность появления события
во всех опытах одна и та же:
Рх = Рг = . . . в Рг = . . . = Рп = />,
ТО
М [X] = пр\ D [X] = npq, (8.3.9)
а это — уже знакомые нам числовые характеристики
с. в, X, имеющей биномиальное распределение с
параметрами пир, которые мы вывели иным способом в
п. 5.1. >
Задача 5. Математическое ожидание и
дисперсия числа появлений события в
серии зависимых опытов. Производится серия из
п зависимых опытов, в каждом из которых может
появиться или не появиться событие А; вероятность его
появления в ?-м опыте равна р<; вероятность его
совместного появления в г-м и ;-м опытах равна Рц (в общем
случае для зависимых опытов Pu^PiPj). Найти м. о. ц
дисперсию числа X появлений события А во всей серпи
опытов.
Решение. Формула (8.3.5) для М [X] сохраняет
силу:
М [X] - S Pi-
Чтобы найти дисперсию D [X], применим к св. Х =
п
*=2 Uu где Ui — индикатор события А в i'-м опыте, тео-
i=l
рему о дисперсии суммы:
D [X] - 2 D [?/,] + 2 2 *у> (8'ЗЛ0)
i=l i<j
где Ki} — ковариация св. Uu Uj. Выразим ковариацию
через м.о. произведения (см. формулу (8.2.19)):
Случайная величина Ut • Uj имеет только два возможных
значения: 0 и 1; она равна нулю, если хотя бы одна из
величин Ui или ?/,• равна нулю, и равна единице только
если Ui = \, f/j = 1, то есть и в i-м, и в /-м опытах
событие А произошло:
8 3. ПРИМЕНЕНИЕ ТЕОРЕМ О ХАРАКТЕРИСТИКАХ 281
откуда
Ktj = PtJ - ptpjm
Подставляя в (8.3.10), получим:
D [X] - i Рт + 2 2 (Ру - ЛЛ). (8.3.10')
i ij
В случае, когда опыты независимы, Рц = ptph и формула
(8.3.10') переходит в уже знакомую нам формулу (8.3.8).
Рассмотрим частный случай, когда все опыты
производятся в одинаковых условиях:
Pi = Рг = . . . = Рп = Р\ Рц в Const = Р.
Тогда М [X] = пр, а формула (8.3.10') дает:
D[X] = npq + (/г- 1)п(Р- р2), (8.3.11)
где g = 1 — р, Р — вероятность появления события А
сразу в двух опытах — все равно, каких. >
Задача 6. Математическое ожидание и
дисперсия св. X, имеющей
гипергеометрическое распределение (п. 5.4).
Решение. Напомним, в каких условиях возникает
гипергеометрическое распределение: производится
вынимание п шаров из урны, в которой а белых и b черных
шаров; случайная величина X—число белых шаров
среди вынутых:
Рт = р (X - т) = С?СГт/С2+ъ @ < т < а).
Рассмотрим п вниманий шаров как п зависимых
опытов, производимых в одинаковых условиях. Вероятность
события А = {появление белого шара) во всех опытах
одна и та же и равна р = а/(а + Ь). Согласно решению
предыдущей задачи
М [X] « пр = па/(а + Ъ). (8.3.12)
Найдем дисперсию св. X по формуле (8.3.11).
Вероятность того, что любая пара шаров будет белой, равна
р_ а е-1 . flBSJL
a + b a + b-V ч а + Ь
и формула (8.3.11) дает:
D [X] = *.
1 J
282 гл. 8. числовые характеристики функций
В п. 5.4 мы уже приводили эти формулы для м. о. и
дисперсии гипергеометрического распределения. >
Задача 7. Математическое ожидание и
дисперсия среднего арифметического из
п независимых наблюдений случайной
величины X. Имеется св. X с м. о. пгх и дисперсией Dx;
над ней производится п независимых наблюдений,
давших результаты Хи Х2, ..., Хп (п «экземпляров» св. X).
Вычисляется их среднее арифметическое:
i=l
Найти м. о. и дисперсию с в. Y.
Решение. По формуле для м.о. линейной функции
(см. формулу (8.2.9)) находим:
пх = — »тх = тХ9 (8.3.14)
то есть м. о. среднего арифметического из п независимых
наблюдений св. X равно ее м.о. тх.
По теореме о дисперсии линейной функции (см.
формулу (8.2.13))
D [Y] - 4 2 D №] - * - т« <8'3-15>
п is=1 п
то есть дисперсия среднего арифметического из п
независимых наблюдений св. X в п раз меньше дисперсии
самой с. в. X. Отсюда
Gy^oju, (8.3.16)
то есть при увеличении числа опытов п с к. о. их
среднего арифметического уменьшается обратно
пропорционально 1/п. >
Задача 8. Математическое ожидание а
дисперсия частоты события при п
независимых опытах. Производится п независимых
однородных опытов, в каждом из которых может произойти
или не произойти событие А\ вероятность события А во
всех опытах одна и та же и равна р. Случайная
величина р* — частота событий Л, то есть отношение числа X
появлений события в п опытах к общему числу
8 3 ПРИМЕНЕНИЕ ТЕОРЕМ О ХАРАКТЕРИСТИКАХ 283
опытов п:
р* = Х/п. (8.3.17)
Найти м. о. и дисперсию случайной величины р*.
Решени е. С. в. X имеет биномиальное
распределение с параметрами п7 р\ ее м. о. равно тх = пр; ее
дисперсия Dx = npq, где q = 1 - р. Из формулы (8.3.17)
следует, что
М [p*j - М [Х]/п = пр/п = р, (8.3.18)
т. е. м. о. частоты события в п однородных опытах равна
его вероятности в одном опыте.
Находим дисперсию
D [р*] = D [Х]/п2 « npq/n2 = pq/n, (8.3.19)
т. е. дисперсия частоты события в п независимых
однородных опытах равна pq/n, где q « 1 — р — вероятность
непоявления события в одном опыте. >
Задача 9. Математическое ожидание и
дисперсия числа опытов до й;-го
появления события А. Производится ряд независимых
опытов, в каждом из которых событие А появляется с
вероятностью р. Опыты ведутся до тех пор, пока событие А
не появится к раз, после чего опыты прекращаются.
Найти м. о. и дисперсию случайной величины Y{h) —
число опытов, которое будет проведено.
Решение. Представим св. Y{k) в виде суммы:
к
v(b) y у
где Xi —число опытов до первого появления события А
(включая первое появление события А);
Х2 — число опытов от 1-го до 2-го появления события
А (включая 2-е);
Х{ — число опытов от (i — 1)-го до i-ro появления
события А (включая f-e);
Хк — число опытов от (к — 1)-го до /с-го появления
события А (включая /с-е).
Из п. 5.3 мы знаем, что с. в. X, имеет
«геометрическое + 1» распределение с параметрами m = l/p и С»
284
ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
= q/p2. Но точно такое же распределение с теми же
параметрами имеет и каждая из остальных св. Xt (i =
~2, ..., к). Отсюда
M[F(h)]
Цр = к/р;
(8.3,20)
Задача 10. Числовые характеристики
числа опытов, нужного для получения
заданного результата А. Производится ряд опытов,
в общем случае — зависимых, с целью достижения задап-
ного результата Л. С возрастанием числа опытов т
вероятность достижения результата Ау естественно, не
убывает. Задана неубывающая функция целочисленного
аргумента т = 0, 1, 2...:
G (т) = Р{при первых т опытах событие А появилось
хотя бы один раз).
G(m)
На рис. 8.3.1 показана зависимость G(m). Для
наглядности (и только) точки соединены отрезками прямых.
После достижения
результата А опыты прекращаются.
Случайная величина У — число
опытов, которое придется
произвести. Найти м. о. и
дисперсию св. У.
Решение. Допустим
временно, что опыты
неограниченно продолжаются и после
того, как достигнут результат А,
Назовем i-й опыт
«необходимым», если до него результат
А еще не был достигнут, и «излишним», если уже был
достигнут.
Рассмотрим случайную величипу ?/<, равную 1, если
1-й опыт необходим, и 0, если излишен (индикатор
«необходимости» i-то опыта):
1, если i-u опыт необходим,
Од если i-й опыт излишен^
/77
8.3 ПРИМЕНЕНИЕ ТЕОРЕМ О ХАРАКТЕРИСТИКАХ 285
или, что равносильно,
II, если в предыдущих i— 1 опытах результат А
не достигнут,
О, если достигнут.
Ряд распределения с. в. СЛ:
Щ : U-Jj-^-dI. (8-3.21)
Заметим, что t/t всегда равна 1 (первый опыт всегда
необходим). По ряду распределения (8.3.21) находим:
0-С(I - 1) + 1 Ц - G(i - 1)] - 1 - G(i - 1),
Очевидно, интересующая нас величина Y есть общее
число необходимых опытов, то есть
Найдем м. о. и дисперсию с. в. У. По теореме
сложения математических ожиданий
Итак,
S С (то)]. (8.3.22)
rn=O
Для нахождения дисперсии вычислим сначала второй
начальный момент св. Y:
Возводя сумму в квадрат, имеем
Таким образом,
а2 (Л - М [f tf'l + 2М Г2 C/if/il - 2 М [U\] +
+ 2 2 М [СОД. (8.3.23)
286 ГЛ 8 ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
Согласно ряду распределения (8.3.21)
М [U\] « О- G(i - 1) + I2 f 1 - G(i - 1)] = 1 - G(i - 1).
(8.3.24)
Найдем М [C/jf/j] при i</. Случайная величина ?/,?/,
тоже имеет два возможных значения: 0 и 1. Она равна
единице, только если обе случайные величины равны
единице: ?/, = ?/,= 1, т. е. если оба опыта — i-ii и ;-й —
необходимы; для этого требуется, чтобы более поздний
опыт — /-й — был необходим, а вероятность этого равна
1 —G(y--l). Ряд распределения св. UiUj (i < j) имеет
вид:
1
G U -1)
1 - С (/- 1)
Откуда
М [UiUj] = 1 - G (/ - 1) (/ < /). (8.3.25)
Сумма 2 M[UiUj] представляет собой двойную сумму
i<)
по i = 1, 2, 3, ... и по / = i + i, i + 2, i + 3...:
OO 00
2 M [UiUj] = 2 2 M [f/it/j]. (8.3.2G)
Подставим выражения (8.3.24)-(8.3.26) в (8.3.23)
а,Щ-2A-С(*-1)) + 22 2 A-G(/-1)) =
2 A — G(m)) + 2 2 m(l — G(m)). (8.3.27)
m=0 r»—0
Следовательно,
OO
M [У] A - M [Y]) + 22m(l-C (m)). > (8.3.28)
тп—О
Рассмотрим ряд примеров на применение решенпых
выше задач.
8.3 ПРИМЕНЕНИЕ ТЕОРЕМ О ХАРАКТЕРИСТИКАХ 287
Пример 1. Ведется наблюдение с помощью
радиолокатора за группой, состоящей из пяти объектов, i-й
объект за время наблюдения обнаруживается с
вероятностью Pi (i = 1, 2, 3, 4, 5); /?, = 0,1; рг = 0,2;
/>з = 0,3; а = 0,4; /75 = 0,5.
Найти м. о. числа объектов, которые будут
обнаружены.
Решение. Обозначим X — число обнаруженных
объектов. Согласно решению задачи 3,
М [X] = 2 Pi - 0,1 + 0,2 + 0,3 + 0,4 + 0,5 = 1,5. *
Пример 2. В условиях предыдущего примера
известно, что события At = (обнаружение i-ro объекта} и
Aj = (обнаружение /-го объекта) зависимы. Кроме
вероятностей р^ заданы еще вероятности Рц обнаружения
пары объектов: г-то и /-го (i<j):
Pli2 = 0,03; Plt3 = 0,04; PM = 0,02; P1>5 = 0,04;
Р2 з = 0,08; Р2,4 = 0,09; Р2>5 = 0,09; Р3,4 = 0,03;
Найти м. о. и дисперсию числа X обнаруженных
объектов.
Решение. М [^] = 1^ как и в примере 1. По
формуле (8.3.10')
5
Ас - S PiQ* + 22 (Pis - PiPj) =
i=l i<j
= 0,1-0,9 + 0,2-0,8 + 0,3-0,7 + 0,4-0,6 + 0,5-0,5 +
+ 2 . [@,03 - 0,02) + @,04 - 0,03) + @,02 - 0,04) +
+ @,04 - 0,05) + @,08 - 0,06) + @,09 - 0,08) +
+ @,09 - 0210) + @,08 - 0,12) + @,20 - 0t15) +
+ @,21-0,20)] = 1,01, ^
Пример З. Производится стрельба по резервуару с
горючим независимыми выстрелами; вероятность попада-
пия в резервуар при каждом выстреле равна 0,2. Первый
попавший в резервуар снаряд вызывает течь горючего,
второй воспламеняет его. Как только произошло
воспламенение, стрельба прекращается. Найти м. о., дисперсию
288 ГЛ. 8 ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
и с. к. о. числа X снарядов, которое придется
израсходовать. Найти приближенно число снарядов /V, которое
нужно иметь в распоряжении, чтобы их хватило для
воспламенения резервуара.
Решение. Согласно решению задачи 9
М[Х]-А-10; z>,-^-40; а,- /40«6,32.
Максимальное практически возможное число снарядов,
которое придется израсходовать, получим, прибавляя к
М [X] (из осторожности) не Зох, а Аох и округляя до
целых единиц:
10+ 4-6,32 «35. *>
Пример 4. Проводится ряд тестов с целью
локализации неисправности технического устройства (ТУ);
после первого теста неисправность локализуется с
вероятностью 0,2; после двух тестов — с вероятностью 0,6;
после трех тестов — с вероятностью 0,9; четырех тестов
всегда достаточно для локализации неисправности.
Случайная величина Y — число тестов, которое придется
провести. Найти числовые характеристики св. Y — м. о. /п„,
дисперсию Д,, с. к. о. оу.
Решение. Этот пример можно решить, пользуясь
результатами, полученными в задаче 10 этого п.
В данном случае G@)«0; G(l)==0,2; GB) = 0,6;
GC) = 0,9; GD)=l; G(m)=i при m>4. По формулам
(8.3.22), (8.3.28):
= 1 + 0,8 + 0,4 + 0,1 = 2,3;
ос
Dy = mv(l — my) + 2 2 mA — G (m)) = 2,3 A - 2,3) 4-
тя = О
+ 2@*1 + 1-0,8 + 2-0,4 + 3-0,1) = - 2,99 + 3,8 = 0,81,
ay = 0,9. >
Пример 5. Работают независимо друг от друга га —
==20 накопителей на магнитных лентах (НМЛ).
Вероятность выхода из строя в течение суток для каждого из
НМЛ равна р = 0,2. Найти м.о., дисперсию и с. к. о.
числа X НМЛ, которые выйдут из строя в течение суток.
8 3. ПРИМЕНЕНИЕ ТЕОРЕМ О ХАРАКТЕРИСТИКАХ 289
Решение. Согласно решению задачи 3
М[Х] = пр = 20-0,2 = 4;
О[Х] =npq = 20-0,2-0,8 -3,2; ах
ах
Пример 6. Условия совпадают с условиями
примера 5, но с той разницей, что НМЛ выходят из строя
зависимо друг от друга; вероятность того, что выйдут из
строя i-n и /-й НМЛ для всех пар НМЛ одна и та же
и равна Р = 0,05. Найти м. о., дисперсию и с. к. о. числа
X вышедших из строя за сутки НМЛ.
Решение. Математическое ожидание с. в. X
остается тем же, что п в примере 6:
М [X] = пр = 4.
Дисперсиго пайдем согласно решению задачи 5 (формула
(8.3.11)). Поскольку все вероятности рг и Р1$ одинаковы:
п я=г П == О 9 f / ss 4 9 9П\ • Р === Р — П С)К /птта nnnv
Pi p — w,? \i —• i, ?, ..., ?aj) , г tj ~ i — u,uj ^для всех
i^j), а число всех возможных пар НМЛ с различными
номерами (*</) равно
С» _ ?^ll? _ 190-
формула (8.3.11) дает
D[X]=* 20 0,2 •0,8+20-19(Р-р2) =
= 3,2 + 380@,05 - 0,04)'= 3,2 + 3,8 - 7,0,
*2,65. ^
Пример 7. Производится п = 600 бросаний мопе-
ты; случайная величина р* — частота появления герба:
р*=*Х/п, где X —число появлений герба (п. 1.3). Найти
м.о. случайпой величины /?*, ео дисперсию и с. к. о.
Пользуясь «правилом трех сигма», найти диапазон
практически возможных значений с. в. р*. Проверить,
укладывается ли частота появления герба при п = 660
бросаниях, полученная в примере из п. 1.3, в этот диапазон.
Решение. Согласно решению задачи 8 данноЛ) п.
имеем:
М [/>*] = р - 0,5;
DIP*] - ?2
п
а[р*] = у/) [р*] « 2,04 • Ю-2; Зо [р*]« 0,0612.
10 Теория вероятностей и ее
инженерные приложения
290 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
Диапазон практически возможных значений с. а. р*:
0,5*0,061, т. е. от 0,439 до 0,561; результат р* = 0,505,
полученный в примере из п. 1.3, в этот диапазон
укладывается. >
Пример 8. Для уточнения определения массы тела
на точных весах производят п = 40 взвешивании и осред-
няют их результаты:
п
Y i V У
л = — Zd А*«
где Х{ — результат г-го взвешивания. Систематической
ошибки весы не дают. Среднее квадратическое
отклонение одного взвешивания равно о* —3 (мг). Найти
среднее квадратическое отклонение случайной величины У—
среднего арифметического из п — 40 взвешиваний.
Решение. Согласно решению задачи 7 данного
пункта (формула (8.3.16))]
Пример 9. Сколько раз нужно произвести
взвешивание тела в условиях примера 8 для того, чтобы
среднее квадратическое отклонение св. У не превышало
,0,1 (мг)?
Решение. Имеем:
отсюда Vn^frj', n>900. Итак, достаточно и = 900
взвешиваний. >
Пример 10. В партии из N изделий имеется К
доброкачественных и (iV — К) дефектных. Из этой партии
наугад выбираются п изделий без возвращения.
Определить м. о. и дисперсию числа X доброкачественных
изделий среди п выбранных.
Решение. Очевидно, с. в. X имеет
гипергеометрическое распределение с параметрами а -* К; b**N — К; п.
В соответствии с формулами (8.3.12) и (8.3.13) получим:
K+N-K
8.4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ РАЗНЫХ ФУПКЦИЙ 291
Если рассматривать св. Y — число дефектных изделий
среди п выбранных, то
n-M[X] = ;
D[Y]=D[X\. >
8.4. Числовые характеристики
часто встречающихся в инженерной практике
функций случайных величин
Задача 1. Числовые характеристики
минимальной из двух величин: случайной X
и неслучайной а. Имеется
непрерывная св. X с плотностью /(#); - ' Тх \
с. в. Y связана с X зависимостью: а "" 1П*- 1 J
У-minU, а}, (8.4.1)
где а — неслучайная величина. /о х
Найти числовые характеристи- Рис.841
ки — м. о. и дисперсию — с в. У.
Решение. Соотношение (8.4.1) можно записать в
виде:
X при Х<а\
а при A^a.j х '
График функции у = min (х, а} показан на рис. 8.4.1.
По формуле (8.1.10) для непрерывной св. с
плотностью }(х) находим м. о. случайной величины У:
оо а
J min(х, а}f{x)dx~ J xf{x)dx
ОО О
+ a j / {x) dx - j ж/ (х) с*х + с [1 — F (а)], (8.4.3)
а — о©
где F(x)— функция распределения с, в. X,
292 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
По формуле (8.1.12) находим второй начальный
момент св. У:
оо
аа [Y] - М [У2] - J (min {хх а})« /(*) dx =
— ОО
а оо а
- J xif(x)dx + ailf(x)dx^ J x*f(x)dx + a*(l-F(a)),
—оо а —оо
{8.4.4)
Откуда
D [У] - а2 [Y] - те}. (8.4.5)
Если с. в. X дискретна и имеет ряд распределения
= Р{Х«=а:4} (i = l, 2, .... п), то
n (a) n
*, а} /?i = S ^iPi + а 2 Pit (8*4.6)
il i(a)+l
где (а)— номер максимального из возможных значений
с. в. X которое не больше а: х(а) < а.
Аналогично найдем
аа [Л - 2 «?Pi + a2 S Pi. > (8,4,7)
il i()+l
Пример 1. Напряжение Х, подаваемое на вход
ограничителя, распределено по нормальному закону с
параметрами тх и ах. Ограничитель работает по принципу
F~mintf, a}.
Найти характеристики wiy и Z?y напряжения Y на выходе
ограничителя.
Решение. По формуле (8.4.3J
ax 1/2я
+ o ,-L expl —-—^-Ых =
J У2я a, K I 2a* J
- a, [т {Ф (т) + 0,5} + ^ exp {- Щ, (8.4.8)
8.4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ РАЗНЫХ ФУНКЦИЙ 293
где т = (а — тх)/ах; Ф (х) — функция Лапласа.
Дисперсию находим через второй начальный момент:
оо
dx
+ а* [0,5 - Ф(т)] - 2а^±°^ ГТ. (8.4.9)
(8.4.10)
Если тх = а, то т = 0; ту = тх — ох/ Vln\ Dv ¦¦ а? (я —
-1)/Bя). >
Пример 2. В ВЦ за смену поступает случайное
число X информационных документов (ИД), подчиненное
закону Пуассона с параметром М [X] = тх. Число ИД У,
обрабатываемых в ВЦ в смену, не может превышать
величины а (целое число): y = min{X, а}. Найти
характеристики случайной величины Y,
Решение. По формуле (8.4.6)
„к ^_ тк
Тпу
2, тх ^-т*. , _ X1 ""х ^-mv
и ( о ъ
k — тГ Г
k=l \ fe=0 J
= тхЛ (а — 1, тх) + а A — R (а, т*)), (8.4.11)
2дЙ
А0
Заметим, что мы доказали равенство
> 0 и це
(8.4.12)
а
ml • -щ- е-п* = тлД (а - 1, тя) (а > 0 и целое).
294 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
Если а = О, то ^ к -~- е~Шх = 0. Для нахождения ВеЛИ-
чины а2[У] найдем (с учетом равенства (8.4.12))
следующее выражение:
(а - 22 тх) + тлД (а - 1, тхJ (8,4.13)
где а > 1.
Следовательно,
(a — 22 тх) + mxR {а — 1, тх) + а2 A — R (a, m*)).
(8,4.14)
Откуда
D [У] - а2 [У] - т5 - тУ? (а - 2Х тх) + mxR(a-l% mx) +
+ а? A - R (а, тх)) - т| [Д (а-1, тх)]2^а2[1-Д(а, тл)]2-
— 2тхаД(а— 1, тж)[1 —Д (а, тх)] (а>1). > (8.4.15)
Задача 2. Числовые характеристики
максимальной из двух величин: случайной X
и неслучайной а. Имеется не-
z-max{a:,cj^ прерывная с. в. X с плотностью
1{х). Св. Z связана с X
зависимостью
I Л7 Л |Д ПРИ X
шах {X, а} — v F
' 1л при
а х (8.4.16)
Рис. 8.4.2 _ ? „ ,__ ,
График функции Z = max (л, а)
показан на рис. 8.4.2, где а имеет тот же смысл, что и в
задаче 1 этого пункта.
Найти числовые характеристики: м. о. и дисперсию
св. Z.
8.4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ РАЗПЫХ ФУНКЦИЙ 295
Решение. По аналогии с решением задачи 1 этого
пункта имеем:
т2 = М [Z] =*
а оо оо
= a J /(х) dx + J х/ (x) dx = aF (a) + J x/ (x) dxx (8.4.17)
—oo a a
oo
a3 [Z] = аЧ (a) + J x2f (x) dx. (8.4.18)
a
Если с. в. X дискретна, то
(a) n
S 2 (8.4.19)
(a) n
S 2 ?Л. (8.4.20)
Дисперсию найдем по формуле
D [Z] - a, [Z] - mf. > (8.4.21)
Пример З. При сборке электронной схемы
применяется резистор, имеющий случайное сопротивление,
распределенное по нормальному закону с параметрами пгх а
сх\ при этом отбирается только такой резистор, у
которого сопротивление не менее заданного а. Таким
образом, сопротивление отобранного резистора Z = max{X, а).
Найти числовые характеристики случайной величины
Z — резистора, отобранного для установки в схеме.
Решение. Выразим величину тл через уже
найденную величину mv (см. (8.4.3)):
а оо оо во
т2 =. а J f(z)dx+§ xf(x) dx + «j f(x) dz—a§f(x) dx +
—oo a a a
a a
+ J xf (x) dx — j '*/ (x) dx = a + mx — my. (8.4.22)
— 00 «-00
Аналогично найдем величину aa[Z] через уже найденную
величину a2[Y] (см. (8.4.4)):
«8 [Z] = о2 J / (х) dx + j x*f(x) dx =
в-.а* + лЙ + о2-а«[П (8.1.23)
296
ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
Учитывая, что с. в. X распределена нормально с
параметрами тх и ах, имеем:
mz = тх + ох [т (Ф (т) + 0,5) + ехр {- QJYzk] (8.4.24)
а2 [Z] = а2 [Ф (т) + 0,5] + (т2х + о2х) @,5 - Ф (т)) +
(8.4.25)
где т = (а — тх)/ох, Ф(х) — ^функция Лапласа. >
Задача 3. Случайная величина Y
определяется следующим образом через
случайную вели ч и н у X:
(8.4.26)
+ Bахтх + oIt) ехр[?
У
ъ
а
0
-/
а
Рис.
7Г
ь &
8.4.3
Ъ < X.
График этой зависимости
представлен на рис. 8.4.3.
Зная закон распределения
случайной величины X, найти числовые
характеристики случайной величины У.
Решение. Если случайная величина X
непрерывна, то
= aF(a) + xf(x) dx + b [1 — F(b)], (8.4.27)
a
b
a2 [Y] = аЧ (a) + J *2/(*) cb + b2 [1 - F (ft)]; (8.4.28)
где /(я)— плотность распределения случайной
величины X.
Если X дискретна, то
(а) (Ь) п
my = fl2pi+ Ц artfi + Ъ 2 Pil (8.4.29)
а2 [У]
(а) (Ь)
а2 2 Pi + 2
i |(
sfo + Ь2 2
Ь
(8,4.30)
8.4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ РАЗНЫХ ФУНКЦИЙ 297
где (а)—номер максимального пз возможных значений
случайной величины X, меньшего (или равного) а, (&) —
номер минимального из возможных значений случайной
величины X, большего, чем 6; pi = Р {X = х$ш >
Пример 4. На вход стабилизатора подается
напряжение X, имеющее нормальное распределение с
параметрами тх, ох. Стабилизатор работает по алгоритму (8.4.26).
Найти характеристики на выходе стабилизатора.
Решение. По формулам (8.4.27) и (8.4.28) находим
0,5,
+ Ь [025 - Ф (хь)] = а [Ф (т„) + 0,5] + тх [Ф (ть) - Ф (т.)] +
+ ^= [<ГТ«/2 - <rT*/2] + Ъ [0,5 - Ф (ть)], (8.4.31)
где
т« =(« — тх)/ах; хь = (Ь — тх)/ох;
а2 [Y] = а2 [Ф (та) + 0,5] + (а% + т%) [Ф (хь) - Ф (т„)] +
+ 6* [0,5-0(^I. (8.4.32)
Если участок (а, Ь) симметричен относительно точки
тх и длина его равна 2Д, то п (г)
b-mx тх + Ь-тх
л _т.т а~т* Д.-
—т, В этом случае ту = тх,
Рис. 8.4.4
а2 [У] = ml + Д2 + 2 (о2 - Д2) Ф (т) - -^1 те-^2/2;
-2т^], (8.4.33)
298 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
При т -* О (А -»• 0) мы в пределе имеем дело с
идеальным стабилизатором напряжепия: Y-+тх и Dy-*0. При
т-»*<» (А-> оо) никакой стабилизации напряжения не
будет: У = Х и Dy = Dx. На рис. 8.4.4 показан график
зависимости (8.4.33). >
8.5. Числовые характеристики суммы
случайного числа случайных слагаемых
Задача 1. Случайная величина Z
представляет собой сумму случайного числа
случайных слагаемых.
где Xi (i = 0, 1, 2, ...); У—случайные величины, Хо*=*
в 0 — не случайная величина. Случайная величина У не
зависит от слагаемых Хи имеет характеристики ту и Dy
и может принимать целочисленные значения 0, 1, 2, ...
. •., А, ...; система св. Xt (г —1, 2, .,.) имеет
характеристики: м.о; nti A = 1, 2, #..) и ковариационную матри-
[00]
ХгХ}\ (/, / = 1, 2, •..). Если в сумме
нет слагаемых (У — О), то она равна нулю потому что
Х0 = 0 (/710 = 0; D0 = 0).
Найти числовые характеристики с. в. Z: тг и Dt.
Решение. Пусть нам известен закон
распределения с. в. У:
Рассмотрим гипотезу, состоящую в том, что {У — fch
Условное математическое ожидание случайной величины
Z при этой гипотезе будет:
S M[Xj-2 mi9 (8.5.2)
i i
По формуле полного математического ожидания
(8.1.20) получим:
m,-M[Z] - 2 M[Z|r-*].p* « 2 B *ч)рк. (8.5,3)
ft—0 fc=0 \i=0 /
8.5. ХАРАКТЕРИСТИКИ СУММЫ СЛУЧАЙНОГО ЧИСЛА 299
Если св. Xi (при i>0) распределены одинаково, то
т{ — тх 0 = 1, 2, ...) и выражение (8.5.3) примет вид:
00 / ft \ ОО 00
тг = 2B тх I Pk = 2 kmxpk = %2 Дфь = тхту.
ft=O \i=0 / А=0 fc=O
(8.5.4)
Особо отметим, что формулы (8.5.3) и (8.5.4)
справедливы как для зависимых, так и для независимых с. в,
Х< (* = 1,2, ...).
Аналогично найдем второй условный начальный
момент случайной величины Z
Г/ ft \ / ft \ -J ft ft
L \i=o / \i=o / J 1=0^=0
Откуда, по формуле полного м. о.,
00
а2 [Z] = М [Z2] = 2М[г2|7 = I:].й =
-2j2o|o(^i^; + ^ii)]pft. (8.5.6)
Если случайные величины Xi (г = 1, 2, ...) некоррели-
рованы, то Кц = О при i=^;; Ku = Dit В этом случае
а2 [Z] - 2 f 2 2 ЩЩ + 2 iDil p*. (8.5.7)
Если случайные величины Xt (i = 1, 2, ...)
одинаково распределены и одинаково коррелированы гц = г} то
М [Хг] = тг = тх\ D [Хг] - ЛГ«4 = Z?x;
В этом случае:
оо
-mv)rDx. (8.5,8)
300 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
Дисперсию случайной величины Z найдем по формуле:
Dz - D [Z] = а2 [Z] — то} -
= mlDy + mvDx + rDx (a2 [Y] - щ). (8.5.9)
Если случайные величины Х{ (i = l, 2, ...) одинаково
распределены и некоррелированы, то
?2 e m|/)y + Wy/)x. (8.5.10)
Рассмотренная задача имеет большое практическое
значение. >
Пример 1. Рассматривается работа
вычислительного цептра (ВЦ), в который ежесуточно вводится
случайное число У информационных документов (ИД),
распределенное по вакоиу Пуассона с параметром а (ту = ?>„==
= а). Каждый ИД содержит случайное число знаков Х\
которое не зависит от того, сколько имеется знаков в
других информационных документах. Известны М [X] =» тх и
D[X]=ssDx. Определить м.о. и дисперсию числа знаков Z,
вводимых в ВЦ в течение суток.
Решение. Очевидно, что Z = 2 ^i5 по формулам
(8.5.4) и (8.5.10) получим:
mz = <x*mx\ (8,5.11)
D*-a(mZ + Dx). (8,5.12)
Например, если а « т„ = Д, = 100 (ИД), тж«500
(знаков), ох — У/?я = 100 (знаков), то тг —100 • 500 —
= 50000 (знаков);
а,« у/?;« У 100B5 000 + 10000) «5090 (знаков).
Заметим, что если коэффициент вариации числа
знаков в ИД равен Ох/тх*=*0,2, то коэффициент вариации
числа знаков, вводимых в ВЦ в течение суток, будет
Ог/тг» 0,102, т. е. величина Z существенно «менее
случайна», чем X. >
Пример 2. Анализируется работа по наладке
сложного электронного прибора (ЭП), которая проводится
в несколько попыток. Каждая попытка наладить ЭП
завершается успехом с вероятностью р независимо от того,
сколько до этого проводилось таких попыток и как долго
они длились. Длительность i-on попытки наладить ЭП
8.5. ХАРАКТЕРИСТИКИ СУММЫ СЛУЧАЙНОГО ЧИСЛА 301
есть случайная величина Т% с характеристиками М [Т(\ —
= m и D [Тг] — D (i = 1, 2, .. .)• Случайные величины
Г* независимы между собой и не зависят от числа
попыток наладить ЭП.
Требуется найти математическое ожидание и
дисперсию времени Т, затраченного на наладку ЭП.
Решение. Очевидно, что время Т будет равно:
где случайная величина Y имеет «геометрическое +1»
распределение:
l/ D
По формулам (8.5.4) и (8.5.10) получим:
М [Т\ - т/л (8.5.13)
D [Г] «- m*q/p2 + Dip. (8.5.14)
Так, например, если вероятность наладить прибор в
одной попытке р = 0,5, a m = 2 (часа); а = VZ? «=• 1 (час),
то М [Т] -2/0,5 = 4 (часа).
а [Г]- /DlTj- /10-3,16 (час). >
Рассмотрим еще один пример, связанный с суммой
случайного числа случайных слагаемых.
Пример 3. За время пролета космического
летательного аппарата (КЛА) в окрестностях кометы он
подвергается «бомбардировке» различными частицами,
образующими «атмосферу» (кому) кометы. Частицы в
атмосфере кометы образуют трехмерное пуассоновское
поле точек с параметром а(й)=за0/А, где А —расстояние
от КЛА до поверхности кометы. Каждая частица имеет
случайную массу G, распределенную по закону Релея
G.9.26) с математическим ожиданием g. Энергия
соударения частицы с КЛА равна GW2, где v — скорость
пролета КЛА в атмосфере кометы, которая считается
постоянной. Вероятность р того, что частица, попавшая
в КЛА, пробьет его защитную поверхность, равна
вероятности того, что энергия ее соударения с КЛА
302 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
превысит пороговый уровень \х:
Расстояние до поверхности кометы как функция времени
определяется по формуле
где U — момент пролета КЛА на минимальном
расстоянии от кометы; h0 — минимальное расстояние между КЛА
и кометой; fet — заданный коэффициент.
Требуется определить м. о. и дисперсию с. в'. Z —
числа пробоин на защитной поверхности КЛА.
Решение. Введем индикатор события А = {пробой
поверхности) для каждой частицы:
1 — если i-я ударившаяся в КЛА частица
пробивает защитную поверхность КЛА;
о — если г-я ударившаяся в КЛА частица
не пробивает защитную поверхность КЛА.
Тогда
у
где У — число соударений частиц с поверхностью КЛА
за время его пролета около кометы.
По условиям задачи случайная величина Y имеет
распределение Пуассона. Найдем ее м. о. Сначала найдем
м. о. числа соударений частиц с поверхностью КЛА,
которое произойдет на интервале времени (t, t + dt)
полета КЛА.
По определению, опо будет равно объему
пространства, в котором пролетит КЛА за это время (s*v-dt),
умноженному на плотность частиц в этом пространстве
$-va dt
(ot,(h(t)): 2; , где 5 —площадь «сечения» КЛА.
hi (' ~ 'о) + К
Математическое ожидание с. в. У найдем по формуле:
оо
s-vadt
8.5. ХАРАКТЕРИСТИКИ СУММЫ СЛУЧАЙНОГО ЧИСЛА 303
Так как t = 0 — пачало полета КЛА, то
оо
Найдем величину р:
_ exp |- (^j Д jr)} b
(8.5.15)
где g — м. о. массы частицы.
По формулам (8.5.4) и (8.5.10) получим:
М [Z] = ар; D [Z] = р2а + pqa =*ар(р + q) = apt
т.е. M[Z]=D[Z].
В следующей гл. будет доказано, что св. Z — число
пробоин на защитной поверхности КЛА распределено по
закону Пуассона, поэтому М [Z] = D [Z]. ^
Пример 4. Рассматривается формирование
железнодорожного состава, состоящего из грузовых вагонов.
Число вагонов в составе Y случайное с параметрами
т„ = 200 и оу = 8. Вес перевозимого ^-м вагоном груза
является св. Xt с характеристиками тя = 50 (тонн) и
о» — 3 (тонны). Найти характеристики (м. о. и с к. о«)
веса Z, перевозимого составом, если вес груза каждого
вагона не зависит от веса груза других вагонов.
Решение, Очевидно, что
4-1
По формулам (8.5.4) и (8.5.10) находим:
М [Z] = тг = тх-ту = 10000 (тонн),
D [Z] « 502-64 + 1800 - 161800 (тонн2),
a [Z] - 402,2 (тонн).
По «правилу трех сигма» находим практически
возможный диапазон перевозимого составом груза:
т2 ± За, - 10000 ± 1206 (тонн). >
304 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЯ
Задача 2. Случайная величина Z
определяется через случайные величины Y и
Xi A = 0, I, 2, ...) следующим образом:
min{Y,a>
Z = 2 Xh (8.5.16)
i=-0
где Y — целочислепная случайная величина, независимая
от случайных величин Xt (i = l, 2, ...); с. в. Xt
представляют собой систему независимых одинаково
распределенных случайных величин, Х0 = 0; а>1, целое; задай
закон распределения случайной величины У и числовые
характеристики случайной величины Х{: тх и Dx (i>0).
Требуется найти числовые характеристики случайной
величины Z.
Решение. Обозначим
F«min{7, a}, 18,5Л7)
Тогда
v
В соответствии с решением задачи 1 этого п. (см. (8.5.4)
и (8.5.10)): ш2 ¦¦ mv*mx; Dz — ^Dv + тД)х. Величины
mv и Z)o были определены в задаче 1 п, 8.4 ((8,4,6) a
(8.4.7)):
mv = М [т!п{Ул а}] - 2 кр. + а 2 Ри (8.5.18)
fe0 Я ft-a+1
а2 [I - М [(min {У, а}J] - 2 к% + *2 S Pk. (8«5'19)
! <*2 [V] — mix
где Ph eP {У ¦¦ к} (к ят 0? 1, #,. tb)— закон распределения
случайной величины У. >
Рассмотрим инженерное приложение этой задачи.
Пример 5. В ВЦ ежесуточно поступает случайное
число У информационных документов (ИД),
распределенное по закону Пуассона с параметром а; обработке
подлежит не более а ИД; каждый ИД имеет случайное
число знаков Х{ с характеристиками тх и Dx. Требуется
определить числовые характеристики случайной
величины Z — числа знаков, вводимых в ВЦ в течение суток.
8.5, ХАРАКТЕРИСТИКИ СУММЫ СЛУЧАЙНОГО ЧИСЛА 305
Решение. По условию рк = Р {Y = к] = аке~а/к\.
Откуда (см. (8.4.12))
а ос
т0 = 2 й/>ь + а 2 рь = а^(а — 1;ос) + а[1 — /?(а,a)]t
(8.5.20)
где R (a, a) = P {Y ^ a} — распределение случайной
величины У, подчиненной закону Пуассона с параметром а.
В соответствии с формулой (8.4.14) имеем
(а-1, а)+а2[1~Д(я, а)],
(8.5.21)
откуда
Dv = a2 [F] — ml « a2/? (a — 2, a) + аД (a — 1, a) +
+ a2 [1 — R (a, a)] - а2 [Я (a - 1, a)]2 —
- 2aai? (a - 1, a) [1 - R (ax a)] - a2 [1 - R (a% a)]2, (8.5.22)
Приведем численный пример: my«=a=100 (ИД
в сутки) m, —500 (знаков); ax = 100 (знаков); a = a =
=» 100. Характеристики потока поступающих в ВЦ
документов и распределение числа знаков в ИД такие же,
как и в примере 1 этого пункта, но в нашем случае
вводится в ВЦ в сутки не более 100 ИД (а = 100).
В п. 10.2 будет показано, что при больших значениях
параметра а имеет место приближенное равенство
A0.2.27): Л (те, а) « Ф((т + 0,5-а)/Уа)+0,5; Ф{х)-
функция Лапласа; проведем расчеты:
«0,5-0,02-0,48;
015 + ф(^)«
« 0,5 + 0,02 = 0,52;
(а - 2Х а)« 0,5 + Ф (^l±|b-j = 0i5 + ф^_ 1|^
« 0,5 - 0,06 - 0,44.
306 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
Следовательно,
mv = 100-0,48 + 100-A — 0,52) = 48 + 48 = 96;
а2 [V] = 1002-0,44 + 100-0,48 + 100*-0,48 = 9248;
А> = а2 [у] — т*° = 9248 - 921С = 32.
Таким образом:
тг = mv-mx = 96-500 а; 48 000 (знаков);
В z = mlDv + тД == 250 000-32 + 96-10 000 « 896 • МИ?
о2 = /Д « 2993;
коэффициент вариации
ог 2993 п ПГ9/
7^7 - 48000 = °^0G24'
Мы видим, что по сравнению с условиями примера 1,
среднее число вводимых в ВЦ знаков снизилось
относительно мало (было 50000 —стало 48000), но
коэффициент вариации изменился сильно (был 0Д02 —стал
0,0624), т. е. общее число знаков стало почти не
случайным. >
8.6. Числовые характеристики минимальной
и максимальной из двух случайных величин
Задача 1. Случайная величина Y
определяется как минимальная из двух св.:
где Х{ и Х2 независимые непрерывные случайные
величины с плотностями fi{xi) и )г(Хг). Найти числовые
характеристики случайной величины Y.
Решение. Рассмотрим гипотезу, состоящую в том,
что случайная величина Хг попала в элементарный
интервал (я2, x2 + dz2); вероятность этой гипотезы есть
элемент вероятности f2(x2)dx2. Найдем условное м. о.
случайной величины У при этой гипотезе по формуле
'(8.4.3), заменяя в ней величину а на х2, f(z) на ()
uF(x) uaF^)
М [У | х2] - j *,/, (хх) dxx + х2 [1 - Fx
8 6. ХАРАКТЕРИСТИКИ МИНИМУМА И МАКСИМУМА 307
Тогда по интегральной формуле полного математического
ожидания (8.1.20) получим:
оо
М [7J - М [min {Xv Xt}] = J M [Y | *2] /2 fo) dxt =
— оо
оо / Х2 \
- J I J *ifi{*i)<toAu{x2)dxt +
—оо \—оо /
оо
+ J *2 [1 — Fi (x2)] U fo) ЛЧ = mXl + тн —
— ОО
ОО 00
- J *Л(*1)Л(*1)&я- J *шРЛ*ш) f,(*,)*** (8-6.1)
— 00 —СХ5
По формуле (8.1.22) найдем a,z[Y]:
а2 [У] - М [(min {Xlt X2}J] = а2 [XJ + а2 [Х8] -
оо оо
- j «^.(xJM*,)^- j ZFx^fMdxv (8.6.2)
— 00 —ОО
где a2[-Xi], а2[^г] — вторые начальные моменты случайных
величин Хг и Х2 соответственно. Дисперсию найдем по
формуле
Если случайные величины Xt и Хг распределены
одинаково, то
оо
М [Y] - 2тх - 2 J xF (x) f (x) dx, (8.6.3)
— 00
00
a2 [Y] - 2a2 [X] — 2 J *2F (a;) / (ж) Лг. > (8.6.4)
Пример 1. Для повышения надежности
срабатывания автоматической парашютной системы установлено
два радиовысотомера, работающие независимо друг от
друга. Оба высотомера настроены на срабатывание на
высоте h\ ошибка измерения высоты распределена
равномерно в пределах зоны нечувствительности
радиовысотомера ±Д, систематических ошибок нет. Надежность
работы каждого высотомера равна р = 1 — q. Автоматиче-
308 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
екая система срабатывает, как только один из
высотомеров покажет значение высоте, равное h. Требуется
определить математическое ожидание и дисперсию высоты К,
на которой срабатывает автоматическая парашютная
система.
Решение. Рассмотрим две гипотезы: Я2
автоматическая парашютная система срабатывает при исправной
работе обеих высотомеров, Я4 — автоматическая система
сработает при исправной работе одного из высотомеров.
Очевидно,
Р (Я,) - Р2/(Р2 + 2pq); Р (Нг) = 2pq/(p* + 2pq).
Обозначим с. в. Уиг — высоту срабатывания парашютной
системы при наличии гипотезы #2. Следовательно,
где Xly X2 — независимые, одинаково распределенные с. в.,
распределенные равномерно в интервале (А — Д; А + Д).
Для упрощения вычислений введем центрированные
случайные величины
Xi-Xi-h; Хг = Хг-}ь.
Плотность и функция распределения центрированных
случайных величин:
/(*)«1/BД) при z<=(— Д, Д);
0 при #< — Д;
F(x)
Д)/BД) при
1 при х>А.
В этом случае
о о
min {Хи Х2) = min {Xu Х2) + А.
По формулам (8.6.3), (8.6.4), паходим
А
-А
8.6. ХАРАКТЕРИСТИКИ МИНИМУМА И МАКСИМУМА 809
Следовательно,
М [Ун2] =M[min{X11 X2}] =M[min{i1( X2} + h] -Л—§¦'
М [П2] = М [(min {ХХ1 Х2})*] =^-2}Иу;
]]J = A.
Очевидно, что
так как при гипотезе Ht работает только один высотомер.
Следовательно,
h A
ft з
м 1У2] - м\у2нЛ'Р(нх) + мГу!г21-Р(я2)
откуда
Обычно вероятность срабатывания высотомера в
парашютных системах довольно высока, поэтому величина
рг/(р2 + 2pq) близка к единице. Например, если р=»
= 0,9999, то Pz/(p2 + 2pq) = 0,9998. Поэтому с достаточной
точностью можно считать, что
где тх ж Dx — математическое ожидание и дисперсия
высоты срабатывания каждого высотомера. >
Пример 2. Анализируется работа вычислительной
системы (ВС), состоящей из двух блоков, работающих
независимо друг от друга. Время безотказной работы 2\
и Т2 блоков — независимые случайные величины,
распределенные по законам Эрланга kt и кг порядков с па-
310 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
раметрами Xi и Я2 соответственно. Для работы ВС
безусловно необходима работа каждого блока. Требуется найти
характеристики времени Т безотказной работы ВС.
Решение. Очевидно, что r = min{ri, Г2К В п. 6.4
было показано, что плотность и функция распределения
случайной величины Т{, распределенной по закону Эр-
ланга к{ порядка с параметром Л», определяются по
формулам
il
Fi @ = 1 - 2 (W г~ЧХ \п\ (i » 1, 2).
Воспользуемся формулой (8.6.1) и найдем интеграл вида
оо
J
Ус+м1 ( К Y
Заметим, что М [fi] = к^Х^, М [Т2] = кг/к2.
Следовательно, по формуле (8.6.1) получим:
М[тт{Г1(Г2}1 =
V
/1 -о
С помощью аналогичного приема получим:
М[(тт{7\,Г2}J] =
Хг1 чг1 (n + kl + i
) П=0
8.6. ХАРАКТЕРИСТИКИ МИНИМУМА И МАКСИМУМА 311
В частности, когда случайные величины 7\ и Г2
распределены по показательным законам с параметрами Л4
и К2 (&i «1, кг = 1), получим:
М [min {Tv Т2)} _ _* ; М [(min {Ти Г,})»]
j
Л1 2
D [min {Г ГЛ]
)
Задача 2. Случайная величина У
представляет собой максимальную из двух
случайных величин:
F — maxUTj, Х2),
где X,, Хг — независимые непрерывные случайные вели-
чипы с плотностями /i(Xi) и /2(#2). Найти числовые
характеристики случайной величины У.
Решение. Применяя прием, использованный в
задаче 1 этого пункта и пользуясь формулами (8.4.17) и
(8.4.18), получим
М [У] - М [max {Хи Х2}\ - mXl + т*2-М [min {Xv X2}] -
ОО 00
- J *Л(*х)/1(^*1+ j ^xfe)/a(^)^a; (8.6.7)
- «2 I^il + «, [X,] - М [(min {Xv XJf] -
00 00
- J *;*,(*i)/i(*i)<ki+ J ^,w/,w<bi. (8.6.
Если случайные величины Xh X2 распределены
одинаково, то
М [Y] - М [max {Xv X2}} - 2 J" a:F (x) / (х) dx; - (8.6.9)
—00
00
М Щ - М [(max {Xv Xt)f] - 2 J *V(z) /(x) dx. >
(8.6.10)
Пример 2. С целью увеличения времени Т
безотказной работы вычислительной системы (ВС) ее компо-
312 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
нуют из двух независимо работающих ЭВМ, время
безотказной работы которых равно Тх и Т2. Случайные
величины Ti и Т2 распределены по законам Эрланга кх и
кг порядков с параметрами К{ и К2 соответственно. ВС
считается работоспособной, если работает хотя бы одна
из ЭВМ. Следовательно, Г==тах{Г1, Тг). Найти
числовые характеристики св. Т.
Решение. По формулам (8.6.7), (8.6.8)' имеем
М [max {Tv T2}] - -J±- + ¦?- - М [тт{Г1г Т2)), (8.6.11)
(8б12)
где M[min{TvT2}] и M[(min{TvT2}J] определяются
по формулам (8.6.5) и (8.6.6) соответственно. Если
случайные величины Ti и Т2 распределены по
показательным законам с параметрами hi и к2 (/с! = А:2=1), то
Mlm*x{Tv.T2}] = ± + ±-^
Л1 Л2
8.7. Числовые характеристики модулей
функций случайных величин
Задача 1. Случайная величина
У=|Х-а|, (8.7.1J
где X — непрерывная св. с плотностью /(#),
а—-неслучайная величина. Требуется найти числовые
характеристики Шу и Ц, с. в. У.
Решение. Функция
{а — X при X ^ а;
X —а при Х>а N '
8.7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ МОДУЛЯ
313
следовательно,
00
J \x— a\f(x)dx = j (a — x)f(x)dx
(a: — a)f(x)dx = a[2F(a)- 1] + 2 J ж/ (*) &c — mx;
а о
(8.7.3)
со oo
<HlY]- J |x-o|«/(a;)At- j (x-aJf(x)dx =
— 00 —OO
- a2 [X] — 2am* + a2, (8.7.4)
где a2 [X] — второй пачальный момент с. в. X, тх — ее
м. о. >
Пример 1. Ремонтная бригада располагается в
точке а линейного участка газопровода, длина которого I
(рис. 8.7.1). Известна плотность распределения f(x)
fix)
I
• х
I X
Рис. 8.7.1
Рис. 8.7.2
случайной точки X на газопроводе, где возникает
неисправность. Кривая распределения f(x) приведена на
рис. 8.7.2*). Найти характеристики св. У —расстояния
до места расположения неисправности, которое
необходимо проехать ремонтной бригаде.
Решение. Случайная величина У определяется по
формуле (8.7.1), а характеристики — по формулам (8.7.3)
и (8.7.4).
Если неисправность на газопроводе возникает с
постоянной плотностью вероятности в любой его точке, то
/(а:) = 1// при яе @,1);
10 при х<1\
х/1 при же (О,/);
1 при х>1.
*) Эта кривая распределения имеет нелинейный характер, так
как некоторые участки газопровода чаще выходят из строя,
чем другие.
314 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
В этом случае
I
Найдем величину агат, при которой щ достигает
минимального значения:
дту/да шш Bа — 1)/1 - 0; amin = 1/2; mUmin - I/A.
Заметим, что если ремонтную бригаду располагать тх
одном из концов линейного участка газопровода (а — 0
или a = Z), то в этом случае ту*=1/2, т. е. среднее
расстояние увеличится в два раза. Найдем остальные
характеристики:
a2 [Y] = а2 [X] — 2атх + а2 = Р/3 — al + a2;
Dy - а2 [Г] - ml - Р/3 - а/ + а2 - (а2 - la + Р/2J/Р,
При а = 0 (или а - /); Dyee0 = Р/12; оУа==0 = г/ /12.
При а - //2; Z)^//2 - Р/48; аУа=|/2 - Z/ /48 «
Мы видим, что при расположении ремонтной бригады
на одном из концов линейного участка газопровода
среднее квадратическое отклонение расстояния от места
расположения бригады до места расположения
неисправности также увеличивается в два раза по сравнению с
минимальным. >
Задача 2. Рассмотрим модуль разности
св. F— \Xi~-Х21, где Xt и Хг независимые непрерывные
св., имеющие п.p. U{xx) и fz(x2).
Требуется найти числовые характеристики св. Y.
Решение. Рассмотрим гипотезу, состоящую в том,
что
Х2е(х2; x2 + dx2).
Ее вероятность — элемент вероятности: fz(x)dx. Условное
м. о. случайпой величины Y при Х2 = я2 было найдено в
предыдущей задаче 1 ((8.7.3)), где вместо величины а
нужно подставить величину хг:
00
М [У | Хг - *,] = х, [2Ft (х3) - 1] + 2 j xjx {xx) dxt - m^.
(8.7.5)
8.7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ МОДУЛЯ 315
По формуле полного математического ожидания (8.1.20)
получим
М[У]- J
— 00
оо j 1
- 2 J x2F, (x.) /2 (x,) dx2 + 2 j j xjj (xa) Л?! /2 (x.) i*a -
U J
- m*2 - mxu (8.7.6)
Из симметрии условий примера относительно величин
Xi и Xz следует, что
ОО / ОО \ 00
J J *l/x(*l)<kl|/l(*l)<k|- J *
— ОО \—00 / —00
.Тогда
00
М[У)-2 J ar2F1(x2)/2(x2)dx2 +
00
+ 2 j x1F2{x1)fl{xl)dxl-mXl-mH. (8.7,7)
—00
Так как выражение случайной величины Y
симметрично относительно Xj и Х2, то формулу (8.7.7) можно
переписать в другом виде:
М[У]-2
ОО /ОО \
+ 2 J I J «к/, (^) dx2 Д (zx) Acj - т%1 - тх%. (8.7.8)
-оо \Xl /
Второй начальный момент случайной величины Y можно
найти непосредственно:
Так как случайные величины независимы, то
а2 IY] « М [У2] - М [X; - 2ХХХ2 + X*] -
- ^xt + DH + (mXl - mX2J. (8.7.9)
816 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
Пример 3. Анализируется поиск информации на
магнитной ленте. Начало записи располагается с равной
вероятностью в любой точке Xi на магнитной ленте
длиной I и (рис. 8.7.3). Головка лентопротяжной^
механизма в момент начала поиска с равной вероятностью па-
ходится в любой точке Х2 магнитной ленты. Скорость
перемотки ленты постоянная
Х2 Xf и равна v.
-Jj ' »' • ' f~ x Определить м. о. и
дисперсию времени Т перевода
Рис. 8.7.3 головки из точки Хг в
точку Х^
Решение. Очевидно, что в данном случае
тпхг - гпн _ 1/2; . Дсх - Ас2
Рассмотрим св. Y = \Х{ — Хг\ — расстояние между Хх и
Хг. По формуле (8.7.8) находим
По формуле (8.7.9) находим
а2 [Y] - DH + DH
откуда
Dy - а2 [У] - m* - Г/18; а, - УЦ, - Z/C /2 ).
Время Т = F/y, следовательно,
М [Т] - М [Г]/у = //(Зу);
D [Г] = D [F]/i;2 - /2/A8i;2);
Пример 4. Рассматривается система п
независимых одинаково распределенных нормальных св. (Хи
Х2, ..., Хп) с характеристиками: тпХ{ = 0; оХ{ — a (i -¦
-1,2, ...,n).
Требуется найти характеристики: м.о. и дисперсии—'
следующих функций этих св.:
а) Уп=?*?; (8.7.10)
i
8.7, ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ МОДУЛЯ 317
п
б) гп = ±^Х\ = Уп/п; (8.7,11)
1 = 1
(п \1/2
2Х? =(Ynf2; (8.7.12)
(л \1/2
4\2*П ~(V/2. (8.7.13)
Решение, а) Обозначим Х\«yir найдем
характеристики У<:
М [(Г, - myj1] - М [Ц] - 2myiM [Г,] +
+ < = М[У?]
В соответствии с формулой F.3.12I
откуда
D [Г4] - D [X?] - За4 - о* - 2а4.
Следовательно,
М [Г„] - 2 М [Х\] - wa2, (8.7.14)
D [У«] - S D [X\] - 2na4. (8.7.15)
Если a = l, то распределение случайной величины Yn
называются %г («хи квадрат») — распределением, тогда
M[X2] = n; D[X2]-2az. (8.7.16)
б) св. Zn связана линейной зависимостью со св.
Yn: Zn~ Yn/n, следовательно,
М [Zn] - М [Yn]ln - a2; (8.7.17)
D [Zn] - D [Уп]/л« - 2о*/п. (8.7.18)
в) Закон распределения и числовые характеристика
св. Ra были определены в п. 7.10 (G.10.36) —G.10.38)).
318 ГЛ. 8 ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
г)" с.ь.уп связана со св. Rn линейной зависимостью
Vn=RJMn\ следовательно,
M{Vn] = M[Rn)/Vn; (8.7.19)
D[Vn] = D[Rn]/n. > (8.7.20)
Случайные величины Уп, Zn, Rn и Vn, рассмотренные
в этом пункте, находят широкое применение в
математической статистике.
8.8. Комплексные случайные величины
При изучении различных случайных явлений в ряде
случаев бывает удобно пользоваться комплексными
случайными величинами. Комплексной
случайной величиной называется св. вида:
X = Xi + *X2, (8.8.1)
где^Х^, Х2 — действительные случайные величины, i=*
— У—1 — мнимая единица. Случайная величина Xt
называется действительной частью, а случайная величина
Хг — мнимой частью
комплексной с. в. X.
Комплексная случайная
величина
X-Xi-tXt (8.8.2)
называется сопряженной с
комплексной с. в. X.
Комплексную с. в. X можно
изобразить случайной точкой с
координатами (Xlt X2) или
случайным вектором R на комплексной плоскости xfix%
(рис. 8.8.1).
Случайная величина R — длина случайного радиуса-
вектора /?, называется модулем (или абсолютной
величиной) комплексной св. X:
R = | X | = Ух* + Х22 - УЗГХ. (8.8.3)
Случайная величина R является действительной.
Случайный угол 0, который случайный радиус-вектор
R образует с положительпым направлением оси 0х{1 на*
зывается аргументом комплексной случайной величины
8.8. КОМПЛЕКСНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 319
X. Действительная с. в. 0 определяется из выражения:
^ (8.8,4)
Математическим ожиданием комплексной случайной
величины X = Xt + iXz называется комплексное число
mx = mx + imx%. (8.8.5)
Центрированной комплексной случайной величиной
называется случайная величина
Х-Х-гоя-Х1-тЯ1 + * (Ха - гоЯ|) - ix + iX2, (8.8.6)
о о
Xv Х2
где Xv Х2—действительные центрированные случайные
величины.
Дисперсией комплексной с» в. X = Хх + iX2
называется м.о. квадрата модуля соответствующей
центрированной с. в.:
Dx = D [X] - М [ | X |«] - М [XX], (8,8.7)
"о о о
где ХшшХ1—1Хй.
Найдем произведение
о "о о оо о о ол
XX - {Хг + tXt) (Хг — iX2) = X* + XI (8.8.8)
Пользуясь теоремой сложения математических
ожиданий, которая доказана в п. 8.2, а именно: м.о. суммы
св. равно сумме их математических ожиданий, получим:
Dx - М [XX] - М [Х\ + Х22] - М [Х\] + М [Х22] =
= DXi + DX2, (8.8.9)
т. е. дисперсия комплексной св. есть действительное
неотрицательное число, равное сумме дисперсий
действительной и мнимой части.
В соответствии с формулами (8.8.3) и (8.8.4)
случайную величину X можно выразить через полярные
координаты Л, 9 случайной точки X на плоскости х{0х2
X - R cos 0 + IR sin 0, (8.8.10)
320 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
Пользуясь формулами Эйлера, выражение (8.8.10)
можно записать в виде
X = Reie. (8.8.11)
Рассмотрим две комплексных св.:
Х=*Х% + iX2i У - Yt + lYt. (8.8.12J
Ковариацией Кху двух комплексных св. X и Y пазы-
вается м. о. произведения центрированной комплексной
о
с. в. X на центрированную комплексно-сопряженную
о
св. Y:
кху = м [ху\ = м f(i1 + dt)(yi - *у*)] =
00 00 00 00
- М [X.Y, + X2Y2 + i (XtYt - XxY2)l
Пользуясь теоремой сложения математических
ожиданий и вынося песлучайный множитель i за зпак
математического ожидания (см. п. 8.2) получим:
Кху - КЯхУг + КХгУ2 + l (JfVi - Kx;Vl), (8.8.13)
где КХ{У.— ковариация действительных с. в. Х{ и Yj (i =
-1.2; / = 1, 2).
Ковариация двух комплексных св. X и Y является
в общем случае комплексным числом. Особо отметим,
что определенная таким образом ковариация Кху двух
комплексных с. в. X и У не равна ковариации Кух двух
комплексных св. У и X. Проводя аналогичные
преобразования для Кух получим:
Кух - KXiyx + КХЛ - i (KX2Vi - КХ;У2) = Кху1 (8.8.14)
т. е. ковариация двух комплексных св. У и X равна
комплексно сопряженной ковариации двух комплексных
св. Хи У.
Комплексные св. X и У называются независимыми,
если независимы их действительные и мнимые части, т. е.
/*.Л*1, *2, У и У2) = /х(яп, *г)-Ъ(Уи Уг)- (8.8.15);
В этом случав
К*Л = К*#% в К*г*х " ^Vi = ° <8.8.16)
8.9. ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ 321
и выполняется условие:
М[Х.У] = М[Х].М[Г] =
= (М [Хг] + 0Л [Х2]) (М [YJ + 1М [Г2]), (8.8.17)
т. е. м. о. произведения комплексных независимых с. в.
равно произведению м. о. этих с. в.
8.9. Характеристическая функция
случайной величины и ее свойства
Для доказательства центральной предельной теоремы,
которое будет изложено в п. 10.2, А. М. Ляпунов ввел
метод характеристических функций,
который нашел широкое применение при решении различных
вероятностпых задач.
Рассмотрим комплексную св.
У = е«* = ехр{*Ш, (8.9.1);
где X — действительная с. в., закоп распределения
которой известен, ? —параметр, г = У—1 — мнимая единица.
Характеристической функцией с. в. X называется м. о.
комплексной с. в. Y:
Ъх (t) = М [Y] = М [eitx]. (8,9.2)
Характеристическая функция безразмерна, а параметр
t имеет размерпость, обратную размерности св. X.
Пользуясь формулами (8.8.10) и (8.8.11), можно
показать, что комплексная св. У (8.9.1) представляет
собой едшшчпый радиус-вектор со случайным углом tX
на комплексной плоскости. Следовательно, М [Y] также
представляет собой единичный вектор, но с неслучайным
углом на комплексной плоскости, откуда Ifl^fjl^l.
Для дискретной св. X, принимающей значения хи
хг, ..., хп с вероятностями ри р2, ..., рп,
характеристическая функция определяется как сумма:
¦«W-|el\ (8.9.3)
для непрерывной с. в. X с плотпостыо /(#J-=KaK
интеграл:
ПО
J eUxf(x)dx. (8,9,4)
II Теория вероятностей и ее
инженерные приложения
322 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЯ
Таким образом, характеристическая функция $.,•(/)
непрерывной с. в. представляет собой преобразоваыю Фурье
плотности распределения и однозначно определяемся
этой плотностью. Отсюда следует, что плотность
распределения f(x) также однозначно выражается через
характеристическую функцию i}x(t) обратным
преобразованием Фурье: •
C.9.5)
Характеристическая функция неслучайной величины а
равна
^(f)ee?«*t (8.9.6)'
Выведем основные свойства
характеристической функции.
1. Характеристическая функция с. в. Z — аХ+ b
выражается через характеристическую функцию $x(t) св.
X формулой
г%(t) = M [eii(aX+b)] = eif4x (at). (8.9.7)
2. Если у св. X существует начальный момент к~го
порядка &и[Х], то существует к-я производная
характеристической функции и выражается формулой
@ = -^ М [eitx] - ikM [XheiiXl
При t -> 0 получим:
Откуда
а,[Х]=^>@)Г\ (8.9.8)
3. Характеристическая функция суммы независимых
случайных величин Хи ..., Хп равна произведению
характеристических функций слагаемых.
Действительно, пусть
и заданы характеристические фупкции Qh(t) св. Xk (к =
— 1, ..., п). Требуется найти характеристическую фупк-
8 9. ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ 323
цию ®z(t) св. Z. По теореме умножения м.о. (8.2.23)
получим:
<М0 = М f exp [it Д хХ\ = М \ П exp {itXk} 1 =
= П М [exp ОВД = Д *хк (t). (8.9,9)
Л^1 fc=l
4. Из свойств 1 и 3 следует, что если Z = 2 Д/А + Ь
и с. в. Хи XZi ..., Хк, ..., Хп независимы, то
02 (/) = ехр {«Ь}Д O«fc КО* (8.9.10)
Пример 1. Найти характеристические функции
следующих случайных величин:
1) св. Хи принимающей значение 0 и 1 с
вероятностями q и р (р + # = 1) — индикатора события Л,
происходящего с вероятностью р\
2) св. Х2, распределенной по биномиальному закону
с параметрами п и р\
3) св. Х3, распределенной по закону Пуассона с
параметром а;
4) с в. Х4, имеющей геометрическое распределение
с параметром /?;
5) св. Х5, распределенной с постоянной плотностью
на участке (а, Ь);
6) св. Х6, распределенной по нормальному закону с
параметрами тх и ох;
7) св. Хь распределенной по закону Коши,
симметричному относительно точки а с плотностью /(#) = —^
1 + ()/
8) с в. Х8у имеющей распределение Лапласа,
симметричное относительно точки а с плотностью / (я) ==»
9) св. Х9, имеющей гамма-распределение с
параметрами п и X (см. F.4.1));
10) св. Хш подчиненной показательному закону с
параметром К с плотностью f(x) = Xe~%x (К > 0; х>0).
324 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
Решение. 1. Так как св. Xt принимает значения
О и 1 с вероятностями q и р, то
Oi(t)=*eU9q + eitlp = q + peu. (8.9.11);
2. Вероятность Рт того, что св. Х2 = т (иг = О, 1, ...
#.., п) определяется по формуле Рт = C™pmqn~m,
следовательно,
= 2 С (ре»)тЯп-т = (q + Реи)\ (8.9.12)
т=о
3. Вероятность того, что св. Х3 = А: (/с = 0, 1, 2, ...)
определяется по формуле Рк — аке-а/к\, следовательно,
оо
= е~а-еа<и 2^ТГ" e~aeit = e-e(l-*W), (8.9.13)
так как ^ (aeif)V^! = еае при |aeif|<oo.
4. Вероятность того, что св. Xi^k (& = 0, 1, 2...),
определяется по формуле рк = qhp, следовательно,
#4 @ - 2 eithqhP = 1Р/{1 - ?^')] 2 (?*")* A - ?«'О =
ft=0 /1=0
—ff^Ot (8.9.14)
так как 2 (<??*')* A ~ Qeit) в 1-
/1=0
5. Плотность св. Х5, распределенной равномерно на
интервале (а, Ь), определяется по формуле /(#) ==
«=1/F — а) (х^(а1 Ь))у следовательно:
ь
#6 (t) = J е|(яДр/(Ь - а) = (е"ь - e«e)/(«6 - ita) =
а
b a)t]. (8.9.15)
8.9. ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ
325
6. Плотность св. Хб, распределенной нормальпо с
параметрами т и а, определяется по формуле / (х) =
а 1/2я
(х-тГ
^5 \% следовательно
(х-тпJ
г — т = у I
dx = dy I
оо
gKm Г* it
?V5f J*
dy =
oo (v-ito*\* ла%
eitm Г» I /io ) ~
—7=r \ e x ' e 2 t
У2п J
= dz
itm-
t'o*
• <8-9-16)
так как последнее подынтегральное выражение
представляет собой нормальную плотность с параметрами т =
= 0; о и интеграл от нее в бесконечных пределах равен
единице.
7. Плотность св. Хь распределенной по закону Ко-
ши, симметричному относительно точки а, можно
записать в виде
Следовательно,
— 00
^i«a Г» gtta
Я J l±
— 00
oo
*) В [6] показало, что — \ ~
я J 1
). (8,9.18)
dy =
326
ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
8. Плотность св. Х8, распределенной по закону
Лапласа, симметричному относительно точки а, имеет вид:
Следовательно,
1 Ь>0). (8,9.19)
I (о; — а)/Ь = у
I dx = bdy
В первом интеграле проведем замепу перемепных
Ь + 1 щ во втором у{1 — йЬ) — у, В этом случае
0
г 0
J
L—оо
1. (8.9.20)
9. Плотность св. Х9, имеющей гамма-распределение
с параметрами п и X, определяется но формуле
/(«) = X(Xx)""f«"**r(n) (*>0; X>0; n>i)'f (8.9.21);
где
оо
Г (п) - J xn~le~*dx {п > 1) (8,9,22)
о
— (/i— 1)!
— известная гамма-функция. При и целом
(w^ 1). Следовательно,
n)
— U)
так как интеграл равен Т(п) (см. (8.9.22)),
10. Так как гамма-распределение при п = 1
превращается в показательное распределение с параметром X
(см. п. 6.4), то для св. Х10 получим характеристическую
8.9. ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ 327
функцию в виде:
*«<*) —зс=т*- > (8-9-24)
Пример 2. Для случайных величии,
фигурирующих в пупктах 1, 2, 5, б примера 1, найти числовые
характеристики с помощью аппарата характеристических
функций.
Решение.
1. Oi" @)/** = ~(q + pe»)/ih |t-« - pe«|*=o - p = M [X\].
Следовательно, M[Xj = M [^i]= P> D [Xj — p — p- = pq-
- л (g + pe1')"-1 peil Uo = np = M [X,];
+ n(q + peu)n ' pei(]|(=o — n(n — I)pz + np = M [X\].
D [X2] = M [XI] - (M [X2]f = п*р* - np* + np-n2p2=npq.
Э) ! t(ibeitb-iaeita)-(eitb-eUl
3.
(=o
X
= (раскроем неопределенность 0/0 (при <->0)
по правилу Лопиталя) = -^ X
e (b — a)
ibeitb - iaeita + t [{ibf eitb - (la)* eita] - (ibeitb - iaeita}
(=o
~ 2 F - a)
Апалогичпо находим
D [X5J - M [XI] - (M [X5]J = F - a)V12.
4. ¦&; @)/j = Г1 [exp {Jim - *W/2) (^ - ^2) b=o
328
ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
@)/t2 = Г2 [exp {itm — №/2} (im — la2f +
+ (- о2) exp {itm - t2o*/2}] |(=0 = m* + a2 = M [X*];
8.10. Метод линеаризации функций
случайных величин
Выше в этой главе было показапо, как, зная закон
распределения случайных аргументов, можпо находить
числовые характеристики функций этих аргументов. Во
многих случаях можпо обходиться даже без закопов
распределения случайных аргументов, а пользоваться
только аппаратом числовых характеристик и находить
числовые характеристики функций (м. о., дисперсию, другие
моменты) как функции числовых характеристик
аргументов. Особенно простые соотношения существуют
между числовыми характеристиками функций и числовыми
характеристиками аргументов в случае, когда эти
функции являются линейными.
В инженерной практике очепь часто встречаются
такие функциональные зависимости, которые, будучи
нелинейными, могут быть приближеппо заменены
линейными в диапазоне возможных значепий случайпых
аргументов. Например, сопротивление схемы, изображенной
па рис. 8.10.1, определяется по формуле
Л = RfitRJ (ИЛ + ЛА + Л2Л3)
(8.10.1)
и представляет собой пелинеппую
функцию: Л~ф(Л1, Л2, Л3).
Однако такую нелинейную
функцию можпо приближенно заменить
линейной (линеаризовать), если
диапазон возможных значепий аргументов мал. В конкретпом
приборе сопротивление можно представить в следующем
виде:
Рис. 8.10.1
где г{ (?~1, 2, 3) — м. о. случайпой величины Л,
(номинальное значение сопротивления Л*); ДЛг — ошибка
изготовления сопротивления Л(.
8.10. ЛИНЕАРИЗАЦИЯ ФУНКЦИЙ СЛУЧАЙНЫХ ВЕЛИЧИН 329
Эти ошибки, в зависимости от точности изготовления,
колеблются в диапазоне нескольких процентов от
номинальных значений, и величину R в формуле (8.10.1)
можно приближенно заменить линейной функцией св.
Д,=»г, + ДД, (t=l, 2, 3).
Линеаризацией функции называется приближенная
замена нелинейной функции линейной. Заменив
нелинейную функцию случайных аргументов линейной, мы
получаем возможность паходить числовые характеристики
функций по числовым характеристикам аргументов.
Метод линеаризации функций случайных аргументов
находит широкое применение в различных инженерных
задачах при определении числовых характеристик
различных параметров работы приборов и механизмов,
находящихся под воздействием случайных возмущений.
Рассмотрим сначала задачу линеаризации функции
одного случайного аргумента:
где X и Y — непрерывные с. в.
Из курса высшей математики известно, что любая
непрерывная дифференцируемая функция у = у(х) может
быть разложена в ряд Тейлора в окрестности точки а:
(8.10.2)
где
Ф'(о). (8.10.3)
С математической точки зрепия линеаризация
функции одного случайного аргумента У —ф(Х) есть
приближенное представление этой функции первыми двумя
членами ряда Тейлора; при этом разложение проводится
в окрестности точки тх = М[Х]. Это приближение будет
тем точнее, чем меньше диапазон возможных значений
случайного аргумента.
Применяя такую приближенную замену нелинейной
функции у = ф (х) линейной, получим
у = ф(х) = ф (иг,) + ф' (тх) (# - Шх).
Такое же приближенное линейное соотношение связывает
330 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
и случайные величины У и X:
или Х (8.10.4)
Выводя эту формулу, мы перешли от случайных
величин X и У к неслучайным # и у, так как, строго
говоря, по случайной величине дифференцировать нельзя.
В дальнейшем мы иногда позволим себе не быть столь
строгими, и переход от случайных величин к не
случайным будем подразумевать при вычислении производных.
На рис. 8.10.2 дана геометрическая интерпретация
линеаризации функции одного случайного аргумента. Ли-
неаризовапная функция у =* ср (тх) + ср' (тх) (х — тх) есть
Рис, 8,10.2
не что иное, как уравнение касательной к кривой
у = ф (х), проходящей через точку К с абсциссой тх и
ординатой ф(тх). Линеаризация состоит в том, что
участок кривой ф(я) для диапазона же(а, A) приближенно
заменяется отрезком касательной.
Если такая замена нелинейной функции ф(х)
линейной ф(/пх) + <р'(/пх) (# — тх) удовлетворяет нас по
точности, то мы можем произвести линеаризацию зависимости
между случайными величинами У и X, т. е. заменить
ее линейной:
Y = q>(mx) + q>'(mx)X
и найти числовые характеристики — ту и Dy — случайной
величины У так, как это делают для линейных функций
(см. формулы (8.2.9) и (8.2.13)):
Шу - М [Y] - М [ф (X)] - Ф (mx)t (8.10.5)
Dy - D [У] - [Ф' (/я,)]» Д* (8.10,6)
8.10. ЛИНЕАРИЗАЦИЯ ФУНКЦИЙ СЛУЧАЙНЫХ ВЕЛИЧИН 331
откуда
c,-lq>'(m,)lo.. (8-10-7)
Будем называть функцию, мало отличающуюся от
линейной в диапазоне практических возможных значений
аргумента, почти линейной.
Из формул (8.10.5) —(8.10.7)" следует, что
математическое ожидание почти линейной
функции приближенно равно той же функции
от математического ожидания аргумента,
а ее дисперсия приближенно равна
дисперсии аргумента, умноженной на квадрат
производной функции в точке,
соответствующей м. о. аргумента.
Остановимся, кстати, на одной подробности. Может
показаться, что приближенная замена участка кривой
ф(#) участком касательной менее точна, чем замена ее
участком секущей в том же диапазоне. Но мы выбираем
замену участком касательной потому, что, во-первых, это
проще, и, во-вторых, как правило, плотность f(x)
непрерывной с. в. X больше в областях, близких к ее
математическому ожиданию тя, чем по краям диапазона ее
возможных значений; значит, наилучшее приближение
нелинейной функции к линейной должно осуществляться
там, где плотность аргумента максимальна, а это обычно
бывает вблизи математического ожидания (как,
например, для нормального закона).
Пример 1. Случайная величипа У обратна св. X:
У-1/Х;
св. X распределена равномерно в интервале A,2). Най-
сти числовые характеристики с. в. У методом
линеаризации и сравнить их с точными значениями этих
характеристик.
Решение. Находим:
m.-B + i)/2-l,5; Д< = B-1O12 = 1/12;
<р' (х) - - I/*2; (q/ (mx)? « (I/mlJ - 0,1975;
ту = у(тх) *= 1/1,5 « 0,6667;
Dy - (q>' {mx)f Дс & 0,01646; ау « 0,1283.
332 ГЛ. 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
Точные значения характеристик пайдсм по формулам
а,
оо 2
] у(х) f(x)dx = \ l>dx
со
J
2
1
In
1
\x\
-In
-
2 =
0,6931;
0,5;
D [У] - а2 [Y]
0,5 — 0,69312& 0,01955;
0,1398. >
Аналогично тому, как производилась линеаризация
функции одпого случайного аргумента, выполняется
линеаризация функции от нескольких с. в. Хи X2i ..., Х„,
образующих систему. Пусть
У «*<р(Х|, Х2, ..., ХпI
причем функция ф дифференцируема по каждому из
своих аргументов и почти линейна в области их
практически возможпых зпачепий. Известны числовые
характеристики системы: математические ожидания ти тг1 ..., тп
и ковариационная матрица
к„
Разложим фупкцию q>(xu x2i >.м хп) в ряд Тейлора в
окрестности точки (ти т2, ..., тп) и ограничимся линей-
пыми членами разложения. С геометрической точки
зрения это равносильно замене уравнения поверхности
ф(#1, #2, .,., хп) в /г-мерпом пространстве касательной
плоскостью к этой поверхности:
Ф (хи х2% • ¦.х хп) & Ф (mlf..., тп) +
+ 2 9«i (тЬ • • • т тп) (Х\ —1П\)*
Следовательно, с. в. Y может быть приближенно пред-
8.10. ЛИНЕАРИЗАЦИЯ ФУНКЦИЙ СЛУЧАЙНЫХ ВЕЛИЧИН 333
ставлена в виде линейной функции системы с. в.
(Xiy ..., Хп):
Ф(mv .. .х тп) + 2 Ф** (щ, м.^п) (Хг — тг)
'' f U
= ф \М>1у • . . х ffln) + JIj фзс* (^u • • м "^n) ^i« (8.10.8)
Применяя к этому выражению формулы (8.2.9) и (8.2.13)
получим:
т^у^ф(?М1, ..., тпп)| (8.10.9)
где для краткости введено обозначение:
Формулу (8.10.10) можно записать через средние
квадратические отклонения и коэффициенты корреляции:
где ri;« = jj-?- — коэффициент корреляции случайных
величин Х{ и X). Если случайные величины Xh ..., Ха не-
коррелированы, то
Пример 2. Определить числовые характеристики
сопротивления схемы, изображенной на рис. 8.10.1, если
номинальные значения сопротивлений М [R^ = гх =
« 800 ом; М [Я2] — г2 » 900 ом; М [В3] » г3 « 1000 ом,
ошибки в изготовлении сопротивлений распределены
равномерно в интервале ±1% номинального значения
сопротивления и не зависят от ошибок изготовления других
сопротивлений.
334 ГЛ, 8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
Решение.
-Я = ф (Я„ Rt, Я8) = RtRtR3/ (Д,Яг + Д.Я, + R2R3);
D [Лх] = B • 800- 10~2)Vl2 да 21,3 (омJ;
D [Д8] =B-900-10-2J/12 ж 27,0 (омJ;
D [R3] - B-1000- 10-2Ol2 « 33,3 (омJ.
По формуле (8.10.9) находим:
М [R] Я ф (ГХ, г„ Г3) = 8Q0.90Q + 800-ЮОО + 900-1000^298(ОМ)-
Определим значения частных производных
= (900-ЮООJ ^ 81-Ю10 ^
= (800-900 + 800-1000 + 900-ЮООJ 2422-108 ^
(9*\ А (Л1ДзJ ^ (800-ЮООJ _ 0,64 _
\д*ш)» \(ЛЛ + ЛЛ + ЛЛ)*/т 5-86-1012 ^5'86^
» 0,109;
_ (800-900^ д*№м
5,86-1012 5,86-102
По условию сопротивления независимы (#о=*0); по
формуле (8.10.12) находим
з
D [R] - 2 (SJ D №1« 0,1382.21,3 + 0,1092-27 +
+ 0,08852-33,3 « 0,406 + 0,321 + 0,260 & 0,987 (омJ;
a [R] - УЩЩ - 0,993 (ом).
Заметим, что если коэффициент вариации каждого
сопротивления в схеме, изображенной на рис. 8.10.1
равен:
Г1 Г2
8.10, ЛИНЕАРИЗАЦИЯ ФУНКЦИЙ СЛУЧАЙНЫХ ВЕЛИЧИН 335
то коэффициент вариации сопротивления всей схемы
будет
УРЩ_ 0,993 ^AAAogo
1Щ] ™ -298" ~ (}>00333>
что свидетельствует о меньшем относительном разбросе
сопротивления схемы по сравнению с отдельными
сопротивлениями.
Если бы рассматриваемая схема состояла из.
номинально одинаковых сопротивлений:
М [Rj = M [R2] = M [R3] - 900 (ом),
то мы получили бы
D [Я*] - 27 (ом)' (I - 1, 2,_ 3); М [R] - -^ = 300 (ом),
[dRjm [dRjm [dR3jm C.9002J ~ 9 *
D[R] = 3($У D[^] = З.4.9.З
/lRj-1 (om);
М[Л] -3oo-
Мы видим, что характеристики схемы практически
остались теми же, что и для схемы с разными
сопротивлениями. >
ГЛАВА 9
ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
СЛУЧАЙНЫХ ВЕЛИЧИН
9.1. Закон распределения функции
одного случайного аргумента
В предыдущей гл. мы познакомились с методами оп-»
ределения числовых характеристик функций с. в. и
показали, что для их отыскания не требуется знать законы
распределения этих функций, а достаточно знать законы
распределения аргументов. Как было показано, во многих
случаях инженерной практики при нахождении числовых
характеристик функций с. в. можно обойтись даже без
законов распределения аргументов — достаточно знать
лишь числовые характеристики этих аргументов.
Однако нередко в инженерных приложениях
возникает и задача определения законов распределения функции
с. в. Обычно это требуется при определении вероятности
попадания этих функций в различные области их
возможных значений.
В этом пункте мы будем решать следующую задачу.
Имеется непрерывная с. в. X с плотностью /(#); св. У
выражается через с. в. X функциональной зависимостью
Г-Ф(Х). (9.1.1)
Требуется найти закон распределения с. в. У.
Рассмотрим сперва случай, когда функция (р(Х)
строго монотонна, непрерывна и дифференцируема в
интервале (а, Ь) всех возможных значений с. в. X. Функция
распределения G(y) св. У определяется по формуле
G{y)-P{Y<y). (9.1.2)
Если функция ф(я) монотонно возрастает на всем
участке возможных значений св. X (рис 9.1.1), то
событие (У < у) эквивалентно событию {X < г|?(у)}, где
ty(y)~x есть функция, обратная фупкцпп ф(я)=г/.
Из строгой монотонности ф(#) следует однозначность
9.1. ФУНКЦИЯ ОДНОГО СЛУЧАЙНОГО АРГУМЕНТА
функции ${у). Имеем
337
J f(x)dx. (9.1.3)
Дифференцируя это выражение по величине у,
входящей в верхний предел интеграла, получим п. р.
случайной величины У:
8 (У)
dG(y)
dy
Если функция ф(#) на участке (а, Ь) возможных
значений св. X монотонно убывает (рис. 9.1.2), то событие
У
У
у=р(х)
Y<y
Рис. 9.1.1 Рис. 9.1.2
{Y<y} эквивалентно событию {Х>$(у)}. Следовательно,
ь
J f(x)dx. (9,1.5)
Дифференцируя G(y) по переменной у, входящей в
нижний предел, получим п. р. случайной величины У:
8(У) = ^ = - /(*(?)) ¦' (У) *)• (9.1.6)
Так как плотпость не может быть отрицательной, то
формулы (9.1.4) и (9.1.6) можно объединить в одну:
s(y)=s:f(^{y) W(y) I- (9.1.7);
Если с. в. X дискретна и имеет ряд распределения
X :
\Pi\
|Pn
(9Л>8)
¦) В формулах (9.1.3) и (9.1.5) диапазон возможных значений
с. в. X может быть (—оо, оо), т. е. а = —оо; Ь = оо,
338 ГЛ, 9, ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
то возможные значения Y = ф (X) определяются из
выражения гл = ф(#г) (^ = 1, 2, ..., /г); при этом имеет
место равенство
В{У«Ы-Р{Г-ф(^)>-Л. (9.1.9)
Задача 1. Закон распределения
линейной функции одного случайного аргумен-
т а. Частным случаем мопотонной функции является
линейная функция у =-ах + Ь, где а, Ь — неслучайные
величины. Пусть Y есть линейная функция непрерывной
с. в. X с плотностью /(#):
Найдем, пользуясь формулой (9.1.7), плотность
распределения g(y) случайной величины У. В данном случае
обратная функция <^{y)s=s{y — b)/a; ее производная ^'(г/) —
= 1/а; модуль производной 1/|а|. Формула (9.1.7) дает
Ту > (9.1.10)
Пример 1. Случайная величина X распределена по
показательному закону
Случайная величипа У линейно выражается через X:
Найти плотность распределения с. в. У.
Решение. В данном случае обратная функция
г|)(?/) = B —1/)/3. Условие
(у<2) х>0 в формуле (*) для
1 oV "" \° (У>2) у переходит в условие
9 Г ' у = 2-Ъх<2\ по
формуле (9.1.10) получим
/ ч _ [е{у~2) при у < 2,:
gW^l 0 при */>2.'
График плотности g(y)
показан на рис. 9.1.3. >
Рис. 9.1.3 Пример 2. Найти
п. р. линейной функции
Y — аХ+ Ъ нормально распределенного аргумента X с
характеристиками тх и а*.
Решение. По формуле (9.1.7) имеем
9.1. ФУПКЦИЯ ОДНОГО СЛУЧАЙНОГО АРГУМЕНТА
339
а это есть нормальный закон с характеристиками ту~
= amx+b\ Dy = a2ol; оу=\а\ах. Таким образом, в
результате линейного преобразования
нормально распределенной св. X получаем
св. У, также распределенную по
нормальному закону. >
Пример 3. Непрерывная с. в. X распределена по
закону Коши в простейшем
(каноническом) виде: У
1
/(*)¦
с. в. У связана
мостью:
с нею
зависиНайти плотность
распределения с в. У.
Решение. Так как функ- Рис. 9.1.4
ция у = 1 — хг монотонна
(монотонно убывает) на всем участке (—°°, °°)\
применим формулу (9.1.7). Решение оформим в виде двух
столбцов; в левом будут помещены обозначения функций,
принятые в общем решении задачи; в первом —
конкретные функции, соответствующие данному примеру,
W(y)\
Пример 4. С. в. X распределена по тому же закону
Коши /(#)= 1/[яA + #2)]; св. У есть величина,
обратная X:
Найти ее плотность g(y).
Решение. График функции у = 1/х показан на
рис 9.1.4. Эта функция терпит разрыв второго рода (пе-
340
ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
рескакивает с —°° на +<») при я = 0; но обратная
функция х = 1/у однозначна, поэтому можно применять ту же
формулу (9.1.7), которая выведена для монотонной
функции. Решение снова оформим в виде двух столбцов
(слева — общий, справа — частный случай):
У = Ф (х)
W(y)\
1/[л A + я*)];
У = 1/х\
х = 1/у;
т. е. обратная величина Y = 1/Х тоже, как и X, имеет
распределение Коши. >
Пример 5. Скорость соударения молекул X
распределена по закону Релея с параметром о:
2os
Количество выделяемой энергии У при соударении
молекул определяется по формуле
1 — * ] (с>0— неслучайная величина).
Найти п. р. с. в. Y,
Решение. При х>0 функция ф(Х) монотонна.
Решение примера снова располагаем в виде двух
столбцов (слева общий случай, справа — частный конкретный
случай):
/И
У = <Р (*)
Wiy)\
@<у<с);
@<у<с);
c/[2(c-y)(-\nl(c-y)/c]I/2]
@<у<с);
@<у<с). >
9.1. ФУНКЦИЯ ОДНОГО СЛУЧАЙНОГО АРГУМЕНТА
341
Пример 6. Радиус круга X распределен по закону
Релея с параметром о:
Найти закон распределения св. У — площади круга.
Решение. Св. У = пХг — функция монотонная при
следовательно, с в. У имеет показательный закон
распределения с параметром —г* >
2яа
Пример 7. Через точку а, лежащую на оси Orj,
проводится прямая ab под углом X к оси Orj (см.
рис. 9.1.5). Угол X распределен равно-
а
мерно в интервале!—j; + -у). Найти
закон распределения св. У —
абсциссы точки пересечения прямой ab с
осью 0?.
Решение. /0l)=
I ¦' (У) I я л , ^z 2# - Следовательно,
1 + У /а а
т. е. с. в. У распределена по закону Коши. >
Пример 8. Напряжение X распределено по
нормальному закону с параметрами тх, ох\ стабилизируемое
напряжение У определяется по формуле
а при X ^ а;
Y = X при а < X ^ Ь;
6 при Ъ<ХЩ
Найти функцию распределения с. в. У.
Решение. С.в. У —смешанная:
Р{У _ а) - Р {Х<а} - Ф [(а- тх)/ох] + 0,5;
342
ГЛ, 9, ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
где Ф (х)— функция Лапласа. Функция распределения
с. в. У имеет вид:
0 при
G {у) = Ф [(у — тх)/ах] + 025 при а •
1 при
На рис. 9.1.6 показан график G(y). В общем случае, если
f(Hy)
а ь у
Рис. 9.1.6
функция распределения с. в. X есть F(z), то
10 при
F(y) при а'
1 при у > b. ^
Пример 9. Стабилизатор напряжения работает
таким образом, что ограничивает напряжение сверху:
[X при
' [а при
Найти функцию распределения с. в. У, если задана
функция распределения с. в. X — F(x).
Решение. По аналогии с решением предыдущего
примера получаем
|0 при у<а;
(F(y) при а<у. >
Пример 10. Стабилизатор напряжения X работает
таким образом, что ограничивает напряжение снизу:
max
а при X^а;
X при а < X,
Найти функцию распределения св. У, если задана
FLxl~ Функция распределения с. в. Х9
9.1. ФУНКЦИЯ ОДНОГО СЛУЧАЙНОГО АРГУМЕНТА
343
Решение. В соответствии с решением примера 8
получаем
\F (у) при а<г/;
" 10 при у < а. >
Рассмотрим теперь случай, когда функция у = ч>(х)
на участке (а, Ь) возможных значений с. в. не монотонна
(рис. 9.1.7). В этом случае обратная функция х = ^(у)
неоднозначна.
Число значений обратной функции ty(y) зависит от
того, какое у мы взяли; обозначим эти значения ^(j/),
Рис. 9.1.7
Фг(у)\ ..., ^i(j/)\ ... Событие Y<y равносильно
попаданию св. X в один из неперекрывающихся отрезков,
отмеченных жирной линией на рис. 9.1.7, где
соответствующая часть кривой у — (р(х) лежит ниже прямой у; в
нашем случае эти отрезки будут: от а до \f>i(j/); от ^{у).
до ^з(у)У от $ь(у) до $ъ{у) и т. д.; последний отрезок
может кончаться точкой Ь, а может и одной из точек
^i(y) (это несущественно). Попадания точки X в эти
отрезки — события несовместные; по правилу сложения
вероятностей
= № (У)> Ь (У))} + Р ix е (г|>4 {у), ф5 (у))} + .. ¦ -
- J f{x)dx+ j f(x)dx+ J f{x)dx+..>
Учитывая правило дифференцирования интеграла по
переменной, входящей в его пределы (а именно:
производная интеграла по такой переменной равна значению
подынтегральной функции от верхнего предела,
умноженному на производную верхнего предела минус значение
подынтегральной функции от нижнего предела, умножен*
344 ГЛ. О ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
ное на производную нижнего предела), получим в нашем
случае
+ fib(У))Ь(У)- /W>a(у))Ь(у) + .., (9.1.11)
В тех точках, где ф(х), пересекая прямую у, убывает
(начало соответствующего участка оси абсцисс, для
которого Y<y), производная г|/ (у) отрицательна; она же
входит в сумму (9.1.11) со знаком минус; в тех точках,
где (р(х) возрастает, i|/(i/) (конец участка) она имеет
знак плюс. Производные постоянных а и Ъ равны нулю,
поэтому безразлично, фигурируют ли точки а и Ъ в виде
начала или конца какого-либо участка. Все члены в
формуле (9.1,11) положительны, и она принимает очень
простой вид:
к
g(y) - 22 /(Ь(У))\Ь(УI (9.1.12)
где к — число значений обратной функции,
соответствующее данному #, г|),(г/); ф2(у); ...; % (у)— значения
обратной функции, соответствующие данному у.
Задача2. Закон распределения модуля
случайной величины. Задача ставится следующим
образом: дана непрерывная с. в. X с плотностью f(x) на
участке (—ооэ +оо); случайная
величипа У связана с нею
соотношением:
У-1X1.
Найти плотность раснределе-
0 <р2(У) ос пия с- Вв у.
Рис. 9.1.8 Решение. Функция у =
= \х\ не монотонна; ее график
показан на рис. 9.1.8. Обратная функция при данном у
^еЛочДва значешш: +t(y).e-0, biv) = y. По формуле
(9.1.12) получим:
111 =f{-y) + f(y) {y>0)
(9.1.13)
^отрицательной случайная величина Y быть не может).
В частности, если плотность }(х) симметрична
относительно начала координат, т. е. /(-*) =/(я), формула
9.1. ФУНКЦИЯ ОДНОГО СЛУЧАЙНОГО АРГУМЕНТА
345
(9.1.13) даст:
Задача 3. Закон распределения
квадрата случайной величины. Пусть непрерывная с. в.
X имеет плотность /(#); найти плотность распределения
ее квадрата.
Решение. Функция у = & не монотонна
(рис. 9.1.9); *i (у) = —ViT; *a(»l-V». Формула (9.1.12);
() ()() ()()()
ном случае, когда с. в. X имеет нормальное
распределение с параметрами тх = 0; ох = 1;/(•?) = е~х ^1 к 2л, с. в.
Y имеет распределение
Кривая этого распределения показана на рис. 9.1.10. >
-V» 0 Уу
Рис. 9.1.9
12 3т/
Рис. 9.1.10
До сих пор мы рассматривали только случай, когда
аргумент функции Y = ср (X) — непрерывная случайная
величина. Теперь рассмотрим более простой по существу,
но более сложный в записи случай, когда аргумент X —
дискретная с. в. с рядом распределения
X
Некое «подобие» ряда распределения с. в. Y даст таблица
Pi
...
.. .
хп
Рп
Ф(*х)
Pi
Ф(*2)
Р*
i • •
• • «
фК)
Рп
Чтобы сделать из нее ряд распределения, нужно,
во-первых, расположить значения, стоящие в верхней строке,
в порядке возрастания, а, во-вторых, объединить те из
346
ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
них, которые окажутся равными (в силу
неоднозначности обратной функции), и сложить соответствующие
вероятности. Полученный таким образом ряд а будет рядом
распределения св. У.
Пример 11. Дискретная св. X имеет ряд
распределения
— 2
0,3
— 1
од
0
0,1
1
0,3
2
0,2
Построить ряд распределения ее квадрата
У-Х2.
Решение. «Неупорядоченный» ряд распределения
имеет вид:
4
0,3
1
0,1
0
0,1
1
0,3
4
0,2
Расположим значения св. У в порядке возрастания,
объединим равные и сложим их вероятности; получим
ряд распределения с в. У:
Y :
Пример 12. Число X неисправностей на участке
высоковольтной линии в течение года имеет
распределение Пуассона с параметром а. Общий материальный
ущерб от этих неисправностей пропорционален квадрату
их числа:
0
0,1
1
0,4
4
0,5
где с > 0 — неслучайная величина. Найти закон
распределения этого ущерба.
Решение. Ряд распределения X имеет вид:
X :
ае
а2е~а/2\
т
ате-а/т\
Так как значения У возрастают вместе со значениями X
и среди них нет совпадающих (обратная фупкция на
участке 0, 1, ..., т, ... однозначна), то ряд
распределения У имеет вид:
У :
0
е"а
с
ае-°
4с
а2е-°
2
...
...
т\
ате-а
т\
...
9.2. ПОЛУЧЕНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 347
9.2. Получение случайной величины
с заданным распределением путем
функционального преобразования
Здесь мы рассмотрим важную для практики работы
с ЭВМ задачу о получении св. У с заданным
распределением путем функционального преобразования другой
с. в. Эта задача часто встречается при моделировании
случайных явлений на ЭВМ методом статистических
испытаний (метод Монте-Карло). Задача ставится
следующим образом: в нашем распоряжении имеется с. в. X
с заданной плотностью f(x). Спрашивается, какому
функциональному преобразованию У = ср(Х) ее надо
подвергнуть, чтобы св. Y имела заданное распределение?
В практике работы с ЭВМ исходной случайной
величиной X является непрерывная св. X, распределенная
с постоянной плотностью на интервале @,1):
при *<=(<), 1)Л*)
)
о при **<01)) ('2<1)
Пусть мы хотим, чтобы путем функционального
преобразования У = ф(Х) из нее получилась св. с заданной ф.р,
G(y). Докажем, что для
этого надо подвергнуть
с. в. X функциональному
преобразованию
Y = G-X(X), (9.2.2)
где G~l (x)-~ функция,
обратная требуемой
функции распределения G(y).
Изобразим функцию Y<y
распределения G(y) на рис 9.2.1
графике (рис 9.2.1). Если
эта функция непрерывна и строго монотонна, то и
обратная функция G~*(x) также непрерывна, В этом случае
функция распределения с в. Y
G(y) G(y)
J J
(y)
J
oo 0
(9.2.3)
что и требовалось доказать.
¦) Значение такой с. в. получают на ЭВМ с помощью так на-
вываемых «датчиков случайных чисел» (или «псевдослучайных
чисел»).
348
ГЛ, 9, ЗАКОЫЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
Следовательно, для получения значения у
непрерывной св. Ус функцией распределения G(y) нужно
поступать следующим образом:
1. «Разыграть» на ЭВМ значение х с. в. X,
распределенной равномерно на интервале @,1) (программа
RANDO для ЕС ЭВМ, программа RANDU для ЭВМ СМ 4,
операторы RANDOMIZE, RND для персональных ЭВМ).
2. Найти обратную функцию G^(x) по отношению
к G(y) и вычислить значение у св. У по формуле
Если св. У дискретная, то ее ф. p. G(y) представ*
ляет собой ступенчатую функцию (рис 9.2,2) и обратная
функция G"l(x) не однозначна. Поэтому формула (9.2.2)
Рис. 9.2.2
не может быть применена для получения значения с. в. У.
Ранее в п. 3.3 было показано, что Р {Y = Уг} = Pi (i =*
= 1, ..., п) равно величине скачка ф. p. G(y) в точке yi
(рис 9.2.2). Таким образом, участок оси ординат от 0
до 1 можно разбить на п непересекающихся отрезков:
A^OjpJ; А2 = (рх; р1 + рг\\
= (Pi + Рг> Pi + Pi + Рз\'< • • -, Ai =¦
' (Pi + Pa + • •. + Pi-v Pi + Pi + • • • + P»]» • •.» A«
(9.2.4)
при этом длина i-го отрезка Д,- равна pt (/==1, 2, ..., п).
Тогда можно предложить следующий способ «розыгрыша»
значения у св. У, имеющей ряд распределения
Pi
Уг
Р2
...
Уп
Рп
9.2. ПОЛУЧЕНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
349
1. Разбить интервал @, 1) на непересекающиеся
участки Д< (i — 1, 2, ..., п) длиной piy p2, ..., рп.
2. «Разыграть» на ЭВМ значение х с, в. X,
распределенной равномерно в интервале @, 1).
3. Определить, какому из интервалов Д< принадлежит
значение х с.в. X. Если х^At, то св. У = у{.
Действительно,
..., п).
Заметим, что указанный способ разбиепия не
единственно возможный, но его можно предложить как наиболее
простой.
Если св. У смешанная, то ее ф. p. G(y) имеет
скачки, горизонтальные участки и участки монотонного
возрастания (рис. 9.2.3). На рис. 9.2.3 изображена функция
распределения смешанной св. У, имеющая три
дискретных значения {уи г/2, */з) с вероятностями plf p2i p3, два
участка непрерывного возрастания: (уи у2]; (у3, yj и
один горизонтальный участок (у2, Уз]*
В случае смешанной с в. У поступают следующим
образом:
1. Разбивают интервал @, 1) па к + l
непересекающихся интервалов, где к — число дискретных значений
св. У, I — число участков, где функция G(y)
непрерывна и строго монотонна. Порядок такого разбиения
показан на рис 9.2.3.
2. «Разыгрывают» на ЭВМ значение х с. в. X,
распределенной равномерно на участке @, 1).
350 ГЛ. 9, ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
3. Если значение х с. в. X попадает на интервал Д*
(#еДг), отвечающий скачку функции распределения в
точке уи то полагают У = у{ (/ = 1, 2, ..., 4).
4. Если значение а; ев, I попадает на иптервал А;,
на котором G(y) непрерывно возрастает, то полагают
у-ОТг(х) (/ = 13 2, ..., Z), (9.2.5)
где GJ1 (х) — функция, обратная функции G(y) па /-м
участке непрерывного возрастания.
Если необходимо получить значения уи у2, ..., уп
системы непрерывных с. в. (Уь У2, ..., У„), имеющей
функцию распределения G(yu t/2, ..., i/ft), то поступают
следующим образом. На основании формулы G.8.14')
запишем:
/J-J
?
— 00
Правило получения значений i/i, г/2, ..., ул системы
св. (Fi, У2, ..., Уп) сводится к следующему:
1. «Разыгрывается» значение Xi с. в. Xh
распределенной равномерно в интервале @, 1), и по ф.p. G1(i/1)
получаем yt — значение св. Yt: yx=zGl1(xl), гдеС^ (xx) —
функция, обратная функции Gi{y).
2. Разыгрывается значение х2 с в. Х2, распределенной
равномерно в интервале @, 1), и по ф. p. G2{i(y2\yi)
получаем у2 — значение с в. У2: Уг—^г]! (Ж21 ^i)> гДе
^2ii (X21 i/i) — функция, обратная функции G2|1 (j/2l 1/1).
В качестве аргумента у{ ф. p. G2li(y2\yi) берется то
зпачепие уи которое было получено в пункте 1.
3. Разыгрывается значение х3 с в. Х$1 распределеп-
ной равномерно в интервале @, 1), и по ф. p. G3|it2(j/3lyi>
у2) получаем у3 — значение с. в. У3. В качестве
аргументов уи у% ф.p. G3llt2(ys\yi, Уъ) берутся значения yt и i/2,
полученные в пунктах 1, 2 и т. д.
Если с в. У1? У2, ..., Yn независимы, то
G {уи Уг, .... Уп) = Gi (yi) • G2 (y2)... Gn (yn).
В этом случае задача упрощается. Разыгрывают значе-
9.2. ПОЛУЧЕНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 351
ние х{ св. X, и по ф.p. Gi(y{) определяют значение ух
с в. У1? затем разыгрывают значение хг с в. Х2 и по
ф. p. G2(y2) определяют значение у2 св. У2 и т. д.
Пример 1. Получить значение дискретпой св. У,
распределенной по закону Пуассона с параметрОхМ а =1.
Решение.
Р {Г -*>-¦? *~в в Т? <* - <U, 2, 3, ...).
По формуле (9.2.4) находим интервалы Д*:
Ао - @, е-*);
{) {
fc=0 fc«0
4 4 k
где 2 P (^ « fc) = 2 if ^ я Л (/' a); Ao e (°; °'3679];
At-@,3679; О,7358];"Д8-@,7358; 0,9197], ...
Пусть, например, в результате розыгрыша с. в. X
приняла значение х = 0,3758. Следовательно, is4lf и
значение уев. У будет равно единице (г/= 1). >
Пример 2. Получить значение с в. У,
распределенной по закону Релея с параметром о ~ 1.
Решение. G(y)«l-ехр{-у72> (у>0)';
Пусть например, в результате розыгрыша с в. X
приняла значение х = 0,6738; тогда значение с. в. У будет
у = (- In A - 0,6738)-2I/2 « 1,497. »»
Пример 3. Выходное напряжение У стабилизатора
имеет функцию распределения
0 при у<110;
1 при 130 < у,
где Ф(я) — функция Лапласа, у выражается в вольтах.
Преобразуя с. в. X, распределенную равномерно на
интервале @, 1), разыграть значение св. У*
352 ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
Решение. Св. У— смешанная:
р {Y = 110} = фA10~120) + 0,5 « 0,1587;
Р {У = 130} - 0,5 - Ф A3°^120) « 0,1587.
График G(i/) показан на рис. 9.2.4.
Начинаем с розыгрыша значения х с. в. X. Если это
значение попадет па
интервал Д4 = @; 0,1587], то
У примет значение у =
= z/i = 110 [вольт]; если
аеД1а=@Д587; 0,8413], то
у - 10-Ф-1^-0,5)+120
[вольт], где ф-1 (х) —
функция, обратная
функции Лапласа Ф{х); если
х еД2 = @,8413; 1], то
но по 130 х у = у2=130 [вольт]. Пусть,
Рис. 9.2.4 например, в результате
розыгрыша с. в. X
приняла значение х — 0,7453, значит, х^Ах;
0,7453 = Ф [(у - 120)/10] + 0,5; (у - 120)/10 -
= Ф-4 @,2453) «0,66,
отсюда значение с. в. У будет
у - 120 + 6,6 = 126,6 [вольт]. >
Пример 4. Разыграть значения у{ и у2 системы
св. (Yu У2), если св. F4 распределена по
показательному закону с тпУ1 = 2, ас в. У2 — по нормальпому
закону; случайные величины Уь У2 зависимы: условная
плотность с. в. У2 при Yi = yt равна
Решение.
G, Ы - 1 - ехр {-у,/2> (у, > 0)",
откуда
Ух - СГ1 («i) = - [In A - *!>] -2 @ < Ж1 < 1);
откуда
9.3. ФУНКЦИЯ ДВУХ СЛУЧАЙНЫХ АРГУМЕНТОВ 353
Пусть в результате двукратного розыгрыша с. в. Xt
п Х2 припяли значения х{ ~ 0,3872 и хг = 0,6387.
Соответствующие им значения у{ и у2 будут:
у, - -In A - 0,3872) ¦ 2 « 0,9794,
у2 = 0,9794 + Ф" @26387 — 0,5)« 1гЗЗЗ. ^
9.3. Законы распределения фупкции
двух случайных аргументов
Рассмотрим функцию двух случайных аргументов
Хг] (9.3.1)
и найдем функцию распределения с. в. F, считая
известной плотность j(xu х2) системы (Xit Хг).
Сделаем гипотезу, состоящую в том, что Х%^\х2, хг +
+ dx%). Вероятность этой гипотезы Р{^2 ^fe» хъ + ^2)} ^
( \
(
J /(^11^2)^1] dx2* В предположении,
-00 J
что эта гипотеза имела место, найдем условную
функцию распределения, т. е. условную вероятность события
{Y < у} при условии Хг — хг:
J /in (*i |*.)<fclf (9.3.2)
.*2)<У)
где /m(^ilxj)e /(^1, #2)//2(?2)— условная п. р. случайной
величины Xi.
Область интегрирования в (9.3.2) определяется из
условия, что при фиксированном значепии переменной х2
функция <p(si, x2)<y. Применяя интегральную формулу
полной вероятности, получаем
- j (
j /(хрхЛАсЛДг,. (9.3.3)
(ф(*1,«!)<у) J
12 Теория вероятностей и ее
инженерные приложения
354 ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
Мы могли начать с того, что зафиксировать значелие
с. в. Хи а не с. в. Х2, поэтому
00
П J
-oo \(V(xvx2)<y)
f(xvx2)dx2)dxv (9.3.4)
)
Последние две формулы можно объединить:
JJ f(xvx2)dxxdx2i (9.3.5)
(()<)
где область интегрирования на плоскости xfix2
определяется из условия ф(х1} х2)<у. Дифференцируя (9.3.5)
но величине у, найдем плотность распределения с. в. Y:
В случае, если с. в. Х{ и Х2 независимы, их плотность
Нхи х»)*=1Лх1)ви{Хг), и формулы (9.3.3) —(9.3.5)
примут вид:
оо
- I t I fi(xt)dx%)f1(x^dxv (9.3.6)
-oo \(<((xvx2)<V) J
Задача 1. Система св. (Xh Хг) имеет
совместную плотность /(*<, хг). Найги плог-
и ость распределения их произведения:
F-Xi Хг.
Решение. Зададимся некоторым значением у и
построим на плоскости XtOx2 область, где у{хи хг)=*
— х{ -х2<у (заштрихованная область Ь(у) на рис. 9.3.1).
Эта область ограничена двумя гиперболами, асимптоты
которых совпадают с осями координат. По формуле
(9.3.5) находим функцию распределения св. Y:
G(y)~
(9.3,7)
9 3 ФУНКЦИЯ ДВУХ СЛУЧАЙНЫХ АРГУМЕНТОВ
355
Дифференцируя это выражение по у, получил! плотность
распределения с. в. Y:
о °°
(9.3.8)
Пример 1. Случайная точка (<Y,, Хг) распределена
равномерно в квадрате К со стороной I (рис. 9.3.2).
/УЖуУУ
Рис. 9 3.1
Рис. 9.3.2
Найти закон распределения площади Y прямоугольника
R со сторонами Хи Хг: Y = X, Х2.
Решение. Очевидно, что в пашем примере св. Хх
и Х2 независимы:
А (лп > —
@<xz< 1).
Область интегрирования (xt - x2< у) заштрихована на
рис. 9.3.3. По формуле (9.3.6) получим:
С (у)- JJ c/x^-l-. JJ
1 1
«1-jd*! J ^ = y(
Окончательно имеем:
0 при у ^ О;
— In у) при 0<у*
1 при у>\.
Дифферепцируя это выражение по у, получим п. р.
356 ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
случайной величины У:
8{у) = — In у @<г/<1). ^
Задача 2. Система св. (Xi, Х2) имеет
совместную п. р. /(д-i, х2). Найти п. p. #(#) их
отношения У = XJXi9
Решение. Зададимся некоторым значением у и
построим на плоскости xfix2 область D(y)} где ф(хь я2) =
=¦ xz/xi < i/ (заштрихованная область Z)(i/) на рис. 9.3.4).
О
V
Й
¦
Х1'Х2
= У
у
/ ' / ' /
' 'у' '
0
х2
#1
Рис. 9.3.3
По формуле (9.3.5) находим
случайной величины У:
Ряс. 9.3.4
функцию распределения
И
. (9.3.9)
Дифференцируя это выражение по у, найдем п. р.
случайной величины Y:
О
8 (У) J *i/(*i.
> (9.3.10)
Пример 2. Найти п. р. отношения XJX2 = У двух
независимых нормально распределенных с. в. Xlt X2 с
характеристиками я^ — /п2 =* 0; аА; а2.
Решение. Сперва найдем п. р. случайной величины
7 - y^/ai - (Xt/Oi)/ (X«/a«). Обозначим Xt/d - Xt;
X2/a2 — X2. В соответствии с решением примера 2 п. 9.1
с. в. Xi и Хг будут распределены нормально с характе-
9.4 СУММА ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН
357
ристиками /тг1 = т2 = 0; О1в02в1. По формуле (9.3.10)
п. р. случайной величины У будет определяться из
выражения
Х1 У2х: Х1 У Х\
я A + ?)'
Следовательно, с. в. 7 распределена по закону Когаи;
по формуле (9.1.10) получаем:
тоже закон Коши. >
Пример 3, Случайная точка
\Xh X2) распределена
равномерно внутри круга к радиуса г—1.
Найти п. р. случайпой величины
УХ/Х
Р е ш е п и е. Функция
распределения G(y) есть относительная
площадь области D (у) (рис. 9.3.5): G(y)=—farctg у + -5-)
Рис. 9,3.5
откуда
g(y)
dG (у)
— тоже закон Коши.
9.4. Закон распределения суммы
двух случайных величин. Композиция
двух законов распределения
На практике часто возникает надобность находить
закон распределения суммы случайных величин.
Пусть имеются система (Xlf Хг) двух непрерывных
с. в. и их сумма
Найдем плотность распределения с. в. У. В
соответствии с общим решением предыдущего пункта, находим
358
ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
область плоскости xt0x2, где хх-\-х2<у (рис. 9.4.1):
ос A/-»1 \
С С С Г у-»!
"¦ Vl// в 1 / V^l^ ^2) «^l"^2 ) 1 ) / \XV X*> aX2| aXl»
(D(y)) -00 I ~oo )
(9.4.1)
Дифференцируя это выражение по у, получим п. р.
случайной величины Y = Хх + -XV.
оо
г {у) = j /(^; у — *i) ^i- (9.4.2)
—©о
Так как функция ф(^1, х2)~xt + х2
симметрична относительно своих
аргументов, то
оо
J / \У 2* 2/ 2*
— оо
Если с. в. Xi и Х2 независимы, то формулы (9.4.2)
и (9.4.3) примут вид:
оо
— 00
оо
(9.4.5)
В случае, когда складываются независимые с. в. Хг
и Х2, говорят о композиции законов
распределения. Произвести композицию двух законов
распределения — это значит найти закон распределения суммы
двух независимых св., распределенных по этим законам.
Для обозначения композиции законов распределения
применяется символическая запись
«-W., (9.4.6J
которой по существу обозначаются формулы (9.4.4) или
(9.4.5).
Пример 1. Рассматривается работа двух
технических устройств (ТУ). Сначала работает ТУ*; после его
выхода из строя (отказа) включается в работу ТУ2.
Рремепа безотказной работы ТУЬ ТУ* — Хх и Х2 —
независимы и распределены по показательным законам с
9 4 СУММА ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН 359
параметрами К{ и кг. Следовательно, время Y
безотказной работы ТУ, состоящего из ТУ* и ТУ2, будет
определяться по формуле
Y - Хх + Хг.
Требуется найти п. р. случайной величины Y — т. е.
композицию двух показательных законов с параметрами
hi и Kz:
(9.4.7)
Решение. По формуле (9.4.4) получим (у>0)
^"ХЛ ^ -^ (Г* - Г^) (у > 0).
(9.1.8)
Если находится композиция двух показательных
законов с одинаковыми параметрами (kt — ^^Я), то в
выражении 1,9.4.8) получается неопределенность типа 0/0,
раскрывая которую, получим:
Сравнивая это выражение с выражением F.4.8),
убеждаемся в том, что композиция двух одинаковых
показательных законов (Ki «* Я2 = X) представляет собой
закон Эрланга второго порядка (9.4.9). При композиции
двух показательных законов с различными параметрами
Xi и К2 получают обобщенный закон Эрланга второго
порядка (9.4.8). >
Задача 1. Закон распределения
разности двух св. Система св. (Хи Х2) имеет совместную
п. p. ]{xh хг). Найти п. р» их разности F*=Xi — X2.
Решение. Для системы с в» (Хи — Xz) п. р. будет
/(*i, -*i)» т. е. мы разность заменили суммой.
Следовательно, п. р. случайной величины У будет иметь вид (см.
(9.4.2), (9.4.3)): '
g{v)- J /(Jri,*i-0)<fci- j Пь-У,гъ)*хЛ. (9.4.10)
360 ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
Если с. в. Xi и Х2 независимы, то
со со
g(y)= ,f /i (*i) /2 (*i - У) d*i = j 1Лхг-уIг^г)^х2. >
— оо —00
(9.4.11)
Пример 2. Найти п. р. разности двух независимых
показательно распределенных с. в. с параметрами Я4 и Х2.
Решение. По формуле (9.4.11) получим
S (У)
i (*i) /2 (*i — У) d*v
Рассмотрим два случая:
а) у>0:
g(y)
б)
На рис. 9.4.2 изображена п. р. g{y). Если
рассматривается разность двух независимых показательно
распределенных с. в. с одинаковыми параметрами (kt = кг = К),
Рис. 9.4.2
то giy)^ he xlyl/2 — уже знакомый закон Лапласа
(рис. 9.4.3). >
Пример 3. Найти закон распределения суммы двух
независимых с. в. Х{ и Х2, распределенных по закону
Пуассона с параметрами а* и аг.
9.4. СУММА ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИИ
361
Р е ш е п и е. Найдем вероятность события {Х{ + Х2
т) (т = 0, 1, 2, ...).
P{^ + X2 = m}= 2 P{Xl = k}-P{X2 = m-k)
«7 -а
; - /r)!
Следовательно, св. Y == Xx + Xz распределена по закону
Пуассона с параметром аB) = «i + аг, >
Пример 4. Найти закон распределения суммы двух
независимых с. в. Х4 и Х2, распределенных по
биномиальным законам с параметрами пх\ р и п2\ р соответственно.
Решение. Представим св. Хх в виде:
2
где Х|Х) — индикатор события А в /-м опыте:
A) |1 — если в j-м опыте событие А произошло,
1 ~~ [О — если в 1-м опыте событие А не произошло.
Ряд распределения с. в. Х^ имеет вид:
0
g = l — p
1
Р
Аналогичное представление сделаем и для с в. Х2:
где Xf^ — индикатор события А в /-м опыте:
0
1
Р
Xf : ——
Следовательно,
у - х, + х2
2
n1+n2
302 ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
1де Х/,1НB)если индикатор события Л:
0
1
Р
Таким образом, мы показали, что с. в. У есть сумма
(ni + nz) индикаторов события Л, откуда следует, что
с. в. У распределена по биномиальному закону с
параметрами (л, + пг), р.
Заметим, что если вероятности р в различных сериях
опытов различны, то в результате сложения двух
независимых с. в., распределенных но биномиальным законам,
получится с в., распределенная не по биномиальному
закону. >
Примеры 3 и 4 легко обобщаются на произвольное
число слагаемых. При композиции законов Пуссона с
параметрами аи а2, ..., ат снова получается закон
Пуассона с параметром а(т) =* at + а2 +... + ат.
При композиции биномиальных законов с
параметрами (пи р); (я2, р); ..., (пт, р) снова получается
биномиальный закон с параметрами (fymj, р), где п{т)»
« тг4 + пг +... + пт.
Мы доказали важные свойства закона Пуассона и
биномиального закона: «свойство устойчивости». Закон
распределения называется устойчивым, если при
композиции двух законов одинакового типа получается закон
того же типа (различаются только параметры этого
закона). В п. 9.7 мы покажем, что таким же свойством
устойчивости обладает нормальный закон.
9.5. Закоп распределения функции
нескольких случайных величин.
Композиция нескольких законов распределения
Рассмотрим задачу об отыскании закона
распределения св. У, представляющей функцию системы св. (Ж\,
Аг2, ..¦, Хп) с плотностью /(х,, х2, ...» х„):
У^Ф^, Х2, ..., Хп). (9.5.1)
Сделаем гипотезу, состоящую в том, что подсистема
с. в, [Хг, Х8, ..., Хп) лежит в пределах элементарного
9.5. ФУНКЦИЯ НЕСКОЛЬКИХ СЛУЧАЙНЫХ ВЕЛИЧИН
363
(/г—1)-мерного параллелепипеда, примыкающего к
точке {хг, х3, ..., хп):
' *n + dxn)
2, Х3, ».., Xп) I
в.з... ,п (^2» тз' • • • I ^n) dx2dx3 ... АгП|
где
/2,3,..., П^2' <Г3? • • •» ^") == J / \*^1» ^2» • • •»
— оо
Тогда, применяя тот же прием, что и в п. 9.3, получим:
J <n-l> J
j J
j хп)<у) J
X /2,з,....п(^21 • • •» ^i) ^r2 • • • ds«. (9.5.2)
Последнюю формулу можно записать в векторном виде:
/Й(/х, (9.5.3)
где х —(xf, х2, ..., хп).
Если случайные величины не зависимы, то формула
(9.5.2) принимает вид:
оо оо
...fn{xn)dx%...dxn. (9.5.4)
Задача 1. Закон распределения суммы
нескольких случайных величии. Пусть (Хи
Х2, ..., Х„)—система непрерывных случайных величин
с плотностью f(xh х2, ..., ?и), а с. в. Y равна их сумме:
у-
(9.5.5)
364
ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
п
Функция у = хг+ 2 х% (при #< = const; t = 2, ..., л)'
i—2
является монотонной функцией аргумента Xi.
Следовательно, применяя тот же прием, что и в случае
суммирования двух св. (п. 9.4), получим
СО 00
- J <-« 1
— 90 —00
X
X /2 п (х21 ..., яп) dx2 ... dxn.
Из соображений симметрии последнюю формулу можно
переписать в виде:
у-
= J <n> J \ J /л|1,в|...|Л-1,Л + 1 n (я*|*и • • •
— 00 —OO \ — ЭО
¦ • *) %h-li Xh+U • . м ^n) dj:^J /j|2 A-l,/i+l,.*.,^(^i» • • •
Дпфферепцируя последнюю формулу по j/, получим:
7 7/ п \
Xdxt>.. dxh^1dxk+i *.. dxa* (9.5.6)
Если случайные велпчипы независимы, то
.. • /п (д?л) rfxx... drfc-xd^ft+i ... fik». (9.5.7)
Формула (9.5.7) выражает композицию п законов
распределения и может быть записана в символическом виде
*-/i •/»•...• а, (э.бл:
Задача 2. Закон распределения
линейной функции п случайных величин. Найдем
функцию распределения и плотность распределения
П.5. ФУНКЦИЯ НЕСКОЛЬКИХ СЛУЧАЙНЫХ ВЕЛИЧИН 365
с. в. Y:
Y - S агХг + Ь.
Рассмотрим график функции у = а1х1 + 2j<iiXi + b при
г—2
1 f = 2 l
;. =const
const
a:,
Рис. 0.5.1
фиксированных значениях z< (г = 2, ..., п) (рис. 9.5.1,а,
9.5.1, б). При а{ > 0 получим
G(i/)= J (n-i) J j
— ОО —00 \ —О
/l|2 nOril*2, ...
¦2... dxn; (9.5.8)
- I(и-1) I f[y/ai — [ 2 ^i + ь)Ai; *я. •. м «n) x
—oo —oo \ \t—2 // /
При «t < 0 получим
oo oo / oo
X dr2 ... dxn. (9.5.9)
— oo — oo
,.., xn) dxt) /2 n (x2, ...,zn)dz2... dxn\ (9.5.10)
7 7 ( ( n
= — J (n-!> J /10/01—1 2 «Й +
X«te,v..(fe». (9.5.11)
306 ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
Формулы (9.5.9) и (9.5.11) можно объединить в одну
? 7 ( In \ I
g(u) = signax J (n-n j / ylax — 2 <*i*i + Ь к,
#2, . .., xnj dx2 ... drn. (9.5.12)
Исходя из симметрии задачи, формулу (9.5.12) можно
переписать в виде:
ОО СО /
—-oo —с» \
\ / \
)/ , .. ., xn )dxL .. .
(А =1,2, ...,/z). (9.5.13)
Если с. в. Х{ (i = 1, 2, ..., дг) независимы, то
оо оо
= sign ah J (n-i) j /j (tx) ... /*_! (x^i) X
— oo —oo
X Д I ///afe — I 2 <ЗД + Ь ] lak)
v via ;/ у
... fn{xn) dxx ... dxh^1dxh+1 ... dxn.
(*« 1,2, ...,/*). (9.5.14)
Пример 1. Рассматривается работа п ТУ, которые
включаются последовательно: сперва работает ТУ,,
затем ТУ2 и т. д. Время Т безотказной работы ТУ,
распределено по показательному закону с параметром 1< и
не зависит от времени работы других ТУ (/ = 1, 2, ...
..., п). Время Т(п) безотказной работы такой системы
получится сложением времен работы отдельных ТУ:
Найти закон распределения и числовые характеристики
с. в. 7\п), т. е. произвести композицию п показательных
законов распределения с параметрами Ai, Я,2, . • •» ^п.
9.5. ФУНКЦИЯ НЕСКОЛЬКИХ СЛУЧАЙНЫХ ВЕЛИЧИН 367
Решение. Введем следующие обозначения
7\,2 = 7\ + Т2;
Т 1,2,3 ~ Т\гг "Г 13, • • ., i 1,2 k ~ *1,2 А-1 * Tfa . . .
Закон распределения каждой из введенных с. в.
представляет собой композицию законов распределения. Методом
математической индукции можно доказать, что п. р.
суммы п независимых с. в. 7\, Г2, ..., Тп, распределенных
по показательным законам с параметрами Xt, Х2, ..., Х„
имеет вид
*(«>
@ - (- 1Г' П ^i 2 -т-^ (t > 0); (9.5.15)
«-' i П
ф. р. случайной величины ^(п) определяется так:
!! ~е (*>0). (9.5.16)
hfii
Закон распределения св. Т{п) называется
обобщенным законом Эрланга n-vo порядка. Для
обобщенного закона Эрланга л-го порядка м, о, и дисперсия
равны:
[п -1 п
-2-V. (9.5.17)
Обобщенными законами Эрланга n-го порядка удобно
аппроксимировать различные законы распределения
неотрицательных случайных величин,
368 ГЛ. 9, ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
При Kt = кг = ... = \п = Х получаем закон Эрлаттга
n-го порядка (п=1, 2, ...), рассмотренный в п. 6.4:
- 1, to) Л « 1 -Я(л- 1, to)
(9.5.18)
где P(fc, a) - aVVil; R(m, a) - 2
/<=о
В соответствии с формулами (9.5,18) можно доказать
следующие свойства функций Р(к, а) и /?(яг, а):
а
00
1 - R(к, а) = J Р(к, a) da; JP(ft, a) da - Я (оо, а) = i;
(9.5.l())
.Числовые характеристики с. в. Т(п) распределенной по
закону Эрланга n-го порядка, равны:
М[Г(я,]-?; D[r(n)] = ^; о[Г(п)]=1^-. (9.5.20)
Закон Эрланга гс-го порядка тесно связан со
стационарным пуассоновским потоком с интенсивностью К.
Случайная величина 7\П), распределенная по этому закону,
Рпс. 9.5.2
представляет собой интервал времени, содержащий п
интервалов между событиями в этом потоке (рис. 9.5.2).
На рис. 9.5.3 изображено семейство законов Эрланга п-то
порядка для »«1, 2, .,., 5, 6 и А«1. При /г = 1 мы
получаем показательный закоп.
9.5. ФУНКЦИЯ НЕСКОЛЬКИХ СЛУЧАЙНЫХ ВЕЛИЧИН 369
В следующей главе будот доказано, что при
увеличении п закон Эрланга тг-го порядка неограниченно
приближается к нормальному.
Определенным «неудобством» при применении закона
Эрлапга п-то порядка является увеличение м. о. и
дисперсии с. в, Т(П) с увеличением п (см. (9.5.20)). Поэтому
я-г
в инженерных приложениях часто используют норм и-
рованпый закон Эрлапга л - г о порядка,
по которому распределена св. Т{п):
Tw-Tw/n. (9.5.21)
Применяя формулу (9.1.10) для п. р. линейной функции
с. в., получим:
Обозначим Хп = пКу тогда
t
, Kt);
(9.5.22)
370
ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
Формулы (9.5.22) определяют плотность и ф. р. н о р-
мирова иного закона Эр л аи га я-го порядка;
числовые характеристики с. в. Т{п) = Т{п)/п найдем
вынося 1/п из-под знака м.о. и l/п2 из-под знака дисперсии:
= ~*Г '* ^ I * (П)\ === у' ^ I (n)J === —
Л ПК
м
(9.5.23)
Из этих формул видно, что с увеличением п м. о.
случайной величины Т(п) не мепяется, ее с. к. о.
неограниченно уменьшается; соответственно,
коэффициент вариации стремится к нулю. На рис. 9.5.4
1 2 t
Рис. 9 5.4
изображено семейство нормированных законов Эрланга
для и«1, 2, 3, 4, 5, 6 и Х- 1.
Плотность св. Т(п) (или Г(л>), распределенной по
эакону Эрлаига n-го порядка, представляет собой
частный случай гамма-распределения (п. 6.4) при п
целом. Следовательно, характеристическая функция с. в,
У(п) будет определяться по формуле
(9-5-24)
9.5. ФУНКЦИЯ НЕСКОЛЬКИХ СЛУЧАЙНЫХ ВЕЛИЧИН 371
а для с в. Т(п) — по формуле
Ът(х\ = ^J^ в М" = / п \п (95.25)
(*«-<*)" (^-ix)n (m-jxAJ V ^
Предел этого выражения, как известно из курса
математики,
Нш ?я (х)
lim
71-*оо
Г
- e~i\ (9.5.26)
Следовательно, при п -*- <» св. Г(П) «стремится»
(точнее — сходится по вероятности) к неслучайной величине
l/XlTtnI—* l/h\ так как предельное выражение для
\ ^ /
характеристической функции совпадает с
характеристической функцией неслучайной величины (8.9.6). >
Пример 2. Найти закон распределения суммы трех
независимых с. в. Хи Х?„ Х8, каждая из которых
распределена равномерно на интервале (—а; а):
/<(х,)-1/Bа) при хг^(-а, а); (i-1,2,3).
Решение. Обозначим Y = X, + Хг + Х3. Найдем пер-
вопачально закон распределения св. F,,2 e Xi + X2, т. е.
-2а-а О
Ti42<V>
а 2а
Рис. 9.5.5
Jo -2а -а О а 2а За у
Рис. 9.5.6
проведем композицию двух равномерных законов
распределения.
По формуле (9.4.5) получим
оо
j /i (У— *«>/«
0.
при |(/|>2а;
1»1<2а.
Сумма X1 + AF2=y'if2 распределена но закону
равнобедренного треугольника (закону Спмпсона) на участке
{-2а, 2а) (рис. 9.5.5).
372
ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
Рассмотрим св. У—У^ + Хз. По формуле (9.4.5)
проведем композицию закона Симпсопа и равномерного
распределения:
Кривая распределения
рабол (рис. 9.5.6). >
— | у 1
16а3
За8-И
при |у I
при а
при \у\
состоит из трех отрезков
па9.6. Закон распределения минимума
(максимума) двух случайных величин.
Закон распределения порядковых статистик
В этом пункте мы рассмотрим прежде всего такое
функциональное преобразование с. в., которое
заключается в выборе максимальной (минимальной) из двух
величин.
Задача 1. Закон распределения миниму-
случайпых величин. Дана
непрерывная система с. в. (X,, Хг) с
п. p. f(xu хг). Найти функцию
распределения с. в. У:
Y = min^, Х2) =
при ХХ^Х21
при J
[Х2
Х2.
Решение. Найдем
сначала Р{?>у} = Р{Х1>У;Х2>
> у). Область D(y), где Xt > у и Хг> у показана на
рис. 9.6.1. Вероятность попадания точки (Хи Х2) в
область D(y) равна
Р{У >у} = 1 -G(y) - P{(XV X2) <=D(y)} -
-F(oo, oo)-F(y, oo)-F(oo, y)+ F(y, y) =
9.6. МИНИМУМ (МАКСИМУМ) СЛУЧАЙНЫХ ВЕЛИЧИН 373
где F(xi<t хг)—функция распределения системы с. в.
(X|, X2), F{(xx), Рг(я2) — функции распределения с. в.
Х{ и Хг соответственно. Следовательно,
i(y)-F(y, у). (9.6.1)
Для определения п. p. g(y) нужно найти производную
правой части (9.6.1):
!
! I(y,x2)dx2;
— oo
00
dFl (у)
dy
dF2 (у)
dy
Для отыскания —J' рассмотрим полный
дифференциал функции F(yh уг):
Отсюда
dFjy, y)
У)
~-
«-OO —00
dx2
= J f(y,x.2)
+ J /(*i, y)dxv
Плотность распределения с. в. Y:
g(y)-fiQt) + Ш- J /(^ ^)*r?a- J /(^i. V)d*v (9-6-2)
—oo — oo
Если с. в. Хи %г распределены одинаково, то
oo
G (у) - IF (у) - F (у, у); g (у) = 2/ (у) - 2 j / (у, х2) dx2.
(9.6.3)
374 ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
Если с. в. Хи Х2 независимы, то F(xu х2) = Fl(xl)F2(xz);
Xl)=fi{Zi)h{Xt) И
g(y) = /i iy) (i - *". (у))
1(y)F2(y), \
U (у) A - ^i (у))- J
Если с. в. Xt, X2 независимы и распределены одинаково
с п. p. /iW = /2W=/W, то
F(y)B-F(y)); g(y) - 2/ЫA - F(y)). > (9.6.5)
Пример 1. Рассматривается работа ТУ, состоящего
из двух блоков Bt и Б2, совместная работа которых
безусловно необходима для работы ТУ. Времена работы
блоков Bi и Б2 представляют собой независимые с. в.
Xi и Х2 распределенные по показательным законам с
параметрами Xi и Х2. Требуется найти закон распределения
св. У — времени работы ТУ.
Решение. Очевидно, что
ь Хг).
По формулам (9.6.4) находим:
т. е. минимум двух независимых случайных величин,
распределенных по показательным законам с
параметрами Ki и А,2, распределен тоже по показательному закону
с параметром Ху + Хг* >
Задача 2. Закон распределения
минимальной из п независимых с л у ч а й ных в е-
л и ч и н. Дана система п независимых с. в. {Хи Х2, ...
..., Хп) с п. р. Л(х,), /2(^2), ..., fa{xH). Найти ф. р. и
плотность с. в. Y = min{Zb ..., Хп).
Решение. По определению
1-Р{(Х1>у)(Х,>у)...(Хя>у))шш
П П), @.6.6)
} П
»=1 1=1
где Fi(у) = Р{Х{<Ly} — функция распределения с. в.
9 6 МИНИМУМ (МАКСИМУМ) СЛУЧАЙНЫХ ВЕЛИЧИН 375
X, (f-1,2, .... в);
^Г1 " 2 f> (У) П A - Fi (tf)V(l - F} (У))- (9-6.7)
^Г П
Если величины Х1у ..., Х„ распределены одинаково, то
g(y) = nf(y)(l^F(y))n; G(i/) = l_(l_F(^))n. >
(9.6.8)
Пример 2. Рассматривается работа
автоматизированной системы (АС), состоящей из п подсистем. Для
работы АС необходима работа всех п подсистем; время
безотказной работы i-й подсистемы Т{ распределено по
показательному закону с параметром А< A = 1, 2, ..., п)
и не зависит от времени работы других подсистем.
Определить закон распределения времени Т{п) безотказной
работы АС.
Решение. Очевидно, что
T™=mmlTi9 Тг, ..„Г,, ..., TJ.
По формуле (9.6.G) находим функцию распределения
с. в. Гп)
где ^(/)= 1 — e-Xii (/ > 0). Отсюда
сся4о - 1 -П (i -1 + *"v) -
где
Таким образом, закон распределения с. в.
Т{п) — минимальной из п независимых св.,
распределенных по показательным
законам, также является показательным; при
этом его параметр (\{п%) равен сумме параметров Xf этих
показательных распределений. Из этого следует, что
м[7т(пI 1- — >! • D\TW\
IVIli J-"«(/<)~" и ' UL J
376
ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
Можно показать, что закон распределения св. Г(п)
при достаточно большом п будет сходиться к
показательному закону, даже если св. 7\ (i —1, 2, ¦ .., п) не
распределены по показательным законам. Покажем это па
примере одинаково равномерно распределенных св.:
В этом случае
10 при t < 0;
t/n при 0<t<n; (i =
1 при п < t
При п -> сю получаем
0 при
A — t/nf при
1 при п< t
при t < 0;
при t > 01
а это есть ф. р. показательного закопа.
Таким образом, можно сделать вывод, широко
применяемый в инженерных приложениях: если какое*
либо устройство состоит из достаточно большого числа
элементов п, работа которых безусловно необходима для
работы устройства, то закон распределения времени Т{п)
безотказной работы устройства близок к показательному
с параметром, определяемым по формуле
2М
г=1
где Ы [Т{] — среднее время безотказной работы i-го
элемента.
Поток отказов такого устройства будет близок к пуас-
соновскому с параметром Х(и). >
Задача 3. Закон распределения
максимальной из двух случайных величин. Дана
непрерывная система св. (Хи Х2) с плотностью f(xi9x2).
Требуется найти закон распределения с в.
rlf X2}.
Решение. По определению,
- P{Y<y} = P{max{Xlf X2}<y} = F(y, у), (9.6.9)
9 6. МИНИМУМ (МАКСИМУМ) СЛУЧАЙНЫХ ВЕЛИЧИН 377
где F(xu x2) — функция распределения системы (Xh X2).
F(xv х2) == j j /to, x2)dxxdx2;
— оо —оо
У У
'У)= j j f(xi,x2)dx1dx2.
— оо —оо
Дифференцируя это выражение, как делали раньше,
получим:
у у
g (У) = J / ('i. У) <**i + j / (У. *г) *Хг- (^6.Ю)
~оо —оо
Если случайные величины Xh X2 распределены
одинаково, то
g(y) = 2 j' f(xv y)dxl. (9.6.11)
Если случайные величины Хи Хг независимы, то
G(y)-Fl(y)F2(y);
g (У) = /i (У)РМ + U (У) Рг (У).
Если случайные величины Хи Х2 независимы и
распределены одинаково, то
С(у) = (Р(у)У; g(y) = 2f(y)F(y). (9.6.13)
Пример 3. Работа ТУ не может быть начата
раньше того, как будет окончена сборка двух его блоков Bt
и Б2. Время сборки блоков Б, и Б2 представляет собой
систему независимых св. Х{ и Х2, распределенных по
показательным законам с параметрами Я, и Хг. Требуется
найти плотность св. У —времени окончания сборки
обоих блоков ТУ.
Решение. Очевидно, что У = тах{Х1, XJ.
Плотность распределения св. У определяется по формуле
(9.6.12)
8
(У) = V1У A - е~^) + V"'2" A - e'hV) {у > 0).
Этот закон не является показательным. >
Задача 4. Закон распределения
максимальной из п независимых случайных во-
378 ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
личин. Дана непрерывная система св. (Xh Хг, ..., X,,)'
с плотностью 1(хи х2, ..., хп). Найти закон
распределения случайной величины
У-тах«„ ..., XJ.
Решение. По определению
G{y)-*P{Y<y}-P{m*x{Xv ...,Xn}<p}-
-Р{^1<»| *л<У, -.->Xn<y) = F(y,y, ...,»), (9.6.14)
где F(zi, #2, •.., #п)—функция распределения системы
(Хи Х2, ..., Х„). Дифференцируя, найдем плотность
распределения:
п У У
J (n-i J
idxi+i . .. dxn. @.6.15)
Если случайные величины Хи ..., Хл независимы, то
^гП^(^ (9.6.16)
fi
где Fj(Xj) — ф.р. св. Хл; /;(х,)—ее плотность.
Если св. Хи ..., Хп независимы и распределены
одинаково {Fi{y) = F(y)\ h(y) = j(y) (i = l, ..., л)), то
Пример 4. Работа ТУ не может быть начата
раньше того, как будет окончепа сборка всех п его блоков:
Б|, Б2, ..., Б„. Времена сборки блоков Бь ..., Бд
представляют собой систему п независимых св. (Хи ..., Хл),
распределенных по показательным законам с
параметрами Xi, ..., Хп.
Требуется найти плотность св. Y — времени
окончания сборки всех п блоков ТУ.
Решение. Очевидно, что Y**m&x{Xit ..., XJ. Но
формуле (9.6.16) имеем
9.6. МИНИМУМ (МАКСИМУМ) СЛУЧАЙНЫХ ВЕЛИЧИН 379
+ S (K + h + h)e-(Xi+
п
п - 2 ?*у
...+(-1)«-'2 Я,е '"" • >
Задача 5. Закон распределения
порядковых статистик. Рассмотрим непрерывную
систему одинаково распределенных, независимых св. (Xh
Аг2, ..., Хп) с ф.p. F(x) и п. p. J(x). Расположим
значения, принятые случайными величинами Xlf Х2, ..., Хп,
в порядке их возрастания и обозначим:
X(i) —- случайная величина, принявшая наименьшее
из значений: (ХA) = min {Xu Х2, ,.., XJ);
Х{2) — вторая по величине принятого значения из
случайных величин Xly X2i ..., Хп\
Х(т) — т-п по величине принятого значения из
случайных величин Xh Xz, ..., Хп;
Х(п) — наибольшая ио принятому значению из
случайных величин Xiy Х2, ..., Хп (A'(n) = max{X,,
X2,...,XJ).
Очевидно,
Случайные величины ХA), ХB), ..., Х(п) называются
порядковыми статистиками.
Формулы (9.6.8) и (9.6.17) дают законы
распределения крайних членов X(i) и Х(п) системы (*).
Найдем функцию распределения F{m){x) св. Х(т).
Событие {Х(т)<х} состоит в том, что т св. из системы
п с. в. (А74, Х2, ..., Хп) будут меньше х и (/г — т) с в.
будут больше х. Так как св. Х{ (i — l, 2, ..., /г)
независимы и одинаково распределены, то Р {Хг < х) == F (х)
Р{Х{>х} == 1 — F(x). Нам нужно найти вероятность
того, что в п независимых опытах событие КХ{ < х)
появится ровно т раз. Примеияя биномиальное распределение,
получим
F(m) (х) - Р {Х1т) < х) - 2 СИ (f (ж))* A - f (^))"-ft,
Л=тп
(9.6.18)
380 ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
откуда, дифференцируя, найдем:
/(т) (*) - F[m) (х) - п](х) С™Ц (F (х))"-1 A - F{х)Гт.
(9.6.19)
При т=1 (9.6.19) дает ранее полученную формулу
(9.6.8), при т = п — формулу (9.6.17).
9.7. Законы распределения функции
от нормально распределенных
случайных величин
Нормально распределенные с. в. играют значительную
роль в различных инженерных приложениях.
Аналогичную роль играют и функции нормально распределенных
с. в.
В этом пункте мы будем рассматривать следующую
задачу. Дана функция системы нормально
распределенных с. в. (Xt, X2i ..., Хп):
Х21 .... X.)
Требуется найти закон распределения св. Y.
Задача 1. Закон распределения
линейной функции п нормально
распределенных случайных величин
Y = 2 <цХ{ + Ъ. (9.7.1)
Решение. Рассмотрим первоначально случай, когда
число аргументов я = 2. По формулам G.9.1), (8.3.2')
и (9.5.14) имеем
f 1
9 7. ФУНКЦИИ НОРМ РАСПРЕДЕЛЕННОГО АРГУМЕНТА 381
где
в = -
ft/ — b — a]nxl у — b ~ alml-\- a2m2 тЛ
l ""T5
С = . —— Н — т, (у—Ъ— а,т
+
Следовательно (см. (п. 7.9)),
g(y) = [(^па1)/я/Bла1а2
После преобразовании получаем
где
my — M [F] = a^h + a2m2 + b;
o~y = D [У] = afci + a^ + 2a1a2r12alo2.
Таким образом, мы показали, что линейная функция
системы двух нормально распределенных св. (Xh X2)
распределена нормально.
Методом математической индукции этот результат
может быть обобщен на случай системы п нормально
распределенных св.: линейная функция (9.7.1) системы п
нормально распределенных св. (Х1у Х2, ..., Хп) с
математическими ожиданиями (mit m2, ..., тпп), дисперсиями
(aj, a,, ..., (Jn) и нормированной корреляционной
матрицей 11гч11 распределена нормально (9.7.2) с
характеристиками:
п п
Щж 2 а%т% + Ь\ о\« 2 afcf + 22 diujrijOiOj. >(9.7.3)
il il i<
Мы показали, что нормальный закон является
«устойчивым» по отношению к линейному преобразованию.
382 ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
Устойчивость нормального закона по отношению к
линейному преобразованию в значительной мере
определяет его широкое применение в инженерной практике.
Во многих случаях реакция Y технического устройства
(ТУ) (или системы) на входные возмущения (Хь ...
..., Хп) может быть описана линейной (или
линеаризуемой) функцией. Часто эти возмущения представляют
собой нормально распределенные св. Поэтому реакция
ТУ на эти возмущения также представляет собой
нормально распределенную с. в. В следующей главе будет
показан более сильный результат, состоящий в том, что
при определенных условиях линейная функция (9.7.1)
распределена приблизительно нормально, даже если
система св. (Хи X2i ..., Хп) имеет не нормальное
распределение. Другими словами, реакция ТУ на входные
возмущения во многих случаях если не точно, то
приближенно представляет собой нормально распределенную с. в.
Задача 2. Распределение %2. Пусть имеется
п независимых одинаково распределенных нормальных
случайных величин Хи Х2, ..., Хп с математическими
ожиданиями, равными нулю и дисперсиями, равными
единице:
a[X*] = l (к = 1, 2, ..., л).
Обозначим сумму квадратов этих случайных величии
Х2=2*1 (9-7.4)
и найдем закон распределения случайной величины х2;
это распределение называется «х2-распределениехМ».
Решение. В задаче 3 п. 9.1 было показано, что
плотность распределения квадрата Y нормально
распределенной случайной величины с м.о., равным нулю, и
дисперсией, равной единице (F = .Y2), имеет вид:
Характеристическая функция с. в. У равна:
оо
Ф„(9 - М [<?!'у] - J (еше-
9 7 ФУНКЦИИ НОРМ РАСПРЕДЕЛЕННОГО АРГУМЕНТА 383
Этот интеграл был нами вычислен; он равен (см.
(8.9.23)):
1/2 // а \1/2
/()
п
Очевидно, что %2 = ^ Yk, где У* имеет то же распреде-
ление и ту же характеристическую функцию, что и
св. У.
В соответствии со свойством 3 характеристических
функций (см. (8.9.9)) имеем:
П/2
Из этого следует (см. (8.9.23)), что х2-распределенпе
представляет собой гамма-распределение с параметрами
К = 1/2 и /г/2, где п — число суммируемых квадратов
случайных величин, следовательно, плотность
распреде2
ления с. в. х2 имеет вид:
(97-5)
Пользуясь свойством 2 характеристических функций
(см. (8.9.8)), можно показать, что
М If] - М [{2 *?] = 'Ь. D [Х2] - D [j| X?] - 2*.
(9.7.6)
Число п суммируемых квадратов св. называют
числом степеней свободы х2"РаспРеДеления- Х2-Рас~
пределение широко применяется в математической
статистике. >
Задача 3. Закон распределения суммы
квадратов независимых одинаково
распределенных нормальных св., имеющих
пулевые математические ожидания.
Решение. Пусть Xh Х2, ..., Хп — нормально
распределенные независимые св.:
Yn - Ъ К (9.7.7)
причем М [Xh] - 0; D[XA] = o2 (к = 1, 2, ..., п).
384 ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
Пронормируем каждую из св. Хк, деля ее на а:
Очевидно,
М [Zk] = М [Xh/a] = 0;
Из ранее доказанного следует, что с в. Yn/o2 =
Zk будет иметь х2-распределенпе:
откуда
т. е. с. в Yn представляет собой линейную функцию с. в.
X2. В соответствии с решением задачи 1 п. 9.1 плотность
распределения св. Yn будет (см. (9.1.10))'
(9.7.8)
Числовые характеристики св. Yn будут М [Yn] = по2
и D [Yn] = 2/ia4. Закон распределения с. в. Yn широко
применяется при статистической обработке
экспериментальных данных. >
Задача 4. Закон распределения
среднего арифметического квадратов
независимых одинаково распределенных
нормальных св., имеющих нулевые
математические ожидания и одинаковые дисперсии.
Решение. Случайная величина
где М [Xft]=0; D [Xk] - а2 {к = 1, 2, ..., п). С. в. Zn
представляет собой линейное преобразование св. Yn (см.
(9.7.7)):
9.7. ФУНКЦИИ НОРМ РАСПРЕДЕЛЕННОГО АРГУМЕНТА 385
следовательно, п. р. случайной величины Za будет (см.
(9.1.10)):
_ (я/2)*" n/2-i wy/Bq«) (9 7 10)
ояГ (л/2) * V '
В соответствии с формулами (8.2.3) и (8.2.4)
M[Zn]-a2; D [Zn] - 2a4/*. >
Распределение с. в. Zn также широко применяется в
статистике.
Задача 5. Закон распределения корня
квадратного из суммы квадратов
независимых одипаково распределенных н о р-
Mjaльных с. в., имеющих пулевые
математические ожидания.
Решение. Случайная величина
= 1/
(9.7.11)
где М [Хк] - 0; D [Хк] = а2.
Закон распределения и числовые характеристики с. в.
Rn были определены в п. 7.10 (см. G.10.33) —
G.10.38)). >
Задача 6. Закон распределения модуля
нормально распределенной с. в.
Решени е. Пусть с. в. X имеет нормальное
распределение с параметрами иг, о; случайная величина Y
определяется так:
F-UI; (9.7.12)
находим:
(9.7.13)
гдет = М[Х]; o2 = D[X] и Ф(х)'— фупкция
Лапласа. Плотность распределения с. в. Y будет:
(у—шJ (--?/—я*J
1-e" + a-W<"~ СУ>0). (9.7.14)
13 Теория вероятностей и ее
инженерные приложения
3S6 ГЛ. 9, ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
Если т == 0, то
(J) (9.7.15)
> (9.7.16)
Задача 7. Логарифмически нормальное
распределение. Говорят, что неотрицательная св.
У имеет логарифмически нормальное распределение,
если ее натуральный логарифм
1пУ-Х (9.7.17)'
имеет нормальное распределение. Требуется найти закон
распределения св. Y:
Y = e*. (9.7.18)
Решение. Пусть параметры нормального закона,
по которому распределена св. X, равны т, а. Найдем
соответствующее логарифмически нормальное
распределение. Функция е* монотонна, поэтому плотность св. Y
найдем по формуле (9.1.7):
(9.7.19)
где
о у 2,п [ 2o
Следовательно,
* (9.7.20)
Задача 8. Ограниченный нормальный
закон. При контроле качества изделия по параметру
X, распределенному по нормальному закону с
характеристиками М [X] » т и D [л] «а о2, отбраковываются
изделия, имеющие значение параметра X меньше величины
а или больше величины fi- Найдем закон распределения
св. Y — значения контролируемого параметра изделия,
прошедшего контроль, и св. Z — не прошедшего
контроль.
9.7. ФУНКЦИИ НОРМ РАСПРЕДЕЛЕННОГО АРГУМЕНТА 387
Решение. Вероятность р того, что изделие пройдет
контроль, будет:
где /(д:) = ехр{-(^~тJ/Bа2)}/аУ2я; Ф(х)— функция
Лапласа.
По интегральной формуле Бейеса C.4.9) получим
плотность распределения св. Y —- значения параметра X
Q а т
Рис. 9.7.1
О ос
т
Рис. 9.7.2
для изделия, прошедшего контроль:
при у ф (ос, р).;
(9,7.21)
388 ГЛ. 9, ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
Аналогично найдем плотпость распределения св. Z —
значения параметра X для изделия, не прошедшего
контроль. Эта плотность gi{z) отлична от нуля только вне
промежутка (a, fS), a именно
*,(*)
(9.7.22)
где
Заметим, что />t + р2 — 1 — р есть вероятность того, что
изделие не пройдет контроля.
На рис. 9.7.1 и 9.7.2 показаны графики п. p. gv{y)
"*«(*)• >
9.8. Вероятностная смесь распределений.
Закон распределения суммы случайного
числа случайных слагаемых
В инженерной практике нередко встречаются задачи,
в которых закон распределения случайной величины сам
является случайным и зависит от того, какое из полной
группы несовместных событий (гипотез) Яь //2, ..., Нл
имело место. Требуется найти «полный» эакон
распределения случайной величины с учетом того, что он с
какими-то вероятностями может быть тем или другим.
Пусть, например, имеется техническое устройство
(ТУ), состоящее из п элементов. В ТУ с вероятностью
Pi работает 1-й элемент (и только он один). Задапы ве-
п
роятностирх, р2, , •», рп] 2Р| в 1.Если работает J-й
элемент, то связанный с ТУ случайный параметр X имеет
заданное распределение (функцию распределения Ft(z)
или плотность АОО). Требуется найти полный
(«усредненный») закон распределения параметра X с учетом
случайности номера работающего элемента.
Другой пример: поступающее к потребителю изделие
может принадлежать тому или другому из заводов —
9.8. ВЕРОЯТНОСТНАЯ СМЕСЬ РАСПРЕДЕЛЕНИЙ 389
производителей: Зь 32, ..., Зл; если оно принадлежит
2-му заводу, время Т его безотказной работы — случайная
величина с плотностью fi{t). Известны вероятность рг
того, что изделие принадлежит заводу 3* f i = 12 2Х ,. ^ и;
Требуется найти полную («усредненную»)
плотность распределения j(t) времени Т безотказной
работы изделия.
Решим поставленную задачу в общем виде. Имеется
случайная величина Х\ об условиях опыта, в результате
которого она принимает то или другое значение, можно
сделать п взаимоисключающих гипотез: #lf //2, ..., Нп.
Вероятности гипотез известны:
Если имеет место гипотеза #*, функция распределения
св. X равна Fi(x). Требуется найти полную
(«усредненную») функцию распределения F (х) случайной
величины X с учетом случайности ее закона распределения.
По определению
F(x)-P{X<x).
Найдем эту вероятность по формуле полной вероятности
с гипотезами Ии //2, ,.., //„:
F (х) - 2 Р (Я*) F{ (x) - 2 P/i (х). (9.8,1)
i=l i=l г
Если св. X непрерывна, то, дифференцируя (9.8.1),
получим выражение для ее плотности:
f(x) = F'(x) = ^Pih(x). (9.8.2)
Нетрудно убедиться, что функция распределения (9.8.1)
и плотность (9.8.2) обладают свойствами функции
распределения и плотности: F(x) не убывает при возраста-
оо
оо
; J f(x)dx-i.
0
Возникающее таким образом распределение
называется вероятностной смесью распределений.
390 ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
Найдем математическое ожидание и дисперсию
смешанного распределения (9.8.1) или (9.8.2). По формуле
полного математического ожидания находим:
М [X] = 2 /У"ь (9-8.3)
где Шх — условное м. о. случайной величины X при
условии, что имела место гипотеза //*.
Может показаться, что и дисперсию случайной
величины X можно найти точно таким же способом; но это
не так (в ее выражение входят условные
математические ожидания, различные при разных гипотезах), что
касается второго начального момента агСТ, то он, как
н.о. квадрата св. X, находится аналогично (9.8.3): по
формуле полного математического ожидания
а2 [X] - М [X*] - Д РР? [X], (9.8.4)
Д
4г)
где с4г)[Х]— второй начальный момент св. X при
гипотезе Н{.
Дисперсия с. в. X вычисляется по формуле
(9.8.5)
Пример 1. В партии изделий, состоящей из N
экземпляров, Ni изготовлены заводом 31? JV2 — заводом 32
(Nt + N2 — N). Время безотказной работы изделия
завода 3t имеет показательное распределение с параметром
A,i, завода 32 — показательное распределение с
параметром Я2. Найти плотность f(t) времени безотказной
работы изделия наугад выбранного из партии в N изделий.
Решение. Имеем две гипотезы:
Hi — изделие принадлежит заводу 31?
#2 — изделие принадлежит заводу 32.
Вероятности гипотез
Смешанная плотность
РЛв' + PaV"Xa* (* > °). (9.8.6)
Распределение (9.8.6) в общем случае уже не будет
показательным. >
9.8. ВЕРОЯТНОСТНАЯ СМЕСЬ РАСПРЕДЕЛЕНИЙ 391
Задача 1. Закон распределения суммы
случайного числа случайных слагаемых.
Рассмотрим с. в. Z, представляющую собой сумму
случайного числа случайных слагаемых:
у
Z « 2 Хн (9.8.7)
где случайные величины Хг независимы между собой и
имеют одинаковую плотность /(#)» а дискретная св. Y
не зависит от величин Хг (г —О, 1, 2, ,..) и принимает
неотрицательные целочисленные значения 0, 1, 2, ...
..., /с, ... Известно распределение дискретной с. в. Y:
ph = P{Y = k} (ft-0, 1, 2, ...)<
¦ч
Требуется найти закон распределения св. Z,
Решение. Сделаем гипотезу, состоящую в том, что
с. в. Y приняла значение к > 0. В этом случае условная
плотность с. в. Z представляет собой композицию к
плотностей f(x); обозначим эту композицию
/<»>-/»/¦...,,,/.
h раз
Если св. Y приняла значение 0, то в сумме нет ни
одного слагаемого: Z = 0, и это значение обладает
отличной от нуля вероятностью; в нем функции
распределения G(z) случайной величины Z имеют скачок,
равный /?о.
При z, отличном от 0, функция G(z) непрерывна.
Найдем ее выражение. По формуле полной вероятности
G (z) = P {Z < г} - 2 P/W (г), (9.8.8)
h
где Fih) B) — функция распределения суммы к
независимых случайных величин с плотностью f(x).
Итак, случайная величина Z—-величина смешанного
типа; она имеет одно значение 0 с отличной от нуля
вероятностью /?0, а при Z > 0 представляет собой
вероятностную смесь распределений с плотностями f{ (х);
производпая G(z) равна
*M-C'(*)-Spfc/W(*). > (9.8.9)
Пример 2. Рассматривается работа ремонтной
бригады. За ограниченное время t приема заявок на опре-
392 ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
деленный вид ремонтных работ поступает случайное
число заявок F, распределенное по закону Пуассона с
параметром а; прием заявок за время t неограничен. Закон
распределения времени Т{ ремонта по j-й заявке —
показательный с параметром \х (?=1, 2, ...). Случайные
величины Ti независимы, одинаково распределены и не
зависят от числа принятых заявок Y. Найти закон
распределения и числовые характеристики времени Т
выполнения всех заявок, поступивших за время t: T = 27\.
Решение. Вероятность того, что за время t
поступит ровно к заявок на ремонт, равна:
^ = Л-7И (й = 0, 1,2, ...).
Если не поступит ни одной заявки (& = 0)\ то время
ремопта будет равно пулю: То = 0.
Если поступит к заявок, время ремонта будет
распределено по закону Эрланга к-то порядка (см. F.4.8)):
- 1)! = \\Р(к - 1, jut^)
где Р(к, а) —табличная функция пуассоновского
распределения (приложение 1). Случайная величина Т
является смешанной, принимающей значение ? = 0 с
вероятностью р0; при ?>0 F(t) пепрерывна и имеет производ-
ную F'@-S pkfk) (t).
В данном примере с. в. Т представляет собой сумму
случайного числа случайных слагаемых
у
Т = 2 Tk, где Го = О, а св. Тк (к>0) распределена по
fe=0
закону Эрлаига &-го порядка.
Таким образом, закон распределения св. Т
представляет собой при t > 0 вероятностную смесь законов
Эрлапга 1-го, 2-го, ..., к-то, ... порядков с вероятностями
ри />2, ..., Рь .. ¦
Найдем м.о. и дисперсию св. Г. По формуле (8.5.4)
находим м. о. случайной величины Т:
=o \i=o
9.8. ВЕРОЯТНОСТНАЯ СМЕСЬ РАСПРЕДЕЛЕНИЙ 393
В нашем случае М [То] = 0; М [Т\] = 1/j.i, следовательно,
Дисперсия св. Т равна (см. (8.5.10))
D[rj - (М [Г,])»- D[Y] + D[f4].M [Y\ = ± + 42 « ^,
так как
Задача 2. Вероятностное /?, g
преобразование пуассоновского распределения.
Своеобразной задачей на вероятностные смеси
распределений является задача, которую мы назовем «задачей
вероятностного р, q преобразования пуассоновского
распределения».
Рассматривается с. в. X, распределенная по закону
Пуассона с параметром а. Со св. X связана св. Y
следующим образом:
1) если св. Х = 0, то св. Y принимает значение,
равное нулю с вероятностью, равной единице;
2) если св. Х=1, то св. Y может принимать два
значения: 0 и 1:
3) если св. Х = к (к = 2, 3, ...), то св. У может
принимать значения 0, 1, ..., тп, ..., к и имеет
биномиальное распределение с параметрами к, р;
O|Z = /c}
11 X - ЛЬ
Pry w> I V
|Г == m| A =
(9.8.10)
(заметим, что формулы (9.8.10) справедливы и для
fc = 0; 1). По формуле полной вероятности имеем
ХР{Х = *} + ...; (9.8.11)
394 ГЛ 9 ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
св. X распределена по закону Пуассона с параметром
а, поэтому Р {X = k} = ahe~a/k\. С учетом формул (9.8.10)
получим:
Р {У = 0} = 1 .*-e + ae"aq + aV"V/2 + ...
. .. + ahe~aqh/k\ + .. . = fj ahe'aqh/k\ =
ft=0
= e-a{l-q) ? (aq)he'aq/k\ « Гор.
(9.8.12)
Таким образом, мы доказали, что при вероятностном р, <?
лреобразовании пуассоновского распределения с
параметром а получается также пуассоновское распределение,
но с параметром ар. (Этим мы, в частности, доказали,
что число пробоин в примере 3 п. 8.5 распределено по
закону Пуассона.) >
Пример 3. В АСУ за сутки поступает случайное
число X информационных документов (ИД),
распределенное по закону Пуассона с параметром а. Каждый из
поступивших ИД с вероятностью р является срочным
(независимо от вида других ИД) и требует
приоритетной обработки.
Требуется определить закон распределения числа
срочных ИД У, поступивших в АСУ за сутки.
Решение. В соответствии с решением задачи 2
этого п. св. Y будет распределена по закону Пуассона с
параметром ар:
M[Y] = Dm = ap; Р{У - к} - ^ <Гор.
Например, если величина а = 100 и р = ОД, то М [У] = 10.
9 8 ВЕРОЯТНОСТНАЯ СМЕСЬ РАСПРЕДЕЛЕНИЙ 395
С помощью таблицы приложения 1, можно найти
вероятность того, что в АСУ за сутки поступят 8
срочных документов:
Пример 4. Для условий примера 3 этого пункта
найти закон распределения числа Z поступивших
несрочных ИД в АСУ за сутки.
Решение. Очевидно, что св. Z будет распределена
по закону Пуассона с параметром aq, так как
вероятность того, что поступивший в АСУ ИД будет
несрочным, равна 1 — р = q. >
Пример 5. Показать, что случайные величины У и
Z, рассмотренные в примерах 3 и 4 этого пункта, цеза-
висимы.
Решение. По условию
где с. в. X, У и Z распределены по законам Пуассона с
параметрами а, ар, aq соответственно (<7 = 1 —/?).
Следовательно, имеют место равенства-
qm-k
С другой стороны,
т
- A; Z =¦ т — Щ, (**)
Если с. в. У и Z независимы, то
Р {У = к; Z = т - к} = Р {Y ---= к) Р {Z = т - к}
(необходимое и достаточное условие независимости с. п.
У и Z). В этом случае равенство (**) примет вид:
m
A! ' (m - A)!
.fc! (т — A)! ml ml *d к\ (/я — A)l ml
/i=0 h=Q
396 ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
V m\pq л „ .
т. к. 2^ ы <т__ mi" 1 как сумма вероятностей оппомиаль-
ного распределения с параметрами т, р. Таким образом,
мы доказали, что св. У и Z независимы. >
Замечание: св. X и У (или X и Z) будут
зависимы. Найдем ковариацию К^ и коэффициент
корреляции гху. Запишем равенство
Z = X-Y
и найдем дисперсию левой и правой части (см. (8.2.13) )i
Dz = Dx + Dy-2Kxy.
Так как св. X, У, Z распределена по законам Пуассона
с параметрами а, ар, aq (q = 1 — р), то aq » а + ар — 2^,
откуда
ЛГху - ар - М [Г] - 1Э[Л;
Гх2/« кху/( Vdx. Vdv) = /p.
Задача 2 легко обобщается на случай многомерного
преобразования пуассоновского распределения.
Задача 3. Вероятностное многомерное
Ри Рг, Рз, ..., рп преобразование пуассоновско-
/
го распределения! Zj P* — 1 )• Дана с в. X,
распределенная по закону Пуассона с параметром а. Эта св. X
подвергается преобразованию: с вероятностью рг
получаем св. Yu ..., с вероятностью />* — св. У*, ..., с
вероятностью рп — с в. У„, таким образом, как это делалось
в задаче 2 этого п.
Если св. Х = 0, то св. Yi принимает значение,
равное нулю, с вероятностью, равной единице; если св.
Х=»1, то св. Yi может принимать два значения: 0 и 1;
если св. X — 2, то с.в. Yt может принимать три
значения: 0, 1 и 2;
2} = A-;>.)*; Р{Г{ = 1|Х = 2} =
Р {Y{ = 21X =5 2} = pf и /Т. д. Указанная процедура
справедлива для любого ? = 1, 2, ..., п.
9.8. ВЕРОЯТНОСТНАЯ СМЕСЬ РАСПРЕДЕЛЕНИЙ 397
Требуется определить закон распределения системы
св. (Yu У2, ..., Yn).
Решение. В соответствии с решением задачи 2
этого пункта св. Y{ будет распределена по закону
Пуассона с параметром яр,. Для доказательства этого
достаточно обозначить величину Pi — р и 1 — pi = q. Но в
качестве i-ro номера можно рассматривать любой (i =
= 1, 2, ..., /г), следовательно, система с в. (Yu У2, ...
,.., Yn) будет представлять собой систему св.,
распределенных по законам Пуассона с параметрами ариарг,...
..., арп. Кроме того, в соответствии с решением примера
5 этого п. св. Yu 72, ..., Yn будут независимы. При
этом выполняются следующие равенства:
Х= 2 Yu a = 2 ар . >
Пример 6. В АСУ в сутки поступает случайное
число X информационных документов (ИД),
распределенное по закону Пуассона с параметром а. Каждый из
поступивших ИД может с вероятностью pt (г =1,2,...
..., п) относиться к г-му виду, независимо от других ИД
71 \
2р{ = 1 I.Требуется определить закон распределения
св. Yi — число поступивших ИД i-ro вида ((» 1,2, ...,п).
Решение. В соответствии с решением задачи 3
св. Yi будет распределена по закону Пуассона с
параметром apt (;=1, 2, ..., п)\ св. Yh Y2, ..., Yn будут
независимы. >
Замечание, св. X и У* (i = l, ..., п) будут
зависимы, так как
X - ? Yt.
i
Задача 4. Вероятностное многомерное
преобразование /?ь рг, ..., рт биномиального
т
распределения с параметрами п, р ( 2Pi == 1 ]•
Дана с в. X, имеющая биномиальное распределение с
параметрами /г, р. Эта св. X подвергается независимому
преобразованию: с вероятностью pi = kjn получается
св. Yi (i = l, ¦.., т), при этом кг — такие целые по-
398 ГЛ. 9. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
т
ложительиые числа, что их сумма равна п\ ^1ц = тг. Тре-
буется найти закон распределения системы св. (YuY2i...
..., Ут). Читателю предлагается доказать с помощью
приемов, примененных в задачах 2 и 3 этого пункта, что
св. У4| ..., Ym будут независимы и иметь бипомиальное
распределение с параметрами (Аг±, р), (/с2, /?), ...
..., (km, p) соответственно; при этом будет выполняться
равенство
т
X - 2 Yi.
ГЛАВА 10
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
ТЕОРИИ ВЕРОЯТНОСТЕЙ
ЮЛ. Закон больших чисел
Математические закопы теорий вероятностей
получены в результате абстрагирования реальных
статистических закономерностей, свойственных массовым
случайным явлениям. Опыт учит, что, наблюдая массовые
однородные случайные явления, мы обнаруживаем в них
своеобразные закономерности, определенного типа
устойчивости. С некоторыми из них мы уже познакомились
в начале нашего курса; например, с тем, что при
большом числе однородных независимых опытов частота
события Р* (А) становится устойчивой, приближается
(сходится по вероятности) к его вероятности Р(^).
Другой пример: при увеличении числа опытов, в каждом
из которых св. X принимает какое-то значение, среднее
арифметическое наблюденных значений св. X становится
устойчивым, приближается (сходится по вероятности)
к ее математическому ожиданию. Оба эти положения
представляют собой частные случаи так называемого
закона больших чисел. Физическое содержание этого
закона может быть сформулировано так: при очень
большом числе случайных явлений
средний их результат практически перестает
быть случайным и может быть предсказан
с большой степенью определенности.
В узком смысле слова под «законом больших чисел»
понимается ряд математических теорем, в
каждой из которых для тех или иных условий
устанавливается факт приближения средних характеристик большого
числа опытов к определенным постоянным,
неслучайным величинам. С некоторыми частными формами
закона больших чисел, касающимися поведения частоты
события при большом числе опытов, а также среднего
арифметического большого числа наблюденных
значений случайной величины мы уже встречались ранее, но
на описательном, до-математическом уровне. В данном
400 ГЛ, 10. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
пункте мы докажем некоторые относящиеся сюда
теоремы. Все эти доказательства опираются на неравенство
Чебышева, которое является для них леммой. Докажем
его в первую очередь.
Неравенство Чебышева. Для любой
случайной величины X, имеющей математическое ожидание
гпх и дисперсию Dx, справедливо неравенство:
Р{\Х-тх\^а}^% A0.1.2)
где а — любое положительное число.
Неравенство A0.1.2) ограничивает сверху вероятности
больших отклонений с. в. от ее математического
ожидания.
Докажем неравенство A0.1.2) спачала для
непрерывной с. в. X с плотностью f{x)> Событие А, состоящее в
том, что отклонение случайной величины X от ее
математического ожидания тх будет не меньше, чем а:
представляет собой попадание случайной точки X за
пределы участка {тх — а; тх-\-а) на оси абсцисс
ос ос
D тх~ос тх /7У"СС х
Рис. 10.1.1
(рис. 10.1.1); на рос. 10.1.1 эта зона оси абсцисс
(включая крайние точки тх — а и тх + а) отмечены жирной
линией и жирными точками*). Вероятность попадания
X в эту зону
J f(x)dx+ J /(*)&?-1- J f{x)dx. (ЮЛА)
+ mа
J
*) Для непрерывной случайпой величины X Р|Х = тх — а} =
_. р |Х = тх+ а}= 0, но мы не будем отбрасывать знак равенства
в AQ-.1.3), имея в виду дальнейший переход к дискретным и
смешанным с. в.
10.1. ЗАКОН БОЛЬШИХ ЧИСЕЛ 401
Теперь вычислим дисперсию случайной величины X:
+ 00 ОО
Dx- j (x-mxfj{x)dx = J \x-mxff{x)dx, A0,1,5)
— oo —oo
Заменим в правой части A0.1.5)' всю область
интегрирования па множество точек, для которых (х — тхJ**
>а\ от этого интеграл увеличиться не может:
тх~а оо
Dx> J \x-mx\*f(x)dx + j \z-mx\*f{x)dz.
—oo ™,х-+а
A0.1.6)
Теперь заменим в правой части A0.1.6) величину
\х — тх\2 на величину а2, не превосходящую ее; от этого
опять-таки выражение A0.1.6) больше не станет:
Ас>а2 J f(x)dx + a* J f(x)dxl A0.1.6')
—oo Wx+a
то есть
A0.1,7)
Деля обе части A0.1.7) на a2>0, получим
доказываемое неравенство Чебышева A0.1.2).
Совершенно аналогично доказывается неравенство
Чебышева и для дискретной случайной величины, имеющей
значения хи хг, ... с вероятностями ри p2j ...; вместо
интегралов в формулах A0.1.4), A0.1.6), A0.1.6у) ставятся
суммы, распространяемые на те значения #<, для которых
\xi — mx\ >a. Предоставляем читателю проделать эти
выкладки самостоятельно. Для смешанной случайной
величины X соответствующие формулы будут содержать как
суммы, так и интегралы.
Пользуясь неравенством Чебышева A0.1.2), оценим
сверху вероятность того, что случайная величина X с
любым законом распределения отклонится от своего
математического ожидания не меньше, чем на Зах, где ах =
= УД*; полагая в A0.1.2) a = 3a*, получим:
Р {| X - тх | > За*} <a?/Ca*)« = 1/9, A0.1.8)
то есть для любой случайной величины вероятность не^
выполнения «правила трех сигма» не превышает 1/9.
402 ГЛ. 10. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Сформулированное правило, вытекающее из
неравенства Чебышева и относящееся к любой случайной
величине с любым законом распределения, дает нам в первом,
грубом приближении «правило трех сигма» — пользуясь
этим правилом, мы никогда не ошибемся больше, чем
на 1/9 вероятности. В действительности, для
большинства случайных величин, встречающихся на практике,
ошибка «правила трех сигма» существенно меньше.
Рассмотрим несколько примеров на применение неравенства
Чебышева при а = За*, в каждом из которых сравним
точное значение Р {| X —- тх | ^ Зох) с его верхней
оценкой 1/9.
v Пример 1. Случайная величина X— индикатор
события А с вероятностью р — имеет два возможных
значения: 0 с вероятностью g = l~jj и 1 с вероятностью р:
X:
<?
1
р
Мы знаем, что тх = р\ Dx = pq (см. п. 3.3). Вычислим,
пользуясь распределением (*), точное значение
вероятности Р{|Х— р|^3 у pq\\ нетрудно убедиться, что опо
зависит от Того, какова вероятность р:
р<!0,1;
при
при
при
0,1<р<0,9;
р ^ 0,9.
q.
IX —
Действительно, при р = 0,1, 3Vpg = 0,3; единственное
значение св. X, отклоняющееся от р = 0,1 больше, чем
на 0,3, есть 1, а его вероятность равна р\ то же будет
и при р<0,1. Для больших вероятностей /?^0,9
единственным значением св. X, отклоняющимся от р
больше, чем на Зах, будет 0, а его вероятность равна
Из (**) видно, что вероятность события
3* 31/pq не больше, чем р при малых р и не больше, чем
1— p = q при больших р\ значит, она ни при каких
условиях не превосходит 0,1, что меньше, чем 1/9,
даваемое неравенством Чебышева. При значениях 0<р<0,9
ошибка «правила трех сигма» вообще равна нулю. >
Пример 2. Случайная величина X имеет
биномиальное распределение с параметрами пир:
-pi Л-0,1,2, .... n).
10.1. ЗАКОН БОЛЬШИХ ЧИСЕЛ 403
В этом случае шх = пр\ Зох = 3}'рдп. Вероятность
невыполнения «правила трех сигма»
Р [\Х - пр\^3 V^q) =Р {X ^пр - 3
V /oft ft n—ft . in пк ft n-h
где
- f лг/7 + 3 V^npq — если это число целое,
}Гпр + 3 V^rcpg] + 1 — если число пр + 3 Vnpq дробное^
[х] — целая часть числа х.
Подсчеты для конкретных значений пир
показывают, что эта вероятность существенно меньше 1/9.
Предоставляем читателю проверить это самостоятельно. >
Пример 3. Непрерывная с. в. X распределена
равномерно на участке от а до Ь:
J 1/F —а) при же (а, Ь)х
/Wel0 при хф(ахЪ).
Перенесем начало отсчета в точку с абсциссой
\а + Ь)/2, то есть отцентрируем св. Х\ при этом ее м.о.
станет равным нулю, а дисперсия не изменится; обозначим
Ъ — а = с > 0 длину участка, на котором распределена
о
равномерно с. в. X. Центрированная с. в. X распределена
равномерно па участке (—с/2; с/2); ее с. к. о. равно
ох = с/BУЗ). Рассмотрим участок 0 ± Зах, вероятность
о
непопадания точки X в который требуется найти.
Правая его граиица_0 + За* имеет абсциссу Зс/BУЗ) =
— УЗ с/2; так как УЗ с/2 > с/2, эта точка лежит за
пределами участка (—с/2; с/2) и вероятность попадания
правее ее равна нулю; так же равна нулю вероятность ее
попадания левее точки с абсциссой — УЗ с/2. Значит,
в случае равномерного распределения «правило трех
сигма» действует безошибочно; вероятность его
невыполнения равна нулю. >
Пример 4. Случайная величина X распределена по
показательному закону с плотностью
f(x) = Xe~Kx при х>0.
Его характеристики: тх = ох=1/Х.
¦ 04 ГЛ. 10. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Отклонение с. в. X от тх больше, чем на Зах,
возможно только в большую сторону, так как тх — За*
отрицательно. Вероятность невыполнения «правила трех сигма»:
Р {X > тх + За*} =
= Р {X > 1А + ЗА} = Р {X > Щ = 1
где F(x) = 1 — ехр {—Ха:} — функция распределения с. в. X.
Отсюда
Р {X > тя + За,} - 1 - A - <Г4ХД) = <Г4« 0,0183.
Итак: для показательного закона вероятность
невыполнения «правила трех сигма» равна 0,0183; это
значительно меньше, чем 1/9 «0,1111, но все же не
пренебрежимо мало. Показательное распределение — одно из
наименее благоприятных для применения «правила трех
сигма» — почти в 2% случаев значения св. X выходят
за пределы интервала тх + Зах. >
Пример 5, Случайная величина X распределена по
нормальному закону с параметрами шио,
Вероятность невыполнения «правила трех сигма»
в 1 - р {| X - т | < За} = 1 - 2Ф (За/а) - 1 - 2Ф C),
где Ф (#)— функция Лапласа.
По таблице значений функции Лапласа (см.
приложение 2) имеем ФC) « 0,49865, откуда
р {| х - т | > За} « 1 - 2.0,49865 = 0,0027,
т. е. для нормального закона только ничтожная доля
значений св. (менее 0,3%) выходит за пределы
интервала т ± За. >
Исторически «правило трех сигма» возникло именно
для случая нормального распределения, где оно
выполняется с очень высокой точностью, но при более
«либеральных» требованиях к точности его можно примепять
и к другим случайным величинам.
Опыт учит, что для большинства случайных величии,
встречающихся в инженерной практике, «правило трех
сигма» выполняется с довольно высокой вероятностью,
и для того, чтобы ориентировочно представить себе
диапазон практически возможных значении с. в., можно
отложить от м. о. т в ту или другую сторону по За.
Переходим к рассмотрению различных форм закона
больших чисел. Во всех этих формах утверждается ус-
10.i. ЗАКОН БОЛЬШИХ ЧИСЕЛ 405
тойчивость средних: при неограниченном увеличении
числа опытов п их средний результат приближается
(сходится по вероятности) к некоторому постоянному,
неслучайному числу.
Термином «сходится по вероятности» мы уже
пользовались раньше; теперь дадим ему четкое математическое
определение.
Пусть имеется последовательность
случайных величин:
Говорят, что эта последовательность сходится по
вероятности к неслучайной величине а, если при
неограниченном увеличении п вероятность события
{\Хп — а\<г) (где г > 0 — произвольно малое
фиксированное число) стремится к единице.
Иначе говоря, каковы бы ни были произвольно малые
наперед заданные числа е > 0 и б > 0, всегда найдется
такое большое число N, что для всех номеров,
начиная с N
Р {| Хп — а К в} > 1 — 6 (n>N). A0.1.9)
Докажем две теоремы, принадлежащие П. Л. Че-
бышеву.
1-я теорема Чебышева (называемая иногда
просто «законом больших чисел») состоит в следующем.
Пусть имеется с. в. X с м.о. тх и дисперсией Dx; над
этой св. X производится п независимых опытов, в
результате которых она принимает значения /Хи Х2, . ¦.
..., Хп (п «экземпляров» случайной величины X).
Рассматривается среднее арифметическое всех этих
значений, зависящее от п:
Случайные величины Yn образуют последовательность;
первая теорема Чебышева утверждает, что она сходится
по вероятности к математическому ожиданию св. X:
Yn^mx,*) A0.1.11)
П-»оо
*) Знаком > обозначепа сходимость по вероятности; ииог-
Р
да применяют обозначение *"«
406 ГЛ. 10. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
т. е. среднее арифметическое наблюденных в п
независимых опытах значений случайной величины сходится
по вероятности к ее математическому ожиданию при
п-+ «\
Доказательство 1-й теоремы Чебышева.
Найдем м. о. и дисперсию св. Yn. По теореме сложения
математических ожиданий
но все св. Хи Хг, ..., Хп распределены одинаково и
имеют математическое ожидание тж, поэтому
Вынося из-под знака дисперсии 1/п2 и применяя
теорему сложения дисперсий для независимых с в.
Хи Х2, ..., Х„, найдем:
i=l
Применяя к св. Yn неравенство Чебышева, в котором
положим а = е, где е — сколь угодно малое наперед
заданное положительное число, получим:
Р {| Yn - тх | > е} < ДсДгсе2). A0.1.12)
Как бы ни мало было 8, всегда можно выбрать п
таким большим, чтобы правая часть A0.1.12) стала
меньше сколь угодно малого положительного числа 6; поэтому
при достаточно большом п
а вероятность противоположного события
Р {| Yn - тх |< в} > 1 - б, A0.1.13)
а это, мы знаем, равносильно сходимости по вероятности
ЮЛ. ЗАКОН БОЛЬШИХ ЧИСЕЛ 407
Yn к тх:
Yn~mx, A0.1.14)
и первая теорема Чебышева доказана.
Эта теорема может быть записана и в другом ппде:
обозначая Zn = Yn — mx, получим
Zn^0, A0.1.15)
и вообще, если случайная величина Уп при п -> оо
сходится по вероятности к постоянной а, то это значит,
что разность между Yn и а при п ->¦ «> сходится по
вероятности к нулю. Именно в такой форме мы будем
записывать сходимость по вероятности во второй теореме
Чебышева.
2-я теорема Чебышева. Только что доказанная
1-я теорема Чебышева относилась к случаю, когда все
с. в. Хи Х2, ..., Х„ были независимы и имели одно и то
же распределение, а значит, одно и то же м.о. тпх и одну
и ту же дисперсию Dx. Теперь мы рассмотрим случай,
когда условия независимых опытов меняются, то есть их
результаты представляют собой неограниченную
последовательность независимых с. в. Хи Х2, ..., Хп, ... с
различными, в общем случае, математическими ожиданиями
mXi и дисперсиями DH (iel, 2, ..., п, ...). Обозна-
п
чим снова Yn — A/л) 2 %\ и докажем, что если все
дисперсии DX{ ограничены сверху одним и тем же
числом D:
DX.^D (г = 1,2, ...,», ...), (Ю.1.16)
то разность между средним арифметическим наблюден-
них значений случайных величин и средним
арифметическим их математических ожиданий сходится по
вероятности к нулю*).
*) Может возникнуть вопрос: почему в этом случае мы не
говорим, что среднее арифметическое наблюденных значений
случайных величин при п -*• оо сходится по вероятности к среднему
арифметическому их математических ожиданий (так иногда и
формулируется 2-я теорема Чебышева)? Потому что в данном слу-
п п
чае как A/л) 2 Л\, так и A/л) 2 тх% зависят от л, а понятие
«сходимость по вероятности» определено нами только для
постоянной величины а, не зависящей от п.
408 ГЛ. 10. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Доказательство снова проведем, применяя
неравенство Чебышева к Уп. Для этого найдем
М[У„1=4-1
Dl
•у „
i =ssl
п
-г=1
A0.1.17)
Согласно неравенству Чебышева
или, учитывая A0.1 Л7),
Учитывая, что все дисперсии DX{ (i == 1, 2, ..., п)
ограничены сверху величиной D, и заменяя в A0.1.18)
все DXi на Z), мы можем только усилить неравенство;
поэтому
4
Как бы ни было мало произвольное наперед
заданное е, всегда можно выбрать п таким большим, чтобы
правая часть A0.1.19) стала меньше произвольного
малого 6; поэтому
<8t A0.1.20)
откуда, переходя к противоположному событию, получим
доказываемое неравенство:
: 7,ТП:
•hCi
<е >1-6. A0.1.21)
Закон больших чисел может быть распространен и на
зависимые случайные величины.
Пусть Xi, Х2, ..., Х„, ...— зависимые случайные
величины с математическими ожиданиями тх , ..., тЖп и
iO.i. ЗАКОН БОЛЬШИХ ЧИСЕЛ 409
О О
ковариационной матрицей || К^\\ = ||М [XiXj] ||, размеры
которой зависят, разумеется, от я. Математическое
ожидать
ние случайной величины Yn = A/я) 2 Х\ по-прежнему
г = 1
п
равно тУп = A/п) 2 wx.. Для зависимых случайных
величин дисперсия суммы равна сумме всех элементов
ковариационной матрицы; отсюда
Наложим на элементы ковариационной матрицы
условие, состоящее в том, чтобы двойная сумма в формуле
A0.1.22) возрастала при п -* оо медленнее, чем п2\ тогда
Jim ОУп = 0. A0.1.23)
П-*оо
Теорема Маркова состоит в следующем: если с. в.
Xi, ..., Хп — зависимые случайные величины с
математическими ожиданиями mx^...,mXn и дисперсиями
DXii ..., DXn,удовлетворяющими условию A0.1.23), то
разность между их средним арифметическим и средним
арифметическим их математических ожиданий сходится
по вероятности к нулю:
A0.1.24)
Доказательство. Применим к величине Yn
неравенство Чебышева
п
: — — 7, тХ{
D
Уп
е
A0.1.25)
Так как по условию A0.1.23) при п-+оо Dyn-+0, то
при произвольно малом е можно выбрать п настолько
большим, чтобы правая часть A0.1.25) стала меньше
любого б > 0
2
п i=1
410 ГЛ. 10. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
а вероятность противоположного события
«-42 «*«
i
<¦}>*-
что и доказывает сходимость по вероятности к нулю раз-
71
ности между Yn и — ^ mXi в формуле A0.1.24).
г=1
Помимо различпых форм закона больших чисел,
в теории вероятности имеются еще разные формы так
называемого «усиленного закона больших чисел», где
доказывается не «сходимость по вероятности», а
«сходимость с вероятностью единица» различных средних к
неслучайным средним; в виду относительной неважности
этих форм для технических приложений, мы на них
специально не останавливаемся.
Докажем два следствия закона больших чисел A-й и
2-й теорем Чебышева).
1. Теорема Бернулли. При неограниченном воз-
растании числа п независимых опытов, в каждом из
которых событие А появляется с вероятностью р, частота
события А сходится по вероятности к его вероятности р.
Эту связь между частотой и вероятностью мы уже
устанавливали (без специального доказательства);
теперь мы ее выведем как следствие закона больших
чисел.
По определению, частота события есть отношение
числа появлений событий в п опытах к числу опытов п:
p*n(A) = Rn/n. A0.1.26)
Представим случайную величину Rn в виде суммы
индикаторов события А:
где Х< —ипдикатор события А в i-u опыте:
{0 если в г-м опыте событие А не появилось
1 если в i-м опыте событие А появилось,
Частота A0.1.26) есть пе что иное, как среднее
арифметическое п наблюденных значений
случайной величины X —индикатора события А
10.1. ЗАКОН БОЛЬШИХ ЧИСЕЛ 411
в одном опыте. Напомним, что м.о, индикатора события
равно его вероятности р. Согласно теореме Чебышева
?1->оо
РпИ)"^р, что и доказывает теорему Бернулли*).
Теорема Бернулли относится к случаю, когда все
опыты производятся в одинаковых условиях, и вероятность
появления события А во всех них одна и та же и равна
/?. К более общему случаю, когда вероятности ри /?2, ...
,.., /?„, ... различны, относится теорема Пуассона.
Пусть производится неограниченное число п
независимых опытов, в каждом из которых может появиться
событие А, причем его вероятность в i-u опыте равна /?,-.
Теорема Пуассона утверждает, что при п -> <»
разность между частотой событий А и средним
арифметическим его вероятностей сходится по вероятности к нулю:
]П-^0. A0.1.27)
Доказательство. Теорема Пуассона — следствие
2-й теоремы Чебышева. Действительно, величина
п
Рп (А) = A//г) 2 %i есть среднее арифметическое
индикаторов события А в 1-м, 2-м, ..., мм, ..., гс-м опытах.
Случайная величина X имеет м. о. mXi = pi и дисперсию
D*i == Pi(l — Pi) (п- 3.3); дисперсии DX{ при любом i
ограничены сверху одним и тем же числом D = 0,25
(максимальным значением Pi(l-Pi), достигаемым при /?i = 0,5).
Применяя вторую теорему Чебышева к среднему
арифметическому индикаторов, убедимся в справедливости
теоремы Пуассона.
Закон больших чисел во всех его формах имеет
большое значение в практических применениях
вероятностных методов, в частности, в инженерной практике. Выше
мы уже убедились, что для нахождения числовых
характеристик функций случайных величин (например,
ошибок приборов и механизмов) зачастую не требуется
знания законов распределения аргументов, а достаточно
*) Заметим, что доказать эту теорему (как и сам Борнулли
ее доказывал) можно было бы и без ссылки на теорему Чебышева,
а просто исходя из биномиального распределения с. в. /?п, но это
доказательство было бы довольно громоздким,
412 ГЛ. 10. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
знать их числовые характеристики — м. о., диснерсию,
матрицу ковариаций. Каждая из этих характеристик есть
не что иное, как математическое ожидание
какой-то случайной величины; в частности, D [Хг] = М [X*],
о о
Кц = М [Х{Х}], а на основании закона больших чисел
можно каждое из этих математических ожиданий
приближенно заменить средним арифметическим
наблюденных значений соответствующей св. при достаточно
большом числе опытов; мало того, можно даже оценить
ошибку, вытекающую из такой замены (о том, как
это делается, мы расскажем в следующей главе).
Теорема Бернулли позволяет нам приближенно
определять вероятности событий в опытах, не сводящихся к
схеме случаев, по частотам этих событий при достаточном
числе опытов (гл. И).
Менее известная и менее популярная теорема
Пуассона дает возможность приближенно находить среднюю
вероятность события А в серии опытов, одинаковость
условий которых трудно гарантировать.
Важное значение в инженерной практике имеет
теорема Слуцкого, которая в определенном смысле
является следствием закона больших чисел и его
различных форм (мы здесь приводим ее без доказательства).
Если случайные величины Хп, Ynj..., Wn при
возрастании п сходятся по вероятности к соответствующим не-
случайным величинам х,у,..., w: Xn ~~^^x; Yn~^*y;...
. • •; Wn —^ w, то любая рациональная функция Д(Х«,
У», ..., Wn) сходится по вероятности к неслучайной
величине R(x, у, ..., w) (если R{x, у, ..., w) не
обращается в бесконечность).
В частности, любая степень Rh(Xny Yn, ..., Wn) при
&>0 сходится но вероятности к Rh(x1 у, .,., w):
Rh{Xn, rnt .... Wn)^Rk(x, у, ..., w). A0.1.28)
Одно из инженерных приложений этой теоремы
следующее. Входные воздействия на техническое устройство
(ТУ) представляют собой случайные величины Хп, У„,...
..., Wn, сходящиеся по вероятности при увеличении п
к неслучайным. Выходная величина ТУ определяется по
формуле R(Xni Уп, ,.., Wfl), где Л —рациональная функ-
10.2. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА 413
ция. В этом случае при достаточно большом п в качестве
выходной величины ТУ можно приближенно
рассматривать неслучайную величину R{x, у, ..., w).
Заметим, что никаких ограничений на зависимость
(или независимость) с. в. Хп, Уп, ..., Wn при этом не
накладывается.
10.2. Центральная предельная теорема
Одно из важнейших положений теории
вероятностей — так называемая центральная предельная теорема.
Как и закон больших чисел, она имеет ряд форм. Во
всех формах закона больших чисел устанавливается факт
сходимости по вероятности каких-то случайных величин
к постоянным, не случайным — при увеличении п —
числа опытов или числа наблюдаемых случайных величин.
В данном пункте мы рассмотрим другую группу
предельных теорем, а именно теоремы, определяющие
условия возникновения нормального распределения (закона
Гаусса). Такие условия часто встречаются на практике,
что и объясняет широкую распространенность
нормального закона в случайных явлениях природы.
Кое-что об этих условиях (на чисто описательном
уровне) мы уже говорили раньше (гл. 6), там, где
впервые встретились с нормальным распределением. А
именно, нормальное распределение возникает тогда, когда
суммируется много независимых (или слабо зависимых)
случайных величин, сравнимых по порядку своего
влияния на рассеивание суммы.
В практической деятельности инженера такая обста-
повка встречается нередко.
Пусть, например, рассматривается отклонение У„
выходного параметра большой интегральной схемы (БИС)
от номинала. Это отклонение (при известных
допущениях) может быть представлено как сумма п
элементарных отклопепий, связанных с отдельными причинами:
Yn=2Xb A0.2.1)
где, например,
Ari — отклонение, вызванное влиянием температуры;
Х2 — отклонение, вызваппое влиянием влажности
воздуха;
414 ГЛ. 10. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Х3 — отклонение, вызванное ошибкой ввода какого-
либо параметра;
Х4 — отклонение, вызванное недостаточной чистотой
материала изделия;
и т. д.
Число п этих элементарных отклонений весьма
велико, как и число п причин, вызывающих суммарное
отклонение Yn; обычно слагаемые Хи Х2, ..., Хп
сравнимы по порядку своего влияния на рассеивание суммы.
Действительно, если бы какая-то из случайных величин:
Хи Х2, ..., Хп оказывала существенно большее влияние
на рассеивание суммы, чем все остальные, было бы
естественно Припять специальные меры для того, чтобы
устранить главную причину рассеивания; поскольку
такие меры не предпринимаются, можно предположить, что
оставшиеся случайные слагаемые сравнимы по порядку
своего (равномерно малого) влияния на рассеивание
суммы.
Нормальный закон широко распространен в технике;
в большинстве случаев ошибки измерения параметров,
ошибки выполнения команд, ошибки ввода различных
величин в техническое устройство распределены по
нормальному (или близкому к нормальному) закону; такая
ошибка обычно может быть представлена в виде суммы
многих «элементарных ошибок» X,-, каждая из которых
связана с отдельной, практически независимой от
других, причиной.
Именно в применении к теории ошибок был впервые
обоснован Лапласом и Гауссом нормальный закон.
Нормальный закон широко распространен в биологии:
вес, размер и другие параметры представителей
растительного и животного мира во многих случаях имеют
нормальное распределение, так как их разброс вызван
суммарным воздействием многих факторов, среди
которых нет доминирующих по своему влиянию.
Центральная предельная теорема в различных ее
формах устанавливает условия, при которых возникает
нормальное распределение и нарушение которых ведет к
распределению, отличному от нормального.
Различные формы центральной предельной теоремы
различаются между собой условиями, накладываемыми
на распределения образующих сумму случайных
слагаемых Х1а Х2, ..., Хп. Чем жестче эти условия, тем легче
10.2. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА 415
доказывается теорема; чем они шире, тем труднее
доказательство. Здесь мы докажем одну из самых простых
форм этой теоремы, а именно, центральную
предельную теорему для одинаково
распределенных слагаемых.
Теорема. Если Хи Х2, ..., ХП9 ...— независимые
случайные величины, имеющие одно и то оке
распределение с математическим ожиданием m и дисперсией о2,
то при увеличении п закон распределения суммы
Yn = 2 Xk A0.2.2)
неограниченно приближается к нормальному.
Доказательство. Проведем доказательство для
случая непрерывных случайных величин (для
дискретных оно будет аналогичным). Применим для этого
аппарат характеристических функций*). Согласно свойствам,
доказанным в п. 8.9, характеристическая функция суммы
A0.2.2) равна произведению характеристических
функций слагаемых. Случайные величины Хи Х2, ..., Хп
имеют одну и ту же плотность /(#), а значит и ту же
характеристическую функцию Qx(t). He нарушая общности,
можно перенести начало отсчета всех случайных величин
Хи Х2, ..., Хп в их общее математическое ожидание гп\
это равносильно их центрированию и, значит, тому, что
м. о. каждой из них будет равно нулю.
Напомним, что характеристическая функция каждой
из св. Xh (А = 1, 2, ..., п), по определению, равна (см.
(8.9.4))
00
О» («)- j eitxf(x)dx, A0.2.3)
—оо
где i ¦* V—1 — мнимая единица. Характеристическая
функция случайной величины Уп равна произведению п
характеристических функций слагаемых (см. 8.9.9):
Разложим функцию bx(t) в окрестности точки t = О
в ряд Маклорена с тремя членами:
Оя@ - 0,@) + (>;@) t + [*^@)/2 + а(*)] t\ A0.2.5)
где производные берутся по ?; а\t)-+0 при t-+0.
*) Заметим, что этот аппарат был создан А. М. Ляпуповым
специально для доказательства центральной предельной теоремы.
416 ГЛ. 10. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Найдем значения &х@); К@); $1@).
Полагая в формуле A0.2.3) ? = 0, имеем:
<М0)-
по свойству плотности распределения f(x).
Продифференцируем A0.2.3) по t:
оо счэ
K{t)= J ize-itxf(x)dx = i j xeitxf(x)dx. A0.2.6)
— 00 7-00
Полагая в A0,2.6) ? = 0, получим:
00
Ь'х @) = i J xf (x) dx = М [X]t
— 00
где М [X] — математическое ожидание св. X с
плотностью f(x). В пашем случае все случайные величины
Xit X2j ..., Хп имеют плотность f(x), а их общее м. о.
равно нулю; поэтому
о; (О =- о.
Продифференцируем A0.2.6) еще раз:
00
ti(t)~- \ xVtxf{x)dx.
— ОО
Полагая t = 0, получим
{?@)-
а это есть не что иное, как дисперсия
центрированной св. X с плотностью ](х) (со знаком «минус»).
Следовательно,
Подставляя в A0.2.5) 0,@)= 1; <?@) = 0 и О* @)
— а2? получим
Обратимся к случайной величипе Yn. Мы хотим
доказать, что при увеличении п ее закон распределения
10.2. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА 417
приближается к нормальному. Для этого перейдем от пес
к линейно связанной с Yn «нормированной» случайной
величине
2п«=Уп/(оУп)\ A0.2.7)
Эта величина удобна тем, что ее дисперсия но
зависит от п и равна единице при любом п. В этом нетрудно
убедиться, рассматривая Zn как линейную функцию
независимых случайных величин Хи Х21 ..., Хп, каждая из
которых имеет дисперсию о2.
Если мы докажем, что с. в. Zn имеет нормальное
распределение, это будет означать, что и с. в. Уп, линейно
связанная с 2„, распределена нормально.
Вместо того, чтобы доказывать, что закон
распределения с. в. Zn при увеличении п приближается к
нормальному, докажем, что ее характеристическая функция,
однозначно определяющая плотность, приближается к
характеристической функции нормального закона с теми
же, что у Zni параметрами: т?п = 0; oZn = 1 (8.9.10).
Найдем характеристическую функцию с. в. Z. Из
свойства (8.9.7) характеристической функции (п. 8.9) имеем:
где ОУп — характеристическая фупкция с. в. Yn. Из
A0.2.4) и A0.2.8) имеем:
Или, пользуясь формулой (*)',
К @ = I1 - [т - а Ма ^)I 'W)}n. A0-2-9)
Прологарифмируем это выражепие:
In Фг„ @ = п In {l - [^ - a (t/{o У л))] Р/(в*п)}.
Введем обозпачепие
[^ _ а (t/(a Vn))] <2/(«o2) = х. A0.2.10)
Тогда
In #*„(*) = л In A-х). A0,2,11)
14 Теория вероятностей и ее
инженерные приложения
418 ГЛ. 10. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Будем неограниченно увеличивать п; при этом
величина и, согласно A0.2.10), будет стремиться к нулю.
Разложим In A-х) в ряд по степеням и и ограничимся
одним членом разложения (остальные при п -> «> станут
пренебрежимо малыми):
Тогда
limlnfl Zji(t) = lira n-{—H)=li
П-»оо П-*оо П-»ао
Z2/2 + lira а(*/(о /л)) Р/о*.
Но функция а'@ стр?мится к нулю при ?-*0;
следовательно, Hm a(t/(a Vп)) = 0 и liming @ = — *2/2,,
П-*О0 П-»ОО
откуда lim 0^(^ = 6"' 2, а это есть не что иное, как
П-»оо
характеристическая фушщия случайной величины,
распределенной по нормальному закону с параметрами
т«0, о-1 (см. (8.9.16)).
Таким образом, мы доказали центральную
предельную теорему для частного случая одинаково
распределенных слагаемых. Другие, более общие (и более
сложные) формы центральной предельной теоремы мы
приведем без доказательства.
Теорема Ляпунова. Пусть Хи X2i ..., Хп —-
независимые случайные величины с математическими
ожиданиями лц, тх%1 .. ¦, шХп и дисперсиями Д^, Ас2,
• • • х Dxn, причем при п -> оо
lim 2|Х 7 S^J -0, A0.2.12)
0
где Xk == Xk — m^.
A. M. Ляпунов доказал, что при п -* оо закон
распределения случайной величины
Yn=2>Xk A0.2.13)
неограниченно приближается к нормальному.
Смысл условий A0.2.12) состоит в том, чтобы в сум-»
ме A0.2.13) не было слагаемых, влияние которых на
рассеивание суммы подавляюще велико по сравнению с
10 2. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА 419
влиянием всех остальных, а также не должно быть
большого числа случайных слагаемых, влияние которых на
рассеивание суммы исчезающе мало но сравнению с
суммарным влиянием остальных.
Наиболее общим (необходимым и достаточным)
условием справедливости центральной предельной теоремы
является условие Линдеберга: для любого т > О
lim A / 2 D{) 2 f (* - mxf П (х) dx = 0,
п-»оо \ / i=i / г=1 ° г-—
A0.2.14)
где /,(#)' — плотность распределения св. Xt, гп1=М[Х1]
(i = 1, 2, ..., гг).
Однако пользование условием Липдеберга на
практике затруднительно, так как нам редко бывают в
точности известны законы распределения случайных величин
X, (j-lf2,..., п).
Исторически первой доказанной формой центральной
предельной теоремы явилась теорема Лапласа, состоящая
в следующем. Если производится п независимых опытов,
в каждом из которых событие А появляется с
вероятностью р, то при больших п справедливо приближенное
равенство:
//^}-Ф(а), A0.2.15)
где Yn — число появлений события Л в п опытах; q ==
= 1 — р\ Ф(х) — функция Лапласа.
Выведем формулу A0.2.15) как следствие
центральной предельной теоремы для одинаково распределенных
слагаемых. «Нормированная» случайная величина
Zn={Yn-np)/U^, A0.2.16)
связанная с Yn липейной зависимостью, строго говоря,
дискретна, так же дискретна с. в. У„, распределенная
по биномиальному закону, но при большом п ее
значения расположены на оси абсцисс так тесно, что можно
ее рассматривать как непрерывную, с плотностью
распределения f(z). Случайная величина Yn имеет
биномиальное распределение с параметрами п, р; ее
математическое ожидание М [Yn] = np', ее дисперсия равна
D [Yn] = npq. НайдвхМ числовые характеристики случай-
420 ГЛ. 10. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИЙ ВЕРОЯТНОСТЕЙ
ной величины A0.2.16) как м, о. и дисперсию линейной
функции от с. в. Ук. Имеем:
М [Zn] = (М [Уп] - пр)/ V^fq = (пр - пр)/ V^pq - 0
D[Z,J-1; o[Zn]-U
Таким образом, случайная величина Zn A0.2.16)
имеет не зависящие от п числовые характеристики т = 0,
о=1 (потому мы и перешли к св. Zn от Yn).
п
Учитывая, что Yn ¦= 5 %и где Х{ — индикатор собы-
тия А в 1-м опыте, убеждаемся, что св. Zn A0.2.16)
есть сумма п независимых одинаково распределенных
случайных величин. Применяя центральную предельную
теорему для одинаково распределенных слагаемых,
убеждаемся, что при большом числе опытов п с. в. Zn имеет
распределение, близкое к нормальному, с параметрами
т ~ 0; о = 1, откуда и следует справедливость формулы
A0.2.15).
Теорема Лапласа дает возможность приближенно
находить вероятности значений случайных величин, рас-
нределенпых по биномиальному закону при больших
значениях параметра щ при этом вероятность р не должна
быть ни слишком большой, ни слишком малой.
Практически можно судить о возможности замены
биномиального распределения нормальным по тому,
выполнены ли при данных пир условия:
np-3bifq>0; пр + Sy'npq <п. A0.2.17)
Если эти условия соблюдены, то можпо вычислять
вероятности Ри = Р {Yn = к} как приращение
нормальной функции распределения па участке от Л до Л+1:
Рк = р {Yn - к} « F (к + 1) - F (k)t A0.2.18)
где F (х) — функция распределения нормального закона:
-т\/о). A0.2.19)
Подставляя в A0.2.19) т=*пр и o^l/npq, получим:
F(«)- 0,5 + Ф{{х - np)linpq). A0.2.20)
Вычисляя приращение этой функции на участке от
к до к + 1, получим:
y A0.2.21)
10.2. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА 421
Теорему Лапласа A0.2.15) можно записать в
несколько ином виде, если перейти обратно от нормированной
св. Zn A0.2.16) к св. Yn — числу появлений события
в п опытах, связанной с Zn линейной зпргтгимостыо:
Уп = l/npqZn + np.
Фупкция распределения случайной величины Yn при
большом п будет сколь угодно близка к нормальной
функции распределения с параметрами ту — пр\ оу ==»
Р {Yn < у} = F (у) = 0,5 + Ф ((у -
а вероятность попадания случайной величдпы Yn на
любой участок от а до р приближенно равна
откуда — другая форма записи теоремы Лапласа:
A0.2.22)
npq
Рассмотрим ряд примеров, в каждом из которых для
решения задачи следует применить ту или другую форму
центральной предельной теоремы.
Пример 1. Имеется п идентичных технических
устройств (ТУ), время безотказной работы каждого 1-го из
которых — случайная величина 7\, распределенная по
показательному закону с параметром К, одинаковым для
всех ТУ. Число п собранных в такую систему ТУ
достаточно велико. Случайные величины 7\, 7'2, ..., Т{, ...
..., Тп независимы между собой. В случае отказа ?-го
ТУ происходит мгновенное и безотказное переключение
на следующие но порядку (i+l)-e ТУ (i + Kn).
Общее время Г безотказной работы системы ТУ равно
сумме времен Т{:
п
Г = S Тг- A0.2.23)
Найти приближенно вероятность того, что система ТУ
проработает безотказно время, не меньшее заданного т:
A0.2.24)
(поскольку с в. Т непрерывна, знак равенства можно
отбросить).
422 ГЛ. 10. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИЙ ВЕРОЯТНОСТЕЙ
Решение. Согласно центральной предельной
теореме для одинаково распределенных слагаемых, с. в. Т
A0.2.23) будет распределяться приближенно по
нормальному закону с параметрами:
п п
m = м[Т] = 2м[Tt] = -j-; Dm
Находим приближенно вероятность A0.2.24):
Р{Г>т}-1-Р{7><т}=»1-^(тI
где F(t)— функция нормального распределения с
параметрами
m = пД; о = Уп/К.
Для нормального закона функция распределения
равна:
где Ф(х)— функция Лапласа.
Поэтому
Пример 2. Станок с числовым программным
управлением выдает за смену гс=1000 изделий, из которых
в среднем 2% дефектных. Найти приближенно
вероятность того, что за смену будет изготовлено не менее
970 доброкачественных (недефектных) изделий, если
изделия оказываются доброкачественными независимо друг
от друга.
Решение. Вероятность р изготовления
доброкачественного изделия: р = 0,98, Y — число
доброкачественных изделий; число независимых опытов п = 1000.
Проверяем, выполнены ли условия A0.2.17); находим
М [Г] - пр = 980;
4,43;
пр - За, « 980 - 13,3 > 0; пр + Зау < 1000.
Следовательно, пользоваться нормальным законом
можно; применяя теорему Лацласа в форме A0.2.22),
10.2. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА 423
находим:
Р {Y > 970} = Р {970 < Y < оо}«015-ф(^^-)« 0,988.
Итак, искомая вероятность достаточно велика (равна
0,988), но все же с вероятностью 0,012 можно ожидать,
что число доброкачественных изделий за смену будет
меньше, чем 970. >
Пример 3, Для условий предыдущего примера
определить, на сколько доброкачественных изделий «у
должен быть рассчитан заготовленный для них бупкер,
такой, чтобы вероятность его переполнения за смену не
превысила 0,01.
Решение. Найдем у из условия
P{y<V}^P{^<T} = 1-0,01 = 0,99.
Ищем такое значение у = y, прп котором функция
распределения случайной величины Yn
F (!/)= 0,5 + Ф((у -ту)/оу)= 0,99,
то есть Ф((т - 980)/4,43)= 0,99 - 0,5 = 0,49.
По таблиц функции Лапласа (см. приложение 2)
находим аргумент, при котором функция Лапласа равна
0,49; он приближенно равен 2,33; отсюда
2,33; у « 980 + 10,32 » 990. *
Пример 4. Железнодорожный состав состоит из п
вагонов; вес каждого вагона в тоннах — случайная
величина X с м. о. тх и с. к. о. <тж. Число вагонов п —
большое (несколько десятков). Локомотив может везти вес
не больше q (топп); если вес состава больше q (тонн),
приходится прицеплять второй локомотив. Найти
вероятность того, что одного локомотива не хватит для
перевозки состава.
п
Решение. Обозначим Q = 2 %г ве& состава. На
i
основании центральной предельной теоремы при
достаточно большохм п с. в. Q распределена приближенно по
нормальному закону с параметрами тя = птх\ оч =
У У по*.
424 ГЛ. 10. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Искомая вероятность равна единице минус функция
распределения случайной величины Q:
Р{<?> ff) - 1 - [0,5 + Ф ((?- тхп)/{ Vnax)l >
A0.2.25)
Пример 5. Решить предыдущую задачу, по если
состав содержит Wt вагонов, п2 платформ и п3 цистерн;
вес Xi вагона имеет математическое ожидание т1 и
дисперсию Di\ вес платформы Х2 — характеристики m2, D2y
вес цистерны Х3 — характеристики т3, D3. Величины пи
Di; n2j D2; n3i Dz имеют один и тот же порядок,
причем пи п2, п3 достаточно велики.
Решение. По теореме Ляпунова (условия которой
выдержапы, так как число п — п^ + п2 + п3, вообще,
конечно) можно утверждать, что при достаточно большом
п вес состава Q имеет приближенно нормальное
распределение с характеристиками
зз
mq "= 2 ПгГП\\ Dq = 2 niDh Oq = V Dq.
Вероятность того, что одного локомотива не хватит
для перевозки состава, приближенно подсчитывается по
формуле
mq)/Gq). >
Пример 6. Показать, что при большом значении а
вероятности Р^ = Р {X = к} для с. в. X, распределенной
по закону Пуассона с параметром а, можно
приближенно подсчитывать по формуле
A0226)
Д_ф;
\ Va 1 \ V
где Ф(^)— функция Лапласа.
Решение. В примере 3 п. 9.4 мы показали, что
распределение Пуассона устойчиво по отношению к
операции сложения. Поэтому с. в. X можно представить в
виде:
10.2. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА 425
где Хг — независимые, одинаково распределенные с. в.,
распределенные по закону Пуассона с параметром а/п.
С другой стороны, при достаточно большом « св. I по
центральной предельной теореме будет иметь
приближенно нормальное распределение с параметрами тх = а;
Дс = а. Следовательно, Р{Х = /с}= "?f*<?~a будет
приближенно равна вероятности того, что с. в. X,
распределенная по нормальному закону с параметрами тх = а; Д* =
= а, попадет в интервал (/с —0,5; к + 0,5):
Эта формула дает вполне удовлетворительный по
точности результат при а>20. Из A0.2.26) следует, что
Щгп, а)=^Р(к, а)«Фр+^~а) + 0,5. > A0.2.27)
Пример 7. ТУ состоит из большого числа п
одинаковых элементов, работающих независимо. Каждый
элемент имеет очень малую вероятность отказа р. Пользуясь
аппаратом характеристических функций, вывести
расчетные формулы для определения закона распределепия с. в,
X — числа отказавших элементов.
Решение. Случайная величина X распределена по
биномиальному закону с параметрами пир:
Р{Х = т} = Спр q
Характеристическая функция св. X (см. (8.9.12))
имеет вид:
il) [
Разложим эту функцию по малому параметру р и ог*
раничимся четырьмя членами:
C + реи)п « 1 — пр A — еи) +
Разложим также характеристическую функцию с. в. X,
распределенной по закону Пуассона (см. (8.9.13)) с
параметром пр (считая его малым):
-Пр{1- е"
е")
426 ГЛ, 1OS ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Если величина пр мала {пр < ОД), то можно
приближенно считать, что {q + peli)n « e-npd-e**) Hj
следовательно,
P(X — m\ — Гтптпп~т ~ (ПР^ p-np (if) О 9Я^
Так, при w==108 и p = 10" (w/? = 0,l) имеем
m
(^p) —np
ml
m
C™pm qn-m
Mm np
ml
0
0,904837
0,904837
3
0,000151
0,000151
l
0,090484
0,090484
2
0,0045240
0,0045240
2
0,999996
0,999996
т. е. совпадение очень точное. >
Пример 8. Произвести аппроксимацию нормального
закона с параметрами тх и Dx законом Эрланга тг-го
порядка с параметром К (см. F.4.8)).
Решение. На основании центральной предельной
теоремы можно считать, что с. в. Т(пI распределенная по
закону Эрланга гс-ого порядка (га>10), будет
приближенно распределена по нормальному закону с
параметрами М [Г(п>] — п/к; D [Т(п)] = w/Я2. Следовательно, с. в.
X с нужным нам нормальным распределением
определяется через Т(п) формулой
X - Т(п) - п/Х + тх,
а величина К определится из условия
Dx = D [1\п)] - п/Х\
откуда _
Х- Vn/VDX. >
Пример 9. Провести аппроксимацию нормального
закона с параметрами тх и Dx с помощью суммы п не-
10.2. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА 427
зависимых с. в. Хь ..., Хп, распределенных равномерно
в интервале @, 1).
Решение. На основании центральной предельной
теоремы при большом п случайная величина
Уп - 2 xi
распределена приближенно по пормалыюму закону с
параметрами
М [Yn] = пМ [Хг] = ^-; D [Уп] = nD [Хг] « JL
Нужную нам случайную величипу X представим как
линейную функцию случайной величины Yn:
X = aYn + b. A0.2.29)'
Находим /
тх = а-тг + b; D*= a i&-
Откуда находим коэффициенты а и Ъ в формуле A0.2.29)
а -
Итак, чтобы получить случайную величину X,
распределенную приближенно по пормалыюму закону, падо
сложить достаточно большое число п независимых
случайных величин, распределенных равномерно в интервале
(О, 1) и подвергнуть их сумму линейному
преобразованию A0.2.29).
В практике работы с ЭВМ при моделировании
случайных явлений получают нормально распределенные
случайные величины именно таким способом Опыт
показывает, что вполне удовлетворительную точность
можно получить уже при п = 6; числа п = 10 -f- 12 за глаза
достаточно. >
Пример 10. В кассе учреждения имеется сумма
d = 3500 (руб.). В очереди стоит гс = 20 лиц. Сумма X,
которую надо выплатить отдельному лицу — случайная
величина с математическим ожиданием тл=150 (руб.)
и средним квадратическим отклонением а* = 60 (руб.).
Найти вероятность того, что суммы d не хватит для
выплаты денег всем людям, стоящим в очереди.
Решение. На основании центральной предельной
теоремы для одинаково распределенных слагаемых при
428 ГЛ. 10. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
большом п (а п = 20 практически можно считать
«большим»), случайная величина
п
Yn = 2j Xif
где Х{ — сумма, которую надо выплатить ?-му лицу,
имеет приближенно нормальное распределение с
параметрами:
тУп = п. тх\ Dyn = nDx; оУп
или
Шуп = 20-150 = 3000; оУп = /20- 60 « 268;
Р {Гп> 3500} - 0,5 — Ф (C500 - 3000)/268)« 0,032.
Итак, с вероятностью около 3% имеющейся в кассе
суммы не хватит для выплаты всем, стоящим в
очереди.
Пример И. В условиях предыдущего примера:
какую сумму а нужно иметь в кассе для того, чтобы
вероятность того, что ее не хватит для выплаты всем
стоящим, стала равна 0,005?
Решение. Имеем условие Р {Yn > а) = 0,5 — Ф ((а—
- 3000)/268) = 0,005, т. е. Ф((а-3000)/268)-= 0,495.
По таблице Ф(х) приложения находим аргумент
функции Лапласа, при котором она равна 0,495:
п oOUU ОГО *}ПС\Л
—2ё8~ ^ 2'58' откУДа а = 3691*
Итак, сравнительно небольшого увеличения суммы а
(от 3500 до 3691) достаточно для того, чтобы
гарантировать выплату всем с очень высокой вероятностью
0,995. >
Пример 12. Монета подбрасывается я = 1000 раз.
Рассматривается св. X — число выпавших гербов.
Определить интервал возможных значений с. в. X,
симметричный относительно м. о. этой с. в., в который она
попадает с вероятностью 9* = 0,997.
1000
Р е ш е н и е. X =* 2 Хь где Х{ — число выпавших гер-
i=l
бов при 1-м бросании:
|0— если при i-м бросании выпала цифраг
\ если при 1-м бросании выпал терб.
м
|0
\l
10.2. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА ^29
М [Хг] = 0,5; D [Хг] = 0,5-0,5 = 0,25 (i - 1, 2, ..., 1000)
1000
m, = M[I]=2M [Хг] = 0,5.1000 - 500;
1000
J5X = D [X] - 2 D [Хг] - 0,25.1000 = 250;
На осповапии цептралыюй предельной теоремы с. в. X
распределена нормально, следовательно,
Р (| X - тх | < е} - 2Ф (-pj = 0 = 0,997; Ф (iL)«0,4985.
По таблицам Ф(х)— функции Лапласа паходим:
— » 2,97; е «0-^2,97 « 15,8 • 2,97 « 47,0.
Искомый интервал будет:
(гоя-в; тх + е)-E00-47; 500 + 47)-D53; 547).
Итак, с очень большой вероятностью 9* = 0,997 можно
утверждать, что число выпавших гербов будет заключено
в пределах от 453 до 577 (об этом уже говорилось в
п. 1.1). >
ГЛАВА 11
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
11.1. Предмет и задачи
математической статистики
Ранее в книге мы уже говорили (правда, довольно
бегло) об экспериментальных, статистических аналогах
таких понятий теории вероятностей, как «вероятность
события», «функция распределения», «плотность
вероятности», «математическое ожидание» и т. д. и о том, как
можно по статистическим аналогам приближенно
оценивать интересующие нас характеристики. В данной
главе, опираясь на уже знакомый читателю
математический аппарат, мы рассмотрим эти вопросы более
подробно.
Математической статистикой называется наука,
занимающаяся методами обработки опытных данных, полу-
ченпых в результате наблюдений над случайными
явлениями. Любой такой результат можно представить как
совокупность значений, принятых в результате п опытов
какой-то случайной величиной или системой случайных
величин. Поэтому все изложение здесь будем вести на
языке случайных величин.
Перед любой наукой ставятся, в порядке возрастания
сложности и важности, следующие задачи: 1) описание
явлений; 2) анализ и прогноз; 3) выработка
оптимальных решений.
Стоят такие задачи и перед математической
статистикой.
Пример задачи первого типа: в наше распоряжение
поступил статистический материал. Как его упорядочить,
представить в наиболее удобном для обозрения и анализа
виде? Какими формами таблиц, графиков лучше всего
воспользоваться?
Пример задачи второго типа: как, на основании
статистических данных, оцепить, хотя бы приближенно,
интересующие пас характеристики, папример, м. о.,
дисперсию и с. к. о. случайной величины, пад которой велись
ii.i. ЗАДАЧИ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 431
наблюдения? С какой точностью, при дапном количестве
опытов, будут оцениваться эти характеристики?
Пример задачи третьего типа: пазпачить число
опытов га, достаточное для того, чтобы разница между
частотой события р* и его вероятностью р с достаточно
большой вероятностью не превзошла заданной величины е,
или для того, чтобы ошибка от замены математического
ожидания средним арифметическим (опять-таки с
достаточно высокой вероятностью) была не больше
заданной. Одной из характерных задач третьего типа является
задача проверки правдоподобия гипотез. Ставится она
так: в нашем распоряжении имеется совокупность
опытных данных, относящихся к одной или нескольким
случайным величинам. Спрашивается, противоречат ли эти
данные той или другой гипотезе? Например, гипотезе о
тохМ, что случайная величина X распределена по
закону с плотностью /(.г), или о том, что две случайные
величины X, Y пекоррелированы и т. п. Все такие
задачи решаются по определенной схеме: выбирается
какая-то мера отклонения R экспериментальных данных
от гипотетических, являющаяся функцией наблюденных
в опыте значений; находится (точно или приближенно)
закон распределения с. в. R и, на основе этого закона,
вычисляется вероятность того, что с. в. 7? примет
значение не меньшее, чем то значение г0, которое
фактически зарегистрировано:
r0). (li.i.i)
Если эта вероятность очень мала, то можно считать
событие R>rQ практически невозможным, а опытные
данные противоречащими гипотезе; последнюю
нужно отвергнуть. Если же она не мала, то опытный
материал не противоречит выдвинутой гипотезе
(хотя и не подтверждает ее).
Таким образом, в результате проверки правдоподобия
гипотезы может быть сделан один из выводов: 1)
отбросить гипотезу, как противоречащую опытным данным;
2) не отбрасывать гипотезу, считать ее приемлемой.
Напомним читателю, что назначение той вероятности,
которую следует считать «очень малой», в значительной
мере условно и носит на себе неизбежно черты
произвола; но не носят ли ее на себе в той или иной мере
все решения, которые мы принимаем в нашей
практической деятельности? Ни одно из них мы не принимаем
432 ГЛ. 11. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
послушно, с закрытыми глазами, слепо доверяясь какой-
то теории. Размышляющий, оценивающий,
сопоставляющий человеческий разум всегда должен первенствовать
в любой задаче выбора решения. Теория должна
подсказать человеку разумный выбор, оценить последствия
каждого варианта выбора, и в этом ее основное
назначение.
МатвхМатическая статистика не представляет
исключения. Она помогает экспериментатору лучше разобраться
в опытных данных, полученных в результате наблюдений
над случайными явлениями; оцепить, значимы или не
значимы наблюденные факты; принять или отбросить те
или иные гипотезы о природе явления.
D настоящей главе мы рассмотрим вкратце и в
самом элементарном виде задачи всех трех типов:
способы описания результатов опыта; способы обработки
опытных данных и оценки по ним интересующих нас
характеристик случайного явления; наконец, способы
выработки разумных решений.
Сделаем одно замечание, относящееся ко' всей главе.
В ней мы будем одни н те же величины рассматривать
то как случайные, то как неслучайные. Пусть читателя
не смущает этот кажущийся парадокс. Дело в том, что
до опыта, пока он еще не выполнен, значения случайных1
величии еще неизвестны. После того, как опыт уже
произведен, эти случайные величины приняли вполне
определенные значения я, значит, уже не случайны. При
решении некоторых задач математической статистики мы
будем рассматривать результаты наблюдений как случай-^
шло, находить их числовые характеристики, законы
распределения и т. д. Если же в этом надобности не будет,
мы ограничимся рассмотрением результатов серии опытов
как самых обычных, неслучайных величин.
11.2. Первичная статистическая
совокупность. Ее упорядочение.
Статистическая функция распределения
Если наблюдаемая с. в. X дискретна, то
статистическим аналогом ряда распределения является
статистический ряд, полностью аналогичный ряду распределения
с. в. X, с той разницей, что вместо вероятностей р% =•
и Р {X = я*} в нем стоят частоты соответствующих со-
ii.2. ПЕРВИЧНАЯ СТАТИСТИЧЕСКАЯ СОВОКУПНОСТЬ
433
бытии: pi = Р*{Х = хг). На этом вопросе мы больше
не будем останавливаться. Гораздо сложнее (и чаще
встречается на практике задача обработки опытов над
непрерывной св. X. Займемся описанием
результатов серии из п независимых опытов, в каждом из
которых зарегистрировано значение непрерывной с. в. X,
и простейшей обработкой этих результатов.
Первое, что попадает в наши руки — это протокол,
в котором зарегистрированы: номер опыта к и значение xh,
которое приняла в этом опыте с. в. X. Такой протокол
мы будем называть первичной статистической
совокупностью. Это — совсем еще не обработанный
статистический материал.
II р н м е р. Измерено п = 100 сопротивлений
определенного вида. В табл. 11.2.1 приведены: номер опыта к
и соответствующее значение сопротивления xh (в омах).
Таблица 11.2.1
к
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
xk
87
85
91
94
102
80
75
102
99
101
100
120
122
101
88
80
97
92
91
94
ft
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
xh
82
111
115
99
96
101
115
100
97
91
87
116
121
101
123
97
95
88
104
111
k
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
xh
88
90
101
95
93
92
88
94
98
99
102
101
122
99
97
95
105
112
116
118
h
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
xh
108
95
99
92
100
118
103
102
89
90
94
106
112
122
100
92
93
82
111
102
h
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
xh
84
105
110
102
104
107
120
108
107
98
96
106
110
115
95
109
111
103
88
108
Рассмотрение и осмысление таблицы такого типа
(особенно при большом числе опытов п) затруднительно,
и по ней практически нельзя представить себе,характер
распределения с. в. X. Первый шаг к осмыслению
материала — это его упорядочение, расположение в по-
434
ГЛ. 11. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
рядке возрастания значений с. в. Протокол результатов
опыта, в котором они перенумерованы и расположены
в порядке возрастания, будем называть упорядоченной
статистической совокупностью, В табл. 11.2.2 приведены
те же данные, что в табл. 11.2.1, но расположенные в
порядке возрастания значений с. в. X. Номер значения
будем обозначать i (в отличие от номера опыта к). Если
в таблице 11.2.1 одно и то же значение встречается
несколько раз, будем писать его столько раз, сколько оно
встретилось.
Таблица 11.2.2
i
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
xi
75
80
80
82
82
84
85
87
87
88
88
88
88
88
89
90
90
91
91
91
i
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
92
92
92
92
93
93
94
94
94
95
95
95
95
95
95
96
96
97
97
97
г
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
xi
97
98
98
99
99
99
99
99
100
100
100
100
101
101
101
101
101
101
102
102
г
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
xi
102
102
102
102
103
103
104
104
105
105
106
106
107
107
108
108
108
109
НО
110
г
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
хг
111
111
111
111
112
112
115
115
115
116
116
118
118
120
120
121
122
122
122
123
По упорядоченной статистической совокупности типа
табл. 11.2.2 можно уже построить статистическую
функцию распределения:
F*(x) = P*{X<x}. A1.2.1)
Функция F* (х) — разрывная ступенчатая функция,
непрерывная слева, равная нулю левее наименьшего
наблюденного значения с. в. X и единице — правее
наибольшего. Теоретически она должна иметь п скачков,
где п — число опытов, а величина каждого скачка должна
быть равна 1/п — частоте наблюденного значения с. в.
Практически, если одно и то же значение наблюдалось
li.2. ПЕРВИЧНАЯ СТАТИСТИЧЕСКАЯ СОВОКУПНОСТЬ
435
несколько раз, соответствующие скачки сливаются в один,
так что общее число скачков равно числу различных
наблюденных значений с. в. Каждый скачок в точке Xi
равен «кратности» 1г значения Хг в статистической
совокупности, деленной на число опытов гс.
Например, для данных табл. 11.2.2 статистическая
функция распределения F*(x) ведет себя следующим
образом: до точки # = 75 (и включая ее) она равна пулю;
в ней F*(x) совершает скачок, равный 1/тг = О,О1 и
сохраняет значение 0,01 до точки х = 80 (включая ее);
здесь она делает скачок, равный 2/п = 0,02, становится
равной 0,03 и сохраняет это значение до точки х = 82
(включая ее) и так далее.
Вычисляя таким образом функцию F*(x), получим
таблицу ее значений на интервалах между скачками
(табл. 11.2.3).
75 <
80 <
82 <
84 <
85 <
,87 <
88 <
89 <
90 <
91 <
92 <
93 <
94 <
95 <
96 <
97 <
98 <
99 <
100 <
X
*<75
С*<80
Cs<82
-*<84
С*<85
С*<87
-я<88
С*<89
С*<90
С я<91
Ся<92
Ся<93
-дг<94
С*<95
Ся<96
С*<97
^ж<98
:а:<99
С х < 100
: * < 101
F* (х)
0
0,01
0,03
0,05
0,06
0,07
0,09
0,14
0,15
0,17
0,20
0,24
0,26
0,29
0,35
0,37
0,41
0,43
0,48
0,52
ас
101 < х ^
102 < х з
103 < х <
104 < z s
105 < ж ^
106 < х $
107 < х <
108 < х <
109 < ж <
110 < я? <
111 < я <
112 < Ж
115 < * <
116 <Ж
118 < ж
120 < х <
121 < х <
122 < я ^
Ta6j
^ 102
^ 103
S 104
? 105
?106
С 107
?108
?109
? 110
?111
?112
? 115
?116
? 118
? 120
? 121
С 122
? 123
123
гида 11.2.3
F* (х)
0,58
0,64
0,66
0,68
0,70
0,72
0,74
0,77
0,78
0,80
0,84
0,86
0,89
0,91
0,93
0,95
0,96
0,99
1,00
По материалам этой таблицы строим график функции
F*(x) (рис. 11.2.1). Жирными точками, как всегда,
помечены значения функции в точках разрыва.
Рис. 11.2.1, в отличие от табл. 11.2.1, уже дает
некоторое представление о характере распределения с. в. Х\
разумеется, самое общее представление, так как ясно,
ГЛ. И. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
\
V
1 f
-
-
-
-
-
V
v
1
123 SO
CN
oo
776 ;
CM
сэ
708 \
CO
C3
702
C5
CO
s]
cc
CN
CO
Q
CO
°O
CM
CO
- a
li.3. ГРУППИРОВАННЫЙ СТАТИСТИЧЕСКИЙ РЯД 437
что некоторые особенности кривой F*(x) случайны и
связапы с выбором именно тех, а не других сопротивлений
для измерепия. Другие 100 опытов дали бы несколько
иной график функции F*(x), но общая тенденция
сохранилась бы. При неограниченном увеличении п скачки
кривой F*(x) станут более мелкими; кривая F*(x)
станет плавпее, будет приближаться (сходиться по
вероятности) к функции распределения F(x) случайной
величины X. Тем не менее, такой громоздкий и трудоемкий
способ получения функции распределения F(x) вряд ли
может быть рекомендован (не забудем, что каждый опыт,
вообще говоря, стоит денег). На практике применяются
другие, более простые способы построения законов рас-
пределепия случайных величии по опытным даппым.
11.3. Группированный статистический
ряд. Гистограмма
Для того, чтобы составить себе общее представление
о законе распределения с. в. X, незачем фиксировать
каждое наблюдепное зпачепие и строить статистическую
функцию распределения F*(x). Этим целям лучше
служат группированный статистический ряд
и гистограмма.
Для построения группированного статистического
ряда весь участок оси абсцисс, на котором расположены
' значения с. в. X, наблюдавшиеся в опыте, делится на
участки или «разряды». Длины разрядов необязательно
брать равными друг другу: бывают случаи, когда на тех
участках оси абсцисс, где наблюденные значения X
располагаются гуще, удобнее брать разряды более мелкими,
а там, где реже — более круппыми (или объедипять два
или более равных по длине разрядов в один). Границы
разрядов удобно брать «круглыми» числами.
Группированным статистическим рядом называется
таблица, где в верхней строке указаны разряды: от — до
(знак -г), в нижней — соответствующие им частоты:
X:
h
причем 2 Рг == 1*
i=i
Частота р\ события {X^(xh xi+l)} вычисляется как
отношение числа U опытов, в которых значение с. в. X
р* 1 ?\ 1-
Xk-\ * Xh
Pi
438
ГЛ. 11. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
попало в i-й разряд (х{ ч- xi+i), к общему числу п
произведенных опытов.
Сразу же возникает вопрос: а как быть, если
значение с. в. X попало в точности на границу между
разрядами? К какому разряду его отнести? Это неважно:
можно отнести значение либо к левому разряду, либо к
правому (ведь вероятность того, что непрерывная с. в. X
примет заранее заданное значение, равна пулю); мы
остановимся на более симметричном «справедливом»
правиле: если значение с. в. попало в точности на границу
разрядов, разделить его поровну между соседними
разрядами и прибавить по 1/2 к числам 1{ для обоих
разрядов.
Построим группированный статистический ряд для
св. X, рассмотренной в предыдущем п. (табл. 11.2.1,
11.2.2, 11.2.3). Выберем границы разрядов «круглыми»:
G0-4-80); (80 + 90); (90ч-100); A00ч-НО); A10 ч-
.4-120); A20 4-130).
Подсчитывая количество значений с. в., попавших в
каждый разряд (считая половинки от попавших в
границу между разрядами) и деля на число опытов п = 100,
получим группированный статистический ряд:
Разряды
704-80
Частоты 1 0,02
Разряды
Частоты
1004-110
0,29
804-90
0,14
110-4-120
0,15
90-4-100
0,34
1204-130
0,06
A1.3.1)
Деля каждую частоту р\ на длину соответствующего
разряда Д| = xi+i — x* = 10, получим таблицу плотностей
частоты /i:
Разряды
Плотпость частоты
Разряды
Плотность частоты
70-4-80
0,002
1004-110
0,029
804-90
0,014
1104-120
0,015
904-100
0,034
1204-130
0,006
11.3. ГРУППИРОВАННЫЙ СТАТИСТИЧЕСКИЙ РЯД
439
Откладывая по оси абсцисс разряды и строя па
каждом разряде как на основании прямоугольник площади
Pi, получим гистограмму — статистический аналог
кривой распределения (рис. 11.3.1)*).
0,0k-
70 80 90 100 110 120 130 х
Рис. 11.3.1
Имея в своем распоряжении группированный
статистический ряд, мы можем приближенно построить
статистическую функцию распределения F*(z). В качестве тех
значений х, для которых
вычисляется F*(x),
естественно взять границы
разрядов. Так, например,
для с. в. X,
рассмотренной в предыдущем
пункте, пользуясь
группированным статистическим
рядом A1.3.1), находим:
F* G0)
Р*{
= 0;
F* (80)
¦ 0,02;
70
130 х
0f 16; F* A00) - Р* {X < 100} =0,50;
*) В рассмотренном выше примере число опытов было
сравнительно невелико (п = 100) и, соответственно ему, мы взяли
очень псболыноо число разрядов (к = 6), Вообще говоря, для
построения (хотя бы ориентировочного) закона распределения пе-
прерывной с. в. X по опытным данным и число опытов п, и
число разрядов к должны быть существенно больше. Ориентировочно
можпо назвать число опытов п, необходимое для того, чтобы с
удовлетворительной точностью представить себе распределение
интересующей нас с. в. X: оно должно быть порядка нескольких
сотен. Соответственно число к разрядов, на которое делится
интервал наблюдавшихся значений с. в., должен быть больше, чем
в рассмотренном нами примере; обычпо его выбирают
порядка 12 4- 20.
440 ГЛ. 11. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
F* A10) = Р* {X < 110} = 0,79; F* A20) = Р* {X < 120} =
= 0,94; F*A30) = l.
График статистической функции распределения
показан на рис. 11.3.2 (точки соединены отрезками прямых),
11.4. Выравнивание статистических распределений
Во всяком статистическом распределении неизбежно
присутствуют элементы случайности, связанные с
тем, что число опытов ограничено, что произведены
именно те, а не другие опыты, давшие именно те, а не
другие результаты. Только при очень большом числе
опытов эти случайности сглаживаются, и явление
обнаруживает в полной мере присущие ему закономерности.
На практике мы почти никогда не располагаем таким
большим числом опытов (наблюдений) и вынуждены
считаться с тем, что любому статистическому
распределению присущи в той или иной мере черты случайности.
Случаен ступенчатый вид статистической функции
распределения непрерывной св.; случайна форма
гистограммы, ограниченной тоже ступенчатой линией.
Неудобно пользоваться такими негладкими функциями при
дальнейшем их преобразовании. Поэтому на практике часто
приходится решать вопрос о том, как подобрать для
данного статистического распределения аналитическую
формулу, выражающую лишь существенные черты
статистического материала, по не случайности, связанные
с недостаточным объемом
-F(x) f*(x) опытных данных. Такая
задача называется
задачей выравнивания
статистических распределений.
Обычно выравниванию
5^-, подвергаются гистограм-
/\ ч. мы. Задача сводится к
g*T I 1 1 1 1 1 т^—. тому, чтобы заменить ги-
х стограмму плавной кри-
Рис. 11.4.1 ной, имеющей достаточно
простое аналитическое
выражение, и в дальнейшем пользоваться ею в качестве
плотности распределения f(x) (рис. 11.4.1).
Как подобрать наилучшим образом плавную кривую,
выравнивающую "гистограмму? Это задача в
значительной мере неопределенная, как и любая задача об акали-
11.4. ВЫГЛВИИВЛНИЕ РАСПРЕДЕЛЕНИЙ
441
тическом представлении эмпирических функций.
Например, если несколько полученных в опыте точек на
плоскости хОу расположены приблизительно по прямой
(рис. 11.4.2), естественно возникает идея заменить эту
зависимость линейной функцией. Если зависимость явно
нелинейна (рис. 11.4.3), в качестве аппроксимирующей
У
О
х
0
х
Рис. 11.4.3
fix)
Рис. 11.4.2
кривой выбирают параболу, и т. д. При сглаживании
эмпирических зависимостей очень часто исходят из
«принципа наименьших квадратов», считая,
что наилучшим приближением в данном классе функций
является то, для которого сумма квадратов отклонений
обращается в минимум. Вопрос о том, в каком
именно классе функций следует искать наилучшее
приближение, решается уже не математически, а исходя из
соображений, связанных с
физикой решаемой задачи, с
учетом характера эмпирической
кривой и степени точности
наблюдений. Иногда
принципиальный вид функции,
выражающей исследуемую
зависимость, известен заранее из
теоретических соображений; из
опыта же требуется получить
лишь некоторые числепные па-
раметры, входящие в
выражение функции.
Аналогично обстоит дело и с задачей выравнивания
статистических распределений. Принципиальный вид
выравнивающей плавной кривой f(x) выбирается заранее,
исходя из условий возникновения с. в. X, а иногда просто
из соображений, связанных с внешним видом
гистограммы. Например, гистограмма, изображенная на рис. 11.4.1,
явно наводит на мысль о нормальном распределении,
а на рис. НАЛ —о показательном.
X
Рис. 11.4.4
442 ГЛ. 11. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Условия возникновения случайной величины также
должны учитываться при выборе типа выравнивающей
кривой. Если, как это нередко бывает на практике, с. в. X
складывается из многих независимых или слабо
зависимых слагаемых, сравнимых по порядку своего влияния
на рассеизание суммы, естественно в качестве
выравнивающей взять нормальную плотность:
/(д?)-[1/(оУ2я)]ехр{-(а;-то)а/Bо8)} A1.4.1 J
и подбирать, исходя из опытных данных, только
параметры m и о в выражении A1.4.1). Если же, например,
с. в. X есть расстояние между соседними событиями
потока, то в качестве выравнивающего закона можно взять
показательный (см. п. 6.2) или какой-нибудь из законов
Эрлапга (см. п. 6.4).
При этом необходимо иметь в виду, что любая
аналитическая функция /(х), с помощью которой
выравнивается гистограмма, должна обладать основными
свойствами плотности:
/(*)>0; J f(x)dx=L A1.4.2)
— 00
Что касается параметров, входящих в выражение
функции /(я), то их подбирают так, чтобы наилучшим
образом согласовать выравнивающее аналитическое
распределение со статистическим. При этОхМ пользуются
различными методами; чаще всего — методом
моментов, состоящим в том, чтобы важнейшие моменты — м. о.,
дисперсия, иногда высшие моменты: |л3, щ у
выравниваемого и выравнивающего распределений
совпадали*).
Пример. Угол ф, определяющий высоту
наблюдаемого объекта над горизонтом, измеряется с помощью
специального прибора. Случайная величина X—ошибка
измерения угла ср. С целью исследования точности прибора
произведено п = 500 измерений этой ошибки (в
тысячных долях радиана). Результаты измерений сведены в
группированный статистический ряд:
*) Моментами выше четвертого порядка пользоваться
нерационально, так как точность вычисления момептов резко падает с
увеличением их порядка,
11.4. ВЫРАВНИВАНИЕ РАСПРЕДЕЛЕНИЙ
443
X:
Разряды
Частоты р\
Число
попаданий в j-й
разряд п.
Разряды
Частоты /?*
Число
попаданий в i-й
разряд Пц
(_4)Ч-(-3)
0,012
6
0-М
0,240
120
(_3)-r(-2)
0,050
25
1-2
0,176
83
(-2L-
0,144
72
24-3
0,092
46
(-i)-^o
0,266
135
34-4
0,020
10
A1.4.3)*).
Построить гистограмму распределения. Выровнять
статистическое распределение с помощью нормального
закона:
подобрав параметры т и а так, чтобы сохранить
неизменными первые два момента статистического
распределения: математическое ожидание и дисперсию.
Решение. Для этого нужно знать статистическое
среднее тх и статистическую дисперсию Dx св. X. Мы
знаем (п. 10.1), что при большом числе опытов п
среднее арифметическое наблюденных значений с. в.
сходится по вероятности к ее м. о., а средпее арифметическое
их квадратов — ко второму начальному моменту а2[Х].
В данном случае мы не располагаем всеми
наблюденными п = 500 значениями с. в. X, да если бы и располагали,
вычисление моментов (без помощи ЭВМ) было бы
слишком трудоемким. Ограничимся определением так
называемых «грубых» моментов по группированному ряду
A1.4.3). Делается это так: выбирается в качестве
«представителя» i-ro разряда его середина и этому значению
444 ГЛ, it. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
хг приписывается частота Р\. Приближенное значение
статистического среднего тх найдем как сумму
произведений всех Xi ua р% *
ml = — 3,5-0,012 — 2,5.0,050-1,5-0,144-0,5-0,266 +
+ 0,5-0,240 + 1,5-0,176 + 2,5-0,092 + 3,5-0,020« 0,168,
Статистический второй начальный момент:
а* [X] = (— 3,5J.0,012 + (- 2,5J.0,050 + (-1,5J-0,144+
+ (_0,5J- 0,266 + 0,52-0,240 + 1,52.0,176 + 2,52-0,092 +
+ 3,52-0,020 « 2,126;
вычитая из а2 [X] квадрат среднего значения \w<xj\
-3 -2 -1 0 1 2 3 к ос
получим статистическую дисперсию:
_ Dl & 2,098,
откуда а* = |/ D*x « 1,448.
Полагая в выражении нормальной плотности
т-0,168; а = 1,448
и пользуясь таблицей приложения 4 в [4], получим
значения на границах разрядов:
/(_4) = 0,0045; /(-3) = 0,0256;
/(-2) = 0,0895; /(-1) = 0,1986;
/@) = 0,2740; /A) = 0,2343;
/B) = 0,1244; /C) = 0,0435.
Гистограмма и выравнивающая ее нормальная
кривая распределения f(x) показаны на рис, 11.4.5.
i 1.5 КРИТЕРИЙ СОГЛАСИЯ х* 445
11.5. Критерий согласия %г
В настоящем пункте мы коснемся одной из задач
третьего типа — проверки правдоподобия гипотез.
Предположим, мы хотим установить, противоречат ли
опытные данные гипотезе о том, что с. в. X распределена по
такому-то закону? Для ответа на такой вопрос
пользуются так называемыми критериями согласия, из которых
мы остановимся только на одном, чаще всего
применяемом, так называемом критерии %2 Пирсона.
Изложим идею этого критерия сначала для случая
дискретной с. в. X с возможными значениями хи xZi ...
• .., xh. Предположим, что произведено п независимых
опытов, в каждом из которых с. в. X приняла
определенное значение. На основе этих опытов составлен
статистический ряд распределения с. в. X:
Pl
A1.5.1)
где рг «¦ щ\п— частота события {X = #J, га<— число
опытов, в которых появилось это событие (t=l, 2, ...
..., /с). Мы выдвигаем гипотезу Я, состоящую в том,
что с. в. X имеет ряд распределения:
11 Х2 I ' * • I Хг I • * • \xh
а отклонения частот р% от вероятностей pi объясняются
случайными причинами. Чтобы проверить
правдоподобность этой гипотезы, надо выбрать какую-то меру
расхождения статистического распределения с
гипотетическим.
В качестве меры расхождения R между
гипотетическим распределением A1.5.2) и статистическим A1.5.1)
при пользовании критерием %г берется сумма
квадратов отклонений Pi — р статистических вероятностей
р* от гипотетических piy взятых с некоторыми «весами» с»:
R-^cdpl-PiY. (и.5.3)
% Коэффициенты с< вводятся потому, что отклонения,
относящиеся к разным значениям р{, нельзя считать
равноправными но значимости: одно и то же по абсолютной
446 ГЛ. 11. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
величине отклонение р% — Р\ может быть
малозначительным, если сама вероятность рг велика, и очень заметным,
если она мала. Поэтому естественно веса с» взять
обратно пропорциональными вероятностям ри Но с каким
коэффициентом попорциональности?
Пирсон доказал (мы этого делать не будем), что если
положить
ct^n/pt, (И.5.4);
то при большом числе опытов п закон распределения
величины R обладает весьма простыми свойствами: он
практически не зависит от закона распределения с. в. X
и мало зависит от числа опытов гс, а зависит только от
числа значений с. в. к и при увеличении п приближается
к распределению %2 (п. 9.7). При таком выборе
коэффициентов d мера расхождения R обычно обозначается %2:
или, вводя величину п под знак суммы и учитывая, что
Pi = Щ/п, где щ — число значений в ?-м разряде {i =
к
= 1, 2, ,.., к); 2 пг = п, получим
i=i
R = X2 = 2 («i - nPifl{nPi). A1.5.5)
i=l
Распределение х2? к&к мы знаем, зависит от
параметра г, называемого «числом степеней свободы». При
пользовании критерием A1.5.5) число степеней свободы
полагается равным числу разрядов к минус число
независимых условий («связей»), наложенных на
частоты Pi. Примерами таких условий могут быть:
S Л « U (И.5.6)
i = l
если мы требуем только того, чтобы сумма частот была
равна единице (это требование накладывается
во всех случаях); или же
k
2 A1.5.7)
если мы требуем, чтобы совпадало статистическое среднее
И.5 КРИТЕРИЙ СОГЛАСИЯ х2 447
с гипотетическим, или же
2(*i-/n*JA =А« (Н.5.8)
i = i
если мы требуем, кроме того, еще п совпадения
дисперсий и т. д.
Для распределения %2 составлены таблицы (см.
таблицу приложения 3). Пользуясь ими, можно для каждого
значения %г и числа степеней свободы г найти
вероятность р того, что величина, распределенная по закону %z,
превзойдет это зпачение. В таблице приложения 3
входами являются: значение вероятности р и число
степеней свободы г; числа, стоящие в таблице, представляют
собой соответствующие значения %2.
Распределение %2 дает возможность оценить
расхождение между гипотетическим распределением A1.5.2)
и статистическим A1.5.1). Если вероятность р очень
мала (не превосходит выбранного нами зпачения «уровня
значимости» а, такого, что событие с вероятностью а
считается уже практически невозможным), это значит,
что опытпые данные противоречат гипотезе Я,
состоящей в том, что св. X имеет распределение A1.5.2):
эту гипотезу надо отбросить. Если же вероятность р
не мала, можно признать расхождения между
теоретическим и гипотетическим распределениями
несущественными и отнести их за счет случайных причин.
Гипотезу II можно считать правдоподобной, или, по крайней
мере, не противоречащей опытным данным.
Подчеркнем, что большое значение вероятности р
(папример, близкое к единице) отнюдь не
свидетельствует о большом правдоподобии гипотезы Я. Это может
говорить, например, о том, что опытные данные
сознательно «подгонялись» под желательное нам
распределение (или просто о том, что число опытов п недостаточно
велико, чтобы распределение величины R стало близко
кх2Ь
Критерий согласия %2 можпо примепять и для
непрерывных случайных величин, если, группируя
статистический ряд, приближенно заменить непрерывную с. в. X
дискретной с возможными зпачепиями хt, х2, ..., ?*, ...
.,., xhi где Xi — середипа г-го разряда (п. 11.3):
Р'г
• • #
р:
• « •
*
Pk
X: " ; ; :, A1.5.9)
448
ГЛ. 11. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
a Pi — частота попадания с. в. X в i-й разряд:
р* = щ/п;
щ — число значений св., попавших в i-й разряд (i='
h
= 1, 2, ..., к); 2«i=^
i=l
Пусть мы хотим выровнять (сгладить)
статистическое распределение A1.5.9) с помощью гипотетической
плотпости j{x). Будем поступать точно так же, как для
дискретной с. в. X, заменяя частоты Pi их
гипотетическими значениями: pi = P (^g (%i, xi+i)} —т. е.
вероятность попадания с. в. X в i-ii разряд, вычисляемая по
формуле:
J f(x)dx;
вместо числа значении с. в.
берется число разрядов к.
Во всем остальном поступаем и рассуждаем так же,
как для дискретной с. в.
Пример 1. Произведено гс = 800 наблюдений над
случайной величиной X, возможные значения которой:
#ie0; #2=1; ...; ?f+i = i; ...; Яп — Ю. Результаты 800
опытов представлены в виде таблицы:
Значение х^
Число появлений п{
Значение хг
Число появлений п{
0
1
25 1 81
5 1 6
106
80
2
124
7
35
3
146
8
16
4
175
9 1 10
6 I 6
Требуется оценить правдоподобие гипотезы Я,
состоящей в том, что X распределена по закону Пуассона
с параметром а, равным статистическому среднему
наблюденных значений св. Х.Б качестве уровня
значимости принять а = 0,15.
Решение. Деля пг на п, получим группированный
статистический ряд. Собственно говоря, оп пам не
нужен, так как в формуле A1.5.5) фигурируют не частоты
Pit а только числа п{; приводим здесь этот ряд для
наглядности.
U.5. КРИТЕРИЙ СОГЛАСИЯ
449
*
Pi
xi
*
Pi
0
0,031
5
0,132
1
0,101
6
0,100
2
0,155
7
0,044
3
0,183
8
0,020
4
0,219
9
0,008
10
0,008
Найдем статистическое среднее mxt
ml
* - 0-0,031 + 1-0,101 + 2-0,155 +
+ 3-0,183 + 4-0,219 + 5-0,132 + 6-0,100 + 7-0,044 +
+ 8-0,020 + 9-0,008 + 10-0,008 «&
Вычислим вероятности р<, соответствующие закону
Пуассона, по формуле:
а1 -а
е
где а = т* — 3,716.
"По найденному значению а = 3,716 рассчитываем ве«
роятности р{:
х\
Pi
*i
Pi
0
0,0243
6
0,0890
1
0,0904
7
0,0472
2
0,1680
8
0,0219
3
0,2081
9
0,0091
4
0,1933
5
0,1437
10
0,0033
По формуле {11.5.5)' находим значение %*:
10
Число степеней свободы г в данном случае равно
числу значений случайной величины (ft = 11) минус едини*
15 Теория вероятностей и ее
450 ГЛ. П. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
ца (первое условие: 2 р% = 11 и минус еще единица —
совпадение гипотетического м. о. со статистический: г^3
— И—1—1 = 9. По таблице приложения 3 находим для
г = 9 и 5С2 = 15, р = 0,1. Таким образом, в данном
примере гипотеза II о пуассоновском распределении с. в. X
противоречит опытным данным и ее надо отбросить,
так как р « ОД < а достаточно мала. >
Пример 2, Пользуясь критерием согласия х2
Пирсона, определить, не противоречит ли опытным данным
гипотеза о том, что св. X, приведенная в п. 11.4
(статистическое распределение A1.4.3)), распределена по
нормальному закону с теми же м. о. и дисперсией, уровень
значимости а = 0,1.
Решение. Определяем число степеней свободы г
распределения х2; оно равно числу разрядов А; = 8 минус
8
число наложенных связей: 1) 2 Pi в U 2) w = mx =
- 0,168; 3) ах - VTTX - <? -1,448; г - 8- 3 = 5.
Составим таблицу вероятностей попадапии с. в. X,
подчиненной нормальпому закону с параметрами m =
«=0,168 и а = 1,448 в разряды
Разряды
Вероятности р{
Разряды
Вероятности р^
(-4Ж-3)
0,0126
0-М
0,2668
(-3L-
-Н-2)
0,0522
1-г2
0,1789
(-2L-
-Н-1)
0,1422
2-3
0,0770
(-1L-0
0,2433
34-4
0,0212
A1.5.10)
Пользуясь данными таблиц A1.4.3) и A1.5.10),
вычислим значение х* [п в 500):
8
Я» =. 2 («i - npifKnpi) = 3Л99.
По таблице приложения 3 при г« 5 и х2 я 3,99
находим значение р»0,55; это свидетельствует о том, что
выдвинутая нами гипотеза о нормальности распределения
с. в, X не противоречит опытным данным. >
Н.б. ОЦЕНКА ЧИСЛОВЫХ ХАРАКТЕРИСТИК 451
11.6. Оценка числовых характеристик
случайных величин по ограниченному
числу опытов
Выше мы рассмотрели некоторые задачи
математической статистики, относящиеся к обработке опытных
данных. Это были задачи нахождения закона распределения
с. в. по результатам опытов. Для того, чтобы такая
задача имела смысл, нужно располагать достаточно
обширным статистическим материалом, порядка нескольких
сотен опытов (наблюдений). Однако на практике нередко
приходится иметь дело со статистическим материалом
весьма ограниченного объема — с двумя-тремя десятками
наблюдений, часто даже меньше. Это обычно связано с
дороговизной и сложностью каждого отдельного опыта.
Такого ограниченного материала явно недостаточно для
того, чтобы найти заранее неизвестный закон
распределения случайной величины, но все же он может быть
использован для получения некоторых сведений о ней;
например, на основе ограниченного статистического
материала можно определить — хотя бы ориентировочно,—
важнейшие числовые характеристики с. в.:
математическое ожидание, дисперсию, иногда —- высшие моменты.
На практике нередко бывает, что вид закона
распределения известен заранее, а требуется найти только
параметры, от которых он зависит (например, т и а для
нормального закона). Наконец, в некоторых задачах
закон распределения с. в. вообще несуществен, а требуется
знать только ее числовые характеристики.
Рассмотрим вопрос об определении числовых
характеристик с. в. X по результатам п независимых опытов.
Допустим, что опыты еще не произведены, их
результаты нам неизвестпы, случайны. Обозначим Х{
значение, которое примет с. в. X в i-u опыте; результаты
опыта — п независимых случайных величин:
Хи Х2, ..., Xit ..., Хп. A1.6.1)
Будем рассматривать их как п «экземпляров»
случайной величины X, каждый из которых имеет тот же
закон распределения, что и сама с. в. X.
Предположим, что мы хотим определить (пусть
приближенно) по результатам п опытов A1.6.1) пекоторый
параметр а, связанный с законом распределения с. в. X.
Будем называть приближенное значение параметра а его
452 ГЛ. ii. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
оценкой. Любая оценка, вычисляемая на основе
экспериментальных данных A1.6.1), есть функция этих
случайных величин и, значит, тоже случайная
величина. Обозначим а оценку параметра а:
х1,..., хл). (И.6.2)
Например, естественной оценкой для математического
ожидания тх с. в. X является среднее
арифметическое ее наблюденных значений:
i, (н.6.3)
г=1
(в других случаях выбор оценки может быть не столь
очевидным, как мы убедимся ниже).
Итак, любая оценка а параметра а — случайная
величина — функция п случайпых величии Хи Х2, ..., Хп
(п «экземпляров» случайной величины X). Закон
распределения этой с. в. а зависит от закона распределения
с. в. X и от вида функции ср, выражающей а через
Хи Х2, ..., Хп, а значит и от числа опытов п. Этот закон
распределения может быть найден методами теории
вероятностей; иногда он, на наше счастье, оказывается
довольно простым. Предъявим к оценке а ряд требований,
которым она должна удовлетворять, чтобы быть в
каком-то смысле «доброкачественной» оценкой.
Естественно потребовать от оценки а, чтобы при
увеличении числа опытов п она приближалась (сходилась
/^ П + оо \
по вероятности) к искомому параметру а \а >а .
\ & }
Оценка, обладающая таким свойством, называется со-
стоятелъной.
Кроме того, желательно, чтобы, пользуясь величиной
а вместо а, мы по крайней мере не делали
систематической ошибки в сторону завышения или
занижения, т. е. чтобы выполнялось условие:
М [а] - а. A1.6.4)
Оценка, обладающая таким свойством, называется
несмещенной.
Наконец, желательно, чтобы выбранная несмещенная
оценка была как можпо менее случайной, т. е. обладала
по сравнению с другими минимальной дисперсией:
D[a]=:min, A1,6.5)
11.6. ОЦЕНКА ЧИСЛОВЫХ ХАРАКТЕРИСТИК 453
Оцепка, обладающая таким свойством, называется
эффективной.
На практике не всегда удается удовлетворить всем
этим требованиям. Например, иногда формулы для
вычисления эффективной оценки слишком сложны, и
приходится удовлетворяться другой оценкой, дисперсия
которой несколько больше. Иногда применяются — в
интересах простоты расчетов — незначительно смещенные
оценки.
Так или иначе, при выборе оценки любого параметра
желательно ее критическое рассмотревие со всех
вышеупомянутых точек зрения.
Здесь мы ограничимся нахождением — по результатам
опытов A1.6.1) оценок для математического ожидания
m и дисперсии D случайной величины X: М [X] —пг;
D[X D
Мы уже упоминали, что естественной оценкой для
математического ожидания m случайной величины X
является среднее арифметическое ее наблюденных значений
(или статистическое среднее):
п
^{. A1,6.6)
Нетрудно убедиться, что эта оценка состоятельна:
согласно закону больших чисел (п. 10.1) при увеличении
числа опытов п она сходится по вероятности к
математическому ожиданию m случайной величины X.
Посмотрим, является ли эта оценка несмещенной?
Для этого найдем ее математическое ожидание:
i=l J i=l i=
A1.6.7)
то есть оценка m для m является несмещенной.
Найдем дисперсию этой оценки:
D [m] = D [т*] = 42° ^ " h 2 D = f • (И-6-8)
Эффективность или неэффективность оценки зависит
от вида закона распределения с. в. X. Можно доказать
(мы этого делать не будем), что если с. в, X распреде-
454 ГЛ, И. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
лена нормальпо, то оценка т = т* для математического
ожидания т является и эффективной.
Перейдем к оценке для дисперсии D. На первый
взгляд наиболее естественной представляется
статистическая дисперсия D*, то есть среднее арифметическое
квадратов отклонений значений X, от среднего:
A1.6.9)
Проверим, состоятельна ли эта оценка? Выразим ее
через статистический второй начальный момент, т. е.
через среднее арифметическое квадратов наблюденных
значений:
п
2 Xfm2 A1.6.10)
Первый член в правой части — средне*1
арифметическое наблюденных значений случайной величины X2
сходится по вероятности к ее м.о.: М [X2] = а2 [X].
Второй член сходится по вероятности к т2; вся величина
A1.6.10) сходится по вероятности к а2 — пгг ==/). Значит,
оценка A1.6.9) состоятельна.
Проверим, является ли она также и несмещенпой?
Подставим в A1.6.9) вместо т его выражение A1.6.6)
и произведем указанные действия:
Так как статистическая дисперсия D* не зависит от
того, где выбрать начало координат, выберем его в
точке яг, то есть отцентрируем все случайные величины
Xh X2j , t., Хп. Тогда
п
Найдем м, о. величины /)*:
"-^м 21? -4м[2ад].
И.6. ОЦЕНКА ЧИСЛОВЫХ ХАРАКТЕРИСТИК 455
Но М [х\] - Dx M [XiXj] - 0, и формула A1.6.12)
дает:
М [Z)*] = ^i2z)-42 M[iA] = ^Z). A1.6.13)
Отсюда видно, что величина D* не является
несмещенной оценкой для дисперсии Z); ее м. о. не равно Z),
а несколько меньше. Пользуясь оценкой D* вместо D,
мы будем совершать некоторую систематическую
ошибку в меньшую сторону. Чтобы ее ликвидировать,
достаточно ввести поправку, умножив L>* на п__ ^ тогда
мы получим несмещенную оценку для дисперсии:
" ~~ " n-V
равную статистической дисперсии, умноженной па п и
деленпой на п — 1:
п
D = j~ 2 (Хг - тJ A1.6.14)
или, выражая D через статистический второй начальный
момент,
5-{т 2 *?-»•] A-
При больших значениях п поправочный множитель
п/(п— 1) становится близким к единице, и его
применение теряет смысл.
А теперь, произведя уже все необходимые выкладки,
мы можем забыть о том, что результаты п опытов
случайны, и записать их в виде последовательности
известных чисел:
и сформулировать правило приближенного нахождения
математического ожидания m и дисперсии D случайной
величины X по опытным данным. В качестве
приближенных значений (оценок) этих характеристик нужно
взять:
п п
» = »»¦ - 4 2 **; D = jJ^ 2 (*« - mf, A1.6.16)
456 ГЛ. 11. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Вместо второй из формул A1.6.16) часто бывает
удобнее пользоваться выражением
1-И^Л- (И-6.17)
Можно доказать (мы этого делать не будем), что
тага
кои же поправочный множитель п_ л нужно вводить
и при вычислении несмещенной оценки для ковариации
двух с. в. X и Y:
Кху = М [XYU
а именно, если в результате п опытов получено п пар
значений случайных величин X и Y:
то несмещенная оценка для их ковариации будет:
п
где
^xy можно вычислять и по равносильной A1.6.18)
формуле:
*** - 4 2 ЗД* - ^^ I Г=Т
(И.6.20)
Оценку коэффициента корреляции с. в. X и У
находят по формуле:
Д (Н.6.21)
Пример 1. Произведено 20 измерений входного
напряжения X и выходного напряжения Y (в вольтах) на
входе и выходе технического устройства (ТУ);
результаты сведены в таблицу:
11 6. ОЦЕНКА ЧИСЛОВЫХ ХАРАКТЕРИСТИК
457
i
Уг
i
хг
Ух
1
-15
— И
И
-4
—2
2
3
-3
12
-9
3
3
15
3
13
21
И
4
48
9
14
55
19
5
-5
—2
15
-17
— 12
6
-37
-17
16
-15
1
7
-22
-9
17
15
13
8
-2
-3
18
-4
5
9
3
5
19
-39
-13
10
И
7
20
1
0
A1.6.22)
Найти оценки для числовых характеристик системы
св. (X, YI
20
• ю
- 50 -зо -ю •.
-10 -
10 30
50 X
-20 г
Рис. 11.6.1
Решение. На рис. 11.6.1 приведены эти
статистические данные в виде точек на плоскости хОу. По
формуле A1.6.6) находим оценки тх и ту:
20 20
»* 4 УП
Т 71 >"N^ П ООП
тУ - 20 AJ »* ~ 4*w'
1
458 ГЛ. 11. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
По формуле A1.6.14) находим несмещенные оценки
для дисперсий и с. к. о.:
20
Ас = —j 2 (*t "*" ^J ^ 559; ** в К #* « 232б;
i
По формуле A1.6.20) находим оценку для кова-
риации:
[20 -|
откуда, по формуле A1.6.21) находим оценку для
коэффициента корреляции с. в. X и У:
г*у - RJWx-By * 0,921.
Мы видим, что между X и 7 существует довольно
тесная (причем положительная) корреляционная
зависимость, что видно и из рис. 11.6.1.
11.7. Точность и надежность оценок
числовых характеристик
случайной величины
В предыдущем пункте мы показали, что
подходящими (состоятельными и несмещенными) оценками для
математического ожидания т и дисперсии ^случайной
величины X являются т и D A1.6.16). Эти оценки как
функции п случайных величин Хи Х2, ..., Хп сами
представляют собой случайные величины.
Разумеется, заменяя т и D их оценками т и Д мы
совершаем какую-то ошибку; интересно оценить эту
ошибку и найти вероятность рв того, что она не
превзойдет какого-то е (эта величина г характеризует
точность оценки, а вероятность (Je — ее надежность).
Здесь мы изложим только элементы теории точности и
надежности оценок; при этом будем предполагать, что
число опытов п не слишком мало (порядка десятков).
Чтобы оценить точность и надежность оценки,
нужно знать ее закон распределения. На наше счастье, он
во многих случаях оказывается близким к нормальному.
11.7. ТОЧНОСТЬ И НАДЕЖНОСТЬ ОЦЕНОК 459
Действительно, среднее статистическое значение с. в. X:
представляет собой сумму сравнительно большого числа
п независимых случайных величин и, согласно
центральной предельной теореме, имеет распределение, близкое
к нормальному, с математическим ожиданием
п
М [т] - ~ 2 М [ХЛ я 4 #n'm e w (И.7.1)
и дисперсией
и, значит, средним квадратическим отклонением:
о [in] = W/n = o/i'n, A1.7.3);
где о — с. к. о. случайной величины X.
Для того, чтобы приближенно найти параметры
нормального закона, по которому распределяется оценка т,
можно, не вдаваясь в излишние тонкости, приближенно
заменить в формулах A1.7.1), A1.7.3) неизвестные нам
параметры m, D их оценками m, D. Получим:
М[т]жт; D[m]&~; a[m] & l/^. A1.7.4)
Допуская, что с. в. т имеет нормальное
распределение с параметрами A1.7.4), найдем приближенно
вероятность того, что оценка т отклонится от своего
математического ожидания меньше, чем на е:
A1.7.5)
о [ml
где Ф(х)—функция Лапласа.
Пример 1. При обработке результатов тг = 20
независимых опытов получены оценки математического
ожидания и дисперсии m = 4,52 и D = 2,35. Найти
вероятность того, что, полагая m — m == 4,52, мы не совершим
ошибки, большей, чем е = 0,Зв
460 ГЛ. 11. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Решение, По формулам A1.7.4) находим:
М (т] « 4,52; D [т] « 2,35/20 = 0,1175; о [т] « 0,343.
По формуле A1.7.5) имеем:
р {| т- т | < 0,3} = 2Ф @,3/0,343)& 2 • 0,3093 « 0,618,
Итак, вероятность того, что ошибка от замены т на
m не превзойдет 0,3, не настолько велика, чтобы считать
это событие практически достоверным. >
Пример 2. Тот же вопрос, что в примере 1, но
число опытов п = 100 {т = 4,52, D = 2,35),
Решение.
D [т] = 2,35/100 - 0,0235; о [т] « 0,1533.
Р (| т — т| < 0,3} я 2Ф @,3/0,1533) « 2-0,4748 « 0,95,
Итак, «надежность» того, что, заменяя т на т, мы
совершим ошибку не больше е = 0,3 при п = 100 опытах
примерно равна 0,95. Если нам требуется большая
надежность или большая точность при той же надежности,
придется увеличить число опытов п. >
Теперь займемся точностью и надежностью оценки
D для дисперсии D. Как мы знаем, эта оценка —
несмещенная, и ее математическое ожидание равно Z)t
Запишем эту оценку в виде:
Можно показать (мы этого делать не будем)\ что при
п > 20 оценка В, независимо от распределения с. в. Хг
распределена приближенно нормально, с параметрами
M[D]-Di D[D] = ^--^^D\ A1.7.7)
где ^4 и D — соответственно четвертый центральный мо*
мент и дисперсия случайпой величины X.
Величину |л4 можно в принципе приближенно
заменить ее оценкой |л4:
J) (Х4 - т*)«) ^ (Н.7.8)
но такая оценка при малом числе опытов дает большие
11.7. ТОЧНОСТЬ И НАДЕЖНОСТЬ ОЦЕНОК 461
ошибки. Если закон распределения с. в. X известен, то
величину (ы4 можно подсчитать. Например, для
нормально распределенной св. X ja4 = 3ZJ, откуда (см. A1.7.7))
Заменяя в последнем выражении величину D ее
оценкой D, получим:
A1.7.9)
Если с. в. X распределена равномерно на интервале
(а, ?),то
™ — 80 ' U ~~ 12 «
откуда
DfDj^^ + ^g2; a[5]«KD[zf]. A1.7.10)
В случае, если закон распределения с. в. X нам
неизвестен, рекомендуется в практических задачах
пользоваться приближенным равенством A1.7.9).
Пример 3. Для условий примера 1 найти
приближенно вероятность р того, что, полагая D = D = 2,35 мы
не совершим ошибки больше, чем е == 0,50. ^
^Решение. По формуле A1.7.7) находим М [D]«
«Z?==2,35. Воспользуемся второй формулой A1.7.9) для
приближенного определения с. к. о. случайной величины
В: а[Щ » У2/(л-1)Я « 0,762.
Найдем вероятность того, что нормально
распределенная с. в. D отклонится от своего м. о. D меньше, чем
на 0,5:
p = P{\D-D\<0,5} = 2Ф@,5/0,762)» 0,488.
Таким образом, вероятность того, что ошибка от
замены дисперсии D ее оценкой В не превзойдет 0,5,
равна р»0,488; эту вероятность нельзя считать
большой. >
462 ГЛ. 11. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
11.8. Оценка вероятности по частоте
В данном п. мы рассмотрим вопрос об оценке
вероятности события по его частоте в серии из п опытов.
Начнем с того, что сколько-нибудь
удовлетворительное представление о вероятности р события А можно
получить только из обширной серии опытов, при
большом п (см. хотя бы пример, приведенный в п. 1.3,
где частота события А = {появление герба} очень
медленно, как бы «нехотя», приближается, сквозь ряд
случайных колебаний, к его вероятности /? == 0,5).
При сравнительно малом п задача оценки
вероятности по частоте, о точности и надежности этой оценки,
является довольно сложной, и мы не будем на ней
останавливаться*). Рассмотрим задачу при достаточно
большом п и решим ее приближенно, как выше (в п. 11.7)
решали задачу об оценках числовых характеристик
случайной величины.
Пусть произведено п опытов, причем в X из них
событие А произошло, а в (п — Х)-~ не произошло.
Частота события А выражается формулой
р* = Х/п. '(И.8.1 J
Так как опыты независимы, то с. в. X распределена
по биномиальному закону с параметрами пир. Мы
знаем (п. 5.1), что м. о. случайной величины X,
распределенной по биномиальному закону, равно пр, где п —
число опытов, р — вероятность «успеха» (появление
события А) в каждом опыте, а дисперсия св. X равна
npq, где q = 1 - р.
Теперь представим с. в. X в виде суммы п случайных
величин:
Х- 2*|, A1.8.2)
где Xi — индикатор события А в i-м опыте:
A, если в i-u опыте А произошло,;
Х- —
г [0х если в i-м опыте А не произошло, (i = 1, 2, ..., п),
*) Желающие могут познакомиться с нею по любой книге,
специально посвященной математической статистике,
например, [10].
it.8. ОЦЕНКА ВЕРОЯТНОСТИ ПО ЧАСТОТЕ 463
Из центральной предельной теоремы мы знаем, что
при достаточно большом п сумма п независимых
случайных величин распределена приблизительно нормально;
значит, с. в. X можно считать распределенной по
нормальному закону с параметрами пр и Vnpq. Ее линейная
функция р* = XI п имеет также нормальное
распределение с параметрами:
М [/>*]- р, A1.8.3)
Из того, что математическое ожидание частоты р*
события А равно р, следует, что р* является не см е-*
щенной оценкой для р (то, что эта оценка
состоятельна, следует из теоремы Бернулли (п. 10.1)).
Чтобы оценить точность приближенного равенства
р «р*, найдем вероятность того, что ошибка этого
равенства не превысит е:
). A1.8.5)
Пример 1. Найти вероятность того, что при и=*
— 600 бросаниях монеты (см. пример в п. 1.3) ошибка
от замены вероятности частотой не превысит е = 0,05.
Решение. В данном случае р = q = 0,5;
Р{\Р* — 0,51 < 0,05} - 2Ф @,05 • 24г5/025) ж 0,986.
Итак, с довольно высокой вероятностью 0,986 можно
утверждать, что при я = 600 бросаниях монеты ошибка
от замены вероятности частотой не превысит 0,05. >
В данном примере наша задача облегчалась тем, что
вероятность появления герба р нам была известна зара~*
нее (так что, собственно, незачем было заменять ее
частотой). В большинстве практических задач вероятность
р заранее неизвестна; из положения можно выйти,
заменив в формулах A1.8.4) и A1.8.5) вероятность р ее
приближенным значением /?*, а вместо q поставив q* =»
¦=1 —р*. Формула A1.8.5) приближенно запишется
в виде:
(^) A1,8.6)
Пример 2. Произведено п = 400 опытов с целью
определения вероятности р события 4. Из этих 400 опы*
464 ГЛ. 11. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
тов в 101 появилось событие Л. Найти вероятность того,
что приняв р « р* = 101/400, мы не сделаем ошибки
больше, чем е = 0,02.
Решение, р* * 0,253, д* « 0,747; р*д* » 0,189.
0,642. (Н.8.7)
УО,253-0,747
Итак, вероятность того, что ошибка приближенного
равенства р « 0,253 не превзойдет 0,02, не очень велика
и составляет около 64%. >
Пример 3. Сколько опытов п надо произвести в
условиях предыдущего примера, чтобы ошибка
приближенного равенства р«р* не превысила 0,02 с
вероятностью не меньше, чем 0,9?
Решение. Будем исходить из того, что частота
события А при увеличенном числе опытов останется
приблизительно той же, как и при и = 400 (все наши
расчеты носят ориентировочный характер). Нам нужно,
чтобы 2Ф @,02 V и/0,4349) было не меньше, чем 0,9, т. е.
Ф@,02Уп/0,4349)^0,45. Найдем, пользуясь таблицей
приложения 2, то значение аргумента, при котором
функция Лапласа становится равной 0,45; оно приближенно
равно 1,64; отсюда
0,02 Уп > , « . у- 1,64*0,4349 ^ or gg
n>1271f V
Рассмотренный пример поучителен тем, что
показывает, какое грандиозное число опытов требуется, чтобы
добиться удовлетворительной точности определения
вероятности по частоте. Обычно мы определяем
вероятности событий по значительно меньшему числу опытов;
надо отдавать себе отчет в том, что точность
приближенного равенства р »/?*, как правило, невелика и, значит,
нет смысла сохранять большое число значащих цифр в
полученной таким образом вероятности.
К изложенному вопросу об оценке вероятности по
частоте тесно примыкает другой, имеющий большое
практическое значение вопрос о значимости расхождений
между двумя частотами.
Пусть произведено две серии, состоящих
соответственно из щ и пг опытов. В каждом из них регистрировалось
появление или непоявление одного и того же события Ач
11.8. ОЦЕНКА ВЕРОЯТНОСТИ ПО ЧЛСТОТВ 465
В первой серии событие А появилось в kt опытах, во
второй — в к2 опытах, причем частота события А в
первой серии получилась больше, чем во второй: Pi = ^i/^i>
> Р2 = к2/п2. Разность между двумя частота получилась
равной г0:
рГ-Л-г„. (И.8.8)
Спрашивается, значимо или не зпачимо это
расхождение? Указывает ли оно на то, что в первой серии
опытов событие А действительно вероятнее, чем во второй,
или расхождение между частотами надо считать
случайным?
При решепии этой задачи мы воспользуемся
классическим в математической статистике приемом нуль-
гипотезы. Нуль-гипотеза Но состоит в том, что
различия в вероятностях не существует, то
есть обе серии опытов произведены в одинаковых
условиях, а расхождение г0 объясняется случайными
причинами. Выдвинув нуль-гипотезу, подсчитывают вероятность
того, что при этой гипотезе расхождение превзойдет
наблюденное г0. Если эта вероятность очень мала (меньше
той вероятности а, при которой мы уговорились считать
событие практически невозможным), то нуль-гипотезу
надо отбросить, как противоречащую опытным
данным; если же вероятность не очень мала, гипотезу Но
отбрасывать не надо, а расхождение г0 можно объяснить
случайными причинами.
В данном случае нуль-гипотеза Но состоит в том, что
обе серии опытов однородны и что вероятность р
появления события А в них одна и та же, приближенно
равная частоте, которая получится, если обе серии смешать
в одну:
p^p*^(ki + ki)/(ni + nt]. A1.8.9)
При достаточно больших щ и п2 каждая из
случайных величин pt; р* распределена практически
нормально, с одним и тем же и.о.: /?«/?*. Что касается
дисперсий Dt и D2 в первой и второй сериях, то они различны
и равны соответственно:
(И.8.10)
Случайная величина R = рх — р2 также имеет
приближенно нормальное распределение с математическим
466 ГЛ. 11. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
ожиданием mR, равным нулю, и дисперсией
DR = Dt + D2«piA -pl)/ni + piA -p*2)/n2r A1.8.11)
откуда
+ Л A - Р*гIп%. (И.8.12)
Вероятность того, что с. в. R примет значение, не
меньшее, чем наблюденное в опыте г0, равна
Р{#>г0}»Р{Л >г0) - 1 -FB(r,)t
где FB(#) — функция распределения с. в. Д.
Из п. 6.3 мы знаем, что для пормального закона
функция распределения равна:
В нашем случае
откуда
^ (Ц.8.13)
Если вероятность A1.8.13) очень мала (не
превосходит выбранного уровня значимости а), то гипотезу Яо
следует отбросить, как противоречащую опытным данным;
если же она не слишком мала, можно отнести
расхождение между частотами за счет случайных причин.
Пример 4. Два стрелка, соревнуясь, дали по
одинаковым мишеням из одинакового оружия первый —
двадцать выстрелов, второй — шестнадцать (^ = 20; и2 = 16).
Первый попал в «десятку» ki = 16 раз, второй к2 = 10 раз;
Л .- W = 0,8; Р.* - -{у « 0г625; р{ > р*2: г0 - 0,800 -
-0,625 = 0,175.
Второй стрелок утверждает, что различие частот
случайно, что вообще он стреляет так же хорошо, как
первый. Проверить правдоподобие этой гипотезы, считая за
уровень значимости а = 0,02,
11.9. ПРОВЕРКА ЗНАЧИМОСТИ РАСХОЖДЕНИЙ 467
Решение. По форхмуле A1.8.12) находим:
0,8-0,2 , 0,625-0,375 П/(сло
-^р- + 1б7 «0,1503.
1б
По формуле A1.8.13):
Эта вероятность заметно превосходит принятый
уровень значимости а = 0,02; гипотеза //0 = (стрелки
стреляют одинаково метко} не противоречит опытным
данным. >
11.9. Проверка значимости расхождении
между двумя средними
В данном пункте мы рассмотрим задачу, подобную
той, которую мы решали в п. 11.8 (проверка значимости
расхождений между двумя частотами).
Пусть имеется две серии опытов; первая состоит из
пи вторая — из пг опытов. В каждой серии
регистрировались значения какой-то с. в. X. Первая серия дала
среднее значение тг = I Д] X*1 I / п^ вторая т2 =
п21 где индексами A) и B) вверху отмечены
значения, припятые с. в. X в первой и второй сериях
опытов. Оказалось, что тх > т2, а разность между ними
равна
г0 = ml — ml>0.
Спрашивается, является ли значимым это
расхождение, или же его можно объяснить за счет случайных
причин? Уровень значимости принят равным а.
Снова выдвинем нуль-гипотезу Яо, состоящую в том,
что в первой и второй сериях мы имеем дело с одной и
той же с. в. Её м. о. приближенно равно
статистическому среднему, взятому по материалам всех опытов (без
468 ГЛ. 11. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
разделения на серии):
A1.9.1)
а дисперсия, вычисленная через второй начальный
момент (для простоты берем слегка смещенную оценку /)*,
без цоправки (щ + пгI(пх + п2 — 1); при больших гс, и
щ этот поправочный коэффициент близок к единице),
равна:
Л*-(IS WV + 2 [^)?)/(«1 + «2)-(^J. (Н.9.2)
\г=1 г-1 //
Теперь рассмотрим две случайные величины: Ft и
У г — средние значения с. в. X в первой и второй сериях:
i1 2 i1
и найдем их числовые характеристики:
i; D [Уа]
Разность двух средних значений
R = Fi — У2 = wj
имеет математическое ожидание
и дисперсию, равную сумме дисперсий величин 7j и F2:
DR « D*/ni + D*/n2 = {п1 + пг)О*/{щ • п2),
откуда
а « V in 4-и \ Г)*/ (п . п \ /Л Q KY
Вероятность того, что с. в. R примет значение, не
меньшее, чем наблюденное в опыте г0, равна
- 1 - К(Д <г0} = ^л(г0), A1.9.6)
где FnL%l— функция распределения с, в. /?t
11.9. ПРОВЕРКА ЗНАЧИМОСТИ РАСХОЖДЕНИЙ 469
В п° 6.3 мы нашли выражение нормальной ф. р.:
F(a;) = 0t5 + <
откуда
Подставляя в A1.9.6), получим:
Р{Я>го} = О,5-Ф(-2.
A1.9,7)
Если эта вероятность очень мала (меньше принятого
уровня значимости а), то расхождение между двумя
средними Yi — Y2 = R надо признать значимым3 а нуль-
гипотезу Но отбросить, как противоречащую опытным
данным; если она недостаточно мала — признать
гипотезу #о правомочной и отнести расхождение за счет
случайных причин.
Пример. Испытано два образца ЭВМ одной и той
же марки; для каждой проводились опыты по измерению
времени безотказной работы Т (суток). Для первого
образца проведено п{ = 20 опытов, для второго щ =
= 16 опытов*). Результаты обеих серий опытов (время
безотказной работы в часах) сведены в таблицу:
Таблица 11.9.1
JSft опыта г
1
2
3
4
5
6
7
8
9
10
1-й
образец
10,1
9,2
7,8
14,5
16,1
3,2
4,9
8,8
11,4
20,2
2-й
образец
8,6
10,2
3,8
4,9
19,0
10,0
5,4
4,3
12,2
8,6
JSft опыта г
11
12
13
14
15
16
17
18
19
20
1-й
образец
6,1
12,3
14,4
10,5
2,2
18,3
22,4
6,6
3.4
10,5
2-й
образец
14,4
15,2
6,1
0,5
2,8
4,6
—
—
Среднее: тп1 = 10,65; т2 = 8,13.
*) В целях простоты вычислений мы взяли такое 7меренное
число опытов.
470 ГЛ. 11. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Большее среднее время безотказной работы первого
образца как будто говорит в пользу его большей
надежности:
10,65 > 8,13.
Спрашивается, является ли это расхождение
значимым (при уровне значимости а = 0,05), или его можно
объяснить случайными причинами?
Решение. Среднее по обеим сериям:
з^ , ^ <_^
п + п ^ п + п
20 + 16 х + 2 х + 2
Средний квадрат по обеим сериям:
а* « Щ&. « Ю1,39; Я* « 101,39 - 9,522« 10,76.
По формуле A1.9.5) (R « т\ - mj = 2,52):
~ 1,10;
} = 0,5 — 0B,52/1,10)» 0,021.
Полученная вероятность заметно меньше принятого
уровня значимости а = 0,05, поэтому гипотезу Яо
следует отбросить как противоречащую опытным
данным: первый образец действительно дает в среднем
большее время безотказной работы, чем второй.
Заметим, что сравнительно небольшого изменения
опытных данных было бы достаточно, чтобы прийти к
противоположному выводу. Например, если бы разность
Го имела значение не 2,52, а, например, го=1,8, мы
получили бы
Р {R > г0} = 0,5 - Ф A,636) » 0,051,
а это уже превзошло бы уровень значимости а = 0,05,
и нам не пришлось бы отбрасывать гипотезу Но. >
В двух последних пунктах мы пользовались весьма
грубым аппаратом для проверки правдоподобия гипотез;
более тонкий аппарат излагается в специальных курсах
математической статистики (например, [1]). Однако для
прикидочных расчетов вполне можно обойтись и
вышеизложенными приемами, памятуя о том, что уровень
значимости а назначен нами достаточно произвольно.
ПРИЛОЖЕНИЯ
Приложение 1
а"*
Распределение Пуассона Р (т, а) = —г е"~Л
0
1
2
3
4
5
X
0
1
2
3
4
5
6
X
0
1
2
3
4
5
6
7
0,1
0,9048
0,0905
0,0045
0,0002
0,6
0,5488
0,3293
0,0988
0,0198
0,0030
0,0004
1
0,3679
0,3679
0,1839
0,0613
0,0153
0,0031
0,0005
0,0001
0,2
0,8187
0,1638
0,0164
0,0019
0,0001
0,7
0,4966
0,3476
0,1217
0,0284
0,0050
0,0007
0,0001
2
0,1353
0,2707
0,2707
0,1804
0,0902
0,0361
0,0120
0,0037
0,3
0,7408
0,2222
0,0333
0,0033
0,0002
0,8
0,4493
0,3595
0,1438
0,0383
0,0077
0,0012
0,0002
3
0,0498
0,1494
0,2240
0,2240
0,1680
0,1008
0,0504
0,0216
0,4
0,6703
0,2681
0,0536
0,0072
0,0007
0,0001
0,9
0,4066
0,3659
0,1647
0,0494
0,0111 '
0,0020
0,0003
4
0,0183
0,0733
0,1465
0,1954
0,1954
0,1563
0,1042
0,0595
0,5
0,6065
0,3033
0,0758
0,0126
0,0016
0,0002
5
0,0067
0,0337
0,0842
0,1404
0,1755
0,1755
0,1462
0,1044
472
ПРИЛОЖЕНИЯ
П р одолжение
X
8
9
10
11
12
13
14
15
X
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
1
в
0,0025
0,0149
0,0446
0,0892
0,1339
0,1606
0,1606
0,1377
0,1033
0,0688
0,0413
0,0225
0,0126
0,0052
0,0022
0,0009
0,0003
0,0001
2
0,0009
0,0002
7
0,0009
0,0064
0,0223
0,0521
0,0912
0,1277
0,1490
0,1490
0,1304
0,1014
0,0710
0,0452
0,0263
0,0142
0,0071
0,0033
0,0014
0,0006
0,0002
0,0001
3
0,0081
0,0027
0,0008
0,0002
0,0001
8
0,0003
0,0027
0,0107
0,0286
0,0572
0,0916
0,1221
0,1396
0,1396
0,1241
0,0993
0,0722
0,0481
0,0296
0,0169
0,0090
0,0045
0,0021
0,0009
0,0004
0,0002
0,0001
4
0,0298
0,0132
0,0053
0,0019
0,0006
0,0002
0,0001
9
0,0001
0,0011
0,0050
0,0150
0,0337
0,0607
0,0911
0,1171
0,1318
0,1318
0,1186
0,0970
0,0728
0,0504
0,0324
0,0194
0,0109
0,0058
0,0029
0,0014
0,0006
0,0003
0,0001
5
0,0653
0,0363
0,0181
0,0082
0,0034
0,0013
0,0005
070002
10
0,0000
0,0005
0,0023
0,0076
0,0189
0,0378
0,0631
0,0901
0,1126
0,1251
0,1251
0,1137
0,0948
0,0729
0,0521
0,0347
0,0217
0,0128
0,0071
0,0037
0,0019
0,0009
0,0004
0,0002
0,0001
ПРИЛОЖЕНИЯ
473
см
О)
а
н
о
ч
§
«б
g
СО
СО
00
г»
со
ю
00
о
СО
S
СО
о
8
790
см
о
см
ОЭ
со
см
о
SJ*
О5
ОЭ
о
595
о
ОЭ
тЧ
О
00
оэ
§
399
о
о
о
000
о
о
о
\п
со
LO
г-
о
см
О
749
8
СО
S
см
СО
оэ
LO
о
567
о
см
4J4
ю
о
со
S
380
S
со
039
о
ггэ
О
¦чч
"*"
СО
СМ
о
•*ч
642
о
г»
см
о
¦«-ч
Г—
00
ОЭ
О
483
ОЭ
О
LO
оэ
о
ОЭ
о
СО
00
о
317
00
о
я
079
см
о
СО
LO
803
Ч[Ч
431
00
Ю
О
со
00
со
СО
307
СО
О
со
ОЭ
см
см
LO
см
СМ
см
оэ
117
со
о
СО
ОЭ
00
о>
-&
00
280
00
см
со
СО
003
о
СО
СО
СО
см
СО
-гч
910
2
см
155
о
о
см
см
см
я
ОЭ
чН
см
566
см
СО
см
см
см
vf
00
S
540
8
оэ
см
3
оэ
497
оэ
СО
191
ю
о
о
оэ
ю
см
г»
LO
см
857
см
со
а
ю
см
а
891
со
см
ю
СО
со
см
г-
со
см
'со
см
907
см
см
ю
225
СО
о
см
ю
00
см
о
со
см
00
см
935
см
СО
со
см
Is*
со
СО
см
035
см
8
г-
СО
см
vf
см
СО
см
115
со
см
.«.
ю
см
о
см
СО
со
ю
о
со
785
со
ю
о
со
V1H
см
о
СО
226
оэ
см
со
СО
оэ
см
оэ
со
ОЭ
см
103
оэ
см
882
00
о
со
со
со
со
со
со
398
СО
СО
¦^ч
vf
00
см
со
639
со
Ч--1
СО
см
со
<ч_н
см
а
859
со
315
ОЭ
о
V*
см
СО
со
S-
ОЭ
LO
СО
769
LO
СО
со
ю
ю
со
vf
со
со
083
S
о
00
со
VI*
СО
я
375
341
о
00
см
00
СО
8
00
со
900
СО
00
пэ
СО
г-
со
со
ОЭ
со
286
СО
СО
о
со
VP
о€
S
650
S
я
364
•чч
о
СО
ОЭ
ОЭ
со
796
ОЭ
СО
СО
оэ
со
LO
СО
оэ
со
ю
см
со
ю
СО
о
оэ
со
^
г»
00
686
00
со
СО
оэ
384
см
1-^
<ЧЧ
см
СО
466
OS
со
оэ
886
о
vf
см
00
о
оо
LO
со
о
490
о
о
см
403
со
чрН
О5
00
со
со
ю
о
со
922
см
S!*
СО
см
S
см
507
см
VT
со
см
о
см
см
073
см
а
419
474
ПРИЛОЖЕНИЯ
I
00 OS t> CM О
О sp CM CO t>»
sP sP COO CO
sP lO CD t- N
sp sp sP sP sP
OS SP OS 00 -*ч
CD t> OS LO CD
^ Ю 00 *н CO
00 00 00 OS OS
o«o t*^
CM sp CO О CO
Ю CD C- 00 00
OS OS OS OS OS
sP *<Г sp sp Sp
Ю CM CD LO Ю
CM CO CM OS CO
SP Ю CO CD t>-
Osp CO
f CO SP
^ со
sP
CM f
4- ю со
CO 00 00 OS O5
CD CM CO f« CD
О CO CM О Ю
Ю CC Ь 00 00
O5 «<t» vP CD CO
!>• iO CO CM Ю
^-« см •^н оэ ю
VP Ю CD CO t>-
ЧРЧРЧрЧр^р
N О О ^ vf
Is* О VP •*" CNl
О Ю 00 ^ CO
Х00СОФО5
C1-*O Ю "^
O5 C3 CM Oi lO
sJ<COC- f~ 00
О "^ О5 CD lO
CO CD О 00 О
i-n 00 О
-*-1 со vp
b II^ CO
CO CO -<P vP 4-i
•<P Ю Ob 00 »<P
3J С СГ« Ь ^*
CM CM ОС ««-1 CO "г* С
ОС СМ 1^ СО С
CS SP !>• О С
Г- ОС СО OS OS
sP *^ sP ^-З* *^
00M
CO OS О 00 vf
flOl>- t4- 00
en en a OS os
см ю о ^ oo
CO OS OS t^ CO
CM CM Ю CD CD
CO 00 ^P CO О
OS CO l^- О CM
t^ 00 00 O3 OS
^ P f p P
CO Ю CO «^ CO
v*ooa г- со
VP Ю CO t- 00
OS OS OS OS OS
sfsrsr sr st*
OS ЧР • .
cc oc oo <:
CO s
* LO CO I»
sf sr sf
CM ^ CO О Ю
00 SP -Ч-" ^ vp
oo со г- о см
«> 00 00 O. OS
vp sp ЧР vp sp
coooo о со
SP Ю CO t- 00
OS OS OS OS OS
p P p vp sp
00 00 CM t^-
CO CM CO Ю
*«ч О OS CO vji
00 СО СО OS СМ
cospiocot-- t^ooooooos
CO О vp О Ю
•«ч CD !>• CO CM
Sf ЮСО N 00
a: os os as a;
rrf sf sf
00 О MO CO
vp CO COCO OS
sp CO CO sf и
со vp m со t>
sp sp sr sp vp
00 Г* Ю CO CNl
ЫО vr 1С О
t- "M CO OS ^J
t- oo oo oo os
sp sp sp vp sp
CO Г- sp (>J C5
OS sp CD lO ^
со ю cc r^ oo
Os o: C: OS os
sp vp sp sp sp
.. . jS
СО lO lO sP ^ч
COsp LOCO «>•
sP spsp spsp
Ю sp О 00 О
Oi *r« -** CM 00
I— CM CD O. 4-i
t^ 00 00 00 OS
sp sp spsp sP
OS sP CO sP- CO
CO LO CO t^» 00
OS OS OS OS OS
spsp sp sP sP
i^f^sH Csf CM~CM CM «rJ
Ю CD t^ CO OS
LO
SP
со"
со"
н
0.499S9997
0,499968
0,49977
0,49865
e
Приложение 3
X
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0,95
0,004
0,103
0,352
0,711
1,145
1,635
2,17
2,73
3,32
3,94
4,58
5,23
5,89
6,57
7,26
0,90
0,016
0,211
0,584
1,064
1,610
2,20
2,83
3,49
4,17
4,86
5,58
6,30
7,04
7,79
8,55
Значения
0,80
0,064
0,446
1,005
1,649
2,34
3,07
3,82
4,59
5,38
6,18
6,99
7,81
8,63
9,47
10,31
X в зависимости от г и
оло
0,148
0,713
1,424
2,20
3,00
3,83
4,67
5,53
6,39
7,27
8,15
9,03
9,93
10,82
11,72
0,50
0,455
1,386
2,37
3,36
4,35
5,35
6,35
7,34
8,34
9,34
10,34
11,34
12,34
13,34
14,34
Р
0,30
1,074
2,41
3,66
4,88
6,06
7,23
8,38
9,52
10,66
11,78
12,90
14,01
15,12
16,22
17,32
0,20
1,642
3,22
4,64
5,99
7,29
8,56
9,80
11,03
12,24
13,44
14,63
15,81
16,98
18,15
19,31
0,10
2,71
4,60
6,25
7,78
9,24
10,64
12,02
13,36
14,68
15,99
17,28
18,55
19,81
21,1
22,3
0,05
3,84
5,99
7,82
9,49
11,07
12,59
14,07
15,51
16,92
18,31
19,68
21,0
22,4
23,7
25,0
476
ПРИЛОЖЕНИЯ
о
о
о
о
,20
о
,30
о
о
о
о
с—
о
о
00
о
О)
о
G3
о
/
00
СО
см
*
in
а
см
00
as
in
и
см
m
•ч-l
со
ОЭ
CD
О5
со
CD
Г-
см
СО
со
см
«г*
in
ел
sf
со
со
in
со
о
о
см
S
о
СО
00
СЛ
00
см
о
26,
со
см
см
СО
см
Vf
CD
СО
см
S
о
ел
со
СЛ
00
•чН
8
см
27,
о
СО
см
см
00
8
см
00
СО
-чН
о
СЛ
со
SF
00
см
о
in
со
см
см
cS
СЛ
ч-Ч
Й
16
СО
см
3
о
8
СО
СЛ
см
см
со
см
ел
со
см
со
о
см
00
я
со
СЛ
см
СП.
00
со
8
со
см
ел
см
со
•ч-н
см
о
со
со
CD
о
см
см
см
см
3
о
см
со
я
о
СО
см
со
см
см
§
СЛ
СЛ
00
о
со
8
см
8
со
29
27,
00
со
см
о
8
18
со
СО
in
со
со
см
S
S
8
см
00
со
см
СЛ
оо
г-
СО
СО
см
ел
S
СО
8
00
со
см
см
со
см
со
см
см
00
СЛ
я
00
со
15,
со
см
о
8
ел
и
со
8
со
СО
см
см
см
а
а
00
ю
со
Й
со
со
о
СО
со
а
со
со
см
СО
см
3
00
со
СО
со
см
8
¦чН
8
ю
см
00
со
00
см
со
я
in
см
см
ел
ЧН
ел
см
00
00
со
см
8
in
со
со
СЛ
см
in
in
CM
со
CM
со
а
СЛ
00
в
СПИСОК ЛИТЕРАТУРЫ
1. Ван дер Варден Б. А. Математическая статистика.— М.!
ИЛ, 1960.
2. В е н т ц е л ь Е. С. Теория вероятностей.— М.: Высшая школа, 1999,
576 с.
3. В е н т ц е л ь Е. С, О в ч а р о в Л. А. Теория вероятностей,—
М.: Наука, 1973.-360 с.
4. В о н т ц е л ь Е. С, О в ч а р о в Л. А. Прикладные задачи
теории вероятностей.— М.: Радио и связь, 1983.— 416 с.
5. Г н е д е н к о Б. В. Курс теории вероятностей.— М.: Физматгиз,
1988.- 406 с.
6. Г р а д ш т е й н И. С, Рыжик И. М. Таблицы интегралов,
сумм, рядов и произведений.—М.: Физматгиз, 1971.— 100 с.
7. Коваленко И. Н., Филиппова А. А. Теория
вероятностей и математическая статистика.— М.: Высшая школа, 1982.—
256 с.
8. Мешалкин Л, Д. Сборник задач по теории вероятностей,—
М.: МГУ, 1972.
9. Овчаров Л. А. Прикладные задачи теории массового
обслуживания,— М.: Машиностроение, 1969.— 324 с.
10. П у г а ч е в В. С. Теория вероятностей и математическая
статистика.— М.: Наука, 1979.— 495 с.
11. Сборник задач по теории вероятностей, математической
статистике и теории случайных функций (под редакцией А. А.
Свешникова).—М.: Наука, 1965.—656 с.
12. С м и р н о в Н. В., Д у д и н - Б у р к о в с к и й И. В. Теория
вероятностей и математическая статистика в механике,—М.:
Физматгиз, 1965.— 554 с.
13. Т у т у б а л и н В. Н. Теория вероятностей. Краткий курс и
научно-методические замечания.— М.: МГУ, 1972.
14. Ф е л л е р В. Введение в теорию вероятностей и ее
применение в 2-х т.- М.: Мир, 1984 - т. 1 - 528 с, 1984 — т, 2 — 752 с.
ОСНОВНЫЕ СОКРАЩЕНИЯ
БИС — большая интегральная схема
ИД — информационный документ
м. о.— математическое ожидание
п. р.— плотность распределения
с. в.— случайная величина
с. к. о.— средпее квадратическое отклонение
ТУ — техническое устройство
ф. р.— функция распределения
ЭВМ — электронная вычислительная машина
ОГЛАВЛЕНИЕ
Предисловие 3
Введение 5
Глава 1. Основные понятия теории вероятностей ... 15
1.1. Случайное событие. Его вероятность 15
1.2. Непосредственный подсчет вероятностен .... 21
1.3. Частота или статистическая вероятность события . . 28
Глава 2. Аксиоматика теории вероятностей. Правила
сложения и умножения вероятностей и их следствия ¦ , 37
2.1. Элементарные сведепия из теории множеств ... 37
2.2. Аксиомы теории вероятностей и их следствия.
Правило сложения вероятностей 41
2.3. Условная вероятность события. Правило
умножения вероятностей 50
2.4. Примеры применения основных правил теории
вероятностей , 58
2.5. Формула полпой вероятности ..««•«• 69
2.6. Теорема гипотез (формула Бейеса) , » , , 76
Глава 3. Случайные величины. Их законы распределения 82
3.1. Понятие случайной величины. Закон распределения.
Ряд распределения дискретпой случайной величины 82
3.2. Функция распределения случайной величины. Ее
свойства 87
3.3. Функция распределения дискретпой случайной
величины. Индикатор события 92
3.4. Непрерывная случайная величина. Плотность
распределения * ... 94
3.5. Смешанная случайная величина # • • . • . 104
Глава 4. Числовые характеристики случайных величин » 107
4.1. Роль и назначения числовых характеристик.
Математическое ожидание случайной величины .... 107
4.2. Моменты. Дисперсия. Среднее квадратическое
отклонение • . • • 115
Глава 5. Некоторые важные для практики распределения
дискретных случайных величин 129
5.1. Биномиальное распределение » 129
5.2. Распределение Пуассона . , 135
5.3. Геометрическое распределение 146
5.4. Гипергеометрическое распределение • . . • • 150
ОГЛАВЛЕНИЕ 479
Глава 6. Некоторые важные для практики распределения
непрерывных случайных величин 153
6.1. Равномерное распределение 153
6.2. Показательное распределение 158
6.3. Нормальное распределение 161
6.4. Гамма-распределепие и распределение Эрланга . . 173
Глава 7. Системы случайных величин (случайные
векторы) 177
7.1. Понятие о системе случайных величин .... 177
7.2. Функция распределения системы двух случайпых
величин 179
7.3. Система двух дискретных случайных величин.
Матрица распределения 183
7.4. Система двух непрерывных случайных величин.
Совместная плотность распределения 190
7.5. Зависимые и независимые случайные величины.
Условные законы распределения 194
7.6. Числовые характеристики системы двух случайных
величин. Ковариация и коэффициент корреляции . 213
7.7. Условпые числовые характеристики системы
случайных величин (X, У). Регрессия 220
7.8. Закон распределения и числовые характеристики п-
мерпого случайного вектора 223
7.9. Двумерное нормальное распределение • , . , 230
7.10. Многомерное нормальное распределение , . . 243
Глава 8. Числовые характеристики функций случайных
величин ¦ . * 258
8.1. Математическое ожидание и дисперсия функции 258
8.2. Теоремы о числовых характеристиках функций
случайных величин 267
8.3. Применение теорем о числовых характеристиках к
решению инженерных задач 276
8.4. Числовые характеристики часто встречающихся в
ипженерной практике функций случайных величин 291
8.5. Числовые характеристики суммы случайного числа
случайных слагаемых 298
8.6. Числовые характеристики минимальной и
максимальной из двух случайных величин .... 306
8.7. Числовые характеристики модулей функций
случайных величин « . • . . 312
8.8. Комплексные случайные величины 318
8.9. Характеристическая функция случайной величины
и ее свойства , 321
8.10. Метод линеаризации функций случайпых величин , 328
Глава 9. Законы распределения функций случайных
величии ,,,..,. 4 t ...... 336
9.1. Закон распределения функции одного случайного
аргумента «,..•, 336
9.2. Получение случайной величины с заданным
распределением путем функционального преобразования 347
9.3. Закон распределения функции двух случайных
аргументов ,,,,.,, 353
ОГЛАВЛЕНИЕ
9.4. Закон распределения суммы двух случайных
величип. Композиция двух законов распределения . . 357
9.5. Закон распределения функции нескольких
случайных величин. Композиция песколышх законов рао-
пределепия ¦ 362
9.6. Закон распределения минимума (максимума) двух
случайных величин. Закон распределения
порядковых статистик 372
9.7. Законы распределения фупкций от нормально
распределенных случайных величип 380
9.8. Вероятностная смесь распределений. Закон
распределения суммы случайного числа случайных
слагаемых , . , 388
Глава 10. Предельные теоремы теории вероятностей . , 309
10.1. Закон больших чисел 309
10.2. Центральная предельная теорема 413
Глава 11. Элементы математической статистики , , , 430
11.1. Предмет и задачи математической статистики , . 430
11.2. Первичная статистическая совокупность. Ее
упорядочение. Статистическая функция распределения . 432
11.3. Группированный статистический ряд. Гистограмма 437
11.4. Выравнивание статистических распределений . . 440
11.5. Критерий согласия %2 445
11.6. Оценка числовых характеристик случайных величин
по ограниченному числу опытов 451
11.7. Точность и паденшость оценок числовых
характеристик случайной величины 458
11.8. Оценка вероятности по частоте 462
11.9. Проверка значимости расхождений между двумя
средними 467
Приложения , 471
Список литературы 477
Основные сокращения , 477