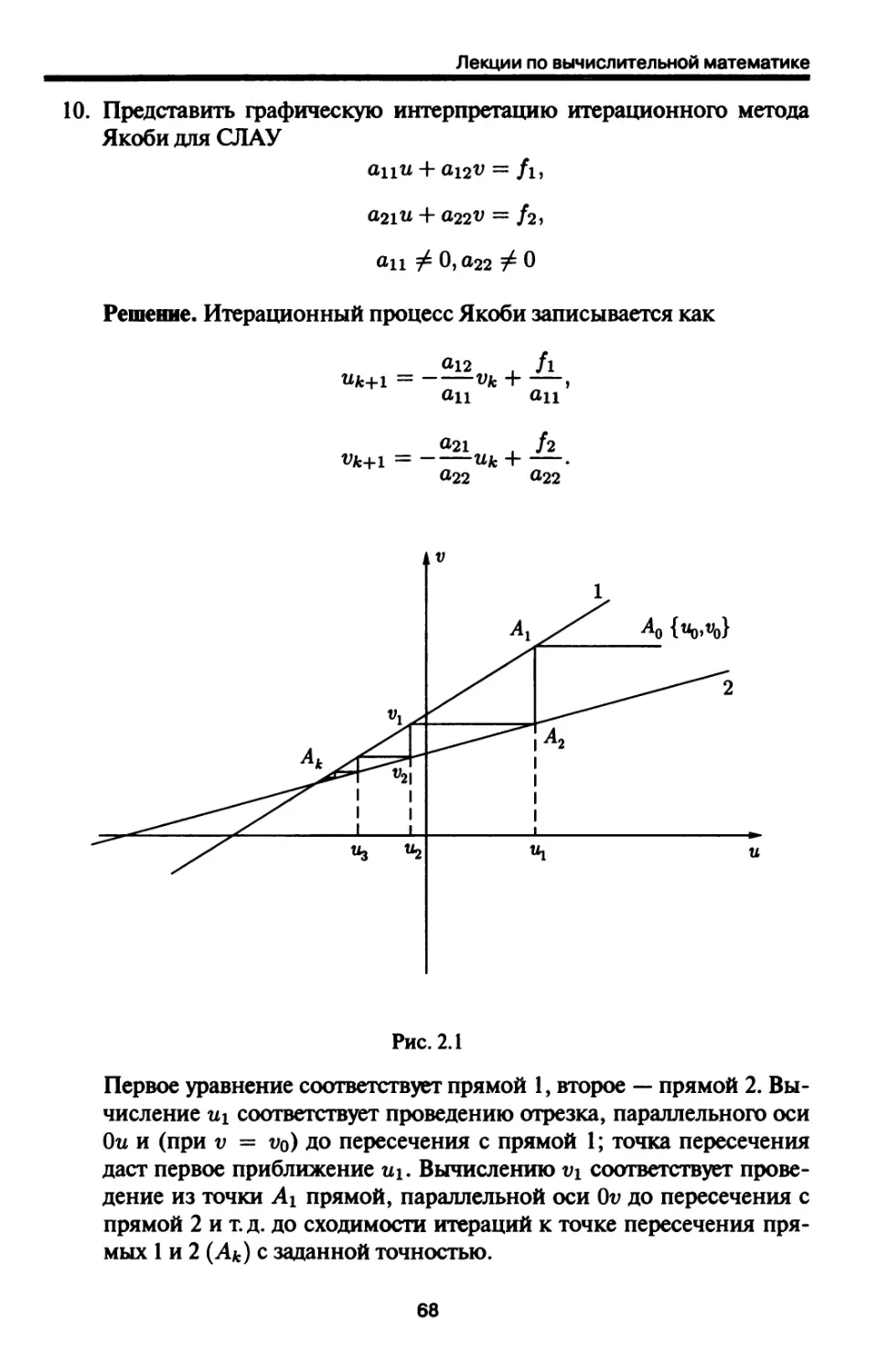
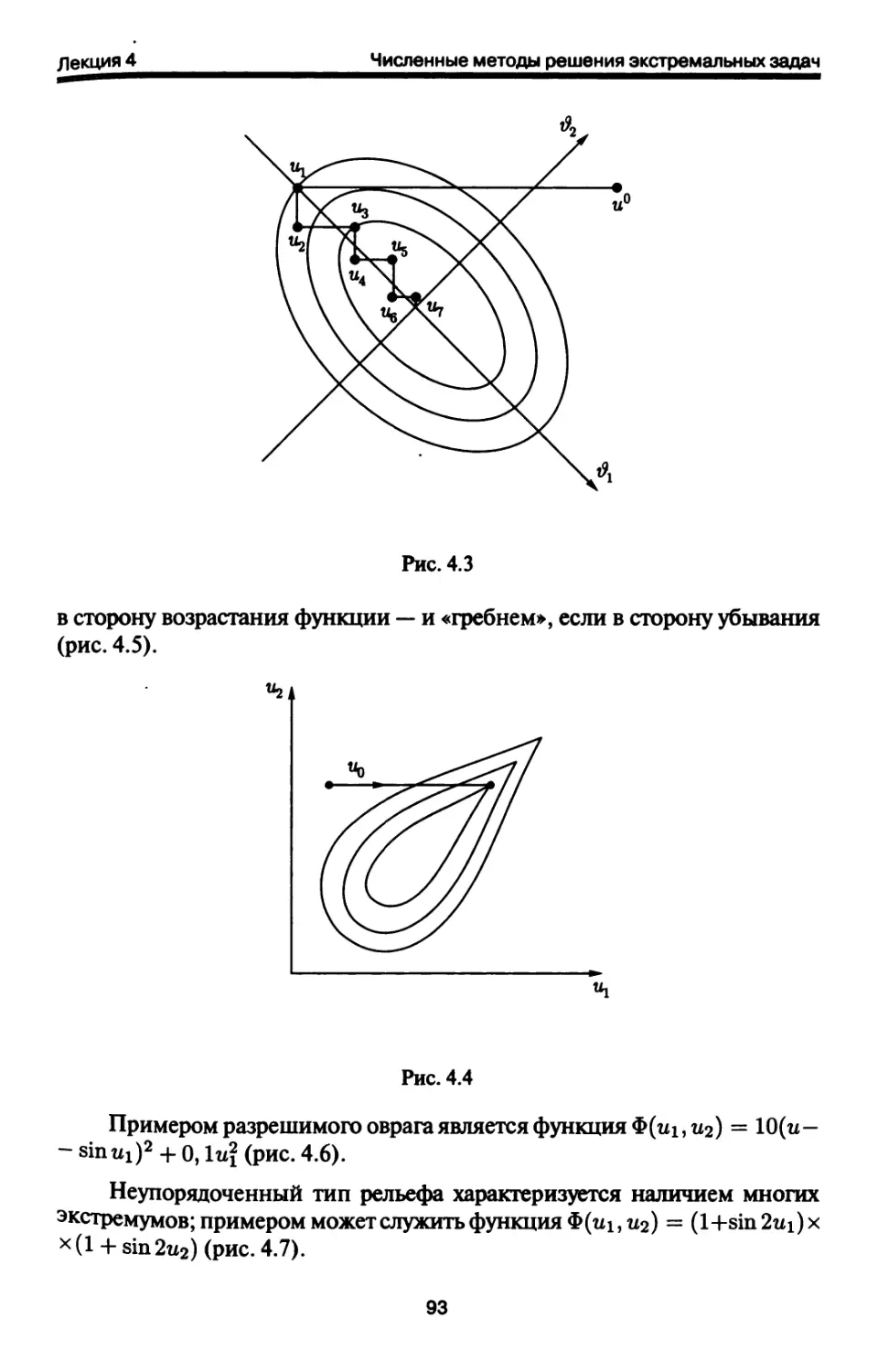
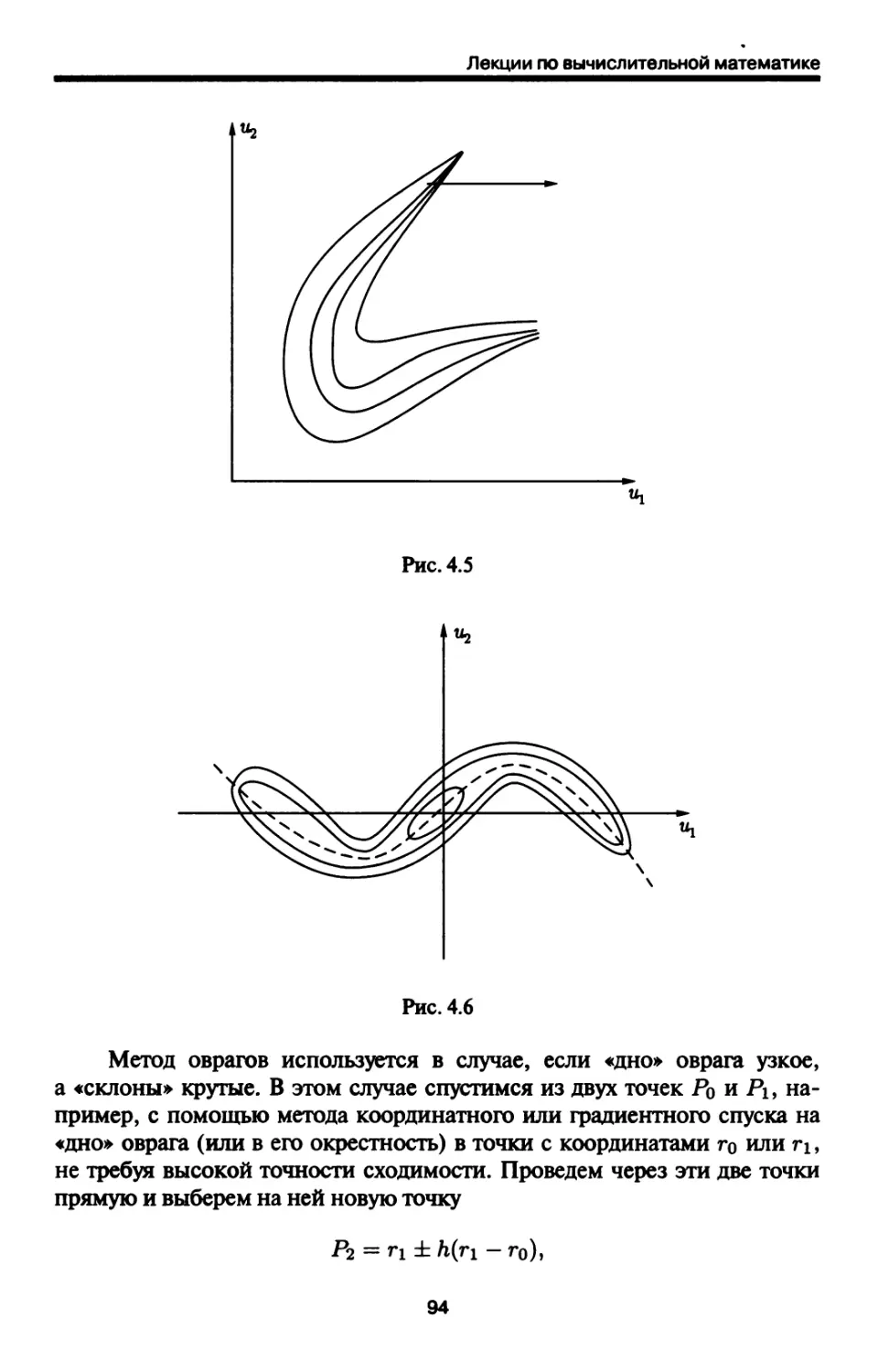
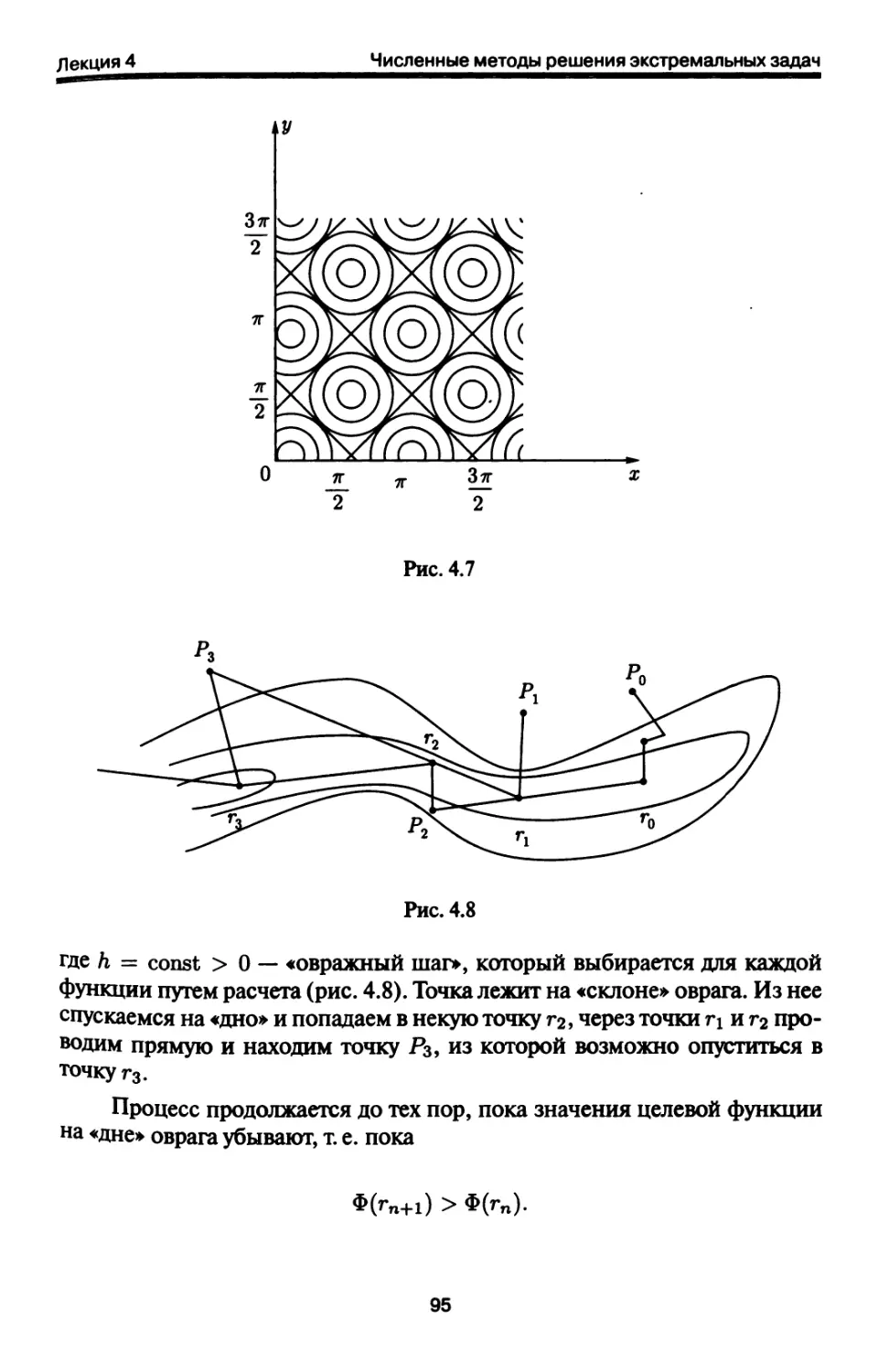
Автор: Петров И.Б. Лобанов А.И.
Теги: вычислительная математика численный анализ математика
ISBN: 5-94774-542-9
Год: 2006
Текст
Основы информационных технологий
И. Б. Петров, А. И. Лобанов
ЛЕКЦИИ
ПО ВЫЧИСЛИТЕЛЬНОЙ
МАТЕМАТИКЕ
Учебное пособие
Интернет-Университет БИНОМ.
Информационных Технологий Лаборатория знаний
wwnw.intuit.ru www.lbz.ru
Москва
2006
УДК 519.6@75.8)
ББК22.19я73
ПЗО
ПЗО Петров Игорь Борисович
Лекции по вычислительной математике: Учебное пособие /
И.Б. Петров, А. И. Лобанов. — М: Интернет-Университет
Информационных Технологий; БИНОМ. Лаборатория знаний, 2006. — 523
с: ил., табл.- (Серия «Основы информационных технологий»)
ISBN 5-94774-542-9 (БИНОМ. ЛЗ)
ISBN 5-9556-0065-5 (ИНТУИТ.РУ)
В курсе лекций рассматриваются основные понятия и методы вычислительной
математики. Курс содержит как лекции, посвященные классическим численным
методам анализа и линейной алгебры, так и решению дифференциальных уравнений.
Особое внимание уделяется решению систем уравнений в частных производных
гиперболического типа. Большинство лекций снабжено задачами для рассмотрения
на семинарских занятиях и для самостоятельного решения.
УДК 519.6@75.8)
ББК22.19я73
Издание осуществлено при финансовой и технической поддержке
издательства «Открытые Системы», «РМ Телеком» и Kraftway Computers.
Полное или частичное воспроизведение или размножение каким-либо
способом, в том числе и публикация в Сети, настоящего издания допускается
только с письменного разрешения Интернет-Университета
Информационных Технологий.
По вопросам приобретения обращаться:
«БИНОМ. Лаборатория знаний»
Телефон D95) 157-1902,157-5272,
e-mail: Lbz@aha.ru, http://www.Lbz.ru
© Интернет-Университет
Информационных
icnv _ л Технологий, 2006
ISBN 5-94774-542-9 (БИНОМ. ЛЗ) © БИНОМ. Лаборатория
ISBN 5-9556-0049-3 (ИНТУИТ.РУ) знаний, 2006
О проекте
Интернет-Университет Информационных Технологий — это первое
в России высшее учебное заведение, которое предоставляет возможность
получить дополнительное образование во Всемирной сети. >Ш>-сайт
университета находится по адресу www.intuit.ru.
Мы рады, что вы решили расширить свои знания в области
компьютерных технологий. Современный мир — это мир компьютеров и
информации. Компьютерная индустрия — самый быстрорастущий сектор
экономики, и ее рост будет продолжаться еще долгое время. Во времена
жесткой конкуренции от уровня развития информационных технологий,
достижений научной мысли и перспективных инженерных решений зависит
успех не только отдельных людей и компаний, но и целых стран. Вы
выбрали самое подходящее время для изучения компьютерных дисциплин.
Профессионалы в области информационных технологий сейчас
востребованы везде: в науке, экономике, образовании, медицине и других
областях, в государственных и частных компаниях, в России и за рубежом.
Анализ данных, прогнозы, организация связи, создание программного
обеспечения, построение моделей процессов — вот далеко не полный список
областей применения знаний для компьютерных специалистов.
Обучение в университете ведется по собственным учебным планам,
разработанным ведущими российскими специалистами на основе
международных образовательных стандартов Computer Curricula 2001 Computer
Science. Изучать учебные курсы можно самостоятельно по учебникам или
на сайте Интернет-Университета, задания выполняются только на сайте.
Для обучения необходимо зарегистрироваться на сайте университета.
Удостоверение об окончании учебного курса или специальности
выдается при условии выполнения всех заданий к лекциям и успешной сдачи
итогового экзамена.
Книга, которую вы держите в руках, — очередная в многотомной
серии «Основы информационных технологий», выпускаемой Интернет-
Университетом Информационных Технологий. В этой серии будут
выпущены учебники по всем базовым областям знаний, связанным с
компьютерными дисциплинами.
Добро пожаловать в
Интернет-Университет Информационных Технологий!
Анатолий Шкред
anatoli@shkred.ru
Об авторах
Петров Игорь Борисович, доктор физико-математических наук,
профессор, заведующий кафедрой информатики МФТИ. Область научных
интересов: математическое моделирование в динамике деформируемого
твердого тела, математическое моделирование в биологии и медицине,
численные методы, современные методы преподавания информатики и
вычислительной математики. Автор более 200 научных и
учебно-методических работ.
Лобанов Алексей Иванович, доктор физико-математических наук,
профессор. Область научных интересов: математическое моделирование
в динамике высокотемпературной плазмы, математическое
моделирование в биологии и медицине, численные методы. Автор более 150 научных
и учебно-методических работ.
Оглавление
Предисловие 13
Лекция 1. Предмет вычислительной математики. Обусловленность
задачи, устойчивость алгоритма, погрешности вычислений. Задача
численного дифференцирования 15
1.1. Обусловленность задачи 17
1.2. Влияние выбора вычислительного алгоритма на результаты
вычислений 19
1.3. Экономичность вычислительного метода . . . 21
1.4. Погрешность метода 22
1.5. Элементы теории погрешностей 23
1.6. Задача численного дифференцирования 24
1.7. Задачи 28
1.8. Задачи для самостоятельного решения 30
Литература 31
Лекция 2. Численное решение систем линейных алгебраических
уравнений 32
2.1. Постановка задачи 32
2.2. Согласованные нормы векторов и матриц 34
2.3. Обусловленность СЛАУ. Число обусловленности матрицы . 36
2.4. Прямые методы решения СЛАУ 39
2.4.1. Метод исключения Гаусса 40
2.4.2. Модификация метода Гаусса для случая линейных
систем с трехдиагональными матрицами — метод
прогонки 44
2.4.3. LU-разложение 45
2.4.4. Метод Холецкого (метод квадратного корня) .... 46
2.5. Итерационные методы решения СЛАУ 48
2.5.1. Метод простой итерации 48
2.5.2. Влияние ошибок округления на результат
численного решения 50
2.5.3. Методы Якоби, Зейделя, верхней релаксации .... 51
2.6. Вариационные итерационные методы 54
2.6.1. Связь между вариационной задачей и задачей
решения СЛАУ 54
2.6.2. Методы градиентного и наискорейшего спуска ... 56
2.6.3. Метод минимальных невязок 56
Лекции по вычислительной математике
2.6.4. Метод сопряженных градиентов 57
2.7. О спектральных задачах 58
Литература 70
Лекция 3. Численное решение переопределенных СЛАУ. Метод
наименьших квадратов 72
3.1. Пример использования метода наименьших квадратов (МНК) 72
3.2. Понятие о методах решения плохо обусловленных СЛАУ . 79
3.3. Задачи 80
3.4. Задачи для самостоятельного решения 82
Литература 83
Лекция 4. Численные методы решения экстремальных задач ... 85
4.1. Поиск безусловного минимума функции 85
4.2. Методы спуска 91
4.2.1. Метод покоординатного спуска 91
4.2.2. Метод градиентного спуска 96
4.2.3. Метод наискорейшего спуска 96
4.3. Задачи математического программирования 98
4.4. Задачи 101
4.5. Задачи для самостоятельного решения 102
Литература 103
Лекция 5. Численное решение нелинейных алгебраических
уравнений и систем 104
5.1. Сжимающие отображения. Итерации. Метод простых ите-
раций(МПИ) 104
5.2. Метод Ньютона 108
5.3. О вариационных подходах к решению нелинейных систем
уравнений 112
5.4. Метод Чебышёва построения итерационных процессов
высшего порядка 112
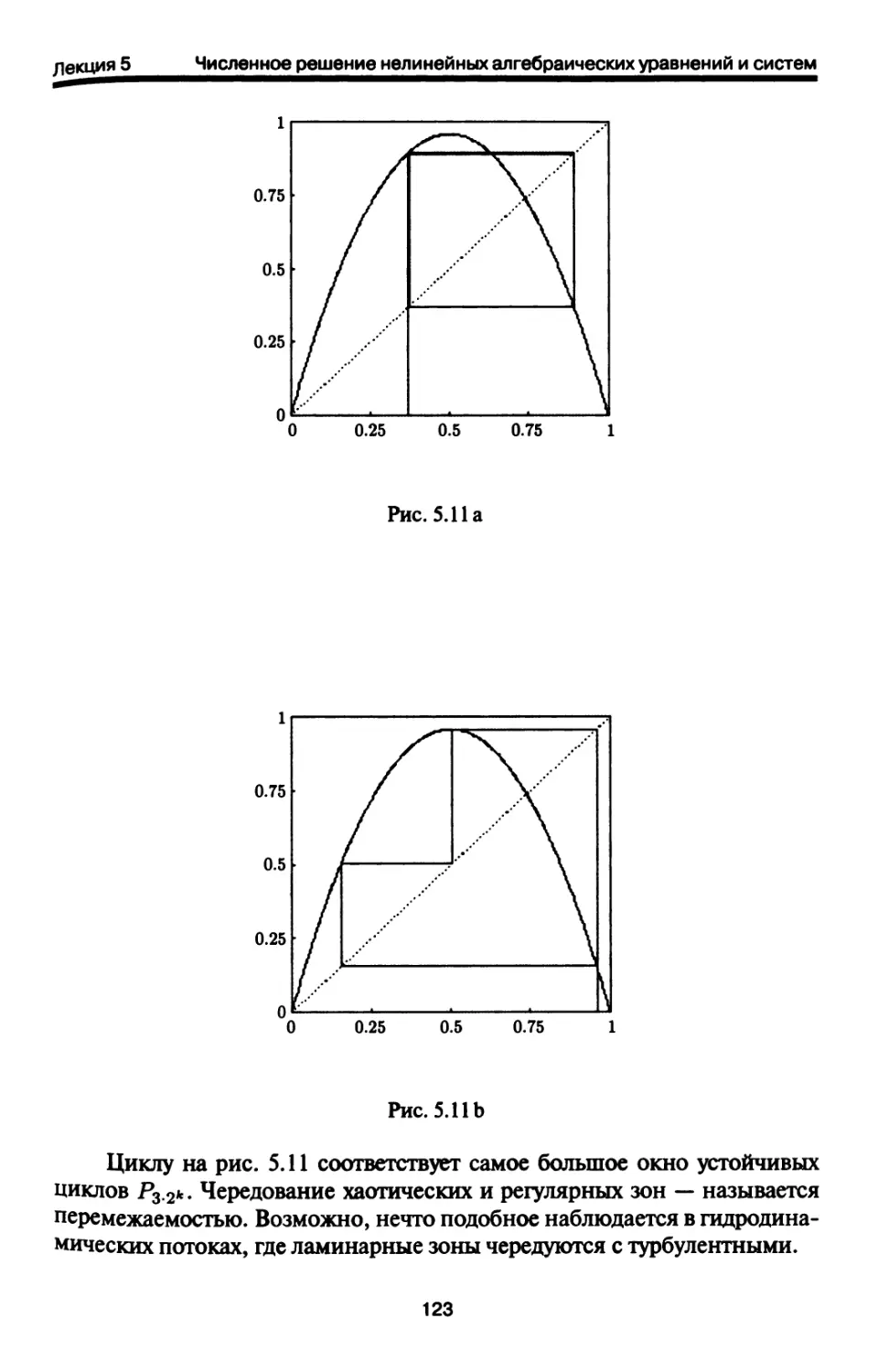
5.5. Разностные отображения в нелинейной динамике 113
5.6. Задачи 124
5.7. Задачи для самостоятельного решения 131
Литература 132
Лекция 6. Интерполяция функций 133
6.1. Постановка задачи интерполяции 133
6.2. Кусочно-линейная интерполяция 134
6.3. Интерполяция обобщенными полиномами 135
6.4. Полиномиальная (алгебраическая) интерполяция 136
6.5. Теорема об остаточном члене интерполяции 137
6
Оглавление
6.6. Интерполяционный полином в форме Ньютона 139
6.6.1. Разделенные и конечные разности 139
6.6.2. Интерполяционный полином в форме Ньютона . . 141
6.7. Многочлены Чебышёва и минимизация остаточного члена
интерполяции 141
6.8. Обусловленность задачи интерполяции. Постоянная Лебега 142
6.9. Интерполяция с кратными узлами 143
6.9.1. Замечание о тригонометрической интерполяции . . 145
6.10. Кусочно-многочленная глобальная интерполяция(сплайны) 143
6.11. В-сплайны 151
6.12. Интерполяция функций двух переменных 154
6.13. Задачи 155
6.14. Задачи для самостоятельного решения 159
Литература 160
Лекция 7. Численное интегрирование 162
7.1. Квадратурные формулы интерполяционного типа
(формулы Ньютона—Котеса) 162
7.2. Оценка погрешности квадратурных формул 166
7.3. Кратные интегралы 168
7.4. Квадратурные формулы Гаусса 169
7.5. Вычисление интегралов от функций с особенностями ... 173
7.6. Идея метода Монте-Карло 174
7.7. Задачи 175
7.8. Задачи для самостоятельного решения 178
Литература 180
Лекция 8. Численные методы решения задачи Коши для систем
обыкновенных дифференциальных уравнений 181
8.1. Базовые понятия 181
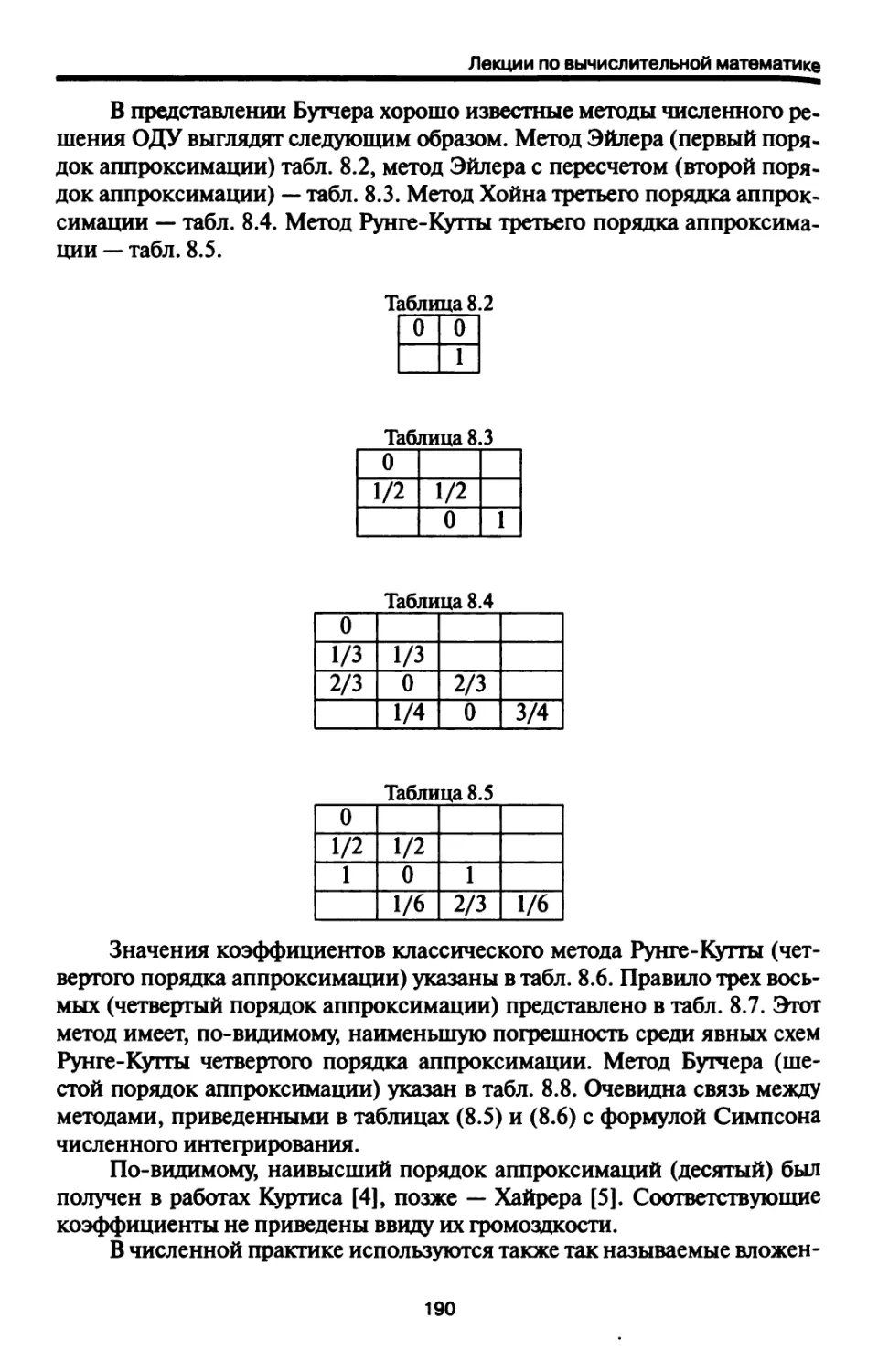
8.2. Методы Рунге-Кутты 186
8.3. Методы Адамса 197
8.4. Оценка погрешности 200
8.4.1. Автоматический выбор шага интегрирования .... 200
8.5. Устойчивость методов Рунге-Кутты 202
8.6. Задачи 207
8.7. Задачи для самостоятельного решения 212
Литература 216
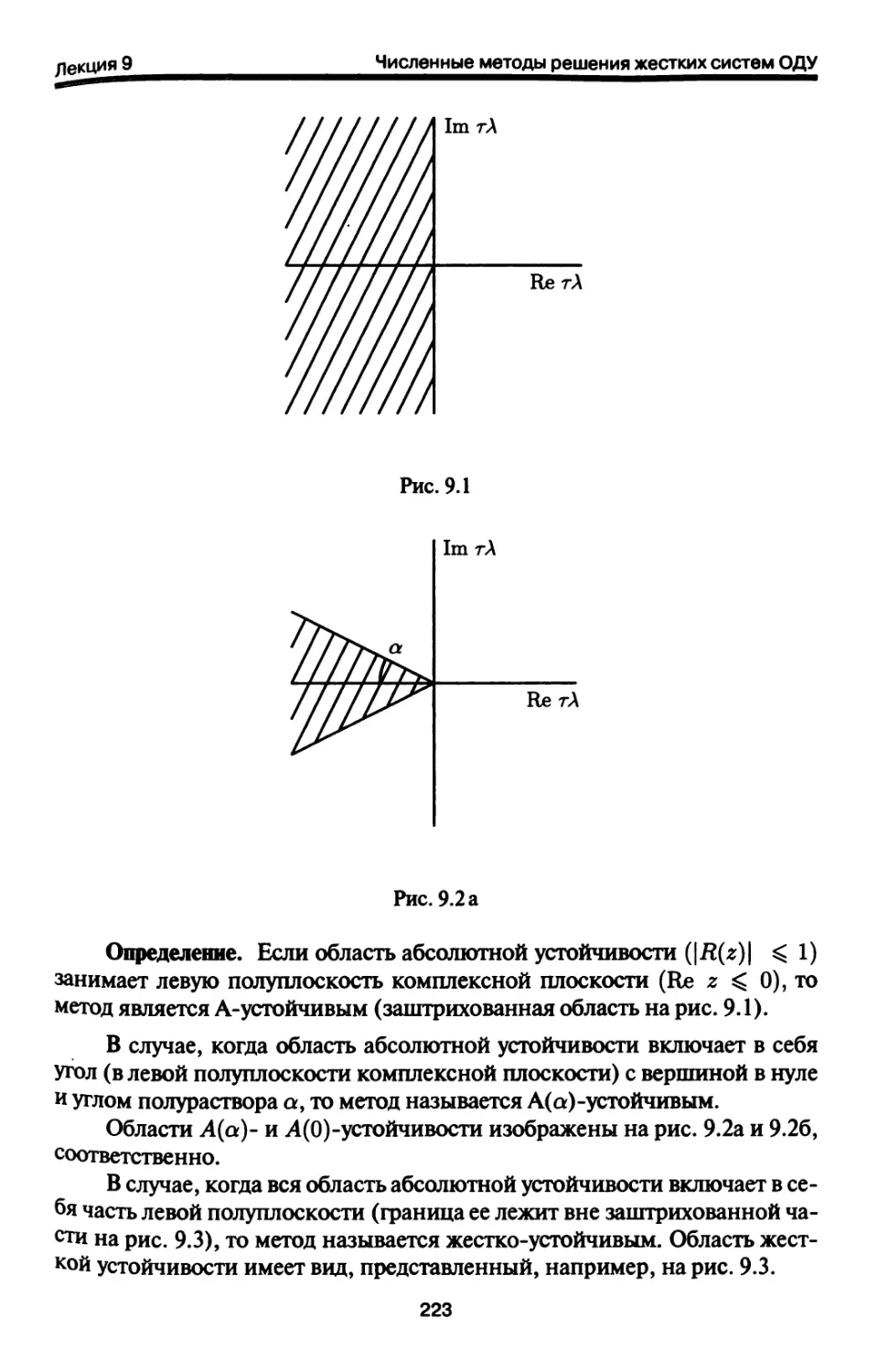
Лекция 9. Численные методы решения жестких систем
обыкновенных дифференциальных уравнений 218
9.1. Явление жесткости. Предварительные сведения 218
9.2. Сингулярно-возмущенные задачи 224
Лекции по вычислительной математике
9.3. Решение линейных ЖС ОДУ и вычисление матричной
экспоненты 229
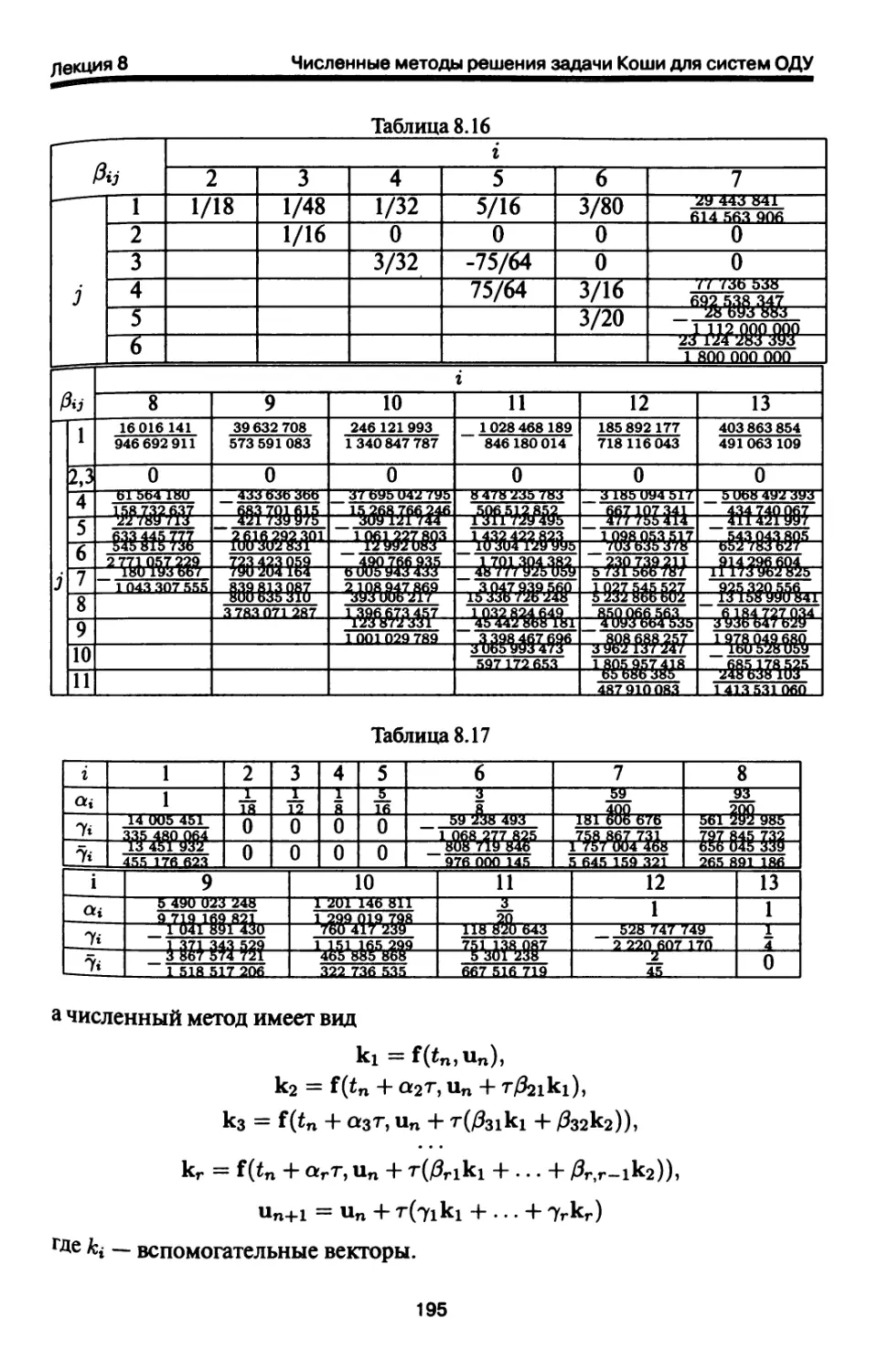
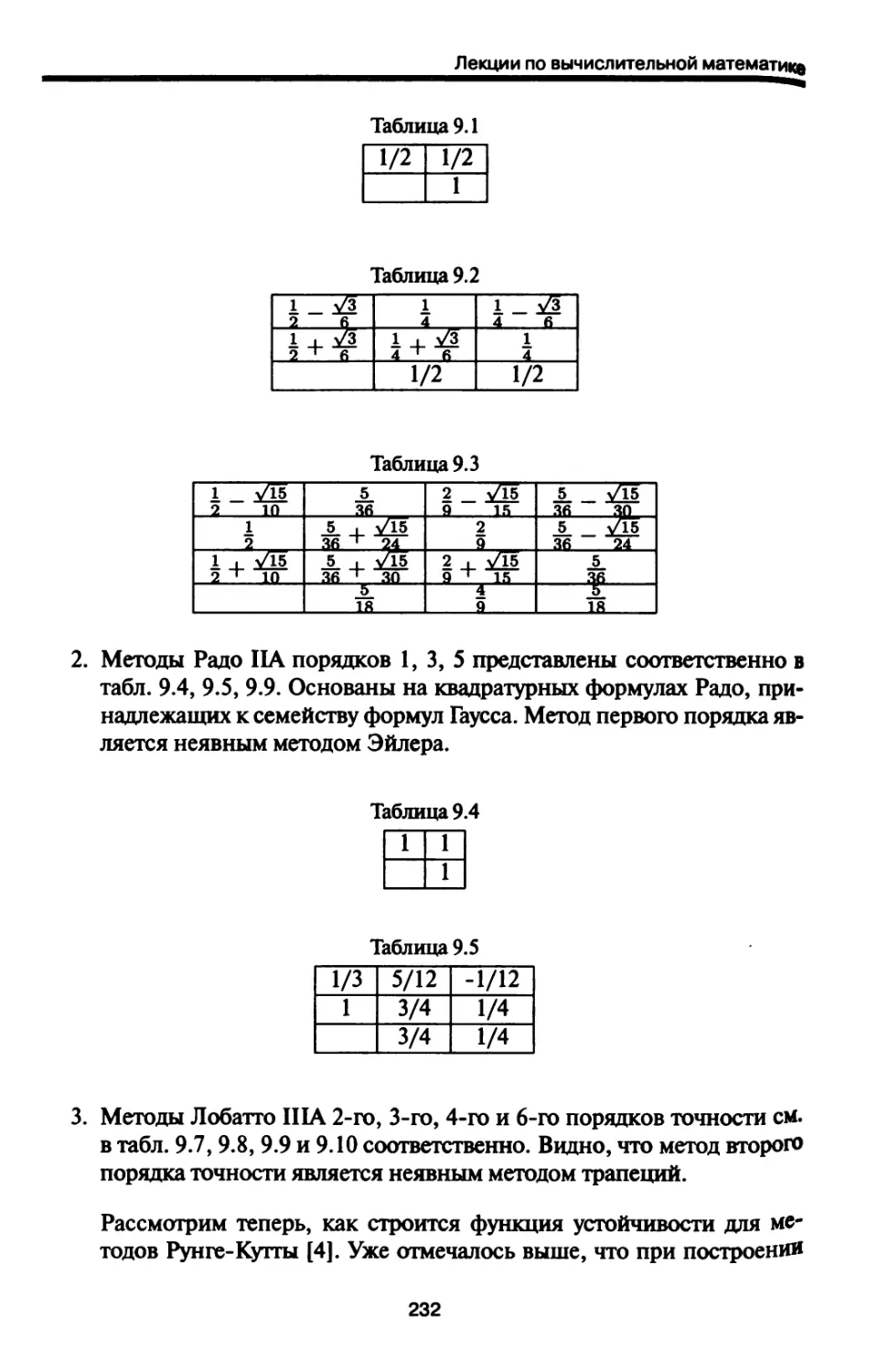
9.4. Численные методы решения ЖС ОДУ. Семейства неявных
методов Рунге-Купы и Розенброка 230
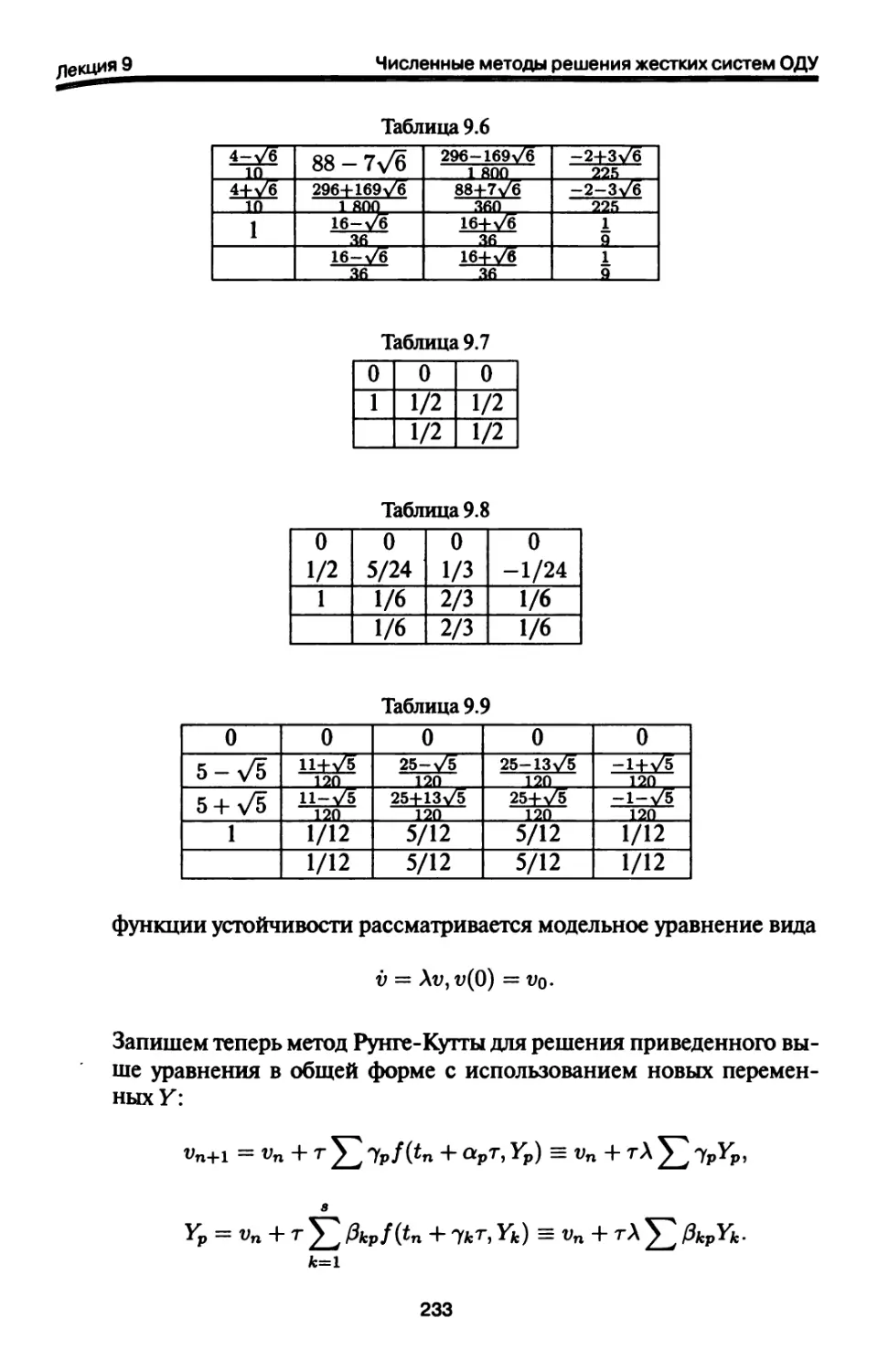
9.5. Формулы дифференцирования назад и методы Гира.
Представление Нордсика 236
9.6. Задачи для самостоятельного решения 239
Литература 245
Лекция 10. Численное решение краевых задач для систем
обыкновенных дифференциальных уравнений 247
10.1. Краевая задача для линейной системы ОДУ первого порядка 247
10.2. Метод дифференциальной прогонки. Понятие о жестких
краевых задачах 250
10.3. Краевая разностная задача Штурма-Лиувилля для
обыкновенного дифференциального уравнения второго порядка . 253
10.4. Пятиточечная прогонка 257
10.5. Матричная прогонка 258
10.6. Численное решение нелинейных краевых задач 259
10.6.1. Метод стрельбы 259
10.6.2. Метод квазилинеаризации (метод Ньютона) 260
10.6.3. Аппроксимация граничных условий 260
10.7. Краевые задачи на собственные значения для
обыкновенных дифференциальных уравнений 263
10.8. Решение краевой задачи методом Фурье 264
10.9. Задачи 266-
10. ЮЗадачи для самостоятельного решения 270
Литература 274
Лекция 11. Исследование разностных схем для эволюционных
уравнений на устойчивость и сходимость 275
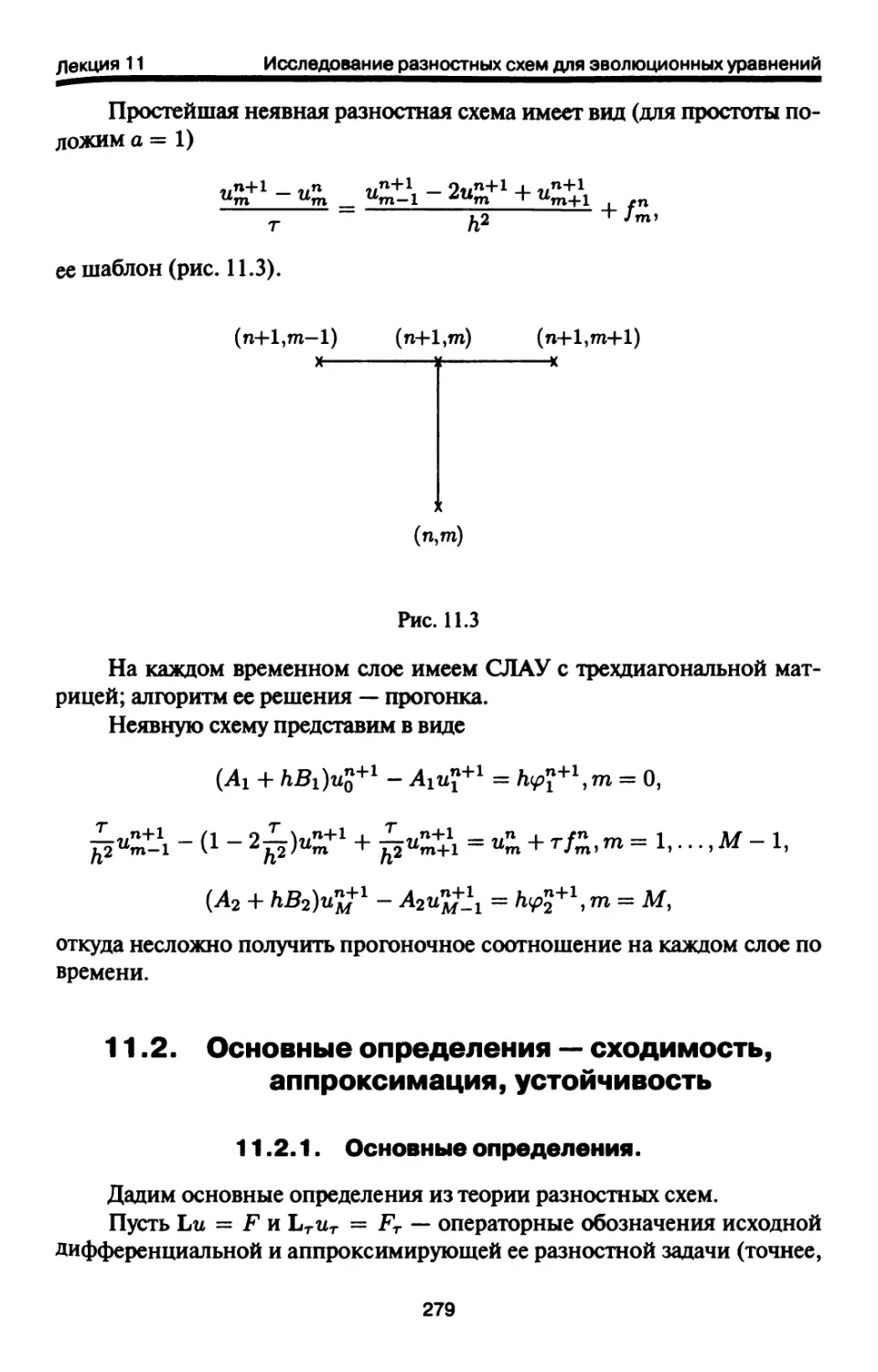
11.1. Постановка некоторых задач для уравнений
математической физики 275
11.2. Основные определения — сходимость, аппроксимация,
устойчивость 279
11.2.1. Основные определения 279
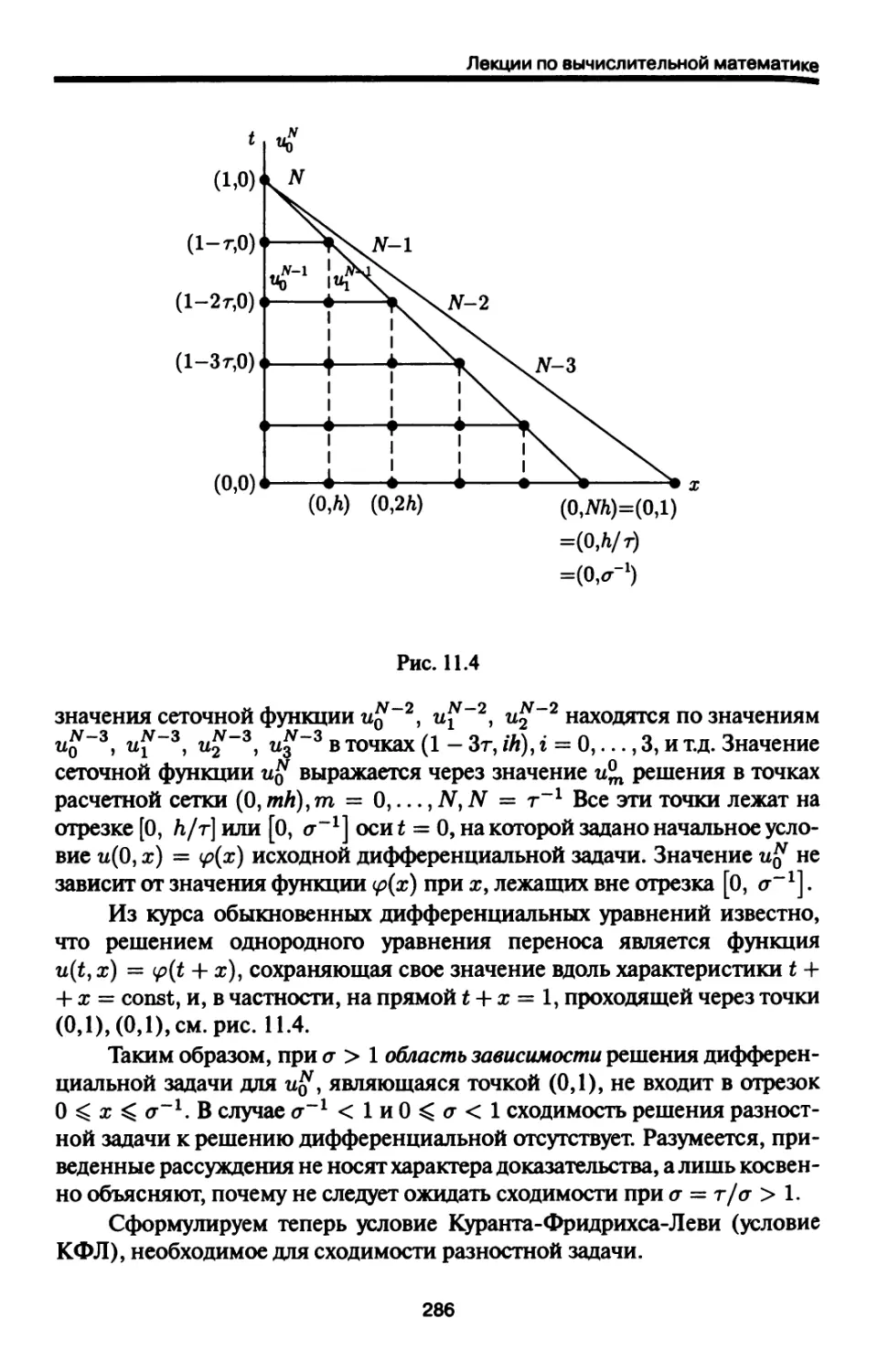
11.2.2. Необходимое условие сходимости разностной
схемы Куранта, Фридрихса, Леви (условие КФЛ) .... 285
11.3. Элементы теории устойчивости разностных схем 287
11.4. Задачи 302
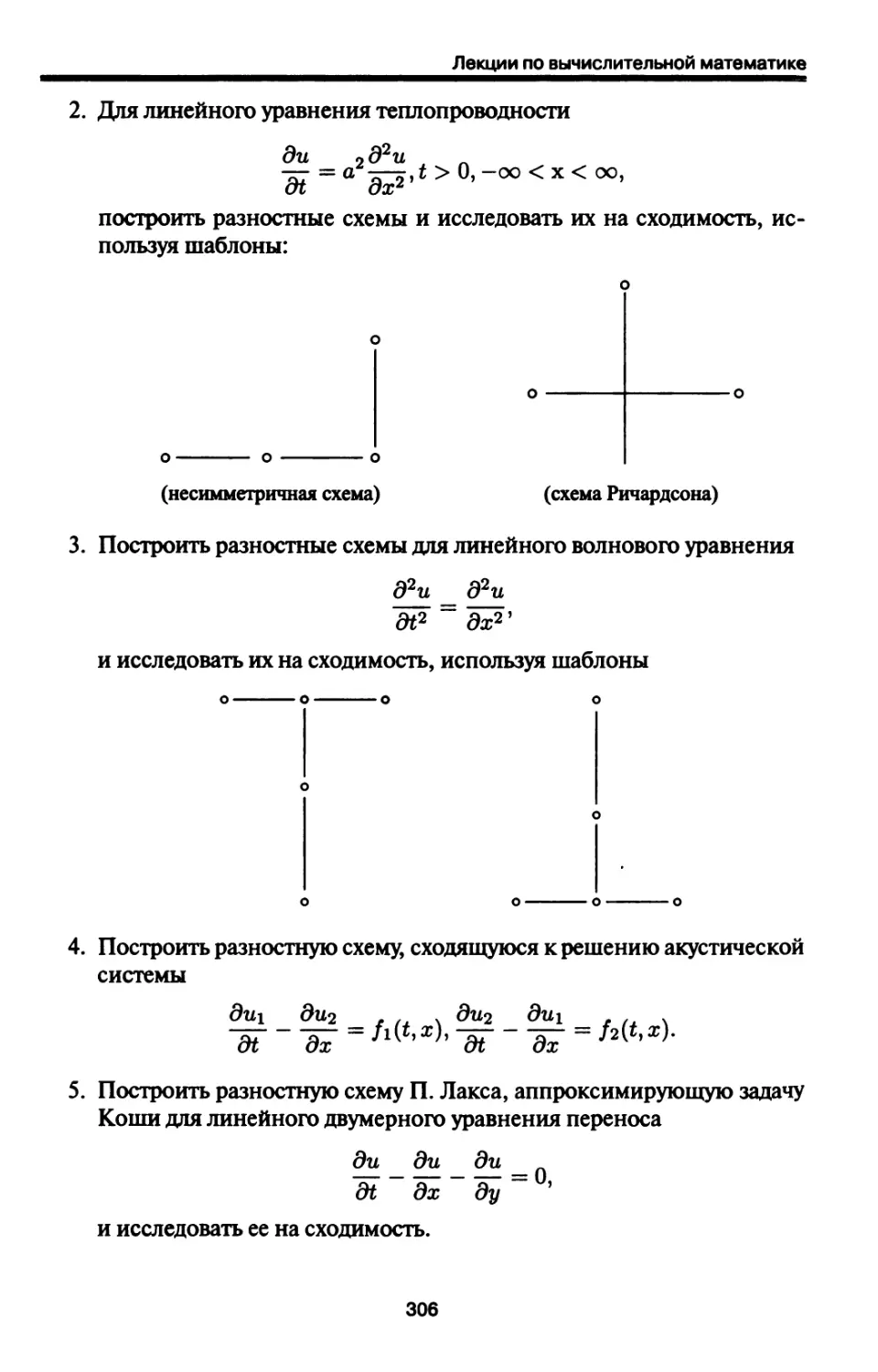
11.5. Задачи для самостоятельного решения 305
Литература 307
Оглавление
Лекция 12. Численное решение дифференциальных уравнений в
частных производных параболического типа на примере
уравнения теплопроводности 308
12.1. Постановки задач для уравнений параболического типа . . 308
12.2. Разностные схемы для численного решения нелинейного
уравнения теплопроводности 312
12.2.1. Неявная схема с нелинейностью на нижнем слое . . 312
12.2.2. Схема с нелинейностью на верхнем слое 312
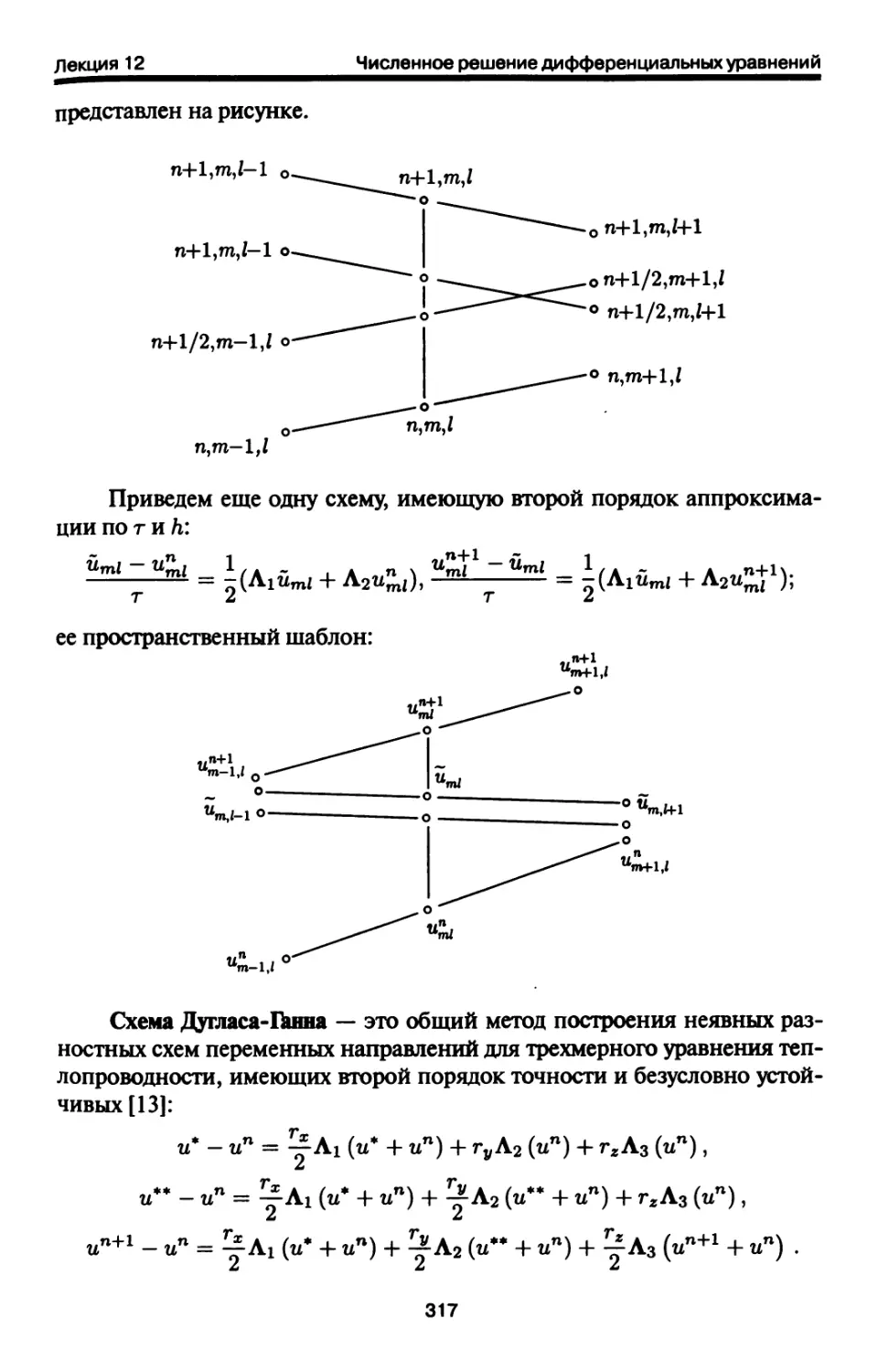
12.3. Разностные схемы для численного решения многомерного
уравнения теплопроводности 315
12.4. Исследование сходимости разностных схем для
многомерного уравнения теплопроводности 318
12.5. Задачи 320
12.6. Задачи для самостоятельного решения 325
Литература 330
Лекция 13. Численные методы решения уравнений в частных
производных гиперболического типа (на примере уравнения переноса) 332
13.1. Простейшее линейное уравнение переноса 332
13.2. Квазилинейные уравнения гиперболического типа.
Характеристики квазилинейных уравнений 334
13.3. Численные методы решения уравнений в частных
производных гиперболического типа на примере линейного
уравнения переноса 336
13.4. Численные методы решения уравнений в частных
производных гиперболического типа для квазилинейного
уравнения переноса 342
13.5. Методы регуляризации численных решений с большими
градиентами 347
13.6. Гибридные схемы (метод Р. П. Федоренко) 350
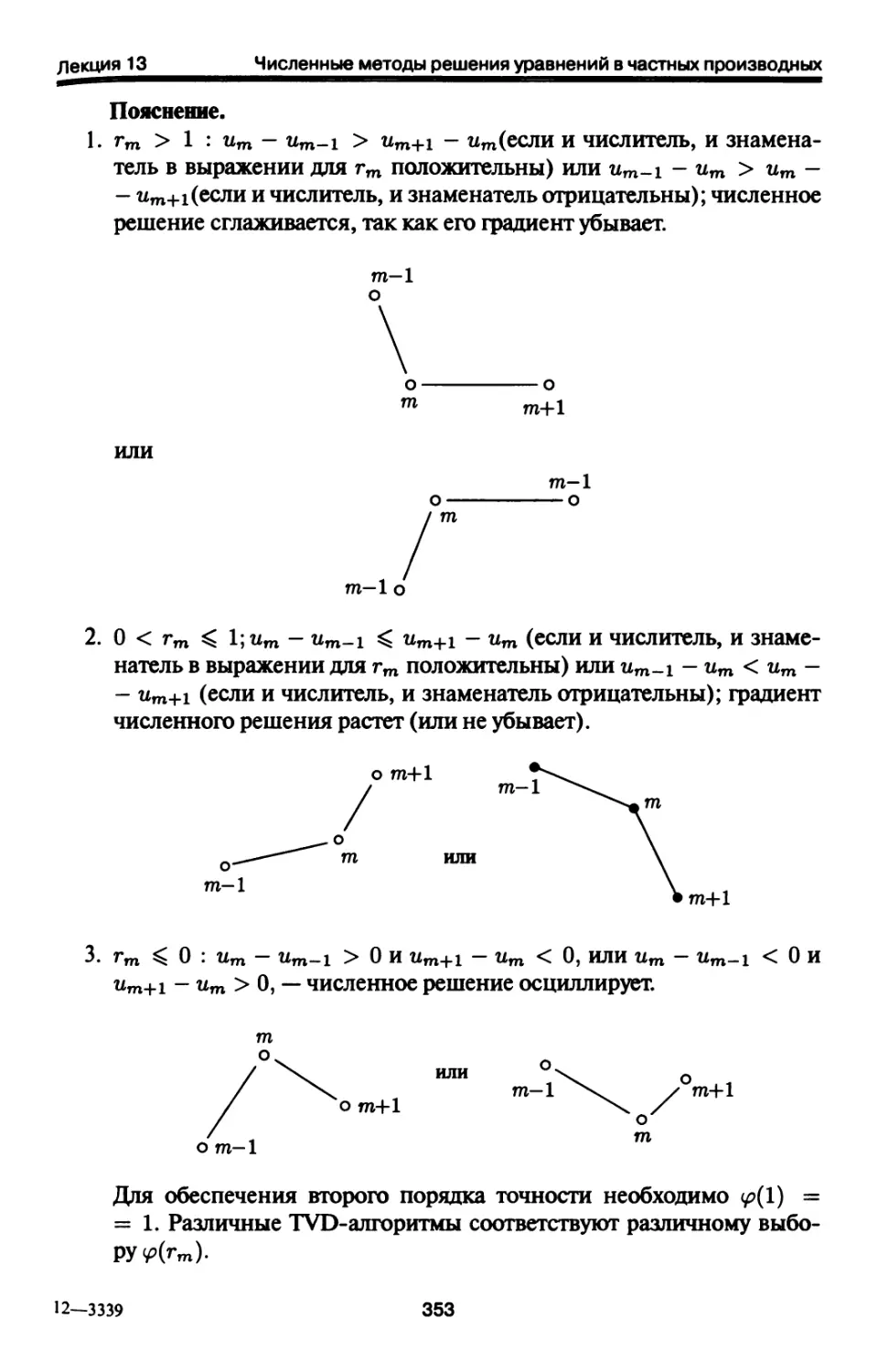
13.7. Схемы с уменьшением полной вариации (Total Variation
Diminishing, схемы Хартена) 351
13.8. Идеи построения сеточно-характеристических методов и
анализ разностных схем в пространстве неопределенных
коэффициентов 354
13.9. Задачи 362
13. ЮЗадачи для самостоятельного решения 374
Литература 379
Лекция 14. Введение в методы численного решения уравнений
газовой динамики 381
14.1. Формы записи одномерных уравнений газовой динамики . 381
9
Лекции по вычислительной математике
14.2. Методы Лакса-Вендроффа и Мак-Кормака 385
14.3. Сеточно-характеристический метод для численного
решения уравнений газовой динамики (М.-К. М. Магомедова-
А. С. Холодова) 386
14.4. Разностная схема И.М. Гельфанда для численного решения
одномерной системы уравнений газовой динамики 388
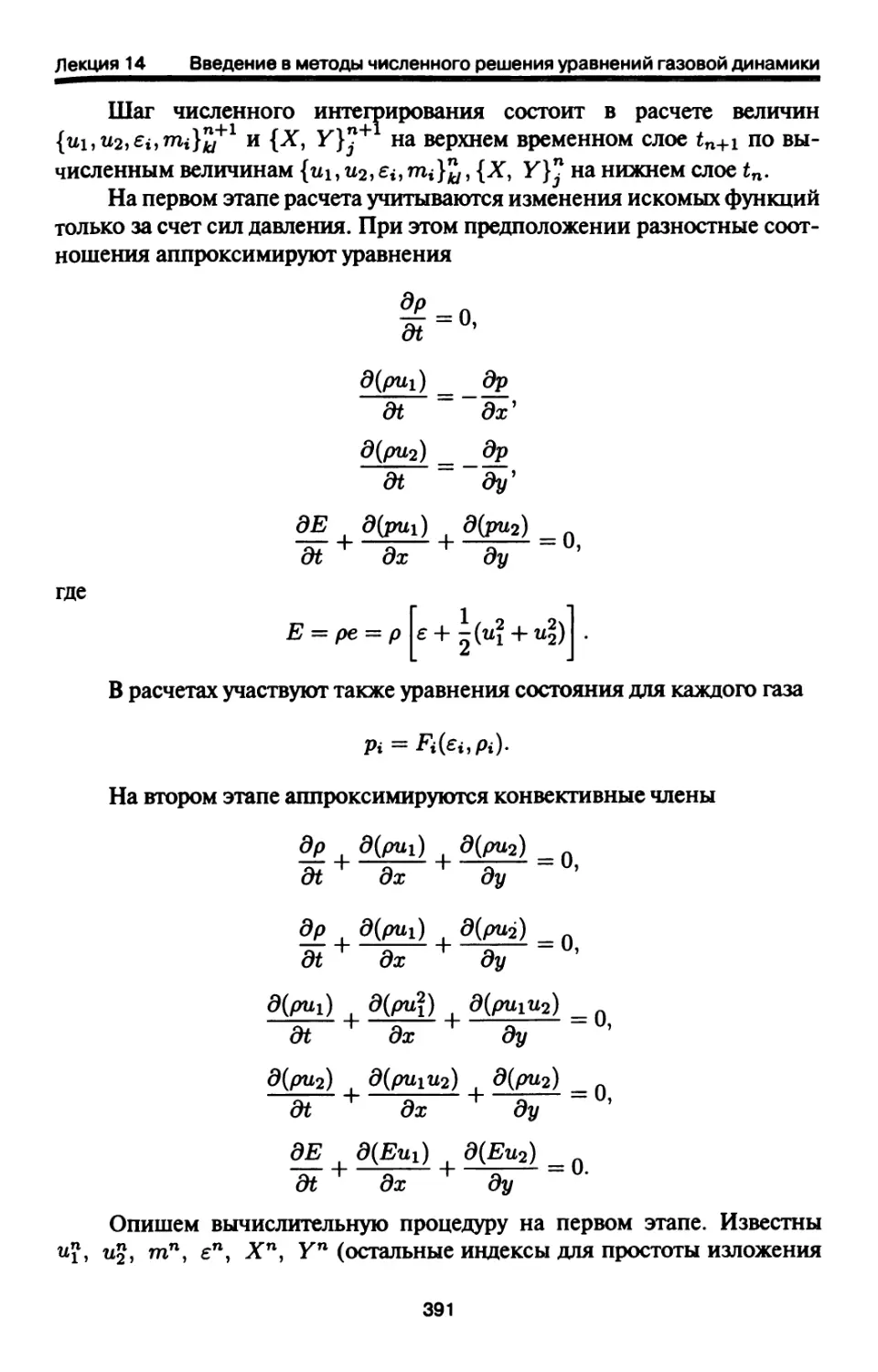
14.5. Метод частиц в ячейках Харлоу (PIC method:Purticle-In-Cell) 390
14.6. Задачи для самостоятельного решения 395
Литература 397
Лекция 15. Численное решение уравнений в частных производных
гиперболического типа с большими градиентами решений .... 399
15.1. Потоковая форма представления разностных схем 399
15.2. Гибридные схемы 400
15.3. Гибридные схемы и пространство неопределенных
коэффициентов 401
15.4. Метод коррекции потоков Бориса-Бука 404
15.5.Т\Т)-схемы 405
15.6. ENO-схемы 408
15.7. Разностные схемы для квазилинейного уравнения переноса 410
15.8. Однопараметрическое семейство неявных схем 412
15.9. TVD-схемы для квазилинейного уравнения с
антидиффузией 413
15. lOTVD-схемы для линейных систем уравнений
гиперболического типа 415
15.1 Шетод С. К. Годунова 417
Литература 420
Лекция 16. Численное решение уравнений в частных производных
эллиптического типа на примере уравнений Лапласа и Пуассона 424
16.1. Постановка задачи. Простейшая разностная схема «крест».
Устойчивость схемы «крест» 424
16.2. Методы решения сеточных уравнений 428
16.2.1. Метод простых итераций 429
16.2.2. Метод простых итераций с оптимальным параметром 430
16.2.3. Чебышёвское ускорение метода простых итераций . 434
16.2.4. Метод переменных направлений 437
16.2.5. Методы Якоби, Зейделя, верхней релаксации .... 440
16.3. Попеременно-треугольный итерационный метод 442
16.4. Сводка результатов по итерационным методам решения
сеточных уравнений 445
16.5. Основные идеи многосеточного метода Р. П. Федоренко . . 446
ю
Оглавление
16.6. Построение разностных схем для эллиптических
уравнений на нерегулярных сетках. Монотонные схемы (подход
АХ.Холодова) 448
16.7. Задачи 451
16.8. Задачи для самостоятельного решения 452
Литература 458
Лекция 17. Понятие о методах конечных элементов 459
17.1. Вариационный подход Ритца 460
17.2. Общая схема метода Ритца 462
17.3. Формулировка проекционного метода Галеркина 465
17.4. Пример построения схемы конечных элементов 467
17.5. Построение базисных функций 469
17.6. МКЭ для нестационарных уравнений 474
17.7. Решение нелинейных уравнений с помощью МКЭ 477
17.8. Задачи для самостоятельного решения 478
Литература 478
Лекция 18. Методы расщепления 479
18.1. Понятие о методах расщепления 479
18.2. Метод расщепления первого и второго порядка точности
пот 480
18.2.1. Локально-одномерные схемы 480
18.2.2. Схемы Кранка-Никольсон 482
18.2.3. Общая формулировка методов расщепления .... 482
18.2.4. Схемы расщепления для уравнения теплопроводности483
18.3. Методы двуциклического покомпонентного расщепления . 484
18.4. Методы расщепления с факторизацией оператора 489
18.4.1. Факторизованная схема расщепления 489
18.4.2. Неявная схема расщепления с приближенной
факторизацией 490
18.4.3. Метод «предиктор-корректор» 491
Литература 493
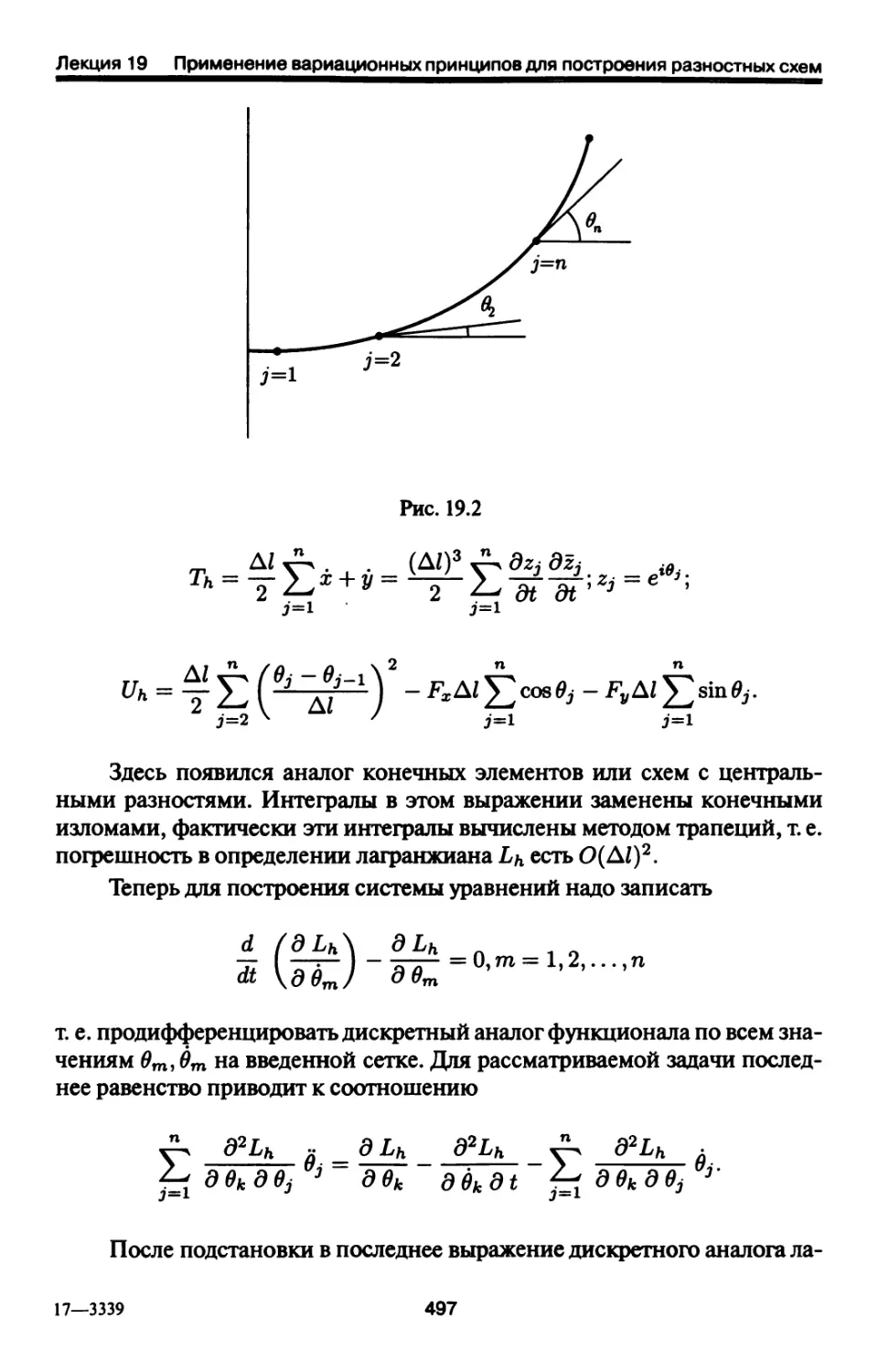
Лекция 19. Применение вариационных принципов для построения
разностных схем 494
19.1. Пример использования принципа наименьшего действия
(Гамильтона) 494
19.2. Вариационные схемы для решения задач газовой динамики 498
19.3. Вариационная схема для уравнения теплопроводности на
криволинейной сетке 502
19.4. Задачи для самостоятельного решения 507
Литература 509
11
Лекции по вычислительной математике
Приложение. Параллельные вычисления на кластерах из
персональных компьютеров в математической физике 510
1. Введение 510
2. Расчет электрического поля установки РС-20 с
использованием кластера из персональных компьютеров 512
3. Математическая модель и выбор численного метода .... 513
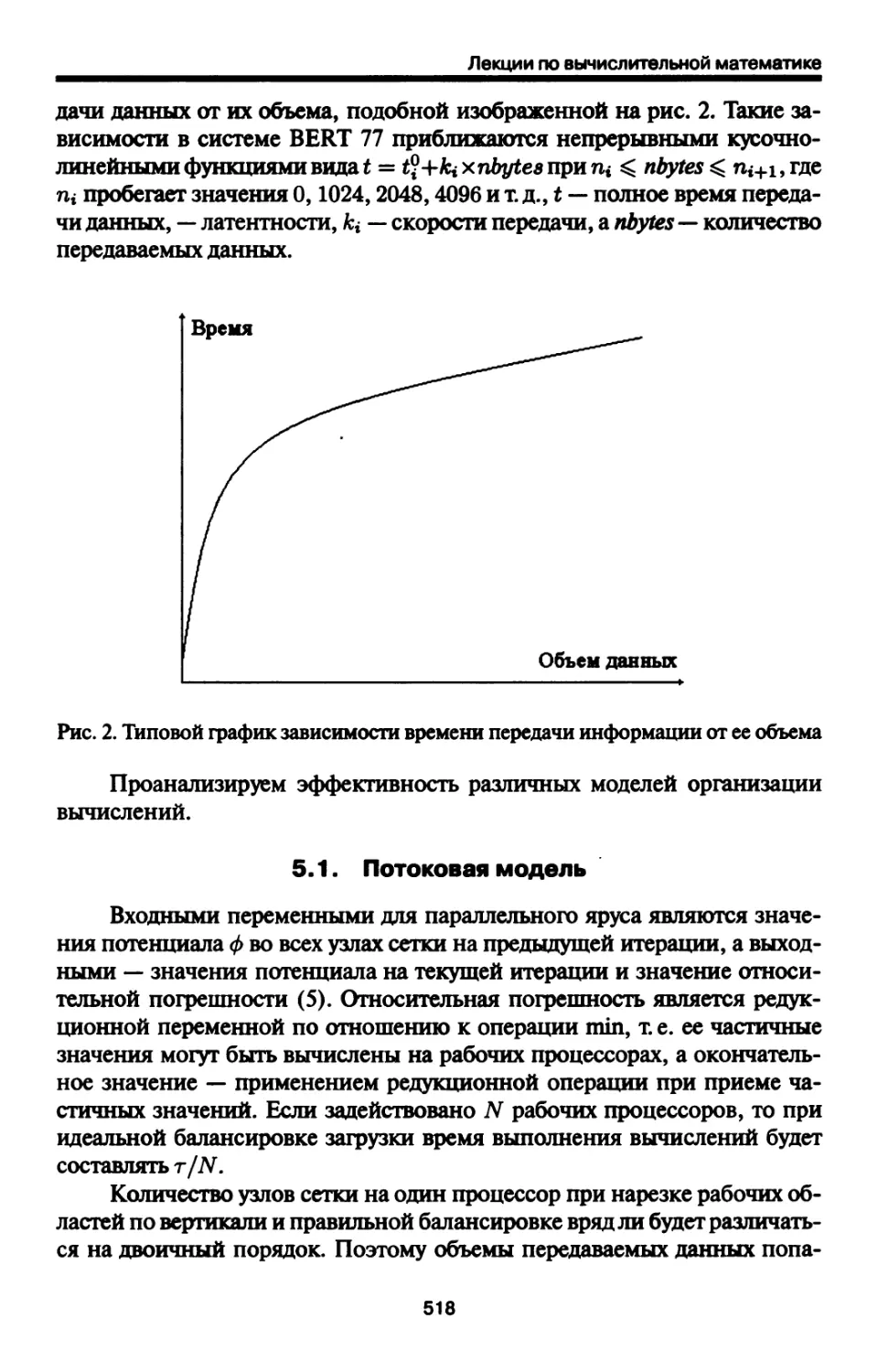
4. Модели организации параллельных вычислений для
комплексов с распределенной памятью 514
Потоковая модель 515
Статическая модель 516
5. Выбор модели организации параллельных вычислений . . 517
5.1. Потоковая модель 518
5.2. Динамическая модель 519
5.3. Статическая модель 519
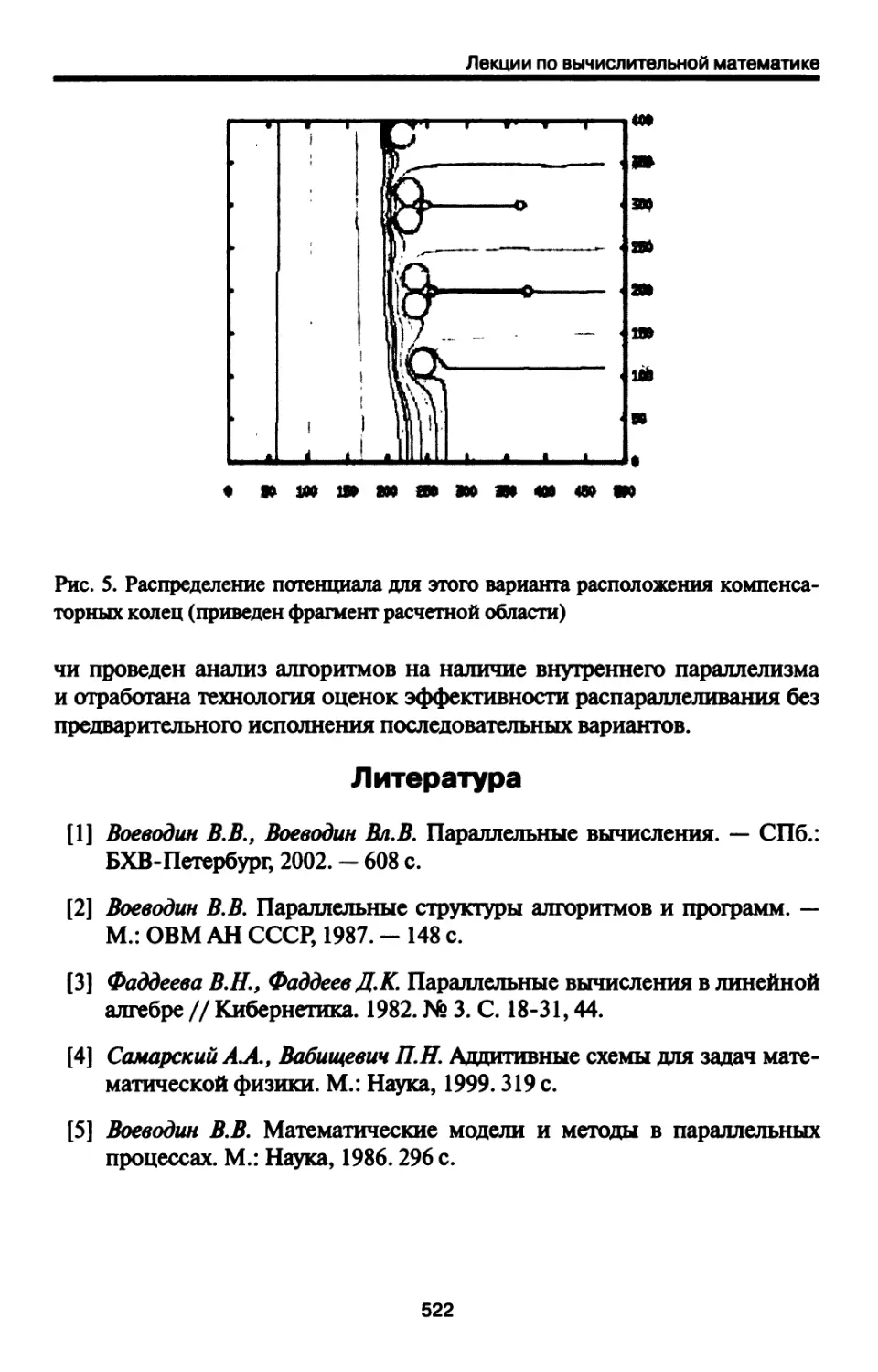
6. Заключение 521
Литература 522
12
Предисловие
В последнее время в России издается довольно много книг по
вопросам вычислительной математики. При написании учебников их
создателям приходится решать противоречия между строгостью изложения
и компактностью, сжатостью информации, между классическими
темами и новым материалом, между необходимостью описывать те разделы,
которые далеки от научных интересов авторов, и желанием уделить
больше внимания любимой теме. Все эти противоречия встали и перед
авторами данного курса. Насколько успешно их удалось преодолеть, судить
читателям.
За основу данной книги были взяты курсы вычислительной
математики, которые в течение ряда лет читались студентам факультетов
общей и прикладной физики, молекулярной и биологической физики,
проблем физики и энергетики МФТИ. Слушатели этих курсов — не
профессионалы-вычислители, а исследователи, специалисты в
предметной области. Но логика современного развития науки привела к тому, что
успех исследования во многом определяется эффективностью
применения вычислительной техники и численных методов. В этой связи авторы
посчитали необходимым дать студентам представление и о сравнительно
современных численных методах. В силу быстрых изменений,
происходящих сейчас в вычислительной математике, издать курс, на 100
процентов удовлетворяющий потребностям сегодняшнего дня, просто
невозможно.
В книгу включены идеи, методы, разделы, которые не являются
обязательными и при первом прочтении могут быть опущены. Такие лекции
помечены звездочками. Отметим, что термин «лекция» несколько
условен. В книгу входит годовой курс, число лекций в году составляет 30-33.
В книге 19 лекций, в силу того что под лекцией здесь понимается
тематический раздел, который может включать в себя материал нескольких
реально читаемых лекций.
Большинство лекций книги (все основные и некоторые
необязательные) снабжены задачами для разборов на семинарских занятиях и
для самостоятельного решения на компьютере с использованием либо
пакетов программ, либо оригинальных программ, составленных
самими обучающимися. По мнению авторов, без самостоятельной реализации
основных алгоритмов и простых вычислительных процедур невозможно
глубокое понимание предмета. В конце каждой лекции приведен список
литературы — это источники, которыми пользовались авторы при
написании курса, и специальная литература, более подробно освещающая те
13
Лекции по вычислительной математике
или иные разделы. Списки литературы не претендуют на полноту, а лишь
отражают вкусы и научные пристрастия авторов.
Все замечания можно направлять по электронной почте по адресам
alexey@crec.mipt.ru или petrov@mipt.ru.
Авторы выражают свою искреннюю благодарность всем коллегам по
кафедре вычислительной математики МФТИ за внимание и помощь в
работе, первому заведующему кафедрой академику О. М. Белоцерковскому
за доброжелательную поддержку. Особая благодарность В. С. Рябенькому,
Р. П. Федоренко, А. С. Холодову, учителям авторов, которые передали им
свои знания и любовь к предмету. Доценты Е. Н. Аристова, О. А. Пырко-
ва, Т. К. Старожилова и старший преподаватель В. Д. Иванов прочли
части книги в рукописи и высказали ряд конструктивных замечаний и
предложений. Много сил и энергии потратили Е. А. Евсюкова, Д. В. Кибарди-
на и Е. Р. Павлюкова при технической подготовки рукописи. Авторы
также благодарны Ж.И.Утюшевой и М.С.Гриневой за предоставленные
конспекты лекций.
14
Лекция 1 Предмет вычислительной математики
Лекция 1. Предмет вычислительной математики.
Обусловленность задачи, устойчивость алгоритма,
погрешности вычислений. Задача численного
дифференцирования
Первая лекция носит вводный характер. На простейших примерах
иллюстрируются понятия численного алгоритма, устойчивость и
обусловленность задачи. На примере задачи численного дифференцирования
вводится метод неопределенных коэффициентов для получения
приближенных формул. Рассматривается некорректность задачи численного
дифференцирования.
Ключевые слова: алгоритм, обусловленность задачи, устойчивость
алгоритма, погрешности вычислений, задача численного
дифференцирования, метод неопределенных коэффициентов.
Первое применение вычислительных методов принадлежит
древним египтянам, которые умели вычислять диагональ квадрата за
конечное количество действий. Они также могли находить квадратный корень
из 2, скорее всего, с помощью алгоритма, в дальнейшем получившего
название формулы Герона, а еще позднее — метода Ньютона:
С именем среднеазиатского врача, философа и математика Аль-
Хоремзи связано понятие алгоритма. Разработкой вычислительных
методов занимались Л. Эйлер, которому принадлежит, по-видимому, первый
численный метод дня решения обыкновенных дифференциальных
уравнений, И. Ньютон, О. Л. Коши, Ж. Л. Лагранж, А. М. Лежандр, П. С.
Лаплас, А. Пуанкаре, П. Л. Чебышёв и многие другие известные математики.
Решающую роль в развитии вычислительной математики как
самостоятельной науки сыграли немецкий математик Карл Рунге и русский
математик, механик и кораблестроитель А. Н. Крылов.
В наше время вычислительная математика
получила.значительный импульс в 1950-е годы, что было связано с развитием
ядерной физики, механики полета, аэродинамики спускаемых
космических аппаратов. В дальнейшем решались задачи, связанные не
только с расчетами действия ядерного взрыва и обтеканием боеголовок
стратегических ракет. Численные методы нашли свое применение в
15
Лекции по вычислительной математике
таких областях как динамика атмосферы, термогидрография,
физика плазмы, механика горных пород и ледников, синергетика,
биомеханика, теория оптимизации, математическая экономика и др.
Наиболее наукоемки и требуют максимальных вычислительных
ресурсов задачи физики, механики и электродинамики сплошных сред.
К ним относятся системы уравнений в частных производных
Эйлера, Лагранжа, Максвелла и др., кинетической теории газов
(уравнения Власова, Берда), а также задачи многомерной оптимизации.
Развитие многих вычислительных методов — заслуга ученых,
неразрывно связанных с МФТИ. Среди них следует упомянуть академиков
А. А. Дородницына, О. М. Белоцерковского, А. А. Самарского, членов-
корреспондентов РАН А.С.Холодова, Б.Н.Четверушкина,
Ю.П.Попова, С. П. Курдюмова, профессоров В. С. Рябенького, Э. Э. Шноля,
Р. П. Федоренко, Л. А. Чудова, В. Ф. Дьяченко, И. М. Гельфанда, Г. А. Тир-
ского, А. П. Фаворского.
Вычислительная математика отличается от других математических
дисциплин и обладает специфическими особенностями.
1. Вычислительная математика имеет дело не только с
непрерывными, но и с дискретными объектами. Так, вместо отрезка прямой
часто рассматривается система точек {tk}%=0, вместо непрерывной
функции /(х) — табличная функция {fk}%=o, вместо первой производной —
ее разностная аппроксимация, например,
Такие замены, естественно, порождают погрешности метода.
2. В машинных вычислениях присутствуют числа с
ограниченным количеством знаков после запятой из-за конечности длины
мантиссы при представлении действительного числа в памяти ЭВМ.
Другими словами, в вычислениях присутствует машинная погрешность
(округления) 8м - Это приводит к вычислительным эффектам,
неизвестным, например, в классической теории обыкновенных
дифференциальных уравнений, уравнений математической физики или в
математическом анализе.
3. В вычислительной практике большое значение имеет
обусловленность задачи, т.е. чувствительность ее решения к малым изменениям
входных данных.
4. В отличие от «классической» математики выбор вычислительного
алгоритма влияет на результаты вычислений.
5. Существенная черта численного метода — экономичность
вычислительного алгоритма, т. е. минимизация числа элементарных операций
при выполнении его на ЭВМ.
16
Лекция 1 Предмет вычислительной математики
6. Погрешности при численном решении задач делятся на две
категории — неустранимые и устранимые. К первым относят погрешности,
связанные с построением математической модели объекта и
приближенным заданием входных данных, ко вторым — погрешности метода
решения задачи и ошибки округления, которые являются источниками малых
возмущений, вносимых в решение задачи.
Специфику машинных вычислений можно пояснить на нескольких
элементарных примерах.
1.1. Обусловленность задачи
Пример 1.1. Вычислить все корни уравнения
х4 - 4х3 + 8х2 - 16х + 15.99999999= (х - 2L - 1(Г8 = 0.
8
Точное решение задачи легко найти:
(х - 2J = ±1(Г4,
xi =2,01; х2 = 1,99; х3,4 = 2 ± 0,01г.
Если компьютер работает при 6м > Ю~8, то свободный член в
исходном уравнении будет округлен до 16,0 и, с точки зрения
представления чисел с плавающей точкой, будет решаться уравнение (х - 2L = 0,
т. е. xi,2,3,4 = 2, что, очевидно, неверно. В данном случае малые
погрешности в задании свободного члена « 10~8 привели, независимо от метода
решения, к погрешности в решении « 10~2.
Пример 1.2. Решается задача Коши для обыкновенного
дифференциального уравнения 2-го порядка:
u"{t) = u(t),t*(O) = l,u'@) = -1.
Общее решение имеет вид
u(t) = 0,5[ti@) + и'@)]е* + 0,5[u@) - и'@)]е-*.
При заданных начальных данных точное решение задачи: и(х) =
= е"~е, однако малая погрешность 8 в их задании приведет к появлению
члена 6ег, который при больших значениях аргумента может
существенно исказить решение.
Пример 1.3. Пусть необходимо найти решение обыкновенного
дифференциального уравнения
и = 10и, и = u(t),
17
Лекции по вычислительной математике
Его решение: u(t) = uoe10^~to\ однако значение u(to) известно
лишь приближенно: u(to) « Wq, и на самом деле и* (t) = ^)
Соответственно, разность и* -и будет
Предположим, что необходимо гарантировать некоторую заданную
точность вычислений е > 0 всюду на отрезке t е [0,1]. Тогда должно
выполняться условие
|u*(t)-u(t)|<e.
Очеввдно, что max \u*(t) - u(t)\ = \и * A) - и{1)\ = \иХ - щ\ е10*1"*0).
*€[01]
Отсюда можно получить требования к точности задания начальных
данных5: \v,q - uo| < 5,5 ^ е е0 при ?0 = 0.
Таким образом, требование к заданию точности начальных данных
оказываются в е10 раз выше необходимой точности результата решения
задачи. Это требование, скорее всего, окажется нереальным.
Решение оказывается очень чувствительным к заданию начальных
данных. Такого рода задачи называются плохо обусловленными.
Пример 1.4. Решением системы линейных алгебраических
уравнений (СЛАУ)
J
|l00u+1001v =
является пара чисел {1,1}.
Изменив правую часть системы на 0,01, получим возмущенную
систему
= 11.01
v
с решением {11.01; 0.00}, сильно отличающимся от решения
невозмущенной системы.Эта система также плохо обусловлена.
Пример 1.5. Рассмотрим полином
(х - 1)(х - 2)... {х - 20) = х20 - 210х19 + ...,
КОРНИ КОТОРОГО Xi = 1, Х2 = 2,. . . , Z20 = 20.
Положим, что коэффициент (-210) при xig увеличен на « 10~7.
В результате вычислений с 11-ю значащими цифрами получим
совершенно иные корни: х\ = 1,00;хг = 2,00;хз = 3,00;х4 = 4,00; Хб =
= 5,00; х6 = 6,00; х7 = 7,00; х8 = 8,01; х9 = 8,92; хю,п = 10,1 ± 0,644г;
18
Лекция 1
Предмет вычислительной математики
глада = H,8±l,65t;xi4,i5 = 14,0±2,52i;xi6,i7 = 16,7±2,81i;zi8,i9 =
= 19,5 ± 19,4i; х2о = 20,8.
Причина значительного расхождения также заключается в плохой
обусловленности задачи вычисления корней рассматриваемого
выражения.
1.2. Влияние выбора вычислительного алгоритма
на результаты вычислений
Пример 1.6. Пусть необходимо вычислить значение выражения
ту-
Избавившись от знаменателя, получаем (у/2 - IN = C - 2>/2K =
= 99 - 70>/2.
Полагая а) у/2 « | = 1,4, в) у/2 « j| = 1,41F) и рассматривая
эти приближения как разные методы вычисления, получим следующие
результаты:
V2
7/5
17/12
(V2-1)"
0,004096
0,005233
C - 2y/2f
0,008000
0,004630
99 - 70\/3
1
-0,1F)
Очевидно, что столь значительное различие в результатах вызвано
влиянием ошибки округления в задании \/2.
Пример 1.7. Вычисление функции sin x с помощью ряда Тейлора.
Из курса математического анализа известно, что функция синус
представляется своим рядом Тейлора
X
X X
причем радиус сходимости ряда равен бесконечности — ряд сходится при
любых значениях х.
Вычислим значения синуса при двух значениях аргумента. Пусть
сначала х = 0,5236C0°). Будем учитывать лишь члены ряда, большие,
чем 10~4. Выполнив вычисления с четырьмя значащими цифрами,
получим sin@.5236) = 0.5000, что соответствует принятой точности.
Пусть теперь х = 25,66A470°). Если вычисления по данной
формуле проводить -с восемью значащими цифрами, то получим абсурдный
результат: sin B5,66) « 24 (учитывались члены ряда, большие, чем 10~8).
Разумеется, выходом из создавшейся ситуации может быть
использование формул приведения.
19
Лекции по вычислительной математике
Пример 1.8. Вычисление функции ех с помощью ряда Тейлора.
Из курса математического анализа известно, что экспонента
представляется своим рядом Тейлора
X2 X3
е* = 1 + *+2Г + - + ...,
радиус сходимости этого ряда также равен бесконечности.
Приведем некоторые результаты расчетов (ехм — значения
экспоненты, вычисленные на компьютере).
X
1
20
-1
-10
-20
ех
2,718282
4,8516520 108
0,3678795
4,5399930 Ю-5
2,0611537-10"9
2,718282
4,8516531-108
0,3678794
-1,6408609 Ю
1,202966
Выходом из этой ситуации может быть использование для
отрицательных аргументов экспоненты формулы
Естественно ожидать рост ошибок округления при вычислении
рассматриваемой функции при больших значениях аргумента х. В этом
случае можно использовать формулу ех = еп+а = епеа, где п = [ж].
Пример 1.9. Рассмотрим следующий метод вычисления интеграла
1
1п= (xnel-xdx,n = l,2...
Интегрирование по частям дает
1 1
In = fxnd(-el-x) - x" • e1"* + fe1-* ¦ d(xn) = -1+ /"nx"-^1'
rdx,
откуда следует Io = j el~xdx = e - 1 « 1,71828. In = /i/n_i - l,n ^ 1.
о
Тогда
h = 1 • /о - 1 « 0.71828, h = 2Д - 1 « 0.43656, /3 = 3/2 - 1 « 0.30968,
/4 = 4/3 - 1 w 0.23872,1Ъ = 5/4 - 1 « 0.1936, /в = 6 • /5 - 1 « 0.16160,
/7 = 7/6 - 1 » 0.13120, /8 = 8/7 - 1 « 0.00496, /9 = 9/8 - 1 « -0.55360,
/ю = 10 • /9 - 1 « -6.5360
20
Лекция 1 Предмет вычислительной математики
Очевидно, что отрицательные значения при п = 9,10 не имеют смысла.
Дело в том, что ошибка, сделанная при округлении /о до 6-ти значащих
цифр сохранилась при вычислении Д, умножилась на 2! при
вычислении h, на 3! — при вычислении h, и так далее, т. е. ошибка растет очень
быстро, пропорционально п!.
Пример 1.10. Рассмотрим методический пример вычислений на
модельном компьютере, обеспечивающем точность SM = 0,0005.
Проанализируем причину происхождения ошибки, например, при вычитании
двух чисел, взятых с точностью до третьей цифры после десятичной
точки и = 1,001, v = 1,002, разность которых составляет Д = \vm - им\ =
= 0,001.
В памяти машины эти же числа представляются в виде
им = иA + &lf),vM = v(l + Slf), причем |<^| ^ 5М и \SVM| ^ 6М-
Тогда wm-w» и 51f, vm - v « vSvM.
Относительная ошибка при вычислении разности им - ум будет
равна
s= {им - ум) -(и-у) = (им - и) -
= =
(и - г;) (и - v) (u-v)
Очевидно, что S =
цифры могут оказаться неверными.
—6 хл
26
= х» т-е- ж* значапдае
Пример 1.11. Рассмотрим рекуррентное соотношение ul+i = qui9
г ^ 0, uo = a, g > 0, u» > 0.
Пусть при выполнении реальных вычислений с конечной длиной
мантиссы на i-м шаге возникла погрешность округления, и вычисления
проводятся с возмущенным значением и™ = щ + 5», тогда вместо щ+\
получим uflx = q(ui + Si) = wi+i -h gJ», т. e. u+i = qSu г = 0,1,....
Следовательно, если |g| > 1, то в процессе вычислений
погрешность, связанная с возникшей ошибкой округления, будет возрастать
(алгоритм неустойчив). В случае \q\ ^ 1 погрешность не возрастает и
численный алгоритм устойчив.
1.3. Экономичность вычислительного метода
Пример 1.12. Пусть требуется вычислить сумму 5=1 + х + х2 +
+ ... + х1023 при 0 < х < 1. Для последовательного вычисления х, х2 =
= х-х,..., х1023 = х1022 х необходимо проделать 1022 умножения, а затем
столько же сложений.
21
Лекции по вычислительной математике
Однако если заметить, что 5 = L гх_х , то количество
арифметических действий значительно уменьшается; в частности, для вычисления
хю24 требуется всего 10 умножений: х2 = х • х; ж4 = (хJ(хJ,..., х1024 =
= (»)•»(«)•".
Пример 1.13. Вычисления значений многочленов. Если вычислять
значение многочлена Р(х) = ao+aix+a2x2+.. .+anxn «в лоб», т. е.
вычислять значения каждого члена и суммировать, то окажется, что
необходимо выполнить (п2 + [п/2]) умножений и п сложений. Кроме того, такой
способ вычислений может привести к накоплению ошибок округления
при вычислениях с плавающей точкой.
Его очевидным улучшением является вычисление каждого члена
последовательным умножением на х. Такой алгоритм требуй* Bп - 1)
умножение и п сложений.
Еще более экономичным алгоритмом является хорошо известная в
алгебре схема Горнера:
Р(х) = ((... ((апх + an-i)x + ап-2)х + ... + а0),
требующая п операций сложения и п операций умножения. Этот метод
был известен в средние века в Китае под названием Тянь-Юань и был
заново открыт в Европе в начале XIX века англичанином Горнером и
итальянцем Руффини.
Пример 1.14. Рассмотрим систему линейных алгебраических
уравнений (СЛАУ) вида Аи = f, и = {щ,..., un}T, f = {Д,..., /п}т, с тревдиа-
гональной матрицей
А =
( bi ci 0 ... 0
CL2 &2 C2 ... 0
О аз Ьз сз ... О
О ... О ап Ьп
Если проводить решение такой системы без учета специфической
структуры матрицы (например, с помощью метода Гаусса), то количество
арифметических действий будет порядка п3, если же учесть эту структуру,
то количество операций можно уменьшить до п.
1.4. Погрешность метода
Оценим погрешность при вычислении первой производной при
помощи соотношения: f'(x) « f(+hyf()
h)-f(x) = [/(x)^fef(x)-hO(fe)]-/(x) = +
h h
22
Лекция 1 Предмет вычислительной математики
где 0{К) есть погрешность метода. В данном случае под погрешностью
метода понимается абсолютная величина разности f'(x) - Я*±АЬЯ*11
которая составляет O(h) (более точно §/"@ , где ? € [х, х + h]).
Если же взять другой метод вычисления производной f'(x) «
« Их+ь)-^(х-н) 9 то получим, что его погрешность составляет O(/i2), это
оказывается существенным при малых h. Однако уменьшать h до
бесконечности не имеет смысла, что видно из следующего примера. Реальная
погрешность при вычислении первой производной будет
Д = \ max |/"@I + ^ = O(h) + O(h~l),
поскольку абсолютная погрешность вычисления значения функции за
счет машинного округления не превосходит Ц**-.
В этом случае можно найти оптимальный шаг h. Будем считать
полную погрешность в вычислении производной А функцией шага h.
Отыщем минимум этой функции. Приравняв производную A'h(h) к нулю,
получим оптимальный шаг численного дифференцирования
Лопт = 2
\
шах |/''@Г
€[*х+Ь]
Выбирать значение h меньше оптимального не имеет смысла, так
как при дальнейшем уменьшении шага суммарная погрешность начинает
расти из-за возрастания вклада ошибок округления.
1.5. Элементы теории погрешностей
Определение. Пусть и и и* — точное и приближенное значение
некоторой величины, соответственно. Тогда абсолютной погрешностью
приближения и* называется величина Л(и*), удовлетворяющая
неравенству
Определение. Относительной погрешностью называется величина
), удовлетворяющая неравенству
и-и"
5{и*).
и*
Обычно используется запись и = n*(l ± 8(и*)).
23
Лекции по вычислительной математике
Определение. Пусть искомая величина и является функцией
параметров ti,... tn е П, и* — приближенное значение и. Тогда предельной
абсолютной погрешностью называется величина
?>(u*)= sup |u(*i,...,tn)-u*|,
(ti,...,tn)€n
Предельной относительной погрешностью называется величина
Пусть |tj - *j| ^ Д(^)> 3 = 1тп- приближенное значение и* =
= u(tl,..., ?*). Предполагаем, что и — непрерывно дифференцируемая
функция своих аргументов. Тогда, по формуле Лагранжа,
Отсюда |и(«1,...,«п)-и*| < Dx(u*) = ? Ь^ Д(^), где Ъ, =
ii
= sup
n
J
Можно показать, что при малых р = ^/(Д(^)J +... + (Д(?* )J эта
оценка не может быть существенно улучшена. На практике иногда
пользуются грубой (линейной) оценкой
|u(tb..., «„)-!»•! <Х?2(и#), г» D2(u*)
Несложно показать, что
a) A(±t{±,..., ±i*) = A(tJ) + ... + Д(??), предельная погрешность
суммы или разности равна сумме предельных погрешностей.
b) Предельная относительная погрешность произведения или
частного приближенного равна сумме предельных относительных
погрешностей
1.6. Задача численного дифференцирования
В пункте 1.2 уже была введена простейшая формула
численного дифференцирования. Рассмотрим задачу приближенного вычисления
значения производной подробнее.
24
Лекция 1 Предмет вычислительной математики
Пусть задана таблица значений х». В дальнейшем совокупность
точек на отрезке, на котором проводятся вычисления, иногда будут
называться сеткой, каждое значение х{ — узлом сетки. Пусть сетка —
равномерная, и расстояние между узлами равно h — шагу сетки. Пусть узлы
сетки пронумерованы в порядке возрастания, т. е.
хо = а,
Xj =а + j/i,,j = 0,1,..., N
Пусть f(xj) = fj — функция, определенная в узлах сетки.
Такие функции будут называться табличными, или сеточными функциями.
Считаем, кроме того, что рассматриваемая сеточная функция есть
проекция (или ограничение) на сетку некоторой гладкой нужное число раз
непрерывно дифференцируемой функции f(x). По определению
производной
J v ' д*-о Ах
тогда, если шаг сетки достаточно мал, по аналогии можно написать
формулу в конечных разностях, дающую приближенное значение
производной сеточной функции:
nxi) M /fa+*)-/fa). AЛ)
Если параметр h достаточно мал, то можно считать полученное
значение производной достаточно точным. Погрешность формулы A.1)
оценена в пункте 1.2. Как показано выше, при уменьшении шага сетки h
ошибка будет уменьшаться, но при некотором значении h ошибка
может возрасти до бесконечности. При оценке погрешности метода
обычно считается, что все вычисления были точными. Но существует ошибка
округления. При оценке ее большую роль играет машинный е — мера
относительной погрешности машинного округления, возникающей из-за
конечной разрядности мантиссы при работе с числами в формате с
плавающей точкой. Напомним, что по определению машинным е
называют наибольшее из чисел, для которых в рамках используемой системы
вычислений выполнено 1 + е = 1. Тогда абсолютная погрешность при
вычислении значения функции (или представлении табличной функции)
есть f(xj) • е. Максимальный вклад погрешностей округления при
вычислении производной по формуле A.1) будет 2^ffi'c, тогда, когда члены в
знаменателе A.1) имеют ошибки разных знаков.
Пусть k = max |/(x)|, максимум ищется на отрезке, на котором
вычисляются значения производных. Тогда суммарная ошибка, состоящая
25
Лекции по вычислительной математике
из погрешности метода и погрешности округления, есть Д =
М2 = тах|/"(х)|.
Для вычисления оптимального шага численного
дифференцирования найдем минимум суммарной ошибки, как функции шага сетки Ц* -
- ^ = 0, откуда
Если требуется повысить точность вычисления производных,
необходимо воспользоваться формулами, имеющими меньшие погрешности
метода. Так, из курсов математического анализа известно, что
= lim f(x + Ax)-f(x-Ax)
J K ' дх-о 2Дх
По аналогии напишем конечно-разностную формулу
/'(х,) « /(*i + fcW(»i-fc). A.2)
A.2) — формула с центральной разностью. Исследуем ее на
аппроксимацию, т. е. оценим погрешность метода. Предположим, что функция,
которую спроектировали на сетку, трижды непрерывно дифференцируема,
тогда
*i) у + /"'(* + **)
-h) = f(xj) - /'(*;) h + f"(*,)? - Г(Xi e2h)
Погрешность метода определяется 3-й производной функции.
Введем Ms = max |/"'(я)I > тогда суммарная погрешность при вычислении
хе[а,Ь)
по формуле с центральной разностью есть
M3h2 ke
3 + h1
для вычисления оптимального шага, находя минимум погрешности, как
функции шага сетки, имеем ^^ - ^| = о, откуда hopt = уЩ-
Для более точного вычисления производной необходимо
использовать разложение более высокого порядка, шаг hopt будет увеличиваться.
Формула A.1) — двухточечная, A.2) — трехточечная: при
вычислении производной используются точки (узлы) Xj (узел входит с нулевым
коэффициентом), Xj + /i,Xjf - h — совокупность узлов, участвующих в
26
Лекция 1
Предмет вычислительной математики
каждом вычислении производной, в дальнейшем будем иногда называть
сеточным шаблоном.
Введем на рассматриваемом отрезке шаблон из нескольких точек.
Считаем, что сетка равномерная — шаг сетки постоянный,
расстояния между любыми двумя соседними узлами равны. Используем для
вычисления значения первой производной следующую приближенную
(конечно-разностную) формулу:
A.3)
шаблон включает I точек слева от рассматриваемой точки Xj и га
справа. Коэффициенты а* — неопределенные коэффициенты. Формула
дифференцирования может быть и односторонней — либо /, либо т могут
равняться нулю. В первом случае иногда называют (на наш взгляд, не
слишком удачно) такую приближенную формулу формулой
дифференцирования вперед, во втором — формулой дифференцирования назад.
Потребуем, чтобы A.3) приближала первую производную с точностью O(fti+m).
Используем разложения в ряд Тейлора в окрестности точки Xj.
Подставляя их в A.3), получим
Г ?
k=-l
= -Г^
_ w +...+/«(«iM>kirfc«-i+...
Потребуем выполнение условий:
afc = 0,
к2 п ^ кп п
су = о,...5>*-^- = о,...
A.4)
Получаем систему линейных алгебраических уравнений для
неопределенных коэффициентов a A.4). Матрица этой системы есть
/ 1
-1
I2
Н)
i . . .
\ " ¦ •
Вектор правых частей
3
@,
1
-Z + 1 ...
(/-IJ ...
(-l + lf :..
1,0,...,0)т.
27
1
га
т2
т3
Лекции по вычислительной математике
Определитель данной матрицы — детерминант Вандермонда. Из
курса линейной алгебры следует, что он не равен нулю. Тогда
существует единственный набор коэффициентов а, который позволяет найти на
шаблоне из A + / + га) точек значение первой производной с
точностью O(ft'+m).
Для нахождения второй производной можно использовать ту же
самую формулу A.3) с небольшой модификацией
только теперь ? kak = 0, ? акк2 = \.
Очевидно, что и данная система уравнений для нахождения
неопределенных коэффициентов имеет единственное решение. Для получения
с той же точностью приближенных значений производных до порядка I +
+ т включительно с точностью O(hl+m) модификации формулы A.3) и
условий A.4) очевидны, набор неопределенных коэффициентов
находится единственным образом.
Таким образом, доказано следующее утверждение. На сеточном
шаблоне, включающем в себя N +1 точку, с помощью метода
неопределенных коэффициентов всегда можно построить единственную формулу для
вычисления производной от первого до N порядка включительно с
точностью O{hN).
Утверждение доказано для равномерной сетки, но на случай
произвольных расстояний между сеточными узлами обобщение проводится
легко.
Так как на практике вычисления проводятся с конечной длиной
мантиссы, то получить нулевую ошибку невозможно.
Читателям предлагается оценить значение оптимального шага при
вычислениях по формулам типа A.3) самостоятельно.
1.7. Задачи
1. Найти абсолютную предельную погрешность, погрешность по
производной, линейную погрешность для функции и = t10, если заданы
точка приближения t* = 1, значение функции и* в этой точке и
погрешность ДГ = 10~1.
Решение: обозначим b = sup \u't(t)\ = sup Ю-*9 = 10A,1)9 «
|| ||
23,...
Абсолютная предельная погрешность может быть определена как
D(um) = sup \t10 - 1| = (l.lI0 - 1 « 1,5...
|ti|<oi
28
Лекция 1 Предмет вычислительной математики
Оценка погрешности и при вычислении значения функции по
максимуму производной и линейная оценка соответственно будут D\(u*) =
= ЬА(Г) = 2,3...;D2(u*) = |7@)| Д(**) = 1.
2. Дать линейную оценку погрешности при вычислении неявной
функции ^(u,ti,t2,...,tn) = 0, если известны точка приближения
{*i» • • • >*пЬ значение функции в точке приближения и* и погрешность
в определении аргументов AtJ,..., Д**.
Решение. Дифференцируя по tj, получим
+ _=0
ди dtj dtj
откуда
dtj Kdtjndu) '
При заданных {?J,..., ?*}, можно найти и* как корень уравнения
<р(и, t\, *2, • • -Лп) = 0, а затем — значения
(«•.«I К)
откуда можно получить линейную оценку погрешности функции Д^*).
3. Вычислить относительную погрешность в определении значения
функции
и = ху2г3,еслих* = 37,1,2/* = 9,87,2* = 6,052, Да:* = 0,3, Ду* =
= 0,11,Дг* = 0,016.
Решение:
6(и) = 6{х*) + 26(у*) + Щг*) = 3.8 • 10.
4. Оценить погрешность в определении корней квадратного
уравнения <?(u,?i,*2) = и2 + tiu + *2 = 0, если заданы приближения
Пусть it* — решение уравнения
и *2 +t\u* +1\ = 0.
Из формулы
29
Лекции по вычислительной математике
получим
du и*
Ь2(р) = — = J__.
Следовательно, линейная оценка будет
1.8. Задачи для самостоятельного решения
1. Найти абсолютную предельную погрешность, погрешность по
производной и линейную оценку погрешности для функций и = sin*,
Заданы точка приближения t = t* и погрешность At.
2. Определить шаг т, при котором погрешность вычисления
производной и'(?), приближенно вычисляемой в соответствии с
формулами
u'{t) « ^ т)\) ^
не превосходит 103. Известно, что \u"(t)\ ^ 1, К"(?)| ^ 1 для
любых^.
3. Пусть для вычисления функции и = f(t) используется частичная
сумма ряда Маклорена
причем аргумент задан с погрешностью Д* = 10~3.
Найти п такое, чтобы погрешность в определении функции и(у)
по данной формуле не превышала Д?. Рассмотреть отрезки t e
[О, 1], t е [10, И].
Предложить более совершенный алгоритм для вычисления
функций u(t) = sin t, u(t) = e* на отрезке t e [10, 11].
30
Лекция 1 Предмет вычислительной математики
4. Определить оптимальный шаг численного дифференцирования г
при использовании для вычисления производной приближенной
формулы
, _ u(t - 2т) - 8(t - г) + 8(t + г) - u(t + 2т)
имеющей четвертый порядок точности, если известно, что
М5, а значения функций вычисляются с точностью е.
5. Вычислить относительную погрешность в определении значения
функции и(х, у, z) = x2y2/zAc, если заданы
х* = 37,1, у* = 9,87, z* = 6,052, Д(л*) = 0,1;
Д(у*) = 0,05; Д(г*) =0,02.
Литература
[ 1 ] B.C. Рябенький. Введение в вычислительную математику. — М.: Физ-
матлит,2000.294с.
[2] Н. В. Бахвалов, Н. П.Жидков, Г. М. Кобельков. Численные методы. —
М: Лаборатория Базовых Знаний, 2002.632 с.
[3] В. И. Косарев. 12 лекций по вычислительной математике. — М.: Изд-
во МФТИ, Физматкнига, 2000.220 с.
[4] А. А. Самарский. Введение в численные методы. М.: Наука, 1997.
234 с.
[5]. А. А. Амосов, Ю.АДубинский, Н. В. Копченова. Вычислительные
методы для инженеров. — М.: Высшая школа, 1994.544 с.
[6] Д. Каханер, К. Моулер, С. Нэш. Численные методы и программное
обеспечение. — М.: Мир, 1998.575 с.
31
Лекции по вычислительной математике
Лекция 2. Численное решение систем линейных
алгебраических уравнений
Рассматриваются наиболее употребительные приближенные методы
решения систем линейных алгебраических уравнений. Вводятся
согласованные нормы векторов и матриц. Вычисляется число обусловленности в
различных нормах. Анализируется влияние ошибок округления на погрешность
результата. Дается понятие о спектральных задачах. Для самосопряженной
матрицы рассматривается метод вращений поиска собственных значений.
Ключевые слова: системы линейных алгебраических уравнений,
согласованные нормы вектора и матрицы, обусловленность системы,
число обусловленности матрицы, прямые методы, метод Гаусса,
метод Гаусса с выбором главного элемента, Ш-разложение,
итерационные методы, метод простых итераций, методы Якоби, Зейделя,
верхней релаксации, метод наискорейшего спуска, метод
сопряженных градиентов, спектральные задачи, метод вращений.
К численному решению систем линейных алгебраических
уравнений (СЛАУ) сводятся многие задачи математической физики.
Математические модели, представляющие собой СЛАУ большой размерности,
встречаются в математической экономике, биологии и т.п. Теория
получения приближенных решений СЛАУ—часть вычислительной линейной
алгебры. Сама вычислительная линейная алгебра, по-видимому,
является наиболее обширной темой во всем курсе вычислительной математики.
По прикладной линейной алгебре существует обширная литература'(на-
пример, [1, 2, 3,4, 5]), а программы, реализующие наиболее популярные
алгоритмы вычислительной линейной алгебры, являются неотъемлемой
частью прикладного программного обеспечения, в частности,
современных математических пакетов.
2.1. Постановка задачи
Рассмотрим СЛАУ вида
Au = f, B.1)
32
Лекция 2 Численное решение систем линейных алгебраических уравнений
где А — невырожденная (det А^О) квадратная матрица размером пхп
(\
&11 &12 • • • &1п 1
0>п1 Оп2 ••• 0>пп
u = {ui,..., un}T — вектор-столбец решения, f = {/ь..., /п}т — вектор-
столбец правой части.
Так как матрица системы — невырожденная, Д = det А ф 0, то
решение системы B.1) существует и единственно.
Из курса линейной алгебры [6] известно правило Крамера
нахождения решения. Так, каждый компонент вектора неизвестных может быть
вычислен как
где Дг — определитель матрицы, получаемой из А заменой г столбца
столбцом правых частей. Однако несложные арифметические оценки
позволяют понять, что использование этой формулы приводит к
неоправданно большим затратам машинного времени [3]. Так, например, если
одно слагаемое в Д вычисляется за 10~6 с, то время расчета для п = 100 на
существующих в момент написания книги компьютерах будет
измеряться годами.
На самом деле в настоящее время с помощью компьютеров
численно решаются СЛАУ намного более высокого порядка (примерно до
п « 106). Такие решения осуществляются при помощи прямых или
итерационных численных методов. Прямые методы позволяют в
предположении отсутствия ошибок округления (при проведении расчетов на
идеальном, т. е. бесконечноразрядном компьютере) получить точное
решение задачи за конечное число арифметических действий. Итерационные
методы, или методы последовательных приближений, позволяют
вычислить последовательность {и*}, сходящуюся к решению задач при к —> оо
(на практике, разумеется, ограничиваются конечным к, в зависимости от
требуемой точности).
Однако неточность в задании правых частей и элементов матрицы
А может приводить к значительным погрешностям при вычислении
решения B.1). В первой лекции на примере было показано, что такое
явление наблюдается в случае плохо обусловленной системы. Остановимся
подробнее на важном вопросе оценки погрешности решения СЛАУ.
Для этого напомним некоторые сведения из функционального
анализа, которые понадобятся в дальнейшем.
2—3339 33
Лекции по вычислительной математике
2.2. Согласованные нормы векторов и матриц
В векторном n-мерном линейном нормированном пространстве
введем следующие нормы вектора:
кубическая:
IH^ max Ы, B.2а)
октаэдрическая:
евклидова (в комплексном случае — эрмитова):
/ « \ »/2
B.2в)
Рассмотрим квадратную матрицу А и связанное с ней линейное
преобразование v = Аи, где v, и е Ln (Ln — n-мерное линейное
нормированное пространство). Норма матрицы определяется как действительное
неотрицательное число, характеризующее это преобразование и
определяющееся как
ПАИ = sup JM B.3)
||u||#0 IMI
Укажем некоторые свойства нормы матрицы:
|| А|| = 0 тогда и только тогда, когда А = 0.
Заметим, что норму матрицы B.3) называют подчиненной норме
вектора. Говорят, что норма матрицы А согласована с нормой вектора и,
если выполнено условие
Нетрудно видеть, что подчиненная норма согласована с
соответствующей метрикой векторного пространства. В самом деле
= sup W > ^ °ТКуда
| llull llull
34
Лекция 2 Численное решение систем линейных алгебраических уравнений
Согласованные с введенными выше нормами векторов нормы
матриц будут определяться следующим образом:
1 .
== /maxA'(A*-A).
/тах
Покажем, как получается выражение для согласованной нормы
матрицы \\А\\г, соответствующей норме вектора ЦиЦ^
Вычислим норму вектора || Au||x:
||Аи||1=шах
г
Hj\) max\щ\ =
з 3 ' з
откуда пилг1 ^ max^ | a»j|. По определению нормы матрицы как
точной верхней грани отношения ^j^, шах^) |а^| = || A||x, если
существует вектор, на котором точная верхняя грань достигается.
Покажем, что таким вектором является, например, v* =
= {signal, • • •, signal}7, при этом допустим, что максимум в последнем
неравенстве достигается при i = к.
Поскольку ||vfc|| = А:,то Y,akjVj = Е \akj\ = тах^ К,|.
э з г з
Тогда, в соответствии с выражением для первой нормы вектора,
получаем
з
Таким образом, точная верхняя грань в рассмотренном неравенстве
достижима и действительно || А|| х = max ]Г) |о# |.
Для третьей нормы B.2в) ||А||3 = sup иплг* = sup
з
Аи,Аи) _
и и)
и •• - и Т ^"' /
35
Лекции по вычислительной математике
Заметим, что матрица В = А* А — симметричная. Без ограничения
общности предположим, что все собственные числа матрицы различны.
Матрица обладает всеми действительными собственными значениями,
и каждому собственному числу соответствует собственный вектор. Все
собственные векторы взаимно ортогональны. Можно рассмотреть орто-
нормированную систему собственных векторов u>i,..., шп; Ах,..., An —
соответствующие им собственные значения. Любой вектор и можно
представить в виде своего разложения по базису из собственных векторов:
€iu>i. Кроме того, (А* А) о;» = AiU?». Поэтому
/(А* Аи, Аи) /v^(^6wi»6«i)
SUD 4 / 7 г = SUP 4 / У ^TZ Z Г" =
Hull^oy (u>u) ||и||^Оу i HZiViAiUi)
причем точная верхняя грань достигается при и = о?». Действительно,
supW , , = SUP\Л*(А*А) = л/тахАг(А*А),
т.к. А*Аа;» = Aid;», откуда (A*Aw»,о;») = А»(о;»,^),
В важном частном случае симметричной (самосопряженной)
матрицы А имеем А^*А = А^2 = |А^|2 , поэтому ||А||3 = max |Aj^|.
2.3. Обусловленность СЛАУ. Число
обусловленности матрицы
Понятия согласованных норм матриц и векторов позволяют
оценить погрешности, возникающие при численном решении СЛАУ. Пусть
и матрица, и правая часть системы заданы с некоторой погрешностью,
тогда наряду с системой
Аи = f B.4)
рассматривается система
(А + ДА) (и + Ди) = f + Af. B.5)
36
Лекция 2 Численное решение систем линейных алгебраических уравнений
Теорема. Пусть правая часть и невырожденная матрица СЛАУ B А)
вида Аи = f, и € Ln,f б Ln, получили приращения Af и ДА
соответственно. Пусть существует обратная матрица А'1 и выполнены условия
ЦАЦ ^ 0,//J'pcjj11 <l,*deiA= ЦАЦ • || А1|. В этом случае оценка
относительной погрешности решения || Ди|| / ||и|| удовлетворяет неравенству
II Аи» д /||Af|| ЦААЦЧ
in "i-^Ji^n v iifii и ah ;•
Доказательство.
Из B.5) следует, что Аи = A-1(Af - ДА и - ДА Аи). Переходя в
этом равенстве к норме и использовав неравенство треугольника,
получаем
||Ди|| < ЦА!! ||Af|| + ЦА-1!! ЦДАЦ ||и|| + ЦА!! ЦДАЦ ||Ди||, или
11**11 ^ ЦА!! Ш. Ilfll+IJA-1!!^ ЦАЦ ||u||+||A-i||A||Jl^ ||Au||.
Вводя обозначение /х(А) = ЦА!! • ||А||, перепишем последнее
равенство в виде
Заметим,^) Д ^ ||и|| т.к. ||f|| = ||Au|| ^ ||А||. ||u||.
Тогда для оценки относительной погрешности решения
окончательно получим
||Ди|| М . \\M\\ || ДА||
ПнГ ^ 1-мл^иAтГ + W >' B-6)
При АА « 0 получаем оценку при наличии погрешности только
правых частей
Hull * м
если в B.5) положить ДА • Ди « 0, то
37
Лекции по вычислительной математике
В результате получено важное соотношение, показывающее, на
сколько возрастают относительные ошибки решения СЛАУ в случае наличия
относительных ошибок при задании правых частей и элементов матриц.
Величина
B.9)
называется числом обусловленности матрицы А. Число обусловленности
определяет, насколько погрешность входных данных может повлиять на
решение системы B.1). Почти очевидно, что всегда \i ^ 1. Действительно
При fi« 1 -г 10 ошибки входных данных слабо сказываются на
решении и система B.1) считается хорошо обусловленной. При \х » 102 ч-103
система является плохо обусловленной.
Пример. Решением системы
Г ЮОи + 99v = 199
будет пара чисел и = v = 1.
Внесем возмущение в правые части системы:
J lOOu + 99v = 198,99
При этом решение заметно изменится: и = 2,97; v = —0,99.
Воспользовавшись выбранными согласованными нормами, получим
« 05 10
= 199,
Sf = llfll « 0,5 • 10 (это очень малая величина),
ll*ll
^ = 199,/и = 199 • 199 * 4 • 104.
Значит, 6и = -ЧдИ ^ рЛ^|1 « 4 • 104 • ^ = 2, что согласуется с
результатами решения возмущенной и невозмущенной задач. Для
невозмущенной задачи || Ди|| » 2, ||и|| = 1.
Рассмотрим еще одно важное свойство. Число обусловленности
матрицы, как было показано ранее, можно определить, как Su/Sf ^
ju(A), если ДА « 0 при 8и = ^п^. Можно ли найти более тонкую оценку
отношения 6 и/5 /, учитывающую зависимость обусловленности СЛАУ
38
Лекция 2
Численное решение систем линейных алгебраических уравнений
от выбора правых частей? В этом случае параметр обусловленности
системы, вообще говоря, зависит и от f, и от А(, и удовлетворяет неравенству
i/(f, At) ^ 0 = *^$- • ]|^[f • Его можно определить как точную верхнюю
грань отношения |у no Af, что соответствует наихудшей ситуации. Тогда
Af
H
; sup ¦
lull
НА
Далее,
Т1|А-'||-й =
с другой стороны
•sup
f Hull
infI/(f) = inf||A
-И
-1
Параметр z/(f), характеризующий обусловленность системы,
зависит от правых частей. Более тонкая его оценка есть i/(f) = ||-А. х|| Д,
причем 1 < i/(f) < /х. Так как такую оценку провести не всегда
возможно, то чаще используется точная верхняя грань || А1| || А||. Такая оценка,
конечно, может быть существенно завышенной.
Можно также показать, что для симметричной матрицы А имеет
место \i =
max Ад
А
min
А
, т. е. обусловленность СЛАУ зависит от ее
спектральных свойств. Это следует из определения третьей нормы мат-
и соотношения ||А~1||О =
max,
рицы ||А||з =
предлагается доказать самостоятельно.
которое
2.4. Прямые методы решения СЛАУ
Трудность численного решения рассматриваемых СЛАУ
определяется видом матрицы А. Легко получается решение системы с
диагональной матрицей, в этом случае система распадается на п линейных
уравнений, каждое из которых содержит лишь одну неизвестную величину. Для
39
Лекции по вычислительной математике
диагональной системы очевидны явные формулы
ик = fk/akk,k = 1ч-п.
В случае треугольной матрицы
&11 &12 . . . din \
О U22 .. 0>2п
О 0 ... апп )
из последнего уравнения получаем ип = fn/a>nn, (о>н ф 0, т. к. Д =
Решая систему линейных уравнений с треугольной матрицей «снизу
вверх», для ик имеем
Uk = (Л ~
dkk
Можно оценить количество арифметических действий,
затрачиваемых на решение такой системы. Оно составляет О(п2).
Пусть теперь система уравнений имеет матрицу общего вида.
Стандартная схема такого решения разделяется на два этапа: прямой ход —
приведение матрицы к треугольному виду, и обратный — вычисление
решения системы.
2.4.1. Метод исключения Гаусса
Рассматривается система уравнений
¦ ... + ainun = /ъ
¦•• +a>2nUn = /2, /2 10)
- • • • + аппип = /п.
Прямой ход метода Гаусса состоит в следующем. Положим, что
ац ф 0 и исключим их из всех уравнений, начиная со второго, для чего ко
второму уравнению прибавим первое, умноженное на -a2i/an = -г/21,
к третьему прибавим первое, умноженное на -ам/ац = -щг и т.д.
После этих преобразований получим эквивалентную систему:
+ ... + ainun = /1,
а\2и2 + ... + а\пип = /2\
40
Лекция 2
Численное решение систем линейных алгебраических уравнений
в которой коэффициенты и правые части определяются следующим
образом:
alj = ач " Vna>ij\ fi = fi - Wi; ij = 2,...,n.
Теперь положим a22 Ф 0. Аналогично, вычислив множители второго
шага -а\2/а22 = ~Vi2 (i = 3,... ,п), исключаем u2 из последних (п - 2)
уравнений системы B.17). В результате преобразований получим новую
эквивалентную систему уравнений
+ ai2u2 4- ai3u3 + ... + ainun =
a\2u2 4- <43u3 -f ... + a?nun = /21
§ ... + a\nun = /|
в которой a^ = a^ - т&2а^; /i2 = // - mij2\ i, j = 3,...,п. Продолжая
алгоритм, т. е. исключая щ (г = к -f 1,..., п), приходим на п - 1 шаге к
системе с треугольной матрицей
B.12)
... + а\пип
... + a\nun = /j
4-...
Обратный ход метода Гаусса позволяет определить решение
системы линейных уравнений. Из последнего уравнения системы находим ип\
подставляем это значение в предпоследнее уравнение, получим un_i.
Поступая так и далее, последовательно находим ип-2, un_3,..., и\.
Вычисления компонент вектора решения проводятся по формулам
Л
2кк
-^ * = n-l,n-
и2 = — (ft -
а22
и\ = —(/1 -
an
... - а\пип),
... - ainun).
41
Лекции по вычислительной математике
Этот алгоритм прост и легко реализуем при условии, что ац Ф О,
а22 / Ои т.д. Количество арифметических действий прямого хода «
2/Зп3, обратного « п2. Это уже приемлемая для современных
компьютеров величина.
Рассмотрим метод Гаусса с позиции операций с матрицами. Пусть
Ai — матрица системы после исключения первого неизвестного
ац а\2 a\z
01 i
0 а\2 азз
din
«к
«к
ft /I /i\i
= \/l)/2)-i/n/
Введем новую матрицу
/ 1
-»721
-%1
О
О
О
О
1
О
О
О
о о
1
Очевидно, Ai = NiA, fi = Nif. Аналогично, после второго шага
система приводится к виду A2u = f2, где А2 = N2Ai, f2 = N2fi,
А,=
«и
«13
ain
О а\2 4j ... а\п
О 0 а\3 ... а\п
О О
1
0
0
0
1
-»?32
0
0
1
... 0
... 0
... 0
О
После п-1 шага получим An_iu = fn_i,An_i = Nn_i-An_2,fn_i =
= Nn_ifn_2,
/ ац ai2 ахз ... a\n
0 a22
0 0
An_i =
«23
«L
Nn_1 =
\ 0 0 0 ...
/10... 0 0 \
0 1 ... 0 0
0 0 ... 1 0
V 0 0 ... -щ,п-1 1
42
Лекция 2
Численное решение систем линейных алгебраических уравнений
В итоге получаются матрица и вектор An_i = Nn_i.. .N2N1A,
f(n_i) = Nn_i... N2Nif, откуда А = Nf 1Щl... N^x • Ап_ь При этом
/1 0 0 ... О \
1 о о
T/21 1 0
Г731 0 1
0
0
0
0 0
1-1 -
.. 1
( 1 О
О 1
0 1 0
О Т732 1
о
о
\0 ta О
о о \
о о
О О ... 1 О
% 0 0 ... %,„-! 1 ,
После введения обозначений U = An_i, L = N^NJ1
/1 0 0 ... О \
1721 1 0 ... О
^, где
L =
0
получим A = LU.
Это представление матрицы А называется LU-разложением (на
произведение нижней и верхней треугольных матриц L и U). Прямой
ход метода Гаусса можно рассматривать как один из вариантов
представления матрицы в виде произведения двух треугольных матриц, или LU-
разложения. Его можно провести и другими способами.
Вспомним «отрицательный» пример из лекции 1. Пусть необходимо
решить систему
-l(T7tli+tt2 = l,
и\ 4- 2^2 = 4.
Исключая и\ из первого уравнения и подставляя во второе, получим
U2 = A07 + 4)/A07 + 2). После вычислений с семью значащими цифрами
получаем их = 0,000000, и2 = 1,000000, что неверно (см. второе
уравнение). Теперь исключим и\ из второго уравнения и подставим в первое.
При этом получим иг = 1+2.10-у- После вычислений с той же точностью
имеем: и2 = 1,000000, и\ = 2,000000, что является правильным
решением (с заданным количеством значащих цифр).
В реальных вычислениях используются методы с выбором главного
(или ведущего) элемента. Выбор главного элемента по столбцам
реализуется следующим образом: перед исключением и\ отыскивается шах \ац\.
43
Лекции по вычислительной математике
Пусть максимум достигается при г = к. В этом случае меняются
местами первое и к уравнения (или в матрице меняются местами две строки)
и реализуется процедура исключения.
Затем отыскивается max \a\2 |, и процедура поиска главного
элемента в столбцах повторяется. Так же реализуется выбор главного элемента
по строкам: перед исключением щ отыскивается шах|ajy |. Если
максимум достигается при г = к, то у и\ и и* меняются номера, то есть
максимальный элемент из коэффициентов первого уравнения окажется на
месте аи, и т. д. Наиболее эффективным является метод Гаусса с выбором
главного элемента по всей матрице. Во многих методах важным является
п
условие диагонального преобладания \ац\ ^ Yl \atj\ Для * = 1, • • ,п, при
выполнении которого проблемы, появляющиеся в методе Гаусса, не
возникают. Если для всех строк матрицы выполняются строгие неравенства,
то говорят о строгом диагональном преобладании.
Полученное решение можно улучшить следующим образом. Пусть
г1 = f - Аи1 есть невязка, допущенная при решении рассматриваемой
системы (и1 — полученное численное решение) за счет ошибки
округлений. Очевидно, что погрешность е1 = и - и1 удовлетворяет СЛАУ Ае1 =
= г1, так как Ае1 = Аи-Аи1 = f - Аи1.
Решив последнюю систему, получаем е1, после чего уточняем
решение: 9 11
иг = и1 + е1.
Эту процедуру можно продолжить.
2.4.2. Модификация метода Гаусса для случая линейных
систем с трехдиагональными матрицами — метод
прогонки
В приложениях часто возникают системы линейных уравнений с
матрицами специального вида. В дальнейшем, например, при
интерполяции функции сплайнами, при решении задачи Штурма-Лиувилля, при
численном решении уравнений теплопроводности, уравнений Лапласа
и Пуассона придется иметь дело с системами, матрицы которых имеют
ненулевые элементы лишь на главной диагонали и еще на двух
диагоналях — одной под главной, одной над главной. Такие матрицы называются
трехдиагональными. Для решения систем с трехдиагональными
матрицами существует экономичный (требующий малого количества памяти и
арифметических действий) вариант метода Гаусса — прогонка. В
англоязычной литературе метод прогонки называется алгоритмом Томаса.
Подробнее о свойствах метода прогонки речь пойдет в лекции 10 в связи с
решением разностными методами задачи Штурма—Лиувилля.
44
Лекция 2 Численное решение систем линейных алгебраических уравнений
2.4.3. LU-разложение
Среди прямых методов численного решения СЛАУ широко
используется также LU-разложение матрицы А и метод Холецкого (или метод
квадратного корня).
Если матрица А представима в виде произведений матриц LU, то
СЛАУ может быть представлена в виде
(LU)u = f. B.13)
Перепишем B.13), вводя вспомогательный вектор v, в следующем
виде
Lv = f,Uu = v. B.14)
Решение СЛАУ свелось к последовательному решению двух систем
с треугольными матрицами. Первый этап решения системы Lv = f:
= /n,
откуда можно вычислить все vk последовательно по формулам
Далее рассмотрим систему Uu = v или
+ ...
nnUn = Vn,
решение которой находится в обратном порядке, т. е. при к = п — 1,..., 1
п
по очевидным формулам Uk = d^ (vk — Z) dkj Uj). Условия существова-
ния такого разложения даются следующей теоремой [5] (без
доказательства).
Теорема. Если все главные миноры квадратной матрицы А отличны
от нуля, то существуют единственные нижняя и верхняя треугольные
матрицы L = 1ц и U = dij такие, что А = LU. При этом все диагональные
коэффициенты матрицы L фиксированы и равны единице.
45
Лекции по вычислительной математике
Опишем алгоритм нахождения элементов Ujdij матриц L, U.
Выписав равенство А = LU в компонентах, получим
0>2п
\ 0>п1 0>п2 • • • 0>пп
1 0 ... О \ /dn dia ... dm
hi 1 ... О 0 d22 ... d2n
\lnl In2 ... 1 / V ° 0
Выполнив умножение матриц, приходим к системе линейных
уравнений размером пхп:
dn = ац, d\2 = ai2,..., d\n = ain,
= «22, • • •, h\d\n + d2n — U2n,
относительно неизвестныхdxu di2,..., din, fei, ^22, • • •, d2n, /ni, Ini, • •, dnn
Специфика этой системы позволяет решить ее последовательно. Из
первой строки находим d\j = aij(j = 1,..., n).
Из уравнений, входящих в первый столбец приведенной выше
системы, находим 1ц = an/dn,i = 1,... ,п. Теперь можно из уравнений
второй строки найти d2j = a2j - l2idij,j = 2,..., п, а из уравнений,
входящих во второй столбец, получим li2 = d22(ai2 - lndi2), г = 2,...,п и
так далее. Последним вычисляется элемент
п-1
= dnn - 22,
k=l
Можно выписать общий вид этих формул:
ij = dij - 2^ hkdkj,
fУ = di3l
Приведение матриц к треугольному виду аналогично приведению
матрицы в методе Гаусса и также требует количества арифметических
действий порядка О(п3), точнее, « 2п3.
2.4.4. Метод Холецкого (метод квадратного корня)
Пусть матрица рассматриваемой линейной системы А —
симметричная, т. е. aij = ay/, положительная матрица. Тогда она представима в
46
Лекция 2
Численное решение систем линейных алгебраических уравнений
виде А = LL
LT =
т, где
/ In
0
{ о
0 .
¦ ¦ hn
¦¦ Inn )
V-
1
/ hi
In
\ hn
0
/22
hn
- I \
... Inn )
Далее, как и в случае LU-разложения, решение СЛАУ Аи = f
сводится к последовательному решению двух линейных систем с
треугольными матрицами Lv = f, LTu = v, для решения которых требуется
примерно 2п2 арифметических действий.
Первая из этих линейных систем
= /1,
= /2,
+ . . . + innVn = /n,
она легко решается. Для решения получаем очевидные формулы
Вторая система уравнений есть
-f li2U2 + . . . + hnUn = V\M2U2 + • • • + hnUn = V2, . • .
Из нее находим значения переменных щ в обратном порядке по
формуле
j=JH-l
Определенной опасностью при реализации этого метода являются
возможная близость к нулю 1ц и отрицательность подкоренных
выражений при вычислении 1ц (последнего не должно быть при симметричной
положительной матрице А)
Элементы матрицы L находим из уравнения LLT = А,
приравнивая соответствующие элементы матриц LLT и А. В результате получим
47
Лекции по вычислительной математике
систему уравнений
In = аи»
1ц1ц = а»1,г = 2,.. .,п,
*21+4г = а22,
Ulhl + ^22 = Ui2, i = 3, . . . , П,
'fcl + **2+ ••• + *** =0>kk,
Uihi + Ы&2 + ... + Ukhk = a>kk,i = к + 1,... ,n.
Решение этой системы легко находится:
1ц = у/аи,
hi = <Hi/hiii = 2,...,n,
fi2 = (ai2 - Iiihi)/l22, г = 3,..., n,
hk = (o>ik - Uihi - Ы*2 - ... - U,k-ih,k-i)/hkii = к 4-1,... ,n,
Метод также называется методом квадратного корня.
Внимание! Не следует путать матрицу (оператор) L с оператором
А1/2 — квадратным корнем из самосопряженного положительного
оператора.
2.5. Итерационные методы решения СЛАУ
2.5.1. Метод простой итерации
Рассмотрим систему линейных алгебраических уравнений
Au = f.
Проведем несколько равносильных преобразований. Умножим обе
части системы на один и тот же скалярный множитель г, затем прибавим
к правой и левой частям системы вектор и. Систему уравнений можно
теперь записать в виде, удобном для итераций:
u = Bu + F, B.15)
где В = Е - г A, F = rf.
48
Лекция 2 Численное решение систем линейных алгебраических уравнений
Теперь построим последовательность приближений к решению
системы. Выберем произвольный вектор uo — начальное приближение к
решению. Чаще всего его просто полагают нулевым вектором. Скорее
всего, начальное приближение не удовлетворяет B.15) и, следовательно,
исходной системе. При подстановке его в исходное уравнение возникает
невязка r0 = f - Auo. Вычислив невязку, с помощью B.15) можно
уточнить приближение к решению, считая, что
Ui =Uo +ТГ().
По первому приближению снова вычисляется невязка, процесс
продолжается. В ходе итерации получаем iifc+i = u* + тг*, г* = f - Аи*.
Эквивалентная формулировка метода, называемого методом простых
итераций, заключается в следующем. Решение B.15) находится как предел
последовательности {uo, ui, u2,...} приближений, члены которой
связаны рекуррентным соотношением (оно эквивалентно приведенному
выше, из записи исключен вектор невязки):
щ+! = Ви* + F, B.16)
uo = 0 (или любому произвольному вектору). Если предел такой
последовательности существует, то говорят о сходимости итерационного
процесса к решению СЛАУ.
Существуют другие формы записи метода итераций, например
ufc+i = (E-TA)u* + rf. B.17)
Канонической формой записи двухслойного итерационного процесса
называется следующая:
^^^. B.18)
При Б* = Е, т* = г последняя формула соответствует однопара-
метрическому итерационному процессу — рассмотренному выше методу
простых итераций. При D* = Е, т* = {т*, к = 1,..., п} — п-шаговому
явному итерационному процессу, при D* = D', ть = 1 — методу простой
итерации без итерационного параметра. В случае, когда D ф Е,
итерационный метод называется неявным — для вычисления следующего
приближения к решению придется решать (как правило, более простую, чем
исходную) систему линейных уравнений.
Теорема (достаточное условие сходимости метода простой итерации).
Итерационный процесс B.16) сходится к решению U СЛАУ Аи = F со
скоростью геометрической прогрессии при выполнении условия: ||В|| ^ q < 1.
49
Лекции по вычислительной математике
Доказательство.
Пусть U — точное решение системы B). Вычитая из B.16)-B.15),
получим и*- U = B(ufc_i-U), или, обозначив погрешность ел = Ufe-U,
получим для эволюции погрешности уравнение вк = Ве&_1.
Справедлива цепочка неравенств: ||iifc-U|| = ||е*|| ^ ||В|| • ||€fc-i||
**
Отсюда следует, что при q < 1 lim u* = U.
fc-*oo
Из неравенства \\ek\\ ^ qk ||eo|| можно получить оценку количества
итераций,необходимых для достижения точности е, т. е. для выполнения
условия ||и* - U|| = \\ek\\ < е. Эта оценка имеет вид к ^ f In тт^тг) / big.
Теорема (критерий сходимости метода простой итерации (без
доказательства)). Пусть СЛАУ B.15) имеет единственное решение. Тогда для
сходимости итерационного процесса B.16) необходимо и достаточно, чтобы
все собственные значения матрицы В по абсолютной величине были меньше
единицы.
Сравним по количеству арифметических действий прямые и
итерационные методы. Метод Гаусса без выбора главного элемента при п > 1
требует » (§™3) арифметических действий; метод простой итерации
B.16)« Bп2 • /), где J — число приближений, необходимое для
достижения заданной точности. Значит, при / < n/З метод итераций становится
предпочтительнее. В реальных задачах, в основном, /«п. Кроме того,
итерационные методы можно делать более эффективными, изменяя
итерационные параметры. В ряде случаев итерационные методы
оказываются более устойчивыми по отношению к накоплению ошибок округления,
чем прямые.
2.5.2. Влияние ошибок округления на результат численного
решения
Будем трактовать суммарный эффект ошибок округления при
выполнении одного итерационного шага как возмущение правой части в
итерационном процессе
ufc = BuM+F. B.19)
Результат вычислений на каждой итерации при наличии ошибок
округления представим в виде
uf = Bu^1+F + <Jfc, B.20)
где 6k — суммарная погрешность округления. Норму разности между
реальным и идеальным (т. е. в отсутствии ошибки округления) результатами
50
Лекция 2 Численное решение систем линейных алгебраических уравнений
расчетов получим, вычитая B.19) из B.20). Учтем, что ||В|| < q < 1,
-x|| -I-
Так как начальное приближение задано точно Ци^ — ио|| =0.
Обозначим S = max ||<$i|| и вычислим сумму членов геометрической прогрес-
t
сии. Получим ||u^ — Ufc|| < S3-^- < Y^~, то есть погрешность, вносимая
в решение из-за конечной разрядности мантиссы, не зависит от
количества итераций. Этот результат является характеристикой устойчивости
рассматриваемого вычислительного процесса.
2.5.3. Методы Якоби, Зейделя, верхней релаксации
Представим матрицу А в виде
, B.21)
где L и U — нижняя и верхняя треугольные матрицы с нулевыми
элементами на главной диагонали, D — диагональная матрица.
Рассматриваемая СЛАУ может быть переписана в следующем эквивалентном виде:
Lu + Du + Uu = f.
Построим два итерационных метода
= f
+ Dufc+i + Uujk = f,
или, соответственно,
D-HL + U)ufc + D~4 B.22)
ufc+1 = -(L + D^Uiifc + (L + D)-^. B.23)
Очевидно, что эти формулы описывают итерационные процессы
вида B.16), если положить в B.22)
В = -D-^L + U), F = D"xf
51
Лекции по вычислительной математике
или
В = -(L + D)^ Р = (L + D)-Xf.
Эти итерационные процессы называются методами Якобы и Зейде-
ля. Представим их в компонентной записи. Метод Якоби будет иметь вид
(перенесем итерационный индекс к вверх):
Метод Зейделя можно представить следующим образом
+ + O2W
^lUknt\ - /n)/ann.
Эти формулы легко выводятся, если учесть, что элементами
матрицы D являются da = а#1.
Теорема (достаточное условие сходимости метода Якоби).
Итерационный метод Якоби сходится к решению соответствующей СЛАУ, если
выполнено условие диагонального преобладания
,...,п. B.24)
3=1
(МО
Доказательство.
Выполненные условия B.24) означает, что в любой строке матрицы
перехода
г\ ai2 Qi3 ain—1 ain \
U21 Q Q23 Д2п —1 a2ti
a22 O22 * * ' <*22 O22
ann ann a>nn ' ' ' лпп /
сумма модулей элементов меньше единицы. В этом случае по крайней
мере одна из норм матрицы В меньше единицы. Тогда выполняется
достаточное условие сходимости метода простых итераций. ¦
52
Лекция 2
Численное решение систем линейных алгебраических уравнений
Теорема (критерий сходимости итерационного метода Якоби). Для
сходимости итерационного метода Якоби необходимо и достаточно, чтобы все
корни уравнения
0,21
0>2п
= 0
по модулю не превосходили единицы.
Доказательство.
Легко проверить, что в силу диагональное™ D имеет место
det(B - АЕ) = det [-
= det(-D). det [(L+U) + DA].
Собственными значениями матрицы В = -D~1(L + U) являются
корни уравнения
det[(L + U) + DA]=0,
которые в соответствии с критерием сходимости метода простой
итерации должны быть по модулю меньше единицы.
Аналогичную теорему можно доказать и для метода Зейделя, однако
матрица в этой теореме будет иметь другой вид:
Аоц
\
\Cb22
\cbni
Аапп
Теорема (достаточное условие сходимости метода Зейделя (без
доказательства)). Пусть А — вещественная, симметричная, положительно
определенная матрица. В этом случае итерационный метод Зейделя сходится.
Доказательство этой теоремы сводится к проверке того, что
выполнение условий теоремы для матрицы А = L + D + LT влечет
выполнение условия сходимости итерационного метода с матрицей перехода —
(L + D)^. СЛАУ с вещественной матрицей А такой, что det А ф 0
может быть симметризована умножением на матрицу Ат:
(ATA)u = ATf
(симметризация Гаусса).
53
Лекции по вычислительной математике
Развитием метода Зейделя является метод релаксации. В этом
методе вводится итерационный параметр г, называемый параметром
релаксации. Представим метод релаксации в матричной форме:
(rLiifc+i + Dufc+i) + (r - l)Dufc + rUufc = rf.
Выбирая т, можно существенно изменять скорость сходимости
итерационного метода. Выразим Ufc+i
ufc+i = -(D + rL)-1 [(г - 1)D + тЦ uk + r(D + тЦ'Ч.
В общем случае задача вычисления тогтг (оптимального
итерационного параметра) не решена, однако известно, что 1 < тот < 2. В этом
случае итерационный метод называется методом последовательной
верхней релаксации или SOR — Successive Over Relaxation. Иногда встречается
термин «сверхрелаксация» при 1 < rOirr < 2. При 0 < г < 1 имеем метод
нижней релаксации.
2.6. Вариационные итерационные методы
2.6.1. Связь между вариационной задачей и задачей
решения СЛАУ
Пусть и € Ln , где Ln есть n-мерное евклидово пространство.
Рассмотрим квадратичный функционал от и, называемый функционалом
энергии:
Ф(и) = (Аи,и)-2(Г,и) + с,
где А — линейный оператор, f е Ln, с — константа. Этот функционал
совпадает с квадратичным функционалом Ф(и) = (А*и, и) — 2(f, и) + с,
где А* — сопряженный к А оператор. Действительно, (Аи, и) = (и, А* и)
по определению сопряженного оператора и (и, А* и) = (А* и, и) в силу
коммутативности скалярного произведения. Тогда
1,А , 1/А„ ч /А + А* \
так как -(Аи, и) + -(А*и,и) = (—^—и'и ) •
Без ограничения общности предположим, что оператор А —
самосопряженный, А = А*. В противном случае будем рассматривать задачу
с оператором |(А + А*) при решении вариационной задачи.
Будем также считать, что А — положительный оператор, т. е. А > О,
это означает, что для любого ненулевого вектора и выполнено (Аи, и)>0.
54
Лекция 2 Численное решение систем линейных алгебраических уравнений
Поставим задачу об отыскании элемента v, придающего наименьшее
значение функционалу Ф(и):
Ф(у) = min Ф(и).
u€Ln
Теорема. Пусть А = А* > 0. В этом случае существует
единственный элемент v e Ln, придающий наименьшее значение
квадратичному функционалу Ф(и) = (Аи, и) — Bf, и) + с, являющийся решением СЛАУ
Au = f.
Доказательство.
СЛАУ Аи = f имеет единственное решение v, поскольку А является
невырожденным оператором в силу его положительной определенности.
Покажем, что в этом случае при Av - f = 0 для любого вектора Д имеет
место Ф(у 4- Д) > Ф(у), т. е. при u = v достигается минимум
квадратичного функционала Ф(и).
Действительно,
Ф(у+Д)=(А(у+Д), v+A)-2(f, v+Д)+с =
= (Av, v) + (Av, Д) + (АД, v) + (АД, Д) - 2(f, v) - 2(f, Д) + с =
= (Av, v) + 2(Av, Д) + (АД, Д) - 2(f, v) - 2(f, Д) + с =
= [(Av, v) - 2(f, v) + c] + 2(Av, Д) - 2(f, Д) + (АД, Д) =
= Ф(у) + 2(Av - f, Д) 4- (АД, Д) = Ф(у) + (АД, Д) > Ф(у),
т. е. при Av = f и любом Д имеет место min Ф(и). Докажем, что верно и
обратное утверждение. Если элемент доставляет минимальное значение
функционалу энергии, то он является решением системы линейных
уравнений Av = f. Из курса математического анализа известно, что в точке
минимума должно выполняться условие grac^(u) = 0, А > 0.
Вычисляя градиент, приходим к условию минимума функционала grad<?(u) =
= 2 Аи - 2f = 0. Таким образом установлена эквивалентность
вариационной задачи (отыскание элемента, придающего минимум Ф(и)) и задачи о
нахождении решения СЛАУ. ¦
Заметим, что СЛАУ с самосопряженным и положительно
определенным оператором А представляют собой важный класс задач в
математической физике, в частности, они возникают при решении краевых
задач для эллиптических уравнений. При необходимости можно
произвести симметризацию по Ibyccy исходной системы.
55
Лекции по вычислительной математике
2.6.2. Методы градиентного и наискорейшего спуска
Метод градиентного спуска состоит в нахождении следующего
приближения в итерационном процессе из предыдущего, путем смещения в
направлении градиента функционала
Ф(и) = (Аи,и)-2(Г,и) B.25)
= и* - а* • grs^(ufc), B.26)
где А — положительно определенная симметричная матрица; а* —
параметр, определяемый из заданных условий; например, из условия
минимума величины
Ф[ик-ак-&еАФ(ик)].
В этом случае итерационный метод называется методом
наискорейшего спуска. Так как grad Ф(и) = 2(Au - f), то B.26) приобретает вид
Ufc+i = и* - тк(Аик - f), где тк = 2а*, B.27)
что соответствует записи итерационного метода в форме B.17). Здесь тк
является итерационным параметром, который в методе наискорейшего
спуска определяется из условия минимума функции Ф(т*,и*+1) по тк.
Найдем условие этого минимума:
О = 2(Аи*+1 - f,(u*+i)'rfc) = -2(Au*+1 - f, Aufc - f).
Здесь учтено соотношение: (Au',u) = (u',A*u) = (Au,u'),
поскольку A = А* и (v, Aw) = (Aw, v) в силу самосопряженности
оператора А. Подставим в последние равенства u*+i из B.27), получим (Аи* —
- f - тк А(Аи* - f), Аи* - f) = 0, откуда следует
(Аи* - f, Аи* - f) - т*(А(Аи* - f), Аи* - f) = О,
тк = (Аи* - f, Аи* - f)/(A(Au* - f), Аи* - f), или г* = jfe^Jy. где
г* = Аи* - f.
Вектор г* называют вектором невязки.
2.6.3. Метод минимальных невязок
Этот итерационный метод определяется следующим образом. Пусть
u*+i = и* - г*г*, как и ранее, г* = Аи* - f. Итерационный параметр т*
на каждой итерации выбирается так, чтобы минимизировать евклидову
норму невязки r*+i. Заметим, что итерационный процесс un+i = un +
+ тпгп может быть представлен в равносильном виде в терминах невязки
56
Лекция 2 Численное решение систем линейных алгебраических уравнений
rn+i = гп+т„ Аг„. Тогда для квадрата евклидовой (третьей) нормы
невязки получаем условие
Для отыскания минимума невязки на следующей итерации
приравняем нулю производную последнего выражения по итерационному
параметру г*. Получим равенство
-2(Аг*,г*) + 2т*(Аг*, Arfc) = 0.
Из последнего соотношения находим значение итерационного
параметра
(Arfc,Arfc)'
2.6.4. Метод сопряженных градиентов
Этот метод применяется для решения систем уравнений с
самосопряженной положительной матрицей А = А* > 0. Оптимизируем
градиентный метод, выбирая параметры т таким образом, чтобы на
последующем шаге невязка была ортогональна всем предыдущим. На первом шаге
невязку ищем аналогично методу наискорейшего спуска. Получим
невязки, образующие ортогональный базис. На последнем шаге невязка
становится равна нулю, так как пространство конечномерно, и единственный
элемент, ортогональный всем базисным векторам конечномерного
пространства — нулевой. Получаем точное решение за конечное число шагов
(прямой метод). Однако этот метод работает не всегда, так как при плохой
обусловленности матрицы он становится вычислительно неустойчивым.
Идея метода состоит в следующем. Выбираем произвольное
начальное приближение и вычисляем по нему вектор невязки г° = Au° ~ f,
тогда первое приближение и1 = и0 + тьг°.
Из условия ортогональности невязок на двух первых шагах находим
значение итерационного параметра то = - (^л^у •
Построим такое приближение, чтобы учитывались две
предыдущие — трехслойный итерационный метод. Фактически, при
построении его применяется процесс ортогонализации Грамма-Шмидта. Если
(Агп"~2, г11) = 0, то гп~~2, г*1 — ^сопряженные невязки.
Имеем метод сопряженных градиентов.
Все невязки уменьшаются по норме, поэтому данный метод
эффективен даже для плохо обусловленных задач, т.к. на определенном шаге
можно оборвать вычисления и получить приближение к решению с
заданной точностью. Тогда этот метод становится итерационным.
57
Лекции по вычислительной математике
Приведем последовательность расчетных формул одного из
вариантов метода сопряженных градиентов.
Ui = (E-riA)uo-fr1f,
и*+1 = afc+i(E - Tfc+i A)u* + A - afc+i)ufc_i + a*+iTfc+if, B.28)
где
ai = 1 afc+i = 1 7 г , A; = 1,2,...
В вычислительной практике этот метод используется при
умеренном числе обусловленности, больших п и неизвестных границах спектра
матрицы А, как итерационный метод, поскольку к0 обычно достаточно
большое число. Подробнее о методах сопряженных градиентов можно
прочитать в [2].
2.7. О спектральных задачах
Спектральные задачи — вычислительно наиболее трудоемкие
задачи в прикладной линейной алгебре. Различают полную и частичную
проблемы собственных значений. В первом случае необходимо отыскать
ВСЕ собственные числа матрицы, во втором — лишь максимальное по
абсолютной величине собственное число. Различают также
самосопряженную спектральную задачу и задачу для произвольной матрицы.
Очевидно, самосопряженная проблема решается проще — спектр
самосопряженной матрицы всегда действительный.
Рассмотрим два алгоритма для самосопряженных матриц. Первый —
степенной алгоритм, для вычисления наибольшего по абсолютной
величине собственного числа. Выбираем произвольный ненулевой вектор ио
и строим последовательность векторов
= Аи*.
Легко показать, что выражение
х (Aufc,Ufc)
приближает максимальное по абсолютной величине собственное
значение с точностью О(\н/\н-1)к. Здесь Xn/Xn-i — отношение самого
58
Лекция 2 Численное решение систем линейных алгебраических уравнений
большого по модулю собственного числа матрицы к следующему по
абсолютной величине.
Для решения полной самосопряженной проблемы собственных
значений применяется метод вращений.
Определение собственных значений самосопряженной матрицы А
эквивалентно отысканию такой ортогональной матрицы Т, что
Л = Т'АТ,
матрица Л — диагональная. Среди всех ортогональных преобразований
данное минимизирует сумму квадратов внедиагональных элементов
исходной матрицы. Построим итерационный метод, минимизирующий эту
сумму на каждой итерации. Пусть каждое преобразование подобия на
каждой итерации содержит лишь одну матрицу вращения А = ТУу АТу,
где матрица Т^ есть матрица поворота в плоскости и»и, на угол а. Эта
матрица отличается от матрицы А только двумя строками и двумя
столбцами (с номерами i и j). Так как евклидова норма матрицы не
изменяется при ортогональных преобразованиях, то легко получить
соотношение между суммами квадратов внедиагональных элементов старой и
новой матриц:
4 - 24 + \ ((% -а*)sin 2а +2а»;cos 2аJ •
Очевидны условия минимизации суммы в левой части последнего
равенства. Следует на текущей итерации выбирать индексы так, чтобы
выполнялось условие |<ц,| = max|a#|, a угол поворота выбирается из
условия 0 = ((ay - аи) sin 2а + 2ау cos 2аJ. Тогда он удовлетворяет
условию tg 2а = -^-,|а| ^ ?.
Независимо от наличия кратных собственных значений метод
вращений обладает квадратичной сходимостью.
Выбор максимального по модулю внедиагонального элемента —
затратная операция, поэтому часто реализуется метод вращений с
барьерами. Его идея состоит в следующем. При переборе внедиагональных
значений вращение производится тогда, когда значение элемента по
абсолютной величине превосходит некоторую величину (барьер). Если все
элементы меньше барьера, его значение уменьшается, например, на
порядок, и снова начинается циклический перебор внедиагональных
элементов. Подробнее о методе вращений смотри в [1].
Другие алгоритмы решения спектральных задач описаны в
специальной литературе [1, 3,10].
59
Лекции по вычислительной математике
Задачи
1. Методом Гаусса решить систему линейных уравнений Ах = f, где
А=
или
5xi + 0 • Х2 Н- хз = 11,
2xi -f- 6 • Х2 + 2хз = 8,
-3xi + 2 • х2 + 1Ох3 = 6.
Решение. Расширенная матрица А имеет вид
ац аи ai3 Л \ / 5 О 1 11
= | u2i a22 a23 h = 2 6-2 8
t3i а32 азз /з / \ -3 2 10 6
Разделив элементы первой строки на ведущий элемент ац = 5
получаем первую опорную строку A,0,0.2,2.2).
Далее умножим ее на a2i = 2 и вычтем из второй строки, после чего
умножим опорную строку на аз1 = 3 и вычтем из третьей. Получаем
матрицу Ai
А =
Вторая опорная строка — результат деления второй строки
матрицы Ai на
а\2 = 6:
@, 1, -0.4, 0.6)
Матрицы А2 после умножения опорной строки на 2 и вычитания ее
из третьей
А =
ац
0
0
ai2
Й22
&32
ai3
U23
ЛЗЗ
м
Л =
Л/
/1 0
0 6
\0 2
0.2
-2.4
10.6
2.2
3.6
12.6
an
0
0
ai2
<Z22
0
ai3
Ct33
Л ^
Л
/з >
\ (l
- °
0
6
0
0.2
-0.4
11.4
2.2
0.6
11.4
60
Лекция 2 Численное решение систем линейных алгебраических уравнений
Третья опорная строка (результат деления третьей строки на 11,4)
есть @,0,1,1).
Матрица Аз будет
A 0 0,2 2,2
0 1 -0,4 0,6
0 0 1 1
Обратный ход метода Гаусса.
Система уравнений с матрицей А3
xi + 0 • х2 + 0,2х3 = 2,2,
х2- 0,4х3 = 0,6,
х3 = 1.
Разрешая эту систему, начиная с последнего уравнения, получим
Хз = 1, Х2 = 1, Х\ = 2.
Определитель матрицы det А можно вычислить как произведение
ведущих элементов
detA = 5-6-11,4 = 342.
2. Показать, что решение системы линейных уравнений
xi + 2х2 + Зхз + 4х4 = 2,
Xi + 3X2 + Хз + 2X4 = -1,
2xi + Зх2 + 8х3 + 7х4 = 10,
2xi + 5х2 + Зхз 4- 7х4 = 3
методом Гаусса невозможно.
Решение. Преобразование матрицы рассматриваемой системы бу-
1 2 3 4 2 \ /12342
0 1-2-2-31 101-2-2-3
0 -1 2 -1 6 |* 0 0 0 -3 -3
0 1-3-11/ \00 -1 1 2
Поскольку а§3 = 0 то вычисление третьей опорной строки
невозможно.
61
Лекции по вычислительной математике
3. Показать, что
М(А)
max А» (А)
5
minAi(A)
t
Рассмотреть случай симметричной матрицы А.
Решение. Для собственного вектора ш, соответствующего
наибольшему по модулю собственному значению матрицы, выполняется
равенство Аш=Xuj, откуда
||АИ1 = |тахА<||М|.
Учитывая, что ||Аи>|| ^ ||А|| ||ц;||,получим ||А|| ^ maxAi(A) .Для
i I
обратной матрицы А максимальным по модулю является соб-
. Объеди-
ственное число rninA , откуда ЦА!!
няя два последних неравенства, получим
minAi(A)
maxAi(A)
minAi(A)
В случае симметричной матрицы А(А* = А) имеем
||А||з = х/Атах(А*А) = л/Атах(А2) = y/^JA) = |Атах(А)|,
т. к. из Aoji = XiWi следует (Ао;»J = А?и;?. Аналогично
Тогда/х(А) = ||А||з
= |Amax(A)|/ |Amin(A)|.
4. Найти число обусловленности матрицы А, выразив его через число
обусловленности матрицы В, если А = В*В > 0.
Решение. Для самосопряженной положительной матрицы А имеем
IA = sup
||||
(и, Аи)
(U, U)
62
Лекция 2
Численное решение систем линейных алгебраических уравнений
Тогда
НАМ II A -HI (U,All)
= А о A L L = sup —, ^- sup
311 ll3 ||||#o (uu) ;
(Bu.Bu)
(u,u)
sup
(u,u) I
(B~1u,B-1u)
(u,u)
(u,u)
откуда
5. Показать, что норма матрицы
согласована с нормой вектора
Решение.
t=i
3=1
t=l
Положим
Покажем, что существует вектор v, для которого достигается
равенство. В качестве такового можно взять вектор v с компонентами
Vi =0,г^ k,vk = 1.
Таким образом, норма матрицы ||А||2 = шах ^2 \uij\ согласована с
нормой вектора ||и||2 = ? \щ\.
ii
63
Лекции по вычислительной математике
6. Дана жорданова клетка порядка п
( 1
О
d
1
О
d
о о \
о о
0
0
0
0
0
0
... 1
d
...
...
1
0
d
1
А =
Найти /х( А) и оценить возмущение в компоненте и\ решения
системы Аи = f, если компонент /п вектора / возмущен на величину е.
Решение. Из Аи = f следует, что и = А~1(.
С помощью обратной подстановки ип = 1, un_i = ... находим
компоненты матрицы
0
0
0
0
1
0
0
0
-d ...
1
0 ...
0 ...
... (-d)n
... {-d)n-A
i
0
(-d)«
Ы)"-3
-d
1
В этом случае ИА^ = 1 + \d\, || А1| = l + |d| + rf» +... + \d\n~l =
- 13FT'
Видно, что при \d\ > 1 матрица А плохо обусловлена, при |d| < 1 -
хорошо. При п = 20 и d = 5 имеем /х(А) « 1014.
Компонент ui решения возмущенной системы u = A-1f будет
где ui — компонент решения невозмущенной системы Аи = f
Отсюда видно, что при |d| > 1 возмущение в п компоненте
вектоl
ра f увеличивается в компоненте и\ вектора и в \d\n~l раз, а при
\d\ < 1 — в \d\n~l раз убывает.
7. Пусть в системе линейных уравнений
1*1+ 0,99^2 = /ь
0,99ui + и2 = h
64
Лекция 2 Численное решение систем линейных алгебраических уравнений
вектор f = (/i,/2)T получает приращение Af = (?/i,<5/2)T, а
решение получает приращение Аи = (<5иь <5и2)т, Найти наименьшее
число /i, при котором независимо от f и Af выполняется оценка
||Af 1|
"М ||f|| *
IN
Решить задачу, используя нормы матриц \\-\\г , ||-||2, ||-||3.
Решение. Для возмущенной задачи А(и+Аи) = f+Af, из
линейности системы следует AAu = Af. Для возмущения решения
выполняется равенство Аи = A Af. Тогда ||Ди|| ^ ||A-i-||A||.^.|J|.
Отсюда сразу следует ||Ди|| ^ \\^~г\\ ' НА11 ^щ"" llull > так кзк
Д < 1|д«11-
Тогда искомая оценка будет JlpjjjH ^ ЦА!! • ||А|| ^щ^. Обозначим
1л = ЦА'1!! • ||А||. В этом случае наименьшим числом, при
котором выполняется оценка Hjj^ < А*^щ^' является \i = || А1| • || А||.
Это — число обусловленности системы уравнений. Численное
решение в соответствующих нормах получается легко.
8. При заданном фиксированном f найти наименьшее число v, при
котором независимо от Af выполняется оценка
|| Af |1
Найти такую правую часть системы f, которой соответствует
наименьшее I/, а также само это значение при использовании третьей
нормы матрицы.
шсшение*
По условию задачи и ^ |^| • |щ|[. Рассмотрим, какие значения
может принимать это число. Точная нижняя грань для такой
оценки, очевидно, inf v = В • sup " ul'.n ". Так как надо най-
ти оценку, не зависящую от начального возмущения (при решении
конкретной задачи оно, очевидно, неизвестно), получим
= inf „ = \\А-1\\.Щ
65
Лекции по вычислительной математике
Для точной нижней грани выполнено infi/(f) = ЦА!! х
х (sup N .,f,| " ) =1. Можно оценить и точную верхнюю грань:
Таким образом, 1 < v ^ /x.
Ответим на вопрос, при каких f достигается sup v и inf v. Для это-
f f
го используем разложение вектора правой части системы по
базису из собственных векторов матрицы А2 (без ограничения
общности полагаем, что такой базис существует). В этом базисе ^j^ =
Для самосопряженной положительной матрицы А* = А > 0
получаем
|Amin(A)|
\
tZl = J!Au!i<
Hull
В то же время
для самосопряженной положительной матрицы Ч^- = |А*(А.)|
В случае А* = А > 0 получаем sup Jjgjl = |Am(UC(A)| inf l|Au;
= |Amin(A)|.
Таким образом,
SUP ИПЗГ = >Am«c(A*A);8up V? = V%»a*(A*A),
inf
u
66
Лекция 2 Численное решение систем линейных алгебраических уравнений
9. Выписать формулы итерационных методов Якоби, Зейделя,
верхней релаксации для СЛАУ
или
2и + v = 1,
= -1.
Оценить количество итераций для метода Якоби.
(Решение системы: и = 1; v = -1).
Итерационные методы Якоби, Зейделя, релаксации соответственно
записываются
1 1
= ~2Vk + r
1 1
= ttfcf
ИЛИ Xfc+i = BXfe + f,
/ 0 -0,5 \
B-V-0,5 0 J«
1 1
2Vk 2'
1 1
A r)Ufc h A Vfc),
= A - r)vk - ^A + uk).
Оценка количества итераций проводится по формуле
к « Ь — / Ь ||В|| = In 10/ In i
67
Лекции по вычислительной математике
10. Представить графическую интерпретацию итерационного метода
Якоби для СЛАУ
= /2,
Решение. Итерационный процесс Якоби записывается как
ик+1 = -^vk + А,
an an
Q>21 . Н
= икЛ .
Рис. 2.1
Первое уравнение соответствует прямой 1, второе — прямой 2.
Вычисление и\ соответствует проведению отрезка, параллельного оси
Ои и (при v = v0) до пересечения с прямой 1; точка пересечения
даст первое приближение щ. Вычислению v\ соответствует
проведение из точки А\ прямой, параллельной оси 0v до пересечения с
прямой 2 и т. д. до сходимости итераций к точке пересечения
прямых 1 и 2 (Ак) с заданной точностью.
68
Лекция 2
Численное решение систем линейных алгебраических уравнений
11. При каких a, b сходится метод простой итерации и*+1 = Ви* -h f,
где
а Ь О
В= | Ь а Ь
О Ъ а
Решение. Для того, чтобы метод простой итерации сходился к
решению соответствующей СЛАУ, необходимо и достаточно, чтобы все
собственные значения матрицы В по модулю были меньше
единицы: |At| < 1. Решаем характеристическое уравнение
det(B - АЕ) =
а-А
Ь
О
6 О
а-А Ь
Ь а-А
= (а-А)
а-А
-Ь
О а-А
Ь а-А
= (а - А) [(а - АJ - Ь2] - 62(а - А) =
= (а - А)(а - А - V2b)(a - А + л/26) = О,
откуда получим условие сходимости итерационного метода
|а| < 1,|а±\/26 <1.
12. Найти условие сходимости итерационных методов Якоби и Зейделя
для СЛАУ Аи = f с матрицей А вида
Решение. Для метода Якоби
+ f, где B = -
U).
Имеет место уравнение:
Во; = Аи;, где А и ш — собственное число и собственный вектор,
соответственно. В таком случае -D(L + U)u; = Аи;, или: (L + U +
4- AD) из = 0, откуда (предполагаем наличие нетривиальных
решений у последней СЛАУ):
det(L + U + AD) = 0.
69
Лекции по вычислительной математике
Решим это уравнение:
det
Ха Ь О
Ь Ха Ъ
= 0,
0 Ь Ха
откуда получим условия сходимости итерационного метода Якоби:
Для метода Зейделя имеем
• В = -(D +
В таком случае
, Во; = Аи;.
откуда следует уравнение
det(AL + AD + U) = 0,
Вычислив детерминант, придем к алгебраическому уравнению
det
Ха Ь 0
А6 Ха Ь
0 АЬ Ха
= аХ2(а?Х-2Ь2) =
В таком случае, поскольку Ai^ = О, A3 = 2^, получим условие
сходимости метода Зейделя: | < 2~ *. Видно, что в данном случае
условия сходимости для обоих методов совпадают.
Литература
[1] Воеводин В.В. Вычислительные основы линейной алгебры. М.:
Наука, 1977. 303 с.
[2] ГолубДж., ВанЛоун Ч. Матричные вычисления. М.: Мир, 1999.548 с.
[3] ДеммельДж. Вычислительная линейная алгебра. Теория и
приложения. М., Мир, 2001.429 с.
[4] Фадеев А.К., Фадеева В.Н. Вычислительные методы линейной
алгебры. СПб.: Лань, 2002.736 с.
70
Лекция 2 Численное решение систем линейных алгебраических уравнений
[5] Воеводин В.В., Кузнецов ЮЛ. Матрицы и вычисления. М.: Наука,
1984.320 с.
[6] Беклемишев Д.В. Курс аналитической геометрии и линейной
алгебры. М.: Наука, 1980.240 с.
[7] Рябенький B.C. Введение в вычислительную математику. М.: Физ-
матлит,2000.294с.
[8] Бахвалов Н.В., Жидков Н.П., Кобельков Г.М. Численные методы. М.:
Лабо-ратория Базовых Знаний, 2002.632 с.
[9] Косарев В.И. 12 лекций по вычислительной математике. М.: Изд-во
МФТИ, Физматкнига, 2000.220 с.
[10] Коновалов Л.Н. Введение в вычислительные методы линейной
алгебры. Новосибирск, Наука, 1993.158 с.
[11] Амосов АЛ, Дубынскый Ю.А., Копченова Н.В. Вычислительные
методы для инженеров. М.: Высшая школа, 1994.544 с.
[12] Вержбицкий В.М. Численные методы. Линейная алгебра и
нелинейные уравнения. М.: Высшая школа, 2000.266 с.
71
Лекции по вычислительной математике
Лекция 3. Численное решение переопределенных
СЛАУ. Метод наименьших квадратов
В лекции рассматриваются методы решения переопределенных систем
уравнений. Обсуждается вопрос о выборе базиса на погрешность результата.
Вкратце описываются итерационные методы решения плохо обусловленных
систем линейных уравнений.
Ключевые слова: переопределенная система, метод наименьших
квадратов, обобщенный многочлен, конечный ряд Фурье.
3.1. Пример использования метода наименьших
квадратов (МНК)
Приведем простой пример получения переопределенной системы
линейных уравнений. Такого рода задачи часто встречаются, например,
при обработке результатов экспериментов.
Пусть / — линейная (или близкая к линейной) функция
аргумента х: /(х) = и\х + uo- В точках Xk известны значения функции /(х*).
Тогда uo,ui — коэффициенты, которые необходимо подобрать так, чтобы
выполнялись условия u\Xk + uq = Д, к = 0,1,2,3,4, Д = /(х*).
Получим систему пяти уравнений относительно двух неизвестных.
Это — переопределенная система. Она не имеет классического решения,
так как в общем случае не существует прямой, проходящей через все 5
точек (это возможно только тогда, когда какие-либо три уравнения
полученной системы линейными преобразованиями сводятся к двум
другим — система линейно зависима).
Рассмотрим общий случай. Пусть коэффициенты {г*о, и\}
необходимо определить по результатам п +1 измерения. Введем функцию, равную
сумме квадратов невязок т> = u\Xk + щ — Д
¦tio-ЛJ. C.1)
Примем за обобщенное решение переопределенной СЛАУ такие
{uo,ui} для которых Ф(ио,их) принимает наименьшие значение. Для
определения обобщенного решения из условия минимума суммы
квадратов невязки получаем систему двух уравнений, имеющую классическое
72
Лекция 3 Численное решение переопределенных СЛАУ
решение:
ди ди\
Выбор функции Ф(ио,и1) имеет некоторый произвол. Например,
возможно каждому измерению придать некоторый вес &&. От набора
таких весовых множителей зависело бы решение системы. В этом случае
функция Ф будет
k=0
Если в качестве невязки выбрать г* = \u\Xk + щ - Д |, то получим
задачу линейного программирования на отыскании минимума функции
з
Ф(иги2) = 52 \UlXk + uo - ДI •
к=0
Получившийся таким образом функционал, вообще говоря,
недифференцируем. Для решения задачи нельзя использовать метод
наименьших квадратов.
Произвол имеется и в выборе базисных функций. Вообще говоря,
можно было бы записать невязку гк в виде
= 1,..., п,
где (fj (x) — некоторые функции, образующие базис, например, тригоно-
р
метрические: (pj(x) = sin(/x) . Выражение ? Uj(pj(x) называется обоб-
i=o
щечным полиномом. В приведенном выше примере в качестве базисных
функций были выбраны степенные функции <pj{x) = xj. Обобщенный
полином превратился в алгебраический.
В случае выбора произвольной системы базисных функций
переопределенная СЛАУ и функционал Ф(ио, ..., ир) будут
ио<Ро(хо) + ... + ир<рр(х0) = /о,
п р
,...,«„) = "
i=0 j=0
73
Лекции по вычислительной математике
Отыщем обобщенное решение методом наименьших квадратов.
Приравнивая все частные производные по компонентам обобщенного
решения к нулю |~ = 0 (условия минимума) и изменяя порядок
суммирования, получаем СЛАУ
Р / п \ п
5Z ( *52<РЖхд<Рк(Хг) I Uj =^fi<Pk(Xi), к = 0, . . . ,р,
j=0 \t=0 / i=0
ИЛИ
Система метода наименьших квадратов имеет вид Du = f с
матрицей D, элементами которой являются скалярные произведения (^, щ,) =
п
— S 4>э(х)ч>к{х\) Это — матрица Грамма. Ее свойства известны из курса
линейной алгебры, эта матрица симметричная и положительно
определенная. Таким образом, решение исследуемой СЛАУ существует и
единственно. В правой части системы стоят проекции свободного члена ис-
п
ходной задачи на подпространство базисных функций (</?, f)=^2<
1=0
Здесь учтено, что J^ = 2 ? <Pk(*i) Ё Щщ(хг) "ЛЬ или» в Р^"
i=0 \j=0 )
вернутом виде
(Xi) (Uo <Po(Xi) + UiV?o(^i) + - • . + Up(fp(Xi) - f(Xi)) = 0,
г=0
n
^ (/?l(Xt) (Uo yo(^i) ~b ^1 ^l(Xi) + . . . -|- Upy?p(Xi) — /(X{)) = 0,
i=0
(^i) + Ui <fi(Xi) -f . . . + Up <ft>(Zi) - /fai)) = 0.
i=0
Часто выбирают <рк{х) — xfc, в этом случае система уравнений
принимает следующую форму:
i=0 i=0
74
Лекция 3 Численное решение переопределенных СЛАУ
Эта система может быть легко выписана в компонентах:
i=0
\i=0 / t=0
t=0
В случае использования ортонормированных систем базисных
функций <Pj(x)9 т. е., при выполнении условия {чрк, <pj) = Skj решение
прини^^ 22
j j
мает простой вид и0 = ^^у = ||w)ir2(vo,/);ui = \\<pi\\~2(<pu /);••• uv =
= ||<^р|Г2(^р,/). Поскольку система функции ортонормирована, то ||^|| =
= 1 и Uk = (<Pk,f),k = 1,..., п. Эти коэффициенты называются
коэффициентами Фурье, а обобщенный многочлен с этими коэффициентами —
обобщенным многочленом Фурье. В частности, в качестве базисных можно
использовать ортогональную систему функций на [-тг,7г] : {sinA;x,cosA;x}
к = 1,..., п. Такие представления называют отрезками
тригонометрических рядов Фурье или конечными рядами Фурье.
Докажем теорему о методе наименьших квадратов, обобщающую
изложенную информацию.
Запишем переопределенную СЛАУ
... + aipup = Д,
пп1Щ + . . . + dnpUp = /n, П > p. C.2)
где линейные нормированные пространства Lp и Ln имеют размерности
Р и п соответственно. Перепишем C.2) в матричной форме:
Au = f,
(аи ... aVi
ащ ... ащ
75
Лекции по вычислительной математике
Наряду с основным скалярным умножением в Ln
? C.3)
введем скалярное умножение с весовой матрицей В:
[х,у]п = (Вх,у)п, В = В* > 0,х, у е Ln C.4)
Оба этих умножения удовлетворяют аксиомам скалярного
умножения элементов линейного пространства. Матрица В является весовой и
определяет вклад невязки каждого слагаемого суммы C.1). Система C.2)
не имеет классического решения. Определим обобщенное решение этой
системы как элемент линейного пространства v, придающий
наименьшее значение квадратичной форме:
<&(u) = [Au-f,Au-f]n.
Теорема. Пусть столбцы матрицы А линейно независимы, mse. ранг
А равен р. Тогда существует единственный элемент р-мерного евклидова
пространства v € Lp, являющийся обобщенным решением системы C.2), и
решением СЛАУ
A*BAu = A*Bf, C.5)
состоящей из р скалярных уравнений относительно неизвестных ^
доставляющий минимум квадратичной форме
Доказательство.
Покажем, что решение СЛАУ А* В Аи = A*Bf существует и
единственно. Введем обозначение q* e Ln для вектора — к столбца матрицы
системы А:
Несложно показать, что матрица D = А*ВА системы C.5) есть
квадратная матрица р х р. Элемент dij этой матрицы, стоящий на
пересечении i строки и j столбца, есть d{j = (qi? Bq^O1 = (Bqi? qj)n = [q», qj]n,
в силу коммутативности скалярного произведения d^ = dy/, что означает
самосопряженность матрицы D : D = D*.
Покажем, что матрица D невырождена и положительно определена.
Напомним, что (f,A?)n = (A*f,?)p;fi e Ln, ? G Lp. Это равенство
проверяется непосредственно, если записать обе его части в развернутом
76
Лекция 3 Численное решение переопределенных СЛАУ
виде. Невырожденность матрицы D следует из того, что ранг матрицы А
равен р.
В таком случае 0 < [Ах,х]п = (ВАх,Ах)п = (А*ВАх,х)р =
= (Dx,x)p. Поскольку D невырождена и положительно определена, то
C.5) имеет единственное решение v G IP. Теперь покажем, что v —
единственное обобщенное решение системы. Для любого вектора Д Ф О
выполнено Ф(у + Д) > Ф(у):
Ф(у + Д) = [A(v + Д) - f, A(v + Д) - f]n =
= [Av - f, Av - f]n - 2 [Av - f, АД]П + [АД, АД]П =
= Ф(у) + 2 [Av - f, АД]П + (БД, Д)р = Ф(у) + (БД, Д)р > Ф(у),
что и требовалось доказать. ¦
При доказательстве использовалось
[Av - f, АД]П = (B(Av - f), АД)П = (A*BAv - A*Bf, Д)р = О,
поскольку A*BAv = A*Bf.
Так как матрица D = А*ВА — симметричная и положительно
определенная, то для численного решения полученной СЛАУ можно
воспользоваться итерационными методами.
Если система векторов {q*}?=1 оказывается ортонормированной,
т-е- fat» <Ъ*1 = uiji'J = 1» • • >Р>то матрица D оказывается единичной. Ее
элементы и есть скалярные произведения [q», q,-]. В этом случае
решением системы будет
u = A*Bf.
Следует отметить, что если базисные функции (fi(x), i = 0,... ,р не
выбираются специальным образом, то при достаточно больших р (р ^ 5)
полученная СЛАУ оказывается плохо обусловленной. Строки матрицы
D = А* В А могут оказаться почти линейно зависимыми. Простейшим
примером такого почти линейно зависимого базиса является система
функций х*, г = 1,... ,р при больших р. В этом случае желательно
использовать ортогональные функциональные базисы, однако такой выбор
не всегда возможен и удобен.
Для примера возьмем в качестве базисных функций степенные,
обобщенный полином в этом случае будет
j=0
77
Лекции по вычислительной математике
Скалярные произведения на отрезке [0,1], записанные в
интегральной форме (т. е. при п —> оо), будут иметь вид
В таком случае СЛАУ после применения МНК, т. е. минимизации
1
функционала Ф(и) = f (F(x) — f(x)Jdx, где F(x) — заданная функция,
о
будет:
1
1 1 Г , 4J
+ -иг + ... + ^jUp = J F(x)dx,
о
1 [ тх ^J
... + ^-j-?Up = у x/(x)dx
1 1
2"° + 3
или
где
Матрица Hp+i называется матрицей Гильберта. Это классический
пример плохо обусловленной матрицы. Число обусловленности очень
быстро растет с ростом р. Так при р = 1 /х = ||Н|| • ЦН)! « 20, при
р = 9/х « 1013. Если получим СЛАУ для дискретной системы точек, т. е.
Для (<Pj,<fk) = Е «• »(^ji/) = ? *i7(*i) «i = i, то ее матрица будет
t=0 i=0
асимптотически приближаться к матрице Гильберта Hp+i при п —> оо.
78
Лекция 3 Численное решение переопределенных СЛАУ
3.2. Понятие о методах решения плохо
обусловленных СЛАУ
Улучшить качество численного решения СЛАУ метода наименьших
квадратов возможно, если использовать различные преобразования
матрицы А.
Большинство прямых методов решения линейных систем основано
либо на замене исходной системы Аи = f (А — квадратная матрица) на
эквивалентную CAu = Cf, либо на представлении матрицы А в виде
произведения других матриц, таких, чтобы новая система либо решалась
более просто, либо была лучше (по крайней мере, не хуже) обусловлена,
чем исходная.
Подход, использующий спектральную эквивалентность матриц А и
С (в смысле границ спектра собственных значений), основан на
умножении А на близкую в некотором смысле матрицу С. Последняя матрица
выбирается таким образом, чтобы произведение было близким к
единичной матрице (при этом С Ф А, так как обращение плохо
обусловленной матрицы приводит к накоплению вычислительных ошибок. Число
обусловленности матрицы СА у, = Amax/Amin будет близко к единице.
Метод энергетически эквивалентных операторов оказался эффективным
при численном решении сеточных уравнений при разностной
аппроксимации уравнений в частных производных эллиптического типа.
Идея предобусловливания СЛАУ состоит в том, чтобы вместо
исходной системы Аи = f решать систему А'и' = Р, где А' = С АС, и' =
= Си, f' = C"xf, матрица С выбирается так, чтобы она была
симметричной положительной, хорошо обусловленной.
Определение. Матрица Q с вещественными элементами qij является
ортогональной, если
Q* = Q
Пусть матрица С невырождена. Тогда она представима в виде
C = QR,
где Q — ортогональная, a R — верхняя треугольная матрицы. В качестве
матрицы Q часто используется симметричная ортогональная матрица Н:
Н = Е - 2wwT,
где w - произвольный вектор-столбец, такой, что (wTw) = 1. Матрица
(w, wT) есть произведение вектора-столбца w на вектор-строку wT
(преобразование Хаусхолдера или метод отражений).
79
Лекции по вычислительной математике
Заметим, что симметричность матрицы Н (матрицы отражений)
показывается непосредственной проверкой; ортогональность Н можно
показать следующим образом:
ННТ = (Е - 2wwT)(E - 2wwT) =
= Е - 2wwT - 2wwT + 4wwT • wwT =
= E - 4wwT - 4w(wTw)wT = E,
TaKKaKwTw = 1.
Матрица СЛАУ представляется в виде А = HTR, после чего
решается эквивалентная система уравнений Ru = Hf.
3.3. Задачи
1. Для функции /(ж) = у/х на отрезке [0,1] построить многочлен
F(x) = uo + u\x среднеквадратичного приближения со скалярными
произведениями:
Решение. Введем базисные функции <ро(х) = 1, ipi(x) = ж, и
вычислим скалярные произведения
1 1
2
(<АьЫ = / l2cb = l,((piy<pi) = / x2dx =-,
0 о
1 1
/1 С
xd*= 2'(/>^o)= /
о о
1
/2
y/xxdx = -,
о
Для вычисления коэффициентов получим СЛАУ
^l 2
W0+2Ul = 3'
112
2U0+3Ul = 5'
откуда uo = ^,ci = |,F(x) = ^ + f x.
80
Лекция 3 Численное решение переопределенных СЛАУ
2. Получить СЛАУ
С22Х + С21У = /2,
если она задана в форме метода наименьших квадратов: А* В Аи =
(Oil O12
O21 O22
О31 O32
Решить эту систему для случая оц = 032 = 1,021 = 012 = 2,031 =
Решение. Проведем необходимые вычисления:
/ аи а21 а31 \ ( 1 0 \ / °п
\ ai2 a22 032 / V ° 1 )
= ( ОЦ 021 О» \/1 0\/ ^
V Oi2 O22 O32 / V ° ! / \ *
2
/з
(
all + а21 ~Ь~ а31 ОцО12 + O21O22
¦ O21O22 + O31O32 Oi2
= / wi \ _ / an/i +a2i/2 +a3i/3 \
\ ^2 / V ai2/! + a22/2 + a32^3 / '
@11012-1-021022+031032) г11+(а12+о22+Оз2)гх2 = 012/1+022/2+032/3-
Решение в числах предлагается найти читателям.
3. С помощью метода наименьших квадратов найти коэффициенты
полинома второй степени f(x) = uo + u\x + U2X2, если таблица
измерений задана {хи Л}1Г=о •
Решение. Переопределенная система уравнений:
= Д,А: = 0,1,... ,n,
определяет функционал
п
Ф(ио,...,ип) =
к=0 fc=O
81
Лекции по вычислительной математике
Условия минимума последнего
ЭФ
дик
= 0.
После проведения алгебраических преобразований получим для
коэффициентов систему линейных уравнений
\к=0
к=0
к=0
\k=0
\fc=0
к=0
к=0
\fc=0
\fc=0
\fc=0
k=0
3.4. Задачи для самостоятельного решения
1. Заданатаблица{хя:,/А:}, А; = 0,1,...,п,п > 1.
Найти линейную функцию /(х) = ах+/3, минимизирующую
функционал Ф(а,/3) = Е (Л ~ ахк - /?J.
к=0
Используя этот результат, решить переопределенную СЛАУ
х + у = 3, х + Зу = 7,2ж - у = 0.2, Зх + у = 5.
2. Пусть В — квадратная матрица размером п х n, u — n-мерный
вектор, Ф(х) — функционал, Ф(х) = (Ви - их, Ви - их). Доказать,
что Ф(х) достигает минимума при х = (Ви, и)/(и, и).
3. Барометрическое давление изменяется с высотой по закону р =
= aebh.
Определить коэффициенты а, Ь по результатам наблюдений,
приведенных в таблице (h — высота в метрах над уровнем моря; р —
давление в мм рт. ст.):
h
р
0
760
270
737
840
686
1452
636
2116
584
3203
508
82
Лекция 3
Численное решение переопределенных СЛАУ
4. Скорость корабля связана с мощностью его двигателя формулой
Р = ао + аз*;3 (Р — мощность в лошадиных силах, v — скорость
в узлах).
Определить ао, аз по табличным данным.
V
р
6
423
8
805
10
1378
12
2357
13
2893
5. Найти приближение многочленом третьей степени методом
наименьших квадратов для функции f(x) = sin(Trx) по значениям в
точках хо = —1, xi = -0,5, Х2 = 0, ха = 1.
6. Вычислить матрицы А*ВА и А*В и найти решение системы
уравнений вида A*BAu = A*Bf, если заданы матрицы А, В и вектор
f.
А =
/ 1
2
1
\s
1
-1
3
1
\
)
7. Функция f(x) = v/l + sin2(z - 1) приближенно заменяется
тригонометрическим многочленом Р(х) = ао + aisinx + bicosx +
+ d2 sin 2x + &2 cos 2х по десяти точкам хо,..., хд с помощью метода
наименьших квадратов.
Опишите алгоритм вычисления коэффициентов ao, ai, 6i, a<i, Ьч-
8. Доказать, что прямая, проведенная по методу наименьших квадра-
Е Vi*i E
тов, проходит через точку с координатами х1 = W... , у' = -\
2ш* У* 2L
Литература
[ 1 ] Рябенький В. С. Введение в вычислительную математику. М.: Физмат-
лит,2000.294с.
[2] Бахвалов Н.В., Жидков Н.П., Кобельков Г.М. Численные методы. М.:
Лаборатория Базовых Знаний, 2002.632 с.
[3] Каханер Д, Моулер К., Нэш С. Численные методы и программное
обеспечение. М.: Мир, 1998.575 с.
83
Лекции по вычислительной математике
[4] ГолубДж., ВанЛоун Ч. Матричные вычисления. М.: Мир, 1999.548 с.
[5] Форсайт Дж., Малькольм М., Моулер К. Машинные методы
математических вычислений. М.: Мир, 1980.279 с.
[6] Коновалов А.Н. Введение в вычислительные методы линейной
алгебры: Новосибирск. М.: Наука, 1993.158 с.
84
Лекция 4 Численные методы решения экстремальных задач
Лекция 4. Численные методы решения
экстремальных задач
Рассматриваются наиболее употребительные методы поиска минимума
функций нескольких переменных.
Ключевые слова: функционал, целевая функция, стационарная
точка, метод перебора, метод золотого сечения, метод парабол, метод
покоординатного спуска, градиентного спуска, метод
наискорейшего спуска, математическое программирование.
4.1. Поиск безусловного минимума функции
Определение. Пусть на множестве J7, состоящем из элементов и
линейного метрического пространства определена скалярная функция Ф(и).
1. Говорят, что Ф(и) имеет локальный минимум на элементе и*, если
существует его конечная е-окрестность, в которой выполнено
Ф(и*)<Ф(и),||и-и1<е D.1)
2. Ф(и) достигает глобального минимума в U на элементе и* (строгий,
абсолютный минимум), если имеет место равенство
Ф(и*) = ЫФ(и) D.2)
Замечание. Если U — числовая ось, решается задача на нахождение
минимума функции одного переменного, если U — n-мерное векторное
пространство, имеется задача на нахождение минимума функции п
переменных, если U — функциональное пространство, то решается задача на
отыскание функции, доставляющей минимум функционалу (задача
оптимального управления или динамического программирования).
Если к D.1) или D.2) добавляются условия
F? <Ф<(и)<^\г = 1,...,/,
(uk IF* — числа, а Ф» — заданные функции), то это задача поиска
условного минимума, если подобные ограничения отсутствуют, то это задача
85
Лекции по вычислительной математике
поиска безусловного минимума. Причем, если функции Фг(и) линейны,
задача поиска условного минимума называется задачей линейного
программирования, если хотя бы одна из этих функций нелинейна, то
имеется задача нелинейного программирования. Обе эти задачи вместе с
задачей динамического программирования в теории оптимального
управления называются задачами математического программирования.
Говорится о поиске минимума функции, не ограничивая общности,
так как максимум функции Ф(и) является минимумом функции -Ф(и).
Ф(и) называют целевой функцией.
Отметим связь между задачами вычисления корней системы
нелинейных алгебраических уравнений (СНАУ) и задачи минимизации.
Пусть на множестве U e Ln решается система нелинейных
уравнений
/i(wb...,un)=0,
Определим целевую функцию следующим образом:
l,...,tin) =
к=1
В области U справедливо Ф(и) ^ 0, причем минимальное значение
Ф(и) имеет при и = и*, где и* — корень рассмотренной системы. Поэтому
ее решение эквивалентно поиску минимума Ф(и) в U. Если Ф(и) строго
больше нуля, то система решений не имеет.
Теперь положим, что необходимо найти минимум целевой функции
Ф(ге), у которой существуют первые производные. В этом случае задача
сводится к решению СНАУ
^0
дип
Точка, являющаяся решением указанной СНАУ, называется
стационарной. Однако не всякая стационарная точка может быть точкой
локального минимума целевой функции.
Следующую теорему приведем без доказательства.
86
Лекция 4 Численные методы решения экстремальных задан
Теорема. Пусть функция Ф(и) дважды непрерывно
дифференцируема. Тогда достаточным условием того, чтобы стационарная точка и*
была точкой локального минимума, является положительная определенность
матрицы Гессе
(
д
Отметим, что методы отыскания минимума Ф(и) нередко
оказываются более эффективными, чем методы численного решения СНАУ.
Метод перебора.
Пусть U = [а, 6], т. е. отрезок числовой оси. Разобьем его на п равных
частей с узлами в точках щ = a + i(b - а)/щ i = 0,..., п.
Вычислив значение Ф(и) в этих точках, найдем путем сравнения
точку и*, в которой
ф(и*) = min Ф(щ).
Далее полагаем: и* « umin, Ф* « Ф(и*). Погрешность в определении
и* этого простейшего метода не превосходит числа
Этот метод прост, но неэкономичен, особенно когда ищется
минимум функции многих переменных. Например, в гиперкубе U =
= {0 < щ ^ 1,1 ^ % ^ 10} с разбиением каждого из отрезков (по каждой
из координат) на 10 частей, с быстродействием 106 операций в секунду
потребуется около 107 с (примерно 4 месяца) для нахождения пипФ(и),
если предположить, что количество арифметических действий,
необходимое для вычисления значений Ф(и) в каждой точке требует тысячи
арифметических операций. Этот метод можно сделать более
эффективным, если сначала определить минимум с грубым шагом, затем уже
искать минимум с меньшим шагом на том из отрезков [х%, ?i+i], на котором
предполагается наличие минимума; можно и далее уточнять решение
задачи таким же образом.
Усовершенствованием этого метода являются методы исключения
отрезков, дихотомии (деления отрезка пополам) и золотого сечения. В
них отрезок [а, Ь] делится на 4 части выбором внутри отрезка точек ui, U2,
в которых вычисляются значения целевой функции. Сравнив ее значения
в этих точках, можно сократить отрезок поиска точки минимума,
перейдя к отрезку [а,и2], если Ф(иг) < Ф(и2) или [tii,ft], если Ф(иг) ^ Ф(и2).
Эту процедуру можно продолжить.
87
Лекции по вычислительной математике
В методе дихотомии точки щ, и2 выбираются близко к середине
отрезка и\ = ь+д-Д, U2 = fr+*+A, где Д достаточно мало. Поскольку
отношение ^з^ > je^ близко к 1/2, такой выбор объясняется стремлением
обеспечить максимальное относительное уменьшение отрезков.
В конце вычисления в качестве приближенного значения и* берется
середина последнего отрезка. В результате п итераций длина отрезка бу-
дет Дп = Ь? + (? + 2^т + • • • + |)д = ъг + A - ?)Д, т.е. точность
определения и* составляет еп = Дп/2.
Находя п из условия еп ^ ?, получим количество итераций,
необходимое для достижения данной точности
^. Ь-а-А
Если в предыдущем неравенстве положить А малой, то
Ь-а
Метод золотого сечения.
Расположим точки иь п2 на [а, Ь] так, чтобы одна из них стала бы
также пробной, но уже на новом отрезке, после исключения части
исходного отрезка. Это позволит уменьшить количество вычислений,
поскольку необходимо будет вычислить значение Ф(и) лишь в одной из пробных
точек, так как во второй оно уже известно.
Найдем расположение таких точек, для чего рассмотрим отрезок
[О, 1] и, для определенности, положим, что при его уменьшении
исключается его правая часть.
1-т
0,5
1-т
Ц | «J
Рис. 4.1
Пусть U2 = т, тогда симметрично расположенная относительно
центра отрезка точка имеет координату и\ = 1 - г (рис. 4.1).
88
Лекция 4 Численные методы решения экстремальных задан
Пробная точка щ отрезка [0,1] перейдет в пробную точку г4 = 1 - т
нового отрезка [0, г]. Условием деления отрезков [0, 1] и [0, г] в одном и
том же отношении точками г*2 = тии2 = 1-т является равенство
или т2 + т-1 = 0,
т 1 — т
откуда находим положительный корень
«0,61803...,
Для отрезка [а, Ь]
ui = а +—-—(Ь-а)\и2 = а +—-—(Ь-а)
Замечания.
1. Точки iti, u2 обладают следующим свойством: каждая из них делит
отрезок [а, Ь) на две неравные части так, что отношение длины всего
отрезка к длине его большей части равно отношению длин большей
и меньшей части. Точки, обладающие таким свойством, называются
точками золотого сечения, введенного Леонардо да Винчи.
2. На каждой итерации отрезок поиска минимума уменьшается в
одном и том же отношении
\/5-1
поэтому в результате п итераций длина становиться равной
Ап = тп(Ь-а).
Следовательно, точность еп определения точки и* после п итераций
равна
An 1,>/5-1чП/, ч
?п = ~2~ = 2 *—2—^ ^ " п^
а условие окончания вычислительного процесса будет еп ^ е.
Метод парабол.
Методы, использующие исключение отрезков, основаны на
сравнении функций в двух точках пробного отрезка, учитываются лишь
значения функции в этих точках.
89
Лекции по вычислительной математике
Учесть информацию о значениях функции между точками
позволяют методы полиномиальной аппроксимации. Их основная идея
заключена в том, что функция Ф(и) аппроксимируется полиномом, а точка его
минимума служит приближением к и*. Разумеется, в этом случае кроме
свойства унимодальности (т. е. наличия единственного минимума на
рассматриваемом отрезке), необходимо на Ф(и) наложить и требования
достаточной гладкости для ее полиномиальной аппроксимации.
Для повышения точности поиска и* можно как увеличивать степень
полинома, так и уменьшать пробный отрезок. Поскольку первый прием
приводит к заметному увеличению вычислительной работы и появлению
дополнительных экстремумов, обычно пользуются полиномами второй
(метод парабол) или третьей (метод кубической интерполяции) степени.
Алгоритм поиска минимума состоит в следующем.
Выбираем на пробном отрезке три точки ui, U2, из такие, что ui <
U2 < U3 И Ui ^ U* ^ U3.
Построим параболу (квадратичный полином)
Q(u) = ао + ai(u — ui) + а2(и — и\)(и — U2),
график которой проходит через точки (щ, /(ui)), (иг, /A*2)), (мз,
Коэффициенты а*, А; = 1,2,3 находим из системы уравнений
Q(ui) = /(in),
Q(u2) =
Q(us) =
откуда
\ai =
a2 =
u2-ui
/Ы-/Ы
U3 — U2 L Us — Ui U2 — Ui
Точку п минимума Q(u) находим, приравнивания его производную
к нулю:
U= "(U1+U2-— ) =
2, а2
1 Г/ , ч (/2 - /l)(^3 ~ U2) и /з - Д /2 - /l у.]
= X \Ц\ -т и2) /( ) .
2[ u2—u\ U3—ui u2—ui]
Далее полагаем: и* « п (очередное приближение точки минимума).
Эту процедуру можно продолжить до достижения необходимой точности,
выбирая новые точки и&, к = 1,2,3. Для этого можно использовать
методы исключения отрезков, используя в качестве двух пробных точек и2 и
п, таких, чтои2, п € [1*1,113].
90
Лекция 4 Численные методы решения экстремальных задач
4.2. Методы спуска
Основная идея методов спуска состоит в том, чтобы построить
алгоритм, позволяющий перейти из точки начального приближения и0 =
= {uj,..., и%} в следующую точку щ = {uj,..., и?} таким образом,
чтобы значение целевой функции приблизилось к минимальному.
4.2.1. Метод покоординатного спуска
Этот метод является редукцией поиска функции многих
переменных к последовательности поиска минимумов функции одной
переменной. Пусть и0 eU — начальное приближение к минимуму Ф(и).
Рассмотрим Ф(щ) = Ф(^о,..., и%) как функцию одной переменной
т при фиксированных и§,..., м° и находим одним из приведенных
методов поиска минимума функции одной переменной
minгФ(п1,и^,...,и5).
Полученное значение иь доставляющее минимум <?(ui),
обозначим и}; при этом
Далее, при фиксированных значениях u\,v%,...,u°n ищем
как функции от иъ\ соответствующее значение щ обозначим и\\ при этом
Этот процесс продолжаем аналогичным образом и для оставшихся
координат; в результате получим
Таким образом, переходим из точки щ в точку tii. Этот процесс
повторяется до тех пор, пока не будет выполнено условие выхода из
итераций, например:
где е > 0 — заданная точность.
Пример. Найти минимум функции двух переменных
ф(и) =ul
91
Лекции по вычислительной математике
Щ
ч \
\ \
J h
Рис. 4.2
Выбрав некоторую точку начального приближения, например, и0 =
= B,2), получим минимум целевой функции за два шага, так как ее
линии уровня — окружности с центром в начале координат (рис. 4.2).
Если же целевой функцией является, например
Ф(и) = Ъи\ + 5г*2 4- 8^11*2,
которая поворотом системы координат на угол -45° и преобразованием
V\ + V2 (—Vl + V2)
U\ = т=—5W2 = 7=
у/2 у/2
приводится к виду Ф'(г;) = v\ + 9v|, то ее линиями уровня являются
эллипсы v\/9 + v\ = с2 поэтому спуск будет иметь иной характер (рис. 4.3).
Можно показать, что покоординатный спуск реализуется
(сходится к точке минимума) при условии существования вторых
производных Ф^Ф" ,Ф„1и2, причем Ф^ 7* аг > 0,Ф^2 ^ а2 > 0,|Ф2111а| <
аз, ахаг > of Изломы приводят к подъему. Этот метод сходится
достаточно медленно, а при наличии так называемых «оврагов», очень медленно.
Разделим «рельефы», образуемые линиями уровня — на два типа:
«котловинный» и «овражный». В первом случае линии уровня похожи на
эллипсы, а функция вблизи своего минимума практически не изменяется при
изменении переменных. Этот случай можно назвать простым (рис. 4.4).
Рельеф овражного типа имеет либо точки излома (рис. 4.4), либо
участки с большей кривизной («разрешимый овраг»). Если линии
уровня — кусочно-гладкие, то выделим на них точки излома,
геометрическое место которых назовем истинным «оврагом», если угол направлен
92
Лекция 4
Численные методы решения экстремальных задач
Рис. 4.3
в сторону возрастания функции — и «гребнем», если в сторону убывания
(рис. 4.5).
Рис. 4.4
Примером разрешимого оврага является функция Ф(иь г^) = 10(и—
2 + 0,1и\ (рис. 4.6).
Неупорядоченный тип рельефа характеризуется наличием многих
экстремумов; примером может служить функция Ф(г*1,и2) = (l+sin2ui)x
*A + sin 2u2) (Рис. 4.7).
93
Лекции по вычислительной математике
Рис. 4.5
Рис. 4.6
Метод оврагов используется в случае, если «дно» оврага узкое,
а «склоны» крутые. В этом случае спустимся из двух точек Pq и Pi,
например, с помощью метода координатного или градиентного спуска на
«дно» оврага (или в его окрестность) в точки с координатами го или п,
не требуя высокой точности сходимости. Проведем через эти две точки
прямую и выберем на ней новую точку
Р2 =
- r0),
94
Лекция 4
Численные методы решения экстремальных задач
Зтг
2
тг
т
Зтг
2
Рис. 4.7
Рис. 4.8
где h = const > 0 — «овражный шаг», который выбирается для каждой
функции путем расчета (рис. 4.8). Точка лежит на «склоне» оврага. Из нее
спускаемся на «дно» и попадаем в некую точку г2, через точки т\ и г2
проводим прямую и находим точку Рз, из которой возможно опуститься в
Процесс продолжается до тех пор, пока значения целевой функции
на «дне» оврага убывают, т. е. пока
Ф(гп+1) > Ф(гп).
95
Лекции по вычислительной математике
4.2.2. Метод градиентного спуска
Напомним, что градиент функции &с8АФ(и) = (^г,..., ^) есть
вектор, ортогональный линиям уровня целевой функции, а его
направление совпадает с направлением наибольшего роста Ф(и) в данной точке.
В точке минимума grad Ф(и) = 0.
Построим итерационный процесс следующим образом:
ик+\ = ик - г • grad Ф, но = а,
где г — шаг спуска (итерационный параметр). Итерации продолжим до
выполнения заданного условия окончания процесса поиска минимума,
например
Пример. Рассмотрим функцию двух переменных Ф(и1, иг) = ^
2J.
В соответствии с методом градиентного спуска получим
1 1 и1
4=г4-ту,
= и1 - т • 2и1-
Пусть начальное приближение щ = {1; 1}; г = 0,1.
Тогда щ = {0,95; 0,80}; и2 = {0,9025; 0,6400}; и3 = {0,8574; 0,5120};
= 0,446.
Если взять г = 2, то и\ = {0; -3} и Ф(и\) = 9, в то время как
min Ф(и) = 0. Выбор шага оказывается существенным в этом методе,
поэтому чаще используются методы с переменным шагом.
4.2.3. Метод наискорейшего спуска
В методе градиентного спуска выберем шаг г так, чтобы функция
Ф(и) максимально уменьшала свое значение:
$(ufc+i) = ттФ(и* — г
В предыдущем примере выбор шага в точке щ сводится к задаче о
поиске минимума функции
откуда г = 10/9, поскольку
4(«i) = i(ttJ-r^J + («g-2n«8J = i
96
Лекция 4 Численные методы решения экстремальных задач
На следующих шагах т будет зависеть от и\, к > О, г = 1,2.
Общий случай этого метода, а также метод сопряженных
градиентов рассмотрены в лекции, посвященной численным методам решения
систем линейных алгебраических уравнений.
Отметим следующее важное обстоятельство. Решение
экстремальных задач в Vх зачастую сопряжено со значительными трудностями,
особенно для многоэкстремальных задач. Некоторые из этих трудностей
исчезают, если ограничиться рассмотрением только выпуклых функций на
выпуклых множествах.
Определение. Функция Ф(и), заданная на выпуклом множестве U е
Ln, называется выпуклой, если для любых точек щ v e U и любого а е
[О,1] выполнено:
Ф [аи + A - a)v] < аФ(и) + A - а)Ф(у).
Определение. Функция Ф(и) называется строго выпуклой, если для
всех а е (О,1) выполнено строгое неравенство
Ф [аи + A - a)v] < аФ(и) + A - а)Ф(ь).
Это определение имеет наглядный геометрический смысл: график
функции Ф(и) на интервале, соединяющем точки щ v лежит ниже хорды,
проходящей через точки {щ Ф(и)} и {v, Ф(^)} (рис. 4.11).
Для дважды непрерывно дифференцируемой функции Ф(и)
положительная определенность матрицы Гессе Ф?М есть достаточное условие
строгой выпуклости.
Теорема. Пусть Ф (и) *— выпуклая функция на выпуклом множестве U,
и е U. Тогда любой ее локальный минимум на U является одновременно и
глобальным.
Глобальный минимум строго выпуклой функции Ф(и) на выпуклом
множестве U достигается в единственной точке.
Доказательство.
Предположим противное, т. е. щ — точка локального, а и* —
глобального минимума Ф(и) на U, и* Ф щ и Ф(ио) > Ф(и*). Отсюда, с учетом
выпуклости Ф(и) имеем
Ф [аи * +A - а)и0] ^ аФ(и*) + A - а)Ф(и0) < Ф(и0).
При а —> +0 точка и = аи* + A - а)и° попадает в сколь угодно ма-
лую окрестность uq. Поэтому полученное неравенство Ф(и) < Ф(ио)
противоречит предположению о том, что uq — точка локального минимума
(первая часть теоремы доказана).
4—3339
97
Лекции по вычислительной математике
Рис. 4.9 •
Пусть и^\и^ — две различные точки глобального минимума. Из
строгой выпуклости Ф(и) следует, что для всех а е [0,1] выполняется
строгое неравенство Ф [аи^ + A - а)и^2)] < аФ(и^1>}) + A - а)Ф(и^) =
= Ф* = min Ф(и), что противоречит предположению о том, что и^, г№ —
точки глобального минимума. ¦
4.3. Задачи математического программирования
Под линейным программированием понимают часть
экстремальных задач, рассматривающую минимизацию линейных функций и
переменных при наличии дополнительных линейных условий трех типов:
1шпФ(и);Ф(и) =
щ ^ 0; 1 ^ г ^ п;
D.3)
t=l
n
Каждое из этих условий определяет полупространство,
ограниченное гиперплоскостью; вместе эти условия определяют выпуклый п-мер-
98
Лекция 4
Численные методы решения экстремальных задач
ный многогранник J', являющейся пересечением полупространств.
Условия типа равенств выделяют из n-мерного пространства (п — т)-мерную
плоскость. Ее пересечение с М дает выпуклый (n — m)-мерный
многогранник G. Таким образом, задача состоит в том, чтобы найти минимум
линейной функции Ф(и) в многограннике G.
G — выпуклый многогранник (возможно и неограниченный),
поэтому внутри него линейная функция Ф(и) не может достигать
минимума. Показывается, что ее минимум, если он существует, достигается в
какой-то из его вершин. Теоретически задача линейного
программирования достаточно проста: необходимо вычислить значение функций в
конечном числе точек — вершинах многогранника, сравнить их между
собой и найти среди них наименьшее. Однако трудность заключается в том,
что в экономических задачах количество переменных порядка 102 -=-104,
поэтому решение оказывается достаточно сложным.
Пример. Рассмотрим следующую простую задачу линейной
оптимизации на плоскости: найти тшФ(и) = c\U\ + C2U2 при ограничениях
0,22^2 =
О, U2 ^ 0.
Рис. 4.10
Неравенства щ ^ 0 и г*2 ^ 0 выделяют I квадрант плоскости (щ, иг),
а линейная функция Ф(и) = c\U\ + C2U2 при определенных ci, сг задает в
этом квадранте семейство прямых уравнением с\и\ + C2U2 = d (d
неизвестно) (рис. 4.10).
Лекции по вычислительной математике
Рис. 4.11
Вообще говоря, ограничения в форме равенств могут быть
следующего типа: отсутствует, одно ограничение, два ограничения (последний
случай соответствуют рассматриваемому). Пусть СЛАУ в данном
примере имеет единственное решение и* = (ui, uj).
Если выполнены неравенства щ ^ 0, ич ^ 0, то и* и есть решение
задачи линейной оптимизации, a min Ф(и) = с\и\ + C2u? (рис. 4.11).)
Если же, например, и\ < 0 и и\ < 0 то задача линейного
программирования неразрешима, так как по условию решения находится внутри
первого квадранта. В данном случае ограничения определяют
единственное решение рассматриваемой задачи, а целевая функция принимает
«навязанное» значение Ф(г**). Процесс решения оказался весьма простым.
Если бы имелось больше условий типа неравенств и меньше равенств,
рассмотрение оказалось бы более сложным.
Пример. Графическое решение задачи
пипФ(и) = —Зг*1 —
ui + 2u2 ^ 7,
+ и2 ^ 8,
100
Лекция 4 Численные методы решения экстремальных задач
приводит к решению и* = C,2) и Ф(и*) = -15. Для решения задачи
рассматриваются линии уровня функции Ф(и), т. е. семейство параллельных
прямых — 3i*i — Зг*2 = d = const.
Нормальный к этим прямым вектор -Ф'и(и) указывает направление
убывания целевой функции. Решением задачи и* является одна из
вершин многогранника, образованного прямыми системы неравенств.
4.4. Задачи
1. Свести задачу о нахождении решения системы нелинейных
уравнений
\ v - 5 • 10e-(u+t;) = О,
к вариационной задаче в области п = {\и - О,1| ^ 0,1; \v - 0,1| ^
0,1}.
Решение. Решение системы сводится к нахождению условий
минимума функционала
Ф(щv) = (u-5- HrVvJ + (и- 5 • KTV^)J.
2. Свести задачу о нахождении минимума функции
Ф(и, v) = и4 + v4 - и2 - v2 в области п > {\и\ ^ 1; \v\ ^ 1}.
к решению системы алгебраических уравнений.
Решение. Задача о нахождении минимума функции Ф(щ v) сводится
к решению системы уравнений |^ = 0, Ц = 0.
3. Найти значения {ж, у}, при которых достигается минимум функции
Решение. Вычислим частные производные |?, |? и приравняем их
к нулю. Получим систему двух нелинейных уравнений Зх2 - Ъу =
= 0, -Зх + Зу2 = 0. Решениями этой системы являются пары
{0,0}, {1,1}. Подстановкой убеждаемся, что вторая точка является
точкой глобального минимума.
4. Методом деления отрезка пополам найти точку локального
минимума для функции /(х) = х3 + е~х - х на отрезке [0,1] с точностью
€ = 10~2.
Решение. Обозначим границы отрезка ао = 0,6о = 1 и зададим ф =
= 6 = Ю-3.
101
Лекции по вычислительной математике
Вычислим / feg+ьр-М « о, 2324 и / (*а±Ь±±\ « о, 2307. Так как
второе значение меньше первого, то положим {аь bi} = {0.4990,1}.
Продолжая далее, получим {02,62} = {0,4990; 0,7505}, {аз,Ьз} =
= {0,6238;0,7505}, {аА,ЪА} = {0,6861; 0,7505}, {а5,Ь5} =
= {0,6861; 0,7191}, {о6,Ьб} = {0,7016; 0,7191}, {а7,Ь7} =
= {0,7101; 0,7198}.
5. С помощью метода Ньютона найти минимум функции F(t) = sin t-
— cost, to = —0,5.
Решение. Найдем точку минимума функции F(t) как корень
уравнения F'(t) = 0. Для этого построим итерационный процесс
Ньютона:
При t0 = -0,5 имеем F'(t0) = cost + sint » 0,3982, F"(t0) = -
-sin to + cos to « 1,3570, t\ = to - §2ffff « -0,7934. Дальнейшие
вычисления дают t2 = -0,7854, t3 = -0,7854.
4.5. Задачи для самостоятельного решения
1. Найти точку локального минимума функций:
/(ж, у) = Зх2 - 2ху/у + у - 8х + 8,
/(ж, у) = ж3 + 8у3 - бжу + 1,
/(ж, у) = 2ж3 - жу2 4- 5ж2 -I- у2.
2. Найти точку локального минимума функций:
/(t)=3t4-8t3+6t2,
102
Лекция 4 Численные методы решения экстремальных задач
/2 о
используя методы дихотомии и сведения вариационной задачи к
решению алгебраического уравнения.
3. Найти точки локального минимума функций
/(ж,у) = (х2 + у2 - IJ + (у - xsinxJ,
/(х, у) = х3 + 8у3 - бху + 1,
/(х,у) = (х - ЗJ + (у - 2J + (х - у - 4J,
/(х, у) = 2х3 - ху2 + 5х2 + у2
методом покоординатного спуска.
Литература
[1] Федоренко Р.П. Введение в вычислительную физику. — М.: Изд-во
МФТИ, 1994.526 с.
[2] Калыткин Н.Н. Численные методы. — М.: Наука, 1978.512 с.
[3] Амосов А.А., Дубинский Ю.А., Копненова Н.В. Вычислительные
методы для инженеров. М: Высшая школа, 1994.544 с.
[4] Бирюков СИ. Оптимизация. Введение в теорию. Численные методы.
М.:МЗ-пресс,2003.244с.
ЮЗ
Лекции по вычислительной математике
Лекция 5. Численное решение нелинейных
алгебраических уравнений и систем
Рассматриваются численные методы решения нелинейных уравнений
и систем. На основе принципа сжимающих отображений
рассматриваются условия сходимости итерационных методов. Доказывается квадратичная
сходимость метода Ньютона. Рассматривается задача о динамике
простейшего нелинейного дискретного отображения — логистического. Дается
понятие о бифуркациях дискретного отображения.
Ключевые слова: итерации, метод простой итерации. Терема о
неподвижной точке. Метод Ньютона, метод хорд, дискретные
отображения, бифуркации.
5.1. Сжимающие отображения. Итерации. Метод
простых итераций(МПИ)
Рассмотрим системы нелинейных алгебраических уравнений,
записанные в векторном виде.
Система нелинейных алгебраических уравнений
f(u) = 0 E.1)
может быть также представлена в равносильном виде
u = F(u), E.2)
где u e Ln Ln — n-мерное евклидово пространство. Как правило, для
нелинейной системы переход от формы записи E.1) к равносильному
виду E.2) осуществляется не единственным образом.
Поставим в соответствие системе E.2) итерационный процесс,
определяющий последовательность итераций (последовательных
приближений к решению). Соответствующий итерационный процесс
записывается в форме
= F(ufc), uo = а, к = О,1,.... E.3)
Для дальнейшего изложения потребуется понятие отображения.
Отображением называется закон, по которому каждому элементу х
некоторого множества X однозначно сопоставляется определенный элемент
104
Лекция 5 Численное решение нелинейных алгебраических уравнений и систем
у множества У (X может совпадать с У). Это соотношение между
элементами х е X и у € У записывается как у = /(ж) или / : х —> у. Говорят, что
отображение / действует из X в Y(f : X -> У). Отображение f : X ^ X
называют преобразованием множества X, это отображение /
преобразует множество X в себя. В функциональном анализе и линейной алгебре
вместо термина «отображение» часто употребляется термин «оператор», в
случае, если X и У — числовые множества, употребляется термин
«функция».
Определение. Область П е LN называется выпуклой, если наряду с
любыми двумя точками а е п и Ь е п она включает все точки отрезка
[а, Ь], т. е. точки с координатами и = а + t(b — а), где 0 < t ^ 1.
Определение. Отображение v = F(u) называется сжимающим в
замкнутой выпуклой области П, если существует такое число 0 < q < 1,
что
p[F(ui),F(u2)] ^ qp(uuu2)
при любых ui,U2, принадлежащих области П, здесь p(ui,U2) —
расстояние между элементами. В линейном нормированном пространстве
Приведем без доказательства одну из основных теорем
функционального анализа.
Теорема (принцип сжимающих отображений). Всякое сжимающее отоб
ражение имеет в п одну и только одну неподвижную точку и* € п.
Более подробно о сжимающих отображениях и другие теоремы о
неподвижных точках можно найти, например, в [1,2, 3J.
Теорема (о сжимающем отображении [1,5]).
Последовательность {щ}, к = 0,1,... элементов n-мерного
евклидова пространства, порожденная итерационным процессом
Ufc+i =F(UA:),Uo =а,
сходится к решению U системы нелинейных алгебраических уравнений и =
= Р(и), если отображение
v = F(u)
является сжимающим; при этом выполнено
p(uo,ui).
105
Лекции по вычислительной математике
Доказательство.
По определению сжимающего отображения
= p[P(ufc),F(iUk-i)] ^
^ ... ^ qkp(uo, Ui) = qkp0.
В таком случае получим цепочку неравенств при р > к:
p(up,ufc) ^ p(up,up_i) + ...
^ qp Po + ... -f q Po ^ q Po 2^ Я* = Po* __ •
t=0 ^
В соответствии с критерием Коши существования предела
последовательности, последовательность и* стремится к пределу U, поскольку
правая часть неравенства стремиться к нулю при к —> оо.
Напомним критерий Коши сходимости числовой
последовательности: последовательность {ик}, к = 0, 1, ... является сходящейся, если
для любого положительного числа е существует номер N такой, что при
всех к > N и любых натуральных р расстояние между членами
последовательности ик и Ufc+i меньше е, т. е. \ик - ик+р\ < е .
Напомним критерий Коши для последовательности элементов
метрического пространства: последовательность {и*}, к = 0, 1, ...
является сходящейся, если для любого е > 0 существует номер N такой, что при
всех к > N и любом натуральном р расстояние р(ик, щ+р) < е.
Продолжим доказательство. Переходя в последнем неравенстве к
пределу при р —> сю , получим
p(U,ufcKp0-^.
Покажем, что U есть корень уравнения E.2)
p[U,F(U)] <p(U,ufc+1)+p[u*+1>F(U)] = p(U,ufc+1)+p[F(ufe),F(U)]
fc+i fc+i fc fc+i
^ Poz + gp(ufc,U) ^ po- + qpo- = 2p0-
1q 1q 1q
z+ gp(ufc,U) ^ po+ qpo2p0
1-q 1-q 1-q l-q
Поскольку к выбрано произвольно, а левая часть от fc не зависит, то
р [U, Р(Ц)] = 0, или U = F(U).
В случае скалярного уравнения имеем в = u* + t(uk+i - щ),
|«k+i - ufc| = |F(iifc) - F(uk-i)\ <
< max\F'@)\ \uk - ufc_i| ^ . . < (max\F'F)\)k |«i - uo|,
A A
106
Лекция 5 Численное решение нелинейных алгебраических уравнений и систем
откуда следует условие сходимости итерационного процесса max | F (и) | <
q < 1. Отрезок Д включает в себя всю последовательность Uk, Uk ? Д, к =
= 0,1,2,...
В случае решения системы нелинейных уравнений достаточным
условием сходимости итерационного процесса будет ||F'(u)|| < 1, где
F' (и) — матрица Якоби. ¦
Теорема (без доказательства). Пусть область G e Ln выпуклая, и е G
а компоненты i*i(u) вектор-функции F(u) = (Fi,..., Fn)t имеют
равномерно непрерывные производные первого порядка. Положим, что норма
матрицы Якоби
/ 0Fi dFx \
dFndFn
dui"' дип/
не превосходит некоторого числа 0 ^ q < 1, m.e.||Y|| ^ q < 1 для всех
ueG.
В этом случае отображение v = F(u) является сжимающим в
области G, т.е. p(F(ui),F(u2)) ^ gp(ubu2), или ||F(ui) - F(u2)|| <
g||ui — u2|j.
Геометрическая интерпретация метода простой итерации для
скалярного случая Uk+i = F(uk) приведена на рис. 5.1. Алгоритм метода
простых итераций таков.
1. Локализуем корень, приближенно определяем, на каком отрезке он
находится. Вопрос локализации корня не решается
алгоритмически, это, скорее, вопрос искусства вычислителя, хотя во многих
случаях локализовать корень достаточно легко.
2. Выбираем точку щ на оси 0и.
3. Вычисляем F(uo).
4. Определяем точку щ по значению F(uo):
4.1. Пересечение горизонтальной прямой АА' с прямой v = и есть
точка С {ОА = vi, АС = и{)
4.2. Очевидно, что горизонтальная координата точки С и есть wi
4.3. Опустим перпендикуляр из С на и. Поскольку О А = щ9 то
in — значение на первой итерации.
107
Лекции по вычислительной математике
Рис. 5.1. Геометрическая интерпретация метода простых итераций
5. Аналогично строим точки и2, щ,. Получившаяся диаграмма носит
название лесенка Ламерея.
Метод релаксации. Без ограничения общности рассмотрим
скалярный случай. Положим F(u) = u + rf(u) и построим итерационный
процесс Ufc+i = uk + r/(wfc), uq = a.
Тогда F'(u) = 1 + rf'(u) и г выбирается из условия I-F^u)! < 1,
причем, чем меньше значение \F'(u)\, тем быстрее будет сходиться
итерационный процесс. В частности, если положить F'(u) = 0, то, г =
= - [f'(u)]~l, а формулы итерационного процесса будут
1
5.2. Метод Ньютона
Как и выше, необходимо найти решение уравнения f(u) = 0. Пусть
ик есть к приближение решения (к итерация). Следующее приближение
ищем в виде ик+\ = ик + Аик, разложив функцию f(u) в ряд Тейлора с
точностью до членов первого порядка: /(зд+Ди*) = /(«*)+/?(«*)• Ди*+
+ О(А2ик).
Пренебрегая членами O(A2Uk), получим линеаризованное
уравнение для определения
=ик-
= a.
108
Лекция 5
Численное решение нелинейных алгебраических уравнений и систем
Это уже знакомая формула, полученная в результате оптимизации
релаксационного варианта метода простой итерации.
Для системы уравнений матрица Якоби Ги(и*) будет
а метод Ньютона выглядит следующим образом:
= ft + (f?
где fi =
/i(ui,..., ип). Приходим к СЛАУ вида А(Ди) = -f, где Ди
Tf = (/i,/2,...,/n)T, Аи € Ln,f € Ln, Ащ
Рис. 5.2. Геометрическая интерпретация метода Ньютона в одномерном случае
Геометрический смысл метода Ньютона в одномерном случае
проиллюстрирован на рис. 5.2. Заменим f(u) в точках ик — каждом
приближении к корню — касательными. За следующее приближение по методу
Ньютона примем значение и точки пересечения касательной с осью
абсцисс. Метод Ньютона называют также методом линеаризации или
методом касательных.
109
Лекции по вычислительной математике
Теорема о квадратичной сходимости метода Ньютона [2,4].
Сформулируем и докажем теорему для одномерного (скалярного)
случая. Аналогичная теорема будет справедлива и для систем
нелинейных уравнений.
Теорема. Пусть существуют первые две ограниченные производные
f(u) и, кроме того, существует [/и(и)]~г; причем имеют место оценки
l/uul ^ С^М/'М]1 ^ Ci (отображение f (и) равномерно невырождено),
а начальное приближение выбирается из условия
q < 1.
Тогда метод Ньютона сходится с квадратичной скоростью сходимости.
Доказательство.
Разложим /(uk+i) в ряд Тейлора в окрестности f(uk),
ограничившись квадратичными членами разложения:
f(uM) = f(uk) + /i(ttfc) Auk + 0{A2uk).
Здесь введено обозначение Auk = uk+i —uk. Переходя к абсолютной
величине и учитывая, что для метода Ньютона f{uk)+f'u{uk) Auk = 0, или
Дг* = -lfL(u)]~lf(uk), ПОЛУЧИМ
2 ^ СС2 \f(u)\2
= O(A2uk) ^ C2 - A2uk = C2 \\fi(u)]-lf(uk)\2 ^ С2С2 \f(uk)\2 ,
так как
Введем в рассмотрение невязку как rk = \f(uk)\, получим rk+i ^
Crg, где С = С2С?.
Можно выписать цепочку соотношений r\ ^ Cr\,r2 ^ Cr\ ^
С3г$,гз < Ст\ ^ С7т%, и т.д., в результате для невязки на к итерации
получается выражение гк < С~1(Сг0Jк .
Неравенства гк+\ ^ Ст\ игк ^ С~1(СгоJ являются определением
квадратичной скорости сходимости.
Для сходимости итерационного процесса Ньютона достаточно,
чтобы было выполнено условие, следующее из последнего неравенства: Сго =
= С |/(г*о)| ^ q < 1. Отсюда следуют ограничения на начальное
приближение, в частности, |/(ио)| ^ 1/С- Теорема доказана. ¦
Замечание. Несложно показать, что погрешность, определяемая,
как ек = р(ик — U), или, в скалярном случае, ек = \ик — ?/|, убывает
110
Лекция 5 Численное решение нелинейных алгебраических уравнений и систем
квадратично. Для этого разложим f(uk+i) в окрестности Uk в ряд Тейлора
до первого члена (или линеаризуем /(ufc+i))
f"
f(u>k+i) « f{uk) + f{uk)(uk+i - ик) + y 2
Так как в методе Ньютона приближения находятся достаточно
близко к корню уравнения и Uk+i « U, получим
о = №) =
Разделив полученное равенство на f'u{uk), приходим к оценке U -
" \ик - $Й] = 2@?) (и - м^J' откУДа СЛ(*Ует U - (ик -
\U - Uk\2, Uk € А, к — 0,1, Левая часть последнего
неравенства по формуле Ньютона равна ek+i = \U — Uk+i\ • В таком слу-
m*x\f"($)\
чае ?fc+i < Се\, где С = 2\f'{uk)\ » 0ТКУДа последовательно находим
Итерационные процессы, имеющие третий и четвертый порядок
сходимости, представляются формулами
ик+г-ик п
Отметим, что итерационные методы высших порядков
используются достаточно редко вследствие повышенных требований к гладкости
функций и необходимости вычисления ее производных и обратных к ним
величин.
Иногда для численного решения нелинейных алгебраических
систем уравнений, чтобы не вычислять на каждой итерации обратную
матрицу, используют упрощенный метод Ньютона
ufc+i = ufc - [f ~х(ио)] ~l f (и*), uo = а.
Этот метод оказывается приемлемым, поскольку начальное
приближение в методе Ньютона обычно выбирается достаточно близким к кор-
ню уравнения.
Методом секущих (или разностным методом Ньютона)
называется итерационный метод, в котором вместо производной вычисляется
ш
Лекции по вычислительной математике
разностное выражение f'(uk) « fiph)-fipk-\) ^ откуда Ufc+1 = Uk __
5.3. О вариационных подходах к решению
нелинейных систем уравнений
Рассмотрим систему нелинейных уравнений f(u, v) = О, д(щ v) = О,
Рассмотрим функционал Ф(и, v) = /2(u, г;) Н- д2(щ v).
Так как Ф неотрицателен, то найдется точка {п, v} такая, что {п, г;} =
= arg min Ф(и, v), но min Ф(и, v), очевидно, достигается при /(и, г;) = О,
^(u, v) = 0, т. е. на решении исходной системы уравнений.
Построим итерационный процесс, соответствующий методу
градиентного спуска
где Тк — параметр, который выбирается, например, из условия
минимальности Ф(и/ь+1,т;^+1) в данном направлении (метод наискорейшего
спуска), {pk,qk} — вектор, определяющий направление минимизации.
На каждом шаге итераций решается задача минимизации Ф по одному
аргументу.
5.4. Метод Чебышёва построения итерационных
процессов высшего порядка
Предположим, что существует функция д(и), обратная к /(и). При
этом и = g[f(u)],U = 0@). Пусть, кроме того, f(u) непрерывна и
имеет необходимое число непрерывных производных на отрезке, внутри
которого лежат все члены последовательности {и*}, к = 0,1,...
Обратная функция имеет такое же количество непрерывных производных, как
и /(и). Разложим функцию g(f[v]) = g(h) в ряд Тейлора в окрестности
корня — точки w = /(и).
Тогда, учитывая, что и = g[f(u)], w = /(w), h = f{v), получим
g@) = U «u-
112
Лекция 5 Численное решение нелинейных алгебраических уравнений и систем
Можно показать, что итерационный метод
имеет порядок сходимости п + 1. Для вычисления производных
обратной функции и = д [f{u)] воспользуемся правилом дифференцирования
сложной функции:
О = «<«[/(*)] - [/Si3 + 3«<a>[/(ti)] • /gj • /gj
О = РB)[/М] ¦ [/A)Ы]2 + 9il)[f(u)] • /gj,
gj • /gj
5.5. Разностные отображения в нелинейной
динамике
Рассмотрим последовательность чисел Uk+\ € R (R — множество
вещественных чисел), каждый член которой связан с предыдущим
рекуррентным соотношением
tifc+i =/(tifc,Ufc_i,...,tii,fc), E.4)
где fc g N (N — множество натуральных чисел). Соотношения E.4)
называются разностными отображениями (уравнениями) с дискретным
аргументом.
Такие уравнения появляются при моделировании процессов, в
которых величина и рассматривается через определенные промежутки
времени. Например, еще в середине XIX века Ферхюльст для описания
динамики популяционной системы предложил измерять ежегодно
численность особей Uk, где А; — номер года. Относительная численность Uk+i
полагалась пропорциональной численности в к год, однако она начинает
убывать, когда животных становится много (и& сравнимо с 1):
tifc+i = /(и*), E.5)
где
/(и*) = Aufc(l - ufc), u0 = a. E.6)
Другой пример из экономической области — задача о банковских
сбережениях. Пусть щ — денежный вклад, растущий в соответствии с
постоянным процентом 8, по закону:
= A + 5)ик = ... = A + 8)кщ>.
113
Лекции по вычислительной математике
Пусть далее законодательный орган, желая воспрепятствовать
такому обогащению вкладчика, издает закон о том, чтобы процент убывал
пропорционально и*, т. е.
Тогда счет в банке изменился бы по закону
= [l + So (l - —)] ttfc, E.7)
т. е. в соответствии с моделью E.6).
Так как ик е [0,1], то А е [0,4]. Отображение E.6) называется
логистическим. К нему можно также придти, применив простейший из
численных методов решения обыкновенных дифференциальных
уравнений — явный метод Эйлера (лекция 8) для решения дифференциального
уравнения динамики популяции (уравнения Ферхюльста)
й = \иA-и),и@) = а E.8)
где и — численность популяции. Вводя шаг по времени, получим
разностный аналог уравнения E.8):
= Aufc(l - ик), и0 = a, E.9)
т
откуда получаем
uk+i=auk-pul E.10)
a = At + 1, /? = At.
И отображение E.7), и отображение E.10) легко приводится к виду
E.6). Достаточно произвести очевидную замену переменных. Для E.10)
эта замена будет /х = a, Zk = jjftifc. Как двумерное обобщение
логистического отображения можно рассматривать отображение Хенона
uk+i = 1 - аи\ + ук, y*+i = /ft**, Щ < 1, E.11)
или
uk+i = 1 - olu\ +Cuk-i. E.12)
К довольно известным двумерным дискретным моделям относится
также отображение Чирикова, предложенное для моделирования
поведения незатухающего ротатора, возбуждаемого внешними толчками:
= ик - asin2/fc,2/fc+i = ук + uk+i. E.13)
114
Лекция 5 Численное решение нелинейных алгебраических уравнений и систем
Рассмотрим подробнее свойства отображения:
= \икA - Ufc), uo=a.
Заметим, что /@) = /A) = 0 и max f(u) = /@,5) = А/4, то при
0 < А < 4 интервал X = [0,1] отображается в себя, ие X.
Введем обозначения
/2 = /(/(и)), /3 = /(/(/(и))), /* = /(/... /(и)...).
Последовательность /, /2,..., Д,... называется траекторией
отображения и обозначается {/fc(uo)}o°.
Определение. Точка а € X (X — множество, включающее в себя
все значения отображения E.4)) называется предельной точкой
траектории {fk(uo)}kLo, если существует последовательность fci < fc2 < ... <
кп —> со такая, что/кп —> а,п = 1,2,
п—юо
Рассмотрим вначале случай 0 < А < 1. На X = [0,1] существует
только одна предельная (или неподвижная) точка х = 0. Любая
последовательность, {/*(мо)}^о сходится к предельной точке рассматриваемого
отображения х = 0. Если рассматривается популяционная модель, то это
означает, что рассматриваемая популяция не может выжить.
Из теоремы о сжимающем отображении следует, что
последовательность {uk}%L0 сходится к своей предельной точке, если |/?| ^ 1.
В этом случае точка называется притягивающей. При выполнении
условия |/4| > 1 точка называется отталкивающей.
Графическое изображение траектории (лесенка Ламерея)
представлено на рис. 5.3.
Теперь рассмотрим случай 1 < А < 3.
В случае, когда А > 1 — неподвижная точка, и = 0 становится
отталкивающей, поскольку |/'@)| > 1, а на отрезке [0,1] появляется другая
неподвижная точка и\ = 1 — А.
Производная для рассматриваемого отображения \f'{u{)\ =|2—А| <1.
Точка щ при 1 < А ^ 3 явлйется притягивающей.
Отметим, что при 1 < А ^ 2 производная fr(u\) > 0 и траектория
{fk{u0)}<j?=l стремится монотонно к и\ (рис. 5.4); при 2 < А ^ 3
производная /'(ui) < 0 и траектория приближается к и\ немонотонно,
поочередно принимая значения то меньше, то больше этого значения.
При А = 3 точка и\ остается притягивающей, но значение
производной в этой точке является предельным: |/'(^i)l = 1-
115
Лекции по вычислительной математике
0.75
0.25
0 0.25 0.5 0.75
Рис. 5.3
0.75
0.25
0 «о 0.25 0.5 0.75
Рис. 5.4
При значениях параметра логистического отображения А = 1 и Л =
= 3 неподвижная точка этого отображения теряет устойчивость и
появляется либо другая устойчивая неподвижная точка, как это произошло в
первом случае, либо притягивающий цикл; определение цикла будет дано
ниже. Качественное изменение поведения решения (траектории
отображения) при изменении параметра называется бифуркацией.
Пусть теперь 3 < А ^ 1 + \/б. Как уже отмечалось, при значении
параметра А = 3 происходит бифуркация: неподвижная точка иъ = 1 -
116
Лекция 5
Численное решение нелинейных алгебраических уравнений и систем
- А из притягивающей превращается в отталкивающую: \f'(u)\ > 1 при
X > 3. После того как точка стала отталкивающей, рассмотрим корни из,
U4 уравнения /2(и) = и, или Х2и2 - А(А + 1)и + (А + 1) = 0.
Заметим, что если щ — предельная точка отображения /(и) = и ,
то она является также и предельной точкой отображения /2(и) = и.
Действительно, /2(tii) = f(f(ux)) = f{ui) = ui , где ui — любая
предельная точка рассматриваемого отображения, отличная от корней уравнения
fi(u) = и. Тогда, зная два корня уравнения /2(и) = и точки щ, и± легко
находятся как корни квадратного уравнения, они есть
1)±у/2А-ЗА2-3
2А
Эти корни связаны соотношениями
В данном случае говорят, что отображение имеет цикл периода 2,
который будем обозначать Р2. Его наличие, например, в популяционной
модели говорит об изменении численности особей с периодом в 2
единицы времени. Траектория для случая такого цикла изображена на рис. 5.5.
Можно считать, что неподвижная (предельная) точка отображения есть
цикл периода 1.
Переход от цикла Pi (предельная точка логистического
отображения) к циклу Рг называют бифуркацией рождения цикла (удвоения
периода).
0.75
0.5
0.25
\
0 0.25 0.5 0.75 1
РИС. 5.5
117
Лекции по вычислительной математике
Определение. Точка а е X называется периодической периода т,
если /т(а) = о и /*(а) Ф а при 0 < г < га.
Отметим, что каковы бы ни были попарно различные точки мь
t*2,..., ит, если положить /(щ) = Ui+i, г = 1,2,..., га - 1 и f(um) =
= мь то рассматриваемое отображение будет иметь периодическую
траекторию периода т: щ, мг, • •., ит, ui, М2,..., мт,...
Если к тому же /(м) имеет первую производную, то в окрестности
каждой из точек щ выполнено
или
Будем рассматривать /т(м) как сложную функцию. Пользуясь
правилом дифференцирования сложной функции, получим
m
п
k=l
\U -
Если
п ГЫ
< 1, то траектория {fk{v>o)}kLo приближается к
циклу {mi, ..., Mfc}, или {ик}™=1. Такой цикл называется притягивающим
— мультипликатором цикла. Цикл может
циклом, а величина
т
п
fc=l
быть как притягивающим, так и отталкивающим.
Определение. Цикл Рт = {mi, ...,ит} отображения / : X —> X,
переводящего множество X в себя, называется притягивающим, если
существует число ко, такое, что для любого к > ко траектория {fk(uo)}^=o
распадается на m последовательностей, каждая из которых сходится к
точкам mi ,..., Urn соответственно.
Достаточным условием существования притягивающего
(отталкивающего) цикла является выполнение неравенства /л(Рт) > 1, где
ц(Рт) — п f(uk),u € Рт — мультипликатор цикла.
Отметим интересные свойства функции /2(м), в частности, ее
график пересекается с прямой у = и не только в неподвижных точках
рассматриваемого отображения, mi, мг, но и в точках цикла Рг. Таким
образом, можно сказать, что бифуркация рождения цикла обусловлена
потерей устойчивости одной предельной точки и появлением двух
устойчивых предельных точек отображения /2(м). На рис. 5.6а, в показано
поведение функции /2(м) при разных значениях параметра А (А = 2,8; А = 1 +
+ \/5).
118
Лекция 5 Численное решение нелинейных алгебраических уравнений и систем
О 0.25 0.5 0.75
О 0.25 0.5 0.75
Рис. 5.6
При увеличении Л у отображения появляются новые неподвижные
точки. Мультипликатор цикла Ръ вычисляется следующим образом:
Ки3,и4) = f(u3)f(u4) = Л2A - 2u3)(l - 2щ) = 4 + 2А + А2.
Очевидно, что |/х(глз, и±)\ < 1» если 3 < А < 1 + \/б, тогда цикл Рг —
притягивающий. Траектория {/fc(uo)}j?=o притягивается циклом {щ,ид}
и подпоследовательность {/r2*(uo)}gio сходится к одной точке цикла, а
{/2/с+1К)}2°=о-к другой.
Знак мультипликатора дает информацию о характере приближения
траектории к циклу. В частности, если 3 < А < 1 + д/5, то
подпоследовательности {/2fc(uo)}jbLo и {/2/e+1(wo)}fcLo» начиная с некоторого и,
являются монотонными, одна из них возрастающая, а другая — убывающая,
что зависит от знаков /'(из) и f'(ui).
При 1 + \/5<А<1 + \/б значение мультипликатора /х < 0, и
подпоследовательности {/2*(uo)}i?=o и {/2/с+1(мо)}?1о приближаются к точкам
{^з, и4} немонотонно.
Рассмотрим теперь случай 1 + \/б < А < 3,54...
При А = 1 + \/б происходит вторая бифуркация удвоения периода.
Цикл {из,гб4} из притягивающего превращается в отталкивающий,
1/*(**з»И4)| > 1 ПРИ А > 1 + >/б. Появляется новый притягивающий
Цикл Р4:
= f(u5),u7 = /(tie), tig = f(u7),ub = /(ug).
119
Лекции по вычислительной математике
Для популяционной динамики это означает, что численность
особей колеблется с периодом 4 единицы времени. Соответствующий
график приведен на рис. S.7.
1
0.75
0.5
0.25
0
/
s—
Д
/
\
0 0.25 0.5 0.75 1
Рис. 5.7
При Л « 3,54 цикл Р± периода 4 становится отталкивающим,
5, .,^8I > 1; при этом появляются притягивающий цикл Ре
периода 8. Дальнейшее увеличение параметра Л будет приводить к появлению
циклов Pi б, Р32 и т.д. Происходит каскад бифуркаций удвоения периода.
Заметим, что рассмотренный простой процесс имеет сложное
поведение. Наблюдается каскад бифуркаций при увеличении величины Л;
кроме того, все циклы, которые при этом встречаются, имеют период 2Р.
Эта важнейшая закономерность, которая прослеживается не только в
расчетах, но и в природе! Рассмотренные бифуркации при увеличении Л
можно наглядно представить на бифуркационной диаграмме (рис. S.8).
Диаграмма получается, если обозначить через Ль Лг те значения А, в
которых происходят бифуркации, а через Ai, A2,... при которых и = 0,5
является элементом циклов Р2, Pi,...; по вертикальной оси откладываются
значения предельных точек отображения. Обозначим за di, &i,...
величины, равные расстоянию между х = 0,5 и ближайшим к нему
элементом цикла Рг при А = А*. Численный эксперимент показал, что Л* и А*
при достаточно больших к ведут себя, как геометрическая прогрессия со
знаменателем S = 4,66920..., т. е.
lim
= 6.
fc->oo Afc+2 — -
Отношение dk/dk+i имеет предел, равный а = 2,50290
120
Лекция 5
Численное решение нелинейных алгебраических уравнений и систем
Эти закономерности были замечены американским математиком
фейгенбаумом.
Рис. 5.8
При дальнейшем увеличении А последовательность {и*}?10
приобретает хаотический характер (А = Аоо « 3,569), что видно на рис. 5.9.
0.75
0.25
2 2.5 3 3.5
Рис. 5.9
121
Лекции по вычислительной математике
Примечательно, что каскады Фейгенбаума имеют фрактальный
характер (т. е. сохраняют подобие при изменении масштабов, рис. 5.10а, в).
0.95
0.78
0.73
3.4 3.5 3.5 3.6 3.7
0.868
3.54 3.55 3.56 3.58 3.59
Рис. 5.10
Изучение графиков функций f2(u) и fl(u) показывает, что их
фрагменты вблизи максимумов близки друг к другу, более того, они
отличаются лишь масштабами. Оказывается, что такое же подобие имеет место
для функции /2*, п > 1 при А = А*, и выполняется тем точнее, чем
больше п. Если положить и' = и-1/2 (в дальнейшем штрих будем опускать) и
считать а коэффициентом растяжения вдоль осей, то для некой
симметричной функции д (и), определенной на отрезке [-1,1], можно получить
следующее функциональное уравнение:
которое универсально определяет а:
9@) = -
Вблизи максимума д(х) должна быть близка к квадратичной
параболе, причем д@) = 1. В теории универсальности показывается, что эта
функция вычисляется с помощью ряда
д (и) = 1 - 1,52763и2 + 0,104815и4 - 0,0267057и6 + ...
Пусть теперь А = 3,83. В этом случае из хаотической области,
изображенной на рис. 5.10, появляется устойчивый цикл Рз (рис. 5.11а, b
представляют циклы в последовательные моменты времени).
122
Лекция 5 Численное решение нелинейных алгебраических уравнений и систем
1
0.75
0.5
0.25
0
s—^
/
у
/ \
\
\
0 0.25 0.5 0.75 1
Рис. 5.11а
0.75
0.5
0.25
/
/•¦•••¦¦¦
/
V
\
\
0.25 0.5 0.75
Рис.5.11Ь
Циклу на рис. 5.11 соответствует самое большое окно устойчивых
циклов Р3.2*. Чередование хаотических и регулярных зон — называется
перемежаемостью. Возможно, нечто подобное наблюдается в
гидродинамических потоках, где ламинарные зоны чередуются с турбулентными.
123
Лекции по вычислительной математике
5.6. Задачи
1. Методами простых итераций и Ньютона решить уравнение
х2 -е~х = 0,х0 € [0.5, 1].
Решение. Метод простых итераций будет Xk+i = е~^,хо = 0,75,
F(x) = е-*, №(х)\ < 1 прих € [0.5, 1].
Приведем таблицу приближений до точности |xs — «4| < Ю.
к
0
0,75
1
0,6873
2
0,7091
3
0,7015
4
0,7042
5
0,7032
Метод Ньютона запишется как
Результаты расчетов:
к
Хк
0
1
1
0,7330
2
0,7038
3
0,7035
2. Построить итерационные методы для вычисления корней
уравнения
х3 + Зх2 - 1 = 0.
Использовать метод простых итераций.
Решение. Все три корня данного уравнения лежат на отрезках
[-3,-2], [-1,0], [0,1].
Построим итерационный процесс для вычисления первого корня,
лежащего на отрезке [-3, -2]:
хк+1 = х^2 - 3,F(x) = X - 3,
= |-2х~3| < i < 1,
т. е. для начального приближения хо ? [-3, -2] метод простых
итераций сходится.
Для вычисления двух оставшихся корней, лежащих на отрезках
[-1,0] и [0,1], построим итерационный метод
= ±(хк + 3)~2 , F(X) = ±(хк + 3)~2 .
124
Лекция 5 Численное решение нелинейных алгебраических уравнений и систем
Поскольку для рассматриваемых отрезков \F'X (x) | =
то этот итерационный процесс сходится к корням
рассматриваемого уравнения.
3. Исследовать сходимость итерационного метода релаксации для
численного решения уравнения вида /(х) = 0:
=хк-т /(х*)> x0 = a, f'(x) > 0.
Решение. Итерационный метод релаксации записывается как
xk+i = F(xk),x0 = 0,
F(x) = x-r/(x).
Из условия того, что отображение является сжимающим,
получим \F(x) - F(y)\ = \х - у - т(/(х) - /(у))| ^ q \х - у\, где q =
= max |1 - rf (x + а(х - у))\, 0 < а < 1.
Положим 0 < /^in ^ /; ^ /Ьж тогда q(r) = maxfll - r/^in|,
Отсюда видно, что итерационный процесс будет сходиться, если
|1 - т?твх\ < 1, или г < 2//^, а оптимальное значение параметра,
при котором q = gmin достигается при |1 - rf'm{Ti\ = |1 - r/^
Г = То = 1
4. Построить метод простых итераций и итерационный процесс
Ньютона для системы уравнений
д(х,у) = 2х2 - ху - 5х + 1 = 0.
Решение. Графики функций /(х, у) и д(х, у) приведены на рис. 5.12.
Метод простых итераций запишем как
Хк+i =yfc-31gxfc,
= 2xfc H 5,
Хк
125
Лекции по вычислительной математике
Рис. 5.12
Матрица Якоби для такого процесса запишется как
J =
Ш
Несложно проверить, вычислив норму матрицы Якоби, что для
приведенного начального приближения достаточное условие
сходимости не выполняется.
Рассмотрим другой итерационный процесс:
Хк+1 =
J
F(x,y) =
Матрица Якоби для этого итерационного метода будет
5+1/ х
-1 2%/2л/ж(у-|-5)-1
2>/x+31gx U
126
Лекция 5
Численное решение нелинейных алгебраических уравнений и систем
В окрестности начального приближения условие сходимости
выполнено. Таблица первых пяти приближений будет
к
X
У
0
3,4
2,2
1
3,426
2,243
2
3,451
2,2505
3
3,466
2,255
4
3,475
2,258
5
3,480
2,259
5. Построить итерационный метод Ньютона для вычисления $/а,а>0,
neR.
Решение. Найдем корень уравнения
/(*) = хп - а = 0.
Метод Ньютона для этого уравнения запишется
~Хк f'(xk)-Xk
п
а 1
В частности, при п = 2 имеем
6. Получить расчетные формулы метода Ньютона для численного
решения системы двух нелинейных уравнений /(х, у) = 0, д(х, у) = 0.
Решение. Положим x*+i = Axk, y*+i = Ук + Ду*, 1(хк,Ук) = fk,
получим
откуда
IJ*
9x
-1
127
Лекции по вычислительной математике
-A («)»
"Я*
-Л(Й).+9*'4
(«).(*).-(*).(«)."
'i. * Jn
-1
-л
-5fc
-5fc
*\ +/fcM.
fc Wife
4(«);
где Л* =
цы
a/:) (f
гд у /J(k \ — матрицаЯкоби, X^, Y^ — матри-
Xfc =
= (-л (в).
,Yfc =
-Л
-Sfc
Тогда запишем расчетные формулы для итерационного метода
Ньютона:
= ук 4- Аук.
7. Найти приближенное решение системы двух нелинейных
алгебраических уравнений ж3 - у3 -1 = 0, ху3 - у - 4 = 0, используя метод
Ньютона.
= уо = 1,5.
Пусть /(х, у) = х3 - у3 - 1,д(х, у) = ху3 -у- 4.
Начальное приближение можно найти графически: xq
128
Лекция 5 Численное решение нелинейных алгебраических уравнений и систем
Матрицы Jfe, Xfc, Yfc в этом случае будут
-2ук
-yk-4 3xky*k
-2ук \
Следующее приближение вычисляется по формуле Ньютона:
Xk+i = Хк + ТГТ, 2/fc+i = Ук + ТТТ*
IJfcl
Результаты вычислений первых двух итераций приведены в таблице
(точность ? « 10~3).
к
0
1
2
хк\Ук
1,5;
1,5
1,502397
1,547059
1,5020396
1,545570
fk',9k
0,12500
-4,33750
-0,002170
0,015844
0,0000017
0,000019
IJfcl
71,71875
77,73277
IX*
-0,171875
0,0277988
|Yfc|
-3,3750
0,1153255
8. . Найти приближенное решение системы трех нелинейных
уравнений х2 + у2 + z2 = 1,2х2 + у2 - 4г = 0, Зх2 - 4у + z2 = 0, используя
метод Ньютона. За начальное приближение решения выбрать точку
хо = уо = *о = 0,5.
Решение. Обозначим F = (х2+2/2+22-1,2х2+у2-4г,Зх2-4у+г2)т,
Bх 2у 2z
Ах 2у -4
6х -4 2^
Соответственно, для точки начального приближения вычислим
@,25 + 0,25 + 0,25-1
0,5 + 0,25-2,00
0,75-2,00 + 0,25
Jo =
,detJ0 = -40^0,
5—3339
129
Лекции по вычислительной математике
Вычислим первое приближение
/0,5
х = хп — J-1Fn = I 0 5 I —
\0,5
-0,25
-1,25
.-1.00
Для второго приближения
@,8752 + 0,5002 + 0,3752-1
2-0.8752 + 0,5002-4-0,375
30,8752-40,500 + 0,3752
B 0,875 2 0,500 2 0,375
4 0,875 2 0,500 -4
6-0,875 -4 2-0,375
detJi = -64,75,
-15,25 -3,75 -4,75
-23,625 -2,625 9,625
0,15625\
0,28125 ,
0,43750/
1,750 1 0,750'
3,500 1 -4
5,250 -4 0,75
64,75
-19,25 12,25 -1,75
По формуле Ньютона получим
х2 = xi -
. /-15,26 -3,75 -4,75\ /0,15625\ /0,78981\
+—— -23,625 -2,625 9,625 I • 0,28125 = 0,49662 .
Ь4'75\ -19,25 12,25-1,75,/ Ц43750/ \0,36993;
Аналогично находим третье приближение, которым и ограничимся:
@,78521\
0,49662 .
0,36992/
130
прюхия 5 Численное решение нелинейных алгебраических уравнений и систем
5.7. Задачи для самостоятельного решения
1. Исследовать возможность применения трех итерационных
процессов
= -e"Xfc,
для численного решения уравнения х + lnx = 0, имеющего корень
х«0,6.
2. Исследовать сходимость процесса простой итерации в зависимости
от начального приближения для численного решения уравнения
х - 2х = О,
имеющего корни х\ = 1, хг = 2.
3. Предложить процессы простых итераций для решения уравнений
cosx
о
* = о,
х = 1п(х + 2) (уравнение имеет два корня),
е"х = cos х (для поиска ближайшего к нулю корня).
4. Предложить итерационный процесс Ньютона для вычисления
решений систем уравнений
= 1024,
\ 2x + cosy = 2.
5. Предложить методы простых итераций и Ньютона для численного
решения нелинейных уравнений:
X
x2-20sinx = 0,
х2*-1 = 0,
\/х + 1 - - = 0,
х
arctg(x - 1) + 2х = 0.
131
Лекции по вычислительной математике
6. С помощью методов дихотомии и Ньютона найти точку локального
минимума функции f(t) = е~г +13 - t, с точностью е = 10~6.
Литература
[1] Колмогоров АН., Фомин СВ. Элементы теории функций и
функционального анализа. М.: Наука, 1981.
[2] Бабенко К.И. Основы численного анализа. М.: Наука, 1986.744 с.
[3] Коллатц Л. Функциональный анализ и вычислительная математика.
М.: Мир, 1969.448 с.
[4] Федоренко Р.И Введение в вычислительную физику. М.: Изд-во
МФТИ, 1994.526 с.
[5] Н. В. Бахвалов, Н. П. Жидков, Г. М. Кобельков. Численные методы -
М: Лаборатория Базовых Знаний, 2002. - 632 с.
[6] Лобанов А.И., Петров И.Б. Вычислительные методы для анализа
моделей сложных динамических систем. Ч. 1. М.: МФТИ, 2004.168 с.
[7] Вержбицкш B.U. Численные методы. М.: Высшая школа, 2005.
866 с.
[8] Шарковский АН., Майстренко Ю.А., Романенко Е.Ю. Разностные
уравнения и их приложения. Киев: Наукова думка, 1986.279 с.
[9] Ахромеева Т.С., Курдюмов СП., Малинецкий Г.Г., Самарский А.А.
Нестационарные структуры и диффузионный хаос. М.: Наука, 1992.
541с.
132
лекция 6 Интерполяция функций
Лекция 6. Интерполяция функций
Рассматривается задача алгебраической интерполяции.
Обусловленность задачи исследуется на основе рассмотрения константы Лебега.
Доказывается теорема об остаточном члене интерполяции. Выводятся формулы
алгебраической интерполяции с кратными узлами. Рассматривается задача
гладкого восполнения функции (локальными и нелокальными сплайнами),
а также естественный базис в пространстве сплайн-функций — В-сплайны.
Ключевые слова: интерполяция, обобщенный полином, метод
неопределенных коэффициентов, интерполяционный полином
в формах Лагранжа и Ньютона, постоянная Лебега, кусочно-
линейная интерполяция, сплайны, В-сплайны.
6.1. Постановка задачи интерполяции
Пусть задана совокупность узлов интерполяции или сетка на
некотором отрезке [а, Ь]. В простейшем случае сетка — равномерная, т. е.
расстояние между соседними узлами одинаково. В дальнейшем также
рассмотрим неравномерные сетки.
1. Совокупность узлов {tn}n=o> гп = а + пт,т = (b- a)/N, t € [a, b].
2. Сеточная проекция функции f(t) на [a,6], т.е. таблица /п =
= if(tn)}n=o 5 эту таблицу задает оператор ограничения на сетку
или рестрикции (от английского restriction) R.
Задача состоит в том, чтобы по таблице /п восстановить
непрерывную функцию. Обозначим ее через F(t). Разумеется, она
отличается от исходной функции /(?), причем такое восстановление
неоднозначно и осуществляется оператором интерполяции I. Сама
функция F(t) называется интерполирующей или интерполянтом. Необходимо
оценить потерю информации при действии этого оператора, т. е.
величину \f(t) - F(t)\, зависящую от типа оператора интерполяции и свойств
/(), в частности, ее гладкости. Таким образом, имеем схему:
133
Лекции по вычислительной математике
6.2. Кусочно-линейная интерполяция
Простейший способ интерполяции — кусочно-линейная,
требующая минимальных требований на гладкость функции /(?). При таком
способе интерполяции соседние точки (tnifn) и (?n+i,/n+i) соединяют
отрезками прямых
Теорема. Пусть f(t) — Липшиц непрерывная функция, т.е. \f(ti) -
с |ti —12\, /иогда |/(t) - F(*)| < c
Примечание. Если сетка неравномерная и г = max(?n+i - tn), то
теорема верна и для этого случая.
Доказательство.
Пусть ? € [?n,?n+iL обозначим г = tn+i - tn. Тогда t = tn + ос • г;
О < а < 1. В силу линейности F(?) имеем равенство F(t) = a/n+i + A -
-a)/».
Оценим разность
- Л*I = l«
Поскольку /n+i = /(^п ч- г), имеем
+ г) - /(tn + ат)| ^ |сA - а)г| =
= сA - а)г, т. к. О < а < 1.
Аналогично |/п - /(^)| ^ саг. В таком случае \f(t) - F(t)| < 2a(l -
- а)ст ^ ст/2. ¦
Замечание. Простой аппарат кусочно-линейной интерполяции
позволяет ввести объекты, на которых базируется один из наиболее
известных современных численных методов — метод конечных элементов.
Сетке tn ставится в соответствие набор базисных функций (pn(t), каждая из
которых сопоставляется своему узлу tn, причем (pn(tk) = ??, <Pn(tn-i) =
= <Pn(?n+i) = 0, <pn(tn) = 1, а в остальных точках она вычисляется с
помощью кусочно-линейной интерполяции.
Функция F(t) в этом случае представляется в виде
N
п=0
134
Лекция 6
Интерполяция функций
В вычислительной математике часто используется кусочно -
полиномиальная интерполяция. Так, эрмитовым кубическим интерполянтом
называется кусочно-кубический интерполянт с непрерывной
производной, кубическим сплайном называется кусочно-кубический интерполянт
с двумя непрерывными производными. О сплайнах речь пойдет ниже.
6.3. Интерполяция обобщенными полиномами
N
Для того чтобы функция (обобщенный полином) F(t) = ? un<Pn(t)
n=0
была интерполирующей, необходимо выполнение условий: F(tk) = Д,
к = 0 -г N, где Д — значения функции в точках интерполяции. Для
коэффициентов обобщенного полинома получаем систему уравнений:
или в векторной форме
Au = f,
где
А =
... <PN(tN)
, U = ( U0
f=( /о Л ... Лг )Т.
Теорема (доказывается в курсе линейной алгебры). Для того чтобы
решение задачи интерполяции существовало и было единственным, необходимо
и достаточно, чтобы система базисных функций ipn(tk) была линейно
независима.
Теорема (доказывается в курсе линейной алгебры). Для того чтобы
система функций y>n(tk) была линейной независимой в точках to,..., ?п,
необходимо и достаточно, чтобы определитель матрицы Грамма
С = А*А =
135
Лекции по вычислительной математике
был отличен от нуля. Здесь каждый элемент матрицы Грамма имеет вид
N
i=0
В случае, если система функций {<Pj}q ортогональна на множестве
точек {tj,}?, решение задачи интерполяции значительно упрощается
(напомним, что система функций {щ }" является ортогональной на
множестве точек {tj}", если (<р*, щ) = 0 при k^jn (<pk, щ) ф 0 при k = j для
всех* = 0, l,...,N;j = 0,l,...,n).
Дело в том, что матрица Грамма для ортогональной системы
функций диагональна, и ее определитель отличен от нуля (всякая
ортогональная система функций заведомо линейно независима). Линейная система
уравнений представляется как А* Аи = A*f, или Си = Ь, где С = А* А,
b = А * f — вектор, а ее решение в случае А * А = Е есть и = А * f.
Примером ортогональной системы являются показательные
функции e2nikt* на множестве точек tj = j/N, j = 0,1,..., N (на отрезке [0,1]).
6.4. Полиномиальная (алгебраическая)
интерполяция
В этом случае (uk(t) = tk) СЛАУ для определения коэффициентов
имеет вид
Щ + Uit0 + . . . + UNt" = /о,
+ . . . + UNti = /l,
UQ
" = fN,
а ее определитель
det
/ 1
\ !
tN
t% ...
отличен от нуля, если узлы интерполяции попарно различны. Это
известный из курса линейной алгебры определитель Вандермонда.
Ответ на вопрос о существовании и единственности решения СЛАУ
оказывается — утвердительным - решение задачи алгебраической
интерполяции всегда существует и единственно, но при больших N система
136
Интерполяция функций
оказывается плохо обусловленной. Однако решение этой задачи можно
выписать в явном виде
N
Ls(t) = ^2 fn •</>%&),
n=0
где <p%(t) = П j^zf- — базисные функции, являющиеся полиномами
i=0 п *
хфп
степени N, каждый из которых сопоставлен со своим узлом сетки так, что
<p%(tk) = Я?• Заметим, что правильнее было бы писать Ьц(г> {tn}, {/п}),
т. е. интерполянт зависит от t, сетки и сеточной функции. Такой вид
записи алгебраического интерполяционного полинома не единственен.
Выписанный полином называется интерполяционным полиномом в форме
Лагранжа. Он удобен для теоретического рассмотрения, но на практике
часто оказывается более удобной другая форма представления —
полином в форме Ньютона, о котором речь пойдет ниже.
6.5. Теорема об остаточном члене интерполяции
Введем понятие остаточного члена интерполяции для оценки
погрешности
F.1)
Теорема. Пусть функция f(t) имеет на отрезке [а, 6] N + 1
N
ограниченную производную. Тогда RN(t) = rN+i)\ П (* — tj) • /^+1'(?)» г&е
Доказательство.
Рассмотрим функцию
*(z) = f(x) -LN(x) -^(*)%l^tZl^'}"-t!!y
имеющую, по крайней мере, N +1 производную. По условию, эту
производную имеет /(х), а два остальных члена — полиномы.
Кроме того, ф{х) на [а, Ь] имеет, по крайней мере, N + 2 нуля.
Их можно указать. Точки х = tn{n = 0, ..., N) — нули, поскольку
f(tn) = L(tn), а последнее слагаемое обращается в них в нуль. N + 2
нулем является точка х = t в силу определения остаточного члена. Далее,
поскольку между каждыми двумя нулями непрерывно
дифференцируемой функции имеется хотя бы один нуль ее производной, на [а, 6]
имеется хотя бы N + 1 нуль ф1. Применяя это рассуждение к ф", фш\... можно
показать, что существует точка f € [а, Ь] такая, что \
137
Лекции по вычислительной математике
Вычислим N 4- 1 производную правой части выражения для F(x) с
учетом того, что L(N+1) = 0. Кроме того, в точке f
[«ЕйИВйЩ - |^.тогШ/<-.(а_й,(!) .^j..
= 0, откуда получим выражение для R.N(t): #лг(*) =
Рассмотрим некоторые важные следствия этой теоремы.
Следствие (точность интерполяции на равномерной сетке). Положим,
что tn = пт, т = (Ь — a)/N, t € [a, b], — сетка равномерная. В этом случае
имеет место оценка
Доказательство.
Пусть * = ^ + ат, а € [0,1], к = 0,1,..., N - 1.
N
Тогда t - tn = fcr + ат - nr = (к + а - п)т; откуда П (* - *п) =
п=0
N N
= rN+1 П (к + а - п). Можно показать, что П \к + а - п\ ^ N\. Оста-
п=0 п=0
точный член оценивается следующим образом: R,N(t) = ^///+Jp П (* —
- tn), поэтому с учетом приведенных оценок получим
Рассмотрим, как ведет себя оценка в задаче экстраполяции при
удалении точки t от интервала [*о,?лг]. При t e [tN,tN + г] имеем |ЛлК*)| ^
max |/(N+1)(C)I, поскольку "п* \к + а - п\ ^ (N 4-1)!. При
t *+] ' ' п=0
t e [tN 4- г,*аг + 2т] |Ллг(«)| < (ЛГ + 2)rN+1 • max |/<N+«@|. так
как П
n=0
и так далее.
138
Лекция 6
Интерполяция функций
Видно, что ошибка экстраполяции растет быстро, но не сразу:
экстраполяция допустима на интервалах ~ О(т).
6.6. Интерполяционный полином в форме Ньютона
6.6.1. Разделенные и конечные разности
Определение. Пусть задана система узлов {tn}^=0, tn € [а, 6], to =
= а, tN = Ь.
Разделенные разности нулевого порядка в точке U совпадают со
значениями функции /(ti);
Разности первого порядка определяются для двух точек U, ?»+1
равенством
/(t)
77»
H+l — Н
разности второго порядка — для трех точек U, ti+i, ti
fU . . \ f(U+liU+2) -/(*i>
/l4,ti+i,t<+2J = T 7 »
4+2 — 4
разности порядка fc — для к + 1 точки по рекуррентной формуле
'™ u+k-u
Методом математической индукции можно показать, что
к
П
r=0
a)
b) существует точка ?е [а,6]такая,чтоА:!/(^,^+ь...,^+л) =
Отсюда следует, что разделенная разность есть симметричная функция
своих аргументов ?»,..., U+k и она не изменяется при их перестановке.
Для удобства введем таблицу разделенных разностей:
to
«2
/(«о)
/(*l)
/(«2)
/(*п)
/(*0,«l)
f(tut2)
f(to,t\,t2)
f(tn-2,tn-i,tn)
/(*o,...,t»)
139
Лекции по вычислительной математике
Пусть сетка — равномерная. Тогда конечной разностью первого
порядка функции f(t) в точке tk с шагом г называют величину Д Д = Д+i -
- Д, где Д = /(?*)» второго порядка — величину
Д2Д = ДД+1 - ДД = Д+2 - 2Д+1 + Д,
третьего
Д3Д = ДД+3 - ЗД+2 + ЗД+1 - Д = Д+з - ЗД+2 + ЗД+1 - Д,
четвертого
Д4Л = Л+4 - 4Д+з + 6Д+2 - 4Д+1 + Д,
причем
ДПЛ = Д"/**! - Д-1/*,* > 1, Д°Л = Л-
Методом математической индукции доказывается формула
где С* = 8i(jx_a)\ - биномиальные коэффициенты.
Нетрудно показать, например, используя формулу Лагранжа, что
существует точка ? е [а, Ь] такая, что rn/(n) (f) = Дп Д, tk € [а, 6], поэтому в
вычислительных методах используется приближенная формула
аналогичная тем формулам численного дифференцирования, что были
получены в первой лекции методом неопределенных коэффициентов.
Заметим, что введенные конечные разности называют «разностями
вперед». Аналогично можно ввести «разности назад»:
ДД = Д - Д-1, Д2Д = ДД - ДД-1 = Л - 2Д_! + Д-2,...
и центральные разности
ДД = Л+1/2-ДД-1/21Д2Л = ДЛ+1/2-ДЛ-1/2 = Л+1-2Д+Л-1, ¦ • •,
Д»Л = Ап-г/к+1/2 - Д" А-1/2-
Иногда для обозначения первых конечных разностей вперед и назад
используют обозначения Д+Д, Д~ Д.
140
лекция 6 Интерполяция функций
6.6.2. Интерполяционный полином в форме Ньютона
Интерполяционный полином может быть записан с
использованием введенных выше разделенных разностей. Такая форма его записи
называется интерполяционным полиномом в форме Ньютона. Полином
имеет вид
Nn(t) = f(tl) + f{tlM){t - h) + ... + /(tb ... ,tn+i)(* - *l) ...(*- tn).
To, что это интерполяционный полином, может быть доказано,
например, методом математической индукции. Отметим, что полином в
форме Ньютона напоминает ряд Тейлора, а остаточный член
интерполяционного полинома — остаточный член этого ряда. Достоинством записи
интерполянта в форме Ньютона является то, что для повышения
порядка полинома нет необходимости в его полной перестройке; достаточно
лишь добавить к уже полученному выражению еще одно или
несколько слагаемых. С помощью разделенных разностей можно оценивать
погрешность интерполяции. Читатели могут предложить способ контроля
точности вычислений, основанный на использовании разделенных
разностей.
6.7. Многочлены Чебышёва и минимизация
остаточного члена интерполяции
Многочленом Чебышёва первого рода называется функция Tn(t) =
= cos (n arccos ?), где t € [— 1, 1], n = 0,1,...
Убедимся в том, что функция Tn(t) действительно является
многочленом. При п = 0 и п = 1 имеем T0(t) = 1, Ti(t) = t
Положив 0 = arccos t, получим Ti(t) = cos0,Tn(?) = cosn0,
Tn-i(t) = cos(n-lH,Tn+i(?) = cos(n+1H. По формуле суммы косинусов
cos(n+1 H+cos(n—1H = 2 cos 0 cos п0, и справедливо рекуррентное
соотношение Tn+iW+Tn-ife) = 2Г1(*)Гп(*),илиГп+1(*) = 2trn(t)-Tn_i(t).
Отсюда следует вид записи полиномов Чебышёва: Т2 = 2t2 - 1,Тз(?) =
= 4t3 - 3t,T4(t) = 8t4 - 8t2 + 1 и так далее. Функции Tn(t) являются
многочленами степени п со старшим членом 2n~ltn.
Введем также нормированные многочлены Чебышёва fn(t) = |У^.
Нули многочлена Чебышёва находятся из очевидного уравнения
Tn{t) = cos(narccost) = 0, откуда tm = cos(^z^7r),m = 1,2,...n,t G
[-1,1]. Для произвольного отрезка [а, Ь] нули полинома Чебышёва
получаются очевидным линейным преобразованием, выражения для них
будут^ = ^H-^cos(^^7r) ,m= 1,2,... п. Легко отыскиваются также
точки экстремумов полинома Чебышёва, для них \Tn(t)\ = 1 и на отрезке
* € [—1,1] точки экстремумов естьtm = cos(^7r),m = 1,2,.. .п.
141
Лекции по вычислительной математике
Нас интересует решение следующей задачи на минимакс: найти
min < max
чтобы путем выбора узлов сетки минимизировать остаточный член
интерполяции. Эта задача была решена П. Л. Чебышевым.
Теорема Чебышева (без доказательства). Среди всех многочленов
степени п ^ 1, со старшим коэффициентом ап равным единице, наименьшее
уклонение от нуля, равное 21~п, имеет нормированный полином Чебышева
Это свойство полиномов Чебышева, наименьшее уклонение от
нуля, можно сформулировать по-другому: для любого полинома Pn(t) =
= tn + an-itn~x + ... + оо, отличного от fn(t) справедливо 21~п =
= max |fn(t)| < max \Pn(t)\,te [-1, 1].
Если в качестве интерполяционных узлов выбрать нули полинома
Чебышева, то произведение П (t - tj), а также Rn(t) будут наименее
уклоняющимися от нуля.
6.8. Обусловленность задачи интерполяции.
Постоянная Лебега
В процессе вычислений значения интерполируемой функции
известны с некоторой погрешностью. При работе на вычислительной
машине ошибки округления неизбежны. Возникает вопрос о
чувствительности интерполяционного полинома к ошибкам начальных данных
(обусловленности задачи интерполяции) и к ошибкам округления (вопрос
вычислительной устойчивости). Интерполяционный полином —
оператор, линейный по отношению к значениям интерполируемой функции. С
учетом погрешности начальных данных полином в форме Лагранжа
может быть записан следующим образом:
N N
п=0 п=0
причем слагаемое
n=0
142
Лекция 6 Интерполяция функций
характеризует чувствительность к ошибкам начальных данных и
ошибкам вычислений. Нас интересует оценка
N
max \AN(t,6f)\ ^ 1NS;S= max \Sfn\,lN = max V \<p?(t)\,
t€la,o| t?[a,b\ t€la,6] *—^
коэффициент In называется постоянной Лебега.
Введем в рассмотрение еще один объект. Пусть ]Г) |^f (x)| —
сумма модулей всех базисных функций. Обозначим ее L (х) = J2W (х)\ ~"~
функция Лебега (сетки). Тогда константа Лебега In = sup L (x).
x€[a,6]
Так как функция Лебега зависит лишь от расположения узлов сетки,
то и константа Лебега зависит лишь от введенной сетки. Обусловленность
и устойчивость задачи интерполяции зависят от константы Лебега.
Если рассматривать оператор интерполяции как оператор проекции
(проектор), переводящий элемент одного пространства (пространства
сеточных функций) в другое (пространство непрерывно
дифференцируемых функций), то постоянная Лебега есть норма такого оператора
проекции. Подробнее об этом в [7].
Конечно, реальная погрешность при интерполяции будет заведомо
меньше, чем приведенная выше оценка. Тем не менее, оценка является
достижимой (это свойство нормы оператора). Наихудшим
распределением погрешности будет такое распределение, когда погрешности
максимальны и меняют знак от точки к точке. То, что при этом будет достижима
приведенная выше оценка, следует из вида функции Лебега и каждой из
базисных функций. Предлагаем читателям соответствующие построения
провести самостоятельно.
Приведем (без доказательства) примерные оценки роста
постоянной Лебега в зависимости от числа узлов сетки. Константа Лебега растет
примерно как In ~ 2N для равномерной сетки и In ~ \n(N) для сетки
с чебышевским набором узлов. Доказано, что рост константы Лебега для
последней сетки асимптотически стремится к минимально возможному,
и сетка с чебышевскими узлами близка к оптимальной для задач
интерполяции.
6.9. Интерполяция с кратными узлами
Определение. Пусть в узлах сетки {tn}^=0 заданы не только
значения функции f(tn), но и значения ее производных f'{tn),f"{tn),...,
/(*n-i) (tny g этом случае узел tn называется кратным, а число кП9 равное
количеству заданных значений производных в п узле — кратностью узла.
143
Лекции по вычислительной математике
Доказывается теорема о существовании единственного полинома
, удовлетворяющего условиям
N = ко + кг + ... + км - 1.
Такой полином называется полиномом с кратными узлами.
Отметим два частных случая.
а) в точке t = t0 заданы/о,/о,...,/oN) (Л/= 0, ko = N + l).
Тогда многочлен P#(?), удовлетворяющий этим условиям, может
быть записан как
t=0
Это — ряд Тейлора, который является интерполянтом с кратным
узлом в точке t = to кратности N + 1.
б) Пусть на концах отрезка [*о, ?1] заданы значения /о, Д, /о, f[(M =
= l,fc0 = 2М = 2,ЛГ = 3). Тогда P3(t0) = /о,Р&о) = f
= /{, а интерполянт имеет вид
= /0
здесь г = ti -t0.
Такой многочлен называется кубическим интерполяционным
многочленом Эрмита.
Теорема без доказательства. . Пусть f(t) имеет N + 1 ограниченную
производную на отрезке [а, 6]. 7огда погрешность интерполяционного
многочлена Эрмита степени N выражается формулой
где tn — интерполяционные узлы, п = 0,..., М, fc» — кратность г узла, ? е
Поставим теперь следующую задачу: построить
кусочно-кубическую интерполирующую функцию, непрерывную на отрезке [а, Ь] со
своими двумя первыми производными.
144
Лекция 6 Интерполяция функций
Обозначим такую функцию S(t); значения производных в узлах tn
обозначим тп = Sf(tn). Если задать в узлах tn, tn+i значение функции и
ее первой производной, то получим эрмитов кусочно-кубический
полином
2 Шп "• 2
или
5(г) = fn(l-z)\l+2z)+fn+1z\3-2z)+mnTnz(l-TJ-mn+lTnz2(l-z),
где гп = *n+i -tn,z = (t- tn)/rn, mn = S"(?n).
6.9.1. Замечание о тригонометрической интерполяции
Для периодической функции f(t) с периодом Т естественно строить
приближение с использованием функций <pn(t) = an cos ^ + 6n sin ^
Тригонометрическая интерполяция состоит в замене f(t) тригонометри-
N N
ческим многочленом FN(i) = ]П <pn(i) = ао+ 5^ (ancos ^+bnsin ^),
п=0 п=1
коэффициенты которого находятся при решении СЛАУ Fuitk) = f(tk),
к = 1,..., 2N + 1, *2N+i - to = Г, здесь {г*}^ — последовательность
узлов интерполяции.
6.10. Кусочно-многочленная глобальная
интерполяция(сплайны)
Определение. Пусть на отрезке [а, Ь] задана система узловых точек
{гп}п=о- Сплайном Sm(t) называется определенная на [а,6] функция,
имеющая I непрерывных производных и являющаяся на каждом
интервале (?n-i, tn) многочленом степени т.
Определение. Дефектом сплайна называется разность d = т-l
между степенью сплайна и показателем его гладкости Z.
Замечание. Для сплайнов также используется обозначение Sm,d(?)*
Если сплайн строится так, чтобы выполнялись условия Sm(tn) = f(tn),
где f(t) — интерполируемая функция, то он называется
интерполяционным сплайном. В соответствии с определением, кусочно-линейная
функция является интерполяционным сплайном первой степени дефекта 1,
кусочно-квадратичная функция с первой непрерывной производной —
145
Лекции по вычислительной математике
интерполяционным сплайном второй степени дефекта 1. Наиболее
известным в приложениях является интерполяционный кубический сплайн
дефекта 1 (естественный сплайн), который будем обозначать S(t).
Определение. Кубическим сплайном дефекта 1, интерполирующим
на отрезке [а, 6] заданную функцию f(t), называется функция S(t),
удовлетворяющая следующим условиям:
1. S(tn) = f(tn) — условие интерполяции в узлах сетки {tn}n=o-
2. S(t) е С2[а, Ь]9 т. е. является непрерывной вместе с двумя первыми
производными.
3. На каждом отрезке [?n,?n+i], S(t) является кубическим
многочленом; п = О, ...,ЛГ- 1.
4. На краях отрезка [а, Ь] заданы краевые условия. Наиболее часто
употребляются следующие:
(a)S'(a) = /'(a), S'(b) = f'(b);
(b) S"(a) = /"(a), S"{b) = f"(b); часто полагают S"(a) = S"{b) =
= 0;
(c) S(a) = 5F), S'(a) = S"(b); эти условия называются
периодическими, т. е. интерполируемая функция является
периодической с периодом Ь-а.
Покажем, что эта задача имеет единственное решение.
Теорема. Интерполяционный кубический сплайн S(t),
удовлетворяющий условиям 1-3 и одному из краевых условий 4, существует и
единственен.
Доказательство.
Пусть S(z) — эрмитов кубический многочлен, который на каждом
отрезке [?n, ?,,+i], п = 0,..., N- 1, представлен как
S(z) = fn(l-zJ(l+2z)+fn^l-z2C'2z)+mnrnz(l'-zJ--mn+1Tnz2(l-z)J
где rn = tn+1 - tn, z = (t - tn)/Tn, mn = S'(tn). Тогда
(/n+i-/n)F-12z) 6г-4 6z-2
& if) = 2 гТПп hmn+i ,
q"(+ _i_ c\\ — g/ / 4m 2т
О \ln -ГУ))— О
Tn T,
n
Qtt,. nx afn - fn-i 2mn-i 4m.
^ n+l
Tn_i Tn_i
146
Лекция 6 Интерполяция функций
Условие непрерывности второй производной S"(tn + 0) = S"{tn - 0)
будет
rnmn_i + 2ran -I-
о Л /n+l - /n /n-/n-l^ _ Tn-1 _ ,
V rn Tn-1 / Tn_i+Tn
После добавления краевых условий получаем систему из N +1
уравнение с iV + 1 неизвестным mn. Для краевых условий первого типа
(заданы первые производные) система выглядит как
rnmn_i + 2mn + Sn
mN = /^.
Для условий второго типа (заданы вторые производные)
rnran_i + 2mn -h
_i_ o™ o/n ~ /n-i tN-i „
-i + 2miv = о 1 7r~JN-
tn-i 2
Аналогично получается СЛАУ для третьего типа краевых условий.
Во всех случаях матрицы СЛАУ оказываются трехдиагональными
симметричными, со строгим диагональным преобладанием и, как
показывается, положительно определенными, а, следовательно, и
неособенными. Следовательно, решение СЛАУ существует и единственно. Отсюда
следует существование и единственность решения задачи о построении
кубического сплайна. ¦
Приведем еще одно доказательство этой же теоремы.
Доказательство.
Рассмотрим неравномерную сетку: tn - tn-i = rn_i, ?n+i - tn = rn.
В узлах сетки определены значения функции: /п-ъ /n, /n+i- Пусть тп —
значение второй производной в точке tn (пока неизвестное!). На отрезке
[ для второй производной кусочно-кубического сплайна имеем
S't't = — (mn(*n+i - t) + mn+i(t - *n)). F.2)
147
Лекции по вычислительной математике
Так как сплайн — полином третьей степени, то его вторая
производная — линейная функция. Интегрируем F.2) по t, получаем (на отрезке
I ™>n+i2Шп2)
Интегрируя последнее соотношение еще раз, получаем:
S(t) = -L(mn(tn+1 -1K + mn+1(* - tnK)+
6rn
+Ctn(tn+l-t)+l3n+l(t- tn).
An — константа интегрирования. После второго интегрирования
положим Ant + Вп = ((Зп - an)t + an*n+i - ^n^n, т. е. вместо двух констант
Лп, Бп введем две новые константы, более удобные для дальнейших
выкладок.
Из условий S(tn) = /n, 5(*n+i) = /n+i, получаем:
- ГПп+±Г% й й /n+1 ™>n+iTn
/n-1-l = 7 + РпТп => Рп = — g •
л _ /п+1 ~" /п (уу1п-ц - тп)тп
тп о
Приравняем первые производные в tn справа и слева S't(tn + 0) =
= S't (tn - 0), получим систему уравнений для определения
коэффициентов сплайна:
/п ~ /п-
ГП_! 6
~ /n (шп-ц — mn)rn
" 2 2+ ^ 6 '
которая дополняется соответствующими граничными условиями. В
случае свободного сплайна mo = ms = 0.
Систему для определения коэффициентов, называемых моментами
кубического сплайна, можно записать в матричной форме
AM = F,
148
Лекция 6
Интерполяция функций
где А — квадратная матрица:
А =
О
0 ...
а ...
а±а ...
О 0 \
0 О
о О
О О О .
М и F — векторы-столбцы:
М = (mi,m2,...,m//_i) ,
TN-1 Tff+TN-1
^ (h~h /l-/o /3-/2
V Ti To T2
П
Ttf
Матрица А симметрична, имеет свойство диагонального
преобладания и, как можно показать, положительно определена, а
следовательно, неособенная. Значит, решение рассматриваемой СЛАУ существует и
единственно. Следовательно, и задача о построении кубического сплайна
имеет единственное решение. Для других типов краевых условий
доказательство проводится аналогично. Метод решения такой СЛАУ, который
будет рассмотрен в лекции 10 — прогонка.
Теорема (без доказательства). Для функции f(t) € С4[а, Ь] и
интерполирующего ее сплайна S(t), построенного на сетке {tn}?Lo* имеют место
следующие неравенства:
гдеМ4 =
, г =
- *»)•
Отсюда следует, что при г —> 0 последовательность функций 5^ (?),
* = 0,1,2 (кубический сплайн и первые две его производные) сходится,
соответственно, к ^
Теорема (экстремальное свойство кубических сплайнов) (без
доказательства). Пусть сплайн S(t) интерполирует функцию f(t) на системе узлов
{tn}n=o;to = a,tN = Ь.
149
Лекции по вычислительной математике
Тогда S(t) с краевыми условиями S"(a) = S"(b) = 0 доставляет минимум
функционалу
ь
j[F'\t)\4t
среди всех функций F(t) e С% [а, 6], т. е. функций, имеющих интегрируемые
ь
с квадратом вторые производные (/ [F"(t)Jdt) сходится на отрезке [а, Ь]) и
а
интерполирующих f(t) на отрезке [а, Ь].
Локальный сплайн. Локальная форма сплайн-интерполяции
предложена В. С. Рябеньким [9, 10]. Рассмотрим неравномерную сетку: tn -
- tn-i = ftn-i, ?n+i - *n = hn. В узлах сетки определены значения
функции: /n-i, /п» /n+i- Не вдаваясь в детали, приведем важные для
практического использования формулы в случае постоянного шага сетки h =
= const.
Построим интерполяционный полином второго порядка Рг(х) в
форме Ньютона (d - fn)/h:
«n-1
tn
*n+l
/n-1
/n
/n+1
fn —' /n — 1
/n+l~/n
h
/ni_2/n+/n+i
, /n) = /n-1
/n-1 — 2/n -h /n+1 /, . w, _
h2
Этот полином приближает / на отрезке [?п-ь
F.4)
с точностью до
o(h2). Рассмотрим теперь полином
/п+2 ~ З/п+1 + 3/п - /n-1
представляющий собой аппроксимацию функции / на отрезке [tn-i,
с непрерывными первой и второй производными. В [1] доказано, что
выражение F.4) аппроксимирует /im^ с порядком o(ft3~m) во всех точках
отрезка. Так как коэффициенты сплайна зависят от значений функции
лишь в 4-х соседних точках и для определения коэффициентов F.4) не
требуется решать систему линейных уравнений, такая кусочно-гладкая
интерполяция называется локальным сплайном.
150
Лекция 6 Интерполяция функций
Замечание. Qs(t, fn) уже не обладает экстремальным свойством.
6.11. В-сплайны
Сплайны с локальным носителем. (В-сплайны). В последнее
время в вычислительной практике широкое распространение получили В-
сплайны (от английского слова bell — колокол), сосредоточенные на
конечном носителе. Они используются как для интерполяции функций, так
и в качестве базисных функций при построении методов типа конечных
элементов.
Для подробного ознакомления с приложениями В-сплайнов и В-
сплайнами произвольной степени рекомендуется обратиться к [5, 6] и
современным публикациям, например, в журнале «Математическое
моделирование» [14]. В данной лекции ограничимся наиболее
распространенными случаями В-сплайнов порядка 2 и 3, см. также [11].
Определение. В-сплайном, или базисным сплайном степени N - 1
дефекта 1 относительно узлов {и}"*^ называется функция
BN-hn(t) = BAT-i(tn,t»+i, • • .,*»+*,*) = N ^Г V
- tj)
Пусть tn+i = tn+гт, т. е. рассматривается случай равномерной сетки.
Рассмотрим несколько частных случаев В-сплайнов.
1. N = 2. В этом случае сплайн строится наиболее просто.
= 2, («»-!
tn-*n+l)(tn-"
~~ Qmax (^n+2 ~ Qmax
(^ — tn)(tn+2 —
-J [(^n — Omax — 2(in+i — t)
151
Лекции по вычислительной математике
или
( 1
+ 2t
-1) = 0,
B(t) =
-L@-0 + in+2-t) = ;-
Это функция «крышка» или «крышечка». Она часто используется в
качестве базисной функции в методах конечных элементов.
L
Рассмотрим случай В-сплайна 2-го порядка, задаваемого формулой
2 ? — tk-2
Sk(x) =
tk-l - tk-2
, ^ г. х 1
1 + 2х - х2;х =
2-х2; х =
t-tk
-, t
A - xJ; x = * <fc+1 ,t € [tfc+i,«M-2].
При i < tk-2,t > tk-2,Sk(x) = 0. Построенный сплайн обладает
следующими свойствами:
(a) S#fc-2) = 5;(ifc+2) = 0;
(b) S{tk-i) = S(tk+i) = 1;
(c) 5(^_2) = 5(tfc+2) = 0.
При интерполяции функций можно поступить таким способом.
Заметим, что для интерполяции с помощью сплайна необходимо
потребовать выполнения условия
152
Лекция 6 Интерполяция функций
где Ь — коэффициенты интерполяции, S — В-сплайн, индекс
указывает на точку носителя, в которой сплайн достигает своего
максимума. Система таких соотношений, естественно, дополняется
граничными условиями. Известно [5], что получившаяся система для
определения коэффициентов разложения будет иметь тревдиаго-
нальную матрицу с диагональным преобладанием при выполнении
ограничения на^цлины соседних шагов: они должны различаться не
более чем в
2. N = 4 (кубический В-сплайн) имеет вид
*>г, п\Ч — TIJ 1Л n ~ '/max ~ 4l*n+l — tJmax
- *)Lx
K
/та
или, после несложных упрощений:
Базисные сплайны заданной степени являются линейно
независимыми функциями и образуют базис в функциональных
пространствах, что можно использовать для представления с их помощью
других функций этих же пространств. Любая, например, кусочно-
постоянная функция на отрезке, составленном из равных
интервалов, может быть единственным образом представлена как
линейная комбинация В-сплайнов нулевой степени, любая кусочно-
линейная функция — В-сплайнов первой степени и т.д. Базисные
153
Лекции по вычислительной математике
сплайны играют существенную роль при построении численных
методов решения задач математической физики, например, метода
конечных элементов в теории приближения функций, при решении
задач компьютерной графики.
Для последнего класса задач также используются функции Берн-
штейна:
*»(« _ Nl (b-t)N-n(t-a)n
"nW~ n\(N-n)\ (b-a)N
n = 0,...,iV,?e [a,b].
Функции Бернштейна иногда записывают в форме рекуррентного
соотношения:
i = 0,... ,nf Bjy+1(*) = 0.
Такие рекуррентные последовательности применяются с целью
уменьшения ошибок округления.
Функции Бернштейна являются базисными для построения кривых
Безье, активно использующихся в компьютерной графике и
техническом дизайне, появившихся в результате работ Безье и де Касти-
льо над формами автомобилей фирм Рено и Ситроен. Подробнее о
функциях Бернштейна в [12].
6.12. Интерполяция функций двух переменных
Пусть сетка образована пересечением прямых х = хп, п = 0,..., N
и у = ут,т = 0,...,M,/nm = f(xniym) - значение функции в узле
хп, Ут- Воспользуемся, например, аппаратом кусочно-многочленной
интерполяции. Для этого сначала реализуется кусочно-многочленная
интерполяция заданной степени по х на каждой прямой у = ут. Затем при
каждом значении х = хп реализуется кусочно-многочленная
интерполяция по у с учетом значений функции, полученных на первом шаге. Так, в
случае кусочно-линейной интерполяции по обоим переменным этот
метод приводит (для случая прямоугольника х е [xn,zn+i],y ? [yn,2/n+i])
к интерполяционному многочлену
г?, х f (gSn+l)(yym+l) , f Qg3?n)(l/ym+l) ,
г \Х,У) — /nmT w \ + /n+l,m7 Г7 Г+
(Xn - Xn+l)(ym - Ут+l) (Xn+1 - Xn)(ym - Ут+l)
(x - xn+i)(y - ym)
154
Лекция 6 Интерполяция функций
Сходным образом можно провести последовательную лагранжеву
интерполяцию, но при каждом фиксированном значении га, затем — при
каждом фиксированном значении п с учетом первого шага
интерполяции. Общая формула такого интерполянта аналогична одномерной
формуле для интерполяционного полинома в форме Лагранжа:
/1'\rVj
Если ja, /в, Id — значение функции /(x, у) в вершинах А, В,
некоторого треугольника на треугольной расчетной сетке, то вычислить
приближенное значение функции внутри этого треугольника можно с
помощью билинейной функции /(х, у) « F(x, у) = ax + by + с, находя
коэффициенты а, 6, с из условий
= /в,
где {ха, ул}, {^в, 2/в}, {a:D, 2/d} — координаты вершин А, В, D.
Погрешность такой интерполяции для функции /(х, у) с непрерывными
вторыми производными будет O(h2), где h — длина наибольшей стороны
треугольника ABD.
6.13. Задачи
1. Выписать интерполяционные полиномы первой и второй степени в
форме Лагранжа и Ньютона.
Решение. Интерполяционные полиномы первой и второй степени в
форме Лагранжа:
-«а)
(t-tO)(t-t2)
155
Лекции по вычислительной математике
где to, t\, *2 — узлы интерполяции, /(ti), /(*г), /(*з) — значения
интерполируемой функции.
Интерполяционные полиномы первой и второй степени в форме
Ньютона:
/(Ут)
2. Сравните количество арифметических действий, требуемое для
вычисления интерполяционного полинома, записанного в двух
формах:
LN(x) = а0 + t(ai + t(a2 + ?(... (an_i + Cnt)...))) (схема Горнера)
Решение. В первом случае для вычисления значения в одной точке
требуется ^(п + 1) умножений и п сложений. Во втором — п
умножений и п сложений.
3. Задана система узлов интерполяции:
Какова погрешность интерполяции, если п = 3?
Решение. Сделаем замену переменных в выражении для
остаточного члена
Получим
Полученный кубический полином имеет на [-1; 1] экстремумы в
точках
В таком случае шах |Я3(*)| = ||As(t)|| = (t?2"ffi-
156
Лекция 6 Интерполяция функций
4. Предложите простой рекуррентный алгоритм вычисления
коэффициентов а» (г = 0 ч- N - 1) интерполяционного полинома
Ps(t) = ао 4- ax{t - t0) + ... + an(* - t0)... (t - tjv-i).
Решение. Для коэффициентов полинома получаем систему
линейных уравнений с треугольной матрицей:
ао = /о,
-to) = /ь
- to){t2 - h) = /2,
Оо + CL\(tN — to) + ... 4- CLN(tN — to) ... (tN — tiV-l) = /AT»
которая легко решается от первого уравнения к последнему:
|
5. Оценить погрешность приближения функции \nt'(t' = 1,23) при
помощи интерполяционного полинома второй степени по точкам
1,1; 1,2; 1,3.
Решение. Остаточный член интерполяции будет
RN(t) =
при N = 2 имеем:
max |/C)(t)|
ti,i;i,3] ^ v "
е = \f(x) - L2(t)\ < i^^ |(t - to)(t - tt)(t - *a)|,
max |/C)(*)l = r-^«1.5-
[1,3;1,2]\J Wl 1-1,3
В таком случае
e = |ln(t') - L2(t)\ < ^ |A,23 - 1,1)A,23 - 1,2)A,23 - 1,3)| w
157
Лекции по вычислительной математике
6. Показать, что погрешность интерполяции может быть выражена
следующим образом:
- LN(t) = (t -10)...(*- is)fit, t0,...,
где /(?, to,..., to) — разделенная разность порядка N.
Решение. Из выражения для разделенной разности порядка N + 1
f(tN)
получим выражение для f(t):
Тогда
(t - to) • • • (* - to) • /(*, to,..., to).
Сравнивая полученное выражение с выражением для остаточного
члена интерполяции Rs(t) = f(t) - L(t) = ^(N+1ffl (t -to)...(t-
- to)» приходим к выводу, что для некоторой точки ? е [?0, to] имеет
место соотношение между разделенной разностью и производной
порядка N +1:
7. Пусть значения функции /(?) заданы в узлах интерполяции ^ь^^з-
Построить функцию g(t) = а%~^*, для которой выполнялось бы
условие интерполяции: p(ti) = f(U),i = 1,2,3 (задача дробно-
линейной интерполяции).
Решение. Из условий интерполяции g(U) = a%ffi** = f(U),i =
= 1,2,3 получаем систему трех линейных уравнений:
— do/2 = ?2/2*
158
Лекция 6 Интерполяция функций
Вводя обозначения
-t
и применив метод последовательного исключения неизвестных,
получим
а0 = B*„ Дп/ Дп+i/ - /» *n 6nf)/6n(tf),
ах = /п - 2ДП/Дп+1/,Ьо = -tSn{tf)/6nf.
Здесь учтено, что *n(t/) = tn*n/ 4- /ntl
Разумеется, знаменатель дробно-рационального выражения не
должен обращаться в нуль на рассматриваемом отрезке.
6.14. Задачи для самостоятельного решения
1. Покажите, что интерполяционный полином в форме Лагранжа
может быть построен в соответствии со следующими рекуррентными
формулами: L0(t) = /(*0),
Ln(t) = Ln_x(t) + [f(tn) - Ln_i(t)] + -^г,
3
2. Построить интерполяционный кубический полином Рз(*)= Л <М*,
i=0
для которого выполнено РзA) = 1, РзB) = 2, РзC) = 2, аз = 1.
3. Построить интерполяционный полином в форме Лагранжа для
функций f(t) = |t|, /(*) = *2 по узлам -1; 0; 1; и -2; -1; 0; 1; 2.
4. Оценить погрешность интерполяции функции f(t) = sin t на
отрезке [0; тг/4 ] по трем равноотстоящим узлам.
5. Оценить, какое количество узлов интерполяции потребуется на
отрезке [0; тг/4 ] для обеспечения точности е = 10~3 при
интерполяции функции sint.
159
Лекции по вычислительной математике
6. Привести примеры непрерывных функций, для которых расходится
последовательность интерполяционных полиномов (на
равномерной сетке).
7. Какой величины необходимо выбрать шаг интерполирования г для
обеспечения точности е ^ 10~4 интерполяции функции f(t) =
= \/i, t e [1; 103] при линейной и квадратичной интерполяции?
8. Пусть имеется таблица функции f(t) = sint в равноотстоящих
точка {tn}o> причем max(?n+i - tn) = т. При каком г линейная интер-
п
полиция позволит восстановить f(t) с точностью е < 10~4? Тот же
вопрос для квадратичной интерполяции. Решить задачу для случаев
равномерной и неравномерной сеток {tn}o-
9. Как оценить погрешность интерполяционного процесса, если
интерполируемая функция задана таблично?
10. По заданным значениям функции
t
f
1
-6
2
-1
2,5
15,6
3
16
найти значение t, при котором f(t) = 0 (решение уравнения f(t) =
= 0 для заданной функции методом обратной интерполяции).
11. Построить линейный и кубический сплайны по значениям
функции f(t) в точках {0,1}и {0,1,2} соответственно.
12. Показать, что система линейных алгебраических уравнений для
определения коэффициентов сплайна F.3) всегда имеет
единственное решение. Показать, что для этой системы устойчив метод
прогонки. Оценить число обусловленности системы F.3) в случае,
когда Лп = ft не зависит от номера узла.
Литература
[1] Федоренко Р.П. Введение в вычислительную физику. М.: Изд-во
МФТИ, 1994.528 с.
[2] Рябенький В. С. Введение в вычислительную математику. М: Физмат-
лит,2000.294с.
[3] Марчук Г.И. Методы вычислительной математики. М.: Наука, 1989.
608 с.
160
Лекция 6 Интерполяция функций
[4] Вержбицкий В.М. Численные методы математический анализ и
обыкновенные дифференциальные уравнения. М: Высшая школа,
2001.382 с.
[5] Завьялов Ю.С., Квасов Б.И., Мирошниченко В.Л. Методы сплайн-
функций. М.: Наука, 1980.352 с.
[6] Завьялов Ю.С., Леус В.А., Скороспелое В А. Сплайны в инженерной
геометрии. М.: Машиностроение, 1985.224 с.
[7] Вершинин В.В., Завьялов Ю.С., Павлов НН. Экстремальные свойства
сплайнов и задача сглаживания. Новосибирск: Наука, 1988.104 с.
[8] Самарский АА., ГулинА.В. Численные методы. М: Наука, 1989.430 с.
[9] Бабенко К.И. Основы численного анализа. М.: Наука, 1986.744 с.
[10] Рябенький В. С, Филиппов Л. Ф. Об устойчивости разностных
уравнений. М.: Гостехиздат, 1956.160 с.
[11] Рябенький В. С. Метод разностных потенциалов для некоторых задач
механики сплошной среды. М.: Наука, 1987.320 с.
[12] Ши Д. Численные методы в задачах теплообмена. М.: Мир, 1988.
544 с.
[13] Каханер Д., Моулер К., Нэш С Численные методы и программное
обеспечение. М.: Мир, 1998.575 с.
[14] Калиткин НН. и др.// Математическое моделирование. 1994, т. 6,
№4, с. 77-110,1997, т. 9, №6, с. 67-81,1997, т. 9, №9, с. 107-116.
6-3339 161
Лекции по вычислительной математике
Лекция 7. Численное интегрирование
Исследуются простейшие квадратурные формулы интерполяционного
типа — прямоугольников, трапеций, Симпсона. Для оценки реальной
погрешности формул используется правило Рунге. Дается понятие о
квадратурных формулах Гаусса. Рассматриваются методы вычисления
многомерных интегралов.
Ключевые слова: квадратурные формулы интерполяционного типа.
Правильные квадратурные формулы. Кубатурные формулы.
Квадратуры Гаусса.
Введение. В данной лекции будет рассматриваться задача
численного интегрирования. Формулы численного интегрирования функций
одного переменного называют квадратурными формулами. Задача
приближенного вычисления определенного интеграла (на отрезке или по
многомерной области) фактически разбивается на две самостоятельные
подзадачи. Первая — это интегрирование таблично заданной функции
(полученной, например, при проведении лабораторного эксперимента). В
таком случае априорная информация о гладкости подынтегральной
функции отсутствует, весьма ограничены возможности в выборе узлов
интегрирования. Для этой задачи наиболее эффективными будут
квадратурные формулы интерполяционного типа и правило Рунге оценки
погрешности.
Вторая задача — подсчет значения определенного интеграла от
известной функции. При этом самая ресурсоемкая операция с точки
зрения вычислений — подсчет значения функции. Желательно построить
численный метод, позволяющий получать как можно более высокую
точность при наименьшем количестве вычислений, при этом выбор узлов
квадратурных формул целиком в руках вычислителя. В этом случае
наиболее эффективными окажутся квадратурные формулы типа Гаусса.
7.1. Квадратурные формулы интерполяционного
типа (формулы Ньютона-Котеса)
Простейшую квадратурную формулу (формулу численного
интегрирования) можно получить следующим образом. Пусть необходимо
вычислить интеграл
= jf(t)dt.
162
лекция 7 Численное интегрирование
Положим, что f(t) на рассматриваемом отрезке [a, ft] не изменяется
(f(t) « const). Тогда / = /(?)(ft - а), ? € [а, Ь]. Если f = ^, то получим
формулу прямоугольников с центральной точкой
Конечно, для константы приведенная выше формула точна —
говорят, что построенная квадратурная формула будет точна на полиномах
степени 0. Легко можно доказать, что формула прямоугольников с
центральной точкой будет давать точное значение и в случае линейной
функции. Для всех других функций эту формулу будем рассматривать как
приближенную.
Если предположить, что функция f(t) на отрезке интегрирования
[а, ft] достаточно близка к линейной, то можно заменить приближенное
значение интеграла / площадью трапеции с высотой (ft - а) и
основаниями /(а) и /(ft). Тогда получается формула трапеций
В общем случае квадратурные формулы получаются при помощи
интегрирования интерполяционного многочлена, аппроксимирующего
подынтегральную функцию. Семейство квадратурных формул,
получающихся таким образом, называется формулами интерполяционного типа
(формулы Ньютона—Котеса).
Введем на отрезке интегрирования сетку, определим значения
функции в узлах сетки. Узлы в дальнейшем будем именовать узлами
квадратурной формулы (или квадратуры). Пусть, как и в задаче интерполяции,
имеется совокупность узлов {tn}n=0 ,tn = a + nr,T = (b- a)/N, t ? [a, ft].
Пусть также задана таблица /n = {f(tn)}n=o- Отрезок fo,?fc+i] далее
иногда будем называть элементарным отрезком.
Заменим подынтегральную функцию ее интерполяционным
полиномом в форме Лагранжа. Будем полагать, что
ь ь
Jf(t)dt*Jbn(t)dt.
Рассмотрим некоторые частные случаи.
Формула трапеций. На отрезке [tk,tk+i] проводим замену
подынтегральной функции интерполяционным полиномом первой степени:
tfc+l —
163
Лекции по вычислительной математике
после чего, выполнив интегрирование по элементарному отрезку,
получим приближенное значение интеграла на [?*,
h « iftb+l " tk) [/(t*+l) + /(**)] = у
После суммирования интегралов по всем элементарным отрезкам
[tk, tk+i ] получаем формулу трапеций для отрезка [а, 6]:
к=0 к=0
к=о
Ha равномерной сетке (сетке с равноотстоящими узлами) при тк =
= г = F - a)/N полученная формула принимает вид
ЛГ-1
'«\ Е i/(**)+/c*+i)] = 5[/(to)+2f{ti)+• • •+2/(^-i}+/(*nI •
fc=O
Формула Симпсона. Заменим подынтегральную функцию f(i) на
отрезке [tk-i,tk] интерполяционным полиномом (в форме Лагранжа)
второй степени. Для простоты положим т = F - a)/N = tk- tk-i = const
для всех к — сетка на отрезке интегрирования равномерная. Тогда
f (t-tk-1/2)(t-tk) (t-tfc-iKt-tjfe)
+л йГ^Ж=^^ = ?[(t" tk-l/2){t"
-2(t - tfc-i)(t - tk-l/2)fk-i/2 + (t- tk-i)(t - ^_
После вычисления интеграла от полинома получим приближенное
значение интеграла по элементарному отрезку
6 L,№-
Суммируя по всем элементарным отрезкам [?*_1, ?*], получим
= ? (/о + 4/i/2 + 2Д + 4/з/2 + .
164
лекция 7 Численное интегрирование
где д = f(tk), fk+1/2 = /(**+**+!). формулу Симпсона можно также
записать, не используя дробных индексов:
если локальную формулу получать путем интегрирования
интерполяционного полинома второй степени по отрезку [?*_ь
= |(Л_1 + 4Д
где F(?) — интерполяционный полином, построенный на отрезке
[t*-b tfc+i] по точкам ?*-1, tfc, **+ь В этом случае Л/" — число разбиений
отрезка на элементарные отрезки — должно быть четным.
Еще одна используемая на практике квадратурная формула
интерполяционного типа— так называемое «правило 3/8». Она получается при
замене подынтегральной функции интерполяционным полиномом
третьей степени, построенным по четырем точкам. Расчетные формулы для
правила 3/8 приведем без вывода:
3,/2а + Ь\ 3,/а + 26\ 1Г/1Л1
8; ("8"J + 8f ("Г") + 8/F)J
Квадратурные формулы интерполяционного типа более высокого
порядка применяются достаточно редко.
Конечно, существуют и формулы интерполяционного типа более
высоких порядков. Они не применяются на практике по следующим
обстоятельствам. Любая формула интерполяционного типа записывается в
виде
м
k=0
Во всех приведенных выше формулах коэффициенты а& были
положительными. Такие квадратурные формулы называются правильными
квадратурными формулами. При использовании полиномов более
высоких степеней получаются квадратурные формулы, не являющиеся
правильными.
Для степени интерполяционного полинома более 7 среди
коэффициентов встречаются отрицательные. Д. Пойа показал, что
п
lim y^|anjb| =oo,
fcO
165
Лекции по вычислительной математике
где апк — веса квадратурной формулы, получающейся при замене
подынтегрального выражения интерполяционным полиномом степени п. Такое
увеличение суммы абсолютных значений коэффициентов связано с
быстрым ростом постоянной Лебега при алгебраической интерполяции на
равномерной сетке.
Подробнее о свойствах квадратурных формул интерполяционного
типа можно прочитать в [6].
7.2. Оценка погрешности квадратурных формул
Погрешность квадратурных формул может быть оценена, например,
с использованием остаточного члена интерполяционного полинома:
/
RN{t)dt
max XJ _,, n
п (* - tk)
k=0
Из последней формулы следует, что квадратурная формула точна,
если подынтегральная функция является многочленом степени не
выше N.
Получим, например, локальную оценку погрешности для формулы
трапеций, используя формулу для остаточного члена интерполяционного
полинома 1-го порядка:
12
Тогда погрешность по всему отрезку [а, Ь] будет составлять
-*. - 12 12 v- -г
Другой способ получения погрешности квадратурных формул
состоит в следующем. Рассмотрим интеграл по элементарному отрезку
tfc+i
= J f(t)dt,
tk
№ = f(z) + f'{z){t -z) + !l(t-zJ + ... + R(t - г),
166
Лекция 7 Численное интегрирование
где z e[tk, *fc+i] — некая опорная точка, тогда для приближенного
значения интеграла верно
tfc+i
Д = f(z)Tk + ?т1+г)т1 + ...+ J R(t- z)dz, тк = **+1 - tk.
tk
Коэффициенты ?, 77,... зависят от производных f'(z), f"{z),...
С другой стороны, любая из рассмотренных квадратурных формул
представима в виде
Д = rk(afk + 6Д+1/2 -1-
Заменяя в этой формуле значения функций / в точках Д, Д+1/2, Л+i
ее разложением по формуле Тейлора, получим
Тк = f(z)rk + 6
Сравнивая разложения для Д, Д, легко заметить, что вместе с
первым слагаемым совпадают и другие слагаемые до (тп - 1)-го порядка, так
Разность же несовпадающих слагаемых будет, очевидно, оценкой
погрешности квадратурной формулы на интервале [^,^+1] : ?k =
= IД - Д| < v max |/^| rjf*+1, где v — константа.
[*fc,*fc+i]
Если просуммировать локальные погрешности по всем интервалам
[**» *fc+i]> то получим оценку погрешности квадратурной формулы по
всему отрезку [а, Ь]:
= \I-I\^v(b- a) max |/(m)| тп
где т = maxTfc на неравномерной сетке, или т = (b- a)/N на
равномерной. Число тп называется порядком точности квадратуры.
Получим теперь погрешность формулы прямоугольников (со
средней точкой) для Тк = т = const:
погрешность формулы трапеций
167
Лекции по вычислительной математике
погрешность формул Симпсона (с дробными и без дробных индексов
соответственно)
лD)«
Ь — а Л4ъ.ч 4
2880
max
max
180 [а,Ь]
г4.
Заметим, что если функция f(t) имеет только три непрерывных
производных, то оценка погрешности формулы Симпсона ухудшается на
порядок:
7.3. Кратные интегралы
Рассмотрим, для примера двукратный интеграл по прямоугольной
области п(а < х < Ь,с < у < d). Аналогично одномерному случаю,
в соответствии с формулой прямоугольников (со средней точкой)
заменим функцию ее значением в точке пересечения диагоналей прямоуголь-
6 d
ника. В таком случае получим / = // f(x,y)dxdy « Sf(^, ^), где
а с
S = тхту, тх = (Ь - а), Ту = (d - с). Если разбить прямоугольник на
прямоугольные ячейки Si, то получим аналог формулы прямоугольников со
средней точкой в виде суммы по i:I « X)^t/(^t,2/i), где 5» — площадь
i
г-ой прямоугольной ячейки, х»,у» — координаты точки пересечения ее
диагоналей.
Применим теперь формулу Симпсона для вычисления двукратного
интеграла путем редукции к методу вычисления одномерного интеграла,
зачем представим двойной интеграл как
Ъ d Ь d
I = j jf(xyy)dxdy = jdx J /(x,y)dy.
Сначала применим формулу Симпсона для вычисления внешнего
интеграла:
Г d
6
.с
d d 1
f(a,y)dy + 4 j /(l±*,y)^ + J f(b,y)dy\.
168
Лекция 7 Численное интегрирование
Теперь применим формулу Симпсона для каждого из трех
полученных интервалов:
d
h = J f(a, y)dy « ^ [/(a, c) + 4/(a, ^) + /(a, d)] ,
С
С
,—) + /(—,d)j,
,^/(Ь,с) + 4/(Ь,^) + /(Ь,<
С
Подставляя приближенные формулы для вычисления интегралов
1,12, /з в формулу для вычисления /, получим
2, с) -I- /(a, d) + /(Ь, с) -
а' "T)+^(bj"T")+^(^"'c)+/(^jd)Г16f ("'" J г •
Если область интегрирования не является прямоугольной, то ее
можно сделать подобластью большей по площади прямоугольной
области, которую в свою очередь разбить на прямоугольные ячейки. Ячейки
в этом случае разделяются на внутренние, к ним применяются
приведенные формулы численного интегрирования, и граничные, не
прямоугольные, площади которых вычисляются по более сложным алгоритмам. При
этом приближенное значение интеграла, например, при использовании
формулы средних, можно записать как / да ? ^вн + Z) ^т» гДе ^вн — ПРИ"
ближенное значение интегралов по внутренним ячейкам, /^ — по
граничным, г, j — номера ячеек с площадями 5» и Sj.
7.4. Квадратурные формулы Гаусса
Поскольку формулы Ньютона—Котеса являются
интерполяционными, очевидно, что они не могут успешно использоваться для
получения формул высокой точности по причине неустойчивости
интерполяционного процесса для многочленов высокого порядка. Как отмечалось
выше, постоянные Лебега растут с увеличением количества узлов интерпо-
ляции для равномерной сетки как 2N. По этой причине обычно использу-
*отся полиномы степени от нуля до трех (соответственно, формулы пря-
169
Лекции по вычислительной математике
моугольников со средней точкой, трапеций, Симпсона, 3/8).
Вычисление с их помощью интегралов от функций, обладающих высокой
степенью гладкости, например, близким к полиномам высокой степени,
представляется нерациональным. В выражение для погрешности этих формул
входят первая, вторая или четвертая производные. Погрешность
определяется низким порядком производной при высокой степени гладкости
интегрируемой функции. Этих недостатков лишены квадратуры Гаусса.
Формулировка задачи построения квадратурных формул,
поставленная Гауссом, такова.
Для заданного количества точек, а именно, для (iV-b 1) точки, найти
такое расположение узлов и такие веса с», чтобы квадратурная формула
N
t=0
была точной для полиномов как можно более высокой степени, т. е.
чтобы rN(t) = 0.
Пояснение. Для некоторых классов функций существуют
квадратурные формулы с rN(t) = 0, которые называются точными. Примером
такого класса функций являются полиномы
N
к=0
на отрезке [а, Ъ]. Определим на этом отрезке узлы ^,г = 1,...,ЛГи веса а
так, что
N
I
г=0
Представим Рдт(г) в виде интерполяционного полинома
при этом остаточный член интерполяции полинома равен нулю:
Тогда из предыдущего условия следует
а к=0
170
Лекция 7 Численное интегрирование
где Сг являются базисными функциями полиномов Лагранжа.
Квадратурная формула
N
является точной для любого полинома степени N. Оказывается, эта
формула может быть точной и для полиномов более высокой степени,
а именно, 27V+1, что используется при построении квадратурных формул
Гаусса.
Пусть формула численного интегрирования имеет вид
ь
1 = / f(t)dt = cof(to) + cif(ti) + ... + cNf(tN) + rN,
a
где Ci — веса, tn — остаточный член квадратуры.
Положим, что существует многочлен Рм (t) степени М > N, для
которого квадратурная формула точна, т. е. г^ = 0 при f(t) =
f(t) = PM(t) = ао + axt + a2t2 + ... 4- aMtM,
где at — коэффициенты. В этом случае получим
а0 Idt + ai Itdt + a2 ft2dt + ... + aM ftMdt =
= cq(uo + d\to -f- d\
+ci(ao + CL\ti + а2Ьг
-\-Cn(uq + CLltpf + Q
Приравняем выражения в обеих частях равенства при а3\
ь
со + с\ -К • • • + см = / dt = /о,
a
&
= Jtdt = IU
а
171
Лекции по вычислительной математике
Получается нелинейная система из М+1 уравнения с 2(N+1)
неизвестными с», U. Отсюда следует, что максимальное значение М есть 2N +
+ 1. Решение этой системы или исследование на его существование и
единственность в общем случае затруднительны. Ниже будет рассмотрен
пример получения квадратурной формулы Гаусса таким путем для двух
узлов.
Гаусс решил эту задачу более простым (в смысле реализации, но не
решения!) способом, доказав следующую теорему. Приведем ее без
доказательства.
Теорема. Если в качестве узлов U, г = 0,..., N в квадратурной форму-
ле используются нули полиномов Лежандра qtq+\(t), а веса Сг вычисляются
по формулам
-1 fc=O
то квадратурная формула
} N
точна для полиномов степени 2N + 1.
Напомним, что полиномы Лежандра образуют ортогональную
систему функций на отрезке [-1; 1]:
1 1
Jqi(t)qj(t)dt = O при г ф j; jqi(t)qj(t)dt ^0 при i=j.
Первые несколько полиномов Лежандра будут qo(t) = l,()
= t,q2(t) = ±Ct2-l),q4(t) = ^C5*4-30*2 + 3),... рекуррентная и общая
формулы имеют вид:
(n + l)g«+i(i) = Bn + l)tqn(t) - ngn_i(*),
Заметим, что рекуррентные формулы, связывающие три полинома
порядка п-1,пип + 1 уже встречались для полиномов Чебышева. Такие
рекуррентные формулы существуют для всех систем ортогональных
полиномов.
172
Лекция 7 Численное интегрирование
Погрешность квадратурной формулы Гаусса на отрезке будет rpt (t) =
=, 22<"+1)+1а*/<2<"+1>>@, при этхш ? е [-1,1]. Для ? е [а,6]
формула остаточного члена будет rN(t) = (Ь - аJ<"+1>+1а*/<2<*+1»@,
причем коэффициент а// быстро убывает с ростом N. Здесь as =
[(Nl)!]4
Формулы Гаусса обеспечивают высокую точность уже при
небольшом количестве узлов (от 4 до 10) В этом случае аг « 5 • 10~7, аз «
« б • 10~10,а4 « 4 • 103. В практических же вычислениях число
узлов составляет от нескольких сотен до нескольких тысяч. Отметим также,
что веса квадратур Гаусса всегда положительны, что обеспечивает устой-
N
чивость алгоритма вычисления сумм Y, <kf(U)-
i=0
7.5. Вычисление интегралов от функций с
особенностями
Пусть требуется вычислить несобственный интеграл
б
от функции, обращающейся в бесконечность в некоторой точке с € [а, Ь].
В этом случае интеграл обычно разбивают на два
6 ( c-6i Ь \
|/(t)A= ton | j f(t)dt + I f(t)dt\.
a 62—>0 у a c+62 )
Числа Si и $2 выбирают малыми величинами так, чтобы
выполнялась оценка:
J f(t)dt
где е — заданное малое положительное число (точность вычисления
интеграла). После этого по квадратурным формулам вычисляют определен-
с—6\ Ь
ные интегралы Д = J f(t)dt и /2 = / f(t) dt с точностью е/4 каждый.
а с+62
После таких вычислений за приближенное значение интеграла с особен-
ь
ностьюпринимают/ f(t)dt «Д+/2 (сточностьюе).
а
173
Лекции по вычислительной математике
Другой способ вычисления интеграла от функции особенностью,
называемый методом Канторовича выделения особенностей, состоит в
следующем. Представим подынтегральную функцию в виде суммы:
f(t)dt = Jg(t)dt + I [/(«) - g(t)) dt
При этом g(t) подбирают так, чтобы она была интегрируемой, а
разность [/(?) - g(t)] — ограниченной.
1
Пример. Пусть необходимо вычислить I = f t dt o .
о \АA+*2)
Представим I как сумму двух интегралов J = h + h, где h =
Интеграл Д вычисляется аналитически, а 7г, поскольку
подынтегральная функция ограничена, можно вычислить по квадратным
формулам.
Аналогично можно поступить и в следующей задаче:
е dt= r—f-dt+ I- ^-tL*.
0 0 0
Интегрирование быстро осциллирующих функций типа / =
ь
— / f(t)eiwtdt можно проводить, заменив f(t) на интерполяционный по-
а
Ь
лином, / « / PN(t)eiwtdt. Этот интеграл вычисляется явно.
а
7.6. Идея метода Монте-Карло
Метод Монте-Карло используется, как правило, для вычисления
кратных интегралов. Рассмотрим задачу вычисления интеграла по
многомерному кубу:
11 1
0 0 0
Для его вычисления можно построить кубатурные формулы,
используя процедуру последовательного интегрирования, заменяя кратный
174
Лекция 7 Численное интегрирование
интеграл / на
11 1
I = f dti J dt2... J dtnf(tut2,...,tn).
0 0 0
Проблема вычисления подобных интегралов заключается в том, что
при росте размерности задачи объем вычисления значительно
увеличивается, а задача численного интегрирования превращается из довольно
простой в одну из самых сложных и трудоемких. По этой причине
приведенные выше квадратурные формулы используются обычно для решения
одно-, дву- и трехмерных задач.
Для вычисления интегралов по гиперкубу высокой размерности
обычно используется метод Монте-Карло. Суть его состоит в том, что
генерируется последовательность случайных точек единичного п-мерного
куба t\, *2, • • •»*n € Rn ; очевидно, что чем больше точек участвует в
вычислительном процессе, тем больше точность расчета.
Пусть теперь необходимо взять интеграл по области ft,
принадлежащей n-мерному кубу, причем, ft выделяется неравенствами
»(**)< 0, j = l-s-J, k = l + K.
Далее генерируется последовательность случайных чисел,
равномерно распределенная в единичном гиперкубе, и для всех точек
проверяются неравенства gj(tk) ^ 0. Если они выполнены, т. е. tk € ft, то
вычисляются значения /(?&), прибавляющиеся к сумме.
Пусть вычислено М точек, из которых К попали в ft и накоплена
к
сумма ? f(tk).
fc=i
Среднее по объему ft значение функции / вычисляется по формуле
/ = |р-, где Sn = К/М, In — кратный интервал по ft.
С другой стороны, это же значение можно приближенно вычислить
как сумму:
Приравнивая эти выражения, получим:
Л/Г 1 1
I ^ /(*)' откуда 1п ~ J7
M
7.7. Задачи
1. Получить локальную и глобальную оценки погрешности для
формулы трапеций.
175
Лекции по вычислительной математике
Решение. Локальную оценку погрешности получим, используя
формулы для истинного члена интерполяционного полинома:
SN =
max
N
П (*-*»)
В случае формулы трапеции имеем
Погрешность для всего отрезка [а, Ь] будет следующей (г
-a)(N,trn = nT) :
= (Ь -
n=l
2. Получить квадратурную формулу Гаусса для двух узлов на отрезке
t e [-1,1].
Решение. В случае двух узлов N = 1 (количество отрезков
разбиения), M = 2,JV + 1 = 3 (степень полинома). Узлы tn и веса Сп
должны удовлетворять следующей системе уравнений:
N
N
n=0 J
В данном случае система уравнений будет:
1
со + d = I ldt = 2,
-i
i
f
-i
176
Лекция 7 Численное интегрирование
У
-1
1
-1
откуда получим
со = с\ = 1; to = *i = -т=.
Формула Гаусса записывается как
1
-1
Эта формула будет точной для полиномов третьей степени.
3. Предложить способ вычисления интеграла
Решение. Представим интеграл / как сумму двух интегралов
y/i
о о о
Первый интеграл 1\ вычисляется аналитически: h = 1,6.
Поскольку подынтегральная функция в /2 трижды непрерывно
дифференцируема и ограничена, то /2 можно вычислить, например, по
формуле прямоугольников с центральной точкой:
4. Предложить способ уточнения приближенного значения интеграла
по квадратурной формуле, при вычисленных значениях этого
интеграла при двух шагах интегрирования: h и h/2 (правило Рунге).
177
Лекции по вычислительной математике
Решение. Интеграл / может быть представлен в виде
где Ip(h) — приближенные значения интеграла, вычисленные по
формуле с порядком точности р с шагом ft, Ip (|) — значение
интеграла, вычисленное по той же формуле с шагом вдвое меньшим.
При малых ft константы С и С\ близки. Этот факт тоже
необходимо доказывать. Доказательство труда не представляет — пользуясь
теоремой Лагранжа о среднем, легко получить, что эти величины
отличаются на O(ftp). Тогда получим
P{h) + си» = г Q) + ад (§) « р Q) + 1С Q
откуда следует
Подставив С во вторую формулу для вычисления /(с, ft/2), получим:
" • + 2Р - 1 '
Во-первых, эта простая формула позволяет относительно дешевым
способом уточнить вычислительное значение интеграла с шагом
ft/2. Во-вторых, получаем возможность контролировать точность
численного интегрирования путем вычисления значения интеграла
дважды (с шагами ft и ft/2).
Примечание. Легко получается аналог правила Рунге при
вычислении интеграла для табличной функции. Необходимо лишь с
использованием одних и тех же квадратурных формул вычислить
интеграл с шагом таблицы ft и затем повторить вычисления, выкинув
половину точек, с шагом 2ft.
7.8. Задачи для самостоятельного решения
1. Предложить алгоритмы вычисления интегралов от быстро
осциллирующих функций:
1 2
/sinlOOx, f 1ЛЛ . ,
/ — dx, / coslOOxlnxcte
178
Лекция 7 Численное интегрирование
(формулы Филона. Подробнее о них в [3]).
2. Предложить алгоритм вычисления интегралов:
1,5 1 1
,х
ех Г arctgx ( Vx3 +1
X J X J yJX
0 0 0
1 11
/cosx —1 f cosx f xsinx
-—S—dx^ -^b,J m—)dx,
0 0 0
oo 0 1
/1 - cosx _ / sinx _ / ln(l + x) .
7=r-dx, / dx, / —i ^dx.
Xv/X J X J X
1 1 0
3. Доказать, что формула Симпсона точна, если подынтегральная
функция есть произвольный многочлен третьей степени.
4. Определить число тг по формуле
используя формулы прямоугольников с центральной точкой,
трапеций, Симпсона.
5. Оценить число разбиений отрезка для вычисления интеграла
1
/ sinx2dx
о
по формуле прямоугольников с центральной точкой для
достижения точности е = 10~4. Тот же вопрос для подсчета интеграла
1
/ exp(x2)dx.
о
6. Оценить погрешность при вычислении интеграла
dx
+ х2
о
179
Лекции по вычислительной математике
по формуле прямоугольников с центральной точкой, трапеций,
Симпсона.
7. На элементарном отрезке [xi,Xi-\] подынтегральная функция
аппроксимируется кубическим сплайном:
S<n> = ап + Ьп(х - хп) + Ц(х - хпJ + ^(х - хп)\
Вывести соответствующую формулу сплайн-квадратуры и
исследовать ее точность.
Литература
[1] Калиткин Н.Н. Численные методы. М: Наука, 1978.512 с.
[2] Березин И.С., Жидков Н.П. Методы вычислений. Т. 2. М.: Физматгиз,
1962.464 с.
[3] Косарев В.И. 12 лекций по вычислительной математике. М: Изд-во
МФТИ, Физматкнига, 2000.220 с.
[4J Федоренко Р.П. Введение в вычислительную физику. М.: Изд-во
МФТИ, 1994.528 с.
[5] Каханер Д., Моулер К., Нэш С. Численные методы и программное
обеспечение. М.: Мир, 1998.575 с.
[6] Бабенко К.И. Основы численного анализа. М.: Наука, 1986.744 с.
180
Лекция 8 Численные методы решения задачи Коши для систем ОДУ
Лекция 8. Численные методы решения задачи Коши
для систем обыкновенных дифференциальных
уравнений
Подробно рассматриваются методы типа Рунге-Кутты, менее
подробно — Адамса. Формулируются н доказываются утверждения об устойчивости
методов Рунге-Кутты на устойчивых и нейтральных по устойчивости
траекториях.
Ключевые слова: методы Рунге-Купы, Адамса, таблицы Бутчера,
аппроксимация, устойчивость, сходимость, устойчивые траектории,
нейтральные траектории.
8.1. Базовые понятия
Рассмотрим численные методы решения задачи Копта для
обыкновенных дифференциальных уравнений (ОДУ) вида
dt -'<*•">• <> °' (8Л)
и@) = и0,
а также систем ОДУ
—jj- = f (t, U),
u@) = uo,
где
U = (Wb U2,. . . , Um)T, f = (/i, /2,. .., fm)T
— векторы столбцы искомых функций и правых частей соответственно.
К аналогичной форме приводится задача Коши для обыкновенного
Дифференциального уравнения (системы уравнений) порядка выше
первого, вида
du dm~1w\
dtm -*V". - dt>-->
u@) = oo,
181
Лекции по вычислительной математике
если положить
du\ du2 dum-i
di db dz
dum
щ@) = Oi_i,i = 1, 2, ..., m.
Введем в расчетной области t € [О, Г] точки (узлы расчетной
сетки) {?п = пт, п = 0, 1, ..., ЛГ}, в которых вычисляется искомое
решение. Совокупность узлов называется расчетной сеткой, (сеточной
областью), г — шагом интегрирования. Здесь для простоты введена
равномерная сетка. В реальных расчетах применяются и неравномерные сетки.
Введем сеточную функцию иТ, определенную в узлах сетки и
представляющую собой совокупность приближенных значений искомой
функции, UT — проекцию точного решения искомой задачи на сетку и /г —
значения правой части в узлах сетки.
Введем вслед за [1] также операторное обозначение
дифференциальной задачи
где
!?-/(*, «), <>0;f=( 0, *>0;
u@), t = 0; \ u0, t = 0;
и аппроксимирующей разностной задачи
Lr(uT) = Fr, (8.3)
где LT — обозначения разностного оператора, FT — проекция F на
расчетную сетку. Заметим, что ииит являются элементами соответственно
функционального и конечномерного пространств. Определим основные
понятия теории разностных схем [1,2].
Определение. Решение задачи (8.3) ит сходится при г -+ 0 к
решению исходной задачи (8.2), если
при г —> 0.
При этом, если имеет место оценка
то имеет место сходимость порядка р.
182
Лекция 8 Численные методы решения задачи Коши для систем ОДУ
Определение. Говорят, что задача (8.3) аппроксимирует задачу (8.2)
на ее решении, если невязка
при г —> 0, где rr = LT(Ur) - Fr; при этом, если имеет место оценка
то говорят, что имеет место аппроксимация порядка р.
Определение. Задача (8.3) устойчива, если из соотношений
Lr(uT)-Fr=ST,
Lt(vt)-Ft=Vt
следует
II *т - «К С2 (Ц6.Ц + |||*.||) , С2 ф С2(т).
Теорема 1 (В. С. Рябенъкого-П. Лакса). Решение задачи (8.3)
сходится к решению исходной задачи (8.2), если задача (8.3) устойчива и
аппроксимирует задачу (8.2); если аппроксимация имеет порядок р, то сходимость
также имеет порядок р.
Доказательство.
В силу аппроксимации имеем оценку: ||гг || ^ С\тр. Тогда из
определения устойчивости, положив vT = С/г, получим
IIиг - Ml < С2 \\гт\\ ^ С2Сп* = Ст*,
поскольку в данном случае
Ы1 = о
и, кроме того,
Приведем примеры простейших разностных уравнений,
аппроксимирующих (8.1):
2т 'ч
183
Лекции по вычислительной математике
Первая из схем называется явной (явная схема Эйлера), вторая —
неявной (неявная схема Эйлера). Алгоритмическая реализация первой
схемы — бегущий счет (рекуррентная формула), второй — решение
нелинейного алгебраического уравнения на каждом временном шаге.
Для реализации третьей схемы необходимо задание функции ип в
двух точках: tonti. Один из возможных вариантов — решение на первом
шаге нелинейного уравнения вида:
Un+1~TUn-1 = 1 [fitn-г, «n-i) + /(*n+i, «n+i)]
прип = 1.
В данном случае проявляется несовпадение формальных порядков
дифференциального и разностного уравнений (дифференциальное
уравнение первого порядка, разностное — второго).
Один из первых методов приближенного решения обыкновенных
дифференциальных уравнений — разложение в ряд Тейлора.
Дифференцируя по t исходное уравнение (8.1), получим
Таким образом, можно написать приближенное равенство:
i=0
Полагая
получаем приближенное значение u{t) в точке t = ?n+i- При J = 1 и
*n+i - *п = т = const получаем метод Эйлера:
un+i = ип 4- т/п.
Этот способ не получил распространения в практике решения
дифференциальных уравнений из-за необходимости вычисления производных u(t),
где г = 1-S- /. По затратам машинного времени он заметно уступает другим
методам, о которых будет идти речь далее.
В настоящее время в практике решения жестких систем ОДУ
применяют так называемые многозначные методы, основанные на
разложении в ряд Тейлора и вычислении производных. О жестких системах ОДУ
будет рассказано ниже.
184
Лекция 8 Численные методы решения задачи Коши для систем ОДУ
Рассмотрим еще один способ получения простейших одношаговых
расчетных схем для численного решения уравнения (8.1), для чего
напишем равенство
t
u(t + r) = u(t) + / u\t + г) dr.
о
После аппроксимации интеграла в правой части по формуле
прямоугольников и замене его на величину ru'(t), получим
или
ti(* + r) = u(t) + r/(t, и) + О(т2),
поскольку u'(t) = /(?, и).
Опуская член О(т2) и обозначая t = tn, t + г = ?n+i, u(t) = uny u(t +
4- r) = un+i, получим метод Эйлера.
Если рассматриваемый интеграл заменить формулой трапеций,
получим
U(t + Г) = U(t) + I [||'(«) + v!(t + Г)] + О(Г3),
откуда имеем
Этот метод называется неявным методом трапеций. Для того чтобы
метод был явным, его делают двухэтапным:
= **п + r/(/n, tin),
= Un + -[f(tnyUn) + /(tn+
где un+i — вспомогательная величина, вычисляемая на промежуточном
этапе. Если этот же интеграл приблизить формулой прямоугольников со
средней точкой, то получим
u(t + г) = u{t) + ти1 (* + I) 4- О(г3).
Снова воспользовавшись дифференциальным уравнением (8.1),
преобразуем последнее выражение к виду
u(t + г) = u{t) + г/ [t + I, « (t + I)] + О(т3).
185
Лекции по вычислительной математике
Соответствующий неявный метод имеет вид
ип+х =un+rf [tn + ^, и
для его явной реализации можно воспользоваться следующей двухэтап-
ной формулой:
= Un + j
-,
8.2. Методы Рунге-Кутты
Наиболее распространенными при численном решении
обыкновенных дифференциальных уравнений являются методы Рунге-Кутты. Их
принято представлять в следующей форме [3].
Определение, г-шаговый явный метод для численного решения
задачи Коши для обыкновенного дифференциального уравнения (8.1):
= f(tn
ип
(8.4)
kr = f(tn + arr, ип + т (Priki +'... + A-.r-ifo)),
Un+i = un + r Gifei + ... + 7rfcr),
где к{ — промежуточные вспомогательные величины.
Коэффициенты, определяющие конкретный метод, могут быть
представлены в виде таблицы Бутнера (табл. 8.1). Нулевые коэффициенты C13,
как правило, в таблице Бутчера не указывают.
Таблица 8.1
0
а2
аз
аг
/?21
031
71
#32
&2
72
0ГТ-1
7г-1
Ъ
186
Лекция 8 Численные методы решения задачи Коши для систем ОДУ
Обычно также используют условие, предложенное Куттой без
объяснений и не являющееся обязательным [3]:
Получим простейшие методы Рунге-Кутты. Для этого введем
погрешность
г
з=о
и представим ее в виде разложения в ряд Маклорена
h
где ^ /р+1\|Г^дН ~" остаточный член ряда; 0 < в < 1.
Будем полагать (что можно сделать соответствующим выбором
коэффициентов)
В таком случае разложение для f (т) имеет более простой вид:
^>@т) ,
*{Т) (р + 1)! Т '
где р — порядок точности метода.
1. Пустьр = 1,г = 1. Тогда
?(т) = u(t + г) - «(«) - ттп/(«, и),
отсюда
Г@) = «"(* +г).
Видно, что условие ?@) = 0 выполняется лишь при 71 = 0, что
соответствует методу Эйлера, при этом
где Яг — невязка, имеющая первый порядок малости по т.
187
Лекции по вычислительной математике
2. Рассмотрим более сложный случай: р = 2, г = 2. Тогда
?(т) = u(t + г) - u(t) - T7i/(t, u) - T*y2f(t + а2т, и + faiTf(t, и)).
Вводя обозначения
,U = U-\-02\Tf{t, U),
получим следующие выражения для производных погрешности ? по
аргументу г:
?{т) = «'(* + т) - -nf(t, и) - -»/(«, «)-
-па[«а#(*. в) + A
Г(т) = и"(* + г)-272[oa/[(t, в
Г (г) = «"(< + г) - Зта[о^/Й(*, fi)
+/32i/l(*.u)/(«,«)]+o(r).
Поставив в эти выражения следующие равенства:
получим
= 0,^@) = (l-7i-
/i(«, u)/(«, u),
Г@) = A - 37ao3)/S(*f u) + B -
+A-
Второе из полученных соотношений выполняется при 71 + 72 = 1»
третье — при 1 - 272^2 = 0,1 - 272Д21 = 0.
Таким образом, имеется три алгебраических уравнения и четыре
параметра. Эти уравнения определяют однопараметрическое
семейство схем. Задавая один из параметров, можно получать
различные методы Рунге-Кутты с аппроксимацией второго порядка. При
формально одинаковом порядке аппроксимации они будут
обладать различными свойствами (устойчивостью, реальной
погрешностью).
188
Лекция 8 Численные методы решения задачи Коши для систем ОДУ
Так, при 7i = 1/2, имеем 72 = 1/2, аг = 1,/fei = 1; метод будет
выглядеть следующим образом:
Положив 7i = 0, имеем 72 = l,c*2 = 1/2,/З21 = 1/2;
соответствующий метод будет:
3. При p = 2, r = 3 получаем систему уравнений для коэффициентов:
«2 =#21,<*3 = &
а3 (а3 - а2) - /?32а2 B - За2) = 0,
= 1/6,7гаг + 7заз = 1/2,71 + 72 + 7з = 1,
имеющую бесконечное множество решений. Расчетные формулы
одного из возможных методов имеют вид
fci = rf{tn, un), k2 = г/ ltn Н- -, un + у J ,
= iin H-
6
В случае р = 4, г = 4 имеем двухпараметрическое семейство методов
Рунге-Купы, из которого наиболее известен следующий «классический»
метод:
,fc2 = r/Un + ^, tin + yj,
2fc2
6
189
Лекции по вычислительной математике
В представлении Бутчера хорошо известные методы численного
решения ОДУ выглядят следующим образом. Метод Эйлера (первый
порядок аппроксимации) табл. 8.2, метод Эйлера с пересчетом (второй
порядок аппроксимации) — табл. 8.3. Метод Хойна третьего порядка
аппроксимации — табл. 8.4. Метод Рунге-Кутты третьего порядка
аппроксимации — табл. 8.5.
Таблица 8.2
0
0
1
Таблица 8.3
0
1/2
1/2
0
1
Таблица 8.4
0
1/3
2/3
1/3
0
1/4
2/3
0
3/4
Таблица 8.5
0
1/2
1
1/2
0
1/6
1
2/3
1/6
Значения коэффициентов классического метода Рунге-Кутты
(четвертого порядка аппроксимации) указаны в табл. 8.6. Правило трех
восьмых (четвертый порядок аппроксимации) представлено в табл. 8.7. Этот
метод имеет, по-видимому, наименьшую погрешность среди явных схем
Рунге-Кутты четвертого порядка аппроксимации. Метод Бутчера
(шестой порядок аппроксимации) указан в табл. 8.8. Очевидна связь между
методами, приведенными в таблицах (8.5) и (8.6) с формулой Симпсона
численного интегрирования.
По-видимому, наивысший порядок аппроксимаций (десятый) был
получен в работах Куртиса [4], позже — Хайрера [5]. Соответствующие
коэффициенты не приведены ввиду их громоздкости.
В численной практике используются также так называемые вложен-
190
Лекция 8
Численные методы решения задачи Коши для систем ОДУ
Таблица 8.6
0
1/2
1/2
1
1/2
0
0
1/6
1/2
0
2/6
1
2/6
1/6
Таблица 8.7
0
1/3
2/3
1
1/3
-1/3
1
1/8
1
-1
3/8
1
3/8
1/8
Таблица 8.8
0
1/2
2/3
1/3
5/6
1/6
1
1/2
2/9
7/36
-35/144
-1/360
-41/260
13/200
4/9
2/9
-55/36
-11/36
22/13
0
-1/12
35/48
-1/8
43/156
11/40
15/8
1/2
-118/39
11/40
1/10
32/195
4/25
80/39
4/25
13/200
ные формулы Рунге-Кутты [3,6,7], в которых наряду с соотношением
= ип
... + 72^2)
(8.5)
используется соотношение того же вида, но с другим набором весовых
множителей
, (8.6)
причем порядки аппроксимации в них различаются: q — порядок
аппроксимации (8.6), ар — (8.5). В этом случае порядок метода указывается, как
Р(я)у а таблица Бутчера имеет вид табл. 8.9. Последнюю строчку в этой
таблице иногда называют оценщиком погрешности.
Приближения точного решения с разными остаточными членами
(8.5) и (8.6) позволяют оценить погрешность численного метода,
полученную в конкретном расчете, и служат для повышения точности еще на
один порядок в каждой точке или (что бывает чаще) для автоматического
выбора длины следующего шага интегрирования (см. 1).
191
Лекции по вычислительной математике
Таблица 8.9
0
«2
«3
Otr
Ui
V>2
/hi
Al
A-i
7i
7i
032
A*
72
72
...
Ar-1
7r-i
7r-i
7r
7r
Приведем несколько наиболее известных вложенных методов Рун-
ге-Купы. Метод Фельберга 2C) представлен в табл. 8.10, метод Ческино
2D)-втабл. 8.11.
Таблица 8.10
0
1
1/2
1
1/4
1/2
1/6
1/4
1/2
1/6
0
4/6
Таблица 8.11
0
1/4
1/2
1
1/4
0
1
1
1/6
1/2
-2
-2
0
2
2
4/6
0
1/6
Метод Кутты-Мерсона 4E) приведен в табл. 8.12. Этот метод —
наиболее простой среди вложенных методов Рунге-Кутты порядка 4E),
поскольку требует небольшого числа обращений к функциям вычисления
правых частей системы уравнений (8.1) и имеет простые коэффициенты.
Таблица 8.12
0
1/3
1/3
1/2
1
1/3
1/6
1/8
1/2
1/2
1/6
1/6
0
0
0
0
3/8
-3/2
-3/2
0
2
2
2/3
0
1/6
192
Лекция 8
Численные методы решения задачи Коши для систем ОДУ
Для S этапного метода Кутты-Мерсона 4E) приведем подробные
расчетные формулы:
+ ^ " +
ki=Tf(tn,
т
Рассмотрим вкратце другие вложенные методы и соответствующие
им таблицы. Метод Фельберга 4E) представлен в табл. 8.13, метод Дорма-
на-Принса 5D) — в табл. 8.14 (см. также [6]).
Таблица 8.13
0
1/4
3/8
12
1
1
2
1/4
3/32
1 У32
2 197
439
Щ
8
27
25
21fi
16
9/32
2 107
-8
9
0
0
3 6BU
о э44
2 565
1 408
6 656
12 825
845
4104
4 104
2 1У7
4 104
5в 4.ЧП
14
4Я
1
~50
0
55
Этот метод замечателен тем, что он не только минимизирует
остаточный член в оценщике погрешностей, но и требует меньшей памяти
Для хранения таблицы коэффициентов метода. Действительно,
последняя строка C совпадает с одной из строк у.
С методом Фельберга более высокого порядка 7(8) можно
ознакомиться в [ [8]], значения его коэффициентов приведены в табл. 8.15.
Среди современных методов решения нежестких систем ОДУ
наилучшие результаты дает метод Дормана-Принса 8G). Он обладает
наименьшей погрешностью среди всех схем порядка 8, коэффициенты
указаны в табл. 8.16,8.17. С вложенными формулами Рунге-Кутты, разрабо-
в 90-х годах, можно ознакомиться в монографии [10].
7—3339
193
Лекции по вычислительной математике
Таблица 8.14
0
1/5
3/10
4/5
|
1
1
1/5
3/40
44/45
19 STI
6 561
9 017
W
Щ
5 Г79
57 6ПП
9/40
-56/15
'2Ь 360
2 187
355
33
0
0
0
32/9
64 44»
*ш
500
1 UP
500
1113
7 571
729
49.
[25
\Ш
[25
Ш
Ш
НО
5 163
1 1о/
6 784
2 18*
92 097
339 2ПП
11
l?V
2 1ПП
0
40
Методы Рунге-Кутты — это одношаговые методы, так как
позволяют найти значение искомой функции в точке ?n+i используя только
значение функции в точке tn. При этом не учитывается информация о
функции, накопленная на предыдущих этапах расчета. Такая информация
может быть полезна при решении жестких задач или при автоматическом
выборе следующего шага интегрирования.
Один из способов учета предыстории заключается в использовании
общих многошаговых методов. Частный случай — методы Адамса —
рассмотрен в следующем параграфе. Другой способ учета описан в 1.
Таблица 8.15
0
2/27
1/9
1/6
5/12
1/2
5/6
1/6
2/3
1/3
1
0
1
2/27
1/36
1/24
5/12
1/20
-25/108
31/300
2
-91/108
'J'Sb'S
4100
3/205
41/840
0
1/12
0
0
0
0
0
0
0
0
0
0
0
0
1/8
-25/16
0
0
0
0
0
0
0
0
0
0
25/16
1/4
125/108
0
-53/6
23/108
_Mi
0
~Ш
0
0
1/5
-65/27
61/225
704/45
-976/135
44УЬ
1025
0
4496
102ft
0
0
125/54
-2/9
-107/9
311/54
82
-6/41
-На
34/105
34/105
13/900
67/90
-19/60
2133
4100
-3/205
21 УЗ
41OO
9/35
9/35
3
17/6
&
-3/41
51
9,1
9/35
9/35
-1/12
_45_
1в4
3/41
Iftd
9/280
9/280
I»
41
6/41
12
41
9/280
9/280
0
0
41/840
0
1
0
41/840
0
41/840
Общие условия аппроксимации методов Рунге-Кутты и барьеры Бутче-
ра. Вернемся к общей записи метода Рунге-Кутты (8.4) и
соответствующей таблице Бутчера. Рассматривается задача ^^ = f {t, u),
u@) = uo,
194
Лекция 8
Численные методы решения задачи Коши для систем ОДУ
Таблица 8
Таблица 8.17
i
<*i
1i
li
1
1
14 005 451
335 480 064
13 451 932
455 176 623
i
7i
7i
2
0
0
3
75
0
0
9
5 490 023 248
1 041 891 430
1 371 343 529
* 86* 5/4 721
1 518 517 206
4
8
0
0
5
rfi
0
0
6
8
59 238 493
1 068 277 825
808 719 846
976 000 145
10
1 201 146 811
1 299 019 798
_}
760 417 239
151 165 29
322 736 535
9
7
400
1
t
11
118 iPlb 643
751 i jo 087
5 301 2o8
667 516 719
181 606 676
758 867 731
L /57 004 468
i 645 159 321
8
93
200
561 Ш 985
797 845 732
656 0
265 f
12
1
528 747 749
2 220 607 170
45 339
91 186
13
1
1
0
а численный метод имеет вид
k2 = f(tn + a2r, un
k3 = f (in + a3r, un
где fcj
kr = f (tn + arr, un
un+i = un +
_ вспомогательные векторы.
+ /?32к2)),
... + /3r,r-ik2)),
.. + 7rkr)
195
Лекции по вычислительной математике
Наряду с явными, рассмотрим также неявные методы Рунге-Купы,
определенные как
= f (tn + o:2r, un + r
arry
un+i = un
таблица Бутчера для неявных методов примет вид
«1
<*3
ar
(hi
Ai
/?rl
7i
/?12
Ai
/З32
)9r2
72
A,r-1
#2,r-l
/?3,r-l
Prr-1
7r-l
LJOf
г^Зг
/?rr
7r
Для вывода условий аппроксимации общего метода Рунге-Кутты
необходимо действовать так же, как описано выше. Для этого введем
погрешность
и представим ее в виде разложения в ряд Маклорена. Приравнивая
члены при одинаковых степенях шага г, получим условия аппроксимации
метода. Для того чтобы метод имел порядок 3, необходимо выполнение
следующих условий: г
Е-*-1»
i=l к=1
i=l fc=l 1=1
i=l ifc=l /=1
196
Лекция 8 Численные методы решения задачи Коши для систем ОДУ
причем эти выражения упрощаются, если воспользоваться
необязательными условиями Купы. При повышении порядка аппроксимации
метода возникают дополнительные условия на коэффициенты, система зна-
яительно усложняется.
Для того чтобы построить аппроксимирующую схему (метод Рунге-
Кутты) необходимо найти набор коэффициентов метода. Как было
показано выше, в случае двух стадий метода такой набор коэффициентов — не
единственный, существует континуум методов второго порядка
аппроксимации. Континуум решений система уравнений порядка для явных
методов Рунге-Купы имеет и в случае явных методов с тремя или четырьмя
стадиями. Но для пятистадийного метода система уравнений порядка
является несовместной. Это утверждение было доказано Бутчером и носит
название «первый барьер Бутчера». Его обычно формулируют в виде
теоремы [3].
Теорема (первый барьер Бутчера). Среди явных методов Рунге-Кутты
с числом стадий пять не существует методов пятого порядка
аппроксимации.
Для повышения порядка до пятого приходится использовать шести-
стадийные методы. При увеличении числа стадий возникает второй
барьер Бугчера — порядок аппроксимации метода, начиная с семи стадий,
оказывается уже на 2 ниже, чем число стадий. При увеличении порядка
аппроксимации метода приходится значительно увеличивать число
стадий — барьеры Бутчера встречаются чаще.
Наличие такого барьера — одно из следствий быстрого роста
констант Лебега при интерполяции на равномерной сетке. Дело в том, что
явные методы Рунге-Кутты тесно связаны с квадратурными формулами
интерполяционного типа. Достаточно очевидно, что классический
метод Рунге-Кутты порядка 4 основан на применении формулы Симпсона,
а правило 3/8 — на одноименной квадратурной формуле. Как было
показано в лекции 7, с повышением порядка аппроксимации квадратурные
формулы перестают быть правильными, а это следствие роста
константы Лебега. Тогда и появляются барьеры Бутчера при построении методов
Решения систем ОДУ.
От этого недостатка свободны некоторые неявные методы,
основанные на квадратурных формулах Гаусса.
8.3. Методы Адамса
Для решения ОДУ или систем ОДУ существуют одностадийные
методы Адамса (линейные многошаговые методы), суть которых
заключали в следующем.
197
Лекции по вычислительной математика
Пусть известно приближенное решение в некоторых узлах
расчетной сетки: tni ?п-ъ • • •, tn-m. В окрестности этих узлов заменим f(t, x(t))
интерполяционным полиномом, записанным в форме Ньютона ([1, 2], а
также лекция 6):
n, *n-l, *»-2, *n-3)(t-*n)(*-*n-l)(t-*n-2) + .-.
Для того чтобы вычислить решение в точке п +1, запишем его в
интегральном виде
tn + l tn+i
un+i =un+ J /(*, ti(t)) A = У /(*) A
и подставим в него интерполяционный полином с переменным шагом
Wn + Tnf(tn) + у /(tin, Wn_i)+
2
«n» «п-ь «„-a) + 5j Br^ + 8rnrn_x+
12
Здесь rn = tn+i - tn, /(unj tin-i), /(«n, ttn-i, ttn-2) и т.д. -
разделенные разности.
Эта формула четвертого порядка точности. Если опустить
последнее слагаемое, то получим формулу третьего порядка, если опустить еще
и предпоследнее, то — второго, и т. д. Если же положить тп = const, то
формула значительно упростится:
г2 5 3
un+i = ип + т/п + — Аг/п + — т3Д2/п + - т4Д3/п,
где Akfn — fe-я конечная разность.
Для того чтобы начать вычисления по данному варианту метода
Адамса, необходимо знать решение в четырех точках. Это можно сделать,
например, с помощью методов Рунге-Кутгы. Кроме того, коэффициент
при погрешности, например, для метода четвертого порядка точности
Рунге-Кутты существенно меньше соответствующего коэффициента ддя
метода Адамса.
198
лекция 8 Численные методы решения задачи Коши для систем ОДУ
Первые четыре метода Адамса, от первого до четвертого порядка
точности с постоянным шагом интегрирования, представляются в виде
- /п - - /п_1 1 ,
/55 _ 59 , 37 , 9 . \
ип+1 = ип + т ^- /„ - - /„_! + - /п_2 - - /п_з j •
В общем виде методы Адамса могут быть записаны следующим
образом:
ki
= ип + т
i=o
Значительно большее значение в вычислительной практике имеют
неявные методы Адамса, которые можно записать как
3=0
Первые четыре неявных метода имеют вид
к = 0 ; un+i = ип + т/п+1,
к = 1 : un+i = wn + r f - /n+1 + - fn J ,
/ + / ^
+ ^2/n 12 ^n
19 ^5Г
_/n__/n.1 +
Первая и вторая формулы — неявный метод Эйлера и неявный
метод трапеций соответственно. Порядок аппроксимации приведенных
методов — с первого по четвертый соответственно.
Для к = 8 коэффициент 7j можно представить в виде таблицы
(табл. 8.19) и ввести следующие обозначения: А^г/п = Ajfn - AJ/n-i —
«разности назад», щ — коэффициенты, которые можно представить в ви-
Де таблицы (для к = 8 табл. 8.20). Для к = 1 получается уже знакомый
явный метод Эйлера.
199
Лекции по вычислительной математике
Таблица 8.18
J
ъ
0
1
1
2
~2
3
~24
4
— 720
5
-ш
6
-8П4ЯП
7
-2ТТа5
8
33 У53
Я Й2Я ЯОО
Таблица 8.19
3
Vi
0
1
1
?
2
5
Т?
3
л
4
5
288
6
7
5 257
17 280
8
1 U7U U17
Ч в2Я 800
8.4. Оценка погрешности
8.4.1. Автоматический выбор шага интегрирования
Рунге предложил простое правило оценки точности метода,
основанное на проведении вычислений с разными шагами интегрирования.
Основная идея правила Рунге заключается в следующем.
Погрешность численного метода порядка р - 1 в точке U = гт
представляется в виде
Если выполнить аналогичные вычисления с шагом вдвое
меньшим, г/2, то получим
После вычитания из первого соотношения второго
откуда
гр 2P - 1
Подставив выражение для С во второе соотношение, получим
т.е. погрешность метода, с точностью О(т*+1) оценивается по простой
формуле
е =
2Р-1 - 1'
200
Численные методы решения задачи Коши для систем ОДУ
Это правило используется не только для оценки погрешности
вычисления, но и для автоматического выбора шага интегрирования. Для
эТОго на каждом шаге вычисления производятся трижды: с шагом тис
двумя шагами т/2. Полученные значения ип и игп используются для
вычисления реальной погрешности е (точнее, оценки ее главного члена).
Если величина е превышает некую заданную (или заранее выбранную)
константу so, то шаг интегрирования уменьшается; если, напротив, е
существенно меньше го, то г увеличивается.
Разумеется, алгоритмы выбора шага интегрирования могут
основываться и на иных принципах. Например, можно выбрать г
адаптирующимся к решению: уменьшать при увеличении абсолютной величины
производной и увеличивать при ее уменьшении, т. е. вычислять т, как
функцию от ||и?||.
Управление длиной шага в методах Рунге-Кутты осуществляется на
основе сравнения с некоторой задаваемой величиной Т,
характеризующей требования к погрешности на каждом шаге численного
интегрирования системы.
Пусть используется метод с порядком аппроксимации р. Тогда
главный член погрешности метода е, определяемый по правилу Рунге, или,
в случае использования вложенных методов Рунге-Кутты,
представляющий собой модуль разности между приближениями к решению,
вычисленными по формулам (8.5) и (8.6), имеет вид
Положим теперь Т = С2 т*^1. Тогда для величины максимального
значения нового шага интегрирования rnew получаем
1/&Н-1)
Tnew — ,
где /3 — так называемый гарантированный множитель. Он служит для
того, чтобы в случае резкого уменьшения шага (например, при выходе на
жесткий участок при решении умеренно жестких систем) численный
метод оставался устойчивым.
Кроме того, гарантированный множитель помогает избежать
слишком быстрого увеличения величины шага интегрирования в случае, когда
Реально полученная погрешность мала. Обычно величина гарантийного
множителя принимается за 0,5; 0,8; 0,9 или @,25 + 0,38)гНр+1\
Если при выполнении очередного шага погрешность е не превосхо-
Дит величины Т, то шаг считается принятым, а дальнейший расчет
продолжается с шагом rnew, в противном случае шаг считается отклоненным,
и проводится пересчет с новым значением шага для перехода от tn
201
Лекции по вычислительной математике
На практике применяют модернизации алгоритма выбора шага. Так,
если реальная ошибка е мала, то предлагаемый алгоритм позволяет
выбрать очень большой шаг по т. В таком случае применяют алгоритм
Г / /Г\1/(р+1)\1
in ^ Дпах, max l/?min, /3 f — J I \ .
Tnew = Г • mill
Здесь /?max,/?mm — максимальное и минимальное разрешенное
изменение шага интегрирования.
Другая возможность регулировки шага численного интегрирования
для методов Рунге-Купы заключается в объединении достоинств
методов Рунге-Купы и Адамса. Первые из них допускают легко
регулировать шаг интегрирования, а вторые помнят часть предыстории изменения
функции.
Более тонкий алгоритм управления величиной шага получается с
учетом величины ошибки на предыдущем шаге
-/?
''"new
т. е. фактически гарантийный множитель зависит от ошибки на
предыдущем шаге. Обычно при таком выборе управления длиной шага полагается
Такой выбор регулировки шага повышает устойчивость численных
методов Рунге-Кутты не очень высокого порядка. Для метода Дормана-
Принса порядка 8G) лучшие результаты дает /3 « 0,04.
В [10] показано, что такой метод выбора шага является решением
задачи оптимального управления с учетом пропорциональной обратной
связи и интегральной обратной связи. Там же показано, что оптимальный
выбор показателей степени есть а « 0,7/{р + 1), /3 « 0,4/(р + 1).
8.5. Устойчивость методов Рунге-Кутты
Для исследования устойчивости методов Рунге-Купы для
численного решения задачи
«f(t,u), u@) = uo
представим ее дискретный аналог в виде
Un+1r~Un=F(tn,un), (8.8)
здесь F(?, x) — функция приращения метода Рунге-Кутты, которая,
конечно, связана с функцией правой части системы ОДУ.
202
Лекция 8 Численные методы решения задачи Коши для систем ОДУ
Теорема 2 (Устойчивость методов Рунге-Кутты [3, 9]). Пусть f(t,x)
Дипшиц-непрерывна по второму аргументу, т. е.
причем это условие выполняется для каждого t,CФ С(т) и Ст < 1.
Тогда разностное уравнение (8.8) устойчиво и имеет место оценка
||un - vn|| < eC2*||uo - vo|| + -^—. (8.9)
Здесь un, vn —решения близких систем разностных уравнений:
Un-hl " Un
г
Vn+1 - Vn
us— максимальная погрешность при вычислении правой части системы,
т. е. для всех п (включая нуль)
а постоянная Съ незначительно отличается от С.
Сформулируем вначале следующую лемму.
Лемма 1. Пусть С — постоянная Липшица для функции правых частей
системы (8.1), тогда функция приращения F(?, u) для метода (8.8)
удовлетворяет следующему неравенству:
где
С2 = C(J2 Ы
Суммирование в правой части последнего равенства ведется по
каждому индексу от 1 до г — числа стадий метода. Число сумм в скобках,
конечно, тоже равно г. Отметим также, что если в таблице Бутчера все
коэффициенты неотрицательны (такой метод Рунге-Кутты, по аналогии с
методом численного интегрирования, назовем правильным), то из условий
порядка (аппроксимации) будет следовать, что в скобках стоят первые г
членов разложения еСт в ряд Тейлора. Отсюда необходимое требование
203
Лекции по вычислительной математике
(в формулировке теоремы) к малости Ст. В случае наличия отрицатель-
ных коэффициентов в таблице Бутчера константа Липшица С2
увеличится незначительно — число стадий метода конечно и невелико (в
настоящее время известны методы максимум с 17 стадиями, [6]).
Доказательство данной леммы довольно простое, но громоздкое.
Читатель может проделать это самостоятельно.
Доказательство теоремы.
Рассмотрим эти близкие уравнения. Вычитая из первого уравнения
второе, получим
||un - vn|| +r||F(t,un) -F(t,vn)|| + 2re (8.10)
или, учитывая условие Липшица,
A + C2r)||un - vn|| + 2re.
Здесь константа C2 — постоянная Липшица функции приращения
метода Рунге-Кутты, выражение для нее приведено выше в
формулировке леммы 1.
Далее, применяя последовательно это неравенство, получим
оценки:
||ui - vi|| < A + C2t)||uo - vo|| + 2rc,
||u2-v2|| ^ (l+C2r)||ui-vi||+2re ^ A + C2tJ||uo-v0||+2t?[1+A+C2t)],
||u3 - v3|| < A + C2r)||u2 - v2|| + 2re ^
< A + C2rK||uo - vo|| + 2re[l + A + C2r) + A + C2r)%
откуда, после суммирования прогрессии, имеем
||un - vn|| < A + C2r)n||uo - vo|| (
Далее полагаем A + C2r)n = A + C2r)tlT » eCat при C2r < 1.
После подстановки экспоненты в последнюю оценку получим
неравенство (8.9). ¦
204
Лекция 8 Численные методы решения задачи Коши для систем ОДУ
Заметим, что экспоненциальный множитель в неравенстве (8.9) при
больших t велик, а оценка, в наиболее общем случае, в предположении
Липшиц-непрерывности функции F(u), неулучшаема. Однако в
некоторых важных частных случаях эту оценку можно улучшить, рассматривая
более тонкие свойства рассматриваемой функции. Докажем следующее
утверждение [9], рассматривая задачу Коши для системы ОДУ.
Утверждение. Пусть матрица
строго отрицательна, т. е.
для любых f, u и а > О (траектория, в окрестности которой выполняется
это условие, называется устойчивой).
Тогда при интегрировании правильным методом Рунге-Купы к-го
порядка аппроксимации погрешность приближенного решения есть О(тк
при любом t > О при выполнении условий ат < 1.
Утверждение будет доказано, если в оценке устойчивости метода не
будет содержаться множитель ect.
Доказательство.
Из полученного в теореме 2 неравенства (8.9) имеем
||un+1 - vn+1|| < ||(un - vn) + т (F(un) - F(vn))|| + 2rey
где F(u) — функция приращения метода Рунге-Кутты для систем ОДУ.
Оценим норму разности в правой части неравенства, используя
более точные свойства функции F(u), чем Липшиц-непрерывность:
1
F(u) - F(v) = F(u + s(u - v))|*lj = / ^F(u + s(u - v))ds =
0
1
= / F'(u + s(u - v))(u - v)ds.
о
Здесь произведена замена переменных u(s) = v + s(u - v).
Поскольку
l
u — v = / (u — v) ds,
о
205
Лекции по вычислительной математике
то получаем, что
||(u-v) + r(F(u)-F(v))|| =
1 1
j (E + rF'u(u + s(u - v))) (u - v) ds < / И E + rF'ull || u - v|| da.
о о
(8.11)
Оценим норму || E + rF'u || . Для этого сначала оценим квадрат нор-
НЕ + гГ.||" . sup
= sup
Здесь использовано определение нормы матрицы (лекция 2)
= sup
где В — матрица, ? — вектор из рассматриваемого пространства.
При малых г, пренебрегая членами порядка О(т2), из последнего
неравенства получаем требуемую оценку:
Тогда из (8.11) имеем
1
ЦБ +-rF'J|||u - v||<b < A - or)||u -
о
откуда
||un+i - Vn+iH ^ A - or)||un - vn|| + 2re.
Рассмотрев, как и ранее, цепочку неравенств
||ui - vi|| < A - ат)||ио - vo||
||u2 - v2|| < A - ат)\\щ - vi|| +
получим
Ни» - vn|| < A - ar)n||uo - vo|| + 2™\~_%\пат) '
или
||un - vn|| < A - ar)n||uo - vo|| + -. (8.12)
a
Утверждение доказано. ¦
206
Лекция 8 Численные методы решения задачи Коши для систем ОДУ
Пусть теперь (A(u)f,?) ^ 0 т.е. рассматриваются нейтральные,
или «не неустойчивые» траектории исследуемой системы обыкновенных
дифференциальных уравнений. В этом случае аналогичным образом
показывается, что
2
Тогда, проведя аналогичные выкладки, получим
||un+i - vn+1|| < A + С2т2) ||и» - vn
откуда
Для метода к-то порядка аппроксимации е = О(тк), к ^ 0. В этом
случае решения близких систем на п-ы шаге по времени отличаются на
величину
||un - vn|| ^ eC2r2n||uo - vo|| + O(rk~l). (8.13)
Отсюда видно, что при п ~ г (или tn = пт ~ г) численное
решение имеет точность О(тк~г). Другими словами, на конечных
интервалах времени t ~ ОA) точность метода О(тк), на больших же временах
t ~ О(т~1) точность понижается до t ~ О(тк~1).
Такие случаи возникают, когда имеется необходимость проводить
численные расчеты при исследовании процессов с большим количеством
колебаний, вращений и т.д. Важно отметить то, что полученные
оценки погрешности численного решения получены с использованием более
сильных, чем условие Липшиц- непрерывности, свойств правых частей
рассматриваемых дифференциальных уравнений.
8.6. Задачи
1. Семейство явных методов Рунге-Кутты
Пусть дана следующая система обыкновенных дифференциальных
уравнений:
y = f(*;y),
У@) = у0.
Для численного решения задачи проведем следующие вычисления:
k2 = f(tn + с2т,уп
207
Лекции по вычислительной математике
8-1
= Щп + са г, уп + г
Г=1
Уп+i =
Р=1
где a9b9c — действительные числа (вектор уп считается известным,
т. к. уо — начальные условия, по этим значениям можно найти ух
и т.д.).
Численный метод называется явным методом Рунге-Кутты порядка
S или S-стадийным.
Будем также записывать метод Рунге-Кутты в виде таблицы Бутче-
ра — таблицы коэффициентов метода:
0
с8
0
Ь21
bsl
ai
0
0
Ь32
а2
0
0
Ь88-1
a8-i
0
0
0
а8
Для метода порядка S вывести условия, связывающие
коэффициенты таблицы Бутчера, необходимые для обеспечения р-го порядка
аппроксимации метода (р^ s).
Указание 1. Разложить проекцию на сетку точного решения задачи
Коши в ряд Тейлора в окрестности точки tn. Использовать
следствия исходного дифференциального уравнения, например:
dt
ду dt
ду
Указание 2. Для простоты все вычисления провести для случая
одного нелинейного уравнения. Требуемые условия приведены в [3,
с. 153,162]. В качестве упражнения найти все явные методы Рунге-
Кутты с5 = р = 3,5 = р = 4.
2. Семейство неявных методов Рунге-Кутты
Метод вида
ki = f (tn + cit, yn + т
208
Лекция 8 Численные методы решения задачи Коши для систем ОДУ
8
, уп + т
z=i
а
Уп+i = +
где ki,..., ks определяются как решение нелинейной системы
уравнений, называется неявным методом Рунге-Кутты порядка S (S-
стадийным). Как будет выглядеть для него таблица Бутчера?
Вывести условия аппроксимации порядка р на решении (р=1,2,3,4;
5 = 2).
Следует обратить внимание на то, что для определения kb k2,, k5
необходимо решать систему нелинейных уравнений. Какова ее
размерность?
В чем состоит особенность методов с bij = 0 при j > г?
(Это так называемые полуявные или диагонально-неявные
методы).
3. Управление длиной шага
(а) Система ОДУ решается с помощью метода Рунге-Кутты
порядка аппроксимации р > 1. Описать алгоритм выбора шагов
интегрирования, таких, чтобы достигнутая погрешность на
каждом из них не превосходила заданную величину е.
Решение. Пусть переход от значения уп к yn+i осуществляется
с шагом h. Тогда в результате работы метода получим
уп+1 = ~
где уп+1 — точное решение задачи, взятое в точке n+1, C/ip+1 —
главный член погрешности, постоянная С зависит как от
коэффициентов конкретного метода, так и от решения задачи.
(Из решения задачи 8.1 следует, что разложения yn+i и уп+1 в.
ряд Тейлора совпадают до членов с номерами р+1
включительно).
Осуществим теперь переход от уп к yn+i за два этапа, используя
тот же метод Рунге-Кутты с шагом h/2. Тогда имеем
=»+i = yn+i + 2C(/i/2)p+1 + O(/ip+2). (8.15)
Так как С оценивается через максимальное по абсолютной
величине значение (р + 1)-й производной на отрезке [?n, tn+i],
209
Лекции по вычислительной математике
можно считать, что в последнем выражении константа
совпадает с константой в предыдущем равенстве. Используя два
равенства, возможно либо явно вычислить Chp и исключить его
из (8.15), повысив точность аппроксимации на порядок,
либо поступить следующим образом. Вычитая из (8.15) равенство
(8.14), имеем
отсюда главный член погрешности (8.15) будет равен
<8Л6>
Необходимо выбрать шаг интегрирования hnew таким
образом, чтобы главный член погрешности не превосходил
заданное значение (CAJ+J < е):
AnewV+yn+1-^
\ h ) 1-2-1-
откуда имеем
h. (8.17)
Если же на текущем шаге погрешность (8.16) превышает е , то
шаг считается отклоненным и расчет выполняется снова со
значением, найденным по формуле (8.17).
(Ь) Система ОДУ решается с помощью явных методов р и р +1
порядка аппроксимации. На каждом шаге погрешность расчетов
не должна превышать е. Как выбрать длину шага
интегрирования?
Рассуждаем аналогично тому, как это сделано в пункте 1. При
расчете методом р порядка аппроксимации имеем
ар + 1 порядок дает
„?# = y»+i + Х2^+2 + O(/iP+3). (8.19)
Отсюда сразу получаем Chp+l ~ у?+х - y^Xl- ®ти величины
сравниваются с заданной точностью.
210
Лекция 8 Численные методы решения задачи Коши для систем ОДУ
Существует семейство методов Рунге-Кутты, таких, что члены
погрешности для результата старшего (р +1) порядка
минимизируются, а вычисление погрешности р-го порядка
используется лишь для управления длиной шага. При этом для порядка
р и р+1 коэффициенты Ь, с в таблице Бутчера B.4.1) совпадают,
а различаются лишь коэффициенты а. Кроме того, Ь8* = ах(ур).
Такие методы построены Дорманом и Принсом и носят их имя.
4. Рассмотрим уравнение Ферхюльста (логистическое уравнение),
описывающее динамику численности популяции:
у), (8.20)
У@)=2/о;0<г/о< 1,а>0.
(a) Решить уравнение (8.20) точно, учитывая, что это уравнение в
разделяющихся переменных. Получившаяся кривая — график
точного решения — носит название логистической кривой.
(b) Рассмотреть для (8.20) явный метод Эйлера:
Уп+i = Уп + тауп A - уп). (8.21)
При каких шагах т метод является устойчивым?
Решение. При t —> оо точное решение (8.20)
асимптотически стремится к единице. Очевидно, что последовательность
уп = 1 является и решением (8.20). Непосредственно
проверяется, что (8.21) аппроксимирует (8.20) с точностью О(т). В
случае, если метод (8.21) устойчив, то решение (8.21) сходится к
решению (8.20) и должно выполняться неравенство
|уп+1 - 1| < \Уп - 1| •
Если рассмотреть (8.21) как запись метода простых итераций
для (8.20), то он должен сходиться к корню у = 1 при любом
начальном приближении уо, лежащем между 0 и 1.
Перепишем (8.21) в виде
zn+i = bzn(l - Zn)y zn = —Уп;Ь= 1+та (8.22)
та 4-1
и для (8.22) воспользуемся результатами, полученными в
Лекции 5. Таким образом, условия устойчивости для (8.21) будут
следующими:
Ь = 1 + та < 3, откуда г < 2/а.
211
Лекции по вычислительной математике
(с) Описать сценарий развития вычислительной неустойчивости
для задачи (8.21), можно воспользоваться материалом лек-
#ции 5. Следует обратить внимание на то, что когда метод
неустойчив, в отличие от линейных задач, модуль разности
численного и точного решений остается ограниченным при
любом сколь угодно большом t при 2/а ^ г < 3/а.
8.7. Задачи для самостоятельного решения
5. Для уравнения Ферхюльста (8.20) рассмотреть неявный метод
Эйлера
= Уп + rayn+i(l - 2/n+i). (8.23)
Для определения 2/n+i можно воспользоваться (8.23), решая его как
квадратное уравнение. Что можно сказать про устойчивость
такого метода? Как правильно выбрать корень квадратного уравнения
(8.23)?
6. Реализовать явный и неявный методы Эйлера и метод Рунге-Кутты
порядка аппроксимации 4 для системы уравнений Лотки-Вольтерра
«хищник—жертва», которая описывает динамику простейшей
экосистемы:
х = ах — ху,
у = Ьху- су,
х@)=хо >
Здесь х — безразмерная численность «жертв», у — численность
«хищников», а, 6, с — положительные константы, Ь < 1.
Построить графики численных решений на фазовой плоскости (х, у)»
Построить там же график точного решения. Объяснить полученные
результаты. Что будет в случае, когда конечное время, до которого
происходит расчет, Т > 1?
Построение тонного решения, в [13, с. 36]. На фазовой плоскости
точному решению соответствует кривая
&у_ __ (Ьх - с)у
dx x(a - у) '
212
Лекция 8 Численные методы решения задачи Коши для систем ОДУ
Вводя другую параметризацию кривой у(х), получим, что она может
быть описана системой уравнений
dy у
dr
dx
dT
a —
X
bx-
v1
Эта система легко интегрируется, а после исключения параметра г
находим первый интеграл исходной системы.
7. Решить численно систему из предыдущей задачи, когда скорость
размножения жертв является периодической функцией времени:
a (t) = аоA + sin(u;?)), и — параметр. Что происходит с решением
при увеличении ш!
8. Уравнение Ван-дер-Поля [3, с. 115-119]
у@) = ус > 0; у'@) = 0,0 ^ t < 30, а> 0@ + 1000)
описывает нелинейные колебания в различных системах.
(а) Проинтегрировать уравнение численно явными методами Рун-
ге-Купы различных порядков. При каких шагах т методы
становятся неустойчивыми?
Указание: представить уравнение в виде системы
V1 = -Р,
р' = ар(у2 - 1) + 2/,
или в виде
(представление Льенара).
(Ь) Реализовать для уравнения Ван-дер-Поля следующие
полуявные методы Рунге-Кутты:
7 0 71 = ^ (или
1-7
Какой порядок аппроксимации они имеют? Устойчивы ли они?
213
Лекции по вычислительной математике
9. Уравнение Эйлера
Решить численно задачу о колебаниях в системе, где и
возвращающая сила, и коэффициент вязкого трения убывают со временем
(уравнение Эйлера):
х+ ! + Ю0^= О,
где* € [1, 100],хA) = 1,хA) = 1.
Использовать для численного решения сетки с шагом г = 0,1
(a) явный метод Эйлера;
(b) неявный метод Эйлера;
(c) методы Рунге-Кутгы порядка 2,3,4.
Уменьшить г вдвое. Что происходит с решением? Какому решению
верить?
Сравнить численное решение с точным.
Указание. Будем искать точное решение в виде х = ta, где а, вообще
говоря, комплексное. Рекомендации можно найти в [14].
10. Уравнение Эйлера
Рассмотрим более простую систему без трения:
х + 100^ = 0.
Выполнить пункты предыдущей задачи. В чем заключается
разница? Точное решение уравнения можно найти в [ 14] или решить
уравнение самостоятельно, положив х = cba.
11. Уравнение Хатчинсона
Одной из модификаций уравнений Ферхюльста является уравнение
Ферхюльста с запаздыванием (уравнение Хатчинсона):
Заметим, что в качестве начальных условий необходимо задавать
y(t) при t G [-1,0], т. е. не в одной точке, а на отрезке.
214
Лекция 8 Численные методы решения задачи Коши для систем ОДУ
(а) Аналитически решить уравнение так называемым методом
шагов. Задавая конкретную функцию y(t) = g(t) при t e [—1,0]
(начальные условия), интегрируем уравнение Хатчинсона на
полуинтервале при t e]0, 1]:
Зная y(t) на [0,1], можно найти y(t) на [1,2] и т.д.
Если положить y(t) = 1/2 при t e] - 1,0], y(t) = t,y(t) = e"*,
что происходит в точках t = 1,2,3,... п,...?
(Ь) Построить численный метод интегрирования уравнение
Хатчинсона. Найти решение в случае
при а < тг/2, а = тг/2, а > тг/2.
О численном решении уравнений с запаздыванием [3, с. 304-
319].
12. Уравнение Минорского
у + 2гу + о;2?/ + 2^ (t - 1) = еу3 (t - 1)
встречается в различных механических и электротехнических
задачах, в которых имеется запаздывание и нелинейность (здесь ryu,q —
постоянные, 0 < е < 1). Построить численное решение, задавая
начальные данные на отрезке t G [—1,0]. Рассмотреть зависимость
решения от параметров г, и, q. В качестве одного из характерных
случаев значений этих параметров рассмотреть следующие: г = -1, q =
= ( — 1)П, LJ = П7Г.
Подробное качественное исследование уравнения Минорского
представлено в [12, с. 191-211].
13. Уравнение Тннбергена
у + by(t - 1) = e[y(t - I)]3, 0 < е < 1
получено при исследовании циклов в судостроительной
промышленности. Предполагается, что время постройки одного судна
постоянно (и принято за единицу). Превышение темпа закладки
новых судов над средним теоретическим темпом закладки
пропорционально нелинейной функции у - (е/Ь)у3. Для рассматриваемого
215
Лекции по вычислительной математике
случая е > 0 уравнение показывает, что при возрастании
отклонения судостроители должны реагировать относительно более
консервативно из-за недостатка материалов, рабочей силы и т. п.
Решить уравнение численно, задавая начальные данные на отрезке
t е [—1,0]. Рассмотреть характерные режимы: 1) 0 < Ь < 1/е, 2)
Ь » тг/2,3) Ь > тг/2.
Показать, что в интервале 0 < 6 < тг/2 решение уравнения ведет
себя так же, как решение линейного уравнения (е = 0). Исследование
поведения решения уравнения Тинбергена имеется в [12, с. 180-
184].
Литература
[ 1 ] Рябенький В. С. Введение в вычислительную математику. М.: Физмат-
лит,2000.294с.
[2] Бахвалов Н.В., Жидков Н.П, Кобельков Г.М. Численные методы. М:
Лаборатория Базовых Знаний, 2002.632 с.
[3] Хайрер Э., Нерсетт С, Ваннер Г. Решение обыкновенных
дифференциальных уравнений. Нежесткие задачи. М: Мир, 1990.512 с.
[4] Curtis A.R. High-order Explicit Runge-Kutta Formula, Their Uses, and
Limitations // J.Jnst.Math.Applics. 1970. V. 16. P. 35-58.
[5] Hairer E. A Runge-Kutta Method of Order 10 // J.Jnst.Math.Applics.
1978. V. 21. P. 47-59.
[6] DormandJ.R., Prince PJ. A Family of Embedded Runge-Kutta Formulae
//J.Comp.Appl.Math. 1980. V. 6. P. 19-26.
[7] Prince PJ., DormandJ.R. High Order Embedded Runge-Kutta Formulae
//J.Comp.Appl.Math. 1981. V. 7. P. 67-78.
[8] Fehlberg E. Classical Fifth-, Sixth-, Seventh and Eighth Order Runge-
Kutta formulas with step size control. NASA Technical Report. 1968,287.
Extract published in // Comptuting. 1969. V. 4. P. 93-106.
[9] Федоренко Р.П. Введение в вычислительную физику. М.: Изд-во
МФТИ, 1994.528 с.
[10] Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных
уравнений. Жесткие и дифференциально-алгебраические системы.
М.: Мир, 1999.685 с.
216
Лекция 8 Численные методы решения задачи Коши для систем ОДУ
[11] Лобанов А.И., Петров И.Б. Вычислительные методы для анализа
моделей сложных динамических систем. Ч. I. M.: МФТИ, 2000.168 с.
[12] Пинии Э. Обыкновенные дифференциально-разностные уравнения.
М.: ИЛ, 1961.248 с.
[13] Арнольд В.И. Обыкновенные дифференциальные уравнения. 3-е изд.
М.: Наука, 1984.272 с.
[14] Малинецкий Г.Г. Задачи по курсу нелинейной динамики / В кн.:
Новое в синергетике. Загадки мира неравновесных структур. М.: Наука,
1997. С. 215-262.
217
Лекции по вычислительной математике
Лекция 9. Численные методы решения жестких
систем обыкновенных дифференциальных
уравнений
Дается понятие жесткой системы (ЖС ОДУ). Рассматриваются
неявные методы Рунге-Кутгы и Гйра для решения ЖС ОДУ. Исследуется
устойчивость методов.
Ключевые слова: жесткие системы ОДУ, спектр матрицы Якоби,
А-устойчивость, асимптотическая устойчивость, жесткая
устойчивость, неявные и диагонально-неявные методы Рунге-Кутты,
методы Розенброка, методы Ikpa, представление Нордсика.
9.1. Явление жесткости. Предварительные
сведения
Рассмотрим в качестве примера две задачи Коши для систем
обыкновенных дифференциальных уравнений (ОДУ) [1,2]:
1 . 1
и = аи+ - v,v = — v,
с начальными данными и@) = щу v@) = vq; здесь а ~ 0A), е < 1; и
линейную систему с постоянными коэффициентами
и = 998u + 1998v,
• v = -9 ,
u@) = v@) = 1.
Решением первой задачи Коши являются функции
v(t) = voe-*'',
а второй —
= 4е~* - Зе000'
«(*) = 4е~* - Зе
218
Лекция 9 Численные методы решения жестких систем ОДУ
В обоих случаях решение состоит из двух экспонент: быстро
убывающей и относительно медленно изменяющейся. Отметим, что
абсолютные величины собственных значений матриц рассматриваемых
линейных систем ОДУ при их представлении в виде
и = Аи,
(и — вектор-столбец, А — матрица с постоянными коэффициентами)
существенно различаются. Так, в первом случае Ai « D?)~\ \2 ~ 0A); во
втором: Ai « -1, А2 = 10~3. В обоих случаях имеем:
При моделировании физических процессов причина такой
разницы в собственных числах заключена в существенно различных
характерных временах процессов, описываемых системами ОДУ. Наиболее часто
подобные системы встречаются при моделировании процессов в
ядерных реакторах, при решении задач радиофизики, астрофизики, физики
плазмы, биофизики, химической кинетики. Последние задачи часто
могут быть записаны в виде [3]:
t=i i=i
где Uk — концентрации веществ, участвующих в химических
реакциях, скорости протекания которых характеризуются коэффициентами а^.
В качестве примера приведем одну из систем химической кинетики,
описывающую изменение концентрации трех веществ, участвующих в
реакции для случая полного перемешивания [1].
Пример 1. Обозначим концентрации трех веществ, участвующих в
реакции, через щ, и2 и из, тогда
иг = -4 • 10~V + 104u2u3,
й2 = l(T2ui - 104и2щ - 3 • 107тх|,
Участки решения, характеризующиеся быстрым и медленным его
изменением, называются пограничным слоем и квазистационарным режи-
, соответственно.
219
Лекции по вычислительной математике
Трудности численного решения подобных систем ОДУ, получивших
название жестких (определение жесткой системы приведено ниже),
связаны с выбором шага интегрирования. Дело в том, что характерные
времена исследуемых процессов могут различаться более чем в 1012 раз.
Следовательно, если при численном решении системы
u = f(u)
выбирать шаг из условия
г ||f'u(u)|| « 1,
то он будет соответствовать самому быстрому процессу. В данном случае
затраты машинного времени для исследования самых медленных
процессов будут неоправданно велики. По этой причине имеются следующие
альтернативы в выборе подхода к численному решению рассматриваемых
задач.
1. Численно решать систему ОДУ с шагом
т. е. с учетом характерных времен всех процессов, описываемых
данной системой.
2. Решать систему ОДУ с различными шагами, соответствующими
физическим процессам с существенно различными характерными
временами. В этом случае необходимо задавать условия перехода к
другому шагу интегрирования.
3. «Пренебречь» быстропротекающими процессами и численно
рассматривать лишь медленные, проводя интегрирование с шагом,
превышающим характерные времена быстрых процессов. В этом
случае придется конструировать численные методы, позволяющие
проводить расчеты с шагом
r>||f#u(u)|r1.
Определение ([3]). Система ОДУ для задачи Коши
называется жесткой, если спектр матрицы Якоби
J = {f'u(u)}
разделяется на две части.
220
Лекция 9 Численные методы решения жестких систем ОДУ
1. Жесткий спектр:
ReAi(u) ^ -До, |bn Afc| < |ReAfc|, к = 1 -г- Nx
(Аг — собственные значения матрицы Якоби); Ло > О
2. Мягкий спектр:
|Aj| ^Ao,j = l^^2,Ao>0.
При этом Ло < Ло.
Отношение Ло/Ао называется показателем жесткости системы.
В дальнейшем будем полагать Ао ~ 0A).
Проблему численного решения жестких систем ОДУ рассмотрим на
примере модельной линейной системы вида
u = Bu,u@) = u0. (9.1)
Ее точное решение задается формулой
+
где константы интегрирования bj, bk соответствуют жесткой и мягкой
частям спектра; 11,,о;* — собственные векторы матрицы Якоби,
соответствующие собственным значениям А,, А*.
В этом решении видны две части: первая (жесткая) убывает как е~Ло*
на временном интервале [to, O(AqX)] (пограничный слой), вторая заметно
изменяется на интервале [^^(Л^1)] (квазистационарный режим).
Если провести аппроксимацию линейной системы ОДУ с помощью
явного метода Эйлера
или
Un+i = (E + rB)un,
то общее решение такой системы разностных уравнений будет иметь вид
Ni N2
? ? к. (9.3)
Второе слагаемое в этом решении аппроксимирует второе слагаемое
в точном решении (9.2), а первое быстро растет и приводит к абсурдному
Результату.
221
Лекции по вычислительной математике
Теперь проведем аппроксимацию линейной системы ОДУ (9.1) с по-
мощью неявного метода Эйлера:
- = Bun+i,
или
un+i = (E + rB)-1un.
Общее решение такого разностного уравнения имеет следующий
вид:
jf=i fc=i
В этом случае второе слагаемое ведет себя так же, как и точное
решение, а первое стремится к нулю как (гЛо)~п, т. е. его поведение
качественно совпадает с точным в области пограничного слоя.
В практике численных исследований жестких задач часто не нужно
изучать поведение решения в пограничном слое, и можно
воспользоваться неявными методами. Но в случае необходимости исследовать этот слой
можно с шагом г < AjJ.
Устойчивость методов численного интегрирования жестких систем
ОДУ обычно исследуется на примере скалярного уравнения
и = Аи, и@) = и0. (9.4)
Положим, что численный метод, применяемый к решению этого
уравнения, может быть записан в виде
un+i = R(z)un> z = тА,
где R(z) называется функцией устойчивости [1, 4]. О построении
функции устойчивости речь пойдет ниже.
Определение. Численный метод для решения уравнения (9.4)
является абсолютно устойчивым, если выполнено условие
1ВД1 < 1.
Из определения следует, что |un+i| ^ |и„|.
Это требование является естественным при Re z ^ 0, поскольку в
таком случае модуль точного решения есть невозрастающая функция.
Множество всех точек г, для которых \R(z)\ ^ 1, называется
областью абсолютной устойчивости.
222
Лекция 9
Численные методы решения жестких систем ОДУ
1
/А
/////
1
Im тХ
RerA
Рис. 9.1
Im гЛ
а
RerA
Рис. 9.2 а
Определение. Если область абсолютной устойчивости (|Д(г)| < 1)
занимает левую полуплоскость комплексной плоскости (Re z ^ 0), то
метод является А-устойчивым (заштрихованная область на рис. 9.1).
В случае, когда область абсолютной устойчивости включает в себя
Угол (в левой полуплоскости комплексной плоскости) с вершиной в нуле
и углом полураствора а, то метод называется А(а)-устойчивым.
Области А(а)- и Л@)-устойчивости изображены на рис. 9.2а и 9.26,
соответственно.
В случае, когда вся область абсолютной устойчивости включает в
себя часть левой полуплоскости (граница ее лежит вне заштрихованной
части на рис. 9.3), то метод называется жестко-устойчивым. Область
жесткой устойчивости имеет вид, представленный, например, на рис. 9.3.
223
Лекции по вычислительной математике
Im тХ
* * ж г ж * <*
RerA
Рис. 9.2 b
ImrA
Рис. 9.3
Определение. Численный метод называется L-устойчивым, если он
А-устойчив и если
\R(z)\ ->0, при Re rA -> -со.
В частности, рассмотренный выше неявный метод Эйлера является
L-устойчивым. Решения, полученные такими методами, будут
затухающими.
9.2. Сингулярно-возмущенные задачи
Рассмотрим простейшую нелинейную жесткую систему А. Н. Тихо-
224
прюхия 9 Численные методы решения жестких систем ОДУ
нова [5] (сингулярно-возмущенная задача Коши с малым параметром при
производной):
ей = /(u, v),
v = д{щ v),
0<е< 1,
или j
и = - f(u, v),
v = д(щ v),
с начальными условиями
и@) = uo,v{0) = vo.
Из характеристического уравнения находим:
¦Л-А \f'
= А2-А (i
det
т. е. Ai — жесткая, а А2 — мягкая часть спектра.
Первое, что хотелось бы сделать, — упростить задачу, положив е « 0.
В этом случае система приобретает вид:
/(*,*) = 0,
v = д(щ v),
и@) = uo,v(O) = vo
и описывает траекторию, проходящую по кривой /(u, v) = 0. Эта
кривая играет существенную роль в решении исходной системы ОДУ.
Однако полностью поведение решения упрощенная (невозмущенная) система
описывать не будет, поскольку начальные данные не обязательно должны
лежать на этой кривой.
Для того чтобы понять эту ситуацию, рассмотрим фазовый портрет
конкретной системы ОДУ вида:
1 о
ей = v - - vr + щ
о
V = —U,
u@) = uo,v@) = vo. .
8—3339 225
Лекции по вычислительной математике
D
Рис. 9.4
Эта система эквивалентна нелинейному уравнению второго
порядка — уравнению Ван-дер-Поля. Приведенный выше вид иногда
называется представлением Льенара. Подробнее о свойствах рассматриваемой
задачи можно прочитать в [6, 7, 8,9].
Кривая /(u, v) = О для этого случая изображена на рис. 9.4. Она
делит плоскость щ v на две части: / > 0 и / < 0; вдали от кривой, поле
скоростей du, dv направлено почти горизонтально влево (вправо) в
зависимости от знака /. На самой кривой выделяются две устойчивые ветви
АВ и CD, где fu < 0, и неустойчивая ветвь BD, на которой f'u > 0.
Опишем теперь качественно поведение траектории рассматриваемой
системы ОДУ, состоящей из следующих участков.
1. Пограничный слой А1 А. На этом участке за малое время О(е)
траектория из точки {щ, vo} переходит в е-окрестность кривой / = 0.
Здесь траектория почти горизонтальна и приближенно
определяется дифференциальным уравнением
и = - f(u, v),
v(t) « vo,
u@) = uq.
(//? > 9, так как /, g ~ O(l), 0 < e < 1).
В окрестности кривой /(u, г;) = 0 имеем f'u < 0, поэтому допустима
оценка
dt
226
Лекция 9 Численные методы решения жестких систем ОДУ
откуда видно, что f(u, vo) стремится к нулю как экспонента с
показателем \ f'u, т. е. / становится малой величиной (« 0) за время
га» а = О(е).
2. Квазистационарный режим. Движение точки {u(t), v(t)}
продолжается уже по участку кривой АВ, /(и, г;) = 0 и описывается
системой
/(*,«) = 0,
г; = д(и, v).
На этом участке за время ЬАв ~ ОA), что видно из второго
уравнения, точка подвигается от А к В, пока система ОДУ устойчива.
В случае невозмущенной системы точка могла бы и далее
продвигаться по участку BD, но для полной системы эта ветвь
оказывается неустойчивой (f'u > 0) и траектория «срывается» на устойчивую
ветвь CD в точке В, в которой f'u = 0.
3. Пограничный слой. На участке ВС точка (u(?), v(t)}
«перескакивает» из В в С за малое время О(е); движение здесь, как и на ветви
АВ9 приближенно описывается уравнениями
и = - /(u, v),
v(t) « const.
4. Квазистационарный режим. Движение по ветви CD, как и по ветви
АВ, описывается уравнениями
/(", v) = 0,
v = д(щ v),
И ДЛИТСЯ tcD~O(l).
5. Пограничный слой. На неустойчивой ветви DA также, как и на
ветви ВС, происходит скачок из точки D за время гол ~ О(е) в
устойчивую точку А, и т. д.
Такое поведение траектории (замкнутая кривая) называется
предельным циклом. Для жестких систем периодические решения
называют иногда релаксационными колебаниями [6, 7].
^ Таким образом, это характерно для жестких систем, траектория
состоит из чередующихся участков быстрого (за время t ~ О{е)) и
медленного (за время t ~ ОA)) изменения решения.
227
Лекции по вычислительной математике
Рассмотрим проблемы, которые могут возникнуть при численном
интегрировании подобных жестких систем ОДУ. Численное
интегрирование в зоне пограничного слоя, если оно необходимо исследователю,
проблемы не составляет. Требуется лишь выполнение условия
В зоне квазистационарного режима часто оказывается, что
интегрирование с таким шагом слишком дорого. Можно, правда, разрешить
уравнение /(u, v) = 0 (и = ip(v)) относительно и и далее интегрировать
его, предварительно реализовав алгоритм перехода на другой шаг:
v = g(v, (p(v)),
однако в случаях более сложных, построение подобных численных
методов может оказаться отдельной сложной задачей.
Чаще всего в практике численных расчетов целесообразно
использовать неявные схемы. В случае ЖС ОДУ неявные схемы
предпочтительнее из соображений устойчивости. Так, рассматриваемую задачу можно
аппроксимировать системой дискретных уравнений:
- и* 1
= -
Эта система нелинейных уравнений может быть решена численно,
например, методом Ньютона. Иногда полагают, что неявные схемы
позволяют проводить численное интегрирование сквозным методом с
большим шагом т. Рассмотрим, к чему это может привести.
Первый пограничный слой будет пройден за один шаг:
их =uo + -
так как e <^т,тд мало.
Далее следует процесс численного интегрирования на устойчивой
ветви АВ. В окрестности точки В поведение численного решения по
неявной схеме осложняется. Это связано с тем, что рассматриваемая
система в данной окрестности может иметь более одного решения. При
этом, по крайней мере, одно из решений нелинейной алгебраической
системы может лежать на неустойчивой ветви CD кривой f(u, v) = 0.
Возможно, что при выборе большего шага интегрирования получится
именно это нефизическое решение, к которому сойдутся итерации.
228
лекция 9 Численные методы решения жестких систем ОДУ
Такую опасность необходимо всегда учитывать при проведении
численного интегрирования по неявным схемам с большим шагом.
9.3. Решение линейных ЖС ОДУ и вычисление
матричной экспоненты
Рассмотрим один из наиболее простых численных методов решения
жестких линейных систем ОДУ [10], основанный на представлении
решения в явном виде
un+i = eBrun
для линейных систем жестких ОДУ вида
u = Bu,u@) = uo.
Его численная реализация связана с вычислением матричной
экспоненты. О свойствах матричной экспоненты (и в целом функций от
матриц) можно прочитать в [11]. Использование для этого разложения в ряд
Тейлора
представляется непригодным, так как простые оценки показывают, что
по вычислительным затратам этот алгоритм сопоставим с методом
Эйлера с шагом г ||В|| < 1:
Следовательно, для того, чтобы fc-й член разложения ряда Тейлора
был, по крайней мере, порядка ОA), необходимо выполнение условия
^Я, илиг||В||
470 соответствует условию численного интегрирования с шагом т||В|| < 1.
Количество членов ряда при этом N ~ г||В|| » 1, что неприемлемо для
Решения.
Представим экспоненту в следующем эквивалентном виде:
229
Лекции по вычислительной математике
При этом значение параметра р выбирают таким, чтобы
и можно было использовать ряд Тейлора с небольшим количеством
членов. Действительно, в этом случае
что вполне приемлемо при соответствующем выборе параметра р.
В этом алгоритме сначала вычисляют матрицу
к=1
затем D2P путем последовательных перемножений. При таком способе
вычисления матрицы также имеется опасность, связанная с тем, что при
некоторых р, Ао,Ло слагаемые, соответствующие мягкой части спектра,
окажутся много меньше единицы (и слагаемых, соответствующих
жесткой части). В этом случае предпочтение отдается представлению
eAr= lexp (--
-л2"
а последовательность вычислений имеет вид
D = E + ^B;C = D; С = (С2)р.
При этом на мягкой части спектра, поскольку т|Л_, | <С 1, имеем
нажесткойчасти,посколькутеперьрнебольшиеит|Л^|/2р > 1,получим
оценку , .
что уже приемлемо для вычислений.
9.4. Численные методы решения ЖС ОДУ.
Семейства неявных методов Рунге-Кутты и
Розенброка
Рассмотрим другие методы для численного решения как линейных
жестких систем ОДУ вида (9.1), так и нелинейных систем общего вида
u = f(t;u),u@) =uo
230
лекция 9 Численные методы решения жестких систем ОДУ
й автономных ЖС ОДУ
u = f(u), u@) = uo,
см. также [1, 4, 9, 13, 14, 15, 16]. Из соображений устойчивости
метода предпочтение естественно отдать неявным методам. Простейшими из
лих являются:
1. неявный метод Эйлера (приведем его вид для случая автономной
ЖС ОДУ, для неавтономной системы формулы очевидны):
un+i — un
- = f (un+i), uo = a;
2. метод трапеций
- Un f(lln+i, tn+i) + f(un, tn)
= U0=a;
3. метод прямоугольников (правило средней точки)
un+i — un . ч
= i(un+1/2, tn+i/2),uo = a,
где
*n+l + tn Un+i + Un
*n+l/2 = ^ >Un+l/2 = ^ *
Среди одношаговых методов для решения жестких систем
наиболее известны методы Рунге-Купы. Все приведенные в данном
параграфе формулы можно рассматривать как частные случаи неявных одно- и
двухстадийных методов из этого семейства. Не останавливаясь на
получении приводимых коэффициентов, выпишем наиболее известные из
формул Рунге-Купы, используя таблицу Бутчера. О представлении методов
Рунге-Кутты в виде таблиц Бутчера — в лекции 8.
Отметим, что в отличие от рассматриваемых выше явных методов,
при использовании неявных схем Рунге-Кутты матрица коэффициентов
метода в таблице Бутчера — заполненная, и для определения
вспомогательных векторов, входящих в функцию приращения, приходится решать
систему нелинейных алгебраических уравнений.
1. Методы Гаусса соответственно 2-го, 4-го, и 6-го порядков
представлены в табл. 9.1,9.2,9.3. Основаны эти методы на соответствующих
квадратурных формулах Гаусса, рассмотренных в лекции 7. Первый
метод совпадает с правилом средней точки. Второй метод D-го
порядка) носит название метода Хаммера-Холлинсворта.
231
Лекции по вычислительной математике
Таблица 9.1
1/2
1/2
1
Таблица 9.2
~ fi
1 ^15
2 1П
1
2
1 , л/15
2 + UT
1
4
4 • fi
1/2
Таблица 9.3
A.
Ш + ^W
5
2_
5 +
i
<
fi
i
4
1/2
2
)
J.
.4fi
_5_
\/15
VT5
~ 24"
5
?
5
2. Методы Радо IIA порядков 1, 3, 5 представлены соответственно в
табл. 9.4, 9.5, 9.9. Основаны на квадратурных формулах Радо,
принадлежащих к семейству формул Гаусса. Метод первого порядка
является неявным методом Эйлера.
Таблица 9.4
1
1
1
Таблица 9.5
1/3
1
5/12
3/4
3/4
-1/12
1/4
1/4
3. Методы Лобатто IIIA 2-го, 3-го, 4-го и 6-го порядков точности см.
в табл. 9.7,9.8,9.9 и 9.10 соответственно. Видно, что метод второго
порядка точности является неявным методом трапеций.
Рассмотрим теперь, как строится функция устойчивости для
методов Рунге-Кутты [4]. Уже отмечалось выше, что при построения
232
Лекция 9
Численные методы решения жестких систем ОДУ
Таблица 9.6
4-л/6
4W6
1П
1
88-7v/6
296+169л/6
16-л/б
3fi
296-169>/6
1 8ПП
88+7л/6
ЯЯП
16+л/б
3fi
164-л/6
зя
-2+Зл/б
-2-W6
22Й
Q
Q
Таблица 9.7
0
1
0
1/2
1/2
0
1/2
1/2
Таблица 9.8
0
1/2
1
0
5/24
1/6
1/6
0
1/3
2/3
2/3
0
-1/24
1/6
1/6
Таблица 9.9
0
5-VE
5 + \/Ь
1
0
1/12
1/12
0
25-л/5
12П
25+13>/5
120
5/12
5/12
0
25-13ч/5
120
25+\/5
5/12
5/12
0
120
120
1/12
1/12
функции устойчивости рассматривается модельное уравнение вида
v = \v,v@) =vo.
Запишем теперь метод Рунге-Кутты для решения приведенного
выше уравнения в общей форме с использованием новых
переменных У:
2 7P/(*n + арт, Yp) = vn + тЛ ^ -ypYp,
0kPf(tn + 7*т, Yk) =vn^r
233
Лекции по вычислительной математике
Приведенные выше формулы можно рассматривать как систему
линейных уравнений относительно новых переменных Yi,..., У*, un+1
следующего вида:
-Z012 • • • -Zf3is 0 \
— Z022 • • • — zfcs О
)
-Z42
Y2
Необходимо выразить vn+i через vn. Для этого воспользуемся
правилом Крамера. Ответ можно записать в следующей форме:
_ det(E - zB 4- zeaT)
Xn+1 " det(E-zB) Xni
где E — единичная матрица размера S x 5, В — матрица
коэффициентов fa, входящая в таблицу Бутчера, е — единичный вектор
размерности S (столбец), ат — строка коэффициентов 7ь входящая
в таблицу Бутчера, 5 — число стадий метода Рунге-Кутты.
Условием устойчивости метода будет
det(E-zB)
Одноитерационные методы Розенброка. Розенброком был предложен
класс неявных методов, в котором не решается система нелинейных
уравнений. В простейшем случае для автономной системы уравнений методы
типа Розенброка могут иметь вид [3]
(Е - атВ - Ьт2В2)
= f [un + erf (tin)].
Здесь В = f?(un) — матрица, постоянная на данном шаге по
времени. Параметры а, 6, с подбираются таким образом, чтобы обеспечить
максимально возможный порядок точности.
Например, для схемы третьего порядка точности получим
а = 1,077; 6 = -0,372; с =-0,577.
Такую схему иногда называют методом с одной итерацией, имея в
виду, что вычисление обратной матрицы сравнимо по количеству ариф-
234
Численные методы решения жестких систем ОДУ
метических операций с одной итерацией метода Ньютона.
Преимущество методов типа Розенброка перед прочими классами численных
методов ЖС ОДУ заключается в том, что для определения решения на
верхнем временном слое необходимо решать уже линейную систему
алгебраических уравнений.
Рассмотрим связь между методами Розенброка и Рунге-Кутты.
Определение ([9J). 5-стадийный метод Розенброка для решения
автономной системы ЖС ОДУ имеет вид
= rf un
V
S
un+i =un + ^
k=i
где /?, 7, /z — управляющие коэффициенты метода. Как и выше, матрица
Якоби правой части системы В вычисляется по данным в точке tn. Связь
последних формул с выражениями для явных методов Рунге-Кутты
очевидна.
Несколько сложнее представляются методы Розенброка в случае
неавтономной ЖС ОДУ [9]:
= Tf \tn
V
j 3
Вывод условий порядка методов Розенброка — достаточно громозд-
Кий, и всем заинтересованным читателям можно рекомендовать
разобраться в выкладках в книге [9]. Отметим, что широкое распростране-
ние получают в последнее время вложенные методы Розенброка
высокого порядка аппроксимации, имеющие очень хорошие вычислительные
качества. Возможно, что новые методы типа Розенброка способны будут
вытеснить из вычислительной практики наиболее распространенные до
этого в вычислительной практике методы Гира.
235
Лекции по вычислительной математике
9.5. Формулы дифференцирования назад и
методы Гира. Представление Нордсика
В предыдущей лекции вкратце был изложен альтернативный
методам Рунге-Купы подход к построению численных методов для решения
ОДУ, основанный на расширении шаблона разностной схемы. При пере*
ходе от точки tn к ?n+i использовались значения решения (или функций
от него) в предыдущих точках. Полученные численные методы (первые
схемы такого рода были получены Адамсом) носят название линейных
многошаговых. Однако применение методов Адамса для решения ЖС
ОДУ приводит к неутешительному результату. Отчасти он обоснован
результатом, полученным Далквистом.
Теорема (Далквиста (или второй барьер Далквиста) [8, 9]). Не суще-
ствует А-устойчивыхлинейных многошаговых схем с порядком
аппроксимации выше второго.
Попробуем ввести другой класс линейных многошаговых методов —
это так называемые формулы дифференцирования назад (или ФДН-
методы) [8].
Общий вид ФДН-метода таков:
к
un+i + ^Г aiun+i-j = Tj8fn+i, (9.5)
где коэффициенты о, выбираются из условий аппроксимации
метода. В отличие от методов типа Рунге-Купы, при использовании ФДН-
методов нелинейная система алгебраических уравнений для
определения un+i имеет меньшую размерность, следовательно, требуется меньшее
число операций для нахождения решения.
Семейство А(а)-устойчивых ФДН-методов с достаточно большим
значением угла полураствора а носит общее название методов Гира.
Коэффициенты методов Гира, представленных в виде (9.5), приведены в
таблице 9.10 (см. также книгу [13]).
Величина к характеризует количество точек в шаблоне и порядок
аппроксимации ФДН-метода. В первом столбце таблицы также приведен
угол полураствора а для А(а)-устойчивых методов. ФДН-методы с
порядком аппроксимации 7 и выше безусловно неустойчивы.
К очевидным недостаткам методов ФДН (как, впрочем, и других
многошаговых) является необходимость разгонного участка и
трудности при автоматическом выборе шага. Существует эквивалентная форма
ФДН-методов, методы Нордсика, в которой эти недостатки
преодолеваются сравнительно легко. В некоторых источниках они не выделяются
236
Лекция 9
Численные методы решения жестких систем ОДУ
~~ к
1
¦"" 2
3(86)
4G3,35)
5E1,84)
6A7,84)
Таблица 9.10.
В
1
2/3
6/11
12/25
60
ш
ьии
147
-1
1/3
-2/11
-3/25
—12
W
1U
147
Коэффициенты методов Гира
-4/3
9/11
16/25
75
47
—72
147
-18/11
36/25
—'200
Ж
147
-48/25
300
"Ж.
4UU
147
а4
—300
137
450
147
147
в самостоятельный класс методов, а называются ФДН-методами в
представлении Нордсика.
Рассмотрим в качестве примера построение метода Нордсика [2, 8]
для модельной задачи
(9.6)
и введем также в рассмотрение вектор Нордсика
т2 тк
Z = (ЦТи' <
в который, кроме искомого значения функции, включены
приближенные значения первых к производных в узлах сетки. Для того чтобы
осуществить переход к следующему значению zn+i необходимо задать
правила вычисления компонентов вектора z по данным в текущий момент
времени. Вслед за [2, 8] ограничимся рассмотрением случая к = 3. Для
этого разложим (9.6) в ряд Тейлора в окрестности tn:
г2
г3
—
(9.7)
Для записи ряда использован остаточный член в форме Лагранжа. Кроме
того, используем следующие следствия приведенного выше разложения:
ти'п+1 = ти'п
(9.8)
(9-9)
(9.10)
а конкретное значение ^ выберем из условий аппроксимации уравнения
(96)
237
Лекции по вычислительной математике
Подставляя последнее равенство в (9.8), получим:
4^-и<4>@ = r(/n+i - Я), (9.11)
а /? выражается через компоненты вектора Нордсика:
Заманчивая идея подставить выражение (9.11) во все соотношения
(9.7),(9.8),(9.9),(9.10) приводит к неустойчивому методу (см. [2, 8]). При
этом (неустойчивый) метод имеет четвертый порядок аппроксимации.
Основная идея метода Нордсика заключается в том, чтобы, несколько
«испортив» порядок аппроксимации, добавляя в выражения (9.7), (9.8),
(9.9), (9.10) представление (9.11), добиться максимальной устойчивости
метода при приемлемом порядке аппроксимации.
Окончательный ответ для представления Нордсика можно записать
в следующем кратком виде:
zn+1 = Pzn + l(r/n+i - efPzn), (9.12)
где матрица Р — треугольная матрица Паскаля, определяемая
соотношением (для произвольного числа компонентов вектора Нордсика к): Pij =
= C{j @ ^ % ^ j < к) здесь С\ — биномиальный коэффициент. В
противном случае Р^ = 0. Вектор ei определяется как @,1,0,0,..., 0), а вектор
1 — как A0,1,12,... ,h), значение 1 выбирается из условия нормировки.
Относительно первого компонента вектора Норсдика un+i система
уравнений нелинейна, все остальные переменные входят в систему линейным
образом.
Для рассматриваемого случая к = 3 Норсдик получил набор
коэффициентов I = C/8,1,3/4,1/6) из условий минимума погрешности и
обращения в нуль собственных чисел матрицы М = Р - lef Р. Можно
получать набор коэффициентов для метода Гира в представлении
Норсдика, например, из условий жесткой устойчивости (например,
ослабленного требования L-устойчивости, когда требуется лишь \R(z)\ —> 0 при
Re т\ —> -со). В этом случае для рассмотренного выше примера Z =
= F/11,1,6/11,1/11).
Покажем, что последний из приведенных методов Нордсика
эквивалентен методу ФДН Гира при к = 3. Для этого просто для трех
последовательных шагов по времени исключаем из формул типа (9.7), (9.8), (9.9),
(9.10) (точнее, из (9.12)) значения производных решения. После
нетрудных преобразований получим формулу Гира. Другой рассмотренный
вариант метода Нордсика приведет к одной из неявных формул Адамса.
Подробнее в [8].
238
Лекиия 9 Численные методы решения жестких систем ОДУ
Отметим, что метод Гира в представлении Нордсика оказывается
самостоятельно стартующим. При старте можно положить вектор
Нордсика для данной задачи равным, например, zo = (uo, 0,0,..., 0), что
позволит начать вычисления, но приведет к уменьшению порядка
аппроксимации. Таким образом, многозначный (по введенной в [2]
терминологии) вариант метода Гира обладает переменным порядком
аппроксимации: стартуя как метод первого порядка, по завершении разгонного
участка метод стремится к максимально возможному для данной
формулы порядку.
Отметим также, что для системы с релаксационными колебаниями
лучшие результаты могут давать многозначные методы Гира не очень
высокого порядка аппроксимации.
9.6. Задачи для самостоятельного решения
1. Модель Филда-Нойса «орегонатор»
Простейшая математическая модель периодической химической
реакции Белоусова-Жаботинского состоит из трех уравнений:
уг = 77,27(у2 4- yi(l - 8,375 •
У2 = тт~27^3 ~ ^ +
уз = 0,161(yi -уз).
На то, что система жесткая, указывают большие различия в
константах скоростей реакций — есть процессы быстрые и есть
медленные.
Так как переменные системы — концентрации (НВЮ2, Вг~ и Ce(IV)
соответственно) то начальные условия для системы следует
выбирать положительными, как правило, близкими к 0. Конечное время
интегрирования системы Г* = 800.
О системе подробнее, например, в [8,9,17].
2. Уравнение Ван-дер-Поля
Типичным примером жесткой задачи малой размерности является
уравнение Ван-дер-Поля [8,9,18,19]. Его возможно записать в виде
системы
2/i = 2/2,
?-1) + У1), (9.13)
239
Лекции по вычислительной математике
или в виде
V3
(9.14)
(представление Льенара). Считаем, что параметр а — большой.
В расчетах рассмотреть два случая: а = 103 и а = 106. Для тестов
обычно полагают yi = 2, 2/2 = 0.
Конечное время интегрирования системы, записанной в виде (9.13),
Тк = 20.
Периодические решения жестких систем ОДУ иногда называют
релаксационными автоколебаниями [18, 19].
Дополнительный вопрос: указать преобразование, переводящее
представление (9.13) в представление Льенара (9.14).
3. Система Ван-дер-Поля и траектории-утки
Рассмотрим неавтономную систему уравнений Ван-дер-Поля:
Й=аИу
2/2 = -yi
Как и в предыдущей задаче считаем, что а = 103 и а = 106, у\ =
= 2, 2/2 = 0. Рассмотреть численно случаи 0<А<1и1<Л<
^
О траекториях-утках в системе Ван-дер-Поля см. [19] (строгое
математическое исследование) и [20](популярное изложение).
4. Суточные колебания концентрации озона в атмосфере
Рассмотрим простейшую математическую модель колебаний
концентрации озона в атмосфере [2]. Она описывается следующей
неавтономной системой ОДУ:
+ 2k3(t)y2
2/2 = 0,
2/1 = fciyi2/2 ~ ^22/12/3 ~
240
Лекция 9 Численные методы решения жестких систем ОДУ
В данной модели уравнения описывают изменение концентрации
атомарного кислорода, молекулярного кислорода и озона
соответственно. Считается, что изменения концентрации молекулярного
кислорода невелики. Начальные значения для задачи таковы:
yi@) = 106(см-3)*, У2@) = 3,7- 1016(см-3), у3@) = 1012(см),
значения констант скоростей химических реакций
А* = 1,63 • 1(Г16, к2 = 4,66 • 106.
Две другие химические реакции зависят от локальной
освещенности участка земной поверхности и приближаются следующим
выражением:
_ Г exp(-Ci/sina;t), sin a;* > 0,
-\ 0, sinu;*<0,
где ш = тг/43 200с, сз = 22,62, с± = 7,601. Значения констант
скоростей обращаются в нуль ночью, резко возрастают на рассвете,
достигают максимума в полдень и падают до нуля на закате. Конечное
время интегрирования Т* = 172800 с (двое суток).
Данная система является жесткой ночью и умеренно жесткой в
светлое время суток.
5. Уравнение Бонгоффера-Ван-дер-Поля
Рассмотрим еще один пример жесткой задачи малой размерности,
имеющей периодическое решение [19,21].
2/2 = -У1 - ЬУ2 + с-
Здесь а = 103 и а = 106, уг = 2, у2 = 0.
Уравнение описывает протекание тока через клеточную мембрану.
Постоянная компонента тока с в безразмерной записи системы
такова, что0<с<1,6> 0.7* = 20.
6. Сингулярно-возмущенная система — модель двухлампового
генератора Фрюгауфа.
Система более высокой размерности, имеющая решение в виде
релаксационного цикла, приведена в [18] (см. также [21]). Она имеет
вид:
e±i = -a(yi - у2) 4- <р{хх) - х2,
241
Лекции по вычислительной математике
ех2 = а{уг - у2) + <р(х2) - xi,
2/1 =хи
2/2 = х2.
Здесь а > 0 — константа порядка единицы, функция <р(и) =
= -tgGm/2),zi@) = х2@) = 0,yi = 2, у2 = 0,Г* = 20,е =
= нг3,ю-6.
7. Простейшая модель гликолиза
Простейшая модель гликолиза описывается уравнениями
следующего вида [21]:
2/1 = 1 - 2/12/2,
2/2 = осу2 12/1 - -
предложенными Дж. Хиггинсом. В системе /3 = 10, а = 100, 200,
400, 1000. Начальные условия для системы: yi@) = 1,2/2@) =
= 0,001, Г* = 50. Решение этой системы — релаксационные
автоколебания (жесткий предельный цикл).
8. Пример жесткой системы — модель химических реакций Робертсона
Один из первых и самых популярных примеров жесткой системы
ОДУ принадлежит Робертсону A966) и имеет вид, типичный для
моделей химической кинетики — в правой части системы стоят
полиномы второй степени от концентраций (сравните с орегонато-
ром).
Система Робертсона имеет вид [9]
2/i = -0.04yi + 1042/22/з>
у2 = 0.04yi - 1042/22/з -3-10
Начальные условия для системы таковы: 2/i@) = 1, 2/2@) = 0,
2/з@) = 0. Рассматриваются следующие величины отрезка
интегрирования: Тк = 40 (в работе Робертсона рассматривался именно
такой отрезок интегрирования), Г* = 100,1000,..., 1011. О свойствах
задачи см. в [9].
242
лекция 9 Численные методы решения жестких систем ОДУ
9. Модель дифференциации растительной ткани
Данный пример из [9] — типичный случай биохимической модели
«умеренной» размерности (современные модели, например,
фотосинтеза включают сотни уравнений подобного типа). Хотя данная
модель является умеренно жесткой, тем не менее, ее лучше решать с
помощью методов, предназначенных для решения ЖС ОДУ.
2/1 = -1.71yi + 0.43г/2 + 8.232/3 + 0.0007,
у2 = 1.71J/1 - 8.75у2,
уз = -Ю.ОЗуз + 0.43г/4 + 0.0352/5,
t/4 = 8.322/2 + 1.71у3 - 1-122/4,
уъ = -1.7452/5 + 0.43уб + 0.43у7,
у6 = -2802/62/8 + 0.692/4 + 171у5 - 0.43у6 + 0.69у7,
у7 = 280у6У8 - 1.87»7,
У* = -2/7-
Начальные значения всех переменных системы равны 0, кроме
уг@) = 1 и 2/g@) = 0.0057. Длина отрезка интегрирования Т* =
= 421,8122.
10. Задача Е5
Еще одна модель химической реакции из [9], получившая свое
название Е5 в более ранних публикациях.
2/з = Ау± - Вухуг - МСу2у3
У4 = Вугу3 - Су4.
Начальные условия: у\ @) = 1,76 • 10, а все остальные переменные
равны 0. Значения коэффициентов модели следующие: А = 7,89 •
100, В = 1,1 • 107, С = 1,13 • 103, М = 106. Первоначально задача
ставилась на отрезке Т* = 1000, но впоследствии было обнаружено,
что она обладает нетривиальными свойствами вплоть до времени
Тк = 1013 (подробнее см. [9]).
Обратить особое внимание, что в процессе расчетов приходится
иметь дело с очень малыми концентрациями реагентов (малы
значения 2/2,2/з и 2/4)• Как «подправить» постановку задачи Е5?
243
Лекции по вычислительной математике
11. Уравнение Релея
Уравнение Релея во многом похоже на уравнение Ван-дер-Поля [21 ].
Рассматривается задача вида
х-/*A-х2)х + х = 0.
Решить задачу, записав уравнение Релея в виде системы ОДУ
Начальные условия: х@) = 0, х@) = 0,001, д = 1000, Тк = 1000.
12. Экогенетическая модель
Рассмотрим пример системы уравнений, которая описывает
изменения численности популяций двух видов и эволюцию некого
генетического признака а. Система ОДУ имеет вид
а = еB - 7ах).
Параметры задачи таковы: е ^ 0,01,0 ^ хо ^ 3,0 < уо ^ 15, ао =
= о, Тк = 1500. Наличие малого параметра в третьем уравнении
системы показывает, что генетический признак меняется медленнее,
чем численность популяций. Решение системы — релаксационные
колебания.
Задача описана в статье [22].
13. Экогенетическая модель
Еще один пример жесткой системы описан в статье [22]. Более
интересный случай — численность двух популяций зависит от
взаимодействия между ними и двух медленно меняющихся генетических
признаков.
х = xBai - 0,5х - а\aj2y),
у = уBа2 - oti2alx - 0,5у),
di = еB - 2aia^22/),
d2 = е{2 - 2а]~2а2х).
Параметры задачи таковы: е ^ 0,01,0 ^ хо ^ 40,0 ^ уо < 40, аю =
= O,a2o = 10,Tfc = 2000.
244
Лекция 9 Численные методы решения жестких систем ОДУ
Рассмотреть также модификацию предыдущей системы [22]:
х = xBai - 0, Ъх - a?aj3y),
6ц = е{2 - 3a?aj3y),
d2 = еB - 3aJ" 3a|x).
Параметры задачи: е ^ 0,01,0 ^ хо ^ 40,0 < уо < 40, аю = 0, аго =
= 10,Tfc = 2000.
Литература
[1] Уатт Дж. Холл, Дж. (ред.) Современные численные методы
решения обыкновенных дифференциальных уравнений. М.: Мир, 1979.
312 с.
[2] Каханер Д., Моулер К., Нэш С. Численные методы и программное
обеспечение. М.: Мир, 1998.575 с.
[3] Федоренко Р.П. Введение в вычислительную физику. М.: Изд-во
МФТИ, 1994.528 с.
[4] Деккер К., Вервер Я. Устойчивость методов Рунге-Кутты для жестких
нелинейных дифференциальных уравнений. М.: Мир, 1988.334 с.
[5] Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные
уравнения. М.: Наука, 1980.
[6] Мищенко Е.Ф., Розов Н.Х. Дифференциальные уравнения с малым
параметром и релаксационные колебания. М.: Наука, 1975.248 с.
[7] Мищенко Е.Ф., Колесов Ю.С., Колесов А.Ю., Розов Н.Х.
Периодические движения и бифуркационные процессы в сингулярно-
возмущенных системах. М.: Наука. Физматлит, 1995.336 с.
[8] Хайрер Э., Нерсетт С, Ваннер Г. Решение обыкновенных
дифференциальных уравнений. Нежесткие задачи. М.: Мир, 1990.512 с.
[9] Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных
уравнений. Жесткие и дифференциально-алгебраические задачи.
М.: Мир, 1999.685 с.
245
Лекции по вычислительной математике
[ 10] Теоретические основы и конструирование алгоритмов задач
математической физики. / Под. ред. К.И. Бабенко. М.: Наука, 1979.
[11] Гантмахер Ф.Р Теория матриц. 4 изд. М.: Наука, 1988. 552 с.
[12] Оран Э., Борис Дж. Численное моделирование реагирующих
потоков. М.: Мир, 1990.660 с.
[13] Вычислительные процессы и системы. Вып. 8 / Ред. Г.И. Марчук. М.:
Наука, 1991.380 с.
[14] Ракитский Ю.В., Устинов СМ., Черноруцкий И.Г. Численные методы
решения жестких систем обыкновенных дифференциальных
уравнений. М.: Наука, 1979.160 с.
[15] Лохов Г.М., Подзоров СИ., Щенников В.Вл. Методы численного
исследования жестких систем нелинейных обыкновенных
дифференциальных уравнений. Уч. пособие. 2-е изд. М.: МФТИ, 1997.140 с.
[16] Лебедев В.И. Функциональный анализ и вычислительная
математика. М.: Физматлит, 2000.296 с.
[17] Колебания и бегущие волны в химических системах: Пер. с англ. /
Под ред. Р. Филда, М. Бургер. М.: Мир, 1988.720 с.
[18] Мищенко Е.Ф., Розов Н.Х. Дифференциальные уравнения с малым
параметром и релаксационные колебания. М.: Наука, 1975.248 с.
[19] Мищенко Е.Ф., Колесов Ю.С., Колесов А.Ю., Розов Н.Х.
Периодические движения и бифуркационные процессы в сингулярно-
возмущенных системах. М.: Наука. Физматлит, 1995.336 с.
[20] Малинецкий Г.Г. Хаос. Структуры. Вычислительный эксперимент.
М.: Наука, 1998 (или Эдиториал УРСС, 2000.)
[21] Ланда П.С Нелинейные колебания и волны. М.: Наука. Физматлит,
1997.496 с.
[22] Кондратов А.С., Хибник А.И. Экогенетические модели как быстро-
медленные системы. / В кн.: Исследования по математической
биологии. Пущино, 1996. с. 88-123.
246
Лекция 10 Численное решение краевых задач для систем ОДУ
Лекция 10. Численное решение краевых задач для
систем обыкновенных дифференциальных
уравнений
Рассматриваются численные методы решения краевых задач. На
примере линейных краевых задач иллюстрируется применение различных
вариантов метода прогонки — дифференциальной прогонки, разностной
трехточечной прогонки, пятиточечной прогонки, матричной прогонки,
периодической прогонки. Для нелинейных краевых задач рассмотрены методы
стрельбы и квазилинеаризации. Дается представление о методах решения
спектральных задач (задач на собственные значения). Обсуждается вопрос о
применении метода Фурье при решении краевых задач для разностных
уравнений, аппроксимирующих исходную дифференциальную задачу.
Ключевые слова: Метод стрельбы. Метод прогонки. Матричная
прогонка. Дифференциальная прогонка. Жесткие краевые задачи.
Метод квазилинеаризации. Задача Штурма-Лиувилля. Метод Фурье.
10.1. Краевая задача для линейной системы ОДУ
первого порядка
Рассмотрим линейную систему ОДУ первого порядка
at
с краевыми условиями
Ru@) + Su(L) = q,
где u, f, q — n-мерные векторы, A(t), R(t), S(t) — матрицы размера пхп.
Для приближенного решения задачи введем расчетную сетку {tn}%=o
и за приближенное решение примем сеточную функцию {ип}%=0 .
Рассмотрим методы построения приближенного решения.
Метод построения фундаментальных решений аналогичен
известному по курсу дифференциальных уравнений способу построения
общего решения системы линейных уравнений первого порядка. Решение
представляется в виде
247
Лекции по вычислительной математике
Здесь Uk(t) есть полная фундаментальная система решений
однородной задачи
, К — 1, Z,. . ., П
at
с начальными данными, например
где единица стоит на к месте, т. е. в качестве начальных данных
используются векторы и*@) = е*. Важно, чтобы решения однородной задачи
составляли систему линейно независимых функций. Каждая такая функция
ищется численно как решение соответствующей задачи Коши, используя
методы, описанные в лекциях 8 и 9.
Пусть й(?) — частное решение неоднородной системы
с нулевыми начальными условиями п@) = 0. Тогда неопределенные
коэффициенты ctk находятся из краевых условий
Ru@) + Su(L) = q, или
SQ(L) + S[]T akuk(L)} = q.
Последнее соотношение представляет собой СЛАУ относительно
коэффициентов а± размерности п.
Полную фундаментальную систему решений однородной задачи
можно получить, используя, например, схему второго порядка точности
(метод трапеций)
Un+l -
= Ап+1/2 ^ »Ап+1/2 = A \tn + -J ,
un+1 = (E - ~
Частное решение получаем аналогично:
-пп А un+i + йп
2
г
248
Лекция 10 Численное решение краевых задач для систем ОДУ
по@) = 0,или
Оп+1 = (Е - ? А) [(Е + I A) Un + rfn+1/2] , по = 0.
Приведем пример, когда решение задачи методом построения
фундаментальных решений не проходит. Рассмотрим систему уравнений
du f dv
Подобные системы ОДУ моделируют, например, процессы
прохождения излучения или потоков элементарных частиц (гамма-излучение,
потоки нейтронов) через разные среды (атмосфера, защита ядерных
реакторов) в приближении оптически толстого слоя. Коэффициенты a, b ~ 50
характерны для защиты реакторов. Найдем общее решение этой задачи с
помощью метода фундаментальных систем в виде линейной комбинации
двух решений однородных ОДУ:
где {ui,vi) и (u2,v2) — решения двух однородных систем (в дальнейшем
для простоты будем полагать, что п — v = 0.) Тогда
п1 = at;1, v1 = ftul, ti^O) = 1, уг@) = 0;
u2 = av2, v2 =
u2@) = 0, v2@) = 1,
а коэффициенты ax и a2 находятся из краевых условий.
Общее решение такой системы, как известно, представляет собой
сумму двух экспонент
(аналогичным образом решение представляется и для иг, V2), где а», 6», г =
= 1,2 находятся из решения задачи, С»; г = 1,2 — произвольные посто-
-А а
янные; Ai и Аг — корни характеристического уравнения
Ь -А
= 0.
Решая характеристическое уравнение, получаем Ai,2 = ±Vab « ±50. По-
лученное решение есть сумма двух экспонент: одной, быстро растущей
(~ e50t), и второй, быстро убывающей (~ е0*). Искомое же решение
есть функция, близкая к Uoe~5Ot (в случае задачи с защитой ректора Щ —
249
Лекции по вычислительной математике
падающий поток нейтронов; задача защиты — значительное его
ослабление, приблизительно в е50 раз).
Слагаемые с быстрорастущими экспонентами должны взаимно
уничтожиться. Получение же численного решения - весьма трудная задача,
поскольку численное решение имеет большую и быстро возрастающую
погрешность. Пусть им = и{\ + е) ~ e5Ot(l + 10~12), т.е. начальная
погрешность имеет порядок 102. Она возрастает при вычислениях
примерно в e50t раз — даже при умеренных t это очень большое число.
10.2. Метод дифференциальной прогонки.
Понятие о жестких краевых задачах
Рассмотрим метод дифференциальной прогонки, не приводя
доказательства его устойчивости. Покажем, что с помощью этого метода
можно решить рассмотренную выше задачу. Будем искать решение в виде
u(t) = a(t)v(t)+0(t),
где а и /? — пока неизвестные функции (прогоночные коэффициенты),
для которых необходимо получить дифференциальные уравнения.
Продифференцируем это соотношение
и = av + av 4- Р
и подставим в него уравнения системы и = ау+/, v = Ьи+д. В результате
получим, что av + / = av + a(bu + g) + /3 . Подставим в полученное
соотношение уравнение и = av + /3. Тогда av + f = av + ba2v + Ь/За +
После приведения подобных членов имеем равенство
v(a + Ьа2 - а) + (/? + b/За + ад - /) = 0.
Приравнивая к нулю коэффициенты при v и единице, получим два
дифференциальных уравнения для прогоночных коэффициентов:
а + Ьа2 - а = 0,
0 + а/ЗЬ + ад - / = 0.
Дополним их начальными условиями. Левое краевое условие вида
и@) = С/о запишем в виде прогоночного соотношения и@) = a@)v@) +
+ /?@), полагая а@) = 0, /?@) = С/о. Таким образом, получаем начальные
данные для двух задач Коши для a(t) и /?(?), которые могут быть решены
численно.
250
лекция 10 Численное решение краевых задач для систем ОДУ
Теперь разрешим правое краевое условие. На правой границе
отрезка интегрирования имеем условие v(l) = 0 и прогоночное соотношение
при t = 1: u(l) = a(l)t;(l) + /3A), откуда получаем u(l) = /3A).
Далее воспользуемся уравнением v = bu+g, подставив в него
прогоночное соотношение u = av + /3, получим дифференциальное уравнение
для v:
Интегрируя эту задачу справа налево, попутно определяем u(t):
u(t) = a(t)v(t)+p{t).
Метод дифференциальной прогонки оказывается весьма
эффективным при решении линейных систем дифференциальных уравнений с
переменными коэффициентами. Очевидно, что все приведенные выше
соотношения верны без изменения и для таких систем.
Рассмотрим теперь общую постановку жесткой краевой задачи,
неявно содержащую большой параметр. О жестких системах и задаче Коши
для них речь шла в предыдущей лекции. Рассматривается линейная
система du
— = Au + f,t€ [a,6],
N
(dt, u(a)) = / ^ disU8(a) = q^ i = 1,..., fc, к < N,
8=1
N
(a*, uF)) = J2 <w*>)=«i,»=*+1,..., #,
8=1
Здесь A — постоянная матрица размером N x N (дальнейшие
рассуждения будут справедливы и для систем уравнений с переменными
коэффициентами). Определители систем линейных алгебраических
уравнений, которыми являются краевые условия на обоих концах интервала
интегрирования, полагаются отличными от нуля.
Определение. Рассматриваемая краевая задача для ОДУ является
жесткой, если спектр собственных значений матрицы А можно разделить
на три части.
1. Левый жесткий спектр, для которого справедливо ReAj ^ -Ло,
|bnAj| < Ло,Ло > 1, г = 1,..., Ni.
2. Правый жесткий спектр, для которого ЫеЛ? ^ Ло, |ЬпЛ?| < Ло, г =
= iV! + l,...,iV2.
3. Мягкий спектр |Ai| ^ Ао, г = iV2 + 1,..., N.
251
Лекции по вычислительной математике
Отношение Ло/Ао > 1 является параметром, характеризующим
жесткость системы. В дальнейшем будем полагать А0(Ь - а) > 1, Ло(Ь -
- а) ~ ОA).
Общее решение такой системы имеет вид
u(t) = f7'eA.''n{+ ?
t=l i
где fij, ft?, u>i есть собственные векторы матрицы А, соответствующие
трем частям спектра. Понятна качественная структура этого решения,
содержащего как левый, так и правый пограничные слои. Будем
полагать, что количество собственных значений в каждой из трех частей
спектра не изменяется. Особенность жестких краевых задач состоит в
том, что их решениями являются ограниченные функции. Для них
верно || и || < С (||f|| + ||q||), ||f || и ||q|| — нормы правых частей в системе
ОДУ и краевых условиях, соответственно. Для численного решения
задачи можно использовать такую же схему второго порядка, как и ранее.
Рассматриваем класс вычислительно корректных задач, для которых С =
= ОA)<ехр(Л0(Ь-а)).
В дальнейшем будем полагать величину ||А||(Ь - а) « Ло(Ь - а)
большой, а величину ехр(||А||(Ь — а)) « ехр(Ло(Ь - а)) — очень
большой. В приложениях такие задачи встречаются наиболее часто.
Важно отметить и то, что не все возможные постановки задач для
жесткой системы приводят к вычислительно корректным алгоритмам.
Показывается, что необходимыми (и почти достаточными) условиями
корректности являются следующие неравенства: к ^ N\, (N - к) ^ 7V2 -
- 7Vb т. е. число краевых условий на левом конце отрезка
интегрирования не должно быть меньше быстро убывающих вправо решений, на
правом конце — не меньше быстро убывающих влево решений. В
противном случае краевая задача оказывается вычислительно некорректной, так
как С = О(ехр(Л0F - а))).
Проблемы, которые возникают при численном решении жесткой
краевой задачи, были уже рассмотрены: суммирование функций
порядка eLt, как известно, приводит к потере точности и накоплению
вычислительных ошибок. Вторая проблема состоит в следующем. Для
вычисления коэффициентов а«, входящих в общее решение неоднородной
системы (а оно состоит из суммы частного решения неоднородной системы
N
и общего решения однородной u(t) = йо + ? atUi), приходится решать
плохо обусловленную СЛАУ (d», п(Ь) + ^2 а»и»(Ь)) = q», г = к + 1,..., N.
252
лекция 10 Численное решение краевых задач для систем ОДУ
10.3. Краевая разностная задача
Штурма-Лиувилля для обыкновенного
дифференциального уравнения второго
порядка
Задача Штурма-Лиувилля для обыкновенного дифференциального
уравнения второго порядка часто встречается в приложениях.
Рассмотрим линейную задачу
^ + Bu = D,t = a, A0.1)
at
A^
at
где коэффициенты д, h, s, вообще говоря, являются функциями
независимого переменного t.
Для разностной аппроксимации рассматриваемой краевой задачи
введем равномерную разностную сетку {?п}см *п = пт, т = (b - a)/N
и определим на этой сетке сеточную функцию {ип}$ .
Коэффициент д9 вообще говоря, может не иметь первой
производной. Такая задача может возникнуть, например, в случае расчета
установившегося распределения температуры в задаче стационарной
теплопроводности с контактным разрывом. Представим разностную задачу в виде
1 f un+i-un ип-ип-Л un+i-un_i
~ I Pn+l/2 0П-1/2 I + Пп — + 8nUn =
9n+i/2 =
,uN -uN-i , ,
A h D Un = U , t = 0.
Контактный разрыв при этом помещается в узел с номером п. В этом
случае фактически аппроксимируется тепловой поток через границы
ячейки разностной сетки, для уравнения теплопроводности получается
консервативная разностная схема — подробнее смотри в лекциях, посвя-
Щенных численному решению уравнений в частных производных.
253
Лекции по вычислительной математике
Выписанные выше соотношения определяют простейшую
разностную схему. Под разностной схемой здесь и ниже понимается
совокупность разностных уравнений для определения значений сеточной
функции внутри расчетной области, дополненная соответствующими
начальными и граничными условиями для этой сеточной функции.
Для определения значений сеточной функции получается СЛАУ с
трехдиагональной матрицей
anun-i - bnun
= dn, n = 1,..., N - 1,
гдеап = ^Zl- &,cn = ^±^ + ^,6n = an + cn-hn,dn = /n,fe0 = ?-
Эта СЛАУ представима в каноническом виде A'u = d, где А' —
матрица
А' =
( -b0 со 0 ... О ^
п\ —Ь\ С\ ... О
О а2 -Ь2 ... О
О О О ... -bN
u, d есть векторы-столбцы
d =
Трехдиагональные матрицы часто возникают при численном
решении краевых задач как для обыкновенных дифференциальных
уравнений, так и для уравнений в частных производных. Ранее матрица
подобной структуры встречалась при построении сплайна Шонберга
(лекция 6). Характерная особенность таких матриц заключается в том, что
при большой размерности матрица имеет ленточную структуру — все
элементы вне ленты (главная диагональ матрицы и по одной диагонали
над и под ней) нулевые. В общем случае численное решение СЛАУ iV-ro
порядка требует O(N3) арифметических действий и O(N2) ячеек
памяти. В численных методах большую роль играют экономичные алгоритмы,
в которых количество арифметических операций пропорционально
количеству неизвестных — O(N).
К таким алгоритмам относится метод трехточечной разностной про-
гонки, появление которого в России связано с именем И. М. Гельфанда,
254
Лекция 10 Численное решение краевых задач для систем ОДУ
в англоязычной литературе такая прогонка называется алгоритмом
Томаса. Экономия памяти очевидна — необходимо хранить только три
диагонали исходной матрицы (три одномерных массива). Рассмотрим
экономичный вариант метода Гаусса, предназначенный для решения подобных
систем.
Решение ищется в виде прогоночного соотношения
Un-l = PnUn + tfn, П = 1, . . . , N,
где рп и qn — прогоночные коэффициенты, подлежащие определению.
Левое краевое условие также записывается в виде прогоночного
соотношения
О) «о
do bo
Где р! = со/Ьо, Qi = -do/bo (заметим, что если А > 0 и В < 0, то 6о > со,
0<р< 1).
Получим рекуррентные формулы, позволяющие последовательно
вычислить р2» <72> Рз,<7з и т. д. вплоть до pn^Qn-
Подставив равенство un-i = PnUn + Qn в уравнение апип-\ — Ьпип +
n+i = dn, получим ап(рпип + qn) - bnun + CnUn+i = dn, или
on — anpn
Сравнивая эту запись со стандартным видом прогоночного
соотношения
видим, что для прогоночных коэффициентов должны выполняться
равенства
Сп d
Pn+l = h 7ПГ>
о аР
Эти формулы определяют прямой ход прогонки.
Из краевого условия на правом конце отрезка интегрирования
- b^UN = (In и прогоночного соотношения un-i = Pnun + 4n
находим величину им.
Далее последовательно вычисляются остальные неизвестные ипп =
= ЛГ — 1,..., lun_i = PnUn+qn. Это — обратный ход алгоритма прогонки.
Теперь, после того как описан прогоночный алгоритм, исследуем его
На Устойчивость.
Для этого рассмотрим вычисление прогоночного коэффициента рп
(т-е. этап прямого хода прогонки). В идеальной арифметике этот ко-
эФфициент равен pn+i = ьп-?пРп1 в конечноразрядной арифметике —
255
Лекции по вычислительной математике
Pn+i = Vn+i + Дп+ъ где Дп+1 — погрешность, связанная с
округлениями на всех предшествующих этапах вычислений. Полагая An+i малой,
исследуем изменение этой погрешности с ростом п. Для этого запишем
соотношение между Дп и Дп+1 в виде
Рп+1 + Дп+1 = + ?п,
Ьп -От\Рп + &п)
где еп — погрешность вычислений правой части и машинного
представления коэффициентов ап, Ь„, Сп. Следовательно, Дп+1 складывается
из двух составляющих — локальной погрешности еп и наследственной
Дп+1.
Полагая Дп < рп при Дп > 0,рп > 0 и опуская члены порядка
О(Д2), получим оценку
Дп+1 « , °" + 7Г^~П2 Дп + ?п'
Ьп - QP?(о ар)
Отсюда, учитывая, что pn+i = bw_cJnPn, получим требуемую оценку
для эволюции погрешности
Дп+1 = ^+1Дп + еп,п = 0,...,^-1. A0.2)
Сп
Докажем следующую теорему.
Теорема. Если выполнены условия диагонального преобладания \Ьп\ >
\а>п\ + \сп\ и хотя бы для одной строки матрицы системы имеет место
строгое диагональное преобладание (\Ьп\ > \а>п\ + \сп\) • Пусть, кроме того,
0 < р\ < 1. Тогда алгоритм прогонки устойчив.
Доказательство.
Докажем утверждение теоремы для случая, когда во всех строках
матрицы выполнено условие строгого диагонального преобладания. На
случай нестрогих неравенств обобщение доказательства очевидно.
1. Пусть выполнено условие диагонального преобладания и 0 < р\ <
1. Для определенности положим ап > 0, Ьп > 0, Сп > 0.
Кроме того, pn+i = ь в» _. < а ,г°пл п = ,. ,п°?л п \ < '.
да следует 0 < pn+i < 1.
2. Покажем, что ^ « 1 + сг, Дх < A + ст)До + е.
Для этого вспомним выражения для коэффициентов линейной
системы, полученной при разностной аппроксимации исходного
уравнения второго порядка.
_ ffn-l/2 _ hn_ ^ ffn-1/2 _ , _ y2v
256
лекция 10 Численное решение краевых задач для систем ОДУ
Сп =
0П+1/2 hn ^ 9п+1/2
г2 2г
Вернемся к выражению для эволюции погрешности A0.2). С учетом
полученных оценок имеем Дп+1 ^ ^^п + ?п- Так как ^ « 1 + ст, то
Дп+i ^ 0- + ст)^п + еп, где с — константа Липшица дляпфункции g{t).
Считаем, что на каждом шаге ошибка округления не превосходит
предельного значения, т. е. 0 ^ еп ^ е.
Из цепочки неравенств
Д2 ^ A + стJ До + е [1 + A + ст)],
Дз ^ A + стKДо + е [1 + A + сг) + A + стJ] ,
будет следовать оценка Дп < A 4- ст)п До + ^"ffing- Используя
известные из математического анализа неравенства, последнюю оценку можно
записать в виде
Дп ^ естпД0 + естп—, стп = ct.
с#
При ct ~ ОA) погрешности не накапливаются (для краевых задач
это реальное условие), поскольку в расчетах т > е, где е — машинный
эпсилон (подробнее в лекции 1).
Аналогичное утверждение доказывается и для второго прогоночного
коэффициента qn+i = ь^~р"; алгоритм устойчив при выполнении тех
же условий.
Покажем устойчивость обратного хода прогонки.
При обратном ходе вычисления проводятся по формулам ип =
= Pn+iun+1 + gn+i, откуда, учитывая, что и™ = ип + Дп и и%+1 = un+x +
+ Дп+ь получим Дп = Рп+1 Дп+i +вп, где Дп — наследственная
погрешность, еп — погрешность округления на п шаге. Очевидно, что
обратный ход прогонки устойчив при выполнении условия 0 < рп < 1, или
°
10.4. Пятиточечная прогонка
При численном решении краевых задач для обыкновенных
дифференциальных уравнений 4-го порядка возникают СЛАУ с пятидиагональ-
й матрицей вида:
= /о,
- diu2 + eiu3 = /i,
257
Лекции по вычислительной математике
апип-2 - hnun-i + CnUn - dnun+i + enun+2 = /n, n = 2,..., N - 2,
-3 - bN-lUN-2 + CN-lUN-1 ~ ds-l
CLnUn-2 —
Алгоритм решения таких систем — пятиточечная прогонка,
формулы которой выводятся аналогично формулам для трехточечной прогонки.
Приведем их окончательный вид. В прогоночном соотношении появятся
три коэффициента (р, д, г):
Прогоночные коэффициенты находятся по формулам
Pn+i = [dn + gn(anPn-i - Ьп)] /Аи п = 2,3,..., iV - 1,
Pi = do/co,p2 = (di - qibi)/Du
rn+i = [/n - anrn_i - rn(anpn_i - bn)] /Dn, n = 2,3,..., N,
= en/Dni n = 1,2,3,..., N - 2, ^ = eo/co,
= Cn - angn_i + Pn(anPn-i - bn), n = 2,3,..., N,
Достаточными условиями устойчивости пятиточечной прогонки
являются диагональное преобразование и неравенства
\рп\ + Ы < l,n= l,...,iV- 1,|р^| < 1.
10.5. Матричная прогонка
Представим прогоночные соотношения для системы уравнений
второго порядка
-BoUo - C0Ui = Do,
AnUn_i - BnUn + CnUn+i = Dn>n = 1,2,3,... ,N - 1,
ANV - BNUN = D^,
где Un и Dn — векторы, Cn, An, Bn — матрицы.
258
Лекция 10 Численное решение краевых задач для систем ОДУ
Обратный ход прогонки выполняется в соответствии с формулами
qn+i>
Здесь рп+1 — матрица, qn+i — вектор.
Окончательный вид формул для прямого хода матричной прогонки
будет
рп+1 = (Вп - АпРп)-1^, п = 1,2,3,..., N - 1,
Pi = B^" Со;
qn = (Bn- AnPn^^Anqn -Dn),n = 1,2,3,.. .,iV,
Q.1 == ^^п **о-
Этот алгоритм называется методом матричной прогонки. Можно
показать, что алгоритм матричной прогонки устойчив, если ||рп|| < 1 для
1 ^ п ^ N; матрицы Во и (Вп - Апрп) невырождены.
10.6. Численное решение нелинейных краевых
задач
10.6.1. Метод стрельбы
Рассмотрим систему нелинейных ОДУ:
f = f(u); t € [О, L],
F[u@), u(L)]=O, u, f,F€/T\
Введем пока неизвестный вектор а размерности п такой, что
{ и@) = а '
и решим соответствующую задачу Коши, например, методом Рунге-
Кутты; получим решение и(?,а). Используя краевые условия, получаем
нелинейную систему алгебраических уравнений
F(a, u (L, a)) = 0, или F(a) = О,
которая решается численно методом Ньютона или простых итераций.
Отметим, что левая часть данной системы при использовании метода
стрельбы задается не в виде функции, а алгоритмически — процедурой
259
Лекции по вычислительной математике
вычисления значений функции на правом краю отрезка интегрирования
как решения соответствующей нелинейной задачи Коши!
10.6.2. Метод квазилинеаризации (метод Ньютона)
Рассмотрим простейшую разностную аппроксимацию краевой
задачи для ОДУ второго порядка
следующего вида:
т2 '"' ' ° Ь 2'
Зададим некоторые начальные приближения u° = <р(?п) к искомой
функции и построим итерационный процесс, воспользовавшись
линейным приближением функции правой части
-О),
где г является итерационным индексом, а начальное приближение <p(tn)
удовлетворяет граничным условиям <р@) = Unp{L) = [/2.
На первой итерации, т. е. при г = 0, получаем первое приближение к
искомому решению, решая методом трехточечной прогонки разностное
уравнение
Полученное первое приближение вновь подставляем в
линеаризованную разностную задачу и методом прогонки получаем второе
приближение. Аналогично поступаем и далее, до достижения заданной точности
в соответствии с условием ||ui+1 - гх* || ^ е.
10.6.3. Аппроксимация граничных условий
Для простоты выше рассматривались краевые задачи, для которых
задавались граничные условия первого рода, т. е. на границе
рассматриваемой области задавалось значение функции. Тогда трудностей с
аппроксимацией граничных условий не возникало. Несколько сложнее обстоит
дело при задании граничных условий второго и третьего рода (условий на
производные и смешанные условия). Ограничимся описанием способов
аппроксимации лишь для граничных условий второго рода.
260
Лекция 10 Численное решение краевых задач для систем ОДУ
Рассмотрим вначале линейную задачу с постоянными коэффициен-
""" сРи Аи
u'@)=a,u'(l)=6,
и соответствующую ей разностную задачу
Цп-ц ~ 2ип + Un-i
^2+ h 2т 5ttn = ^п'
заменив при этом производные в граничных условиях по формулам од-
носторонего дифференцирования первого порядка
и\ — и$ = та, un — Wisr-i = тЬ.
В результате получили разностную схему для аппроксимации
дифференциальной задачи. Несмотря на то, что во внутренних узлах
разностные формулы приближают дифференциальные уравнения со вторым
порядком аппроксимации, решение по этой схеме получается только с
первым порядком из-за понижения порядка аппроксимации в граничных
точках. Естественно было бы повысить порядок схемы до второго во всех
точках, включая граничные.
Наиболее распространены три способа.
1. Использование формул одностороннего дифференцирования более
высокого порядка точности. Эти формулы разбирались в лекции
1. Подход очевиден, однако имеет недостаток — матрица системы
уравнений для определения решения будет уже не тревдиагональ-
ной, следовательно, алгоритм прогонки неприменим. Можно
избавиться от этого недостатка, проведя перед численным решением
системы соответствующие алгебраические преобразования. Они в
случае применения конкретной формулы численного
дифференцирования для аппроксимации граничных условий свои, но
достаточно очевидны.
2. Использование фиктивной ячейки (фиктивного узла). Рассмотрим
расширение сеточной области. Введем в рассмотрение узлы с
индексами 0 и N + 1, находящиеся формально за пределами
рассматриваемой области. Пусть в них тоже определено значение сеточной
функции. Тогда узел с индексом 0 выступает как внутренний узел, и
в нем может быть записано соотношение
+ h 2т =
261
Лекции по вычислительной математике
при этом можно для граничного условия использовать формулу для
вычисления производной со вторым порядком аппроксимации по
формуле центральных разностей Ц1^гц~1 = а. Из этих двух
уравнений осталось только исключить значение в фиктивном узле
(фиктивной ячейке).
Такой метод аппроксимации граничных условий очень хорошо
зарекомендовал себя при решении нелинейных задач для уравнений в
частных производных. В таком случае значения сеточной функции
в фиктивных точках не исключаются из системы, а тоже находятся
численно.
На правом конце отрезка формулы аналогичны. Не составляет тру.
да обобщить этот подход и для граничных условий третьего рода.
3. Использование ряда Тейлора. Для формулы на левой границы
области интегрирования щ - щ = та в явном виде выпишем главный
член невязки:
Используя само дифференциальное уравнение, можно выразить
значение второй производной функции в окрестности границы:
откуда следует
Заменив в последнем соотношении производную на конечную
разность, получим
tti -Mo т ии\ -up
—т— 2 "° "~ —г
Осталось только привести это соотношение к виду, удобному для
использования в методе прогонки.
В случае линейных уравнений с постоянными коэффициентами два
последних способа приводят к одному и тому же выражению для
значения сеточной функции в граничном узле. Для нелинейных уравнений эти
способы будут различаться, но каждый из них приводит к повышению
порядка аппроксимации граничных условий и, следовательно,
разностной схемы.
262
Лекция 10 Численное решение краевых задач для систем ОДУ
10.7. Краевые задачи на собственные значения
для обыкновенных дифференциальных
уравнений
Краевые задачи на собственные значения достаточно часто
встречаются в физических приложениях. Например, это задача определения
собственных колебаний струны, сводящаяся к ОДУ вида
В приведенном уравнении краевые условия зависят от способа
закрепления струны.
Это и задачи собственных колебаний упругого стержня (ОДУ
четвертого порядка), нахождения энергетических уровней атома водорода,
вычисление критических нагрузок в теории стержней и оболочек и др.
В задачах на собственные значения добавляется еще один
пристрелочный параметр — Л, поэтому эти задачи часто решаются
методом стрельбы. Приведем простейший пример — одно дифференциальное
уравнение первого порядка с двумя краевыми условиями (второе краевое
условие появляется из-за присутствия неизвестного параметра А):
-J + /(M,A) = 0,u@) = t*i,
at
Если не учитывать правое краевое условие, то получим задачу Коши.
Ее численное интегрирование приводит к некому значению на правом
конце, зависящему от Л и, вообще говоря, не равному иг. Варируя
параметр А, можно добиться выполнения правого краевого условия с
некоторой заданной точностью. При этом, разумеется, используются методы
численного нахождения корней алгебраического уравнения, обычно
метод касательных.
Второй пример — краевая задача на собственные значения для ОДУ
второго порядка с нулевыми краевыми условиями:
u@) = u(L) = 0.
Поскольку это уравнение второго порядка с неизвестным
параметром А (собственное значение дифференциального оператора), то для его
263
Лекции по вычислительной математика
решения требуется третье условие. Однако в силу линейности и
однородности задачи решение определяется с точностью до произвольного по*
стоянного множителя, что и является неявным заданием третьего
условия. Его можно задать, например, следующим образом:
du(a) _
dt
Трудности при использовании метода стрельбы возникают, если
соответствующая задача Коши плохо обусловлена, а также в случае жестких
краевых задач. В этих случаях появляется сильная зависимость
численного решения от пристрелочного параметра Л.
В качестве тестового примера для сравнения с результатами
численного расчета удобно использовать модельную краевую задачу на
собственные значения:
имеющую точное решение
2
АЛ=(—J ,«*(«) = sinf—J,* = 1,2,...
Непосредственной подстановкой показывается, что решениями
соответствующей разностной задачи на собственные значения
un-i — 2un + un+i
2 + Лип = 0, п = 1,2,..., N - 1, tN = L, и0 = uN = О,
являются собственные значения и собственные функции
А
откуда видно, что
4 . Trfcr тгА: 2
т. е. имеет место сходимость решения разностной задачи к решению
дифференциальной задачи А? —> А^ .
т—О
10.8. Решение краевой задачи методом Фурье
Рассмотрим разностную задачу
ип-\ — 1un + Un+1
^2 = ~fn,n= 1,...,JV-l,uo = tijv =0,tN = L.
264
пвкция 10 Численное решение краевых задан для систем ОДУ
Построим ее решение в виде разложения по базису из собственных
функций разностного оператора:
Этот оператор имеет полную ортонормированную систему собственных
функций u>k(tn) = yj\ sin кк<?п), к = 1,..., N - 1, тп = tn, которые
соответствуют собственным значениям оператора Рт(и): \к = ? sin2 ^.
Будем искать решение в виде
N-1
ип = u(tn) = ^2 ckVk(tn), п = 1,..., N - 1,
к=\
где Ск — пока неизвестные коэффициенты Фурье. Для нахождения этих
коэффициентов представим правую часть разностного уравнения в виде
суммы Фурье
N-1 N-1
fn = ^2 fkuk(tn), ГДе А = U^k) = ^2 fiUk{U)T.
к=1 t=l
Подставим выражение для ипу fn в виде сумм Фурье в исходное
разностное уравнение
N-1 N-1
к=1 fc=l
ИЛИ
N-1 N-1
CfcPT [cJfc(tn)j = - / .
к=1 к=1
откуда, с учетом соотношения
получим
N-1 N-1
«А,*«?.
k=l
Таким образом, получено решение разностного уравнения в виде
суммы Фурье. Несложные арифметические подсчеты показывают, что
265
Лекции по вычислительной математике
метод прогонки, требующий O(N) арифметических действий для числен*
ного решения этой же разностной задачи (из них 2(N — 1) умножений и
N—1 деление) оказывается более экономичным, чем метод Фурье,
требующий O(N2) действий B(N - IJ умножений и N - 1 деление).
Преимущества метода Фурье сказываются при решении двумерных разностных
уравнений с постоянными коэффициентами.
10.9. Задачи
1. Пусть краевая задача имеет вид
6, A0.3)
где нелинейная функция / не зависит явно от первой
производной у'х. В 1924 году Б. Нумеров предложил следующий метод
аппроксимации задачи A0.3):
Vn+i - 2yn + Vn-i = h2[fn + ^(/n+i - 2/п + /n-i)], (Ю.4)
где введено обозначение/^ = /(?&, у*).
В чем заключается отличие метода Нумерова от аппроксимации
вида A0.5):
Уп+i - 2уп + Уп-i = Л2/п? (Ю.5)
Описать алгоритмы численного решения нелинейных
алгебраических систем A0.4) и A0.5). В случае A0.4) и/ = /(х) это — алгоритм
прогонки.
Решение. Выпишем главный член погрешности аппроксимации
разностного уравнения A0.4). Для этого подставим в разностное
уравнение проекцию на сетку точного решения задачи A0.3). Следует
отметить, что конкретный вид решения не важен, достаточно
только, чтобы решение существовало. Предположим также, что оно
четырежды непрерывно дифференцируемо.
Раскладывая проекции точного решения в правой части A0.4) в ряд
Тейлора до четвертого порядка включительно, убедимся, что все
нечетные производные взаимно уничтожатся, а четные дадут
следующее выражение для главного члена погрешности аппроксимации:
1 /74
Уп+i - 2у„ + уп-1 = у"(хп) + ^2-^{хп) + O(h4).
266
Лекция 10 Численное решение краевых задач для систем ОДУ
Из уравнения A0.3) следует, что во всех внутренних точках области
выполняется равенство
переходя в последнем равенстве к разностной аппроксимации
правой части, можно учесть явно главный член погрешности
аппроксимации в A0.S). Приводя подобные слагаемые в A0.4), получаем
аппроксимацию Нумерова
h2
Уп+1 ~ 2уп + Уп-1 = — (/п+1 + Ю/п + /n-l),
которая приближает исходную задачу во внутренних точках
сеточной области с четвертым порядком.
Такая идея разумного распоряжения правой частью для
неоднородных и нелинейных задач приводит к компактным (возможно,
название не слишком удачное — термины «компакт» и «компактный»
уже давно заняты в математике под совсем другое!) разностным
схемам — схемам повышенного порядка точности на нерасширенном
шаблоне. Действительно, и в элементарном шаге вычислений для
A0.4) и для A0.5) участвуют только три точки. Вопросам
построения компактных разностных схем для нелинейных уравнений в
частных производных посвящена монография [7].
В случае, когда правая часть явно зависит от первой производной,
либо не получается компактной схемы, либо схема перестает быть
экономичной. Действительно, чтобы не ухудшить порядок
аппроксимации, необходимо вычислять значение первой производной в
соответствующих узлах со вторым порядком. Если во всех точках
использовать формулу с центральной разностью, то расширится
шаблон схемы — в каждом шаге элементарных вычислений
должно теперь участвовать пять точек. Если для точки с индексом п
использовать формулу с центральной разностью, а для точек с
индексами П + 1ИП-1 — соответствующие формулы для односторонней
производной, то для каждой точки шаблона придется вычислять
заново значения функции /. При использовании классического вида
аппроксимации Нумерова при каждом элементарном вычислении
производится лишь однократное обращение к функции
вычисления правой части — лишь для /п+ь значения /п и /n_i уже
получены при вычислениях для точки с индексом п - 1. Так как время
вычислений, как правило, определяется в таких задачах именно
количеством обращений к правой части, то вычисления замедляются
в три раза.
267
Лекции по вычислительной математике
2. Для численного отыскания периодического с периодом «единица»
решения уравнения
где f,q,p — заданные функции, используется разностная схема.
Предложить модификацию метода прогонки (периодическая
прогонка) для решения данной задачи.
Решение. Рассмотрим следующую краевую задачу для уравнения
Штурма-Лиувилля
y"+p(x)yf + q(x)y = f(x)
с условиями периодичности
где р принимает значения 0 и 1. Отметим, что пока период
решения считается известным. Отрезок [0, 1] возможно рассматривать
без ограничения общности, так как любой отрезок можно
перевести в единичный неособым линейным преобразованием, при этом
вид уравнения существенно не изменится (функции pnq
умножатся на постоянный множитель).
Краевая задача с условиями периодичности решается методом
циклической прогонки. Запишем дискретный аналог уравнения:
Уп-Ц - tyn + Уп-1 , Уп+1-2/п-1 , ,
д2 г ?п 2ft qnVn =
Очевидно, что оно аппроксимирует дифференциальную задачу со
вторым порядком на равномерной сетке. На случай неравномерной
сетки рассматриваемый метод легко обобщается.
В силу периодичности дискретное уравнение должно выполняться
во всех точках сетки, включая граничные. Кроме того, в силу
граничного условия при р — О, уо = Улг+1, система сеточных
соотношений примет вид:
- Ьоуо
-1 - Ьпуп
268
Лекция 10 Численное решение краевых задач для систем ОДУ
o>nVn-i -
где ak = 1 - 0,5p*ft,6fc = 2 - qkh2,ck = 1 + 0,5pkh,u>k = fkh2.
Матрица системы линейных уравнений получается «почти трехдиа-
гональной» — от трехдиагональной ее отличают всего два элемента
в углах матрицы.
Обобщение стандартных прогоночных соотношений (для
трехточечной прогонки) на периодический случай будет иметь вид
Уп-1 = апУп + Рп + 1VN-
Из приведенного выше соотношения для уо сразу получаем, что
аг = со/Ьо, /?i = -/о/Ьо, 7i = ^о/Ьо- Теперь несложно получить
рекуррентную зависимость для прогоночных коэффициентов:
ск а о>кРк - f
P =
bk - akak' bk - akak' bk -
По приведенным выше формулам получаются значения
коэффициентов для всех уравнений с номерами меньше, чем N. Подставим
теперь прогоночные соотношения в последнее уравнение линейной
системы. В итоге с учетом введенных выше обозначений получаем
- bNyN + cNy0 = ipn,
а это соотношение, сгруппировав члены, можно переписать как:
Ум = MN2/o + ^,
где введены обозначения
_ -Cn _ <PN -
Qn(oln + 7n) bN'
Теперь выражение для значения сеточной функции уп-\
подставляем в прогоночные соотношения. Получается выражение,
связывающее уп-1 с у0:
Отсюда получаем следующие рекуррентные соотношения:
269
Лекции по вычислительной математике
Отметим, что эти коэффициенты вычисляются в обратном
порядке — аналог обратного хода прогонки. Последнее соотношение
приводит к явному выражению для уо- В результате получаем
Теперь информации для определения значений искомой функции
во всех точках сетки (еще один ход прогонки) достаточно.
Алгоритм периодической прогонки был предложен А. А. Абрамовым.
10.10. Задачи для самостоятельного решения
1. Рассмотреть две краевые задачи:
у" = еу, у@)=а, »A) =6, (Ю.6)
у" = -е*, 2/@) =а, уA)=Ь. A0.7)
(а) Найти решения этих задач, положив а = 1 и сделав замену ух =
(b) Найти решение методом стрельбы при а = 1 и различных Ь. Что
происходит при 0 < Ь < 1,499719998? При Ъ > 1,499719998?
[[6] С. 110].
(c) Решить задачу A0.6) методом Нумерова A0.4) с
линеаризацией по Ньютону. Сколько узлов сетки необходимо, чтобы найти
решение с точностью е = 10~4?
2. Рассмотреть нелинейную сингулярно-возмущенную1 краевую задачу:
еу" = (У'J, У(О) = 1, »@) = 0,0 < е « 1.
(a) Получить точное решение задачи [[8], С. 11]. Для этого следует
сделать замену у'х = р(у).
(b) Предложить и реализовать численный метод решения задачи.
Сравнить полученное решение с точным. Исследовать
поведение погрешности численного метода при е —> 0.
1 Сингулярно-возмущенными задачами называются задачи с малым параметром при
старшей производной.
270
Лекция 10 Численное решение краевых задач для систем ОДУ
3. Рассмотрим краевую задачу
где g е N — натуральное число, 0 < е < 1.
Получить численное решение задачи в случаях:
а) и(х) = х2,А> 1,В> 1,
б) и{х) = х2,А= \,В> 1 или А > 1, В= 1,
в) и(х) = \х\ ,А> 1,В> 1,
г) и(х) = \х\ ,А= 1,Б> 1.
Что происходит с решением при увеличении ql (В численных
расчетах задать е = 10,10,10~4).
Теоретически задача исследована в [[8], С. 170—171]. В случае и{х) =
= |х| появляется внутренний пограничный слой — узкая область в
окрестности х = 0, где у отличны от |х|.
4. Решить численно краевую задачу:
у@) = А, 7/A) = В, \А\ < V2, |В| < v/2, 0 < е < 1.
Решением этой задачи являются так называемые пиковые, или пич-
ковые, структуры. В [[8], с. 171-174] исследованы свойства
решений и приведены графики восьми линейно независимых решений.
Там же показано, что при фиксированных Аи В существует по
четыре линейно независимых решения, таких, что
lim y(x, е) = 0
при всех х, за исключением точек xi = г/п,г=1,п — l,n G N(n ^ 2),
где lim y(x, е) = \/2.
Найти численно такие структуры для п = 2, п = 3, выбирая
соответствующее начальное приближение при линеаризации по Ньютону.
(Положить е = 10,1(Г3,10).
271
Лекции по вычислительной математике
5. Известно, что краевая задача
А<-1, у@)=В>1
имеет решение с внутренним пограничным слоем в точке х = 1/2
[[8], С. 175]. Исследовать, как его толщина зависит от параметра е.
Какое начальное приближение надо использовать при решении
задачи методом линеаризации?
Известно, что при А = О, В = 0 данная краевая задача имеет еще два
решения, кроме тривиального (у = 0). Найти их численно.
Всего у этой задачи счетное множество решений.
6. Исследовать следующую сингулярно-возмущенную задачу:
2/@) = уо, 2/A)=2/1,я{0) = 0
в зависимости от вида функции а(х). Рассмотреть поведение
решения при е —> 0. Удалось ли получить пограничный слой типа
всплеска?
7. Решить численно задачу на нахождение собственных значений и
собственных функций волнового уравнения [ [1], С. 180—206]:
у" = -к2у,у@)=уA) = 0.
(a) Сравнить полученные решения с известными точными кп =
= 71тг,2/п — sin(n7rx) (n — положительное целое число).
(b) Использовать этот же алгоритм для получения решения при
больших к. С какими трудностями пришлось столкнуться? Как
можно улучшить используемый алгоритм?
(c) Рассмотреть данную задачу для других граничных условий,
например, у'@) =уA) = 0.
8. В цилиндрических координатах задача на собственные значения
имеет следующий вид:
у@) = 1,уA) =0.
272
Лекция 10 Численное решение краевых задач для систем ОДУ
Собственными функциями этой задачи являются цилиндрические
функции Бесселя нулевого порядка, а собственными значениями
задачи будут нули этих функций:
кг = 2,404826, к2 = 5,520078,
fc3 = 8,653728, fc4 = 11,791538.
Показать, что подстановка у = -4U приводит уравнение к виду,
для которого можно применять метод Нумерова. Решить численно
спектральную задачу. Сравнить результаты расчета с точными
собственными значениями, приведенными выше.
9. Частица в потенциальной яме
Найти численно все уровни энергии частицы в потенциальной яме
с потенциалом U(x) = -2sech2x и соответствующие им функции
распределения.
Указание: уровни энергии есть собственные значения Л* уравнения
Шредингера у" + (А - U(x))y = 0 с условиями у(+оо) = у(-оо) =
= 0, а соответствующие им собственные функции и есть функции
распределения.
Данный результат важен для решения уравнения Кортвега-Де
Фриза, поэтому обсуждается в [9, С. 11—17].
10. Частица в потенциальной яме
(a) Получить аналитическое решение уравнения Шредингера для
случая прямоугольной и параболической потенциальных ям и
сравнить его с численными решениями, найденными
обычным методом второго порядка аппроксимации с
использованием алгоритма прогонки и методом Нумерова.
(b) Рассмотреть случай, когда потенциал имеет зеркальную
симметрию относительно х = 0. При этом собственные функции
системы будут четными или нечетными относительно х = 0,
причем четность или нечетность чередуется с ростом
квантового числа (энергии). Проверить этот эффект численно. Каким
способом в этом случае можно в два раза сократить объем
вычислений при расчете собственных значений для потенциалов?
(c) Проверить численно, что для заданного потенциала две
волновые функции у\ и ух, соответствующие разным собственным
значениям А и Л', являются ортогональными: / у\(х)у\< (х) = 0,
как это следует из квантовой механики.
273
Лекции по вычислительной математике
11. Частица в поле с потенциалом Тоды
Рассмотреть движение частицы в поле с потенциалом Тоды ([10,
с. 87-89]):
х = 1 - ех.
Это уравнение можно трактовать как движение частицы в поле с
потенциалом U (х) = ех — х.
Найти численно все периодические решения, удовлетворяющие
следующим граничным условиям:
х@) = хA20) = 0,
х@) = хA20) = А
и дополнительному условию А ^ 10.
Как период колебаний зависит от А? Сколько решений получается?
Литература
[1] Федоренко Р.П. Введение в вычислительную физику. М.: Изд-во
МФТИ, 1994.528 с.
[2] Калиткин Н.Н Численные методы. М.: Наука, 1978.512 с.
[3] Самарский А.А., Николаев Е.С. Методы решения сеточных
уравнений. М.: Наука, 1978.590 с.
[4] На Ц. Вычислительные методы решения прикладных граничных
задач. М.: Мир, 1982.294 с.
[5] Бахвалов Н.В., Жидков НП., Кобельков Г.М. Численные методы. М:
Лаборатория Базовых Знаний, 2002.632 с.
[6] Хайрер Э., Нерсетт С, Ваннер Г. Решение обыкновенных
дифференциальных уравнений. Нежесткие задачи. М.: Мир, 1990.512 с.
[7] Толстых А. И. Компактные разностные схемы и их применение в
задачах аэрогидродинамики. М.: Наука, 1990.230 с.
[8] Чане К., Хауэрс Ф. Нелинейные сингулярно-возмущенные краевые
задачи. М.: Мир, 1988.248 с.
[9] Лэм Дж. Введение в теорию солитонов. М.:Мир, 1981. Могилев:
Бибфизмат, 1997.294 с.
[10] Ланда ПС. Нелинейные колебания и волны. М.: Наука-Физматлит,
1997.496 с.
274
Лекция 11 Исследование разностных схем для эволюционных уравнений
Лекция 11. Исследование разностных схем для
эволюционных уравнений на устойчивость и
сходимость
В лекции рассматриваются методы исследования устойчивости
разностных схем для линейных эволюционных уравнений в частных
производных (гиперболического и параболического типов) Обсуждается применение
спектрального признака устойчивости, энергетического признака, условия
Куранта, Фрццрихса и Леви для гиперболических уравнений.
Формулируется и доказывается теорема (В. С. Рябенького-П. Лакса) о связи
аппроксимации, устойчивости и сходимости для линейных разностных схем.
Ключевые слова: аппроксимация, устойчивость, сходимость.
Теорема П. Лакса-В.С. Рябенького. Спектральный признак
устойчивости. Энергетическая устойчивость.
11.1. Постановка некоторых задач для уравнений
математической физики
Напомним некоторые корректные постановки задач для уравнений
в частных производных, которые будут встречаться в дальнейшем.
Задача Коши для уравнения теплопроводности.
Найти функцию u(t, х) в области х е (-оо, оо), t e [О, Г],
удовлетворяющую уравнению
ди д2и ?, ч
и начальным данным и@, х) = uo(x), где щ(х) — заданная функция.
Смешанная задана для уравнения теплопроводности.
Найти функцию u(t, х) в области х € [О, X], t е [О, Т],
удовлетворяющую уравнению
ди д2и
начальным данным u@,x) = ио{х) и краевым условиям, записанным в
общей форме Ах j%u(t, 0) + Вги(г, 0) = </?i(t), -A2?u(t, X) + B2u(t, X) =
275
Лекции по вычислительной математике
Смешанная задана для уравнения переноса.
Найти функцию u(t, х) в области х е [О, X], t е [О, Т],
удовлетворяющую уравнению (для определенности положим с > 0):
ди ди
начальным данным Коши
и левому краевому условию
Смешанная задача для волнового уравнения.
Найти функцию u(t, х) в области х е [0, X], ? е [0, Т],
удовлетворяющую уравнению
д2и 2д2и ЖЙ ч
+ f{t)
с начальными данными
/л ч ди@,х)
w@,o;) = iio,—^-Z=
и краевыми условиями г*@, ^) = <pi(t), u(X, t) =
Эллиптическая краевая задача (уравнение Пуассона).
Найти функцию г*(х, г/) в области х е [0, Х]> у € [0, У],
удовлетворяющую уравнению
8 д2и
и краевым условиям u(x,0) = <pi(x),u(x,Y) = <p2(x),u@,Y) =
Простейший способ построения численных решений для уравнений
в частных производных — метод сеток. В дальнейшем, наряду с методом
сеток, будем рассматривать и другие подходы к численному решению
задач, например, вариационные, методы конечных элементов.
Рассмотрим постановку разностной задачи в методе сеток на
примере одномерного уравнения теплопроводности.
Для решения одномерной смешанной задачи для уравнений в
частных производных параболического типа область определения искомой
функции покрывается расчетной сеткой с узлами в точках {?п, хт}, п =
= 0,..., N, т = 0,..., М, tn = пт, xm = mh, г = T/N, h = Х/М, где г, h —
шаги сетки по времени и пространству соответственно. Приближенным
276
Лекция 11
Исследование разностных схем для эволюционных уравнений
решением задачи назовем сеточную функцию {u?j. Верхний индекс в
такой форме записи сеточной функции традиционно указывает на номер
слоя по времени, нижний (нижние) — на номер узла сетки по
пространственной координате (рис. 11.1).
Рассмотрим подходы к построению численных алгоритмов для
приближенного решения уравнений в частных производных.
«ь
РИС. 11.1
Явная разностная схема для приближенного решения уравнения
теплопроводности во внутренних узлах сетки (не принадлежащим границе
сеточной области) имеет вид
С"ч
= а
/т =
Под разностной схемой понимается совокупность разностных
уравнений для определения значений сеточной функции внутри расчетной
области, дополненная соответствующими начальными и граничными
условиями для этой сеточной функции. Шаблон схемы,
представляющий собой конфигурацию расчетных узлов в области интегрирования,
используемых на каждом элементарном шаге вычислений, показан на
рис. 11.2.
Эта схема аппроксимирует дифференциальное уравнение во
внутренних точках (узлах) области интегрирования, т. е. при п = 1,..., N -
- 1, т = 1,..., М — 1. Проведем аппроксимацию начальных данных и
краевых условий:
ит =
), ГП = 0 -г М, U0 € О7Т,
277
Лекции по вычислительной математике
(п,га+1)
Рис. 11.2
|n = ! ^
м
для определенности положим А*, В* ^ О, к = 1, 2.
Расчет ведется по рекуррентной формуле на каждом временном слое
отп = 1доп = ЛГотга = 1дот = М-1во внутренних узлах; слой п =
= 0(t = to) соответствует начальным данным, лучи m = 0(х = Хо) и
т = М(х = хм)— левому и правому краевым условиям.
Запишем явную схему в виде
=< + ?«-1 - 2< + <+1) + г/».
По этой формуле последовательно, на каждом слое вычисляется
сеточная функция во внутренних узлах области интегрирования.
Для завершения расчета слоя t = ?n+i необходимо вычислить и?+1
и гх^, для чего разрешаем левое и правое краевые условия относительно
этих величин:
f n+i _ mf »? fjn+1 _
0 " i4i+/iBi ' м "
где u?+1 и ujj!^1 уже вычислены ранее. Реализация одного шага по
времени занимает О(М) арифметических операций, всех слоев — O(NM)
операций.
Явными схемами называются такие разностные схемы для
эволюционных уравнений, когда данные на следующем слое по времени
находятся непосредственно из данных на предыдущем слое без решения
алгебраических систем уравнений. Если же на верхнем временном слое для
определения значений сеточной функции необходимо решать систему
алгебраических уравнений, то схема называется неявной.
278
Лекция 11 Исследование разностных схем для эволюционных уравнений
Простейшая неявная разностная схема имеет вид (для простоты
положим а = 1)
um um цтп-1
Г ft2
ее шаблон (рис. 11.3).
Km)
Рис. 11.3
На каждом временном слое имеем СЛАУ с трехдиагональной
матрицей; алгоритм ее решения — прогонка.
Неявную схему представим в виде
(Аг + hBx)u^1 - Am?*1 = h^\m = 0,
?<t\-(l-2^)^
(А2 + hB2)unJl - A2ur^ll = hrt+\m = M,
откуда несложно получить прогоночное соотношение на каждом слое по
времени.
11.2. Основные определения — сходимость,
аппроксимация, устойчивость
11.2.1. Основные определения.
Дадим основные определения из теории разностных схем.
Пусть Lu = F и Lrur = FT — операторные обозначения исходной
дифференциальной и аппроксимирующей ее разностной задачи (точнее,
279
Лекции по вычислительной математике
параметрического семейства задач); L и Lr — соответственно,
дифференциальный и разностный операторы, и е п,иг е пт — решения
дифференциального и разностного уравнений, принадлежащие
соответствующим функциональным пространствам, F € а>, FT e шт — правая часть
исходного уравнения и ее проекция на расчетную сетку. Считается
известным способ получения проекции непрерывной функции на сетку. В
простейшем случае используются значения функции, вычисленные в узлах
сетки. Индекс г в этой операторной записи указывает на всю
совокупность сеточных параметров. Можно сказать, что для дискретной задачи
имеется не один оператор, а совокупность различных операторов,
зависящих от набора параметров.
Например, задачу Коши для линейного одномерного уравнения
переноса
можно представить в виде
Здесь
du du
Lu = ( dt dx1
iu(O,x),t = i
Одна из аппроксимирующих эту задачу разностных схем (правый
уголок) имеет вид
или в операторной форме
LT«T = FT
где
{ «m.
FT = { Я"'
FT
280
Лекция 11 Исследование разностных схем для эволюционных уравнений
Определение 1. Говорят, что решение ит сходится к решению при
г —> 0, если ||пт - UT\\ —> 0, где Ur — проекция точного решения на
разностную сетку; причем, если имеет место оценка \\ur -Ur\\ ^ стр,
с Ф с(т), то сходимость имеет порядок р.
В качестве примера исследуем на сходимость разностную схему для
задачи Коши для обыкновенного дифференциального уравнения (схема
Эйлера)
^L^A 0) «о-в,
аппроксимирующую простейшее ОДУ
^ + Au = 0, z€[0,l], u(O) = a.
Из разностного уравнения
ип = A - \т)ип-1
найдем его общее решение:
un = a(l-Ar)n, или un = a(l-Ar)tn/r.
Решение дифференциальной задачи легко находится:
u(t) = ae~xt.
Величина погрешности решения, входящая в определение сходимости,
тогда будет Дп = а |A - Ar)tn/r ~ e"Atn |.
Представим A - Ат)*я/Г в виде
A - Ат)*"/Г = ехр(^ 1пA - Аг)) = ехр - Г-Аг + ^ + О(г3I =
т г I 2 J
= е"^ fl + ^pi + О(т2)] [1 + О(т2)] = е-л*« + ^A2tne"At- + О(т2).
Тогда
Л2/
un = ae-At" + ra^e-At" + O(r2),
и, следовательно,
281
Лекции по вычислительной математике
т. е. разностная схема имеет первый порядок сходимости. К сожалению,
чтобы исследовать схему на сходимость, необходимо знать точное
решение дифференциальной задачи. Обычно разностные схемы
исследуются на аппроксимацию и устойчивость, откуда по теореме П. Лакса и
В. С. Рябенького и следует сходимость, по крайней мере, для линейных
задач.
Пример разностной задачи, аппроксимирующей рассматриваемое
уравнение:
^ 3
Можно показать, получив общее решение разностной задачи, что
эта схема не является устойчивой и, следовательно, не имеет место
сходимость решения к точному решению дифференциальной задачи.
Определение 2. Говорят, что разностная задача аппроксимирует
дифференциальную на ее решении, если норма невязки, возникающей при
действии разностного оператора на сеточную функцию — проекцию на
сетку точного решения
стремится к нулю при г —> 0; если выполнена оценка ||гг|
Ск ф ci(r) (константа, входящая в правую часть неравенства, не зависит
от сеточных параметров), то имеет место аппроксимация порядка р.
Приведем пример исследования разностной схемы на
аппроксимацию, для чего напомним следующие соотношения, полученные с
помощью разложения проекции точного решения на сетку в ряд Тейлора в
окрестности одного из сеточных узлов:
U(t + г) = U(t) + rU't{t) + T^U't'{t) + ^U?\t) + ^U?\t) + 0{тъ)
Щг) « )^U(T) = Щг) + r
U<{t) « U{t)-U{t-T) = Щг) _ r + o{r%
т I*
r)-U(t-r) = ^ +
U{t -t) = U(t) - rU't(r) + T^U't'{r) - T^U?\t) + ^C/tD) + O(t5);
282
Лекция 11 Исследование разностных схем для эволюционных уравнений
Рассмотрим задачу Коши для уравнения переноса
•щ - ^ = /(«,«), -оо < х < оо,0 < t < Г,
и@, х) = <р(х), -оо < х < оо.
Введем разностную сетку и положим
?, х) ^ u(t + г, х) - u(t, х) du(t, х) ^ u(t, х + ft) - ц(?, х)
Получим введенную выше схему «правый уголок».
Положив, что функция и(?, х) имеет ограниченные вторые
производные, получим выражения для главных членов погрешности
аппроксимации, т. е. тех членов, которые определяются минимальными степенями
сеточных параметров.
xm) h d2u(tn,xm)
+ 2 " ^
r " at +2
Тогда для невязки верно равенство LTUT = F(tm, xm) + rr, или, так
как в силу самого дифференциального уравнения
\ / itn,zm
= -57--S- I +rr-
\ / itn,xm
Здесь невязка гт определяется выражением
Td2u(tniXm) hd2u(tn,Xm) t ^
Так как \\гТ \\ = 0(г + Л), то разностная схема имеет первый порядок
аппроксимации по г и ft.
Аналогично можно получить выражение для невязки разностной
схемы
г Л*
аппроксимирующей уравнение теплопроводности
ди д2и _
dt дх2 "
283
Лекции по вычислительной математике
После соответствующих вычислений получим
Td2U ft2 d*U ( 2 ,4ч и и г\( , и2\
rT=2dfi-l2dF tniXm + °{T 'Н% |Ы| " °{Т + Н)-
Таким образом, схема обладает первым порядком аппроксимации
по г и вторым по Л.
Определение 3. Говорят, что разностная задача является устойчивой,
если из соотношений
Lrur — FT = fr,LTvr — FT = rjry
следует в смысле выбранной нормы
||ur-i/r|| ^ С2(||?г|| + ||*7т||), причем эта оценка равномерная, с2 ф с2(т).
Теорема (П. Лакса-В. С. Рябенького). Решение линейной разностной
задачи сходится к решению дифференциальной, если разностная задача
устойчива и аппроксимирует дифференциальную задачу на ее решении. При
этом порядок аппроксимации совпадает с порядком сходимости.
Дадим еще одно эквивалентное определение устойчивости
разностной задачи, применимое лишь для линейных разностных операторов.
Как будет видно ниже, даже для линейных дифференциальных задач
возможно построение нелинейных разностных схем.
Определение 4. Линейная разностная задача устойчива, если при
любой правой части FT она имеет единственное решение ит, причем
\\иТ\\ ^ С \\FT\\, и данная оценка равномерна по сеточным параметрам
СфС(т).
Покажем, что из устойчивости задачи в смысле второго определения
следует ее устойчивость в смысле первого определения.
Вычтем из разностного уравнения LruT = FT «возмущенное»
разностное уравнение (положим для простоты г\т = 0):
LTvT = Fr+fr.
Получим в силу линейности разностного оператора
Lr(uT -vT) = fr.
В силу определения 4 справедливо неравенство
284
Лекция 11 Исследование разностных схем для эволюционных уравнений
откуда и следует справедливость в смысле определения 3, так как ?г в
этом неравенстве играет роль правой части, аит - vT — искомой
функции. Можно также показать справедливость обратного утверждения.
Заметим, что в силу произвольности ?г, из последнего неравенства следует
единственность решения разностного уравнения.
В теории разностных схем также вводится определение
корректности разностной задачи.
Определение 5. Семейство разностных уравнений
LTur = Fr
считается корректным, если:
— его решение существует и единственно при любых правых частях
FT € u)F\
— существует константа С, независящая от т, такая, что при любых FT
выполняется оценка ||ur|| < С \\FT\\.
Первое условие эквивалентно существованию оператора L~\
второе — равномерной по т ограниченности L, т. е. константа С является
универсальной для всего семейства уравнений.
Заметим также, что условие ||ur|| < С||^т|| означает непрерывную
равномерную по т зависимость решения разностной задачи от правой
части.
Это неравенство является введенным ранее определением
устойчивости разностной задачи.
11.2.2. Необходимое условие сходимости разностной схемы
Куранта, Фридрихса, Леви (условие КФЛ)
Рассмотрим разностное уравнение
аппроксимирующее задачу Коши для уравнения переноса
Очевидно, что значение иХ сеточной функции в точке A,0)
выражается через значения и*~1 и и^1 в точках A - т,0), A - г, К). В свою
очередь, значения и$~1 и и^~1 находятся по значениям сеточной
функции ч%~2, uf, и?'2 в точках A - 2т,0), A - 2т, ft), A - 2т, 2ft),
285
Лекции по вычислительной математике
@,ft) @,2Л)
@,М)=@,1)
Рис. 11.4
N-2
'О
U
N-2 ,.N-2
находятся по значениям
значения сеточной функции ц
ио~3у u?~3i и2~31 из~3 в точках A - Зг, /А), г = 0,..., 3, и т.д. Значение
сеточной функции щ выражается через значение и^ решения в точках
расчетной сетки @, mh), т = 0,..., N, N = г Все эти точки лежат на
отрезке [0, h/r] или [О, а~г] оси t = 0, на которой задано начальное
условие и@, х) = <р(х) исходной дифференциальной задачи. Значение и^ не
зависит от значения функции <р(х) при х, лежащих вне отрезка [0, а].
Из курса обыкновенных дифференциальных уравнений известно,
что решением однородного уравнения переноса является функция
u(t, x) = (p(t -h х), сохраняющая свое значение вдоль характеристики t +
+ х = const, и, в частности, на прямой t + х = 1, проходящей через точки
@,1), @,1),см. рис. 11.4.
Таким образом, при а > 1 область зависимости решения
дифференциальной задачи для и^', являющаяся точкой @,1), не входит в отрезок
0 ^ х ^ а. В случае а <1иО^ст<1 сходимость решения
разностной задачи к решению дифференциальной отсутствует. Разумеется,
приведенные рассуждения не носят характера доказательства, а лишь
косвенно объясняют, почему не следует ожидать сходимости при а = т/а > 1.
Сформулируем теперь условие Куранта-Фридрихса-Леви (условие
КФЛ), необходимое для сходимости разностной задачи.
286
Лекция 11 Исследование разностных схем для эволюционных уравнений
Пусть некая точка А принадлежит области определения решения
u(t, х) и значение функции и(А) зависит от значения некоторой
функции <р(х) в точках х, принадлежащих множеству п(А), которое, в свою
очередь, принадлежит области определения функции (р(х).
Положим, что для приближенного вычисления решения уравнения
\ju = F используется разностная схема LruT = Fr, причем, значение
решения в точке Ах расчетной сетки, ближайшей к А, полностью
определяются значениями функции <р на множестве пх(Ах). Для того чтобы
имела место сходимость ит —> и при h —> 0, разностная схема должна
быть устроена так, чтобы при сколь угодно малых значениях
пространственного шага h в произвольной окрестности любой точки области fi(A)
имелась точка множества пх(Ах).
Другими словами, разностная схема должна быть устроена так,
чтобы область зависимости разностного уравнения учитывала область
зависимости решения исходного дифференциального уравнения. В
противном случае сходимости ожидать, вообще говоря, нельзя. Если же
разностная задача аппроксимирует дифференциальную, то необходимое условие
сходимости КФЛ является также необходимым условием устойчивости
схемы. Отметим, что условию КФЛ можно придать форму теоремы.
11.3. Элементы теории устойчивости разностных
схем
Канонической формой двухслойной линейной разностной схемы
называется ее запись в виде
U+1"U = fn, A1.1)
В и А — операторы, действующие в пх. Рассматриваем случай, когда для
этих операторов выполнено условие (Аи, и) > /х(и, и), где /л —
положительное число, и — произвольный ненулевой элемент пространства
сеточных функций. Тогда оператор А называется положительным,
записывается А > 0. Требуем и В > 0. Пока не оговорено иное, рассматриваем
случаи самосопряженных операторов.
Если В = Б, то разностная схема называется явной. Рассмотрим
для примера разностную схему с весами для одномерного уравнения
теплопроводности
7|п+1 __ 7/п
Ьа_Ъг. = ?ЛХХ<+1 + A - ?)ЛххгС * € [0,1],
где
п = 0,..., N - 1, т = 0,..., М - 1.
287
Лекции по вычислительной математике
В случае ? = 0,5 эта схема называется схемой Кранка-Никольсон.
Для записи схемы с весами в каноническом виде положим
и, обозначив Un = (iff, tig,..., ufa_г )т, получим форму записи В
+ Aun = 0, где В = Е + т?А.
В случае неравномерной сетки каноническая форма записи схемы
будет
Un+1""Un fn, fn = (/r,...,/^_1)T (П.2)
Иногда схему с весами записывают в виде
Заметим, что канонический вид разностной схемы аналогичен
итерационному методу решения СЛАУ Аи = f. Эта аналогия не
является формальной — переход от СЛАУ к итерационному методу A1.1)
может быть интерпретирован, как замена стационарного уравнения Аи =
= f нестационарным. Решение последнего при стационарных граничных
условиях стремится к решению стационарного при стремлении времени
к бесконечности.
Отличие состоит в том, что в последнем случае операторы В, А и
функция f не зависят от п и итерационный параметр г не обязательно
должен стремиться к нулю.
Введем величину (Аи, и) — энергию оператора А, а также
энергетическую норму вектора:
||u||A = (Au, иI/2.
Говорят, что эта норма порождается оператором А.
Рассматривается задача Коши для оператора — однородного
разностного уравнения A1.1); и0 = (р.
Дадим два определения.
Определение б. Разностная схема A1.1) устойчива по начальным
данным, если для решения A1.1) выполняется оценка:
||un+1|| <Afi||p||,Vtn еиг -узлы сетки по*, A1.3)
причем константа М\ не зависит от сеточных параметров.
Будем рассматривать также неоднородное уравнение,
соответствующее A1.1):
n+l_ „п
= -Aun + f(xm, tn). A1.4)
г
288
Лекция 11 Исследование разностных схем для эволюционных уравнений
Определение 7. Говорят, что разностная схема A1.4) устойчива по
правой части, если для решения A1.4) в любой момент времени
выполняется условие
||un+1|| <M2||f||, A1.5)
причем константа Мч не зависит от сеточных параметров.
Определение 8. Разностная схема A1.1) равномерно устойчива по
начальным данным в энергетической норме, порождаемой некоторым
оператором R = R* > О, если 3 р > 0 : V tn выполнено:
||Un+l||R<p||Un||R
и при этом рп ^ Mi, p и Mi не зависят от сеточных параметров.
Обычно рассматриваются случаи р = Мi = 1 или р = 1 + ст, Мi =
Если разностную схему в каноничной форме представить в виде
Un+1 = RrUn + тВ~ fn,n = 0,. . . ,iV— l,Rr = Rr(?n)>
то оператор Rr = Е-тВ А называется оператором послойного
перехода разностной схемы A1.1). Нетрудно заметить, что условие равномерной
устойчивости по начальным данным эквивалентно ограничению нормы
оператора R^: ||Rr|| < р, а в силу условия рп ^ С и ограниченности норм
степеней оператора R: ||R?|| ^ С.
Для оценки нормы оператора R" можно воспользоваться
собственными значениями этого оператора — корнями уравнения det ||Rr-AE|| =
= 0.
Если А — собственное значение, aw- соответствующий ему
собственный вектор, то RtU> = Аи;. Поэтому R?u; = Апа>, откуда ||R?|| ^
|АГ\таккак||Н»«|| = |A|nIMI < I|R?II М-
Последнее неравенство должно выполняться при любом п. Оно
невыполнимо, если |А|П с увеличением п будет неограниченно расти, так
как ||RJ|| ^ С. Этого не произойдет, если на А будет наложено
условие |А| ^ 1 + ст, константа с не зависит от сеточных параметров, с =
= ОA),т < 1. Последнее условие называется необходимым
спектральным признаком устойчивости (признак фон Неймана).
Рассмотрим разностную задачу Коши для линейного уравнения
переноса
LTuT = FT,
где
——, п = 0,... ,N — 1, т = 0,...,М — 1,
JO—3339 289
Лекции по вычислительной математике
F =//^1 П = °'"-'ЛГ' т = 0,...,Л/-1,
\ Vm, п = 0, га = 0,..., М,
Условие ее устойчивости записывается в виде неравенства
Для однородного уравнения переноса это условие принимает вид
Последнее неравенство означает устойчивость разностной схемы по
начальным данным. Оно должно выполняться, в частности, в случае,
если u^ = ipn является произвольной гармоникой при представлении
начальных условий в виде ряда Фурье (важно лишь знать, будет ли эта
гармоника неограниченно расти по времени). Возьмем в качестве
начального условия произвольную гармонику и^ = eiotm, где а — вещественный
параметр.
Решение однородной разностной задачи в этом случае ищется с
помощью метода разделения переменных. На каждом временном слое
решение разностной задачи ищется как произведение и!^ = Aneiam.
Спектр оператора послойного перехода А(а) легко ищется
подстановкой в разностное уравнение. Например, для однородного
уравнения переноса с постоянными коэффициентами после преобразований
wm+1 = A - ^)^m + ^m+i» гДе а — T/h = const — безразмерный
параметр — число Куранта (в числитель дроби входит скорость переноса,
которая в рассматриваемой задаче равна единице). Для спектра
оператора перехода имеем А(а) = A - а) + aeia. -
Для решения вида и!^ = Xneiam справедливо \\и!^\\ = ||Aneiam|| =
= ||А- • и°т\\ < |А"| • |К||, или шахК| = |АЯ| • max|t&|, поэтому для
выполнения условия устойчивости max |u?j ^ С • max lu^l необходимо
m m
выполнение неравенства |А(а)|п ^1 + Ст.
Константа в правой части последнего неравенства не зависит от
сеточных параметров.
Спектральным признаком это условие называется потому, что
каждая гармоника eiam является собственной функцией оператора
послойного перехода uj^+1 = RruJ^. В частности, для рассмотренного выше
примера с уравнением переноса RrW^ = A - a)u^ + сги^г.
Множество точек А(а) на комплексной плоскости состоит из
собственных значений оператора перехода — спектр оператора. При этом
считаем а е [0,2тг]. Сфррмулируем теперь спектральный признак
устойчивости в этих терминах. Спектр оператора перехода с п на п +1 времен-
290
Лекция 11 Исследование разностных схем для эволюционных уравнений
ной слой должен лежать в круге радиуса 1 + Ст на комплексной
плоскости.
В приведенном примере спектр оператора не зависит явно от г
поэтому условие устойчивости может быть записано в виде |А(а)| ^ 1.
Такое условие иногда называется условием строгой устойчивости.
В [6] показано, что строго устойчивые схемы можно построить лишь для
таких дифференциальных задач, для которых справедлив принцип
максимума, т. е. максимальное и минимальное значения решение
дифференциальной задачи принимает на границе расчетной области.
Вернемся к модельному уравнению переноса. В данном случае спектр
представляет собой окружность с центром в точке A — а) и радиусом а на
комплексной плоскости. При ст < 1 эта окружность лежит внутри
единичного круга, касаясь его в точке А = 1(а = 0), при а = 1 совпадает с
единичной окружностью, при а > 1 находится вне единичного круга.
Приведем еще один пример исследования на устойчивость
разностной задачи:
n = 0,..., N - 1, m = 0,..., M - 1, a > 0.
Эта схема аппроксимирует задачу Коши для уравнения
теплопроводности.
После подстановки решения в виде гармоники Фурье, умноженной
на коэффициент перехода, и1^ = Aneiam в разностное уравнение,
получим уравнение для спектра оператора послойного перехода
e-2 + e л
a г^ = 0.
h2
г
После очевидных преобразований получим
где а' = ra/h2 — аналог числа Куранта для параболических уравнений
(иногда его называют параболическим числом Куранта)
При изменении а спектр А(а) пробегает значения l-4a' < A(a) < 1,
а для выполнения условия устойчивости необходимо 1 - 4а' ^ -1, или
<?' ^ 1/2, откуда г <^.
Аппроксимация этого же дифференциального уравнения с
помощью неявной схемы приводит к следующему выражению для спектра А(а):
и 1
, как и ранее, о' = ra/h2.
291
Лекции по вычислительной математике
В этом случае условие устойчивости выполнено при любом
соотношении сеточных параметров. В таких случаях говорят, что схема
безусловно устойчивая.
Теорема 3. Для задачи Коши
nn+i_ ип
В — = -Aun;u° = <p A1.6)
условие В ^ | А необходимо и достаточно для устойчивости в
энергетической норме, порождаемой А, т. е.
Неравенство в последней теореме имеет смысл операторного неравен-
ства, т. е. для любого ненулевого вектора выполнено (BU, u) ^ \ (AU, и).
Доказательство.
Достаточность. Умножим A1.6) скалярно на уг = цП"^-цП ? тогда
получим
(Вутэ уг) = -(Aun, yT).
Ввиду того, что
r = i(
u ^(u + uj _ i ^ r = i(u + u) _ lyT
последнее равенство можно представить как уравнение:
((В - I А) ут, ут) + ^ (A (un+1 + un), un+1 - un) = 0. A1.7)
В силу самосопряженности A, (Aun, un+1) = (Aun+1, un) и тогда
(A (un+1 + un), un+1 - un) = (Aun+1, un+1) - (Aun, un).
Из A1.7) следует
((В - I A) yr, yT) + -^ (||и-+1|Ц - ||u»||i) = 0. A1.8)
В случае В ^ \ А получим, что ||un+1||^ ^ II^^IIa- Отсюда следует
устойчивость в норме ЯА по начальным данным.
Необходимость. Пусть ||un+1||A ^ IIu°Ha- Используем равенство
A1.7) (оно называется энергетическим тождеством). В случае п = 0 из
A1.7) следует:
2т ((В - I A) w, w) + (Аи1, и1) = (Аи0, и0) = (А<р,<р).
292
Лекция 11 Исследование разностных схем для эволюционных уравнений
Это равенство может быть выполнено лишь в случае
((b-Ia)w,w)>0.
В силу того, что В = В* > 0, существует В. Так как <р —
произвольный элемент нашего пространства сеточных функций, tow =
= -ВА<^> — произволен. Последнее равенство выполнено при
любых (р, значит В - | А ^ 0.
Теорема доказана. ¦
Теорема 4. Пусть А, В — постоянные самосопряженные
положительные операторы. Тогда условие В ^ | А необходимо и достаточно для
устойчивости по начальным данным в энергетической норме, порождаемой
оператором В:
1К+1||в ^ 1М1в.
Таким образом, получим следующее правило исследования
устойчивости двухслойных разностных схем.
1. Приводим схему к каноничному виду.
2. Исследуем свойства оператора А. Если он является
положительным, самосопряженным и независящим от п, проверяется условие
Рассмотрим теперь устойчивость схемы Кранка-Николсон для
уравнения теплопроводности. Эта схема введена в рассмотрение в начале
данного параграфа. В операторном виде она записывается так:
„П+1 „П 1
г 2
Запишем ее в каноническом виде:
(.+ia)S=L=?~
Аи".
По доказанной ранее теореме, данная схема устойчива по
начальным данным в На в случае, если
В = Е+-А^-А=>Е>0 (что всегда верно).
I* I»
Тогда, в энергетической норме, порождаемой оператором А, схема
Кранка-Николсон безусловно устойчива.
293
Лекции по вычислительной математике
Схема с весами. Можно действовать также, как и для схемы Кранка-
Николсон, а можно несколько иначе. Для общей записи схемы с весами
un+i _
+ A(<nin+1 + A - <r)un) = О
т
иногда употребляется сокращенная форма
— + Аи(<7) = 0, здесь UW = <run+1 + A - <j)un.
Умножив это разностное уравнение на А слева, получаем:
пИ _ ц
— + (тип+1 + A - а)ип = О,
т
(А + атЕ) — + un = 0.
Тогда необходимое и достаточное условие устойчивости в норме,
порождаемой оператором Б (т. е. в евклидовой норме)
(А + <ттЕ) > I Е, А + (а - Л rE > 0.
Так как А = А* > 0, домножим обе части последнего неравенства
на А, тогда Е + (а - 1/2)тА ^ 0 — условие устойчивости схемы с весами.
Следствие. Неявная схема (а = 1) безусловно устойчива в норме \\.\\ =
= (., .)х/2 (аналог нормы L2).
Докажем теперь, что из равномерной устойчивости однородной
разностной схемы следует устойчивость по правой части.
Рассмотрим уравнение
В ——=-^ 4- Aun = <рп.
Умножив это равенство скалярно на 2туг = 2т цп+^-цп ^ получим
2т ((В - I А) ут, уг) + (Aun+1, и"*1) = (Aun, un) + 2т (<рпу уг)
(это — энергетическое множество для неоднородного уравнения). Кроме
того,
((u, v) = (А-1 Аи, v) = (Аи, А-Ч) < ||u||a IM|A-t),
(Vй, Уг) ^ ||уг||в ||fPn||B-i
(аналог неравенства Коши—Буняковского).
294
Лекция 11 Исследование разностных схем для эволюционных уравнений
Теперь используем ^-неравенство
тогда получаем
2т ((В - Т- А) ут, ут) + (Aun+\ u"+1) <
< (Aun, u") + ^- ||9n|||-. +2те1\\уг\\1,
2т ((B A - ?l) - T- A) yT) yr) + (Aun+\ un+1) <
Выбираем e: 3-^77 = 1 + e, тогда можно написать
2тA - ?l) ffB - i±? га) ут> уЛ + (Au"+\ u"+1)
Пусть В — ^^ г А ^ 0, е > 0, е не зависит от сеточных параметров
получаем
l|iin+1||i^ Hu-lli + ^rll^H^.
Откуда сразу следует
l|un+1||i < ||u°||i + 1±? г JT 1И&-Х. (И.9)
fc=O
Таким образом, для неоднородной разностной схемы доказана
следующая теорема.
Теорема. Для разностной схемы вида
где А — постоянный (т. е. не зависящий явно от п) положительно
определенный самосопряженный оператор, а В удовлетворяет условию
295
Лекции по вычислительной математике
где е > О не зависит от сеточных параметров, выполнена априорная
оценка (\\.9).
Вообще, в силу того, что разностная схема устойчива по начальным
данным при В = В* > 0, из равномерной устойчивости по начальным
данным следует устойчивость по правой части.
Так как В = В* > 0, то 3 В, тогда
un+l _ un + rB
ИЛИ
где Т = Е — тВ А — оператор послойного перехода.
Равномерная устойчивость по начальным данным означает, что
||Tun||R ^ p||un||R. Тогда из предыдущего равенства с использованием
неравенства треугольника получим
Применяя оценку п раз, получим априорную оценку для
устойчивости по правой части с использованием энергетической нормы,
порождаемой оператором R = R* > 0 :
]Г p
fc=O
Теперь попробуем обобщить полученные результаты на случай
операторов, зависящих от времени.
Для начала рассмотрим аппроксимацию типа Кранка-Николсона
un+l _ un un+l + n
при этом (AnV>, *l>) ^ 0, V n.
Самый простой способ рассмотрения этого уравнения — разрешить
его (в операторном виде) относительно un+1:
~1
un+1 = (Е + I An)~1 (E - I An) un = Tnun.
Оценим ||ТП||. Воспользуемся тем, что
+^А") (перестановочность).
296
Лекция 11 Исследование разностных схем для эволюционных уравнений
((fA")-1 (E-JA») v, (В+5 А-) (Е - JA») v)
||Tn 2= sup -Ь / =
" 1М|*> (v,v)
- т{Аф,
+ ^
Факт, что IKE-aAJCE + crA)-1!! < 1, Va > 0, А = А* > 0, носит
название леммы Келлога.
Для сеточной функции используем норму ||v|| = (v, vI/2.
Подобный результат уже был получен при постоянном (не зависящем от
времени) А.
Везде в доказательствах существенную роль играет то, что А=А* >0.
Может получиться так, что А > 0, но А Ф А* :
А = А, + А*, А, = \ (А + А*), Ак = \(А- А*).
В этом случае многие свойства разностных схем аналогичны
доказанным выше.
Может быть так, что А8 = О, А = А*. Тогда
(Av, v) = -(Av, v) = О
в силу кососимметричности оператора А. Например:
um ~um . um+l urn-l = q
r 2h
/ 0 1 0\
A=l -1 0 II, A = Afc, (Av,v) = 0 Vv.
V о -io/
Теорема (об устойчивости по начальным данным для
несамосопряженного оператора А (без доказательства)).
Разностная схема
г
297
Лекции по вычислительной математике
равномерно устойчива по начальным данным, если
(а - 0,5)т||Аи||2 + (Аи, u) ^ О,
причем для ее решения справедлива оценка
Таким образом, рассмотрен вопрос об устойчивости разностной
схемы, записанной в операторной канонической форме
un+l _ un
В + Aun = 0 A1.10)
в случае В = В* > 0, А = А* > 0, причем А и В — постоянные матрицы.
Рассмотрим более сложные случаи, в частности схему с весами
——^-^ + Аи(<7) = 0, A1.11)
где А — кососимметрический оператор: А = -А*, тогда (Ау, у) =
= (у, А*у) = -(Ay, y)V у. Пример таких схем — простейшие
разностные схемы для уравнения переноса:
,
г 2ft
Представим разностную схему A1.11) в каноническом виде A1.10)
un+l __ un
В + Aun = 0, где В = Е + ат А.
г
Заметим, что (Ви, и) = (и, и) + ат (Аи, и) = (и, и) = ||и||2.
Кроме того, V и : ||и|| ^ 0 верно (Ви, и) > 0. Тогда 3 В~\ и, сделав
замену, и = В-1х, имеем:
Н|2 =
Ч В-Ьс) = (В-^, х) < НВ-^Н • ||х||,
цв-1х|| < ||х|| и ЦВ-1!! < 1.
Схема A1.10) представима в виде
Bun+1 = Bun - тAun = 0; un+1 = un - rB Aun = 0
(разрешенный относительно верхнего временного слоя вид).
298
Лекция 11 Исследование разностных схем для эволюционных уравнений
Найдем (Bun+1, un+1).
(Bun+\ un+1) = (Bun - rAun, un - тВ~1Аип) =
= (Bun, un) - r [(Aun, un) + (Bun, B^AiT)] + r2(Aun, B Aun).
В этом случае идеология доказательства оказывается похожей на
доказательство устойчивости методов Рунге-Кутты на нейтральных по
устойчивости траекториях в лекции 8. Первое слагаемое в квадратных
скобках равно нулю, оценим второе слагаемое:
В = Е + от А = Е - сгтА + 2ат А = В* + 2атА;
(Bun, B^Au") = (B*un, В Aun) + Чат (Aun, B^Au");
первое из слагаемых в левой части выражения — нуль. В результате
имеем:
||un+1||2 = ||un||2 - Bа - IJt^B^Au*, Aun, B^Aii"). A1.12)
Если сг ^ 0,5, то | |un+11| ^ | |un11, и схема устойчива по начальным
данным. Можно показать, что она также будет устойчива и по правой
части.
Пусть теперь а < 0,5. Из A1.12) следует, что
||un+1||2 ^ ||un||2 - Bа - 1)т2||А||2 1КЦ2 < A + cor)||un||2,
гдесо = A-2а)т||А||2.
Если г11 А| |2 ^ С2, то в случае а < 0,5 разностная схема будет
равномерно устойчива с р = у/1 + сог ^ е°'5с°г. Из устойчивости по начальным
данным и в этом случае следует устойчивость по правой части.
Рассмотрим пример: уравнение Шредингера движения частицы во
внешнем поле (т = 1)
или, после обезразмеривания, получим
Если внешнего поля нет, можно потенциальную энергию частицы U
положить равной нулю. На отрезке [0; 1] можно записать разностную схе-
^У «с комплексными коэффициентами», аппроксимирующую уравнение
299
Лекции по вычислительной математике
Шредингера:
-г Аф{а) = О,
(\ 1 1 W
Можно формально умножить правую и левую части A1.13) на г и
воспользоваться приведенными выше результатами. Получим, что в
случае а ^ 0,5 схема устойчива, а при а < О,5 возникает условие
устойчивости вида
Так как 11Л11 = ^, то окончательно получаем условие
где С2 — константа, определяющая р-устойчивость схемы. При этом
погрешности все равно экспоненциально возрастают! В энергетической
норме На условие устойчивости будет
которое не выполняется при любом т. Следовательно, в
энергетической норме устойчивых разностных схем для уравнения Шредингера при
а < 0,5 нет.
Рассмотрим разностную схему
,)<" = о.
V 2ft
Здесь В = Е; А = diag (—^ 0 ^) — трехдиагональная матрица;
| (А + А*) = 0 — оператор А кососимметрический.
В случае а ^ 0,5 схема устойчива. При а < 0,5 имеем условие
устойчивости
а2 ат 4сгЛ
г 713 < С2 =* "Г < »
4л^ д а
но ошибки все же экспоненциально возрастают как е0^1-2*)*2*, где к —
число Куранта. По спектральному признаку при а = 0 схема неустойчива.
Очевидно, что для уравнения Шредингера нет устойчивых схем в
случае а < 0,5 и при использовании метода конечных элементов.
Действительно, будем рассматривать дискретную схему
300
Лекция 11 Исследование разностных схем для эволюционных уравнений
где В = В*. Условие устойчивости в энергетической норме приведет к
операторному неравенству вида
В силу положительности -Л, приходим к противоречию
о > 5(-Л) > о.
В завершение экскурса в теорию устойчивости разностных схем
рассмотрим разностную схему более общего вида:
u_ „п
B(t) — + A(t)uw = if.
Пусть, как и ранее, выполнено условие самосопряженности
A(t) : A(t) = Am(t) >O,te [0; Г], B(t) > 0;
A(t) — Липшиц-непрерывен по t.
|([A(t) - A(* - r)] x, x)| < rc(A(t - t) x, x).
Введем энергетические нормы, зависящие от времени:
ЯА : (A(t) u, u) = ||u||i(t).
Воспользуемся введенным ранее энергетическим тождеством:
(Ц»»+1 — 11П\
Учтем, что
- r)y(t),y(t)) + ([A(t) - A(t - r)]y(t),y(t))
в силу Липшиц-непрерывности. Тогда получаем
те) х (А(* - т)ип, ип) + 2т
un+1 — Un\
, ^— J .
301
Лекции по вычислительной математике
Теперь если B(t) - ?-Ц& > 0, то при <p(t) = 0 сразу имеем
< A + тс)(А(« - т)и», u") =
= A + re) ||u»||iw < ^(OJu1, u1) < ect||u°||i@.
Отсюда и следует устойчивость: из энергетического тождества при
п = 1 получим, что схема устойчива по начальным данным. Устойчивость
по правой части будет следовать из устойчивости по начальным данным.
Таким образом, случай операторов, зависящих от времени,
принципиально не отличается от случая постоянных операторов, лишь нормы
устроены несколько по-другому.
Аналогичные теории строятся и для трехслойных разностных схем,
условия устойчивости также получаются на основе энергетических
тождеств в виде операторных неравенств.
11.4. Задачи
1. Построить разностную схему, аппроксимирующую задачу Коши для
уравнения переноса
— - — =/(t,s),tt@,s) = v(x),-oo<x<oo,t >0
с помощью аппроксимации первых производных со вторым
порядком точности.
Решение. Аппроксимация уравнения переноса со вторым порядком
точности по схеме с центральными разностями
„.п+1 ».п—1 ».п ~,п
итп ~um um+l um-l fn _ n AT I ™ 1 К/Г 1
2^ 2h =/m,n = 0,...,iV-l, m= 1,...,M-1.
Для аппроксимации начальных условий необходимо задать не
только u^ = ipm , но и значение и^, которое можно вычислить с
помощью, например, формулы Тейлора:
Поскольку % - ga = f(t, х) и «(О, х) = ф), то
>-"«?¦ А-
302
Лекция 11 Исследование разностных схем для эволюционных уравнений
В таком случае аппроксимация задачи будет
ит Цт+1 Цт-1 _ fn Q дг -. т_1 Л/-1
2 2/i ~~ '**' "~ ' * * *' ' "~ '#' *'
В этом примере пришлось конструировать дополнительное второе
начальное условие, поскольку исходное дифференциальное
уравнение имеет первый порядок, а разностное — второй.
2. Исследовать устойчивость разностной схемы
ит -ит цтп+1 цш-1 г / п 9?/п 4- ?/п ^ - fn
аппроксимирующей задачу Коши для уравнения переноса.
Решение. Воспользуемся спектральным признаком. Подставляем в
разностную схему решение в виде: и!^ = \neima и рассматриваем
однородное уравнение.
Получим
А - 1 eima - e~
г 2/1
откуда
А(а) = 1 + га sin а - 2а* sin2 —, а = г — число Куранта.
2 а
Вычислим фаницы спектра. Для этого вычислим
|А (а)|2 = (l - 2а2sin2 |J + a2 sin2 а,
а затем расстояние 1 - | А|2. Проведем необходимые вычисления:
(l - 2а2 sin2 ^) + a2 sin2 а = 1 - 4а2 sin2 ^ + 4а2 sin2 a =
= 1 + 4<т4 sin4 ^ + (-4а4 sin4 | + a2 sin2 a) =
303
Лекции по вычислительной математике
= 1 + 4а4 sin2 - + (-4аг sin2 - + <т24 sm2 - cos2 —) =
= 1 + 4a4 sin2 | + [-4a2 sin2 | + a24sin2 |(l - sin2 |)] =
Условие устойчивости выполнено, если правая часть
неотрицательна, что достигается при а ^ 1.
3. Исследовать устойчивость явной разностной схемы
Г ft2 Л2
п = 0,..., N - 1, т = 1,..., М - 1, / = 1,..., L - 1,
аппроксимирующую задачу Коши для уравнения в частных
производных
ди д2и д2и _
at дх2 ду2 ~
Решение. Воспользуемся спектральным признаком устойчивости
фон Неймана, представив разностное решение в виде
После подстановки в разностное уравнение, получим
а = ^,
(а,/?) = 1 - 4<rsin2 ^ - 4asin2 -,
откуда следует 1 — 8а ^ А(а, /3) ^ 1. Окончательно условие
устойчивости разностной схемы будет а < 1/4.
4. Исследовать на устойчивость разностную схему
„п+1 1Ъп цП „п
Urn Urn _AUm+l Um = 0>П = 0, ¦ ¦ ¦ , ЛГ - lfm = 0y. . . , M - 1,
Г Д
(где u = (ubU2)T, — вектор, А = f J , — матрица 2 х 2),
аппроксимирующую систему уравнений в частных производных
ди\ du2 Л 9^2 5^1 Л du A ди
0 = 0А=°г>000<х<00
304
Лекция 11 Исследование разностных схем для эволюционных уравнений
Решение. Подставим в разностную схему решение в виде
п — \п ( ui \
После подстановки в разностное уравнение, получим
(А - 1)и° - a(eia - 1)Аи0 = 0, а = т/h - число Куранта.
Это уравнение можно рассматривать как векторную запись СЛАУ
относительно и0
Система имеет нетривиальное решение только тогда, когда
определитель матрицы обращается в нуль, т. е.
откуда
Ах = 1 - а + aeia, А2 = 1 + а - aeia.
Эти два корня пробегают окружности радиуса а с центрами в точках
1 — а и 1 + ст. Условие устойчивости не выполнено ни при каком
значении числа Куранта.
11.5. Задачи для самостоятельного решения
1. Для задачи Коши для линейного уравнения переноса
ди ди
+0
построить разностные схемы и исследовать их на сходимость,
используя шаблоны:
Разностная схема, построенная на симметричном трехточечном
шаблоне, называется схемой П. Лакса.
305
Лекции по вычислительной математике
2. Для линейного уравнения теплопроводности
ди 2д2и
<>0<
построить разностные схемы и исследовать их на сходимость,
используя шаблоны:
(несимметричная схема) (схема Ричардсона)
3. Построить разностные схемы для линейного волнового уравнения
д2и д2и
dt2 " дх2'
и исследовать их на сходимость, используя шаблоны
4. Построить разностную схему, сходящуюся к решению акустической
системы
диг ди2
ди2 дщ
5. Построить разностную схему П. Лакса, аппроксимирующую задачу
Коши для линейного двумерного уравнения переноса
ди ди ди _
~dt ~ ~дх ~ ~ду ~ '
и исследовать ее на сходимость.
306
Лекция 11 Исследование разностных схем для эволюционных уравнений
Литература
[1] Годунов С.К., Рябенький B.C. Разностные схемы, введение в теорию.
М.: Наука, 1977.400 с.
[2] Федоренко Р.П. Введение в вычислительную физику. М.: Изд-во
МФТИ, 1994.526 с.
[3] Самарский АА. Теория разностных схем. М: Наука, 1983.656 с.
[4] Самарский АА., Вабищевич П.Н., Матус Т.П. Разностные схемы с
операторными множителями. Минск, 1998.441 с.
[5] Самарский А.А., Гулин А.В. Численные методы математической
физики. М.: Научный мир, 2003. 316 с.
[6] Жуков А.И. Метод Фурье в вычислительной математике. М.: Наука,
1992.128 с.
Лекции по вычислительной математике
Лекция 12. Численное решение дифференциальных
уравнений в частных производных параболического
типа на примере уравнения теплопроводности
В лекции рассматриваются разностные схемы для решения
линейного уравнения теплопроводности, нелинейного уравнения теплопроводности.
Приводится пример интегро- интерполяционного метода для построения
разностных схем. Отдельно рассматриваются экономичные схемы решения
многомерных задач для уравнения теплопроводности — переменных
направлений, дробных шагов, Дугласа-Гкнна.
Ключевые слова: явная разностная схема. Неявная разностная
схема. Интегро-интерполяционный метод. Квазилинейное уравнение
теплопроводности. Консервативная схема. Методы переменных
направлений. Схема Дугласа- Ганна.
12.1. Постановки задач для уравнений
параболического типа
Рассмотрим численные методы решения уравнений
параболического типа.
Одномерное линейное уравнение теплопроводности (диффузии).
Напомним постановку соответствующей смешанной задачи:
/(«,х),*€[0,Г||*€[0,Х]. A2.1)
Здесь а = a(x,t) > О, Для того чтобы задача была поставлена
корректно, необходимо задать начальное условие
и граничные условия
B ^ = Х'
О свойствах решений линейного уравнения теплопроводности
подробнее в [1, 3].
308
Лекция 12 Численное решение дифференциальных уравнений
Одномерное квазилинейное уравнение теплопроводности
(диффузии):
^ ^[^]/(n), t€[0,T],*€[0,X]. A2.2)
Уравнения такого вида встречаются в теории горения, астрофизике,
физике плазмы, теории сверхпроводимости Гинзбурга-Ландау, динамике
популяций и других приложениях. Здесь а(и) > 0 при любых значениях
и
и, кроме того, / a(z)dz < +оо. Для глобальной ограниченности решения
о
оо
также требуется выполнение условия / -#у = оо. Для корректной поста-
1
новки задачи необходимо задать одно начальное и два граничных
условия. Подробнее о квазилинейных уравнениях теплопроводности в
книгах [4, 5,6,7,8].
Двухмерное линейное уравнение теплопроводности (диффузии):
^ |^ 0,*е[о)т])х€[о,х])уе[о,У]. A2.3)
Для численного решения уравнения A2.1), по-видимому, наиболее
известной является параметрическая двухслойная шеститочечная
разностная схема вида
J
A2.4)
где?€[0,1].
При f = О имеем явную схему ц^ г""цш = aUm~1~2^iUmfl,
устойчивую при а = ^ ^ |, с порядком аппроксимации О(т, к2).
При f .= 1 имеем неявную схему ц"* г""ц^ = а"™'1" ЦД +Цт^1,
устойчивую при любых г, Л, с порядком аппроксимации О(т, /г).
При ^ = 1/2 разностный метод называется схемой Кранка-Николь-
сон: 2fii^2t = t(<t\-y-HCyt + <-!-2<+цп+1) Схемаустойчива
при любых шагах г, ft и имеет порядок аппроксимации О(т2, ft2). Эта
схема, в отличие от двух предыдущих, не является монотонной, т. е. она может
Давать осцилляции разностного происхождения на решениях, имеющих
большие градиенты.
Схема, имеющая второй порядок точности по г и четвертый по /i,
получается на расширенном шаблоне с учетом разностной
аппроксимации главного члена невязки. При исследовании аппроксимации явной
309
Лекции по вычислительной математике
двухслойной схемы получим
= At» + T-u'lt - |uW + 0{r\ h%
Произведя аппроксимацию первого и второго слагаемого в правой
части (в невязке) рассматриваемого равенства и учитывая следствия
исходного уравнения теплопроводности
получим новую схему повышенного порядка точности:
Л2
2 ^ баг; Л* "U>
Трехслойная параметрическая схема для численного решения
одномерного линейного уравнения теплопроводности имеет вид
Г
_Л П -
[1
ft2
при г/ = 0,5, f = 1 ее порядок аппроксимации равен О(т2, Л2).
Недостатком схемы является трехслойность и, следовательно, необходимость
ставить дополнительное условие на м{@, х).
Соответствующий шаблон имеет вид
п+1
-о п
п-1
m-1 m т+1
310
Лекция 12
Численное решение дифференциальных уравнений
В случае если коэффициент теплопроводности а зависит от времени
и координат, консервативную схему можно получить, используя интегро-
интерполяционный метод (положим, для простоты f(t,x) = 0).
Напомним, что разностная схема называется консервативной, если
выполняются следующие условия. В дифференциальной задаче выполняется
некий закон сохранения. Соответствующий закон сохранения
выполняется и на сеточном уровне. Если же в дифференциальной задаче
имеется несколько законов сохранения, а при переходе к сеточному описанию
все они получаются как следствие нашей разностной схемы в результате
алгебраических преобразований, то схема называется полностью
консервативной.
Как правило, при записи уравнений в частных производных
законам сохранения соответствует дивергентная форма записи. Для
уравнения теплопроводности роль такого закона сохранения играет
непрерывность теплового потока.
m-l/2
m+1/2
о
m-1
т
¦
(
m+1
n+1
n+1/2
n
Для этого запишем уравнение в дивергентной форме:
— + -?— = 0, где W = -ait, х) - тепловой поток,
at ох ох
ИЛИ
" Wdt = °*
S Г
Произведем аппроксимацию последнего интеграла по
прямоугольному контуру с узловыми точками (п, т - 1/2), (п, m + 1/2), (п + 1, m +
+ 1/2), (n+1, m-l/2):
iin h - Wn+l/2r - ?An+1 . h A- Wn~*~1/2r - 0
^+1/2' "m
m-l/21
Отсюда, учитывая вид
ei/.
2 ^flni
yn+1 цт , n+1 tn+1 m 1
h +am+l/2 fc j'
311
Лекции по вычислительной математике
-/-_ |„п цт"цт-1 , ..п+1 Цт ~ цт-1 \
-l/2 ~ 2 I am-V2 Д +am-l/2 ^ I >
(
2h
+ ¦ am+l/2 I am-l/2 и
12.2. Разностные схемы для численного решения
нелинейного уравнения теплопроводности
12.2.1. Неявная схема с нелинейностью на нижнем слое
где am+1/2 вычисляется следующим образом:
n n
ат+1/2 - a ^^5 +
An - 2°(Цт>О(Цт+1)
^ ат+1/2 - ^СЯ^С+Л'
На верхнем слое по времени решение находится с помощью метода
прогонки. Недостаток схемы заключается в необходимости выполнения
условия, ограничивающего шаг по временигт || f'u \\ < 1.
12.2.2. Схема с нелинейностью на верхнем слое
(необходимость ее реализации появляется, когда условие г ||/?
оказывается трудновыполнимым):
am ~ um _ L I лп+1 цт+1
7 " h ^m+1/2 ft "m-1/2 ft ^ ^ ^m •
Для реализации алгоритма прогонки проведем линеаризацию
функции в правой части, то есть используем итерационный метод Ньютона
312
Лекция 12 Численное решение дифференциальных уравнений
в функциональных пространствах (метод квазилинеаризации). Пусть и^
есть % приближение к и?+1; необходимо вычислить и%+г.
Тогда
Для вычисления значений сеточной функции на следующем
временном слое имеем СЛАУ с трехдиагональной матрицей:
am+1/2
Итерации продолжаются до выполнения условия
При реализации шеститочечной схемы с переменным
коэффициентом теплопроводности и нелинейной правой частью f(u) итерационный
процесс может иметь следующий вид:
r 2h[\
/ иП , * — Un Un —Un л \ 1
+ lai+l/2 ^ an-l/2 д 1 =f(um) + fu(um)(um " t*m).
Здесь также была применена линеаризация функции f(u).
Отдельно рассмотрим важный частный случай а = ик. В довольно
грубом приближении уравнение описывает тепловые волны,
образующиеся в высокотемпературной плазме и при образовании сверхновых звезд.
С\л О V Q / *
Оь ОХ ОХ
Начальное условие для этой задачи и(х, 0) = 0, граничные условия —
u@,t) = Ctk, Urn u(x,t) = 0.
Будем искать автомодельное решение задачи, т. е. решение,
зависящее не от двух переменных t и ж, а от одной, являющейся их
комбинацией:
г) = х — Dt, D = const.
313
Лекции по вычислительной математике
Часто под автомодельными понимают решения, зависящие от
безразмерных комбинаций независимых переменных. Введенную
переменную иногда называют переменной бегущей волны. В этом случае
du_dudri_ -п— &Ц-&Ц
тогда рассматриваемое уравнение приобретает вид
-Dv! = (ики'у.
Штрихом здесь обозначено дифференцирование по новой
переменной т/. Скорость распространения волны, обозначенная здесь через D,
будет определена ниже. После интегрирования обыкновенного
дифференциального уравнения получим
-Du = ик • и'г
Постоянную интегрирования полагаем равной нулю, так как
должно выполняться условие непрерывности теплового потока на фронте
тепловой волны. Далее
-D = uk-l-u't
или (uk)'v = -kD, откуда ик(т]) = -kDq или u(rj) = VkD • (-r/I/fc.
Интересуют только положительные решения при ц ^ 0, т. е. при
х ^ Dt При г) > 0 положим и(г)) = 0. В таком случае обобщенное
решение (так как в точке г\ = 0 получается разрыв первой производной)
рассматриваемой задачи будет иметь вид
W \ 0 , »/>0.
Скорость фронта тепловой волны легко определяется из граничного
условия: i
D = у/Ск/к.
Квазилинейное уравнение вида
ди д
имеет качественно различные решения при разных параметрах /си/. Но
в окрестности теплового фронта при распространении тепла по
нулевому фону все эти решения имеют одинаковую асимптотику, решения в
окрестности фронта устроены так же, как и у рассмотренной выше задачи
о распространении тепловой волны.
314
Лекция 12 Численное решение дифференциальных уравнений
12.3. Разностные схемы для численного решения
многомерного уравнения теплопроводности
Численное решение даже простейших уравнений параболического
типа сильно усложняется, если в задаче имеется в наличии более одного
пространственного измерения. Условие устойчивости для многомерных
схем накладывает столь жесткие ограничения на шаги по времени, что
расчет по ним практически невозможен. Необходимо применять
неявные схемы. Представим разностную схему для численного решения
двумерного уравнения теплопроводности
ди _ д2и д2и
'di~"d^ + dy2
в виде
здесь
„п+1
+
ml
h2 i"*-,,,! - h2
х у
Получена линейная система с разреженной (блочной) матрицей.
Однако вид этой матрицы таков, что алгоритм пятиточечной прогонки
в данном случае не применим.
Можно предложить схему расщепления по направлениям, или
локально-одномерную схему (метод дробных шагов, Н. Н. Яненко [7]):
-umi
Соответствующий пространственный шаблон схемы будет
Um-l,l О
315
Лекции по вычислительной математике
Для аналогичной трехмерной задачи
dt" дх2* ду2 + dz2
можно предложить локально-одномерную схему дробных шагов
n+1/З _ п n+2/З _ n+1/З
Umlp Umlp A n+1/З Umlp Umlp A n+2/З
= AlUl 1 = ^Ul
mlp »
n+2/З
Порядок аппроксимации этих схем: О(т, hi, h%) в двумерном случае
и О(т, hl.h^hD — B трехмерном.
Порядок аппроксимации этой схемы по времени можно увеличить
до второго, если провести усреднение операторов Aiu!^lp(i = 1 -г 3),
аппроксимирующих вторые производные по координатам х»(г = 1 -5- 3):
n+1/З n
Umlp "~ Umlp A
T
n+2/З _ n+1/З
mlp mlp л
T
mlp mlp a
T
r, n+1/З
Umlp
n+1
3LS mlp "• V
?)un+1/3l
m'P
n+2/З
где 0 < ? < 1, причем при ^ = 1/2 порядок аппроксимации схемы
будет О(т, hx2, Лу2, h2z) Эта схема Кранка-Николъсон устойчива при любых
т, /ix, hyi hz; ее шаблон для двумерной задачи
= Ах
316
Лекция 12
Численное решение дифференциальных уравнений
n+l,m,/
представлен на рисунке.
n+l,m,/-l о-
n+l,m,/—1 о
n+l/2,m-l,/ о
п,т—1,1
Приведем еще одну схему, имеющую второй порядок
аппроксимации по г и Л:
ит1 ~ и
ее пространственный шаблон:
ит1 ~
Схема Дугласа-Ганна — это общий метод построения неявных
разностных схем переменных направлений для трехмерного уравнения
теплопроводности, имеющих второй порядок точности и безусловно
устойчивых [13]:
и* - ип = ±Аг (и* + ип) + гуА2 (ип) + г2А3 (ип),
и" - ия = ^Ai (и* + ип) + rfA2 (и** + ип) + ггАз (ип),
un+1 - un = ^Ai (и* + ип) + ^А2 (и** + ип) + ^Аз (un+1 + ип) .
317
Лекции по вычислительной математике
Верхние индексы * и ** обозначают промежуточные значения,
координатные индексы г, j, к опущены во всех членах уравнений, Лг —
компоненты разностного оператора теплопроводности. На каждом шаге метода
возникает система линейных уравнений с трехдиагональной матрицей,
решаемая методом прогонки. Схема Дугласа-Ганна безусловно
устойчивая. В настоящее время это наиболее удачная из схем расщепления в
трехмерном случае.
12.4. Исследование сходимости разностных схем
для многомерного уравнения
теплопроводности
Простейшая явная разностная схема для численного решения
двумерного уравнения теплопроводности
ду2
получается путем замены производных конечными разностями
= ttm-l,l - 2<1 + «Сц,1 , </-! ~ 2< + <
г
или, в операторной форме,
Л.п+1
Исследование спектральной устойчивости этот схемы (и^ =
= Ane<em+W, а, /3 € [0,2тг]) приводит к следующему результату для
спектра оператора послойного перехода:
2 ^ 4^ sin2
А(а, /?, г, hx, hy) = l- 4-^- sin2 ^ - 4-^- sin2 -,
hi 2 Aj 2
откуда получаем условие устойчивости
1
Для неявной схемы
318
Лекция 12 Численное решение дифференциальных уравнений
исследование на устойчивость по спектральному признаку дает
т. е. схема устойчива при любых а, /?.
Приведем исследование спектральной устойчивости для схемы
переменных направлений.
Рассмотрим переход с нижнего на верхний временный слой. В
таком случае можно положить u^i = eiQtm+i/3'; сомножитель Ап опускаем,
так как рассматривается один переход с n-го на (п + 1)-й слой в
предположении, что известно решение на n-ом слое (можно было бы написать,
u^i = Сегат~*~г01, где С = Ап, но в этом нет смысла, так как С в
дальнейших выкладках сократится).
Тогда на первом этапе получим um/ = Aiu^z, а на втором —
Вычисление Ai и А2 дает
l-4_|sin2f l-4?sin2f
Л Л
Окончательно спектр оператора послойного перехода представим в
виде произведения спектров на каждом промежуточном этапе.
Схема безусловно устойчива.
Исследование схемы расщепления на аппроксимацию проведем на
примере локально-одномерной схемы для двумерного уравнения
теплопроводности
Запишем эти уравнения в операторной форме
(Е - тА^пгщ = tCz, (E - rA2)un+1 =
Подействуем на обе части второго уравнения оператором (Е - тК\):
(Е - тЛхХЕ - тЛзХ!1 = (Е - т
319
Лекции по вычислительной математике
Так как
(E-rAi)fimi = tC то (Е-
Это уравнение приводится к виду
Последнее слагаемое в правой части является величиной порядка
О(т) и определяет погрешность аппроксимации.
Если правая часть f(t, x, у) не нулевая, то схему можно переписать,
например
12.5. Задачи
1. Исследовать на аппроксимацию и устойчивость схему Ричардсона
п+1_ п-1
m 2rm = 7?Лжжип, с шаблоном
аппроксимирующую уравнение теплопроводности ^ = aii7-
Решение. В силу симметрии шаблона схемы несложно заметить, что
ее порядок аппроксимации О(т2, h2).
Подстановка решения в виде и^ = Aneiam дает квадратное
уравнение для определения спектра оператора послойного перехода Л2 +
+ ^f A sin2 ^-1 = 0, один из корней которого при любом значении
параметра а по модулю больше единицы, т. е. рассматриваемая
схема безусловно неустойчива.
320
Лекция 12
Численное решение дифференциальных уравнений
Выходом из данной ситуации оказывается замена в выражении
кела-Дюффорта):
величины < на "n'4"w+1 (схема Фран-
и]
п+1 _ п.п-
ит
2т h2
со следующим шаблоном:
которая разрешается явно относительно и?*1 и безусловно
устойчива.
Однако она обладает лишь условной аппроксимацией: 0{т2, Л2, г2/Л2
и таким образом, сходимость возможна лишь при т/h -> 0.
2. Исследовать на аппроксимацию и устойчивость схему Саульева
бегущего счета
(четные слои, счет справа налево)
л.П+1 л,П уП
= а-
(нечетные слои, счет слева направо) со следующим шаблоном:
И—3339
321
Лекции по вычислительной математике
Решение. Путем подстановки решения в виде иЧ^ = Aneiam,
несложно проверить, что схема безусловно устойчива.
Невязка каждого из двух уравнений, вычисленная относительно
точек, отмеченных крестиками, имеет порядок О(т2, ti2, т, Л, т/К).
Сложение же невязок из двух рассматриваемых уравнений дает
погрешность O(r2,h2, r2/h2), аналогичную схеме Франкела-Дюфорта.
Схема Саульева допускает значительное улучшение. Достаточно
только вычислить значения функции в рамках перехода с данного
слоя на следующий два раза — бегущим счетом слева направо и
бегущим счетом справа налево — и усреднить результаты. Свойства
такого метода расчета предлагается исследовать самостоятельно.
3. Исследовать на аппроксимацию и устойчивость схему Алена-Чена
_
с шаблоном
Ответ. Во-первых, несмотря на то, что в правую часть входит
значение функции uj}*1, вычисляемое на верхнем слое, разностное
уравнение разрешается относительно м?+г. Схема безусловно
устойчива, что является ее достоинством при реализации, однако она имеет
порядок аппроксимации О(т, h2,r/h2), т. е. схема является условно
аппроксимирующей.
4. Выяснить, является ли явная четырехточечная схема Um ~Un
= аАххип с шаблоном
монотонной. Монотонные разностные схемы (по Фридрихсу) — это
схемы, которые при записи в виде, разрешенном относительно v%fl
при значениях сеточной функции во всех остальных точках
шаблона, имеют неотрицательные коэффициенты. Монотонные
разностные схемы не дают паразитные осцилляции в решении. Придумать
322
Лекция 12 Численное решение дифференциальных уравнений
доказательство утверждения, что из монотонности разностной
схемы следует ее устойчивость, предлагается самостоятельно.
Решение. Представим рассматриваемую схему в виде
где а = 1 - ^f ,#1 = ос-1 = ^, откуда видно, что схема является
монотонной при выполнении условия ctk ^ 0,fc = -1,0,1 то есть
при г ^ т?. Эта схема условно монотонная.
Заметим, что неявная четырехточечная схема является монотонной,
а схема Кранка-Никольсон — условно монотонная.
о
Исследование монотонности параметрической двуслойной схемы в
оо
виде UJJ+1 = 53 amV>m+k, дает (выкладки опускаем ввиду их гро-
моздкости):
оо
4- ^ ак{иш-к
4ar (h + y/h2 -I- 4f ar)
1 ^—> -
/2
-2
Коэффициенты ах при х ^ 1 неотрицательны, коэффициент с*о
неотрицателен при выполнении условия:
< B-Qfe2
Г^4аA-02'
Отсюда видно, что, за исключением неявной четырехточечной
схемы с ? = 1, все неявные схемы являются монотонными лишь при
условии т ~ h2.
323
Лекции по вычислительной математике
5. Исследовать на устойчивость и аппроксимацию трехслойную схему
г ft ~" xxUm
с шаблоном
о о о
Ответ. Простое исследование на аппроксимацию данной схемы
путем разложения функций в ряд Тейлора дает О(т2, ft2). Схема
безусловно устойчива. Кроме того, схема монотонна.
6. Показать, что решение задачи
) = 0, u@,t)=ctl/a, u(x,0)=0
представляет собой бегущую волну, распространяющуюся с
конечной скоростью, причем при а > 0 на фронте волны решение терпит
разрыв первой производной (т. е. является обобщенным решением).
Предложить какие-нибудь разностные схемы для численного
решения данной задачи, например, применив интегро-интерполяцион-
ный метод [3]. Почему в этом случае нельзя переписать уравнение в
виде
ди ад2и 2
продифференцировав правую часть по х, а затем заменить
производные их разностными аппроксимациями?
Решение. Построим решение задачи в переменных бегущей волны:
и = и@ = и(х - vt), (x-vt^ 0), и = 0. A2.6)
Подставив A2.6) в исходное уравнение, получим следующее
обыкновенное дифференциальное уравнение:
а(Л[)[. A2.7)
324
Лекция 12 Численное решение дифференциальных уравнений
Это уравнение интегрируется по f:
к - vu = auau'v A2.8)
где к — константа интегрирования.
Выражение, стоящее в правой части A2.8), есть поток величины и,
а уравнение A2.8) является некоторым законом сохранения. В
точке фронта и = О, в силу непрерывности потока справа и слева от
фронта A2.8) должно выполняться, отсюда следует к = 0.
Так как интересуют только нетривиальные решения A2.5),той Ф 0,
и можно разделить правую и левую части на и. Тогда получим
-v = еша-Ц = -(«% A2.9)
откуда u=[<f(x-vt)]1/a.
Из краевых условий при х = 0 имеем v = aca/a. Наличие разрывов
производной легко проверяется. Уравнение A2.5) записано в
дивергентном виде, которому будет соответствовать консервативная
схема.
В [9] использован несколько отличный подход к решению задачи.
В [4] рассмотрен общий случай, когда коэффициент
теплопроводности есть функция К(и):
Подробнее про разностные схемы для аппроксимации уравнения
E.3.1) в [4, с. 441-463].
12.6. Задачи для самостоятельного решения
1. Используя условие устойчивости Куранта-Фридрихса-Леви,
определить, какие из разностных схем, шаблоны которых приведены
ниже, не будут устойчивыми:
-о о ———^— о о о -
325
Лекции по вычислительной математике
2. При каком соотношении шагов г и h явная разностная схема
для уравнения теплопроводности имеет порядок аппроксимации
O(t2,/i4)?
3. Показать, что параметрическая разностная схема
при весе ? = \ - ^ имеет порядок аппроксимации О(т2, ft4).
4. Для аппроксимации уравнения A2.2) использована схема
^m wm-l
где fcm+i/2 вычисляется следующим образом:
(а) кт+1/2 = §(«)• + «
(d) k 1/9-flW
Выражения a)-d) суть некоторые аппроксимации <ша, взятые на
предыдущем слое по времени между узлами um,um+i. Какой из
вариантов предпочтительнее? Почему не работают в окрестности
фронта средние гармонические — с) и d)?
Реализовать схемы а) и Ь) на ЭВМ, сравнить численное решение с
точным (см. выше). Почему при больших числах Куранта
наблюдается отставание фронта волны в численном решении от точного
значения [9]?
5. Режимы с обострением
Рассмотрим уравнение
)'а>0'а>0^>0- (Ш0)
326
Лекция 12 Численное решение дифференциальных уравнений
Построить численно решение A2.10) в случаях а) C = а +1, 6) /3 <
u(-oo, t) = 0,u(+oo, t) = 0,ti(*, 0) =
В чем качественное различие случаев а) (так называемый S-режим
с обострением), б) (#5-режим), в) (LS-режим)? (См. [5, глава 2], [4,
С. 172-206]). В случае а) численно проверить справедливость
формулы полуширины локализации тепла: I = ку^т- Как решение
зависит от амплитуды начального возмущения ио?
6. Автомодельные решения и автомодельные переменные
В случаях 1-3 будем искать решение уравнения A2.10) в виде [5,
С. 32-62], [4]:
(a) Найти функции g(t),(p(t).
(Ответ: g(t) = A - t/tf)~1/2, <p (t) = A - */tf) *2"^-*>\ tf —
положительный параметр).
(b) Какому дифференциальному уравнению удовлетворяет при
этом функция /(О? Решить численно получившееся
уравнение для /(?) с условиями
с дополнительным требованием faf^=i = 0.
(с) Задавая /(?) при t = 0 в качестве начальных условий для
A2.10), сравните поведение численного решения с
автомодельным. (Так как известны g(t), ф(г) и /(?), то тем самым
найдено u(x, ?)V?0 < t < tf). Что происходит при t —> tf?
7. Тепловой кристалл
Рассмотрим уравнение
ди , 9 лди , д ад
к+к
Попытайтесь качественно исследовать свойства решений этого
уравнения.
327
Лекции по вычислительной математике
В случае а = /? - 1 > 0, к\ ф кг рассмотреть задачу со следующими
граничными условиями:
при х < 1/Аг, иначе 0. Здесь п< 0 — действительное число.
Рассмотреть случаи
и = -1/а, п < -1/а, - 1/а < п < 0.
Решить задачу численно и сравнить полученное решение с
аналитическим. Решение тепловой кристалл описано в [4, с. 148-155].
8. Остановка тепловой волны
Модифицируем задачу 6:
положив г = 0,1.
(a) Выполнить пункты задачи 6. Как влияет малый линейный сток
на поведение решения?
(b) В случае а = /3 -1 найти автомодельное решение, аналогичное
рассматриваемому в задаче G).
Указание. Рассмотреть последовательность замен
ди
= ea€tdt.
Каким станет уравнение A2.11) в переменных v, х, П
(с) Рассмотреть задачу о формировании теплового кристалла для
уравнения A2.11).
9. Неустойчивость Тьюринга
Рассмотрим систему
ди „ д2и
328
Лекция 12 Численное решение дифференциальных уравнений
dv ,.
с условиями
ди
дх
х=0
ди
дх
х=1
х=0
= 0,
причем а + d < 0, ad - ftc> 0. При этих условиях особая точка @,0)
системы и = аи + bv, v = си + dv устойчива. Пусть, без ограничения
общности, а > 0.
(a) Найти условие, когда внесение в систему диффузии приводит
к потере устойчивости однородного стационарного решения.
Указание. Рассмотреть преобразование Фурье по
пространственной переменной. Исследовать на устойчивость особые
точки получившейся системы ОДУ.
(b) Подобрав коэффициенты а, Ь, с, d и ?>i, Дг, удовлетворяющие
условиям, найденным в пункте 1, получить при численном
счете так называемые структуры Тьюринга. Под структурой
Тьюринга здесь понимается пространственно-неоднородное
решение с волновым числом fe, таким, что ReA(A;2) = 0; %f?w = 0
при записи решения в виде [ ) = ( Cl ) ext~ikx. В случае
V v ) \ С2 /
линейной задачи эти структуры будут возрастать по амплитуде
при t —> оо, в случае нелинейного уравнения (следующая
задача) бесконечный рост становится невозможным, структура
стабилизируется за счет нелинейности.
10. Распределенный брюсселятор
Рассмотрим систему уравнений типа реакция-диффузия, где для
описания химических реакций использована модельная система
«брюсселятор». В литературе эта постановка имеет название
«распределенный брюсселятор»:
9v п 2 d2v
- = Bu-u*v + D2J-i
с граничными условиями
329
Лекции по вычислительной математике
и начальным условием и(х, 0) = А(\ + ecos u;z),v(?,0) = В/A.
Это — система уравнений «брюсселятор» с учетом диффузии
компонентов.
(a) Пусть В > A + Ay/Di/D2J,Di < D2. Рассмотреть
образование структур Тьюринга в случаях д = Ay/Di/D2,n <
0.207,0.207 < \i < 2.418, ^ > 2.418.
Когда можно пользоваться явной разностной схемой? Когда
необходима неявная схема?
(b) Пусть теперь Di > D2,A > 1. Что происходит в системе?
Почему для расчетов необходимо применять неявные схемы?
Какую схему расщепления по физическим процессам можно
предложить для решения задачи? Примеры расчетов
приведены в книге [15], качественное исследование — в [14, С. 403-
407].
11. Схема «Классики»
Для двумерного уравнения теплопроводности используется схема
«классики». Как и в схеме Саульева, расчет осуществляется в два
этапа:
hi
в случае, если Z + т + п — четное,
+«as.
hi
i
в случае, если 1 + т + п — нечетное.
Явная или неявная эта схема? Исследовать ее на аппроксимацию
и устойчивость. Зачем нужно «перепрыгивание» — смена порядка
обхода узлов при переходе со слоя на слой по времени?
Применить эту схему к расчету предыдущей задачи.
Литература
[1] Тихонов АН., Самарский АЛ. Уравнения математической физики.
М., Изд-во МГУ, 2002.
330
Лекция 12 Численное решение дифференциальных уравнений
[2] Владимиров B.C. Уравнения математической физики. М: Наука,
1984.
[3] Соболев С.Л. Уравнения математической физики. М.: Наука, 1992.
[4] Самарский А.А.у Галактионов В.А., Курдюмов СП., Михайлов А.П.
Режимы с обострением в задачах для квазилинейных параболических
уравнений. М.: Наука, 1987.480 с.
[5] Ахромеева Т.С., Курдюмов СП., Малинецкий Г.Г., Самарский А.А.
Нестационарные структуры и диффузионный хаос. М.: Наука, 1992.
544 с.
[6] Курдюмов СИ, Куркина Е. С. Тепловые структуры в среде с
нелинейной теплопроводностью. / В кн.: Будущее прикладной математики.
Лекции для молодых исследователей. Под ред. ГГ. Малинецкого. М.:
Едиториал УРСС, 2005.512 с.
[7] Яненко Н.Н. Метод дробных шагов решения многомерных задач
математической физики. Новосибирск: Наука, 1967.196 с.
[8] Годунов С.К., Рябенький B.C. Разностные схемы, введение в теорию.
М.: Наука, 1977.400 с.
[9] Федоренко Р.П. Введение в вычислительную физику. М: Изд-во
МФТИ, 1994.526 с.
[10] Самарский А.А. Теория разностных схем. М.: Наука, 1983.656 с.
[11] Самарский А.А., Вабищевич П.Н., Матус Г.И Разностные схемы с
операторными множителями. Минск, 1998.441 с.
[12] Марнук Г.И. Методы расщепления. М: Наука, 1988.263 с.
[13] Андерсон Д., ТаннехиллДж., Плетчер Р. Вычислительная
гидромеханика и теплообмен: в 2-х т., Т. 1: Пер. с англ. М.: Мир, 1990.384 с.
[14] Ланда НС Нелинейные колебания и волны. М.: Наука-Физматлит,
1997.496 с.
[15] Хайрер Э., Нернсет С, Ваннер Г. Решение обыкновенных
дифференциальных уравнений. Нежесткие задачи. М.: Мир, 1990.512 с.
331
Лекции по вычислительной математике
Лекция 13. Численные методы решения уравнений
в частных производных гиперболического типа (на
примере уравнения переноса)
В лекции дается понятие о простейших разностных схемах для решения
линейного уравнения переноса. Приводится вид некоторых часто
употребляемых схем. Обсуждаются способы конструирования гибридных разностных
схем. Обсуждаются вопросы обобщения на квазилинейный случай. Дается
первоначальное представление о способах регуляризации решений с
большими градиентами. Вводится понятие схем с уменьшением полной вариации
(TVD). Рассматриваются основные идеи метода конструирования
разностных схем в пространстве неопределенных коэффициентов.
Ключевые слова: линейное уравнение переноса, характеристика,
квазилинейное уравнение переноса, дивергентная форма,
консервативная разностная схема, регуляризация, сглаживание, схемная
вязкость, антидиффузия, гибридные схемы, TVD-схемы, пространство
неопределенных коэффициентов, первое дифференциальное
приближение.
13.1. Простейшее линейное уравнение переноса
Рассмотрим простейший пример уравнений в частных
производных. Пусть в некотором объеме движущейся жидкости находится
пассивная примесь, т. е. такая, наличие которой не меняет принципиально
характер движения. Например, это может быть маркер — краска,
чернила или мелкие частицы, которые специально добавлены в жидкость для
визуализации течений. Тогда изменение концентрации примеси в любом
сколь угодно малом объеме равно потоку примеси через границы объема
в единицу времени (закон сохранения массы), и можно записать,
устремляя рассматриваемый объем к нулю
ди
— = -div(uv),
где и — концентрация пассивной примеси, v — скорость течения
жидкости. Пусть жидкость несжимаема и
divv = 0.
332
Лекция 13 Численные методы решения уравнений в частных производных
Тогда из двух предыдущих соотношений сразу следует уравнение
5j+vgradu = 0. A3.1)
ot
Равенство A3.1) будем в дальнейшем называть уравнением переноса
пассивной примеси или линейным уравнением переноса. Кроме A3.1),
будем рассматривать и одномерное уравнение переноса
ди ди ,,~ ~v
а также неоднородное уравнение переноса
где / — заданная функция, играющая роль источника (стока).
Неоднородным уравнением переноса описываются системы, в
которых пассивная примесь может вступать, например, в химические
реакции. Если уравнения переноса описывают распространение
планктона, то в правой части будет стоять функция, описывающая размножение
планктона и его пассивную утечку (например, за счет его поедания
рыбами). О неоднородных линейных моделях речь пойдет ниже.
Уравнения вида A3.1, 13.2, 13.3) традиционно рассматриваются в
курсах обыкновенных дифференциальных уравнений [1,2].
Причина этого кроется в следующем обстоятельстве. Рассмотрим
систему ОДУ
x = v, A3.4)
соответствующую A3.1). Это — уравнение характеристик для линейного
уравнения переноса. Если функция и является первым интегралом A3.4),
то она является решением A3.1). Иными словами, вдоль характеристики
решение однородного уравнения переноса сохраняет постоянное
значение.
Упражнение. Найти в явном виде уравнение характеристики для A3.2).
В какое уравнение перейдет неоднородное уравнение переноса A3.3)
вдоль характеристики?
Для корректной постановки задач для линейного уравнения
переноса начальные и граничные условия необходимо ставить на некоторой
гиперповерхности. Так как решение уравнений переноса
распространяется вдоль характеристик, то начальная гиперповерхность должна быть
трансверсальной ко всем характеристикам (не иметь точек касания с
характеристиками). Кроме того, если для однородного уравнения переноса
333
Лекции по вычислительной математике
какая-либо характеристика имеет с начальной гиперповерхностью более
одной общей точки, то значения начальной функции во всех этих точках
должны быть равны между собой. Все эти условия достаточно очевидны,
если вспомнить физический смысл уравнения переноса.
Отметим, что наличие характеристик можно считать условием
того, что система имеет гиперболический тип. Так, если система уравнений
произвольного порядка п имеет п действительных характеристик, будем
называть ее гиперболической. Таким образом, линейное уравнение
переноса имеет гиперболический тип.
13.2. Квазилинейные уравнения
гиперболического типа. Характеристики
квазилинейных уравнений
Рассмотрим теперь более сложные примеры уравнений первого
порядка в частных производных. Уравнение вида
ди х—4 ди .
где / = f(t,Xi,u),Ck = Cfc(^,Xi,u), будем называть квазилинейным
уравнением (переноса) [1,2]. Естественно предположить, что все функции,
входящие в запись A3.5), достаточно гладкие (подробнее в [1]). Для
квазилинейных уравнений также существует понятие характеристики. В
соответствии с [ 1,2], уравнения характеристик для A3.5) будут иметь вид
u = f.
Последние соотношения для характеристик легко переписываются
в координатах:
Рассмотрим пример нахождения характеристик для квазилинейного
уравнения.
Уравнения газовой динамики моделируются уравнением Хопфа:
ди ди „
334
Лекция 13 Численные методы решения уравнений в частных производных
Для вывода уравнения Хопфа рассмотрим одномерную среду,
состоящую из частиц, которые движутся по инерции. Считаем, что движение
происходит вдоль прямой. Запишем для частиц второй закон Ньютона:
ди dudx ди ди
Найдем характеристики уравнения Хопфа: & = и, ^ = 0. Таким
образом, характеристики уравнения Хопфа — семейство линий х = а +
+ W,w = b.
Отметим, что линейное уравнение можно рассматривать как
частный случай квазилинейного уравнения. При этом можно ввести
определение характеристики для линейного уравнения аналогично
характеристике для квазилинейного уравнения. Заметим, что характеристика
квазилинейного уравнения, вообще говоря, определяется в пространстве
более высокой размерности, чем для линейного уравнения.
Характеристики линейного уравнения, определенные выше, в этом случае
совпадают с проекциями на гиперплоскость (xi,... ,хп) характеристик
квазилинейного уравнения. В частном случае для однородных
квазилинейных уравнений можно рассматривать характеристики на гиперплоскости
(xi,..., хп). Тогда характеристики уравнения Хопфа можно считать
прямыми линиями x(t) = х@) + u(x@),0)t. На практике при построении
численных методов часто именно эти линии и считаются
характеристиками уравнения Хопфа.
Используя метод характеристик, можно решать уравнения Хопфа.
Рассмотрим в качестве примера уравнение Хопфа с начальным условием
u(x,0) = ch~2(x). Построим характеристики для данной задачи,
пользуясь начальными данными. Вдоль каждой характеристики значение
функции остается постоянным. Можно построить решение вплоть до
момента времени, когда характеристики начинают пересекаться. После этого
решение уравнения Хопфа в классическом смысле перестает
существовать. Далее существует лишь разрывное обобщенное решение типа ударной
волны. На разрыве (фронте ударной волны), вообще говоря, необходимо
ставить дополнительные условия. Пересечение характеристик и
образование ударной волны в решении также называют градиентной
катастрофой. Более подробная информация о свойствах уравнения Хопфа в [3].
Конечно, возможно найти численное решение уравнения Хопфа в виде
ударной волны. Речь об этом пойдет ниже.
335
Лекции по вычислительной математике
13.3. Численные методы решения уравнений в
частных производных гиперболического
типа на примере линейного уравнения
переноса
Двухслойные разностные схемы. Линейное одномерное уравнение
переноса, как отмечалось выше, имеет вид A3.3)
ди ди л
— + с— = 0, с = const;
Наряду с линейным уравнением переноса, в следующем параграфе
будем рассматривать также квазилинейные уравнения. Простейшее
квазилинейное уравнение гиперболического типа — уравнение Хопфа A3.5).
Оно интересно тем, что моделирует уравнения газовой динамики.
Запишем его в двух формах:
(дивергентная форма). Отметим, что дивергентная форма записи
отражает наличие некоторого закона сохранения. В случае уравнения Хопфа это
закон сохранения импульса. В другой форме,
^ + u^ = 0, 0<^T, (Kz<oo. A3.7)
at ox
Эту форму записи иногда в дальнейшем будем называть
характеристической. Отметим, что для линейных уравнений с постоянными
коэффициентами нет принципиальной разницы между характеристической и
дивергентной формами. Для уравнений с переменными
коэффициентами эта разница возникает даже в линейном случае. При использовании
различных форм записи для построения разностных схем возникают
численные методы с разными свойствами.
Для корректной постановки начальной и краевой задач необходимо
корректно задать начальные и граничные условия. Они для
рассматриваемых ниже задач имеют вид
и@, х) = ipi(x), 0 < х < оо;
u{t, 0) = (p2(t), O^t^T.
Для определенности пока положим о 0.
Решением задачи Коши для уравнения A3.3) является «бегущая
волна»:
u(t,x) = *(*-<*),
336
Лекция 13 Численные методы решения уравнений в частных производных
где с — скорость переноса, а функция Ф(х-с^) определяется из начальных
или граничных условий. Характеристики уравнения имеют вид х - d =
= const и при постоянной скорости переноса являются прямыми
линиями. Решение однородного уравнения A3.3), как отмечено выше,
остается постоянным вдоль характеристики, поэтому начальные и граничные
условия переносятся вдоль этих линий. В случае неоднородного
уравнения вдоль характеристики оно превращается в обыкновенное
дифференциальное уравнение.
Приведем вид двухпараметрического семейства двухслойных
разностных схем первого и второго порядков точности [4]:
2/i Um ~ 2т h?
где применены обозначения
- Um, A~Um = Um- Wm-1,
Д")ит = Д+г1т + Д"ит = um+i - um_i,
= Д+(Д-гхт) = Д+(ит - г*т-!) =
Рассмотрим теперь конкретные разностные схемы решения
модельного линейного уравнения переноса.
Схема П. Лакса (трехточечная схема) получается при 7 = 0, q = 1. Ее
порядок аппроксимации О(т + h2 4- Л2/т). Здесь и далее порядок
аппроксимации приводится для модельного уравнения переноса с
постоянными коэффициентами. В случае переменных коэффициентов в схему надо
внести необходимые изменения. При этом естественно линейное
уравнение рассматривать как частный случай квазилинейного.
Схема является условно устойчивой, т. е. при выполнении условия
Куранта а = cr/h ^ 1. Отметим здесь, что величина а играет
определяющую роль при исследовании разностных схем на аппроксимацию и
337
Лекции по вычислительной математике
устойчивость. Она называется числом Куранта. Исследование
разностной схемы на устойчивость для линейного эволюционного уравнения с
постоянными коэффициентами можно провести с использованием
спектрального признака (фон Неймана).
Приведем разностные уравнения для схемы Лакса во внутренних
точках расчетной области:
- 0,5«+1 + <_i) <+i - <-i
2ft
На рисунке приведен шаблон для схемы Лакса. Напомним, что
шаблоном разностной схемы называется конфигурация узлов, значения
сеточной функции в которых определяют вид разностных уравнений во
внутренних (не приграничных) точках сетки. Как правило, на рисунках с
изображениями шаблонов точки, участвующие в вычислении
производных, соединяются линиями.
о (n+l,m)
при а>0
) (n,m)
о (n+l,m)
при а<0
(п,т)
Схема Кураита-Изаксона-Риса (КИР), которую иногда также
связывают с именем С.К. Годунова, получается при 7 = 0, q = asign с. Ее
порядок аппроксимации О(т + ft). Схема КИР условно устойчива,.т. е. при
выполнении условия Куранта а = ст/h ^ 1. Приведем разностные
уравнения для схемы Куранта-Изаксона-Риса во внутренних точках
расчетной области:
Щп tV+c"m Ц"-1=0, О О,
с<0.
Эти схемы, имеющие также название схемы с разностями против
потока (в англоязычной литературе — upwind) могут быть записаны в ви-
338
Лекция 13 Численные методы решения уравнений в частных производных
де
<+!-<, * < О,
Их преимущество состоит в более точном учете области зависимости
решения. Если ввести обозначения
a, a ^ О, _ 1, , |ч ( 0, а ^ О,
0, а<0, а = 2(° " W) = { а, а < О,
то обе схемы можно записать в следующих формах:
(потоковая форма разностного уравнения);
= < - \а{ипт+1 - <_х) + М«+1 - 2<
(здесь явно выделен член со второй разностью, придающий устойчивость
схеме);
1^М
(уравнение в конечных приращениях).
Рассмотрим также метод неопределенных коэффициентов для
построения разностной схемы правый уголок первого порядка точности для
уравнения переноса
— - — = ^(*,х),т.е. приа = -1.
Схему можно представить в виде
LruT =
Схема Куранта-Изаксона-Риса тесно связана с численными
методами характеристик. Дадим краткое описание идеи таких методов.
339
Лекции по вычислительной математике
Две последние полученные схемы (при разных знаках скорости
переноса) можно интерпретировать следующим образом. Построим
характеристику, проходящую через узел (?п+ъЯт), значение в котором
необходимо определить, и пересекающую слой tn в точке х' = хт - ст. Для
определенности считаем, что скорость переноса с положительна.
Проведя линейную интерполяцию между узлами xm-i и хт на
нижнем слое по времени, получим
(/\ *^т •? •? Хт—1
х ) = ит-\ ?— + ит д =
= -^Um-1 + A " у
Далее перенесем вдоль характеристики значение ип(х') без
изменения на верхний слой ?п+ь т. е. положим um+1 = ttn(x/). Последнее
значение естественно считать приближенным решением однородного
уравнения переноса. В таком случае
= A - а)ит + otim-i,
или, переходя от числа Куранта снова к сеточным параметрам,
,
и
т-1
т.е. другим способом пришли к уже известной схеме «левый уголок»,
устойчивой при а = cr/h < 1, с > 0. При а > \ точка пересечения
характеристики, выходящей из узла (?n+i,xm), с n-м слоем по времени
расположена левее узла (?n, xm_i). Таким образом, для отыскания
решения ит+1 используется уже не интерполяция, а экстраполяция, которая
оказывается неустойчивой.
Неустойчивость схемы «правый уголок» при с > 0 также очевидна.
Для доказательства этого можно использовать либо спектральный
признак, либо условие Куранта, Фридрихса и Леви. Аналогичные
рассуждения можно провести и для случая с < 0 и схемы «правый уголок».
o(n+l,m)
Неустойчивая четырехточечная схема получается при 7 = 0, q = 1, ее
порядок аппроксимации О(т + h2). Сеточные уравнения для разностной
340
Лекция 13 Численные методы решения уравнений в частных производных
схемы будут иметь следующий вид:
2ft
Схема Лакса-Вендроффа возникает при 7 = 0, q = а. Порядок
аппроксимации схемы Лакса-Вендроффа есть О(т2 + h2). Схема устойчива
при выполнении условия Куранта о = ст/h ^ 1.
Эту схему можно получить либо методом неопределенных
коэффициентов, либо путем более точного учета главного члена погрешности
аппроксимации. Рассмотрим процесс вывода схемы Лакса-Вендроффа
подробнее. Проводя исследование предыдущей четырехточечной схемы на
аппроксимацию (а исследование это довольно элементарно и сводится к
разложению функции проекции на сетку точного решения
дифференциальной задачи в ряд Тейлора), получим для главного члена погрешности
т 2ft dt дх
При выводе выражения для главного члена погрешности аппроксимации
использовано следствие исходного дифференциального уравнения
переноса ^г = с21^7» которое получается путем дифференцирования
исходного уравнения A3.3) сначала по времени t9 затем по координате х и
вычитанием одно из другого получившихся соотношений.
Далее, заменяя вторую производную во втором слагаемом в правой
части с точностью до О(Л2), получим новую разностную схему,
аппроксимирующую исходное дифференциальное уравнение с точностью О(т2 +
+ Л2). Сеточные уравнения для схемы Лакса-Вендроффа во внутренних
узлах расчетных сеток есть
т ' " 2ft ^2 ft2
Неявная шеститочечная схема возникает при q = 0; при 7 = 0,5 ее
порядок аппроксимации О(т2 + ft2), при 7 = 1- O(r + ft2).
Построить шаблоны схемы при 7 = 0,5 и при 7=1.
Неявная нецентральная схема. Рассмотрим случай q = asign с. При
7 = 0,5 порядок аппроксимации — О(т2 + ft). При 7 = 1- О(т + ft).
Упражнение. Нарисовать шаблон схемы при 7 = 0,5 и при 7 = 1-
Последние две разностные схемы носят названия схем Ландау-Мей-
мана-Халатникова и Карлсона, соответственно.
341
Лекции по вычислительной математике
Явная схема Бима-Уорминга
Бим и Уорминг предложили изменить метод Мак-Кормака,
используя на обоих этапах односторонние разности одинаковой
направленности; для линейного уравнения переноса эта схема будет
h
| д ( д
г h h2
При подстановке первого уравнения во второе, получим
Шаблоны двух- и одноэтапной схем имеют вид
о п+1
о п+1
х х ~
¦о п о о о
пг— 2 т—1 т т—2 т—1 т
Эта же схема может быть записана в приращениях
13.4. Численные методы решения уравнений в
частных производных гиперболического
типа для квазилинейного уравнения
переноса
Рассмотрим теперь простейшие разностные схемы для уравнения
Хопфа.
Обобщение на случай уравнения Хопфа схемы П. Лакса имеет вид
т h
Здесь, очевидно, используется дивергентный вид уравнения A3.6).
342
Лекция 13 Численные методы решения уравнений в частных производных
Упражнения. Рассмотрим схему Лакса-Вендроффа для уравнения
Хопфа. Пусть начальные условия для задачи Коши поставлены
следующим образом: u(z,0) = ch~*(x). Тогда уравнение Хопфа имеет первый
+<х>
интеграл: / u(x,t)dx = const. Проверить, что приведенная выше схема
—оо
является консервативной, т. е. в ней на сеточном уровне автоматически
выполняется тот же закон сохранения.
Построить аналогичную схему с использованием
характеристической формы записи уравнения Хопфа A3.9). Будет ли она
консервативной?
Схема условно устойчива при выполнении условия Куранта (точнее,
обобщения условия Куранта) ^ max |ti?J ^ 1. Здесь и ниже, как и ранее
в A3.7), / = 0,5 и2. При этом предполагается, что течение достаточно
гладкое, момент градиентной катастрофы еще не наступил, в решении
нет ударных волн и других разрывов.
Схема Куранта-Изаксона-Риса. Обобщение схем КИР на
квазилинейный случай (при использовании дивергентной формы записи
уравнений) очевидно.
- П+1 «.П /П fn
ат ит , Jm+1 Jm _ л п ^ с\
fn _ fn
Схема устойчива при выполнении условия Куранта ? max |w^| ^ 1.
Обобщение схемы Лакса-Вендроффа (схема предиктор-корректор).
Для квазилинейных уравнений (а также линейных уравнений с
переменными коэффициентами, неоднородных уравнений и т. п.) схема Лакса-
Вендроффа становится более сложной. Для ее построения необходимо
ввести так называемые полуцелые точки (точки с дробными индексами).
На первом этапе (предиктора) значения в полуцелых точках
вычисляются по приведенной выше схеме — обобщению на квазилинейный случай
схемы Лакса:
СУД - 0.«+i <) /+1 /
т/2
- 0.5
т/2 + h ~U>
343
Лекции по вычислительной математике
на втором этапе (корректор) используется схема «чехарда» (трехслойная
схема на крестообразном шаблоне, которая не входит в семейство A3.8)):
С
n / f
Схема Лакса-Вендроффа принадлежит к так называемым
центральным схемам. Ее шаблон симметричен. На первом этапе рассчитываются
значения сеточной функции в полуцелых точках шаблона на
промежуточном слое (*m_i/2, xm_i/2), (*n+i/2, Zm+1/2), на втором этапе
вычисляется решение на верхнем слое в точке (?n+i, zm). Схема устойчива при
выполнении условия Куранта.
Аналогично строятся схемы Лакса-Вендроффа для линейных
неоднородных уравнений.
Нецентральная схема Мак-Кормака (предиктор-корректор).
Как и приведенная выше схема Лакса-Вендроффа, схема МакКор-
мака состоит из двух этапов. Рассмотрим построение схемы МакКормака
для однородного уравнения A3.7). Первый этап (предиктор) имеет вид
= 0,
r ft
Цщ-1 — Цщ /m "" /m-1 = q
Г ft "~ '
т. е. используется схема «явный правый уголок». Второй этап —
корректор:
— - — — 4- т л. т" = 0.
г 2ft
Таким образом, расчет на первом этапе по схеме «правый утолок»,
на втором — «левый уголок».
Другая схема Мак-Кормака имеет вид
и — ип fn — fn
Г ft
/ ~ /т
т
Ц^1 - 0, 5(ЦШ + пт) /т+1 - /т = Q
г 2ft
Такие разностные схемы называют нецентральными. К их
преимуществам относят отсутствие полуцелых индексов, более простую постановку
граничных условий. В линейном случае схемы Мак-Кормака совпадают
344
Лекция 13 Численные методы решения уравнений в частных производных
со схемой Лакса-Вендроффа. Схемы имеют второй порядок
аппроксимации по обеим переменным, схемы устойчивы при выполнении условия
Куранта.
Схема Русанова (центральная схема третьего порядка точности).
Для построения схемы Русанова вводятся не только полуцелые
точки, но и два слоя промежуточных точек с дробными индексами. Первый
этап схемы Русанова (переход к слою 1/3) имеет вид
п
т/3
ее второй этап есть схема «чехарда»
n+2/З п /П+1/3 __ /П+1/3
2г/3 Л
а третий этап
,.п+1 _ 7/п о /n+2/З f n+2/З
24ft +
^ -Кч + <-а) = 0.
На первом этапе производится расчет по схеме Лакса, на втором —
по схеме «крест» («чехарда»). Последнее слагаемое третьего этапа
вводится для обеспечения устойчивости схемы (член, пропорциональный
разностной аппроксимации 4-й производной).
Схема является условно устойчивой при выполнении условия
Куранта и условия 4ст2 - а4 < и < 3.
Нецентральная схема Уоршшга-Кутлера-Ломакса 3-го порядка
точности.
Первый этап:
n+1/З п *п _ fn
+ U
2r/3
^/ «.и fn fn
um-l ~ um-l , /m ~~ /m-1
2T/3/3 Л
345
Лекции по вычислительной математике
Второй этап:
С+2/3 -
,"+2/3
ит+1 ~
Третий этап:
-U
2т/3
0,5«+
2г/3
,,"+1 _ ,,
Г
+ С+1/3) ,
+ ^n+1/Зч
^n+1/З лП+1/3
2Л °'
^n+1/З _ ^n+1/З
2h
п „ rn+1/3 ^n+1/З
m , ^ Jm+
+ 8'
1 »т—1 ,
h '
¦pTt i Q ^Tl
J 1 *• ^J 0
^ - 4<_х + <_2) = 0.
Последний член добавляется для устойчивости схемы, которая
является условно устойчивой при выполнении условий Куранта.
Неявная схема Бима-Уорминга.
Схема Бима-Уорминга имеет вид:
7,П+1 _ 7/П
Рассмотрим алгоритм расчетов по схеме Бима-Уорминга.
Линеаризуем функцию /?+1:
Jm '
о 1цт am/ J
Здесь мы воспользовались тем, что функция / не зависит явно от
времени, иначе формулы будут выглядеть несколько иначе. Тогда будем
иметь равенство
A[Fn(un+l _ ип Л = 0
Проведя аппроксимацию производной (df/dx)^ центральными
разностями, получим искомую неявную разностную схему:
— ^Г^т-1 * ит-1 +ит "+" 4Л^^1 ' U1 =
346
Лекция 13 Численные методы решения уравнений в частных производных
В результате для аппроксимации уравнения Хопфа получается
система линейных алгебраических уравнений с трехдиагональной
матрицей, алгоритм численного решения которой — один из вариантов
трехточечной прогонки.
13.5. Методы регуляризации численных решений
с большими градиентами
Кроме основных понятий теории разностных схем —
аппроксимации, устойчивости, сходимости — на практике существенную роль
играют дополнительные свойства разностных схем. Среди таких свойств
упомянем монотонность. Не существует общепринятого определения
монотонности разностной схемы. Пока, до рассмотрения разностных схем в
пространстве неопределенных коэффициентов, воспользуемся
определением, данным Борисом и Буком в [5,6].
Под монотонными далее будем понимать такие разностные схемы,
в которых не увеличивается число локальных экстремумов (минимумов
и максимумов численного решения) по сравнению с числом локальных
экстремумов в решении точной задачи. Кроме того, монотонные схемы
не должны увеличивать по абсолютному значению уже имеющиеся
экстремумы.
Свойство монотонности разностной схемы очень полезно при
расчете разрывных решений. К сожалению, доказанная для линейного
уравнения переноса теорема С. К. Годунова гласит, что среди линейных
разностных схем (термин «линейный» уточним чуть ниже) не существует
монотонных с порядком аппроксимации выше первого.
Зачастую в практических задачах схемы первого порядка
аппроксимации не могут обеспечить требуемую точность численного решения.
При использовании немонотонных схем для получения численных
решений с большими градиентами, появляются осцилляции разностного
происхождения. По этой причине в численных методах часто
используется регуляризация численных решений. Рассмотрим наиболее
распространенные методы регуляризации.
Сглаживание численного решения на верхнем слое (метод Л. А. Чудова).
Вычисленное с помощью немонотонной разностной схемы
значение функции в точке хп корректируется следующим образом:
йт = A - 2а)ит + aum-i
причем при а = 0,5 значение йт является средним арифметическим
йп = 0,5(um_i
347
Лекции по вычислительной математике
Для того чтобы понять действие сглаживающего оператора,
представим явную схему для численного решения линейного одномерного
уравнения теплопроводности
ди
_ ^
dt ~ адх2
т. е. при а = ат/h2 сглаживание аппроксимирует диссипативный член,
пропорциональный второй производной по координате. Понятно, что
скорректированное решение будет устойчивым при а ^ 0,5. Для
снятия этого ограничения можно ввести алгоритм неявного сглаживания. Он
имеет вид
йт = A - 2а)йт + cmm_i + cmm+i.
Подробнее о сглаживании по Л. А. Чудову можно прочитать, например,
в [7].
Апщижсимационная вязкость.
Рассмотрим схему первого порядка аппроксимации, для численного
решения модельного однородного уравнения переноса A3.3)
Ъп+Си™ Цт-1= 0
исследование которой на аппроксимацию дает следующее выражение для
главных членов ошибки аппроксимации (главных членов невязки):
Таким образом, с точностью до членов второго порядка,
аппроксимируется уравнение
ди ди д2и
+
где аналог коэффициента теплопроводности 7 = т^A ~ т) ~ так назы"
ваемый коэффициент аппроксимационной вязкости, а член
ch сгд2и
именуется аппроксимационной вязкостью. Его действие —
сглаживание численного решения. Слагаемые в правой части уравнения
переноса, пропорциональные второй производной, моделируют диссипативный
348
Лекция 13 Численные методы решения уравнений в частных производных
эффект. Однако эта вязкость является свойством выбранной разностной
схемы первого порядка аппроксимации. Здесь в уравнение не вводятся
никакие дополнительные члены и не используются сглаживающие
операторы. Рассматриваемое уравнение носит название первого
дифференциального приближения разностной схемы. Все схемы первого порядка
аппроксимации будут обладать схемной вязкостью.
Упражнение. Некоторая разностная схема для решения уравнения
переноса A3.3) первого порядка аппроксимации обладает
отрицательным коэффициентом схемной вязкости. Что можно сказать о других
свойствах этой схемы (устойчивость, сходимость, монотонность)?
Искусственная вязкость.
Для регуляризации решения, полученного с помощью
немонотонных разностных схем с порядком аппроксимации выше первого можно
вводить так называемую искусственную вязкость. Этот способ
регуляризации решения был предложен фон Нейманом и Рихтмайером для
численного решения системы уравнений газовой динамики. В рамках
данной лекции ограничимся рассмотрением модельного линейного
уравнения переноса.
Идею искусственной вязкости можно проиллюстрировать на
примере, вообще говоря, неустойчивой схемы
л.П+1 -.П
для решения линейного одномерного уравнения переноса A3.3).
Для того чтобы сделать эту схему устойчивой, введем в правую часть
член порядка погрешности аппроксимации, моделирующий диссипатив-
ный эффект, так называемую искусственную вязкость. Получим
следующую задачу:
brU =?Т ^ >
где ?Имт+1 ~ 2пт + um-i) ~~ искусственная вязкость, величина порядка
главного члена погрешности аппроксимации (невязки) ? —
коэффициент искусственной вязкости. Исследование этой схемы на устойчивость с
помощью спектрального признака дает г < 0,5, §^ ^ 1, где г = j?, а =
= ^. При f = 0,5 для рассматриваемого линейного уравнения получим
схему Лакса-Вендроффа.
Упражнение. Построить четырехточечную схему с искусственной
вязкостью для квазилинейного уравнения (уравнения Хопфа в форме
A3.5) и в форме A3.6)).
Методы коррекции потоков Бориса—Бука.
Рассмотрим идею введения схемной антидиффузии, предложенную
Борисом и Буком в [5, 6]. Пусть Lrur = 0 — схема первого порядка
349
Лекции по вычислительной математике
точности, аппроксимирующая линейное одномерное уравнение
переноса A3.3) и обладающая аппроксимационной вязкостью.
Уменьшим влияние последней на численное решение, введя так
называемые потоки антидиффузии (терминология авторов метода):
Kt1 =Um- -(Фт+1/2 - Фт-1/2),
где йт — решение, полученное по упомянутой схеме, Фт±1/2 — потоки,
имеющие вид
, fm+l/2 -T
Фт+1/2 = jj Ut
€m-l/2-T
Фщ-1/2 = ?
При fm_i/2 = fm+i/2 разностное уравнение имеет вид
Таким образом, идея метода коррекции потоков состоит во введении
сглаживающего оператора определенного вида. Метод коррекции
потоков описан, например, в [5].
13.6. Гибридные схемы (метод Р. П. Федоренко)
Идею построения гибридных схем, изложенную в [11], рассмотрим
на традиционном примере схемы "уголок"
LrUr = Ъп Ъп + U™ "™-* = О
г h
ддя численного решения модельного уравнения переноса
ди ди л
Ьи=т+д-х=°-
Разложения сеточных функций проекции на сетку точного решения
дифференциальной задачи в ряд Тейлора дает
г д2и h д2и
Поскольку дат = |^7, что показывается дифференцированием
рассматриваемого уравнения переноса по t и по х, полученное выражение
может быть представлено в виде
мп+1 _ ип ип —ип л Л т т2
350
Лекция 13 Численные методы решения уравнений в частных производных
Аналогичным образом можно получить и схему третьего порядка
точности:
^_х - <_2) = 0.
Введем разностный анализатор гладкости численного решения,
сравнивая конечные разности первого и второго порядков:
7=1 о,
и представим полученную схему в виде:
?/n+1 — ип ип —ип, *s т х2
г h 2rKh h2)
Таким образом, в областях с большим градиентом численного
решения 7 = 0 и расчет ведется по схеме первого порядка точности, в области
же гладкого решения 7 = 1 и расчет ведется по схеме второго порядка,
(при А = 0 имеем схему первого, при А = оо - второго порядка точности).
Аналогичный анализатор можно ввести и для схемы третьего порядка
аппроксимации.
Заметим, что гибридные схемы, построенные выше для
аппроксимации линейного уравнения переноса, уже нелинейные —
коэффициенты переключения зависят от локальных свойств решения. Таким образом,
в соответствие линейному дифференциальному оператору ставится
нелинейный. Для таких схем не обязана выполняться теорема С. К. Годунова,
и можно ожидать, что на пути введения нелинейности для
гиперболических систем и уравнений можно построить монотонные или близкие к
монотонным схемы высокого порядка аппроксимации.
13.7. Схемы с уменьшением полной вариации
(Total Variation Diminishing, схемы Хартена)
Схемы с уменьшением полной вариации (сокращенно их называют
TVD-схемами) описаны, например, в [8, 12]. Для построения схемы
рассмотрим полную вариацию численного решения. Она определяется
следующим образом:
Vax(un) = JT K+i-u?|. A3.9)
j=-oo
351
Лекции по вычислительной математике
Схема будет TVD, если
Var(un+1) ^ Var(tin). A3.10)
Суть построения TVD-схем можно понять, представив схему Лакса-
Вендроффа для численного решения модельного уравнения переноса в
виде
<+1 = < - и« - и» _х) - (/«+1/2 - /?_1/2), (mi)
где а = ст/h, /m+i/2 = 0,5<тA - <r)(um+i - ит) — антидиффузионные
потоки. Схема похожа на метод коррекции потоков, но одношаговый. Эта
схема не монотонна. Сделаем ее монотонной, ограничив
антидиффузионные потоки введением функций ip(rm):
)cr(l - (J){um+i -
аналогично для ?т_х /2- Здесь </? — ограничитель,
отношение прилежащих градиентов у>(гт) выбирается так, чтобы A3.11)
была TVD-схемой, причем в расчетах обычно полагают rm = "^"".T^+e,
где е — малое число. m m
Можно показать, что условием устойчивости схемы является
неравенство
О < <р(гт) < minBrm, 2) при гт > О и (р(гт) = 0 при rm < 0.
Простейшим ограничителем является выбор конечных разностей в
соответствии с принципом минимальных производных Колгана:
г\'тп/ -> Jm+i/'Z л4 '
Приведем пример другого ограничителя:
{minB, rm),rm > 1,
minBrm,l), 0<rm^l,
0, rm < 0.
или
¦{
minmodB,rm),rm > 1
minmod(l,2rm),0 < rw <
где min modfoy) = 8^ж+81кпу min(|x|, \y\).
352
Лекция 13 Численные методы решения уравнений в частных производных
Пояснение.
1. rm > 1 : tim — um-i > um+i - ит(если и числитель, и
знаменатель в выражении для гт положительны) или ит-\ - ит > ит-
- um+i(eam и числитель, и знаменатель отрицательны); численное
решение сглаживается, так как его градиент убывает.
или
т-1
о
\
о
m
о
т+1
т-1
о
т
т—1 о
2. О < гт ^ \\иш - wm-i ^ um+i - ит (если и числитель, и
знаменатель в выражении для гт положительны) или um_i - ит < ит -
- wm+i (если и числитель, и знаменатель отрицательны); градиент
численного решения растет (или не убывает).
о т+1
т-1
т
или
3. гт ^ 0 : ит - Um-i > 0 и um+i - ит < 0, или иш - um-i < 0 и
um+i - ит > 0, — численное решение осциллирует.
или
"о т+1
о'т-1
Для обеспечения второго порядка точности необходимо </?A) =
= 1. Различные TVD-алгоритмы соответствуют различному выбо-
12-3339 353
Лекции по вычислительной математике
Дивергентный вариант TVD-схемы:
*С+1 = Кг - J(/m+l/2 - /т-1/2),ГДе
/т "» Jm+1 Q / fn /n\ i ФУТт) („ ~\( tn гп\
q = sigiK7m+i/2, число Куранта а = у.
13.8. Идеи построения
сеточно-характеристических методов и
анализ разностных схем в пространстве
неопределенных коэффициентов
Идея построения метода.
Продемонстрируем основные идеи построения
сеточно-характеристических методов на примере решения простейшего линейного
уравнения переноса:
+ ? = /(М)> c = const>0 <13Л2>
с соответствующими начальными и граничными условиями.
Известно, что A3.12) имеет характеристику, определяемую
уравнением характеристики:
dx
Tt=a
и вдоль нее превращается в обыкновенное дифференциальное уравнение
(ОДУ):
!-'«>¦
В частности, для однородного уравнения A) значение функции и
вдоль характеристики не меняется. На сведении уравнения в частных
производных к ОДУ построены так называемые методы характеристик.
Методы сеток основаны на введении в области интегрирования
уравнения разностной сетки, сеточного шаблона, т. е. совокупности узлов
сетки, используемых для замены дифференциального уравнения (в малой
области) разностным аналогом (аппроксимацией). При анализе
аппроксимации обычно используются разложения проекции на сетку точного
решения дифференциальной задачи в ряд Тейлора.
Рассмотрим класс методов, в которых одновременно использован и
сеточный, и характеристический подход.
354
Лекция 13
Численные методы решения уравнений в частных производных
vr\x
п+1
т-2
т-1
т
т+1
Рис. 13.1
В области интегрирования введем разностную сетку:
tn = п • г, хт = га • ft; п = О,1,2,3,...; га = 0, ±1, ±2, ±3,...
Значение решения A) в узлах сетки обозначим через и^. Для
перехода на следующий временной шаг сетки будем использовать явный
пятиточечный шаблон (рис. 13.1). Необходимо вычислить значение uJJ*1,
используя значения и на п слое по времени. Проведем из точки п + 1, га
характеристику с наклоном А до пересечения со слоем tn в точке V. Тогда
вдоль характеристики значение u^+1 выражается через и?, например, как
A3.13)
Выражение A3.13) получено, как аппроксимация обыкновенного
дифференциального уравнения вдоль характеристики методом трапеций.
Проводя ту или иную интерполяцию для нахождения значения и? по
точкам слоя tn, получим различные разностные схемы для определения uj^+1
на данном шаблоне.
О физическом смысле условия Куранта.
Пусть а = г • A/ft — число Куранта. В случае А = const очевидно,
что выбором т и h можно добиться G = 1 или а = 2. В этом случае
характеристика, проведенная через точку uJJ^1, попадет в узел разностной
сетки, где значение и^_г (или и^_2 соответственно) известно точно. Для
однородного уравнения происходит перенос значения в точку it^+1 вдоль
355
Лекции по вычислительной математике
характеристики. Если 2 ^ а > О, то для определения значения и"
приходится решать задачу интерполяции, а для а > 2 — задачу экстраполяции
по узлам сетки. Известно, что вторая задача, как правило, неустойчива.
Точку V назовем областью влияния дифференциального уравнения A),
а точки шаблона, по которым проводится интерполяция — областью
влияния разностного уравнения. Для устойчивости разностной схемы
необходимо, чтобы область влияния дифференциальной задачи лежала
внутри области влияния разностной — это проявление условия КФЛ.
Пространство неопределенных коэффициентов.
Запишем разностную схему в виде
+ A3.14)
k=-2
где коэффициенты ак будем искать из условий аппроксимации,
раскладывая uJJ*1, u^+k в ряды Тейлора в окрестности точки (?п, хт). Оставляя
свободными два коэффициента (например, а_2 , од), получаем условия
аппроксимации порядка О(т + h):
a_i = -A + а - 3 • а_2 - а0),
ai = -A-а + а_2-ао).
Примем свободные коэффициенты за координатные оси
линейного пространства с евклидовой метрикой. Каждая точка этого
пространства будет соответствовать разностной схеме первого порядка
аппроксимации. Кроме того, можно выделить множество схем порядка О(т + h2)
а0 = 1-а + 3-а_2 A3.15)
и единственную на данном шаблоне схему третьего порядка
аппроксимации с порядком О(т + Л3):
Остальные коэффициенты находятся с использованием A3.15) и A3.16).
Введем пространство коэффициентов (а_2, од). Тогда любая точка
в этом пространстве есть разностная схема с порядком аппроксимации
O(r+h). Прямая A3.15) отделяет в пространстве множество схем с
порядком О(т + Л2) (рис. 13.2), на ней лежит единственная точка —
аппроксимация О(т + Л3). Должна быть также и точка с порядком аппроксимации
О(т2 + /i2).
356
Лекция 13
Численные методы решения уравнений в частных производных
Зафиксируем какое-либо число Куранта, например, а = 0,5.
Применим к разностной схеме A3.14) с неопределенными коэффициентами
спектральный признак устойчивости (фон Неймана). Получится кривая,
которая определяет границу устойчивости разностных схем в
пространстве неопределенных коэффициентов.
7
<*-2
Рис. 13.2
Для схем первого порядка выпишем первое дифференциальное
приближение:
u't + аи'х = — A - а2 - а0 + За-i) и%х.
т
Можно также выделить множество таких схем, что aM ^ 0. Это —
монотонные схемы (заштрихованный многоугольник на рис. 13.2).
Среди монотонных схем можно найти схему с наименьшей ошибкой
аппроксимации. Это точка многоугольника, которая при данном а лежит ближе
всего к прямой со схемами второго порядка аппроксимации.
Закончим рассмотрение примера с модельным линейным
уравнением переноса:
u't + си*х = 0.
На выбранном шаблоне любая разностная схема, как указывалось
ранее, представляется в виде
u™ =
В случае монотонной схемы можно оценить норму погрешности.
Заметим, что погрешность v определяется тем же разностным уравнени-
357
Лекции по вычислительной математике
ем A3.14), тогда с использованием первой нормы (максимум абсолютной
величины)
в силу аппроксимации
Отсюда следует, что монотонные разностные схемы всегда
устойчивы. В общем случае можно рассматривать многослойные шаблоны для
уравнения переноса (рис. 13.3)
7/n+i _
и записывать условия порядка для аппроксимации соответствующего
порядка:
Е а = 0
монотонная
3-х точечная
"схема"
X-
Рис. 13.3
Исключая два коэффициента из условий порядка, можно от
пространства неопределенных коэффициентов {а?} перейти к
пространству {d?}, размерность которого на 2 меньше, например:
358
Лекция 13 Численные методы решения уравнений в частных производных
где, конечно, точки @; -1) и @; 1) не включаются в суммирование.
Условие устойчивости в пространстве неопределенных коэффициентов имеет
вид
1<7«, Ч>)\ ^ 1,
где q есть спектр оператора послойного перехода. Эта величина
определяется из условия
и дополнительного требования
Основная гипотеза: Разностным схемам, которым в пространстве
{d?}, соответствуют близкие друг к другу точки (в смысле
р = y/(&i, ах) - (аг, аг)) по своим свойствам также близки.
Расширяя шаблон, как и в случае пятиточечного шаблона,
можно строить области схем высокого порядка аппроксимации, монотонные
схемы (о? ^ 0) и т. д.
Монотонные разностные схемы в пространстве неопределенных
коэффициентов занимают некий выпуклый многоугольник, вершины
которого определяются довольно просто: это все возможные при данном
числе Куранта а трехточечные разностные схемы, причем для
характеристики, проходящей через v%+l9 одна точка схемы лежит выше (левее)
характеристики, а другая ниже (правее), см. рис. 13.3.
Метод построения разностных схем в пространстве неопределенных
коэффициентов для квазилинейных систем уравнений
гиперболического типа (к ним относятся системы уравнений механики сплошных сред,
в частности, газовой динамики, механики деформируемого твердого
тела (МДТТ) и т.п.) допускает обобщение и на многомерные случаи.
Подробное описание можно найти в монографии [9]. Здесь же
многомерные обобщения рассматриваться не будут. Они приводят к эффективным
численным методам для нестационарных многомерных задач.
Исследовав схемы A3.14) на устойчивость по спектральному
признаку, получаем множество устойчивых схем, а потребовав выполнения
условия oik ^ 0 для всех точек шаблона, получаем множество схем с
положительной аппроксимацией (монотонных по Фридрихсу схем). На
рассматриваемом шаблоне устойчивые схемы существуют при 2 ^ а > 0 (для
а>0).
Множество схем с положительной аппроксимацией не пересекается
с множеством схем с порядком аппроксимации выше первого, как это
следует из теоремы С. К. Годунова.
359
Лекции по вычислительной математике
Первое дифференциальное приближение. Дисперсионная и диссипа-
тивная ошибки
Поскольку решения дифференциальной задачи и разностного
уравнения принадлежат разным функциональным пространствам, что
порождает определенные трудности при теоретическом анализе свойств
разностных схем, для такого исследования возможно рассматривать
разностные операторы в том же пространстве. Будем считать, что
разностные схемы удовлетворяются функциями непрерывного аргумента в
каждой точке рассматриваемой области.
Обычно ограничиваются рассмотрением уравнений, в которых
оставлены члены в разложении в ряд Тейлора проекции точного решения на
сетку по г и ft, порядок которых совпадает с порядком погрешности
аппроксимации схемы. Получающиеся при этом уравнения называют
первым дифференциальным приближением (ПДП).
Для схемы первого порядка E) при выполнении условия F) первым
дифференциальным приближением будет
v!t + а • их = <Ji • h • ихх, где Si = const. A3.17)
Из уравнения A3.17) исключены члены со второй производной и'и,
с использованием так называемой продолженной системы:
<); = о,
Иногда уравнение A3.17) называют П-формой (параболической
формой) первого дифференциального приближения. Если производные по
времени не исключаются из ПДП, то имеем Г-форму (гиперболическую
форму) ПДП, которая, как правило, не применяется в исследованиях как
малоинформативная.
При Si > О уравнение A3.17) можно трактовать как присутствие в
схеме некоторой диссипации (схемной вязкости). Ее наличие
проявляется в расчетах в виде размазывания точного решения, причем его
интенсивность увеличивается при ухудшении аппроксимации (увеличении
шага К). В этом случае говорят, что ошибка схемы носит диссипативный
характер. Если схемная вязкость получается отрицательной, то приходим к
обратной задаче теплопроводности. Как известно из курсов
математической физики, такая задача поставлена некорректно. А соответствующая
разностная схема при исследовании по спектральному признаку
оказывается неустойчивой — по ПДП можно сделать вывод об устойчивости
схемы.
360
Лекция 13 Численные методы решения уравнений в частных производных
Для более высокого (второго) порядка ПДП имеет вид
' < = <J2-/i2t4'^. A3.18)
Уравнение A3.18) обладает дисперсией, т.е. разные
пространственные гармоники разложения начального возмущения в ряд Фурье
распространяются по сетке с разными скоростями. Говорят, что ошибка носит
дисперсионный характер. Сеточная дисперсия легко получается, если
искать частное решение последнего уравнения в виде комплексной
экспоненты: и = \(t) ехр(гкх). Подробнее о ПДП в [4].
Интересна связь ПДП и исследования свойств схем в пространствах
неопределенных коэффициентов. Так, для схем первого порядка
расстояние от точки в пространстве неопределенных коэффициентов до прямой
схем высокого порядка A3.15) по абсолютной величине равен
коэффициенту 6i в уравнении A3.17), а знак определяется положением внутри
области устойчивости.
Понятие о гибридных схемах
Численные расчеты по разностным схемам высокого порядка
показывают, что осцилляции нефизического характера появляются в
окрестности разрывов решения или его первой производной. В связи с этим
возникает идея построения численного метода, имеющего высокий порядок
аппроксимации на участках гладкого решения, в то время как в
окрестности разрывов функций или их производных применяется монотонная
схема (с положительной аппроксимацией) первого порядка.
Можно формализовать этот подход:
;7-оA)р + A-7)-оB)р).
р=-2
1 + BЬ-1)
7 . л
ит\
Um\ + \ит Um-l\
где a(l)p — коэффициенты первой схемы (высокого порядка
аппроксимации), применяемой в области гладкого решения, аB)р —
коэффициенты второй (монотонной) схемы, 7 — весовой коэффициент,
вспомогательный параметр Ь характеризует гладкость решения (очевидно, что Ь =
= 0, при и = const), A; — коэффициент гибридности — целое число из
диапазона 2 ^ к < 10.
При этом реализовано достаточно гладкое переключение со схем
высокого порядка аппроксимации на монотонные схемы.
361 *
Лекции по вычислительной математике
13.9. Задачи
1. Для линейного уравнения переноса
ди _ ди
~dt~~dx
предложить схему N + 1 порядка аппроксимации.
Указание. Рассмотреть невязку, образующуюся при замене
дифференциального уравнения разностным
ит ит цт+1 ат _ q
Решение. Проведем исследование разностного уравнения на
аппроксимацию. Для этого представим сеточные функции u^+1 и
u^+i в виде разложения проекции на сетку точного решения
дифференциальной задачи в ряд Тейлора:
= < + h «С + ^ («X + ^ (О1 + ? Hv)l + ¦¦¦+
и^=и»т+т кс+% ю1+^ («п;+^ ю:+• • •+
Отсюда получим с учетом того, что и[к^ = и^ :
ит цтп+1
— \Щ их)т + Г^'
где гт — невязка, вычисляемая в точке (tn, xm) по формуле
гТ = 1(г - ft)< + |(т2 - Л2)<' + i
= Е TikTT
fc=l(К +1
а = т/h — число Куранта.
362
Лекция 13 Численные методы решения уравнений в частных производных
Аппроксимация частных производных высоких порядков,
входящих в выражение для невязки с помощью конечных разностей,
приводит к соотношению
1 N к 1
В таком случае, после переноса суммы по к в выражении для
невязки в левую часть, получим разностную схему искомого порядка
аппроксимации:
или
Эта схема легко распространяется на уравнение
ди _ ди
если учесть, что
"v ч " дхк+1'
2. Доказать устойчивость разностной схемы
_ f n
аппроксимирующую задачу Коши для уравнения переноса
х€ (-00,00), u@,x) = у?(х), x€(-oo,oo),
используя второе определение устойчивости:
||ит||<с||/||приа= J<1.
363
Лекции по вычислительной математике
Решение. Перепишем разностную схему в виде, разрешенном
относительно следующего слоя по времени
Определим норму в пространстве сеточных функций как
||iir || = sup KJ = max sup |<J .
n
n,m
Если 1 - a ^ 0, то справедлива оценка
В таком случае
Отсюда видно, что при /? = 0 норма решения \и^\ не
возрастает при возрастании п — выполняется принцип максимума.
Поскольку правая часть в полученном неравенстве не зависит от т, то
||
Аналогично
max |u^| < max |u^| -h r max|/?|.
Сложение этих неравенств дает
откуда получаем, с учетом того, что tn = пт:
max|</>m|+*n+i max
m m,n
364
Лекция 13 Численные методы решения уравнений в частных производных
При этом учтено, что
Таким образом, получим
3. Построить явную разностную схему первого порядка точности для
аппроксимации линейного уравнения переноса ^ - |^ = /(?,х),
используя ее запись в общем виде через неопределенные
коэффициенты
на шаблоне «явный правый уголок».
Решение. Будем подбирать коэффициенты Ci таким образом,
чтобы выполнялось условие аппроксимации первого порядка LTUT =
Разложение сеточных функций и^4 и г4^+1 в ряды Тейлора в
окрестности точки хт, tn приводит к равенствам
Подстановка этих разложений в разностную схему с
неопределенными коэффициентами дает
LrC/T = & С
= (ex + с2 + <*)< + сгт(и[)^ + czh{<)nm + О(т2 + h2) =
(ci + с2
поскольку можно считать независимыми переменными шаг по
пространству и число Куранта, а для шага по времени получаем
очевидное выражение г = аД, а = const.
365
Лекции по вычислительной математике
Здесь использованы очевидные равенства для дифференциального
оператора
ди т ди ди ди т
L+L
Для выполнения условия аппроксимации первого порядка
необходимо выполнение условий порядка
Ci<jh=\+O(h),
С1+С2 + С3 = 0 +
Если положить O(h) = 0, поскольку это некое число, стремящееся
к нулю при измельчении шага, то условия порядка примут вид
c\ah = 1,
ci + c2 + с3 = 0,
ci + сз = 0.
Эта схема линейных алгебраических уравнений имеет единственное
решение:
1 _i G—1 I _i t
Получили коэффициенты уже известной разностной схемы первого
порядка аппроксимации на заданном шаблоне:
_ fn
Несложно проверить, что учет O(h) привел бы к незначительной
коррекции результата.
Конечно, выбранная разностная схема легко получается и из
других соображений. Но с помощью метода неопределенных
коэффициентов удается построить схемы с хорошими свойствами для более
сложных уравнений и систем.
366
Лекция 13 Численные методы решения уравнений в частных производных
4. Исследовать на спектральную устойчивость разностную схему на
шаблоне квадрат
Yr («и + <+1) ~ «+1 - О)
1- о] = /
аппроксимирующую линейное уравнение переноса
ди ди .
+ °
Решение. После подстановки в схему гармоник Фурье
п __ \niam
ит — л е >
получим выражение для спектра оператора послойного перехода
_ v l-iatZa/0
т = т/h — число
Тогда |А(а)| = 1 и рассматриваемая схема безусловно устойчива.
Этого следовало ожидать, так как аппроксимация производной по
времени производится как на нижнем, так и на верхнем временном
слое. Однако решение на верхнем слое выписывается в явном виде,
поскольку правое условие ставится на левой границе. Поэтому
схему иногда относят к явным схемам бегущего счета. Расчетная
формула будет
?/п+1 _ п , ° - 1 / п+1 _ п ч , fti+1/2
ит+1 — ит + а + j Vwm Um+J + T/m/
т+1 — ит + а + j Vwm Um+J + T/m+l/2*
Схема обладает вторым порядком аппроксимации по времени и
пространственной координате.
5. Получить дисперсионное соотношение для разностных схем
первого и второго порядка сходимости для аппроксимации нелинейного
уравнения »
dv dv л
0? + и-^ = 0, где и ф const,
и, вообще говоря, зависит от решения.
Указание. Использовать дисперсионное соотношение для данного
дифференциального уравнения в виде eAte**, где к — волновое
число, Л = — uki.
367
Лекции по вычислительной математике
Решение. Будем искать дисперсионное соотношение для
разностного уравнения в виде
,,n _ pX{k)tn ikxm _ Хпт+ikmh
После его подстановки в схему правый уголок первого порядка
аппроксимации, получим
откуда следует
Сравним дисперсионное соотношение для дифференциального и
соответствующих разностных уравнений.
Пусть ^ = 1. Имеет место совпадение A(fc) и А(т,й,А;), однако этот
случай мало интересен для вычислительной практики, поскольку и
может меняться в ходе решения задачи. Для проведения
дисперсионного анализа схем положим kh < 1, имея в виду то, что h —
малый параметр, а аппроксимация тем лучше, чем меньше волновое
число, т. е. чем более гладким является исследуемое частное
решение. Заметим, что для расчетной сетки с шагом h обычно
реализуются волновые числа к « 2nh~1.
В таком случае дисперсионное соотношение будет
а = ит/h— число Куранта,
а частное решение примет вид
exp(ik(mh — ипт)) • exp I —-uk2(h — ит)пт 1 .
Первый сомножитель совпадает с соответствующим частным
решением дифференциального уравнения, второй является
особенностью разностного решения; его поведение при различных т, ft, к
представляет особенный интерес. При и < 0, h - ит > 0, как
видно из этого решения, рассматриваемую схему нельзя
использовать для проведения расчетов. Второй сомножитель имеет порядок
368
Лекция 13 Численные методы решения уравнений в частных производных
ехр(/с2 \и\ htn), он быстро растет при к ~ ft, h —> 0, г —> 0.
Аналогичная ситуация получается и при и > 0, ft - иг < 0. При и < 0, ft -
- иг > 0 второй сомножитель затухает с ростом tn тем быстрее, чем
больше к, или чем меньше Л — длина волны частного решения вида
exp(ikx). Таким образом, численное решение, полученное по схеме
уголок, отличается от точного, в котором все гармоники
сохраняют амплитуду с ростом ?п, наличием затухающего множителя для
гармоник с большими волновыми числами (или малыми длинами
волн). Действие этого сомножителя приводит к сглаживанию
решений, имеющих разрыв в начальных данных.
Для разностной схемы Лакса-Вендроффа второго порядка
Кй + О - <г« - с-i) + \ WU - 2С + Си) = о
дисперсионное соотношение будет
А = г In jl + a(e-ikh - 1) 4- 2uh(l - a)sin2 у j ,
для длинноволновых гармоник с kh < 1
А (г, /i, Л) » -tfcu + i^(h2 - и2т2) = A(fc) + г*3^-A - a2).
6 о
Из полученных соотношений можно сделать следующий вывод.
Решения исходного уравнения переноса имеют вид волн с волновым
числом к, которые движутся вправо со скоростью п, так как
v(t,x) = exp(ifcr + X(k)t) = exp(ik(x — ut)).
Решения разностного уравнения имеют вид
v(tn,xm)= exp(ikxm + A(r, Л, fc)tn) =
= exp (ifc |xm - u [l - у (Л2 - u2r2)] tny) =
= exp (ik {xm - u [1 + Ujb(fc)] tn}),
где введено обозначение
и (Л222)
369
Лекции по вычислительной математике
Последнее выражение означает, что разностные решения уже не
имеют вид волн, движущихся с одной и той же скоростью. Теперь
каждая волна со своей частотой движется с собственной скоростью
и = Uk [1 + и(к)]. Разумеется, при малых к и скорости и* мало
отличаются от и, но высокочастотные волны движутся со скоростями,
заметно отличающимися от скорости переноса. Кроме того, в схеме
Лакса-Вендроффа гармоники со временем не затухают, численное
решение не сглаживается со временем. Начальный волновой пакет
и и определенный им начальный профиль решения, изменяются с
течением времени из-за рассогласования фаз. Это приводит к
потере монотонности профиля v(x), если он был вначале монотонным,
и появлению осцилляции разностного происхождения. Появление
сеточной дисперсии — одно из проявлений эффекта Гиббса,
подробнее об эффекте Гиббса в [16].
6. Акустическая система описывает распространение плоских
звуковых волн. Поставим для нее задачу Коши:
ди 1др др 2ди
р = const, с = const,
и(х, 0) = uo(z), р(х, 0) = ро(х),
t > 0, —оо < х < оо,
где и — скорость движения среды, р — давление, р — плотность
среды, с — скорость звука в среде.
a) Представить акустическую систему в интегральной форме.
b) Преобразовать акустическую систему к виду системы с
разделенными переменными.
c) Предложить разностную схему первого порядка точности для
ее решения.
Решение.
а) Проинтегрировав акустическую систему по произвольной
области с границей G, получим:
ф pudx - pdt = 0,
г
d> ^dx- pudt=0.
370
Лекция 13 Численные методы решения уравнений в частных производных
Ь) Умножим второе уравнение на {рс)~1, затем сложим с первым
и вычтем из него. Получим систему двух уравнений
рс) дх
'cdi
или, после введения обозначений (инвариантов Римана) R =
= и+^8 = и--*? система запишется в виде двух уравнений
переноса:
dR 9R_Q &?_ —-о
(jt С/Х (jt OX
Эта система позволяет выписать общее решение:
R = f(x-ct), S = g(x + ct).
Здесь fyg — произвольные непрерывно дифференцируемые
функции, определяемые из начальных условий. В терминах
инвариантов Римана можно определить и значения естественных
переменных и,р:
u=-(f(x-ct)+g(x-
Замечательное свойство инвариантов Римана R, S заключается в их
постоянстве вдоль прямых x-ct = const, и х + ct = const или ^jr =
= ±с — характеристик акустической системы.
Если задавать начальные данные w(x,0) = (р(х)р(х1О) = ф(х),
-оо < х < оо, то связь начальных данных и инвариантов Римана
будет
V(x) = \(f(x)+g(x))Mx) = f [/(*)-*(*)],
откуда получим
рс рс
Следовательно, решение системы в этом случае
\ ^К* " ct) + Ф(х + ct)),
371
Лекции по вычислительной математике
Для численного решения системы, записанной в инвариантах Ри-
мана, можно применить схему Куранта-Изаксона-Риса:
или
Известно, что данная схема имеет первый порядок аппроксимации
и является устойчивой при выполнении условия КФЛ: ^ ^ 1.
7. Заменить смешанную задачу для волнового уравнения
эквивалентной ему парой уравнений в частных производных
первого порядка.
Решение. Введем новые переменные
X
v(t, x) = J ^^-dV, F(t, x) = j f{t, V)dr,.
0 0
Функции u(t,x),v(t,x), что несложно проверить, удовлетворяют
акустической системе уравнений
ди dv л dv оди
х
,t;@,x) = f
о
Введем в рассмотрение параметрическую схему для численного ре
шения этой системы:
о < 6
372
Лекция 13 Численные методы решения уравнений в частных производных
Исследование полученной двухпараметрической разностной
схемы на спектральную устойчивость дает условия устойчивости: f i +
+ ?2 ^ 1, о2 B?i - 1) B?г — 1) > —1, <г = х- ОТСК)Да видно, что если
?i ^ 0,5 и $2 ^ 0,5, то схема устойчива при любых числах Куранта и
сеточных параметрах, если & + & ^ 1> но один из параметров
меньше 0,5, то схема условно устойчива при г < ?B?i - l)Bf2 - I).
Пусть f i = $2 = 0,5. Тогда полученная схема является безусловно
устойчивой и обладает вторым порядком аппроксимации по обоим
переменным.
8. Исследовать на сходимость схему «крест» с шаблоном
о
для численного решения волнового уравнения ^г - |^т = 0.
Решение. Запишем разностную схему:
T „, um zum т Um цт-1 *ит ^ цт+1 _ n
br-r- ^ Д2 "О-
Исследование на аппроксимацию дает выражение для главного
члена невязки
Схема имеет второй порядок аппроксимации. Исследуем схему на
устойчивость по спектральному признаку. Для спектра оператора
послойного перехода получается
А2 - 2 (l - 2а2 sin2 ^) А + 1 = 0, а = т/h — число Куранта.
По теореме Виета, произведение корней Ах А2 = 1, и условие
устойчивости выполняется, если |Ai| = |Аг| = 1. Для полученного
квадратного уравнения с действительными коэффициентами это
означает, что его корни являются комплексно сопряженными. Это
возможно лишь в случае, если дискриминант
D(a) = 4<72sin2a
373
Лекции по вычислительной математике
будет отрицательным. Условие устойчивости будет выполнено для
всех гармоник, если а < 1.
13.10. Задачи для самостоятельного решения
1. Для линейного однородного уравнения переноса ^ + а|^ = 0, а =
= const > 0 построить разностные схемы первого, второго и
третьего порядков аппроксимации, используя шаблоны, приведенные на
рисунках.
2. Для линейного однородного уравнения переноса ^ + |^ =0,
построить разностную схему, имеющую второй порядок по
времени и четвертый по координате, используя шаблон с точками
3. Исследовать устойчивость параметрической схемы
1— I Ot -Ь A — оп I = 0. ос ? 10.11 = О
г 2[ 2Л 2Л J
для численного решения линейного уравнения переноса.
4. Определить, при каких значениях а схема
С - «т-1
аппроксимирующая линейное однородное уравнение переноса,
является устойчивой.
374
Лекция 13 Численные методы решения уравнений в частных производных
5. Для численного решения линейного уравнения переноса
ди_ди ди
dt~ дх* ду
предложить разностные схемы первого и второго порядков
точности; исследовать их на сходимость.
6. Исследовать на сходимость схему предиктор-корректор:
предиктор
т/2
Um-l/2 - Um-l/2
r/2
корректор
т/2
аппроксимирующую уравнение переноса
dt^ дх
7. Исследовать на сходимость схемы, имеющие шаблоны
для численного решения уравнения переноса
ди ди л
— -f а— = 0, а = const > 0.
at ox
8. Предложить устойчивые схемы первого и второго порядка
аппроксимации для численного решения акустической системы
__=0 ^ Q
dt дх ' 5t 5x
которую можно представить в матричной форме:
375
Лекции по вычислительной математике
9. Используй характеристические свойства уравнения переноса
ди ди .
— + а— =0, а = const > 0
at ox
построить аппроксимирующую разностную схему на шаблонах,
приведенных на рисунках
10. Предложить гибридную разностную схему для численного
решения линейного однородного уравнения переноса, использующую
два опорных шаблона, изображенных ниже:
11. Исследовать на сходимость схему с шаблоном
(п+1,га) о
(п,га— 1) о-
(п,т)
о (n-l,m-l)
для численного решения линейного однородного уравнения
переноса.
12. Исследовать на устойчивость схему с искусственной вязкостью
т +а 2ft
для решения уравнения переноса
ди
Л2
ди ди Л
•77" + а— = 0, а = const > 0.
от ах
376
Лекция 13 Численные методы решения уравнений в частных производных
13. При каких значениях ? эта схема совпадает со схемами Лакса,
Куранта-Изаксона-Риса, Лакса-Вендроффа?
14. Показать, что разностные схемы Лакса и Куранта-Изаксона-Риса
удовлетворяют условию TVD.
15. Акустика
Рассмотрим нестационарное течение жидкости, охватывающее
ограниченную область. Требуется предсказать звуковое поле,
излучаемое на большом расстоянии от области течения. Акустическая
аналогия этой задачи состоит в решении неоднородного волнового
уравнения:
fid2
здесь а0 — скорость распространения звука в покоящейся
жидкости, (р — искомый потенциал скорости, q — интенсивность
источника.
Если жидкость несжимаемая, то ао —> оо и волновое уравнение
переходит в уравнение Лапласа.
Все волны обладают некоторыми общими свойствами. Одним из
важных свойств большинства волн является сохранение энергии.
Другое свойство состоит в том, что полное смещение среды в волне
обычно весьма мало. Поскольку волновое уравнение имеет второй
порядок как по пространственным переменным, так и по
времени, оно обратимо, если только в уравнении не присутствуют члены,
описывающие диссипативные процессы. Следовательно, в
алгоритмах для волнового уравнения нежелательны диссипативные
ошибки, приводящие к уменьшению амплитуды решения. Выполнение
условия обратимости решения в алгоритме гарантирует, что моды
не затухают, когда алгоритм устойчив. Поскольку волны часто
распространяются на весьма большие расстояния, алгоритм,
применяемый для расчета их поведения, должен давать минимальное
численное затухание. Наилучшие из подобных алгоритмов являются
почти неустойчивыми или могут быть легко переведены в
неустойчивое состояние за счет малых ошибок аппроксимации,
дополнительных нецентрированных слагаемых в разностном уравнении или
нелинейных эффектов, которые не появляются при линейном
анализе устойчивости.
(а) Реализовать разностный алгоритм для численного решения и
рассмотреть поведение решений волнового уравнения,
представленных в виде суммы двух волн <р (x,t) = Д(?) + /2G7), где
377
Лекции по вычислительной математике
f = х - aottf = я+oo*. Для этого задать в начальный момент
времени (t = 0) потенциал возмущенного движения (р(х) в виде
функции, например, Д (?), отличной от нуля только на участке
0 < х0 ^ ?о-
(b) Исследовать распространение волн, если область их
распространения с одной стороны ограничена. Как учесть
взаимодействие волны со стенкой в численном расчете?
(c) Рассмотрим систему дифференциальных уравнений:
dp dv
dv dp
at = ~ао^-
Уравнения имеют периодические решения вида
где р(к) и v(k) — комплексные величины, к — волновое число,
отвечающее направлению х. Это действительная величина,
которая с длиной волны моды связана соотношением Л = 2тт/к.
Реализовать следующую конечно-разностную аппроксимацию
системы:
пп пп-1 п-1/2 _ п-1/2
PJvP ^ Vl/2
At - *
n+1/2 n-1/2
Здесь переменная р определена в центрах ячеек в старый и
новый момент времени. Скорость v определена на границах
ячеек и в моменты, промежуточные по отношению к тем, в
которые определена плотность. Подобные сетки называются/>де/*е-
сенными. Разностная схема называется явным алгоритмом
«чехарда» на разнесенной сетке. Вывести условие устойчивости для
этой схемы.
(d) Для акустической системы реализовать неявный
конечно-разностный алгоритм:
! Atop |>Г+1/2 ~ "jLl/2)
Pi PJ " 2 [ Дх
г _
" Vi/2 ~
378
Лекция 13 Численные методы решения уравнений в частных производных
Расчетная сетка здесь разнесена по пространству, но не по
времени. Новые значения р и v теперь определяются
одновременно на одном и том же шаге по времени. Исследовать
устойчивость этой схемы.
Одной из хороших проверок алгоритма является следующая
процедура. Провести расчет на большое число шагов по
времени, затем остановить его, изменить знак St и затем выполнить
обратный расчет задачи до начального времени t = 0.
Более подробно качественные свойства рассмотренных здесь
алгоритмов обсуждаются в [18, С. 145-154].
Литература
[1] Тихонов АН., Васильева А.Б., Свешников А.Г. Дифференциальные
уравнения. 3-е изд. М.: Наука. Физматлит, 1998.232 с.
[2] Арнольд В.И. Дополнительные главы теории обыкновенных
дифференциальных уравнений. М.: Наука, 1982. 302 с. Современное
переиздание этой книги: Арнольд В.И. Геометрические методы в теории
обыкновенных дифференциальных уравнений. Ижевск: Ижевская
республиканская типография, 2000.400 с.
[3] Самарский АА, Попов Ю.П. Разностные методы решения задач
газовой динамики. М.: Едиториал УРСС, 2002.480 с.
[4] Шокин Ю.И., Яненко Н.Н. Метод дифференциального приближения.
Применение к газовой динамике. Новосибирск, Наука, 1985.364 с.
[5] Борис Дж.П., Бук Д.Л. Решение уравнения непрерывности
методом коррекции потоков. / В кн. Вычислительные методы в физике.
Управляемый термоядерный синтез. М.: Мир, 1980. с. 92-141.
[6] Boris J.P., BookD.L.//}. Comput. Phys., 1973, Vol. 11, pp. 38-69.
[7] Пасконов B.M., Полежаев В.И., Чудов Л А. Численное моделирование
процессов тепло- и массообмена. М.: Наука, 1984.288 с.
[8] Куликовский АГ., Погорелое Н.В., Семенов АЮ. Математические
вопросы численного решения гиперболических систем уравнений. М.:
Физматлит, 2001.608 с.
[9] Магомедов М.-К.М., Холодов А.С Сеточно-характеристические
численные методы. М.: Наука, 1988.288 с.
379
Лекции по вычислительной математике
[10] Годунов С.К., Рябенький B.C. Разностные схемы, введение в теорию.
М.: Наука, 1977.400 с.
[11] Федоренко Р.П. Введение в вычислительную физику. М.: Изд-во
МФТИ, 1994.526 с.
[12] Флетчер К. Вычислительные методы в динамике жидкостей. М.:
Мир, 1991.240 с.
[13] Белоцерковский ОМ. Численное моделирование в механике
сплошных сред. М.: Физматлит, 1994.442 с.
[14] Лобанов А.И., Петров И.Б., Старожилова Т.К. Вычислительные
методы для анализа моделей сложных динамических систем, ч. П.
Учебное пособие. М.: МФТИ, 2002.154 с.
[15] Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных
уравнений и их приложения к газовой динамике. М.: Наука, 1978.687 с.
[16] Жуков А.И. Метод Фурье в вычислительной математике. М.: Наука,
1992.128 с.
[17] Галанин МЛ. Численное решение уравнения переноса. / В кн.:
Будущее при-кладной математики. Лекции для молодых исследователей.
Под ред. ГГ. Малинецкого. М.: Ециториал УРСС, 2005.512 с.
[18] Оран Э., Борис Дж. Численное моделирование реагирующих
потоков. М.: Мир, 1990.661 с.
380
Лекция 14 Введение в методы численного решения уравнений газовой динамики
Лекция 14. Введение в методы численного решения
уравнений газовой динамики
Лекция не обязательна при первом прочтении книги. В лекции
приводятся некоторые часто употребляемые численные методы решения
уравнений газовой динамики. Особое внимание уделено идее конструирования
разностных схем из семейства сеточно- характеристических.
Ключевые слова: уравнения газовой динамики. Характеристическая
форма. Дивергентная форма. Пространство неопределенных
коэффициентов. Сеточно-характеристические разностные схемы.
Искусственная вязкость. Метод частиц в ячейках.
Рассмотренные в предыдущих лекциях разностные методы решения
уравнений в частных производных демонстрировались на примере
либо линейных задач, либо достаточно простых нелинейных уравнений с
хорошо изученными свойствами. Такие задачи в реальной
вычислительной практике обычно служат тестами для отработки методов решения
более сложных нелинейных систем. Традиционным объектом приложения
численных методов служат уравнения механики сплошной среды (МСС).
Основных причин тому три. Первая — все математические модели МСС
известны достаточно давно, хорошо исследованы и являются частью
научной классики. Вторая — математические модели МСС нелинейны. Как
правило, у линеаризованных уравнений очень узкая область применения.
Третья — в результатах решения задач МСС на протяжении всего XX
века была практическая заинтересованность, вызванная бурным развитием
авиации, осуществлением наукоемких ядерных и космических программ
в разных странах.
В данной книге ограничимся самой простой моделью МСС —
уравнениями газовой динамики. Основная идея лекции — демонстрация идей
и методов вычислительной математики, рассмотренных выше, в
приложении к реальным задачам.
14.1. Формы записи одномерных уравнений
газовой динамики
В основе построения математических моделей, описывающих
поведение жидкостей и газов, лежит понятие о сплошной среде. Из
молекулярной физики известно, что среда состоит из отдельных частиц
(молекул, ионов, электронов, атомов), расстояние между которым существен-
381
Лекции по вычислительной математике
но больше их собственных размеров. Длина свободного пробега
частицы I (расстояние, пройденное частицей между двумя столкновениями)
тем меньше, чем больше частиц заключено в единице объема, чем больше
плотность среды. В механике жидкостей и газов рассматриваются среды,
содержащие в единице объема большое количество частиц (много
больше, чем число Авогадро — число частиц в одной грамм-молекуле
вещества, NA « 6 • 1023 (г • моль)).
В таких средах можно рассматривать лишь некоторые усредненные
характеристики, не занимаясь изучением поведения каждой частицы в
отдельности. В этом предположении заключается идея модели сплошной
среды, непрерывно заполняющей пространство.
Количественным критерием применимости приближения
сплошной среды может служить неравенство 1/L < 1, где L — характерный
пространственный размер задачи (например, размер тела при внешнем
обтекании потоком газа). В газах при нормальных условиях / да A0 -5-10~6)
см, поэтому приведенное условие для тел с размером более 1 см
выполняется с достаточной точностью. Предложение о сплошности среды, по-
видимому, берет свое начало от Эйлера, впервые рассмотревшего газ как
непрерывную деформируемую субстанцию. Не вдаваясь в особенности
получения уравнений газовой динамики (этой теме посвящено большое
количество литературы, [1,2, 3]), приведем их в окончательный вид.
Эйлерова (недивергентная) форма одномерной системы уравнений
газодинамики имеет вид
до до ди
-~ + и-^- + р— = 0 (уравнение неразрывности), A4.1)
ot ох ох
ди ди 1 вр ,
— + и— = — (уравнение движения),
от ох р ох
де де 1д(ри) ,
— + и— = 1^ (уравнение энергии),
где е — удельная энергия, равная е = е + \,е — удельная внутренняя
энергия, и — скорость газа, р — плотность среды, р — давление, t —
время, х — декартова координата. Эту же систему уравнений в частных
производных можно представить в матричной (характеристической) форме
где U — вектор-столбец, А — квадратная матрица 3x3.
Система замыкается уравнением состояния
/(р, е, р) = О,
382
Лекция 14 Введение в методы численного решения уравнений газовой динамики
которое, например, для идеального газа имеет вид
Р __л
где 7 — безразмерная постоянная, равная отношению теплоемкости
газа при постоянном давлении и теплоемкости при постоянном объеме —
постоянная адиабаты.
В системе, записанной в матричной форме A4.2), учтено, что
давление есть функция температуры (или удельной внутренней энергии) и
плотности р = р(р, е) следовательно,
др_дрдр дрде_
дх~~ дрдх дедх'
Не занимаясь выводом формул (это делается простыми
алгебраическими преобразованиями), представим другие виды записи уравнения
энергии, справедливые для приведенного выше уравнения состояния:
ди л
э-х = 0'
dp dp о ди ^
где с = у/чр/р — адиабатическая скорость звука,
dS , dS п
dS. п d . д д
или -|г = 0, где г|, = _+„_,
5 = т{ерI~1 — энтропия. Она, как следует из последней формулы,
сохраняется вдоль траектории частицы идеального газа, т. е. на траектории
уравнения
Дивергентная форма уравнений газовой динамики получается при
записи соответствующих законов сохранения в интегральной форме.
Если затем совершить предельный переход, то дифференциальная запись
уравнений будет
2?
0, A4.3)
383
Лекции по вычислительной математике
или в матричной форме
dR dQ
2 2
где К = {р,ри,р(е+Ц-)}ту Q = {ри,ри2 + p,/m(e + Ц- + ^)}т.
2 2 р
Интегральная форма этих уравнений получается при использовании
теоремы Гаусса-Остроградского
/!г ^ f ~ Qdt) =
п
где Г — граница замкнутой области интегрирования п в плоскости t, x.
Здесь u{t,x),p{t,x),p{t,x) — скорость, плотность и давление газа
соответственно. В механике сплошных сред вводится эйлерово и лагранже-
во описание поведения среды. В первом случае наблюдатель
полагается неподвижным, например, стоящим на берегу реки. Соответственно
расчетная сетка будет неподвижной (фиксированная эйлерова сетка). Во
втором случае полагаем, что наблюдатель движется вместе со средой,
например, находится на лодке, плывущей по течению реки. В этом случае
лагранжева расчетная сетка будет двигаться вместе с частицами среды.
Л агранжева форма одномерных уравнений газовой динамики имеет
вид
8а 18W
/ \-1
где / = [щ] 1^и^ соответственно эйлерова и лагранжева координаты,
связь между которыми дается последним уравнением. Эта система в
одномерном случае может быть записана в другом виде. Если ввести лагран-
жеву массовую координату гу(^), связанную с лагранжевой координатой
? дифференциальным уравнением Ш = р@,?), в массовых координатах
последняя система запишется как
du dp л
+ = 0
384
Лекция 14 Введение в методы численного решения уравнений газовой динамики
dv _ ди
dt dvf
Эта система дополняется уравнениями, связывающими лагранжевы
и эйлеровы координаты
dx dx@,rf)
~dt = U^ ' ^' eft? = V^ ' ^'
где v = р — удельный объем.
14.2. Методы Лакса-Вендроффа и Мак-Кормака
Если система уравнений газодинамики записана в дивергентной
форме
dt + дх и'
то запись разностных схем, соответствующих методам Лакса-Вендроффа
и Мак-Кормака, аналогична их записи для численного решения
уравнения переноса (лекция 13).
Так, схема Лакса-Вендроффа может быть представлена в следующем
виде:
т/2
(первый этап);
т/2 + h ~U'
+ h
Qm+1/2 - Qm_1/2
(второй этап).
Схему МакКормака представим следующим образом:
Qm+1 ~ Qm _ n
U
Rm-1 - Rm-1 Qm ~ Qm-1
(первый этап);
13—3339 385
Лекции по вычислительной математике
{ QmQm-i =Q
г 2/i
(второй этап).
Так как использована дивергентная форма записи исходных
уравнений, то можно ожидать, что полученные таким образом схемы окажутся
консервативными. О консервативных схемах газовой динамики
подробнее в [4,5].
14.3. Сеточно-характеристический метод для
численного решения уравнений газовой
динамики
(М.-К. М. Магомедова-А. С. Холодова)
Этот метод (точнее, семейство методов) наиболее эффективен при
численном решении задач, для которых существенным являются учет
волновых процессов в сплошной среде. Подробнее о методе в книге [6],
детальное описание — в монографии [7].
Матрица А системы уравнений газовой динамики, записанной в
форме
р
• = (р,ще)т,А= | \% и
р/р
имеет вещественные собственные числа Ai = и + с, А2 = и, Аз = и — с
и соответствующие им собственные векторы, о;» (например, левые,
которые находятся при решении системы линейных алгебраических
уравнений o>iA = AiC*;*). Таким образом, одномерная система уравнений
газовой динамики является квазилинейной системой гиперболического
типа.
Матрица из левых собственных векторов, записанных в строку,
является матрицей перехода в базис из собственных векторов матрицы А:
Матрица А представима в виде А = fi^Aft, где Л — диагональная
матрица, состоящая из собственных чисел матрицы А:
A = diag(AbA2,A3).
386
Лекция 14 Введение в методы численного решения уравнений газовой динамики
Для получения разностной схемы введем обозначения
А+ = 1(А + |А|), А- = ±(А - |А|),а = т/Л.
t=nr
Рис. 14.1
Умножим каждое из уравнений исходной системы газодинамики,
записанных в матричной форме на и>и в результате получим
dU
или, учитывая, что о;» — левый собственный вектор,
Построим разностную аппроксимацию полученной системы
уравнений в частных производных с учетом знака собственных чисел (или
направления характеристик). Для облегчения восприятия ограничимся
простейшим методом первого порядка аппроксимации
туп
-Um
_ туп
+ f = 0
Приведенное выше разностное уравнение может быть записано в
матричной форме
387
Лекции по вычислительной математике
или в виде, разрешенном относительно верхнего слоя:
= UJ, - о
или в компактной форме:
U^1 = 1С + <т(-В+Д-и + В-Д+U)-
где
В+ = П^А+П, В" = «"^"П.
Учет направления характеристик позволяет получать устойчивые
разностные схемы для системы уравнений газовой динамики. Сеточно-
характеристические схемы позволяют гибко менять форму шаблона в
зависимости от локальных свойств решения задачи. Существует обобщение
методов на случаи двух и трех пространственных измерений. В сочетании
с методом неопределенных коэффициентов сеточно-характеристические
схемы дали очень хорошие результаты не только в традиционной
газовой динамике, но и в механике деформируемого твердого тела,
магнитной гидродинамике [6,7].
14.4. Разностная схема И.М. Гельфанда для
численного решения одномерной системы
уравнений газовой динамики
Система уравнений газодинамики решается в области t ^ 0, ц ?
[О, X], отрезок интегрирования разбивается на интервалы узлами {rji}Q .
Все интервалы заполнены газом, что соответствует приближению
механики сплошной среды. Величины на интервалах считаются кусочно-
постоянными. При численном решении определяются шесть функций:
и, р, е, Т, v, х — скорость, давление, удельная внутренняя энергия,
температура, удельный объем, эйлерова координата.
Для решения задачи используется система одномерных
нестационарных уравнений в частных производных, описывающих поведение газа
в лагранжевых переменных G7 — лагранжева координата):
dv du
~dt~d^= '
du t d(p + Q) _A
dt+ dv "u'
388
Лекция 14 Введение в методы численного решения уравнений газовой динамики
дт, ~9
dx
Tt=u. A4.5)
Здесь а(Г, v) — заданный коэффициент теплопроводности,
4 v\dn drjlJdrj
— искусственная вязкость Рихтмайера-Неймана, /л — коэффициент
искусственной вязкости. Очевидно, что Q Ф О если щ < 0, при этом |^ < О
или §f > 0. Так как плотность со временем увеличивается, происходит
сжатие газа. В зонах разрежения, где |^ > 0 и Q = 0, искусственная
вязкость действует только в зонах сжатия.
Коэффициент теплопроводности зависит от температуры и задается
как
а(Г, v) = Г7а(Т, v), 7 > 1, ai ^ а ^ а2, ai > 0.
Начальные данные для рассматриваемой задачи будут
ti(O,if) = wo, x(O,ry) = х0> t/@,4) = t*>, T@,i7) = To.
Условия на границах выбираем следующие:
^ ), T(t,X) = T2(t),
При численном интегрировании полагаем, что значения функций
и, Г,, v, х известны на п слое и задача состоит в вычислении этих же
функций на п+1 слое. Сеточные функции umn+i, T^^/2, v^\/2, zmn+i
вычисляются с помощью неявной разностной схемы.
В результате разностная схема записывается как
= 0,771 = 1,. . .,М,
|
Г
hm =*7т+1/2 -^т-1/2»^= 1, . . . , Af — 1, A4.6)
1 Li «+1J + «+ЛJ «J + к -^
г [ т+1/2+ 4 т+1/2 4
389
-т+1/2
Лекции по вычислительной математике
п+1 / , х-^\»г-|-1 тгЧ-11 _
грП+1 rpn+1 rpn+1
1т+Ъ/2 1гп+1/2 1т+1/2
"т+1/2 I ™т+1 "т
Лт+1/2 = Г7т+1 -77т, Ш= 1,...,М - 1,
0^ т 0 ??м
К этим уравнениям системы добавим разностное выражение для
вычисления искусственной вязкости
Qm+l/2 = 7Г~\
с фиктивным краевым условием Qm+i/2 = 0 и интерполяционное
выражение ДЛЯ рт
_ fem-1/2 • Pm+1/2 + fem+l/2 ' Pm-1/2
~ ^ TT
Схема имеет второй порядок аппроксимации по координате, а при
весовом коэффициенте, равном 0,5, и второй порядок по времени,
причем все точки спектра лежат на единичной окружности. Подробнее о
данной схеме в [10].
14.5. Метод частиц в ячейках Харлоу (PIC
method:Particle-ln-Cell)
Метод PIC разработан Харлоу в Лос-Аламосской лаборатории (США)
в 60-х годах прошлого века для расчета процессов с большими
деформациями исходной области интегрирования (расплескивание, разрушение).
Область интегрирования покрывается фиксированной в
пространстве расчетной сеткой, шаг которой h постоянен по обеим координатам
х, у, ячейки занумерованы двумя индексами к, I.
В центре ячейки вычисляются величины ujjy, и?ш (компоненты
скорости газа), е^к1,т^ы где i — номер вещества, е^ — удельная
внутренняя энергия газа с номером г, гп^ — масса этого вещества. Если этого
вещества в ячейке нет, то в ней и энергия, и масса полагаются равными
нулю.
Предположим, что в каждой ячейке содержится несколько частиц
E—10), каждая из которых характеризуется координатами X?, YJ1 массой
fXj, ij — номер вещества, из которого состоит частица с номером j.
390
Лекция 14 Введение в методы численного решения уравнений газовой динамики
Шаг численного интегрирования состоит в расчете величин
{ui,U2,?i,mt}?+1 и {X, Y}"+ на верхнем временном слое ?n+i по
вычисленным величинам {ub U2, ?», гпг}%, {X, У}" на нижнем слое tn.
На первом этапе расчета учитываются изменения искомых функций
только за счет сил давления. При этом предположении разностные
соотношения аппроксимируют уравнения
at '
_
at дх'
д(ри2) dp
at ay'
дЕ д(рщ) d(jm2) _
at+ дх + ay
где
= pe = pie+ ±(и1 + и
В расчетах участвуют также уравнения состояния для каждого газа
На втором этапе аппроксимируются конвективные члены
д{ри2) _ п
at + ~ЫГ + ~ду~ - и>
dp , d(pui) . d(puj)
at+ дх + ау ~ '
d(puiu2) д(ри2) _
at + дх + ду
эд а(Дщ) а(Дп2)
а< дх ду
Опишем вычислительную процедуру на первом этапе. Известны
uj, uj, mn, en, Xn, У" (остальные индексы для простоты изложения
391
Лекции по вычислительной математике
опускаются). Сначала рассчитывается давление р?, исходя из
предложения равенства давлений на границе двух сред р\ = рг = • ,или
К этим уравнениям добавляется условие ? Ъ — Л2, поскольку 7» —
часть объема h2 ячейки, занимаемого газом с номером г. По известной
массе г газа находим его плотность: р» = т"/7ь а по известной удельной
энергии е? — давление р» = Fi(e?, 7»~1т?)-
Затем по закону Дальтона находится давление, р^, которое
приписывается к центру ячейки /с, 2. Система нелинейных алгебраических
уравнений решается, вообще говоря, итерационным методом. В случае
р = pfi(e) выписывается ее явное решение. Далее находим
предварительные значения расчитываемых величин, которые обозначим как
пх, иг, т, ё. Первое из уравнений ^ = 0 — закон сохранения массы —
на сетке приобретает вид га#/ = т?ш. Поскольку на первом этапе |? =
= 0, то два следующих разностных уравнения — уравнения движения —
записываются как
Здесь
i
Последняя из рассчитываемых величин — энергия. Дискретный
аналог уравнения энергии в методе частиц в ячейках будет
Ёу- Е% Pfc+l/2,f • ttltfc+l/2ti ~Pfc-l/2,I ' Ultk-l/2tl
Рк,Н-1/2 Ц2,*,/+1/2 Pk,l-l/2 U2k,l-l/2
Здесь
п+1/2 _ \
о,п+г/2 -
4
392
Лекция 14 Введение в методы численного решения уравнений газовой динамики
Вычислим величину eJJ — энергию. Напомним, что е = р(е + ц
Тогда eft2 есть энергия в ячейке ft x ft:
где pft2 — масса ячейки, равная mfa = ? тш- В таком случае, с учетом
закона сохранения массы,
= in
Вычислим величину [(ft2p)^]^ , имеющую смысл полной
внутренней энергии в ячейке, зная массу т?к1 и удельную внутреннюю энергию
еЗы вещества.
теперь имеется алгоритм вычисления Ек1 и, следовательно,
Из соотношения
находим величину полной удельной внутренней энергии Ей- Однако
искомыми являются значения удельной внутренней энергии для каждого
вещества. Пусть Дв» — изменение удельной внутренней энергии г
вещества за первый этап шага по времени по г веществу. Зная тг (масса г
вещества), запишем полное приращение полной удельной внутренней
энергии в ячейке (Де) и приравняем его к уже полученному полному
приращению
Для определения изменения количества каждого газа нужно сделать
некое правдоподобное предположение, например, считать, что все
одинаковы. Тогда N Aeiki = ejjj - e?z и, соответственно, ёш = е"к1
На этом первый этап расчета (предиктор) закончен.
Рассмотрим второй этап расчета.
Движение частиц описывается обыкновенными
дифференциальными уравнениями
393
Лекции по вычислительной математике
которые могут быть приближены, например, с использованием
явного метода Эйлера. Тогда дифференциальные уравнения заменяются
разностными уравнениями
= хр + ™lp, ypn+1 = урп + ™2р,
где скорости частиц й*, щ определяются интерполяцией величин пь йг в
ячейках, окружающих р частицу.
После этого рассчитывается перенос массы и вычисляется новая
масса каждой ячейки. Для этого выделяются три группы частиц:
• частицы, оставшиеся при переходе на п +1 слой в пределах ячейки,
которые, очевидно, не вносят изменений в массу, импульс, энергию
новой ячейки, т.е. (X^Ypn) <Е шф(Х^\Т^1) € «>& где ч>ц -
обозначение старой ячейки,
• частицы, покинувшие ячейку ш^: (Х?, Ypn) e wy,
• частицы, перешедшие из соседних ячеек: (Хр, Ypn) g Uij,
На шаг по времени накладывается ограничение
h
т <
что означает запрет на перемещение частицы за один шаг больше, чем на
одну ячейку. Перемещение в данном методе возможно только в соседнюю
ячейку. Предположим, что каждая р частица, перешедшая на п+1 шаге по
времени в соседнюю ячейку, переносит в нее массу тр. Это означает, что
значение массы rriiki считается путем сложения масс всех частиц типа г,
для которых (Х?+\ Урп+1) € Uij
Процедура вычисления импульса выполняется следующим образом.
Компоненты полного импульса частиц в ячейке (к, I) могут быть
вычислены, как mjfjui,*/, mjjjlfe.jw, ПРИ этом р частица, покинувшая ячейку ш^,
уносит импульс mpt!i,fc!,mpie2,M* Изменение импульса в 5^ за один шаг
по времени будет
здесь символы суммирования означают суммирование по частицам (р),
покинувшим данную ячейку и пришедшим в нее, соответственно. После
394
Лекция 14 Введение в методы численного решения уравнений газовой динамики
вычисления компонентов импульса каждой ячейки вычисляются
компоненты СКОРОСТИ tijj1, tfJjJ1.
Частица типа г, переходящая из 5*е в другую ячейку, переносит
полную энергию
АЕР = тр
ш + 5 ]¦
Тогда можно вычислить энергию i вещества в ячейке и>ы на
промежуточном шаге:
\ (J +
iPei L
При t = ?n+i полная удельная энергия изменится на величину
где знаки суммирования снова означают суммы по всем частицам,
покинувшим ячейку шы и пришедшим в нее, соответственно. Далее получим
с-П+1 = Jl J?n+l _ I Г
miki
Отметим недостатки этого метода. Во-первых, это дискретность
плотности, что приводит при небольшом количестве частиц в ячейке к
скачкообразным изменениям плотности. Во-вторых, аппроксимация
исходных уравнений достигается при количестве частиц, стремящемся к
бесконечности. Кроме того, этот метод требует значительно большего
количества памяти, чем конечно-разностные методы, так как наряду с
физическими характеристиками узлов необходимо хранить и свойства
частиц в ячейках.
Подробное описание метода частиц в ячейках в [11].
14.6. Задачи для самостоятельного решения
1. Волны Римана
Выпишем нелинейную систему уравнений одномерных движений
идеальной сжимаемой жидкости в случае баротропных процессов.
Она состоит из уравнения Эйлера
395
Лекции по вычислительной математике
уравнения неразрывности
до ди до
и условия баротропности
Уравнения позволяют определить плотность р и скорость и в
зависимости от координаты х и времени t. Система не имеет решений,
зависящих только от х ± aot, но оказывается возможным найти
решение этой системы, представляющее собой плоскую волну и
являющееся обобщением решений вида f(x ± aot). Будем искать такие
решения системы, для которых скорость и является функцией
только плотности р. Частные решения системы уравнений носят
названия решений Римана; соответствующие этим решениям движения
называются волнами Римана f(x ± aot).
(а) Доказать, что в рассматриваемом течении скорость можно
определить по формуле
«=*/#-¦
J у d
Обозначим ^ = а2 (о) и введем величину с = и + а. Какой
физический смысл имеет величина с?
(Ь) Задав начальный профиль возмущения плотности, численно
решить уравнение для р (x,t):
а) для случая адиабатических движений совершенного газа
G=1,4):
б) задав самостоятельно некоторую зависимость давления от
плотности, р = /(р).
396
Лекция 14 Введение в методы численного решения уравнений газовой динамики
(c) Описать качественное поведение решения р(х, t). Указать,
какие требования к численному методу предъявляет
возникновение в потоке скачков уплотнения. Вывести зависимость р(р),
при которой не возникает эффекта опрокидывания волны
сжатия Римана. Дать физическую трактовку полученного
соотношения. Провести численный расчет течения с полученной
зависимостью р(р).
(d) Доказать, что рассмотренные решения Римана можно
определить как такие решения, для которых имеется семейство
прямолинейных характеристик.
(e) Поставить условия существования центрированных волн
Римана, когда
и = и0 f(x/t), р = р0 <p(x/t).
Течения подобного типа — частный случай автомодельных
течений, когда решение зависит от некоторой комбинации
независимых переменных. Проиллюстрировать численными
расчетами особенности распространения центрированных волн
Римана.
Литература
[1] Седов Л.И. Механика сплошной среды, т. 1, 2. М.: Наука, 1976.
[2] Лойцянскый Л.Г. Механика жидкости и газа. М.: Дрофа, 2003.840 с.
[3] Овсянников Л.В. Лекции по основам газовой динамики. Москва-
Ижевск: Институт компьютерных исследований, 2003.336 с.
[4] Самарский А.А., Попов Ю.П. Разностные методы решения задач
газовой динамики. М.: Едиториал УРСС, 2002.480 с.
[5J Попов Ю.П. О консервативности разностных схем. / В кн.: Будущее
прикладной математики. Лекции для молодых исследователей. Под
ред. ГГ. Малинецкого. М.: Едиториал УРСС, 2005.512 с.
[6] Белоцерковский О.М. Численное моделирование в механике
сплошных сред. М.: Физматлит, 1994.442 с.
[7] Магомедов М.-К.М., Холодов А.С. Сеточно-характеристические
численные методы. М.: Наука, 1988. 288 с.
397
Лекции по вычислительной математике
[8] Годунов С.К., Забродин А.В. и др. Численное решение многомерных
задач газовой динамики. М.: Наука, 1976.400 с.
[9] Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных
уравнений. М.: Наука, 1978.687 с.
[10] Федоренко Р.П. Введение в вычислительную физику. М.: Изд-во
МФТИ, 1994.526 с.
[11] Харлоу Ф.Х. Численный метод частиц в ячейках для задач газовой
динамики. Вычислительные методы в гидродинамике. М.: Мир. 1967.
460 с.
[12] Флетнер К. Вычислительные методы в динамике жидкостей. М.:
Мир, 1991.240 с
[13] Андерсен Д., ТаннехиллДж., Плетчер Р. Вычислительная
гидромеханика и теплообмен. М.: Мир, 1990. т. 1,2.
[14] Оран Э., Борис Дж. Численное моделирование реагирующих
потоков. М.: Мир, 1990.661 с.
Лекция 15 Численные методы решения уравнений в частных производных
Лекция 15. Численное решение уравнений в
частных производных гиперболического типа с
большими градиентами решений
Лекция продолжает тему предыдущей лекции и также является
необязательной. В ней рассматриваются некоторые идеи, нашедшие свое
применение для построения разностных схем решения задач механики сплошной
среды. Рассматриваются способы построения гибридных схем для задач с
большими градиентами решения, описываются идеи TVD- и ENO-схем. Вкратце
описываются разностные схемы, построенные на основе решения задачи о
распаде произвольного газодинамического разрыва (схемы С.К. Годунова).
Ключевые слова: потоковая форма представления разностных схем,
регуляризация, сглаживание, антидиффузия, гибридные схемы,
пространство неопределенных коэффициентов, TVD-схемы, ENO-
схемы, метод С. К. Годунова.
15.1. Потоковая форма представления
разностных схем
Рассмотрим линейное одномерное уравнение переноса
ди ди
— + а— = 0, а = const.
at ох
Приблизим его при помощи схем «левый уголок» и «правый уголок»
в зависимости от направления переноса (схемы
Куранта—Изаксона—Риса [1] или С. К. Годунова [2]):
ha ; =0, а > 0, ha—-1—; =0, а < 0.
г h т h
Можно объединить форму записи приведенных выше выражений и
записать схему как
{ % о - = %~число
Введя обозначения а+ = \{а + |а|),а~ = |(а — |а|), приведенную
выше объединенную запись можно представить еще в двух формах:
399
Лекции по вычислительной математике
или
Представим разностную схему в потоковом виде, для чего введем
функции /^j/2» /m-i/2 так> что Данные на следующем слое по времени
можно представить в виде
ит =ит~~ a(/m+l/2 ~~ /т-1/2)'
Тогда простое сравнение выражений даст возможность записать
потоки, для них легко получаются выражения
/m+l/2 = 9 Wttm+1 + Um) ~ Щ
/m-i/2 = \(« + <-i) " si
В [3] приведен общий вид неявной схемы, записанной в потоковом
виде
ГДе fm±l/2 = A "
выражение для /^±\/2 аналогично выражению для /^
Введем также двухпараметрическое семейство разностных схем [4]
П+1 П | ' / /П Jn \
в которых потоки будут определяться в зависимости от направления
переноса а. Они также будут зависеть от значений параметров:
= /
+ Cl-a-/?)< + /
+ A - a - /?) <+1 + /Jti», в < О,
15.2. Гибридные схемы
Для построения первой гибридной разностной схемы в работе [5]
использовалось следующее представление (а > 0):
<+1 = < - у« " <-i) + ~ (l -
400
Лекция 15
Численные методы решения уравнений в частных производных
где 7 — параметр гибридности. От него зависит порядок разностной
схемы, по которой будет производиться расчет в областях с большими
локальными градиентами решения. В цитируемой работе [5]
7 =
«m+l -
<А
ит ит-1
ит ~ ит-1
A5.1)
При А = 0 схема имеет первый порядок точности, при сколь
угодно больших А — второй. Можно повысить порядок аппроксимации этой
схемы до третьего:
+ ~ (l - у) {«,+1 - 2
В [21] схему, записанную в потоковой форме представления,
предложено сделать гибридной, вводя потоки:
/?+1/2 = \ {«+1 " О ~
при такой записи о = a J в области гладкого решения и <j = signa в
области с большими градиентами решения. Переключатель между «гладким»
и «негладким» решениями может быть построен аналогично A5.1).
Другие способы построения переключателей описаны в [6, 7]. В [6]
построены сеточно-характеристические гибридные схемы.
15.3. Гибридные схемы и пространство
неопределенных коэффициентов
Повышать точность метода также можно, если использовать
разложение сеточной функции и^и в ряд Тейлора в окрестности точки
{tn,Xrn). В общем случае любая разностная схема представляется в
виде суммы по точкам шаблона с неопределенными весовыми
множителями [8]:
где v = 1,0, -1 — номера слоев по времени, входящих в шаблон
(шаблоны с более чем 3 слоями по времени рассматривать не будем), \i =
= 0, ± 1, ± 2,... — пространственные узлы точек сеточного шаблона
401
Лекции по вычислительной математике
", xm+At), а? — неопределенные коэффициенты. Если v не
принимает положительных значений, то схема явная, в противном случае —
неявная. Если все а? неотрицательные, то схема монотонная по Фридрихсу
или схема с положительной аппроксимацией.
Учитывая продолжения исходного дифференциального уравнения
= (-1)
к }
L
dtkdxl
полученные дифференцированием исходного однородного уравнения
переноса по независимым переменным к + I - 1 раз, получим после
подстановки разложения проекции точного решения уравнения переноса на
сетку wJJ^ в разностную схему A5.2):
ди ди 5о hSidu fv^cPu htSs&u h2S4
dt +пдх~ rM+ r 9x+ 2т дх2+ 3!г 9х3 4!г дх
A5.3)
откуда получим выражения для условий порядка, соблюдение которых
необходимо для того, чтобы разностная схема аппроксимировала
дифференциальную задачу
а = ar/h — число Куранта, к = 0,1,2,... — порядок аппроксимации,
который может быть достигнут.
Из условий аппроксимации видно, что для получения первого
порядка точности О(т, h) необходимо и достаточно выполнения условий
i)a^ = O. A5.4)
Для получения схем более высокого порядка аппроксимации
необходимо использовать условия порядка с более высокими к.
Для построения разностных схем с заданными свойствами в [9]
предложено ввести линейное пространство неопределеннных
коэффициентов {<*?}, в [10] на основе такого подхода предложена теория
построения разностных схем повышенного порядка точности, в [6] —
теория построения гибридных схем, наиболее близких в этом пространстве
к монотонным по евклидовой норме.
Существует несколько определений монотонной схемы. Они,
вообще говоря, не эквивалентны. Одно из определений приведено выше —
это неотрицательность коэффициентов разностной схемы при записи в
виде, разрешенном относительно точки (tn+1, xm). Монотонная схема по
402
Лекция 15 Численные методы решения уравнений в частных производных
Борису и Буку — схема, не увеличивающая число экстремумов в
разностном решении задачи по сравнению с количеством экстремумов в точном
решении задачи. Дадим еще одно определение монотонной схемы.
Определение. Схема называется монотонной, если из условия
+ ит ^ 0 следует uJJ^ + и%+г ^ 0 для всех га.
Для системы уравнений в частных производных гиперболического
типа
где А — квадратная матрица с постоянными коэффициентами размера
п х n, u = (щ,..., un)T — вектор-столбец, разностную схему можно
представить в виде [11] (см. также лекцию 14):
^ - <_i) + ^ I А| «+1 -
ИЛИ
+ (О |А| П) (iCh - 2< + tC_i)} ,
где А = diag(Afc) — диагональная матрица из собственных значений
матрицы А, 17 — матрица размера п х п, строками которой являются левые
собственные векторы матрицы А. Если матрица А невырожденная и все
ее собственные числа действительны, то система имеет гиперболический
тип, а матрица системы может быть представлена в виде произведения
трех матриц А = П^АП. Матрица перехода в базис из собственных
векторов в данном случае есть матрица из левых собственных векторов
матрицы системы, так как матрица А несамосопряженная. Обратную
матрицу к матрице перехода также надо вычислять непосредственно — как
правило, в задачах механики сплошных сред матрица перехода не
ортогональная, обратная матрица не равна транспонированной.
Эту же схему можно записать в виде
< = < {A
где А" = 0,5(А + |А|), А+ = 0,5(А - |А|), или
IC+1 = < - I {(П-Ч-П) (iCn - О - (П^А+П) « + хС-г)} ,
где Л+ = 0,5(А - |А|), Л" = 0,5(А + |А|),
403
Лекции по вычислительной математике
Если по аналогии со скалярными потоками /?+\/2» -C-i/2 ввести
векторные потоки fm+i/2, fm-1/2» то разностная схема A5.2) может быть
представлена в виде:
<+1 = 1С - ?(fm+l/2 - fm-1/2),
raefm+1/2 = \
i {(П-'АПЖ,, + <) - (П-1 |A| O)(iCn -
fm_1/2 = I
{(O
Для одномерной квазилинейной системы уравнений газовой
динамики разностная схема выписана подробно в предыдущей лекции. В
квазилинейном случае потоки fm+i, fm_i можно представить в виде
fm+l/2 = \
Матрицы, входящие в приведенные выше формулы, выписаны в
лекции 14.
15.4. Метод коррекции потоков Бориса-Бука
Метод коррекции потоков предложен в [12], как схема «предиктор-
корректор». На этапе «предиктор» погрешность метода вносит в
численное решение поток численной диффузии (вязкости), на этапе
«корректор» водятся потоки искусственной антидиффузии, уменьшающие их.
Пусть йт — численное решение, полученное после предиктора.
Корректор представляется в виде
С1 = йт - {fm+l/2 ~ fm-l/2),
где определены антидиффузионные потоки fm+\/2 = M(um+i - um),
/m-1/2 = M^m-t2m_i) через границы xm+i/2,xm_1/2,(/i —коэффициент
антидиффузии).
404
Лекция 15 Численные методы решения уравнений в частных производных
В [13] предложен общий вид корректора:
причем коэффициенты антидиффузии вычисляются с помощью подхода,
предложенного в [6,10].
15.5. TVD-схемы
Идею схем TVD (Total Variation Diminition), т. е. схем с уменьшением
полной вариации, представим на примере схемы Лакса-Вендроффа [14]:
„,П+1 Л.П ^Т/лтп Л,П \ ( ?ГЪ ГП \
ит = ит - ^\Um " um-l) ~ (Лп+1/2 ~ Лп-1/2)»
/т+1/2 = у A ~ ar)(fZm+i - пт), /т-1/2 = ^A - ат)(пт - Um_i).
Эта схема немонотонная, но в отсутствии последнего слагаемого
(/т+1/2 ~ fт-1/2) она была бы монотонной. Этот факт можно
проинтерпретировать следующим образом: антидиффузионные потоки в
схеме Лакса-Вендроффа слишком велики и приводят к появлению
осцилляции. Следовательно, эти потоки необходимо ограничить, например, как
/ )A )(U - йт).
Поток /т+1/2 ограничивается некой функцией <p(rm), называемой
ограничителем или лимитером. Параметр гт вычисляется по формуле
ит - ит-1
его можно назвать показателем гладкости решения.
Для гладких решений rm « 1, при больших же градиентах гт « 0.
Функция <р(гт) выбирается так, чтобы схема относилась к классу
TVD, т. е. чтобы уменьшалась полная вариация на следующем слое по
времени, TV(un+1) < TV(un). Выражение для полной вариации есть
п=оо
TV(un) = Y2 |um+i — ит|• Это условие более слабое, чем условие мо-
т=—оо
нотонности разностной схемы.
Для того чтобы полная вариация уменьшалась, достаточно выбрать
лимитер следующим образом:
0 < <p(rm) ^ min Brm, 2), rm > 0,
405
Лекции по вычислительной математике
причем для обеспечения второго порядка аппроксимации необходимо,
чтобы ч>A) = 1.
Другой ограничитель имеет вид
{minB,rm),r > 1,
minBrm,l),0<r^l,
0,r<0.
Заметим, что вместо свободных параметров в этой схеме вводится
функция-ограничитель, а сама схема является одношаговой. Иногда в
расчетах полагают
_ um-um-i+e
где малая величина е (е « 1СГ5 ч-10~10) играет роль шумового фильтра.
Вместо условия уменьшения полной вариации разностной схемы
можно ввести более слабое ограничивающее условие TVD(un) < С,
причем пт ^ С (схемы TVB).
В [15,16] разностную схему для численного решения уравнения
переноса предложено представить в виде
arrj.
где {m±i/2 ^ 0; или
В соответствии с [16], эта схема будет монотонной, если выражение
в скобках неотрицательно. Монотонность схемы может быть достигнута
выбором коэффициента ?m±i/2, как функции от г. Как и ранее, rm =
= ^"у. Выбор весового множителя осуществим в соответствии с
правилом
О, rm < О,
(с+ЬA-6))-2с6„ 1 ¦ Х^«
^55—Гт' А "Г 0 < ?Vn<2>
Гт > 2.
Здесь 5, с, Ь — константы, 0 < S < 1; если с + Ь =? 0 получаем
схему второго порядка аппроксимации, причем, при с = 1/3 и 6 = 2/3 —
третьего порядка везде, кроме точек разрыва функций.
406
Лекция 15
Численные методы решения уравнений в частных производных
Отметим, что, по-видимому, основные идеи, использованные при
построении TVD и ENO схем, впервые были описаны В. П. Колганом
в [17] и Р. П.Федоренко [5]. Схема с различными шаблонами, которую
можно рассматривать как развитие идеи гибридных схем Р. П. Федоренко [5],
предложенная Колганом, имеет вид
Кг ~ §?(Д + Д~>т = 0, |Дит_2| :
и? - ^Д-<, |Дит_2| ^ |Дит-1|, |Дит|
|Aum_2
\Aum\
Здесь использованы обозначения Аит = um+i - um, А~ит = ит-
- Um-U (Д + А")ит = Um+i - иш-и (ДД")ит =
Соответствующие шаблоны показаны на рисунках ниже.
Рассмотрим способ конструирования TVD-схемы. Произвольную
четырехточечную схему (три точки на нижнем временном слое) можно
представить в виде <+* = и^ + С^+1/2Ат+1/2и - С-_1/2Дт_1/2и, где
введены потоки Am+i/2U = v>m+i - um, Дт_1/2гА = ит - wm_i.
Положим, что коэффициенты схемы удовлетворяют условиям С^+1/,2 ^ О,
^m-i/2 ^ О» ДЛЯ всех ш- Тогда приведенная разностная схема является
TVD-схемой. Покажем, что это так. Для этого вычислим полную
вариацию
rv(un)= f; !<+!-<!= f; |дт+1/2ип|.
Запишем разностную схему в операторном виде и^1 = Lu^, где
J, =и^+С++1/2Дго+1/2и-С-_1/2Дт_1/2и. Покажем, что TK(un+1) <
(ип), или TV(Lun) < TV(un). Оценим величину Дт+1/2«п+1,
учитывая, что tC+\ = u^+1 + С++3/2Дт+з/2« - С-+1/2Дт+1/2и;и^,+1 =и^ +
+ Ст+1/2дт+х/2« - С-_1/2Дто_1/2ч. Тогда
A - с
IДт+3/2«|
407
Лекции по вычислительной математике
откуда следует
- f; i дт+1/2«п+1|< f; (i-c:_1/2-
15.6. ENO-схемы
Рассмотрим построение схемы типа ENO, предложенной в [4], для
уравнения переноса. Основная идея этих схем заключается в
использовании двух (или более) шаблонов для обеспечения двух традиционно
противоположных свойств: второго (или третьего) порядка точности и
монотонности без наличия аппроксимационной или искусственной вязкости.
Обычно используются две базовые схемы: с центральными и
односторонними разностями, а также с условием переключения, зависящим от
значения производных (первой и второй) и знака скорости переноса.
Рассмотрим один из вариантов построения этого метода, для
численного решения линейного уравнения переноса. Запишем схему в
потоковой форме
а сами числовые потоки будем вычислять по формулам, в которые введем
неопределенные пока коэффициенты:
а<+2A - а - /?)<+1 + /?<, а < О,
аи»_2 + A-а-/?)<_
Выпишем первое дифференциальное приближение (ПДП) разностной
схемы (лекция 13). Для этого выпишем проекцию точного решения
уравнения переноса на введенную разностную сетку, разложим в ряды
Тейлора в окрестности любой точки шаблона и приведем подобные
слагаемые. В получившемся дифференциальном уравнении оставим главные
члены невязки. Кроме того, как более информативную, рассматриваем
П-форму, после всех вычислений получим
ди ди
408
Лекция 15 Численные методы решения уравнений в частных производных
Из ПДП следует, что при а = 0 = 0 получаем схему первого порядка,
при а = 0, /3 = 1/2 — второго порядка с центральными разностями, а =
=-^0=0— второго с ориентированными разностями.
Потребуем, чтобы коэффициент при второй производной в
первом дифференциальном приближении схемы с центральными
разностями обратился в нуль. Это означает, что в схеме отсутствует схемная (ап-
проксимационная) вязкость. Отсюда получим
Если ввести аналог числа Куранта а = ^, то данное условие можно
записать более компактно: 0 = О,5A - с).
Для схем с ориентированными разностями @ = 0) условие
равенства нулю аппроксимационной вязкости дает
а l-\a/r\h
Исследование обеих схем на монотонность, которое здесь
опускается, приводит к условиям Дт+1/2и ^ 2B-<т) Am-i/a** Для схемы с
центральными разностями, и Дт+1/2и < 2^1j"^Am_1/2u для схемы с
ориентированными разностями. Объединение этих условий дает условие
монотонности обеих схем:
m~1 ^ A < Д
2B-<7)
Можно выделить монотонные разностные схемы без
аппроксимационной вязкости, если реализовать переключение с одной схемы на
другую.
Для такой монотонной схемы можно выписать окончательный вид
потоков. Формулы для потоков выпишем через число Куранта.
/m+l/2
если
С 3—ал.п 1—<тл.п л ^ П
- J ~Um 2~um-l» a ^ U
I ~wm+l 2~um+2»a<lJ
(a • Аи • A2u)m+1/2 > 0;
j 1 - asigna n 1 4- crsigna
/m+l/2 = 2 Um+1 H 2
если
(a - Ди - Д2и)т+1/2 < 0.
409
Лекции по вычислительной математике
Здесь применяются обозначения Дт+х/2и = um+i-um, A2um+i/2 =
- Дит.
15.7. Разностные схемы для квазилинейного
уравнения переноса
Рассмотрим теперь нелинейное уравнение переноса, записанное в
дивергентной форме
и соответствующей характеристической форме, которая легко получается
из дивергентной:
- + a(u)^ = 0,a(u) = ?. A5.6)
В дивергентной форме записи этого квазилинейного уравнения
переноса величина / играет роль потока. Представим явную трехточечную
разностную схему для численного решения A5.5) или A5.6) в потоковой
форме
?1 /?-1/2). A5.7)
2 [/? +
/m-1/2 = \ [/m-1 + /m " ^m-l/2) ' Aum_1/2] ,
ry — коэффициент при второй разности в разностной схеме, если а =
= const.
В случае схемы Куранта-Изаксона-Риса (или схемы с разностями,
ориентированными против потока — upwind scheme) имеем
fm-1/2 = 2^m + •^m "" |am—1/21 (% -
для сокращения записи введена скорость переноса, вычисляемая по
формуле
a(tim),(ttm+i-um)=0.
410
Лекция 15 Численные методы решения уравнений в частных производных
В квазилинейном случае совпадавшие в линейном случае схемы
будут приводить к разным разностным уравнениям, соответственно,
будут различаться и численные решения из-за разности погрешностей
аппроксимации. В случае квазилинейного уравнения для схемы Лакса-
Вендроффа выражения для потоков будут иметь следующий вид:
[/ +fm~- ^
I/ + /
Для схем Куранта-Изаксона-Риса и Лакса-Вендроффа
коэффициенты r/(am±i/2) будут иметь значения |am±1/2| и %(ат±1/2J
соответственно. Если, например, функция г/(х) = |х| при |ж| « е, где е — малое
число (порядка величины аппроксимационной вязкости для разностной
схемы первого порядка Куранта-Изаксона-Риса), то полагают г)(х) = |х|
ПрИ |х| ^ ?, 7)(х) = Х ?/ ГфИ |х| < ?.
Введем обозначение 7m+i/2 = 2aam+1/2, тогда величины потоков
/m±i/2 можно переписать как
- ^ Ьт-
1/2
Здесь введены обозначениЖ5Gт+1/2) = 2ar7(am+i/2),QGm+i/2) =
= 2a77(am_1/2I /m+i = /т + ат+1/2 Дт+1/2и. Подставляя эти выражения
для численных потоков в A5.7), получаем
<+* = < + С++1/2Дт+1/2 . и" - С-_1/2Дт_1/2гЛ A5.8)
ГДеС?+1/2 = \ [QGm+l/2) - 7т+1/2] уС^1/2 = ^ [QGm+l/2) +7m+l/2] ,
откуда следует
Ст+1/2 + Cm+l/2 = QGm+l/2)-
В случае линейного уравнения переноса с постоянным
коэффициентом (постоянной скоростью переноса) Qm+i/2 = 2a|a|,7m+i/2 =
= 2acr,77 = \а\ . Условие устойчивости такой схемы имеет вид т ^
Построенная разностная схема относится к классу TVD-схем, что
непосредственно проверяется. Схема обеспечивает выполнение условия
TV(un+l) ^ TV(un) с учетом неравенств С^+1/2 > О, С^_1/2 ^ О,
Cm+l/2 + Cm+l/2 < Х Д™ ЛЮбЫХ т«
411
Лекции по вычислительной математике
15.8. Однопараметрическое семейство неявных
схем
Рассмотрим однопараметрическое семейство неявных разностных
схем для численного решения нелинейного уравнения переноса. Схемы,
принадлежащие этому семейству, запишутся следующим образом:
весовой множитель меняется от нуля до единицы: 0 ^ 9 < 1.
Потоковая форма записи этих квазилинейных уравнений будет
<tl = < - *(/m+l/2 " /m-1/2), /m±l/2 = A -
Такая запись однопараметрического семейства схем включает в себя
как явные (при в = 0), так и неявные (например, при в = 1, в = 0,5)
разностные схемы.
Для вычисления числового потока будем использовать формулы
/m+l/2 = л (/m+1 + /m + ?\n+l/2)> /m-1/2 = « (
где дополнительные слагаемые для вычисления потока в полуцелых
точках есть
Подстановка выражений для потоков в исходную однопараметриче-
скую разностную схему приводит к следующему выражению:
|0 {/m+l-
ИЛИ
412
Лекция 15 Численные методы решения уравнений в частных производных
где i%? — величины, вычисляемые на п слое по времени, кроме того,
в левой части прибавили и вычли величину /?+\ введено обозначение
Фт±1/2 = r/(am±l/2)(l ~ Qmil/г) + г)ш±\/2$т±\/2-
При способе вычисления локальной скорости переноса в
соответствии с правилами
ат+1/2 = < ?тЧ'*и 1 п
/ ^fer» Дт_1/2и^0,
^т-1/2 = < "т-1/2»
[ а(ит), Дт_1/2и = 0,
получим разностную схему
или, в чуть сокращенной форме записи,
2Дт+1/2и -
Алгоритм решения приведенного разностного уравнения —
прогонка.
15.9. TVD-схемы для квазилинейного уравнения с
анти диффузией.
Повысить порядок аппроксимации TVD-схем можно, введя в
уравнение переноса антидиффузионный член
ди д л л;
где дополнительный антидиффузионный поток имеет порядок
погрешности аппроксимации и вводится по формуле / = /i/z(cr, u)^.
Очевидно, что это дополнительное слагаемое в исходном уравнении
будет иметь вид
д ди.
413
Лекции по вычислительной математике
Таким образом, проведена коррекция потока, компенсирована ап-
проксиммационная вязкость. Хартен предложил модифицировать поток,
введя в него функцию Р:
/m+l/2 = X
причем разные TVD-схемы различаются выбором этого слагаемого Р.
В исходном варианте разностной схемы, предложенной Хартеном, эта
функция выбиралась следующим образом:
/т±1/2 = \
= 0>
/m±l/2 = 2
Эта схема, тем не менее, приводила к заметному размазыванию
разрывов в решении.
Приведем также другие виды ограничительной функции. Общий
вид записи лимитера будет один и тот же:
a Qm+i/2 может выбираться из следующих вариантов:
Qm+i/2 = minmod(Am+i/2u, Am-i/2u
+ minmod(Am+i/2u, A
Qm+1/2 = min mod (Am_i/2u, Am+i/2w, Am+3/2u),
Qm+i/2= min mod BДт_1/2и, 2Дт+1/2и), 2Дт+3/2и, 0,5(Дт+3/2и+Дт_1/2)).
Еще один вариант выбора лимитера в уравнении квазилинейного
типа будет
-Pm+l/2 = - [^(am+l/2)Qm+l/2 +4(am+l/2)(l ~ От+1/2)] Д
С согласованным выбором функции Qm+i/2 = Qm+i/2 • Am+i/2it.
414
Лекция 15 Численные методы решения уравнений в частных производных
Введем обозначения показателей локальной гладкости решения
. _ т1/2 + _
и представим функции Q(r~, г+), входящие в выражения для
ограничения потока, в виде
Q(r~~,r+) = minmod(l,r~) +minmod(l,r+) — 1,
Q(r~,r+) = min mod (r~,r+),
Q(r-,r+)=minmodB,2r-,2r+,0,5(r--hr+)).
Итак, напомним основные идеи, направленные на построение TVD-
схем повышенного порядка точности:
— построение гибридных схем, аналогичных методу коррекции
потоков [17];
— построение схем с модифицированным по Хартену потоком [18];
— построение схем, основанных на методе Годунова второго порядка
аппроксимации [20, 21].
15.10. TVD-схемы для линейных систем уравнений
гиперболического типа
Построим разностную схему типа TVD для случая одномерной
системы линейных уравнений в частных производных гиперболического
типа, к которым относятся, например, системы уравнений акустики или
теории упругости.
Запишем систему как и ранее в матричной форме представления
ди А ди л
+А0
где и — вектор-столбец искомых функций, А — квадратная матрица
п х п с постоянными коэффициентами, t, x — независимые
переменные. Пусть матрица А имеет п действительных собственных чисел А* и
собственных векторов и>г- Без ограничения общности можно считать, что
среди этих собственных чисел нет кратных, а соответствующие
собственные вектора образуют базис.
415
Лекции по вычислительной математике
Тогда возможен переход к базису из собственных векторов, в
котором матрица системы диагонализуется, сама система запишется как
где А — диагональная матрица из собственных чисел матрицы A, ft —
матрица, строками которой являются соответствующие левые
собственные векторы. Последнее уравнение можно переписать следующим
образом:
dR dR
где R = Пи — инварианты Римана.
Разностную схему для численного решения уравнения в
инвариантах представим в виде:
-jjSrn + fm+1
Здесь g = r/ft, a <pm+i/2 вычисляется аналогично скалярному
случаю, с учетом того, что вместо am+i/2 необходимо брать А^+1/2, г —
номер собственного значения, вместо Am+i/2u: Um+i/2 =
)
Явную схему TVD второго порядка точности типа
предиктор-корректор для численного решения нелинейной системы уравнений
гиперболического типа представим в виде:
-(Um + lO - |(fm+i - fm),
__fl4~l
um =
где компоненты вектора <^m
Функция, входящая в выражение для лимитера, вычисляется
mmi
n _ J + minmod(Um+i/2, Um+3/2) - Um+1/2,
Vm+i/2- ^ minmod(Um+1/2,Um,1/2,Um+3/2),
min modBUm_1/2,2Um+i/2,2Um+3/2,0,5(Um_1/2+Um+3/2)).
416
Лекция 15 Численные методы решения уравнений в частных производных
15.11. Метод С. К. Годунова
Широко распространенный метод С. К. Годунова для получения
численных решений с особенностями разрывного характера основан на
решении задачи о распаде разрыва [2, 21-22]. В газовой динамике
хорошо известно точное решение этой задачи и рассмотрены все возможные
конфигурации решений. Положим, что начальные данные есть кусочно-
постоянные функции на сетке ^
Um+l/2 = u[tn,0,5(z
Например, для системы уравнений газовой динамики и = {и, р, е}.
Иногда начальные данные задают в ячейках с целыми номерами
Решение задачи строится следующим образом. В окрестности
каждого узла хт (или xm+i/2 при другой нумерации) решается задача о
распаде разрыва независимо от других возмущений. Это решение используется
до того момента, когда волна, образовавшаяся от разрыва в точке хт, не
встретится с волной, идущей от точки xm+i. Далее полагаем, что и при
t = tx = г решение также приближается кусочно-постоянными
функциями
1 г
h J
h = zm+i — xm,
или, на сетке с отличной нумерацией узлов
Хт+1/2
u^ = - J u
«m-l/2
Представим систему дифференциальных уравнений в частных
производных, записанную в дивергентном виде,
dt + дх
в интегральной форме
(Щ + %)dtdx = j{Sdx - Pdt) = 0,
G dG
14—3339 417
Лекции по вычислительной математике
где G — некая односвязная область, 3G — ограничивающий ее
замкнутый контур, S, Р — функции от и. Для этого выберем в качестве G ячейку
{(tn, ?n+i) x {xm, Xm+1)} и получим интегральное уравнение
l tn+1 aJm+1 *n+l
S(tn,x)dx- J P(t,xm+1)dt- J S(tn+I,x)dx+ J P(t,xm)dt = 0.
%m *n Em *n
Первый и третий интегралы вычисляются просто по формуле
средних — функции на отрезке [xm, xm+i] кусочно-постоянны. Положив все
функции кусочно-постоянными и на отрезке [?n, ?n+i] в силу автомодель-
ности решения задачи Римана относительно переменных (x/t), получим
равенство
Snm+1/2h - Р» +1т - S?+\/2h + Р» г = О,
или, разделив правую и левую части на произведение rft,
или ^^т + prn+i/2-^m-i/2 = 0 при другой индексации.
При этом потоки PJ^, PJ^+1 вычисляются при помощи решения
задачи о распаде разрыва, которая сводится к решению системы
нелинейных уравнений.
Повышение порядка аппроксимации схем типа Годунова,
основанных на решении задачи распада разрыва (или солверов Римана)
реализуется путем использования кусочно-линейной аппроксимации искомых
величин внутри ячеек (в отличие от кусочно-постоянного их
представления в методе Годунова) и различных алгоритмов пересчета по времени
(алгоритмов типа предиктор-корректор) [19, 20].
Рассмотрим один из таких методов. Пусть внутри ячеек для всех
сеточных функций заданы кусочно-линейные распределения
где Q^ — вектор наклонов функций и внутри ячейки. При этом
изменение этой функции по времени внутри ячейки будет
А
at ~ Адх~
Предиктор (первый шаг) выглядит следующим образом:
пт - U" f« + SQS.) - f« - $Qm) _ n
г + h ~U;
418
Лекция 15 Численные методы решения уравнений в частных производных
Um 2 на промежуточном слое п + 1/2 вычисляем, как среднее
арифметическое
На втором шаге — корректор — получим, используя метод конечных
объемов
"m+1 ~ Кг , fm+l/2 ~ *т-1/2 _ п
г + h ~U'
где, fm±i/2 = /(umii/2), а функции \im±i/2 определяются из решения
задачи Римана со следующими начальными данными:
0.
Эта схемы была получена в работах [27, 29]. В качестве начальных
данных можно выбирать, не изменяя порядок точности, например, такие:
^ 1 ^Q^+i,m+1/2 0
/ / 0.
Простым способом вычисления наклона Qm в ячейке с номером m
для сеточной функции ит, обеспечивающим устойчивость схемы,
является использование функции min mod (у, z)=0,5(sign2/+sign^) min(|y|,|z|),
которая выбирает наклон с минимальным значением модуля, при
условии, что знаки обоих аргументов совпадают (при разных знаках
аргументов эта функция равна нулю):
Qm = minmod( , ).
Подобный алгоритм предиктор-корректор можно использовать и
для системы уравнений, записанной в характеристической форме:
При этом предиктор имеет вид
1 un
„n+1/2 _ um "Гцт _ n _
В качестве корректора используем, например, полученную ранее
сеточно-характеристическую схему
hill A l«j hll? Л l^ ^ U
419
Лекции по вычислительной математике
с учетом того, что начальные данные являются кусочно-постоянными:
h
Qw =0.
Литература
[1] Courant T.R., Isacson E, Rees М. On the solutions of nonlinear hyperbolic
differential equations by finite differences. // Commun. Pure and Appl.
Math. 1952. v. 5. № 5. PP. 243-254.
[2] Годунов С.К., Забродин А.В., Прокопов Т.П. Разностная схема для
двумерных нестационарных задач газовой динамики и расчет обтекания
с отошедшей ударной волной. //ЖВМиМФ. 1961. т. 1. № 6. С. 1020-
1050.
[3] Yce H.C. Construction of Explicit and Implicit Symmetric TVD Schemes
and Their Applications. //J. of Сотр. Physics. 1987. Vol. 68. PP. 151-179.
[4] Гущин В.А., Коньшин В.Н. Численное моделирование волновых
движений жидкости. Сообщения по прикладной математике. /
Препринт ВЦ АН СССР. 1985. 36 с.
[5] Федоренко Р.П. Применение разностных схем высокой точности для
численного решения гиперболических уравнений. // ЖВМиМФ.
1962. т. 2 № 6. С. 1122-1128.
[6] Петров И.Б., Холодов А.С. О регуляризации разрывных численных
решений уравнений гиперболического типа. // ЖВМиМФ. 1984. т.
24. №8. С. 1172-1188.
[7] Leer B.Van. Towards the ultimate conservative difference scheme. II.
Monotonicity and conservation combined in a second-order scheme. //
J. of Appl. Phys. 1974. v. 14. № 4. PP. 361-370.
[8] Магомедов М.-К.М., Холодов А.С. Сеточно-характеристические
численные методы. М.: Наука, 1988.288 с.
[9] Холодов А.С. О построении разностных схем с положительной
аппроксимацией для уравнений гиперболического типа. // ЖВМиМФ.
1980. т. 20. №6. С. 1601-1620.
420
Лекция 15 Численные методы решения уравнений в частных производных
[10] Холодов А.С. О построении разностных схем повышенного порядка
точности для уравнений гиперболического типа. // ЖВМиМФ. 1980.
т. 20. №6. С. 1601-1620.
[11] Магомедов К.М., Холодов А.С О построении разностных схем для
уравнений гиперболического типа на основе характеристических
соотношений //ЖВМиМФ 1969. т. 9. № 2. с. 373-386.
[12] Boris J.R, Book D.L. Flux-corrected transport. I. Shasta a fluid transport
algorithmthatworks.//J.ofC.Ph. 1973. Vol 11. № 1. PP. 38-69.
[13] Воробьев О.В., Холодов А.С. Об одном методе численного
интегрирования одномерных задач газовой динамики. // Математическое
моделирование. 1996. т. 8. № 1. С. 77-92.
[14] Lax P.D., B.Wendroff Difference schemes for hyperbolic equations with
high orders of accuracy. // Comm. Pure. Appl. Math. 1964. v. 17. № 3. PP.
381-398.
[ 15] Vyaznikov К К, Tishkin V.F., FavorskiiЛ.Р. One way to Construct Higher-
Order Accurate Monotonic Difference Schemes for Systems of Hyperbolic
Equations. // MMCE. 1994. v. 2. № 2. PP. 189-212.
[16] Вязников К.В., Тишкин В.Ф., Фаворский А.П., Шашков М.Ю.
Квазимонотонные разностные схемы высокого порядка точности. /
Препринт ИПМ АН СССР. 1987. № 36.27 с.
[17] Калган В.П. Применение принципа минимальных значений
производной к построению конечно-разностных схем для расчета
разрывных решений газовой динамики. // Ученые записки ЦАГИ. 1972. т.
3. № 6. С. 68-77.
[18] Harten A.J. High resolution schemes for hyperbolic conservation laws. //
J. Comput. Phys. 1983. v. 49. PP. 357-393.
[19] Родионов А.В. Повышение порядка аппроксимации схемы С.К.
Годунова. //ЖВМиМФ. 1987. т. 27. № 12. С. 1853-1860.
[20] BovrelM., Montagne J.L. Numerical study of a non-centered scheme with
application to aerodynamics. //AIAA Paper. 1985. №. 85-1497. [Idem, in
AIAA7th Comput. Fluid Dyn. Conf. Cincinnati, Ohio, 1985, July 15-17.
A Collect. Techn. Papers, 88-97, AIAA, New York].
[21] Куликовский A J. у Погорелое Н.В., Семенов А.Ю. Математические
вопросы численного решения гиперболических систем уравнений. М.:
Физматлит, 2001.608 с.
421
Лекции по вычислительной математике
[22] Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных
уравнений и их приложения к газовой динамике. М.: Наука, 1978.687 с.
[23] Куропатенко В.Ф. О разностных методах для уравнений
гидродинамики. Тр. МИАН СССР, 1966. Т. 74. С. 107-137.
[24] Родионов А. В. Монотонная схема второго порядка аппроксимации
для сквозного расчета неравновесных течений. // ЖВМиМФ. 1987.
т. 27. № 4. С. 585-593.
[25] Leer В. Van. On the relation between the upwind-differencing schemes of
Godunov, Engquist-Osher and Roe. // SIAM J. Sci. Stat. Comput. 1984.
vol. 5. №1, PP. 1-20.
[26] Engqist В., Osher S. One-sided difference approximations for nonlinear
conservation laws. // Math. Comput. 1981. vol 36. № 154. PP. 321-351.
[27] Osher S. Numerical solution of singular perturbation problems
and hyperbolic system of conservation laws. // In: North Holland
Mathematical Studies. 1981. vol. 47. PP. 179-205.
[28] Roe PL The use of the Riemann problem in finite differences. / Lect.
Notes Phys. 1981. Proc. 7th Int. Cont. Numer. Meth. Fluid Dynamics.
June 23-27.1980. vol. 141. PP. 354-359.
[29] Roe PL Approximate Riemann problem solvers, parameter vectors, and
difference schemes. // J. Comput. Phys. vol. 43. № 2. PP. 357-372.
[30] Miller G.N., Pucket E.G. A high-order Godunov method for multiple
condensed phases. //J. Сотр. Phys. 1996. vol. 128. № 1. PP. 134-164.
[31] MillerG.N., Colella P. A high-order eulerian Godunov method for elastic-
plastic flow in solids. //J. Сотр. Phys. vol. 167. № 1. PP. 131-176.
[32] Leer B. Van. Towards the ultimate conservative difference scheme. V. A.
second-order sequel to Godunov's method. // J. Сотр. Phys. 1979. v. 32.
№1. PP. 101-136.
[33] Меньшов И.С. Повышение порядка аппроксимации схемы Годунова
на основе решения обобщенной задачи Римана. // ЖВМиМФ. 1990.
т. 30. №9. С. 1357-1371.
[34] Моисеев Н.Я. Об одном способе повышения точности решений в
разностных схемых, построенных на основе метода С.К. Годунова. //
Вопросы атомной науки и техники. Сер.: Методики и программы
численного решения задач математической физики. 1988. вып. 1. С.
38-45.
422
Лекция 15 Численные методы решения уравнений в частных производных
[35] A. Harten ENO Schemes with Subcell Resolution. // Journal of
Computational Physics. 1989. v. 83. pp. 148-184.
[36] Harten A. Uniformly High Order Accurate Essentially Non-oscillatory
Schemes. //J. of Сотр. Ph. 1987. vol. 71. PP. 231-303.
[37] Jee N.S. Construction of explicit and implicit symmetric TVD schemes
and their application.//!. Сотр. 1987. v. 68. Nq 1. PP. 151-179.
[38] Ершов СВ. Монотонная ENO-схема повышенной точности для
интегрирования уравнений Эйлера и Навье-Стокса. //
Математическое моделирование. 1994. Т. 6. № 11. С. 63-75.
[39] Ильин С.А., Пшофеев Е.В. Сравнение квазимонотонных разностных
схем сквозного счета на задаче Коши для одномерного линейного
уравнения переноса. // Математическое моделирование. 1992. Т. 4.
№ 3. С. 62-75.
Лекции по вычислительной математике
Лекция 16. Численное решение уравнений в
частных производных эллиптического типа на
примере уравнений Лапласа и Пуассона
В лекции разбираются постановка простейшей разностной задачи для
уравнений Лапласа и Пуассона в прямоугольной области (схема «крест»).
Дается обзор методов решения сеточных уравнений. Вкратце
описываются идеи современных методов решения эллиптических уравнений в области
произвольной геометрии — многосеточный метод и метод построения
мажорантных разностных схем в пространстве неопределенных коэффициентов.
Ключевые слова: схема крест, разностный принцип максимума,
методы решения сеточных уравнений, метод простых итераций, чебы-
шевский набор параметров, методы Якоби, Зейделя, верхней
релаксации, трехслойный итерационный метод, метод переменных
направлений, коэффициенты Фурье, попеременно-треугольный
итерационный метод, многосеточный метод Р. П. Федоренко,
мажорантные разностные схемы.
Среди всех типов уравнений математической физики
эллиптические уравнения с точки зрения вычислителей стоят особняком. С одной
стороны, имеется хорошо развитая теория решения эллиптических
уравнений и систем. Достаточно легко доказываются теоремы об
устойчивости разностных схем для эллиптических уравнений. Во многих случаях
получаются априорные оценки точности расчетов и числа итераций при
решении возникающих систем сеточных уравнений. С другой стороны,
системы сеточных уравнений, возникающие при решении уравнений
методами сеток, имеют большую размерность и плохо обусловлены. Для
решения таких систем разработаны специальные итерационные методы.
16.1. Постановка задачи. Простейшая разностная
схема «крест». Устойчивость схемы «крест»
Будем рассматривать двухмерное уравнение Пуассона
д2и д2и
в единичном квадрате 0<х^1,0^у<1с краевыми условиями первого
рода на границе расчетной области Г:
((р — заданная на границе функция).
424
Лекция 16
Численное решение уравнений в частных производных
В случае прямоугольной области граничные условия удобно
записать в следующем виде:
Для простоты выкладок введем равномерную расчетную сетку с
узлами {a?m, yi}, т, I = 0,1,..., М с равным количеством шагов по каждому
пространственному направлению, сеточную область D — совокупность
всех узлов сетки, включая граничные, и сеточную функцию umi. В этом
случае шаги по координатам предполагаются равными. В случае
неравных шагов по каждому направлению полученные результаты не
изменятся, а запись уравнений станет более громоздкой.
о (т,/+1)
о (ггМ-1)
Выбираем простейший пятиточечный шаблон разностной схемы
«крест». На этом шаблоне аппроксимирующее разностное уравнение
легко выписать. Для этого производные заменим вторыми разностями:
Um-U -
h2 h2
где h — шаг по координатам, или в операторной форме
~Jmh
Эту же разностную схему можно записать в каноническом виде для
разностных схем для эллиптических уравнений:
-(um-u
h2fml.
425
Лекции по вычислительной математике
Такую каноническую запись не следует путать с канонической
формой записи итерационного метода, которая встретится ниже.
Такая схема обладает вторым порядком аппроксимации по обеим
координатам. Это легко показать, применяя разложение в ряд Тейлора
функции — проекции точного решения на сетку — вплоть до членов
четвертого порядка включительно. Проведем такое разложение для одного
из операторов, стоящих в данном разностном уравнении:
цт-1-2цт + цт+1 (д2и\ h2
AlUm = __ = ^_^ + _^^
Здесь учтено разложение проекции точного решения в ряд Тейлора
ди\ h2 (д2и\
ит+1 = и(хт+1) =Um + h^^ +
и аналогичное разложение для um_i.
Для рассматриваемого двухмерного уравнения получим выражение
для главного члена невязки
\ди ди] h2 \&u ди]
Рассмотрим устойчивость полученной схемы. Отметим, что методы
исследования на устойчивость, применяемые для эволюционных
(зависящих от времени) уравнений, здесь не работают. Действовать
приходится на основе определения устойчивости.
Сформулируем и докажем две леммы, которые облегчат процедуру
доказательства устойчивости разностной схемы.
Лемма 1. Пусть сеточная функция umi определена на сетке (хт,
yi)(m,l = О,...,М) и во всех внутренних узлах сетки удовлетворяет
уравнению "m-м-а^-н^м + um,f-1-2u^+uWtffl = ^ прицт в0 всех
внутренних узлах сетки правая часть этого уравнения неотрицательная:
fmi ^ 0. Тогда наибольшее значение сеточная функция umi достигает хотя
бы в одной точке границы сеточной области.
Доказательство.
Предположим, что существует такая внутренняя точка области, в
которой сеточная функция принимает наибольшее значение. Пусть это
точка с индексами г, j. Перепишем разностное уравнение, несколько
перегруппировав члены в левой части:
((
426
Лекция 16 Численное решение уравнений в частных производных
В силу сделанного предположения, хотя бы одна из скобок в левой
части отрицательна, а остальные неположительны. Тогда в левой части
стоит отрицательное число, в то время как в правой — положительное
(по условиям леммы). Получившееся противоречие возникло из-за
предположения о том, что максимальное значение сеточная функция
принимает во внутренней точке сеточной области. Лемма доказана. ¦
Лемма 2. Пусть сеточная функция umi определена на сетке (xm, yi)
(т, I = О,..., М) и во всех внутренних узлах сетки удовлетворяет
уравнению um-ifi-2umi+ttm+ifi + ttm^-i^ttmi+ttm^ti = ^ причем во всехвнутрен-
них узлах сетки правая часть этого уравнения неположительная: fmi ^ 0.
Тогда наименьшее значение сеточная функция umi достигает хотя бы в
одной точке границы сеточной области.
Доказательство от противного практически повторяет
доказательство предыдущей леммы.
Лемма 3 (сеточный принцип максимума). Каждое решение разностного
уравнения Лапласа ^-м-^уШт+м + *w-i-2u?f+um,,fl = Q достигает
своего минимального и максимального значения на границе сеточной
области.
Доказательство очевидно — это объединение утверждений леммы 1
и леммы 2.
Введем норму сеточной функции как
||uTO/|| = max \umi\.
ml€D
Для доказательства устойчивости теперь надо доказать однозначную
разрешимость разностной задачи для уравнения Пуассона с любой
правой частью и любыми граничными условиями, получить оценку
Здесь в правой части стоит норма правой части задачи, записанной
в операторном виде, ||/|| = max \fmi\ + max \<pmi\. Первый максимум в
ml?D ml€dD
этой сумме берется по всем внутренним точкам, второй — по всем точкам
сеточной границы.
Докажем однозначную разрешимость разностной задачи.
Рассмотрим сеточное уравнение Лапласа с нулевыми граничными условиями.
В силу принципа максимума такая задача имеет лишь тривиальное
решение. Но сеточная система — это система линейных уравнений. Если
система с нулевой правой частью имеет лишь тривиальное решение, то
она однозначно разрешима при любой правой части.
427
Лекции по вычислительной математике
Заметим, что в точной арифметике действие разностного оператора,
приближающего дифференциальный оператор Лапласа, на
произвольный полином второй степени совпадает по результату с действием
дифференциального оператора — погрешность аппроксимации, как следует
из приведенной выше оценки, будет нулевая. Рассмотрим
вспомогательную функцию
где R — радиус окружности с центром в точке @,0) и включающей в себя
рассматриваемую область. В данном случае R = у/2. Эта функция иногда
называется мажорантой ГЬршгорина.
Индекс h означает, что рассматривается сеточная проекция
мажоранты. Обратимся к сеточной функции Wmi = umi — Р^ и применим
к ней разностный оператор Лапласа. Получим Aiwmi + A2Wmi = fmi +
+ max \fmi I во всех внутренних точках области. Отсюда следует, что свое
m/€D
наибольшее значение рассматриваемая сеточная функция достигает на
границе сеточной области в соответствии с доказанной леммой 1. Но,
как легко убедиться, на границе области сеточная функция wmi = umi -
— Р^ принимает только отрицательные значения. Тогда umi — Р^ < 0
во всех точках сеточной области, включая граничные. Рассмотрим
сеточную функцию Vmi = umi + P^. Проведя такие же рассуждения, придем
к неравенству иШ1 + P^i > 0 во всех точках сеточной области, включая
граничные.
Объединяя полученные результаты, находим
K.I ^ \Р*а\ < \R2 max, \fml\ + mgj> fowl,
откуда следует неравенство ||umj|| ^ max(l, i?2/4) ||/||. Таким образом,
устойчивость самой разностной схемы доказана.
16.2. Методы решения сеточных уравнений
При решении эллиптических систем существенная часть
вычислительной работы — решение возникающих сеточных уравнений.
Фактически для нахождения сеточной функции решения надо получить решение
системы линейных уравнений большой размерности с разреженной
матрицей специального вида. При аппроксимации уравнения Лапласа или
Пуассона на регулярных сетках матрица системы самосопряженная.
Методы решения таких систем рассмотрим ниже. Перед чтением данного
раздела рекомендуется просмотреть лекцию 2.
428
Лекция 16 Численное решение уравнений в частных производных
16.2.1. Метод простых итераций
Наиболее эффективные алгоритмы для численного решения
полученной СЛАУ — итерационные. Действительно, прямые методы требуют
вычисления обратной матрицы, обратная матрица получается
заполненной. Пусть и^ — начальное приближение, выбирать которое
желательно как можно ближе к искомому решению, и^, %Рш1,... — последующие
приближения. Верхний индекс в данных обозначениях указывает номер
итерации.
Если выполняется условие
где Umi — проекция точного решения на сетку, то итерационный метод
является сходящимся. Оценка сходимости при этом может быть получена
в виде
где с — константа, 0 < q < 1. Итерации продолжаются до тех пор,
пока не выполнено условие Ци^1 - г^Ц ^ е, где е — заданная точность.
В таком случае можно оценить количество итераций, необходимое для
достижения этой точности г « []n(e/c)/]nq] + 1. Квадратные скобки в
этой записи — операция взятия целой части числа.
Метод простых итераций записывается для системы сеточных
уравнений в следующем виде: иг^ = ulml + r(Auinl - fmi), если точка
принадлежит внутренней части сеточной области, и и1т1 = ipmi если точка с
индексами ml принадлежит границе сеточной области. Здесь Л = Лх +Лг,
г — итерационный параметр. Количество арифметических операций при
реализации метода простых итераций ~ O{N2).
Получим формулу для эволюции погрешности. Вычтем из
итерационной формулы vl?i = uj^ + т(Ли* - f )mi очевидное тождество um/ =
= umj + т(Ли - f )mi во внутренних точках, а из равенства и^1 = и^
вычтем тождество и™* = umj в граничных узлах. Тогда получим г^1 =
= г^+тЛг^ rjjjj1 = 0, во внутренних и граничных узлах соответственно.
Здесь rjnZ = uj^ - umi — невязка на i итерации.
В таком случае для сеточной функции невязки rmj, равной нулю на
границе, ее эволюция описывается уравнением
Для оценки сходимости итерационного процесса необходимо
перейти к неравенству для норм, например евклидовых, и оценить норму
оператора перехода
429
Лекции по вычислительной математике
откуда получим
Наиболее простым для этих целей является метод Фурье (или
спектральный анализ оператора перехода).
Непосредственной проверкой доказываются два следующих
утверждения. Семейство функций ^ = sin(rr^L) являются собственными
функциями оператора Ль им соответствуют собственные значения Ар =
Здесь р — номер собственного значения (собственной функции),
га — номер сеточного узла; р = 1,..., М — 1.
Для этого необходимо непосредственной подстановкой убедиться в
истинности равенства
или
1 Г . (тП—1)р7Г . 77Ш7Г . (?П+1)шг1
м м \
Семейство функций Ф^ = <р?^ является собственными
функциями оператора Л, соответствующие собственные значения есть А**7 =
Равенство ЛФ^ = -АР9Ф^ также проверяется непосредственной
подстановкой.
В дальнейшем необходимо будет знать границы спектра Amin = А1 =
= I = ? sin2 ~7 ^ я*2!так как Af » 1, Л = 1/М,
\(М-1) г 4 . 2(М-1OГ 4 . 2 7Г 4
Для Ар9 имеем / ^ \pq ^ L, где I « 2?r2,L « 8//i2 = 8М2. Легко
также оценить число обусловленности системы сеточных уравнений.
16.2.2. Метод простых итераций с оптимальным параметром
Представим сеточную функцию невязки г^, равную нулю на
границе, в виде разложения по базису из собственных функций разностного
оператора (Ф^ — собственные функции оператора Л)
при этом выполняется равенство Парсеваля
430
Лекция 16 Численное решение уравнений в частных производных
Далее, используя это разложение, получим
г1 = (Е + тА)г° = (Е + тЛ) ]Г CpqV™ =
РЯ
Р9
Здесь используется то, что A - r\pq) являются собственными
числами оператора (Е + тЛ). При сложении равенств тЛ^ = -гЛ^ и Еф^ =
= (р^п получаем (Е+тЛ)^ = A—тА)^. Легко получается оценка нормы
этой сеточной функции на первой итерации:
< да |1-тА| vT^ = да l1-^! 1И1 •
Для последовательности итераций также легко получается
стандартная оценка нормы
Отсюда видно, что значение q вычисляется, как тах{|1 — т1\, |1 —
— тЬ\}, а условие сходимости q < 1 выполняется при 0 < г < 2/L.
Границы спектра разностного оператора уже оценены в предыдущем пункте.
Для определения параметра г, обеспечивающего максимальную
скорость сходимости, необходимо решать следующую оптимизационную
задачу:
min( max ll — тА|).
Так как max 11 - т\\ достигается на правой или левой границе
интервала [1, L], то выполняется равенство max |1—т\\ = тах{|1—т1\, |1—тЬ\}.
В таком случае необходимо определить г, при котором достигается
min{max(|l — т1\, |1 — тЬ\)} , или tq = arg [minmax(|l — т1\, |1 — тЬ\)).
где то — оптимальный итерационный параметр.
Как показано на рис. 16.1, minmax(|l — rl\, |1 — тЬ\) достигается
при |1 — т1\ = |1 — тЬ\. Справа от точки В при любых г максимальна
функция |1 — тЦ, слева — функция |1 — т1\, и тогда минимум от
искомого максимума достигается в точке В. Отсюда получим 1-т/ = -A-
— тЬ). Следовательно, значение оптимального итерационного параметра
т0 равно т0 = j^i.
431
Лекции по вычислительной математике
,' \\-А
Рис. 16.1
Оптимальное значение функции, отвечающей за скорость
сходимости, будет
= 1 - TOl = 1 -
¦1 =
L-l
L + l
1-2/х,
где ц = L/1 — число обусловленности системы сеточных уравнений.
Количество итераций, соответствующее этому методу, легко
оценивается:
lne
+ 1-
lne
Lln(l-21/L)J '-"U-Ja/L) -21— ¦*]•
Пусть расчеты приводятся с точностью е = 10~5 на сетке 100 х 100,
тогда оценка числа итераций дает при / « 2тг2 и L = SN2 i « ^^ In 105 «
« 2 • 104 итераций.
Показатель сходимости q0 = 1 - 2/х « 0,9995.
Параметр /х = L/Z — число обусловленности матрицы (лекция 2);
чем оно больше, тем медленнее сходятся итерации. Напомним
(лекция 2), что в n-мерном линейном нормированном пространстве Ln
вводятся три наиболее употребительных нормы вектора:
Hullj = max|ut|,i = 1,.. .,n,
432
Лекция 16 Численное решение уравнений в частных производных
t=l
Hulls =
которым, в соответствии с определением согласованной нормы
матрицы А
сопоставляются нормы матрицы А с элементами ai3\
\\А\\г =та
Показывается, что для симметричной матрицы А число
обусловленности 11 может быть представлено в третьей норме:
Р min|Ai| Г
Таким образом, доказана следующая теорема.
Теорема. Рассмотрим итерационный метод и1^1 = и^ +
- fmi)y с оператором Л = Л* > 0 для численного решения разностного
аналога уравнения Пуассона |^ + ^т = Дя> J/) ^ помощью аппроксимирующей
его разностной схемы
Пусть I uL— минимальное и максимальное собственные числа
оператора Л соответственно.
Если итерационный параметр г удовлетворяет условию 0 < г < 2/L,
то последовательность итераций и* сходится к проекции решения исходного
дифференциального уравнения, причем выполнено неравенство \\vx\\ ^ qx \ \ v° 11,
где параметр 0 < q < 1 определяется следующим образом:
g = max{|l-W|,|l-rL|}.
433
Лекции по вычислительной математике
Параметр q принимает наименьшее значение q0 при г = т0 =
Приэтомдо = ±$? * 1 -2J;.
16.2.3. Чебышёвское ускорение метода простых итераций
Рассмотрим итерационный метод с выбором параметра г на каждой
итерации:
i1 i i
Соответствующие соотношения для эволюции невязки имеют вид:
После разложения невязок на двух соседних итерациях по базису из
собственных функций сеточного оператора получим равенство
Для коэффициентов разложения и компонентов невязки
справедливы следующие равенства:
3=1
РЯ
.(
Оценим погрешности на г шаге итераций
max
[)
Вновь приходим к минимаксной задаче: найти такую
последовательность итерационных параметров {т,}*^, чтобы выполнялось
min max
{rj} A€[I,L]
Заметим, что П A —г,-Аи) есть полином (относительно г) степени г.
Задача — сделать его наименее уклоняющимся от нуля на отрезке [/, L].
434
Лекция 16 Численное решение уравнений в частных производных
Эта задача, как известно, решена Чебышевым, а корни этого полинома
являются нулями полинома Чебышева (лекция 6):
+ l L-l irpj-1
Достаточно громоздкие выкладки, которые опускаются, дают в
результате оценку скорости сходимости метода с оптимальным набором
параметров q « 1-2у^1//х, и числа итераций, необходимого для достижения
заданной точности г « | ^ In е"1 + 1.
Пусть расчеты приводятся с точностью е = 10~5 на сетке 100 х 100,
тогда оценка числа итераций и скорости сходимости есть q « 0,968, г «
360. «Цена» каждой итерации — приблизительно ЮМ2 операций.
Однако метод итераций с чебышевскими параметрами в таком виде
оказывается неустойчивым по двум причинам: рост ошибок округления
в расчетах и некоторые свойства нулей полиномов Чебышева, в
частности, сгущение т^1 — величин, обратных корням полинома —- к границам
спектра. Не останавливаясь на доказательстве неустойчивости чебышев-
ского итерационного процесса, заметим, что для ее устранения
необходимо переставить итерационные параметры не в их естественном поряд-
i
ке, а так, чтобы все частичные произведения П A - TjX) не возраста-
ли бы вблизи границ спектра при любом i. Эта необходимо, поскольку
частичное произведение, относящееся к правой части спектра со
сгущающейся чебышевской сеткой, очень быстро растет из-за больших
величин A—TjX). Задача упорядочения итерационных параметров достаточно
сложна, ее решение связано с именами В. И. Лебедева, В. П. Финогенова,
А.А.Самарского и Е.С.Николаева [4]. Приведем результат ее решения
для г = 2Г, где г — количество сомножителей в произведении (число ите-
i
раций) П A - г,Л), г — натуральное число.
При г = 2 перебираем корни полинома Чебышева в их
естественном порядке (в фигурных скобках указываем номер корня) {1,2} или в
порядке убывания номера {2,1}. Далее последовательность номеров
корней получаем следующим образом. Каждый номер корня меняется на
пару чисел: первое число — номер корня, второе — дополняет сумму в
каждой паре до значения г + 1BГ + 1). Таким образом, при i = 4
получаем два упорядоченных набора. Из последовательности {1,2}
получаем {1,4,2,3}, а из {2,1} - {2,3,1,4}. Действуя аналогично далее, имеем
при i = 8 {1,8,4,5,2,7,3,6} в первой последовательности чебышевских
параметров или {2,7,3,6,1,8,4,5} во второй последовательности.
Следующий шаг дает i = 16{1,16,8,9,4,13,5,12,2,15,7,10,3,14,6,11} в первой
435
Лекции по вычислительной математике
последовательности чебышевских параметров или {2, 15, 7, 10, 3, 14, 6,
И, 1, 16, 8, 9, 4, 13, 5, 12} — во второй. Построение таких
упорядоченных наборов легко можно продолжить. Приведенное упорядочение
является универсальным — оно обеспечивает устойчивость любых методов,
где необходим чебышевский набор итерационных параметров.
Обычно при реализации чебышевских методов задаются
последовательностью из 32 или 64 параметров и делают серию итераций.
Если невязка велика, то результат серии используют в качестве
начального приближения для следующей серии итераций, если невязка мала, то
решение считается найденным. Такая упрощенная реализация работает
несколько медленнее, чем «честное» чебышевское ускорение, но весьма
эффективно.
Приведем итерационные формулы трехслойного метода Чебышева,
который не уступает предыдущему по скорости сходимости, однако не
требует изменения порядка выбора итерационных параметров. В
качестве платы за удобство использования метода затраты памяти становятся
несколько большими. Формулы трехслойного метода будут
= ai+1(E - tA)u< + A - ai+xK + rai+if,i = 1,2,...
где г = 2/A + L),ai = 2,ai+1 = 4/D - р2а*),р = (L - l)/(L + /)•
Можно показать, что погрешность г* удовлетворяет оценке
Трехслойный метод Чебышева можно также представить в
следующем виде:
и1 = (Е - тА)и° + rf, ui+1 = ^i(E - тАК - ^V + —rf,
7t+i 7t+i 7t+i
гдег = l,2,...,r ^ ^
Трехслойный метод Чебышева в настоящее время применяется
значительно чаще двухслойного при численном решении уравнений
эллиптического типа.
Каноническая форма записи трехслойного итерационного метода
(к которым и относится приведенный трехслойный метод Чебышева)
есть
Bui+1 = ai+i(B - Ti+iAK + A - Qi
436
Лекция 16 Численное решение уравнений в частных производных
Ви1 = (В - nA)u° + nt,
* = 1,2
Если оператор В — единичный, то трехслойный итерационный
метод называется явным, в противном случае — неявным. Заметим, что
каноническая форма записи двухслойного итерационного метода имеет вид
eui+1-u* А { с
В + Агх* = f.
Если оператор В — единичный, то двухслойный итерационный
метод называется явным, в противном случае — неявным.
Каноническая форма записи трехслойного итерационного метода
получается из двухэтапного итерационного процесса. На первом этапе
(предиктор) используется метод
где и — промежуточное значение. Второй этап — корректор:
В трехслойных схемах используются два итерационных параметра:
Ti и а» причем при а» = 1 трехслойная схема переходит в двухслойную.
Рассмотренные методы основываются на следующих свойствах
оператора А:
— самосопряженность: А = А*,
— положительная определенность: А > 0,0 < I < А» < L; для
реализации алгоритма необходимо знание только границ спектра
оператора.
16.2.4. Метод переменных направлений
Еще большие успехи при попытках ускорить итерационные
методы были достигнуты при использовании методов переменных направлений.
Можно показать, что решение нестационарной задачи
dt " дх2 + ду2 ''
со стационарными граничными условиями и\Г = <р будет стремиться к
некоторому стационарному пределу при t —> оо или при п —> оо. В этом
437
Лекции по вычислительной математике
пункте п — количество шагов по времени при решении рассматриваемого
дифференциального уравнения в частных производных разностным
методом. В этом случае итерационный параметр г играет роль шага по
времени, отличие состоит лишь в том, что итерационный параметр не
обязан быть малым, хорошая аппроксимация нестационарного уравнения не
требуется.
Представим метод переменных направлений в следующем виде:
« - fmU ^ ^ = Лхпы + A2UJ+1 - fml
Уравнение для эволюции погрешности получается, если из
приведенных формул ВЫЧеСТЬ ТОЖДеСТВО ит1~ит1 = AiUml + A2Umj - / :
т ~~ ii.1» ffii ~t~ 11.2' mli т ^I'tnl ' 2 ml *
Представим rm/ и rmi в виде разложения по базису из собственных
функций:
p.q pq
и рассмотрим эволюцию погрешности за одну итерацию. ФР9, как и
ранее, собственные векторы разностных операторов Ai и Лг, СрЯ —
коэффициенты Фурье; невязка г{т1 обращается в нуль на границах области
интегрирования.
Используя разностное уравнение для rmi представим связь между
невязкой на предыдущей итерацией и невязкой на промежуточном слое
в виде
(Е - rh^fmi = (Е + тК2)г\п1.
Используя представление Фурье, получим
РЯ РЯ
откуда после действия операторов Ai и Л2 на суммы, получаем
? ср,A + тА*)Ф«' = ? 4,A - тЛР)Ф^.
РЯ РЯ
Здесь Ар и Xя — собственные значения разностных операторов Лх и
Л2@ < I < Лр, 0 < Xя ^ L, / « тг2, L « 4iV2), N — число шагов по
каждому пространственному измерению рассматриваемой системы разностных
уравнений. В силу единственности разложения сеточной функции по
базису ФР9, получаем соотношение для коэффициентов Фурье
. 1-тХя {
438
Лекция 16 Численное решение уравнений в частных производных
Аналогично, после спектрального анализа второго этапа расчета,
получим
- т\р 1- .„ t
м 1 + тА*^9 1 + т\я
Введем обозначение
и(т) = max I- г
тогда для коэффициентов разложения справедливо неравенство \<*+l | ^
/x2(r) |cj^|, следовательно, для нормы невязки имеем условие ||ri+1|| ^
М2(т)|И|, так как Цг^Ц = ЦЕ^Ф^Ц < WZ^U^W <
M2IIZH^1*^!! = А*2НГ<1|1 поскольку справедливо равенство Парсеваля.
Необходимо обеспечить наиболее быструю сходимость, минимизировав
коэффициент /х(г).
Найдем оптимальное значение параметра г, обеспечивающее min /г(г
Для этого необходимо решить задачу
= arg < niin max
6\ г |_A€[/,L]
1-rA
гА|
которая решается так же, как и ранее. Простой графический анализ
|| || {||||}
функции
приводит к результату
=ш
ш
Минимум /i(r) достигается, как и в предыдущем случае, при ^а| =
^^, откуда сразу получается 2 = 2т§IL, то = l/VlL.
Вычислим значение //(то) = \~\ijfc « 1 — 2у/Г[Ь. Погрешность
за одну двухэтапную итерацию убывает, таким образом, в q = р2 « 1 —
/1
Количество итераций, необходимое для достижения заданной
точности, можно оценить как i « ln! = \ Jk lne".
4y/l/L * у *
Скорость сходимости итерационного процесса для приведенного
метода приблизительно такая же, как и для процесса с чебышевским
набором итерационных параметров. Эти результаты могут быть
сформулированы в виде теоремы.
Естественным обобщением приведенного итерационного процесса
представляется замена одного итерационного параметра г набором г».
Выбор этих параметров приводит к минимаксной задаче
• /
mm < max
I I
1J
1 + TjA
439
Лекции по вычислительной математике
решение которой представляется в виде громоздкого алгоритма, который
здесь не приводится. Для этого метода имеем оценку числа итераций для
достижения заданной точности г « Ins In L/l.
16.2.5. Методы Якоби, Зейделя, верхней релаксации
Для системы сеточных уравнений, полученных при использовании
схемы «крест»
2 Цуп+1, I цт,!-1
h? + h2 Jml
запишем итерационный метод Якоби. Расчетные формулы (верхний
индекс, как обычно, показывает номер итерации) для этого метода будут
h? + h2
га, / = 1,..., М - 1, КМ = 1, с условиями на сеточной границе ujj1 /г =
Если в явном виде выразить и1^, получим каноническую форму
записи сеточного метода, правую часть берем на предыдущей итерации,
левую — на текущей:
) +
Количество итераций, требуемое для вычисления решения с
точностью е9 оценивается по формуле
Метод Зейцеля, учитывающий результаты вычислений на г + 1
итерации, записывается для рассматриваемого уравнения Пуассона
m, Z = 1,..., M - 1, ЛМ = 1, с условиями на сеточной границе u^/r =
= Uml.
Напомним, что хотя метод Зейделя неявный, но его реализация
оказывается простой, если правильно установить последовательность
вычислений. В каноническом виде формулы для метода Зейделя есть
«Ы = \(U + 4 + <} + <) +
440
Лекция 16 Численное решение уравнений в частных производных
Сначала из последнего уравнения, используя граничные условия
и*+г = Uoi и и1^1 = C/io, находим ujf1. Затем, зная uj|х, можно
аналогично найти и\~21 и так далее. Значения сеточной функции
вычисляются в следующем порядке изменения индексов: A,1), A,2),..., A, М -
-1),BД),B,2),...,B,М-1),(М-1,1),(М-1,2),...,(М-1,М-1).
Оценка количества итераций, необходимых для достижения точности е,
есть г« ^-lne.
Метод Зейделя сходится быстрее метода Якоби, однако число
итераций также оценивается как O(N2) = O(L/l). В случае метода верхней
релаксации система представляется в виде
(L + U + D)u = f,
где L и U — нижняя и верхняя треугольные матрицы с нулевыми
диагоналями, D — диагональная матрица. Вводится параметр 1 < т < 2 и
итерационные формулы записываются в виде Lu*+1 + Uu* + D | ^- +
+ A - ^)и*] = '• При т = 1 получаем метод Зейделя.
Рассмотрим реализацию метода верхней релаксации для разностной
аппроксимации уравнения Пуассона. Переписав разностную схему в
виде
выпишем расчетные формулы для метода релаксаций:
ТП — 1,/ 171,I— 1 , 171+1,1 171,1+1
ft2 + Л2
Последовательность вычислений в методе релаксаций такая же, как
и в методе Зейделя. Уравнения представляются в виде
< + <} $<? « + <) + 4A )<
решение u^Jj1 вычисляется так же с левого нижнего угла области
интегрирования. Основное преимущество метода верхней релаксации перед
методом Зейделя состоит в существенном ускорении скорости сходимости
при соответствующем выборе параметра т. Не проводя исследований на
сходимость, приведем их окончательный результат. Необходимое
количество итераций для достижения точности е равно i « ^ lne, h = 1/М.
441
Лекции по вычислительной математике
Отметим также, что для реализации этих трех методов не требуется
знания спектра задачи. При оптимальном выборе итерационного параметра
в методе верхней релаксации знание границ спектра позволяет ускорить
сходимость метода.
16.3. Попеременно-треугольный итерационный
метод
При аппроксимации уравнений Пуассона или Лапласа получается
система сеточных уравнений
Au = f,
без ограничения общности считаем оператор (матрицу системы)
самосопряженным и положительно определенным. Сеточный оператор
Лапласа самосопряжен — это легко доказать, но отрицателен. Для того чтобы
получить систему уравнений с положительным оператором, достаточно
правую и левую части системы умножить на -1. Здесь А — квадратная
матрица размером N х N.
Зададим матрицу R = {г# } :
{
О,
В таком случае А можно представить в виде суммы двух треугольных
матриц А = R + R*.
R и R* — нижняя и верхняя треугольные матрицы, а их
диагональные элементы совпадают. Далее будем рассматривать систему
сеточных уравнений как операторное уравнение в конечномерном евклидовом
пространстве (унитарном в комплексном случае).
Попеременно-треугольный итерационный метод (ПТИМ) может
быть представлен в каноническом виде
Здесь В — самосопряженный положительный оператор. Его часто
называют оператором предобуславливания. Для рассматриваемого
метода оператор предобуславливания представляется в виде произведения
где Е — единичный оператор, и — параметр (действительное число).
442
Лекция 16 Численное решение уравнений в частных производных
При известных и и т значение uk+i находится в два этапа. Сначала
вычисляется невязка на итерации г* = Аи* - /, а затем решается система
матричных уравнений
Поскольку матрицы (Е + сЛ1*) и (Е + иК) являются треугольными,
то эти уравнения решаются значительно проще, чем исходное.
Для формулирования теоремы о ПТИМ введем понятие
операторного неравенства: будем полагать, что А < В, если для любой сеточной
функции, не равной нулю тождественно, выполнено неравенство
((A-B)u,u)>0.
Теорема (без доказательства). Пусть А = R + R* и существуют
положительные постоянные 6 и А, при которых выполнены неравенства
Пусть также и = -т=» т = —^—, гдеч\ = —?—6 /-г-\, 72 =
удД *Yi +T2 2A' /л\/"'
7Ьгда двухэтпапный итерационный метод
сходится, причем для его погрешности справедлива оценка
гдер =
В качестве S можно взять минимальное собственное значение Amin
оператора А, либо любую положительную постоянную 5 ^ Amin. Можно
показать, что Д ^ Атах, А > 6, где Атах — максимальное собственное
значение оператора А.
Рассмотрим применение ПТИМ к численному решению уравнения
Пуассона (знак минус ставим для удобства записи):
= fmh
443
Лекции по вычислительной математике
с нулевыми граничными условиями
ит0 = UmN = Щ1 = UNi = 0.
Эта задача может быть представлена как операторное уравнение, где
Aumi = —(Ai+A2)um/m, 2 = 19..., JV* — 1. Оператор будет
самосопряженным и положительным.
Далее необходимо представить матрицу А в виде А = R+R* и
определить константы 6 и Д.
Рассмотрим разностную аппроксимацию уравнения Пуассона по
схеме * крест», переписав схему в эквивалентном виде:
,l-l\ I f
h\
Тем самым представили оператор А как сумму двух операторов А =
= R + U, где
)¦
При этом матрица оператора R является нижней треугольной, а
матрица R* — верхней треугольной (в этом легко убедиться, записав
рассматриваемую систему в виде СЛАУ). Можно также показать, что
оператор U является сопряженным оператором к R, т. е. А = R + R*.
Также показывается, что S = ^sin2^ = Amin(A),A = ^ ^
?cos2f = Amax(A).
Воспользовавшись формулами для тиц получим
h2 h /i2(l + sin^) 2h
^ 2тг' sin ^A + 3 sin ^) тг
Оценка количества итераций для этого метода дает
N. _х
= —Ine x.
2
г « л , =
Напомним, что границы спектра для рассматриваемого оператора
L » 8N2,l » 2тг2 и N » f v/X/Z.
Алгоритм вычисления ujj1, в соответствии с ранее приведенными
формулами двух этапов ПТИМ будет таков.
Лекция 16 Численное решение уравнений в частных производных
Первый этап:
п йт,1+1 - Uml
h {h
второй этап:
Xml Um-U , Uml
uol — u, um0 — u.
Уравнение для um/ нужно начинать решать от точки т = N - 1, / =
= iV - 1, учитывая, что на границе сеточной области сеточная функция
равна нулю. Таким образом, вычисления ведутся рекуррентно. Система
решается, начиная с правого верхнего угла области до левого нижнего
угла. Система линейных уравнений, соответствующая второму этапу,
решается аналогично, но вычисления здесь начинаются в точке m = 1,1 = 1
и заканчивается в точке т = N — 1,1 = N — 1.
Метод по своим идеям напоминает схему Саульева, рассмотренную
ранее в одномерном варианте при решении уравнений параболического
типа.
Использование в ПТИМ набора чебышевских итерационных
параметров приводит к следующему результату. Расчетные формулы для
метода таковы:
T
R*, В = (E + u;R*)(E + cjR),
r0 _ 2
1 + 7# jJ ° 7i + 72'
- 7i/72
ry =
+ 7i/72'
Bj - 1)тг . t
J =COS 2i 'J = l,...i».
Для проведенного примера 71 « 2sin ^, 72 « 1 + sin ^, ^ «тг/i.
Оценка количества итераций будет г =
16.4. Сводка результатов по итерационным
методам решения сеточных уравнений
После рассмотрения самых распространенных методов решения
сеточных уравнений получена возможность сравнить итерационные мето-
445
Лекции по вычислительной математике
ды по количеству итераций, необходимых для достижения точности е.
Приведем только выражения для сомножителя, пропорционального
числу узлов сетки.
Ш^- — методы Якоби и простых итераций с оптимальным выбором
параметра,
^ — метод Зейделя,
^ — метод верхней релаксации,
^¦г — метод простых итераций с чебышевским набором параметров,
\г%- — методы переменных направлений и
попеременно-треугольный,
10L — попеременно-треугольный метод с чебышевским набором
параметров,
^ 1п(|М) — метод переменных направлений с чебышевским
набором параметров, 7 « 3,2.
16.5. Основные идеи многосеточного метода
Р. П.Федоренко
Вернемся к рассмотренному выше вопросу о сходимости
итерационных методов решения систем сеточных уравнений, получающихся при
решении уравнений Лапласа или Пуассона. Выше был проведен
спектральный анализ итерационных методов решения такой системы.
Вернемся, например, к результатам исследования метода переменных
направлений. Для него установлено равенство для коэффициентов
разложения в конечный ряд Фурье невязки
t+i _ 1 ~ тХР ~ _ 1 - г АР 1 - г А? {
Из этого выражения следует, что коэффициенты при
высокочастотных составляющих (т.е. при достаточно больших А при
фиксированном г) убывают достаточно быстро, в то время как при низкочастотных
гармониках (А « 0) коэффициенты убывают медленно. Такой же эффект
существует и для других итерационных методов.
Рассмотрим сеточное уравнение Пуассона
fmi, A6.1)
и, кроме того, уравнение
A2emi = rmh A6.2)
446
Лекция 16 Численное решение уравнений в частных производных
где г — невязка, е — погрешность решения. Если известно приближенное
решение задачи A6.1), то, решая A6.2), можно найти решение исходной
системы по формуле
но решение задачи A6.2) по сложности точно такое же, как и решение
исходной задачи.
Если применять итерационный метод A6.1), сделав несколько
итераций, то приближенное решение задачи будет известно, а невязка
станет плавно меняющейся функцией — в разложении в конечный ряд
Фурье будут отсутствовать высокочастотные составляющие. Невязка будет
хорошо представляться на более грубой сетке, тогда размерность
вспомогательной системы A6.2) понизится.
Введем сетку с шагом 2h и рассмотрим на ней задачу A6.2).
Размерность системы сеточных уравнений получилась в четыре раза
меньше, чем размерность исходной системы. Предположим, что есть средство
эффективно решать такие задачи. После этого для восстановления
решения надо найти невязку на более подробной сетке. Строим оператор
интерполяции с грубой сетки на подробную. Очевидно, что ошибка
интерполяции будет иметь высокочастотный компонент. Тогда используем
полученное решение (низкочастотные компоненты погрешности погашены
на грубой сетке, остались только высокие частоты) в качестве
начального приближения и делаем несколько сглаживающих итераций. Этот этап
называется коррекцией с грубой сетки.
Схема приближенного построения решения получается следующей.
1. Решается уравнение A6.) на подробной сетке, проводится
несколько сглаживающих итераций,
2. По приближенному решению находится невязка rmi = Aiumi +
3. Ищется ограничение (проекция) невязки на грубую сетку.
4. На грубой сетке решается уравнение Aiemi + A2emj = rmj.
5. Строится оператор интерполяции решения на подробную сетку,
значения невязки пересчитываются на подробную сетку.
6. На подробной сетке проводится несколько сглаживающих
итераций для уравнения Aiemi + A2emi = rmj.
7. Ищется решение по формуле Umi = umi + emj.
Выполнение пункта 4 — решения сеточной системы — может
оказаться трудоемким, поэтому внутри этого шага алгоритма можно еще раз
447
Лекции по вычислительной математике
перейти к более грубой сетке. Многосеточный метод состоит в
рекурсивном повторении данной процедуры до тех пор, пока не будет получена
система малой размерности, которая может быть эффективно решена
прямым методом (например, Гаусса или сопряженных градиентов).
Простейшая реализация многосеточного метода — каскадный
алгоритм. Он предусматривает последовательное решение задач на сетке со
все большим числом узлов, а интерполяция решения с более грубой
сетки используется в качестве начального приближения. Для
самосопряженных эллиптических задач часто используется V-цикл. Сначала ищется
решение на подробной сетке, затем проводится последовательно
вычисление невязок на все более грубых сетках, затем -— несколько коррекций
с грубой сетки и сглаживающие итерации на все более и более
подробных сетках. Для несамосопряженных задач лучше зарекомендовал себя
W-цикл, когда сначала вспомогательная система решается на
последовательности все более и более грубых сеток, затем идут итерации на все
более подробных сетках, затем снова итерации на грубых сетках и затем —
на подробных вплоть до сетки с максимальным числом разбиений.
Впервые многосеточный метод предложен в [10]. Более подробно о
многосеточных методах и реализации многосеточных алгоритмов можно
прочитать в [8] и статьях Н. С. Бахвалова с соавторами и Ю. В.
Василевского с соавторами в [9].
16.6. Построение разностных схем для
эллиптических уравнений на нерегулярных
сетках. Монотонные схемы (подход
А.С.Холодова)
В этом разделе будем следовать статье [11]. Кроме уравнений
Лапласа и Пуассона, в этом разделе будем рассматривать произвольные
уравнения эллиптического типа. Рассмотрим задачу
ихх + ei2uxy + e22U>yy + е\их + е2иу = /(а:, у, и)
с условиями на коэффициенты
em(x,y,u) = {emj},
га,/= 1,2, j = l,...,J, e22>ei2/4.
Последнее условие обеспечивает эллиптичность задачи. Задача
решается в произвольной замкнутой области с несколькими несвязными
границами. Предположим сначала, что область не содержит входящих
448
Лекция 16 Численное решение уравнений в частных производных
углов (т.е. таких, величина которых больше тг). В случае со
входящими углами в решении эллиптических задач возникают особенности, во
многих случаях необходимо сочетание численных методов и
аналитических (асимптотических методов в окрестности входящего угла),
подробнее в [12]. Индекс j — номер узла сетки; для простоты выкладок узлы
сетки нумеруются одним индексом.
Запишем разностную схему для аппроксимации приведенного выше
уравнения в каноническом виде
— точки, принадлежащие шаблону схемы (см. ниже), / ^ 5, причем
неопределенные коэффициенты удовлетворяют условию монотонности
осы ^ 0. Здесь К — общее число внутренних сеточных узлов с одно-
индексной нумерацией, гь..., г/ — номера расположенных достаточно
произвольно в области интегрирования внутренних и граничных
сеточных узлов, aki — неопределенные коэффициенты. Часть этих
коэффициентов (или все, если 1 = 5) определяются условиями аппроксимации
первого порядка или второго порядка на решениях исходного
уравнения. Эти условия получаются стандартно — проекция точного решения
на нерегулярную сетку раскладывается в ряд Тейлора в окрестности
точки Uk- После несложных, но громоздких выкладок получаем, что
следующие условия обеспечивают первый порядок аппроксимации:
- 0.5X«(ei - Х>(е\ + Д, - elx)/Z + Ytely)) = 0,
i
i - 0.5X?(e2 + Х<(е2/и - eie2 + e2x)/3 - ВД - e2y))) = 0,
0.5Xi(ei2 + Xi(e2 + ei2x - 2euei)/3 + r<(ei + ei2y))) = 0,
? - X?(e22 ~ Xi(e12e2 + e22ex - e22x)/3 + У^(е2 + ем»))) = 0,
A) = - 52аыХ?{1 - e1Xi)/3)/2 = 0.
15—3339 449
Лекции по вычислительной математике
Суммирование ведется по всем тючкам, включенным в шаблон. Если
к приведенным выше условиям добавить условия
- el2Xi) - Х?(е22 - е\2)) = О,
- el2Xt)) = О,
0! = - ? akiXf /6 = 0,02 = - J2 <*ыХ?Ъ/2 = 0,
то схема имеет второй порядок аппроксимации на решениях. Здесь
введены обозначения Xi = xi - Хк, У% = у% - Ук-
В обычных разностных методах шаблон фиксирован (т. е. все
внутренние точки сетки имеют одинаковое число соседей). В данном
подходе для каждой рассчитываемой точки к = 1,..., К специальным
образом подбираются соседи (сеточный шаблон) так, чтобы выполнялись
условия неотрицательности коэффициентов а** в канонической форме
записи разностной схемы. Эти условия обеспечивают неотрицательность
разностного оператора (мажорантность схемы).
Получающийся в результате решения уравнений для условий
аппроксимации первого порядка и неравенств, обеспечивающих
монотонность схемы, для каждого к = 1,..., К набор коэффициентов а^
приводит к знакопостоянной линейной (или нелинейной для квазилинейных
уравнений) системе уравнений
Au = b,
0 ... 0 -aUl 0 ... 0 -aUl 0
0 0 ... 0 -aKil 0 ... 0 -секи
Условия неотрицательности неопределенных коэффициентов
обеспечивают выполнение достаточных условий сходимости и принципа
максимума, в том числе, при разрывных граничных условиях. Тогда
простейший итерационный метод Якоби
является сходящимся.
450
Лекция 16 Численное решение уравнений в частных производных
Можно показать, что при весьма слабых ограничениях на
расположение сеточных узлов в области интегрирования такие схемы могут быть
конструктивно построены. Этот же подход распространен на случай схем
со вторым порядком аппроксимации на решениях.
16.7. Задачи
1. В современных формулировках метод релаксации
рассматривается с черно-белым (шахматным, красно-черным) упорядочением
узлов. Назовем все внутренние узлы сетки черными, если для них
сумма значений индексов четная, все прочие внутренние узлы назовем
белыми. Получить расчетные формулы метода верхней релаксации
для сетки с черно-белым (шахматным, красно-черным)
упорядочением узлов.
Решение. Заметим, что при расчетах белые узлы соседствуют
только с черными, и наоборот. Тогда с учетом этого расчетные формулы
будут для всех белых узлов
l
_f
to ' L9
а для всех черных
11— t . t •+- U __ .¦•> A I it1 *. 1
= /mb
Последовательность вычислений для такого варианта будет
несколько отличаться от первоначальной формулировки метода
релаксаций. Сначала ищется значение на следующей итерации для всех
белых узлов, затем — для черных. Такой итерационный метод
очевидным образом связан со схемой «классики» для решения
параболических уравнений.
2. Пусть число внутренних узлов равно 9. Выписать в матричном
виде сеточные уравнения при классической формулировке схемы
«крест» и для случая черно-белого упорядочения узлов. Для
простоты рассмотреть вариант, когда значения функции на границе
области равны нулю.
Решение.
В «классическом» варианте сеточная система есть
-Аи = f,
451
Лекции по вычислительной математике
где
А =
/4-10-10
-14-10 -1
0-14
-1 0 -1
0
0
0
0
-1
0
0
0
0
—
0
0
0
0
-1
0
-1
0
0
0
-1
0
0
0
0
0
-1
0 >
0
0
0
0
-1 О
4 -1
-1 4
0-14-10-1
-10-14-10
0-10-14
0 0 0 0 0-10-1
-1
U =
fll,f 12, /l3, /21, /22, /23, /31, /32,.
а в случае черно-белого упорядочения узлов сетки
-Аи = f,
где
А =
/4 0 0 0 0-1-10 0 \
04000-10-10
0 0 4 0 0-1-1-1-1
000400-10-1
0000400-1-1
-1 -1-10 0
-1 0-1-10
О
0 0 0
4 0 0
0-1-10-10 0 4
О 0-1-1-10 О О
U =
=—h (/11,/13,/22,/31,/зз,/12,/21»/23»/32)
16.8. Задачи для самостоятельного решения
1. Будем рассматривать только частные типы краевых задач для
поля (р9 зависящего от двух пространственных переменных (х, у),
удовлетворяющего уравнению
452
Лекция 16 Численное решение уравнений в частных производных
В задачах электростатики у> — это потенциал, a S соответствует
плотности заряда; в стационарной тепловой задаче <р —
температура, S — локальная скорость выделения или поглощения тепла.
Будут рассматриваться граничные условия Дирихле, в которых
значения (р задаются на некоторой замкнутой кривой в плоскости (х, у) и,
возможно, на некоторых дополнительных кривых внутри области.
Реализовать численные алгоритмы, основанные на:
(a) непосредственной аппроксимации дифференциального
оператора и решении системы сеточных уравнений методом
Гаусса;
(b) применении итерационного алгоритма.
а) Для уравнения Лапласа, S(x,y) = 0, рассмотреть
численное решение для простейших граничных условий (типа
констант или линейных функций).
б) Для уравнения Пуассона вычислить разность потенциалов
между двумя зарядами как функцию расстояния между
ними и сравнить полученные значения с аналитическими.
в) Изменить программу так, чтобы можно было задавать на
некоторых внешних и внутренних границах условия
Неймана. Изучить решения с такими граничными условиями.
г) Вместо граничных условий Дирихле задаются
периодические граничные условия. Тогда потенциалы на левой и
правой, а также на верхней и нижней границах области
произвольные, но равные по величине друг другу. Т. е. для
всех г и j <рц = ipm; <рц = y>Nj. Уравнения с такими
условиями описывают пространственно-периодическое
распределение плотности заряда в кристалле. Модифицировать
программу и решить уравнение Пуассона с этими
граничными условиями.
2. Для решения приведенной выше задачи с различными граничными
условиями реализовать алгоритм быстрого дискретного
преобразования Фурье (алгоритмы такого преобразования описаны,
например, в [4,8]).
3. Модель малярной кисти Подробнее об этой задаче и других примерах
установившихся течений жидкости в [13, С. 232—240].
При окраске стены кистью, часть краски остается на стенке в
виде слоя за кистью. Рассмотрим приближенную модель процесса.
Предположим, что кисть состоит из большого числа параллельных
453
Лекции по вычислительной математике
и равноотстоящих друг от друга пластин, которые совместно
скользят по плоской стенке, в направлении их контакта со стенкой вдоль
оси х. Предположим, что пластины имеют бесконечные размеры в
направлениях осей х и г, так что результирующее движение
представляет собой установившееся течение одного направления.
Уравнение движения имеет вид
д2и
Здесь и — скорость течения жидкости.
Оси координат удобно связать с пластинами, тогда граничные
условия для течения в канале между двумя соседними пластинами будут
и = О при у = 0 и у = 6, 0<2<оо,
и = U при z = 0, 0 < у < Ь.
а) Получить численное решение поставленной задачи. Сравнить
результат с точным решением
и(у ~\ = ?L V 1с-ппг/ьстП7Гу
5lu b '
Объяснить, как реализован алгоритм для вычисления
значений функции точного решения.
б) Получить оценку толщины слоя жидкости, который будет
оставаться на стенке позади кисти, при предположении, что все
пластины имеют заднюю кромку при одном и том же
значении х. Использовать формулу для объемного расхода жидко-
Ь оо
ста, вытекающей из одного канала: Q = / / и dydz. Сравнить
о о
со значением для точного решения Q — AUb2, A « 0,27.
в) Указать недостатки рассмотренной модели. Определить
характер их влияния на решение.
4. Стационарное движение несжимаемой вязкой
жидкости в цилиндрических трубах
Рассмотрим движение несжимаемой вязкой жидкости в
цилиндрической трубе произвольного поперечного сечения. Обозначая
градиент давления || = -G(t), получим уравнение движения в виде
454
Лекция 16 Численное решение уравнений в частных производных
fp- + f^T = -™, где /i — коэффициент вязкости, и — скорость
течения жидкости. Требуется решить уравнение, подчиняющееся
граничным условиям, с помощью которых задаются градиент давления
и значения и при определенных у и z.
(a) Решить задачу для трубы круглого поперечного сечения, для
которой и = 0 на границе трубы, т. е. при г = у/у2 + г1 =
= а. Сравнить численные результаты с точным решением и =
= j- (а2 — г2). Получить численно величину объемного расхода
а
жидкости через произвольное сечение Q = j и 2nrdr, сравнить
о
ее с точным значением Q = 2L§-^. Предложить, как можно
использовать данную величину для контроля точности
численного расчета.
(b) Получить решение задачи для трубы эллиптического
поперечного сечения с полуосями b (по оси у) и с (вдоль оси z).
Сравнить результат численного решения с точным распределением
скорости
Самостоятельно вывести величину объемного расхода
жидкости и сравнить ее точное значение с численными данными.
(с) Вычислить распределение скорости в трубе прямоугольного
поперечного сечения со сторонами у = mfe, z = тс (для
определенности пусть с > Ь). Получить точное решение для
скорости и расхода, сравнить его с численным значением.
Указание. Для получения точного решения учесть, что разность
и ~ f Ь ~» представляет собой четную функцию как от у, так и
от z, которая удовлетворяет уравнению Лапласа и равна 0 при
у = mb. '
S. Гравитационные волны
Примером нестационарных течений жидкости являются волновые
движения с колебаниями отдельных частиц. Рассмотрим волны на
поверхности жидкости, возникающие в результате того, что
поверхность выведена из состояния равновесия и колеблется под
действием силы тяжести. Такие волны называются гравитационными.
Гравитационные волны описываются уравнениями нестационарных
течений идеальной несжимаемой жидкости.
455
Лекции по вычислительной математике
Пусть начальное возмущение заключается в отклонении
жидкости от состояния равновесия. Предположим, что этим начальным
возмущением являются мгновенные добавочные давления,
вызванные, например, порывом ветра. Возникающие при этом движения
будут потенциальны: V = V</?. Уравнение неразрывности
обращается в уравнение Лапласа:
Уравнения движения Эйлера приводятся к интегралу Коши-Лаг-
ранжа следующего вида:
где gz представляет собой потенциал сил тяжести.
Пусть течение медленное, тогда квадратом скорости в последнем
уравнении можно пренебречь. Кроме того, так как <р определяется
с точностью до произвольной функции, зависящей от времени, то
это уравнение можно переписать в виде
р д(р
р ot
Граничные условия. Предположим, что жидкость ограничена снизу
непроницаемой поверхностью. На этой поверхности ставим
условие непроницаемости на нормальный компонент скорости: Vn =
= |? = 0. Свободная поверхность (граница жидкости с газом) будет
плоскостью, которую примем за координатную плоскость ху. На
свободной поверхности жидкости давление р равно давлению газа
над жидкостью (ро). Граничное условие для скорости на свободной
поверхности
Начальные условия. Пусть возмущенная поверхность в начальный
момент (t = 0) определяется уравнением z = f(x,y). Тогда при t =
= о, z = 0 справедливо соотношение ^ = —gf(x,y). Начальные
скорости возникают в результате действия импульса давления, рав-
т
ного Jpdr. Потенциал скорости в начальный момент можно пред-
0
ставить в виде
ч> = —/i(*>y)-
456
Лекция 16 Численное решение уравнений в частных производных
Плоские волны. Рассмотрим волновое движение, называемое
плоскими волнами. В этом случае свободная поверхность будет
представлять собой цилиндрическую поверхность с образующими,
параллельными оси у. Пусть жидкость ограничена плоским
горизонтальным дном, отстоящим от свободной поверхности на
расстояние h. Тогда для искомого потенциала скорости у?(х, г, t)
справедливы соотношения
1 * dz v'
Начальные условия заменим требованием периодичности по
времени t и координате х искомого решения.
(a) Построить аналитическое решение поставленной задачи,
представив искомую функцию в виде <р = 0(t)X(x)Z(z). Показать,
что полученное решение — результат наложения четырех
колебаний.
(b) Получить численное решение и сравнить его с аналитическим.
Определить профиль волны ?(х, у, ?), используя соотношение
^ д dt '
Прогрессивные волны. Провести численное исследование частного
случая плоских волновых движений, который определяется
потенциалом скорости вида
<р = Aekz cos(kx — at).
Профиль волны в этом случае имеет вид
С = sin(fcx — at).
9
Описать основные закономерности рассматриваемого движения
жидкости. Чему равен период волны, частота колебаний? Вывести
формулу для траекторий частиц жидкости и сравнить ее на графике
с траекторией, получаемой в численном решении.
457
Лекции по вычислительной математике
Литература
[1] Рябенький B.C. Введение в вычислительную математику. М.: Физмат-
лит,2000.294с.
[2] Федоренко Р.П. Введение в вычислительную физику. М.: Изд-во
МФТИ, 1994.526 с.
[3] Самарский АЛ. Теория разностных схем. М.: Наука, 1983.656 с.
[4] Самарский А.А., Николаев Е.С. Методы решения сеточных
уравнений. М.: Наука, 1978.590 с.
[5] Марчук Т.Н. Методы вычислительной математики. М., Наука, 1989.
608 с.
[6] Иванов В.Д., Косарев В.И. и др. Лабораторный практикум "Основы
вычислительной математики". М.: МЗ Пресс, 2003.193 с.
[7] Самарский А.А., Гулин А.В. Численные методы математической
физики. М: Научный мир, 2003.316 с.
[8] ДеммельДж. Вычислительная линейная алгебра. Теория и
приложения. М., Мир, 2001.429 с.
[9] Современные проблемы вычислительной математики и
математического моделирования, Том 1. М. Наука, 2005.343 с.
[10] Федоренко Р.П. Релаксационный метод решения разностных
эллиптических уравнений. // ЖВМ и МФ, 1961, т. 1, № 5. с. 922-927.
[11] Холодов А. С. Монотонные разностные схемы на нерегулярных
сетках для эллиптических уравнений в области со многими
несвязными границами. // Математическое моделирование. 1991. Т. 3. № 9. С.
104-113.
[ 12] Марчук Г.И., Шайдуров В.В. Повышение точности решений
разностных схем. М.: Наука, 1979.320 с.
[13] БэтчелорДж. Введение в динамику жидкости. М.: Мир, 1973.758 с.
458
Лекция 17 Понятие о методах конечных элементов
Лекция 17. Понятие о методах конечных элементов
Лекция дает первое представление о классе методов конечных
элементов. Приводятся вариационная и проекционная постановки задачи.
Рассматривается применение МКЭ к стационарным и нестационарным задачам.
Вкратце обсуждаются вопросы устойчивости методов конечных элементов
при решении нестационарных задач. Рассматривается общая схема
применения методов конечных элементов к решению многомерных задач
математической физики.
Ключевые слова: метод конечных элементов, вариационная
формулировка, метод Ритца, проекционная формулировка, метод Галер-
кина, базисные функции, функции с финитным носителем,
согласованный базис.
Основная идея метода конечных элементов, базирующая на
методах Бубнова, Галеркина и Ритца, была предложена Р. Курантом в 1943 г.,
но осталась незамеченной, опередив потребности практики. В 50-х годах
прошлого века с появлением первых компьютеров возникла
необходимость в разработке новых инженерных подходов к численному решению
задач со сложной геометрией, в которых области интегрирования
разбивались на подобласти. Такие подобласти (носители финитных базисных
функций, об этом ниже) и получили название конечных элементов.
Рис. 17.1
Методы конечных элементов (МКЭ) в настоящее время, пожалуй,
самые распространенные в мире численные методы. К их достоинствам
относятся:
459
Лекции по вычислительной математике
1. возможность счета на неравномерных сетках, в двумерном и
трехмерном случаях для областей сложной геометрии;
2. «технологичность» методов (уточнение далее).
Современные МКЭ возникли в 50-е годы XX века при решении
задач теории упругости.
Самая распространенная статическая задача — задача о
нагруженной конструкции
Д и = -2, и \дп = 0,
а область ft — сложная. Например, область может иметь вид,
представленный на рис. 1. Каждая простая подобласть — конечный элемент.
В настоящее время под МКЭ понимают целые семейства
вариационных (Ритца) и проекционных (Галеркина или Бубнова-Галеркина)
методов.
17.1. Вариационный подход Ритца
Рассмотрим две задачи:
U и{х) ее -(*(*) и'я(х))'ж +р(х) и(х) = /(*), A7.1)
u@) = a; и(Х) = Ь;
к(х) ^ fc0 > 0; р{х) ^ 0.
Ь2 и(х, у) = -div (fc(x, у) grad и(ху у)) +р(ж, у) и(ху у) = д(ху у),
A7.2)
к(х, у) > к0 >0;р(х, у) ^0.
Эти задачи похожи: A7.1) является одномерным случаем более
общей задачи A7.2). Уравнения A7.1) и A7.2) записаны в самосопряженной
форме. Поставим задачам A7.1) и A7.2) в соответствие функционалы
х
Ji(u) = J (fc«J +pu2 - 2/u) dx A7.3)
о
и
/2(u) = fl{k{Vu, Vu) + pu2 - 2gu)dxdy. A7.4)
460
Лекция 17 Понятие о методах конечных элементов
Будем рассматривать пространство функций w e W\ (пространство
Соболева) с нормой
IN
X
= / (w2 + {w'xJ) dx для одномерного случая,
о
ff 2л л , ff fdwV , /ftfA2,, ^
= // w*dxdy+ / / ( -5- J 4-1 -5- I dxdj/ для двумерного случая
7У У7 V^/ V^J//
Это — функции с ограниченным интегралом.
Теорема 5. Среди всех функций w € W\, удовлетворяющих граничным
условиям, решение задачи A7.1) придает наименьшее значение функционалу
A7.3), а решение A7.2) — функционалу (П А).
Доказательство.
Докажем это утверждение для одномерного случая, а доказательство
для уравнений A7.2,17.4) оставим в качестве упражнений.
Введем ?(х) = w(x) - и(х). Поскольку w(x) e W\, а и(х) — дважды
непрерывно дифференцируемая функция, то ?(х) € И^1 и?@) = ?(Х) = 0.
-2/?)dx +
о
X
= h(u) + I (Щ'хJ +p?2) dx+ I 2?(pu - /) dx + 2 / ku'xgx dx =
000
q +J2tt-(ku'x)x+pu-f)dx,
0. A7.5)
Третье слагаемое в A7.5) равно нулю в силу граничных условий для
функции f; последнее слагаемое равно нулю, так как и — решение A7.1);
второе слагаемое — неотрицательное. Следовательно, минимум
функционала h{w) достигается, когда J(g) = 0, т. е. f = 0 или, что то же самое,
w(x) = u(x). ¦
461
Лекции по вычислительной математике
Чуть сложнее эта теорема доказывается для двумерного случая, где
надо воспользоваться теоремой Остроградского-Гаусса. Таким образом,
решение соответствующей задачи в частных производных A7.2) или
краевой задачи для ОДУ A7.1) сводится к задаче минимизации некоторого
функционала.
В том случае, если функционал A7.3) или A7.4) ограничен снизу, то
экстремаль функционала — минимум, и численный метод, который будет
построен ниже, носит название метода Ритца. Чаще, когда нет
необходимости тщательно исследовать постановку задачи, говорят об
экстремальной точке, стационарной точке функционала и т.д.
17.2. Общая схема метода Ритца
Решение задачи A7.1) ищут в виде
ix), A7.6)
k=i
где 1>(F(x),...,iI>n(x) — базисные функции в W^^ix) удовлетворяет
граничным условиям, а *ф?(х) при к ^ 1 такие, что ^@) = ф?(Х) =
= 0. Если суммирование в A7.6) происходит до бесконечности, то эта
формула дает точное решение задачи A7.1). Так как рассматривается
конечное число базисных функций, то получаем лишь приближенное
решение. Примером базисных функций для метода Ритца может служить
тригонометрический базис, а в качестве приближенного решения
получим конечный отрезок ряда Фурье.
Подставив A7.6) в A7.3), получаем
h(uN) - Е Е ад
p=l q=l
r=l
A7.7)
Находим минимум функционала A7.7) из условия ?% } = 0,
получаем систему из N линейных уравнений для определения
коэффициентов Ск- Затем объявляем A7.6) решением задачи.
Точно так же поступаем и для функционала A7.4). Число
уравнений в системе для определения коэффициентов тоже будет N (у
базисной функции только один индекс!). Вид функционала будет аналоги-
462
Лекция 17 Понятие о методах конечных элементов
чен A7.7), но вместо интегралов по отрезку будут стоять двойные
интегралы по рассматриваемой области пространства п, а вместо
производных — градиенты.
Первая проблема, которая возникает в методе Ритца — выбор
подходящего базиса. Как от набора функций ф? (х),..., ф% (х) зависит
решение? Как оценить ошибки?
Существуют два типа базиса: глобальный базис для метода Ритца и
базис из функций с финитным носителем.
Для того чтобы решения по методу Ритца сходились к точному,
необходимо и достаточно, чтобы V д е W% иУ е > О существовала
линейная комбинация
N(x) ее <(х) + ? С^(х),такая, что||^ - д\\щ < е,
если вычисления проводятся точно.
Допустимый базис для применения в методе Ритца si
g = l,...,W.
На отрезке [0,1] допустимые базисы: ф*Ц = хA - x)TjBx - 1), где
Tj(x) — j-й полином Чебышева; фУ = xJ(l - х).
Матрица системы линейных уравнений для определения
коэффициентов разложения по базису метода Ритца получается заполненной.
В случае использования «неудачных» базисов ее число обусловленности
достаточно велико.
Технологичность метода Ритца заключается в следующем. Матрица
соответствующей системы является самосопряженной с диагональным
преобладанием при правильном выборе базиса. Можно решать систему
быстро сходящимися итерационными методами.
Рассмотрим простейший вариант метода Ритца с использованием
базиса функций с финитным носителем. Напомним, что носитель
функции — множество точек х, для которых ф^{х) Ф 0. Введем разбиение
отрезка [0, X] точками Xj (сетку): 0 = хо < х\ < ... < хм = X. Строим
базисные функции:
X-XN-1
XN-XN-i '
Xj <
463
Лекции по вычислительной математике
Рис. 17.2
Можно проверить, что фУ € W\[О, X]. Интегралы и
производные определяются в смысле обобщенных функций — недостаток базиса!
Достоинством этого базиса является то, что базисные функции почти
ортогональны.
Пусть
тогда
Xj
*i+l
Xj-1
1
- xj) Jt2dt =
Xj+i - Xj Xj+i - Xj
dx =
0 T>"
6 "
6 '
а все остальные скалярные произведения равны нулю.
Также достаточно легко берутся интегралы, включающие в себя
производные базисных функций. Носитель каждой такой базисной функции
464
Лекция 17 Понятие о методах конечных элементов
называется конечным элементом, а метод Ритца с использованием такого
базиса — первый метод из семейства МКЭ. Иногда конечным элементом
также называют саму базисную функцию с финитным носителем.
17.3. Формулировка проекционного метода
Галеркина
По-прежнему рассматриваем задачи A7.1) и A7.2).
В дальнейшем будет рассмотрен класс дифференциальных
операторов. Главный недостаток метода Ритца — применимость лишь к
дифференциальным задачам, допускающим вариационную формулировку, т. е.
в линейном случае L — самосопряженный положительно определенный
оператор (все собственные числа L положительны).
Наряду с формулировкой A7.1) и A7.2) будем использовать запись,
определяющую слабое (обобщенное) решение:
(Ьщ v) - (/, v) = 0, A7.8)
где v — любая функция из рассмотренного ранее функционального
пространства W^, а скалярное произведение определено как
х
(щ v) = / и(х) v(x) dx в одномерном случае;
о
(u, v) = / / и(х, y)v(x, y)dxdy в двумерном случае.
п
Равенство A7.8) определяет обобщенное решение задачи. Известно,
что если и — классическое решение задачи, то оно является обобщенным
решением в смысле A7.8). Обратное, по понятным причинам, неверно —
в W\ «больше» функций, чем в С1 или С2. У задачи может существовать
обобщенное решение, но не существовать классического.
Рассмотрим конечномерное подпространство пространства W\ с
введенным базисом:
ф^ — базисные функции в W\\ они обязаны обладать теми же
свойствами, что и базисные функции для метода Ритца. Рассмотрим теперь
для A7.8) конечную систему весовых функций из W\ : v?,..., v#. Вместо
A7.8) рассмотрим конечную систему проекций на весовые функции.
16—3339 465
Лекции по вычислительной математике
Введем также обозначение
R = LuN -f A7.9)
здесь R — невязка. Тогда, после подстановки разложения по базисным
функциям в A7.8), получим систему соотношений
(Я, v?) = (LtA t/jft - (/, v"). A7.10)
Минимум невязки в пространстве, определяемом функциями
vf,..., г/$ достигается тогда, когда невязка принадлежит его
ортогональному дополнению: (Я, v?) = 0 для всех к. Теперь надо потребовать,
чтобы весовые функции образовывали базис в W\. Естественно в качестве
весовых функций использовать уже имеющиеся базисные ф^,... ,^$.
Тогда получаем проекционный метод Галеркина.
В итоге для определения коэффициентов разложения по базису из
конечных элементов имеем систему соотношений вида
3=1
или в матричной форме:
Это же соотношение получается и при выводе системы уравнений
для коэффициентов в методе Ритца.
При вычислении скалярных произведений использовалась
самосопряженность линейного дифференциального оператора L. Но при
выводе соотношения A7.10) самосопряженность оператора не
использовалась! Значит, метод Галеркина можно обобщать и на случай
несамосопряженного (и нелинейного!) дифференциального оператора. При
использовании в качестве базисных функций «функций-крышечек», введенных
выше, получаем вариант МКЭ. Для задач A7.1) и A7.2) метод будет давать
те же соотношения, что и метод Ритца.
466
Лекция 17 Понятие о методах конечных элементов
17.4. Пример построения схемы конечных
элементов
Для уменьшения числа выкладок считаем, что
hi = /ii+i = h для всех i(hi = х» - Xi_i).
Рассмотрим несамосопряженный аналог задачи A7.1):
-*(*) и% + ?(х) < + р(х) и(х) = /(я),
u@) = a; ti(l) = 6;
Л(х) ^ fco > 0; р(х) ^ 0.
Найдем сопряженное уравнение:
1
I (-ku" + qv! + pu- f)-vdx =
= —ku' • v
о
1 111
n + / ufct/ dx + #ш; гу — I u(qv)f dx+ puvdx — I fvdx =
О 0 0
1 1
Г члены определяемые \ f t , , / n, 4// , , ,
< > - / fvdx + / ((fo;) - qv +pv • udx.
\ граничными условиями J J J J
о о
Из этого соотношения легко получить условия, при которых L±L*.
Теперь запишем разложение по базису:
j
подставляем в исходное дифференциальное уравнение:
(к( ) (V + f с А" А + («*) (*» + Ус*»\ *»
)
467
Лекции по вычислительной математике
Рассмотрим отдельно каждое слагаемое в левой части:
Первые два слагаемые в правой части получаются в силу того, что
носители базисных функций финитны. Последнее слагаемое в правой
части получается интегрированием по частям. Зачем необходимо
интегрирование по частям? На первый взгляд (Ф^)^ = 0. Но эта
производная базисной функции — обобщенная функция, следовательно, в
скалярных произведениях появятся J-функции, при интегрировании возникнут
сложности.
В итоге после всех необходимых вычислений коэффициент перед С к'
12 1
-Ck-i • k{xk-i/2) - + Ск • к{хк) - - Cfc+i • к(хк+1/2) ^.
Функция к(х) считается кусочно-постоянной на
соответствующих отрезках, можно использовать какую-либо другую
аппроксимацию (к<рУ)'х, учитывая что к(х) — заданная функция.
Первые два слагаемые в правой части A7.11) зависят от граничных
условий и относятся к правой части системы уравнений для
определения Ск-
Рассмотрим теперь
Коэффициенты при Ск будут следующие:
-Ск-1 - q(xk-i/2)' 2 + °k ' Я(*к)' 0
468
Лекция 17 Понятие о методах конечных элементов
Здесь опять предполагается, что функция q(x) кусочно-постоянная.
Последнее слагаемое с р(х) дает выражение
- + Ск -р(хк) -g- + Cfc+i -p(xfc+1/2) -,
т. е. при «плохом» способе вычисляемых интегралов фактически
получаем конечно-разностное соотношение, похожее на аппроксимацию Нуме-
рова.
Вместе с тем, существует значительное отличие. Сеточная
функция — это функция, заданная таблично. Решение (приближенное)
МКЭ — это не сеточная функция, а элемент W\.
17.5. Построение базисных функций
Математическая основа МКЭ — метод Галеркина и вариационный
метод Ритца — развиваются, начиная со второго десятилетия XX века.
Прогресс в МКЭ последних лет заключается именно в построении
наборов базисных функций, обладающих достаточной гладкостью — так
называемых согласованных базисов.
Базис из «крышечек» в двумерном случае. Процесс построения
базисных функции включает в себя:
а) триангуляцию области — разбиение на треугольники, каждый из
которых является носителем своей базисной функции;
б) построение базисных функций.
Требования к триангуляции (обозначения на рис. 17.3).
dD=S
Рис. 17.3
469
Лекции по вычислительной математике
1. Между точками S и Sh с помощью нормалей к S устанавливается
взаимно-однозначное соответствие, расстояние между
соответствующими точками не превосходит Si h2 (h — сеточный параметр).
2. Длины сторон треугольников и их площади лежат в пределах [Ы\ ,]
и [ft27i, Л272], где h, h, 71»72 — положительные константы, не
зависящие от Л.
3. Существует непрерывное взаимно-однозначное преобразование ?>Л
на область, границы которой параллельны осям координат, или
составляют с ними угол тг/4. Преобразование линейно внутри
каждого треугольника и переводит последний в равнобедренный
прямоугольный треугольник с катетами, равными h.
Простейший пример построения триангуляции.
1. Область D вписываем в прямоугольник.
2. Строим в прямоугольнике равномерную сетку с шагом h (рис. 17.4).
\
/
)
¦
/
г
\
/
)
*-
Л
Л
J
Рис. 17.4
Рис. 17.5
3. Ближайшие к границе D узлы сетки сдвигаем на границу D
(рис. 17.5).
4. Разбиваем четырехугольники внутри Dh диагоналями (рис. 17.6).
5. Убираем все ячейки, пересечение которых с Dh пусто (рис. 17.7).
Построение базисной функции — «крышечки». Фиксируем
вершину Pi какого-либо треугольника. Составляем список соседей — вершин,
принадлежащих треугольникам, имеющим вершину Pi. Пусть в списке
470
Лекция 17
Понятие о методах конечных элементов
\
Л
\
к
\
\
\
\
А
\
V
Рис. 17.6
Рис. 17.7
есть вершины Q\ и фг, принадлежащие треугольнику 1 (рис. 17.8). В этом
треугольнике представляем
I _ У-1/i _ Х~У2
V2'yi X1'V2
1-
УР1 -У1
1/2-VI
X1-1/2
Тогда для точки
рДя, у) =
k=i
К сожалению, базисных функций типа «кры-
шечек» может не хватить для решения
уравнений второго (по пространственной производной)
порядка. До сих пор рассматривались уравнения
второго порядка. Перейдем теперь к модельному
уравнению
0, X]
A7.12)
с какими-либо граничными условиями.
Будем искать решение в соответствии с
методами МКЭ:
Рис. 17.8
A7.13)
где фУ обладают финитным носителем. Подставляем разложение A7.13)
в A7.12). Отвлекаясь от членов с граничными условиями, отнесенными к
471
Лекции по вычислительной математике
pQ , при умножении на ф[* имеем
)
Отсюда следует, чтобы первая сумма в A7.14) вычислялась,
желательно, чтобы базисы ф[* были гладкими:
, X],
а сходимость МКЭ следует понимать в норме W$ [О, X].
Примеры согласованных базисных функций. Если используется базис
из «крышечек», то в каждом узле (при стыковке конечных элементов)
решение МКЭ будет иметь разрыв первой производной. Это происходит из-
за выбора базиса МКЭ. Сама искомая функция непрерывна.
Допустим, необходимо найти решение, обладающее непрерывной
первой производной.
Строим набор функций базиса:
{4>x (x) }m; m = ^—"; (p — нечетное положительное число).
Считаем, что размер конечного элемента равен 1. Для одномерной
сетки всегда найдется линейное преобразование (свое для каждого
элемента!), переводящее данный элемент в отрезок длины 1. Положим, что
базисная функция есть
(р{(х) = 0, еслих^ [-1; 1],
а на каждом отрезке [-1; 0], [0; 1] — полином степени р. В точках х = ± 1
ipi(x) и все ее производные до порядка т - 1 равны нулю. В точке х = 0
= 1.
472
Лекция 17
Понятие о методах конечных элементов
Введем
(в случае равномерного разбиения отрезка на конечные элементы). Тогда
{Vij}j = O, ..., tf;i = l, ..., m-базис.
Рассмотрим случай р = 1. Тогда га = р — 1, на каждом отрезке
функция линейна. Приходим к набору из «крышечек».
Возьмем р = 3, тогда то = 2. Строим набор базисных функций.
Фиксируем г = 1. На отрезках [-1; 0], [0; 1] получаем полином
степени 3.
<pi(x) = ао + а\х + а2х2 + а3х3(на[-1; 0]).
Условия: ^l(-l) = 0, ^1 @) = 1, vi(-l) =
= 0, vi@) = 0 определяют коэффициенты
оо = 1; а\ = 0; аг = -3; аз = -2.
В итоге на отрезке [-1; 0]
Аналогично поступаем на отрезке [0; 1],
там имеем
График базисной функции <pi(x)
представлен на рис. 17.9.
Пусть теперь г = т = 2. Строим набор
такой, что
4- бгх2 Н- бзх3.
Из условий у^С1) = 0, <Р2A) = 0, у?2@) = 0, ?>2@) = 1 получается
(р2(х) = A - хJх при 0 ^ х ^ 1.
Аналогично, ^г(х) = A - хJх при -1 ^ х < 0. График функции
изображен на рис. 17.10.
Базис является согласованным, если для уравнения степени не выше
р + 1 все базисные функции непрерывны (принадлежат Ст).
473
Лекции по вычислительной математике
Что представляет собой метод Галерки-
на при использовании такого базиса? Теперь
в точках сетки (межэлементных) необходимо
знать не только функцию и, но и ее первую,
вторую,..., (га - 1)-ю производную по х:
N
+ и'х(а
N
6 величин
6 величин
Рис. 17.10
Отметим, что u(a+jh) и и'х(а+
+ jh) определяются численно при
решении уравнений методом Галер-
кина.
Увеличилось число базисных
функций и коэффициентов
разложения.
Заметим также, что матрица
системы — разреженная, но уже
не трехдиагональная (если порядок
системы выше второго).
Согласование в двумерном
случае. Надо сшивать следующие
величины (рис. 17.11): 18 величин в
узлах плюс 3 значения нормальных
производных на гранях.
Получается 21 условие, значит
необходимо иметь 21 произвольную
константу. Полином должен иметь
достаточно высокую степень
(члены до ж5, у5). Поэтому в
многомерном случае, как правило,
используются несогласованные базисные
функции или с низким (га = 1) порядком согласования.
17.6. МКЭ для нестационарных уравнений
Рассмотрим простейшую МКЭ-аппроксимацию уравнения
теплопроводности:
ди д2и
~dt=Ddl?
дх
т=1,2
дхду
(А),
дхт
(А),
6 величин
Рис. 17.11
474
Лекция 17 Понятие о методах конечных элементов
с соответствующими граничными и начальными условиями. Будем
искать решение в виде
Используя подход Галеркина, получаем (в базисе из «крышечек»)
1 dCj-г 2 дСл, 1 dCj+1 D
Это — система дифференциально-разностных уравнений. Теперь
необходимо заменить производные по времени разностными отношениями.
Заметим, что «явная» схема (когда в правой части стоят
коэффициенты разложения на предыдущем слое по времени С]1) уже не является
явной, в соответствии с определением явных методов, данном выше:
ft1-*?.! 2 С?"-СТ 1 С«?-С?+1 D
в ; +з —т—+е —т— w
и на n + 1-м слое все равно необходимо решать систему уравнений
методом прогонки. Причиной этого вычислительного неудобства является
то, что система дифференциальных уравнений для определения
зависимости коэффициентов разложения — это система обыкновенных
дифференциальных уравнений, но не записанная в нормальной форме Коши.
Попытаемся исследовать схему на устойчивость спектральному
признаку фон Неймана. Подставив в приведенное выше разностное
уравнение
Су = Xneij{py
получаем выражение для спектра оператора послойного перехода Х((р):
^-^ [ei<p + 4 + е-*] = к [ei{* 4- 2 + е"^],
о
где к = D -fa. Отсюда видно, что устойчивость метода конечных
элементов опять определяется безразмерной комбинацией параметров
разбиения (размера конечного элемента, шага по времени) и коэффициента
теплопроводности — параболическим аналогом числа Куранта.
Преобразуем уравнение для А:
А-1 _ к B cos ч>-2)
6 ~~ 4 + 2 cos (p '
А = 1 — 6fc —-, откуда условием устойчивости будет к ^ -.
cos (p + 2 6
475
Лекции по вычислительной математике
Имеет смысл пользоваться «неявной схемой» (правая часть берется с
верхнего слоя по времени) или аппроксимацией типа Кранка-Никольсон.
Продолжим рассмотрение применения МКЭ к нестационарным
уравнениям. Как и ранее, смотрим задачу для уравнения
теплопроводности
ди д2и
dt " Эх2'
Выбирая базис из «крышечек», представляем решение в виде
Подставляя последнее уравнение в исходное и применяя стандартную
процедуру метода Галеркина, получаем систему дифференциальных
уравнений
1 dCj-г 2 dCj I dCj+1 _D
6~dT + 3~dT + 6~dr-l?{Cj-1~2Cj +
(шаг сетки считается постоянным), или, в матричном виде
При этом, в любом базисе
В = В* > О, А = А* > 0.
Тогда
3 В1/2 : В^В1/2 = В.
Матрица В1/2 — самосопряженная положительно определенная.
Можно записать последнее уравнение A7.15) в виде
BV2B1/2 — = Цг АВ/2В1/2С.
dt h?
Введем вектор z = В/2С и умножим последнее соотношение слева на
В/2, тогда получаем
% = S ВАВ/2. = § Р z. A7.16)
at hz hz
Таким образом, из неявной системы A7.15) получена «явная» система
A7.16) — перед вектором производных нет матричного множителя.
476
Лекция 17 Понятие о методах конечных элементов
Запишем для A7.16) схему Кранка-Николсон:
zn+i _ zn = g_ B-1/2AB/2(zn+1 + zn). A7.17)
Вопрос об устойчивости схемы A7.17) можно решить следующим
образом. Умножим A7.17) на zn+1 + zn. Получаем соотношение:
(zn+\ zn+1) - (zn, zn) = I (B-1/2AB/2(zn+1 +zn), (zn+1 +zn));
||z»+1||2 = ||zn||2+|(P(zn+1+zn),(z"+1+zn)) ^ ||zn||2-^ ||zn+1+zn||2
в силу того, что А < 0 (спектр оператора А уже известен). Последнее
неравенство и означает безусловную устойчивость метода.
17.7. Решение нелинейных уравнений с помощью
МКЭ
Рассмотрим в качестве простейшего примера уравнение Хопфа
Его решение, как и ранее, ищем в виде A7.14), при этом
по-прежнему используем базис из «крышечек». После вычислений получаем
1 dCj-x 2 dC3; 1 dCi+1 2
б ~~dT + з "dT + 6 1Г"^гад-
A7.19)
Если написать дискретизацию A7.19) неявным образом (по
величинам на п + 1-м слое по времени или по аналогии со схемой Кранка—
Николсон), то получается нелинейная относительно С?+1 система. Ее
необходимо решать с помощью метода Ньютона. Можно линеаризовать
A7.19) в окрестности С]1, считая, что
Тогда A7.19) преобразуется в следующую линейную относительно
величин на п + 1-м слое по времени запись:
(;+1) ?+l?? = о.
477
Лекции по вычислительной математике
Эту систему можно решать, используя метод немонотонной
прогонки — гибрид метода прогонки и алгоритма Гаусса с выбором ведущего
элемента.
Возможен и другой подход — линеаризация исходного уравнения
A7.18) и решение получившейся последовательности линейных
уравнений для определения приближенного решения задачи.
За рамками этой лекции, кроме технических подробностей,
остались численные методы, основанные на применении минимизации
функционала квадрата невязки — методы наименьших квадратов, а также
методы граничных элементов для решения эллиптических задач.
17.8. Задачи для самостоятельного решения
1. При решении задачи с использованием метода Ритца на отрезке
[0,4] используются глобальные базисы
2) f,xD-x),x2D-z),...,x"D-x);
°> 4>4 V1 4/'
Описать достоинства и недостатки каждого из этих базисов.
Литература
[1] Марчук Г.М., Агошков В.И. Введение в проекционно-сеточные
методы. М.: Наука, 1981.414 с.
[2] Стренг Г.,Фикс Дж. Теория метода конечных элементов. М.: Мир,
1977.
[3] Самарский А.А., Тулин А.В. Численные методы математической
физики М.: Научный мир, 2003. 316 с.
[4] Ши Д Математическое моделирование задач тепло- и массообмена.
М.: Мир, 1988.544 с.
[5] Ректорис К. Вариационные методы в математической физике и
технике. М.: Мир, 1985.590 с.
478
Лекция 18 Методы расщепления
Лекция 18. Методы расщепления
Лекция знакомит с идеями построения экономичных разностных схем
для уравнений математической физики, основанных на методах
покомпонентного расщепления (локально-одномерные схемы) и на принципах
расщепления по физическим процессам.
Ключевые слова: методы расщепления, схема Кранка-Никольсон,
локально-одномерные схемы, расщепление по физическим
процессам, расщепление с факторизацией оператора.
18.1. Понятие о методах расщепления
Рассмотрим дифференциальную задачу для уравнения в частных
производных с постоянными коэффициентами:
-^ + Au = 0;s€fix, teuu u\r = ur,u(t0) = u0. A8.1)
at
Здесь оператор А ^ 0 — положительный дифференциальный
оператор с постоянными коэффициентами. В запись оператора А входят
производные по пространственным переменным. Для любого
ненулевого элемента выполнено (Ау>, </?) ^ 0. Г — граница области
интегрирования fix; A — разностный оператор, аппроксимирующий А. Можно
проверить, что разностное уравнение
1/ I 11
+ЛЦ „+tt = 0,u° = uo A8.2)
аппроксимирует A8.1) со вторым порядком по г (схема
Кранка-Никольсон). Заметим, что A8.2) можно трактовать как результат попеременного
применения явной и неявной схем первого порядка аппроксимации,
записанных на интервалах [?n, ?n+1/2], [?n+1/2,
n+l/2 _ n
U Л
т/2
^ + Лип+1 = 0. A8.3)
479
Лекции по вычислительной математике
Исключая из уравнений A8.3) значения функции на
промежуточном слое по времени (с полуцелым индексом), получим A8.2). Если А =
= А(*),то
+ А"" о =0 A8.4)
un+1 = (Е + ^ЛП)-1(Е - -Лп)гЛ
7"
при этом разностный оператор также является положительным:
(Апи,и) ^0,
а решение на следующем слое по времени может быть записано в
операторном виде следующим образом:
или
где Tn = (Е + JЛП)(Е - \Лп).
Для доказательства устойчивости полученного разностного
уравнения умножим скалярно A8.4) на (ип + un+1)/2, получим
= 0 A8.5)
2т
Так как в силу положительности разностного оператора (Апи, и) ^ 0,
то из A8.5) следует, что ||wn+1|| ^ ||un||, чем и обеспечена устойчивость
схемы. Если разностный оператор Л (пространственные разности)
выбран в виде полусуммы разностных операторов на верхнем и нижнем
слоях по времени |(ЛП+1 + Лп) = Лп+1/2, то схема имеет второй порядок
аппроксимации по т.
18.2. Метод расщепления первого и второго
порядка точности по г
18.2.1. Локально-одномерные схемы
Положим, что дифференциальный оператор А и соответствующий
ему разностный оператор Л можно представить в виде суммы
операторов, каждый из которых включает производные лишь по одной
пространственной переменной и разности лишь вдоль одного направления
соответственно. Всего пространственных направлений N. Такие
дифференциальные и разностные операторы будем называть локально-одномерными.
480
Лекция 18 Методы расщепления
И дифференциальный, и разностный операторы записываются в виде
суммы локально-одномерных:
N N
Для однородной задачи можно выписать схему расщепления по
направлениям:
т
un+2/N _ Un+1/N
= 0.
Получена система разностных уравнений, каждое из которых не
аппроксимирует исходное дифференциальное, но может быть легко решено
(методом прогонки вдоль соответствующего направления, если
разностные операторы содержат лишь первые и вторые разности). Тем не менее,
последовательно примененные друг за другом, они дают на следующем
слое по времени решение с разумной точностью. Говорят, что имеет
место суммарная аппроксимация — результирующий оператор послойного
перехода получился аппроксимирующим. Описанный выше способ
называется иногда методом дробных шагов, и уже встречался при решении
многомерного уравнения теплопроводности.
Для неоднородной задачи один из возможных вариантов схемы
расщепления имеет вид
4*
Т
un+2/N _ Un+1/N
= fn.
Возможны и другие способы учета правой части, например,
введение ее во все уравнения с весовыми множителями, которые подбираются
из условий наилучшей суммарной аппроксимации (минимизации
ошибки аппроксимации на следующем слое по времени).
481
Лекции по вычислительной математике
Приведенные выше схемы расщепления по направлениям
абсолютно устойчивы.
18.2.2. Схемы Кранка-Никольсон
Рассмотрим обобщение схемы Кранка-Никольсон на случай
многомерных уравнений с локально-одномерными операторами. Положим,
N
как и ранее, Л = ? Л». Если коэффициенты разностного оператора яв-
но зависят от времени, они берутся на промежуточном временном слое
Л = A(?n+1/2). Для простоты изложения рассмотрим двумерный случай.
Схему расщепления по направлениям представим в виде
un+l/2 _ ип Un+1/2 + ип
+Ах = 0
+1 _ un+l/2 ип+1 + un+l/2
+ Л
а решение на следующем слое по времени в операторной форме
выписывается как un+1 = Tnun. Для оператора послойного перехода получается
следующая формула:
Т» = (Е + ^ ^ ^ ^
При выполнении условия
\ IIAill < 1
схема устойчива, обладает вторым порядком аппроксимации по времени,
если операторы Ai, Л2 коммутативны, и первым — если нет.
18.2.3. Общая формулировка методов расщепления
Заменим локально-одномерные дифференциальные операторы Ai
разностными операторами на каждом шаге по времени tn < t ^ tn+\-
Представим схему расщепления в следующем общем виде:
U
г
un+2/N _ un+l/N
= о,
1 = 0.
482
Лекция 18 Методы расщепления
Условие устойчивости такой схемы расщепления будет
\\CiCi-i... Ci || < 1 + сг, с = const,
Двухслойная схема расщепления с весовыми коэффициентами
представлена в виде
^- + Аг [A - а)«» + aun+l'N] = О,
г 1
Л2 [A - a)un+l'N + aun+2'N] = 0,
ЦП+^ + AN fA - a)u^
= 0.
Если в этой схеме расщепления положить веса верхнего и нижнего
слоев по времени равными, 7 = 0,5, то в случае коммутирующих
операторов Лг (каждый такой разностный оператор аппроксимирует со вторым
порядком соответствующий локально-одномерный дифференциальный
оператор) схема будет иметь второй порядок аппроксимации и по
времени. Если при этом каждый оператор А* ^ 0, то схема будет абсолютно
устойчивой.
18.2.4. Схемы расщепления для уравнения
теплопроводности
Рассматриваем нестационарное уравнение теплопроводности
— - Аи = 0, t ? fit, {*, У, z} е fi.
Здесь оператор Лапласа определен как Д = d2/dx2+d2/dy2+d2/dz2.
Его также можно записать в виде суммы трех локально-одномерных
операторов А = Ах + Ху + А2. Соответствующие разностные операторы
будут А = Ахх 4- ЛуУ + А2„ где Ахх = ^-i,Jfc-2u^fc+um+1|Jfc шалошчно
определяются операторы вычисления второй разностной производной и
по остальным направлениям Луу, Л22
Локально-одномерная схема для уравнения теплопроводности будет
un+l/3
Г
un+2/3 _
Г
-.П
1
1
un+l/3
483
Лекции по вычислительной математике
Для повышения порядка аппроксимации можно использовать схему
свесами
^- + Ахх [A - а)ип + аип+1<3] = О,
-.n+2/З -.n+1/З г т
Ц ~" [A -а)^1/3 + <ти"+2/3] = О,
_ 7,п+2/3
= 0.
18.3. Методы двуциклического покомпонентного
расщепления
Для этих методов отсутствует требование коммутативности
операторов Л».
Будем рассматривать численное решение A8.1) не на одном шаге по
времени, отрезке [?n, *n+1], а на двух последовательных шагах [?n~\ tn+1].
Пусть теперь разностные локально-одномерные операторы зависят явно
от времени, тогда они определены в середине отрезка Л» = Ai(tn).
Запишем схему расщепления:
un-l/2 _ ^n-1 Un-V2 . ип-1
+ А -2 =0,
ип _ ип-1/2 ип + ип-1/2
; +Л2 =0,
ип+1/2 _ ип и и
х?=0. A8.6)
7" ^
В операторной форме этот метод записывается как un+1 = Tnun~\
где введено обозначение
^Лх) (Е- 1Ах) (В+ ^Лз) (Е - ^
Если локально-одномерные операторы положительны Ai(t) > 0,
то при достаточной гладкости решения и элементов матриц Ai(t) схема
A8.6) абсолютно устойчива и аппроксимирует A8.1) со вторым порядком.
484
Лекция 18 Методы расщепления
Для неоднородного дифференциального уравнения fjf+Au =
/разностная аппроксимация метода расщепления может быть представлена в
виде
(Е + Т-К2) (ип - тГ) = (Е - 1
(Е + Т-\2) ип+1'2 = (Е - 1
где fn = f(tn).
В операторной форме записи решение неоднородной задачи
имеет вид: un+1 = TV1 + 2TT%T%fn, где введены обозначения Тп =
= ТуТ^Т^Ту Т? = (Е + \А?)~ (Е- Щ).
Представим разностную аппроксимацию неоднородного
дифференциального уравнения с помощью последовательного применения
операторов А1,...,Адг,Лдг,...,Ai:
(Е + ?Л„) (и" - г Г) = (Е - |Ajv) un~l'N,
(Е + T-KN) un+l'N = (Е - ^AN) (un + тГ),
Рассмотрим примеры использования метода двуциклического
расщепления для некоторых задач математической физики.
Пример 1. Трехмерное нестационарное уравнение диффузии,
область интегрирования — параллелепипед. Полагаем, что в вертикальном
направлении (ось Oz) коэффициент диффузии в вертикальной плоскости
7 зависит от координаты, что характерно для задач геофизики, /х —
коэффициент диффузии в горизонтальной плоскости. Задача может быть
представлена в виде
ди д ди
485
Лекции по вычислительной математике
Сведем решение рассматриваемой трехмерной задачи к
последовательному решению трех одномерных задач. Первая задача имеет вид
т dz*1 dz +/'
она описывает диффузию в вертикальной плоскости. Вторую и третью
задачи запишем
ди2 _ д2и2 дщ _ (Риз
dt " * Эх2 ' dt " М ду2 '
Теперь рассмотрим разностную аппроксимацию исходного
дифференциального уравнения
ди ,. . . ч
— + (Ai + А2 4- Л3)и = /, где
Л2М = -TJ
7m-l/2 , J
J
A3M = T^iUm+ijk Umjfc) + T
flz |_ nz flz J
Разностная схема двуциклического покомпонентного расщепления
приобретает вид
un+l/6 + ип
=0,
un+2/6 1 ^
un+4/6 _ un+3/6
un+3/6 _j_ un-|-2/6 yn+1/2
un-f 5/6 _ un u + w
; +Л2 = 0,
_|_ n
n+5/6
20-
Пример 2. Сопряженное нестационарное уравнение переноса и
диффузии
•щ + (Ах + А2 + А3)м = /,
486
Лекция 18 Методы расщепления
где операторы определены как
d(vxu) д2и . d(v2u) д2и А d(v3u) д ди
Здесь vi, V2, уз — компоненты вектора скорости, и — концентрация
субстанции, а — коэффициент поглощения субстанции внешней средой,
(т>0.
Соответствующую схему расщепления представим в виде
=0,
un+2/6 _ un+l/6
r+ Aa2
un+3/6 _ un+2/6 un+3/6 _j_ Mn
+ Лз г
;
un+4/6 _ Mn+3/6
+Лз
Mn+5/6 _ Mn+4/6 ^n+5/6 . M
+ л
+5/6
= 0'
7+ Al2
где разностные операторы аппроксимируют соответствующие локально-
одномерные дифференциальные операторы. Так для рассматриваемой
задачи
iffc) H
y Lily
3U = ft" ~-^-(um+li:,/k " Umjk) + J^
Отметим, что в рассматриваемой задаче на каждом этапе может быть
проведено расщепление и по физическим процессам. Для простоты
рассмотрим двухмерное уравнение конвекции-диффузии
ди
487
Лекции по вычислительной математике
в котором компоненты скорости движения среды vi,v2 удовлетворяют
уравнению неразрывности:
дх + ду
Первый этап расщепления задачи по физическим процессам связан
с переносом, на нем решается разностный аналог уравнения
дщ d(vi,u) d{v2,u)
dt^ дх ^ ду
Второй этап расщепления описывает процессы диффузии и
поглощения субстанций
— - /i Аи + <ти2 = /.
Пример 3. Расщепление по физическим процессам системы уравнений
газовой динамики (метод крупных частиц).
Система
ui, ti2 — компоненты вектора скорости v, P — давление газа, р —
плотность, е — внутренняя энергия.
Первый (Эйлеров) этап. Измеряются лишь величины, относящиеся
к ячейке в целом, а жидкость внутри каждой ячейки сетки считается
моментально замороженной. Расчет производится по формулам,
аппроксимирующим уравнения
^ = о
ди,др ди2 0Р _
р + 0^ + 0
486
Лекция 18 Методы расщепления
На втором (Лагранжевом) этапе происходит движение газа массы
через границы эйлеровых ячеек и перераспределение массы, импульса,
энергии по пространству; определяются поля параметров течения газа.
Аппроксимируется система уравнений
гv) = 0, ^ + div(pW2v) = О,
18.4. Методы расщепления с факторизацией
оператора
18.4.1. Факторизованная схема расщепления
Пусть для решения дифференциальной задачи
at
используется разностная схема Bun+1 = Fn, где Fn = (В - тА)ип + rfn,
п=0,1,...
Пусть для вычисления Fn затрачивается O(N) действий, число
арифметических операций пропорционально числу узлов сетки N. Такие
разностные операторы называются экономичными.
Пусть Bi (i = 1,2,..., N) — экономичные разностные операторы,
такие, что Bit; = F.
Назовем схему разностной схемой с факторизоеанным оператором В,
если возможно его представление в виде
В = В1В2 • •. Bjy.
Эта схема будет также экономичной, так как для решения
разностного уравнения по-прежнему потребуется O(N) действий. В самом деле,
решение уравнения
1
может быть найдено в результате последовательного решения р
уравнений
Bitii = Fn,
B2u2 = ui,
489
Лекции по вычислительной математике
здесь i = 2,3,..., N. Тогда un+1 = us- В записи задачи введены
обозначения ui = un+1/N,..., щ = un+i/N,..., un-i = t^+n^1 — промежуточные
значения.
Схемы с факторизованным оператором иногда называются также
факторизованными схемами. Устойчивая схема с факторизованным
оператором В, которая представляет собой произведение конечного числа
операторов Bi,..., Вдг, является экономичной схемой.
Пример. Метод переменных направлений (продольно-поперечная
схема). Приведем запись схемы для решения линейного двумерного
уравнения теплопроводности. Расчетные формулы есть
--П+1/2 __ -.71
U г U - (Ai«-+l/« + Л2и«) = Г,
un+l _ „п+1/2
F
Тогда, исключая un+1/2, получим в операторной форме записи
(В - IAi) (В - Т-\2) un+1 = (В + jAi) (Е + IАа) ип,
или BiB2un+1 = Fn, где Bi = Е - |АЬ В2 = Е - §А2, Fn =
EA)(EiA)
E)(i)
Разностная схема может быть представлена в виде факторизованный
схемы расщепления:
18.4.2. Неявная схема расщепления с приближенной
факторизацией
Рассмотрим неявную разностную схему
+ Aun+1 = 0,n = 0,1,..., А = 53 А*, А4 > 0. A8.7)
r i=i
Представим разностную схему A8.7) в виде
(E + rA)un+1 = un. A8.8)
490
Лекциями* Методы расщепления
Факторизуем разностную схему A8.8) приближенно с точностью до
членов порядка О(т2). Для этого заменим в A8.8) оператор Е + тЛ на
факторизованный
(Е + tAi)(E + тЛ2)... (Е + tAn) = Е + тЛ 4- r2R,
где введено обозначение
Врезультате приходим к неявной схеме с приближенной
факторизацией
Bun+1 = un, В = П В», Bi = E + тА»,
t=i
или
Эта схема абсолютно устойчива, имеет первый порядок
аппроксимации.
18.4.3. Метод «предиктор-корректор»
Основная идея методов типа «предиктор-корректор» заключается в
следующем. На каждом отрезке [tn, tn+l] задача решается в два приема:
сначала по схеме первого порядка аппроксимации и со значительным
запасом устойчивости находится решение в момент времени ?n+1/2 = tn +
+ т/2 — предиктор. После этого на втором этапе расписывается исходное
уравнение по схеме более высокого порядка аппроксимации (чаще
всего, второго) — корректор. Основная идея семейств таких методов близка
к идее построения методов типа Рунге-Кутты для обыкновенных
дифференциальных уравнений.
Представим эту схему как следующую схему расщепления:
un+l/4 _ ип
rj2 +
un+l/2 _ nn+l/4
491
Лекции по вычислительной математике
Если в этой схеме расщепления исключить un+1/4, то получим
последовательность расчетных формул
далее, исключив, Лип+1/2, получим
+ л
(е+-Л2)
Если для разностных операторов выполнены условия \ ||Л»|| < 1,
Ai ^ О, Л2 ^ 0, а коэффициенты разностной схемы явно не зависят от
времени, то при достаточной гладкости решения дифференциальной
задачи разностная схема абсолютно устойчива и аппроксимирует исходную
задачу со вторым порядком.
Далее рассмотрим случай, когда оператор Л представляется в виде
суммы операторов Л»: Л = $^Л». Пусть все эти разностные операторы
i
положительны. Метод «предиктор-корректор» можно записать в виде
последовательности расчетных формул
Эта последовательность после исключения промежуточных этапов
сводится к одному разностному уравнению
^^ + А П (в + 1а,)"V + lfn+1/2) = Г+1/2-
i=N
Приведем пример построения такой схемы. Для нестационарного
трехмерного уравнения теплопроводности
ди 2^дЧ
492
Лекция 18 Методы расщепления
получим следующую разностную схему типа «предиктор-корректор»
un+l/6 _ ип
ф +
ип+1/3 _ ип+1/6
т/2
т
Далее, исключая промежуточные слои, получим схему, записанную
в каноническом виде
un+l_un n+u r
+ Л -I- —(AiA2 + Л1Л3 + Л2Л3) +
Т 2» 4 Т
т3. un+1-un п
+-5-Л1Л2Л3 = 0.
О Т
Схема абсолютно устойчива (для коммутирующих операторов),
имеет второй порядок аппроксимации по г и /it. Конечно, при практическом
решении задач на компьютере используется именно последовательность
разностных операторов. Канонический вид схемы удобен для ее
теоретического исследования.
Литература
[1] Белоцерковский ОМ. Численное моделирование в механике
сплошных сред. М.: Физико-математическая литература, 1994.442 с.
[2] Марнук Г.И. Методы расщепления. М.: Наука, 1988.263 с.
[3] Ковеня В.М., Яненко Н.Н. Методы расщепления в задачах газовой
динамики. Новосибирск: Наука, 1981.263 с.
493
Лекции по вычислительной математике
Лекция 19. Применение вариационных принципов
для построения разностных схем
В необязательной лекции приводятся примеры использования
вариационных принципов Лагранжа и Гамильтона для построения разностных схем
на основе вариации дискретного аналога лагранжиана (гамильтониана)
системы.
Ключевые слова: вариационные принципы Лагранжа и
Гамильтона. Разностная схема на неравномерной сетке. Консервативные
разностные схемы.
Вариационный принцип Ритца, позволяющий получить МКЭ для
уравнений в частных производных эллиптического типа, в том числе и
на нерегулярных сетках, рассматривался в лекции 17. Далее для решения
нестационарных задач в основном использовался проекционный
вариант МКЭ (метод Галеркина). Тем не менее, многие задачи
математической физики допускают вариационную постановку. Некоторые
величины и законы сохранения могут играть особую роль для задач (пример —
закон сохранения гамильтониана для консервативной системы).
Необходимы разностные схемы (или численные методы), позволяющие
учитывать специфику задачи и вариационные постановки.
Сделать это можно двумя способами. Первый — использовать
вариационные принципы для дискретных аналогов соответствующих
функционалов. При этом обычно получаются консервативные схемы. Второй
способ — построение разностных схем обычными методами (конечных
разностей), а затем их модификация, направленная на минимизацию
погрешности аппроксимации законов сохранения.
Рассмотрим первый (вариационный) подход.
19.1. Пример использования принципа
наименьшего действия (Гамильтона)
Рассматривается задача о движении твердого нерастяжимого
стержня длиной 1. Пусть он закреплен в точке 0, а на другой конец стержня
действует сила F(t) (рис. 19.1). Требуется определить движение стержня.
Начальная форма стержня считается заданной.
Возможное решение: записать уравнение движения — получится
уравнение гиперболического типа; поставить граничные условия; по-
494
Лекция 19 Применение вариационных принципов для построения разностных схем
F(t)
Рис. 19.1
строить разностную схему. Но в задаче допускаются сколь угодно
большие колебания стержня.
Другой способ приближенного решения. Введем в — угол
отклонения от оси х — как функцию длины дуги s, времени t. Тогда имеем
8
х= I cos 0(s', t) ds',
о
a
у = I sin 0(s', t) ds'.
Кинетическая энергия стержня есть
а потенциальная энергия складывается из упругой энергии (изгиба) и
работы внешней силы F(t):
U =
ds-Fxx(l,t)-Fyy(l,t)
(соответствующие коэффициенты полагаются равными 1).
495
Лекции по вычислительной математике
Лагранжиан системы есть L = T -С/, так что
(g) ds-
0 0 0
1 1
-Fx /cosOds-Fy I sin0 ds.
о о
Согласно принципу Гамильтона, функционал действия достигает
экстремального значения на истинном движении. Отсюда следует, что
d_ fdL\ dL
dt \дв) дв ~
и получается уравнение движения для 0:
1
I G cos @(s, t) - 0(<т, t)) 0(<т, t)da = 0"(s, t) + Fy sin в - Fx cos 0-
o
l
- I G sin @E, *) - 0(<r, t)) 02(a, t) da.
о
0@, t)=0; ^@,0 = 0;
1 - «; a < 5, 0 ^ s ^ 1;
Имеем интегро-дифференциальное уравнение для определения
0(«, t), причем как строить его разностную аппроксимацию —
непонятно.
Отметим, что G(s, а) есть функция Грина для задачи
W" = -g(8), U)'@) = W(l) = 0.
Теперь введем дискретный аналог лагранжиана Lh. Для этого
разобьем стержень на п отрезков одинаковой длины А/ (и одинаковой массы).
Каждый отрезок характеризуется углом наклона 0*. Тогда (см. рис. 19.2)
О 3
Д/ cos 6k = А/ У^ cos вк\
k=i
j
sin °k\
496
Лекция 19 Применение вариационных принципов для построения разностных схем
Рис. 19.2
dzj iBj
Здесь появился аналог конечных элементов или схем с
центральными разностями. Интегралы в этом выражении заменены конечными
изломами, фактически эти интегралы вычислены методом трапеций, т. е.
погрешность в определении лагранжиана Lh есть О(Д/J.
Теперь для построения системы уравнений надо записать
d (dLh\ dLh
т. е. продифференцировать дискретный аналог функционала по всем
значениям 0т, вт на введенной сетке. Для рассматриваемой задачи
последнее равенство приводит к соотношению
d2Lh
d2Lh
_ ^
двк двкдь jr[ dek
После подстановки в последнее выражение дискретного аналога ла-
17—3339 497
Лекции по вычислительной математике
гранжиана и выполнения дифференцирования по всем вк,вк, получаем:
п
= п4(в1-г - 20,
+7i2(Fy cos 9i - Fx sin 00 -
sin (*« ~
(известно, что n Al = 1 по построению).
Таким образом, при использовании сеточного аналога
вариационного принципа Гамильтона получена дифференциально-разностная
система уравнений (дифференциальная по времени, разностная по
пространственным переменным).
Рис. 19.3
Несколько затруднительно решать эту систему как систему
обыкновенных дифференциальных уравнений, так как она не приведена к
нормальной форме Коши. Однако с последней
дифференциально-алгебраической системой можно работать и решать ее. Алгоритмы решения
основаны на том, что gik — сеточный аналог функции Грина. Обратная
матрица — сеточная аппроксимация оператора второй производной.
Подробное изложение метода решения в [1].
19.2. Вариационные схемы для решения задач
газовой динамики
Более интересные разностные схемы получаются для многомерных
задач. Особенно плодотворным вариационный подход оказывается при
решении задач механики сплошной среды.
498
Лекция 19 Применение вариационных принципов для построения разностных схем
Рассмотрим следующий пример. В бесконечном объеме (вакууме)
находится область ft, занятая газом (см. рис. 19.3). Масса газа га =
= / р dV, р(х, у, z) — плотность среды,
п
Движение системы подчиняется следующим уравнениям:
+ grad P = О (движение);
р
at
-7- + /xiivW = 0 (неразрывность);
at
de
р — + PdivW = 0 (закон сохранения энергии);
at
, P, е) = 0 (уравнение состояния).
Эти уравнения приведены в лагранжевых переменных. Напомним,
что полная производная определена как j-t = ^ + (W, V). Здесь все
обозначения традиционные, через W обозначена скорость движения среды,
а через V — элемент объема. Рассматривается случай невязкого
нетеплопроводного газа. Запишем лагранжиан для движения среды, представив
ее как систему частиц, а затем устремим число частиц в бесконечность.
-T-U-j &
П п Q
Движение среды должно доставлять минимум функционалу
действия
t
S
о
По закону сохранения массы S(pdV) = 6(dm) = 0. Найдем SS —
= j L{r)dr.
оду сохранения м
вариацию S:
t t
6S= f SL(t) dr= f dr f ((W, SW) - Se) dm.
о on
Согласно первому началу термодинамики в предположении адиаба-
тичности процесса,
Используя кинематическое соотношение
499
Лекции по вычислительной математике
получим, что
Тогда
ss = -
p —— + grad P) Sr
t
I (W, Sr) pdV + / dr Л (Sr, n)P4r = 0.
SI J о ° дп
Независимые вариации траекторий Sr полагают равными нулю при
г = 0 и г = L Считая также (Sr, п)\дп = 0, получим, что вариация
лагранжиана равна нулю на решении системы уравнений Эйлера газовой
динамики.
Рис. 19.4
Рассмотрим дискретный аналог функционала действия. Для этого
введем в п сетку с ячейками, пронумерованными по левому нижнему
углу. При отображении ft на квадрат сетка отображается на равномерную
квадратную сетку (см. рис. 4). Тогда
Lh =
B <У>2 + у2
где rriij = pijVij — масса ячейки (pij — ее плотность) < и2 + v2 > —
усредненная по ячейке плотность кинетической энергии
<u2+v2>ij=-
[, fc=O
500
Лекция 19 Применение вариационных принципов для построения разностных схем
Условие адиабатичности течения имеет следствием для дискретной
системы выражение rriij ddj = -Pij dVij.
Кинематические соотношения (уравнения движения для узлов
сетки) есть
dt ~~Ut" dt "VtJ'
Объем каждой ячейки вычисляется в предположении, что границы
ячейки — отрезки прямых:
Vij = 2 [fo+lj ~ xij+l)(yi+l.?+l - Vij) ~ (xi+lj+l - xij)(Vi+lj ~ 2/ii+l)]-
Теперь необходимо получить соответствующую систему
дифференциально-разностных соотношений, аппроксимирующих уравнения
Эйлера.
Запишем функционал действия
t
Sh = J Lh(r) dr
о
и найдем его вариацию:
s (^ o
Е § S^i Е <i. i+k)+Е \ 5^i Е uw. j+*)+Е ра
Первое слагаемое в последнем равенстве можно переписать как
1 1 И
(иЪ ' H nHbji) = MijUijSuij = Mij -^ Sxij
где
Mij = т (^it-ij + rrii-ij-i + mi:7- + mij-i).
501
Лекции по вычислительной математике
После преобразований получаются следующие соотношения:
д V
м"
т. е. возникает система дифференциально-разностных уравнений
движения.
Уравнение адиабатичности трактуется, как уравнение для
определения энергии:
\
J
Система дифференциально-разностных соотношений замыкается
уравнением состояния.
Теперь, заменяя производные по времени на конечные разности,
получим разностную схему для решения уравнений газовой динамики на
нерегулярной подвижной сетке. Обычно для решения таких уравнений
используются явные разностные схемы. Подробнее о вариационных
методах получения схем для уравнений газовой динамики в [2].
19.3. Вариационная схема для уравнения
теплопроводности на криволинейной сетке
Рассмотрим линейное уравнение теплопроводности
——hdiv (—fcgrad и) = О A9.1)
о г
с условиями
(—fcgrad и, п) = О
в ограниченной области п с криволинейной границей. При этом нигде
в U уравнение не вырождено, т. е. к(х, у) > 0 во всех точках области,
включая граничные.
502
Лекция 19 Применение вариационных принципов для построения разностных схем
Рис. 19.5
В области Л каким-либо образом введена сетка с
четырехугольными ячейками. Сетка считается связной, т. е. для любых двух вершин
ячеек существует ломаная, их соединяющая и состоящая из ребер ячеек
(рис. 19.5).
Пусть сетка построена так, что существует преобразование,
переводящее область п в параллелограмм (прямоугольник) с равномерной
сеткой внутри. Тогда координатные линии ж, у переходят в координатные
кривые криволинейного базиса ?, г/.
Перепишем уравнение A9.1) в виде системы
fcgradu = O.
Рассмотрим функционал
Найцем SF[u]:
A9.2)
= / f-2di
2divW Su - 2Su ^ - 2uJUu) dx dy,
6^' W) = 2 ( -^-, SVf ) = 2 { -V-, -
503
Лекции по вычислительной математике
Отсюда при ^ 6и = 0 минимум функционала достигается на
решении уравнения теплопроводности.
Для построения разностной схемы введем дискретный аналог
функционала Fh(Wh), т. е. в дискретном аналоге основной расчетной
величиной будет поток тепла.
Прежде чем построить функционал, рассмотрим ячейку разностной
сетки (рис. 19.6). Температуру Uij и коэффициент теплопроводности (или
температуропроводности) к^ отнесем к центру ячейки (точке
пересечения диагоналей). В дальнейшем считаем, что термодинамические
величины постоянны во всей ячейке. Векторы теплового потока отнесем к
углам ячейки (рис. 19.6), а к центрам соответствующих ребер — проекции
потоков на координатные оси. Считаем, что г увеличивается по мере
увеличения координаты f; j — по мере увеличения rj; проекции векторов
потока направлены вдоль соответствующих координатных линий. Заметим,
что проекции потоков для двух ячеек сонаправлены с векторами внешней
нормали, а для двух — противонаправлены.
Рис. 19.6
Проинтегрируем уравнение
504
Лекция 19 Применение вариационных принципов для построения разностных схем
по элементарной ячейке разностной сетки. Имеем:
^ - wv ii+1r* ii+i + w^ yT^ „•) = o,
A9.4)
где Г — длины соответствующих ребер, Sy — площадь элементарной
ячейки.
Так как координаты всех вершин выпуклого четырехугольника
известны, то поиск длин, площадей и углов — элементарная
геометрическая задача.
Уравнение A9.4) — дискретный аналог уравнения A9.2). Если
возможно определить все потоки в моменты времени tn, ?n+1, а после
применить аппроксимацию A9.2) по времени с какими-либо весами, то будет
построена разностная схема для расчета температуры.
Учтем, что
2и^ = -2udivW.
ut
Построим дискретный аналог A9.3):
ZujJ^Iw -
A9.5)
Скалярные квадраты, входящие в первое слагаемое дискретного
аналога функционала, выражаются через контравариантные проекции
следующим образом (рис. 19.7):
^j j - 2WvijWii+lj
SID. (p2
и т.д.
Знак «+» или «—» определяется по правилу: компоненту потока
приписывается знак «+», если проекция потока сонаправлена с внешней
нормалью, а знак «-» — если противонаправлена. Таким образом, для
углов ячейки (pi и <^з получим знак «+» в последнем слагаемом (проекции
одинаковых знаков), а для углов <р2 и <^4 — знак «-»(проекции теплового
потока в произведении разных знаков).
505
Лекции по вычислительной математике
i+lj
Рис. 19.7
Для получения явной схемы положим в A9.S) вес верхнего слоя по
времени а = 0 и дифференцируем A9.5) по всем W$ ^, Wv ^.
Приравнивая производные нулю, получим схему для определения потоков, затем
из A9.4) ищем все и?+1.
Для построения неявной схемы в A9.4) считаем а = 1, а вместо
A9.5) пишем следующую дискретизацию:
ип+1 _ п 1
Sij ij i3 =
l,p=O
Выражая отсюда неизвестное пока значение и^1 в A9.5), получим
выражение, зависящее от и?, {И^+1}, {W^+1}, причем Fh(Wh) есть
сумма квадратов контравариантных проекций.
Дифференцируя, получим линейную систему уравнений для
определения потоков. Можно показать, что матрица системы будет обладать
следующими свойствами:
1. А = А*>0;
2. А имеет ленточную структуру;
3. А является разреженной.
Можно применить эффективные итерационные методы решения
системы.
Доказано, что неявная схема будет безусловно устойчивой, а
явная — условно устойчивой.
506
Лекция 19 Применение вариационных принципов для построения разностных схем
Метод легко обобщается на случай к = к(х, у, и), если уравнение не
вырождается. Кроме того, метод может быть обобщен и на случай других
граничных условий (не обязательно отсутствия потоков). В этом случае
в функционал A9.3) добавляются соответствующие интегралы по
границам, а в A9.5) — суммы по поверхностям.
Подробнее об этих схемах можно прочитать в [2].
19.4. Задачи для самостоятельного решения
1. Уравнение Кортевега-Де Фриза
Одно из самых замечательных уравнений математической
физики — уравнение Кортевега-Де Фриза (сокращенно КДФ) часто
записывают в виде
щ - 6иих + иххх = О
или
щ + пйх = йххх.
(a) Найти преобразование, переводящее эти формы записи друг в
друга.
(b) Рассматриваем задачу для уравнения щ - 6иих + иххх = 0 в
области х € [—10; 10] с условием периодичности.
Для решения иногда используют трехслойную разностную
схему на шаблоне рис. 19.8 (третья производная расписывается
по пяти точкам симметричным образом, некоторые
коэффициенты могут обратиться в нуль). Исследовать ее на
аппроксимацию и устойчивость. Какое условие устойчивости получено?
Построить разностную схему на шаблоне, напоминающем
шаблон схемы Саульева для решения уравнения
теплопроводности (рис. 19.9а, б).
Рис. 19.8
507
Лекции по вычислительной математике
Тис. 19.9
Исследовать получившиеся схемы на аппроксимацию и
устойчивость. Можно ли использовать прогонку для вычислений на
верхнем слое?
(с) Уравнение щ - 6иих + иххх = 0 имеет бесконечное число
законов сохранения. Укажем несколько из них:
/
/
udx = consti,
u2dx = const2
Как построить консервативную разностную схему, чтобы на
сеточном уровне выполнялись законы сохранения $ udx =
= const?
(d) Особую роль играет третий из приведенных выше законов
сохранения. Он является гамильтонианом для уравнения щ -
— 6иих + иххх = 0, т. е.
dt~dx\6u)'
Здесь ^ — вариационная производная функционала h ,способ
получения разностной схемы, сохраняющей гамильтониан
системы.
Решение. Запишем сеточный аналог гамильтониана Д:
+оо
f- E
Контрольный вопрос: почему /J1 аппроксимирует Д с
точностью O(h2)?
508
Лекция Применение вариационных принципов для построения разностных схем
На сеточном уровне взятие вариационной производной
означает дифференцирование по всем и!^ и деление на h. Тогда
получаем сеточную запись вариационной производной:
5и = hdvT = m
Аппроксимируя дискретный аналог D.4.3) с естественным для
этого вторым порядком по h, получаем
2 - 3(um-lJ Um+2 ~ 2um+l + 2um-l ~ Цщ-2
dt 2h
un+l_un-l
Заменяя производную по времени разностью т 2тт и вы"
числяя правую часть на п слое, получаем одну из схем пункта 2.
Конечно, возможны и другие аппроксимации гамильтониана,
варьирование которых приводит к другим разностным схемам.
Все они будут записываться на симметричных шаблонах, на
сеточном уровне для этих схем также будет выполняться закон
сохранения / udx = const.
Удастся ли получить вариационную схему на несимметричном
шаблоне типа Саульева?
Литература
[1] Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных
уравнений. Жесткие и дифференциально-алгебраические системы.
М.: Мир, 1999.685 с.
[2] Самарский А.А., Колдоба А.В., Повещенко Ю.А, Тишкин В.Ф.,
Фаворский А. П. Разностные схемы на нерегулярных сетках. Минск, ЗАО
"Критерий", 1996.196 с.
509
Приложение.
Параллельные вычисления на кластерах из
персональных компьютеров в математической
физике
В. Е. Карпов, А. И. Лобанов
В Приложении на примере решения конкретной задачи по
проектированию установки рассмотрены основные схемы распараллеливания численных
методов.
Ключевые слова: параллельные вычисления, кластер, метод Якоби,
статическая модель, динамическая модель, потоковая модель,
внутренний параллелизм.
1. Введение
Одним из источников сложных задач, описываемых уравнениями в
частных производных, является современная физика плазмы. Для
исследований в области управляемого термоядерного синтеза создаются
установки, способные генерировать мощные энергетические импульсы.
Актуальными становятся вопросы моделирования динамики плазмы в таких
установках.
Соответствие с экспериментами дает численное моделирование на
основе сложных математических моделей. При этом резко возрастает
объем выполняемых расчетов. Лет 10—12 назад использовать полные
модели не позволяли возможности вычислительной техники. Сейчас
требуется применение параллельных вычислительных систем. Для
проведения параллельных расчетов разрабатываются специальные методы.
Однако существует ряд апробированных методов и комплексов программ
для обычных компьютеров. Анализ их внутреннего параллелизма и
адаптация для выполнения на параллельных ЭВМ становятся необходимыми.
Один из способов повышения производительности ЭВМ —
развитие элементной базы, ведущее к уменьшению времени выполнения
процессором элементарных операций. Согласно эмпирическому
закону Мура (Мооге) [1], производительность процессоров удваивается
каждые полтора года, но конечному пользователю требуется решение задачи
уже сейчас. Неудовлетворенные запросы заставляют разработчиков
компьютерных систем искать другие способы повышения
производительности, например, за счет совмещения по времени выполнения операций
несколькими физическими устройствами.
510
Приложение. Применение вариационных принципов для построения разностных схем
Идея одновременного использования двух и более устройств в
вычислительных машинах стала внедряться с конца 1950-х годов.
Первоначальные изменения в конструкции не затрагивали алгоритмических
основ решения задач. Они допускали совместную работу нескольких
программ, требуя более совершенной организации процесса выполнения
заданий, но практически не позволяли ускорить решение задачи.
Существенного повышения производительности удалось добиться
после внесения в архитектуру ЭВМ принципов параллельной
обработки данных. Известные приемы конвейеризации этапов выполнения
различных команд процессора, применение в одном процессоре
нескольких функциональных устройств позволяют ускорить решение задачи на
уровне машинных команд. Такой параллелизм используется при работе
процессоров с очень большим командным словом — VLIW-процессоров
(Very Large Instruction Word). На современном этапе этот параллелизм
скрыт от прикладного программиста. Ответственность за его
эффективное использование возлагается на разработчиков процессоров или
компиляторов.
Наибольшего увеличения производительности удалось достичь с
появлением параллельных вычислений. Термин «параллельные
вычисления» относится к ускорению решения задач за счет одновременного
использования нескольких процессоров. Параллельные вычисления стали
особенно популярными в конце 80-х—начале 90-х годов XX века.
К применению параллельной техники оказались не готовы
специалисты, освоившие программирование на последовательных машинах.
Потребовалось создание алгоритмов, пригодных для реализации на
параллельных ЭВМ. Научная мысль одновременно продвигалась в двух
направлениях. Первым стало исследование на параллельность уже
существующих алгоритмов для последовательных компьютеров [2]. Вторым —
разработка новых алгоритмов, специально предназначенных для
параллельных комплексов [3, 4].Необходимое условие для параллельной
реализации алгоритма — наличие у него внутреннего параллелизма, т. е.
существование ярусно-параллельной формы с большой шириной ярусов.
В концепции неограниченного параллелизма [5] лежит предположение о
том, что вычислительная система не накладывает никаких ограничений
на алгоритм. Тогда это же условие полагается достаточным. Опыт
реализации показал ошибочность предположения о достаточности. На
машинах с одной архитектурой алгоритмы могли показывать высокую
эффективность, в то время как на машинах с другой архитектурой эти же
алгоритмы работали медленнее своих последовательных версий. Но анализ
алгоритмов на наличие внутреннего параллелизма необходим для любой
параллельной программы, а концепция неограниченного параллелизма
позволяет получить оценку максимально возможного ускорения.
511
Лекции по вычислительной математике
Для сложных задач такой анализ — весьма трудоемкий процесс. При
его проведении используются различные инструментальные программы.
По большей части это компиляторы, которые не только автоматически
выявляют наличие внутреннего параллелизма, но и готовят пригодный к
параллельному исполнению машинный код.
Для вычислительных комплексов с распределенной памятью
наличие у программы значительного внутреннего параллелизма еще не
означает, что она будут эффективно работать. Свою роль здесь начинает
играть соотношение времен выполнения параллельных частей программы
и обменов информацией между процессорами. Если у пользователя есть
возможность снять временной профиль последовательной программы на
своей вычислительной системе, то эти соотношения могут быть учтены.
В качестве примера использования параллельных технологий
рассмотрим задачу модернизации экспериментальной установки.
2. Расчет электрического поля установки PC-20
с использованием кластера из персональных
компьютеров
Установка РС-20 была создана в Курчатовском институте и
первоначально предназначалась для проведения радиационно-биологических
исследований. Необходимость проведения экспериментов по созданию
сверхмощных импульсов тока потребовала модернизации для
увеличения напряжений и плотности заряда, пропускаемого через плазменный
прерыватель тока.
Первоначально эскиз конструкции установки выглядел как
спайка двух коаксиальных конденсаторов различного диаметра, внешние
обкладки которых соединены металлической поверхностью (рис. 1). В
больший конденсатор помещена диэлектрическая вставка, представляющая
собой полый усеченный конус. В полиэтиленовую вставку врезаны пары
компенсаторных колец. Каждая пара соединена между собой плоскими
металлическими кольцами, проходящими через диэлектрик. Внутри всей
установки поддерживается вакуум. Внешние обкладки конденсаторов
заземлены. На внутренний цилиндрический электрод подается
постоянное напряжение. К компенсаторным кольцам подведены постоянные
напряжения, увеличивающиеся от нижнего кольца к верхнему. Требуется
определить потенциалы и напряженность электрического поля внутри
установки, а также оптимальную форму и расположение
компенсаторных колец.
512
Приложение. Применение вариационных принципов для построения разностных с*ем
Рис. 1. Первоначальный эскиз установки RS-20
3. Математическая модель и выбор численного
метода
Ввиду осевой симметрии целесообразно перейти в цилиндрическую
систему координат (г, z, в). Распределение потенциала электрического
поля ф описывается уравнением Лапласа:
д
д
F)
На металлических поверхностях значения потенциалов заданы
эскизом конструкции. Так как корректно поставить граничные условия на
верхнем и нижнем срезе конденсаторов не представляется возможным,
будем считать, что конденсаторы продолжаются в обе стороны на
бесконечное расстояние. В этом случае на входе и выходе установки получаем
граничные условия вида
ln(r)-ln(n)_ , ln(r)-ln(ra) i
f2
G)
^ In(r2)-ln(n)
Рассматриваемая область не является односвязной (имеются
внутренние границы на компенсаторных кольцах). Кроме того, известно, что
в плоском случае в окрестности угловых точек решение ведет себя как
const + г *, где C — величина угла. Для входящих углов, у которых C > тг
(в данном случае это точка стыка коаксиальных конденсаторов),
производные от решения стремятся к бесконечности как г i "г.
Наличие угловой точки предполагает высокие напряженности
электрического поля и требует подробных сеток для расчета потенциала.
Коэффициент диэлектрической проницаемости среды е терпит разрыв на
границе раздела сред вакуум — диэлектрик.
513
* Лекции по вычислительной математике
Целесообразно использовать для решения поставленной задачи один
из явных методов, характеризующихся высокой степенью внутренней
параллельности. Применялась пятиточечная разностная аппроксимация,
при этом система линейных уравнений решалась итерационным методом
Якоби:
+1 ~ Ф Ф ~~ ^
ТК?п+\,тГ+ еп-^тZ)+
4rn>m T*f Air+ 2' Alr_
- ^n|m • У>п|т-</>п,т-1ч n
€n,m-h 7 ) = 0,
где верхний индекс указывает на номер итерации. Индексы + и -
относятся к величинам шагов сетки справа и сверху от рассматриваемой
точки и слева и снизу, соответственно. Для учета разрыва коэффициента
диэлектрической проницаемости в качестве значения е в полуцелых точках
вблизи границы раздела сред выбирались средневзвешенные значения.
Использовался следующий критерий выхода из итераций:
J
<Pn
(9)
4., Модели организации параллельных вычислений
для комплексов с распределенной памятью
Эффективность работы параллельных программ на вычислительных
комплексах с распределенной памятью определяется тремя
составляющими:
• степенью внутреннего параллелизма алгоритма;
• количеством данных, передаваемых между процессорами;
• степенью равномерности загрузки процессоров.
Существуют другие факторы, влияющие на производительность. Но
их учет относится к компетенции производителей компиляторов, в то
время как ответственность за три выше перечисленных фактора ложится
на плечи прикладного программиста. Степень внутреннего параллелизма
является свойством выбранного алгоритма и никак не связана с
организацией совместной работы процессоров. Количество передаваемых
данных и равномерность загрузки вычислительных мощностей, напротив,
напрямую связаны с моделью организации параллельных расчетов. При
514
Приложение. Применение вариационных принципов для построения разностных схем
анализе эффективности параллельной версии алгоритма используется не
количество данных, а время их передачи. Скорость передачи одного и
того же количества данных в рамках одного вычислительного
комплекса может полагаться постоянной, что позволяет сравнивать между собой
разные модели организации вычислений. Переход к другому
вычислительному комплексу требует повторного сравнения эффективностей
моделей.
Для многопроцессорных компьютерных систем с распределенной
памятью существуют три модели организации параллельных
вычислений: потоковая, динамическая и статическая. Рассмотрим особенности
каждой из них на примере.
Пусть задан следующий фрагмент программного кода:
do k = 1, maxiter
doi = 1,n
enddo
enddo
print *,a
Для внутреннего цикла массивы а и b являются входными (они
требуются для вычислений на любом процессоре). Массив а относится и к
выходным, так как «полный» массив требуется, по крайней мере, на
одном процессоре после завершения параллельных вычислений.
Потоковая модель представляет собой модель вычислений по
классической схеме master-worker и требует наличия двух программ с
различными кодами. Все вычисления, за исключением параллельных частей
алгоритма, выполняются только на главном процессоре (master).
Параллельные части выполняются на рабочих процессорах (workers). Для
приведенного выше фрагмента кода организация вычислений в потоковой
модели выглядит следующим образом:
master (фрагмент программы 1)
do k = 1, maxiter
(балансировка загрузки рабочих процессов и передача им
соответствующих частей ранее вычисленных массивов а и Ь)
(сбор вычисленных частей массива а от рабочих процессоров для
последующего использования)
enddo
print*,a
515
Лекции по вычислительной математике
worker (фрагмент программы 2)
(прием своей части массивов а и b и границ цикла)
doi = imin, imax
enddo
(отправка вычисленной части массива а главному процессору)
В потоковой модели входные данные рассылаются в необходимых
объемах всем рабочим процессорам, что требует значительного времени
на передачу. Выходные данные собираются только главным процессором,
на что требуется меньшее время.
Динамическая модель является видоизменением потоковой модели.
Для ее работы и на главном, и на рабочих процессорах запускается один и
тот же исходный код. Вычисления выполняются на всех процессорах (за
исключением операций вывода, выполнение которых может быть
возложено только на главный процессор). Фрагмент кода при динамической
организации вычислений может иметь следующий вид:
do k = 1, maxiter
(балансировка загрузки процессов)
doi = imin,imax
enddo
(рассылка вычисленной части массива а на все другие процессоры и сбор
информации от них)
enddo
print *,a (возможно, только на главном процессоре)
В динамической модели входные данные никогда не передаются между
процессорами. Вместо этого производится широковещательная
рассылка выходных данных по окончании параллельного яруса. Сравнительная
эффективность моделей организации вычислений определяется
количеством входных и выходных данных для каждой параллельной части
программы. Обе модели (и потоковая, и динамическая) могут применять
динамическую балансировку загрузки процессоров непосредственно перед
выполнением параллельного яруса.
Статическая модель организации вычислений похожа на
динамическую, но все передачи данных определяются их фиксированным
распределением по процессорам. Оно не может изменяться во время
работы программы. Все процессоры выполняют идентичные вычисления.
516
Приложение. Применение вариационных принципов для построения разностных схем
После завершения параллельного яруса у каждого процессора есть свой
срез общего объема информации. Передачи данных определяются не
необходимостью выполнения параллельных частей программы, а
способом их дальнейшего использования. Модельный фрагмент кода для
статической модели может быть записан:
do k = 1, maxiter
do i = imin, imax
enddo
enddo
(рассылка и сбор вычисленной части массива а)
print *,a (возможно, только на одном процессоре)
Статическая модель позволяет уменьшить объемы передачи
информации между процессорами. Она позволяет также решать задачи,
требующие большого объема данных, которые принципиально не могут быть
решены в последовательном режиме из-за технических ограничений. Но
в статической модели невозможна динамическая балансировка загрузки
процессоров, что может ухудшить производительность программы при
неправильном распределении данных.
5. Выбор модели организации параллельных
вычислений
Для решения уравнения (8) был выбран достаточно простой
алгоритм, внутренний параллелизм которого практически очевиден. Тем не
менее, для определения эффективной модели распараллеливания
целесообразно использование системы анализа программ на параллельность
BERT 77 (http://www.plogic.com/bert-des.html). BERT 77 опирается на
полученные оценки выполнения элементарных конструкций языка
программирования FORTRAN 77 без предварительного исполнения
анализируемой программы. Эти оценки строятся для каждой тройки:
вычислительная система, компилятор, система коммуникации. Были проведены
исследования для разных комбинаций компонентов тройки. Они
показали, что времена выполнения программных конструкций (включая
вычисление выражений, организацию циклов, доступ к элементам
многомерных массивов, организацию вызовов функций и подпрограмм) могут
быть оценены при использовании небольшого количества (порядка 200)
предварительно вычисленных времен выполнения элементарных
операций для конкретной пары «вычислительная система—компилятор».
Эксперименты по измерению скоростей передачи информации для
различных коммуникационных систем приводят к зависимости времени пере-
517
Лекции по вычислительной математике
дачи данных от их объема, подобной изображенной на рис. 2. Такие
зависимости в системе BERT 77 приближаются непрерывными кусочно-
линейными функциями вида t = ??+fctx nbytes при щ ^ nbytes ^ n*+i, где
щ пробегает значения 0,1024,2048,4096 и т. д., t — полное время
передачи данных, — латентности, кг — скорости передачи, a nbytes—количество
передаваемых данных.
Время
Объем данных
Рис. 2. Типовой график зависимости времени передачи информации от ее объема
Проанализируем эффективность различных моделей организации
вычислений.
5.1. Потоковая модель
Входными переменными для параллельного яруса являются
значения потенциала ф во всех узлах сетки на предыдущей итерации, а
выходными — значения потенциала на текущей итерации и значение
относительной погрешности E). Относительная погрешность является
редукционной переменной по отношению к операции min, т. е. ее частичные
значения могут быть вычислены на рабочих процессорах, а
окончательное значение — применением редукционной операции при приеме
частичных значений. Если задействовано N рабочих процессоров, то при
идеальной балансировке загрузки время выполнения вычислений будет
составлять r/N.
Количество узлов сетки на один процессор при нарезке рабочих
областей по вертикали и правильной балансировке вряд ли будет
различаться на двоичный порядок. Поэтому объемы передаваемых данных попа-
518
Приложение. Применение вариационных принципов для построения разностных схем
дут на один участок кусочно-линейной аппроксимации, скажем, на
участок j. Скорость передачи информации на нем составляет к3 байтов в
единицу времени. Если главный процессор будет отправлять рабочему
процессору с номером i nbyteSi байт, то время передачи составит tl =
= t°j + kj x nbytei. Полное время передачи входных данных главным
процессором при использовании 8-байтовых данных будет t = N х t® +
+kj x nnodesx 8, где nnodes—полное число узлов расчетной сетки.
Независимо от значений N и j это время на порядок превышает время
выполнения одной итерации. Даже без анализа передачи выходной информации
видна неэффективность модели на имеющейся конфигурации
вычислительной системы.
5.2. Динамическая модель
В динамической модели передача входных данных от главного
процессора к рабочим отсутствует. Но вычисленные значения потенциала и
относительной погрешности должны быть широковещательно разосланы
всем процессорам. Аналогично получаем ту же оценку времени
вычислений на одном процессоре — т/N и оценку снизу для времени передачи
данных t = N х t*j + kj x (N - 1) х {(nnodes/N) +1) x 8, которые
доказывают неэффективность применения и этой модели.
5.3. Статическая модель
Как правило, статическая модель характеризуется наименьшим
количеством обменов информацией между процессами, но требует
тщательной предварительной балансировки загрузки процессоров.
Удобно обеспечить баланс загрузки для случая 6 процессоров,
распределяя между ними области ответственности, как показано на рис. 3.
Процессор, отвечающий за верхний и нижний срезы, будет загружен
меньше, чем остальные, но можно поручить ему отображение
текущего состояния решения задачи. Незначительное ухудшение балансировки
получается при разделении средних областей ответственности пополам,
а верхнего и нижнего срезов между разными компьютерами для 12
процессоров.
При идеальной балансировке для N процессоров время выполнения
каждой итерации по-прежнему будет т/N. Для следующей итерации
процессоры должны обменяться с соседями значениями потенциалов на
граничных слоях, передав два слоя, и приняв два слоя от них. Это займет не
более чем ^ = 4 х ^ + ^ х ^^ х g)
секунд, где nnodesr — количество узлов в одном радиальном слое, а
константы tOj и kj выбираются для объема передаваемой информации nnodesr x
8 байт. Оценка ускорения может быть получена как t/(t/N +1).
519
Лекции по вычислительной математике
б
з Ъ
2 «fc.
-'- 1
5 Mb
б
т* 0.5 Mb
4* 0 4 Mb
Г^ 0.3 Mb
--Л. 0.2 Mb
r# 01Mb
^ 0Mb
DvlV 115CJ
нности для 6 процессоров при использо-
Рис. 3. Разделение на области от
вании статической модели вычислений
Если проводить проверку условия выхода из итераций (9) на каждой
итерации, то дополнительно потребуется рассылка значения частичной
погрешности по всем процессорам. Это приведет к дополнительным
затратам на пересылку, в лучшем случае, \og(N - 1) х (?? + fci x 8) секунд.
Исправить ситуацию возможно, вычисляя значение погрешности не
на каждой итерации, а, скажем, после каждой 100-й итерации. Рискуем
выполнить лишние 100 итераций, что составляет доли процента от их
общего количества, но при этом дополнительные коммуникационные
затраты не влияют на эффективность работы программы.
Предварительная оценка ускорения вычислений на имеющемся
комплексе с использованием пакета PVM составляет 5,7 раза для 6
процессоров и 10,1 раза для 12 процессоров. Реальное ускорение, естественно,
будет несколько меньше из-за невозможности точной предварительной
балансировки загрузки процессоров в статической модели. Проведенный
расчет с использованием коммуникационного пакета PVM показал
реальное ускорение по отношению к последовательному варианту 5,03 раза
для 6 процессоров и 8,7 раза — для 12.
520
Приложение. Применение вариационных принципов для построения разностных схем
На основе расчетов вариантов модернизации установки было
принято решение изменить форму компенсаторных колец и распределение
потенциала на кольцах. Окончательный вариант приведен на рис. 4.
Вычисления показали значительное снижение напряженности внутри
диэлектрика в области нижних компенсаторных колец (рис. 5) и
позволили сделать вывод об отсутствии пробоя. Данный вариант был принят за
основу модернизации установки РС-20.
Рис. 4. Окончательный вариант расположения компенсаторных колец
6. Заключение
Рассмотренный пример относится к решению сравнительно
простой задачи математической физики. Динамика плазмы (в частности,
в РС-20) описывается гораздо более сложной системой уравнений в
частных производных. Однако эта задача позволяет проанализировать
методы организации параллельных вычислений и отладить технологию
применения кластеров для сложных расчетов. В задачах динамики плазмы,
например, наиболее эффективной оказывается динамическая модель
организации вычислений.
Но и приведенная задача представляла практический интерес. Во-
первых, для физиков. Модернизированная установка активно
эксплуатируется. Во-вторых, для математиков-прикладников. На примере зада-
521
Лекции по вычислительной математике
i
> m
i
IP
So»
Ш. - ° -¦
¦111 —'
tot
и»
л
so
i
Рис. 5. Распределение потенциала для этого варианта расположения
компенсаторных колец (приведен фрагмент расчетной области)
чи проведен анализ алгоритмов на наличие внутреннего параллелизма
и отработана технология оценок эффективности распараллеливания без
предварительного исполнения последовательных вариантов.
Литература
[1] Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. — СПб.:
БХВ-Петербург, 2002. — 608 с.
[2] Воеводин В.В. Параллельные структуры алгоритмов и программ. —
М.: ОВМ АН СССР, 1987. - 148 с.
[3] Фаддеева В.Н., Фаддеев Д.К. Параллельные вычисления в линейной
алгебре // Кибернетика. 1982. № 3. С. 18-31,44.
[4] Самарский АА., Вабищевич П.Н. Аддитивные схемы для задач
математической физики. М.: Наука, 1999.319 с.
[S] Воеводин В.В. Математические модели и методы в параллельных
процессах. М.: Наука, 1986.296 с.
522
Учебное издание
Петров Игорь Борисович
Лобанов Алексей Иванович
ЛЕКЦИИ ПО ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКЕ
Учебное пособие
Литературный редактор Я. Черкесова
Корректор Ю. Голомазова
Компьютерная верстка А. Широбоков
Обложка М. Автономова
Подписано в печать 31.07.2006. Формат 60x90 Vi6-
Гарнитура Тайме. Бумага офсетная. Печать офсетная.
Усл. печ. л. 33,0. Тираж 2000 экз. Заказ № 3339.
ООО «ИНТУИТ.ру»
Интернет-Университет Информационных Технологий, www.intuit.ru
Москва, Электрический пер., 8, стр.3.
E-mail: admin@intuit.ru, http://www.intuit.ru
ООО «БИНОМ. Лаборатория знаний»
Москва, проезд Аэропорта, д. 3
Телефон: D95) 157-1902,157-5272
E-mail: Lbz@aha.ru, http://www.Lbz.ru
Список книг Интернет-Университета Информационных Технологий
Алгоритмы, структуры данных, вычисления
1. Лекции по вычислительной математике, А.И. Лобанов и др., 2006, 528 с.
2. Цюфы и алгоритмы. Структуры данных. Модели вычислений, В.Е. Алексеев,
В.А. Таланов, 2006, 320 с.
3. Нейрокомпыотерные системы, М.С. Тарков, 2006,144 с.
4. Нечеткие множества и нейронные сети, Г.Э. Яхъяева, 2006, 320 с.
Архитектура ЭВМ
5. Архитектура и технологии IBM eServer zSeries, Э.К. Лекцкий и др., 2005,640 с.
6. Архитектуры и топологии многопроцессорных вычислительных систем,
А.В. Богданов и др., 2004,176 с.
7. Основы микропроцессорной техники, 3-е изд., Ю.В. Новиков и др., 2006,360 с.
8. Основы теории и организации ЭВМ, В.В. Гуров и др., 2006, 272 с.
Безопасность информационных технологий
9. Основы информационной безопасности, 3-е изд., В.А. Галатенко, 2006, 208 с.
10. Основы сетевой безопасности: криптографические алгоритмы и протоколы
взаимодействия, О.Р. Лапонина, 2005,608 с.
11. Стандарты информационной безопасности, В.А. Галатенко, 2006, 264 с.
Интернет-технологии
12. Flash MX для профессиональных программистов, МА Капустин и др., 2006,512 с.
13. Основы web-технологий, П.Б. Храмцов и др., 2003, 512 с.
История и социальные вопросы
14. Основы права интеллектуальной собственности, AT. Серго и др. 2005, 344 с.
Операционные системы
15. Операционная система Iinux, Г.В. Курячий и др., 2005, 392 с.
16. Операционная система Solaris, Ф.И. Торчинский, 2005,472 с.
17. Операционная система Unix, Г.В. Курячий, 2004,320 с.
18. Основы операционных систем, 2-е изд., В.Е. Карпов и др. 2006, 536 с.
Разработка приложений
19. Введение в анализ, синтез и моделирование систем, В.М. Казиев, 2006,248 с.
20. Введение в теорию программирования, СВ. Зыков, 2004, 400 с.
21. Интеграция приложений на основе WebSphere MQ, В А Макушкин и др., 2005,336 с.
22. Компонентный подход в программировании, В.В. Кулямин, 2006,464 с.
23. Объектно-ориентированный анализ и проектирование с использованием UML и
IBM Rational Rose, A.B. Леоненков, 2006,320 с.
24. Основы менеджмента программных проектов, И.Н. Скопил, 2004, 336 с.
25. Основы тестирования программного обеспечения, В.П. Котляров, 2006, 360 с.
26. Программирование в стандарте POSIX, В.А. Галатенко, 2004, 560 с.
27. Проектирование информационных систем, В.И. Грекул и др., 2005, 296 с.
28. Стили и методы программирования, Н.Н. Непейвода, 2005,320 с.
Сетевые технологии
29. Основы локальных сетей, Ю.В. Новиков и др., 2005, 360 с.
30. Основы сетей передачи данных, 2-е изд., В.Г. Олифер и др., 2005,176 с
Системы и языки программирования
31. Основы программиромния на С#, ВА Биллиг, 2006,488 с.
32. Основы программирования на PHP, H.B. Савельева, 2005,264 с.
33. Основы программирования на языке Пролог, ПА Шрайнер, 2005,176 с
34. Основы функционального программирования, Л.В. Городняя, 2004,280 с.
35. Программирование на Java, НА. Вязовик, 2003,592 с.
36. Программирование на языке Pascal, ТА Андреева, 2006, 240 с.
37. Сборник заданий по основаниям програмиировання, В.В. Пупышев и др., 2006,352 с.
38. Язык программирования Python, PA Сузи, 2006,328 с.
39. Язык программирования Си++, 2-е изд.,АЛ. Фридман, 2004, 264 с.
40. Язык Си и особенности работы с ним, Н.И. Костюкова и др., 2006, 208с.
41. Data Mining, ИА Чубукова, 2006, 384 с.
42. Основы SQL, Л.Н. Полякова, 2004, 368 с.
43. Основы баз данных, С.Д. Кузнецов, 2005,488 с.
44. Основы проектирования приложений баз данных, И.Ю. Баженова, 2006, 328 с.
Человеко-машинное взаимодействие
45. Интеллектуальные робототехнические системы, ВЛ. Афонини др., 2005,208 с.
Основы информатики и математики
46. Математическая теория формальных языков, АЕ. Пентус и др., 2006,248 с.
47. Начала алгебры. Часть 1, АВ. Михалев, АА Михалев, 2005,272 с.
48. Преподавание информатики и математических основ информатики, под. ред.
АВ. Михалева, 2005,144 с.
49. Common Intermediate Language и системное программирование
в Microsoft .NET, AM. Чеповский и др., 2006, 328 с.
50. Основы программирования, В.В. Борисенко, 2005, 328 с.
51. Работа с текстовой информацией. Microsoft Office W>rd 2003,0.Б. Калугина,
B.C. Люцарев, 2005,152 с.
52. Работа с электронными таблицами. Microsoft Office Excel 2003,0.Б. Калугина,
B.C. Люцарев, 2006,240 с.
Информационные технологии от первого лица
53. Технология программирования, АН. Терехов, 2006,152 с.
Архитектура информационных технологий
54. Архитектура и стратегия. "Инь" и "янь** информационных технологий,
А Данилин, А Слюсаренко, 2005, 504 с.
55. Готовы ли Вы к войне за клиента? Стратегия управления взаимоотношениями с
клиентами (CRM), П. Черкашин, 2004, 384 с.
56. OpenView. Network Node Manager. Разработка и реализация корпоративного
решения, Джон Бломмерс, 2005, 264 с.
57. Объектно-ориентированное конструирование программных систем + CD,
Бертран Мейер, 2005,1232 с.
58. Я могу работать в современном офисе + CD, А Прохоров, 2005,264 с.
INTUIT.RU
ЛОКАЛЬНАЯ
ВЕРСИЯ
1.01
ТВОЙ ПУТЬ
К ЗНАНИЯМ
дистанционное обучение
без подключения
к Интернету
Автономная система обучения учебным программам Интернет-Университета
Информационных Технологий. Подключение к интернету не обязательно. В
системе имеется более 70 учебных курсов, предусмотрены возможности сдачи
тестов и экзаменов. Система поддержиавает многопользовательскую работу на
одном компьютере.
Рекомендуемые системные требования
Операционная система: Windows 98/ME/NT/2000/XP/2003
Минимальные требования к аппаратуре: Pentium III, HDD 300MB, RAM 128Mb,
вндеорежим 800x600 true color, CD-ROM
12x,i