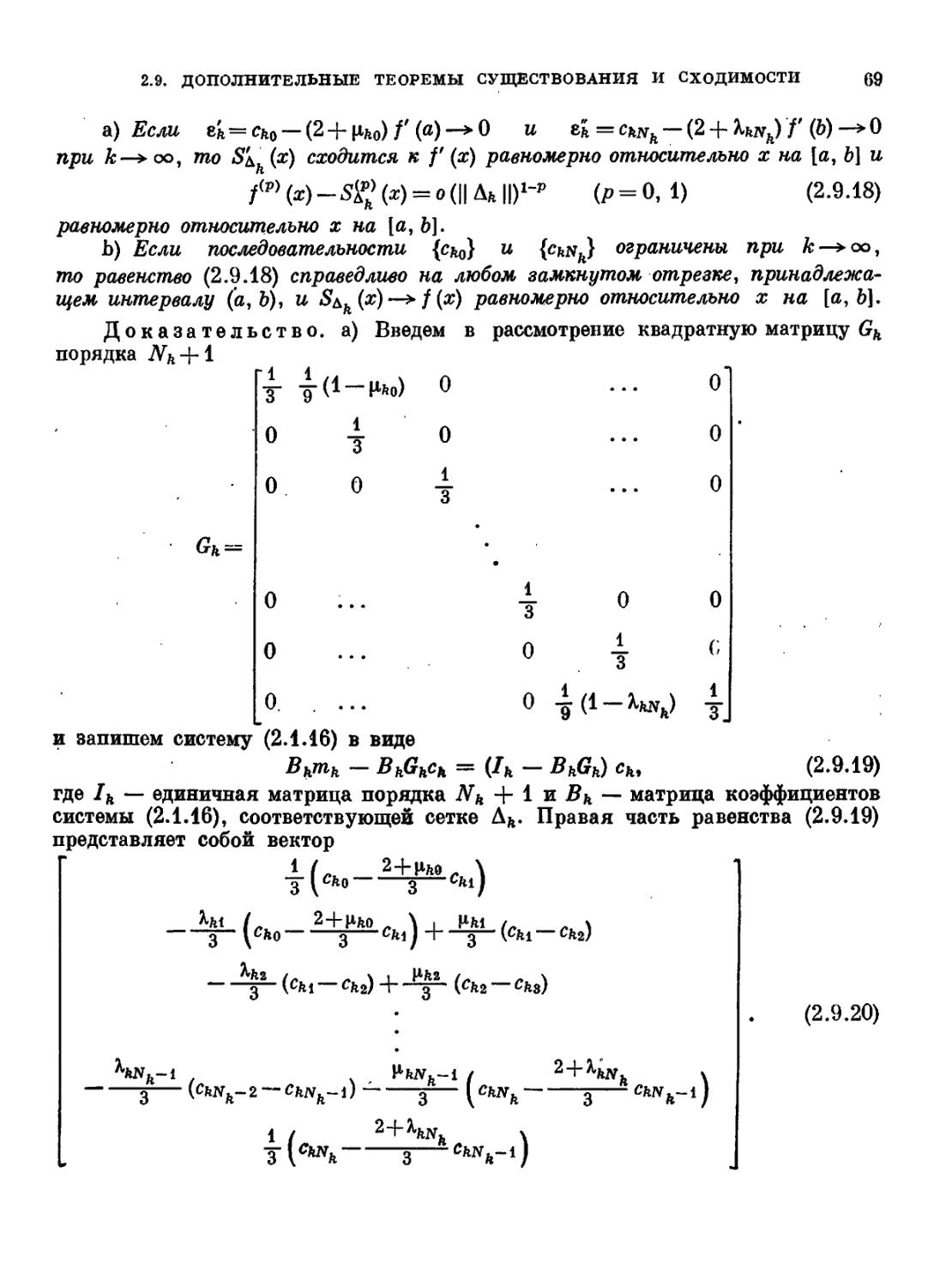
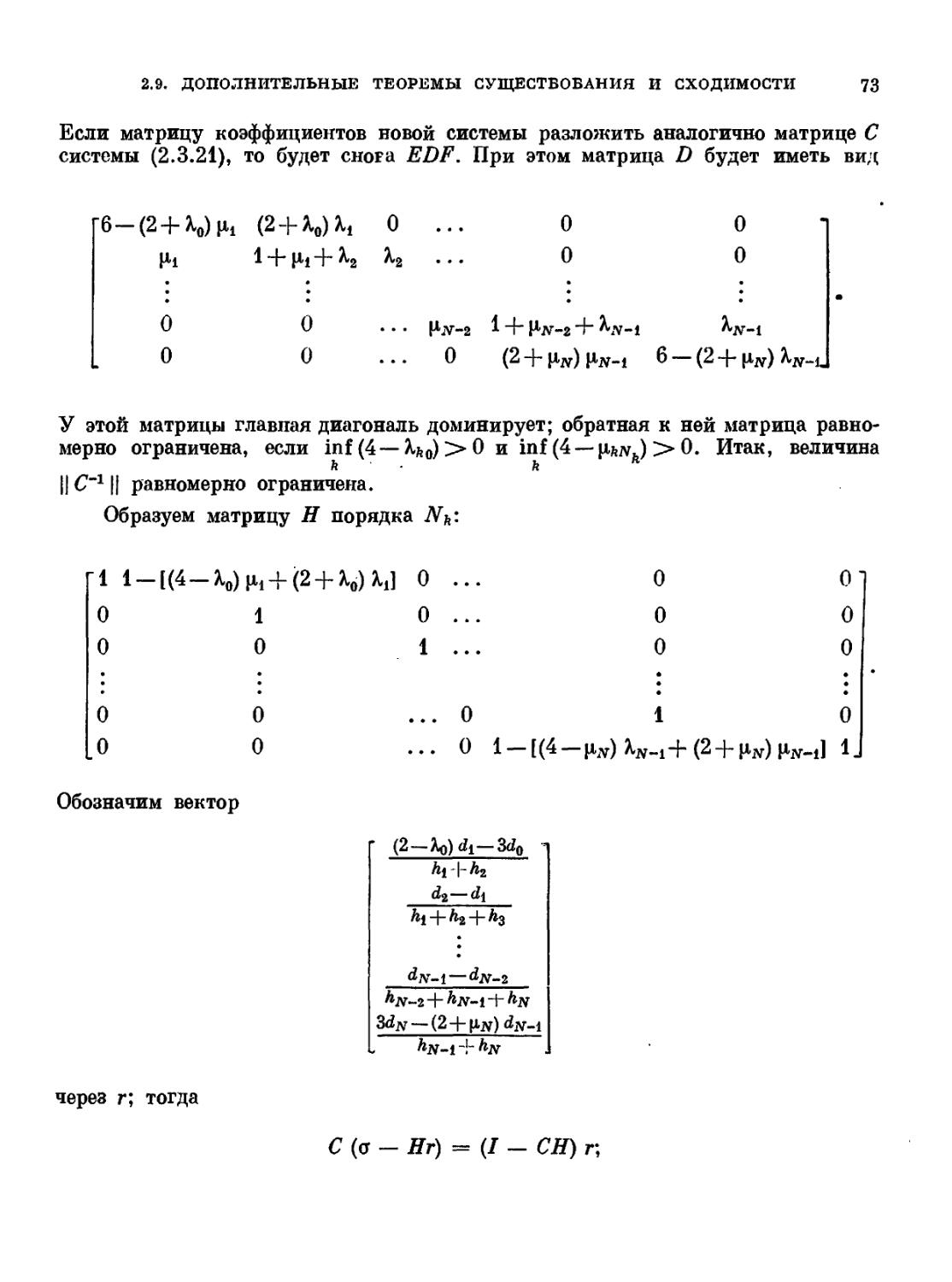
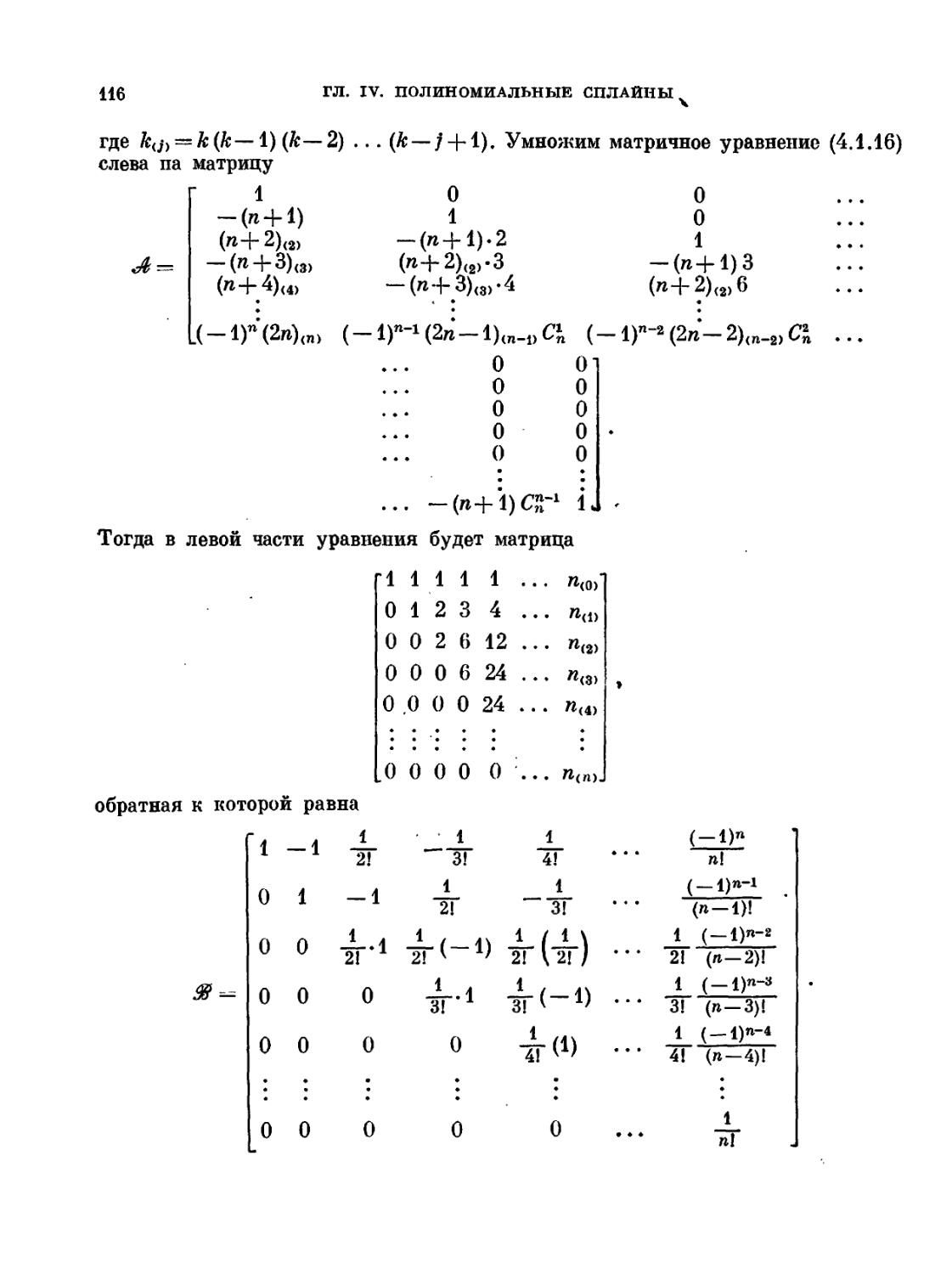
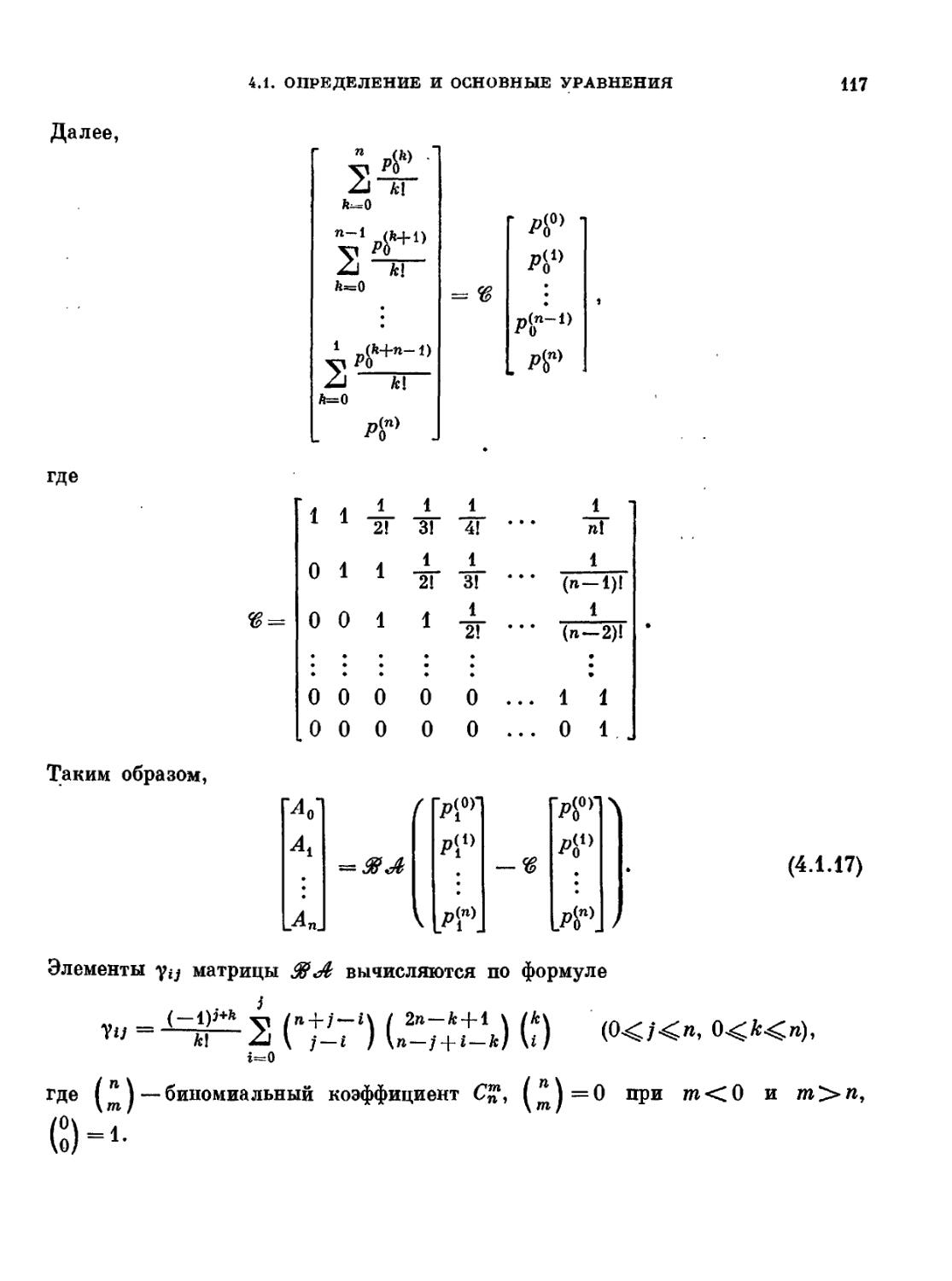
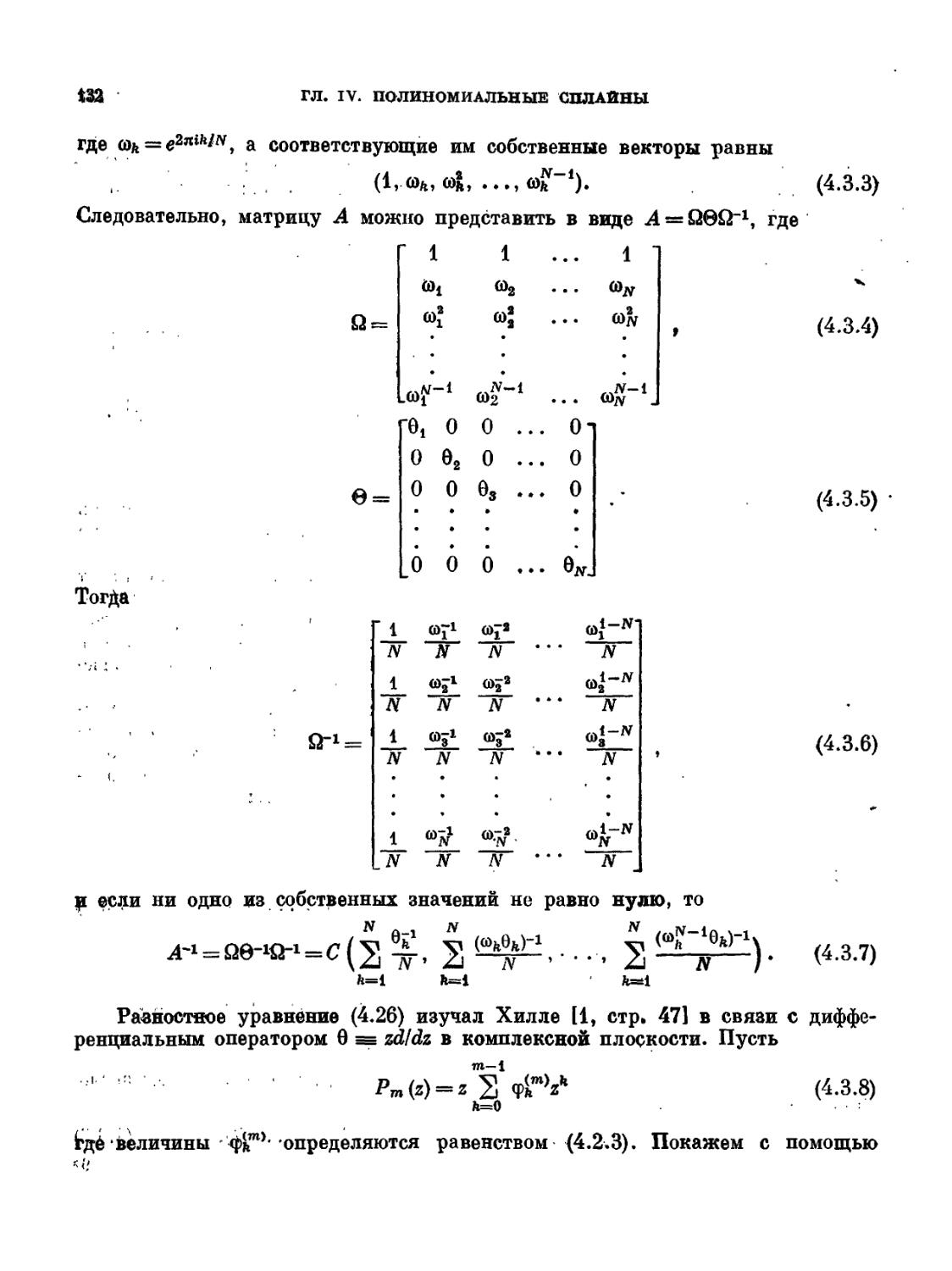
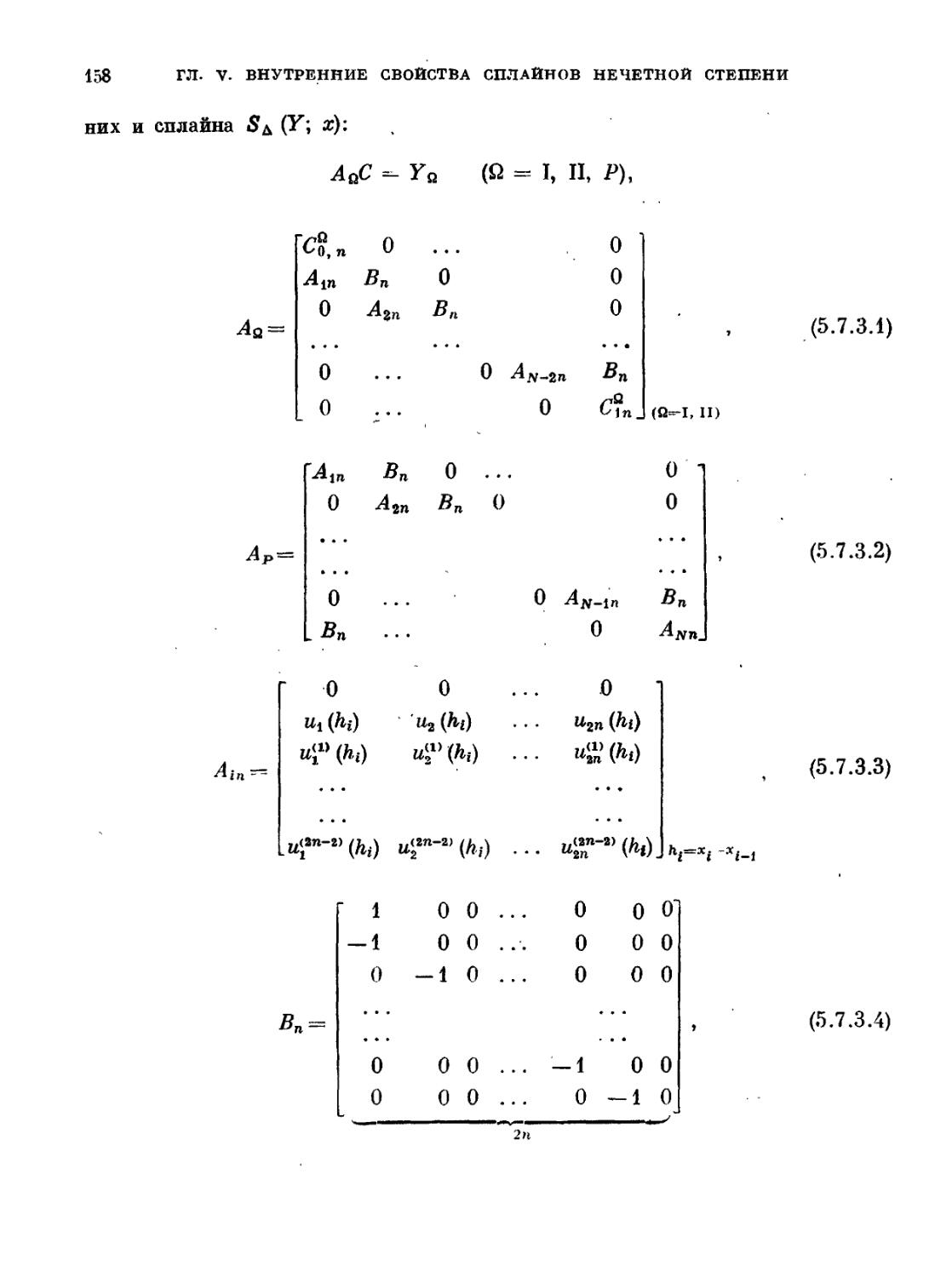
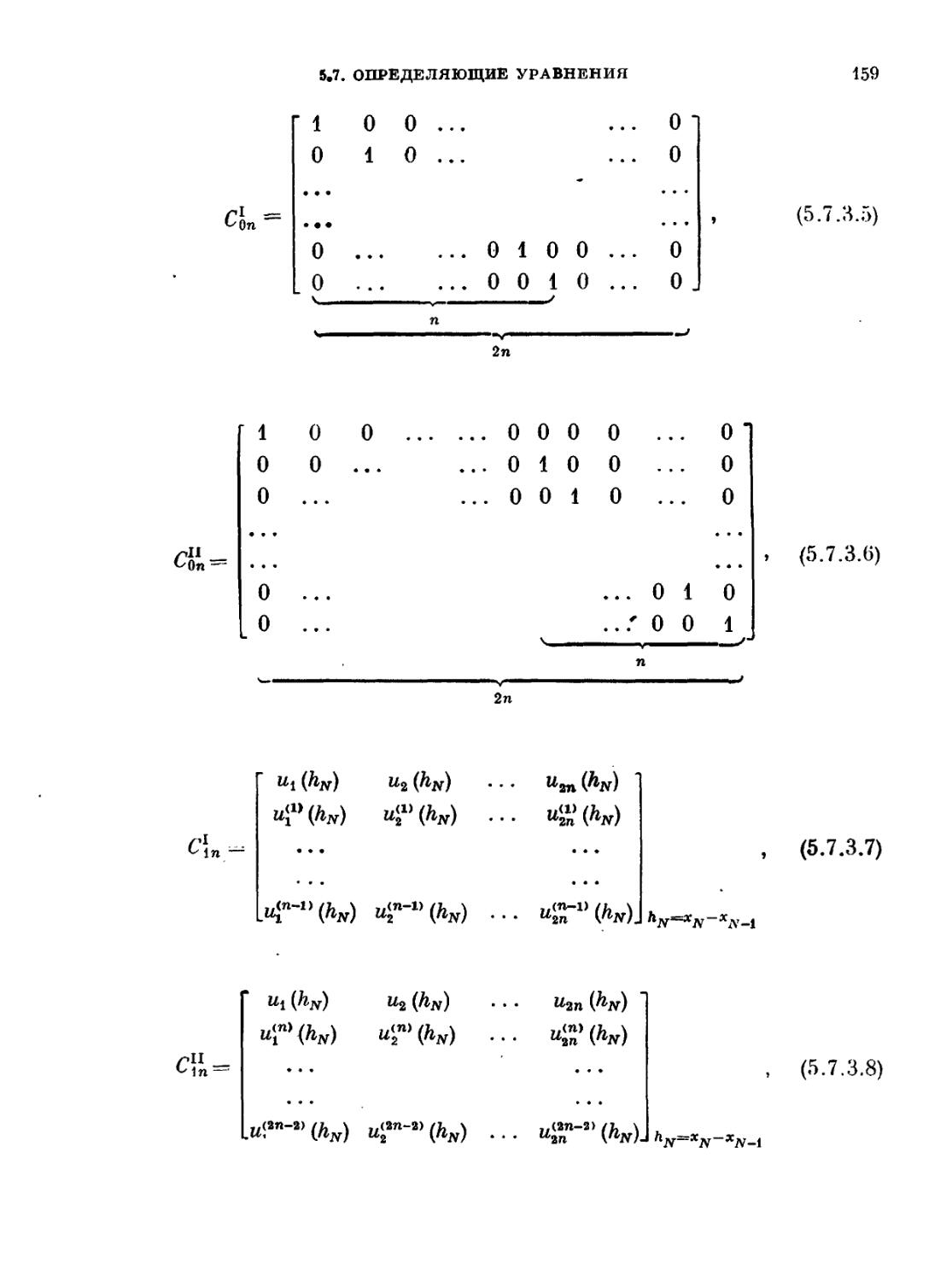
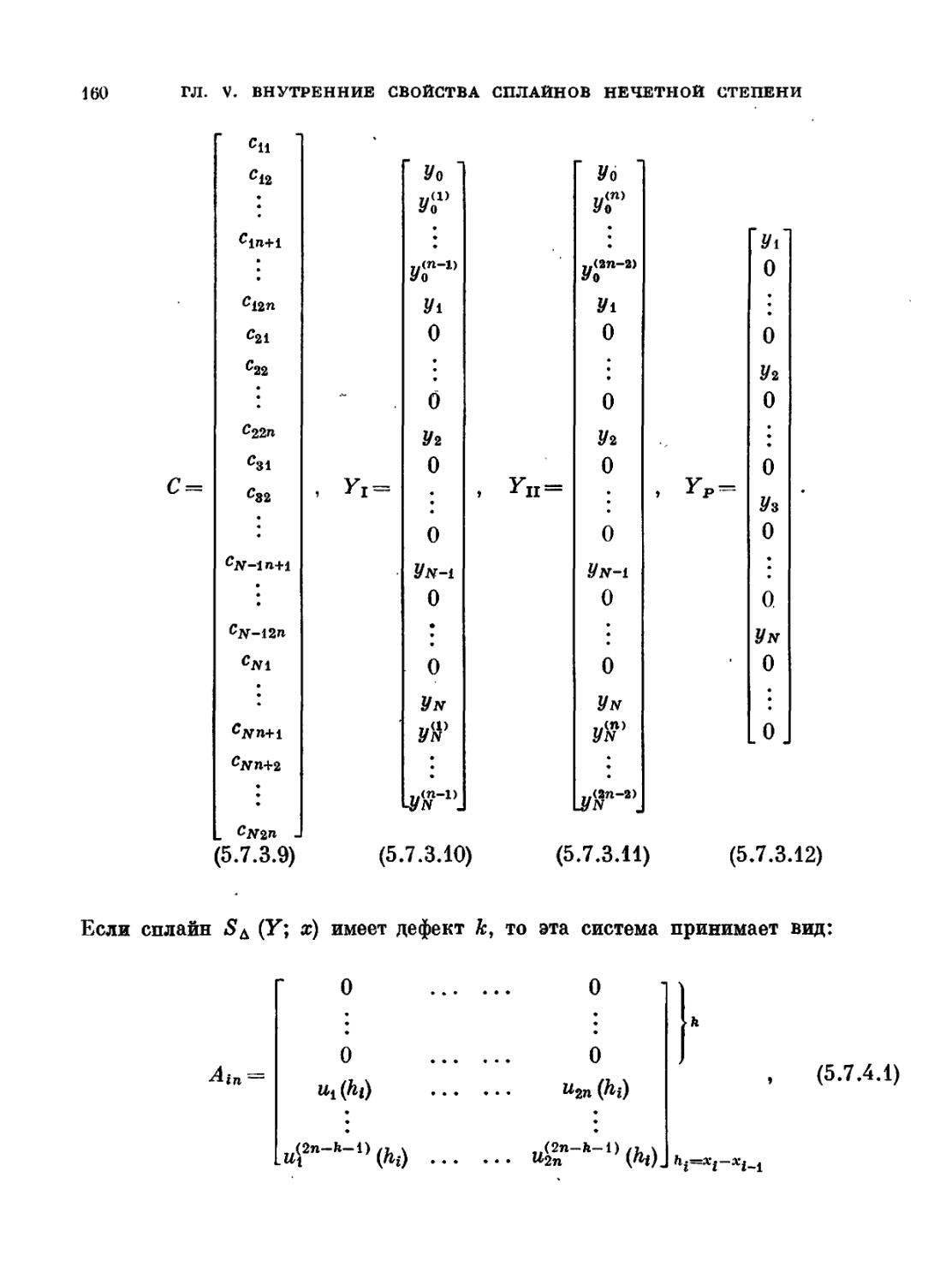
Текст
Дж. АЛ БЕРГ, в. НИЛЬСОН, Дж. УОЛШ
ТЕОРИЯ СПЛАЙНОВ
И ЕЕ ПРИЛОЖЕНИЯ
Перевод с английского
Ю. Н. Субботина
под редакцией
С. В. Стечкина
с добавлениями
С. Б. Стечкина и Ю. Н. Субботина
Издательство «Мир» Москва 1972
ТЬе ТЬеогу о! ЗрИпез
аш! ТЬеп* АррНсаИопз
Д. Н.
А1гсгаП КезеагсЬ ЬаЪогаЪопез
Еаз1 НаПГогй, СоппесИси1
Е. N. N115011
РгаН & ^УЫЬпсу А1гсга{* Сотрапу
ЕазЪ Наг1!ог<1, СоппесИсиЬ
Д. Ь. \Уа1зЬ
о! Магу1ап<1
СоИеде Рагк, Магу1ап<1
1967
АсаAет1С Ргезз №\и Уогк апй Ьои<1оп
ДК 518.5
Монография посвящена изложению основ теории кусочно-полиномиаль-
кусочно-полиномиальных приближений и некоторых ее применений. Это новое направление в тео-
теории приближений, которое в настоящее время усиленно развивается главным
образом американскими математиками. Активное участие в его разработке при-
принимают и авторы монографии, среди которых Дж. Уолш — видный амери-
американский ученый, известный советским читателям по переводу его монографии
«Интерполяция и аппроксимация рациональными функциями в комплексной
области».
Кусочно-полиномиальные, или, как их теперь называют, сплайн-прибли-
сплайн-приближения, имеют ряд преимуществ перед обычными полиномиальными приближе-
приближениями, в частности при решении задач на быстродействующих вычислительных
машинах.
Книга представляет большой интерес для специалистов по теории прибли-
приближений и по вычислительной математике, а также для инженеров и вычислите-
вычислителей, студентов и аспирантов университетов и институтов с отделениями при-
прикладной математики.
Редакция литературы по математическим наукам
Инд.2-2-3
1-72
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Теория сплайнов и сплайн-аппроксимаций представляет собой весьма
важный и интенсивно развивающийся раздел теории приближения функций.
Во многих задачах сплайны являются более естественным аппаратом прибли-
приближения, чем многочлены. К таким задачам относятся практически важные га да-
дачи интерполирования и сглаживания функций, численного дифференцирования,
численного интегрирования функций, а также численного интегрирования
дифференциальных уравнений. В теоретических исследованиях сплайны появ-
появляются как решение различного рода вариационных задач теории приближений
(задачи о поперечниках). Безусловно, у сплайнов большое будущее.
В вычислительную математику и теорию приближений сплайны прони-
проникали постепенно, на протяжении длительного времени. Первой ласточкой
здесь надо считать «метод ломаных Эйлера» интегрирования обыкновенных
дифференциальных уравнений. В теории приближений они появились по край-
крайней мере с эпохи Лебега и Джексона как вспомогательные средства для дока-
доказательства теоремы Вейерштрасса и «прямых теорем» теории полиномиальных
приближений. Приближения сплайнами естественно возникают также при
исследовании квадратурных формул. С уклоном в задачи вычислительной
математики сплайн-аппроксимации систематически исследовал и активно
пропагандировал И. Шёнберг (США). Как промежуточное приближение
они появились в глубоких исследованиях Н. П. Корнейчука о приближе-
приближении дифференцируемых функций. Отметим еще работы В. М. Тихомирова по
поперечникам функциональных классов и Ю. Н. Субботина по функцио-
функциональной интерполяции, в которых с неизбежностью также появляются
сплайны.'
В Настоящее время знакомство с основными свойствами и приложениями
сплайнов необходимо как специалистам по теории приближений, так и при-
прикладникам, использующим результаты и методы этой теории.
6 ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
В предлагаемой читателю монографии Алберга, Нильсона, Уолша изла-
излагаются некоторые важные вопросы теории сплайнов. Изложение рассчитано
на широкий круг математиков, инженеров и прикладников и поэтому является
далеко не полным. В конце книги помещены добавления переводчика и редак-
редактора перевода, где освещается ряд задач, не затронутых в основном тексте.
Отметим, однако, что общий характер книги не позволил нам рассмотреть
с должным вниманием задачи о поперечниках.
Я надеюсь, что появление этой книги будет способствовать развитию
теории сплайнов и ее более широкому использованию в прикладной матема-
математике.
С. Б. Стечкин
Глава I. ВВЕДЕНИЕ
1.1. Что такое сплайн?
Целесообразно книгу по теории сплайнов начать с определения сплайна
в его простейшей и наиболее употребительной форме и объяснить происхо-
происхождение этого термина. В течение многих лет чертежники использовали длин-
длинные тонкие рейки из дерева или какого-либо другого материала в качестве
лекал, проводя с их помощью плавные кривые через заданные точки. Эти
рейки, или сплайны, закрепляют на месте, подвешивая к ним в некоторых
точках свинцовые грузила. Изменяя положение точек, в которых подвеши-
подвешиваются грузила, а также положение сплайна и грузил, при достаточном числе
грузил можно добиться, чтобы сплайн проходил через заданные точки.
Если рассматривать рейку (сплайн чертежника) как тонкую балку, то
имеет место закон Бернулли — Эйлера
М (х) = Е1 [ИВ. (я)],
где . М (х) — изгибающий момент, Е — модуль Юнга, / — геометрический
момент инерции и Я (х) — радиус кривизны кривой, совпадающей с дефор-
деформированной осью балки. При незначительных изгибах Я (х) можно заменить
на 1/у"(х), где у (х) — деформированная ось балки. Таким образом,
Поскольку грузила по существу действуют как простые опоры, функция М (х)
между точками закрепления грузил изменяется линейно.
Математическим сплайном называют приближенное представление дефор-
деформированной оси рейки кусками кубической параболы (обычно различными
между каждой парой смежных грузил) с определенными разрывами производ-
производных, допускаемых в точках прикрепления грузил (где стыкуются два поли-
полинома).
Математический сплайн простейшего вида непрерывен и имеет непрерыв-
непрерывные первую и вторую производные, а третья производная может претерпевать
в точках соединения разрыв с конечным скачком. Это соответствует рейке,
имеющей непрерывную кривизну, скорость изменения которой разрывна
в точках прикрепления грузил. Для многих важных применений эта математи-
математическая модель сплайна чертежника достаточно близка к действительности.
На практике чертежник не помещает грузила в заданных точках, через
которые должен проходить его сплайн. Более того, обычно между заданными
8 ГЛ. I. ВВЕДЕНИЕ
точками и грузилами нет взаимно однозначного соответствия. Бели же исполь-
используется математический аналог, то обычно в качестве заданных точек берут
точки соединения, причем число заданных точек совпадает с числом точек
соединения (включая концы).
В следующем разделе мы кратко изложим историю новейших исследова-
исследований по математической теории сплайн-аппроксимаций. Из этой истории станут
ясными некоторые свойства сплайнов, а также будет понятно расширение
этого -понятия по сравнению с аппроксимирующим инструмент чертежника.
1.2. Последние достижения в теории сплайнов
Аппроксимация сплайнами в ее современном виде впервые появилась
в статье Шёнберга [1]. Как указано в разд. 1.1, существует очень тесная связь
между теорией сплайнов и расчетом балок. В работе Сокольникова [1, стр. 1—4]
дается краткий, но очень четкий обзор развития методов расчета балок. В нем
предвосхищены некоторые из недавних достижений в теории сплайнов, в частно-
частности свойство минимальной кривизны. Как отметил Шенберг [1], приближения,
применяемые в страховом деле, также включают в себя понятия, тесно«вязы-
вающие их со сплайнами.
После 1946 г. Шёнберг и некоторые его ученики продолжили изучение
сплайнов и моносплайнов. В частности, Шёнберг и Уитни [1; 2] впервые полу-
получили признаки существования некоторых интерполяционных сплайнов. К во-
вопросу существования сплайнов нечетной степени с интерполяцией в точках соеди-
соединения возможен теперь более простой подход, разработанный Албергом, Ниль-
соном, Уолшем* [2; 8]; при этом подходе используется основное интегральное
соотношение, полученное Холлидеем 11] для кубического сплайна 5Д (/; х),
интерполирующего функцию / (х) на сетке А:
ь ь ь
| Г (*) I2 их = | | 81 (/; *) I2 ** -V \ I Г (*) - 81 (/; х) |2 их.
а
Мы будем называть это интегральное соотношение первым интегральным
соотношением. Вывод его основан на следующей теореме Холл идея.
Теорема (Холлидей). Пусть даны сетка Д: а = х0 <; Х\ <; . . .
. . . < х^ — Ь и действительные числа {^} A = 0, 1, . . ., ./V). Среди всех функ-
функций / (х), имеющих на [а, Ь] непрерывную вторую производную и таких, что
/ (л^) = уг (г = 0, 1, . . ., Щ, сплайн 5Д (/; х) с точками соединения в Х(, для
которого 5д (/; а) = 5д (/; Ь) — 0, минимизирует интеграл
ь
\?'(х)\г&с. A.2.1)
Эта теорема и метод ее доказательства послужили толчком для развития
многих разделов современной теории сплайнов. Так как интеграл A.2.1) часто
1.2. ПОСЛЕДНИЕ ДОСТИЖЕНИЯ В ТЕОРИИ СПЛАЙНОВ 9»
дает хорошее приближение для интеграла от квадрата кривизны кривой
У — 1 (#)» то свойство, сформулированное в теореме Холлидея, часто называют
свойством минимальной кривизны. Очевидна также тесная связь этой теоремы
с минимизацией потенциальной энергии, затраченной на отклонение балки 1).
Мы рассмотрим некоторые обобщения простого кубического сплайна.
Для этих обобщений известны аналоги теоремы Холлидея, но, поскольку в новых
условиях нет аналога кривизны, мы будем говорить о свойстве минимальной
нормы. Это вполне обосновано, ибо в каждом случае можно указать соответ-
соответствующее гильбертово пространство Ж, в котором интеграл A.2.1) или его-
аналог равен квадрату нормы функции / (х).
Лишь в 1964 г. был развит подход к изучению сплайнов с точки зрения
гильбертовых пространств. В этом году авторы (Алберг, Нильсон, Уолш [4—7]}
ввели некоторые ортонормальные базисы пространства $в, состоявшие цели-
целиком из сплайнов или, выражаясь точнее, из эквивалентных классов сплайнов.
Для любого ортонормального базиса пространства Ж функция / (х) из Ж при
любом целом положительном N имеет среди линейных комбинаций первых N
элементов базиса элемент наилучшего приближения. Пусть ||»||<§#— норма
в Ж, 1!г (х) (I = 1, 2, . . .) — элементы базиса и
Функция ||/~ V \\&е принимает наименьшее значение, когда а% совпадают
с коэффициентами при XIх (х) (* = 1, 2, . . .) в разложении функции / (х) по
элементам полного базиса.
Желательно получить другую характеристику элемента наилучшего при-
приближения, особенно если она сможет облегчить его определение. Такую харак-
характеристику действительно можно указать. Алберг, Нильсон, Уолш в работе [11
получили следующий результат: если дана сетка Д: а = х0 <; Х\ <; . . . < хк —
= Ь, то среди всех простых периодических кубических сплайнов на Д сплайн,
интерполирующий периодическую функцию в точках сетки, осуществляет
наилучшее приближение в предыдущем смысле, В дальнейшем этот результат
был распространен на целый ряд других случаев: Алберг, Нильсон, Уолш-
[2, 4, 5, 7, 9], де Бур [3], Шёнберг [7], Гревиль [2], де Бур, Линч [1, 2].
В гл. III, V и VI настоящей книги изучаются с точки зрения гильбертова
пространства соответственно кубические сплайны, полиномиальные сплайны
нечетной степени и обобщенные сплайны. Пусть Ж обозначает функциональное
пространство классов функций; мы покажем, что при соответствующем выборе-
нормы Ж будет гильбертовым пространством. Однако в дальнейшем вместо <Ш
мы будем употреблять другие обозначения.
Далее, различные авторы исследовали сходимость сплайнов и их произ-
производных 5да) (/;, х) к /<«) (ж), когда норма сетки || Д || = шах \ x^+^ — X; \ стре-
стремится к нулю. Первые результаты в этом направлении получены в работе Албер-
*) Потенциальная энергия, затраченная на отклонение балки, пропорциональна интег-
интегралу от квадрата кривизны деформированной оси балки (Сокольников [1, стр. 2]).
40 ГЛ. I. ВВЕДЕНИЕ
га, Нильсона, Уолша [1] для кубических сплайнов; при этом использовалось
первое интегральное .соотношение. Бели функция / (х) принадлежит про-
пространству С2 [а, Ь] и сплайн 5Д (/; х) интерполирует ее в' узлах сетки, то
#да> (/; я) сходится равномерно относительно х к /<«) (я) при а = 0, 1. Более
подробный анализ был проведен Албергом и Нильсоном [1—3]. В частности,
было показано, что если / (х) принадлежит С% [а, Ь], то 51 (/; х) сходится рав-
равномерно к /" (я) при условии, что распределение узлов сетки приближается
к равномерному и || А || -*■ 0. Это ограничение на сетку позднее было снято
Шармой и Мейером [1, 2].
Биркгоф и де Бур [1, 2] показали, что если / (а;) принадлежит С4 [а, Ы, то
(а-0,1, ...,4) A-2.3)
при условии ограниченности величины Дд = тах || А \\1{хг — а^-О. При более
слабых требованиях, которым должна удовлетворять функция / (#), щпример
для / (х) 6 С [«, Ь] или / (а;) ^ С1 Ь» Ы> соответствующие свойства сходимости
были получены Албергом, Нильсоном, Уолшем [12]. Кроме того, сходимость
полиномиальных сплайнов нечетной степени изучалась Албергом, Нильсоном,
Уолшем [2, 9], Шёнбергом [41 и Циглером [1], многомерных сплайнов — Албер-
Албергом, Нильсоном, Уолшем [4, 7, 10], обобщенных сплайнов — Албергом, Ниль-
Нильсоном, Уолшем [5, 7, 10].
Многие из этих результатов о сходимости зависят от тонкой структуры
системы линейных уравнений, определяющих сплайны. В гл. II и IV теория
сплайнов излагается с этой точки зрения. В то же время некоторые результаты
о сходимости можно получить, не прибегая к этим определяющим уравнениям.
В частности, для полиномиальных сплайнов степени 2тг — 1 таким способом
можно установить сходимость вплоть до производных (тг *— 1)-го порядка.
Более того, с помощью интегрального соотношения
ь ь
(*) Ох, A.2.4)
выведенного Албергом, Нильсоном, Уолшем [10], при различных ограниче-
ограничениях можно доказать сходимость вплоть до производных Bп — 2)-го порядка.
Это было сделано для обобщенных сплайнов, частным случаем которых являют-
являются полиномиальные сплайны нечетной степени. Интегральное соотношение
A.2.4) называют вторым интегральным соотношением; для подходящего
функционального пространства оно следует из теоремы Рисса о представлении
линейных функционалов. Этот подход развивается в гл. III, V и VI. При усло-
условии ограниченности величины ЯА основным здесь будет результат
п-а-1 (а = 0, 1, ..., 2л-1). A.2.5)
Для кубических сплайнов этот результат слабее, чем A.2.3). В общем случае
вопрос о возможности замены 2ге — а — 1 на 2тг — а остается открытым.
Теория сплайнов развивалась в нескольких направлениях. Особенно
важны обобщения на многие переменные. Первый шаг быд сделан Биркгофом
1.2. ПОСЛЕДНИЕ ДОСТИЖЕНИЯ В ТЕОРИИ СПЛАЙНОВ Ц
и Гарабедяном [1], до первое удачное обобщение получил де Бур [1, 2], дока-
доказавший как существование, так и единственность определенных бикубических
интерполяционных сплайнов1). Позднее Алберг, Нильсон, Уолш [4, 11] рас-
распространили первое интегральное соотношение на сплайны нескольких пере-
переменных. В результате этого для целого ряда многомерных сплайнов были
доказаны существование, единственность, свойство минимальной нормы и свой-
свойство наилучшего приближения. Вопросы сходимости были сведены к анало-
аналогичным вопросам для одномерных сплайнов, ответы на которые были известны.
Многомерные сплайны рассматриваются в гл. VII и VIII.
Обобщение в другом направлении заключается в замене оператора /Jп,
«вязанного с полиномиальным сплайном степени 2тг — 1 (здесь 2? г= д,1йх),
оператором Ь*Ь, где
Ь а ап (х) Бп + ап_4 (х) Я" + . . . + ао(х) A.2.6)
и Ь* — оператор, формально сопряженный с Ь. Теперь в каждом интервале
•сетки сплайн $ (я) должен удовлетворять уравнению Ь*Ь8 — 0 вместо ОШ8 =
— 0. Сплайны, определенные таким образом, называются обобщенными сплай-
сплайнами. Первый шаг в этом направлении сделал Шенберг [7], рассмотревший
«тригонометрические сплайны». Затем последовало полное обобщение: Гре-
виль [1], Алберг, Нильсон, Уолш [5, 7, 10], де Бур, Линч [1]. Более абстракт-
абстрактный подход к теории сплайнов развили Аттиа [1] и его коллеги из Гренобля.
Оператор Ь = О (О — а) рассматривался Швайкертом Ш; он назвал
получившиеся у него сплайны «сплайнами в напряженном состоянии». При
надлежащем выборе а эти сплайны по сравнению с кубическими имеют некото-
некоторые преимущества, а также и некоторые недостатки; в частности, с их помощью
можно избежать появления лишних точек перегиба, но при этом кривизна
«будет концентрироваться вблизи точек соединения. Обобщенным сплайнам
посвящены гл. VI и VIII.
Сард [1] уделил значительное внимание приближению линейного функцио-
функционала X другим линейным функционалом <$, таким, что остаток М а X — X
аннулирует полиномы степени п — 1. При естественных ограничениях выпол-
выполняется равенство
ь
0 (И; A.2.7)
ядро &С {&', V) называется ядром Пеано. Сард [1] искал такой функционал X,
•чтобы интеграл
ь
( Ф' *\2 гН
г) В дальнейшем мы применяем следующую, терминологию: / (г, $) будет называться
дважды кубическим полиномом (а не бикубическим), если / (<, «) — кубический полином
по I для каждого $ и кубический полином по 5 для каждого I. Дважды, кубический сплайн
совпадает с дважды кубическим полиномом в каждом частичном прямоугольнике, опре-
определенном двумерной сеткой.
12 ГЛ. I. ВВЕДЕНИЕ
принимал наименьшее значение; для целого ряда функционалов X ему уда-
удалось найти такие X. В 1964 г. Шёнберг показал, что при слабых ограниче-
ограничениях на X среди функционалов X вида
& = «о/ М + <*Л М + • • • 4-
оптимальный функционал X получается, когда #/ = Х8± (/; ж), где 5Д (/; ж) —
простой (см. ниже) полиномиальный сплайн (степени 2тг — 1), интерполирую-
интерполирующий функцию / (х) на сетке А: а = х0 <С а^ < . . . < а:^ = Ь. Этот результат
был обобщен (Алберг, Нильсрн, Уолш [8], Алберг, Нильсон [6]) на функциона-
функционалы X вида
2
где /> -С л — 2 и некоторые коэффициенты ац с самого начала полагаются'
равными нулю. Для обобщенных сплайнов равенство A.2.7) принимает вид,
ь
Я/ = | Ж (Л; О Ь/ @ <й,
где ядро е%* {&\ г) зависит от Ь (см. также де Бур и Линч [2]). Эти вопросы
изучаются в гл. III, V, VI и VIII.
При обобщении результатов Шёнберга о приближении функционалов,
потребовалось ввести сплайны несколько иного рода. Характер этих различий:
частично позволяет выявить следующую терминологию.
Сплайн порядка 2п называется простым, если его Bп — 1)-я производная
претерпевает разрыв только в узлах сетки. В большинстве случаев мы будем,
рассматривать простые сплайны. Если во внутреннем узле хг сетки допускают-
допускаются разрывы производных, начиная с Bп — к — 1)-й, то говорят, что сплайн:
имеет дефект к в точке хг. Если сплайн имеет дефект к во всех внутренних
узлах сетки, то гбворят, что он имеет дефект к. В дальнейшем мы будем счи-
считать, что 0 ^ к ^ п. В этой терминологии решение уравнения Ь*Ь1 — 0 имеет
на [а, Ъ] дефект 0, а простой сплайн имеет дефект 1.
Требование, чтобы некоторые коэффициенты а,ц в A.2.8) заранее были:
нулями, часто налагает на применяемые сплайны еще более сложные и нере-
нерегулярные условия непрерывности. Такие сплайны называются гетерогенными^
их мы подробно рассмотрим в гл. VI и VIII. Они были введены Албергом».
Нильсон ом, Уолшем [8] при изучении аппроксимации линейных функционалов.
Работа Голомба и Вайнбергера [1] об «оптимальном» приближении линей-
линейных функционалов очень тесно связана с теорией сплайнов. Во многих случа-
случаях фигурирующие в их приближениях функции и (х) являются интерполяцион-
интерполяционными сплайнами. Но это не отмечается в упомянутой работе; исследование-
протекает в ином направлении, и функции и (х) появляются только как реше-
решение вариационной задачи. Теорема Холлидея, выясняющая связи этих иссле-
исследований с теорией сплайнов, не упоминается. Позднее эту связь осознал Сек-
реет [2].
Глава II. КУБИЧЕСКИЕ СПЛАЙНЫ
2.1. Введение
Естественно начинать изучение сплайнов с кубических сплайнов. Тесная
«вязь последних со сплайнами чертежника, возникающая в результате их замены
тонкими рейками, открывает многие их важнейшие свойства и объясняет
значительную часть их приложений к задачам численного анализа.
Сплайны успешно применяются в элементарных процессах интерполяции
и приближенного интегрирования. Однако наиболее важна их эффективность
в численном дифференцировании. В значительной степени это объясняется
присущей им быстротой сходимости. Кроме того, свойства наилучшего прибли-
приближения и минимальной нормы, развитые в гл. III, также содействуют этой
эффективности.
В этом вводном разделе наряду с основными уравнениями, определяющими
сплайн, приводятся методы, необходимые- для простых применений. Затем
в разд. 2.2 и 2.3 излагаются вопросы существования и сходимости, представ-
представляющие наибольший интерес. В разд. 2.4 и 2.5 рассматриваются сплайны с рав-
равномерными узлами и даются специальные формулы численного дифференци-
дифференцирования и интегрирования для этого случая. В разд. 2.6 обсуждается приме-
применение сплайнов для вычерчивания кривых по точкам. В разд. 2.7 и 2.8 сплайны
применяются для численного решения линейных дифференциальных уравне-
уравнений и интегральных уравнений. В конце главы выводятся свойства сходимости
и существования, требующие более тонких методов анализа.
При определении математического сплайна отрезок а ^ х ^ Ь делится
на части точками, соответствующими положениям грузил:
Д: а = х0 <С XI <С . . . <С х1^ = Ъ.
Кроме того, задаются соответствующие ординаты:
У- Уо> У±
Ищется функция <УД (У; х), которую мы будем обозначать <5Д (х) или <УД,У (х)
(и #д,у, если х нас не интересует), непрерывная на [а, Ь] вместе со своими
первой и второй производными, совпадающая с кубическим полиномом на каж-
каждом отрезке х^_! -^ х-^. х}- (/ = 1, 2, . . ., IV) и удовлетворяющая условиям
Яд (У; *у) = У^ (/ = 0, 1, . . ., Щ.
Функцию <5Д (У; х), или <5Д (я), называют сплайном относительно сетки Д
или сплайном на А, интерполирующим значения У] в узлах сетки. Сплайн
называется периодическим с периодом Ь — а, если
О) (р = 0, 1,2).
14 ГЛ. II. КУБИЧЕСКИЕ ЙПЛАЙНЫ
По традиции обозначим через М; «моменты» 5д (х^ (/ = 0, 1, . . ., )
хотя они не являются истинными моментами балки в обычном смысле этого
слова. В силу линейности второй производной на [я/_1, ХА
B.1.1)
где Л/ = X} — а:;_1. Проинтегрируем дважды обе части равенства B.1.1) и, вычи-
вычислив константы интегрирования, получим
1
щ 1 ь} 6
Из B.1.3) находим односторонние пределы производной:
^^ М=^. ■ B.1.4)
Согласно B.1.1) и B.1.2), функции 81. (х) и 5д (х) непрерывны на [а, Ь].
Из непрерывности функции 8'ь(х) в точках х; с учетом равенств B.1.4)
получаем
% *±р%гД!1=11!Ь. B.1.5)
Для периодического сплайна равенства B.1.5) Ц =. 1, 2, . . ., N — 1) дают
систему N — 1 уравнений относительно Ми М2> . . ., Му» Мы требуем в этом
случае, чтобы уравнение B.1.5) было также справедливо для У = N.• Здесь
в силу периодичности* должны выполняться соотношения у# = уо> М1^ = Мо,
УN+^ = Уи Мм+1 = Ми ^N+1 — Ъ\-
Чтобы определить величины Мо, Ми • • •» М-^ для непериодического
сплайна, надо задать два дополнительных условия, так называемые «краевые
условия». Задание наклонов сплайна в точках а и & приводит к аналогу двойной
консольной балки. Пусть 5Д (а) = у'о, 8к(Ь) = у'м, тогда из B.1.4) имеем
Выбор Мо = 0, Мн = 0 соответствует расположению простых опор на концах.
Условие , . . '•;.'.
, • ; ... . Мо — ЯЖ! = 0, 1.>
эквивалентно расположению простой опоры в точке х_± = (х0 — Яж1)/A — Я)
и требованию, чтобы вся кривая на отрезке #_1 ^ х ^ х^ совпадала с кубиче-
кубическим полиномом. Обычно берут Я ==. 1/2.
2.1. ВВЕДЕНИЕ
" 15
Мы будем также рассматривать более общие краевые условия
2М0 + 'к^М^ = й0, \1цМх_1 + 2М^ — с?^. B.1.6)
Введем обозначения
* == А I ?! ' г^-' ^ ~~" ^ « === » » • • • I •*" — ■"•/ •
Тогда условия непрерывности B.1.5) принимают вид
B.1.7)
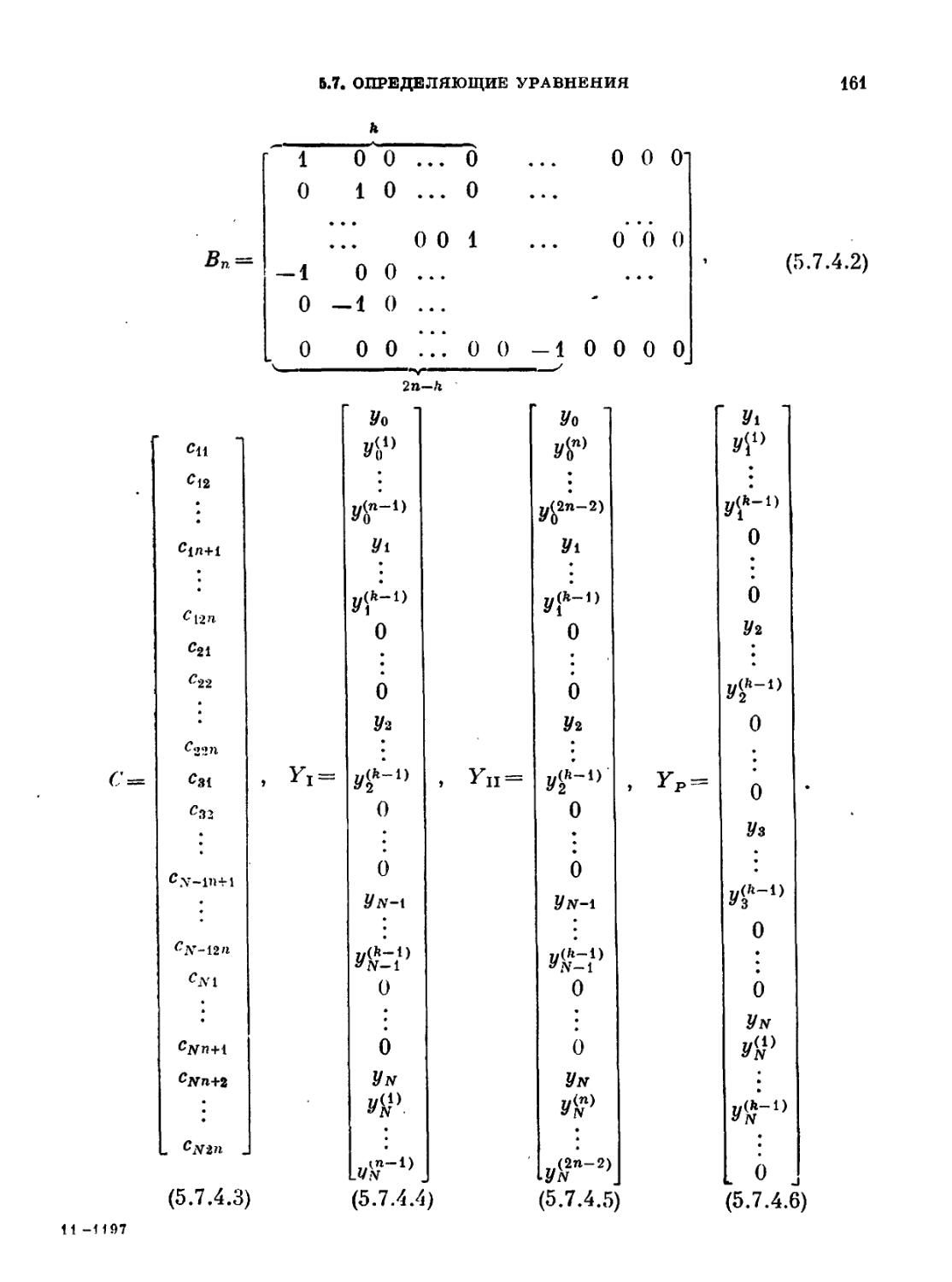
Уравнения B.1.6) и B.1.7), определяющие непериодический сплайн, можно
записать теперь в матричной форме
Ма
-2
0
К
2
Цо
0 ...
/\/4 • • •
2 ...
0
0
0
0
0
0
0
■0
0
О
$N-2
B.1.8)
0 0 0
0 0 0
0 0 0 ... 0 \1„ 2
где й/ — правая часть равенства B.1.7). Определяющие уравнения для перио-
периодического сплайна имеют вид
0 0
Мг
мч
- 2 %1 0 ..
0 ьц 2 ..
О
О
о
о
0
О
0 0 0
0 0 0
ьо о
2
0
О
2
B.1.9)
$N-
N-2
где М0 = МК, К =
Во многих случаях более удобно работать с наклонами /
а не с моментами М]. Тогда на отрезке [х;-и х;] справедливы равенства
{J( )Л (X — «/-1J(Х*— X)
! / Ц ^ / /
ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
д [X) — ГП)-Х
.д-За)
ч
+
B.1.11).
Отсюда находим
81 (х) --= -
и
B.1.12)
_-—_-
B.1.13)
Из . требований непрерывности второй производной 5"д (х) в точках
(/ = 1, 2, ..., #— 1) находим
или, в более удобной форме,
A.1.15)
В непериодическом случае при общих краевых условиях 2т0 4- [Лол*! =■ с0,
-! + 2т№ = с^ система уравнений принимает вид
т0
2
0
*
•
•
0
0
.0
2
•
•
*
0
0
0
0 .;.
И • • •
2 ...
•
0 ...
б ...
0 ...
0
0
0
•
•
2
0
0
0
0
•
•
•
2
0
0
0
•
•
*
0
2
B.1.16)
с?—правая часть равенства B.1.15).
2.1. ВВЕДЕНИЕ
17
В периодическом случае получаем
о
0
0
0
0
0
0
0
0
0
0 0 0
0 0 0
о о
0
7712
771о
, B.1.17)
0
Краевые условия в терминах величин М] классифицируются следующим
образом:
при х = а:
(И)
(ш)
при д; =
A1)
(Ш)
и в терминах величин т^
(I)
A1)
(Ш)
A)
(И)
B.1.18)
при х = а:
при х = Ь:
B.1.19)
кг
(ш)
2—1197
18 ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
Здесь у1 и ун — заданные значения второй производной сплайна на концах
отрезка. Эти два множества краевых условий равносильны, если
_ ^Ау , с 2—
Нетрудно проверить, что правые части равенств B.1.7) и B.1.15) равны
утроенным значениям в точке х$ соответственно второй и первой производных
параболы, проходящей через точки (жу_1, У}-1), (#/, у;) и {х^+х, у^+^) и имеющей
вертикальную ось. Этот факт особенно важен в связи с задачей вычерчивания
кривой по точкам с помощью сплайнов более высокого порядка; он исследован
подробно в гл. IV.
Для решения системы уравнений B.1.8) или B.1.16) имеется очень
аффективный алгоритм. Рассмотрим уравнения
и образуем вспомогательные величины (к= 1, 2, ..., тг)
B.1.20)
Последовательно исключая л4, .*.., хп^ из 2-го, . . ., ге-го уравнений, полу-
получаем эквивалентную систему
+ ик (к = 1, . . ., п — 1),
откуда последовательно определяем хп, . , .'; ^.
Для матриц с доминирующей главной диагональю, с которыми мы
главным образом имеем дело, эта процедура устойчива в том смысле, что ошибки
быстро затухают @<Сск1рк < 1). Заметим также, что величины рк и д& зависят
от сетки Аи не зависят от значений ординат 'в узлах сетки. Это позволяет для
фиксированной сетки А один раз вычислить значения {рк} и {д&} и использо-
использовать их при построении сплайнов с различными ординатами в узлах сетки.
2.2. СУЩЕСТВОВАНИЕ, ЕДИНСТВЕННОСТЬ И НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ 19
Этот метод распространяется на периодические сплайны. Рассмотрим
первые п — 1 уравнений системы
+ ^2^2 + С%ХЪ — ^2»
B.1.21)
из них выразим хи #2» • • •» ^п-1 через #п и найдем ж„ И8 последнего уравне-
уравнение. В дополнение к уже определенным величинам ръ, д&, ик вычислим для
к — 1, 2, . . ., п величины
^г Eо=1)- BЛ-22)
Тогда первые ге — 1 уравнений системы B.1.21) запишутся в виде
хк = ЯкХн+1 + 8кхп + ик (к = 1, . . ., п — 1).
Положим
хк = Нхп + ик (* = 1, 2, ..., л-1); B.1.23)
тогда
«л (*п = 1),
"& К = 0).
Отсюда находим ?п_1, . . ., ^1, г>п-ъ • • •» ^1» определяем хп из уравнения
а затем вычисляем #п_1, . . ., ^ по формуле B.1.23).
Заметим, что если все коэффициенты ак, Ьк и ск постоянны, то величины
рк и дь можно найти, ретив разностное уравнение второго порядка. Действи-
Действительно, положим рк = Ъ,к1Нк.1 (к0 = 1), ак = а, ^ = &и.^ = с для всех &;
тогда из равенств B.1.20) получим соотношения
равносильные разностному уравнению
К — &&ь-1 + аскк_2 = 0.
Аналогичным свойством обладают и периодические сплайны.
2.2. Существование, единственность и наилучшее приближение
Для большинства представляющих интерес случаев доказательство суще-
существования сплайна требует применения теоремы Гершгорина (см. Тодд 1,
стр. 2271), в которой утверждается, что собственные значения матрицы (а,-,)
2*
20 ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
(^ / — 1, 2, . . ., п) лежат в объединении кругов
\ X \ц\ (<
Зфг
комплексной плоскости. Матрица с доминирующей главной диагональю
(| ап I > 2 I аи I) невырожденна. В матрицах, фигурирующих в уравнени-
ЗФ1
ях B.1.9) и B.1.17), сумма 2 I аи I всегда равна 1, в то время как ац = 2.
Н1
В B.1.8) и B.1.16) главная диагональ будет доминирующей, если Я,о, ц^, ц0,
%к меньше 2 по абсолютной величине.
Таким образом, периодический кубический сплайн с заданными ордина-
ординатами в узлах сетки всегда существует и единствен; он задается формулой B.1.2),
где величины М; однозначно определяются из B.1.9). То же верно, в частно-
частности, для непериодического сплайна, имеющего консольные концы {т0 и тя
заданы), или простые краевые опоры (Мо = Мк = 0), или заданные краевые
моменты, или простые опоры в точках за пределами концов сетки (например,
Мо = ХМи Мя — цМ^_1, 0 < Я < 1, 0 < \1 < 1).
Общая теорема существования, охватывающая более широкий класс
непериодических кубических сплайнов, доказывается в разд. 2.9. Там нам
понадобятся специальные свойства матрицы коэффициентов.
Заметим, что множеству величин М) может соответствовать более чем один
сплайн, так как при замене у) на у^ + им?/ Л- С при постоянных т и С правая
часть равенства B.1.7) не изменяется; это же относится и к краевым услови-
условиям B.1.18). Таким образом, «Уд (У; х) + тх + С — #д (У; х), где у3 = ул +
-\- тХ] + С. В периодическом случае можно лишь утверждать, что #д {У; х) ■+-
+ С = 5д (?; х) при у] = уз 41 С. (Единственной периодической линейной
функцией является константа.)
Можно также поставить вопрос о произвольности величин М$ и ту. Всегда
ли существует сплайн, связанный с произвольно заданным множеством вели-
величин М] или т^? Просуммировав соответствующие числа из B.1.5) при / =
= 1, 2, . . ., ЛГ, получим необходимое условие для периодического сплайна:
М} = 0.
Можно показать, что допустимо любое множество значений М}, удовлетворяю-
удовлетворяющих этому соотношению. Обозначим левую часть равенства B.1.5) через
тогда предыдущее уравнение дает ^Ф,/ = 0. Положим (ух—у^IЬ,^ = с; тогда
У}-У'}-! _
Из равенств B.1.5) получаем
2.2. СУЩЕСТВОВАНИЕ, ЕДИНСТВЕННОСТЬ И НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ 21
Итак,
У^= УN +
Уг = У\ +
Эта система уравнений имеет однопарамстрическое семейство решений (пара-
метр Ун) тогда и только тогда, когда с = [ 2 ^ (ф1 + • • • + %-1)]Ка — &)>
3=2
т. е. когда с — известная функция от заданных значений М). Нетрудно заме-
заметить, что для непериодических сплайнов на величины М-} нет ограничений.
Соответствующая задача для наклонов щ несколоко сложнее. Обозначим
левую часть равенства B.1.14) через Зч|э/ и положим (^1 — УяIЩ = с; тогда
из B.1.14) при / = 1, ...,.№ получим
Ч + (-
я,
Эти уравнения совместны тогда и только тогда, когда
... + ( — 1IУ~1'ф1 + (— 1)^с = с, что равносильно условию
3=1
Получившаяся система уравнений имеет однопараметрическое семейство реше-
решений (уь . . ., Ун) тогда и только тогда, когда
Ограничимся здесь случаем, когда сетка равномерна. Если Л" нечетно, то эти
требования равносильны условиям ^1+^2 + -.-+^^ = 0 и с = % +
+ -фз + . . . + 'фл. Если N четно, то двупараметрическое семейство решений
Уг$ = У& + & (^ ■+ • • • + ^2^-1), Уг}+1 = Ук + *** + А* (^2 + • • • )
(параметры ^^ и с) существует тогда и только тогда, когда
22
ГЛ. И. КУБИЧЕСКИЕ СПЛАЙНЫ
т. е.
т>1 + гпз + • • • + иг#-1 = т-2 + т4 + . . . + т^ = 0.
^ Рассмотрим экстремальную задачу, из которой станет ясна роль уравне-
уравнений B.1.7) и B.1.14). Пусть функция /* (х) непрерывна. Для данной сетки Д
положим // = / (я?/) и обозначим череа #д (/; х) периодический сплайн, интер-
интерполирующий / (х), или непериодический сплайн, удовлетворяющий краевым
условиям B.1.Ш). Таким образом, 5Д (/; х}) = //.
Пусть 5д (х) — любой кубический сплайн на Д. Образуем интеграл
ъ
Е= [[Г (х) - Яд (х)? ах. •
с'
а
Величина Е — это мера приближения функции /* (х) функцией Яд (х) на отрез-
отрезке [а, Ь]. Пусть М] = 5д (х}). Раскрывая скобки и интегрируя по частям,
получаем
N
Е=-
где /о = /лг, /о = /^, Мъ = МК, если /(ж) и
ционарной точке функции #
имеют период &—а. В ста-
ста-1.2. ....*-!). B.2.2)
В периодическом случае стационарная точка существует, если для / = 1,2,...
. . ., N выполняется второе соотношение. Соотношения B.2.2) эквивалентны
уравнениям B.1.8) при краевых условиях B.1.181) или уравнениям B.1.9).
Следовательно, функция Е имеет стационарную точку тогда и только тогда,
когда Яд (х) аз Яд (/; х).
Покажем, что эта стационарная точка в действительности является точ-
точкой минимума. Обозначим через (ЛГ0, Ми . . ., Мк) ет {Ми • • •» Мя) реше-
решения системы уравнений B.2.2) для непериодического и периодического случаев
соответственно, т. е. М; = Яд (/; х}). Преобразуем' выражение для Е следую-
следующим образом: заменим М; в B.2.2) на М; и умножим полученные уравнения
2.3. СХОДИМОСТЬ 23
д —Мо, —Ми - • •, —Мк соответственно, а затем прибавим их к правой
части равенства B.2.1):
е
=\ [/"(х
ь N
(X))' ^ + 2
[Г (X))
а г=1
_ IV
= | [Г (*)
Заметим, что первый и третий интегралы правой части не зависят от выбора ]
Поэтому ясно, что Е принимает наименьшее значение при 5д (х) — 5д (/; х).
Это свойство называют свойством наилучшего приближения интерполяционного
сплайна. В гл. III это и другие аналогичные экстремальные свойства иссле-
исследуются более тонкими и сильными средствами.
2.3. Сходимость
Эффективность сплайнов при аппроксимации можно объяснить в значи-
значительной степени их замечательными свойствами сходимости. Если функция
/(«>(а:) непрерывна на отрезке [а, Ь] (д == 0, 1, 2, 3, 4), то сплайны ^д (/; х)
сходятся к функции / (х) на последовательности сеток Д по крайней мере со
скоростью || А ||а, где || Д |] = тах А/. (Для сравнения со степенью сходимо-
сходимости более общих аппроксимативных последовательностей см. Дэвис [1, гл. XIII].)
Аналогично производные 5др) (/; я) сходятся к /<р) (х) @ <: р ^ д) по крайней
мере со скоростью || Д \\а~р. При этом в некоторых случаях требуется, чтобы
в соответствующих сетках отношение максимума длины интервала к минимуму
длины интервала было ограничено, но во многих представляющих интерес
случаях достаточно, чтобы предел норм сеток был равен нулю. Более того,
эти скорости оптимальны.
Для установления сходимости необходимо знать некоторые свойства
матриц, обратных к матрицам коэффициентов в B.1.8), B.1.9), B.1.16) и
B.1.17). Если Хо, \1х или А,Л-, ц0 по абсолютной величине меньше 2, доказатель-
доказательство сходимости относительно просто. В этом разделе мы будем рассматривать
именно такой случай. Изучение более специфических свойств обратной матри-
. цы, необходимых для общего случая, мы отложим до разд. 2.9.
24 ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
Пусть В — квадратная матрица порядка га, и- пусть норма элемента
х = ^, . . ., хп) в га-мерном пространстве определяется равенством
шах
Для нахождения индуцированной нормы матрицы В запишем линейное пре-
преобразование, задаваемое этой матрицей, в виде
п
У, = .2
Тогда
у || = шах | У! |< || ж || тах
г ^
так что индуцированная норма матрицы В удовлетворяет неравенству
п
р|15<
хфО IIх II 1 ТТ
?— 1
Обозначим через ^* индекс строки, дающей максимальное значение для
п
2 \Ъц\, и положим
1-1
{1, если Ы*з>-0,
— 1, если &*$<0.
Тогда
3=1 }~1
2
г 3=1
откуда
Предположим, что главная диагональ матрицы В является доминирующей.
Для данного х выберем к так, что \\х || = \ хк \. Тогда
г 'з=1
п
>тт(\Ьи\
2.3. СХОДИМОСТЬ 25
Так как В'1 существует и х = В~1у, то для нормы матрицы В'1 мы получаем
оценку
И55 ^{(||
Обозначим через Л и А матрицы коэффициентов в B.1.8) и B.1.9) соот-
соответственно. Бели в B.1.8) Хо и (х^ по абсолютной величине меньше 2, то
в непериодическом случае
|| Л-1 || < тах [B - А,,,)-1, B - ц*)-1, 1], B.3.1)
а в периодическом
||Л-1||<1. B.3.2)
Пусть В я В обозначают матрицы коэффициентов в B.1.16) и B.1.17),
причем в первой из них | ц0 | < 2 и ) Я№ | <; 2. Тогда
Ц В-1 || < тах [B - ро)-\ B - Х„)-1, 1],
Зададим теперь на отрезке [а, Ь] последовательность сеток
А*: а = хк0 < хк± < . . . < хкПк = Ь,
положим
и определим норму сетки Дй:
|| АЛ || = тах
B.3.3)
B
B.
B.
.3.4)
3.5)
.3.6)
Нас будут интересовать последовательности {Ай}, для которых || Дй || -*- О
при к-> оо. Иногда мы будем предполагать выполненным также дополнитель-
дополнительное ограничение на сетки Д&:
.= тах ^х^-<Р<оо. B.3.7)
В частности, это ограничение предполагается выполненным в первой теореме
сходимости.
Теорема 2.3.1. Пусть на отрезке [а, Ь] заданы непрерывная периоди-
периодическая функция / (х) и последовательность сеток Ай, удовлетворяющая условию
B.3.7) и такая, что Ит || Ай || = 0. Если периодический сплайн 5Дй (х) интер-
й-»-оо
полирует функцию / (х) в узлах сетки Ай, то
/ (*) ~ #д* (х) = о (|| 1 ||) B.3.8)
26 ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
равномерно относительно х на (а, Ь]. Если, кроме того, функция / (х) удовлет-
удовлетворяет на [а, Ь] условию Липшица порядка а@<а<^1), то
/ (х) - 5Дл (х) = О (|| Д, уа) B.3.9)
равномерно относительно х на [а, Ь]. В непериодическом случае равенства
B.3.8) справедливо, если интерполяционный сплайн удовлетворяет краевым
условиям B.1.18Ш), зир тах(| А*о|, 1ц*лгА|) <2 и ||ДА ||2(|йю| + 1<*отк|) ->0
при к—>оо. Если, кроме того, /(ж) удовлетворяет условию Липшицй по-
порядка а@<а^1), то B.3.9) справедливо при условии ограниченности
последовательности || Д& ||2~а (| д,^ \ +1 йтк \ )•
Доказательство. Из формулы B.1.2) получаем для
B.3.10)
где ради сокращения записи опущен индекс сетки к.
Обозначим через А$ элементы матрицы, обратной к матрице коэффициен-
коэффициентов в B.1.8). Тогда
Пусть (о (б, /) — модуль непрерывностит функции / (х) на отрезке [а, Ъ].
Заметим, что коэффициенты при М^\ и М; в равенстве B.3.10) не превосходят
по величине Л|/Зб/2. В силу условия B.3.7)
/)) B.з.Ц)
откуда
Щ (I М,^ \ + | М,\) < 2 || Л-1 || Fр2ш (|| Д ||, /) + || Д2 || (| <*в | + | й
B.3.12)
В периодическом случае с учетом неравенства B.3.2) получаем
Щ (| М,^ | + I М} |) < 2 || I-1 || 6^ш (|| Д ||, /) < 12р2со (|| Д ||, /).
В непериодическом случае из B.3.10) и B.3.12) имеем
-/(*) к!-§-<*(н д и, я+-^г и А~х
Ясно, что соответствующее неравенство справедливо также для периодиче-
периодического случая. Таким образом, B.3.8) доказано.
2.3. СХОДИМОСТЬ 27
*
Бели функция / (х) удовлетворяет на отрезке [а, Ь] условию Липшица
порядка а@<а^1), т. е. если существует такая константа К, что для
любых х и х' из [а, Ь]
I /(*)-/ (*') К К | х - х' |а,
то правую часть неравенства B.3.11) можно заменить на $2К || Д ||а; тогда
Для периодических функций
Теорема доказана.
Очевидно, что для краевых условий B.1.19Ш) можно доказать соответ-
соответствующую теорему; при этом мы требуем, чтобы выполнялось неравенство
вир тах (| щ0 М ^лл-ь I) < 2. Кроме того, для справедливости соотношения
B.3.8) мы требуем, чтобы || ДА || (| с&0 | +1 сьяк |) —*• О при к—> оо, а для спра-
справедливости соотношения B.3.9) — чтобы величины || Дй Ц11 (\ск0 \-{- \ скг^к |)
были равномерно ограничены относительно к±
Здесь целесообразно отметить, что некоторые свойства сплайнов анало-
аналогичны свойствам полиномов, исследованных Фейером. Фейер [2] доказал, что
если полином § (х) степени 2ге — 1 в узлах Чебышева |^п) 6 [—1» 11 (к = 1,2,...
. . ., п) удовлетворяет неравенствам | # Aьп)) I <! А и | §' A^п)) | <^ Б, то
I 8 (х) I <^ 4 + ^ъВ на ^—1» И» причем числа Яп не зависят от полинома § (х)
и Яп ->- 0 при ?г -*- с». Еще' раньше (в работе [1]) он доказал, что если полином
Хп (х) степени 2ге — 1 интерполирует в узлах Че0ышева функцию / (ж), непре-
непрерывную на отрезке I—1, 1], и Х'п (%ьп)) = 0, то Хп (х) сходится равномерно на
[-1, 1] к/.(*).
Рассмотрим для сплайна 5д (х) представление B.1.10), справедливое,
даже если 5Д (х) не принадлежит классу С2 [а, Ъ]. Положим о — (х — &/_<)/&/
на [д^_ь х}\; тоща
5Д (о;) = т;_1^ A — оJ о — т}к;О* A — а) +
+ у,-1 A - аJ Bа + 1) + У/©1 B A - а) + П.
Следовательно, если | уь | ^ Л и | тпй | -^ 5, й = 0, 1, . . ., Л, то для х
из отрезка \х;_и х^\
Таким образом, доказана
Лемма 2.3.1. #слм кубический сплайн 5д (о;) во всех узлах произвольной
сетки А из [а, Ь] удовлетворяет неравенствам
28 ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
то для всех х ^ [а, Ь]
Важно отметить, что в этой лемме 5Д (х) — кусочно кубический полином
с непрерывной первой производной. Относительно второй производной не было
сделано никаких предположений. Пользуясь терминологией, которую мы под-
подробнее объясним в следующих главах, будем называть такой сплайн сплайном
дефекта 2. Сплайны с непрерывной второй производной будем называть сплай-
сплайнами дефекта 1. Сплайн, на всем отрезке [а, Ь] совпадающий с кубическим
полиномом, будем называть сплайном дефекта 0.
Пусть на отрезке [а, Ь] задана сетка Д, и пусть сплайн 5Д (я) дефекта 2
интерполирует непрерывную функцию / {х) в узлах сетки Д и его производ-
производная в этих узлах равна нулю. Тогда справедлив следующий аналог теоремы
Фейера [11:
Лемма 2.3.2. Пусть на отрезке [а, Ь] заданы непрерывная функция
/ (х) и такая последовательность сеток Дй, что || Дй || -»- 0 при &->• со. Если
сплайн 8&к (х) дефекта 2 интерполирует функцию / (х) в узлах сетки- Д& и его
производная в этих узлах равна нулю, то последовательность {8&к (х)} схо-
сходится к / (х) равномерно на 1а, Ъ]. Точнее,
Доказательство. Так как «на концах каждого отрезка 1^-ь }
заданы значения кубического полинома и его первой производной, то суще-
существование таких сплайнов очевидно. Далее, сплайн 5Дй (х) изменяется монотон-
монотонно на каждом отрезке [а^-ь х^]. Пусть х € [я^-1, х^]; тогда
У — ближайший к х конец указанного отрезка.
В следующей лемме на рассматриваемые сплайны налагаются более слабые
ограничения. Ее доказательство очевидно.
Лемма 2.3.3. Пусть на отрезке [а, Ь] заданы последовательность сеток
Дл и два сплайна §Ак и ^Дй, совпадающие в узлах сетки. Если || Дл || -> О,
шах Г$д (хц) | IIДИ1 -» 0 и шах | Гд. (хю) \ \\ Дл || -* О
при к—>оо, то
равномерно относительно х на [а,
2.3. СХОДИМОСТЬ 29
Вернемся к теореме 2.3.1. Сплайны 8&к (х) дефекта 2 из леммы 2.3.2 без
дополнительных ограничений на сетки Дй сходятся к / (х) равномерно на [а, 6].
Если же выполнено условие B.3.7) и величины \\ А-1 || и \\"А~Х || в B.1.16)
и B.1.17) равномерно ограничены относительно к, то сплайны 8Ак (х) из
теоремы 2.3.1 удовлетворяют соотношению
шах | 8к (хю) | || ДЛ Ц -* 0.
Отсюда в силу леммы 2.3.3 5Дд (х) — 8&к (х) -*- 0 равномерно относительно х
на [а, 61, а в силу леммы 2.3.2 8 Ак (х)-*~ { (х) равномерно относительно х
на [а, 6]. Этот вариант доказательства теоремы 2.3.1 более ясно указывает
на роль условия B.3.7).
Если предположить, что производная /' (х) непрерывна на [а, 61, то интер-
интерполяционный сплайн и его производная сходятся соответственно к / (х) и /' (х).
В этом случае нет необходимости налагать на последовательность сеток допол-
дополнительное ограничение B.3.7).
Теорема 2.3.2. Пусть на отрезке [а, Ь] заданы последовательность
сеток Д&, || Дй |[ -> 0 при к-*- 0, и функция / (х) € С1 [а, Ь]. Если интерполя-
интерполяционный сплайн 8&к (х) удовлетворяет краевым условиям B.1.191) или является
периодическим вместе с функцией / (#), то
/(р>(д0-Л*Ч*) = °A1Л*111~Р) (Р = 0, 1) B.3.13)
равномерно относительно х на [а, 61. Если /' (#) удовлетворяет на [а, 61 усло-
условию Липшица порядка а @ <С а ^ 1), то
^ (р = 0, 1) B.3.14)
равномерно относительно х на [а, 61.
Доказательство. Положим в непериодическом случае
г ( )т / (Д /
а в периодическом внесем соответствующие изменения. Для данной сетки ДЛ
обозначим через Вк матрицу коэффициентов в B.1.17) или B.1.16) при крае-
краевых условиях A) и с уравнениями Зтк0 = 3/' (а) = сйо, Зт^ = 3/' F) г скх
вместо первого и последнего уравнений системы B.1.16). Тогда
30
ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
где Д — единичная матрица порядка
дическом случае равна
0
1
или .№&. Правая часть в неперио-
непериоа в периодическом
о
{ску
Норма каждого из этих векторов не превосходит соC||Ад||, /')-^Зсо(|| Ад ||, /'),
и, следовательно, ИяЦк-Ч.е^КНДк1 ||*3ю(|| Ай ||, /')<3©(|| Ал ||, /')• Далее,
в периодическом случае существует такая точка 1&/€ 1#й/-и хк% что х/з Ск} =
= /'(|й^). То же верно для 1-^7-^^ — 1 в непериодическом случае, причем
здесь сй0 = 3/'(а), с^=*3/' F). Итак, \\тк-&||<4ю(|| Ай||, /')•
Отсюда и из B.1.11) для а: ^ [х^-ь хы\ получаем (опуская индекс сетки к)
\2_1
/ 4
X
(^-/»-(»»ы-Й-1)+ (/5-/5-1I
Так как |/'(*У-(/у-&-1)/М<®(л/./'). То
I/'(*)-«% (*)|<-|-«» (II а II,/').
В частности, для функции, удовлетворяющей условию Липшица порядка а,
Так как сплайн 5Д (#) интерполирует функцию / (х) в узлах сетки А, то на
[ ]
-^-1| А || о) (|| А||, /'),
где у — ближайший к х конец отрезка [#/_1г ^1. Теорема доказана.
2.3. СХОДИМОСТЬ
31
Случай общих краевых условий B.1.19Ш) мы рассмотрим в разд. 2.9.
По существу тот же метод доказательства применяется,«когда функция
/ (х) имеет на отрезке [а, Ь] непрерывную вторую производную. В следующей
теореме результаты Шармы и Мейера [1, 2] несколько обобщаются, ибо на функ-
функцию / (х) налагаются более общие условия.
Теорема 2.3.3. Пусть / (я) 6 С* [а, Ъ] и на отрезке [а, Ъ] задана такая
последовательность сеток {Д&}, что || Д& || -*- 0 при к -»- оо. Если сплайн 8±к (х)
интерполирует функцию / (х) на сетке Д& и удовлетворяет краевым услови-
условиям B.1.181) или B.1.18и), или если функции 8&к (х) и / (х) периодические, то
(Р = 0, 1, 2) B.3.15)
удовлетворяет на [а, Ъ] усло-
услоравномерно относительно х на [а, Ь]. Если /"
вию Липшица порядка а @ < а ^ 1), то
= 0, 1, 2)
B.3.16)
равномерно относительно х на [а, 6].
Доказательство. Положим Мк = (Мк0, Мки ..., Л/ь^ )т, йк =
= Dо> 41» •••> 4лгй)Т в непериодическом случае и Мк=(Мки ..., Мк^к)т,
4 = (йки - - •» йшк)Т в периодическом. Пусть ^4Л обозначает матрицу коэффи-
коэффициентов системы B.1.8) или B.1.9), соответствующую сетке Дд. Тогда B.1.8)
(при краевых условиях A)) и B.1.9) можно записать в виде
Ак [Мк~ ак) = (/*-у Ак) 4, B.3.17)
где 1к — единичная матрица. Правые части равны (опущен индекс сетки к)
32 ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
Заметим, что в периодическом случае величина й?/6 равна разделенной раз-
разности / [а^.!, X;, Х]+1\ (Гильдебранд [1, стр. 381). То же верно для / -ф О и / ф N
в непериодическом случае:
1 1
Отсюда -^ й} — у /" (|/) для некоторой точки %} из интервала (ж/-!, х^). Из фор-
формулы Тейлора с остаточным членом в форме Лагранжа следует, что для неко-
некоторой точки |о, х0 <С 1о < хи
Аналогичное утверждение справедливо для й^.
Таким образом, |(/й-1 А) 4||<й>C||Дй|Ь Л<3(о(|| ДА |Ь Л, а по-
поскольку || 4Г111-^1» из B.3.17) получаем *
4 й||<11 А * 11
4- й*||<11 -А* 11-Ц (А —I" Л*) й||<Зю(||Дк||, Л-
Ясно, что ||/й —-|"^||<ю(||Дй||, Л и, следовательно, ||МЛ —
<;4со(|| ДЙЦ, /*). Так как функция 81 (х) кусочно линейна, то
|, Л.
В частности, если /"(д;)^^Ыра, т. е. /" (х) удовлетворяет условию Липшица
порядка а с константой К, то из предыдущего неравенства получаем
Так как 5д (ж^) = /(ж^), то по теореме Ролля на каждом интервале
(^М, ж^) существует точка |^, для которой /' (|ь/) = Ядй(|^). Таким
образом, на этом интервале
] | ДЛ || <о(|| Дк ||, Л.
-5кк (х) 1 = | ] [/" (*) -5дй (х)]
С помощью повторного интегрирования находим, что
| /(х) -5дк И 1<у || А* ||2 со (|| А* ||,
Результат справедлив и для краевых условий B.1.1811), если первое и последнее
уравнения системы B.1.8) записать в виде ЗМь0 = 3/" (а) =е= йй0 и ЗЛ/ь№ =
соответственно. В этом случае по-прежнему || Ак ||-<1.
2.3. СХОДИМОСТЬ 33
Отметим, что увеличение гладкости функции / (х) улучшает сходимость
интерполяционных сплайнов. Биркгоф и де Бур [1] доказали, что если после-
последовательность интерполяционных сплайнов 5дЛ (х) удовлетворяет краевым
условиям A), выполняется B.3.7) и /да (х) абсолютно непрерывна на [а, Ь],
то 8%к (х) сходится к /*' (х) равномерно. Далее, если функция / (х) имеет
на [а, Ь] непрерывную четвертую производную, то /(г) (х) — 8$ (х) =
= О (|| Дй || -р) (р = 0, 1, . . ., 4) равномерно относительно х на [а, Ь]. Приве-
Приведем простое доказательство более сильного результата.
Теорема 2.3.4. Пусть на отрезке [а, Ъ) заданы функция / (х) ^ С8 [а, Ъ]
и последовательность сеток {Д&}, для которой выполнено условие B.3.7) и
|| А^ [I —>- 0 при к—*~ оо. Тогда для интерполяционного сплайна 8&к (х), удовлет-
удовлетворяющего краевым условиям B.1.181) или B.1.18Н), а также для периодического
сплайна, если функция / (х) периодическая,
(р = 0, 1,2,3) B.3.18)
равномерно относительно х на [а, Ъ]. Если /* (х) удовлетворяет на [а, Ь] усло-
условию Липшица порядка а @ < а ^ 1), то
/*> (*) -Й? (*) =0 (||А*|13+в^"*) (Р = 0, 1, 2, 3) B.3.19)
равномерно относительно х на [а, Ь],
Доказательство. Рассмотрим сначала систему B.1.8). Положим
^ = 1 и через
°>- к,
обозначим третью производную сплайна на отрезке \х^и х^). Вычтем из каж-
каждого уравнения системы B.1.8) предыдущее:
B.3.20)
Разделим уравнения B.3.20) последовательно на (&! + к2), (&1 + А2 + 3)>
2 + А3 + Й4)> • • •, (йлг-2 + Л^_! + А^), (А^_! + А^). Обозначим через г =
('*1» г2, . . ., гЛ-)т вектор-столбец получившихся правых частей, т. е.
г е [/О, /ь/2
Г1~ь
(/=2,
3-1197
34
ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
Здесь I//, /л-ь • • •» //+*! = / [#/> #л-ь • • •» #/+ь1 есть &-я разделенная разность
функции / (о;) в точках X}, а?_/+±, . . ., &/+&• Заметим, что
Таким образом, из B.3.20) находим
1—
B.3.21)
^^ + 1-
Матрица коэффициентов этой системы при "К\ = . . . = Я^_4 —-^ имеет доми-
доминирующую главную диагональ, но в общем случае главная диагональ не будет
доминирующей. Однако матрицу С системы B.3.21) можно представить в виде
произведения матрицы с доминирующей главной диагональю на две диаго-
диагональные матрицы:
С = ЕйР,
где
Е
0
A
A — ^N-^N-
|*1 [Ад ♦
о
о
о
2.3. СХОДИМОСТЬ
35
1*1
О
О
.0
О О
1 + (*2 + ^3 ^3
I * •
О 0
о
О
О
Ясно, что ПЛ-Ч
Если для всех г, / интервалы сетки удовлетворяют соотношению
то
1
Кроме того,
Отсюда следует, что
Пусть а=(а1? ..., а^)т; тогда из уравнения Со = г получаем
1 —1*4A+ А.0
Л
+ ^2)^2
0
О
О
О
О
о
Так как сумма элементов каждой строки матрицы / — С равна нулю, то пра-
правая часть последнего равенства имеет вид
~ 2)
3*
36
ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
Если производная /'* (х) непрерывна на отрезке [а, Ь\, то величину | гу+1 — гу |
можно сделать сколь угодно малой. Так как A— ц^+д ^ 1 + р, то при
достаточно малом значении нормы || А || ступенчатая функция 8% (х) будет
равномерно близка к /"' (х). В самом деле, \Г}+1 — г^ | -^ <о D || Д ||, /да) -^
< 4(о (|| А ||, Г) и
II о - г || < || С-1 || || (/ - С) г || < #2<о (|| А ||, Г),
как || Г ()
где К2 = 8 A + 2Р) A + Р) Р2
[_1, #/1, то в результате получаем
Так как || Г (*) - г, || < со C || А ||, /-)
на отрезке [ 1
I Г (*) - -51 (*) К C + К2) со (|| А ||, Г). B.3.22)
Если/*" (я) удовлетворяет на [а, 6] условию Липшица порядка а, О < а ^ 1, то
I Г <*) - 81 (х) | = О
равномерно относительно х на 1а, Ь]. В частности, если /D> (о;) непрерывна
на [а, Ь], то
шах
\Г(х)-81(х)
При доказательстве теоремы для краевых условий B.1.18Н) требуются лишь
незначительные изменения: первое и последнее уравнения системы B.1.8)
следует записать в виде ЗМ0 = й0 = 3/" (а) и ЪМ^ = й№ = 3/" F), величины
1 + Я4 и 1 + Н-лг-1 в первой и последней строках равенств B.3.20), B.3.21)
и в матрице Б следуем заменить соответственно на 2 + Х4 и 2 + Ц^-1*
В периодическом случае также необходимо несколько изменить матрицу
коэффициентов. В этом случае С•= БйР, где
1—
о
о
Р —
о
о
ЩН-2
0
О
о
о
о
о
о
о
о
О
о
о
о
О
2.3. СХОДИМОСТЬ 37
При этом учитывается, что в периодическом случае %1%2 ... Х^ = [Х1[Х2 • • • Не-
Неограниченность величины || С || доказывается так же, как раньше, и мы
опять получаем неравенство B.3.22).
Так как третья производная 81(х) претерпевает в узлах сетки разрывы
с конечным скачком, то нельзя установить неравенство для вторых производ-
производных простым интегрированием. Для изучения второй производной исследуем
вторую разделенную разность:
Шй. Л • Л 1
2
—щ ) (*м-*)
В силу равенства B.1.5) и интерполяционного свойства сплайна 8^
Очевидно, что для х
Из этого соотношения и из неравенства B.3.22) имеем
тах
I, Л-
Применив теорему Ролля и проинтегрировав, получим, как и раньше, требуе-
требуемые неравенства для | /' (х) — 5д (ж) | и | / (х) — 5Д (а;) |. Теорема доказана.
Следующие два свойства] дополняют эти первоначальные сведения
о сходимости сплайнов. Здесь мы лишь сформулируем эти свойства, а дока-
доказательство приведем в разд. 2.9 и 3.12.
Бели / (х) имеет на [а, Ь) непрерывную четвертую производную и сетки Д&
удовлетворяют условиям || Д& || -> 0 при к -> оо, || Дй ||/ппп Нк} ^ Р < оо,
и тах | %к1 — 1/2 | -> 0 при к -*- оо, то
I
Нт тах
\\ Аи II
_ /ш {хь л
= 0.
38
ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
Таким образом, скачки третьей производной сплайна непосредственно связа-
связаны с четвертой производной 'аппроксимируемой функции.
Подводя итог, можно сказать, что скорость равномерной сходимости раз-
разности /(Р> (х) —
к нулю равна о
Г~
Р), если / (х) принадлежит
классу Су [а, Ь] (у = 0, 1, . . ., 4; 0 -< р ^ 7)» и равна О (|| Д& ||4~р), если
/ (х) принадлежит классу С* [а, Ь] @ ^ р <^[ 3). В разд. 3.12 будет показано,
что если функция / (х) не совпадает с кубическим полиномом, то скорость
сходимости не может быть выше О (|| Ал ||*~р).
2.4. Равные интервалы
Бели сетка А, заданная на отрезке [а, Ь], является равномерной, то обрат-
обратные матрицы для матриц коэффициентов систем B.1.8), B.1.9), B.1.16) и B.1.17)
принимают относительно простую форму. Это позволяет непосредственно при-
применять сплайны к стандартным задачам численного анализа.
Введем определитель порядка п
Аг (V =
г
2
1-Х
0
0
X
2
0
0
0 ...
А • . •
• • •
0 ...
0 ...
0
0
1-Х
0
0
0
2
1-Х
0
0
X
2
и положим /)_1 (X) = 0^ 2Э0 (А,) = 1 и
разностному уравнению.
Бп (X) - 2Бп_1 (X) +
так что
B.4.1)
(X) = 2. Тогда Бп (X) удовлетворяет
-Х) Вп.2 (X) = 0,
Пусть Оп = Оп A/2), До -= 1,
; тогда
B.4.2)
B.4.3)
Рассмотрим определитель порядка п
2 а
1 2 *
1 о
2 .
2.4. РАВНЫЕ ИНТЕРВАЛЫ 39
Здесь (?1(а) = 2. Положим <?0(а) = 1, <?-1(а) = 0; тогда для ?г>1
и <2П (а) удовлетворяет тому же самому разностному уравнению, что и Оп.
Для определителя | А | матрицы коэффициентов системы B.1.8) справедливы
равенства
А 1 = 2<?„ (|1„) -11$^ (Ы = 2<2„ A0) -~ цЖ-1 (Х,о). B.4.5)
Элементы матрицы Л-1, обратной к матрице коэффициентов системы B.1.8),
в случае равномерной сетки можно найти из алгебраических дополнений транс-
транспонированной матрицы:
А
Для равномерной сетки обратная матрица А'1 в периодическом случае
имеет особенно интересный вид. Она является циркулянтом (Мюир [1]). Каж-
Каждая строка получается сдвигом предыдущей на один элемент вправо. Свойства
таких матриц играют важную роль при изучении полиномиальных сплайнов;
мы подробно рассмотрим эти свойства в гл. IV. ^
Если сетка равномерна, то в периодическом случае для определителя | А \
матрицы коэффициентов в B.1.9) выполняется соотношение
-4 Р*-2 + (-2I~К- B-4-7)
Пусть йо^» ^\ • • •» й$-1—элементы первой строки матрицы Л. Положим
4& Г «? тогда
Элементы <$** можно найти непосредственно из алгебраических дополнений
матрицы коэффициентов (эта матрица симметрическая):
1). B.4.9)
Для определителя |5| матрицы коэффициентов системы B.1.16) справед-
справедливы равенства
— "о" Л^м^ (ц0) = 2^ (Я^) — -к- Цо^-1 (Л^); (^.4.10)
40 ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
так как для системы B.1.17) В = А, то
В непериодическом случае легко заметить, что момент
N
вычисляется по формуле
N-2
3=2
при условии, что сплайн принимает значение /_/ в точке Х} = а-\-]к. Далее,
+ А Ь А\4А
ЛГо1 -2ЛП1 Ч-^Гг1 = -6ЛЙ1 + A—2Ло) ^г'о1 A^1),
Лгл?-2 - 2^Г^-1 + Лш1 = - б^Глг1-1 + A - 2М ЛГл? (I # ЛГ -1),
A<1-<ЛГ-1),
Лдг-1^-2 — 2Ап-1х-1 + -4;у-1л- = 2 — 6-4^-ш-1 + -4лг-юA. — 2ц^).
Таким образом, мы получаем следующее представление для моментов:
лг
В периодическом случае
^|=-р-2^4^+-р-л- B-4-12)
Величины Л^1 и Л^1 быстро убывают с ростом | I — / |, так что при вычисле-
вычислении М} необходимо сохранять только несколько членов, центрированных
относительно X;. Кроме того, часто можно использовать предельные значения
2.4. РАВНЫЕ ИНТЕРВАЛЫ 41
коэффициентов при N -»- оо в B.4.11) и B.4.12); это дает значительное упро-
упрощение при применении сплайнов.
Положим
Тогда непосредственно из равенства B.4.3) находим, что
гп+1_ 8п+1 рп_11
Уп~ г—$ ♦ т — 2+а
Учитывая, что 2 + а — — B + 1/ст) = 1^3, получаем
Для непериодических сплайнов особый интерес представляют случаи,
в которых Яо = р,^ = а. Случай а = 1 связан с краевыми условиями B.1.181);
а = 0 — с краевыми условиями B.1.18Н); а = —2 приводит к параболиче-
параболическому выходу. Последний случай связан с условиями Мо = М^ М^-1 = М^
имеющими особое значение, когда не известны ни краевые моменты, ни краевые
наклоны. Свойства существования и сходимости таких сплайнов мы рассмо-
рассмотрим в разд. 2.9.
Нетрудно заметить, что для тг>1
г» ~ 2 + а
Таким образом, для 0<1^;<!ЛГ и для г = / =
л (а) _ 2 A — дД«) + до A —
г» ~" 2 + а '
\А\ _B + ааJ —а2"B —аа-1J B.4.14)
л-1 -
так что
-а^-1 Bа + а)] [2+ао-ош~2^~1 Bа + а)] /п^/г
B.4.15а)
и
, ^
B+аа)а—
Для 0</<ЛГ
.
42 ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
так что
<Л0 B.4.15с)
Чтобы завершить вычисление Л^, заметим, что в силу равенств B.4.6)
А^ — А~$ для О <С I <С N1 0<.^<.N и Лг/ = Л^_{^_,- для остальных значе-
значений г, /.
Для упомянутых ранее трех случаев имеем:
Краевое условие A) (а = 1)
.-1 _
5 ~
Краевое условие ' (п) (а = 0)
А$ =0 @</<ЛГ).
Параболический выход (а = — 2)
2.4. РАВНЫЕ ИНТЕРВАЛЫ 43
Чтобы найти элементы В"$ для равномерной сетки, в равенствах B.4.6)
надо заменить А,о, \кц на |л0, А,^. В периодическом случае В\] = А\1. Для
наклона тг имеем следующий аналог соотношения B.4.11):
IV N-1
^ _! „_4 ^, ! 3
3=1
ЛГ-1
Г>~1 /Л ^ ^ \ ^ жэ— 1 4 I ^ 3
, 3 „_1 ,
B.4.16)
Из рассуждения, следующего за B.1.9), видно, что для определения значений
В11 из формул B.4.15а) — B.4.15с1) величину а в рассматриваемых трех слу-
случаях надо взять равной 0, 1, 2 соответственно. Поэтому в первых двух случа-
случаях из предыдущего вытекает, что В$ совпадают с Л^1, а а = 2 дает пара-
параболический выход.
Параболический выход (а = 2)
02N-23-1)
"-2) @<
— О*
Для периодического сплайна вместо B.4.16) имеем
N-3 }
о
где квадратные скобки обозначают целую часть.
Предельные значения при N —-> оо величин Лу/ весьма полезны.
В самом деле,
44
ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
при этом ошибка аппроксимации равна
Даже в непериодическом случае, учитывая, что а»—0,268, получаем хоро-
хорошее приближение (за исключением интервалов вблизи концов). Значения !)
для /с^7 равны
й=012345 67
> = 0,57735 —0,15470 0,04145 —0,01111 0,00298 —0,00080 0,00021 —0,00006
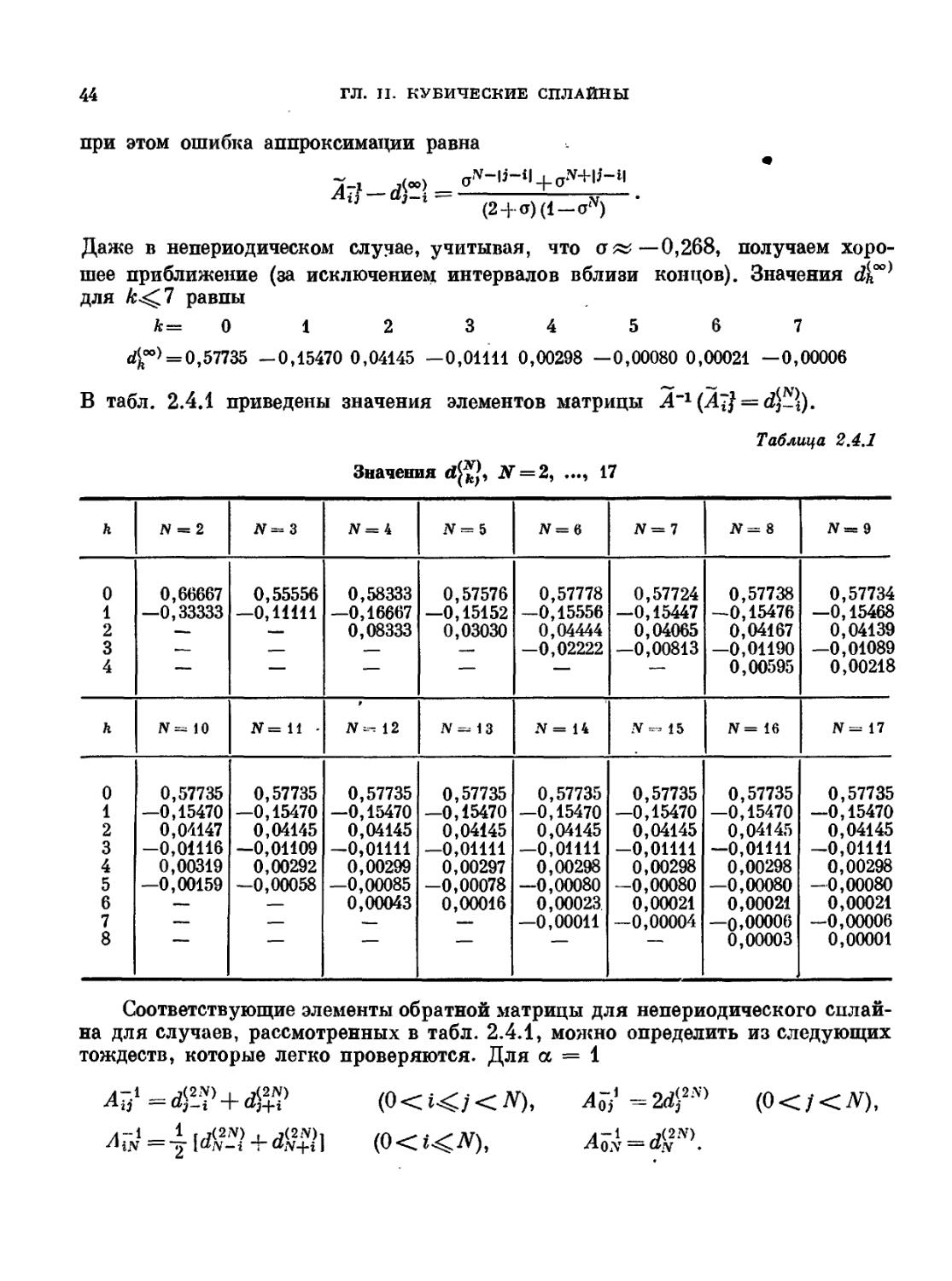
В табл. 2.4.1 приведены значения элементов матрицы
Значения й{^\ .У = 2, ..., 17
Таблица 2.4.1
к
0
1
2
3
4
к
0
1
2
3
4
5
6
7
8
N = 2
0,66667
—0,33333
ГС=^ 10
0,57735
—0,15470
0,04147
-0,01116
0,00319
—0,00159
лг=з
0,55556
—0,11111
# = 11 -
0,57735
—0,15470
0,04145
—0,01109
0,00292
—0,00058
0,58333
—0,16667
0,08333
9
ЛГ~ 12
0,57735
—0,15470
0,04145
—0,01111
0,00299
—0,00085
0,00043
0,57576
—0,15152
0,03030
ЛГ= 13
0,57735
—0,15470
0,04145
—0,01111
0,00297
-0,00078
0,00016
0,57778
-0,15556
0,04444
-0,02222
ЛГ= 14
0,57735
—0,15470
0,04145
—0,0И11
0,00298
-0,00080
0,00023
—0,00011
0,57724
-0,15447
0,04065
—0,00813
ЛГ=- 15
0,57735
—0,15470
0,04145
-0,01111
0,00298
—0,00080
0,00021
-0,00004
ЛГ=8
0,57738
—0,15476
0,04167
-0,01190
0,00595
ГС= 16
0,57735
—0,15470
0,04145
—0,01111
0,00298
—0,00080
0,00021
—0,00006
0,00003
0,57734
—0,15468
0,04139
—0,01089
0,00218
IV = 17
0,57735
—0,15470
0,04145
—0,01111
0,00298
-0,00080
0,00021
—0,00006
0,00001
Соответствующие элементы обратной матрицы для непериодического сплай-
сплайна для случаев, рассмотренных в табл. 2.4.1, можно определить из следующих
тождеств, которые легко проверяются. Для а = 1
@ <
Л),
?BЛ;)
2.5. ПРИБЛИЖЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ 45
Для а = 0
А7? = ^!? - Л^Р @ < «</ < ЛО, V - 0 @ < /
= у B + аJ [^ГОД - #">аГ >] (О < *
Для а = — 2
'Н2>«Я? (О < *
Элементы В$ для а = 2 находим из соотношений
«5* -^-«-«дег,» (р<к/<#),
г2) - й^гД'1 (о < к Щ,
2.5. Приближенное дифференцирование и интегрирование
К наиболее важным приложениям сплайнов в численном анализе и обла-
областях, где их подвижность и гибкость особенно очевидны, относится их приме-
применение в численном дифференцировании и интегрировании. Из теоремы 2.3.4
ясно, что при приближенном интегрировании даже для неравных промежутков
процесс имеет четвертый порядок точности. При приближенном дифференци-
дифференцировании ошибка равна О (А8), но к этому можно кое-что добавить. Получающие-
Получающиеся производные непрерывны в узлах сетки. Это явление частично объясняется
свойством наилучшего приближения, приведенным в разд. 2.2, и частично
свойством минимальной кривизны, которое изучается в гл. III.
Для периодического сплайна из равенств B.1.15) следует, что
Н
=3 2 Н
*=1
а для непериодического сплайна —
IV-!
3 ч
46 ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
В случае равномерной сетки выполняются соотношения B.4.16) и B.4.^
Для неравномерной сетки величины В$ обычно вычислять нецелесообразно
Для вычисления наклонов т,} следует непосредственно использовать алго
ритм, указанный в конце разд. 2.1, либо вначале применить его для вычи
сления моментов М}-, а затем найти наклоны из соотношений B.1.4):
B-5.3)
Небольшая перегруппировка членов в равенствах B.5.1) и B.5.2) приво-
приводит к важному свойству наклонов лгг: из равенства B.5.1) получаем
= 3 2
_
а из равенства B.5.2) —
'У~2 / — /
Г
2
-г
3=2
<* B.5.5)
Можно показать, что для равномерной сетки сумма
^ В-1 Ь-1»
является сглаживанием величин (/; —//_1)/А/ в смысле Шёнберга [1], а вычи-
вычисление Ш] включает дополнительное усреднение таких сумм. Аналогичные
выводы можно сделать относительно соотношения B.5.5).
Однако здесь нужно снова отметить, что правая часть равенства B.1.15)
равна наклону в точке х$ параболы, проходящей через точки (я/_ь У;-О,
(я/, ^), (я/+1, У}+\)^ следовательно, эти наклоны парабол представляют сгла-
сглаживание величин щ.
Тот факт, что т^ представляет сглаживание величин (// — //-О/А, заметно
отличает поведение т^ от поведения М}. Из B.1.7) видно, что вторые разде-
разделенные разности / 1а:/_1, <с/, Х]+\\ в свою очередь представляют сглаживание
величин Л//.
Эти характеристики важно принимать во внимание, когда сплайны при-
применяются к задачам, в которых требуется гладкость вторых производных.
К задачам такого типа относится определение картины линий тока для течения
сжимаемого газа. В этом случае для устойчивости численного процесса надо
найти значения кривизн линий тока с максимально возможной точностью.
Оказывается, что сплайн можно эффективно применить для определения вторых
производных с помощью следующего приема: сначала обычным методом находим
2.5. ПРИБЛИЖЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
47
наклоны линий тока, затем строим сплайн, интерполирующий найденные накло-
наклоны, и берем в качестве требуемой второй производной производную от сплайна.
Пример 2.5.1 позволяет пояснить действие этого приема при расчете типич-
типичной линии тока внутри сопла. Здесь М; — вторая производная обычного
ПРИМЕР 2.5.1
Определение наклонов и вторых производных
для контура сопла
(наклоны на концах заданы)
ж
0
1
2
3
4
5
6
7
8
9
10
11
12
•13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
У
5,160
5,110
5,070
5,020
4,972
4,921
4,860
4,738
4,528
4,228
3,829
3,373
3,094
2,985
3,100
3,375
3,720
4,050
4,380
4,700
5,000
5,280
5,550
5,580
6,050
6,275
6,500
6,700
6,890
7,070
7,250
У
—0,04400
—0,04450
—0,04780
—0,04924
—0,04923
—0,05083
—0,08343
-0,16442
—0,25486
—0,36231
—0,45763
-0,38834
-0,19400
0,00043
0,21077
0,32662
0,34276
0,32733
0,32793
0,31094
0,28830
0,27586
0,25826
0,25110
0,23733
0,22458
0,21433
0,19308
0,18334
0,18354
0,16250
м
-0,00490
0,00380
—0,01031
0,00743
—0,00741
0,00420
—0,06941
—0,09257
—0,08830
—0,09423
-0,12878
0,26736
0,12135
0,26724
0,15369
0,07801
-0,04571
0,01483
-0,01362
—0,02037
-0,02492
0,00004
-0,03524
0,02093
-0,04848
0,02299
—0,04349
0,00099
-0,02046
0,02082
—0,06292
у" (сплайн от
сплайна)
—0,00145
—0,00255
—0,00266
—0,00087
0,00186
—0,01135
—0,05907
—0,09313
—0,08270
-0,12118
—0,04087
0,15803
0,19970
0,20913
0,17807
0,05750
—0,01209
—0,00700
—0,00440
-0,01245
—0,01635
—0,01530
—0,01258
—0,00867
—0,01557
—0,00891
—0,01754
—0,01646
—0,00577
-0,00331
-0,00960
сплайна, у) — вторая производная сплайна от сплайна. В обоих случаях
использовались краевые условия Мо = Ми Мц^ = Мк.
Интеграл от сплайна по отрезку [а, Ь] получаем непосредственно из соот-
соотношения B.1.2). Имеем
\
Ы+1$
Л,-
24
B.5.6)
48
ГЛ. Т1. КУБИЧЕСКИЕ СПЛАЙНЫ
и, следовательно,
B.5.7)
Как и в случае численного дифференцирования, для неравных интервалов
предпочтительнее вычислить вначале моменты М) с помощью алгоритма,
указанного в конце разд. 2.1, а затем найти значение интеграла B.5.7). Для
равномерной сетки
Ъ N • Л'
) 8ь{х)йх = Ъ2л 2 2"^ 2 '
а 3—1 3—1
В периодическом случае получается просто правило трапеций, поскольку
здесь М\ + . . . + Мя — 0.
Суммирование левых частей равенств B.1.5) для непериодического сплай-
сплайна дает
N-2
B.5.8)
Таким образом, равенство B.5.7) для равномерной сетки принимает вид
АЗ
- ^- BМ0 + М1
Для краевых условий, в которых
имеем дело, справедливо равенство
B.5.9)
и с которыми мы в основном
-з#. Положим
= ЕЛ (а) =
тогда в силу B.4.11)
BМ0
-1- (/0 + /„ -а/4-
^г B/0 + Л 4-
~
Из B.4.6) получаем
2.5. ПРИБЛИЖЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ 49
а учитывая B.4.14), имеем
Е ^
0
Аналогичное равенство выполняется для 0<С]<С.М:
^"'+а?B.5.10)
Заметим, что Ео = 1 —*■/&. Таким образом, равенство B.5.9) принимает вид
ь
N-2
2 (*+Т^) /,. B.5.11)
3=2
Приведем алгоритм, с помощью которого можно для произвольного а быстро
вычислить коэффициенты в B.5.11). Положим Сгп=1{ — 2)П2?П; тогда
Далее, пусть
р — 2бд-2 + &п-з р __
Легко проверить непосредственно, что
и для
Следовательно,
Значения этих величин для малых тг приведены в табл. 2.5.1.
Коэффициенты для случая й0 = Лм = 0, а = 0 даны в табл. 2.5.2, а для
случая <20 = й# = 0, а = —2 в табл. 2.5.3. Первую из этих таблиц можно
найти в работе Холлидея [1]; здесь она приведена для удобства. В таблицах
представлены только числители, а знаменатели указаны лишь в левой части
каждой строки.
Любопытно отметить, что для 1, 2 и 3 интервалов получаются соответ-
соответственно правило трапеций, правило Симпсона и правило трех восьмых. В гл. V
и VI будут детально исследованы основные соотношения между сплайнами
4—1097
Таблица 2.5.1
п
—3
—2
—1
0
1
2
3
4
5
6
7
8
9
10
4
—1
0
1
—4
15
—56
209
-780
2911
—10864
40545
—151316
564719
2
—1
2
—7
26
-97
362
—1351
5042
—18817
70226
—262087
978122
-1
—1
5
—19
71
—265
989
—3691
13775
—51409
191861
—716035
2672279
—
—2
1
~Чъ
-1/5
~2/7
-6/!9
-7и
_1»/71
-2в/97
-71/265
-*7/Зв2
1/5зо
Таблица 2.5.2
Чш 1 1
1/8 3 10 3
1/ю 4 11 И 4
1/м .11 32 26 32 Ц
1/зв 15 43 37 37 43 15
1/т 41 118 100 106 100 118 41
1/142 56 161 137 143 143 137 161 56
153 440 374 392 386 392 374 440 153
209 601 511 535 529 529 535 511 601 209
Таблица 2.5.3
Чг 1 1 '
з 1 4 1
Чв 3 9 9 3
!/зв 13 44 30 44 13
!/9в 35 115 90 90 115 35
!/44 16 53 40 46 40 53 16
1/зео 131 433 330 366 366 330 . 433 131
1/492 179 592 450 504 486 504 450 592 179
1/44в 163 539 410 458 446 446 458 410 539 163
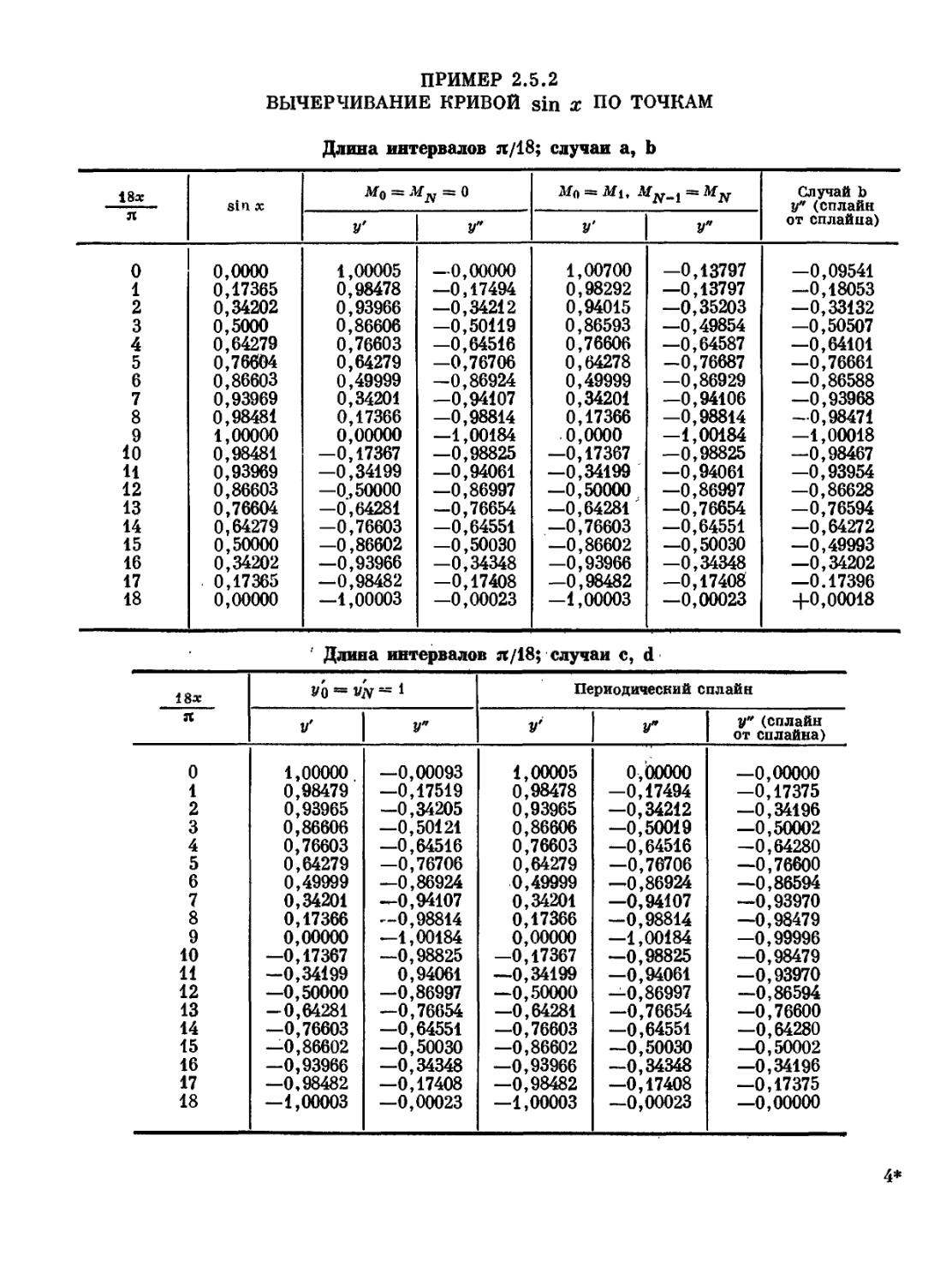
ПРИМЕР 2.5.2
ВЫЧЕРЧИВАНИЕ КРИВОЙ 8Ш X ПО ТОЧКАМ
18*
Л
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
81п х
0,0000
0,17365
0,34202
0,5000
0,64279
0,76604
0,86603
0,93969
0,98481
1,00000
0,98481
0,93969
0,86603
0,76604
0,64279
0,50000
0,34202
0,17365
0,00000
Длина интервалов л/18
У
1,00005
0,98478
0,93966
0,86606
0,76603
0,64279
0,49999
0,34201
0,17366
0,00000
-0,17367
—0,34199
—0,50000
-0,64281
—0,76603
—0,86602
—0,93966
—0,98482
—1,00003
У
—0,00000
—0,17494
—0,34212
—0,50119
-0,64516
-0,76706
—0,86924
—0,94107
-0,98814
—1,00184
—0,98825
—0,94061
—0,86997
—0,76654
-0,64551
—0,50030
-0,34348
—0,17408
-0,00023
; случаи а,
Ь
У
1,00700
0,98292
0,94015
0,86593
0,76606
0,64278
0,49999
0,34201
0,17366
0,0000
—0,17367
—0,34199
—0,50000
—0,64281
—0,76603
—0,86602
—0,93966
—0,98482
-1,00003
У
-0,13797
—0,13797
—0,35203
—0,49854
—0,64587
-0,76687
—0,86929
—0,94106
-0,98814
-1,00184
—0,98825
—0,94061
—0,86997
—0,76654
—0,64551
—0,50030
-0,34348
—0,17408
—0,00023
Случай Ь
У (сплайн
от сплайца)
—0,09541
—0,18053
—0,33132
-0,50507
—0,64101
—0,76661
—0,86588
—0,93968
-0,98471
—1,00018
-0,98467
—0,93954
—0,86628
-0,76594
—0,64272
—0,49993
—0,34202
—0.17396
+0,00018
Длина интервалов я/18; случаи с,
18*
Я
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
V'
1,00000
0,98479
0,93965
0,86606
0,76603
0,64279
0,49999
0,34201
0,17366
0,00000
—0,17367
—0,34199
—0,50000
-0,64281
—0,76603
—0,86602
-0,93966
—0,98482
—1,00003
у = 1
У
—0,00093
—0,17519
—0,34205
—0,50121
—0,64516
—0,76706
—0,86924
—0,94107
—0,98814
—1,00184
-0,98825
0,94061
—0,86997
-0,76654
-0,64551
—0,50030
—0,34348
—0,17408
—0,00023
Периодический сплайн
У'
1,00005
0,98478
0,93965
0,86606
0,76603
0,64279
0,49999
0,34201
0,17366
0,00000
-0,17367
—0,34199
—0,50000
—0,64281
—0,76603
—0,86602
—0,93966
—0,98482
—1,00003
у"
0,00000
—0,17494
—0,34212
—0,50019
—0,64516
—0,76706
—0,86924
—0,94107
-0,98814
—1,00184
-0,98825
—0,94061
—0,86997
—0,76654
—0,64551
—0,50030
—0,34348
—0,17408
—0,00023
у" (сплайн
от сплайна)
—0,00000
-0,17375
—0,34196
—0,50002
—0,64280
—0,76600
—0,86594
—0,93970
—0,98479
-0,99996
—0,98479
—0,93970
-0,86594
—0,76600
—0,64280
—0,50002
—0,34196
—0,17375
—0,00000
4*
52
ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
18*
я
0
2
4
6
8
10
12
14
16
18
0,00000
0,34202
0,64279
0,86603
0,98481
0,98481
0,86603
0,64279
0,34202
0,00000
Длина интервалов л/9; случаи а,
Мо = М# = 0
У
0,99989
0,93962
0,76600
0,49995
0,17363
—0,17362
-0,49996
—0,76599
—0,93962
—0,999992
у"
—0,0
—0,34533
—0,64950
-0,87481
-0,99489
-0,99472
—0,87505
-0,64916
0,34569
0,00022
Ь
У'
1,02734
0,93227
0,76797
0,49942
0,17377
-0,17366
—0,49995
М), 76599
—0,93962
-0,99992
у
—0,27235
-0,27235
—0,66905
-0,86957
-0,99629
—0,99435
—0,87515
-0,64917
—0,34569
+0,00022
Случай Ь
у" (сплайн от
сплайна)
—0,19056
—0,35391
—0,62260
—0,87575
—0,98078
—0,98612
—0,86531
—0,64285
—0,34200
—0,00011
Длина интервалов л/9; случаи с,
18х
л
0
2
4
6
8
10
12
14
16
18
з/о = ук = *
V'
1,00000
0,93959
0,76600
0,49945
0,17363
—0,17362
—0,49996
—0,76599
-0,93962
-0,99992
-0,00105
—0,34504
-0,64957
—0,87479
—0,99489
—0,99472
—0,87505
—0,64916
—0,34569
—0,00022
Периодический сплайн
V'
0,99989
0,93962
0,76600
0,49995
0,17363
—0,17362
—0,49996
—0,76599
—0,93962
—0,99992
V
0,00000
0,34533
0,64950
0,87481
—0,99489
—0,99472
—0,87505
—0,64916
—0,34569
-0,00022
у" (сплайн от
сплайна)
0,00000
—0,34198
—0,64279
—0,86589
—0,98469
—0,98469
—0,86589....
—0,64279
—0,34198
0,00000
и формулами численного интегрирования, а также связь сплайнов с прибли-
приближением линейных непрерывных функционалов.
В примере 2.5.2 приближение сплайнами применяется для вычисления
первой и второй производных функции зт х на отрезке [0, 2я]. При этом
берутся интервалы длины я/9 и я/18. В таблице указаны значения вторых
производных, при вычислении которых использовались моменты М$, а также
вторые производные сплайна от сплайна. Применение различных краевых
условий позволяет оценить степень их влияния на приближение. Мы рассма-
рассматриваем 4 случая: а) Мо — Мц = 0; Ь) Мо = Ми Мк^ = Мк; с) заданы
точные значения у\ и у'^, д) сплайн периодический. Ввиду симметрии значе-
значения приведены лишь на отрезке [0, я].
Вычисление у" с помощью сплайна от сплайна показано для случаев Ь)
и й), в которых применен тот же тип сплайнов, что и в основном вычерчивании
по точкам. При сравнении со значениями зт х становится очевидным улучше-
2.6. ВЫЧЕРЧИВАНИЕ КРИВОЙ ПО ТОЧКАМ 53
ние приближения у", вычисленное таким способом. Заслуживает внимания
качество периодического приближения у' и периодического сплайна от сплайна
приближения у" как для интервала длины я/18, так и для интервала длины л/9.
Превосходное качество приближения второй производной с помощью
периодического сплайна от сплайна получается при учете 6 десятичных знаков
в данных и в аппроксимации
I,-= 2 9/4Л»
справедливой для больших N.
2.6. Вычерчивание кривой по точкам
Конкретная цель большей части исследований, посвященных одномерным
сплайнам, состоит в вычерчивании кривой по точкам. Тем не менее такое вычер-
вычерчивание остается искусством, и необходимо указать некоторые технические
приемы, используемые при применении сплайнов в этом искусстве. -»
Обычно желательно применять более или менее равномерные распределе-
распределения точек сетки. Если длинный и короткий интервалы расположены рядом,
то часто возникают колебания, вовсе не свойственные исходным данным.
Влияние краевого условия, выбранного для данной дуги, если этот выбор
сделан неудачно, быстро затухает по мере удаления от крайних точек дуги.
При вычерчивании кривой по точкам часто бывает необходимо более-или менее
точно определить наклон в конце дуги. Выбор краевого условия действительно
оказывает некоторое влияние на величину этого наклона. Бели крайние точки
являются точками перегиба, то можно использовать условие Мо = М^ = 0.
При отсутствии оснований для другого выбора можно полагать Мо = М\,
•Л/^-1 — М я. Однако построенная кривая может оказывать резкое воздействие
на поведение величин М] вблизи концов, которому данное краевое условие,
по-видимому, противоречит. В этой ситуации часто применяются более общие
краевые условия: Мо = ХоМ^ Мя — РиМц^, где Хо и ц№ подбираются
в соответствии с этим поведением.
Аналогичная задача возникает при вычерчивании по точкам вблизи конца,
в котором наклон и кривизна уменьшаются по величине, например при вычер-
вычерчивании кривой у = Ух, 0 ^ х ^ 10, вблизи конца х = 10. Поведение этой
кривой не соответствует естественному ходу кубического полинома и вычер-
вычерчивание по точкам не даст хорошего результата, если существенно не увеличи-
увеличивать промежутки сетки при приближении к концу х = 10. Вблизи конца х = 0
хорошему вычерчиванию этой кривой по точкам с помощью сплайна мешает
также наличие здесь вертикальной касательной.
Некоторые трудности, возникающие при вычерчивании кривой по точ-
точкам, можно исключить подходящей заменой координат. Однако во многих
задачах появляются трудности по существу, и необходима техника применения
сплайнов,: позволяющая их обходить. Очень эффективным оказывается
параметрическое представление. Пусть на дуге С последовательно расположи-
54 ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
ны N 4- 1 точек Р^ (ж/, у]) (/ = 0, 1, . . ., АГ), и пусть 5; обозначает суммар-
суммарную длину хорд
5
/ 2
г=1
Мы строим сплайны, зависящие от 5 и проходящие через точки (х^ $>) и (г^-, $,-)
соответственно. Можно приближенно вычислить длины отрезков получившейся
кривой х — х ($), у = у (в) и построить новые сплайны для х и у в зависимо-
зависимости от суммарных длин хорд, но этот шаг обычно не приводит к заметному
изменению самой кривой.
Весьма поучительный пример дает приближенное представление абсциссы
х и ординаты у единичной окружности с помощью периодического сплайна,
зависящего от суммарных длин хорд. При использовании 8 точек (на расстоя-
расстоянии 45° друг от друга) максимальная ошибка не превосходит 0,00112 радиуса.
Для 12 точек (на расстоянии 30° друг от друга) максимальная ошибка равна
0,000165 радиуса. Интересно отметить, что даже для 4 точек ошибка составляет
менее 1%. Заметим, что таким путем удается с помощью сплайна эффективно
выполнить параметрическое представление.
Преимуществ при таком представлении много. Геометрическая конфигура-
конфигурация дуги в этом случае имеет гораздо меньшее значение, чем, для обычных
сплайнов. Вычерчивание с помощью сплайна простой замкнутой кривой,
заданной полярными координатами г и 6 с полюсом внутри кривой, будет эффек-
эффективным, если любой луч, исходящий из полюса, пересечет кривую не более
одного раза и не совпадет с касательной к кривой. При использовании сум-
суммарных длин дуг таких ограничений не требовалось. Можно даже строить
по точкам пространственные Кривые, образуя сплайны для х, у и г в зависимо-
зависимости от длин хорд или длин дут..
Нужно, разумеется, позаботиться, чтобы кривые, проходящие через точки,
действительно обладали требуемыми свойствами непрерывности. Применение
единого сплайна для вычерчивания кривой, состоящей из дуги окружности
и касательной в ее конце, приводит к колебаниям вблизи соединений, обуслов-
обусловленным разрывом кривизны. Если кривая (в двумерном случае, когда у зависит
от х) имеет в некоторых точках разрывы наклонов и кривизны, то для ее при-
приближения сплайном следует или выбирать именно эти точки в качестве узлов,
или располагать узлы соответствующим образом вблизи точек разрыва кривиз-
кривизны. Во втором случае сама точка не должна выбираться в качестве узла сетки.
При параметрическом вычерчивании по точкам, когда в качестве параметра
берется суммарная длина хорд, положение лучше. Соответствующее располо-
расположение интервалов оказывается удовлетворительным, даже если точка разрыва
кривизны берется в качестве узла сетки.
2.7. Приближенное решение дифференциальных уравнении
Сплайны часто с успехом применяются при решении задачи Копш и крае-
краевых задач для обыкновенных дифференциальных уравненийД Предлагаемый
метод пригоден в общем случае, но мы ограничимся сейчас двухточечной крае-
2.7. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 55
вой задачей для уравнения второго порядка:
Ьу = у" + р (х) у' + ^ (х) у = г (х) (а < х < Ь), „ ?
а^ (а) + а2/ (а) = а0, Ь^ (Ь) + &У'(&) = &
Введем фундаментальные сплайны, связанные с краевым условием B.1.181):
так будем называть N + 3 независимых сплайнов Лд>& (я) (& = 0, 1, . . ., IV)
и ВАуъ(х) (к = О, IV), образующих базис для всех кубических сплайнов, опре-
определенных на сетке Д: а = х0 <. х^ . . . < хы = Ь. Зададим эти фундамен-
фундаментальные кубические сплайны условиями
^д, к (ж>)=бц} и=о, 1,..., #),
-4д.к (*|) = О (*=О,ЛГ), А = 0, 1, -...ЛГ,
= 0 . G = 0,1, ...,Л0, ( * ' ^
& = 0, ЛГ,
где бь/ — символ Кронекера. ■»
Кубический сплайн, интерполирующий решение дифференциального урав-
уравнения и удовлетворяющий краевым условиям B.1.181), можно представить
в виде
#Д (У; х) = 2 Ль. о (*) У (*/) + / (а) Да. о (ж) + у' Ф) Да. N (ж). B.7.3)
Обозначим
,4д (у; ж) = у (*) - ^д "(у; *>• -" B-7-4)
Если существует единственное решение у (х) задачи B.7.1), принадлежащее
классу С2 [а, Ы, то #^а) (у; х) = о (|| Д Ц2~°) (а = 0, 1, 2) равномерно относи-
относительно а: на [а, Ь]. Если функция у (х) имеет производные более высокого
порядка, то в соответствии с результатами разд. 2.3 порядок стремления функ-
функции Яд0 (у; х) к нулю также более высокий.
Принимая во внимание равенство B.7.4), запишем
)$ь(у; х)-г(х) = Оь(у; х),
где #д (у; х)= —ЕЪ (у; х) —р (х) Яд (у; х)—д (х) Яд (у; х), так что Яд (у; х) =
= о(||1||). Подставляя B.7.3) в B.7.1), получаем
,м{х)-г(х)=С&(у;х). B.7.5)
Таким образом, ординаты У} — у{х}) (/ = 0, 1, ..., IV) и наклоны у'0 = у' (а),
м = у'(Ъ) удовлетворяют уравнениям
/
I « = 0. 1 т. B.7.6)
56
ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
Введем (
)бозначения:
>
и пусть матрица Яд
*
•
•
*
0
Уь=(#о' Уъ У и
Яд=(О, Оь(у;х
Яд = (а0, гад,
имеет вид
«1
•
•
■
0
• • ■ • г/»»
о), -..,<
0
•
*
•
0
'а (у; *л
• » •
... ьл
• • • Лш/лл.
ш • •
•
), 0)т,
0
•
•
•
0
•
•
•
Тогда
НдУь = Лд + Сгд»
Величины Gд (^; х$, конечно, не известны. В предлагаемом методе Gд
заменяют нулем и находят приближенное значение У* из уравнения НАУ% =
— Яа- Если матрица Яд1 существует и || Яд^д || —> 0 при ||А||—^0, то репю-
ния уравнения
ЯдУд = Дд B.7.7)
определяют сплайны, равномерно сходящиеся на [а, Ъ] к у (х). В частности,
эти условия выполняются, если нормы || Яд1 || равномерно ограничены.
Для иллюстрации рассмотрим краевую задачу
B.7.8)
Здесь матрица Яд имеет вид
О 1
Лд, о [р^о) Д» О \^О/ ^'
к, о ад ^д.оад
у @) = у A) = 1.
0
—а2
о
^, ^ ад
о
*д, лг ад
В'к, о
. О
, о
О
—а2
О
О
Умножим уравнение B.7.7) на квадратную матрицу порядка
1 0 ... О О'
О
О
О
О
О 0 ... О 1
B.7.9)
2.7. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
57
где А — матрица коэффициентов системы B.1.8) при А,0 = |л^=1. Тогда урав-
уравнение B.7.7) примет вид
о
о
о
о
о
о
1
6
О
о
о
О
о
6
-Ща2 -~ 2а2
6
О
О
и <-у2
Л—2а2
О
О
о
я3(я3+я4)
•
•
•
О
О
о
о
о
о
о
о
о
о
о
о
О
О"
О
О
О
О
__6_
О
•
'Уо'
Уо
У1
Уъ
Уз
•
*
Ух
=
1
0
0
0
0
•
0
.1
B.7.10)
Заменим здесь —у'о 4- (уг — уо№ на щ и у$ — (у^ — ук^1Кгг на ик. Затем
поменяем местами первое и второе, последнее и предпоследнее уравнения
этой системы. В результате получим
6
О 1
О
О
О
0
О
О
6
Тца2
О
О
О
О
О
О
о
о
о"
0
0
0
6
Щ
Уо
Ук
"о"
1
0
1
[0
58
ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
Ясно, что если число || А || достаточно мало, то матрица коэффициентов имеет
доминирующую главную диагональ и норма обратной матрицы равномерно
ограничена.
В этом процессе вектор ошибки С?д умножается на матрицу B.7.9), норма
которой ограничена, и на матрицу, обратную матрице коэффициентов систе-
системы B.7.10), норма которой также ограничена. Отсюда следует сходимость
сплайнов к функции у (хI В самом деле, при || А || -*- 0
\У' Ы ~
- Ух, У* М -
0.
В табл. 2.7.1 приведено точное решение (с 5 десятичными знаками) крае-
краевой задачи у" — ЮОу = 0, 0 ^ х ^ 1, у @) = у A) = 1, а также ее прибли-
приближенные решения, построенные с помощью сплайнов, определенных на сетках
Таблица 2.7.1
X
0,00
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
Точное
значение у
1,00000
0,60657
0,36799
0,22332
0,13566
0,08263
0,05070
0,03170
0,02079 .
0,01520
0,01348
1
0
0
0
0
0
ЛГ=10)
,000000
—
,35107
—
,12343
,04390
,01075,
,01065
у(*>
1,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
Г= 20)
00000
60333
36406
21975
13277
08042
04906
03049
01987
01444
01277
Точное
значение у'
-9,9991
—
—
—
—
—
—
—
—
—
у' (N = 10)
—10,1152
—
—
—
—
—
—
у' (N=20)
—10,1028
—
—
.
—.
—
—
—
—
—
с 11 и 21 узлами. Решение этой задачи имеет вид у = сЬ. 10 (х — 0,5)/сЬ 5.
Ввиду симметрии в таблице представлены значения лишь для половины отрез-
отрезка [0, 1}.
Необходимо отметить, что с помощью формулы B.7.3) можно получить
приближенное решение на всем отрезке. Это особенно важно, когда для даль-
дальнейших вычислений требуется знать решение краевой задачи в различных
точках отрезка [а, Ь]. Важный пример дает координатный самописец, для
которого часто бывает нужна интерполяция в большом количестве промежу-
промежуточных точек.
Нелинейные дифференциальные уравнения эффективно решаются с помо-
помощью сплайнов, когда последние применяются в сочетании с методом квази-
квазилинеаризации, развитым Беллманом и Калабой [1]. Здесь задача
У" =1 (*, У, У'), а < х < &;
Л [у (а), у' (а)\ = 0, В [у (Ь), у' (Ъ)] = 0
2.7. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
59
решается итерационным методом
0п+1 = /у(#, Уп, У'п) (Упы — Уп)-гТу' & Уп, Уп) {Уп+1 ~Уп)
с линеаризованными краевыми условиями
Лу [уп (а), Уп (а)] [уп+1 (а) — уп (а)] + А'у> [уп (а), у'п (а)] [у'п+1 (а) — Уп (а)) = О,
В'у [Уп (*>), Уп (Ь)] [Уп*1 (Ь) ~ Уп F)] + В'у [уп (Ь), У'п (Ь)] 1Уп+1 (Ь) - Уп (Ь)} = 0.
В случае равномерной сетки моменты для ранее введенных фундаментальных
сплайнов можно найти непосредственно с помощью результатов разд. 2.4.
Краевые условия имеют вид B.1.181), так что в матрице коэффициентов А систе-
системы B.1.8) к0 = ц^ = 1.
Таким образом,
, N (%о) ВЪг N (х0)
- 6
к
0
0
0
0
0
0
. 0
6
к
3/й2
0
0
0
0
0
0
6
к
3/7
0
0
-6//г2
0
0
- г/к2
-Ъ/к2
-б//*2
3/Ь*
0
0
. . .
• • •
• ♦ •
. . .
-6//12
ЗА2
о'
О
3/Ь2
-6/й2
6/Л
О
О
О
О
О
О
3//г2
— в/к
О
0
О
О
О
О
О
6/А
Формулы для элементов обратной матрицы А'1 приведены в разд. 2.4.
Фактически мы имеем
—а")
-1
60 ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
где А^^=А]^@<:^<:N, 0</<.№) и Л# = Лй1-,^-* для всех г и /. Эти
величины можно найти, применяя методы разд. 2.4, или их можно вычислить
непосредственно, принимая во внимание, что аР + о~к и сгп—ок являются
4
р
решениями разностного уравнения мп+2 + 4мп+1 -Ь ип = 0.
2.8. Приближенное решение интегральных уравнении
Рассмотрим линейное интегральное уравнение
ь
А, B.8.1)
где 1{х) и ЯГ (я, *) непрерывны, а.<ж<;&, а<]*<;Ь. Введем ЛГ + 1 фундамен-
фундаментальных сплайнов Лд,^(а;) (/ = 0, 1, . ..,.№), удовлетворяющих краевым усло-
условиям М0 = Ми Му-1 — Мц. Таким образом,
^д.^'(Ж|) —б^ 0", / = 0, 1, .
Интерполяционные сплайны этого типа имеют вид
N
где уз = у (X}). Если >?д (х) = у (х) — 5д (х), то
а
Если функции /(#) ж ^ (х, <) принадлежат классу Са[а, Ь] (а = 0, 1, 2, 3), то
Дальше мы делаем почти то же, что в предыдущем разделе в случае
линейного дифференциального уравнения: полагаем Оь(х})-— 0 (/ = 0, 1, ..., Щ
и находим у0, уи ..., #№ из уравнений
N Ь N
2 0г-4д, г (X,) = / (Ж,) + % ^ К (Х}, $
г=0 а
Интегралы
ь
2.8. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
61
определяем точно, если это возможно (заметим, что АА>г — кусочно кубический
полином), или же вычисляем приближенно. В последнем случае можно, напри-
например, каждую функцию К (а^, I) заменить интерполяционным сплайном, и тогда,
поскольку фундаментальные сплайны Лдг ({) известны, для вычисления этих
интегралов потребуется лишь небольшая дополнительная работа.
Итак, нам необходимо решить следующую систему уравнений:
4J
/ц-1
22
Уо "
У\
Уг
•
"-/о"
— /1
-и
*
Если 1 не является собственным значением однородного интегрального
уравнения, то доказательство сходимости найденных так сплайнов к точному
решению при || А || -*• 0 опирается на соответствующее доказательство для
случая, в котором для приближенного интегрирования применяется правило
трапеций (см. Гурса и Бергман [1]).
С алгебраической точки зрения при применении к интегральным уравне-
уравнениям сплайны обычно проще брать в стандартной форме B.1.2). В качестве
примера рассмотрим интегральное уравнение, связанное с двухточечной крае-
краевой задачей B.7.8):
1
у (х) = 1 + [ К (х, Г)у (*) йгу B.8.2)
где
{а2 (х — 1) г при 0 <; г <; х,
о?х ({ — 1) при ж^г<[1.
Заменим у (х) сплайном <?Л (х), определяемым из соотношений
Х1 1 ,
уг = 1 + а2 (хг — 1) \ ?<5Д (*) сИ + а2х{
о
(г = 0, 1, . . ., АГ).
Так как у0 = ух = 1, то число уравнений можно уменьшить на 2. Для
0 < I < N имеем
62 ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
Х1
5=1+1 хм
х,-
*М
После вычисления интегралов получаем для равномерной сетки (кг —
1 ^ ЛГД1)
1=1
1-1
ЛГ—1
Умножая соответствующие члены 2, 3, ..., г-го уравнений системы B.1.8)
на 1, 2, ..., (г —1) и складывая их, находим:
г-1
Аналогично
Применяя соотношения B.1.5), связывающие А/,-_1, ЛГ4, М^+1, получаем
(АГ —
12
2.8. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
63
Заметим, что М0=а?у0=-а? = у№@), Мл=-а2^=1а2 = |/"A) и, следовательно,
выполняются краевые условия B.1.18П).
Величина М{ выражается через уи ..., ук-\ с помощью равенства B.4.11),
в котором А$ определяются (разд. 2.4) для краевых условий (п):
При четном N получаем для уг (г = 1, 2, ..., N/2) следующую систему уравнений:
^ = 1+-180 A—2") +-30 1в
где
а
В табл. 2.8.1 приведено для сравнения точное решение (см. разд. 2.7) при
N = 20.
Таблица 2.8.1
X
0,00
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0 50
Точное
значение у
1,00000
0,60657
• 0,36799
0,22332
0,13566
0,08263
0,05070
0,03170
0,02079
0,01520
0,01348
Приближенное
решение, по-
построенное с по-
мощью сплайнов
1,00000
0,60656
0,36802
0,22334
0,13568
0,08264
0,05070
0,03170
0,02080
0,01520
0,01348
Из равенства B.8.2) видно, что в рассмотренном примере у" (х) — а?у (х) =
= 0. В общем случае краевые условия для сплайна можно найти, продиффе-
продифференцировав интегральное уравнение и получив тем самым ограничения на Мо
и М ц.
Рассмотренный пример охватывает значительную часть схемы, применяе-
применяемой в общем случае, когда для приближенного вычисления требуемых инте-
интегралов само ядро К (х, г) при каждом фиксированном х{ заменяется интер-
интерполяционным сплайном.
64
ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
2.9. Дополнительные теоремы существования и сходимости
Существование интерполяционного сплайна доказано в разд. 2.2 в пред-
предположении, что в системе B.1.8) | Хо | <С 2 и | р,^ | <С 2, или при ана-
аналогичных ограничениях на систему B.1.16). Чтобы расширить эти результаты,
необходимо детальнее исследовать свойства матрицы коэффициентов систем
B.1.8) и B.1.16). Сейчас мы закончим доказательство общей теоремы суще-
существования*
Теорема 2.9.1. Периодический сплайн 5Д (х) с заданными ординатами
Ум Уи • • • » Ух = Уо в узлах сетки А: а = х0 <С х^ <С . . . •< ж№ = Ь всегда
существует. Непериодический сплайн, удовлетворяющий краевым условиям
B.1.18Ш) [или B.1.19т)], существует, если Хо •< 4 и р,к <С 4 (или
{х0 < 4 и Хк< 4).
Чтобы завершить доказательство, остается рассмотреть непериодический
случай, в котором Хо <С 4 и р,№ <С 4. (Случай [х0 •< 4 и Я№ •< 4 эквивалентен
рассматриваемому.) Для к >• / положим
-Х* 2
B.9.1)
и условимся, что этот определитель равен 2, 1, 0 при к = /, к — / — 1, к =
= ; — 2 соответственно. Разложим определитель B.9.1) по правилу Лапласа
B.9.2)
или, в терминах непрерывных дробей,
*»>1-
B.9.3)
Это соотношение между трехдиа тональными матрицами (континуальными
матрицами) и непрерывными дробями указано Эйткеном [1, стр. 126].
В гиперкубе 0 ^ Хг -^ 1 ()' ^ I -^ к) левая часть равенства B.9.3) пред-
представляет собой дробно линейную функцию каждого из своих аргументов.
По теореме Гершгорина в этом гиперкубе ее знаменатель отличен от нуля.
Если ^ = . . . = Хк = 0, то И (^, . . ., %к) = 2м+1 (к > / — 1). Таким
2.9. ДОПОЛНИТЕЛЬНЫЕ ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И СХОДИМОСТИ 65
образом, функция Т) (Х>, . . ., %к) положительна в гиперкубе и принимает
там свое наибольшее и наименьшее значения в точках, в которых X* равно О
или 1 для всех г.
Если А^-и = 0, то левая часть равенства B.9.3) равна 1/D — X./). Если
Х/+1 = 1, то она равна 1/3 или 1/4 в зависимости от того, 0 или 1 равно Х/+2-
Следовательно, если 0 ^ X* ^ 1 (/ ^ (; -^ к), то
Заметим, что
и по индукции докажем следующую лемму.
Лемма 2.9.1. Если 0 < Хг < 1 (/<*<*) и & > /, то
д(Ь-;+1)/2^ д.— . нечетн0>
2.3(й-^/2, &-/ ч
Разложим определитель Х> = /> (Хо, • • ., Х^) матрицы коэффициентов
системы B.1.8) сначала по элементам первой строки, а затем по элементам
последней строки:
[, ..., Хд-_|) — 2Х0 A — Х^) и (л2, ..., л^_1) ■—
Отсюда найдем:
" D — Хо) D — Х№) 0 (Х2,,..., Х^.з) для Х{— О, Х^.! = 1,
2 D —Х0)/)(Х2, ..., Х№_2, 0) * для Х! = 0, Х№_1 = 0,
О = ч
2D — Х^) г/A, Х2, .. ., Л-^-_2) Для Л>1~1, Л-^_| = 1,
A, Х2, ...,Х^_2, 0),, для Х1=1, Я^-1 —0.
Из неравенства B.9.5) для Хо <С 4 и [х# <С 4 следует, что определитель Э матри-
матрицы коэффициентов системы B.1.8) удовлетворяет неравенству
Г з<"-3>/2, N нечетно, 1
/)> [штC,4-Х0)].[ттC,4-М]-1 о о(Д'-4)/2 дг \>°- B-9-7)
I 2 «3й ;/ , N четно, ^
Теорема полностью доказана.
Распространим теперь теоремы 2.3.2 и 2.3.3 на более общие краевые усло-
условия. Для этой цели надо использовать свойства элементов обратной матрицы,
которые и сами по себе представляют значительный интерес. Эти свойства
связаны со скоростью убывания величины элементов обратной матрицы по мере
их удаления от главной диагонали.
5-Н97
66 ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
Элементы матрицы Л, обратной к матрице коэффициентов системы B.1.8),
можно найти непосредственно из алгебраических дополнений матрицы А.
Таким образом,
B.9.8)
где А.^ = 1 — (х^1 и /> — определитель матрицы коэффициентов.
Нам нужны две леммы о свойствах этих элементов. Разложим определитель
Т) (X/, . . ., Л-ь) для / <С к по минорам первой строки:
Я (** . . ., К) = 20 (
При /? (X/, ..., кь) ф 0 имеем
Д (А,/+1, ..., Хк) _ (
"
Это отношение равно х/2, если ^/+1 = 1, и 2/D — ^), если Х/+1 = 0. Кроме
того, оно является билинейной' функцией каждого из своих аргументов. Бели
О-^Хг-^1 для ]<СК.к и•%,} <С 4, \лк <С 4, то знаменатель положителен.
Тогда можно показать, что
. Г1
Разложив определитель О (к}, ..., А,&) по минорам последней строки,
получим для 0-^1|<^1 (] <.Кк) и ^<4, ^й<!4 неравенство
2 ^$ Лд
Анализируя доказательство неравенства B.9.4), нетрудно заметить, что
при 0<^<1 и<г<к) и Я4 4
При тех же самых условиях аналогичным образом выводим неравенство
Сформулируем первую из нужных нам лемм.
2.9. ДОПОЛНИТЕЛЬНЫЕ ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И СХОДИМОСТИ
67
Лемма 2.9.2. Для
целого р, 0<Лг
(О<г<ЛО, (%<4 и любого
тах Г4-, -гЛ-1 3"<р)/2, р нечетно,
р четно,
B.9.13)
тт
тах
тах
:Гт-Л-]
.[1,2-5—1 :
Доказательство. Для нечетного
, N—р нечетно,
N—р четно,
, B.9.14)
В
р
(Яо, ..
2)
I)
-1, ...,
В силу неравенств B.9.9) и B.9.11) это отношение заключено между вели-
величинами
Ш1П Ь' 43^] (Т) ' таХ \ ] ()
Для четного
(%р, ...,
В
В
Т> (Ягу_2, ..., Ядг)
и в силу неравенства B.9.11) это отношение заключено между величинами
1 \р/2-1 Г 1 1 П / 1 \р/2-1
Г1 1
шах [-, --
Неравенство B.9.13) доказано. Из B.9.10) и B.9.12) аналогично выводится
неравенство B.9.14).
Следует отметить, что неравенства B.9.13) и B.9.14) точные, так кэк при
подходящих значениях Я; они обращаются в равенства.
Лемма 2.9.3. Для %0 < 4, 0 < Хг < 1 @ < ъ <
0ЛГ
< 4 и
' — р нечетно,
' — р четно.
B.9.15)
5*
68 ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
Доказательство. Разложим определитель Т) (Х,о, . • ., А, л) по пра-
правилу Лапласа:
и (л0» • • •» ^ю ~ & (^-о> • • ч ^р) ^ И-р+ь • • ч А^) —
— ^ (^-о» • • ч ^р-О А,р A — ^-р+0 ^ (^-р+2» • • •, Ъ-гг)- B.9.16)
Если О^р^д — 2 ид-^Л^, то это разложение можно записать в виде
О (Л-о» • • ч Л-Дг) == ^ (Л-0» • • ч
ч ^7>) ^ (^р+1> • • ч ^д-г)Лд-1 A —
О & (Ь+2 • * ч
.. ., А,к), B.9.17)
при этом мы считаем, что О (Х,^ . . ., X/) = 0, если ] — I — 2. Средний член
неравенства B.9.15) при 0<Ср<С? — 2 ид<Л^ равен
для ^р=° и К=и
Т 4-1° (^Р+И • • • т ^а)| Для ^р = О И Я,д = О,
A X)^(XX)^ для Хр=1 и Ха = 1,
] ^ (^р+1» • • • 9 "в-1) ~~2 ■ в-1 \"Р+1» • • ч Л-д-г) 2" ( Р+1/
1 ' 1 —1
Я A А)# (^ ^)} ДЛЯ
Здесь использованы соотношения 1> (О, /1 ) (^
В (X,;, ..., ^-1,1) = 2В (%}, ..., Яй-1). Рассматривая случаи Х,р+1 = 0, Л,р+1 = 1,
Х,?_1 = 0, Лд_4 = 1 и учитывая неравенства B.9.9) и B.9.10), получаем
Для завершения доказательства осталось применить лемму 2.9.1.
Распространим теперь теоремы 2.3.2 и 2.3.3 на более общие краевые
условия:
Теорема 2.9.2. Пусть на отрезке [а, Ь] заданы функция /(ж) из класса
С1 [а, Ь] и последовательность сеток {Д&}, ||Аь||—^0 при к~->оо. Пусть
сплайн 8&к {х) интерполирует функцию / (х) в узлах сетки Дь и удовлетворяет
краевым условиям B.1.19Ш), и пусть т{D —ий0)>0, т{D — %шь) ~> О
к к п
и последовательности {ць0} и {^шЛ ограничены при к—>оо.
2.9. ДОПОЛНИТЕЛЬНЫЕ ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И СХОДИМОСТИ
69
а) Если г'к = сн - B + \1к0) /' (а) -+ 0 и
( к я
к —> сю, то 5д (#) сходится к /' (а;) равномерно относительно х на [а, Ъ] и
= о (|| Д* ||)^
= сШк - B +
о
= 0,
О
я) /' (Ь)
[а
B.9.18)
равномерно относительно х на [а,Ъ].
Ь) Если последовательности {с^} и {сияк} ограничены при к—>оо,
то равенство B.9.18) справедливо на любом замкнутом отрезке, принадлежа-
принадлежащем интервалу (а,Ь), и 8&к(х)—>{(х) равномерно относительно х на [а, Ь].
Доказательство, а) Введем в рассмотрение квадратную матрицу 0к
порядка
■Що) 0 ... О
П
т
О
О
1
О
О
О
о
о
о
о
3
о
о
о
О 4A-
и запишем систему B.1.16) в виде
Вктк - Вкпкск = {1к - Вкпк) сЛ, B.9.19)
где 1к — единичная матрица порядка Ык + 1 и Вк — матрица коэффициентов
системы B.1.16), соответствующей сетке Д&. Правая часть равенства B.9.19)
представляет собой вектор
Т\Ск0~
--Х-(см-<Ъ2)Ч-
B.9.20)
70 ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
Заметим, что величина 1/зсь*@<*<^) равна значению производной /'(|)
в некоторой точке | из интервала {х^, #г-н). Таким образом, норма вектора
B.9.20) не превосходит большей из двух величин
л . 2-\-ккм
4-1елН о—-2в>(|| АьН, /') + 3(о(||ДйЦ, /').
Из равенств B.9.8) и леммы 2.9.3 вытекает, что нормы || Вй11| ограничены
относительно к. Таким образом, в силу B.9.19)
\\тк-Скск\\->0
при к—>оо. Следовательно, \\0кск — [/' (хъо), V (х]ц), ..., /' (хтк)] II —>-0,
поскольку
Заключительная часть доказательства проводится точно по схеме доказатель-
доказательства теоремы 2.3.2.
Ь) Пусть выполнены условия второй части теоремы. Для отрезка
[а', Ъ'\ <= (а, Ь) по крайней мере п'к = 1 + (а' — а)/|| Д& || точек сетки Дй
лежат слева от точки а' и по крайней мере п"к = 1 + (Ь — Ь')/|| Дй || точек
сетки Дь лежат справа от точки Ь' (учитываются также и точки, совпадающие
с а' и Ъ'). При образовании сумм, которые представляют компоненты вектора
тк — (*кск из равенства B.9-19), связанные с узлами сетки из отрезка [а', Ь'],
мы видим, что первая, вторая, предпоследняя и последняя компоненты век-
вектора B.9.20) умножаются на величины, не превосходящие соответственно
{1, ^
(см. равенства B.9.8) и лемму 2.9.2). Так как п'к и пк неограниченно возрастают
при к -*- оо, то
Нт{ тах \тк] — /' (хк})]} = 0.
2.9. ДОПОЛНИТЕЛЬНЫЕ ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И СХОДИМОСТИ 71
Равномерная сходимость на отрезке 1а', Ъ'] последовательностей {5дл (х)}
и {5дй (х)} соответственно к функциям / (х) и /' (х) устанавливается обычным
образом.
Чтобы установить равномерную сходимость на отрезке [а, Ъ] последова-
последовательности {5д (х)} к функции/ (х), заметим, что при выполнении условия Ъ)
из метода доказательства случая а) следует, что величины т^ равномерно
ограничены относительно к. Отсюда равномерная сходимость последователь-
последовательности {5д (х)} к функции / (х) вытекает непосредственно из B.1.10). Отметим,
что член, содержащий ум-1 и Ук}> является кубическим полиномом с экстре-
экстремумами в точках #ь;_1 и х^ и, следовательно, изменяется монотонно между
этими точками.
Справедливость следующих утверждений очевидна.
Следствие 2.9.2.1. Пусть выполняются условия теоремы 2.9.2.
Если /' (х) удовлетворяет на [а, Ь] условию Липшица порядка а @ <С а ^ 1)
и е'н = О (|| Д& ||а), то правую часть равенства B.9.18) можно заменить на
О (|| А* ||1+а'р) (р = 0, 1).
Следствие 2.9.2.2. Если производная /' (х) существует, ограничена
для всех х 6 1«, Ь] и непрерывна на отрезке [а', Ь'\ <= (а, Ь), то 8'ък (х) -> /' (х)
равномерно на [а', Ь'\ и 5д (#) -> / (а;) равномерно на 1а, Ъ].
Теорема 2.9.3 доказывается точно так же, как теорема 2.9.2. Мы ограни-
ограничимся здесь лишь ее формулировкой.
Теорема 2.9.3. Пусть на отрезке [а, Ь] заданы функция /(#) из класса
С2 [а,Ь] и последовательность сеток {Д&}, || А&|| —>0 при к—>оо. Пусть сплайн
#д (а;) интерполирует функцию / (х) в узлах сетки Дь и удовлетворяет крае-
вым условиям B.1.18111), и пусть т{D — "Кь.о)> 0, Ш{D — ^шь) >0 и последова-
к н А
тельности {^0} и {\*-шк} ограничены относительно к.
а) Если г'к - йк0 - B + Хк0) Г (а) -» 0 м еЦ = Оьяк - B 4- Цалгй) Г (Ь) -► 0
дгрм Л—>оо, то |5д. (а;) сходится равномерно на [а,Ь] к /" (х) и
\!™(х)-8%(х)\ = о(\\Ак\\2-р) (р = 0, 1, 2) B.9.21)
равномерно относительно х на [а, Ь].
Ь) Если последовательности {^к0} и {&шЛ ограничены относительно к,
то равенство B.9.21) справедливо на любом отрезке [а', Ь'] а (а, Ь). Более того,
последовательности {8'ьк (х)} и {5д (х)} сходятся равномерно на [а, Ь) к функ-
функциям /' (#) и / (х) соответственно.
Справедливы также аналоги двух предыдущих следствий.
72 ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
Следствие 2.9.3.1. Пусть выполняются условия теоремы 2.9.3. Если
V (х) удовлетворяет на отрезке [а, Ь] условию Липшица порядка а @ < а ^ 1)
и е'к = О (|| ДА ||а), г'ь, — О (|| Дй ||а), то правую часть равенства B.9.21)
можно заменить на О (|| Ай \\2+а~^) (р = О, 1, 2).
Следствие 2.9.3.2. Если вторая производная /"(х) существует, ограни-
ограничена для всех х$[а,Ъ] и непрерывна на [а\ Ь'] <= (а, о), то 8ьк (х) —»/"(х)
равномерно на [а\Ь'\ и 8^ (х)—>{(р)(х) равномерно на [а,Ь\ для р — О, 1.
Очевидно, что можно установить ряд других аналогичных результатов.
Например, существование второй производной /* (х) можно заменить равно-
равномерной ограниченностью разностных отношений. Можно доказать сходимость
в единственной точке, если известно, что в этой точке существует вторая произ-
производная (Алберг, Нильсон [3]).
Займемся теперь третьей и четвертой производными.
Теорема 2.9.4. Пусть на отрезке [а, Ь] заданы функция / (х) из класса
С3 (а, Ъ] и последовательность сеток {Ль}» удовлетворяющая условиям
Пусть сплайн 5дй (х) интерполирует функцию / (х) в узлах сетки Дь и удовле-
удовлетворяет краевым условиям B.1.18Ш), и пусть ш(D — А,ьо)>0, т!D-— (д,й^ь)>0
к к к
и последовательности {кко} и {рш^ ограничены относительно к. Если величины
Г И,
стремятся к нулю при к—хх»! то для х^[а, Ь]
\/(р)(х)-3($(х)\ = о(\\ Ай||3~р) (р=0, 1, 2, 3).
Если, кроме того, /"(я) удовлетворяет условию Липшица порядка сс(О <Ссс<;1)
и обе величины г'ъ и г"ъ равны О (|| А» ||а), то на отрезке [а, Ь]
р) 0> = 0, 1, 2, 3).
Доказательство. Заменим первое и последнее уравнения системы
B.3.21) уравнениями (опущен индекс сетки к):
[6- B + Хо)
B + М ^-1<т„., + [6 - B + р„) Х„н] ^.^ =
2.9. ДОПОЛНИТЕЛЬНЫЕ ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И СХОДИМОСТИ
73
Бели матрицу коэффициентов новой системы разложить аналогично матрице С
системы B.3.21), то будет снова ЕйР. При этом матрица /) будет иметь вид
О
О
О
О
О
О
О
О
О
О
У этой матрицы главная диагональ доминирует; обратная к ней матрица равно-
равномерно ограничена, если т{D— А,й0)> 0 и т!D — ^шь) > 0. Итак, величина
к ■ й й
II С II равномерно ограничена.
Образуем матрицу Н порядка ЛГ*:
О 1
О 0
* •
О О
о о
Обозначим вектор
о ...
1 ...
... О
... О 1
B-А<
))а1—за0
[~\- Ь/2.
1—й\
•
•
•
О
О
О
О
о
о
о
через г; тогда
С (<т - Нг) = (I — СН) г,
74
ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
правая часть представляет собой вектор
- 6щ + B +
- [D
+ B + К
1 —
[1 - 6^.2 + B + ^) ХЬ_4] {г^ - [D - II») Х^ + B +1%)
Скорость, с которой величина || (/ — СН) г \\ стремится к нулю, теперь
очевидна, и утверждения теоремы следуют из ограниченности || С Ц.
В заключение приведем довольно любопытное свойство сходимости к /D) (х).
Ради простоты рассмотрим лишь случаи периодических кубических сплайнов,
хотя соответствующие рассуждения проходят и для непериодического сплайна.
Рассмотрим скачок третьей производной сплайна в точке х}- и положим
Величины а^ удовлетворяют уравнениям
О
1 —
1 —
1 —
1 —
1—
1—
0
О
1 — Ипг-
Вычтем из (/ + 1)-го уравнения ;-е и новое уравнение разделим на /&/_!
+ / + ^: имеем
B.9.22)
2.9. ДОПОЛНИТЕЛЬНЫЕ ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И СХОДИМОСТИ
75
где
есть четвертая разделенная разность / 1:г/_2,
^ х;+и
о
и 97- = A —
о
Умножим строки матрицы Б на
A4 •..
а столбцы—на
-2J ЦЛГ-1
о
0
о
о
о
М-ЛГМ-1
Напомним, что в периодическом случае Х1 ... ^ = 14 ...
получим матрицу
0 ... О
результате
Если для рассматриваемых сеток Ай выполняется неравенство
Ц Ай ||/тт ^ <^ р < оо, то норма обратной матрицы || Б'1 \\ равномерно огра-
ограничена относительно к. Обозначим через О^ сумму элементов ;-й строки
матрицы Б:
Если сетки
при
оо стремятся к асимптотически равномерным, т. е.
шах "
з
76 ГЛ. II. КУБИЧЕСКИЕ СПЛАЙНЫ
ТО
тах
С;
1
0.
Вообще пусть С — диагональная матрица с диагональным элементом 0}
на ;-й строке. Тогда у матрицы О'Ю — / сумма элементов каждой строки
равна нулю.
Запишем уравнение B.9.22) в виде
Пусть четвертая производная /D) (х) непрерывна на Га, Ь]. Величина 4^- отли-
отличается от /<4> (я^) на О (|| А ||). Таким образом, || (/ — &!)) % || -*■ 0 при
|| А || -> 0. Так как норма обратной матрицы || I) || равномерно ограничена,
то очевидно, что || б — Б'Ю'Юё \\ -*• 0. Бели при || А || -»- 0 сетки стремятся
к асимптотически равномерным, то || б — 2§ ][-+■ 0. Итак, мы доказали следую-
следующую теорему.
Теорема 2.9.5. Пусть на отрезке [а, Ь] заданы функция /(&) из класса
С*[а, Ь] и последовательность сеток {А&}, удовлетворяющая условиям Нш || Д& \\ =0
и зир || Аь \\/т\п]1ь} — $<Со°. Если эти сетки при к—»оо стремятся к асимп-
к з . ■
тотически равномерным, то
"Ь7-гО) — $Г (хм—0) П
хы) =0.
Пт тах
Глава III. ВНУТРЕННИЕ СВОЙСТВА
КУБИЧЕСКИХ СПЛАЙНОВ
3.1. Свойство минимальной нормы
Изложение теории кубических сплайнов в гл. II не выясняет их внутрен-
внутренней структуры. Исторически эта внутренняя структура сплайнов оказалась
хорошо скрытой; прошло более десятилетия после введения сплайнов Шёнбер-
Шёнбергом [1], прежде чем было открыто первое из их внутренних свойств. Это свой-
свойство, называемое свойством минимальной нормы, было установлено Холлидеем
[1]. Прежде чем сформулировать и доказать теорему Холлидея, мы введем
некоторые понятия и обозначения.
Через &Сп{а, Ь) будем обозначать класс функций /(ж), определенных
на отрезке [а, Ъ], имеющих абсолютно непрерывную (п — 1)-ю производную
и ге-ю производную, принадлежащую пространству Ь2 (а, Ь). Через е/Гр(а, Ь)
обозначим подкласс функций из &Рп(а, 6), которые вместе со своими п— 1
первыми производными имеют непрерывное периодическое продолжение
с периодом Ъ — а на числовую прямую (—оо, <х>).
Функция / (х) принадлежит типу Г, если ее первая производная обра-
обращается в нуль при х — а и х = Ъ. Две функции принадлежат одному и тому
же классу эквивалентности типа I, если их разность принадлежит типу Г.
Сплайн 8{х) можно различными способами представить с помощью конеч-
конечного числа параметров. Бели в качестве двух таких параметров в пред-
представлении сплайна приняты 8'(а) и 8'(Ь). то говорят, что представление имеет
тип I и сплайн 8(х) принадлежит типу I. Аналогично говорят, что функция
/ (х) принадлежит типу II', если ее вторая производная обращается в нуль
при х — а и х = Ь. Две функции принадлежат одному и тому же классу экви-
эквивалентности типа II, если их разность принадлежит типу 1Г. Представлением
типа II для сплайна 5 (х) называется представление, в которое явно входят
3"(а) и 8"(Ь). Говорят, что сплайн 8(х) принадлежит типу II, если он пред-
представлен таким способом. Понятие типа облегчает дальнейшее исследование
кубических сплайнов; позднее при рассмотрении сплайнов, отличных от куби-
кубических, это понятие будет видоизменено.
Теорема 3.1.1 о свойстве минимальной нормы сформулирована здесь
в несколько более общем виде по сравнению '• первоначальной формули-
формулировкой, но ее доказательство не отличается от д жазательства, данного Хол-
Холлидеем.
Теорема 3.1.1. Пусть даны сетка А: а = х0 < Х{ <С ... < хм = Ъ
и последовательность У — {уг} (I = 0, 1, . . ., ./V). Среди всех функций
./ (х) ^ <г/?2(а, 6), для которых / (я,) = уи кубический сплайн 5Д (У\ х) типа II
78 ГЛ. III. ВНУТРЕННИЕ СВОЙСТВА КУБИЧЕСКИХ СПЛАЙНОВ
минимизирует интеграл
ь
I2 их.
а
Более того, сплайн 5Д (У; х) — единственная допустимая функция, минимизи-
минимизирующая этот интеграл.
Доказательство. Если / (х) ^ &Р* (а, Ь) ж / (#г) = уь то
ъ ь ь
| Г (х)-8"А (У; х) |2 йх= ^ | /" (х) |* <&—2 Г /" (х) 81 (Г; а:) их + ^ 15д (У; *) |« Дг=
а а а а
Ъ Ь Ь
— Г 1 /" (т\ |2 А* 9 Г И" (т\ 9* (V' т\\ <?* (У- гЛЯг Г I Ял IV' т\
V V V
а а а
Далее,
( {Г (х) - 81 (У; х)} 81 (У; х) их = 2 \ {Г И -^ <У5 *)> ^а (У; »
И
{/" (а:) -51 (У; х)} 81 (У; х) их =
'; *) 12 - ? {/' И - •& (у; ж)> ^ (^; *) ^ -
(У; х)} 81 (У; «) [^ - {/ (д?) -Яд (У; х)} 81 (У; *) Ц^ =
так как функция $д (У; о;) постоянна на каждом отрезке [х^и хД и / (я*) =
= 5Д(У; х1) = у1 (г = 0, 1, ..., -/V). В силу непрерывности произведения
{/' (*) -5к (У; х)} 81 (У; ж) на [а, &]
Ь ■ N ■
{Г (х) -81 (У; х)} 81 (У; х) их = 2 {/' (*) - 51 (У; х
а г=1
' (д?)-5к(Г; х)}8!(У; ») |^=0.
3.2. СВОЙСТВО НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ 79
Последнее равенство справедливо, так как по условию сплайн «5Д (У; х) при-
принадлежит типу 1Г Отсюда следует, что
ь ь ь
\Г (х)\*с1х- ^ \81(У; х)\*йх^ \ \Г(х)-81(У; х)\Ых. C.1.1)
Правая часть равенства (ЗЛ.1) обращается в нуль, только если #д (У; х) =
= /" (#), т. е. если 5Д (У; х)==1 (х) + Ах + В. Так как по условию
5д (У; хь) = / (хг) (I = О, 1, . . ., IV), то равенство возможно лишь, когда
5Д (У; х) — / (х). Теорема доказана. Равенство C.1.1) называют первым инте-
интегральным соотношением.
Содержание теоремы Холлидея предвидели в какой-то мере еще первые
исследователи упругих балок, начиная с Бернулли и Эйлера (см. Сокольни-
Сокольников [1, стр. 1]), но абстрактная формулировка, простота доказательства Хол-
Холлидея и интегральное соотношение C.1.1), доказанное этим методом, являются
важным достижением. Однако Холлидей не продолжил эту тему дальше и не
исследовал далеко идущие следствия первого интегрального соотношения.
3.2. Свойство наилучшего приближения
Введем в ^(а, Ъ) полунорму
ь
11/11= '
и для фиксированной функции / (х) € ёТ2 (а, Ь) рассмотрим || / — 5Д ||, где
#д (х) — кубический сплайн заданного типа, определяемый фиксированной
сеткой Д: а = х0 < х± < . . . <; х-^ = Ъ. Возникает вопрос: минимизирует
ли сплайн #д (х), интерполирующий функцию / (х) на сетке А, величину
|| / — 5д (х) ||? В разд. 2.2 для некоторых важных случаев на этот вопрос дан
положительный ответ; мы сформулируем результат для периодического случая.
Теорема 3.2.1. Пусть даны сетка Д: а = х0 <; хг <С . . . < а;^ =Ъ
и функция / (х) 6 &С% (а, Ь). Среди всех периодических кубических сплайнов
8^{х) интерполяционный сплайн <5Д (/; х) минимизирует ||/—<5д ||. Если
сплайн 5д (х) также минимизирует || / — <5д ||, то 5д (х) = 5Д (/; х) + сопз*.
Доказательство теоремы 3.2.1, содержащееся в разд. 2.2, классическое;
оно использует определение стационарных точек. В разд. 3.4 мы обобщим рас-
рассуждения Холлидея и приведем изящное доказательство, которое обходит
определение стационарных точек и распространяется с периодического случая
не только на сплайны типа I и II, но и на сплайны, не являющиеся простыми.
Сейчас мы не будем давать полное определение простого сплайна, а скажем
80
ГЛ. III. ВНУТРЕННИЕ СВОЙСТВА КУБИЧЕСКИХ СПЛАЙНОВ
лишь, что кубический сплайн называется простым, если он принадлежит классу
С2 (а, Ъ).
Свойство, выраженное теоремой 3.2.1, называют свойством наилучшего
приближения (Алберг, Нильсон, Уолш [1]). Подобно свойству минимальной
нормы и другим важным внутренним свойствам, исследуемым нами дальше,
его можно получить в качестве простого следствия из первого интегрального
соотношения, которое само (как видно из доказательства Холлидея свойства
минимальной нормы) следует из очень общего тождества, справедливого при
выполнении определенных условий. Это тождество играет важную роль в тео-
теории сплайнов и полезно в случаях, когда методы, подобные методу стандарт-
стандартной минимизации, примененному при доказательстве теоремы 3.2.1, становятся
очень громоздкими. Однако, если прямые методы (такие, как в гл. II) приме-
применить можно, они обычно дают более точные результаты. Это, в частности,
относится к скоростям сходимости. Сейчас мы получим указанное тождество
в явном виде и используем его в качестве краеугольного камня в теории
сплайнов.
3.3. Основное тождество
Мы сможем вывести вышеупомянутое тождество ив то же время сделать
более ясными условия, при которых справедливо первое интегральное соотно-
соотношение, если, как и в рассуждении Холлидея, дважды проинтегрируем по частям
интеграл
ь
{Я2/ (*) - #2ЯД (х)} Я2ЯД (х) дх.
Новое обозначение IJ/ (х) вместо /" {х) поможет сделать обобщения в гл. VI
более естественными. В результате двукратного интегрирования по частям
на каждом интервале (ж*_ь хг) сетки А: а = х0 <с х^ <С . . . <С хк = Ъ имеем
Х1
\ {О2/ (х) -
х)}
(х) ах = {Я/ (х) -
х)}
4-1
- {/ (X) - Яд (X)}
(X)
Х1
Г
(х) |*« -
1
{X) ^ =
х) - /Mд (*)} Д*5д (х) |*|^ - {/ (х) - Яд (х)} 0»5д (х) |^_1
так как #45д(яг)=0, если х^(х^и х$. Поэтому в силу непрерывности
{Я Я# )} #2#
{Я/ (х) -ИЗа (х)} #2#д (х) на [а, Ъ)
ъ
14 (т\ ГJ.СД (<г\\ Л2С. /г\ А*
/г\ |ь X*
\Х) \а — 21л
г=1
х)-Б8& (х
X)| * « ^О.О«1у
3.4. ПЕРВОЕ ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ 81
Обычно функция 1>35д (х) претерпевает разрывы в узлах сетки Д; это вызы-
вызывает появление суммы
{=1 1—1
Заменим в тождестве
ъ
Н/-вГ||*=11/||*-2 ^{^/(^-^^(«И^^^-НуИ1 C.3.2)
а
§(х) на 8&(х) и воспользуемся равенством C.3.1); получим основное тождество
II /- Яд II2=II / II2 - 2
{ () - Яд И} Д 3Яд (*) &1] = II Яд ||«, C.3.3)
справедливое для любой функции / (х) иэ класса гТа (ат Ь) ж для любого про-
простого сплайна 5Д (х), определенного на произвольной сетке Д: а = хо<Сх1 < ...
• • • ^^, X ^у == О.
3.4. Первое интегральное соотношение
Если <5Д (х) — 5д (/; х) 4- сопз1, то в основном тождестве сумма
обращается в нуль. Если, кроме того, / (х) ^ йГр (а, 6) и 5Д (#) ^ ^*р (а, &),
или / (х) — 5Д (х) принадлежит типу Г, или 5Д (#) принадлежит типу 1Г,
то основное тождество сводится к первому интегральному соотношению. Ясно,
что эти условия лишь достаточные, а не необходимые, так как, в частности,
можно потребовать, чтобы выполнялись краевые условия смешанного типа.
Можно не требовать непрерывности 5д (х) и все же получить первое интеграль-
интегральное соотношение, если предположить, что первая производная сплайна #д (х)
интерполирует /' (х) в узлах сетки Д; даже это не исчерпывает всех возможно-
возможностей. Учитывая эти замечания, получаем теорему 3.4.1 как прямое следствие
основного тождества.
Теорема 3.4.1. Если функция /(а:) принадлежит классу &С* (а, Ъ),
сплайн 5д (/; х) интерполирует ее на сетке Д: а = #0 <С %\ <С - ••<С## = &
и выполнено любое из условий: а) функция / (х) и сплайн <5Д (/;, х) периодические,
Ь) разность / (х) — /5д (/; х) принадлежит типу Г, с) сплайн 5Д (/; х) при-
принадлежит типу II', то
6—1197
82 ГЛ. 1Т1. ВНУТРЕННИЕ СВОЙСТВА КУБИЧЕСКИХ СПЛАЙНОВ
Далее, по теореме 3.4.1
±,т\\ — II/ — лд,гП .> и.
Следовательно, для любой функции / (я), удовлетворяющей условиям / (хг) =
— Уь (^ = 0, 1, . . ., ^) и принадлежащей классу <йГ2 (а, &),
ь
• т\ I2 /7т* г* \ \ ^ /'А I2 /7-г
, х; | а»с -^ I | / \Х) \ ах,
а
причем равенство здесь имеет место тогда и только тогда, когда Яд (/; х) —
= /" (о;). Таким образом, свойство минимальной нормы непосредственно сле-
следует из первого интегрального соотношения. Как мы уже видели, метод
доказательства этого соотношения указан Холлидеем.
Если ^0 = ух и функция / (х) вместе со сплайном Яд (х) принадлежит клас-
классу йГ| (а, Ь), то из теоремы 3.4.1 вытекает следующая теорема.
Теорема 3.4.2. Пусть даны сетка А: а = х0 < хг < . . . < я^- — Ь
и последовательность У = {уг \^> — 0, 1, . . ., М\ у0 = ух}. Среди всех функ-
функций / (х) 6 ^р (я> Ъ), для которых / (#{) = уь (I — 0, 1, . . ., ЛГ), периодический
сплайн <5д (У\ х) минимизирует интеграл
ь
I Г (*) I2 их.
а
Более того, он является единственной допустимой функцией, минимизирующей
этот интеграл.
Заметим, что если у0 — ^^, Яд (У', х)р — периодический интерполя-
интерполяционный сплайн для У, а 5Д (У; х) — соответствующий сплайн типа 1Г, то
ь ь
^ \8Ъ(У; х)\*<1х^ \ |ЯД(Г; х)р |2 дх,
а а
причем равенство выполняется только тогда, когда
Яд (Г; х)р = Яд (Г; х) + Ах + В = Яд (Г; *),
так как сплайны Яд (У; а:)р и Яд (У; а:) принимают одно и то же значение
в точках х = аих — Ъ. В этом смысле теорема 3.1.1 сильнее, чем теорема 3.4.2.
Сформулируем еще один аналог теоремы 3.1.1.
Теорема 3.4.3. Пусть даны сетка А: а = х0 < XI < . . . < х$ = &
м последовательность У — {у„, у^, Уг | ^ = 0, 1, . . ., #} С5 ^
2 (
р
м последовательность У — {у„, у^, Уг | ^ = 0, 1, . . ., #}. Сре5м всеа:
ций / (ж), принадлежащих е/Г2 (а, Ь) м удовлетворяющих условиям / (#
(е = 0, 1, . . ., Л) м /' (ж^) = у\ (^ = 0, Л''), сплайн Яд (У; а:) тмгеа I м
миними-
3.4. ПЕРВОЕ ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ 83
вирует интеграл
ь
" ' /" (х) |2 их. C.4.1)
Более того, он является единственной допустимой функцией, минимизирующей
этот интеграл.
Доказательство. Все, кроме единственности, следует непосред-
непосредственно из теоремы 3.4.1. Для доказательства, единственности! заметим, что
если функция # (х) также удовлетворяет условиям теоремы 3.4.3 и минимизи-
рует интеграл 3.4.1, то в силу теоремы 3.4.1
или и (*) в Яд (X; х) + Ах + В=е=За (У; х), ибо #<«> (а) = Яда) (У; а)
(а = 0, 1). Если опущено условие 5д (У; хг) = у\ (г = 0, ЛГ), то сплайн
типа 1Г, интерполирующий на сетке А последовательность У, минимизирует
интеграл C.4.1).
Сплайн 5Д (х) данного типа линейно зависит от своих значений в узлах
сетки А и от значений своих производных в точках х = а и х — Ь. Это вытекает
из равенств B.1.2), B.1.8) и B.1.9). Следовательно, при различного рода
условиях
Яд (/ + Г. *) = Яд (/; а) + Яд (к *), C.4.2)
хотя это разложение, вообще говоря, не единственно. Укажем полезные наборы
краевых условий, при выполнении которых разложение C.4.2) не только спра-
справедливо, но и единственно:
а) все разности Яд (/;*)—/ (я), #д (§\ х) — § (х) и 5Д (/ + #; х) —
— / (х) — § (х) принадлежат типу Г;
Ь) все сплайны Яд (/; я), 5Д (#; х) и 5Д (/ + #; х) принадлежат типу 1Г;
с) все сплайны #д (/; х), 5Д (§"; х) и 5д (/ + 8\ х) периодические.
В частности, для некоторых краевых условий на <5Д (/ — «Уд; х) и
Яд (/; *)
Яд (/ - 5Д; х) = 5Д (/; *) - Яд (*). C.4.3)
Так, если сплайн 5Д (/ — #д; а:) периодический, принадлежит типу IV или
таков, что 5д (/ — 5Д; х) -~ I (х) + 8А (х) принадлежит типу Г, то справед-
справедливо не только равенство C.4.3), но и основное тождество и оно записывается
в виде
Отсюда следует, что ||/ — <УД || >> ||/ — #д>/ ||. Если сплайн 5Д (/ — 5Д; а:)
принадлежит типу 1Г, то можно изменить условие Ь) и все же сохранить раз-
6*
84 ГЛ. III. ВНУТРЕННИЕ СВОЙСТВА КУБИЧЕСКИХ СПЛАЙНОВ
ложение C.4.2), потребовав лишь, чтобы разность 5Д (/; х) — 5Д (х) принад-
принадлежала типу 1Г. Это доказывает теорему 3.4.4, обобщающую теорему 3.2.1.
Заметим, что наиболее сильный результат получается, когда / (х) — 5Д (/; х)
принадлежит типу Г, ибо в этом случае на #д (х) не налагается никаких
условий.
Теорема 3.4.4. Пусть даны сетка А: а = х0 <. х^ <С . . . <С х& = Ь
и функция /(я) из класса <&Сг (а, Ь). Если сплайны 5Д (х) и 8А (/; х) удовле-
удовлетворяют одному из условий', а) / (я), 5Д (х) и 3А (/; х) принадлежат классу
$%% (а, &), Ь) 5Д (х) — 5д (/; х) принадлежит типу 1Г, с) / (х) — 5Д (/; х)
принадлежит типу Г, то
Если здесь выполняется равенство, то 3А (х) г= 5Д (/; х) + Ах + В {в перио-
периодическом случае А = 0).
Разложение C.4.2) следует из существования такого множества парамет-
параметров, от которых сплайн <5Д (х) зависит линейно и которые вместе с требования-
требованиями непрерывности полностью определяют сплайн #д (х). Эти параметры назы-
называют определяющими значениями,
3.5. Единственность
При обсуждении единственности и < существования различных сплайнов
в настоящей главе мы опирались до сих пор на результаты гл. II. Все сформу-
сформулированные теоремы справедливы и их справедливость не зависит ни от суще-
существования, ни от единственности, хотя, если бы не было по крайней мере
существования, теоремы были бы пустыми. Многие теоремы существования
и единственности из гл. II получены относительно просто, благодаря наличию
у соответствующих матриц доминирующей главной диагонали. Фактически неко-
некоторые важнейшие свойства ограниченности матриц, нужные при доказательстве
теорем сходимости в гл. II, были также получены из этой доминантности, а из-за
ее отсутствия в случае сплайнов более высокой нечетной степени в гл. IV уста-
установлены весьма ограниченные теоремы существования и единственности.
Б гл. V мы обойдем эти трудности, применив первое интегральное соотношение
(в более общей форме).
Чтобы продемонстрировать применение первого интегрального соотноше-
соотношения, докажем с его помощью основные теоремы существования и единствен-
единственности для кубических сплайнов.
Теорема 3.5.1. Пусть даны сетка А: а = х0 <С х^ <С . • . <С хк = Ь
и функция / (х). Если выполнено любое из условий: а) функция / (х) и сплайн
д?д (/; х) периодические, Ь) / (х) — «5Д (/; х) принадлежит типу Г, с) / (х) —
— 5д (/; х) принадлежит типу 1Г, то интерполяционный сплайн <5д (/; х}
является единственным.
3.6. СУЩЕСТВОВАНИЕ 85
Доказательство. Предположим, что одному и тому же условию
а), Ь) или с) удовлетворяют два сплайна 5Д (/; х) и 5Д (/; я), интерполирую-
интерполирующих функцию / (х) в узлах сетки А. В каждом из этих случаев разность
^л (/; х) — <^л (/; х) интерполирует нулевую функцию % (х) и по теореме 3.4.1
выполняется первое интегральное соотношение. Таким образом,
откуда
5А(/;ж)
Так как оба сплайна <5Д (/; х) и 5Д (/; х) интерполируют функцию / (х) в узлах
сетки А, то А — В — 0.
При доказательстве теоремы 3.5.1 функция / (х) служила только для
определения такого вектора, что сплайны 5^ (/; х) и 5Д (/; х) интерполируют
его в узлах сетки А. Первое интегральное соотношение применялось не к / (х),
а к г (ж), так. что дифференцируемость или даже непрерывность функции / (х)
несущественны и ее можно считать произвольной функцией на [а, Ъ].
Замечание 3.5.1. Единственность, доказанная в теоремах 3.1.1,
3.4.2 и 3.4.3, влечет единственность рассматриваемых здесь сплайнов. Однако
в случае с) требуется провести рассуждения несколько более тщательно.
3.6. Существование
Теперь мы можем дать другое доказательство существования интерполя-
интерполяционных сплайнов типов I, II и периодических сплайнов. Это доказательство
переносится на более общие случаи.
Теорема 3.6.1. Пусть даны сетка А: а — х0 <. #1 < . . . < х1У = Ъ
и функция / (х). Тогда в каждом классе эквивалентности типа I или II сущест-
существуют сплайны <5Д (/; х) типа I или II, интерполирующие функцию / (х) в узлах
сетки А. Если / (а) = / (Ь), то существует периодический сплайн, интерполи-
интерполирующий / (х) на А.
Доказательство. Так как функция / (х) рассматривается только
в узлах сетки, ее можно изменить так, чтобы ее значения на А оставались
теми же, а новая функция / (х) принадлежала любому наперед заданному клас-
классу эквивалентности типа I или типа II. В силу теоремы 3.5.1, если сплайн
•^л (У; х) существует, то он является единственным. Сплайны, о которых идет
речь, существуют, если матрицы систем B.1.8) и B.1.9) невырожденны. Обе
эти системы можно записать в виде
АМ = Г, C.6.1)
86 ГЛ. III. ВНУТРЕННИЕ СВОЙСТВА КУБИЧЕСКИХ СПЛАЙНОВ
где А — матрица, М и У — векторы. Компоненты вектора М равны значе-
значениям <5д (/; х) в узлах сетки А. Бели уравнение C.6.1) имеет два- различных
решения М, то существуют два различных периодических сплайна или два
различных сплайна из одного и того же класса эквивалентности типа I (или
типа II), интерполирующих функцию / (х) в узлах сетки А. Это противоречит
теореме 3.5.1, следовательно, уравнение C.6.1) имеет единственное решение.
Так как единственность решения уравнения C.6.1) для одного У влечет един-
единственность решения для любого У, то А'1 существует, и теорема доказана.
Хотя теорема 3.6.1 устанавливает существование обратной матрицы Л,
метод доказательства не позволяет оценить || А'1 ||. В этом смысле теорема 3.6.1
хуже теорем существования из гл. П. Ее преимущество состоит в ее общности.
Более того, первое интегральное соотношение вместе со вторым интегральным
соотношением (разд. 3.9) компенсируют в значительной степени отсутствие
оценок для \\ А'1 \\.
3.7. Общие уравнения
Матричные уравнения B.1.8) и B.1.9) из гл. II были выведены в пред-
предположении, что вторая производная^ сплайна 5Д (х) непрерывна и кусочно
линейна. В гл. IV мы получим аналогичные уравнения для сплайнов нечетной
степени более высокого порядка; но только при ограничениях типа равномерно-
равномерности сетки эти уравнения имеют простой вид. Вообще всегда есть система пример-
примерно N уравнений с тем же самым числом неизвестных, где N — число интерва-
интервалов сетки. Однако представление сплайнов нечетной степени более высокого
порядка через эти величины становится значительно сложнее, чем в случае
кубических сплайнов (ср. разд. 4.1). Возможность применения аналогичного
метода для обобщенных сплайнов, исследуемых в гл. VI, не ясна, поскольку
предположение о линейности не выполняется. Следовательно, каждый слу-
случай требует специального подхода.
Даже в случае обобщенных сплайнов можно непосредственно написать
систему 2и./У уравнений с 2пЫ неизвестными, где снова N — число интервалов
сетки иге — порядок соответствующего дифференциального оператора. Более
того, на каждом интервале сетки нетрудно выразить сплайн через эти величи-
величины. Возникающие при этом матрицы таковы, что лишь незначительное число
их элементов отлично от нуля. Это позволяет использовать на счетно-решающих
устройствах специальные процедуры обращения, которые очень сокращают
объем памяти, требуемой для выполнения обращения. Однако появляющиеся
здесь матрицы имеют тот недостаток, что при стремлении длин интервалов
к нулю они стремятся к вырожденной матрице. Более того, когда возможно
специальное представление, размер системы уравнений обычно бывает зна-
значительно меньше.
Чтобы вывести эти уравнения, изменим нашу прежнюю точку зрения
и построение кубических интерполяционных сплайнов будем рассматривать
как проблему склеивания вместе N решений. дифференциального уравнения
Я4/ = 0, C.7.1)
3. 7 ОБЩИЕ УРАВНЕНИЯ
87
каждое из которых удовлетворяет уравнению на различных открытых интер-
интервалах сетки А: а — х0 < х^ < . . . <С хк = Ъ; при этом построенный сплайн
Яд (/; #) должен интерполировать заданную функцию / (х) в узлах сетки А,
удовлетворять определенному множеству краевых условий и принадлежать
классу с%?3 (а, Ъ).
Любое решение уравнения C.7.1) является линейной комбинацией четырех
линейно независимых решений щ (х) A = 1, 2, 3, 4), которые можно выбрать
так, что ир @) = 6г_4/ (у = 0, 1, 2, 3). В частности, иг (х) — х%~ 1A — 1)!.
Поэтому на любом отрезке агг_4 ^ х ^ хг
4
#д (/; «) - 2 *М (*-*м). C.7.2)
1
Так как 8ь(^\x^) = ^(x^)—у^^ то сн^у-^ (I — 1, 2, ...,ЛГ). Чтобы сплайн
5д(/;#) принадлежал классу с/Г3 (а, Ь), необходимо выполнение условий
4 4
C.7.3)
Бели
Л) @) =
(Ь0, 1, 2; 1 = 1, 2, ..., ЛГ-1).
(/; а;) принадлен^ит типу I, то дополнительно получаем
4
2
4
2
?=1
а если 5д (/; ж) принадлежит типу II, то
4
2
3=1
В периодическом случае
4
I
4
= у0 = у№, 2 с
3=1
Положим
0
0
0
1
1
0
0
0
0
1
0
0
0
0
0
0
0
0
C.7.4)
C.7.5)
(&=0, 1, 2). C.7.6)
C.7.7.1)
C.7.7.2)
ГЛ. III. ВНУТРЕННИЕ СВОЙСТВА КУБИЧЕСКИХ СПЛАЙНОВ
Г1 0 0 0]
о-|_О 1 0 0]'
"
1 0 0 0
0
1 ° ° °
о О 1 0
(«» — «»-
— х^у
C.7.7.3)
C.7.7.4)
C.7.7.5)
C.7.7.6)
У=(Уо>иу'<> + $у1, уь
Тогда
С
0, 0
где для сплайнов типа ]
А =
для сплайнов типа I]
А =
~с\
А
0
0
.0
'Со1
А±
0
0
.0
= (
, 0,
0
1 В
А
0
0
0
в
А«
0
0
для периодических сплайног
■
А=-.
Аг
0
0
в
в
Аг
0
0
Си, с12,
г/2,о,
о ..
о ..
*
• *
0 ..
0 ...
0 ..
0 ..
в
0 ..
0 ..
0 ...
в ...
0 ...
0 .,.
АС
. 0
. 0
. 0
•
. 0
. 0
. 0
. 0
• А>
. 0
0
0
л№
0
Сц, С21
У"\ У"\ У"\ / • Л /0 )
у,^—1)'-', и} и, ?/^5 оун \~ РУм1
. 0
0
0
с»
(а=1, Р = 0);
0"
0
0
с11
(а = 0,р=1);
0 '
0
-1 В
д
C.7.
т. CГ7.
C.7.
C.7.7
•
C.7.7
C.7.7
7.7)
7.8)
7.9)
.10)
.11)
.12)
3.8. СХОДИМОСТЬ ПРОИЗВОДНЫХ НИЗШИХ ПОРЯДКОВ
89
и вектор У вместо C.7.7.8) имеет вид
У - (уи О, 0, 0, уг, 0, . . ., Уя, О, 0, 0)т. C.7.7.13)
В каждом случае матрица А не вырождена, ибо из представления C.7.2) коэф-
коэффициенты Сц определяются однозначно. Таким образом, как и при доказатель-
доказательстве теоремы 3.6.1, два различных решения уравнения C.7.7) дают два различ-
различных интерполяционных сплайна, что противоречит теореме 3.5.1. Так как
сп — Уг-\ (г = 1, 2, . • ., .ЛО, то размер системы уравнений легко можно умень-
уменьшить с 4гаЛГ до ЪЫ
3.8, Сходимость производных низших порядков
Исследуем теперь сходимость последовательности интерполяционных
сплайнов {#д№, /} ^ = I, 2, . . .), определенных на последовательности сеток
{Д№: а = х§ < х * < . . . < х% — Ъ}, || Д№ || -»- 0 при N -> оо. Здесь, как
и в гл. II, не предполагается, что А^ е Алг2 при N1 ^ Ы2- Сделаем одно важ-
важное для последующих рассуждений замечание. Так как сплайн 5д^ (/; х) интер-
интерполирует функцию / (х) в узлах сетки А№, то в силу теоремы Ролля на каждом
интервале х^_± <С х •< хУ (ъ = 1, . . ., т^ существует такая точка яг№, что
/Ч*»)^^ (/;*!»)• C.8.1)
В дальнейшем нам потребуется аналогичное утверждение о том, что на каждом
интервале хУ_2<Сх<хУ (г = 2, ..., тК) существует такая точка яглг, что
/'(*«*)-$1„ (/;««»)• C.8.2)
Теорема 3.8.1. Пусть даны функция /(#) из класса <йГ2(а, Ь) и после-
последовательность сеток {Д№: а = х* < х1* < ... < х% =${N=1,2, ...), || Д^-1| -»-0
при Лг->оо. Пусть соответствующая последовательность интерполяционных
сплайнов {^Ду,/} (N=1, 2, ...) удовлетворяет одному из следующих условий:
а) /(я)€б#р(а, Ь) и сплайн 8^A; х) периодический (N—1,2, ...), Ь) /(я) —
— 8\х{1;х) принадлежит типу Г (# = 1,2, ...), с) 5д№(/;а;) принадлежит
типу IV (N=1,2, ...). Тогда
{$ C.8.3)
= 5д^ (/; х^). При-
При№ (/; х) и 1, получим
равномерно относительно х на [а, Ь].
Доказательство. Пусть хц^^[х^_1, х^] и /' (
менив неравенство Буняковского — Шварца к /* (х)—
х) | = | ^ {Г (х) -
; х)} их
^"^*
ж.
х
90 ГЛ. III. ВНУТРЕННИЕ СВОЙСТВА КУБИЧЕСКИХ СПЛАЙНОВ
Из свойства минимальной нормы получаем
^1у/2, C.8.4)
где К = ||/ ||. Если А1 е А^ (./V = 1, 2, . . .), то в качестве К можно взять
Ц/ — 5д1} / ||, поскольку в этом случае сплайн 5д1 (/; х) является сплайном
на А1У и можно применить свойство наилучшего приближения. Так как точки
хги существуют в каждом интервале сетки, то можно среди них выбрать такую,
что | х — х1к | ^ || А л ||. Отсюда и из неравенства C.8.4) следует, что
#дд. (/; х) ->■ /' (я) при N -*• оо равномерно относительно х на 1а, Ь]. Аналогично
для любой точки х можно найти такой индекс г, что х^_г ^ х ^ хУ и
х
где х есть х^-1 или х™ в зависимости от того, какая из этих точек ближе к х.
Следствие 3.8.1.1. Если А,сД№ (ЛГ = 1, 2, ...), || Ая || ->-0 при ^У->оо,
и сплайн #д№(/; ^) (ЛГ== 1, 2, ...) принадлежит заданному классу эквивалент-
эквивалентности типа II, то равномерно относительно х на [а, Ь]
Нт $5§ (/; а?)« /<а> (ж) (а - 0, 1).
Доказательство. Здесь в силу свойства наилучшего приближения
можно положить #=Ц / — 5а!, /1| •
Следствие 3.8.1.2. Пусть функция /(#), последовательность сеток
{Д#} (ЛГ= 1, 2, ...) и последовательность сплайнов {5д^ (/; #)} {И■=■ 1, 2, ...)
удовлетворяют условиям теоремы, 3.8.1 щш следствия 3.8.1.1. Гог5а
(а = 0, 1) C.8.5)
равномерно относительно х на [а, Ъ].
3.9. Второе интегральное соотношение
Рассмотрим более подробно полунорму
ь ь
У/ц2_ Г | 4»(х\ 12лх^ [ \^*^(х)\*с1х C.9.1}
а а
Если / (я) € е% (а, Ь), то для любого сплайна 5д(яг), определенного на сетке А:
ь
= 2 ( {/J/И-^25д(а:)}2^. C.9.2)
3.9. ВТОРОЕ ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ 91
Интегрируя по частям, получаем
- {/ И - Яд (*)} {Я3/ (х) - Щ^
+ ] {П*)-8а(х)}{ОЧ(х)~№ь(х)}Л*- C.9.3)
Из равенств C.9.2), C.9.3), непрерывности на отрезке [а, Ъ] функции
{/?/() О8)}{О(х) — Д2Яд(а;)} и равенства
ь
а
находим, что
II /-Яд II2 = {Д/ И - ЯЯд И} {Д2/ (а?) - Д2Яд (а?)} |2-
{/ (*) - Яд (х)} ВЧ (х) ах. C.9.4)
Тождество C.9.4) в теории сплайнов очень важно. Оно справедливо для любой
функции $(х) из класса <йГ4 (а, Ь) и любого простого сплайна Яд (#), определен-
определенного на произвольной сетке Д:а = х0 <С XI <; . . . <Схк = 6. При некоторых
условиях на сплайн Яд (<е) это тождество принимает вид
ь ь
||/-Яд||2== | {#2/(*)-#2ЯдИР^- ^ {/(*)-5д-(а:)}1)«/(х)Л? C.9.5)
а
и называется вторым интегральным соотношением. В частности, следующая
теорема вытекает непосредственно из тождества C.9.4).
Теорема 3.9.1. Пусть даны функция /(я) из класса $С* (а, Ь) и сетка
А: а = х0 <С #1 <С . . . < Хх = 6. Л?слм сплайн Яд (/; я) интерполирует функ-
функцию / (#) на сетке А и удовлетворяет одному из условий: а) / (х) — Яд (/; х)
принадлежит типу Г, Ь) / (х) — Яд (/;, х) принадлежит типу II', с) сплайн
Яд (/; х) периодический и / (#) € ^"р («» &)>
Ь
« ( {/ (х) - Яд (/; х)} БЧ (х) Ох. C.9.6)
92 ГЛ. III. ВНУТРЕННИЕ СВОЙСТВА КУБИЧЕСКИХ СПЛАЙНОВ
Замечание 3.9.1. Если / {х) 6 &Сг (а, 6), то утверждение «/ (х) —
— 5Д (/; х) принадлежит типу II'ь не корректно, так как /" (х) может не суще-
существовать в точках х = а или х = Ъ. В данной теореме / (х) 6 &С* (а, Ь) и поэтому
утверждение имеет смысл.
3.10. Улучшение оценки порядка сходимости
Пусть функция / (х), последовательность сеток {д} ( ,,)
и последовательность сплайнов {5дл,.,/} № = 1, 2, . . .) удовлетворяют усло-
условиям теоремы 3.9.1. По тем же соображениям, что и прц доказательстве тео-
теоремы 3.8.1,
(« = 0, 1), C.10.1)
а в силу второго интегрального соотношения
ъ
.C-200/2
< | Г 1Д4/(х)IдЛ1/2 { аир I /(ж) — 8^Ц\ х) |}1/2 ||-Д^ ||C-2<х>/2 (а = 0, 1).
C.10.2)
Положим а = 0 и подставим получившееся неравенство в правую часть нера-
неравенства C.10.2):
а
где
<{ Г |/>*/(«) I Ас)" {вир \П*)-8*1Г№*)\УЛ-\\Ь*\\'''> (ЗЛО.3.1)
C.10.3.2)
Снова положим в C.10.3.1) а = 0 и подставим получившееся неравенство
в правую часть неравенства C.10.2). Повторив этот процесс к раз, получии
C.10.3.1), но теперь
C.10.4)
ЗЛО. УЛУЧШЕНИЕ ОЦЕНКИ ПОРЯДКА СХОДИМОСТИ 93
Так как это верно для любого натурального к, то
ь
| Д* ||3-а (а = 0, 1). C.10.5)
Можпо дать более простое доказательство неравенства C.10.5). В самом деле,
из C.10.2) вытекает, что
зир | / (а?)-5Д (/;*)!<:
,3/2
Если
аир
то все доказано; в противном случае
вир | / (х) -8^ (/; *) |1/2< { ( I ^Ч И | Ох] II Ддг 1|3/2, C.10.6)
так что неравенство C.10.5) справедливо при а = 0. Подстановка C.10.6)
в C.10.2) дает общий случай»
Итак, доказана
Теорема 3.10.1. Пусть даны функция }(х) из класса ()
и сетка Д№: а = хо<Сх1< ... <;о;дг = Ь, ЦД^Ц-^0 при N-+■00. Если сплайн
Зд^ (/;х) интерполирует функцию / (х) в узлах сетки Д^ и удовлетворяет
одному из условий: а) /(яг)—8^. (}; х) принадлежит типу Г (.#=1,2, ...),
Ь) /(ж) — 8^0; х) принадлежит типу 1Г, с) /(ж) ^^*р(а, Ь) и сплайн
8&х И'Iх) (#= 1, 2, ...) периодический, то
ь
8ир | /(«> И-^ (/; г) |< Г |!>*/ (*) | <2х || Д„ ||3"а (а = 0, 1).
Замечание 3.10.1. Если C.10.1) заменить более точным неравенством
| /(а) (*)-$$«> (/; Ж) |< (|) 4-а || /-5Ддр,, || ||Ддг||^3-2а>/2 (а-0, 1), C.10.7)
доказанным в разд. 3.8, то получим
зир \Р*Чх)-&>(Кх)\^(±уа\1ВЧ(*)\**\\Ь*\\'-а (а = 0,1). C.10.8)
94 ГЛ. III. ВНУТРЕННИЕ СВОЙСТВА КУБИЧЕСКИХ СПЛАЙНОВ
3.11. Сходимость производных высших порядков
Пусть даны функция / (х) из класса $Г4(а, Ь), сетка А: а = хо<х1< ...
... <_хы=Ъ и сплайн 5д (/; х). Вновь запишем для жг_1<а:<а:^ (< — 1, ..., ./V)
равенство C.7.2):
4
—агм). C.11.1)
3=1
Пусть б1^ (с, й] обозначает а-ю разделенную разность с постоянным шагом про-
произвольной функции §(х) на произвольном отрезке [с, Д\; положим 6$ [с, й]~
Тогда существует такая точка х^ ^ [х(.и х& что
д^ (а=0, 1, 2, 3),
откуда "*
4
,.,) (а-0, 1, 2, 3) C.11.2)
и при Ц А ||->-О
(а = 0, 1, 2, 3). C.11.3)
Заметим, что функции Ца> (х) (;' = 1, 2, 3, 4; а = 0, 1, 2, 3) непрерывны
на отрезке [О, Ъ — а] и, следовательно, равномерно непрерывны и ограничены
на [О, Ь — а]. Когда || А || ->• 0, эти функции остаются фиксированными,
а изменяются только точки, в которых они вычисляются. Таким образом, для
достаточно малого числа || А || система C.11.2) разрешима и каждый коэф-
коэффициент сг7 является линейной комбинацией четырех величин 6зд Л#г-ь ^|)
(а = 0, 1, 2, 3). Кроме того, с помощью теоремы 3.10.1 получаем соотношения
|С1 C.11.4.1)
I °8д, / [Яг-1, XI] — Ь) [Х1-1, Хг]\= '
№ )/()} \Ц!1.9 (З.Ц.4.2)
{ [Хг-и %г] — 8/ [Хг-и Хг] \ =
C.11.4.3)
3.11. СХОДИМОСТЬ ПРОИЗВОДНЫХ ВЫСШИХ ПОРЯДКОВ 95
+3 { (
1х) | <&.|| Д II3 М> C.11.4.4)
где к1 = Х1 — Х1-1. Если положить 7?д = тах{|| А ||//&г}, то предыдущие неравен-
г
ства можно записать в виде
ъ
| б|д> 1 [хм, *,] - 6? [^г-±, *,] | < BаЛд)а | | Я*/ (*) | <22г • || А Ц30
а
(а-0, 1, 2,3). C.11.5)
Учитывая замечание 3.10.1, в правой части неравенства C.11.5) можно полу-
получить дополнительный множитель 1/4.
Теорема 3.11.1. Пусть даны функция }(х) из класса &Р*(а,Ъ) и после-
последовательность сеток {А^: а = х$ <х™ < ... <х^ —Ь} (./V *= 1, 2, ...), || А^ || —» О
при Л"—>оо. Пусть величины, ■ДдДР= шах || А№ ||/(#^ — ^^-1) ограничены
1=1,. • • , Я»^
относительно N и сплайн Зд^Д/; х) (Л" = 1, 2, ...) интерполирует функцию
/(ж) в узлах сетки А^ и удовлетворяет одному из условий', а) /(ж)—Зд^/; х)
принадлежит типу V (N=1, 2, ...), Ь) /(ж) — 5д№(/; #) принадлежит типу 1Г
м А! ^ Адг (Л^ = 1, 2, ...), с) /(х) €&?% (а, Ь) и сплайны Яд^ (/; х) периодические.
Тогда
(а> (*) = ^ (/; х) + О (|| ДдгН3-") (а = 0, 1, 2, 3) C.11.6)
равномерно относительно х на [а, Ь].
Доказательство. Так как для некоторой точки ^ ^[х^_1, хУ]
*?[ян, *|] = /<а) (*&) (а = °» 4» 2» 3), C.11.7)
то из C.11.5) следует, что
зир |/(а>(*)| (а = 0, 1,2,3).
96 ГЛ. III. ВНУТРЕННИЕ СВОЙСТВА КУБИЧЕСКИХ СПЛАЙНОВ
Правая часть неравенства по условию ограничена относительно N.. Так как
матрица системы C.11.3) при N-*-оо стремится к тождественной матрице
равномерно как относительно N, так и относительно расположения отрезков
1а:г-_1, X}], то все коэффициенты с,^, определяющие сплайны ^д (/; х) (./V =
= 1, 2, . . .), равномерно ограничены относительно N. Поэтому для а <С 4
величины | 5д^(/; х) | равномерно ограничены относительно N. В частности,
существует такое действительное число В, что | 5д^ (/; х) \ ^ В для любого N.
Так как для любой точки х существует такое г, что х ^ 1а^г, #Г1» то из равен-
равенства C.8.2) получаем
р
[о,Ь]
и, более общо,
|/<«>(*)-$2»)(/;*)|<2{ вир |/<•>(*) | + В} || Ая||8-а (а = 0, 1,2).
№ *=[о,Ь]
Кроме того,
зир |/<»(*) | + В> Ц Д„ Ц»,
ж=[о, Ь] ,
и теорема доказала.
Замечание 3.11.1. При а = 0, 1 теорема 3.10.1 гарантирует более
точные оценки скорости сходимости. Возможно, даже более важно то, что
в ней нет дополнительных условий на сетки, в то время как в теореме 3.11.1
величины йд должны быть ограничены относительно N.
3.12. Ограничения на порядок сходимости
В разд. 3.10 и 3.11 мы установили, что
/«х)(;г) = ^(/;а:)+О(||А^||8-а) (а«0, 1,2,3). C.12.1)
Кроме того, в гл. II с помощью более специальных методов было показано, что
/(а) (я) = ^«> (/; х)+О (|| А„ ||4-а) (а-0, 1, 2, 3, 4), C.12.2)
хотя константы и ограничения на сетки не одни и те же в обоих случаях.
ъ
В частности, константа в равенстве C.12.1) пропорциональна \/ 1/<3>], а кон-
а
станта в C.12.2) (когда / (х) € С4 (а, Ъ)) пропорциональна ||/**>|| ; здесь
3.13. ПРИЛОЖЕНИЯ К ТЕОРИИ ГИЛЬБЕРТОВА ПРОСТРАНСТВА 97
использованы стандартные обозначения
и
1/(«) I-
В замечании 3.11.1 указывается на различие ограничений, налагаемых на сетки
Сейчас мы установим ограничения па скорость сходимости.
Теорема 3.12.1. Пусть даны функция / (х) из класса С* (а, Ь) и после
дователъность сеток {А№}, |[ Д№ || -»- 0 при N ->■ оо, и пусть К = зир Ял <С
л 'у
< оо. Если при \1 >■ О
/ («)=Ч, (/; *)+° (иА* и44*) C-12-3)
равномерно относительно х на [а, Ь], то
(ж) = 0.
Доказательство. Точпо так же, как в разд. 3.11, можно пока-
показать, что
Так как б|д [х^_1, х% ]^=0 для всех ^, то для любого е>0
для всех достаточно больших N. Кроме того, б*[ж^_1, х^) — /<4> (хш) для неко-
некоторой точки #,-№ из отрезка [ж(*[_1,л:^]: Так как функция /D> (л:) равномерно
непрерывна на [а, Ь], то
| /<4> (х) | < | /D> И - /<4> (*1ЛГ) | +1 /<4> (*<ЛГ) |< 2е,
если значение || А№ || достаточно мало. Теорема доказана.
3.13. Приложения к теории гильбертова пространства
Введенный в разд. 3.1 класс сЗГ2 (а, Ь) при соответствующей факторизации
является гильбертовым пространством со скалярным произведением
ь
•• C.13.1)
Ясно, что семейство Р± ?сех кубических сплайнов на произвольной фиксиро-
фиксированной сетке А: а = х0 <С х\ <С .1. . <С хн = Ь образует линейное подпро-
7-1197
98 ГЛ. III. ВНУТРЕННИЕ СВОЙСТВА КУБИЧЕСКИХ СПЛАЙНОВ
странство пространства е5Г2(а, Ь). Так как непериодический кубический сплайн
определяется своими значениями в узлах сетки Д и значениями своих первых
производных в точках х = #0, х — хк (которые можно взять в качестве ег»
определяющих значений1)), то это подпространство {Ы + 3)-мерно или
(./V + 1)-мерно, если считать эквивалентными две функции, разность которых
линейна на отрезке [а, Ь]. В этом смысле подпространство Рд периодических
кубических сплайнов имеет размерность ./V — 1. Поскольку подпространства
^д и ^д конечномерны, они замкнуты в с5Г2 (а, Ь) относительно нормы
II / II = (/, /I/2, C.13.2)
индуцируемой скалярным произведением C.13.1). Если Ь.\ а Д2, то ^д с:
а Рь. и ^д4 ^ ^д2* Процесс ортогонализации Грама — Шмидта позволяет
ввести в^ди Рд ортонормальный базис 2).
Пусть А^ <^ Д^+1» обозначим через [^д^+1 — ^д^ подмножество в ^д^+1,
состоящее из сплайнов #д^+1 (я), равных нулю в узлах сетки Д^ и таких, что
их первые производные равны нулю в точках х = а и х = Ь. Таким образом,
1^д^+1 — ^д#1 — эт0 подмножество в /5'длг+1, состоящее из сплайнов, опреде-
определяющие значения которых на А^ равны нулю. Аналогично [Р&.г^+1 — ^д^ "~
это подмножество в ^Рд^+1» состоящее из сплайнов, определяющие значения
которых на А^ равны нулю. Напомним, что если {^} (г = 1, 2, . . .) —
последовательность взаимно ортогональных подпространств пространства
г%* (а, Ь), то бесконечная прямая сумма
Роо = VI 0 У2 © • • •
является наименьшим линейным подпространством пространства Ж% (а, Ь),
содержащим все конечные прямые суммы
V^®V2®.. .®У„ ^ = 1, 2, . . .)
и замкнутым относительно нормы C.13.2). Элемент V ^ У» имеет единственное
представление
оо
V =
где V^ е Уг {I = 1, 2, . . .).
Пусть на отрезке [а, Ь] задана последовательность сеток {А№} (лУ— 1, 2, ...)г
1. Если ИфИ, то множества [Р^ — Р^{] и [^д]у—^Д]у1] имеют
общим только нулевой сплайн. Для определенности пусть N^>N. Тогда если
сплайн 8(х) принадлежит множеству [Рьх—Рьх^]* т0 эт0 сплайн на А^.
!) Здесь и в оставшейся части гл. III предполагается, что определяющие значения
совпадают с компонентами Щ!\-\-$у\ и у г вектора У [C.7.7.8) или C.7.7.13)], связанного
с рассматриваемыми сплайнами.
2) Ради простоты рассуждений мы будем говорить здесь о сплайнах, а не о классах
эквивалентности сплайнов.
3.14. СХОДИМОСТЬ ПО НОРМЕ
Если 8 (х) принадлежит также множеству [Рь^—^д^_ 4 ], то его определяющие
значения на Д^ равны нулю. Следовательно, 8 (х)— это сплайн на сетке Д^,
определяющие значения которого на Д^ равны нулю, а потому 8(х) = 0. Заме-
Заметим, что ёТ|(а, Ь) плотно в #Г2(а, Ь), но не является замкнутым подпростран-
подпространством пространства еЗГ2(а, Ъ). Возникает вопрос: когда для заданной последо-
последовательности сеток {А^} соответствующие последовательности линейных про-
пространств {^д^} и {А^} таковы, что
,Ь), C.13.3)
В разд. 3.14 мы рассмотрим важные достаточные условия, при которых
справедливы разложения C.13.3) и C.13.4). Пусть / (х) — любая функция
из <2# (а, Ь) и {иг (х)} — ортонормальный базис для /"Д(я>. Так как ^д^^
еёТ2(а, Ь), то для доказательства справедливости разложения C.13.3) доста-
достаточно показать, что
Нт||/- 2 (/, Р|)р«П = 0. C.13.5)
N-►00 {=1
Аналогичное замечание относится к Рд^ и ёТ| (а, Ь), ибо последнее простран-
пространство плотно в ёТ2 (а, Ъ). В разд. 3.14 мы покажем, что компоненты, составляю-
составляющие разложение C.13.3), взаимно ортогональны, так что это разложение имеет
смысл. То же относится и к разложению C.13.4).
3.14. Сходимость по норме
В этом разделе мы докажем две важные теоремы. Первая теорема посвя-
посвящена сходимости, и ее можно было доказать еще в разд. 3.8.
Теорема 3.14.1. Пусть на отрезке [а, 61 заданы функция /(я) из клас-
класса &2(а,Ъ) и последовательность сеток {Д^} (N=1, 2, ...), Д^ с= А^+1 и
|| Адг || —>0 при N—+.00. Если сплайн 8^(р, х) (Лг= 1, 2, ...) интерпо-
интерполирует функцию / (х) на сетке Д# и удовлетворяет одному из условий:
а) Цх) — 8ька\х) принадлежит типу Г (Л/"= 1, 2, ...), Ь) / (х) — Зд^ (/; х)
принадлежит типу IV (ЛГ= 1, 2, ...), с) /(ж) и 8^ (/; х) (Л^ = 1, 2, ...) при-
принадлежат классу ёТ^ (а, Ь), то
Ит||/-5д„ /||==0. C.14.1)
Доказательство. Пусть N^<:N2. Так как 5Д^ (/; х) € ёТ2(а, Ь)
й сплайн Зд^ (/; х) интерполирует 5д^8 (/; х) на сетке Д^ и удовлетворяет
7*
100 ГЛ. III. ВНУТРЕННИЕ СВОЙСТВА КУБИЧЕСКИХ СПЛАЙНОВ
одному из условий а), Ь) или с), то в силу свойства минимальной нормы
/Н- C.14.2)
Поэтому последовательность действительных чисел {|| <5Д /})} монотонно
возрастает и снова по свойству минимальной нормы ограничена сверху числом
|| / ||. Отсюда следует, что она является последовательностью Копш. Так же,
как при выводе неравенства C.14.2), заключаем, что к сплайнам «УДдг и »$ДлГ2
можно применить первое интегральное соотношение. Тогда
115^+р./-Ч.^||2==:||^+р./112-11^./112 (Р = 1>2> ♦••) C-14.3)
и, следовательно, {5Д^(/; х)} —последовательность Коши в №(а,Ь). Так как
Пространство Ь2(а,Ь) полно, то существует такая функция #(х) ^Ь2 (а, Ь), что
ъ
Пт \{8(х)-8Ъ„A;х)}*ах = 0. C.14.4)
а
Пусть
|; C.14.5)
в силу неравенства Буняковского — Шварца
а
Ъ
Учитывая C.14.4), получаем, что
Ит\0(х)-8'ь (/;«)|=-0 C.14.6)
равномерно относительно х на [а, &], ибо по теореме 3.8.1
Нт|/* (*)-&*(/;*) НО C.14.7)
равномерно относительно х на [а, Ь]. Так как правая часть неравенства
\Г (х)-6(х)\<С\Г (х)-3'ь„A; х)\ + \0(х)-8'^(!; х)\
как угодно мала, то /' (х) в* О (х) и, следовательно, /* (х) — д (ж). Теорема
доказана.
Теорема 3.14.1 и следующая лемма играют основную роль при доказатель-
доказательстве справедливости разложений C.13.3) и C.13.4).
3.14. СХОДИМОСТЬ ПО НОРМЕ 101
Лемма 3.14.1. Пусть на отрезке [а, Ь] заданы две сетки Д4 и Дг,
Д4 <= А2. Если сплайны 3± (х) и 5Д (х) таковы, что <5Д (х) обращается в нуль
в точках сетки А4 и 8±1 (х) принадлежит типу 1Г, или 8±2 (х) принадлежит
типу Г, или оба сплайна #д4 (#) и 8^ (х) периодические, то (8^^ 3^ = 0.
Доказательство. Пусть сетка А4 определяется точками а =
х0 <С #1 •< . . . <С ж№ = Ь. Дважды проинтегрируем («5^, «Уд^ по частям:
| 811{х)81%{х)йх =
Лемма доказана.
Теорема 3.14.2. Пусть задана последовательность сеток {}
(Л" = 1, 2, . . .), А^ с: А^+1 и || А№ ||-> 0 при N -+ оо. Для каждого N
пусть Р^!^ обозначает линейное пространство кубических сплайнов на А№,
Рд^ — подпространство периодических сплайнов и /^ — подпространство
кубических сплайнов типа 1Г.
оо
а, Ь) = ^ © Д ©;[^- ^длт_1] « ^Доо, C.14.8)
-Ч.!^^- C.14.10)
Доказ ательство. Докажем лишь равенство C.14.8), а C.14.9)
и C.14.10) доказываются аналогично. По определению пространство ^Доо
замкнуто, так что
где Сд^ — ортогональное дополнение в Рь.^. Так как ^д0О^е5Г2(а, Ь), то необ-
необходимо лишь доказать, что если /(#)€#Г2(а, Ь), то ^(х)^Р^.оо. Пусть сплайны
»5дд, (/; х) (Л^= 1, 2, ...) типа I интерполируют функцию {(х) в узлах сетки А^
и для каждого Л" разность ,/ (х) — 8^ (/; х) принадлежит типу Г. Тогда
по теореме 3.14.1
./|| = О. C.14.12)
ЛГ->оо
102 ГЛ. III. ВНУТРЕННИЕ СВОЙСТВА КУБИЧЕСКИХ СПЛАЙНОВ
Это доказывает теорему, так как пространство ^Доо замкнуто и по лемме 3.14.1
составляющие его подпространства ортогональны.
Замечание 3.14.1. При доказательстве равенств C.14.9) и C.14.10)
надо взять последовательность {«Уд^ (/; #)}, состоящую соответственно
из сплайнов типа IV и периодических сплайнов. В C..14.9) множество
[^ду — ^д^ 4] для каждого N представляет собой семейство сплайнов типа
1Г, определяющие значения которых на сетке Д^+1 равны нулю. В периодиче-
периодическом случае надо учесть, что &Р%(а, Ь) плотно в 5Г2(а,4>). Более подробно эти
вопросы рассматриваются в разд. 6.14.
3.15. Канонические сеточные базисы и их свойства
Пусть на отрезке [а, Ь] задана последовательность сеток {А^}
(/V =в-1, 2, . . .), Д^ <= А^+1. Предположим, что у нас есть ортонормальный
базис для ^д. Распространим его до ортонормального базиса для ^д ,
построив ортонормальный базис для ортогонального дополнения [/Доо — ^д^
к /^ относительно ^дто. Для этого построим для каждого N ортонормальный
базис для [^д^ — ^д^- Тем же методом (с небольшими изменениями) можно
построить ортонормальные базисы для [^дто — ^дА1 и ЬРд^ — />д1 ]. Если
II А№ || -»- 0 при Лг->-оо, то из теоремы 3.14.2 следует, что таким способом
можно построить явные ортонормальные базисы для еЗГ2 (а, Ь). Эти ортонормаль-
ортонормальные базисы для [Р^ — ^д 1, [^дто — ^д1] и [Рд^ — Рд 1 будем называть
сеточными базисами.
Обозначим через М множество всех различных узлов последовательности
сеток {Адг} (# = 1, 2, . . .), не содержащихся в сетке А4. Так как множество
М счетно, его можно занумеровать:
М = {Ри Ры . . .}. C.15.1)
Если нас интересует сеточный базис лишь для 1-^д^ — ^д4!» то множество М
будет содержать лишь конечное число элементов; обозначим это множество
через Ми- Пусть сетка Аи получена добавлением точки Р1 к сетке А1, и пусть
сплайн ц,1 (х) типа Г на сетке Аи таков, что (ьц (Р1) = 1 и (л4 (х) = 0 в точках
сетки А!. Если сетка Аи получена добавлением точки Рг к сетке А1г_1
(Аю = А1), то сплайн |лг (х) типа Г на сетке Ац таков, что [1( (Рг) = 1
и р,г (х) = 0 в точках сетки Дц_1. В силу леммы 3.14.1 последовательность
{\11 (х)} A = 1, 2, . . .) состоит из взаимно ортогональных сплайнов типа Г
и по построению образует базис для [^д1оо — ^д^, где
Положим
5« Ж) = Т77ИГ С-*. 2,...). C.15.2)
3.15; КАНОНИЧЕСКИЕ СЕТОЧНЫЕ БАЗИСЫ И ИХ СВОЙСТВА
ЮЗ
Последовательность E* (х)} A = 1, 2, . , .) ортонормальных сплайнов типа Г
образует базис для [Рь1оо— ^д^- Если мы поступим, как в предыдущем слу-
случае, но потребуем, чтобы сплайны (л* (х) имели тип 1Г или были периодическими,
то получим сеточные базисы соответственно для [Р'^1оо— Р\^ и 1^Рд1оо — Р&.^
(необходимые дополнительные определения очевидны).
Эти базисы не единственны, ибо построение зависит от того, как занумеро-
занумеровано множество М. Более того, это не те базисы, которые нам нужны для
[Р^ — Р^], [Р'ь,» — Р'^] и [РДоо — Р^]. Однако если для] каждого N про-
процесс исчерпает точки сетки Д# прежде, чем будут занумерованы все точки для
сеток с большим номером, то получатся как раз требуемые сеточные базисы.
Выделим один естественный способ нумерации такого типа и назовем полу-
полученные сеточные базисы каноническими сеточными базисами: для каждого Лт
пронумеруем слева направо узлы, принадлежащие сетке Ая, но не принадле-
принадлежащие предыдущим сеткам. Таким образом, канонический сеточный базис
определяется однозначно и зависит лишь от данной последовательности седок.
Однако любой сеточный базис будет каноническим относительно вспомога-
вспомогательной последовательности сеток {Ац} A = 0, 1, 2, . . .), использованной
при его построении.
Лемма 3.15.1. Пусть последовательность сеток {Ддг} (N—1,2,...),
Адг с= Адг+ц определяет канонический сеточный базис {5* (х)} (I = 1,2, ...)
для [Р^-Р^], [Р'^-Р1^] или [Р^-Р^]. Пусть {А1{} (г = 1,2, ...)-
соответствующая последовательность сеток, использованная при построении
базиса (8г(х)}. Тогда
(сс = О, 1; г = 1, 2, ...)•
C.15.3)
Доказательство. Пусть сетка
Д
<х[<. ...
у
= Ь. Для любой точки х
определяется точками а = х1<С
, Ъ] можно найти такой интервал
^2аф что $г (я|_2) — «^ (&}) = 0, поскольку сплайн З^ (х) равен нулю в точ-
точках сетки Дн-1. Следовательно, можно найти такую точку Хг^ [ж*._2, х\],
что 8[(хц) = 0. Отсюда и из неравенства Буняковского — Шварца выводим, что
Если х^[х}_гх\], то либо
шая общности, можно считать, что
(), либо 8г(х^ = 0. Поэтому, не нару-
нару(а:*._1)=0. Итак,
и лемма доказана.
104 ГЛ. III. ВНУТРЕННИЕ СВОЙСТВА КУБИЧЕСКИХ СПЛАЙНОВ
Заметим, что для каждого N существует такое число 1№, что Д№ = Д«^.
Таким образом, если || Д^ Ц -*- 0 при N ->• оо, то || Д^ || ->• 0 при I -*■ оо.
Если мы предположим, что || Дн || -> 0 при г -> оо с приемлемой скоростью,
то получим следующую теорему.
Теорема 3.15.1. Пусть для некоторого К >■ 0, не зависящего от г,
канонический сеточный базис {8{ (х)} (ь = 1, 2, . . .) удовлетворяет условию
|| Д1г || ^ КН. Тогда существует такое действительное число В > 0, что
2
1=1
Доказательство. В силу леммы 3.15.1
2 {^ (^)}2<2 2 II Аи Н8<2Л? В Г3 < оо,
г=1 г=1 г=1
а теорема доказана.
Замечание 3.15.1. Условия, налагаемые на {А^} в теореме 3.15.1,
обычно можно проверить, исходя из свойств {АЛг}, благодаря наличию связи
между двумя последовательностями сеток.
3.16. Остаточные члены
Пусть даны функция / (х) из класса &Р2 (а, Ь) и сетка Д4: а = х0 < х^ < . . .
. . . < хк — 6, и пусть сплайн 5Д1 (/; х) принадлежит типу I, интерполирует
функцию / (х) на сетке А4 и разность / (х) — 5Д1 (/; х) принадлежит типу Г.
Исследуем остаточный член
Д(*)=/И-ЯД1(/; *). C.16.1)
Добавим к узлам сетки А4 середины всех ее интервалов — получим новую сетку
А2; с ней проделаем то же самое и т. д. В результате появится последователь-
последовательность сеток {А^} (ЛГ = 1, 2, . . .), для которой Д^ <= Д№+1 и || Д№ |[-> 0 при
.№-->-оо. Каждая сетка Д№ содержит B2У~1^Г + 1) узлов. Пусть {5г- (х)}
(г = 1, 2, . . .) — канонический сеточный базис для [^дто — Рь^ и (Аи)
(I = 1, 2, . . .) — соответствующая ему последовательность сеток. Тогда
= 2,3, ...).
Так как C.16.2)
то
II Аи' 1К11 А^ II =^_- II А. 11<^!!г11, C.16.3)
3.16. ОСТАТОЧНЫЕ ЧЛЕНЫ 105
поскольку 1^2]У~1ЛГ. Итак, условия теоремы 3.15.1 выполнены и для неко-
некоторого положительного действительного числа В
Положим
«5 (ж) = 2 {Яг- И}2 их < В < оо. C.16.4)
г=1
Кп {х, г) = 2 5г (х) 8Цг) (п = 1,2, ...). C.16.5)
г=1
Тогда в силу ортонормальности функций 5* (г)
Ь п+р
I {Кп+Р (ж, г)-кп (х, о}2 А = 2 • № (*)>*• C-16'-6>
а ■ г=п+1
Из C.16.6) и C.16.4) следует, что для каждой точки х ^ [а, Ъ] последователь-
последовательность {Кп (я, г)} (га = 1, 2, . . .) является последовательностью Коши
в I? (а, Ь), а из неравенства Буняковского — Шварца следует, что для каждой
точки х ^ [а, Ь] она является последовательностью Коши также и в Ь {а, Ъ).
Пусть К (я, *) — ее предел.
ъ
В силу C.16.4) и C.16.6) интеграл \К(х,{)*сИ равномерно ограничен
а
относительно х. Таким образом, К (я, I) ^ V- ([а, Ъ] х [а, Ъ]) и
ь ь
Г К (ж, *) /" @ Л = Нт ^ Кп (ж, 0 /" @ А =
а
п
п
= Нт 2 (Я /) Я* (я) = /(*) —
Итак, доказана
Теорема 3.16.1. Пусть даны функция /(ж) из класса &Сг (а, Ъ) и сетка
А4: а = ж0 <: ж4 <С . . . <; хк = Ь. Пусть сплайн 5Д (/; ж), интерполирующий
4 0 <: 1 С <: к у ^,1 (/; ), рплрую
функцию /(ж) в узлаж сетки А4, принадлежит типу I и разность /(я
— ^Д! (/»* я) принадлежит типу Г. Тогда существует ядро К (ж, ^) 6
6 ^2 ([а, Ых[а, Ь1), которое для каждой точки х ^ [а, Ь] принадлежит про-
пространствам Ь (а, Ь) и V1 (а, Ь), м
ъ
К (х) = / (*) - $Д1(/; Ж) = ^ ^ (ж, 0 /" (*) Л. C.16.7)
106 ГЛ. III. ВНУТРЕННИЕ СВОЙСТВА КУБИЧЕСКИХ СПЛАЙНОВ
Замечание 3.16.1. Аналогичные ядра можно получить для интерпо-
интерполяционных [сплайнов типа 1Г и для периодических интерполяционных сплай-
сплайнов. Заметим, что эти ядра не зависят от функции / (х).
3.17. Преобразования, определяемые сеткой
Сард [1] широко использовал остаточные члены вида C.16.7) при анализе
целого ряда аппроксимаций. Существование ядер К (ж, *)жв случае, когда
в формуле C.16.7) вторая производная /" (х) заменяется произвольной произ-
производной, доказано при очень общих условиях. Первоначальные результаты
в этом направлении восходят к Пеано 11]. В гл. V мы докажем существование
ядер для сплайн-аппроксимаций, в которых основную роль играют производ-
производные, отличные от второй. С более общей точки зрения подошел Гревиль [11,
изучивший существование таких ядер в случае, когда /" (х) в формуле C.16.7)
заменяется линейным дифференциальным оператором Ь порядка п.
Пусть с помощью к + 1 функций а* (х) и сетки Д: а = х0 <С х± < . . .
^ . . < хк = Ь определено семейство преобразований вида
= Ц о, (*)/(«!). C.17.1)
{=--0
Гревиль 11] установил, что если для линейного дифференциального оператора Ь
C.17.2)
а
то для каждой точки х из [а, Ь] интеграл
ь
& C.17.3)
принимает наименьшее значение, если а; (х) в C.17.1) выбираются так, чтобы
функция Г/ (х) была обобщенным сплайном типа 1Г, интерполирующим / (х)
в узлах сетки Д. Этот результат представляет собой частичное распространение
результатов Шёнберга [6] по приближению линейных функционалов на более
общий случай. В гл. VI мы дадим полное распространение результатов
Шёнберга на обобщенные сплайны.
Наряду с преобразованиями C.17.1) можно рассмотреть преобразования
несколько более общего вида:
к
Г/ (*) = 2 «I (*) / (**) + Ъо (х) Г Ы + Ь| (х) Г Ы, C.17.4)
г=0
где дополнительные функции Ъо (х) и Ь\ (х) также принадлежат классу
Жп (а, Ь). Здесь мы ограничимся случаем п = 2 и рассмотрим ей*2 (а, Ь) как
3.17. ПРЕОБРАЗОВАНИЯ, ОПРЕДЕЛЯЕМЫЕ СЕТКОЙ 107
гильбертово пространство со скалярным произведением
ъ
(/. 8) = \ Г (*) ** (*) &;+ /' («) *' («) + /' (Ь) ** (Ь); C-17.5)
а
ари этом будем отождествлять функции, отличающиеся на постоянное слагае-
слагаемое. Кроме того, мы будем считать, что Т и Вт линейно отображают <йГ2 (а, Ь)
в себя. Нас интересует вопрос: при каких условиях на функции а* (х) (I —
= 0, 1, . . ., &), Ьо (х) и &1 (х) величина || Ет || будет минимальной?
Пространство <йГ2 (а, Ь) можно представить в виде
т? (а, Ь) = /'д © <?д, C.17.6.1)
где
С!д = [Ж* (а, Ь) - /'д] C.17.6.2)
— ортогональное дополнение к Р&, т. е. (тД совпадает с множеством всех функ-
функций из е/Г2 (а, &), которые обращаются в нуль на А и первые производные кото-
которых равны нулю при х = а и х = Ъ. Таким образом, для / (х) ^ (?д
ЕТЦх) =/(*), C.17.7)
откуда || Кт И ^-1 для всех допустимых преобразований Т. Постоянная функ-
функция / (х) эквивалентна нулевой функции, так что в этом случае Г/ должно быть
эквивалентно 0. Следовательно, если мы хотим, чтобы на пространстве е2Г2 (а, Ь)
с указанными отождествлениями было определено преобразование Г, мы долж-
должны потребовать, чтобы сумма
ь
г=0
была постоянной относительно х.
Пусть в качестве функций аг (х) выбраны кубические сплайны типа Г
на сетке Д (так что аг (х/) = бу), в качестве Ьо (х) — кубический сплайн на Д,
который обращается в нуль в каждой точке сетки А и первая производная кото-
которого равна 1 в точке х0 и нулю в точке %ав качестве Ь± (х) — кубический
сплайн, аналогичный Ъо (х), но с переставленными значениями первых про-
производных. Тогда Г/ (х) будет проекцией функции / (х) на Р^. Сумма
2 а, (х)
г=0
будет постоянной относительно х; на самом деле она тождественно равна 1.
В этом случае линейные отображения Т и Ят будут проекторами, а соответ-
соответствующие линейные подпространства Р& и (тД будут ортогональными дополне-
дополнениями. Из всего этого следует, что
II Т || = || Нт || = 1. C.17.8)
При таком выборе преобразования Т оно не только будет проектором, но как
проектор будет больше любого другого проектора в классе рассматриваемых
108 ГЛ. III. ВНУТРЕННИЕ СВОЙСТВА КУБИЧЕСКИХ СПЛАЙНОВ
преобразований, поскольку пространство нулей любого другого проектора
вида C.17.4) должно содержать &д. Если же Т не является проектором, то в
Т [&Р* (а, Ь)] найдется лучшее приближение для / (ж), чем Г/ (х). Если Т —
проектор и Т\ >■ Т — также проектор, то Т^ (х) дает по крайней мере такое
же хорошее приближение для / (я), как и Г/ (х). Здесь мерой качества прибли-
приближения Г/ (х) к / (х) служит малость величины || /?г/ ||.
Незначительно изменив представление C.17.4), можно определить два
соответствующих класса преобразований, где сплайны типа 1Г непериодические
сплайны играют ту же роль, что и сплайны типа I для преобразований
C.17.4).
3.18. Связь с ракетной техникой
Чтобы максимизировать полезный груз, доставляемый ракетой, мы долж-
должны минимизировать интеграл от квадрата приложенного ускорения (Зейферт
[1, 10-2-2]). В поле, свободном от тяготения, это равносильно минимизации
интеграла от квадрата полного ускорения. Если заданы начальное и конечное
положения и скорости, а также время полета, то из теоремы 3.4.3 следует, что
координаты оптимальной траектории являются* кубическими функциями
от времени. Этот вывод согласуется с обычным (формальным) анализом задачи
(Зейферт [1, 10-3-11). Если, кроме того, заданы промежуточные положения
в моменты времени, отличные от начального и конечного, то решением будет
траектория, координаты которой являются сплайнами относительно времени.
Это также следует из теоремы 3.4.3. Отметим, что нет надобности предпола-
предполагать приложенное ускорение непрерывным, достаточно считать его интегрируе-
интегрируемым с квадратом. При обычном анализе задачи оптимизация ограничивается
профилями ускорения, имеющими вторые производные по времени, чтобы обо-
обосновать двойное интегрирование по частям. При доказательстве теоремы 3.4.3*
дифференцируется только сплайн, а не функция из класса <йГ2 (а, Ь), на кото-
которой осуществляется оптимизация.
Глава IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ
4.1. Определение и основные уравнения
Естественно попытаться распространить понятие кубического сплайна
на кривые, составленные из кусков полиномов произвольной фиксированной
степени, и получить для этих кривых свойства, аналогичные установленным
в предыдущих главах для кубических сплайнов. Цель этой главы — ввести
полиномиальные сплайны и рассмотреть их алгебраические свойства. В сле-
следующей главе будут подробно исследованы внутренние свойства полиномиаль-
полиномиальных сплайнов нечетной степени.
Первый важный момент, на который надо обратить внимание при переходе
к полиномиальным сплайнам,— это существенная разница между сплайнами
четной и нечетной степени. Оказывается, например, что полиномиальные сплай-
сплайны четной степени, интерполирующие заданную функцию в узлах сетки, могут
не существовать. По этой причине определение интерполяционного сплайна
нечетной степени, которое в действительности приводит к ожидаемому рас-
распространению свойств кубического сплайна, для сплайнов четной степени
должно быть другим.
Рассмотрим сначала число степеней свободы. Полиномиальные сплайны
степени 2/г — 1 на сетке Д: а = х0 <С х\ <С . . . <С Хи = Ъ зависят от 2пЫ
произвольных постоянных. Требование непрерывности производных порядка
О, 1, . . ., 2/г — 2 в каждом внутреннем узле сетки дает Bп — 1) (№ — 1)
условий. Остальные N -\- 2п — 1 степеней свободы распределяются на интер-
интерполирование в N + 1 узлах сетки и на /г — 1 краевых условий в каждом из кон-
концов X = Яд, X = Яд-.
. Для сплайнов степени 2/г степеней свободы всего B/г + 1) N. Требование
непрерывности производных порядка 0,1, . . ., 2/г — 1 во внутренних узлах
сетки дает 2/г (ТУ — 1) условий. Остальные 2п -\- N составляют /г краевых усло-
условий в точках х = х0 и х = хк и по одному условию интерполяции в каждом
интервале. Естественно взять в качестве N точек интерполяции середину
каждого интервала сетки,
В этой главе мы не делаем попытки полностью описать сплайны четной
степени. Они вводятся главным образом в ситуациях, где в сочетании со сплай-
сплайнами нечетной степени они дают более ясную общую картину.
Итак, мы требуем, чтобы полиномиальный сплайн 5Д (х) степени к на сетке
Д интерполировал заданную функцию / (х) в узлах сетки, если к нечетно,
и в точках
1г{1 = 1, 2, . . ., N1 *«-1 <&<
НО ГЛ. IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ
если к четно. Периодические сплайны степени 2п — 1 и 2п удовлетворяют,
кроме того, условиям $дв)(#0 + 0) = 5Д9> (я^ — 0) для д = 0, 1, . . ., 2/г — 2
и д = 0, 1, . . ., 2/г — 1 соответственно.
Согласно формуле Тейлора с остаточным членом в интегральной форме
Коши,
к-2 ' х •+
^7)
Для сплайна степени 2/г—1 запишем это разложение в виде
2п-3 Ь
М*«)~ 2 •хГ(^-а)>г^)(а)+Bп1.зI 1 (**-*J+п-3Я12п-2>(*)^ D.1.1)
где для т>0
хт, х>0.
В этих обозначениях единичная ступенчатая функция со скачком в точке
х = 0 имеет вид х\.
Так как функция 5д2п~2) (ж) линейна на каждом интервале (ж/_ь X;),
а первый член в правой части равенства D.1.1) — полином степени 2п — 3
по хг, то, вычислив центральные разделенные разности
"г
при ЛГ>2л —2 и п— 1<а<^ЛГ — /г+1, получим
2п-2 V Г ГсBп-2>/~ \ Х3~~1 | сBп-2)
D.1.2)
Если /г>1, то д,{хг~гI/<И= — п(хг — г)*. Проинтегрируем по частям правую
часть равенства D.1.2):
•B»-2)Bп-1)]«м/~
4.1. ОПРЕДЕЛЕНИЕ И ОСНОВНЫЕ УРАВНЕНИЯ Ш
Bп-2)Т°г м
+ ~$г 2
3=1
хо)+ -Г
где М^^)
Функция б2- (х—ж^2" при ж^л:/-! тождественно равна нулю, а при х>х}+х
совпадает с полиномом степени 2л —3. Следовательно, 62п~2б| (хг — ху)^1 = О
при *</ — п и г>/ + /г. Если *>1, то {хг — хо)^-2+ [(«« — «ОГ-
( J1B^ — 1)^ — полином степени 2/г —3 по я*. Таким^образом,
если г>га. Для г = га — 1 коэффициент при Мо можно записать в виде
Bп-2)! О1 I. Bп-1)А1
С помощью простого вычисления разностей можно показать, что
г+п-1
[]
[]
Для /г—1<;г<!^ —га+1 равенство D.1.2) имеет вид
П АцМ^вГ^ьЫ, D.1.5)
где
при этом в соответствии с D.1.4) полагаем
B»-1)| Д
112 ГЛ. IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ
В периодическом случае мы полагаем Ху^х = х} — (Ь — а) и Х;+х = х$ +
-1- (Ь — а) и учитываем периодический характер сплайна 5Д (х). В силу
сказанного выше член с Мо в формуле D.1.3) исчезает и равенство D.1.5)
выполняется для каждого узла сетки.
Так как величины А1} не зависят от сплайна 5Д (х), ^о в равенстве D.1.5)
его можно заменить функцией #2п~2, которая на той же сетке сама является
сплайном степени 2/г — 1. Тогда в силу D.1.5)
г+п-1
B/1-2)! 3 А13=1 (л-1<1<Лг-л+1). D.1.7.1)
3=г-п+1
Аналогично если сплайн 8&(х) заменить функцией х*п~г, то получим
г+п-1 г+п-1
Bп-1)! 2 ХгМ}= 2 X] (/г-1<*<ЛГ-./г+1). D.1.7.2)
3=г—п+1 з'=г—п+1
В периодическом случае равенства D.1.7.1) и D.1.7.2) справедливы для всех I.
Дополнительное важное свойство заключается в том, что А ц ^ 0. В самом
деле, рассмотрим функцию
Легко видеть, что Ф(р)(а;) = 0 (р = 0, 1, ..., 2/г —2) для х^.х^1 и
B/г — 1)! (х — х^
фB«-2, {х) = ) {2п-1)! {хН1-х)
I
Г B/г
I 0,
Таким образом, первые 2п — 2 .производных нигде не отрицательны, поэтому
все разделенные разности порядка 2/г — 2 в равенстве D.1.6) не отрицательны.
В периодическом и в непериодическом случае, когда
п — 1<1<7\Г — п+1,
уравнения для сплайнов имеют вид D.1.5). Кроме того, в непериодическом
случае краевые условия дают дополнительно 2/г — 2 соотношений. При
задании краевых условий мы ограничимся сплайнами нескольких определен-
определенных типов.
Под простым сплайном степени 2п — 1 будем понимать полиномиальный
сплайн степени 2/г — 1, принадлежащий классу Сгп~г [а, Ь]. Далее, будем гово-
говорить, что полиномиальный сплайн степени 2п — 1 и вообще функция (когда
из контекста ясно, чему равно п) принадлежат типу Г, если их первые п — 1
производных обращаются в нуль при х = .а и х = Ь. Две функции принадлежат
одному и тому же классу эквивалентности типа I, если их разность принад-
принадлежит типу Г. В этом же смысле (снова когда из.контекста ясно, чему равно п)
мы будем говорить, что функция / (х) принадлежит типу 1Г, если /<р> (а) =
= /(р> (Ь) — 0 для р = /г, /г + 1» • • •» 2/г — 2. Две функции принадлежат
одному и тому же классу эквивалентности типа II, если их разность принад-
принадлежит типу Н'. Как и раньше, сплайн принадлежит типу I, если/(р) (а) и /<р> (Ь)
4.1. ОПРЕДЕЛЕНИЕ И ОСНОВНЫЕ УРАВНЕНИЯ ИЗ
(р — 1, 2, . . ., п—\) явно входят в представление, сплайна как независимые
параметры, и сплайн принадлежит типу II, если, в его представление явно
входят /<Р) (а) и /<Р) (Ь) (р = п, п + 1, . . ., 2/г — 2). Во всех этих случаях зави-
зависимость от величин /<р) (а) и /<р) (Ь) должна быть линейной.
Чтобы задать краевые условия для сплайнов типов I и II, образуем разделен-
разделенные разности вида D.1.1). Пусть [#0, хи ♦ . ., х;\к и [х0, х^, . . ., х^\ обозна-
обознак \
0,
чают соответственно разделенные разности от хк и х\ относительно точек
#о, #ь . • ., X}. Тогда из D.1.1) получаем тем же методом, что и при выводе
D.1.3), уравнения
2п-3
I Мр Г,л 12П-2 I
"г ^2п 2)! I"- ' * °' ''"' 3 °^+ '
Bп —1I
D-1.8)
где ? = 1, 2, . . ., 2п — 3 и ^ '(а;) = б| (аг — я/)*". Последняя сумма в D.1.8)
распространяется лишь на индексы 1, . . ., <?, поскольку ^- (дгй) = 0 при &<^
Для сплайнов типа I мм исключаем неизвестные величины Зд9> (а)
(д = п, п -|- 1, . . ., 2/г — 3) и получаем л — 1 уравнений относительно
Л/о, М{, . . ., Л/гп-з* Для сплайнов типа II мы рассматриваем D.1.8) лишь
при <? = п, /г + 1, ..., 2/г — 3 и получаем /г — 2 уравнений относительно
Л/о, Л/4, . . ., Мгп-з» которые вместе со спецификой выбора Мо для сплайнов
типа II вновь дадут п — 1 уравнений. Если вместо D.1.1) применить соотно-
соотношение
2п-3 Ъ
*а(*|) = 2 ТГ^-^^^ + Тг^Ж I й2п-2)<«) («.—О?"'*. D-1.9)
то у нас будет аналогичное множество п — 1 краевых условий при х = 6.
Таким образом, N + 1 — 2 (/г — 1) стандартных уравнений вида D.1.5) вместе
с 2/г — 2 краевыми условиями дадут 7^ + 1 уравнений относительно Мо,
М\, . . .., А/"л»
Если Л" < 2ге, то стандартные уравнения вида D.1.5) не применяются
и определяющие уравнения выводят только из равенств D.1.8) и их аналогов,
связанных с D.1.9). 3 этой связи заметим, что условие N 1> п — 1 необходимо
для существования сплайна типа II. Проинтегрировав п — 1 раз на отрезке
хо ^ х -к* Х1 тождество
8-1197
114 ГЛ. IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ
и воспользовавшись условием 5д^ (а) = /(в) (а) (я = п, ч. ., 2п — 2), выра-
выразим $1в) (а?!) ^ = п, п + 1, . . ., 2га — 2) через единственный параметр М^
Проинтегрировав 1$д2п~2) (х) на отрезке ж4 <^ х ^ х2, выразим 5Д9) (х2)
(д яг п, и + 1, . . ., 2п — 2) через параметры Ми М2- Наконец, проинтегри-
проинтегрировав 5д2п~2) (я) на отрезке а^_1 •< а: <! я^» выразим 5^ (Ь) (? = п, п + 1, . . *
. . ., 2п — 2) через параметры Ми • • •» Мх. Так как величины 5дв> (Ь)
^ = п, п + 1, . . ., 2/г — 2) заданы, то в точке Ь остается N — п + 1 сте-
степеней свободы, так что N^71 — 1. Следующие п интегрирований приводят
к N — га-Ъ1+и = .ЛГ-Ъ1 степеням свободы и, значит, к возможности
интерполяции заданной последовательности {/,-}: 5Д (я,-) = /^ (/ = 0, 1, . . ., Лг).
Для полного определения сплайна надо выразить производные 8)Р {х;)
(9 = 1, . • ., 2п — 3; / = 0, 1, . . ., IV) через параметры М] и через значе-
значения 5Д (X]), которые сплайн интерполирует в узлах сетки А.
Интегрируя функцию
^ ^. D.1.10)
на отрезке лг/-1-^^^ж;, получаем
— 2), D.1.11)
где
D.1.12)
Заменив в D.1.1) а на X} и при п — 1^/^^—п-\-\ вычислив разделенные
разности, получим систему уравнений для определения величин В^. Для четного
р имеем
2п-3
D.1.13)
хг
я11}! 2 ^тСЛш+Атм)^^1""*»I11^ О/)» D.1.14)
4.1. ОПРЕДЕЛЕНИЕ И ОСНОВНЫЕ УРАВНЕНИЯ
115
(х
■
Ы
-м-»/- Bп-2)!
1
~" Bп-1)!
ш=г+1
Для нечетного /7 используем разделенные разности
D.1.15)
В итоге система уравнений для определения величин Вк] (к = 1, 2, . . ., 2л — 3)
имеет треугольную матрицу коэффициентов, и метод ее решения очевиден.
Перейдем к другому методу построения стандартных соотношений D.1.5)
для сплайна. В прежнем методе алгебраическое вычисление разделенных раз-
разностей Ь\п~2Ь] (хг — я/)^-довольно утомительно.
Нам потребуется такой полином р {о) степени 2/г + 1, первые п производ-
производных которого в точках а = 0(и а = 1 заданы:
рЮ @) = ^*>, ' р(*> A) = р\* (к = 0, 1 п).
Запишем полином р(о) в виде
Условия в точке а = 1 дают систему
1 1 1
71+1 71 + 2 1
(П
1
^-Ь1)B>
Г Л,
п
п
й1
_ „(п)
D.1.16)
116
ГЛ. IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ
где кф — к{к— 1) (к— 2)
слева па матрицу
1
-(и-
(к — / + 1). Умножим матричное уравнение D.1.16)
О
1
G1+1).2
"' ,-3
«•4
О
О
О
О
О
О
О
О
о
о
Тогда в левой части уравнения будет матрица
Г1 1 1 1 1 ...
О 1 2 3 4 ...
О О 2 6 12 ...
О О О 6 24 ...
О О О О 24 ...
Л<1>
0000 0
п1Ю.
обратная к которой равна
/И __
1 —1 — —
1 * 2!
0 1 1 ~
и 1 1 2!
1
4!
1
""зГ
О О
О О
о о
• *
о о
о —-•
о о
3!
о
о
О
о
о
1
-(/г+1K
(/г+2)BN
л'1 ^"/(П-2) ^П
(-1)"
п!
( 1) ... о,
1
21
3!
(_1)П-2
(п-2)!
(п-3)!
(_1)п-4
4! (п-4)!
п!
4.1. ОПРЕДЕЛЕНИЕ И ОСНОВНЫЕ УРАВНЕНИЯ
117
Далее,
где
Таким образом,
п
2
2
1
2*
1
)
•
(Ь+п-1)
Л!
т)(л— 1)
1
0
0
•
•
*
0
0
1
1
0
*
*
*
0
0
2!
1
1
•
*
*
0
0
1
3!
1
2!
1
*
•
*
0
0
1
4!
!
!
*
*
*
0
0
1
иг
1
1 1
О 1
тЛ0"
А,
•
Ап.
ф Л,
•— <м <т&
(
\
Р{0)~
Р{1)
:
р(п)
*
*
Элементы у^ матрицы 98Л; вычисляются по формуле
г=0
D.1.17)
где ( п \ — биномиальный коэффициент С^, ( п) = 0 при т < 0 и т >► /г,
118
ГЛ. IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ
Произведение матриц 38Л;% имеет более простой вид
1
(п\Bп-\-1\ (п—1\/2п\
\0)\ п ) { 0 )\ п)
/2п +
п~1
п
2п
/п-(-2\ /2п+1\ /»"И\ / 2п \
I 2 И п-2 / . V 2 7 \п-2)
1 (п — 2\Bп — 1
Г V 0 / V п
1 /п—1\/2п —
2Т\ 1 ) \ п-
Л/Л\ /2п-1\
2! ^2 И п-2 )
1 /1\ /п + 2\ Л-/°\ /л + 1
-1 /2\ /п
гЗ\/п+2\ 1 /2\ /п+1 \
^2/ \п—2/ п! \2/ \п—2)
* •
(—1)" / п + 1 \ / п + 2 \ (_1)п / п\ / п + 1 \
•" (л-1)! V п ) \ 0 / п! иД 0 |.
D.1.18)
и с его помощью легче вычислить полином
п ' -.
D.1.19)
аЬ 1
п
=ж-1г 2 (~*)? (п"А
где
На отрезке гн<«^^ сплайн 8ь(х) совпадает с полиномом степени 2л—1.
Рбозначим его через 8^^(х):
п-1
1)
, D.1.21)
Тогда для <? =/г, /г+1, ..., 2п — 1
п-1
г>«A)},
.1.22)
й=0
?3- (х,)^Гп^1й @)},
4.1. ОПРЕДЕЛЕНИЕ И ОСНОВНЫЕ УРАВНЕНИЯ 119
где
еы1)- -4 2 <-* Г V') (") (»+л».. D'1'23)
1
В частности,
-2)!- D.1.24)
Если потребовать, чтобы производные 5д9) (х) были непрерывны в точке X}
для д = п, л+1, ..., 2/г—2, то для этих значений ^ будет 5^,-(ж/) =
Й^), т.е.
п-1
\. D.1.25)
Обозначим 5дв)(ж/) через 8\дК Тогда в каждой точке X] получим л—1 урав-
уравнений (д — п, ...,2/г—2)
!»-! @) [( -
+}ТВы-1 A) 55?|^ =
Ё +1^1, A) Я<ЭД + ГЙ> 1 * @) [(-1)*« Л5+, А* -Л?А
. D.1.26)
Если /г — 1 ^ г■< N—11+1, то уравнения D.1.26) при I — п.+ 1^/^1 +
+ ге — 1 дают B/г — 3) (/г — 1) соотношений относительно B/г — 1) (/г — 1)
переменных
?) (/ = * — п + 1, . .,., * + п — 1; ? = 1, 2, . . ., /г — 1).
Исключая из них 8\ф (] = I — п + 1, . . ., I + ?г —- 1; ^ = 1, 2, . . ., /г — 2),
выводим уравнения для сплайна относительно переменных
120 ГЛ. IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ ч
Если мы хотим, чтобы уравнения для сплайна были записаны в терминах вели-
величин М), надо с помощью равенства D.1.11) выразить 5$1) и 8^п~{) через
М}-и М}, 8\Ч2\ и 8\ч) (# — 0, 1, . . ., п — 2), подставить эти значения в D.1.16)
и, как прежде, выполнить процесс исключения. В итоге получим соотноше-
соотношения, эквивалентные D.1.5).
В качестве иллюстрации проведем построение для сплайна пятой степени.
Функции Г20 (<*), Т21 (о), Т22 (а) здесь имеют вид
2
5=о
2
откуда
Г2'о(О) = -60, Г2'1'@)=-36, Г2'2'@)=—9,
Г2'о'A)= -60, Га'И1)= -24, Г2'2'A)= -3,
Гй> @) = 360, Т$ @) = 192, Г$> @) - 36,
^ -360, ГЙ}A)= -168, ГЙ^!)^- -24.
В силу равенств D.1.22)
пг г а» о».
м - 360 %!-- 360 -^+192 -р +168 -ф + 36 -^-- 24 ^.
^+360^ 1в8^ 12^^^
М,- -360^+360^- 1в8-з^- -192^-24^
так что
Снова применяя равенства D.1.22), находим
- §) + 6 ^5. - ^ (9Л/у + 2ШН),
D.1.29)
4.1. ОПРЕДЕЛЕНИЕ И ОСНОВНЫЕ УРАВНЕНИЯ 121
Требование непрерывности Яд" (х) в точке х^ приводит к уравнению
-81 • 12 8з~81-1
{А 4
DЛ-
а непрерывность 8ь(х) в точке X] с учетом D.1.28) дает
2 , /4 + М ,_ 2 ,
2 , 6 ^ 6 ^-5а
А; А/
Запишем уравнения D.1.25) и D.1.26) в точках ж7-_4, ж/, ж^-+1 и исключим
из них 5}_2, 55_„ 5^, 55+1, 5^+2. Тогда получим
120
+ 120
\ (А; + А/+1) (АМ + А; ■+
_1
120 (А/+1 + А/+2) (Л,
Нам осталось лишь потребовать выполнения краевых условий. Выпишем
их для сплайнов типа I, хотя развитые методы в равной степени можно при-
применить для сплайнов типа II. Уравнения D.1.25) и D.1.26) при х = а исполь-
используются для того, чтобы удовлетворить условиям непрерывности 5д (х) и 5д" (х)
в точках Хх и х2. Пятым уравнением служит первое из уравнений D.1.22) (зна-
(значение 3'0' задано). Исключение переменных 8[, 8'гж 8'а дает два условия на вели-
122 ГЛ. IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ
чины Мо, Ми М2, М3:
к\ Мо Г
120 1
120
М2
120
А2А3(ЗА2+2А3)
120 (Л, + Аз) (*! + *. +Аз)
&1 А1^А2 А2 ^
12 А!+А2\ А2 *1 I] 4*11 *! °^ 2 -Г
В силу симметрии из этих соотношений можно непосредственно получить соот-
соответствующие краевые условия в точке х = Ь\
Вычислив величины Л//, определим значения 5$_ь 8^ #2-1 и 5} и тогда
D.1.21) даст представление для 5д (х) на отрезке [я/_*, Х]\. Если исключить
8^-2 из двух соотношений непрерывности в точке ^_4 и затем ^.^
же соотношений в точке х^, то получатся два уравнения относительно
и 5$, из которых находим, что
1 \_ 1 8,-8ы
к)- Н к
120
120 '
И наконец, 5,_! т 8] находим из равенств D.1.28).
Очевидно, что применение полиномиальных сплайнов, заданных на нерав-
неравномерной сетке, затруднительно. Большая часть этих трудностей связана с тем,
4.2. РАВНЫЕ ИНТЕРВАЛЫ
123
что величины М] уравнениями сплайна определяются неявно. В разд. 4.5
мы введем сплайны пятой степени максимального дефекта; они менее сложны
и очень удобны для применения.
4.2. Равные интервалы
В теории, полиномиальных сплайнов особенно важны полиномиальные
сплайны, заданные на равномерной сетке. В этом случае положим Ь, = (Ь — а)Ш
и обозначим через А = # — 1 разностный оператор, связанный со сдвигом к,
т. е. Е1 (х) = / (х + &)• Запишем уравнения D.1.5) и D.1.6) в виде
А?П~г) = B»-
D.2.1)
B»-1I 6*
Fу, как и раньше, обозначает разделенную разность). Так как б* [(г — /
= 6! [((-/) Ц2Г\ то
Пусть /г=1 и
2, ..., п-1).
Тогда
D.2.3)
/Л 2 4^
Таким образом,
2п-2
1 Х^
га— 1)! 2]
Bга— 1)!
А2п-2
где о\— центрально-разностный оператор Е~гА2.
Величины фйп> для четного п связаны со сплайнами четной степени с точ-
точками интерполяции в узлах сетки. Однако удобно рассматривать все множе-
множество этих величин. Укажем па связь между нисходящими разностями функции
хп в точке х = 0 («разностями нуля», Фриман [1, стр. 123]) и (п — 1)-ми разное
стями функции (#)". Обозначим Акхт 1^=0 через А'Ют; тогда для разностей
с единичным шагом
г-Б<-')'('
. 1 4- 7*
7
)
D.2.6)
124
ГЛ. IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ
При т = 3 это равенство очевидно. В качестве иллюстрации приведем таблицу
А»
дп*.
В горизонтальном прямоугольнике указаны значения
ном параллелограмме — значения О3, ДО3, Д203, Д303.
Следующие равенства очевидны:
ф(т, +
) + (ф(
(т)
т — 2
=фГ + (фГ+фГ+Фот)) + (Ф2т) + 2ф
ф'Д
в диагональ-
диагональщ _ 2)
)+...
т — 2
т — \
3
Разрешая их относительно фйт>» получаем равенства D.2.6).
Разпости нуля удовлетворяют рекуррентному соотношению
Д*0т+1 - к (Дй0т + Д^О1"). D.2.7)
Покажем, что величины фйт) удовлетворяют рекуррентному соотношению
ФР =
D.2.8)
4.2. РАВНЫЕ ИНТЕРВАЛЫ 125
В самом деле, в силу D.2.6)
(* +1) Фй'" + {т-к) фйГ» =
"-1 ./т_Л —1 + /'
п х . /т Ь
й V 7 + 1
+ (т-к) 2 (-1)'AП~** + /) А^0ж^. D.2.9)
Далее,
(т-к-\
]( ]], D.2.10)
и член в
/к+}\ /Л + У\
квадратных скобках равен нулю, поскольку &1 I = (у +1) I I .
/т\ ( т \ (т+1\
Кроме того, I ♦1+1?,/|1 — I 1/1 I» так что левая часть в D.2.10) равна
[/т — к— 1 + А /т —Л—1 + А1 /те —Л—1 + А
(те —Л + А /те —Л —1 + А
.. ^ + (Л+1_/)^ ^ ^. D.2.11)
Таким образом, правая часть в D.2.8) равна
й-1
(т — к— 1 + А1 ,, <
-/)( . Ч Д^О1". D.2.12)
С другой стороны, в силу D.2.7)
к
7
126 ГЛ. IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ
(-1)''[~(*-/>(
Здесь последнее слагаемое равно нулю, и соотношение D.2.8) доказано.
Приведем значения нескольких первых членов множества {фйт>} (индекс т
относится к строке, к— к диагонали):
т = 1 1 к=0
т = 2 1 1 &=1
т = 3 14 1 й=2
тгс=4 1 И 11 1 к=Ъ
т = 5 1 26 66 26 . 1 &=4
т=6 1 57 302 302 57 1 к=5
тте = 7 1 120 1191 2416 1191 120 1 Ь=6.
Нетрудно заметить, что соотношения D.1.27) для сплайнов пятой степени
в случае равномерной сетки примут вид
- \М^2+ 26Л/М+66Л/;+ 26Л/^+1+ Л/^21 =
Проиллюстрируем теперь применение сплайнов четвертой степепи, заданных
на равномерной сетке. Учитывая тождество D.1.1), имеем
и, вычисляя разности, как при выводе равенств D.1*5), получаем
^. D.2.14)
Чтобы [получить полную систему уравнений для сплайнов типов I и II,
надо выразить D.1.8) в более простой форме. В случае равномерных сеток
система D.1.8) (# = 1, 2, ..., 2л —3) принимает вид
<4-2-15)
4.2. РАВНЫЕ ИНТЕРВАЛЫ
127
(Оператор А во втором и третьем членах правой части равенства D.2.15) дей-
действует на индекс и Ясно, что А9 (О ^п~2 |г=о == А'О2".)
При выводе представления для сплайна <?А (х) и его производных на отрез-
отрезке [ж/_1, Я/1 гораздо удобнее в рассматриваемой ситуации заменить D.1.11)
равенствами (р = 0, 1, 2, . . ., п — 1)
Bр)!
Bр)\Н
1 Bр-2*)|
D.2.16)
2| ^ Bр-2
Из условия непрерывности 8%п~9) (х) и 5Д2П) (х) в точке X} вытекает, что
Аи = В1}, ~М1=-2~А1}. D.2.17)
По индукции немедленно получаем, что для р = 1, 2, ..., /г —1
М§ &2Ю-2 }Л Л2
= \АР1. D.2.18)
_!, = $;. D.2.19)
BР)! А
Кроме того, для р = п
—2)! ^а-Г "-
Bп—1)! А "+" Bп—3)! • ^~г--
Запишем эту систему разностных уравнений в виде
' М;/Н '
Аи
■ 0"
0
0
D.2.20)
где
2!
4!
-^ о
2!
о
о
Bп—2)! Bп-4)!
2! Г
62
2
2п—1)! Bп-3)!
— Н
3!
D.2.21)
128
ГЛ. IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ
В периодическом случае, а также в непериодическом случае при п — --*/-*
^ЛГ —л-|-1 умножим слева обе части равенства D.2.20) на сопряженную
матрицу оР*. Пусть | & \ — определитель матрицы ^, а />*, —элементы
матрицы йГ**. Тогда
1*1
1*1.
D.2.22)
откуда
Сравнивая равенства D.2.23) и D.2.5), видим, что
б\П-1
и поэтому
D.2.23)
D.2.24)
2п-2
-жгго 2
D.2.25)
Л=0
Разумеется, это тождество можно получить непосредственно, разлагая опре-
определитель |<^|, но вычисления при этом несколько усложняются.
Оператор в правой части равенства D.2.24) можно записать в виде
2!
4!
к*
Т
о
б2
о
о
B^—2)! V1—*'»
B1)! B*-2)!
B1 + 2)! B01
к2
2!
Л*
4!
Л*
вГ
62
2
Л»
2!
Т
0
0
б2
2
*1 ±1 —^ О
о
о
о
Bп-4)! Bп-6)!
А2П-2
B»-2)! Bга-4)!
62
2
"
0
62
2
4.2. РАВНЫЕ ИНТЕРВАЛЫ .
129
2!
к*
_б2
2
&2
2!
О
о
о
О
о
B1—2)! B1—4)! B1 — 6)!
B0!
Обозначим
Bг-2)! Bг-4)!
2!
_^1
4!
62
2
Г
«-г-1
<?п (X) =
X
Г
1Г
"бГ
— л;
Т
1
~Ж
0
1
Ж
0
0
• • •
• • *
• « «
0
0
0
1
Bп-2)! Bп-4)!
1 1
21
1
2!
Bп-2)! '•* ■ ••* 4!
тогда разложение по минорам первого столбца дает равенство
1 л / ч ■ _^_0 /х
а\ Ч:п-2 г1'
D.2.26)
D.2.27)
справедливое для /г!>2, если положить ^ = 1/2!. Запишем (?п (х) в виде
Тогда , ■ • ...
п~ 2 п—1 ' п—к—1
2„ , Л _ X* хк~г . ^
п-1
) _ "VI и-1 VI «п
Л=1
откуда
D.2.29)
9-1197
130
ГЛ. IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ
В частности,
Далее, заметим, что
и по ипдукции получим
к*
2!
1
1Г-
— х
D.2.30)
4! 2!
Л»
2!
4Т
ДО
6Г
Т
Т
0
—
2!
0
0
0
0
0
0
Bп—2)! Bп—4)! Bп—6)!
Bп)! Bп—2)! Bп—4)
Отсюда и из D.2.26)
2!
41
— л;
2!
Х2ч п—г-1
Вернемся к определению
равенств D.2.16)
D.2.31)
для сплайнов типов I и II. В силу
й=1
D.2.32)
"Г
Если величины М; найдены, то для сплайнов типа I значения 5д" (а)
(д = га, ...,2га — 3) можно определить из равенств D.2.15), переписанных
в виде
2п-3
Bп-2)!
5=1
; й;3. СУЩЕСТВОВАНИЕ
131
Аналогично определяются величины З^а) (д == 1, 2,."•«.*;;.> п-*-А) для сплай-
сплайнов типа II. После того как будут вычислены все величины 8)?\а)
(д = 1, . . ., 2п — 3), значения 8^{х]) можно найти с помощью интегрирова-
интегрирования. Дважды интегрируя по частям, получаем . ■
й=0
-<>м *
3-1
■2
4.3. Существование
Для полиномиальных сплайнов, заданных на неравномерной сетке, очень
трудно провести доказательство существования, основанное непосредственно
на свойствах матрицы коэффициентов. Заметим, что даже в случае равномер-
равномерной сетки матрица коэффициентов для сплайнов седьмой степени не имеет
доминирующей главной диагонали (сравните таблицу коэффициентов в разд. 4.2).
Существование полиномиальных сплайнов нечетной степени, удовлетво-
удовлетворяющих свойству наилучшего приближения или минимальной нормы, как
и в случае кубических сплайнов, следует из первого интегрального соотноше-
соотношения. Эти свойства мы рассмотрим более подробно в гл. V.
Что касается периодических полиномиальных сплайнов, заданных на рав-
равномерной сетке, то их существование можно доказать- непосредственно. Более
того, при доказательстве обнаруживаются некоторые свойства матрицы коэф-
коэффициентов, представляющие также самостоятельный интерес. Матрица коэф-
коэффициентов системы D.2.1) является циркулянтом порядка N1
А —
01
аа
D.3.1)
=1, 2, ...,
ак = 0 в остальных случаях.
Хорошо известно (см. Эйткен [1] или Мюир [1]), что собственные значе-
значения матрицы А равны
*-4 (*=1, 2, ...,Л0, D.3-2)
9*
132
ГЛ. IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ
где щ = е2п1к№, а соответствующие им собственные векторы равны
. A,.ю*,«*, ...,©""'). D.3.3)
Следовательно, матрицу А можно представить в виде А — ШЬОг1, где
1 1 ... 1
со?
о)!
Тогда
и)? 0J; ...
е4 о о ... о
о е2 о ... о
о о е3 ... о
• • • •
• ♦ • •
О 0 0 ... влг
1 ю^1 а>г2
ЛГ-1
_1_
N
щ
2
N
саг»
N
[V N
И если ни одно из собственных значений не равно нулю, то
к=±1
D.3.4)
D.3.5)
D.3.6)
Разностное уравнение D.26) изучал Хилле [1, стр. 47] в связи с диффе-
дифференциальным оператором 6 == ъсИйг в комплексной плоскости. Пусть
т-1
1 == 2 2^ Фй 2 D.о.о)
й=0
где величины фьт>' определяются равенством D.2.3). Покажем с помощью
-' 'о.
4.3. СУЩЕСТВОВАНИЕ
индукции, что
Для те=1 имеем
Предположим, что
тп—2
г У,
Дт-1 *
A—г)т '
где ф})т) = ф^1 = 1 для всех ;гс>1. Тогда
т—2 т—1
— г)
»
так как Фаш) = (&4-1) фК?"'" + (те — А) Ф^!". Из равенства D.3.10) получаем
ЛB) = 2, РтB)=2И^т-1B) + A-2)/>т-1 (г)] A»> 1). D.3.11)
С помощью индукции можно также показать, что полином Рт (г) имеет
т — 1 различных действительных отрицательных нулей. Заметим, что Р% (г) =
= г (г + 1)» так что —1 является нулем полинома Р2 (г). Предположим, что
полином Рт-\ (г) имеет т — 2 различных отрицательных нулей. (Очевидно,
что он обращается в нуль в точке г = 0.) Так как значения Рт-1 (я) действитель-
действительны (х = Ке г), то между двумя последовательными нулями полинома Рт-\ (х)
должен быть нуль производной Р'т-\ (х). Таким образом, Рт-1 {х) и Рт (х)
одновременно не обращаются в нуль, за исключением точки х = 0. В нуле
производной Рт-1 (х) полиномы Рт-\ {х) и Рт (х) имеют противоположные
знаки. Старший коэффициент полинома Рт (х) равен 1, так что Рт (х) ->- +оо
или Рт (х) ->• — оо при х ->■ — оо в зависимости от четности или нечетности т.
Итак, Рт (х) имеет нуль между каждыми двумя последовательными нулями
производной Рт-1 (я) и ну ль левее самого левого нуля полинома Рт_1 {х).
Кроме того, Рт @) = 0 и, так как Р'т @) > 0, то между 0 и самым правым
нулем производной Рт-1 (^) должен быть нуль полинома Рт (х). Следовательно,
Рщ 0е), кроме нуля в точке х = 0, имеет т — 1 различных отрицательных
нулей.
Теперь уже легко показать (и не одним способом), что фьт) = фт^-ь-
Отсюда будет следовать, что обратная величина каждого нуля полинома
Рт B)/г является также нулем этого полинома и Ргп (—1) = 0« Поэтому для
периодических сплайнов нечетной степени все собственные значения 8Ь отличны
от нуля. Фактически из равенства D.3.2), где ак — а^+2-ь A <С к ^ $), видно,
что все они действительны. Итак, матрица А в этом случае не вырождена.
134 ГЛ. IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ
Заметим, что (—1) является 7У-м корнем из единицы, только если N четно.
Таким образом, для сплайнов четной степени матрица А не вырождена, если N
нечетно. Это завершает доказательство следующей теоремы.
Теорема 4.3.1. Периодические интерполяционные полиномиальные
сплайны степени 2/г — 1, заданные'На равномерной сетке, содержащей N интер-
интервалов B/г — 1 ^ ./V), всегда существуют. Периодические интерполяционные
полиномиальные сплайны степени 2/г -^ N существуют, если число N нечетно.
4.4. Сходимость
Для полиномиальных сплайнов до сих пор не установлены все свойства
сходимости, аналогичные свойствам сходимости, рассмотренным в гл. II и III
для кубических сплайнов. Если функция / (х) принадлежит классу Са [а, Ъ]
(О-^ Я ^ 2/г — 1) и сплайн 5Дь (х) интерполирует ее в узлах сетки Д&,
Нт || Дь || = 0, и удовлетворяет определенным (довольно общим) краевым
условиям, то можно ожидать, что
. /доИ-^И = о(||АПГр) @О<:д<2>г-1), D.4.1)
если только в случае производных порядка 2/г — 1 величины Лдй =
= 1тах || Д,, \\1{хы — хкг^)\ ограничены.
В работе Алберга, Нильсона, Уолша [91 рассматривается сходимость
последовательности периодических полиномиальных сплайнов, интерполирую-
интерполирующих функцию / (х) из класса С2п~2 1а, Ъ] для асимптотически равномерных
сеток. Несколько позже Циглер [1] доказал сходимость периодических интер-
интерполяционных сплайнов без предположения об асимптотической равномерно-
равномерности сеток. Алберг и др. [10] дали оценки порядка сходимости обобщенных
сплайнов для функции /(г) из класса Сп[а, Ь] и из класса С2п [а,, Ъ].
В последнем случае сетки удовлетворяют условию B.3.7) (см. гл. V и VI).
В гл. V будет доказано, что если / (х) € &Сп (а, Ь), то
{х) = О(\\ Д* И""*
Кроме того, если величины Лд ограничены и /(#)(|С2п[а, Ь], то
Как и в случае кубического сплайна, ухудшение оценки сверху связано лишь
с методом доказательства.
Для того чтобы получить более точные соотношения D.4.1), как для кубиче-
кубических сплайнов, по-видимому, необходимо использовать свойства матрицы,
обратной к матрице коэффициентов системы уравнений, определяющих сплайн.
Но пока, кроме некоторых специальных случаев, эти свойства еще не изучены.
В этом разделе устанавливается ряд результатов, касающихся сходимости
общих полиномиальных сплайнов нечетной степени при априорном предполо-
предположении, что матрица, обратная к матрице А коэффициентов системы уравнений
4.4, СХОДИМОСТЬ
135
для сплайнов, описанной в разд. 4.1, обладает некоторыми нужными свой-
свойствами. В разд. 4.5 подробно обсуждаются периодические полиномиальные
-сплайны, заданные на равномерных сетках.
Теорема 4.4.1. Пусть на отрезке [а, Ь] даны функция / (х) из класса
С2п~г [а, Ь] и последовательность сеток {Ай}, || Дй || -> 0 при к-*- оо. Пусть
■сплайн 8&к (х) интерполирует функцию / (х) в узлах сетки Ай и разность
У (х) — 8&к (х) принадлежит типу Г, или типу IV, или сплайн 8&к (х) периоди-
периодический (последнее при условии, что функция / (х) периодическая и принадлежит
классу С2п~* (—оо, оо)). Если матрица Ал1, обратная к матрице Ак коэффи-
коэффициентов системы D.1.5), равномерно ограничена относительно к, то
2п-2)
D.4.2)
равномерно относительно х на [а, Ъ]. Если производная рп~2 (х) удовлетворяет
на [а, Ъ\ условию Липшица порядка а @ < а ^ 1), то
1р) (р = 0, 1, ..., 2п-2) D.4.3)
равномерно относительно х на [а, Ь].
Доказательство. Опустим индекс сетки к и обозначим через М
вектор (Мо, Л/1, . . ., ММ)Т. Пусть А —матрица коэффициентов системы
уравнений для сплайна. Запишем систему в виде
АИ = а. (АЛЛ)
Если сплайн $д (х) периодический, то система D.4.4) точно совпадает с систе-
системой D.1.5) (I — 1, 2, . . ., Ы). Здесь вектор в, равен (д^, . . ., с?^) и
&1 = б*п~7 (**)• D.4.5)
Таким образом,
А [И - B/г - 2)!<2] = [/ - Bп -2)\А] й, D.4.6)
где единичная матрица / имеет порядок N. В силу D.1.7) правая часть равен-
равенства D.4.6) есть вектор
Bп-2)! 2
Bп-2)!
3=1
Bп-2)!
3=1
136 ГЛ. IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ
Величины Ац неотрицательны и, следовательно, в силу D.1.7) равномерно
ограничены относительно к. Более того, Ац = 0 для / <С1 — п+1 и />
> ъ + п — 1, а для I — и + 1< 1
| а3 - Лг | < а> (B/г - 2) || Д ||, /<2">). D.4.7).
Из D.4.6) и D.4.7) вытекает, что
|| М - B/г - 2I й Ц < || А-1 || а) (B/г - 2) || А ||, /<2">). D.4.8)
Дальше доказательство для периодического случая проходит обычным
образом. С помощью B/г — 3)-кратного применения теоремы Ролля и того фак-
факта, что сплайн $д (х) интерполирует функцию / (х) в узлах сетки А, находим,
что в любых 2й — 2 последовательных интервалах есть по крайней мере одна
точка I, в которой 5<Д2П~3)A) = /BП~8) A). Отсюда
ас
/BП-3) ф _ 5B„-3) ф = | [/B„-2) ^ __ 5B«-2) ф ] ^^
И
тах |/BП-3)(ж)-5к2п-3) (ж)|<B/г-3) [[Л1| ю(Bп-2 || А||, /BП~2)) || А ||.
Продолжая этот процесс, получаем соотношения D.4.2) и D.4.3) для перио-
периодического случая.
Займемся теперь сплайнами типа П. Здесь доказательство отличается
от доказательства, примененного в периодическом случае, наличием п — 1
краевых условий в каждом конце отрезка [а, Ь]. Так как мы заранее предпола-
предполагаем, что обратные матрицы А'1 равномерно ограничены (существование
их доказывается в гл. V), то остается лишь показать, что правая чаеть равен-
равенства D.4.6) стремится к нулю.
Рассмотрим уравнения D.1.5) для г = п — 1, п, . . ., N — п + 1.
В дополнение к ним имеем п — 1 соотношений
М0 = /BП-2)@), D.4.9.1)
2»-3
ч {/[*о,аЧ *д]~
2 ^ИЛ =
4
[0,4-* *д-
9 = га, ге-р 1, ..., 2/г—3.
(Соотношения D.4.9.2) следуют из D.1.8).)
Для полинома р (х) степени не выше 2/г — 2 правая часть D.4.9.2) точно
равна р<2п~2> (хоIBп — 2)!. Поскольку для таких полиномов равенства D.1.8)
выполняются тождественно, положим р (х) = #2п~2/B/г — 2)!. Тогда в D.1.8)
каждая из величин М^ равна 1. Итак, мы представили коэффициенты при М$
в D.1.8) в виде
^ 10, хг — а, . . ., хд — а]2п.
Следовательно,
4.4.
Я
' 2^
5=0
сходимость
, 1
Ч-п+И Bп—2)!
137'
Осталось показать, что правая часть в D.4.9.2) стремится к 8%п~2) (хо)/Bп — 2) Г
при || А || —>0. Пусть полином р(х) степени 2/г —2 удовлетворяет условиям;
а=0, 1, ..., 2ге —2.
Тогда
2п-2
(*)- 2 4-
откуда
2п-3
Р [#0> •С1» • • •» Яд] —
1
так что правую часть равенства D.4.9.2) можно записать в виде
4
[0, аг,-а, ..., хя-
4-
?BП-2)
(а).
D.4.10)
Здесь первое слагаемое является отношением д-х разделенных разностей отно-
относительно х0, д?1, . . ., хя функции Р = 5д — р» первые 2п — 2 производных
которой обращаются в нуль в точке #0, и функции х2п'2.
Исследуем более общую задачу вычисления отношения разделенных раз-
разностей двух к раз дифференцируемых функций:
ь ..., хк]
D.4.11)'
в [ХО, «1, ..., Хк]
Заметим, что йню разделенную разность можно записать в виде (Дэвис [1, стр. 46])<
Р[Х
0, X
х0
х^ х\ ... х\~^ Р (я,
.Л-1
1 г г2 г''
«8
. D.4.12)
138
ГЛ. IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ
Рассмотрим функцию (Гурса, Хедрик [1, стр. 10])
•<р (х) =
х0
1 х1 х\
о
Хк-1
X
X2
х(
X
*=} <?(*»._,)
X
Эта функция при х = ж0, #1, . . ., хк-\ равна нулю. Если взять К в виде D.4.11),
тго ф (хк) = 0. Таким образом, ф' (х) на интервале (я0, хк) обращается в нуль
к раз, ф" (х) обращается в нуль (к — 1) раз, . . ., <р(|1) (х) обращается в нуль
один раз. Обозначим через | точку интервала (х0, хк), где ф(й) (х) = 0. Так
как
(*) =
то
0\х0,Х1 хк]
Поэтому первый член в D.4.10) равен
Bя—2)Bп —3) ... B»-д-
и предел этого выражения при || Д ||->0 равен нулю. Из D.4.10) следует теперь,
что правая часть в D.4.9.2) при || Д ||->- 0 стремится к 8Aп~2) (хо)/Bп — 2I.
■Оставшаяся часть доказательства для сплайнов типа II проходит, как в пре-
предыдущем случае.
Доказательство для сплайнов типа I мы проводить не будем. Здесь нет
никаких новых идей, и доказательство главным образом связано с непосред-
непосредственным, но довольно утомительным процессом исключения величин 8% (а),
^д*1», • • ., 84"-»(а) из равенств D.1.8).
Укажем некоторые важные случаи, когда нормы || А~г \\ равномерно огра-
ограничены и, следовательно, применима сформулированная теорема. В работе
Алберга, Нильсона, Уолша [9, теорема 4] показано, что она справедлива
для периодических сплайнов, заданных на последовательности асимптоти-
асимптотически равномерных сеток {Дь}, т. е. сеток Дл, для которых Ц Дь || —>• 0 и
тах | 1/2 — Н^+1/(Н1^ + Ъм+1) 1-^0, в частности, для периодических
•сплайнов на равномерных сетках, которые мы в дальнейшем рассмотрим.
4.4. СХОДИМОСТЬ . 139
Второй общий результат относится к случаю, когда условия гладкости
аппроксимируемой функции ослабляются, но на сетку налагаются дополни-
дополнительные ограничения. B.3.7).
1
Теорема 4.4-2. Пусть на отрезке [а, Ь] заданы функция / (х) из класса
•Ся [а, Ь] @ <1 д ^ 2/г — 3) и последовательность сеток {Дь}, || Д& || —>— 0 при
к ->■ оо и 7?дь = шах || Д& ||/(«й/+1 — хк}) <*С Р < °°- Пусть нормы \\ Аи1 \\
равномерно ограничены. Если полиномиальный сплайн 8±к (х) степени 2/г — 1
интерполирует функцию / (х) на сетке Ан и разность / (х) — 5дй (х) принад-
принадлежит типу Г или типу 1Г, или сплайн 8Ак(х) периодический (последнее при
условии, что функция / (х) периодическая и принадлежит классу Ся (—оо, оо)),
то
ь(х)=О(\\Ак\\«-р) (р-0, 1, ..., а). D.4.13)
Если производная /(9) (х) удовлетворяет на отрезке [а, Ь] условию Липшица
порядка а @ < а ^ 1), то
Г(*)-$%{х)-О(\\Ак\\*+а-р) (/, = 0, 1, ..., д). D.4.14)
Доказательство. Как и в предыдущей теореме, доказательство
приведем лишь для периодических сплайнов и сплайнов типа II. При ц ■<
<С2п — 2 разделенная разность (индекс сетки опускаем) / [ ]
удовлетворяет неравенству
Можно показать, что правые части в D.4.9.2) удовлетворяют аналогичному
неравенству с постоянным множителем, стоящим перед
Из равномерной ограниченности норм || А'11|, уравнений D.1.5) (с учетом D.4.9))
и т. д. следует, что
шах || А !!■"-«-■ |АГу|<Л:в©[(д +1)|| А ||,/<«>]<
Отсюда
В периодическом случае в силу D.1.13)
X
«(ЦА||,/(9>) Ср-1,2, ....
для некоторого числа /Гр, не зависящего от индекса сетки. Это неравенство
справедливо также в непериодическом случае, если п — 1<^/<^^ — и + 1.
Применение краевых условий дает аналогичное неравенство для 0 ^ / <
1 ЛГ 1/ЛГ
ГЛ. IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ
Из равенства D.1.11) получаем теперь, что для некоторой другой кон-
константы К*
и а и,
и, следовательно,
*/
Так как 5д (х}) = / (х}) и / [х^, ..., хД = Зд^ (&) = /<9> (|2) для некоторых
точек |4 и |2 из интервала (а^_д+1, х'ц.д^I то на отрезке [ж;_4, ж,]
(х) - /<*> (х) = [8^ (х) - 8^ {х,
Таким образом, соотношения D.4.13) и D.4.14) доказаны для р = д. Спра-
Справедливость этих соотношений для р <С я вытекает из, повторного интегрирова-
интегрирования и применения интерполяционных свойств.
Заметим, что доказательства предшествующих теорем опираются на свой-
свойства ограниченности величин М;, а не непосредственно на ограниченность норм
|| Аи1 ||. Пусть функция / (х) принадлежит классу С2п~2 [а, Ъ\. Если | Мк] |<!
^ В 0 = 0, 1» • • •» ^ь5 А = 1, 2 . . .) и последовательность сеток вложенау
то можно показать для интерполяционных полиномиальных сплайнов 8аъ(х)->
что последовательность {8%^~2) (х)} сходится равномерно на [а, Ь] к /<2п<^> (х)
(Алберг и др. [9, теорема 3]). С другой стороны, можно снять требование вло-
вложения сеток, если допустить, что сплайны ^гд") (х) равностепенно непрерыв- '
ны. В самом деле, в силу интерполяционных свойств и теоремы Ролля
812^2) (х) — /<2п-2> (х) по крайней мере в одной точке из каждых 2» — 2 после-
довательных интервалов, и поэтому
| /<2»~2> (х)-8%™ (х) |<а> [(п-1) || А» ||, /^~2>1 + <» [(/г-1) || Д, ||, &%-»].
Далее, можно показать (Алберг и др. [9, стр. 237]), что если сетки вложены
и сплайны (#дй(#)} интерполируют произвольную функцию /(я), определен-
определенную на отрезке [а, Ь], а производные 8%^~2) (х) равностепенно непрерывны
и ограничены в какой-то точке, то производная рп~2(х) существует и
8%"-2){х)->р2п-2)(х) равномерно на [а, Ъ].
Теорему 4.4.2 можно переформулировать следующим образом:
Теорема 4?4.3. Пусть на отрезке [аг Ь] заданы функция / (х) из класса
Сй [а, Ь] @ ^ д ^ 2д — 3) и последовательность сеток {Аь}, || Д& || ->• 0 при
к ->■ оо. Допустим, что полиномиальные сплайны 8±к (х) интерполируют функ-
функцию / (х) в узлах сетки Ак и
Ит тах | М^ 11| Дй ||2П-«-2 = 0.
4.5. СПЛАЙНЫ ПЯТОЙ СТЕПЕНИ ДЕФЕКТОВ 2 И 3 141
Тогда равномерно на [а, Ь]
Доказательство. Доказательство аналогично доказательству пре-
предыдущей теоремы, только вместо неравенства D.4.16) надо воспользоваться
тем, что по условию левая часть этого неравенства стремится к нулю.
4.5. Сплайны пятой степени дефектов 2 и 3
Первое интегральное соотношение, выведенное в гл. III для кубических
•сплайнов, обобщается в гл. V на сплайны нечетной степени. Мы покажем там,
что для функции / (х) из класса Сп [а, Ь] и полиномиального сплайна степе-
степени 2п — 1 это соотношение справедливо, если
2 2 [/(П-р> (») - якп-р) (х)] ж*»-» (х) & = о.
Мы не рассматриваем пока, при каких условиях на сплайны справедливо
это равенство. Заметим лишь, что для простого сплайна (т. е. сплайна,
принадлежащего классу С2п~2 [а, Ь]) члены при / = 0, 1, . . ., N — 1; р =
= 1,2,..., п — 1 исчезают в силу непрерывности $кп+1)~1> (я) в точке X;. Члены,
■содержащие множитель 81ьп~1у (ж>), обращаются в нуль ввиду равенства
В гл. V будет показано, что условие непрерывности производных
) ^ можно заменить условием
для всех р, удовлетворяющих неравенству 1-<д-<Р-<п — 1 (д задано).
В случае сплайнов пятой степени максимальный допустимый дефект равен 3
(Я = 1). Здесь ЗТ (х}) = #» (х}) (р-0, 1, 2; / = 1, ..., ЛГ-1).
При создании алгоритмов .численного интегрирования и дифференцирова-
дифференцирования или интерполирования аналитически заданной функции часто бывает
полезно воспользоваться интерполяционными процессами более высокого
порядка. В этих алгоритмах сплайны дефекта, превышающего 1, находят
.важное применение.
Другое применение этой идеи, представляющее и самостоятельный интерес,
включает использование сплайнов максимального дефекта, когда только сама
функция / (х) известна или ее можно подходящим образом определить в узлах
сетки. Здесь мы вначале аппроксимируем требуемые производные некоторым
вспомогательным способом, таким, как полиномиальная интерполяция 1).
Для сплайнов пятой степени дефекта 3 найдем приближенные значения
производных /^ и /5 с помощью параболической интерполяции. Пусть функция
*) На эффективность сплайнов пятой степени максимального дефекта в сглаживании
кривых и на их связь с правилом Симпсона и правилом трех восьмых указал С. Ауслендер.
142 ГЛ. IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ
Щ = Щ (#) (О <С / <С .№) совпадает с параболой, проходящей через точки:
( /О ( и) ( &0 Т
к
D.5.1)
(Я, = 1 — ц; = к^1/(к] + ^+1), как и в гл. II).
Сплайн #д (х) пятой степени дефекта 3 определяется на отрезке [х^, ягД
условиями
(/и) й (/О (^) = м?° (**) (Р = 0, 1, 2). D.5.2)
Имеем
D.5.3>
Пусть кубический полином а (а) удовлетворяет условиям а @) — а' @) .=-
= а' A) = 0, а A) = 1. Тогда
а (а) = За2 — 2а8. D.5.4)
Полином пятой степени, совпадающий на [х;_1, я,-] с ^д (ж), можно записать
в виде
и,-_1 (х) [1 — а; (ж)] + щ (х) щ (х), D.5.5)
где о^ (х) = а[(х — х^/к^].
Отметим в связи с этим, что первая и вторая производные в точке х^ равны,
взвешенным средним наклонов т]-и т^ т^+^ и моментов Л//_4, М^ М^+1
простого кубического сплайна (см. B.1.15) и B.1.7)). Для равномерных сеток
это дает сглаживание в смысле Шёнберга первой и второй производных куби-
кубического сплайна. На практике было обнаружено, что иногда вычерчивание кри-
кривой по точкам с помощью такого сплайна пятой степени дает преимущество-
по сравнению с простым кубическим сплайном.
Важно также заметить, что сплайн пятой степени дефекта 3 полностью
определяется аппроксимируемой функцией и ее первой и второй разделенными
разностями. Для определения такого сплайна не нужно решать никакой систе-
системы уравнений. Кроме того, достаточно четырех параметров, чтобы описать
полином пятой степени на [х/_1, я,-]. Таким образом,
5д (X) -
х-х$) I*} {х-) + {Х~~*')Ш и) (х})] ъ (х). D.5.6>
4.5. СПЛАЙНЫ ПЯТОЙ СТЕПЕНИ ДЕФЕКТОВ 2 ИЗ 14&
Так как
то
*А *)(*)}■ D-5-
Сплайны этого типа тесно связаны с численным интегрированием. Имеем
ж*
Заметим, что при такой аппроксимации использованы лишь значения /;-_2
1 ^и //> /ли* Положим X} — &/_! — /&, Х}_1 — х/_2'=^+1—Х] = ХН. Тогда
1 / (ж) их — ._. .. л. { — /у_2 + [6Я A + Я) +1 ] (/;-1 ~\-1$) — //-и}• D.5.8)
При Я = —1/3 процесс заключается в интегрировании по трем интервалам
длины Н — к/3 с абциссами х;_и ^_2, ж;+1, а;у, расположенными в указанном
порядке. В результате получаем правило трех восьмых
При А, = —1/2 процесс заключается в интегрировании по двум интервалам
длины Н = к/2 с расположением абсцисс Х;_1, Х;_г = аг^+1» ЖУ« При таком,
выборе Я квадратурная формула совпадает с правилом Симпсона
Х1
Допустим, что X выбрано так, что коэффициенты при /^_4 и /,• обращаются
в нуль, т. е.
Тогда мы получаем квадратурную формулу Гаусса второго порядка:
444 ГЛ. IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ
Можно ожидать, что сходимость таких сплайнов эффективно сравнивается
со сходимостью кубических сплайнов. В силу D.5.7) на отрезке [#/_1, Х}\
(х) - Г (*) | = | \Щ-1 (*,-,) A ~о) + Щ {х!) а-Г(х)] +
+ 10а A - а) A - 2а) [и•_ 4 (в/-1) - и • (*,)] | <
<12+КЗ/2]а)(ЦД||, Г). . D.5.10)
Если /(я) принадлежит классу С11 [а, 6], то на отрезке [х^
- /' (х) = [Ц^ - /' (х)] |- {^1 Л; [иЗ_ 1 (х^) A -а/ И) + Щ (*,) а; (х)
2 -1I «5
Если 0<СР <;к^Н}+1 <;р для всех сеток А(Р фиксировано), то
-Отсюда следует, что
| /' (*)-& И |<соп8*.ю(|| А ||, /'). D.5.11)
Наконец, если / (х) принадлежит классу С [а, Ь], то
и снова, если 0<СР <;к^Н^ <^ для всех сеток А, то
Отсюда следует, что
| / (а) -$а И |<соп81-о> (|| А ||, /). D.5.12)
Можно также распространить на сплайны пятой степени идеи Фейера,
описанные в связи с доказательством теоремы 2.3.1. Исследуем сплайн пятой
степени дефекта 2, интерполирующий функцию / (х) из класса С [а, Ъ] в узлах
сетки А на отрезке 1а, Ъ] и имеющий производную, равную нулю в каждом
из этих узлов. Ограничимся здесь периодическими сплайнами пятой степени
и функциями / (х) с периодом Ь — а, принадлежащими классу С (—оо, со).
Снова обозначим этот сплайн через 8ь(х) и положим для удобства
= 5д {X}). Из равенств D.1.22) получаем
&(,. го- //~/-?-1 -60 1 МГ*-3^-!
ДД(ж,-У)-—^ щ Н ^
D *>
4.6. СХОДИМОСТЬ ПЕРИОДИЧЕСКИХ СПЛАЙНОВ НА РАВНОМЕРНЫХ СЕТКАХ 145
В силу непрерывности 18% в точке х$
или. в обозначениях гл. II,
= 20 К/^1-//)Ам1 (У*/н)-К//-/ы)/М (*/н/М /4 5 14)
Здесь норма матрицы, обратной к матрице коэффициентов, ограничена
независимо от сетки А. Если функция /(#) непрерывна и тах|| А ||//г;-<р,
то |^|||Д||2<1/а-20Р2Bр —1)©(||Д||,/). Из D.5.13) заключаем, что неза-
независимо от сетки Д можно аналогично оценить 8%. (х)) || Д ||3, а из D.1.27)
заключаем, что то же верно для $%у (Х} — 0) || Д ||4 и Зд'^ + О) || Д ||4. Так как
на отрезке [х^ь Х]\ „
[81 («^ -Л» (^-,) -I]
]
то из предыдущих рассуждений вытекает, что при выполнении условия B.3.7)
разность / (х) — 5Д (х) можно сделать произвольно малой, если число || А ||
достаточно мало. Таким образом, доказана
Теорема 4.5.1. Пусть на отрезке [а, Ь] задана последовательность
сеток {Аи}, удовлетворяющая условию B.3.7) и такая* что Нт||Дь|| = 0. Если
периодический сплайн 5д (х) пятой степени дефекта 2 интерполирует непре-
рывную периодическую функцию /(ж) периода Ъ — а и §ь.(х) = 0 в точках
сетки Ад, то последовательность {8ьк (х)} сходится равномерно к / (х) при
к-*~оо.
4.6. Сходимость периодических сплайнов
на равномерных сетках
В разд. 4.3 было показано, что матрица коэффициентов системы D.2.5),
которая после умножения на Bп—1I становится циркулянтом порядка ТУ,
^ \Тп-1 » ТП » •••» Т2П-2 ». ^' ' • * ' ^' ТО ' Т1 » •••» Тп-2 /' \*±.О.1)
не вырождена. Сейчас мы покажем, что норма обратной матрицы при фиксиро-
фиксированном п равномерно ограничена относительно N.
10-1197
146 ГЛ. IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ
В разд. 4.3 было установлено, что функция
2п-2
<?(*) = * 2 ФГ-ХJЬ D.6.2)
имеет только действительные отрицательные нули, отличные от —1. Собствен-
Собственные значения матрицы D.6.1) равны числам ^ (о)й)/о)Ц~1, где щ — ехр Bкп1/Щ.
Таким образом, собственные значения этой матрицы отличны от нуля. Теперь
нужное нам свойство вытекает из следующей теоремы.
Теорема 4.6.1. Обозначим через С% последовательность циркулянтов
&\ <4Й\ ..., а]^>), к = 1, 2, ...,ичереза)(/=—т-\-2,—лг+3, ...,т)—данные
действительные или, комплексные числа. Пусть а(*> = а,- (/ = 1, ..., т), а<*> = а^_лт.
(к\ з к
^^'-=Nь — яг+ 2, ..., ЛГй), а) ' = 0 # остальных случаях. Если полином #(г) =
т
= 2 а^2^+т-2 не имеет нулей, по модулю равных 1, то С& существует
;=-т-|-2
и нормы \\Сь11| ограничены относительно к.
Доказательство. Обозначим через Р& матрицу перестановок
порядка ДГй*.
Рк = С@, 1, 0, ..., 0).
Тогда РкС (а№>, а(*>, ..., а#>) = С (а#>, ..., а^),^ и
ДА н
= Рпт+ *
где /& — единичная матрица порядка ЛГЙ. Так как полином д (г) не имеет нулей,
по модулю равных 1, то существует круговое кольцо г4 < | г \ < г2, содержащее
в себе | 2 | = 1, в котором д (г) ф 0. В этом круговом кольце функцию
[2~тп+1 д (г)] можно разложить в абсолютно сходящийся степенной ряд
00 00
2 Ь}%К Так как || Рк \\ = 1 (норма максимума строки), то ряд 2 Ъ)Р1
5=1—00 }= — °°
сходится в этой норме к матрице Си1, обратной к Ск. Кроме того,
нсгМк 2
где правая часть зависит только от а_т+2, . . ., ат.
Из теоремы 4.4.1 теперь непосредственно следует
Теорема 4.6.2. Пусть периодическая функция / (х) с периодом Ь — а
принадлежит классу С<2п~2>(—оо, оо) и на отрезке [а, Ь] задана последователь-
последовательность равномерных сеток {Ак} (]] Ак ]| -> 0). Если периодический полиномиаль-
4.6. СХОДИМОСТЬ ПЕРИОДИЧЕСКИХ СПЛАЙНОВ НА РАВНОМЕРНЫХ СЕТКАХ 147
ный сплайн 8& (х) степени 2п — 1 (п > 1) интерполирует функцию / (х)
в узлах сетки Дй, то
Г-2-р) {Р = О, 1, 2 2п-2)
равномерно относительно х на [а, Ь]. Если производная /Bп-2) (х) удовлетворяет
на отрезке [а, Ь] условию Липшица порядка а (О <С а <^ 1), то
^ (р = 0, 1 2/г-2)
равномерно относительно х на [а, Ь].
В следующей теореме функция / (х) имеет большую гладкость.
Теорема 4.6.3. Пусть периодическая функция / (х) с периодом Ь — а
принадлежит классу С12п~1У (—оо, оо). Если периодический полиномиальный
сплайн 8&к (х) степени 2п — 1 интерполирует функцию / (х) в узлах равномер-
равномерной сетки Дй а [а, Ь] (к — 1, 2, . . .), то равномерно относительно х на
[а, Ъ) .
^ 1), D.0.3)
где З^ъ^ (х*д есть правый или левый предел последовательности {8^~и (х)}
в точке хк}. Если. /Bп~1) (#) удовлетворяет на [а, Ъ] условию Липшица порядка
а@<а<;1), то
/(р)И-51Рй)(Ж)=О(||Дй||2п-1+а-р) (Р = 0, 1 2п-1) D.6.4)
равномерно относительно -х на [а, Ь].
Доказательство. Положим (опуская индекс сетки к)
Вычитая члены каждого уравнения системы D.2.5) из соответствующих членов
последующего уравнения, получаем
2п-2 _Л „ _„ «
»_!]. D.6.5)
Таким образом, если С —циркулянт D.6.1), а—вектор (а4, ..., алгй) и г—век-
г—вектор правых частей системы D.6.5), то
{±). D.6.6)
10*
148
ГЛ. IV. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ
Правую часть равенства D.6.6) можно представить в виде
й=0
2-2
учитывая, что г_/ = гл-А_у, ^Nк+^ — ^^. Норма этого вектора не превосходит
<Зи-3)а>(||Дл||, Л), так что
С другой стороны, на отрезке [х^, х$\
Так как
= 0^ на отрезке
аир
то
—1) + B/г —1I
Ц
Равенства D.6.3) и D.6.4) для р = 2/г — 1 доказаны. С помощью интегрирова-
интегрирования и интерполяционных свойств сплайна 5д (х) их можно обычным способом
получить и для меньших значений р (см. теорему 2.3.3).
Аналогично обобщается теорема 2.9.5. Мы только сформулируем результат.
Теорема 4.6.4. Пусть периодическая функция / (х) с периодом Ь — а
принадлежит классу Сгп (—оо, оо). Если периодический полиномиальный
сплайн 5дй (х) степени 2п — 1 интерполирует функцию / (х) на равномерной
сетке Аь с: [а, Ъ] (к = 1, 2, . . .), то
Нт щах
'*
к
-0)
= 0.
Другие результаты о сходимости связаны с ослаблением требований к/ (х).
Мы изложим их в следующей теореме, которая вытекает из теоремы 4.4.2.
4 6. СХОДИМОСТЬ ПЕРИОДИЧЕСКИХ СПЛАЙНОВ НА РАВНОМЕРНЫХ СЕТКАХ 149
Теорема 4.6.5. Пусть периодическая функция / (х) с периодом Ъ — а
принадлежит классу С4 (—оо, оо) (О <С <? <С 2тг— 2). Если периодический
полиномиальный сплайн 5дА (х) степени 2тг — 1 интерполирует функцию / (х)
на равномерной сетке Д^ с: [а, Ъ] (к = 1, 2, . . .), то
/О» (х)-3% (х)=о(\\ Ал |'ГР) @<р<?) D.6.7)
равномерно на [а, Ь] относительно х. Если /(в^ (х) удовлетворяет на отрезке
[а, Ъ] условию Липшица порядка а (О <С а ^ 1), то
/(Р) (х)-8?> (х)=О(\\ А» ||9+а-р) @<р<д) D.6.8)
равномерно относительно х на [а, Ы..
Глава V. ВНУТРЕННИЕ СВОЙСТВА ПОЛИНОМИАЛЬНЫХ
СПЛАЙНОВ НЕЧЕТНОЙ СТЕПЕНИ
5.1. Введение
По своему содержанию эта глава очень близко примыкает к гл. III, и почти
каждая теорема, полученная для кубических сплайнов в гл. III, имеет здесь
свой аналог. Основное изменение здесь сводится к тому, что при рассмотрении
полиномиальных сплайнов степени 2/г — 1 (п >• 1) мы заменяем функциональ-
функциональное пространство а%*а(а, Ъ) функциональным пространством &Сп (а, Ь) и скаляр-
скалярное произведение
ъ
Пх)ё"{х)йх E.1.1)
скалярным произведением
ъ
</■*)=$ Г (*) ёт (*) «**. E.1.2)
В гл. IV уже были выявлены некоторые затруднения, связанные со сплайнами
четной степени, и указаны некоторые пути преодоления части этих затрудне-
затруднений. В этой главе особенно важно требование, чтобы рассматриваемые сплай-
сплайны были нечетной степени, и это требование нельзя ослабить.
Для изучения внутренних свойств обобщенных сплайнов, в том числе
и полиномиальных сплайнов нечетной степени, необходимо задать в простран-
пространстве е%*п (а, Ь) скалярное произведение (/, §). Это можно сделать, если сплайны
удовлетворяют (всюду, кроме узлов сетки) самосопряженному дифференциаль-
дифференциальному уравнению порядка 2/г
А8А = 0. E.1.3)
Тогда оператор А можно представить в виде
А = Ь*Ь, E.1.4)
где Ь — линейный оператор порядка /г, а Ь* — его формально сопряженный.
Скалярное произведение определяется формулой
(/, «) = { (Ы) (х) .{Ь§) (х) Ли E.1.5)
Эта точка зрения развивается в гл. VI в предположении, что оператор Ь имеет
действительные и неособенные коэффициенты. Для комплекснозначных сплай-
5.2. ОСНОВНОЕ ТОЖДЕСТВО
151
нов на [а, Ь] можно развить аналогичную теорию, слегка изменив определе-
определения (/, §) и Ь*.
Мы не будем приводить тех доказательств, которые в основном повторяют
доказательства, данные в гл. III для кубического случая, а только сформули-
сформулируем соответствующие теоремы. Как правило, мы будем обращать внимание
только на различия в доказательствах. В частности, доказанные здесь тео-
теоремы существования и единственности требуют некоторого уточнения.
5.2. Основное тождество
Пусть на отрезке [а, 61 заданы сетка А: а = х0 <; х1 <с ... <Сх# = Ь,
полиномиальный сплайн 5Д (х) степени 2л — 1 и функция / (х) 6 &Сп (а, Ь).
Тогда
-2
(х)ах-
причем второй интеграл в правой части можно записать в виде
Ь . N Х1
N Х1
= 2 ) {/<П) (*) - Лп) (*)> ^1
11 х
Интегрируя и раз по частям, получаем
E.2.1)
х) - $1П) (х)} 8Р (х) их =
п
откуда
(х) -Лп) (*
Ар-
о
П—1
о X* (
а=1
(х) \Ь-
3 ^{{8%>(х)}*Aх. E.2.2)
152 ГЛ. V. ВНУТРЕННИЕ СВОЙСТВА СПЛАЙНОВ НЕЧЕТНОЙ СТЕПЕНИ
При выводе этого тождества мы воспользовались непрерывностью функции
{/"-« (х) _ $1п-а) (я)} E?+а-1> (х) на отрезке [а, Ь] при а = 1, 2, . . ., п - 1
и не ставили никакого другого условия, кроме того, чтобы сплайн 5Д (х) был
простым полиномиальным сплайном степени 2п — 1 на Д и функция / (х) при-
принадлежала классу Жп (а, Ь). Равенство E.2.2) называют основным тождеством
для простого полиномиального сплайна степени 2п — 1 на сетке Д.
5.3. Первое интегральное соотношение
Из основного тождества непосредственно следует, что если сплайп 5Д (/; х)
интерполирует функцию / (х) на сетке Д и удовлетворяет какому-либо множе-
множеству краевых условий, то
ь ь ь
I {/(п) (х)У0х= ^ {^П)(/; х)}Ых + [{/^ <*)-$?>(/; х)}Ых.
а а а
Это равенство называют первым интегральным соотношением для полиномиаль-
полиномиального сплайна степени 2/г — 1, интерполирующего на сетке Д функцию / (х)
из класса &Сп (а, Ь).. Справедлива
Теорема 5.3.1. Пусть даны сетка Д: а = х0 <. ж4 <1 . . . < хИ — Ъ
и функция / (х) из класса <Жп (а, Ь). Если сплайн 8& (/; х) интерполирует
функцию / (х) на сетке А и удовлетворяет одному из условий: а) разность
/ (х) — #д (/; х) принадлежит типу Г, Ь) сплайн 5Д (/; х) прцнадлежит
типу 1Г, с) сплайн 5Д (/; х) и функция / (х) периодические, то
ъ ь ь
(п) Йп) E.3.1)
а а а
Ясно, что можно применить краевые условия смешанного типа. Более
того, можно, как указано в гл. III, ослабить условия непрерывности на сплайн
•$• а (/; х) и его производные и все же получить первое интегральное соотноше-
соотношение, требуя лишь, чтобы определенные производные сплайна 5Д (/; х) интер-
интерполировали соответствующие производные функции / (х) в узлах сетки Д.
Эти дополнительные интерполяционные условия заменяют непрерывность
функции {/(п-а)(я) - 5?"а) (/; х)} Лп+в-4) (/; х) на отрезке [а, Ы Возмож-
Возможность эту выражает
Теорема 5.3.2. Пусть даны сетка Д: а = х0 < ж4 <1 . . . < ж^ = Ь,
функция / (х) из класса №п (а, Ь) и сплайн 5Д (х) из класса &Сгп~и (а, Ь) (к ^ п).
Пусть $д2п) (х) === 0 на каждом открытом интервале сетки Д и 5(да) (х) интер-
интерполирует в узлах сетки /(а) (х) (а = 0, 1, . . ., А: — ^ж^амж^б при а =^= 0).
- 5?> (а)}2
5.4. СВОЙСТВО МИНИМАЛЬНОЙ НОРМЫ 153
если выполнено одно ив условий: а) / (х) — 5Д (х) ^принадлежит типу Г, Ь) 5Д (х)
принадлежит типу IV, с) сплайн 5Д (х) и функция / (х) периодические.
Замечание 5.3.1 В периодическом случае здесь и в ряде других
теорем требуется также, чтобы бьшо 5Д (/; а) — / (а) и #да) (/; а) = •5гда) (/; Ъ)
(а = 0, 1, ..., 2га —2). Могут понадобиться и условия Я?* (/; а) = /(а)(а)
(а = 0, 1, ..., к-1), Яда)(/;а)=5'да)(/;&) (а-0, 1, ..., 2га-/с-1).
5.4. Свойство минимальной нормы
В качестве непосредственного следствия из первого интегрального соот-
соотношения для полиномиальных сплайнов степени 2га — 1 получаем аналог
свойства минимальной нормы кубических сплайнов. Сформулируем этот
результат и основные краевые условия, при которых он справедлив.
Теорема 5.4.1. Пусть на отрезке [а, Ь] даны сетка Д: а — х0 <С #4 <С . . .
. . . <С хк — Ь и произвольная функция / (х), имеющая га — 1 производных в точ-
точках х = а и х = Ь. Тогда среди всех функций д (х) из класса &Сп (а, Ь), интер-
интерполирующих функцию / (х) на сетке Д, сплайн 5Д (/; х) типа IV минимизирует
интеграл
ь
E.4.1)
Если функция $ (х) такова, что / (х) — § (х) принадлежит типу V, или если
/ (х) ид (х) — периодические функции, то интеграл E.4.1) минимизируется
сплайном, интерполирующим функцию / (х) в узлах сетки Д и удовлетворяю-
удовлетворяющим тем же самым условиям, что и функция д (х).
Требования гладкости, наложенные на 5Д (/; х), как и в теореме 5.3.2,
можно ослабить. Введем следующую терминологию. Пусть даны сетка Д:
а = х0 < а?! <С . . . < Хх = Ь и такая функция 5Д (х) из класса &С%п~к (а, Ь),
что 5ДП> (х) = 0 на каждом открытом интервале сетки Д. Функция $д (х),
удовлетворяющая этим условиям, называется полиномиальным сплайном
степени 2/г — 1 дефекта к. Мы предполагаем, что 0 -^ к <^ тг. В этой терми-
терминологии простой сплайн на Д имеет дефект 1, а полином степени 2га — 1 имеет
дефект 0.
Теорема 5.4.2.,Пусть на отрезке [а, Ь) даны сетка Д: а = хо<Сх
. . . -< хк = Ь и произвольная функция / (х), имеющая га — 1 производных
в точках х = аих = Ъик — 1 (&<^га) производных во внутренних узлах сет-
сетки Д. Тогда среди всех функций $ (х) из класса &Сп (а, Ь), интерполирующих
функцию / (х) _в узлах сетки Д и таких, что во внутренних узлах сетки Д
(х) г= /(а) (*) (а « 1, 2, ...,*- 1),
154 ГЛ. V. ВНУТРЕННИЕ СВОЙСТВА СПЛАЙНОВ НЕЧЕТНОЙ СТЕПЕНИ
сплайн типа IV дефекта к минимизирует интеграл E.4.1). Если функция § (х)
такова, что / (х) — # (х) принадлежит типу Г, или если / (х) и $ (х) — перио-
периодические функции, то интеграл E.4.1) минимизируется интерполяционным
сплайном дефекта к, удовлетворяющим тем же самым условиям, что и функ-
функция е(х).
Пусть функция § (х) удовлетворяет условиям теоремы 5.4.1 или 5.4.2
и минимизирует интеграл E.4.1). Тогда она отличается от соответствующего
интерполяционного сплайна Яд (/; х) на решение уравнения />п/ = 0. Это
следует непосредственно из первого интегрального соотношения. Кроме того,
разность % (х) — Яд (/; х) должна обращаться в нуль на Д и, в зависимости
от дополнительно наложенных условий, в определенных точках сетки некото-
некоторые из ее производных также должны обращаться в нуль. Если число таких
интерполяционных требований не меньше /г, то можно ожидать, что # (х) =
зз Яд (/; х). В частности, это верно, когда сетка А содержит по крайней мере
п точек. Далее, если функция § (х) периодическая, то разность # (х) — Яд (/; х)
также периодическая и, следовательно, является константой, причем равной
нулю, ибо % (а) = Яд (/; а). В разд. 5.6 мы рассмотрим этот вопрос более
подробно*
5.5. Свойство наилучшего приближения
Полиномиальный сплайн Яд (я), заданный на сетке А, зависит линейно
от своих значений в узлах сетки и от значений своих производных. Более того,
он полностью определяется этими величинами. Эти утверждения справедливы
независимо от того, равен дефект сплайна 1 или нет. В частности, эта линей-
линейная зависимость сплайна отражается в уравнениях D.1.5), D.1.8), D.1.11) —
D.1.13), E.7.3), E.7.4) и E.12.3). Таким образом, при соответствующем выборе
краевых условий
Яд (/ + & х) = Яд (/; х) + Яд (г, х). E.5.1)
Самые полезные из таких разложений получаются, если выполняется одно
из условий:
а) все три разности Яд (/ + 8\ х) — (/ + ё) (я), Яд (/; ж) — / (я)
и Яд (§; х) ■— $ (х) принадлежат типу Г;
Ь) Яд (/ + #; х) и #д (/; х) + 5Д (#; х) принадлежат типу II';
с) Яд (/ -|- #; я), 5Д (/; х) и Яд (#; х) — периодические сплайны.
Одно из наиболее важных следствий разложения E.5.1) состоит в том,
что если § (х) = —5д (я), то при выполнении любого из условий а), Ь), с)
Яд (/ - 5Д; х) = Яд (/; х) - Яд (х). E.5.2)
Когда разложение E.5.2) связано с условием Ь), предполагается, что сплайны
Яд (#), Яд (/; х) и —Яд (§; х) принадлежат одному и тому же классу экви-
эквивалентности типа II. При выполнении условий а), Ь) и с) разложение E.5.2)
справедливо, даже если дефект сплайнов Яд (/ — Яд; ж), Яд (/; х) и Яд (х)
больше 1. Если мы определим сплайн Яд (/ — Яд; х) так, чтобы выполнялось
5.5. СВОЙСТВО НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ 155
первое интегральное соотношение, то, как в гл. III, получим
ь ь
^ {/<«> (х) - ЯГ (*)>■ 0х=$ {5Г (/ - 5Д; *)}2 ах +
а а
а
Ь
E.5.3)
Отсюда непосредственно вытекают теоремы 5.5.1 и 5.5.2.
Теорема 5.5.1. Пусть даны сетка А: а = х0 <С #1 < . . . <С Жд- = Ъ,
сплайн 5Д (ж) м функция / (ж) мз класса &Сп (а, Ь). ^слк сплайн 5Д (/; а;) интер-
интерполирует функцию / (ж) на сетке А м / (ж) — 5Д (/; а?) принадлежит типу Г, то
Г {/<»> (ж) —5кП) (ж)}айа;> | {/(п) (ж)-5кП) (/; ж)}2^г. E.5.4)
а а
Если рассматриваются лишь сплайны #д (х) из заданного класса эквивалент
ности типа II, то интеграл
E.5.5)
а
минимизируется сплайном, интерполирующим функцию / (х) в узлах сетки А
и принадлежащим тому же классу эквивалентности. Если функция] (х) и сплайн
5Д (х) периодические, то интеграл E.5.5) также минимизируется сплайном,
интерполирующим / (х) на сетке А.
Теорема 5.5.2. Если на отрезке [а, Ъ) заданы сетка А: а — х0 <С
<.Х1<....<Хц = Ъ, функция / (х), сплайн |5Д (х) дефекта к (к ^ п) и сплайн
•^д (/'» х) дефекта к, интерполирующий функцию / (х) в узлах сетки А и такой,
что / (х) ~ #д (/; я) принадлежит типу V и 5да) (/; ж) интерполирует /(а) (ж)
(а = 1, . . ., к — 1) во внутренних узлах сетки А, то справедливо неравен-
неравенство E.5.4). Кроме того, если 5Д (х) принадлежит заданному классу эквива-
эквивалентности типа II или функция / (х) и сплайн 5Д (х) периодические, то инте-
интеграл E.5.5) минимизируется соответствующими сплайнами 5Д (/; х) дефек-
дефекта к, которые интерполируют / (х) в узлах сетки А и производные 5да) (/; х)
которых интерполируют /(а) (х) (а = 1, 2, . . ., к — 1) во внутренних узлах
сетки А.
Если сплайн <УД (х) также минимизирует интеграл E.5.5) и для него
выполняются условия теорем 5.5.1 или 5.5.2, то разность 5Д {х) — 5Д (/; х)
удовлетворяет уравнению Ипу = 0. В периодическом случае эта разность
постоянна.
156 ГЛ. V. ВНУТРЕННИЕ СВОЙСТВА СПЛАЙНОВ НЕЧЕТНОЙ СТЕПЕНИ
5.6. Единственность
Вопрос о единственности полиномиальных сплайнов степени 2/г — 1
на сетке А: я = г0 < а;1 < ^ < . . . < а;^ = Ь легко сводится к вопросу:
равен ли тождественно нулю полином Р (х) степени п — 1, обращающийся
в нуль в узлах сетки А и обладающий некоторыми другими свойствами? Если
этот полином Р (х) принадлежит типу I' или является периодическим, то он
равен нулю тождественно. В этих двух случаях сетка А может состоять ровно
из двух точек х = а и х = Ь. Если Р (х) принадлежит типу 1Г, то ситуация
совершенно.иная, поскольку требование, равенства нулю производных поряд-
порядка а (а = п, п -{- 1, . . ., 2/г — 1) при х = аих = Ьяе дает дополнительных
ограничений на полином Р (х). В этом случае для того, чтобы полином Р (х)
был равен нулю тождественно, если он обращается в нуль в узлах сетки А,
сетка должна содержать по крайней мере п точек. Но если потребовать, чтобы
производные Р(а) (х) (а = 0, 1, . . ., к — 1) обращались в нуль во внутренних
узлах сетки А, то полином Р {х) будет равен нулю тождественно, когда
к № — 1) > п - 2 и Р (а) = Р (Ъ) = 0.
Заметим, что нулевая функция г (х) представляет собой полиномиальный
сплайн степени 2п — 1 для любого целого числа п > 0. Нулевая функция
2 (х) принадлежит не только типу Г, но и типу 1Г, а также является периоди-
периодической. Кроме того, 2 (х) можно интерпретировать как сплайн степени 2п — 1
на Д дефекта к, к — 1 производных которого интерполируют нулевую функ-
функцию во внутренних узлах сетки Д. Наконец, г (х) минимизирует интеграл
ь
их. E.6.1)
Рассмотрим любые два сплайна 5д (х) и 5д (х) на сетке Д, разность кото-
которых обращается в нуль на А и принадлежит типу Г, 1Г или является периоди-
периодической. Так как сплайн 5д (х) — 5д (х) интерполирует функцию г (х) == 0
на сетке Д, то
ь
" 1) (х) - 5(дп) (ж)}2 ах - 0. E.6.2)
В силу непрерывности подинтегрального выражения сплайны ^д (х) и 5д (х)
отличаются на полином степени п — 1, обращающийся в нуль на А и при-
принадлежащий типу Г, 1Г или являющийся периодическим. Справедлива
Теорема 5.6.1. Пусть даны сетка А: а = ^ < Ж( < . . . < хк — Ь
и функция / (х). Тогда в каждом классе эквивалентности типа I существует
не более одного сплайна, интерполирующего функцию / (х) в узлах сетки Д.
Если / (а) = / F), то существует не более одного периодического сплайна, интер-
интерполирующего функцию / (х) в узлах сетки Д. Наконец, если N' ;> п — 2, то
в каждом классе эквивалентности типа II существует не более одного сплайна,
интерполирующего функцию / (х) в узлах сетки Д.
5.7. ОПРЕДЕЛЯЮЩИЕ УРАВНЕНИЯ 157
Аналогично если полиномиальные сплайны #д (х) и 5Д (х) степени 2/г — 1
лета к (к^. п) таковы, что 5Д (хг) = 5Д (хг) (г = 0, 1, . . ., IV), 5да) (я,) =
= 5да) (хг) (I — 1, 2, . . ., N — 1; а = 1, 2, . . ., к — 1) и разность 5Д (я) —
— «Уд (х) принадлежит типу Г, 1Г или является периодической, то, как и преж-
прежде, можно утверждать, что равенство E.6.2) выполняется. Это доказывает
теорему 5.6.2, из которой теорема 5.6.1 вытекает как частный случай.
Теорема 5.6.2. Пусть даны сетка Д: а = х0 <С х1 <С . . . «< хк = Ъ
и функция / (х), имеющая к — 1 производных в каждом, внутреннем узле сет-
сетки Д. Тогда в каждом классе эквивалентности типа I существует не более одного
полиномиального сплайна 5Д (/; х) степени 2/г — 1 дефекта к (к ^ /г), интер-
интерполирующего функцию / (х) в узлах сетки Д и такого, что 5да) (/; х) = /(а) (х)
(а = 1, . . ., к — 1) во внутренних узлах сетки Д. Аналогично если / (а) =
= / (Ь), то существует не более одного периодического сплайна дефекта к, удов-
удовлетворяющего тем же интерполяционным требованиям. Наконец, в каждом
классе эквивалентности типа II существует не более одного такого сплайна
при условии, что к (ТУ — 1) ^ п — 2.
5.7. Определяющие уравнения
Как видно из уравнений D.1.5) — D.1.13), представление, полученное
для полиномиальных сплайнов нечетной степени в гл. IV, довольно сложно.
Мы заменим сейчас эти уравнения системой, аналогичной системе из разд. 3.7.
Пусть щ (х) = хЧЦ - 1)! (/ = 1, 2, . . ., 2п). Тогда и$а> @) = 6,_1а,
и функции щ (х) образуют фундаментальную систему решений дифференциаль-
дифференциального уравнения
#27 =■- 0. E.7.1)
Итак, любое решение уравнения E.7.1) можно представить в виде
2п
(*)- E.7.2)
Так как для данной сетки Д полиномиальный сплайн 5Д (х) удовлетворяет
уравнению E.7.1) на каждом открытом интервале ^_!<С а? <С«г A=1,2, .. .,^,го
5Д (х) = 2 сцщ (х — а?|_1).
Это представление единственно, ибо функции щ (х) линейно независимы. Сле-
Следовательно, множество коэффициентов су (I = 1, 2, . . ., М; / = 1, 2, . . ., 2/г)
однозначно определяет сплайн 5Д (х), и обратно, если сплайн &д (х) суще-
существует, то он однозначно определяет множество коэффициентов су.
Используя представление E.7.2) и условия непрерывности и интерполя-
интерполяции, наложенные на сплайны типа I, II и на периодические сплайны, мы полу-
получаем следующую систему уравнений для вычисления коэффициентов су, а через
158
ГЛ. V- ВНУТРЕННИЕ СВОЙСТВА СПЛАЙНОВ НЕЧЕТНОЙ СТЕПЕНИ
них и сплайна 5д (У; х):
АпС - Уп (Й = I, II, Р)г
,п
, п
0
1П
0
0
0
Вп
Агп
ш • •
0
Вп
0
Ухп Вп 0 ...
О Ащ Вп О
О
Вп
О
Щ (Иг)
О
о
о
о
• * •
Вп
0
@-1, И)
О 1
О
О
О
1ЛГП_
О
и
2П
1
-1
0
* ♦ •
0
0
0
0
-1
0
0
0 ..
0 ..
0 ..
0 ..
0 ..
0
0
0
. —1
0
0
0
0
• • *
0
1
0
0
0
0
0
E.7.3.1)
E.7.3.2)
E.7.3.3)
E.7.3.4)
2п
5.7. ОПРЕДЕЛЯЮЩИЕ УРАВНЕНИЯ
159
1 —
1
О
О
О
о о
1 О
п
О1ОО
0 0 10
2п
О
о
о
о ]
E.7.3.5)
1
0
0
0
0
о
о
о
0 0 0 0
0 10 0
0 0 10
...0 1
...'0 0
п
О
о
о
О
1
E.7.3.6)
(М Щ (кх)
и
?»
■1) (М
• < ы
,(П-1)
, E.7.3.7)
11
,,(п) си \
BП-2)
, E.7.3.8)
160
ГЛ. V. ВНУТРЕННИЕ СВОЙСТВА СПЛАЙНОВ НЕЧЕТНОЙ СТЕПЕНИ
С12
с21
С22
С31
С82
сN-^2п
Уо
У\
о
о
Уг
О
О
УМ-1
о
О
Ум
У®
Уо
„BП-2)
Уо
о
*
о
Уг
О
О
о
о
У*
BП-2)
У1
о
*
о
У2
о
о
Уз
о
О.
Ум
о
о
E.7.3.9)
E.7.3.10) E.7.3.11) E.7.3.12)
Если сплайн 5Д (У; х) имеет дефект к, то эта система принимает вид:
О
*
о
Bп-Ь-1)
О
О
Bп-й-1)
E.7.4.1)
6.7. ОПРЕДЕЛЯЮЩИЕ УРАВНЕНИЯ
161
к
Вп
1
0
— 1
0
0
0
1
♦ ♦ •
• • •
0
0
0
0
0
0
0
... 0
... 0
0 0 1
• * •
• • *
.'.! о о
0
• • •
о'
*
-10 0
0
• •
0
• •
0
о-
0
0
E.7.4.3)
2п-Л
G =
т'
л
л
л
С мп
С21
•
С&П+2
» ■'I
Уо
•
•
Ух
•
0
•
•
0
У2
•
0
*
0
*
0
•
•
•
0
Улг
•
(Н—1)
у =
Уо
У1
о
о
Уг
2
О
о
о
*
о
Ух
E.7.4.2)
E.7.4.4)
E.7.4.5)
Ух
О
*
о
Уг
О
о
Уг
О
»
»
О
Улг
I о
E.7.4.6)
11 -1197
162 ГЛ. V. ВНУТРЕННИЕ СВОЙСТВА СПЛАЙНОВ НЕЧЕТНОЙ СТЕПЕНИ
Существование сплайна 5Д (У; х) связано с существованием матрицы,,
обратной к Ап. Этот вопрос мы исследуем в следующем разделе. Для перио-
периодического сплайна у нас есть уравнения для случая #1а) (/; а) = /(а) (а)
(а = 0, 1, . . ., к - 1), Яда) (/; а) =[8{Р (/; Ь) (а = 0, 1, .. ., 2/г - к - 1)..
5.8. Существование
В разд. 5.6 доказана единственность интерполяционного полиномиального
сплайна нечетной степени, а в разд. 5.7 установлено, что каждому полиноми-
полиномиальному сплайну 5д {х) нечетной степени соответствует единственное множе-
множество коэффициентов сц (г = 1, , . . ., ТУ*, / = 0, 1, . . ., 2/г — 1). Следова-
Следовательно, если уравнение
имеет не только нулевое решение, то функцию г (х) == 0 интерполируют два
различных сплайна, что противоречит теоремам 5.6.1 и 5.6.2. Таким образом,,
обратная матрица А&- существует и справедливы следующие две теоремы,
которые дополняют теоремы 5.6.1 и 5.6.2.
Теорема 5.8.1. Пусть на отрезке 1а, Ь] заданы сетка А: а = х0 «С
<Сж1<С...<Сж^ = 6« функция / (#). Тогда в каждом классе эквивалентности
типа I существует единственный сплайн, интерполирующий / (х) в узлах-
сетки Д. Если / (а) = / (Ь), то существует единственный периодический сплайн,
интерполирующий / (х) в узлах сетки Д. Наконец, если N >• п — 2, то в каж-
каждом классе эквивалентности типа II существует единственный сплайн, интер-
интерполирующий / (х) в узлах сетки Д.
Теорема 5.8.2. Пусть на отрезке [а, Ь] заданы сетка Д: а = х0 <С.
<х1 <С . . . <С.хк = Ь и функция / (х), имеющая к — 1 производных в каждом-
внутреннем узле сетки Д. Тогда в каждом классе эквивалентности типа I суще- '
ствует единственный полиномиальный сплайн 5д (/; х) степени 1п — 1 дефек-
дефекта к (&<С п), интерполирующий / (х) на А и такой, что $да) (/; х) = /(а) (х}
(а = 1, . . ., к — 1) во внутренних узлах сетки Д. Аналогично если / (а) =
= / (Ъ), то существует единственный периодический сплайн дефекта к, удов-
удовлетворяющий тем же условиям интерполяции. Наконец, если к (./V — 1) !>-
;> п — 2, то существует единственный сплайн в каждом классе эквивалент-
эквивалентности типа II.
Теоремы существования и единственности, доказанные в настоящей главе,,
непосредственно вытекают из свойства минимальной нормы, и их можно было-
бы получить до доказательства свойства наилучшего приближения. Это важно,
так как при доказательстве последнего свойства в разд. 5.5 мы предполагали,
существование вспомогательного сплайна 5Д (/ — 5д; х).
Теорема существования интерполяционных кубических сплайнов из гл. III
слабее теоремы, полученной в гл. II другими методами. Из результатов гл. IV
5.9. СХОДИМОСТЬ ПРОИЗВОДНЫХ НИЗШИХ ПОРЯДКОВ 163
следует, что применение этих методов к полиномиальным сплайнам нечетной
степени приводит к теореме существования, в которой требуется, чтобы сетки
были почти равномерными. В связи с этим понятна важность теорем 5.8.1
и 5.8.2.
5.9. Сходимость производных низших порядков
Пусть функция / (х) принадлежит классу <г#"п (а, Ь) и сплайн $д (/; х)
интерполирует ее в узлах сетки А: а = х0 <С х\ <С . . . «< хк = Ь. Многократ-
Многократно применяя теорему Ролля, получаем, что в каждых а последовательных
интервалах $да) (/; х) интерполирует /(а) (я) @ .< а < п) по крайней мере
в одной точке. Обозначим эту точку через ха. Тогда
X
1;х)}0х. E.9.1)
Если указанные точки интерполяции ха лежат по обе стороны от х, то интер-
интервал интегрирования можно выбрать так, чтобы выполнялось неравенство
Если же такие точки интерполяции лежат по одну сторону от х, то множитель
Ч2 следует опустить. Для последовательности сеток {А^}, у которой || Адг || -*- О
при N ->■ оо и х не совпадает ни с а, ни с Ъ, при достаточном большом N
точка х лежит между такими точками интерполяции, так что множитель Ч2 сох-
сохраняется. В частности, этот множитель сохраняется, когда / (х) — $д (/; х)
принадлежит типу Г или функция / (х) и сплайн $д (/; х) принадлежат
«; (а, Ь).
Пусть а. = п — 1. Тогда
X
| 2, E.9.2.1)
*П-1
где
ь
/*=| {/<"> (Х)-Й° (/; *)>« их E.9.2.2)
о
и В — г1% или 5=1. Многократно повторяя эти рассуждения, приходим
к неравенству
E.9.3)
11*
164 ГЛ. V. ВНУТРЕННИЕ СВОЙСТВА СПЛАЙНОВ НЕЧЕТНОЙ СТЕПЕНИ
Б силу свойства минимальной нормы (теорема 5.4.1)
^Ш'ахУ'2. E.9.4)
Отсюда и из E.9.3) заключаем, что справедлива
Теорема 5.9.1. Пусть даны функция /(я) из класса Жп(а,Ь) и после-
последовательность сеток {Д^: а = хо <х™ ... <^х^к = Ь), ||Д^||—->0 при Л^—» оо.
Если сплайн 5д^ (/; х) интерполирует / (х) в узлах сетки А^ (N = 0, 1, 2, ...)
и удовлетворяет одному из условий: а) разность /(я)— 5д^(/;я) принадлежит
типу Г (N = 0, 1, 2, ...), Ь) функция /(я) и сплайн 5Ддг(/;я) периодические
(N=0,1,2,...), с) сплайн ЗддД/; х) принадлежит типу IV {N=0,1,2,...), то
E.9.5.1)
Н А,НBп-2а-1)/2 {} {/<"> (*)}*<**}1/2. E.9.5.2)
а
Если выполнено условие с), то для х = а и х — Ь множитель 2~Bп~2а~1)/2
следует опустить. Наконец, если выполнено условие й) ДосА№ и
;ж) принадлежит типу 1Г, то в E.9.5.1) к E.9.5.2)
следует заменить на
Легко сформулировать аналог теоремы 5.9.1 для сплайнов типов I и II
дефекта к. Однако для большей общности рассмотрим полиномиальные сплай-
сплайны дефекта к, для которых /(а) (хь) = 5да) (/; 2|) (а —0, 1, ...,& — 1) не только
во внутренних узлах сетки А, но ив точках а и Ь. Для полного определения
сплайна в непериодическом случае потребуем дополнительно выполнения
условия
)(/;^) = 0 (а = /г, /1+1, ..., 2/г-А-1;г = 0, Щ. E.9.6)
В периодическом случае должно быть $да) (/; а) = $да) (/; 6) (а = 0, 1, ...
. . ., 2/г — к — 1). Назовем эти сплайны, как периодические, так и неперио-
непериодические, интерполяционными сплайнами типа к.
5.10. ВТОРОЕ ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ
Для интерполяционных сплайнов типа к справедливо первое интеграль-1
ное соотношение и, следовательно, для них можно доказать свойство мини-
минимальной нормы, единственность, существование и свойство наилучшего при-
приближения. С помощью этих четырех свойств можнр получить аналог тео-
теоремы 5.9.1. Доказательство мы опускаем, так как оно протекает по той же
схеме.
Теорема 5.9.2. Пусть на отрезке [а, Ь] заданы функция / (х) из класса
$Гп{а,Ъ) и последовательность сеток (А^: а = #оУ<я7*< • • • <С#т^ — &Ь
|| Д^ || —»- 0 при N-+00. Если сплайн 8^ (/; х) интерполирует функцию
/ (х) в узлах сетки Д^ и удовлетворяет одному из условий: а) Зд^ (/; х) —
сплайн типа & (ЛГ = 0, 1, . . .), Ь) / (х) принадлежит классу а%"(а, Ь)
и 5д (/; х) — периодический сплайн типа &, то
1{а){х) = 8%{1;х) + ча{х) '(а = 0,1 /г-1), E.9.7.1)
где
\\< (*~2*+2I/2 (»-2»+1I ... ||Bп-2а-1)/2 Г \
) К- 2Bп-2а-1)/2 (а-2*+ 2)! " *" " и
E.9.7.2)
5 случае а) множитель 2~Bп~2а~1)/2 опускается при х = а и х = Ъ, если а>
>> Аг — 1. Л?с/ш в неравенстве E.9.7.2) множитель п — 2А; + 2 меньше 1, то он
заменяется на 1.
Замена множителя ]/га (/г — 1) ... (а + 1) в E.9.5.2) множителем
уп _ 2к + 2 (га — 2& + 1I/(а — 2& + 2)! в E.9.7.2) обусловлена тем, что
если Яд (/; х) —сплайн типа А, то 8^к~{) (/; ж) интерполирует /BЙ~1) (я;) по край-
крайней мере один раз в каждом интервале сетки. Таким образом, 8^к~ (/; х) в этом
случае обладает интерполяционными свойствами, обычно характерными для
первой производной. Если т — неположительное целое число, то в неравенстве
E.9.7.2) полагаем т\ = 1.
5.10. Второе интегральное соотношение
Соотношения, полученные в разд. 3.9 и 3.10, можно распространить обыч-
обычным образом на полиномиальные сплайны степени 1п — 1. Пусть
ь
(/, 8)= |/>п/Яп^ E.10.1)
а
И
1/2 E.10.2)
166 гл- V- ВНУТРЕННИЕ СВОЙСТВА СПЛАЙНОВ НЕЧЕТНОЙ СТЕПЕНИ
Кроме того, пусть Даны сетка Д: а = х0 < Х\ < . . . <.хк = Ь и полино-
полиномиальный сплайн #д (х) степени 2/г — 1 на Д. Бели функция / (х) принадле-
принадлежит классу е%Г2п (а, 6), то
Ь N Х1
5 {/*я> («) —^Х0 («)}• Лр = 2 ( {ГИ-5ГИ}2^. E.10.3)
Проинтегрируем по частям каждый интеграл в правой части равенства E.10.3)
п раз:
(х) — 8ка) (х\\
И-Яд (*)) {/BП) И-^12я) И) с2г, E.10.4)
п
II/—52
Ь - . .
| E.10.5)
Тождество E.10.5) является аналогом тождества C.9.4). При определен-
определенных условиях на равность / (х) — 5д (х) тождество E.10.5) сводится к соот-
соотношению
ъ
. E.10.6)
о
которое мы будем называть вторым интегральным соотношением. Заметим,
что для сплайна $д (/; х) типа к, интерполирующего функцию / (х) на сетке Д,
второе интегральное соотношение, вообще говоря, не выполняется. Однако
справедливы следующие две теоремы.
Теорема 5.10.1. Пусть даны сетка Д: а = х0 < Х\ <С . . . <С Хц = Ь
и функция / (х) из класса е%Г21г (а, Ь). Если полиномиальный сплайн 8& (/; х)
степени 2/г — 1 интерполирует функцию / (х) в узлах сетки Д и удовлетворяет
одному из условий: а) / (х) — 5Д (/; х) принадлежит типу Г, Ь) / (х) — #д (/; х)
принадлежит типу 1Г, с) функция / (х) и сплайн $д (/; х) периодические, то
5.11. УЛУЧШЕНИЕ ОЦЕНКИ ПОРЯДКА СХОДИМОСТИ 167
Теорема 5.10.2. Пусть даны сетка Д: а = х0 <С х{ <С . . . <С хк — Ь
<и функция / (х) из класса $Сгп (а, Ь). Если полиномиальный сплайн 8& (/; х)
степени Ъг — 1 дефекта к интерполирует функцию / (х) в узлах сетки Д,
удовлетворяет условию
5(а> (/;*!> = У00 (а*) (а=1, 2, ...,&— 1; 1 = 1, 2,...,^—1) E.10.7)
и одному из уЪловий: а) / (х) — 5д (/; х) принадлежит типу I', Ь) / (х) — <5д (/; х)
принадлежит типу II', с) функция / (х) и сплайн 5д (/; х) периодические, то
Как мы уже отмечали, для сплайнов типа к второе интегральное соотно-
соотношение обычно не выполняется. Но для сплайнов, удовлетворяющих несколько
(измененным краевым условиям
(а = 0, 1, . . м к — 1; а = щ п + 1, . . ., 1п — к — 1; ъ = 0, Щ, E.10.8)
-второе интегральное соотношение справедливо. В этом случае справедливо
также свойство наилучшего приближения, но отсутствует свойство минималь-
минимальной нормы. Такие интерполяционные сплайны называют сплайнами моди-
модифицированного типа к. Сплайны типа II являются сплайнами модифицирован-
модифицированного типа I.
5.11. Улучшение оценки порядка сходимости
В этом разделе мы рассуждаем почти так же, как в разд. 3.10. Из нера-
неравенства E.9.3) вытекает, что при подходящем значении константы Ка
ь
\/(«> (х)-3^ (/; *) |<Яа { | {/<"> (х)-3?> (/; х)}*их] Ч* \\ Д ||Bп-2а-1)/2.E.11.1)
а
Если справедливо второе интегральное соотношение, то неравенство E.11.1)
эквивалентно неравенству
{ ^ )-5д(/; х)}
а
•откуда
зир
{зир | / (х)-Яд (/; х) |}1/21| Д \\^~^~^\ E.Ц.2)
X
168 ГЛ. V. ВНУТРЕННИЕ СВОЙСТВА СПЛАЙНОВ НЕЧЕТНОЙ СТРПЕНИ
Положим, как в разд. 3.10, а = 0и решим неравенство E.11.2) относительно
зир|/(я) — 5д(/; х)\, считая, что /(я)^5д(/; х). Итак,
X
5ир | /[(*)_5Д (/; Х) |<ЛГ02\//<^> (х) || Д ||*»< E.11.3)
х а
С учетом неравенства E.11.2) получаем
|/(а) (х)-^ (/; х) |<ад, Vрп~Ъ (х) || Д ||2«"«-*. E.11.4)
а
Теперь мы можем переформулировать теоремы 5.9.1 и 5.9.2.
Теорема 5.11.1. Пусть даны функция / (х) из класса &Сгп (а, Ь) и по-
последовательность сеток
|| Д.^ [[ -> 0 при N ->- оо. #а/ш сплайны 8^ (/; #) интерполируют функцию
/ (ж) к удовлетворяют одному из усЛоёий: а) разность / (ж) -^ 5д^ (/; ж) дрм-
надлежит типу Г (ТУ = 0, 1, . . .), Ь) функция? (х) и сплайн Зд^ (/; х) перио-
периодические ^ = 0, 1, . . .), с) разность / (ж) — 5Д^ (/; #) принадлежит типу IV
Щ = 0, 1, . . .), то
(а = 0, 1, ...,/г-1), E.11.5,1)
п (п-1) ... (а+ 1) (п-1)! 2-Bп-а-1)\/
E.11.5.2)
выполнено условие с), то угри х — а и х = Ь множитель 2-<2п~а-1>
опускается.
В новом варианте теоремы 5.9.2 участвуют сплайны модифицированного
типа к, а не сплайны типа к.
Теорема ,5.11.2. Пусть даны функция / (х) из класса &Сгп (а, Ь) и по-
последовательность сеток
II Д# Ц-^0 пРи N ->■ оо. ^сли сплайны 5д^ (/; ж) интерполируют функцию
/ (#) м удовлетворяют одному из условий: а) 5д^ (/; ж) — сплайн модифициро-
модифицированного типа к (ТУ = 0, 1, 2, . . .), Ь) / (х) 6 е^|п (а, Ь) и #д^ (/; #) — перио-
периодический сплайн типа к (ТУ = 0, 1, 2, . . .), то
(х) (а = 0, 1, ...,/г-1), E.11.6.1)
5.12. СХОДИМОСТЬ ПРОИЗВОДНЫХ ВЫСШИХ ПОРЯДКОВ 169»
где
I % <*> К {П~2%2-2Н^\ +1)!>2 2-(Л—-» \//<-1> (х) || Д„ Ц2—1. E.11.6.2)-
В случае а) множитель 2~^2п~а~1> опускается, когда х — а или х = Ь и а^-к..
Если в E.11.6.2) множитель п — 2к + 2 меньше 1, то он заменяется на 1.
5.12. Сходимость производных высших порядков
Пусть даны сетка Д:а = хо<.х1< . . . <.Хц = Ьи функция / (х) из клас-
класса $С2п (а, Ь). Пусть полиномиальный сплайн 5д (/; х) степени 2п —,1 интер-
интерполирует функцию / (х) на сетке Д и удовлетворяет неравенству
Д1Г. E.12.1),
Для разделенных разностей
бед,/ 1**-и **] (*=1. 2, ...,^; а = 0, 1, ...)
с равномерным шагом, где б^ [^_4, ж^] = «5д (/; ^_1) = /(а;м)» можно найти.
такие точки яа*, ям^^а^я*» что
(г=1, 2, ...,^;а = 0, 1, ...,2и-1). E.12.2)
В качестве следствия отсюда получаем, что при достаточно малых значе-
значениях || А || можно использовать уравнения
б!д> / [я*-!, хг] = 2 сци\а) (ха1~хг_1) (г = 1,2, ... ЛГ; а = 0, 1, ..., 2п— 1)
E.12.3)
для определения коэффициентов сц, ибо при || Д || —> О
2п
2
равномерно как относительно номера, так и относительно расположения-
отрезков [х^, х{\. Более того, так как оператор 6" [а, Ъ] линеен относительно /,
то
= \ б!д> /-/ [ям, хг] |, E.12.4>
откуда
3> ,[Хг-ь хг\-Ь? [хм, хг) |<Bа/?д)аК^/^^ (х) || Д \\2п~а'х
а
(г = 1, 2, ..., ЛГ; а = 0, 1, ..., 2п — 1), E.12.5.1)
-170 ГЛ. V. ВНУТРЕННИЕ СВОЙСТВА СПЛАЙНОВ НЕЧЕТНОЙ СТЕПЕНИ
тде
Теорема 5.12.1. Пусть даны функция /(я:) из класса Ж2П(а, Ь) и по-
-следовательностъ сеток
||Д^||-»-0 при ДО ->- оо. Пусть величины ,йд^ заданы равенством E.12.5.2)
и ограничены относительно ДО. Если полиномиальный сплайн 5Д^. (/; х) степе-
степени 1п — 1 интерполирует функцию / (х) ни сетке Д^- и удовлетворяет одному
из условий: а) / (х) ■—5д^(/;'я) принадлежит типу Г (ДО = 1, 2, . . .),
Ь) / (х) — 5д^ (/; х) принадлежит типу 1Г (ДО = 1, 2, . . .), с) функция / (х)
и сплайн 5Д2УГ (/; х) периодические (ДО = 1, 2, . . .), то
1{а)(х) = 8^(!;х) + О(\\А„\\2п-а-1) (а = 0, 1 2л-1) E.12.6)
равномерно относительно х на [а, Ь].
Доказательство по существу такое же, что и у теоремы 3.11.1.
Аналогично доказывается теорема 5.12.2, которую можно сравнить с тео-
?ремой 5.11.2. В тех случаях, когда применима теорема 5.11.2, она точнее
«(в частности, это верно при к >• 1). Детали доказательства последнего утверж-
утверждения теоремы 5.12.2 приведены в разд. 6.12.
Теорема 5.12.2. Пусть даны функция / (х) из класса з/Г2п (а, Ь) и по-
последовательность сеток
II &N 11->■ 0 пРи ДО->- оо. Пусть величины ,йд^ заданы равенством E.12.5.2)
«м ограничены относительно ДО. Если полиномиальные сплайны #д^ (/; х) степе-
степени 2п — 1 интерполируют функцию / (х) в узлах соответствующих сеток Дл-
и удовлетворяют одному из условий: а) 5д „ (/; х) — сплайн модифицированного
типа к (ДО = 1, 2, . . .), Ь) / (х) 6 <г%?|п (а, Ь) и #д^ (/; я) — периодический
^сплайн типа к (ДО = 1, 2, . . .), то
;-а-й) (а = 0, 1, ...,2л-*) E.12.7)
•равномерно относительно х на [а, 6]. Кроме того, равномерно относительно х
Нт Й^ (/; х) = /(«) (х) (а = 0, 1, ...
5.13. Ограничения на порядок сходимости
Результаты, касающиеся ограничений на порядок сходимости кубических
«сплайнов (разд. 3.12), без существенных изменений переносятся на полино-
полиномиальные сплайны нечетной степени. В общем случае
8"—1) (а=0- *
5.14. ПРИЛОЖЕНИЯ К ТЕОРИИ ГИЛЬБЕРТОВА ПРОСТРАНСТВА 171
При а = 0, 1, . . ., п — 1 на сетки не налагают никаких ограничений, но при
а = п, . . ., 2п — 1 величины .йд^ должны быть ограничены относитель-
относительно N. Для равномерных сеток и периодических сплайнов (разд. 4.6, теорема
4.6.3) известен более сильный результат:
/(а)И=^(/; *) + О(||Д„||2п-а) (а = 0, 1 2/1-1). E.13.2)
ь
В случае E.13.1) скорость сходимости пропорциональна V Bп~1) (х), а в слу-
а
чае E.13.2) для функции / (х) из класса С2.п (а, Ъ) она пропорциональна
11/2П(I1
(I
Скорость сходимости в E.13.2) неулучшаема относительно || Д^ ||. Справед-
Справедлива следующая теорема, доказательство которой аналогично доказательству
теоремы 3.12.1.
Теорема 5.13.1. Пусть дана последовательность сеток {Д^}, || Д^||->-
-*- 0 при N -*■ оо. Пусть величины Дд^ ограничены относительно N. Если функ-
функция / (х) принадлежит классу С2п (а, Ь) и при \1 >> О
/ (х) = Яд„ (/; х) + О (|| Д„ 1Р*") E.13.3)
равномерно относительно х па [а, 6], то
/Jп/ = 0.
Замечание 5.13.1. Сплайны, рассматриваемые в теореме 5.13.1,
не обязаны иметь дефект 1. Основное условие здесь -— это выполнение равен-
равенства E.13.3).
5.14. Приложения к теории гильбертова пространства
Продолжим обсуждение, начатое в разд. 3.13. Если в классе $Сп (а, Ь)
•задать псевдоскалярное произведение формулой
ъ
(А 8) = | /(П) И ё1Щ И ^ E.14.1)
и отождествить функции, отличающиеся на полином степени п — 1, то он ста-
станет гильбертовым пространством; без этих отождествлений и без этого скаляр-
скалярного произведения (/, §) класс &Сп (а, Ь) будет просто линейным пространством.
Пусть дана сетка Д: а — х0 <С х\ <С . . . < х^ — Ъ. Обозначим через ^д (/г, к)
«емейство полиномиальных сплайнов степени 2п — 1 дефекта к (к ^ /г). Как
линейное подпространство пространства &Сп (а, Ь) это семейство имеет раз-
размерность к (IV —1) + 2/г, а как гильбертово пространство, в котором отожде-
отождествляются сплайны, отличающиеся на полином степени п — 1, оно имеет
размерность к ^ — 1) + п. Семейство Рд (и, к) периодических полиномиаль-
полиномиальных сплайнов на Д степени 2/г — 1 дефекта к является подпространством про-
пространства ^Рд (/г, к). Как линейное пространство (без каких-либо отождествле-
отождествлений) Рд (п, к) имеет размерность N1$, а как гильбертово пространство (с ото-
172 ГЛ. V. ВНУТРЕННИЕ СВОЙСТВА СПЛАЙНОВ НЕЧЕТНОЙ СТЕПЕНИ
ждествлением сплайнов, отличающихся на константу) Рд (/г,- к) имеет раа-
мерность N1$ — 1. Если сетка А2 содержит сетку Д4, то ^Д1 (га, к) — подпро-
подпространство в Рь (п, к) и РД1 (п, к) — подпространство в РДа (га, к). Так как
^д (и, &) и Рь Ь1, к) конечномерны, то они замкнуты. Пусть Д4 с: Д2; обозна-
обозначим через [РьАп, к) — Рь.(п, к)] и [РДа (/г, к) — РД1 (и, &)] сплайны соот-
соответственно из г д2 (/г, А;) и *Дг (/г, к), определяющие значения которых (вклю-
(включая любые производные 1)) в узлах сетки Д4 равны нулю. Когда нам понадобит-
понадобится, мы будем применять аналогичные обозначения для других пространств.
Ортогональность составляющих подпространств в разложениях, фигурирую-
фигурирующих в оставшейся части этого раздела, доказывается в разд. 5.15. Заметим,
что линейные пространства [Р&1 (п, к) — -^4М (и» А)] и т. д. в отличие от прот
странств Р& (п, к) не изменяются при отождествлении функций, отличающихся
на полином степени п — 1. Таким образом, даже после отождествления эле-
элементы этих пространств можно считать функциями, а не классами эквивалент-
эквивалентности.
Пусть последовательность сеток {А^} на [а, Ь] вложеиа, т. е. Д^ с: Дл-+1
С = 1, 2, . . .). Тогда
E.14.2.1)
(и, к) =
л> *л л
E.14.2.2)
Определим Р^ (п, к) и РДео (п, к) как бесконечные прямые суммы
Р&м (п, к) = /^ (га, &) © 2 © [^лг (ге, *) — ^Адг.! (»»/«)] E.14.3.1)
и
00
Рьм (га, ж) = РД1 (ге, А:) © 2 ф [^а^ (п, к) — Рддг_1 (га, А:)]. E.14.3.2)
Ясно, что
РДоо (и, /с) с= Р^ (п, к), E.14.4.1)
Р^ (га, к) е йГп (а, 6). E.14.4.2)
В разд. 5.15 мы докажем для кфО, что РАво (га, &) = &Сп (а, 6) и
^Аоо (п> ^) = ^п (а» &)» если только Ц Д^ || ->- 0 при N ->■ оо. Так как по
определению пространства ^Доо (га, к) и РДов (га, /с) замкнуты относительно
нормы
II/II = (/,/I/2, E.14.5)
!) Здесь и в оставшейся части этой главы мы будем рассматривать только такие опре-
определяющие значения, запись которых в E.7.3.10), E.7.3.11) или E.7.3.12) связана с сеткой А
5.15. СХОДИМОСТЬ ПО НОРМЕ 173
то для доказательства сформулированного только что утверждения достаточно
показать, что каждое из пространств ^Доо (га, к) и Рд^ (га, к) плотно в &Сп (а, Ъ).
Но сначала мы вьщелим два важных дополнительных подпространства в Р& (п, к).
Это семейство полиномиальных сплайнов на А типа II' степени 2га — 1 дефекта
к и семейство полиномиальных сплайнов на А типа к степени 2га — 1 *). Обозна-
Обозначим эти подпространства через Р'ь (га, к) и Тд (п, к). Заметим, что Р'ь (га, к) а
си Тд (га, к) а р^ (п, к). Если на отрезке [а, Ь] дана последовательность
-сеток {Адг}, Адг с: А^+1 ^ = 1,2, . . .), то с помощью подпространств Р'ь (га, к)
и Гд (га, к) определим бесконечные прямые суммы Р'^ (га, &) и Т^ (га, &):
л. (и. *)-^_, (и, А)], E.14.6.1)
(га, к) - ГД1 (га, А) © 2 © [Гд (п, Л) -Гд (га, А)]. E.14.6.2)
П разд. 5.15 мы покажем, что для
Т\> (л, *) = ^ато (л, Л) - ^п (а, Ь), E.14.7)
если ЦАдгЦ-^0 при Л
5.15. Сходимость по норме
Теорема 5.15.1. Пусть заданы последовательность сеток {Ад*: а — х§'<С
<... <«2ЛГ = Ь}, А^с=АЛГ+1(Л'=1, 2, ...), ЦД^Ц-^Ога^Л^-^оо, дбукк-
/ (л:) мэ класса Ш41 (а, Ъ) и последовательность полиномиальных сплайнов
^(/;я)} степени 2га—1 дефекта к (&<п). ^елм 5Д^ (/; а^ = /(«) (х%)
(а = 0, 1, ..., к — 1; г = 1, ..., Шдт — 1) для каждого N и выполнено одно из усло-
условий: а) }(х)—8а(^;х) принадлежит типу V (И— 1, 2, ...), Ь) 5Д (/; а;)
принадлежит типу IV (N=1,2, ...), с) 5ду(/; ж) принадлежит типу к
(&Т = 1, 2, ...),(!) / (ж) и 8ьК (/; ж) принадлежат классу &С% (а, Ъ) (N — 1,2, ...),
то ||/ — 5д„ /Ц-э-0 при ЛГ-^оо.
Доказательство. Так как в этих случаях выполняются свойство
минимальной нормы и первое интегральное соотношение, то доказательство
протекает точно так же, как и для теоремы 3.14.1. При этом га-я и (га — 1)-я
производные играют соответственно роль второй и первой производных в дока-
доказательстве теоремы 3.14.1.
Замечание 5.15.1. Норма в теореме 5.15.1 определяется как норма
гильбертова пространства, т. е.
II/ II = (/,/I/2. E.15.1)
х) Сплайн принадлежит типу к, если для некоторой функции /(я) он является интер-
интерполяционным сплайном типа к.
174 ГЛ. V. ВНУТРЕННИЕ СВОЙСТВА СПЛАЙНОВ НЕЧЕТНОЙ СТЕПЕНИ
Как уже отмечалось, если подпространство У$ ортогонально подпространству
Ь 2 фГ», E.15.2)
то У — наименьшее замкнутое подпространство, содержащее все составляю-
составляющие подпространства Ук. Кроме того, можно выбрать базис для У, который
будет расширением на У базиса для каждого У^. Следовательно, теорема 5.15*2
вытекает из теоремы 5.15.1, ибо плотное замкнутое подпространство совпадает
со всем пространством *).
Теорема 5.15.2. Пусть на отрезке [а, Ь\ задана последовательность
сеток {Д^}, А^ <= Д^+1 (ЛГ = 1, 2, . . .), || А^ ||-> О при N-+00. Тогда
РА„ (/г, к) =П„ (и, к) = Т^ (и, к) = Шп (а, Ь), E.15.3.1)
(/г, к) =&Сп(а, Ь). E.15.3.2)
В разд. 3.14 был по существу развит аналогичный подход и для аналогов^
наших прямых сумм Рью (и, к), Р'А<ю (/г, к), Т^ю (л, к) и Рью (тг, к) было
показано, что составляющие подпространства попарно ортогональны, так что-
указанные разложения являются разложениями в смысле гильбертова про-
пространства. Эти утверждения справедливы и в нашем случае. Приведем лемму,
обобщающую лемму 3.14.1.
Лемма 5.15.1. Пусть на отрезке [а,Ъ] заданы две сетки А4 и А2^
А4с:А2, и пусть полиномиальные сплайны 8&г(х) и 8ь2(х) на Д4 и А2 соот-
соответственно имеют степень 2п — 1 и дефект к(к^.п). Если 8$(х) (а = 0, 1,...
...,&— 1) обращается в нуль во внутренних узлах сетки А4 и выполнена
одно из условий: а) »5'д1 (х) принадлежит типу 1Г, Ь) 8&2 (х) принадлежит
типу Г, с) 5^ (х) и 8±2 (х) принадлежат типу к и 8$ (а) = 8$ (Ь) = О
(а — 0, 1, ..., к — 1), й) 8^1 (х) и 5д2(ж) принадлежат классу 8Р%(а,Ъ)
и 5Й}(а) = 0 (а = 0, 1, ..., А:-1), то
Доказательство. Пусть сетка Д4 определяется точками а =
= Ь. Тогда
Ь N «I
| Й> (х) 52> (*) ** =
а 1—1 4_4
После гс-кратиого интегрирования по частям получаем
- 2 {2 (-1)"+1 йГ* М «Й*-" (А 1?М1 - о-
11 о1
2 {2
1=1 о=
Лемма доказана.
Плотность подпространства Рд (п, А;) в о#*« (а, 6) доказывается в разд. 6.14.
00
д
00
5.16. КАНОНИЧЕСКИЕ СЕТОЧНЫЕ БАЗИСЫ И ИХ СВОЙСТВА 175-
Рассмотрим любую из бескопечных прямых сумм ^Доо (/г, к), Р'Адо (/г, к)г
(п, к), Рд (гс, к); например,
-00 V ' '' 0
^ (л, к) = ^д, (л, к) © 2 © Г*а„ («, *) - *а„ 4 (л, А)]. E.15.4>
N=2
Если 8ьК$[Р1К(п, к)~ Р^_%(п, к)], то 5^ (ж) (а = 0, 1, . ..,/с — 1) обращается
в пуль во внутренних узлах сетки А^-1 и принадлежит типу Г. Таким обра-
образом, применима лемма 5.15.1 и, следовательно, E.15.4) — ортогональное разло-
разложение.
Теорема 5.15-3. Пусть на отрезке [а, Ъ] задана последовательность
сеток {ДдгЬ Длг <= Длг+1 (-ЛГ = 1, 2, . . .) и |] А^ |] ->• 0 при N -»- оо. ^
бесконечные прямые суммы
Л», *)], E.15.5.1).
E.15.5.2),
{п, к) - ГА1 (и, к) © § ф [№ (/г, /с) - Гд^ (я, к)], E.15.5.3>
оо
РАоо (п, к) -РА1 (и, к) © 2 © [^а- (», А) - Рллг , (/г, Л)] E.15.5.4)
N=2 л—I
являются ортогональными разложениями относительно скалярного произведе-
произведения E.14.1) и все они тождественно совпадают с пространством &Сп (а, Ь).
5.16. Канонические сеточные базисы и их свойства
В разд. 3.15 были введены канонические сеточные базисы для <2Г2 (а, Ь}
и Ш% (а, Ъ). Аналогичные базисы можно построить для &Сп (а, Ь) и <$?$ (а, Ъ).
Мы сейчас построим такие базисы для Рьт (/г, к), ^дм (/г, к), Т^ю (п, к)
и Р&ю (п, к), а в силу теоремы 5.15 у нас получатся различные ортонормальные
базисы для Шп (а, Ь) и Ш% (а, Ь). Приведем построение сеточного базиса лишь
для пространства Рьт (п, к), так как для остальных пространств построение
по существу совпадает с этим. Даже здесь мы упрощаем процесс по сравнению
с разд. 3.15, ограничиваясь единой простой нумерацией узлов сетки и тем
самым не рассматривая сеточные базисы, которые не являются каноническими.
Пусть на отрезке [а, Ъ] задана последовательность сеток {А^}, А^ с:
с= А^+1 (ЛГ = 1,2,...). Обозначим через М множество всех различных точек,
содержащихся в сетках Д^, но не принадлежащих сетке А4. Занумеруем точкиг
множества М: Рь Р2, - • • • Начинаем нумеровать их (слева направо) с точек
сетки Д2, затем нумеруем точки сетки А3 и т. д. В каждом случае точки, пред-
предварительно уже занумерованные, пропускаются. Определим теперь новую-
76 ГЛ. V. ВНУТРЕННИЕ СВОЙСТВА СПЛАЙНОВ НЕЧЕТНОЙ СТЕПЕНИ
зюследователыюсть сеток {пт} (то = 0, 1, 2, . . .), где я0 = А1, я4 = Д4 [} {Р4}
и вообще ят = ят_1 у {Рт}- Предположим, что нам дан ортонормальный
•базис для Рь% (п, к). Построим ортонормальный базис для [Р^^ (п, к) —
^ ( &)Ь распространив данный базис до ортонормального базиса для
те (, )
Допустим, что для каждого то (то = 1, 2, . . \) полиномиальные сплайны
] (х) (] = 1, 2, . . ., к) на лт типа Г степени 2п — 1 и дефекта к таковы,
что производные Н^) (х) (а = 0, 1, . . ., к — 1) обращаются в нуль на зтт_4,
а сами сплайны Нт} (х) ортонормальны. Такие сплайны можно получить, при-
применив процесс ортогонализации Грама — Шмидта к сплайнам #т; (х) ■(/ = 1,
2, . . ., к) типа Г на Ат, производные §<&) (х) (а — 0, 1, . . ., к — 1) которых
обращаются в нуль в узлах сетки Ат_4 и удовлетворяют условию $<&) (Рт) —
■— 6<?+1. Положив для ъ = к (то — 1) + У, где к (то — 1) <С 1*Скт,
8г (и, к; х) = кп; (х) (т « 1, 2, . . ., / = 1, 2, . . ., А), E.16.1)
лолучим требуемый ортонормальный базис для [^д,,,, (/г, к) — Р&1 (п, к)].
В самом деле, подмножество {$* (/г, к; х) \ г = 1, 2, . . ., &то} представляет
собой ортонормальный базис для [РПт (п-> Щ — ^т (и, АI (то = 1, 2, . . .)
и для каждого ^(^ = 1,2,...) сплайны ^ (/г, к; х), которые вместе со свои-
зш первыми к — 1 производными не обращаются в нуль в каждом узле сетки
Д V, составляют ортонормальный базис для [Р/^К. (п, к) — 7?1д1 (п, к)]. Если
не возникнет неопределенности, будем обозначать ^г (п, к; х) через 5^ (х)
и /^д (/г, к) через Т^д.
Множество 5^ (ж) (I = 1, 2, . . .) вместе с заданным ортонормальным
базисом для Р&1 называют каноническим сеточным базисом для Р&ю\ его ана-
аналоги для ^дм, Гд^ и Рд^ называют каноническими сеточными базисами для
этих пространств. Из теоремы 5.15 непосредственно вытекает
Теорема 5.16.1. Пусть на отрезке [а, Ъ] задана последовательность
сеток {Адг}, А^ с: А^+1 (N = 1,2,...) и || Д^ || -> 0 при N ->- оо. Тогда
■^Доо С71» ^)» ^Доо (ге> ^) и ^А» (л» ^) имеют канонические сеточные базисы,
которые являются ортонормалъными базисами для &Сп (а, Ь), а РДоо (п, к)
имеет канонический сеточный базис, который является ортонормалъным бази-
базисом для Ш% (а, Ь) и &Сп (а, Ъ).
Замечание 5.16.1. В теореме 5.16.1 Шп (а, Ъ) и &Рр (а, Ь) рассма-
рассматриваются как гильбертовы пространства со скалярным произведением, опре-
определенным равенством E.14.1).
Дадим аналог леммы 3.15.1, содержащий крайне важную информацию
о модуле величин 8\а) (х) (а — 0, 1, . . ., п — 1).
Лемма 5.16.1. Пусть с помощью последовательности сеток {А^}, А]\гс:
сДдг-н (N--1,2, ...), построен канонический сеточный базис {31{п, к\ х)}
для пространства [Р& (п, к) — Р^(п,к)], [Р'ь (п, к) — Р'ьх(п, к)], [Гд (гс, /с)—
■5.16. КАНОНИЧЕСКИЕ СЕТОЧНЫЕ БАЗИСЫ И ИХ СВОЙСТВА 177
— Т^(п, к)] или [Рь^ (п, к) — Рд^/г, к)]. Пусть {лт} (т = 0, 1, ...) —после-
—последовательность сеток, использованная при его построении. Тогда для
(п, к; х)\^.Ка\\лт.1\\Bп-2а-1)/2 (& = 0, 1, ..., п-\), E.16.2.1)
где
К«= 2-Bп-2«-1)/2 (а==()> ^ _^ п_1} E.16.2.2)
Для |^м(п^)-4(пД)] и [Гдто(ге, А:) —7'Д1(ге, &)] множитель 2~Bп~2а~ХI2
опускается, когда х — а и х — Ъ. Если в равенстве E.16.2.2) множитель
п — 2к-\-2 меньше 1, то он заменяется на 1.
Доказательство. На отрезке [а, Ъ], кроме, быть может, точек
х = а и х = Ъ, можно найти такие точки хг, что *5Г1П~1> (#0 =0 и | х — хь \ .<
^х/2 Vй — 2& + 2 || ящ_4 ||. Это следует из возможности многократного
применения теоремы Ролля и из того, что 5|А~1) (х) обращается в нуль в каж-
каждом узле сетки ят_1. Отсюда и из неравенства Буняковского — Шварца
2. E.16.3)
Рассуждая так же в отношении З^1* (х) и используя неравенство E.16.3)
вместо неравенства Буняковского — Шварца, получаем
E.16.4)
Продолжая этот процесс, приходим к неравенству E.16.2). Так как изменения,
требуемые при х — а и х — Ь для [/^ — Р'ьх\ и [ГДоо — ТА%], тривиальны,
то лемма доказана.
В заключение разд. 5.16 приведем теорему 5.16.2, играющую важную
роль в разд. 5.17 и 5.18.
Теорема 5.16.2. Пусть канонический сеточный базис {81 (х)} таков,
что || лт || — О A/яг). Тогда существуют такие действительные числа 5а>0,
что
1) (а = 0, 1, ...,/г-2). E.16.5)
Доказательство. Для некоторых положительных постоянных К и Ва
<00 (а = 0'!' ..-,л-2). E.16.6)
Теорема доказана.
12-1197
178 ГЛ. V. ВНУТРЕННИЕ СВОЙСТВА СПЛАЙНОВ НЕЧЕТНОЙ СТЕПЕНИ
Замечание 5.16.2. Было бы желательно вывести E.16.5) и для
а = п — 1, но неравенства E.16.2) недостаточно точны- Это будет ясно позд-
позднее, когда мы получим точные аналоги неравенств E.16,2) для обобщенных
сплайнов, из которых будет видно, что общность наших методов приводит
к неточности для малых степеней.
Замечание 5.16.3. В наших рассуждениях само собой предпола-
предполагалось, что сетка Д1 = я0 имеет достаточно много узлов, так что сплайны
81 (п, к\ х) = 8г (х) существуют. Кроме того, мы использовали соотношение
I = к (т — 1) + и где к (т — \) <. 1-^.кт, введенное нами раньше. Теперь,
говоря, что Нт || Ддг || = 0 или что какой-то базис является каноническим
N-►00
сеточным базисом для $Сп (а, Ь) или з/Г" (а, Ъ), мы будем дополнительно пред-
предполагать, что || Лг || — О A/0-
5.17. Ядра и интегральные представления
В разд. 3.16 мы определили ядра, дающие интегральное представление
для остаточного члена
Я(х) =/(*) -5Д(/; х). E.17.1)
Определим теперь такие ядра На (п, к\ х, *), что для функций / (х) из класса
<Ш/ (Я, О)
ъ
(х) =^На(п,к; х, I) /00 @ йг + РЙ>4 (х). E.17.2)
а
Если / {х) 6 Жп (а, Ъ), то / (х) — 5Д (/, х) 6 &Сп (а, Ь) и поэтому E.17.2)
справедливо и для E.17.1). Остаток Рп~1 (я) представляет собой полином сте-
степени п — 1; более подробно мы рассмотрим его в конце этого раздела.
Теорема 5.17.1. Пусть функция / (х) принадлежит классу Шп(а, Ь)
или &Р%(а, Ъ) и последовательность {81 (п, к; х)} (I = 1, 2, ♦ . .) вместе
с базисом {иг (л, к\ х)} (& = 1, 2, . . ., т) для Р^ (л, к) образует канониче-
канонический сеточный базис, который является ортонормальным базисом для Шп (а, Ь)
или &С% (а, Ъ). Тогда для всех х из отрезка [а, Ъ)
ь
/о») (х) - Нт Г Яа„ (/г, к; х, г) /<»> (г) л+ Р{А (х)
]У->оо •»
а
(а = 0, 1, ...,/г —1), A5.17.3.1)
где Рп_! (х) — полином степени п — 1 и
т N
Я (п и. г 4\ У „(а) (г\ п(п) (А 4- V. Д^а* (г\ Я^ A\ (Ъ 17 Ч 2^
г=1 г=1
причем сходимость равномерна относительно х ^ [а, Ь].
5.17. ЯДРА И ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ 179
Доказательство. Пусть при построении {^ (я:)} применяется
последовательность сеток {яг} A — 0, 1, . . .). По предположению || тс2 || ->■ О
при ъ -*■ оо; следовательно,
(х) - Шп
2
г=1
откуда
т N
= Ит { 2 (»ь /) Ца) И + 2 №. /) ^а> (*I + ^-1 (*)> E.17.4)
гу г1 41
то
Ж) « Цщ Г { 2 И{«> (Я!) И}») @ +
(*), E.17.5)
и по теореме 5.9.2 сходимость равномерна относительно х. Отсюда немедленно
вытекает утверждение теоремы, так как равенство E.17.5) выполняется для
а = 0, 1, . . ., п — 1.
Доказательство теоремы 5.17.1 использует поточечную сходимость функ-
функций 1§'да) (/; х) к /<а> (х). Таким образом, для соответствующего канонического
сеточного базиса для ^Д(Ю или РДоо справедливо г)
Следствие 5.17.1. Пусть функция] (х) принадлежит классу К2п (а, Ъ)
или Кр1 (а, Ъ) и последовательность {81 (ге, к\ х)} A=1,2,.. .) вместе
с щ (п, к; х) (г = 1, 2, . . ., т) образует канонический сеточный базис для
■^а» \п-, Щ или РДве (/г, к), который является ортонормальным базисом для
пространства <г%Г2п (а, Ь) или &С™ (а, Ъ) соответственно. Тогда для всех х из
отрезка [а, Ъ\ и а = 0, 1, . . ., 2/г — к — 1 выполняется равенство E.17.3).
Замечание 5.17.1. Отметим, что НаК (п, к; х, г) получается из
■^а-1лг (п1 &> хч 0 формальным почленным дифференцированием относи-
относительно х.
В теореме 5.17.1 не устанавливается существование в Ь (а, Ь) требуемых
ядер Иа (/г, к\ х, I) для каждого х. Однако мы покажем, что при а = 0, 1, ...
. . ., п — 2 ядро Н^ (/г, к; х, г) существует и принадлежит I? (а, Ъ); оно
представляет собой предел в смысле среднеквадратического частичных сумм
Н (/г, к; х, г).
Теорема 5.17.2. Пусть последовательностью сеток {яг} (г = 0, 1, . . .),
заданной на отрезке [а, Ь], определяется канонический сеточный базис, кото-
который является ортонормальным базисом для $Сп (а, Ь) или (Ж^ (а, Ъ). Если функ-
х) Предполагается, что для вспомогательной последовательности сеток {л^} (» = 1, 2,...)
величина Ля как функция от г ограничена.
12*
180 ГЛ. V. ВНУТРЕННИЕ СВОЙСТВА СПЛАЙНОВ НЕЧЕТНОЙ СТЕПЕНИ
ция Нак(п, к; х, г) определена равенством E.17.3.2), то последовательность
{Нап} (а = 0, 1, . . ., п — 2; N = 1, 2, . . .) как функция от I является
последовательностью Коши в Ь2 (а, Ь) и, следовательно, последовательностью
Коши в Ь (а, Ъ). Если На (/г, &; х, г) (а = 0, 1, . . ., п — 2) — ее предел, то
ь
/«*> (х) =^На (п, к; х, I) /(«) (*) д* + Р{А (*), (а = 0, 1, ..., п- 2), E.17.6)
а
где Рп-1 (х) — полином степени п — 1. Сходимость равномерна относительно
х 6 [а, Ь], и Яа (/г, к; х, I) получается из Яа_4 (п, к; х, I) формальным почлен-
почленным дифференцированием по х.
Доказательство. Так как сеточный базис ортонормален, то из
леммы 5.16.1 получаем
Ъ Ь Л'+р
2
а а ^=
N4-33
Ш) E-17.7)
Итак, для а -^ п — 2 мы имеем последовательность Коши, и равенство E.17.6)
следует из E.17.3); это завершает доказательство, так как пределы существуют
равномерно относительно х ^ [а, Ь].
Сделаем несколько замечаний о сеточных базисах. При выборе базисов
для Еь^ /"д^ 71д1 и Рд4 мы могли считать их линейными пространствами (без.
отождествлений), а не гильбертовыми. Например, можно выбрать базис для
^д,» содержащий п независимых полиномов степени, меньшей п. Бели ^д4
рассматривается как гильбертово пространство, то эти базисные элементы
тождественны нулевому сплайну. Но такое построение непротиворечиво, так
как эти полиномы ортогональны каждому элементу из ^д4, в том числе и самим
себе. Включение их в базис позволяет выразить ^д^/; х) в виде
т N
{8,, /) Ма) (х) + РЙ>4 (х) E.17.8)
и, следовательно, доказать теорему 5.17.1 и следствие 5.17.1. Здесь полиномы
степени, меньшей п, представлены в базисе членом Р^п-\ (%), а остаток базиса
[щ (п, к; х), щ (/г, к; х), . . ., ит (/г, к; х)]
представлен суммой
т
2
г=1
5.18. ПРЕДСТАВЛЕНИЕ И ПРИБЛИЖЕНИЕ ЛИНЕЙНЫХ ФУНКЦИОНАЛОВ 181
С другой стороны, можно рассмотреть Р^ как гильбертово пространство с орто-
нормальным базисом и^ (п, к; х), щ (п, к; х), . . ., ит (п, к; х), а затем опре-
определить Рп-\ (х) формулой
т
Рп-1(*) = 5Д1 (/;«)-2 и,щ)ий(х). E.17.9)
Равенство E.17.8) будет также справедливо *). Оба варианта согласуются
с формулировкой наших теорем.
5.18. Представление и приближение линейных функционалов
В этом разделе мы исследуем представление линейных функционалов
с помощью интегралов, а также рассмотрим приближение функционалов дру-
другими функционалами и выведем интегральное представление для остаточного
члена. В отличие от разд. 3.17 мы не ограничимся случаем точечных функцио-
функционалов Хх'- / -*- / (х)- Мы докажем теоремы о представлении, относящиеся
к типу, изученному Пеано [1] и Сардом [1]; их связь с теорией сплайнов впер-
впервые осознал Шёнберг [6]. Мы приняли другой, новый подход, довольно общий,
в значительной мере использующий результаты, полученные здесь и в гл. III.
В итоге мы доказываем теоремы в одном смысле более сильные, а в другом более
слабые, чем те, которые получены Пеано, Сардом и Шёнбергом.
Пусть функция / (х) принадлежит классу Шп (а, Ь) или &С% (а, Ь) и линей-
линейный функционал X, определенный на Ш41 (а, Ь) или &С% (а, 6), действует
по формуле
ИО (Ч<:п-1), E-18.1)
;=0 а
где |1/ (г) — функции ограниченной вариации на [а, 61. Подробно функциона-
функционалы такого типа описаны Сардом [1, гл. I]. Исследуем возможность представ-
представления #<>/ в виде
ь
Рп-1, E.18.2)
где функция Н {I) не зависит от / (х) и принадлежит пространству I? {а, Ъ),
а /*„_! (х) — полином степени п — 1. Как и в предыдущем разделе, установим
сначала более общий результат о существовании последовательности функций
{#л- (п, к; ^} № = {, 2, . . .) из класса &Сп-к (а, Ь), для которой
ь
= Ит I* НК (га, к; I) /<«> (г) <2* + %°Рп-х- E.18.3)
N-+00 V
х) В формуле E.17.9) под щ(х) понимается конкретный член из класса эквивалент-
эквивалентности, а не сам класс.
182 ГЛ. V. ВНУТРЕННИЕ СВОЙСТВА СПЛАЙНОВ НЕЧЕТНОЙ СТЕПЕНИ
Теорема 5.18.1. Пусть функция 1 (х) принадлежит-классу Шп (а, Ь)
или е%Гр (а, Ъ) и последовательность {8г (п, к; х)} (г = 1, 2, . . .) вместе
с {иг (п, к; х)} (г = 1, 2, . . ., т) образует канонический сеточный базис,
который является ортонормалъным базисом для $Сп {а, Ь) или $Ср (а, Ь). Если
X — линейный функционал E.18.1), то
ь
Х°/= Ит Г Н„(п, к; 1){п A)й1 + Х°Рп-ь . E.18.4.1)
а
где
т N
Н„ (и, к; х) = 2 а, и(Г (х) + 2 & $п) (ж)» E.18.4.2)
2 () 2
г=-=1 1=1
а« = 2 ] "^ ^ й^ ^ (г ^ 1, 2, ..., т), E.18.4.3)
Л Ь
Р« - 2 1 ^^ (*>й^ E) С я 1. 2, ..., Л) E.18.4.4)
3=0 а
к Рп_4 (ж) — полином степени п — 1 ♦
Доказательство. Представим /<а>(ж) (<х = 0, 1, ..., п—1) в виде
т . N
/(«> (х) = 11т { 2 (/, И|) ^а) (*) + 2 (/, М ^
Л'-».оо {=1 1=1
где сходимость равномерна относительно х. Тогда
Т) Ь т N
[ {
(/. »|) «Iй («) + 2 С/. ^|) З? (8)} фу E) + Яо^4.
Так как сходимость равномерна относительно х, то
Л Ь т N
=шп 2 ({2 (/,^)^)
^"ЙХ 1й
г=1
По определению
ь
нп> и) *<п> и) й1, E.18.5)
5.18- ПРЕДСТАВЛЕНИЕ И ПРИБЛИЖЕНИЕ ЛИНЕЙНЫХ ФУНКЦИОНАЛОВ 183
так что после подстановки значепий (/, щ) и (/, 51*) и изменения порядка
суммирования получаем
т г\ Ь
а г=1 }=0 а
+ 2 [2
Теорема доказана.
N Т)
2 [21
{=■1 э'=0 а
Следствие 5.18.1. Пусть функция} (х) принадлежит классу &Сгп (а, Ъ)
или <2%?рп (а, Ъ) и последовательность {5^ (п, к; х)} (г = 1, 2, . . .) вместе
с {щ (и, к; х)} A, 2, . . ., т) образует канонический сеточный базис, который
является ортонормалъным базисом для &Сп (а, Ь) или &С% (а, Ь). Если линейный
функционал X имеет вид
1\ Ъ
#о/=2 ( /"}@^(«) (л<2я-2), E.18.6)
г=о а
где |Х; (^) — функции ограниченной вариации на [а, Ь], то равенство E.18.4)
справедливо, только теперь г\ ^ 2/г — 2.
Для функционалов вида
п ь
Хо{ = 2 ) /0) (О Й1*И«) (ч<2п-2), E.18.7)
где |х^ (г) — функции ограниченной вариации на [а, Ь], мы получаем пред-
представления специального вида E.18.2).
Теорема 5.18.2. Пусть {яг} (г = 0, 1, . . .) — последовательность
сеток на [а, Ь\, определяющая канонический сеточный базис, который является
ортонормалъным базисом для <Жп (а, Ь) или <&С™ (а, Ь). Если функция Н^ (п, к; х)
задана равенством E.18.4) (с учетом того, что х\ -^ п — 2), то {Нх (п, к; х)}
№ = I, 2, . . .) является последовательностью Коши в & (а, Ь) и, следова-
следовательно, последовательностью Коши в Ь (а, Ъ). Если Н (п, к; х) — ее предел, то
ь
Хо} = ^ Н (/г, к; I) /<п> {г) йг + #°Р„-4, E.18.8)
где Рп_1 (х) — полином степени п — 1.
Доказательство. Теорема доказывается по существу так же,
как теорема 5.17.2.
184 ГЛ. V. ВНУТРЕННИЕ СВОЙСТВА СПЛАЙНОВ НЕЧЕТНОЙ СТЕПЕНИ
Сейчас мы уже можем рассмотреть приближение линейного функционала
X вида E.18.1) линейными функционалами вида
Во/= 2 2 ау/«> (*,) (*<»). EЛ8-9)
определенными совокупностью констант а^ A — 0, 1, . . ., г; / = 0, 1, ...
. . ., к — 1) и сеткой А: а = х0 < хх <С . . . <. хт = Ь. Пусть ^ A) —
кусочно-постоянная функция со скачками а^ в точках хг A = 0, 1, . ., г).
Тогда E.18.9) принимает вид
к-1
#°/ = 2 (/(Л(*)<*М«). E.18.10)
]=0 а
где \х}- (I) — функции ограниченной вариации на 1а, Ь], и наши теоремы о пред-
представлении функционалов применимы. Пусть функции^ (п, к', х), и2 (п, к; х), ...
. . ., ит (п, к; х) образуют базис для Р& (/г, к), а последовательность
{$* (/г, к; х)} (г = 1, 2, . . .) распространяет этот базис до ортонормального
базиса для &Сп (а, Ь). Аналогично можно рассмотреть подпространство Гд (/г, к)
или Рд (/г, к) (в случае К% (а, Ь))\ некоторые трудности встречаются при рас-
рассмотрении пространства Р'ь (/г, к) (для х — а и х = Ь).
Сделаем теперь два важных замечания. Первое касается коэффициентов Eг.
Так как 8^ (хг) = 0 (а = 0, 1, . . ., к — 1; ; = 0, 1, . . ., г, I = 1, 2, . . .),
то все коэффициенты рг A = 1, 2, . . ., АО, заданные равенством E.18.4.4),
в формуле для В обращаются в нуль. Это происходит потому, что мера щ (*)
сосредоточена в узлах сетки А; более того, это верно для каждого N. Следова-
Следовательно, если применить теорему 5.18.1 или 5.18.2 к X — В, то коэффициенты р$
будут определяться только оператором X и не будут зависеть от В. Второе
замечание состоит в том, что
т
о г=
^и) (/г, к; г) /<«> (*)} Л + «оРп_ь E.18.11)
и из доказательства теоремы 5.18.1 видно, что
Ь N
#о/^.#о$Д)/ + Ит Г { 2 Мп)(*)/т) (*)}</*• E.18.12)
1
|1 1Г,
а г=1
Так как коэффициенты а^ в E.18.9) можно подобрать так, чтобы выполнялось
равенство
Я°/ = ХоЗь;, E.18.13)
то получаем следующие две теоремы.
5.18. ПРЕДСТАВЛЕНИЕ И ПРИБЛИЖЕНИЕ ЛИНЕЙНЫХ ФУНКЦИОНАЛОВ 185
Теорема 5.18.3. Если линейный функционал X имеет вид E.18Л),
а линейный функционал В — E.18.13), то
а Ь-1
где
и ъ
ь N
— &от — ЦШ \ < >, р»О1 1/1, Л: Г) Гк (С) |- ЙС, 10.1О.14.1)
{ (л</г) E.18.14.2)
3—0 а
и функции |л? ($) (/ = 0, 1, . . ., х\), определяемые только оператором X,
имеют ограниченную вариацию на отрезке [а, Ь].
Теорема 5.18.4. Если линейные функционалы X и В имеют вид
соответственно E.18.7) и E.18.3), то
ь
Х°{-Во{= Г Н (/г, к; I) /<п> (I) да, E.18.15.1)
а
где Н (/г, к; Ь) принадлежит пространству Ъ% (а, Ъ) и является пределом в смы-
смысле среднеквадратического функции
т N
Н„ (п, к; I) =-■ 2 а^|п) (/г, к; 0+ 2 Р«ЯП> ("' ^ ')> E.18.15.2)
г=1 1=1
П Ь
щ = 2 ] «Iя (л' А; 5) ^ E)' E.18.15.3)
п ь
^ (ге' *; 5) ^' (*)• E.18.15.4)
Функции |л,- («) имеют ограниченную вариацию и зависят только от функцио-
функционала X, в определение которого они входят. Если В — любой линейный функцио-
функционал вида E.18.9) и X — В аннулирует полиномы степени, меньшей п, то
ь
#о/ — Во/= [н (/г, к\ I) /<п> {г) ае, E.18.16)
а
где Н (/г, к; I) принадлежит пространству Ь2 (а, Ь) и определяется, как в тео-
теореме 5.18.2. Кроме того, интеграл
ь
[ {Н (/г, к; г)}2 аЧ E.18.17)
а
принимает наименьшее значение, когда В удовлетворяет условию E.18.13).
186 ГЛ. V. ВНУТРЕННИЕ СВОЙСТВА СПЛАЙНОВ НЕЧЕТНОЙ СТЕПЕНИ
Применение методов этого раздела к точечным функционалам %х'' / -*- / (х)
рассматривается в гл. VI. Там исследуются также другие функционалы, пред-
представляющие значительный интерес. Например, если нежелательно, чтобы ап-
аппроксимирующий функционал В включал значение функции / (х) в точке хи
то, казалось бы, можно просто положить в E.18.9) ащ = 0. Однако тогда усло-
условие E.18.3) будет, вообще говоря, нарушено. Но существуют и такие аппрокси-
аппроксимирующие функционалы, для которых при этом условие E.18.3) не нарушается.
Это свойство полезно при выводе формул для численного интегрирования
методом последовательных приближений, так как для устойчивости процесса
часто бывает нужно устранить в этих формулах некоторые значения функции
и ее производных.
Глава VI. ОБОБЩЕННЫЕ СПЛАЙНЫ
6.1. Введение
К изучению полиномиальных сплайнов нечетной степени возможны два
подхода: 1) алгебраический, состоящий главным образом в подробном изучении
системы линейных уравнений, определяющих сплайны, и 2) подход, исполь-
использующий внутренние свойства сплайнов и основные интегральные соотношения
между функциями из классов з%*п (а, Ъ) и Ж2п (а, Ъ) и аппроксимирующими
сплайнами. Первый подход весьма эффективен при изучении кубических и дваж-
дважды кубических сплайнов, но его роль заметно падает даже для полиномиаль-
полиномиальных сплайнов более высокой нечетной степени. Для обобщенных сплайнов
в настоящее время нет алгебраической теории, но для некоторых частных
случаев обобщенных сплайнов можно достаточно хорошо развить специальные
разделы этой теории. Подход, основанный на внутренних свойствах, применим
и в случае обобщенных сплайнов и достигает здесь своей полной силы. В настоя-
настоящей главе эта теория представлена как продолжение внутренней теории поли-
полиномиальных сплайнов.
Пусть Ь — линейный дифференциальный оператор, заданный формулой
Ь = ап (х) Дп+ ап_4 (х) Д*-1 + . . . + а0 (х),\ F.1.1)
где функции а; (х) (/ = 0, 1, . . ., п) принадлежат Сп [а, Ь] и ап (х) фО
на [а, Ь]. Обозначим через Ь* оператор, формально сопряженный к Ь:
*).} + ав(«). F.1.2)
Если на отрезке 1а, Ь] задана сетка Д: а = х0 <. х^ <;...<; хк = Ь, то
обобщенным сплайном дефекта к @ <^ к ^ л) относительно сетки Д называется
функция 5Д (х) из класса 8Р2п-к (а, Ь), удовлетворяющая дифференциальному
уравнению
Ь*Ь8А = 0 F.1.3)
на каждом открытом интервале (хг-и щ) (г = 1, . . ., .№). Мы будем говорить,
что сплайн 5Д (х) имеет порядок 2гс, когда нам нужно будет указать порядок
оператора Ь*Ь, определяющего 5Д (х).
188 ГЛ. VI. ОБОБЩЕННЫЕ СПЛАЙНЫ
Если к — 0 и оператор Ь имеет аналитические коэффициенты, то 5Д (х) имеет
непрерывные производные всех порядков и удовлетворяет уравнению F.1.3)
всюду на [а, Ъ]; в этом случае непрерывность Bп — 1)-й производной влечет
непрерывность 2д-й и всех высших производных. Таким образом, для этого
важного класса дифференциальных операторов условие равенства нулю дефек-
дефекта равносильно непрерывности всех производных сплайна. Для обычных сплай-
сплайнов (дефект 1) допускаются разрывы Bп — 1)-й производной, но только в узлах
сетки. Вообще дефект сплайна указывает, насколько сплайн не удовлетворяет
уравнению F.1.3) на отрезке [а, Ь\.
6.2. Основное тождество
Пусть дай дифференциальный оператор Ь порядка п и его формально сопря-
сопряженный Ь*. Тогда
^ {х)Ь*о(х),. F.2.1.1)
где билинейная форма Р [и (я), V (х)] определена равенством
Р[и(х), и{х)]= 2 2 (-1)|1и("-й)ИК-;И^И}^. F.2.1.2)
Перегруппируем правую часть в F.2.1.2):
Р[и(х), V(ж)] = П2 и*"-'"» (х) У (-1)к{ап-иъ (*) Ч И)<й>- F-2-2)
0 й0
Пусть теперь даны сетка' Д: а — хо<х1<1 ... <.хк — Ъ и обобщенный
сплайн 8ь.(х) на ней степени 2п. Если в уравнении F.2.1) положим и(х)=?
=-1(х) — 8ь(х) и V (х) — Ь8& (х) и проинтегрируем его по отрезку [х^, хг]
($ = 0, 1, ..., к), то получим
| Ь {/ {х) - 8А (х)} Ь8А (х) ах =
п-1 з
3=0 й=0 1-1
поскольку Ь*Ь8ь (х) — 0 на (ж^, ж^). Следовательно, из общего тождества
а
Ь Ь
) — Яд (ж)] ^д (ж) йх— [ {Л5Д (ж)}2 йж F.2.4)
а
6.3. ПЕРВОЕ ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ 189
и равенства F.2.3) вытекает, что
ь ь
а а
N п-1 3
-2
й-0
1 . F.2.5)
Тождество F.2.5) называют основным тождеством для обобщенных сплайнов.
При его выводе учитывалось, что 1) 5Д (х) представляет собой сплайн относи-
относительно сетки А и 2) функция / (х) принадлежит классу <ЗГП (а, Ь).
6.3. Первое интегральное соотношение
При определенных ограничениях на сплайн 5Д (х) основное тождество
имеет вид
Ь Ъ- Ь
Г 11,/(а) |» Жв = \\Ь8ь(?;х)р0х + [ | 1т/(ж) - ^д (/; ж) |« Л» F.3.1)
а
и называется первым интегральным соотношением для обобщенных сплайнов.
Если дефект сплайна Зд (х) равен к, то производные {Ь8& (я)}(П~3) (/ = 0,1,...
. . ., к) в узлах сетки Д претерпевают разрыв. Обозначим
%(У{+()()У> (г = 0, 1, ...,л-1); F.3.2)
тогда рг EД; ж) совпадает с коэффициентом при {/ (х) — 5Д (х)} п"г в равен-
равенстве F.2.3). Так как для г ;> п — к функции |3Г (|5Д; х) в узлах сетки могут
быть разрывными, то мы вместо требования непрерывности потребуем, чтобы
разность /(«) (х) — 5ДЯ) (х) (а = 0, 1, . . ., к — 1) обращалась в нуль во вну-
внутренних узлах сетки Л; если, кроме того, выбраны подходящие краевые условия
в точках х = а и х = Ь, то равенство F.3.1) справедливо.
Одно допустимое множество краевых условий мы получим, если потребу-
потребуем, чтобы разность / (х) — 5Д (х) обращалась в нуль в точках х = а ж х = Ь
и принадлежала типу Г; другое —чтобы разность Цх)—8Ьк{х) обращалась
в нуль в точках х = аш х = Ъ и сплайн $д (х) принадлежал типу 1Г. Подчерк-
Подчеркнем здесь, что понятия типа Г и типа II' зависят от оператора Ь. Говорят,
что функция / (х) принадлежит типу Г, если производные /<а> (х) обращаются
в нуль в точках х = а ш х = Ь при а = 1, 2, . . ., п — 1, где п — порядок
оператора Ь. Говорят, что функция / (х) принадлежит типу 1Г, если произ-
производные {ЦУа^ (а = 0, 1, . . ., п — 2) обращаются в нуль в точках х = а
жх = Ъ. Для !, = /)" эти определения совпадают с прежними 1). Классы эквива-
Они равносильны требованию рв(/; в) = ра(/; Ь) = 0 (а = 0, 1, ..., п—2).
190 ГЛ. VI. ОБОБЩЕННЫЕ СПЛАЙНЫ
лентности и т. д. можно ввести аналогично тому, как это сделано в гл. III и V.
Как и прежде, сплайн будем называть простым, если он принадлежит
классу С2п-'* (а, Ъ).
Для обобщенных интерполяционных сплайнов типа к это условие также
и достаточно; обобщенный сплайн 5Д (/; х) дефекта к на Д называется интер-
интерполяционным сплайном типа к, если 5дс) (/; х) (а = 0, 1, . . ., к — 1) интер-
интерполирует значения /<а> (х) во внутренних узлах сетки А и {Ь8А (ж)}<а> = 0
(а = 0, 1, . . ., п — к — 1) в точках х = а и х = Ь. В периодическом случае
разность/(«> (х) — 5да)(/; х) (а = 0, 1, . . ., к — 1) должна обращаться в нуль
во всех узлах сетки А и сплайн 5Д (/; х\ должен принадлежать классу
С2п-к~1 (а, Ь). Сформулируем условия, при которых справедливо первое инте-
интегральное соотношение F.3.1).
Теорема 6.3.1. Пусть на отрезке [а, Ь] заданы сетка А: а = х0 <С
<С XI <С . . . < ху = Ь и функция / (х) из класса е%Г(п) (а, Ь). Если для обобщен-
обобщенного сплайна 5Д (/; х) дефекта к на А
во внутренних узлах сетки А и, кроме того, выполнено одно из условий: а) / (х) —
— 5Д (/; х) принадлежит типу Г и/ (хг) — 8А (/; я,) = 0 (I = 0, ТУ), Ь) / (х;) —
— 5Д (/; X}) = 0 (г = 0, ТУ) и 5Д (/; х) принадлежит типу 1Г, с) &д (/; х)
принадлежит типу к, А) /(а) (#г) — 8^ (/; хг) — 0 (а = 0, 1, . . ., к — 1;
I — 0, 1, . . ., Щ, функция / (х) принадлежит &С% (а, Ь) и сплайн 8А (/; х)
периодический, то первое интегральное соотношение F.3.1) справедливо.
Первое интегральное соотношение справедливо для более широкого, чем
в теореме 6.3.1, класса обобщенных сплайнов. Сплайны этого более широкого
класса обладают тем свойством, что в точках сетки задаются некоторые их
первые п — 1 производных. В отличие от сплайнов дефекта к для таких сплай-
сплайнов нет необходимости задавать в узлах сетки какие-то определенные производ-
производные, можно в различных узлах задавать различные производные. Например,
можно задать четные производные в узлах с четным номером, а нечетные —
в остальных узлах, при этом функцию / (х) считать четной производной. Кроме
того, производные 5да) (х) (а = 0, 1, . . ., п — 1) должны быть непрерывными.
Если 8$ (#г) = /^ {хг), то не обязательно требовать непрерывности функции
рп_/_1 EД; х) в точке хг, а если 5д} (хг) ^=/0) (я*)> т<> должно выполняться
равенство
Цт Рп-^^д; х)^ Нт рп-МЯд; х). F.3.3)
0 0
^—0
0)
Наконец, если Яд* (х) Ф /0) (х) при х = а или х = Ь, то функция
Рп-^-1 («^д» х) должна в этих точках обращаться в нуль. Сплайны, удовлетво-
удовлетворяющие всем перечисленным условиям, называют гетерогенными. Для гетеро-
гетерогенных сплайнов непосредственно из основного тождества вытекает
6.4. СВОЙСТВО МИНИМАЛЬНОЙ НОРМЫ 191
Теорема 6.3-2. Пусть на отрезке [а, Ь) даны сетка А: а = х0 < х^ <
<С . . . <С Хи — Ь и функция / (х) из класса &Сп (а, Ь). Если производные
) (а = 0, 1, . . ., /г — 1; г = 0, 1, . . ., ТУ) гетерогенного сплайна
(/; я) на А заданы и 5?) (/; я*) = /(а) (хг), то
ь ь ь
| A; х)\Ых+
6.4. Свойство минимальной нормы
Если выполнены условия теоремы 6.3.1 или 6.3.2, то из первого интеграль-
интегрального соотношения следует, что
ь ь
а а
Сохраним для обобщенных сплайнов терминологию полиномиальных сплайнов
и будем называть это экстремальное свойство свойством минимальной нормы;
при Ь = /)п неравенство F.4.1) выражает свойство минимальной нормы для
полиномиальных сплайнов.
Теорема 6.4.1. Пусть даны сетка А: а — х0 < аг4 < хИ — Ь и после-
последовательность У = {уга \ I — 0, 1, . . ., N; а — 0, 1, . . ., к — 1}. Среди
всех функций / (х), принадлежащих классу $Сп (а, Ь) и таких, что /<а> (#,) — У(а
(г = 0, 1, . . ., IV; а = 0, 1, ; . ., к — 1), обобщенный сплайн 8& (У; х) типа
к, если он существует, минимизирует интеграл
ь
{Ц{х)}*йх. F.4.2)
\
Если функция § (х) также минимизирует интеграл F.4.2), то § (х) и «Уд (У; х)
отличаются на решение уравнения Ь{ = 0. Кроме того, если уОа — уМа {а. —
— 0, 1, . . ., к — 1), то среди всех функций, принадлежащих классу Ш1^ (а, Ь),
периодический обобщенный сплайн типа к, если он существует, минимизирует
интеграл F.4.2) и является единственным с точностью до периодического реше-
решения уравнения Ц — 0.
Для Аг == 1 и Ь = /)п теорема 6.4.1 сводится к основному утверждению
теоремы 5.4.1. Хотя теорему о минимальном значении интеграла F.4.2) можно
сформулировать при других условиях, мы формулируем ее только для гетеро-
гетерогенных сплайнов, а другие возможные теоремы рассматриваем как частные
случаи теоремыь 6.4.2.
Теорема 6.4.2. Пусть даны сетка А: а = а;0 < ^ < . . . < х?? = Ь
и последовательность У — {Уш^, где совокупность значений ъ составляет неко-
некоторое подмножество множества 0; 1, . . ., N и совокупность значений с^ состав-
192 ГЛ. VI. ОБОБЩЕННЫЕ СПЛАЙНЫ
ляет подмножество множества 0, 1, . . ., п — 1, которое, вообще говоря,
может меняться вместе с I. Тогда среди всех функций / (х) из класса &Р1п) (а, Ь),
для которых /(ос^ (х() = у1а. при $^аг {У, гетерогенный обобщенный сплайн,
если он существует и полностью определяется последовательностью У, мини-
минимизирует интеграл
ь
^х)}*Aх. F.4.3)
Если функция % (х) удовлетворяет тем же самым условиям, что и сплайн, и так-
также минимизирует интеграл F.4.2), то д (х) и 5Д (У; х) отличаются на реше-
решение уравнения Ц = 0.
Существование обобщенных сплайнов на каждой сетке и для всех опера-
операторов Ь гарантировать нельзя; обычно они существуют, когда узлов сетки
достаточно много. В отличие от полиномиальных сплайнов мы не можем указать
явно, сколько узлов необходимо для существования обобщенных сплайнов.
Поэтому в теоремах 6.4.1 и 6.4.2 мы в явной форме требуем существования
сплайнов EД (/; х) (в случае полиномиальных сплайнов мы требовали, чтобы
число узлов было достаточно велико). Более подробно этот вопрос мы обсудим
в разд. 6-7.
6.5. Единственность
При изучении единственности можно непосредственно применить методы
гл. III и V и получить нужные результаты. Необходимо только отметить, что
если два обобщенных сплайна 5Д (У; х) и 5Д (У; х) интерполируют на А соот-
соответствующий вектор У, то их разность 5Д (У; х) — 5Д (У; х) является обоб-
обобщенным сплайном того же типа, но она интерполирует нулевой вектор. Кроме
того, эта разность обладает в узлах сетки теми же свойствами непрерывности,
что и сплайны 5Д (У; х) и 5Д (У; х). Теперь с помощью свойства минимальной
нормы нетрудно доказать, что 5Д (У; х) — #д (У; х) = 0. Таким способом
доказываются следующие две теоремы.
Теорема 6.5.1. Пусть даны сетка А: а = х0 < #4 < . . . < ж^ = Ь
и вектор У == {^а \ I — 0, 1, . . ., N; а = 0, 1, . . ., к — 1}. Пусть опе-
оператор Ь и сетка А таковы, что если ^ = 0м #(а) (я*) = 0 (I — 0, 1, . . ., ./V;
а = 0, 1, . . ., к — 1), то % (х) == 0. Тогда существует не более одного обоб-
обобщенного сплайна 5Д (У; х) типа к на А, для которого 5да> (У; хг) = у1а
A = 0, 1, . . ., -/V; а = 0, 1, . . ., к — 1), и периодический обобщенный сплайн
типа к также является единственным.
Теорема 6.5.2. Пусть даны сетка А: а = х0 < #4 < . . . <С а;я = Ь
и вектор У =■ {ую,}, где совокупность значений I составляет некоторое подмно-
подмножество множества 0, 1, . . ., И, а совокупность значений аг составляет под-
подмножество множества 0, 1, ... м п — 1, которое может меняться вместе с г.
Пусть оператор Ь и сетка А таковы, что если Ь% == 0 и #(а*) (х^ = 0 для всех
б.в. ОПРЕДЕЛЯЮЩИЕ УРАВНЕНИЯ
193
допустимых значений г и аи то $ (х) == 0. Тогда сущ гствует не более одного
гетерогенного сплайна && (У; х), удовлетворяющего условиям 5д * (У; хг) =
— у1а. для всех допустимых значений ^ иаь если только вектор У достаточен
для определения 8& (У', х).
6.6. Определяющие уравнения
Пусть функции щ (х)> . . ., и2п (х) образуют на отрезке [а, Ъ] фундамен-
фундаментальное множество решений дифференциального уравнения Ь*Ь{ = 0 и и\а) (а) —
= ^«+1 (/ = 1» 2, . . ., 2/г; а = 0, 1, . . ., 2га — 1). Если задана сетка А:
а = х0 <С XI <С . . . <С хк = Ъ, то на каждом интервале х1_1 <С х <Схг (г =
= 1, . . ., Ы) обобщенный сплайн 5Д (х) имеет единственное представление
2п
;=1,
Принимая во внимание требования интерполяции, непрерывности и краевые
условия, получаем для определения 2пЫ коэффициентов сц систему 2пЫ линей-
линейных уравнений. Вопрос о существовании решения этой системы отложим
до разд. 6.7, а здесь лишь выведем соответствующие уравнения для ряда важ-
важных случаев.
Для того чтобы получить из уравнений E.7.4) и E.7.3) соответствующие
уравнения для периодических обобщенных сплайнов и обобщенных сплайнов
типа I дефекта к, необходимо произвести следующие изменения.
A) Равенство E.7.4.1) записать в точке хг, а не &г.
B) Равенство E.7.3.7) записать в точке хн, а не к#.
' C) Равенство E.7.4.2) заменить равенством
и1 (хд Щ (хг) • • • ^2п
и\
и'2п
Щ
BП-Й-1)
и
п
F.6.2.1)
В случае обобщенных сплайнов типа II необходимо произвести изменения A)
и C) и заменить равенства E.7.3.6) и E.7.3.8) равенствами
1 0 ... О
{Ьщ}а
{Ьщ}
{Ьи2п}1
(п-2).
(п-2)
а
F.6.2.2)
13-1197
194
.ГЛ. VI. ОБОБЩЕННЫЕ СПЛАЙНЫ
И
11
Щф)
{Ьщ}ь
Щ(Ъ)
{Ьи2}ь
(Ь)
;»-2)
|(п-2)
F.6.2.3)
Для обобщенных сплайнов типа к надо проделать то же, что для сплайнов
типа II, но только равенства E.6.2.2) и E.6.2.3) заменить равенствами
1
О
О
{Ьщ}а
О
1
о
о
О
О
О
И
»1 (Ь) .
Лп-к-1)
О
,(п-к-1)
F.6.2.4)
и. Ф)
и'2(Ь)
Щп (Ь)
и2п Ф)
п-к-\)
F.6.2.5)
В формулах F.6.2.2)—F.6.2.5) через {2д7}са> обозначена а-я производная в точ-
точке х = с. Поскольку коэффициенты линейного дифференциального оператора Ьг
вообще говоря, непостоянны, мы должны вычислять функции щ (х) в точках хг>
а не Нг, ибо в общем случае функция щ (х — а) не есть решение уравнения
Ц = 0 даже тогда, когда щ (х) является решением.
Гетерогенные сплайны могут быть различного характера и требуют инди-
индивидуального подхода. Однако следует отметить, что в каждом внутреннем
узле сетки производные 5да> (х) (а = 0, 1, . . ., п — 1) непрерывны. Кром&
того, в этих узлах либо заданы производные $да) (х), либо предполагается
непрерывность функции ру EД; аг) (а = 0, 1, . . ., п — 1; а + ? = п — !)•
6.7. СУЩЕСТВОВАНИЕ . 195
Эти условия дают 2/г (ТУ — 1) линейных уравнений. В точках х = а и х = Ь
либо задаются значения производных 5да) {х), либо предполагается, что функ-
функция р\ EД; х) в этих точках обращается в нуль (се, = 0, 1, . . ., п — 1;
а + у = п — 1). Это дает еще 2/г уравнений, так что всего получается 2пN
уравнений; как раз столько же и неизвестных коэффициентов сц. При выводе
системы уравнений, связанной с гетерогенными сплайнами, следует помнить,
что р\ EД; х) линейно зависит от 5Д (х), т. е.
2п
Р\ (ЯД? Х) = 2 СЦР, (И/, X) (*!-!<*<«!). F.6.3)
^1
6.7. Существование
Теперь уже мы подготовлены к тому, чтобы применить проведенный в трех
предыдущих разделах анализ и доказать существование обобщенных сплайнов.
Доказательство проходит по той же схеме, что и соответствующие доказатель-
доказательства в гл. III и V.
Теорема 6.7.1. Пусть даны сетка А: а = х0 <С х1 < . . . <С ху = Ь
и вектор? У == {у1а \ г = 0, 1, . . ., ТУ; а = О, 1, . . ., к — 1}. Пусть опера-
оператор Ь и сетка А таковы, что если Ь§== А и #(а> (хг) = О (I = 0, 1, . . ., ТУ;
а = 0, 1, . . ., к — 1), то # (х) == 0. Тогда существуют обобщенный сплайн
5Д (У; х) типа к на А, удовлетворяющий условиям 5да> (У; хь) = у1а (I =
= 0, 1, . . ., N1 а — 0, 1, . . ., Аг — 1), и периодический обобщенный сплайн.
. Доказательство. В силу теоремы 6.4,1 если сплайн 5Д (У; х)
существует, то он единствен. Кроме того, в разд. 6.6 мы видели, что $д (х)
можно найти из системы линейных уравнений
АС = У, F.7.1)
где С — вектор коэффициентов с^, Л — матрица и У — заданный вектор.
Так как два различных множества коэффициентов сц определяют два различ-
различных сплайна, то уравнение АС = 0 имеет единственное решение и, следова-
следовательно, обратная матрица А~г существует. Теорема доказана.
Аналогично доказывается существование. гетерогенных сплайнов.
Теорема 6.7.2. Пусть даны сетка А: а = х0 ■< я4 < . . . <; я^ = Ъ
и вектор У == 0/{а}> г^е совокупность значений а* составляет некоторое под-
под0 1 1
р 0/{а}> у * р
множество множества 0, 1, . . ., п — 1, а совокупность значений I составляет
подмножество множества 0, 1, . . ., ТУ, которое меняется вместе с и Пусть
оператор Ь. и сетка А таковы, что если Ь% == 0 и #<а> (х^) ?=. 0 для всех допусти-
допустимых значений I и а(, то § (х) == 0. Тогда сущесгщуещ гетерогенный сплайн
5Д (У; х), удовлетворяющий условиям 5Д '• (У; хг)■•=* уга1 для всех допустимых
значений г и а*, если только вектор У достаточен для. определения 8А (У; х).
13*
196 ГЛ. VI. ОБОБЩЕННЫЕ СПЛАЙНЫ
Доказательство существования опирается на установленную ранее един-
единственность. Вопросы единственности в свою очередь связаны с вопросом о том,
как часто решение / уравнения Ь*Ьу = 0 и производные этого решения могут
обращаться в нуль на [а, Ь], не обращаясь в нуль тождественно. Для специаль-
специальных дифференциальных операторов Ь, таких, как Ь = /)п, на этот вопрос
можно дать вполне определенный ответ. В общем случае ситуация менее опре-
определенная. Однако известны два основных результата, доказательства которых
очевидны и потому мы их не приводим. Первый результат состоит в том, что
для каждого оператора Ь существует свое максимальное число, характери-
характеризующее, сколько раз решение уравнения Ь*Ьу = 0 и определенные его произ-
производные могут обращаться в нуль, не обращаясь в нуль тождественно. К сожа-
сожалению, точно это максимальное число неизвестно. Второй результат таков:
в любом достаточно малом интервале 2га независимых нулевых интерполяцион-
интерполяционных условий на функцию у (х) и на определенные ее производные вынуждают
ее обратиться в нуль тождественно; максимальная длина такого интервала
также неизвестна.
6.8. Наилучшее приближение
Как обобщенные сплайны типа к, так и гетерогенные сплайны зависят
линейно от своих определяющих значений. Таким образом, в обоих случаях
Яд (/ - Я х) = ЯА (/; х) - Яд (8; х).
Пусть даны сетка А: а = х0 < х1 < . . •<ялг = Ь и функция / (х) из класса
&Сп (а, Ь). Для любого сплайна Яд (х) на А
Яд (/ - Яд; я) = Яд (/; х) - Яд (Яд; х) =
= Яд (/; х) - 8А{х)
при условии, что определяющие значения сплайнов Яд (/; х), Яд (Яд; х) и
5Д (/ — Яд; х) равны соответственно значениям функций / (х), Яд (х) и / (х) —
— Яд (ж) в узлах сетки; при этом требования непрерывности также должны
быть совместными. В силу свойства минимальной нормы
или
|| /-Яд ||2-|1 Яд,/-Яд ||2 = || /_ЯД-ЯД>/+ЯД ||*,
откуда
II/ -Яд || > ||/- Яд,/ ||.
Это доказывает следующую теорему.
Те о р е м а 6.8.1. Пусть даны сетка Д: а — х0 < я4 < . . . < хк — Ь
и функция / (#) из класса $%* (а, Ь). Среди всех обобщенных сплайнов Яд (я)
типа к на & интерполяционный сплайн Яд (/; х), для которого Яда) (/; хь) ==
=* рй* (хг) (I — 0, 1, ..• ., Л"; а = 0, !,...,& — 1), если он существует,
6.9. СХОДИМОСТЬ ПРОИЗВОДНЫХ НИЗШИХ ПОРЯДКОВ 197
минимизирует интеграл
ь .
^{Ц (х) - Ь8А (ж)}2 Ох. F.8.1)
а "....'■
Если сплайн 8А (х) также минимизирует интеграл F.8.1), то 8± (х) и 8& (/; х)
отличаются на решение уравнения Ьу = 0. Далее, если функция / (х) и сплайн
#д (х) периодические, то интерполяционный сплайн типа к также минимизи-
минимизирует интеграл F.8.1) и он является единственным с точностью до периодиче-
периодического решения уравнения Ьу = 0.
Справедлива также
Теорема 6.8.2. Пусть даны сетка А: а — х0 < . . . < а;^ = Ь и функ-
функция / (х) из класса &Сп {а, Ь). Среди всех обобщенных гетерогенных сплайнов
8А(х) на А, определенных заданными условиями непрерывности и заданными
определяющими значениями 8^1 (хь), где совокупность значений г составляет
некоторое подмножество множества 0,1, . . ., Ы, а совокупность значений а*
составляет подмножество множества 0, 1, . . ., п — 1, которое меняется
вместе с I, интерполяционный сплайн 8& (/; х), удовлетворяющий условиям
5д 1 (/; хг) = / (хг) г для всех допустимых значений Ьиаг {если только эти усло-
условия достаточны для его определения), если он существует, минимизирует инте-
интеграл F.8.1). Если сплайн 8^\х) также минимизирует F.8.1), то 5Д {х)
и 8^ (/; х) отличаются на решение уравнения Ьу = 0.
6.9. Сходимость производных низших порядков
При обсуждении сходимости мы ограничимся обобщенными сплайнами
типа к. Укажем, однако, что и у периодического обобщенного сплайна типа к,
обобщенного сплайна типа I дефекта к и обобщенного сплайна типа II дефекта к
также есть регулярно расположенные точки, в которых сплайн и его произ-
производные интерполируют значения функции / {х) и соответствующих ее произ-
производных. Поэтому здесь, как и в разд. 5.9, применима теорема Ролля и, следова-
следовательно, для перечисленных сплайнов можно получить аналогичные свойства
сходимости. Мы сформулируем соответствующие теоремы, но значительную
часть обсуждений и доказательств проведем только для сплайнов типа А:. Гете^
рогенные сплайны, которые мы рассматриваем, имеют иррегулярности в свой-
свойствах интерполяции и непрерывности, связанные с начальной сеткой данной
последовательности сеток {А^} (Ы = 1, 2, . . .); мы будем предполагать, что
А1 ^ Адг № — 1, 2, . . .). Упрощения можно достичь за счет требования,
чтобы в узлах сетки А^, не принадлежащих Аь выполнялось условие
•^д^ (/» х) — / (х) и сплайн 5Длг (/; х) имел в этих узлах дефект 1 (разд. 1.2).
В этом разделе сходимость доказывается так же, как в разд. 5.9, с одним лишь
важным исключением, относящимся к применению неравенства Минков-
ского.
198 ГЛ. VI. ОБОБЩЕННЫЕ СПЛАЙНЫ
Пусть даны функция / (х) из класса &Сп (а, Ь) и последовательность обоб-
обобщенных сплайнов {#д»г (/; х)} № = 1» 2, . . .) типа к. Бели (А#: а ~ х$ <С
<^<а;^<. ..<ж|; = Ь} —соответствующая последовательность сеток,
то 5Й! (/; х^) = /<а) {х?) Н = 0, 1, . . ., т^; а = 0, 1, . . ., к — 1). Много-
кратно применяя теорему Ролля, получаем, что $1°^ (/; х) интерполирует /(а) (х)
при а !> 2Аг по крайней мере один раз в каждых а — 2к -\- 2 последовательных
интервалах сетки и при 0 ^ а ^ 2к — 4 по крайней мере один раз в каждом
интервале сетки. Следовательно, для каждой точки х из [а, Ь] можно найти
такую точку хаК, что 5д°^ (/; хаК) = /(а) (жа2^) @^ а <; п) и | ж — хаТГ |-<
^ Яа || Ад- II, где Ка = а — 2А; 4- 2, если 2А; ^ а ^ п — 1, д Ка = 1, если
0 ^ а ^ пип BА;, га — 1). Кроме того, если х не совпадает ни с а, ни ^ Ъ и N
достаточно велико, то узлы интерполяции лежат по обе стороны от я, и тогда
Ка = (а — 2к +' 2)/2 при 2к ^ а ^ га — 1. Таким образом,
8
F.9.1.1)
• F.9.1.2)
Здесь, как и в предыдущих главах, мы использовали неравенство Буняков-
ского — Шварца. Повторим этот процесс для а = п — 2, но вместо неравен-
неравенства Буняковского — Шварца применим неравенство F.9.1). Тогда получим
^^ F.9.2)
а в общем случае
№> (/ *)
(а = 0, 1, ..., п — 1). F.9.3)
С помощью неравенства F 9.3) оценим величину 3 сверху и в свою очередь
подставим эту оценку в F.9.3). Тем самым докажем равномерную сходимость
функций 5^ (/; х) к /(а) (х) (а = 0, 1, . . ., п — 1) для х 6 Ы, Ы
По определению
И-^(/; х)}, F.9.4)
а в силу неравенства Минковского
.. ь ь
[о, (х) Ип {/ (х)-8А„ (/; »)}!• й^} 1/2< { | [Ь {/ И - 5дА. (/;
а
6.9. СХОДИМОСТЬ ПРОИЗВОДНЫХ НИЗШИХ ПОРЯДКОВ 199
. Ь
... + {] [«о (*) {/ (х) -8*,, (/; *)р Ох} 1/2. F.9.5)
а
Перенесем часть членов налево и воспользуемся неравенством F.9.3):
ь
{Д/ (*) - Ь3ь„ (/; *)}* <&}1/2, F.9.6.1)
а
где
ЛГ-1= ш! |а»(ж
2() р |^()|{1}^|||| F.9.6.2;
3=0
Так как ап (х) ф 0 и коэффициенты а; (ж) (/ = 0, 1, . . ., п) непрерывны на
отрезке 1а, Ы, то при достаточно малом значении || А^ || константа К. положи-
положительна и ограничена. Таким образом, если выполняется свойство минимальной
нормы или свойство наилучшего приближения и А1 ^ А^ (Ы ^ 1), то кон-
константа / ограничена. Отсюда вытекает справедливость следующих двух теорем.
Теорема 6.9.1. Пусть дани функция /(х) из класса &Рп(а,Ь) и после-
последовательность сеток (Ддг: а = х^ <С х± <... • <С х^ — 6} (IV—{, 2, ...),
|}ЛЛг||-*-0 при Л^-*-ос. Если последовательность обобщенных сплайнов
{Зд^у (/; х)} (IV—1, 2, ...) дефекта к такова, что
Л2(/;*?)-/(а)(*Г) (« = 0, 1, ..., к-1; 1 = 1, 2, ...,.т„-1),
и выполнено одно из условий: а) все сплайны 8&К (/; х) принадлежат типу к,
Ь) функция 1(х) принадлежит классу 8Рр(а, Ь), 8^ (/; х?) — /(а> (х1?)
(а=-0, 1, ..., к— 1; г —0) ц все сплайны 'З'д^/; ^) периодические, с) разность
] (х) — Яд^ (/; х) обращается в нуль при х—а и х-=Ъ и принадлежит типу Г
(Л^ — 1, 2, ...), с1) разность / (гс) — Яд^ (/; ж) обращается в нуль при х — а
и х — Ь, А1^Ан^>1) и 5д (/; %) — 8ьк({', х) принадлежит типу 1Г ^ =
— 1, 2, ...), то 5ля а —0, 1, ..., ге —1 последовательность (<5'д^(/; ж)} сд:о-
дится равномерно на [а, Ь] к /(а) (х) и
И - Й# (/; х)\ = О (|| А„ ||(*»-*«»-*)/»). F.9.7)
Теорема 6.9.2. Пусть даны функция / (х) из класса &Сп (а, Ь) и последо-
последовательность сеток (Д^: а = ^<^<... <^ = Ь} ^ = {, 2, ...), || Ддг || ~*-0
200 ГЛ. VI. ОБОБЩЕННЫЕ СПЛАЙНЫ
при N-+00, Дх е Ддг (N^1). Пусть последовательность обобщенных гетеро-
гетерогенных сплайнов {5д^(/; х)} (ТУ— 1, 2, ...) такова, что сплайн Яд^ (/; х)
имеет дефект 1 в каждом узле сетки Д^, не принадлежащем. Дъ и интер-
интерполирует функцию / (х) в этих точках. Пусть для каждого значения I
из некоторого подмножества множества 0, 1, ..., тА и для значений а?
из подмножества множества 0, 1, ..., п— 1, зависящих от г, «о не завися-
зависящих от Н, выполняются условия З^. (/; хЬ — ^а0 (х\). Пусть эти интерпо-
ляционные условия достаточны для определения каждого сплайна 6д (/; х).
Тогда для а = 0, 1, ..., п — 1 последовательность 8*?^ ({; х) сходится равно-
N
мерно на [а, Ь) к /(а) (х) и справедливо равенство F.9.7).
6.10. Второе интегральное соотношение
При выводе первого интегрального соотношения мы пользовались-
тождеством
, F.10.1)
связывающим линейный дифференциальный оператор Л и его формально
сопряженный Ь*. Пусть даны сетка Д: а = хо<Сх1<.... <#дг = & и функция.
/ (х) из класса &Сгп (а, Ъ). Положим и(х)={ (х) — 5д (х) и V (х) -- Ь? (х) — //6'д (х),
где Яд (х) — обобщенный сплайн на Д, соответствующий оператору Ь. Тогда
^ A-1, 2, ..., Л"). F.10.2).
Обозначим
Рг (/ - 5Д; х) = 2 (~ IK' [вп-1*/ И {^/ И ~ ^Д (^)}]0>) (г=0, 1, ..., /г -1);.
3=0
F.10.3)
тогда Р[/(х) — 8& (х), Ь/(х) — Ь8&(х)] можно записать в виде
F.10.4)-
в.Ю. ВТОРОЕ ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ
201
Эта формула вытекает из F.2.2), и обозначение, принятое в ней, согласуется
с обозначениями в разд. 6.3. Из F.10.2) и F.10.4) следует, что
Г {Ы(х)-Ь8А(х
г=1 3=0
Ь
4- ( {/ {х) - 5д (х)} Ь*Ь{ (х) ах.
F.10.5)
Если сумма
2
С!
(б.ю.6)
обращается в нуль, то из F.10.5) получаем соотношение
ь
йх= \
F.10.7)
а
а
называемое вторым интегральным соотношением для обобщенных сплайнов.
Если 5да* (#0= / (#0 @^а<Сл) во внутреннем узле ж* сетки, то соответ-
соответствующий член в сумме F.10.6) в точке х% равен нулю. С другой стороны,
при /(а) (г,-) Ф «5гда> (#г) вклада в сумму в точке #* также не будет, если
Шп
= 11т
^—0
F.10.8)
Если /(а) (ж) — 5да> (х) Ф 0 при х = а и х~ Ъ, то для того чтобы не было вклада
в сумму, мы требуем, чтобы в соответствующей точке функция рп-а-1 (/ — Зд» х)
обращалась в нуль. Эти рассуждения доказывают следующие две теоремы.
Теорема 6.10.1. Пусть даны сетка А: а = х0 <.хх<С ... <Схк = Ь
и функция /(#) из класса &Сш(а, Ъ). Если обобщенный сплайн 5д(/; х) на Д
дефекта к таков, что 8^ (/; а?*) =/(а> (а?|) (а = 0, 1, ..., & —1; г = 1, 2, ...
..., N — 1) и выполнено одно из условий', а) <5да) (/; ж^) =/(а> (Жг) (а = 0, 1, ...
..., Аг— 1; 1 = 0, ЛГ) к {ЬНхй — ЬЗьф ^)}(а) = 0 (а = 0, 1, ..., п — к-1;
1 — 0, ТУ), Ь) функция / (ж) принадлежит классу &Сгр (а, &), сплайн 8& (/; ж)
периодический и 8^ (/; х*) = /(а) (а;г) (а = 0, 1, ..., /с—1; г = 0), с) разность
{(х) — 5д(/, ж) обращается в нуль при х—.а и х = Ь и принадлежит типу Г,
A) разность / (г) — 5д (/; #) обращается в нуль при х — а и х — Ь и принад-
принадлежит типу 1Г, то
х)
их
{/ (х) - Яд (/; х)
202 ГЛ. VI* ОБОБЩЕННЫЕ СПЛАЙНЫ
Теорема 6.10.2. Пусть даны сетка Д: а — хо<Сх1<..,. • <.&к — Ь
и функция / (#) из класса а%2п(а, Ь). Пусть обобщенный гетерогенный сплайн
<5д(/; х) на Д удовлетворяет условию 8^г) (/; х{) = /(аг-) (жг), когда совокупность
значений I составляет некоторое подмножество множества 0, 1, ..., ТУ и сово-
совокупность значений а* составляет подмножество множества 0, 1, ..., п—1,
зависящее от I, и эти интерполяционные условия достаточны для определения
сплайна <5д(/; х). Если Яд^ (/; ж*) ^*=/(а) (ж*) для некоторого 1A = 0, 1, ..., ТУ)
и некоторого а(а = 0, 1, ..., п— 1), положим,
НШ рл-а-Л/ — Яд; Я)= ИШ Рп-а-1 (/ —
+0 —0
при 1=^=0, гфЫ и
при Ь — 0 м./ш г = ТУ. Тогда
ь ь
^ {Ь1 (х) -Ь8ь (/; х)У йх=^{1 (х) -Яд (/; *)} ^^/ [х) <2г.
а а
6.11. Улучшение оценки по рядка . сходимости
Для большинства интересующих нас обобщенных сплайнов из F.9.1.2),
F.9.3) и F.9.6) вытекает, что
ъ
'Кп., ...Ка {
а
(а = 0, 1, ..., /1-1). F.11.1)
Условия, при которых выполняется неравенство F.11.1), приведены в разд. 6.9,
и там же указаны значения констант К и Ка (а = 0, 1, . . ., п — 1). Неравен-
Неравенство F.11.1) выполняется даже для гетерогенных сплайнов, если || Д^ || умно-
умножить на соответствующую константу, но при условии, что точки иррегулярно-
иррегулярности в свойствах непрерывности и интерполяции содержатся лишь в ограничен-
ограниченном числе сеток из рассматриваемой последовательности. Если мы предполо-
предположим, что справедливо неравенство F.11.1) и второе интегральное соотношение,
то те же рассуждения, что и в разд. 5.11, приведут к неравенству
н /(а) -й&/" ~ < кг Кп~1 {Кп~* - • • к«J к«-1 * • • к° V[Пь"д» ||2п~1~а
а
(а = 0, 1, ..., п— 1). F.11.2)
Чтобы была видна аналогия с гл. V, в неравенстве F.11.2) использовано
обычное обозначение
11/11— ^р |/(*)| F.11.3)
6.11. УЛУЧШЕНИИ ОЦЕНКИ ПОРЯДКА СХОДИМОСТИ 203
и специальное обозначение
Ь $
УИ\г.= }\Ь*Ь1(х)\дх. F.11.4)
о
Фактически мы доказали следующие две теоремы.
Теорема 6.11.1. Пусть даны последовательность сеток {А^: а —
— х^<С.х^<С ... <%тк — Ъ} (N — 1, 2, ...), ||А^||->-0 при #->-оо, и функ-
функция /(х) из класса &2п(а,Ъ). Если последовательность обобщенных сплайнов
{<5д^(/; #)} (N = 1, 2, ...) такова, что *Й^(/; а^) —•/(а) (**) (а —0, 1, ...
..., к — 1; 1—1, 2, ..., л% — 1) и выполнено одно из условий: а) разность
/(х)—8^(/;х) (N=1,2, ...) обращается в нуль при х = а и х — Ь
и принадлежит типу V, Ъ) функция /(я) принадлежит классу ё%рП(а, Ь),
сплайн 5д (/; х) периодический и / (х0) = 8)^! (/; х0) (а = 0, 1, ..., к — 1;
N = 1, 2, ...), с) разность / (г) — Яд^ (/; х) обращается в нуль при х = аи х = Ь,
принадлежит типу IV и Д4 е Д^ (#— 1, 2, ♦..), й) функции /(а) (а;) —
^~~ № \ \ / * ■^/ / \^" *~"~ ^1 "^ * • ■ ■ > '■' ^~~ ^ / ™ \*^И^У л # ^ Л -- I # • •** II \^^ "~~" ^? -^ * • " ■
..., п — к—1) обращаются в нуль при х = аих — Ь (N=1, 2, ...), то равно-
равномерно по х на отрезке [а, Ь]
Теорема 6.11.2. Пусть даны функция / (х) из класса Ж п (а, Ь) и последо-
последовательность сеток
II Д# II ->- 0 при N-+00 и Д4 е Д^ Щ ^> 1).
Пусть последовательность обобщенных гетерогенных сплайнов {«^д^ (/; х)}
(# = 1, 2, . . .) такова, что каждый гетерогенный сплайн 8/^1^ (/; х) имеет
дефект 1 в каждом узле-сетки Д#, не принадлежащем Д4, и интерполирует
функцию / (х) в этих узлах. Пусть для совокупности значений I, составляющей
некоторое подмножество множества 0, 1, . . ., т\, и для значений аг, состав-
составляющих подмножество множества 0, 1, . . ., п — 1, зависящее от г, но не
зависящее от N, выполнено условие 8*?^ (/; х\) = /(а»> (х\). Если в требованиях,
N
налагаемых на гетерогенный сплайн, заменить рг («Яд,/; х) на рг (/ — •З'д,/'» %), то
/(а) (я?) = 8]?% (/; х) + О (|| Дл, И211-*) (а = 0, 1, . . ., п - 1)
равномерно относительно х 6 Ы, Ь], если только условия интерполяции доста-
достаточны для определения сплайна 8±к (/; х).
204 ГЛ. VI. ОБОБЩЕННЫЕ СПЛАЙНЫ
6.12. Сходимость производных высших порядков
Пусть даны сетка Д:а = а;0<;х1<;. . . < хн = 6 и функция/ (х) из клас-
класса &С%п (а, Ь). Если обобщенный сплайн Яд (/; х) дефекта к вместе со своими
первыми к — 1 производными интерполирует на А функцию / (х) и ее первые
к — 1 производных, то 5гда) (/; х) интерполирует /(а> (х) по крайней мере один
раз в каждых а — 2к + 2 последовательных интервалах сетки при 2к ^ а ^
^ 2/г — к — 1 и один раз в каждом интервале при 0 ^ а ^ 2к. Таким образом,
• 1 \/ \Х)—<5д Ц, X)} ОХ
А || (а = 0, 1, ..., 2/г — к — 1), F.12.1)
где константа #а определяется, как в разд. 6.9, но теперь для значений а
вплоть до 2/г — к — 1, а% — подходящим образом выбранная точка, в кото-
которой 5да) (/; х) интерполирует /(а) (х). Следовательно, если мы оценим сверху
величину ||/(а+1)— Яд^1* И», независимо от || А^ ||, то будет доказана сходи-
аюсть 8^ (/; х) к /(а) (х) (а = 0, 1, . . ., 2/г — к — 1) при Ц Д^ |[ ->- 0.
Известно, что при я^_1 ^ х ^ х-г
2п
(х), F.12.2)
где функции щ (х) и коэффициенты Сц определены в разд. 6.6. Если коэффициен-
коэффициенты с^ ограничены при || А || ->• 0, то величины || 8^} ||«> (а = 0, 1, . . ., 2/г —
— к — 1) также ограничены, а так как и || /<а> ||«о (а = 0, 1, . . ., 2/г — к — 1)
ограничены, то отсюда следует нужная нам сходимость. Для доказательства
ограниченности коэффициентов сц воспользуемся методами разд. 5.12. Для
некоторой точки ха1 из отрезка [я^_1, х{]
<ЕА,, [*м, *!] =<5'да) (/; «а,)- F-12.3)
Более того, в разд. 6.11 было показано, что
/-1, F.12.4)
где В0 = К{Кп_1}^Кп_2 ... Ко. В силу F.12.2) и F.12.3)
2п
2 С^5а) («а,) (а = 0,1, ...,2/г-1;1 = 1, 2, ...
F.12.5)
Оцепим левую часть равенства F.12.5):
и х{] < {2аЛд}« В0\Г [Пь \\ А Ц2"-" +1«? [«м, ^г! I
A = 1, 2, ..., #; а = 0, 1, ..., 2/г—1), ( ' ' '
6.12. СХОДИМОСТЬ ПРОИЗВОДНЫХ ВЫСШИХ ПОРЯДКОВ 205
где
-|1А|1 ,. F.12.6.2)
Величины
< •
(а=0, 1, ...,2/1-1)
при || Д || ->- 0 стремятся к нулю равномерно как относительно номера, так
и относительно положения отрезка [#*_ь х{). Так как функции щ (х) образуют
фундаментальную систему решений уравнения Ь*Ь1 — 0, то коэффициенты
ограничены, если только ограничены величины Л?д.
Теорема 6.12.1. Пусть даны функция / (х) из класса е/Г2П (а, Ь), после-
последовательность сеток Д^: а = хо <.Х1 < ... "Сх^ — Ь^ = 1,2, ...), ЦД^Ц-^О
при N-+00, и последовательность обобщенных сплайнов {8^ (/; х)} (ТУ =
= 1,2,...) дефекта к. Если 8{*> (/; жГ) = /<а> (а?) (а = 0, 1, ..., к — 1; * =
= 1, 2, ..., тц — 1) и выполнено одно из условий: а) 8^ (/; х^) = /<а> (хГ)
<а = 0,1, ...,*-1; 1 = 0, т^), {^д„ (/; а:Г)-^/(хГ)}(а) = 0(а = 0, 1 п-
— к— 1; г = 0, игдт) к Д4 е Д^ (ТУ — 1, 2, ...), Ь) функция / (х) принадлежит
классу Ж? (а, Ъ), 8%* (/; *Г) = /<а> (л?) (а = 0, 1, ...,*-1; 1 = 0;^ = 1,2, ...)
« каждый сплайн 8^A; х) периодический, с) разность /(х) — 8АкA;х) обра-
обращается в нуль при х = а и х = Ъ и принадлежит типу Г (N — 1,2, ...),
4) разность / (х) — б'д^ (/; ж) обращается в нуль при х = а и х = Ь и принадле-
принадлежит типу IV и Д4е Д^(ТУ = 1, 2, ...), то последовательность {8%^ (/; х)}
сходится равномерно на [а, Ъ] к функции /<а> (х) (а = 0, 1, ..., 2/г — к— 1) к
/(а) (я) = Яд^ (/; *) + 0(|| Д^||2п~а~й)» яри условии, что величины Л^, опреде-
определенные равенством F.12.6.2), ограничены.
Теорема 6.12.2. Пусть даны функция /(х) из класса &Сгп{а,Ь)у после-
последовательность сеток Ддг: а = хо < х* < ... < ж^ = 6, ТУ — 1, 2, ..., || Д^ || -> 0
при N->- со, и последовательность обобщенных гетерогенных сплайнов {8& (/; х)}
(N=1, 2, ...). Пусть сплайн 8^ (/; ж) имеет дефект 1 <? каждом узле
сетки Д^, ке принадлежащем Д4, м интерполирует функцию / (ж) в а^шх
узлах. Пусть для совокупности значений а*, составляющих некоторое под-
подмножество множества 0, 1, ..., /г—1, зависящее от I, но не зависящее от ТУ,
•выполнено условие 8^ (/; #!) = /(«> (ж|). Ясли в требованиях на гетерогенные
сплайны заменить рг^д,/; #) «а Рг (/ —^д,/,* ж), пго равномерно по х на отрез-
отрезке [а, Ъ]
^ -«-1) (а-0, 1, ..., 2/г-2), F.12.7)
206 ГЛ. VI. ОБОБЩЕННЫЕ СПЛАЙНЫ
если только величины НА ограничены и интерполяционные условия доста-
достаточны для определения сплайна 8^(^;х).
Замечаниеб.12.1. Если5'^(/;аг?')==/(«)(я:|лг) (а-0, 1, ...,& — 1) в узлах
сетки, не принадлежащих Д4, и каждый сплайн 5^ (/; х) имеет дефект к
в этих узлах, то равенство F.12.7) справедливо для а = 0, 1, ..., 2п — к — 1Г
по показатель 2/г—а—1 надо заменить на 2/г — а — к.
Слегка изменив рассуждения, использованные при доказательстве двух
предыдущих теорем, можно доказать следующую теорему.
Теорема 6.12.3. Если выполнены условия теоремы 6.12.1 или 6.12.2,
то равномерно относительно х на [а, Ь]
Ит8^1 (/; х) -/<а> (х) (а = 0, 1, ..., 2п- 2). F.12.8)
Доказательство. В самом деле,
F.12.9)
Далее, в силу ограниченности коэффициентов Сц относительно N производные
■$л°2 (/» х) (а = 0, 1, . . ., 2/г — 2) равномерно ограничены и равностепенна
непрерывны на интервалах сетки (в качестве значения производной в узлах,
где условие непрерывности нарушено, берем односторонний предел). В любом
интервале (хг-_4, х{) можно найти такие точки х^а и х^а, что
F.12.10)
Так как 6"+л = 6| + б", то для завершения доказательства остается приме-
применить неравенство Треугольника.
6.13. Ограничения на порядок сходимости
Если функция / (х) принадлежит классу С2п [а, Ь], то указанную в теоре-
теореме 6.12.1 оценку можно улучшить, но лишь до определенной границы. Для
кубических сплайнов эта граница дана в разд. 3.12, а для полиномиальных
сплайнов нечетной степени — в разд. 5.13. Для обобщенных сплайнов этот
вопрос исследуется аналогично.
Теорема 6.13.1. Пусть последовательность сеток {А.у} С#" = 1»
2, . . .) такова, что ]| А^ |] -+■ 0 при N-^-00 и Я = зир /?Длг <С с». Пусть
N
функция / (х) принадлежит классу С2п (а, Ь) и \1 >• 0. Если для последователь-
последовательности обобщенных сплайнов {Яд^ (/; х)} (ЛГ = 1, 2, . . .) дефекта к
1 (х) = Яд„ (/; х) + О (|| Д„ ЦЯЧ*) F.13.1)
6.13. ОГРАНИЧЕНИЯ НА ПОРЯДОК СХОДИМОСТИ 207
равномерно относительно х на [а, 6], то
ь*и (х) == о.
Доказательство. С помощью методов разд. 6.12 можно показать,
что при выполнении условий теоремы
Ит 8$ (/; х) = /<*> (х) (а = 0, 1, ..., 2»), F.13.2)
ЛГ->оо
при этом на каждом шаге надо заменить 2/г — а — 1 на 2/г — а + М" Как
следствие отсюда получаем, что
Ь*Ы (х) = 11т {Ъ*Ц (х) - Ь*Ь8А (/; *)} =-- 0
для почти всех х. Теорема доказана.
Ограничения, наложенные в теореме 6.13.1 на приближаемую функцию
и приближающую последовательность интерполяционных сплайнов, не являют-
являются единственно возможными. В гл. IV нам встречались другие ограничения
подобного характера. Для обобщенных сплайнов они имеют следующий вид.
Теорема 6.13.2. Пусть даны функция / (х) из класса С [а, Ь] и после-
последовательность сплайнов {8ьц (/; х)} (Ы — 1, 2, . . .), интерполирующих функ-
функцию / (х) на последовательности сеток {А^-} (N = 1,2,.. .), || А^ || ->- 0 при
к Если
2п
/; *) = 2 4*
1
и коэффициенты с$ ограничены относительно ./V, то функция / (х) принадле-
принадлежит классу С2""*1 [а, 61.
Доказательство. В силу ограниченности коэффициентов с$ после-
последовательности {5д^ (/; х)} (а = 0, 1, . . ., 2п — к — 1) равномерно ограни-
ограничены и равностепенно непрерывны. Следовательно, можно найти такую функ-
функцию Ра (ж), что для подходящей подпоследовательности сеток {Ат} (т =
= 1, 2, . . .)
Й» (/; х)=Ра(х) (а-0, 1, ..., 2п-к-1)
то
равномерно относительно х на [а, 6]. Таким образом, каждая функция Ра (х)
непрерывна. Более того, так как сходимость равномерна, то
X
ТИ-»-»
а
х
п — Л—2)
208 ГЛ. VI. ОБОБЩЕННЫЕ СПЛАЙНЫ
Итак, функция /^ (х) принадлежит классу С2*"'* [а, Ь] и совпадает с функ-
функцией / (ж), ибо они обе непрерывны и в силу интерполяционных свойств после-
последовательности (<5Д^ (/; х)} совпадают на множестве, плотном в [а, Ь]. Теорема
доказана. .
Замечание 6.13.1. Условия интерполяции можно заменить сходи-
сходимостью последовательности сплайнов к / (х).
6.14. Приложения к теории гильбертова пространства
Как показано в разд. 5.1, класс Жп (а, Ъ) со скалярным произведением
ь
х)дх F.14.1)
становится гильбертовым пространством после отождествления функций, отли-
отличающихся на решение уравнения Ц — 0. Если на отрезке [а, Ь\ задана после-
последовательность сеток {А^} (ЛГ = 1, 2, . . .), Д^ <и А^+ь то, как в гл. V,
можно образовать конечномерные подпространства /*д^ (к, Ь), состоящие из
всех обобщенных сплайнов дефекта к на Д^, и подпространства [-^д^ {(к, Ь) —
— ^д^ (к, Ь)], состоящие из тех элементов подпространства ^д^+1 (к, Ь), опреде-
определяющие значения *) которых на А^ равны нулю. Аналогично можно образовать
подпространства Р&К(к, Ь) и [Рд^+1(&, Ь)—Р^К{к, Ь)\ периодических сплайнов,
подпространства Р"^(кг Ь) и 1^д^+1 (к, Ь) — Р'ь^к, Ц\ сплайнов типа II'
и подпространства Гд^ (к, Ь) и и д№+1 (к, Ь) — Гд^ {к, Ь)\ сплайнов типа к.
Можно также рассмотреть линейные подпространства гетерогенцых сплай-
сплайнов, удовлетворяющих тем же условиям непрерывности в узлах, но имеющих
другие определяющие значения. Мы ограничимся рассмотрением гетерогенных
сплайнов, которые в точках сетки, не принадлежащих А19 имеют дефект к.
Обозначим подпространства, аналогичные подпространствам Р^ы (к, Ь) и
1^д„+1 (К Ц - Р^ (к, Ц], через #д„ (к, Ь) и 1#д„+1 (к, Ь) - #д„ (к, Ц\
соответственно. Если не будет возникать недоразумений, мы не будем указы-
указывать зависимость от к и Ь, например вместо Р^К (к, Ь) будем писать просто
Рь.К* Подчеркнем особо, что, задавая различные условия непрерывности, кото-
которым должны удовлетворять гетерогенные сплайны в узлах сетки Ль мы полу-
получаем различные подпространства НА^ Образуем бесконечные прямые суммы
(к, Ц =^Д1 (К Ь) 0 Д 0 [Рь„+1 (*, Ц -*ь„ (К Ц], F.14.2.1)
D, Ь)-Рья{к, Ц], ' F.14.2.2)
АГ=1
х) Под «определяющими значениями» мы понимаем здесь и в оставшейся части
гл. VI заданные значения сплайна и его производных.
6.14. ПРИЛОЖЕНИЯ К ТЕОРИИ ГИЛЬБЕРТОВА ПРОСТРАНСТВА 209
^к, Ц-П„(к, Ц], F.14.2.3)
(к, Ц - Тн (к, Ь) © Д 0 [Та№+1 (к, Ц - Т^ (к, Ц\% F.14.2.4)
(*, Ь) -ЯД1 (&, Ь) ф| © [Яд^+1 (*, Ь) -Яд^ (/с, Щ. F.14.2.5)
Д
Ортогональность составляющих подпространств доказана в разд. 6.15. В том
же разделе показано, что если ]| А^ || ->• 0 при N ->- оо, то все эти бесконечные
суммы, за исключением, быть может, ?дв (к, Ь), совпадают друг с другом
и тождественно равны Жп (а, Ь).
В гл. V мы установили, что пространство <г%*" (а, Ъ) при натуральном п
плотно в &Сп (а, Ь) относительно нормы
ь
11/11 — Г Г \Т)п4 (т\ 12 ЛГ1 *'2 (а \А 31
а
Покажем сейчас (теорема 6.14.1), что сумма е5Гр(а, Ъ) + Рп-1 (а> &) плотна
в &Сп (а, Ь) относительно нормы
ь
|| / ||ь = 11 Щ (х)]2 сЬ}1/2, F.14.4)
а
определенной скалярным произведением F.14.1). Здесь Рп-\ (а, Ъ) — линейное
.пространство полиномов на [а, Ь] степени п — 1, а е5Гр(а, Ь) + Рп-\ (а, Ъ) —
линейное пространство, натянутое на е5Гр(а, Ь) и Рп-\ (а, Ъ).
Теорема 6.14.1. Линейное пространство Жр(а, Ъ) + Рп-\ (а, Ь) плот-
плотно в з/Гп (а, Ь) относительно нормы
ъ
1/2
Если Ь = /)п, то &С^ (а, Ь) плотно в Жп (а, Ъ).
Доказательство. Рассмотрим сначала частный случай Ь == /)п.
Пусть дана произвольная функция / (х) из класса &Сп (а, Ь). Так как #п/ (я)
принадлежит I»2 (а, Ь), то /)п/ (х) разлагается в ряд Фурье, частичная сумма
которого является периодической функцией на [а, Ь]. Каждую из частичных
сумм можно проинтегрировать п раз и выбрать константы интегрирования
(положив их равными нулю) так, чтобы получившаяся функция РК (х) была
периодической. Так как || / —7^ ||я« ->■ 0 при N ->■ оо, то для частного слу-
случая Ь == /)п теорема доказана.
14—1197
210 ГЛ. VI. ОБОБЩЕННЫЕ СПЛАЙНЫ
Для доказательства теоремы в общем случае покажем, что сходимость
относительно нормы \\-\\вп влечет сходимость относительно нормы ||*||ь» ГДО
п — порядок дифференциального оператора Ь.
Та!? как е%Гр(а, Ь) плотно в &Сп (а, Ь) относительно нормы П'У^п, то можно
найти такую последовательность функций {Р м (х)} (ДГ = 1, 2, ...) из с/Гр(а, Ь)г
что ||/—Ри\\вП-*-0 при N ->- оо. Заменим последовательность {^^ (х)}
последовательностью {7^ (х)} (# = 1, 2, . . .), где Рк(х) = Ру (х)-}-Р^ (х).
Полином Рх (х) степени п — 1 выбран так, что Р{а) (а) = /(а) (а) (а = 0, 1, ...
..., п — 1). Применяя неравенство Буняковского — Шварца, получаем
ь
{п)Ру/\ F.14.5.1)
F.14.5.2)
F.14.5.гг)
а
Ь
где константы К} (/ = 0, 1, . . ., /г — 1) не зависят от N. Из определения
Ь [/ (х) — Т^у (х)], неравенства Минковского и неравенств F.14.5) имеем
ъ ь
а а
Ъ Ь
1/2<к
а а
откуда следует, что ||/ — Р^ ||ь ->- 0 при N ->- с», и теорема доказана.
В гл. III было показано, что &С% (а, Ъ) является гильбертовым простран-
пространством относительно нормы ||*|1о2, в гл. V аналогичное утверждение доказано
для е%Гп (а, Ь) и нормы П'П^п- Здесь мы покажем, что е5Гп (а, Ь) является гиль-
гильбертовым пространством и относительно нормы |Н1г,- Если принять во внима-
внимание псевдохарактер нормы, то при соответствующих нормах все свойства,
кроме полноты пространства, становятся очевидными. Последнее свойство
также легко доказать.
Теорема 6.14.2. Пространство Шп (а, Ь) полно относительно нор-
нормы ||.||ь.
Доказательство. Предположим, что {/^} (Лг — 1, 2, . . .)
последовательность Коши относительно нормы ||«||ь« Тогда {Ь{я} Ш
6.15. СХОДИМОСТЬ ПО НОРМЕ 211
2, . . .) — последовательность Коши в Ь2 (а, Ь). Так как пространство 1?
полно, то эта последовательность сходится к некоторой функции % (х) из II (а, Ь).
Если / (х) — решение г) уравнения Ц (х) = § (х), то / (х) принадлежит &Сп (а, Ь)
и II /л- — / Иь ->■ О ПРИ N -*■ оо. Таким образом, <Жп (а, Ь) полно относительно
нормы \\-\\ь.
6Л5. Сходимость по норме
Теорема 6.15-1. Пусть заданы функция /(#) из класса ЗРп(а,Ь),
последовательность сеток {Дл-: а = х^ <С.х^<С ... <С#^ —^(N—1, 2, ...),
Дау с Д№+1, ||Адг||—>0 при ./V—»оо, и последовательность обобщенных сплайнов
{•^АдЛ/; х)} С^—1, 2, ...) дефекта к. Если сплайн 8ь.^(/; х) интерполирует
функцию / на сетке А*, /(а) (х*) - 5^ (/; ^) (а- 1, 2, ..., к— 1; I = 1, 2, ...
..., т^— 1) (./V ^ 1, 2, ...) и выполнено одно из условий: а) / (х) — 8^ (/; х) при-
принадлежит типу Г (#=1, 2, ...), Ь) / (х) — Яд^ (/; х) принадлежит типу IV
(ЛГ=1, 2, ...), с) /(•) (**) = 5к^ (/; ^) (а = 1, 2, ..., к-1; < = 0, т^; ЛГ =
=^1, 2, ...) и каждый сплайн 8^A; х) принадлежит типу к, д) ^а)(х^) =
= <5гл^(/; ф (а^1» 2, ..., &—1; г-0; Л"=1, 2, ...), функция Цх) при-
принадлежит классу <2%*р (а, Ь) и каждый сплайн 8^ (/; х) периодический, то
Нт
Доказательство. Так как 3& (/; х) можно считать интерполяцион-
интерполяционным сплайном для 5д^ (/; х) (М > 1), то последовательность {|| б'д^ (/; х) ||ь}
(ЛГ=1, 2, ...) монотонно возрастает и ограничена сверху величиной Ц/Ць.
Это вытекает из первого интегрального соотношения, из которого также сле-
следует, что
Так как последовательность {|| ^а^, / ||ь) сходится, то {5д^(/; х)} — последова-
последовательность Коши относительно нормы Ц-Ць- Как и в разд. F.9.6), легко пока-
показать, что при достаточно малом значении ЦАдгЦ Для некоторой положитель-
положительной постоянной К, не зависящей от N,
Таким образом, {8%^(}; х)} — последовательность Коши в Ь2 (а, Ъ). Если
предел в Ь2 (а, Ь) этой последовательности и
X
1) В качестве решения можно взять решение в смысле Каратеодори (см. Сансонв
и Конти [1, стр. 11]).
14»
ГЛ. VI. ОБОБЩЕННЫЕ СПЛАЙНЫ
ТО ■ ■ . •
-аI/2 { Г
а
и при ТУ—> оо правая часть неравенства F.15.1) стремится к нулю. Отсюда
следует, что /(п~4) {х) == О (х) на [а, 6], поэтому
, Шп 11^-/11^ = 0. F.15.2)
Далее,
-^ (о:) —^^^ (/; о:) |<:F —аI/2 || /_б'^, /|1х>«+ I /^"^ (^~^-^ (/' а> >' .
F.15.3.1)
»{1; а)
+ |/(п~2) (а)-^72) (/;«)!» F.15.3.2)
п
(п-*> (а)-^7Й (/; а)|. F.15.3л)
Из этих неравенств при достаточно большом ТУ получаем
где К — положительная постоянная, не зависящая от N. Теорема доказана.
Те же рассуждения можно применить к последовательности гетероген-
йых сплайнов, так что справедлива
Теорема 6.15,2. Пусть даны функция /(ж) из класса &Сп(а, Ь), после-
последовательность сеток {ДЛт: а~х^<.х^<с ... <-х^ =Ь) (№ — 1, 2, ...), А^ сг
сгДет+1, ЦАдгЦ—>0 при ТУ—> оо, и последовательность обобщенных гетероген-
гетерогенных сплайнов, удовлетворяющих условиям теоремы 6.9.2. Тогда
Приведем непосредственные аналоги леммы 5.15.1 и теоремы 5.15.3 для
обобщенных сплайнов.
6.16. КАНОНИЧЕСКИЕ СЕТОЧНЫЕ БАЗИСЫ 213
Лемма 6.15.1. Пусть на отрезке [а, Ъ] заданы две сетки Д4 и Д2, А1 с
сг А2 и два обобщенных сплайна 5Д1 (х) и 5д2 (х), удовлетворяющих в узлах
сетки Д4 одним и тем же условиям непрерывности. Если в узлах сетки Д4 заданы
одни и те же значеиия сплайнов и их производных и определяющие значения
сплайна 8&2(х) в узлах сетки Д4 равны нулю, то
(ЯД1, 8^ь = 0.
Доказательство. Пусть сетку Д4 определяют точки а — х0 <С
<С хх <: . . . <: хн — Ь. Тогда
г=1
N
г=1
1
1=1 *«-*
Последняя сумма равна нулю потому, что если какое-нибудь ее слагаемое
не аннулируется непосредственно другим слагаемым (в силу непрерывности),
оно умножается на определяющее значение сплайна 8&2 (х) на А4 и обращается
в нуль. Это доказывает лемму, из которой в свою очередь следует
Теорема 6.15.3. Пусть на отрезке [а, Ъ) задана последовательность
сеток {А^} Щ = 1, 2, . . .), А^- с: А^+1 и II Ал- 1 ] —*— 0 при N ->■ оо. Тогда
бесконечные прямые суммы F.14.2) представляют собой ортогональные разложе-
разложения относительно (/, §)ь и, кроме, быть может, РДой (к, Ь), совпадают с
$Сп (а, Ь). Для РДоо (к, Ь) справедливы включения
&С% (а, Ь) = РАоо (к, Ь) = &Сп (а, Ь).
6.16. Канонические сеточные базисы
Мы не будем здесь давать определение и построение канонических сеточ-
сеточных базисов для РАсо (к, Ь), ^Дво (к, Ь), ГДво (к, I) и РДи (к, Ь), так как это
делается точно так же, как в гл. V. Однако аналог леммы 5.16.1 формулируется
и доказывается иначе. Доказательство более сложно в том смысле, что нужно
еще показать, что если 5^ (Ь; х) — элемент канонического сеточного базиса,
связанного с линейным дифференциальным оператором Ь порядка и, то
|| 5, (I; х) \\вп ^К\\8г (Ь; х) \\ь, F.16.1)
где положительная постоянная К не зависит от г. Эта постоянная нам понадо-
понадобится при выводе аналога неравенства E.16.2).
214 ГЛ. VI. ОБОБЩЕННЫЕ СПЛАЙНЫ
Итак, мы следуем разд. 6.9. Так как определяющие значения сплайна
5$ (Ь; х) равны нулю во всех узлах сеток, предшествующих сетке л^ (последо-
(последовательность сеток {пг} A = 0, 1, . . .) возникает при построении каноническо-
канонического сеточного базиса), то в качестве функции / (х) можно взять нулевую функ-
функцию. Таким образом, в F.9.1) можно положить
* ъ
/2 = ^ {^п) (I; х)У их. F.16.2)
Далее, тем же методом, что и в разд. 6.9, доказывается существование кон-
константы К, не зависящей от I, при которой выполняется неравенство F.16.1).
Следовательно, существуют такие положительные постоянные Ка, не завися-
зависящие от г, что справедлив аналог леммы 5.16.1. Для этих постоянных нет про-
простого представления, так что мы не будем приводить их явного значения.
Лемма 6.16.1. Пусть канонический сеточный базис {8{ (Ь; х)} A = 1, 2, ...)
для [Р^(к,Ь)-Р^{кЬ Р{кЬ)ПЛкЬ Т(кЦТ(кЦ
(к, Ь)~Н^(к, Ь)] или [Р^(к, Ь)~Рд4 (Л, Ц] определяется с помощью
последовательности сеток {Адг} (N = 1,2, ...), Л^ с: Адг+1. Пусть при построе-
построении сплайнов 8г (Ь; х) использована соответствующая последовательность
сеток {я*} A — 0, 1, 2, ...). Тогда существуют такие постоянные Ка, не зави-
зависящие от I, что
\3[а) (Ь; х)\^Ка\\л1-1\\Bп-2а-1)/2 (а=0, 1, ..., п-1). F.16.3)
С помощью этой леммы можно доказать следующий аналог теоремы 5.16.2.
Теорема 6.16.1. Пусть канонический сеточный базис {81 (Ь; х)}
A = 1,2, . . .) таков, что \\ я^|| = О A/г)« Тогда существуют такие действи-
действительные числа ра ;> 0, что
8а (х) = 2 {^а) (^; ^)}2<Р« @<а</г-2). F.16.4)
г=1
Элементы 5г (Ь; х) канонического сеточного базиса не только ортогональ-
ортогональны, но при Адг си А^+1 базис для ^д^+1 получается просто расширением бази-
базиса для ^Дд,- Пусть сетка Адг задана точками а — х0 <С гг4 <С . . . <С хк = Ь.
Если для построения базиса для ^Ддг используются фундаментальные сплайны
•Я* (Адг; х), определяющие значения которых во всех точках, кроме хь равны
нулю, а в этой точке лишь одно из них равно единице, то не только сохра-
сохраняется ортогональность, но при переходе от ^Ддг к Р^к 4 нет необходимости
строить полностью новое множество базисных элементов. Эта ситуация в ка-
какой-то степени аналогична использованию интерполяционной формулы Ньютона
вместо интерполяционной формулы Лагранжа. Если надо, добавить точки
интерполяции, то приходится полностью построить новое множество фунда^
6.17. ЯДРА И ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ 215
ментальных многочленов Лагранжа (Дэвис [1, стр. 41]); в то же время, чтобы
учесть новые точки интерполяции, достаточно только дополнить новыми
членами интерполяционную формулу Ньютона.
6.17. Ядра и интегральные представления
В настоящем разделе мы приведем для обобщенных сплайнов аналоги
теорем разд. 5.17. Все теоремы справедливы также и для гетерогенных сплай-
сплайнов. Так как доказательства несущественно отличаются от прежних, то мы
их опускаем.
Теорема 6.17.1. Пусть функция / (#) принадлежит классу &Сп (а, Ь)
или <&Ср{а,Ъ) и сплайны {8[(Ь, к; х)} A = 1, 2, ...) вместе с {щ (Ь, к; х)}
A — 1,2, ...,т) образуют канонический сеточный базис для Р^ (к, Ь), Р'^ (к, Ь),
Т^ (к, Ь), #Доо (к, Ь) или РДоо (к, Ь), который является ортонормалъным бази-
базисом для <&Сп (а, Ь) или &С%(а, 6). Тогда для каждой точки х из [а, Ь]
\){) {х) (а = 0, 1, ..., я-1), F.17.1)
а
где ЬО (х) == 0 для х^[а, Ь] и
Нах (Ь, к; х, г) =
= I! *4а)(Ь, к; х)Ьщ (Ь, Л; 0 + 2 $а> (Ъ *; х) Ь81 (^ *; 0. F.17.2)
г=1 г=1
причем сходимость в F.17.1) равномерна относительно х из [а,Ь].
Следствие 6.17.1. Пусть функция /(х) принадлежит классу &Сгп (а, Ь)
или <2/Г|,п(а, Ь) и сплайны {8г (Ь, к; х)} (ъ= 1, 2, ...) вместе с {щ (Ь, к; х)}
(б= 1, 2, ..., т) образурт канонический сеточный базис (см. сноску на стр. 181)
для Рьм (к, Ь), Р'Аоо (к, Ь), ГДоо (к, Ь), ЯДоо (к, Ь) или РДоо (к, Ц, который яв-
является ортонормалъным базисом для е/Гп(а, Ъ) или &С%{а, Ъ). Тогда равенство
F.17.1) справедливо для всех х^[а, Ь] и а = 0, 1, ..., 2п — 2. В случае гете-
гетерогенных сплайнов предполагается, что максимальный дефект не превосходит к.
Теорема 6.17.2. Пусть последовательность сеток {я*} (I - 0, 1, 2, ...)
на [а,Ъ] определяет канонический сеточный базис для ^Доо (/с, Ь), Р'^ао(к, Ь),
Ть^ф, Ь), Нь^^Ь) или Р^оо(к, Ь), который является ортонормалъным
базисом для &Сп (а, Ь) или ЗРр (а, Ь). Если функция Нак (Ь, к; х, I)
задана равенством F.17.2), то {Нах} (а = 0, 1, ..., п — 2; N-- 1, 2, ...)
для всех х является последовательностью Коши в Ьг (а, Ъ) и, следовательно,
последовательностью Коши в Ь (а, Ъ). Если На (Ь, К; х,1) (а = 0, 1, ..., п— 2) —
ее предел, то для функции / (х) из класса <Жп (а, Ъ) или &С* (а, Ь)
2^6 ГЛ. VI. ОБОБЩЕННЫЕ СПЛАЙНЫ
Ъ
/<а) (х) = ^ Яа (Ь, к; х, 1)Ц (г) &1 + 0{а) (х), F.17.3I
а
где ЬО (х) = 0 для х ^ [а, Ь]. Кроме того, сходимость равномерна относительно
х^[а, Ь] и На (Ь, к; х, г) получается из Н^^ {Ь, к; х, г) формальным диффе-
дифференцированием по х.
Замечание 6.17.1. Мы предполагали, не оговаривая это особо, чта
сетки {я*}, применяемые при построении канонического сеточного базиса для
е5Гп(а, Ь) или &С% {а,*Ь), удовлетворяют условию || я* || = О^Ц).
6.18. Представление и приближение линейных функционалов
Для обобщенных сплайнов можно сформулировать и доказать аналог»
всех четырех теорем, приведенных в разд. 5.18, но так как доказательства
в основном остаются прежними, мы не будем их здесь повторять. Рассмотрим
несколько примеров приближения линейных функционалов, в которых при
аппроксимации интеграла берутся равноотстоящие значения подинтегральной
функции. Эти примеры рассматривал Сард [1, гл. II]; они иллюстрируют метод,,
которым в теории сплайнов можно получить многие из его многочисленных
«наилучших приближений». Мы дадим также приложения теории обобщенных
сплайнов к вычислению собственных значений линейного дифференциального-
оператора. В конце этого раздела укажем применение гетерогенных сплайнов
к приближению точечных функционалов %х: /->-/(:г).
Теорема 6.18.1. Пусть функция /(х) принадлежит классу &Сп{а,Ъ)
или &р(а,Ъ) и сплайны {8{ (к, Ь\ х)} A = 1,2, ...) вместе с {щ (к, Ь; х)}
A—1,2, ..., т) образуют канонический сеточный базис для рА0О{к, Ь),
Р'ь.^ (к, Ь), Ть^ (к, Ь), ЯД(х> (к, Ь) или Рд^ (к, Ь), который является ортонор-
малУным базисом для &Сп (а, Ь) или &Ср (а, Ь). Если линейный функционал X
имеет вид E.18.1), то
ь
#о/ = Нт Г Нк{к, /,; г)Ц{г)д,1-\-%оО, F.18.1.1)
.№->-оо Л
а
где
то л?
Н„ (к, Ь; х)= 2 оцЬщ (к, Ь; 0+ 2 Р«ВД (к, Ь; х), F.18.1.2)
1=1 {=1
т| Ь
^-0 а
г\ Ь
..., т), F.18.1.3)
F.18.1.4)
3=0 а
и ЬО(х) = 0 для всех х из отрезка [а, Ь].
6.18. ПРЕДСТАВЛЕНИЕ И ПРИБЛИЖЕНИЕ ЛИНЕЙНЫХ ФУНКЦИОНАЛОВ 217
Следствие 6.18.1. Пусть функция / (х) принадлежит классу 8%2п(а,ЬУ
или Ж1п(а,Ъ) и сплайны {8г (к, Ь; х)} (г = 1,2, ...) вместе с {щ (к, Ь; х)}
(г = 1,2, ..., п) образуют канонический сеточный базис для ^^(к, Ь),
^"^{к, Ь), Тцк<х>{к,Ь), НАоо(к, Ь) или Р^оо(к, Ь), который является ортонор-
мальным базисом для Шп{а,Ъ) или $%р(а,Ь). Если линейный функционал X
имеет вид
п ъ
#о/=2 р^^ФПО, F.18.2)
3=0 а
где \Ь){1) — функция ограниченной вариации на [а, Ь], то справедливо равен-
равенство E.18.1), но только теперь т)<2п — к—1.
Замечание 6.18.1. И в теореме, и в следствии из нее функция О (х\
зависит от/ (х), но ядро Я^ (к, Ь\ х) не зависит от/ {х). Доказательство по суще-
существу использует равномерность сходимости подпоследовательности сплайнов^
и их производных к функции / (х) и ее производным, а не скорость этой сходи-
сходимости. Поэтому, учитывая теорему 6.12.3, в следствии 6.18.1 нужно требовать,
чтобы к] было меньше 1п — 2, а не 2/г — к — 1.
Теорема 6.18.2. Пусть функция / (х) принадлежит классу &Сп (а, Ь)
или &Ср(а,Ъ) и сплайны {8 г {к, Ь; х)} A=1,2, ...) вместе с {щ (к, Ь; х)}-
A—1,2, ..., т) образуют канонический сеточный базис для Р>^0О(к, Ь),
Р'^оо{к, Ь), Т^оо(к, Ь), Н^оо(к, Ь) или Р^оо(к, Ь), который является ортонор-
малъным базисом для &Сп (а, Ь) или Ш"у> (а, Ь). Если линейный функционал X
имеет вид E.18.1), где Ц-^п — 2, то последовательность {Я^ (к, Ь; х)} является
последовательностью Коши в Ь2 (а, Ь) и, следовательно, последовательностью*
Коши в Ь{а, Ь). Если И {к, Ь; х) — ее предел, то
ь
Хо}= \ Н(к, Ц 1)ЦA)й1 + Х<>а, F.18.3>
а
где ЬО (х) = 0 для всех 'х ^ [а, Ь].
Сформулируем теперь аналоги теорем 5.18.3 и 5.18.4 о приближении
лилейных функционалов.
Теорема 6.18.3. Если линейный функционал X задается формулой
E.18.1), а линейный функционал В таков, что
В*1 = Ьо8ь,и F.18.4>
где 8ь{1; х) — интерполяционный сплайн для функции / (х) из класса &Сп(а, Ъ)
или №%(а, Ь), представляющий собой линейную комбинацию функций {щ (к, Ь; х)}
(г =1,2, ,.., т) и О(х), то
Ь N
Х°{ — Бо/ = 1пп Г {V $1ЬЗг(к, Ь; {)\ Ц{1)аЧ, F.18.5.1)
а 1=1
218 ГЛ. VI. ОБОБЩЕННЫЕ СПЛАЙНЫ
■где
т| Ь
а . X* Г о О") (Ъ. т . о\ /I.. , /о\ /,• л о л/Л /А 4 Я К О\
Рг — 7\ 1 <^г \у"> л-1! 8) О)*} \8) \1 = \., 6, . . •, *У )ч ^О.Ю.О.лу
2=0 а
а ц^(я) (/ = 0,1, ..., т]) — функции ограниченной вариации на [а, Ь], связан-
связанные с оператором X представлением F.18.1).
Теорема 6.18.4. Если линейный функционал X имеет вид E.18.1),
а линейный функционал В удовлетворяет условию F.18.4), причем ц <; п — 1, то
ь
Х°1 — Во! = Г II (к, Ь; I) Ц (I) аЧ.
а
Функция Н (к, Ь; I) принадлежит пространству I/2 (а, Ь) и является преде-
пределом в смысле среднеквадратического последовательности
N
Ни (к, Ь; х) = 2 р\'^ (&> Ь; х), F.18.6.1)
г=1
где
Р* = 2 ? ^ ^' Ь; 5) а& № (Л< »); F.18.6.2)
3=1 а
функции {А/ (§) имеют ограниченную вариацию на [а, Ь] и зависят только от X
(снова / (х) — функция класса $Сп (а, Ъ) или е/Тр (а, Ь)). Если В — любой линей-
линейный функционал вида E.18.9) и X — В аннулирует решения уравнения Ц (х) =
= 0, то для к << п
ь
Н (к, Ь; г) Ь] (Г) йг, F.18.7)
а
где функция Н (к, Ь\ Ь) принадлежит I? (а, Ь) и определяется, как в теоре-
теореме 6.18.2, только теперь X следует заменить на X — В. Кроме того, интеграл
ь
{Н (к, Ь; *)}2 <й F.18.8)
а
принимает наименьшее значение, если В удовлетворяет условию F.18.4).
ь
Замечание 6.18.2. Если на коэффициенты аи, фигурирующие в фор-
формуле E.18.9), наложены дополнительные ограничения, то условие F.18.4)
не всегда удовлетворяется. Однако, как правило, можно добиться выполнения
условия F.18.4), используя гетерогенные сплайны. Это, в частности, можно
■сделать, если некоторые из коэффициентов а и должны быть нулями. Кроме
того, если функция / (х) принадлежит классу &Сгп (а, Ь) или з^Гр71 (а, Ь), то в тео-
6.18. ПРЕДСТАВЛЕНИЕ И ПРИБЛИЖЕНИЕ ЛИНЕЙНЫХ ФУНКЦИОНАЛОВ 219
реме 6.18.3 условие г\ <С п в равенстве E.18.1) следует заменить условием
г\ <С Ъг — 2. Напомним, что дефект к сплайна никогда не превосходит п, т. е.
порядка оператора Ь.
Рассмотрим теперь приближение интеграла
1
Х*1 = | / (х) Ах F.18.9)
функционалами вида
Во! = а4 (-1) + аа/ @) + а/A). F.18.10)
Можно было бы рассмотреть произвольный отрезок [а, Ь] и положить
F.18.11)
но вычисления при этом становятся более громоздкими. К тому же, допу-
допуская упрощение F.18.9), мы не теряем общности, так как
1
} }
а —1
и потому
что эквивалентно равенству F.18.11).
Потребуем дополнительно, чтобы для линейных функций приближение
было точным. Тогда по теореме 5.18.4 (или 6.18.4)
1
#0/ — Во /= Г Нв @ Я2/ (*) <И F.18.12)
-1
и интеграл
1
{Нв (ОJ й% F.18.13)
I
принимает наименьшее значение, когда #о/ = Х<>8^^, где #д (/; х) —
кубический сплайн типа 1Г, интерполирующий функцию / (х) на сетке А:
—1 < 0 < 1. Пусть
^ О
тогда
*^д (/; #) = ^и^! ((х) -\~ спщ (х) + СщЩ (х) + С14^4 (ж) (—1-^#^0), F.18.15.1)
о Д ^у , «1/^ — ^21 1 \ / "Т" ^22 2 к / "| ^'23'*3 \ / ~1 24 4 \ / \ '^^•'*' "^%- ■'■/ IV/» АО» АО»»ьу
220 ГЛ. VI. ОБОБЩЕННЫЕ СПЛАЙНЫ
И
0 0 0 0
%о8ь?1 — Сц \ Щ (х) их + с12 I щ {х) скс + с^ \ щ(х) Ах-{-си \ и4(х)с1х-{-
-1 -1 Л -1
1111
+ С21 \ Щ (х) их-\- с22 \ и2 (х) их ~\- с23 \ и9 (х) Ах-\~ с24 \ щ (х) их.
Ъ I Ъ Ъ
Поскольку
1 0
ущ (х)Aх = 1, \ щ(х)с1х=1,
0 -1
1 О
\ и2 (х) их = 1, \ щ (х) их — — у,
о
} 8 6
0 -1
1 О
щ (х) йх — ^, Г щ (х) Aх — — ^,
О -1
ТО
Из интерполяционных свойств сплайна #д (/; х) вытекает, что
— 1) - с14 — с12 + у с13 —-^ с14,
1 1
/ A) =г с21 + с22 + у с23 + -^-
24,
а условия непрерывности производных #д (/; х) и Яд. (/; а?) в точке х = О
дают с12 = с22 и с13 = с23- И наконец, так как сплайн принадлежит типу 1Г, то
О = с43 — с14, 0 = с23 + с24.
Итак,
= ^2 Я = С14 = —С24
И
Кроме того, с14 = /@), так что
6.18. ПРЕДСТАВЛЕНИЕ И ПРИБЛИЖЕНИЕ ЛИНЕЙНЫХ ФУНКЦИОНАЛОВ 221
Отсюда следует равенство
л _ 3/(-1)-6/@)Ч-3/A)
с13 — ^ ,
из которого в свою очередь вытекает, что
Эта формула называется правилом 3—10—3; ее получил Сард [1, стр. 42],
непосредственно минимизируя интеграл F.18.13).
Если потребовать, чтобы функционал В был точен для полиномов второй
степени, то с меньшим усилием можно получить более известную квадратурную
формулу. В этом случае
1
Хо{ - Во! = \ Пв {г) Я8/ (I) ЛЬ, F.18.17)
ж интеграл F.18.13) принимает наименьшее значение, когда Бо/ = #о#д/,
где #д (/; х) — сплайн пятой степени типа 1Г, интерполирующий функцию
У (х) на сетке А. Так как функция
)= х+
интерполирует / (х) на А и является сплайном пятой степени типа 1Г на А,
то в силу единственности сплайна #д (/; х)
Яд (/; х) = у (х).
Следовательно,
/(_1)-2/@)+/A) +2/@)=
«5
эта формула известна под названием формулы Симпсона. Ее также получил
Сард, непосредственно минимизируя интеграл F.18.13). Кроме того, Сард
показал, что если функционал В точен для полиномов третьей степени, то
остаток имеет вид
| нв {I) Я4/ {г) <к. F.18.19)
При этом интеграл F.18.13) также принимает наименьшее значение, когда
функционал В определяется по формуле Симпсона.
Вывод этой формулы с помощью теории сплайнов приводит к серьезным
трудностям, так как полиномиальные сплайны седьмой степени типа 1Г опре-
определяются на А неоднозначно. Один из возможных сплайнов — полином у (х)
второй степени, определяемый равенством F.18.18); он дает формулу Симпсона.
Если же к сетке А добавить любую четвертую точку р, то па новой сетке А
полиномиальный сплайн 5д (/; х) седьмой степени типа IV определится
222 ГЛ. VI. ОБОБЩЕННЫЕ СПЛАЙНЫ
однозначно и совпадет с кубическим полиномом, интерполирующим / (х)
на Д. Если #о/ = ^о5Л)у и функционал В точен для кубических полино-
полиномов, то равенство F.18.19) справедливо, и при таком выборе В интеграл F.18.13)
принимает наименьшее значение.
Пусть
и (х) = -=-:— ;
тогда кубический полином и (х) обращается в нуль на А и равен 1 в точке р.
Кроме того,
Яд (/; х} = у (х) + {/ (р) - у (р)} и{х)
и %°8ь,; = %°У + {/ (р) — У (р)} Х°и = #оу. Итак, мы подтвердили
хорошо известный результат, что формула Симпсона точна для кубических
полиномов, и указали, все еще в соответствии с Сардом, аппроксимирующий,
функционал вида F.18.10), точный для кубических полиномов. При этом
остаточный член представим в виде F.18.19) и интеграл F.18.13) принимает
наименьшее значение, когда функционал В определяется из формулы Симпсо-
Симпсона. Кроме того, мы показали, что добавление четвертого узла к сетке А
и рассмотрение аппроксимирующих функционалов В вида
Во! = а/ (-1) + Щ @) + с/ A) + й/ (р)
не приводят к улучшению приближения интеграла относительно меры F.18.13).
Мы разобрали примеры, в которых участвовали только полиномиальные
сплайны; теперь нам понадобятся обобщенные сплайны. Рассмотрим задачу
вычисления собственных значений линейного дифференциального операто-
оператора F.1.1) при условии, что задано п линейно независимых вспомогательных,
условий, каждое из которых требует, чтобы функция / (х) или одна из ее пер-
первых п — 1 производных обращалась в нуль в некоторой точке отрезка [а, Ь].
Ограничимся простым случаем, когда вспомогательные условия заданы только
на концах отрезка. Пусть
/(аг> (а) = 0 A = 1,2 I; Щф ау, * ф /), ^
/<*/> (Ь) - 0 (/ = 1,2 /; V* ф У^, * Ф Я,
где I -\- I — п и все числа аг и у^ меньше п. Пусть дана сетка А: а = х0 <С
<С хх <С . . . <С Хц — Ь и ^2~д обозначает семейство простых обобщенных сплай-
сплайнов 5д (Ь; х), связанных с оператором Ь и удовлетворяющих краевым усло-
условиям F.18.20) и дополнительным условиям
рп_а1_! EУ, а) - 0 (I - 1, 2, . . ., /),
* F.18.21)
Рп-у,-1 (Яд; Ь) = 0 (У = 1,2,..., /),
где функция ру (ь>; гс) определяется формулой F.3.2). Кроме того, мы пред-
предполагаем, что если Ьу === 0 и у удовлетворяет условиям F.18.20), то у =■ 0.
6.18. ПРЕДСТАВЛЕНИЕ И ПРИБЛИЖЕНИЕ ЛИНЕЙНЫХ ФУНКЦИОНАЛОВ 223>
Прежде чем приступить к задаче о собственных значениях, связанной \
с оператором Ь и условиями F.18.20), рассмотрим задачу нахождения решения
неоднородного уравнения
х) = е (х), а < х < Ь, F.18.22)
удовлетворяющего условиям
/(а*> (а) =АЬ (I = 1, 2 /; а, ф а,, * ^ ;), 6 18 23)
/(V,) F) = в, (] = 1,2 /; уг ^ у,-, * =^ ;),
где / + / — л и числа а$ и уу меньше п. Если решение соответствующего одно-
однородного уравнения удовлетворяет условиям @.18.23) и можно найти частное
решение уравнения F.18.22), удовлетворяющее однородным краевым услови-
условиям F.18.20), то неоднородное уравнение также разрешимо.
Заметим, что ^"д — пространство со скалярным произведением
а
Пусть его размерность равна т и {иь (Ь; х)} (г = 1, 2, . . ., т) — его орто-
ортогональный базис. Пусть {Р(} (г = 1, 2, . . .) — последовательность различных
точек из [а, Ь), отличных от узлов сетки Д. Образуем последовательность сеток
{п(} (г = 1, 2, . . .), начиная с п0 = А и последовательно добавляя по одной
точке /^ в порядке их нумерации, причем последовательность {Рг} должна
быть такой, чтобы выполнялось условие || я* || — О A/г)- Таким образом,
можно ввести такие дополнительные ортонормальные сплайны 5г (Ь; х), удов-
удовлетворяющие краевым условиям F.18.20) и F.18.21), что последовательность
(«!?г (Ь; х)} (г = 1, 2, . . .) вместе с {иг (Ь; х)} {I — 1, 2, . . ., т) образует
канонический сеточный базис для Шп (а, Ь). Пусть функция / (х) удовлетво-
удовлетворяет уравнению F.18.22) и краевым условиям F.18.20). Тогда по теореме 6.17.2,
если краевые условия F.18.20) однозначно определяют решение дифференци-
дифференциального уравнения F.18.22), то
ь
/ (х) = | Я (Ь; х, г) Ц @ &, F.18.24)
а
где Н (Ь; х, г) — предел в смысле среднеквадратического последовательности
{Я* (Ь; х, 0} № = 1, 2, . . .),
то N
#* (Ь; х, г) -- 2 щ (Ь; х) Ьщ (Ь; I) + 2 #* (ь'> х) Ь8г (ь'> *)• F.18.25)
г=1 1—1
Применяя лемму 6.16.1, получаем
\5г(Ь;х)\<СК(±)п~1/2 (г-1,2, ...). F.18.26)
;224 ГЛ. VI. ОБОБЩЕННЫЕ СПЛАЙНЫ
Решение / (х) уравнения F.18.22), удовлетворяющее условиям F.18.23), имеет
вид
ь
/(*)-<? (х) -Ь ^ Н (Ь; х, *) 8 (О <й, F.18.27)
а
где С1 (#) — решение соответствующего однородного уравнения. Ядро Н (Ь; х, г)
можно интерпретировать как функцию Грина.
Задача о собственных значениях уравнения
Ъо (х) = Хи (ж), F.18.28)
где функция V (х) удовлетворяет условиям F.18.20), эквивалентна задаче
о собственных значениях интегрального уравнения
ь
и(х) = \\Н (Ь; х, г) V @ <И. " F.18.29)
Но последняя задача имеет важное преимущество перед первой, поскольку
Н (Ь\ х, I) в случае п ^ 2 представляет собой предел в среднеквадратическом
вырожденных ядер Ну {Ь\ х, I). В этом случае приближенное решение нахо-
находится из интегрального уравнения с вырожденным ядром. При обосновании
аппроксимации и установлении скорости сходимости можно использовать
неравенство F.18.26).
Применение обобщенных сплайнов в подобных задачах не ограничивается
специальными краевыми условиями F.18.20). В общем случае требования
на краевые условия должны быть такими, чтобы выполнялось первое инте-
интегральное соотношение. Если дана сетка А: а = жо<;а;1<;...'<^^ = &
и линейный дифференциальный оператор Ь, то первое интегральное соотноше-
соотношение выполняется, если
Е *Ч/-$д,/, ^д,/Ц?м -0, (E.18.30)
1
где Р (и, V) — билинейная форма оператора Ь. В силу условий интерполяции
и непрерывности, наложенных на сплайн 5Д (/; х), равенство F.18.30) прини-
принимает вид
*\ 1ьа = 0. F.18.31)
Следовательно, если разность / (х) — 8& (/; х) удовлетворяет линейным одно-
однородным краевым условиям, при которых уравнение F.18.22) имеет единствен-
единственное решение на отрезке [а, Ь\, и Ь8А (/; х) удовлетворяет сопряженному мно-
множеству краевых условий, то равенство F.18.31) справедливо. Дальше теория
развивается, как и прежде.
Другое важное замечание состоит в том, что если дан самосопряженный
дифференциальный оператор К — Ь*Ь, где Ь не имеет особенностей на [а, 6],
то можно с помощью тех же методов решить уравнение
Щ (х) = * (*), F.18.32)
6.18. ПРЕДСТАВЛЕНИЕ И ПРИБЛИЖЕНИЕ ЛИНЕЙНЫХ ФУНКЦИОНАЛОВ 225
удовлетворяющее самосопряженным линейным однородным краевым услови-
условиям, гарантирующим справедливость равенства F.18.31). Такими условиями
будут, например, условия
/(«) (а) = /(<*> (Ь) = 0 (а = 0, 1, . . ., п — 1). F.18.33)
При их выполнении
ь
/ (х) = ^ Н (Н; х, г) Щ (О <Й, F.18.34) '
а
где Я (К; х, I) — равномерный предел последовательности {Н^ (Н; х, *)}
(ЛГ = 1, 2, . . .),
т N
Н„ (Д; х, г) = 2 Щ (Ь; х) щ (Ь; 0 + 2 ^ (Ь *) ^1 (^; *)• F.18.35)
1=1 г=1
Равенство F.18.34) можно доказать так же, как равенство F.18.24). Следует
только заметить, что в этом случае
ь ь
^ Ь81 {Ь; х) Ц (хHх= ^ 8г (Ь; х) Ь*Ц (х) йх.
а а
Аналогичные замечания относятся к задаче о собственных значениях
уравнения
Л/ (х) = Я/ (х).
Если порядок оператора Я равен 2, то оператор Ь имеет первый порядок.
Поэтому неравенство F.18.26) слишком слабое для установления равномерной
сходимости Нк (Н; х, ()кЯ (Н; х, г). Однако, если в наш канонический сеточ-
сеточный базис добавлять новые узлы, двигаясь слева направо, и на каждом шаге
вводить точку, делящую пополам интервал сетки, то равномерность сходимо-
сходимости можно будет доказать. Здесь важно, что базисные элементы 8г (Ь; х) тожде-
тождественно равны нулю всюду, кроме двух смежных интервалов сетки, разделен-
разделенных узлом из соответствующей сетки щ, в котором сплайн «5^ (Ь; х) интерполи-
интерполирует ненулевое значение. Так как сплайн 5* (Ь; х) единствен и оператор Ь
имеет первый порядок, то достаточно потребовать только непрерывности
сплайна 5г (Ь; х), а не его производных. Таким образом, если бы сплайн
5* (Ь; х) не обращался в нуль тождественно на интервале сетки, в обоих кон-
концах которого он равен нулю, то это бы противоречило его единственности, ибо
тогда существовал бы другой сплайн с теми же свойствами интерполяции
и непрерывности, что и у сплайна 5$ (Ь\ х), переопределенного так, что он
на рассматриваемом интервале сетки обращается в нуль. Итак, для любой
точки х из отрезка [а, Ъ] на каждом шаге только два базисных элемента не обра-
обращаются в ней в нуль. Так как на каждом шаге сеточные интервалы делятся
пополам, то равномерная сходимость следует из леммы F.16.1).
В заключение этой главы приведем пример, в котором для приближения
линейного функционала X требуются гетерогенные сплайны. Пример взят
15—1197
226 ГЛ. VI. ОБОБЩЕННЫЕ СПЛАЙНЫ
из численного анализа или, более точно, из области численного интегрирова-
интегрирования обыкновенных дифференциальных уравнений. Предположим, что инте-
интегрирование ведется с постоянным шагом. Так как зависимость от длины шага
линейна, то можно считать ее равной единице. Рассмотрим два последователь-
последовательных интервала, определенных точками хп^, хп, хп+и в качестве этих точек
можно взять 0, 1, 2 соответственно. Таким образом, дана сетка 0 <; 1 < 2
и надо получить формулу для вычисления значения функции / (х) в точке
х — 2, зная ее значения в точках х — 0, х = 1 и значения ее первой производ-
производной во всех трех точках. Мы хотим, чтобы для кубических полиномов аппрокси-
аппроксимация была точной. (Здесь предполагается, что найдены удовлетворительные
значения функции / (х) и производной /' (х) в точках х = 0иж = 1ис помо-
помощью предварительной формулы и дифференциального уравнения получено
приемлемое значение /' (х) в точке х = 2 для использования его в уточняющей
формуле.) Наконец, мы хотим, чтобы уточняющая формула была линейной
функцией пяти величин / @), / A), /' @), /' A), /' B) и чтобы эти величины
полностью отражали зависимость формулы от функции / (х).
Из общей теории следует, что, если линейный функционал X, определяе-
определяемый равенством Х°! == / B), удовлетворяет этим условиям, то его можно
приблизить с помощью гетерогенного полиномиального сплайна Яд (/; х)
седьмой степени. Имеем
/ B) = Яд (/; 2) + М B),
где остаточный член М B) можно представить в виде
9.
М B) = \Н B, г) Я4/ (х) йг. F.18.36)
о
Интеграл
B, *)}2 йг F.18.37)
о
принимает наименьшее значение, когда в качестве аппроксимирующего функ-
функционала взят сплайн Яд (/; 2). Сплайн Яд (/; х) полностью определяется
условиями
Яд(/; 0)=/@), Яд(/; 1) = / A);
Яд (/; 0) = /' @), Як (/; 1) = /' A), Як (/; 2) = /' B);
}; 1 + 0) = Яда) (/; 1-0) (а = 0, 1, 2, 3, 4, 5);
Г; 0) = 0 (а = 4, 5);
2) = 0 (а = 4, 5, 7).
Если щ {х)« х1-1 A = 1,2, ..., 8) и
F.18.38)
Г сПи1 (Х) + С12**2 (х) + • • • + С&и& (Х)» 0"^ х
Яд (/; х) = | ^^ (х)+с22щ («)+...+ с2Вщ (х), 1
6.18. ПРЕДСТАВЛЕНИЕ И ПРИБЛИЖЕНИЕ ЛИНЕЙНЫХ ФУНКЦИОНАЛОВ
227
то условия F.18.38) дают 16 линейно независимых уравнений для выраже-
выражения 16 величин сц через / @), / A), /' @), /' A) и /' B). Точное решение этой
системы приводит к формуле
43
43
F.18.39)
полученной Сардом [1, стр. 83]. Сард указал также, что это решение устойчиво
и сходится в смысле Далквиста [1]. При численном решении системы, поро-
порожденной условиями F.18.36), получаются следующие значения коэффициентов:
А.» 0,1860464/
_35
43
« 0,8139536,
^ « 0,3488372,
-§-«1,209302,
■М-» 0,2558140.
F.18.40)
15*
Глава VII. ДВАЖДЫ КУБИЧЕСКИЕ СПЛАЙНЫ
7.1. Введение
До сих пор мы изучали только теорию одномерных сплайнов, но она легко
обобщается на бблыпие размерности. В одномерной теории сплайнов основную
роль играли простые кубические сплайны, а в двумерной теории основными
будут простые дважды кубические сплайны (разд. 1.2). В этой главе мы огра-
ограничимся простыми двумерными сплайнами, общий случай рассмотрим в гл. VIII.
Пусть на плоскости задана прямоугольная область &: а ^ I ^ Ь; с ^ 5 ^
<1 А. Если даны две одномерные сетки А*: а = Ьй<си<С....<Ц1^ = Ъ ж Д8:
с = «о < 51 < • • • < 8м = &, т0 двумерная сетка п — {Рц} A = 0, 1, ...
. . ., ЛГ; ; = 0, 1, . . ., М), где Рц = (**, $/), разбивает область № на прямо-
прямоугольники
№;•: ^-1 < * < Ь\ Ъ-1 < в < «Л A = 1,2,..., ЛГ; / = 1, 2, . . ., М).
Функция »9Я ({, з) называется простым дважды кубическим сплайном относи-
относительно сетки я, если 1) она совпадает с бикубическим полиномом на каж-
каждом прямоугольнике Мц и 2) принадлежит классу С\ (М), где С? {М) — семей-
семейство функций / {г, з), определенных на №, п-я частная производная которых,
включающая не более г дифференцирований относительно каждой переменной,
существует и непрерывна.
Как и в одномерном случае, можно провести различие между сплайном
и его представлениями. Можно представить двумерные сплайны в виде линей-
линейной функции конечного числа линейно независимых параметров; выбор этих
параметров, так называемых «определяющих значений», осуществляется не
единственным образом. В этой главе мы ограничимся определенной, но важной
группой таких представлений. Сплайн имеет представление типа!, если в число
его определяющих значений входят следующие значения его частных произ-
производных:
а) -Ц±- в узлах {Ри} A = 0, #;/ = 0, 1 М),
Ь) -Ц±- в узлах {Ри} (г = 0,1, ..., М; ; = 0, М), G.1.1)
с) ^ в узлах {Ри} (I = 0, N1 / = 0, И).
Остальные параметры, необходимые для единственности представления сплай-
сплайна 6 я (I, з), иногда не выделяют; в случае интерполяционных сплайнов на я
они совпадают со значениями сплайна #я (г, з) в узлах сетки зт. Аналсп'7чно
7.2. ЧАСТИЧНЫЕ СПЛАЙНЫ 229
сплайн имеет представление типа II, если в число его определяющих значений
входят следующие значения его частных производных:
а) -^ь- в узлах {Ри} (* = 0, ЛГ; ; = 0, 1 М),
- в узлах {/>„} A = 0,1 #;; = 0, М), G.1.2)
с) -Щ&- в узлах
Двумерные сплайны называются периодическими по I, если #я B, $).,
дЗл (*, «)/д* и д2#„ B, $)/ей2 — периодические функции с периодом Ъ — а по {.
Аналогично определяется сплайн, периодический по $. Сплайн называется
дважды, периодическим, если он периодический по I и по 5 с периодами Ъ — а
ж А — с соответственно. Наиболее удобно в качестве определяющих значений
дважды периодического сплайна взять его значения в точках {Рц} A=1,2,...
. . ., И; 7 = 1, 2, . . ., М). Такой сплайн называют дважды периодическим
интерполяционным сплайном на п. Иногда слова «дважды» и «на зт» мы будем
опускать.
Если значения G.1.1) равны нулю, то говорят, что сплайн принадлежит
типу Г. Если значения G.1.2) равны нулю, то говорят, что сплайн принадле-
принадлежит типу II'. Как и в одномерном случае, разделим функции / ({, з), опре-
определенные на &, на классы эквивалентности типа I и типа II: будем говорить,
что две функции принадлежат одному и тому же классу эквивалентности типа I,
если их частные производные G.1.1) определены и совпадают. Функции, для
которых величины в G.1.1) определены и равны нулю, называются функциями
.типа Г. Аналогично определяются функции типа II и функции типа 1Г.
Однако в отличие от одномерных аналогов эти определения зависят
от выбора сетки, ибо они зависят и от количества узлов сетки, и от их распо-
расположения на границе области М-
Исторически теория двумерных сплайнов отстала от ее одномерного анало-
аналога более чем на 15 лет. Первую попытку обобщения предприняли в 1960 г.
Биркгоф и Гарабедян [Ц. Год спустя де Бур 12] заложил основы теории дву-
двумерных сплайнов, установив существование простого сплайна типа I, интер-
интерполирующего функцию / B, «) на прямоугольной сетке. Свойства минимальной
нормы, наилучшего приближения, сходимости и ортогональности получили
в 1964 г. Алберг, Нильсон и Уолш [4, 10].
Прежде чем развивать дальше теорию дважды кубических сплайнов, рас-
рассмотрим одно полезное обобщение.
7.2. Частичные сплайны
Пусть даны прямоугольник М\ а ^ I -^ Ъ, с ^ 5 ^ й, сетка А*: а = 20 <С
<:^^<...•<:IN = Ъ^![N-\-1 функций /,- ($) (I = 0, 1, . . ., ТУ), определен-
определенных на отрезке с ^ 5 ^ й. Для каждогр 5 можно образовать одномерный куби-
кубический сплайн #д (У ($); {) типа 1Г, где
Г («) = 1/о («), А («) /И*IТ. G.2.1)
230 ГЛ. VII. ДВАЖДЫ КУБИЧЕСКИЕ СПЛАЙНЫ
Аналогично, если /0 («) = /^ ($), то можно образовать периодические сплайны
#д (У («); 2) или, если дополнительно даны две функции §0 («) и ц^ ($), можно
образовать сплайны типов I и II; при этом дополнительные производные по I
в точках ^ = аи< = 6 для данного значения 5 полагаются равными значениям
функций Цо ($) и 8х («) соответственно. При фиксированном 5 выполняются
в одномерном смысле свойства минимальной нормы и наилучшего приближе-
приближения. Если функции /* ($) (г = 0, 1, . . ., Щ, #0 ($) и ц> ($) принадлежат про-
пространству Ь (с, й)> то и #д, (У («); г), д8м (У ($); *)Ш, д*8Аг (У ($); {)Шй
принадлежат этому пространству, поскольку сплайн Яд (У («); ?) линейно
зависит от функций /{ («), §0 ($), ^^ («) и они полностью отражают его зависи-
зависимость от 5. В таком случае теорема 7.2.1 служит типичным примером теорем,
справедливых для частичных сплайнов. Ее доказательство немедленно следует
из теории одномерных сплайнов. За исключением нескольких замечаний,
касающихся сходимости и действия линейных операторов на частичные сплай-
сплайны, мы предоставляем читателю самому перенести всю теорию одномерных
сплайнов на частичные сплайны.
Теорема 7.2.1. Пусть дани сетка А*: а = *0 < *1 < • • • < *л" = &
и функций /^ («) A = 0, 1, . . •, Щ из Ь (с, д). Среди всех функций / B, «),
определенных в прямоугольнике №\ а 4^1 ^.Ъ, с^«^й, совпадающих с рг ($)
при I = %% A = 0, 1, . . ., ./V) и при каждом 8 ^ [с, 6) принадлежащих классу
з% (а, Ь), частичный сплайн 5д (У ($); {) типа 1Г, где вектор У ($) задан
формулой G.2.1), минимизирует интеграл
с а
и является единственной допустимой функцией, минимизирующей этот инте-
интеграл.
При измельчении сетки А* функции Яд4 (У («); Ь) и д8&{ (У ($); 1)/д{ для
каждого 5 сходятся соответственно к / {{, з) и д] (^, з)/д{ равномерно относи-
относительно I. Если интеграл
]
а
равномерно ограничен относительно 5, то сходимость также равномерна отно-
относительно 5. Важно заметить, что в силу линейной зависимости Яд4 (У («); г)
от /, E) (I = 0, 1 ЛГ), ^0 (<) и §„ (з)
для всех а, для которых производная даУ (з)/д8а определена. На самом деле
это соотношение выполняется для достаточно хороших линейных операторов.
7.3. СВЯЗЬ ЧАСТИЧНЫХ СПЛАЙНОВ С ДВАЖДЫ КУБИЧЕСКИМИ СПЛАЙНАМИ 231
Далее,
\ 8* (У (з); I) из — Яд ( Г У ($) й$; А .
с ' .с
В дальнейшем мы будем рассматривать простые частичные сплайны. Так назы-
называются только что введенные одномерные сплайны, если они при фиксирован-
фиксированном значении 5 являются простыми.
7.3. Связь частичных сплайнов
с дважды кубическими сплайнами
Введение частичных сплайнов облегчает построение дважды кубических
сплайнов; оно сводит его к построению одномерных сплайнов.
Пусть функция / (*, «) задана в прямоугольнике №: а ^ I -^ Ъ, с ^ 5 ^ <2.
Если сетка я; на № определяется одномерными сетками А*: а = ^0 <С ^1 <С • • •
• • ♦ <. *^ = Ь и А8: с — $0 < $! <С . . . <. 8М — & и для / (*, $) существуют
частичные производные G.1.1), то молшо положить
и для I = 0, 1, . . ., N построить сплайн #д8 (/*; «) типа I, интерполирующий
разность /$ («) — |5д8 (/*; «) принадлежит типу Г. Пусть
() ()
и ($) на Д8 и такой, что р /$ () д8 (/*; ) рд у у
#а8 (ёь 8) (г = 0, Щ — аналогичный сплайн для функций §0 (з) и ^^ («).
Обозначим через #я (/; ^, «) частичный сплайн типа I, определенный сплайна-
сплайнами #д8 (/*; «) (Ь = 0, 1, . . ., Щ и |5д8 (§г; з) (г = 0, ]У). Легко проверить,
что 8я (/; I, 8) — простой дважды кубический сплайн, интерполирующий
функцию / B, «) на сетке п. Следует только заметить, что при ^г-1-^^-^^г
-I- В10 (г) 8ь$ (вг0; 8)+В1к Ц) 8ь$ (**; «), G.3.2)
где Ац (г) (/ = 0, 1, . . ., ./V) и Вц (^) (; = 0, ЛГ) — кубические полиномы
относительно I. Но так как при «7_1-<^ «-<^ 5? (/ = 0, 1, . . ., М) функции
#а8 Иь 8) (I = 0, 1, . . ., Щ и #д8 (§г; з) (г — 0, Л^) являются кубическими
полиномами относительно 5, то в каждом прямоугольнике Мц\ 1%-\. ^ ^-^ 1%,
8^-^ •< 5 <; «у (I = 1, 2, . . ., АГ; / = 1, 2, . . ., М) функция #я (/; *, у) совпа-
совпадает с двойным кубическим полиномом. Из способа построения ясно, что
^я (/; *» 5) принадлежит классу С\ (№).
Это построение доказывает существование по крайней мере одного про-
простого дважды кубического сплайна типа I, интерполирующего функцию / B, «)
в узлах сетки п и такого, что разность/ {{, 8) — #я (/; г, 8) принадлежит типу Г.
При этом естественно сразу же возникает вопрос о единственности, ибо можно
получить второй такой сплайн, поменяв ролями переменные 8 ж I. Единствен-
Единственность будет довольно просто доказана после распространения на дважды куби-
232 ГЛ. VII. ДВАЖДЫ КУБИЧЕСКИЕ СПЛАЙНЫ
ческие сплайны свойства минимальной нормы. Можно также установить един-
единственность, исследовав более тщательно равенство G.3.2).
Аналогично строятся периодические сплайны и сплайны типа II, интер-
интерполирующие функцию / B, з) на сетке п. Заметим, что кубические полиномы
по « и I, к которым сводится сплайн #„ (/; 2, з) на границе каждого прямо-
прямоугольника №ц, дают достаточно информации для определения сплайна
&я (/; 2, «) на Мц1). Эти кубические полиномы можно получить из одномерных
сплайнов, участвующих в построении сплайна #я (/; $, $). Так как при его
построении используются значения функции / (*, $) и некоторых ее производ-
производных лишь в конечном числе тояек, то функция / B, $) является по существу
произвольной функцией на М-
7 Л» Основное тождество
Пусть функция / (г, «) принадлежит классу С\ (Я) и прямоугольник М:
л <1 2 <1 Ь; с<^5<1й с помощью сетки п разбит на прямоугольники №ц\
*г-1 < * < <!»' *;-1 < 5 < 5^ (г = 1, 2, . . ., АГ; / = 1,2,.. -., М; *0 = а^х =
= Ъ, $й = с, $м = д). Тогда очевидно, что
2
с а с а
а ь
8) д*Зп(г, 8)\ 2
Г
с а
с а
Преобразуем последний член в правой части, дважды интегрируя его по частям
относительно I:
с в
3 1^21Р "~^25Р
с 1=1
Н
х) Это утверждение нуждается в пояснении, а именно: такие величины, как д*8л/д8 дг,
в вершинах прямоугольников <%1) получены в результате построения одномерных сплайнов,
интерполирующих д81д& вдоль линий «=«/_! и *=*/, и последующего дифференцирова-
дифференцирования по *.
7.4. ОСНОВНОЕ ТОЖДЕСТВО
233
и дважды по частям относительно $:
а ъ
Г Г
) )
с а
М
1=1
I)
Отсюда и из равенства G.4.1) выводим тождество
а ь й ь а ь^
^ ^ у^ (/*> 1/1» } V щ) К, ^** ^* } V V ^ ^
с а
с а
]У
^=^
с а
г
т*
" G-4.2)
Его называют основным тождеством; в нем #я B, «) является двойным куби-
кубическим полиномом в каждом прямоугольнике Ми (г = 1, 2, . . ., ./V; ; =
= 1, 2, . . ., Л/). При его выводе не предполагалось, что функция #я (^, «)
принадлежит классу С\ (М)- Если же такое предположение сделать, то #я (I, $)
будет простым дважды кубическим сплайном на № и тождество G.4.2) при-
примет вид
\ \
с а
а р
а ь
с а
с а
д*8я (<, 8) Л
д$2 д№ Г
си
М N
Г д^и *>
[ да
да
1 1
М
— 9
+ 2
д&д1
}| ■■■■ ' ■ I |
Iй" I1*
G.4.3)
234 ГЛ. VII. ДВАЖДЫ КУБИЧЕСКИЕ СПЛАЙНЫ
Важно заметить, что, хотя производная дь8п (I, $)/д$2 д*8, вообще говоря,
не обязательно непрерывна на прямой I = ^, но ее левосторонний и право-
правосторонний пределы при 1-*-1} непрерывно зависят от 5. То же верно и для
производной дь8я (?, 8)/д$* дР, если поменять ролями переменные $ и {. Эти
свойства простых дважды кубических сплайнов были использованы при
сведении основного тождества к виду G.4.3),
7.5. Первое интегральное соотношение
При различных дополнительных условиях основное тождество приводится
к интегральному соотношению
с а с а
а ь
которое называется первым интегральным соотношением. Это снова непосред-
непосредственное обобщение одномерной ситуации. Для простых интерполяционных
дважды кубических сплайнов справедлива
Теорема 7.5.1. Пусть даны, прямоугольник М'. а-</;<;Ь, с-<5<^й
и сетка п, определенная одномерными сетками А*: а = $0 <С ^ <С . . . <^^N ~ &.
и А8: с = $0 <С $1 <С . . . <С $м =• д» Если простой дважды кубический сплайн
8п B, «) интерполирует на сетке п функцию / {{, $) из класса С\ (И) и выпол-
выполняется одно из условий: а) / (г, в) — |5Я (/; /;, 5) принадлежит типу Г,
Ь) 8п (/; {, в) принадлежит типу 1Г, с) функция / (^, $) и сплайн 8Я (/; г, в)
дважды периодические, то
с а с а
с а
Разумеется, первое интегральное соотношение справедливо и при других
краевых условиях.
7.6. Свойство минимальной нормы
В качестве непосредственного следствия из теоремы 7.5.1 получаем обоб-
обобщение на дважды кубические сплайны свойства минимальной нормы, харак-
характерного для одномерных сплайнов.
Теорема 7.6.1. Пусть даны прямоугольник М\ а -^ г -^ Ь, с -^ 5 <1 й,
сетка л, определенная одномерными сетками ^ а = 1^ <Ц\ <С . . . <С I^ = Ъ
7.7 ЕДИНСТВЕННОСТЬ И СУЩЕСТВОВАНИЕ 235
и А8: с = з0 < ^1 <С . . . <С $м = <2, и множество действительных чисел {/^}
A = 0, 1, . . ., ЛГ; / = 0, 1, . . ., Л/), где значения /у связаны с узлами сетки.
Тогда среди всех функций / (?, $) из класса С\ (М) сплайн типа II', интерпо-
интерполирующий значения /у «а я, минимизирует интеграл
Кроме того, если частная производная д/B, $)/д* задана в точках (^-, $?)
(г = 0, ТУ; / = 0, 1, . . ., М), частная производная д/ ({, 8)/дз задана в точках
Ьгу */)(* = О, 1, . . ., АГ; / = О, М) и д2/ (*, $)ЛЙ Оз — в точках (*ь *,) (г = О,
Ы; / = О, М), то соответствующий интерполяционный сплайн типа I мини-
минимизирует интеграл G.6-1). Если /0</ = {ю- (/ = 0, 1, . . ., М) и /{0 = ^м
(г = 0, 1, . . ., Щ, то интеграл G.6.1) принимает наименьшее значение,
когда в качестве функции / B, $) выбран дважды периодический интерполяцион-
интерполяционный сплайн1).
Любая другая функция, минимизирующая этот интеграл, отличается от
указанных сплайнов на решение уравнения д*?/дх%ду2 = 0, удовлетворяет
нулевым интерполяционным условиям и принадлежит типу Г, 1Г или является
дважды^периодической. Множество таких решений бесконечномерно.
7.7. Единственность и существование
Единственность дважды кубических интерполяционных сплайнов типов
1 и]П, а также дважды периодических сплайнов легко следует из единствен-
единственности в одномерном случае. Рассмотрим типичный случай дважды периодиче-
периодических интерполяционных сплайнов. Пусть два дважды периодических сплайна
#я (/*> *» 5) и ^я (/; *> 5) интерполируют на сетке я функцию / (Л, $), заданную
на прямоугольнике \$. Тогда их разность #я (/; ^, з) — 8„ (/; г, $) представ-
представляет собой дважды кубический сплайн, интерполирующий нулевую функцию
2 (г, з) на сетке я, и при I = %% или 5 = $^ она тождественно равна нулю, ибо
совпадает с периодическим сплайном, определяющие значения которого равны
нулю. А так как в /?*/ разность сплайнов совпадает с бикубическим поли-
полиномом, который на границе Кц обращается в нуль и удовлетворяет уравне-
уравнению д*{A,з)/д1?д$* — 0, то она равна нулю тождественно.
Теорема 7.7.1. Пусть даны прямоугольник М: а-^г^Ь, с<>.<й
и сетка л, определенная одномерными сетками Д<: а = 40 <С ^ < . . . < ^ =
= Ь и Д8: с = з0 <. 81 < . . . <. зм = Л. Если функция / (I, 8) задана на М,
простой дважды кубический сплайн 8Я (/; I, 8) интерполирует ее на сетке п
и выполняется одно из условий: а) / ({, з) — #я (/; {, з) принадлежит типу Г,
Ь) / (*» $) — #я (Л *» 5) принадлежит типу 1Г, с) функция / {I, з) и сплайн
8Я (/; ^, 5) дважды периодические, то сплайн 8п (/; ^, 5) является единственным.
х) Формулировка теоремы и последующие рассуждения авторов были неточны. При
переводе эти неточности устранены.— Прим. перев.
236 ГЛ. VII. ДВАЖДЫ КУБИЧЕСКИЕ СПЛАЙНЫ
Замечание 7.7.1. Так как функция / (*, 5) определена только в узлах
сетки, то в теореме 7.7.1 утверждается, что в любом классе эквивалентности
типа I или II существует не более одного сплайна, интерполирующего функцию
/ (*, з) на сетке п.
V
Доказательство существования одномерных кубических сплайнов в гл. III
основано на изучении системы линейных уравнений, обеспечивающих выпол-
выполнение условий интерполяции и непрерывности, наложенных на сплайн. В этом
случае из доказанной единственности следовало, что система линейных урав-
уравнений разрешима. В двумерном случае не вполне очевидно, как записать про-
простым способом конечную систему линейных уравнений, обеспечивающих тре-
требуемую непрерывность сплайна #я (/; 2, $) и ого производных вдоль прямых.
Однако здесь существование вытекает из построения сплайна $„ (/; {, $), выпол-*
пенного в разд. 7.3, поскольку при этом построении требовалось лишь сущест-
существование одномерных сплайнов. А раз существование установлено, можно
выписать соответствующую систему независимых линейных уравнений, исполь-
используя структуру дважды кубических сплайнов в каждом прямоугольнике Мц
(см. Алберг и др. 111]).
7.8. Наилучшее приближение
Так как сплайн линейно зависит от своих определяющих значений, то для
интерполяционных сплайнов относительно сетки л при соответствующем
выборе краевых условий
Я« (/ + ё\ *, *) = Я* (/; и 8) + Яя (§; *, 5). G.8.1)
В частности, разложение G.8.1).справедливо, если выполнено одно из усло-
условий: а) #я (/ + Г» *, 8) — 8п (/; I, в) — #я (#; г, з) принадлежит типу Г,
Ь) #я (/ + 8; г, з) — 8п (/; г, §) — 8п {§; *, $) принадлежит типу П\ с) функ-
функции / (г, §), $ ({, з) и сплайны #я (/ + Г> ^, 8), 8п (/; г, з) и $„ (#; ^, з) дважды
периодические.
Если разложение G.8.1) применить к разности / ({, з) — #я (*, $), где
^я (*» 5) — произвольный простой сплайн относительно сетки я, то в силу
свойства минимальной нормы
а ь
с а
а ь а ь
= $ $ {Г (*, «)-%(*, 8)-8нпи-8п; г,
с а с а
а ь а ь
с а со
если только краевые условия таковы, что #я (#я; I, з) = #я (г, $). Отсюда
легко получить свойство наилучшего приближения простого дважды кубиче-
кубического сплайна.
7.9. ФУНДАМЕНТАЛЬНЫЕ СПЛАЙНЫ 237
Теорема 7.8.1. Пусть даны прямоугольник М: а -^ ^ -^ Ь; с -^ $ ^ й
и сетка п, определенная одномерными сетками А*: а = 20 <С ^ . • • <С ^N ~ Ъ
и Д5: с = 80 <С 8х <С . . . <С 8М = Л. Если функция / ({, з) принадлежит классу
С\ (№), простой сплайн 8п (^, $) определен сеткой п, простой сплайн 8Я (/; {, в)
интерполирует функцию / ({, з) на п и разность / (*, $) — ^я (/;, г, $) принад-
принадлежит типу Г, то >
а ь а ъ
с а с а
причем с точностью до решения уравнения д4/ ({, з)/д^ дЬ2 = 0 сплайн
8п (/; Ь, з) является единственным, удовлетворяющим этому неравенству. Если
требуется, чтобы все функции были дважды периодическими или принадлежали
заданному классу эквивалентности типа II, то неравенство G.8.2) справедливо,
когда в качестве 8Я (/; I, &) взят соответствующий интерполяционный сплайн.
В дважды периодическом случае сплайн 8Я (/; г, з) является единственным
с точностью до периодического решения, а в остальных случаях — с точностью
до произвольного решения уравнения д4/ (г, 8)/дз* дг% = 0.
7.9. Фундаментальные сплайны
Фундаментальные сплайны уже встречались в этой книге в разд. 2.7; они
также очень полезны при интерпретации представления G.3.2) для дваж-
дважды кубических сплайнов. В очень широком смысле фундаментальные сплайны
можно определить как сплайны, у которых одно определяющее значение равно
единице, а все другие равны нулю. Функции
А, (*НЛу (*), *м<*<*| A=1, 2 М; / = 0, 1 М),
A = 1,2 ЛГ), G.9.1)
(«==1,2
фигурирующие в равенстве G.3.2), являются одномерными фундаментальными
сплайнами. Кроме того, справедливы одномерные представления
м
Ъ Щ^ дП^*м) A = 0, 1 Щ,
3=0
м
Ъ *м)
)=0
Ял, (я,; 0-2 А, (,) °Щ^й + в0 М Щ^> + ВМ
3=0
где ^4/E), В0(з) и Вм (з) — соответствующие одномерные фундаментальные
сплайны, определенные сеткой А8: с = $0 <; «4 <; . . . <; $м = й.
238 ГЛ. VII. ДВАЖДЫ КУБИЧЕСКИЕ СПЛАЙНЫ
Подставим в G.3.2) представления G.9.2):
N М М
М N
**/) I у р а „ч эли, »0) ,
3=0 г=0
1=0
, 5) ^^ , G.9.3.1)
где
. A = 0,1, ...,ЛГ;/ = О, 1 М),
A = 0, ЛГ;У = О, 1 М),
G 9 3 2)
-О,[ЛГ; /-О, АО.
Ясно, что Сц ({, з), Иц (г, $), Ец (г, з), Р^ (I, з) — двумерные фундаменталь-
фундаментальные сплайны, необходимые для представления сплайна 8Я (/; г, $). Из равенств
G.9.3.2) видно, что они представляют собой произведения одномерных фунда-
фундаментальных сплайнов. Таким образом, хотя сплайн #л (/;, {, $), вообще говоря,
не равен произведению функции от I на функцию от 5, но его можно представить
в виде конечной суммы таких произведений.
7.10. Свойства сходимости
Свойства сходимости дважды кубических сплайнов фактически непосред-
непосредственно вытекают из представления G.3.2), которое с учетом G.9.1) можно
записать в виде
8*Ц\ *> «)- 21 А* @Ял5(/У, 8) + ВоA;)8ьАёо; «) + **(*)$*.<**; «) G.10.1)
{=0
Следовательно,
Иш 5„ (/; I, 8)« 2 А^ @ / («ь ') + 5о @ д-Щг^ + В«
и
Ит Ит 8„{[;{, *) = /(*, в).
А,||-О||Дв||-*.О
7.11. ВТОРОЕ ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ 239
Если функция / {г, з) принадлежит классу С* (М), то сходимость равномерна
как относительно *, так и относительно 5 и повторный предел можно заменить
двойным пределом. Дифференцируя #я (/; I, з) и рассуждая аналогично, заклю-
заключаем, что справедлива
Теорема 7.10.1. Пусть даны прямоугольник М: а ^ I ^ Ь; с ^ 5 -^ д,
и сетка я, определенная одномерными сетками Д(: а = 10 <; {г <С . . . <С ^ = Ь
и А8: с = 50 <С $1 <С . . . <С §м = А. Если функция / ({, з) принадлежит классу
С\ (М) и || я || -*• 0, то ду8я (/; г, 8Iд$а д$ равномерно относительно {из схо-
сходится к д7/ (*, 8)/д8адг&, где у = а + р < 2, а < 1, р < 1, и
Если функция / (г, 5) принадлежит классу С\ (М), то
(||3-Ч||А.||3-а). . G.10.3)
Далее, равенство G.10.3) выполняется для 'у = а + Р-^6, а^З, Р-^3 при
условии, что отношение норм сеток к минимальному расстоянию между смеж-
смежными узлами остается равномерно ограниченным, когда \\ А 8|| и || А* || стре-
стремятся к нулю. В этом случае показатели 3 — Р и 3 — а можно даже заменить
на А — Р^4 — а соответственно.
Замечание 7.10.1. В теореме предполагается, что сплайн 5Я (/; I, з)
удовлетворяет краевым условиям, которые по существу диктуются теорией
одномерных сплайнов. В частности, теорема 7.10.1 справедлива, если сплайн
#я (/; г, з) интерполирует функцию / ({, з) на сетке я и разность / (г, з) —
— ^я (/; *» 5) принадлежит типу Г или 1Г. Теорема справедлива также, если
функция / ({, з) и сплайн #я (/; {, з) дважды периодические. Для того чтобы
можно было применять соотношение G.10.2), сплайны #я (/; I, з) должны рас-
рассматриваться только из фиксированного класса эквивалентности типа II.
7.11. Второе интегральное соотношение
Для дважды кубических сплайнов существует аналог второго интеграль-
интегрального соотношения
3 3 1 д*д* д&д** ) ага8-
с а
а ь
-И
с в
при подходящих краевых условиях, но так как с помощью представления G.10.1)
можно получить свойства сходимости дважды кубических сплайнов непосред-
240 ГЛ. VII. ДВАЖДЫ КУБИЧЕСКИЕ СПЛАЙНЫ
ственно из свойств сходимости одномерных сплайнов, то значение этого тожде-
тождества не так велико. В теореме 7.11.1 указываются условия, при которых спра-
справедливо тождество G.11.1). Эта теорема доказывается по той же общей схеме,
по которой было установлено первое интегральное соотношение для дважды
кубических сплайнов.
Теорема 7.11.1. Пусть даны прямоугольник №\ а ^ I ^ Ь; с ^ 5<^ &
и сетка я, определенная одномерными сетками А*: а = *0 <; ^ . . . <; ^ = Ь
и Д5: с = з0 <С 81 <С . . . <С $м = д>. Если функция / ({, з) принадлежит классу
С\ (М), сплайн 8п (/; г, $) интерполирует ее на сетке л; и выполняется одно
из условий: а) / ({, з) — 8Я (/; {, з) принадлежит типу Г, Ь) / ({, з) —
— #я (/; {, з) принадлежит типу 1Г, с) функция / ({, з) и сплайн 8Я (/; I, з)
дважды периодические, то *
\ \ г \
- г
с а
7.12. Прямое произведение гильбертовых пространств
Пусть #1 и Яг — сепарабельные гильбертовы пространства с базисами
{е{) A = 1, 2, . . .) и {//} 0? = 1, 2, . . .) соответственно, и пусть Я — линей-
линейное пространство, натянутое на {пи} = {ег, /у} A = 1, 2, . . .; ; = 1, 2, . . .).
Положим
(Ау. Мн = (««• «Оя!-^. /|)я„ G.12.1)
где (•, «)я! и (•, «)я2 — скалярные произведения. Пользуясь линейностью,
доопределим (•, «)^ до скалярного произведения на всем Н. Положим
|| и \\Е = (и, и)У2; G.12.2)
тогда Н можно пополнить относительно нормы И • 11я и расширить скалярное
произведение (•, «)^ на это пополнение. Обозначим пополненное пространство Н
через Н, а расширенное скалярное произведение через (•, «)я. Легко прове-
проверить, что Н — сепарабельное гильбертово пространство относительно (•, -)н.
Более детально эта конструкция изучалась Сардом [1, стр. 354].
Мы занялись обсуждением прямого произведения гильбертовых про-
пространств, так как хотим образовать прямое произведение пространств Жп (а, Ъ)
и (Жп{с, 6). В гл. III мы рассматривали пространство о/Г2 (а, Ъ) как псевдо-
псевдогильбертово пространство со скалярным произведением
ь
</,«)«$ /" (*) 8" @ Л
а
и построили для него несколько ортонормальных базисов. Для наших целей
наиболее полезным из этих базисов оказался канонический сеточный базис.
7.12. ПРЯМОЕ ПРОИЗВЕДЕНИЕ ГИЛЬБЕРТОВЫХ ПРОСТРАНСТВ 241
Пусть последовательность {ц$ (*)} A = 1, 2, . . .) образует канонический сеточ-
сеточный базис для Шг(а, Ь), а {^ ($)} (/ = 1, 2, . . .) образует канонический
сеточный базис для з%Га(с, д). Пусть задан прямоугольник М: а ^ ^^ Ъ; с^.
-^ 5-^ й. Обозначим через &Сг(<й) прямое произведение пространств Шг(а, Ь)
и &Сг (с, а). Тогда
с а
будет скалярным произведением для &Сг(М), ибо
Г Г Г Я4»* @ *у (») 0*и*О*>*(»I ^л Г «/а »/*\ л* Г •
с а
Это соотношение позволяет интерпретировать з/Га (М) как пространство классов
функций на М, а символическое произведение щи^ — как поточечное произведе-
произведение функций иг (И) и V^ ($). Но для наших целей необходимо отождествить функ-
функции, отличающиеся на функцию, линейную относительно I и 5.
Покажем, что С\ (М) с: Жг (М).
Пусть последовательность сеток {пы} (И— 1, 2, ...) па М определена
одномерными сетками Д^: а — $' << ^ < ... <С ^ — Ъ и Д^: с = 5^ •<; $х < ...
... <С 81ты — й, причем сетка 1гм содержит в себе сетку я^, если Му>М.
Пусть соответствующая последовательность сплайнов {«5^д^(/; г, $)} (ЛГ= 1, 2, ...)
интерполирует на этих сетках функцию /(/, 5) из класса С\(М). Так как при
М>N сплайн 8Ы(};1,8) интерполирует на сетке пк сплайн 8М(};1;,8),
то в силу первого интегрального соотношения
а ь
3 3 \ 5^^ ^2-^г—^
с а
-1!
с а с а
Отсюда вытекает, что последовательность действительных чисел
с а
монотонно возрастает и ограничена сверху величиной
а ь
р г
) )
с а
16-1197
242 ГЛ. VII. ДВАЖДЫ КУБИЧЕСКИЕ СПЛАЙНЫ
и потому последовательность
И±А\ —1 2 ^
есть последовательность Коши в 1/а(^) и ее предел $((, з) также принадлежит
I/2 (М). Продолжая, как в гл. III, полагаем
в I
с а
и получаем
( __ ( (
; г, *)__ ( дЧ(а, с) д*8к(!\ а, с)}
с а
Теперь из теоремы 7.10.1, определения §•(<, 5) и неравенства Буняковского
Шварца заключаем, что
откуда
Следовательно,
т. е.
N-+00
Теорема 7.12.1. Пусть даны прямоугольник &\ а ^ I ^ Ь\ с ^ « ^ й
и последовательность сеток {лк} (Л" = 1, 2, . . .), определенная одномерными
сетками А^: а = ^7 < ^ < • . • < ^ = & " А^: с = «^ < «? <. - • •
. . . <С 5^ = й. Пусть || пм || ->• 0 при N -> оо и сетка я,у содержит сетку
Пх> при Лг' <С Л^ х). 1?сл1* функция /(*, 5) принадлежит классу С\{№), сплайн
-8у (/; ^, 5) интерполирует ее на Пу и выполняется одно из условий: а) / (*, 5) —
— ## (/; 2, 5) принадлежит типу Г (ТУ = 1, 2, . . .), Ь) 5^ (/; г, $) принад-
принадлежит типу IV (ЛГ = 1,- 2, . . .), с) функция / (#, 5) и сплайн 8у (/; *, 5}
(ЛГ = 1, 2, . . .) дважды периодические, то
Нт || /—
Следствие 7.12.1.
Можно положить ||яЛ'11 = тах{|| Д^||, || А^ ||}.
7.13. МЕТОД ФУНДАМЕНТАЛЬНЫХ СПЛАЙНОВ 243
7.13. Метод фундаментальных сплайнов
В разд. 7.9 мы показали, что можно построить дважды кубические фунда-
фундаментальные сплайны, попарно перемножая кубические фундаментальные
сплайны. В настоящем разделе мы используем это и другие свойства фунда-
фундаментальных сплайнов для приближения решений дифференциальных уравне-
уравнений в частных производных второго порядка. Пусть функция / (?, $) определена
на прямоугольнике &:а^.{4^.Ь; с ■< 5^ А и принадлежит классу С\{№).
Если ортонормальный базис {иь B, 5)} (г = 1, 2, . . .) для &С% {М) представляет
собой прямое произведение канонических сеточных базисов для &Сг{а, Ъ)
и 8С% (с, д), то
= 0, G.13.1.1)
а ь
Г Г
с а
Кроме того, если постоянные 61г 62» &з> &4 выбраны надлежащим образом1), то
/ (*, 5) = Ъх + Ъ4 + Ъ38 + Ъ& + 2 а&1 (*» «). G.13.2)
1=1
Положим
= 1, 2, . . .) * G.13.3)
и рассмотрим только подходящую подпоследовательность. Тогда можно счи-
считать, что сплайны #^ (/; I, 8) интерполируют функцию / {г, 5) и к ним приме-
применима теорема 7.10.1. Таким образом, для у = а + р
, ») , дУ5„ (/; I, у) дУДу (/; *, ») _
где 0< а, р < 4 и / («, 5) = ^^ (/; ^, 5) + ^дг (/; ^, 5). В равенстве G.13.4)
через Д^ и Д^ обозначены одномерные сетки, возникающие при построении
канонических сеточных базисов, с помощью которых были получены функции
иг {г, 8) (г = 1, 2, . . ., IV). Заметим, что если функция / (г, 8) принадлежит
классу С\ {М), а не С\ {М), то в силу теоремы 2.3.4 теорема 7.10.1 остается спра-
справедливой и сходимость сохраняется для О^а, р* -^ 2; но здесь скорость сходи-
сходимости меньше и оценить ошибку, как мы это сделали в предыдущем случае,
нельзя. Итак, хотя при доказательстве сходимости мы будем пользоваться
равенством G.13.4), наш метод применим и при менее ограничительных условиях.
*) Это возможно не для любой функции / (*,*) из С\ ($). Например, если / (*, ») == И,
то аг = О (г = 1,2, ...), но *4^&1 + Ь2*+&з*+М*' В дальнейшем представление G.13.2) не
используется.— Прим. перев.
16*
244 Г«Т. VII. ДВАЖДЫ КУБИЧЕСКИЕ СПЛАЙНЫ
Пусть на № заданы дифференциальное уравнение в частных производных
вида
й1 ({, $) 11ц + а2 (г, з) 118г + ад (г, в) 1188 + а4 (*, 5) Иг +
{, в) С78 + а6 (*, 5) V + § (г, з) = 0 G.13.5)
и множество таких краевых условий, что задача корректна в смысле Адамара.
Это значит, что уравнение G.13.5) имеет единственное решение V ({, з), непре-
непрерывно зависящее от множества исходных данных. Так как мы собираемся лишь
продемонстрировать метод, то рассмотрим только случай, когда уравнение —
эллиптического типа и на границе области № решение V (г, 5) принимает
заданное значение / (т), где т — длина дуги вдоль границы, причем производ-
производная /" (т) непрерывна вдоль*каждой стороны прямоугольника №. Следователь-
Следовательно, / (т) определяет также значения 118({, в) вдоль вертикальных сторон прямо-
прямоугольника № и значения С/*($, в) вдоль горизонтальных сторон прямоугольни-
прямоугольника &. Наконец, мы предполагаем, что коэффициенты уравнения G.13.5) и гра-
граничные данные достаточно гладкие, так что I/ (Я, 5) принадлежит классу
С\ {№). Предположение эллиптичности и гладкости не умаляет общности мето-
метода, но позволяет сделать изложение более доступным.
Пусть сплайн 5^ ({/; I, $) интерполирует функцию V ({, з) и разность
V (г, з) — 8х (И; I, з) принадлежит типу Г (ЛГ = 1, 2, . . .)• В обозначениях
разд. 7.9 сплайн 5^ (II; г, з) принимает вид
?«• (Р; и я) - 2 2 и (п, з}) аг (I) А, (в)+
~\~ 2 {Рг (а-> 8}) ^о @ ~\~^1(Ь, »,/) Вп (I)} А^(з
з=о " хУ
+ 2 {РЛ*и с)В0(8) + 118(и, C)Вт (8)}А
г=0 л
+178г (а, с) Во (I) Во (з) +178{ F, с) ВП^Т (I) Во (в) +
(а, д) Во (г) Втк (в) +1781 (Ь, й) ВЛд. (*) 5т^ (в). G.13.6)
Если положить
|йв)-» G.13.7.1)
то уравнение G.13.5) запишется так:
Ы7 + и (*, 5) - 0. G.13.7.2)
Следовательно,
I, з) - -§ [г, 8) - ЬЕ„ (Щ *, *), G.13.8)
7.13. МЕТОД ФУНДАМЕНТАЛЬНЫХ СПЛАЙНОВ 245
и, выбирая N достаточно большим, можно, учитывая равенство G.13.4), сде-
сделать член ЬЕЫ A7; {, з) произвольно малым по абсолютной величине. Если
мы потребуем, чтобы равенство G.13.8) выполнялось в точках (^-, 8/) (г =
= 0, 1, . . ., тг^; / = 0, 1, . . ., т^), то получим (тг^ + 1) (т^ + 1) линей-
линейных уравнений относительно неизвестных
* = 1, 2, ..., пы— 1; / = 1, 2, ...,т„ — 1),
#а* (**, «/) (г = 0, гс^; / == 0,
Для определения остальных величин 17 (^, 5;), 17* (^, $/), 1/8 (^, $/), фигури-
фигурирующих в равенстве G.13.6), используются исходные данные. В матричной
форме эти уравнения принимают вид
Л^ = 6^Н-#*, G.13.10)
где А я — матрица коэффициентов, V^ — вектор неизвестных, Оу — вектор,
связанный с функцией — § (г, $) и граничными данными, и Е^ — вектор,
связанный с функцией — ЬЕМ A7; I, $). Хотя существование обратной матри-
матрицы ^й1 не гарантировано, но оно очень вероятно, так как решение 17 ({, з)
существует и единственно, а функцией 17 ({, з) сплайн «5^ (^'» *» 5) опреде-
определяется однозначно. Если предположить, что ^4^х существует и || А^Ех || ->- 0
при N -*- с», то решения Vк аппроксимирующих уравнений
А„п„ = О„ G.13.11)
определяют дважды кубические сплайны 5^ (^, $), сходящиеся к 17 ({, з) при
N-+00. Скорость сходимости зависит от оценок G.13.4) и поведения мат-
матрицы А$. Заметим, что сплайн 5^ A7; {, з) удовлетворяет не краевым усло-
условиям, а лишь сплайн-аппроксимациям краевых условий. Таким образом,
важно, что задача корректна. Если прямоугольник Л разбит примерно
на 100 прямоугольников, то матрицу ^4^ можно обратить численно с помощью
метода исключения, в других случаях обычно применяются итеративные
методы. Так как А% ({), А) (в), Вг (г) и В} (в) — кубические сплайны, то их
нахождение сильно облегчается. Полученные приближения не будут полностью
численными, поскольку равенство G.13.6) (или оно же, но с более удобной
перегруппировкой членов) дает также промежуточные значения. Это позволяет
использовать полученные приближения в аналитических исследованиях. Послед-
Последняя особенность остается также в силе при применении метода для численного
решения обыкновенных дифференциальных уравнений. Так как ошибка равна
А"мЕы, то оценку для ошибки можно получить в процессе вычисления. Если
требуется вычислять значения функции в большом числе промежуточных
точек, то метод фундаментальных сплайнов выгоднее методов такой же точ-
точности, которые дают лишь значения 17 ({, з) в узлах сетки.
246 ГЛ. VII. ДВАЖДЫ КУБИЧЕСКИЕ СПЛАЙНЫ
7.14. Иррегулярные области
До сих пор мы изучали дважды кубические сплайны, заданные только
в прямоугольных областях. Результаты легко распространить и на другие
области, например на области, состоящие из конечного числа прямоугольников.
В определении для таких областей представлений типов I и II величины, зада-
задававшиеся ранее равенствами G.1.1) и G.1.2) соответственно, задаются теперь
вдоль сторон прямоугольников, параллельных оси {. То же относится и к сто-
сторонам, параллельным оси 5. Величины, определяемые условием (с) из G.1.1)
и G.1.2), должны задаваться в каждой вершине прямоугольников. Первое
интегральное соотношение, свойства минимальной нормы, наилучшего при-
приближения и другие свойства дважды кубических сплайнов, полученные для
прямоугольной области, непосредственно обобщаются на области, указанные
Рис. 1.
выше. Мы предоставляем читателю самостоятельно исследовать такие области,
а сами займемся областями или, возможно, более уместно сказать, «поверхно-
«поверхностями», которые при подходящем преобразовании отображаются в прямоуголь-
прямоугольник М. Отображения могут не быть взаимно однозначными (и даже просто
однозначными) и поэтому не всем функциям на М будут соответствовать функ-
функции на первоначальной поверхности.
Рассмотрим поверхность #, изображенную на рис. 1. Предположим, что
на поверхности 5 даны точка Ро и семейство {Г^} гладких кривых на 5, соеди-
соединяющих точку Ро с точками (?, расположенными на границе Г поверхности #.
Мы считаем, что граница Г также является гладкой кривой в том смысле, что
каждая из описывающих ее координат имеет непрерывную вторую производную
относительно длины дуги, соответствие между точками (? и кривыми Г^ взаим-
взаимно одназначно и любая пара этих кривых пересекается только в точке Ро.
Семейство {Г^} заполняет поверхность в том смысле, что через любую точку
Р на 5 (кроме точки Ро) проходит точно одна кривая из нашего семейства.
Пусть й (Р, Р') обозначает расстояние между точками Р и Р', измеряемое
по кривой Гс, проходящей через точку Р. Ясно, что функция й (Р, Р') опре-
определена не для произвольной пары точек Р и Р' из #, но если Р и Р' можно
соединить кривой |Г^, то это можно сделать единственным способом, так что
д, (Р и Р') в этом случае определено. Далее, пусть € (Р) — расстояние, изме-
измеряемое вдоль кривой Г против часовой стрелки от фиксированной точки (?0
на Г до точгёи <?р, единственной точки на Г, для которой точка Р лежит на
7.14. ИРРЕГУЛЯРНЫЕ ОБЛАСТИ 247
кривой Т<2р. Положим
Тогда каждой точке Р поверхности 5, не лежащей на кривой Г^о, можно поста-
поставить в соответствие пару чисел Ы (Р), 5 (РI, причем эта пара определяется
однозначно. Для точки Р Ф Ро, лежащей на Г^о, таких пар будет две: [0, 5 (Р)]
и \1, 8 (Р)], где / — длина кривой Г, а для точки Ро — бесконечное множество:
пары У, 0], где 0 <! I <; /. Таким образом, отображение Р: Р ->- [г (Р), 5 (Р)],
хотя и не однозначно, переводит 8 в М'. 0^^<! /; 0 <1 $ <1 1. При этом кривая
Рц ((} ф <20) переходит в прямолинейный отрезок ^ = { (О), параллельный
оси в. Кривая Г^о отображается в два прямолинейных отрезка I = 0 и I = /,
точка Ро — в прямолинейный отрезок 5 = 0 и кривая Г — в прямолинейный
отрезок 5 = 1. Заметим, что, не будучи однозначным, Р имеет однозначное
обратное отображение Р~г, ибо каждая точка B, $) в М является образом точно
одной точки поверхности 5. Следовательно, для каждой функции / (Р), опре-
определенной на 5, существует единственная функция / ({, з) = / [Р~х B, $)].
В силу гладкости кривых Г и Гд некоторые частные производные функции
/ (Р) можно выразить через частные производные функции / (I, $) и обратно.
Итак, каждой функции / (Р), заданной на 5, можно поставить в соответствие
интерполяционные сплайны 5 (/, Р), которые на самом деле интерполируют
соответствующие функции / ((, з) = / [Р'1 ({, $)], заданные на М- Существенно,
что функции / ({, з) принадлежат классу С\ {№), постоянны на отрезке 5 = 0
и являются периодическими относительно I.
Построим еще одно отображение, которое также может оказаться полез-
полезным. Предположим, что вместо семейства кривых Г^, соединяющих точку Ро
с граничными точками (?, у нас есть семейство заполняющих поверхность глад-
гладких кривых {Гд,ф'}, где обе точки (? т& (?' лежат на Г. Рассмотрим два случая:
1) через каждую точку поверхности #, кроме двух точек (?0 и <^1, лежащих
на Г, проходит единственная кривая Гд, ц> нашего семейства и 2) существует
одна особая точка Ро, через которую проходят все кривые Г$, $» нашего семей-
семейства. Если особой точки нет, поставим в соответствие каждой точке Р и& 8
координату г (Р), равную расстоянию, измеряемому вдоль Г в направлении
против часовой стрелки, от точки (?0 до граничной точки (?Р, первой встретив-
встретившейся нам точки кривой Г<э <эр/, проходящей через Р. Заметим, что граничная
точка <2Р встречается нам раньше точки (^1.
Кроме того, мы предполагаем, что Г — спрямляемая жорданова кривая,
так что наша поверхность # односвязна. Пример такой поверхности показан
на рис. 2. г (Р) однозначно сопоставляется точке Р, если 0 соответствует точке
(?о и расстояние /' от точки (?0 до (?1, измеряемое вдоль кривой Г против часовой
стрелки, соответствует точке <?!•
Точке Р, отличной от (?0 и от ()и можно единственным образом поставить
в соответствие вторую координату
248 ГЛ. VII. ДВАЖДЫ КУБИЧЕСКИЕ СПЛАЙНЫ
для Р — <20 и Р = (>1 функция 5 (Р) не определена, и величины 5 ((?0) и 5
могут принимать любое значение между 0 и 1. Как и прежде, отображение
8(Р))
переводит поверхность # в прямоугольник ^?:0^^^/'; 0<^5^1. Отобра-
Отображение Р вновь не однозначно, но обратное к нему однозначно, так что с функ-
функцией / (Р), заданной на #, можно связать функцию / (*, $) = / [Р~г (*, $)],
заданную на М. Теперь можно определить интерполяционные сплайны 5 (/г Р)
так же, как и раньше. В этом случае они принадлежат классу С\ (М) и постоян-
постоянны на отрезках { = 0 и I — V. ,
Если различать кривые Г$, у и Г^, я (они имеют противоположное
направление), то мо^кно считать прямоугольник М\ 0-^^-<!/; 0<^$<11,
где / — длина кривой Г, образом области. Отображение Р переводит кривые
Рис. 2.
Г$|<?' и Т<2'г <2 в прямолинейные отрезки Ь = сопз* и I' = соп81. Числа I
и I', связанные таким образом, называют сопряженными, а точки {I, §)
{г', 1 — 5) называют сопряженными точками. В этой терминологии интересую-
интересующие нас функции из класса С\ {М) постоянны на отрезках I = О, I = /', перио-
периодичны по г и равны в сопряженных точках.
Если особая точка Ро существует, то требуется некоторая модификация.
Возьмем в качестве точки $0 произвольную точку на Г и определим Ь (Р),
как и раньше. Нам нужно поставить в соответствие точке Ро координату 5
независимо от кривых Г^ ^ нашего семейства. Для точек Р, расположенных
на кривой Г^ д> между @Р и Ро, положим
2 йЩр, Р0) '
а для точек Р, расположенных на кривой Г<зр ^ между точками Ро и Рр>,
положим
■ И1+тИ$-)- <7Л4-3-2>
= "И
Если мы различаем кривые Тя, ^ и Г^', я, то прямоугольник М'. а ^ I <; /;
О <^ 5 ^ 1 опять можно считать образом рассматриваемой области. Соответ-
Соответствующие функции из класса С\ {М) периодичны по I, постоянны вдоль отрезка
5 = 1/2 и равны в сопряженных точках (*, 5) и (*', 1 — 5). Этот случай изо-
изображен на рис. 3.
7.15. ПРЕДСТАВЛЕНИЕ ПОВЕРХНОСТИ 249
Во всех предыдущих рассуждениях мы не требовали, чтобы поверхности
были плоскими. Таким образом, кривые Г, Гф, Г^, ^ не обязаны быть пло-
плоскими. Отображение Р'. Р -»■ [г (Р), з (Р)] задает множество внутренних коор-
координат на поверхности #. Важно отметить, что кривые Г, Гс, Гв| я> можно
приблизить одномерными сплайнами в смысле приближения их внутренних
Рис. 3.
координат х). Итак, можно построить поверхности, определенные лишь конеч-
конечным числом точек, и использовать их для приближения других гладких поверх-
поверхностей. Можно доказать не только поточечную сходимость, но также сходи-
сходимость касательных плоскостей и кривизн. Более подробно эти идеи развиваются
в разд. 7.15.
7.15. Представление поверхности
Распространим идеи разд. 7.14 на другие классы поверхностей. Рассмо-
Рассмотрим три класса поверхностей: 1) гладкие поверхности, гомеоморфные сфере,
2) гладкие поверхности, гомеоморфные тору, и 3) гладкие поверхности, гомео-
гомеоморфные цилиндру конечной длины. Первый класс рассмотрим более подробно,
а для двух других укажем лишь необходимые изменения. Возможны две раз-
различные точки зрения: можно попытаться приблизить данную поверхность дру-
другой поверхностью, определяемой конечным числом точек, а можно попытаться
сразу определить поверхность (разумным, но не обязательно единственным
способом), задавая конечное число ее точек.
Мы примем последнюю точку зрения, ибо она представляется более важной.
Пусть дано N + 1 множеств точек, причем точки каждого множества компла-
компланарны. Обозначим соответствующие плоскости через ^^ (/ = 0, 1, . . ., ДО
и предположим, что в плоскости ^^ содержатся т; -\- 1 точек (}ц
A = 0, 1, . . ., ту), (?0/ = Bтл, описывающих приближенно простую
замкнутую кривую Г/, причем кривые Гои Г ^вырождаются в точки. Допустим,
что точки (?0; (/ = 0, 1, . . ., Щ компланарны. Мы будем считать плоскости
^^ упорядоченными в том смысле, что они параллельны и направленное
расстояние от любой плоскости й, до Й.|+1 положительно (это условие
не является необходимым). Схематично эта ситуация изображена на рис. 4.
*) Приближают обычно только конечное число кривых Г<э или Гд д,, и они служат
для определения линий решетки, параллельных оси «.
250
ГЛ. VII. ДВАЖДЫ КУБИЧЕСКИЕ СПЛАЙНЫ
Пусть каждая точка (?ц определяется своими прямоугольными координа-
координатами (хц, уф 2ц). Обозначим через п, ((?^, <2^) длину суммарной хорды
ют <2ц до <?Ь7-, соответствующей увеличению первого индекса от I до к, а через
^ длину всей суммарной хорды, т. е. 1} = д, ((H;, (?т /). Тогда для каждого
(/ = 0, 1, . . ., ]У) можно определить три периодических сплайна 5;- (Х(г1; $),
ЧЛ*
Рис. 4.
^ (Уи'у 8) и $/ Bф 5)> интерполирующих соответственно значения х^,
и %н в точках 5 = 5^- (I = 0, 1, . . ., т}), где
1 = 0, 1, ..., Л1,;/ = О, 1, ...,
G.15.1)
Разобьем единичный отрезок
О = 5П < «1 < •.. •
с помощью сетки А:
Л = у
52/г =
и зададим в каждом множестве п; новое множество точек Р^, вычислив значе-
значения 5^ (Хф 5), $^ (уф з) и ^- (г{;-; 5) в точках 5 — 50, 51г . . ., $2ь- В част-
частности, ^0^== Ро^ = Ры^ и = 0, 1, . . ., Щ, Р{о = ^оо (г = 0, 1, ..., 2/е)
И Р4лгн=<?Одг A = 0, 1, .. ., 2Й).
В каждой плоскости ^^ построим новые периодические сплайны, интерпо-
интерполирующие координаты точек Рц в узлах сетки А. Обозначим эти сплайны через
8; (х; з), 8^ (у; з) и 8^ (г; §); вообще говоря, они не интерполируют исходные
координаты, но можно надеяться, что соответствующие им плоские кривые
близки к оригиналу Г;. Эти кривые обладают тем ценным свойством, что
их координаты определяются периодическими сплайнами с общей сеткой А
Зададим для фиксированного г и д= I + к (тос! 2к) множество #-коор-
динат:
\ 8<])ч • • • »
7.15. ПРЕДСТАВЛЕНИЕ ПОВЕРХНОСТИ 251
и аналогичные множества ^-координат и 2-координат. Тогда получим 2к различ-
различных упорядоченных множеств координат. Заметим, что множества, соответ-
соответствующие г — О и г = 2к, отождествляются, а множества, соответствующие
гид, отличаются только порядком. Эти множества координат можно исполь-
использовать для определения 2к ориентированных замкнутых пространственных
кривых, образованных периодическими сплайнами ЗТ% (х; г),^1 (у; {) и 2Г% (г; г),
интерполирующими значения этих координат. Зависимость переменной { от
точек интерполяции определяется равенствами
где А{Рц, Рц) — длина суммарной хорды между точками Рц и Рц, соответ-
соответствующей увеличению второго индекса от / до /. Точке (?0# всегда соответствует
параметр г = 1/2, а точке (?Оо в силу периодичности сплайнов — и 2 = О,
и г = 1. Как правило, этими значениями исчерпываются все значения I, в кото-
которых интерполируются исходные точки (^ (кроме случаев г = О, г = 2к
и г = к, в которых все точки интерполяции совпадают с исходными точ-
точками @0;).
Напомним, что сплайны $~г (х; г), ЗТг (у; г) и $~1 (г; I) строятся на сетке
А*: 0 = ^0 < {н < . . . < 1Ь2К — 1, которая меняется вместе с г. Чтобы
устранить эту зависимость, построим на единичном отрезке 0 ^ 2 -^ 1 сетку п
§ — 1ц <а\ < * • • <С г N ~ -% <
и вычислим значения сплайнов ^г(х;г), ^((у; I) и $~г (г; I) для этих новых
значений г. Мы получим тогда 1к новых множеств координат. Образуем новые
периодические сплайны $~п1 (х; г), УЯ1 (у; г) и ЗТл% (г; {), интерполирующие
новые координаты в узлах общей сетки я. Здесь г принимает значения
О, 1, ...,2к и Згяо(х;*) = Згп2к(х;{), ^„0(у,*) = ^л2к(У',1), Уя0 (*;*) =
= ^л2кB'> $)■ Наконец, вычислим значения этих сплайнов при фиксированном
I] и построим периодические сплайны 8±^ (х; з), 8^^(у; з) и <5д,/ (г; 5) отно-
относительно сетки Д. Для каждого / этими координатными функциями определяют-
определяются простые замкнутые кривые, аналогичные исходным кривым, но только
теперь у нас 2-Л^ + 1 кривых, а не N + 1, так как мы учитываем ориентацию.
Периодические одномерные сплайны
Ущ (х; г), ЗГя1 (у; г), ЗГп1 (г; г) (I = 0, 1 2к), G.15.3.1)
Яд.; (*; 5), Яд,,- (у; з), 8А^ (г; *) (/ = 0, 1 2Щ G.15.3.2)
дают значения х, у и г на линиях решетки единичного квадрата №\ 0.^2 <^ 1;
О -^ 5-^ 1» определяемых сетками п и А. Нетрудно понять, что эти одномерные
сплайны содержат достаточную и непротиворечивую информацию, позволяю-
позволяющую считать х, у, 2 дважды кубическими сплайнами на №, которые для равно-
252 ГЛ. VII. ДВАЖДЫ КУБИЧЕСКИЕ СПЛАЙНЫ
мерных сеток я; и А удовлетворяют соотношениям симметрии:
х (*; 8) = х{1-г, 1 - 5),
у Ц, в) = у A — *, 1 — 5),
* (*,*) = г A — *, 1 — 5), G.15.4)
[х (О, 5), у (О, 5), г @, 5) = <?00,
Но это верно только когда сделаны отождествления, необходимые для G.15.4)
и для периодичности сплайнов, т. е., когда поверхность, описываемая коорди-
координатами х (Я, 5), у {г, з) и 2 (г, §), гомеоморфна сфере. Без отождествлений
G.15.4) она больше похожа на две сферы с общим северным полюсом.
Для поверхностей, гомеоморфных тору, две кривые Го и Г^ не вырож-
вырождаются, а отождествляются. Следовательно, сплайны по своей природе перио-
периодичны относительно г и нет необходимости удваивать рассматриваемые поверх-
поверхности, чтобы сделать их периодическими. Это значительно упрощает процедуру.
Для поверхности, гомеоморфной конечному цилиндру, сплайны относительно I
принадлежат типу I или II. Это не вызывает затруднений, необходима лишь
дополнительная информация для определения требуемых производных в кон-
концах цилиндра.
Переменные 5 и г, участвующие в этих построениях, могут применяться
в ситуациях, когда поверхность удваивается четное число раз. В более огра-
ограничительных ситуациях часто бывают удобнее другие переменные. В частности,
во многих случаях в качестве переменной 5 берут угол между прямой, соединяю-
соединяющей точку на кривой Г, с фиксированной точкой, и фиксированной прямой,
проходящей через фиксированную точку. Если поверхность тороидальна,
то аналогичную замену можно осуществить и в отношении г. Для поверхности,
гомеоморфной конечному цилиндру, в качестве одной из переменных часто
берется сама координата ъ. Если возможно использовать независимые пере-
переменные, подобные указанным выше, то можно значительно сократить число
переопределений поверхности для получения в конце концов прямоугольной
сетки (иногда поверхность даже совсем не надо переопределять).
7.16. Поверхности Кунса
Метод Кунса [1] представления поверхностей заключается в том, что прямо-
прямоугольная область М ' а <^ г ^ Ъ; с 4^ 5 ^ А делится на прямоугольники.
&и- Ь-1<* < и, $/-1 < *< *; (ь = 1, 2, . . ., Щ } = 1, 2, . . ., М) и на
каждом прямоугольнике определяется поверхность 5 ({, з), совпадающая
вдоль каждой из четырех сторон этого прямоугольника с одной из заданных
кривых /* ($) (ъ — 0, 1, . . ., Щ, & (г) (/ = 0, 1, . . ., М), • определенных
на прямолинейных отрезках, разбивающих М на прямоугольники Мц. Это
осуществляется так, чтобы первые частные производные 8 ({, 8) в направлении
нормали к стороне прямоугольника Мц (назовем их нормальными произвол-
7.16. ПОВЕРХНОСТИ КУНСА 253
ными) зависели только от значений граничных данных в концах стороны и от
значений первой производной граничных данных там же (вдоль стороны).
В частности, для каждого прямоугольника Мц имеем # (?, $,-_!) = #/_1 СО»
**-1<!<-< <г, и д8 (?, 8)/дз\8==8, ?г-1 •< ? •< ?*, зависит только от величин
/;_1 ($,_!), /у_1 (я*), /^-1 (^г_1), Г}-1 (зд (и от некоторых величин, не зависящих
от граничных данных). Следовательно, функцию ц>_.1 (?) можно переопределить
на отрезке ?*-1-<?-<^ (пока значения ^_1 (?) и ^_! (?) в точках ?4_1 и ?г-
не изменяются), не меняя нормальной производной функции 5 (?, з). Кроме
того, в построение вводится достаточная симметрия, так что нормальная про-
производная функции б1 (?, з) непрерывна вдоль границы между двумя смежными
прямоугольниками.
Хотя для достижения этих целей не существует единого метода, мы опи-
опишем сейчас один метод, тесно связанный с теорией сплайнов.
Пусть функции #у_1 (?) и & (?) определяют значения функции # (?, в)
вдоль прямых 5 = $;_! и 5 = я,- соответственно, а функции ]г_1 (з) и /г- ($) опре-
деляют ее значения вдоль прямых I — гг^ и I = 1Х соответственно. Эти четыре
функции определяют значения функций # (?, $), д8 (?, з)/дз и дЗ ({, зIдг в вер-
вершинах прямоугольников 31ц. Зададим значения смешанной производной
д23 (?, з)/дз д{ в вершинах прямоугольников Мц некоторым фиксированным,
но произвольным образом. (В смежных прямоугольниках значения должны
быть непротиворечивыми.) Тогда в каждом прямоугольнике №ц существует
единственный бикубический полином 8A;, з), определенный этими 16 вели-
величинами.
Положим
{-
-зA, а» (-2
I
G.16.1)
*,(«. ») = {/<-, (»)-5(«,.„ .)} {-2 A^1Т3
5,Л *) = {Ш-$(*„ .)} {-2 (^^K
Тогда функция
4
5 (I, в) = 8 Ц, з) + 2 8г (I, з) G.16.2)
1=1
будет обладать нужными свойствами.
Легко найти функцию о (?, 5). Для этого допустим, что Мц — квад-
квадрат с единичной стороной, и пусть
Л (?, 5) = E - 8^.^K {Оц (? - 1^^ + «12 (* - Ьг-Х? + «13 «-1-0 + «14} +
+ E - 8^.^J {а21 (? - 1^K + «22 (* - Ч-дг + «23 {I - и-х) + «24> +
+ (.9 — 8^.^) {а31 {I — ^_!K + а32 (? — *1-1)8 + «33 (^ — ?|-1) + «34} +
{ 3 G.16.3)
254
Тогда
ГЛ. VII. ДВАЖДЫ КУБИЧЕСКИЕ СПЛАЙНЫ
д8
дЗ
За14 + 2а24 =
'1-1. 8>-1
«24 == ^ (^-1» 5У) — «34 — «44»
03
—«34;
— «зз —'
+ 2а аз —-
М)~ «43 —
^
и + За
— «33 ^34'
«11+ «12+ «21+ «22 =
12
а22 =
•I, 5/) —«13 —«14—«23 —«24 —«31 —
— «32 — «33 — «34 — «41 — «42 — «43 — «44»
08
да
ц+ 2а12 + Зад! -|- 2а22 •=
9ац + база + 6а2, -«- 4а22 =
За14 — 2а23 —
— ^24 — «31 — «32 '— «33 — «34»
08
«13 — «23 — «Э«31
"«32 — «33 «л141 — "«42 — «43»
525
Кроме того, нам заданы следующие значения:
55
5*
08
^1
01
7.16. ПОВЕРХНОСТИ КУНСА
255
_эз_
Ч' 87-1
■е' / \ д&
**, &4
'(• *]
= Л(«/).
7-1
Непосредственной проверкой убеждаемся, что функция # ({, з) обладает нуж-
нужными свойствами. Если мы хотим задать нормальную производную функции
# B, 5) вдоль границ прямоугольников Мц, то требуются весовые функции
5-й степени, для высших производных необходимы полиномы более высокой
степени.
Однако весовые функции могут быть и не полиномами. Например, можно
потребовать, чтобы $ {I, з) и аналоги полиномиальных частей равенств G.16.1)
удовлетворяли уравнению Ь*Ь8 = 0 при фиксированном I ж уравнению
М* М8 — 0 при фиксированном з (Ь и М — линейные дифференциальные
операторы, I,* и М* — их формально сопряженные). Если функции /* ($)
и #/ @ удовлетворяют одному и тому же дифференциальному уравнению
Ь*Ыь == М*Мк = 0 Bп-го порядка), так что надо задать информацию только
в вершинах прямоугольников №ц, то поверхности Кунса представляют собой
двумерные сплайны 51 (*, 5), где каждый из одномерных сплайнов, полученных
при сужении сплайна 8 (г, з) на какую-то линию решетки, имеет дефект п
в каждом узле сетки на этой линии. Так как Куне рассматривал по существу
каждый из прямоугольников Мц отдельно, а не все вместе, то надо допускать
дефект равным п.
Глава VIII. ОБОБЩЕННЫЕ СПЛАЙНЫ
ДВУХ ПЕРЕМЕННЫХ
8.1. Введение
Содержание настоящей главы тесно связано с содержанием гл. VII. Однако
здесь наше внимание сосредоточено на сплайнах |5Я (Я, $), которые в каждом
прямоугольнике Мц удовлетворяют одновременно двум дифференциальным
уравнениям: дифференциальному уравнению по переменной I и дифферен-
дифференциальному уравнению (не обязательно связанному с первым) по переменной 5.
Мы не требуем здесь, чтобы одномерные сплайны, полученные фиксированием
одной из переменных, были простыми. Если рассматривать фиксированную
переменную как параметр, то все сплайны такого однопараметрического семей-
семейства будут иметь общую сетку; мы цредполагаем также, что они обладают
одинаковыми свойствами непрерывности во внутренних узлах сетки и удовлет-
удовлетворяют краевым условиям одного и того же типа.
Мы связываем рассматриваемые сплайны с теорией гильбертова простран-
пространства, строя прямые произведения двух гильбертовых пространств одномерных
сплайнов. Кроме того, мы получаем некоторые характеристики сплайнов,
охватывающие свойства наилучшего приближения и минимальной нормы,
устанавливая условия, при которых справедливо первое интегральное соот-
соотношение. Вопросы поточечной сходимости двумерных сплайнов мы сводим к
аналогичным вопросам для случая одномерных сплайнов, где ответ из-
известен.
Применяемые здесь методы с большими или меньшими трудностями
обобщаются на большее число переменных: построение прямого произведения
более чем двух гильбертовых пространств не вызывает затруднений; однако
установление условий, при которых справедливо первое интегральное соотно-
соотношение, сопряжено со значительными вычислительными трудностями, связан-
связанными главным образом с громоздкостью рассматриваемых выражений. Поэтому
мы ограничиваемся лишь двумерным случаем. Хотя это и можно было бы сде-
сделать, мы не будем останавливаться на применении обобщенных двумерных
сплайнов для представления поверхностей.
8.2. Основные определения
Пусть даны прямоугольник .52: а ^ Ь 4Щ Ь\ с ^ 8 ^ д, и два дифферен-
дифференциальных оператора
и = ап (*) И? • + ап_1 (*) ДГ1 • + . . . Н а0 (*)., '
(8.2.1)
Ь8 = Ьт (*) Б™ • + Ът_ь (8) ОТ'1 • + ... + Ьо @..
8.2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ 257
Здесь Ъь = 6,13.1, О8 — 613зх коэффициенты а1 ({) (с — О, 1, . . ., п) имеют
непрерывные п-е производные, ап (г) Ф О на [а, Ъ]; коэффициенты Ъ^ ($)
(/ — О, 1, . . ., т) имеют непрерывные тгс-производные, Ът(8)ф0 на [с, 3]. Обо-
Обозначим через Ь* и Ь* операторы, формально сопряженные к операторам Ьг
и Ь8. Наконец, пусть сетки Д<: а ={0 < 1Х <;...< Ьы — Ъ и Д8: с = $0 <С
<С §1 <С . . . <С зм = А определяют сетку я, разбивающую прямоугольник М
на ИМ прямоугольников Мц (г = 1, 2, . . .,^; / = 1, 2, . . .,
Определение 8.2.1. Функция #я ({, з) называется двумерным обоб-
обобщенным сплайном на М относительно сетки п, связанным с операторами Ьг
и Ь8, если а) для каждой точки 5 из [с, 6} она является гетерогенным сплайном
на [а, Ь] относительно сетки Д^, связанным с оператором Ь^ и Ь) для каждой
точки Ь из [а, Ь) она является гетерогенным сплайном на [с, 3] относительно
сетки Д8, связанным с оператором Ьа.
Интересно исследовать важность требования, чтобы выполнялись
условия Ь*^8Л = 0 и Ь*Ь88Я = 0 внутри каждого прямоугольника №ц.
Если Ь*Ь(8Я — 0 в прямоугольнике Мц, то в этом прямоугольнике
#л (I, «) — а4 (г, /; 5) щ (Г} + «з (и /; 5) и2 (I) + . . . +а2п (г, /; 5) и2п ({),
где функции и1 ({) (I — I, 2, . . ., 2п) образуют фундаментальную систему
решений уравнения Ь$1ци — 0. Тогда из условия Ь*Ь88п — 0 получаем
0 = ЦЬ8а{ (г, ;'; 5) щ ({) + Ь*Ь8а2 (I, /; 5) и2 @ + . . .
. . . + Ь*Ь8а2п (I, г, 8) и2п (*).
Следовательно, Ь*Ь8ак (г, /; §) = 0 (к = 1, 2, . . ., 2/г), так что
«л (г\ /; 5) = сА1 (г, /) ^1 (§) + ск2 (г, /) у2 (*) + ••• Ч
где функции VI (з) (/ = 1,2,..., 2т) образуют фундаментальную систему
решений уравнения Ь*Ь^ = 0. Таким образом, для B, $) из №
2п 9.т
I, /) ил (*) У| E). (8.2.2)
Из представления (8.2.2) видно, что, если производная да8я {Ь, )
непрерывна при I — 1и то и производные д^+а8я {г, вIд& д$ (р =0, 1, . . ., 2т)
также непрерывны при I = $1, кроме, быть может, точек B,-, $,•) (/ = 0, 1, ...
. . ., М). Аналогичный результат справедлив, если переменные ^ и з поменять
ролями. Заметим, что в силу представления (8.2.2) можно менять поря-
порядок дифференцирований при вычислении частных производных функции
#Л (*, 5).
17-1197
258
ГЛ. VIII. ОБОБЩЕННЫЕ СПЛАЙНЫ ДВУХ ПЕРЕМЕННЫХ
8.3. Основное тождество
Билинейную форму Р (и, и), связанную с линейным дифференциальным
оператором Ьг, можно записать в виде
п-1
р [и, и) = 2 в*"-'» (*) & {Ьи V, *), (8.3.1.1)
3=0
где
ыи, V, ^-^(-
(8.3.1.2)
(В разд. 6.2 мы обозначили р/ (Ь, Ь8п\ 2) через ру (8Я; I).) Так как рассмат-
рассматриваемые здесь функции зависят от двух переменных I и 5 и нам даны два опера-
оператора Ь{ и 1/8, то мы слегка изменим обозначения:
п-1
0
«.».5; 0.
Р^ (Ьи V, 8; 0 - Д (- ЗД* {ли-м @ у (*.
■=Х
V,
(8.3.2.1)
(8.3.2.2)
(8.3.2.3)
(8.3.2.4)
Пусть функция /B, §) задана в прямоугольнике №: а ^ I ^ Ь; с ^ 5 ^ Л
и ее частные производные, содержащие не более п дифференцирований по I
и не более т дифференцирований по 5, непрерывны в №. Пусть А*: а — {0 <.
< *! <С . . . < 1К = Ь и Д8: с = 50 <; в4 < . . . < 8М = ^ определяют на №
сетку я и 5Я (I, з) является сплайном на М относительно этой сетки, связанным
с операторами Ьг и Ь8. Рассмотрим интеграл
л ь
1
8, V, г; 8)= 2 (-Лв)г{Ь»-м(«)»('.
1 0
с а
Так как 1Л1ц8п {I, в) = 0 и Ь*Ь88п (*, $) = О внутри каждого прямоугольг-
ника №ц, то
й N п- I
с 1=1 з = 0
N М п-1т-1
- Ь 2л 2л 2л и* и* \?& 8> л*1*»
«; 0
1=0
'1-1
'* • (8.3.3)
8А-1
8.4. ТИПЫ СПЛАЙНОВ 259
Если в тождестве
а ь ль
с а с а
а ъ а ь
-2
с а с а
заменим / правой частью равенства (8.3.3), то получим тождество
а ь
с а
с а с а
N М п-1т-1
-2 2 2 2
й=1
Ц1 Г* , (8.3.4)
называемое основным тождеством для обобщенных двумерных сплайнов. Хотя
функции р/ допускают разрывы в узлах сетки или вдоль линий решетки, но они
имеют точки разрыва лишь первого рода, и поэтому вычисления, связанные
с нахождением величины /, надо проводить в терминах левосторонних и право-
правосторонних пределов.
8.4. Типы сплайнов
С помощью сетки А: а = {0 < й <С . . . <!? ^ = Ь на отрезке [а, Ь] можно
определить различные сплайны, отвечающие одному и тому же линейному диффе-
дифференциальному оператору Ь. Любой конкретный сплайн #д (?) зависит от конеч-
конечного числа независимых параметров, которые мы называем определяющими
значениями; 5Д (?) есть результат конкретного задания численных значений
этих параметров. Если таких параметров к и каждый их них может принимать
любое действительное значение, то мы получаем ^-параметрическое семейство
сплайнов ^д относительно сетки А. Семейство Р± состоит из сплайнов, отли-
отличающихся только заданием численных значений этих параметров и, следова-
следовательно, обладающих в точках сетки одинаковыми свойствами непрерывности.
В этом смысле семейство ^д определяет тип сплайна.
Для некоторых классов сплайнов мы уже ввели в рассмотрение понятие
фундаментального сплайна, т. е. сплайна, для которого все значения парамет-
параметров равны нулю, кроме одного, равного единице. Таким образом, с семейством
РА можно связать к линейно независимых сплайнов ег (г) (г = 1, 2, . . ., к)
и рассматривать его как линейное пространство с элементами ег (I) в качестве
17*
260
ГЛ. VIII. ОБОБЩЕННЫЕ СПЛАЙНЫ ДВУХ ПЕРЕМКННЫХ
базиса. Это значит, что, если Яд (I)
то
@ = 2 ад @-
(8-4.1)
Фундаментальными сплайнами являются, например, сплайны, о которых
говорится в следующих двух определениях х).
Определение 8.4.1. Пусть Яд (*) ^ Р±. Семейство РА называется
семейством гетерогенных сплайнов явного типа, если каждый коэффициент аг
в равенстве (8.4.1) можно определить (до некоторой степени независимо от рас-
рассматриваемого сплайна Яд {г)) как значение производной 5да) (Ь) в каком-нибудь
узле сетки А для некоторого а (а = 0, 1, . . ., п —1). Если ни одна из произ-
производных 5да) (*|) (а = 0, 1, . . ., п — 1; I — 0, 1, . . ., N — 1) не участвует
в определении коэффициентов аи то функция ра {V Ь8А; *) непрерывна при
I = 1{ ($ = 1, 2, . . ., N — 1) или обращается в нуль при I = Ьг A = 0, Щ.
Большинство из рассмотренных нами сплайнов были сплайнами явного
типа (нри подходящем выборе базисных элементов). Данное определение
{в частности, его двумерный аналог) в значительной степени облегчает форму-
формулировку многих основных результатов.
Определение 8.4.2. Пусть Еп — семейство двумерных сплайнов
на М' относительно сетки я, и пусть базис состоит из к сплайнов к1 ({, »)
{I — 1, 2, . . . , к). Семейство Ря называется семейством гетерогенных сплай-
сплайнов явного типа, если из равенства
2
1= 1
8)
(8.4.2)
вытекает, что каждый коэффициент аь можно определить (до некоторой степени
независимо от рассматриваемого сплайна !$„ (г, $)) как значение частной про-
производной 6^'1^8Я ($, 8)Ша дзу в каком-нибудь узле сетки я для некоторого числа
а + V (а = 0, 1, . . ., п — 1; у — 0, 1, . . ., т — 1). Если ни одна- из про-
производных да^8я (I, 8Iдьад8ч (а = 0, 1, . . ., п ~ 1; у = 0, 1, . . ., т - 1;
г = 0, 1, . . ., -/V; У = 0, 1, . . ., М) не участвует в определении коэффициен-
коэффициентов а{, то функция р\ [Ь8, ра (Ьь ЬгЬ88п, я; г), г; з] во внутренних узлах
{Ь„ 5/) сетки непрерывна 2) либо по Ь, либо по'«, или обращается в нуль либо
непрерывна вдоль границы в узлах (^, 5,) (в граничных узлах сетки, не совпа-
совпадающих с угловыми точками), или обращается в нуль в точках (^-, я,-) (в угло-
угловых точках).
х) Эти определения не охватывают все классы сплайнов, например периодические
сплайны. Но нетрудно дать определения для всех нужных случаев.
2) Утверждая, что функция / (г, «) в точке (**, «/) непрерывна по *, мы подразумеваем,
что, если пределы /(*, ^+0) и /(*,$,-—0) различны, то они оба непрерывны по г. '
8.5. ПЕРВОЕ ИНТЕГРАЛЬНОЕ СООТНОШЕНИЕ 261
Когда мы говорим, что сплайн #я (I, з) интерполирует функцию / ({, з)
на сетке п, то понимаем под этим, что #я A, з) = / ({, з) в узлах сетки п. Дадим
более строгое определение.
Определение 8.4.3. Пусть семейство Ря состоит из сплайнов явного
типа и сплайн 5Я (/; I, з) принадлежит Рп. Сплайн Я,, (/; г, з) называется
сплайном сильной интерполяции для функции / ({, з), если его частные произ-
производные, фактически участвующие в определений 8.4.2, интерполируют соответт
ствующие частные производные функции / ({, з) в указанных узлах сетки п.
8.5. Первое интегральное соотношение
Теорема 8.5.1. Пусть функция / ({, з) задана на прямоугольнике
М'. а ^.1 ^ Ъ, с-^з-^й и ее частные производные, содержащие не более п
дифференцирований по I и не более т дифференцирований по з, непрерывны на $,.
Пусть сетки
и
Д8: с = 50 <С $1*<С • • • <С з^ = д, >
определяют на М сетку п. Если 8Я (/; г, з) представляет собой сплайн на №
относительно п, связанный с операторами Ьг и Ь3, и является сплайном сильной
интерполяции для / ({, з) на п, то справедливо первое интегральное соотноше-
соотношение
ль а ь
({, в)}3 йг из =
с а с а
а ь
{Ь3Ьг1 ({, з) —Ь8Ьг8я (/; г, з)}2 <И из.
с а
Доказательство. В силу основного тождества и тождества (8.3.4)
для доказательства теоремы достаточно показать, что величина / равна нулю.
Специальный вид представления (8.2.2) для сплайна 5Я (/; I, з) позволяет
убедиться в справедливости следующих двух замечаний: 1) слагаемые, соответ-
соответствующие внутренним узлам ({(, з^) сетки, не дают вклада в величину /, если
в этих узлах производная да+У8я (/; г, зIдр- дз"* интерполирует да+г/ (?, зIд1а дз"*
или функция Рг [Ь8, ра Aц, Ь8Ьг8я, з\ г), г; з\ непрерывна либо по I, либо
по 5, и 2) слагаемые, соответствующие граничным узлам сетки, не дают вклада,
если р\, [Ь8, ра (Ь(, Ь3Ьг8п, з\ I), I; з] обращается в нуль в этих узлах, либо
непрерывна в них как функция, рассматриваемая лишь на границе прямоуголь-
прямоугольника М- Но условия пунктов 1 и 2 выполнены, поскольку #я (/; I, з) являет-
является сплайном сильной интерполяции для / (I, з) на д. Теорема доказана.
262 ГЛ. VIII. ОБОБЩЕННЫЕ СПЛАЙНЫ ДВУХ ПЕРЕМЕННЫХ
8.6. Единственность
Сформулируем теперь свойство минимальной нормы для двумерных сплай-
сплайнов. Это свойство весьма полезно при исследовании единственности интерпо-
интерполяционных сплайнов; как и раньше, оно вытекает из первого интегрального
соотношения.
Теорема 8.6.1. Пусть даны прямоугольник М: а ^ { ^ Ь; с ^ 5 ^ А,
сетка п, определенная одномерными сетками А*: а = *0 < Ь^ <. . . . <. {я = Ь,
А8: с = $0 <$!<!.•. <С вдг = й, и семейство Ря сплайнов заданного типа.
Если функция / {I, з) определена на М и ее частные производные, содержащие
не более п — 1 дифференцирований по I и не более т — 1 дифференцирований
по з, непрерывны на М, а частные производные, содержащие п дифференцирова-
дифференцирований по I и т дифференцирований по з, непрерывны в каждом прямоугольнике
М и если 8ЯЦ; 2, $) — сплайн сильной интерполяции для / (И, з), то
ль а ь
| {Ь8Ьг8я (/; *, *)}2 &1 Оз.
с а
Еслвдано семейство Ря явного типа, то любое решение уравнения Ь$Ь^ =
= 0 принадлежит Ря г). В частности, нулевая функция 2 ({, з) (нулевой сплайн)
будет элементом семейства Ря.
Определение 8.6.1. Если в Ря существует лишь один сплайн, кото-
который удовлетворяет уравнению Ь8Ьг8я = 0 и является сплайном сильной интер-
интерполяции для 2 (*, $), то говорят, что семейство Ря обладает свойством единст-
единственности.
Заметим, что если функция 5Л ({, з) на линиях решетки одномерных сплай-
сплайнов сильной интерполяции для нулевой функции равна нулю, то из представ-
представления (8.2.2) видно, что она равна нулю тождественно.
Теорема 8.6.2. Если семейство Ря обладает свойством единственности
и 8п (/; 2, в) — сплайн сильной интерполяции для функции / ({, з), удовлетворя-
удовлетворяющей условиям теоремы 8.6.1, то сплайн 8Я (/; Ь, з) является единственным.
Доказательство. Разность любых двух сплайнов сильной интер-
интерполяции для / ({, з) является сплайном сильной интерполяции для г{1, з).
В силу первого интегрального соотношения эта разность удовлетворяет урав-
уравнению Ьа1ц8я = 0 и, следовательно, тождественно равна нулю. Теорема дока-
8ана.
8.7. Существование
После того как получены фундаментальные сплайны, образующие базис
для семейства Ря сплайнов заданного типа, нетрудно построить для функции
/ ({, з) сплайн сильной интерполяции #я (/; I, з) из семейства Ря — достаточно
Вообще говоря, это утверждение неверно (см., например, разд. 7.6 и стр. 243, где
0* Х д2М2).— Прим. перев.
8.7. СУЩЕСТВОВАНИЕ 263
найти лишь некоторые частные производные функции / (г, $). Но здесь важно,
что фундаментальные сплайны существуют и известны.
Отметим, что двумерные сплайны выражаются через одномерные. Из этого
факта, в частности, следует представление (8.2.2). Пусть в прямоугольнике
М: о,<^.1 4^Ъ', с^«4^с помощью одномерных сеток Аг: а = ^() <С и <С . . .
, . , < ^ = Ь и Д,: с = *0 < «1 < . . . < «^ = й определена сетка п. Из пред-
представления (8.2.2) видно, что в каждом прямоугольнике Мц надо определить
Апт коэффициентов Сц. Если мы надлежащим образом запишем систему линей-
линейных уравнений для нахождения коэффициентов си (всего таких коэффициентов
4птЙМ), то для установления разрешимости этой системы можно будет вос-
воспользоваться свойством единственности. В самом деле, если бы соответствую-
соответствующая однородная система имела два решения, то для нулевой функции были бы два
сплайна из Ря сильной интерполяции, что невозможно.
Однако, чтобы получить соответствующую систему уравнений для су,
условия на 5Я (/; 2, в) должны гарантировать выполнение первого интеграль-
интегрального соотношения. В каждом внутреннем узле AЬ з>7) таких условий Атп:
а) производные да+У8я (/; {, з)/д1а дз^ (а = О, 1, . . ., п — 1, у = 0, 1, ...
. . . , т — 1) в точке (^, $;) непрерывны и по ^ и по 8 (это дает Зпт условий),
Ь) производная дь+у8я (/; I, 8I др^ дз? интерполирует д«+?/ (г, $)/д*а д& или
функции рг [Ь8, ра {Ьи ЬгЬ*8я, в; г), I + 0; в] и РУ1Ь8, ра Aг8, ЦЬ88Я, з; г),
$ — 0; а] непрерывны по I в точках (^, »7) при а = 0, 1, . . ., тг — 1; у =
= 0, 1, . . ., т — 1 (переменные I ъ. з можно поменять ролями).
Таким образом, кроме того случая, когда выполняется условие а) и первая
альтернатива в условии Ь), в узле (I*, $?) необходимо удовлетворить не четырем,
а пяти условиям. Так как условия, которые должны выполняться в граничных
узлах сетки, остаются неизменными, то создается впечатление, что в некоторых
случаях число условий превосходит число имеющихся в распоряжении коэф-
коэффициентов. Следовательно, можно ожидать (по крайней мере формально),
что коэффициенты с1} должны удовлетворять более чем АптИМ условиям.
Однако в действительности эти условия не всегда оказываются переопределен-
переопределенными.
Например, пусть Р^ — семейство сплайнов явного типа на [а, Ь], а ^д —
семейство сплайнов явного типа на отрезке [с, й\. Обозначим через {И,1 (I)}
{г = 1, 2, . . ., к) множество фундаментальных сплайнов, связанных с Е^ ,
и через {цу ($)}(/ = 1, 2, ...,/) множество фундаментальных сплайнов, свя-
связанных с Р& . Рассмотрим линейное пространство Ря, порожденное множест-
множеством {Нг ({) §] ($)} (г = 1, . . ., к; / = 1,..., I) попарных произведений.
Предоставляем читателю самому проверить, что Ря состоит из двумерных сплай-
сплайнов на М относительно зт; на самом деле Ря будет даже семейством сплайнов
явного типа. Заметим, что в данном случае г)
Р«.[4, Р« (Ьи ЬгЬМёз, * *) Ъ «1 = Ра (А,, Ь8&; з) ра (Ьг, {{к; I). (8.7.1)
!) Для этих сплайнов, согласно (8.7.1), в каждом внутреннем узле сетки должны
выполняться лишь 4 условия. Можно показать, что в данном случае во внутренних узлах
сетки имеется 4(ЛГ— 1) (.ЛГ—1) пт условий ив граничных узлах сетки 4(-ЛГ-1-ЛГ4-1)
условий, т. е. всего 4АГЛГлто условий.
264 ГЛ. VIII. ОБОБЩЕННЫЕ СПЛАЙНЫ ДВУХ ПЕРЕМЕННЫХ
Понятие частичных сплайнов можно также использовать (как и в гл. VII)
для построения двумерных обобщенных сплайнов. Но и здесь оба семейства
сплайнов, участвующих в построении, должны быть явного типа. Тогда будет
справедливо первое интегральное соотношение и в силу единственности пере-
переменные I и в можно будет (как и в гл. VII) поменять ролями.
8.8. Сходимость
Обоснование сходимости, данное в разд. 7.10, можно с таким же успехом
применить и здесь, так что задача сходимости в двумерном случае сводится
к задаче сходимости в одномерном случае. Только теперь, чтобы можно было
изменять порядок дифференцирований, надо потребовать еще непрерывности
функции / (?, 5) и достаточного числа ее частных производных. Теорема 8.8.1
служит типичным примером теорем сходимости, доказанных таким способом.
Ее доказательство проводится по схемам разд. 7.10, и поэтому мы его опускаем.
При желании можно также оценить скорость сходимости посредством скоростей
сходимости рассматриваемых одномерных сплайнов.
Теорема 8.8.1. Пусть даны прямоугольник .<%: а ^.1 <1 Ь; с^5^й
и последовательность сеток {я^} (к — 1, 2, . . .) на №, определенная последова-
последовательностями {А?: а = *$ < г\ <С • • • < Ь%к = Ъ) (к = 1, 2, . . .) и {А?: с =
= «5 < ^ < . . . < «^ = Л} (к = 1, 2, . . .). Пусть функция / B, 5) имеет
на М непрерывные частные производные, содержащие не более щ дифференциро-
дифференцирований по I и не более т^ дифференцирований по 8, и пусть {8Я (/; ^, $)} (к —
= 1, 2, . . .) — последовательность двумерных сплайнов, связанных с линей-
линейными операторами Ьь и Ьа вида (8.2.1); тг ^ щ, т ^ т4. Если для каждого гк
равномерно по 8 и № и для каждого $*
)
г- («=0.1....,
равномерно по I и 8%, то
равномерно по 8 и {.
8.9. ПРИЛОЖЕНИЯ К ТЕОРИИ ГИЛЬБЕРТОВА ПРОСТРАНСТВА 265
8.9. Приложения к теории гильбертова пространства
Если даны прямоугольник М: а^ 1; 4^. Ъ; с ^ 8 ^. Л и канонические сеточ-
сеточные базисы {#г {Ьг; *)} (Ь = 1, 2, . . .) и {8^ {Ьа; $)} (/ = 1, 2, . . .) для про-
пространств &Сп (а, Ь) и &Ст (с, й) соответственно, то можно образовать прямое
произведение этих пространств в смысле гильбертова пространства (Сард
11, стр. 354]). Обозначим это прямое произведение через е%?ш {№)• Его можно
интерпретировать как замыкание относительно полунормы
ь л
1Т Т •( I .г л\ 12 ^7+ Л а / О О А \
1-1*1-1 ъ\ \Ъ) 8) I \ХЪ по 1О.<7..1)
а с
(здесь отождествляются функции, отличающиеся на решение уравнения
Ьг^ = 0) пространства функций, порожденного попарными произведениями
элементов канонических базисов для &СП (а, Ь) и &Ст (с, <3). Следовательно,
функции I
,; *) 8Л (Ьа\ 8) (I = 1, 2, . . .; / = 1, 2, . . .) (8.9.2)
образуют базис для $С%, {№).
Обозначим через С^ {М) пространство функций / (г, $), а-я частная
производная которых, содержащая не более Р дифференцирований по I и не
более у дифференцирований по 5, непрерывна на М- В этой терминологии
Сптт(М) и Сгйт) (№) — подпространства пространства ЖтШ)-
Если функция / (г, з) принадлежит С^^ПМ), то ее можно представить
в виде
/ (*, ■*)= ё («, «) + ^ацЗц (** 8), (8.9.3)
где
ь а
ЬЗ 'л 1 1 / \ ^ > "/ *^ 2 /Уд О I IV • о 1 С^о С^^ у ( ~~~> х у м^ • • »^ У ■ А ^ ы^ • • •) ^
а с
Ь%Ь9% ({, 8) = 0.
Из теоремы 8.8.1 следует, что при достаточно слабых ограничениях сходи-
сходимость равномерна относительно г и 5. Поступая, как в разд. 5.17, получаем
представление
ь а
/ {{, з) — § (#,- §) -\- \ \ К {$, 8\ I', §') 2!/B!/8/ (^', §') с?5' ей', (8.9.4.1)
а с
где
Я ({, з; г', в) = Ит 2 ^о1 (^» 5) ЬгЬэЗи (*', «')• (8.9.4.2)
Уравнение (8.9.4), как и в разд. 6.18, можно использовать для решения
дифференциальных уравнений в частных производных вида
^ *, 5) = / ((, 8) (8.9.5)
266
ГЛ. VIII. ОБОБЩЕННЫЕ СПЛАЙНЫ ДВУХ ПЕРЕМЕННЫХ
и соответствующей задачи о собственных значениях. Недостаток этого метода
состоит в том, что произвольный дифференциальный оператор в частных про-
производных, вообще говоря, нельзя представить в виде (8.9.5). Кроме того, метод
применим лишь для прямоугольных областей .$?. Чтобы устранить последнее
ограничение, можно специальным образом подобрать координаты, как это
описано в разд. 7.14, но обычно выбор координат нарушает разложение
вида (8.9.5), если оно было справедливо.
Что касается приближения и представления линейных функционалов,
то здесь ситуация намного лучше. Одна из причин заключается в том, что
линейные функционалы часто определяются внутренне, а не в терминах кон-
конкретной координатной системы. Например, пусть
ц = / (Р) м,
(8.9.6)
где И — односвязная замкнутая область, звездообразная относительно
точки Ро, и &А — элемент площади. Введем в Б полярные координаты г и 0
с полюсом в точке Ро. Пусть г = § @) — граница области И. Практически
в качестве функции % @) можно взять простой кубический сплайн относительно
переменной 0. Введем новые координаты
тогда
1 2Я
I!
0 0
/(Р,
а)
дг
ар
дв
Ж
дг
да
дв.
да
а) <ф Да =
(8.9.7)
а) § (аK р й$ Оа. (8.9.8)
о о
Этот пример показывает, что координатную систему в области И можно
ввести так, что область изменения координат станет прямоугольной. После
перехода к прямоугольной области большой класс функционалов можно пред-
представить и приблизить так же, как в гл. V и VI. Расхождения с одномерными
методами не вызывают затруднений.
ЛИТЕРАТУРА
А л б е р г, Н и л ь с о н (АЫЬег1? I. Н., N П я о п Е. N4
1. Сопуегдепсе ргорегИез о! *Ье зрНпе й*, МоЫсез Ат. Маш. 8ос. A961), 61Т-219.
2. Сопуегдепсе ргорегИез о! Ше зрНпе й*, 1п1егп. Соп§г. Ма1Ь. 31оскЬо1т, 1962.
3. Сопуегдепсе ргорегМез о! *Ъе зрНпе Й*, /. 8ос. 1п4. Арр1. Магк., 11 A963), 95—104.
4. Сопуегдепсе ргорегМез о! депегаНгей зрНпез, МоШез Ат. Маш. 8ос. A964), 64Т-485.
5. Ог*ЬодопаШу ргорегИез о! зрНпе йшсМопз, /. МаЬк. АпаЬ. Арр1., 11 A965), 321—327.
6. ТЬе арргох1та*1оп о! Нпеаг {ипс110па1з, /. 8ос. 1п&. Арр1. Маш., Нитег. Апа1., 8ег.
В, 3 A966), 173—182.
Алберг,Нильсон, Уолш (АЫЬегд I. Н., N113011 Е. N.. \У а 1 з Ь I. Ь.)
1. Вез* арргохнпайоп ргорегйез о! *Ье врИпе й*, /. МаНъ. Меск., 11 A962), 225—234.
2. Вез1 арргох1таИоп апа сопуег^епсе ргорегИез о! Ы^Ьег огйег зрНпе Й1з, НоПсез Ат.
МаШ. 8ос. A963), 63Т-103.
3. ОгШо^опаШу ргорег*1ез оНЬе зрНпе Гипс*1оп, МоПсез А т. Маш. 8ос. A964), 64Т-338.
4. Ех*гета1, ог1Ьодопа1Лу, апй сопуег^епсе ргореШев о! тиШ-сИтеп810па1 зрНпез, N0-
Псез Ат. МаОг. 8ос. A964), 64Т-339.
5. РипЛатепЫ ргорегйез о! &епегаНгес1 зрНпез, Нойсев А т. Ма(к. 8ос. A964), 64Т-451.
6. ШдЬег-огйег зрНпе 1П*егро1а*)оп, ЫоПсев Ат. Маш. 8ос. A964), 64Т-494.
7. Рипс1атеп*а1 ргореШез о! гепегаНхей арНпез, Ргос. N0*. Асай. 8а. 1/8А, 52 A964),
1412-1419.
8. СепегаШей зрНпез апй 1Ье Ьез1 арргох1таИоп оС Нпеаг {ипсИопаЬ, ЫоИсев Ат. МаШ.
8ос\ A965), 65Т-125.
9. Вез1 арргстпШюп апй сопуегдепсе ргорегИез о! Ы^Ьег огйег зрНпе арргох1таИопз,
/. Ма1к, Меск., 14 A965), 231—244.
10. Сопуег^епсе ргорег*1ез о! зепегаНгей зрНпез, Ргос. Ыаг. Асай. 8с1. 1/8А, 54 A965), 344—
350.
11. Ех1гета1, ог*Ьо§опаН1у, апй сопуегдепсе ргорегИез о{ ти111-Й1тепз10па1 зрНпез, /.
МаШ. Апа1. Арр1., 11 A965), 27—48.
12. Сопуег^епсе ргорегйез о! сиЬ1с зрНпез, НоПсев Ат. Ма1к. Зое. A966), 66Т-47.
Аттиа (А**е1а М.)
1. ОёпёгаНзаиоп Йе 1а йеНпШоп е4 йез ргорпеЧез йез «зрПпе {ипсМош, СотрЬ. В.епй.,
260 A965), 3550-3553.
Беллман, Кал аба (В е 11 т а п К. Е., Ка1аЬа К. Е.)
1. Мойегп апа1уЦс апс1 сотри1аЦопа1 те1Ьос1з 1П зегепсе апс! таШетаИсз, Атз1егс1ат,
1965.
Биркгоф (В1гкЬо!1 О.)
1- Еггог Ьоипйз !ог арНпе Й4з, Койсев Ат. Ма(к. 8ос. A964), 64Т-296.
Биркгоф, де Бур (В 1 г к Ь о Н С, йе Воог С.)
1. Еггог Ьоипйа Гог зрНпе т1егро1а1юп, /. Ма(к. Ме1к., 13 A964), 827—835.
Биркгоф, Гарабедян (В 1 г к Ь о { { С, СагаЪесПап Н.)
1. ЗтооШ аийасе тЪегроЫюп, /; Маш. Ркув., 39 A960), 258—268.
Гильдебранд (Н11с1еЬгапс1 Р. В.)
1. 1п1гоаис1юп 4о питепса1 апа1у818, Кетяг Уогк, 1956.
Голомб, Ваинбергер (Оо1отЬ М., "\Уе1пЬегдег Н. Р.)
1. ОрМта! арргох1таИоп апй еггог Ьоипйз. Оп питепса1 арргох1та1юп, Ргос. Зутр.
МаШ. Кез. Сеп^ег, Ш1У. "\У18сопзт, Арп1 1958, рр. 117—190.
268 ЛИТЕРАТУРА
Г р ч в и л ь (О г с V 1 1 ] е Т. N. Е.)
1. ]Читпепса1 ргосейигез !ог т1егро1а1лоп Ьу зрПпе Гипсиопз, МаШ. Кез. СспЪег ТесЬ.
Зшптагу Кер1. 450, И8 Агту, 11шу. о! Шзсошнп, 1964.
2. 1п1егро1аИоп Ьу депсгаНгей ярПпе {ипсИопз, Ма1Ь. Вез. Сеп1ег ТесЬ. 8иттагу Вер1.
476. 118 Агту, Ь'шу. о{ \\715сопзт. 1964.
3. Китепса! ргоседигез !ог 1п4егро1а11оп Ьу зрНпе {ипсИопз. /. Зое. 1пЛ. Арр1. Маш..
МитеНса1 Апа1., 8ег. В. 1 A964), 53—68.
Г у р с а, Бергман (С о и г з а I Е„ Вегдтапп 8.)
1. А соигзе т та1Ьетаиса1 апа1уз18, уо1. III, раг1 2, N6%' Уогк, 1964.
Гурса, Хедрик (О о и г я а I Е., Н е A г 1 с к Е. П.)
1. А соигзе 1П та1Ьета1:1са1 апа!уз18, уо1. I, Воз1оп, 1904.
Далквист (Б а Ь 1 д и 1 з I О.)
1. Сопуег^епсе апй з1аЬШ1у 1п 1Ье пишег1са1 ШедгаИоп о^ огA1пагу сИГГегепНа! е^иа^^опз,
Маш. 8сапа.. 4 A956), 33—53.
Де Бур Dе Воог С.)
1. ВшиЫс «зрНпс» 1п1егро1аиоп, ЫоИсе$ Ат. Маш. Зое. A961), 579-24.
2. ВкиЫс зрПпе 1Шсгро1аиоп, /. Ма1Н. Рку$., 41 A962), 212—218.
3. Вез1 арргох1та11оп ргорегИез о! зрНпе Сипсиопз о{ 0AA ^еегее, /. Ма1к. Меск., 12 A963),
747-749.
Д е Б у р. Л и н ч (A е В о о г С. Ь у п с Ь П. Е.)
1. Сепег&1 &рНпе {ипс110пз апA 1Ье1г т1п1тит ргорегйез, МоНсе$ Ат. Маш. 8ос. A964),
64Т-456.
2. Оп «рНпез апй Ше1г т1ттит ргореШез, /. МаШ. МесЬ., 15 A966), 953—969.
Джонсон (I о Ь п з о п К. 8.)
1. Оп топозрПпез о! 1еазЬ с1су1аИоп. Тгат. Ат. Маш. Зое, 96 A960), 458—477.
Д э вис (Б а у 13 Р. 3.)
1. 1п1егро1аШ>п апй арргох^таНоп, N6^ Уогк, 1963.
Зейферт (8 е 11 с П Н. 8., ей.)
1. 8расе ТесЬпо1о?у, Кечу Уогк, 1959.
Куне (Соопз 8. А.)
1. 8ийасез !ог сотри1ег-а1с1сс1 Aез1§п оГ зрасе Пдигез. 1964 (не опубликовано).
Л а н д и с, Н и л ь с о н (Ь а п A1 з Р.. N I 1 8 о п Е. N0
1. ТЬе Aе1егт1паиоп о! 1ЬегшоAупа1П1С ргорегИез Ьу й}гес1 йгйегепИаИоп 1есЬп1Я
Ргодг. 1п1егп. Коз. ТЪеппоДуп. Тгапзрог1 Ргорег^ез, Ат. 8ос. МесЬ. Епдгз, 1962.
М ю и р ( М и 1 г Т.)
1. А 4геаЙ8е оп 4Ье ЪЬеогу о^ с1еЪеппшап1я, Ке\у Уогк, .1960.
П е а н о (Р е а п о О.)
1. Кез4о пе11е !огти1е Й1 диаAга1;иге ехргеззо соп ип 1п1едга1е йе{1П11о. АШ Ассай.
Ыпсег, Деп<1. С1<ше 8с1. П§. МаЬ. На1. E), 22 A913), 562—569; Ореге 8сеИе Кота, 1
A957), 410-418.
С а н с о н е, Конти (8 а п я о п е С Соп И В.)
1. ]Чоп-1теаг (Ш!егеп1ла1 едиаИопз, N6^ Уогк, 1964.
Сард (8 а г й А.)
1. Ыпеаг арргох1та(юп «МаШетаиса1 8игуеу8» № 9, Ат. МаШ. 8ос, РгоУ1Aепсе, 1963.
Секрест (8 е с г е 8 I Б.)
1. Вез1 1п1;ея^а1{оп Гогти1аз апй Ьез4 еггог Ьоипйз, Магк. Сотр.. 19 A965), 79—83.
2. Еггог Ьоипйз !ог ]п48гро1а11оп апA сИНегепИаНоп Ьу 4Ье изе о{ зрНпе {ипсМопз. /. Зое.
1пй. Арр1. Магк., Nите^. Апа1., 8ег. В, 2 A966), 440—447.
Сокольников (8 о к о 1 п 1 к о И I. 8.)
1. Ма1петаИса1 Шеогу о! е1азМс]'1у, ЛТе\у Уогк, 1956.
Тайльхаймер, Старквезер (Т Ь е 11 Ь е 1 т е г Р., 81агк\уеа1Ьег \\г.)
1. ТЬе {агппд о\ зЫр Ппез оп а Ы§Ь-зреес1 сотри1ег, МитеНса1 ТаЫе& АШ СотригаИоп.
15 A961). 338-355.
Тейлор (Т а у 1 о г А. Е.)
1. 1п1гос1исМоп № {ипс1юпа1 апа1уз1з, Ке\у Уогк, 1958.
Т о д д (Т о й A I., ей.)
1. 8игуеу о! питепса! апа!уз18, Кечу Уогк, 1962.
ЛИТЕРАТУРА 269
Ф е й е р (Р е ^ ё г Ь.)
1. Шег 1п1егро1аМоп, ИасЬг. Сез. ЧЯЪз. СоШп§еп, Ма1Ь. РЪуз!к. К1., 1916.
2. Б1е АЪзсЬаЧгипд етез Ро1употз т ешет 1п1егуа11е, \уепп 8сЬгапкеп Мг зете ДУег1е
ип<1 егз1;еп АЫеНипдзлуеПе т ешге1пеп Рипк1еп Дез 1п4егуа11ез дедеЪепепзтс[, ипй Шге
Ап^епЙипд аи! (Не КопуегдепгГга^е НегтНезсЬеп 1п1егро1а1юп8геШеп, Ма1к. %.. 32
A930), /.26-457.
Фриман (Ргеетап Н.)
1. МаШетаИсз !ог ас1иапа1 з1и<1еп18, уо1. II, СатЬпйде ЬТП1У. Ргезз, Ьопс1оп, Ие\у Уогк,
1949.
X и л л е (Н 111 е Е.)
1. Апа1уИс (ипсИоп 1Ьеогу, уо1. II, Воз1оп, 1962.
X о л л и д е й (II о 11 а й а у 3. С)
1. 8тоо1Ьез1 сигуе арргохппаИоп, Маш. ТаЫе$ АМ$ Сотпри.1., 11 A957), 233—243.
Ц и г л е р G, 1 е в 1 е г 2.)
1. Оп 1Ье сопуег§епсе о{ п-ЬЪ. ог<1ег зрНпе ГипсИопз, Иоисез Атп. Зое. A965), 65Т-354.
Шарма, Мейер (8 Ь а г т а А., М е 1 г А.)
1. Сопуегдепсе ог зрНпе 1ипсЦопз, МоИсез А т. МаШ. 8ос. A964), 64Т-496.
2. Бедгее о! арргсттаУоп о! зрНпе 1п1егро1аИоп, /. МаШ. Меск., 15 A966), 759—767.
Ш в а й к е р т (8 с Ь \у е 1 к е г I Б. О.)
1. Ап 1П1егро1аИоп сигуе изт§ а зрНпе 1П 1епз1оп, /. Мазк. Рку$., 45 A966), 312—317.
Шёнберг (8сЬоепЬегд 1.1.)
1. СоШпЪиНопз 1о ргоЫет о! арргсштаИоп о! еди1<Иаиш1; <1а1а Ьу апа1уИс ^ипсИопз,
()иаг1. Арр1. Маш., 4 A946), 45—99, 112—141.
2. Оп Ро1уа Ггедиепсу !ипсИопз апй 1Ъе1Г Ьар1асе ггапзГогтз, /. Апа1. Ма1к., 1 A951),
331-374.
3. 8р1те ГипсИопз, сопуех сигуез, апA тесЬап1са1 ^иас^^а1;V1^е, Вий. Ат. Маш. Зое, 64
A958), 352-357.
4. 8рПпе т1егро1а1юп апй гЬе ЫдЬег йепуаИуез, Ргос. N01, Асай. 8ы. 118А, 51 A964),
24—28.
5. 8рНпе т1егро1а1юп апй Ьезг яиаAга!;иге {огти1ае, ВиЫ. Ат. Маш. 5ос, 70 A964),
143-148.
6. Оп 1пе ЬезЦ арргохгтаиоп о{ Нпеаг орега^огз, КотМ. Мей. Акай. \Уе1еп$сНар. Ргос,
йег. А, 67 A964), 155—163.
• 7. Оп 1п§опотсШс арНпе 1п1егро1а11оп, /. Ма1к. Меск., 13 A964), 795—825.
8. Оп 1п1егро1а1;1оп Ьу зрНпе ГипсИопя апй Из Ш1П1та1 ргореШез. «1п1егпа11опа1 Зепез
о! 1^итепса1 Апа1уз18», уо1. 5. рр. 109—129, Асайстхс Ргезз, Ие^ Уогк, 1964.
9. 8р1те ГипсИопя ап<1 гЬе ргоЫет о{ дгадиаНоп, Ргос. №аг. Асай. Зсг. [/8А, 52 A964),
947—950.
10. Оп топозрНпез о! 1еаз1 AеУ1а11оп апй Ьез1 ^иа<1^а^и^е Гогти1ае, /. Зое. 1пй. Арр1. МаШ.,
;\итег.' Апа1., 8ег. В, 2 A965), 145—170.
Шёнберг, Уитни (8сЬоепЬегд I. I., "\У Ь 1 I п е у А.)
1. 8иг 1а розШуИё йез с1ё1егттап1з бе 1гапз1а11опз йе {опсИопз <1е Ггёяиепсе йе Р61уа
ауес ипе аррИса^оп аи ргоЫёте с1'1п1егро1аиоп раг 1ез {опсИопз «зрНпе», Сотри Кепи.,
228 A949), 1996-1998.
2. Оп Ро1уа !геяиепсу ГипсИопв. III, Тгат. Ат. МаШ. Зое, 74 A953), 246—259.
Эйткен (А 1 I к е п А. С.)
1. Бе1епптап1з апй таШссз, ЕсПпЬигдЬ, Ьопйоп, 1958.
Эскер (А 8 к с г В.)
1. ТЬе врНпе сигуе, а зтооШ 1п1егро1аИпд1ипс11Оп ияес1 1П питег1са1 Йез1дп о{ зЫр-Ипез,
;Хогй. ТШкг. 1п1огт. ВекапйПм, 2 A962), 76—82.
ДОБАВЛЕНИЯ
С. Б. Стечкин, Ю. Я. Субботин
§ 1. Полиномиальные сплайны первой степени
Функцию <?1 (х) называют сплайном первой степени на сетке
А: а — х0 < XI < ♦ ♦ . < хп = 6, A.1)
если она непрерывна на [а, Ь] и совпадает с линейной функцией на каждом
из отрезков [хг, х1+х\ (г = 0, 1, . . ., п — 1).
Полиномиальные сплайны первой степени (ломаные) с успехом приме-
применяются в качестве промежуточного приближения. Эта идея восходит к Лебегу
(см., например, [7]*)), который использовал промежуточное приближение
ломаными для доказательства теоремы Вейерпгграсса о полноте множества алгеб-
алгебраических многочленов в пространстве С (О, 1). В дальнейшем этот метод раз-
развивался в работах Н. П. Корнейчука, например, в [12].
Сформулируем некоторые результаты о приближении интерполяционными,
сплайнами первой степени. Пусть функция / (х) непрерывна на отрезке [0, 1]'
и сплайн ^1 (х) интерполирует ее в узлах хк = к1п, к = 0, 1, . . ., п.
Обозначим через Н& и РРЯ,» классы функций, модуль непрерывности со F, /)•
и соответственно модуль непрерывности первой производной со F, /') кото-
которых не превосходит заданного модуля непрерывности со (б). В. Н. Малоземов
[17] доказал следующие две теоремы.
Теорема 1. Если со (б) — выпуклый модуль непрерывности, то
1/п
аир [|/И-^(х)||с=1 ^
Теорема 2. Для произвольного модуля непрерывности со (б)
1/п
зир вир I /' (х) — 8[ (х) I = п [ со Ц) дХ. A.4>
Обобщение равенства A.2) дано В. Ф. Сторчаем [26].
х) Жирные цифры в квадратных скобках указывают номер работы в списке литературы
к этим добавлениям. Светлые цифры отсылают к основному списку.
§ 1. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ ПЕРВОЙ СТЕПЕНИ
271
Теорема 3. Если со F) — выпуклый модуль непрерывности, то
A.5)
Равенство A.2) получается отсюда предельным переходом при р -*- оо.
Приближения ломаными функций класса Н& для произвольного со (б)
рассматривались в работе А. С. Логинова [14], где доказана
Теорема 4. Если со F) щк О, то для любого п = 1, 2, . . .
шах |/(*)-$!И1
<Т •
зир /(со, гс) = -~-
F)^0 ^
A.6)
00
*5^4 (а;) — ломаная с вершинами в точках (к/п, {(к/п)), к = 0, 1, ..., п.
Докажем теорему 2. Пусть
И
= шах
п
Так как
ТО
1/п
\ 5 (х) их = О,
к/п
\ п *~
1/п
со
1/п
Покажем, что для функции
272
где
/1
1/п
^
^ 0
($0(х)^Н&), выполняется равенство
вир | /'0 (х) —,
В самом деле,
тах 1
Далее,
/о (*) -^ И И тах [
ДОБАВЛЕНИЯ
1/п
0
Ч.М1-
1/п
п | ю(/
0
:о*.
■Г-
) Й2, СО 1
1
о*.
■
1
1/п
Интегрируя это неравенство от 0 до 1/п, получаем
1/п
\
О
Следовательно,
1/п
тах | /„ ^л:) — ^ (х) | = ге \ со (?) Д.
Теорема доказана.
§ 2. Интерполяционные параболические сплайны
2.1. Существование и сходимость. Здесь рассматриваются сплайны четной
степени, узлы которых находятся посредине между узлами интерполяции.
Впервые такие сплайны на равномерной сетке изучал Шёнберг [1].
Пусть заданы непрерывная периодическая функция / (х) с периодом Ь — а
и сетка
А: а = х0 < XI < . . . < хп = Ь. B.1)
Функцию «!?2 (х) называют периодическим сплайном второй степени с периодом
Ъ — а, интерполирующим функцию / (х) на сетке А, если
2) 82 (х) имеет непрерывную первую производную и 8 (х) = ^ при
1 + жй)/2 -^ х <1 (хк + ял+1)/2, где 5Гг — константы, к = 1, 2, . . ., га,
+ 1 о,
3) #2(*л) =/Ы, * = 0, 1, ...,»•
§ 2. ИНТЕРПОЛЯЦИОННЫЕ ПАРАБОЛИЧЕСКИЕ СПЛАЙНЫ 273
Положим ... •«
хь> /г —0, 1, ...,/г,
х
Представим 82 (х) в виде
82 (х) = ^2 (а) + Я; (а) (х-а) + $
О
и потребуем, чтобы выполнялось условие 82 (хк-1, хк, яй-и) =/(«й-1, *й,
/с = 1, 2, . . ., п. Тогда
т^рЯ-1+з«+тг^»Г 5;+1=8/ <*-• *»■Жкм)- : ;'B:2)
к = 1, 2, ..., /г, о о = Оп, Оп-Н ^ *^1«
Матрица коэффициентов системы B.2) обладает доминирующей щавной
диагональю, следовательно, система имеет единственное решение. Неизвестные
1^2.(а) и #2 (а) находятся из условий интерполяции. Таким образом, при п ^-1
существование и единственность периодического интерполяционного сплайна
второй степени доказаны.
Положим
= тах
Лемма 1. Если сплайн 82 (х) второй степени интерполирует в узлах
сетки B.1) непрерывную периодическую функцию / (х) с периодом Ь — а, то
у<16шах т(^/) , B.3)
1<й€ *Л
тах |«|< 16 шах
к. '
Если, кроме того, $ (х) имеет непрерывную первую производную, то
/'). B.5)
Доказательство. Пусть у = тах (а, р) = тах тах (ак, рь); тогда
к
из равенств B.2) получаем
Т B.6).
18-1197
274 ДОБАВЛЕНИЯ
откуда
/)}<16тах
Ы^п пк
+ в1Л|)-/'(Ж|-в1Лм)}<16©(«, /'),
Далее, в силу B.2)
о л о
~3" 1/(^1-1» «1»«1+1)|<"з- 1^| +
я^гга
Лемма 1 доказана.
Лемма 2. Если периодическая функция 1{х\ с периодом Ъ — а имеет
непрерывную вторую производную /" (х) и сплайн 82 (х) второй степени интер-
интерполирует эту функцию в узлах сетки B.1), то
Доказательство. Заменим в B.2) к на к +1 и вычтем из второго
равенства первое; получим
Положим
ел = | 81+1 — 81 \, ег = тах ек.
к
Тогда
8 + 8 (Лм + ^Х^ + Л^О ^ ^ 8{кг + к1+1) + 8(*м + *,) + 2
т. е. е4/4 ^ 2© (б, /"). Лемма доказана.
Теорема 1. Если периодический сплайн 82 (х) второй степени интер-
интерполирует в узлах сетки B.1) непрерывную периодическую функцию / (х) с перио-
периодом Ъ — а и Ь = тах пк, то
к
, Ц/.(*)■.- ^2 («У II - тах | Ш - 82 (х) \ < © F, /) + №, B.8>
X» = 8 тах й^1© (&й, /).
Л1
§ 2. ИНТЕРПОЛЯЦИОННЫЕ ПАРАБОЛИЧЕСКИЕ СПЛАЙНЫ
275
Доказательство. Для хг < х <. ж*+1 имеем @ < Я, < 1)
(б, л + I A -
где хг < я:', а:" <С х1+1. Положим Я, =
-1. Тогда
— ^д'1 (я^+^ — *)» 1 — А, =
X'
Применяя теперь неравенство B.3), получаем утверждение теоремы.
Следствие. Если / (х) € 1лр 1, т. е. ю (б, /) = 6, то при любом
расположении узлов
11 Т IД/} ^^~ Л о 100} 11 ч^С^ У О •
\\ Л \ / Й \ / I I ^*^» *
т. е. интерполяционный процесс всегда сходится.
Теорема 2. #сды функция / (#) с периодом Ъ — а имеет непрерывную
первую производную, то
|| /СО (С) - 5$« (с) || < ЛГ^-'ш'Сб, /') (г = 0, 1), B.9)
где К0 = 8,5; Я4 = 17.
Доказательство. Пусть х — произвольная точка отрезка [а, Ь)
и хг <^ #.^ х1+1 для некоторого г. Так как / (хк) = 82 (^й), к = г, 1 + 1,
то существует такая точка |, а:г <С | <; а:г+1, что /' (!) = 5, (|). Тогда
(б, я+18'2 (|) -5; (х) |=
С помощью B.5) получаем неравенство B.9) при 1 = 0. Далее, для а?#
х ■
(*) - 82 (х) | =
- 8'
8,5б(о F, /),
где у — ближайший,к х конец отрезка [хи х1+1]. Теорема 2 доказана.
18*
2.76 ДОБАВЛЕНИЯ
Теорема 3. Если функция / (х) с периодом Ь — а имеет непрерывную
вторую производную, то
||/(г) {х) _ 5<о (Х) || ^ АгЬ*-*<* (б, /") (I = О, 1, 2), B.10)
где Ао = 9/4, Ах = 18, А2 = 18.
. Доказательство. Пусть хк <С я: <С #ь+1 и число 2? таково, что
§ (х) = 0, где $ (г) = / (г) — #2 (г) — П (г — <гь) (г — а:й+<). В силу интер-
интерполяционных свойств сплайна #2 (#) и выбора числа Л
§(х) = §(хк) ■= йг(жй+1) = 0.
По теореме Ролля существуют такие точки 1Ь |2> ^й <С ^1» 1г < ^й+ь чт0
§' A0 = / Aг) = 0. Так как функция %' (г) непрерывна на отрезке Ць |2Ь
то в некоторой точке ^ функция | %' A) | достигает своего наибольшего значе-
значения. Следовательно, в этой точке либо а) §" (|) = 0, либо б) §" (% + 0)
и §" (% — 0) имеют противоположные знаки; пусть для определенности
€■ (I + °) > °» ё" A - 0)< 0- Здесь §" (I + 0) и #" A - 0) - соответственно
правосторонняя и левосторонняя производные функции %' (г) в точке |. Обо-
Обозначим через /" (х) — 8" (х ± 0) ту из двух величин /" (х) — 8Цх -\- 0),
/" (х) — #2 (х — 0), которая больше по абсолютной величине. В случае а)
В случае б)
/" A) - ^ а + 0) - 2Я > 0,
Г F) - Ч F - 0) - 2П < 0.
Следовательно,
% B.11)
Пусть теперь #й <^ х ^ ^ь+1* Тогда
| /" (*) - 81 (х) | < | /" («) - 81 (х ± 0) |. B.12)
Из интерполяционных свойств сплайна 82 (х) получаем / (жг) — 82 (хг) = 0,
I = к — 1, к, Л: -V- 1- Рассуждая далее, как в случае функции § (г), устанавли-
устанавливаем, что либо существует такая точка т), что /" (г\) — 81(ц) = 0, либо
/" (т^) — 8К2 (ц + 0) и /" (-л) — ЗЦц — 0) имеют противоположные знаки.
Применяя лемму 2 и, возможно, неравенство || 8к+2 — 8к || <^ 2 || 8к+1 — 81 |[,
находим, что
I г (х) - з; (х ± 0) | < | г (*) - Г (ц) + з; (ц + о> - з; (х ± 0) |<
< 2со F, Г).+ 16@.F, /") = 18со F, П< B-13)
§ 2. ИНТЕРПОЛЯЦИОННЫЕ ПАРАБОЛИЧЕСКИЕ СПЛАЙНЫ 277
Положим в B.13) х = \. Тогда в силу B.13) и B.11)
/ \ С //*»\ I л*00 А2 /А ^"\
По теореме Ролля существует такая точка |0, хк <. Ъо <. хк+1, что /' (^й) —
*— ^2 Но) = 0. Поэтому для хк < х < хк+±
| /' (х) - 82 (х) |< [/" @ - 5;' (*)] Л < 18б(о F, /").
Теорема доказана.
Для полиномиальных сплайнов второй степени справедливы аналоги боль-
большинства теорем из гл. II настоящей книги. Мы остановимся здесь лишь на дока-
доказательстве аналога теоремы 2.9.1.
Пусть на отрезке [а, Ъ] заданы сетка А: а = х0 <С х^ <С'. . . <С хп = Ъ
и функция / (х). Функцию 82 (#) назовем интерполяционным сплайном- второй
степени для функции / (х) на сетке А, если
1) первая производная 8'2 (х) непрерывна на [а, Ъ],
2)
п»
-1, 2 п-1),
где 8ъ (к = 0, 1, ..., п) — константы.
Этими условиями непериодический сплайн второй степени определяется
неоднозначно, так как он имеет п -\- 3 параметра, а интерполяционные свойст-
свойства дают лишь п + 1 условий. Поэтому нужно наложить еще 2 условия (крае-
(краевые условия) на ^2 (х). Можно потребовать, например, чтобы выполнялось или
а) 8; = 8п = 0, или б) 81 = /" (*0), 8"п = /" (хп), или в) 82 (х0) - /' (хо)г
З'ъ (хп) = {'(хп)- В терминах {81} условия в) принимают вид
Н° *- Ч Ч ^ B.14)
) /' (т
У \Хт
Так же, как для кубических сплайнов, можно рассмотреть краевые условия
общего вида
278
ДОБАВЛЕНИЯ
где Хо, \1п, й0 и а\ — заданные числа. Воспользуемся обозначениями разд. 2.1
основного текста:
л \ / • л о
Тоща с учетом соотношения B.2) для к = 1, 2, . . ., га
получаем систему уравнений для нахождения величин
,тг-1).
- 1 и условий B.15),
О
0
0
0
0
0
0
0
0
0
0
0 0 0
0 0 0
Ю о о
0
0
81
81
•
С"
-2
-'.
1
•
"г
B.16)
где д,к = 8/ (хк_1, хк, хк+1), к = 1, 2, . . ., п — 1. Если величины 8к най-
найдены, то сплайн 82 (%) однозначно определяется, из условий интерполяции.
Поэтому вопрос о единственности интерполяционного сплайна 82 (х) сводится
к вопросу единственности решения системы B.16). Сформулируем аналог тео-
теоремы 2.9.1.
Теорема 4. Непериодический сплайн 82 (х), имеющий заданные орди-
ординаты уо, уи * . ., уп в узлах сетки А: а = х0 <С х^ <С . . . <С хп = Ъ и удов-
удовлетворяющий краевым условиям B.15), существует и является единственным,
если только Я.о <С 9, \1п <С 9.
Эту теорему можно доказать по схеме доказательства теоремы 2.9.1. Поэто-
Поэтому детали доказательства мы опустим. Положим для к > /
В (X], ..., Хк) =
X; О
3 Я-7+1
о
о
о
о
о
о
о
о
О О
о о
0
3
1-Хъ
B.17)
Как и при выводе'неравенств B.9.4), можно показать, что при
</<*<&) " .. . . ■
^ ' \ \. ^г ("^+2» • • •» "&) 1
B.18)
§ 2. ИНТЕРПОЛЯЦИОННЫЕ ПАРАБОЛИЧЕСКИЕ СПЛАЙНЫ 279
Далее, у :
Докажем с помощью индукции, что справедлива
Лемма 3. #слм 0<;Я^1 (/<;&<;&) и &>/, то
У
B.19)
Разложим определитель И = Б (Я,о, ..., Яп) матрицы коэффициентов
системы B.16) сначала по элементам первой строки, а затем по элементам
последней строки:
Б = (!, , пО цД*! (!, , па)
М 5..., Я,п_а). B.20)
Поскольку определитель /)—линейная функция как относительно Хи так
и относительно Хп_и то он принимает свои наибольшее и наименьшее зна-
значения, когда Х± равно 0 или 1 и %п-\ равно 0 или 1. Поэтому при оценке
определителя В снизу можно ограничиться лишь этими значениями %х и Хп-1>
В силу B.20) "' - ч ■.•■•'.:
_ г.- :.'
(9 — Ч)(9 — [1п)Б(К •••"» К-*) при ^ = 0, ^-1=1»
(90)(, 2, Дп_2) при Я4 =
при Я1==1, Яп_! = 1,
, ...Дп_2, 0) при Х4=1, Хп_1 = 0. .„ .
Отсюда и из неравенств B.18) и B.19) для Я0<;9 и р,л<;9 вытекает,
что определитель Ь матрицы коэффициентов системы B.16) удовлетворяет
неравенству
А Г 8<п)/2, п нечетно! . ;
/»Гшт(8, 9-Я0).шт(8, О-М^ }
^. п чеТН0 } ^
Теорема доказана. • ■
2.2. Пример расходимости. Из теоремы 1 следует, что если бп =
= тах | х\% — х\п) | -> 0 и б^^ -> 0, где Ьп = 8 тах НТп <» (Ьы, /)» Н1п —
0^1^1 I
—1
280 ДОБАВЛЕНИЯ
— хц.\ — XI \ то последовательность сплайнов 8п (х) второй степени, интер-
интерполирующих функцию / (а:) в узлах сетки
а < 4П) < 4П) < • • • < 4П) = ь> B-21)
равномерно сходится к / (х) при п-*- оо. Первый пример расходящегося интер-
интерполяционного сплайн-процесса построил Норд [44] для случая кубических
сплайнов. Отметим, что в примере Норда / (а:) 6 Ыр.1/3. Функция / (х) при-
принадлежит классу 1лр а @ < а <; 1), если | / (х + к) — / {х) |<; №. Мы пока-
покажем, что существуют такая последовательность сеток B.21) и такая функция
/♦ (х) из класса 1лр а @ < а <. 1), что последовательность сплайнов #п (х)
второй степени, интерполирующих функцию /* (х) на этих сетках, не сходит-
сходится к /* (х).
Положим
*-» * т ' B.22)
71 == ^, о, • • •,
{/!(*), 0<а:<1,
.^(-а:), -1<ж<0,
0, х = 0.
B.23)
Продолжим функцию /*(а:) периодически с периодом 2 на всю ось х. Ясно,
что функция /*(#) принадлежит классу Ыр а.
Построим последовательность {8п (х)} периодических сплайнов второй
степени, интерполирующих функцию /* (х) в узлах
если A + е)<2A—а),
0<а<1. B.24)
если A + е)>2 A—а),
Для сокращения записи положим х^ = — 1/тг, х^ = 1/ге, х2 = \1п +
X} = (/ — 1)/тг, / = 3, 4, . . ., тг -+- 1. Заметим, что в силу четности функции
/*(#) и симметричности узлов относительно точки 0 сплайны »?„ (а:) являются
четными. Это следует из единственности интерполяционного сплайна. Отсюда,
в частности, вытекает, что, хотя для всех сплайнов #п (х) точка 0 служит точ-
точкой склейки, но в этой точке сплайны 5^ (а:) имеют непрерывную вторую про-
производную и 8'п @) = 8п (#0 = 8'п (#_1). Следуя схеме рассуждений Норда,
д окажем, что справедлива
§ 2. ИНТЕРПОЛЯЦИОННЫЕ ПАРАБОЛИЧЕСКИЕ СПЛАЙНЫ 28%
Лемма 4. 5"п {х^1п2+& -/*- О при п -> оо.
Доказательство. "Допустим, что 8п (х^ = апп2+е, где ап -> О
при гс -»- оо. В силу определения функции /*(я) и равенств B.2)
^а). B.25)
так как 1/и+1/и&<;1/(га — 1), п = 2, 3, ... ♦ Из B.25) находим, что
= (- 1)п 8/гB-«)Р - (8яР-»4- 3)
По предположению Оп —> 0, а в силу B.24) Р>-2 и E-|-е+1<.B — а)
Поэтому существует такое число пь что при всех /г>-/г1
; (х2) |<9и<2а>Э, п>щ. B.26)
Еще раз применяя равенства B.2), получаем
и складывая соотношения B.25) и B.27), имеем
Р-1 ?, , > 8Н З/»
= - Ж (*2) + О [5; (х2)] + О <»*-•) + о (га2+8), B.28)
поскольку
Кроме того, B — а)<B — а)р, 2 + е = 1+1 + е<р + A— а)Р =
= B — а) р. Следовательно,
\8"п (х3) | = 3 | 8"п (х2) | + о
Отсюда и из B.26) вытекает, что для всех п, превосходящих некоторое число-
^2 >• ^1»
. B.29)
282 ДОБАВЛЕНИЯ
Далее, . .
Заметим, что
IГ(
Таким образом,
% («о = -я; (*2) - бя; («>> +
л из B.26) и B.29) вытекает, что для всех п, превосходящих некоторое число
B.30)
Покажем по индукции, что для I = 3, 4, . . ., п
: I 5; (в1+1) | > з 15; '(*,) | >
Для I = 3 это верно, так как
Пусть неравенство B.31) верно для г = к !> 3, Из равенств B.2) имеем
5; (^-4) + 65; ы + 5; («к+1) = аду («к+1> - 2/ ы +/ (^.о!
(«к)-|-| 5; (**-!> |-
> б 15; («») 1 -1 зап (аь-д I -
>6\8п(хк)\-Ъ\8п(хк-1)\>Ь\8"п(хк)\>
>60/гB-а>&.
'Следовательно,, . -.'.
О другой стороны, с помощью1 неравенства B.4) выводим, что
31 при достаточно больших -то получаем ;противоречие. Лемма 4 доказана.
§ 2. ИНТЕРПОЛЯЦИОННЫЕ ПАРАБОЛИЧЕСКИЕ СПЛАЙНЫ 283
Теорема 5. Для любого О<;а<; 1 существуют такая функция / (х)^ 1лра
и такая последовательность узлов {х^Уъ^о, что последовательность сплайнов
{8п (х)} второй степени, интерполирующих /(#) в узлах {хкп)}, не сходится
к Цх). Более того, для некоторой подпоследовательности {}
(#) — 8Пк(х)\\р—*оо при к
где
1
(Г
1
тах
Доказательство. Пусть / (х) = /* (х), где /* (х) определяется по фор
муле B.23), и пусть узлы {а4п)} имеют вид
7' ± (т4""^)' ±7',
Тогда в силу леммы 4 существует такая подпоследовательность {щ}, пи —■> оо
при &—* оо, что 15п& (а?!) | = | Опл | /г^+е, где | а«й | > с>• 0. Заметим, что в силу
неравенства Гёльдера
где р -{-д~х = 1. Поэтому теорему достаточно доказать для р—1. Имеем
ипк
Так как
О /лЛ О" /->. \ / /»Й \ 1_ /* /-г \
1 / 4 \ 1
ТО
* >и1_ 2+8- _4 4_>Л_ е-1^.; 1_
так что при 8 ;> 1 получаем, что 1пк -*- оо при к —-> оо.
284 добавления
Обозначим через Яш,е класс непрерывных периодических функций / (х)
с периодом 2, модуль непрерывности ю F, /) которых не превосходит заданно-
заданного модуля непрерывности ю F). При этом ю F) удовлетворяет следующему
условию: существует такое число {$, что б1"9» F&) ->- оо при 6 ->- 0. Ясно, что
Р >» 1. В силу свойств модуля непрерывности можно считать, что Р ^ 2. Дока-
Докажем для случая р = оо обобщение теоремы 4.
Теорема 6. Существует такая функция /2 (х) ^ #м,е, что последова-
последовательность сплайнов {8п (х)} второй степени, интерполирующих ее в узлах
^). ±4-±4 ±1.
не сходится к ней.
Доказательство. Определим функцию /2(х) аналогично функции
/* (х), только вместо B.22) положим
00
— <??<? —1— п — 2 3
Предположим, что 8п(х1) = апв>(п-$) п&+1, где а„-^0 при п—*оо. Тогда
в силу B.25)
8п(х2) = 8/г*Р [/2 (х2)-/2 (х,)] - (8/гР-1 + 3) 5;(^ =
= 8тг2Р (— 1)пю (/г-Р) — (8/г2^ + 3
Таким образом, начиная с некоторого номера щ,
B.32)
Из первого равенства в B.28) имеем
поскольку
О при п—>оо
§ 3. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ НА РАВНОМЕРНОЙ СЕТКЕ 285
Итак, начиная с некоторого номера щ^-щ,
п>щ. B.33)
Как и в лемме 4, доказывается, что, начиная с некоторого номера п3^щ,
18№п (хп) |>20".Зп-3/г2М^р), »>л». B-34)
С другой стороны,
= 16гс2Рсо (п-^Х^би2* [тг^1 +1] ю (/г-Э), B.35)
так что при достаточно больших п получаем противоречие. Следовательно,
существует подпоследовательность {«&}, для которой \аПк\^>с'>0. Поэтому
пьФ)\>
Теорема доказана.
/2 (-^
при к —> оо.
Замечание. Рассмотрим класс функций Н%, модули непрерывности
ю F, /) которых не превосходят заданного модуля непрерывности ю F). При
этом ю F) удовлетворяет следующему условию: существует такая последова-
последовательность {Рп}> Рп ^> 2, Рп •< п 1П 3/1п ге (начиная с некоторого номера), что
со (п~^п) п^гГ1 ->. сю. Тогда найдутся такая функция / (#) 6 #ю и такая после-
последовательность узлов, что соответствующая последовательность интерполяцион-
интерполяционных сплайнов расходится. Для доказательства достаточно применить рас-
суждения, использованные при доказательстве теоремы 6, но только с заменой
р на р„. В силу B.34) и B.35)
Заключительная часть доказательства проводится, как в теореме 6.
Следствие. Если в предыдущем замечании ю F) = б 1п? б (у > 1),
то существуют функция / (х) с модулем непрерывности б 1п? б и последова-
последовательность узлов, для которых соответствующая последовательность интер-
интерполяционных сплайнов расходится к +оо.
Для доказательства достаточно взять р„ = п 1п 3/1п п, п^>2.
§ 3. Полиномиальные сплайны на равномерной сетке
Рассмотрим приближение непрерывных функций, заданных на всей оси,
интерполяционными сплайнами на равномерной сетке. Мы приведем оценки
остаточного члена, а также формулы, удобные для приложений.
286 ДОБАВЛЕНИЯ
Функцию 5Г (х, к) называют сплайном степени г, определенным на равно-
равномерной сетке {тк}, если
1) производная 5'|.г) (х, к) непрерывна на (—оо, оо),
2) 5Г (*, Л) = ЗД,
C.1)
где %т — константы, [у\ — целая часть числа у и т — О, ± 1, ± 2, ....
Сплайн #г (я, к) интерполирует функцию / (х) в узлах {тк}, если #г (тк, к) =
= / (тк). Впервые такие сплайны рассматривались Шёнбергом [1]. Нетрудно
заметить, что сплайнов «§> (х, к), интерполирующих функцию / (х) в узлах
{тк}, бесконечно много. В работе [27] показано, что если
[тк) || = зир | Ад/ (тк) \ <С оо,
т
где
г
№{ (тк) = 2 (- 1)Г~ЙС?/ Ий + А:М,
Й=О
то существует единственный сплайн #г (х, к), интерполирующий функцию
/ (х) в узлах {хк} и имеющий ограниченную г-ю производную. При этом
00
где уг=[г/21,
^гИ=тгЕ 2 (-
1=0 й=0
и хр(р= 1, 2, ..., уг, —1 <ХрР <х? _! < ... <я:1<0) — нули полинома
Р2ь(х).
Пусть г-я производная сплайна 5Г (х, к) определена равенствами C.1)
и C.2). Тогда
X
8Г (х,к) = Рг.х (х) + -^-щ ^ (х - г)г-18У» (Ь, к) й1, C.4)
М8г(тк, к) = Ы$(тк), т = 0, ± 1, ± 2,
где Рг-г (х) — полином степени не выше г — 1. Если потребовать, чтобы сплайн
8г(х,к) совпадал с функцией /(я) в г различных узлах {т&}, то полином
РТ-\(х) будет однозначно определен и разность 1(х)—8т(з>,к) будет обра-
обращаться в нуль во веех уэлах {гпк}^ Например, если в качестве г узлов выбраны
§ 3. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ НА РАВНОМЕРНОЙ СЕТКЕ 287
точки 0, /ь, ..., (г — 1)к, то [28]
г—1'
ЕД^/(О)—Д^ф(О)
г^ @$ (х, к), C.5)<
где . .
Практически, если к мало, то для уменьшения ошибки надо для определения*
Рг-1 (х) брать более редкую сетку.
Теорема 1. Если функция / (х) непрерывна вместе со своей к-й произ-
производной, к 4^. г, и || Ад/ (тк) || <1 Р (к) <С оо, то существует единственный
сплайн 8г (х, к), интерполирующий / (х) в узлах {тк}, т = 0, ± 1, ± 2, . . .,.
м удовлетворяющий неравенству
—5Г (х, Л) ||ос—. оо><^ (г, к, р) (ог+1_р (Л, /(^>) (()</><*) C.6>
где
(Л/)= вир зир
—оо<х<оо <|
и. константа А (г, к, р) зависит только от г, к и р.
Доказательство. Пусть г-я производная сплайна 5"г (я, к), интерн
полирующего функцию/(ж) в узлах {тк}, определяется равенствами C.1) и C.2).
Докажем, что для такого сплайна справедливо неравенство C.6). Возьмем
произвольную точку х и выберем такое целое число п, что
а* = Зпр (г - р + 1) к < х < 3 (п + 1) р (г - р + 1) к = ап+1. C.7)
Будем считать, что р <г (по поводу случая р = к — г см. [281). В силу
интерполяционных свойств сплайна и теоремы Ролля на каждом интервала
{тк, тк -\- рк) существует по крайней мере одна точка х', для которой
/<*» {х') = 8{Г {х', к).
В частности, на интервале C.7) существуют по крайней мере г — р + 1 точек
для которых
66,,+,,
г—р+1 (
588
ДОБАВЛЕНИЯ
Отсюда и из C.4)
4п)
Представим Рг-
г = 1, 2, ..., г—р+1.
по формуле Лагранжа:
г-р+1
где (ог_р+1 (ж)- (х-х[т) (х-х™) ... (я-4-Ум). Тогда
а
п+1
г-р+1
2
где
г-р+1
Если ап
Заметим также, что
то при выполнении условий C-8)
7Н1
С
В силу, неравенства Лебега (см., например, [181)
г-р+1 '
C.9)
C.10)
C.11)
C.12)
1=1
где Еп (/; а, Ь) — наилучшее приближение функции / (х) на отрезке [а, Ь]
алгебраическими многочленами степени не выше п, а
г-р+1
Ьг-7, — тах
§ 3. ПОЛИНОМИАЛЬНЫЕ СПЛАЙНЫ НА РАВНОМЕРНОЙ СЕТКЕ
289
— константа Лебега соответствующего интерполяционного процесса. При выпол-
выполнении условий C.8)
Ьг-р < Л2 (г, р), C.14)
где Л2 (г, р) зависит только от г и р.
Далее воспользуемся следующим результатом Уитни (см. [481):
Еп (/; а, Ь) < Лл'вир | А?+1/ (*) I. ' C-15)
где Ап зависит только от п и не зависит от длины интервала, а верхняя грань
берется по всем значениям ги(, для которых а ^ х, х + (п + 1) * -^ Ь. Отсю-
Отсюда, в частности, следует, что
Учитывая соотношения C.2), C.10) —C.15), получаем
< Ад (г, р) а>г.р+1 (Л, /<р>) + Л, (г, р) &г"р вир
^А* (г, р) оь^м (Л, /(р))+Л (г, р) Грсог+1 (Л, /).
В силу свойств модуля гладкости
*, /г) -5Г (о», Л) | <
и неравенство C.6) доказано.
Докажем единственность. Пусть сплайн
теоремы. Тогда при Ь,^ =
(а»,
г»
Н) удовлетворяет условиям
» г)
А{
Л?
Из этой оценки вытекает, что последовательность (ДГ) ограничена и, как уже
отмечалось, такая последовательность однозначно определяется равенства-
равенствами C.2).
Следствие 1. При выполнении условий теоремы 1
(г, к,
Следствие 2. Если функция / (х) удовлетворяет условиям теоремы 1
и является периодически с периодом 2я, а Н = 2л/п (п — натуральное число), то
шах
<А(г, к,
р зтои* из представления C.2) следует, что сплайн 8г(х, 2я/п) также
имеет период 2л.
19-1197
290 ДОБАВЛЕНИЯ
Замечание. При выполнении условий следствия 2 правая часть равен-
равенства B) сворачивается в конечную сумму
А—О Р—I 4
(лг = О, 1, ..., тг— 1).
Пусть УУГ обозначает, множество непрерывных функций / (х) с периодом 2я,
имеющих непрерывные производные вплоть до (г — 1)-го порядка, причем
(V—1)-я производная удовлетворяет условию Липшица
Для класса РУГ В. М. Тихомировым [32] получен следующий Окончательный
результат.
Теорема 2. Если функция /(#) принадлежит классу РУГ и периоди-
периодический сплайн 8г-1 (х, п/п) степени г — 1 интерполирует ее в узлах {яг//г}
(г = 0, 1, ..., 2/г), то
зир ||/(я) — 8г-1(х, я/»)||с(о,2я) = ^г«"г, п=1, 2, ..., C.17)
А"г — константа Фавара
7П=0
Так.как совокупность сплайнов 8г-1 (ж, я/») образует 2тг-мерное подпро
странство пространства С @, 2я) непрерывных периодических функций с перио-
периодом 2я, то равенство C.17) дает оценку сверху для поперечника
С @, 2я)) = ш! вир ш! || / (ж)-у (х)
ЬС(О, 2я) /сш- Ь
с
где 1гт есть т-мерное подпространство пространства С @, 2я). В этой же
работе [32] доказано, что эта оценка является точной, т.е. что
и, кроме того, вычислены поперечники класса
в пространстве С (—1, 1) непрерывных непериодических функций, заданных
на отрезке [—1, 1]. При этом существенную роль играют функции хпТ(Ь),
обобщающие полиномы Чебышева и представляющие собой решение экстре-
экстремальной задачи
(-1.1)-||*Г- 2 (-1)к+1(«-Ф+Г- 2 Я*'8||с(-1,1) =
т г—1
шах|Г-2 (-1)"+1(<-«*)!-2
1^*«1 А=1 ' 8=0
§ 4. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ СПЛАЙНОВ 291.
где нижняя грань берется по всем а8, т ^ п и —1 ^ ^ ^ Ь2 ^ . . . ^ {т ^ 1.
Экстремальным тг-мерным подпространством для класса РГГ. вновь будет под-
подпространство сплайнов степени г — 1, но в этом случае узлы сплайна уже
не равномерные и связаны с узлами функции хп_гг(().
§ 4. Некоторые приложения сплайнов
4.1. Приближенное решение краевой задачи и задачи Коши. Схема
применения сплайнов для численного ^Т
7Г6Г
р _^2^^1-^
1в раздГ]27Г6сновногоГтекста. Аналогичную схему использовал И. Петерсон [21];
"кроме того, он получил некоторые оценки уклонения аппроксимирующего
решения от точного решения. Сформулируем его результат.
Пусть кубический сплайн 8(х) задан на сетке А: а=хо<Сх1<. . .<Схп — Ь
и 5 (х() = уг, хг = (Ъ — а) 1/п, г = 0, 1, ...,». Положим 5 {х^г) = 1/1/г»
# (Яп-1/г) = Уп-1/2, где х1/2 = (Ь — аI2п, хп.Ч2 = (Ъ — а) Bп — 1)/2п.
Требуется найти приближенное решение краевой задачи
У' + Р(*)У' +Я(х)У = г(х), D.1)
У (а) - У (Ъ) = 0.
Будем искать решение в виде кубического сплайна # {х). Из краевых
условий сразу получаем, что 5 {а) = у0 = 8 (Ъ) = уп = 0. Наложим допол-
дополнительно условие
8" (У) + Р (У) 8' (у) +д(у)8 (у) = г (у), D.2)
где у — #1/2, #1, #2, . • ., жп-1» #71-1/2' Таким образом, у нас есть система п + 1
уравнений с п + 1 неизвестными у1/2, у и У г, • • •» Уп-и Уп-т-
Теорема 1. Если функции р (#), ^ (х) и г (х) непрерывны на отрезке
[а, Ь] и задача D.1) имеет единственное решение при любом г (х), то систе-
система D.2) при достаточно большом п имеет единственное решение, причем
у^(х) —точное решение задачи D.1) и
о) F, /) = тах тах |/(#+*) — /(^) I.
Остановимся более подробно на приближенном решении с помощью сплай-
сплайнов второй и третьей степени задачи Коши для дифференциального уравнений
первого порядка
У' =- / (*, у), 0 < х < Ь, у @) = Уо. D.3)
Предлагаемый метод был развит в работе Лоскалзо и Талбота [40].
Пус*ть 7*= {(#, I/), 0<<г<Ь} и функция /(ж, у) имеет непрерывные
(т — 2)-е частные производные в Т, т^-2. При т = 2 предполагается, что
функция / (#, у) непрерывна в Т. Кроме того, она удовлетворяет условию
19*
292 добавления
Липшица
1/(*. У1>-/(*. У) \<Ь\У1-У I, 0<яг<6,
где Ь — абсолютная постоянная. Эти условия, в частности, гарантируют
единственность решения задачи D.3).
Приближенное решение задачи D.3) будем искать в виде сплайнов 8т (х)
степени т дефекта 1. Пусть узлы сплайна 8т (%) равномерны: {Ж| — гк}7 I =
= О, 1, . . ., п; п> т, к = Ып. Положим
где у'@) = /@, ув), /@) = а/@, Уо)/««+(«/(О, У0)%)/@, Ув) и-*• Д- Для
определения коэффициента а0 потребуем, чтобы функция 5 (х) удовлетворяла
уравнению D.3) в точке х = Н: ^%
8' (к) = / (Л,
Пусть функция] 5 (#)| определена на отрезке (V — 2) к <1 я: ^ (V — 1) к.
Положим
т-1
. (V—
и найдем коэффициент ау_! из условия
^ (V» = / [V*, 5т (V*)], V- 1,2 П. D.4)
В работе [40] показано, что при т !> 4 этот процесс неустойчив, а при
т = 2 и 7» = 3 справедливы соответственно следующие теоремы.
Т е о р е м а 2. Если / (#, у) ^ С2 на Г, то существует такая константа
К, что для всех к <С 21Ь и всех х ^ [0, Ь]
\ 82 (х) -у(х)\< Кк\ \ ЗР (х) - у™ (х) | Кк3~\ 1 = 1,2.
Здесь у (х) — точное решение задачи D.3) и
)] &=1, 2, ..., п-1.
Теорема 3. ^сли / (#, у) ^ С3 «а 7\ то существует такая константа К,
что для всех Н < Ъ/Ь и для всех х € [а, Ъ\
~\ г = 0, 1, 2, 3. D.5)
Здесь у (х)—точное решение задачи D.3) и
Докажем теорему 3.
§ 4. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ СПЛАЙНОВ 293
Лемма 1. Если к <С т1Ь, то сплайн 8т (ж), определяемый соотношения-
соотношениями D.4), существует и является единственным.
Доказательство. Запишем D.4) в виде
}, D.6)
где
т-1
й=0
При к <С т1Ь отображение % = ц^ B) является непрерывным строго сжимаю-
сжимающим, следовательно, имеет единственную неподвижную точку. В самом деле,
пусть 2 = §н (*), 21 — §н (Ь). Тогда
(т—
где Ь — константа Липшица для функции / (х, у). Лемма доказана.
Рассмотрим на отрезке [О, Ь] семейство % кубических сплайнов 8{х) =
= 5"з (х) дефекта 1 с узлами в точках сетки А: 0 = х0 <С хц <С . . . <С хп = Ь,
XI — Ы1п, Ь = 0, 1, . . ., п. На любом отрезке [кк, (к + 2) &], 0^ к <
<С к + 2 ^ п, сплайн 8{х) из % зависит от 5 линейных параметров, так что
величины
8(М), 8'(гк), I = к, к + 1, к + 2, D.7)
линейно зависимы.
Лемма 2. Для любого сплайна 8 {х) из %
8(кк + Щ — 8{Щ *= ^[8'(кк + 2й) + 45" (кк + &) + 5'(АА)]. D.8)
Доказательство. Пусть
2 2
*=0 * * 1=0
Тогда
-«-«!+-»• а2 —о" Н1 — т
294
ДОБАВЛЕНИЯ
Так как это соотношение справедливо для любого сплайна из
— —а2,
— Ро—?1 —
то
_1_
6
Определитель этой системы
1_
2
= — 2а2,
! — —2а2,
_ 7
— й ^^
1
0
0
0
0
1
1
1
2
1
6
0
0
-1
0
0
0
0
О
-1
-2
О -4-
_ 1
~~ 2
1
2
1
6
-1
1
2
24
отличен от нуля, так что для любого фиксированного а2 система имеет един-
единственное решение. В частности, при а2 — 1
ао=—1, оц^О, а2 = 1, Ро^з", Р^Т' Рз^-^»
и D.8) доказано.
Лемма 3. Для к <; д/Ь решение двухшаговой разностной схемы
Уг+2—Уг =4"
, Уд
(Л
+ / (Л + 2Л, у,
(* = 0, 1, . : ., п-2),
D.9)
/ начальных условиях у0 = 8 @), у{ = 8 (к) единственно и уг = 8 (гй),
г = 0, 1, . . ., п, еде 8 (х) определяется с помощью равенств D.4) при т = 3.
Доказательство. Пусть значения у0, у1? . . ., уг+1 (* ^- 0) заданы.
Тогда из D.9) уг+2 находится однозначно, так как при к<С.Ъ1Ь отображение
2 = "Фа (*) = с + 1/3&/' (^ + 2й, ^) непрерывно и строго сжимающее и поэтому
имеет единственную неподвижную точку. Так как последовательность E (гк)}
в силу леммы 2 также удовлетворяет соотношению D.9), то лемма 3 доказана.
Лемма 4» Существует такая константа К, что для к <С ЫЬ
I у (Л) - 5 (Л) | < Кк\
где у(х) — точное решение задачи D.3) и 8 (х) — 8$ (х).
§ 4. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ СПЛАЙНОВ
295
Доказательство. Так как
то
-хУD)® • DЛ°)
Докажем сначала, что при к<.3/Ь функция ао = ао(к) ограничена. Положим
Л2 , , /»3
Тогда при
Так как
= ао, то
(к,
^у1) -у'0-кУ;
где М не зависит от к. Так как /& принимает лишь значения Ып, п — натураль-
натуральное число, то между 21Ь и 3/Ь имеется лишь конечное число значений к, и пото-
потому функция а0 = а0 (к) ограничена для всех к — Нп = Ып < 3/Ь. Отсюда
и из D.10) вытекает оценка
| 8(к) -у(к)\ = О ОТ. D11)
Далее,
- у' (к) | = | / [к, 8(к)] -1[к,у (к)) | <
< Ь | 8{к) -у{к)\ = О (к9),
т. е.
следует, что
Из определения
Из этих двух представлений для 8'(к) находим, что а0 = ут + О (к). Вновь
применяя равенство D.10), получаем утверждение леммы.
. Так как начальные данные в методе Милна — Симпсона D.9) имеют чет-
четвертый порядок точности, то вычисленные с помощью этого метода значения
5 Aк) также имеют четвертый порядок точности [38, стр. 248], т. е. для некото-
296 ДОБАВЛЕНИЯ
рой константы К, не зависящей от к,
I * Ы - У Ы К КН\ D.12)
где у (х) — точное решение и хк = &6/гс, & = О, 1, . . ., п. Далее,
| $'(«*) - у' (**) |=|/ [«*, 8(хк)] -1\хк; у (хк)] | <
' < Ь | 8(хк) - у (хк) | < КШ. D.13)
Лемма 5. Пусть функция у (а?) принадлежит классу С* (О, 6) м точки
хк и хк+1 —хк г\- Ь, лежат на отрезке [О, Ь\. Если полином. :
Р (^) =)Р з И = а0 + а4 (ж — а?&) + а2 (ж — о;й)а + а3 (х —
удовлетворяет условиям
О (Н% Р (хк+1) = у2 = у (хк+г) + О (^),
|1 '
о
(х) ~ Р@ (*) | - 0 (Л4) (<гк < с < хк+и г -О, 1, 2, 3). D.15)
Доказательство. Положим сик — у{хк) — ух, акЛ.^~у (а?й+1) — у2, «* =
= у'(#ь) — ^, ай+1 = /(;гА+1) — Уг- Тогда в силу интерполяционной формулы
Эрмита (см, например, [71, стр. 66)
где ■?! (л:) интерполирует точные значения функции у (х) и ее производной
у' (х) в узлах хк и #ь+1. Из представления D.16) получаем
В силу теоремы Ролля существуют такие точки |4, ^, хй<|1 <|<лга+1, что
^(^)—/A0 = 0 и Р*(|)—^(^) = 0. Следовательно, для яй<ж<яй+1
| у" (х) - РГ (*) I = I У" И -У" в) + ^Г (I) ~ Рх (*) 1=11Г (*) - У* (I) | =0 (Щ, D.18)
X
-Р'х{х) | = ^ [у*(х)-Р;(«)] Ас| = 0ОТ D.20)
§ 4. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ СПЛАЙНОВ 297
х
D.21)
Из D.16) —D.21) вытекает D.15). Лемма доказана.
Так как при выполнении условий теоремы 3 точное решение у (х) и при-
приближенное решение 5 (х) — 89(х) удовлетворяют на каждом отрезке [хк, хк+1],
& = О, 1, . . ., п — 1, условиям леммы 5, то теорема 3 доказана.
Сплайны и обобщенные сплайны находят применение также при прибли-
приближенном вычислении собственных значений и собственных функций само-
самосопряженного дифференциального уравнения (см., например, [41], [36]).
4.2. Наилучшие квадратурные формулы. Остановимся на [одном важ-
важном частном случае наилучшего приближения линейных функционалов, а имен-
именно на задаче о наилучших квадратурных формулах для некоторых классов
функций. Обозначим через И^ класс функций, непрерывных на отрезке [0, 1],
имеющих абсолютно непрерывную (г — 1)-ю производную и г-ю производную,
удовлетворяющую неравенству
Не
} D.22)
Если, кроме того, функции и их производные вплотьудо (г — 1)-го порядка
являются периодическими с периодом 1, то такой класс функций будем обозна-
обозначать через Й^$.
Поставим в соответствие интегралу
1
I
лвадратурную формулу
п
или, в более общем случае, квадратурную формулу
т п
2 2 <*ьз /(8) Ы (т <г - 1). D.23)
•=0 А=0
Положим
т п
(/) - К / (*) Л> - 2 2 а^(8) М (»< г - 1). D.24)
/ (*) Л> - 2 2 а^(8) М (»< г - 1).
298
ДОБАВЛЕНИЯ
Если / (яг)
находим, что
то с помощью формулы Тейлора в интегральной форме
(=0
г—1
8=0 &=0
т п
1=т
Для того чтобы величина
«=оь=о
т п
8=0 й=0
Я = зир Я (/)
@Л 1.D.25)
D.26)
была конечной, необходимо, чтобы квадратурная формула была точной для
полиномов степени, не превосходящей г — 1, т. е. чтобы выполнялись равенства
п
(/ + 1)!
»
Г Г
Г
пк8
т~
D-27)
()
8=0 Й=0
Сформулируем задачу о наилучшей квадратурной формуле для класса функ-
функций ]Уд. При этом возможны две постановки задачи.
При заданных узлах {хъ} требуется найти такие веса {а^}, чтобы на классе
функций И^ остаток Я (/) принимал наименьшее значение, а также указать
его величину, т. е. найти Я* и {а*8}, для которых
т п
Я* = зир
(х)
D-28)
Эта задача восходит к Сарду* и, как уже отмечалось в основном тексте, ею
занимались при выполнении условий D.27) Сард (т — 0, д = 2, хк — к1п,
к = 0, 1, . . ., гс), Шёнберг (т > 0) и другие..
Вторая постановка принадлежит А. Н. Колмогорову (см. например, [19],
стр. 5). Он ищет наилучшую квадратурную формулу, когда вариируются
не только веса, но и узлы квадратурной формулы. Для класса И^ требуется
найти такие значения {а|в}, {х*} и Я#, что
т п
= зир
Г / {х) Ах- 2 2 а
^5 оло
,=ол=о
т{
D.29)
§ 4. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ СПЛАЙНОВ 299
Сформулируем некоторые результаты, полученные в этом направлении.
Большая их часть представляет собой дальнейшее развитие идей С. М. Николь-
Никольского ([19], [20]). В частности, в этих работах показано, что при выполнении
условий D.27)
т п
л
где 1//> + 1/д= 1 A-^р, д-^оо). Таким образом,
1 т п
D30)
8=0 Й=0
причем коэффициенты акз, удовлетворяют условиям D.27).
Отметим, что для функций подкласса Щд класса ТРд, удовлетворяющих
условиям
формула D.30) справедлива без дополнительных ограничений D.27), т. е. в D.31)
нижняя грань берется по произвольным {а^} и {хк}. Для этого случая в рабо-
работе [19] приведены наилучшие квадратурные формулы и значения величин Д,
длят =0, г = 1, 2;д = оои произвольных натуральных чисел п. Там же
(см. также [20]) найдены наилучшие квадратурные формулы и величины В*
для т = г — 2, г четно, г ^- 2, д = оо, п — произвольное натуральное число.
Для тех же значений т, г, п и д = 1 наилучшая квадратурная формула полу-
получена А. И. Киселевым (см., например, [19], стр. 107).
Для класса УУЦЧ при произвольном д, 1 .<; д <1 с», М. Б. Аксень и А. X. Ту-
Турецкий [1] доказали следующую теорему.
Теорема 1. Среди квадратурных формул вида D.23) наилучшей для
класса И^ов при 1 ^ д ^ оо, т = г — 2, г четно, г ^ 2, и произвольном нату-
натуральном п является квадратурная формула с узлами
х% = 2 (к + 1) к, к = 0, 1, . . ., п,
и весами
г~—: & = 0, 1, ..., п— 1,
,/—2,
D.32)
300 ДОБАВЛЕНИЯ
и Кгр(х)—полином степени г с коэффициентом при #г, равным единице,
менее уклоняющийся от нуля в метрике Ьр(—1, 1), т. е.
1 ' . г-1
1/Р
з=0
При этом
,A)
Частные случаи этой теоремы при д = 2, г = 2 и при д = 2, г *— произ-
произвольном четном числе были получены ранее в работах Г. Я. Доронина [81
и И. И. Ибрагимова и Р. М. Алиева [9] соответственно.
Аналогичные результаты М. Б. Аксень и А. X. Турецкий получили для
класса И^ в предположении, что квадратурная формула точна для полиномов
степени не выше г — 1. В этом случае
.9 = 0, 1, ..., т,
где
и остальные коэффициенты а& определяются по формулам D.32), где надо
заменить Н на Н^
Н. Е. Лушпай [15] рассмотрел случай т = г — 1. Оказывается, что наилуч-
наилучшие квадратурные формулы для т = г — 2 совпадают с наилучшими при
т = г — 1, если г четно. Мы не будем выписывать соответствующие формулы
для других значений г. Отметим, что аналогичный результат независимо был
получен Каутским [39]. Для класса У?\ Н. Е. Лушпай [16] нашел наилучшие
квадратурные формулы вида D.23), точные для константы, при т = г — 1,
г=1, 2, 3, . . . ит — г — 2, г — четное число, г> 2. В частности доказано,
что при г = 1, 2 и т = 0 наилучшей для класса Ш% среди квадратурных
формул вида
I
является формула прямоугольников
2л
1т
о ь=о
В дальнейшем Н. П. Корнейчук и Н. Е. Лушпай [13] нашли наилучшую квадра-
§ 4, некоторые приложения сплайнов 301
турную формулу для класса ИЧ при т = г — 2, т = г — 3 (г нечетно, г ^ 3).
Аналогичные результаты получены ими для классов И^1 и ТУ\.
Как видно из равенств D.27), вывод наилучшей квадратурной формулы
для классов \Уд тесно связан с наилучшим приближением конкретной функции
A — Ь)г сплайнами степени г — 1 дефекта т — 1с п нефиксированными
узлами в метрике пространства Ьр @, 1), р-1 + ^-1 = 1. В следующем разделе
мы кратко обсудим вопросы наилучшего приближения сплайнами.
4.3. Наилучшие приближения сплайнами некоторых классов функций.
В § 1 уже отмечались работы Н. П. Корнейчука, связанные с наилучшим
приближением классов функций УУТНЮ сплайнами степени г +1 с нефиксиро-
нефиксированными узлами ис(г+ 1)-й производной, не превосходящей по абсолютной
величине заданной константы К. Обозначим через Й^"!/© класс функций с перио-
периодом 2л;, непрерывных на всей оси и имеющих непрерывные производные вплоть
до г-го порядка, причем модуль непрерывности со(/(г\ б) г-й производной
не превосходит заданного модуля непрерывности со (б). В этих работах для
выпуклого модуля непрерывности иг^5 даны характеристические свойства
сплайна наилучшего приближения в С @, 2л;) для функций из класса УУГН&
и вычислена величина наилучшего приближения. Характеристические свойства
сплайнов наилучшего приближения изучались также Джонсоном, Шумейке-
ром, Райсом и др. (библиографию см., например, в [47]).
Другое направление исследований — изучение порядков приближения
некоторых классов функций сплайнами с фиксированными и нефиксированны-
нефиксированными узлами ([24; 29; 30; 35]).
Функцию 5 {х) = 8тп (х) будем называть сплайном порядка (т, п),
если 1) она т — 1 раз непрерывно дифференцируема и 2) существует такое
разбиение 0 = х0 <С Х\ <;. . . <С а?ц = 1 отрезка [0, 1] на \х ^ л частей,
что на каждом отрезке [хк, хк+х\ функция 8тп (х) совпадает с некоторым мно-
многочленом степени не выше т.
Рассмотрим задачу об изучении наилучших приближений сплайнами
некоторых классов функций Щ. Пусть
(/)р = ш! || / (*) - 8пп (х) ць„@) 1} A < р < оо), D.33)
8тп
где нижняя грань берется по всем сплайнам порядка (т, п) с произвольными
узлами. Положим
Етп (Я») = зир Етп (/)р. D.34)
В работе Ю. Н. Субботина и Н. И. Черных [30] доказана
Теорема 1. Пусть 1 ^ р, ^ ^ оо, функция / (х) имеет абсолютно
непрерывную производную /<т> (х) (т > 1) и ||/(т+1)|1ь (О, 1) -< 1- Тогда
V0'
Оценка на рассматриваемом классе функций точна по порядку при /г->-оо.
302 добавлкния
Отметим, что задачу о нахождении и оценке величины D.34) можно поста-
поставить также для интерполяционных сплайнов с нефиксированными узлами.
Сформулируем один результат в этом направлении, который легко следует
из теоремы 4 работы [30]. Пусть И^ есть класс непрерывных функций на отрез-
отрезке [0, 1], имеющих абсолютно непрерывную первую производную и вторую
производную, удовлетворяющую неравенству || /" ||ь @,1) <; 1 A <; р •< оо)*
Тогда
), D.36)
3~1K~
где с4 = 1, Сое = 1/2, сд={(д — 1) Bд —1)~1}C~1K~ A<д<оо) и нижняя грань
в D.36) берется по ломаным, вписанным в /(х) в точках (хк, }(хк)), хк—
произвольные числа, удовлетворяющие неравенствам
О = жо<ж1<....<а;„='1. , D.37)
Оценка сверху для еп (И^|) вытекает из неравенства C4) работы [30].
Для оценки снизу достаточно рассмотреть функцию
\
где
V _ЯD*_1),
1 1А I _/\1/с/о_лв'—1 * ■ *
далее функция 5 (^) продолжается с периодом 4/г на всю ось. Заметим, что
о
Ясно, что каковы бы ни были узлы D.37), ломаная, вписанная в
л
в точках (хк, 1*(хк)), уклоняется от /• (х) не менее, чем на \ из (и) пи, т. е.
\ из (и) пи, т.
о
Равенство D.36) доказано.
§ 4. НЕКОТОРЫЙ ПРИЛОЖЕНИЯ СПЛАЙНОВ 303
Сравним этот результат с приближением функций того же класса впи-
вписанными ломаными на фиксированной сетке D.37). Имеем
хк+1
тах
— 1
1/9'
тах "
хк
Пусть 6 = ^—х0. Тогда пример функции
где
Применяя неравенство Гёльдсра, получаем
(Т
хк
^тах тах | (-—г|~) ^ц-! ^~\х —.х ) —Г?!—Г II/1№-^
где 6= тах (хь+1 — хь). Поэтому для фиксированных уэлов {х\)
D.39)
П) \ П (»)+/; (в) (х- 6), 6<х<1,
где /! (х) строится так же, как в предыдущем примере строилась функция /* (х),
только к следует положить равным 6/2 и
показывает, что в неравенстве D.39) на самом деле имеет место знак равен-
равенства, т.е.
еп(Щ) = -^-8BA-1)/д. D.40)
В частности, наилучшими фиксированными узлами для функций класса И^
являются равномерные узлыГ
304 ДОБАВЛЕНИЯ
В. Л. Великий [4] изучал приближение функций / (х) из класса Н& сплай-
сплайнами 82г-1 (я) степени 2г — 1 дефекта г, интерполирующими функцию / (х)
в фиксированных узлах D.37) и такими, что 5&-1 (хг)= 0, к = 1, 2, . . ., г — 1;
1 = 0, 1, . . ., п. Им показано, что для таких сплайнов справедлива оцен-
оценка A.5) и что константу 8/2, вообще говоря, уменьшить нельзя. Кроме того,
он доказал, что для этих сплайнов при р = 1 и выпуклом модуле непрерывно-
непрерывности ю (б) выполняется равенство A.4).
Укажем здесь также на исследования А. Н. Колмогорова [11] (см. также
[5], стр. 89—106), связанные с приближением в метрике пространства С @, 1)
некоторых классов г раз дифференцируемых функций сплайнами степени г,
г-я производная которых не превосходит заданной константы К, и с приложе-
приложением полученных результатов для оценок энтропии пространства дифференци-
дифференцируемых функций.
Ю- А. Б рудный и И. Е. Гопенгауэ [2, 3] развивают теорию локальных
наилучших приближений, началом которой послужила работа П. Л. Чебыше-
ва [34]. При этом фактически рассматривается приближение функций сплай-
сплайнами степени п дефекта п.
В работе Алберга, Ни лье она, Уолша [9], Шёнберга [45], Нитше [42, 43],
А. А. Попова, Б. X. Сендова [22] рассматриваются также обратные теоремы
для сплайн-аппроксимаций.
§ 5. Многомерный случай
В этом параграфе рассматриваются частичные сплайны 8 (х1, х2, . . ., хп)
степени 2р + 1 дефекта р по каждой переменной. Формулируемые здесь резуль-
результаты принадлежат В. С. Рябенькому [23] (см. также 124], стр. 158—168).
Пусть ограниченная функция 1|) {хи • » •, хп) задана в уэлах (х^ хп)
сетки, хь = тгк A = 1,2,.. ., п), ть = 0, ±1, ± 2. Положим
Д*г/ = / («=1,2, ...,га),
— /(Ж4, ..., «!_!, XI, Хц.и . .., Хп) A = 1, 2, . . ., П),
л,ж • • * А* * * • *« А * • * 4 • * *'
и
СьО|))= зир —Г&М ^ («1. • • • > *п) . E.1)
Л-1, * • * • «СП Л **'
Справедлива следующая теорема:
Теорема 1. Для всякой ограниченной функции ^(х1, . . ., а:п), задан-
заданной на сетке (ж4, . . ., ж„) и любого натурального числа р найдется функция
§ 5. МНОГОМЕРНЫЙ СЛУЧАЙ 305
8(%х, ...» хп), обладающая следующими свойствами:
1) функция 8(х1, . . ., хп) определена на всем пространстве и совпадает
с яр в узлах сетки;
2) функция 8(хх, . . ., хп) имеет непрерывные производные до порядка р
включительно по всевозможным комбинациям Хх, х2, • • ., хп;
3) справедливы неравенства
(к = 0, !,...,/>), E.2)
где константа С (р) зависит только от р.
Мы не будем приводить полное доказательство теоремы, а укажем лишь
вид функций 8 (х±, .\ ., хп), которые фактически являются частичными сплай-
сплайнами (определение см. в разд. 7.1 основного текста) степени 2р + 1 дефекта р
по каждой переменной.
Пусть п = 1 и Рг (Ф, х) (I = 0, 1) — многочлен степени не выше р, совпа-
совпадающий с функцией г|э (х) в р + 1 точках х = ш, (ъ -\- 1) Л, . . ., (г '+ Р) й*
Построим интерполяционный многочлен Эрмита (> (ф, ж) степени не выше
2р + 1, удовлетворяющий условиям
, 0) = <&р0 (у, 0)
йхк
(к = 0, 1, . . ., р), и положим # (х) == () (яр, х), 0 ^ х ^ к. На отрезках
тк ^ х ^ (т -\- 1) к функция I? (х) строится аналогично, только за начало
отсчета следует взять точку х = тк.
Пусть оператор Ь переводит указанным способом функцию яр (ж) одного
переменного, определенную в точках х = тк (т = 0, ±1, ±2, . . .), в функ-
функцию # (х), определенную всюду. Через Ьг обозначим оператор Ь, когда он
применяется к функциям яр {х\, .... хп) одного переменного а;,-, х( = тк (осталь-
(остальные переменные рассматриваются как параметры). Тогда функция
# (#ь . . ., хп) = ЬпЬп-х • . . Ьх*\> («ь • ♦ ., хп) E.3)
удовлетворяет всем условиям теоремы.
Положим в формуле E.1) Ле4 = Л?®, ..., кп — кп, где к\ — фиксированные
числа, к\ + к\ + ... + к%, = А;0, и пусть верхняя грань берется только
по {хХУ —, хп). Наряду с величиной Ско (яр) рассмотрим также величину
ОО 00
Х1=—оо Хп=—оо 1 п
Не нарушая общности, можно считать к=1.
20-1197
306
ДОБАВЛЕНИЯ
Введем функционал
— 00
1/в
где нижняя грань берется по функциям Р (х1г . . ., а^), определенным на всем
пространстве и совпадающим в целых точках с функцией $ (хи . . ., хп). Рас-
Рассмотрим всевозможные функции г|э, для которых Ск0 (ф)9 <С оо. В работе 131]
вычислена норма функционала
и построен линейный метод
= М) (хи . . ., я„),
продолжающий функции г|э (хи , . .,
пространство и такой, что
заданные в целых точках, на все
В частном случае тг == 1, д = оо функция Р# (х) совпадает с интерполяцион-
интерполяционным сплайном степени &° дефекта 1 (см. § 3). Позднее Шёнберг [461 дал решение
этой задачи при гг = 1, д = 1, 2, оо, причем для % = 2 указал наилучшее
продолжение для индивидуальной функции $ (х). В этом случае функция
Р# (х) совпадает с интерполяционным сплайном степени 2к9 — 1 дефекта 1.
Ограниченность нормы || х\ || доказана ранее С. Л. Соболевым [25] с по-
помощью метода В. С. Рябенького.
Функции 5 (#!, . . ., хп), определенные равенством E.3), можно исполь-
использовать для приближения гладких функций. Справедлив следующий резуль-
результат [24].
Теорема 2. Пусть функция / (х±, . . ., хп) имеет всевозможные непре-
непрерывные производные до некоторого порядка д включительно. Обозначим через
/ (#ь . . ., хп) функцию, определенную лишь в точках (т^, . . ., тпк) (тг =
= 0, ±1, ±2, . . .; 1 = 1, 2, . . ., п) и совпадающую в этих точках с функ-
функцией / (#1, . . ., хп). Для заданного натурального числа р, р ^> д, построим
функцию
где 1ц —оператор, описанный выше. Тогда
ЛИТЕРАТУРА 307
и ..., хп)
дх\1 ... дх*п дх]1...
(р) зир тах
+ +
*
п
п
(*<«),
константа С\ (р) зависит только от р.
Приближение функций многих переменных сплайнами и их приложения
исследуются также в ряде работ Ю. С. Завьялова [48—52].
ЛИТЕРАТУРА
1. Аксень М. Б.,Турецкий А. X.. Наилучшие квадратурные формулы для неко-
некоторых классов функций, Весцъ АН БССР, сер. физ.-матем., 1 A966), 15—27.
2. Брудный Ю. А., Гопенгауз И. Е., Приближение кусочно-полиномиальными
функциями, Изв. АН СССР, сер. матем., 27, № 4 A963), 723—743.
3. Брудный Ю. А., О локальных наилучших приближениях функций многочленами,
ДАН СССР, 161, № 4 A965), 746—749.
4. Великий В.Л., О наилучшем приближении сплайн-функциями на классах непре-
непрерывных функций, Матем. заметки, 8, № 1 A970), 41—46.
5. В и т у ш к и н А. Г., Оценка сложности задачи табулирования, Физматгиз, М., 1959.
6. Г а л к и н П. В., О разрешимости задачи периодической сплайн-интерполяции. Ма-
Матем. заметки, 8, № 5 A970).
7. Г о н ч а р о в В. Л., Теория интерполирования и приближения функций, Гостех-
издат, М.— Л., 1954.
8. Доронин Г. Я., К вопросу о формулах механических квадратур, Сборник научных
трудов Днепропетр. инж.-стр. ин-та, № 1—2 A955), стр. 210.
9. Ибрагимов И. И., Алиев Р. М., Наилучшие квадратурные формулы для неко-
некоторых классов функций, ДАН СССР, 162, № 1 A965), 23—25.
10. К а чм а ж С, Ш т е й н г а у з Г., Теория ортогональных рядов, Физматгиз, М.,
1958.
11. Колмогоров А. Н.,0 некоторых асимптотических характеристиках вполне огра-
ограниченных метрических пространств ДАН СССР, 108, № 3 A956).
12. К о р н е й #г у к Н. П.. О наилучшем приближении непрерывных функций, Изв. АН
СССР, сер. матем., 27, № 1 A963), 29—44.
13. К о р н е й ч у к Н. П., Л у ш п а й Н. Е., Наилучшие квадратурные формулы для
классов дифференцируемых функций и кусочно-полиномиальное приближение, Изв.
АН СССР, сер. матем., 33, № 6 A969), 1416—1437.
14. Логинов А. С, Приближение непрерывных функций ломаными, Матем. заметки,
№ 2 A969), 149—160.
15. Л у ш п а й Н. Е., Наилучшие квадратурные формулы для некоторых классов функ-
функций, Изв. вузов, матем., 12 A969), 53—59.
16. Л у ш п а й НЕ., Наилучшие квадратурные формулы на классах дифференцируемых
периодических функций, Матем. заметки, 6, № 4 A969), 475—482.
17. М а л о з е м о в В. Н., Об отклонении ломаных, Матем. заметки, 1, № 5 A967), 537—
540.
18. Н а т а н с о н И. П., Конструктивная теория функций, Гостехиздат, М.— Л., 1949.
19. Никольский СМ., Квадратурные формулы, Физматгиз, М., 1958.
20. Н и к о л ь с к и й С. М., К вопросу об оценках приближений квадратурными форму-
формулами, УМН, 5 , № 2 C6), A950), 165—177.
20*
308 ДОБАВЛЕНИЯ
21. Петере он И., О кусочно-полиномиальной аппроксимации, Изв. АН Эст. ССР.,
сер. физ.-матем. и техп., 1 A962).
22. Попов В. А., С е н д о 6 Б. X., О классах, характеризуемых наилучшим приближе-
приближением сплайн-функциями, Матем. заметки, 8, № 2 A970), 137—148.
23. Р я б е п ь к и й В. С, Об устойчивости конечноразностных схем и о применении метода
конечных разностей к решению задачи Коши для системы уравнений с частными произ-
производными, Диссертация. МГУ, 1952.
24. Рябенький В-С,Филиппов А. Ф., Об устойчивости разностных уравнений,
М., 1956.
25. Соболев С. Л., Лекции по теории кубатурных формул, часть 2, Новосибирск, 1965,
стр. 170.
26. С т о р ч а и В. Ф., Об отклонении ломаных в метрике Ью, Матем. заметки, 5, № 1
A969), 31—37.
27. С у б б о т и н Ю. Н., О связи между конечными разностями и соответствующими про-
производными, Труды Матем. ин-та АН СССР, 78 A965), 24—42.
28. Субботин Ю. Н., Поперечники класса \УГЬ в Ь @, 2зх) и приближение сплайн-
функциями, Матем. заметки, 7, № 1 A970), 43—52.
29. Субботип Ю. Н., Об одном линейном методе приближения дифференцируемых
функций, Матем. заметки, 7, № 4 A970), 423—430.
30. Субботин 10. Н., Черпых Н. И., Порядок наилучших сплайн-приближений
некоторых классов функций, Матем. замет.ки, 7, № 1 A970), 31—42.
31. С у б б о т и н Ю. Н., Функциональная интерполяция в среднем с наименьшей п-ъ
производной, Труды Матем. ин-та АН СССР, 88 A967), 30—60.
32. Т и х о м и р о в В. М., Наилучшие методы приближения и интерполирования диффе-
дифференцируемых функций в пространстве С (—1, 1)\ Матему сб., 80 A22), № 2 A0), A969),
290—304.
33. У л ь я н о в П. Л-. О некоторых свойствах рядов по системе Шаудсра, Матем. за-
заметки, 7, № 4 A970), 431—442.
34. Ч е б ы ш с в П. Л., Теория механизмов, известных под названием параллелограммов,
Полное собрание сочинений, т. И, М.— Л., 1947, стр. 23—51.
35. В 1 г к Ь о I С, Ьоса1 зрИпе арргохппаЦоп Ьу тотеп(8, 2. Ма1к. Меск., 13, № 9 A967).
36. С 1 а г 1 е I Р. С, 8 с Ь и И г М. Н., V а г % а К. 8., ]Читепса1 теИюдз о{ ЫдЬ-огДег
ассигасу Гог попИпеаг Ьоипдагу уа1ие ргоЫетз, Мит. Ма1к., 12 A968), 120—133.
37. С 1 с з 1 е 1 з к 1 2., Оп Нааг 1ипсЦоп8 апд оп 1Ье БсЬаидег Ьая18 о{ 1Ье зрасе С [0, 1],
Акад. Ро1. 8е1., 8ег. та1Ь., аз1г. е1 рЬуз., 7, № 4 A959), 227—232.
38. Н е п г I с 1 Р., Б1зсге1е уапаЫе теШосЬ т огйтагу <ШегепИа1 едиа1юпя, Ке\у Уогк,
1962.
39. К а и I з к у I., ОрИта1 диас1га1иге Гогти1ае апд тшшш1 топозрНпез т Ь9, 1оиг.
Аш1г. Ма1к. 8ос, 21 № 1 A970), 48—56.
40. Ь о з с а 1 7. о Р. В., Та1Ьо1 Т. Б., 8рНпе ТипсШт арргох1та1шл 1ог зоЫНопз о!
огдтагу <ШЛсгспМа1 едиаНол», 8ьат /. Аитег. Апа1., 4, № 3 A967), 433—445.
41. N8116161' Р., 8сЬгапкеп {иг сНе ЕгдепмгеПе §емгоЬпНсЬег БШегеп11а1д1е1сЬип§еп
о!игсЬ 8р1те-Арргох1таиоп, Иит. Ма1к., 14, A970), 346—354.
42. N 11 я с п е, 8а1ге уот 1аскзоп-Вегпз1;е1п-Тур Шг (Не АрргохшаНоп пи1 8рИпе-Рип-
с«оп, Магк. Ъ., 109, № 2 A969), 97—106.
43. N 11 з с Ь е, 11ткелгза1ге Шг 8рНпе-Арргох1та1юп, Сотро&Шо Ма1к., 21, 4 A969), 400—
416.
44. N о г а 8., АрргохппаЦоп ргореШеа оГ Ше зрНпе Ш, В1Т, 7 A967), 132—144.
45. 8сЬоепЬег§ I. I., 8рИпе 1п1егро1аИоп апй 1Ье Ы§Ьег дег1уа11уе8, КитЬег 1Ьеогу
Д апа1уз!3, N6^ Уогк, 1968, рр. 279—295.
ЛИТЕРАТУРА 309
46. 8сЬоепЬег§ I. I., Саг<Нпа1 т1егро1аиоп ап<1 зрИпе йшсИопз, 1оиг. Арргох. ТНеогу,
2, № 2 A969), 167—206.
47. 8с Ь и ш а к е г Ь. Ь., АррпттаИоп Ьу зрИпе НипсМопз под редакцией ОгеУ1е11е
Т. N. Е., Асайехтс Ргезз, N6^ Уогк, 1969, рр. 65—85.
48. Завьялов В- С, Применение вычислительных систем для решения сложных задач
проектирования в машиностроении, : сб. ^Вычислительные системы, вып. 38, Ново-
Новосибирск, 1970.
49. Завьялов Ю. С, Интерполирование кубическими многозвенниками, сб. Вычисли-
Вычислительные системы, вып. 39, Новосибирск, 1970.
50. Завьялов Ю. С, Интерполирование бикубическими многозвенниками,сб. Вычисли-
Вычислительные системы, вып. 38, Новосибирск, 1970.
51. Завьялов Ю- С, Экстремальное свойство [кубических многозвенников и задача сгла-
сглаживания, сб. Вычислительные системы, вып. 42, Новосибирск, 1970.
52. Завьялов Ю. С, Экстремальное свойство бикубических многозвенников и задача
сглаживания, сб. Вычислительные системы, вып. 42, Новосибирск, 1970.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Балка консольная 14
Второе интегральное соотношение для сплай-
сплайнов дважды кубических 239
кубических 86, 90, 91
обобщенных 200, 201
полиномиальных 165, 166
Вычерчивание кривой по точкам 13, 53
Гетерогенные сплайны 190
явного типа 260
Гильбертова пространства теория для сплай-
сплайнов кубических 97
обобщенных 208
полиномиальных 171
Дважды кубические сплайны простые 228,
233
типа I 228, типа Г 229, типа II 229,
типа II' 229
частичные 229, 231
— периодические сплайны 229
Дефект сплайна 12
кубического 28
обобщенного 187
полиномиального 153
пятой степени 122, 141, 142
Дифференциальный оператор 106, 222
Единственность сплайнов дважды кубиче-
кубических 235
двумерных 262
кубических 84
обобщенных 192
— — полиномиальных 156, 157
Интерполяционный сплайн типа к 164, 190
Иррегулярные области 246
Краевые условия 14, 15, 17, 18, 20, 29, 48,
53, 55, 65, 68, 83
Кубические сплайны 10, 13, 22, 55, 84
Кунса поверхности 252
Моменты 14, 15
Наклоны 14, 15, 55
Обобщенные сплайны И, 187, 255
двумерные 257
Ограничения на порядок сходимости 96,
170, 171, 206
сетки 25
Определяющие значения 84, 98, 208, 226
Ортогональность сплайнов 101
Основное тождество для сплайнов дважды
кубических 223
двумерных 258, 259
кубических 81
обобщенных 189
полиномиальных 151, 152
Остаточные члепы 105, 106
Параболические сплайны 272
Первое интегральное соотношение 8, 79
для сплайнов дважды кубических
234
двумерных 261
кубических 30, 81, 86
обобщенных 189
полиномиальных 152
Периодические сплайны 13, 14, 15, 25, 110,
145
Полиномиальные сплайны 109
Порядок сплайна 12, 187
Представление поверхности 249, 252
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
311
Приближенное решение дифференциальных
уравнений 13, 54
в частных производных 244
задачи Коши и краевой задачи 54, 56,
291
интегральных уравнепий 60
Простые сплайны 112, 190
Прямое произведение гильбертовых прост-
пространств 249
Пятой степени сплайны 120, 14, 142
Равномерные сетки 46, 48, 145
Равные интервалы 38, 125
Расходимости пример 279» 280
Свойство минимальной кривизны 9
нормы 8, 9
для сплайнов дважды кубических
234
кубических 77, 82
обобщенных 191
полиномиальных 153
частичных 230
— наилучшего приближения для сплайнов
дважды кубических 236
кубических 23, 79, 80
обобщенных 196
полиномиальных 154
—, частичных 230
Сглаживание 46, 142
Сеточные базисы 102, 103 .
канонические для сплайнов кубиче-
кубических 102, 103
обобщенных 213
полиномиальных 175, 176
Собственные значения матрицы 131, 132
Собственных значений проблема 222, 224
Сопряженные точки 248
числа 248
Сплайн 7, 8, 9, 11, 13, 14, 15, 22, 25, 55
— от сплайна 47
Сплайны в напряженном состоянии И
— нечетной степени 109
— сильной интерполяции 261
-типа I 77, 112, ИЗ, 189, 228
Г 77, 112, ИЗ, 189, 229
II 77, 112, ИЗ, 189, 229
И' 77, 112, ИЗ, 189, 229
к 164, 170, 173, 190
модифицированного 167, 170
— четной степени 109, 123, 272
Степень сплайна 10, 109
Суммарная длина хорды 54
Существование сплайнов дважды кубиче-
кубических 235
двумерных 262
гетерогенных 195
кубических 64
обобщенных 195
полиномиальных 131
Сходимость для сплайнов дважды кубиче-
кубических 238
двумерных 264
кубических 23, 64, 89, 94
обобщенных 197, 204, 205
полиномиальных 134, 145
— по норме для сплайнов кубических 99
обобщенных 211
полиномиальных 173
Фундаментальные сплайны дважды кубиче-
кубические 237, 243
кубические 55, 59
Циркулянт 33
Частичные сплайны 229
Эквивалентности классы 77, 189—190
Явный вид сплайна 260
Ядро 105, 106, 178, 215
ИМЕННОЙ УКАЗАТЕЛЬ
Аксень М. Б. 299, 300
Алберг (АЫЬег$ I. Н.) 6, 8, 9, 10, 11, 12,
72, 80, 134, 138, 140, 229, 236, 304
Алиев Р. М. 300
Аттиа (АМе1а М.) И
Ауслендер (Аиз1епдег 8.) 141
Каутский (КаШзку I.) 300
Киселев А. И. 299
Колмогоров А. Н. 298, 304
Конти (СопИ К.) 211
Корнейчук Н. П. 5, 270, 301
Куне Соопз 8.) 252
Беллман (ВеПтап К. Б.) 58
Бергман (Вегдтапп 8.) 61
Бернулли (ВегаоиШз I.) 79
Биркгоф (В1гкЬой О.) 10, 33, 229
Брудный Ю. А. 304
до Бур (ДеВоог С.) 9, 10, И, 12,33, 229
Вайнбергер (\УетЬегдег Н. Р.) 12
Великий В. Л. 304
Лебег (ЬеЬездие А.) 5, 270
Линч (ЬупсЬ К. Е.) 9,11, 12
Логинов А. С. 271
Лоскалзо (Ьозса1зо Р. К.) 291
Лушпай Н. Е. 300
Малоземов В. Н. 270
Мейер (Ме1Г А.) 10, 31
Мюир (Мтг Т.) 39, 131
Гарабедяп (СагаЬеШап И.) И, 229
Гильдебранд (НПйеЬгапй Р. В.) 32
Голомб (Оо1отЬ М.) 12
Гопенгауз И. Е. 304
Гревиль (СгеуШе Т. N. Е.) 9, 11, 106
Гурса (Соигза1 Е.) 61, 138
Далквист (БаЬкпшЬ С.) 227
Джексон Aаскзоп Б.) 5
Джонсон AоЬпзоп О. С.) 301
Доронин Г. Я. 300
Дэвис (БаУ18 Р. I.) 23, 137, 215
Завьялов 10. С. 307
Зейферт (Зейег* Н. 8.) 108
Ибрагимов И. И. 300
Калаба (Ка1аЬа К. Е.) 58
Каратеодори (СагаШеЪйогу С.) 211
Никольский С. М. 299
Нильсон (ЫПаоп Е. И.) 6, 8, 9, 10, 11,
12, 72, 80,134, 138,140, 229, 236, 304
Ницше (ТШзсЬе I.) 304
Норд (Иогй 8.) 230
Пеано (Реапо С.) 106, 181
Петерсон И. 291
Попов В. А. 304
Райе (Влсе 1.К.) 301
Рябенький В. С. 304, 306
Сансоне (Запзопе О.) 211
Сард (8агй А.) 11, 106, 181, 216, 221, 222,
227,240, 265, 248,298
Секрест (8есге$1; Б.) 12
Сендов Б. X. 304
Соболев С. Л. 306
Сокольников (8око1ткой I. 8.) 8 9, 79
Стечкин С. Б. - 6, 270
ИМЕННОЙ УКАЗАТЕЛЬ
313
Сторчай В. Ф. 270
Субботин 10. Н. 5, 270, 301, 306
Талбот (Та1Ьо1 Т. Б.) 291
Тихомиров В. М. 5, 290
Тодд (Тойа I.) 19
Турецкий А. X. 299, 300
Холлидей (НоНаДау I. С.) 8, 49, 77,
79, 80, 82
Циглер B1е§1ег 2.) 10, 134
Чебышев П. Л. 304
Черных Н. И. 301
Уитни (АУЬПпеу А.) 8, 289 Шарма (ЗЬаппа А.) 10, 31
Уолш (\Уа1зЬ I. Ь.) 6, 8, 9, 10, И, 12, 80, Швайкерт (8сЬ\иге1кег* Б. О.) И
134, 138, 140, 229, 236, 304 " "* ' '
Фейер (Щёе Ь.) 27, 28, 144
Фриман (Ргеетап Н.) 123
Хедрик (Нейпск Е. К.) 138
Хилле (НШе Е.) 132
Шёнберг (ЗсЬоепЬегд I. I.) 5, 8, 9, 10, И,
12, 46, 77, 106, 142, 181, 272, 286, 298,
304, 306
Шумейкер (ЗсЬшпакег Ь. Ь.) 301
Эйлер (Еи1ег Ь.) 5, 79
Эйткеп (АНкеп А. С.) 64, 131
ОГЛАВЛЕНИЕ
Предисловие редактора перевода Г>
Глава I. Введение 7
1.1. Что такое сплайн? 7
1.2. Последние достижения в теории сплайнов 8
Глава II. Кубические сплайны 13
2.1. Введение 13
2.2. Существование, единственность и наилучшее приближение . . 19
2.3. Сходимость 23
2.4. Равные интервалы 38
2.5. Приближенное дифференцирование и интегрирование 45
2.6. Вычерчивание кривой по точкам 53
2.7. Приближенное решение дифференциальных уравнений ... 54
2.8. Приближенное решение интегральных уравпепий 60
2.9. Дополнительные теоремы существования и сходимости ... 64
Глава III. Внутренние свойства кубических сплайнов 77
3.1. Свойство минимальпой нормы 77
3.2. Свойство наилучшего приближения 79
3.3. Основное тождество 80
3.4. Первое интегральное соотношение 81
3.5. Единственность 84
3.6. Существование 85
3.7. Общие уравнения 86
3.8. Сходимость производных низших порядков 89
3.9. Второе интегральное соотношение 91
3.10. Улучшение оценки порядка сходимости . 92
3.11. Сходимость производных высших порядков 94
3.12. Ограничения на порядок сходимости 96
3.13. Приложения к теории гильбертова пространства 97
3.14. Сходимость по норме 99
3.15. Канонические сеточные базисы и их свойства 102
3.16. Остаточные члены 104
3.17. Преобразования, определяемые сеткой 106
3.18. Связь с ракетной техникой 108
ОГЛАВЛЕНИЕ 315
Глава IV. Полипомиальпые сплайны 109
4.1. Определение и основные уравнения 109
4.2. Равные интервалы 123
4.3. Существование 131
4.4. Сходимость 134
4.5. Сплайны пятой степени дефектов 2 и 3 141
4.6. Сходимость периодических сплайнов на равномерных сетках . . 145
Глава V. Внутренние свойства полиномиальных сплайнов нечетной сте-
степени 150
5.1. Введение 150
5.2. Основное тождество 151
5.3. Первое интегральное соотношение 15?
5.4. Свойство минимальной нормы 153
5.5. Свойство наилучшего приближения 154
5.6. Единственность 156
5.7. Определяющие уравнения 157
5.8. Существование* 162
5.9. Сходимость производных низших порядков 163
5.10. Второе интегральное соотношение 165
5.11. Улучшение оценки порядка сходимости 167
5.12. Сходимость производных высших порядков 169
5.13. Ограничения на порядок сходимости 170
5.14. Приложения к теории гильбертова пространства 171
5.15. Сходимость по норме 173
5.16. Канонические сеточные базисы и их свойства 175
5.17. Ядра и интегральные представления 178
5.18. Представление и приближение линейпых функционалов .... 181
Глава VI. Обобщенные сплайны 187
6.1. Введение 187
6.2. Основное тождество 188
6.3. Первое* интегральное соотношение 189
6.4. Свойство минимальной нормы 191
6.5. Единственность 192
6.6. Определяющие уравнения 193
6.7. Существование 195
6.8. Наилучшее приближение 196
6.9. Сходимость производных низших порядков 197
6.10. Второе интегральное соотношение 200
6.11. Улучшение оценки порядка сходимости 202
6.12. Сходимость производных высших порядков 204
6.13. Ограничения на порядок сходимости 206
6.14. Приложения к теории гильбертова пространства 208
6.15. Сходимость по норме 211
316 ОГЛАВЛЕНИЕ
6.1В. Канонические сеточные базисы 213
6.17. Ядра и интегральные представления 215
6.18. Представление и приближение линейных функционалов . . . 216
Глава VII. Дважды кубические сплайпы , 228
7.1. Введение 228
7.2. Частичпыс енлайпы 229
7.3. Связь частичных сплайнов с дважды кубическими сплайнами . . 231
7.4. Основное тождество 232
7.5. Первое интегральное соотношепис 234
7.6. Свойство минимальной нормы 234
7.7. Единственность и существование 235
7.8. Наилучшее приближение 236
7.9. Фундаментальные сплайны 237
7.10. Свойства сходимости 238
7.11. Второе интегральное соотношение 238
7.12. Прямое произведение гильбертовых пространств 240
7.13. Метод фундаментальных сплайнов 243
7.14. Иррегулярные области 246
7.15. Представление поверхности 249
7.16. Поверхности Кунса 252
Глава VIII. Обобщенные сплайны двух переменных 256
8.1. Введение 256
8.2. Основные определения 256
8.3. Основное тождество 258
8.4. Типы сплайнов . . . • 259
8.5. Первое интегральное соотношение 261
8.6. Единственность 262
8.7. Существование 262
8.8. Сходимость 264
8.9. Приложения к теории гильбертова пространства 265
Литература 267
Добавления. С. В. Стечкин, Ю. Я. Субботин 270
§ 1. Полиномиальные сплайны первой степени 270
§ 2. Интерполяционные параболические сплайпы 272
§ 3. Полиномиальные сплайны па равпомерпой сетке ....... 285
§ А. Некоторые приложения сплайнов . 291
§ 5. Многомерный случай 304
Литература 307
Предметный указатель * 310
Именной указатель 312
УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Ваши замечания о содержании книги,
ее оформлении, качестве перевода и'другие
просим присылать по адресу:
129820 Москва, И-110, ГСП,
1-й Рижский пер., д. 2
« Издательство «Мир»
Дж. Албер-г, Э. Пильсон, Дж. Уолш
ТЕОРИЯ СПЛАЙНОВ
И ЕЕ ПРИЛОЖЕНИЯ
Редактор Л. Б. Штейнпресс
Художник О. Я. Коняхин
Художественный редактор В. И. Шаповалов
Технический редактор Е. Н. Лебедева
Сдано в набор 26/Х1 1971 г,
Подписано к печати 10/1У 1972г.
Бумага № 1,70Х9(П/1в=10 бум. л.
Усл. печ. л. 23,40
Уч.-изд. л. 21,35 Изд. К» 1/5627
Цена 2 р. 04 к. Зак. 1197
ИЗДАТЕЛЬСТВО «МИР»
Москва, 1-й Рижский пер., 2
Московская типография № 1 й
Главполиграфпрома Комитета по печати
при Совете Министров СССР
Москва, Трехпрудный пер., 9
Издательство «Мир»
в 1973 году
выпустит пишу
РОКАФЕЛЛЕР Р. Выпуклый анализ, Принстон,
1970, перевод с английского, 27 л.
Первая в мировой литературе монография, специально
посвященная комплексному анализу — сформировавше-
сформировавшемуся совсем недавно разделу анализа, занимающемуся
изучением выпуклых функций. Эти функции привлекли
особое внимание исследователей в пятидесятых годах
нашего века, когда выяснилось, какую огромную роль
они играют в задачах линейного программирования, тео-
теории игр и теории оптимальных процессов при наличии
ограничений. Исследование выпуклых функций проводит-
проводится в книге во всех аспектах: алгебраическом, топологи-
топологическом, с точки зрения двойственности, представления
в виде неравенств и т. д. Большое внимание уделено при-
приложениям. Автору удалось сочетать доступность учебника
и обстоятельность монографии. Это делает его труд инте-
интересным для широкого круга математиков различных спе-
специальностей — от студентов до научных работников.
ВНИхМАНИЮ ЧИТАТЕЛЕЙ!
Только предварительный заказ
н а к н и г и в магазинах, торгующих
научно-технической литературой,
обеспечит своевременное получение
интересующих вас книг.
Издательство «Мир»
в 1973 году
выпустит книгу
СТЕЙН Э. Сингулярные интегралы и дифференциальные
свойства функций, Принстон, 1970, перевод с английско-
английского, 19 л.
Книга посвящена теории функций многих действитель-
действительных переменных. В ней систематически изложены резуль-
результаты исследований последних десятилетий по сингуляр-
сингулярным интегралам и связанным с ними интегральным пре-
преобразованиям, по мультипликаторам интегралов Фурье,
граничным значениям гармонических функций многих
переменных и, наконец, по классификации свойств диф-
ференцируемости функций на основе их представимости
интегралами типа потенциала или поведения их разно-
разностей. Подобный подход к изучению дифференцируемости
функций многих переменных не освещен в отечественной
литературе.
Книга написана чрезвычайно ясно и сочетает все каче-
качества хорошего учебника с обстоятельностью монографии.
Она, несомненно, заинтересует математиков многих спе-
специальностей, прежде всего специалистов по теории функ-
функций и теории дифференциальных уравнений, и будет
полезна преподавателям, аспирантам и студентам универ-
университетов и пединститутов.
ВНИМАНИЮ ЧИТАТЕЛЕЙ!
Только предварительный заказ
на книги в магазина #, торгующих
научно-технической литературой,
обеспечит своевременное получение
интересующих вас книг.