ENGINEERING
THERMODYNAMICS
by
M. T. HOWERTON
Professor of Chemical Engineering
University of Denyer
D. VAN NOSTRAND COMPANY
PRINCETON, NEW JERSEY
TORONTO
INC.
LONDON
NEW YORK
ТЕРМОДИНАМИКА г"
ДЛЯ ИНЖЕНЕРОВ
Перевод с английского
канд. хим. наук Т. Н. Капцовой
В. К. Урбанович
Под редакцией проф. К. В. Астахова

ИЗДАТЕЛЬСТВО «МЕТАЛЛУРГИЯ»
МОСКВА 1966
№>09 &
Оглавление
От редактора русского издания
BIBJ IOTFKA
ЧернНвського техноло-
Ичного (нститугу
т.
Предисловие ...................................................
7
26
Глава 1. Первый закон термодинамики............................... 29
1.	Закон сохранения массы и энергии...................  29
2.	Внутренняя энергия.................................. 30
3.	Теплота ............................................ 34
4.	Работа ............................................. 34
5.	Баланс энергии...................................... 37
6.	Уравнение Бернулли.................................. 39
7.	Изменение энергии в однофазной системе с постоянным
составом ............................................... 40
8.	Изменение теплоемкости с	температурой............... 49
9.	Изменение энергии в однофазной системе постоянного
состава при стационарном	процессе.................... 53
10.	Изменение энергии при фазовом превращении........... 59
11.	Изменение энергии при химических реакциях.........	62
Задачи.................................................. 67
Глава 2. Уровни внутренней энергии.................................. 69
1.	Внутренняя энергия............................... 69
2.	Квантовая теория................................. 70
3.	Распространение волн в упругой среде............. 72
4.	Волновое уравнение для атомных систем............ 74
5.	Поступательная энергия свободной частицы......... 76
6.	Поступательные энергетические уровни частицы	в	ящике	77
7.	Энергетические уровни жесткого ротатора.......... 79
8.	Энергетические уровни гармонического осциллятора	.	.	83
Задачи ................................................... 90
Глава 3. Статистические распределения............................... 91
1.	Одна группа частиц на энергетическом уровне........... 91
2.	Несколько частиц на одном энергетическом уровне ...	92
3.	Распределение	Больцмана............................... 97
4.	Распределение	Ферми—Дирака............................ 98
5.	Распределение	Бозе—Эйнштейна......................... 100
6.	Распределение Больцмана как приближение для иераз- ,
личимых частиц.......................................... 103
7.	Вычисление X......................................... 103
8.	Поступательная сумма состояний....................... 104
9.	Вырождение поступательных энергетических уровней . .	105
*
10	Вычисление ц........................................... ИЮ
II,	Сумма состояний для жесткого ротатора................. ЮН
12.	Сумма состояний для гармонического	осциллятора .	.	.	109
Задачи............................................. 113
Глава 4. Статистическое вычисление	термодинамических	функций	...	114
1.	Внутренняя анергия............................. 115
2.	Теплоемкость................................... 119
3.	Число размещений для наиболее вероятного распределе*
ния .................................................. 128
4.	Изменение энергии в замкнутой однофазной системе опре-
деленного состава .................................... 130
5.	Теплота ............................................. 131
6.	Работа .............................................. 132
7.	Энтропия ............................................ 132
8.	Энтальпия .........................................   146
9.	Свободные энергии.................................... 146
Задачи................................................... 148
Глава б. Эмпирическое определение термодинамических функций ...	149
1.	Правило фаз ......................................... 149
2.	Вывод дифференциальных уравнений..................... 150
3.	Интегрирование частных дифференциальных уравнений
первого порядка ...................................... 156
4.	Экспериментальные данные pvT......................... 158
5.	Алгебраическое уравнение состояния................... 163
6.	Обобщенный фактор сжимаемости........................ 169
7.	Термодинамические графики и таблицы.................. 183
Задачи .................................................. 188
Глава 6. Второй закон термодинамики ............................... 189
1.	Введение ............................................ 189
2.	Самопроизвольный переход теплоты..................... 190
3.	Самопроизвольное расширение газа..................... 191
4.	Самопроизвольное необратимое смешивание двух идеаль-
ных газов ............................................ 193
5.	Обратимость ......................................... 194
6.	Превращение теплоты в работу......................... 196
7.	Обратимые циклы теплового двигателя.................. 197
8.	Полезная работа...................................... 201
9.	Рассеянная энергия................................... 203
10.	Термодинамический анализ процессов .................. 207
Задачи .................................................. 210
Главе 7. Термодинамические свойства растворов...................... 212
1.	Однофазные растворы переменного состава.............. 212
2.	Парциальные мольные величины......................... 213
3.	Влияние состава иа парциальные мольные величины . . .	214
4.	Химические потенциалы................................ 218
5.	Вычисление парциальных мольных величин............... 221
Задачи .................................................. 231
Глава 8. Критерий равновесия....................................... 232
1.	Общий критерий равновесия............................ 232
2.	Критерий термического равновесия..................... 233
3.	Критерий фазового равновесия......................... 234
4.	Критерий фазового равновесия, выраженный через сум-
му состояний.......................................... 235
5.	Критерий равновесия, выраженный через свободную
энергию Гельмгольца................................... 237
5
в. Критерий фазового равновесия, выраженный через хи-
мический потенциал . . . •............................. 238
7.	Критерий фазового равновесия, выраженный через фу-
гитивность ............................................ 238
8.	Критерий химического равновесия..................... 245
9.	Вычисление фугитивности............................. 246
10.	Вычисление коэффициента активности.................. 257
11.	Влияние температуры на фугитивность и коэффициент ак-
тивности ............................................... 261
Задачи ................................................. 263
Глава 9.	Фазовое равновесие......................... 264
1.	Равновесие твердое вещество — пар чистого компонента 264
2.	Адсорбция пара иа твердых поверхностях.............. 269
3.	Равновесие пар — жидкость для чистых компонентов 272
4.	Равновесие пар — жидкость для смесей................ 273
Задачи ................................................. 292
Глава 10. Химическое равновесие................................... 292
1.	Вычисление константы химического равновесия ....	294
2.	Определение равновесного состава.................... 298
3.	Параллельные реакции................................ 304
4.	Температура адиабатных реакций...................... 311
Задачи ................................................. 314
Литература ....................................................... 315
Приложения ....................................................... 317
ч
I
ч
(I
t «• .4
>
От редактора русского издания
Предлагаемый советским читателям перевод книги Говертона
«Термодинамика для инженеров» может служить хорошим учеб-
ным пособием по применению термодинамики к решению ряда
технологических задач. Эту книгу нельзя отнести к числу учеб-
ников по термодинамике, поскольку основные принципы этой
науки в ней изложены недостаточно четко и без надлежащей на-
учной строгости.
Основное достоинство книги состоит в раскрытии форм при-
менения термодинамики к решению тех или иных конкретных
теоретических задач химической технологии. С этой точки зре-
ния книга не имеет себе равных на русском языке.
Автор, широко образованный педагог, прекрасно сознавая
огромное значение статистической термодинамики для решения
технических задач, показал формы и методы использования ос-
новных результатов статистики Больцмана и квантовых стати-
стик Бозе — Эйнштейна и Ферми — Дирака при рассмотрении
важнейшйх понятий термодинамики, как например внутренней
энергии, теплоемкости, энтропии и т. д.
Автор в своей книге пользовался различными системами единиц
измерения, заимствуя в ряде случаев из соответствующих источни-
ков сложные уравнения с многочисленными коэффициентами. Каж-
дый коэффициент расшифровывался самостоятельными формулами,
которые отвечают применению английских единиц измерения (см.
уравнения на стр. 182, 227, 256 и др.). Приведение этих уравне-
ний к новому виду, отвечающему использованию обычных единиц
измерения, было бы уже не переводом текста автора, а переработ-
кой его. Кроме того, приходилось считаться с тем, что некоторые
коэффициенты в уравнениях состояния получены отдельными иссле-
дователями экспериментально. В связи с этим редактор счел необ-
ходимым сохранить оригинальный вид этих уравнений, а также
рассмотренных в книге примеров, дав, однако, во всех случаях в
скобках значения полученных решений в общепринятых единицах
измерения. Все же справочные материалы даны в общепринятой
системе единиц измерения.
Ниже приведены данные по переходу от единиц одной систе-
мы к единицам другой системы.
7
Единицы л и н ы
1 yd (yard) = 3ft (foot) «= 36 in (inch) » 0,9144 x; 1 ft «==
 0,3048 Mi 1 in — 2,54 cm.
Единицы площади
lyd® = 0,836 л®; 1 ft® = 0,092 x®; 1 in® = 6,452 cm*.
Единицы объема
1 yd8 = 0,02832 № = 28,32 л\ 1 in8 == 16,39 см?\ 1 gal (gal-
lon) « 3,7852 a.
Единицы веса
1 sh ton (short ton) = 907,185 кг = 2000 lb (pound);
1 long ton = 1016,05 кг;
11b = 16 oz (ounce) = 0,4536 кг;
1 oz = 28,35 г.
Единицы удельного объема
1 ft3/lb = 0,06243 х3/кг.
Единицы удельного веса
1 lb/ft3 = 16,0185 кГ/х3
Единицы давления
1 lb/ft® = 4,88 кг/м2-,
1 lb/in®(psi) = 702,7 кг/м2 = 0,0703 кг!см2 = 51,71 мм рт. ст.
Единицы измерения температуры
. оС=(Т-32. t °F = 1>8 t °C + 32; Т °К = -f- Т °R; 7 °R =
v	1 , О	У
о	Л/° F
=4-7 °К; At °C = 44-.
О	1 ,о
Единицы количества теплоты
1 Btu (British thermal unit) = 0,252 ккал = 107,53 кГм\
1 Рсц (Paund centigrad unit) = 1,8 Btu = 0,4536 ккал.
Единицы теплового потока
1 Btu/(ft® h) = 2,71 ккал/(м2-ч); 1 Pcu/(ft2-h) = 4,878 ккал (№-ч)
Единицы удельной теплоемкости
1 Btu/(lb-°F) = 1,0 ккалЦкг °C).
Коэффициент теплопроводности
1 Btu/(ft-h °F) = 1,488 ккал/(м-ч °С);	1 Btu/(in-h-°F) =
= 17,88 ккал1(м-ч°С).
Коэффициент теплопередачи
1 Btu/(ft®h-°F) = 4,882 ккал/(м*-ч-°С); lPcu(ft®.h.°Q=
=3,878 ккал1(м2 ч- °C)
8
Обозначения
yd — ярд;
ft — фут;
in — дюйм;
gal — галлон;
long ton — длинная тонна;
ton — короткая тонна;
1b — фунт;
oz — унция;
°F — градусы Фаренгейта;
°R — градусы Ренкина;
Btu — Британская тепловая единица — количество теплоты,
необходимое для нагревания 1 фунта воды на 1 °F
при 68 °F (20 °C);
Рсц — количество теплоты, необходимое для нагревания
1 фунта воды на 1 °C (при 20 °C).
XI Генеральная конференция по мерам и весам в 1960 г. при-
няла в качестве единой системы для измерения почти всех физи-
ческих величин Международную систему единиц, сокращенно
обозначаемую латинскими буквами SI (Sistem international).
На русском языке эта система единиц обозначается буквами СИ.
В Советском Союзе система СИ введена как предпочтительная
с 1 января 1963 г.
Международная система единиц построена на шести основных
единицах (метр, килограмм, секунда, ампер, градус Кельвина,
свеча) и двух дополнительных угловых единицах (радиан, сте-
радиан). Три первые основные единицы позволяют образовать
производные единицы для всех механических величин, а каждая
из трех остальных единиц дает возможность образовать производ-
ные единицы для величин, не сводимых к механическим явлениям,
ампер — для электрических и магнитных величин, градус Кель-
вина — для тепловых величин, свеча — для величин в области
фотометрии.
Основные единицы СИ перечислены в табл. I, в которой ука-
заны также и их сокращенные обозначения.
Метр — единица длины, равная 1650763,73 длин волн в ва-
кууме излучения, соответствующего переходу между уровнями
2р10 и 5ds атома криптона 86.
Килограмм — единица массы, равная массе международного
прототипа килограмма.
Секунда — единица промежутка времени, равная
1/31556925,9747 тропического года для 1900 г. января 0 в 12 ч
эфемеридного времени.
Ампер — единица силы неизменяющегося тока, который, про-
ходя по двум параллельным прямолинейным проводникам бес-
конечной длины и ничтожно малого кругового сечения, располо-
9
Таблица 1
ОСНОВНЫЕ ЕДИНИЦЫ СИ
Величина	Единица намерения	Сокращенные обозначения	
		русскими буквами	латинскими буквами
Длина	метр	м	m
Масса	килограмм	кг	kg
Время	секунда	сек	s
Сила тока	ампер	а	А
Термодинамическая тем-	градус Кельвина	°к	°К
пература Сила света	свеча	св	cd
женным на расстоянии 1 м один от другого в вакууме, вызвал бы
между этими проводниками силу, равную 2  10"7 единиц силы
Международной системы на каждый метр длины.
Градус Кельвина — единица измерения температуры по тер-
модинамической температурной шкале, в которой для темпера-
туры тройной точки воды установлено значение 273,16 °К-
Свеча — единица силы света, значение которой принимается
таким, чтобы яркость полного излучателя при температуре за-
твердевания платины была равна 60 св на 1 см2.
Дополнительные единицы СИ приведены в табл. II.
Таблица II
ДОПОЛНИТЕЛЬНЫЕ ЕДИНИЦЫ СИ
Величина	Единица измерения	Сокращенньк русскими буквами	обозначения латинскими буквами
Плоский угол Телесный угол	радиан стерадиан	рад стер	rad sr
Радиан — угол между двумя радиусами круга, вырезающий
на его окружности дугу, длина которой равна радиусу.
Стерадиан — телесный угол, вершина которого расположена
в центре сферы и который вырезает на поверхности сферы площадь,
равную площади квадрата со стороной, равной радиусу сферы.
Производные единицы СИ с указанием сокращенных обозна-
чений русскими и латинскими или греческими буквами и разме-
ров приведены в табл. III—VII.
10
Тдблица III
ПРОИЗВОДНЫЕ ЕДИНИЦЫ ГнЮСТГЛНСТВА И ВРЕМЕНИ
Величин!	Еднниця измерения	Сокращенные обозначения	
		русскими буквами	ЯЛТИНСКИМИ буквами
Площадь	квадратный метр	л«	тя
Объем	кубический метр	м3	т8
Частота	герц	гц	Hz
Линейная скорость	метр в секунду	м/сек	m/s
Линейное ускорение	метр на секунду в квад- рате	м/сек3	m/s“
Угловая скорость	радиан в секунду	рад/сек	rad/s
Угловое ускорение	радиан на секунду в квадрате	рад/сек3	rad/s*
Таблиня IV
МЕХАНИЧЕСКИЕ ЕДИНИЦЫ
Величина	Единица измерения	Сокращенные обозначения	
		русскими буквами	латинскими буквами
Плотность (объемная масса) Количество движения Момент количества дви- жения Момент инерции Сила Момент силы Давление, напряжение Модуль упругости, мо- дуль сдвига, модуль объем- ного сжатия Поверхностное натяжение Удельный вес Динамическая вязкость Кинематическая вязкость Энергия, количество ра- боты Мощность	килограмм не кубический метр килограмм-метр в секун- ДУ килограмм-квадратный метр на секунду килограмм-квадратный метр ньютон ньютон-метр ньютон на квадратный метр ньютон на квадратный метр ньютои на метр ньютон на кубический метр ньютон-секунда на квад- ратный метр квадратный метр на се- кунду джо уль ватт	кг/м3 (кг-м)/сек (кг-м3)/сек кг-м3 н н-м н/м3 н/м3 н/м н/м3 (н-сек)/м3 м3/сек дне вт	kg/ms (kg-m)/s (kg -тя)/8 kg-ms N N-m N/ma N/m2 N/m N/m8 N-s-m2 m2/s J W
И
Таблица V
ЭЛЕКТРИЧЕСКИЕ И МАГНИТНЫЕ ЕДИНИЦЫ
		Сокрсщишис	обозначения
Величина	Единица измерения	РУ и Кими буквами	латинскими буквами
Количество э. ктричест ва, электрический заряд Плотность электрическо- го тока Разность электрических потенциалов, электродви- жущая сила, электричес- кое напряжение Напряженность электри- ческого поля Электрическая емкость Абсолютная диэлектри- ческая проницаемость Электрическое сопротив- ление Удельное электрическое сопротивление Электрическая проводи- мость Удельная электрическая проводимость Электрическая энергия Магнитный поток Магнитная индукция Магнитодвижущая сила, разность магнитных потен- циалов Индуктивность, взаим- ная индуктивность Абсолютная магнитная проницаемость	кулон ампер на квадратный метр вольт вольт на метр фарада фарада на метр ом ом-метр сименс сименс на метр джоуль вебер тесла ампер геири генри на метр	К а/м* в в/м ф ф/м ом ОМ‘М сим сим/м дж вб тл а гн гн/м	с А/ш2 V V/m F F/m е Q-m S S/m J Wb T A H H/m
г I
В табл. VIII приведены температурные шкалы и формулы
перевода единиц температуры.
Для пересчета в единицы СИ приведены таблицы переводных
множителей: для единиц длины — табл. IX, для единиц вре-
мени, площади, объема — табл. X, для единиц массы, плотности,
удельного веса, силы — табл. XI; для единиц давления, работы,
энергии, количества теплоты — табл. XII; для единиц мощности,
теплового потока, теплоемкости, энтропии, удельной теплоемко-
сти и удельной энтропии — табл. XIII; для единиц плотности
теплового потока, коэффициентов теплообмена (теплоотдачи) и
теплопередачи, коэффициентов теплопроводности, температуро-
проводности и температурного градиента — табл. XIV.
12
Таблица VI
ТЕПЛОВЫЕ единицы
Величин*	1 Единиц* измерения	Сокря1цеииыо обозкичспни "	
		русскими букпямц	латинскими буквами
Количество теплоты, внутренняя энергия изо- хорно-изотермический по- тенциал (свободная энергия Гельмгольца), изобарно- изотермический цотенциал (свободная энергия Гиб- бса), энтальпия	джоуль	дж	J
Удельная теплота (фа- зового превращения, хи- мической реакции)	джоуль на килограмм	дзю/кг	J/kg
Т еплоемкость системы; энтропия системы}	джоуль на градус	дж!град	J/deg
Удельная теплоемкость; удельная энтропия	джоуль на килограмм - градус	джЦкг-град)	J/(kg-deg)
Тепловой поток	ватт	вт	W
Коэффициент теплообме- на, коэффициент теплопе- редачи Поверхностная плотность теплового потока	ватт на квадратный метр- градус	ет1(м2-град)	W/(m2-deg)
	ватт на квадратный метр	вт/м2	W/m2
Коэффициент теплопро- водности	ватт на метр-градус	втЦм-град)	W/(m-deg)
Коэффициент температу- ропроводности	квадратный метр иа се- кунду	м.2/сек	m2/s
Температурный градиент	градус на метр	град/м	deg/m
При рассмотрены наряда вопросов в настоящей книге встре-
чаются различные величины, являющиеся основными в физике
и термодинамике, поэтому ниже приведена табл. XV численных
значений этих величин в международной системе СИ.
Многие теоретические выводы и математические выкладки,
приведенные в книге, были тщательно проверены, и замеченные
в них ошибки исправлены при переводе. Однако значительная
часть таких выводов и выкладок, а также численных расчетов не
была проверена и сохранена в том виде, в каком она была в под-
линнике.
По поводу некоторых положений, выдвинутых автором книги,
можно сделать ряд критических замечаний.
Первое замечание касается истолкования соотношения Эйнш-
тейна Е = тс2, которое дано автором недостаточно четко и не
совсем правильно. Это соотношение впервые было установлено
Эйнштейном как одно из следствий специальной теории относи-
тельности. В последние годы в связи с многочисленными исследо-
ваниями различных ядерных реакций его справедливость была
13
!Таблица VII
световые единицы и единицы энергетической фотометрии
		Сокращенные	обозначения
Величина	Единица измерения	/ русскими буквами	латижкнмн буквами
Световой поток Световая энергия Светиость Освечиваиие Яркость Освещенность Количество освещения Волновое число Энергия излучения Объемная плотность энергии излучения Поток излучения Поверхностная плотность потока излучения Энергетическая свет- ность, энергетическая осве- щенность Энергетическое количест- во освещения	люмен люмен-секунда люмен иа квадратный метр свеча-секунда НИТ люкс люкс-секунда метр в минус первой степени джоуль джоуль иа кубический метр 1 ватт ватт на квадратный метр ватт на квадратный метр джоуль на квадратный метр	лм лм*сек лм/м* св-сек нт лк лк. сек \/м дж дж/м* вт вт/м2 вт/м2 дж/м2	1m Im - s lm/m2 cd -s nt lx lx-s 1/m J J/m3 W W/m2 W/m2 J/m2
много раз экспериментально подтверждена. Поэтому правиль-
ность этого соотношения не вызывает никаких сомнений. Если
иметь в виду материю как объективную реальность, а энергию как
важнейший ее атрибут, то из факта прямой пропорциональности
между энергией материального объекта Е и его массой т Е = тс2
(причем коэффициентом пропорциональности является универ-
сальная постоянная с2) следует, что масса этого объекта представ-
ляется таким его свойством, которое обязано наличию у этого
объекта энергии. Следовательно, материальному объекту при-
суща та или иная масса постольку, поскольку он обладает неко-
торым количеством энергии и масса объекта по существу является
мерой количества содержащейся в нем энергии. Утверждение
автора о взаимном превращении массы и энергии является недо-
разумением. Исходя из сказанного выше о массе как о свойстве
материи, обусловленном наличием у последней энергии, второе
из параллельных высказываний автора: «энергия не может быть
создана из ничего и не может быть уничтожена», «масса не может
быть создана из ничего и не может быть уничтожена» абсолютно
неверно. В нем автор в скрытой форме отождествляет понятия
«масса» и «материя», что, конечно, неправильно и не соответст-
вует формуле Е = тс2.
14
g
а
Ч
о
я
ТЕМПЕРАТУРНЫЕ ШКАЛЫ И ФОРМУЛЫ ПЕРЕВОДА ЕДИНИЦ ТЕМПЕРАТУРЫ
15
Тдблица IX
ГН PI ИОДНЫЕ МНОЖИТЕЛИ ДЛЯ ЕДИНИЦ ДЛИНЫ
« /
Единица измерения	Сокращенны* обозначении		Переводный множитель /
	русскими буквами	латинскими или греческими буквами	
Метр	м	ш	/ 1
Слнтиметр	см	ст	/ 1 СЛ4=10~® M
Миллиметр	мм	тт	/ 1 л«л1=10'3 м
Микрометр (микрон)	мкм	р.т	/	1 Л«КИ=10“в М
Нанометр	нм	пт	1 кл=10~в м
Ангстрем	—	А '	1 А= io-м м
Икс-единица	—	X	1=Х=1,00206-10-13 м
Ярд (Брит.)	—	yd (UK)	1 ярд (Брит.) = =0,9143984 м
Ярд (США)	5—	yd (US)	1 ярд (США) = =0,9144018 м
Ярд	—	yd	1 ярд=0,9144 м (точно)
Фут	—	ft	1 фут=0,3048 м (точно)
Дюйм	—	in	1 дюйм=0,0254 «(точно)
Миля	—	mile	1 миля = 1609,344 м (точно)
Морская миля	—	n. mile	1 морская миля=1852 м (точно)
Морская сажень	—	—	1 морская сажень = =1,8288(точно)
Световой год	св. год	1- y.	1 св-гэд=9,4605 • IO16 и
Астрономическая едини- ца длины	а. е. д.	AU	1 а.е.д.=1,495-1011 м
Парсек	пс	PC	1 пс= 3,260 св-мт= =3,084-1010 м
На основании исследований советских ученых (К. А. Пути-
лова, А. И. Бачинского и др.) отчетливо выявилось понятие о
теплоте как части внутренней энергии, рассматриваемой в момент
перехода при контакте от одного объекта к другому в результате
неупорядоченных соударений молекул и атомов обоих объектов
на поверхности контакта. Такой переход имеет место вследствие
разности температур обоих объектов, хотя бы и бесконечно ма-
лой. Поэтому, написав выражение первого начала термодина-
мики
dt/ = 6Q+8A,
в котором d(J — дифференциал внутренней энергии системы;
8Q — бесконечно малое количество теплоты, сообщенное системе;
8/1 — бесконечно малое количество работы, выполненное вдоль
сил, действующих на систему, можно сказать, что изменение
внутренней энергии системы может быть осуществлено только
двумя формами передачи энергии — в виде теплоты и в виде
работы. Таким образом, первое начало термодинамики является
16
Таблица X
ПЕРЕВОДИМ!! МНОЖИТЕЛИ ДЛЯ ЕДИНИЦ ВРЕМЕНИ. ПЛОЩАДИ, ОВЪЕМА
	Сокращенные обозначения		
Единица измерения^	русским и буквами	лагни сними буквами	Переводный множитель
Секунда	\ Минута	\ Час	1 . Сутки Год i Квадратный метр ар Os	Гектар >	Квадратный	ярд vj ф	Квадратный	фут Квадратный дюйм Квадратная миля Руд Акр Кубический метр Литр Кубический ярд Кубический фут Кубический дюйм Галлон (Брит.) Галлон (США) Пинта (Брит.) и Жидкая уиция (Брит.) Жидкая унция (США) Бушель (Брит.) Бушель (США)	сек мин Ч м* а га Z М3 Л	S min h d а m* а ha yd2 ft2 in2 sq. mile m3 1 yds Г ft3 in3 gal (UK) gal (US) Pt (UK) fl. oz (UK) fl.oz(US) bu (US)	I 1 мин—60 сек 1 ч==3600 сек I сутки=86400 сек 1 год = 31556925,9747 сек (на 1900 г.) 1 1 а=100 м2 1 аа= 104 м2 1 квадратный ярд = =0,836127 м2 1 квадратный фут = =0,0929030 м2 1 квадратный дюйм= =6,4516-IO4 At2 (точно) 1 квадратная миля = =640 акров= 2,58999 • 10е м2 1 руд= 1011,71 м2 1 акр=4046,8б м2 1 1 л=1,000028.10-3 л3 1 кубический ярд = =0,764555 м3 1 кубический фут = =0,0283168 л» 1 кубический дюйм = =16,3871-10-е м3 1 галлон (Брит.) = =4,54609-Ю-3 л3 1 галлон (США) = =3,78543-Ю-3 м3 1 пиита (Брит.) = =0,568261-Ю-3 л3 1 жидкая уиция (Брит.)=28,4130.10-« м3 1 жидкая унция (США)=29,5737-10-в м3 1 бушель (Брит.) = =36,3687-10-3 м3 1 бушель (США) = =35,2393-10-3 м3
Б1БЛ1ОТЕКА
Черн1г1вського техноло-
г1чного Ihctmtvtv
17
2—1503
облицв XI
ПЕРНиОДНЫТ! МНОЖИТЕЛИ ДЛЯ ГД1ПТИН МАССЫ, ПЛОТНОСТИ, УДЕЛЬНОГО ВЕСА,
СИЛЫ	/
Единицы измерения	1 F	 Сокращенны» обоаиачения			Переходный множитель
	русскими буквами	Латинскими буквами		
Килограмм	кг	kg		1 /
Тонна	т	t		1 m=1000 кг
Техническая единица	(кгс-сек*)/м	kgf-s2/m		1 (кгс-сек2)/л=9,80665 кг
массы				(точно)
Фунт (Брит.)	—	lb (UK)		1 фунт (Брит.)= «0,453592338 кг
Фунт (США)	—	lb (US)		1 фунт (США)= =0,4535924277 кг
Слаг	—	slug		1 слаг= 14,5939 кг
Гран	—	gr		1 гран=64,79891-10-® кг
Унция	—	oz		1 унция=28,3495-10-3 кг
Тонна (Брит.)	—	ton		1 тонна (Брит.)= =1016,05 кг
Килограмм на куби- ческий метр	кг/м3	kg/m3		1
Грамм на кубический сантиметр	г/см3	g/cm3		1 г/сл*=1 т/л3=103 кг/м3
Тонна на кубический метр	т/м3	t/m3		
				
Грамм иа миллилитр	г/мл	g/ml		1 г/лл=999,972 кг/л3
Фунт на кубический	—	lb/ft3		1 фунт на кубический фут=
фут				= 16,0185 кг/л3
Ньютон на кубичес- кий метр	н/м3	N/m3		1
Килограмм-сила иа	кгс/м3	kgf/m3		1 кгс/л3=9,80665 н/л3
кубический метр				(точно)
Фунт-сила на кубн-	—	lbf/ft3		1 фуит сила на кубический
ческий фут				фут= 157,087 н/л3
Ньютон	н	N		1
Дина	дин	dyn		1 дин=10-6 н
Стен	—	sn		1 стен=103 н
Килограмм-сила	кгс, кГ	kgf		1 кгс=9,80665 н (точно)
Тонна-сила	тс	—		1 тс=9,80665 103 н (точно)
Фунт-сила	—	Ibf		1 фунт-сила=4,44822 н
18
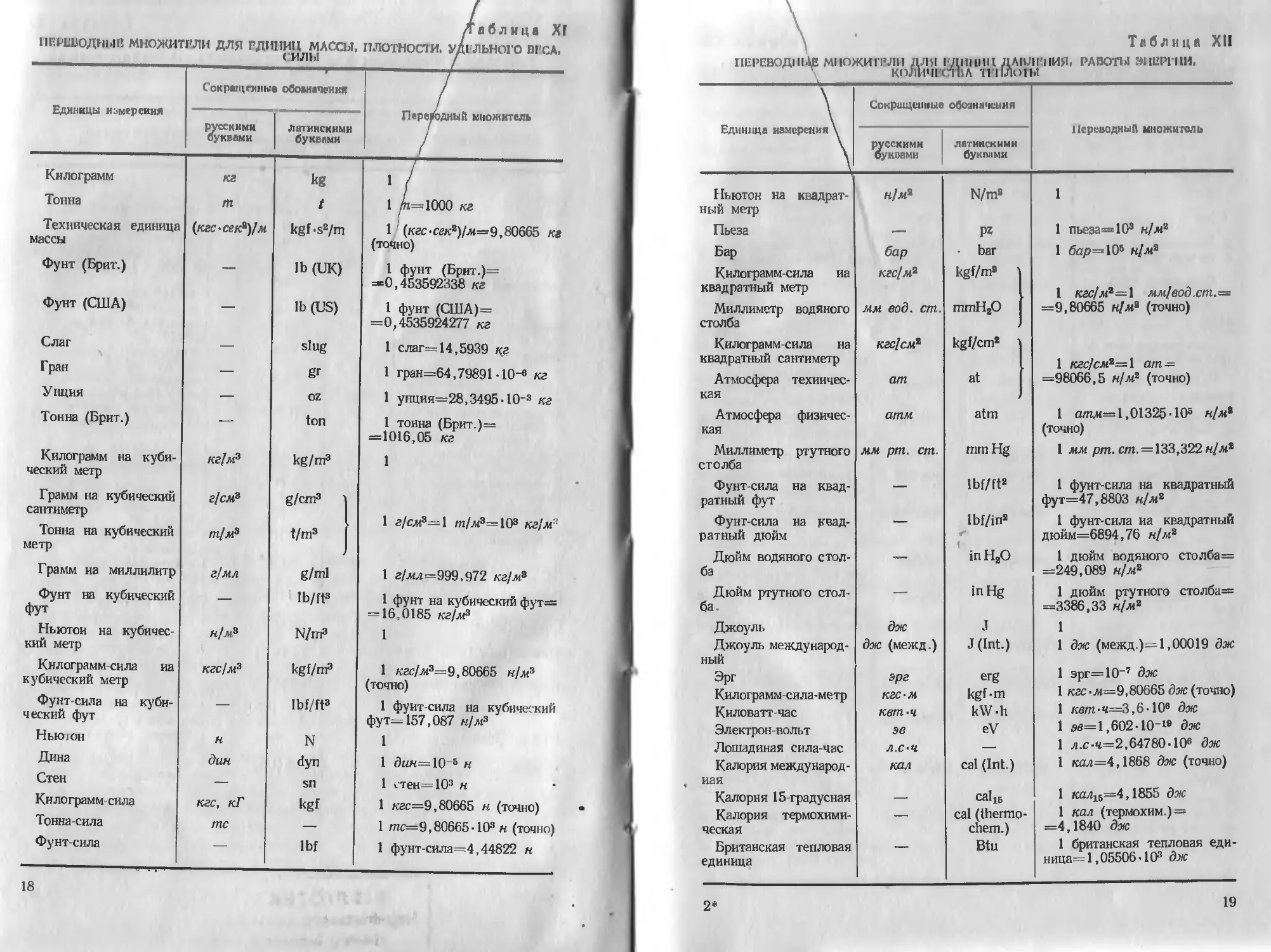
Таблица XII
ПЕРЕВ0ДП1ДВ МНОЖИТЕЛИ ДЛЯ I Д1Н111Ц ДЛНЛИПИЯ. РА ВОТЫ ЭНЕРГИИ.
КОЛИЧГСП11А 11 11ЛО1Ы
—	1 	III I,	—1 Единица камер ния\^	Сокршцепиые обозначения		НсреводныП множитель
	русскими буквами	латинскими бу КПД ми	
Ньютон на квадрат-	н/л2	N/m2	1
ный метр			
Пьеза	—	Р?	1 пьеза=103 н/л2
Бар	бар	bar	1 бар=106 н/л2
Килограмм сила иа	кгс[м2	kgf/m2	
квадратный метр			1 кгс/мг=1 мм1вод.ст.=
Миллиметр водяного столба	мм вод. ст.	mmHsO	—9,80665 н/л2 (точно)
Килограмм-сила на	kscJcm1	kgf/cm2	
квадратный сантиметр			1 кгс/см2=1 ат—
Атмосфера техиичес-	ат	at	—98066,5 н/л2 (точно)
кая			
Атмосфера физичес-	атм	atm	1 атм=1,01325-106 н/л2
кая			(точно)
Миллиметр ртутного	мм рт. ст.	mm Hg	1 лл рт. ст. = 133,322 н/мг
столба			
Фунт-сила на квад-	—	lbf/ft2	1 фунт-сила на квадратный
ратный фут			фут=47,8803 н/л2
Фунт-сила на квад-	—	lbf/in2	1 фунт-сила иа квадратный
ратный дюйм			дюйм=6894,76 н/л2
Дюйм водяного стол-	.*1»	in H2O	1 дюйм водяного столба=
ба			=249,089 н/л2
Дюйм ртутного стол-	—.	inHg	1 дюйм ртутного столба=
ба.			=3386,33 н/л2
Джоуль	дж	J	1
Джоуль международ-	дж (межд.)	J (Int.)	1 дж (межд.)=1,00019 дж
НЫЙ			
Эрг	эрг	erg	1 эрг=10-7 дж
Килограмм-сила-метр	кгс-м	kgf-m	1 кгс -л=9,80665 дж (точно)
Киловатт-час	квт-ч	kW-h	1 квт-ч=3,&-10в дж
Электрон-вольт	эв	eV	1 $«=1,602-10-1® дж
Лошадиная сила-час	Л.С’Ч	—	1 л.с-ч=2,64780- 10е дж
Калория международ-	кал	cal (Int.)	1 кал=4,1868 дж (точно)
иая			
Калория 15-градусная	—	calis	1 кал16=4,1855 дж
Калория термохими-	—	cal (thermo-	1 кал (термохим.) =
ческая		chem.)	=4,1840 дж
Британская тепловая	—	Btu	1 британская тепловая еди-
единица			ница= 1,05506-103 дж
2*
19
аблица XIII
ПН’1 ПОЛНЫЕ МНОЖИТЕЛИ ДЛЯ I ДИНИИ МОЩНОСТИ. ТЕПЛО1Г1ГО ПОТОКА.
ТЕПЛОЕМКОСТИ. ЭНТРОПИИ, УДЕЛЬНОЙ ТЕПЛОЕМКОСТИ И УДШ1|>ПОЙ ЭНТРОНШI
Единица измерения	Соирпщчшы» обозначения		Переводный миожитель
	русскими буквами	латинскими буквами	
			1
Ватт	вт	W	1
Эрг в секунду	эрг/сек	erg/s	1 эрг/сек= 10-’ вт
Килограмм-сила-метр в секунду	кге-м/сек	kgf -m/s	1 кгс-м/сек-= =9,80665 вт (точно)
Лошадиная сила	Л.С.	—	1 л.ч.=735,499 вт
Лошадиная сила (Брнт.)	—	hp	1 л. с. (Брит. )= =745,700 вт
Килокалория между- народная в час	ккал/ч	kcalint/h	1 ккал/ч= 1,163 вт (той но)
Калория междуна- родная в секунду	кал/сек	caljnt/s	1 кал/сек—4,1868 вт (точно)
Британская тепловая единица в час	—	Btu/h	1 британская тепловая единица в час=0,293071 вт
Джоуль на градус	дж/град	J/deg	1
Эрг на градус	эрг/град	erg/deg	1 эрг/град= =10-’ дж/град
Килокалория на гра- дус	ккал/град	kcal/deg	1 ккал/град — =4,1868 • 103 дж/град (точ- но)
Калория на градус	кал/град	cal/deg	1 кал/град— =4,1868 дж/град (точно)
Британская тепловая единица на градус Фа- ренгейта	—	Btu/deg F	1 британская тепловая единица на градус Фарен- гейта =4,89911•103 дж/град
Джоуль на кило- грамм-градус	дж/(кг- град)	J (kg-deg)	1
Эрг на грамм-градус	эрг/ (г град)	erg/(g-deg)	1 эрг/(гград)= = 10'4 дж/(кг-град)
Килокалория иа ки- л о грамм-градус	ккал/(кг-град)	kcal/(kg • deg)	1 ккал/(кг-град)= =4,1868 • 103 дж/(кг/град) (точно)
Калория на грамм- градус	кал/(г-град)	cal/(g-deg)	1 кал/(г-град)= = 4,1868-103 дж/(кг-град) (точно)
Британская тепловая единица на фунт-градус Фаренгейта		Btu/(lb-degF)	1 британская тепловая единица на фунт-градус Фаренгейта=4,1868 • 103 дж/(кг-град) (точно)
20
Таблице XIV
III РГНПДНЬП МНОЖИП ЛИ ДЛЯ ЕДИНИЦ ПЛОПКЧЛИ Т) ПЛО1ИЧ <! IIOiucA,
КОЭФФИИИ1 HIGH II 11ЛОО1.М1 НА (II НЛООГДАЧИ) И И 1IJIOI1I РГ'ДАЧИ.
КОЭФФИЦИЕНТОВ И НЛоПРОНОДШМ 1И. 11 Mill РАТУГОНРОИОДИОСТИ
И 11 МШ'РАТУРНО! О I РАДИЫПА
Единица измерения	Сокращенные o6o.iiiu<kiiii>i		Переводный множитель
	\ русскими буквами г	латинскими буквами	
Ватт на квадрат-	вт/м2	W/m*	1
ный метр			1 вт/см2 =№ etn/м2-
Ватт на квадрат-	вт/см2	W/cm2	
ный сантиметр			l эрг/(см2-сек)— = 10*3 вт/м2
Эрг иа квадратный сантиметр в секунду	эрг!(см2-сек)	erg/(cma-s)	
Килокалория на квадратный метр-час	ккал/(м2-ч)	kcal/(in2-h)	1 ккал/(м2-ч)= = 1,163 вт/м2 (точно)'
Калория на квад- ратный сантиметр-	кал/(см2-сек)	cal/(cm2-s)	1 кал/(см2 сек)= =4,1868-101 вт/м2 (точно)*
секунду		Btu/(ft2-h)	
Британская тепло- вая единица иа квад- ратный фут-час	—		1 британская тепловая единица на квадратный фут-час=3,15461 вт/м2
Британская тепло- вая единица на квад- ратный фут-секунду		Btu/(ft2-s)	1 британская тепловая единица на квадратный фут-секунду = 1,13566X X 104 вт/м2
Британская тепло- вая единица иа квад- ратный дюйм-секун- ДУ		Btu/(in2-s)	1 британская тепловая единица на квадратный дюйм-секуиду — 1,63535 X X 10е вт/м2
Ватт на квадрат-	вт/(м2 -град)	W/(m2-deg)	1
ный метр-градус			1 вт/(см2-град)= =104 вт/(м2-град)
Ватт иа квадрат- ный сантиметр-гра-	вт/ (см2 -град)	W/(cm2-deg)	
дус Эрг на квадратный сантиметр-секуиду-	эрг/(см2  сек • град)	erg/cm2-s- deg)	1 эрг/(см2-сек-град)=: = 10-3 вт/(м2-град)
градус Килокалория на квадратный метр- час-градус	ккал/(м2-ч-град)	kcal,'(m2  -h-deg)	1 ккал/(м2-ч-град)= = 1,163 вт/(м2  град) (точ- но)
Калория на квад- ратный сантиметр-	кал/'см2  сек • град	cal/(cm2-s- deg)	1 кал/(с м2-сек-град)= —4,1868-104 втЦм* -град)
секунду-градус		Btu/(ft2-h- •degF)	1 британская тепловая единица на квадратный фут-час-градус Фаренгей- та=5,6783 вт/(м2-град)
Британская теп- ловая единица на квадратный фут-час- градус Фаренгейта			
Британская тепло- вая единица на квадратный фут-се- кунду-градус Фарен- гейта		Btu/ft2-s-  deg F)	1 британская тепловая единица иа квадратный фут- секунду-градус Фаренгей- та=2,04418-104 вт/(м2Х Хград)
Ватт на метр гра-	вт/(м-град)	W/(m-deg)	1
дус			
21
Продсурктие шиПлицы XIV
Еднишц намерения	Сокращенные обозначении		llep/водиый множитель
	русскими буквами	ЛАТИНСКИМИ буквами	
Ватт на сантиметр-	вт/(см-град)	W/(cm-deg)	. -у 		 1 вт/(см-град)~*
градус Эрг на сантиметр-	эрг /(см-сек-град)	erg/(cm-s-	ta/Ю2 втЦм-град) 1 эрг/(см-сек-град)=
секунду-градус Килокалория на	ккал/(м-ч- град)	•deg) kcal/(m • h •	= 10~ь вт/(м-град) 1 ккалЦм-ч-град)—
метр-час-градус Калория на сан-	кал/(см-сек-град)	•deg) cal/(cm-s-	=1,163 вт/(м-град) (точ- но) 1 кал/(см- сек- град)=
тиметр-секунду-гра- дус Британская тепло-		deg) Btu/(ft-h-	=4,1868-102 вт/(м-град) ( точно) 1 британская тепловая
вая единица на фут- час-градус Фарен- гейта Британская тепло-		• deg F) Btu/(ft-s-	единица на фут-час-градус Фаренгейта= =1,730741 вт/(м-град) 1 британская тепловая
вая единица на фут- •секунду-градус Фа- ренгейта Британская теп-		•degF) Btu/(in-s-	единица на фут-секунду- градус Фаренгейта= =6,23067  103 вт/(м-град) 1 британская тепловая
ловая единица на дюйм-секунду-гра- дус Фаренгейта Квадратный метр	м2/сек	•degF) m2/s	единица на дюйм-секунду- градче Фаренгейта= =7,47681.10* втЦм град) 1
иа секунду Квадратный сан-	см2/сек	cm2/s	1 см2/сек=10~* м2/сек
тиметр на секунду Квадратный метр	м2/ч	m2/h	1 ж2/ч=2,7778х
ла час Квадратный фут		ft2/h	ХЮ-4 м2/сек 1 f квадратный фут на
на час Квадратный фут		ft2/s	час=25,8064-10-в м2/сек 1 квадратный фут на се-
«а секунду Квадратный дюйм		in2/h	кунду=0,0929030 м2/сек 1 квадратный дюйм на
на час Квадратный дюйм		in2/s	час=17,92111 • 10-6 м2/сек 1 квадратный дюйм на
-на секунду Градус на метр	град/м	deg/m	секунду=6,4516х X 10~* м2/сек (точно) 1
Градус на санти- метр	град/см	deg/cm	1 граЗ/сл«=100 град/м
Градус Фаренгей-	—	degF/ft	1 градус Фаренгейта иа
та на фут Градус Фаренгей-		degF/in	фут= 1,82269 град/м 1 градус Фаренгейта на
та на дюйм			дюйм=21,8723 град/м
22
Таблиц# XV
HrKOrOI'UR 0С11ОН11Ы1 ФИ IH'II'CKIII ШЛИЧИНЫ В CUCTFMI' СИ
Фнимчаскм млячмиа
Численно нипченнг
и системе CN
Внесистемно-
(ничейно
Постоянная тяготения 7
Число молекул в одной
килограмм-молекуле
Объем 1 килограмм-мо-
лекулы идеального газа при
нормальных условиях
Универсальная газовая
постоянная
Постоянная Больцмана
Число Фарадея
Постоянная Стефана-
Больцмана а
Постоянная Планка h
Заряд электрона
Масса покоя электрона
Масса покоя протона
Масса покоя нейтрона
6,67-10-н мя/(кг-секя)
6,025-10»’ кмоль-i
22,4 л»
8,31 дж/(кмоль-град)
1,38-Ю-»3 дж/град
9,65-107 к) кг-же
5,67-10 8 ет/(мг  град*)
6,625  10-34 дж  сек
1,602-10-» к
9,11-10-** кг
1,672-Ю-27 кг
1,675-10-»’ кг
„ „„„	(«-атм)
0,082 (моль-град)
1,36-10 1 (см2-сек-град*)
5,49-10"4 а.е.м
1,00759 а.е.м.
1,00899 а е.м.
выражением общего закона сохранения энергии в применении
к тепловым явлениям. Автор книги, близко подойдя к правиль-
ному толкованию понятий «теплота» и «работа», недостаточно
четко сформулировал первый закон термодинамики, полагая его
тождественным равенству Д£ = Ате2, которое по существу
значительно шире по содержанию первого закона термоди-
намики.
Второй закон термодинамики автор также сформулировал
не на термодинамической, а на статистической основе — «изоли-
рованная система, свободная от одухотворенного выбора, сама
произвольно стремится перейти в состояние, которое может осу-
ществиться наибольшим числом способов». Поэтому неудивитель-
но, что прежде чем подойти к описанию содержания второго за-
кона термодинамики и его следствиям, автор сравнительно под-
робно остановился на статистическом подходе к рассмотрению
термодинамических процессов и термодинамических функций,
и такие понятия, как энтропия, термодинамические функции
U — TS « U — TS + pv, появились в книге раньше, чем было
рассмотрено содержание второго закона термодинамики. Из-
лагая содержание последнего, автор высказывает мысли, по су-
ществу примыкающие к признанию тепловой смерти мира; так,
он утверждает, что второй закон термодинамики эквивален-
23
тен утверждению Клаузиуса «Энтропия мира стремится к мак-
симуму». В советской термодинамической и философской лите-
ратуре давно уже раскрыт антинаучный смысл этого утверждения,
коль скоро мир нельзя рассматривать как конечную изолирован-
ную систему, а к тому же в космосе могут протекать и протекают
такие процессы, которые непосредственно не подчиняются зако-
нам термодинамики конечных систем. Вот почему выше было ука-
зано, что книга Говертона едва ли может заменить учебник по
термодинамике. Кроме того, автору свойственна некоторая не-
последовательность. Так, например, автор ссылается на знаме-
нитое правило фаз Гиббса, в то же время по существу не дает его
вывод. Очевидно, читатель должен быть знаком с выводом этого
правила, а кроме того, должен иметь отчетливое представление
о понятиях «фаза», «компонент» и «число степеней свободы». По-
следнее понятие становится особенно ясным при наличии теоре-
тического вывода правила фаз. К сожалению, в книге нет такого
вывода, как нет и тщательного анализа понятий о фазе и ком-
поненте.
Как мы уже указывали, автор в ряде случаев избегает строго-
го подхода к тем или иным термодинамическим понятиям. На-
пример, по сути дела он не провел различия между понятиями
«равновесный» и «обратимый» (процессы). Как известно, про-
цесс является равновесным (квазистатическим), если он состоит
из непрерывной совокупности равновесных состояний системы.
Обратимый же процесс — это такой процесс с рассматриваемой
системой, выполнив который она может вернуться в исходное
состояние без изменений в ней самой и в системах, внешних по
отношению к ней. В подавляющем большинстве случаев равно-
весные процессы являются обратимыми, однако можно привести
пример, когда равновесный процесс не является обратимым.
В описании политропных процессов автор отошел от общеприня-
того понимания понятия «политропный процесс». В отличие от
принятого в советской термодинамической литературе автор
определяет политропный процесс как такой процесс с идеальным
газом, который удовлетворяет условию pifi — const, в котором
величина 8 лежит между единицей и величиной отношения CplCv.
Поэтому изотермический, адиабатный и многие другие процессы
не являются, по мнению автора, политропными. В указанном
ограничении величины 8 и состоит отличие понимания политроп-
ного процесса автором от принятого советскими термодина-
миками.
К сожалению, в русской терминологии нет термина, аналогич-
ного английскому термину «fluid», объединяющему газы и жид-
кости. Поэтому перевод этого термина дан словом «газ», что,
конечно, несколько ограничивает смысл текста перевода по срав-
нению с текстом подлинника, хотя при внимательном чтении
перевода становится ясно, идет ли речь только о газе, или о газе
и жидкости одновременно.
24
Как уже было упомянуто, при нсрсподе в основном была со-
хранена терминология автора, поэтому функции U — TS и
U — TS + ри назнапы, как в последнее время принято в зару-
бежной термодинамической литературе, соответственно как сво-
бодная энергия Гельмгольца и свободная энергия Гиббса, т. е.
приведен дословный перевод названий этих функций, принятых
в подлиннике. Первая из них обозначена буквой A: U — TS — А,
а свободная энергия Гиббса — буквой F: U— TS + ри-
Опять-таки эти обозначения отличаются от принятых в советской
литературе. Термин «fugacity» не имеет в советской литературе
однозначного перевода, поэтому в настоящей книге он передан
словом «фугитивность».
Принятый в подлиннике термин «грамм-моль» в переводе за-
менен на термин «моль», поскольку термин «моль» и есть сокра-
щенное название «грамм-молекулы». Вместе с тем при переводе
сохранен термин «фунтомоль» как более краткий взамен правиль-
ного термина «фунто-молекула».
Несмотря на тщательный просмотр текста перевода, я все же
допускаю возможность наличия в нем отдельных неточностей.
Поэтому заранее признателен читателям за указание недостат-
ков русского текста.
Проф. К. В. Астахов
25
Предисловие
Основные законы термодинамики достаточно широки, чтобы
найти разнообразные применения в физике, химии и технике.
В результате развития термодинамики появилось много различ-
ных точек зрения при рассмотрении отдельных вопросов. Тем
не менее оказалось возможным в пределах данной книги ограни-
читься основными понятиями и рассмотреть такие применения,
которые относятся к превращению теплоты в работу, а также в
качестве специальных примеров процессы с переносом вещества
а системы с химическими реакциями.
Эта книга может служить руководством при изучении основ-
ных принципов термодинамики с элементарным приложением
их в нескольких областях техники. Так как законы термодинами-
ки основаны на прямом экспериментальном наблюдении суммар-
ных свойств, они являются по своей природе эмпирическими.
Несмотря на то что применения, основанные на этих законах, мо-
гут быть сформулированы в конкретных количественных мате-
матических выражениях, термодинамические величины, такие
как температура, давление, энергия и энтропия, не могут быть
интерпретированы физически без ссылки на принятые теории
по строению материи.
Использование теории строения вещества для интерпретации
термодинамических величин не может ни исключаться, ни ума-
ляться при эмпирическом развитии термодинамических соотно-
шений. Любое соотношение, основанное на структурной модели,
идентичное эмпирическому термодинамическому соотношению,
является подтверждением принятой структурной модели. Толко-
вание термодинамических величин в терминах структурной тео-
рии имеет важное значение.
Это положение аналогично ежедневному наблюдению за вре-
менем восхода солнца в течение нескольких лет в различных
точках поверхности земли. Эти эмпирические данные могли бы
быть скорректированы, и время восхода солнца могло бы быть вы-
ражено как математическая функция дня, года, широты, долготы
26
и высоты. Гака я корреляция была бы полезна в ряди применений,
по она не исчерпывает сведений о природе системы, к которой
относятся наблюдаемые данные. Эта корреляция могла бы быть
сделана только относительно физической модели солнечной си-
стемы. На основе правильной модели можно было бы вывести
уравнение, которое предсказало бы время восхода солнца в дан-
ный день в определенном месте. Если такое предсказание сопо-
ставить с эмпирической корреляцией, это могло бы служить под-
тверждением принятой модели солнечной системы и могло быть
использовано для интерпретации эмпирических данных.
Основываясь на таком рассуждении, были введены элемен-
тарные понятия квантовой и статистической механики для интер-
претации эмпирической стороны классической термодинамики.
Квантовое представление об энергетических уровнях использо-
вано для интерпретации внутренней энергии. Статистические тео-
рии приведены для того, чтобы показать, что термодинамические
энергии и энтропия являются средними или статистическими
свойствами системы в целом. Это позволяет понять основные поло-
жения второго закона, обоснование третьего закона и шкалу абсо-
лютных энтропий. Также представлены методы вычисления теп-
лоемкости и абсолютной энтропии идеальных газов. Численные
значения абсолютной энтропии особенно важны для анализа си-
стем с химическими реакциями. После рассмотрения этих основ-
ных положений технические применения даны в виде обычных
термодинамических соотношений.
Книга состоит из двух основных разделов. В гл. 1—6 изло-
жены основные законы и их интерпретация с соответствующими
вычислениями и применениями к чистому компоненту или систе-
мам с постоянным составом. Эти главы включают основной ма-
териал, который используется во всех областях техники. В гл.
7—10 рассмотрены переменные составы и применение основ-
ных законов к фазам и системам с химическим равновесием. Для
того чтобы сохранить изложение на должном уровне, основной
материал ограничен в объеме и многие частные применения умыш-
ленно опущены.
Хотя представленный материал не является новым и ориги-
нальным, книга построена так, что можно легко перейти от тео-
ретических положений к практическим применениям, которые
в ней не указываются. В гл. 1 дано краткое введение к термодина-
мическим рассуждениям и расчетам, основанным только на зако-
нах сохранения энергии. Глава 2 — библиографическая; в ней
довольно подробно описаны выражения для квантованных энер-
гетических уровней. Хотя для детального изучения математиче-
ской стороны необходимо знание основ учения о дифференциаль-
ных уравнениях, полученные результаты могут быть использо-
ваны без применения дифференцирования. В гл. 3 изложены тео-
рии статистического распределения, необходимые для понимания
внутренней энергии и энтропии. Распределение Максвелла —
27
Больцмана дает, в частности, основу дня статистического вычис-
ления термодинамических свойств. В гл. 2 рассмотрено при-
менение статистических выводов для вычисления термодинами-
ческих свойств с числовыми расчетами для идеального газа.
В гл. 5 представлены методы для вычисления изменений термоди-
намических свойств неидеальных газов и жидкостей с помощью
использования эмпирических данных pvT и уравнений состояния.
Обсуждение второго закона термодинамики в гл. 6 основано
непосредственно на статистических выводах, взятых из гл. 3 и 4.
Так как энтропия определена как функция состояния, анализ
обратимых циклических тепловых двигателей и необратимых
процессов дается как естественное применение основных прин-
ципов.
Элементарные свойства растворов описаны в гл. 7, а в гл. 8
выведен критерий равновесия. Применение его к системам с
фазовым и химическим равновесием включая изменения пере-
менного состава, рассмотрено в гл. 9 и 10.
При попытке применить числовые расчеты к нескольким раз-
личным областям возникает проблема единиц. В настоящее время
не существует твердо установленных единиц, которые годились
бы сразу для всех случаев применения. Однако перевод единиц
из одной системы в другую представляет определенные трудно-
сти. В^'этой книге переход от одной системы единиц к другой све-
ден к минимуму путем подбора наиболее удобной системы единиц
для каждой данной задачи. Выбор единиц обычно диктуется
имеющимися в наличии данными. В большинстве случаев отдает-
ся предпочтение метрической системе с выражением энергии в
калориях, массы в граммах, температуры в градусах Кельвина
(или в стоградусной шкале). При применении английской систе-
мы единиц энергия выражается в британских тепловых единицах,
масса в фунтах и температура в градусах Рэнкина (или Фарен-
гейта). Перевод единиц из одной системы в другую редко бывает
необходим. Например, величина, выраженная в кал/(моль °К),
имеет то же числовое значение в брит. тепл. ед./(фунт-моль °R).
Следовательно, теплоемкости и энтропии имеют одинаковое чис-
денное значение в обеих системах.
ГЛАВА 1
Первый закон термодинамики
Законы классической термодинамики основаны на непосред-
ственных эмпирических наблюдениях и как таковые полностью
не зависят от каких-либо теорий, которые были или будут пред-
ложены для объяснения физической природы материи и энергии.
Количественные соотношения, основанные на законах классиче-
ской термодинамики, могут быть выражены в величинах экспери-
ментально измеряемых свойств.
Вопреки обычному пониманию термина «динамика», класси-
ческая термодинамика имеет дело только с превращениями энер-
гии и их влиянием на измеряемые макросвойства системы без
учета детального механизма, имеющего место при самих превра-
щениях. Интерпретация механизмов таких превращений может
быть дана только на основе приемлемой модели или теории при-
роды вещества и энергии. Так как рассмотрение таких механизмов
дает более глубокое понимание других эмпирических соотноше-
ний, то основные принципы квантовой и статистической механики
могут быть использованы для объяснения изменений в макросвой-
ствах системы с помощью величин ее микро- или молекулярных
свойств. Использование этих теорий при развитии и объяснении
термодинамических соотношений приводит к появлению отдель-
ной дисциплины, именуемой «статистической термодинамикой»,
которая особенно необходима для объяснения термодинамических
функций внутренней энергии и энтропии и для установления кри-
терия состояния равновесия.
Законы и соотношения классической термодинамики сначала
будут обсуждены с эмпирической точки зрения. Затем они будут
рассмотрены и интерпретированы на основе статистической термо-
динамики.
1.	Закон сохранения массы и энергии
Понятие «энергия» медленно развивалось на протяжении ряда
веков. Человек непосредственно через ощущения мог легко
установить, что тело в движении ведет себя и реагирует иначе,
29
чем п состоянии покоя; горячее тело ведет себя иначе, чем холод-
ное. Некоторые тела даже в состоянии покоя выделяют шергию
в виде теплоты при использовании их в качестве топлива.
Хотя и можно было легко сделать качественные наблюдения,
однако объяснение их оставалось неясным и запутанным, при-
мером чего может служить теория теплорода, которая рассмат-
ривала теплоту как жидкость, аналогичную воде. Только с про-
ведением количественных измерений в течение последних двух
столетий понятие «энергия» было выяснено и точно определено.
Теперь можно экспериментально показать, что масса и энергия
взаимно превращаемы и что общая масса и энергия сохраняются
при всех известных превращениях. Понятие сохранения массы
и энергии теперь принято как основной закон термоди-
намики.
Хотя масса и энергия не являются независимыми величинами,
изменение массы вследствие изменения энергии незначительно
за исключением реакций, протекающих с чрезвычайно большим
энергетическим эффектом. Например, изменение массы, соответ-
ствующее изменению энергии, равной 1 000 000 брит. тепл. ед.
(2,5-Ю8 кал), может быть вычислено по уравнению Эйнштейна:
ДЕ = Дтс2
к
и равно приблизительно 2,6-10~8 фунта (1,2-10—Б г). По этой
причине масса и энергия могут рассматриваться как независимые
для всех физических процессов и химических реакций, включаю-
щих обычные валентные силы. Для этих случаев закон сохране-
ния массы может быть сформулирован независимо от закона со-
хранения энергии.
Энергия не может быть ни создана, ни уничтожена. Масса
не может быть ни создана, ни разрушена. Эти утверждения мо-
гут быть использованы независимо от измеряемой ошибки в боль-
шинстве технических приложений и могут быть приняты как пер-
вый закон термодинамики.
Экспериментальные наблюдения показывают, что энергия
может проявляться в нескольких различных формах. Например,
энергия тела и его измеряемые свойства — такие как темпера-
тура и давление — могут изменяться под действием теплоты или
работы. Применение первого закона требует предварительного
рассмотрения различных форм энергии.
2.	Внутренняя энергия
С макроскопической точки зрения энергию системы, соответ-
ствующую ее массе, называют внутренней энергией. Внутренняя
энергия — это свойство системы, которое полностью определяется
ее состоянием и известно как «функция состояния». Изменение
внутренней энергии при переходе системы из одного состояния
30
в другое строго определенное и не зависит от мехшпнма, пьнвив-
шего эго и пленение.
С молекулярной точки зрения внутренняя энергия системы
есть сумма всей кинетической и потенциальной энергии частиц,
составляющих эту систему. Эта энергия распределена между по-
тенциальной и кинетической энергиями частиц внутри ядра
каждого атома, потенциальной и кинетической энергиями коле-
бания атома в молекуле, кинетической энергией вращения групп
атомов внутри молекулы, кинетическими энергиями вращатель-
ного и поступательного движений молекулы как таковой и, нако-
нец, межмолекулярной потенциальной энергией внутри сис-
темы .
Различные виды внутренней энергии могут быть грубо клас-
сифицированы как «независимые от температуры» и «зависимые
от температуры». При значениях температуры и давления, обыч-
но встречающихся в инженерной практике, электронная и ядер-
ная энергии в основном не зависят от температуры и составляют
внутреннюю энергию системы при температуре абсолютного нуля.
Энергии поступательного, вращательного и колебательного дви-
жений зависят от температуры и составляют часть внутренней
энергии, которую содержит тело при температуре выше абсолют-
ного нуля. Эту часть внутренней энергии обычно рассматривают
как термическую энергию. Она представляет наибольший интерес
в термодинамике.
В настоящее время абсолютные величины электронной и ядер-
ной энергий не могут быть определены, но изменения в величи-
нах этих энергий можно оценить эмпирически по данным теплот
образования или сгорания для конкретных рассматриваемых
соединений. Значительные сдвиги произошли в области опреде-
ления величин различных видов термической энергии. Например,
на основании классической кинетической теории газов вычисле-
но, что средняя энергия поступательного движения в идеальном
газе составляет 3/2 RT. Так как поступательному движению мо-
лекулы в свободном от поля пространстве соответствуют три сте-
пени свободы (по одной на каждую ось координат), то х/2 RT
внутренней энергии должна приходиться на каждую степень сво-
боды.
Полуколичественное определение средней внутренней энер-
гии вращения и колебания возможно в том случае, если на каж-
дую степень свободы вращения приходится 1/2 RT и на каждую
степень свободы колебания RT (по х/2 RT на потенциальную
и кинетическую энергии колебания соответственно). При опре-
делении общего числа степеней свободы в молекуле каждый атом
рассматривается как материальная точка с тремя степенями
свободы. Таким образом, молекула, состоящая из п атомов, будет
иметь Зп степеней свободы. Следовательно, одноатомная моле-
кула обладает суммарно тремя степенями свободы, каждая из
которых соответствует поступательному движению. Если рас-
31
сматривать атом как материальную точку, то одноатомная моле-
кула не должна обладать ни вращательной, ни колебательной
энергией. Двухатомная молекула обладает в сумме шестью сте-
пенями свободы, три из которых поступательные, две вращатель-
ные (пренебрегая вращением атомов но валентной связи) и одна
колебательная. Нелинейная трехатомная молекула обладает в
сумме девятью степенями свободы, из которых три поступатель-
ные, три вращательные и три колебательные.
В табл. 1, согласно классической теории, приведены величины
вкладов во внутреннюю энергию Е от каждой степени свободы F
для одноатомных, двухатомных и нелинейных трехатомных .мо-
лекул.
Таблица 1
КЛАССИЧЕСКАЯ СОСТАВЛЯЮЩАЯ МОЛЕКУЛЯРНОЙ ВНУТРЕННЕЙ ЭНЕРГИИ
Формы движения	Одноатомная молекула		Двухатомная молекула		Нелинейная трех- атомная молекул.1	
		E/RT	F	E/R.T	F	E/RT
Поступательное движение .	3	3/2	3	3/2	3	3/2
Вращение		0	0	2	1	3	3/2
Колебание		0	0	1	1	3	3
Сумма ....	3	—	6	—	9	—
Классическое представление о внутренней энергии частично
подтверждено эмпирическими данными по теплоемкости. Термин
«теплоемкость» первоначально использовали для определения
количества теплоты, необходимой для изменения температуры
единицы массы какого-либо материала на один градус. Однако
было найдено, что теплоемкость является функцией условий,
при которых происходит нагревание. Например было найдено,
что количество теплоты, необходимое для нагревания единицы
массы газа на один градус, значительно больше, если газ рас-
ширяется при постоянном давлении в процессе нагревания, чем
то количество теплоты, которое потребовалось бы для нагревания
газа при постоянном объеме. Кроме того, имеет значение темпе-
ратурный интервал, в котором происходит нагревание. Поэтому
существует несколько различных видов теплоемкости, каждый
из которых характерен для какого-либо процесса нагревания.
В настоящее время количество энергии, присущее системе,
определяется как внутренняя энергия, а не как теплота, поэтому
термин «теплоемкость» потерял свое прямое значение. Тем не
менее его пока еще широко используют для обозначения хорошо
известного свойства системы. Особый интерес представляет тепло-
емкость при постоянном объеме Cv, которая определяется как
32
скорость изменения внутренней анергии единицы массы при из*
[менении температуры при условии постоянства объема:
(1-1)
Эта частная производная может быть функцией и температуры,
и давления.
Так как Cv измеряет скорость изменения внутренней энергии
с изменением температуры при постоянном объеме, то прибли-
женное значение Со может быть получено прямым дифференци-
рованием значения внутренней энергии (табл. 1) по температуре.
Теплоемкости идеальных газов при постоянном объеме и постоян-
ном давлении приведены в табл. 2.
Таблица 2
ТЕПЛОЕМКОСТИ ИДЕАЛЬНЫХ ГАЗОВ. БРИТ. ТЕПЛ.'ЕД. (ФУНТ-МОЛЬ-»К)
[«ал/(люль.°К)|
Формы движения	Одноатомная молекула		Двухатомная молекула	Трехатомная молекула	
	с°	СР	cv 1 СР	Ср	СР
При комнатной температуре и ниже
Поступательное движение . . .	...| 3	5	3	5	3	5
Вращение		  i °	0	2	2	3	3
Сумма		• •  1 3	5	5	7	6	8
При очень высоких температурах
Колебание		0 ♦	0	2	2	6	6
Сумма 		3	5	7	9	12	14
Теплоемкость идеальных газов при постоянном давлении Ср,
может быть получена р помощью соотношения
Cp = Cv-\- R,
где R — газовая постоянная для идеального газа, численно
равная 1,987 кал/(моль °К).
Для одноатомной молекулы по классической теории Со равно
3 кал/(моль°К.) и Ср равно около 5 кал/(моль-°К). Эти значения
не зависят от температуры, что согласуется с экспериментальны-
ми данными. Соответственно классической теории для двухатом-
ных молекул Cv равно около 5 кал/(моль-вК), а
Ср = 7 кал Кмоль °К). В действительности Ср для большинства
двухатомных молекул составляет около 7 кал/(моль-вК) при
комнатной температуре и приближается к 9 как к пределу при
очень высоких температурах. Это указывает на то, что колеба-
3—1503
33
тельная энергия для двухатомных молекул обычно миля при
компппюй температуре, tio постепенно возрастает с повышением
температуры до тех пор, пока не будет достигнуто значение 1/?
на одну колебательную степень свободы для теплоемкости, по-
лученной при высокой температуре. $•
Если колебательная составляющая ничтожно мала при ком-
натной температуре, Ср для нелинейных трехатомных молекул
должна быть равна 8 кал/(моль К) при комнатной температуре
и приближаться к 14 как к максимуму при высоких температурах.
Это предположение находится в соответствии с экспериментами.
3.	Теплота
Внутренняя энергия системы может быть изменена добавле-
нием или расходом энергии в форме теплоты. Теплота является
переходной формой энергии из одной области в другую под влия-
нием разности температур. Скорость этого перехода пропорцио-
нальна разности температур. В соответствии с этим определением
теплоты нельзя говорить, что энергия, содержащаяся в веществе,
является теплотой. Энергия может быть передана системе в виде
теплоты, но внутри системы она превращается во внутреннюю
энергию и не сохраняется как теплота.
Теплота — переходная форма энергии. Ее количественная
оценка должна зависеть от механизма этого перехода. Так как
классическая термодинамика не рассматривает подробно меха-
низм теплопроводности, конвекции и радиации, количество
перенесенной теплоты может быть вычислено термодинамически
только при наблюдении влияния процесса ^переноса теплоты на
свойство системы и окружающей среды.
4.	Работа
Внутренняя энергия системы может быть также изменена
добавлением или расходом энергии в форме работы. Работа яв-
ляется формой энергии в процессе перемещения под действием
силы. Как сила, так и перемещение необходимы для того, чтобы
передать энергию в форме работы.
Обычная форма работы — это результат изменения объема,
вызванного действием внешнего давления. В этом случае дей-
ствие силы может быть вычислено как произведение внешнего
давления и площади, на которую это давление направлено. Сме-
щение удобно вычислить как изменение объема и, деленное на
площадь поперечного сечения А. Следовательно, выполненная
работа w равна произведению силы рА и перемещения Av/А, т. е.
w — (рА) (Av/А)=р Av,	(1-2)
где р — постоянное давление, производящее изменение объема
Av.
34
Если изменение объема происходит п несколько стадий, при
чем в каждой стадии отдельно действует постоянное давление, то
общая выполненная работа будет рання сумме произведений
рДи для каждой стадии:
(1-3)
Если действие давления непрерывно в процессе изменения
объема, проделанная работа может быть выражена интегралом
и
w — \ pdv.	(1-4)
ч
Чтобы вычислить этот интеграл, необходимо знать соотноше-
ние между действующим внешним давлением и объемом системы
в течение всего процесса.
Работа и теплота являются формами энергии в процессе ее
переноса. Количественная оценка энергии зависит от механизма
переноса. Примером может служить работа, совершенная при
и ютермическом расширении одного моля идеального газа от 10
до 1 атм. Однако точное количество работы зависит от частного
пути, по которому происходит расширение, как показано в при-
мере 1.
Пример 1. Определить количество выполненной работы
при изотермическом расширении 1 моля идеального газа от 10
до 1 атм для каждого из следующих случаев.
А.	Расширение газа происходит в одну стадию от 10 до 1 атм
при условии постоянного внешнего давления, равного 1 атм.
Б. Расширение происходит в две стадии. В первой стадии
газ расширяется от 10 до 5 атм при постоянном внешнем давле-
нии 5 атм. Во второй стадии газ расширяется от 5 до 1 атм при
постоянном внешнем давлении 1 атм.
В.	Расширение происходит в три стадии. В первой стадии
1аз расширяется от 10 до 5 атм при постоянном внешнем давле-
нии 5 атм\ во второй стадии он расширяется от 5 до 2 атм при
постоянном внешнем давлении 2 атм-, в третьей стадии — от 2
до 1 атм при постоянном внешнем давлении 1 атм.
Г. Расширение происходит в 9 стадий с постепенным пони-
жением внешнего давления соответственно на 1 атм.
Д. Расширение происходит при бесконечно большом числе
стадий, причем для каждой стадии внешнее давление на беско-
нечно малую величину меньше, чем внутреннее давление газа.
При расширении газа для каждой стадии работа равна произ-
ведению постоянного внешнего давления на изменение объема.
В указанном примере внешнее давление всегда является конеч-
ным давлением для каждой стадии расширения. В этом случае
проделанная работа выражается уравнением (1-2):
ау = р2До.
3*
35
Для 1 моля идеального газа
Av «	*£ « - «HetzzM
Р» Pl	PiPi
тде pt и p4 — начальное и конечное давления в цилиндре соот-
ветственно. Тогда работа, выполненная в одну стадию,
w = ^(Ра —р,) _  ЯГДр
Pi	Pi
и общая работа для каждого случая
RTVAp
Результаты работы, выполненной в каждой стадии для раз-
личных случаев, приведены ниже:
А
Б
В
Г
10	1	0,900
10	5	0,500
5	1	0,800
		1,300
10	5	0,500
5	2	0,600
2	1	0,500
		1,600
10	9	0,100
9	8	0,111
8	7	0,125
7	6	0,143
6	5	0,167
5	4	0,200
4	3	0,250
3	2	0,334
2	1	0,500
 1,930
По мере того,
как ДР в каж-
дой стадии
приближается
к нулю, вся
выполненная
работа стре-
мится к вели-
Д
чине
Pi
— RT С — = RT In— = ЯГ In 10 = 2,303 RT.
J Р	Р»
pi
В случае А выполненная работа составляет 0,900 в слу-
чае Б 1,300 RT', в случае В 1,600 RT. Если расширение выпол-
нено в 9 стадий, как в случае Г, работа составляет 1,930 RT. Оче-
видно, величина выполненной работы возрастает с ростом числа
стадий. В пределе при бесконечно большом числе стадий внешнее
36
давление по существу рпппо внутреннему давлению во всех слу-
чаях и внутреннее давление может быть шмелено н интеграле
внешним давлением. При этих условиях Величина выполненной
работы составляет 2,303 RT. Это выражает максимальное коли-
чество работы, которое можно получить нри изотермическом
расширении газа от 10 до 1 апгм.
Графически результаты работы изотермического расширения
идеального газа показаны на рис. 1.
10 г	10 г
О 0,2 0,6 0,6 в,в 1,0 О 0,2 о,If 0,6 0,8 1,0
v/RT,amn-f	if/KT,amtr*
9 0,2 0,6 Ofi 0,8 1,0
Рис. 1. Работа изотермического расширения идеального газа:
a—w=0,900 RT; б—ш= 1.300 ЯГ; е—№=1.600 RT; г—№=1.900 ЯГ; с1—№=2,303 ЯГ
Основные условия для получения максимальной работы от
системы требуют, чтобы движущая сила и сила сопротивления
были уравновешены во всех случаях. Такой процесс можно на-
чать «равновесным», или «обратимым», поскольку только беско-
нечно малые изменения в силах действующей и противодейству-
ющей будут вызывать процесс, обратный своему направлению.
Такой процесс является предельным — к нему можно прибли-
жаться, но нельзя достигнуть в действительности. Он является
стандартным или относительным процессом, с которым можно
сравнить реально выполненные процессы.
5.	Баланс энергии
Применение закона сохранения энергии к специальным си-
стемам следует рассматривать как баланс энергии, при этом
имеется в виду энергия, которая сообщается системе, отводится
37
от нес и накапливается внутри системы при протекании того или
иного процесса. Наиболее часто встречаются два типа процессов:
процессы в закрытых системах и процессы, протекающие стацио-
нарно. Процесс в закрытой системе — это такой, при протекании
которого нс происходит добавления или удаления вещества из
системы. В процессах, протекающих стационарно, вещество
вводится в систему с постоянной скоростью и с той же скоростью
удаляется из нее, так что во время процесса не происходит; на-
копления вещества в системе.
При процессе в закрытой системе энергия может добавляться
или удаляться из системы только двумя путями, а именно в виде
теплоты или работы. Если Q — вся теплота, сообщенная системе,
w___вся работа, выполненная системой, и ДЕ — возрастание
внутренней энергии, то баланс энергии для процесса в закрытой
системе может быть представлен, соотношением
Q — w-\-AE.	(1'5)
Несмотря на то что теплота и работа — формы энергии в мо-
мент перехода и, следовательно, являются функциями пути или
механического перехода, разность между Q и w полностью опре-
деляется начальным и конечным состоянием системы и не зависит
от какой-либо промежуточной стадии процесса.
Для стационарно текущих жидкостей действуют два допол-
нительных вида изменения энергии вследствие возможного из-
менения в скорости потока вещества и в изменении высоты при
прохождении им через систему. Разность между кинетической
энергией при входе в систему и выходе из нее дает соотношение
т (ul—u№gc,
где т _ масса вещества, проходящего через систему в единицу
времени;
и — его линейная скорость;
gc — константа перехода размерности массы к размерности
силы.
Изменение потенциальной энергии, вызванное изменением вы-
соты при введении вещества в систему и выводе его из нее, можно
представить в виде соотношения
m(z2—z^glgc,
где z — высота по отношению к стандартной плоскости потенци-
альной энергии; g — ускорение силы тяжести.
Кроме того, различают обычно механическую работу пере-
мещения через границы системы и работу, выполненную над си-
стемой жидкостью, входящей в нее и покидающей ее. В этом
случае общая работа, выполненная единицей массы жидкости,
проходящей через систему, составит
к’общ = + Psve — Pivi >	(1 ’6) ;
38
где ws — механическая работа перенося через 1‘раиицы системы
некоторым механическим устройством, например насосом или
турбиной; PjV, - работа, совершенная над системой, когда еди-
ница массы входит в нее; р8о4 — работа, совершенная системой,
1 огда единица массы уходит из нее; р — давление жидкости и
f — объем единицы массы. Произведение pv иногда называют
«работой потока».
Полный баланс энергии стационарного процесса на единицу
массы жидкости в единицу времени равен
Q = wt + Д (pv) + ДЕ + Д (	4. Az-?-.	(1-7)
\ z8c /8с	'
В этом уравнении появляется сумма ДЕ и A(pv). Довольно
часто такую сумму можно определить, не вычисляя отдельно ДЕ
и A(pv). Поэтому ее обозначают как «изменение энтальпии» и
определяют по уравнению
АН = ДЕ + Д (pv).	(1-8)
С помощью изменения энтальпии Н общий баланс энергии
стационарного процесса на единицу массы жидкости может быть
представлен уравнением
<2 = щ,5_!_ДД + д/^_\_|_Дг-^>	(1-9)
\	)	Вс	'
(». Уравнение Бернулли
Если при стационарном процессе рассматривать только еди-
ницу массы вещества, то баланс энергии для нее определяется по
уравнению (1-5). Если все процессы, происходящие при стацио-
нарном изменении системы, обратимы, то работа, выполненная над
единицей массы, может быть вычислена с помощью давления си-
стемы согласно уравнению (1-4)
к-обР== Jptto.	(1-10)
Так как в действительности работа совершается не при обра-
тимом процессе, то количество выполненной работы меньше
на величину F — энергию, рассеянную при трении. Поэтому ба-
ланс энергии для единицы массы может быть изображен в виде
Q—ДЕ = w— J pdv—Е.
Заменяем (Q — АЕ) в уравнении (1-7):
§pdo=ws+A(pv) 4-Д (-^)+Д2|- + Е. (I-1I)
39
Используя математическое соотношение
A(pv)-f/Mto + jvdp,
уравнение (1-11) можно написать так:
—^vdp =w, +Д	+	(1-12)
Уравнение (1-12) — обычная форма уравнения Бернулли для си-
стемы со стационарно протекающим процессом.
Вычисление энергии, рассеянной при трении, требует подроб-
ных знаний механизма процесса и лежит вне области термодина-
мики. Термодинамический анализ главным образом направлен
на вычисление максимальной механической работы, совершенной
процессом. Максимальная механическая работа получается в ре-
зультате обратимого процесса, для которого F — 0. При незна-
чительных изменениях кинетической и потенциальной энергии
уравнение (1-12) превращается в следующее выражение для мак-
симальной или обратимой механической работы:
ws ——§ vdp-	(1-13)
7. Изменение энергии в однофазной системе
с постоянным составом
Процесс при постоянном объеме
Изменение внутренней энергии системы удобнее всего опре-
делять с помощью теплоемкости при постоянном объеме, вычис-
ляемой по уравнению (1-1). Для процесса при постоянном объеме
ДЕ = fadT.	(1-14)
Работа, выполненная при течении процесса в закрытой систе-
ме при постоянном объеме, равна 0, так как любые перемещения
отсутствуют. Следовательно, теплота, добавленная системе при
течении процесса при постоянном объеме, равна изменению внут-
ренней энергии. Путем сочетания уравнений (1-5) и (1-14) полу-
чаем
Q = AE=Jc^T.	(1-15)
Так как Д(ро) — v&p, то для процесса при постоянном объеме
изменение энтальпии может быть вычислено с помощью уравне-
ний (1-8) и (1-14):
=	+	(1'16).
40
Для жидкостей н Твердых тел величина v&p обычно быпиет ис-
шачителыш по отношению к Изменению внутренней энергии,
тогда
ДНдаДЕ.	(1-17)
Для одного моля идеального газа пДр = 7?ДТ в процессе
при постоянном объеме и
ДД = J С^Т + J RdT= j (С„Ч- R) dT - J Cpdf.	(1-18)
Процесс при постоянном давлении
Для процессов при постоянном давлении изменение энталь-
пии наиболее удобно вычислять с помощью теплоемкости при
постоянном давлении. По определению
СНН’	(1-19)
11оэтому для процессов при постоянном давлении
\H = [cpdT.	(1-20)
Так как работа выполнена при процессе в закрытой системе
при постоянном давлении и А(ро) равно рДо, то добавленная
геплота равна изменению энтальпии на основании уравнений
(1-5), (1-8) и (1-20):
Q==AE + pAo=.AE = Jcpd?.	(1-21)
Поскольку изменение объема при термическом расширении
жидкостей и твердых тел весьма мало, то произведение pAv
обычно незначительно по сраднрнию с АЕ и
Q = AE^AE.	(1-22)
Для одного моля идеального газа рАи = /?АТ в процессе при
постоянном давлении и
Q=AE-=AE + EA7.	(1-23)
Комбинируя уравнения (1-20) и (1-23), имеем
Q = JcpdT = \Е + ^RdT,	(1-24)
из которого следует
&Е —§ (Cp—R)dT = \С^Т.	(1-25)
41
H.wtncpMtifiecKtul прицеп
Из уравнений (1-14) и (1-25) п'идпо, что изменение внутренней
энергии идеального газа всегда равно J С,ДТ и не зависит от ка-
кого-либо изменения объема или давления; оно равно пулю,
если начальная и конечная температуры одинаковы. Другими
словами, внутренняя энергия идеального газа является функ-
цией только температуры.
Из уравнений (1-18) и (1-20) следует, что изменение энтальпии
газа всегда равно J CjiT и не зависит от какого-либо изменения
объема или давления; оно также равно нулю, если начальная
и конечная температуры одинаковы. Последнее заключение прямо
вытекает из закона Бойля, по которому объем идеального газа
обратно пропорционален давлению при условии постоянства темпе-
ратуры. Таким образом, р^х= p2t?2 для любых двух состояний при
одной и той же температуре и A(pv) = 0. Так как ДЕ = 0 для
этих двух состояний, то и АН = 0.
Вычисление выполненной работы при изотермическом расши-
рении или сжатии проиллюстрировано в примере 1, где особое
внимание обращено на зависимость выполненной работы от меха-
низма процесса. Если внешнее давление ра постоянно, то процесс
необратим, и работа может быть вычислена по уравнению
ш = ра ——=/?тГ-^—Ра-1.	(1-26)
P1J [Pi Pl J	'	'
Если конечное давление системы равно внешнему давлению, урав-
нение (1-26) приобретает вид, приведенный в примере 1.
С термодинамической точки зрения интерес в основном пред-
ставляет вычисление работы, произведенной при обратимом про-
цессе. Для жидких и твердых систем произведенная работа обыч-
но незначительна, так как объем таких систем почти не зависит от
приложенного внешнего давления. Чтобы вычислить интеграл
уравнения (1-4) для газовых систем, необходимо знать соотноше-
ние между давлением и объемом. В обратимом процессе разница
между давлением внутри системы и внешним давлением практи-
чески равна нулю и внутреннее давление может быть заменено
внешним.
Для одного моля идеального газа интеграл уравнения (1-4)
для изотермического обратимого процесса приобретает следующее
выражение:
02
w = RT f-^- = /?Tln-^- = /?Tln-^-.	(1-27)
J V	P2
VI
Это же самое уравнение было получено в примере 1 упрощенным
способом.
42
Так кпк изменение ннугренией энергии при течении изотер
мического процесса в системе из твердого тела, жидкости или
идеального газа практически равно нулю, то теплота, сообщен-
ная системе, равна произведенной работе.
Адиабатный процесс
Адиабатный процесс — это такой процесс, при котором не
происходит теплообмена между системой и внешней средой.
Следовательно,
Q = 0	(1-28)
и
ДЕ.	(1-29)
При процессе в закрытой системе, который является адиабат-
ным и протекает при постоянном объеме,
Q = ui=—ЛЕ = 0.	(1-30)
При адиабатном процессе в системе из одного моля идеального
1аза, теплоемкость которого не зависит от температуры, урав-
нение (1-29) принимает вид
щ = Со(Г1-Г2) = СоГ1( 1-yf).	(1-31)
Так как процессы расширения и сжатия чаще сопровождаются
изменением давления, чем изменением температуры, то для вы-
числения выполненной работы необходимо знать соотношение
между изменениями давления и температуры.
Уравнение (1-29) в дифференциальной форме имеет вид
pdv^—CjdT,	(1-32)
где р, v и Т — переменные величины. При обратимых процессах
давление, объем и температура связаны соответствующим урав-
нением состояния, В этом случае при дифференцировании закона
идеального газа
pdv + vdp = RdT.	(1-33)
Подставляя уравнение (1-33) в уравнение (1-32), получаем
vdp^(Cv + R)dT = CfjdT.	(1-34)
С помощью закона идеального газа подстановка v в функции
р и Т в уравнении (1-34)и последующее разделение переменных
дают уравнение, содержащее в качестве переменных величин
только давление и температуру:
Rdp-=CpdT-	<Ь35)
43
Поскольку мы приняли, что теплоемкость по зависит от тем-
пературы, уравнение (1-35) может быть проинтегрировано:
/?1п-£1. -Ср In(1-36)
Pl	"j
Уравнение (1-36) может быть решено для отношения конеч-
ной и начальной температур в функции отношения давлений:
<ьз7>
Используя уравнение (1-37), из уравнения (1-31) получаем
выражение для работы, выполненной при течении адиабатного
обратимого расширения или сжатия одного моля идеального газа,
для которого теплоемкость не зависит от температуры:
	(1-38)
Уравнение (1-38) часто записывают иначе, используя отно-
шение теплоемкости при постоянном давлении к теплоемкости
при постоянном объеме:
k = 5р.	(1-39)
Применение соотношения Ср — Со= 7? для идеального газа при-
водит к следующему выражению для теплоемкости в функции k:
R _k— 1
ср- k’
(1-40)
(1-41)
Подставляя уравнения (1-40) и (1-41) в уравнение (1-38), по-
лучаем
RT
k —
Соотношение между изменением объема и давления может
быть получено с помощью уравнения (1-37) и уравнения состоя-
ния идеального газа
Рг _	( Vi	\ / Тг \ _ ( Vi	\	/	Рг^ \ с
Pi	\v2/\7i/	\ Цг	/	\	Pi / Р'
ilk 5
Рг ^_ /	t>i \	Ср = / J4 \С»	=	(3 V
Pl \	)	\ Vt J	\Vi I '
(1-43)
(1-44)
44
Уравнение (1-44) можно записать тпьж<" и виде
Pivi P»vi const.
(1-45)
Уравнение (1-42) может быть получено непосредственно из
равнений (1-45) и (1-4).
Работа, произведенная во время необратимого адиабатного
процесса расширения или сжатия идеального газа при условии
постоянства внешнего давления, может быть вычислена с помощью
уравнения (1-31). Если рх — начальное давление системы, рй —
конечное давление системы и ра — постоянное внешнее давление,
то
= <М6>
Уравнение (1-47) представляет собой отношение начальной тем-
пературы к конечной для необратимого адиабатного расширения
пли сжатия идеального газа при постоянном давлении в функ-
ции давления. Это отношение аналогично уравнению (1-37) для
обратимого процесса.
Работу и изменение внутренней энергии можно легко вычис-
лить, определив отношение конечной температуры к начальной
с помощью уравнения (1-47) и подставив его численное значение
в уравнение (1-31).
Политропные процессы
Термин «политропный» используют для обозначения разл ич-
пых процессов в идеальных газовых системах, не являющихся
изотермическими или адиабатными. Работу, выполненную при
течении такого процесса, удобно вычислять, используя форму
уравнений, полученных для адиабатного обратимого процесса
в идеальной газовой системе с заменой величины k эмпирической
постоянной 8. При политропных процессах уравнения (1-45),
(1-37) и (1-42) принимает вид
Pii>J = p2t4 = const,
‘ а _ / Ра \ в
71	\ Pi )
6-1	,
__ Pivi I____f Рг \ в
»- 1	\ Pi )	
(1-48)
(1-49)
(1-50)
45
Эмпирнчвския пистоянния 8 может быи> произвольной вели-
чиной между единицей и k. Если величина 8 приближается к
единице, то вычисленные величины w, Q и Л/? приближаются к
таковым для изотермических обратимых процессов в системе из
идеального газа. Если же величина 8 приближается к k, то вы-
численные величины w, Q и Д£ приближаются к таковым для
адиабатного обратимого процесса в системе из идеального газа.
Пример 2. Вычислить произведенную работу, передачу
теплоты и изменение внутренней энергии для каждого из следую-
щих процессов.
А. Из сосуда емкостью 1 фут3 (28,3 л) идеальный газ, нахо-
дящийся первоначально под давлением 10 атм, начинает выте-
кать в окружающее пространство, где давление равно 1 атм и
температура 535 °R (297 °К). Предполагается, что газ вытекает
достаточно медленно, так что сосуд и содержимое его сохраняют
постоянную температуру.
Этот процесс можно представить себе как процесс в закрытой
системе, если считать системой то количество газа, которое ос-
тается в сосуде при конечных давлении и температуре. Во время
процесса это количество газа может быть рассмотрено как от-
деленное свободно двигающимся поршнем от остальной массы
воздуха. В этом случае давление понижается очень медленно, так
что процесс можно рассматривать как изотермическое обратимое
расширение идеального газа.
Исходя из уравнения состояния идеального газа можно опре-
делить количество газа, остающегося в сосуде при конечных
температуре и давлении:
т = ^- = (1-1/0,73-535) фунт-моль.
л\Л 2
Согласно уравнению (1-27), выполненная работа
w = mRT In (&-} = п’9^ In 10 = 6,30 брит. тепл, ед. (1,59 ккал).
\ р2 /	U,i О• ОоЭ
Так как процесс является изотермическим, то
ДЕ = 0
для любого идеального газа передача теплоты равна выполнен-
ной работе:
Q = [2? = 6,30 брит. тепл. ед. (1,59 ккал).
Б. Повторить вычисление, принимая, что объем теплоизоли-
рован и процесс протекает адиабатно. Если истечение газа на-
столько медленно, что процесс можно рассматривать как обрати-
мый, то конечную температуру можно определить по уравнению
(1-37). Для одноатомных идеальных газов с независимой от тем-
46
псратуры Cv з брит. тепл. ед. (фунт-моль °R) |3 кал/(моль К)1
и Ср = 5 брит- 'спл. ед./(фут-моль "R) 15 кал/(люль’К)1
7	( 10 )	0,398,
где газовая постоянная Z? приблизительно равна 2 брит,
гепл. ед./(фунт-мол b°R) 12 калЦмоль °К)1,
Т8 = 0,398-535 = 213 °R (118° К).
Количество газа, остающегося в конце процесса,
/тг = (1 -1/0,73 - 213) фунт-моль.
Согласно уравнению (1-38), работа
Ц>= пАо53951о (1—0,398) = 6,21 брит. тепл. ед.(1,56 ккал).
В этом случае Q 0 и
ДЕ = —w,
пли
аг? 3-(213—535) с ni	/1 ес \
ДЕ =—0 73.21з”^“ ~—6,21 брит. тепл. ед. (—1,56 ккал).
Для идеального газа с независимыми от температуры Со =
5 брит. тепл. ед./(фунт-моль °R) 15 кал/(моль °К)1 и Ср —
7 брит. тепл. ед./(фунт-моль °Е) [7 калЦмоль ОК)1 конечная
температура и изменения энергии имели бы иные числовые зна-
чения. В этом случае конечная температура была бы
2
Г2= 535/10 7 =535/1,93 = 277 °R(154 °К).
Количество газа, остающееся в объеме в цонце процесса, было бы
т = (1 -1/0,73 277) фунт-моль
и произведенная работа составила бы
и>= п5’—9|=-(1 — 1/1,93) = 6,38 брит. тепл. ед.(1,61 ккал).
В. Повторить вычисления, принимая, что сосуд теплоизоли-
рован и процесс адиабатный, а клапан сосуда внезапно широко
открывается и давление в сосуде через гипотетическую диа-
фрагму или с помощью поршня мгновенно падает до атмосфер-
ного. В этом случае процесс необратим и конечная температура
определяется уравнением (1-47). Для идеального газа с независи-
47
мымн от температуры Со «> 3 брит. тепл. ед./(фунт моль- К)
13 кал/(моль•°К)1 и Са 5 брит, тепл. ед./(фунт-моль "R)
15 кал/(моль К)1
3 + 1
Т. "2 ТУ 1,6 ПК4П
7Г “3------0,640
2 +*
и
Ts = 535  0,640 = 342 °R (190,08 °К).
Количество газа, остающегося в сосуде,
tn = (l • 1/0,73-342) фунт-моль.
В этом случае w и —Д£ можно определить по уравнению (1-46):
w — —&Е =	(1 —0,640)= 2,31 брит. тепл. ед. (0,58 ккал).
Для идеального газа с независимыми от температуры Со =
— 5 брит. тепл. ед./(фунт-моль°R) [5 кал/(моль °К)1 и Ср =
= 7 брит. тепл. ед./(фунт-моль °R) [7 кал/(моль-°К.)] конечная
температура была бы
72_-Г + -10_2л6_
Л 5	,	3,5
и	2 +1
Т2 = 535 • 0,743 = 397 °R (217 °К).
Выпол ненная работа была бы
w — — A£ = -^^Vq 307“^ =2,37 брит. тепл. ед. (0,597 ккал).
Г. Повторить вычисления, принимая, что процесс является
не изотермическим и не адиабатным, а политропным с величиной
8, равной 1,3. В этом случае конечную температуру можно опре-
делить по уравнению (1-49):
^=(то)и-°’И7
и
Т2 = 535 0,587 = 314 °R (175,2 °К),
Ч исло молей, остающееся в сосуде, равно
tn = (1 • 1/0,73-314) фунт-моль,
а работа по уравнению (1-50)
w = п 7о h!8,7,' ? п (1 —0,587) = 6,42 брит. тепл. ед. (1,62 ккал).
48
Для идеального газа с немпнсимой от температуры С, «*
3 брит. тепл. ед./(фунт-моль “R) 13 кал/(молъ °К)1 изменение
внутренней энергии составит
ЛЕ=-^-^1у3.3i4~L- = —2,89 брит. тепл. ед. (—0,728 ккал).
И < общего баланса энергии
<2 = ДЕ 4-и>,
Q =—2,89 + 6,42s=3,53 брит. тепл. ед. (0,89 ккал).
Для идеального газа с независимой от температуры Со =
б брит. тепл. ед./(фунт-моль-°Ю 15 кал/(моль °К)1
ЛЕ = —5-~	- = — 4,81 брит. тепл. ед. (—1,21 ккал)
У, / О • «5
и
Q——4,81 + 6,42=1,61 брит. тепл. ед. (0,406 ккал).
8.	Изменение теплоемкости с температурой
Для того чтобы вычислить интегралы для ДЕ и Д//в уравне-
ниях (1-14) и (1-20), теплоемкость должна быть выражена в за-
висимости от температуры. Согласно табл. 2, теплоемкость одно-
атомного газа, например такого как гелий, аргон или неон, не
зависит от температуры и равна 3 кал/(моль • °К) при процессах
при постоянном объеме и 5 кал/(моль °К) при процессах при
постоянном давлении. Таким образом, для одноатомных идеаль-
ных газов
г2
ДЕ=Ус^Г = 3(Т2—7\)	(1-51)
Т1
и
Та
Д//= [ С1ДТ = 5(Т„—Т1).	(1-52)
Г1
Для всех других веществ теплоемкость изменяется в некоторых
пределах с температурой. Характер изменения зависит от агрегат-
ного состояния вещества и сложности молекулы. В среднем интер-
вале температур у большинства жидкостей и твердых тел, а так-
же у некоторых двухатомных идеальных газов теплоемкость воз-
растает линейно с температурой согласно соотношению
Ср = а-(-ЬТ,	(1-53)
где а и Ь могут быть определены эмпирически. В этом случае
г2
HH=^(a + bT)dT=\a+ b(r* + Tl> (Т2—7\).	(1-54)
л
4-1503
49
Средняя геплормкость может бып» определена следующим образом.
ДЯ-С^^-Л).	(1-65)
При линейном изменении Ср с температурой
С а I Мг» + Л)
^1>т	“ "Г 2
(1-56)
и является такой же, как и истинная теплоемкость при средней
температуре или среднее арифметическое от истинной теплоемкости
для двух температурных пределов Т\ и Тг. Для идеальных газов
Cv—Cp—R
и
Cm = Cpm-R.	(1-57)
Для более сложных газов теплоемкость не может быть выраже-
на линейной функцией от температуры. Наиболее удобным эмпи-
рическим соотношением является простой степенной ряд
(?p = «W + cF-	(1-58)
На практике обычно ограничиваются тремя членами этого ряда.
В этом случае
г2
ДЯ - J (а + ЬТ + сТ8) dT = Jo + А (Т2 + Л) +
п
+4(7’1 + 7’2T1 + 7D](T2-7’j)	(1-59)
и Срт между температурами Г, и Тй определяют следующим об-
разом:
Срт = а + А (Т2 + 7\) + 4 (Т| + Т87\ + Т>).	(1 -60)
Данные по теплоемкости ряда газов представлены в прило-
жении 1 для достаточно низких давлений, так что газы могут рас-
сматриваться как идеальные. Эмпирические постоянные для урав-
нения теплоемкости в форме уравнения (1-58) приведены в при-
ложении 2. Эти постоянные согласуются с данными теплоемкости
приложения 1 для температурного интервала 300—1500 °К с
указанным максимальным отклонением.
Значения средних мольных теплоемкостей газов представлены
в приложении 3 для стандартной температуры 298 °К (25 °C), т. е.
величины, приведенные в приложении 3 для температур Т °К,
означают среднюю величину теплоемкости между 298 °К и темпе-
ратурой Т °К- Произведение средней теплоемкости на разность
температур (t —25) °C дает изменение энтальпии между 25 °C
и темпепатурой ГС в кал!(моль °К)-
50
Средние теплоемкости в приложении 3 могут быть исполню*
пипы для вычислении в две стадии изменения штчльпнн между
1Вумя температурами tt и t;
(кН от /, до = от 25 до fB)-*(A// от 25 до tt),
где
(АЯ от 25 до t2)^(Cpm между 25 и t3)(t2—25)
и
(АЯ от 25 до t1) = (Cpm между 25 и	—25).
Пример 3. Вычислить количество перенесенной теплоты,
выполненную работу, А£ и АЯ при нагревании 1 моль гелия от
Г)(Ю до 1000 °C при постоянном объеме и постоянном давлении.
Принять, что газ ведет себя как идеальный во всем интервале
температур и давлений.
Постоянный объем
В процессе при постоянном объеме не происходит никаких
перемещений и работа равна нулю. Перенесенная теплота в этом
случае равна .изменению внутренней энергии
Q^bE^CjlT.
Теплоемкость при постоянном объеме гелия не зависит от
юмпературы и равна 3 кал/(моль °К).
Q = ЛЕ = 3(1 000—500) = 1500 кал/моль.
Для процесса при постоянном объеме
АЯ = А£ 4- f Ар.
Для идеального газа при постоянном объеме
уАр=/?АТ,
АЯ = 3 (1000—500) + 1,987-(1000—500) = 2494 кал/моль.
Постоянное давление
В процессе при постоянном давлении выполненная работа рав-
на pAv. Для идеального газа при постоянном давлении
рАо = £АТ = 1,987 (1000 — 500) = 994 кал/моль.
Из баланса энергии и определения энтальпии для процесвов
при постоянном давлении
Q = АД + рДо = АЯ = \cpdT.
4*
51
Теплоемкость при постоянном дянленнп гелия нс чивисиг от
температуры и равна
3-4-1,987 4,98) калЦмоль “К),
Q ДЯ-4,987(1000—500)->2494 кал/моль,
АЕ —। ДЯ—рДо - 2494—994 —> 1500 кал/моль
Пример 4. Вычислить перенесенную теплоту, выполнен-
ную работу, ДЕ и ДЯ при нагревании 1 моль двуокиси углерода
от 500 до 1000 °C при постоянном объеме и постоянном давлении.
Принять, что газ ведет себя как идеальный во всей области тем-
ператур и давлений.
Постоянный объем
В процессах при постоянном объеме выполненная работа рав-
на нулю. Перенесенная теплота в таком случае равна изменению
внутренней энергии
Q = AE —
Так как данные по теплоемкости для двуокиси углерода в
отношении Ср точнее, чем в отношении Со, то удобнее сначала
вычислить ДЯ. Согласно уравнению (1-18),
ДЯ = ^7
для идеального газа в процессе при постоянном объеме. Измене-
ние энтальпии может быть вычислено с помощью эмпирических
постоянных приложения 2 или значений средней теплоемкости
для температур между 298 °К (25 °C) и Т °К в приложении 3.
Среднюю теплоемкость между 500 и 1000 °C можно вычислить
подставляя эмпирические постоянные для двуокиси углерода в
уравнение (1-60):
Срт=6,214+ 10,396-IO"3 (1237 + 573)/2—3,545 1(Гв (1237г +
4-1237 5734-5732)/3;
Срт=6,214 + 9,60—3,18= 12,94 калЦмоль  °К);
АН — 12,64 (1000—500) = 6320 кал/моль.
Используем среднюю теплоемкость между 25 °C и температурой t\
АН между 25 и 1000°С= 11,92 (1000—25)= 11,620 кал/моль,
АН между 25 и 500 °C = 10,77 (500—25) = 5,ПО кал/моль,
АН между 1000 и 500 °C = 6,510 кал/моль.
Приняв последнюю величину для ДЯ, имеем
Q = ДЕ = ДЯ — vAp = ДЯ—RAT = 6510 — 1,987 ( 1000—500) =
= 5516 кал/моль.
52
Пости.чиш* дабленш
При постоянном дивлспин
&у»рДц-/?ДТ 1,987-(WOO—500) 994 кал/молы,
Qx=AE-\-pAv*=AH =6510 кал/моль-,
АЕ — АН—pAv АН RAT 6510 —994 5516 кал/моль.
9.	Изменение энергии в однофазной системе
постоянного состава при стационарном процессе
Изотермические обратимые процессы, в которых изменения
кинетической и потенциальной энергии незначительны
Для процессов, в которых изменения кинетической и потен-
циальной энергии незначительны, уравнение (1-7) принимает вид
Q = tjysДД-|- Д (pv).	(1-61)
Для изотермических процессов, включающих несжимаемую жид-
кость или идеальные газы,
ДЕ = 0	(1-62)
и уравнение (1-61) становится следующим:
Q = ws + A(pv).
(1-63)
Для несжимаемых жидкостей обратимая механическая работа
может быть вычислена согласно уравнению (1-13):
ws = —§vdp = —vAp.	(1-64)
Кроме того,
A(pv) = vAp.	(1-65)
С помощью уравнений (1-64) и (1-65) уравнение (1-63) принимает
вид
<2^0.	(1-66)
Таким образом, обратимые изотермические стационарные про-
цессы, в которых изменения кинетической и потенциальной энер-
гии незначительны, являются также адиабатными для несжимае-
мых жидкостей.
Если среда — идеальный газ, A(pv) = 0 для изотермических
процессов, то уравнение (1-63) можно записать так:
Q=ws= -§vdp = -RT^- = RT ln-g-.
pi
(1-67)
53
Слодошгголыю, вСЯ энергия, введенная n нидс механической
работы в изотермический стационарный процесс с идеальным га-
юм, в конечном счете удаляется ил системы в форме теплоты
Выражение для обратимой механической работы идентично урав-
нению (1 27) для общей обратимой работы при изотермическом
расширении идеального газа в закрытой системе.
Адиабатные и обратимые процессы, в которых изменения
кинетической и потенциальной энергии незначительны
Для адиабатных процессов, в которых изменения кинети-
ческой и потенциальной энергии незначительны, уравнение (1-9)
принимает вид
ws=—ЬН — — ДЕ—Д(ро).	(1-68)
Для несжимаемых жидкостей
ws——v\p (обратимый процесс),	(1-69)
ДЕ = Ус^Т,	(1-70)
Д(ру) —пДр.	(1-71)
Подстановкой этих выражений в уравнение (1-68) получим
(1-72)
Таким образом, процесс является изотермическим. Этот ре-
зультат согласуется с заключением, вытекающим из уравнения
(1-60), о том, что обратимые изотермические стационарные про-
цессы для несжимаемых жидкостей также адиабатны.
Применяя уравнения (1-68) к идеальным газовым системам,
имеем
tos= - fCpdT.	(1-73)
Так как условия устанавливают чаще в отношении давления,
чем в отношении температуры, то необходима функциональная
зависимость для изменения температур от изменения давления.
Уравнение (1-73) для обратимого бесконечно малого изменения
примет вид
vdp = Cpd7\
Для одного моля идеального газа
(1-74)
Считая, что Ср не зависит от температуры, уравнение (1-74) можно
проинтегрировать, в результате чего
in-p-.	(1-75)
CD Pl 1 1
54
Уравнение (1-76) может быть решено дли отношения гемпернгур
в функции отношения давлений:
(1-76)
Это уравнение тождественно уравнению (1-37) для обратимых
адиабатных процессов в идеальных газовых закрытых системах.
При условии, что теплоемкость не зависит от температуры,
уравнение (1-68) может быть записано так:
w,-CeT,[	(1-77)
Используя уравнения (1-39), (1-40) и (1-41), уравнение (1-77)
может быть выражено в следующем виде:
k-i	fc-i
w - Г 1—k = !P1M 1 — ( P~V . (1-78)
s (k — 1) I \ Pi / J л —![ \Pi/ '
i де	—объемная скорость потока для одного моля идеального
газа.
Если система не производит и не поглощает работу, урав-
нение (1-68) принимает вид
ЛЯ = 0.	(1-79)
В этом случае адиабатный стационарный процесс с идеальным га-
зом, в котором изменения кинетической и потенциальной энергии
ничтожны, является также изотермическим. Для реальной жид-
кости возможны изменения температуры, так как энтальпия —
функция и температуры и давления.
Изменения кинетической и потенциальной энергии
Для процессов, которые не являются ни адиабатными, ни изо-
термическими, уравнение Бернулли в виде уравнения (1-12),
вероятно, наиболее удобно для вычисления механической энергии.
При отсутствии какой-либо выполненной или поглощенной работы
ws равно нулю и уравнение (1-12) принимает вид
(1-80)
Для горизонтальных процессов без трения уравнение (1-80) ста-
новится следующим:
Р	. / /;2 \	~ .
(1-81)
Оно выражает соотношение между изменением в системе давления
и изменением линейной скорости течения жидкости (флюида).
55
Для несжимаемых жидкостей уравнении (1-81) может быть пы
ряжено кпк
*(*-₽,)'	(Ь82)
Уравнение (1-82) находит практическое применение для опре-
деления линейной скорости течения на основании измерения
давления в двух различных сечениях потока. Так как объемная
скорость течения несжимаемых жидкостей должна быть одинакова
в двух поперечных сечениях
то
(1-83)
Выражение для линейной скорости во втором поперечном се-
чении можно получить из уравнения (1-82) с помощью уравнения
(1-83):
На практике в уравнение (1-84) вводят эмпирический коэф-
фициент для учета рассеяния энергии вследствие трения и дру-
гих необратимых процессов. Уравнение (1-84) также находит
применение для сжимаемых жидкостей, когда изменение давления
достаточно мало по сравнению с абсолютным давлением. В таких
случаях изменение удельного объема среды незначительно.
В процессах, при которых выполняется или поглощается ра-
бота, механическая работа может быть задана каким-либо спо-
собом или она становится неизвестной величиной, определяемой
по уравнению (1-12). Если механическая работа неизвестна, зна-
чения кинетической и потенциальной энергии должны быть вы-
числены каждое в отдельности.
Для большинства технических применений в земных условиях
отношение местного ускорения силы тяжести к постоянной пере-
вода размерности gc должно быть взято равным единице. Кроме
того, чтобы изменение потенциальной энергии было более
1 брит. тепл. ед./фунт-моль (0,55кал/моль), необходимо изменение
в высоте более 778 футов (237 м), так что обычно изменение вели-
чины потенциальной энергии сравнительно невелико в про-
цессах, сопровождающихся значительным количеством перене-
сенной теплоты или большим температурным изменением. При
тех же самых условиях величина кинетической энергии также
часто незначительна, поскольку необходимо изменение в линей-
ной скорости от нуля до 100 фут/сек (30,5 м!сек), чтобы обусловить
изменение кинетической энергии приблизительно на 0,2 брит,
тепл. ед./фунт-моль (0,11 кал!моль).
56
Пример 5. Определить затраченную работу и перепое
теплоты в окружающее пространство при обратимом иютермн-
ческом сжатии I фуит-моль/мии (454 моль/мин) среды (флюида)
от 1 до 10 атм в условных стационарного процесса, принимая,
что изменения кинетической и потенциальной энергии незначи-
тельны.
А. Припять, что среда — жидкая вода при 60 °F (289 °К).
Б. Принять, что среда — пар в состоянии идеального газа
при 1000 °R (555,5 °К).
Решение
А. Работа, необходимая, чтобы накачать 18 фунтов (8200 г)
жидкой воды удельным объемом 0,016 фут3/фунт (1 см*/г) от 1 до
10 атм в изотермическом стационарном процессе может быть
вычислена по уравнению (1-64):
ws= —18-0,016(10 — 1)-14,7-144 =
= —5500 фут(фунт-сила)/мин =—0,167 л. с.
Численная величина отрицательна, так как работа произведена
над системой.
Согласно уравнению (1-66), обратимый процесс является так-
же адиабатным, и поэтому теплота в окружающее пространство
не переходит.
Б. Работа, требуемая для сжатия той же массы среды в виде
пара в состоянии идеального газа при 1000 °R (555,5 °К) в изо-
термическом обратимом стационарном процессе, может быть
вычислена по уравнению (1-67):
ws=—1,987-1000-In 10=—4570 брит. тепл.
ед./мин(—1150 ккал/мин)——4570-778/33000=—108 л. с.
Согласно уравнению (1-67), эта же величина является также
скоростью переноса теплоты в окружающее пространство.
Большая разница в величинах работы, вычисленной в приме-
рах А и Б, показывает огромное преимущество в перекачке сред
в жидкой фазе по сравнению с паровой фазой.
Пример 6. Определить необходимую работу и темпера-
турные изменения при обратимом адиабатном сжатии 1 фунт-
моль/мин (454 моль!мин) среды от 1 до 10 атм в условиях стацио-
нарного процесса, принимая, что изменения кинетической и по-
тенциальной энергии незначительны.
А. Принять, что среда — жидкая вода с начальной температу-
рой 60 °F (289 °К).
Б. Принять, что среда — пар в состоянии идеального газа с
начальной температурой 700 °R (115,6°К) и с независимой от
температуры теплоемкостью при постоянном давлении 8,5 брит,
тепл. ед./(фунт-моль-°R) [0,5 кал/(моль
57
Решены
А. Согласно уравнению (1-69), работа, Требуемая для панк
танин 18 фу и гоп (8200 <•) жидкой воды с начальной температурой
60 °F (289 *'К) от 1 до 10 атм при адиабатном обратимо протека
ющем процессе, при условии, когда изменения кинетической и
потенциальной энергии незначительны, равна
ш,«=- 18.0,016.(10 —1)14,7-144 =
= - 5500 фут (фунт-сила)/мин =—0,167 л. с.
По уравнению (1-72) процесс является также изотермическим,
поэтому температура не изменяется.
Б. Работа, требуемая для сжатия 1 фунт-моля (454 моля) па-
ра, взятого при температуре 700 °R (115,6 °К) от 1 до 10 атм
при обратимом адиабатном стационарном процессе, выражается
уравнением (1-77). Изменение температуры определяется по
уравнению (1-76):
2
£ = (4^=1,718.
Конечная температура
7\ = 1,718-700= 1200 °R (393,4 ° К),
а выполненная работа
u>s =—8,5-700-(1 —1,718)=—4260 брит. тепл.
ед./мин =—4260-778/33,000 — —101 л. с.
Пример 7. Определить минимальную работу, требуемую
для перекачки 100 гал/мин (378,5 л/мин) при 60 °F (289 °К) не-
сжимаемой среды из железнодорожной цистерны в бак, располо-
женный выше цистерны. Принять, что разность уровней между
входным и выходным отверстием составляет 30 футов (9,144 лг).
Принять также, что линейная скорость среды и общее давление
систем одинаковы для этих двух отверстий.
Для стационарных условий уравнение (1-12) имеет вид
—&z['g )=—^0 ФУТ (ФУнт-сила)/ФУнт'масса (—8,97 Мн/кг).
Если среда — газолин плотностью 6,25 (фунт-масса)/гал
(0,75 г/см3), то массовая скорость потока должна быть равной
625 (фунт-масса)/мин (284 кг/мин), а минимальная требуемая
работа
ws——30-625= — 18,750 фут (фунт-масса)/мин=—0,57 л. с.
чтобы обеспечить возрастание потенциальной энергии.
58
Если бы средой была сериал кислота плотностью 16,3 (фунт-
масса)/гал (1,84 е/с.м8), то массовая скорость течения равнялась
бы 1530 (фунт-масса)/мни (69Б ке!мин), а минимальная работа
ws— —30 1530»= —45,900 фут(фунт-сила)/мии => — 1,39 л. с.,
чтобы обеспечить возрастание потенциальной энергии.
10.	Изменение энергии при фазовом превращении
Тремя различными фазами или агрегатными состояниями ве-
щества считаются твердое, жидкое и газообразное. Конкретная
фаза, в которой данная масса вещества действительно существует,
определяется общим количеством энергии, которым обладает си-
стема. Для данной массы вещества твердая фаза содержит мини-
мальное количество внутренней энергии, а газовая фаза — мак-
симальное; внутренняя энергия жидкой фазы занимает промежу-
точное место между энергиями твердой и газовой фаз.
В твердой фазе внутренняя энергия почти полностью состоит
из колебательной энергии атомных частиц и потенциальной энер-
гии, обусловленной силами притяжения между частицами. Потен-
циальная энергия относительно невелика, и межатомные расстоя-
ния малы. В этих условиях силы притяжения так велики, что
частицы находятся в жесткой структуре, а кинетические энергии
перемещения и вращения практически отсутствуют.
Добавление энергии при температуре и давлении, соответ-
ствующих плавлению, приводит к увеличению потенциальной энер-
гии и межатомных расстояний до такой степени, что жесткая
структура нарушается, и твердая фаза переходит в жидкую. Уве-
шчение расстояния между частицами позволяет им приобрести
некоторое количество поступательной и вращательной энергии.
Общая энергия на единицу массы, поглощенная при переходе из
твердой фазы в жидкую, называется «скрытой теплотой плавле-
ния». Так как поступательное и вращательное движение частиц в
жидкой фазе при точке замерзания сильно затруднено, то эта
фаза почти подобна твердой фазе при тех же температуре и дав-
юнии. Однако частицы жидкой фазы при температуре кипения
больше удалены друг от друга и имеют большую свободу в по-
ступательном и вращательном движении.
Добавление энергии при температуре кипения и соответствую-
щем давлении настолько увеличивает потенциальную энергию,
что позволяет частицам отойти друг от друга на относительно
большие расстояния, и вещество из жидкого состояния переходит
в газовую фазу. В газовой фазе силы притяжения между части-
цами слабы, и частицы получают свободу независимого переме-
щения и вращения. Общая энергия на единицу массы вещества,
поглощенная при переходе из жидкой фазы в газовую, называется
«скрытой теплотой испарения».
59
Скрытия теплота фа юного превращения сообщается при усло-
виях постоянства давления и мджет быть вычислена как измене
нис энтальпии. Для большою числа веществ изменение энтальпии
фазового превращения может быть определено эмпирически при
температуре превращения и атмосферном давлении. Так как жид-
кости и твердые тела почти несжимаемы, на скрытую теплоту и
температуру плавления давление влияет очень мало. Однако па-
ровая фаза может подвергаться сильному сжатию, и на скрытую
теплоту и температуру испарения давление влияет весьма сущест-
венно.
Вообще температура кипения возрастает с увеличением дав-
ления. Поскольку температура кипения и давление возрастают,
то плотность пара увеличивается, а плотность жидкой фазы умень-
шается до тех пор, пока при определенных температуре и давлении
плотность и другие свойства этих двух фаз не станут идентичными.
Эти значения температуры и давления определяют критическую
точку. По мере приближения к критической точке свойства двух
фаз становятся более близкими и энергия, требуемая для превра-
щения вещества из одной фазы в другую, уменьшается. В крити-
ческой точке скрытая теплота парообразования становится равной
нулю. При температуре выше критической невозможно получить
более одной фазы при любом давлении.
Скрытая теплота парообразования для температур и давлений,
отличающихся от нормальной точки кипения и 1 атм, может
быть установлена методом, разработанным в примере 5. В этом
примере принято, что паровая фаза ведет себя как идеальный газ,
так что метод пригоден только для давления ниже 2 атм. Сущест-
вуют также полуэмпирические методы оценки скрытой теплоты
испарения.
«Пример 8. Скрытая теплота парообразования воды равна
970,2 брит. тепл, ед/фунт (539 кал1г) при 212 °F (373,2 °К) и 1 атм.
Определить скрытую теплоту при 80 °F (300 °К) и 0,00136 атм,
допуская, что жидкость несжимаема и пар ведет себя как идеаль-
ный газ.
Так как разность энтальпии для двух состояний не зависит
от пути перехода от одного к другому, то переход из начального
состояния в конечное можно представить как ряд стадий, для
каждой из которых изменение энтальпии может быть вычислено.
Сумма отдельных изменений энтальпий равна общей разности
энтальпии для начального и конечного состояний.
Удобный способ вычисления скрытой теплоты испарения воды
при 80 °F (300 °К) показан на рис. 2. Этот способ должен обяза-
тельно включать стадию испарения при 212 °F (373,2 °К) и 2 атм,
для которой известно изменение энтальпии. Начиная с жидкой
воды при 80 °F (300 °К) и 0,00136 атм, температура и давление
должны изменяться до 212 °F (373,2 °К) и 1 атм в две стадии.
В первой стадии давление увеличивается с 0,00136 до 1 атм
при постоянной температуре 80 °F (300 °К). Предполагается, что
60
объем остается постоянным, изменение внутренней wiepi ин ранни
нулю, а изменение энтальпии вычисляется кик гЛр, где и — объем
1 фунта (464 е) воды при 80 °F (300 "К) Для первой стадии
ЛЯ,- 1/62,4 (1—0,00136)-14,7-144/778 =
= 0,043 брит. тепл, ед/фунт (0,0239 кал!г).
Во второй стадии вода нагревается от 80 °F (300 °К) до 212 “F
(373 °К) при постоянном давлении 1 атм. Так как теплоемкость
Рис. 2. Изменение энтальпии при испарении
воды практически равна 1 брит. тепл. ед/(фунт °F) (1 кал1г) во
всем температурном интервале, то
Д/72= 1,00-(212—80)= 132 брит. тепл. ед/фунт(73,2 кал1г).
В третьей стадии вода переходит из жидкого состояния при
212 °F (373,2 °К) и 1 атм в пар также при 212 °F (373,2 °К)
и 1 атм, причем изменение энтальпии известно:
ДЯ8 = 970,2 брит. тепл. ед/фунт(539 кал/г).
В четвертой стадии пар расширяется изотермически от 1
до 0,00136 атм при постоянной температуре 212 °F (373,2 °К).
Если пар ведет себя как идеальный газ, изменение энтальпии
при этом равно нулю:
ДЯ4=0.
•1
В пятой стадии пар охлаждается от 212 °F (373,2 “К) до
80 eF (300 иК) при постоянном давлении 0 00136 атм. Средняя
теплоемкость пара во всем температурном интервале составляет
около 8,08 брит. тепл, ед/фунт-моль (4,6 кал/моль). Тогда измене-
ние энтальпии для пятой стадии
А//в= (8,08/18)(80—212) »
—59,2 брит. тепл. ед/фунт(—32,9 кал/г).
Сумма отдельных изменений энтальпий равна 1043 брит. тепл,
ед/фунт (579 кал 1г), что приблизительно равно скрытой теплоте
испарения воды при 80 °F (300 °К) и 0,00136 атм. Так как изме-
нение энтальпии на первой стадии всегда незначительно, то в
пределах сделанных выше допущений увеличение скрытой теп-
лоты определяется разностью между средними теплоемкостями
жидкости и пара, умноженной на изменение’температуры:
\ ~ \ 4“ [Срт (ж) Срт (пар)] (Т.2 7\).
11.	Изменение энергии при химических реакциях
Изменение энтальпии в результате химической реакции ре-
агентов в их естественном состоянии при 25 °C и 1 атм до про-
дуктов также в их естественном состоянии при 25 °C и 1 атм
называется «стандартной теплотой реакции» при 25 °C. Хотя
стандартные теплоты реакции для всех возможных реакций не
приводятся, изменение энергии при реакции может быть вычисле-
но, если стандартная теплота образования или стандартная теплота
сгорания известна для каждого отдельного исходного вещества
и продукта реакции.
Стандартная теплота образования — это изменение энталь-
пии при образовании соединения при 25 °C и 1 атм из его элемен-
тов в свободном виде в их естественном состоянии при 25 °C и
1 атм. Стандартная теплота сгорания — это изменение энтадьпии
при реакции данного вещества с элементарным кислородом, взя-
тыми каждый при 25 °C и 1 атм при условии образования опреде-
ленных продуктов при тех же температуре и давлении. Продукты
сгорания определяются элементами, составляющими исходное
соединение. Углерод окисляется до двуокиси углерода, водород —
до воды (жидкой), азот не окисляется, но образует газообразный
азот, и сера обычно окисляется до двуокиси серы.
Теплота данной реакции может быть определена с помощью
ряда таких реакций образования и сгорания, которые в сумме
составили бы изучаемую реакцию. Сумма изменений энтальпии
индивидуальных реакций будет тогда изменением стандартной
энтальпии данной реакции. Если величины теплот образования-
известны для всех рассматриваемых соединений, то стандартная-
теплота реакции может быть получена вычитанием суммы теплот
62
образования исходных веществ из суммы теплот образовании ко-
нечных продуктов реакции. Если теплоты сгорания нлиестпы для
всех рассматриваемых соединений, стандартная теплом реакции
может быть получена вычитан нем суммы теплот сгорания конеч-
ных продуктов из суммы теплот сгорания исходных веществ.
Обычно теплоты образования известны для неорганических соеди-
нений, а теплоты сгорания — для органических.
Если начальное и конечное условия отличаются от 25 °C и
1 атм, изменение энтальпии может быть вычислено с помощью
нескольких стадий, выбранных так, чтобы можно было определить
изменение энтальпии для каждой отдельной стадии. Так как речь
идет о химической реакции, то одна из этих стадий должна вклю-
чать все расчеты для реакции от начальных до конечных продук-
тов, взятых каждый при 25 °C и 1 атм, поскольку это является
Рис. 3. Изменение энтальпии при химической реакции
условием, при котором обычно определяют изменение энергии
при реакции. Например, если исходное вещество А при начальной
температуре ТА и давлении /?А и исходное вещество В, взятое
при температуре Тв и давлении рв, образует смесь конечных про-
дуктов 7? и S при температуре Тр и давлении рр, изменение энталь-
пии можно определить по схеме, приведенной на рис. 3.
Эти расчеты можно иллюстрировать следующими примерами.
Пример 9. Определить стандартную теплоту реакции,
протекающей при 25 °C, исходя из данных теплот образования,
приведенных в приложении 4:
SO2 (г) + Vs о2 (Г) 4- Н2о (ж) = H2SO4 (ж).
Реакция образования		A/7f, ккал] моль
SO2(r)-	-^S + O2 (г)	4-70,960
Н2О (ж) —	->Н2 (г)-р/2О2 (г)	4-68,317
Н2 (г) + S + 2Оа (г)-> Н25О4(ж)_________—193,910
SO2 (г) + %О2(г) + Н2О (ж) — Н25О4(ж)	- 54,633
63
Таким образом, в результата реакции получении 100%-ной
H,SO« из SOs,Oe и поды при 25°C выделяется 54,633 ккал теплоты
па каждый моль полученной кислоты. Если эта кислота раство-
ряется в воде с образованием водного раствора, то выделяется
дополнительно 22,990 ккал теплоты.
АН, ккал!моль
H2SO4(w) + х НДж) —* HjSO^ (води. р-р) — 22,990
Стандартная теплота реакции равна теплоте образования ко-
нечного продукта минус сумма теплот образования исходных ве-
ществ.
Пример 10. Определить стандартную теплоту следующей
реакции при 25 °C по данным теплот сгорания:
С2Н4(г) + Н2О(ж) —> СаН5ОН(ж).
Реакция сгорания	А/4е, ккал/моль
С2Н4(г) 4- ЗО2(г)-* 2СОа (г) + 2Н2О(ж)	— 337,234
2СО2(г) + ЗН2О(ж) > С2Н5ОН(ж) + ЗО2(г) + 326,700
С2Н4(г) + На0(ж) —> С2Н5ОН(ж)
— 10,534
При получении этилового спирта из этилена и воды при 25 °C
выделяется 10,534 ккал теплоты на моль спирта. Стандартная тепло-
та реакции в этом случае равна теплоте сгорания вещества (эти-
лена) минус теплота сгорания продукта (этилового спирта). Роль
воды как реагента в этом расчете включена в данные по теплотам
реакции сгорания. Результат расчета получается как небольшая
разность между двумя относительно большими числами. Малый
процент ошибки в данных теплот сгорания дает большой процент
ошибки в вычислении теплоты реакции.
Пример 11. Определить стандартную теплоту следующей
реакции при 25 СС, используя теплоты образования и теплоты
сгорания:
СаС2(гп) 4- 2Н2О(ж)--> С2Н2(г) 4- Са(ОН)2.
Реакция сгорания, и образования	АН, ккал/моль
СаС2----Са 4- С2	4-15,000
2СО2(г) 4- Н20(ж) —* С2Н2(г) 4- 5/2О2	4- 310,620
Са 4- О2 4- Н2-> Са(ОН)2	— 235,800
2С4-2О2----»2СО2(г)	—188,104
Н2О(ж)----->Н24-1/2О2	+ 68,317
СаС2 + 2На0(ж)
С2Н2(г) 4- Са(ОН)2
—29,967
64
При получении гязообрилил<> iiuciплена нщролизом кйрбида
кальция при 25 °C выделяется 29,967 ккал теплоты на моль ацетиле-
на. Поскольку в одном и том же расчете используются и теплоты
образования, и теплоты сгорания, то нельзя сделать общих вы-
водов. Заметим в этом случае, что теплота образования двух мо-
лей двуокиси углерода входит в расчет, несмотря на то что дву-
окись углерода не участвует в рассмотренной выше реакции.
Пример 12. Котел, топящийся метаном, температура ко-
торого равна 20 °C и давление 1 атм при 20%-ном избытке воз-
духа с температурой 30 °C и давлением 1 атм, дает продукты
сгорания при 300 °C и 1 атм. Питающую воду первоначально при
25 °C и 1 атм перекачивают через экономайзер, чтобы повысить
ее температуру перед поступлением в бойлер. Учитывая полное
сгорание (без окиси углерода) и не учитывая потерь теплоты в
окружающее пространство, определить количество пара в фун-
тах при 350 °C и 10 атм, образующееся на каждые 1000 фут3
(28317 л) метана.
Баланс энергии для этого стационарного процесса представ-
лен уравнением (1-9). Пренебрегая изменениями потенциальной
И кинетической энергии, можно представить баланс энергии урав-
нением
Q=ws-\-&H - 0.
Численные вычисления проводятся в расчете на использова-
ние 1 моля метана и образование s граммов пара, полученных
из s граммов питательной воды. Если считать питательную воду
несжимаемой, то механическая работа, требуемая для перекачки
ноды в систему, выражается так:
tt>s= — vAp=— s 1 (5—1)55^1= — 0,1 s кал.
Перед вычислением изменения энтальпии необходимо опреде-
лить количество воздуха и газообразных продуктов сгорания.
Для полного окисления одного моля метана требуется минимум
дни моля кислорода. Получается один моль двуокиси углерода
и дна моля водяного пара. 20%-ный избыток кислорода означает,
то введено 1,2 2 — 2,4 моля кислорода и 0,4 моля остается в
общем объеме газообразных продуктов. Так как кислород получен
in атмосферы, то (79/21) 2,4 — 9,03 моля азота также входят в
»нстему в потоке воздуха и покидают ее с газообразными продук-
1пми сгорания. Эти величины суммированы следующим образом.
Мтериальный баланс:
СН4 + 2О2---* СО8 4- 2НгО,
Вошло в систему, моли		Покинуло систему, моли	
сн4	1,0	СО2	1,0
о2	2,4	о2	0,4
N2	9,03	N2 Н2О	9,03 2,0
•• 1603
65
Мещпп
{моль
20’С, 1атм
КшЛОррд
2,0 ноль
!0°С,1отн
МвШ
< нт '*» I моль
iS'C.luniN
/ iMMb
/28"С,1отм
к Bq fa
' 2 моль
25°С,1атм
щдщд
44 ноль
26 °C,I атм
COi
- 1моль
М"С,1аюм
-О*- 2 моль 2 ноль
loot, 1атм	300 °C,I атм
Кислород
..... $	04 моль
300°Ц1атн
Азот
9,03 моль
30°С,1атн
Азот	д Азот.
9,03 моль —---------------— 3,03 моль
25‘С,1атм	300°с,1итм
Вода	Оа£_	№
-77 ____®_77 З,г -%— S.S
$,1шт т^1атм 360°С,1атм	350°С,10атм
Рис. 4- Изменение энтальпии при окислении 1 моля метана
Изменение энтальпии может быть вычислено по схеме, приве-
денной на рис. 4. Изменения отдельных энтальпий вычислены
ниже, кал:
AH,= 1-8,50-5 = +43;
ДНг = 2,4 7,03 (25—30) =—84;
Д/73 = 9,ОЗ-6,97-(25—30) = —315;
ДЯ4 = ДЯе при 25 °С= —212798;
ЛЯ5 = 1 10,11 • (300 —25) = + 2780;
Д//в = 2 [18-1 (100—25)4-9,717] = +22 134;
ДТ/7 = 2  8,28 • (300—25)—8,09 (100—25) = + 3340;
Д/7а = 0,4-7,29-(300—25) = +802;
ДНв = 9,03-7,04 (300—25)= + 17 500;
Atflo = s-l-(100—25) + 9717/18= +615s;
AHu = (s/18)-8,36-(350—25)—8,09 (100—25)= + 117 s;
ДЯ12 = (изотермическое сжатие, идеальный газ) = 0;
AH+&ys= —166 660 +732 s—0,1 s = 0;
Для s баланс энергии равен
s= 166,660/731,9 = 227 г пара/моль метана.
Число молей метана в 1000 фут3 (28317 л) метана при 20 °C и
1 атм может быть получено по закону идеального газа:
—^'60 фунт-моль/1000 фут3 (1180 моль/28317 л)-,
О ft о * 1 )О' Z/Уо
227 -2,6 = 590 фунтов (265 кг) пара при 350 °C и 10 атм на
1000 фут3 (28317 л) метана при 20 °C и 1 атм.
66
Задачи
1.	Определить количество пгргдвнноП теплоты иуполпеипой работы, ил-
меиепне виутргпней энергии и изменение энтальпии при сжатии 1 моля идеал».*
кого газа от динления 1 атм при следующих условиях:
а)	изотермическое сжатие при постоянном внешнем давлении 10 атм
и температуре 600 “R (4,6 °C);
б)	изотермическое обр тимое сжатие при 500 °R (4,5 °C);
в)	адиабатное сжатие при постоянном внешнем давлении 10 атм и перво*
начальной температуре 500 °R (4,5 °C).
Считать, что в качестве газа взят гелий;
г)	адиабатное обратимое сжатие при начальной температуре 500 °R
(4,5 °C) Предположить, что газ — гелии;
д)	повторить пункты «в» и «г», пр|дполагая, что газ идеальный с Ср= 7
брит. тепл. ед./(фунт-моль•°R) (7 кал/моль), не зависящей от температуры.
2.	Повторить задачу 1 для 1 моля жидкой воды. Предположить, что плот
ность ие зависит от температуры и давления.
3.	При изотермическом сжатии 1 моля гелия, первоначально взятого при
500 °R (4,5 °C) и 1 атм, 2000 брит, тепл ед (504 ккал) теплоты переходит в
окружающую среду. Определить конечное давление, если:
а)	сжатие осуществляется при постоянном внешнем давлении 10 атм;
б)	сжатие производится обратимо.
4)	При адиабатном сжатии 1 моля гелия, первоначально взятого при
500 °R (4,5 °C) и 1 атм, температура газа повышается до 750 °R (144 °C)
Определить конечное давление, если:
а)	сжатие осуществляется при постоянном внешнем давлении 10 атм;
б)	сжатие производится обратимо.
5.	Определить скорость переноса теплоты и минимальную мощность
(л. с.), необходимые для сжатия 1 моль!мин идеального газа при первоначаль-
ных температуре 500 °R (4,5 °C) и давлении 1—10 атм при следующих усло-
виях, пренебрегая изменением кинетической и потенциальной энергии (ста-
ционарный процесс):
а)	изотермическое сжатие гелия;
б)	адиабатное сжатие гелия;
в)	повторить пункты «а» и «б» для азота, считая его идеальным газом с
теплоемкостью при постоянном давлении Ср = 7 брит. тепл. ед./(фунт-моль-°R)
\7 кал (жоль-°К)1, не зависящей от температуры.
6.	Повторить задачу 3 для 1 моль!мин жидкой воды. Предположить, что
плотность не зависит от температуры и давления.
7.	Стационарный компрессор используется для сжатия 1 моль!мин гелия
от 1 до 10 атм. За компрессором следует холодильник, который отводит теплоту
сжатия Газ поступает в компрессор при температуре 500 °К (4,5 °C) и выходит
из холодильника при температуре 550 °R (32,3 °C) Предположить, что компрес-
сор работает в адиабатных условиях и обратимо. Пренебрегая изменениями
кинетической и потенциальной энергии, определить скорость отвода теплоты
от холодильника.
8.	Идеальный газ проходит со скоростью 1 моль/мин через вентиль, пони-
жающий давление, в изолированный трубопровод, причем давление в этом тру-
бопроводе снижается от 100 до 15 фунт/дюйм2 (от 7,03 до 1,05 кН см2). Если
температура в начале потока 30 °C, определить температуру в конце потока по
понижению давления. Считать, что изменения кинетической и потенциальной
энергии незначительны, а теплоемкость 7 брит, тепл ед (7 кал) не зависит от
температуры.
9.	Садовый шланг, несущий воду с избыточным давлением 10 фунтов на
дюйм2 (0,703 кГ/см2), дает небольшую течь. Не учитывая все потери на трение,
определить максимальную высоту струи и максимальную вертикальную ли-
нейную скорость струи при вытекании воды из шланга.
10.	Вода при 60 °F (15,6 °C) течет через горизонтальную стандартную
трубу [с внутренним диаметром 1,049 дюйма (2,67 см)) при массовой скорости
истечения, равной 100 фунт/мин (45,4 л!мин) ц избыточном давлении 600 фун-
5*	67
топ нл I дюйм’ (4,218 кПсм*), Ниеле ирохождиши воды чсрее чпстичпо откры
тый отнль избыточное давление и трубе цпдает до 8 фунтов ив I дюйм*
(0,38 кГ/гм*). Определить потерю еиергил в минуту, обусловленную турбулент-
ностью в вентиле. Считать, что труба полностью изолирована, определить
температуру воды при выходе из вентиля.
11	Пар в цилиндре при 200 °C охлаждается при постоянном давлении
в I атм до жидкой воды при 26 °C. Вычислить количество теплоты и выполнен-
ную работу. Предположить, что пар ведет себя как идеальный газ и что жид-
кость несжимаема.
12.	Жидкий аммиак, текущий по трубе при температуре —33 °C и давле-
нии 5 атм, расширяется, проходя через частично открытый вентиль, до давле-
ния 1 атм и нагревается до —16 “С. Определить изменение энтальпии.
13.	В термостатированном цилиндре содержится 1 моль трихлорметаиа
при 61,2 °C и 1 атм. Определить количество выполненной работы при переносе
1000 кал от термостата в цилиндр при постоянном давлении 1 атм. Предполо-
жить, что пар ведет себя как идеальный газ.
14.	Определить теплоту реакции при 25 °C и 1 атм для каждой из сле-
дующих реакций:
a)	SO2(r) +-у О2(г)---> SO/r);
б)	СаО + Н2О-----> Са(ОН)2:
в)	СаСО3----> СаО + СО2;
г)	2NaCl + СаО + СО2----> Na2CO3 + СаС12.
15.	Определить теплоту реакции при 25 °C и 1 атм для каждой из следу-
ющих реакций, используя данные по теплотам сгорания:
а)	Н2О(г) +С2Н4(г)----> С2Н6ОН(ж);
б)	С2Н4(г) + -у О2----» C;jH4O (г) (окись этилена);
в)	С2Н4О (г) + Н2О(ж)---» С2Н4О2(ж) (этиленгликоль).
16.	Определить теплоту образования при 25 °C и 1 атм с помощью теплот
сгорания, приведенных в приложении 4 для каждого из следующих органиче-
ских соединений: а) метана (г); б) октана (ж); в) этилового спирта (ж);г) эти-
ленгликоля (ж);
17.	Определить теплоту реакции при 500 °К и 1 атм для реакций:
a)	N2 + ЗН2 —2NH3;
3
б)	HjS + -у О2 ----> SO2 + Н2О (г);
в)	SO2 + -у О2-----> SO3;
г)	С3На + 6О2(г) -г—» ЗСО2(г) + 4 Н2О(г).
18.	1/10 моля жидкого бензола и 1 моль кислорода помещены в бомбу
постоянного объема при 25 °C. Реакция окисления протекает адиабатно до свое-
го полного завершения. Определить конечную температуру реакционной смеси.
19.	Смесь водорода и окиси углерода (в отношении 2 моля водорода к
1 молю окиси углерода) загружают в каталитический реактор при температуре
600 °К и давлении 30 атм. Предполагая, что процесс протекает адиабатно и
смесь ведет себя как идеальный газ, вычислить процент превращения окиси*
углерода и водорода в метанол, если температура реакционной газовой смеси
достигает 700 °К-
20.	Газотурбинный двигатель расходует за один час 9 кг жидкого нормаль-
ного октана. Предполагая полное сгорание со стехиометрическим количеством
воздуха до двуокиси углерода, водяного пара и азота при адиабатных условиях,
определить максимальную мощность (л. с.1ч). Воздух и топливо поступают при
25 °C, выхлопные газы выходят с температурой 1000 °C.
68
ГЛАВА 2
Уровни внутренней энергии
Основные положения и уравнения классической термодинами-
ки дают четкое и точное описание поведения материи и энергии.
Так как термодинамические концепции не зависят от той или
иной теории строения вещества, уравнения термодинамики на-
ходят широкое применение, но этот же самый факт затрудняет
физическую интерпретацию термодинамических уравнений и со-
держание термодинамики остается эмпирическим и абстрактным.
Механическая интерпретация этих концепций становится воз-
можной и эмпиризм в значительной степени можно исключить,
если основные концепции будут тесно связаны с теорией строения
вещества. Таким путем проверяется правильность современных
теорий строения вещества. В настоящее время считают, что ве-
щество состоит из молекул, в свою очередь состоящих из атомов,
построенных из таких элементарных частиц, как электроны, про-
тоны и нейтроны. Элементарные чйстицы обусловливают свойства
атомов, атомные свойства определяют свойства молекул, а моле-
кулярные свойства определяют наблюдаемые свойства системы.
Поэтому, зная свойства молекул, можно вычислить все наблюдае-
мые термодинамические свойства системы, состоящей из большого
числа молекул.
Хотя механическая модель атома или молекулы не может быть
четко определена, математические законы, определяющие свойст-
ва и поведение индивидуальных атомов и молекул, теперь твердо
установлены с помощью квантовой механики.
Общие свойства сложной системы, составленной из большого
числа индивидуальных молекул, могут быть вычислены методами
статистической механики и интерпретированы с точки зрения
свойств индивидуальных молекул.
1.	Внутренняя энергия
Современное научное представление о системах дает основание
считать, что поступательные, вращательные и колебательные со-
ставляющие внутренней энергии квантуются в форме дискретных
69
яюргетнчсСкнХ уровней. Таким обрпзом если л,—число моле-
кул, каждая из которых имеет врергню то общая внутренняя
энергия
Е •* Еп(«<(
где суммирование распространено на все возможные энергетиче-
ские уровни. Для тех систем, в которых энергия взаимодействия
между молекулами незначительна (например, идеальный газ),
каждая форма энергии может быть вычислена отдельно.
Уровни поступательной энергии могут быть приближенно
определены, если рассматривать молекулу как свободную ча-
стицу, движение которой ограничено заданной областью про-
странства. Вращательные энергетические уровни могут быть приб-
лиженно оценены, если рассматривать вращающуюся молекулу
как жесткую систему определенных размеров. Колебательные
энергетические уровни могут быть приближенно определены, если
считать различные виды колебаний гармоническими. В действи-
тельности различные виды энергии в молекуле не являются строго
независимыми, когда все виды движения происходят одновременно.
Например, расстояния между атомами и углы между связями в
молекуле не фиксированы, но изменяются около некоторых
равновесных значений вследствие колебательных движений; дли-
на равновесной связи сама по себе — функция вращательной
энергии; силы притяжения между молекулами будут изменять
и вращательную, и колебательную энергии. Эти различные эф-
фекты приводят к взаимодействию или возмущающему влиянию
одного вида энергии на другой. Поправки на такое влияние могут
быть сделаны только для более простых молекул, хотя они обычно
относительно малы.
Для тех систем, в которых силы притяжения между молеку-
лами достаточно велики, например в жидком или твердом состоя-
нии, различные формы энергии не могут быть рассмотрены как
независимые, и квантование энергетических уровней должно быть
проведено относительно целой системы из п молекул. В данной
книге квантованные энергетические уровни поступательного дви-
жения, жесткого ротатора и гармонического осциллятора будут
вычислены при допущении, что они не зависят друг от друга.
2.	Квантовая теория
Экспериментальные данные об энергии могут быть получены
по испусканию или поглощению веществом излучения. Такие
сведения о тепловом излучении и атомных спектрах накаплива-
лись 1 течение многих лет. Ранние попытки объяснить наблюдае-
мое тепловое излучение, применяя классические законы Ньютона
к атомным системам, были только отчасти удовлетворительны.
Например, в излучении абсолютно черного тела количество излу-
ченной энергии для короткие волн мало; оно возрастает с увели-
70
пением длины полны до максимальной величины и с длльисйишм
ростом длины полны снопа уменьшается, приближаясь к пулю.
Основы» «ясь на классических представлениях, Рэлей и Джинс
предсказали часть кривой для длинных волн, в Вин установил
характер изменения кривой с изменением температуры. Однако
классические представления не позволили предсказать всю кри-
вую от коротких до длинных волн.
Планк, стремясь разрешить проблему, впервые получил эмпи-
рическое уравнение кривой зависимости энергии от длины волны,
а затем попытался разработать механизм излучения, который со-
ответствовал бы эмпирическому уравнению. Он смог показать,
что система из гармонических осцилляторов с прерывным излуче-
ниеи энергии позволяет объяснить форму кривой. Однако мысль,
что излучение энергии происходит порциями (квантами), не согла-
совывалась с классической теорией, поэтому квантовая гипотеза
была принята неохотно.
В 1913 г. Бор применил квантовую гипотезу к атомным систе-
мам]^ вывел теоретически наблюдаемый спектр атома водорода.
Ранее спектр был описан уравнением, содержащим эмпирическую
постоянную Ридберга, которую по теории Бора можно вычислить
с помощью известных физических постоянных, включая постоян-
ную Планка h. Успех квантовой гипотезы в объяснении излуче-
ния черного тела и спектра атомарного водорода обеспечил твер-
дую основу для развития новой механики, которая может дать
все результаты классической механики и правильные ответы
на вопросы, которые классическая механика ие могла разре-
шить.
Другой проблемой XIX в. была природа светового излучения.
Существовали две основные теории, подтвержденные надежными
экспериментальными наблюдениями. Такое наблюдаемое свойство
как дифракция, свидетельствовало о том, что свет подчиняется
закону упругих воли и его почти полностью можно объяснить
электромагнитной теорией Максвелла. Однако фотоэлектриче-
ский эффект чужд волновой теории света и мог быть объяснен
только при условии допущения корпускулярной природы
света.
Эти параллельные теории противоречили одна другой до того
момента, когда было открыто, что поток электронов, который мож-
но рассматривать как поток реальных частиц, мог при некоторых
условиях обнаруживать дифракцию на решетке, т. е. явление,
свойственное волнам.
Логическое объяснение этих явно двойственных свойств может
быть найдено при проведении экспериментов. В экспериментах
по изучению фотоэлектрического эффекта наблюдалось действие
индивидуальных фотонов, ударяющихся о твердую поверхность.
В экспериментах по дифракции измерялся статистический эффект
от большого числа фотонов и электронов. Таким образом, веще-
ство и излучение можно считать состоящими из дискретных ча-
71
стин, статистическое поведение которых можно объяснить соот-
ношением, имеющим мытемитическую форму, эквивалентную со-
отношению для распространения Ъолн в упругой среде.
3.	Распространение волн в упругой среде
Уравнение распространения волн вдоль упругой струны и
уравнение распространения продольных волн в упругой среде
имеют аналогичные математические формы. На рис. 5 изображена
часть поперечной волны на упругой струне с постоянной линейной
Рис. 5. Поперечная волна на
струне
плотностью р, длиной ds при равно-
мерном натяжении т. Амплитуда в
точке х и в момент времени 0 рав-
на V. Суммарную вертикальную си-
лу, действующую на каждый элемент
струны, можно выразить уравнением
т (sin <р2—sinipj).
При условии, что радиус кривиз-
ны достаточно большой,
. /dW\
sinq)8^tgq>2=^5x^,
smcpj^tgq^^ J
ds st: dx.
Суммарная вертикальная сила
может быть также выражена с по-
мощью вертикального ускорения
элемента струны:
или
р д2чг _
дх2'
(2-1)
Уравнение (2-1) выражает амплитуду волны как функцию расстоя-
ния х и времени 0. При условии, что внешняя сила не действует
на струну, отдельная волна будет перемещаться, не изменяя фор-
мы вдоль по струне с постоянной скоростью.
Выше суммарная вертикальная сила, действующая на струну,
была выражена уравнением
т (sin <р2—sin <Pj).
72
Если радиус кривизны велик, то •лсмент струны можно принять
как часть дуги, и тогда
(slncp,—siiKpJ-Cvj—Ф>) —
где г — радиус кривизны. Результирующая сила, действующая
внутрь на элемент струны, равна —у—. При устойчивой форме
волны эта сила уравновешена внешней инерционной силой, рав-
ной р^с> , где с — линейная скорость элемента волны. Следо-
вательно,
ds ds-c*
т — = р ——
г г г
и скорость волны выражается уравнением
Подстановка величины с в уравнение (2-1) дает
й2ф _ 1 а2Ф
дх2 ~ с2 ’ д02 ‘
(2-2)
Распространение продольных волн выражается аналогичным
уравнением, если функцию Т рассматривать как плотность среды.
В этом случае модуль упругости Е заменяет натяжение струны т,
масса единицы объема Т заменяет массу единицы длины р и ско-
рость распространения волны будет иметь вид
Если распространение звуковых волн в идеальном газе происхо-
дит изотермически, то модулем упругости будет давление р и
скорость звука будет равна
В действительности распространение звуковых волн в возду-
хе по существу является адиабатным процессом и модуль упру-
гости ближе всего к величине kp, где k — отношение теплоем-
кости при постоянном давлении к теплоемкости при постоянном
Q
объеме Таким образом, скорость звуковых волн в воздухе
0 1
v \ ЧГ / •
Уравнение, выражающее распространение звуковых волн в
идеальном газе, может быть выведено комбинацией баланса массы,
73
баланса iiieprmi, бпллпса сил и урпгпспия состояния для среды
Для случая трех измерений уравнение принимает форму
где x, у и z—независимые пространственные переменные.
Функцию Y уравнения (2-3) можно рассматривать как ампли-
туду поперечной волны или как плотность среды для продольной
волны, а также можно считать функцией вероятности, если урав-
нение применено к световому излучению.
4.	Волновое уравнение для атомных систем [32J
Значительный вклад в основу этой проблемы внес Гейзенберг,
выдвинув принцип о невозможности одновременного измерения
двух сопряженных переменных. Например, если точно известно
положение частицы, то такое свойство, как количество движения,
даже теоретически не может быть точно измерено. Если наблю-
даемое количество движения частицы точно установлено, то по-
ложение частицы не может быть определено. В действительности
любое свойство не может быть точно измерено и известная степень
теоретической неопределенности остается при каждом измерении.
Порядок величин этих неточностей дается соотношением
АхАр > h,
т. е. произведение неточностей в этих двух измерениях по порядку
величины равно постоянной Планка h.
Хотя этот принцип весьма общий, численная величина h
является такой, что неточности не проявляются для окружающих
нас тел с их массами и скоростями. Однако когда мы имеем дело
с массой и скоростью фотонов и атомных частиц, неточности могут
быть оценены и любая теория, с помощью которой можно попытать-
ся описать поведение этих частиц, должна исходить из этих не-
точностей. Интересно заметить, что если бы численная величина h
была близка к единице вместо 6,625 X 10"27 эрг сек, вычисление
траектории мяча или ружейной пули было бы невозможно; могла
бы быть вычислена только вероятность того, что данный пред-
мет можно обнаружить в определенном объеме и что он обладает
количеством движения в заданном интервале. Ньютоновские
законы движения, очевидно, справедливы для обычных систем
только потому, что постоянная Планка — очень маленькая ве-
личина.
На основании соотношения Эйнштейна для энергии фотона
может быть получено уравнение для выражения зависимости дли-
ны волны от массы фотона:
е = ftv = -у- = тс2,
74
из которого
Еще в 1925 г. де Бройль по аналогии предположил, что любой
частице с массой т и скоростью v должна соответствовать длина
волны, выражающаяся соотношением
.	(2-5)
mv	'	'
В то время не было экспериментальных доказательств, чтобы
подтвердить это предположение. Однако несколько лет спустя
гипотеза де Бройля была подтверждена опытами по дифракции
электронов Девисоном, Джермером, Томпсоном и др.
Применяя соотношение Эйнштейна и гипотезу де Бройля к
волнам частиц, получаем
е == ftv = у- = тис.	(2-6)
Количество движения частицы может быть выражено в
виде
₽
mv=-7.	(2-7)
Общая энергия частицы — это сумма кинетической и потенциаль-
ной энергий:
e = -i-mu2 + V. ’	(2-8)
♦
Согласно уравнению (2-8), количество движения частицы
mo = ]/2m(e—V) .	(2-9)
С помощью уравнений (2-7) и (2-9) скорость волны может быть
выражена через массу и энергию частицы
Подставляя выражение для скорости волны в уравнение
(2-3), получаем
aw aw aw _ 2m(е — г» aw	,9...
ах2 + а«/а + аг2 г2 ае2*
Теперь нужно найти решение уравнения (2-11) в виде функ-
ции, которая должна быть конечной, непрерывной и давать конеч-
ную величину для интеграла от 'F2dx по всей области. Конечный
результат для этого интеграла свидетельствует о том, что частица
75
н«ходится внутри заданной области изменения переменных.
Только те функции, которые удовлетворяют <тнм требо они им,
приемлемы для решения физических проблем
Можно попытаться решить уравнение (2 11) для стационар-
ного состояния (т. е. тех энергетических состояний, которые не
являются функцией времени и соответствуют стоячим волнам),
используя решение в форме
'1Г = ф ехр (—2itiv0)=ф exp — 2г/
0
h
где ф— функция только пространственных координат. Уравне-
ние для независимой от времени волновой функции может быть
получено подстановкой этого решения в уравнение (2-11):
где
Это уравнение впервые было получено Шредингером. Наличие
величины i в принятом решении указывает на то, что функция ф
не имеет реального физического смысла. Свойства этого уравне-
ния таковы, что приемлемые решения получаются только в том
случае, если энергия имеет определенные дискретные значения.
Величины е, для которых уравнение имеет приемлемые значения,
интерпретируются как допустимые значения энергии системы.
В следующих разделах уровни энергии нескольких весьма
упрощенных, но важных систем будут получены при использо-
вании уравнения (2-12).
5. Поступательная энергия свободной частицы [17, 32]
Простейшей возможной физической системой является части-
ца с массой т, движущаяся в направлении х без воздействия на
нее силы. Одномерное волновое уравнение для этой системы по-
лучается из уравнения (2-12). Для этой системы переменные у
иг — постоянные параметры и потенциальная энергия равна нулю.
Следовательно, уравнение (2-12) принимает вид
Оно является линейным дифференциальным уравнением второго
порядка с постоянными коэффициентами, и решение его может
быть записано в форме
1 1
ф = A sin (Me)2 х+В cos(Me) 2 х.
76
Так как тригонометрические функции — периодические, то функ*
ция будет оставаться конечной на протяжении исех значений по
ременной х, если (Mt) им ет действительное значение. Следе-
вателыю, энергия не квантуется и может иметь любое положитель-
ное значение между нулем и ос.
6. Поступательные энергетические уровни частицы
в ящике [17, 32]
Эта проблема рассматривает частицу, вынужденную двигаться
в ограниченной области пространства, определенного прямо-
угольным ящиком с размерами ребер а, b и с. Волновое уравне-
ние для этой системы дано уравнением (2-12). Решение этого диф-
ференциального уравнения с частными производными с тремя
неизвестными переменными можно получить, если принять, что
ty — X(x)Y(y)Z(z)t
где X — функция только х;
Y — функция только у,
Z — функция только Z.
Подстановка этого решения в уравнение (2-12) дает
1 д*Х . 1 дгУ , 1 d*Z ,	„	...	„
х ' дх2 + у z'dz2+M(e Vx	V2) —Q,
где V = Vx -}- Vy -|- V2 — потенциальная функция, описывающая
ящик. В этом случае желательно иметь потенциальную энергию,
равную нулю во всех точках внутри ящика, непрерывно возра-
стающую до бесконечности на границах ящика. Поместив начало
координат в одном углу ящика, можно математически описать
потенциальную энергию следующим образом:
V2 = 0 для 0 < х < a; V2=co при х = 0 или х = а;
1^ = 0 для 0<#<й; 1^ = 00 при у=0 или у~Ь-,
V2 = 0 для 0<z<c; У2=оо при z=0 или z = c.
Так как первые три члена дифференциального уравнения —
независимые друг от друга функции, сумма которых всегда по-
стоянна, то каждый член уравнения должен быть постоянным.
Если ввести ех, еу и ег, представляющие собой неопределенные
параметры, связанные уравнением
е— ех+ег/ + ег»
77
то дифф рслциальиое уравнение с частными производными распа-
дается па три обыкновенных дпффгрсчщилльных уравнения:
^ + M(.x-Vx)X-0;
™+M(tv-Vy)Y -0;
Для области внутри ящика Vx = 0 и уравнение относительно х
приобретает вид
^- + МехХ = 0.
dx* 1 х
Это уравнение математически эквивалентно уравнению для
свободной частицы и решение его может быть выражено в форме
1 1
Х = A sin (А4ех) 2 х 4-В cos (Л4ех)*2 х, 0 < х < а,
где А и В — произвольные постоянные.
Для области за пределами ящика потенциальная энергия —
бесконечно большая величина, и единственно возможное решение
дифференциального уравнения
X = 0, 0 > х > а.
Для того чтобы функция была непрерывной во всей области
изменения х, два решения должны совпадать на границах ящика.
Поэтому при х = Q
1 1
0 = A sin (Л4ех)2 0 + В cos (Afex)2  0.
Это условие требует, чтобы произвольная постоянная В была
равна нулю.
На другой границе х = а.
1
0 = A sin (AleJ 2 а.
Чтобы решение имело смысл, А не должно быть равно нулю.
Поэтому
sin(A4ex)2 -а = 0.
Это условие выполняется, если
1
(Мех) 2 -а= тх,
78
где Пд-—целое число. Следовательно, диффе|х‘11циал1|11ос урав-
нение имеет приемлемое реш пне только для дискретных знпч<
ний «*, данных выряжен нем
** Rm I „	>
где М заменено его значением ..у-—.
Аналогичные решения могут быть получены для функций У
и Z, и поступательные уровни энергии частицы, вынужденной
двигаться в ящике с размерами а, Ь и с, даются уравнением
• = -«+^+е. = ДЧ(?Г+№Г + (	(2-13)
Это указывает на то, что поступательная энергия движущихся в
ограниченной части пространства частиц квантуется и что только
те значения энергии, которые определяются целыми квантовыми
числами пх, пу и пг, будут приемлемыми решениями волнового
уравнения.
7. Энергетические уровни жесткого ротатора (17)
В некотором приближении двухатомная молекула может быть
рассмотрена как две материальные точки, жестко связанные, как
указано на рис. 6, так, что расстояние между ними постоянно и
Рис. 6. Двухатомный жесткий ротатор
равно г. Поместим начало координат в центре тяжести и пусть
полярные координаты одного атома будут а, 6 и ф, а координаты
другого атома — Ь, 6 и ф. В прямоугольных координатах кинети-
ческая энергия первой частицы равна
,2
79
g кинетическая энергия пчорой частицы равна
^[(^У+(1)'+(^)‘] '¥[(")+(•'"•«) (#)*]-
Общая кинетическая энергия составит тогда
тха« +таЬ° I / dO \« ... / dtp\*
2 Ц di )	lsin Ц di ) J*
Сумма т^а2 4- тгЬ2 — не что иное, как момент инерции I
системы, и для общей кинетической энергии можно написать вы-
ражение
которое аналогично выражению кинетической энергии для одной
частицы с массой /, находящейся на поверхности сферы с радиу-
сом, равным единице. Волновое уравнение может быть выражено
в полярных координатах путем замены декартовых координат:
x = rsin6cos(p,
у = г sin 6 sin ф,
z = rcos 6.
Уравнение для частицы с массой I на сфере с единичным радиусом
(г — 1) без действующей силы (V = 0) будет иметь вид
1 д V  д dtp \	1 dstp 8п2/е , л	/о 1
sin е \S n6 ‘<99 )+sine •л₽2+ [Л2 Ф —°»	(2-И)
где е — вращательная энергия молекулы. Это дифференциальное
уравнение с частными производными с двумя независимыми пере-
менными может быть разделено на два обычных дифференциальных
уравнения, если решение записать в форме
ф = 0(6)-Ф(ф).
Подстановка этого рещения в уравнение (2-14) дает
sin0 д / . д дв \	8п*/е . „ й	1 д2Ф	,о ,е
ае \ sln6 de )+ л2"~ sln 6	ф "ay2*	(2'15)
Так как левая часть этого уравнения не зависит от правой части,
то каждую часть можно считать равной произвольной постоянной.
Обозначим ее т2. Величина т является просто постоянной и ее
не следует смешивать с массой. Уравнение для Ф тогда примет вид
^+тгФ = 0,	(2-16)
80
которое имеет решение в форме
Ф ^sirim<p4-2Jcosmq>.	(2-'17)
Для того чтобы функция Ф была однозначной и имела конечное
значение, она должна быть периодической с периодом 2л, т. е.
sin ш ф  sin m (ф 4- 2~) = sin ш ф cos 2r ш 4- cos m ф sin 2nm
и
cosm ф = cosm (ф 4* 2л) = cos m ф cos 2лт—sin тф sin 2лт.
Для этого нужно, чтобы cos 2л т = 1 и sin 2л т = 0, что спра-
ведливо только в том случае, если ш — целое число.
Уравнение для 0 можно записать в виде
где
(2-18)
к- 87I*Ze
Л2
Уравнение может быть преобразовано в более удобную форму
с заменой х = cos 0; так как 0 меняется в области от 0 до 2л, то х
будет иметь значение от +1 до —1. Делая эту подстановку, по-
лучим
а	S—2х f+к -1^16=°-	(2Ч9)
иЛ	V**'* I	1 л I
Это уравнение — линейное уравнение второго порядка с перемен-
ными коэффициентами и имеет форму уравнения Лежандра.
Вследствие наличия члена функция становится бесконеч-
ной при х = ±1. Дальнейшая подстановка для зависимой пере-
менной
ш
• 0 = (1-х2)ти
(2-20)
превратит уравнение (2-19) в уравнение, в котором коэффициент
при зависимой переменной постоянен. Таким образом,
(!-xa)g -2х(т4-1)^- + [У-т(ш+1)]о=0. (2-21)
Решение для v в форме бесконечного ряда можно получить,
если принять
v = Eakxn+ks.
(2-22)
6—1503
81
Постоянные величины м и 8 могут быть определены подстановкой
выражения (2*22) в дифференциальное уриннеппе
| fe)'xw+**“’,	(2-23)
Ей*(п4-/л)(п ф ks—l)xn+*’-a,	(2-24)
Подставляя выражения (2-22), (2-23) и (2-24) в уравнение (2-21),
имеем
£йа (п Ц- ks) (п Ц- ks — 1) хп+**-2— Ей* [(ш 4-/гз4-п)(т4-
4-As4-n4-l)—TV]xn+A’ = 0.	(2-25)
Значение величины s определяется как разность между показа-
телями степеней х соседних членов ряда; в этом случае
s = (п 4- ks)—(п 4- ks—2) = 2.
Так как коэффициент при каждой степени х в уравнении (2-25)
должен быть равен нулю, то величину п можно определить, при-
няв коэффициент в соответствующем члене ряда (2-25) при низшей
степени х равным нулю (допустив, что а0 #= 0). Этим членом при
k, равном нулю, является а0-п(п—1) хп~2, в котором п равно
нулю или единице. Каждое значение п будет определять решение
в виде независимого ряда. С помощью коэффициента члена, со-
держащего x2k, рекурентная формула для коэффициентов при
п = 0 может быть выражена следующим образом:
«А+1 _ (m4~2*) (m 4-2*4-!) —ТУ
ак	(2*4-1) (2*4-2)	•
Подобная же формула для. п = 1
Qfe+i   (m 4~ 2* 4~ 1) (m 4~ 2* 4~ 2) — N	/о л-тч
ak ~	(2*+2) (2* + 3)	•
Так как предел каждого выражения равен единице при k -* оо,
то каждый ряд должен сходиться в области —1 < х < 1; но каж-
дый ряд является расходящимся при х = ± 1 и за пределами
этих значений. Следовательно, никакой ряд не может представить
приемлемую волновую функцию.
Однако в случае, когда N имеет значение целого числа, опре-
деляемого произведением (т 4* 2A)(m 4- 26 4* 1), коэффициент
ak+1 и все последующие коэффициенты ряда при и — 0 равны
нулю, и бесконечный ряд вырождается в полином степени 2k,
который является конечным при х, равном 4-1 и —1; подобным
образом ряды при и, равном единице, вырождаются в полином,
когда TV = (т + 2^ 4- 1)(т 4- 2Л 4- 2). В каждом случае общее
решение для v можно выразить как сумму полинома и бесконеч-
ного ряда. Так как ряды неприемлемы для волновой функции, то
полиномы представляют единственно возможное решение.
82
Поскольку m и Л — целые числя, величина N, необходимая
для обрпзоннпня полинома и получении приемлемой волновой
функции, может быть пырпжена
Л/-/(/4-1)Л	(2-28)
где / - m 4- 2k для п 0 пли m 4- 2k 4- 1 для п — 1; / может
иметь значения всех положительных целых чисел. Так как k
должно быть положительно, |ш| </. Следовательно, по опре-
делению N допускаемые энергетические уровни жесткого ротатора
будут
и
e, = 8^/(/4-l). /=1, 2, 3...	(2-29)
t
Величины ег дают энергетические уровни относительно основ-
ного вращательного нулевого уровня при / = 0.
Полиномы, полученные выше, известны как присоединенные
полиномы Лежандра степени / и порядка m и обозначаются сим-
волом Р™(х) или P“(cos 6). Приемлемая волновая функция для
жесткого ротатора может быть записана в виде
ф = ф (ф) @ (6),
ф = [Л sin тф 4- В cos тф] DP™ (cos 6),	(2-30)
где А, В и D — постоянные величины. Для данного значения /
система имеет определенную энергию, выраженную уравнением
(2-29). Однако для каждой величины / величина ш, может прини-
мать значение всех целых чисел от —/ до 4-/, включая 0; так что
m может иметь (2/4- 1) различных значений для данной величины
/. Это можно объяснить тем, что система, обладающая определен-
ной энергией, может иметь (2/ 4- 1) различных состояний. Явле-
ние, в котором несколько состояний системы соответствуют одной
и той же или приблизительно одной и той же энергии, называется
«вырождением»; в вышеприведенном случае говорят, что система
имеет (2/ 4-1) — кратное вырождение.
8. Энергетические уровни гармонического
осциллятора [17, 32]
В задачах о жестком ротаторе расстояние между атомами в
двухатомной молекуле рассматривается постоянным. Действи-
тельно, расстояние может меняться около равновесного значения
вследствие колебательного движения атомов вдоль оси связи.
В некотором приближении колебание можно рассматривать как
6*
83
гармоническое, т. <-. сила, действую!ция па частицу, пропорции,
пальпй отклонению частицы от положения равновесия (рис. 7),
В двухатомной молекуле каждый атом колеблется около по-
ложения равновесия. Если никакая внешняя сила нс действует на
систему, то количество движения одного атома равно количеству
движения другого:
"Л '".-у--	<2-31)
Сумму отклонений хх и ха можно выразить в функции расстояний
,п.	тг
НЧ—I-----------------Mod
между атомами (х):
х=хе4-х1 + х!!.
После дифференцирования
“ Xf
X -
Рис. 7. Гармонический осцил-
лятор
dx___dxi_ dxt,
dt~ ~di+~dt •
dx
С помощью этого равенства находим величину и подставляем
ее в уравнение (2-31):
=т;
[dx____dxj "I
~dt ~dT J ’
/	.	, dx-t dx
dx ___ dx
~df~^ht •
dXi_ тут%
1 di m1 -|- ma
где p — приведенная масса	. Таким образом, колебание
двух атомов в двухатомной молекуле может быть представлено
как колебание частицы с массой р около положения равновесия.
Так как сила, действующая на частицу, пропорциональна от-
клонению частицы от положения равновесия и направлена к этой
точке, то баланс сил, согласно классической механике Ньютона,
даст
d2X . , л
Р -^ + ^ = 0,
d2x . k А
----х=^0.
dt* 1 р
Последнее равенство есть дифференциальное уравнение второго
порядка с постоянными коэффициентами, решение которого мо-
жет быть записано в виде
х = A sin j/" A14- В cos j/"A t.
84
Допустим, что частица нгр1юпачйЛЫ1о пыпедепа пл состояния по-
коя в крайнем ее отклонении от положения раппопесия, и тогда
определим граничные условия:
если f«"0, то х*"Х0,
если t — 0, то  0.
at
Применим второе граничное условие:
=	_ cos уА-0— By± sin]/A-0 = 0.
Для того чтобы выполнялось это условие, коэффициент А должен
быть равен нулю. Используя это заключение вместе с первым гра-
ничным условием, получим
x0 = BcosO.
Следовательно, коэффициент В равен х0. Таким образом, решение
будет иметь вид
X — Хо COS У — t.
“а
Чтобы эта функция воспроизводила то же значение х после
каждого полного цикла, переменная У-у- t должна быть равна
2лп, где п — число циклов, совершенных за время /. Число цик-
лов в единицу времени называется «собственной частотой колеба-
ния», которая определяется выражением
s/J-	<2-32>
Потенциальная энергия системы вычисляется как отрицатель-
ная работа, выполненная частицей, проходящей расстояние х
против действующей силы —kx'
V = —J (—kx)dx = ~~ kxs.
о
Приведенная выше классическая трактовка гармонического-
осциллятора являетсй только приближенной, если частица имеет
атомные размеры. Волновое уравнение для одномерного гармони-
ческого осциллятора таково:
S’ + 7? ( е - 4 kx*} Ф = °-’	<2'33>
85
в нем исиольэоипнл классическая величина погепциалышИ я1ер-
гни. Введя обозначения
Р*-Т:
перепишем волновое уравнение:
^-+(а_р«х«)ф 0.	(2-34)
Это дифференциальное уравнение, являющееся линейным урав-
нением второго порядка с переменными коэффициентами, не
может быть решено каким-либо известным методом; ему можно
придать более удобную форму следующей подстановкой:
^ + (т“е*)Ч>=0.	(2-35)
Чтобы найти решение этого уравнения, рассмотрим первый
предельный случай, когда Е настолько велико, что величиной
можно пренебречь:
^-В2Ф = 0.	(2-36)
Решение этого уравнения должно иметь примерно следующий вид:
4
ф — се
Его можно проверить дифференцированием:
£2
A-ce*T.(=t5),
= 1].
Для больших значений Е величиной ±1 можно пренебречь по
отношению к Е2, так что уравнение (2-36) справедливо. Решение
+ —
се 2 не приемлемо, так как становится бесконечным при Е -► оо,
_Е2_
однако решение се 2 удовлетворительно. Этот анализ подтверж-
«С
_ |«
дает, что ураиш ш«- (2 36) должно содержать множитель е~ .
Следовательно, решение а форме
I»
Ф = е н(Е)
остается возможным. Подстановка его в уравнение (2-35) дает
+ ( “ - 1)и = 0.	(2-37)
Решение для и может быть найдено в форме бесконечного ряда:
и — 2аЛЕт+*’,
и' = SaA (т + ks) 1,
и" = Lak (т + ks) (т 4- ks — 1) gm+*»-2.
Подставляя эти величины в уравнение (2-37), имеем
Yak(тks)(m-^ks — 1)£т+Л5-24- f “---------1 — 2 (m 4-£s)j5m+fts=0,
Так как s— разность между показателями степеней у сосед-
них членов ряда, то в этом случае она равна двум. Первый член
получается при k — 0:
а0-т(т— 1)Е"*-2,
откуда
m =0; 1.
Коэффициент при ?п+гк равен
1 —2 (т 2k)j ak-n (m-\-2k-}-2)(m-\-2k-)-1),
из которого может быть получена рекурентная формула для коэф-
фициентов:
[“ 1
-д- — 1 — 2 (т 4- 2k)
__________"___________________J
ak (m-|-2fe 4-l)(m 4*2fe + 2)’
Поскольку предел (aA+1/a*) стремится к нулю по мере того,
как k приближается к бесконечности, ряд принимает такую же
форму, как е£2для больших значений k. Решение для ф—е 2 и стало
__а
бы тогда е 2ее“ = е 2. Однако из этого ряда нельзя получить
приемлемую волновую функцию. Если в рекурентной фор-
муле (т 4- 2k) = -2"(-|— 1) = я, ряд будет вырождаться в по-
87
липом, который конечен во всей области изменения переменных.
Этот полином известен как «полипом Эрмита степени п», обозна-
чаемый Нп(х). Решение для ф тогда будет:
о
ф(Е)-се //«(£)•
Эта функция интегрируема в пределах — ±оо и является прием-
лемой волновой функцией.
Величины энергии, необходимые для таких решений, могут
быть определены из условия
1 /
2Д ₽
= п.
где п может быть любым положительным
числом, включая нуль:
-“- = 2п + 1 = 2
По определению аир
« +
£ \
2
Если принять классическое представление об основной частоте,
го колебательной энергии гармонического осциллятора можно
придать вид
s, = hv [ti -]—2~^‘	(2-38)
Это уравнение указывает, что основной колебательный энер-
гетический уровень гармонического осциллятора не равен нулю,
когда п = 0, но равен половине кванта энергии. Не теряя общности
энергетические уровни можно отнести к основному колебательно-
му энергетическому уровню, равному половине кванта; в таком
случае
е, — n-Jiv	(2-39)
Относительно
е,о = Ц-Ь.
П р и мер 1. Определить три наибольших длины волны в
вращательном спектре йодистого водорода (Ш), принимая, что
-88
молекула — жесткий ротатор со средним межатомным расстоя-
нием 1,604 А.
Линия спектра поглощения, пяблюдясмля женерлмеитальио,
сочетается с некоторым количеством энергии, эквивалентным раз-
ности между соседними шсрп?тическлмл уровнями. Длина волны,
соответствующая каждой линии, выражается уравнением Эйн-
штейна:
Де
Разность между соседними вращательными энергетическими
уровнями может быть вычислена по уравнению (2-29):
Де “-ет-1</+1><7+2>-/(/+|)1.
*•—sJt2«+>).
Длина волны вращательного спектра может быть тогда Определена
по уравнению
х_ 4^ 1с
hU+l)-
Момент инерции двухатомной молекулы может быть вычислен
по формуле
I — mfl* + т2Ь2,
где а и b — расстояния атомов от центра тяжести. Момент инер-
ции может быть выражен в функции межатомного расстояния
d — a-\-b,
если использовать равенство моментов количества движения:
OTjO = т2Ь.
Из последних двух уравнений
а =	b = mid
т1 + тг ’	т1 + тг ’
Подстановка этих выражений в уравнение момента инерции дает
mlmZ ^2
mt + т»
Для йодистого водорода
! = 1Д27 4L604  10-^ = 0 427.10-88 г.CJftS
1	128-6,02-Ю23	U,4Z/ г см .
. _W.O,427-10-se-3-10i° _ 0,076
Л ~ 6,"624  Ю-2' (/ + 1) “7 + 1 СМ'
89
Пнж» предстпнлспы длины воли, вычисленные пи приведенной
яыш' формуле.
!	Ж	X, гм ' (р»семи гяно)	Х, ем (иолуч Пи)
0	1	0.07Ы	0,078
I	2	0,0380	0,039
2	3	0,0254	0,026
Разность между вычисленными и наблюдаемыми величинами
можно объяснить невыполнимостью допущения о жестком рота-
торе.
Задачи
I.	Определить (эра) величину первых десяти поступательных уровней
энергии молекулы водорода в состоянии идеального газа в ящике размером
2.	Определить (эрг) величину первых десяти различных вращательных
энергетических уровней молекулы водорода как жесткого ротатора и указать
вырождение каждого из них.
3.	Каково отношение низшего энергетического уровня поступательного
движения (пх= пу= пг= 1) молекулы водорода к низшему энергетическому
уровню атома гелия для одинаковых пространственных ящиков?
4.	Каково отношение поступательного энергетического уровня молекулы
водорода в задаче 1 к энергетическому уровню молекулы водорода при тех же
2	2
п... п, для ящика размером 1X —X — сл?
и	3 5
5. Каково отношение вращательного энергетического уровня молекулы
водорода в задаче 2 к вращательному уровню, соответствующему той же вели-
чине / молекулы Н—D, если каждую молекулу считать жесткой и межатомные
расстояния принять одинаковыми?
6. Определить величину (эрг) первых пяти колебательных энергетичес-
ких уровней гармонического осциллятора с частотой колебания, равной
JO10 цикл!сек.
ГЛАВА 3
Статистические
распределения
Из выражений для поступательных, вращательных и колеба-
тельных уровней энергии индивидуальной молекулы энергия си-
стемы молекул идеального газа могла бы быть вычислена, если
бы было известно распределение энергии по энергетическим уров-
ням, т. е. число молекул на каждом данном энергетическом уровне.
Однако для систем, действительно встречающихся в практике,
число молекул так велико, что это распределение невозможно
определить прямым способом. Вместе с тем когда имеется очень
большое число молекул, статистическое вычисление распределе-
ния энергии может быть выполнено достаточно точно.
Вообще наблюдаемые макроскопические (термодинамические)
свойства системы обусловливаются статистическим поведением
микроскопических частиц, и точность статистического вычисления
полностью определяется числом присутствующих частиц. Напри-
мер, имеется конечная вероятность того, что в данный момент
времени все молекулы воздуха .в большом объеме собрались одно-
временно в одном небольшом месте; но вероятность этого настоль-
ко мала, что ею легко можно пренебречь. В среднем можно считать,
что молекулы равномерно распределяются по всему объему.
Однако отклонения от равномерного распределения молекул
газа могут наблюдаться в любой ясный день. В верхних слоях
атмосферы число молекул в единице объема достаточно мало,
и могут осуществляться мгновенные местные отклонения от сред-
ней плотности, что вызывает рассеивание солнечного света, обус-
лавливающее голубой цвет неба. Квантованные уровни энергии
будут относиться к частицам. В идеальном газе энергетические
уровни являются свойством молекулы, в твердом теле — свойст-
вами кристалла.
1. Одна группа частиц на энергетическом уровне [19]
Рассмотрим сначала систему, состоящую из п различимых
частиц, обладающих различными количествами энергии. Если
обозначить энергии, соответствующие отдельным частицам, через
91
«и вц еа--' ел> 10 общая энергии системы будет равна £е£. Обще ,
число рнллпчных способов, которыми осущестиляется отдельный
тип распределения, можно найти подсчетом числа способов, ко-
торыми данные энергетические уровни могут быть заняты различ-
ными частицами. Согласно одному методу подсчета, энергетические
уровни распределяются по различимым частицам таким образом,
что сначала должен быть занят только один уровень. Для за-
нятия первого энергетического уровня в! имеется п различных
возможностей, так как любая из п частиц может занять этот уро-
вень. После того как первый уровень будет занят, появится
(п — 1) различных возможностей для занятия второго уровня
е2, (п — 2) возможностей для занятия третьего уровня е8 и т. д.
до тех пор, пока все п энергетических уровней не будут заняты.
Общее число всех различных способов w, с помощью которых
осуществляется энергетическое распределение, равно произведе-
нию отдельных возможностей, т. е.
w = n(n—1) (л—2) (н—3).. .3-2 •1 = п!	(3-1)
То же самое выражение может быть получено иным методом,
путем предоставления частице занять один уровень из всей си-
стемы п энергетических уровней.
Для занятия первой частицей одного из п энергетических уров-
ней имеется п возможоостей, так как этой частицей может быть
занят любой из п уровней. После того как первая частица займет
один уровень, останется (п — 1) различных возможностей для
занятия энергетического уровня второй частицей, (п — 2) воз-
можностей для занятия энергетического уровня третьей частицей
и т. д., пока все п частиц не займут все п энергетических уровней.
Общее число различных способов занятия частицами энергети-
ческих уровней выражено уравнением (3-1).
В этом случае обмен частицами энергетических уровней при-
ведет к новому состоянию системы с данным распределением, од-
нако величина w не изменится, так как она зависит от общего числа
частиц или энергетических уровней.
2. Несколько частиц на одном энергетическом
уровне (17)
Рассмотрим следующую систему, состоящую из п различных
частиц, распределенных по k энергетическим уровням таким
образом, что имеется nt частиц, каждая с энергией е1( п2 частиц,
каждая с энергией е2, и nk частиц, каждая с энергией еА. Общее
число частиц равно Еп£; общая энергия системы равна Еп£е£.
При занятии частицами энергетического уровня ех имеется п
возможностей для его занятия первой частицей, так как любая
из первоначальных п частиц может быть на этом уровне.
Если вторая частица должна иметь энергию е1( то будет
п(п — 1) возможностей для двух частиц иметь ту же самую энер-
-92
гию, за исключением числа возможностей, относящихся к груп-
пированию и нары, включающие те же самые две частицы, в ко-
торых два члена пары отличались бы только порядком размеще-
ния двух частиц. Действительно, порядок размещения не имеет
значения, и два членя пары представляют одно и то же состояние.
Следовательно, общее число различных комбинаций, в которых
две частицы могут иметь одинаковую энергию, составляет только
.; другими словами, обмен частиц, имеющих одинаковую
энергию, пе дает нового состояния системы. Это положение мо-
жет быть иллюстрировано подсчетом числа различных комбина-
ций, в которых четыре частицы, обозначенные А, В, С и D, могут
иметь попарно одинаковую энергию. Произведение 4x3 ука-
зывало бы, что возможны двенадцать комбинаций, представлен-
ных сочетаниями АВ, AC, AD, В А, ВС, BD, СА, СВ, CD, DA,
DB и DC. В действительности комбинации АВ и ВА представляют
одно и то же состояние и не могут быть различимы. Подобно этому
каждая пара АС и С A, AD и DA, ВС и СВ, BD и DB, CD и DC
представляет одно состояние и, следовательно, имеется только
шесть различных состояний вместо 12.
Для первых трех частиц, соответствующих энергетическому
уровню ех, число различных комбинаций составит
_ <п~2)
2	'	3	•
Для частиц на энергетическом уровне ех число различных ком-
бинаций равно
„ (n—1) (П —2)	(n— fh + 1)
п-^2—.—з—;-------------П1—
t
После того как пг частиц будет отнесено к первому энергетиче-
скому уровню ея, число способов, с помощью которых первая из
оставшихся частица займет энергетический уровень е2, будет рав-
но (п — пг), т. е. любая из оставшихся (и — nt) частиц может за-
нять второй уровень. Число различных способов, с помощью
•которых первые две из оставшихся частицы займут второй уро-
вень, составит ———п*———————. Общее число способов, ко-
торыми осуществляется данное распределение частиц, будет
Z	О	Z
(п — щ — па + 1) . (л — П1--nk-i- 1)
п2	пд
.Так как п =	+ п8 + ... nk, приведенное выше уравнение
может быть записано следующим образом:
rt!	/Г)
W — nilntln3l...nk\ ~ Г1(п/!)'	'	’
93
В »гом случае обмен частиц между •ii<‘pre*i,ii4ecKiiMii уровнями
обусловит понос состояние сне гемы и окажет влияние па величину
КУ. Величина и» зависит по только от общего числа частиц, по также
от их числа па каждом «пергетпческом уровне. Например, переход
частицы с (Пергетического уровня et на уровень еа и одновремен-
ный переход частицы с энергетического уровня е8 па уровень
е2 оставит общую энергию системы практически неизменной, если
(еа — ej як (еа — es). Ojwajcq величина ц> может быть заметно
изменена. До перехода
nl
W, = —;—:—;------г;
1	/ц! п2! п81.. .пк\
после перехода
w _______________21____________.
а (П1-1)!(п2+2)!(Пз-1)!...п«1’
Wi = (П1-1)1(а2+2)1(п3-П1---^1 = (n2+ 1) (па + 2) __п|_
102	П11 П21 «з!  	П1«3	П]И3 '
Теперь задача заключается в том, чтобы определить, какое число
частиц могло бы быть на каждом отдельном энергетическом уровне
для того, чтобы w достигло своей максимальной величины. В при-
мере 1 описан метод прямого подсчета для определения распреде-
ления, которое можно осуществить наибольшим числом способов.
Однако такой метод возможен только в том случае, если число
энергетических уровней и число частиц были бы достаточно малы.
Пример 1. Рассмотрим систему из десяти частиц, распре-
деленных на четырех энергетических уровнях, имеющих относи-
тельные величины энергии 1, 2, 3 и 4, так, чтобы общая относи-
тельная энергия была равна 20. Требуется определить, какое из
различных распределений может быть осуществлено наибольшим
числом способов.
Одно возможное распределение десяти частиц на энергетических
уровнях таково, что все десять частиц располагаются на энерге-
тическом уровне 2. Общая энергия системы составит тогда 20.
Очевидно, имеется только один способ, которым это распределе-
ние можно осуществить, т. е. обмен частиц на том же уровне не
дает нового состояния системы. Применение уравнения (3-2)
дает значение w, равное единице.
Второе распределение может быть получено перемещением
одной частицы с уровня 2 на уровень 1 и другой частицы с уровня
2 на уровень 3. Общая энергия равна 20. Теперь применение урав-
нения (3-2) к этому распределению дает значение w, равное 90.
Таким образом, это распределение можно осуществить 90 различ-
ными способами.
Если в первоначальном распределении две частицы переме-
щаются с уровня 2 на уровень 1, а две других частицы — с уров-
ня 2 на уровень 3, то общая энергия составит 20. Однако w теперь
равно 1260. При перемещении тред частиц с уровня 2 на уровень 1
94
и трех частиц с уроыгя 2 на уровень 3 общая »нергня останется
рапной 20, по ш возрастет до 4200.
В этом случае значения w могут быть вычислены для всех рас-
пределений, имеющих общую энергию 20. Результаты приведены
н табл, 3. Числа в графе — «Уровни «иергни» показывают число
час гни па энергетическом уровне.
Таблица 3
РАСПРЕД! Л1.ПИЕ ЧАСТИЦ ДЛЯ л-10. к-4 И О1ИЦ1 Й ЭНЕРГИИ .-20
№ по пор.	Уровни энергии					Число состоя- ний %
		2	J	4		
1	0	10	0	0	1		
2	1	8	1	0	90	0,2
3	5	0	5	0	252	0,6
4	2	7	0	1	360	0,8
5	6	1	0	3	840	1.9
6	6	0	2	2	1260	2,8
7	2	6	2	0	1260	2,8
. 8	4	2	4	0	3150	7,0
9	4	4	0	2	3150	7,0
10	3	4	3	0	4200	9,4
11	3	5	1	1	5040	Н.2
12	5	1	3	1	5040	11,2
13	5	2	1	2	7560	17,0
14	4	3	2	1	12600	28,1
Сумма . .	• •	• •	• •	i •• 1	44 803	J 100,0
В примере 1 отмечены 44803 различных способа осуществления
определенных условий. Из них около 28% принадлежит одному
конкретному распределению.
В этом примере рассматривается только 10 частиц и четыре
энергетических уровня. Если число частиц станет больше (напри-
мер, ЮВ * * * * * * * * * * * * * * 23) и число энергетических уровней возрастает во много
раз, то всегда останется одно определенное распределение, которое
будет значительно преобладать над остальными. Например, более
99,9% всех возможных состояний могут соответствовать одному рас-
пределению. Это конкретное распределение, которое осуществляет-
ся максимальным числом способов, определяет термодинамические
свойства системы, поэтому всеми другими распределениями можно
пренебречь.
Если число частиц и энергетических уровней становится очень
большим, могут быть использованы методы расчета для вычисле-
ния изменения и>, основанные на изменении «населенности» энерге-
тических уровней. Так, в пределе w достигнет максимальной ве-
личины, когда
dw — 0.
(3-3)
95
Так как In ш также будет максимальным, когда w мякснмпльно, то
всегда должно выполняться условие
din и; 0.	(3-4)
Поскольку d In w вычислить намного легче, чем dw, то уравнение
(3-4) может быть использовано вместо уравнения (3-3).
. Логарифмируя уравнение (3-2) получаем
]n&y=ln(n!)—Е ln(nt!).	(3-5)
В любой реальной системе число частиц будет настолько велико,
что может быть использовано приближенное соотношение Стир-
линга для логарифма факториала. Одна из форм этого соотноше-
ния следующая:
1пп! = п1пл—п,	(3-6)
если п достаточно велико. Сочетание уравнений (3-6) и (3-5) дает
lnu» = nlnn—n—Enzln(nz)4-En,;	(3-7)
так как п равно то
In w — п In п—Е tii In n,-.	(3-8)
Любое перераспределение частиц по энергетическим уровням
должно быть выполнено таким образом, чтобы общее число частиц
и общая энергия системы оставались неизменными.Условия, опре-
деляющие наиболее вероятное распределение частиц по энерге-
тическим уровням (или наиболее вероятное распределение энер-
гии среди частиц), таковы:
1.	Общее число частиц постоянно:
dn='Ldni — Q.
2.	Общая энергия системы постоянна:
de = Eez dnz = 0.
3.	In w максимальный:
d In w = — E In (nz) drij = 0.
Эти три уравнения могут быть скомбинированы по методу
неопределенных множителей Лагранжа. Первое уравнение надо
умножить на чистое число X, второе уравнение — на постоянную
р., имеющую размерность, обратную энергии; складывая три урав-
нения, получаем
X dn 4- pde 4- d 1 п w = 0;
EX dnt 4- E|*ez дп£—E In (nz) dn£ — 0;
E [X 4- |*ez—In n£] dn£ = 0.
96
Хотя все <)п( не являются иезпписимыми, однако можно доказать,
что каждое слагаемое в сумме должно был. ровно 0 и тогда
In ьу будет максимальным. Таким образом для каждого ела
гаемого
111  К р / <
nt •	(3-9)
Если параметры X и р вычислены, наиболее вероятное число ча-
стиц, имеющих данную величину энергии е, может быть опреде-
лено из уравнение (3-9).
3. Распределение Больцмана [17]
Небольшое изменение рассмотренного выше случая имеет
место, когда у нескольких энергетических уровней одинаковые
или почти одинаковые энергии. Вместо пх различимых частиц,
относящихся к одному уровню энергии elt имеется группа gt
различных уровней с энергией ех; п2 частиц относятся к группе
g2 уровней с энергией е2 и т. д. Внутри данной группы на отдель-
ном уровне нет ограничений для числа частиц. Общее число ча-
стиц равно Еп£; общая энергия в равна Ее,п,..
При занятии частицами первой группы gt энергетических
уровней 8j имеется g^ возможностей для первой частицы, так
как любая из первоначальных п частиц может занять любой из
gt уровней. Так как порядок занятия частицами группы уров-
ней, имеющие одинаковую энергию, несуществен, то произведение
дает число возможностей для первых двух частиц. Для nt частиц
на gi уровнях энергии ех число различных способов равно
i „х п — 1 п — 2	п — n, + 1
Ы gi—gi—--------g. —.
По сравнению с данными п. 2, число различных способов, кото-
рыми пг частиц могли бы быть распределены на gx уровнях энер-
гии ег, больше в gp раз, чем для частиц, расположенных на
одном уровне энергии ev
Распространяя этот вывод на распределение п частиц по k
группам энергетических уровней, получаем
«--(ft*)*
(n —nt —n2+ 1) (и —П,—Пд------nk+ 1)~
П2
w  ------———
nj п21 • •

"k
nin(gft)
П(пд)
(3-10)
7—1503
97
С помощью приближенной формулы Стирлинга для In (и!) имеем
1П№ Л1ПП Х/2/ In .
Si
Наиболее пероятное распределение можно найти при следующих
условиях:
1.	dn £ дп(» 0;
2.	di == £в,- dnt = 0;
3.	d In w — — £ п,- In ( -~Л dtii — 0.
\Si )	'
С помощью метода неопределенных множителей Лагранжа
можно найти, что
£ |к + ре£—Inf \ д^ — 0.
Т ак как каждый член суммы должен быть равным нулю, то
ln-^- = * + pv,
«z = gi е* е^‘ =	С3'11)
Это выражение отличается от уравнения (3-9) наличием мно-
жителя g{, который указывает на число уровней с энергией е,-
и называется фактором вырождения. Про соответствующий уровень
говорят, что он «^-кратно вырожден».
Уравнение (3-11) имеет форму закона Больцмана распределе-
ния энергии и закона Максвелла распределения молекул по
скоростям и известно как функция распределения Максвелла —
Больцмана.
4.	Распределение Ферми — Дирака [17]
В предыдущих разделах частицы считались фиксированными
в пространстве и, следовательно, были;отличимы одна от другой.
Однако это ограничение неприменимо для свободных электронов
в металле. Считают, что эти электроны имеют поступательную
энергию и могут свободно двигаться во всем объеме системы таким
же образом, как молекулы в газовой фазе; отсюда происходит
выражение «электронный газ», иногда применяемое для этого
типа систем. Поэтому электронные частицы следует рассматри-
вать как неразличимые. Однако в отличие от молекул газа, элек-
троны ограничены принципом запрета Паули, утверждающим,
что не может быть двух электронов с одинаковыми квантовыми
числами, а следовательно, с равными энергиями.
98
Дли •того случая рассмотрим группу изд, уровней >пергнн в,,
содержащих /ц частиц (щ < #,), вторую группу gt уровней эпср
гин eg, содержащих л, частиц, и т. д.; частицы теперь будем рас
сматривать неразличимыми и примем, что на уровне пе может быть
больше одной частицы. Для k групп общее число частиц равно
Еп,; общая эпср! пя равна Ее£л£.
При распределении частиц па уровнях первой i руппы первая
частица будет иметь gt различных возможностей своего размеще-
ния, поскольку она может быть на любом из gx уровней. Вторая
частица должна иметь (gt — 1) различных возможностей своего
размещения, если не учитывать того, что из-за неразличимости
частиц обмен первых двух частиц не дает нового состояния си-
стемы; следовательно, число различных способов для распреде-
ления первых двух частиц равно
gi(gi —1)
2
Число способов д^ля первых трех частиц составляет
gi (gi — В (gi —2) .
2’3’
число различных способов для лг частиц на gx уровнях в таком
случае составит
о — О (gt~ 2)	(gi —«14-1) .^_gj___
2	3	щ	nJCgi —«J!’
Подобное выражение можно получить для каждой группы
уровней; так как распределение в любой группе не зависит от
распределение в другой группе, общее число способов для
Используя приближенное соотношение Стирлинга
In (л£!), In (&!) и 1п(&— п£)!, получим
In W = 1 [g£ In gt —tli In nt—(gi — til) In (gi—nz)].
Распределение энергии, для которого w максимально,
найти из следующих условий:
1. Общее число частиц постоянно:
dn=Ednz —0.
Общая энергия постоянна:
de—Ее£йп£ = 0.
групп
(3-12)
для
легко
7*
99
3. hi ьу максимальный:
d In w « 4-1 In (	— 1 j dnt •» 0
Используя метод неопределенных множителей Лагранжа, пай»
дем
Е ^Х-|- |А8/ -f- In — 1 j дп( 0.
*
Так как каждый член суммы должен быть равен нулю, то
П1
ni =
gj
е е *+1
(3-13)
Эту функцию распределения впервые вывел Ферми, а затем
применил Дирак к свободным электронам металла; она известна
как распределение Ферми — Дирака и отличается от распреде-
ления Больцмана для различных частиц на член (4-1) в знаме-
нателе.
5. Распределение Бозе — Эйнштейна [17]
Статистический анализ для системы молекул идеального газа
подобен анализу для свободных электронов в металле, за исклю-
чением того, что нет ограничений для числа молекул газа, кото-
рые могут находиться на отдельном энергетическом уровне.
Как и ранее, рассмотрим систему, состоящую из группы gr
уровней энергии заполненных пг молекулами, второй группы
g2 уровней энергии е2, заполненных п2 молекулами, и т. д. При-
мем, что молекулы неразличимы и нет ограничений для числа их
на любом энергетическом уровне какой-либо группы. Общее чис-
ло молекул составляет Еи£. Общая энергия равна Еп£еР
При распределении молекул на уровнях первой группы первая
молекула будет иметь различных возможностей своего разме-
щения, поскольку она может быть на любом из gt уровне. Если
добавляется вторая молекула, то будет gt возможностей для
размещения обеих молекул на одном и том же уровне;
кроме того, вследствие доводов, приведенных в и. 4, будет gl^~-
возможностей для размещения этих молекул на различных уров-
нях. Следовательно, общее число способов, с помощью которых
две молекулы могут быть размещены на gx уровнях, равно
g,gl (1 + bfl) &£1.
too
Если добавляется третья молекула, то будет gt возможностей
для того, чтобы все три молекулы заполнили одни и тот же уро-
вень; g^gi— 1) возможностей, чтобы две молекулы находились
на одном и том же уровне н одна — на другом уровне, и
2	3
возможностей для того, чтобы все три молекулы находились на
разных уровнях. Рассуждения о двух молекулах, находящихся
вместе на одном уровне, и третьей — на другом уровне аналогич-
ны рассуждениям для двух различимых частиц. Пару молекул
можно рассматривать как одну частицу, которая отлична от од-
ной молекулы, трактуемой как вторая частица. Общее число
способов, которыми три молекулы могут разместиться на gt
уровнях, составит тогда
ft+g.tei-O+s,
После добавления четвертой молекулы появится gt возмож-
ностей для того, чтобы все четыре молекулы заполнили один и
тот же уровень, gt(gi — 1) возможностей, чтобы три молекулы
были вместе на одном уровне и одна молекула — на другом уров-
не, “ возможностей для того, чтобы две молекулы были
вместе на одном уровне и две другие молекулы — на двух различ-
ных уровнях, и, наконец,
„ (gi — О (gi —2) (gi —3)
Ki 2*3*4
возможностей, чтобы все четыре молекулы заняли четыре различ-
ных уровня. Число способов, которыми четыре различные моле-
кулы могли бы занять gx уровней, составит
й + gitei—1) + ?| lg‘7'1 + gi (8*~‘;te!~2) +
+g,	- g, [1 + fif-'] X
xz i i	Si—11 Г i । Si~ 1]_„	(gi+l)	(gi + 2)	(gi + 3)
x [' +	—4~]-£i	2	3	4	•
Распространяя эти рассуждения на молекул на gt уровнях,
найдем общее число способов
g. [' +	+ V][' +	••[> + ^]=
_ 0 tei + 1) (gi + 2) (gt + 3) (gt + щ — 1) = (gi + щ— QI
2	‘	3	’	4	n	«J (gi— 1)1 ‘
191
Для гвзов gi обычно намного больше, чем nlt н приведении»
выше вырвжение может быть зппрсапо как
+?)' „пи « Ъ 1.
Подобное выражение будет получено и для каждой другой
группы, так что общее w для k групп может быть записано с удо-
влетворительным приближением:
“,“П <Х"г’(3’И)
Используя приближенные соотношения Стирлинга, найдем
In tv = Е [(gr, + и,) In (gt + n,)—n{ In tii—gi In g J.
Наиболее вероятное распределение будет найдено при соблю-
дении условий:
1.	Общее число частиц постоянно:
dn — Е dtii — 0.
2.	Общая энергия постоянна:
de = Ее,- дп( = 0.
3.	In w максимальный:
d In w = Е In 4- 1 j drij — 0.
Используя метод неопределенных множителей Лагранжа,
получим
Е ре,- In -|- 1 j dnt — 0.
Т ак как каждое слагаемое этого выражения доджно быть равно
нулю, то
Si _ g—Hai_J.
ГЦ	’
>-A~_T-	(3-16)
Это распределение впервые вывел Бозе в 1924 г. для систем све-
товых квантов. Эйнштейн применил его к идеальным газам. Оно
известно как распределение Бозе — Эйнштейна и содержит в
знаменателе слагаемое (—1) вместо (4-1) в распределении Ферми —
Дирака.
102
6.	Распределение Больцмана как приближение
для неразличимых частиц
Общее число различных способов распределения для тех слу-
чаев, когда выполняются условия Ферми — Дирака,
w . П g.
2	3	Л/ *
Общее число различных способов распределения для тех слу-
чаев, когда выполняются условия Бозе — Эйнштейна,
___гт о (£<+1) (£<+2) (gi +3)	8i-\-ni—1
UT-llg, 2	.-3	- ----.
Если gt» nf, выражение для w в обоих случдрх сводится к
w=nei^-‘L	(3-16)
Это выражение для w аналогично тому, которое было найдено в
п. 3 для различимых частиц, деленному на постоянную величину
и!. Множитель п! не фигурирует в уравнении (3-16) вследствие
того, что частицы рассматриваются как неразличимые. Если это
приближенное выражение для w использовать для нахождения
наиболее вероятного распределения энергии, то получится выра-
жение, идентичное уравнению (3-11) для распределения Больц-
мана, так как постоянный множитель п! не влияет на величину
d In w. Таким образом, распределение Больцмана для различимых
частиц может быть использовано как приближенное выражение для
неразличимых частиц, когда gt » nz.
7.	Вычисление А
Параметр А может быть вычислен при условии, что
п = S nt.
Для распределения Больцмана
Таким образом, А может быть вычислена в функции общего числа
частиц и суммы, которая содержит слагаемые для каждого энерге-
тического уровня, который может занять каждая частица
системы. Эту сумму называют «суммой состояний частицы» и
определяют уравнением
i.^'Lgie^i.	(3-18)
103
Хотя тот ж<- общий принцип применен к распределениям Фер-
ми—Дирака и Бозе Эйнштейна, цппое алгебраическое выражение
для X не может Сыть получено.
8.	Поступательная сумма состояний
Сумма состояний, определяемая уравнением (3-18), содер-
жится во всех статистических термодинамических соотношениях.
В частности, поступательную сумдеу состояний используют при
вычислении параметра р.
Поступательные энергетические уровни частицы, заключен-
ной в ящике с размерами а, b и с, относительно основного нуле-
вого уровня выражаются уравнением (2-13):
. _ Г/ \* I / nV \* I { пг \а1
Если это выражение используют для определения энергетических
уровней, то каждый уровень энергии отличается от любого друго-
го уровня, а следовательно, фактор вырождения gt равен единице.
Сумма состояний для этого случая имеет вид
z = £ец,( = £ ехр (	\ exp (	\ ехр • (	.-г \
z ъе д,ехр^	) exp^ gm fc2 jexp 8m с2 )•
Величины
1	h2p /i2[x	Л2[л
8та2 ’ Smb2 И 8тс2
имеют очень малые численные значения, главным образом вслед-
ствие очень малого значения h. Оледркгтлъно, изменение на еди-
ницу квантовых чисел пх, nv и пг даст только очень незначитель-
ную разницу между значениями последующих членов рядов. При
этих условиях суммирование по всем энергетическим состояниям
очень близко к процессу интегрирования. Следовательно,
104
где v— объем системы, рпвиый abc. Значение ноступптельпой
суммы состонппй получнсгся относительно поступательного основ
кого пулевого энергетического уровня. Величина суммы состоя-
ний может быть получена относительно любого энергетического
уровня е0 умножением па фактор с’*’”.
9.	Вырождение поступательных энергетических
уровней
Хотя энергетические уровни для поступательного движения
по существу квантуются, они достаточно близки друг к другу,
чтобы их можно было рассматривать как непрерывный спектр
для вычисления суммы состояний. Логично рассматривать груп-
пу уровней как обладающих одинаковой или почти одинаковой
энергией. В пределе число состояний, имеющих одинаковую или
почти одинаковую энергию, эквивалентно числу состояний, имею-
щих энергию между е и в + de. Для того чтобы определить это
число состояний, их можно рассматривать как узлы решетки,
образованной тремя квантовыми числами пх, nv и пг, отложенных
по трем декартовым координатам. Каждый узел решетки с коор-
динатами пх, пу и пг представляет собой состояние системы.
При поступательном движении уравнение, определяющее си-
стему, таково:
а2 Ья с2 hB
Математически оно эквивалентно уравнению эллипсоида
о	СИЛ I
где р — величина, равная  .
Так как различие между энергетическими состояниями очень
мало, сумма всех энергетических состояний между 0 и е может
быть представлена почти как объем эллипсоида для положитель-
ных значений переменных (Квантованные числа являются дей-
ствительными и положительными целыми числами).
4	1
Общий объем эллипсоида ул abc р3. Только -у часть этого
объема определяется положительными значениями переменных,
так что число состояний, имеющих энергии между 0 и е, равно
з
1 4л / 8пк \ 2	,
I—З--(Т) йЪс-
Число состояний, имеющих энергии между е и в + de, можно
получить дифференцированием:
(3-20)
105
11одстявляя -то в выражение для суммы состояний и Заменив сум»
мирование интегрированием, получаем
f
ел
У Г 1
_ v	4nmvy2m I
«" L’gte*	—-j Ц e la9t-,
4nmvV 2m /"«
1	' 3J
2-(-(x)S
(3-21)
Это выражение тождественно уравнению (3-19).
1Q, Вычисление р
Параметр р теперь может быть вычислен из условия, что
E=Eezn,..	(3-22)
Средняя термодинамическая энергия получается с помощью функ-
ции распределения Больцмана; она точна для различимых частиц
и дает очень хорошее приближение для неразличимых частиц:
П{ = ек е,1г‘,
где
ек— —п—	и
r8ie^ z
Заменяя nz в уравнении (3-22), получаем
(3-23)
Дифференцируя z по р н считая объем постоянным, имеем
(3-24>
Следовательно, средняя термодинамическая внутренняя энергия
может быть целиком выражена в функции суммы состояний и
ее производной по р при постоянном объеме:
Е = 2L (	= п (	.	(3-25)
2 \ Л, \ d!J- )v
106
Средняя анергия поступательного движении молекулы идеаль-
ного газа теперь может быть вычислена из поступательной суммы
состояний	3 / 2пт \ 2	РГ) * 3 lnz«? In	j2	2 Inp + lno;	(3-26) 		J	(3-27) \ 01х /р	2 Р ’	'	’ Et=~-n-(	L\.	(3-28) \ /
Из кинетической теории газов известна средняя поступатель-
ная внутренняя энергия идеального газа
Et=~- nkT.
(3-29)
Сравнивая уравнения (3-28) и (3-29), можно сопоставить стати-
стический параметр и абсолютную температуру, определенную по
закону идеального газа, с помощью соотношения
{*=—(3-30)
Это соотношение показывает, что абсолютную температуру
можно интерпретировать как статистическое свойство, определяе-
мое поведением большого числа молекул. Сама по себе концеп-
ция ^температуры теряет свое значение, когда число молекул
мало. Например, вполне разумно измерять температуру газа
в объеме 1 фут3 (28,3 л) при обычном давлении, когда число мо-
лекул в этом объеме порядка 1010 или больше. Однако если в со-
суде создать вакуум до такой степени, чтобы в нем было только
10 молекул, то понятие «температура газа» потеряет смысл, по-
скольку число молекул недостаточно для обеспечения статистиче-
скою распределения энергии. Любой прибор, измеряющий тем-
пературу, введенный в сосуд, покажет температуру, определяе-
мую скоростями энергетического обмена (главным образом путем
радиации) между измеряемым прибором и стенками сосуда. Одна-
ко указанную этим прибором температуру нельзя рассматривать
как температуру 10 молекул газа в сосуде. Во всех последующих
уравнениях термодинамические свойства будут выражены в зна-
чениях абсолютной температуры Т вместо р.
107
11. Сумма состояний для жесткого ротатора
Сумма состояний может быть теперь выражена в функции тем-
пературы вместо (I с помощью уравнений (3-30) и (3-18):
z S gt exp (— J у	(3-31)
Сумму состояний жесткого ротатора можно вычислить из этого
выражения и квантового условия, выраженного для энергетиче-
ских уровней жесткого ротатора уравнением (2-29):
8^т /оч-О.
где / — целое число, значение которого лежит в пределах от 0
до оо. Учитывая, что каждый энергетический уровень вращения
(2/ 4- 1)-кратно вырожден,
x=S(2/+l)exp(-----1).	(3-32)
В этом случае, как и для поступательной суммы состояний, сум-
мирование может быть заменено интегрированием:
СО
Z
Й2 \
beikf ) / О’+1)
(3-33)
(2/+1)ехр
(3-34)
Уравнение (3-34) строго применимо к жестким двухатомным мо-
лекулам, в которых ядра различны. Для гомоядерных двухатом-
ных молекул с нулевым ядерным спином условия симметрии огра-
ничивают число энергетических уровней до половины уровней для
гетероядерных молекул. По этой причине сумму состояний, да-
ваемую уравнением (3-34), следует разделить на фактор о:
8л2/ kT
ah2 •
(3-35)
где о = 1 для гетероядерных двухатомных молекул и а = 2 для
гомоядерных молекул.
Вращательная сумма состояний для многоатомной нелинейной
жесткой молекулы может быть представлена аналогичным выра-
жением:
JL !
<WJT. (3-36)
108
где 1Х, 1у и глмвпые моменты инерции около трех иращптель*
пых осей. Число симметрии в дли нелинейной, многоатомной жест-
кой молекулы легко определить кик число неразличимых поло-'
жений, в которых молекула может находиться в результате про-
стого жесткого пращейия.
12. Сумма состояний для гармонического осциллятора
Сумма состояний для гармонического осциллятора может быть
вычислена по уравнению (3-31):
z = Egzexp
с помощью выражения для квантовых энергетических уровней
гармонического осциллятора (2-39)
ez = nz/iv,
где е(- отнесена к основному уровню -^-hv. Если рассматривать
колебательные уровни как невырожденные (т. е. щ = 1), то
г = Еехр(-^у	(3-37)
Так как постоянная Планка h входит в выражение (3-37) в первой
степени, то суммирование не может быть аппроксимировано инте-
грированием. В этом случае сумма может быть вычислена непо-
средственно с помощью математического соотношения
1	_Д-л .	(3-38)
так что
=	(3-39)
где
h.4
Х~ kT •
Пример 2. Определить распределение энергии по посту-
пательным энергетическим уровням для идеального газа.
Как было отмечено выше, энергетические уровни поступа-
тельного движения достаточно близки друг к другу, так что их
можно без большой погрешности рассматривать как непрерывный
спектр. При этом условии распределение энергии может быть вы-
ражено в функции доли общего числа частиц, обладающих энер-
гией между е и е + de. Число энергетических уровней с энерги-
ей между е и е + de дано уравнением (3-20) По уравнению (3-21)
вычисляют поступательную сумму состояний.
109
Подстановки этих уриинений в закон распределения Вольцмана
дает выражение для доли общего числа частиц, имеющих энергию
между е и е •+ de:	•
I
Т 
2 i е
Полагая, что г - т=-,
к!
ЧТ
-д- Л.
(АТ)2
d
d
dr.
Рис. 8. Заполнение поступательных
энергетических уровней
2	-L
На рис. 8 приведен график функции г2ё~' в зависимости
от г. Относительное число частиц с энергией, лежащей в задан-
ном интервале, изображается
частью площади между кривой
и осью г. Например, доля об-
щего числа частиц, имеющих
энергию между 0,5 kT и 0,6 kT,
определяется, заштрихованной
площадью, равной 0,48-0,1, или
0,048; т. е. 4,8% частиц имеют
энергию в этом интервале.
Для удобства энергетичес-
кие уровни можно разделить
на группы с интервалом энер-
гии 0,1 kT. Если непрерывная
кривая на рис. 8 аппроксиро-
вана ломаной линией с интер-
валом энергии 0,1 kT, значение
абсциссы для каждою верти-
кального отрезка, умноженное
на 0,1, представляет долю об-
щего числа частиц с энергией,
соответствующей данному ин-
тервалу энергии.
Область под кривой между
абсциссами, соответствующими
ординатам нуль и 1,0 kT, ука-
зывает на то, что около 41% частиц имеют энергию, лежащую в
интервале от нуля до 1,0 kT и аналогично область под кривой
между ординатами нуль и 4 kT указывает, что свыше 90% частиц
имеют энергию 4 kT или меньше.
Пример 3. Определить наиболее вероятное распределе-
ние энергии для системы несимметричных двухатомных жестких
8г.2/АТ
ротаторов, в которых —— равно 100. В соответствии с урав-
110
нениями (3-11) и (3-17) доля общего числи чиспщ на ка кдим
уровне
п _	‘
^8 it kT
Согласно уравнению (3-34), сумма состояний жесткого ротатора
„ V „ ~ ~kf 8п®/ kT	. nn
-	z=S^e	—&—=100.
Для жесткого ротатора фактор вырождения равен
giв 2/ +1
и энергетические уровни даны выражением
kT WlkT1”^4 100	•
Ниже приведены для каждого уровня целые числа / и соответст-
вующие им величины:
_ЛЖ)	_ /(/+!)_
1 ЛЖ) 27+1	(2/+1)е	100	1	7(7+1)	2/4-1	(2/4-1)«	100
0	0	1	1,00	16	272	33	2,17
1	2	3	2,94	17	306	35	1,64
2	6	5	4,70	18	342	37	1,20
3	12	7	6,21	19	380	39	0,97
4	20	9	7,36	20	420	41	0,61
5	30	11	8,15	21	462	43	0,43
6	42	13	8,55	< 22	506	45	0,29
7	56	15	8,57	23	552	47	0,19
8	72 .	17	8,29	24	600	49	0,12
9	90	19	7,73	25	650	51	0,08
10	ПО	21	7,00	26	702	53	0,05
И	132	23	6,14	27	756	55	0,03
12	156	25	5,25	28	812	57	0,02
13	182	27	4,35	29	870	59	0,01
14	210	29	3,54				z= 100,41
15	240	31	2,82				
Сумма 100,41 представляет действительное значение враща-
тельной суммы состояний и находится в близком соответствии с
приближенной классической суммой состояний, равной 100.
В этом случае числа в правой колонке для каждого энергетиче-
ского уровня представляют приближенно процент общего числа
частиц, имеющих соответствующую энергию (рис. 9).
Пример 4. Определить относительную плотность колеба-
тельных энергетических уровней системы гармонических осцилля-
торов, имеющих основную частоту 1 • 1013 цикл!сек при 300, 500 и
111
1000 К. Доля общего числа осцилляторов на данном энергетиче-
ском уровне дана выражением
ч ‘
nt е ~^Т
П	•/ »
1е~ *т~
где фактор вырождения энергетических
осциллятора принят за единицу. Для
уровней гармонического
каждого колебательного
=>вг
% с
и 6 
a
2
Рис. 9. Заполнение энерге-
тических уровней двухатом-
ного жесткого ротатора для
WIkTIh* = 100
о
S= е
20	00 60 ' 80 ' 1Q0
Число частиц, %
б
О
8
20	00	60 80 ЮС
Чцсло частиц, 7о
в
4 -
^1=^
Q~ 20 .00 60	80 100
Число'частицъЯв
Рис. 10. Заполнение энергети-
ческих уровней гармонического
осциллятора при:.
а—300 °К; б—500 °К: в—1000°К
энергетического уровня можн^ написать
е/	/iv
Тг —	х>
где п, — целое число.
Сумма состояний для системы гармонических осцилляторов
определяется уравнением (3-39)
— — -	1	е*
__ kr _ _________1_ = _®___
_ х__е_х
Для этой системы
ftv 6,624-10~27-Ы013 _ 477
Х~ kt ~	1,381-10-мГ Т '
График заполнения энергетических уровней гармонического
осциллятора при 300, 500 и 1000 °К показан на рис. 10.
JI2
Расчеты энергетических уровней гирмоничсскоги исциллятора
приведены в табл. 4.
	Таблица 4 ЭНЕРГЕТИЧЕСКИЕ УРОВНИ ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА					
"и	—ЬБ93 л в	и	л	—0.96В л е	и	ч л	-0,477 л t	0	J4 л
	Т-ЗОО °к, х—1.693, Z—1.253		Т-600 “К. Х-0.95Б. z-1.625		Г-1,000 °к, X—0,477, Z-2.630	
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 оо	1,000 0,202 0,041 0,008 0,002	0,798 0,161 0,033 0,006 0,002	1,000 0,384 0,148 0,057 0,022 0,008 0,003 0,001	0,615 0,236 0,091 0,035 0,013 0,003 0,002	1,000 0,620 0,384 0,238 0,148 0,092 0,057 0,035 0,022 0,013 0,008 0,005 0,003 0,002 0,001	0,380 0,236 0,146 0,091 0,056 0,035 0,022 0,013 0,008 0,005 0,003 0,002 0,001
Z	1,253	1,000	1,625	1,000	2,63	1,000
Задачи
1.	Сколькими способами можно расположить систему из девяти различных
частиц в трех сосудах так, чтобы первый сосуд содержал две частицы, второй
сосуд содержал три частицы и третий сосуд — четыре частицы?
р
2.	Какова средняя поступательная кинетическая энергия — молекулы
п
идеального газа при 300 ° К (эрг)?
По рис. 8 определить, на каком поступательном энергетическом уровне
наибольший процент частиц.
F
3.	Какова средняя энергия двухатомного жесткого ротатора-?
п
Какова средняя энергия нелинейного многоатомного жесткого ротатора?
4.	По рис. 9 определить, каково значение / вращательного уровня, на
котором наибольшее число частиц.
Для какого значения / на вращательном энергетическом уровне будет наи-
большее число частиц, если двухатомная вращательная сумма состояний рав-
на ’200?
8—1503
ГЛАВА 4
Статистическое вычисление
термодинамических функций
Термодинамические функции определяются наблюдаемыми мак-
роскопическими свойствами системы. Макроскопические свойства
определяются свойствами и статистическим поведением молекул
в системе. Все молекулярные и статистические данные, необхо-
димые для вычисления термодинамических функций, содержатся
в сумме состояний, определяемой уравнением (3-31):
z = Sg-,exp
Вычисление суммы состояний позволяет определить все тер-
модинамические свойства.
Для того чтобы вычислить сумму состояний, нужно иметь све-
дения, относящиеся к энергетическим уровням молекул в системе.
Данные по термическим энергетическим уровням вращения и ко-
лебания могут быть получены из рамановских, инфракрасных и
ультрафиолетовых спектров. Ультрафиолетовый спектр и спектр
рентгеновских лучей дают сведения об электронных энергетиче-
ских уровнях. Так как спектроскопическое определение энергетиче-
ских уровней исключительно точно, то предпочитают эти данные.
Для некоторых классов соединений, в частности углеводородов,
такие данные используют для вычисления термодинамических
функций в известных температурных пределах.
Хотя в настоящее время даже спектроскопические данные не-
достаточны для обычного применения этих расчетов ко всем ве-
ществам в широком диапазоне условий, тем не менее значения
термодинамических функций для состояния идеального газа
могут быть с большой точностью использованы при расчете
суммы состояний для поступательного движения, жесткого вра-
щения и гармонического колебания, если незначительно влияние
одного вида энергии на другой. Вычислять термодинамические
функции для неидеального газового, жидкого и твердого состоя-
ний удобнее всего с помощью эмпирических уравнений состояния.
114
1. Внутренняя (пергия
Внутренняя жергия системы из п частиц может быть выражена
в функции энергетических уровней отдельных частиц и абсолют
ной температуры с помощью уравнений (3-18), (3-23) и (3-30).
_ *Z
Е = п*81*1'-^-.	(4-1)
Обозначив
г= >	(4-2)
и полагая п равным числу частиц в 1 моле, мольную внутреннюю
энергию можно выразить следующим образом:
E = RT (4’3)
где — nk для 1 моля.
Внутренняя энергия может быть также выражена в функции
суммы состояний согласно уравнениям (3-25) и (3-30). Для 1 моля
Е = ЯтЧ-дт-\ .	(4-4)
Численные значения поступательных, вращательных, колебатель-
ных и электронных энергетических уровней, определенных по
спектроскопическим данным или вычисленных с помощью кван-
товой механики, обычно выражают относительно самого низкого
или основного уровня молекулы. Если такие значения используют
для вычисления внутренней энергии, полученная внутренняя
энергия представляет собой избыточную энергию относительно
основного состояния системы, когда все частицы находятся на
самом низком энергетическом уровне при температуре абсолют-
ного нуля. Для процессов, в которых общее число частиц данных
молекулярных объектов остается постоянным, изменения внутрен-
ней энергии могут быть вычислены без сведений об основном со-
стоянии. Однако если число частиц данных молекулярных объек-
тов изменяется, как в химической реакции, то для вычисления
изменения внутренней энергии процесса должна быть известий
разность между основными состояниями различных соединений.
При отсутствии конкретных спектроскопических данных о
молекулярных энергетических уровнях внутренняя энергия мо-
жет быть вычислена с достаточной степенью приближения из
поступательных, энергетических уровней частицы в ящике (или
потенциальной яме), вращательных энергетических уровней жест-
кого ротатора и колебательных уровней гармонического осцилля-
тора. Так как поступательные энергетические уровни вычисляются
8*
115
в свободном от поля пространстве, их применение ограничено
системами, приближающимися к состоянию идеального газа, в
которых силы притяжения между «молекулами незначительны.
1. Поступательная составляющая мольной внутренней энер-
гии идеального газа может быть вычислена непосредствен ной
подстановкой уравнения (2-13) для поступательных энергетиче-
ских уровней в уравнение (4-3). Как уже говорилось в гл. 3 п. 8,
суммирование при вычислении суммы состояний может быть за-
менено достаточно точно интегрированием для всех масс, ббльших
массы атома водорода, и для температур, ббльших, чем несколько
градусов Кельвина. В этом случае поступательную составляющую
мольной внутренней энергии идеального газа наиболее просто
вычислить с помощью клас-
сической суммы состояний
по уравнению (3-19) с р,
I 1
равным ( —^-1:
з_
* 12пт kT \ 2
z. — I —»,8— 1	&’>
'	\ h2 )
lnzz —-g-ln +
Q
_|_ -g- In T + In v.
Рис. И. Внутренняя энергия и теплеем- Подстановка этого соотноше-
кость двухатомного жесткого ротатора ния в уравнение (4-4) дзет
в зависимости от величины i>~2IkTlh2	'
RT, (4-5)
которое совпадает с классическим значением внутренней энергии
одноатомого идеального газа.
Вращательная составляющая мольной внутренней энергии
двухатомной молекулы, приближенно принятой жестким ротато-
ром, может быть вычислена подстановкой выражения для энер-
гетических уровней, данных уравнением (2-29), в уравнение (4-3).
Для этого случая
е / К2 «
r==~kT= Ьк21 kt i 0+0
и
§. = 2/4-1.
Внутренняя энергия двухатомного жесткого ротатора представ-
лена как функция температуры на рис. 11. Расчеты иллюстриро-
ваны примером 1.
Эти расчеты показывают, что для всех температур свыше той
8л2/й	Е	'
когда —-------Т — 5, значение приближаете я к классической
величине, равной единице.
116
Так кик нее двухатомные молекулы, кроме водорода, имеют
момент и перин и, равный 1 (г/молъ)А* или больше, классическая
величина является достаточно точным приближением для всех
температур свыше ~120 К и только в редких случаях она спра-
ведлива для температур свыше 50 *К.
Классическое значение можно получить непосредственно.
если вышеприведенное суммирование аппроксимировано интегри-
рованием. Эта предельная величина наиболее удобно вычисляется
подстановкой классической
вращательной суммы состоя-
ний, данной уравнением
(3-35), в уравнение (4-4).
Таким образом,
№IkT
ahs ’
8-2/Л
/gjnzr\ _ 1
I дТ I T 
X	/О
Подстановка этого соотно-
шения в уравнение (4-4) для
1 моля дает
Ет = КТ. (4-е)
Рис. 12. Внутренняя энергия и тепло-
емкость гармонического осциллятора в
зависимости от величины 1/х =
=(А/Ь)Т = Т°К/ 1,438 w см-i
Аналогично, если классическую сумму состояний для нелиней-
ной жесткой молекулы, данной уравнением (3-36), подста-
вить в уравнение (4-4), то
£, = 4^’	<4-7>
Так как сумма состояний для гармонического колебания может
быть легко вычислена без аппроксимирования, то составляющая
внутренней энергии на каждую степень свободы гармонического
колебания может быть вычислена непосредственно подстановкой
уравнения (3-39) в уравнение (4-4). Таким образом,
1
117
Испильзошише уравнения (4-4) в расчете на I моль дает
£ <4*»)
где к равно для каждой степени свободы гармонического коле-
бания. Эта функция представлена иа рис. 12.
Величина, заключенная в уравнении (4-8) в скобки, изменяет-
ся от 0 до 1 и зависит при этом от частных значений v и Т. Для
данного значения v величина в скобках приближается к нулю по
мере приближения Т к нулю (х-*оо); эта величина приближается
к единице по мере приближения Т к бесконечности (х-* 0).
В сложных молекулах, содержащих шесть и более атомов, не-
сколько атомов могут вращаться как группа вокруг оси связи по
отношению к остальной части молекулы.
Такое движение называется внутренним вращением. Сумма
состояний для одной такой группы, вращающейся свободно вокруг
оси связи, дается соотношением
।
/8^прйТ\2
zCB=^-A-^—	(4-9)
Приведенный момент инерции аналогичен приведенной массе и
вычисляется как
(4-Ю)
где IА — момент инерции вращающейся группы;
1В — момент инерции остальной части молекулы (каждый мо-
мент инерции отнесен к оси связи вращения);
п — число симметрии вращающейся группы по отношению
к оси связи вращения.
Например, вращение одной метильной группы по отношению
к остальной части молекулы углеводорода (в частности, этана)
вокруг связи углерод — углерод характеризуется числом сим-
метрии, равным трем.
Вообще, внутреннее вращение не является свбодным, а затруд-
нено потенциальным барьером. Для очень большого потенциаль-
ного барьера внутреннее вращение вырождается во вращательное
колебание, для которого сумма состояний приближается к урав-
нению (3-39). Следовательно, величина суммы состояний для внут-
реннего вращения будет изменяться между максимальной вели-
чиной для свободного вращения, выраженной уравнением (4-9),
и минимальной величиной, равной единице, для сильно затруд-
ненного вращения, выраженной уравнением (3-39), когда v (а
следовательно, и х) достаточно велико. Вычисление суммы состоя-
118
ifiiй для промежуточного случим несколько сложно и не рлссматрн
ается. Однако методы расчета составляющей заторможенного
прощения для теплоемкости и шгропии будут продстиплсны "
пн. 2 и 7.
Составляющая мольной внутренней энергии каждого свобод-
ного внутреннего вращения может быть вычислена подстановкой
суммы состояний, выраженной уравнением (4-9), в уравнение
(4-4):
/dlnzCI)\ 1	1
\ дт )v~ Т •
Есв = ~2-^Т.	(4-11)
2. Теплоемкость
Теплоемкость при постоянном объеме определяется равенством
Выражение для теплоемкости в функции энергетических уровней
и абсолютной температуры может быть получено дифференцирова-
нием уравнения (4-1) по температуре при условии постоянного
объема:
__ S gj г2 е~'__/ Z gj re-r \2
R ^gie~r '£gie~r ) •
(4-12)
где
г
ч
kT •
Теплоемкость какого-либо вещества может быть вычислена
прямой подстановкой значений энергетических уровней в урав-
нение (4-12). В настоящее время наиболее точным методом опреде-
ления теплоемкости является метод, основанный на определении
энергетических уровней с помощью спектроскопических данных.
При отсутствии достаточного количества спектроскопических
данных теплоемкость идеального газа можно вычислить, прибегая
к приближенным допущениям о жесткости ротатора и гармониче-
ском осцилляторе путем использования выражений (2-29) и (2-38)
квантовой механики для энергетических уровней соответственно.
Расчеты теплоемкости для жесткого ротатора иллюстрированы
примером 1. Эти вычисления указывают, что теплоемкость двух-
атомного жесткого ротатора приближается к классической ве-
личине 7? для значения Т, большего, чем 1,25. Для всех
газов, кроме водорода, классическое значение является достаточно
точным приближением для всех температур выше 50 ”К.
119
Пример 1. Вращательную составляющую внутренней
энергии для жестких двухатомных молекул можно вычислить по
уравнению (4-3), используя уравнение (2-29) для вычисления
энергетических уровней:
£	1 gi re-r
RT 3 igTF7'1
где
fssWAr/(/+1) И &-2/ + 1.
Вращательная составляющая мольной теплоемкости жесткой
двухатомной молекулы может быть вычислена по уравнению (4-12):
Cv _ £gzz-2e~r_/ S gt re ' \2
Я ^gie~f \%gie-r ) ‘
Суммы в этих уравнениях вычислены ниже для случая, когда
rr. <	_	...	. ч
~h2—T=l и г==/(Л-1):
/	Si	Г	Г е	Si Г е	ег	gj^ Г е
0	1	0	1,00	1,00000	0	0
1	3	2	7,40	0,40600	0,8120	1,624
2	5	6	4,05-102	0,01230	0,0740	0,444
3	7	12	1,64-106	0,00004	0,0005	0,006
1,41834	0,8865	2,074
Подставляя
сумму в вышеприведенные уравнения, получаем
Е 0,8865 л сос
Я7 = Mi83= °’626
и
Со = 2J374 _/0,8865 \2 _
R ~ 1,4183	\1,418з) ~
Подобные вычисления могут быть выполнены для других значе-
8п2/А
ний	—Т и представлены графически, как показано на рис. 11.
Эти вычисления указывают, что величина возрастает от нуля
при абсолютном нуле температуры до масимального значения,
8те27й
равного '"-'1,1, когда——Т равно 0,8; затем приближается к
8п2/й
единице для значений —— Т, больших, чем 1,25. Для всех га-
зов, кроме водорода, температура в этой точке меньше, чем 50 °К.
Подобные вычисления для поступательной составляющей те-
плоемкости с использованием выражения квантовой механики для
120
икр i этических уровней указывают, что классическая величина
теплоемкости достаточно точна при температурах выше К)'К*
Следовательно, для всех температур выше, чем 60 ‘ К, суммы в
уравнении (4-12) могут быть приближенно замшены интегралами
и классическую поступательную и вращательную составляющие
теплоемкости идеального газа можно вычислить с помощью при-
ближенных классических поступательной и вращательной сумм
состояний по уравнениям (3 19) и (3-35) соответственно.
Теплоемкость может быть выражена в функции суммы состоя-
ний либо подстановкой уравнения (3-31) в уравнение (4-12), либо
дифференцированием уравнения (4-4) по температуре при условии
постоянства объема:
Ср = /?Гтг(^а2\ Н-2Т
\	iv
V.
(4-13)
Классические значения поступательной и вращательной со-
ставляющих теплоемкости идеального газа могут быть вычислены
подстановкой соответствующих классических сумм состояний в
уравнение (4-13). Вместе с тем те же выражения можно получить
дифференцированием по температуре приближенного классиче-
ского выражения для внутренней энергии в функции температуры
при условии постоянства объема.
Дифференцирование уравнения (4-5) по температуре при по-
стоянном объеме дает классическую поступательную составляю-
щую для мольной теплоемкости идеального газа:
(CD)Z =	7? як 3 калЦмоль  °К).
(4-14)
Дифференцирование уравнения (4-7) по температуре при по-
стоянном объеме дает классическую вращательную составляющую
мольной теплоемкости для жесткой линейной молекулы:
(Ср)г = R як 2 калЦмоль • °К).
(4-15)
Дифференцирование уравнения (4-7) по температуре при посто-
янном объеме дает классическую вращательную составляющую
мольной теплоемкости для жесткой нелинейной - многоатомной
молекулы:
(Ср)г=-|-₽~Зксл/(люльоК).	(4-16)
Составляющая мольной теплоемкости на каждую степень сво-
боды гармонического колебания может быть получена подстанов-
кой в уравнение (4-12) квантово-механического выражения (2-38)
для энергетических уровней или подстановкой в уравнение (4-13)
суммы состояний гармонического осциллятора по уравнению
(3-39) или же наиболее легким способом — дифференцированием
121
у равнения (4-38) по температуре при постоянстве объема. Резуль-
татом в каждом случае будет
<>/Ц(ЛГ1)«]’	<4-17>
Av
где х = -gjr. Величина функции, заключенная в скобки в уравне-
нии (4-17), изменяется от нуля при низких температурах (комнат-
ная температура и ниже) до единицы при очень высоких темпера-
турах. Вычисление теплоемкости для гармонического осциллятора
приведено в примере 2.
Пример 2. Колебательная составляющая внутренней
энергии гармонического осциллятора определяется выражением
Е _ х
RT ~ ех — Г
/w	-
где х — а колебательная составляющая теплоемкости гар-
монического осциллятора
Cv __ х2е*
~R~ ~ "(ех—I)2*
Эти величины изображены на рис. 12 как функции
1 kT Т	orz „
--=-7— = , Лоё~(Т в Ков см х).
х Нч	1,438(0'	’	'
Расчеты показывают, что теплоемкость увеличивается от нуле-
вого значения при температурах абсолютного нуля до значения,
приближающегося к единице, для значений ~ > 2,0. Для колеба-
тельного волнового числа 1000 см"1 эта точка соответствует тем-
пературе ~300 °К, для колебательного волнового числа 500 см"1
эта точка соответствует температуре 1500 °К.
Кривая также показывает, что при комнатной температуре
300 °К колебательная составляющая теплоемкости меньше 0,15 7?
для колебательного волнового числа большего, чем 1000 см"1.
Колебательная теплоемкость возрастает с увеличением темпера-
туры, ио понижается с увеличением волнового числа.
Уравнение (3-17) также можно применить к теплоемкости твер-
дого вещества, если принять, что только колебательная энергия
существенна и что все виды колебания одинаковой частоты. В этом
случае теплоемкость для трех колебательных степеней свободы на
моль может быть выражена равенством
(е*—1)2’
которое является уравнением Эйнштейна для теплоемкости твер-
дого простого вещества. Согласно этой теории, все твердые простые
вещества должны иметь одинаковую теплоемкость, если сравнивать
122
их при одной и той ж< величине х. Эти теория опраодынмтся для
температур выше 20 "К. Ниже 20“К предсказанные теорией вели-
чины оказываются ниже экспериментальных. Для высоких тем
ператур величина становится малой и теплоемкость приближается
к максимальной величине, равной 3 /? для всех веществ, что нахо-
дится в соответствии с историческими наблюдениями Дюлонга
и Пти.
Для температур, близких к абсолютному нулю, следует при-
менять теорию Дебая для теплоемкости твердых тел. Эта теория
принимает во внимание колебательные частоты в пределах от нуля
до максимальной величины vm, определяемой размерами твердого
кристалла. Согласно этой теории, приближенное уравнение для
мольной теплоемкости твердого кристалла в области, близкой к
абсолютному нулю, ^южет быть выражено формулой
где 0 — параметр, равный для данного вещества. Теория
Дебая предсказывает, что теплоемкость кристаллических веществ
должна быть пропорциональна кубу абсолютной температуры в
области, близкой к абсолютному нулю. Для высоких температур
эта теория также предсказывает величину теплоемкости, прибли-
жающуюся к 3 7?, в соответствии с экспериментальными наблю-
дениями.
Составляющая теплоемкости, относящаяся к свободному внут-
реннему вращению, может быть получена дифференцированием
уравнения (4-11) по температуре при условии постоянства объема:
(Qcb = ^-^-	(4-18>
Для сильно затрудненного вращения эта составляющая прибли-
жается к величине, выраженной уравнением (4-17) для гармони-
ческого колебания. Составляющая теплоемкости, соответствующая
внутреннему вращению для промежуточных потенциальных
барьеров, была вычислена Питцером и Гвином (29, 34]. Резуль-
таты их вычислений представлены на рис. 13 в виде зависимости
суммы состояний, полученной по уравнению (4-9) для свободного
вращения, от величины где V — потенциальный барьер для
внутреннего вращения и Т — абсолютная температура.
При температурах выше 50 °К величины поступательной и вра-
щательной составляющих внутренней энергии и теплоемкости со-
ответствуют классической теории равномерного распределения
энергии, согласно которой на каждую степень свободы приходится
V2 RT внутренней энергии. Однако вопреки классическому вы -
воду о том, что две степени свободы или RT внутренней энергии
приходятся на каждое колебание по уравнениям (4-8) и (4-17),
123
следует, что вся колебательная составляющая внутренней анергии
равна RT и теплоемкости 7? только при бесконечно высокой тем-
пературе. Эти выражения находятся fi соответствии с экспери-
ментальными наблюдениями, согласно которым для большинства
веществ колебательная составляющая внутренней энергии и теп-
лоемкости незначительна при комнатной температуре и ниже ее
и приближается к максимуму только при высокой температуре.
. Д Чтобы вычислить колебательную составляющую теплоемкости,
.необходимо знать частоту каждого вида колебания в молекуле.
Рис. 13. Составляющая теплоемкости (Cp)hr, со-
ответствующая внутреннему вращению для про-
межуточных потенциальных барьеров [29, 34]
Такие данные могут быть получены с помощью анализа инфра-
красных и рамановских спектров. Согласно уравнению (2-32),
•собственная частота гармонического осциллятора характери-
зуется выражением
где k — силовая постоянная;
р. — функция двух масс осциллятора, равная —.
Имеющиеся в наличии данные указывают, что силовая постоянная
отдельной связи незначительно влияет на всю структуру молекулы.
Если массы осциллятора таковы, что тх намного меньше т2,
то величина р, почти равна величине т1( так что величина
практически не влияет на р. Например, если осциллятор пред-
ставляет собой Н — CR3, величина р- по существу равна массе
атома водорода, независимо от структуры группы —CRa.
Так как силовая постоянная почти не зависит от структуры
группы —CR3, то частота колебания связи Н—С по существу оди-
накова во всех молекулах. Это обобщение может быть распростра-
124
иено на ряд других встречающихся связей. Однако следует быть
осторожным при расширении итого обобщения на случаи, когда
две массы осциллятора имеют величины одного порядка.
Наблюдение характеристических частот связи приводит к
представлению о колебаниях растяжения связей и о колебаниях
в изгибании связей. Колебание растяжения связей рассматри-
вается как периодическое изменение длины связи, и колебание
изгибания рассматривается как периодическое изменение угла
связи. Эта классификация имеет большое значение в тех случаях,
когда молекула содержит только несколько атомов и не приме-
нима к сложным многоатомным молекулам.
Численные значения силовой постоянной и характеристиче-
ские частоты свяли для ряда широко известных связей представле-
ны в табл. 5 [22]. Силовая постоянная является непосредственной
мерой величины силы связи. Следует заметить, что силовые по-
стоянные для ординарных, двойных и тройных связей углерод —
углерод очень близки к отношению 1 : 2 : 3. Вследствие весьма
высоких численных значений частот молекулярных колебаний
характеристические частоты связи, представленные в табл. 5,
выражены через волновое число (ш), определяемого как частота
(v), деленная на скорость света, или как величина, обратная
длине волны:
® = 3.10Ю = ~х~см	(4-19)
В значениях волнового числа величина х, содержащаяся в
выражении колебательной составляющей внутренней энергии и
темплоемкости, становится равной <
_ Ь _ 6,624.10-г7.3-1010-а>
kT 17381 .lO-i’T ’
1,438о>
- т
(4-20)
Для более детального ознакомления с вопросом о колебатель-
ных частотах тех или других молекул см. работу Герцберга «Инф-
ракрасные и рамановские спектры» и «Спектры двухатомных мо-
лекул» [22].
Пример 3. Определить теплоемкость окиси углерода при
300, 1000, 1500 и 2000 °К как идеального газа при давлении 1 атм.
Окись углерода является двухатомной молекулой, имеющей три
поступательных степени свободы. Поступательная составляющая
з
теплоемкости при постоянном объеме равна -у А? и вращательная
составляющая равна R при всех температурах выше 50 °К. Так
как Ср идеального газа равна Cv + R, Ср окиси углерода может
быть вычислена как 3,5 R плюс колебательная составляющая.
125
Твблици В
СИЛОПЫГ ПОСТОЯННЫЕ и ХАРАКТЕРИСТИКА ЧАСТОТЫ СВЯЗИ [22]
Килсбання растяжении			Ишписиие угли синий	
связь	К-Ю‘» t)UH/CM	<i), t М 1	связь	ш, см 1
—с—н	4,79	2960		
=с-н	5,10	3020	/•••••у н czc-h	1000
=с—н	5,85	3300		
—0—н	7,66	3680	X X А / Ml	1100
—N—Н	6,35	3350		
-S-H	—	2570	X /1 ! ° 41	700
с	4,50 9,6	900 1650		
* \с=с			XXX VI/ о 1 о	1450
—с=с	15,59	2050		
с=о	18,53	2143	ЛН с 1	1450
				
\с=О	12,1	1700	о .•111 м о	300
126
Про^>ляевние таОл. Б
Колебании растяжении	। Илменениа угла синаи
свпэь	к-II)"» OllHltM	W, слТ*	саявь	W, см
			хн	
—GtN	17,73	2100	о }	
			Н	.1600
—С—F	5,96	1100		
-С-С1	3,64	650		
				330
—С—Вг	3,13	560	с J	
			^С1	
^С—J	2,65	500		
Колебательная составляющая теплоемкости, вычисленная для
каждой температуры, представлена ниже для основного волнового
*|ирла 2143 см'1 для связи С=О.
т°, к	X	(экспери- ментальная)	/ р (рассчитанная)	Ср («1
300	10,272	0,003	3,503/2=6,97	6,97
1000	3,082	0,479	3,979 7?=7,91	7,93
1500	2,054	0,712	4,212/2=8,37	8,42
2Q0P	1,541	0,823	4,323/2=8,59	8,67
Примечание.		С вычислена в Р	кал/(моль-°Ю-	
Пример 4. Определить теплоемкость водяного пара при
300, 1000, 1500 и 2000 °К как идеального газа при давлении 1 атм.
Молекула водяного пара представляет собой трехатомную моле-
кулу, имеющую три поступательных степени свободы. Поступа-
тельная составляющая теплоемкости при постоянном объеме
3	3
равна -g-/? и вращательная составляющая равна -у/? при всех
температурах выше 50 °К. Так как Ср идеального газа равно
Ср + R, Ср Н2О может быть вычислено как 4/? плюс колебатель-
ная составляющая.
127
Молекула водяного пара имеет три колебательных степени
свободы, из которых две относится к растяжению связей и одна —
к изменению уела связи. Колебательная составляющая теплоем-
кости для каждой температуры вычислена ниже для основного
волнового числа, равного 3700 см-1, относящегося к растяжению
связи О—Н, и волнового числа 1600 ел"1, относящегося к изме-
нению угла связи.
>
Растяжение связи
г. °к	х= 1.438-3700/Г	
300	17,735	——
1000	5,321	0,278 7?
1500	3,547	0,767 7?
2000	2,660	1,144 7?
Изменение угла связи
Т. СК 1,438-1600/T
300	7,669
1000	2,301
1500	1,534
2000	1,150
__1
(/-I)2 ]
0,027 7?
0,655 7?
0,825 7?
0,897 7?
т. »к	(эксперимен- тальная)	. р (рассчитанная)	СР 1471
300	0,027 7?	4,027 7?=8,00	8,03
1000	0,933 7?	4,933 /?=9,80	9,86
1500	1,592 7?	5,592/?=11,11	11,13
2000	2,041 7?	6,041 7?=12,00	12,01
•Примечание. С& вычислена в калЦмоль-^К}.
3.	Число размещений для наиболее вероятного
распределения
Хотя распределение энергии по Больцману может быть исполь-
зовано как для различимых, так и для неразличимых частиц,
число способов, которыми осуществляется это наиболее вероят-
ное распределение энергии, зависит от того, являются частицы
различимыми или неразличимыми.
Для различимых частиц число способов, которыми может осу-
ществляться данное распределение энергии, представлено урав-
нением (3-10):
w = п! П —г-
128
Используя приближенное соотношение Стирлинга для логарифма
факториила в виде равенства (3-6), имеем
1﹫«п1пп-}- Е п{ In	(4-21)
Число способов, при которых имеет место наиболее вероятное рас-
пределение энергии, может быть найдено подстановкой закона
распределения Больцмана для tit в уравнение (4-21). Распреде-
ление Больцмана для nt может быть выражено в функции суммы
состояний с помощью уравнений (3-11), (3-17), (3-18) и (З-ЗО):
•/
^~~g^kT.	(4-22)
Полагая, что W — число способов, которыми осуществляется
наиболее вероятное распределение, принимаем
_ *< *<
lnW = nlnn + -^ Zgie ^ln-^-е^.
in W = п In п + In	Е glе~	-J- £ gl е~
Используя уравнения (3-31) и (4-1), имеем
z F
1п)^ = п1пп+п1п — +-^-;
lnlF=lnz«(4-23)
Сумма состояний для п различимых частиц может быть определена
как	*
Z = zn.	(4-24)
В функции суммы состояний для системы из п различимых частиц
ln№ = lnZ+-.	(4-25)
Для системы	неразличимых частиц	приближенное	выражение
для числа способов,	реализующих данное	распределение энергии,
дано уравнением (3-16):
где gl » nt.
Применив приближенное соотношение Стирлинга для ln(nfl),
найдем
1пщ= Enz рп — 4- lj.
Если уравнение (4-22) закона распределения Больцмана исполь-
зовать для замены п<( то число способов, которыми достигается
9—1503
129
наиболс. вероятное распределение энергии, удовлетворяет соот-
ношению
1,,иХ",п7Г+\%	(4-26)
Определив сумму состояний для системы из п неразличимых
частиц равенством
zn
пГ’
Z
(4-27)
уравнение (4-26) можно написать в той же форме, что и уравнение
(4-25):
In U7 = In Z+	(4-28)
Этим теоретическое развитие статистической термодинамики
завершено. Уравнение (4-28) содержит все основные сведения, ко-
торые термодинамика может дать относительно свойств системы
и обеспечить логическую основу для всех термодинамических
анализов. Сумма состояний Z определяется энергетическими
уровнями, абсолютной температурой и общим числом частиц,
составляющих систему; величина W определяется видом распре-
деления энергии системы среди различных частиц, т. е. числом
частиц на каждом дискретном энергетическом уровне.
Хотя величины 1Г и Z теоретически очень важны, однако они
слишком громоздки для практического применения. Следовательно,
необходимо представить их связанными с более удобными и упо-
требимыми величинами тех или иных свойств.
4.	Изменение энергии в замкнутой однофазной
системе определенного состава
Явное выражение для внутренней энергии в функции W, Z и Т
может быть полу^рно преобразованием уравнения
E = AT(lnU7—InZ) = /feTln^-.	(4-29)
Согласно правилу фаз Гиббса, состояние замкнутой однофаз-
ной системы фиксированного состава может быть полностью опре-
делено двумя независимыми переменными. Следовательно, изме-
нение внутренней энергии такой системы можно выразить мате-
матетически как функцию изменения температуры и объема:
Изменение внутренней энергии может быть выражено в функ-
ции изменения W и Z путем нахождения частных производных
130
уравнения (4-29). Дш|х|к рсицировапне уравнения (4-29) но тем
пературе при постоянном объеме дает
T^^^dT+(k\nW)dT-kT х
х ( dT—(Л In Z) с/Г.
Используя уравнения (4-4) и (4-29) получаем
/ dE \ Tidk\n}X/\	.
\^)od7^T\~dT~)vd1’	(4'31)
Дифференцируя уравнение (4-29) по v при постоянной темпера-
туре, имеем
(М2)
С помощью уравнений (4-31) и (4-32) получаем
dE = Td(k In W) — kT	j dv.	(4-33)
Согласно первому закону термодинамики, замкнутая система
может испытывать изменение внутренней энергии только в резуль-
тате обмена теплотой и работой с окружающей средой. Так как
для этой системы изменение объема указывает на передачу энергии
в форме работы, то второе слагаемое уравнения (4-33) можно отож-
дествить с работой, обратимо выполненной системой. Ограничение
в виде обратимости необходимо, так как коэффициент при dv
представляет собой свойство системы, а именно — давление си-
стемы:
Рсист^^(-^г)г.	(4-34)
Произведение давления системы на dv представляет собой ра-
боту, выполненную системой только при обратимом пропессе.
Если второе слагаемое уравнения (4-33) рссматривать как об-
ратимую работу, выполненную системой, то первое слагаемое
можно рассматривать как теплоту, сообщенную системе при том
же обратимом процессе:
8<?обР = ^1пГ.	(4-35)
5.	Теплота
Отождествление теплоты, сообщенной системе во время обра-
тимого процесса, с Tdk In W дает наглядное представление о
превращении теплоты во внутреннюю энергию. Так как W опре-
деляется числом частиц на каждом энергетическом уровне, вели-
чина W может быть изменена перемещением частиц с одного уров-
ня на другой. Следовательно, добавление теплоты системе уве-
9*
131
личипает IV и рнутрсникио -игргию системы, вызывая перемещение
части с более низких энергетических уровней на более высокие.
Система получит повое значение IV и соответствии с повой вели-
чиной внутренней энергии. Влияние процесса передачи теплоты
Рис. 14. Влияние теплоты и работы
на энергетические уровни и распреде-
ление частиц одноатомного идеаль-
ного газа:
а—нагревание при постоянном объеме;
7'2>7'i;	£2>£i: W2>Wi; б адиабатное
обратимое расширение; 72<7Т;	£г<£1;
|p,2=lV'i: в—изотермическое расширение;
T2=Ti; Ег=£1; Wre>uz1J
при постоянном объеме и ра-
боты на энергетические уров-
ни и распределение частиц
одноатомного идеального га-
за показано на рис. 14.
Важно заметить, что ве-
личина IV остается постоян-
ной при адиабатном обрати-
мом процессе, т. е. не изме-
няется распределение часгиц
на энергетических уровнях.
6.	Работа
Работа, выполненная си-
стемой при таком обратимом
/31nZ\
процессе, как kT ) dv,
позволяет объяснить превра-
щение внутренней энергии в
работу. Так как теплота не
переносится при обратимом
адиабатном расширении, то
величина IV не изменяется.
Следовательно, изменения
внутренней энергии могут
происходить только через
изменения самих значений
энергетических уровней.
Выражение (2-13) для энергетических уровней поступательного
движения содержит слагаемые, зависящие от размеров системы.
Так как совершенная работа вызывает изменения размеров си-
стемы, то выполненная работа изменяет значение энергетических
уровней. Работа, выполненная системой, увеличивает объем и
снижает значения энергетических уровней; результате внутрен-
няя энергия уменьшается. Работа, выполненная над системой,
уменьшает объем и увеличивает значения энергетических уров-
ней, в результате внутренняя энергия повышается.
7.	Энтропия
В любой системе, содержащей достаточное число частиц, чтобы
установилось статистическое распределение энергии, численное
значение IV достигает астрономических размеров. Поэтому наи-
132
более удобно вычислять работу непосредственно в яаииснмости от
величины А In W, содержащейся в уравнении (4-29). Эта величина
может быть определена с помощью удобной термодинамической
функции — энтропии S и уравнения (4-ЗБ), которое связывает
переход теплоты при обратимом процессе с Td(k In W). Ifepenn-
шем уравнение (4-35):
«dS.	(4-36)
Это уравнение, однако, определяет только изменение функции
энтропии через перенесенную теплоту при обратимом процессе
и абсолютную температуру. Изменение энтропии между двумя
любыми состояниями может быть получено интегрированием урав-
нения (4-36):
S-AlnlF+(S0—AlnlF0).	(4-37)
Абсолютную шкалу энтропии можно построить, установив
величину энтропии произвольно выбранного стандартного со-
стояния. Определять абсолютную энтропийную шкалу наиболее
удобно, произвольно придав постоянной интегрирования
(So — A In Го) значение, равное нулю для стандартного состоя-
ния при температуре абсолютного нуля. Утверждение, что
So = k In 1^0 при температуре абсолютного нуля, составляет
основное положение третьего закона термодинамики в его наибо-
лее общей форме. Действительно, для многих кристаллических
веществ все атомы находятся на самом низком или основном уров-
не при’температуре абсолютного нуля. Для этого полностью упо-
рядоченного состояния, когда = 1, In 1Г0 = О и So должно
быть равно нулю. Согласно этому
S = AInF	(4-38)
для любого состояния. .
Так как W — функция состояния, то энтропия также является
функцией состояния. • ’
Уравнение для S в функции суммы состояний может быть по-
лучено подстановкой уравнения (4-38) для k In W и уравнения
(4-4) для Е в уравнение (4-28):
(4-39)
. Поступательная энтропия идеального газа может быть вычисле-
на с помощью определения Z для неразличимых частиц и посту-
пательной суммы состояний для молекулы идеального газа.
Для неразличимых частиц
133
Используя приближенное соотношение Стирлинга для In (nl),
найдем
|||Z п In и — п Inn + n.
Подстановка в уравнение (4-39) дает
S = nfc[lnz — lnn-f-1 + т(д^ \
\ оГ I
\	/V.
(4-40)
Согласно уравнению (3-19), поступательная сумма состояний для
идеального газа
lnzf = -|-ln-“ +А in 7 +In о;	(4-41)
Для 1 моля идеального газа nk = R и v = 82,06 Tip смЧмоль
(Т в °К и р в атм). Так же т = Л4/(6,02 1023), где М — масса
грамм-молекулы, k = 1,3804 10-1в эрг!°\ и /г = 6,624  10-27 эрг-сек.
С помощью этих величин уравнение (4-41) принимает вид
In= -|-In33,0 101а + 1п82,06+-|-1пМ+-|-1пТ—1пр. (4-43)
Подставляя уравнения (4-42) и (4-43) в уравнение (4-40), получим
поступательную составляющую мольной энтропии идеального
газа:
=	~ InT-ln р-1,155].	(4-44)
Для идеального газа при 25 °C и 1 атм
St =2,98InМ 4-25,98 кал/(моль-°Ю-	(4-45)
Вращательная составляющая мольной энергии для жесткой
линейной молекулы может быть получена с помощью определения
z для различимых частиц и суммы состояний для жесткого рота-
тора. Для различимых частиц
Z = z".
Подставляя z в уравнение (4-39), получаем
S=nfc[lnz + T(-^^) ].
(4-46)
134
Согласно уравнению (3-36), сумма состояний для линейного
жесткого	ротвтора имеет вид 8n4kr In zr = In	+ In / + in T—In a;	(4-47) td\nzr \	1 \ dT ) “ T '	(4-48) \	/p
Момент инерции I в вышеприведенном соотношении выражен в
г!{частица) см2. При наличии молекулярной модели удобнее
всего выражать момент инерции в (г! моль) А8. Если
/'=/(6,02  )088)1016,	(4-49)
то мольная энтропия для линейного жесткого ротатора становится
равной
Sr = /? [In/' +In Т—Ina—2,20].	(4-50)
При 298 °К
Sr = 7? [In/' — In a+ 3,49].	(4-51)
Сумма состояний для нелинейной жесткой молекулы может
быть приближенно определена уравнением (3-36):
, Г__	3	1
/ /и 8n2kT \ 2 ,r Г Г , 2
,----№~ ) ЦХ1у1г) ’
где 1Х, 1у и 1г — главные моменты инерции. Если моменты инер-
ции выражены в гЦмоль-А2), то мольная энтропия для нелиней-
ной жесткой молекулы
sr=R -j_inT+-Lin(/;/;/;) —ina—2,70].	(4-52)
При 298 ° К
Sr = 7? [41п(/;/*/*)“ 1по + 5>85]-	(4‘53)
Момент инерции для двухатомной молекулы легко вычислить
по соотношению
/ = /п1аа + т2Ь2,	(4-54)
где а — расстояние массы ггц от центра тяжести;
b — расстояние массы т2 от центра тяжести.
Момент инерции может быть выражен в функции расстояния
между массами:
d = a + b.	(4-55)
Если сумма моментов около центра тяжести равна нулю, то
ггца + тгЬ — 0.	(4-56)
135
Решая уравнения (4-5Б) и (4-Б6) одновременно для а и Ь, нм>« м
аои_Л'«а -х-
nij “j" /Ид ’
mt тг
Подстановка значений а и b в уравнение (4-54) дает
/=.
mt + т2 г ’
где р. — приведенная масса.
Произведения главных моментов инерции нелинейной жесткой
многоатомной молекулы наиболее удобно вычислить с помощью
следующего выражения:
1х1у1г = АВС — AF2 —BE2—CD2—2DEF,
(4-57)
(4-58)
где
А
=	(У[—у)2 + £ пц (z(—z)2;
=	+ у£
=-- £m(.(z/?+г0-[2(т^ + £(m,.zf)2]/£/nf;
= £mf (xf—х)а + £ m, (z£— z)2\
В =Lml(xtA-^)—x'Lmixi—zhtrift,
= £m, (х? 4- г!)—^(т;х,.)2 + £(/п<гг)а]/£т/;
= £mz (x£—x)2 + £ mt (У1—у)2;
C ^Lm^xl + yi)—x^mix—y Ътш,
(x2 + y})—[£(mfxz)2 + £(mi«/z)2]/£fn/;
= £/пДх£—x) (y—y)-,
I = E/n.x,^—(Ет^^Ет^/Ет^
£ I = £mz (x{—x) (zt — z)\
I = £/nzxzz(-—(£m,xz)
J^’Emiiy— y)^—z);
~ _ ZniiXj .
X Ymi ’
,7—
У ~ Ynit '
- ^niiZi
Уравнение (4-58) выведено в предположении, что атомы мо-
лекулы — материальные точки, связанные невесомой жесткой
136
свивыо; xt, yt и zt — дскартопые координаты атомов и х, у и г—
координаты центра тяжести относительно произвольно выбран-
ных осей координат. Хотя выбор осей координат произволен, тем
не менее удобно принять по крайней мере одну ось вдоль главной
связи или плоскости симметрии молекулы
Модель молекулы строится па основе известных величин длин
и углов связи. Для большинства многоатомных молекул возможно
несколько молекулярных моделей с мало отличающимися величи-
нами момента инерции. Любая модель, построенная на основе
принятых длин связи и углов, будет пригодна для целей вычисле-
ния энтропии.
Длина связи или расстояние между атомами определяется в
первую очередь размерами атомов, соединенных связью. Вообще,
чем больше атомы, тем больше длина связи. Для настоящей цели
кажущийся радиус может быть принят для отдельного атома та-
ким, чтобы сумма кажущихся радиусов атомов была равна длине
связи. На длину связи в некоторой степени также влияет прочность
связи: чем прочнее связь, тем короче длина. Поэтому кажущийся
атомный радиус будет изменяться с типом связи; например, ка-
жущийся атомный радиус углерода для одинарной ковалентной
связи равен 0,77 А, для двойной связи он понижается до 0,67 А
и для тройной связи до 0,60 А.
Валентные силы индивидуальных атомов строго направлены
в пространстве, и угол между двумя ковалентными связями атома
является прежде всего свойством атома; общая молекулярная
структура только незначительно влияет на него. Обобщенные дан-
ные по длинам и углам связей суммированы в табл. 6.
Составляющая мольной энтропии на каждую степень свободы
гармонического колебания может быть вычислена с помощью
суммы состояний, выраженной уравнением (3-39):
1
Zo
1 — е
hv
lnzp=—ln(l—е w);
Av
Подстановка левой части этого уравнения в уравнение (4-46) для
1.моля дает
Sp= Я	- In (1 - e"*)j,	(4-59)
где
_ h'j   1,438 <о
Х~ АГ Г '
137
Таблиц* 6
УСРЕДНЕННЫЕ ВЕЛИЧИНЫ РАССТОЯНИЯ И У1 ЛОЦ С ндЗИ (22]
'тт •••'	1	" Связь	А	Связь	Угол
			
н,	0,74	^С-Н хн	108°
СИ	1*. 12		
-с-н	1,09	ХН —с^н	112°
=С—н	1,07	АН	
sC—Н	1,06	С = С J чч	120’
—С—с	1,57		
=С—с	1,47		
—с=с	1,35		
—CsC	1,21		
—С—F	1,39		
—С—С1	1,71	II хъ о 1 X	112°
С Вг	1,95 2,00		
—С—J			
138
Продолж нив табл, в
С»я>*	, А	Связь	Угол
Г ы	1,48 1,16 1,25 1,54		
X	’	। л	п	п 1	II	NI о z :		г__х о II о	123°
—0—н	0,96	3 Z Т 3	106°
—N—Н	1,01		
—S—Н	1,33	oQ г	105°
0.	1,21	s\> . н	92°
0 о	1,48 1,09		
Na			
—N— N—	1,13	XN -N^ 'Н	111°
139
Составляющую свободного внутреннего вращения можно вы-
числить, используя сумму состояний, выраженную уравне-
нием (4-9):
1п гС1 = 4"1п 'л«- + 4 ,n Z"p + 4|п Т~1п М
/01пггв\ 1	1
\ дТ jv " 2 ' Т"
Подставляя левую часть этого уравнения в уравнение (4-46),
для 1 моля получаем
•SCb = -^^4 1п^пр + 4	1пп— °>520
где /пр — момент инерции, (г/моль)  А2;
п — число симметрии.
При 298 °К
*^св — R [~2~ Zr'₽ Inn-j-2,32 ,
(4-60)
(4-61)
Составляющая энтропии сильно затрудненного вращения бу-
дет приближаться к величине, определяемой уравнением (4-59)
Рис. 15. Уменьшение энтропии свободного
внутреннего вращения в зависимости от потен-
циального барьера [29, 34]
для гармонического колебания. Составляющая энтропии внутрен-
него вращения для промежуточных потенциальных барьеров мо-
жет быть вычислена по методу Питцера и Гвина [341. Результаты
их вычислений приведены на рис. 15 как разность между энтро-
пиями свободного SCBOC и затрудненного 5затр внутреннего враще-
140
пня в функции суммы состояний для свободного вращения И
значения где V — мера потенциального барьера, Т — абсолют-
ная температура. Вообще, потенциальный барьер обусловливает
понижение составляющей энтропии от внутреннего вращения.
Пример Б Определить энтропию окиси углерода в состоя-
нии идеального газа при 25 °C и 1 атм. По данным Герцберга
[22], межатомное расстояние составляет 1,128 А и частота колеба-
ния связи 2143 см'1.
Поступательную составляющую при 298 °К можно вычислить
по уравнению (4-45). Для молекулярного веса, равного 28,
S* = 2,98 In 28 + 25,98 = 35,93 кал/(моль °К).
Вращательная составляющая энтропии при 298 °К для двух-
атомной молекулы выражена уравнением (4-51). Для двух атомов
с атомным весом 12 и 16 момент инерции вычисляется согласно
уравнению (4-57):
Г = -2g-(l,128)s= 8,74 (г/моль) А2.
Для двухатомных молекул с разными ядрами число симметрии
а = I. Следовательно, вращательная составляющая
Sr= 1,987 [In 8,74+ 3,49]= 11,28 кал/(моль-°К).
Колебательную составляющую энтропии следует вычислить по
уравнению (4-59). Для окиси углерода при 298 °К
х = 1,438 2143^ = 10,35.
Для этого значения х колебательная составляющая энтропии мень-
ше 0,001 кал/(моль °К).
Энтропия как сумма поступательной, вращательной и
колебательной составляющих будет равна в таком случае
47,2 кал/(моль °К). Эта величина хорошо совпадает с величиной
47,3 кал/(моль °К) [47].
Пример 6. Определить энтропию водяного пара в гипоте-
тическом состоянии идеального газа при 25 °C и 1 атм. По данным
Герцберга [22], длина связи Н—О в молекуле воды равна 0,958 А
и угол между связями Н—О—Н равен 104°27'. Частота колебания
вдоль связи Н—О приблизительно равна 3700 см'1 и частота
колебания, изменяющая угол Н—О—Н, равна около 1600 см'1
(рис. 16).
Поступательную составляющую энтропии следует вычислить
по уравнению (4-45). Для молекулярного веса 18
S; = 2,98 In 18 + 25,98 = 34,60 кал/(люль-°К)
141
Вращательная составляющая энтропии нелинейной молекулы
при 298 °К определяется уравнением (4-53), а произведение момен-
тов инерции — уравнением (4-58). МоЛекула воды трехатомная
с двумя одинаковыми атомами,
она имеет плоскость симметрии,
проходящую по биссектрисе угла
связи Н—О—Н и перпендикуляр-
ную плоскости трех атомов. Сле-
довательно, молекула воды имеет
число симметрии а, равное двум.
Ниже вычислено произведение
Рис. 16. Модель молекулы
воды
моментов инерции относительно
произвольно выбранной системы
координат, имеющей атом кисло-
рода в начале и ось г в плоско-
сти симметрии. Все три атома лежат на плоскости х — г. Коорди-
наты трех атомов приведены в ангстремах:
xi	V,	г1			mt	mtxi	mi*i	mizi
	Hi	-0,755	0	0,592	1	—0,755	0	0,592
	На	0,755	0	0,592	1	0,755	0	0,592
	0	0	0	0	16	0	0	0
			0	0	1,184
	“х=0; 'у	=0; 2=1,184/18=0,0659 А.			
	Х-—Х	У1-у	гГг	т£(Х-Х)2	«Д!/,—Г)2	
№	—0,755	0	0,526	0,570	0	0,277
Н2	0,755	0	0,526	0,570	0	0,277
0	0	0	—0,066	0	0	0,070
			1,140	0	0,624
		Х)(Й—14	тДх—x)(z—z)		т^-у)	-3
	И»	0	-0,390	0	
	Н2	0	0,390	0	
	0	0	0	0	
		0	0	0	
	Согласно	уравнению (4-58)			
		А = 0,624,	,	£> = 0,		
		В = 1,764,	Е = 0,		
		С= 1,140,	В = 0;		
Гх Гу 1'г = 0,624 1,764• 1,140 = 1,26 (г/моль)  А2;
Sr = /?	In (1,26)—In (2) + 5,85 j = 5,27 R =
= 10,50 кал!моль -*K).
Для колебательных частот в молекуле воды колебательная
составляющая энтропии при 298 °К меньше, чем 0,01 калЦмоль °К).
142
Следовательно^ энтропия может бить определена инк сумма посту*
нательной и вращательной составляющих:
S St4-Sr 34,GO4 10,50- 45,10 калЦмолъ °К).
Пример 7. Определить энтропию хлористого этила в со*
стоянии идеального газа при 25 °C и 1 атм. Использовать характе-
ристические длины связи, углы и колебательные частоты из табл,
4 и 5.
Поступательная составляющая при 298 °К вычисляется по
уравнению (4-45) для молекулярного веса, равного 64,5:
S, « 2,98 In (64,5) + 25,98 = 38,4 кал/(моль °К).
Вращательная составляющая энтропии для нелинейной много-
атомной молекулы при 298 °К выражена уравнением (4-53), а про-
изведение моментов инерции — уравнением (4-58). На рис. 17
изображены две проекции модели молекулы хлористого этила,
приведены углы между связями и расстояния между атомами мо-
лекулы. Молекула не имеет элементов симметрии, так что систе-
ма координат выбрана произвольно с началом координат у атома
углерода метильной группы. Ось х совпадает со связью С—С и
одна связь С—Н метильной группы и связь С—С лежат на пло-
скости х — г.
Координаты атомов и необходимые величины для подстановки
в уравнение (4-58) приведены ниже.
	Х1	«1	г1	т1	ml*i	miVl	mizi
Н1	—0,332	—0,885	0,510	1	—0,332	—0,885	0,510
Н2	—0,332	0,885	0,510	1	—0,332	0,885	0,510
н3	—0,332	0	—1,020	1	—0,332	0	—1,02
н«	1,872	0,885	0,510	1	1,872	0,885	0,510
Нв	1,872	—0,885	0,510	1	1,872	—0,885	0,510
С1	0	0	0	12	0	0	0
С2	1,54	0	0	12	18,50	0	0
С1	2,085	0	—1,670	35,5	74,2	0	—59,3
				64,5	95,44	0	—58,28
x=l,48; у=0; г=—0,903.
143
	ц Г"		mz(«z_^«		(»/_*)•
Н’ —1,81	—0,885	1,413	3,27	0,782'	2,00
Н» —1,81	0,885	1,413	3/27	0,783	2,00
И» —1,81	0	-0,100	3,27	0	0,01
Н« 0,39	0,885	1,413	0,14	0,782	з;оо
Н» 0,39	—0,885	1,413	0,14	0,782	2,00
О —1,48	0	0,903	26,30	0	9,8
С« 0,06	0	0,903	0,04	0	9,8
С1 0,605	0	-0,77	13,00	0	21,1
			49,43	3,128	49,07
						
	mz(xz-x)(!/z	-v)	mz(Xz-Jj(2/-2)		-»)
Н‘	1,60		—2,56	—1,25	
Н«	—1,60		—2,56	1,25	
Н»	0		0,18	0	
Н*	0,35		0,55	1,25	
Н6	—0,35		0,55	—1,25	
О	0		—16,05	0	
С®	0		0,60	0	
С1	0		—16,33	0	
	0		—35,62	0	
Подставляя найденные выше величины в уравнение (4-58),
получаем
Д = 3,13+ 49,07 = 52,20,	D=0,
В = 49,43 + 49,07 = 98,50,
С = 49,43+ 3,13 = 52,56
Е = —35,62,
Г = 0;
гг = ABC—BE2 = 52,20.98,50.52,56 -98,50- 35,62* =
= 145,00 г/(моль-А?).
Подставляем произведения моментов инерции в уравнение
(4-53) с а = 1:
£г=7?Щ-1п 145,00 + 5,851= 11,78Я = 23,4 кал/(моль-'К)
Составляющая свободного внутреннего вращения метильной
СН3-группы по отношению к СН2С1-группе при 298 °К выра-
жена уравнением (4-6D. Приведенный момент инерции определяет-
ся уравнением (4-10), где 1А вычислен как момент инерции ме-
тильной группы относительно оси по С—С связи, а 1В вычислен
как момент инерции СН2С1-группы также относительно ови по
С—С связи.
Га = 3 1 1,022 = 3,12 = (г/моль)  А2;
1в = 2 • 1 • 1,022 +1 • 35,5  1,672 = 101,08 (г/моль)  А2;
/'р= 3,12-101,08/104,2 = 3,03 (г/моль)• А2.
44
11одставля>п n уравнение (4 61) число симметрии, рапное трем,
для метильной\группы относительно связи С—-С, получим
R	In(3,03)—1п(3)4-2,32|« 1,77/?«3,50 кал/(моль *К).
Sc
Вычисляя сумму состояний для свободного вращения по урав-
нению (4-2), имеем
Внутреннее вращение в молекуле хлористого этила не является
по существу свободным; оно затруднено потенциальным барьером
V, оцененным в 3700 калЦмоль °К). Согласно рис. 15, энтропий-
ная составляющая свободного внутреннего вращения должна
была бы уменьшиться приблизительно на 1,6 кал/(моль ®К) для
—-— = 0,276 и — 6,25. Следовательно, действительная энтро-
^св
пия для заторможенного вращения
Sa.Bp = 3,50 — 1,60 = 1,90 кал/(моль• °К)
Составляющая энтропии на каждый вид колебания выражена
уравнением (4-59). Каждый из восьми атомов молекулы хлористо-
го этила имеет три степени свободы, что для молекулы в целом
соответствует двадцати четырем степеням свободы. Три степени
свободы относятся к поступательному движению, три — к вра-
щению, одна — к внутреннему вращению и семнадцать степеней
свободы остаются для колебаний.
Виды колебаний в молекуле этихлорида можно приближенно
проанализировать, если рассматривать молекулу как систему
трех тел: группы СН3, группы СН2 и атома хлора. Такая система
должна иметь три колебательных степени свободы, обусловленные
колебанием растяжения связи С—С, колебанием растяжения свя-
зи С—С1 и колебанием изменения угла связи С—С—С1. Остаю-
щиеся четырнадцать колебательных степеней свободы могут быть
отнесены за счет различных колебаний вдоль связей С—Н и из-
менения угла между связями. Относительно высокие их частоты
приводят к незначительной величине составляющей энтропии
при 298 °К.
Составляющая энтропии на каждый отдельный вид колебания
приведена ниже.
Растяжение связи
Тип связи	<о, см-1	X	S
с—н	2960	14,3	0,00005 7?
с—с	900	4,35	0,0700 7?
С—С1	650	3,13	0,1878 7?
0,2578 7?
10—1503
115
Изменение угл| связи
Тип евижи 11-	И), гл"1 1000	X 4,83*	S 0,250 W
А—с FI.v	1450	7,00	0,029 R
н - / С	С	330	1,59	0,635R
			0,905 R
Общая колебательная составляющая энтропии при 298 °К
равна в таком случае 1,163 7? или Sv — 2,3 кал/(моль-°К). Сумми-
руя составляющие, получаем
S, кал/(лолб-°К)
Поступательное движение	......	38,4
Вращение...................... 23,4
Внутреннее заторможенное вращение	.	1,9
Колебание...................... 2,3
66,0
8. Энтальпия
Несмотря на то что термодинамическая система или процесс
могут быть рассчитаны полностью с помощью внутренней энергии
и энтропии, а также давления, объема и температуры, некоторые
сочетания этих свойств встречаются достаточно часто, поэтому
удобно ввести вторичные функции первичных свойств. Одна из
таких функций называется энтальпией и определяется уравне-
нием (1-3):
Н — Е-\-ру.
Из уравнения (4-4) для Е и уравнения (4-34) для р величина И
может быть выражена в функции суммы состояний:
//“w’[(re(),+(4w)J	<4'62>
9. Свободные энергии
Для анализа равновесных систем при условии постоянного
объема удобна функция, называемая «свободной энергией Гельм-
гольца», которая определяется соотношением
А = Е— TS.	(4-63)
Выражение для А в функции суммы состояний может быть полу-
чено сочетанием уравнений (4-29), (4-36) и (4-63):
А~ — ATlnZ.	(4-64)
146
Положительная сторона введения свободной энергии Гельмгольца
заключается d том, что »та шсргия является непосредственной
мерой суммы состояний при условии постоянной температуры.
Вторая функция свободной энергии, называемая «свободной энер-
гией Гиббса» и определяемая уравнением
F~H-TS = A + pv,	(4-65)
является полезной, когда анализируется равновесная система
при условии постоянства температуры и давления. В функции
суммы состояний она имеет вид
F =	+	.	(4-66)
Ниже приведены термодинамические функции в значениях
функции состояния:
E = /T(ainZ/51nT)r;
Cv = k (d2 In Z/d In2 T)v 4- (d In Z/d In T)D;
S = k [In Z + (d In Z/d In Т)о];
p = kT(d In Z/du)r;
pv = kT (d In Z/d In v)T\
H — kT [(d In Z/д In 7%+(.9 In Z/д In o)r];
A = — kTlnZ;
F — —kT [In Z—(d In Z/d In n)r];
Z — для различимых частиц (вращение и колебание);
гп
Z = для неразличимых частиц (поступательное движение).
Термодинамические законы — статистические и классиче-
ские — даны в табл. 7.
Таблица 7
ТЕРМОДИНАМИЧЕСКИЕ ЗАКОНЫ
Первый закон
Статистический Классический	/ £=S nflt | d£=iie/dn£--|-Xn/de; d£=BQ—MF
	Второй зако и
Статистический	1 S=fe In W 1 dS=kd In W
Классический	bqr dS= — T
10
147
Продолжение гаСл, 7
Статистический
Классический
Третий вякли	j
Sv*k In Wo при абсолютном нуле для любого ве-
щества (дли содершеины' кристаллов 1Г0 1 и
So 0)
S0“0 при абсолютном пул< для совершенных крис
таллов
---------------------,---------------
Объединенные первый и второй законы
(замкнутая система; работа расширения)
Статистический
E=kT In W—kT In Z
dE=kTd In W—kT (д *" dv
\ dv JT
Классический
dE—TdS—pdv
Задачи
1.	Окись углерода и азот представляют собой два двухатомных газа с
одинаковым молекулярным весом, равным 28 При 300 °К и 1 атм они имеют
7
классическую теплоемкость — R, указывающую на то, что при этих условиях
колебательная энергия незначительна. Межатомное расстояние у азота (1,094А>
также очень близко к межатомному расстоянию для окиси углерода (1,128 А);
однако энтропия азота в состоянии идеального газа при 298 °К и 1 атм состав-
ляет 45,77 по сравнению с 47,30 для окиси углерода. Требуется дать количе-
ственное объяснение этого различия.
2.	Двуокись углерода и сернистый газ представляют собой два трехатом-
ных газа с аналогичным химическим составом. Несмотря на то что колебатель-
ная составляющая теплоемкости двуокиси углерода превышает таковую для сер-
нистого газа почти на 0,35 кал! моль при 300 ° К. теплоемкость при постоянном
давлении углекислого газа при 300 °К и 1 атм равна 8,89 кал/(моль ° К.) по
сравнению с 9,54 кал/(мольК) для сернистого газа. Какой вывод о молекуляр-
ной структуре этих газов можно сделать из этих термодинамических данных?
3.	Определить абсолютную энтропию этилена в состоянии идеального
газа при 298 °К и 1 атм при условии, что все атомы лежат в одной плоскости
и двойная связь между атомами углерода не допускает внутреннее вращение
Использовать обобщенные данные по углам связи и расстояниям, приведенные
в табл. 5, а также характеристические частоты связи из табл. 4. Вращательное
число симметрии этилена равно 4.
4	Определить число способов или размещений, которыми может осуще-
ствляться наиболее вероятное распределение энергии для одного моля гелия
в состоянии идеального газа при 298 °К и 1 атм.
5.	Показать, что при температуре абсолютного нуля, когда все частицы
находятся на самом низком энергетическом уровне, мольная энтропия опреде-
ляется формулой
~ R1° 8о<
где ga — фактор вырождения для основного энергетического уровня.
6.	Используя статистические методы, определить теплоемкость при по-
стоянном давлении сероводорода как жесткого вращательно-гармонического'
осциллятора при 1000 4К и 1 атм. Основные колебательные частоты сероводо-
рода равны: = 2611 ел-1, ша = 2684 см~1, ws = 1290 см'1.
148
ГЛАВА 5
Эмпирическое определение
термодинамических функций
За последнее время был достигнут значительный прогресс
в вычислении термодинамических функций непосредственно из
суммы состояний для некоторых веществ, по поведению прибли-
жающихся к идеальному газу. Однако вычисление термодинами-
ческих функций для реальных газов и жидкостей затруднено из-
за отсутствия сведений о межмолекулярных силах. Изменение
термодинамических функций реальных газов и жидкостей наи-
более удобно вычислять с помощью эмпирических уравнений для
макроскопических свойств или эмпирического уравнения состоя-
ния. Для количественного вычисления необходимо выразить тер-
модинамические функции в зависимости от измеримых макроско-
пических свойств, таких как давление, объем, температура, тепло-
емкость и состав.
1.	Правило фаз
Число независимых переменных, которое должно быть извест-
но для того, чтобы охарактеризовать состояние системы, опреде-
ляется правилом фаз Гиббса. Для многокомпонентных, многофаз-
ных систем определенной массы
F^C—P 4-2,
где F — число степеней свободы или число интенсивных пере-
менных, которое нужно определить;
С — число независимых переменных компонентов;
Р — число фаз.
Для однофазного чистого компонента или гомогенного раствора
определенной массы и состава Р и С равны единице и число сте-
пеней свободы равно двум. Таким образом, состояние системы
можно определить, зная значения любых двух интенсивных пе-
ременных: температуры, давления или удельного объема.
149
2.	Вывод дифференциальных уравнений
Для однофазного чистого компонента или гомогенного рас-
твора постоянного состава все количественные вычисления бази-
руются на основном соотношении, полученном комбинацией урав-
нений (4-33), (4-34) и (4-36):
dE=TdS—pdv,	(5-1)
тде
Е — внутренняя энергия;
Т — абсолютная температура;
S — абсолютная энтропия;
р — общее давление системы.
Это уравнение по существу содержит все основные данные, ко-
торые можно получить из термодинамического анализа замкнутой
системы с объемом в качестве единственного внешнего параметра;
оно является отправной точкой для вывода конкретных рабочих
уравнений. В сочетании с определением других термодинамиче-
ских функций, таких как энтальпия, теплоемкость и свободная
энергия, а также с помощью правила частного дифференцирова-
ния, это уравнение дает выражение для полного дифференциала
любой термодинамической величины в функции р, о, Т. Если извест-
ны свойства, адэкватные р, v, Т, то дифференциальное уравнение
можно проинтегрировать, чтобы получить изменение термодинами-
ческой функции при переходе системы из одного состояния в другое.
Дифференциальное уравнение для полного дифференциала
термодинамической величины в функции измеримых свойств
системы может быть получено следующим способом.
1.	Выразить полный дифференциал термодинамической вели-
чины <р в функции ее частных производных по двум произвольно
выбранным независимым переменным х и у, используя математи-
ческое уравнение
 (5'2)
2.	Получить второе выражение для полного дифференциала
термодинамической функции <р, комбинируя определение этой
функции с уравнением (5-1).
3.	Вычислить первую из частных производных, входящих в
уравнение (5-2), делением уравнения, полученного в п. 2, на dx,
приняв затем постоянство у. Другую частную производную урав-
нения (5-2) можно вычислить делением уравнения, полученного
в п. 2, на dy, введя затем условие, что х постоянно.
4.	Любые частные производные энтропии, полученные в п. 3,
могут быть вычислены дифференцированием каждого уравнения,
полученного в п. 3 по второй переменной, приняв во внимание,
150
что вторые смешанные частные производные однозначной функ-
ции равны
<Я<р б*<р
~<^сду дудх *
5.	Вычислить полный дифференциал dtp в функции р, v и Г,
используя подстановку для частных производных в уравне-
нии (5-2).
Эти расчеты проиллюстрированы ниже примерами. Наиболее
важные частные производные приведены ниже.
Внутренняя энергия
(dE/dT)v—Cv
(дЕ/др)о=Ср(дТ/др\,
(dE/dT)p = Cp~P(dvldT)p
(dE/dv)p = Cp(dTldv)p~P
(dE/dv)T= T(dpldT)v—p
(дЕ1др)т = —T (dvldT)p—p(dvldp)T
Энтропия
(dS/dT)„=Cv/T
(dS/dp)o=(Cv/T)(dT/dp)o
(dS/dT)p = Cp/T
(dSldv)p^(Cp/T)(dTldv)p
(dS/dv)T — (dp/dT)v
(dS/dp)T = -(dv/9T)p
Энтальпия
(дН/дГ)р=Ср
(dH ldv)p = Cp (dT/dv)p
(дН /др)„ = Cv 4- v (др/дТ)р
(дН ldp)v = Cv (дТ/др)р + v
(дН/др)т = —Т (dv/dT)p + v
(дН /dv)T = Т (dp/dT)v + v (dp/dv)T
Теплоемкость
(dCv/dv)r^T^pldT\
(дср/др)т= -Т(д^тр
Cp-Cv^ ~T(dv/dT)2p(dv/dp)T
15 >
Функции свободной чл epi и и
(W7>'-$
(dA/dv)j = —р
(dF/dT)p^ -S
(dF/dp)T—v
Полный дифференциал термодинамической функции может
•быть получен подстановкой соответствующих выражений для
частных производных в уравнение (5-2).
Пример 1. Внутренняя энергия как функция температуры
и объема.
Общее изменение внутренней энергии замкнутой системы по-
стоянного состава может быть выражено в функции изменений
температуры и объема с помощью уравнения (5-2) для полного
дифференциала:
+(!)/»•
(5-3)
Первая из частных производных — теплоемкость при постоян-
ном объеме
(fr)o=c°-	(5'4)
Другая частная производная может быть вычислена в функции
давления, объема и температуры по уравнению (5-1):
dE = TdS—pdv.	(5-1)
Разделив это уравнение на dv и принимая температуру постоян-
ной,
Деля уравнение (5-1) на dT и принимая затем постоянным объем,
получим
(эг).=7'(^).=с-	<М)
Вторыми смешанными производными уравнений (5-5) и (5-6)
будут
д*Е  гр d2S ( dS \	/ др \	/е
~§vdT ~ ‘ dvdt + ( dv L \дТ )	'°"'>
\ IT \ /V
и
=	(5-8)
\dTdv ) dTdv	4	'
152
Так как вторые смешанные производные энтропии и внутренней
энергии равны, из уравнений (6-7) и (5-8) следует
(6-9)
Подставляя уравнение (5-9) в уравнение (5-5), получаем
(5-10)
Окончательно выражение для общего изменения внутренней энер-
гии в функции р, v, Т и Со может быть получено подстановкой
уравнений (5-4) и (5-10) в уравнение (5-3):
dE

dv.
(5-Н)
Пример 2. Энтальпия как функция температуры и дав-
ления. По аналогии можно получить выражение для изменения
энтальпии как функции температуры и давления. По определению
полного дифференциала
,rr idH \ (дН \	,
dH~ \дТ )dT + \fy)T dp'
(5-12)
теплоемкости при постоянном давлении Ср
(™\ = С
Р
и энтальпии Н = Е 4- pv
dH = dE-\- pdv 4- vdp.
(5-13).
(5-14)
Подстановкой уравнения (5-14) в (5-1) получаем
dH~TdS + vdp.
(5-15).
Разделив уравнение (5-15) на dT и принимая давление постоян-
ным, имеем
Дели уравнение (5-15) на dp и принимая температуру постоянной,
получим
I 4- и -
т
(5-17>
153
с помощью
(5-18)
(5-19)
и энтропии
(5-20)
Найдем вторые Смешанные ирон шоДИыС фунКШ'П //
уравнений (6-16) и (5-17):
и	\oTcip ) удТдр )
дЧ1 т[ d*S \,(dS_\ , (dv\
дрдТ \дрдТ ) + \ йр )г+\&г )р‘
'Так как вторые смешанные производные энтальпии
равны, то уравнения (5-18) и (5-19) дают
(&S \ _	/ дг> \
\др )т-~[дТ у
Подставляя уравнение (5-20) в уравнение (5-17), имеем
(d£)r-T(£-)+v-	(6’2|)
Окончательно подстановка уравнений (5-13) и (5-21) в уравнение
(5-12) приводит к нужному соотношению общего изменения эн-
тальпии в функции р, v, Т и Ср.
ан = с^т-\т (fi-)	] dP- (5-22)
Пример 3. Энтропия как функция, температуры и объема.
Уравнение для энтропии в функции температуры и объема легко
вывести, используя предыдущие соотношения. По определению
полного дифференциала
(5-23)
Из уравнения (5-6)
/ dS \ _ Cv
\dT)v Т-
Из уравнения (5-9)
Следовательно,
ds=cv^-+^Ydv' (5-24)
Пример 4. Уравнение для энтропии в функции темпера-
туры и давления может быть получено из предыдущих соотноше-
ний:
<иб>
Из уравнения (5-16) следует
/as\ =Ср
7”
154
из уравнения (5-20) находим
I dS \ I dv \
Следовательно,
dS Ср^--(^\ dp.	(5-26>
Пример 5. Зависимость теплоемкости от объема и давле-
ния.
Выражения для зависимости теплоемкости от объема и давле-
ния можно легко получить, исходя из определения. Теплоемкость
при постоянном объеме
С°~\дТ )v-
Дифференцируя это уравнение по v при постоянной Т, получаем
/0Со\ = д*Е
\ dv ) т dTdv ’
Дифференцируя уравнения (5-10) по Т при постоянном v,
I д2Е \ — т( д2р \
\ dvdT ) \дТ2 )v‘
Из уравнений (5-27) и (5-28) находим
/ dCv \ ____________________™ / 2р \
\	\^2 V
Теплоемкость при постоянном давлении
Cp=$hp‘
Дифференцируем это уравнение по р при постоянной Т".
( дСр \ _ д2Н
\ др )т дТдр ‘
Дифференцируем уравнение (5-21) по Т при постоянном р:
д*Н _	т( d2v \
дрдТ	1 \дТ2 )р-
Из уравнений (5-30) и (5-21) находим
/дСР \ _ _т( д2а\
\ др )т \^2 )Р
(5-27)
имеем
(5-28)
(5-29)
(5-30)
(5-31)
(5-32)
155
С П'«МОЩЬЮ
(5-18)
(5-19)
и энтропии
(5-20)
Найдем вторые смешанные производные функции Н
уравнений (б-16) и (6-17):
/ дЧ! \	„ft d“.S \
и	\йТЭр )	1 \&Гдр )
341 т( &S \.(3S\ , / dv \
ЗрдТ 1 \дрЗТ )±\др )r~r \йТ- )р’
Так как вторые смешанные производные энтальпии
равны, то уравнения (5-18) и (5-19) дают
(3S \   / до \
)г-	{от )р-
Подставляя уравнение (5-20) в уравнение (5-17), имеем
&}T--T&)'+V- <5'21>
Окончательно подстановка уравнений (5-13) и (5-21) в уравнение
(5-12) приводит к нужному соотношению общего изменения эн-
тальпии в функции р, v, Т и Ср:
dH = CpdT—|Т	) -v ] dp.	(5-22)
Пример 3. Энтропия как функция температуры и объема.
Уравнение для энтропии в функции температуры и объема легко
вывести, используя предыдущие соотношения. По определению
полного дифференциала
dS=^dT + ^)r*.	(5-23)
Из уравнения (5-6)
(0S
Из уравнения (5-9)
/ 3S \ _/ др \
\-^)Т-\дт V
Следовательно,
=	(5-24)
Пример 4. Уравнение для энтропии в функции темпера-
туры и давления может быть получено из предыдущих соотноше-
ний:
+	(5-25)
Из уравнения (5-16) следует
/&S\ = С₽
\дТ)р Т;
154
пэ урппиеппя (Б- 0) походим
Следонателыю,
(5-26).
Пример 5. Зависимость теплоемкости от объема и давле-
ния.
Выражения для зависимости теплоемкости от объема и давле-
ния можно легко получить, исходя из определения. Теплоемкость
при постоянном объеме
Со
Дифференцируя это уравнение по о при постоянной Т, получаем
/ас0\ = д*Е
\ dv ) т dTdv '
(5-27)
Дифференцируя уравнения (5-10) по Т при постоянном v, имеем
\ _т{^Р_\
dvdT \ дТ* )v’
(5-28).
Из уравнений (5-27) и (5-28) находим
dCv \ _ т [ д2р \
)т
Теплоемкость при постоянном давлении
С₽=(^)р-
Дифференцируем это уравнение по р при постоянной Г:
/ дС„ \ _ й27/
\ др ]т дТдр '
(5-29)
(5-30)
Дифференцируем уравнение (5-21) по Т при постоянном р:
Из уравнений (5-30) и (5-21) находим
155
Пример 6. Соотношение мемву Ср и Cv. Соотношение
между теплоемкостью при постоянном давлении и теплоемкостью
урав-
при поспи...ом объеме можно легко получить, используя
яения (5-24) и (5-26) для изменения энтропии:
'	' р
с,-с.-т (*
‘v
dv,
V
(5-33)
V
p
Полная производная v по Т
dv _ г о
dT
(5-34)
Подставляем уравнение (5-34) в уравнение (5-33):
p
pl
Принимаем в уравнении (5-34) объем постоянным:
(5-35)
(5-36)
p
Используя это выражение для последнего члена уравнения (5-35),
получаем
с»~с»=г (£).(£), <5‘37)
Уравнение (5-36) может быть также использовано для придания
уравнению (5-37) следующего вида:
или
(5-38)
3.	Интегрирование частных дифференциальных
уравнений первого порядка
Интегрирование дифференциальных уравнений в частных про-
изводных первого порядка вида
d<p =	+ dy	(5-39)
\ дх/у \ ду )к
156
по существу проводят в две стадии. Эти стадии можно иллюстри-
ровать 1 рафиком (рис. IB), на котором переменная представлена
как функция х для двух фикспровя..... i пачепий у. Если значе-
ния х, и yt определяют начальное состояние системы, а х2 н у« —
конечное ее состояние, то общее изменение <р между начальным и
конечным состояниями может быть вычислено в результате сле-
дующей двухступенчатой операции.
1.	Определить частное изменение ф между (х1( yj и (х2, ух)
по пути А на рис. 18 вычисле-
нием интеграла
•'Э
(дФк= f (—) ^х(5-40)
для фиксированного значения
У = yl-
ч.	Определить частное из-
менение ф между (х2, i/J и
(х2, %) по пути В вычислени-
ем интеграла
<72
(5-41)
VI
Рис. 18. Функция двух независи-
мых переменных
для фиксированного значения х = х2. Общее изменение ср равно
Дф = (Дф)й + (Аф)х2.
(5-42)
С другой стороны, общее изменение ф может быть вычислено
с помощью двухступенчатого процесса вдоль пути С и пути D.
1. Определить частное изменение ф между (х„ у^ и (хх, у2)
по пути С вычислением интеграла
иг
<5-43)
4/1
для фиксированного значения х = хх.
2. Определить частное изменение ф между (xn z/2) и (х2, у2)
по пути D вычислением интеграла
*2
(i<M(£V	<6-44>
. *1
для фиксированного значения у = у2.
Общее изменение ф выражается суммой
Дф = (Д ф)Х) +(Дф)^.	(5-45)
157
Путь, выбранный дли интегрирования, определяется нмеющн
мнся данными по условиям нуги.
Вычисление этих интегралов требует конкретных данных о
соотношении давления, объема и температуры между начальным
и копенным состояниями системы. Такое соотношение обычно на-
зывают риТ-свойствами системы или уравнением состояния.
Обобщенное уравнение состояния в виде функции суммы состоя-
ний можно получить из уравнения (4-34) для давления системы.
Умножаем уравнение (4-34) на объем системы о:
ри=== nkT (	(5-46)
\ о in V )т
и вводим число молей т:
_ре_=/Д1пг_\
тРТ \ д In v 1т
Из суммы состояний для системы частиц в поле нулевого потен-
циала, выраженного уравнением (3-19), следует
Таким образом получаем обычную форму закона идеального газа.
Для реальных газов и жидкостей роТ-свойства непосредствен-
но связаны с силами притяжения и отталкивания между молеку-
лами. В настоящее время межмолекулярные силы в реальных
газах и жидкостях недостаточно хорошо известны для применения
общего уравнения (5-47), поэтому роТ-свойства реальных газов
и жидкостей должны быть определены экспериментально и вы-
ражены как эмпирическое соотношение.
4. Экспериментальные данные pvl
На рис. 19 представлены три типичные ро-изотермы реального
газа для температуры выше критической, равной критической и
для температуры ниже критической. Для сравнения приведена pv-
изотерма идеального газа для той же температуры выше крити-
ческой, что и для реального газа. Если температура ниже
~2,5-кратной критической температуры и давление меньше
~10-кратного критического давления, то реальный газ имеет
объем меньший, чем идеальный газ при тех же температуре и дав-
лении (или меньшее давление, если сравнение производят для
одинаковых температур и объемов). При давлении, большем
10-кратного критического давления, изотерма реального газа
пересекает изотерму идеального газа и объем реального газа ста-
новится больше, чем объем идеального газа при тех же температу-
ре и давлении.
158
Ниже этой точки пересечения силы притяжений между моле-
кулами реальною ia.<a уменьшают объем до зш|чсши1, меньшего,
чем объем идеальною га та при тех же массе, температуре и дав-
лении. При достаточно высоких плотностях (высокие давления
и небольшой объем на единицу массы) силы отталкивания между
молекулами становятся настолько значительными, что объем
реального газа не может быть уменьшен до объема, занимаемого
идеальным газом той же массы при тех же температуре и давле-
нии. В этой же точке пересечения противоположно направлен-
ные силы отталкивания и притяжения по существу компенсируют
друг друга.
По мере того как температура приближается к значению, при-
мерно равному 2,5-кратной критической температуре, точка пе-
ресечения имеет место при
все более и более низком
давлении, пока температура
не достигнет такого значе-
ния, при котором ро-изо-
терма реального газа пол-
ностью лежит выше изотер-
мы идеального газа. Эта тем-
пература, выше которой объ-
ем реального газа всегда
больше, чем объем идеаль-
ного газа даже при очень
низких давлениях (в пределе
р = 0), известна как точка
Бойля.
Если имеются экспери-
ментальные данные для реа-
льного газа для всей обла-
Рис. 19. pv-изотермы реального и иде-
ального газа [1]
сти рассмотренных условий, дифференциальные уравнения табл. 7
можно графически проинтегрировать. Однако когда нижним пре-
деле м интегрирования является очень низкое давление (в пре-
деле р-~0), площадь под ро-изотермой становится неопределяе-
мой. В этом случае более удобно определять остаточный объем а
как разность между объемами идеального и реального газов при
тех же температуре и давлении:
Рид Рреал!	(5-49)
а=—-------v для 1 моля газа.	(5-50)
Положительная сторона применения остаточного объема вид-
на из экспериментального наблюдения того, что при низких дав-
лениях (обычно 1 атм и ниже) изотерма идеального газа прибли-
жается к изотерме реального газа таким образом, что а остается
конечной и по существу постоянной величиной. На рис. 20 пред-
ставлены типичные кривые зависимости остаточного объема от
159
диплении. При высоких давлениях (примерно в 10 рла выше кри-
тическою диплопия) объем реального гйэй больше, чем объем
идеального газа при тех же температуре и давлении, так что
а — отрицательная величина. Для температур выше точки Бойля
а отрицательна для всех давлений. Для температур ниже точки
Бойля объемы реального и идеального газов становятся равными
в точке пересечения изотерм и а = 0. По мере понижения давле-
ния а обычно возрастает и затем приближается к достаточно по-
стоянной величине при низких давлениях. Для температур в
области критической и ниже а обычно максимальна при соответ-
ствующем давлении.
Принимая, что а остается конечной при р—~0, можно получить
конечное значение интеграла для пределов с очень малыми дав-
лениями. Это допущение не исключает того, что при низких дав-
лениях газы ведут сеоя как иде-
альные, так как критерий
------* 1 по мере р-* 0 (5-51)
pv
при этом выполняется. В этом слу-
чае
— = 1 +^=1+р -^-^(5-52)
pv	v	RT — ар
RT л
и в пределе — приближается к
единице при р-*-0.
Рис. 20. Зависимость остаточного
объема от давления
Если для вычисления изменений термодинамических функций
используют экспериментальные данные, выраженные через оста-
точный объем, то частные производные также удобно выразить в
функции а вместо общего объема. Интегралы могут быть затем
вычислены с помощью кривых, выражающих зависимость а от
р и Т, подобно кривым, изображенным на рис. 20.
Пример 7. Определить изменение энтальпии, внутренней
энергии и энтропии для 1 моля двуокиси углерода между 100 °C,
1 атм и 100 °C, 1000 атм, используя экспериментальные данные
работы [331.
Фактор сжимаемости, приведенный в этой работе, представ-
ляет собой отношение действительного произведения pv при тем-
пературе Т и давлении р к произведению pv при стандартных
условиях: 0 °C и 1 атм. Для двуокиси углерода объем 1 моля
при стандартных условиях равен 22264 см3. Следовательно,
объем двуокиси углерода при любых температуре и давлении
составляет 22264 f/p, где f — фактор сжимаемости [33].
Остаточный объем для двуокиси углерода может быть вычислен
из формулы
а RT — ZmAf
р .
16»
Численное значение RT при 273 “С райпо 22414 (смЧмоль) (атм).
Остаточный объем а двуокиси углерода при 100 “С и О 1000 атм
представлен на рис. 21.
Рис. 21. Зависимость остаточного объема дву-
окиси углерода от давления.
Дифференциальное уравнение для изменения энтальпии при
изменении давления при постоянной температуре выражено урав-
нением (5-21):
Значение объема может быть выражено в функции а по урав-
нению (5-50):
Дифференцированием по Т при постоянном р получаем
Подставляем правую часть равенства в уравнение (5-21):
(2«\ -т(А\
\ др )т ' дТ )р
(5-53)
Интегрированием при постоянной температуре получаем
(ДН)т = - j‘ Ja - Т (] dp.	(5-54)
11—1503
161
Интеграл удобно вычислять и дна приема. Интеграл ««//) и
пределах 1—1000 атм при носюш/ной температуре 100 'С можно
вычислить непосредстигиии как площадь под изотермой и р
при 100 °C (см. рис. 21). Эта площадь равна 480 кал/моль.
Значение частной производной (-77—) можно получить с
V/ / р
помощью графического дифференцирования изобар а — Т, изоб-
Рис. 22. Зависимость остаточного
объема двуокиси углерода от тем-
пературы (цифры иа кривых обо-
значают давление в атм).
раженных на рис. 22. Отрица-
тельные значения этой произ-
водной для температуры 100 °C
графически представлены как
функция давления на рис. 23.
Рис. 23. Зависимость част-
ной производной—104
от давления при 100 °C.
Изменение энтальпии между начальным и конечным состоя-
ниями можно вычислить по уравнению (5—54):
ДЯГ= —[480—373 (—3,85)] = —1920 кал/моль.
Величину Д£ можно легко вычислить из определения энтальпии:
=	—Д (ро).
Значение Д(ро) можно найти по уравнению состояния (5-50):
pv—RT—ар.
162
Так как начальная и конгчн я темперитуры одинаковы, то
А(рп) = ед1 — ед„;
A (pv) - (0,071 1 4- 0,U 15-1 000]	= 363 кал/моль,
&Е = —1920 —363= —2283 кал/моль.
Изменение энтропии можно вычислить по уравнению (5-26).
При условии постоянной температуры
i (>)/”•
Подстановкой производной по температуре уравнения (5-50) при
условии постоянного давления получаем
(AS)T= - [ [£-(А-\ ]dp
J Lp \оТ /р\
или
(JS),-StaA.+ ( (ЛА dp.
Pz J \ дТ / р
Вычисленный с помощью кривой на рис. 23 интеграл равен
—3,85 кал/(моль-°К). Так как In — представляет собой из-
менение энтропии идеального газа, то интеграл выражает раз-
ность между изменением энтропии реального газа и изменением
энтропии идеального газа для заданных начальных и конечных
давлений:
(AS)r= —1,987 In 1000—3,85=—13,7—3,85 =
= —17,55 кал /(моль-сК).
5. Алгебраическое уравнение состояния
Попытки привести в соответствие данные pvT и выразить их
соотношение в алгебраической форме были более или менее успеш-
ны для некоторых газообразных соединений, но до сих пор еще
нет полностью удовлетворительного соотношения pvT для жид-
костей в требуемом интервале температуры и давления.
Уравнение, которое связывает давление, объем и температуру,
известно как уравнение состояния. Одним из простейших и наи-
более употребимых уравнений состояния является закон идеаль-
ного газа:
pv=mRT.	(5-55)
Это соотношение объединяет в одно уравнение наблюдения Бойля,
Шарля и Гей-Люссака за поведением газов в условиях, близких
11*
163
к атмосферному давлению и комнатной температуре. Уравнение
хороню выполнимо при условии больших объемов на единицу
массы (малой плотности), когда молекулы газа настолько удале-
ны друг от други, что силы притяжения между ними незначитель-
ны. Уравнение просто по форме и относительно просто в применс
иии к большинству случаев. Даже если закон идеального газа не
строго выполняется, его можно использовать для получения бы-
строй оценки параметров по сравнению с другими уравнениями
состояния.
При использовании закона идеального газа для вычисления
изменений термодинамических функций получаются простые со-
отношения, которые выражают внутренние свойства, обусловлен-
ные незначительностью межмолекулярных сил и молекулярного
объема. Например, чтобы вычислить изменение внутренней энер-
гии, согласно уравнению (5-11), необходимо вычислить частную
производную г) • Для 1
моля идеального газа
RT
р=----
v
V
И
(5-56)
Следовательно,
RT А
—Р = ——Р = °
v	V
и
dE^C^dT.
(5-57)
(5-58)
Таким образом, изменение внутренней энергии идеального газа
не зависит от давления и объема и является функцией только тем-
пературы.
Подобно этому для вычисления изменения энтальпии по урав-
/ dv \
нению (5-22) следует вычислить частную производную ( дТ~ 1 .
Для 1 моля идеального газа
RT
V— —
Р
и
(5-59)
\дТ р
Следовательно.
(J”L\ = т(— \ — и = — — о=0	(5-60)
\ др /т \ дТ /р	р
и
dH = CDdT.
(5-61)
164
Таким образом, изменение энтальпии идеального газа не записи г
от давлении и объема и является функцией только температуры.
Изменение энтропии идеального газа можно легко вычислить
в функции температуры у объема подстановкой уравнения (5-56)
в уравнение (5-24):
dS = Cu~+R-^~.	(5-62)
Аналогичное выражение в функции температуры и давления мож-
но получить подстановкой уравнения (5-59) в уравнение (5-26):
dS = Ср у- — R -р-.	(5-63)
Применение закона идеального газа к уравнениям (5-29) и
(5-32) показывает, что теплоемкость идеального газа не зависит
от давления и объема. Действительно, дифференцируя уравне-
ние (5-56) по температуре при условии постоянства объема, полу-
чаем
Затем дифференцируем уравнение (5-59) по температуре при ус-
ловии постоянства давления:
\ =0.	(5-65)
\ дТ1 )р	'	'
Наконец, применение закона идеального газа к уравнению
(5-37) приводит к тому, что разность (Ср — CD) равна газовой
постоянной R, в чем можно убедиться подстановкой уравнений
(5-56) и (5-59) в уравнение (5-37):
Ср—Cv = T^-.^- = ^L.R=R.	(5-66)
V р pv
Ван-дер Ваальс один из первых сделал попытку видоизменить
закон идеального газа с учетом отклонений на примере данных
pvT для углекислого газа, полученных Эндрюсом. Он получил
соотношение
( p + -^(v-b)=RT,	(5-67)
где а и b — эмпирические постоянные;
. v — мольный объем.
Ван-дер-Ваальс интерпретирует слагаемое -° - как поправку
на силы притяжения между молекулами и постоянную Ь, как по-
правку на объем, занимаемый самими молекулами. Реальные
молекулярные объемы связаны с силами отталкивания между
165
молекулами и представляют собой «сферы влияния», в которые
другие молекулы не могут проникать. Для больших объемов па
единицу массы слагаемое незначительно но отношению к р,
постоянная b незначительна относительно v и уравнение сводится
к закону идеального газа.
Экспериментальные данные свидетельствуют о том, что изо-
терма pv, соответствующая критической температуре, имеет на-
клон, равный нулю, и точку перегиба при критическом давлении.
Установлено математически, что
=0;
\ 0v /ткр
(^\	= 0.
\ ди* / ткр
(5-68)
Применяя эти критерии к уравнению состояния Ван-дер-Ваальса,
получаем, что постоянные а и b связаны с критическими постоян-
ными уравнениями:
д_ 27	.
64 Ркр
_ RT кр  икр .
8Дкр 3
Ркр^кр _ 3
RTKp 8 
(5-69)
(5-70)
(5-7.1)
Подставляя значения для а и b в уравнение состояния Ван-дер-
Ваальса, получаем уравнение в функции приведенных перемен-
ных:
( Рпр +4") (3%-1) = бТ’пр.	(5-72)
\ °пр /
где
р . „	_ v . rj, _ Т
РпР~ о ’ &пр~ V ’ 7пр— Т '
Ркр	икр	1 кр
Эти отношения называются приведенным давлением, приведен-
ным объемом и приведенной температурой соответственно.
Из уравнения (5-72) следует, что все вандерваальсовские газы
должны иметь идентичные руТ-свойства, если сравнивать их при
одинаковых приведенном давлении и приведенной температуре.
Принято говорить, что газы при одинаковых приведенных давле-
нии и температуре находятся в соответственном состоянии.
Несмотря на то что из уравнения состояния Ван-дер-Ваальса
можно сразу предсказать, каково будет отклонение от поведения
идеального газа, все же оно недостаточно для точной оценки ко-
личественных вычислений. Были получены развернутые урав-
166
пенни состоянии, которые вполне* точно предсказывали поведе-
ние реальных газов и широком диапазоне условий. Наиболее из-
вестны из них: уравнение Битти-Брпджсмаиа с пятью эмпири-
чески определяемыми постоянными и уравнение Бенедикт —
Вебб — Рубина, содержащее восемь эмпирических постоянных.
Хотя эти уравнения могут предсказать рпТ-свойства газа в пре-
делах нескольких десятых процента, сложная математическая
форма затрудняет их применение. Отсутствие числовых значений
для эмпирических постоянных также ограничивает их примене-
ние для большого числа газов, в частности углеводородов, при
обычных температурах и давлениях. Тем не менее потребность
в более точных данных pvT для широкого диапазона температур
и давления и развитие вычислительной техники для решения
сложных алгебраических уравнений стимулирует использование
таких уравнений состояния в обычных технических расчетах.
Уравнение состояния Битти — Бриджемана [4] таково:
pv^-RT

)-Л0(1—(5-73)
Уравнение состояния Бенедикт — Вебб — Рубина имеет вид
p = RTd+ ( RTB0-A0-^y*+(RTb-a)cP +
+ aado + cd^^^-.	(5-74)
Пример 8. Определить изменения энтальпии, внутренней
энергии и энтропии для двуокиси углерода при переходе от со-
стояния при 100 °C, 1 атм к состоянию при 100 °C, 1000 атм с
использованием уравнения состояния Ван-дер-Ваальса.
Так как уравнение Ван-дер-Ваальса не может быть решено
явно относительно v, то оно неудобно для вычисления частной
/йу \	[ дН \
производной \^) » входящей в уравнение (5-21) для
Изменение энтальпии при переходе от начальных условий к ко-
нечным легче вычислить интегрированием выражения для изме-
нения энтальпии в зависимости от изменения объема при постоян-
ной температуре.
Переход от независимой переменной р к v можно легко осу-
/йо \
ществить подстановкой I — I из уравнения (5-36) в уравнение
(5-21):	Р
Умножая уравнение (5-21) на J , получаем
/ дН \ / др \ _ / дН \  у, / др \ । у / йр \
\ др ) т\ dv )т \ dv /т \ дТ )v \ dv /т
167
Решаем уравнение Вен-дср-Ваальса относительно р:
RT .а,
Г v—b v*
( дР \ . R .
I in. ~ 1 S3 ..HI» I
\дТ/е v—b
/ dp \	RT . 2а .
[----1 вч----------------:
\ dv /т	(v—b)*	V*
/ дН \	 RTb	2а
\ dv /т (о — b)* v*
Интегрированием по объему при постоянной температуре полу-
чаем
(дн)г= к—<5-75>
(»! — b) (v2 — Ь) ViV2 J
Значения постоянных а и b можно определить по критическим
постоянным с использованием уравнений (5-69) и (5-70). Для дву-
окиси углерода
[Ткр=304°К;
ркр = 73 атм-,
а = (27/64) (0,08206)2 (304)2/73 = 3,58 атм (л/моль)2;;
b = 0,08206 • 304/8  73 = 0,0427 л./моль.
Объем при начальных и конечных условиях определяют из
уравнения Ван-дер-Ваальса методом последовательных прибли-
жений. Значение v, удовлетворяющее уравнению Ван-дер-Ваальса
при 373 °К и 1 атм, равно 30,50 л/моль; тогда (t-y — Ь)-~
— 30,46 л!моль. Значение v, удовлетворяющее уравнению Ван-
дер-Ваальса при 373 °К и 1000 атм, равно 0,0573 л/моль; тогда
(о2 — Ь) = 0,0146 л!моль.
Подстановкой этих значений в уравнение (5-75) получаем
[0,08206.373-0,0427	2-3,58 1
{tXlij'T  I	л л- I
[ 30,46-0,0146	30,5-0,0573]
X (30,5—0,0573)=—35,32 л-атм/моль——856 кал!моль.
Этот результат сравним с величиной —1920 кал!моль, полу-
ченной в примере 7 на основании экспериментальных данных и
нулевого значения для идеального газа.
^Е — АН—A (pv);
Л (pv)~p2v2—PiVr = [1000 -0,0573—1 30,5] х
х 1,987/0,08206 = 649 кал/моль;
168
ДЕ « —856 — 649 « — 1605 кал/моль,
/ dS \	/ др \. .
\ dv /т \ дт
В»
ДЕ- [ (ДА dv,
J \0Т/е
щ
ДЕ= С 7?-*L- = /?ln^=^;
J	v — Ь	vt — b
01
AS = — 1,9871n	_ 1,987 In 2085 =
0,0146
= —15,2 кал/(моль °K).
Это значение сравнимо с разностью энтропий идеального газа при
I атм и 1000 атм:
A S = — 1,9871п	=—13,7 калЦмоль  °К).
6.	Обобщенный фактор сжимаемости
Обобщенное уравнение состояния представлено уравнением
(5-47). Однако пока нет возможности вычислить непосредственно
сумму состояний системы, в которой действуют значительные меж-
молекулярные силы. Так как сумма состояний не может быть
вычислена непосредственно, то уравнение выражают в виде сте-
пенного ряда:
-^=2=1+—+ 4 + 4+--->	(5-76)
RT	v va Vs
где Z — фактор сжимаемости;
В, С и D — вириальные коэффициенты.
Эти коэффициенты являются функциями температуры и вну-
тримолекулярной потенциальной энергии. Хотя значения вто-
рого и третьего вириальных коэффициентов получены на основа-
нии предположенной функции потенциальной энергии между мо-
лекулами, расчеты сложны и результаты в настоящее время при-
меняют лишь частично.
Из-за отсутствия прямого метода вычисления возникла необ-
ходимость эмпирически найти фактор сжимаемости, определяе-
мый уравнением (5-76). Обширные экспериментальные наблюде-
ния подтвердили вывод из уравнения состояния Ван-дер-Ваальса
о том, что все газы имеют одинаковый приведенный объем, если
их сравнивают при одинаковых приведенных температуре и дав-
лении. Эти наблюдения привели к обобщенному, хотя и прибли-
женному утверждению, называемому «законом соответственных
169
состояний». Одна из форм закона может быть представлена мате-
матическим выражением
упр f 1 (T'itpi Pup)-	(Б-77)
Из определения опр и Z получаем
<5'78)
икр	крР ^КрРпр
Из уравнений (5-77) и (5-78) следует, что
Z == / 2 (ГПр, Рпр> 2кр).	(5-79}
Согласно уравнению (5-71), величина ZKp «вандерваальсов-
ского газа» постоянна и равна 0,375. Все газы Ван-дер-Ваальса,
имеют одинаковый фактор сжимаемости при данных приведенных
температуре и давлении. Действительно, величина ZKp для боль-
шинства веществ падает в узком пределе с 0,25 до 0,30. Следова-
тельно, в первом приближении фактор сжимаемости может быть
выражен как функция только приведенной температуры и при-
веденного давления:
2 = /з (ТпР, рПр).	(5-80)
Опубликованы многочисленные выражения фактора сжимае-
мости, основанные на уравнении (5-80). Большая точность наблю-
далась при использовании ZKp в качестве третьего определяющего
параметра в соответствии с уравнением (5-79). На рис. 24 пред-
ставлена зависимость фактора сжимаемости от рп„ при ZKP =
= 0,27 [251.
Применение фактора сжимаемости при вычислении термодина-
мических функций требует, чтобы частные производные давления,
объема и температуры были выражены в функциях Z, Ткр и ркр.
Полученное дифференциальное уравнение можно затем проинте-
грировать графически аналогично тому, как это было сделано в
примере 7. Действительно, два метода расчетов могут быть сде-
ланы с помощью соотношения между а и Z:
-^= — +1=—;	(5-81)
pv V	Z
а  1 — Z
"ЯТ~ р *
Пример 9. Определить разность энтальпии, внутренней
энергии и энтропии для состоянии при 100 °C, 1 атм и 100 °C,
1000 атм, используя обобщенное выражение для фактора сжи-
маемости.
Так как уравнение состояния, выраженное через фактор сжи-
маемости, может быть точно решено для объема, изменение эн-
тальпии можно л^гко вычислить по уравнении? (5-21). Частная
170
Рис. 24. Зависимость фактора сжимаемости от приведенного давления Z^— 0,27 [25]:
область низкого давления; б—область высокого давления (цифры на кривых обозначают приведенную температуру)
тшонзонпжэ doujno$
171
производная объема по температуре при условии постоянства
давления может быть выражена в функции фактора сжимаемости
дифференцированием уравнения (5-76):
f*L\ !ZR,(*LA(1L\
\&т )р p p )\дТ Ip
Подставляем это выражение в уравнение (5-21):
/ dll \ = _ РЛ / &Z \
\ др /т р \ дТ )р
Интегрированием при условии постоянства температуры полу-
чаем
Ра
Так как Z обычно выражают в функции приведенных параметров,
интеграл легче всего вычислить относительно приведенной тем-
пературы и приведенного давления:
Ткр	J Wnp / Рпр Рпр
£пр.1
Значение интеграла определяют графическим интегрированием по
dZ
дТ
кривой —как функции рГ1Р при в диапазоне давления от
Рпр
Рпр.1 ДО Рпр.2-
Критическая температура двуокиси углерода 304 °К и крити-
ческое давление 73 атм. Следовательно, в этом примере
7’пр = 373/304 =1,23;
Pnp.i= 1/73-0,0137;
Рпр.2 = ЮОО/73-13,7.
/ dZ \
Частная производная ( т— 1 может быть вычислена графиче-
W-'np'pnp
ским дифференцированием кривых при значении Тпр, равном 1,23,
при различных приведенных давлениях (рис. 25). Величина на-
клона при Тпр 1,23 для каждого приведенного давления де-
лится на приведенное давление и наносится на график как функ-
ция приведенного давления (рис. 26 и 27).
Площадь под кривой дает величину интеграла (безразмерную),
равную 2,145. Эта величина, умноженная на (—RT^p Тк^, дает
значение изменения энтальпии:
(Д //)г = — J, 987 • 1,232 • 304 - 2,145 = — 1960 калЦлоль.
172
Так как изменение .птальпии идеалыни-о газа с изменением
давления при постоянной температуре равно нулю, то величина
интеграла между нулевым давлением и р„р представляет собой
разность между энтальпиями
реального и идеального газов
при одних и тех же темпера-
туре и давлении:
Hi-Hl „
OZ \ rfpnp
дТпр / Рпр Рпр
Так как интеграл — функ-
ция только Ткр и ркр, то его ве-
личина может быть определена,
как указано выше, и изображе-
на как функция Ткр и ркр (рис.
28 и 29). Изменение энтальпии
реального газа между любыми
двумя состояниями при одина-
ковой температуре, но разных
давлениях может быть опреде-
лено из соотношения
Н2 — Нг = Н2—Н*2 Ht — Hj
Лф	^кр	Т Кр
так как
Рис. 26. Зависимость вели-
чины (dZldTrP)pnplpnp от
давления, Т,,р = 1,23.
1,6
Ц
1,3
V
1,0
*о<)
|0Л
$0,7
§ 0,6
В»Л
g- 1,0
6
§ ол
0,6
О'/
W 11	1,2 1,3 1JS
Приведенная тенператураТпр
Рис. 25. Зависимость фактора
сжимаемости от приведенной тем-
пературы, ZKP= 0,27 [25] (цифры
на кривых обозначают приведен-
ное давление).
Рис 27. Зависимость вели-
чины (1 — Z)/pIip от давле-
ния, Тпр = 1,23.
173
(Н-Н)]ТКр,кал1(№Ль °К)
Рис. 28. Зависимость энтальпии от приведенного давле-
ния, ZKp=0,27 [25] (цифры на кривых обозначают при-
веденную температуру).
Рис. 29. Зависимость энтальпии от
приведенной температуры, ZKP = 0,27
(25] (цифры на кривых обозначают при-
веденное давление).
174
Jh рис. 28 следует, что
"*rZ/ * -6,4 при Тпр - 1,23 и Ряр 13,7;
' *Г
^1-0 при 7’11р»1,23 и р„р 0,0137.
Т'кр
Следовательно,
= —6,4 — 0
Т'кр
и
Я2—Ях = 304 (—6,4)=—1945 кал!моль.
Изменение внутренней энергии может быть вычислено из оп-
ределения энтальпии:
ЕЕ = &Н—Д (pv)
и Д(ри) можно вычислить по уравнению состояния:
pv = ZRT.
В этом случае начальная и конечная температуры равны, так что
Д (pv)T = RT (Z2—Zx) = 1,987 • 373 • (1,42 — 1) = 311 кал/моль,
Д£=—I960—311 =—2271 кал!моль.
Изменение энтропии наиболее просто вычислить по уравне-
нию (5-20):
/ as \ ____I dv \
\ др )т \ дТ /р
Выраженное в функции фактора сжимаемости уравнение приоб-
ретает вид
/ as \	ZR	RT f dZ \
V др )т	р	Р \ дТ )р
Так как отношение — стремится
уравнение легче интегрировать в
к бесконечности при р-*0,
форме
\ др )т р	Р Р \ дТ / р
Интегрированием в приведенных координатах получаем
₽пр 2	Рпр 2
(AS)r=/? In ^±+7? С	(l-Z)-^-/?Tnp f
Pnp.2	J	Pnp	‘	Pnp
₽up.l	pnp.l
175
Первый член п правой части уравнения выражает изменение штро-
пии идеального газа между начальным и конечным состоянием.
Интеграл но втором слагаемом правой части вычислен с помощью
кривой на рис. 27 и равен 0,702 (безразмерный). Интеграл в по-
следнем члене уравнения вычислен также с помощью кривой на
рис, 26 и равен 2,145 (безразмерный). Тогда изменение энтропии
(Л5)г = — 1,987 In 1000+1,987 • 0,702 — 1,987•1,225- 2,145 -
= —13,71 + 1,40—5,24=—17,55 калЦмоль °К)
Рис. 30. Зависимость энтропии от приведенного
давления ZKp = 0,27 [25] (цифры на кривых обо-
значают приведенную температуру).
Вычисление интегралов в пределах давления от 0 до рпр дает
рпР.1
(s1-s;)-(s;-s;)=(s1-s1*)=/? f (i-z)^₽—
•o'	Pnp
₽прд
-WI7D f
J \ v/np /p Pnp
Интегралы являются функциями только Tnf и рпр и представляют
собой разность между энтропией реального газа и энтропией идеаль-
ного газа при одинаковых температуре и давлении. Интеграл
176
может быть определен при различных птчсниях Тпр и р1ф; откло-
нение энтропии (S — S*) изображено па рис. 30 как функция 7'„р
и р„р.
Из рис. 30 следует, что
SB—SJ  —3,8 при 7^ = 1,23 и рпр=* 13,7;
5г—SJ« 0 при Тпр=в 1,23 и рпр"«0,0137;
(Sg—Si)—(SJ—S;)“ —3»8 калЦмоль °К).
Для идеального газа
SJ — s; = — 1,987 In 1 000 = — 13,7 калЦмоль  °К);
Sa—St = —13,7—3,8= —17,5 кал/(моль-°К).
Результаты примеров 7, 8 и 9 суммированы для сравнения в
табл. 8, чтобы иллюстрировать влияние уравнения состояния на
вычисленные изменения термодинамических свойств двуокиси
углерода для состояний при 100 °C, 1 атм и 100 °C, 1000 атм.
Таблица 8
ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА ДВУОКИСИ УГЛЕРОДА
Термодина- мические величины	Единица измерения	Идеальный газ	Эксперимен- тальные дан- ные, пример 7	Данные Ван- дер-Ваальса, пример 8	Фактор сжи- маемости, пример 9
дн Д(ри) Д£ AS	кал/моль кал/моль кал/моль калЦмоль -’К)	0 0 0 —13,71	—1920 363 —2283 —17,55	—856 649 —1505 —15,2	—I960 311 —2271 —17,55
Если экспериментальные данные принять за основу для срав-
нения, с помощью обобщенного выражения фактора сжимаемости
можно получить достаточно точные результаты для двуокиси угле-
рода в диапазоне выбранных условий. Хотя вычисление значения
AS с использованием уравнения Ван-дер-Ваальса достаточно
удовлетворительно, величины АЕ и АТ/ весьма неточны. Вычисле-
ние величин показывает, что надежность принятого уравнения
состояния зависит от того, какая функция вычисляется: внутрен-
няя энергия более чувствительна к уравнению состояния, чем
энтропия.
Примеры 7—9 также иллюстрируют, что внутренняя энергия
реального газа уменьшается по мере изотермического возрастания
давления до тех пор, пока фактор сжимаемости меньше единицы во
всей области условий. Если начальные условия для углекислого
газа 20 °C, 1 атм, а конечные 100 °C, 1000 атм, закон идеаль-
ного газа должен предсказать возрастание энтальпии
~746 кал/моль при повышении температуры на 80 °C; в действи-
12—1503
177
талыюсти «нталышя реальною Газп понизится примерно па
1174 кал!моль.
Пример 10. Определить изменение теплоемкости двуоки-
си углерода вследствие изменения давления от 1 атм до 1000 атм
при постоянной температуре ~100°С, учитывая эксперименталь-
ные данные по определению остаточного объема, обобщенное вы-
ражение для фактора сжимаемости, уравнения состояния Ван-
дер-Ваальса и Бенедикт — Вебб — Рубина.
Согласно уравнению (5-32)
/ дСр \ у, / д2у \
\~др)т \дТЧр'
Вторая частная производная может быть найдена в функции
остаточного объема путем дифференцирования уравнения (5-50)
по температуре при условии постоянства давления:
/ даа \________________________/ д2у \
\dTVp~ \ дТ2 / р
Подставляем уравнение (5-82) в уравнение (5-32):
/ дСр\ д2а \
\ дР Jt	\ffT2lp
Изменение теплоемкости с изменением давления при
температуре находим вычислением интеграла:
(5-82)
(5-83)
постоянной
(5-84>
и
Интеграл можно вычислить с помощью графика второй произ-
/ д2а \
водной при температуре Т как функции давления. Вторую
производную можно найти графическим дифференцированием
кривых, в которых первая производная представлена как функ-
ция температуры для некоторых давлений в интервале от 0 до
1000 атм. Первые производные были вычислены графическим
дифференцированием кривых на рис. 22. Значения вторых произ-
водных представлены как фукнции давления на рис. 31. Графиче-
ское интегрирование с помощью кривой на рис. 29 приведено для
давления от 0 до 1000 атм и результаты представлены на рис. 32.
Согласно рис. 32, изменение величины теплоемкости углекислого
газа при 100 СС от 0 до 1000 атм составляет 11,0 калКмоль °К).
Так как изменение теплоемкости углекислого газа между 0 и
1 атм незначительно, то фактически рассматривается изменение
теплоемкости между 1 и 1000 атм.
Изменение теплоемкости с изменением давления можно также
вычислить в зависимости от обобщенного фактора сжимаемости.
Согласно уравнению (5-76),
и =----,	(5-85)
Р
178
Псрвия и вторая производные от v по Г при условии постоянною
давления равны соответственно:
Подставляем уравнение (5-87) в уравнение (5-32):
RT
Р
(5-89)
₽|
р
Интеграл уравнения (5-89) можно выразить в функции приве-
денных координат (рис. 33):
'ПР(^р)рпр
Рпр
dpnv. (5-90)
Подынтегральное выражение уравнения (5-90) можно вычислить
по графику обобщенного фактора сжимаемости способом, анало-
гичным описанному выше для
экспериментальных данных по
определению остаточного объ-
ема. Подынтегральное выраже-
ние было вычислено для Тпр =
= 1,23 и результаты представ-
Рис. 32. Теплоемкость двуокиси угле-
рода при 100 °C:
/—остаточный объем; 2—фаитор сжимаемо-
сти; 3—по уравнению Бенеднкт-Вебб-Рубина;
4—по уравнению Ван-дер-Ваальса
fl 100 200 300 4flfl 500 00
Давление, атм
Рис. 31. Зависимость второй про-
изводной остаточного объема по
температуре при 100 °К от давле-
ния двуокиси углерода.
лены как функция приведенного давления на рис. 32 [251. Изме-
нение теплоемкости газа при 7пр = 1,23 между двумя любыми зна-
чениями-давления можно получить графическим интегрированием
12*
179
кривой на рис. 3'2. Значение интеграла определено для рт," 0 < 14
и изображено графически на рис. 33 для сраипеппя с величина-
ми, определенными на основе экспериментальных данных.
Определенное (рис. 33) изменение теплоемкости углекислого
газа при 100 °C (Т„р 1,23) между 0 и 1000 атм (рпр 13,7) со-
ставляет 8,1 калЦмоль °К) Лайерсон, Гринкорн и Хуген сделали
более подробные вычисления. Результаты этих вычислений пред-
ставлены на рис. 34 для Тпр от 0,8 до 3,0 и рпр от 0 до 4,0.
Предварительные вычис-
ления, основанные на экспе-
риментальных данных и обоб-
щенном соотношении для фак-
тора сжимаемости, включают
два последовательных графи-
ческих дифференцирования
после графического интегри-
Рис. 34. Зависимость мольной тепло-
емкости от приведенного давления,
ZKp = 0.27 125] (цифры на кривых
обозначают приведенную темпера-
туру):
---------пар (васыш );-------жидкость
(насыщ)
Приведеююе давление рпр
Рис. 33. Зависимость ин-
теграла уравнения (5-90) от
приведенного давления для
двуокиси углерода при
100 °C.
рованря. Хотя вычисление достаточно точно, графическое изоб-
ражение неизбежно содержит ошибку в результатах вычисления,
поэтому кривые на рис. 33, построенные на основании этих
результатов, только приблизительны.
Вычисления с помощью графика можно избежать применением
подходящего уравнения состояния. В этом случае вычисленные
результаты зависят от качества аналитического уравнения, связы-
вающего /wT-свойства газа. Такие вычисления проиллюстриро-
18Э
вини ниже применением уравнений состояния Ван-дер-Ваальса
и Бенедикт — Вебб — Рубина.
Вычисления, основанные па строгом соотношении Ср и Cvr
выражены уравнением (5-38):
Для идеального газа
с;—с;=л.
Вычитаем уравнение (5-91) из уравнения (5-38):
/ др \2
Cp—C,p—(C0—C*v)—T-L-^—^v -R.
/ др \
\ де )т
Интегрируем уравнение (5-29):
(5-91}
(5-92)
(5-93}
Согласно уравнению состояния Ван-дер-Ваальса,
(5-67)
(5-94)
(5-95)
(5-96)
Как следует из уравнений (5-93) и (5-95), Cv— C*v = 0 и теплоем-
кость при постоянном объеме вандерваальсовских газов не зави-
сит от объема и давления.
' .Подставляем уравнения (5-94) и (5-96) в уравнение (5-92):
(5-97)
18Г
Для двуокиси углерода
а 3,58 атм (л/моль)*;
Ь ««0,0427 л/моль.
При 373 °К уравнение (5-67) принимает вид
Ра™ = 30,6/(о—0,0427)—3,58ДЯ
и из уравнения (5-97) получаем
( С„ —С;, калЦмоль  °К) = 1,987-------------!-------.
(V \2
------1 — 1
v — Ь /
Для v =s= 0,10 фут3/фунт-моль (0,006 л! моль)
р = (30,6/0,573)—(3,50/0,01)= J84 атм-,
рпр= 184/73 = 2,52;
Ср—CJ= 1,987/(4,27 0,10(0,10/0,573)2—1] =
= 6,63 кал/моль -°К).
Следовательно, изменение теплоемкости углекислого газа при
100 °C между 0 и 184 атм (рпр — 2,52) составляет 6,63 калЦмоль -°К)
Повторяя вычисления для нескольких значений v, можно уста-
новить соотношение между Ср—Ср и рпр. Такое соотношение,
•основанное на уравнении Ван-дер-Ваальса, представлено на
рис. 33 для сравнения с величинами, определенными по экспери-
ментальным данным и обобщенного выражения фактора сжимае-
мости. По данным рис. 33, величина Ср— Ср при 1000 атм (рпр =
— 13,7) равна 0,72 калЦмоль -°К).
Подобным образом кривая, выражающая соотношение между
(Ср — Ср) и давлением углекислого газа, может быть построена
на основе уравнения состояния Бенедикт — Вебб — Рубина с
использованием параметров (фут3/фунт-моль и СК) для углекисло-
го газа, установленных Кобе [12];
Ло = 10322,8; а = 8264,46;
Вв = 0,799492;	в = 1,0582;
Со= 1,69301-10’; с= 2,91979 10’
7= 1,384000	а = 0,348000.
Изотерма ри для углекислого газа при 100 °C была получена
подстановкой этих параметров в уравнение (5-74):
р„м = 491 d— 566d2—42,9d3 + 195d« + 441 d3 (1 +
+ yd2)/^,	(5-98)
182
где d — мольная плотность, фупт-моль/фут’. Урмннсние для
(Ср — Ср), основанием» на ураиненпп состояния (кпсднкт —
Вебб — Рубина, вывел Слсджескпй 138, 391:
I	2C„d	2с	„"la
Т	+ B.Rd +	+ b№-	d« (1 + 7^) e"vrfS]
/	с„\
ЯТ + 2 BaRT — A0—-^-]d + 3(bRT — a)d» + 6aad* +
\	‘9 /
Cd*
+^f3+M9-2(^)2i
(5-99)
Подстановкой параметров углекислого газа при 100 °C получаем
С____С* —
________[10,73-}- 19,85d11,37d2 — 19,4da (17d2)/tvda]2_________
10,73 — 24,8d — 2,93d2 + 25,7d* + (9,66d2/eYda) (3 + 3?d2 — 2 (-yd2)2]
4-33,75d—42,1 (e^2— l)/eTd3-}-29,ld2/eVda—
—10,73, фунт/дюйм2 [фут3фунт-моль)/°Н]. (5-100)
Для d = 1,35 фунт-моль/фут® p = 1000 атм из уравнения
(5-98) и Ср — Ср = 28,7 фунт-дюйм2 (фут3/фунт-моль) °R =
= 28,7-1,987/10,73 = 5,3 кал!моль  °К).
7. Термодинамические графики и таблицы
Обширные вычисления, аналогичные приведенным в примерах
7, 8 и 9, были выполнены для наиболее обычных газов и проил-
люстрированы таблицами для некоторых интервалов температур
и давлений. Для этих газов разность термодинамических функций
для двух конкретных состояний может быть вычислена непосред-
ственно по табличным данным. Приведенные значения функций в
этих таблицах относятся к произвольно выбранному стандарт-
ному состоянию, т. е. эти значения показывают разность термо-
динамических функций между их величинами для стандартного
состояния- и для состояния с заданной температурой и давлением.
Важно обратить внимание, каковы стандартные состояния, если
сравниваются величины, взятые из различных источников.
В некоторых случаях удобны данные в виде диаграмм и графи-
ков. Выбор частной функции как независимой переменной зави-
183
сит от конкретного применения. Для исследования процессов
нитрования и испарения при постоянном давлении наиболее
удобен график зависимости давления'от энтальпии, а объем, энтро-
пия и температура рассматриваются как параметры. Для изуче-
ния циклов тепловых двигателей был найден удобный график
зависимости температуры от энтропии; объем, энтальпия и давле-
ние были приняты в качестве параметров. Диаграмму Молье, на
которой представлена энтальпия как функция энтропии, а объем,
температура и давление приняты в качестве параметров, широко
используют в расчетах процессов сжатия и расширения. Частная
форма того или иного графика не имеет принципиального значе-
ния, поскольку все графики содержат одни и те же данные и мо-
гут дать одинаковые результаты.
Термодинамические диаграммы для отдельных веществ можно
построить, используя рис. 28 и 30, вычерченные на основе обобщен-
ного фактора сжимаемости. Пример 11 иллюстрирует построение
таких диаграмм для двуокиси углерода при температуре 25 и
150 °C и давлений 1—1000 атм.
Пример 11. Построить диаграмму Молье перегретого
углекислого газа для температуры 25—150 °C и давления 1—
1000 атм. За основу для вычислений принять, что энтальпия
двуокиси углерода равна 8500 кал!моль, а энтропия равна
•5,06 кал/(л*оль-°К) при 25 °C и 1 атм.
Первая стадия построения заключается в вычислении энталь-
пии при нескольких температурах между 25 и 150 °C в состоянии
идеального газа при 1 атм. Согласно уравнениям (5-22) и (1-59),
изменение энтальпии с температурой может быть выражено в
виде
АЯ* = f С^Т = [ а + ± (Т2 + Л) + (7* + 7271 + 7?)1 (Т2—ТО-
J	L	4	J
Таблица 9
ЭНТАЛЬПИЯ УГЛЕКИСЛОГО ГАЗА (Н»=8500 кал/моль ПРИ 298 °К я 1 атл)
Температура			Давление, атм							
			1		10 (рпр=0.137)		100 (Рп	р-1-37)	1000 (р,	1р-13.7)
•С	°К	т пр	ДН»	н*	Н*-Н	н	н*—н	н	н*-н	н
25	298	0,98	0	8500	103	8397	2580	5920	2660	5840
50	342	1,06	227	8727	79	8648	1580	7147	2450	6277
75	348	1,14	460	8960	66	8894	970	7990	2150	6810
100	373	1,22	697	9197	52	9145	760	8437	1945	7252
125	398	1,31	940	9440	42	9398	610	8830	1750	7690
150	423	1,39	1190	9690	39	9651	500	9190	1520	8170
Примечание. Н* обозначает состояние идеального газа.
184
Используя коэффициенты теплоемкости двуокиси yi лерода из
приложения 2 и полагая 1\ ранной 298 иК, получаем
А//* - | 6,214 110,396/2 10я)| (74 298)—[3,646/(3 X
X 101)] (Т9 + 2987' + 298®)) (Т—298).
Величины Д/7* и /7* приведены в табл. 9 для температуры 25 °C
и выше.
Согласно уравнению (5-63), изменение энтропии идеального
газа выражается так:
AS- = JCp-<-^J *.
С помощью коэффициентов для теплоемкости двуокиси углерода,
приведенных в приложении 2, и полагая 7\ равной 298 °К, на-
ходим
AS* = 6,214 In121396(Г_298)_ 3-542 х
298	\ 103 / 4	’	2-10’
X (72—298®) — 1,987 In (р/1).
Величины AS* и S* при некоторых температурах и давлениях
представлены в табл. 10.
Отклонения величин энтальпии и энтропии от соответствую-
щих вейичин для идеального газа, полученных по кривым рис. 28
и 30 при некоторых температурах и давлениях, также приведены
в табл. 10 и 11.
Рнс. 35. Диаграмма энтальпия — температура
для двуокиси углерода
. На рис. 35 изображены кривые изменения действительной
энтальпии как функции температуры в зависимости от давления,
принятого как независимый параметр. На рис. 36 представлены
кривые изменения действительной энтропии как функции темпе-
ратуры в зависимости от давления, также принятого как неза-
висимый параметр. Значения энтальпии в качестве независимого
185
Таблица 16 ЭНТРОПИЯ УГЛЕКИСЛОГО ГАЙА (3*=51,06 кал/(Аоль-°К.) ПРИ 298 °К и 1 атм}			Давление, атм		ат1=ап<л mi	сл 2)	SSSWfc	
				SfcSgSS cDin-M* eoeooi	
					
			—R In 1000	СО СО со СО сО СО 1 1 1 1 1 1	
		100 (Рпр = 1.37)	I	СО	Ch Ь- b- ООО Ю Ь- —1 СО С4 СО — сч сб СО СО Tf Tf* ’t* Tf*	
			CQ J <0	СЧ Ю Ю IQ С Ю CO oo —* co CM 03 ь- co см — — О	
			со	’-’fC'lOOrt Ct co co Ch co CM CM co CO ^F IQ	
			-7? In 100	Ю ЮЮ LO Ю V »™* *“* ——"4 V-—’ ч—* —— О ООО ОС 1 1 1 1 1	i
			Ю (Рпр°0.137)	i	СО	— <M Ю to co vf <o bp о co ct> ch	
			со J СО	COClCOlOb CM CM — — oo о” о о о о o' - 3	
			» со	О СМ О ь- СО — Г rF СМ О ю 00 ------ о ФЬЬССОО rf* rf* TF -ЧГ rf« g	
			-R In 10	§ b~ b~ b- |>. b- b" lOWlfliOWiO § Tf Tf Th Tj- «Ф II 1 i II 1 к	
		-	СО	(ООь.’ФЮОО н Ob- — Г- CO v — — (M CO CO rr u ЮЮЮЮЮЮ b	
			 AS*	tr co — 00 О (M 2 b- ’d* О <O CO те О О — (M <М СО 'О о	
	Температура	о.		* b- СО rf (М —‘ О О О — 04 СО СО (V о — — — — — Е	
				ж 00 СО 00 сооо СО 2 СЬ(М Tf о- О(М »* (М со СО СО со Tf* ф S	
		и о		1 ® ю о Ю Q ш о счюь-осчю С	
параметра, мятые и» рис. 35,
изображены кривыми па рис. 36.
С помощью этого построения на
рис. 36 представлена энтропия
как функция температуры и
давления.
На рис. 37 те же данные
приведены в виде диаграммы
Молье энтальпия — энтропия в
зависимости от температуры и
Рис. 36. Диаграмма энтропия — тем-
пература для двуокиси углерода.
Рис. 37 Диаграмма энтальпия —эн-
тропия для двуокиси углерода.
186
Давления КПК h?.,uhhi нмых параметров, форма графика ii.i рас. 37
особенно удобна, так как пересечение кривых, соответствующих
определенным температуре и давлению, дает точку, ио которой
штальпия может быть определена ординатой, а энтропия — абс-
циссой. По диаграмме Молье процесс с постоянной энтальпией
(например, процесс расширения по Джоулю — Томпсону) изоб-
ражается горизонтальной прямой линией, а процесс с постоян-
ной энтропией (нзоэитропийпый) изображается вертикальной
прямой.
Пример 12. Перегретый углекислый газ при стационарных
условиях (100 'С, 100 атм) расширяется адиабатно, проходя че-
рез редуктор с понижением давления до 1 атм. Определить ко-
нечную температуру и изменение энтропии.
Пренебрегая изменением кинетической и потенциальной энер-
гии, считать, что изменение энтальпии для этого процесса равно
нулю, так, что конечная температура может быть определена по
данным табл. 10 (рис. 36 или рис. 37); тогда найдем, что она будет
немного меньше 25 °C. Изменение энтропии может быть определе-
но по данным табл. 11 (см. рис. 35 или 36) и составит 51,0 — 42,3 =
— 8,7 кал!(моль °К).
Пример 13. Определить максимальное количество работы,
которое может быть получено при обратимом и адиабатном рас-
ширении двуокиси углерода с начальной температурой 50 °C и
изменением давления от 5 до 1 атм при прохождении через тур-
бину.
Для этого обратимого адиабатного процесса изменение энтро-
пии равно нулю и ws равно —ДТ/. Интерполяцией данных по
рис. 37 определяем, что энтропия при начальных условиях равна
48,5 кал/(моль °К) и энтальпия 8680 кал/моль. Энтальпия при
1 атм и той же самой энтропии составляет 7850 кал/моль.
Исходя из этого
Wg-'-—АН = 8680—7850=—830 кал/моль.
Так как для двуокиси углерода отклонения от законов идеального
газа при давлении 1 атм весьма невелики и теплоемкость лишь
немного изменяется с температурой ниже 50 °C, конечная тем-
пература может быть установлена достаточно точно из соотношения
г2
И; — Н; = J CpdT = Ср (7\ — 323).
323
В этом случае
Я* = 7850 кал/моль-,
.	Я* = 8500 кал/моль-,
Ср = 8,89 кал / (моль-СК)',
Т2—323 = 2g5p.-8500 = _72 ок
8,89
Т2= 323—72= 251 °К(—22 °C).
187
Зидачи
1.	Определить количество переданной теплоты и выполненной работы во
время сжатия 1 моля окиси углерода при начальных температуре 500 °R
(4,5 °C) и давлении от 1 атм до 100 атм при следующих условиях. Использо-
вать в виде уравнения состояния обобщенный фактор сжимаемости.
а)	изотермическое сжатие при Б00 °R (4,5 "С) и постоянном внешнем леп-
лении 100 атм;
б)	изотермическое обратимое сжатие при 500 °R (4,5 °C);
в)	адиабатное сжатие при постоянном внешнем давлении 100 атм;
г)	адиабатное необратимое сжатие.
2.	Опр делить скорость передачи теплоты и минимальную мощность
4л. с.), необходимые для сжатия до 100 атм 1 моль/мин двуокиси углерода от
начального состояния 500 °R (4,5 °C) и 1 атм при протекании стационарного
процесса при следующих условиях:
а)	изотермическое обратимое сжатие;
б)	адиабатное обратимое сжатие.
3.	Для обеспечения стационарного процесса применяют компрессор для
сжатия<44 фунт!мин (20 кПмин) двуокиси углерода от 1 атм до 100 атм.
Затем холодильник отводит часть теплоты сжатия. Газ поступает в компрес-
сор при температуре 500 °R (4,5 °C) и покидает холодильник при температуре
550 ° R (32,3 °C). Предполагая, что компрессор работает адиабатно и обратимо
и изменения кинетической и потенциальной энергии незначительны, опреде-
лить скорость передачи теплоты от холодильника.
4.	Углекислый газ подается со скоростью 1 моль!мин через редуктор в
изолированный трубопровод, и давление понижается с 10 атм до 1 атм. Тем-
пература газа при входе в редуктор 100 °C. Определить температуру после по-
нижения давления. Изменениями кинетической и потенциальной энергии пре-
небречь.
5.	Повторить задачи 1—4 для водорода, азота, сероводорода н аммиака.
6.	100 фунт!мин (45,4 кГ1мин) пара при 300 фунт/дюйм8 (21,2 кГ/см2)
и 1320 °R (460,1 °C) расширяются адиабатно н обратимо до 30 фунт/дюйм2
(2,1 кПсм2). Определить мощность турбины в л. с.
7.	Использовать диаграмму обобщенного фактора сжимаемости для на-
хождения изменения энтальпии и энтропии пара между 1000 °F (537,8 °C),
1000 фунт/дюйм2 (70,3 кГ1см2) и 200 °F (93,3 °C), 20 фунт/дюйм2 (1,4 кГ/см2).
Сравнить полученные результаты с данными для пара в приложении 3.
8.	Повторить задачу 7 при условии, что уравнение состояния Вертело
справедливо в виде
/ 9	27 \
_ Ро _	[ 128	64 I
Z - RT - ! + ^Гпр- Гз у рпр.
ГЛАВА 6
Второй закон термодинамики
1.	Введение
Второй закон термодинамики, как и первый, основан на на-
дежных экспериментальных данных, полученных в результате
следующих наблюдений: теплота самопроизвольно переходит
из области высоких температур в область низких температур,
газы самопроизвольно перетекают из области высокого давления
в область низкого давления, два различных газа самопроизвольно
смешиваются и теплота не может быть количественно превращена
в работу в периодически действующей тепловой машине. Объясне-
ние этих наблюдений основано на молекулярной структуре ве-
щества. Однако экспериментальные наблюдения отражают пове-
дение не отдельных молекул, а статистическое поведение большой
группы молекул. Следовательно, второй закон термодинамики,
который основан на наблюдении макроскопических свойств, по
природе своей является статистическим и справедливость его
ограничена законом статистики.
Второй закон термодинамики может быть сформулирован сле-
дующим образом: «Изолированная система, свободная от одухотво-
ренного выбора, самопроизвольно стремится к такому состоянию,
которое осуществляется наибольшим числом способов».
Это утверждение означает только то, что изолированная си-
стема первоначально не находится в таком состоянии, которое
может быть осуществлено наибольшим числом способов, но стре-
мится путем всевозможных перегруппировок к тому, чтобы воз-
растало число способов осуществления ее состояния.
Невынужденный переход системы от одного состояния к дру-
гому называется «самопроизвольным процессом». Самопроизволь-
ные процессы происходят только в том случае, когда конечное
состояние изолированной системы более вероятно, чем начальное
состояние.
Вследствие идентификации энтропии с числом способов осу-
ществления состояния системы второй закон может быть выражен
через энтропию следующим образом: «Изолированная система,
свободная от одухотворенного выбора, самопроизвольно стремит-
189
ся к cocioHiihio с максимальной «нтроппей». Аналогично утверж-
дение Клпулпусл: «Энтропия мира стремится к максимуму».
Сущность jnix формулировок , весьма глубока. Вселенная,
рассматриваемая в целим, является вполне изолированной систе-
мой, и все самопроизвольные процессы, происходящие в пей, при-
водят к наиболее вероятному состоянию. Это, по-видимому, зна-
чит, что вселенная первоначально существовала в состоянии низ-
кой вероятности.
Рис. 38. Самопроизвольный переход
теплоты в изолированной системе.
2.	Самопроизвольный переход теплоты
Справедливость формулировок второго закона может быть
проиллюстрирована обычно наблюдаемым самопроизвольным пе-
реходом теплоты из области высокой температуры в область низ-
кой температуры. Учитывая определение давления по уравнению
(4-34) и энтропии по уравнению (4-38), уравнение (4-33) можно
записать так:
dE = kTd\nW— pdv — TdS —pdv.	(6-1)
Рассмотрим теперь систему, состоящую из двух резервуаров
или фаз, обозначенных А и В (рис. 38). Чобы сосредоточить вни-
мание на процессе перехода
теплоты от А к В и обратно,
систему следует полностью
изолировать от окружающей
среды и собственные объемы
двух тел принять постоян-
ными.
В начальный момент те-
ло А имеет внутреннюю
энергию ЕА, температуру ТА
и величина W для него бу-
дет WA, тело В имеет внут-
реннюю энергию Ев, темпе-
ратуру 7’в и величина W для
него будет W в. Для бесконечно малого количества теплоты, пе-
реданного от тела А к телу В, изменение внутренней энергии
тела А может быть вычислено согласно уравнению (6-1):
dEA = kTAd\nWA—pAdvA = TAdSA—pAdvA. (6-2)
Изменение внутренней энергии тела В:
dEB — kTsdlnW в—pjjdv^ = ТrflSB—p^lvB.	(6-3)
Поскольку объем каждого тела остается постоянным
dvA = dvB=0	(6-4)
и
BQ= —4₽Л = (ШВ,	(6-5)
190
где численное значение положительно, когда теплота переходит
от А к В, и отрицательно, когда теплота переходит от О к Л.
При этих условиях уравнения (6-2) и (6 3) могут быть напи-
саны в виде
J?-	dSA,	(6-6)
ТА
^- = kdlnWB=dSB.	(6-7)
тв
Из уравнений (6-6) и (6-7) следует
ЭД	= Win (ВД = d (SA+Sfl).	(6-8)
‘ А1 в
Произведение (UZ^ITg) представляет собой общее число пере-
группировок при наиболее вероятном распределении энергии для
объединенной системы, изолированной от окружающей среды.
Эксперимент показывает, что теплота передается от тела А
к телу В только в том случае, если ТА > Т в. Используя обозна-
чения, принятые в уравнении (6-5), находим, что численное зна-
чение 8Q при этих условиях положительно. Если ТА < Тв, то
теплота будет перехоить от тела В к телу А и численная
величина 8Q будет отрицательной. В любом случае величины
kd In (1Гл№й) и d(SA + SB) будут положительны. Другими сло-
вами, самопроизвольный переход теплоты всегда приводит к уве-
личению значения (1ГЛЙ7В) и общей энтропии в изолированной
системе. Процесс самопроизвольного перехода теплоты будет про-
должаться до тех пор, пока ТА не будет равно Тв и в этой точке
величины d In (1ГЛЦ7В) и d(SA + SB) будут равны нулю. Иначе
говоря, состояние термического равновесия будет тогда, когда
(WAW в) и общая энтропия изолированной системы достигнут
максимальной величины.
3.	Самопроизвольное расширение газа
Другой обычно наблюдаемый самопроизвольный процесс —•
расширение газа из области высокого давления в область низкого
давления. Действительно, самопроизвольное вытекание газа из
области низкого давления в обласЛ высокого давления не невоз-
можно, но чрезвычайно маловероятно из-за большого числа мо-
лекул, входящих в реально наблюдаемую систему, например изо-
лированную систему, составленную из сообщающихся сосудов
одинаковых размеров, содержащих в целом пять молекул. На
основании простой статистики можно заключить, что система бу-
дет содержать две молекулы в одном сосуде и три молекулы в
2	ГА	1
другом сосуде около — времени. Около — времени четыре моле-
191
кулы будут находиться п одном сосуде и одна милскула в друюм,
и лишь случайно все пять молекул могут оказаться в одном со-
суде и пи одной в другом. '
Это свидетельствует о том, что в короткие промежутки времени
молекулы самопроизвольно движутся из сосуда, содержащего
две или меньше молекул (низкое давление) в сосуд, содержащий
три или больше молекул (высокое давление). Однако частота та-
ких событий быстро уменьшается, если число молекул в системе
возрастает. В реальной наблюдаемой системе число молекул обыч-
но так велико, что вероятность самопроизвольного перехода ве-
щества из области низкого давления в область высокого давления
фактически мала. Только в верхних областях атмосферы число
молекул на единицу объема настолько мало, что можно обнару-
жить самопроизвольные отклонения от средней плотности. Кажу-
щийся голубой цвет неба можно объяснить преломлением света
в области, где наблюдаются флуктуации плотности.
Самопроизвольное расширение газа можно исследовать коли-
чественно путем рассмотрения изолированного сосуда, разде-
ленного на две части А и В с помощью свободно двигающегося
поршня, первоначально закрепленного подвижным штифтом в
определенном положении.
Давление в части А будет рА, а давление в части В — рв.
Если принять, что скорость перехода теплоты между этими ча-
стями достаточно велика, то температурный градиент, обуслов-
ленный процессами расширения и сжатия, мгновенно выравни-
вается. Хотя температура в изолированной системе может изме-
няться, все же предполагается, что она одна и та же во всех частях
системы.
Изменение внутренней энергии части А может быть выражено
с помощью уравнения (6-1):
dEA = kTd\nWA -тг Pa^va-	(6-9)
Для части В	
dEB — kTd\nWB—Р[4ив.	(6-10)
Для изолированной системы	
dEAA-dEB=0	(6-U)
и dvA-[-dvB=^)-, dvA— —dvB.	(6-12)
Из вышеприведенных уравнений следует	
ИТАп (WAWB) = Td (SA + SB) = (pA-pB) dvA.	(6-13)
Эксперимент показывает, что когда рА > рв, часть А расши-
ряется и dvA будет положительна. Наоборот, если рА < рв,
то часть А будет сокращаться п dvA будет отрицательна. В каждом
случае величины (рА — Pe)dvA и kTd In (№д№в) будут положи-
192
гельпы. Другими слонами, самопроизвольное расширение газа
приводит к увеличению произведения (1^лWB) и общей энтропии
изолированной системы. Самопроизвольное расширение буде.т
происходить до тех пор, пока рА нс станет ранным рв, при этом
d In (WAWB) и d(SA + Sn) будут равны пулю. Иначе говоря,
состояние равновесия наступает в том случае, если (WAWB) или
общая энтропия изолированной системы достигнут максимальной
величины.
4.	Самопроизвольное необратимое смешивание
двух идеальных газов
Самопроизвольное смешивание идеальных газов можно иссле-
довать количественно, если рассматривать изолированный сосуд,
разделенный на две части А и В выдвижной перегородкой. Пред-
полагается, что первоначальные температура и давление оди-
наковы во всей системе. Так как общая внутренняя энергия остает-
ся постоянной для изолированной системы, температура при сме-
шивании идеальных газов не изменится. Применяя уравнение
(6-1), определяем для каждой части объема:
dEA = kTdlnW А—pdvA,	(6-14)
dEB = kTd\nWB—pdvB.	(6- ft)
Складывая уравнения (6-14) и (6-15), получаем
/sTdln (WAWB) = pdvA + pdvB.	(6-16)
Так как и температура и давление будут постоянны при смеши-
вании, то
P = NA- = Nb-*L=(Na+Nb)-^,	(6-17)
VA VB	V
где v — vA + vB — общий объем изолированной системы. Делая
соответствующую подстановку в уравнение (6-16), получаем
fofln (ГЛГЙ) = dS = R [NAdimA+N^d\nvB]. (6-18)
Перед удалением перегородки в сосуде объем, относящийся
к компоненту А, был равен vA, а объем, относящийся к компонен-
ту В, был равен vB. После удаления перегородки объем, относя-
щийся к каждому компоненту, стал равен общему объему изоли-
рованной системы v. Таким образом, объем, соответствующий
обоим компонентам, увеличится при удалении перегородки и
d In v для обоих компонентов будет положительным. Следова-
тельно, удаление перегородки приводит к увеличению произведе-
ния (WAWB), и газы будут самопроизвольно смешиваться с обра-
зованием гомогенной смеси во всем объеме системы.
13-1503
193
Изменение энтропии при смешении может быть вычислено
интегрированием уравнении (6-18) между ннчпльным и конечным
объемом для каждого компонента:'

7? 2VJn — Ч-А^п — .
VA
(6-19)
Согласно уравнению (6-17) объемная доля равна мольной доле
для смесей идеального газа:
na ~va у .	Nв _VB
na + nb v a’na+nb V В‘
AS смешения для 1 моля смеси можно тогда получить делением
уравнения (6-19) на общее число молей (NA + NB):
ASCM = —7? [хА1пхА + хв1пхв].	(6-20)
5.	Обратимость
Вышеприведенные выводы, относящиеся к самопроизвольным
изменениям, применимы только к изолированным системам. На
практике большинство наблюдаемых систем не являются изоли-
рованными, и поэтому важно определить изолированную систему,
прежде чем применять к ней концепции второго закона термоди-
намики. Вообще изолированную систему обычно определяют как
рассматриваемую систему плюс окружающую ее среду. Окружаю-
щая среда обычно включает в себя источник теплоты для получе-
ния и отдачи энергии в форме теплоты и источник работы, содер-
жащий устройства для получения и отдачи энергии в форме ра-
боты. Земная атмосфера может быть рассмотрена как источник
теплоты и как источник работы.
Рассмотрим цилиндр с газом как систему, окруженную источ-
никами теплоты и работы. Этот цилиндр и источники вместе со-
ставляют изолированную систему, к которой применимы концеп-
ции второго закона термодинамики.
Например, цилиндр с идеальным газом при давлении 10 атм
и комнатной температуре представляет собой рассматриваемую
систему, окруженную атмосферой с давлением в 1 атм и при ком-
натной температуре. Как показано в примере 1 (стр. 199), само-
произвольное расширение от 10 атм до 1 атм может происходить
разными путями с различными количествами теплоты и работы,
обмениваемыми цилиндром и окружающей средой для каждого
пути.
Так как конечное состояние идеального газа внутри цилиндра
одинаково для всех путей, то изменение в числе способов осуществ-
ления начального и конечного состояния газовой системы будет
одно и то же для каждого отдельного пути.
194
Численное значение изменения In WZ гнза между начальным и
конечным условиями легко вычислить в функции энтропии с по-
мощью соотношения
АД 1 нГв = £Sg - fe’.	(6-21)
Q для обратимого изотермического расширения 1 моля идеального
газа от 10 до 1 атм равна RT 1п 10, a ASg == /? 1п10. Соответст-
вующее изменение In Wt между начальным и конечным состоя-
ниями будет
AlnIF, = 1п^ = ^*- = A in 10.
a We. k k
(6-22)
Для 1 моля j равно 6,02 1023. Таким образом, отношение W
для конечного состояния газа к W для начального состояния
будет
W'
_ g2 — 106,02-Ю23
Wgl
(6-23)
Вследствие получающихся астрономических величин для изме-
нения W более удобно рассчитывать термодинамические процессы
в функции энтропии.
Хотя изменение энтропии газа в цилиндре равно R In 10 для
всех путей, изменение энтропии окружающего пространства
будет различным для каждого пути. Его можно получить деле-
нием действительного количества теплоты, полученного от окру-
жающей среды, на абсолютную температуру окружающей среды.
Ниже приведено изменение энтропии для изотермического расши-
рения идеального газа по стадиям, описанным в примере 1:
Стадия........ а
Газовая система	.	2,303	R
Окружающая	среда	—0,900 7?
Общее изменение
энтропии	1,403 R
в	с	d	е
2,303 7?	2,303 7?	2,303 7?	2,303 7?
—1,300 7? —1,600 7? —1,930 7? —2,303 7?
1,0037?	0,7037?	0,373 7?	0,000 7?
Все изменения энтропии в окружающей среде отрицательны,
так как теплота передается от окружающей среды газовой системе.
Общее изменение энтропии для изолированной системы из
газа плюс окружающая среда показывает, что для полностью
обратимого пути е изменение общей энтропии изолированной си-
стемы равно нулю. Для полностью обратимого процесса общее
число способов осуществления состояния изолированной системы
одно и то же и в начале и в конце процесса. Хотя газа в ци-
линдре увеличивается в 1()б-02-ю23 раз> для окружающей сре-
ды уменьшается во столько же раз, так что произведение №gU7s
для полностью изолированной системы остается постоянным.
13*
195
Для всех необратимых процессов штропня и общее число спо
собой осуществления состояния пзолпровпниой системы W W',
увеличиваются. Для этих путей HZ. для окружпющей среды умень-
шается в мсныиее число раз, чем возрастает, так что произве-
дение 1Р£1Г,для изолированной системы возрастает.
В этом примере принято, что температуры системы и окружаю
щего пространства одинаковы. Если в окружающей среде темпе-
ратура выше, чем в газовой системе, изменение энтропии для
окружающего пространства будет менее отрицательным, чем
значение, приведенное выше. Это приводит к более положитель-
ному общему изменению энтропии для изолированной системы:
газ плюс окружающая среда; даже на стадии е изменение общей
энтропии будет положительным. Это показывает, что переход
теплоты из области высокой температуры в область низкой — не-
обратимый процесс.
6.	Превращение теплоты в работу
Изотермическое расширение идеального газа является про-
стой иллюстрацией процесса количественного превращения теп-
лоты в работу. Работа, совершенная по отношению к окружающей
среде, происходит за счет эквивалентного количества теплоты,
полученной от окружающей среды. Однако этот процесс не может
продолжаться после того, как давление в цилиндре достигнет
наиболее низкого давления окружающей среды. Для того чтобы
продолжить процесс, система должна вернуться к первоначаль-
ному состоянию. Но восстановление состояния потребовало бы по
крайней мере такой же работы, как работа, полученная во время
расширения; таким образом, эффективность изотермического
расширения для получения только работы была бы сведена
к нулю.
Теплота может быть полностью превращена в работу при не-
периодическом процессе; при периодическом процессе она может
-быть превращена в работу только частично. Непрерывное превра-
щение теплоты в работу требует применения циклических процес-
сов с периодическим возвращением к первоначальному состоянию.
Для того чтобы получить максимальное превращение теплоты в
работу, все стадии в цикле должны быть обратимы. Простейшим
возможным циклом считается тот, в котором количество теплоты
поглощается обратимо из единственного источника при темпера-
туре 7j. При этом теплота частично превращается в работу, а
частично передается обратимо единственному теплоприемнику
при температуре Т2, которая обязательно должна быть меньше
температуры 7\. Стадии изотермического переноса теплоты могут
состоять из расширения или сжатия газа при постоянной темпе-
ратуре с помощью сдвига фазового равновесия системы, когда
температура и давление остаются постоянными, или сдвига хи-
мического равновесия газовой системы путем изменения давления
196
при постоянной температуре. Все другие стадии в цикле обяза-
тельно должны быть адиабатными.
Термодинамическая эффективность такого никла определяется
отношением совершенной работы к поглощенной теплоте. После
каждого полного цикла система возвращается к своему первона-
чальному состоянию, так что изменение внутренней энергии ра-
ботающего газа для одного цикла равно нулю. Баланс энергии
для одного цикла примет вид
ДЕ = Qj + Qa —w = 0.	(6-24)
Численная величина Qs будет всегда отрицательна, так как тепло-
та уносится от системы. С помощью уравнения (6-24) можно вы-
разить коэффициент полезного действия цикла'
(6-25)
<21	<21
Так как конечное состояние системы после каждого цикла
такое же, как и начальное состояние системы, то изменение энтро-
пии работающего газа для одного цикла также равно нулю:
=	+	=	(6-26)
1 1	1 2
Перегруппировкой слагаемых получаем
А.	(6-27)
Qi Л
Подставляя отношение температур вместо отношения количеств
теплоты в уравнение (6-25), можно выразить коэффициент полез-
ного действия цикла полностью в функции температур источника
и теплоприемника:
— =1—(6-28)
<2t Ti
Уравнение (6-28) указывает на то, что все обратимые циклы,
протекающие между одними и теми же двумя температурными
уровнями источника и теплоприемника, будут иметь одинаковую
эффективность превращения теплоты в работу. Коэффициент по-
лезного действия будет функцией только двух температур и не
будет зависеть от частных обратимых процессов и отдельных ра-
ботающих газов, которые используются в цикле. Уравнение (6-28)
также свидетельствует о том, что чем выше температура источника
теплоту и ниже температура теплоприемника, тем ближе эффек-
тийность превращения приближается к единице.
7.	Обратимые циклы теплового двигателя
Один из простейших обратимых циклов теплового двигателя —
цикл Карно. Анализ этого цикла имеет историческое значение в
развитии термодинамики. Цикл Карно использует идеальный газ
197
n качестве рабочего газа и соверпыегся в четыре ступени, как ио
казано па рис. 39. Па первой ступени идеальный газ расширяется
обратимо и изотермически от давлений pt до давления />4 при тем-
пературе 1\. Количество теплоты, эквивалентное выполненной
работе, поглощается при постоянной температуре 7\. Па второй
ступени газ расширяется обратимо и адиабатно от давления ра
и температуры до давления р3 и температуры Тг. Третья сту-
пень представляет собой обратимое изотермическое сжатие от
давления р3 до давления р4 при температуре Т2. Количество теп-
лоты, эквивалентное работе сжатия, отдается при постоянной
температуре Тг. Давление р4 специально выбирается так, чтобы
Рнс. 39. Обратимый цикли-
ческий тепловой двигатель
Рнс. 40. Цикл Карно с идеальным га-
зом:
Л—изотермическое расширение; В—адиабатное
расширение; С—изотермическое сжатие; D—ади-
абатное сжатие
обратимое адиабатное сжатие в четвертой ступени возвращало
систему к ее первоначальным условиям рх и 7\. Коэффициент
полезного действия цикла Карно может быть представлен как
функция 7\ и Т2 и выражается уравнением (6-28).
На диаграмме р — v (рис. 40) количество теплоты, поглощае-
мое при температуре 1\ во время изотермического расширения'на
первой ступени, эквивалентно площади под кривой между дав-
лением рг и р2. Количество теплоты, отданное во время изотерми-
ческого сжатия на третьей ступени при температуре Т2, эквива-
лентно площади под кривой между давлением р3 и р4. Работа,
выполненная при адиабатном расширении на второй ступени,
равна понижению внутренней энергии и представляет собой пло-
щадь под кривой между давлениями р2 и Рз- Работа адиабатного
сжатия на четвертой ступени равна повышению внутренней энер-
гии и представляет собой площадь под кривой между давлением
р4 и рг. Так как вторая и четвертая ступени находятся между
198
двумя одинаковыми гемперптуриымп уровнями, уменьшение
внутренней энергии идеального газа на второй ступени равно по»
иьпнению внутренней энергии па четвертой ступени."Следователь-
но, работа адиабатного расширения па второй ступени равна ра-
боте адиабатного сжатия четвертой ступени и площадь под кривой
между давлениями ра и ря равна площади под кривой между
давлениями pt и pi. Так как изменение внутренней энергии для
полного цикла равно нулю, вся проделанная работа эквивалентна
разности между количеством теплоты, поглощенным в первой сту-
пени, и количеством теплоты, отданным на третьей ступени, и
может быть представлена площадью, ограниченной кривыми на
рис. 40. Отношение этой площади к площади под изотермой пер-
вой ступени представляет собой коэффициент полезного действия
цикла.
Хотя цикл Карно — относительно простой процесс для превра-
щения теплоты в работу, любой другой обратимый цикл, в кото-
ром происходит теплообмен с окружающей средой только при
двух фиксированных температурах, приведет точно к таким же
результатам. В цикле Карно происходит теплообмен с окружаю-
щей средой только во время изотермических расширения и сжат ия
идеального газа.
В других возможных циклах теплообмен с окружающей средой
может происходить при постоянной температуре во время фазо-
вого изменения. Такие обратимые циклы иллюстрируются в при-
мере 1.
Пример 1. Цикл начинается с состояния 1 фунта (453,6 а)
жидкой воды при 212 °F (100 °C) при давлении ее пара
14,7 фунт/дюйм2 (1,03 кГ/см2). На первой ступени цикла теплота
поглощается при постоянных температуре и давлении до тех пор,
пока вода полностью не превратится в пар. Вторая стадия —
обратимое адиабатное расширение, во время которого температура
понижается и часть пара конденсируется. Так как во всех случаях
присутствуют две фазы, давление системы всегда соответствует
давлению водяного пара при данной температуре. Если адиабат-
ное обратимое расширение ограничено 101,76 °F (39 °C) и давле-
нием 1 фунт/дюйм2 (0,07 кГ/см2), система будет содержать ~12%
жидкости и ~88% пара.
Исходя из этого третья ступень представляет собой неполную
конденсацию при постоянных температуре и давлении до тех пор,
пока система не будет содержать ~90,3% жидкости и 9,7% пара.
Затем обратимое адиабатное сжатие должно вернуть систему в
первоначальное состояние.
На протяжении одного цикла двигатель будет поглощать
970,2 брит. тепл. ед. (245 ккал) теплоты на 1 фунт (453,6 а) воды
при 212 “F (100 “С) и 1 атм и будет производить работу, равную
157,1 брит. тепл, ед (39,6 ккал) с коэффициентом полезного дейст-
вия, равным 16,2%. Этот коэффициент тот же самый, что и для
цикла Карно или любого другого обратимого цикла, совершающе-
199
	i				
			ч	°.	s.	S. «	§	"	«	о	0» е 2 й	42.9
					
		ед.			
		т. тепл.	180 1150,0 8,35 975,0	"*	°	со i	s‘	s	170.3
		О,			
3	<0				
ТОЙ ФА-	§ с о ь	gc.	СП	хф	о	LO —'	со	ю	о LO	-Г СО	Г-	О	г- со	©	-Г	1,7564 0,1200 0,1920	0,3120
	33 О)	£			
					
4И ДЛЯ	Z	*:	со	о ь-	00	со хф	ю	о	й 6	о 00	о	2 Й	*	Ь 00	о	о	917,4
С J3 < X	а> Й О	футЗ I	г-	О со —4	со	о о	со	о	-е -	~	-	СП О	СО	О	04	СО О.	S	хф хГ	О СП	-	04 04	О	СО	32,41
СП					
ВЕЛИЧИНЫ МАССЫ, ОБЪЕМА ЭНТРОПИИ И	Температура	Давление	1	Масса		со	со	со хГ	Tt-	ТГ	О Ю	io	LO	о Xf	Х?Х	СО	СО хг	О	хГ cQ	чГ	454,3
		кГ/сл^ фунт	о	О	LO	еО О	о	сп	о о	О	ОО °	°.	”1 —’	—	о	о	О	О	О О	СО	Ь- О	Q	с? °	.	Я. т-х’	со	о	О о о	I о
			 1,03 1,03 0,07 0,07		
		С* 5 д 1	14,7 14,7 1,0 1,0		
		о с	ООО	о о	о	со	со		
		Ь о	со	о 04	04	—	Г? —	—	О	О 04	04	х—	*-		
	Точка | на 1	Фаза рнс. 41		•Л	л	л О	О	о §	1	1 к	S	°-	s	m*	•	1 * ё X ё	К с 04	СО		
200
i оси между Двумя одинаковыми температурными уровнями, что
можно выразить с помощью уравнения (6-28)
Величины массы и объема, энтальпии и энтропии каждой
фазы для каждой из четырех точек (1—4) приведены в табл. 11 и
12. В табл. 12 приведены изменения объема, энтальпии и эитро-
Рис. 41. Диаграмма обратимого цикли-
ческого теплового двигателя, работаю-
щего с использованием воды:
I—испарение при 100 °C, 1,03 кГ/смЯ-, //—адиа-
батное расширение с частичной конденсацией;
Ш- частичная конденсация при 39 °C, I атм;
/V—адиабатное сжатие с полной конденсацией
пии для каждой стадии (/—IV) процесса. Диаграмма обратимого
циклического теплового двигателя дана на рис. 41.
Таблица 12
ИЗМЕНЕНИЕ ОБЪЕМА. ЭНТАЛЬПИИ И ЭНТРОПИИ ДЛЯ КАЖДОЙ СТАДИИ ПРОЦЕССА
	Объем Д с		Энтальпия ДН	
Стадии	футЗ	л	брит. тепл, ед-	ккал/моль
I. Изотермическая . . . П. Адиабатная	 III. Изотермическая . . .	26,8 267,2 —261,2	758 7562 —7403	970,2 —166,8 —813,1	245,0 —42,0 —205,4
IV. Адиабатная		—32,4 0	—917	9,7 0	2,44 0
Примечание. №=245,0—205.4 =39,6 ккал. К. П. Д.=(39,6/245,0)100=16,2%.
8.	Полезная работа
 Максимальную работу, которую гможет выполнить частная
система по отношению к окружающей среде при практически наи-
более низких давлении pff и температуре То, получают, когда все
процессы, включающие ступени теплообмена, обратимы и конеч-
ные давление и температура системы равны р0 и То. Частная си-
201
стема может быть представлена как цилиндр с газом плюс обрлти-
мый циклический тепловой двигатель для выполнения ступеней
обратимого теплообмена, как показано на рис. 42. Окружающая
среда будет состоять из атмосфе-
Рис. 42. Полезная работа
ры при давлении р0, теплоприем-
ника с температурой То и из ис-
точника работы для выполнения
или поглощения механической ра-
боты.
Система может обмениваться
выполненной работой с окружаю-
щей средой в результате обрати-
мый циклов теплового двигателя
и в результате изменений давле-
ния и объема в цилиндре. Обмен
работы между цилиндром и ок-
ружающей средой, связанный с
изменением давления и объема,
можно разделить на две части.
Первая часть состоит из обмена
механической работы, происходя-
щей между цилиндром и источни-
ком работы; вторая часть пред-
ставляет собой обмен работы,
выполненной атмосферой при по-
стоянном давлении р0 вследствие
изменения объема в цилиндре. Общую работу, выполненную
системой, можно выразить уравнением
= Юдв-J- №ц + р0 (Vo —V),
(6-29)
где ц>дв — работа, выполненная тепловым двигателем;
и)ц — механическая работа, выполненная цилиндром;
Po(vo — и) — работа, выполненная против атмосферного давления.
На основании общего баланса энергии замкнутой системы об-
щая работа, выполненная системой,
w = Qo — Д.Е.	(6-30)
Обратимый теплообмен между системой и теплоприемником при
температуре То можно вычислить по температуре теплоприемника
и изменения энтропии системы
Qo = TobS.	(6-31)
Подставляя произведение T0&S в уравнение (6-30), выполненную
максимальную работу можно выразить полностью через функции
состояния:
= Чцв + “’и + Ро (v0—v) = Te&S—bE.	(6-32)
202
Работа, выполненная плд атмосферой, Itc может быть исполь-
зована для любой полотой цели. Полезной работой можно счи-
тать только ту часть общей максимальной работы, которую можно
использовать дли совершения полезной механической работы, а
именно и?Д|, и а>ц:
W’-w„4-po(Vo—0.	(6-33)
где — полезная работа.
Следовательно,
=	=	Д£ —p0(f0—V).	(6-34)
Для процесса, происходящего полностью при постоянном дав-
лении р0,
wn~T0&S—&H.	(6-35)
Для обратимого стационарного процесса, когда потенциальные
и кинетические эффекты незначительны, при вычислении макси-
мальной механической работы Q принимается равным Т0Д5
[см. уравнение (1-9)]:
дац = 7’0Д5—ЬН.	(6-36)
9.	Рассеянная энергия
Для полностью обратимых процессов в замкнутой системе одна
часть изменения внутренней энергии, представленная полезной
работой и работой, выполненной против атмосферного давления
p0(v0 — 0> способна совершить работу над окружающей средой,
в то время как другая часть, представленная произведением
T0&S, переходит в виде теплоты к теплоприемнику и полностью
непригодна для совершения работы любого вида. Поэтому произ-
ведение T0/\S иногда называют «рассеянной энергией».
Максимальное количество работы получается только тогда,
когда все стадии процесса обратимы. Любая необратимость в про-
цессе ведет к уменьшению количества выполненной работы.
Термин «рассеянная энергия» употребляется также в другом смыс-
ле, чтобы показать, что энергия, первоначально пригодная для
выполнения работы, была превращена в теплоту необратимым
процессом и стала бесполезной для выполнения работы. Это ко-
личество энергии называется также «потерянной работой».
Энергия, превращенная в рассеянную энергию необратимым
процессом в изолированной системе, может быть интерпретиро-
вана и вычислена как минимальное количество работы, необхо-
димое для восстановления первоначально изолированной системы
до ее начального состояния при условии, что вся теплота, израс-
ходованная во время восстановления процесса, передана тепло-
приемнику при практически самой низкой температуре То. Для
того чтобы работа восстановления была минимальной, процесс
203
посстпиоплоипя должен быть обратным. Если количества и-плоты
и работы, которыми обменшипотся составные части изолирован
ной системы при необратимом процессе, используются вновь об
рятимым путем, то нериоНичалышн внутренняя энергия каждой
составной части будет по крайней мере частично восстановлена;
однако первоначальные температура и давление для каждой со-
ставной части не будут достигнуты.
Для того чтобы полностью восстановить первоначальные усло-
вия, над системой должна быть выполнена обратимо дополнитель-
ная работа №0- Так как эта дополнительная работа должна быть
выполнена при условии постоянства внутренней энергии, экви-
валентное количество теплоты Qo должно быть обратимо передано
теплоприемнику при температуре То. Это приведет к изменению
энтропии теплоприемника, равному Так как процесс полного
‘ о
восстановления проводится необратимо, это изменение энтропии
теплоприемника должно быть также равно общему изменению
энтропии первоначально необратимого процесса в изолированной
системе. Так как Qo равно w0, то
-2°-= ш°- = у AS,
то То ’
где EAS — сумма всех изменений энтропии, происходящих в
изолированной системе при необратимом процессе. Следовательно,
минимальную работу восстановления, или энергию, ставшую рас-
сеянной из-за первоначально необратимого процесса, можно вы-
числить с помощью следующей формулы:
w0 = То Е AS.	(6-37)
Пример 2. Количество теплоты Q передано от источника
теплоты с температурой Т непосредственно теплоприемнику с
температурой То. Общее изменение энтропии для этого необрати-
мого процесса переноса теплоты
V AS = ——-То)
т0 т тть
Количество энергии, ставшей рассеянной этим необратимым про-
цессом, может быть вычислено как
т0 v as=qL=A.
Это выражение можно рассматривать как количество работы,
которое можно было бы получить, если количество теплоты Q
сообщить обратимому циклическому тепловому двигателю, рабо-
тающему между двумя источниками теплоты с температурами Т
и (рис. 43).
204
Оно тпкже представляет собой минимальное количество рабо-
ты, необходимое для восстановления теплового источника до его
первоначальных условий. Обратимый воспроизводимый процесс
показан на рис. 43. Для того чтобы передать количество теплоты Q
в верхний тепловой источник с температурой Т, от внешнего источ-
1 — ~ , а
от нижнего источника с температурой То потребуется количество
Так как количество теплоты, равное Q,
было первоначально добавлено нижнему источнику, избыток.
Рис 43. Рассеянная энергия (потерянная работа).
Обратимый воспроизводимый процесс
равный Q— q(~~^ =	—"у5)’ Д°лжен быть взят от этого
источника и передан теплоприемнику в окружающей среде для
того, чтобы восстановить первоначальные условия.
Это количество теплоты, переданное теплоприемнику, обяза-
тельно равно работе, необходимой для приведения в действие
теплового двигателя. Оно может быть интерпретировано как
энергия, ставшая рассеянной вследствие первоначального необ-
ратимого перехода теплоты.
Пример 3. В необратимом изотермическом расширении
идеального газа в примере 1,А (гл. I, стр. 35) работа, выполнен-
ная газом, составила 0,9 RT и изменение энтропии изолированной
системы было равно 1,403 R. Изолированная система в этом слу-
чае состоит из цилиндра с идеальным газом, термостата с темпера-
турой Т и резервуара работы, который поглощает работу расши-
205
рения (рис. 14). Ураипеине (0-31) свидетельствует о том, что ко-
личество энергии, ставшей рассеянной при лом необратимом рае
ишрении, составляет 1,403 RT0.
Для того чтобы вычислив. <то непосредственно, следует ис
пользовать обратимый процесс восстановления. Сначала коли-
чество работы 0,900 RT, выполненной необратимым расширением,
будет повторно и обратимо приложено к цилиндру идеального
газа. Во время этого обратимого сжатия количество теплоты, рав-
Обратимый воспроизводимый процесс
Рис. 44. Рассеянная энергия (потерянная рабо-
та). Необратимое изотермическое расширение иде-
ального газа в изолированной системе
ное 0,900 RT, будет передано термостату, который восстановит
первоначальные условия. Если принять, что термостат и система
имеют одинаковую температуру, этот процесс можно считать об-
ратимым процессом передачи теплоты. Однако давление в цилинд-
ре составит теперь только е0,в0, или 2,46 атм, вместо первоначаль-
ных 10 атм. Поэтому нужно приложить дополнительное коли-
чество работы, равное RT In или 1,403 RT. В результате
равное количество теплоты должно быть взято от газового цилинд-
ра. Но так как температура системы равна Т, то прямой переход
этого количества теплоты в теплоприемник при То будет необра-
тимым процессом. Следовательно, необходим обратимый процесс
переноса теплоты.
206
Согласно одному из методой осуществления обратимого Про-
цесса переноса теплоты, количество теплоты, ранное 1,403 RT,
должно быть сообщено обратимому тепловому двигателю.
Двигатель должен выполнить работу, равную 1,403 R Т
и отдать количество теплоты Q » 1,403 RT0 тепло-
приеминку с температурой То. Работа, совершенная тепло вым
двигателем, могла бы быть использована, чтобы уменьшить н еоб-
ходимую работу для восстановления. Таким образом, миним аль-
ная работа, требуемая для восстановления системы в перв ©на-
чальное состояние,
w0 = 1,403 RT~r 1,403	( 1 — А) = 1,403 RT0,
что равно Qo. Тот же результат получается из произведени я тем-
пературы теплоприемника и общего изменения энтропии, об услов-
ленного необратимым процессом.
Пример 4. Вычислить рассеянную энергию относительно
теплоприемника с температурой То, если 0,21 фунт-моля/(95,3 мо-
ля) О2 при температуре Т и давлении р смешиваются необратимо
с 0,79 фунт-моля (359 молей) N2 при той же температуре Т и об-
щем давлении р. Следует считать, что газы ведут себя как идеаль-
ные.
Согласно уравнению (6-20), изменение энтропии вследствие
необратимого смешивания
ДЗсмеш = R [0,21 In — 4- 0,79 In —1 = 1,987 0,513 =
с [	0,21	0,79J
= 1,02 брит, тепл, ед./(фунт-моль-°Н) [1,02 к.ал/(моль • ®К)].
Энергия, ставшая рассеянной вследствие необратимого смешива-
ния, равна 1,02 То кал/(моль-°К), если То выражена в ®К-
Это значение можно интерпретировать как минимальное ко-
личество энергии, необходимое для восстановления системы до ее
первоначального состояния относительно теплоприемника с тем-
пературой То. Например, если самая низкая температура тепло-
приемника в окружающем пространстве равна 80 °F, или 540 °R
(300 °К), то минимальное количество работы, необходимое для р аз-
деления 1 фунт-моля (454 моля) воздуха на О2 и N2 при тех же
температуре и давлении составит 1,02 540, или 550 брит. тепл,
ед./фунт-моль (305 кал/моль).
10.	Термодинамический анализ процессов
Концепция о полезной работе и рассеянной энергии применима
в теоретических расчетах физических процессов. Так как эти
величины выражаются в функции состояния и температуры тепло-
207
р <	•
приемника, они могут быть вычислены из известных начальные и
конечных условий и не зависят от механизма процесса.
Например, поток горячего газа в промышленном процессе
представляет собой потенциальный источник для получения ра-
боты относительно окружающей температуры.
Пример 5. 2000 фунт/ч (908 кг/ч) тяжелого жидкого
топлива теплоемкостью 0,6 брит. тепл. ед./фунт-моль • °R) х
Х[0,6 кал/(моль-°К)] вытекает из отверстия в дне сосуда при
температуре 1000 °R (555,5 °К). Определить полезную работу отно-
сительно окружающей среды,температура которой 520 °R
(288,8 °К).
Максимальная работа, которая может быть получена при
охлаждении топлива от 1000 R (555,5 °К) до 520 °R (288,8 °К),
выражена уравнением (6-36). При условии постоянства давления
изменение энтропии топлива составит
AS——0,61п~~^-=—0,391 брит. тепл. ед./фунт-моль-°R)
[—0,391 кал / (моль-° К)].
Изменение энтальпии будет
ДЯ = 0,6(520—1000)=—288 брит. тепл, ед./фунт-моль
(—160 кал/моль).
Возможная максимальная работа
^ = [520 (—0,391) ф-288]-2000^? 168,000 брит,
тепл, ед./ч (93,3 ккал/ч), или 66,2 л. с.
Результаты примера 5 представляют собой максимальную
мощность при охлаждении топлива до температуры окружающей
среды. Тот же анализ можно использовать для вычисления мощ-
ности при частичном охлаждении топлива.
Пример 6. Определить возможную мощность при охлажде-
нии 2000 фунт/ч (908 кГ/ч) жидкого топлива теплоемкостью
0,6 брит. тепл. ед./(фунт-моль °R) [0,6 кал/(молъ °К)1 от 1000 °R
(555,5 °К) до 800 °R (444,4 °К) относительно окружающей среды,
температура которой 520 °R (288,8 °К). В этом случае
AS =—0,6 In=—0,134 брит. тепл. ед/(фунт-моль °R)
[—0,134 кал /(моль -°К)];
Д// = 0,6(800—1000)=—120 брит. тепл, ед./фунт-моль
(— 66,6 кал/моль)-,
wrnax = [520-(—0,134) 4-120]-2000 =100,600 брит. тепл.
ед./ч (55,5 ккал/ч) или 39,5 л. с.
208
Механизм для получения этой работы можно выразить в виде
обратимого циклического процесса теплового двигателя, рабо-
тающего между температурой топлива и температурой окружаю-
щей среды 520 °R (288,8 °К). В этом случае начальная температу-
ра изменяется от 1000 °R (555,5 °К) до 800 °R (444,4 °К) и урав-
нение (6-28) для коэффициента полезного действия теплового
двигателя должно быть записано в дифференциальной форме:
1—
где Т — переменная.
Тогда бесконечно малое количество теплоты, перешедшее дви-
гателю, может быть вычислено по понижению энтальпии топлива:
8Q= — dH~~ CpdT;
= -CpdT [ 1 -= To Cp^-—CpdT.
Интегрированием в пределах начальной и конечной температур
получаем уравнение
w = T0Cp\n^~ СР(Т2-Т\),
которое является разновидностью уравнения (6-36) для процессов
при постоянном давлении. Наибольшее количество работы может
быть получено в том случае, когда конечная температура источни-
ка Т2 достигает температуры теплоприемника То.
Так как уравнение (6-36) применимо к любому стационарному
обратимому процессу, его можно использовать для вычисления
минимальной работы, необходимой для холодильника или тепло-
вого насоса.
Пример 7. Определить минимальную мощность, требуе-
мую для охлаждения 100 фунт-молей/мин (45360 моль!мин) воз-
духа от 550 °R (305,5 °К) до 500 °R (277,8 °К) при температуре
окружающей среды 550 °R (305,5 СК). Применение уравнения
(6-36) к 1 фунт-молю (454 моля) воздуха с теплоемкостью
7 брит. тепл. ед/(фуит-моль °R) [7 кал!(моль °К)1 дает
Д3= — 71п^=—0,666 брит. тепл. ед./(фунт-моль-^)
[—0,666 кал/моль  °К]’,
АЯ —7(500—550) —
= —350 брит. тепл, ед./фунт-моль (—194.5 кал/моль);
550(—0,666)+ 194,5 =
=—16 брит. тепл. ед./(фунт-моль) (—8,88 кар/моль).
14-1503
209
Для 100 фунт-молей (45360 молей) воздуху в 1 мин
®m|n = (-16)-100 =
— —1600 брит. тепл. ед./мин(—888 кал/мин), или —37,7 л. с.
Пример 8. Определить минимальную мощность, необхо-
димую для нагревания 100 фунт-молей (45360 молей) воздуха в
1 мин от 500 ®R (277,8 °К) до 550 °R (305,5 °К) при температуре
окружающей среды 500 °R (305,5 °К)-
= 0,666 брит. тепл. ед./(фунт-моль-°R) [0,666 кал](моль• ®К)];
ДЯ = 7(550—500) =
= 350 брит. тепл. ед./(фунт-моль) (194,5 кал/моль)-,
№min = 500-0,666 — 350 =
= 17 брит. тепл. ед./(фунт-моль)(—9,43 кал/моль).
Для 100 фунт-молей (45360 молей) воздуха в 1 мин
wmin = (—17)-100 =
= 1700 брит. тепл. ед./мин.(—943 кал/мин), или—40 л. с.
Задачи
1.	Цикл Карно работает с 1 молем гелия в качестве рабочего газа. На пер-
вой ступени газ расширяется изотермически и обратимо от 10 до 5 атм при
постоянной температуре 1000 °R (555,5 °К)- На второй ступени газ расширяется
адиабатно и обратимо от 5 атм при 1000 °R (555,5 °К) до 1 атм. Затем система
возвращается к своим первоначальным условиям в две ступени: сначала изо-
термическим сжатием, затем адиабатным сжатием. Вычислить w, Q, АЕ и AS
для каждой ступени, а также для полного цикла. Показать, что коэффициент
полезного действия, выраженный отношением произведенной работы к пере
данной теплоте при 1000°R (555,5 °К), равен 1 —
П
2.	Проследить работу цикла в задаче 1 на диаграммах давление —объем
и температура — энтропия. Абсолютная энтропия гелия при 25 °C и 1 атм
равна 30,13 кал/(лоль-°К).
3.	Определить полезную работу 1000 брит. тепл. ед. (252 ккал) теплоты
источника теплоты с темпер турой 1000 °R (555,5 °К) относительно теплопри-
емника с температурой 600 °F (315,5 °C).
4.	Определить полезную работу от теплоты при получении работы 1 фунта
(454 г) пара в цилиндре при 212 °F (100 °C) и 1 атм относительно окружающей
среды с температурой 70 °F (21,1 °C) и давлением 1 атм. Разработать обрати-
мый механизм для получения работы.
5.	Определить минимальную мощность, необходимую для того, чтобы при-
вести в действие тепловой насос, с помощью которого 10 000 брит. тепл, ед./ч.
(2520 ккал/ч) должны быть переданы комнате с температурой 70 °F (21,1 °C)
от окружающей среды с температурой 0°F (—18 °C). Сколько теплоты будет
взято при этом от окружающей среды?
210
6.	Компрессор мощностью 1000 л. с. сжимает 1 моль!мин гелия от 1 атм
и 500 °R (277,8 °К) до 10 атм. Компрессор работает адиабатно, а еле ующий
за иим холодильник охлаждает сжатый газ до 550 ° R (305,5 °К). Определить:
а)	количество теплоты, отводимое холодильником;
б)	температуру газа между компрессором и холодильником;
в)	работает ли компрессор обратимо?
г)	рассеянную энергию только в ступени необратимого сжатия относи-
тельно теплоприемника с температурой 500 °R (277,8 °К);
д)	общую рассеянную энергию при совместной работе компрессора и хо-
лодильника относительно теплоприемника с температурой 500 °R (277,8 °К).
7.	Какова должна быть минимальная мощность (л. с.) и скорость передачи
теплоты в холодильник при сжатии 1 моля гелия от 1 атм и 500 °R (277.8 °К)
до 10 атм и 550 °R (305,5 °К), считая, что сам компрессор работает обратимо.
8.	Обратимый циклический тепловой двигатель работает между источни-
ком теплоты с температурой 1000°R (555,5 °К) и теплоприемником с темпера-
турой 700 °R (388,8 °К). С какой скоростью теплота должна переноситься от
источника, чтобы получить максимальную мощность двигателя в 5 л. с. С ка-
кой скоростью теплота будет передаваться теплоприемнику?
9.	От газа, текущего по трубе при давлении 50 фунтов на дюйм® (3,5 кПсм1)
и температуре 60 °F (15,6 °C), берется проба с помощью эвакуированной сталь-
ной бомбы емкостью 0,1 фут® (2,8 л), присоединенной в схему таким образом,
чтобы газ мог проходить в бомбу через частично открытый вентиль до тех пор,
пока давление в бомбе не станет равным общему давлению в трубе. Процесс
взятия пробы считать адиабатным. Определить общее изменение энтропии для
гелия и двуокиси углерода в отдельности.
10.	Поток насыщенного пара при 220 °F (104,4 °C) впускается непосред-
ственно в поток холодной воды при 60 °F (15,6 °C), чтобы повысить температуру
воды до 160 °F (71,1 °C). Определить отношение массы пара к массе воды, из-
менение общей энтропии на фунт полученной смеси и рассеянную энергию
относительно теплоприемника с температурой 60 °F (15,6 °C).
14
ГЛАВА 7
Термодинамические
свойства растворов
I.	Однофазные растворы переменного состава
Для однофазного чистого компонента или гомогенного раство-
ра с определенным составом такие экстенсивные свойства, как
объем, внутренняя энергия, энтальпия и энтропия, являются
функциями общей массы системы и таких двух интенсивных свойств,
как температура и давление. Для однофазного раствора с
переменным составом экстенсивные свойства — функции двух
интенсивных свойств и массы каждого отдельного компонента.
Если G — экстенсивное свойство однофазного раствора, то
G = <₽(p. Т, Na, Nb...Nc),	(7-1)
где Na, Nb...Nc масса (или число молей) каждого отдельного
компонента соответственно, а давление и температура произволь-
но выбраны как две независимые интенсивные переменные.
Для того чтобы определить экстенсивное свойство раствора,
нужно знать вклад каждого отдельного компонента в общую ве-
личину G для раствора. Вклад, который вносит компонент в общую
величину G для раствора, может быть определен путем исследова-
ния изменения свойства G раствора, вызванного изменением мас-
сы компонента i. Согласно определению полного дифференциала,
общее изменение G, вызванное изменением каждой из независи-
мых переменных уравнения (7-1), равно
<7-2>
где сумма содержит слагаемые для каждого компонента в растворе.
Постоянство массы каждого компонента, за исключением компонен-
та i, предполагается для каждой частной производной под зна-
ком суммы.
При условии постоянства температуры и давления
(7-3)
А	,Р
212
2.	Парциальные мольные величины
Частная производная (dGIdNдт, р измеряет скорость измене-
ния свойства G с изменением массы N t компонента i при условии
постоянства температуры, давления и масс всех других компонен-
тов. Если Nt измерено числом молей, то производная называется
«парциальная мольная величина» и обозначается Gt. В идеальном
случае скорость изменения G с изменением Nf равна величине G
для 1 моля чистого компонента i, обозначаемой Gz. Например,
если свойство G есть объем раствора, добавление 1 моля компо-
нента i к раствору в идеальном случае привело бы к увеличению
объема раствора, равному объему 1 моля чистого компонента г,
т. е. vt. Добавление Nt молей компонента i привело бы к увеличе-
нию объема раствора, равного На рис. 45 представлена
величина G для идеально-
го раствора в зависимости
от числа молей компонен- ь
та i при условии, что тем-
пература,'давление и чис-
ло молей всех других
компонентов остаются по- §
стоянными. Этот график §>
представляет собой линей- |
ную зависимость, и нак- §
лон прямой (dGldN{)Tt р,
или парциальная мольная
Рис. 45. Парциальная мольная вели-
чина:
/—идеальный раствор, 2—неидеальиый раствор
величина О£, постоянна и
равна величине С£ для
1 моля чистого компонен-
та i. Наклон представляет
собой вклад 1 моля компо-
нента i в общее свойство G
раствора и не зависит от
количества присутствую-
щего компонента i. Вклад TV£ молей компонента i в общее свой-
ство G идеального раствора равен G£JV£. Таким образом, общая
величина G для идеального раствора при условии постоянства
температуры и давления составит
с
G^G^.
А
(7-4)
Обычно растворы не бывают идеальными и график зависимости
G от Nt не является линейным. Наклон кривой dG!dNt, или пар-
циальная мольная величина, не является постоянной, но пред-
ставляет собой функцию числа молей компонента i в растворе.
На этом графике число молен всех компонентов, за исключением i,
213
строго задано и величина -Nt определяет состав раствора. Та-
ким образом, парциальная мольная величина неидеального рас-
твора должна рассматриваться как функция состава раствора.
Если все количество раствора определенного состава разделить
на несколько частей, скорость изменения Gt с изменением 7VZ,
или парциальная мольная величина, будет одной и той же для
каждой части, т. е. парциальная мольная величина является
интенсивным свойством, зависящим от состава, но не зависящим
от общей массы раствора.
В растворе, содержащем 1 моль компонента i, парциальная
мольная величина при данном составе представляет собой вклад
компонента i в общее свойство G раствора. Например, если свой-
ство G есть объем раствора, то вклад 1 моля компонента i в общий
объем раствора не равен объему 1 моля чистого компонента i,
т. е. (г;), но является парциальным мольным объемом v( при опре-
деленной концентрации. В растворе, содержащем Nt молей ком-
понента i,_вклад компонента i в общее свойство G раствора со-
ставит Nfit. Следовательно, общая величина G для неидеального
раствора при данных температуре и давлении составляет
с ।
G=£GzJV£.	(7-5)
А
При постоянных температуре и давлении полный дифферен-
циал G, согласно уравнению (7-5), будет иметь вид
С	с
dG^G^^N^.	(7-6)
А	А
Для того чтобы это уравнение согласовывалось с уравнением (7-3)
с
V^G^O.	(7-7)
А
Уравнение (7-7) обычно служит для проверки и сопоставления
экспериментальных данных.
3.	Влияние состава на парциальные мольные величины
В приведенных выше уравнениях числа молей отдельных ком-
понентов считались независимыми переменными, а общее число
молей раствора рассматривалось как зависимая переменная.
Если число молей какого-либо компонента i изменилось, в то
время как число молей всех других компонентов осталось постоян-
ным, общее число молей раствора также обязательно изменится.
Однако если общее число молей раствора принять постоянным,
214
то число молей отдельных компонентов не будет больше незави-
симым из-за соотношения
с
У 7Vz = aconst.
А
В этом случае число молей компонента i не может изменяться не-
зависимо от чисел молей других компонентов в растворе.
Для 1 моля раствора уравнения (7-5), (7-3) и (7-7) будут соот-
ветственно
g^^Gtxt;	(7-8)
А
dg^G^x	(7-9)
А
Й
С
£хДС, = 0.	(7-10)
А
где х{ — мольная доля, определяемая соотношением
Nt
Y —
a g — мольное свойство:
G
VNt •
Согласно соотношению £xz — 1, все мольные доли xt не яв-
<Ю
ляются независимыми и G не равно —— Это соотношение можно
использовать для исключения одного из xz, а именно для раствора,
содержащего компоненты А, В...С:
Хс— 1 —ХА Хв—... —Xq_v
Уравнение (7-8) примет вид
(7-11)
А
Так же, если Edxz = 0, то
dxc= —dxA—dxB—...—dxc_j
и уравнение (7-9) становится
с-1
dg^(G-Gc)dXi.	(7-12)
А
215
Теперь все xt— независимые и полный дифференциал для g как
функции хА, xB...xc_t при постоянной температуре и давлении
равен
С-1
’ А
(7-13)
Сравнивая уравнения (7-13) и (7-12), имеем
Gt~Gc.
(7-И)
dg =
дх{
Подстановкой уравнения (7-14) в уравнение (7-11) получаем выра-
жение Gc:	Сс=г-^,<-	(7-15)
Исключая Gc из уравнений (7-14) и (7-15), получаем выражение G(-.
g<“*+«)-!><(» <™>
Уравнение (7-16) дает выражение парциальной мольной величины
для всех компонентов, кроме С. Уравнение (7-15) дает выражение
парциальной мольной величины компонента С.
Для бинарного раствора компонентов А и С уравнение (7-15)
принимает вид
=	(7-17)
а уравнение (7-16) принимает следующий вид:
Сд=^ + (1-Хд)(Д).	(7-18)
Так как (1 —хА) — хс и (—dx^ — dxc, то уравнение (7-18) мо-
жет быть записано как
GA-g-xc(^)
(7-19)
или
£~(л~)хс+Сл-
(7-20)
На графике g как функции хс (см. рис. 45), уравнение (7-20)
является уравнением прямой линии с тем же наклоном, что и
касательная к кривой g — хс в точке хс, отсекающая отрезок GA
на оси ординат.
216
Уравнение (7-17), записанное в форме
(7-21)
выражает уравнение той же прямой в функции хА и Gc. Таким
образом, парциальные мольные величины компонентов в бинар-
ном растворе могут быть получены с помощью касательных, про-
веденных.к кривым g — хА или g — хс для данного состава. От-
резок, отсекаемый касательной в точке хА— 1, равен GA, отрезок,
отсекаемый касательной в точке хс = 1, равен Gc.
При графическом определении парциальных мольных величин
из экспериментальных данных большую точность можно полу-
чить, если пользоваться значениями отклонения свойств от по-
ведения идеальных растворов, чем производить вычисления через
абсолютные величины. Концепцию об остаточном объеме, исполь-
зованную раньше для выражения отклонения действительного
объема газа от объема идеального газа при тех же самых темпера-
туре и давлении, можно применить к любому экстенсивному тер-
модинамическому свойству раствора путем определения избыточ-
ного количества той или иной величины по соотношению
(7-25)
А ёид. р-р ёреал. р-р,	(7-22)
где
ёид.Р-р=Е£Л-	(7-23)
Дифференцируем уравнение (7-22) по хА при условии постоянства
температуры и давления:
( ^L\ = ( ^ид^р \  dg	(7-24)
\дхА/ \ дхА I	дх А
Дифференцируем уравнение (7-23) по хА для бинарного раствора:
д8пд. Р Р \  	/ Вид. р-р	8 с
" д^~) -SA — ёс	-
Поставляем уравнение (7-25) в уравнение (7-24):
/ ДА \ __ 8ид. р-р — gc  ^8	_ 2g\
)	хА	дхА	' ' '
и уравнение (7-26) в уравнение (7-21) для бинарного раствора:
g= (§НД. p-p-gc)	Ъ +GC-	(7-27)
Преобразованием уравнения (7-27) получаем
gH«.p-p-g = A = ^*д + (&-Л).	(7-28)
217
Таким образом, разность между мольным количеством Gc
чистого компонента С и парциальной мольной величиной Gc ком-
понента С в растворе состава хА можно получить по величине от-
резка, отсекаемого на оси ординат касательной, проведенной к
кривой А — хА в точке хА. Парциальную мольную величину мож-
но получить из тождества -
@с — ёс—(ёс — Gc).
Уравнение (7-10) используют обычно как основное уравнение при
определении изменения GA и Gc с изменением состава. Для би-
нарного раствора
xAdGA+XfdGc — 0.	(7-29)
При хс как независимой переменной можно вывести соотношение
(7-30)
В любой точке хс должно выполняться следующее соотношение
между двумя наклонами кривых:
дхс __ ___ ХА _ __1 ~ХС
двА ХС	ХС
дхс
(7-31)
Если хс = 0, то или величина (дСА1дх^ равна нулю, a (dGcldxc)
конечна, или (dGAldxc) конечна, a (dGcldxc) бесконечно велика.
Если хс — 0,5, то {<)GAldX(^ и (dGcJdxc) равны, но противополож-
ны по знаку. Если х = 1,то или (двс1дхс) равна нулю и (dGA!dxc)
конечна, или (дСс!дх^ конечна, a (dGA/dxc) бесконечно велика).
4.	Химические потенциалы
Если рассматривать систему с фазовым или химическим рав-
новесием, особенно важное значение имеют такие функции, как
полный дифференциал внутренней энергии, энтальпии, свобод-
ных энергий Гельмгольца и Гиббса. Для однофазных открытых
систем эти функции можно выразить с помощью уравнения (7-2):
"-(“Vs+(£V (7-32>
‘'H=(^)„/s+(^)s/₽ +ЖИ (МЗ)
218
“л-&\/r4%\.K*+№}r,dN* <7-34>
+2(Д)Г,;** <7-з5>
Первые два частных дифференциала в правой части каждого урав-
нения ограничены постоянным числом молей каждого компонен-
та. Эти дифференциалы для гомогенных растворов постоянной
массы и состава можно вычислить по уравнению (6-1):
dE = TdS—pdv.	(7-36)
Из этого уравнения следует, что	
/дЕ \ 	гр \dS к	(7-37)
и	
/дЕ\ _ п \ dv Is	Р'	(7-38)
Энтальпия равна	
dH = dE-\- pdv 4- vdp.	(7-39)
Сложив уравнения (7-39) и (7-36), получаем	
dH — TdS + vdp.	(7-40)
Из этого уравнения следует, что	
/ дН \	(7-41)
и	
/5Я \ ) = V. \дР Is	(7-42)
Тогда свободная энергия Гельмгольца	
dA = dE —TdS—SdT.	(7-43)
Сложив уравнения (7-34) и (7-36), получаем	
dA = —SdT—pdv.	(7-44)
Из этого уравнения найдем	
—S	(7-45)
И /дА \ _	„ \ dv )г	Р'	(7-46)
219
Свободная энергия Гиббса
dF=dH—TdS—SdT.
Сложив уравнения (7-47) и (7-40), получаем равенство
dF='—SdT -\-vdp.
Из этого уравнения следует, что
и
(7-47)
(7-48)
(7-49)
(7-50)
Подставляя значения этих частных производных при постоянном
составе в уравнения (7-32)—(7-35) и перенося их в левую часть
уравнения, получаем
dE-TdS±pdv^(j^ sdNp,	(7-51)
dH-TdS^vdp^X	dN •	(7-52)
dA + SdT + pdv^^^^dNp.	(7-53)
dF + SdT—vdp = J ( ^7 ) dNt.	(7-54)
Из уравнений (7-36), (7-40), (7-44) и (7,48) можно получить сле-
дующее равенство:
dE—TdS + pdv = dH—TdS—vdp — dA-{- SdT+pdv =
= dF + SdT-vdp.	(7-55)
Так как левые части в уравнениях (7-51)—(7-54) равны, то равны
и суммы правых частей. Поэтому частные производные для каж-
дого отдельного компонента должны быть равны в каждой сумме.
Следовательно,
дЕ \	/ дЯ\ __/_дА_\ _( дЕ\
dN‘)s,<>
Гиббс первый установил важность этих частных производных при
исследовании равновесия систем и назвал их «химическими по-
тенциалами». Обычно спи обозначаются знаком р.
220
5.	Вычисление парциальных мольных величин
Экспериментальные данные
Объем раствора — наиболее легко наблюдаемое и измеряемое
экстенсивное термодинамическое свойство раствора. Следова-
тельно, эмпирическое определение парциальных мольных величин
зависит в первую очередь от наличия данных о соотношении
объема и состава раствора при условии постоянства температуры
и давления.
Экспериментальные наблюдения показывают, что объем даже
неидеальных газов складывается почти аддитивно и образую-
щаяся смесь газов по своему поведению близка к идеальному газу.
Однако объем большинства жидкостей не является аддитивным
свойством и образующиеся растворы по своему поведению сильно
отклоняются от идеальных. Степень отклонения от поведения
идеальных растворов можно рассматривать в связи с межмолеку-
лярными силами, которые относительно малы в смеси газов, но
могут быть достаточно большими в жидких растворах. Рас-
смотрим парциальные мольные величины в применении к этим
растворам.
Если есть данные относительно объема раствора или плот-
ности как функции состава, то парциальный мольный объем мож-
но вычислить непосредственно с помощью уравнений (7-15) и
(7-16). Вычисление значительно упрощается, если раствор со-
стоит только из двух компонентов; в этом случае применяют
уравнения (7-17) п (7-18). Эти расчеты иллюстрированы примером 1
для раствора этиловый спирт — вода.
Пример!. Вычислить парциальные мольные объемы как функ-
цию состава в системе этиловый спирт—вода при 25 °C и 1 атм*.
На рис. 46 показана зависимость мольного объема раствора эти-
ловый спирт — вода от концентрации.
Вычисленные величины избыточного мольного объема раство-
ра в зависимости от концентрации представлены на рис. 47. Отре-
зок, отсекаемый касательной в точке, где мольная доля спирта
равна нулю, показывает избыточный парциальный мольный объем
воды; отрезок касательной в точке, где мольная доля спирта равна
единице, показывает избыточный парциальный мольный объем
спирта. Значения парциального мольного объема спирта и воды,
полученные вычитанием избыточного парциального мольного
объема чистого компонента в зависимости от концентрации,
представлены на рис. 48.
Парциальный мольный объем воды достигает максимума и
парциальный мольный объем спирта — минимума в точке пере-
* Данные о плотности раствора см. в «Справочнике физ.-хим.-техн. вели-
чин» Изд-во «Советская энциклопедия», 1931—1933
221
гиба кривой состав — объем на рис. 46 и кривой избыточного
мольного объема на рис. 47. Если бы раствор этиловый спирт —
вода был идеальным, то кривая состав — объем (см. рис. 46)
Рис. 46. Зависимость мольного
объема раствора этиловый
спирт— вода от концентрации
при 25 °C и 1 атм.
Рис. 47. Зависимость мольного
избыточного объема раствора
этиловый спирт — вода от кон-
центрации при 25 °C и 1 атм
Рис. 48. Зависимость парциаль-
ного мольного объема этилово-
го спирта и воды от концент-
рации спирта при 25 °C
и 1 атм.
была бы прямой линией, связывающей мольные объемы чистых
компонентов, и парциальный мольный объем каждого компонента
был бы равен мольному объему чистогр компонента.
22?
Уравнения состояния для смесей
При отсутствии экспериментальных данных о свойствах рас-
твора парциальные мольные величины можно вычислить с помощью
уравнения состояния смесей. Такое уравнение состояния должно
содержать переменные состава, а также температуру, давление и
объем. Так как рпТ-свойства определенного состава могут быть
выражены в той же форме, что и свойства чистого соединения, то
переменные состава лучше всего ввести в уравнение состояния пу-
тем выражения каждого из параметров как функции концентра-
ции.
Исследователи пытались найти различные способы для выра-
жения параметров уравнения состояния как функций концентра-
ции^ параметров чистого компонента. Битти и Икехара [51 предло-
жили использовать линейную комбинацию для параметров с
размерностью объема первой степени и линейную комбинацию
квадратных корней для параметров с размерностью объема вто-
рой степени. Например, если уравнение состояния Ван-дер-
Ваальса выбрать для выражения ргТ-свойств смеси, его можно
записать так:
RT _____а_т_
Vm — bm	&т
(7-57)
где ит — объем 1 моля
(7-58)
(7-59)
смеси и
1
am=(S^'A2)2;
6т=ЕхД,
чистых компонентов; xt — мольная доля
где at и bt — параметры
компонента в смеси.
Исходя из теоретических рассуждений, основанных на кине-
тической теории газов, Ван-дер-Ваальс предположил, что пара-
метры в уравнении состояния для бинарной смеси могут быть
выражены общим соотношением
km=k1x?1+2klt2x1x2+k2x&)	(7-60)
где /?х и k« — параметры чистых компонентов; и х^ — соответ-
ствующие мольные доли в смеси, A1j2— комбинация из и k<>.
Если km представить как линейную комбинацию kr и Л2 в соответ-
ствии с уравнением (7-59), то klf2 можно вычислить как среднее
арифметическое kr и k2. Таким образом, уравнения (7-59) и (7-60)
примут вид
+ 2А, >2xtx2 4- k2x[ = ktxt 4- k2x2,
h _	+ ^2
«1.9—	2
где
(7-61)
1,2
Если km представить как линейную комбинацию квадратных
корней из ki и k2 в соответствии с уравнением (7-58), то в мож-
223
но вычислить как среднее геометрическое kr и Л2. Таким образом,
уравнения (7-58) и (7-60) примут вид
где
1 1
'Г	-р k2X2 = (^ %! -р ^2
(7-62)
Выражение для парциального мольного объема можно получить,
используя уравнение Ван-дер-Ваальса и уравнение (7-16). Диф-
ференцируем уравнение (7-57) по х{ при постоянных температуре
и давлении:
~ ){Vm ~ ЬтУ
дх;	1 2cm \vm Ъп^2
(7-63)
Затем дифференцируем уравнение (7-58) по х{:
2а2Ю-а?).
(7-64)
Xj выпадает из уравнения (7-58) из-за соотношения = 1,
примененного, чтобы сохранить независимость оставшихся моль-
ных долей.
Дифференцируем уравнение (7-59) по х( после исключения Xj.
(7‘65)
Подставляя уравнения (7-63) — (7-65) в уравнение (7-16), полу^
чаем

1 д д
t „ 2 (at2 —	—
(bi — bfn) — zam
1 2om
(vm — bmy
RTv*m
(7-66)
или, после преобразования
1 | Ьщ  2 Omai .(Vm	bm)2
vm________RT ~ v*m
vi~Vm i_2am. (vm-bm)2
RT ... v»m '
(7-67)
Для бинарной смеси уравнение (7-66) сводится к следующему урав-
нению:
(fci — bs) — 2 [ах + / ojCj (x2 — Xi) — a2x2]
RT<?m
l—2am
(Vm — bmy
Wn
(7-68)
224
Аналогичные методы комбинации параметров чистых компонентов
и концентраций были предложены для других уравнений состоя-
ния. Например, если уравнение состояния Битти — Бриджмена
использовать для смесей, то параметр Ло в уравнении (5-73) вы-
числяется с помощью линейной комбинации квадратных корней
из параметров чистых компонентов; другие четыре параметра вы-
числяются линейной комбинацией параметров чистых компонен-
тов [41:
А>=1^0М2]г;
Во =
a=ExjCii;
b = ЕхД;
С— LXjCi.
(7-69)
Уравнение состояния Бенедикт — Вебб — Рубина с успехом было
использовано для жидких смесей и для газообразных смесей со
следующей комбинацией параметров [61:
4=^ ОМ2 Г;
Во — ExtBot;
^«[ЕхДС^]»;
т=[Ех((у()~Г;
а=рэд3]3;
1
&=[Ех,(^р3;
[ЕхДсУ7]®;
1
<х = [Ех/а,) 3 ]3.
(7-70)
Используя эти соотношения для определения параметров смеси,
выражение для парциального мольного объема, основанное на
уравнении состояния Бенедикт — Вебб — Рубина, можно дать
в виде
_1_
d
1 1
1 + [(Во<+В0)~ 2 (Ло, Ло)2 //?Т-2(С0Д)2 /RTs]d
1 1
+ 3[(^2)3-(afO2)3//?T]d2
i	i
-|- (3/ЛТ) [о(о,а2)3 + а(а/22)] 3 ] d6
1
4- (3/^Т3) (С, С2)3 d2( 14- т<И/е^
i
—(2c/R.T3) d2 (yd?)2 (Vj/y) 2 /е'*да
14-2 [BO—(AJRT)—(C^RT3}] d4- 3 p-(a//?T)] d2
(7-71)
4- 6aad6/RT 4- (3c/7?T3) d2 (1 4- yd2)/e^
—^clRT3)d2(yd2)2leyd2
15—1503
222
Обобщенное уравнение состояния для смесей можно записать
с помощью среднего фактора сжимаемости Zm:
(7-72)
где Zm— функция давления, температуры и состава смеси. Если
использовать закон Амага об аддитивности объемов, то средний
фактор сжимаемости представляет собой линейную комбинацию
факторов сжимаемости чистых компонентов, причем каждый из
иих должен быть взят при температуре и общем давлении смеси:
7m=ExiZz.
Однако в этом случае образовавшаяся смесь представляет собой
идеальный раствор и парциальный мольный объем данного ком-
понента в смеси равен мольному объему чистого компонента:
7 RT
v^v^Z^.
Если использовать закон Дальтона об аддитивности давлений,
то средний фактор сжимаемости представляет собой линейную
комбинацию факторов сжимаемости чистых компонентов, причем
каждый из них должен быть взят при температуре системы и дав-
лении чистого компонента для общего объема смеси.
В соответствии с псевдокритической точкой метода Кэй сред-
ний фактор сжимаемости для смеси может быть получен из обоб-
щенного фактора сжимаемости для чистых компонентов путем
определения псевдокритических температуры и давления смеси.
Псевдокритическую температуру определяют как среднюю мольную
величину критических температур чистых компонентов, псевдо-
критическое давление — как среднюю мольную величину крити-
ческих давлений чистых компонентов:
Ткрт=г^Ткр1-,	(7-73)
Ркр т~ (•	(7"74)
Из этих величин можно вычислить псевдоприведенные темпе-
ратуру и давление для смеси:
Тпрт=ТТ—,	(7-75)
1 кр гп
Рпрт=-^~.	.(7-76)
Ркр m
Эти приведенные параметры затем используют для определе-
ния среднего фактора сжимаемости для смеси по графику обоб-
щенных факторов сжимаемости для чистых компонентов.
Пример 2. Определить парциальные мольные объемы эта-
на и гептана в паровой фазе смеси и в жидкой фазе раствора как
226
функции концентрации при 400 °К и 20 атм, используя уравне-
ния состояния Ван-дер-Ваальса и Бенедикт — Вебб — Рубина.
По уравнению состояния Ван-дер-Ваальса
для этана
аг = 1391 атм • (фут3/фунт-моль)а;
br — 1,028 фут3/фунт-моль;
для гептана
а2 = 7931 атм  (фут8/фунт-моль)2;
Ь2 = 3,311 фут8/фунт-моль.
Объемы смеси для данного состава можно определить методом
последовательных приближений из уравнения состояния Ван-
дер-Ваальса при 400 *К и 20 атм, используя постоянные для
смеси, вычисленные по уравнениям (7-58) и (7-59). Например в
растворе, содержащем 20% (мол.) этана и 80% (мол.) гептана,
%i — 0,20;
х2 = 0,80;
I	i
ат = (1391 2 -0,204-7931 2 -0,80)а=6300 атл1-(фут3/фунт-моль)а;
Ьт— 1,028-0,20 4-3,311-0,80 = 2,854 фут3/фунт-моль;
RT — 1,315- 400 = 526 атм-(фут’/фунт-моль).
Подставляем полученные результаты в уравнение состояния:
p = 526/(vm—2,854)—6300Д&.
Допустив, что vm равно 4,34 фут’/фунт-моль, найдем .
р= 526/(4,34 — 2,854)—6300/4,34а = 20 атм.
Следовательно, согласно уравнению Ван-дер-Ваальса, моль-
ный объем раствора, содержащего 20% (мол.) этана и 80% (мол.)
гептана при 400 °К и 20 атм, равен 4,34 фут8/фунт-моль, или
0,271 л!моль. Мольный объем раствора для других концентраций
может быть вычислен подобным способом. Вычисленные моль-
ные объемы растворов приведены на рис. 49.
Парциальные мольные объемы могут быть вычислены с по-
мощью графика мольного объема раствора этан — гептан как
функции концентрации (рис. 49) по способу, описанному в при-
мере 1; вместе с тем парциальные мольные объемы могут быть
15*
227
определены аналитически по уравнению (7-68) для бинарной сме-
си, содержащей 20% (мол.) этана и 80% (мол.) гептана:
2 [ах-\-Уa(х2—jq)—а2х2] = 2 [ 1391 • 0,20 +
4 УТ391 7931 (0,80 —0,20)—7931 • 0,80] = —
— 8150 атм (фут3/фунт-моль)2;
(Ьх — b2) = 1,028—3,311 — —2,283 фут3/фунт-моль.
Для этого раствора было найдено, что vm равен 4,34 фут3/фунт-моль
при 20 атм и 400 °К- Подставляя эти значения в уравнение (7-68),
получаем
7 - 4 44 > A RA / - 2-283 - К - 8150)/Б26] (1,486/4,34)* ]
Uj —1 _ J2-6300/(526-4,34)] (1,486/4,34)*	]'»
t\ = 4,34 + 0,80(—1,31) = 3,29 фут3/фунт-модь(0,205 л/моль).
Таким же образом находим парциальный мольный объем геп-
тана в растворе:
?2 = 4,34—0,20 (—1,31) = 4,60 фут8/фунт-моль (0,287 л/моль).
Парциальные мольные объемы для других составов могут быть
вычислены аналогичным способом (см. рис. 45).
Хотя уравнение состояния Ван-
Рнс. 49. Зависимость мольного
объема раствора этан— гептан,
вычисленного по уравнению
состояния Ван-дер-Ваальса, от
концентрации этана х при
400 °К и 20 атм
дер-Ваальса относительно про-
сто в применении к вычислению
свойств смеси, точность вычислен-
ных результатов сомнительна.
Для получения надежных резуль-
татов следует применять очень
точное уравнение состояния. Из-
вестно, что по уравнению состоя-
ния Бенедикт — Вебб — Рубина
риТ-свойства углеводородов и их
смесей вычисляются с ошибкой
только в несколько десятых про-
цента. Для того чтобы показать
влияние уравнения состояния на
величину вычисленных свойств
раствора, были определены пар-
циальные мольные объемы смеси
этан — гептан с помощью уравне-
ния состояния Бенедикт—Вебб —
Рубина и результаты сравнены с
результатами, полученными по
уравнению Ван-дер-Ваальса.
Уравнение состояния Бене-
дикт — Вебб — Рубина наиболее
применимо в форме уравнения
228
(5-74). Когда его применяют для смесей, параметры могут быть
вычислены в функции параметров компонентов и мольных долей
согласно соотношениям (7-70). Ниже приведены параметры
смеси, содержащей 20% (мол.) этана и 80% (мол.) гептана, вы-
численные с точностью до третьего знака с помощью параметров
чистых компонентов, указанных в приложении 7. В качестве
единиц измерения использованы атмосфера, л/моль и градус
Кельвина.
1 ।
Д, = 0,20-4,15556 2 + 0,80 -17,5206 2 ]2= 13,5;
Во = [0,20  0,062772 4- 0,80 • 0,199005] = 0,1725;
1 1
Со= [0,20-17,9592 2 4- 0,80- (474- 574) 2]2-104= 335-104;
1	1
а = [0,20-0,345160 3 4-0,80 • 10,36475 3]3 = 6,65;
1	1
Ь = [0,20-0,0111220 3 4-0,80-0,151954 3]3 = 0,104;
1 1
с = [0,20 32,7670 3 4- 0,80 • 2470 3 ]3 • 103 = 150 104;
1	1
а = [0,20-0,243389 3 4-0,80 4,35611 3]3 10-3 = 3,00 10-3;
1 1
у = [0,20 • 1,18000 2 4- 0,80 • 9,0000 2 ]2 • 10-2 = 6,80 • 10-2.
Изотерму давление — плотность при 400 °К получаем подста-
новкой этих значений в уравнение состояния:
ратм = 32,824d—28,74d2—-3,23d3 4-0,01995d® 4-
4-9,38d3(l 4-0,068d2)/e°’oe8'i2.
Приняв, что d = 6,11 моль! л, найдем, что р = 20 атм. Следо-
вательно, мольная плотность раствора при 400 °К и 20 атм рав-
на 6,11 моль/л и мольный объем равен (6,II)-1, или 0,164 м!моль.
Мольные объемы раствора для других концентраций могут быть
вычислены аналогичным способом. Результаты нанесены графи-
чески на рис. 50.
Парциальные мольные объемы можно найти графически из
рис. 50 либо вычислить аналитически по уравнению (7-71). Для
смеси, содержащей 20% (мол.) этана и 80% (мол.) гептана при
400 °К, параметры для этана в уравнении (7-71) имеют величины,
определенные ниже с точностью до третьего знака:
(Во£-Во) = 0,235;
1
2(Л0,Л0)2 /РТ = 0,456;
1
2(CoiCo) 2//?Г3=0,301;
229
_L J. )
з [(W3 —(a»°2)3 Ж] = °>081;
1 1
(3/ЯТ) [сг(а/12) 3 + a (<¥*2)3 ] = 1,49  IO'8;
1
(3/7?T8) (qc2) 3 = 0,238;
I
2c(v£/t)2/Z?T3 = 0,237;
2	(Bo - AQ/RT-CO/RTS) = -1,749;
3(fe—a//?T)= —0,294;
baa/RT = 3G5 10~s;
ЗсЖ3 = 0,856:
2с//?Г3 = 0,571,
Рис. 51. Зависимость парциальных
мольных объемов растворов этан — геп-
тан от концентрации этана, вычис-
ленных:
--------по уравнению Ван-дер-Ваальса;
---------- по уравнению Бенедикт-Вебб-Ру-
бнна
Мольный оЛен раствора, л/моль
Рис 50. Зависимость мольного
объема раствора этан— гептан,
вычисленного по уравнению
состояния Бенедикт — Вебб —
Рубина, от концентрации этана
х при 400 °К и 20 атн
230
Если эти величины подставить в уравнение (7-71), то выражение
для парциального мольного объема этана в функции мольной плот-
ности раствора примет вид
1—0,521d—0,081++149-1(Г5+ +
-j-	+ 0,238+(1 + 0,068+)/е°>Обад2—
- _	—0,237г/2 (0,068+)2/e°’088d2
Vh~ 1 — 1 ,749г/ —Ь” 294г/2 + 36 5—~
+ 0,856+(1+O,O68+)/e°’oe8d2—
—0,57 Id2 (0,068+)2/е°>овадг
Аналогично выражение для гептана:
fl —2,092г/—0.350++417 10~5+ +
-3-	4- l,00+(l + О,О68+)/ео>ооад2 —
-	.	— 0,650 (0,068+)2/+0tiM2
H ~	1 — 1,749rZ—0,294+ + 365-10~6++
+ 0,856+(1+0,068+)/e0’008d2—
—0,571+ (0,068+)2/e0»0e8d2
Вычисленная мольная плотность этого раствора соответствует
величине 6,1 моль/л при 400 °К и 20 атм. Подстановкой этого
значения в уравнения (7-77) и (7-78) получаем
vE~ 0,104 л/моль-,
уя= 0,174 л!моль.
Вычисленные величины для других концентраций нанесены гра-
фически на рис. 51 для сравнения с парциальными мольными
объемами, вычисленными по уравнению состояния Ван-дер-
Ваальса.
Задачи
1.	Каков будет объем раствора при 25 °C, полученный при смешивании
50 см3 этилового спирта и 50 см3 воды? Какую часть общего объема раствора
можно отнести к каждому компоненту?
2.	Используя данные для фактора сжимаемости, определить мольные
объемы для паровой фазы смеси этана и гептана при 400 °К и 20 атм в интер-
вале концентрации 0,5—1,0 мольных долей этана, принимая, что раствор иде-
альный. Каковы парциальные мольные объемы этана и гептана при этих усло-
виях?
3.	Применить критерий, выраженный уравнением (7-31), к нескольким
точкам на кривой для парциальных мольных объемов на рис. 48 и 51.
ГЛАВА 8
Критерий равновесия
1.	Общий критерий равновесия
Предсказание условий, определяющих фазовое и химическое
равновесие систем, одно из наиболее важных применений прин-
ципов термодинамики. По второму закону термодинамики изоли-
рованная система, свободная от одухотворенного выбора, будет
самопроизвольно стремиться принять то состояние, которое может
осуществляться наибольшим числом способов. Это положение
можно использовать, чтобы установить критерий равновесия, по-
тому что то состояние изолированной системы, которое характе-
ризуется наибольшим числом способов осуществления, и может
быть названо «равновесным состоянием».
Рассмотрим изолированную систему, состоящую из несколь-
ких фаз /, k, I, ...р. Фаза / содержит п} частиц, распределяющих
энергию Е} между собой Ц различными способами; фаза k содер-
жит tik частиц, распределяющих различными способами энер-
гию Ek, и так далее. Для всех фаз, составляющих изолированную
систему, общее число способов, которыми все частицы Хну рас-
]
пределяют между собой общую энергию JjEy, будет ПЦ, посколь-
I	i
ку все j независимы друг от друга.
Любое самопроизвольное изменение, происходящее внутри
системы, приводит к увеличению общего числа способов осуществ-
ления состояния системы. Так как состояние равновесия характе-
ризуется полным отсутствием стремления к самопроизвольному
изменению, система будет находиться в состоянии равновесия,
когда Пйу достигнет своего максимального значения. Следо-
вательно, критерий равновесия для изолированной системы может
быть выражен уравнением
dnfiy = 0.	(8-1)
Вообще, когда число частиц и число энергетических уровней
велико, скорость изменения общего числа состояний системы
пропорциональна скорости изменения числа состояний, характе-
232
ризующихся наиболее вероятным распределением энергии, так
что действительный критерий равновесия для изолированной
системы может быть выражен уравнением
(8-2)
Так как InniF/ будет максимальным при максимальном
П IF/, то в равной мере справедливым и более удобным Критерием
равновесия для изолированной системы является требование
(/1пПГу = йЕ1пГу = 0.	(8-3)
2.	критерий термического равновесия
Выводы п. 2 гл. 6 для теплопереноса между двумя фазами изо-
лированной системы могут быть распространены на многофазную
изолированную систему. Изменение в in IF/ фазы / при условии
постоянства состава может быть вычислено по уравнению (6-1):
Ы1п№.-=^4-	dv.-.
Производя суммирование по всем фазам изолированной системы и
применяя уравнение (8-3), получим для состояния равновесия
ULd In Wj = Е + Е	dv,- = 0.	(8-4)
Для изолированной системы общая энергия и общий объем по-
стоянны:
Ed£/ = 0;	(8-5)
ЕеЦ.=0.	(8-6)
Уравнения (8-4), (8-5) и (8-6) могут одновременно удовлетворяться
только при условии, если температура и давление для всех фаз
одинаковы:
Ty-Tft=...Tp;	(8-7)
p,= pft=...pp.	(8-8)
Следовательно, состояние равновесия будет существовать в
изолированной системе только в том случае, если температура и
давление будут одинаковы во всей системе.
Для отдельной многофазной системы, находящейся в тепловом
контакте с окружающей средой, общее число способов осуществ-
ления состояния может возрасти не только в результате тепло-
обмена между фазами внутри системы, но и в результате теплооб-
мена между системой и окружающей средой. Так как состояние
полного равновесия может наступить только в том случае, если
энергия распределена между фазами таким образом, что темпера-
233
тура Т и давление р одинаковы для всех фаз, уравнение (8-4)
может быть записано в виде
6Ы1п№7=^—(8-9)
Если общий объем постоянен, то Ldvj равна нулю и если 8Q —
общее количество теплоты, полученное системой от окружающей
среды, то UdEj = 8Q; тогда уравнение (8-9) примет вид
fcMlnW7,—^- = 0.	(8-10)
Произведение k^d In Wf представляет собой дифференциал эн-
тропии рассматриваемой неизолированной системы; —-диф-
ференциал энтропии окружающей среды. Общий дифференциал
энтропии изолированной системы, состоящей из рассматриваемой
системы и окружающей среды, при равновесии равен нулю.
3.	Критерий фазового равновесия
Критерий фазового равновесия может быть установлен при
рассмотрении системы из двух или более фаз, находящихся в кон-
такте, так что вещество, как и теплота, может переноситься че-
рез границы раздела фаз. Хотя многофазную систему следует рас-
сматривать замкнутой относительно обмена веществом с окружаю-
щей средой, теплообмен между ними возможен.
Так как система замкнута относительно массы, то общее число
частиц любого компонента будет постоянным, т. е. ^dn^ будет
!
равно нулю, если ntl обозначает число частиц компонента i в фазе
/ и суммирование распространено на все фазы. Следует допустить,
что перенос частиц от одной фазы к другой не влияет на энергети-
ческие уровни каждой фазы. Это предположение означает постоян-
ство объема для газовой фазы и незначительные изменения объема
для жидкой и твердой фаз. Все фазы будут иметь одинаковые тем-
пературу и давление, хотя температура и давление всей системы
в целом могут изменяться при переносе вещества и теплоты.
Изменение числа способов осуществления фазы /, вызванное в
результате изменения температуры и переноса частиц компонен-
та I, можно найти дифференцированием уравнения (4-28) по тем-
пературе и числу частиц компонента i в фазе / при условии по-
стоянства объема и числа частиц всех других компонентов:
(тйг')г,.Л +	)„и	^)т,.,ап‘'+
(8-П>
234
Используя уравнение (4-4) и проводя суммирование по всем фазам,
получаем
к. *
'	(8-12)
Произведение StdEj/dn,-^ >vflntj обозначает скрытую теп-
L
лоту, необходимую для перехода dn-частиц компонента i из фазы
j при постоянных температуре Т и объеме v; он показывает обмен
теплотой с окружающей средой, необходимый для поддержания
постоянной температуры. Произведение Х(<?Е,/дТ)njVJdT обозна-
i
чает явное изменение энергии в системе вследствие изменения
температуры dT; он также выражает обмен теплотой с окружаю-
щей средой. Полагая BQ равным сумме этих двух теплот, урав-
нение (8-12) можно записать в виде
(843)
I
Так как переход теплоты и перенос вещества могут происхо-
дить независимо друг от друга, то критерий термического равно-
весия, выраженный уравнением (8-10), должен выполняться неза-
висимо от какого-либо межфазового переноса вещества фазы.
В случае, если 8Q = 0, уравнение (8-3), выражающее общий кри-
терий равновесия для изолированной системы, также применимо.
В любом случае критерий фазового равновесия, допускающего
переход компонента i, выражается следующим образом:
/
Ednz/~0.
.Для замкнутой системы
(8-14)
(8-15
Уравнения (8-14) и (8-15) выполнимы
/ д InZ,-
если частная производная (^--——
фаз.
одновременно в том случае,
р. одна и та же для всех
4.	Критерий фазового равновесия, выраженный
через сумму состояний
Если все фазы системы — твердые фазы одного и того же чи-
стого вещества, то
Z? = z«/
235
и
In Z.j — tijXn Zj.
Так как сумма состояний для частицы не зависит от числа ча-
стиц, то
ainZy \
dni /
= Inz,-.
т>°/ ‘
Так как состояние равновесия требует, чтобы частные производные
были равны для каждой фазы, то In z, а следовательно, и г должны
быть одними и теми же для каждой твердой фазы чистого компо-
нента при равновесии. Этот критерий может быть также выражен
в виде равенства единице отношения сумм состояний для любых
двух фаз:
-^-=1.	(8-16)
Температура, при которой это соотношение выполняется,
называется «температурой фазового перехода».
Для равновесия между твердой фазой s и газовой фазой g
для одного и того же чистого вещества
Zs=z"s;Zg = -"*;
ng!
lnZs = njnz,; lnZg ~ nghizg—nglnng + ne.
При выводе последнего равенства использована приближенная
формула Стирлинга для In ng!:
<31nZs \
dns )t,vs
Так как частные производные должны быть одинаковы при равно-
весии для всех фаз, то критерий равновесия твердая фаза —
пар для чистого соединения может быть выражен соотношением
lnzs = 1п-^-;
пе
zs = ^
пе
или
%- = пе.	(8-17)
zs
Температура, для которой это соотношение выполнимо, называется
«температурой сублимации».
226
5.	Критерий равновесия, выраженный через
свободную энергию Гельмгольца
Свободная энергия Гельмгольца для фазы j многокомпонент-
ного раствора выражается через сумму состояний уравнением
(4-64):
Af= -ATlnZ,.	(8-18)
Критерий фазового равновесия, выраженный через свободную энер-
гию Гельмгольца, можно получить дифференцированием урав-
нения (8-18) по числу частиц компонента i в фазе j при постоян-
стве температуры, объема и числа частиц всех других компонен-
тов:
dAj \__________ы / dlnZy \
дпц IT,vj	\ дпц /гр/
(8-19)
Подставляя левое выражение в уравнение (8-14), получаем
У (дА'\
\дпц iTyVj
dnu = 0.
(8-20)
Так как количество компонента i в системе определенно, то
£ <Ц/=0.
/
(8-21)
Уравнения (8-20) и (8-21) выполнимы одновременно только в том
случае, если частные производные (dAj/dn^j fOj одинаковы для
всех фаз.
Сумма в уравнении (8-20) представляет собой изменение сво-
бодной энергии Гельмгольца для всей системы при переходе ком-
понента i из одной фазы в другую при постоянстве температуры
и объема, причем число частиц других компонентов в каждой
фазе поддерживается постоянным. Суммирование уравнения (8-20)
по всем компонентам дает общее изменение А при межфазном
переходе частиц всех компонентов при постоянстве температуры и
объема. Так как каждый отдельный член такой суммы должен
быть равен нулю, то критерий равновесия можно выразить сле-
дующим образом:
^ц=£о = О. (8-22)
’	" \oriii jT,v/	"
< i
237
6. Критерий фазового равновесия, выраженный
через химический потенциал
Если частная производная уравнения (8-19) выражена в функ-
ции числа молей, а не числа частиц, то, согласно уравнению (7-56),
оиа означает химический потенциал:
SAj \
dNu)
7
(8-23)
Так как число молей компонента прямо пропорционально числу
частиц, то критерий фазового равновесия требует, чтобы химиче-
ский потенциал каждого компонента был одинаковым во всех
фазах.
Критерий равновесия, выраженный через свободную энергию
Гельмгольца, применим к системе только при условии постоян-
ства температуры и объема. Однако химический потенциал может
быть отнесен к другим термодинамическим функциям при иных
ограничивающих условиях. Согласно уравнению (7-56), крите-
рий равновесия может быть выражен через любую из следующих
частных производных, определяющих химический потенциал:
ц	=	‘	(7'56)
' ХдНи’т,», \dNtj)Ttp XdUiils^ \dNii)s,p
7. Критерий фазового равновесия, выраженный
через фугитивность
Если независимые переменные — температура и давление, то
химический потенциал компонента i в одной из фаз многокомпо-
нентной многофазной системы можно выразить через свободную
энергию Гиббса:
= К	(8-24)
\ oNi/ т,р
Из-за недостатка сведений об абсолютной величине внутрен-
ней энергии нет данных о свободной энергии раствора как функ-
ции числа молей компонента. Однако химический потенциал мож-
но выразить через парциальный мольный объем, который можно
вычислить поданным непосредственных экспериментальных наблю-
дений плотностей раствора или с помощью эмпирического урав-
нения состояния.
Дифференцируя уравнение (8-24) по давлению при условии
постоянства температуры и числа молей всех компонентов, полу-
чаем
/	\ =	(8-25)
\ др )т др
238
Так как F — непрерывная функция Nt и р, то вторые смешанные
производные должны быть равны
\ dNj ,'р  \ др /	(8-26)
др	dNi
Для раствора постоянного состава
= v.	(8-27)
\ др Jtn i
Комбинируя уравнения (8-25), (8-26) и (8-27), получаем
(8-28)
Интегрируем уравнение (8-28) в пределах р* и р при условии
постоянно# температуры:
₽
Н—и!= J	(8-29)
р*
Если нижний предел интеграла настолько мал, что смесь ведет
себя как идеальный газ, парциальную мольную свободную энер-
гию компонента в растворе при давлении р* (величина р*, а так-
же величины Н*, S* и F* (см. ниже) — параметры идеального
раствора] можно вычислить через мольную свободную энергию
чистого компонента и его мольную долю в растворе.
Свободная энергия Гиббса
F^H—TS.	(8-30)
Смесь идеальных газов образует идеальный раствор, поскольку
общий объем смеси равен сумме объемов чистых компонентов во
всем диапазоне состава. Следовательно, общая внутренняя энер-
гия смеси равна сумме внутренних энергий чистых компонентов
и общая энтальпия смеси равна сумме энтальпий чистых компонен-
тов:
NiH^	(8-31)
Однако смешение идеальных газов — это необратимый про-
цесс, и общая энтропия раствора должна быть больше, чем сумма
энтропий чистых компонентов. Сумма энтропий чистых компонен-
тов равна	а общая энтропия смеси
(8-32)
239
Энтропию смешения можно вычислить, применяя выводы, полу-
ченные в п. 4, гл. 6 к многокомпонентной смеси идеальных газов.
Согласно уравнению (6-19)
Ni
—R S ЛГДп	(8-33)
IV i
Следовательно,
s* = s ^iSi—R £ (tylnty-tyln 2	(8-34)
Свободная энергия смеси идеальных газов получается подстанов-
кой уравнений (8-31) и (8-34) в уравнение (8-30):
F* = S Nfl'i-T £ N& + RT	(tylnty—ЛГДп £ ^).(8-35)
Первые два слагаемых представляют собой суммы свободных
энергий чистых компонентов. Следовательно,
F* = S	+ RT [ 2 (ЛГДпЛ^) — £ ЛГДп(£ АГ,)], (8-36)
где F* — мольная свободная энергия чистого компонента I в со-
стоянии идеального газа при давлении р*.
Парциальную мольную свободную энергию компонента i
можно найти дифференцированием уравнения (8-36) по при
условии постоянства Т, р* и числа модей всех других компонен-
тов:
-?5=f!+S 2 $4
откуда
F*t=F't+RT\nxt.
(8-37)
Для случая, когда нижний предел давления р* достаточно
мал, так что раствор представляет собой идеальный газ при
давлении р* и температуре Т, уравнение (8-29) можно записать в
виде
р
^i-—F*l — RT\nxl-\- J V/dp.
р*
(8-38)
Для чистого компонента изменение свободной энергии при
условии постоянной температуры получаем интегрированием урав-
нения (8-27):

(8-39)
240
Выражение для химического потенциала через мольную свобод-
ную энергию чистого компонента получаем вычитанием уравне-
ния (8-39) из уравнения (8-38):
р _
Pz=Fz+Z?Tlnxz+J (v{— vt) dp.	(8-40)
Р*
Для идеального раствора парциальный мольный объем равен
мольному объему чистого компонента, и уравнение (8-40) прини-
мает вид
Н = Л +	(8-41)
Уравнение (8-41) включает уравнение (8-37) как частный случай
для смеси идеальных газов.
Интеграл в уравнении (8-40) выражает разность между хими-
ческим потенциалом компонента в растворе и химическим потен-
циалом компонента в идеальном растворе при тех же составе,
температуре и давлении. Он был назван «избыточным химическим
потенциалом» или «избыточной парциальной мольной свободной
энергией», определяемой соотношением
р
^=^(Vi-Vi)dp.	(8-42)
р*
Избыточный химический потенциал — функция только со-
става и используется для измерения степени отклонения свойств
реального раствора от свойств идеального раствора.
Общее выражение для свободной энергии раствора таково:
F= 2 ад= S	(8-43)
Подставляя в это уравнение значение [\, взятое из уравнения
(8-41), получаем, что свободная энергия идеального раствора
при давлении р и температуре Т
2 NiFi + PT S^lnx,.	(8-44) •
Уравнение (8-44) применимо к идеальным растворам и вклю-
чает уравнение (8-36) как частный случай для смеси идеальных
газов. Величина —j?EA^zlnxz может быть интерпретирована
как энтропия смешения для идеального раствора; она включает
в себя уравнение (8-33) как частный случай для энтропии смешения
идеальных газов.
Из-за отсутствия численных значений для абсолютных внутрен-
них энергий неизвестны величины свободных энергий даже для
чистых веществ, поэтому численные значения химических потен-
циалов не могут быть определены с помощью уравнения (8-38).
16—1503
241
Однако если одно и то же относительное давление р* использует-*
ся для каждой фазы в системе, то величина (р,- — Fl) должна быть
одной и той же для каждого компонента в любой фазе при равно-
весии. Следовательно, правая часть уравнения (8-38) может быть
использована для расчета равновесия системы.
Если одну из фаз многофазной многокомпонентной системы
можно рассматривать как смесь идеальных газов во всем диапазоне
давления от р до р*, то
и интеграл уравнения (8-29) можно вычислить следующим образом:
Р(—F} = [ RT = RT\n £-.	(8-45)
.) Р	Р*
р*
Подставляя значение интеграла в уравнение (8-38), получим
Pz—Л = ЯЛп^ + ЯЛп -£-=ЯЛп XiP .	(8-46)
Р*	Р*
Перепишем это равенство в иной форме:
Pz — (F*t—RT\np*) = RT\nxiP.	(8-47>
Если давление р* настолько мало, что система ведет себя как
идеальный газ, то член (FI — RT In р*) — функция только
температуры, как показано ниже.
д ( F*t — flTlnp*'
др*
-Т
RT
др* lr р*
(8-48)
Для идеального газа
р*
в
Подставляя это равенство
ние (8-27), получаем уравнение
— 7?Г1пр* ’
уравнение (8-48) и используя уравне-
др*
—v\ — О,
(8-49)
5FJ
которое указывает, что (FI — RT In р*) — функция только тем-
пературы.
Таким образом, при данной температуре уравнение (8-47)
показывает, что величина х{р или парциальное давление смеси
идеальных газов может служить мерой химического потенциала.
242
Для реальных неидеальных растворов удобно использовать
функцию, первоначально введенную Льюисом [281, который не-
сколько упростил уравнение (8-45) для смеси идеальных газов в
применении к неидеальным растворам. Эта функция, названная
«фугитивностью», в частности, определяется соотношением
р	_
ft—J Vidp=RT\n-^.	(8-50)
р*
Так как это уравнение определяет только отношение фугитивно-
стей, то для более полного определения необходимо, чтобы фуги-
тивность компонента в растворе приближалась к парциальному
давлению компонента по мере приближения общего давления к
нулю, т. е.
---> 1 при р-—> 0.	(8-51)
XiP
Это требование означает, что все системы приближаются к состоя-
нию идеального газа при давлении, стремящемся к нулю. Таким
образом, если нижний предел давления р* таков, что раствор
ведет себя как идеальный газ, то
~П = х(р*.	(8-52)
Подставляем уравнение (8-52) в уравнение (8-50):
р — 77 = ЯЛп	.	(8-53)
1	х(р*
Подставляя уравнение (8-37) в уравнение (8-53), получаем
ft—Л = ЯЛп-£.	(8-54)
В результате преобразования уравнение (8-54) можно выра-
зить следующим образом:
=ЯЛп/, -|- (F4—ЯЛ пр*);	(8-55)
химический потенциал можно выразить через фугитивность и
слагаемое (PJ — ЯТ In р*), которое, согласно уравнению (8-49), —
функция только температуры. Таким образом, при данной тем-
пературе химический потенциал ft является линейной функцией
In ft и критерий равновесия можно выразить через фугитивность.
Точнее, так как химический потенциал компонента один и тот же
для всех фаз многофазной системы при равновесии, то фугитив-
ность компонента также должна быть одной и той же для каждой
фазы при равновесии.
16*
243
Поскольку абсолютное численное значение химического по-
тенциала не может быть определено, то абсолютное численное
значение фугитивности можно определить либо непосредственно
по экспериментальным данным, либо с помощью эмпирического
уравнения состояния. Поэтому в дальнейшем равновесные си-
стемы будут рассматриваться с помощью фугитивности, а не хи-
мического потенциала.
Из уравнений (8-38) и (8-54) исключаем (p.z — Fty:
р
RT\nf( = j Vidp + RTln(xtp*).	(8-56>
p*
Слагаемое, содержащее p*, может быть исключено из урав-
нения (8-56) путем использования математического соотношения
р
RT^-^- = RTlnp—RTlnp*.
р* Р
Подставляя выражение для RT In р* в уравнение (8-56), полу-
чаем
р
RTlnfi = j* ( dp + RTlnxft. (8-57)
p*
Уравнение (8-57) позволяет вычислить компонента в растворе
состава xt, поскольку есть данные о величине vt во всей области
давления от р* до р при постоянных температуре и составе.
Для чистого компонента vt •= vp, xt = 1; ft — и уравнение
(8-56) сводится к следующему:
р	р
7?Т1п^ = J vtdp -|- RTlnp* = j
р*	р*
v(—dp + RTlnp. (8-58)
Р /
Подставляя выражение для RT In р* в уравнение (8-56), полу-
чаем
р
RTlnfi= J (п,—vfidp + RTlwcfo,
р*
(8-59)
где fi — фугитивность чистого компонента i при температуре
Т и давлении р.
Уравнение (8-59) можно также записать в виде

(8-60)
244
где tz называют «коэффициентом активности», определяемым от-
ношением
р
1пт< = “ f (Ч—Ч) dP-	(8'61)
Ki J
p*
Для идеального раствора vt = vt, a ?(= 1, и уравнения (8-59)
и’ (8-60) сводятся к следующему равенству:
(8-62)
Коэффициент активности можно связать с избыточным хими-
ческим потенциалом с помощью уравнений (8-61) и (8-42):
txf.	(8-63).
8. Критерий химического равновесия
Критерий равновесия, выраженный через свободную энергию
Гельмгольца уравнением (8-22), может быть выражен и через
другие термодинамические функции при различных ограничи-
тельных условиях. Применяя уравнения (7-51) — (7-54) для го-
могенных растворов к одной фазе j многокомпонентной много-
фазной системы, получаем следующие соотношения:
(dAj)TVj — (dFf)Tp = (dHi)Sjp^(dEjlspi = J] pydNij. (8-64)
i
Складываем эти уравнения для всех фаз:
{dA)To = {dF)Tp=f{dH)Sp — (dE)Sx)= £ 2	(8-65).
1 i
Согласно уравнению (8-22) каждый из этих членов при равновесии
равен нулю. Следовательно, при равновесии
2	(8-бб>
1 i
Так как химический потенциал каждого компонента при равновесии
одинаков в каждой фазе, сумма	идентична для всех
i
фаз. Таким образом,
Е S Р S 0.	(8-67}
/ i	i
245
где Р чирло фаз. .Необходимо, чтобы для каждой фазы
£^ = 0.	(8-68)
/
Это соотношение особенно важно для установления равновес-
ного состава химической реакционной системы. Оно также ука-
зывает, что все термодинамические уравнения, которые первона-
чально были выведены для гомогенных систем постоянного соста-
ва, также справедливы для равновесных систем переменного со-
става.
9. Вычисление фугитивности
Фугитивность компонента в растворе можно вычислить по
уравнению (8-57), если есть данные, относящиеся к величинам
парциальных мольных объемов во всей области давлений от нуля
до давления системы. На практике, однако, не бывает достаточно-
го количества данных для непосредственного применения урав-
нения (8-57). Обычно отсутствуют данные о парциальном мольном
объеме для компонентов в паровой фазе, парофазную смесь счи-
тают идеальным раствором и фугитивности компонентов вычис-
ляют с достаточной точностью по уравнению (8-62).
В настоящее время в литературе есть немало данных по
парциальному мольному объему для компонентов в жидкофазных
растворах. Однако для непосредственного вычисления фугитив-
ности компонента в жидкофазном растворе нужны не только дан-
ные о парциальном мольном объеме компонента в жидкой фазе
и данные о парциальном мольном объеме газовой фазы того же
состава при малом давлении, но и данные во всей области: от дав-
ления, при котором начинается конденсация, до давления, при
котором происходит кипение. В этом случае система не может
физически осуществляться одной фазой. Следовательно, фуги-
тивность компонента в жидкофазном растворе нельзя определить
только на основе экспериментальных данных о парциальном
мольном объеме. С помощью уравнений состояния для смесей мож-
но установить непрерывное математическое соотношение для
двухфазной области и связать все парофазные и жидкофазные
состояния. Однако вычисленные величины фугитивности для
жидкой фазы весьма чувствительны к математической форме урав-
нения состояния для двухфазной области и рассчитывать их сле-
дует с особым вниманием.
Фугитивность чистых компонентов
Хотя фугитивность чистого компонента сама по себе имеет
небольшое значение, тем не менее она оказывается полезной ве-
личиной в вычислении фугитивности компонента идеального га-
246
зового раствора согласно уравнению (8-62). Фугитивность чистого
компонента можно вычислить непосредственно из уравнения
(8-58):
в котором подынтегральное выражение, согласно уравнению
(5-49), является остаточным объемом. Следовательно,
In —
р
faip-
о
(8-69)
Уравнение (8-69) наиболее удобно для вычисления фугитивности,
если есть экспериментальные данные pvT для всей области дав-
лений — от нуля до давления системы.
Пример 1. Определить фугитивность двуокиси углерода
при 100 *С и 1000 атм. График зависимости остаточного объема а
от давления при 100 °C для двуокиси углерода приведен на рис. 21.
Площадь под кривой между нулевым давлением и 1000 атм равна
19,8 л-атм. Подставляя эти данные в уравнение (8-69), получаем
In—
Р
19,8
0,08206-373
— 0,647;
1000
ео,«47
= 522 атм.
Хотя уравнение (8-69) применимо даже тогда, когда система
находится в жидкой фазе при конечном давлении, фугитивность
чистого жидкого компонента удобнее вычислить с учетом того, что
при температуре и давлении, соответствующих фазовому равно-
весию системы, фугитивность жидкой фазы равна фугитивности
паровой фазы. Следовательно, фугитивность жидкости в точке
кипения может быть определена вычислением фугитивности пара
при тех же температуре и давлении.
Если фугитивность вещества известна при каком-либо давле-
нии и температуре, ее можно вычислить при другом давлении и
той же температуре с помощью уравнения (8-58) для двух различ-
ных давлений:
Р2
ln-^- = -1 [	(8-70>
11 xi J
pi
Для большинства жидкостей объем по существу не зависит от
давления в широкой области давления. При этом допущении урав-
нение (8-70) можно написать так:
In fj.— v^ — Pi'>
Л RT
(8-71>
247
Таким образом, фугитивность жидкости при данных температуре
и давлении можно вычислить согласно соотношению
р (р—Р)
= кг
(8-72)
где fL — фугитивность жидкости при определенной температуре
и давлении;
fp — фугитивность пара при давлении, соответствующем тем-
пературе системы;
vL — средний мольный объем жидкости для интервала между
давлением пара Р и давлением системы р.
Уравнение (8-72) можно также получить, если написать урав-
нение (8-69) как сумму трех интегралов:
р	р	р
1П7-~йг f a°dp+-^ J 'Мр~ J V- <8'73)
О	Р	Р
В пределах от 0 до Р система находится в паровой фазе и, соглас-
но уравнению (8-69), первый интеграл представляет собой
fG
In др.. В пределах от Р до р система находится в жидкой фазе, и
второй интеграл, согласно уравнению (8-70), представляет собой
изменение фугитивности жидкости. Следовательно, уравнение
(8-73) принимает вид
, fL , $ , vL(P-P) . р
In — = In 4----------In—
P P RT	P
(8-74)
и может быть записано в том же виде, что и уравнение (8-72).
Пример 2. Определить фугитивность жидкого гептана
при 400 °К и 20 атм. Давление пара гептана при 400 °К состав-
ляет 2,19 атм.
Газофазные объемы гептана были измерены в диапазоне тем-
ператур 275—350 °C и давления 25—315 атм [40]. Данные были
обработаны согласно уравнению состояния Битти — Бриджемана;
были определены постоянные для гептана. В области низкого
давления уравнение Битти — Бриджемана для гептана может
'быть представлено приближенным выражением
v + ( Во —
RT I
Р
КГ
V2
248
Если v > 10 л/моль, значения остаточного объема для паровой
фазы при 400 °К можно точно вычислить из выражения
и соответствующее давление рассчитать из соотношения
RT
Р = —т~'
+ а
Для значений Ао = 54,520. Во = 0,70816 и RT =
= 32,824 л-атм/моль при 400 °К — Во^ =0,95 можно вы-
числить следующие значения для аир:
V, л/моль.............. 10	20	50	со
а, л/моль.............. 1,05	1,00	0,97	0,95
р, атм................. 2,97	1,56	0,644	0
При 400 °К средняя величина а для гептана между 0 и 2,19 атм
равна 0,98. Следовательно, фугитивность гептана в паровой фазе
и в жидкой фазе при 400 °К и 2,19 атм может быть получена
непосредственно по уравнению (8-69):
1п_1_=--------0,98-2,19 в_0()654;
2J9	0,08206-400
fG = 2,19/e°>066 = 2,05 атм.
Средний мольный объем жидкого гептана между 2,19 и 20 атм
при 400 °К может быть определен по экспериментальным данным;
он равен 0,169 л/моль. Таким образом, согласно уравнению (8-66),
фугитивность жидкого гептана при 400 °К и 20 атм равна
fL — 2,05 е0,169 (20-2.19)/0,08206-400.
fL = 2,05-1,096 = 2,25 атм.
При отсутствии экспериментальных данных аналитическое
выражение для фугитивности можно получить сочетанием урав-
нения (8-58) с соответствующим уравнением состояния. Например,
подстановка уравнения Ван-дер-Ваальса в уравнение (8-58) дает
ln/!=ln_^_ + _L—	(8-75}
(о— b) (v— b) RTv
При выводе этого равенства были использованы следующие соот-
ношения для нижнего предела:
о°°-Ь =с“ =	, ~== 0.	(8-76)
р* V
249
Аналогично этому выражение для фугитивности, основанное на
уравнении состояния Бенедикт — Вебб — Рубина [71
Inf = In 7?Td + А (RTBa-A0-^d + ~ (RTb-a)d2 +
+ 6- aad6 4--	( е —4- — + yd2 Y	(8-77)
Пример 3. Определить фугитивность двуокиси углерода
при 100 °C и 1000 атм, используя уравнения состояния Ван-дер-
Ваальса и Бенедикт — Вебб — Рубина.
Уравнение Ван-дер-Ваальса
Мольный объем двуокиси углерода при 100 °C и 1000 атм был
определен в примере 8 (гл. 5). Он равен 0,0573 л!моль. При этом
были использованы величины
RT — 0,08206  373 = 30,6 л  атм/моль;
а = 3,58 атм (л/моль)2-,
Ь = 0,0427 л/моль.
Подставляя эти величины в уравнение (8-75), получаем
Inf =6,50;
f = 660 атм.
Величина в 660 атм намного ближе к экспериментальной, чем
величина 1000 атм, которая была получена на основании закона
идеального газа. Однако остается ошибка 26,4% по сравнению с
величиной 522 атм, полученной в примере 1 на основании экспе-
риментальных данных.
Уравнение Венедикт — Вебб — Рубина
Несколько лучший результат для фугитивности двухокиси
уI лерода можно получить при использовании постоянных урав-
нения состояния Бенедикт — Вебб — Рубина, определенных Ко-
бе [12]:
Д = 10322,8; а = 8264,46;
Во = 0,799492; 6=1,0582;
С. = 1,69301 10°; с = 2,91971 • 10®;
у = 1,384000; а = 0,348000.
Эти параметры выражены в фут3/фунт-моль и °R. pv-изотерму для
двуокиси углерода при 100 °C можно получить подстановкой этих
значении в уравнение (5-74):
Ра™ = 49 Id—566d2— 42,9d3 4- 195d6 4-
4-441d3(l 4- l,384d2)/<«1-384d2.
250
Предполагается, что d — 1,35 фунт-моль/фут3, р = 1000 атм.
Следовательно, мольная плотность двуокиси углерода при 100 °C
и 1000 атм равна 1,35 фунт-моль/фут3.
Выражение для фугитивности двуокиси углерода получено-
подстановкой приведенных выше значений параметров в урав-
нение (8-77):
In (/, атм) = In 419rf—2,3Irf—0,13Id2 +0,476d5 +
0,90d2
e^3 — 1
fd2

где у = 1,384.
Для
d =1,35 фунт-моль/фут3;
In /= = 6,16;
f —495 атм.
Погрешность этой величины составляет — 5,2% по отноше-
нию к величине 522 атм, основанной на экспериментальных дан-
ных.
Пример 4. Определить фугитивность жидкого гептана при
400 °К и 20 атм, используя уравнения состояния Ван-дер-Ваальса
и Бенедикт — Вебб — Рубина.
Уравнение состояния Ван-дер-Ваальса
В этом примере
RT = 1,315 • 400 = 526 атм (фут3/фунт-моль);
а = 7931 атм (фут3/фунт-моль)2;
b == 3,311 фут3/фунт-моль.
С помощью этих величин мольный объем жидкого гептана при
400 °К и 20 атм был вычислен по уравнению состояния Ван-дер-
Ваальса. Он равен 4,7 фут3/фунт-моль. Подстановкой этих величин
в уравнение (8-75) получаем
In/=1,92;
/ = 6,8 атм.
Величина 6,8 атм намного больше величины 2,25 атм, опреде-
ленной в примере 2 на основании экспериментальных данных.
Этот результат показывает, что уравнение состояния Ван-дер-
Ваальса непригодно для вычисления фугитивности жидкой фазы.
251
Уравнение состояния Бенедикт — Вебб — Рубина
В этом примере:
RT = 0,08206 -400 = 32,824 атм л/моль-,
Др= 17,5206; а — 10,36475;
Во = О,199005; 6 = 0,151954;
Со = 474,574-104; с = 247-104;
Т = 9,00-1(Гг; а = 4,35611-10~3.
Численные значения этих параметров даны в атм, л, моль и °К.
Мольная плотность жидкого гептана при 400 °К и 20 атм
была определена. Она равна 5,72 моль!л. Это соответствует моль-
ному объему 0,175 л!моль, который хорошо согласуется с экспери-
ментальным значением 0,169 л!моль, использованным в примере
2. Подстановка этих величин в уравнение (8-77) дает
lnf=0,81;
f = 2,25 атм.
Эта величина согласуется с величиной фугитивности для жидкого
гептана, полученной в примере 2 на основании эксперименталь-
ных данных, и указывает на то, что уравнение состояния Бене-
дикт — Вебб — Рубина может быть использовано для оценки ве-
личины фугитивности жидких углеводородов.
Фугитивность чистого вещества можно вычислить на основа-
нии закона соответственных состояний подстановкой уравнения
состояния, определенного выражением (5-76)
Р
в уравнение (8-58):
р
In _ Г (1 —7)	(8-78)
Р J	Р
о
Отношение называется коэффициентом фугитивности и обозна-
чается v
v = —.	(8-79)
Р
Интеграл в уравнении (8-78) можно вычислить с помощью
соответствующей диаграммы для фактора сжимаемости (см.
рис. 24). После вычисления интегралов коэффициент фугитивности
наносят на график как функцию приведенных температуры и
давления, как показано на рис. 52.
252
Рис. 52. Зависимость коэффициента фугитивности
от приведенного давления, ZKp= 0,27 (251 (цифры
на кривых обозначают приведенную температуру).
г”г Для области на диаграмме сжимаемости, где изотермы
Z— рпр — прямые линии, проходящие через точку Z — 1,
Рпр — 0, изотермы могут быть представлены уравнением
Z—l=mpnp,
(8-80)
где т — постоянная, равная тангенсу угла наклона прямой.
Таким образом,
Рпр
Подстановкой в интеграл уравнения (8-78) получаем
г
In — = т
Р
рпр
J ^Рпр = тРпр
Используя уравнение (8-80), имеем
-£_==empnp==ez-i.	(8-81)
Р
Это соотношение достаточно точно выполняется для области
Z > 0,6 и рпр < 2,5.
253
.Для более ограниченной области Z > 0,80 и рпр < 2,5 соот-
ношение можно еще более упростить, используя степенной ряд
для ez-1, когда (1 — Z) меньше, чем 0,20:
_L = ez-i= 1 + (Z—1) = Z	(8.82)
Р
или
v = Z.
В этой области коэффициент фугитивности и фактор сжимаемости
примерно равны. Уравнение (8-82) можно также записать в виде
Р J?L
v
Если
р* = -^,
V
то
где р* — давление, которое идеальный газ имел бы при темпера-
туре и объеме системы.
Пример 5. Определить фугитивность двуокиси углерода
при 100 °C и 1000 атм, используя диаграмму обобщенного фактора
сжимаемости. Величина интеграла в уравнении (8-78) была опре-
делена в примере 9 гл. 5 (см. рис. 27). Она равна 0,702 (безразмер-
ная). Таким образом,
In (//1000)= —0,702;
/= 1000e°-7C2 = 495umi.
При Тпр = 1,225 и рпр = 13,7 величина коэффициента фуги-
тивности, взятая из рис. 52, равна ~0,50:
/=1000-0,50 = 500 атм.
Эта величина хорошо соглсуется с величиной 522 атм, получен-
ной в примере 1 на основании экспериментальных данных.
Фугитивность компонентов в смеси
В настоящее время вычисление фугитивности компонентов в
смеси почти полностью основано на применении приближенного
уравнения состояния к уравнению (8-59). Правильность вычислен-
ных величин может быть проверена использованием их для пред-
сказания условий фазового равновесия системы в виде темпера-
254
туры, давления и состава, которые могут быть измерены экспери-
ментально. Этот прием подтвержден работой Бенедикта для
углеводородных систем.
Если уравнение (7-66) для парциального мольного объема,
основанное на уравнении состояния Ван-дер-Ваальса, подставить
в уравнение (8-59), то можно получить следующее выражение для
фугитивности компонента:
|цГ _____RTxi। bi 2 j/~tirncti
(vm — bm) (vm — bm)	RTV
(8-83)
Это соотношение основано на правилах для получения параметров
смеси, выраженных уравнениями (7-58) и (7-59). Для бинарной
смеси
.	= («Л 4- ага2х^.
Для чистого компонента уравнение (8-83) принимает вид уравне-
ния (8-75).
Аналогичное выражение, основанное на уравнении состояния
Бенедикт — Вебб — Рубина, получается, если уравнение (7-71)
для парциального мольного объема подставить в уравнение
(8-59) [6]:

1пД. = In (RTx,d) + (Во+В0/)-2^^—
___2 (С»О><)2
’ RTS
d + ~
з ___(д2ар 3 I d2 +
RT
1	И
а (а2а()3 + a (a2az)3 ps +
5RT
(8-84)
Пример 6. Определить фугитивность компонентов рас-
твора, содержащего 20% (мол.) этана и 80% (мол.) гептана при
400 °К и 20ш/ш, используя уравнения состояния Ван-дер-Ваальса
и Бенедикт — Вебб — Рубина.
255
Уравнение состояния Ван-дер-Ваальса
значения параметров, определенных в примере 2
Используя
(гл. VII):
RT = 526 атм (фут8/фунт-моль);
at = 1391 атм (фут8/фунт-моль)а;
а2 = 7931 атм  (фут8/фунт-моль)а;
£>!= 1,028 фут8/фунт-моль;
bs — 3,311 фут8/фу нт-моль;
ат = 6300 атм  (фут8/фунт-моль)а;
Ьт— 2,854 фут8/фунт-моль;
найдем
2 Уата! = 2 У6300 -1391 = 5920 атм  (фут8/фунт-моль)8;
2 ]/ ата2 = 2 У5300 • 7931 = 14105 атм  (фут8/фунт-моль)2.
' 1,486	526-4,34	2’35’
при 400 °К и 20 атм.
Мольный объем раствора был вычислен в примере 2 (гл. VII),
он равен 4,34 фут8/фунт-моль при 400 °К и 20 атм. Подставляя
эти значения в уравнение (8-83), получаем
. г , 526-0,20 . 1,028	5920
1п/. = 1п----:'	—
п 1,486
fY = 10,5 атм
Аналогичным способом
. т . 526-0,80
lnf? = In
3,311	14,105	, со
---	------------- = 1,ио,
1,486	1,486	526-4,34
/а — 5,4 атм при 400 °К и 200 атм.
Для сравнения были вычислены фугитивности компонентов на
основании уравнения состояния Бенедикт — Вебб — Рубина.
Подставляя значения параметров компонентов из примера 2
(гл. VII) в уравнение (8-84), получаем выражение для фугитив-
ности этана в функции плотности раствора:
In?! = In 32,824-0,20d—0,522^—0,0405da-|- 29,9- 10-6d6-|-
2
_ 1
+ 0,238 (d2/^2) е
—0,237 (d8/^) x
7d2
е^-1
'(d2
!_____
2
X
(8-85)
где 7 — для раствора равно 0,068.
256
Аналогично выражение для фугитивности гептана в функции
плотности раствора имеет вид
1пД,= In 32,824 •0,80d—2,092d—0,175d2 4-
4- 83,5  ICF-VP 4-1,0 (d2/e^)
—0,656(d2/e^2) _e---
evda — 1_______£
74P	2
1 —1 _ T<|
yrf2	2 ]’
(8-86)
Мольная плотность этого раствора вычислена в примере 2
(гл. VII). Она равна 6,11 моль!л при 400 °К и 20 атм. Подставляя
эту величину в уравнения (8-85) и (8-86), получаем для этана:
ft = 16,6 а/тш при 400 °К и давлении 20 атм и мольной доле,
равной 0,20; /2 = 1,67 атм при 400 °К и давлении 20 атм и моль-
ной доле, равной 0,80.
10. Вычисление коэффициента активности
Согласно уравнению (8-61), коэффициент активности в раство-
ре выражается интегралом:
р
RTXxv^ — j (v{—vt)dp.	(8-61)
p*
Интеграл измеряет отклонение свойств раствора от идеального
поведения. Хотя интеграл может быть вычислен посредством при-
ближенного уравнения состояния, этот расчет эквивалентен вы-
числению фугитивности компонента в растворе и не имеет особых
преимуществ перед методами, рассмотренными в п. 9.
Независимый подход к вычислению коэффициента активности
был найден при использовании избыточной парциальной мольной
свободной энергии с помощью уравнения (8-63). Согласно этому
уравнению, коэффициент активности компонента в растворе свя-
зан с избыточной парциальной мольной свободной энергией соот-
ношением
<8'87>
где FE — общий избыток свободной энергии раствора,
FE = £ N;VE.	(8-88)
Избыток свободной энергии раствора есть функция температуры,
давления и состава и по существу содержит все факторы, вызы-
вающие отклонение раствора от идеального поведения.
Сочетая уравнения (8-87) и (8-88), получаем
£ = Е К (С ) = S "fib (8'89)
17—1503
257
На основании статистической теории были выдвинуты различ-
ные предложения для выражения избыточной свободной энер-
гии как функции концентрации. Так как микроструктура жид-
кого раствора неизвестна, каждое предложение обязательно
основывается на упрощенной модели жидкости и содержит опре-
деленные ограничения. Однако полученные соотношения полез-
ны для сопоставления экспериментальных данных. Дальнейшие
успехи в определении коэффициентов активности несомненно
позволяют проверить уже установленные методы.
Рассмотрим сильно упрощенную, однако важную систему, со-
держащую пА молекул компонента А и пБ молекул компонента В.
Предположим, что молекулы двух компонентов одинаковых раз-
меров, так что каждая молекула А находится в непосредственной
близости к с окружающим молекулам и каждая молекула В также
находится в непосредственной близости к а окружающим молеку-
лам. Если раствор очень разбавлен по отношению к компоненту В
(т. е. пв < мл), большинством молекулярных контактов будут
контакты А — Ди раствор будет приближаться по своему по-
ведению к идеальному со свойствами, близкими к свойствам чи-
стого компонента А. Подобно этому, если раствор очень разбавлен
по отношению к компоненту А (т. е. пА < пв), то большинством
молекулярных контактов будут контакты В — Ви раствор будет
приближаться по своему поведению к идеальному со свойствами,
близкими к свойствам чистого компонента В. Таким образом,
отклонение от поведения идеального раствора будет наблюдаться
в области, где заметную роль играет число контактов А — В,
и в первом приближении избыток свободной энергии можно при
нять пропорциональным числу контактов между молекулами А
и молекулами В:
РЕ~САВ,	(8-90)
где САВ — число контактов А — В в системе.
Рассматривая молекулу Д, окруженную о-частицами, можно
вычислить среднее число контактов А — В в области распределе-
ния А и В. В среднем доля этих а-частиц, приходящаяся на молеку-
лы Д, будет равна мольной доле А в системе пА/(пА -Ь пв); доля
а-частиц, приходящаяся на молекулы В, будет равна мольной
доле В в системе пв1(пА + Нд). Таким образом, каждая молекула
А будет находиться в контакте с <тв/(пА + пв) молекулами В и
во всей системе, содержащей пА молекул Д, будет апАпв1(пА +
•Т пв) контактов между молекулами А и молекулами В, т. е.
Сдв = -^-.	(8-91)
«л + яв
Переводя в этом уравнении число молекул в число молей и подстав-
ляя в уравнение (8-90), получаем
дг N
FE = A'—^—в~,	(8-92)
"a + nb
258
где А' — коэффициент пропорциональности, включающий а й
число Авогадро. На основании принятых допущений мольная
избыточная свободная энергия будет пропорциональна мольной
доле А и мольной доле В:
j-!±-=A^b.	(8-93)
Избыточная парциальная мольная свободная энергия компо-
нента А получается дифференцированием уравнения
Na при постоянных температуре и давлении:
N Iй
----------------------------------— = А'х2в.
na + nb\
dFE \
™а)тр
Подставляем уравнение (8-94) в уравнение (8-87):
1йюТд= ——- = Ахв,
610 ГА 2.303RT
где А = А '/2,303 RT.
Подобным образом для компонента В
lgioTB = ^-
(8-92) по
(8-94)
(8-95)
(8-96)
и£ =
i А
Эти соотношения для бинарной смеси впервые получил Маргу-
лес. Они являются простейшими выражениями коэффициентов
активности как функции состава. Однако с помощью этих простых
соотношений могут быть вычислены коэффициенты активности
очень немногих реальных систем, поэтому необходим более тща-
тельный анализ для получения соответствия с экспериментом.
Более точный анализ, кроме взаимодействия между двумя молеку-
лами в группе, учитывает взаимодействие между тремя молекула-
ми в группе. Например, взаимодействие между двумя молекуламиД
и одной молекулой В должно рассматриваться так же, как взаимо-
действие между двумя молекулами В и одной А. Однако сложная
природа жидкого раствора и много неизвестных факторов, которые
влияют на поведение неидеального раствора, делают нереальным
строгий анализ; поэтому становится необходимым эмпирический
подход.
Обобщенный эмпирический метод для вычисления избыточной
свободной энергии как функции состава предложил Воль [541.
Метод заключается в выражении мольной свободной энергии рас-
твора в виде эмпирической функции состава, выраженной через
эффективный мольный объем q и обобщенную объемную долю z
для каждого компонента определенную соотношением
Zj^qjXj! qiXt,	(8-97)
где Xj — истинная мольная доля компонента /, и сумма содержит
слагаемые для каждого компонента в растворе, включая компо-
нент /.
17*
259
Согласна данным Воля, взаимодействие между парами неоди-
наковых молекул в бинарной смеси выражается членом 2a12zJLz2,
где а12 — эмпирическая постоянная взаимодействия. Подобным
образом молекулярное взаимодействие в группе из трех молекул
выражается членом 3a112ziz2 и Зар^г^, где czll2 — эмпирическая
постоянная для группы, содержащей две молекулы компонента 1
и одну молекулу компонента 2; а122 — эмпирическая постоянная
для группы, содержащей одну молекулу компонента 1 и две моле-
кулы компонента 2. Такое рассуждение может быть распростра-
нено на любое число компонентов и любое число молекул в группе.
Таким образом, избыточная свободная энергия на единицу
объема бинарной смеси может быть разложена в ряд следующего
вида:
_Д£
Л'1 + Л',
---------= 2a112ZjZ8 + 3tz112z*z2 + За^г^ -)-- (8-98)
+ ягхг
Используя члены уравнения (8-98), соотношение z2 4- z2 — 1
и приняв
А — (2e12 4- За122)
В = (2aJ2 За122) д2,
получим выражение для мольной избыточной свободной энергии
раствора:
FE (Qixi + г1г2 (P'qiti ?ггг)
<7i<72
Умножая уравнение (8-99) на общее число молей и используя
определение г по уравнению (8-97), можно выразить общую из-
быточную свободную энергию в функции чисел молей отдельных
компонентов:
рЕ __ NiN2	+ A'q2N2)	(8-100)
(vA+^г)*
Избыточная парциальная мольная свободная энергия компо-
(8-100) по
нента / получается дифференцированием уравнения
Ni при условии постоянства температуры и давления:
Vw'Л₽ L \	/ 1
Используя уравнение (8-87), получаем
IgioVi = А [Д + 2 (в —Д ) ],
(8-101)
(8-102)
Д = Д'/2,303ЯТ;
B — B'I2,3O3RT.
260	'
Подобным образом для компонента 2 получаем
igio Т2 —
В-|-2/Л —
\	<72
(8-103)

Если эффективные мольные объемы равны, — = 1, z = х и если
<?2
к тому же А = В, то получается упрощенное соотношение Мар-
гулеса, выраженное уравнениями (8-95) и (8-96). При условии,
что = 1, но A =f= В, уравнения (8-102) и (8-103) приобретают
развернутую форму соотношений Маргулеса, которые оказались
полезными для обработки экспериментальных данных:

(8-104)

(8-105)
При условии, что — — A/В, уравнения (8-102) и (8-103)
?2
приобретают форму соотношений ван-Лаара:
lgT1 =	= Igy..=	Axj _ ГД	I2 *1 + *2 Z5	J Bxl	А	
		. X I X to м r ।	।	2 *
	Г в Г	L <4 *1 J	2
(8-106)
(8-107)
Эти соотношения впервые получил ван-Лаар на основании
уравнения состояния Ван-дер-Ваальса. Хотя строгость вывода
ван-Лаара сомнительна, результаты оказались полезными для об-
работки экспериментальных данных.
Эмпирические параметры А и В в вышеприведенных отношениях
зависят от температуры, и уравнения верны только при условии
постоянства температуры и давления. Методы вычисления пара-
метров и коэффициентов активности обсуждаются в гл. IX.
11. Влияние температуры на фугитивность
и коэффициент активности
Все приведенные выше соотношения для фугитивности и коэф-
фициента активности были ограничены условиями постоянства
температуры. Зависимость фугитивности от температуры можно
получить с помощью уравнения (8-50), которое определяет отно-
шение фугитивностей в функции химического потенциала:
|хг-Ё? = /?ПпД.	(8-50)
261
Первая производная уравнения (8-50) по температуре при постоян-
стве давления и состава имеет вид
(ОЛ _=ят(-пЦ —+/?1пД (8-Ю8)
\dT)pN \dT)pN \ffr)pN [дТ JPN -fl
Так как fl — фугитивность компонента в смеси идеальных газов, то
B = xiP*
и
/ a in if \ _ о
\ ST JpN
Сочетанием уравнений (8-50) и (8-108) получаем
_(dZL\ — рт( d}nfi\ I f;	(8-109)
\дТ )pN \дТ Ipn~* \ дТ / pn' Т Т'	'
Первая производная уравнения (7-49) по Nj при постоянном дав-
лении
Согласно определению парциальной мольной величины, уравне-
ние (8-110) может быть написано в виде
(w'L—5-	(W11)
Дифференцируем уравнение (4-65) по TV£ при условии постоянства
температуры и давления:
(8-112)
Зависимость фугитивности от температуры можно получить
сочетанием уравнений (8-109), (8-111) и (8-112):
I	(Hl-Hi \ .	(8-113)
\ дТ I pn \ RT2^ / pn
Коэффициент активности в функции фугитивностей, выражен-
ный уравнением (8-60), имеет вид
lnyf = lnf£—In —lnx£.	(8-114)
Дифференцируем уравнение (8-114) по температуре при условии
постоянства давления и состава:
_р1п7Г\ pin/А	(8-115)
\ дТ ]pN \ дТ fpN \ &Г )pN
262
Зависимость коэффициента активности от температуры можно по-
лучить с помощью уравнений (8-113) — (8-115):
5 In 7/ \ _ / Hi —Hi \
дТ )pN \ RT2 )pn
(8-116)
где в случае смеси идеальных газов парциальная мольная энталь-
пия равна мольной энтальпии чистого компонента, т. е. Щ — Н\.
Задачи
1.	Сумму состояний для чистого трехмерного кристалла, считая его сово-
купностью гармонических осцилляторов, можно выразить уравнением
kT
п
Z =z” =
(1 _ е-ху
где е0 — основной энергетический уровень при условии, что каждая частица
кристалла имеет три вида колебания равной частоты (х = MkT)
Применить критерий уравнения (8-16) для определения температуры фа-
зового перехода твердой фазы А в твердую фазу В, если (еоВ — egA) равно
3000 кал/моль и vA равно 2\в- Принять, что температура достаточно высока,
чтобы значение х было мало, и величину (1— е~х) можно приближенно заменить
на х.
2.	Вычислить изменение энтропии при смешении 0,20 моля чистого жид-
кого бензола и 0,80 моля чистого жидкого толуола, считая, что смесь образует
идеальный раствор.
3.	Дать определения;
а)	идеального раствора;
б)	химического потенциала;
в)	свободной энергии Гельмгольца;
г)	свободной энергии Гиббса;
д)	фугитивности;
е)	коэффициента активности;
ж)	избыточной свободной энергии.
4.	Определить минимальное количество энергии, необходимое для раз-
деления 1 фунт-моля идеального раствора, содержащего 30% (мол.) бензола,
60% (мол.) толуола и 10% (мол.) ксилола, на чистые компоненты при темпера-
туре теплоприемника 60 °F (15,6 °C).
5.	Определить фугитивность двуокиси углерода при 100 °C и 10 атм при
условии применения уравнения состояния Вертело в форме
/ 9/128	27/64 \
Z — * т I т т3 Рпр-
\ ' пр ‘ пр /
Сравнить полученный результат с фугитивностью, определенной с помощью
графика на рис. 52.
ГЛАВА 9
Фазовое равновесие
Если две или более фаз находятся в тесном контакте, возникает
потенциал, способствующий самопроизвольному переходу вещест-
ва через границы фаз, и система стремится к состоянию равнове-
сия. Состояние равновесия характеризуется комплексом условий,
к которым приближается неравновесная система как к пределу;
в большинстве случаев степень достижения равновесия настолько
велика, что различие между реальным состоянием и равновесным
находится в пределах ошибки опыта. Знание условий равновесия
имеет первостепенное значение в таких технических процессах,
как абсорбция, адсорбция, экстракция, дистилляция, испарение,
высушивание и кристаллизация. Критерий для определения усло-
вий равновесия был разобран в гл. 8. Из всех возможных комби-
наций фаз и веществ ниже будет рассмотрена только двухфазная
система неэлектролитов, в иотором одна из фаз — пар.
1.	Равновесие твердое вещество — пар чистого
компонента
Согласно правилу фаз, двухфазная система из чистого компо-
нента имеет только одну степень свободы. Следовательно, данные
либо температуры, либо давления полностью определяют состоя-
ние системы.
Интересно установить, каково соотношение между давлением
пара и температурой в системе.
Такое соотношение можно получить непосредственно из урав-
нения (5-9) для замкнутых систем постоянного состава:
т
V
Если это равенство применить к твердым или жидким фазам, то
давление и объем будут по существу независимыми и указанием
264
на постоянство объема можно пренебречь. Для обратимых процес-
сов испарения при постоянных температуре и давлении
dH
-dS-T~—1	(9-1}
dv ~ dv Т • dv’	к '
Для двухфазных замкнутых систем
=	+	=	(9-2)
dv — v^dg 4- vtdl = (vg—oz) dg,	(9-3)
где g — число молей пара;
I — число молей жидкости, тогда
dg-}-dl = 0.
Отношение уравнения (9-2) к уравнению (9-3) позволяет вычислить
d//	,
производную в функции мольной теплоты испарения и моль-
ных объемов пара и жидкости:
dl1 Hg—Hi _ х	,9 4v
dv Vg — vi	vg — vi '	v '
При условии, что паровую фазу можно рассматривать как
идеальный газ, а мольный объем твердого или жидкого вещества счи-
тать незначительным по сравнению с мольным объемом пара
RT
Vg-V^V^ — ,
уравнение (9-4) примет вид
Уравнения (5-9), (9-1) и (9-5) могут служить для вычисления накло-
на кривой для давления пара:
_dp __Х₽
dT ~ КГ*
или
dlnp  X	(Q-К \
dT ~RTZ ’	{ '
Уравнение (9-6) — частный вид знаменитого уравнения Клау-
зиуса — Клапейрона, которое обычно используют для определе-
ния скрытой теплоты испарения по величине наклона кривой для
давления пара. При условии, что паровая фаза — идеальный газ,
265
скрытую теплоту испарения можно выразить как функцию тем-
пературы, согласно выводам примера 8 (гл. I):
т	т
l = h + $Cp^T-$CpSdT,	(9-7)
о	о
где Хо можно интерпретировать как гипотетическую или экстра-
полированную скрытую теплоту испарения при температуре абсо-
лютного нуля. Для одноатомных газов Cpg равно | уравне-
ние (9-7) можно выразить в виде
т
d\np=^dT	C^dT- (9’8>
о
Выражение для давления пара получается интегрированием
уравнения (9-8):
т т
l„p=_i+4-lnT-J-^JC^T + i, (9-9)
О о
где i — постоянная интегрирования, характерная для отдельных
веществ. Численные значения постоянной i определены эмпири-
чески для металлов, пары которых образуют идеальный одноатом-
ный газ. Таким образом была установлена справедливость урав-
нения (9-9) [19].
Численное значение постоянной i также было определено ме-
тодами статистической термодинамики. Согласно уравнению (8-17),
критерий равновесия для фазовой системы твердое вещество — пар
выражается отношением
(8-17>
В этом выражении сумма состояний паровой фазы и сумма состоя-
ний твердой фазы должны быть отнесены к одному и тому же осно-
вному энергетическому уровню. Если давление системы мало для
того, чтобы пар можно было рассматривать как идеальный газ,то
=	(9-10}
Подстановкой уравнения (9-10) в уравнение (8-17) получаем
(9-11)
ИЛИ
lnp=ln(feT) —lnzs4-ln-^,	(9-12>
где р можно интерпретировать как давление пара над твердой
266
фазой. Если паровая фаза — одноатомный идеальный газ, то
для нее сумма состояний выражается уравнением
zg	.	(9-13)
где zg относится к основному энергетическому уровню твердой
фазы. Величина Хо обозначает разность между основными энерге-
тическими уровнями паровой и твердой фаз, и ее можно рассматри-
вать как гипотетическую или экстраполированную скрытую теп-
лоту испарения при температуре абсолютного нуля.
Выражение для суммы состояний твердой фазы можно полу-
чить интегрированием уравнения (4-4):
lnzs = J-^dT = J
о
(9-14)
Таким образом, для давления пара уравнение получаем подстанов-
кой уравнений (9-13) и (9-14) в уравнение (9-12):
т
1пр = -^+-2- 1117-f	+	+
о
3	5
+ 1пЦ
(9-15)
Сопоставление уравнений (9-9) и (9-15) показывает, что постоян-
ная интегрирования в уравнении (9-9) может быть представлена в
функции атомной массы и известных универсальных физических
постоянных. Если энергия выражена в кал!моль, температура
в °К, давление в атм и масса в единицах атомного веса, то послед-
ний член уравнения (9-15) равен —3,66. Следовательно,
4=4-1пМ—3,66.	(9-16)
Эта величина, вычисленная на основе статистической термодина-
мики, хорошо согласуется с эмпирическими величинами, вычислен-
ными по экспериментальным данным по давлению пара твердых
веществ [191.
Наиболее удобное выражение для давления пара, пригодное
и для твердой и для жидкой фазы в ограниченном интервале тем-
ператур, можно получить интегрированием уравнения (9-6) при
условии, что скрытая теплота испарения не зависит от темпера-
туры:
lnp=—A+fc.	(9-17)
267
где b — постоянная интегрирования. Если интегрирование вы-
полнено в пределах 7\ — Т2, то
Pi _(Tg— ^1)
h~R' Та7\ •
(9-18)
Эти формы уравнения Клаузиуса — Клапейрона, полученные в ре-
зультате интегрирования, показывают, что график зависимости
Рис. 53. Давление пара легких углеводородов:
1—октан; 2—гептан; 3—гексан; 4—пентан; 5—нормальный бу-
тан; 6—изобутан; /— пропан; Я—пропилен; У—этан; 10—эти-
лен; //—метан
in р от  должен быть прямой линией. Тот факт, что давление
пара большинства веществ действительно можно аппроксимировать
в области низкого давления, позволяет найти удобный способ
нахождения кривой по двум значениям давления пара при извест-
ных температурах или по одному значению давления пара и тем-
пературы (например, нормальная точка кипения при давлении
1 атм) и скрытой теплоте испарения (рис. 53).
268
Это соотношение для жидкостей в области, близкой к крити-
ческим давлению и температуре, следует использовать с осто-
рожностью, потому что по мере приближения температуры к кри-
тической скрытая теплота испарения быстро понижается до нуля;
кроме того, критическое давление обычно бывает настолько вы-
соким, что предположение о том, что пар по поведению идентичен
идеальному газу, неправильно.
2.	Адсорбция пара на твердых поверхностях [15]
Проблема адсорбции пара на твердых поверхностях играет
важную роль в процессах хроматографического разделения, ион-
ного обмена и химического катализа. В этой системе представляет
интерес соотношение между количеством адсорбированного ве-
щества и давлением в системе при данной температуре в условиях
равновесия. Такое соотношение впервые вывел Лангмюр на осно-
вании кинетического анализа скоростей адсорбции и десорбции.
Условия равновесия были установлены путем приравнивания
скоростей двух противоположных процессов. Однако полученные
Лангмюром изотермы адсорбции не зависят от скоростей и меха-
низма процесса и могут быть целиком получены на основе крите-
рия равновесия, выраженного уравнением (8-17), или с помощью
положения, что химический потенциал компонента должен быть
один и тот же в обеих фазах.
Анализ основан на модели твердой поверхности с определен-
ным числом различимых участков, способных адсорбировать мо-
лекулы из паровой фазы.
Если общее число адсорбированных молекул значительно мень-
ше, чем число соответствующих участков, то адсорбированные
молекулы не будут влиять на молекулы в паровой фазе, прибли-
жающиеся к поверхности. Адсорбированные молекулы должны
располагаться в виде некоторого фиксированного монослоя, т. е.
адсорбированное вещество лишается возможности свободного пе-
ремещения по участкам поверхности и толщина его слоя не превы-
шает одной молекулы. Предполагается, что паровая фаза является
идеальным газом.
Следуя выводам из гл. III, п. 2, выведем уравнение для числа
способов, которыми адсорбированные молекулы могут распреде-
ляться на твердой поверхности:
„ (%—1) (щ —2)	<«s —«1 + 1)
2 . 3 -------------
________Hsl_________ns!___ iigl,	zq , q\
(ns—п0)!Пщ! ~ (ns —nQ)! па1’Ппг- ’
где ns — число независимых различных адсорбирующих участ-
ков на твердой поверхности;
269
па — общее число молекул, адсорбированных на поверхности;
tts,
nt — число адсорбированных молекул с энергетическим уров-
нем ez;
Па =
Выражение для In w можно получить с помощью приближен-
ной формулы Стирлинга для логарифма факториала:
In w = In 7-—I +1°	—ДпЛпп, 4- Ен.-.	(9-20)
(ns — na)lna! 1	till \	/
Уравнение (9-20) имеет тот же вид, что и уравнение (3-5), за
исключением постоянного слагаемого (ns!)/(ns— па)\. Так как
наиболее вероятное распределение определяется величиной d In к»,
значение этого постоянного слагаемого не влияет на функцию
распределения, и распределение Больцмана применимо в виде
п,= ^-е кт.
1 га
(9-21)
Наиболее вероятное значение In w получается подстановкой
уравнения (9-21) в уравнение (9-20):
е 
|п » =+ ш [е е-г] in i-
nsl гпа £
In W = In 7----------7 4—«Д’’
(ns — na)lnal kT
(9-22)
(9-23)
Написав уравнение (9-23) в виде
n 1 Z
E — kT In w = — feTTn,——rr ,	(9-24)
(ns—na)lnal	v 1
и сравнив его с уравнением (4-28), можно выразить сумму состоя-
ний для адсорбированной фазы равенством
z — ns!z°a
° (ns — па)! па!
(9-25)
Сумма состояний для идеального газа выражается уравнением
(4-27):
z!=-g.	(9-26)
Критерий равновесия для этой системы удобно выразить соот-
ношением
/ д lnZa \	__/ д In Zg \
\ дпа )т0	\ J Tv
(9-27)
270
Из уравнения (9-25) следует
In Za = In ns! — (ns—na) In (ns—na) + (ns—na)~na In na +
+ na4-«aInza.	(9-28)
Дифференцируем уравнение (9-28) по na:
+'"*»• <9'29)
Из уравнения (9-26) следует
In Zg — rig In zg—rig In rig 4- rig,	(9-30)
а дифференцированием последнего уравнения по rig получаем
/<HnZg\
\ d«g )
= lnzg—In «g.
Tv
(9-31)
Подставляем уравнения (9-31) и (9-30) в уравнение (9-27):
»s —«а _ zg
fla	^a^g
(9-32)
Количество адсорбированного вещества на твердой поверх-
ности может быть выражено через долю занятых активных участ-
ков поверхности:
6 = -^.	(9-33)
С помощью уравнений (9-33) и (9-32) находим
9 =-----------------------------1--
Для идеального газа
pv
"е RT
(9-34)
е==------р-~
Р + zaJRT
(9-35)
Кроме того, для идеального газа
з
^=(тг)т^=<р(П
Следовательно, для данного вещества
только температуры:
zg/t>_
ZaIRT
является функцией

271
Изотерма адсорбции Лангмюра, записанная в виде
выражает соотношение между долями занятой поверхности как;
функциями температуры и давления. При низком давлении, когд^
р < р°, эта функция переходит в прямую линию и имеет наклон
равный При высоком давлении, когда р >> р°, значение функ-
Рис. 54. И зотермы адсорбции Ланг-
мюра (циф ры на кривых обозначают
да вление в системе)
ции приближается к единице
как к пределу, из чего сле-
дует, что все участки заняты.
На рис. 54 эта функция пред-
ставлена кривыми для не-
скольких значений р°.
Изотерма Лангмюра поз-
воляет сделать анализ ад-
сорбции пара, хотя сделан-
ные допущения для ее выво-
да несколько ограничивают
ее применение. Приведенные
расчеты могут быть распро-
странены* на случай много-
слойной адсорбции, что при-
водит к изотерме адсорбции
Брунауэра — Еммета — Тел-
лера НО, 151.
Изотерму Брунауэра —
Еммета — Теллера широко используют для расчета данных ад-
сорбции и измерения площади поверхности [высокопористых
материалов.
3.	Равновесие пар — жидкость для чистых
компонентов
Соотношение, выведенное для равновесия системы твердое ве-
щество— пар, выраженное уравнениями (9-6) и (9-18), в основ-
ном применимо и к системе пар — жидкость чистого компонента
с учетом отмеченных выше ограничений. Давление пара жидкого
чистого компонента можно также вычислить на основании соответ-
ствующего уравнения состояния, которое применимо и для жид-
кой и для паровой фазы с учетом того, что фугитивность паровой
и жидкой фаз одинакова при равновесии.
Зависимость фугитивности парообразного и жидкого гептана
при 400 °К на основании уравнения состояния Ван-дер-Ваальса
от давления приведена на рис. 55 (см. пример 4, гл. 8). Точка пе-
ресечения прямых указывает, что фугитивности двух фаз равны
272
Давление,атн
Рис 55 Зависимость фуги-
тивности парообразного и
жидкого гептана при 400 °К
Ван-дер-Ваальса от давления:
/—паровая фаза; 2—жидкая фаза
(верхние кривые вычислены по урав-
нению Ван-дер-Ваальса, инжние— по
уравнению Бенедикт — Вебб — Рубина}
при давлении 7,3 атм. Вычисленное таким образом давление пара
не совпадает с действительным давлением пара, равным 2,13 атм
при 400 °К- Это указывает на то, что уравнение состояния Ван-
дер-Ваальса не совсем пригодно для
вычисления давления паров угле-
водородов. Для сравнения приве-
дены результаты вычисления по
уравнению состояния Бенедикт —
Вебб — Рубина (рис. 55). Точка пе-
ресечения прямых свидетельствует
о том, что вычисленное значение
давления пара хорошо совпадает
с экспериментальной величиной. Од-
нако экспериментальное давление
пара было использовано при опре-
делении параметров в уравнении со-
стояния Бенедикт — Вебб — Рубина
для гептана, так что результат этого
вычисления не является неожидан-
ным. Расчет показывает, что наи-
большая ошибка возникает при вы-
числении фугитивности для жидкой
фазы. Поэтому важное значение име-
ет выбор математической формы урав-
нения состояния для всей двухфаз-
ной области, где не может физичес-
ки существовать гомогенная система.
4.	Равновесие пар — жидкость для смесей
Обобщенный расчет
Проблема определения условий равновесия пар — жидкость
для смесей основана на том критерии, что фугитивность данного
компонента должна быть одной и той же для каждой фазы. Для ре-
шения этой проблемы необходимо знать температуру, давление и
состав для каждой фазы в системе.
Фугитивность данного компонента в той или иной фазе при
определенных температуре, давлении и составе можно вычислить
по уравнению (8-57):
_	р
In 11 — J_ ( Iv( —
kip RT j \ 1
о
dp.
P J
Для равновесия двухфазной системы пар — жидкость

(9-36)
18-1593
273
для каждого компонента. Подставим вычисленную фугитивность,
данного компонента в уравнение (9-36):	/
=	&-^dp.	(9-37/)
0
Отношение равновесной концентрации компонента в паровой
фазе к равновесной концентрации того же компонента в жидкой
фазе называется «коэффициентом распределения», или «равно-
весным отношением» и обозначается через Кр
=	(9-38>
Сочетая уравнения (9-37) и (9-38), коэффициент распределения
можно выразить через парциальные мольные объемы
р
^=ехр (t£—(9-39>
о
Было немало попыток представить коэффициент распределения
как функцию температуры, давления и состава. Однако так как
интеграл уравнения (9-39) — функция вида и количества каждо-
го компонента в системе, то нельзя вывести общее строгое соотно-
шение для коэффициента распределения. Более того, чтобы вы-
числить интеграл в уравнении (9-39), необходимо знать величины
x/t при постоянных составе и температуре по всей области давлений
от нуля до давления системы. В области давления между давле-
нием системы и давлением при кипении, соответствующем темпе-
ратуре и фазовому составу, of представляет собой парциальный
мольный объем компонента в гомогенной жидкой фазе. В области
давления между нулем и началом конденсации of представляет
собой парциальный мольный объем компонента в гомогенной паро-
вой фазе того же состава. В двухфазной области между давлением
начала конденсации и давлением при кипении величины of не
могут существовать, и уравнение (9-39) не может быть использо-
вано для определения коэффициента распределения.
Тем не менее уравнения состояния для смеси используют
для экстраполяции данных о парциальном мольном объеме на об-
ласть двух фаз и для вычисления фугитивности компонента в жид-
кой фазе. Пригодность уравнения состояния для определения
фугитивности для жидкой фазы зависит не только от точности
передачи ро7'-свойств гомогенных паровой и жидкой фаз, но и от
его математического поведения для той двухфазной области, когда
гомогенная система физически не может существовать.
Расчет условий равновесия жидкость — пар с помощью урав-
нений состояния приведен в примере 1. В нем рссматривается при
менение уравнений состояния Ван-дер-Ваальса и Бенедикт -
Вебб — Рубина для смеси этана и гептана.
\ Пример 1. Определить равновесный состав жидкой и
паровой фаз для смеси этана и гептана при 400 °К и 20 атм,
используя уравнения состояния Ван-дер-Ваальса и Бенедикт —
Вебб — Рубина.
Решение основано на том критерии, что равенства
7S=7i
и
Тн=1н
должны выполняться одновременно. Методы вычисления фугитив-
ностей компонентов в смеси рассмотрены в примере 6 (гл. 8) для
данного состава. Если состав фазы неизвестен, вычисления, дан-
ные в примере 6 (гл. 8), следует
повторить для всех составов.
Результаты таких вычислений,
основанные на использовании урав-
нения Ван-дер-Ваальса, показаны
на рис. 56, где фугитивности ком-
понентов этана и гептана представ-
лены в зависимости от концентра-
ции этана при температуре 400 °К и
давлении 20 атм. Графическим ме-
тодом последовательных приближе-
ний найдено, что фазовые составы,
которые удовлетворяют критерию
равновесия, определяются содержа-
нием 0,22 мольных долей этана в
жидкой фазе и 0,58 мольных долей
этана в паровой фазе. Эксперимен-
тальные данные показывают, что
реальные составы содержат ~0,20
мольных долей этана в жидкой фазе
и ~Ю,85 мольных долей этана в па-
Рис. 56. Зависимость фугитив-
ности компонентов смесей
этап—гептан при 400 °К>
20 атм, вычисленной по урав-
нению Ваи-дер-Ваальса, от
концентрации этана.
ровой фазе.
Для сравнения эти вычисления повторены с использованием
уравнения состояния Бенедикт — Вебб — Рубина для определе-
ния фугитивности компонентов. Результаты представлены на
рис. 57, откуда видно, что равновесие достигается при содержании
0,20 мольных долей этана в жидкой фазе и 0,88 мольных долей
этана в паровой фазе. Эти величины хорошо согласуются с экспе-
риментальными данными. Наибольшее различие между фугитив-
ностями, вычисленными по уравнениям состояния Ван-дер-Вааль-
са и Бенедикт — Вебб — Рубина, наблюдается для жидкой фазы.
Метод, описанный в примере 1, применим к многокомпонент-
ным смесям. Однако для таких смесей фугитивности компонентов
не могут быть представлены как функцци концентрации отдельного
18*
275
Рис. 57. Зависимость фугитивности
понентов смесей этан — гептан
400 °К, 20 атм, вычисленной по ;
I ком-
при
урав-
нению Бенедикт — Вебб — Рубина, от
концентрации этаиа
компонента и необходим строгий аналитический метод последо-
вательных приближений. Этот метод чрезвычайно сложен и его
не применяют в обычной инженерной практике. Однако с развитием
вычислительной техники он, вероятно, будет приемлем. /
Аналогичные вычисления, выполненные для различных сме-
сей углеводородов, подобных рассмотренной в примере 1, с исполь-
зованием уравнения состояния Бенедикт — Вебб — Рубина,
показывают хорошее совпадение рассчитанных величин с экспе-
риментальными данными. Для характеристики многокомпонент-
ной системы недостаточно
знать только температуру
и давление. Если известны
состав одной фазы, а так-
же температура или дав-
ление, точные вычисления
методом последовательных
приближений непригодны.
Для случаев, когда из-
вестны экспериментальные
данные по температуре,
давлению и составу, коэф-
фициент распределения
для каждого компонента
вычисляют для концент-
рации, определен ной экс-
периментально с помощью
уравнения (8-84) и соот-
ношения
к as
где fi — /f при равновесии. Вычисленный коэффициент распреде-
ления хорошо совпадает с коэффициентом распределения, опреде-
ленным непосредственно по экспериментальным данным, согласно
уравнению (9-38). Выражение вычисленных коэффициентов рас-
пределения для двенадцати легких углеводородов как функции
температуры, давления и состава было получено при использова-
нии средней точки кипения как параметра переменного состава
Основное соотношение было представлено в форме 324 диаг-
грамм, охватывающих область давлений от атмосферного до
3600 фунт/дюйм2 (253 кПсмг), область температур от —100 °F
(—73,3 °C) до 400 °F (204,4 °C) и область средней точки кипения
от —225 °F (—140 °C) до 180 °F (82,2 °C). На каждой диаграмме
коэффициент распределения для данного компонента при опреде-
ленном давлении выражен как функция температуры для несколь-
276
ких средних точек кипения. Де Прист I131 предложил соотношение,,
упрощающее интерполяцию, и, кроме того, вывел соотношение,
по которому коэффициент распределения для усредненного соста-
ва представлен как функция только температуры и давления.
Выражение для усредненных коэффициентов оказалось полезным
для предварительной оценки точки конденсации, точки кипения
и фазового состава последующим использованием более точного
соотношения, включающего средние точки кипения как параметры
состава.
Выражение для коэффициента распределения как функции
только температуры и давления по существу допускает, что каж-
дая фаза образует идеальный раствор.
Идеальные растворы
Обобщенное выражение для определения равновесия пар —
жидкость может быть значительно упрощено, если принять, что
каждая фаза — идеальный раствор. В этом случае уравнение
(8-62) может быть использовано для вычисления фугитивности
компонента в смеси исходя из фугитивности чистого компонента
при температуре и давлении раствора и его мольной доли в рас-
творе:
(8-62)
Применение уравнения (8-62) к каждой фазе при равновесии дает
=	(9-40}
Решением уравнения (9-40) для отношения ~ можно получить
выражение для коэффициента распределения компонента в идеаль-
ном растворе в функции фугитивностей чистого компонента для
чистой жидкости и чистого пара при температуре и давлении рас-
твора
(9-41>
X/	ti
То же самое выражение можно получить, применяя уравнение
(9-39) для идеального раствора в каждой фазе; в этом случае
of — vLi, vCi — v°. Тогда
1 I г
exp от I dp
xi	1 f Gw
exp I v;dp
(9-42)
Уравнение (9-42) можно записать в том же виде, что и уравнение
(9-41), если применить уравнение (8-58) к каждой фазе.
277
Так как мольный объем чистого компонента — функция только
температуры и давления, то коэффициент распределения каждого
компонента в идеальном растворе является функцией только
температуры и давления и не зависит от состава. Его можно рас-
сматривать как свойство чистого вещества, не зависящее от вида и
качества других компонентов в растворе. Однако при вычислении
К из сотношения jf/ff возникают трудности из-за того, что для
чистого компонента только одна фаза может существовать фи-
зически при данной температуре и давлении. Поэтому либо ff,
либо /f должна представлять собой фугитивность гипотетического
состояния в зависимости от того, является ли равновесное давле-
ние смеси большим или меньшим, чем давление пара чистого ком-
понента при температуре равновесия. Уравнение состояния для
чистого компонента снова можно использовать для экстраполяции
роТ-свойств в нестабильную область для того, чтобы облегчить
вычисление /f при давлении меньшем, чем давление пара, и
при давлении большем, чем давление пара.
При идеальном растворе задача определения условий фазового
равновесия может быть сведена к двум отдельным и независимым
стадиям. Первая стадия — коэффициент распределения для каж-
дого компонента определяют при данных температуре и давлении
исходя из фугитивностей жидкой и твердой фаз чистого компо-
нента. Вторая стадия — по данным значениям коэффициента
распределения для каждого компонента определяют фазовые со-
ставы, применяя уравнение (9-38) к каждому компоненту с учетом
того, что Sxz — 1 для жидкой фазы и Ъу1 = 1 для паровой фазы.
При бинарных смесях знать две независимые переменные до-
статочно для определения системы, и соотношения чрезвычайно
просты. Для двух компонентов можно нацисать четыре уравне-
ния с четырьмя неизвестными:
Di ~	У 2 — ^2X2'’
1, У14- у 2= 1 •
Если заданы температура и давление, то величины и К2
можно вычислить непосредственно, и четыре переменных состава
будут неизвестными этих уравнений. Из четырех уравнений можно
получить значение в функции и Кг:
(9-43)
Для того чтобы две фазы существовали одновременно в двух-
компонентной системе, коэффициент распределения одного ком-
понента должен быть больше единицы, а коэффициент другого
компонента меньше единицы. Если коэффициенты распределения
обоих компонентов больше единицы при данных температуре и
давлении, то существует только паровая гомогенная фаза; если
278
оба коэффициента распределения меньше единицы, может суще-
ствовать только жидкая гомогенная фаза. В случае, когда опре-
делено значение хг, то три остальных переменных состава можно
вычислить из трех первоначальных уравнений.
Если неизвестна либо температура, либо давление, величины
коэффициентов распределения нельзя определить непосредствен-
но и задачу следует решить методом последовательных прибли-
жений. В этом случае состав одной фазы и температура или давле-
ние должны быть заданы для определения всей системы.
Для многокомпонентной двухфазной системы число степеней
свободы равно числу компонентов. Если исходить из соотношений
Ех, — 1 и £«/,= 1,
одна из переменных состава в каждой фазе не будет независимой,,
и для определения системы должен быть задан состав одной фазы
и температура или давление. Задачи, включающие многокомпо-
нентные смеси, всегда следует решать методом последовательных
приближений.
Пример 2. Определить равновесный состав жидкой и па-
ровой фаз для смеси этана и гептана при 400 °К и 20 атм, допу-
ская, что каждая фаза — идеальный раствор. Использовать диа-
грамму обобщенного фактора сжимаемости для вычисления фуги-
тивностей чистых компонентов. Принять, что фугитивность ком-
понента в жидкой фазе не зависит от давления.
Ниже даны необходимые физические постоянные для этана и
гептана:
₽пап> при
Ткр>	РКр, отм 400 атм
Этан...........	305	48,8	—
Гептан ....	540	26,8	2,19
Фугитивность этана в паровой фазе
Т _ 400_ J
"Р “305~ ’ ’
20 О
48,8	‘
Из рис. 52 следует, что
— = 0,95;
Р
/? = 0,95 20= 19 атм.
Фугитивность гептана в паровой фазе
Так как чистый гептан является жидкостью при температуре
и давлении системы, фугитивность должна быть определена для
гипотетического состояния, для которого предполагается, что геп-
279
тан остается паром при давлении 0—20 атм. Допустимая экстра-
поляция может быть основана на предположении, что остаточный
объем пара сохраняется постоянным во всем интервале давления
от нуля до 20 атм при значении, соответствующем давлению пара.
Значение остаточного объема можно определить из фактора сжи-
маемости с помощью соотношения
При давлении пара гептана при 400 °К
^р = ^ = 0,741;
9 19
^Р = 2^ = 0’081-
Из рис. 22,а следует, что Z = 0,94.
Согласно уравнению (5-81),
а 1—0,94 л пот Л -1
= —2 1Q  — 0,0274 атм
При допущении, что остаточный объем сохраняется постоянным
при этом значении во всем интервале давления от нуля до 20 атм,
интеграл в уравнении (8-69) можно легко вычислить:
20
ln-£-= —	—0,0274 20= —0,548.
о
Тогда вычисленная фугитивность гептана в гипотетическом состоя-
нии пара при 400 °К и 20 атм равна
f° — 20 е-0»648 = 11,6 атм.
Фугитивность жидкого этана
Так как чистый этан — эго пар при температуре и давлении
•системы, фугитивность гипотетического жидкого состояния можно
•было бы определить при давлении пара при 400 °К. Однако в этом
случае температура системы выше критической температуры эта-
на и давление пара должно быть определено с помощью экстрапо-
ляции. По одному методу давление пара экстраполируется за
критическую точку с помощью соотношения Клаузиуса — Кла-
пейрона. Согласно рис. 53, экстраполированное давление пара
этана при 400 °К равно 191 атм.
Используя эту величину для определения приведенного дав-
ления пара, получаем
191 о ni
 Ра>~ 4878 “ 3,91 •
280
При pnp — 3,91 и Тпр — 1,31 коэффициент фугитивности, опреде-
ленный из рис. 52, равен 0,54. Таким образом, фугитивность эта-
на в гипотетическом жидком состоянии при 400 СК и 191 атм
должна быть равна
/£=0,54-191 = 103 атм.
Эту величину можно также считать фугитивностью гипотетического
жидкого состояния при 400 СК и 20 атм.
Фугитивность жидкого гептана
Значение коэффициента фугитивности гептана при 400 °К и
давлении его пара 2,19 атм, как определено выше, равно 0,94.
Следовательно, фугитивность жидкой фазу при этих условиях
равна
0,94 2,19 = 2,06 атм.
Хотя к этому значению давления может быть сделана небольшая
поправка, как в примере 2 (гл. VIII), эта величина будет исполь-
зована как фугитивность при 400 °К и 20 атм.
Коэффициенты распределения для этана и гептана можно те-
перь вычислить, применяя уравнение (9-41) для каждого компо-
нента:
,, flE 103 с
^=-^=-19=5’42:
=	0,177.
п (О 11,6
1Ц
Содержание этана в жидкой фазе можно вычислить с помощью
уравнения (9-43):
!—_ 1—0,177 __ 0.923
—	“ 5,42 — 0,177~ 5,24
Г.	/7
Содержание гептана в обеих фазах и этапа в паровой фазе можно
вычислить следующим образом:
= КЕхЕ = 5,42-0,157 = 0,850;
кн= 1—х£ = 1—0,157 = 0,843;
y„=l—y£= 1—0,850 = 0,150.
Вычисленный состав жидкой фазы состоит из 0,157 мольных
долей этана и 0,843 мольных долей гептана. Состав паровой фазы
определяется 0,850 мольных долей этана и 0,150 мольных долей
281
гептана. Эти величины, полученные при допущении, что раствор
идеальный, хорошо совпадают с экспериментальными величинами,
равными 0,20 мольных долей этана в жидкой фазе и 0,85 мольных
долей этана в паровой фазе. Наиболее вероятный источник оши-
бок в вычислениях заключается в оценке фугитивности гипоте-
тического состояния жидкой фазы этана и паровой фазы гептана.
Паровая фаза в виде идеального газа — жидкая фаза в виде
идеального раствора
Если давление системы настолько низко, что паровую фазу
можно считать смесью идеальных газов, определение условий
равновесия может быть в дальнейшем упрощено. В идеальной
газовой системе фугитивность чистого компонента равна общему
давлению. Так как смесь идеальных газов также образует идеаль-
ный раствор, фугитивность компонента в смеси равна произведе-
нию общего давления на мольную долю, или парциальному дав-
дению. Это составляет содержание закона Дальтона:
=	(9-44)
Кроме того, фугитивность чистой жидкости, находящейся под
давлением ее пара, равна давлению пара, когда паровая фаза
является идеальным газом. Если не учитывать влияние давления
на фугитивность жидкости, то фугитивность компонента в идеаль-
ном жидкофазном растворе
где Р — давление пара чистого компонента при температуре
системы.
При равновесии фугитивности компонента в двух фазах рав-
ны и
Р/ = ^ = /’Л-	(9-45)
Это соотношение составляет содержание закона Рауля. При этих
условиях коэффициент распределения можно вычислить по урав-
нению (9-45) как отношение давления пара к общему давлению:
(9-46)
Пример 3. Определить состав жидкой и паровой фаз для
смеси этана и гептана при 400 °К и 20 атм, считая, что паровая
фаза является идеальным газом, а жидкая фаза — идеальным
раствором. Гипотетическое давление этана при 400 °К было уста-
новлено в примере 2 и равно 191 атм, а давление пара гептана
при 400 СК составило 2,19 атм.
282
На основании этих допущений коэффициенты распределения
могут быть установлены по уравнению (9-46):
Кв-^-9,65;
Ки=2-^=0,Ю8.
Мольную долю этана в жидкой фазе можно вычислить по урав-
нению (9-43):
г — 1 —0,108 _ 0,892	„ 0945
%£~9,55-0,108“ 9,44
Остальные переменные состава вычисляют следующим образом:
уЕ == Х£х£ = 9,55 • 0,0945 = 0,903;
хн= 1 —х£ = 1 —0,0945 = 0,905;
УН = 1 — уЕ = I — 0,903 = 0,097.
Эти вычисленные величины значительно отклоняются от экспе-
риментальных данных, приведенных в примерах 1 и 2.
Паровая фаза как идеальный газ — жидкая фаза как неидеальный
раствор
Для системы, в которой давление настолько низко, что паровую
фазу можно рассматривать как смесь идеальных газов, фугитив-
ность компонента в смеси равна парциальному давлению согласно
уравнению (9-44). Для неидеального раствора фугитивность ком-
понента в смеси удобно выразить через коэффициент активности
согласно уравнению (8-60). Таким образом, критерий равновесия
для этой системы может быть выражен в виде
=	(9-47)
для каждого компонента в системе. Если паровая фаза — идеаль-
ный газ и влиянием давления на фугитивность для жидкой фазы
можно пренебречь, то фугитивность для жидкой фазы чистого ком-
понента равна давлению пара и уравнение (9-47) может быть за-
писано так:
=	(9-48)
Коэффициенты активности можно вычислить по формулам Мар-
гулеса или Ван-Лазра, выведенным в гл. 8, п. Ш Хотя эти форму-
лы применимы к системе при определенных тташературе, давле-
нии и составе, их все же можно использовать для всей области
составов, в которых изменения температуры малы. При бинарной
смеси, у которой точки кипения чистых компонентов отличаются
283
не более чем на 20 °C, эти формулы применимы для всей области
.составов с однозначными параметрами.
В соотношениях, состоящих из двух параметров, эти параметры
вычисляют из экспериментальных данных о фазовом составе при
определенных температуре и давлении. Например, коэффициент
активности каждого компонента в бинарной смеси вычисляют по
уравнению (9-48), если величины х{ и известны. В двухфазных
системах, которые образуют азеотропные смеси, достаточно изме-
рить азеотропный состав только одной фазы, так как составы обо-
их фаз идентичны:
-V =
72	Р2(\—х,)
(9-49)
(9-50)
Параметры в выражении Ван-Лаара для бинарной смеси опре-
деляют, решая уравнения (8-106) и (8-107) одновременно для
/4 и В:
A=lgv.[i+^j’;	(9-51)
в““М1+ййГ-	(9-52)
Если константы справедливы для всей области температур,
коэффициенты активности для других составов жидких фаз мож-
но определить из уравнений (8-106) и (8-107). Поскольку коэф-
фициенты активности для обоих компонентов при данном составе
жидкости известны, соответствующую температуру системы вычи-
сляют методом последовательных приближений при условии, что
п =	+	(9-53)
Значения давлений паров, которые удовлетворяют уравнению
(9-53) при определенных температуре и составе жидкости, исполь-
зуют затем для определения у± и у2 из уравнений (9-49) и (9-50).
Определить температуру системы по методу последовательных
приближений можно во многих случаях путем деления уравнения
(9-50) на уравнение (9-49) и решением относительно ух:
—гЧ-р—	(9'54>
. .	12 л2 Г2
Уравнение (9-54) выражает yt в функции отношения
Даже тогда, когд^ Pz и Рг в большой степени зависят от темпера-
туры, отношение -р- может только немного изменяться в ограни-
ченном интервале температуры. Так как соотношение для коэф-
284
фициентов активности по существу ограничено узкой областью
Температур, отношение часто определяют как среднюю вели-
чину во всей области составов. В этом случае «д определяют не-
посредственно и вычисление температуры системы для любого
состава методом последовательных приближений не является
необходимым.
Пример 4. Построить х — «/-диаграмму для системы
гидразин — вода при общем давлении 760 лип рт. ст., считая
паровую фазу идеальным газом. Система образует азеотропную
смесь приблизительно при 58,5 ° (мол.) гидразина с максималь-
ной точкой кипения 120 °C при давлении 1 атм [531. Скрытая
теплота испарения чистого гидразина равна 9670 кал/моль при
нормальной точке кцпения 113,5 °C и 1 атм. Использовать соот-
ношение Ван-Лаара для определения коэффициентов активности
чистых компонентов в жидкой фазе.
Давление пара чистого гидразина при азеотропной темпера-
туре можно определить с помощью соотношения Клаузиуса —
Клапейрона по уравнению (9-18):
1 „ Р _ 9670	(120- 113,5) = Qnq.
1п760 — 1,987 ’	390-386,5	’
PNaHi=760e°»®09= 936 мм рт. ст. при 120° С.
Давление пара воды при 120 °C равно 1520 мм рт. ст.
Коэффициенты активности компонентов в азеотропном раство-
ре можно определить с помощью уравнений (9-49) и (9-50). Если
коэффициент активности гидразина у1, а коэффициент активности
воды т2> то
760 л о,о	760 л гол.
Т1“936~0,812, Y® ~ 1520 “ °’500’
lgTi=—0,090; lgy2=—0,301.
Постоянные в соотношении Ван-Лаара можно определить по
уравнениям (9-51) и (9-52):
Л = —0,090[ 1 4- ^44^0^1® = -0,090(1 + 2,38)®= -1,028;
В= - 0,302? 1+“’|4^-зо1}Г=—о,301(1+ 0,420)® = -0,607.
Коэффициенты активности
вычислить подстановкой
и (8-107):
при других составах системы
этих величин в уравнения
можно
(8-106)
ё ( А. +1 ,1
у В  хг +
. В
lgYa= - —
I 1 + А ‘ Z )
— 1,028
1,67 J +1Г
Х2 /
— 0,607
2 <
1 + 0,590-^
А
285
Вычисленные величины коэффициентов активности приведены
ниже:
*1	IgYl	IgYz	Vi	1’2
0,0	—1,0280	0,0000	0,0937	1,000
0,1	—0,7290	—0,0152	0,1870	0,966
0,2	—0,5070	—0,0538	0,3110	0,883
0,3	—0,3460	—0,1080	0,4510	0,780
0,4	—0,2270	— 0,1710	0,5930	0,675
0,5	—0,1420	—0,2400	0,7200	0,576
0,6	—0,0826	—0,3110	0,8250	0,489
0,7	—0,0421	—0,3870	0,9070	0,410
0,8	—0,0178	—0,4600	0,9600	0,347
0,9	—0,0039	—0,5350	0,9910	0,292
1,0	0,0000	—0,6070	1,0000	0,247
Так как температура системы 100 СС (точка кипения воды) —
120 СС (точка кипения азеотропной смеси), составы паровой фазы
можно вычислить по уравнению (9-54). При 100 °C давление пара
гидразина определяют по уравнению (9-18):
In	(100-113,5) _
760	1,987 ‘ 373-386,5 ~ и,чэо,
При 120 °C
PN;jh4 = 760 е~0,4ВВ = 482 при 100 °C;
_ 760 _ ।
Р1 482— 1,й/й'
Р2\	1,625 + 1,575
/ср“	2
1,60.
Подстановкой этих величин в уравнение (9-54) получаем

У1 =
Вычисленные составы паровой фа-
зы приведены ниже и на рис. 58:
	Т2 Т1	Х2 XI	0^11,60 (71 )\Х1 )	‘Л
0,0	10,670	оо	ОО	0,000
0,1	5,170	9,000	74,450	0,013
0,2	2,840	4,000	18,180	0,052
0,3	1,730	2,330	6,450	0,134
0,4	1,140	1,500	2,740	0,267
0,5	0,800	1,000	1,280	0,439
0,6	0,593	0,667	0,633	0,612
0,7	0,452	0,429	0,310	0,763
0,8	0,361	0,250	0,144	0,874
0,9	0,295	0,111	0,052	0,951
1,0	0,247	0,000	0,000	1,000
Рис. 58. Равновесный состав
жидкости и пара в системе
гидразин — вода; давление в
системе равно 760 мм рт. ст.
286
Метод расчета равновесия
В предыдущих главах были приведены вычисления фазовых
составов при данной температуре и давлении, независимо от
количества вещества, входящего в каждую фазу. Во многих рас-
четах нередко нужно знать массу или объем вещества в каждой
фазе. Их можно определить из соотношений для равновесия с уче-
том материального баланса для конкретной системы.
Материальный баланс для данной системы можно установить,
рассматривая систему вначале как гомогенную фазу, жидкость
или пар, которая разделяется на две фазы с изменением темпера-
туры или давления. При отсутствии химической реакции мате-
риальный баланс можно выразить через число молей:
F = V+L,	(9-55)
где F — число молей первоначальной гомогенной фазы;
V —• число молей пара;
L — число молей жидкости при конечных условиях.
Если zz — мольная доля компонента i в начальной гомоген-
ной фазе, yt — мольная доля компонента i в конечной паровой
фазе их, — мольная доля компонента i в конечной жидкой фазе,
то материальный баланс для компонента I можно записать:
Fz^Vyt+Lx^	(9-56)
С помощью уравнений (9-55), (9-56) и (9-38) определяем хг:
xi =---V----ге	(9-57)
Л/д-4-1
Учитывая то, что Sx,- = 1, суммированием уравнения (9-57)
по всем компонентам получаем
V
—+ 1
2------V----(9-58)
К/ — +1
Используя заданную величину zL для каждого компонента в на-
чальной гомогенной фазе и равновесные температуру и давление,
уравнение (9-58) можно решить для отношения ~ методом после-
довательных приближений. Действительное значение L можно
получить из уравнения (9-55), если его написать так:
Если требуется определить температуру для отношения
лри заданном давлении, то вначале задают некоторое значение
287
температуры, а затем определяют коэффициенты распределения
из уравнения (9-58). Температура, соответствующая тем значе-
ниям коэффициентов распределения, которые удовлетворяют
уравнению (9-58), и является температурой для отношения
Подобный метод используют и в тех случаях, когда температура
дана, а давление неизвестно.
Для бинарной системы отношение может быть выражено
в функции первоначального состава гомогенной фазы и коэффи-
циентов распределения
гх К,-1
v
к к
гг Т-Ка
(9-59)
Если каждая фаза образует идеальный раствор и известны темпе-
V
ратура и давление, отношение -j- можно определить непосредст-
венно, не применяя метод последовательных приближений.
Пример 5. Используя данные Де-Приста для коэффициен-
тов распределения, приведенные в приложении 9, определить
состав жидкой фазы, которая должна быть в равновесии с паро-
вой фазой, содержащей 60% (мол.) изобутана и 40% (мол.) гексана
при давлении 10 атм.
В этом случае температура равновесия неизвестна, ее и состав
жидкой фазы следует определить методом последовательных приб-
лижений.
Принимаем Т = 250 °F	(121,1 °C),	Тогда	
	У	К	к
Изобутан		. . .	0,60	2,35	0,255
Гексан 		. . .	0,40	0,46	0,870
	1,00		1,125
Так как сумма > 1, принятая температура слишком низка.
Принимаем Т = 270 °F (132,2 °C). Тогда
	У	К	к
Изобутан		. . . .	0,60	2,65	0,226
Гексан 		. . . .	0,40	0,55	0,727
	1,00		0.95'
Так как сумма < 1, принятая температура слишком велика.
Принимаем Т — 265 °F (129,4 °C). Тогда
	У	К	К
Изобутан	 Гексан 		. . . .	0,60 . . . .	0,40	2,60 0,52	0,231 0,769
	1,00		1,000
288
Температура равновесия равна 265 °F (129,4 °C) при 10 атм
и жидкая фаза будет содержать 23,1% (мол.) изобутана и
76,9% (мол.) гексана. Эту равновесную температуру называют
«температурой кипения» жидкой фазы и «температурой конден-
сации» паровой фазы.
Пример 6. Определить состав пара, который будет в рав-
новесии с жидкой фазой, содержащей 30% (мол.) изобутана и
70% (мол.) гексана при 200 °F (93,3 °C). В этом случае давление
неизвестно, его и состав паровой фазы следует определить методом
последовательных приближений.
Принимаем л = 75 фунт/дюйм2 (5,27 кПсм?). Тогда
х Ку =Кх
Изобутан..................... 0,30	2,80	0,840
Гексан....................... 0,70	0,45	0,315
1,00	1,155
Так как сумма Еу, больше единицы, принятое давление слиш-
ком низкое.
Принимаем л = 90 фунт/дюйм2 (6,33 кПсм2). Тогда
х К у = Кх
Изобутан..................... 0,30	2,50	0,750
Гексан....................... 0,70	0,36	0,252
1,00	1,002
Равновесное давление равно 90 фунт/дюйм2 (6,33 кПсм2)
и паровая фаза будет содержать ~75% (мол.) изобутана и 25%
(мол.) гексана.
Пример 7. Определить температуру и давление, при ко-
торых паровая фаза, содержащая 80% (мол.) изобутана и 20%
(мол.) гексана, могла бы существовать в равновесии с жидкой
фазой, содержащей 25% (мол.) изобутана и 75% (мол.) гексана.
Такое положение обычно редко встречается в практике, но
оно представляет собой интересную иллюстрацию того случая,
когда все составы известны, а температура и давление неизвест-
ны. Определим коэффициенты распределения по данным извест-
ных составов:
К (изобутана) =	3,20;
К (гексана) =	= 0,267.
По положению этих величин на номограмме Де-Приста (рис. 2
приложения) равновесные температура и давление равны
100 °F (37,8 °C) и 22 фунт/дюйм2 (1,55 кГ/см2).
Пример 8. Определить число молей жидкости и число
молей пара, получающихся, когда смесь, содержащая 0,5 молей
изобутана и 0,5 молей гексана, приведена в равновесие при тем-
пературе 265 °F (129,4 °C) и давлении 10 атм. По результатам
примера 5 паровая фаза будет содержать 60% (мол.) изобутана и
40% (мол.) гексана, жидкая фаза будет содержать 23,1% (мол.)
изобутана и 76,9% (мол.) гексана.
19—1503	289
Если L — общее число молей жидкости и V — общее число
молей пара, то для числа молей изобутана в системе можно со-
ставить уравнение
0,231 L + 0,60 V= 0,50.
Подобно этому для числа молей гексана в системе можно
составить другое уравнение:
0,769 L + 0,40 V = 0,50.
Решая эти уравнения, получаем
L — 0,271 молей жидкости;
V = 0,729 молей пара.
р
С другой стороны, отношение можно определить непосред-
ственно по уравнению (9-59), в котором
г1 = 0,50; 22==0,50; ^ = 2,6 и Лг = 0,52;
Г2,6 —11
у 1	1—0,52
_У __ _____L___ J ____9 со
L ~ 0,52(2,6—1) о
1 —0,52	2,6
Действительное число молей может быть определено из этого
отношения, учитывая, что общее число молей в системе (£ + V)
равно единице:
£ == __	— -jj-g-qp-y =0,271 моля;
Т+1
v=l—£=1—0,271 = 0,729 моля.
Пример 9. Смесь углеводородов, содержащая 0,30 молей
изобутана, 0,50 молей гексана и 0,20 молей нормального октана,
приведена в равновесие при 250 *F (121,1 *С) и 100 фунт/дюйм2
(7,03 кГ/см2). Определить число молей жидкости и число молей
пара при этих условиях, а также температуру кипения и темпера-
туру конденсации при давлении системы.
Принять температуру кипения равной 215 °F (102,2 °C) при
100 фунт/дюйм2 (7,03 кГ/см2).
	X	К	у = Кх
Изобутан		....	0,30	2,55	0,765
Гексан 		....	0,50	0,43	0,215
Октан		....	0,20	0,10	0,020
	1,00		1,000
200
Принимаем температуру конденсации равной 318 °F (160 °C) при
100 фунт/дюйм2 (7,03 кПсм2). Тогда
	У	К	* = _Е. к
Изобутан . .	. .	0,30	4,81	0,063
Гексан . . . . .	. .	0,50	1,17	0,427
Октан . . . . .	0,20	0,39	0,513
	• ’	1,00		1,003
При 250 °F (121,1 °C) и 100 фунт/дюйм2 (7,03 кПсм^
	Z	К.
Изобутан .	0,30	3,2
Гексан . . .	0,50	0,61
Октан . . .	0,20	0,175
Эти величины используются		в уравнении (9-58) для определе-			
V ния отношения —	методом последовательных			приближений.	
Ниже приведены рассчитанные по			уравнению (9-57) составы		
трехкомпонентных	систем для	заданных значении:			
V Отношение -j- .	1	0,60	0,40	0,33	0,30
Изобутан . . .	0,143	0,164	0,184	0,194	0,199
Гексан ....	0,621	0,585	0,561	0,554	0,559
Октан .	...	0,340	0,290	0,262	0,252	0,247
Сумма 		1,104	1,039	1,007	1,000	0,996
Отношение для которого сумма Ехг = 1, является тре-
буемым решением. К сожалению, сумма Ех, весьма нечувстви-
тельна к изменению отношения , и чтобы получить ответ в
требуемых пределах, нужно с осторожностью использовать ве-
личину которая делает сумму большей или меньшей единицы.
Задачи
1.	По данным рис. 53 определить скрытую теплоту испарения нормального
октана и сравнить ее с величиной, данной в приложении 5.
2.	По приведенным ниже данным определить давление пара над твердым
алюминием при 500 °К. В первом приближении скрытая теплота сублимации
может быть взята как сумма скрытых теплот испарения и плавления:
Абсолютная температура, °К.............. 2022	1760	1557
Давление пара жидкой фазы, мм рт. ст . .	100	10	1
Скрытая теплота плавления при точке плавления 933 ° К равна
2550 кал/моль.
3.	Построить график зависимости температуры кипения и температуры
конденсации (росы) от фазового состава смеси пропана и изобутана при общем
давлении 100 фунт-дюйм2, если:
а)	паровая фаза — идеальный газ и жидкая фаза — идеальный раствор;
б)	каждая фаза — идеальный раствор; справедливо обобщенное выраже-
ние для фактора сжимаемости;
в)	справедлива диаграмма Де-Приста.
19'
291
ГЛАВА 10
Химическое равновесие
Решение задач по химическому равновесию системы основано
непосредственно на критерии, выраженном уравнением (8-68):
£|h/Ww=0.
В системе, включающей одновременно фазовое и химическое
равновесие, химический потенциал идентичен для каждого ком-
понента в каждой фазе системы, поэтому задачу можно решать
относительно какой-нибудь одной фазы. При отсутствии химиче-
ской реакции состав фазы может быть изменен только прохожде-
нием вещества сквозь границы фаз. При наличии в системе химиче-
ской реакции состав даже замкнутой однофазной системы может
изменяться путем превращения одного вещества в другое.
Для замкнутой однофазной системы dNt в уравнении (8-68)
не является независимой величиной, но связано со стехиометрией
химической реакции. Например, если а молей компонента А реаги-
рует с Ь молями компонента В с образованием г молей компонента
R и s молей компонента S в соответствии с реакцией
аА ф- ЪВ rR 4- sS,
то уравнение (8-68) можно записать так:
—аР-д — Ь[хв 4- rp-^4- sy.s = 0.
(Ю-1)
Химический потенциал каждого компонента можно выразить
в функции фугитивности, согласно уравнению (8-50):
Hi = И/ + In -5 .
I I
где индекс нуль означает, что соответствующая величина отно-
сится к произвольно выбранному стандартному состоянию.
292
Подставляем уравнение (8-50) в уравнение (10-1):
А о	-.Or yds	-гг	-is
- W + 111 -^W =•	<10-2)
i\l	f\Ja rOU	r<* fU
I A IB	' A IB
где
Ар-о = гГ-я + в^—ap^ — Ьр.д.	(10-3)
Слагаемые левой части уравнения (10-2) определяются только
стандартным состоянием для каждого компонента и числом молей
для каждого компонента, участвующего в реакции. Правая часть
уравнения выражена через фугитивность каждого компонента
в реакционной смеси при равновесии.
При решении задач по химическому равновесию системы преж-
де всего необходимо определить стандартное состояние для каждо-
го компонента. При рассмотрении систем с химическим равнове-
сием следует выбрать такое стандартное состояние, при котором
фугитивность равнялась бы единице для каждого чистого компо-
нента при температуре реакционной системы. Давление в таком
стандартном состоянии будет различным для каждого чистого ком-
понента.
Стандартное состояние каждого компонента можно также оп-
ределить как состояние чистого компонента в гипотетическом со-
стоянии идеального газа при 1 атм и температуре системы. Для
большинства газов при давлении в 1 атм фугитивность настоль-
ко близка по значеню к 1 атм, что различие между гипотетическим
состоянием идеального газа и реальным состоянием ничтожно.
В этом случае для стандартного состояния давление равно
1 атм и одинаково для всех компонентов. При стандартном состоя-
нии с фугитивностью, равной единице каждого чистого компонен-
та при температуре системы, уравнение (10-2) принимает вид
yr -?s
где мольная свободная энергия используется теперь как химиче-
ский потенциал для каждого чистого компонента в его стандарт-
ном состоянии; AF0 — изменение свободной энергии реакции,
причем исходные вещества и продукты реакции находятся в их
стандартном состоянии.
Экспоненциальный член левой части уравнения (10-4) назы-
вается «константой равновесия реакций» и определяется соотно-
шением
1п/<-=-^.	(10-5)
Численное значение константы равновесия реакции зависит от
определения стандартного состояния и является функцией тем-
293
пературы системы и коэффициентов каждого компонента в урав-
нении химической реакции. Эта константа не зависит от давления
реакционной системы.
Анализ систем с равновесными химическими реакциями мож-
но разделить на две стадии. Вначале вычисляют константу хими-
ческого равновесия из уравнения (10-5); затем с помощью урав-
нения (10-4) определяют равновесный состав реакционной смеси.
1. Вычисление константы химического равновесия
Определение константы химического равновесия по существу
сводится к вычислению изменения свободной энергии реакции при
условии стандартного состояния. Изменение свободной энергии
реакции при условии изотермического стандартного состояния
определяется изменением энтальпии и энтропии согласно выра-
жению
bF° = bH° + TbS°.	(10-6)
Метод вычисления изменения энтальпии реакции зависит преж-
де всего от эмпирических данных теплот образования и теплот
сгорания (см. гл. 1). Имеются различные эмпирические методы
для определения теплот образования. Такие методы применяют,
когда нет прямых экспериментальных данных. Данные по тепло-
там образования и теплотам сгорания обычно относятся к 25 °C
и 1 атм.
Изменение энтропии реакции можно выразить через абсолют-
ные энтропии каждого компонента в его стандартном состоянии:
AS° = rS^ + sS;—aS^ —Ь5д.	(10-7)
Абсолютные энтропии индивидуальных чистых компонентов
при данных температуре и давлении могут быть определены мето-
дами, описанными в гл. 4. Такие вычисления приведены для мно-
гих веществ для температуры 25 °C и давления 1 атм (см. при-
ложение 4).
Таким образом, если известны данные о теплотах образования
или сгорания и абсолютной энтропии каждого компонента реак-
ции, то свободную энергию реакции можно определить также для
25 °C и 1 атм. Однако температура стандартного состояния
не всегда равна 25 °C. Поэтому изменение свободной энергии реак-
ции следует вычислять при температуре стандартного состояния.
Влияние температуры на изменение свободной энергии реакции
лучше всего проявляется в форме зависимости теплоты реакции и
изменения энтропии реакции от температуры.
Влияние температуры на теплоту реакции при условии постоян-
ного давления рассмотрено в гл. 1. Согласно схеме, изображенной
на рис. 3, теплоту реакции при температуре Т можно выразить
294
через теплоту реакции при 298 ®К (25 °C) и 1 атм следующим со-
отношением:
ДЯ^ДЯ^ + рС^Т,	(10-8)
298
где
ЛСр = rCpli + sCps—аСрЛ—ЬСрВ.
(10-9)
Подобным образом влияние температуры на изменение энтро-
пии реакции при давлении стандартного состояния можно выра-
зить соотношением
т
As;=As;9e+J^dT.	(io-ю)
Если теплоемкость каждого компонента выражается как функ-
ция температуры уравнением (1-58)
Ср-а + ЬТ + сТ3,
то интегрированием уравнения (10-8) получаем
Д#;=Да7 + ^72+-^78 + ЛН;,	(10-11)
•*	X	о
где	дя; = дя;ве—Да 298 — 2982 — -	у- 298®;	(10-12)
	Дц = rtZ/j “|“ scz$ айд ДЬ = rbR + sbs—abA— ЪЬВ\ ^с — гсц + scs—acA— bcB.		(10-13>
Аналогично интегрированием уравнения (10-10) получаем
Д5;= Д«1пТ + ДЬТ + ^ 72 + Д5;,	(10-14)
где
Д$°о = Д£»8—Да 1п 298-ЛЬ 298 — ~-298!.	(10-15)
Подстановкой уравнений (10-11) и (10-15) в уравнение (10-6)
получаем выражение для изменения свободной энергии реакции
как функции температуры:
ДЕ^=ДЯ° + (Да— Д5“)7—ДаТ1п7—^Т8 —~-Т*. (10-16)
Константу равновесия реакции затем можно вычислить подста-
новкой уравнения (10-16) в уравнение (10-5). Если принять, что
ДСр — линейная функция температуры, то Дс в уравнении
295
(10-16) будет равно нулю. Если принять, что ДСр имеет постоян-
ное значение и не зависит от темперауры, то и ДЬ и Дс равны
нулю. При условии, что ДСр равно нулю, уравнение (10-16)
упрощается:
де;=дд’-едх;,	(ю-17)
где Д77д и AS" не зависят от температуры и могут быть вычислены
при любой температуре, близкой к стандартной. В этом случае
константа равновесия химической реакции может быть выражена
как функция температуры подстановкой уравнения (10-17) в
уравнение (10-5):
, „ ьн° AS°
+	(10-18)
Согласно уравнению (10-18), зависимость In К от -jr- будет выра-
жаться прямой линией, если ДСр = 0. Это соотношение часто
употребляют для корреляции экспериментальных данных.
В тех случаях, когда данные по теплоемкости как функции
температуры представлены в форме таблиц или графика и неиз-
вестны эмпирические постоянные уравнений для теплоемкости,
как в уравнении (1-58), интегралы уравнений (10-8) и (10-10)
можно вычислить графически и полученные значения ДН?- и
ДХг подставить непосредственно в уравнение (10-6) для ДЕ°Г .
Этот метод проще и короче, чем определение постоянных уравне-
ний для теплоемкостей и использование затем аналитических вы-
ражений.
Для многих веществ свободные энергии образования и In К
образования в зависимости от температуры сведены в таблицы.
Если такие данные известны для каждого компонента реакции, то
изменение свободной энергии для стандартного состояния и кон-
станты химического равновесия можно получить непосредствен-
но из соотношений
ДЕ° => rAF;R + sAF°s—аДЕ;л—ЬДЕ;В; (10-19)
In К — г In К1К+ s In KfS— a In	— bin	(10-20)
Однако величины в таких таблицах с течением времени ока-
зываются недостаточно точными при проверке и необходимо улуч-
шение данных по теплотам образования и абсолютным энтропиям.
Пример 1. Определить константу химического равновесия
при 1000 °К Для реакции
soa 4- -2~ ^2 «—~ so3.
Принять, что фугитивность каждого чистого компонента равна
1 атм в стандартном состоянии при 1 атм и 1000 °К. Данные по
теплотам образования, абсолютной энтропии и постоянным для
296
уравнений теплоемкости приведены ниже (см. приложения 2 и 4):
	so2	О2	SO3
ДЯЪ 298 °К, 1 атм ....	—70 960	0	—94 450
S, '298 °К, 1 атм		59,40	49,00	61,24
а 		7,116	6,095	6,077
в-103 		9,512	3,253	23,537
с-10е 		—3,511	—1,017	—9,687
Единицы: кал, моль, °К.
Теплота реакции при 298 °К и 1 атм равна
А^»98= —94450 + 70960= —23490 фи/моль.
Изменение энтропии реакции при 298 °К и 1 атм:
= 61,24—59,40— 49^— = —22,66 калЦмоль °К).
Суммарные постоянные теплоемкостей:
Да = 6,077 -7,116 —	= —4,087;
ДЬ=( 23,537 — 9,512—	10-3 = 12,397  10~8;
дс=^—9,687 + 3,511 +-Ц^) 10-®=—5,667-10-®.
Величину ДЯ° получают подстановкой полученных численных
значений в уравнение (10-12):
ДЯ°= —23490 + 4,087 298----- 2982 +
 ^667„'10~е -2988= —22770 кал/моль.
«J
Величину Д5“ получают подстановкой тех же значений в урав-
нение (10-15):
Д5°= —22,66 + 4,087 1п298 —12,397-10-® 298 +
+ .5’667J-2~6 -2982=—2,82 калЦмоль °К).
Выражение для изменения свободной энергии реакции как
функции температуры получают подстановкой этих величин в
уравнение (10-16):
ДГТ = — 22770 — 1,27 Т + 4,087 TinТ—I2-’397™!- т*.
При ЮОО°К
ДЕ°= —1064 кал/моль.
297
Константа химического равновесия при 1000 °К получается
подстановкой этой величины в уравнение (10-5):
In К= 1064 1,987 1000 = 0,535.
/(=1,71.
2. Определение равновесного состава
Если значение константы химического равновесия определено
для данной температуры, равновесный состав реакционной смеси
можно вычислить по уравнению (10-4):
Х =	(10-21)
Фугитивность каждого компонента в реакционной смеси можно
выразить через коэффициент активности, фугитивность чистого
компонента и мольную долю, согласно уравнению (8-60):
Применяя уравнение (8-60) к фугитивности каждого компонента,
можно записать уравнение (10-21) так:
К = КуК,Кх,	(10-22)
откуда
л\=44:	<10-23)
(10-24)
„Г /
<10-25)
ХАХВ
Вычисление коэффициентов активности для компонентов в
неидеальной реакционной смеси — сложная проблема, в настоя-
щее время еще не решенная. Поэтому ниже рассматриваются
системы, которые образуют идеальные растворы. Предположение
о том, что раствор ведет себя как идеальный, справедливо для
большинства газообразных систем.
Для идеального раствора коэффициент активности каждого
компонента равен единице и
Kv=l.	(10-26)
298
Фугитивность каждого чистого компонента можно выразить че-
рез коэффициент фугитивности, определяемый уравнением (8-79):
где л — общее давление в системе. Применяя уравнение (8-79)
к фугитивности каждого чистого компонента, уравнение (10-22)
можно записать так:
если
	(10-27)
Г S	
а о	(10-28)
Кр= а b • РаРв	(10-29)
где р — парциальное давление компонента в газовой фазе системы
[см. уравнение (10-32)1.
Если реакционную систему рассматривать как смесь идеаль-
ных газов, коэффициент фугитивности каждого компонента равен
единице и
	Л,= 1.	(10-30)
В этом случае	к=лр=/<хя>	(10-31)
где		(10-32)
	Г S .	а Ь УаУв	(10-33)
	Лп = г+ s—а — Ь.	(10-34)
Мольные доли в уравнении (10-33) не являются независимыми,
но определяются стехиометрией реакции. Если определить пере-
менную как количество одного компонента, вступающего в реак-
цию или образующегося в результате ее, то все мольные доли мож-
но выразить через одну общую переменную, и уравнения (10-27)
и (10-33) можно решить относительно этой неизвестной. Таким
образом может быть определен равновесный состав реакционной
смеси.
Пример 2. Определить равновесный состав реакции
СО+ 2Н2 Z—i CHSOH
299
при 600 °К и начальном соотношении: I моль окиси углерода и
2 моля водорода при следующих условиях:
а)	идеальный газ, давление 1 атм;
б)	идеальный газ, давление 300 атм;
в)	идеальный раствор, давление 300 атм.
Величины теплот образования и абсолютной энтропии каждо-
го компонента приведены ниже (см. приложения 2 и 4):
со	н2 сн3он
ДН°, 298 °К, 1 атм .... —26416	—	—48080
5°/298оК, 1 атм......	47,301	31,21	56,80
Д//;88= —48080 ( 26416— —21664 кал/моль;
kS°iW~ 56,80—47,301 -2-31,21 = —52,92 кал!(моль-° К);
ДК;ой = -21664 + 298-52,91 = —5897 кал!моль.
Коэффициенты для уравнения теплоемкости
Cp=a + bT-] cT2 + dT3
приведены ниже:
	СО	н2	CHSO1I
а . -				 6,726	6,952	4,55
МО2		. . . .	0,04001	-0,04576	2,186
с-10е 		1,283	0,9563	—2,91
41-16»		. . .	—0,5307	—0,2079	-1,92
а- 4,55—6,726—2-6,952=—16,08;
b = (2,186—0,04001 + 2 • 0,04576)  10-2 = 2,238 • 1СГ2;
с = (—2,91 —1,283 —2 0,9563). 16-*= —6,105-10+
d = (—! ,92 + 0,5307 + 2 - 0,2079) • 10 9 = —0,9735  10+
Подставляя эти значения в уравнение (10-12), получаем
Д#° = —21664+ 16,08-298 — 2:.238--1°--2982 +
+ 6,105-10 °- 2983 + 0-973 .1-0— 2984= —17810 кал/моль.
О	>
Подставляя численные значения в уравнение (10-15), полу-
чаем
ДХ; = —52,92 + 16,08 In 298—2,238-10-2-298 +
6,105-10;° 2g82 + 0,9735 -10+ 2д83 = 32кал/^МОль.
’	2	о
300
Подставляя численные значения в уравнение (10-16), получаем
&FT	17810	„„ , 1Rn01	2,238-IO-2 ~ ,
-у —-------у---48,38-|- 16,08 In Т-------g----Т +
, 6,105-10-®	, 0,973-10-»
+------6---Т +--------12--Т 
&F°
При 600 °К -6^ = 18,5;
Д-^воо— 1^,5 600== П084 кал/моль.
Согласно уравнению (10-5),
—s = ~9-31;
К- 0,90-10-4.
Очень большое значение изменения стандартной свободной
энергии и соответственно малое значение константы химического
равновесия указывает на то, что равновесное превращение окиси
углерода и водорода в метанол имеет место, вероятно, значитель-
но ниже 600 °К-
Полагая, что реакционная смесь образует идеальный раствор,
имеем	Ку = 1
и уравнение (10-27) можно записать так:
К = К. УсНзОН-----	(10-35)
^СО'^Н/^2
Число каждого компонента в равновесной смеси вычисляли исходя
из 1 моля окиси углерода и 2 молей водорода. Было получено m
молей метанола при равновесии:
	Число молей	У 1—т
СО . .	. .	1— т	3—2т 2 (1—т)
на. . . СН3ОН	. .	2—2т	3—2m tn
	. .	гл	3—2т
Сумма ,	. .	3—2т	
Подставляя соответствующие мольные доли в уравнение
(10-35), получаем
.	(10-36)
Kv	4(1—m)8	v >
При давлении 1 атм систему можно рассматривать как смесь
идеальных газов, для которых = 1. В этом случае
k=K= 0,900-1 о-4.
301
Решая уравнение (10-36) методом последовательных прибли-
жений, вычисляем т:
/п = 0,400-10-4.
При этих условиях только 0,400 10"2% окиси углерода и водорода
в реакционной смеси вошли в реакцию; степень протекания реакции
незначительна.
Уравнение (10-36) указывает на то, что значение т будет расти
по мере возрастания величины К- Так как К является функцией
только температуры, то значение k будет расти при данной тем-
пературе по мере возрастания давления и по мере понижения зна-
чения Kv.
Полагая, что закон идеального газа справедлив и для дав-
ления 300 атм, величина К, = 1,
Л = 0,900-10-4-3002 = 8,10.
Решая уравнение (10-36) методом последовательного приближе-
ния для т с этими значениями k, получаем, что
m = 0,61.
Даже если константа химического равновесия не зависит от дав-
ления, возрастание давления от 1 до 300 атм увеличит степень
превращения окиси углерода и водорода от незначительной вели-
чины до 61 %. Вычисленный равновесный состав реакционной смеси
на основании закона идеального газа приведен ниже:
Мольная доля
......... 3—1,22	=0,219
2 (1-0,61)
......... 3—1,22	0,438
0,61
СН2ОН ....	“з-1122’^ = 0,343
1,000
В действительности закон идеального газа не является спра-
ведливым при давлении 300 атм и должны быть сделаны поправ-
ки на отклонение от поведения идеальных газов. Коэффициент
фугитивности при заданных значениях Тир наиболее легко
определить по графику, построенному на основании обобщенного
фактора сжимаемости (см. рис. 52):
	Гкр- °К	Ркр, атм	600 'пр	Т	300 р"₽“’
СО . .	. .	133	34,5	4,51	8,7	1,06
н2 . .	33,3	12,8	18,0	23,4	1,20
сн3он	. .	513	78,5	1,17	3,82	0,47
К, = 0,47/1,00 1,22 = 0,326.
302
В этом случае
0,900-10~4-3002
0,326
= 24,8.
Решением уравнения (10-33) методом последовательных приближе-
ний для т получаем, что т = 0,75.
Так как для этой системы < 1, то отклонение от поведения
идеального газа обусловливает больший процент превращения,
чем в том случае, если бы система вела себя как смесь идеальных
газов. Мольные доли компонентов неидеальной реакции смеси
при равновесии таковы:
Мольная доля
1—0,750
С0.......... -3-1,50- =0'167
0,75
СНзОН ....	-3~Г50~ = 0,500
1,000
При этих условиях реакция возможна, даже если константа хи-
мического равновесия очень мала.
Влияние давления на равновесный состав смеси можно объяс-
нить принципом Ле-Шателье — с повышением давления возра-
стают равновесные концентрации компонентов для той части
уравнения реакции, которой соответствует меньший объем. Это
влияние наиболее ярко проявляется в газовых системах; влияние
давления на равновесные концентрации незначительно для мало
сжимаемых жидкостей и твердых веществ.
Наибольшие равновесные концентрации продуктов реакции
всегда связаны со стехиометрией, т. е. компоненты, загружаемые
в реактор, должны быть в том же соотошении, в котором они реаги-
руют (см. пример 2). Присутствие инертного компонента или из-
бытка одного реагирующего вещества всегда вызывает понижение
равновесных концентраций продуктов в равновесной реакцион-
ной смеси.
Пример 3. Определить равновесный состав для реакции
СО Ч-2Н27=± СН8ОН
«
при 600 °К и 300 атм для начального соотношения: 1 моль СО и
3 моля Н2. В этом случае водород присутствует в избыточном ко-
личестве по сравнению с необходимым для полного протекания реак-
ции с окисью углерода. Константа равновесия при 600 °К для этой
реакции была вычислена в примере 2,
303
Число молей каждого компонента в равновесной смеси вычис-
лено на основании того, что взяты 1 моль СО и 3 моля Н2 и при
равновесии получено т молей метанола.
Число молей		Мольная доля
		1—т
СО . .	.	1—т	4—2т
		3—2т
н2 . . .	. 	3—2т	4—2т
СН3ОН .	т	т 4—2т
	4—2т	
Подстановкой соответствующих мольных долей в уравнение
(10-35) получаем
Кл2 , т (4 — 2т)2	,. п
х = k = -(1 -^Г(3 - 2m)2 	•	(10-37)
Следующие величины были вычислены в примере (10-2) для
этой реакции для 600 °F (315,6 СС) и 300 атм:
Я =0,900-КГ4;
К, = 0,326;
/г = 24,8
Решая уравнение (10-37) для т методом последовательных прибли-
жений, получаем, что т — 0,883.
Мольные доли компонентов в равновесной реакционной смеси
равны:
СО.........
Н:.........
СН3ОН . . . .
Мольная доля
1—0,883 __ гп
2 (2—0,883) 0,052
3—1,766 _
2 (2—0,883)	0,553
0,883	_ 0,395
2 (2—0,883)	1,000
Хотя избыток водорода повышает превращение окиси углерода
от 75 до 88%, вместе с тем он понижает мольную долю метанола
в равновесной смеси от 0,500 до 0,395.
3. Параллельные реакции
Во многих реакционных системах возможно протекание более
чем одной химической реакции с теми же исходными веществами
при данных температуре и давлении. Это особенно характерно для
систем, включающих органические соединения. В тех случаях,
когда в различных реакциях участвуют общие исходные вещества
304
или продукты реакции, и в анализ условий равновесия следует
включать все возможные реакции, протекающие одновре-
менно.
Относительно простой, но важной системой является реакция
дегидрогенизации нормального бутана на соответствующем ката-
лизаторе до трех нормальных бутенов: нормального бутена-1
(н — С4), цис-бутена-2(ц = С4) и транс-бутена-2(т = С4). Экспе-
риментальные данные показывают, что относительные количества
трех бутенов определяются критерием термодинамического равно-
весия.
Пример 4. Определить равновесное превращение нор-
мального бутана до бутена-1, цис-бутена-2 и транс-бутена-2 как
функцию температуры в пределах 600— 1Ю0°К при общем дав-
лении 1 атм. Принять, что закон идеальных газов справедлив
при этих условиях.
Ниже приведены некоторые данные по теплотам образования
и абсолютной энтропии1 при условии, что Т — 25 °C, р — 1 атм.
Mif, кал/моль . .
S, кал/(моль
н-С4 С4 — 1 ц-С4=2 т<4»2 На
—29812	280 —1362 —2405	0
74,10	73,48 71,90 70,86 31,21
Теплоемкость [кал/(люло1К)1 некоторых соединений при
р — 1 атм и различной температуре дана ниже.
Г. °к	н-С4	С4=1	ц-С4=2	т-С.1=2	На
298	23,61	21,35	18,86	20,99	6,89
300	23,77	21,45	18,96	21,08	6,90
400	29,80	26,94	24,33	26,02	6,97
500	35,54	31,75	29,39	30,68	6,99
600	40,42	35,82	33,80	34,80	7,01
700	44,61	39,31	37,60	38,38	7,04
800	48,23	42,33	40,87	41,50	7,08
900	51,42	44,95	43,70	44,20	7,14
1000	54,20	47,24	46,15	46,58	7,22
ноо	56,60	49,23	48,28	48,65	7,31
Хотя эмпирические уравнения теплоемкостей есть для всех
рассматриваемых соединений, цель этого примера — иллюстри-
ровать метод вычисления константы равновесия реакции прибли-
женным методом непосредственно по табличным данным теплоем-
кости. Величины констант равновесия реакции, вычисленные в
этом примере, удовлетворительно совпадают с величинами, полу-
ченными по константам равновесия образования, приведенным
в сборнике 1
1 Данные по теплотам образования, абсолютной энтропии и теплоемкости
указанных соединений приведены из сборника «Избранные свойства углеводо-
родов». Национальное бюро стандартов С461, 1947.
20—1503
305
Три одновременно протекающие реакции можно записать сле-
дующим образом:
1.	н-С4 < — н-С4 = 1 + Н2;
2.	н-С4	ц-С4 — 2 + Н2;
3.	н-С4^т-С4=2 + На.
Определение констант равновесия как функции температуры
Для реакции 1:
ДЯ°В8 = 280+ 29812 = 30092 кал/молы,
AS;B3 = 73,48 + 31,21—74,10 = 30,59 калЦмоль  °К).
Для реакции 2;
ДД2В8 ~	1362 + 29812 = 28450 кал/молы,
AS;BB = 71,90+31,21— 74,10 = 29,01 калЦмоль  °К).
Для реакции 3:
ДД°В8 = —2405 + 29812 = 27407 кал/молы,
ДХ°2В8 = 70,86 + 31,21 —74,10 = 27,97 калЦмоль  °К).
Теплоту реакции и энтропию реакции при других температу-
рах можно вычислить по уравнениям (10-8) и (10-10) с использо-
ванием табличных данных теплоемкости при допущении, что кри-
вые зависимостей теплоемкости при постоянном давлении Св и
-2- от температуры могут быть аппроксимированы отрезками
прямых линий с разностью абсцисс в 100 °К.
При этих условиях уравнения (10-8) и (10-10) можно записать
приближенно так:
дн; = дд;В8+е (дср)тдт;	(ю-з8)
д$;=дх;,8+е дт.	(Ю-39)
Вычисленные суммы приведены в табл. 13, в которой для каждой
реакции даны ДС (олефина) + С„(водорода) — С_(бутана), а обо-
/ ДС„ \
значения (ДС„)т и —=— — это средние арифметические в том
или ином температурном интервале. В табл. 14 значения &Нг,
&S°t, &F°t и lg10K вычислены для каждой реакции при некоторых
температурах согласно уравнениям (10-38), (10-39), (10-5) и
(10-6).
306
Таблица 13
СРЕДНИЕ ЗНАЧЕНИЯ (А С ) и (А С /Г )т ДЛЯ 1, 2 и 3 РЕАКЦИЙ ПРЕВРАЩЕНИЯ
Н—БУТАНА
о	ь	о* <3	к X Е	£ йГ	О X ьГ	л	срттх хдт
				Реакция 1			
298	2	4,63	10		1,55	0,03	
300	100	4,58	434	10	1,53	1,28	0,03
400	100	4,11	366	444	1,03	0,840	1,31
500	100	3,20	281	810	0,640	0,517	2,15
600		2,41		1091	0,402		2,67
	100		207			0,326	
700	100	1,74	146	1298	0,249	0,199	3,00
800	100	1,18	92	1444	0,148	0,111	3,20
900	100	0,67	46	1536	0,074	0,050	3,31
1000		0,26		1582	0,026		3,36
	100		10			0,015	
1100		—0,06		1592	0,005		3,37
				Реакция 2			
298	2	2,14	4		0,718	0,014	
300	100	2,09	180	4	0,696	0,535	0,014
400	100	1,50	117	184	0,375	0,271	0,549
500		0,84		301	0,168		0,820
	100		62			0,117	
€00	100	0,39	21	363	0,065	0,034	0,937
700	100	0,03	—13	384	0,004	—0,015	0,971
800	100	—0,28	—43	371	—0,035	—0,050	0,956
900	100	—0,58	—70	328	—0,065	—0,074	0,906
1000		—0,83		258	—0,083		0,832
	100		—92			—0,088	
1100		—1,01		166	—0,092		0,744
				Р еа к	ци я 3		
298	2	4,27	9		1,43	0,028	
300	100	4,21	370	9	1,40		0,028
						1,100	
400		3,19		379	0,800		1,128
20*
307
Г1 рэдолжение табл. 13
			X Е	кГ	о X Д	Д к	^Ср/ Т)т* ХАТ
	100		266			0,613	
500	100	2,13	173	645	0,426		1,741
						0,329	
600	100	1,39	НО	818	0,232		2,070
						0,174	
700	100	0,81	58	928	0,116		2,244
						0,080	
800	•	0,35		986	0,044		2,324
	100		13			0,017	
900	100	—0,08	—24	999	—0,009		2,341
						—0,025	
1000	100	—0,40	—52	975	—0,040		2,316
						—0,049	
1100		—0,64		923	—0,058		2,267
Таблица 14
ТЕРМОДИНАМИЧЕСКИЕ ДАННЫЕ ДЛЯ I, 2 и 3 РЕАКЦИЙ ПРЕВРАЩЕНИЯ Н-БУТАНЛ
Т °К	А НТ Г			tao К
		Реакция 1		
298	30,092	30,59	20,976	
600	31,183	33,26	11,227	—4,089
700	31,390	33,59	7,877	—2,459
800	31,536	33,79	4,504	— 1,230
900	31,628	33,90	1,118	—0,271
1000	31,674	33,95	—2,276	0,497
1100	31,684	33,96	—5,672	1,127
		Реакция 2		
298	28,450	29,01	19,805	
600	28,813	29,95	10,843	—3,950
700	28,834	29,98	7,848	—2,450
800	28,821	29,98	4,837	—1,321
900	28,778	29,96	1,814	—0,440
1000	28,708	29,84	—1,132	0,247
1100	28,616	29,75	—4,109	0,816
		Реакция 3		
298	27,407	27,97	19,072	
600	28,225	30,04	10.201	—3,715
700	28,335	30,21	7Т188	—2,224
800	28,393	30,29	4,161	—1,137
900	28,406	30,31	1,127	0,417
1000	28,382	30,29	—1,908	0,417
1100	28,330	30,24	- 4,934	0,980
I
308
Определение равновесного превращения
Вычислим число молей каждого компонента, присутствующего
в равновесной смеси, исходя из того, что первоначально был взят
1 моль нормального бутана, а в равновесной смеси будет х молей
нормального бутена-1, у молей цис-бутена-2 и г молей транс-бу-
тена-2:
Число молей при равновесии
н-С4	1—(х+у+г)
и-С4=1	х
ц-С4=2	у
т-С4=2	г
Нг	х+у+г
Сумма
1+(*+?/+г)
Применяя уравнение (10-31) к каждой из трех приведенных выше
реакций, получаем три независимые уравнения с неизвестными
х, у, г:
к __________х (х + У + г) гс______ х (х + у + г) .
1 П-(*+«/ +*)П1+ (х +У+*)]	l-(* + J/ + *)a’
К У (х + У + ?)" .
2	1-(х + у+г)* 1 2’
К — г (х Ц- у + г) к
'3	1 _ (х + у + г)2>
Если s — сумма х, у и г, т. е.
S = X-p^-j-Z,
и £ — сумма констант равновесия химической реакции, т. е.
£ = К1 + 7<2 + Х3,
то три соотношения равновесия можно записать так:
=
2	1 — S2
IS	ZS7C
^3=Г_82.
Сложением этих уравнений получаем равенство
^+k8+^3-s14?S2.
которое можно решить относительно s:
S=f-M4 S
[dP + rc)]
(10-40)
(10-41)
(10-42)
(10-43)
309
Величины х, у и г можно получить подстановкой величины "s
из уравнения (10-43) в уравнения (10-40)—(10-42):
х =------1—-у;	(10-44)
[2(S + я)] 2
£ = —;	(Ю-45)
ДО 4-*)} 2
г=~----П-	(Ю-46)
ДО 4- к)] 2
Численные значения констант равновесия, величин х, у и z
V °^ее пРеБРаи*ение бутаназ для температур в интервале 600—
1100 К приведены ниже.
т. °к		Ка	Кз		Е	
600	0,000081	0,000112	0.000193		0,000386	
700	0,00348	0,00355	0,00570		0,0127	
800	0,0589	0,0471	0,0729		0,1789	
900 1000	0,536 3,14	0,363 1,77	0,532 2,61		1,431 7,52	
1100	13,4	6,55	9,55		29,5	
Т, °к	[£(2+D]i/g	X	У	Z	S	
600	0,0196	0,0041	0,0057	0,0099	0,0197	
700	0,114	0,030	0,031	0,050	0,111	
800	0,460	0,128	0,102	0,159	0,389	
900	1,865	0,287	0,195	0,285	0,767	♦
1000	8,00	0,393	0,221	0,326	0,940	
1100	30,0	0,447	0,218	0,318	0,983	
Выход олефиновых углеводородов и общее превращение бутана
в зависимости от температуры показано на рис. 59.
Температура^К
Рис. 59. Равновесное превращение и распределе-
ние продуктов дегидрогенизации бутана прн об-
щем давлении 1 апм в зависимости от темпера-
туры:
/—конверсия; 2—х молей нормального бутена-1; z молей
транс бутеяа-2; 4—у молей цис-бутена-2
310
4.	Температура адиабатных реакций
Во всех предыдущих примерах температура равновесной реак-
ционной смеси была известна. При решении реальных технических
проблем, включающих и работу химического реактивного двига-
теля, учитываются такие условия, когда реагирующие вещества
загружаются в систему при известных температуре и составе и
реагируют по существу при адиабатных условиях. В этих случаях
конечная температура и состав реакционной смеси неизвестны.
Определить максимальную конечную температуру и максималь-
ное превращение можно при допущении, что система достигает
состояния равновесия и что химическое равновесие рассчитывает-
ся одновременно с энергетическим балансом, когда неизвестны
температура и состав.
Типичным примером этого является реакция с водяным паром,
в которой окись углерода и пар реагируют на соответствующем
катализаторе с образованием двуокиси углерода и водорода.
Большой избыток пара используется для достижения высокой сте-
пени превращения окиси углерода. Смесь пара и окиси углерода
подается в большую камеру с катализатором, которая работает
по существу адиабатно. Желательно определение максимальной
температуры и степени превращения.
Пример 5. Определить максимальную температуру и сте-
пень конверсии, достигаемые в адиабатных условиях при проте-
кании реакции
со+н2о?=^со2+нг,
если начальная температура 750 °К и подаваемый в камеру газ
содержит 20% (мол.), Н2> 6% (мол ) СО, 2% (мол.) СО2 и
72% (мол.) Н2О. Газ получается в результате предварительной
реакции между метаном и водяным паром. Принять, что общее
давление равно 1 атм и закон идеального газа выполняется в
этих условиях.
Требуемые данные по теплоте образования, абсолютной энтро-
пии и теплоемкости приведены ниже.
	со	н2о	СО2	Н2
Д Я°, 298 °К, 1 атм	—26 416	—57798	—94052	—
S° , 298% 1 атм	47,301	45,106	51,061	31,211
а	.	6,420	7,256	6,214	6,947
Ь-\№		1,665	2,298	10,396	—0,200
с-10’		-0,196	0,283	—3,545	0,481
Теплота реакции при 298 °C и 1 атм равна
ДТ/288 = —94052-1-26416 4-57798= —9838 кал/моль.
Изменение энтропии реакции при 298 ° К и 1 атм равно
AS;88 = 51,061 4- 31,211—47,301 -45,106 =—10,135 калЦмоль °К).
311
Изменения теплоемкости таковы:
Да = 6,214 + 6,947—6,420—7,255 - —0,515;
ЛЬ = (10,396—0,200 — 1,665 —2,298)  Ю"3 = 6,233-10'3;
Ас = (—3,545+ 0,481 + 0,196—0,283)-10-в = &,151  10-6-
Из уравнения (10-12) следует
ДН° = -9838 + 0,515-298——23?'10~3 (298)2 +
+ —V — (298)3 = —9934 кал/моль.
Из уравнения (10-15) получаем
Д5;= — 10,135 + 0,515 In 298—6,233 10“8 298 +
+ ?_’151_Ц£А (298)2 = — 8,92 кал!моль.
Из уравнения (10-16) следует, что
+ _	+ 8,41 +0,515In
3,151-10-® тг
6	1 •
Величины константы химического равновесия при трех тем-
пературах вычислены из этого уравнения и приведены ниже.
Г, к	A f ° Т	, ,,	А F° 1п/< «= —	К
700	—4,33	2,18	8,85
800	—2,72	1,37	3,93
900	—1,50	0,755	2,13
Число молей каждого компонента, находящегося в равнове-
сии, можно вычислить на основании того, что в конвертер посту-
пает 100 молей газовой смеси и в реакцию вступают m молей окиси
углерода:
Число молей
СО ....	6—tn
Н гО	.	.	72—m
СО2 .	.	.	7+т
Н2. .	.	.	20+т
Сумма . .	100
В этом случае общее число молей газа не зависит от степени
превращения и равновесный состав не зависит от общего давле-
ния. Подстановкой соответствующего числа молей в уравнение
(10-29) получаем соотношение между т и К-
К _ (20 4- т) (2_(-_т)_
Л ~ (6 —m)(72—т) •
312
Это квадратное уравнение может быть решено для т как функ-
ции К:
Г 1-0,284(К—0,0926) (К —1)]4
1	~	‘ (К+ 0,282)2
Щ — -----!-------------------------А—.
0,0257 (К—1)
К+ 0,282
Соотношение между т и температурой можно установить, вы-
числяя величину т для каждого значения константы равновесия,
определенного выше:
т, °к	к	т
700	8,85	5,66	0,944
800	3,93	5,46	0,910
900	2,13	4,85	0,809
Отношение ~ представляет собой долю первоначально взятой
окиси углерода, которая реагирует до установления равновесия.
Энергетический баланс. Для адиабатных стационарных систем,
в которых не производится никакой внешней механической работы,
а изменения потенциальной и кинетической энергии незначитель-
ны, АД — 0. Изменение энтальпии можно вычислить в зависимо-
сти от температуры и числа молей окиси углерода, реагирующих
по следующей схеме:
750 ° К	298 °К 298 °К Т, °К
I	6
20 молей Н2---» 20 молей Н2 . (20+т) мол. Н2 * (20+гн)мол.Нг
2	7
6 мол. СО —» 6 мол. СО\1/,(6—т) мол. СО---* (6—ли) мол. СО
5
3 8
72 мол. Н2О 72 мол Н3О	(72+т) мол. Н2О —► (72+/п)мол.НаО
4	6
2 мол. СО2----* 2 мол. СО2 (2 + т) мол. СО2--* (2 + т) мол. СО2
Вследствие большого избытка пара, используемого в этой реак-
ции, конечная температура изменяется при протекании реакции
незначительно. В небольшом интервале получающихся темпера-
тур средняя мольная теплоемкость каждого компонента между
298 °К и конечной температурой также мало изменяется и может
считаться независимой от конечной температуры. Использование
этого допущения значительно упрощает арифметические вычисле-
ния энергетического баланса.
313
Изменения индивидуальной энтальпии вычислены ниже и
сумма их приравнена к нулю:
АЯ, = 20 7 (298—750) = —63300;
ЛЯ2 = 6 7,20 (298 —750) = —19500;
\Н3 = 72 8,50  (298 —750) = — 276500;
АН4 = 2 10,70. (298 — 750) =—9700;
Сумма... — 369000;
А Я5 — — 9838 т\
АНе = (2) + ш) 7 (7—298);
ДИ7-(6 —т) 7,25(7—298);
ЛН8 = (72 — т) 8,55 (7 — 298);
АЯ9 = (2+т) 10,75(7—298).
Изменение общей энтальпии в зависимости от т и 7 можно
выразить соотношением
820 (7 —298)—369000 —9838 т +1,95 (7 — 298) т = 0.
Это уравнение можно решить относительно прореагировавшей
части окиси углерода как функции конечной температуры
т 136,8(7 — 298) —61500
6 “ —1795(7 — 298)+9838 "
Это уравнение представлено графически
иа рис. 60. Максимальная температура
и превращение определяются пересече-
нием кривой уравнения энергетическо-
го баланса с кривой равновесного со-
стояния. Адиабатная реакционная тем-
пература составляет 807 °К и равно-
весное превращение равно 0,905. Соот-
ветствующая величина т равна 6-0,905,
т. е. 5,43. Равновесный состав реак-
ционной смеси [% (мол.)] определен
ниже.
Рис. 60. Зависимость кон-
версии окиси углерода от
адиабатной температуры ре-
акции;
/—кривая равновесия; 2—энергети-
ческий баланс
СО................ 6—5,43=0,57
Н2О.........	72—5,43=66,57
СО2 ....	2+5,43=7,43
Н2 ......... 20+ 5,43=25,43
Задачи
1.	Определить значение константы равновесия химической реакции
N2+O2^zl±2NO
при 2000 °C, принимая за стандартное состояние для каждого чистого компо-
нента фугитивность, равную единице при температуре системы.
314
2.	Определить равновесный состав системы, первоначально состоящей
из 21% (мол.) кислорода и 79% (мол.) азота, нагретой до 2000 °C при 1 атм
Предположить, что газ ведет себя как идеальный.
3.	Определить давление, необходимое для получения 25% (мол ) аммиака
в реакционной смеси при 500 °C, если исходная газовая смесь содержит водо-
род и азот в отношении 3:1;
а)	принять, что газ ведет себя как идеальный для всех компонентов при
всех давлениях;
б)	принять, что реакционная смесь образует идеальный раствор, но закон
идеального газа не выполняется.	'
4.	Газовая смесь, содержащая 10% (мол.) SO2, 11% (мол.) О2 и 79% (мол )
N2, поступает в контактный аппарат прн 400 °C и 1 атм. Предполагая, что
реактор работает адиабатно и при постоянном давлении, рассчитать макси-
мальную температуру выходящего газа и степень превращения SO2 в SO,.
5.	Определить состав системы, если эквимольиая смесь СОа н Н2О при-
ходит в равновесие при 1000 °К н давлении 1 атм. Расчет произвести при
условии, что одновременно протекают следующие реакции:
СО2 < —l СО-|-~у" 02
и
СО Н2О < ? СО2 Н2
ЛИТЕРАТУРА
1.	Am. Petrol. Inst. Bull., 44, 1953.
2.	Arnold C. W„ Kobe K- A. Chem. Eng. Progr., 1952, 48, 293.
3.	A s t о n J. G., Fritz J. J. Thermodynamics and Statistical Ther-
modynamics, Inc., New York, 1959.
4.	В e a t t i e J. A., Bridgeman О. C. J. Am. Chem. Soc., 1927, 49,
1665; 1929. 51, 19; Proc. Am. Acad. Arts. Sci., 1928, 63, 229.
5.	Beattie J. A., Ikehara S. Proc. Am. Acad. Arts. Sci., 1930, 64,
127—176.
6.	Benedict M., Webb G. B., Rubin L. C. Chem. Eng. Progr ,
1951, 47, 419—422.
7.	Benedict M., Webb G. B., R u b i n L. C Chem. Eng. Progr.,
1951, 47, 449.
8.	Benedict M., Webb G. B., Rubin L C, Friend L. Chem.
Eng., Progress, 1951, 47, 571—584.
9.	Benedict M., Webb G. B., Rubin L. C., Friend L. Chem
Eng. Progress, 1957, 47, 609—619.
10.	В r u n a u e r S., EmmettP. H. and Teller E., J. Am. Chem.
Soc., 1938, 60, 309.
11.	Cooley J. P., Rohrbaugh J. H., Phys. Rev., 1945, 67, 296.
12.	Cullen E. J., Kobe K- A. AIChE J., 1955, 1, 452.
13.	DePriester C. L Chem. Eng. Progr. Symposium Ser., 1953, 7, 49.
14.	D о d g e B. F. Chem. Eng. Thermodynamics, McGraw-Hill Book Compa-
ny, Inc., New York, 1944
15.	D о 1 e, M a 1 k о 1 m. Introduction to Statistical Thermodynamics, Pren-
tice-Hall, Inc., Englewood Cliffs, N. J., 1954.
16.	E d m i ste r W. C., Ruby L. R. Chem. Eng. Progr., 1955, 51, 95F—100F.
17.	Eyring Henry, Walter John and Kimball George E.
Quantum Chemystry, Inc., New York, 1949.
18.	Felsing W. A., Watson G. M. J. Am. Chem. Soc., 1943, 65, 1889.
19.	Gurney R. W. Introdaction to Statistical Mechanics, McGraw-Hill
Book Company, Inc, New York, 1949.
20.	H a 1 1 N. A., I b e 1 e W. E. Engineering Thermodynamics, Prentice-
Hall, Inc., Englewood Cliffs N. J., I960.
21.	Henely E. J., Bieber H., Chemical Engineering Calculations
McGraw-HiH Book Company, Inc., New York, 1959.
315
22.
23.
24.
25.
26.
27.
23.
29-
30.
31.
32.
33
34.
35
36
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47,
48.
49.
50.
51
52
53.
54.
316
Herzberg F. R. S. Molecular Spectra and Molecular Structure. 1»
Spectra of Diatomic Molecules, D. Van Nostrand Company, Inc., 1950;
2, Infrared and Raman Spectra of Polyatomic Molecules, D Van Nostrand
Company, Inc., 1945.
Hirshf elder J. O., Curtiss C. F., Bird R. B. Molecular
Theory of Gases and Liquids, Inc., New York, 1954.
Hougen О A., Watson К. M., Ragatz R. A. Chemical
Process Principles, Part 1, Material and Energy Balances, 2nd Ed., Inc.,
New York, 1954
Hougen O. A., Watson К- M., Ragatz R. A. Chemicat
Process Principles, Part 2, 2nd Ed., Inc., New York, 1959.
Huff V. N„ Gordon S., Morell V. E. NACA, Report 1037.
Lee J. F., Sears F. W. Thermodynamics, Addison-Wesley Publi-
shing Company, Inc., Reading, Mass, 1955.
Lewis G. N., Randall M., Pitzer K- S., Brewer L.
Thermodynamics 2nd Ed., McGraw-Hill Book Company, Inc., New York,
1961.
Li J. С. M., Pitzer R. S. J. Phys. Chem., 1956, 60, 466.
Lydersen A. L., Greencorn R. A., Haugen O. A. Univ,
of Wis. Eng. Exp. Station, Report No 4, 1955.
Obert Edward, Concepts of Thermodinamics, McGraw-Hill Book
Company, Inc., New York, 1960.
Pauling, Linus, Wilson. Introduction to Quantum Mechanics,
McGraw-Hill Book Company, Inc., New York, 1935.
Perry, John H. Editor. Chemical Engineers' Handbook, 3rd
Ed., McGraw-Hill Book Company, Inc., New York, 1950,.
Pitzer K- S., Gwinn W. D. J. Chem. Phys., 1942, 10, 428.
Reamer H. H., Sage В H Lacev W. N. Chem and E.ng.
Data, 1960, 5, 44-—50.
R i b a u d M. G. Pubis, sci. et techn., ministere d'air (France), No. 266,
1952.
Sage В. H. Ind. Eng. Chem., 1950, 42 , 631—637.
Seifearth J. H., Ioffe J. Ind. Eng. Chem., 1952 , 44, 2894
S 1 e d j e s к i E. W. Ind. Eng. Chem., 1951, 43, 2913.
Smith L. B., Beattie J A., Kay W. C. J. Ain. Chem. Soc.,
1937, 59, 1587.
Smith J. M., Van Ness H. C. Introduction to Chemical Enginee-
ring Thermodynamics, 2nd Ed.. McGraw-Hill Book Chompany, Inc., New
York, 1959.
Spencer H. M. J. Am. Chem. Soc., 1934, 56, 2311.
Spencer H. M. J. Am. Chem. Soc., 1942, 64, 2511.
Spencer H. M. J. Am. Chem. Soc., 1945, 67, 1859.
Spencer H. M. Ind. Eng. Chem., 1948, 40, 2152.
Taylor H. S., Glasstone S Treatise on Physical Chemistry,
Vol 2. States of Matter, 3rd Ed., D. Van Nostrand Company, Inc., Prince-
town, N. J., 1951.
U. S. National Bureau of Standards, «Selectid Values of Properties of Hydro-
carbons», Circular, 461, 1947.
U. S. National Bureau of Standards, «Selected Values of Chemical Properties,
Circular», 500, 1952.
U. S. National Bureau of Standards, «Tables of Thermal Properties of Ga-
ses», Circular 564, 1955.
U. S. National Bureau ol Standards, «Selesteds Values of Chemical Ther-
modinamic Properties», Series 3.
Weiss A. H., J о f f e J. Ind. Eng. Chem., 1957. 49, 120,
Wilson E. D., Ries H. C. Principles of Chemical Engineering
Thermodynamics, McGraw-Hill Book Company, Inc., New York, 1956.
Wilson R. Q, Munger H. P. and Clegg J. W. Chem Eng.
Progress Symposium Series, No. 3, Vol 48, 115, 1952.
Wohl K- Trans. ALCbE, 1946, 42, 215.
Приложения
Приложение 1'
МОЛЬНЫЕ ТЕПЛОЕМКОСТИ ГАЗОВ В ИДЕАЛЬНОМ СОСТОЯНИИ.
ка«/(жо.«> °К) [брит. тепл. ед./(фунт-моль-ср)]
По данным работы [49]							
7. К	*		СО	Ог	NO	H2O	СО2
300	6.894	6,961	6.965	7,024	7,134	8,027	8,895
400	6,975	6,991	7,013	7,196	7,162	8,186	9,877 •
500	6.993	7,070	7,120	7,431	7,289	8,415	10,665
600	7,009	7,196	7,275	7,670	7,468	8,676	11,310
700	7,037	7,351	7,450	7,884	7,657	8,954	11,846
800	7,080	7,513	7,625	8,063	7,833	9,245	12,293
900	7,150	7,670	7,786	8,212	7,990	9,546	12,667
1000	7,219	7,815	7,931	8,336	8,126	9,850	12,980
1100	7,309	7,945	8,056	8,440	8,243	10,151	13,243
1200	7,406	8,060	8,161	8,527	8,342	10,444	13,465
1300	7,511	8,162	0,263	8,608	8,462	10,723	13,656
1400	7,617	8,250	8,344	8,674	8,498	10,986	13,815
1500	7,720	8,328	8,418	8,739	8,560	11,233	13,952
		По данным работы [50]				По данным оаботы ГЗА 1	
т. °к	HCI	j С12	Has	so2	so3		NH.,
300	6,964	8,119	8,20	9,54	12	13	8,54
400	6,973	8,438	8,53	10,39	14,06		9,21
500	7,004	8,624	8,93	11,12	15,66		9,95
600	7,068	8,742	9,35	11,71	16,90		10,69
700	7,167	8,822	9,78	12,17	17,86		11,42
800	7,289	8,880	10,21	12,53	18,61		12,14
900	7,423	8,924	10,62	12,82	19,23		12,81
1000	7,560	8,960	11,00	13,03	19,76		13,43
1100	7,693	8,990	11,34	13,20	20,21		13,99
1200	7,819	9,015	11,64	13,35	20,61		14,52
1300	7,936	9,038	11,92	13,47	20,96		15,00
1400	8,043	9,059	12,16	13,57	21	28	15,43
1500	8,141	9,078	12,37	13,65	21	58	15,83
317
Приложение 2
МОЛЬНЫЕ ТЕПЛОЕМКОСТИ ГАЗОВ В ИДЕАЛЬНОМ СОСТОЯНИИ
С* =а ЬТ-\-сТг (298	1500 “К, максимальное отклонение 2%) [42—45]
Соединенно	Формула	a	b-103	c-10'
Воздух .				6,557	1,477	—0,2148
Аммиак		NH3	6,086	8,812	—1,506
Бром		Вг2	8,4228	0,9739	—0,3555
Двуокись углерода		со2	6,214	10,396	—3,545
Окись углерода . .	...	СО	6,420	1 665	—0,196
Хлор		С1,	7,5755	2,4244	—0,9650
Водород	 ...	Н2	6,9469	—0,1999	0,4808
Бромистый водород		НВг	5,5776	0,9549	0,1581
Хлористый водород		НС1	6,732	0,4325	0,3697
Сероводород . . . .	.....	H2S	6,662	5,134	—0,854
Азот . . . •		n2	6,4492	1,4125	—0,0807
Окись азота		NO	6,440	2,069	—0,4206
Закись азота ...	...	N»O	6,529	10,515	—3,571
Кислород		o2	6,0954	3,2533	—1,0171
Фосфин . .	PH3	4,496	14,372	—4,072
Двуокись серы ....	so2	7,116	9,512	—3,511
Серный ангидрид		so3	6,077	23,537	—9,687
Вода		H2O	7,256	2,298	1 ,283
Метан		CH4	3,381	18,044	—4 500
Этан . .	C2H6	2,247	38,201	—11,049
Пропан 		CsH8	2,410	57,195	—17,533
и-Бутан		C^Hjo	4,453	72,270	—22,214
2-Метилпропан		QH10	3,332	75,214	—23,734
н-Пентан ...	.....	GbHla	5,910	88,449	—27,388
н-Гексан 		CaH14	7,477	104,422	—32,471
н-Гептан ,		C,Hle	9,055	120,352	—37,528
и- Октан		Cs'ijg	10,626	136,298	—42,592
Этилен	 ....	C2H4	2,830	28,601	— 8,726
Пропилен			C3H3	3,253	45,116	—13,740
1-Бутен		C4H,	5,132	61,760	—19,322
Цис-2 Бутен		c4H8	1,625	64,836	—20,047
транс-2-Бутен ...	C4H8	4,967	59,961	— 18,147
Ацетилен		C2H2	7,331	12,622	— 3,889
Пропин 		C3H4	6,334	30,990	— 9,457
2-бутин		QHj	5,700	48,207	—14,479
Бензол 		C,He	—0,409	77,621	—26,429
Толуол 		C8H5CH3	0,576	93,593	—31,227
Стирол 		CgH8	4,074	99,731	—33,108
Циклопентан	 Циклогексан	 Метилциклогексан .	. . Формальдегид	 Ацетальдегид	 Ацетон	 Этанол Метанол *		CsHjo C6H12 C6HUCH3 HCHO CH3CHO (CH3)2CO C2H6OH CH3OH	—5,763 —7,701 —4,624 4,498 7,422 5,371 6,990 4,398	97,377 125,675 140,877 13,953 29,029 40,227 39,741 24,274	—31,328 —41,584 —46,698 — 3,730 — 8,742 —15,182 —11,926 — 6,855
Примечание, а, Ь, с—эмпирические постоянные.
• Для температуры 273—1000 °К-
I
СРЕДНЯЯ МОЛЬНАЯ ТЕПЛОЕМКОСТЬ ГАЗОВ МЕЖДУ 299 °К и 7”К*. кал/(моль-°К)[брит. тепл. ед.Дфунт-моль •’!?)]
О)
S
Ж
О)
Я
О
Рассчитано по данным приложения
319
Приложение 4
ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА ЧИСТЫХ ВЕЩЕСТВ ПРИ 25 °C (298.16 °К)
И ДАВЛЕНИИ 1 атм ГАЗООБРАЗНЫХ ВЕЩЕСТВ В ИДЕАЛЬНОМ СОСТОЯНИИ [48]
Соединение	Формула	Состояние	ДНО ккал/моль	S" кал/(моль^ °К)	ДНО ккал/мо гь
Хлористый	А1С13	Твердое	—166,2	40	—152,2
алюминий					•
Окись алюми-	АЦОз	»	—399,09	12,186	—376,77
НИЯ					
Сернокислый	ai2(so4)3	»	—820,98	57,2	—738,99
алюминий					
Аммиак	NH;i	Газообразное	—11,04	46,01	— 3,976
Аргон	Аг	То же	0	36,983	0
У глекислый	ВаСО3	Твердое	—291,3	26,8	—272,2
Хлористый	ВаС12		—205,56	30	—193,8
барий					
Окись бария	ВаО	»	—133,4	16,8	—126,3
Сернокислый	BaSO4		—350,2	31,6	—323,4
барий					
Борная кисло-	Н3ВО3	»	—260,2	21,41	—230,2
та					
Бор	В	»	0,000	1,56	0,000
		Газообразное	+97.2	36,649	+ 86,7
Бороэтан	в,не	То же	+ 7,5	55,66	+ 19,8
Окись бора		Твердое	—302,0	12,91	—283,0
Хлористый бор	ВС13	Газообразное	— 94,5	69,29	— 90,9
		Жидкое	— 100 0	50,0	— 90,6
Бром	Вга	Газообразное	+ 7,34	58,639	+ 0,751
		Жидкое	0	36,4	0
Карбид каль-	СаС2	Твердое	— 15,0	16,8	— 16,2
ция					
Хлористый	СаС12	»	—190,0	27,2	—179,3
кальций					
Гидрат окиси	Са(ОН).,	»	—235,80	18,2	—214,33
кальция					
Окись кальция	СаО		— 151,9	9,5	—144,4
Фосфорнокис-	Са3(РО4)2		—986,2	57,6	—929,7
лый кальций					
Графит	С	»	0	1,3609	0
()кись углеро-	СО	Газообразное	— 26,4157	47,301	— 32,8079
Да					
Двуокись угле-	СО2	То же	— 94,0598	51,061	— 94 2598
рода					
Сероуглерод	cs2		-|- 27,55	56,84	+ 15,55
		Жидкое	-1- 21,0	36,10	+15,2
Четыреххло-	СС|4	Газообразное	— 25,50	73,95	—15,3
рпстый углерод					
		Жидкое	— 33,3	51,25	—16,4
Хлор	С12	Газообразное	0	53,286	0
Окись хрома	Сг2О3	Твердое	—269,7	19,4	—250,2
Окись меди	СиО	»	— 37,1	10,4	—30,4
Закись меди	Си2О	»	— 39,84	24,1	—34,98
320
Продолжение прилож. 4
* Соединение	Формула	Состояние	ДН'^ ккал! моль	о о о 5 О 1 со S	де» ккал/моль
Фтор	f2	r r	! Газообразное	0	48,6 I	0
Гелий	Не	To же	0	30,126	0
Водород	Н2	»	0	31,211	0
Бромистый	НВг	»	— 8,66	47,437	— 12,72
водород					
Хлористый	НС1	To же	—22,063	44,617	—22,769
Цианистый во-	HCN	»	+31,2	48,23	+28,7
дород			+25,2		
		Жидкое		26,97	+29,0
Фтористый водо-	HF	Газообразное	- 64,2	41,47	—64,7
род Йодистый во-	HJ	»	+ 6,20	49,314	+0,31
дород Вода	н,о	»	—57,7979	45,106	—54,6357
		Жидкое	—68,3174	16,716	—56,6902
Сероводород	H2S	Газообразное	— 4,815	49,15	— 7,852 ‘
Йод	+	То же Твердое	+ 14,876 0	62,280 27,9	+ 4,63 0
Закись—-окись	Fe3O4	»	—267,0	35,0	—242,4
железа					
Окись железа	Fe2O3	»	—196,5	21,5	—177,1
Хлористый	РЬС12	»	— 85,85	32,6	— 75,04
свинец					
Окись свинца	PbO	»	— 52,07	16,6	— 45,05
(желтая]	PbO2		— 66,12		— 52,34
Двуокись		»		18,3	
свинца					
Сернокислый	PbS04	»	—219,50	35,2	—193,89
свинец			— 22,54		
Сернистый свинец	PbS	»		21,8	— 22,15
Фтористый	LiF	»	—146,3	8,57	—139,6
литий					
Окись магния	MgO	»	— 143,84	6,4	—136,13
Сернокислый	MgSO4		—305,5	21,9	—280,5
магний					
Двуокись мар	MnO2	»	—124,5	12,7	—111,4
ганца					
Ртуть	Hg	Г азообразное	-|- • 14,54		41,80	+7,59
Неон	Ne	То же	0	34,948	0
Закись никеля	NiO	» Твердое	+ 59,3 — 58,4	57 9,22	-4-51,8 —51,7
Азотная кис-	HN03	Жидкое	— 41,404	37,19	—19,100
лота					
Окись азота	NO	Газообразное + 21,600		50,339	+20,719
Азот	4	То же	0	45,767	0
Закись азота	n2o	Г азообразное	1 + 19,49	52,58	+24,76
Двуокись азо- та	no2	То же	| + 8,091 1	57,47	+12,390
21—1503
321
Продолжение прилож. 4
Соединение	Формула	Состояние	Д//и ккал/моль	SO кал/{моль-°К)	Д/™ ккал/моль
Четырехокись	NaO4	Газообразное	4- 2,309	72,73	423,491
азота Кислород	о2	»	0	49,003	0
Озон	Оз	»	4-34,0	57,09	4-38,9
Фосген	СОС1,	»	—53,30	69,13	—50,31
Фосфор	р	»	4-75,18	38,98	4-66,71
Фосфор	р2	»	4-33,82	52,13	4-24,60
Фосфор	₽4	»	4-13,12	66,90	4- 5,82
Фосфин	РН8	»	4- 2,21	50,2	4- 4,36
Пятихлорис-	РС16	»	—95,35	84,3	—77,59
гый фосфор Хлорокись	РОС13	»	—141,5	77,59	—130,3
фосфора Трехбромис-	PBrs	»	—35,9	83,11	—41,2
тын фосфор Треххлористый фосфор Бромистый	РС1з	»	—73,22	74,49	—68,42
	КВг	Твердое	-93,73	23,05	—90,63
калий Хлорновато-	KCIOs	»	—93,50	34,17	—69,29
кислый калий Хлористый ка-	КС1	»	—104,175	19,76	—97,592
ЛИЙ Йодистый ка-	KJ	»	—78,31	24,94	—77,03
ЛИЙ Карбид крем-	SiC	»	—26,7	3,935	—26,1
НИЯ Четыреххло-	SiCl,	Жидкое	—153,0	57,2	— 136,9
ристый кремний Двуокись	SjOs	Газообразное Твердое	—145,7 —205,4	79,3 10,00	—136,2 —192,4
Бромистое се- ребро Хлористое се-	AgBr	»	—23,78	25,60	—22,930
	AgCl	»	—30,362	22,97	—26,224
ребро Йодистое се-	AgJ	»	—14,91	27,3	—15,85
ребро Азотнокислое	AgNOg	»	—29,43	33,68	— 7,69
серебро • Натрий	Na	Газообразное	4-25,98	36,715	4-18,67
Хлористый	NaCl	Твердое	—98,232	17,30	—91,785
натрий Едкий натр	NaOH	»	—101,99	—	—90,60
Азотнокислый	NaN03	»	—111,54	27,8	—87,45
натрий Двуокись серы	SO2	Газообразное	—70,96	59,40	—71,79
322
Продолжение прилож 4
Соединение	Формула		Состояние		дну ккал/моль		S0 калКмоль- °К)		дгу ккал/моль	
Серный ангид- рид Серная кислота Двуокись оло- ва Окись олова Титан Четыреххло- ристый титан Двуокись ти- тана Двуокись ура- на Шестифторис- тый уран (гек- сафторид урана) Трехокись ура- на Пятиокись ва- надия Окись цинка	so3 HjSO* SnO2 SnO Ti TiCl4 TiO2 uo2 UFe uo3 v2o6 ZnO		Газообразное Жидкое Твердое » » Жидкое Твердое » Газообразное Твердо? » » »		—94,45 —193,91 —138,8 —68,4 +112 —179,3 —218,0 —270 —505 —517 —302 —373 — 83,17		61,24 12,5 13,5 43,069 60,4 12,01 18,6 90,76 54,45 23,57 31,3 10,5		—88,52 —124,2 —61,5 + 101 —161,2 —203,8 —257 —485 —486 —283 —344 —76,05	
Соединение	формула	Состояние		ккал/моль		ккал/моль		о со	£ о •о §	ккал/моль
Метан Этан Пропан н-Бутан Изобутан н-Пентан н-Гексан н-Гептан	CH4 c2H6 c3Hs C4H10 c4hw CsHjg CeH14 C,HJ6	Газообразное To же » » » » /Кидкое Г азообразное /Кидкое Газообразное		—212,798 —372,820 —530,605 -687,982 —686,342 —845,16 —838,80 —1002,57 —995,01 —1160,01		—17,889 —20,236 —24,820 —29,812 —31,452 —35,00 —41,36 —39,96 —47,52 —44,89		44,50 54,85 64,51 74,10 70,42 83,27 62,79 92,45 70,34 101,64		—12,140 — 7,860 — 5,614 — 3,754 — 4,296 — 1,96 — 2,21 + 0,05 ! — 0,91 + 2,09
21
323
Пройолжение прилож. 4
Соединение	Формула	Состояние	д//° с кка.ч/моль	Аш ккал/моль	so Kai/(M0ib' °К)	дг» ккал/молъ
н-Гептан	с,н1е	Жидкое	— 1151,27	—53,63	77,92	+ 0,42
н Октан	с8н18	Газообразное	—1317,45	—49,82	110,82	+ 4,14
		Жидкое	— 1307,53	—59,74 ,	85,50	+ 1,77
Этилен	С2Н4	Газообразное	—337,234	+ 12,496	52,45	4-16,282
Пропилен	С3н„	То же	—491,987	+4,879	63,80	4-14,990
1 Бутен	С4П8	»	—649,757	4 0,280	73,48	1*17,217
] 1,ис-бутен	С4Н8	»	—648,115	—1,362	71,90	+ 16,046
Траис-2-бутен	С4Нв	»	—647,072	—2,405	70,86	4 15,315
Изобутен	С4Н„	»	—646,134	—3,343	70,17	+ 14,582
1 Пентен	с6н10	»	—806,85	—5,000	83,08	+ 18,787
1 Гексеи	СвН12		—964,26	—9,96	92,25	4-20,80
1 Гептен	с,н14		—1121,69	—14,89	101,43	4-22,84
ГОктен			—1279,13	— 19,82	110,61	+24,89
Ацетилен	С2Н2		—310,620	+54,194	47,997	+50,000
Бензол	СвНв	»	—789,08	+ 19.820	64,34	4-30,989
		Жидкое	-780,98	4 11,718	41,30	4-29,756
Толуол	С,Н8	Газообразное	—943,58	+ 11,950	76,42	+29,228
		Жидкое	- 934,50	4 2,867	52,48	4 27,282
Этилбензол	CgHn,	Газообразное	— 1101,13	+7,120	86,15	+31,208
		Жидкое	—1091,03	—2,977	60,99	+28,614
Стирол	СзНе	Газообразное	— 1060,90	1-35,22	—	—
Формальдегид	СН2О	То же	—134,67	—27,7	52,26	—26,2
Муравьиная кислота	СН2О2	» Жидкое	+ 75,70 + 64,57	—86,67 —97,8	60,0 30,82	—80,25 —82.7
Ацетальдегид	С2Н4О	»	—284,98	—39,76	63,5	—31,96
Уксусная кис- лота	С2Н4О2	»	—219,82	116,4	38,2	—93,8
Ацетон	с3н6о	»	—435,32	—44,3	63,72	—27,3
Этанол	С2Н„О	»	—336,82	—56,24	67,4	—40,30
		Жидкое	—326,70	—66,356	38,4	—41,77
Этиленгликоль	С2Н6О2	»	—284,48	—108,58	39,9	—77,12
Окись этилена	С2Н4О	Газообразное	—	—12,19	58,1	— 2,79
Четанол	СН4О	То же	—182,59	—48,16	56,8	—38,70
		ЖВДкое	—173,65	—57,036	30,3	—39,75
324
Приложение 5
КРИТИЧЕСКИ" СВОЙСТВА., ТОЧКА КИПЕНИЯ И СКРЫТАЯ ТЕПЛОТА ИСПАРЕНИЯ
[33, 52]
Соединение	Критическая температура, ° К	Критическое давление, атм	Точка кипения при 1 атм, °К	Скрытая теп- лота испарения при 1 атм ккал/молъ
Аммиак ......	405,6	111,5	239,8	5,581
Бром	584	102	331	7,420
Двуокись углерода . .	304,1	72,9	194,7	6,100
Сероуглерод . .	546,2	76	319,5	6,400
Окись углерода .	133,0	34,53	81,7	1,444
Четыреххлористый угле				
род		556,4	45,0	349,7	7,170
Хлор	417	76,1	239,1	4,878
Фтор .	118	25,0	85,2	1,510
Водород ...	33,24	12,797	20,39	0,216
Бромистый водород . .	363	84	206,4	4,210
Хлористый водород . .	324,6	81,6	188,1	3,860
Цианистый водород . . .	456,7	50,0	298,86	6,027
Фтористый водород . . .	—	—	293,1	1,800
Йодистый водород . . .	424,2	82,0	237,8	4,724
Сероводород ...	373,6	88,9	212,8	4,463
Окись азота 		179	65	121,4	3,292
Азот		126,0	33,5	77,36	1,333
Закиси азота .	309,7	71,7	184,7	3,956
Кислород . .	154,78	50,14	90,19	1,630
Фосген		455,0	56	280,7	5,832
Фосфин		324,5	64,5	185,4	3,490
Двуокись серы	430,4	77,7	263,1	5,950
Серный ангидрид .	491,5	83,8	316,5	9,990
Вода		647,3	218,4	373,2	9,717
У глеводороды
Метан		191,0	45,8	111,67	1,955
Этилен		282,5	50,0	169,5	3,237
Этаи ....	305,5	48,2	184,5	3,517
Ацетилен	308,7	61,6	184,7	4,270
Пропилен . .	364,9	45,6	225,5	4,405
Пропан		370,0	42,0	231,1	4,487
Изобутан	408,15	36,0	261,4	5,089
н Бутан .	...	425,2	37,5	272,7	5,350
1 Бутен .	419,7	39,6	266,9	5.240
Цис-бутен .	428,2	40., 8	276,9	5,580
Транс-2-бутен	428,2	40,8	274.05	5,440
it Пентан . .	470,1	33,3	309,2	6,160
1 -Пентен . .	474	40	303,1	
н-Гексан . .	507,9	29,9	341,9	6,900
н-Гептан 		540,2	27,0	371,6	7,580
н-Октан . .	569,4	24,6	398,8	8,215
2,2,4-триметил пентан .	544	25,4	372,4	7,410
Бензол 		562,1	48,3	353,3	7,350
Толуол г .	593,8	41,6	383,8	8,000
Циклопропан	398	54	240,2		
Циклопентан .	511,8	44,6	322,4	6,525
Циклогексан . .	553,8	40	353,9	7,190
Метилциклогексан	572,3	34,32	373,1	7,580
325
Продолжение прилож. 5
Соединение
| Критическая
температура, °К
Критическое 1Точка кипения
давление, атм при 1 атм, ° К
Скрытая тепло-
та испарения
при 1 атм
ккал/моль
С Н.О-С оединения
Ацетальдегид ...	. .	461	44	293,3	6,500
Уксусная кислота . .	594,8	57,1	391,4	5,830
Ацетон		508,7	46,6	329,35	7,100
Этиловый спирт	516	63,0	351,7	9,220
Этиловый эфир		467,0	35,6	307,8	6,220
Окись этилена . .	469	71	283,7	6,101
Метиловый спирт ....	513,2	78,5	337,9	8,430
Метиловый эфир . . .	400,1	53	248,3	5,141
Изопропанол		509	53	355,36	9,650
п-Пропанол		537	50,2	370 ,‘5	9,890
	Галогениды			
Дихлордифтормета! । . . .	384	39,6	242,7	4,850
Хлористый метил ....	416,3	65,9	248,9	5,150
Фтористый метил . . .	317,8	58,0	195,1	4,230
Трихлорметан		536	55	334,4	7,020
Приложение 6
ЗНАЧЕНИЯ ПОСТОЯННЫХ [атм, л,моль, °К) В УРАВНЕНИИ СОСТОЯНИЯ
ИТТИ-БРИДЖЕМАНА ДЛЯ НЕСКОЛЬКИХ ГАЗОВ [46]
Г.,3	Ао	а	Во	ь	СХ 10~i
Не	0,0216	0,05984	0,01400	0,0	0,0040
N<	0,2125	0,02125	0,02060	0,0	0,101
Аг	1,2907	0,02328	0,03931	0,0	5,99
Н2	0,1975	0,00506	0,02096	—0,04359	0,504
N2	1,3445	0,02617	0,05046	—0,00691	4,20
О2	1,4911	0,02562	0,04624	0,004208	4,80
Воздух	1,3012	0,01931	0,04611	—0,01101	4,34
I»	17,0	0,0	0,325	0,0	4000
со2	5,0065	0,07132	0,10476	0,07235	66.00
NH3	2,3930	0,17031	0,03415	0,019112	476,87
СН4	2,2769	0,01855	0,05587	—0,15870	12,83
с.,н4	6,1520	0,04964	0,12156	0,03597	22,68
с8не	5,8800	0,05861	0,09400	0,01915	90,00
с3н8	11,9200	0,07321	0,18100	0,04293	120,00
1-С4Н8	16,6979	0,11988	0,24046	0,10690	300,00
изо-С4Нв	16,9600	0,10860	0,24200	0,08750	250,00
н-С4Н] q	17,7940	0,12161	0,24620	0,09423	350,00
изо-С4Н1и	16,6037	0,11171	0,23540	0,07697	300,00
и QHW	28,2600	0,15099	0,39400	0,13960	400,00
изо-С6Н12	23,3300	0,15174	0,33560	0,13358	400,00
н-С,Н1в	54,520	0,20066	0,70816	0,19179	400,00
СН3ОН	33,309	0,09246	0,60362	0,09929	32,03
(С2НГ))2О	33,278	0,12426	0,45446	0,11954	33,33
326
ПРИЛОЖЕНИЕ 8
температуры.
Приложение ?
ЭМПИРИЧЕСКИЕ ПОСТОЯННЫЕ (атм, Ммоль, ’К) В УРАВНЕНИИ БЕНЕДИКТ-ВЕБВ-РУБИНА [6].
ГАЗОВАЯ ПОСТОЯННАЯ. Я=0,08207; 7=273,13+/ (°C)
Газ	Ао	в»	Со-10“«	а	Ь	г 10“«	а юз	у. 102
Метан		1,85500	0,0426000	0,0225700	0,494000	0,00338004	0,00254500	0,124359	0,60000
Этилен 		3,33958	0,0556833	0,131140	0,259000	0,0086000	0,021120	0,178000	0,92300
Этан		4,15556	0,0627724	0,179592	0,345160	0,0111220	0,0327670	0,243389	1,18000
Пропилен ....	6,11220	0,0850647	0,439182	0,774056	0,0187059	0,102611	0,455696	1,82900
Пропан		6,87225	0,0973130	0,508256	0,947700	0,0225000	0,129000	0,607175	2,20000
нэо-бутан ....	10,23264	0,137544	0,849943	1,93763	0,0424352	0,286010	1,07408	3,40000
изо-бутилен . . .	8,95325	0,116025	0,927280	1,69270	0,0348156	0,274920	0,910889	2,95945
н-бутан ...	10,0847	0,124361	0,992830	1,88231	0,0399983	0,316400	1,10132	3,40000
и ‘ пентан		12,7959	0,160053	1,74632	3,75620	0,0668120	0,695000	1,70000	4,63000
н-пентан 		12,1794	0,156751	2,12121	4,07480	0,0668120	0,824170	1,81000	4,75000
н-гексан		14,4373	0,177813	3,31935	7,11671	0,109131	1,51276	2,81086	6,66849
н-гептан		17,5206	0,199005	4,74574	10,36475	0,151954	2,47000	4,35611	9,00000
1966 г.
ВЫЙДЕТ В СВЕТ
2-ИСПРАВЛЕННОЕ И ДОПОЛНЕННОЕ ИЗДАНИЕ
МОНОГРАФИИ ЕСИНА О. А. И ГЕЛЬДА П. В.
«ФИЗИЧЕСКАЯ ХИМИЯ
ПИРОМЕТАЛЛУРГИЧЕСКИХ ПРОЦЕССОВ»».
Ч. II
За первое издание этой книги, вышедшей в 1S54 г.
авторам присуждена Международная премии им. Баха.
В монографии дается обстоятельное изло-
жение основ теории процессов получения стали
и обобщается опыт работы советской школы
теоретической металлургии.
Во второй части монографии рассматривают-
ся условия равновесия твердых и жидких фаз»
структурные особенности жидких металлов, сте-
кол и расплавленных шлаков; условия равнове-
сия, механизм и скорость взаимодействия газов
с жидкими металлами и шлаками. Значительное
внимание уделяется молекулярно-кинетическому
анализу различных реакций и взаимодействий с
участием жидких фаз.
Ориентировочный объем книги 50 л.,
цена 3 р. 25 к.
Редактор издательства М II. Заславская
Технический редактор В В. Михайлова
Бумага ,60X90i/i(j 10 254-1 вкл
от 26/V111 1966 г.
Сдано в производство 29/XII 1965 г.
Подписано в печать 26/VIII 1966 г.
—0,13= 10,38 бум. л. 20,75 печ. д.
Уч.-изд- л. 18,31
Заказ 1503 Изд. № 4447
Тираж 8500 экз.
Теыплан 196б п. 36
Цена 1 руб 57 ко
Издательство «Металлургия»
Москва Г-34, 2 й Обвденскин пер., 14
Московская типография № 21. Угрешская ул.» 12