Экстремальные задачи теории приближения - Корнейчук Н.П.

Глава 1. Постановка задач и общие свойства наилучшего приближения
§ 1.2. Общие свойства наилучшего приближении
§ 1.3. Общие теоремы существования и единственности элемента наилучшего приближения
Глава 2. Двойственность экстремальных задач в линейных нормированных пространствах
§ 2.2. Теоремы двойственности в случае приближения конечномерным подпространством
§ 2.3. Соотношения двойственности в случае приближения выпуклым замкнутым множеством
§ 2.4. Критерии элемента наилучшего приближения, вытекающие из соотношений двойственности
Глава 3. Наилучшее приближение фиксированного элемента в пространствах $C$ и $L_p$
§ 3.4. Критерии ближайшего элемента в $C$ и $L_p$ в случае приближения замкнутым выпуклым множеством
§ 3.5. Функции Бернулли и их наилучшее приближение тригонометрическими полиномами в метрике $L$
Глава 4. Наилучшее приближение на классах сверток
§ 4.2. Двойственные соотношения для классов сверток
§ 4.3. Приближение классов сверток тригонометрическими полиномами
§ 4.4. Наилучшие линейные методы для классов сверток
Глава 5. Наилучшее приближение тригонометрическими полиномами классов периодических функций с ограниченной $r$-й производной
§ 5.2. Функции Стеклова и их простейшие свойства
$§ 5.3. Результаты по наилучшему приближению классов $W_{L_p}^r$, вытекающие из общих теорем для сверток$
$§ 5.4. Функции $\varphi_{\lambda r}$ и $g_{nr}$ и их экстремальные свойства$
§ 5.5. Наилучшие линейные методы для классов $W_M^r$, $W_L^r$ и $W_V^r$
§ 5.6. Теорема сравнения Колмогорова и следствия из нее
§ 5.7. Экстремальные свойства функций класса $W_M^r$ в метрике пространства $L_p$
$§ 5.8. Наилучшее приближение класса $W_{L_2}^r$ в метрике $L_2$$
$§ 5.9. Замечание о распространении результатов на классы $W_{L_p}^rK$$
Глава 6. Перестаковки и экстремальные свойства дифференцируемых функций
§ 6.2. Простые функции и их перестановки
§ 6.3. Разложение интеграла на сумму простых функций
$§ 6.7. Теоремы сравнения для $\Sigma$-перестановок при ограничениях на норму в метрике пространства $L$$
$§ 6.8. Теоремы сравнения для $\Sigma$-перестановок при ограничениях на норму в метрике пространства $М$$
§ 6.9. О справедливости результатов для функций произвольного периода $2l$
$Глава 7. Наилучшее приближение тригонометрическими полиномами на классах $W^rH^{\omega}$$
$§ 7.2. Классы $W^rH^{\omega}$$
$§ 7.6. Верхние грани наилучших приближений тригонометрическими полиномами на классах $W^rH^{\omega}$ в пространствах $С$ и $L$$
$Глава 8 Наилучшее равномерное приближение класса $W^rH^{\omega}$ функциями класса $W_{M}^{r+1}K$$
$§ 8.3. Наилучшее приближенно класса $H^{\omega}$ классом $W_M^1K=KH^1$$
Глава 9. Теоремы Джексона и точные константы
§ 9.2. Точная константа и неравенстве Джексона для функций пространства $С$
§ 9.3. Точная константа в неравенстве Джексона для функций пространства $L_2$
§ 9.4. Точная константа и теоремах Джексона для $С^r$ и $L^r$ при нечетных $r$
Глава 10. Поперечники некоторых классов периодических функций
$§ 10.3. Поперечники классов $W_{L_2}^r$ в пространстве $L_2$$
$§ 10.4. Поперечники классов $W_{M}^r$ и $W^rH^{\omega}$ в пространстве $С$$
$§ 10.5. Поперечники классов $W_{V}^{r-1}$, $W_{L}^{r}$ и $W_{M}^{r}$ в пространстве $L$$
§ 10.6. Оценка нечетных поперечников с помощью теоремы о поперечнике шара
§ 10.7. Об экстремальных подпространствах
§ Д.2. Некоторые экстремальные соотношения
Комментарии и библиографические указания
$§ 5.3. Результаты по наилучшему приближению классов $W_{L_p}^r$, вытекающие из общих теорем для сверток$
$§ 5.4. Функции $\varphi_{\lambda r}$ и $g_{nr}$ и их экстремальные свойства$
$§ 5.8. Наилучшее приближение класса $W_{L_2}^r$ в метрике $L_2$$
$§ 5.9. Замечание о распространении результатов на классы $W_{L_p}^rK$$
$§ 6.7. Теоремы сравнения для $\Sigma$-перестановок при ограничениях на норму в метрике пространства $L$$
$§ 6.8. Теоремы сравнения для $\Sigma$-перестановок при ограничениях на норму в метрике пространства $М$$
$Глава 7. Наилучшее приближение тригонометрическими полиномами на классах $W^rH^{\omega}$$
$§ 7.2. Классы $W^rH^{\omega}$$
$Глава 8 Наилучшее равномерное приближение класса $W^rH^{\omega}$ функциями класса $W_{M}^{r+1}K$$
$§ 8.3. Наилучшее приближенно класса $H^{\omega}$ классом $W_M^1K=KH^1$$
$§ 10.3. Поперечники классов $W_{L_2}^r$ в пространстве $L_2$$
$§ 10.4. Поперечники классов $W_{M}^r$ и $W^rH^{\omega}$ в пространстве $С$$
$§ 10.5. Поперечники классов $W_{V}^{r-1}$, $W_{L}^{r}$ и $W_{M}^{r}$ в пространстве $L$$
Автор: Корнейчук Н.П.
Теги: анализ математика
Год: 1976
Похожие
Сплайны в теории приближения
Задачи и управления по курсу "Численные методы"
Экстремальные комбинаторные задачи и их приложения
Теория вероятностей и математическая статистика: основные понятия, примеры, задачи
Текст
                    Ы. П. КОРНЕЙЧУК
ЭКСТРЕМАЛЬНЫЕ
ЗАДАЧИ
ТЕОРИИ
ПРИБЛИЖЕНИЯ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
Москва 1976

518
К 67
УДК 517.5
Экстремальные задачи теории
приближения, 11. П. Корнейчук. Главная
редакция физико-математической литературы
изд-ва «Наука», М., 1976.
В монографии с современной точки
зрения рассматриваются задачи,
связанные с получением точной оценки
погрешности наилучшего приближения на
классах функций и с оптимальным выбором
аппроксимирующего аппарата. Подробно
изложены разработанные в последние годы
новые методы, поз полившие получить
окончательные результаты и ряде
экстремальных задач теории аппроксимации.
Книга предназначена для студентов и
аспирантов математических
специальностей, она будет полезна научным
работникам в области теоретической и прикладной
математики.
Ил л. 21.
Николай Павлович Корнейчук
Экстремальные задачи теории приближения
М., 1976 1\, 320 стр. с илл.
Редакторы Б. И. Голубое. Г. Я. Пирогова
Техн. редактор И. /У/. ЛксеЛьрод. Корректоры О. Л. Сегал, Г. С. Вайсберг
Сдано в набор 18/Ш 1976 г. Подписано к печати 23/VII 1976 г. Бумага 84х108'/з2.
Физ. печ. л. Ю. Условн. печ. л. IG.8. Уч.-изд. л. 10,48. Тираж 7 000 экз. Т-11092.
Цела книги I р. 25 к. Заказ № 544.
. Издательство «Паука»
Главная редакция физико-математической литературы
117071, Москва, B-7I, Ленинский проспект, 15
Ордена Трудового Красного Знамени Ленинградское производстпенно-техниче-
ское объединение «Печатный Диор» имени Л. М. Горького Союзиолнграфпрома
при Государственном комитете Совета Министров СССР по делам издательств,
полиграфии и книжной торговли. 197136, Ленинград. П-136, Гатчинская ул., 26.
., 20204—101 ,А __ © Главная редакция
К л-о / no Ti5" 44-76 физико-математической литературы
i)Od{UZ)-{b издательства «Паука», 1976

ОГЛАВЛЕНИЕ
Предисловие .;.,,, 6
Список основных обозначений 9
Г л а в а 1. Постановка задач и общие свойства наилучшего
приближения 11
§ 1.1 Залами теории приближения 11
§ 1 2. Общие свойства наилучшего приближении 16
§ 1.3. Общие теоремы существования и единственности
элемента наилучшего приближения 20
Глава 2. Двойственноеть экстремальных задач в линейных
нормированных пространствах 23
§ 2.1 Теорема Хана —Батха и отделимость выпуклых
множеств 23
§ 2.2 Теоремы двойствен мости п случае приближения
конечномерным подпространством 24
§ 2.3 Соотношения двойственности в случае приближения
выпуклым замкнутым множеством 28
§ 2.4. Критерии элемента наилучшего приближения,
вытекающие из соотношений двойственности 34
§ 2%5. Двойственные соотношения для задач наилучшего
приближения в пространствах Lp (а, Ь) и С [а, Ь] . . 36
Глава 3. Наилучшее приближение фиксированного элемента
в пространствах С и Lp ; 43
§ 3.1 О существовании и единственности элемента
наилучшего приближения в С и Lp 44
§ 3.2. Теоремы Чебышева и Валле-Пуссена 46
§ 3.3. Критерии элемента наилучшего приближения в
Lp{\ -^р <Соэ) в случае приближения
подпространством 52
| 3.4. Критерии ближайшего элемента в С и Lp в случае
приближения замкнутым выпуклым множеством ,.%. . 56
§ 3.5. Функции Бернулли и их наилучшее приближение
тригонометрическими полиномами в метрике L . . . 59
Глава 4. Наилучшее приближение на классах сверток .... 70
§ 4,1. Свертка функций; основные свойства и неравенства 70
§ 4,2 Двойственные соотношения для классов сверток. . . 73
§ 4.3. Приближение классоп сверток тригонометрическими
полиномами 76
§ 4.4. Наилучшие линейные методы для классов сверток , 85

4 ОГЛАВЛЕНИЕ
Глава 5. Наилучшее приближение тригонометрическими
полиномами классов периодических функций с ограниченной
r-й производной 94
§ 5.1. Классы дифференцируемых функций 94
§ 5.2. Функции Стеклова и их простейшие свойства .... 98
§ 5.3. Результаты по наилучшему приближению классов
WrL , вытекающие из общих теорем для сверток , . 101
v
§ 5.4. Функции ф;г и gnr и их экстремальные свойства . . 104
§ 5.5. Наилучшие линейные методы для классов WrM> WrL
и W[, 109
§ 5.6. Теорема сравнения Колмогорова и следствия из нес 113
§ 5.7. Экстремальные свойства функций класса WrM в
метрике пространства Lp 120
$ 5.8. Наилучшее приближение класса WrL в метрике /.2 . 125
§ 5.9. Замечание о распространении результатов на классы
¦ W, К- 127
Глав а 6. Перестаковки и экстремальные свойства
дифференцируемых функций 129
§ 6.1 Перестановки функций 130
§ 6.2. Простые функции и их перестановки 132
§ 6.3. Разложение интеграла на сумму простых функций 136
§ 6.4. ^-перестановка Ф (/, х) 144
§ 6.5. Основное неравенство 150
§ 6.6. Стандартные v-перестановки Фаг(х) 154
§ 6.7. Теоремы сравнения для ?-перестановок при
ограничениях па норму и метрике пространства L . . . . 158
§ 6.8. Теоремы сравнения для V-перестановок при
ограничениях на норму в метрике пространства М .... 168
§ 6.9. О справедливости результатов для функций
произвольного периода 2/ 175
Глава 7. Наилучшее приближение тригонометрическими
полиномами на классах W'H^ 176
§ 7.1. Модуль непрерывности 176
§ 7.2. Классы WH* 183
§ 7.3. Функции fnr(t) = fnr((o, 0 187
§ 7А. Основная лемма 190
2л
§ 7.5. Оценка функционала /7(J)(g-)= sup [ fgdt . . . . 193
f e на g
§ 7.6. Верхние грани наилучших приближений
тригонометрическими полиномами на классах WIf® в
пространствах С и L 204
§ 7.7. О возможности реализации верхней грани Еп(И^)с
с помощью линейного метода 211

ОГЛАВЛЕНИЕ 5
Глава 8 Наилучшее равномерное приближение класса \V?ft*
функциями класса W^ 1Л" 216
§ 8.1. Переход к двойственной задаче и некоторые
свойства экстремальных функций 216
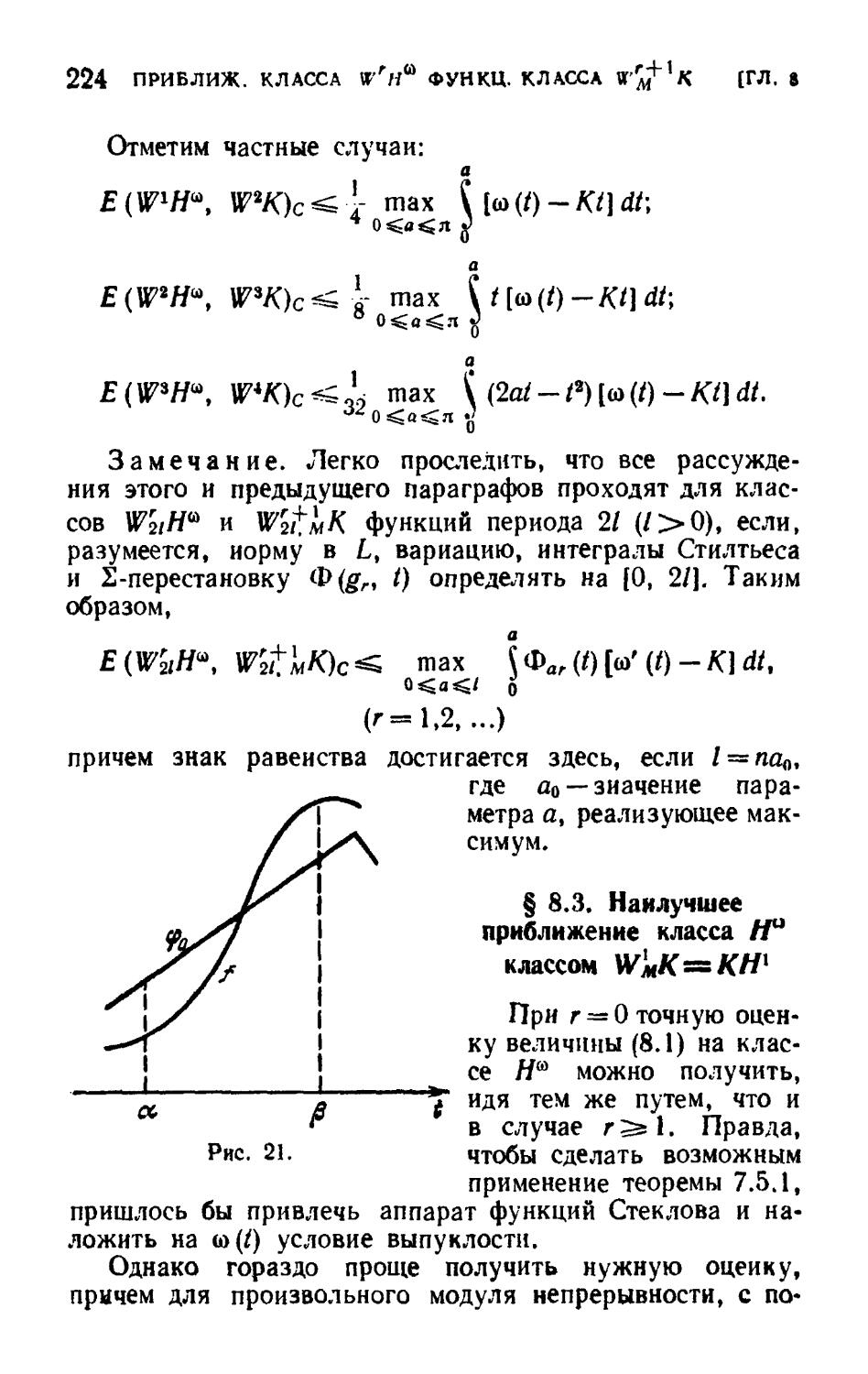
§ 8.2. Опойка приближения на классе Гг//Ы (г ^ I) .... 220
§ 8.3. Наилучшее приближенно класса //w классом
WmK---t-KH1 224
$ 8.4. Другой вывол точной опенки для Hn(WrHUi)c ... 227
Глава 9. Теоремы Джексона и точные константы 230
§ 9.1 Неравенства Джексон* в С и Lp 230
§ 9.2 Точная константа и неравенстве Джексона для
функций пространства С 234
§ 9.3. Точная константа в неравенстве Джексона для
функций пространства L> 237
§ 9.4. Точная константа и теоремах Джексона для С и U
при нечетных г 243
Глава 10. Поперечники некоторых классов периодических
функций 252
§ \0Л Вводные замечания 252
§ 10.2 Теорема о поперечнике шара 254
§ 10.3 Поперечники классов WrLt в пространстве L2 , . , ¦ 258
§'10.4 Поперечники классов WrM и WrI!^ в пространстве С 260
§ 10.5. Поперечники классов W[~l, WrL и WrM в
пространстве L 273
§ 10.6. Оценка нечетных поперечников с помощью теоремы
о поперечнике шара 281
§ 10 7 Об экстремальных подпространствах 286
Дополнение 296
§ Д.1 Неравенства Гельдера и Минковского для интегралов 296
§ Д.2. Некоторые экстремальные соотношения 301
Комментарии и библиографические указания 307
Литература , , 315

ПРЕДИСЛОВИЕ
Теория приближения—одна из наиболее интенсивно
развивающихся областей математики-.
В последние десятилетия наблюдается проникновение
идей и методов теории аппроксимации в самые
различные разделы математической науки, особенно
прикладных направлений. Одновременно с этим перестраивается
и ставится на более широкую и прочную основу
фундамент теории приближения, заложенный классическими
работами Чебышева и Вейерштрасса, Джексона и Берн-
штейна о приближении многочленами индивидуальных
функций и целых их классов.
Задачи апироксимашюнного содержания, задаваемые
на классах функций (или, более общо, на множествах
произвольного банахова пространства), во многих
случаях являются задачами на экстремум: требуется найти
точную верхнюю грань погрешности приближения
заданным методом па фиксированном классе функций или
указать для этого класса наилучший аппарат приближения.
Такого рода задачи и рассматриваются в этой книге.
Однако выбор материала определялся не только
экстремальным характером задач. В основу книги положены
исследования по экстремальным задачам теории
наилучшего приближения функций действительного переменного,
в которых получены окончательные результаты, т. е.
решение доведено до точных констант, и где ни убавить,
ни прибавить уже, в сущности, ничего нельзя.
Следует сказать, что наиболее существенные
результаты окончательного характера получены на классах
периодических функций, что, впрочем, нетрудно
объяснить: классы периодических функций обладают
определенной симметрией экстремальных свойств, в то время
как на экстремальных свойствах функций, заданных на
конечном отрезке, существенно сказывается
возмущающее действие концов промежутка. Рассматривая
экстремальные задачи на конкретных классах функций, мы
в этой книге ограничиваемся периодическим случаем.

ПРЕДИСЛОВИЕ 7
Подчеркнем, что основное содержание книги связано
с задачами наилучшего приближения. Хоти мы и
затрагиваем вопрос о наилучших линейных методах
аппроксимации, широкий круг фактов и результатов,
связанных с экстремальными задачами дли линейных методов,
остался вне рамок книги.
Мы предполагаем знакомство читателя с основными
фактами теории функций действительного переменного
(в частности, с основами теории меры и интеграла
Лебега), а также с элементами функционального анализа,
самыми общими понятиями которого мы оперируем на
протяжении всей книги.
Конечно, .при рассмотрении конкретных задач можно
было бы обойтись без таких терминов, как линейное
нормированное пространство, норма, компактность, оператор и
т. д., но изложение от.этого не стало бы проще и понятнее,
не говоря' уже о том, что оно, конечно, не стало бы короче.
Но дело не только в языке. Идеи и методы
функционального анализа позволили вскрыть глубокие связи
между различными по постановке задачами, получить
утверждения глобального характера, объясняющие с
единой точки зрения целую совокупность частных фактов.
Пример тому —фундаментальные теоремы о
двойственности экстремальных задач в линейных нормированных
пространствах, которые служат в этой книге отправным
пунктом при рассмотрении конкретных случаев.
Автор, впрочем, далек от мысли переоценивать роль
методов функционального анализа при решении задач,
поставленных в конкретных пространствах. Знание
глубоких фактов функционального анализа позволяет
взглянуть на проблему с самой общей точки зрения,
значительно расширить круг возможных подходов к ее
решению, а иногда —сразу указать общую схему, в которую
она укладывается. Однако там, где нужно получить
точную количественную оценку экстремальных свойств
функций конкретного класса, свойств, лежащих, так
сказать, па грани допустимого, там общие методы, именно
в силу своей общности, обычно оказываются бессильными.
Попытки найти точный результат в той или иной
конкретной экстремальной задаче, как правило, где-то
и глубине упираются в некоторую совсем элементарно
формулируемую задачу, связанную с получением простого

8 ПРЕДИСЛОВИЕ
[fa вид и интуитивно легко воспринимаемого, но далеко
не просто доказываемого неравенства. И тут требуется
точкнй анализ, умение найти новый, нестандартный
подход к исследованию глубоко лежащих свойств
функций рассматриваемого класса. Мы стараемся
акцентировать внимание читателя на этих узловых моментах,
приводя подробные доказательства связанных с ними
результатов. Во многих из этих доказательств важную роль
играют геометрические соображения (особенно в главах
5, 6, 7, 10) и суть дела становится прозрачной, если
сделать соответствующий чертеж.
Вопрос о том, какие вспомогательные факты
доказывать, а где можно ограничиться ссылкой, автор
пытается решить, приняв следующий принцип: ссылки делать
только на то, что исчерпывающе доказано в
университетских учебниках по теории функций и
функциональному анализу. Правда, в одном месте мы вынуждены
отступить от этого, на пат взгляд, разумного правила;
в последней главе некоторые результаты по оценке
поперечников базируются на глубокой (хотя интуитивно и легко
воспринимаемой) теореме Борсука, строгое
доказательство которой можно найти лишь в специальной литературе.
Вспомогательный материал по теории функций и
функциональному анализу, который в нужном нам объеме
не содержится в учебниках, включен в виде отдельных
параграфов в те главы, где он нужен. Некоторые факты
общего характера вынесены в дополнение.
Основной материал прочитан автором в виде
спецкурсов в Днепропетровском государственном университете.
В обсуждении новых результатов, включенных в
монографию, активное участие принимали сотрудники кафедры
теории функций этого университета, за что автор
приносит им благодарность. В. М. Тихомиров, В. И. Рубан п
В. Ф. Бабенко прочитали в рукописи отдельные главы
книги, их замечания помогли улучшить изложение
некоторых мест. В частности, В. И. Рубаном предложена
новая схема оценки снизу поперечников при
доказательстве основных теорем § 10.4, позволившая обойтись
без теоремы Борсука. Всем им, а также редактору книги
Б. И. Голубову, очень внимательно прочитавшему
рукопись, автор искренне благодарен.
Н. Корнейчук

СПИСОК ОСНОВНЫХ ОБОЗНАЧЕНИЙ
V —квантор общности: «для всех»
3 — квантор существования: «существует»
Q) — пустое множество
л:е Л — элемент х принадлежит множеству Л
хф Л — элемент .V не принадлежит множеству А
A U В — объединение множеств А и В
А П В — пересечение множеств А и В
Л\5 — разность множеств Лий
А х В — прямое произведение множеств А и В
А а В — множество А содержится в множестве В
{х: Рх\ — совокупность элементов ху обладающих
свойством Рх.
/(Л) —образ множества Л при отображении /
Ri — совокупность всех действительных чисел
#д—'«-мерное евклидово пространство
[а] — целая часть числа а
sign а—величина, равная 1, если а > 0, равная —I,
если а<0, и нулю, если .а = О
inf А — точная нижняя грань чисел, входящих в
множество A czRx
sup Л—точная нерхпня грань чисел, входящих в
множество AdRx
def — по определению
Р*!! = 5х-л —норма элемента х в линейном
нормированном пространстве X
X*— пространство, сопряженное с линейным
нормированным пространством X
/^ — множество функционалов feX* таких, что
/ (х) =- О V* <= /\ где FczX
mes Е — лебегова мера множества Е
dim X — размерность линейного пространства X
sup vrai i/ (/) —существенная верхняя грань функции
^^b
\f(()\ на [а, Ь], т. е. наименьшее из чисел N^RU для
которых неравенство 'f(t) >N выполняется на множе-
стис меры нуль

10 СПИСОК ОСНОВНЫХ ОБОЗНАЧЕНИЙ
С, Lpy М, V — пространства 2я-периодических
функций с соответствующей метрикой
Хг — множество r-х 2л-периодических интегралов
от feX, где X есть С, Lp, M или V
№гх = {/:/е=Л', !/(г).;Л-<1} (г= 1, 2, ...)
Е (х, F) = E (л\ JF)x — наилучшее приближение
элемента х множеством F в пространстве X
Е(Ш, F)x — точная верхняя грань величин Е{х, F)x
по всем х е 301
)x — точная нижняя грань величин sup j!x —
— Лл: 1^ но всем линейным ограниченным операторам А из X
в Fc=A
Тп @ — тригонометрический полином порядка п — 1
р\п-\ — подпространство тригонометрических
полиномов Тп (t) порядка /2 — 1
( i)
rt(, X) —«-мерный поперечник (по Колмогорову)
множества 301 в пространстве X
d'nffil, Л) —«-мерный линейный поперечник
множества Эй в пространстве X
^г*ф — свертка функций g и ф
g * :ТЙ — класс сверток g * ф, где ср е ?Л
1)г (/) — функция Бернулли
<*>(/» /)х —модуль непрерывности функции f в
пространстве к\ <о(/, Ос— ю(Л О
Я'0 —класс функций feC, у которых a)(f, 0^to(/)
ИГгЯ(О(г=1, 2, ...) — класс функций / из Сг, у
которых /<'> е Д"
/(О — убывающая перестановка функции f
Ф(/, х) — ^-перестановка функции f
$>ar (x) — стандартная 2-перестановка
ь
V(/)~ вариация функции / на отрезке [а, Ь]

ГЛАВА 1
ПОСТАНОВКА ЗАДАЧ И ОБЩИЕ СВОЙСТВА
НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ
§ 1.1. Задачи теории приближения
В настоящее время в теории приближения принято
естественным образом выделять три типа, а лучше
сказать, три цикла задач, которые в определенной степени
соответствуют и основным хронологическим этапам
развития исследований в теории аппроксимации.
Эти три цикла задач мы сформулируем з
произвольном линейном нормированном пространстве X и будем на
протяжении всей книги говорить о них как о задачах I,
II или III.
Задача 1. Приближение фиксированного элементе*
А'еХ фиксированным множеством F из X.
В качестве меры приближения естественно взять,
во-первых, величину
?(*, F) = inf {.x-uf, A.1)
GF '
которая в дальнейшем будет называться наилучшим
приближением элемента х множеством F. (Конечно, величина
(\Л) есть не что иное, как расстояние р(х, F) элемента х
от множества F. Но мы с самого начала примем, так
сказать, аппроксимационную терминологию.)
В качестве аппроксимирующего множества F в этой
книге будут рассматриваться подпространства (конечной
или бесконечной размерности), а также выпуклые
замкнутые множества.
Пели существует элемент uQ^F, реализующий в A.1)
точную нижнюю грань, т. е. такой, что
1х—щ1=Е(х, F)y
то i/0 называется элементом наилучшего приближения для х
и множестве F (или ближайшим if x элементом в F).

12 ПОСТАНОВКА ЗАДАЧ И ОБЩИР ВОПРОСЫ ГГЛ. 1
Здесь сразу возникают следующие вопросы,
относящиеся к задаче I:
1) Существует ли для любого х из X в множестве F
элемент наилучшего приближения? Ясно, что для
положительного ответа на этот вопрос необходимо, во всяком
случае, чтобы F было замкнутым.
Множество F, обладающее тем свойством, что для
любого х^Х в нем есть ближайший элемент, называют
иногда множеством существозания. Мы этим термином
также будем пользоваться.
2) Если для любого х е X ближайший элемент в
множестве F существует, то будет ли он единственным (для
любого хеХ)? Ответ на этот вопрос может зависеть как
от структуры множества /\ так и от метрики
пространства X.
Самые общие факты, связанные с существованием
и единственностью элемента наилучшего приближения,
будут приведены в § 1.3 этой главы.
3) Каковы характеристические свойства элемента
наилучшего приближения? Речь идет об указании
необходимых и достаточных условий, которым должен
удовлетворять ближайший к л' элемент в множестве F.
Вопрос о характеристических свойствах ближайшего
элемента является более тонким, чем вопросы
существования и единственности; получение удобных для
практического использования критериев требует учета более
тонкой специфики пространства А" и аппроксимирующего
множества /-'. Нужные нам факты в этом направлении,
для конкретных функциональных пространств будут
изложены в главе 3.
Если F есть множество существования и
единственности, то каждому элементу х ^ X соответствует
единственный ближайший к нему в множестве F элемент
и~Р(х). Этим задан некоторый оператор Р (оператор
наилучшего приближения), отображающий X в F. Ниже
мы увидим, что в общем случае этот оператор не является
аддитивным. Поэтому представляет интерес наряду с
величиной A.1) рассмотреть также меру приближения,
задаваемую выбором линейного оператора А (АХ a F) и
измеряемую величиной

§ 1.11 ЗАДАЧИ ТЕОРИИ ПРИБЛИЖЕНИЯ 13
Можно считать, что оператор А определяет некоторый
линейный метод приближения элементов х е X
множеством F. Этот линейный метод мы тоже будем обозначать
через Л.
Задача II. Приближение фиксированного множества
:ТЧ с: X фиксированным множеством F того же
пространства X.
Если исходить из наилучшего приближения A.1)
элемента х множеством F, то меру приближения в задаче II
естественно определять величиной
Е (ЭМ, F) = sup Е (х, F) = sup inf jjje-tti!, A.2)
которая характеризует отклонение множества Э){ от
множества F.
Элемент хое3I (если он существует), для которого
называют экстремальным (в данном случае наиболее
удаленным) элементом в ЭЙ относительно Z7.
В конкретных случаях задача II может состоять
в том, чтобы точно выразить (или хотя бы оценить)
величину A.2) через характеристики, с помощью которых
задано множество ЭЯ. Практический смысл задачи II
можно видеть в том, что знание величины A.2) позволяет
указать минимальную гарантированную оценку
погрешности приближения любого элемента из ЗЛ с помощью
множества F.
Если же приближение осуществляется с помощью
линейного оператора Л, то нас будет интересовать точная
верхняя грань
sup \x-Ax\ A.3)
а также величина
(:T)tf F)= inf suplx-Axl A.4)
ЛА^д)!
где точная нижняя грань распространена иг все
линейные операторы А, отображающие X в?. Можно сказать,
что величина A.4) характеризует наилучшее линейное
приближение множества 301 элементами множества F.
Линейный оператор A(AXaF) (если он существует),
реализующий в A.4) точную нижнюю грань, т. е. такой,

14 ПОСТАНОВКА ЗАДАЧ М ОБЩИЕ В0ПР06Ы [ГЛ. I
ЧТО
определяет наилучший для Ш линейный метод
приближения.
Ясно, что если А есть оператор из X и /;, то
[x-Axl^E(x, F) VxeX
н, следовательно,
sup i;jc-/lxliSbE(gR, F);
а так как это справедливо для любого линейного
оператора Л (АХ с:/7), то
?(:Wt F) »?(:№, F). A.5)
Разумеется, весьма интересным представляется
выяснение случаев, когда в A.5) будет знак равенства. Если
при этом существует наилучший линейный метод Л, то
sup ;:*- Ла" =?(:)Л, F),
г спад
и можно сказать, что линейный метод А реализует па
множестве ?Л верхнюю грань наилучших приближений
элементами множества F*.
Круг задач первого к второго циклов можно
расширить, если рассматривать приближение элемента х или
множества tW из X некоторой расширяющейся
последовательностью аппроксимирующих множеств
/^с^с.с^с.., A.6)
где индекс п может соответствовать, например,
размерности множества F,,. Из включений A.6) и определения
величины Е(х, F) следует, что для любого х^Х
и, следовательно, для любого множества Ш а X
Теперь можно говорить об изучении числовых
последовательностей Е(ху F,,) и ?(9)t, "F,,), в частности, о
выяснении точной или хотя бы порядковой асимптотики их
при я->оо.

§ 1J] ЗАДАЧИ ТПОРИИ ПРИБЛИЖЕНИЯ 15
Аналогичные задачи при аппроксимации
последовательностью множеств A.6) можно ставить и для величин
A.3) и A.4).
Задача III. Наилучшее приближение
фиксированного множества УЯ cz X заданным классом множеств
{F} из X.
Имеется в виду, что задан класс в каком-то смысле
«равноценных» множеств /\ например подпространств
одной и той же размерности, и требуется выбрать то из
них, которое наименее отклоняется от ЭЛ. Таким образом,
речь идет о выборе для Ж наилучшего
аппроксимирующего множества.
В этой книге задача III будет рассматриваться только
в указанном выше случае, когда \F\=^\Fn} есть
множество всех подпространств в X фиксированной
размерности п. Применительно к этому случаю мы и
сформулируем некоторые аспекты задачи III.
В 1936 г. А. Н. Колмогоров [1] поставил задачу
вычисления величин
Fn
(:W, Fn) (я-I, 2, ...), A.7)
где точная нижняя грань берется по всем
подпространствам Fn размерности п. Для центрально-симметричных
множеств Ш (т. е. таких, что из хеМ следует, что
и —хеЗЯ) величина <1Я(Ю1Ч X) получила название
//-мерного поперечника по Колмогорову множества 3I в
пространстве X. Она равна половине наименьшей «ширины»
множества Ш и характеризует минимальную
погрешность, которую можно обеспечить, приближая 3I
всевозможными /i-мерными подпространствами.
Для произвольного множества Ш поперечник
естественно определить через точную нижнюю грань по
всевозможным сдвигам Fn~\-a подпространств размерности п.
Если существует подпространство F*, на котором
нижняя грань в A.7) достигается, то F% называется
экстремальным подпространством для множества Ш
в пространстве X. Экстремальное подпространство F%
является наилучшим (в классе всех подпространств [Fn\)
аппаратом приближения множества :ТН.
Если минимизировать не наилучшее приближение
?(ЭД| ^я), а наилучшее линейное приближение #(ЯЯ, Fn)

16 ПОСТАНОВКА ЗАДАЧ И ОБЩИЕ ВОПРОСЫ |ГЛ. 1
множества ЭЛ подпространствами Fn размерности я, то
придем к задаче вычисления линейного поперечника
4iOJM, X)==inftf(:W. Fn) (/i = l, 2, ...) A.8)
множества iUt в пространстве X. Из A.5) следует, что
<*;(»?, X)^dft(:W, А') (/г = 1, 2, ...), A.9)
и особый интерес приобретает исследование случаев знака
равенства в A.9) и отыскание соответствующих этим
случаям экстремальных подпространств Fft, для которых
Е(:Ш, «)-?(:№, FS)-=d«(:Wf X) = d;(:W, A).
В настоящее время но каждой из сформ}'лированных
задач 1, II и III имеется значительное количество
фундаментальных исследований, и немыслимо все их
осветить с достаточной полнотой в одной книге. Мы сразу
же очертим круг вопросов, составляющих основное
содержание этой книги, сказав, что главной целью является
изложение результатов, связанных с точным решением
задач II и III о наилучшем приближении фиксированных
множеств в конкретных пространствах периодических
функций. В качестве аппарата приближения в задаче II
будут рассматриваться главным образом подпространства
тригонометрических полиномов фиксированного порядка;
есть, однако, результаты по приближению выпуклым
множеством.
Линейные методы в задаче II будут затронуты лишь
в связи с выяснением вопроса о возможности реализации
с их помощью верхней грани наилучших приближений
на заданном классе функций.
Что касается задачи I, то мы ограничимся
изложением лишь тех фактов но приближению фиксированного
элемента, которые потребуются нам в основных главах,
посвященных задачам II и III.
§ 1.2. Общие свойства наилучшего приближения
При фиксированном аппроксимирующем множестве F
из X величиной A.1) задается на X некоторый
функционал: каждому ,геХ ставится в соответствие число
Е (х, F). Назовем этот функционал функционалом
наилучшего приближения и отаетим некоторые его общие свой-

§ 1.2] ОБЩИЕ СВОЙСТВА НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ 17
ства, считая везде ниже X вещественным линейным
нормированным пространством.
Предложение 1.2.1. Функционал наилучшего
приближения Е (ху F) непрерывен, каково бы ни было
множество F. Если же F — подпространство, то функционал
Е(ху F) является полуаддитивным:
Zi F) A.10)
и положительно однородным, т. е.
?(Ъг, F) = \X\E(x, F), A.11)
где X — любое действительное число (le^),
Доказательство. Пусть х и у —произвольные
элементы из X. Для любого u^F имеем
а переходя слева и справа к нижней*) грани по u^F,
получим
Е(хч F)^lx-yl + E(y9 F),
т. е.
?(*, F)-E(yy F)^\x-y\. A.12)
Так как в A.12) х и у можно поменять местами, то
справедливо неравенство
Е(х, F)-E(y, F)\<>\x-y\% A.13)
из которого немедленно вытекает непрерывность
функционала наилучшего приближения.
Пусть теперь F — подпространство. Для любых ultu2^F
имеем
? (*i -г Ae2, F) = inf j! (xi -|- x2) — и I <
^с ] (х, -Ь лг2) - (иг -\- и2) :| ^с;! л:! - «i|| + \хг- и21,
и переход в правой части к нижней грани по и\ и w2
из F дает A.10).
*) Здесь и в дальнсй|.'1ем мы ради краткости вместо «точная
нижний (верхняя) грань» пишем просто «нижняя (верхняя) грань»

18 ПОСТАНОВКА ЗАДАЧ И ОБЩИЕ ВОПРОСЫ [ГЛ. 1
Далее, если F — подпространство, то для х&Х
и Xe/?i(X=?fcO) можем написать
E(lx, F)= innU-MiWX- inf \х - \ \ -
UGF" '' «?/•' ' К i
не/-"'
и соотношение A.11) доказано. Из него, в частности,
следует (в предположении, что F — подпространство)
равенство
?(-*, F) = E(x, F) (VxezX).
Заметим, что если /;—не подпространство, то
соотношения A.10) н A.11) могут и не иметь места
(простейший пример: X — Ru F~--[~-1, 1|, Xi--^l/2, х2^=\). С
другой стороны, даже если F — подпространство, функционал
наилучшего приближе>гия не является, вообще говоря,
аддитивным. Чтобы убедиться в этом, достаточно в
двумерном евклидовом пространстве R2 элементов х~Ци ?2}
рассмотреть приближениэ элементов -^i = {0, 1} и х2 —
--z -J0, —1} подпространством F—jHi, 0}.
Теперь, предполагая, что F есть множество
существования и единственности, отметим некоторые свойства
оператора наилучшего приближения Я, сопоставляющего
элементу х^Х ближайший к нему элемент и = Р (х)
из F. Оператор Я неявно задается равенством
;:*_р (*)!!=: inf i!*-«ij = ?(;r, F).
Предложение 1.2.2, Ее л 11 F — подпространство
из Ху являнщееся множеством существования и
единственности, то оператор Р является однородным'.
и9 следовательно, нечетным, т. е,
Если, кроме того, подпространство F конечномерно, то
оператор Я непрерывен.
Однородность оператора Р вытекает из цепочки
равенств, в которой используется A.11):

§ 1.2] ОБЩИЕ СВОЙСТВА НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ 19
Докажем непрерывность оператора Р в
предположении, что F конечномерно.
Пусть Ада-^л'о, ит^Р{хт) и uo — P(xQ). Так как
!; *„'*;/( (ю==1, 2, ...)
(сходящаяся последователыюсть ограничена), то
;'а-,„ — ит] =---? (лг,л, ?)<¦:аг,п|;^/С
и, следовательно,
} М/«!' ^ ; "т - х,п ;i + "I л:т ¦ < 2/< (т = 1, 2, ...),
т. е. последовательность \ит\ элементов из F также
ограничена. Предположим, что
В конечномерном пространстве всякое ограниченное
множество компактно, поэтому в \ит\ существует сходящаяся
подпоследовательность. В силу сделанного предположения
найдется такая подпоследовательность \ит }, что
причем и'е/;, ибо F замкнуто. Но и,„ — Р (лгш ) —
элемент наилучшего приближения в F для а-,,.^ поэтому
откуда при /г—>-со,с учетом непропьп^юстн нормы, получим
что невозможно, ибо в силу единственности элемента
наилучшего приближения, если ugeF и иФи<0, то
Полученное противоречие доказывает, что
lim Р(хт) = Р(Хц).
Отметим еще один факт, связанный с понятием
выпуклости.
Напомним определение. Множество D линейного
пространства X называется выпуклым, если вместе с любыми
.двумя точками Xi и хг оно содержит и соединяющий их

20 ПОСТАНОВКА ЗАДАЧ И ОБЩИЕ ВОПРОСЫ [ГЛ. 1
отрезок, т. е, совокупность точек вида axi + (\ — <х)х2,
где 0<а<1.
Предложение 1.2.3. Если F — выпуклое множество
(в частности, подпространство) линейного нормированного
пространства X, то множество Fx элементов наилучшего
приближения для х е X в F является выпуклым.
В случае, когда Fx пусто или состоит из одного
элемента, предложение 1.2.3 тривиально. Пусть Fx не пусто
и состоит более чем из одного элемента. Если иг и u2^FXy
т. е. если
u<=F
то для любого a, O^a^l, элемент п = аи1 + (\ — a) u2
принадлежит F и
Но так как неравенство ||# — uf<d для #<=F
невозможно, то {I jc — tt|| = d, т. е. #eF*.
§ 1.3. Общие теоремы существования и единственности
элемента наилучшего приближения
Не углубляясь в тонкости существования и
единственности, мы здесь докажем лишь несколько общих и
довольно простых утверждений, которые нам потребуются
в следующих главах книги.
Предложение 1.3.1. Любое конечномерное
подпространство * F линейного нормированного пространства. X
является множеством существования.
Нужно показать, что для любого хе X в
конечномерном подпространстве F существует элемент
наилучшего приближения. Фиксируем x^X\F (если яе/7, то
доказывать нечего). Так как F замкнуто, то
inf
ШЯ
ш=1, 2, ... существует элемент
а в силу определения точной нижней грани для каждого
=1, 2, ... существует элемент um^F такой, что

1.31 ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ 21
Последовательность элементов \ит) ограничена, ибо
<d + 1+[.*;! (m-1, 2, ...),
и так как в конечномерном пространстве любое
ограниченное множество компактно, то существует сходящаяся
подпоследовательность \ит}:
lim um. = «0»
/ — со ;
причем uo^F в силу замкнутости F. Теперь, написав
J7 (/=if 2, ...),
в пределе при j-+c& получим
j'.v — ua;i = d, .
т. е. предельный элемент м0 является ближайшим к дг
в множестве /\
Мы можем значительно расширить круг своих
представлений о множествах существования, введя следующее
определение.
Множество F нормированного пространства X
называется локально компактным, если компактно в X любое
ограниченное подмножество из F, т. е. любая
ограниченная последовательность элементов из F содержит
сходящуюся подпоследовательность.
Так как при доказательстве предложения 1.3.1 из
свойств подпространства F мы использовали только ere
замкнутость и вытекающую из конечномерности
локальную компактность, то, буквально повторяя приведенные
выше рассуждения, мы получим следующее утверждение.
Предложение 1.3.2. Любое замкнутое локально
компактное множество F линейного нормированного
пространства X является множеством существования.
Касаясь проблемы единственности, мы здесь укажем
один факт общего характера, когда единственность
обусловлена структурой метрики пространства X.
Норму пространства X называют строго выпуклой.
если с4ера !',•*•!.== 1 в X не содержит отрезков, т. е. из
-¦ лг|i == *. #•; =1,' хФу, следует, что :j ax-f (I — a) y\ < 1
l
()
Строгая выпуклость нормы равносильна тому, что
равенство ||*+0|i = 5*|j-bj|#;i для хфО и уфО возможно,

22 ПОСТАНОВКА ЗАДАЧ И ОБЩИЕ ВОПРОСЫ [ГЛ. 1
только когда х — су (с>0). (Говорят, что в этом случае
пространство X строго нормировано.) Действительно, если
хфу и j:jt[! = ;i#j!= 1, то равенство ах = с(\ — а)у (с>0,
О <а < 1)'невозможно, ибо из него следовало бы, что
а'||л"|| = сA — аMу'|!, а = сA — а) и х = у. Но если ахФ
фс(\—а)у и пространство X строго нормировано, то
х
т, е. норма в X строго выпукла.
Обратно, если норма строго выпукла, хфОу уфО,
хфсу, то элементы
удовлетворяют условиям х' Фу'у ^х'] = \у'\=\л и потому
При сх = jл:j'/('!л:|; +';f/ ,j) последнее неравенство запишется
в виде
так что X строго нормировано.
Предложение 1.3.3. Если норма пространства X
строго выпукла и для xgX в подпространстве F а X
существует элемент наилучшего приближения и{), то этот
элемент единствен.
В самом деле, предположим» что кроме tf0 ближайшим
к л; в подпространстве F является также элемент иг. Тогда
п силу предложении 1.2.3 ближайшим к х в F является
и элемент п = 1 2 (ы(, -j-«i). Поэтому
H-v-Wo) •l-(A--Wi) = =-21.,X"a>2?(.vf F) =
—'-a: —uo;; + ;iA: —«г;.
Так как норма в X строго выпукла и, значит, X
строго нормировано, то
х — //0 =г= с (х — «j) (с > 0).
1:слн теперь с^1, то сразу вщно, что ul = u^ если же
сф1у то
х----A-е) '(ио-сиг)
и, следовательно, хе/;, а тогда ul = ui}--=x.
Предложение 1.3.3 доказано.

ГЛАВА 2
ДВОЙСТВЕННОСТЬ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ
В ЛИНЕЙНЫХ НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
Может быть, одним из самых замечательных фактов
современного анализа явилось установление, в самых
общих терминах, соотношений, связывающих различные
по постановке экстремальные задачи. Эти соотношения,
получившие название теорем двойственности, играют
фундаментальную роль в теории приближения, теории
оптимального управления, математическом программировании.
В этой главе будет доказано несколько утверждении,
сводящих задачу наилучшего приближения в линейном
нормированном пространстве X к двойственной задаче на
вычисление верхней грани в сопряженном пространстве X*.
Эти результаты будут служить отправным пунктом при
решении экстремальных задач в конкретных
функциональных пространствах.
Вывод соотношений двойственности существенньш
образом базируется на теореме Хана —Банаха о продолжении
линейных ограниченных функционалов и на следствиях
из нее, одним из которых является, в частности,
теорема отделимости. Мы сформулируем в § 2.1 эти
утверждения, отсылая интересующихся их доказательством к
учебникам Л. А. Люстерника и В. И, Соболева [1], А. Н.
Колмогорова и С. В. Фомина [1].
§ 2.1. Теорема Хана—Банаха
и отделимость выпуклых множеств
Теорема Хана — Банаха. Всякий линейный
ограниченный функционал /, заданный на линейном
многообразии D линейного нормированного пространства X, может
быть продолжен на все пространство X с сохранением
нормы, т. е. существует линейный ограниченный
функционал ф, заданный на всем X и такой, что:
1) <р (*)=/(*) Va-^D,
2) 1!фЦх— sup >(*)¦= sup -/Wi-i/k
Ж1 кй5!

24 лвопстикиность экстремальных задач ггл. 2
Следствие 1. Для любого элемента л*0<=Л\ х0ф0,
существует функционал /^Х* такой, что J*/^Г = 1 и
Следствие 2. Пусть F — подпространство
линейного нормированного пространства X. Для любого х0 \f
существует функционал /еХ* такой, что:
1) /(.v)«0 V*e=/-\
2) !П=1,
3) f(xo) = E(xo, F)= inf jU0-«!|.
/54
Чрезвычайно важную роль в задачах геометрического
характера играет теорема отделимости выпуклых множеств
(А. Н. Колмогоров, С. В. Фомин [1], стр. 130).
Выпуклое множество D (см. § 1.2) линейного
пространства X называют выпуклым телом, если оно имеет
непустое ядро, под которым понимается совокупность точек
х из D таких, что для любого у ^ X при некотором е —
= ?(#)>0 имеет место включение x-\~ly^D при всех
|/| <е. Если X нормировано, то это равносильно
наличию у D внутренних точек.
Теорема отделимости. Пусть А и В —
непересекающиеся выпуклые множества в вещественном линейном
нормированном пространстве X, причем хотя бы одно из
них является выпуклым телом. Тогда существует
ненулевой функционал /еХ*, разделяющий множества А и В,
т. е. такой у что
§ 2.2. Теоремы двойственности в случае
приближения конечномерным подпространством
В случае, когда аппроксимирующим множеством
является конечномерное подпространство, двойственные
соотношения совсем просто выводятся из теоремы Хана —
Банаха и ее следствий, без привлечения теоремы
отделимости.
Везде X будет обозначать линейное нормированное
пространство, X*— пространство, сопряженное с X,
элементами которого являются заданные на X линейные
ограниченные функционалы / с нормой
|:/|= sup :/(*);.

§ 2.2] ПРИБЛИЖЕНИЕ КОНЕЧНОМЕРНЫМ ПОДПРОСТРАНСТВОМ 25
Теорема 2.2.1. Если хи хъ ..., хп —фиксированная
система элементов пространства Л\ то для любого х е X
:\ п 1
(ft---I, 2 л)
где нижняя грань берется по всевозможным числам Я*,
« верхняя — по всем функционалам f <= X* с нормой || /|] ^ 1,
которые обращаются в нуль на элементах xk. Верхняя
грань достигается на некотором функционале fQ^X*,
?/о',. •• •
Л о к а з а т е л ь с т в о. Пусть F — множество элементов
и ^ X вида
Таким образом, F есть линейное многообразие,
содержащее не более чем п линейно независимых элементов, т. е.
F— конечномерное подпространство в X. Через F1
обозначим множество функционалов /еХ* таких, что
Соотношение B.1), которое мы должны доказать,
перепишется теперь в виде
inf ;U-~ «r.= sup f(x). B.2)
ие/1< ' " fc-.Г1
Если х <= Z7,, то B.2) тривиально, ибо обращается
в равенство 0 = 0. Пусть хфр. В силу предложения 1.3.1
существует элемент uo^F такой, что"
def
\х — ио||= infill — u-j= d,
e/7
причем d>0. Для любого функционала /ef1 с нормой
!/!]=?= 1 имеем
так что
sup f(x)^d. B.3)

26 ДВОЙСТВЕННОСТЬ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ И'Л. 2
С другой стороны, в сил)- следствия 2 из теоремы
Хана —Банаха существует функционал fo^F:- такой, что
7о(.= 1 и fo(x) — d. Это значит, что на самом деле в B.3)
имеет место знак равенства. Теорема доказан.].
Теорема 2.2.2. Если /ь /2> ..., fn — фиксированная
гцстема функционалов из X*, то для любого feX*
ini!f- Ykkflf\~ sup f(x),
ik^- I, 2 n)
где нижняя грань распространена на всевозможные системы
чисел ал, а верхняя берется по всем элементам х^Х
с нормой !!#|'г5г=1, на которых обршцается в нуль каждый
из функционалов /^.
Доказательство. Обозначим через Н множество
элементов х е Х> для которых fk (х) ¦--= 0 F — 1, ..., п).
Ясно, что Я есть замкнутое (в силу непрерывности /*)
линейное многообразие, т. е. подпространство в X.
Наряду с функционалом /^Х* будем рассматривать
его сужение /"// на подпространство Н, т. е. заданный
на Н линейный ограниченный функционал такой, что
/*// (х) -=/ (х) Для всех хезН. Очевидно, что
I///]- Slip fu(.Y)~ Slip J'(X).
л-е// а-с. И
;'A--i^l ,.vi:< I
Продолжением функционала /// иа все пространство X
является не только функционал /, но if .-побои
функционал вида
<Р-/-?/¦*/*, B.5)
где Я/, — произвольные числа, ибо если хе//, то/ft (.г)---О
п cp(x) = /(x) ~f//(x). Покажем, что любое продолжение
функционала fn с Н на X имеет »ид B.5). При этом, не
теряя общности, мы можем считать функционалы [и [ъ ...
..., /„ линейно независимыми. Существует (см., например,
JI. Л. Люстерник, В. И. Соболев |11, стр. 210) система
элементов {хь -v2> :.., хп\ с: X, биортогональная системе
функционалов {/ь /2, .,., /«}, т. е. такая, что // (л:л) = 0,

§ 2.21 ПРИБЛИЖЕНИЕ КОНЕЧНОМ ЕРИ Ы.М ПОДПРОСТРАНСТВОМ 27
если кфг и //(#/) = 1. Если яеХ, то элемент
п
у-=х- ?fk(x)xk
принадлежит Ну ибо
= fi(x)-h(x) = 0 (* = l. 2 n).
Таким образом, люГюп элемент jr e X можно представить
в виде
х = У+ ?fk(x)xk, tj<=H. B. С)
/2=1
Фиксируем fsX* п обозначим через ср продо.лжение
функционала //7 с Я на X. Для любого *^Х, учитывая,
представление B.6), а также то, что tp(^) = f(//)f будем
иметь
(х)
Л-
') - >] /* № / (.\V) !- X] /* (х) ср
т. е. функционал <р представим в виде B.5) с ЯА = Я/?(ср) =
/()
/()
Так как при продолжении норма функционала может
только увеличиться, то для любого набора
коэффициентов Хь
С другой стороны, в силу теоремы Хана —Банаха
существует продолжение функционала /я с # на X, сохраняющее

28 ДВОЙСТВЕННОСТЬ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ {ГЛ. 2
норму, т. е. существует система коэффициентов
(k=ly 2, ..., п), для которой
Теорема 2.2,2 доказана.
Как мы увидим в следующих главах, базируясь
на соотношениях B.1) и B.4), можно построить
эффективные методы решения экстремальных задач теории
приближения в конкретных функциональных пространствах.
Впервые этот путь к точным результатам в задачах
наилучшего приближения использовал С. М. Никольский [3],
§ 2.3. Соотношения двойственности в случае
приближения выпуклым замкнутым множеством
Здесь мы получим существенное обобщение теоремы 2.2.1
на случай, когда аппроксимирующим множеством является
произвольное выпуклое замкнутое множество и, в
частности, произвольное (не обязательно конечномерное)
подпространство.
При выводе двойственного соотношения для
приближения выпуклым множеством ключевую роль будет играть
теорема отделимости.
Основной результат можно сформулировать в. виле
следующего утверждения.
Теорема 2.3.1. Если F — выпуклое замкнутое*)
множество линейного нормированного пространства X, то для
любого элемента хеХ справедливо соотношение
inf l*-u|!= sup [/(*)-sup/(и)], B,7)
где X* — пространство, сопряженное с X. При каждом
х е X/F существует функционал /оеХ* с нормой j|/0]= 1»
реализующий верхнюю грань в правой части B.7).
Укажем весьма простую геометрическую интерпретацию
соотношения B.7) в случае, когда X есть #2 — веществен-
*) Условие замкнутости множества F в теореме 2 3 1
несущественно; оно введено для некоторого упрощения дальнейших выкладок
Кроме того, аппроксимирующее множество обычно предполагаете»
'«ямкиутым.

$ 2.3]
ПРИБЛИЖЕНИЕ ВЫПУКЛЫМ МНОЖЕСТВОМ
29
пая плоскость с прямоугольными координатами хк и хг.
При этом будем иметь "в виду, что в правой части B.7)
верхнюю грань можно брать только по функционалам fX*
таким, что ifl=l и f(f(
м <= F
Линейный функционал /е/?| определяется вектором
а = [аи а2] е /?2, причем jl / f = • а % и / (х) = a,.v, -f ад> Л'1я
любого ^={x4, х2} ^У?2- Если f/!|=lt то tf(x)\ совпадает
с расстоянием точки х от прямой /(/), на которой f(x) ¦¦-
= 0, и для выпуклого замкнутого множества FczR2
Рис. 1.
величина- f(x) — sup /(w), если она неотрицательна, дает
Ы €= /'
расстояние точки х (xzfcF) от ближайшей к ней опорной
к F прямой L(f) (рис. 1). Это расстояние в силу
выпуклости F будет наибольшим, если проекция и0 точки л*
на прямую L(/) = L(/o) будет принадлежать F, т. е. будет
ближайшей к х точкой в множестве F.
Переходим к доказательству теоремы 2.3.1. Считая
множество F фиксированным» введем обозначения:
inf J!*-u|L
B.8)
где 5* —замкнутый единичный шар в Х*э т. е.

30 ДВОПСТВСННОСТЬ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ ГГЛ. 2
Е (х) и N (х) являются неотрицательными числовыми
функциями, заданными на X. Мы должны доказать, что
E(x) = N(x) Vx<=X. B.9)
Так как
/(*)- sup.f(u)~ inf [/(.v)-/(tt)]« inf f(x-u),
то для *<=F функция /V(x), так же как и Е (х),
обращается в пуль, А мы можем в дальнейшем считать, что
X\F
\
Неравенство N (х) •<: Е (х) почти тривиально.
Действительно, если а{) есть элемент наилучшего приближения
для х в множестве F, т. е. Е (х) —jj* — uoj;» т0
N(x)^ sup [/(.v)-f<«0)
•< sup;:/:'iix—w0;;^^;> — w0;i-= я(х).
fes*
Если же элемент наилучшего приближения для х в F
отсутствует, то для любого е>0 найдется элемент их ^F
такой, что
|:* —н,||
Проводя те же оценки, получим
и так как е произвольно, то
N(x)^E(x). B.10)
Доказывая справедливость противоположного
неравенства Е (х) -<~ N (х), отметим сначала следующий простой,
но полезный факт, немедленно вытекающий из
определения нормы функционала.
Предложение 2.3.2. Если f^X*, а т]!>0, то
sup
В самом деле, для всех элементов х из X с нормой
]х{<О\ справедлива оценка
С другой стороны, в силу равенств
)\= SUP f(x)

§ 2.3] ПРИБЛИЖЕНИЕ ВЫПУКЛЫМ МНОЖЕСТВОМ 31
для любого е>0 существует элемент хе, ;,л'е!"< 1 такой,
что
/(¦г«)>.7:- *•
Положив ге = 1]Л'8, будем иметь
причем !ге"-<Т1, так что ввиду произвольности к>0
прег^южоние 2.3.2 доказано.
Теперь, считая х фиксированным, .v ?2 X\F, if заметив,
что Е (х) >() (в силу замкнутости множества Z7),
рассмотрим в пространстве Л открытый шар
U(x9 Е(х)) = >у: у<=Х,:.у-х:<:Е(х)\
с центром в точке х и радиусом Е(х). Очевидно, шар
U (.г, Е(х)) есть выпуклое тело, прячем он не пересекается
с множеством F, ибо если предположить существование
элемента Uj такого, что u{^F и их g (/ (.v, Е(х))> то б уде а
иметь
Е ДО <:::*--и, !;<?(*),
что абсурдно.
Таким образом, к множествам F и U (л', Е (х)) можно
применить теорему отделимости, в силу которой
существует ненулевой функционал /€еХ'* такой, что
f(u)^f(!j) VaeF, Vye'J (x, E(x)).
Так как |./|'=^=0, то, положив Ji—fix\fu получим
функционал /,еХ* с нормой
1/i'=l, B.11)
который также разделяет множества F и U (л% Е (х))\ для
всех meFh всех у ^U (x, E (х)) выполняется неравенство
fiW**h(y). B.12)
Переходя в левой части B.12) к верхней грани по u^F,
а в правой —к нижней грани по j/eL/(.y, ЕДО), получлм
чхгпюикчгие
inf fx(y). B.13)
U{. E{x))
Любой элемент y<^U(x>E ДО) можно представить в виде
+ Ц|| = ||# — .г]<ЕДО; обратно, если]|?"

32 ДВОЙСТВЕННОСТЬ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ [ГЛ. 2
то элемент у = х-\-2, очевидно, принадлежит шару U (ху
Е (л-)). Поэтому
inf Ш= inf f, (х + z) =
i/ E() i;¦;?
= inf M*-*)=M*)- sup /,(г)
I!!<?( !|;<Е()
и соотношение B.13) можно переписать в виде
sup Ы«ХЫ*)- S"P М2)- B-Й)
не/7 ,j2;i<?(x)
Но в силу предложения 2.3.2 и равенства B.11)
sup f, (г) = ?(*),
а потому, с учетом определения B.8) и опять же
равенства B.11), из B.14) будем иметь
Е (х) < U (х) - sup ft (a) ^N(x). B.15)
Соотношения B.10) и B.15) дают B.9).
Остается убедиться, что при каждом фиксированном
,v<=X\F найдется функционал /oeif* с нормой Л/о] =
^ 1, для которого
/оМ- sup Ы«)= sup \f(x)-sup f(u)) = N(x). B.16)
Из определения верхней грани следует, что для
каждого я=1, 2, ... существует функционал fn^S* такой,
что
Л' (*) - ~ < /я W - sup fn (и) <, N (х)9
п U(=F
и, значит,
lim I/„ (х) - sup U (и) I = .V (х). B.17)
Теперь нужно воспользоваться тем, что в
пространстве X* всякое ограниченное множество слабо компактно.
Этот факт в случае, когда X сепарабельно (а в
дальнейшем телрема 2.3.1 будет применяться только к сепара-
бельным пространствам), доказан в учебнике А. Н.
Колмогорова и С. В. Фомина [1J, стр. 188; в общем случае
доказательство этого утверждения можно найти,
например, в книге Н. Даирорда и Дж. Т. Шварца [1], стр. 459.

2.3] ПРИБЛИЖЕНИЕ ВЫПУКЛЫМ МНОЖЕСТВОМ 33
Итак, фигурирующая в B.17) последовательность {/„}
из S* содержит слабо сходящуюся подпоследовательность.
Чтобы не усложнять обозначений, будем считать, что
слабо сходится уже {/„[, т. е. при любом х^Х числовая
последовательность [fa(x)\ имеет предел. Положив
М*)= lim fn(x), B.18)
получим заданный на X линейный функционал /,„ причем
легко проверяется, что /0, так же как и /„, принадлежит
шару S*.
Сопоставив B.17) и B.18), приходим к соотношению
lim
Докажем, что для предельного функционала /0
выполняется B.16). Так как, очевидно,
/0 (л*) — sup /„ (и) -< N (х),
то надо лишь установить невозможность неравенства
Но если
sup /о(«)=Т1>Тэ
а числа е>0 и ei>0 выбраны из условия ft —ех>
>у-М, то найдется элемент uo^F такой, что fu («0)>
>Vi~~8i> а с другой стороны, в силу B.19) для п^пг
будет /я(«о)<Т + е' Следовательно, для всех п^пе
/о Ы - fn («о) > Ti - *1 - У - с > О
в противоречии с B.18).
Норма экстремального функционала /0,
удовлетворяющего B.16), не можит быть меньше единицы. В самом
деле, если li/0;j< 1, то функционал fi^kf{)y где >.= 1/-/у],
очевидно, принадлежит fuapy 5* и
/х (х) — sup fi(u) = kf0 (x) — Я, sup /0 (а) = IN (x) > Л^ (дг),
что невозможно.
Теорема 2.3.1 полностью доказана. Важным ее
частным случаем является следующее утверждение,
обобщающее теорему 2.2.1.

34 ДВОЙСТВЕННОСТЬ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ [ГЛ. 2
Теорема 2.3.3. Если F — подпространство
линейного нормированного пространства X, то для любого
Х
inf ([я —Mf= sup /(*), B.20)
где F1 —множество функционалов feX* таких, что
f(u) = O VueF. Верхнюю грань в правой части B.20)
реализует некоторый функционал fo^F±c нормой !j/oii= 1.
Действительно, если /(^Т71, то для некоторого и' е/7
будет f (и')~афОу и так как Xu'<=F при любом К и
/Яы') = Ла, то при каждом фиксированном *
f(x)-sup
Это значит, что при вычислении верхней грани по /
в правой части B.7) можно рассматривать только те
функционалы f из S*, которые одновременно
принадлежат и множеству F~\ но тогда B.7) запишется в
виде B.20).
Достижимость верхней грани в B.20) следует из
соответствующего факта в теореме 2.3.1.
Ясно, что теорема 2.2.1 содержится в теореме 2.3.3,
и мы могли отдельно ее не доказывать. Но когда речь
идет о приближении конечномерным подпространством
(а именно этот случай будет чаще всего иметь место
в дальнейшем), то незачем для обоснования двойственных
соотношений идти через теорему 2.3.1, если есть более
простой путь.
§ 2.4, Критерии элемента наилучшего приближения,
вытекающие из соотношений двойственности
Теоремы 2.3.1 и 2.3.3 позволяют указать общие
критерии ближайшего элемента в выпуклом замкнутом
множестве или в подпространстве.
Теорема 2.4.1. Пусть F (FФX) — замкнутое
выпуклое множество линейного нормированного
пространства X. Для того чтобы элемент uo^F был элементом
наилучшего приближения в F для х ^ X \ /\ необходимо
и достаточно существование функционала /оеХ* со
следующими свойствами:

§ 2.4J КРИТЕРИИ ЭЛЕМЕНТА НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ 35
i)ii/o!!==i,
2) iU~«o!;=/o(*-«o)>
3) Ы«о)= sup /о (и).
Доказательство. Пусть для элемента uo^F
inf й-зс — u ii ==!;лг — м03 B-21)
и /0 — функционал с нормой ''|/oj—1, реализующий в
соотношении B.7) точную верхнюю грань. Тогда
!i*--«oh=/o(*)--sup/„(«)¦ B.22)
Покажем, что функционал /0 удовлетворяет условию 3)
теоремы. Действительно, если предположить, что
М«о)< sup /оИ,
и учесть оценку
/oW-/oW^i/o!;::^«oh!^-«o'i,
то получим
I1 х - и0I1S* /о (*) - /о ("о) > /о (*) - sup /0 (и)
U(=:F
в противоречии с B.22). Таким образом,
!i*-M=/o W -/о Ы=/о (х-и0)
и необходимость условий 1)~3) для функционала f0
устанонлемт.
ОбрппЮу пусть для элементов х^ Х\ F и Uo<^F
нашелся функционал /оеР, удовлетворяющий условиям
1) —3). Тогда для любого элемента u^F будем иметь
\х- "о!! = /о (х-ио) = /о (л- и) + [/о (и) - fo Ы].
Так как разность в квадратных скобках ввиду условия 3)
неположительна, то
т. е. элемецт и0 удовлетворяет B.21). Теорема 2.4.1
доказана.
Теорема 2.4.2. Пусть F — подпространство
линейного нормированного пространства X. Для того чтобы
элемент и{) е F доставлял наилучшее приближение в F
элементу x^X\F$ необходимо и достаточно существование

36 ДВОЙСТВЕННОСТЬ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ [ГЛ. 2
функционала /оеХ*, удовлетворяющего следующим
условиям:
1) 'i/oHl,
2) j*-Uo!! = M*).
3) /о(«) = 0 Vaef.
Действительно, если
inf Bx-wJH*—"о? («oef) B.23)
не/7
и функционал /0 с нормой i| / [; = 1 реализует верхнюю
грань в B.20), то
!:*-V. = /oM
и для f0 условия 1)—3) выполнены.
Обратно, если для функционала f0 из X* выполняются
соотношения 1) —3), то для любого u^F
!"-*: — «i!r--fo (*-")=/о (*) =?*-М .
т. е. имеет место B.23).
Заметим, что если подпространство F конечномерно,
то теорему 2.4.2 мы могли вывести, базируясь на
соотношении B.1).
§ 2.5. Двойственные соотношения для задач
наилучшего приближения
в пространствах Lp (а, Ь) и С [а, Ь]
С[а,Ь]у как обычно, будет обозначать пространство
непрерывных на отрезке [а, Ь] функций х (t) с нормой
1х}С[а, «,]= max j jc(/) |.
Lp {ay b) A ^ p < oo, Lx (о, й) = L (ay b)) есть
пространство суммируемых (т. е. интегрируемых по Лебегу) на
(CLyb) в р-й степени функций x(t) с нормой
у up
a Loc (a, b) = М (а, 6) — пространство измеримых
существенно ограниченных на (а, Ь) функций x(t)y норма в
котором задается равенством
(а. Ь) = S^CiM (а. 6) p

<S 2.5] ДВОЙСТВЕННЫЕ СООТНОШЕНИЯ В LQ{a, b) И С [а, Ь] 37
Несмотря на существенное различие в задании нормы
в пространствах Lp(ayb) A<р<оо) и L^(ayb)t
многие факты, как мы увидим ниже, будут формулироваться
одновременно для всех 1-^ р ^ оэ. Это связано с тем,
что для x(t) ^ М {а, Ь) (см., например, С. М.
Никольский, [4], стр. 14)
т. е. М (а, Ь) есть предельный случай пространства Lp (a, b).
Посмотрим сначала, как в пространствах С\а,Ь] и
Lp(a,b) реализуется общее соотношение двойственности
B.1) для наилучшего приближения линейными
комбинациями фиксированной конечной системы элементов.
Что касается Lp(ayb) (I <;р<оо), то мы могли бы,
записывая правую часть B.1) для этого случая, сразу
воспользоваться известными в функциональном анализе
теоремами об общем виде линейных ограниченных
функционалов в L(afb) и Lp(afb) A<р<оо). Мы однако
изберем иной путь—через теорему 2.2.2, — который
потребует некоторых (впрочем, весьма небольших) выкладок,
но зато позволит получить нужный результат также и
для Leo (a> b).
Пусть хх (/), х2 (t)t ... , хп @ — фиксированные функции
из Lp(a,b) (ls^ps^oo). Положив
h
h (У) - I xk (/)у (/) dt [у (t) e L,, (a, b); У + Xpl = l),
a
мы зададим в пространстве Lp>(a,b) n линейных
ограниченных функционалов fk (k= I, 2, ... , п).
Действительно, используя при 1<р<сх> неравенство Гельдера
(см. (Д.1)*)), а при р— 1 и р = оо просто заменяя \уA)\
или соответственно \xk(t)] нормой в М(а,Ь), получим
! /* (у) I < \! хк (о у (о! л < f, xfc 5 (a> w f у ¦{, ,e> w.
Таким образом, fk^Lp(a, b) (k=lf 2, ..., n).
*) (Д.1), (Д.2), ... — номера формул из Дополнения в конце
киши.

38 ДВОЙСТВЕННОСТЬ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ [ГЛ. 2
Если *@ —любая функция из Lp(a,b)y то, полагая
мы определим на Lp> (а, Ь) линейный ограниченный
функционал /, f ^ Ц< (а, Ь). Пусть
B.24)
где Я={Яь >.2> • •> К} — произвольный набор числовых
коэффициентов. Ясно, что cpb<=Lp'(a, 6), причем
(at b).
Вычисляя норму функционала ср^ и пользуясь при этом
доказанным в Дополнении соотношением (Д. 12), будем
иметь
sup
С учетом B.24) получаем, что для любых Xk имеет
место равенство
и теорема 2.2.2 приводит к соотношению
min if x - 2]
= min I1/ —
sup
I, 2 я

S 2.5] ДВОЙСТВЕННЫЕ СООТНОШЕНИЯ » Lp (я, Ъ) И С la, b) 39
Если учесть представление функционалов fk и /, то
окончательно получим
j@i] hk()
sup \x{t)y(t)dtt B.25)
У 1 Jfi,.
де у Л хк означает, что
\xk(t)y(t)dt = O.
а
Отметим частные случаи соотношения B.25),
соответствующие случаям р=1 и р = оо:
1'Л1 (a, b)^1 a
А1
sup ]x(t)y(t)dtt B.26)
In |i
Ч II *=* \\M(a.b)
b
sup \x{t)y{t)dt. B.27)
При п=1 и ^(/) = 1 равенство B.25) запишется в виде
ь
inlx(t)-yiLpia,b) = i sup \x(t)y(t)dU B.28)
Рассматривая задачу наилучшего приближения
\\ С [а, 6], мы будем исходить из самого общего случая,
когда аппроксимирующим множеством является
замкнутое выпуклое множество; двойственность для
приближения подпространством получим как частный случай.

40 ДВОЙСТВЕННОСТЬ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ [ГЛ. 2
В учебниках но функциональному анализу
доказывается (см., например, А. Н. Колмогоров, С. В. Фомин
[1], стр. 347), что всякий функционал /eC*[a,i]
представим в виде интеграла Стилтьеса:
ь
= ]x (t) dg (t) Чх (t) e С [a, b]9 B.29)
a
гДе g @ — некоторая функция с ограниченным изменением
на [а, Ь]у причем
Поэтому, если F — некоторое множество из С[а,Ь]> то
для любой функции х@еС[а, b]
sup \f(x) -sup/
fz=C*ia,b\l u<=F
sup
5 x @ ^ @ - sup U (/) dg (ol. B.30)
V (fi) 55 1 п
a
С другой стороны, любой функции g(t) с вариацией
ь
V (g) ^ 1 соответствует задаваемый равенством B.29)
а
функционал /eC*[a,i], причем (см. (Д. 15))
!/(*)! =
\x(t)dg(t)
а
b
гак что S/'l^Vfg). Это значит, что в B.30) на самом
а
деле имеет место знак равенства.
Таким образом, теоремы 2.3.1 и 2.3.3 для случая
Х^=С[я, Ь\ получают следующую формулировку.
Предложение 2.5.1. Если F —выпуклое замкнутое
множество в С [а, Ь], то для любой функции x(t)^C [а, Ь]
inf ix(t)-u(t)lc{a,b} =
(ь ь к
= sup [\x(t)dg(t)-*uv\u(t)dg(t)\. B,31)
V u>«i

в 2.61 ДВОЙСТВЕННЫЕ СООТНОШЕНИЯ В Lp(a, b) И С [at b] 41
В частности, если F — подпространство, то
ъ
inr\x(t)-u(t):C{a,b)= sup ]x(t)dg(t), B.32)
b
V do < i
a
где F'x — множество функций g(t) с ограниченным
изменением на [a, ft], удовлетворяющих условию
Существуют функции g (t) с вариацией на fa, 6],
равной единице, реализующие в B.31) и B.32) точную
верхнюю грань.
Разумеется, что в случае конечномерного
подпространства Г вторую часть сформулированного утверждения мы
могли вывести из теоремы 2.2.1.
Замечание. Соотношения B.31) и B.32) имеют место
при [а, 6] = [0,2/] и в пространстве С2! непрерывных на
всей оси 2/-периодических функций, ибо рассуждения,
которыми они доказаны, в равной степени справедливы
и для функций *(/)^С|0, 2/|, удовлетворяющих условию
л:@)— хB1) и, следовательно, допускающих непрерывное
продолжение с периодом 21 на всю ось.
Укажем конкретную реализацию теорем 2.3.1 и 2.3.3
в случае X = Lp(a, b) A^/?<сю).
Известно (Л. А. Люстерник, В. И. Соболев [1], стр. 193),
что любой функционал /еЦ(й, Ь) A^р<оо) задается
равенством
/(*)«$* @ У @ dt Чх (/) е= 1Р (а, Ь)9 B.33)
а
где y(t)<=Lp>(a% Ь) A/р+ W = 1)» причем
1П = 1Ук„(а.Ь). B.34)
Верно и обратное: каждая функция y(t)^LP'(a, Ь)
определяет равенством B.33) функционал /eL*p(a,i), удовле-

42 ДВОЙСТВЕННОСТЬ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ 1ГЛ. ?
творяющий условию B.34). Поэтому из теорем 2.3.1 и 2.3.3
вытекает
Предложение 2.5.2. Если F — выпуклое замкнутое
множество в Lp(at b) A^/;<оо), то для любой функции
x(t)e=Lp(ay b)
\\
v
Ib b
sup (\x (t)у (/) dt - sup \и (/)у (/) dt) B.35)
В частности, если F — подпространство, то
inf fX (t)-U(t) }L<a,b)= SUP \X(t)y(t)dt B.36)
«ef ' veFX, J
F-1- —множество функций у (t) e L^- (a, 6), 5ля которых
\u(t)y (t)dt = O V«@ sF.
Верхняя грань в B.35) a B.36) достигается на некоторых
функциях y(t) из Lp'(a9 b) с нормой \у \lp,{q,ь,= 1.
Ясно, что при (а, 6)==@, 2/) утверждения
предложения 2.5.2 справедливы и для соответствующих пространств
2/-пориодических функций.

ГЛАВА 3
НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ ФИКСИРОВАННОГО
ЭЛЕМЕНТА В ПРОСТРАНСТВАХ CML
Эта глава в общем плане книги имеет
вспомогательный характер. В ней будет доказано несколько фактов,
связанных с существованием, единственностью и
характеристическими свойствами элемента наилучшего
приближения в пространствах С и Lp. Основное внимание уделено
критериям элемента наилучшего приближения, которые
будут позже использованы при решении других
экстремальных задач.
Рассмотрен также важный для дальнейшего пример
на вычисление наилучшего приближения в метрике L
функций Бернулли.
Наряду с введенными в § 2,5 пространствами С [а, Ь\
и Lp (a, b) будут рассматриваться пространства 2л-перио-
дических функций:
С — пространство непрерывных на всей оси периода
2л функций /(/) с нормой
Lp A ^;р<оо, Lx — L) — пространство 2я-периодических
суммируемых на @, 2л) в р-й степени функций/(/), норма
в котором определена равенством
/2п \\/р
(интеграл везде понимается в смысле Лебега).
М == Loo —- пространство 2л-периодических существенно
ограниченных па всей оси функций /(/) с нормой
Ясно, что если / непрерывна, то i|/.w llf|!c
Условимся еще вместо \ffL писать Ц/Цр, имея б виду,
что Ш!/к |/||fU

44 ПРИБЛИЖЕНИЕ ФИКСИРОВАН. ЭЛЕМЕНТА В С И L [ГЛ. 3
§ 3.1. О существовании и единственности элемента
наилучшего приближения в С и Lp
Заметим сразу, что, как следует из общих
предложений 1.3.1 и 1.3.2, в пространствах С и Lp (l)
равно как и в пространствах С [а, Ь] и Lp(a, b)
любое локально компактное множество и, в частности,
любое конечномерное подпространство является
множеством существования.
В пространствах С и Lv периодических функций
естественным аппаратом приближения являются
тригонометрические полиномы. В дальнейшем через Тп (i) мы всегда .
будем обозначать тригонометрический полином
Тп (t) = а2°- + У (а* cos kt + pA sin kt) C.1)
порядка п—\ (я=1, 2, ...). Система функций
1, cos/, sin/, cos2/, sin 2/, ..., cos(/j — 1)/, sin (« — !)/,
C.2)
линейной комбинацией которых является 7"w@, линейно
независима. Действительно, если
п — \
¦?¦+ 2(aftcos^+p/fesin^)s0»
то, умножая обе части тождества последовательно на
функции системы C.2) и интегрируя по периоду @, 2л),
обнаружим, что все коэффициенты аи и рА равны нулю.
Таким образом, при фиксированном п множество
полиномов C.1) является подпространством (в С или в Lp)
размерности 2п— 1. Мы его будем обозначать Fjn-u & Для
наилучшего приближения функции fs^, где X есть С
или Lp, подпространством /^o-i введем традиционное
обозначение:
( Fj,-i)x= Inf iif-rrtb
Из общего утверждения 1.3.1 вытекает
Предложение 3.1.1. Для любой функции f (t) е Ху
г X есть С или Lp A<р<оо), в подпространстве Fw~x

<§ 3.11 СУЩЕСТВОВАНИЕ И ЕДИНСТВЕННОСТЬ 45
существует полином наилучшего приближения, т. е.
существует тригонометрический полином Т% (/) =* Т% (/, /)
порядка п — 1 такой, что
В пространствах С fa, b\ и Lp(at b) (К р^оо)
функций, заданных на конечном промежутке, одним из
простейших и удобных аппаратов приближения являются
алгебраические многочлены
1 (« = 0, 1, 2, ...). C.3)
При фиксированном п множество многочленов C.3) в силу
линейной независимости функций 1, ty i2, ..., Vх
является подпространством размерности я+1. В силу 1.3.1
справедливо
Предложение 3.1.2. Для любой функции f (/) е
^X[a, fe), 2(9^ A^[a, b] есть С fa, fe| ил« Lp (a, 6), cp<«d^
вс^л: многочленов C.3) при каждом фиксированном п
существует многочлен Р% @ наилучшего приближения, для
которого
Вопрос о единственности элемента наилучшего
приближения не играет роли при решении тех задач,
которым посвящено основное содержание книги, и мы не будем
в него углубляться. Отметим только, что к пространству
Lp A<р<оо) применимо предложение 1.3.3.
Действительно, знак равенства в соотношении
являющемся сокращенной записью неравенства Минков-
ского, при 1 <р<оо возможен лишь при условии f(t) =
¦-= сф (/) (с > 0) (см. Дополнение), поэтому пространство
^A<Р<°°) строго нормировано, а это, как мы уже
знаем, равносильно строгой выпуклости нормы.
Таким образом, в любом подпространстве
пространства Lv или /,,,(а, Ь) при 1<р<оо элемент наилучшего
приближения единствен.
Что касается пространств С и L, то норма их не
является строго выпуклой. Например, в пространстве С,

46 ПРИБЛИЖЕНИЕ ФИКСИРОВАН. ЭЛЕМЕНТА В С И L [ГЛ. 3
положив f(t) = cost, cp(/) = cos2/, будем иметь
ШсН!ф!!с=1,
однако при всех а @<а<1)
Впрочем, для многих важных подпространств, в
частности для подпространства f.^-i тригонометрических
полиномов, единственность элемента наилучшего приближения
как в С, так ив/, имеет место, однако это уже связано
со спецификой самих подпространств.
В следующем параграфе единственность
тригонометрического полинома наилучшего приближения для функций
пространства С будет выведена как следствие из теоремы
Чебышева.
Аналогично обстоит дело с проблемой единственности
и в пространствах С fa, b\ и L(af Ь), норма которых не
является строго выпуклой. Заметим, что среди
многочленов C.3) при фиксированном п для любой функции
/<=C(a, b] многочлен наилучшего приближения единствен
(см. ниже предложение 3.2.4).
§ 3.2. Теоремы Чебышева и Валле-Пуссена
Изложение вопросов, связанных с характеристическими
свойствами элемента наилучшего приближения, мы начнем
со знаменитой теоремы Чебышева о критерии многочлена
наилучшего равномерного приближения. Хотя эта теорема
может быть выведена (совсем не просто, впрочем) из общих
соотношений двойственности, мы приведем здесь ее
традиционное элементарное доказательство, причем как для
периодического, так и для непериодического случаев.
Теорема 3.2.1 (П. Л. Чебышев [1|).
Тригонометрический полином fn (t) доставляет функции f(/)eC
наилучшее равномерное приближение среди всех
тригонометрических полиномов порядка п — 1 в том и только в том
случае, когда на периоде О ^ / < 2л существует 2п точек х%:
в которых разность Д (/) = / (/) — fn (t) достигает по
абсолютной величине максимального значения [ Д |{ = |, Д ||с.

§ 3.2] ТЕОРЕМЫ ЧЕБЫШЕВА И ВАЛЛЕ-ПУССЕНА 47
поочередно меняя знак, т. е.
C.4)
Докажем необходимость условий теоремы. Пусть
fn(t) — полином наилучшего равномерного приближения
для /еС, т. е.
\\f-fn^ = \nV{f~Tn\c = En(f)c^d. C.5)
п
Ясно, что разность A (t) = f(t) — fn (t) имеет нули, ибо
иначе Тп не доставлял бы функции f наилучшего
приближения. Заметим далее, что в силу периодичности функции
условия теоремы инвариантны относительно сдвига
аргумента, т. е. если 2п точек xky обладающих указанными
свойствами, существуют на [0, 2л), то 2п точек yk =¦• xk + a
обладают этими свойствами на промежутке [а, а + 2д),
где а —любое число, и наоборот. Поэтому мы можем
считать, что Д @) = Д Bл) = 0.
Обозначим через е множество точек промежутка @, 2л),
в которых разность Д@ принимает значения ±:d. Среди
точек множества е будем различать еь-точки, в которых
A(/) = d, и ^"-точки, в которых Д@ = — d. Множество е
содержит как е\ так и е~-точки, т. е. график А (/)
обязательно касается обеих прямых у — zLd. Действительно,
если бы было, например, A(/)<d для всех t, то для
полипома Тп(ь\ l) = fn(t) + t-: при достаточно малом е>0
было бы lf — Tn(e)]c<d*, что невозможно в силу C.5).
На промежутке @, 2л) можно выбрать точки zk
@ = го<г!<г2< ... <гт<2л) так, что будут
выполняться следующие условия:
1) Д(гА) = 0 (А«1э 2, ...э/я);
2) каждый из отрезков
*1=фоэ zib а2я[2ь г2], ..., ат = [^_ь zm], om?i = [zm, 2л]
C.6)
содержит хотя бы одну е-точку, причем все е-точки,
лежащие па одном отрезке, одного знака: либо еь-точки, либо
3) знаки е-точек па соседних отрезках ak и
=»1, 2, ..., /я) противоположны (рис. 2).

48 ПРИБЛИЖЕНИЕ ФИКСИРОВАН. ЭЛЕМЕНТА В С И Lp [ГЛ. 3
Чтобы доказать необходимость условий теоремы,
достаточно установить, что число отрезков C.6) не меньше
чем 2п, т. е. что (m+l)/2s^tt.
Положим v = [(m+l)/2| (fa|~ целая часть числа а) и
покажем, что v^n.
Рассуждаем от противного. Пусть v<«, т. е.
v^n — 1, и
M/) = tv(*, O = ^sini^sin^-...sin-bf^-, C.7)
Так как
sin
sin
где a, P и у—некоторые числа, то tv(/), как
произведение v тригонометрических полиномов первого порядка,
Рис. 2.
является тригонометрическим полиномом порядка v.
Поэтому, кроме точек г0, гь ... 22v-i, поЛИ11ОМ Tv@ на
полуинтервале [0, 2л) других нулей не имеет, причем гА —
единственные точки, в которых ty(/) меняет знак.
Пусть a+ — объединение отрезков ok из C.6),
содержащих <?ь-точки, а а —объединение отрезков из C.6),
которые содержат е~-точки. В силу непрерывности найдется
положительное число h > 0 такое, что
d (/e=aJ), C.8)
h (/e=or). C.9)
Теперь выберем в C.7) множитель % по знаку и величине
так, чтобы выполнялись соотношения
sign Д @ = sign tv (t) (t о е), C.10)
max | tv (Я, t)\<h/2. C.11)

§3.2] ТЕОРЕМЫ ЧЕБЫШЕВА И БАЛЛЕ-ПУССЕНА 49
По предположению, v •.<. п—1, поэтому функция Тп (t) -j-
+ xv@ есть также тригонометрический полином порядка
п—\у и мы получим противоречие, если окажется, что
C.12)
Пусть, например, алскт'*. Тогда ввиду C.10) xv(/)> О
во внутренних точках отрезка <ть а так как в точках zk
не только tv(/), но и А (/) обращается в нуль, то в силу
C.8) и C.11) разность Д(/)~ xv(/) в каждой точке / <= ok
но абсолютной величине строго меньше d и, значит,
шах |Д (/) —Tv@i<d. C.13)
Справедливость такого неравенства для аА<=ог
совершенно аналогичным образом вытекает из C.9), C.10),
C.11) и того факта, что Д (ги) — xv (z*) = 0. Таким образом,
неравенство C.13) должно выполняться на каждом
промежутке ak (k= I, 2, ..., m), что равносильно C.12).
Необходимость доказана.
Достаточность условий теоремы Чебышева
устанавливается гораздо проще. Надо доказать, что если для
полинома tn(t) выполнены эти условия, то для любого
полинома Тп (t) будет
Предположив, что это не так, т. е. что для некоторого
полинома Тп (/)
|Г«5ДГ, C.14)
рассмотрим тригонометрический полином Sn (t) = Tn (t) —
— fn (t) (Sn(/)^0), который запишем в виде
Sn (t) = \f (t) - fn (/)] ~ (/ @ - Tn (/)].
Разность в первых квадратных скобках в точках Хы
о которых говорится в условии теоремы, принимает
значения rJi'jA'J, поочередно меняя знак. Поэтому ввиду
C.14), предполагая для определенности, что Д(^)>0,
будем иметь
sign Sn {xk) - sign Л (хк) (k г= 1, 2, ..., 2л).
Но тогда с учетом C.4) полином Sn (t) должен на периоде
[0, 2л) иметь по меньшей мере 2лг — 1 нулей, что для

50 ПРИБЛИЖЕНИЕ ФИКСИРОВАН. ЭЛЕМЕНТА В С И Lp [ГЛ. 3
нетривиального тригонометрического полинома порядка
л— 1 невозможно.
Теорема 3.2.1 доказана.
В качестве следствия из теоремы Чебышева получаем
Предложение 3.2.2. Для каждой функции f €= С
тригонометрический полином наилучшего приближения
(фиксированного порядка) единствен.
В самом деле, пусть
Тогда в силу 1.2.3 полипом 2 [fn (t) + T% (t)] также
доставляет наилучшее приближение функции /, и по теореме
Чебышева существует 2п точек xk (/е=1, 2, ..., 2п) на
периоде, в которых
U (**) - Тп Ш] + U (xk) - Т*п (xk)] = ± 2Еп (f)c C.15)
(A=lf 2,..., 2я).
Каждая из квадратных скобок по абсолютной величине
не превосходит En(f)c> и потому равенства C.15)
возможны, лишь если
/ (xk) - fn (хк) = / (xk) - Т% (xk) = ztEn (/)с,
т. е,
(A=l, 2, ..., 2я).
Остается заметить, что тригонометрические полиномы
порядка я— 1, совпадающие более чем в B/г — 2)-х точках
на периоде, совпадают тождественно.
Критерий, аналогичный теореме 3.2.1, имеет место и
в пространстве С [at b].
Теорема 3.2.3 (П- Л. Чебышева [1]). Алгебраический
многочлен
доставляет функции f ^C[a, b] наилучшее равномерное
приближение на [а, Ь] среди всех многочленов степени п
в том и только в том случае, если существуют п+2
точки xk:

$ 3.2J ТЕОРЕМЫ ЧЕБЫШЕВА И ВАЛЛЕ-ПУССЕНА 51
в которых разность A (t) = / (/) — Рп (t) принимает
значения ±|| Aj|c[o, &i> поочередно меняя знак.
Доказательство необходимости проводится по схеме
доказательства теоремы 3.2.1, исключая, разумеется,
соображения, связанные с периодичностью.
Следует ввести в рассмотрение множество е точек
отрезка [а, &], в которых разность Д (/) принимает
значения iH! &\c[a, ь], выделить отрезки
\а, *i], [^ь г2], — > [*т> b\\ i\(zk) = 0 (А = 1, 2 т),
содержащие сточки только одного знака, причем знак
е-точек меняется от отрезка к отрезку, и убедиться, что
число этих отрезков :??п + 2. Читатель, разобравший
доказательство теоремы 3.2.1, без труда проведет самостоятельно
все выкладки, связанные с рассуждением от противного
и построением поправки
к многочлтеу Рп (/).
Достаточность доказывается так же, как и в
теореме 3.2.1, с-использованием того факта, что
нетривиальны и алгебраический многочлен степени п не может иметь
более чем п нулей.
Из теоремы 3.2.3, аналогично периодическому случаю,
выводится
Предложение 3.2.4. Для каждой функции f^C\a, b]
алгебраический многочлен наилучшего приближения
(фиксированной степени) единствен.
Для оценки снизу наилучшего равномерного
приближения бывают полезны следующие теоремы.
Теорема 3.2.5 (Валле-Пуссеи [lj). Пусть f (/) gC.
Если для некоторого тригонометрического полинома Т% (t)
порядка лг — 1 на периоде [0, 2л) существуют 2п точек хь-
0 < а-! < х2 < ... < х2п < 2л,
в которых разность Л (t) = / (t) — T% (t) принимает значения
с чередующимися знаками:
sign А (**)- — sign Д (^4)^0 (А=1, 2, ..., 2п-1),
то

52 ПРИБЛИЖЕНИЕ ФИКСИРОВАН. ЭЛЕМЕНТА В С И L \ Л. 3
Доказательство. Рассуждая от противного,
предположим, что
En(f)c< min 1Д(**)|-Ч
Если Т„ @ — многочлен наилучшего равномерного
приближения для /, то
и, в частности,
f(xk)-fn(xk)\<4^\f(xk)-rn(xk)\ (*=I, 2 2«).
C.16)
Рассмотрим разность
S* (/) - 7Л @ - П @ = Д @ - [/ @ - Тп (/)]. C.17)
Из C.16) и C.17) следует, что
sign Sn (xk) = sign Д (xk) (k - 1, 2, ..., 2n),
и тригонометрический многочлен Sn(t) порядка лг — 1
должен в силу условия теоремы иметь на |0, 2л) по
меньшей мере 2/г — 1 нулей, что невозможно, ибо ввиду C.16)
Sn(t)^Q.
Совершенно аналогично доказывается
Теорема 3.2.6 (Валле-Пуссен [ 11). Пусть fs=C |а, Ь].
Если для некоторого алгебраического многочлена Рп (/)
степени п существуют я+ 2 точки
в которых разность A(t) — f (/) — Рп (t) принимает
чередующиеся по знаку значения, то
tollf-Pnlcia.ti'S* min |
Рп
§ 3.3, Критерии элемента наилучшего приближения
в Lp (I ^/Koo) в случае приближения подпространством
Заметим сразу, что хотя Lp у нас есть пространство
2п-периодических функций, все рассуждения и результаты
этого параграфа не связаны с периодичностью, так htq
цод Lp можно понимать и Lp@% 2я).

$ 3.3J КРИТЕРИИ БЛИЖАЙШЕГО ЭЛЕМЕНТА В L 53
Рассматривая сначала случай 1<р<Соо, докажем
следующую теорему.
Теорема 3.3.1. Пусть F — фиксированное
подпространство в Lp A<р<оо). Для того чтобы функция
Фо е F доставляла функции /eLp наилучшее приближение
в подпространстве F, необходимо и достаточно выполнение
условия
2л
S Ф @1 / @ - Фо @ i^ sign [/* @ - Фо @1^ = 0 Vcpef.
о
C.18)
Доказательство, Мы можем считать, что fe?F.
Пусть фо @ — функция наилучшего прггбднжения для f
в подпространстве F. В силу предложения 2.5.2 и, в
частности, соотношения B.36) существует функция ho(t)eLP'
A/р+ 1/р'= 1) с нормой [AoV—1 такая, что
\ К (t) ф (t) di = 0 Уф еЕ f C.19)
2л 2л
I/ - Фо I =5/@ Ло @ Л = J [/ @ - Фо @1 Ло @ d/. C.20)
о о
Применяя неравенство Гельдера, можем написать
2л 2я
\ а~Фо)Ло^^ \ i/(o-"<po(o:iMo;d/<
о и
<3/-Фо!р5ЛоЗр'==1/-Фои C.21)
причем в силу C.20) везде здесь должен быть знак
равенства. Это означает (§ Д. I), что (вес выписанные ниже
соотношения справедливы почти всюду)
|Ао@1=«,/@-фь(ОГ1. C.22)
где а —положительная константа. Кроме того, из равенства
2я 2я
5
о
дледует, что
C.23)

54 ПРИБЛИЖЕНИЕ ФИКСИРОВАН. ЭЛЕМЕНТА В С И L [ГЛ. 3
В силу C.22) множество точек, в которых обращается
в пуль только один из сомножителей в левой части C.23),
имеет нулевую меру, и потому из C.23) вытекает
соотношение
sign Ло @ = .sign If (/) — ф0 @1- C.24)
Теперь с учетом C.22) и C.24) будем иметь
Ао (/) = ! Ао @ ! sign Ло (/) =
= «»f @ — Фб @ i" -1 sign [f @ — Фо @1.
что вместе с C.19) дает C.18). Необходимость доказана.
Доказывая достаточность, предположим, что для
функции (poef условие C.18) выполнено. Тогда для любой
фЕ/^ будем иметь
If" Фо % = S (f —ФоI/ —Фо Гl sign (f - Фо) dt =
о
2я
= \ (/-Фо + Ф-ФO-Фо!/7-^п (/-фо)Л==
б
2л
= J V — Ф) i /* — Фо ip x sign (/ — Фо) d/ ^
Так как (р—1)р' = р, а функции f и (р0 принадлежат^,
то if — Фо!*7"-1 eLp'. Поэтому, применяя неравенство Гель-
дера, получим
Итак, для любой функции
т. е.
II / — Фо IU ^ II /" — ФIU»
а это означает, что ф0 есть функция наилучшего
приближения для / в подпростраистве F. Теорема 3.3.1 доказана.

3.31 КРИТЕРИИ БЛИЖАЙШЕГО ЭЛЕМЕНТА В L 55
v
В случае р=1 необходимость условия C.18) требует
некоторых оговорок.
Теорема 3.3.2. Пусть F — фиксированное
подпространство пространства L. Для того чтобы фукция ф0
из F доставляла наилучшее в метрике L приближение
функции fet, достаточно, а в случае, когда множество
точек I, в которых /(О = Фо(О> имеет меру нуль, и
необходимо выполнение соотношения
ы
Ф (/) sign [/ (t) - ф0 @1 dt = 0 Уф е= F. C.25)
Доказательство. Пусть
[/-Фо||1= inf I7-<p]l C.26)
и Ао@ —Функция из M~Lco> реализующая в B.36) при
р = 1 верхнюю грань. Тогда
2я 2л
U - Фо [l = U @ Ао @ Л = jj (/ - ф0) Ао Л.
Таким образом,
2я
Л= 5 |/-Фо1Л. C.27)
5
Если множество точек, в которых /@~Фо@» имеет
меру нуль, то равенство C.27) для функции Ао возможио
тогда и только тогда, когда почти всюду
МО = sign |/@-Фо @1-
2я
Из этого соотношения и того, что jj/z0 @ ф@ d/= 0
о
Уфе/7, следует C.25).
С другой стороны, если для фо^/7 выполнено C.25),
то, какова бы ни была функция (pef, будем иметь
2л 2д
$ 1/-фо|^= 5 (/-фо)^(/-фо)Л=«
о о
2я 2я
о

56 ПРИБЛИЖЕНИЕ ФИКСИРОВАН. ЭЛЕМЕНТА В С И Lp [ГЛ. з
т. е. Цо(() удовлетворяет соотношению C.26). Теорема
3.3.2 доказана.
Переформулируем теоремы 3.3.1 и 3.3.2 для случая
приближения тригонометрическими полиномами.
Предложение 3.3.3. Т ригоно метрический полином
Тп (() порядка п — 1 является полиномом наилучшего
приближения в метрике Lp (l<Cp<ioj) для функции f e Lp
тогда и только тогда, если для любого
тригонометрического полинома Тп (t) того же порядка
f Tn (t) [ / (t) - f n (i) i ^4ign f/ @ - fn @l dt = 0.
Предложение З.З.4. Для того чтобы
тригонометрический полином Тп доставлял наилучшее приближение
в метрике L функции f e L, достаточно, а в случае, когда
mes{/: /(O^^WJ^O» u необходимо выполнение
соотношения
2я
каков бы ни был тригонометрический полином Тп (t)
порядка п — 1.
Утверждения, аналогичные предложениям 3.3.3 и 3.3.4,
имеют место и в случае наилучшего приближения в
пространстве Lp@, 2л) алгебраическими многочленами.
§ 3.4. Критерии ближайшего элемента в С и Lp
в случае приближения
замкнутым выпуклым множеством
Здесь мы переформулируем общий критерий 2.4.1 для
'пространств С и Lp.
Предложение 3.4.1. Пусть Хс есть пространство
С или С [0,2л], F — замкнутое выпуклое множество в Хс
и f е Хс- Функция ф0 из F тогда и только тогда
удовлетворяет соотношению
— Ф ;UC, C.28)

: 3.4] ПРИБЛИЖЕНИЕ ВЫПУКЛЫМ МНОЖРХТВОМ 57
когда существует функция gQ (/) с ограниченным
изменением на [0, 2д], удовлетворяющая условиям:
о
о
2я 2л
3) $ фо dg0 = sup
Действительно, каждому линейному ограниченному
функционалу Y, заданному на С [0, 2л], соответствует
функция g (/) с ограниченным изменением на [0,2л]
такая, что
2л
1f(/)= $/<fc V/eC[0,2n],
о
2п
Поэтому в соответствии с утверждением необходимости
в теореме 2.4.1, если для cpoef имеет место равенство
C.28), то существует функция g0, для которой выполнены
условия 1) — 3).
С другой стороны, если для qo^F можно указать
функцию g0, для которой выполнены 1) — 3), то с учетом
этих условий и (ДЛ5) для любой функции 9GF будем
иметь
г2я 2я -|
\ J cpd?0- \ Фо4вГо
L о о J
5
о
о
т. е. справедливо C.28).
Отметим отдельно частный случай предложения 3.4Л,
когда F —подпространство.

58 ПРИБЛИЖЕНИЕ ФИКСИРОВАН. ЭЛЕМЕНТА В С И L |ГЛ. 3
Предложение 3.4.2. Пусть F —подпространство
пространства Хс, под которым понимаем С или С [О, 2л],
и f <= Хс. Функция ф0 из F тогда и только тогда
удовлетворяет соотношению C.28), когда существует
функция g0 с ограниченным изменением на [О, 2я] такая, что:
1) Уы = 1;
С
2л
2) !!/ —ToiUc; = \fdgo\
о
3) V(pG=F $ q>dgo = d.
о
Предложение Зч4.2 выводится из теоремы 2.4.2 точно
так же, как 3.4.1 выведено из 2.4.1.
Предложение 3.4.3. Пусть F — замкнутое
выпуклое множество пространства Lp (l^p<Oo). Функция
Фое/7 тогда и только тогда удовлетворяет соотношению
=inf Sf-фЦр,
когда существует функция Ао(/) е LP' (l/p+ 1/р' = 1),
удовлетворяющая условиям:
2) 1!/
3) ^
О
Справедливость предложения 3.4.3 немедленно
вытекает из теоремы 2.4.1 и того факта, что любому
функционалу XY <= Ц взаимно однозначно соответствует функция
Ag LP' такая, что
xV(f)=\f(t)h{t)dt V/gLpj
Мы не отмечаем частный случай предложения 3.4.3,
когда F — подпространство, ибо более сильный критерий
для этого случая сформулирован в 3.3.1 и 3.3.2.

S 3.5] ФУНКЦИИ БЕРНУЛЛИ 59
§ 3.5. Функции Бернулли и их наилучшее приближение
тригонометрическими полиномами в метрике L
Функциями Бернулли называют 2л-периодические
функции
Как мы увидим в главе 5, они естественным образом
возникают при получении интегрального представления
дифференцируемых периодических функций. Через
наилучшее приближение функций Dr(x) в метрике L
тригонометрическими полиномами будут выражаться
аппроксимативные характеристики некоторых классов функций.
Так как
D2, (х) = (-l)v 2 ^ (v = 1, 2, ...), C.30)
# (v = 0- 1. 2,...), C.31)
то функции Бернулли с четными индексами четны,
а с нечетными индексами нечетны. Кроме того,
т. е. график D2v(x) симметричен относительно прямых
х = тп (т = 0, ±1, ±2,...), а график D2v.,.i (x) —
относительно точек х = тл,у = 0 (рис. 3). Поэтому, изучая
поведение функций Dr{x)y достаточно ограничиться
промежутком [0, л].
Для функции Dx{x) имеют место равенства
' C.32)
0 (лг-О),
которые легко получить, разлагая стоящую справа
функцию в ряд Фурье. Из определения функций Dr(x)
следует, что
Dr(x)=\D^x(t)dt (r = 2,3,...), C.33)

60 ПРИБЛИЖЕНИЕ ФИКСИРОВАН. ЭЛЕМЕНТА В С И Lp (ГЛ. 3
где константа
соотношение
выбирается так, чтобы выполнялось
2л
в частности, C^.1=^. Таким образом» D{ <= M, Dr
(г ^2).
Из C.32) следует, что Д-(.г) на промежутке <<
<2л есть алгебраический многочлен степени г. Этот
яг
4?
Ate)
п
Рис. 3. Функции Бериулли Ог(х) (г =1,2,3).
многочлен известен в математической литературе как
многочлен Бернулли.
Учитывая вид функции Dt(x) и рекуррентное соотно-
игение C.33), легко понять, что функция D2w(x) строго
монотонна и имеет ровно один нуль на промежутке @, я),
a D2vrt(x), обращаясь в нуль в точках л:=-0 и х = л,
сохраняет знак и имеет один экстремум на @, л)
Гоис. 3).

Ь 3.5] ФУНКЦИИ БЕРНУЛЛИ 61
Для дальнейшего нам потребуется
Предложение 3.5.1. Если /et и имеет период
2л/я, то
я
\ f(x)linkidx = O (fe = l,2, ..., /2—1). C.34)
ipu этом ^*(x)dx --0, то функции f (x) ортогональна
—л
тригонометрическим полиномам порядка п—\.
Действительно, полагая л'- /-|-2л7/, будем иметь
л 2 Мл л
\ cik*f(x)dx^=e ~~ \ eiktf(i)dty
—л —л
/ Ш\ л
т. е. \ 1 - е п ) \ еш\ @ di = 0. Но
—л
1_гп = 1 _ cos 2 *я-- 7
при ?=1, 2, ...,'я—1, поэтому имеют место равенства
л
\ (coskx-\-ismkx)f(x)dx = 0 (*==1, 2, ..., п- 1),.
—л
из которых, получим C.34). Второе утверждение
очевидно.
Из предложения 3.5.1 следует, в частности, что для
тюбого тригонолгетрического полинома Тп{х) порядка п — 1
— л
Основной результат этого параграфа составляет
Теорема 3.5.2. Наилучшее приближение в метрике L
функции Dr (t) доставляет тригонометрический полином
Tnr(t), интерполирующий Dr(t) в нулях cos ni, если г
четно, и в нулях sin/г/, если г нечетно. При этом
(л, г=1, 2,...).

62 ПРИБЛИЖЕНИИ ФИКСИРОВАН. ЭЛЕМЕНТА В С И L [ГЛ. 3
Доказательство. Пусть г четно и
Построим четный тригонометрический полином
Т //\ „ \ П // \ (COS/ — COS/)) ... (COS/ — COS /ft.-t)
У яг W *~ Zi Ur Vk) (cos/*-cos/0 ... (cos/* —cos/*.t) X
(cosj — cos /fr^,). .^ (cos / — cos fя)
(cos tk — cos /fr ,.!>... (cos tk — cos tn)'
обратив внимание ua то, что в k-м слагаемом в
числителе и в знаменателе отсутствуют сомножители, в которых
вычитается cos/*. Полином fnr(t) имеет порядок /г— 1,
ибо числитель дроби в каждом слагаемом есть
произведение п—1 полиномов первого порядка.
Очевидно, что в точках /,- значения fnr(t) и Dr{t)
совпадают, т. е. если положить
то Д(/,) = 0 (/=1, 2, .... /z).
Покажем, что точки /у являются простыми нулями Д(/)
и других нулей на отрезке [0, л] функция Д (/) не имеет.
Предположим, что это не так, т. е. что Д(/) обращается
в нуль на [0, я] в (п+ 1)-й точке или хотя бы один из
нулей ij является кратным. Тогда в силу теоремы Ролля
Д' (/) будет иметь на интервале @, я) по меньшей мере п
нулей. По
и так как Tnr(t), как производная четного полинома,
есть полином нечетный, то Д'(/) является нечетной
функцией, а потому обращается в нуль также в точках 1 = 0
и ? = я. Следовательно, Д' (/) имеет на отрезке [0, л]
/г + 2 нуля и, снова по теореме Ролля, четная функция
Д"(/) должна иметь на [0, я] по меньшей мере /z-j-1 нуль.
Продолжая эти рассуждения, придем к выводу, что
нечетная функция Д^-1) (t) имеет на интервале @, я) п нулей.

§ 3.5] ФУНКЦИИ БЕРНУЛЛИ 63
Так как
то Д(г~1}(/) дифференцируема в интервале @, 2л) и
Д^-D (л) = 0. Но тогда функция
C0S И
являющаяся четным тригонометрическим полиномом
порядка /1—1, должна иметь на @,2л) 2/г нулей, что было
бы возможно лишь в случае, когда Д(/>) (/) есть
тождественная константа. Однако ясно, что полином Тпг (/),
интерполирующий строго монотонную @,л) на функцию Dr(t)
в точках /,-, не может быть тождественной константой,
а потому константой не являются Тп) (t) и Ди) (/).
Итак доказано, что // (/=1, 2, ..., я) — единственные
и причем простые нули функции Д (/) на [0, л]. Если
учесть четность Д(/), то приходим к выводу, что Д(/)
обращается в нуль и меняет знак на периоде [0, 2л]
в точках
(являющихся нулями cos nt) и только в этих точках. Это
значит, что
sign Д (/) - sign [Dr @ - tnr (/)] = ± sign cos /z/. C.37)
Поэтому, каков бы ни был тригонометрический полином
ТпA) порядка /г—1, в силу C.35) и C.37) будем иметь
I Тп @ sign [Dr (t) - fnr (/)] dt = 0, C.38)
—л
и в силу критерия 3.3.4 tnr{t) есть полином наилучшего
приближения для Dr(t) в метрике L.

64 ПРИБЛИЖЕНИИ ФИКСИРОВАН. ЭЛЕМЕНТА В С И Lp [ГЛ. 3
Если г нечетно, то полагаем
/г—1
f, /а _ V Г) / ^ sin t (COS* —COSTi) ... (COS/— COSTfr.j) v/,
^ — COS Tfi-U
1
(cos t — cos T^)... (cos t — cos tb_i)
' (COS Tfe — COS ТЛ+1) ... (COS Tfe — COS Тд_!) »
где Xk^kn/n (k~\, 2, ...n— I). Теперь 7ЯГ(/) есть
нечетный тригонометрический полином порядка п—1,
интерполирующий функцию Dr(/) в точках xk. В силу
нечетности разность Д @ = Dr (/) — fnr (i) обращается в нуль
также и в точках t — О и / — я. Рассуждая от противного
и используя теорему Ролля, как и в четном случае,
убеждаемся, что эти нули для Д (/) простые и других нулей
функция Д (/) на [0, л] не имеет. Поэтому при нечетном г
sign [Dr @ - fnr (/)] = ± sign sin nt C.39)
и ввиду C.35) соотношение C.38) также будет иметь место
для любого Тп((), т. е. полином fnr(t), интерполирующий
Dr (t) (r -¦¦= 2v-|-1, v —0, 1...) в точках kn/n, доставляет
наилучшее приближение функции Dr(t) в метрике L.
Остается подсчитать значение наилучшего приближения
En(Dr)L= \\Dr{i)-fnr{t)\dt.
6
В случае четного г, учитывая C.37) и C.35), будем иметь
Еп (D2v)l = ± \ [Dav @ - f „, 2V (О] sign cos nt dt =
Л
jj D2V @ sign cos nt dt
— 71
Чтобы вычислить значение последнего интеграла,
воспользуемся обобщенным равенством Парсеваля (Г. М. Фнхтен-
гольц [1], стр. 589). Ряд Фурье функции /52v @ записан
в C.30), а разложив sign cos nt в ряд Фурье, будем иметь
оо
sign cos л/ = -я-
= i- /cos /г/ — з" cos 3/г/ + g- cos 5/г/ —.. .V C.40)

§ 3.5]
ФУНКЦИИ БЕРНУЛЛИ
65
Перемножая коэффициенты рядов C.30) и C.40) с
одинаковыми индексами и суммируя полученные произведения,
получим
Таким образом,
к 0
Если же г нечетно, г —2v+l, то с помощью соотно-
шений C.35) и C.39) найдем
Еп (Asv l)/. = "t J [^2v+1 @ - К 2VU (<)] Sign Sin fit dt -
(v-0, 1,...).
Так как
, 4 V sin Bk[-\)nl
- (sin/z/+ si
у sin
.;,
то с учетом C.31) обобщенное равенство Парсеваля дает
I I DkvlI(/)slgnsi.,,./i«™i.(-ir 2 WkTTuP^
fe0
2
п, следовательно,
C.42)
Легко видеть, что равенства C.41) и C.42) можно
объединить в одном соотношении
Еа (Drh - -V ? У^т (п. г -= 1, 2,...). C.43)
Теорема доказана.

66 ПРИБЛИЖЕНИЕ ФИКСИРОВАН. ЭЛЕМЕНТА В С И L [ГЛ. 3
Р
Числовые ряды в правой части C.43) определяют при
г=1, 2,,.. константы, которые будут часто встречаться
в окончательных результатах при решении экстремальных
задач теории функций. Если положить
W^ (r="°> 1. 2f ...), C.44)
то C.43) запишется в виде
En(Dr)L = ?§± (л, г=1, 2,...). C.45)
Постоянные о/С\ известны в математической
литературе как константы Фавара. Не представляет особого
труда подсчитать, что
еГ0=1, е#\ = л/2, еЯГ2 = л*/8, о/С9- л3/24, ...,
причем о/Сг возрастают по четным индексам и убывакл
по нечетным, так что
В заключение этого параграфа вычислим коэффициенты
полиномов fnr(t), доставляющих наилучшее приближение
Dr(t) в метрике L. Ясно, что эти коэффициенты
однозначно определяются условиями интерполяции. Пусть
сначала г четно. Тогда
я—I
и коэффициенты \ikr (k = 0, 1, .. •, п — I) мы должны
найти- из условий
2п *7 лпг\ 2п
т. е.
оо
к=\
л—1

$3.5] ФУНКЦИИ БЕРНУЛЛИ 67
Хорошо известны соотношения
п
V4 sin 2nx
2 cos ix = ™y^^Y' " "- C'48)
1-1
Первое in них получим, умножив и разделив в левой
•пктп каждое слагаемое на sinjc и заменив cosB/~ l)xsinx
рмзпоггыо синусов, а второе —тем же способом, умножив
и разделив левую часть на sin(x/2). Считая п фиксиро-
1ШИПЫМ и полагая d C.47) х=(тп)/Bп), а в C.48) я =
• тп/п (ш = 0, :»:1, iL2, ...), получим соотношения
О (m^2sn) (s = 0, ±1, ±2,...),
У cos i WIJT »•
I/i ¦- I (w/ 2s//),
^ |(_l)«-i_lj (/n^2s/i) E = 0. dbl, ±2,...).
Теперь вернемся к C.46). Суммируя левую и правую
части по / от 1 до пу с учетом C.49) получим
оо оо
/ |\г/2 V 2(—О5 (—0г/ V (—О5
Чтобы вычислить \xJr (/=1, 2, ..., n—1), умножим обе
части C.46) на cos Bi— 1) /л/2л и, заменив произведение

68 ПРИБЛИЖЕНИЕ ФИКСИРОВАН ЭЛЕМЕНТА П С И Lp [ГЛ. 3
косинусов на сумму, просуммируем no L Получим
ОО /1
(~1)Г/2Т 2 ? 2 [cosB/-l)^±in
Вычислив суммы по / с помощью равенств C.49),
придем к соотношению, содержащему из коэффициентов {xkr
только |лу>, и сразу найдем, что
L (^й^4" L Bs«-,y -
s=«0 <; = ! J
s« i
Теперь пусть г нечетно. Полином Tnr (t) в этом
случае имеет вид
П
Условия интерполирования в нулях sin/z/ дают:
V * •
2
Умножим обе части всех этих равенств на sin/-1, затем
заменим произведении синусов на разности косинусов и

S 3.5J ФУНКЦИИ БЕРНУЛЛИ
просуммируем по /. Будем иметь
69
? ===== 1 / = 1
Подсчитывая значения сумм по / с помощью формул
(З.Г)О), получим равенства, содержащие только \\>, из
которых найдем
(—1)<^—IV2
J V
Bsn -f jY jL
^-0
, I.
Bsn~jY
s — 1
sttp - <sVJ <3-52'
(/¦•--1 »-l).
В чинности, при /•' • 1

ГЛАВА 4
НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ
НА КЛАССАХ СВЕРТОК
В этой главе будут изложены результаты по решению
задачи II в случае приближения подпространствами
(в частности, подпространством тригонометрических
полиномов) периодических функций, представимых в виде
свертки.
С и Lp (l^p^oo, Li=L, /оо = Л4), как и в
предыдущей главе, будут обозначать пространства 2я-периоли-
ческих функций с соответствующей метрикой.
Мы будем иногда при наличии параметра аргумент,
по которому вычисляется норма, заменять точкой;
например:
/2л \\/р
tf(-+'W(-)Jp= $ \f(x + t)-f(x)\»dx) .
Отправным пунктом наших рассуждений будут
двойственные соотношения в пространствах Lpy которые мы
вывели в главе 2. Предварительно нужно выяснить
некоторые простые факты, касающиеся сверток функций.
§4.1. Свертка функций; основные свойства и неравенства
Говорят, что функция f(x) является сверткой
функций К @ и ф@ из L, если она представима в виде
2л
/(*)ei$*(*-0q>@<tf> D.1)
6
что символически обозначается так:
(Множитель 1/л перед интегралом в D.1) поставлен лишь
для удобства дальнейших приложений.) Функция f( (t)
в каждом конкретном случае фиксирована и ее называют
ядром свертки. Заметим, что из измеримости и
суммируемости К (t) на @,2л) следует измеримость и сумми-

«4.11 СВЕРТКА ФУНКЦИЙ 71
русмость на квадрате 6<лг, ^<2л К(х — I) как функции
двух переменных.
Из 2я-периодичности функций К(() и ф(/) следует
2л-периодичпость /(лг), а также эквивалентное D.1)
представление
\(t)<e(x-l)dt, D.2)
5
ОРОЕ получается п.ч D.1) заменой x—t^-u.
Mw будем пеоднокр.'шю пользоваться тем фактом, что
иормн |ф||;> но мелиетси при сдвиге или перемене знака
йргументи, по которому она вычисляется:
l-/)ln«l*('—Iр-"*Ги V/. D.3)
П релложгн uv 4.1.1. /:ош К (() ^ Lp A^
то / (л) е= /,Л, причем
!7;^<(«/л)!/С!;/.[Ф:!р. D.5)
У1ействительио, предполагая, что К ^ Lpy с помощью
обобщенного неравенства Минковского (см. Дополнение)
и с учетом D.3) будем иметь
2Я
о
Р
dx\ ^
2Я/2Я
О
2л
откула следует включение f^Lp и неравенство D.4).
Ксли <|)eLp, то аналогичным образом, исходя из пред-
стймлсмгпя D.2), волучим неравенство D.5).
Предложение 4.1.2. Если
K(t)<~Lp (Кр<оо), ф(/)е^

72 наилучший приближение на классах сверток [гл. 4
то свертка f (х) непрерывна на всей оси, причем
\Рх^~1К\уМр^ D.6)
В самом деле, используя неравенство Гельдера, при
любых л" и А будем иметь
2я
-t)-K(x-t)]<p(t)dt
¦-; f
/С (• -J- A) — /С (•) > РФ'>-
Непрерывность / в точке л- следует из того, что при
й-*0 (Л. А. Люстерник, В. И. Соболев [1J, стр. 500 и 100)
Норма ;/vie оценивается опять же с помощью
неравенства Гельдера и с учетом D.3):
2я
:=* «max
•* х
Предложение 4.1.3. 0^
К (t) и ф (/) принадлежит пространству М = Loo,
/(л:) непрерывна и
если
Пусть, например, феМ, Тогда
<»-
2Я

* 4.2] ДВОЙСТВЕННОСТЬ ДЛЯ КЛАССОВ СВЕРТОК 73
если А->0, т. е. f(x) непрерывна. Далее
II Г II '
X
О
max
J
Аналогично, исходя из представления D.2), рассматри-
настся случай /(еМ.
§ 4.2. Двойственные соотношения для классов сверток
Для фиксированной функции f ^ Lp и фиксированного
подпространства F a Lp будем полагать
HU. /;)п- inf '7-Ф.1» (U
Те г) pi» ми 4.2.1. Пусть функция f(x) представима
w nw)e тушки D.1), где К (t)^L, aq> (() <= Lp A <p^ ос),
причем тшшсыо хотя бы одно из условий:
«) /((-/) ' /ч @;
б) подпространство F вместе с функцией if (/) содержит
также и функцию я|з(— /).
77*!г)<! ///)// 1-^.(/^/? //лсе^л л^гто соотношение
j!/Kl//> -МУ- 1/9 + l/?' = 1),
D.7)
<,v)t* б правой части f (x) есть также свертка D.1) с тем же
ядром К @» а Hq' {F) ~" множество функций ф е L^' ma-
что i'<pV^! w
K^Lq[\Lp>y в частности, если К еМ, то D.7)
справедливо независимо от соотношения между р и q.
Доказательство. Из неравенства p^q следует,
что f.pczLqy и если фе?р, то f^LpczLg. Воспользо-
нншпись соотношением B.36) (в случае, если F конечно-
ме))ИО, можно исходить из более просто доказываемого

74 НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ НА КЛАССАХ СВЕРТОК [ГЛ. 4
равенства B.25)), можем написать
E(f,F)g=* sup \f{x)h{x)dx D.8)
heiH{F) §
и, следовательно,
sup ?(/, F)g =
/2л
: -1- sup sup U С К {x-t) ф @ dt\h{x)dx~
2я /2Л \
«- sup sup \\\K(tL(x-t)dt\h(x)dx. D.9)
я.|Ф:|„<1Ле//^)^\^ У
.Дальнейшее основано на применении теоремы Фубиии
(см., например, И. П. Натансон [2], стр. 336) о
возможности перемены порядка интегрирования. Рассмотрим
интеграл
2л /2л \
\\K(t)\{\ \i9(x-t)h(xydx)dt. D.10)
о \о /
Так как А е /^ и при р^д <ре/^, то по неравенству
Гельдера
о
и, значит, интеграл D.10) конечен. Если же K^Lg, то
\
о
и для любой ф е L конечен интеграл
2л /2я
j (
Таким образом, при сделанных предположениях в
условии теоремы 4.2.1 теорема Фубини применима и мы можем
переписать D.9) (поменяв заодно порядок вычисления

* 4.2] ДВОЙСТВЕННОСТЬ ДЛЯ КЛАССОВ СВЕРТОК 75
верхних граней) в виде
sup ?(f,F),=
2л / 2л \
= sup sup [q>(t)[±[K(x-t)h(x)dx]dt. D.11)
С помощью обобщенного неравенства iMmiKOBCKoro
проверяется (как это делалось в § 4.1 для свертки), что функция
2л 2л
У @ = 1 J К (х -1) h (x) dx = 1 j ff (.V) /i (.v -f /) dx D.12)
J К (х 1) h (x) dx j
0 0
принадлежит Lp, если этому простра]{ству принадлежит
К @ или й(/). Следовательно, если /( е LP' (независимо
от соотношения между р и q) или /С €= L, но р?^7 A[>
значит, h^.Lq< czLp')y то 4f e Ip'. Но тогда и силу
соотношения (Д. 12)
sup \ y{t)xV(t)dt = ^\p>. D.13)
^ip^1 о
Теперь заметим, что в случае четности или нечетности
ядра К (t) (условие а) теоремы) функцию D.12) можно
записать в виде свертки:
2
о
Подстлшт D.13) \\ D.11), получим D.7).
litviH же выполнено условие б), то для любой
функции г|) fe F
\^{t)h(—t)dt^ 5 Ч> (— /) А (О Л — О,
о 6
т. е. вместе с функцией h(t) множеству Hq>{F)
принадлежит также и h(—/). Но тогда, заменяя сначала / на — <,
а затем х на —xf будем иметь
!2л :•
\K(-+x)h(x)dx\ =
2л
1 |
~\K(—x)h(x)dx\ . D.14)

76 НАИЛУЧШЕЕ ПРИБЛИЖЕНИИ НА КЛАССАХ СВЕРТОК [ГЛ. 4
Под знаком нормы в последнем выражении стоит свертка
ядра К (t) с функцией h^HQ<{F), и следовательно,
правые части D.7) и D.14) совпадают. А так как в силу
D.11), D.12) и D.13) совпадают и их левые части, то
теорема доказана и при условии б).
Отдельно отметим частный и, может быть, наиболее
важный случай теоремы 4.2.1, когда q~p.
Предложение 4.2.2. Пусть функция f(x) пред-
ставима в виде D.1). Если K(t)^L и выполнено по
крайней мере одно из условий а) или б) теоремы 4.2,1, то
sup E(f,F)p= sup |7 fp _
<i н(Г) DЛ5)
§ 4.3. Приближение классов сверток
тригонометрическими полиномами
Теперь в качестве приближающего подпространства
для функций, иредставимых в виде свертки, будем
рассматривать подпространство F^—i тригонометрических
полиномов
Тп (t) = у 4- 2 («* cos kt + Р* sin Ы>1 <4-16)
порядка п— 1.
Для наилучшего приближения функции /gX, где X
есть Lp или С, полиномами D.16) мы сохраним
обозначение Еп (/)х, т. е. по определению полагаем
Ея (f)x = Е (/, FL- i)x = inf ii/ - Гя i|x.
n
Если 3?J — некоторый класс функций из X, то будем
иногда пользоваться сокращенным обозначением
= sup?n(/)x.
В случае X = LP вместо En(f)L , ?"„C??)^ будем писать
Еп(!)р> Еп(Щр, исключая, может быть, случаи р=1 и
При каждом /7 = 0, 1, 2, ... через Нпх {\Н1р -ic[ //?}
обозначаем множество функций (реХ с нормой [фЦ^^!

§4.3] ПРИБЛИЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИМИ ПОЛИНОМАМИ 77
которые при пт^1 ортогональны всем
тригонометрическим полиномам порядка /z—1, т. е.
о
Заметим, что в силу предложения 3.5.1 в множество Нпх
входят, в частности, функции (рбХ с нормой';ф |'х<с 1,
имеющие период 2л/д и ортогональные константе.
В этом параграфе рассматриваются классы сверток
D.1) с ядром /С (/)(=/„, у которых cpe/Z'i. Эти классы
будем иногда обозначать /C*/f'i. В частности, /С* //* есть
класс функций D.1), у которых I'cpjjx^l.
Соотношение двойственности D.8) для F = Fln^\ с
учетом введенных обозначений запишется в виде
Еп(П„= sup ]f(t)h(t)dt (
JJ о
DЛ8)
Перенося на наш случай теорему 4.2.1, заметим, что
Тп(—t), так же как и Tn(t), является
тригонометрическим полипомом порядка /z, так что условие б) теоремы
4.2.1 заведомо выполнено, а потому при p^q, а если
К (t) с= /,v П 1<р'ч то при любых р и q, справедливо соот-
IIOIUOIIUC
^ sup
D.19)
(Кр,
П частности, для любого суммируемого на периоде
ядра /С (О
ЕЛ(К*Н*)Р& sup ?я(/)р- sup 1/]^ D.20)
A<р<оо, 1/p+l/p'= 1).
Равенство D.20) показывает, что задача о верхней
грани, En(j)p на классе сверток D.1), заданном условием
|iЧ''.'.л ^ 1» сводится к задаче вычисления верхней грани
нормы свертки на множестве /(*#? в сопряженной

78 НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ НА КЛАССАХ СВЕРТОК [ГЛ. 4
метрике Lp>. Можно ожидать, что вторая задача, где надо
оценивать не наилучшее приближение, а норму функции
(хотя и на более тонко задаваемом классе), окажется легче
поддающейся точному решению.
Например, используя особенности равномерной
метрики, легко доказать следующее
Предложение 4.3.1. Если К(/)еМ (иу
следовательно, свертка f(x) непрерывна), то
sup Ш=\:ЕЛ(К)Я (
Действительно, заметив, что вместе с функцией
классу Яр принадлежат также и функции it<p(a±f)
при любом а, а затем пользуясь соотношением D.18),
будем иметь
2л
о
2л
4 sup \K(l)<p(t)dt-=lEn(K),.
.. — т т И • ¦'
SUP !i/!]c = — sup max
Из D.19) (при р=1) и D.21) следует, что если ядро
К (i) свертки D.1) принадлежит пространству М, то
sup En(f)g=±En(K)g (K?<cx)), D.22)
т. е. задача свелась к наилучшему приближению
конкретной функции —ядра свертки.
Если в соотношении D.21) q'=*oo, т. е. феЯ^, то
/ (я) будет непрерывна при любом К @ е L, и те же
рассуждения приводят к равенствам
sup En(f)L= sup |i/fc = ^?«(/C)L, D.23)
справедливым для свертки с любым суммируемым ядром.
В случае интегральной метрики вместо точного
равенства D.21) можно указать для рассматриваемых величин
некоторые оценки сверху.

* 4.3] ПРИБЛИЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИМИ ПОЛИНОМАМИ 79
Если в свертке D.1) ipeffj, то ввиду соотношений
D.17) для любого тригонометрического поликома Tn(t)
2л 2л
/(*)= \[ К (t)v(x-t) dt=l-\[K (t) - Тп (ОМ* - t)dt
и в силу общего неравенства D.5) для сверток
Следовательно, ввиду произвольности многочлена Т„
а так как это верно для любой функции D.1) с фбЯ^
то
sup UlP^~En(K)L (Kp^oo).
Сопоставление этого неравенства с D.20) приводит
к оценке
sup En(f)p<]nEn(K)L (l^P<oo), D.24)
справедливой для любого суммируемого ядра K(t).
При р=1 в D.24), как это видно из D.23), имеет
место знак равенства.
Дальнейшие результаты по решению задачи II на
классах сверток мы получим, наложив на ядро K(t)
дополнительное условие.
Условие Л*. При заданном /z = l, 2, ... существует
натуральное число п#^п и тригонометрический полином
п—1
такие, что для функции
4>*@ = slgn[tf(/)-T8@] D.25)
Почти всюду выполняется соотношение
/«*) = -ф*@. D.26)

80 НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ НА КЛАССАХ СВЕРТОК [ГЛ.4
Ясно, что ф# е М и < ф# ги= 1, если только К (/) "^ Уя @-
В силу D.26)
т. е. Ф* (/) имеет период 2л//75!.. Кроме того, используя
сначала D.26), а затем сделав замену /-ря/л* = ы, с
учетом периодичности будем иметь
2 л, 2 л 2 я
С ф* @ Л = - U* (/ + я/л,) Л = - U, @ d/,
о' о' о
т. е.
Последнее равенство вместе с гя/л^-периодичностью ф*
гарантируют для ф* (/) выполнение соотношений D.17)
(см. предложение 3.5.1), поэтому ф^еЯ^,
Смысл условия А* в том, что фигурирующий в нем
полином Т{\ осуществляет наилучшее приближение ядра
K(t) в метрике Л. Действительно, имеет место
Предложение 4.3.2. Если К (I) удовлетворяет
условию At, то
?¦» (/с)л=;: /с—77, su.
В самом деле, используя вид функции D.25) и ее
принадлежность классу Нпм% для любого
тригонометрического полинома Тп(() порядка п-— 1 будем иметь
[ К-Тя I - f [К (t) - Тя @] sign [К (t) - Тя @] dt ^
6
зг Т [К @ - 7-„ @] ф* (/) Л = f [К @ - П @] ф* (/) Л =
о о
Докажем теперь следующее утверждение, которое
будет играть существенную роль при получении точных
результатов для конкретных классов функций.

* 4.3] ПРИБЛИЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИМИ ПОЛИНОМАМИ 81
Теорема 4.3.3. (С. М. Никольский [3]). Если
функции f и ф связаны между собой равенством
2Л
где ядро К (I) e L и удовлетворяет условию Л л. то для всех
s — 0, 1, ..., п имеют место соотношения
sup Еафм= sup i:/i,, =*~Ea(Kh, D.27)
sup En (f)L = sup 1 fI = J • ?„ {K)L. D.28)
Доказательство, Установим сначала
справедливость соотношений D.27). Второе из них, т. е. равенство
sup \fU = \En{K)L
уже доказано выше (см. D.23)) даже без условия Л*.
Положим для любой функции фе//л| (т. е. ф^М Ц'!)
2л
т? (х) = т* (Ф, *) = 1
D-29)
где Г* (/) —полином из условия Л*. Подставив в D.29)
иод интеграл вместо T%(x — t) соответствующую
тригонометрическую сумму и заменив cosk(x — t) и sinA(x —/)
по известным формулам тригонометрии на сумму и
разность, мы после почленного интегрирования увидим, что
%n(t) есть также тригонометрический полипом порядка
п— 1. Поэтому для любой фе#ль т. е. }^КН
max
1.
2л
2Л

82 НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ НА КЛАССАХ СВЕРТОК (ГЛ.4
Так как H^czH^ (s=l, 2, ..., п), то этим показано,
что
sup En(f)c^*-En(K)L (s = 0, 1, .... n). D.30)
Очевидно, что функция ф*( — t), так же как и <р* (/)
имеет период 2я/я# и принадлежит классу Н%. Поэтому.
если положить
2л 2л
о о
то f# (,v) непрерывна, имеет период 2я/л# и может быть
записана в виде
2л
/• W = i ^ [/С @ - Г^ (/)] ф* (/ - х) dt =
о
2Л
о
где обозначено
Но тогда, учитывая, что ф^ (/) = sign/С* (/), будем иметь
для f = 0, rt I, -»:2, ...
2л
2л
2Л
J К* (/) ф* (/) dt = - А-
Кроме того, так как |!<р#5д1^1, то ^ля всех
2л
2л
\\К V) Jt = I; En(K)L.

i 4.1} ПРИБЛИЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИМИ ПОЛИНОМАМИ 83
Таким образом, функция /* (х) в точках /л/л* (i =
^0, ± 1, :±2, ...) принимает наибольшее по абсолютной
величине значение, последовательно меняя знак. Так как
п#^п, то число этих точек на периоде |0, 2л) не меньше
чем 2п и по критерию Чебышева (теорема 3.2.1)
En(f*)c = U*\\c = ~En(Kh, D.31)
Остается заметить, что /* (х) есть свертка ядра К (t)
с функцией <р*( — /), принадлежащей #ль а значит, и
]ГМ E = 0, 1, ..., п). Поэтому в D.30) на самом деле
имеет место знак равенства и соотношения D.27)
доказаны при всех s = 0, 1, ..., пл причем, как видно из
D.31), обе верхние грани реализует функция f* (x).
Переходим к доказательству соотношений D.28).
Справедливость второго из них сразу усматривается из
сопоставления D.20) при р'=\ (р = оо) с D.27) при s = 0;
sup :;/•/.= sup En(f)c= sup En(f)c=*±En(K)i..
Далее, учитывая включения
Hi а НС с...с //{,»
а также D.23), будем иметь
sup En(f)L^ sup En (/)/.<.¦.^ sup
и все будет доказано, если мы установим, что
sup En(f)L^±En(K)L. D.32)
46//J
Положим /,-==— (/ = 0, ±1, d=2, ...) и для каждого
натурального m4>2njn построим функцию
(в остальных точках).

84 НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ НА КЛАССАХ СВЕРТОК [ГЛ. 4
Ясно, что функции фт имеют период 2л/я*, четны и,
кроме того, как показывает элементарный подсчет,
2Л
о
так что cpme#?. Положим
2л 2л
О * О
где, как и выше, K*(t)^K (t) — T%(t), a T%{t) — полином
из условия Л*. В силу равенства D.18)
Entfmh** SUP \fm{t)h{t)dt,
n О
а так как функция ф# (/) из условия Л* принадлежит
#ль то, применяя теорему Фубини, будем иметь
2л
0
Выше
0
2л
г= \ ф^ (j
.я
'о
/. f
V" о
/ 2л
V Ъ
) {— \ К (< + л^ф* (
\
(/ — Л") ф# ( Л") (XX \
1
мы установили, что
лг) dx] rfi
2л
*0
D.33)
В силу непрерывности функции /# (х) для заданного е > О
можно подобрать такое число тг, что для всех т~>те
будет
;M0!>rJ.k-e D.34)

$ 4,4] НАИЛУЧШИЕ ЛИНЕЙНЫЕ МЕТОДЫ 85
Учитывая D.33) и D.34), а также структуру функции
Ф/я@» будем иметь при //7>/?7е
2л \/т
Еп ifmh 2* $ «Г« @ /* (/) Л = 2л, J (Г,„ (/) U @
О — \;т
а так как fm(x) есть свертка /С(/) с функцией <pOT( —/) из
Н'1> то и подавно
sup En{f)L^±En(K)L-*.
ч е-III
В силу произвольности е неравенство D.32), а с ним и
соотношения D.28) доказаны.
Отметим, что в то время как верхние грани в D.27)
реализуются на конкретной функции f# (x)> в равенствах
D.28) верхние грани не достигаются, а существует лишь
последовательность fm (x) из Hi такая, что
lim En(fm)L= Urn Umk = -\En(K)L.
§ 4.4. Наилучшие линейные методы для классов сверток
В качестве меры приближения функции /бХ (X, как
и выше, есть Lp или С) тригонометрическими полиномами
наряду с наилучшим приближением Еп (J)x мы будем
рассматривать также величину
где Л— заданный линейный оператор, отображающий X
в jFL-i* Этот оператор можно рассматривать как
некоторый линейный метод приближения.
Пусть, как и выше, f(x) есть свертка, т. е.
2л
f(x) = l- J К (х-1) Ф @ dl (/= /<*ф),
О
где K^Lf ф ^ Нър (s = 0, 1, ..,, п— 1), т, е. ф е /,р?
S 1 и при s ^ 1
2л

86 НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ НА КЛАССАХ СВЕРТОК [ГЛ. 4
Ряд Фурье функции (реЯр имеет вид
где штрих при знаке v означает, что в случае s = 0,
т. е. ере Яр,
00
Ф @ ~ %¦ + 2 (а*cos ы + bft sin **>•
С помощью системы чисел
\\\, v} = {|x5, |х5ЬЬ ..., Ил-i; v5, vm, ..., vrt^} (vo = O)
-приведем в соответствие свертке / = /С*Ф
тригонометрический полином
D.35)
(штрих означает, что при $ = 0 слагаемое с нулевым
индексом имеет вид |х0а0/2). Заметим, что ak и ^ —
коэффициенты Фурье функции ф.
Так как
2л
1 Р
ak cos kx + bk sin kx = - \ cos k {x — /) ф (/) dt>
b
2л
1 i*
х-я ут х- Ф@
TO
2Я
// /f. y* ¦] V^ — -- С О iy — i% и v\ en (f) df
b
2л
¦ 0 &t% D.36)

§ 4.4] НАИЛУЧШИЕ ЛИНЕЙНЫЕ МЕТОДЫ 87
где
п— 1
Qno(t\ Ц, v) = &+ 2 Oi*cos*/ + v*sin*0.
п—\
Qns(t\ (I, v)= 2 (I** cos « + vA sin ft/) (s=l, 2, ...,л-1).
Если Д = /С*Ф1, /г=='С*Ф2» то> очевидно,
^i/i + V2 = /С* (Л1Ф1 + Я2ф2),
и потому
UnsDl + Wz\ X\ |lf V) =
= ~ J Q« (х -'; |i, v) [Л1ф1 (О + Я2ф2 (/)] dt -
о
= hUns(fl> Х\ [1, V) + ?v2(/n5 (f2, Х\ |Х, V).
Это значит, что (/л5(|а, v) есть линейный оператор,
отображающий множество сверток в тригонометрическое
подпространство Fln—\* В предположении, что / = /(*ф и
f^Xy положим
*п(К*Н'Р; |л, v)x= sup \f-Uns(f; ц, vI^. D.37)
Эта величина характеризует погрешность приближения
методом, задаваемым системой {ц, v} на всем классе
сверток К*Нр. Метод Uns(\L°, v°), определяемый
коэффициентами
для которого
естественно назвать наилучшим для класса K*HSP среди
всех методов такого типа. Линейный метод, определяемый
оператором Uns(\i, v), мы будем называть (ц, vJs-mcto^^om.
Предложение 4.4.1. При каждом фиксированном
п 1, 2, ... для класса K*HSP (l^p^oo) существует
наилучший ((л, \)$-метод.

88 НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ НЛ КЛАССАХ СВЕРТОК [ГЛ. 4
Доказательство. Покажем сначала, что
есть непрерывная функция векторных аргументов |х и v.
Действительно, полином Uns(f; x\ ц, v) непрерывно
зависит от вектора {ц, v}, а так как норма есть непрерывная
функция своего аргумента, то J — Uns(f'y ц, v)-;* также
непрерывно зависит от {ц, v} при фиксированной
функции f. Затем, используя представление D.36), будем
иметь для двух векторов {ц, v} и {ц', v'} (см. § Д. 2, п. 4)
= | sup J/ — Uns(/; \i, v)f.x - sup fJ-UM (/; v-',v')|x| ^
sup" !|!/-f/ns(/; ц. v)Px-!if-f/ns(/; n', v')!;x;^
sup I !/„(/; ц, v)-Uns{f;ii\ v')j:x =
= sup 1
*e//*pf " о' lx
Теперь общие неравенства для сверток с непрерывным
ядром позволяют написать
F (ц, v)-F(vl\ v')!<
^ sup ^JiQ«(H, vJ-Q^Cm', v')iixS<p!*<
ибо в силу неравенства Гельдера для ф е //р будет
2л
Таким образом, непрерывность F (\x, v) следует из
непрерывности нормы полинома Qns(t\ Щ v) относительно
вектора {|Х, V}.
Теперь заметим, что мы можем брать в расчет лишь
те векторы {ц, v}, для которых, например,
v)-inf F (^

§ 4 41 НАИЛУЧШИЕ ЛИНЕЙНЫЕ МЕТОДЫ 89
и, значит, Р([\, v) ;-<:с, где с —некоторая константа. Но
тогда существует постоянная сг такая, что
\Vk\*^.cu '.vft;<ci (* = s, s+1, ..., л—1).
Это значит, что векторы \\i, v}, для которых ^(ц, v)'. ^с,
образуют замкнутое ограниченное множество в
конечномерном пространстве. Остается вспомнить, что
непрерывная функция F(\x9 v) конечного числа переменных на
замкнутом ограниченном множестве достигает своего
минимума в некоторой точке {|л°, v0}.
Возвращаясь к величине D.37), заметим, что для
любых {ц, v}
Шп(К*Н^ и, v)x^En(K*Hl)x= sup ?„(/)*,
и особый интерес представляют те случаи, когда
наилучший (ц, \-M-метод дает на классе наилучшее
приближение, т. е.
\п\$а(К*Н*Р\ |л, v)x = #n(K*HU |i\ v°)x = ?fl(/C*//p)x.
Теорема 4.4.2. Если К е Af, /по (ц, х)х-метод
является наилучшим для класса сверток К*Нр (I <^ р ^ оо\
s--0, 1, ..,, (« —1)) в метрике С в том и только в том
случае, если \\ху v} есть система {[Д v0}
соответствующих коэффициентов тригонометрического полинома
обращающего в минимум интеграл
2л
В случае р -— ос утверждение теоремы справедливо и при

90 НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ НА КЛАССАХ СВЕРТОК [ГЛ. 4
Доказательство. Используя представление
полилома Uns{f\ x; ju, v) в виде свертки D.36), можем написать
г; х;
2л
- ~ jj [К (х-t)- Qns (x-t; ц, v)] Ф @ dt. D.38)
о
Если s = 0, т. е. феАр и !jcp]p<l, то в силу
соотношения (Д. 12) и того факта, что вместе с ср(/) классу Щ
принадлежит также и <р(х — t)f будем иметь при К^М
= sup max —
= sup —
II г < 1 л
2л
2л
~]
Если же l^;s^./г—1, то аналогичную оценку получим,
используя соотношение двойственности D.18)
6Я(К*Н'Р; ц, v)c =
1
= max sup —
2д
\lK(t)-Qns(t; ц, v)]q>(x-
- inin;; /c - Qns (|i, v) -
Итак, в предположении /СеЛ1
Шп{К*Н%р- щ v)csal?„(/<),.,
причем ясно, что знак равенства здесь имеет место лишь
в том случае, если полином Qn0, или при l^s^n— 1
Q^+^s, тождественно совпадает с полиномом Тп
наилучшего приближения функции К в метрике Lp>. Но тогда
коэффициенты ц* и vk (k = s> s+1, ..., п — 1) должны

$ 4.41 НАИЛУЧШИЕ ЛИНЕЙНЫЕ МЕТОДЫ 91
совпадать с соответствующими коэффициентами
полинома 7Х
Если р = оо, т. е. р'=1, то свертка f (х) непрерывна
и при A'eL, так что все рассуждения тоже проходят,
и мы получим
Теорема 4.4.3. Если ядро К ^ L и удовлетворяет
условию АпУ то (u, v)s-Memod является наилучшим в
метрике С для класса К* Н*м и в метрике L для класса
К*Hi (О <r. s ее п — 1), если он определяется вектором
{jo,*, v*} коэффициентов тригонометрического полинома
Т% из условия А%, При этом
, v)c =
=^n(A'k, D.39,
U, v
= ?я(/С*//1I-^Ея(^). D.40)
Утверждение теоремы 4.4.3 для классов K*Hsm
немедленно вытекает из теоремы 4.4.2 (при р = оо) и
соотношений D.27), если учесть, что Т% есть полином
наилучшего приближения ядра К (t) в метрике L.
Что касается классов /\*Wl, то оценка снизу в связи
с D.28) очевидна:
D.41)
Покажем, что при {ц, v} =={[i*, v*} здесь будет знак
равенства. Если s = 0, то
и, оценивая норму свертки
2л
i(x)-Un0(f; х; ц», v*) = -i-j

92 наилучшей приближение нл классах сверток |гл. 4
в метрике L с помощью неравенства D.4), будем иметь
для любой ср <= НЪ
Следовательно,
Пусть теперь l^s^n— 1. Заметим, что вместе с /С(О
условию Л? удовлетворяет и ядро свертки D.38), т. е.
функция Ki(i) = K(t)-Qns{t\ ц, v), ибо
Кг @ - I Т% (/) - <?Я5 (/; [л, v)] ss /С @ - П (/)
и полином T% — Qns обладает относительно Ki(t) всеми
свойствами, предусмотренными условием А%. С учетом
этого факта, а также соотношения D.20) будем иметь
8Я(К*Н1\ ji*. v*)L« sup к/-!/„(/; [i*f v*)||,-
- sup Es(f-Uns(f;vL\ v*))a,<
\\ф|'1Л/ < !
< sip i/-l/4,(/; ti*. v*)-T^.Mt D.42)
!".<Г:!.\/ < !
где полином xs(x) степени s—1 определен равенством
т,(*)==
2л r- s — 1 -|
= "д" М " + 2 (tlf cos * (* - 0 + vX sin ft (л- - /)) ф@ d/ =
2л
{T*n(x-t)-Qns(x-ti [i*.
Таким образом,
f; x; ц*. v*)-xs(x) =
2л

§ 4.4] НАИЛУЧШИЕ ЛИНЕЙНЫЕ МЕТОДЫ
я, продолжая в D.42) оценку, будем иметь
^ п. \ *\ * '¦
_ 1
93
- max sup
2Л
1 max [ \К(x-t)-T%(x~tLt =
Итак, имеет место оценка
сопоставив которую с D.41), получим все утверждения
теоремы 4.4.3 для классов K*Hl-

ГЛАВА 5
НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ
ТРИГОНОМЕТРИЧЕСКИМИ ПОЛИНОМАМИ
КЛАССОВ ПЕРИОДИЧЕСКИХ ФУНКЦИЙ
С ОГРАНИЧЕННОЙ г-й ПРОИЗВОДНОЙ
Важными классами функций, представимых в виде
свертки, являются классы дифференцируемых
периодических функций. В этой главе будет получен ряд точных
результатов по приближению тригонометрическими
полиномами классов функций, задаваемых ограничениями на
норму г-й производной в той или иной метрике.
Большинство из этих результатов непосредственно вытекает
из доказанных в главе 4 общих теорем о приближении
сверток, но некоторые базируются, кроме того, на
теореме сравнения Колмогорова. Этой теореме и
вытекающим из нее важным следствиям —они потребуются нам
и в следующих главах — посвящен отдельный параграф.
В начале главы вводятся классы функций, а также
аппарат функций Стеклова, которым мы в дальнейшем
будем широко пользоваться,
§5,1. Классы дифференцируемых функций
Через X мы по-прежнему будем обозначать
пространство Lp A^/?<оо) или С, а через Хг (г=1, 2, ...) —
множество г-х периодических интегралов от функций из X.
Поясним: X1 есть множество неопределенных интегралов
Лебега
2л
где ф е Ху причем \ ф (/) dt = 0, так что / (х + 2л) = f (x)\
о
аналогично, имея Хг~г, определяем Хг. Таким образом,
С есть множество г раз непрерывно дифференцируемых
на всей оси 2л-периодических функций, a Lrp —
совокупность заданных на всей оси функций / (х) периода 2л,
у которых (г—1)-я производная /(г~*^(,г) локально абаь

§ 5.1] КЛАССЫ ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЙ 95
лютно непрерывна5') па [0, 2я], я /(г) ^ LP. Вместо ??
будем писать U.
Пусть /<==// (г=1, 2, ...) и
со
f (х) = ¦ 1 - ~j- /^ (g^ cos ?,v -f" &а sin kx) E,1)
ft—l
— ряд Фурье функции f. Так как
2л
afe cos kx + />/< siri kx = - \ / (/) cos >fe (л: — t) at
b
то, интегрируя г раз по частям, с учетом периодичности
f(x) и ее производных, будем иметь
2л.
rt/,cos?.v + bfesin?.v = ~r- \ f (/) sin&(.v — t)dt =
о
2л
2л
2л
b
гак что
2л
аЛ cos kx + bk s\nkx = ±-r jj f^ @ cos [ft (x-0 -Щ dt-
E.2)
Подставив в E.1) и учитывая, что ряд Фурье можно
интегрировать почленно, получим для f (х) интегральное
представление
2л
f (х) = -?• + I- jj Dr (x - t) Г V) dt, E.3)
*) Везде в дальнейшем, говоря об абсолютной непрерывности
«ндпнных на всей оси функций, мы имеем в виду локальную абсо-
;1югиую непрерывность, т. е. абсолютную непрерывность на любом
конечном отрезке (для 2л-периодических функций — на [0, 2л]).
?рывность
и —на [0,

96 НАИЛУЧШЕЕ ПРИБЛИЖ. ПОЛИНОМАМИ КЛАССОВ \X'rLp [ГЛ.5
где
cosffta—"-]
(/-=1,2,...)
— функции Бернулли, рассмотренные в § 3.5.
Через En(f)x, как и в главе 4, обозначаем наилучшее
приближение функции f^X тригонометрическими
полиномами Tn(t) порядка п— 1:
?„(/)* = ?(/, FT2n-i)x= inf Jf-T.lx.
Если ЭЛ —некоторый класс функций из X, то полагаем
%п(Щх=* inf supjf-АПх,
где нижняя грань берется по всем линейным операторам
А, отображающим X в F^n-i-
Так как подпространство Fln—\ содержит константу,
то
En(f + c)x = En(f)x, E.4)
где с —любая постоянная. Поэтому везде в дальнейшем,
где речь будет идти о наилучшем приближении En(f)x
функции E.3), мы можем считать, что ао~-^О, т. е.
рассматривать только те функции /eZ/, которые предста-
вимы в виде свертки:
2л
f (х) = I- jj Dr (x-1) /"»(/) dt (f - D,*n. E.5)
b
Обозначим через WrL (r=l, 2, ...) класс функций /
из Lp4 у которых f(r)\p<:l. При каждом /г -1, 2, ...
в классе WL выделим подкласс WrHl =---WrH"p функций
f<=WrL ортогональных тригонометрическим полиномам
Tn(t) порядка п— 1, т. е. таких, что
Т ? di =* О (А = 0, 1, .... л - 1). E.6)

j; 5.1] КЛАССЫ ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЙ 97
Под Hi = Нпр будем понимать множество функций feLp
с нормой !7pJ*^l, удовлетворяющих соотношениям E.6).
Заметим, что если /е WrHnp (г=1, 2, ...), то
оо
/(*)= S (^cosftx+frjkSinfef), E.7)
ибо, как следует из E.6), коэффициенты Фурье функции f
с индексами, меньшими п, равны нулю.
Но тогда ряд Фурье r-й производной fin(x)9 который
получается формальным дифференцированием ряда E.7),
также не содержит соответствующих членов, т. е. /(г) (х)
тоже ортогональна всем полиномам Тя(х), и, значит,
1кп*=Нпр. Обратно, если fs=-WrLpt ?п<=Нпр и
то /е WrHnP. Таким образом, класс WrHnp мы можем пред-
стпнлнть в виде
WrHnp = Dr*Hnp. E.8)
1?слн через Wl ° обозначить множество функций / е U^?
таких, что J/(x)dv = 0, то для / е Ш71' ° имеет место
о
представление E.5) и, следовательно,
ибо /(г), как производная периодической функции, также
имеет нулевое среднее значение на периоде.
Теперь, с учетом сделанного выше замечания,
связанного с равенством E.4), мы можем написать
En{Wip)x = EH(WrLpQ)x = EH(Dr*Hlp)x. E.9)
Введем в рассмотрение еще классы, задаваемые
ограничениями на вариацию функции или ее производных.
Пусть К —множество 2л-периодических функций /(/),
имеющих ограниченную вариацию (ограниченное
изменение) на отрезке [0, 2л], а V (г=1, 2, ...) —множество
функций / периода 2л, у которых \{r'x){t) абсолютно
непрерывна и /(г) <= V\ V° будем отождествлять с V. Через

98 НАИЛУЧШЕЕ ПРИБЛИЖ. ПОЛИНОМАМИ КЛАССОВ WrLp (ГЛ. 5
Wv (г = 0, 1, ...) обозначим класс функций / е Иг, у
которых
2л
V (/<'>) <1.
Ясно, что
ибо, если f&WL, то
2л
\
о
Добавим к этому, что WHi a Wr~lHv> где Wr~lH'l> есть
подкласс функций f^W\T\ удовлетворяющих E.6).
§ 5.2. Функции Стеклова и их простейшие свойства
Если /eL, то функцию
h
—л
—л
называют функцией Стеклова для /(*). Очевидно, что
fh (x) можно записать также в виде
M*)=i- J /@ л,
А —Л
откуда видно, что //,(*) абсолютно непрерывна и,
следовательно, почти всюду
На рис. 4 приведена функция Стеклова для f (х) -
= sign sinx.
Заметим, что если сама функция / абсолютно
непрерывна, то f'eL и
так что с точностью до множества меры пуль

5.2)
ФУНКЦИИ СТЕКЛОВА
и мы можем в этом случае писать //,(*), допуская, что
операции дифференцирования и перехода к функции Стек-
лова могут выполняться в любой последовательности.
Oh
7
Рис. 4. Функция Стеклова для / (х) = sign sin x.
Предложение 5.2.1. Если [ ^ Lp (l^p^oo), то
1Ш^\!Ъ» EЛ°)
Пгп Ц/л — flP=0. E.11)
В силу обобщенного неравенства Минковского (§ Д. 1)
р ji'p
\/p
2л
~л Го
и E.10) доказано. Далее, опять же используя
обобщенное неравенство Минковского, будем имегь
2Л
\/П
1
2/i"
—л v о
¦¦ml

100 НАИЛУЧШЕЕ ПРИБЛИЖ. ПОЛИНОМАМИ КЛАССОВ TrLp ГГЛ.5
Теперь сразу получим E.11), если воспользоваться хорошо
известной в теории функций теоремой Лебега *), которая
утверждает, что для любой функции / е Lp (Л. А. Люстер-
1шк, В. И. Соболев 11|, стр." 500)
lim./(- + 0~/(-);i^O. E.12)
/-о
Основная идея доказательства соотношения E.12)
состоит в том, что для /еС оно тривиально, а в общем
случае, так как С всюду плотно в Lpy то для любого
е>0 есть функция феС такая, что
и, выбрав б--^б(е) из условия
будем иметь для ; /1 < б
Заметим, что из E.11) следует также соотношение
И'пШр = !/,',. E.13)
h-+ 0
Предложен ие 5.2.2. Если ge V, то
В самом деле,
(
будем иметь
п
-д
0
при
1
2/i
!"(
-/Л
h
п
У
2/1
любом
1
lg(tk
h
h (J_
\ \
— h *
0
разбиении
+t)-g(tk.
, = 2я
i + Ol
dt
I
*) Собственно теоремой Лебега обычно называют это
утверждение в случае р — 1.

§ 5.31 РЕЗУЛЬТАТЫ. ВЫТЕКАЮЩИЕ ИЗ ОБЩИХ ТЕОРЕМ 101
Остается заметить, что gh (t) абсолютно непрерывна, и
потому
Из предложения 5.2.2 следует, что если
(г=-1, 2, ...), то ght=WrL9 а если g<=Wr-xHnVt то ?л е=
е WrHnu ибо ортогональность тригонометрическим
полиномам Tn(t) функции g влечет (в силу определения gh)
ортогональность полиномам Tn(t) и функции Стеклова gh.
Дополнительные сведения о функциях Стеклова,
связанные с понятием модуля непрерывности, будут
отмечены в § 7.1.
§ 5.3. Результаты по наилучшему приближению
классов IV? , вытекающие из общих теорем для сверток
В § 3.5 были отмечены некоторые свойства функций
Бсрнулли Dr(t)t в частности то, что Dx^Mf Dr^C *
(r = 2\ 3, ...) и Dr(—t) = (—l)rDr(t). Было доказано, что
при каждых /г, г=1, 2, ... существует
тригонометрический полином tnr(t) такой, что разность Dr(t) — fnr(t)
меняет знак в нулях cos nt или sin/tf (в зависимости от
четности и нечетн сти г) и что других нулей эта
разность не имеет. Это значит, что
sign [Dr @-Гяг @1 = ± sign sin й(/-|о),
где |о —0 при г нечетном и ?0 = л/Bл) при г четном, и
следовательно, Dr(t) удовлетворяет условию А* при я* = я
и T*n(t)*=fnr(t).
Таким образом, функция Dr (/) удовлетворяет всем
условиям, которые налагались на ядро свертки K(t) при
доказательстве теорем в главе 4, и все эти теоремы мы
можем перенести на рассматриваемый теперь случай
наилучшего приближения функций вида E.5).
Наиболее существенные и, главное, окончательные
результаты нам дадут те утверждения главы 4, которые
сводят задачу к наилучшему приближению ядра К (t)
в метрике L% ибо эта последняя задача для /C(/)=Dr(/)
решена нами в § 3.5.

102 ИАИЛУЧШЕР ПРИ&ЛИЖ. ПОЛИНОМАМИ КЛАССОВ \\\р [ГЛ.5
Из теоремы 4.3.3, соотношений E.8), E.9) и C.45)
немедленно вытекает следующее утверждение.
Теорема 5.3.1. Для всех п9 г = 1, 2,... имеют место
равенства
i= sup 1Гш = -!:Еп(Огк==У?, E.14)
f^rifnM
~ sup lfLl = \En{Dr)L = -^t EЛ5)
где константа Жг определена равенством C.44).
Теперь обратимся к общему соотношению D.19). В нашем
случае оно запишется в виде
E.16)
но так как класс Wt ° = D^HP существенно уже класса
D^fH'p, то соотношения E.9) и E.16) дают для наилучшего
приближения класса WL лишь оценку сверху:
En{np\~En{wt;\^ sup ;./>. E.17)
Однако в E.17) мы сможем поставить знак равенства
если справа [J,\р* заменим на Ejtf)^, т. е. норму
функции / заменим наилучшим приближением константой.
Действительно, в силу D.18)
2л
^(^Л*8 SUP ?»(/Ьв SUP SUP Uhdt-
fewj fevr'I лен! й
Проинтегрировав г раз по частям и учитывая,
а г-й интеграл от А можно взять с нулевым средним
значением на периоде, и тогда он принадлежит WrH^f будем
иметь
En{WrL)q-- sup sup \g(tL(t)dt.

§ 6.3J РЕЗУЛЬТАТЫ, ВЫТЕКАЮЩИЕ ИЗ ОБЩИХ ТЕОРЕМ ЮЗ
Теперь то же соотношение D.18) позволяет написать
равенство
,E<W' (у+у - у+*'-')• <5-18>
из которого, между прочим, следует E.17), ибо Е{ teV
Так как Dr^M, то в силу предложения 4.3.1
sup !/к=4*я(Ог),.
что вместе с E.17) при р = 1 дает оценку
Наконец, заметим, что из D,24) и C.45) вытекает
соотношение
в котором, как это видно из E.14) и E.15), при р=1
и р-~со будет знак равенства.
Привлекая к рассмотрению классы W'v, докажем
следующее утверждение общего характера, полагая, как и
в главе 1,
Е(М, F)x= sup ?(/, F)x- sup inf j|/-q>!Y.
Предложение 5.3.2. Если F — любое nod прост ран-
ство из L, то
L F)L (r-1, 2,...). E.20)
Действительно, из включения Wi cz Wv~l сразу следует,
что
E{Wrv~\ F)L.
С другой стороны, если /е Wrv~\ то ее функция Стеклова
/л ef[, и потому
?(/л, F)L^E{WrLy F)L.
В силу предложения 1.2.1
/¦ (/, F)t<?(/-/ft, F)i-b?(//,, F)L<.]f-fkl + E{fH, F)Lt

104 НАИЛУЧШЕЕ ПРИБЛИЖ- ПОЛИНОМАМИ КЛАССОВ WrLp 1ГЛ. 5
так что
i9 F)L.
В пределе при й-*0, ввиду E.11), будет Е (/, F),.<?(№[, F)L,
а так как это справедливо для любой /е IPV\ то
E{Wrv~\ F)L^E{wi9 F)Lt
и E.2.0) доказано.
Из предложения 5.3.2 и соотношений E.15) сразу
следует, что
En(Wrv-l)L = Em(Wi)L = ^ (л. г=1, 2,...).
Используя тот же прием, связанный с переходом
к функциям Стеклова, легко доказать, что
sup Ш,= sup |7U = ^ (/1,г=1,2,...);
поэтому
?«0n-*l)i- sup |!/ik = f? (/i.r-1,2,...). E.21)
§ 5.4. Функции <ря,г и ^ и их экстремальные свойства
В соотношениях E.14) и E.21) верхние грани
реализуют функции, которые будут играть важную роль и
в следующих главах.
При любом X>0 положим
, ч . . * 4 V sinBv4-l)lx
= 2i+l, i = 0, 1, 2, ...),
л: oo
/ v I* /j\ ij 4 . i4r7 V sin Bv \-\)kx /r no\
Ф;.л W - \ Ф?.,г-1 (О Л ---= л^- (— 1)'<2 >. —2;^i)rii E.23)
Ь
v-=0

§ 5.4]
ФУНКЦИИ ф?/. И gn
105
Таким образом, при г^1 ф>.г(л:) есть r-й интеграл от ф?0
с периодом 2я/Л и средним значением на периоде, равным
пулю.
Из равенств E.22) и E.23) легко усмотреть, что при г
четном функция (р?/ (х) обращается в нуль в точках /я/а
(/ = 0, ±1, ± 2, ...) и график ее симметричен относительно
этих точек и прямых x=Bj-\-1) я/2Я, а при г нечетном
<ЫB/+1)л/2а] = 0 (/-0, ±1, ±2, ...) и график фИ*)
-1
Рис. 5. Функции Ч)„г
= 0, 1Э 2).
симметричен относительно точек (B/+ 1) л/2Я, 0) и прямых
л'=/я/л (рис. 5). Вид функции ц>ю(х) и рекуррентные
соотношения в E.22) и E.23) показывают, что других
нулей функции ф>.г(л:) не имеют и что ц>Кг (х) строго
монотонна между нулями своей производной, а график щх(х)
является выпуклым на каждом промежутке, где ф>г
сохраняет знак (при г^2 — строго выпуклым).
Полагая для ограниченной на всей оси функции /
|;/:1ж= sup !/(*)!,
из отмеченных выше свойств tp}J.(x) и равенств E.22) и E.23)

106 НАИЛУЧШЕЕ ПРИЬЛИЖ. ИОЛИНиМАМИ КЛАССОВ U"? t!VI. 5
выводим соотношения
00
; ф?.. гл1=. Фл, @)¦¦ = -*-г У Cv+iri (/-=1,3,5,...),
Ф,,(*) | = ?? 2 j^TW* (г = 2, 4, 6,...).
Таким образом,
'"ф/Ди-f^ ^«О, 1, 2,...), E.24)
где константы ^/Гг определены равенством C.44).
Из E.24) следует, что при ? = 0, 1,..., г
Так как
T^W-cp;..,^^ (ft = 0. 1, ..., г),
то мы можем сформулировать следующее утверждение:
Предложение 5.4.1. Имеют место соотношенич
" Ф^ 1!л1 -" Ф>.,г и "м = ^ • Ф>.;'аГ*/Г E.25)
(г=1, 2, ...; *=1, ..., г),
Crk —s'f r k'-/l r »
а константы с7Гг определены в C.44)
Через фяг(*) будем обозначать функции щ^(х) в случае,
когда Я —л —целое число >0. Функции ф,/г(,г) имеют
период 2я/« и среднее значение на периоде, равное нулю.
Так как
\Stnr !,Л1 = j фло!!Л1 ^^ 1»
то ф,„ е WrH"w u> как следует из E.24),
[ф«г[с = ^ (л. г=1, 2, 3, ...). E.2G)
Из описанных выше свойств функции q^, следует, что*
на периоде [0, 2л) есть 2я равноотстоящих точек, в кото-

§ 5.4] функции ф?г и gnr 107
nr
рых функция tfnrix) достигает своего наибольшего по
абсолютной величине значения, чередуя знак. Такими
точками являются/л/л (/'== 0, 1, ..., 2/г— 1) при г нечетном
и B/-|- 1)л/2/г (/ —0, 1, ..., 2л —1) —при г четном. В силу
критерия Чсбышева среди всех тригонометрических
полиномов порядка /1 — 1 наилучшее приближение в метрике С
функции флг(г---= 1, 2, ...) доставляет тождественный нуль.
Поэтому Еп (ф«г)с = |:Ф«г!!с и с учетом E.14) и E.26)
приходим к равенствам
Еп{Ум)с = Еп{Чпг)с = :^к = Щг («. г=1, 2, ...),
E.27)
:/;с = ;Фпг;;с=^ (/?, r=i, 2,...).
E.28)
Таким образом, функция фаг(л:) реализует обе верхние
грани в E.14)» т. е. дает максимальную погрешность
наилучшего приближения в С среди всех функций класса
Wm и одновременно имеет наибольшую норму в С среди
функций класса WH'm.
Положим теперь
8пг(х) = 1п<9аАх) (я-1,2,...; г = 0, 1, 2,...).
Свойства функций gnr совершенно аналогичны свойствам
Ф„г; в частности, цпг(х) имеют период 2л//г и нулевое
среднее значение па периоде; поэтому, с учетом равенств
заключаем, что gnr e WHnv с: Wy.
Вычислим норму gnr B метрике L:
о
т. е.
Далее, функция signer (а:) с точностью до знака
совпадает либо с sign sin n-v, либо с sign cos ил- (в зависимости

108 НАИЛУЧШЕЕ ПИ1БЛИЖ. ПОЛИНОМАМИ КЛАССОВ WrLp \ГЛ.Ъ
от четности или нечетности г). В силу критерия 3.3.4
и ортогональности gnr тригонометрическим полиномам
порядка я—1 тождественный нуль и в метрике L
является для gnr(x) (а значит, и для упг(х)) полиномом
наилучшего приближения среди всех тригонометрических
полиномов Tn{t). Это значит, что
En(gn,r ik = [?n,r-iik=^ (я. г«1, 2,...). E.29)
Теперь ясно, что функция gn%r-i(x) реализует обе
верхние грани в E.21), т. е.
E.30)
sup l&V*=lgntr--ui = 'Lzr{n* г==1> 2,...).
E.31;
Что касается класса Wl (г = 1, 2, ...), то в нем не
существует функции, реализующей верхние грани в E.15).
Можно указать, как и при доказательстве соответствующих
утверждений в теореме 4.3.3, лишь последовательность
{/„} с WHI такую, что
lim En(fm)L= lim I/mk = -^- E-32)
m -*¦ oo m -v oo
Действительно, привлекая аппарат функций Стеклова
и положив (при фиксированных /гиг)
I >
где Am « 1/m, получим последовательность функций [fm] с:
с; 1^гЯл, для которой (; fm ^ = Еп (fm)L и при m -> oo
l/ifiJ/.-^iff/i.r-iS/., так что выполнены предельные
соотношения C.32).

§ 5.5] НАИЛУЧШИЕ ЛИНЕЙНЫЕ .МЕТОДЫ 109
§ 5.5. Наилучшие линейные методы
для классов WrM, WrL и Wrv
Мы могли бы, как и в § 5.2, где исследовалось
наилучшее приближение, перенести на классы Wm и WrL
результаты гл. 4 по наилучшим линейным методам. Однако,
может быть, более поучительно будет вывести нужные
факты, непосредственно рассматривая приближение
функций этил классов с помощью тригонометрических полиномов
Un(I\ x\ Я) = у + У Kk(akcoskx + bksinkx), E.33)
где ak и Ьд —коэффициенты Фурье приближаемой
функции /(a), a %k — Xk(n) — числовые множители, находящиеся
в нашем распоряжении.
Ясно, что полином Un(f\ x\ ?.) линейно зависит от f
и, таким образом, заданием коэффициентов Хл мы задаем
некоторый линейный метод приближения, который мы
будем называть Х-методом. Положим
*«(»?; Л)л= sup»/ —?/я(/; ^I!х,
fn
где ЭI — некоторый класс функций, и заметим сразу, что
при любом векторе коэффициентов Я = {ЯЬ Я2, ..., X,,_i}
так что
inf#e(»t; Л)х^Яи(аЯ)х, E.34)
А
где X, как и прежде, есть пространство С или Lp (I ^p^oo).
Если f^Lr (г= 1, 2, ...), то соотношение E.2)
позволяет записать полином Un(j\ x\ К) в виде
*(cosк(x-l)~ f\\ /М @Л =

ПО НАИЛУЧШЕЕ ПРИБЛИЖ ПОЛИНОМАМИ КЛАССОВ U ?р [ГЛ. 5
Учитывая E.3), а также тот факт, что
разность f — Un(f\ Я) мы можем теперь представить
следующим образом:
/ (х) - Un (I; *;
х -1) dt,
E.35)
где
{— \у* \ ^c
(- 1)~ V
= 2r i = l, 2,
= 2/—1; /=1, 2
, 2,...),
a a0 —произвольное число, которое мы выберем позже.
Пусть /€=/-р A<р<оо, г=1, 2, ...), т. е. /(г) е /-р.
Общее неравенство D.5) для сверток применительно к E.35)
позволяет написать
U- Un (/; X) |, < 1 i D, - a2" - 7V (X) Ц !/(-> i'p. E.36)
(При р = со E.35) получим, просто оценивая интеграл
в E.35) по абсолютной величине и заменив 'f{r)(x — t)\
на J7(r> in.)
В правой части E.36), которая дает оценку
приближения Я-методом любой / е 1/р, только сомножитель
!D/.~a0/2 — TnrG.) ]i зависит от находящихся в нашем
распоряжении коэффициентов а0, ль л2, ..., Хп.г и
естественно их выбрать так, чтобы этот сомножитель имел
минимальное значение.
Ясно, что всегда
!;D, - *° - Тпг (I) \ ^ Еп (Dr)L -l! Dr - fnr ('ь E.37)
где 7V @ — полином наилучшего приближения для Dr

2
§5.5) НАИЛУЧШИЕ ЛИНЕЙНЫЕ МЕТОДЫ 111
в метрике L, построенный в § 3.5. Этот полином имеет вид
\? ""
п-1
v*rsin« (r«2i-l; /-1, 2,...),
причем коэффициенты \xkr и vkr нами вычислены (см. C.51)
и C.52)).
Будем считать, что при / нечетном а0 —0. Тогда
полиномы 2~^Tnr(t; X) и fnr(t) имеют одинаковую четность, и
мы поступим наилучшим образом, выбрав \и ..., \п^
и —при г четном —а0 так, чтобы эти полиномы
тождественно совпадали. Для этого надо при каждом
фиксированном п положить ао = |лО/., если г = 2/, и
:°' „ E.38)
Учитывая равенства C.51) и C.52), из E.38) получим
для экстремальных коэффициентов \кг следующие
выражения:
\-kr ^(—
hr =
(A=l, 2, ..., /2-1).
В частности, при /•= 1
E.39)
_
E.40)
Если X ^= {>.1г,... , ^Л ^ Д — вектор коэффициентов E.39)
(г будем полагать фиксированным), то при указанном

112 НАИЛУЧШЕЕ ПРИБЛИЖ. ПОЛИНОМАМИ КЛАССОВ \\TLp [ГЛ. 5
выше выборе а0
Oq/2+ Tnr(t, i)=Tnr(t),
так что при Л, = Л, в E.37) будет знак равенства, а E.36)
запишется в виде
ti-Unfatyl^E^Drhm V/sL;. E.41)
Приняв во внимание C.45), из E.41) получим оценку
^f-}f"l WsL; (Kp<-oi). E.42)
Если feW'Lp, то i/^jp^l и f/-t/nfc *.)',<,*#>•';
переходя в левой части этого неравенства к верхней
грани по / е Wl и используя введенные выше
обозначения, получим соотношение
оо; п, г=1, 2, ...).
E.43)
Наиболее существенным и интересным является тот
факт, что в E.43) при р=\ и р = со имеет место знак
равенства. Это немедленно вытекает из сравнения E.43)
с общим неравенством E.34) и соотношениями E.14) н
E.15).
Так как, кроме того, для любого Я-метода
(это устанавливается теми же рассуждениями, что и E.31)),
то доказаны следующие равенства:
(/i, r-1, 2, ...). E.44)
Сопоставив E.44) с E.14), E.15) и E.21), приходим к
выводу, что ?-метод не только является наилучшим среди
всех Я-методов для класса W'm в метрике С и для
классов Wl и Wv~l в метрике L, но и реализует на этих адас-
сах наилучшее приближение в соответствующей метрике.
Полученные результаты можно сформулировать в виде
следующего утверждения.

< 5.6J ТЕОРЕМА СРАВНЕНИЯ КОЛМОГОРОВА ИЗ
Теорема 5.5.1. Верхнюю грань наилучших
приближений тригонометрическими полиномами Т„ (/) порядка
я—1 на классах Wm (г=1, 2, ...) в метрике С и на
классах Wl и Wrv~l (/"=1. 2, ...) в метрике L
реализует %-метод с коэффициентами E.39). При этом
*AW'm, ^c = En{WrM)c = {<9nr\c = ^ (n, r=l, 2,...);
E.45)
<*n(WrL9 i)L = *n(wV-\ l)L = Ea(WrL)L =
~ En{Wrv-\ = lgn.r-i)L=^ (л, г-1, 2, ...). E.46)
§ 5.6. Теорема сравнения Колмогорова
и следствия из нее
При получении точных результатов в задачах II и III
существенную роль в ряде случаев будут играть
доказанные А. Н. Колмогоровым [2] в 1939 г. утверждения,
известные как теорема сравнения и неравенство для норм
производных дифференцируемых функций.
Излагая эти и сопутствующие им результаты, мы в
значительной степени облегчим себе дальнейшие
рассуждения, доказав предварительно следующую элементарную
лемму.
Лемма 5.6.1. Пусть на отрезке [а, Ь] заданы
абсолютно непрерывные функции g(t) и ф(/), причем ср(/)
строго возрастает и выпукла вверх на [а, Ь\. Если
а)
или
б) g(b) = y(b)y g(a)«p(a)9
то на интервале (а, Ь) существуют точки a u P такие,
wio g (а) = ф (Р) и g (а) > Ф1 (Р) •).
Докажем сначала утверждение леммы в
предположении а). Можно считать, что #(/)>ф(/) на (а, Ь), ибо
иначе последующие рассуждения можно применить
*) Через <р'_ (jc) (<р\ (х)) здесь и в дальнейшем будет обозначаться
левая (правая) производная функции ф в точке х.

114 НАИЛУЧШЕЕ ПРИБЛИЖ ПОЛИНОМАМИ КЛАССОВ Г ?, ГГЛ. 5
к отрезку [аь fr], где я^ — самый правый пуль разности
g(/)-cp(/) на (я, Ь).
Так как g(/) непрерывна, то она принимает в
некоторых точках интервала (а, Ь) значение, равное <p(fe).
Пусть ? —самая левая из таких точек, т.е. b
а
Рис 6
" g(t)<4>(b) (a<it<l) (рис. 6). Функция Ф (/) строго
возрастает, следовательно, ф(Н)<Сф(Ь) и, значит,
Поэтому существует точка а, а<:а<!?, такая, что
ф' (a) <ig' (а). Но так как
то в некоторой точке р, a<p<fc, будет Ф(Р)—?(а).
В силу строгой выпуклости вверх функции ф (/)
выполняется неравенство (pl(P)<q'(a) и, следовательно,
Пусть теперь выполнено условие б). Ясно, что в
некоторой точке а + А, где 6<rA<& —д, будет g(fl + Aj-=
= ф(а). Положим
Тогда ft(a)r=v(fl), g, (fc — A) -=g(fc) >ф (Ь — А), т.е. для
функций ^ и ф выполнено условие а) на отрезке
|а, & —А] и по уже доказанному в некоторых точках at
и Р, я<аа<р<& — А, одновременно выполняются

§5.6] ТЕОРЕМА СРАВНЕНИЯ КОЛМОГОРОВА 115
соотношения
Положив а = ах + Л, получим, что
g (а) = Ф (Р), g (а) > Ф1 (Р) (а, р е (а, Ь)).
Лемма доказана.
Замечание. Наряду с леммой 5.6.1 нам
потребуются также ее варианты, полученные зеркальным
отображением всей картины относительно вертикальных
прямых t^-c (c^b) или горизонтальных прямых y^d, где
d^q>(a), а также суперпозицией этих отображении.
Сделав соответствующий чертеж, читатель легко поймет,
что любой из этих вариантов легко свести
соответствующей заменой переменной к уже рассмотренным.
Пусть Wm (—оо, оо) (г=1, 2, ...) обозначает класс
заданных на всей оси (не обязательно периодических)
функций /(*), у которых (л—1)-я производная f[rU(x)
локально абсолютно непрерывна (т. е. абсолютно
непрерывна на каждом конечном промежутке) и
supvrai |/(г) (*)!< 1.
— 0О<*<00
Иначе говоря, 1^!м(—оо, оо) есть класс г-х интегралов
от измеримых функций, существенно ограниченных
единицей на всей оси. Будем и здесь полагать, независимо
от периодичности,
[/;;с= max \f{x)\; |!/Ь,= sup vrai !/(*)'. E.47)
— 00<ДГ<0Э —0O<JC<0O
Теорема 5.6.2 (теорема сравнения Колмогорова)*).
Пусть f e U?/u (—оо, оо) и при некотором
где ц>1г определена в § 5.4. Если f (а) = Ф;.г(а), то
(при г= 1 в предположении, что производные существуют).
Доказательство. Приг=1 утверждение теоремы
тривиально, ибо | у'^ (х) \ =» 1 везде, за исключением точек
своего экстремума.
¦) Л. И Колмогоров [2].

116 НАИЛУЧШЕЕ ПРИБЛИЖ. ПОЛИНОМАМИ КЛАССОВ \\р [ГЛ. 5
Далее будет работать индукция, но чтобы обеспечить
необходимое «зацепление», докажем следующую лемму.
Лемма 5.6.3. Пустьf <elWm (—со, оо) (*=1, 2,...)
и !;Л!с<!!фц!с- Если теорема 5.6.2 де/жа Зля г = А — 1,
Докажем лемму 5.6.3, рассуждая от противного. Пусть
!"/' [м = ! /' Со) I > • Фх, /,-i '"м ---- [ Фа* V
Так как вместо f (х) мы можем рассматривать функцию
d=/(/ + T)» где х —любое число, то можно считать, что
/'('о)>0 и \<pKk х|Ьи = Фл.л-i Со)- Обозначим через fx и /3
ближайшие слева и справа от /0 нули функции ф;.,*-1@.
которая, следовательно, выпукла вверх на (/1э /2), строго
возрастает на (/lf t0) и строго убывает на (/0, /г)-
Найдется точка a, tx < а < /2, в которой будет /' (а) «^
<Фл,а-1 (а), ибо предположение /' (/)>срх,fe jV) (*х<*<
< ^2) означало бы, что
и, значит, |!/'jci>i;(P/.Ai!c —B противоречии с условием
леммы 5.6.3. Положим Д (t) = yf (/), где число -у. 0<Г
<Y<1, выбрано так, что i!/iI'm =',Ф>„* i |'.м. Тогда
!/{*"I|!д| = Т-Ги<1. т.е. Ле^^Г^-ос.оо). Так
как
Д (а) = у/' (а) < Фа. * i (а), Л Со) = Фл, a i ('«),
то применение леммы 5.6.1 (с учетом замечания к ней,
если /0<а<^) приводит к противоречию с
утверждением теоремы 5.6.2 для г = й— 1. Лемма 5.6.3 доказана,
и мы можем продолжить доказательство теоремы 5.6.2.
Предположим, что теорема 5.6.2 уже доказана при
г=1, 2, ..., Л—1 и для функции / выполнены ее
условия при г — k (k^2). Тогда в силу леммы 5.6.3 'J'\м^
^[Укк-г^м- Не теряя общности, мы можем считать, что
я = а,' т.е. /(а) = фл*(а), и sign/' (а) = sign фи (а) фО.
(Если /'(а) = 0, то доказывать нечего). Рассуждаем от
противного: пусть ;/' (а) (> | ср^л (а) |. Для определенности
будем предполагать, что фх*(а)<0 нф>.А(а)>0, т.е.
функция фхА (/) возрастает в точке а и на промежутке
(tQt а), где /0 — ближайший слева ее минимум, она

5 5.6]
ТЕОРЕМА СРАВНЕНИЯ КОЛМОГОРОВА
117
выпукла вниз (рис. 7). Так как
min / (а:) :> — фХЛ "с = щк (t0),
X
то в некоторой точке т], /0<Л<«, будет/ ft):
г. е.
и, следовательно, разность f (/) —Ф>.*(/) должна в
некоторой точке I <=е ft, а) обратиться в нуль. Так как
функция щк (/) = фх, *_, (/) выпукла
вверх на (tQ, а) и по
предположению /'(а) ;>ф>^ (а), то к
функциям f (t) и Фх,*1(/) на
промежутке (|, а) применима
лемма 5.6.1, которая приводит
к противоречию с
утверждением теоремы для r = k~ 1.
Из теоремы сравнения 5.6.2
вытекает ряд следствий;
некоторые из них имеют
самостоятельное значение.
Предложение 5.6.4. Если
f e Wm (—со, со) и при
некотором Я>0 [!Гк<!!ф>.г|!с, то
E.48)
Рис. 7.
Достаточно, очевидно, проверить справедливость E.48)
для любого г при А=1. Если |:/'|^ = if (a) | >}<&Ам*
то, выбрав точку а из условия ф>г(а)=/(а), будем иметь
«/' (а) | > ! ф{г (а); — в противоречии с теоремой сравнения.
Предложение 5.6.5. Пусть /е IF.m (— со, оо),
И Ч / () ( [
';с <
. ,v - .. , ^ Чс, / (Ы = Фхг (^]о) и [а, Р] — содержащий точку
отрезок, на котором фХг монотонна. Если ф>.г@ «а (а,
возрастает, то выполняются соотношения
—т]0)э
E.49)
E.50)

118 НАИЛУЧШЕЕ ПРИБЛИЖ. ПОЛИНОМАМИ КЛАССОВ \VrLp |ГЛ.5
в случае убывания ф>.г@ #а (а, Р) змакц неравенств в E.49)
« E.50) противоположны, В частности, если /feo) —
=-:Ф/.гЫ = 0, то
I / (go+ и)! < I ц>Кг (г]0 + а) | (- -^< к -S ^-\
Можно считать, что Ео^Ло, т.е. /(тH)-=ф>.г (Ло)» а а
и Р —ближайшие к Ло нули производной щг(() слева и
справа. Предположим, что флЛО возрастает на (a, f?) и
.. Фхг(Ло)^О(рис. 8)(дру-
^ гие случаи
рассматриваются аналогично).
Тогда неравенство
~Y0 ~Р Г / (Ло + и) ^ q>ir (Ло + и)
/ @ ^ ы ^ р — Ло)
_L^^ *kr вытекает из тех
соображений, что если бы
Рис> 8' в некоторой точке
5iDo<b<P) был0
f(ti)>4>>.r(li)> то, используя лемму 5.6.1, мы сразу
пришли бы в противоречие с теоремой сравнения.
Точно так же, опираясь на лемму 5.6.1,
устанавливаем, что
где /0 —нуль фЛг(/) на (а,
Осталось доказать, что
. E.51)
причем уже известно, что / (/0) ^ q>lr (t0) = 0.
Предположив, что E.51) не выполняется, мы окажемся в условиях
одного из вариантов леммы 5.6.1, которая снова
приведет нас к противоречию.
Предложение 5.6.6. Пусть f e H?ai (— °°, оо) и
причем точки т]0 а т], лежат на одном промежутке
монотонности функции ifxr (t), то s c0 — Ei! ^ | Ло — Л1:-
И здесь, учитывая возможность сдвига по
горизонтали, мы вправе считать, что Е0=г|0. Но если

§ 5.6] ТЮРЕМА СРАВНЕНИЯ КОЛМОГОРОВА 119
то из неравенства |Si —t|o|<|4i —По! сразу следовало
бы, что I / (?х) | > j qv (SL) I — в противоречии с
утверждением 5.6.5.
Пусть со (/, t) — модуль непрерывности непрерывной на
всей оси функции fy т. е.
со(/, /)= sup !/(*')
I ;<
Справедливо
Предложение 5.6.7. Если f e Wm (— оо, оо) и
Лс^'флг'о, то
со(/, 0^»(Флг, /) @^<оо).
В самом деле, фиксируем t>0t и пусть ] м' — и*\ <,i.
Существуют точки а' и а" такие, что
и на (а', а") функция ц>\г(х) монотонна. Но тогда в силу
предложения 5^6.6 ¦,&'— а*! *^\ и' — а"", ^/t и потому
7 («') -/ («")! -' Ф>.г (а9) - Ф>, (а") | <о> (Ф,г, 0.
Из теоремы сравнения непосредственно вытекает также
следующее утверждение, известное как неравенство
Колмогорова для норм дифференцируемых функций (А. Н.
Колмогоров [2]).
Предложение 5.6.8. Для любой функции /,
являющейся r-м интегралом от измеримой ограниченной на
всей оси функции, справедливо неравенство
1/'%1<сг* ]/•,!«-*''1Г ВТ (г=1,2, ...,* = 0, 1, ...,/-)
E.52)
где "J]m понимается в смысле E.47),
a ?7f r — константы C.44). Неравенство E.52) точное.
Доказывая неравенство E.52)» заметим, что оно
сохраняется при умножении функции / на любое не
равное нулю число, так что мы, не теряя общности, можем
считать, что |/(г)[и-^ 1. Дело сводится, таким образом,
к доказательству соотношения
4{k))M^crk\j\^k" (r-1, 2, ...; /. = 0, 1, .... г)
для любой 1 е W'm \— со, ее).

120 НАИЛУЧШЕЕ ПРИБЛИЖ. ПОЛИНОМАМИ КЛАССОВ WrLp [ГЛ.5
Так как i|q>xrfof непрерывно зависит от Я, причем
il<F*r !1л1-> 0 при Я-><х>, ('флгйл^оо при Я->0, то
значение '31 можно выбрать таким, чтобы выполнялось
равенство Р/Чс — ^ФъЛ;- В силу предложения 5.6.4 из теоремы
сравнения и соотношения E.25) будем иметь при таком
выборе X
(А^О, 1, ..., г),
что и требовалось. Окончательность неравенства E.52)
следует из того же равенства E.25).
Заметим, что хотя теорема сравнения доказана
А. Н. Колмогоровым при получении неравенства E.52)
и носила вспомогательный характер, на самом деле она
сама по себе имеет глубокий смысл. И неудивительно,
что впоследствии использование этой теоремы позволило
получить ряд новых точных результатов, выясняющих
экстремальные свойства функций. Один из примеров
такого применения содержится в следующем параграфе.
§ 5.7, Экстремальные свойства функций класса Wm
в метрике пространства Lp
Здесь мы опять возвращаемся к рассмотрению 2л-пе-
риодических функций.
Теорема 5.7.1. Пусть ft=WrM (г=1, 2, ...) и
при некотором п=19 2, ... выполнены соотношения
[fh^hnrh E-53)
E.54)
\f(t)dt
max
a, b
Тогда
Доказательство. Нужно показать, что при
выполнении условий теоремы
2 л 2 л я [п
6 6 6
Отметим сразу, что предположения относительно
функции / гарантируют выполнение для функций / и српг ус-

§ 5.7] ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ФУНКЦИЙ ИЗ WrM В Lp 121
ловий теоремы сравнения 5.6.2, и мы при доказательстве
можем опираться на все отмеченные выше следствия из
нее. Кроме того, из E.54) следует, что f (х) обращается
в нуль, и .можно полагать, что / @) = f Bл) =: 0.
Пусть S = {(aki bk)\ — система непересекающихся
интервалов из промежутка @, 2л) таких, что
/Ы =/(**) = <>, |/@ |>0 (ak<t<bk).
Из системы S выделим и перенумеруем отдельно
интервалы Д| = (а/, bf) с длиной bi — Qi>nln и интервалы
6v = (tfVf by) с длиной bv — av^TLfn. Ясно, что в 5 может
содержаться лишь конечное число т интервалов At.
Таким образом,
2я т
l yldt, E.55)
и будем отдельно оценивать каждую сумму.
Исходя из тождества
и меняя порядок интегрирования, получим для
интегралов первой суммы
bi bi
= W J \f{x)\dx\diP-\ E.56)
0 U}
где положено
Аналогично
n флг ;;с
У
I Флг (*)!'<**= J M ^-Wl^]^1. E.57)
где
?v @ = \x: ^ e= @, л/я), ;

122 НАИЛУЧШЕЕ ПРИБЛИЖ. ПОЛИНОМАМИ КЛАССОВ W'Lp ЦЛ.5
Докажем, что для любого /, 0 ==? / *?)' <рл, "с>
I \f(x)\dx^ $ IФ"(х)\** (' = 1.2 т). E.58)
ф|гксируем /, и пусть (aj, Ь\)~- наибольший интервал,
содержащийся в (ait bt) такой, что (рис. 9)
В силу предложения 5.6.5
\ \f(x) \dx+yj (x)' dx ^ J ! V»r
а так как ввиду условия E.54)
b.
я/я
а ?/(/)с:(^, b't), то E.58) доказано.
Из E.56) —E.58), с учетом неравенства E.53),
следует, что
л/п
- J \Vnr(x)\pdx (t = l, 2,..., m)
и, значит,
m \" | флг (x)!" dx. E.59)
о

<* s.?l экстремальны!: свопствА функций из \vm в Lp 123
Теперь займемся оценкой интеграла от *f\p по
промежуткам 6V = (av, &v), длины которых < л/л. В связи с E.55)
и E.59) нам достаточно доказать, что
л /л Bя — т)л/п
2$ |/|Мл;^Bл-//г) jj ;срлг/гк= ^ \4>nr\pdx.
v 6V и о
E.60)
m
Так как mcs |J А/>шя//г, то mcs|J 6ч.^Bя — т) • я/л.
Можно считать, что интервалы 6V перенумерованы в
порядке убывания их длин, т. е. |6j \^\ б2 \^ •• • Каждому
из 2л — т первых интервалов 6v(v = 1, 2, ..., 2п — т)
сопоставим на промежутке [((v — 1)я)/л, vn/n] два
непересекающихся интервала (*v, */v) и (гу, uv) длиной |6vj/2
каждый, на одном из концов которых фЛ/-(лт) обращается
в нуль. (Если флг (\п!п) =¦- 0у то xv= (v— 1)я.'я, Иу = уя/л;
если же фяг (Bv— 1) я/2я) = 0, то yv = zv^ Bv— 1) я/2я).
Обозначив через cv середину интервала 6^ = (а^ bv) и
применяя предложение 5.6.5, получим
6,. av cv
(v-1, 2, ..., 2л-т). E.61)
Теперь заметим, что для v>2n—m
/v-*v) + («v-2v)]e
: v; ; 2я m
I < v < 2n — m
Поэтому, если положить
2rt — m
e= U (["^T111' v]\^v,f/JUBv, «v)} E.62)
v •-- I
и учесть структуру функции уПг(х), то в силу того же
предложения 5.6.5 будем иметь
sup \f(x)\ <- min : ц>аг (х) | (v > 2я ~ т),
6

124 НАИЛУЧШЕЕ ПРИВЛИЖ. ПОЛИНОМАМИ КЛАССОВ W'rLp [ГЛ.5
и, следовательно,
^ llf'Pdx^v^Pdx. E.63)
Сопоставив E.61), E.62) и E.63), получим E.60).
Теорема доказана.
В качестве следствия из нее легко выводится
Теорема 5.7.2. Имеют место соотношения
sup |У;1р^'¦ qv|jp A<р<оо; я, г=1, 2, ...). E.64)
Действительно, для любой /е WrH% неравенство E.53)
выполнено в силу E.28). Из того же соотношения E.28)
следует, что если / е WrH%, то положив
у
где у выбрано так, что среднее значение /, на периоде
равно нулю, и, следовательно, ft e Wr'l']H%, будем иметь
ь
max
\f{t)dt
2 ]
Таким образом, для f^WH% все условия теоремы 5.7.1
выполнены, так что !7 ;р^[ <рп/р- Остается заметить, что
Соотношс}1ия E.64) выявляют еще один аспект
экстремальных свойств функций флл.
Если сопоставить E.17) и E.64), то получим оценку
Покажем, что на самом деле здесь имеет место знак
равенства. При р~\ это нам уже известно (см. E.15)).
Если же р>\ и, значит, lscp'<oo, то в силу E.18)
Еп ( WIp)l = sup Ex (f)p. ^ Ег (фяг)р. -
ибо нижняя грань по с реализуется здесь при с = 0, в чем
мы сразу же убедимся, применив критерий полинома

§ 5.81 НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ КЛАССА \Х'ц В L. 125
(нулевой степени) наилучшего приближения в Lp (§ 3.3)
и учитывая, что
S I Ф*г (х) \р ~l sign флг (а:) Ах = 0.
б
Таким образом,
{p)LP
и мы можем сформулировать следующий окончательный
результат.
Теорема 5.7.3. При всех /г, г=1, 2, ...справедливы
соотношения
В случае р^=со, учитывая, что норма в L функции
<Vnr(x)~4ngnr{x) нами подсчитана в § 5.4, получаем
равенства
E,(WrM)L= sup ]fl = *^L=**?± E.65)
(л, г=1, 2,...).
§ 5.8. Наилучшее приближение класса Wl, в метрике ?2
Ради полноты изложения рассмотрим еще самый
простой случай решения задачи II на классах W[ , когда
точный результат легко получить, используя специфику
метрики пространства. Речь идет о наилучшем
приближении в гильбертовом пространстве L2.
Известно (Г. М. Фихтенгольц Ц|), что если feL2 и
/ (х) ~ °2- + 2 (а>cos kx+
k --1
— ряд Фурье функции / по тригонометрической системе, а
5Л (/, х) = -2°- + У (a* cos fcc + bk sin ^) E.66)

f(t) cos ktdt
126 НАИЛУЧШЕЕ ПРИБЛИЖ ПОЛИНОМАМИ КЛАССОВ W \р [ГЛ.5
— частичная сумма этого ряда, то
En(fh=--\f-Sn(f)l2, E.67)
т. е. наилучшее приближение тригонометрическими
полиномами в метрике L2 функции / доставляют суммы E.66).
Пусть [ ^ I/, (г—1, 2, ...). r-кратным интегрированием
по частям найдем (при k^l)
** p'i^l (г-1,3, 5, ...),
\kr\akr\ (г = 2, 4, 6, ...),
•где akr и /^—коэффициенты Фурье функции f{r)(x).
Аналогично
\kr\akr\ (г=\, 3, 5,...),
{k~r\bkr\ (г = 2, 4,6,...).
Таким образом,
и равенство Парсеваля с учетом E.67) позволяет
написать:
I °° I2
оо ос
k а» П k-'-n
Если же f e W[2, то '!/(гM4-^ 1 и, следовательно,
Еп Фг < -I- V/ e Wl*. E.68)
Далее, ряд Фурье функции / е WrH?2 имеет вид
и, повторяя те же выкладки, основанные на равенстве
Парсеваля, найдем, что
г f I- ^ J у/ € ГЯг. E.69)

§5.9] РАСПРОСТРАНЕНИЕ РЕЗУЛЬТАТОВ НА VrLf)K 127
Функция
sin /глг,
очевидно, принадлежит классам Wlt и WrHn}9 и так как
Sn(fOi x)=0, то
т. е. неравенства E.68) и E.69) на соответствующих
классах неулучшаемы.
Заметив, что суммы S,, (/, х) линейно зависят от /,
можем сформулировать следующее утверждение.
Теорема 5.8.1. Справедливы равенства
= sup \f\ =~ (/i,r-l,2,...). E.70)
§ 5.9. Замечание о распространении результатов
на классы Wl К
Обозначим через W\К A ^р^%оо\ г=*1, 2, ...) класс
функций f^Lp, у которых lfir)lP^K\ в частности, W[pl
есть Wl . Все результаты, полученные в этой главе для
наилучшего и линейного приближения на классах Wl
естественным образом — путем умножения правой части
соотношешш на /(, — распространяются на классы W'LjK.
Это вытекает из следующих простых соображений (X будет
обозначать С или Lp).
Если F — подпространство из Х% то в силу
положительной однородности функционала Е (/, F)x
(предложение 1.2.1)
Переходя к верхней грани по /еЯ7? и учитывая, что
когда / пробегает класс Wlp, функция g — Kf пробегает
весь класс WL /(, буде.м иметь
KE(WLP,F)X=-. sup E(Kf,F)x= sup E(g,F)x,

128 НАИЛУЧШЕЕ ИРИЪЛИЖ. ПОЛИНОМАМИ КЛАССОВ U¦'Lp [ГП.Ъ
т. е.
KE(W'Lp, F)X = E(WLPK9 F)x. E.71)
Если /4 — линейный оператор из X в F и g = Kf
(/С>0), то
и, следовательно,
sup [g-^ = /( sup !!/-Л/!!х, E.72)
fieir; /С /eW'f
а переход к нижней грани по всем таким операторам лает
В частности, если А есть Ji-метод (§ 5.5),
отображающий X в Fjn-u to E.72) запишется, в соответствии с
введенными в § 5.5 обозначениями, в виде
Таким образом, каждая оценка или точное равенство,
полученные выше для наилучшего и линейного
приближения классов Wlp, будут справедливы и для классов
WlpK, если правую часть умножить на /(. В частности,
справедливы неравенства
Еп (WrLpK)p *? Шя [wrhK\ <,КЦ± (я, г - 1, 2. ...).
в которых при р=1 и р = оо везде имеет место знак
равенства. Кроме того, для Х-метода, построенного в § 5.5,
)
= Еп {WIk)l - КЖгп -r (л, г --= 1, 2, ...).

ГЛАВА б
ПЕРЕСТАНОВКИ И ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА
ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЙ
Если проанализировать ход рассуждений, которые при*
вели в главе 5 к точным значениям величин Еп(№м)м и
?«(И^!)л, ™ легко обнаружить, что решающую роль
сыграли соотношения
Igh = [gnt r-1 V = [ 4W hi = SUP \g[Ai. F.1)
Действительно, если fe/-J, то из D.18) с помощью
г-к ратного интегрирования по частям получим
2? 2;t
En (/)„ = sup J / (/) h (t) dt = sup \ p> (t) g (t) dt
и равенства F.1) вместе с экстремальным соотношением
(Д. 12) сразу позволяют написать точные оценки:
sup sup \f(t)g(t)dt
= SUP
sup sup \f(t)g(t)dt =
Однако если вместо W] рассматривать классы, задание
которых связано с более чувствительной, чем норма,
характеристикой — модулем непрерывности (§ 7.1), то здесь
информации, заложенной в соотношениях F.1), уже
недостаточно для получения точного результата. Нужны более

130 ПЕРЕСТАНОВКИ, SKCTPFMAJlЬИЫЕ СВОЙСТВА ФУНК. ГГЛ.6
глубокие свойства функций из WrHpl, определяемые
условиями ортогональности их тригонометрическим полиномам.
Ряд этих новых и более тонких свойств удается
выявить и описать с помощью аппарата перестановок, причем
полученные результаты будут относиться к более широким,
чем WrHp, классам функций.
§ 6.1. Перестановки функций
Пусть ф(#) — неотрицательная и суммируемая на
промежутке (а, Ь) (конечном или бесконечном) и,
следовательно, измеримая и почти всюду конечная на (а, Ь)
О
Рис. 10.
функция. Для всех у^-0 определим т(у) как меру
множества Еу точек х из (а, &), на котором ц(х)^у/
т (у) = mes Eyt Еу={х:х<= (a, b)y <р (х) ^ у].
Функция х = ш(*/), которую называют гшогда функцией
распределения для ф (х)> определена на бесконечном
промежутке 0^г/^ + оо, не возрастает, причем
lim m(*/) = 0.
= b~af tn(-\- oo)
Если т(у) непрерывна и строго убывает, то
существует обратная ей строго убывающая на @, b — а)
функция у — ф(я), которую называют перестановкой функции
Ф (х) в убывающем порядке или убывающей перестановкой
Ф(л-) (рис. 10).
В общем случае т(у) может иметь промежутки
постоянства, а также разрывы первого рода в конечном или

§ 6.1] ПЕРЕСТАНОВКИ ФУПКИИЙ 131
счетном числе точек, и чтобы однозначно определить
обратную функцию, исправим график т (у) следующим
образом. В каждой точке разрыва у{) функции т(у)
дополним ее график отрезком у = у(), т (у0 + 0)^x^rn(yQ — 0),
а затем на каждом промежутке [а, р], где функция т(у)
постоянна, оставим в ее графике одну точку с
координатами, например */=1/2(а + Р), х = тA/2 (а + Р)). Теперь
каждому х% 0<#^& —а, соответствует единственная
точка с координатами (л\ /я1 (х)), и этим определена на
@, Ь — а) функция yz=(p(xI которую мы и будем
называть убывающей перестановкой, или'просто перестановкой,
функции ф(х).
При любом у^О .мера .множества точек ^е@, Ь — а),
в которых ч>(х)^у, равна т(у), что становится
очевидным, если сделать чертеж. Таким образом,
rnes [х: х е @, Ь — а), ф (х) ^у} =
= nies {х: х е (г/, &), ф (х) 7&у} = /и (*/),
откуда, в частности, следует, если учесть определение
интеграла Лебега (И. П. Натансон [2], гл. V, VI), что
\
0
]<p(x)dx= S <p(x)dx. F.2)
В рассуждениях, связанных с использованием
перестановок, полезным бывает
Предложение 6.1.1. Если Е — измеримое множество
из (а, &), то
6> — а то* /:
J Ф (х) dx < J ф (л-) rfx < J ф (х) djt. F.3)
Ь — а — mes ? ? 0
В самом деле, если Ф1(л:)^ф(*) (а<х<Ь), а т!(у)
и т(у) — соответствующие функции распределения для ф!
и ф, то для любого у ^ 0 mi(y)^m (*/), и потому ф! (х) ^
—а). В частности, если положить

132 ПЕРЕСТАНОВКИ, ЭКСТРЕМЛЛЬНЫЕ СВОЙСТВА ФУНК. [ГЛ. 6
то будем иметь
Ь Ь-а _
\ ф (х) dx — \ ф! (х) dx= $ ф1 (х) dx =
Е а О
mes Е __ mos Я __
=» )i ф! (лс) d*< )j ф (х) dx,
6 о
т. е. второе неравенство в F.3) доказано. Чтобы
получить первое, надо положить Ег — (а, Ь)\Е и вычесть
неравенство
mes Et _
^ ф (х) dx < ^ Ф М ^
i-, о
из соотношения F.2).
Отметим два очевидных следствия из предложения 6.1.1.
Предложение 6.1.2. Если
6 _
\ Ф (х) dx > jj ф (х) dxf
то mes?>8.
Предложение 6.1.3. Если
ь~а _
J Ф (х) ^ < J ф (х) d*f
? Ъ—а—6
mo mes ? < S.
Можно сказать, что перестановка <р сохраняет норму
в! и, если ф (х) ограничена, —также и норму в М, ибо
в этом случае <р @) =||q>r:A< {a, />>. Ясно также, что
перестановка, вообще говоря^ не сохраняет вариацию функции <р:
ограниченная функция ф(д:) может иметь на [а, Ь\
бесконечное изменение, а вариация ее перестановки ф на
[0, Ь — а] конечна. Легко представить, однако, функцию,
перестановка которой, в известном смысле, сохраняет
информацию о величине ее вариации на [а, Ь]. Такие
функции рассматриваются в следующем параграфе.
§ 6.2. Простые функции и их перестановки
Непрерывную на всей числовой оси функцию ц(х)
будем называть простой, если ф(х) = 0 вне некоторого
интервала (а, р), -ф(*)|>0 для #^(а, р) и при каж-

fi.2] ПРОСТЫЕ ФУНКЦИИ И ИХ ПЕРЕСТАНОВКИ 133
лом */, 0<</<тах|ф(^)!, уршшенне \*р(х)\=*у имеет
л:
ровно два корпя.
Интервал (а, р) условимся называть основным
интервалом простой функции ц (х). Ясно, что вместе с ф(лг)
простой является также и функция | <р (а*) {.
С простой функцией ф (х) мы будем связывать еще
отрезок [а', Р']с:(а, р), на котором jq> (х) | = тах |ф (х) |,
X
причем, если тах]ф(*)| достигается в одной точке, то мы
х
все же, ради удобства изложения, будем говорить
об отрезке [a', Р'], считая, что а' = р\
В дальнейшем через <р (х) мы будем обозначать
убывающую перестановку функции |<р(*)|. Если положить
6 = р — а, 6' = р' —а', то, очевидно, <р (*) = max | <р (/)!
__ t
для О^х^б', <р(лг) строго убывает на промежутке F', б)
и ф(лс) = О для х^б. Ясно также, что
1 3
Ф @) = max | ф (х); = 9- V (ф).
Если я^! (г/) — функция, обратная к |ф(*)( на (а, а'),
a t|:2 (у) — функция, обратная к |ф(х)| на (Р\ Р), то, оче-
иидно,
« *г {у) - +1 (/у) '°< у^ niax i ф WIV (б-4)
\ х )
Переходя к исследованию дифференциальных свойств
перестановки простой функции, заметим, что равенством
Т(*)НФ(О1 F'<.v<6; a</<a' или р'</<Р)F.5)
заданы непрерывные и монотонные взаимно однозначные
отображения интервалов (а, а;) и (Р\ р) на (б', б). Если
ф (^о) = I ф Ci) H' ф (к) I
то x{)^=12 — t\ (рис. 11). Пусть ^0-)-/ieF', б) и числа /^
и li2 выбраны так, что /1 + Л1е(а, а'), /2 + ^e(f, p)
и выполняются равенства
Ч (х* + Л) = j Ф (/i + Ai) i = , Ф (/а + Л2) |. F.GJ

134 ПЕРЕСТАНОВКИ, ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ФуНК |ГЛ.6
Ясно, что Нг и Л2 имеют разные знаки, причем
' = (/2 + Л2) —(/1 + Л1), и потому, с учетом равенства xQ ==
= /2 — Л» имеем
| A j — | Лж —Ла! — I Лх»-Ы Лз 1- F-7)
Из этого следует, что любой системе {(xkt х^ + цк)\
непересекающихся интервалов на E', Л) равенством (G.5)
Рис И
ставится в соответствие система \{tky tk + qk)\
непересекающихся интервалов на (а, а'), причем
IЧ (*к + %) - Ф (**) i =: Ф (h + Як) - Ф (tk) 1
и
Отсюда сразу следует, что из абсолютной непрерывности
простой функции ф (х) следует абсолютная непрерывность
перестановки <р (х) и, значит, представимость ее в виде
Следующая лемма дает соотношения между
производными простой функции |ф(/)! и ее перестановки ф(*),
вычисленными на одном уровне.
Лемма 6.2.1. Пусть <р(t) — простая функция с
основным интервалом (а, р), у (х) — перестановка функции
*) ф' везде будет обозначать (ф)'; перестановку производной
будем обозначать ф\

§ 6.2] ПРОСТЫЕ ФУНКЦИИ И ИХ ПЕРЕСТАНОВКИ 135
!ф@|. Если
F'<.vo<6, a
и в точках tx и /2 ф@ дифференцируема, то существует
производная ф' (л:0), причем
F.9)
Знак равенства в F.9) имеет место тогда и только тогда,
когда Ф'(<1)--Ф'(<2)'
Доказательство. Сопоставим приращению /i
в точке х0 приращения hx и h2 в точках 1г и /2 так
(рис. 11), чтобы выполнялись равенства F.6). Тогда
! Ф (*о +h) - Ф (Хо) • = ; Ф (tx +Нг) -
Считая для определенности
что ;Aii<|A!, будем иметь
' (tz) I и заметив,
F.10)
Если ф'(Л) = 0, то при ft-*0 из F.10) сразу
получаем все утверждения леммы. Пусть ф' Ц^Ф 0, а, значит,
в силу нашего предположения и ф' (/2) Ф 0. Тогда в точке
//{| = cp(.v0) существуют производные функций ipi (у) и я|J (у)»
обратных к j<p(*)i соответственно на (а, а') и ($', Р).
Поэтому ввиду F.4)
причем т' (//0) Ф 0. Следовательно, производная ф' (х0)
существует и
(ело
Теперь F.8) получается из F.10) при А-*0, а F.9)
следует из F.11), если учесть, что для чисел а и 6, имеющих

136 ПЕРЕСТАНОВКИ, ЭКСТРЕМАЛЬНЫЕ CROPICTBA ФУНК. [ГЛ. 6
разные знаки, справедливо неравенство 4 | ab \ ^ (а — ЬJ>
причем оно обращается в равенство лишь при а = — &,
что доказывает последнее утверждение леммы.
Замечание. Выбирая приращение А
положительным или отрицательным, с помощью совершенно
аналогичных рассуждений придем к неравенствам
FЛ2)
где через /+ (х) и fL (х) обозначены соответственно
правая и левая производные функции / в точке х.
§ 6.3, Разложение интеграла на сумму простых функций
Теперь .можно пояснить общую идею дальнейших
рассуждений, направленных на выявление новых свойств
дифференцируемых функций. Разложив функцию / особым
образом на конечную или счетную сумму простых, мы
сопоставим ей с помощью перестановок некоторую
.монотонную функцию, сохраняющую информацию не только
о норме в /. функции /\ но и о ее вариации.
Пусть D — множество 2я-периодических функций g(x),
имеющих в каждой точке х конечные односторонние
пределы g(x — 0) и g(x + 0). Из этого определения ясно,
что каждая функция g^D ограничена. Менее очевидным
является тот факт, что функции g (x) из D почти всюду
непрерывны (и, значит, интегрируемы по Риману па
любом промежутке конечной длины).
Чтобы убедиться в этом, сопоставим каждой точке
разрыва х функции geD точку (Я, у) плоскости, где
у —любое число, заключенное между двумя неравными
из трех чисел g(x — 0), g(X + Q) и g(x) и не совпадающее
ни с одним из этих чисел. Заметим, что в любой
окрестности (х — S, х + б) есть как точки х> в которых g (x) > у,
так и точки ху в которых g(x)<y.
Пусть М = {х, у} — множество всех точек плоскости,
поставленных указанным выше образом во взаимно
однозначное соответствие точкам разрыва х. Докажем, что М
состоит только из изолированных точек. Фиксируем

$6.3] РАЗЛОЖЕНИЕ ИНТЕГРАЛА НА ПРОСТЫЕ ФУНКЦИИ 137
(х0, #<>) еМ, В силу выбора ордишггы у0 существуют
числа е>0 и 6>0 такие, что в прямоугольнике А - -
== {*о —6<*<*о + & #0 — г<у<Уо + г] нет точек
(ху g(x)) графика функции g(x), причем для всех х
из интервала (х0 —б, х<>), а также для всех х из (х<„ ?0 + 6)
выполняется лишь одно из неравенств: g(x)<yo — г или
g(x)>yo + e. Но тогда в прямоугольник А не попадет
ни одна из точек (Зс, у) из М, отличных от (Зс0, Уо)-
Следовательно, каждая точка множества М есть
изолированная точка этого множества, а потому М не более чем
счетно. Значит не более чем счетно и множество точек
разрыва функции g(x)^D.
По функции g из D определим исправленную
функцию gi следующим образом:
I 0, если g(x + Q)g(x-0)^0.
F.13)
Таким образом, gi(x) совпадает с g(x) в точках ее
непрерывности (т. е. почти всюду), а в точке разрыва g\ (*) = 0,
если числа g(x + 0) и g(x — 0) разных знаков или хотя бы
одно из них равно нулю, gi(x) = 1/2[g(x + 0)+g(x—0)]y
если числа g(# + 0) и g(x — 0) имеют одинаковые
знаки
Из определения исправленной функции gt (x) ясно,
что в каждой точке разрыва х значение gi (x) заключено
между g(x— 0) и g(* + 0)» и потому
2зт 2л
Следовательно, если g(x) из D имеет ограниченное
изменение на [0, 2л], т. е. gel/, то также gx e V и в
каждой точке существуют односторонние пределы gi(x + 0) и
?i(*-0).
Так как gi (л:) совпадает с g (.v) почти всюду, то для
любой точки Хо можно выбрать последовательность {хп}
такую, что хп -> ^о» *п ^ х0 (хя < Д'о) и g (лгл) — gi (xn).
Отсюда сразу следует, что g1(x±0)=*g(xd?0) и,

138 ПЕРЕСТАНОВКИ. ЗКСТРЕМАЛЬНЫЕ СВОЙСТВА ФУНК. [ГЛ.6
с учетом F.13),
lU[gi(x+0)+Sl(x-0)], если gi(x+O)X
**
О, если gi(x
Исправленная функция gi(x) обладает рядом свойств,
аналогичных свойствам непрерывных функций, а именно:
О g\ (x) сохраняет знак в некоторой окрестности
любой точки х, где gi (x) Ф 0;
ii) gx (x) .может .менять знак, только проходя через
нуль;
iii) множество нулей функции gi(x) замкнуто.
Действительно, если gi (*0) ф 0, например gx (х{)) > 0,
то из FЛ4) следует, что gi(x0 — 0)>0, ?itvo + 0)>0, и
потому для всех х, достаточно близких к лг0, будет
gi(x)>0.
Далее пусть g1 (xi) >0, gi(x2)<0 (хг<хг). Положим
*0= sup {0}
В силу уже доказанного свойства i) x1<ZXo<Zx2. Для
хх < х < Хо g! (х) > 0, и потому gi (лс0 — 0) > 0, а из самого
определения точки х0 следует, что ^ (хи + 0) <* 0. Поэтому
с учетом F.14) gi(^o) = O и свойство ii) также доказано.
Наконец, если хп-*х0 и gi(xn) = Q9 то хотя бы одно
из чисел gi(x0 — 0) и gi(xo + 0) равно нулю и,
следовательно, опять в силу F.14) gi (*<)) —0.
Обозначим через Dr множество r-х 2я-периодических
интегралов от функций geD, В частности, /gD1
означает, что
а
где а и с —любые числа, g(t)<=D, причем
Везде ниже мы будем считать, что если / е D1, то /' (дг) эе
iBf (jc) уже является исправленной функцией. Это никак

§6.31 РАЗЛОЖЕНИЕ ИНТЕГРАЛА НА ПРОСТЫЕ ФУНКЦИИ 139
не повлияет на исследование свойств функции f, ибо
исправленная функция отличается от исходной лишь на
множестве меры нуль.
С функцией f^D1 везде ниже будем связывать
точку х^ такую, что
(*)| F.15)
и, следовательно, в силу свойства и) исправленной
функции, Г (хо)=*8(хо)~*0.
Обозначим через Fn множество 1^лей функции g{x)
на [jc0, лсо + 2я]. По свойству iii) исправленной функции /^
замкнуто, а потому его непрерывный образ f (FQ) есть тоже
замкнутое множество. Легко показать, что mes/r(/7o)==0.
Действительно, если G —открытое .множество,
содержащее FQ, a {ak% bk) — составляющие множество G
интервалы, то
*. 6*)]
°k<x<hk 4<K<
\dt= \ \g(t)\dL
Остается заметить, что величину последнего интеграла
можно сделать сколь угодно .малой за счет уменьшении
меры множества G \ Fo.
Пусть f eD1 и f(x)^0. Положим
М = max f(x)t m~ min f (x).
X X
Множество [m, M|\/(Fo) открыто, и потому
(an, bn)[\{ak, Ь„) = ф (
а так как mes/ (F«)=0, то
?(bn-an) = M-tn. F.16)

140 ПЕРЕСТАНОВКИ, ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ФУНК. [ГЛ. б
Обозначая через [f(x)]N срезку функции /(х) числом /У:
сопоставим каждому интервалу (аП9 Ьп) функцию (рис. 12)
fn (X) - [f (Х)\ьп - U (Х)]ая (Хи < X ^Х0 + 2Я)
(точка х0 определена равенством F.15), т. е. в данном
м
J v
h
ип
«п
т
-V-
\
f
\
V
-V
Q о о
Рис 12.
случае /(л*0) = mlnf(x)). Таким образом, по определению
X
—any если ап ^f (x)<bn,
— апч если f(x)^bn,
0, если f{x)<an.
Зафиксируем х, хо<.х<хо + 2л9 и пусть натуральное
число По определено неравенствами
Тогда
а так как для всех п таких, что an^bn(tf fn(x)=~Qf if,
кроме того, ввиду F.16)

§ 6.31 РАЗЛОЖЕНИЕ ИНТЕГРАЛА НЛ ПРОСТЫЕ ФУНКЦИИ 141
то значение f(x) можно пргдстлшпъ в виде
/ W = Ц Ы (х) + / (*о) (х0 < х < х0 + 2л). F.17)
Это верно для любых х из [х0, л-0-г2л], а потому
дг0 -г 2л дго + 2л
$ /(*)<& = ? J /л(дг)^+2л/(лго). F.18)
Ясно далее, что
'§^Л(/«)=$.*1Л (л=1. 2, ...),
где g = /' и
2n, an<f(x)<bn}.
Множества еп не пересекаются, и если д; (^ 1) еп, то
п
g(x}~0. Следовательно,
х0 + 2л А'о -г 2л *о -J- 2л
V (/)=» S \g\dt~Z\\gidt-2 V (Ы. F.19)
Если an<f(jc)<bn, то д-^^о и ff (x)=g(x)^Oi т. е.
точка л: является точкой строгой монотонности функции /.
Поэтому ясно, что fn (x) есть сумма неотрицательных
простых функций ф^(х) с непересекающимися основными
интервалами (о^, E^)с:(л;о, хо + 2п). Так как максимум
каждой из функций уп(х) равен bn^-ani то при каждом п
число их рп конечно. Таким образом,
fn {х) - X (Р« М (хо <x^xQ+ 2я), F.20)
причем
5 /«W^=2 \*n(x)dx F.21)
v tfo-2 Yto). (в-22)
2 Y
i - 1 i

142 ПЕРЕСТАНОВКИ, ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ФУНК. [ГЛ.6
Объединяя F.17) и F.20), получаем разложение
f м « 5 S ф« м+/ м (** < х < *¦+2л> <6-23)
неотрицательной функции /eD1 на простые функции
ср'п(л-). При этом, как это видно из F.18) и F.21), а также
из F.19) и F.22),
иШ) \1 W I dx = 2 2 Г Ч>« W! ^ + 2л! / W i, F.24)
V (fl~2DV(q>& F-25)
¦'-Ч
Если /(x)^0, то, построив описанным способом
разложение для неотрицательной функции —f (х), получим
представление f(x) в виде F.23), где / (х0) = max / (х) ^ 0
и (р^ (лг) — простые функции, отрицательные на своих
основных интервалах. Соотношения F.24) и F.25) при
этом сохранятся.
В общем случае, когда f(x) принимает как
положительные, так и отрицательные значения, представим,
как обычно, / в виде / = /+ + /L, где
U(х) = max {f (x), 0}, f_(x) - min {/(*), 0},
разложим на простые функции отдельно /+ и /., а затем
объединим оба разложения. Мы можем затем для удобства
перенумеровать все входящие в объединение разложений
простые функции одним индексом.
Итак, любую функцию f(x) из D1 можно представить
в виде конечной или счетной суммы:
f ДО = 2 Ф* М + * (хо^х^хо + 2л), F.26)
к
где Ф* (л) — простые функции с основными интервалами

* 6.3] РАЗЛОЖЕНИЕ ИНТЕГРАЛА НА ПРОСТЫЕ ФУНКЦИИ 143
Предыдущими рассуждениями доказано, что
разложение F.26) обладает следующими свойствами:
к
h
2) f/It-SS \
к ak
3) V 2V
4) Если [a*, P?] — отрезки, на которых I Ф* (x)! =
= maxi(pfcWif то интервалы системы {(аь а*)," (Pi, pfe)}
попарно не пересекаются, а любые два основных
интервала (аь р*) и (av, pv) или не имеют общих точек, или
вложены одни в другой так, что если, например, (av, pv) с:
с (afe, р*), то
5) Если *e(a,f aJ)|J(Pi, P,-). то /(х) = ф/(д-) +const,
и если производная у (х) существует, то \' (а*) = ф/ (л:) # О
и ср?(л;) = О (кфг). Это значит, что почти всюду на
2) имеет место равенство
в котором при каждом х не равной нулю может быть
лишь одна из функций ф*(дг), так что
|/'(х)| = 2!фНа-)!. F.27)
Заметим еще, что ряды 2*?*(*) и S^W 0ГРани"
Л? к
ченно сходятся на (дг0, л*0 + 2я), т. е. их частичные суммы
почти всюду ограничены одним числом. Это немедленно
следует из равенств F.26) и F.27), если учесть
ограниченность функций f (х) и /'(*).

144 ПЕРЕСТАНОВКИ, ЭКСТРЕМАЛЬНЫЕ С1ЮЙСТВЛ ФУНК. [ГЛ.6
§ 6.4. 2-перестановка Ф(/, х)
Отправляясь от разложения F.26), виедем
специальный оператор Ф, сопоставив функции f^D1 функцию
ф (/, х) - У, <р* (х) + | d | (О < х < 2я), F.28)
где ср^(х) — убывающая перестановка функции jq^^vI.
Функцию Ф (/, х) будем называть 2-перестановкой
функции /. Из ее определения, а также из отмеченных
в конце § 6.3 свойств разложения F.26) сразу вытекают
следующие свойства:
Г. Ф(/, А') не возрастает па [0, 2л], и если положить
А = sup 6* F# ~- Pfr — #Ar)»
Го Ф(/, x)>\d\ для 0*сл;<А и Ф({, x) = \d\ для
А2
def 2л
2°. [O(№l= \ Ф(Л
О
4°. Ф(Х/, д-)-лФ(/, х)
Пусть s — {k) — множество (конечное или счетное)
индексов-.суммирования в F.26) и F.28). При каждом
фиксированном х, 0<х<А, из множества s всех
индексов будем выделять два подмножества sx (x) и s2 (x)
следующим образом:
Если учесть, что при x~^bk yk (x) = 0, то можем написать
F.29)
Весьма существенно, что при каждом х е=. @, Л) сумма
о1(х) содержит конечное число слагаемых. Действительно,

6.41
2-ПЕРЕСТАП0ПКА <b(f, x)
145
если 6'k<x<Sk, то функции цъ(х) соответствует
интервал (tkj Tk)cz(akj р*) такой, что (рис. 13)
=!
F.30)
В силу свойства 4) разложения F.26) интервалы (/ъ тЛ)
не пересекаются, а так как все они лежат на (д-0, д-0 + 2я),
то их число т = т(х) не превосходит 2я/я. Ясно, что
—
—1~^
1
- 1
\
А
I
!!
К"—М
/_Х
1- !
—i—t—V- i
**'
х
SK
Рис. 13.
в силу того же свойства 4) основные интервалы (a*, $k)
функций ф*(х), входящих в сумму вх(х)у также
пересекаться не могут.
Таким образом,
, F.31)
где т = т (х) < 2л/д*, примем в первую сумму вошли все
функции фу(х), для которых 6v<*<6v. a во вторую—
все функции Ч((х)% для которых 6[^х. Надо иметь
в виду, что при изменении х меняется и состав
слагаемых в каждой сумме правой части F.31).
Исходя из представления F.29) можно выразить
Ф(/, х) через интеграл от /' по некоторому множеству

146 ПЕРИХТАИОВКИ, ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА. ФУНК. [ГЛ. 6
из (я0, хо + 2я). Фиксируем л;^@, Д) и заметим, что
в случае k^.Si(x), т.е. 6^<л:<6л, имеются
непересекающиеся промежутки (tkf Tk) такие, что a^
р;р* и
В случае же (jgs2D т. е. 6*
В соответствии с F.29), учитывая строгую монотонность
функции f (х) на промежутках (а*, а*) и (рь Р*), можем
написать
S 1П'ЛЛ F.32)
где
причем ясно, что ЛхП^г^Ф*
Если положить
f* = [*o. ^о + 2я]\ U {tk% тк),
то Лхи^гС:/7^ и из F.32) получаем оценку
r(t)\dt. F.33;
Теперь займемся оценкой производной 2-лерестановки
Если б^<л:<б^ и в точках tk — th{x) из (aft, a*)
и xft = Tfc(;t) из (Pfr, p^), для которых выполнены
соотношения F.30), функция / (а значит, и ср*)
дифференцируема, то в силу леммы 6.2.1 производная y'k{x)
существует и
I фН*)I < 1! vi (tk) - ф^ (т*) 1 = 1-! г (U) - Г Ы i- F.34)

§6.41 Г-ПЕРЕСТАНОВКА Ф (f, *) 147
Так как f(x) абсолютно непрерывна н, значит, ff (х)
существует почти всюду, то производная q'k(x)
существует почти всюду на F?, 6*) и для нее имеет место
оценка F.34), в которой, как уже отмечалось, точки tk
и тк определяются выбором х.
Если же 0<л:<6* или x>bk, то, очевидно,
Ф*(*) = 0.
Таким образом, каждая из перестановок фЛ (л*) в F.28)
почти всюду д!ф!>еренцируема и при каждом х
существует лишь конечное число т = т(х) функций (рь для
которых <р?(л;)=^О, причем для ;ф*(дг)! справедлива
оценка F.34).
Предыдущими рассуждениями доказано
Предложение 6.4.1. Если /eDx, то почти всюду
на @, 2л)
2М, F.35)
причем для каждого х из @, 2я) может существовать
лишь конечное число т — т (х) <z 2n/x не равных нулю
производных ф*(дг). Для всех значений х из (О, А), в
которых Ф' (/, х) существует {т. е. почти всюду на (О, Д))
справедлива оценка
т
|Ф'(/. Х)\^\ У -4!C('v)-«fC(Tv)>
v=l
12
где сумма распространена на все [непересекающиеся)
интервалы (/v, xv) из (х0, хо-г2п) такие, что
Из первой части предложения 6.4Л легко выводится
следующее утверждение.
Предложение 6.4.2. Для любой функции f^D1
функция Ф(/, х) абсолютно непрерывна на [0, 2я].
Действительно, сходящийся ряд неотрицательных
функций можно интегрировать почленно (И. П. Натансон

148 ПЕРЕСТАНОВКИ. ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ФУНК. [ГЛ.6
[2], стр. 135), и потому, учитывая, что вместе с f
абсолютно непрерывными являются также и функции ср* (х)
и ф^(л'), будем иметь
к k \ х I
— f B ф* (^ * - - Т ф' (Л о <*'•
Таким образом, функция O(f, х), являясь интегралом
от своей производной, абсолютно непрерывна.
Покажем еще, что для односторонних производных
утверждения, сформулированные в предложении 6.4.1,
имеют место в каждой точке.
В самом деле, если f^.Dl, то
= lim= lim .
Л-ОЧ-0 П Л-0 i 0 h
где g<=D и, значит, существует конечный правый предел
g(x + 0). Положив под интегралом g(t) = g(x + O) + $(i)
где р(/)-*0, при t-+x + 0 получим
x-*-h
Iirn -,-
Аналогично проверяется, что в каждой точке f'-(x)—-
~g(x — 0). Ясно, что вместе с f(x) односторонние
производные в каждой точке имеют и все простые функции
Фа (я), входящие в разложение F.26). Если теперь учесть
замечание в конце § 6.1, то приходим к выводу, что
перестановки щ(х) также имеют односторонние
производные в каждой точке, причем для б^б
где th и тк связаны с х равенствами F.30).

§6.4] S-flEP-ECTAHORKA ф (/. «) 149
Таким образом, в формулировке предложения 6.4.1
оценку F.36) можно заменить соотношением
где g = f , которое выполняется в каждой точке х
промежутка (О, А) (при соответствующем выборе знаков).
Нам потребуется еще следующее вспомогательное
утверждение:
Л е м м а 6.4.3. Пусть f<=D\f (хи) - 0 и S = \{аи bt)\ —
конечная или счетная система непересекающихся
интервалов из (х0, Хц + 2п) таких, что:
1) bi-ai^c (/=1, 2, ...);
2) любые два интервала системы S разделяет нуль
функции /. Тогда
bi с
\ х) dx.
i a. 0
Действительно, так как f обращается в нуль, то
в представлении F.26) d = 0, и мы имеем
0!* = 2S S
bi
Но каждая функция фА(/) может попасть в двойную
сумму только один раз, ибо в силу условия 2) леммы
ее основной интервал (а*, р/г) может иметь общие точки
не более чем с одним интервалом системы S. Если учесть
еще, что ввиду условия 1) и предложения 6.1.1
то
i
2 i{
i а. к О
что и требовалось.

150 ПЕРЕСТАНОВКИ, ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ФУНК. [ГЛ.6
§ 6.5. Основное неравенство
Основной результат этой главы составляет следующая
теорема, дающая точную оценку для производной Ф' (Д л*).
Теорема 6.5.1. Если /eD:l, то во всех точках
промежутка @, 2л), в которых Ф'(/, х) существует, т. е.
почти всюду, справедливо неравенство
, t)dt. F.37)
В классе D3 есть функции, для которых в F.37) будет
знак равенства в каждой точке интервала @, Д), на
котором Ф (/, л*) > 0.
Доказательство. Так как 2-перестаиовка Ф(/, х)
инвариантна относительно сдвига аргумента функции /, т. е.
х) Vet,
то, не теряя общности, можно считать, что
и в разложении F.26) мы можем считать *0 = 0.
Если в точке л:е@, Д) (а неравенство F.37) надо
доказывать только для таких точек) существует
производная Ф' (/, х), то в силу предложения 6.4.1
т
i*'(/. *)'!«?-4:У 1ф'»('»)-ф;(т»)!-
V=l
V — 1
F.38)
причем непересекающиеся интервалы (^., xv), имеющие
каждый длину х, расположены на @, 2я). Можно считать,
что
При оценке последней сум\.ы в F.38) мы будем
ориентироваться на применение леммы 6.4.3 и потому должны
обеспечить выполнение условия 2) этой леммы
относительно разделения интервалов интегрирования нулями

5 0.51 ОСНОВНОЙ ПЕРА ВПНСТВО 151
/"(/). Для этого нам, может быть, придется сдвигать
копны интервала (/v, xv) внутрь без уменьшения
абсолютной величины интеграла. Пусть
/v = $ Г @ Л = Г (Tv) - Г Cv) = Фу (Tv) - ФС- (/у)
'v
(v= I, 2, ..., m).
Учитывая расположение точек /fc. и xv на основном
интервале (av, Pv) функции 4'V(-v), заключаем, что /v=^0 и
sign/v — — sign<pv, где sign<b понимается как знак
функции (fv(x) на (av, pv).
Те концы интервалов
(/v, xv), в которых /"
обращается в нуль или имеет
тот же знак, что и /Vf мы
оставляем на месте, пере-
обозначив, однако, их на f у ¦ v
^v И Ту. р u
Пусть sign Г (/?)- Рис 14
=— sign/у. Тогда f(/)
обязательно обращается в нуль на (/Vf tv) и, обозначив
через /у ближайший к tv справа нуль /"(/) (рис. 14),
будем иметь
Аналогично, если f (tv) = — sign /v, то вместо tv возьмем
Ту —ближайший к Ту слева нуль функции /"; абсолютная
величина интеграла при этом также увеличится.
Так как /v<Tv и (t'Vi tv) a (tV9 xv), то мы пришли
к системе непересекающихся интервалов (/у, tv),
расположенных на @, 2л) и таких, что Ту — t'v^x, причем
если /у > 0, то Г (/J) ^ 0, Г (ту) ^ 0;
если /v<0, то Г(/С)^О, Г(т;)<0. l ' j
Кроме того, если положить

152 ПЕРЕСТАНОВКИ, ЗКСТРЕМЛЛЬНЫВ СВОЙСТВА ФУНК. [ГЛ.6
то
! /С I-S* i /vi. sign /; = sign /v = - sign fpv.
Теперь мы можем продолжить оценку F.38)
следующим образом:
т т т Tv
4|Ф'(/, *)i^2 !/v'<2 п'^ 2 Vr(/)d/e F'40)
v-1 v--=I v-1^
Положив /f'nj_ i = *( + 2л, т«_|_1«=Т| + 2л, покажем, что
любые два интервала (/v» Ту) и (/С+ь *v+i) (v=l, -.., /w)
разделены нулем функции /\
Если /v и /v-f i имеют разные знаки, то это сразу
видно из F.39). Пусть /С<0, /0+i<O, причем, очевидно,
следует рассмотреть только тот случай, когда точки tv
-и /Vrl не сдвигались (т. е tC = tv, /v+i = 'v+i) и
ГКХО, Г(';+|)<0. F.41)
В силу нашего предположения функции <ру(л') и «Pv+iM
(мы полагаем фт.ц (х) = срЛ (х — 2л)) положительны на своих
основных интервалах, поэтому
а это с учетом F.41) показывает, что f на интервале
(iv, /(.a.i) обращается в нуль.
Случай /у>0, /vt-j-i>0 рассматривается совершенно
аналогично.
Если теперь положить to~t* — 2л, где /* —нуль
функции /", разделяющий (t'm, тт) и D+i, i'm+\)> то /"(/0)-=
= 0 и на промежутке (tOt tu + 2n) мы находимся в
условиях применимости леммы 6.4.3. Так как тО — tv^x
(v=l, 2, ..., /п), то, оценивая последнюю сумму в F.40)
с помощью этой леммы, сразу получим
4,Ф'(Л *)|<$Ф(Л t)dt
о
и соотношение F.37) доказано.
Покажем, что знак равенства в F.37) имеет место
в каждой точке х е @, л///) для функций / е D3 периода

§ 6.5! ОСНОВНОЕ НЕРАВЕНСТВО 153
2л/л (л=1, 2, ...), нечетных и таких, что
л И У'(ЛЛА (ft ^ i ^ Л \
если к тому же /" строго монотонна на (О, п/Bп))
и (n/Bn)t я/л). Действительно, в этом случае / (kn/n) = 0 и
2п
где простая функция фхМ совпадает с /(д:) на своем
основном интервале @, я/и), а
(Л = 2, 3, ..., 2л),
причем ср*(х) = cpi (л-) F = 2, 3, ..., 2л). Таким образом,
для таких функций
Ф (/, х) - 2«ф! (*) @ *? л-< я/л).
Но так как 4>i'* ^-'": = ф1:.9 +'•» то (лемма 6.2.1)
j - , i __ 1 : ,
4
где ! А'2~ А'х • =л:, дг1 = л/л —лг2 и, следовательно,
4 ; Ф' (/, х) \ = 4 • 2/1! ф! (д-) ==» 2/i I cpj (А'х) — cpj (д-2) | =
dt = 2/i ? фГ «) Л =¦
Здесь мы учли, что /" на @, 2л) есть сумма 2/г простых
функций щ(х)у перестановки модулей которых
совпадают с ф[' (а). Теорема 6.5.1 полностью доказана.
Сделаем важные для дальнейшего замечания.
Замечание 1. Условиям, гарантирующим в F.37)
знак равенства для 0<СЖл//1, удовлетворяют, в
частности, введенные в § 5.4 функции ц>пг(х) и gnr(x) при

154 ПЕРЕСТАНОВКИ, ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ФУНК. 1ГЛ.&
всех г~3, 4, • .., так что
X
Ф' DV. х)--\ \Ф (<р„. , в, t) dt @ < х < я/л), F.42)
о'
а;
Ф' (ff«r. дс) - — -J- 5 Ф 0?«. r-s. О Л @ < дс < я/п) F.43)
&
(г = 3, 4, 5...).
Замечание 2. Рассуждения, связанные с
переходом от системы интегралов (/v, xv) к (t'V9 т'х) при оценке
|Ф'(/, а) в доказательстве теоремы 6.5.1, применимы
К в том случае, когда /" принадлежит D и является
исправленной функцией. Действительно, выбирая точки
t'x и Ту так, чтобы интервалы системы (/(,, xv) (v=l,
2, ..., ш+1) были разделены попарно нулями /", мы
использовали лишь те свойства непрерывной функции,
которыми обладает и исправленная функция из D.
§ 6.6. Стандартные 2-перестановкн Фаг(х)
Основная цель этой главы — выяснение
экстремальных свойств дифференцируемых функций, выражаемых
в виде теорем сравнения. Роль стандартных функции
(функций сравнения) будут играть функции ynr, gnr и
их 2-перестановки. Мы, однако, сможем в ряде случаев
получить более общие результаты, если в качестве
стандартных функций сравнения для Ф(/, х) возьмем
следующую последовательность функций Фаг(х)> непрерывно
зависящих от параметра а > 0:
0 {xi
1

6
О (JCSsa) (г-1, 2,

§6.6]
СТАНДАРТНЫЕ 2-ПЕРЕСТЛНОВКИ Ф (*)
155
Легко подсчитать, что для
Ф«1(*)= \ (а~х
Ф(*) C
Графики первых трех функций представлены на рис. 15,
Отметим следующие свойства функций Фаг(х),
вытекающие непосредственно из их определения:
1) Фаг С**) на промежутке @, а) есть многочлен
степени г как относительно х, так и относительно а.
2) При всех г 5*1 функция Фаг(х) на @, а)
положительна и строго убывает от Флг@) = У/-аг (Уг не зависит
от а) до Фаг(а) = 0.
3)
1
4) Если a<b, то Фаг(х
и г 5* 1.
5) Если а<Ь, то при /
всех 0<л'<а Г
Фаг (А') = Ф'ы (X) (Г = 1, 2),
(/) dt
для 0<jc<b
а
6) При всех 6>0 (не
обязательно целых)
э. г W F.44)
6, r = 0f 1,2,...).
Свойства 1) — 3)
очевидны. Свойство 4) при г=1
также очевидно, а для гг>2
проверяется с помощью
индукции, учитывая
рекуррентную формулу определения
Фаг (х). Свойство 5), для
г=1 и 2 тривиально, а для
Рис 15 Функции Фаг{х)
(/ = 0,1.2).
^3 следует из 3) и 4).

156 ПЕРЕСТАНОВКИ. ЭКСТРЕМАЛЫ-fblF СВОПСТВА ФУНК. (ГЛ. 6
Наконец, проверим соотношение F.44) При г = 0 оно
очевидно. Далее имеем
Ф„1 (to)-{ (а-Вх) = б L(« - х\ „ 0ф„/О> , (х).
Пусть F.44) доказано дли r^k. Тогда для
а —Их
б
д/0 — лг а/0 — х
4 5 { j
а/0—ж
2 J
О
и свойство 6) также установлено.
Покажем, что для всех 0^дг^2я
Фд/п. г (л:) - Ф (Впг, х) (я, г - 1, 2, ...), F.45)
т. е. при а — п/п функции Фаг(х) являются 2-переста-
новками функций gnr.
Действительно, если учесть выкладки, проведенные
в конце доказательства теоремы 6.5.1 для функций,
реализующих знак равенства в F.37), то легко понять,
что
где (pi — перестановка простой, равной -— (j*-— \х\)
функции на (— —-, Yf-J и, следовательно,
Поэтому
Ф (gnU X) = | (Л/Л - А') = Фя/П, Х(Х) @^_Х^ Я/Л).
Далее,
(О Л, ?„2 (-^ ) = 0 (ft = 0, 1, ..., 2

§6.6] СТАНДАРТНЫЕ ^ПЕРЕСТАНОВКИ *>„,.(*) 157
и, как легко подсчитать, перестановка простой функции,
совпадающей на [0, л'/г] с \gn2(x)\t равна — f-?? — **)>
поэтому
„ X) - 2« ^ (-J - *) - А ( J - ;•} = Фл „. 2 (г)
Считая, что F.45) доказано для всех г=1, 2, ..., k— 1,
в силу F.43) и свойства 3) функций Фаг для всех
0^А'<л/а будем иметь
ф'|
Это значит, что Ф (gnk, x) и Фя/П§ к (х) могут отличаться
на @, я/л) только на константу; но так как для
2
то F.45) справедливо и для r = k> а значит, и для всех
г = 0, 1, 2, ...
Функции Ф,„.(А') связаны с константами Фавара C.44)
соотношениями
Флг @) = п'Фя/п. г @) =Ц*- F.46)
(л-1, 2, ...; г = 0, 1, ...),
def 2л л/я
] Фя,r-г ]ь = S Фл. r-i @ Л = пГ \ Ф„/я. f. i @
6 6
F.47)
Действительно, из F.45), свойства 3° 2-перестановки
Ф(/, х) и E.29) следуют равенства
Ф«/Я. г @) - Ф (§„,, 0)= ? V (?„,) - * ''
'' *". r-i k

158 перестановки, экстремальный свойства функ. [гл.6
и, чтобы получить F.46), надо лишь учесть, что в силу
свойства 6) фуптпй Фаг(х) Флг@) = пгФл/п,г@). F.47)
получается из F.46) и равенства
л
Фяг @) = { jj Фя, г-г (I) Л = 11| Фя. г_, |1Ь
о
вытекающего из определения Фаг(х).
Наконец отметим, что для функций Фаг(х) при любом
а>0 имеют место соотношения
]<*>a9^k-lh = CrkWa.r-l\l~k/'(r=l,2,...i * = 0, 1 Г),
F.48)
где с,* — та же константа, что и в неравенстве
Колмогорова E.52), т. е.
Действительно, из определения функций Фаг следует,
что соотношение F.48) можно записать в виде
2Ф«, г * @) = сгЛ [2ФС, (О)]1"^ F.49)
или, учитывая, что Фаг @) — 7/-дГ» в виДе
откуда видно, что F.48) или F.49) достаточно доказать
для какого-нибудь одного значения а. Но положив а = я,
будем иметь, учитывая F.47),
т. е. F.48) справедливо при а = п, а значит, и при
всех а>0.
§ 6.7. Теоремы сравнения для ^-перестановок
при ограничениях на норму в метрике пространства L
Результаты этого и следующего параграфов будут
связаны с оценкой производной Ф' (Д х)% которая, как
было установлено выше, существует для f^D1 почти
всюду. Условимся в дальнейшем, выписывая те или иные

§ 6.7J ТЕОРЕМЫ СРАВНЕНИЯ. ОГРАНИЧЕНИЯ В МЕТРИКЕ L i59
соотношения, содержащие Ф'(/, л'), предполагать, не
оговаривая это каждый раз, что они имеют место на
соответствующем промежутке в точках существования
Ф'(Л х) (т- е- почти всюду). Впрочем, во всех этих
соотношениях можно под Ф'(/\ х) понимать левую или
правую производную, существующую в каждой точке.
Пусть, как и в § 5.1, 1/ —множество 2л-периодиче-
ских функций g(x), имеющих ограниченное изменение
на [0, 2я], a Vr (r=l, 2, ...) — множество r-х
периодических интегралов от geK (при условии, разумеется,
что lg{t)dt = 0), V»=V. Wrv(r = O9 1, ...) есть класс
6 /
функций g e Кг, у которых
Отметим, что VczD, ибо если geF, то в каждой
точке существуют конечные односторонние пределы
g(x + 0) и g(*-0). Следовательно, VczDr (r-l, 2, ...)
и для любой функции /el/1 имеет место разложение
F.26) па простые функции, а также определена 2-пере-
становка Ф (/, х) со всеми описанными в предыдущих
параграфах свойствами.
Лемма 6.7.1. Если g^Wlvf то
а если g e W\>, то
@<х<2л),
@<л:<2я).
F.50)
F.51)
Неравенства точные.
Доказательство. Ясно, что F.50) и F.51) нужно
доказывать только для х из промежутка @, Д), на
котором Ф(#, А') >min'/(*);. Пели gE W\>> то в силу прел
ложения 6.4.1, а точнее —в силу соотношения F.36),
v=l

160 ПЕРЕСТАНОВКИ, ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ФУНК. [ГЛ. б
где интервалы (fVf xY) не пересекаются и все лежат на
промежутке длины 2л. Поэтому
1 2л 1
о *
и F.50) доказано.
Пусть теперь geflPv, причем, не теряя общности,
можно считать, что g"~ исправленная функция из
множества К, содержащегося в D (см. § 6.3.1). Фиксируем
хе@, А). Как и при доказательстве теоремы 6.5.1,
исходя из F.36) и используя свойства исправленной
функции (см. замечание 2 в конце § 6.5), придем к оценке
J V
4 ^
\dl
= } У ;/;!, F.52)
где попарно не пересекающиеся интервалы (^, Tv) с
длинами xv — t'v^x лежат на одном периоде и отделены друг
от друга, а также от точки С-н=/( + 2л нулями
функции g". Таким образом, существуют точки Yv (v = 0, 1,...
"*> ш; Yo = Ym-2jl) такие, что g"(Yv) = 0 и
Ym < ^m f 1 •
На каждом интервале (^v, Tv) найдется точка t|v такая,
что
Действительно, положив • /J! = ^(xv — /v), мы должны
заключить, что неравенство \g"(t)\<i\^ не может
выполняться во всех точках промежутка (^v, Tv)» a потому
в некоторой точке t]v<=(/v, Tv) будет \g"(x\%)\^V".
Итак, у нас есть точки
Yo < % < Yi < Ч2 < Y2 < • • • < Ч/n < Ym = Yo + 2л,
причем g"(Yv) = 0 (v=^0, 1, ..., tn) и
|/;1^1вГЫ|^ (v-lf 2, ..., m);

§ 6.7] ТЕОГЕМЫ СРАВНЕНИЯ'. ОГРАНИЧЕНИЯ В МЕТРИКЕ L 161
поэтому, отправляясь от оценки F.52), будем иметь
т
-J 2 {'! / (Лv) - g" (Yv i) I +1 ?" (Yv) - g" (')v):} *S
т. e. F.51) также доказано.
Знак равенства в F.50) и F.51) имеет место при
всех х бЕ @, п/п) для функций соответственно />л1 и gn2.
Теорема 6.7.2. Если gt=Wv (г = 1, 2, ...) и а > 0
выбрано так, что
Ф(?, 0)^Фаг@), F.53)
то имеют место соотношения
l^'fe. *)!<i<Wr(*)| @<*<a), F.54)
iФ' fe, *) К i Ф^ (а — 0) j (а < х < 2л), F.55)
Ф&, дг)^ФвгМ @^^^2л), F.56)
^ЦФагк. F.57)
Доказательство. Ясно, что F.56) и F.57)
тривиальным образом следуют из F.53) и F.54), так что
доказывать надо только F.54) и F.55).
Заметим сразу, что из F.53) в силу свойств Х-иере-
становки и функций Фв, (*) следует, что при г^2
li = !iS II ^ 2Ф (?, 0) = 2Фв/ @) - • ФИ| ^ [L. F.58)
Если учесть, что
Фа1 (х) = - -\-9 Ф;> (х) = - I @ <л- < а),
то F.54) при ггя1, 2, а также F.55) при г—1 уже
доказаны в лемме 6.7.1. Справедливость F.55) при г=2
для geflPv при условии Ф(§, 0) = Ф<|2@) следует
из того, что в силу F.58)

162 пгрестаиовкн. экстремальные свойства фупк. (гл.
а так как [Ф'^, х) ^ 1/4, то Ф(#', 0)^я/4 и (см.
F.36))
Теперь рассуждаем но индукции. Пусть теорема верна
прн г«=1, 2, ..., Л—1 (АГ-3) и дли gEfv при
некотором а выполнено равенство Ф(#, 0)--=Ф„л@). Тогда
(см. F.58)) 3 Ф (gf) k ^) Фд, *-i :>., и нетрудно заключить,
что будет Ф(#\ 0)^Ф||§* i@). Действительно»
предположив, что Ф(#\ 0)><l)ft>Ji?.1@), мы выберем Ь>0 из
условия Ф(д\ 0) = Ф^>-1@), и так как при г = ?— I
теорема верна, то должно быть ] Фь, k t ]L < jl Ф (^');!/. ^
<1Фд,* iV» что противоречит свойствам функции Фв/.,
ибо fc>«. Таким образом,
0)<Фв.Г1@). F.59)
Повторяя цикл рассуждений, из F.58) и F.59) найдем,
что
<Ф«.*«!1 F-ео)
и
Ф<в". 0)^Фй.*,@). F.61)
Если Ф(^, 0) = Фг<Л-2@) (с<<-а), то ввиду
справедливости теоремы для r = k — 2 будем иметь
!Ф' fe\ х)\^\ Ф;, ^4(х) \ <IФ^, *_4(х)! @ < дг <г),
, х) I < | Ф2. *-*(с- 0); <; Ф;, *-а (с); ^; Ф^. *^2 (д-) I
Таким образом,
IФ'(Г. ^) I ^: фа. *-« W! (о ^*< о). F.62)
Из F.61) и F.62) следует, что разность
или неотрицательна на @, 2л), или меняет знак с
положительного на отрицательный один раз. Но тогда для
функции

5 6.71 ТЕОРЕМЫ СРАВНЕНИЯ ОГРАНИЧЕНИЯ В МЕТРИКЕ I 163
в каждой точке промежутка @, 2л) выполняется
неравенство
Si(a-) ^min {О, ЬХ Bл)},
и так как в силу F.60) б1Bл)^0, то 6i(jr)^0 для
всех 0^х^2л. Поэтому
о о
и применение теоремы 6.5.1 дает
х х
IФ' fe, х) < j J Ф (g*. t) dl < I { Фв,,_, @ dt.
о 5
Остается учесть, что при
а при
X
1
*4
О
= Mm \OakM\***Oak(a-0)\.
Теорема 6.7.2 доказана. Из нее без труда выведем
следующее важное для дальнейшего утверждение.
Теорема 6.7.3. Если geWy (г=1, 2, ,..) и при
некотором а>0
Igh^l^arh F.63)
то:
2) |Ф'(?, лг)^<Тф;/(лг)! @<х<а);
3) разность ФAГ (х) — Ф (.?, .v) или неотрицательна на
(О, 2л), или меняет знак с положительного на отрицатель*
ный <>дин раз;
К X
А) $¦
о

164 ПЕРЕСТАНОВКИ, ЭКСТРЕМАЛЬНЫЕ CBlHlClKA ФУНК. [ГЛ:0
В самом деле, выберем Ь>0 из условия Ф(§, 0) ^
гт" (IV @) (рис. 16); тогда из теоремы 6.7.2 (см. F,57)) и
F.63) следует, что
т. е. Ь^а% и потому
Снова применяя теорему 6.7.2, с учетом свойств
функций Фаг(х) будем иметь
l(D'fe. *)l<i^(*)!<".<ICU-)i @ <*<*),
I ф' fe, а-) | ^; сод, F - ох, ф;, (х)\ (Ь < х < а).
Утверждения 1) и 2) этим доказаны. Из сопоставления
их с F.63) следуют 3) и 4), так же, как соответствующие
--$
я b
Рис. 16.
a
утверждения для Ф (g", x) н Ф(;>^ 2(а*) при доказательстве
теоремы 6.7.2.
В качестве следствия из теоремы 6.7.3 отметим
Предложение 6.7.4. Если для функции g^Wv
(r-~l, 2,...) при некотором а>0 выполнено F.53) или
;6.63), то
}g^\L^]Oatr_kh (*-l, 2, ..., г-1).
Действительно, при сделанных предположениях
Ф(#, О)^Ф^(О) и, следовательно, ig'b*^}®a,r-i]L-
Применяя теорему 6.7.3 к функции g'^W[r\ приходим
к неравенству ф^', 0)^Otf|r_i@), т. е. ||g ^• Фа|Г..2^
и т. д.

§ 6.7] ТЕОРЕМЫ СРАВНЕНИЯ. ОГРАНИЧЕНИЯ В МЕТРИКЕ L 165
Из утверждений 6.7.3 и 6.7.4, с учетом соотношений
F.45), вытекает следующий факт.
Теорема 6.7.5. Если g^Wv (г=«1, 2,...)
Ilu то
IФ' fe> x) I, *s? | Ф' (gnr, л:) | @ < x < л/п),
причем разность Ф (gv, *) — Ф (g*, л:) w^w неотрицательна
на @, 2л), или меняет знак с г на — один раз. В часп>
носпш, все утверждения теоремы справедливы для
функций класса WrylHl.
В пояснении здесь нуждается только последняя фраза.
Но если gelP!l//Z, то g^Wv и, кроме того, в силу
E.31) [fffc^SgirU.
Теорема 6.7.5 при k— 1, в частности, означает, что
среди функций класса Wv наибольшую вариацию на [0, 2л]
при одинаковой норме в /. имеют функции gnr. Из
теоремы 6.7.2 (при а-л/п) следует также, что наименьшую
норму в /. при одинаковой вариации среди функций
класса W[ имеют те же функции gnr.
Чтобы облегчить применение полученных выше
результатов при решении некоторых конкретных экстремальных
задач наилучшего приближения, докажем следующее
утверждение.
Теорема 6.7.6. Если g(=Wv (г= 1, 2, ...) и при
некотором а>0
lg\i.*?\<barV> F-64)
то для любой суммируемой на @, 2л) неотрицательной и
невозрастающей функции ц (/)
Доказательство. С учетом утверждений теоремы
6.7.3 надо рассмотреть лишь тот случай, когда разность
меняет па @, 2л) знак. Пусть

166 ПЕРЕСТАНОВКИ, ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ФУНК. [ГЛ. б
Так как fi (t) ^ 0 и не возрастает, то
2л Я 2л
J и @ 6 (о«// = I|i @в (О Л+ j ji (/) б @ лг»
О 6
^ .u (i|) J 6 (О dt -j- |i (г|) j 6 (/) d/ = [I (i|) \ б (/) dt,
О Г| О
н остается заметить, что в силу F.64) последний
интеграл неотрицателен.
Нам потребуется еще вариант теоремы 6.7.6,
соответствующий случаю /---=0.
Теорема 6.7.7. Если gt=W°v()D\ !|^5/.<!|Ф„9 V и
g(x) обращается в нуль, то для любой суммируемой на
(О, 2л) неотрицательной и невозрастающей функции ц(/)
о о
Действительно, в условиях теоремы V(gf)^l, g^D1
о
и, значит, для g определена I-перестановка <I>(g, л-),
причем так как g(x) имеет нули, то
Ф(?> 0) = » V te) ^-2- =Фв0@)
и, следовательно, Ф(§, ^г)<с 1/2 = Фа0(^) для всех 0<л:<
<а. Поэтому разность 6 (/) = Ф„о (/) — Ф (?, /) пли
неотрицательна на @, 2л), или меняет знак с + на — один
2л
раз. А так как $ 6 (/) Л^О, то остается лишь повторить
о
соответствующие рассуждения из доказательства
теоремы 6.7.6.
Отметим еще несколько фактов, непосредственно
вытекающих из теорем 6.7.2 и 6.7.3.
В формулировке следующего утверждения легко
усматривается аналогия с теоремой сравнения Колмогорова
5.6.2.
Предложение 6.7.8. Если g^Wv (r=l, 2,...) и
при некотором а>0
я), F.65)

§6.7] ТЕОРЕМЫ СРАВНЕНИЯ ОГРАНИЧЕНИЯ В МЕТРИКЕ L 167
то
Доказательство. Если b>0 таково, что Ф(g, 0) =
--Фъ,@), то в силу теоремы 6.7.2 O(g, 1)^ФЬг&)>
а потому, с учетом F.65), ФЬг&) < Фиг (?), откуда сразу
следует, что Ь^а. По теореме 6.7.2, если 0<?<Ь, то
а если /;<;?< а, то
'¦(i>' te. 5) i < 1 ф» (& - о): ^! ф;, F) 1 < | oif ft) ;f
и все доказано.
Следующие два предложения дают аналоги
неравенства E.52) Колмогорова в метрике /. (для периодических
функций).
Предложение 6.7.9. Если feFr"! (/" = 2, 3, ...),то
U{k) ]#. < crU f/)[-*-'г j^y ^-")I' F.66)
гс> c,k — me же константы, что и в E.52). Неравенство
F.66) точное.
Док азател ьство. Если F.66) справедливо для
fs=Vr\ то оно справедливо и для функции Х[ при лю-
2л
бом а. Поэтому мы можем считать, что V (f{r'1})= 1, и
о
дело сводится к доказательству неравенства
:
для любой функции / €= WyT-
Зафиксировав /^IF\/-1, выберем а из условия
A}м,г 1 [l — if \l- В силу 6.7.4 и соотношения F.48) будем
иметь
что и требовалось. Неравенство F.66) усилить нельзя,
ибо для / = gn>r 1 в нем имеет место знак равенства, что
сразу видно, если сравнить ^6.48) и F.45).

168 ПЕРЕСТАНОВКИ, ЭКСТРЕМАЛЬНЫЕ СВОПСТВЛ ФУИК. ГГЛ. 6
П р е д л о ж е и и е 6,7.10. Если ( е Z/ (г = 1, 2, ...), то
(* = 0, 1, ..., г-1). F.67)
Неравенство точное.
Так как //с:Кг1, то при г>2 (G.67) следует из
F.66), ибо для /<=//
V (/(-D) = ;;/(-> ||L.
о
Если же г=* 1 и ?=^0, то F.67) тривиально, ибосю^ 1.
Хотя в Z/ при П:^ 2 нет функции, реализующей в F.67)
знак равенства, но для каждого г = 2, 3,... существует
последовательность функций fme= Wi (например, функций
Стеклова для gn,r i) такая, что
т-*со
и неулучшаемость неравенства F.67) следует из
экстремальности функций ?„,,--1 в теореме 6.7.9.
§ 0.8. Теоремы сравнения для 2-перестаиовок
при ограничениях на норму в метрике пространства М
Чтобы получить аналоги ряда теорем предыдущего
параграфа при ограничениях на норму функции g в
равномерной метрике, нам потребуется следующее утверждение,
базирующееся на теореме сравнения 5.6.2 Колмогорова
и вытекающих из нее следствиях.
Теорема 6.8.1. Если ge WrM (r = 0y 1,...) и
max
a, b
mo
]g(t)dt
F.68)
F.69)
\t<\ Vnr @ dt (O^x^z 2л), F.70)
о о
где через f обозначена убывающая перестановка функции
|/| на [О, 2л\.

§ 6.?] ТЕОРЕМЫ СРАВНЕНИЯ. ОГРАНИЧЕНИЯ В МЕТРИКИ М 169
Доказательство. При г=«0 утверждение теоремы
очевидно, поэтому считаем г.^1. Отметим, что из
условии F.69) и периодичности g(t) следует наличие у
функции g нулей, а в силу инвариантности перестановки
относительно сдвига аргумента можно считать, что?@) = 0.
Положим
Оставляя в стороне тривиальный случай б(/M^0 @
<2л), заметим, что достаточно установить справедливость
неравенства F.70) лишь во всех точках промежутка
@, 2л), являющихся нулями 6@ и правыми концами
интервалов, на которых 6(/)<0.
Пусть в точке ?е @, 2л) в(?) —0 и
Положим
тогда
где
Еу~{х: хе@, 2л),
причем mes/:r = ?. Множество Ez состоит из
непересекающихся интервалов (а,п bk) с: @, 2л) таких, что
(^ </</;,),
и мы сейчас покажем, что при сделанных
предположениях относительно точки ? число т этих интервалов не
больше 2/i.
Предположим противное: пусть в множестве Ег имеется
2/i + l непересекающихся интервалов (akn bk) (k~l, 2, ...
..., 2л+1), удовлетворяющих условиям F.71). Можно
выбрать Л>0 настолько малым, что при каждом k =
гг.-. 1, 2, ..., 2/i+l внутри (ак% Ьп) существует интервал
(ак9 bk)czE^.h9 причем', если

170 ПЕРЕСТАНОВКИ, ЭКСТРЕМАЛЬНЫЕ СПОПСТВА ФУНК. |ТЛ. 6
то для g — Vo<^<? 6@ <0- В силу последнего условия,
если Ф„гF — т) = 2-|-Л, т0 Y>Yo- Очевидно,
Чп !- I
Выберем на промежутке монотонности [0, л/2/i]
функции ФяГ(а') точки а п а' таким образом, чтобы было
1 = ^(^I = ^ + Л (*«1, 2, ..., 2/1 + 1),
Тогда в силу предложения 5.6.6 будем иметь
! а'к - ak ] т> \ а' - а ¦„ | &л — W | ^ | а' - а|
и, значит,
Vo ^ 2 B/i + 1)! а' - а' > 4/2 > а' - а | = у
в противоречии с предыдущим.
Итак, число непересекающихся интервалов (ак, Ьк)%
составляющих множество Ег, не превосходит 2п. Поэтому
количество р отрезков [с,-, d{\ из [0, 2л], каждый из
которых содержит хотя бы одни из интервалов (akt bh) и
удовлетворяет условиям
gfe)=g№)-o, !я@!>0 (ci<t<di)y
тоже не больше чем 2/i. Если а0 и а —точки на [0, л/2/z]
такие, что
фпг (а«) = 0 *), : флг (а) I = ф/|Г (с) =~^(I) = ;
то, применив предложение 5.6.5, получим
фяг @
, 2
Эти неравенства с учетом условия F.69) и того, что
*; Ясно, чго а0 есть 0 или л/2п.

§6.8] ТЕОРЕМЫ СРАВНЕНИЯ. ОГРАНИЧЕНИЯ В МЕТРИКЕ М 171
, позволяют написать
р "I
i=\c.
p dJ
2S \8(t)\dt-2p
1= 1 с,
<fnr @ dt
<x0
¦2p(
An
Vnr (/) dt
\ qw @ dt
«0
-tt0
J ФпЛ
Теорема 6.8.1 доказана. Отметим вытекающее из нее
Предложение 6.8.2. При выполнении условий tneo-
ремы 6.8.1
Если ge=WrHlt (/- = 0, 1,...; л = 1, 2,...). то в силу
соотношении E.28) для g выполнены все условия теоремы
6.8.1, и потому справедливо также
Предложение 6.8.3. Для любой функции g e WrH*M
6 о
Теперь докажем теорему сравнения в терминах 1-пере-
стаповок для функций классов U^w.
Теорема 6.8.4. Пусть g<=WrMr\Dx (/-=1, 2,,..),
g имеет нули и
f.*3c<i!qw!c. F-72)
Тогда в каждой точке промежутка @, л/л) выполнено по
крайней мере одно из неравенств
I<!>'(?. *)\^\WDar. х)\ F.73)

172 перестановки, экстремальные свойства функ. [гл.б
или
x)^d>(Van х). F.74)
При г>^3 неравенство F.73) выполняется обязательно.
Доказательство. Пусть g (t) удовлетвор нет усло-
виям теоремы, причем можно считать, что g@) = -0. Так
как geD1, то определена ^-перестановка Ф(?, *)• В силу
предложения 6.4.1 при фиксированном л:^@, л/л)
\wfe, x)\*z\ 2 I^^*)-^<Tv)'» <6-75)
v=l
где интервалы (/Vf tv) не пересекаются, все лежат на
(О, 2л), причем tv —/v = a* и g(*v) = g(*v)-
Предположим сначала, что m>2/i. Из F.72) следует, что
ь
max
]g'(t)dl
9
а из F.72) и включения gG W\\ в соответствии с
предложением 5.6.4 вытекает, что !!#'U<l!T/i,r-iiU- Таким
образом, к функции g' применима теорема 6.8.1. Положив
/V-=[0, 2л]\ (j (/v> tv)
и за.метив, что
mes Fx =а 2л — тх < 2л — 2/и\
последовательно применяя F.33), F.3) и теорему 6.8 1,
будем иметь
®(g, x)^\ \ {g'(i)[dt^}2 jj YJf)dt^
< о \ Ф* ^--i@dt<\ \ фя,г. 1 (/)Л = Ф(фяг, jr).
о °
Пусть теперь т^2п. Если г=1, то из F.75) сразу
получим
т1'Ы<?<»-;ф'(ф-„*)|.

§ G.ft] ТЕОРЕМЫ СРАВНЕНИЯ. ОГРАНИЧЕНИЯ В МЕТРИКЕ Af 173
Если же г^2, то заметим, что g' е? И^лГ1 и (см. 5.6.4)
\g' \:\\-^ ,'фл,г-1!!л11 так что к gf применимо предложение
5.6.7, в силу которого, исходя из F.75), будем иметь
4!Ф'(?, *)!</n©(g'f x)^2mo(if/nn *) = 4|Ф'(ф«г, х)\.
Поясним последнее равенство. Пусть
4>пг (в0) - 0, вх = 0О Ч- я/л, t0 = V2 @o + »j)
и
Фо @ = . Vnr @ ! (Оо < ' < «i), . Фо @ -0 (^ [б0, Вг]).
Тогда Ф(ф/1Г, л')=2«фо(Аг) и для дге @, л/п)
4: Ф' (Фяг, л:) ; = 2/1; Ф; (t, - jc/2) - ф! (/0 + лУ2);«
«'г, л:).
Остается показать, что при /-г=-3 соотношение F,73)
выполняется обязательно. Если g(l) удовлетворяет
условиям теоремы при г;->:3, то ввиду предложения 5.6.4
1 (*=!• 2, ...,/-)
и к каждой из функций g(/?) применима теорема 6.8.1,
в силу которой
№к)Ъ*?]<рЯ9Г-к1 (А-1, 2, ...f г) F.76)
и, следовательно,
Ф(?(*\ 0)<Ф(фЯ|,.Л> 0) (А —0, 1 г—1). F.77)
Применение же к g{k) уже доказанных утверждений
теоремы 6.8.4 приводит к выполнению в каждой точке хе
е @, л/л) одного из соотношений
Iф' (g(*\ а-)!^;ф'(ф,,^ь х); или ф(^\х)<ф(ф„,г..л, ^),
сопоставление которых с F.77) показывает, что разность
Ф(ф/1,г-*, x) — Q>(g{k), x) или ^0, или меняет знак с -(-
на — один раз. Этот факт вместе с F.76) приводит (как
и при доказательстве теоремы 6.7.2) к соотношению

174 ППРГГЛЛИОВКИ ЭКСТРЕМАЛЬНЫЕ СВОЙСТВА ФУНКЦ ГГЛ.6
и теперь, воспользовавшись теоремой 6.5.1 и равенством
F.42), будем иметь для 0<л;<л/я
Теорема 6.8.4 полностью доказана.
Очевидно, что утверждения теоремы 6.8.4
справедливы для любой функции g^WrH%(]Dl. Отметим,
однако, что для #<~ WlH% {\Dl и ge W2HnM
соотношение F.73) на @, я/я) может и не выполняться.
Например, если gx (х) и ?2М — соответственно первый и
второй периодические интегралы от sign sin 2nx, то для
всех 0<х<л/2и
X
' (ёъ х)! = И Ф (g;, /) dt = я.г=2:
Теорема 6.8.5. Если g^WrM(]Dl (л=1, 2, ...),
и, кроме того,
max
^ 2 [; фп, /-ч-1 "с*
то для любой суммируемой неотрицательной и не
возрастающей на @, 2л) функции ц (t) имеет место неравенство
2л 2л
Действительно, в этом случае для g(/) выполнены
условия теоремы 6.8.1, так что ]g /. *s*iipnr'/, а также
условия теоремы 6.8.4, в силу которой разность Ф(фяг,лг) —
— Ф(§*, лг) или неотрицательна на @, 2л) или меняет
знак один раз с -j- на —. Остается повторить
рассуждения, проведенные при доказательстве теоремы 6.7.6.
Отметим, что условиям теоремы 6.8.5 удовлетворяют,
в частности, все функции ge W'HmOD1 (r=l, 2, ...).
Действительно, в этом случае в силу экстремальных

§ 6.9] О ФУНКЦИЯХ ПЕРИОДА 21 175
свойств цпг будет lg'ic^l4nr\G и если положить
2л
где с выбрано из условия jj G(t)dt = O, toG
6
так что iiGS!c<!!q^/i,r+i!ic и
ь
max
§ 6.9. О справедливости результатов
для функций произвольного периода 2/
В этой главе (гак же, как и в предыдущих), исследуя
свойстга периодических функций, мы считали перисд
равным 2л. Однако созершенио очевидно, что все результаты
автоматически распространяются на функции любого
периода 2/ (/>0), если, разумеется, вариацию, норму
в L, а также ^-перестановку определять по отрезку длины
2/. Вместо <Рпг{х) и gn> (*) роль экстремальных функции
будут играть /--е периодические интегралы (с нулевым
лях
средним значением) от функций соответственно sign sin—.—
и 4!;; sign sin —, т. е. функции сря,(я*.7) и gnr(nx
Этим замечанием мы воспользуемся в главе 8.

ГЛАВА 7
НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ
ТРИГОНОМЕТРИЧЕСКИМИ ПОЛИНОМАМИ
НА КЛАССАХ WrHi0
§ 7.1. Модуль непрерывности
Везде в этом параграфе X будет обозначать
пространство С или Lp A^ср<Сос) 2я-периодических функций
с соответствующей метрикой.
Модулем непрерывности функции [gX в
пространстве X называют функцию
<о(/, /)*= sup :!/(- + ")-/(-)iix @^/< + oc). G.1)
Условимся вместо (о (Д t)L писать со (/, t)pt а вместе
со(/, Ос — просто (о(/, t). Таким образом, по определении:
для /^ С
SUP Inax
= sup ;/(*')-/(*•)!. G. г;
Функцию (о(/, t)p A<:р<ос) называют иногда
интегральным .модулем непрерывности.
Модуль непрерывности G.1) функции /еХ обладает
следующими основными свойствами:
1) © (/, 0)х = 0;
2) со (f, t)x не убывает на промежутке 0 ^ t <C оо;
3) модуль непрерывности G.1) есть полуаддитивная
функция, т. е.
G.2;
4) (o(f, 0л- — непрерывная на полуоси [0, ос) функция
Свойства 1) и 2) немедленно вытекают из определенна
модуля непрерывности. Чтобы доказать неравенство G.2)
достаточно в силу G.1), фиксировав /i>0 и /2>^>
установить, что для любого и ^ 0 такого, что и < ^-|- /2, булсл1

7.1] МОДУЛЬ НЕПРЕРЫВНОСТИ 177
Еоли u*uti или u*^t2, то 8то очевидно. Пусть
тах{/ь ^
тогда
и мы будем иметь
\n-+u)-f(-+Q'ix +
f(-)lx^^(f, Мх + «(/, /2)х,
что и требовалось.
Доказывая свойство 4), заметим сначала, что равенство
lim w(/, 0x = 0 G.3)
при Х~С следует из равномерной непрерывности
функций feC на всей оси, а при X~LP A •¦--. /?<оо) — из
теоремы Лебега, на которую мы уже ссылались в § 5.2.
Таким образом, в точке / = 0 функции со (Л /)Л-
непрерывна справа. Если 0<С/<оо, то в силу G.2),
независимо от знака /г (если только l-'rh>-6), справедливо
неравенство
-<o(/f Ол-!<©(/, "Л Ь
и ввиду G.3) co(f, /-fft).v-*G>(/, 0 при h-+0.
Из полуаддитивности модуля непрерывности w (/, t)x
следует, что для любого натурального п
со (/, «O.v <¦ «со (Л /)х (« -1,2,3,...). G.4)
/Действительно, при п~\ это тривиально, а
предположив, что G.4) верно для /г — &, будем иметь
со(/, (*+1) Ох <«>(/
Если Я —любое положительное число, то вместо G.4)
можно написать
со(/, b/)*<(M-l)<o(f, Ox, G.5)
ибо, обозначив через \К] целую часть X, в силу
монотонности (o(f, ()х и соотношения G.4) получим

178 ПРИБЛИЖЕНИЕ ПОЛИНОМАМИ КЛАССОВ WH** [ГЛ. 7
Укажем некоторые оценки для функций Стеклова
(§ 5.2), связанные с «модулем непрерывности.
Предложение 7.1.1. Если f е 1Р A ¦ ^ р < ос) и
fи —функция Стеклова для f, то
]//Ц>^ {<*(/, Л)Р. G.7)
Неравенство G.6) немедленно следует из полученного
в § 5.2 соотношения
if определения модуля непрерывности о)(/\ /)р. Далее,
так как
fi(V) [
то ввиду G.1) п G.4)
Отметим, что в силу 2л-периоличпостн функции f
о)(/, 0л=о>(/§ л) (/:-л).
В самом деле, если м' > л, то всегда найдется целое
(положительное или отрицательное) число т такое, то
2тк — и \ -.:Г- л. Но тогда
'„/(•-'г ")-/(-):.v = ;i/(- + ")-/(- + 2//n)i:v <:«(/, л)х
и, следовательно, при />л модуль непрерывности
возрастать не может.
В случае Х- С свойства 1) — 4) мочуля
непрерывности (о(/, /) являются характеристическими в том смысле,
что, как мы увичим чуть ниже, любая функция о>(/),
иблудпк пин этими спо/к'тнамн, и такая, что (•>(/) о> (;i)
(/ .. -л), н»ляогся модулем непрерывности некоторой
функции /^С. Поэтому целесообразно ввести понятие модуля
непрерывности вообще, не связывая это понятие с какой-
либо конкретной функцией /\
По определению будем называть моду ie.u
непрерывности заданную на [0, -j- ^^) непрерывную неубывающую и

§ 7,11 МОДУЛЬ НЕПРЕРЫВНОСТИ 179
полуаддитнвную функцию со(/), в нуле равную нулю. Все
эти условия, определяющие модуль непрерывности <о (/),
содержатся в следующих соотношениях:
Ит со (/) = со @) = 0, 0 < © (/2) - (о (/х) ^ со (/2 -
00
Если со (/) — модуль непрерывности, то, полагая
/о (х) = /о (- х) = о> (х) @ *г х < л), f0 (* + 2л) - / (л-),
получим функцию /0 е С, у которой, как легко
проверить, со (/о, /) = ш@ @</<я).
Чтобы облегчить проверку функции со(/) на
полуаддитивность, заметим, что это свойство заведомо
выполняется, если отношение (a(i),t не возрастает (при возра
станин /). Действительно, в этом случае для любых /0
и /2>0 будет
<* h —jf- + к —)'f~ = о)-(/0 + ю (/2).
Если (о @ — выпуклая вверх на [0, оо) функция, т. е.
для любых ti^O и /2^0
асо (/,) + A - а) о (U) < (о (а1± + A - а) /2) @ ^ а ^ 1)
(точки хорды лежат не выше соответствующих точек
стягиваемой ею дуги), то отношение ((о(/) — с]>'(/— с) не
возрастает при каждом с>:*0. Это сразу становится
очевидным, если сделать чертеж (см. также И. П. Натансон [2],
стр. 476). Таким образом, справедливо
Предложение 7.1.2. Всякая непрерывная
неубывающая и выпуклая вверх на [0, -1- оо) функция со(/), в нуле
равная нулю, является модулем непрерывности.
Важными примерами модулей непрерывности являются
функции КГ1 (/^-0), где 0<а<: 1 и /<>0, а также
функции, совпадающие с КР @<Са^1, /С>0) на [0,6]
и с /С6а при /2*6.
В дальнейшем нам придется иметь дело большей частью
с выпуклым вверх модулем непрерывности, поэтому
отметим некоторые его дополнительные свойства, вытекающие
из выпуклости.

180 ПРИБЛИЖЕНИИ ПОЛИНОМАМИ КЛАССОВ \\"ГП® [ГЛ 7
Предложение 7.1.3. Выпуклая вверх функция ^(х)
в каждой внутренней точке промежутка выпуклости имеет
конечные односторонние производные г|I (х) и t|?+ (x),
каждая из которых не возрастает, причем
I/, (*)<4»'-(.v). G.8)
Доказательство. Пусть л* —внутренняя точка
промежутка выпуклости функции i|i и число /г>0 таково,
что х —/г и jf + Л принадлежат этому промежутку.
Вытекающее из определения выпуклости вверх неравенство
V2 [if (л* + Л) -f if (х — Л)] ^ г|) (а*) перепишем в эквивалентном
виде
и заметим, что при ft->0 отношение в левой части, будучи
ограниченным сверху, не убывает, а отношение справа,
будучи ограниченным снизу, не возрастает. Следовательно,
эти "отношения при Л->0 имеют конечные пределы,
равные соответственно г|?';. (х) и г|;1 (.v) и удовлетворяющие
неравенству G.8).
Если Xi п *2~~Две внутренние точки промежутка
выпуклости г|) и a'i<O'2, то для всех 0<A<C.v2 —*i
- Л) ^ г|) (л':) -¦(- г|- (.г2)
и, значит,
В пределе при Л->0 приходим к неравенству ^1
^ф!(д:2), так что, с учетом G.8), тем более я|?1
Предложение 7.1.4. ?слн ® (t) — выпуклый вверх
модуль непрерывности, то
а) «а промежутке 0 < / < оо существуют не
возрастающие неотрицательные односторонние производные со'_ (/)
и co'j. (/), причем со.'. (/) <:col (/);
б) ы (t) — абсолютно непрерывная на [0, оо) функция.
Доказательство. Утверждение а) следует из 7.1.3
и монотонности ю(/). Чтобы доказать б), зададим е>0,
и пусть {(аА, рА)} (Л=1, ..., /г) — система непересекаю-

§ 7.11 МОДУЛЬ НЕПРЕРЫВНОСТИ 181
щихся интервалов таких, что
где б = б (е) определено из равенства со (б) = е. Мы можем
считать, что
Из выпуклости вверх ©(/) следует, что если
то для любого Л>0
®(f1 + A)--©(f2)<©ft + A)--©ft)f
поэтому
о(р1)-со(а1)<со(р1-а1),
2
Суммируя, получим
2 ММ)[|] (РЛ)()
Абсолютная непрерывность выпуклого вверх модуля
непрерывности означает, что
t
со (t) -1 со' (и) du,
о
где о/ (и) существует почти всюду на @, оо) (в силу
монотонности со(/)) и суммируема. Если положить
то со' (и) будет определена в каждой точке / е @, со),
являясь на этом промежутке невозрастающей функцией.
Легко привести пример модуля непрерывности, не
являющегося выпуклой вверх функцией. Пусть при

182
ПРИБЛИЖЕНИЕ ПОЛИНОМАМИ КЛАССОВ WrH<u [ГЛ. 7
0<Л<1 (рис. 17)
(О
G.9)
О h
Без труда проверяется, что эта функция, не будучи выпуклой
вверх, удовлетворяет всем условиям, определяющим модуль
непрерывности и, в част-
ности, полуаддитнвпа.
Имеет место
следующая лемма о выпуклой
мажоранте.
Л ем ма 7.1.5. Каков
бы ни был модуль
непрерывности со (/) =? О,
существует вы пукл ый
вверх модуль непрерывно-
=*• сти со* (/) такой, что
ю (/)<©,(/)< 2© (/)
@</<оо). G.10)
Константа 2 в правой части уменьшена быть не может.
Доказательство. Возьмем в качестве со* (/)
верхнюю границу наименьшей выпуклой области, содержащей
область JO ^i / < со, 0 <? у ^ со (/)!. Ясио, что ш* @) — 0
и со* (/) — непрерывная неубывающая и выпуклая вверх
на [0, со) функция, т. е. о>* (/) есть модуль непрерывности.
Из самого определения следует, что о>@ <; со* (/).
Докажем, что в каждой точке />0 со* (/) <2о>(/),
причем ясно, что нужно рассмотреть только те точки /,
в которых со(/)<(•»./(/). Но если / — такая точка, то
существуют /, и /2 таьне, что
1 f+Л
Рис. 17.
и о)^ (/) линейна па |/ь /2]. Следовательно,
w* (/) = о) A\) !- ^—) --_-,—L (/ — tx) =

§ 7.2] КЛАССЫ \XrH® 183
(О
I-** ®1Ы G 1 п
Но /i</ и, значит, со (/^/о) (/) :<с 1, а так как в силу
G.5)
то
Учитывая эти оценки, из G.11) получим
= I r __B h__ b_ ^ л j_ к ^i__ _ о
л j_ к ^i__
1 ' /2_/t /2-/,
Неравенства G.10) доказаны. Легко подсчитать, что
если наименьшая выпуклая мажоранта о)* (t) построена
для модуля непрерывности G.9), то
так что константу 2 в G.10) уменьшить нельзя.
§ 7.2. Классы WrH«>
Классы функций W'l , которые рассматривались в главе 5,
задавались ограничением на норму r-й производной;
структура r-й производной при этом не учитывалась,
требовалось лишь, чтобы '\f{nip^l.
Более тонкий и в то же время более общий способ
задания классов функций связан с заданием мажоранты
для модуля непрерывности самой функции или ее г-й
производной.
Вели о) (/) — фиксированный модуль непрерывности,
о»(/)е?0, то через /УA> будем обозначать множество
функций f (х) из С, для которых
<и(/, 0<*>@ С^0). G.12)

184 ПРИБЛИЖЕНИЕ ПОЛИНОМАМИ КЛАССОВ \VrfI® [ГЛ. 7
Мы уже отмечали в § 7.1, что для /еС со(/, /) = co(f, л)
для /г^л, поэтому включение /е Яо) равносильно
выполнению неравенства G.12) при 0<^л.
Класс ЯA) можно определить еще как совокупность
всех функций feC, удовлетворяющих условию
if(x')-f(x")\^<o(\x'-x"l) V*\ хГ.
В частности, если <о(/)==/С/а @</<я, 0<а^1), то
Яа) есть класс функций / из С, удовлетворяющих на всей
оси условию Гельдера степени а с константой /<:
Этот класс будем обозначать /\Яа.
Предложение 7,2.1. Класс I\W совпадает с
классом W\vK абсолютно непрерывных функций [ из С, у кото-
рых почти всюду f (х); ^К.
Действительно, если f(=KH\ то / абсолютно
непрерывна, и так как для всех х и h
А
то почти всюду f (x)\^K. С другой стороны, если
WlMK, to
т. е. /
Через И77Уа) (г=1, 2, ...) будем обозначать класс
функций /ее С, у которых /^ е Я*. Под 1РЯ@
понимается Яа).
WKHa по определению есть частный случай класса
WrHb\ когда со (О «КГ @</<-л, 0<ail); таким
образом, / е= Г7СЯа означает, что /gC и /(г) е /СЯа.
Из предложения 7.2.1 следует, что класс WrKHl
совпадает с классом Wr\T]K»
Предложение 7.2.2. При фиксированных со (() и
г— О, 1, 2, ... функции класса WrHlu равностепенно
непрерывны, т. е. для любого е>0 существует 6 = 6 (е) такое,
что из ! х' — х", < 6 следует \ f (xr) — / (^/;) j < е Зля
/ ^"Я;\
При г~о сформулированное утверждение следует из
того, что, выбрав 6^=6(е) из условия (oF)^e, будем

§ 7.2] КЛАССЫ Wr//W 185
иметь для любой функции /еЯ@ и любых х' и х" таких,
что | *' — *"! 6
Если же f e WH* (r^l), то, используя
представление (§ 5.1)
2л
2 $
о
и учитывая, что /(л) €= //а\ можем написать
2л
если только V — л*" <б, где 6=-6(е) выбрано из
условия со F) ¦•¦^ лр/.' Dr у,.
Предложение 7.2.3. При фиксированных оо(/) и
г *= 0, 1, 2, ... класс W/rtf(t) есть выпуклое замкнутое
локально компактное в С множество.
И здесь рассмотрим сначала случай г — 0. Если /i и
[2е№\ то, положив /^a/H-(l--a)/2 @<a<l), для
любых точек х' и д:'7 будем иметь
V) -f A - a) /2 (.v') - a/i (x") - A - a) f2 (?) \ ^
! /i (-V) - /i (-V), + A - a); /2 (x') - f2 (x°)! <
т. e. / e Яо), и выпуклость Яо) установлена.
Пусть далее fn (х) (п = 1, 2, ...) — последовательность
функций из Ни\ сходящаяся к f(x) в метрике С: ;!/„ — f'lc-*-
->-0. Фиксировав х' и х", напишем для любых «=1,2,...
< | / (х') -/„ (лг') I + fn (х') - fn (х") ;-!-,/„ (х") - f (х");,
откуда, оценивая каждое слагаемое справа, получим
! / (х') - / (х") | < «(! х' - х" i) -f 2.; / - /л lie,
а переходя к пределу при п -> jo, убеждаемся, что / <~ Я'°.

186
ПРИБЛИЖЕНИЕ ПОЛИПОМАМИ КЛАССОВ \VrH
VrH®
[ГЛ. 7
Локальная компактность множества /7@ в
пространстве С следует из теоремы Арцела (Л. Л. Люстерник,
В. И. Соболев [1], стр. 236) и предложения 7.2.2.
Рассмотрим случай г^эв 1. Если ft и f2e WrH{>\ то
функция / = a/H-(l — а)/я @<а<1) принадлежит Сг и
тривиально проверяется (как и в случае г ¦•=()), что /{М <= //@.
Докажем замкнутость в С класса WH*. Пусть /я е
gFWw (/«=lf 2, ...) и
lim ¦i/«-/5jc = Of G.13)
так что
(u = l, 2, ...). Записав представления
2Л
заметим, что
-1, 2,...),
=lf 2, ...),
и, значит, существует сходящаяся подпоследовательность
\aonk\> aonk~>Q<\*' Так как /^ <= Hlt} и на каждом периоде
/(,'} обращается в нуль, то для любого х найдется точка
a = ak такая, что л* — а -^я, /,(Я (а) --= 0 и, следовательно,
Таким образом, последовательность \fn]k\ (Л--1, 2,...)
ограничена в С и, ввиду локальной компактности класса
//"\ содержит сходящуюся подпоследовательность. Чтобы
не усложнять обозначений, будем считать, что //(,r)—^ij<,
где i|ieff@ ввиду замкнутости этого класса. Так как
среднее значение на периоде каждой из функций f)[]
равно нулю, то
2:1 2л |
V ^ dt --¦-- \ (if — flih dt <U;! i|5 ~ //(/M ,1c 2л -> О (Л ->^),
о о 'I
2л
т. е. ) г|> @ dt = 0.
о

§ 7.3] функции tnr и) 187
Пусть f# (x) — r-vi периодический интеграл от \p(x) со
средним значением на периоде, равным Оо* 2- Тогда /* е
<= Гг#" и
2л
Имеем
[/«,-/• 1с <
<-?- i «о„Л-ао* I + ^ jj :d, (*- 0! 7«ri @ - * @: ^<
о
Так как, с другой стороны, ввиду G.13) |-/Г„А —/'iC —>-О,
то в силу единственности предела /=--/#, т. е. предел
последовательности {/„} из W'H™ также принадлежит этому
классу.
Локальная компактность класса WrH^(r^ 1), как и
в случае /'=^-0, следует из предложения 7.2.2 и теоремы
Арцела.
Замечание. Утверждения, аналогичные 7.2.2 и
7.2.3, имеют место и для классов WrHl? (r = 0, 1, ...;
W'H^H^) функций/е/-;„ у которых (о(/(г), /)р<«@-
Вместо теоремы Арцела здесь следует воспользоваться
теоремой Рисса (Л. А. Люстерник/ В. И. Соболев [IJ,
стр. 242), равностепенная непрерывность понимается
в среднем в р-п степени.
§ 7.3. ФуНКЦИИ fnr(t)=fnr(<d> t)
В классе WH® (л==0, 1, ...) при выпуклом о(/) есть
«стандартная» функция, на которой реализуются многие
экстремальные свойства функций этого класса, в
частности верхние грани наилучших приближений.
Пусть /„о (*) -- //|0 (со, х) — 2л/71-периодическая нечетная
функция, определенная на [0, л/я] равенствами

188
ПРИБЛИЖЕНИЕ ПОЛИНОМАМИ КЛАССОВ WrH<* [ГЛ. 7
Через fnr(x) = fnr(®> х) (г-*!» 2, ...) обозначим r-й
периодический интеграл от fno(x) со средним значением на
периоде, равным нулю. Таким образом,
$
= 1, 3, 5, ...),
\Lr-i(t)dt (r=2, 4, 6, ,..);
о
/v\ tr 1 о Q . Ь 1 9
% r-fc \X) V — lt *t Ot • • •> « — 1, Z,
г).
Графики первых трех функций \пг (х) изображены на
рис. 18.
Рис. 18, Функции fnr(x) = fnr
(/"«0,1,2)
Предложение 7.3.1. Если ы(t) — выпуклый вверх
модуль непрерывности, то fnrtaWrH® (г— 0, 1,2, ...),
причем
со(U, 0 = »@ @</<-J, л = 1,2, ...). G.14)
Чтобы доказать, что /v e W'H®, надо лишь убедиться
в принадлежности функции /„„ классу Яи), т. е. в юм, что
x', x\ G.15)

§ 7.3] функции fnr{t) 189
Проверим сначала G.15) для х' и *", принадлежащих
промежутку [ — я/2п, я/2п], на котором /я0 строго возра-
стает, принимая на концах наименьшее и наибольшее
(относительно всей оси) значения. Если — п/2п*^х' *^
&%: 0 ^ jt" < л/2/г, то из выпуклости co(t) сразу выводим:
Если же 0<лг'<л;(Г^л/2я, то, используя полуаддитив*
ность модуля непрерывности со(/), будем иметь
i U СО - /-о Ю ! = 2 со Bх") - } ш
причем вследствие нечетности /я0 неравенство G.15) теперь
доказано и для х' и л:/;, принадлежащих промежутку
[~я/2п, 0].
В общем случае, когда *' и х' — произвольные точки
оси, всегда можно указать точки Х\ и х2 на промежутке
[ —л/2/i, л/2я] такие, что |jci — х2\^\х' — х'\ и
и следовательно, в силу уже доказанного,
Доказанное нами соотношение G.15) равносильно тому,
что
о)(/„о, /)<©W (/»0). G.15')
С другой стороны, если 0</^л/л, то
/«о(-$)-и(- {-) = {©@ + ¦[«@ = о)(О,
так что при 0-^t^n/n в G.15') имеет место знак
равенства.
Из самого определения функций fnr (x) следует, что:
а) fnr(x) имеет простые нули в точках kn/n (/г«=0,
z)-. 1, :±2, ...) при г четном и в точках BА—1)л/2л при
г нечетном, которые являются центрами симметрии се
графика;

190 ПРИБЛИЖЕНИЕ ПОЛИНОМАМИ КЛАССОВ WrH® [ГЛ. 7
б) f«л (х) достигает максимального по абсолютной
величине значения в точках kn/n при г нечетном и в точках
Bk— 1) л./1 при г четном;
к) /Яг (л*) монотонна на каждом промежутке
длиной л/н между соседними точками своего экстремума.
Предложение 7.3.2. Имеют место равенства
En(f«r)c = \fnrk (л=1, 2, ...; г = 0, 1, 2, ...) G.16)
En{f«rh = ]fnry (я=1, 2, ...; г = 0, 1, 2, ...). G.17)
Действительно, из отмеченных только что свойств
fnr (х) следует, что на периоде [0, 2л) существует 2п
равноотстоящих точек, в которых fnr (х) принимает
максимальные по абсолютной величине значения, поочередно
меняя знак. В силу критерия Чебышева 3.2.1 наилучшее
приближение функции fnr в метрике С среди всех
тригонометрических полиномов порядка я— 1 доставляет
тождественный нуль, так что справедливо G.16).
Из свойств а) — в) функции fnr следует также, что
(~l)r/2signsin^ (r = 0, 2,4, б,...),
(_ Xr+X)r2s[gn(:osnx (r=lt3, 5,...)
и, значит, в силу предложения 3.5.1 функция fnr(x)
ортогональна всем тригонометрическим полиномам порядка
/i—1. Критерий 3.3.4 полинома наилучшего приближения
в метрике L позволяет заключить, что для fnr (x) таким
полиномом будет, как и в метрике С, тождественный нуль,
а потому верно и G.17).
§ 7.4. Основная лемма
Через #а)[а, Ь\ в этом и в следующих параграфах
будем обозначать класс заданных на отрезке [а, Ь]
функций f(x)y удовлетворяющих условию
!/(*')-/(*") !<co(;*'-*"i) Vjc\ *"е[а, 6],
где со (/) —заданный модуль непрерывности.
Лемма 7.4.1. Пусть суммируемая на промежутке
(а, Р) функция г|) (I) удовлетворяет следующим условиям:
X) интеграл

?л\
ОСНОВНАЯ ЛЕЛША
191
доопределенный нулем вне (а, 0), есть простая функция
в смысле определения § 6.2, т. е. V (х) строго монотонна
на (а, а') и ф'у р) (а<а'^р'<р), Y(p) = 0 и
max
2) яд промежутках (а, а') и (Р\ Р) функция ty
обращается в нуль разве что на множестве меры нуль.
Тогда
sup
функция р(х) определена для а^х^с~(а' + Р'),2
= Т(р (х)) (а<х<а', Ц
^ Р * {х)—функция, обратная р (,v).
/Гслг/ ь) (i) — выпуклый вверх модуль непрерывности, то:
а) в G.18) имеет место знак равенства, причем
верхнюю грань реализуют функции из класса //°'|а, Р] вида
K"l~fo(x)* ?де К — произвольная постоянная и
foix) =
-\io'(p(t)-t)d(
G.19)
С
б) величина /Vf 10 (Ц?) может быть записана в виде
ALW)= $ V (/)<.>'(/) Л, G.20)
о
а9^ V (/) — убывающая перестановка функции \ XV (/) |.
Доказательство. Ниже мы покажем, что в
условиях леммы функции р(х) п pl(x) абсолютно
непрерывны и почти всюду на соответствующих промежутках

192
ПРИБЛИЖЕНИЕ ПОЛИНОМАМИ КЛАССОВ \VrH® [ГЛ. Т
выполняются еоотношения
*@-Ч>И0)р'@ («<*<*), G.21)
Ч> (Р-1 @) (Р-1 @)' = ¦ @ (с<* t ^ P). G.22)
А пока, используя эти факты, получим с помощью
несложных выкладок утверждения леммы.
Заметим, что функция р(х) непрерывно и строго
монотонно отображает отрезок [а, с\ на отрезок [?, Р], причем
О fi'-a' p(t)-t fl-a ос t а! с fi' f>(t)§ Ь
Рис. 19.
p(a) — P, p(c)---c (рис. 19). Полагая ^ = р(г) на (Р', р)
(замена неременной правомерна ввиду абсолютной
непрерывности р(х)), получим для /€=//{?, pi
I г|) @ / (/) dt = - J ^ (о (г)) / (р (г)) pf (г) йг. G.23)
/i' ос
С учетом того, что г|:(/)-=0 почти всюду на (а\ р'), для
любой функции /^Я@[а, р], используя G,21) и G.23),
будем иметь
l$V)f(t)dt+\y(t)f(t)dt
а

§ 7.4]
ОСНОВНАЯ ЛЕММА
193
Аналогично, полагая /»р-1(г) на (а, а') и используя
G.22), найдем
G-25)
Равенство
G.26)
проверяется элементарно с помощью той же замены
переменной / = р*(г). Первая часть леммы доказана.
Пусть теперь о (/) — выпуклый вверх модуль
непрерывности. Тогда о @ есть абсолютно непрерывная функция
(предложение 7.1.4) и
причем ш9 (и) не возрастает. Докажем, что для функции
U(x), определенной равенствами G.19), выполняется
соотношение
Мр(*))-М*)«ю(р(*)-*)
G.27)
Если
Тогда
то
и замена t=*p(z) дает
Р<*>
Теперь из G.27) следует, что в G.24), а в силу G.26) и
в G,25), для функции f**fQ знак неравенства можно

194 ПРИБЛИЖЕНИЕ ПОЛИНОМАМИ КЛАССОВ WrH® [ГЛ. '?
заменить на знак равенства. Так как
то верхнюю грань в G.18) вместе с /0 реализует и любая
функция вида /С±/о. ...
Мы должны еще проверить, что [0^Н^[а9 Р]. Пусть
а-^х' <л;"^р, и сначала предположим, что х' ^с^ л*\
Функция р(л;) — л: непрерывно и строго монотонно
отображает отрезок [а, с] на отрезок [0, 0 — а], поэтому
найдется точка лг0, а^л:0<с такая, что
р(*о) —*о = *" — *'•
Пусть для определенности лг'^#0, тогда #"^;p(*0),
причем хо — х'=:р(хо)~х". Учитывая возрастание /0, будем
иметь
/«(*") - /о (*') I = /о (^') - /«(*') - f/o (f> (хи)) -
+ l/u (^«) - /о (.vf)] + f/o Ю - /«(P (*«)
и так как
/о (Р (*о)) - /о (*о) = » (Р (^о) - А:о) = О) (| *' ~ л:" ;),
то надо доказать, что сумма последних двух квадратных
скобок неположительна. Но производная fl)(x) функции
/о.(лг), как это видно из G.19), не убывает на (а, с) и не
возрастает на (с, р), причем fiW=/o(pW)i поэтому
[/о (*о) - /о (*')] + [/о (V7) - /о
^о Р {Хо)
X' X"
< /' (^о) (хо - л') - /' (Р (*«)) (Р Ы - хГ) - 0.
Если же х' к ^" лежат по одну сторону от точки с,
например а ^ х' <.х' ^ су то, выбрав точку Х\ так, чтобы
было с — jci == л:" — х1 у будем иметь, учитывая уже
рассмотренный случай.

§ 7.4] ОСНОВНАЯ ЛЕММА 195
Принадлежность функции Д, классу Яш[а, Р]
установлена. Остается доказать соотношение G.20). Интегрируя
по частям и замечая, что У (х) сохраняет знак на (а, |3),
а функции о/ (р (/) -/) II 1 — р' (/) положительны на (а, с),
получим
5V (/) со' [р (/) - /] (р' (/) — 1)- л
СО
а
Из определения убывающей перестановки и задания
функции р(х) следует, что для a^t^a'
!?(/)i = 4'[p@~>]. G.28)
Если же a'^kt-r^Ci то р(/) —/*^Р' — а' и для таких /
|Мг(/),= max |V(jc); =
так что G.28) выполняется для всех а^/^сс. Поэтму
@ - /] о»' lp (/) -1\ tl -1/ @] л =
а
fl-а
- JJ У (/) Ю' (/) Л.
Теперь обоснуем правомерность сделанных при
доказательстве леммы выкладок, а именно докажем, что:
а). функции p(jc) и р^) абсолютно непрерывны
соответственно на [а, с] и [с, р];
б) равенства Ч' (jc) -4f (р (х)) и У (р-1 (л:)) = У (л:) можно
почти всюду дифференцировать.
Мы воспользуемся следующими фактами.
Предложение 7.4.2. Если абсолютно непрерывная
на [а, Ь] функция y = f(t) строго монотонно отображает
отрезок ak^t^b на отрезок c^y^d, то для любого
измеримого множества ecz[a, b]
mesf(e) = \f'(l)dt. G.29)

196 ПРИБЛИЖЕНИЕ ПОЛИНОМАМИ КЛАССОВ W ГЯ® [ГЛ. Т
При дополнительном предположении, что f (t) — 0 разве
ито на множестве меры нуль, справедливы также
утверждения:
\) если mes/(e) = 0, то mese = O;
И) для любого е>0 существует б = б(е) такое, что
из mesf (е)<8 следует mese<e;
Hi) обратная функция f~l абсолютно непрерывна на
[с, d\.
Соотношение G.29) очевидно, если е —интервал или
вообще открытое множество. Переход к дополнению
убеждает нас в справедливости G.29), когда е замкнуто. В общем
случае равенство G.29) получим, аппроксимируя е «изнутри»
замкнутыми, а «извне» открытыми множествами.
Теперь утверждение i) сразу получается из G.29) и
предположения, что !/' (t) | >0 почти всюду, рассуждением
эт противного.
Доказывая И), можно, не теряя общности, считать,
что / возрастает, т. е. почти всюду на [а, Ь]
Пусть ф (/) — убывающая перестановка функции ф. Тогда
Ф@>0 для 0<^<6 — а.
При заданном е>0, положив
б- X \f(t)dt,
Ь — а — г
из неравенства
в силу предложения 6.1.3 сразу получим, что mese<e.
Абсолютная непрерывность обратной функции /-1 сразу
следует из ii), если учесть, что
Вернемся к условиям леммы 7.4.1. Очевидно, что
где Ч?!1 —функция, обратная к V (л:) на промежутке ЦТ, р].
Так как \ty(x)\>Q почти всюду на ((Г, Р), то в силу
утверждения Ш) предложения 7.4.2 функция 4V (у) абсо-

§ 7.4} ОСНОВНАЯ ЛЕММА 197
лютно непрерывна на [0, max]?(*)]!, и тогда р(л), как
суперпозиция строго монотонных абсолютно непрерывных
функций, тоже абсолютно непрерывна. Совершенно
аналогично устанавливается абсолютная непрерывность р~г(х).
ДокажехМ далее, что если
Р(х)
j
то почти всюду на (а, а')
Пусть е—множество точек л: из (а, а'), в которых
существует производная V (х) и, кроме того, если z=*p(x),
то в точке г существует V (г), а значит, существует и
производная обратной функции в точке у = 4^ (г). Легко
понять, что mese = a' — а, ибо в противном случае
множество положительной меры отображалось бы функцией
р (х) в множество меры нуль, что невозможно, так как
обратное отображение р~] абсолютно непрерывно. Таким
образом, У (х) и р (л:) дифференцируемы в каждой точке
множества е> т. е# почти всюду на (а, а'). Если#ое?, то
)-У (Р(*о)) L Р(
и при А->0 оба сомножителя в правой части имеют
конечные пределы, соответственно V (р (*0)) и р' (л:0). А так
как, с другой стороны,
то G.21) доказано. Аналогично доказывается и
соотношение G.22). Лемма 7.4.1 полностью доказана. Сделаем к ней
два замечания.
Замечание 1. Если функция ур(() в лемме 7.4.1
симметрична относительно середины у= -«>" (а + Р)
интервала (а, Р) и, следовательно,
то р(л:)— л:==2G — л:) и, как легко проверить,
экстремальная функция /о также симметрична относительно точки у

198 ПРИБЛИЖЕНИЕ ПОЛИНОМАМИ КЛАССОВ \VrH(* [ГЛ. 7
и имеет простой вид:
Принадлежность функции /0 классу #a)[a, Р] в этом
случае может быть установлена гораздо проще.
Действительно, если х' и х" расположены по одну сторону от у,
например y^*'<*"^P» то в силу полуаддитивности
со (О
I /о (*") - /о (*') i = j [со Bх" - 2т) - ю B*' - 2т)] <
^ I со [2 {х" - х')] < со С *" - х91).
Если же a<;jt'<Y<#"^P, то, используя выпуклость
со (/).. будем иметь
IU М - /«(*'); = 2 ^ &х" -2V) + o> Bт ¦- 2х')] ^
Замечание 2. Утверждения леммы 7.4.1 остаются
справедливыми, если снять условие 2), наложенное в ней
на функцию ij) (/). Хотя в этом случае функция р (х) может
и потерять абсолютную непрерывность, однако
производимые при доказательстве леммы замены переменной законны
и равенства G.21) и G.22) справедливы. (Обоснование
этих фактов требует более тонких рассуждений.) Впрочем,
для дальнейшего нам достаточно иметь утверждение леммы
даже в предположении, что yp(t) вообще не обращается
в нуль на (а, а;) и (Р' Р).
2л
§ 7.5. Оценка функционала Fl0(g)= sup \fgdt
Ставя своей целью нахождение точных верхних граней
наилучшего приближения тригонометрическими
полиномами па классах WH*, будем исходить из соотношения

§ 7.5] ОПЕНКА ФУНКЦИОНАЛА F (ё) 199
(см. начало главы 6)
2л
En(f)p= sup lf{r)(t)g(l)dt
справедливого для любой функции f e Ljj.
Если /е= Г'#"\ то р)е№ и, следовательно,
ЕЛ №'№*)/- sup ?„#)„ = sup sup ffetf/,
few7"//*0 /e//a) g&wrHn, о
а так как верхние грани можно вычислять в
произвольном, порядке (см. (Д. 17)), то
En(WrH«)p= sup sup \f{t)g{t)dt G.30)
l7J/tftD о
(/i=lf 2, ..,; r = 0, 1, 2, ...; i<p<oo, l/p+l/pf = 1).
Дело сводится, таким образом, к получению оценки
функционала
2л
^>fe)= sup \f{t)g{t)dty G.31)
точной на классе функций ge WrHnp>> Опираясь на
результаты предыдущей главы, мы сможем решить эту задачу
для выпуклых (о(/) при р' = 1 и р' = оо, причем даже
на более широких классах, чем WrHl и WrH%. При этом
мы будем оперировать понятиями и терминами,
введенными в главе 6.
Начнем с теоремы самого общего характера.
2л
Теорема 7.5.1, Если g^D и $ g(t)dt = O, то.каковбы
о
ни был выпуклый вверх модуль непрерывности со(/),
2л 2л
Fcd (В) = sup If (/) ? (/) Л ^ min ^ Ф (Gc, /) со' (/) Л, G.32)
w" с о

200 ПРИБЛИЖЕНИЕ ПОЛИНОМАМИ КЛАССОВ tt"r//to [ГЛ. 7
Неравенство G.32) темно в том смысле, что для
некоторых функций g^O из D в нем имеет место знак равенства.
Доказательство. Очевидно, мы можем считать,
что g(t) — исправленная функция из D. При любом
с Gc e WlD \\ для Gc (x) возможно представление через
простые функции:
причем почти всюду
k
и последний ряд можно почленно интегрировать. Поэтому
для любой функции [е//й
2л с -f- 2л с + 2л
\ f @?@ ^==s \ f (t)ё@ ^=== \ /@ i _/• ф* @ j Л =
о г с \Y у
где (аь pft) —основной интервал простой функции щ(х).
Из свойства 5) разложения на простые функции (стр. 143)
следует, что если [а?, Р^] —отрезок (или одна точка), на
котором 'j фй (х) | имеет максимальное значение, то на
интервалах (аь а?) и (Pi, Р*) производная <pi(;r) =^(^)=^0.
Поэтому, применив лемму 7.4.1, для каждого интеграла
в правой части G.33) получим оценку
f / Ф; л < * 5 ф^ (о а/ (/) л = f ф* (/) ©' (о rf/.
Сходящийся ряд неотрицательных функций можно
интегрировать почленно и потому
2я 2л
= 5 ^2 ф^ @ч) ©' (О л = f ф (С /) о)' (/) л.
о \ л / о
Так как число с у нас было произвольным, то
неравенство G.32) доказано.

$ 7.5] ОЦЕНКА ФУНКЦИОНАЛА F^ (g) 201
Покажем, что оценка G,32) неулучшаема. Пусть
функция g* (t) из D имеет период 2я/л (л = 1, 2, ,..) и нечетна,
причем
8т (и) = ?* (л/« - «) > 0 @ < и < л/2л).
Интеграл
—я/2л
на промежутке [—я/2/i, —л/2л + 2л] есть сумма 2л
простых функций <р*(*) (й = 0, I, ..., 2л—1) с основными
интервалами (Bk — 1) л/2л, Bk + I) я/2л), причем <р0(л:)
совпадает на [— л/2л, л/2л] с G^ (x) и
(?= 1, 2, ..., 2л— 1).
Привлекая к рассмотрению определенную в § 7.3
функцию /„о@^^ и учитывая 2л/л-периодичность и
одинаковую симметрию графиков g^ и /я0* будем иметь
2л
я/2/i
и 2л ^ g*V)U(t)dt. G.34)
6 -я/2/f
Для последнего интеграла справедлива ситуация, о
которой говорилось в замечании 1 в конце § 7.4, причем
функция fn0(t) является как раз экстремальной в классе
Нш[— л/2л, л/2л! функцией для g^ в смысле леммы 7.4.1,
так что мы можем написать
я/2я я/2/i я/д _
5 г,/«о dt = ^ фо @ U @ л = J Фо @ ©' @ л.
— л/2л — я/2л 0
Подставив в G.34), получим
я/я _
ЛЛ?*M* $ 2лФо@<о'(/)Л =
и
гг/л 2л
= $ Ф (G,, 0 (о' @ dt = J Ф (G,, /) ш' @ Л,
о 6

202
ПРИБЛИЖЕНИЕ ПОЛИНОМАМИ КЛАССОВ WrH(u [ГЛ. 7
причем, как следует из общей оценки G.32), здесь может
быть только знак равенства. Теорема 7.5.1 доказана.
Легко понять, что оценка G.32) точна также для
любой функции вида ±g*(' —Y)» где у — любое число.
Верхнюю грань в //w будет в этом случае реализовать
функция zLfn0(t — у). В частности, оценка G.32) точна
АЛЯ g = gnr К g = ipnr (Г = О, 1, ,..), Ибо фуИКЦИИ (—1)Г/2?яг@
при г четном и (—1)(г~1)/2?лг(* + л/2я) при г нечетном
удовлетворяют всем условиям, которые были наложены
на g4 (/). Положив Yr = 0 При г четном и уг = л/2/г при г
нечетргом и учитывая соотношение F.45), будем иметь
для всех я=1, 2, ... и г = 0, 1, 2, ...
2л
(gnr) =
я/я
л/л
! = $ <1\/п,гч(()(о'A)си, G.35)
6 и
а так как срлг = 4ngnr, то аналогично
2л
о
л/rt
G.36)
Наложив на g(t) определенные ограничения-, из эбщей
теоремы 7.5.1 и теорем сравнения главы 6 выведем более
содержательные оценки для функционала F^ig).
Теорема 7.5.2. Если ge=tt^(r = O, 1, 2, ...,),
$ g(t) dt = 0 и при некотором а>0
о
И I1
minl\g(t)dt\\ <]Фд г-ы!1/,
/770 Зля любого выпуклого вверх модуля непрерывности (о (/)
а
О
/7/?м а = я/д з«^/с равенства в G.37) имеет место для

§7.5] ОЦЕНКА ФУНКЦИОНАЛА F^ig) 203
Доказательство. Положим
где с0 выбрано из условия ]О;^^ЦФл,гч1/.- Применяя
сначала теорему 7.5.1, а затем теорему 6.7.6, в которой
надо положить \i (/) = со' (/) и учесть, что из выпуклости
вверх <o(f) следует монотонность со' (/), будем иметь
^со (?) < $ С'} (G, 0 СО' @ * < J Ф„, г,а (/) СО' (/) Л.
и и
Справедливость последнего утверждения теоремы 7.5.2
сразу усматривается из G.35).
2л
Теорема 7.5.3. Пустьgt=Dr(г = 0, 1,...), 5
о
g(r) ]м ^ 1 м ^^ интеграла
G(x)~\g(i)dt \\G(x)dx = Q)
выполнены соотношения
дрм любом выпуклом модуле непрерывности a>(t)
справедлива оценка
я/я
Знак равенства реализует функция
Доказательство. В силу теоремы 7.5.1
2л
О
где g и G —функции из условия теоремы 7.5.3.
Ясно, чтоG(х) обращается в нуль, G^Drjrl и ¦](
^al, так что мы находимся в условиях применимости

204 ПРИБЛИЖЕНИЕ ПОЛИНОМАМИ КЛАССОВ WrH® [ГЛ. 7
теоремы 6.8.5, в силу которой
л/а л/я
F»(g)< J Ф(ф,.г+ь t)u'(t)dt = 4n J Фя/л,г+1 (/)<»'(')<«¦
о о
Остается учесть равенства G.36).
§ 7.6. Верхние грани наилучших приближений
тригонометрическими полиномами
на классах WH** в пространствах С и L
Теорема 7.6.1. Коков бы ни был выпуклый вверх
модуль непрерывности co(/)f имеют место соотношения
(я = 1>2,...;г = 0, 1,...) G.38)
Доказательство. Равенство G.30) при р~со
запишется в виде
Ea(WrH»)c= sup T^te), G.39)
где Fa(g) — функционал, определенный равенством G.31).
Если g e VT#2 (/- « 1 • 2, ...), a G (*) - интеграл от ^ (/)
с нулевым средним значением на периоде, то Ge WrJtlHl
и в силу E.31) и F.45)
Так как Н7г//? с= \V\r\ то для функции ^(/)
выполнены условия теоремы 7.5.2 при а = п/п и, следовательно,
я/я
(n, г=1, 2, 3, ...).
Чтобы получить аналогичную оценку при г = 0, т. е.
на классе //?, прибегнем к функциям Стеклова,
используя факты, приведенные в § 5.2.
Пусть geWj и

§ 7.6] ВЕРХНИЕ ГРАНИ Еп(ФгН®)х ПРИ Х^С И L 205
2л
где с0 выбрано из условия $ G(x)dx~Q. Ясно, что
о
G&WxHh так что
Если СЛ(*)— функция Стеклова для G(x)y т. е.
— Л
то
причем так как Gл (л:) = #л (*), to GhczClci Dl. Кроме того.
и, значит, для функции Gh выполнены все условия
теоремы 6.7.7 прн а = л/п. Применяя последовательно
теоремы 7,5.1 и 6.7.7, будем иметь
2я Я/л
Fо, Ы < j Ф (G*. О ш' (/) Л < j Фя/Я, о (/) (о' (О Л.
О О
Таким образом, для любой функции /еЯа
J fe» Л < J Фдм о (/)«' (/) Л. G.40)
о о
Так как при Л->0 j^^ffk-^Of то
2л 2я
О О
и в пределе прн h -^0 из G.40) получим
2я Я/л
о
т. е.
J ф*/-.

206 ПРИБЛИЖЕНИЕ ПОЛИНОМАМИ" КЛАССОВ W^Ii** [ГЛ. 1
Итак, доказаны соотношения
SUP Fcofe)^ \ ФЯ/п.гУ)(й'№<и
(л-1, 2, ...; г-0, 1, 2, ...),
которые вместе с G.39) приводят к оценкам
• я/я
Я„ (^гЯС0)с ^ 5 ф*/«. - О<»' @ dt G-41>
О
(/i = lf 2,...; г = о, 1,...).
Так как в силу F.44)
Фл/«, г @ = \г Фдг («0 @ < / < Л/Л)
и, значит,
я /п п
[ Ф.-гм г К) ©' @ Л ~ -М ф-"" СО «' f \ ) Л. G-42)
о Г V '
то, учитывая предложение 7.3.2, для полного
доказательства теоремы 7.6.1 надо только установить, что
я/я
E/«r]c= S Фя/п,Л0«'(/)Л G.43)
б
(д-1, 2, ...; г-0, 1, ...).
Эти равенства нетрудно получить непосредственным
вычислением, учитывая задание функций fnn а также
рекуррентное соотношение
а ч)
Однако проще и, может быть, несколько более поучительно
вывести равенства G.43) из G.35) или G.36).
Действительно, так как
i2v@-(-!)vq>*o@ (v=l, 2, ...),

§ 7.BJ. ВЕРХНИГ ГРАНИ
ПРИ Я «С И I
207
то при г нечетных будем иметь в силу G.36)
2л
',« ' Х Г* Г !
\Jnr>.C*=-^\Jntr lU= 4л
2л
л/л
О
Аналогично, замечая, что
=l, 2, ...),
можем для г четных написать
An
4л
{fn0(t-nl2n)vn,rl(t)
о
dt
л/rt
так что равенства G.43), а с ними и теорема 7.6.1 доказаны;
Заметим, что мы, по существу, доказывали равенство
2л л/л
sup sup \g{t)f (t) dt - \ Фя/Я, л @ со' (О Л,
ge
из которого значение верхней грани Еп (WrH®)c получили,
используя соотношение двойственности G.39).
Интегрируя при гГ^1 по частям в последнем
выражении равенств G.38), получим для верхней грани
En(WrHu))c.euxe такое выражение:
я
G.44)
(л, г=1, 2,...).

208 ПРИБЛИЖЕНИЕ ПОЛИНОМАМИ КЛАССОВ WrH<* [ГЛ. 7
Отметим частные случаи. Прн г = 0 из G.38), а при
г»1, 2 из G.38) или G.44) найдем:
Ея (Яв)с = }fm !|c - A/2) (о (я/л), G.45)
я/я я
я/я я
?/-1 [с - { V «о (/) dt = 1 J (о A) Л,
я/я
8 $
б'
Полагая в G.44) и G.45) со (/) - Kt* @«/*?я, 0<а< 1),
получим
я
^ $.%^1(я-/)<аЛ (я. г-1, 2...)f
Из последних равенств прн а = 1 или непосредственно из
G.38) при (о (t) = Kt вытекают также значения верхних
граней ?я(и7г'1/(Я1)с = ?яAГЯ(/С) (г= 1, 2 ...), найденные
нами в § 5.3.
Теорема 7.6.2. Каков бы ни был выпуклый вверх
модуль непрерывности ыA), справедливы соотношения
Л
я.«х@«'(!)* = ^ \ Фяг(я-/)«)(!)Л G.46)
(п«1, 2, ...; г-0, 1, ...).
Доказательство. Прн /?=1 равенство G.30)
запишется в виде
En{WrH«)L= sup F*ig).
mwrHnM
Пусть g&WrH% (r = 0, 1, 2, ...), G(л:) — интеграл OTg@
со средним значением на период, равным нулю, a Gj (jc) —
интеграл от G(t) также с нулевым средним значением
на @, 2я). Тогда (ЗеГ+К a G, е ^г4Я5#, так что,
в силу экстремальных свойств функции <рлг,

I 7.6) ВЕРХНИЕ ГРАНИ E/l(WrH<u)x ПРИ Х«=С И L
209
Теперь, если r^I, то для каждой функции g из
выполняются условия теоремы 7.5.3, и потому
sup F* (g) < 4/z f Фя/„, г+ ! @ <«>' @ Л. G.47)
Для доказательства справедливости этой оценки при г = 0
опять перейдем к функциям Стеклова. Если #^#м, то
для функций Стеклова gh, Gh и G1A выполняются
неравенства
II gh [м «С 1, I! Ga lie < I! Ф«1 !!с. I; Gih lie < 1 Ф«2 Ь
так что gH удовлетворяет всем условиям, наложенным
иа g в теореме 7.5.3 (при г = 0), а потому для любой
2Я
Я/п
о о
В пределе при h ->0 gh можно здесь заменить на g, поэтому
Л/П
sup
Таким образом, оценка G.47) справедлива при всех
г = 0, 1, 2, ... и /1=1, 2, ...
С другой стороны, используя G.36) при г четном,
имеем
0 sign ч>«, (/)«//
а при г нечетном —
'4rt$ Фя/n,
Фя/Я,fо.
Если учесть G 17) и G.42), то теорема 7.6.2 доказана.
я/л

210 ПРИБЛИЖЕНИЕ ПОЛИНОМАМИ КЛАССОВ • fc-ffl* ГПЛ* Г
Здесь также мы шли к нужному результату- через
доказательство соотношения
2я я/я
sup sup \ gf dl = 4n ^ Фя.я. r+1 @ W @ Л.
ge///Ve//tto о
Частные случаи:
я
О
л
Еп (W'KH*h = -^ [ /*ФЯ, (n-t)dt (r = 0, 1, 2 ...).
о
Последнее-'равенство содержит, в частности (npira=l),
значение верхней грани En(Wrf(Hl)i^En(WrL^ l/C) (г = 0,
1, 2, ...), найденное в §5.3.
В заключение этого параграфа укажем непосредственно
вытекающие из G.38) и G.46) оценки (для выпуклого
вверх со (/)):
Е„ (W'H*)L <, ^ (о !^f) (/г=1,2,...; г= 0, 1,...),
G.49)
ГДе 'r\r^2XrJt.liSKr (r=l, 2, ...), а 5STr — константы C.44).
Действительно, положив
0
замечаем, что i|v @) = Фяг @) и J/M/) Л = $ Фяг (/) Л.
о о
Таким образом, разность t|v (/) — Фяг (/) имеет нулевое
среднее значение на @t л)э положительна на
интервале @, г]г) и отрицательна на (цг, л). А так как со' (/)

§7.7] О РЕАЛИЗАЦИИ ?д (//й)с ЛИНЕЙНЫМ МЕТОДОМ 211
не возрастает, то
п
[ for @ - Фл, (/)]«' ({) dt S* 0, G.50)
т. е.
о
Подставив эту оценку в правую часть G.38), получим
G.48). Совершенно аналогично получается
неравенство G.49).
Знак равенства в G.50), а значит, и в G.48) и G.49)
имеет место в том и только в том случае, когда со' (/) —
= const @</<я/л), т. е. о>(/) = /Г/@^/^л/л).
Что касается чисел г|г, то первые из них равны
причем г|г->-2 при г->оо.
§ 7.7. О возможности реализации верхней грани Еп (//0))с
с помощью линейного метода
В главе 5 подчеркивалось, что на классах Wm и Wl
(r^l, 2, ...) верхнюю грань наилучшего
приближения En(f)c, соответственно Еп(/)/., функции f
тригонометрическими полиномами реализует линейный оператор
Unity (^-метод), построенный на базе сумм Фурье
функции / и сопоставляющий функции f тригонометрический
полином
п-\
1 ), G.51)
где пи и Ьк — коэффициенты Фурье функции f.
Поскольку нам уже известны точные значения
величии Еп(№Н»)с и En(WrHb')L (при выпуклом со(/)), то
естественный интерес представляет выяснение вопроса,
существует ли линейный оператор Л, отображающий С

212 ПРИБЛИЖЕНИЕ ПОЛИКОМАМИ КЛАССОВ ITO/* ГГЛ. 7
в трнгонометр|{ческое подпространство /^-i (в частности,
вида G.51)) такой, что
sup М-АПх = Еп(^Н«)х,
f <= гг//ш
где X есть С или JL.
Мы дадим более или менее исчерпывающий ответ
на этот вопрос лишь в случае г = 0 и Х = С.
Совсем простые рассуждения позволяют решить вопрос
о возможности реализации верхней грани Еп (Нш)с при
выпуклом (*>(/) операторами вида G.51). Если через Н$
обозначить множество 2л/я-периодических функций из Н10
с нулевым средним значением на периоде, то в силу
предложения 3.5.1
и, следовательно, при любом выборе коэффициентов \к
sup [/-U«MJcS* sup
fe//ffi f e //"
Пусть ^ (jc)—функция из Я«, определяемая равенствами
О
Так как ]М!с«7«@)!, то
я/л
j
sup |; / - (У, (f, Я) fc ^ ^ ^j (о (/) dt. G.52)
Если ш(/) —выпуклый вверх модуль непрерывности,
то правая часть неравенства G.52) может быть равна
у (о (л/л) в том и только в том случае, когда функция ы(()
линейна на [0, я/л], т. е. со(/) = /(/ @^*<я/л). Таким
образом, если со (/) —выпуклый, но нелинейный на [0, я/л]
модуль непрерывности, то
inf sup !/-1/^

§ 7.71 О РЕАЛИЗАЦИИ ?„ (Н(% ЛИНЕЙНЫМ МЕТОДОМ 213
В частности, при с
inf sup \f-Un{!,%fc^
= КР- @<а<1)
2 ', п]
Еп(КН*)с.
Более тонкими рассуждениями доказывается тот факт,
что при тех же предположениях относительно (о (/) никакой
линейный оператор из С в fjn-i не дает на классе #w
наилучшего равномерного приближения.
Теорема 7.7.1. На классе //°\ заданном выпуклым
вверх модулем непрерывности со(/), верхняя грань En(Hw)c
реализуется линейным оператором из С в fL-\ тогда
и только тогда, когда (о(/) линеен на [0, п*п].
Доказательство. Если <о(t) = Kt @^/^л/л), то
Нш cz КН1 = ГIvf/C, причем
а на классе W)mK верхнюю грань наилучших
приближений реализует Х-метод.
Рис. 20.
Предположим теперь, что для некоторого выпуклого
вверх модуля непрерывности о)(/)
sup if-
G'53)
где Л— некоторый линейный оператор из С в Fjii-t.
Пусть ф0 (#) ~ четная периода 2п/п функция из класса Яш,
равная со (лг) — 1/2(о (я/д) на [0, л/n]. Определим далее
непрерывные функции q>i(x) и ф2(д:) периода 2л следующим
образом (рис. 20):
Ф1 (*) = Ф2 W = Фо (х) (п!п < х ^ 2л), ф2 (л/2п) = ф0 (л/2п),
ф! линейна на [0, л/д], а ф2 линейна на [0, л/2п] и [л/2п,

214 ПРИБЛИЖЕНИЕ ПОЛИНОМАМИ КЛАССОВ WrH® [ГЛ. 7
я/л]. Функции фг и ф2 также принадлежат классу Я°\
Чтобы убедиться в этом, достаточно проверить неравенства
IФ/ (*') - Ф/ (Л: *?©(!*'- *"!) (/ = 1, 2)
для 0 ^ *' < х" ssc я/л. Но из выпуклости вверх ф! и ф2
на @, л/л), а также того, что Ф/@) = фо@), ф,- (х) ^ фо (х)
(О <; * ^: л/л), сразу следует, что в этом случае
I Ф/ (*") - Ф/ (*')! < Ф/ (^ - *') - Ф/ @) <;
<Фо(^-^)-Фо(О) = ю(^-ДГ/) («=1, 2).
В точках &л/л (^ = 0, I, ..., 2л—I) функции ф0, фх и
ф2 принимают значения db — (о (л/л) с чередованием знака,
поэтому
=\<*\Пп) = Е« (Н"*к (^0,1,2), G.54)
причем существенно, что наилучшее приближение
функциям ф; (/ = 0, 1, 2) доставляет'тождественный нуль.
Из равенств G.53) и G.54), с учетом очевидных
соотношений
ЯлЫс^Лф^-ф/'к^ SUP [Af-Гс
fe//w
следует, что
1 Л% - Ф,- |с = Еп (Ф/)г ^Jw^j (/ = 0,1,2).
Но тогда тригонометрический полином А (фь х) из fJii-i
есть единственный полином наилучшего приближения
для ф/, и в силу предыдущего
Л(ф,, *)=0 (i = 0, 1,2). G.55)
Положим
Ф (х) = J~(о Щ [ф2 (дг) - ф1 (;¦)], G.56)
где Р = |iф1 — Ф«[с- Таким образом, феС, причем
0 (я/л < л: ^ 2 я),

§ 7.7] О РЕАЛИЗАЦИИ Ел(//©)с ЛИНЕЙНЫМ МЕТОДОМ 215
Ф(*) линейна на промежутках [0, л/2/т] и [л/2//, л/л].
Тривиально проверяется, что феЯш. Из G.55), G.56)
и аддитивности оператора А вытекает, что Л (ф, *)=0,
следовательно,
и в силу G.53) должно быть
/ л \ 1 / л \
«,9и;<; 9 со. .
П
Но для выпуклого вверх модуля непрерывности со {()
последнее соотношение возможно (со знаком равенства)
лишь в случае, когда оэ(/) — Kt (О^^^сл/д). Теорема
доказана.

ГЛАВА 8
НАИЛУЧШЕЕ РАВНОМЕРНОЕ ПРИБЛИЖЕНИЕ
КЛАССА Wtf* ФУНКЦИЯМИ КЛАССА W'm xK
§ 8Л. Переход к двойственной задаче
и некоторые свойства экстремальных функций
Заметим сначала, что при фиксированном К класс
xK=WrKHl (г = 0, 1, 2,...), не будучи линейным
многообразием, является (как частный случай класса H^rWw)
выпуклым замкнутым множеством (предложение 7.2.3).
Поэтому, рассматривая W[\txK как аппроксимирующее
множество в пространстве С, мы будем отправляться
от результатов §§ 2.3 и 2.5.
В силу предложения 2.5.1 для любой функцни
f<=C\WrM'*K существует определенная на отрезке [0, 2л]
функция go (/) с вариацией
2л.
такая, что
?"(/, WrM lK)c= inf [f-
2л 2Я
= jj / @ dg0 (/) — sup
6 фе^'/со
Естественно, что функция g{i зависит от f, а также от г
и К, которые мы будем считать фиксированными.
Так как класс WrM^lK (r = 0, 1, 2,...) содержит любую
константу, то для функцни go@» удовлетворяющей
соотношению (8.1), должно выполняться равенство go(Q) =*ш
2л
= goBn), ибо в противном случае
о
2л 2я
sup ^ ф dg ^r sup J ф dg0 = + со,
что несовместимо с (8.1).

S 8.11 ПЕРЕХОД К ДВОЙСТВЕННОЙ ЗАДАЧЕ 217
Продолжив go(t) на всю ось с периодом 2л, получим
2л-периодическую функцию (за ней мы сохраним то же
обозначение g0 (/)) с единичной вариацией на [0, 2л],
удовлетворяющую соотношению (8.1). В дальнейшем,
обращаясь к этому соотношению, мы будем иметь в виду,
что go (t) — функция периода 2л.
Пусть фо@ —функция наилучшего приближения для /
в классе WruT]K. Такая функция всегда существует в силу
локальной компактности и замкнутости класса WrM~ */( в С.
Из предложения 3.4.1 и равенства (8.1) следует, что
функции /, фо и g0 связаны следующими соотношениями:
2л
С/ —ФвОс= $ (f-<to)dgo, (8.2)
о
2Я 2л
sup \ ф dgo = Jj (fo dg0. (8.3)
Представим функцию g0 на отрезке [0, 2л] в виде ?0 =
= ^1 + ^2, где ifi — неубывающая, а ^2 — иевозрастающая
на [0, 2л] функции (И. П. Натансон [2], стр. 205).
Из условия g0@) == g0 Bл) следует, что
Ь Bл) - Ь @) - Ь @) - fc Bл) = IV Ы = [, (8.4)
о *
поэтому, обозначив для краткости ц (t) = / (/) — ф0 (/), будем
иметь
2Я 2я
Из сопоставления этих неравенств с соотношением (8.2),
которое можно записать в виде
вытекает, что
2л 2Я
- ? Е ч Ь $ п ^2 = |! ч ;'с (8.5)

218 ПРИБЛИЖ. КЛАССА Wr Н® ФУПКП. КЛАССА \VrA~iV {K [ГЛ. 8
Равенства (8.5), если учесть (8.4), возможны лишь
в том случае» когда я|*1 постоянна па любом интервале,
где Л (*)<!'г) |!с, а •$* постоянна на любом интервале, где
Ц @ > —'! Ц lie- (В справедливости этого утверждения легко
убедиться, рассуждая от противного.) Для функции g0 ~
— ifi-j-я|.-2 это означает следующее:
1) ёоЬ) постоянна на любом интервале (а, Р), на
котором \\\(t).<:b\}c\
2) .go @ не возрастает на каждом интервале (а, Р), где
Tl@<i!rl|c и не убывает на любом интервале (а, {$), где
Ч@>Чл!!о
Назовем у-интервалом интервал (а, Р), обладающий
следующими свойствами*.
Разность л (/) 5= / (/) — ф0 (/) обязательно принимает
значения, равные как ;, т| !<:» так и — i! ЧКс (иначе ф0 не была бы
функцией наилучшего приближения), поэтому у-интервалы
существуют. Так как колебание функции у\A) на у-интер-
вале равно 2]ц\с, / фиксирована, ф0^ Wr\txK9 то длины
у-ннтервалов ограничены снизу некоторым положительным
числом и количество их на любом периоде (а, а + 2л)
конечно.
Из отмеченных выше свойств 1) и 2) функции #0
следует, что go @ постоянна на каждом ^-интервале и может
менять знак только на отрезках (или в точках) между
соседними, у-интервалами. Так как gQ (t) не есть
тождественная константа, то существуют по меньшей .мере два-
у-интервала, на которых g0 принимает разные значения,
а число перемен знака g0 ua периоде конечно.
Теперь заметим, что прибавление к функции g0 любой
тождественной константы не меняет ни ее вариации, ни
значений интегралов Стилтьеса в (8Л)—(8.3). Поэтому
мы вправе считать, что go(t) определена с точностью до
аддитивной постоянной. Этой постоянной мы распорядимся
различным образом при г— 0 и при г^1.
В случае г = 0, когда речь идет о приближении
функции /еС классом W1mK = KH1, выберем эту постоянную
из условия минимальности нормы !'goi!b т. е. из условия
\ Iga.W, dt = min \ \g0 (t) + k[dt. (8.6)

§ 8.1] ПЕРЕХОД К ДВОЙСТВЕННОЙ" ЗАДАЧЕ
Зафиксировав этим самым функцию g0 (/), выясним
некоторые свойства функции сро@-
Из (8.3) при г = 0, интегрируя по частям и учитывая
B.28) и (8.6), будем иметь
2л 2л
sup J Ф dgo = sup \ q/ (t)g0 (t) dt =
= sup f ч* (t) go (t) dt = K\\g0 (t); dt -
2л
0
f
о
откуда сразу следует, что почти всюду, где g0 (/)=,? О
t). (8.7)
Описанные выше свойства функции g0 позволяют
заключить, что независимо от выбора аддитивной постоянной
найдется у-интервал (а, E), на котором go(t)^0 и
sign go (/) = sign т| (а) (а < / < р).
Сопоставление этого факта с (8.7) приводит к следую:
щему утверждению.
Предложение. 8.1.1. Если f^C\W]uI\ и
mo существует промежуток (a, (J) такой, что
Предложением 8.1.1 мы воспользуемся в § 8.3 при
оценке приближения на классе Яо).
Теперь обратимся к случаю гз* 1. Считая г = 1, 2, 3,...
фиксированным, выберем постоянную, с точностью до
которой определена функция g0 в (8.1)—(8.3), из условия

220 ПРИБЛИЖ КЛАССА Wr Н® ФУНКЦ. КЛАССА Я'^^К [ГЛ. $
и через gr{t) обозначим r-й периодический интеграл от
g0 с минимальной нормой в L. Таким образом, gr^ WrVy
причем функция g0(t) = g{rr) (t) удовлетворяет соотношениям
(8.1)—(8.3) и
2л 2л
\ ;gr (t) j dt = min \ \gr (t) + k i dt. (8.8)
о к о
Из (8.3), (8.8) и B.28), интегрируя поспедовательно г+\
раз по частям, найдем
sup \<fdgb= sup (-I)*" \^»grdt =
- sup (-\Y^\№rdl = K\ \gr\dt =
№m<K q о
2л
Jt?rf«*O
0
2я
-(-1У+1$Ф?+1)^Л (8.9)
о
и, следовательно, почти всюду, где g, (/)=?*= 0,
В частности, если почти всюду \gr (t) |>0, то <pf,r+l)(O
есть (с точностью до множества меры нуль)
кусочно-постоянная функция, принимающая только значения ±К и
меняющая знак на периоде конечное число раз. В этом
случае ф0 есть кусочио-полиномнальиая функция (сплайн),
«склеенная» из многочленов степени r-f 1 так, что фо^Сг,
§ 8.2. Оценка приближения на классе 1Уг//*(г^ О
Если /е WrHM (r= 1, 2, 3, ...), то, проинтегрировав г
раз по частям, получим
где go и gr —функции, введенные в конце предыдущего
параграфа для случая гг> 1. Если о> (/) — выпуклый вверх
модуль непрерывности, то применение теоремы 7.5.1

§ *.21 OUEHKA ПРИБЛИЖЕНИЯ ПРИ г> J 221
к правой части (8.10) дает
ffr. t)dt. (8.11)
f
о о
Пусть число А, 0<Д^2л, определяется тем, что
(? 0° 0^;/<Д и Q>{gr, 0 = 0 для Д</^2л,
В нашем случае функция gr удовлетворяет условию (8.8)
и потому не может сохранять знак на промежутке длины,
большей чем л, поэтому заведомо Д^л. Так как
(см. (8.9))
sup $ Ф*о«/С $ !*г|Л«К$ Ф(е„ /)Л, (8-12)
+| 0 6
то из (8.1), (8.11) и (8.12) вытекает следующая оценка
наилучшего равномерного приближения функции /е WH*
функциями класса №д/м/(:
о
Ясно, что здесь функция gr и число Д зависят от f.
Выбрав *>0 из условия
[!Ф^1к-[;ФЫк=!^к (8.13)
и помня, что gr& Wvt с помощью теоремы 6.7.3
заключаем, что
|ФиОК|Ф'(*г, 01 @</<*). (8.14)
причем из (8.13) и (8.14) следует, что Ь<Д и, значит,
Ь
Если положить
б(/)«Ф*@-Ф(*. 0.
то ввиду (8.13)
2л
о
if применив теорему 6.7.6, будем иметь
л я
\ |w' (/) - /<} б (/) Л = $ «>' @ б (О Л 3* О.
и о

222 приближ класса Vh^ Функи. класса \vr^xK [гл\ 8
Этим установлено, что
Е (/, W lK)c ^ \ К (/) - К] Фы @ dt, (8.15)
где число Ь выбрано из равенства (8.13) по* функции gn
так что в конечном счете Ь зависит от /. Но мы можем
получить общую на классе WH™ оценку, перейдя в
правой части (8Л5) к максимуму но параметру Ь, О^Ь^п.
Таким образом, для любой f e WrH<° (г—1, 2, ...),
в предположении выпуклости о) (/) справедлива оценка
а
E(fy WrMr]K)c^-. max \ [со' (/) - Д'] Фаг (?) dt =
а
«•2 max \iba,t^(a-t)[<i>(t)-Kt\dt. (8.16>
По поводу неулучшаемости оценки (8.16) на классе
WrHw отметим следующее. Бели максимум по а в (8.16)
достигается при а = п/п (/2=1, 2, ...), то знак равенства
имеет- место для функции \пг (§ 7.3), принадлежащей, как
нам уже известно, классу Wh® (при выпуклом а) (/)).
Действительно, в этом случае
max U
- \ Ф*п. г (/) а)' (() dt-К \ Фя/Я. г (t) dt =
О О
= UnrVc-Kri<Vntr+i\c. (8.17)
Но в силу общего неравенства
?п (/)с <?"«(/ — ф)с + ?п (ф)с < / - Цф [с + Еп (Ф)с
для любой (реи?л^!/( будем иметь
Й/«г- ФIc Ss Еп (fnr)c ~ ?rt (ф)с -1!\fnr \\с - ?л (Ф)с
и так как (см. E.27)) ?Лф)с</С[фя,,+1!!сэ то
inf г /яг — Ф i!c S= i /яг ile — /С i! ФЛ. rt-i i;c- (8.18)

§8.2} ОПЕНКА ПРЙБЛИЖПНПЯ ПРИ г>1 223
Из сравнения (8.16), (8.17) и (8.18) вытекает, что
в рассматриваемом случае
inf 5 fnr - ф !!с = 5 fnr ]с - /С!! ф„, *., !!с «
- [/«г (•) - /СФ„, г+1 (• + ?) |!с = ^ Фл/«., @ [»' (/) - К) dt.
6
При фиксировашюм модуле непрерывности со @ для
каждого /2 — 1, .2, ,.. можно выбрать число К = КПг
таким образом, что максимум по а в (8Л6) будет
достигаться при а = я//г. Для этого надо положить
Я.'П ГГ 'Г2
где
Таким образом, имеет место следующее утверждение.
Теорема 8.2.1. Для любого выпуклого вверх модуля
непрерывности со(/) при всех г=1, 2, ... справедливы
соотношения
, . def
?(\«77/«, 1П/г1/0с- sup inf !!/-Ф-1с<
max \
max ^Ф^1(а-01«@-/С/]#- (8.19)
0<< J
К~Кпг выбрано так, что максимум по а
достигается в точке а я* я/л, /по в (8.19) имеет место знак
равенства.

224 ПРИБЛИЖ. КЛАССА
ФУНКЦ. КЛАССА
[ГЛ. 8
Отметим частные случаи:
а
Е (WW, W2K)c ^ г max I [a (t) - Ki\ dt\
E(W2H»,
max [ t [u>(t) -Kt} dt;
max
Bat-
-Kt\ dt.
Замечание. Легко проследить, что все
рассуждения этого и предыдущего параграфов проходят для
классов WwH® и W^jtliK функций периода 2/ (/>0), если,
разумеется, норму в L, вариацию, интегралы Стилтьеса
и 2-перестановку Ф(?г. О определять на [О, 2/J. Таким
образом,
вфл,@К№-*1Я.
(г-1,2,...)
причем знак равенства достигается здесь, если / = па0,
где а0 —значение
параметра а, реализующее
максимум.
§ 8.3. Наилучшее
приближение класса //"
классом WlMK—KW
При л —0 точную
оценку величины (8.1) на
классе Я® можно получить,
^ идя тем же путем, что и
в случае г^1. Правда,
чтобы сделать возможным
применение теоремы 7.5.1,
пришлось бы привлечь аппарат функций Стеклова и
наложить на i&(t) условие выпуклости.
Однако гораздо проще получить нужную оценку,
причем для произвольного модуля непрерывности, с по-
Рис. 21.

§ 8.3] ПРИБЛИЖЕНИЕ КЛАССА ДО КЛАССОМ W*MK 225
мощью предложения 8.1.1. Действительно, используя это
предложение и считая для определенности, что (рис. 21)
и, значит, q>n(t)-*K на (a, |J), будем иметь
Следовательно, для любой I
?(/, 1ГХ,/С)с = 1.7 — Фо i!c ^ i [о> (/, р-
^l max [o)(/, t)-Kt\.
Если учесть, что со(/, /) = const для /^л, то получаем
оценку
4 max [со (/,/)-#/]. (8-20)
Покажем, что на самом деле для любой функции /еС
в (8.20) имеет место знак равенства. Пусть /еС,
f\K KHl и
max [а)(/, 0-*'] = © (Л 'о)-Wo,
')-/(-0НИ/, /о).
а а:', а:" —точки такие, что
Тогда для любой функции
^! / (xf) - f (х") i -; Ф (jo - ф (^') I s* со (/, /0) ~ /с/и,
и, значит,
inf 17 —ФГс^-i
так что для f#W\wK в (8.20) возможен только знак
равенства. Если же f<=WlMK, то ш(/, t)<,Kt и (8.20)
дает 0 --О.
Сформулируем доказанный факт в виде следующего
утверждения.

226 иривлиж. класса wftiKii функц. класса \\'^~{к [гл. 8
Предложение 8.3.1. Для любой функции /еС
имеет место равенство
clef 1
Eif KHi)c=g inf iif-cplic-o max fco(/, /)-
Из предложения 8.3.1 немедленно вытекает
Теорема 8.3.2. Коков бы ни был модуль
непрерывности со @» справедливо равенство
def
= -J max [со (/)-/(/]. (8.21)
Существуют функции f e tfCl\ 5ля которых Е (/,
совпадает с правой частью (8.21).
Действительно, если /еЯA), то со(/, /)^а>(/), и
предложение 8.3.1 сразу дает оценку
l max [co(/)-W]. (8.22)
Пусть /0 (д:) — четная 2л-периодическая функция,
равная <о(х) на [0, я1. Тогда со(/о, /)=со(/) (О^^^л) и,
опять же в силу предложения 8.3.1
Е (/0, КН1)с = I max [о> (/0, /) - Kt] -
О ^^ ^ л
О ^^ ^ л
= -1- max
2
Приведем еще одно довольно простое и элементарное
доказательство неравенства (8.20), не опирающееся на
предложение 8.1.1. (Впрочем, само предложение 8.1.1,
из которого оценка (8.20) вытекает немедленно, можно
доказать с i.oмощью элементарных рассуждений, не
опираясь на глубокие факты главы 3.) Фиксируем / е С\КН\
обозначим для краткости
= max [o)(/, /) — К
* 0</<Л
и положим

§8.4] ДРУГОЙ ВЫ ИОД ОЦЕНКИ ДЛЯ Е n(WH^ 227
Для любых х' и х", считая для определенности, что
Фо (*')< Фо (*") и фо(л:')=гИ'ь л*'), будем иметь
Фо (^") —
,*"-'i — /(/х)— И — /С | ^с' — /х f
Этим доказано, что фо<= KHl= WmK. Далее, по
определению для всех х
т. е.
<fo{x)-f(x)^\i. (8.23).
С другой стороны, фиксируем х, и пусть
Тогда
^ max lco(/, 0 — /С/] — |*.
и, следовательно,
f(x)-^(x)^\i. (8.24)
Из (8.23) и (8.24) видно, что
[/~Фо1с^
и тем более
§ 8.4. Другой вывод точной оценки для ?rt(Wr//w)c
Точную оценку наилучшего приближения
тригонометрическими полиномами на классах WrHl° (r = Qy I» ...)
(при выпуклом cd(Q) можно немедленно вывести из
теорем 8.2.1, 8.3\2 и результатов § 5.4 о точном значении
верхних граней наилучших приближений на классах

228 ПРИБЛИЖ. КЛАССА Wr/fm ФУНКи. КЛАССА Wrj$~XK [ГЛ. 8
Рассматривая сначала случай г^1, выберем число
К = Кпг из условия
а я/л
max \ Фог (О [<¦>' (/) -K]dt= \ Ф„/й., (/) fcof @ - К] dt.
Пусть /е1Г7/ш и ф0 —функция из №мМЛ' такая, что
Учитывая, что (см. E.27), § 5.9 и G.46))
л /я
?«(Фо)с<?«(^л.+ '/Ос = /С^Й1 = /С ^ Фл/«.,(/)dt, (8.25)
о
будем иметь по теореме 8.2.1
?»(/- Фо)с + Еп (Фо)с ^ U - Фо 11с + Еп (фо)с ^
I 4>*n. г @ [со' (t)-K]dt + K \ Ф«/«. г (/) Л -
о о
я/п
Следовательно,
^я (/)с < :;/Л,[с V/ € WrH» (я, г « 1, 2, ...).
В случае г = 0, т. е. когда /еЯй, также вводим
функцию фо ^ U^ai/C, для которой
U-<?o[k = E(f, W'MK)c,
и, опираясь на теорему 8.3.2 и равенства E.27), пишем
оценку
max [©(/)_/f/J +/С ф,
где /С>0 произвольно. В частности, эта оценка будет
верна, если К = /Сй выбрано из условия
max
причем этот выбор всегда можно осуществить, если со (/) —
выпуклый вверх модуль непрерывности.

§ 8.4] ДРУГОЙ ВЫВОД ОЦЕНКИ ДЛЯ Еп (WrH((f)c 229
Выбрав указанным образом К и заметив, что &?х = л/2,
будем иметь
т. е.
En (f)c ^ 2 ^ \ п ) ^f е ^ * (п ~ 1» 2, ...).
Можно заметить, что при r^Q указанный здесь путь
получения точной оценки для Еп(Н0))с> не связанный
с теорией 2-перестановок, проще, чем тот, которым мы
шли в главе 7. В случае же г>1 оба пути получения
точной оценки сверху для tn(WrHll))c идут через
основные теоремы для ^-перестановок и вполне сравнимы пь
сложности.

ГЛАВА 9
ТЕОРЕМЫ ДЖЕКСОНА И ТОЧНЫЕ КОНСТАНТЫ
§ 9.1. Неравенства Джексона в С и Lp
В 1911 г. Джексон [1] доказал, что если feC, то
*я(/)с<к«(л \) (я-1. 2,...), (9.1)
а если f^Cr (г= 1, 2, ...), то
E (/) < ? f/w
п
(я, г = 1, 2, ...), (9.2)
где константы х и кг не зависят ли от /, ни от п. Эти,
а также аналогичные им соотношения в других
функциональных пространствах известны в теории приближения
как теоремы (или неравенства) Джексона. Смысл их
в том, что они дают оценку скорости сходимости к нулю
наилучшего приближения тригонометрическими
полиномами в зависимости от дифференциально-разностных
свойств приближаемой функции.
Неравенства (9.1) и (9.2) Джексон получил,
аппроксимируя функцию / с помощью введенного им линейного
метода, который давал в (9.2) константу хл, хотя и не
зависящую от / и п, но неограниченно возрастающую
при увеличении г. В дальнейшем было обнаружено, что
в (9.2) можно поставить константу, не зависящую и от /-,
и появился интерес к задаче по отысканию точных
констант в неравенствах Джексона. Именно этой задаче
посвящена настоящая глава. Но предварительно мы
покажем, как можно вывести неравенства Джексона в Си
в Lp из результатов, полученных в предыдущих главах.
Если /^С, /^ёconst и со(/, f) —модуль
непрерывности функции / в С, то в силу леммы 7.1.5 существует
выпуклый модуль непрерывности а)* (/) такой, что
со(/, /)-^<М0<2<о(Л О 00). (9.3)

§ 9.1] НЕРАВЕНСТВА ДЖР.КСО11Л В С И Ln 231
Р
Первое неравенство в (9.3) означает, что / е Н®* , а потому
в силу G.45)
Учитывая же второе неравенство в (9.3), можем
написать
Еп (/)с < со (/, -?-) (я -1,2....) V/ е= С. (9.4)
Мы получили неравенство вида (9.1) с заменой со (/, 1/л)
на со(/, л/л). Если речь не идет о точной константе, то
эта замена не имеет значения, так как в силу свойств
модуля непрерывности (§ 7.1)
(с 1 \ ( ? я\ /г 1 \
v ' л / "~"~~ г п / ' v1 л /'
Оказалось, однако, что при отыскании точной константы
в неравенствах Джексона для 2л-периодических функций
удобнее значение модуля непрерывности функции / или
/(г) брать в точке я//г.
Пусть теперь f^Cr (r^l, 2, ...) и а>(/(/*\ /) —модуль
непрерывности r-й производной /(/0 в С. Если выбрать
выпуклый модуль непрерывности со* (/) из условия
то f e WrHm* и в силу соотношений G.44) и F.46) будем
иметь
л
If / /
где гЖг — константы C.44). Заменив со^ (л/л) на 2со (/(г),
я/л) и учитывая, что еТ,.^л/2 (г=1, 2, ...), получим
(л, г=1, 2,...) VfeCr. (9.5)
Перейдем к неравенствам Джексона в пространстве Lp.
Пусть /eLp A<р*?^со) и /л —функция Стеклова
для /. В силу полуаддитивности функционала наилучшего

232 ТЕОРЕМЫ ДЖЕКСОНА [ГЛ. 9
приближения (§ 1.2)
Еп (f)P = Ea(f-fh + fh)p < ?я tf - fh)p + En (fh)p <
Для функций Стеклова в § 5.2 были указаны неравенства
!/-/*(р<и</. h)pt (9.7)
1!ДК-^со(/, 2А)р<^-со(/, Л)р, (9.8)
последнее из которых означает, что fh принадлежит
классу WlpK с константой /f = —со(/, А)р. А так как
в силу E.72)
то
EnVk)p<*\*(f, h)p-^-. (9.9)
Положив А = л/л, из (9.6), (9.7) и (9.9) выводим, что
?л (/)р < -J со (/, -J)p A < р < сю) V/ е Lp. (9.10)
Если /eLj (r=»l, 2, ...), то снова вводим функцию
Стеклова fhf причем, как отмечалось в § 5.2, под"Дг> мы
можем понимать как (/л)(г), так н (f{r))h. Применяя тот
же прием, напишем
Еп(ПР^En(f- fh)p + En (fh)p. (9.11)
Так как (см. (9.7))
то разность / — fh принадлежит классу WrLpK с
константой К = афг\ h)p и в силу E.72)
En{f-h)P^^<*(r\ А)Р. (9.12)
Из неравенства же (см. (9.8))

§ 9.11 НЕРАВЕНСТВА ДЖЕКСОНА В С И Lp 233
руководствуясь теми же соображениями, найдем, что
ЕпЦн)Р^%±];<»{Г\ А),. (9.13)
Подставляя оценки (9.12) и (9ЛЗ) в (9.11) и полагая
h = n/n, будем иметь
Если опять учесть, что <?уГг^я/2 (г=1, 2, ...), то
можем написать
-п)р
п)р (9Л4)
(я, г-1, 2,...) V/eA; A<р<оо).
Отметим, что, в отличие от неравенств (9.4) и (9.5)
для пространства С, соотношения (9.10) и (9.14) мы
получили, используя оценки приближения из главы 5,
доставляемые линейными методами. Из (9.10) и (9.14)
при /? = оо мы получаем неравенства Джексона для
приближения линейными методами функций из С и С. Более
тонкие рассуждения (см. §• 9.4) покажут, что при
нечетных г константы в (9.5) и (9.14) можно уменьшить
по меньшей мере в два раза.
Теперь сформулируем задачу, которой мы будем
заниматься в следующих параграфах этой главы.
Пусть X есть пространство С или Lp A^р<оо),
а Хг есть С или 1/р (Х° = Х). Требуется в неравенстве
?«(/)*<-¦><*>(/">, ")х (9Л5)
указать наименьшую из возможных констант кг. Хотя
мы уже знаем, что в (9.15) можно в качестве кг
поставить константу, общую для всех п и г, наилучшая
константа, вообще говоря, может зависеть как от X, так и
от п и г. Поэтому мы ее будем обозначать через кпг(Х).
Таким образом, задача состоит в отыскании
постоянных
f . Л_ COn.St
(9.16)
где X есть С или Lp (I ^/?<Coc)#

234 ТЕОРЕМЫ ДЖЕКСОНА [ГЛ.9
Аналогичную задачу можно поставить в случае
приближения функций f ^ Хг с помощью линейных
операторов Л, отображающих Хг в подпространство Fln-\
тригонометрических полиномов порядка /г—1. Ясно, что
особый интерес представляет здесь вычисление точной
константы, соответствующей наилучшему для Хг
линейному методу. Таким образом, мы приходим к задаче
отыскания величины
"n~ i ~i- cons!
Так как для любого линейного оператора А из Хг
в Fln—\ и любой feXr
то всегда к'пг (X) ^х/1Г (X). Естественно, что наряду
с вычислением констант xrtr(X) и к'пг(Х) интерес
представляет также выяснение случаев совпадения этих
констант, а также эффективное построение наилучших
линейных методов, которые реализуют это совпадение.
Ответ на эти вопросы получен лишь в немногих
отдельных случаях и, как мы увидим, совершенно
различными путями.
§ 9.2. Точная константа в неравенстве Джексона
для функций пространства С
Мы покажем, что в неравенстве (9.4) независимая
от / и от п константа 1 в правой части является точной,
т. е. уменьшена быть не может. Основную роль при
этом будет играть следующая
Л е м м а 9.2.1. При каждом фиксированном п = 1, 2, ...
для любого г > 0 существует функция f(t)=f (е, /) ф const,
такая, что
?„(/)с>A-^-е}со(/, -J). (9.18)
Доказательство. Фиксируем п и зададим е>0,
причем можно считать, что 0<e<V2- Положим
д:0^ о, xk~--kti-(n-k)fi {k = 1, 2, ..., /2), (9.19)

§9.2] ТОЧНАЯ КОНСТАНТА В ПРОСТРАНСТВЕ С 235
где
л=?. о<р<2.
При таком выборе числа C, как легко подсчитать, будет
Построим непрерывную периода 2л четную функцию
/(/), определив ее на полупериоде [0, я] следующим
образом:
/(**) = (-I)*-" (*=1, 2, .... я),
*=1, 2, .... л—I),
/(/) линейна (с сохранением непрерывности) на
промежутках
(**-Р<;*^хЛ) (*=1, 2, .... л), (дг*^*^** + Р)
(*=1, 2, ..., /2-1).
Докажем, что для построенной функции
*(Л ¦;)-». (9-20)
Заметим сначала, что *2 — *1 = Л + Р, т. е. (х2 —Р) —
— лгх = л/л, а так как по определению / (xi) = 1, / (х2 — Р) =
= 0, то
и теперь для доказательства (9.20) достаточно
установить, что для любых ti и t2 таких, что !/г — t2\*^fi будет
i)f(J|
В силу того, что max |/@!—1, мы можем ограни-
читься рассмотрением случая, когда f(tt) и f(t2) имеют
разные знаки, а ввиду четности / можем считать, что
tu <2^[0> я]. Тогда точки ii и /2 могут быть
расположены только следующим образом:
**<*1<** + Р, ^,г-Р</2<^,1 A <*</!- 1).
Из определения функции / следует, что если,
например, /(**)= 1. то
/(/) (/^

236 ТЕОРЕМЫ ДЖЕКСОНА [ГЛ. 9
а так как t* — tx<h, л'*:1 — хк =Л + Р» то
-/('2)—/('iWCsH
Случай f (xk) — — 1 рассматривается совершенно
аналогично. Соотношение (9.20) доказано.
Теперь введем в рассмотрение тригонометрический
полином
s(rt-l)/)f (9.21)
который можно записать (умножив и разделив на
2sin(f/2)) в виде
, _ 1_ sin (п-1/2)/ /9 92)
Тя(Г'п sin (//2) e (J^Z)
Из (9.21) видно, что
т„@)=1—1-, (9.23)
а используя представление (9.22), нетрудно подсчитать,
что
*n(kh) = ^p- (A=I. 2 я). (9.24)
Далее,
! т„ (л'„) - тп (Щ \ < max ; т'п (/) 11 xft - feft |t
и так как \xk — kh\ — (n — k) p, a
= !si
п . , -¦- . %.j — 1) sin (л —
TO
(9.25)
Из (9.23), (9.24) н (9.25) с учетом значений
функции f в точках (9.19), получаем
т„ (л-*) = |/ (х„) - хп (kh)\ + [т„ (АА) - т„ (дг»)| =
-—) + Mft (*-0, 1, .... п),

§9.3] ТОЧНАЯ КОНСТАНТА В ПРОСТРАНСТВЕ Ц 237
где
Учитывая четность функции / и полинома тя,
заключаем, что разность f{t) — Tn(t) в 2л точках на периоде
(—л, я] принимает значения с чередующимися знаками,
причем эти значения по абсолютной величине больше
чем 1 —1/2п—е. В силу теоремы 3.2.5 Валле-Пуссена
справедливо неравенство
в
которое вместе с (9.20) дает (9.18). Лемма 9.2.1
доказана.
Так как в лемме 9.2.1 г>0 произвольно, то вместе
с (9.4) она приводит к соотношениям
^*(С)<1 (л=1, 2, ...).
Формулируя этот результат в виде теоремы Лжексона,
получим следующее утверждение.
Теорема 9.2.2. Для любой функции feC, /^
^ const, справедливы неравенства
En(f)c«»[f, J) (л=1, 2,...),
причем не зависящая от f и от п константа 1 перед
со(/, п/п) уменьшена быть не может.
§ 9.3. Точная константа в неравенстве Джексона
для функций пространства Lz
Еще один точный результат в рассматриваемой задаче
можно получить, используя специфику пространства 12.
Теорема 9.3.1. Для любой функции f из L>, не
являющейся константой (с точностью до множества меры
нуль), имеют место неравенства
E*V)t<yz<»[f, f\ (л = 1. 2, ...), (9.26)
причем при каждом п константа 1/|/~2 в правой части
уменьшена быть не может.

238 ТЕОРЕМЫ ДЖЕКСОНА fJYI 9
Доказательство. Оценку (9.26) мы выведем
из более тонкого, но тоже пеулучшаемого неравенства
ял Л 1 /2
l\ jj (о2(/, tJ sinntdt\ , (9.27)
справедливого для любой функции / е /<2. Чтобы
получить (9.27), запишем ряд Фурье функции / из L2:
и учтем, что в подпространстве тригонометрических
полиномов порядка п—\ наилучшее приближение функции f
в метрике L> доставляют частичные суммы этого ряда,
т. е. суммы
п — 1
Sn (Л х) = з" + 2 (а* cos ** + b* sin kx)
k---1
и, следовательно,
?« (л.=[ / - sn ф ;;.i - i x (a* cos ь-+^ sin k) j
:= Я
Положив для краткости a| + fc/l = Pb в силу равенства
Парсеваля будем иметь
?ИЛ2 = "!>*. (9-28)
k = n
Оценивая модуль непрерывности со (/, tJ функции /,
заметим, что
со
f(x + u)-f(x)~ У] \\ak(cosku-l) + bks\nku]coskx +
k--=\
+ {bk(cosku— I) —аь sinku] sin/гд:},
так что, опять по равенству Парсеваля,
= я 1] {[fl* (cos 6w - 1) + bk sin Aw]2 + [/?л (cos ku - 1) -
} = 2я У] р| A-cos Аи). (9.29)

* 9.3] ТОЧНАЯ КОНСТАНТА В ПРОСТРАНСТВЕ Ц 239
Поэтому для любого /^Ос учетом (9.28) можем написать
и ^t
> 2я У] р? A - cos W) = 2?*" (/J - 2я >] р? cos kt
к — п k-^n
ИЛИ
Е*„ фг < з ^ V' ')* + я Т Р* COS W- (9-3°)
При i e [0, л/л] умножим обе части неравенства (9.30)
(они неотрицательны) на sin /г^ и проинтегрируем по i
от 0 до я/л; это возможно, так как ряд в правой части
мажорируется па всей оси сходящимся числовым рядом
i]f>?. Получим
л'л
-п Е'п ф, <¦ 2 J ^2 (/. 02 sin nt (it + я У
6 л=«
где
я/я
с^= 5 sin nt cos kt dt. (9.31)
о
Легко проверяется, что crt — 0, с*-^0 {k>n)y поэтому
л/л
^(/)^
\ & tf. fa sin nidt,
о
и неравенство (9.27) доказано.
Из проведенных рассуждений ясно, что знак
равенства в (9.27) будет заведомо иметь место, если
выполнены следующие три условия:
1) со(/, /J = |!/(- + 0—/(Oi ДЛЯ всех 0</*?я/я,
т. е. функция
5/(- + и)-/(-):5 = 2я ? р|A-cos*?/)
не убывает на [0, п/п]\
2) pi = O (A-1, 2 я-1);
со
3) У] р^* = 0, где ck определены равенством (9.31).

240 ТЕОРЕМЫ ДЖЕКСОНА [ГЛ. 9
Все эти условия выполняются, например, для
тригонометрических полиномов вида
f (х) = а0 + аг cos nx + рх sin nxy
которые, следовательно, реализуют в (9.27) знак
равенства.
Чтобы из (9.27) получить (9.26), надо лишь заметить,
что если f(x) отлична от константы, то о)(/, я/лJ>0 и
л п п'п
[ J(f, f)zsinntdt<afi(f, пп) [ sinntdt= •?•©
[ ( п [
0 О
Докажем неулучшаемость оценки (9.26). Фиксируем п
и задав б@<б<я/я), построим четную периода 2л/п
непрерывную на всей оси функцию ?„F, /), полагая
Функция g"^ (б, /) разлагается в ряд Фурье
со
sin «v6 \2
jcos
v=l
причем ^(б, 0)-=1, #„(б, 0^0 для
Положим
Соотношение (9.29) позволяет для нашего случая написать
Так как я„ (б, 0 (как функция от /) не возрастает на
[0, я/п], то учитывая (9.28), будем иметь
?•» /г \ 2 V / sin

§ 9.31 ТОЧНАЯ КОНСТАНТА В ПРОСТРАНСТВЕ 1% 241
так что
и остается заметить, что б может быть сколь угодно
близким к нулю.
Результат теоремы 9.3.1 с учетом обозначений (9.16)
и (9.17), а также того факта, что наилучшее
приближение в L2 реализуется линейным методом, может быть
записан в виде
х„о (L2) = у/по Щ) - ~ (п = 1, 2, ...). (9.32)
Вернемся к неравенству (9.27). Если функция со2 (/\ t)z
выпукла вверх на [0, я/л], то существует линейная
функция l{t) такая, что
Имеем
л/л
\ <о2(/, tJsmntdt=*
о
я п
я я/
= jj К (/, /)а - / @] sin nt + jj [/ @ - (о2 (/, 2яп]] sin nt dt +
о о
я; /л
Первый интеграл в правой части неположителен (и
обращается в нуль, если функция ш2 (/, tJ линейна на [0, л/я]),
второй интеграл равен нулю. Таким образом, приходим
к оценке
*.</>.<рНл$,' (9-33)
справедливой для всякой функции /^L2, у которой
<°2 (Л 0г выпукла вверх на [0, я/л].
Если обозначить через КН}/2 класс функций / из /,2,
для которых (*)(/, tJ'^K\^i\ то в силу. (9.33)

242 ТЕОРЕМЫ ДЖРКСОНА [ГЛ. 9
Нетрудно доказать, что оценка (9.34) неулучшаема
на классе КЩ'2, причем достаточно в этом убедиться,
считая /С=1. При фиксированном л=1, 2, ...
рассмотрим функцию
Так как (см. (9.29) и § 5.4)
со
г I / I \ I / \i" 4 VI 1 —cos Bv-|-1) пи я
. t» (• + «) -*«(•) Ji = ;-,„ 2 B7+1]^— = 2„
\ -=0
то
и, значит, флеЯ]-2. Легко видеть также, что для
функции г|?я (/) выполнены условия 1) —3) (стр. 239),
гарантирующие знак равенства в (9.27), а в силу линейности
ш2(Ф/и Ог на [0» я/л] знак равенства будет при / = фя и
в соотношении (9.33).
Таким образом, доказано, что
Еп (КН\~J = \ V^fn (л -1,2,...). (9.35)
Если /еЦ (/"^1, 2, ...) и по-прежнему р? = р?(/)^-.
^ai + W. где ал и ^ — коэффициенты Фурье функции /,
то в силу (9.28)
по
EhWi^n У (*J'|»Ш. (9-36)
а так как pj (/<^)^A2rp| (/), то
EhW2^n\rEh(J{r))*. (9.37)
Знак равенства в (9.35), а значит и в (9.37), имеет место,
лишь если р* = 0 (A--/1-J-1, /г+ 2, ...), т. е. если / есть
тригонометрический полином порядка п.
Сопоставив (9.37) с (9.27), приходим к оценке
Епф2<:21пГ\п{ со2 (/"¦>,' 02 sin ntdti (V/e/4), (9.38)
I о J

§ 9.41 ТОЧНАЯ КОПСТЛНТА ДЛЯ Сг И if 243
точной на множестве Ц, ибо равенство в (9.38) имеет
место для многочленов вида ао4-а, cos я/+ Pi sin/г/.
Из (9.38), как и в случае г--=0, выводится, что для
любой функции / из Ц, не равной константе, справедлива
оценка
^7@^ -') (л. r-If 2f ...), (9.39)
Вопрос о точной константе в неравенстве (9.39)
остается открытым.
§ 9.4. Точная константа в теоремах Джексона
для Сг и U при нечетных г
В этом параграфе будет построен линейный оператор со
значениями в тригонометрическом подпространстве FJ^-i»
который реализует в неравенствах Джексона для С и //
точную константу при г=1, 3, 5, ...
При h>0 зададим на f—ft, h] последовательность
функций gr(t) следующим образом:
*W (А</<А);
^@=$?ri(«)d" (r = 2, 3, ...),
где уг (—Л*<7/-<0) выбрано так, чтобы обеспечить
выполнение условия
$ вг@Л = 0.
—ft
Положим далее
O2v@-fev(<)-*2v(A) Г—Л<<*;Л) (v = 0, 1, 2, ...),
G2v*i@ = &v4(<) (—Л</<А) (v = 0, I, 2, ...)
и заметим, что
Gr(-h) = Gr(h) = 0 (r=l, 2, ...),
О; @=^1@ (г = 2, 3, ...)

244 ТЕОРЕМЫ ДЖЕКСОНА [ГЛ.9
(при г =^2 последнее равенство выполняется везде, за
исключением точки / = 0).
Функции / е Хг, где Хг будет обозначать С или L?
A^р<оо), сопоставим функцию Стеклова
h h
fh (X) = I jj / (X + t) dt = I jj / (A- - 0 di
-h — h
И ПОЛОЖИМ
Ahr (/, a:) = / (л-) + 2/i 2] g2v (A) /{?v) (x) (9.40)
(r=l, 2, ...).
Лемма 9.4.1. Функцию Ahr(f, x), определенную
равенством (9.40), можно представить в виде
Ahr(f, *)=$ Gr(t)fW(x-t)dt (r=l, 2, ...). (9.41)
—л
Доказательство. Пусть г—1. Тогда из (9.40)
видно, что
Ач(/> x)^f(x)-h(x). (9.42)
С другой стороны, преобразуя правую часть (9.41) при
г = 1, будем иметь
h h
^ Gl{t)r{x-l)dt = --\ jj (l- J}d/(jc-/) =
о о
л
0
\ S
—л —л
—л
так что

§ 9.4] ТОЧНАЯ КОНСТАНТА ДЛЯ Сг И Lr 245
При г~ 1 лемма доказана. Далее действует индукция.
Пусть утверждение леммы справедливо для г=1, 2, ...
..., k— 1. Рассмотрим два случая:
1) k четно, * = 2/. В силу (9.40) Ah%v{f4 x) = Ah%v itf, *),
поэтому, учитывая предположение индукции, а затем
интегрируя по частям, будем иметь
я (л; _ /) dO2/ (/) =-- J /<«/> (л; - 0 О2/ @ Л,
л
J
—л
ибо Gv(-h) = G2i(h)=--Q.
2) А? нечетно, Л = 2/+1- Исходя из (9.40) с учетом
предположения индукции найдем
Л, 2/.1 (Л *) - ЛЛ,2/ (/, л:) + 2hg2/ (h) ft» (x) «
^ v _ t) Gtl (/) Л + ft/ (h) $
I
-h
5
= 5
5 ]
—Л —Л
Лемма 9.4.1 доказана.
Лемма 9.4.2. Имеют место равенства
я/2/i Г (г— 1)/2]
J |()|?^T1 = fr (9.43)
—я/2/i
(п, г=1, 2, ...),
где Жг —константы C.44).
Доказательство. Условимся для сокращения
записи в промежуточных выражениях полагать л/2п = Л.
Пусть г = 2/ — 1 (у = 1, 2, ...). Положив в (9.41) /(*)-
= фя,2/-1 (*) (флгМ —та же функция, что и в § 5.4),
а также д: = 0, и учитывая вид (9.40) функции ЛЛг(/, л:),

246 ТЕОРЕМЫ ДЖЕКСОНА [ГЛ. 9
будем
фя.1/1
иметь
h
—Л
Л
ftv(A) J фя,2,
:оф«о(—ол
' = — J <
—л
л
-ом I1
-л
02/ _! @
Ф«0 ('
\dt.
!)<Н
(9.44)
ибо для \t | < A sign Go/ i (/) = (—I)'"'1 sign ф^0 (t).
Так как, далее,
g2x (h) = (—ly-1 !g2v (h) ], (9.45)
Фл,2м@) = (— iy--zrr9
n
h
,,^2v-i (t) dt = 2фл,а/ av (A) = 2 (-l)/-v • a_
—Л
то (9.44) запишется в виде
,¦ j
/ 1 у/<%>2/-3 / п/о V
V = 0
= (-1)' \\Gihl(t).\dt,
\
—Л
что равносильно (9.43) при г = 2/ — 1.
Теперь пусть г=^2/ (/=1, 2, ...). Полагая в (9.41)
/(*) = фя,2/(* + А) и х^=0, будем иметь, учитывая (9.40),
/ h
Фп.1/ W + 2 ftv (Л) \ ФЯ.2/-2У (^ + А) Л =
v = 0 -^Л
Л h
= ^ 02/(Офло(Л-/)Л = (-1)/ \ \Gv-(t)\dt9 (9.46)
-Л -Л
ибо sign Gv (/) = (-1)/ Фя0 (А - /) (| /1< Л).

§ 9.43 ТОЧНАЯ КОНСТАНТА ДЛЯ С И Lr 247
Если снова учесть (9.45) и то, что
h
\ <P«,2/-2V {t + h)dt = ф/?|2; 2Vrl (Щ — фя§2/-2\ч-1 @) =
—/i
то (9.46) запишется так:
= (-1)/ $ .10,, (/)!*.
—А
что совпадает с (9.43) при г ~2/. Лемма 9.4.2 доказана.
В § 5.5 были рассмотрены линейные операторы Un(X) =
^Unr(k), реализующие на классах W'mK и WlK верхние
грани наилучших приближений соответственно в С и /„.
Было доказано также (см. E.42)), что если /еАг, то
ti-Unrif, Ц!л^^1!г:;л. (9.47)
Введем в рассмотрение операторы Bnrt определенные
на Хг равенством
[{г- D/21
где /Л, как и выше,—функция Стёклова для / и /i — л/2«.
Так как Un.r.2\-+i(f> x, Я,) —тригонометрические полиномы
порядка /г—1, линейно зависящие от /, то Впг также
есть линейный оператор, отображающий Хг в
подпространство Ftn—i тригонометрических полиномов порядка
л-1.
Теорема 9.4.3. Для любой функции |еХг ярм всех
нечетных г--- 1, 3, 5, ... справедлива оценка
'if - Bnr (f) ел <^ «о (/и. ; )л (и - 1. 2, ...). (9.48)

248 ТЕОРЕМЫ ДЖЕКСОНА [ГЛ. 9
Доказательство. Имеем для f e Хг
f(r—U/2J
)-?/i.fr-tvu(A2v). Щх-
(9.49)
Так как fh e Xr+1 и, значит, /^2v> e A/r+1-2v, то в силу
(9.47)
]|cBv) rr /fBv) П;| Т
a < nr-av-ri llh
Из общего неравенства для функций Стеклова
следует, что в нашем случае
и поэтому
(| pBv) tt
|!/л — c/
В силу леммы 9.4.1, учитывая свойства функции Gr(t)
при нечетных г, будем иметь
\Ahr{I)h = l \ Gr(t)j^(x-t)dt\ =
= l\Gr(t)\]"(x-t)-p*(x + t)]dt\ . (9.51)
ii о iix

§9.4] ТОЧНАЯ КОНСТЛНТЛ ДЛЯ Сл И L* 249
Если X = Lp A*^/?<oo), то продолжим оценку
с помощью обобщенного неравенства Минковского:
о
\Gr(t)'P J^ (x-t)-f^
dx) * dt
0
5
—Л
В случае Х = С соответствующая оценка получается из
(9.51) очевидным образом. Итак,
h
I Лпг (f) Ix^l* ff\ v)x 5 I Gr {() i dt. (9.52)
Подставив (9.50) и (9.52) в (9.49) и используя лемму 9.4.2,
получим при нечетных г
$1 2
-л v=o
7 • njx'
и теорема 9.4.3 доказана. Из нее следует, что для любой
f(=Xr(r = 2j-l, /=1,2,...)
) Я
f nix
=1, 2, 3, ...). (9.53)
Покажем, что в случае Х = С и X = L неравенство
(9.53) не может быть улучшено.
Так как в силу определения модуля непрерывности
(§ 7.1)

250 ТЕОРКМЫ ДЖЕКСОНА [ГЛ. 9
то, считая везде ниже, что [фconst, будем иметь
ЕпФх l
ЩИ" чп) ^ 2
Функция Стеклова qv,*(*) Для стандартной функции
ф/irW. очевидно, принадлежит С и при достаточно
малых h
Если учесть, что в силу A.13)
то из (9.54) при Х = С получаем
?() + е(Л) = |г + е(/1) (л, г=1, 2, ...),
где величина е(Л) —»-0 при А-+0 и потому может быть
опущена. Таким образом,
что означает неулучшаемость оценки (9.53) на всем
множестве Сг.
Совершенно аналогично, вводя функцию Стеклова
gn,r 1,л Для функции #„,,.-1 и замечая, что gn%r hh<=Lr и
при малых Л
из (9.54) при X = L получим
+ Pi (Л) =
(л, r=I, 2Э ...),

§ 9.4] ТОЧНАЯ КОНСТАНТА ДЛЯ С И Z/ 251
где ?ХAг)->() при ft->0, так что
J^^W («.'-1.2,...). (9.56)
Ясно, что в связи с (9.53) в (9.55) и (9.56) при
нечетных г на самом деле должен быть знак равенства. Эти
результаты, с учетом того факта, что, как это видно из
теоремы 9.4.3, оценка (9.53) получена с помощью
линейного метода, можно сформулировать следующим образом,
привлекая обозначении (9.1G) и (9.17),
Теорема 9.4.4. Справедливы равенства
(л, / = 1, 2, ...).

ГЛАВА 10
ПОПЕРЕЧНИКИ НЕКОТОРЫХ КЛАССОВ
ПЕРИОДИЧЕСКИХ ФУНКЦИЙ
§ 10.1. Вводные замечания
В этой главе будут изложены некоторые результаты
по задаче III, сформулированной в § 1.1. Речь будет идти
о вычислении поперечников классов функций, причем мы
ограничимся рассмотрением только тех классов
периодических функций, на которых в предыдущих главах
найдено точное значение верхней грани наилучших
приближений тригонометрическими полиномами.
Напомним, что п-мерным поперечником (по
Колмогорову) центрально-симметричного множества ЯЧ в линейном
нормированном пространстве X размерности ^п
называется величина
dn($l9 X) = inf?CNf F,b = inf sup inf ]*-
F F ЯйР
где последний раз точная нижняя грань берется по всем
подпространствам Fn фиксированной размерности п.
Линейный поперечник множества ЗМ в X есть по
определению величина
d'n CMt X) - inf Ш (:l\\ Fa)x = inf inf sup fx-Axjx,
где Л —линейный оператор, отображающий X в Fn.
Из определений вытекает, что с возрастанием п
величины dn и d'n не возрастают. Действительно, пусть Fn —
произвольное подпространство в X размерности п и
{а'ь *2, ..., хп) — элементы, образующие базис Fn.
Добавив к ним элемент хп,л<= X\Fny не являющийся их
линейной комбинацией, получим подпространство Fn^x
размерности п~\- 1, причем так как, очевидно, Fn a Fnvl, то для
любого х е X
inf [х — и^х^ 'п^ ''* — и}х,

§ 10.13 ВВОДНЫЕ ЗАМЕЧАНИЯ 253
т. е. всегда есть подпространство размерности п -f 1,
приближающее любой элемент xe:W не хуже чем Fn. Таким
образом, если иод </0(:W, А') условимся понимать просто
величину sup \\х]к, т. е. приближение множества 301 ну-
левым элементом, то можем написать
<№, XJ*d1(*Dl, X)^...^dn(W9 Х)т*...
Аналогично убеждаемся в том, что
di($)i9 X)s*du$it x)>...>«(аи. X)?*...,
где под d?C0i, X) подразумевается также sup \\x]x-
Отметим также, что из неравенства
справедливого для любого подпространства F,u следует,
что
«МЭМ, Х)^А(ЗМ, X), A0.3)
а из положительной однородности функционала E{fyFn)x
следует, что
4№ X) = \X\dn(M, X) (А €=/?,).
Так как
dn(m, Х)*?,Е(Ш, Fn)x, A0.4)
где Fn~ любое д-мерное подпространство, то результаты,
полученные в главах 5—7, где найдены точные значения
наилучших приближений тригонометрическими
полиномами классов WrAU WrH™ в С, W'L,Wrv и 1ГЯ* выдают
оценки сверху для поперечников этих классов
соответствующей размерности в соответствующих пространствах.
Точно так же в силу неравенства
f Fa)x, A0.5)
справедливого для любого подпространства Fn из X
размерности я, результаты главы 5, связанные с
приближением классов WrM% WL и Wv линейными методами, могут
быть использованы для оценки сверху линейных
поперечников этих классов.

254 ПОПЕРЕЧНИКИ К Л ЛССОП ФУНКЦИЙ ГГЛ. 10
Что касается получения для поперечников точной
оценки снизу, то в ряде случаев эффективным здесь
оказывается применение утверждения, известного как теорема
о поперечнике шара.
§ 10.2. Теорема о поперечнике шара
Сначала мы приведем более слабый вариант теоремы
о поперечнике шара.
Предложение 10.2.1. Если U —замкнутый
единичный шар линейного нормированного пространства X, /п. е.
и размерность X больше чем п% то
Предложение 10.2.1 немедленно вытекает из следующего
почти тривиально доказываемого утверждения, которым
мы воспользуемся также при оценке поперечников
некоторых классов функций.
Предложение 10.2.2. Пусть X —линейное
нормированное пространство размерности, большей чем n,Fn—
его п-мерное подпространство и у> 0. Существует элемент
Уо^Х такой, что [уо1 = у и
Действительно, фиксируем х^^Х\ЕПч и пусть и0 —
элемент из Fny ближайший к #0 (он существует в силу
1.3.1), т. е.
<'ei
inf f лг0 — " 1 ¦*= d>0.
F
Положим 0о = -|-(*о —"о)- Ясно, что 'r/of = Y» и так как
для любого и ^.Fn
то Е(у0, Fn)x^y.
С другой стороны,
Е(Уо* Р
и, значит, Е A/о, Fn)x - у.
ч

§ J0.2] ТЕОРЕМА О ПОПЕРЕЧНИКЕ ШАРЛ 255
Возвращаясь к предложению 10.2.1, заметим, что
неравенство
?(?/, Fn)x*Zl
очевидно, а из предложения 10.2.2 следует, что ?(?/, Fn)x^
^ds I, так что
?(?/, Fn)x=L
Остается заметить, что это равенство справедливо для
любого n-мерного подпространства Fn.
Более глубоким, чем предложение 10.2.1, является
тот факт, что д-мерный поперечник пересечения шара U
с (п+ 1)-мерным подпространством из X тоже равен
единице.
Теорема 10.2.3 (о поперечнике шара). Пусть
М„ч — {п-\- \у мерное подпространство линейного
нормированного пространства X, а ипЛ — замкнутый единичный
шар в Ма*и т- е-
Тогда
Доказательство теоремы 10.2.3 базируется на
следующем факте топологического характера, известном как
Теорема Борсука [1]. Пусть Хпч —линейное
нормированное пространство размерности n + 1, a
Sn—единичная сфера в Хпи т. е.
Если оператор Р (х)у отображающий Sn в п-мерное
линейное нормированное пространство Ynf является
непрерывным и нечетным (Р (—х) = — Р (х)), то существует точка
xQ e S,;, в которой Р (х0) = 0.
Доказательство теоремы Борсука для случая,
когда Xni есть RnJrU т. е. (п+ 1)-мерное евклидово
пространство, мож}ю найти в специальных книгах по
топологии (см., например, Спепьер [1], стр. 344). На общий
(сформулированный выше) случай она переносится
тривиальным образом в силу изоморфизма конечномерных
пространств одинаковой размерности (Л. А. Люстерник,
В. И.Соболев [1], стр. 72).

25G ПОПЕРЕЧНИКИ КЛАССОВ ФУНКЦИЙ [ГЛ. 10
Доказываем теорему 10.2.3. Так как dn (Un]1, X) <z
^^0(?/ядь X)=If то надо показать, что для любого
я-мерного подпространства Fn из X ?(?/„, ь Fn)x**l.
Фиксируем подпространство Fn и рассмотрим сначала
случай, когда норма в X строго выпукла (§ 1.3). В силу
предложений 1.3.1 и 1.3.3 для любого х е X в
подпространстве Fn существует и притом единственный элемент
наилучшего приближения и = Р(х). Оператор Р (х),
отображающий X в Fn% является непрерывным и нечетным
(предложение 1.2.2).
Рассматривая оператор Р (х) на сфере
в силу теоремы Борсука заключаем, что существует
элемент ?eSrt такой, что Р(г)^0. Но тогда, так как Sn с
.czUn,u то
и теорема 10.2.3 для случая строго выпуклой нормы
доказана.
Пусть теперь норма в X не является строго
выпуклой. Вместо пространства X будем рассматривать его
конечномерное подпространство Х\, базисом которого
является система всех линейно независимых элементов из
объединения базисов МпХ и Fny так что МпЛ и Fn
содержатся в XiV. Этот переход, учитывая наши цели, мы
вправе сделать, ибо для х <= МП:1 Е (х, Fn)x = Е (*, Fn)xN.
Затем аппроксимируем норму \x'[ — ^x]xN пространства
-Хд' строго выпуклой нормой следующим образом. Пусть
i:xf —строго выпуклая (например, евклидова) норма в А',у
В силу теоремы об изоморфизме конечномерных пространств
существует число Р>0 такое, что
\х\'^$\х\ VjceXAr. A0.6)
При любом е>0 числовая функция
также является нормой в Хх, строго выпуклой, как и
\\х{{, причем ввиду A0.6)
lH Vxs=XN. A0.7)

§ 10.2] ТЕОРЕМА О ПОПЕРЕЧНИКЕ ШАРЛ 257
Положим
Пели х и у отличны от нуля и уф^х, то (§ 1.3)
и тогда
т. е. норма 'Ijc1,0 удовлетворяет условию строгой
нормированное™, а потому тоже строго выпукла. Кроме того,
из A0.7) и A0.8) видно, что
Пусть Х% есть пространство, полученное из XN
заменой нормы ji*1 на f*!0. К пространству Х% применимы
приведенные выше рассуждения для случая строго
выпуклой нормы, в силу которых существует элемент г*=гее
^ Л1л+1 такой, что
j?l l*"-"^!*-0^1- A0.10)
Чтобы оценить наилучшее приближение элемента г
подпространством Fn в метрике XN, заметим, что в силу
A0.9) для любого u<=Fn
Переходя здесь к точным нижним граням no «e Fn и
учитывая A0.10), будем иметь
Но из A0.9) и A0.10) следует, что ]г[^ 1, т. е. ге?/я+ь
а потому
E(UniU Fa)XN^:EB9 FH)xN>l-z.
Так как е>0 здесь произвольно, то
Е(ияП9 Fn)XN^l
и, значит,
E(Un,u Fn)xz*l.
Теорема 10.2.3 доказана.

258 nom-ргчмпки классов функций ггл ю
Замечание 1. В формулировке теоремы 10.2.3 шар
ип+у можно заменить единичной сферой
Sn={x: х^ия,и ]х[=1};
Действительно, с одной стороны, dn(Sn, Х)*?*
*^dn(Un+u X)-=l, а с другой, при оценке поперечника
снизу мы фактически доказали, что dn(Sn, Х)'^\.
Замечание 2. Если X имеет размерность п+l, то
теорема 10.2.3 содержится в предложении 10.2.1.
Применение теоремы 10.2.3 для оценки поперечников
в конкретных случаях облегчает непосредственно
вытекающее из нее
Предложение 10.2.4. Если множество 5Ш
линейного нормированного пространства X содержит тар yUn±i
радиуса у некоторого (п+1)-мерного подпространства, то
Действительно, из включения yUn^cz^l следует, что
:Qi, X)^d(yUn±u -X)» и остается учесть, что
dn(yUnrli X) =
§ 10.3. Поперечники классов W[2 в пространстве L2
Рассмотрение конкретных случаев вычисления
поперечников начнем с самого простого, когда решение задачи
облегчается особенностью метрики гильбертова
пространства L2.
Заметим сначала, что наилучшее приближение элемента
х е L2 N-мерным подпространством F^ из L* реализуют
суммы Фурье элемента х по ортонормированному базису
Fn, т. е. линейный оператор из Л2 в Fk (С. М.
Никольский [5], т. 11, стр. 155). Поэтому для любого множества
2I с Lz
diV(:tt, /.2)-^(:)?1\ U). A0.11)
Обозначая, как и выше, через Fln-\ подпространство
(размерности 2/г — I) тригонометрических полиномов Tn{t)
порядка п— 1, из соотношений A0,5) и E.70) получаем

§ 10.31 ПОПЕРЕЧНИКИ КЛАССОВ tty?a В Ц 259
оценку
d*.-^.. Q^HWl, FL^J = $n(WlJ = \F A0.12)
(я, r=I, 2, ...).
С другой стороны, при каждом фиксированном г=1,
2, ... рассмотрим в Bп + 1)-мерном подпространстве Fj^
тригонометрических полиномов
п
7Vi@ =у + У
шар п 'Ufn + i радиуса 1/пг, т, е. множество полиномов
Tnvi{t) таких, что \\Tn^i\^n'r. В силу равенства Парсе-
валя это означает, что
A0.13)
Но если Tn+i^.n-rUln.\.\, то, применяя к r-й
производной T{n\.\(t) то же равенство Парсеваля, будем с учетом
A0.13) иметь
I Т{п\ 1 % = л V #' (а\ + Ы) ^ лп*' У] (al + б© < 1,
*-1 4=1
т. е. шар rt^f/^+i содержится в классе №[,•
В силу предложения 10.2.4
Ъп№„ L2)^n-' A0.14)
и так как d2«-i(Wl, Q^d^Wi,, Q, то из A0.11),
A0.12) и A0.14) следуют соотношения
= E {W'u, Fln-\\ = дт («. /¦ = 1. 2, ...).

260 ПОПЕРЕЧНИКИ КЛАССОВ ФУНКЦИЙ [ГЛ. 10
§ 10.4. Поперечники классов Wm и И^7/ю
в пространстве С
В этом параграфе будут доказаны следующие две
теоремы.
Теорема 10.4.1. При всех п> /*~1, 2, ... имеют
место соотношения
</2ДГль C) = dtn-X{WM, С) = ^„(Гдь С)-
««Я_,(ГЛ, C) = En(WrM)c = $n(WrM)c=^9 A0.15)
где Жг — константы C.44).
Теорема 10.4.2. Каков бы ни был выпуклый вверх
модуль непрерывности <о(/), при всех //=1, 2, ...а л~0,
1, ... справедливы соотношения
d2n (W С) - d2n х AW, С) = ?„ (Г'Я^с =
J л,@«'(Мл. A0.16)
о
^ fnr(t)^fnr(®i t) — функции, определенные в § 7.3,
а ФЯг@ определены в § 6.6.
Оценки сверху для нечетных поперечников
рассматриваемых классов дают результаты §§ 5.5 и 7.6Э из
которых в связи с общими соотношениями A0.3)— A0.5)
следует, что
d2nri (W'H«y С) - - Еп (W'№»)c - [fnr [с- (Ю. 18)
Теперь наиболее короткий путь к доказательству сразу
всех утверждений теорем 10.4.1 и 10.4.2 лежит через
оценку снизу четных поперечников классов WHU}. Для
этого нам придется доказать несколько вспомогательных
утверждений.
Для любого вещественного числа а положим
? (*=1, 2, ..., 2п) A0.19)
и сопоставим функции /еС вектор
который, очевидно, линейно зависит от Д

§ 10.41 ПОПЕРЕЧНИКИ КЛАССОВ IV м И «//7Ш В С 2G1
Если /^„ — произвольное подпространство из С
размерности 2/г, то при фиксированном а множество векторов
N(a) = N (ay F,,,)- {?„ (/): / е= F2n\ A0.20)
есть линейное многообразие в R2n размерности не выше
чем 2я. Образно говоря, линейное многообразие N (а)
векторов пространства R2n высекается из F2n системой
точек х*.
Лемма 10.4.3. Каково бы ни было подпространство
F2n из С, найдется а = а0 @ ^ а0 -^ л/п) такое, что
dlmN (а())-.<:2п~ 1,
Доказательство. Если dim N @) ^; 2п — 1, то все
доказано, поэтому дальнейшие рассуждения будем строить
в предположении, что dim N'(Q)'=°2n. Тогда, очевидно,
/V @) совпадает с R2n и каждый из линейно независимых
векторов
с>х = {1, 0,...f0},<?2={0f 1,0 0| ^я = |0 0, 1}
содержится в N @). В соответствии с определением N (а)
это означает, что существуют 2/г функций gi e F2n (i —
=^=1,2,..., 2п) таких, что"
et^bigi) (i-1, 2, ..., 2/0,
т. е.
(k -0 A, 4=1, 2 2/г).
Из линейной независимости векторов ех вытекает
линейная независимость функций gh ибо, если бы, напри*
мер, было
ft @=2^@,
то тогда
*i = со Ы = 2 >vri0 ^ = V },.еи
/ —2 t--r2
что невозможно. Таким образом, функции ?/ (/) (/ = 1,
2, ..., 2/г) образуют в F2n базис. Если }&Fzni то

262 ПОПЕРЕЧНИКИ КЛАССОВ ФУНКЦИЙ
и при любом а
[ГЛ. 10
2/1
Это значит, что N (а) есть линейная оболочка векторов
Mft) (i-l. 2, ..., 2л).
Лемма 10.4.3 будет доказана, если мы установим, что
при некотором а = а0 векторы |ао (gi) окажутся линейно
зависимыми.
Введем в рассмотрение определитель
«.«) -
A0.22)
являющийся, очевидно, непрерывной функцией от а. При
а = 0 с учетом A0.21) имеем
1 0 0 ... 0
0 1 0 ... 0
0 0 0
01
= 1.
Подсчитаем значение D(a) при а = п/п. Заметим, что
= *2+р и потому при всех i=l, 2, 3, ..., 2//
а в силу 2л-периодичности функций
gi Wn") = gi (я/л + 2я) - gj (
Поэтому
0
1
0
0
0
1
0 ...
о ...
0 ...
0
0
0
1
0
0
0 0 0
1 0
1 0 0
0 1 0
0
0
о о
0 1
_. 1
Непрерывная функция D(a), принимая в точках a = 0 и
а = я/п значения разных знаков, должна в некоторой
точке а0 @<а0<я//г) обратиться в нуль. Это значит,
что при a = a0 векторы строк определителя A0.22)
линейно зависимы, А так как векторы строк в A0.22) при

§ 10.4J ПОПЕРЕЧНИКИ КЛАССОВ tt"'u И Vi/r И® В С 2бЗ
а~а0 как раз и есть %a(gi) 0 = 1» 2, ..., 2//), то лемма
10.4.3 доказана.
Теперь будем рассматривать специальные
подпространства, связанные с выпуклым модулем непрерывности <о (/)
(задающим класс WrH{A) и определяемые с помощью
стандартной функции fno{t) — fno(u, 0- Мы расширим область
применения получаемых при этом результатов, если при
построении этих специальных подпространств будем
исходить из функций, являющихся некоторым обобщением
функций /,«,(/).
Зафиксируем п=\, 2, ... и в качестве обобщения
функции fm возьмем произвольную ограниченную периода
2п/п функцию *Fo@i не убывающую на отрезке [0, я/2«]
и удовлетворяющую соотношениям
= — Ч'о [ - -" + и) > 0 @ < и < я/2л).
Таким образом, ^0%= (- \)'\^о Щг^\ »,
очевидно,
Через Ч;г(/) (г= 1, 2, ...) обозначим r-й периодический
интеграл от Ч'о@ с нулевым средним значением на периоде.
Ясно, что 2л/«-периодическая функция xYr(f) ведет себя
точно так же, как и /лг(/), имея те же, что и у fnr{t),
нули, точки экстремума и интервалы строгой
монотонности.
Пусть теперь
а %(/) —2д-периодическая функция, задаваемая на [0,
2л) равенствами
0 (/s [0, 2я)\Д,).

264 ПОПЕРЕЧНИКИ КЛАССОВ ФУНКЦИЙ [ГЛ 10
Так как, очевидно, %(/) (/ = 1, ..., 2п) линейно
независимы, то множество функций вида
2л
/@=2 */*/('). (Ю.23)
где Су —произвольные числа, образует в пространстве М
подпространство размерности 2/2, которые мы обозначим
МЧп- Заметим, что при г;==( — l)^ функция A0.23)
совпадает с Ч;о(/).
Пусть Ai'in, о— множество функций g из M'in, у которых
2 О = 0- A0-24>
Если gG^o, то
2л 2п я/л 2/1
S *wл = 2 с> $ */ол = 5 Ivo(о!л 2 о-о.
0 /==1 А/ 0 /=¦-= 1
поэтому каждая из функций множества АЦп,о может
рассматриваться как r-я (г— 1, 2. ...) производная некоторой
2л-периодической функции из Мг. Через М^ (г = 1, 2, ...)
мы и обозначим множество r-х периодических интегралов
от функций g^M^n о- Таким образом, если /еМ^,, (г =
= 1, 2, ...), то /еЛСсС^1 и
2л /2л \
p)(/)-2^v(/) I>/=oj. (Ю.25)
Мг2п есть, очевидно, линейное многообразие, и нетрудно
понять, что размерность М^п равна 2/г. Действительно,
если Мг,,, о — подмножество функций / из Мг2п со средним
значением на периоде, равным нулю, то из определений
ясно, что между функциями g из М«п,о и функциями /
из МГ2п, о существует взаимно однозначное соответствие,
сохраняющее линейные операции (изоморфизм).
Следовательно, A/ltn, о и Мол, о имеют одинаковую размерность.
Но размерность M'in, о равна 2/г— 1, ибо если gE^o,
то в силу A0.24)

» 10.4] ПОПЕРЕЧНИКИ КЛАССОВ WM И W Н® В С 265
Итак, размерность Ж^ 0 равна 2л — 1, и остается
заметить, что М^, о не содержит функции, тождественно
равной единице, а М[п есть объединение А12н, о и
одномерного пространства констант.
Л е м м а 10.4.4. Пусть при фиксированном п = 1, 2, ...
* *r~^ " (г-1,3,
Если /еЛ1о« (^ = 0, 1, 2, ...) и
шах |/(/л)!<й?г;и, A0.26)
то коэффициенты Cj в A0.23) ара г = 0 и в A0.25) при
г ^ I удовлетворяют неравенству
\С;\^\ (/-1, 2, ..., 2ft).
Доказательство. В случае г = 0 утверждение
леммы очевидным образом следует из определения
функций Чг0 и подпространства М%п.
Рассматривая случай гт&1, заметим, что tkr есть
точки экстремума функции ^(Z). Предположим, что для
/ е Мг2п справедливо A0.26), но в представлении A0.25)
производной /(г) коэффициенты с, удовлетворяют
соотношению
max |с/;
Фиксируем коэф<|)ициент cv такой, что | сх \ = X, причем
можно считать, что cv = (— l)v-1 X, ибо в случае cv =
— (—1)VX вместо /(/) мы будем рассматривать функцию
— /(/). Если положить
/* (/)=[/ @,
то
№ @ = ? ^ О.
/•=1
где cJ^K'^Cf и, следовательно, |г*|^1 (/=1, 2, ..., 2п),
ас5 = (-1)м, Последнее означает, что на промежутке
Av функция /^ (/) совпадает с Чг„@. Рассмотрим разность

266 ПОПЕРЕЧНИКИ КЛАССОВ ФУНКЦИИ [ГЛ. 10
Так как в каждой точке t, где f(t)=?O, выполняется
строгое неравенство \f*{t)\<.\f{t)\, то с учетом AСК26)
будем иметь
max !M'*
Заметив еще, что
*r (*l) = *r VV = V, (tn) = . , . = Г г (*2л)>
приходим к выводу, что разность б (/), принимая в
точках tk значения того же знака, что и Чгг(/), должна по
меньшей мере 2п раз на периоде менять знак. По теореме
Ролля число перемен знака на периоде у производных
б' (I), б" (/), ..., 6^ (/) будет не меньше, чем у б (/), т. е.
не меньше чем 2/2. Но, с другой стороны,
/¦-=1
н, следовательно, б(г) (/) равна нулю на промежутке Ду
и сохраняет знак внутри каждого из промежутков Д;-,
где она не обращается тождественно в нуль. Поэтому
число перемен знака у функции б(г) на периоде не может
быть больше чем 2«— 1. Противоречие доказывает лемму.
Наряду с подпространствами Мг2п (г = 0, 1, 2, ...)
будем рассматривать их сдвиги Моп (Р) — множества функций
^ (/) = Ф (/ — р), где (peAfL a P —любое число. Ясно,
что МЪпф), так же как и М*п> является
подпространством размерности 2/г.
Пусть /? =/?¦ = /*/.-]-Р(?—Ь •..,2/г) —точки экстремуг/а
функции xYr(t — Р) на периоде [р, р + 2л); tk = tk — точк\т
экстремума xVr (t) па [0, 2л). Сопоставим подпространству
М'2п (Р) множество Qr2n (P) векторов
щ (f) = {f С?), f 1$). • • - > f ($«)} (f ^ мг2п (p)).
Ясно, что (?2« (Р) есть линейное многообразие, высекаемое
точками й из подпространства Mr<>n (P). Заметим, что точки
tl жестко связаны с подпространством М5л(Р).
Лемма 10.4.5. При любом Р линейное, многообразие
Qvn (Р) имеет размерности Чпч

$ 10.41 ПОПЕРЕЧНИКИ КЛАССОВ Wм И WrH® В С 267
Доказательство. Пусть /ь f2, ..., /^ — базис
в Mr2n (P). Тогда М<2п (Р) есть линейная оболочка функций
fi(t) (/=1, ..., 2л) и, следовательно, <?2/?(Р) есть
линейная оболочка векторов щ (ft) (t = l, 2, ..., 2/г). Лемма
будет доказана, если мы установим, что эти векторы
линейно независимы.
Предположим противное: пусть существует набор
коэффициентов 7v,- (/= 1, ..., 2/z), не все из которых равны
нулю, такой, что
2л _
1=1
Это равенство означает, что все координаты вектора,
стоящего в левой части, равны нулю, т. е.
2 W5) = 0 (А= 1, 2 2л). A0.27)
Функция
2п
очевидно, принадлежит М^ (Р) и в силу A0.27)
2^Л(ф = 0 (*=1, 2, ...,2л
Если положить g0 (/) =g-(/ + P), то g-0^Alort и
go(/,) = O (kr=lt ...f 2л).
Любая функция вида /Cg*0, где /С — произвольное число,
также, очевидно, принадлежит Mr2nf и для нее
выполняются равенства
/Cgo ('*)== 0 (А=1 2«). (Ю.28)
Если с,-— коэффициенты, определяющие функцию /(go @
(при г = 0) или ее r-ю производную (при г^г1) в
соотношениях вида соответственно A0.23) или A0.25), то из
A0.28) и леммы 10.4.4 следует, что |^1^1 и,
следовательно,

268 ПОПЕРЕЧНИКИ КЛАССОВ ФУНКЦИЙ [ГЛ. 10
Ясно, что при любом К это возможно лишь в том
случае, если glr) (/), а значит, и gu(t) есть тождественный
нуль. Но тогда тождественным нулем является и
функция g(t)y а это означает, что
что невозможно, так как функции // линейно независимы
и не все 5if равны нулю. Лемма 10.4.5 доказана.
Из леммы 10.4.5 следует, что любой вектор Л — 'Лз,
%» •••» Ц<ш\ с числовыми координатами гц, ..., т|2л
содержится в Q2n($), т. е. существует функция /бМ!л (Р),для
которой т|ц(/) = т|. Иначе говоря, имеет место следующее
утверждение.
Предложение 10.4.6. Подпространство Мг2п ф)
интерполирует в точках
f2?—lW'2/7 t-R (r — 0 9 4 fi )
(й^1)я/л-|-р (r=lf 3, 5, ...)
(ft-1, 2, ..., 2/i)
e mo^ смысле, что, каковы бы ни были 2п чисел гц, т]2, ...
..., ibn, существует функция /еЛ15„(Р) такая, что
f(tb = i\k (*--=!, 2, ..., 2/7).
Докажем единственность интерполирующей функции из
^2«(Р). *) Для этого достаточно установить, что равенства
/(/Р)-0 F=1, 2, ..., 2/1)
для f^M^/idJ) возможны только в случае /(/) = 0.
Возьмем Ъ\ линейно независимых векторов vj(n, ц{2\ ...
,.., ц{2п) с координатами ц^, ..., tj^J (/ —1, 2, ..., 2/2), и
пусть //(/) (/=1, ..., 2п) — функции из М'2п (Р), для
которых
ft (^) ^ Ч*] 0'» 6 ^= 1, 2, ..., 2/z),
*) Разумеется мы можем ядесь воспользоваться тем общим
фактом, что линейное отображение /V-мерного пространства XN на N-
мерное пространство YN взаимно однозначно.

s io.4i поперечники классов wrAi и w'h® в с 269
причем ясно, что /=,(*)дьо (/=1, ..., 2л). Из линейной
независимости векторов ц{П следует линейная
независимость функций //, ибо из соотношения, например,
2
Ы0= 2
следовало бы, что
2ft In
2 )
т. е. т|а) = Х4т1B) + ... + Х2лт|Bл\ что невозможно.
Так как Мг2п (Р) имеет размерность 2я, то функции ft
(/=1, ..., 2я) образуют базис в МГ2Пф). Следовательно,
если /еМзЛР) и ^0, то
2>Ы0 ||,|
и в силу линейной независимости векторов к\(П числа
2л
где тах!^|>0, не могут быть все равны нулю, т. е.
не равная тождественно нулю функция из Mr$n (P) не
может в каждой из точек Щ принимать нулевые значения.
Таким образом, доказано
Предложение 10.4.7. Для любой системы чисел
Ль %»..-¦ Ц2п существует единственная функция f из
Л^2/?(Р) такая, что
/(<В) = т|* (*^1, 2,..., 2/0,
где точки /^— $г определены в предложении 10.4.6.
Утверждения 10.4.6 и 10.4.7 потребуются нам в § 10.7.
Переходя непосредственно к оценке снизу четных
поперечников классов ДО""#°\ заданных выпуклым модулем
непрерывности <*>(/), будем считать, что функция lK0(/)f
нл базе которой были построены подпространства М*п и
их сдвиги Л«5я (Р). есть функция /я0 @ = f«о К 0- Чтобы

270 ПОПЕРЕЧНИКИ КЛАССОВ ФУНКЦИЙ (ГЛ 10
подчеркнуть, что речь идет именно об этом частном
случае, будем вместо М<2п писать Мгл {<»)}, а вместо Af$« (P)—
-Л1г2„{р, со}.
Из леммы 10.4.4 нетрудно вывести следующее
Предложение 10,4.8. Если f^Mon\f>, w} (/ = 0,
1, ...) и
max
mo fe ИГЛГ".
В силу инвариантности класса W/(u относительно
сдвига аргумента, можно считать, что 0 = 0. Но если
/еМгяМ и
max
то по лемме 10.4.4 в представлении
2л
где в данном случае
I 0 (/ е= [0, 2л)\Л;),
коэффигиюнты f; удовлетворяют соотношениям
|су'<.1 (/-1, ..., 2/2), A0.29)
которые гарантируют включение f{r) e Я(о. Действительно,
если точки /' и Г лежат на одном промежутке Л,-, то
ибо kyjs^l и fn0&Hlu. Если же Г и Г принадлежат
разным промежуткам Лу, то так как в силу A0.29) 7(/)@!^
^ I /ло @ :» мы можем, учитывая выпуклость <а @, написать:
| /и (/') ^ ^(о (/-); ^: fn0 {п; +: и (Г) \ < ш (| /' - Г;).
Приступим к оценке снизу поперечников d2n(WrH(t\ С).
Сопоставив, как и в общем случае, подпространству
2п{Р, «} линейное многообразие Q^ip, w} векторов
- {/(/Г), f (/?), ..., /D)} (f S M5rt {p, о}),

§ 10.41 ПОПЕРЕЧНИКИ КЛАССОВ W'rM И Wr//° В С 271
введем в Q^jP, ю} норму равенством
1 <fc<2
и будем рассматривать Qon {Р, о>[ как линейное
нормированное пространство, имеющее в силу леммы 10.4.5
размерность 2/7.
Пусть F2n — подпространство в С размерности 2я,
а N (a, F2n) — линейное многообразие векторов
la is) = {§ (*?), g D). • • •, 8(Х2п)} (g e F2B)f
высекаемое из F2n системой точек A0.19). Считаем, что
а выбрано так, что
dimiV(oc, /r2/i) = /rt-^2« — I
(на з^то нам дает право лемма 10.4.3). Этим
зафиксирована система точек \х?}.
Выберем затем р так, чтобы системы точек {$} и \х%}
совпадали. Это можно сделать, так как обе эти системы —
равноотстоящие с одинаковым шагом л/п. Теперь
линейные многообразия N (a, F2n) и Qon {P, ш} высекаются
соответственно из F2n и Mort {p, w} одной и той же системой
точек, за которой оставим обозначение {($} и ясно, что
N (a, Fzn) можно рассматривать как ш-мерное
подпространство пространства Qo« IP» g>}.
В силу предложения 10.2.2 существует вектор
^QSniPt w} (высекаемый некоторой функцией ^е
с нормой
такой, что
С учетом определения нормы в Q$rt {P, со} равенство A0.30)
означает, что
-я

272 поперечники классов функций [гл ю
и в силу предложения 10.4.8 /* е WrH<». Равенство A0.31)
можно переписать в виде
inf max 7* ('S)-e('E) iHMc>
откуда следует, что
inf
и, значит,
Так как это справедливо для произвольного
подпространства F2i из С размерности 2/г, то
<kn(WrH», C):^lfnrlc (/"-О, 1, 2, ...; л=1, 2, ...).
A0.32)
Теперь из A0.18) и A0.32), с учетом общего
соотношения монотонности A0.1) и теоремы 7.6.1, сразу
вытекают все соотношения A0.16), и теорема 10.4.2 доказана.
Так как при w(/) = / @ <г f -.:: я) класс WrH™
превращается в W гм"! (§7.1), а функция fnr (t) — в срл, r.i (t + л/2/i),
то оценка A0.32) в этом случае запишется в виде
d2n(WrMy C)^hnr\x: = ^- («• г-1, 2, ...). A0.33)
Сопоставив A0.17), A0.33), а также общие
соотношении A0.1) и (Ю.2), получим все равенства в A0.15), так
что теорема 10.4.1 тоже доказана.
Отметим, что мы доказали теоремы 10.4.1 и 10.4.2,
не привлекая для оценки поперечников снизу
соображений, связанных с теоремой Борсука и теоремой 10.2.3
о поперечнике шара. В § 10.6 мы покажем, как более
коротким путем получить точные оценки нечетных
поперечников классов W'm и WrH*\ опираясь на предложение
10.2.1.

§ 10.5] ПОПЕРЕЧНИКИ КЛАССОВ Wry \ w? И WrM В L 273
§ 10.5. Поперечники классов Wv~~\ Wl и WrM
в пространстве L
Здесь мы докажем следующие утверждения.
Теорема 10.5.1. При всех п> г=1, 2,
...справедливы соотношения
-^(Ш)л-=^(^)л=^; A0.34)
A0.35)
Теорема 10.5.2. При всех п, г=1, 2, ... имеют
место равенства
d2n(WrM, L) = d2n HU/a,, /^^(Г^-1-^-. A0.35)
Как и в предыдущих случаях, для оценки сверху
нечетных поперечников мы используем верхние грани
наилучших приближений рассматриваемых классов
тригонометрическими полиномами. Из результатов § 5.5 следует,
в частности, что
din 1(Щ~\ L)^Gn(Wrv-lk='-^ (n, r=l, 2, ...),
A0.37)
d:in i(Wu L)^$n(WrL)L = ^ (n, r = l, 2, ...),
A0.38)
а полученное в § 5.7 соотношение E.65) позволяет
написать, что
= ^-^- (я, г=1. 2, ...).
A0.39)
Как и при доказательстве теорем 10.4.1 и 10.4.2,
чтобы получить сразу все равенства в A0.34)— A0.36),
мы будем оценивать снизу четные поперечники. При этом
нам придется существенным образом использовать
теорему Борсука.

274 ПОПЕРЕЧНИКИ КЛАССОВ ФУНКЦИЙ [ГЛ. 10
Пусть Г„о («=1, 2, ...) —множество 2л-периодическнх
кусочно-постоянных функций g(t), которые принимают
значения только -|-1 и —1 и меняют знак на периоде
не более чем 2/г раз.
По поводу последнего условия в определении Г„о
сделаем пояснение: мы говорим, что функция f(t) периода
2л меняет на периоде знак ровно т раз, если можно
указать /я+ 1 точку:
в которых }Aк)Ф0 (k=^0, 1, ..., т) и
причем не существует системы из /н + 2 точек с
аналогичными свойствами.
Через Гпг (/г, г^~\у 2, ...) обозначим множество г-х
2л-периодических интегралов от функций из Гп0,
имеющих среднее значение на периоде, равное нулю. Таким
образом, если geiV, то g{r-l) локально абсолютно не-
2 л
прерывна, g{r) е= Гл0 и $ g{r) (/) dt = 0.
6
Основу всех рассуждений но оценке четных
поперечников в L снизу составляет следующая
Лемма 10.5.3. При всех «== 1, 2, ... а г=-0, 1, 2, ...
для любого подпространства ?гп cr L размерности 2п имеет
место оценка
}glL. A0.40)
Доказательство. Сначала рассмотрим случай
г ^1. Заметим, что если /^л не содержит константу, то
Е (Гдг. /72я)/..= + со (г=1, 2, ...). Действительно, в силу
определения множества Глг, если g*e Vnr (r > 1), то
функция X + g, где X —любая константа, также принадлежит
Глг, поэтому, фиксировав gel\r, будем иметь
?(>v + i?, F2n)L^E(K F2n)L-E(g, F2n)L =
= U|?A, F2n)L-E(g, F2n)L.
Если тождественная единица не принадлежит F2nj то,
в силу замкнутости F2nj ?A, F2/i)l>0 и За счет
увеличения ¦ XI мы можем величину Е (X + g, Fzn)L сделать сколь-
угодна большой.

§ №.Г>] ПОПЕРЕЧНИКИ КЛАССОВ Wrv \ w'L И IV д] В L 275
Итак, доказывая соотношение A0.40) при г ^1, мы
можем считать, что F2n содержит любую константу, т. е.
что в состав некоторого базиса F2n входит тождественная
единица. Пусть
МО. МО. .... *2«@
— базис Finy причем
М/) = 1.
Ниже /?*„ будет обозначать 2я-мерное пространство
векторов
координаты которых связаны условием
Ц ?, = 0. A0.41)
Норму в Щп введем следующим образом:
Ш*= I, \t*'', (Ю.42)
Через S^n-i обозначим сферу в R%n с центром в нуле
и с радиусом 2л:
2л+1
Каждому вектору l^S2n_1 сопоставим 2л-периодиче-
скую функцию go (|, 0 следующим образом. Пусть
k
Ло = 0. %-Д]:^| (A«lf 2 2п+1) (тья + 1 = 2я).
A0.43)
Так как некоторые из координат \k могут равняться
нулю, то % и т]*_1 могут совпадать, но если х\к>х\ь-и
то полагаем
go(t, 0 = signg* Dk-i^t<4k)-
Ясно, что таким образом мы зададим функцию g0(?» /)
во всех точках 0^/<^2л, и остается продолжить ее на
всю ось 2л-периодическим образом.

276 ПОПЕРЕЧНИКИ КЛАССОВ ФУНКИИП \ТЛ. 10
Заметим, что, как следует из определения, число
перемен знака на периоде у go{l, t) заведомо ^2/2+1- Но
так как периодическая функция может менять знак на
периоде только четное число раз, то перемен знака
У go (?, t) на периоде не больше чем 2п, и, значит, gu (?, /) е
еГл0.
В силу A0.41)
f god, t)dt = O
о
и, следовательно, go(c, /) является г-й производной
некоторой функции gr(l, t) из множества Тпг (г=1, 2, ...);
для однозначности будем считать, что
Т
0
Положим далее
где константа с(?) однозначно, в силу непрерывности gn
определяется равенством
о с о
Так как с(Е) является константой наилучшего
приближения в метрике /. функции g>(?, /) из Глг, которая в силу
определения Глг может обращаться в нуль на [0, 2л) лишь
в конечном числе точек, то в силу критерия 3.3.4
2л
S signg?(|, 0^ = 0. A0.44)
о
Теперь с помощью функции gf (g, /) зададим на сфере
S2n-i оператор (Bл — 1)-мерное векторное поле) т(?),
положив
где
x,(g)=Ssign??Gf 0^mi@* (i-l, 2, ..., 2л-1),
о
а ^2@, ..., ezn(t) — функции базиса F2rt.

$10.5] ПОПЕРЕЧНИКИ КЛАССОВ w'v \ \X''L И tt"'M Bi 277
Нечетность оператора т(?) легко проверить, если
проследить все этапы отображения через функции go(l, t),
gr(h t) и gr(b t).
Докажем, что оператор т(?) непрерывен на сфере S2*-i-
Пусть последовательность
векторов, принадлежащих сфере S2n-u сходится в
метрике /??„ к вектору 5={5ь ?2. •••¦ ^2«}, также, очевидно,
принадлежащему 52Л_1. Так как сходимость в
конечномерном пространстве есть сходимость по координатам, то
Игл l)r--lk (*-l, 2 2п).
т —с»
Если для векторов ?(т) определить числа т]1Г) аналогично
A0.43), то, очевидно,
Hm nim> = Л* (*=-!. 2, ..., m),
m-*oo
что, в свою очередь, означает, что если
B^^j/r/elO, 2л|, ?о(!(т),
то mesBm->0 при /п->оо.
Но тогда
2л
= max ' ^D,(jr-/)|ft(s'm). t)-go<&, t)]dt*i
2я
^|0,Ц^1т). /)-go(l, t)\dt =
о
= ~ \DrU I I go (l(m), 0 -go (h t) \dt <
< | J Dr ;!.„ mes flm -> 0 (m-j-oo),
т. е. последовательность функций gr(i(m), /) (m = 1, 2, ...)
равномерно (по норме в С) сходится к функции gy(|, /).
Если заметить, что в силу непрерывности оператора
наилучшего приближения (предложение 1.2.2)
lime (|"->) = с (g),

278 ПОПЕРЕЧНИКИ КЛАССОВ ФУНКЦИЙ ГГ71 10
где с (с(т)) и с (с) — константы наилучшего приближения
в L соответственно для функций gr(l(m\ l) и ?Л(?, /), то
приходим к выводу, что
lirn Hgr? (g<->) — я? (Н) 'к = 0.
т. —оо
Из равномерной сходимости при ш -^ оэ
последовательность функций {g?(l{m\ /)} к g? (I, t) и того факта,
что gf (g, t) обращается в нуль на периоде лишь в
конечном числе точек, следует, что мера множества
В* Н* :/е[0, 2л], signg?^, 0#signgr*(?, /)}
стремится к нулю при /л->:х>. Поэтому
), t)-s\gng*{b
u *
8m
(• 1O Of» }\
I 1, Z , • • « t «-' * -I ) •
Это значит, что последовательность векторов i{l[m))
сходится покоординатно, а значит, и в метрике R$n, к
вектору т(?).
Непрерывность оператора т(?) на сфере S2n-i доказана,
и теперь, с учетом нечетности т(?), можно применить
теорему Борсука. В силу этой теоремы существует
вектор geS2/i-i> для которого x(t) —0, что означает, в силу
задания оператора т(?), выполнение соотношений
2л
\ sign g* (I, I) ег (t) Л = 0 (i == 2,3,..., 2/z).
0
Если учесть, что ei(/)^ 1 и A0.44) выполняется также
и при g = g, то получаем систему равенств
2л
^signg*(|> t)ei(t)dt = O (/=1, 2, ..., 2л),
о
которая означает, что функция sign g?(|, /) ортогональна

§ 10.5] ПОПЕРЕЧНИКИ КЛАССОВ Wy \ WrL И WrM В I 279
всем функциям базиса F2ny а значит, и любой функции 2„
По критерию 3.3.2 наилучшее приближение функции
#?(?, t) в метрике L среди всех функций подпространства
F2n доставляет тождественный нуль.
Итак установлено, что
а так как g*(i, /) е Глп то лемма 10.5.3 для г^П
доказана.
Рассмотрим случай г = 0. В пространстве /?*л-!-1
векторов g = {gb g2, ••> 221-м} с нормой A0.42) рассмотрим
сферу
на которой зададим 2я-мерное векторное поле т (|)
следующим образом. Сопоставим вектору H.eS2rt функцию
gu(l, t)y как и в случае г^1, и положим
^ (I) = f sign g0 (g, 0 e, @ d/ (f« 1, 2 2/г),
0
где ej.(/), ..., e2n(t) — базис аппроксимирующего
подпространства F2/t- Этим самым вектору ?eS2rt поставлен
в соответствие вектор
T(g)HT,(g), T2(g), ..., T2/I(?)}.
Оператор x(t) является непрерывным (это доказывается
значительно проще, чем в случае г^-1) и нечетным.
Поэтому в силу теоремы Борсука найдется вектор |eS2M
такой, что x(fe) = 0, т. е.
т/.(Ю= f sign ft (g, /)M/)d/ = 0 (t = b 2 2/0,
6
и, значит, в силу критерия 3.3.2
причем go(|, f)e Г„о.
Лемма 10.5.3 полностью доказана.
Лемма 10.5.4. Имеют место соотношения
!| <т1! = \^УС и г (/? — 1 2 * г ~ 0 1 2 .. .)•

280 поперечники классов функций [гл ю
Доказательство. При r = Q лемма 10.5.4
тривиальна. Если g^Ynr (r^-l), то, очевидно, geP, причем
V (g{r)) ^ 4/г, №'* ]L = 2л. A0.45)
о
В силу неравенства (G.66) для geKr имеем
Г2Л
\
A0.46)
где
Из A0.45) и A0.46) следует, что для любой
или
к]^4?Жг+1/г'. A0.47)
Остается заметить, что для функции g(() из Гпг с
нулевым средним значением иа периоде, у которой g[r] (/)
меняет знак в точках fai/л, в A0.47) будет знак
равенства, ибо с точностью до знака g(() совпадает с ср,1Г @-
Из лемм 10.5.3 и 10.5.4 вытекает, что
d2n (Г„г, L) ^ \ЖГ^1-' (п = 1, 2,...; г - 0, 1,...).
A0.48)
Соотношение A0.48) позволяет немедленно получить
точные оценки снизу для, четных поперечников
классов и?ль U7i/ и W[ в пространстве L.
Так как, очевидно, rnr^WrM, то из A0.48) сразу
следует неравенство
d2rl(WrM, L)^iJfr^n-r (n, г=1, 2,...),
которое вместе с A0.39) доказывает теорему 10.5.2. (Из
результатов § 10.7 будет следовать, что линейные
поперечники donl^Af, L) также равны \cJfrAltrr.)
Далее, как уже отмечалось, вариация на периоде г-н
производной функции gel\?r не превосходит 4/г, поэтому
множество D/г) Гчг, состоящее из функции вида /(/)--

§ I0.6J ОЦЕНКА НЕЧЕТНЫХ ПОПЕРЕЧНИКОВ 281
), где geTftr, принадлежит классу Wv.
Следовательно,
~-1-с12п(Гпг, L)^%± (r-0, 1, 2...)
и с учетом A0.37) получаем все равенства в A0.35).
Соотношения A0.34) немедленно следуют из A0.35) и
A0.38), если учесть, что, как показано в § 5.3, для любого
подпространства F из L
-\ F)l (r=l, 2,...),
и, значит,
dAwL L) = dx(Wv'\ L) (N, r-1, 2,...).
§ 10,6. Оценка нечетных поперечников
с помощью теоремы о поперечнике шара
Для получения точной оценки снизу нечетных
поперечников классов Wm в С и Wl в L имеется простой и
изящный путь, базирующийся, с одной стороны, на
глубокой теореме 10.2.3 о поперечнике шара, а с другой —
ия экстремальных свойствах полиномиальных сплайнов.
Эти свойства сплайнов представляют интерес и сами
по себе.
Пусть S^n — 2л-мерное подпространство 2л-периоди-
ческих функций вида
2п
где функции у\*к (х) периода 2л задаются на [0, 2л)
равенствами
Через Sr2n (r=l, 2,..) будем обозначать 2я-мерное
подпространство 2л-периодических интегралов от функци-и
f^S'in при дополнительном условии, что Сг + сг + ...
-.. + ^2/1 = 0. Таким образом, если /е Sr2n (r—l, 2,...),
то /еСм и на каждом промежутке [(А— 1) л/«, кп/п]

282
ПОПЕРЕЧНИКИ КЛАССОВ ФУНКЦИЙ
[ГЛ Ю
функция f(x) есть алгебраический многочлен степени г.
(Эти свойства можно было взять в качестве определения
подпространства SS,,.) Функции множества Sj* (r^l)
называют полиномиальными сплайнами степени г дефекта 1
по разбиению [кп/п]. В дальнейшем о них будем говорить
просто как о сплайнах. Рассматривая подпространство Son
при всех /• = (), 1, 2, ..., мы будем иногда условно
называть" сплайнами также и кусочно-постоянные функции
ИЗ Sin.
Лемма 10.6.1. Имеют место соотношения
У^Ьл^Ж^Лс V/SS5, (я, г=1, 2,...); A0.50)
))^^T;lnrif% V/eSf2-« (я, г=1, 2,...). A0.51)
V
о.
Неравенства A0.50) и A0.51) тонные.
Доказательство. В обоих случаях можно считать,
что функция /(л*), а значит, и ее производные не
являются тождественными константами, ибо иначе
доказывать нечего.
Заметим далее, что умножение функции / на любую
постоянную не отражается на неравенствах A0.50) и
A0.51); поэтому A0.50) достаточно доказать для случая
2я
!/1гMд1=1р а A0.51) —для случая У(/(г~1>)= 1. Таким
о
образом, надо установить, что если f
о
Sr2n и
iflc^~f (n9 а=1, 2,...),
= 1, то
A0.52)
а если /
2я
^1 и V (fir 1}) = 1, то
о
Ш/->^ (я. г=1, 2,...).
A0.53)
Равенство Цр)||Д1=1 для /eS^rt означает, что хотя
бы на одном из интервалов ((к— 1) л/я, ?л/я) или f(r) (/) ^
^1, или /(г) (/)==— 1, а тогда, очевидно,

§ J0.6] ОЦЕНИЛ НЕЧЕТНЫХ ПОПЕРЕЧНИКОВ 283
Если г=1, то A0.50) уже доказано, ибо бЗГ^
Пусть г ^2. Неравенство Колмогорова E.52) при k
= г—I запишется в виде
i; /«'-" [с < зГ13ТГ1/г .7 Г!,Г iV",
а так как у нас Ц[гIм = I и имеет место A0.54), то
что равносильно A0.52).
Пусть теперь f e S^1 и
V^'-^-L A0.55)
о
Так как /<'-J> e 55rt, то
где ^(л*) определены в A0.49), и ясно, что вариация
функции [{г~1] (х) на каждом отрезке (&— 1) n/n^t^kn/n
измеряется абсолютной величиной ее скачка в точке kn/n9
т. е. равна ',Сл — сЛ1.ц (c2«:i=^Ci)- Поэтому
в силу чего
и для r=l A0.51) доказано. Если же г^2, то, записав
неравенство F.G6) при Л = г — 1:
1Г) I < <гг l2rrw' i7,r [у а"-»)]17'.
подставим в него условие A0.55) и оценку A0.56). Получим
и A0.51) доказано.

284 ПОПЕРЕЧИНКИ КЛАССОВ ФУНКЦИЙ ГГЛ to
Знак равенства в A0.50) и A0.51), как нетрудно
проверить, имеет место для функций / из Son с нулевым
средним значением на периоде, у которых
fir) (х) - У] crfk (х) (cL - - с2 =¦-, са -... - - с2п).
В частности» равенство в A0.50) и A0.51) реализуют
функции фяг (-г).
Лемма 10.6.1 доказана.
Считая Son (r=U 2,...) подпространством в С,
рассмотрим шар e?frn"rU2n функций из Sj/i радиуса о?Сгп~г\
Если fe^frfVrU2»f то f[r~l) абсолютно непрерывно и
в силу A0.50) и{г)]м-^и т. е. /е= WrM. Это значит, что
шар e%'rn-rU\n содержится в классе W'm, и, применяя
предложение 10.2.4, получаем оценку
4„-х(№'ль C)zze?rrn" (n, r = lf 2,...).
Совершенно аналогично оценивается нечетный
поперечник класса W\T] в L. Шар
в силу A0.51) содержится в классе Wrv~x и предложение
10.2.4 сразу позволяет написать оценку
fVllW'iT1, OssatfVr' (/I, Г= 1, 2, ...).
Так как поперечники в L классов Wv~l и U^L
совпадают, то
da«-i(ift. L)^eTr/r' (я, r=l, 2,...).
Отметим, что точную оценку снизу для нечетных
поперечников классов WHK* в С можно сразу получить
из предложений 10.2.4 и 10.4.8. Действительно, ввиду
10.4.8 для любой функции f e МГ2п {о)} из неравенства
Шс<||Мс следует, что feW'H», т. е, шар \fnr[Uci.
радиуса \fnr\ подпространства М& {со} принадлежит классу

§ 10.6] ОПЕНКА НЕЧЕТНЫХ ПОПЕРЕЧНИКОВ 285
WH®. В силу предложения 10.2.4
d^-iiWH», ОИ/«Лс (/» = !, 2,...; г = 0, 1,...).
В заключение найдем нечетные поперечники класса
Н?2 функций / из Lj, у которых со (/, tJ^Vt.
Считая S\n подпространством в L2, рассмотрим з нем
шар
где р = |
Пусть / е pf/frt и
где t|>(/) определены в A0.49). Тогда
k = l
т. е.
2r.
Далее при 0 < / < л//г
2п
и так как
TO
/ 2ft \i/2
Если же n/n^t^n, то

285 ПОПЕРЕЧНИКИ КЛАССОВ ФУНКЦИЙ [ГЛ 10
Таким образом, из включения / е pt/Sj следует, что
/еЯо2, т. е. pt/гА с: Яз''2, и в силу предложения 10.2.4
<*,„-,(//i-2, ^.р~г{ппУ*. (Ю.57)
В сопоставлении с неравенством (9.35) это дает
следующий результат:
§ 10.7. Об экстремальных подпространствах
Подпространство FN из X размерности N мы назвали
экстремальным для класса 3I, если
Из результатов §§ 10.4 и 10.5 следует, что для
классов WrM и W7r//W («>(/) — выпуклый модуль непрерывности)
в пространстве С, а также для классов W\\% W[r[ и W*i
в пространстве L экстремальными являются
подпространства FL-i тригонометрических полиномов. Относительно
этих иодпростра]гств интересно отметить два
обстоятельства:
1) Подпространство f-Jn-i является экстремальным для
указанных выше классов при всех г и в этом смысле его
можно назвать универсальным.
2) Никакое подпространство размерности 2п не дает
для перечисленных выше классов лучшего приближения,
чем подпространство Fln-\9 имеющее размерность 2п— I.
В частности, добавление к системе
1, cos/, sin/, cos2/, sin2/, ..., cos(n — \)t, sin(/z—1)/
любой еще одной функции не улучшает аппроксиматик-
ных свойств порождаемого системой подпространства
относительно этих классов.
Вопросы, связанные с существованием и описанием
экстремальных подпространств для заданного класса :\)i,
еще недостаточно изучены, и мы здесь приведем лишь
некоторые частные результаты.

§ 10.7] ОБ ЭКСТРЕМАЛЬНЫХ ПОДПРОСТРАНСТВАХ 287
Для классов WrM и Wr~lH* (г=1, 2,...) в
пространстве М, а также для классов №д/> Wi и Wv (г= 1, 2,...)
в пространстве L можно указать еще один интересный
класс экстремальных подпространств четной размерности,
существенно зависящих, впрочем, от г. Таковыми
являются определенные в начале § 10.6 подпространства
So/ полиномиальных сплайнов.
Заметим, во-первых, что Sjn можно рассматривать как
частный случай подпространств Л4о„, которые строились
в § 10.4 по 2л//1-периодической функции Y0(f).
Действительно, если в качестве То(/) взять функцию ^0{t)
периода 2я/я, равную 1 для 0^г/<л//г и равную —1 для
д/71 ^/ <2л//г, то построенные в § 10.4 подпространства
МГ2П будут как раз подпространствами 5[>„. Таким
образом, на сплайны из Son распространяются все результаты,
полученные в § 10.4 для подпространств Мггп (Р) и, в
частности, предложения 10.4.6 и 10.4.7, которые мы здесь
переформулируем для данного конкретного и важного
случая.
Предложение 10.7.1. П(к)пространство сплайнов
Son интерполирует в точках
{ ГB*-1)л/2/1 (г-0, 2, 4,...),
*г \ (*-1)я/л (г-1, 3, 5, ...) (Аг=1, 2, ..., 2/1),
причем, каковы бы ни были 2п чисел Ц\, гJ, ..., щ2л,
ствует единственный сплайн a(t)^Sr>n такой, что
о(/*,) = Ч» (*-1, 2 2я).
В силу предложения 10.7.1 каждой функции /еС
можно сопоставить единственный сплайн стлг(/, /) из S^,
интерполирующий функцию f в точках ikry т. е. такой, что
<*nr(f, W = f(W (A?— 1, 2 2л).
Если ввести в рассмотрение фундаментальные сплайны
U @ = U (ri «"» 0 (»= 1, 2, ..., 2/г) из S^n, определяемые
равенствами
(*=!• 2 2/0,

288 ПОПЕРЕЧНИКИ КЛАССОВ ФУНКЦИЙ [ГЛ. 10
то сплайн спг (/, /) может быть записан в виде
i ---. 1
Таким образом, интерполяционные сплайны onr(ft t)
линейно зависят от / и, следовательно, определяют
некоторый линейный метод приближения.
Оказывается, что относительно классов U?д/ (г = 1, 2,...)
интерполяционные сплайны ст/,,r-i (/» /) "з S^1 обладают
наилучшими аппроксимационными свойствами в метриках М
и L. Это будет немедленно вытекать из следующего
интересного факта.
Теорема 10.7.2. Если f e W'm (г -= 1, 2, ...), то при
.всех t справедлива оценка
\f(t)-on.r i(/, /):^!флг@1 («= 1. 2, ...). A0.58)
где qv(/) — функции, определенные в § 5.4.
Доказательство, Сначала рассмотрим самый
простой случай г=1. Пусть fe Wm = Я1 и, значит,
Функция ол0(/, ^), интерполирующая f (t) в точках
Bfe— 1) л/я, постоянна на каждом промежутке [(?— 1)я/я,
Ля/я) (*=1, 2, ..., 2п). Фиксируем / из [0, 2л), и пусть
(v — 1) я/я ^ / < vn/a. Тогда
/, 01 = 1/@ —
В общем случае при г 5? 2 докажем справедливость
оценки A0.58), рассуждая от противного. Пустьдля
некоторой функции / из 1#/л/(л = 2, 3, ...) в точке /е[0, 2я)
выполняется неравенство
Положив для краткости 6 (t) = / (/) — artf r_i (/, /),
заметим, что точки интерполяции /*|Г_ь в которых S (/)
обращается в нуль, являются также нулями функции
qw@- Ясно, что t=?lk,r 1 и фл/.(/)^0, так что можно

$ 10.7] ОБ ЭКСТРЕМАЛЬНЫХ ПОДПРОСТРАНСТВАХ 289
выбрать число Я, 0<j?/<l, так, чтобы выполнялось
соотношение
Теперь функция
обращается в нуль на периоде @,2л) в точках tkrl
(А—1, ..., 2/i) и еще в точке /, т. е. имеет на [0, 2л) по
меньшей мере 2я + 1 нуль. Применяя теорему Ролля
(если л>2), приходим к выводу, что по меньшей мере
2// -j- I различных нулей должна иметь и функция A(r~2)(/).
Покажем, что это невозможно. Действительно, hSr~ts{t)
является интегралом от функции
Д^1>(/) = лб«г-1)(/)-ф111(/)| A0.59)
причем
Чп
а функции Чч@ определены в A0.49). На каждом
промежутке {к — 1) гг. /г *=', t < Ал/я (А = 1 2//)
и так как 1Я <1, а /(г 1}е//!, то для любых точек /'
и Г из [(*-1)л,71, Ая.'/i) таких, что f(rl) (t')^fir~l} (t")f
будет
?,6(r J> (/') - W-1» (Г): = 11\ j/(r l) (Г) - Г 1) (Г)' <
Следовательно, на любом отрезке [/', f] a [{k— 1) л л,
/?л//0 абсолютная величина приращения функции >.S(r 11(/)
строго меньше абсолютной величины приращения
линейной на [D—1)я/я, Ля/я] функции <prti(/). Поэтому
разность A0.59) может обратиться в нуль на промежутке
[(Л— l)n/riy Ая/я) не более одного раза, а если она меняет
знак в точке vn.'n (СЬ.-v ^; 2/г — 1) (что возможно, если
А1Г п (/) разрывна в этой точке), то по крайней мере на
одном из прилежащих интервалов ((v—1)я/я, vn/n) или
(ул/я, (г+1)л/л) функция Д(г л(/) сохраняет знак.

290 ПОПЕРЕЧНИКИ КЛАССОВ ФУНКЦИИ [ГЛ. 10
Теперь ясно, что функция A{r"v (t) на периоде [0, 2л)
не может обращаться в нуль более чем в 2// точках, а также
не может более чем 2п раз менять на [0, 2л) знак. Но
тогда интеграл от А{Г 1] (/), т.е. функция A(r 2) (t) + c,
может иметь своими нулями только изолированные точки
и число их на [0, 2л) не больше чем 2/г.
Теорема 10.7.2 доказана. Из нее немедленно следует
Теорема 10.7.3. Для любой функции f^WrM {r = 1,2,...)
справедливы соотношения
lf — On.r-iihU<'i<Pnrlc = ^ (« = !• 2, ...), A0.60)
а также
]p> o, « = it 2,...), (io.6i)
в частности,
nrlL^—^ (я=1,2,...). A0.62)
Оценки A0.60) и A0.62) вместе с теоремами 10.4.1
и 10.5.2 показывают, что интерполяционные сплайны
<4r-i (/, 0 из SJaT1 "e только доставляют на всем классе Wm
наилучшее приближение (среди всех функций
подпространства S^T1) в метриках М и L, но и реализуют
поперечники этого класса в соответствующих пространствах,
так что
= d2*(inb Al) = rfJn(rAif Af)=^ (/i, r=lf 2, ...)
A0.63)
(разумеется, при г^>2 метрику М надо заменить на С) и
sup [/ - оп,
Щ (п% r=lf 2, ...).
A0.64)
Подчеркнем еще раз, что интерполяционные сплайны
r~i(f»O Дают эффективно определяемый по значениям

§ 10.7] ОБ ЭКСТРЕМАЛЬНЫХ ПОДПРОСТРАНСТВАХ 291
функции / в точках tk%r i линейный метод приближения,
гарантирующий на классе W'm в метриках М и L самую
минимальную погрешность приближения, какую только
могут дать подпространства размерности 2п.
Покажем теперь, что подпространство S.^ является
экстремальным в пространстве L для классов Wi и ЦРуГ1.
В силу равенств A0.35) нам достаточно для этого
установить, что
EiWu Sr,~\ = ^f- (л, г=1, 2, ...). A0.65)
Будем исходить из соотношения двойственности B.26),
которое в нашем случае запишется в виде
E{i%Sr*-\= sup \f(t)h(t)dt, A0.66)
.1 h 1 м < I (j
где [gL, a ftlS^" означает, что
2л
6
и, в частности,
f /i (/) с// = 0,
и
ибо подпространство S^T1 содержит константу.
Рассматривая наилучшее приближение в
пространстве L сплайнами из S^T* функций / е WrP (^=1, 2, ...;
l^p^oc), обозначим через ^(S^V A/р4-1/р'= 1)
множество функций g из 1^, удовлетворяющих условиям
г-Я]р^ A0,67)
2л
О*
Пусть в A0.66) / е= Wp. Проинтегрировав г раз по
частям и распорядившись при этом соответствующим

292 ПОПЕРЕЧНИКИ КЛАССОВ ФУНКЦИЯ ГГЛ. Ю
образом произвольными постоянными, придем к равенству
?(/, Sjn-')i= sup Uir)(t)g(t)dt,
так что
Е {Wp, S? \ = sup sup U (/) g (t) dt.
(V1*10
Если воспользоваться соотношением B.28) и учесть, что
g(() удовлетворяет условию A0.67), то получим:
Srt7%= sup )g^. A0.69)
Вычислим верхнюю грань в правой части A0.69). Из
условия A0.68), которому удовлетворяют функции
множества tt^Ai (S*/T Ор' следует, что для g e tt?Jw (SJT V
U
б
Но если /et и / JL S^, то
5 f(t)dt = Q (*=1, 2, ...t 2/0, A0.70)
где, как и выше, А* есть полуинтервал [(?— 1)я//1, кл/п).
Действительно, положив
и записав условие / JL Sln в виде
} 0 Vcfc(*=lf 2, ....2/1),
при c^ = sign ал получим
2л
4io равносильно A0.70).

§ 10.71 ОБ ЭКСТРЕМАЛЬНЫХ ПОДПРОСТРАНСТВАХ 293
Таким образом, для любой функции g(t) из Wm E*Г0р'
выполняются равенства
lg'(t)dt = Q (*=1, 2,..., 2/0,
так что, если положить
то
g^ (knlri) = 0 (ft = 0, 1, 2, ..•» 2л — 1),
причем, в силу A0.67),
Докажем, что для всех /
где
w@ (г-0, 2, 4, ...),
)«г(« + я/2«) (г-1,3, 5, ...).
и, следовательно, функция tynr(t) имеет простые нули
в точках kn/n и только в них.
Рассуждая от противного, предположим, что \g+ G)| >
> ф/1/-@' @<<<2л, гфкп/п). Можно выбрать число Я,
0<|Х(<1 так, чтобы выполнялось равенство
и тогда разность
будет иметь на периоде [0, 2л), по меньшей мере, 2/1+ I
нуль (в точках kn/n (? = (), 1, ..., 2н—1) и /). Но это
невозможно, ибо функция h{r) (t) = я|?и0(/) — >^Г) (/) меняет
знак на [0, 2л) ровно 2/1 раз: ^я0@ принимает значения
-t 1 везде, кроме Ъг равноотстоящих точек на периоде,
в которых она меняет знак, a I lg(n (/); < 1 всюду.
Из A0.71) и A0.72) вытекает, что

294 поперечники классов функций [гл. to
Соотношения A0.73) справедливы для любой функции g
из множества Wai (S*Tl)/>'*i легко проверяется, что Цпг е
е WrM(Srwl)p: Поэтому, с учетом A0.69), приходим
к равенствам
S:27\~ sup ]g\> = hnrl> (Ю.74)
(я, r= 1, 2, ...; 1<р<оо, 1/p + l/p'= 1).
Из A0.74) при р=1 получаем A0.65).
Что касается экстремальных подпространств в С для
классов WH\ то здесь интерес может представить
следующее утверждение сбшего характера.
Теорема 10.7.4. Если при некотором г = 0, 1, 2, ...
подпространство Fn (Л/ =1,2,...) является экстремальным
для. класса W[\tx в С, то оно является экстремальным и
для класса WH** в С, при любом выпуклом вверх модуле
непрерывности о>(/).
Доказательство. Рассматривая наряду с W'm также
классы W'mK функций /еСм, у которых /(г~1)
абсолютно непрерывна и ЩгIм^К> заметим, что в силу
равенства (§ 5.9)
V Vv м Л, г л/д; = Л Ь (^ Wx л/, t n )с (А > 0)
подпространство, экстремальное для класса ЦР^/» будет
экстремальным также и для W[\\K при любом /(>0,
В § 8.2 было доказано, что если /е 1Г/"//0), то
Цю'(/)-/С]Фв,(/)Л, A0.75)
где Фаг (/) —хорошо известные нам функции, введенные
в § 6.6. Фиксируем N= 1, 2, ,..,и пусть я = [(Л^ + 1)/2] —
целая часть числа (jV+1)/2. Выберем К = Кп таким
образом, чтобы максимум в правой части A0.75) достигался
при а = я/я, и пусть фо(/) —функция наилучшего
приближения для f в классе W^^Kn» Тогда
я/п
'/С„)с ^ $ [со' (/) -/С„] фя,Я(г (/) Л.
A0.76)

§ 10.7] ОБ ЭКСТРЕМАЛЬНЫХ ПОДПРОСТРАНСТВАХ 295
Если FAr — экстремальное подпространство
размерности N для класса W[\fx (а значит, и для WrjJ~lK^9 то,
используя теорему 10.4.1, будем иметь
= KndN(Wtf\ С) = ^ф^. A0.77)
Так как (см. F.47))
я/л
jj Фя1п.гУ)а-=Ц& (« = 1, 2, ...; г = 0, 1, ...),
и
то оценки A0.76) и A0.77) позволяют написать
я/я
1
Это справедливо для любой f e WH®, а потому
Г//«, f Л')с < Y w' @ ф*/«." @ л =
О
п
и остается заметить, что выражение в правой части есть,
в силу теоремы 10.4.2, Af-мерный поперечник класса WH*
в пространстве С.
Из теоремы 10.7.4 и равенств A0.63) следует, что
подпространство сплайнов Sr.in размерности 2/г, являясь
экстремальным для W[\f\ будет экстремальным
подпространством также и для класса WrHtu при любом выпуклом
вверх со@, т. е. E{WrH", S\n)c~dZn{WrН*у С) = ]/*Л;
(/?-= 1, 2, ...; г = 0, I, ...). (При г = 0С 1^адо заменить
на Л4.)

ДОПОЛНЕНИЕ
§ ДЛ. Неравенства Гельдера
и Минковского для интегралов
1. Неравенство Гельдера для интегралов имеет вид
Л) ($;ф (/)>'*) A/р + 1/р'=*1), (ДЛ)
где f^Lp(a, b) A <р<оо), фе^(а, 6). Записав (ДЛ)
в виде
I! / @ ф @! л < i71! ф Ер- ([Л - \gliya. b)h
а
замечаем, что оно верно также при /7=1 и р^=съ (если
под |ф о понимать [у-.м) и получается в этих случаях
тривиальным образом.
При 1<р<оо неравенство (ДЛ) легко выводится
из следующей леммы.
Л е м м а. ?сли 1 < р < оо w 1/р + 1/// = 1, то для
люэых а^О и b^zQ выполняется соотношение
в котором знак равенства имеет место тогда и только
тогда, когда а=-Ь{Лр"{\ т. е. а? = Ьр'.
Доказательство. Рассмотрим функцию
J ^
Так как т|г (л*) = „г* ! — 1, т|" (л*) — (р — I) лг^ 2, то т) (,г) имеет
абсолютный минимум в единственной точке *=1, причем
min

§ Д.Ц НЕРАВЕНСТВА ГЕЛЬДЕРА И МИНКОВСКОГО 297
Таким образом, для всех д:^0
? + ?>*• (Д-3)
и знак равенства в (Д.З) имеет место только при *=1.
Считая, что а>0 и 6>0 (иначе доказывать нечего),
и положив в (Д.З) x = ab]'^-p) = ab-p'<p, будем иметь
-1 aPb-P' + 'T^ab-p'tp.
Если умножить обе части на Ьр\ то получим (Д.2).
В силу предыдущего знак равенства в (Д.2) имеет
место в единственном случае, когда д61/(|—"> = 1» т. е*
a = bl w~l) или aP = bP\
Доказывая неравенство (Д.1), заметим, что оно
тривиально, если почти всюду :/(/)Ф(/) =0. Поэтому
считаем, что каждая из функций /(/) и ф (/) отлична от
нуля на множестве положительной меры и, следовательно,
Если положить в (Д.2) a=>\f(t)\/A9 b=*\(p(t)\/В, то
получим неравенство
АВ ^ рАР ^ р'Вр' '
справедливое по крайней мере почти всюду на (а, Ь).
Интегрируя по / от а до Ь, найдем
т. е.
а
Знак равенства по доказанному выше возможен здесь
лишь при условии, что
АР Вр'
т. е.

298 ДОПОЛНЕНИЕ
что означает пропорциональность функций [/(/) \р и |ф (/) *>'
(почти всюду на (а, Ь)).
2. Неравенство Минковского для интегралов
представляет собой по сути дела третью аксиому нормы
в пространстве Lp(a, b):
Доказывая его, можно, конечно, считать, что обе
функции f (t) и ср (/) отличны от нуля на множестве
положительной меры, и то же самое справедливо для
/(/) + (). Имеем
Так как !f-|-<p;<p-i>/p' = :/-|-<p>e/-(a, ft), то !/Ч-<Г ;) !^
eLP'(a, Ь)ч и, применив к каждому из двух последних
интегралов неравенство Гельдера, получим
11/+фГ11/!л<li!/-I-ф?dt]lP;/;Р9 (Д.5)
ч« l s / l<(pp'
Таким образом,
Ь /b \ 1/p'
^ I f+ф > л< ^ 1 /-|-ф p dt;. (j/;p-|-[ф;:р),
и чтобы получить (Д.4), надо лишь разделить обе части
, Ъ'р'
на К|
Исследуя возможность знака равенства в (Д.4),
заметим, что для этого необходимо, во всяком случае, выиол-

§ Д.Ц НЕРАВЕНСТВА ГЁЛЪдПРА И МИНКОВСКОГО 299
нение со знаком равенства каждого из соотношений (Д.5)
и (Д.6), написанных в силу неравенства Гельдера.
Следовательно, для знака равенства в (Д.4) необходимо,
чтобы функции \f(t)\P и |ф(/)!рбыли (с точностью до
множества меры нуль) пропорциональны 1/@ -гф(/)!(р~1)р' =
Н/(<) + (')"р. Но если |/(Oi = fii/(O'+4P(Ol и i<p(/)| =
0!, то
f(t)=c<e(t) (с>0). (Д. 7)
Легко проверить, что условие (Д.7) является не только
необходимым, но и достаточным для того, чтобы в (Д.4)
был знак равенства.
3. Обобщенным неравенством Минковского называют
соотношение
р \\/р d ,'> \ 1/р
dx\ <$Ш(*. *)i'd*} dy (R.S)
Чтобы доказать его для 1<р<оо (при р=1 оно
очевидно), положим
b
Если \Jp(x)dx^=Oy то на (а, Ь) почти всюду /(а') = 0,
а
а значит, почти всюду на прямоугольнике (a<ix<iby
c<y<.d) f(x, //) = 0, и мы приходим к тривиальному
ь
случаю. Поэтому считаем в дальнейшем, что ^Jp(x)dx>Q.
Предположим сначала, что
ь
\j?(x)dx< + oo, (Д.9)
а
т. е. J <=Lp(a% ft), а значит, Jp 1^Lp^(at b) (l/p-H/// = 1).
13 силу теорехы Ф/оини
I Jp (х) dx = \j» ' (x): J ! / (х, ;/)! ф^| dx =
V /
.. (Д-Ю)

300 ДОПОЛНЕНИЕ
Применение неравенства Гельдера к внутреннему
интегралу дает
b jb \ I //>' /h \ \ ,'р
\ Jp х (х) \ f (,г, у) \ dx =sc; ^ J*> (x) dx j ; W (,v, у) р d* j .
a \e / \a /
Эта оценка справедлива для почти всех у из (с, d), и,
подставляя ее в (Д. 10), получим соотношение
b fb ^ \;р' d fb \ 1.7?
\jPdx^[ \ Jpdx) JJU f(x, y)\pdx) dy9
a \a ) с .a J
разделив обе части которого на [ jj Jp dx\ придем к (Л.8).
\в /
Теперь освободимся от ограничения (Д.9). Пусть
Тогда почти для всех х е (а, Ь)
Jn (х)"~ j j/ Hi У) \\ dy ^ N (d — c),
с
и следовательно,
b
]J%(x)dx<oo OV>0).
В силу уже доказанного для любого N>0
fb \ ]/р d /b \ 1 'p
%(x)dx\ < W J! / (*• У) % dx\ dy ~c
1 с [a )
d ,b ч \n
и в пределе при iV-^-foo получаем (Л.8).
Заметим, что неравенство (Л.8) можно записать в виде
Р J / (* • У) ^У l| ^ $ ¦!/(•» ^/) • p dy
(норма интеграла не превосходит интеграла от нормы),
причем в такой записи оно будет верным, если Lp(a, h)
заменить на М (а, Ь) или С [а, Ь\ при условии, разумеется,

§ Д.2] НЕКОТОРЫЕ ЭКСТРЕМАЛЬНЫЕ СООТНОШЕНИЯ 301
что соответствующие нормы ]•/(•, у)|| имеют смысл. Таким
образом,
Ш(-> y)dy\ ^-V!f('> y)'\xdy, (Д. 11)
,,c [X с
где под X можно понимать Lp(a, b) (l^p^oo) или
С [я, Ь\.
§ Д.2. Некоторые экстремальные соотношения
1. Если /(/)—фиксированная функция из Lp(a, b)
О^р^оо), то имеет место равенство
w*-:/:, (¦-+;-»)• (ДЛ2)
где, как и в § ДЛ, ради сокращения записи положено
а под Ijgjoo и lg\i понимается соответственно
\п\м = \&\мка. ь) А sup vrai \g(i)\
a<t<b
Пусть сначала 1<р<со. В силу неравенства Гель*
дера
h
так что для любой фе/у(й, Ь) с нормой Цф!р'<1
b
\f(t)ip(t)dt^if}p. (Д. 13)
а
Положим
Фо('/ — :—^~j (Я <1<о).
Так как
| ф0 (/) sp' = *' М == / @ ^
i; / ip p si / i.S

302 дополнение
то фо е Lp> (at b), причем
\]'р' (ь \~р р'
Далее имеем
т. е. функция фо реализует в (Д. 13) знак равенства, и
(Д. 12) для 1<Ср<с>о доказано.
Если р-- 1, то, какова бы ни была функция феМ(а, Ь),
причем для функции ф0 @ = sign / (/) здесь имеет место
точное равенство, так что (Д. 12) доказано и в этом случае.
Рассмотрим, наконец, случай р = оо, когда / е М (а, 6).
Для любой функции ф е ? («, ft) с нормой [ф^^!
Покажем, что всегда существует в множестве L (a, fc)
функция с единичной нормой, для которой левая часть
сколь угодно мало отличается от правой. Зададим е>0,
и пусть
e={t:t<=(a, Ь) 7@ \>:Цм~г}.
Ясно, что mcs(?>»0. Положим
(
mes.
I 0 (*€=(*,
Имеем

§ Д.2] НЕКОТОРЫЕ ЭКСТРЕМАЛЬНЫЕ СООТНОШЕНИЯ 303
и в силу определения множества е
mese
Этим (Д. 12) доказано и при р = оо.
2. Для любой фиксированной непрерывной на отрезке
[а, Ь\ функции /(t) (т. е. для /еС[й, Ь\) справедливо
равенство
v
а
где
i!/:;cH;/ha.*i- max
и верхняя грань вычисляется по всем функциям g(t)>
вариация которых на [а, Ь] не превосходит единицы.
В самом деле, если /GC[a, fc], a ^@ имеет
ограниченное изменение на [a, ft], то при любом разбиении
отрезка [а, Ь] имеем
!с V] i
В пределе при max '/* —/*-i |->-0 получим
$/@<te(/)<j/icVte). (Д.
6
и если V (g) < 1, то
(Д. 16)

304 ДОПОЛНЕНИЕ
Чтобы доказать (Д. 14), осталось указать функцию g(t)
с единичной вариацией на [а, 6], для которой в (Д. 16)
будет знак равенства. Пусть lf\c = !/('о)'» причем
сначала будем предполагать, что a^to<cb. Положим
1п I 0 (а<-*<:*„).
Ясно, что вариация go(/) на [а, Ь] равна единице
(если, конечно, /(<)^ё0) и
$ / @ <fco @ - / (to) [ft (to + 0)-g0 (to - 0)] -
= / Co) sign И'о) = !/(/o)! = Iflc
Если же /0 = Ь» то равенство в (ДЛ6) будет для
функции g(t) -gn(t), равной нулю при a^t<cb и равной
signf(b) в точке Ь,
3. Пусть X и Y — два множества элементов
произвольной природы и каждой паре (л% у), где х(=Х, y^Y>
поставлено в соответствие вещественное число F(x, у).
Иначе говоря, на произведении множеств XxY задана
числовая функция F{xt у).
Имеют место соотношения
sup j sup F (х, у) 1 = sup I sup F (x$ у)} =
- sup F(x% у), (ДЛ7)
()XxY
inf f inf F(x, y)]= inf f inf F(
inF F(x% у)ч (ДЛ8)
sup Г inf F(x9 y)}^ inf Г sup F(x9 y)\ (Д.19)
Из всех соотношений (Д. 17) и (Д. 18) мы докажем
только одно:
del"
яA-е1 sup I sup F (x, y)l --= sup F (ху у) "*- Л;
° A-exl/zev | {K.y)^X*Y
справедливость остальных устанавливается аналогичным
образом.

§ Д.2] НЕКОТОРЫЕ ЭКСТРЕМАЛЬНЫЕ СООТНОШЕНИЯ 305
Предположим сначала, что А<-\-оо. Так как для
любых А'бА и уеК
F{x% */)<Л,
то, переходя слева к верхним граням сначала по у е У,
а затем по х(=Ху получим, что В ^ А. С другой стороны,
по определению точной верхней грани, для любого е!>0
существуют хо^Х и */() е Y такие, что
F (*о. Уо)>л"-С*
Но тогда
Я Ss sup f (л-0, у) ^ F (jf0, ^/o) > Л - е,
т. е. fl>/4—e при любом в>0. Следовательно, В^А
и равенство В ?-А установлено.
Если же А --- М-со, то для любого N>() найдутся
Уо^У и xogX такие, что
и так как
В s* sup /? (л:0, у) ^ f (jfOf
то В тоже равно +оо.
Докажем соотношение (Д. 19). Фиксируя любой
элемент л;0 gX, будем иметь
F{xQf y)<sup F{xty) Vz/еУ,
и значит,
inf F(xOt y)*? inf sup F(xf y).
ye У уе Ухе л
В силу произвольности jf0 из X это неравенство останется
справедливым, если слева перейти к верхней грани по
всем xgX,
4. Пусть на множестве X элементов х произвольной
природы заданы вещественные функции fk(x) в конечном
или счетном числе. Тогда
sup
XG X
inf
(Д.20,
к
5гУ inf Ы*). (Д-21;

306 ДОПОЛНЕНИЕ
Действительно, при каждом фиксированном ^
Чтобы получить (Д.20) и (Д.21), остается, учитывая
произвольность Jo, перейти слева в написанных
соотношениях к верхней, соответственно к нижней, грани по
д-0<= А'.
Из (Д.20) и (Д.21) следует, что
:sup /,(*)- sup /s(Jf)|< sup 7i№-M*)lt (Д.22)
XG.X a:C X Х
|inf /, (x) - inf h(xJs inf i /a (,v) -/2 (дг) |. (Л.23)
Действительно, положив f^(x) = f1(x)—f^(x), будем иметь
в силу (Д. 20)
sup Л (х) < sup /2 (х) + sup /а (х),
ел ех Л
т. е.
sup fx (х) - sup U W <
<; sup i/, (x) - /, (,v)] < sup ! h (x) - h (x) \.
Аналогично устанавливаем, что
sup /2 {x) - sup /, (x) < sup | /i (jf) ~/2 (.v) 5,
ex t=x x
и (Д.22) доказано. (Д.23) выводится из (Д.21)
аналогичными рассуждениями.

КОММЕНТАРИИ И БИБЛИОГРАФИЧЕСКИЕ
УКАЗАНИЯ
К главе 1
§ 1.1. В более общем случае — для локально выпуклых линейных
топологических пространств —задачи I, II и III сформулированы и
исследуются в статье Л. Д Иоффе и В. М. Тихомирова [1], где,
в частности, наряду с поперечником по Колмогорову,
рассматриваются другие понятия поперечника множества.
§ 1.3. Более полное изложение вопросов существования и
единственности элемента наилучшего приближения в линейном
нормированном пространстве можно нлйги, например, в книгах Кизевет-
гера [IJ и Зингера [([. По поводу строгой нормированное™
пространств см Н. И. Ахиезер [1], гл.'l.
К главе 2
§ 2 1. Дополнительная информация по вопросам отделимости
выпуклых множеств содержится в монографии А. Д. Иоффе и
В. М. Тихомирова BJ.
§ 2.2 Теоремы 2.2.1 и 2.2.2 получены С. М. Никольским [3]
§ 2.3. В более общем виде —для отделимых локально выпуклых
топологических пространств —теорема 2.3.1 известна как теорема
Фенхеля— Моро (Фенхель [1|, f2|; Моро [I]) и доказана в книге Л. Д.
Моффе и В. М. Тихомирова [2], а также в обзорной статье этил
же амторов [1], в которой содержится систематическое изложение
общей теории двойственности выпуклых функций и fce приложеиш"
к задачам теории приближения и математического программирования
Приведенное в этой книге доказательство первой части теоремы 2.3.1
для линейных нормированных пространств (соотношение B.7)) сооО
lueuo автору В. М Тихомировым
Вопросам двойственности экстремальных задач и приложениях
к задачам выпуклого программирования и теории приближение
посвящена также? монография Е Г. Гольштейиа |1].
§ 2.4. Критерий 2 4.1 в более общем виде (для локально выпуч
лых пространств) содержи гея в статье &. Д. Иоффе и В. М. Тихо
мирова A). О критериях ближайшего элемента в выпуклом множеств*
см. еще Л. Л. Гаркави [!|, В Н Никольский [II, С. Я- Хавин
сон A|.
§ 25 Равенства B.2G) и B.27) содержатся в статье С. М.
Никольского [3J.

308 КОММЕНТАРИИ И БИБЛИОГРАФИЧЕСКИЕ УКАЗАНИЯ
Отметим еще следующий факт. В случае приближения
конечномерным подпространством в X и в X* мы имеем два соотношения
B.1) и B.4), в известном смысле, симметричные друг другу. Если
X рефлексивно, то есть (Х*)*=Х, то, очевидно, справедливо' и
симметричное B.7) равенство
inf i;/—qv-= sup [/(*)— sup ф(*)], (*)
€НЛ gX еЛ
где fe=.X* и Л —выпуклое замкнутое множество в X*.
В общем случае, однако, соотношение (*) не имеет места, даже
если Л —подпространство (разумеется, бесконечномерное) нХ* Чтобы
убедиться в этом, возьмем Х=г--1. [ — I, 1|, югда Х* = М[— I, 1|, и
множество С[— 1, 1J непрерывных на ( —I, 1] функций является
подпространством в М [— 1, 1]. Пусть /0(/) = sign t (, t, ^ 1), тогда
и* в то же время
sup
П
l-l, ij
ибо. если
\'М0*@Л- sup \
S O УфеС[-1, I],
то je (/)=0 почти всюду
Тот же результат нетрудно получить, если в качестве
аппроксимирующего множества вМ[-1, 1] взять единичный шар в С[— 1, 1J.
К главе 3
§ 3.1. Вопрос об условиях единственности полинома наилучшего
приближения подробно освещен в монографиях Н. П. Ахиезера [1|
и А. Ф. Тимана [1].
§ 3.2. Критерии 3 2.1 и 3.2.3 полинома наилучшего равномерного
приближения, полученные 11 Л Чебышевым [1], обобщались в рач-
личиых направлениях. Одно из наиболее важных обобщений указано
Л. Н. Колмогоровым [3].
§ 3.3. Достаточные условия критерия 3.3.4 получены А А
Марковым [1| (см также Н. И. Ахиезер [1|, гл. 2).
Если ^'—конечномерно (например, Л7-мер но, с базисом if>r ..., tfA^
то критерии 3.3.1 и 3.3.2 можно получить, исследуя обычным путем

КОММЕНТАРИИ И БИБЛИОГРАФИЧЕСКИЕ УКАЗАНИЯ 309
на минимум функцию
2д
р
rf/.
Правда, в этом случае следует предварительно обосновать законность
дифференцирования интеграла Лебега по параметрам Х^
§ 3.5. О многочленах Бернулли см., например, В. И. Крылов
[1|, гл. 1.
Раненство C.36) получено Фа варом [1], [2J, [3]. (См. также
Н И. Ахиезер и М- Г Крейн (IJ).
К главе 4
Основные результаты главы 4, в частности, равенства D.15)
(при р^\л ее) и D.23), теоремы 4,3.3, 4.4.2 и 4.4.3, получены
Г.. М Н и Кольским [3]. Линейные методы D.35) ввел в рассмотрение
Надь [1].
К главе 5
§ 5 2. Аппярат функций Стеклова при исследовании задач теории
приближения используется в книге Н. II. Лхнезера [1|.
§ 5.3. Равенства E.14) получены Фаваром [1|, B|, C|; значение
Еп(уР[\{)м независимо найдено также Н. И. Лхиезером и М. Г. Крей-
ном [1]. Соотношения E.15) и E 21) доказаны С. М Никольским [З].
В цитированных работах получены значения верхних граней
наилучшего приближения тригонометрическими полиномами также на
классах функций, сопряженных с функциями классов WrM и WrL,
Ряд интересных ра^от был посвящен получению аналогичных
результатов на классах сверток с ядром К @ более общего, чем
Dr{t) (г=1, 2, ...), вида Основные трудности здесь возникают при
проверке выполнения условия An или более жесткого (но лучше
обозримого) условия N*n: существует полином 7* с: F^n — i и по
меньшей мере одна точка ^0 «= [0, л/я| такие, что разность К (t) —
— Т* @ меняет знак на |0, 2л| в точках ?0, 50 + л//г, 50 + 2л/л, ...
...» 5и-г Bл — 1) л/2/г и только н них В 1938 г. Надь (!) указал
широкий класс ядер (являющихся, однако, как и Dr (t)t либо
четными, либо нечетными функциями), удовлетворяющих условию /V*.
Много усилий было затрачено на распространение результатов,
полученных для классов WrM и WL (r=I, 2, ...), на случай
дробных г > 0, когда ядро Dr {() (при нецелых г) содержит как синусы,
так и косинусы.
Первый важный шаг был сделан В. К. Дзядыком [1], который
в 1953 г. доказал выполнимость условия N% для Dr(t) при 0 < г <
< 1 В 1956 г. С 13. Слечкин [2J установил аналогичный факт для

310 КОММЕНТАРИИ И БИБЛИОГРАФИЧЕСКИЕ УКАЗАНИЯ
ядер более общего вида:
У
при 0</<1 и г^а^2— г. Интерес к ядрам D* объяснялся,
в частности, тем, что ядром Drr'^~x задаются классы, сопряженные
с ХГ'М и
Полностью задача для дробных классов W[M и WrL была решена
в 1958—1959 гг. В. К. Дзядыком [2], а также Сунь Юн-шеиом [I].
Было доказано, что при всех />0
2д
где
7* —тригонометрический полином порядка п— i, интерполирующий
Dr(t) в точках 1//г(р + /?л) (Л?=П, 2 /г— 1), а р—число, равное
нулю, если 0</^1, и являющееся корнем уравнения
/ |
Bv+ly
~ "»
если г > 1.
Впоследствии В. К- Дзядык [3|. f4| доказал выполнимость
условия N* для широкого класса ядер К (/)» представимых в ннде
периодических интегралов от абсолюпю монотонных функций и
включающих как частный случай ядра Dr (/) и Dj (t) при всех г>0
и любых действительных а
§ 5.5. Равенства E.45) доказаны Фаваром [1], [3|, а также
Н. И. Лхиезером и М Г Крейном [1]; соотношения E.46) получены
С. М. Никольским [3].
В цитированных ныше работах В. К. Дзядыка, С. Б Стечкина
и Сунь Юн-шеиа показано, что в случае дрибпых г>0 наилучшее
приближение ?'л(^м)л1 и ^{^l)l Реализует линейный метод U (/;
х\ \i*t v*), определяемый числами ц? и v|, являющимися
коэффициентами полинома 7* (/), наилучшим образом аппроксимирующего
ядро Dr (/) в метрике L

КОММЕНТАРИИ И БИБЛИОГРАФИЧЕСКИЕ УКАЗАНИЯ 311
§ 5.6. Получению соотношений, аналогичных неравенству
Колмогорова в пространствах Lpt а также на полуоси, посвящено большое
число исследований. Для р=\ точный аналог получил Стейн [1],
дру1 ие случаи рассматривались, в частности, в работах С Б. Стеч-
кина [3], В. Н. Габушина [1|, [2|, Н. П. Купцова [1], В. В. Аре-
ctoi33 [1]; в последней из цитированных работ приведена довольно
обширная библиография по этому вопросу, а также указывается на
связь с другими задачами.
§ 57. Доказательство георемы 5.7.1 следует схеме рассуждений
работы Л. В. Тайкова [1], в которой равенство E.64) получено
в метрике пространств Орлича; соотношение E.65) независимо и
другим путем доказано в работе С. II Туровец [1|.
Отмстим еще, что оценку снизу для lin(*)tt)x для широкой
совокупности функциональных пространств X (включающих С и Lp) и
классов Щ указал А В. Ефимов [2].
К главе 6
Основные результаты главы 6 (§§6 2 —6.8) получены Н. П.
Корнейчуком 110|, [11], [12], |15]; им же введено понятие V-переста-
новки.
Неравенство F.67) ранее другим способом и без учета
периодичности доказал Стейн [1].
Систематическое изложение вопросов, связанных с
перестановками функций (§ 6.1), содержится н монографии Г. Г. Харди,
Дж. Е. Лнттльвуда и Г Полна [1), а также в книге Зигмунда |1],
где используется" термин «равноизмеримые функции».
К главе 7
Основные результаты главы 7 (§§ 7.4—7.6) получены Н. П.
Корнейчуком [10], [11], [15]
Утверждение леммы 7.4 1, за исключением пункта б), получено
независимо Я I]. Корнейчуком [1], [2], |6| и С Б Стечкиным еще
в 1959 г. (c\i примечание в работе II П Корнейчука [1]).
Утверждение пункта 6) леммы 7.4.1 получено Н. П. Корнейчуком [11]
Лемма 7 1.5 принадлежит С Б Стечкшгу (см. Л В.
Ефимов [I])
Частные случаи равенства G 38) (при 0-< г <сЗ) были получены
Н- П. Корнейчуком [3], [4], |8|, |9] в 1961-1963 гг другим
методом (см. главу"8).
Неравенства G 48) и G.49) укачаны И II. Корнейчуком в
заметке [13]
По поводу результатов § 7.7 заметим, что соотношение G.52)
содержится в работах Н П. Корнейчука |3], [8]; георема 7.7.1
получена также Н. II. Корнейчуком E|, [15J (см. также книгу Лоренца
[1], гл, 8)
Классы Я<° и WH® и функции [п, (оз, а), по-видимому,
впервые введены С М Никольским [1], [2J.

312 КОММЕНТАРИИ И БИБЛИОГРАФИЧЕСКИЕ УКАЗАНИЯ
К главе 8
Основные теоремы 8ЯЛ и 8.3.2 доказаны Н. П. Корнейчуком
[3], [81, [12].
Утверждение 8.1.1 получено (иным методом) Н. П.
Корнейчуком [3] в 1961 г. при решении задачи об отыскании верхней грани
/:rt(//w)c. Приведенное в конце § 8.3 доказательство неравенства (8.20)
принадлежит Л. В. Покровскому [I], который, так же как и Л. Ф. Ти-
ман [2], позже рассматривал приближение класса //(!)| классом Н<0*.
В снязи с содержанием § 8.4 отметим, что первые результаты
по вычислению точных значений величин Еп (WrH^)c (при О^г^З)
были получены Н II. Корнейчуком [3], [4], [8], [9] именно g
помощью метода промежуточного приближения. При этом точные оценки
для E{WHi4\ WrKHl)c находились при разных г, вообще говоря,
разными методами, использующими те или иные факты частного
характера. Единый подход был найден, когла с помощью аппарата
i>перестановок были выяснены новые экстремальные свойства диф*
ференцируемых периодических функций, что позволило применить
общий критерии 3.4.1.
Результаты по наилучшему приближению одного класса
функций другим содержатся также в работах Л. В. Тайкова [2J, Ю. Н
Субботина BJ, [5], В. В. Арестова и В. И Габушина [1] и др.
К главе 9
§ 9.1. Различные доказательства неравенств (9.1) и (9 2),
использующие, в частности, полиномы Джексона, можно найти в
монографиях И. П. Натансона [1], В П Гончарова [I], H. И Ахиезера |1],
II. П. Коровкииа [1], А. Ф. Тимана [1]. В двух последних
содержатся неравенства Джексона для О и L'p с абсолютными (хотя,
вообще говоря, неточными) константами.
§ 9.2. Лемма 9.2.1 и теорема 9.2.2 доказаны Н. П.
Корнейчуком [7].
§ 9.3. Все результаты §9.3 принадлежат Н. И Черных [I], [2].
§9.4 Теоремы 9.4.3 и 9.4.4 при /-=1 получил В. В. Жук [1];
при / = 3, 5, 7, ... эти теоремы доказаны Л. А. Лигуном [I].
Некоторые оценки величин нпг и к'пг содержа гея в работах
С Б Стечкина 14], 15], В. И. Бердышева [1J, [2J.
К главе 10
§ 10.2. Теорема 10 2.3 доказана в работе В. М. Тихомирова \\\\
приведенное в тексте книги доказательство заимствовано из
монографии Лоренца [1]
§ 10.3. Результаты, приведенные в § 10.3, содержатся в работе
А Н. Колмогорова [1J, в которой впервые поставлена задача о
вычислении поперечников.

КОММЕНТАРИИ II БИБЛИОГРАФИЧЕСКИЕ УКАЗАНИЯ 313
§ 10.4. Все результаты теоремы 10.4.1 принадлежат В. М.
Тихомирову [11, [2], [31, который в 1960 г. указал эффективный метод
получения оценок поперечников снизу, основанный на теореме 10.2.3,
и впервые нашел точные значения поперечником а пространстве С
Порядковые оценки поперечников классов функций в С были
указаны С. Б. Стечкиным A) в 1954 г.
Что касается теоремы 10.4.2, то нечетные поперечники классов
WH® в С (при условии выпуклости о (/)) получены Н. II.
Корнейчуком [9], [12|, а четные —В. П. Рубаном |1J. Оценки снизу для
d»a-\ (WrHi4\ С), базирующиеся на теореме 10.2.3, приведены в книге
Лоренца |1], гл. 9.
Лемма 10.4.3 принадлежит В. М. Тихомирову C|, лемма 10.4.5 —
В. И. Рубану, который, сообщив автору '^ту лемму, указал путь
получения точных оценок поперечников d2i(WrH*at С), не
опирающийся на теорему Боре у ка-
§ 10.5. Нечегиые поперечники с1гп 1(WI, l) и d2n^(W[rK l)
вычислены независимо Ю. И. Маковозом [1| и Ю. Н. Субботиным
[31, [4] (см. § 10.6), поперечинки J2n_3 {WrM, L) получены Ю. И.
Маковозом [2J. (Речь идет, конечно, о получении точных оценок снизу,
так как оценки сверху уже имелись.)
Четные поперечники классов №?, UP[T~l и Wr^ в пространстве L
найдены В. И. Рубаном. В. И. Рубан сообщил автору приведенное
в тексте доказательство теорем 10.5.1 и 10.5.2, позволившее,
используя общие идеи работы Ю. И. Маковоза [2|, получить точные оценки
снизу для четных поперечников в L всех рассматриваемых классов.
В работе В. Л. Моторного и В. II. Рубана [1| с помощью
аппарата V-перестановок получена точная оценка снизу нечетного
поперечника класса WrHk0 в пространстве L (для выпуклого со (/)), и этим,
в связи с результатами § 7.6, доказано, что
§ 10.6. Соотношение A0.50) доказано В. М. Тихомировым [3],
соотношение A0.51)— Ю. Н. Субботиным C|. Доказательства в книге
значительно упрощены. Неравенство A0.57) получил Ю. И.
Григорян A ].
§ 10.7. Утверждение 10.7.1 в случае нечетных г доказано Албер-
гом/ Нильсоном и Уолшем [2], в случае четных г —Ю. Н.
Субботиным [ 1 ].
Неравенство A0.58) получено Л Л. Женсыкбаеным [1|, который
пришел к нему, исследуя ядро интегрального представления
разности /(/) — оЛ,,.., (/, /). Приведенное в книге доказательство, в
сущности, повторяет рассуждения» с помощью которых В. М.
Тихомиров [3] установил оценку A0.60). Соотношение A0.61) принадлежит
Л. Л Женсыкбаеву [1]. Равенство A0.65) получил Л. Л. Лигун [2]
несколько иным, чем в тексте, способом, использующим результат
В. М. Тихомирова A0.60).
Теорема 10.7.4 доказана Н. П. Корнейчуком |14|. Вопрос о
возможности реализации поперечников d2n(WrH(s)t С) с помощью

14 КОММЕНТАРИИ И БИБЛИОГРАФИЧЕСКИЕ УКАЗАНИЯ
интерполяционных сплайнов рассматривался в работах Н П.
Корнейчука fl4] и [16], где, в частности, установлено, что если
выпуклый вверх модуль непрерывности to (t) не линеен на [0, л/я], то
<v~0, 1, 2, ...).
Приведем еще несколько результатов, связанных с вычислением
поперечников классов периодических функций (непериодический
случай мы, как и в предыдущих главах, ие затрагиваем).
1. Имеют место соотношения (В. И. Рубай [2])
(\ <р<оо).
2. Можно показать, что каков бы ни был модуль непрерывности
(О (/), справедливо равенство
d2n{U<»t C)=2
Оценку снерху для d2n (/7е0, С) легко получить, аппроксимируя
функцию / е/7е0 подпространством Sin,h функций Стеклова g^
построенных для j? e Sin (см. Ю. И. Григорян [IJ, где рассматривается
непериодический случай). Для получения оценки снизу надо
воспользоваться леммой 10.4.3 и теоремой А. Н Колмогорова об оценке
поперечников (см. В. М. Тихомиров [IJ, теорема 2).
3 Пусть п = 2, 3, 4, ... фиксировано. Если модуль
непрерывности о>(/) таков, что для некоторого б @ <б <л/л)
0) (/) = (о (л/я) (л/я — б ^ / ^ д.'/г),
w (/) > со (л/п) (/ > л;п),
то
<**,(//», C)<d2^x(/^, С)
(В И. Рубан [3]).

ЛИТЕРАТУРА
А лбе р г Дж., Нильсон Э., Уолш Дж. (A hi berg J. H.,
N4 1 son E. N., Walsh J. L.)
1 Теория сплайнов и ее приложения, М., «Мир», 1972.
2 Best approximation and convergence pioperUes of higher order
spline approximations, /. Math. Mech. 14 A965), 231—244.
Арестов В. В.
1 О некоторых экстремальных задачах для дифференцируемых
функций одной переменной, Труды МИ АН СССР 138 A975),
3—28.
Арестов В. В, Г а б у ш и н В. Н.
1. О приближении классов дифференцируемых функций, MaieM
заметки 9, № 2 A971), 105—112.
Ахиезер Н. И.
1 Лекции по теории аппроксимации, М-, «Наука», 1965.
Ахиезер Н И и Крейн М. Г.
1 О наилучшем приближении тригонометрическими суммами
дифференцируемых периодических функций, ДАН СССР 15 A937),
107-112.
БерзышевВ И.
1. О теореме Джексона в Lp, Труды МИАН СССР 88 A967),
3—16.
2 Связь между иеравенстном Джексона и оцной геометрической
задачей, Матем. заметки 3, ЛЬ 3 A968), 327 — 338.
Борсук (Borsuk K-)
1 Drei Satze liber die я-dimensionale euklidische Sphere, Fund
Math. 20 A933), 177—191.
Валле-Пуссен (Ch.-J de la Vail ее Poussin)
1. Sur les polynomes d'approximation et la representation appiochee
d'un angle, Bull. Ac. Sc Belgique A910), 808—844.
Габушин В Н
1. Неравенства для норм функций и ее производных в метриках
Lp, Матем. заметки I, Л? 3 A9G7), 291—293.
2. Точные константы в неравенствах между нормами производных
функций, Матем заметки 4, № 2 A968), 221—232.
Гаркавн Л Л.
1 О критериии элемента наилучше-го приближения, Сиб. матем
жури. 5 A964), 472 — 476.
Голь ш теин Е. Г.
1. Теория двойственности в математическом программировании и
ее приложения, М., «Наука», 1971.
Г о и ч а р о в В Л.
1 Теория интерполирования и приближения функций, М., Гостех-
издат, 1954.

316 ЛИТЕРАТУРА
Г р и г о р я н Ю.
1. Поперечники некоторых множеств в функциональных
пространствах, Матем. заметки 13, .Vs 5 A973)» 637 — 644»
Дан форд Н., Шварц Дж. Т
I. Линейные операторы. Общая теория, М., ИЛ, 1964.
Джексон (Jackson D.)
1. Ober die Genauigkeit des Anr.aherung stetiger Funktionen durch
ganze rationale Funktionen gegeben Grades und trigonomelrisclien
Sunimen gegebener Ordnung, Diss., Gottingen, 1911.
Д з я дык В. К.
1. О наилучшем приближении на классе периодических функций,
имеющих ограниченную s-ю производную @<s<l), Изв АН
СССР, сер. матем 17 A953), 135-162.
2. О наилучшем приближении иа классах периодических функций,
определяемых ядрами, являющимися интегралами от абсолютно
монотонных функций, ]{зв ЛИ СССР, сер матем 23 A959),
933-950
3. К вопросу о наилучшем приближении абсолютно монотонных и
некоторых других функций в метрике L при помощи
тригонометрических полиномов, Шв. АН СССР, сер матем. 25 A961),
173-238.
4. О наилучшем приближении на классах периодических функций,
определяемых интегралами от линейной комбинации
абсолютно моноюиных ядер, Матем. замени 16, № 5 A974), 691 —
701.
к и мо в А. В.
Линейные методы приближения непрерывных периодических
функций, Матем. сб. 54, № 1 A961), 51—90.
2. О* наилучших приближениях классов периодических функций
тригонометрическими полиномами, Изв. АН СССР, сер магем.
30 A966), 1163—1178.
Же и с ыкбаев А. А.
1. Приближение дифференцируемых периодических функций
сплайнами по равномерному разбиению, Матем. заметки 13,
JV? G A973), 807 — 816.
Жук В. В.
1. Некоторые точные неравенства между равномерными
приближениями периодических функций, ДАН СССР 201 A967), 263—
266.
Зигмунд (Zygmund A.)
I. Тригонометрические ряды, т. I, M., «Мир», 1965.
Зингер (Singer /.)
1 Сеа niai buna approximare in spatii vecloriale normate prin ele-
mciite din subspatii vectoriale, Editura Aeademiei Republicii
Social fste Romania, Bucuresii, 1967.
Иоффе А. Д., Тихомиров В. М.
1. Двойственность выпуклых функций и экстремальные задачи,
УМН 27, 6 A908), 51-116.
2 Теория экстремальных задач, М., «Наука», 1974.
Кизеветтер (К i e s e wetter H.)
1. Voriesungen iiber Hneare Approximation, Berlin, VEB, Deutscher
Verlag der Wissenschaften, 1973,

ЛИТЕРАТУРА 317
КолмогоровА К.
1. Cber die besste Annaherung von Funktionen eincr gegebenen
Funktionklassen, Ann. of Math. 37 A936), 107—110.
2. О неравенствах между верхними гранями последовательных
производных функций на бесконечном интернале, Учен. зап.
МГУ, вып 30, «Математика» 3 A939), 3—13.
3. Замечание по поводу многочленов П. Л. Чебышева, наименее
уклоняющихся от заданной функции, УМН 3, 1 A948), 216 — 221.
Колмогоров А. Н., Фомин С В.
1. Элементы теории функций и функционального анализа, М.,
«Наука», 1972.
Корнейчук Н П.
1. О приближении функций, удовлетворяющих условию Липшица,
суммами Бернштейна— Рогозинекого, ДАН СССР 125 A959),
258-261.
2. Об оценке приближений функции класса //са)
тригонометрическими многочленами, Сб. «Исследования по современным
проблемам конструктивной теории функций», М., 1961,
148-154.
3. О наилучшем равномерном приближении на некоторых классах
непрерывных функции, ДАН СССР 140 A961), 748 — 751.
4. О наилучшем равномерном приближении дифференцируемых
функций, ДАН СССР 141 A961), 304 — 307.
5. О существовании линейного полиномиального оператора,
дающего на классе функций наилучшее приближение, ДАН СССР
143 A962), 25-27.
6. Об экстремальных свойствах периодических функций, ДАН
УССР, .\ь 8 A962), 993-998.
7.1 Точная константа в теореме Д. Джексона о наилучшем равно»
мерном приближении непрерывных периодических функций,
ДАН СССР 145 (I9G2), 514-515.
8. О наилучшем приближении непрерывных функций, Изв. АН
СССР, сер. матем. 27 A963), 29 — 44.
9. Точное значение наилучших приближений и поперечников
некоторых классов функций, ДАН СССР 150 A963), 1218 —
1220.
10. Верхние грани наилучших приближений на классах
дифференцируемых периодических функций в метриках С и L, ДАН СССР
190 A970), 269-271.
11 Экстремальные значения функционалов и наилучшее
приближение на классах периодических функций, Ичв. АН СССР,
сер. матем. 35 A971), 93—124.
12. Неравенства для дифференцируемых периодических функций и
наилучшее приближение одного класса функций другим, Изв.
АН СССР, сер. мачем. 36 A972), 423-434.
13. Замечание о теореме Джексона для дифференцируемых
функций, Матем. заметки 12, Л° 5 A972), 517 — 522.
14 О равномерном приближении периодических функций
подпространствами конечной размерности, ДАН СССР 213 A973),
525-528.
15. О методах исследования -экстремальных задач теории
наилучшего приближения, УМЛ 29, 3 A974), 9 — 42,

318 ЛИТЕРАТУРА
16, On extremal subspaces and approximation of periodic functions
by splines of minimal defect, Analysis Matliemalica I, №2
A975), 91-101.
Коровки и П. П.
1. Линейные операторы и теория приближении, М., Фнзматгиз,
1959.
Крылов В. И.
1 Приближенное вычисление интегралов, М., «Наука», 1967.
Купцов Н. П
I. Колмогоровекие оценки для производных в L2{0, с0)» Труды
МИЛН 138 A975), 94—117.
Л и г у н А. А.
1. О точных константах приближения дифференцируемых
периодических функций, Матсм. заметки 14, JSfe I (\973), 21—30.
2. Точные константы в /геравенствах типа Джексона и
Колмогорова, Лнтореферат кандидатской диссертации, Днепропетровский
госуииверситет, 1974.
Лоренц (L о г е п t z G. G )
1 Approximation of functions» New York, Holt, Rinehalf and
Winston, 1966.
Люстерпик Л. А., Соболев В И.
1. Элементы функционального анализа, М , «Наука», 1965.
Маковоз Ю П.
1. Поперечники некоюрых функциональных классов в
пространстве L, Изв. АН БССР, сер физ.-матсм., ЛЬ 4 A969),
19-28.
2. Об одном приеме оценки сни^у поперечников множеств в
банаховых пространствах, Матем. сб 87, 1 A972), 136—142.
Марков Л. А.
1. О предельных величинах интегралов в связи с
интерполированием A898), Избр. труды, Гостехиздат, 1948.
М о р о (М о г е j u J. J.)
I. Fonctions convexes en dual He, Fac. des Sciences de Mont pel lier
Seminar de Mathemaliques A962)
Моторный В. П., Рубан В. И.
I. Поперечники некоторых классов дифференцируемых
периодических функций в пространстве L, Матем заметки 17, № 4
A975), 531-543.
И адь Б. (Nagy В )
1. Cber gewlsse Extretna]hagen bei transformSerlen trigonornetrischen
Entwicklungen, Berichte Acad d W'iss , Leipzig 90 A938),
103-134.
Натансон И. П.
1 Конструктивная теория функций, Гостехиздат, 1949.
2. Теория функций вещественной переменной, М , «Наука», 1974
Никольский В. Н.
1. Наилучшее приближение элементами выг.уклых множеств в
линейных нормированных пространствах, Уч. зап Калин, гос.
под. ип-та 29 A903), 85-119
Никольский С М.
1. Приближение периодических функции тригонометрическими
многочленами, Труды МИЛН 15 A945), 1-76,

ЛИТГРЛТУРА 310
2. Ряды Фурье функции с данным модулем непрерывности, ДАН
СССР 52 A946), 191 -194.
3. Приближение фупкиип тригонометрическими полиномами в
среднем, Изв. АН СССР, сер. магем. 10 A946), 207 — 256.
4. Приближение функции многих переменных и георемы вложения,
М., «Наука», 1969.
5. Курс математического анализа, т. II, М., «Наука», 1973.
6. Квадратурные формулы, М., «Наука», 1974.
Покрове к и и Л. В.
I. Об оцюй теореме Л. Ф. Тимана, Фуикц. анализ 1, 3 A967),
93-94.
Рубан В. И.
1. Четные поперечники классов WrH^ в пространстве С*^ Матем.
наметки 15, Л« 3 A974), 387—392.
2. Поперечники одного класса 2л-периоднческих функций в
пространстве I.p (I </?<.o;;), Сборник «Теория приближения
функции и ее приложения», Киев, Институт математики АН УССР,
1974, 119—128.
3. О поперечниках одного класса непрерывных периодических
функций, Тезисы Международной конференции по теории
аппроксимации, Калуга, Г975, 89 — 90
С м е н ь е р (S p a n i е г Е. Н.)
! Алгебраическая топология, М., «Мир», 1971.
Стой и (Stein Е. М.)
1. Functions of exponential type, Ann. Math. 65, № 3 A957),
582 - 592.
Стечкин С. Б.
1. О наилучшем приближении заданных классов функций любыми
полипомами, УМН 9, 1 A954), 133-134.
2. О наилучшем приближении некоторых классов периодических
функций тригонометрическими полиномами, Изв. АН СССР,
сер матем. 20 A956), 043 — 648.
3 Неравенства между нормами производных произвольной
функции, Ada Sci. Math. 26 A965), 225-230.
4. Замечание к теореме Джексона, Труды МИЛН 88 A967), 17—19.
5. О приближении непрерывных периодических функций суммами
Фавара, Труды МИЛИ 109 A971), 20-34.
Субботин Ю. Н.
'1. О кусочно-полиномиальной интерполяции, Матем. заметки 1,
№ 1 A967), 63-70.
2. Наилучшее приближение класса функций другим классом,
Матем. заметки 2, Mb 5 A967), 495--504.
3. Поперечник класса WI. в /. @, 2л) и приближение сплайн-фуик-
циями, Матем. заметки 7, Хя ] A970), 43-52.
4. Приближение сплайн-функциями и оценки поперечников, Труды
МИЛН 109 A971), 35-'6О.
5. Связь сплайн-приближений с задачей приближения класса
классом, Матем. заметки 9, J\fe 5 A971), 501 —510.
Сунь Ю и - ш е н
1. О наилучшем приближении периодических дифференцируемых
функций тригонометрическими поли помами, Изв. АН СССР, сер.
матем. 23 A959), 67 — 92.

320 ЛИТЕРАТУРА
Тай ков Л. В.
1. О приближении в среднем некоторых классов периодических
функций, Труды МИЛН 88 A967). til—70.
2. О наилучшем приближении и среднем некоторых классов
аналитических функций, Матем. заметки 1, № 2 A967), 155—102.
Т и м а н Л. Ф.
1. Теория приближения функции действительного переменного, М.,
Физматпп, I960.
2. Деформация метрических пространств и некоторые связанные
с ней вопросы теории функции, УМН 20, 2 A905), 53 — 87
Тихомиров В. М.
1. Поперечники множеств в функциональных пространствах и
теория наилучших приближении, УМН 15, 3 (I960), 81 -120.
2. Некоторые вопросы теории приближении, ДАН (.ССР 160 A905),
774-777.
3. Наилучшие методы приближения и интерполирования
дифференцируемых функций в пространстве С[—1, 1], Матем. сб. 80,
ЛЬ 2 A909), 290-304.
Т у р о ве ц С. U.
1. О наилучшем приближении в среднем дифференцируемых
функции, ДАН УССР, Л» 5 A%8), 417 — 421.
Ф а в а р (F a v a r d J.)
1. Sur ['approximation des foictions periodiques par des polynomes
trigonometriques, С R Acaci. Sci. (Paris) 203 A930), 1122 — 1124.
2. Application de la formule sommdtoire d'Euler a la demonstration
de (juelques proprietes extremeles des integrals des fonctions
periodiques, Maih. Tidskrift 4 A9%), 81—94.
3. Sur les meilleurs procedes d'ap proxim.it ion de certaines clasess de
fonctions par des polynomes trigononietriques, Bull Sci, Math
61 A937), 209-224, 243-250
Фенхель (F e n с li e 1 W.)
1. On conjugate convexe functions, Canad Journ Math. 1 A949),
73-77.
2. Convex Cones, Sets and Inunctions. Princeton L'niv., 1951
Фи хтенгольц Г. M.
1. Курс дифференциального и интегрального исчисления, т. III,
М., «Наука», I960.
X а в и и с он С Я.
1. Об аппроксимации элементами выпуклых множеств, ДАН СССР
172 A907), 294-297.
X а р д и Г., Л и т т л ьв у д Дж., П о л и а Г,
1. Неравенства, ИЛ, 1948.
Чебышев П. Л.
1. Вопросы о наименьших величинах, связанные с приближенным
представлением функции A859), Сочинения, М.--Л., 1947,
Изд-во ЛИ СССР, т. II, стр. 151-235.
Черных II. II.
1. О неравенстве Джексона в L2, Труды МИЛН 88 A907), 71 -74.
2. О наилучшем приближении периодических функций
тригонометрическими полиномами в U, Матем заметки 2, X» 5 A967),
513-522.