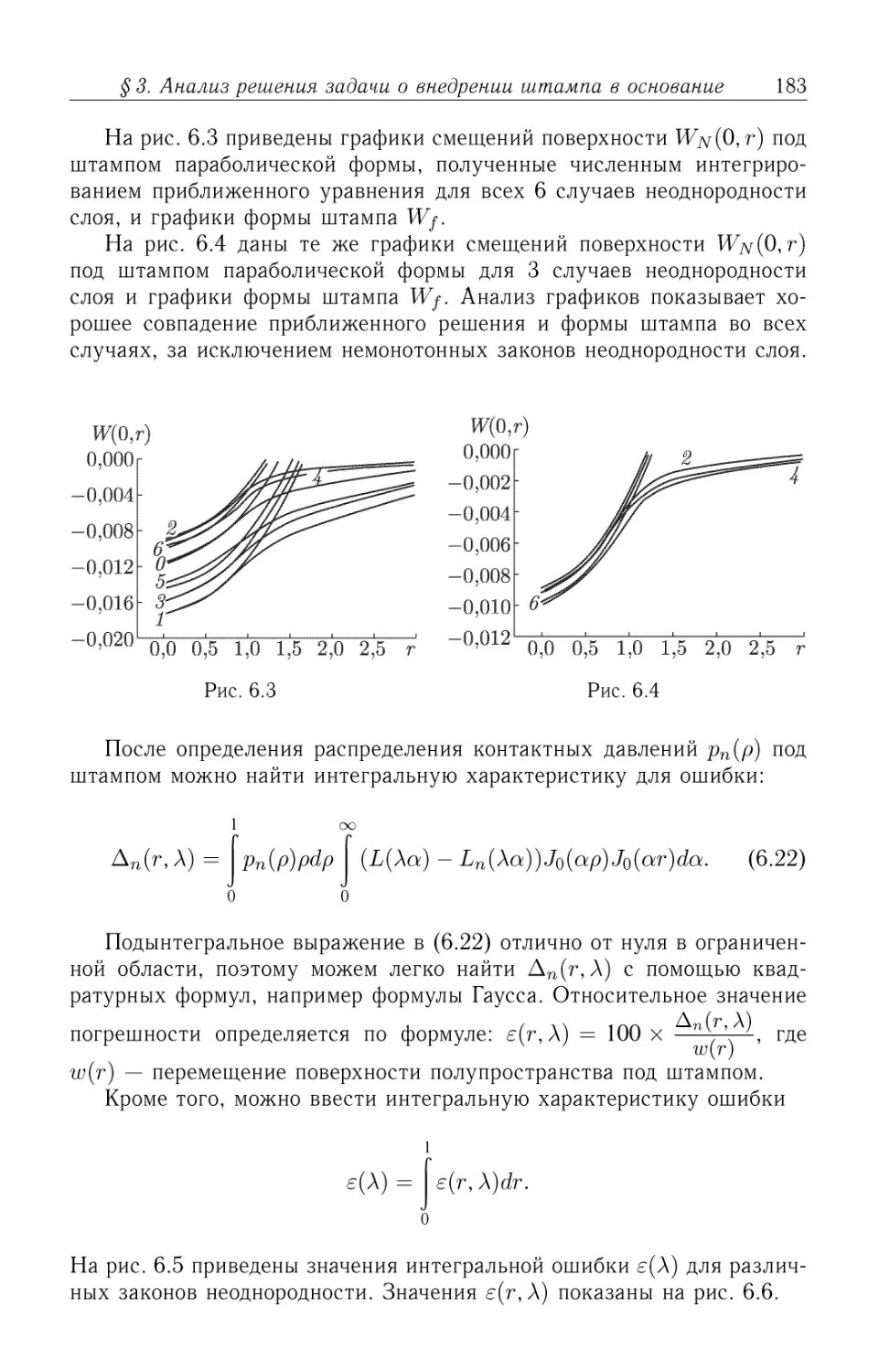
Автор: Айзикович С.М.
Теги: механика деформируемых тел упругость деформация механика физика математика теория упругости
ISBN: 5-9221-0661-9
Год: 2006
Текст
УДК 539.3 ?j Издание осуществлено при поддержке
ББК 22.251 I* dip и: Российского фонда фундаментальных
Д37 ** исследований по проекту 05-01-14058д
Контактные задачи теории упругости для неоднородных сред /
СМ. Айзикович, В.М. Александров, А. В. Белоконь, Л. И. Кренев,
И. С. Трубчик. - М.: ФИЗМАТЛИТ, 2006. - 240 с. - ISBN 5-9221-0661-9.
Монография посвящена разработке и обоснованию новых эффективных
математических методов решения статических контактных задач теории упру-
упругости для неоднородных сред.
Результаты, полученные в работе, дают возможность делать расчеты
и определять параметры контактного взаимодействия функционально-
градиентных материалов и могут быть использованы как в непосредственных
инженерных расчетах, так и при оценке эффективности прямых численных
методов.
Для научных и инженерно-технических работников, специалистов в обла-
области машиностроения, приборостроения и других отраслей современной техни-
техники, а также для преподавателей, аспирантов и студентов вузов, специализиру-
специализирующихся в области механики деформируемого твердого тела.
© ФИЗМАТЛИТ, 2006
© С. М. Айзикович, В. М. Александров,
А. В. Белоконь, Л. И. Кренев,
ISBN 5-9221 -0661-9 и. с. Трубчик, 2006
Введение
Контактные задачи являются центральными в механике деформи-
деформируемого твердого тела, так как контакт — это основной метод при-
приложения нагрузок к деформируемому телу, кроме того, концентрация
напряжений в зоне контакта часто инициирует разрушение материа-
материала. Аналитические решения могут быть получены только для очень
ограниченного класса контактных задач, поэтому важно развивать
численные и численно-аналитические методы их решения.
Особое значение в настоящее время имеют контактные задачи
для неоднородных сред, так как непрерывное изменение механических
свойств по одной из координат характерно для многих тел, что связано
с условиями их создания и эксплуатации.
Расширение температурных диапазонов работы тяжело нагружен-
нагруженных контактов поставило проблемы, связанные с расслаиванием много-
многослойных покрытий, возникновением в них температурных напряжений
при изменении рабочей температуры в зоне сопряжений двух различ-
различных материалов (как правило, материалы, имеющие разные значения
упругих модулей, имеют и разные коэффициенты теплового расши-
расширения).
Преимущества, связанные с увеличением срока эксплуатации изде-
изделий, стимулируют процесс создания функционально-градиентных по-
покрытий и функционально-градиентных соединений, несмотря на все
возрастающую сложность технологии получения таких материалов.
Сегодня интерес к решению задач контактного взаимодействия для
неоднородных материалов поддерживает высокая стоимость и дли-
длительность испытаний на износ, а также необходимость осмысления
результатов этих испытаний.
Развитие трибологии [103] способствовало расширению теоретиче-
теоретических исследований, которые существенно обогатили область неклас-
неклассических контактных задач теории упругости и теоретические основы
трибологии. Контактные задачи для тел с покрытиями относятся к од-
одним из основных задач трибологии. Подложка может быть как дефор-
деформируемой, так и недеформируемой. Покрытия для реальных материа-
материалов — достаточно сложные структуры, неоднородные по толщине [143],
обладающие пористостью, различными свойствами на поверхности
и в зоне, примыкающей к подложке.
Упругие характеристики реальных покрытий могут отличаться в
3-6 раз от упругих свойств подложки. Толщина большинства покры-
покрытий изменяется в диапазоне от 5-10 нм до нескольких миллиметров.
Введение
В настоящее время наибольшее прикладное значение имеют покрытия
с толщиной меньше одного микрона.
При построении общей теории упругости неоднородного тела воз-
возникает необходимость решать все те же задачи, что и для теории
упругости однородных материалов, но появляются и новые достаточно
сложные задачи. В частности, появляется задача определения значений
модуля упругости внутри неоднородного тела. Даже в частных случаях
однородных тонких покрытий, не говоря уже о покрытиях, свойства
которых изменяются по глубине, это сложная задача.
Тела с покрытиями — широко распространенный класс современных
материалов. Синтез современных покрытий направлен на создание все
более тонких покрытий сложной структуры (функционально-градиент-
(функционально-градиентных или многослойных). В большинстве практически важных случаев
свойства покрытий материалов изменяются по одной координате, орто-
ортогональной к образующей поверхности подложки, на которую наносится
покрытие, или просто упрочняется приповерхностный слой основного
материала. Развитые ранее классические математические модели одно-
однородных материалов эти случаи не охватывают, так как при наличии
значительного градиента упругих свойств наблюдаются не только ко-
количественные, но и качественные различия в поведении материалов
с покрытиями. Например, увеличение износостойкости при удачной
конструкции материалов, термостойкость. Но появляются и эффекты
расслаивания, выкрашивания и т.д. Проблема изучения износостойко-
износостойкости покрытий особенно актуальна. На экспериментальное определение
износостойкости покрытий расходуются миллиарды долларов и годы
человеко-часов, но при реальном рассмотрении эксперименты носят
чисто эмпирический характер, так как для покрытия тоньше 2-3
микрон определить достаточно точно упругие свойства и, тем более,
измерить их изменения по глубине без предварительного построения
достаточно точной математической модели контактного взаимодействия
практически невозможно.
Еще одна особенность неоднородных материалов — наличие до-
дополнительных источников концентрации напряжений. В однородных
телах концентрация напряжений возникает в местах резких изменений
геометрии тела и нагрузки. В неоднородных материалах возникает
дополнительная концентрация напряжений в местах резкого изменения
физико-механических характеристик материала (модуля упругости, ко-
коэффициента Пуассона и др.), т.е. по поверхностям сопряжения одно-
однородных элементов.
Разрушение неоднородных материалов определяется совместным
действием температурных напряжений и напряжений от внешней на-
нагрузки, причем чаще всего разрушение начинается в местах концен-
концентрации напряжений. В связи с этим при создании новых материалов
следует учитывать концентрацию напряжений и от физико-механиче-
физико-механической неоднородности на поверхности контакта однородных элементов.
Введение
При расчетах на износостойкость реальных материалов необходимо
учитывать, что вследствие механических, экологических, температур-
температурных и других воздействий неизбежно происходит перераспределение
механических свойств материала в приповерхностных слоях.
Известно, что решения смешанных задач математической теории
упругости для слоистых и непрерывно-неоднородных сред представля-
представляют необходимую основу для решения соответствующих задач термо-
термоупругости, вязкоупругости, теории консолидации [1,2, 48, 130], теории
разрушения и износостойкости неоднородных сред, а методы, применя-
применяемые для их исследования, являются общими для целого класса задач
математической физики.
Первые работы в области контактных задач теории упругости неод-
неоднородных тел, опубликованные в середине 50-х годов прошлого века,
были связаны с расчетом фундаментов и оснований в строительстве,
необходимостью расчета покрытий дорожных одежд [136, 137], а также
касались задач расчета плит на многослойных или непрерывно-неодно-
непрерывно-неоднородных основаниях [63, 80, 81, 92, 93, 125, 126, 132].
Позднее, в конце 80-х годов, интерес к контактным задачам для
непрерывно-неоднородных тел резко возрос в связи с развитием совре-
современных технологий, которые позволили получать покрытия с непре-
непрерывно изменяющимися упругими свойствами.
К настоящему времени опубликовано большое количество работ
по механике как многослойных, так и непрерывно-неоднородных сред.
Обширный список работ, опубликованных до 1982 г., приведен в
библиографическом указателе [142]. Там же предлагается следующая
классификация неоднородных сред: 1) слоистые среды (многослойные);
2) непрерывно-неоднородные; 3) статистические; 4) разнородные.
Данная монография, согласно этой классификации, связана с раз-
разработкой методов решения контактных задач теории упругости для
неоднородных сред второго типа — непрерывно-неоднородных. Мо-
Монография развивает научное направление в области неклассических
контактных задач, созданное в Ростовском университете академиком
РАН И. И. Воровичем.
Постановка и исследование контактных задач для неоднородных
сред, в достаточно общем виде, стали возможны, с одной стороны,
благодаря развитию аналитических методов решения статических и
динамических контактных задач для классических и неклассических
областей, а с другой стороны, вследствие возросших возможностей
вычислительной техники.
Подробный обзор основных результатов для многослойных сред дан
B.C. Никишиным в монографии [2]. Поэтому в данном обзоре мето-
методы, использованные при решении интегральных уравнений, к которым
сводились решения контактных задач для многослойных сред, будут
затронуты только вкратце.
Введение
1. Основные краевые и смешанные задачи для неоднородного
покрытия, лежащего на деформируемом основании. Говоря о кон-
контактных задачах, следует заметить, что осесимметричная контактная
задача для простейшего — двухслойного — многослойного основания
(слой на упругом полупространстве; между слоем и полупространством
предполагается полное сцепление) рассмотрена впервые уже в работе
Б. И. Когана [136]. Для приближенного решения использовался метод
коллокации. Задача о кручении такого основания жестким штампом
рассмотрена в работе Д. В. Грилицкого [ПО], в которой для построения
решения задачи использовался асимптотический метод «больших Л»,
согласно терминологии [90]. Плоская контактная задача рассмотрена
в работе И.М. Вилкова [88], решение получено методом коллокации.
Много внимания контактным задачам для двухслойного основа-
основания (плоской, осесимметричной) уделено в работах Ю.А. Шевлякова,
А. К. Приварникова, В. И. Петришина, В. И. Ильмана, В. Д. Ламзю-
ка [123, 124, 152-155, 190, 191, 193, 194, 227]. В них рассмотрены
случаи как полного сцепления слоя с полупространством, так и от-
отсутствия трения между ними. При решении интегрального уравнения
контактной задачи использованы методы: 1) коллокации; 2) сведения
к линейной алгебраической системе путем аппроксимации полиномом
регулярной части ядра интегрального уравнения [34]; 3) асимптоти-
асимптотический метод «больших Л»; 4) сведения к интегральному уравнению
Фредгольма второго рода и решения его методом механических квадра-
квадратур. То есть методы, эффективные для достаточно больших значений Л.
Для решения практических вопросов, связанных с оптимизацией
свойств закрепленных оснований, возникла необходимость исследо-
исследования в области малых значений характерного геометрического па-
параметра задачи. Однако не было методов, в результате применения
которых получающееся решение носило бы аналитический характер,
что представляет существенные удобства для приложений. Разработке
таких методов и посвящена значительная часть данной работы.
Двухслойное основание подробно исследовалось в работах
Г. П. Александровой [61, 62], в них решения контактных задач
строились с использованием метода «больших Л», при малых
значениях Л определялось только «вырожденное» решение, полученное
из рассмотрения интегрального уравнения путем предельного перехода
при Л —> 0. Приближенными методами осесимметричная контактная
задача для двухслойного основания рассматривалась в работах
Чена, Энгела [241, 248]. Осесимметричную контактную задачу при
наличии сцепления рассматривали В.М. Вайншлельбаум и Р. В. Гольд-
штейн [85]. Работы B.C. Никишина и Г. С. Шапиро [2, 175-178]
посвящены осесимметричным контактным задачам для кругового и
кольцевого штампов, задачи рассматривались как при наличии трения
или сцепления, так и без трения. Для численных примеров брались
два слоя, лежащие на абсолютно жестком основании.
Введение
В работах И. Г. Горячевой и Е. В. Торской проведен анализ напря-
напряженного состояния тел с покрытиями при множественном характере
нагружения [104], исследована периодическая контактная задача для
системы штампов и упругого слоя, сцепленного с упругим основани-
основанием [105], рассмотрено напряженное состояние двухслойного упругого
основания при неполном сцеплении слоев [106] и исследовано влияния
трения на напряженное состояние тел с покрытиями [211].
При рассмотрении более широкой модели с учетом непрерывной
неоднородности среды сведение контактных задач к интегральному
уравнению осложняется необходимостью при построении трансфор-
трансформанты ядра решать краевую задачу для системы дифференциальных
уравнений с переменными коэффициентами.
В ряде ранних работ были рассмотрены некоторые специальные
случаи неоднородности по глубине (степенной, экспоненциальный, ги-
гиперболический, линейный). Заметим, что рассмотренные зависимости
недостаточно точно отражают реальные свойства среды, так как в
указанных случаях предполагается существование точек, в которых
упругие модули равны нулю или бесконечности. Так, в работе Г. Я. По-
Попова [182] приводятся формулы, по которым можно построить инте-
интегральные уравнения для полупространства с экспоненциальной зави-
зависимостью модуля Юнга от глубины. Н.А. Ростовцевым [201] впер-
впервые получено точное решение задачи о действии силы, нормально
приложенной к поверхности изотропного полупространства с модулем
упругости, меняющимся по степенному закону.
В серии работ [250-253] рассматривались основные краевые задачи
для линейной модели неоднородности по глубине для несжимаемого
материала (полупространство или слой на жестком основании).
Контактные задачи для изотропного полупространства с модулем
упругости, меняющимся по степенному закону, рассматривались в ра-
работах Б. Г. Коренева, Л. А. Галина, В. И. Моссаковского, Г. Я. Попова,
Н.А. Ростовцева [201], B.C. Проценко, Ю.Д. Колыбихина, Г. И. Бели-
ка и др. Задача о кручении неоднородного слоя со степенной и экспо-
экспоненциальной зависимостью от глубины рассматривалась в [239]. Зада-
Задачи о кручении неоднородного полупространства для некоторых частных
законов неоднородности рассмотрены B.C. Проценко, Ю.Д. Колыби-
хиным, Г. А. Морарем. Г. П. Коваленко также рассматривал динамиче-
динамические и статические задачи теории упругости для неоднородных сред
частных видов [140].
В работе Б. И. Когана и В. Д. Зинченко [137] задача о напряженно-
деформированном состоянии неоднородного слоя с экспоненциальным
законом неоднородности модуля сдвига при постоянном коэффициен-
коэффициенте Пуассона, сцепленного с однородным полупространством, сводится
к решению системы линейных алгебраических уравнений.
При численной реализации для произвольных законов неоднородно-
неоднородности использовался ряд подходов. В работе Ю.А. Наумова, Ю.А. Шев-
лякова, В. И. Чистяка, П.Х. Демченко, С. Я. Вольского, А. К. При-
Введение
варникова, B.C. Никишина, Г. С. Шапиро [152, 153, 170, 173, 176]
и некоторых других авторов непрерывная зависимость характеристик
среды от глубины аппроксимируется кусочно-постоянными функциями
(многослойными средами).
Следует заметить, что метод аппроксимации произвольной
непрерывной неоднородности среды многослойным пакетом нуждается,
в каждом отдельном случае, в дополнительном исследовании, когда
такая замена является корректной.
В работах Е.А. Кузнецова [144-149] рассматривались контактные
задачи для неоднородного полупространства и полуплоскости, у кото-
которых коэффициент Пуассона является произвольной функцией глубины,
а модуль сдвига постоянный или зависит от глубины специальным
образом. Напряжения и перемещения определяются с помощью неко-
некоторой функции, удовлетворяющей неоднородному дифференциальному
уравнению второго порядка.
Наряду со статическими контактными задачами рассматривались
и динамические контактные задачи. По-видимому, динамические
контактные задачи впервые в общей постановке для произвольных
законов непрерывной неоднородности были изучены в работах В. А. Ба-
бешко, Е.В. Глушкова, Н.В. Глушковой [74](неоднородное полупро-
полупространство), В. А. Бабешко, И. В. Ананьева, В. В. Калинчука, И. Б. По-
Поляковой [64, 65] (неоднородный слой). Исследование динамических
контактных задач для неоднородных полупространства и слоя
отражено в монографии В. В. Калинчука и Т. И. Белянковой [128].
В предлагаемой монографии рассматриваются только статические
контактные задачи. Решения контактных задач для непрерывно-неод-
непрерывно-неоднородного полупространства и полуплоскости в случае произвольного
закона изменения коэффициентов Ламе по глубине были получены
двухсторонним асимптотическим методом [8-10, 12-18]. Трансформан-
Трансформанта ядра интегрального уравнения, к которому сводится задача, и ее
аппроксимация аналитическим выражением специального вида нахо-
находятся численно. После того как аппроксимация трансформанты ядра
интегрального уравнения аналитическим выражением определена, его
решение находится аналитически. Аналитический вид решения удобен
для исследования различных эффектов, связанных с неоднородностью.
Этот метод позволяет строить решения задач для достаточно широкого
класса законов неоднородности.
2. Основные краевые и смешанные задачи для покрытия, лежа-
лежащего на недеформируемом основании. Простейшая модель покры-
покрытия — это однородный слой или клин, сцепленный с недеформируемой
подложкой. Для случая упругого однородного слоя, лежащего на неде-
недеформируемом основании, хорошо известны работы российских ученых
В.М. Александрова, И. Г. Альперина, В. А. Бабешко, М.Я. Беленько-
Беленького, А. В. Белоконя, СЕ. Бирмана, М.М. Бронштейна, И. И. Ворови-
ча, В. А. Кучерова, С. А. Лутченко, В. И. Петришина, B.C. Тонояна,
Ю.А. Устинова, Г. С. Шапиро и др., а также ряда зарубежных ав-
Введение
торов: J.B. Albeas, G.M. Gladwell, W. Т. Kuipers, P. Meijers, E. Me-
lan, S. F. Smith, C. F. Wang. Изучение смешанных плоских задач для
упругого клина началось в конце 60-х годов — это работы В. С. Тоноя-
на, С. А. Лутченко, Г. Я. Попова, М. И. Бронштейна, В.М. Александро-
Александрова, И. И. Воровича, В. В. Копасенко, Б. И. Сметанина, В. Т. Койтера.
Ряд работ, не включающих собственно смешанные задачи, связан с
изучением вопросов об особенностях напряженного состояния вблизи
особых точек сред [182, 229]. В рамках исследования локального
напряженного состояния в вершине составного клина эти вопросы
рассматривались в работах [45, 67, 82, 117, 118, 164, 179, 206, 242,
243, 263, 269, 270]. Было показано, что в окрестности общей вершины
двух сцепленных клиньев могут возникать интегрируемые особенно-
особенности, причем их тип зависит от характеристик материалов в локальной
геометрии соединения.
Для составного клина основные граничные задачи теории упругости
рассматривались в работах А. Г. Акопяна [32, 33], В. Г. Блиновой,
A.M. Линькова [82], М.С. Быркэ [84], В. Д. Ламзюка, А. И. Фе-
денко [155], Б.М. Прокофьева [195] (метод функций податливости),
Н.Б. Сафаряна [204], Чен Дай-Хенга [241] (метод разделения пере-
переменных), Ж. С. Мишуриса [261].
Специальные законы изменения неоднородности по глубине бы-
были исследованы в работах: R. E. Gibson, P. T. Brown [250-253],
рассматривался упругий слой, модуль которого линейно возрастает
с глубиной. В работе [237] исследовалась неоднородная среда для
степенного закона неоднородности. Упругий клин, модуль Юнга кото-
которого является степенной функцией радиуса, исследовался в работах
А. Г. Акопяна [32, 33]. О.Н. Шинджикашвили [229]; В. В. Лапенко
решал задачи для материала, коэффициенты упругости которого яв-
являются степенными функциями радиуса и экспоненциальными по уг-
угловой координате методом разделения переменных [58, 70] и методом
ортогонализации [158]. Для радиально-неоднородного тела задачи тео-
теории упругости исследовались В. И. Андреевым [66] и О. Д. Григорье-
Григорьевым [109]. Заметим, что эти зависимости недостаточно точно отражают
реальные свойства среды, так как в этом случае существуют точки,
в которых упругие модули равны нулю. Методом разделения перемен-
переменных плоская задача теории упругости для неоднородного клина, закон
неоднородности которого является функцией угловой координаты, ре-
решалась в работе Г. Б. Колчина [141].
Задачу о действии сосредоточенной силы на вершину плоского
бесконечного клина, состоящего из материала, чувствительного к виду
напряженного состояния, рассматривал О. А. Чернышов [225].
Кручение цилиндрическим штампом упругого двухслойного осно-
основания рассматривалось в работе [263]. Предполагалось, что модули
упругости слоев являются степенными функциями специального вида.
Температурные воздействия на неоднородный клин рассматрива-
рассматривались в работах [141, 157].
10 Введение
Следует отметить, что контактные задачи для неоднородных сред
имеют ряд особенностей по сравнению с задачами для однород-
однородных сред.
Во-первых, при механической постановке следует учитывать каче-
качественно новую картину распределения контактных напряжений для
существенно неоднородных материалов (эффект отставания основания
от штампа при некоторых значениях геометрических и физических
параметров и т.д.).
Во-вторых, в отличие от однородных сред (полупространство, слой)
трансформанты ядер интегральных уравнений в смешанных задачах
неоднородных сред имеют сложную структуру, необозримую в анали-
аналитическом виде, в общем случае строят только численными методами.
Одной из целей настоящей монографии является разработка и обос-
обоснование эффективных методов решения статических контактных задач
теории упругости для неоднородных сред.
Рассматриваются произвольные общие непрерывные законы измене-
изменения коэффициентов Ламе по глубине среды в случае полупространства
или слоя или по угловой координате в случае клиновидной области.
Развивается полуаналитический метод решения рассматриваемых крае-
краевых задач. Задачи сводятся к решению парных интегральных уравне-
уравнений. Трансформанты ядер парных интегральных уравнений строятся
численно. На основании установленных аналитических свойств данных
трансформант строятся их аппроксимации аналитическими выражения-
выражениями специального вида. Для этих аппроксимаций парных интегральных
уравнений построены замкнутые аналитические решения. Доказыва-
Доказывается, что эти решения являются двухсторонне асимптотически точ-
точными относительно безразмерного геометрического параметра задач.
Аналитическая форма решений интегральных уравнений удобна для
приложений и позволила впервые получить в аналитическом виде ре-
решение задачи о внедрении параболического индентора в неоднородное
полупространство, определить в аналитическом виде форму осадки
поверхности вне штампа в случае неоднородного основания, получить
в аналитическом виде решения задач об изгибе балок и плит на
неоднородном основании.
Часть I
ПОСТАНОВКА КОНТАКТНЫХ
ЗАДАЧ ДЛЯ НЕОДНОРОДНЫХ
ПОЛУОГРАНИЧЕННЫХ
ОБЛАСТЕЙ
Глава 1
КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ НЕОДНОРОДНЫХ
ПО ГЛУБИНЕ ПОЛУПРОСТРАНСТВА
И ПОЛУПЛОСКОСТИ
Настоящая глава посвящена постановке следующих контактных
задач: о сдвиге полосовым штампом неоднородного полупространства
(антиплоская задача); о вдавливании штампа в неоднородную полу-
полуплоскость (плоская задача); о кручении круговым штампом и о вдав-
вдавливании кругового штампа в неоднородное полупространство (осе-
симметричные задачи), — и сведению их к решению интегральных
уравнений. Излагается метод численного построения трансформант
ядер интегральных уравнений и исследуются их свойства. На основа-
основании изучения этих свойств доказывается возможность аппроксимации
трансформант ядер некоторыми аналитическими выражениями. Пред-
Предлагается простой эффективный алгоритм построения дробно-рацио-
дробно-рациональной функции, аппроксимирующей трансформанту ядра. Для част-
частных видов неоднородности построение ядер интегральных уравнений
выполняется в явном виде.
§ 1. Чистый сдвиг полосовым штампом неоднородного
полупространства
1.1. Постановка задачи. Недеформируемый бесконечный поло-
полосовой штамп с плоским основанием жестко сцеплен с поверхностью Г
упругого неоднородного полупространства О. С полупространством
связана декартова система координат x,y,z (рис. 1.1). Штамп контак-
контактирует с полупространством по поверхности у = О, \х\ ^ а. На каждую
единицу длины штампа действует сдвигающее усилие Р, параллельное
оси z. Под действием этого усилия штамп переместится в направлении
оси z на величину г, вызвав в О деформацию чистого сдвига.
Модуль сдвига полупространства с глубиной изменяется по закону
1) G = G0(y), -H^y^O, A.1)
2) G = Gi=G0(-H), -оо <у<-Н. A.2)
Вне штампа поверхность Г не загружена. При сделанных предполо-
предположениях граничные условия задачи имеют вид
(rvz = 0, \х\ > а,
у = 0, ау = тху = 0, { A.3)
\w = г, х < а,
§ 1. Чистый сдвиг полупространства полосовым штампом
13
Рис. 1.1
где w — перемещение вдоль оси z. При (\х\; — у) —> оо напряжения
исчезают. Считаем, что перемещения и напряжения сопрягаются на
границе изменения закона неоднородности:
„. тт _A) B) /,,,0) /}мB) /1 Л\
У — —П, ту — Tyz\ Wy — Wy . A.4j
Требуется определить закон распределения контактных касательных
напряжений под штампом:
ryz \у=о = т(х), \х\ < а A.5)
при условии
Р= I rf?)d?. A.6)
1.2. Вывод интегрального уравнения задачи. При чистом сдви-
сдвиге уравнения равновесия вырождаются в следующее уравнение:
Так как
имеем
дх
и = v = 0,
ду
A.7)
A.8)
о~х = о-у = az = тху = 0;
закон Гука в рассматриваемом случае имеет вид
'^' '^-^v^^- A-9)
Здесь и далее сгж, сгу, az, тху, rxz, ryz — компоненты тензора на-
напряжений; и, v, w — компоненты вектора смещений среды. Всюду
ниже предполагаем известными основные соотношения теории упруго-
упругости [162].
14 Гл. 1. Контактные задачи для полупространства и полуплоскости
Подставляя A.9) в A.7) и используя условия A.1), получим следую-
следующую систему уравнений для определения перемещений w(x, у):
-G/C)(y)—=0, -H^y^O, A.10)
-оо <у<-Н, (Д = ^ + -^). A.11)
Решение уравнений A.10) ищем в виде интегралов Фурье:
сю
Wi(x, У) = ^\ Wi(a' y)e~iaxda (i = 1, 2). A.12)
— СЮ
Подставив Wi(x,y) (г = 1,2) в форме A.12) в A.10) и A.11),
совершив все необходимые дифференциальные операции под знаком
интеграла и приравняв к нулю в полученных соотношениях подынте-
подынтегральные выражения, получим систему обыкновенных дифференциаль-
дифференциальных уравнений относительно функций Wi(a, у) (г = 1, 2):
(Go(y)W(t + Gto(y)W(-Go(yWWl=O, -H^y^O,
Л о A-13)
I W^ — oi W2 = 0, —оо < у < —Я.
Общее решение второго уравнения в A.13) имеет вид
W2(a, у) = Вх(а)е\а\у + В2(а)е-\а\у. A.14)
Из условия ограниченности перемещений при у —> —оо имеем:
В2(а) =0, т.е.
W2(a, у) =Вх(а)е\а\у. A.15)
Условия A.4) можно записать в виде
W\(a, -Я) =W2(a,-H),
A.16)
W[(a,-H) = Wl(a,-H).
Или, используя явный вид W2(a,y) A.15), из A.16) получим
^ ) _яч = |а| • A-17)
Представим искомую функцию т{х) интегралом Фурье:
сю
Tyz\y=0 =т{х) = ^ I T(a)e-iaxda. A.18)
— СЮ
Здесь Т(а) — трансформанта Фурье функции т(х). Обратное соотно-
соотношение имеет вид: ^
Т(а) = | r(^)eia^. A.19)
§ 1. Чистый сдвиг полупространства полосовым штампом 15
Из A.5), A.9), A.12) и A.18) получим
Введем вспомогательную функцию W*(a, у)
W?(a, у) = Wx{a, y)Go(O) \a\T~\a). A.21)
Условия A.17) и A.20) относительно W* примут вид
w?'(«> ~Я) -а A 22)
W?'(a,0) = \a\. A.23)
В силу однородности вид уравнения A.13) относительно функции
W*(a,y) не изменится. Если функция W*(a,y) известна, то, исполь-
используя граничные условия A.3), можно свести задачу к интегральному
уравнению относительно функции Т(а) вида
Wi(a, 0)e~iaxda =
сю
и у we гаж^а = ? |ж| < а. A.24)
2тгСо(О)
— сю
Таким образом, для построения интегрального уравнения данной
контактной задачи необходимо построить функцию W^(a,0) из крае-
краевой двухточечной задачи A.22), A.23) для уравнения A.13).
1.3. Численное построение трансформанты ядра интегрально-
интегрального уравнения. Введем обозначения:
zx = W*(a, у); z2 = W?f(a, у).
Уравнение A.13), считая, что Go(O) ^OVy ? @,—if), перепишем в
виде линейной системы обыкновенных дифференциальных уравнений
первого порядка:
Здесь и (у) = G'(y)G \y), или, в матричной форме:
-г- = Az, -Н < у < 0, A.25)
где матрица А имеет вид
az -v(y)
16 Гл. 1. Контактные задачи для полупространства и полуплоскости
с краевыми условиями A.22), A.23)
1 \у=-н = N , z2\y=o=\a\. A-26)
Решение краевой двухточечной задачи при фиксированном а A.22),
A.23) построим, используя метод, предложенный в работе В. А. Ба-
бешко, Е. В. Глушкова и Н. В. Глушковой [74] для построения транс-
трансформант ядер динамических контактных задач. Для данной задачи он
модифицируется следующим образом.
Ищем z(y) в виде
z(y) = Bi(a)a(a,y)e^y. A.27)
Вектор а(а, у) определяем из задачи Коши при фиксированном а:
^ = Аа-\а\а,-Н^у^0; A.28)
dy
Q>\ \у=-н = 1, й2\у=-н =<*, A-29)
а затем, используя второе условие A.26), находим В\(а) и тем самым
zi(a, 0):
Bi(a) = \а\а~\а,0), A.30)
И?(а, 0) = zx{pt, 0) = ai(a, 0)a^(a, 0) \а\ . A.31)
Далее будем называть этот метод выделения в решении функций,
определяющихся из решения краевой задачи — системы с постоян-
постоянными коэффициентами, методом модулирующих функций. Этот метод
позволяет строить численно трансформанту ядра значительно быстрее
и точнее по сравнению с другими известными методами, в частности,
в работе [74] проведено численное сравнение эффективности этого
метода по сравнению с методом Абрамова [167].
1.4. Чистый сдвиг полосовым штампом неоднородного полу-
полупространства специального вида. Постановка данной задачи пол-
полностью совпадает с п. 1.1, кроме условия A.1). Вместо него полагаем
-H^y^O,
„ A-32)
2) G = Gi= Goe~H, -oo < у < -Я.
В этом случае удается получить аналитическое выражение для
трансформанты ядра. Система уравнений A.13), A.14) становится си-
системой с постоянными коэффициентами:
Г W" + vW - a2W2 = 0, -Я < у < О,
I l У A.33)
\W^ - a2W2 = 0, -oo < у < -Я.
Общее решение первого уравнения A.33) имеет вид
Wi{pt, у) = Сх(а)е*+У + С2(а)е-*-у, A.34)
§ 1. Чистый сдвиг полупространства полосовым штампом
17
где использовано обозначение
Из A.15)-A.17) и A.19) получим следующую линейную систему
алгебраических уравнений относительно С\(а), Czipi), B\(pt)\
o-X+ff
-н =\а\В1{а)е~^н, A.35)
Из A.35), учитывая, что к+к- = —а2, имеем
г ( \
С\(а) =
_ T(«)
Go(O)
а\ + а + ( —а — >zr_ |а
"§ + '
Go(O)
(^+|a|+a2)
,« +a2\ 2QH_a2_x_ a
Для сведения задачи к интегральному уравнению воспользуемся
условием A.3). Имеем
х\ < а,
или
OO
1 Г T(a)
e~iaxda =
2тг I G0@)
da = e, \x
а.
. |a| + a2) e"*" - a - n- \a\
A.36)
Используем A.19) и A.3). Подставим A.19) в A.36), поменяем порядок
интегрирования и произведем замену переменных:
аН = и; Л =
жх = ж/а
A.37)
(всюду далее штрихи опускаем). Тогда A.36) можно представить
в виде
1
1
2тгСо(О)
A.38)
-1
18 Гл. 1. Контактные задачи для полупространства и полуплоскости
Здесь
= 2
о
L(u) =
A.39)
(|гх| + /х) shV + VshV
\u\-
V =
Уравнение A.24) в общем случае, используя замену переменных,
можно привести к безразмерному виду A.38), где связь между L*(a)
и L{u) определяется соотношением
W?(a, 0) = L*(a) = L*(u/H) = L(u). A.40)
§ 2. Кручение жестким круглым штампом
неоднородного полупространства
2.1. Постановка задач. Недеформируемый круглый штамп с
плоским основанием жестко сцеплен с верхней гранью Г упругого
неоднородного полупространства п. С полупространством связана ци-
цилиндрическая система координат r,ip,z (рис. 1.2). Штамп контактирует
с полупространством по поверхности z = 0, г ^ а. К штампу приложен
крутящий момент М, ось которого совпадает с осью z.
Под действием этого момента штамп повернется относительно оси
z на угол г, вызвав деформацию кручения О. Модуль сдвига полупро-
полупространства с глубиной изменяется по закону
i) Lt = LtQ^Z), —?1 ^ Z ^ U,
2) G = Gi=G0(-H), -oo <z<-H. (L41)
В частности, рассматривается также закон неоднородности специаль-
специального вида:
1) G = Goeuz, -
2) G = GX= Goe-H», -oo<z< -H.
Вне штампа грань Г не нагружена. При сделанных предположениях
граничные условия задачи имеют вид
г т = 0, г > а,
z = 0, az=rrz=0, \ Ztp A.43)
I ию = re, r ^ a.
и A-42)
§2. Кручение круглым штампом неоднородного полупространства 19
/
/
/
А
)
J Г
/тB)
„B)
{
н
Z,
с
.———
,———
г—^
0
"\Ю /
Г
/
/
/
Рис. 1.2
При г^оо и 2;^ —оо напряжения исчезают.
Считаем, что перемещения и напряжения сопрягаются на границе
изменения закона неоднородности:
z = -H, т$ = т$, <"=<2). A.44)
Требуется определить закон распределения контактных касатель-
касательных напряжений под штампом:
Tzv\z=0=Ta(r), r^a, A.45)
и связь между приложенным моментом и углом поворота штампа.
2.2. Сведение задачи к нахождению решения интегрального
уравнения. Приведем поставленную задачу к интегральному урав-
уравнению относительно функции та(г). Для этого предварительно найдем
решение вспомогательной задачи о равновесии упругого полупростран-
полупространства со свойствами A.41) под действием скручивающей касательной
нагрузки при z = 0:
o~z = Trz = 0, rZ(p = г (г).
A.46)
Учитывая, что слой подвержен лишь деформации скручивания,
будем искать решение сформулированной вспомогательной задачи
в форме
uz — иг — 0» и(р — u{r, z\
Тогда из трех уравнений Ламе остается одно:
G0(z)
= 0; -
— щг =0, — оо < z < —Н.
О,
A.47)
A.48)
A.49)
20 Гл. 1. Контактные задачи для полупространства и полуплоскости
Здесь 2 2
дг2 г дг dz2'
а напряжения в соответствии с формулами закона Гука примут вид
ar = aip = az=rrz=0, A.50)
Trz = G^, rrin = G (-^ - - ) . A.51)
oz ^ \or r)
Таким образом, необходимо найти решение уравнений A.48), A.49)
при граничных условиях A.46) и условиях сопряжения A.44). Для
этой цели, как известно [210], может быть эффективно использо-
использовано интегральное преобразование Ханкеля. Представим функцию
щ(г, z) (г = 1, 2) в виде
\ A.52)
о
Подставляя щ(г, z) в форме A.52) в A.48), A.49), A.46) и прирав-
приравнивая нулю в полученных соотношениях подынтегральные выражения,
получим систему обыкновенных дифференциальных уравнений отно-
относительно функции Ui(j, z)(i = 1, 2):
G0(z)U['D, z)+G'0(z)U[D, z)-G0(zI2UlA, z) =0, -H^z^O, A.53)
Щ'Ь, z) - 72?M7, z) = 0, - oo < z < -Я. A.54)
Условия A.44) можно записать в виде
Ui(i,-H) = U2b,-H), A.55)
и[{1,-Н) = Щ{1,-Н). A.56)
Из A.45) получим
Здесь T(j) связана с т(г) преобразованием Ханкеля:
A.58)
о
сю
т(г) = T(~f)J\(r~f)~fd~f. A.59)
о
Сравнивая краевую задачу §1 A.13)—A.14), A.17), A.18), A.22)
с данной A.53)—A.57), получим, что они тождественны с точностью
§2. Кручение круглым штампом неоднородного полупространства 21
до обозначений. Таким образом, аналогично § 1, из краевой задачи
A.53)—A.57) мы можем найти численно функцию
C/f G, 0) = СЛG, 0)G0@OT-1G). A-60)
Затем, используя условие A.43), можно записать интегральное
уравнение нашей задачи:
сю
k = ^, r ^ a. A.61)
о о
U*(j, 0) будем далее обозначать L*(j). Используя A.43) и A.58),
A.61) можно представить в виде
G(){O)re, r^a. A.62)
о о
Сделаем замену переменных:
Д = и; А = Н/а; г' = г /а; р' = о/а;
A.63)
L*G)=L(u/H); та(р'а)=т(р)
(далее штрихи опускаем), тогда A.62) можно переписать в виде
1
т(
о о
Для закона неоднородности A.42), аналогично A.41), получим
сю
r(p)pdp I* L(u)Ji(ur\-l)Ji(up\-l)du = \G0@)re, r < 1. A.64)
Замечание 1.1. Полученное тождество краевых задач §§1,2 при
построении трансформант ядер соответствующих интегральных
уравнений известно [90]: если некоторая смешанная задача ма-
математической физики в плоской постановке порождает уравнение
свертки на отрезке, то эта же смешанная задача в простран-
пространственной (осесимметричной) постановке с условием смены гранич-
граничных условий на окружности радиуса а приводит к уравнению вида
а
Ksr = к8{г, p)r(p)pdp = /(r), 0 < г < а,
A.66)
ks(r, р) = L(u)Js(ur)Js(up)du, 5 = 0, 1, 2, ...
о
22 Гл. 1. Контактные задачи для полупространства и полуплоскости
§ 3. Вдавливание штампа в неоднородную
полуплоскость
3.1. Постановка задачи. Пусть недеформируемый штамп взаи-
взаимодействует с поверхностью Г упругой неоднородной полуплоскости О.
С полуплоскостью связана декартова система координат х, у (рис. 1.3).
Штамп вдавливается в О силой Р и моментом М, при этом длина
линии контакта между ними в плане Г' равна 2а. Силы трения на Г'
предполагаются отсутствующими. Вне штампа поверхность Г не на-
нагружена.
У
Н
Ыу) о
МьАг
Рис. 1.3
Коэффициенты Ламе Л и М полуплоскости с глубиной изменяются
по закону
1) Л =
, М =
, - Я < у < О,
2) Л= Л) = Ло(-Я), М = Mi = Мо(-Я), - оо< у< -Я,
A.67)
под влиянием силы Р и момента М штамп переместится в направлении
оси у на величину а + ж/3.
Граничные условия задачи при сделанных предположениях име-
имеют вид
Здесь а + хC — перемещение штампа под действием силы Р и мо-
момента М, "у(х) — форма основания штампа.
§ 3. Вдавливание штампа в неоднородную полуплоскость 23
Предполагаем, что на границе изменения закона неоднородности
имеют место условия сопряжения
(О _ B) (О _ B)
ХУ ~ТхУ'аУ -°у
A.69)
где и и v — смещения вдоль осей х и у соответственно. Индекс
A) соответствует области определения —Н < у < 0, B) соответствует
—оо < у < —Н, при (\х\ ; — у) —> оо напряжения в полуплоскости ис-
исчезают.
Требуется определить распределение контактных нормальных на-
напряжений под штампом:
4') |„=0 =-q(x), \x\^a, A.70)
а также связь между Р, М и а, C.
Здесь основной является задача определения функции распределе-
распределения контактных давлений q(x), поскольку после ее определения связь
между усилиями Р и М, действующими на штамп, и величинами а
и C, находится из условия равновесия штампа:
Р = J g(?)C М = | q@^. A.71)
Возможно рассмотрение случая, когда один из краев или оба края
штампа не врезаются в поверхность полуплоскости. В этом случае на
соответствующих краях должно быть выполнено соотношение
q(±a)=O, A.72)
которое служит для определения полуширины а области контакта
и налагает некоторые ограничения на функцию f(x).
Заметим также, что в силу отсутствия сцепления между штампом и
поверхностью полуплоскости при правильной постановке задачи долж-
должно быть выполнено условие q(x) > 0 для всех \х\ < а.
3.2. Сведение задачи к нахождению решения интегрального
уравнения. Уравнения равновесия для плоской задачи теории упру-
упругости имеют вид [162]
(тх , дтху = q
V A-73)
ау =0
дх ^ ду
24 Гл. 1. Контактные задачи для полупространства и полуплоскости
Связь между напряжениями и деформациями возьмем в форме
A.74)
ди dv~\ Q ди dv
оу ох] ох оу
Напомним, что коэффициенты Ламе Л и М (иногда обозначаемый
G и называемый модулем сдвига) связаны с модулем Юнга Е и коэф-
коэффициентом Пуассона v соотношениями [162]
M G A AJ5)
МГЗЛ + 2М) Л
= А + М ' "=
Подставляя A.74) в A.73), получим следующую систему уравнений:
/л/г . а\^ i л/г л i л/у{ди , С^Л /л
(М + Л)^— + МАг^ + М [ —- + — =0;
4 у^ж \ду дх)
(М + Л)|^ + МА^; + Л70 + 2МХ|^ = 0; A77)
Решение уравнения A.77) ищем в виде интегралов Фурье:
и{х, У) = ^\ U {a, y)e-iaxda,v(x, у) = ± \ V(a, y)e~iaxda. A.78)
Подставляем A.78) в A.77), сделав замену V(a,y) = iV(a, у), анало-
аналогично п. 1.2, имеем систему обыкновенных дифференциальных уравне-
уравнений:
2(
MU" + а(М + K)V' - а2(М + Л)С/ + M't/' + aMV = 0;
о A79)
BM+A)V"-a(M+A)Uf-a2MV+BMf+Af)Vf-aAfU = 0.
Введем вспомогательные функции
Ut(a,y) = -eo\a\U(a,y)/Q(a),
V*(a, у) = -в0 \а\ V(a, y)/Q(a), A.80)
в0 = 2М@) [Л@) + М@)] / [Л@) + 2М@)], г = 1, 2.
а,
§ 3. Вдавливание штампа в неоднородную полуплоскость 25
Здесь Q(a) — трансформанта Фурье искомой функции q(x):
(О
у=о =Ф0=2^ } Q(a)e-iaxda,Q(a)= J q(Oeia^. A.81)
Для сведения смешанной задачи к интегральному уравнению необ-
необходимо построить функцию V\(a,0). После определения V\(a,O) из
условий A.68) получим
сю
~2тг
00 °°_
I Т 7" / \ 7 /^VO^ 7 J- I'll ^-^ / ^Av \ ^-^ / 7 /^VO^ 7 Р / \ \ ^ / Л С\ С\\
\У\(а)е %axda = ——- v J p ye iaxda = f(x), \x\^a. A.82)
При построении V\(a, 0) следуем схеме, изложенной в § 1 при
рассмотрении задачи о чистом сдвиге. Далее все соотношения будем
рассматривать относительно С/* (а, у) и V*(a, у) из A.80), без знака
(*) в записи.
Используя условие A.67), получим, что при у < —Н A.79) вы-
вырождается в систему обыкновенных дифференциальных уравнений
с постоянными коэффициентами. С учетом условий ограниченности
напряжений при у —> —оо общий вид решения системы при у < —Н
имеет вид
U2(a, у) = (dx + \oL\yd2)e\a\y,
V2(a, у) = sgna [d{ - A + Md2 + \а\ yd2) el^.
Здесь d\, d2 — неопределенные постоянные.
Выпишем условия однозначной разрешимости системы A.79) при
-Я < у < 0 (условия A.68)-A.70)).
Граничные условия:
1) следствие из условия отсутствия касательных напряжений на
границе тху = 0
[ Щ \у=0 =0; A.84)
2) следствие из наличия на границе нормальных напряжений (ис-
(использовали A.80))
-Ao(y)aUl + [ЛоЫ + 2М0Ы] V{ \у=0 = в0 \а\. A.85)
Условия сопряжения по перемещениям и напряжениям:
3) Ul(a,y)\y=.H=U2(a,y)\y=.H; A.86)
4) Ща,у)\у=-н=Ща,у)\у=-Н; A-87)
5) МоЫ \U[ + аЩ |у=_я = М, [Щ + аЩ |у=_я; A.88)
26 Гл. 1. Контактные задачи для полупространства и полуплоскости
6) - A0(y)aU1 + [ЛоМ + 2М0(г/)] V{ \у=-н =
A.89)
Условия A.88) и A.89), использовав A.86) и A.87) и A.67), можно
записать в более простом виде
5*)
6*)
и[(<*>У) \у=-н = Щ(а,у)
V{(a,y)\y=-H =Vj(a,y)
=-н,
A.90)
A.91)
Заметим, что в случае многослойного (двухслойного) основания
условия A.88)-A.89) и A.90)-A.91) не эквивалентны.
Введем обозначения
-—• w - V- w - —
dy' ' dy'
Систему уравнений A.79) перепишем в матричной форме
dw
w\ = и;
A.92)
dy
= Aw,
A.93)
где матрица А имеет следующий вид:
О 1 О
о2М + Л М'
А =
а
а
М
о
М
О
м + л
—а
о
М
— OL-
0
м + л
м
М
1
2М; + Л;
2М + Л 2М + Л 2М + Л
2М + Л
w =
W\
A.94)
Численное решение краевой двухточечной задачи A.93), A.84)-
A.87), A.90)—A.91) будем строить методом модулирующих функций
[74]. Ищем w(a, у) в виде
w(a, 2/) = di(a)ai(a,
d2(a)a2(a,
Векторы аДа, ?/) (г = 1, 2) находятся из задач Коши:
dy
1. ai(a, у) |_я = A, а, 1
2. а2(а, у) \у=-н — \аУ>
(г =1,2);
А + ЗМ
U Л + М
Л + ЗМ
Л + М
а +
у=-н
A.95)
A.96)
A.97)
. A.98)
Здесь начальные условия A.97) и A.98) являются следствиями
A.83), A.86)-A.87) , A.90)-A.91).
§ 3. Вдавливание штампа в неоднородную полуплоскость 27
Функции d\(a) и ^(а) определяются из граничных условий A.84)
и A.85):
di(а) (ахB) + аахC)) + d2(a) (а2B) + аа2C)) = О,
di(a) [-A@)aai(l) + (Л@) + 2M@))aiD)] + A.99)
+d2(a) [-Л@)аа2A) + (Л@) + 2М@))а2D)] = воа.
Здесь обозначено
&i{y) \y=o = (ai(l)» aiB), fl^C), fl^D)), г = 1, 2.
Из A.95) окончательно получим
F1*(a,0)=di(a)aiC)+d2(a)a2C). A.100)
Сделав замену переменных аналогично A.37) (всюду далее штрихи
опускаем), A.82) можно представить в виде
1
1 Г /? — т\
-1
оо
, fc(?) = 2 -К"(^) cos utdt, t = ^—г—,
о
^, L(u/F) = V, f{x = fix/a).
3.3. Вдавливание штампа в неоднородную полуплоскость спе-
специального вида. Постановка задачи аналогична задаче п. 3.1, только
условие A.67) возьмем в виде
1) Л = Лое^, М = Мое^, - Я < у < 0,
A 102)
2) Л = Ai = Лое-Я^, М = Mi = Мое-Я^, - оо < у < -Я.
Систему уравнений A.79) можно записать относительно вспомога-
вспомогательных функций A.80) (знак * ниже опускаем) в виде
+ A0)U + 71 Mo?/7 + a7iM0F = 0,
BMo+Ao)T///-a(Mo+Ao)t//-a2MoT/+7iBMo+Ao)F/-a7iAot/ = 0,
7i (у) = 7' -Я" < у < 0, 71 (у) = 0' -оо < у < -Я.
A.103)
Построение общего решения уравнения A.103) при —Я ^ у ^ О
несколько упрощается, если использовать работу [182], согласно кото-
28 Гл. 1. Контактные задачи для полупространства и полуплоскости
рой общее решение A.103) выражается через вспомогательную функ-
функцию ip следующим образом:
дхду дх'
A.104)
2М0 + Ло
_ 2М0 + Ло аУ аУ
Мо дх2 ду2
где (р(х, у) находится из уравнения
1 ду) г 2Мо + Ло дх2
Используем преобразование Фурье
оо
ф,у) = ^ \ Ф(а,у)е-гаЧа. A.106)
— СЮ
Обозначим через A.105) уравнение, полученное в результате под-
подстановки A.106) в A.105). Имеем общий вид решения A.105):
Ф(а,у) = е~°2- [(С{ sinCay + C2 cos(Зау)е-а*у+
+ (С3 sin /Зау + СЛ cos /Зау)еааУ]. A.107)
Здесь использовано то обстоятельство, что корни характеристиче-
характеристического уравнения для A.105) имеют вид
J6 =-аа-0,57 + г/Зск, ?2=?i>
Кз = аа - 0, 57 + г/?а, ^4 = ?з»
аа = 2-3/2 JA/G2 +4а2J + 1б7а2_^_ + у + 4а2, A.108)
- 72 -
Используя граничные условия A.84), A.85), условия сопря-
сопряжения A.86)-A.87), A.90)-A.91) и то, что при -оо < у < -Н
решение имеет вид A.83), получим относительно 6 постоянных
Ci (г = 1, 2, 3, 4), dk (к = 1, 2) при фиксированном а систему 6
линейных алгебраических уравнений. Так как задача, тождественная
построению функции V*(a, 0) для вида неоднородности A.102),
рассматривалась в работе Когана Б. И. и Зинченко В. Д. [137],
здесь получающуюся громоздкую систему уравнений для нахождения
Ci(i= 1, 2, 3, 4), через которые выражается V*(a, 0), приводить
не будем.
§ 4. Вдавливание кругового штампа в полупространство
29
§ 4. Вдавливание жесткого кругового в плане штампа
в неоднородное полупространство
4.1. Постановка задачи. Недеформируемый круглый штамп
вдавливается в верхнюю грань Г упругого неоднородного полупро-
полупространства силой Р. С полупространством связана цилиндрическая си-
система координат г, (р, z (рис. 1.4). Силы трения между штампом и
полупространством предполагаются отсутствующими. Вне штампа по-
полупространство не загружено. Штамп представляет собой осесиммет-
ричное тело с поперечным сечением (г < а) и поверхностью основания
Коэффициенты Ламе Л и М полупространства с глубиной изменя-
изменяются по следующему закону:
1) Л = ЛоB), М = M0(z), - Я < z < 0;
2) Л = Ai = Ло(-Я), М = Mi = Мо(-Я), - оо < z < -Я. ( ' '
/
/
ж
и/1),
с
/ и
/
А
/
«(!)
Jz jTrz
я
0
Щ
Ж
Ж
й
а
Г
/
)
/
/
0
7
/
Рис. 1.4
Как один из частных случаев рассматривается закон неоднородно-
неоднородности специального вида:
Г1) Л = Лоегт, М = Мое2'»',
2) Л = Л[ = Лое-Ят, М = Mi =
-Я
0;
-Я^, -оо < z < -Н.
A.110)
Под действием центрально приложенной силы Р штамп переме-
переместится в направлении оси z на величину 5. Граничные условия при
30 Гл. 1. Контактные задачи для полупространства и полуплоскости
сделанных предположениях имеют вид
!az = 0, г > а,
w = —5(г) = — E — ф(г)), г < а.
A.111)
Предполагаем, что на границе изменения закона неоднородности
имеют место условия сопряжения
(_0) _ _B) A) _ B)
I I zr — ' zr i v z — " z >
z = -H, I A.112)
При (г; — z) -^> oo напряжения в полупространстве исчезают. Тре-
Требуется определить перемещение штампа и распределение контактных
нормальных напряжений под штампом:
а^ \z=0 = -q(r), r^a. A.113)
4.2. Сведение задачи к нахождению решения интегрального
уравнения. При построении интегрального уравнения задачи
воспользуемся замечанием 1.1 (в его справедливости в данном случае
нетрудно убедиться непосредственно) и результатами §3. После
определения функции W*(a, 0) (соответствующей V*(a,0) в §3)
условие A.111) можно записать в виде
Здесь
W?(a,0)Q(a)J0(ar)da = 6(r), r < а. A.114)
о
Q(a)=L(p)J0(ap)pdp, A.115)
о
сю
q(r)= | Q(a)J0(ar)apda. A.116)
о
Или, используя A.115)
а сю
lrq(p)pdp I W?(<y)J0(ar)J0(ap)da = во(ОЩг), г < а. A.117)
о о
Сделаем замену переменных и обозначим
аН = и\ Л = Н/а; г' = г /а; р' = р/а\ W?(a, 0) = L*(u/H);
q(p'a)=T(p); a-lS(r'a) = f(r) (U18)
§ 5. Некоторые общие свойства трансформант ядер
31
(далее штрихи опускаем). Получим, что поставленная задача сводится
к решению интегрального уравнения вида
1, A.119)
во(у) = 2M(j/) (A(j/) + Щу)) (Л(у) + гМ^)), A.120)
где М(у) и Л(?/) — коэффициенты Ламе неоднородного слоя, у — рас-
расстояние от поверхности среды.
§ 5. Некоторые общие свойства трансформант ядер
интегральных уравнений контактных задач для
неоднородных полупространства и полуплоскости,
их аппроксимация
В данном параграфе устанавливаются некоторые общие свойства
функций L(u), характеризующие рассматриваемые классы интеграль-
интегральных уравнений.
На основании установленных свойств предлагаются аппроксимации
этих функций некоторыми выражениями, отражающими эти свой-
свойства, доказывается возможность приближения ими функций L(u).
Предлагается простой метод аппроксимации главной части L(u)
дробно-рациональной функцией.
5.1. Некоторые свойства трансформант ядер рассматриваемых
задач. Рассмотрим асимптотические свойства функций L(u) в за-
задачах §§1,2 для неоднородного полупространства специального вида
A.32) при и —> 0 и и —> оо (выражение A.40)):
VshV х/ _ л/о1^ ||Д. п _
I/ _ л/*/- + и-- " - - 2
Имеем
а) при и —>
L(u) = е2"
0
((
> - IJ
или
и +
^ [C + 2/х + 2/i2)
4/х
L(u) = A + B\u\+Cu2
lim L{u) = A = e2^ = eHv
), A.121)
A.122)
A.123)
32 Гл. 1. Контактные задачи для полупространства и полуплоскости
A.124)
A.125)
A.126)
при /i > О,
< 1 при /х < О,
(В ^ 1 при /i >0,
|Б < 1 при /i < О,
'С > 0 при /х** > /л > /л* > О,
С <0 при 0</i* </i**,
б) при и —> оо
Т / \ 1 I ш^ ш^ ш^ ш^
4 ' 41 9 „2 Я „ 4 1 А 8
или
^ гГ ом
lim
E
-3\
1,
>0 при /i>0,
< 0 при /i < 0,
A.127)
A.128)
A.129)
A.130)
Свойство A.123) означает, что значение 1/@) не зависит от того,
каким образом изменяется неоднородность в слое от Go(O) до Go(—H),
а определяется только самими этими значениями. Графически это
будет выглядеть так: если множество кривых, описывающее некоторые
законы изменения модуля сдвига с глубиной, имеют одинаковые значе-
значения модуля сдвига на поверхности полупространства и на глубине Я,
то графики соответствующих трансформант L(u) в задачах §§1,2 бу-
будут выходить из одной общей точки 1/@) = Go(O)G^(—Я) и сходиться
в одну точку 1/(оо).
Для задач §§3,4 свойства A.128) не меняются, а свойство, анало-
аналогичное A.123), имеет вид
1™ Т(.Л- В(°)
= А,
где
-Щг
1-1
A.131)
A.132)
Для случая многослойных сред свойства функции податливости,
аналогичные A.123), A.128) и A.131), показаны в работах [191, 193].
Во всех рассмотренных задачах эти свойства подтверждаются числен-
численными примерами.
Покажем сохранение свойств A.123), A.128) в общем случае непре-
непрерывной неоднородности для задач §§1,2.
§ 5. Некоторые общие свойства трансформант ядер 33
5.2. Аналитические свойства трансформант ядер интегральных
уравнений антиплоской задачи и задачи кручения для неоднород-
неоднородного полупространства. Ниже покажем аналитическое различие
свойств трансформант ядер интегральных уравнений для непрерывно-
неоднородного полупространства и функций податливости для много-
многослойного [124] полупространства, где в пределах каждого слоя упругие
характеристики не меняются, т.е. слои однородны. Изучим влияние
этого отличия на примере распределения контактных касательных на-
напряжений под штампом для задач §§ 1,2.
Рассмотрим неоднородное полупространство с произвольно и непре-
непрерывно изменяющимся по глубине модулем сдвига G = G(z), так что
lim G(z) = const и для всех z ? (-Н; 0) имеем: G(z) ^ 0, G(z) ^ оо.
Разобьем среду на п + 1 слой (сверху вниз). Введем обозначения:
hi — толщина г-го слоя, Hi — расстояние нижней границы г-го слоя от
поверхности. В каждом таком неоднородном по глубине слое аппрок-
аппроксимируем изменение модуля сдвига экспоненциальным законом вида
G = GkeUkZ, -Hk+X<z<-Hk, fc=l,2, ...,n A.133)
(см. рис. 1.5), так чтобы на границах слоев выполнялись соотношения
непрерывности
G(-Hk) = Gke-V*H* = Gk+xe~v^HK
Считаем, что самый нижний (п + 1)-й слой — однородное полупро-
полупространство. Обозначим
Fk = Gke~VkH\ Fo = G@), Fk_xF^x = e"khk. A.134)
Считаем, что wk (перемещения вдоль оси z) и TyZ (контактные
касательные напряжения) сопрягаются на границах слоев, т. е.
z = -Hk, wk = wk+u t?z=t?+1.
Введем вспомогательные функции Wi(a, z) (i = 1, 2, ..., п)
Wi(a, z) = W*(a, z)G@)\a\T-\a), A.135)
где W*(a, z), T(a) — трансформанты Фурье для задачи §1
(трансформанты Ханкеля — для задачи §2) функций w*(a, z), Tlyz
соответственно.
Сведение задач §§1,2 к нахождению контактных касательных уси-
усилий из интегрального уравнения приводит к необходимости построения
функции W\(a, 0). Ниже будем обозначать данную функцию функцией
L(pt) и называть ее в соответствии с работой [124] функцией податли-
податливости полупространства. Нетрудно убедиться, что построение функции
податливости L(a) задач §§1,2 для среды A.132) в результате исполь-
2 СМ. Айзикович и др.
34 Гл. 1. Контактные задачи для полупространства и полуплоскости
(vk-i,Gk-\
V
я2
X
4i^h\ 1
*h2 2
Hn-1,
hn^ n-1
нп ;
hn n
n+l
Рис. 1.5
зования интегральных преобразований сводится к решению системы
обыкновенных дифференциальных уравнений:
W" - vxW[ - o?Wx =0, - Hi
0;
при условии
=0,
W[(a, 0) = |a
A.136)
A.137)
которое получено из определения вспомогательной функции W{(a, z)
и соотношений закона Гука для чистого сдвига (кручения):
Wl*(a,0)=T(a)G-\0).
Введем обозначения:
Общий вид решения fc-ro уравнения A.136) имеет вид
Wk = Ck
Dkaex*z, -Hk
-Hk+u k= 1, 2, ... , n.
С учетом условий A.135) и A.137), при фиксированном а получаем
линейную систему алгебраических уравнений относительно В, Ci, Di,
i = 1,... , n:
a|; A.138)
KkHk=Sk; A.139)
Ik=Zk; A.140)
СпА+е-Л^ + ^пЛ-е-Л^я- = В \а\ е'^11-; A.141)
D-4#fc
Dfce"
§ 5. Некоторые общие свойства трансформант ядер
35
A.142)
Sk = Ck
Zk =
k= 1, 2, ..., n- 1.
Последовательно снизу вверх исключим неизвестные Ck и Dk из
A.138). Получим следующие выражения для определения правых ча-
частей Sk и Zk уравнений A.138):
п+1
г=к
га+1
i=k
rk-0,5vkVk)shhkQk + UkQkchhkQk, k = n-l, n-2, ..., 2;
Vn = Un= 1, B0(a) = B(a)e-^H";
Pk — Чк e fc , /C = 1, Z, . . . , П, pn+l = 1.
Отсюда функция L(a) (W\(a, 0)) имеет следующий вид:
_ (l«
k\Q\
= Vi(a)Url(a), г = 0, 1, ..., n.
A.143)
A.144)
Свойства L(a) установим на основании свойств функций кг(а). Имеем
\а + 0, Ъкг
h-\(a) =
(\a\ki-0,
= 1+0, 5z/i|a
-l
,,-2\
oo.
На основании A.143)—A.147) найдем
L(a) = 1+0,
a
г=1
-1 i /О/^-2\
a -^ oo.
A.145)
A.146)
A.147)
A.148)
A.149)
36 Гл. 1. Контактные задачи для полупространства и полуплоскости
Используя A.134), соотношение A.148) можно переписать в виде
г=\
_F0 _ Go _ G@)
A
Переходя к пределу при hi —> О, г = 1, 2, ..., n, n —> оо, из A.150)
имеем, что значение НО) не зависит от закона изменения модуля
сдвига по глубине, а определяется лишь значением модуля сдвига на
поверхности и при z —> оо.
Проанализируем установленные свойства A.149), A.150) функции
L(a) в связи с распространенным использованием замены непрерывно-
неоднородной среды многослойной (пакетом однородных слоев). Струк-
Структура асимптотического решения контактных задач при больших Л =
= Нпа~\ где а — полуширина штампа для задачи §1 (радиус
штампа для задачи §2), определяется поведением L(a) при а —> оо
[34, 41]. Для непрерывно-неоднородного полупространства из A.149)
имеем
Ь(а) = 1 + с{\а\~1 +с2а~2 + О(а), а -> оо, A.151)
для пакета однородных слоев [191]
L(a) = l+0,5e-2l^i +O(e~2^hl)t a -> оо. A.152)
Из A.150) следует, что в общем случае непрерывной неоднородно-
неоднородности решение имеет вид ряда по степеням Л и In Л [8, 9, 36], для
многослойного пакета из A.152) соответственно следует, что решение
имеет вид ряда по степеням Л~2 [34].
Непосредственно из построенных методом больших Л асимптотиче-
асимптотических формул [8] видно, что в решении для непрерывно-неоднородной
среды главную часть, связанную с отличием от решения для случая
многослойного полупространства (полуплоскости), характеризует по-
постоянная с\. Из A.149) получим, что
сх =0,5z/i = ]imGf(z)G-l(z), A.153)
в то время как для многослойного пакета с\ = 0.
Таким образом, замена непрерывно-неоднородной среды многослой-
многослойным пакетом в ряде случаев может привести к значительным погреш-
погрешностям в полученном решении. Заметим, что, в отличие от модели в
виде пакета однородных слоев, модель A.133) математически достаточ-
достаточно точно описывает непрерывно-неоднородную среду.
Замечание 1.2. Можно убедиться, что аналогичные различия в
свойствах функций податливости имеют место и в общем случае
§ 5. Некоторые общие свойства трансформант ядер 37
пространственной деформации непрерывно-неоднородного и много-
многослойного полупространств.
Замечание 1.3. В случае неоднородной полосы (слоя), лежащей на
жестком основании,
\\mL(u) = 0. A.154)
Свойством A.154) обладают и все типы оснований, для которых
модуль сдвига (коэффициенты Ламе) растет с глубиной, так что
ИтСо(-Я) = оо (задачи §§1,2), A.155)
lim в(-Н) = оо (задачи §§3,4). A.156)
Методы решения таких задач будут рассмотрены в четвертой
главе. Ниже рассмотрим методы построения решений классов пар-
парных интегральных уравнений, для которых имеют место свойства
A.122), A.127), причем А ф 0. Это контактные задачи как для
непрерывно-неоднородного, так и многослойного полупространств (по-
(полуплоскостей). Причем законы изменения коэффициентов Ламе с глу-
глубиной таковы, что для задач §§1,2:
min Go(—y) > с > О,
уЕ@;оо)
max Go(-y) < с< оо, п 1 ^
lim G^L = const ^ 0.
у^оо Go(-y)
для задач §§3,4:
min ®(-у) > О О,
lim -§^ = const ф 0.
у^оо в(-у)
Замечание 1.4. Условия A.157) и A.158) в случае, если G@) Ф
Ф 0 F@) ф 0), являются также достаточными условиями для то-
того, чтобы можно было применить схему численного построения
L(u), основанную на следующем. Начиная по крайней мере с до-
достаточно больших значений глубины Н можно построить точное
или асимптотическое [135, 224] общее решение уравнений вида:
задачи §§1,2
w + G'(y)^ = 0, -H^y^O; A.159)
38 Гл. 1. Контактные задачи для полупространства и полуплоскости
задачи §§ 3, 4
^ ф ^ = А(у); М = М(у), A.160)
у^О. A.161)
ох
'^ =0, -
оу
5.3. Некоторые аппроксимации трансформанты ядра инте-
интегрального уравнения в контактных задачах для полупространства
и полуплоскости. Обозначим
N
гЛГ/ Л _ТТ
г=1
М
A.162)
A.163)
к=\
Имеем
при и —> О
г=1
м
iff
при
оо
¦й(и) = 1+0@,
м
f (и) =
k=i
Рассмотрим следующее выражение:
L{u) = Ь^(и)+
A.164)
A.165)
A.166)
A.167)
A.168)
Покажем, что выражением A.168) можно аппроксимировать L(u)
со свойствами A.122), A.128). Для этого используем лемму [68].
Лемма 1.1. Пусть четная, вещественная, непрерывная на
всей вещественной оси функция (р(и) обращается в нуль
на бесконечности. Тогда она допускает приближение в С(_оо?оо)
рядами из функций вида
= (и2
A.169)
§ 5. Некоторые общие свойства трансформант ядер 39
Выберем постоянные Ai, Bi (г = 1, ..., N) в A.164) так, чтобы
N
ЦА2гВ~2 = А. A.170)
г=1
Рассмотрим функции
L{u)L"{u). A.171)
Из свойств A.122), A.128), A.164), A.166) и условий A.170) сле-
следует, что Ls(u) удовлетворяют условиям леммы 1.1. Это означает, что
имеет место представление
оо __
La(u) = Y,h(u2 + D2k)-1, A.172)
к=\
или, из A.171)-A.172):
оо ^^
L{u) = L?(u) + \u\^2h(u2 + D2k)-\ A.173)
к=\
Этот результат сформулируем в виде теоремы.
Теорема 1.1. В случае, если трансформанта ядра интегрального
уравнения L(u) обладает свойствами A.122), A.128), она допускает
аппроксимацию выражениями вида A.168).
5.4. Алгоритм построения аппроксимации главной части функ-
функции трансформанты ядра выражением специального вида. При
построении аппроксимации главной части L{u) выражением вида
A.162) для нахождения коэффициентов Ai, Bi (i = 1, ..., N) исполь-
используем следующий алгоритм.
Преобразуем функцию L(u) с помощью отображения 7 = и2/(и2 +
+ (?) с интервала [0; оо) на отрезок [0; 1] (и = сy'VAT ~~ 0 )• Здесь
с — положительная константа, значение которой выбирается так, чтобы
оптимизировать аппроксимацию функции L{u). Аппроксимируем функ-
функции л/lJ^j) и у/1/~1G) на отрезке [0; 1] полиномами Бернштейна TV-го
порядка (или по чебышевским узлам), получим
N , N
A.174)
г=0
где ai, bi — коэффициенты полинома Бернштейна. Если f(x) является
непрерывной функцией на отрезке [0; 1], то коэффициент Bn(x) ап-
аппроксимации этой функции имеет вид
N
bn(x) = y^ j
ra=0
40 Гл. 1. Контактные задачи для полупространства и полуплоскости
Здесь С™ — биномиальные коэффициенты.
Тогда
где коэффициенты а*, Ь* определяются из A.175) после замены пере-
переменной и = 72/(т2 + °2)- Тогда
A.176)
После определения корней числителя и знаменателя A.176) мы
находим значения Ai, Bi (i = 1, 2, ..., TV).
Такая модификация приема, описанного в работе [71], позволяет
избежать наличия TV-кратного корня в знаменателе найденной ап-
аппроксимации, что используется в дальнейшем при построении при-
приближенных аналитических решений парных интегральных уравнений
рассматриваемых задач.
Норму ошибки аппроксимации определим как максимум разности
между точным и приближенным значениями, деленной на точное,
и будем измерять эту ошибку в процентах. Для выбора параметра ап-
аппроксимации с и порядка N можно применить метод перебора. Меняя
значение N от 2 до 28 и параметр с от 0 до 100, определим значения,
при которых достигается минимальная ошибка.
§ 6. Примеры построения трансформант ядер
интегральных уравнений контактных задач для
неоднородного полупространства
Проиллюстрируем основные аналитические свойства трансформант
ядер интегральных уравнений на численных примерах. Рисунок 1.6
соответствует случаю двухслойного основания. На рис. 1.6, в приведе-
приведены построенные численно графики трансформант ядра интегрального
уравнения контактной задачи §4, причем упругие свойства покрытия
отличаются от упругих свойств подложки. Кривая / соответствует
случаю, когда покрытие в 10 раз жестче, чем подложка. Кривая 2
соответствует случаю, когда покрытие в 10 раз мягче, чем подложка.
На рис. 1.6, б приведены кривые разности между функцией транс-
трансформанты ядра L(u), построенной численно, и ее аппроксимацией
выражением Ln(u) вида A.164). Кривые / и 2 соответствуют законам
неоднородности, приведенным на рис. 1.6, а.
§ 6. Примеры построения трансформант
41
0,0
-1,0
ОД 1,0
0,0
ОД 1,0
-ОД
10
о
6
6
4
2
л
\
\
»- —
~-^
===
2
Рис. 1.6
На рис. 1.7 показаны графики трансформант ядер L(u) в случае,
когда упругие свойства покрытия изменяются по линейному закону.
Кривые 1, 2, 3, 4 и 5 соответствуют случаю, когда поверхностные
упругие свойства покрытия отличаются от упругих свойств подложки
соответственно в 2, 4, 6, 8 и 10 раз.
Рис. 1.8, 1.9 иллюстрируют влияние различной скорости изменения
значения модуля упругости по глубине в покрытии однородного упру-
упругого полупространства на функцию L(u) соответствующей контактной
задачи.
Предполагаем коэффициент Пуассона v = 0,333, а модуль Юнга
в неоднородном покрытии изменяется по глубине в соответствии со
42 Гл. 1. Контактные задачи для полупространства и полуплоскости
а О
2 4 6 8 10
Ци
10
5
2 4 6
Рис. 1.7
следующими соотношениями:
Ek(z) =
z<-H,
= 1, ..., 9.
A.177)
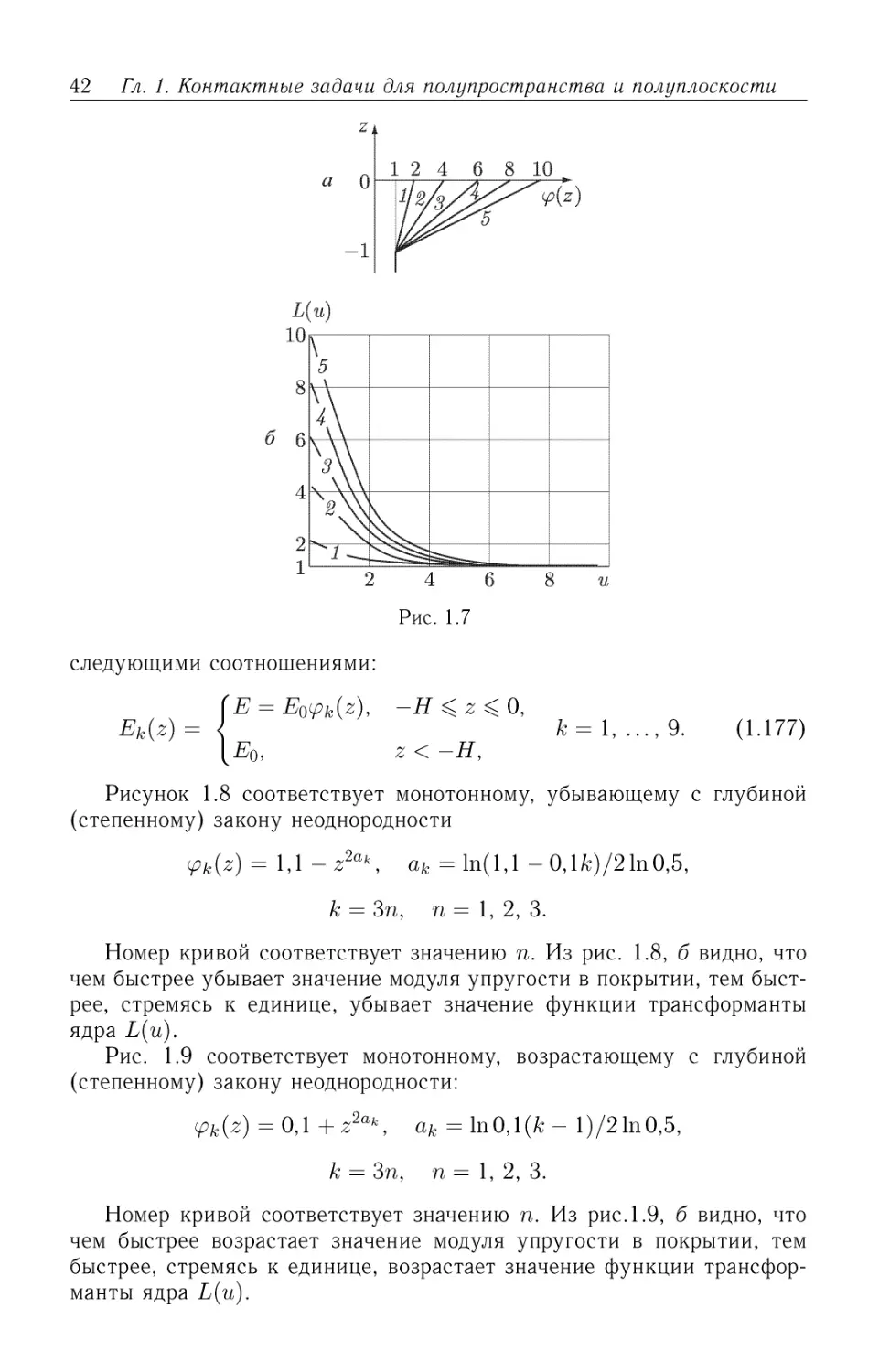
Рисунок 1.8 соответствует монотонному, убывающему с глубиной
(степенному) закону неоднородности
ipk(z) = 1,1 - z2ak,
ak = ln(l,l - 0,lfc)/21n0,5,
k = 3n, n= 1, 2, 3.
Номер кривой соответствует значению п. Из рис. 1.8, б видно, что
чем быстрее убывает значение модуля упругости в покрытии, тем быст-
быстрее, стремясь к единице, убывает значение функции трансформанты
ядра L(u).
Рис. 1.9 соответствует монотонному, возрастающему с глубиной
(степенному) закону неоднородности:
=0,1
z2ak, ak = lnO,l(fc- l)/21n0,5,
= 3n, n = 1, 2, 3.
Номер кривой соответствует значению п. Из рис. 1.9, б видно, что
чем быстрее возрастает значение модуля упругости в покрытии, тем
быстрее, стремясь к единице, возрастает значение функции трансфор-
трансформанты ядра L(u).
§ 6. Примеры построения трансформант
43
ОД 1,0
-1,0
0,0
-1,0
0,1 10
11
9
б 6
\
\
Рис. 1.8
0,0
-1,0
0,1 1,0
ф
X 0,0
ОД 1,0
-1,0
ОД 1,0
б 0,5
9 и
0,0
-1,0
Рис. 1.9
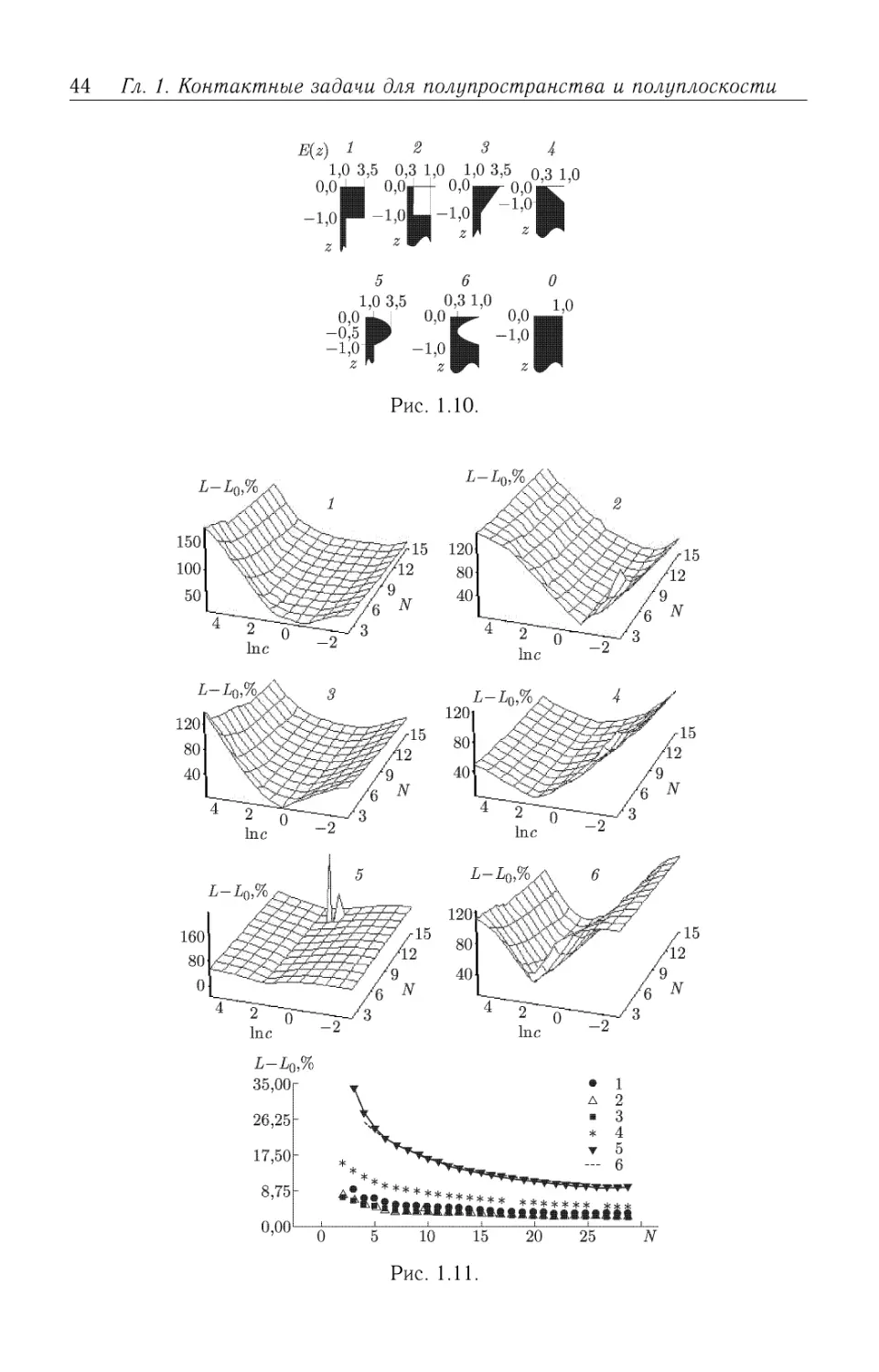
Графики изменения ошибки аппроксимации L(j) в зависимости от
параметров с и N представлены на рис. 1.11. Кривые 1-6 соответ-
соответствуют законам неоднородности, приведенным на рис. 1.10. Большие
значения ошибки для некоторых значений с и N показывают, что
алгоритм построения перестает работать для значений N > 25. Числен-
Численный эксперимент показывает, что для монотонно меняющихся свойств
оснований ошибка лежит в пределах 2-5%, а для немонотонных —
в пределах 10%. Нижний рис. 1.11 соответствует значению с= 1.
44 Гл. 1. Контактные задачи для полупространства и полуплоскости
E(z) 12 3 4
Л'?? 0,3 1,0 1,0 3,5 o,3 1,O
1,0 3,5 0,3 1,0 i о
0,0^ 0,0^ 0,0. '
Рис. 1.10.
0 5 10 15 20 25
Рис. 1.11.
Глава 2
ПОСТАНОВКА КОНТАКТНЫХ ЗАДАЧ ДЛЯ
НЕПРЕРЫВНО-НЕОДНОРОДНОГО ПО ГЛУБИНЕ
СЛОЯ И КЛИНА, НЕОДНОРОДНОГО ПО
УГЛОВОЙ КООРДИНАТЕ, В СЛУЧАЕ
ЗАДАННОЙ ГРАНИЦЫ КОНТАКТА.
ВЫВОД ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
Настоящая глава посвящена постановке следующих контактных
задач: о сдвиге полосовым штампом неоднородного по глубине слоя;
о вдавливании штампа в неоднородную по глубине полосу; о чистом
сдвиге полосовым штампом клиновидной области; о вдавливании штам-
штампа в неоднородный клин. Излагаются методы численного построения
трансформант ядер интегральных уравнений.
Полученные в этой главе результаты используются далее при ап-
аппроксимации трансформант ядер интегральных уравнений некоторыми
аналитическими выражениями.
§ 1. Чистый сдвиг полосовым штампом неоднородного
слоя
1.1. Постановка задачи. Пусть недеформируемый бесконечный
штамп \х\ ^ а, — оо < z < oo с плоским основанием сцеплен с по-
поверхностью упругого, неоднородного по глубине слоя. На каждую
единицу длины штампа действует сдвигающее усилие Р, параллельное
оси z (рис. 2.1). Под действием этого усилия штамп переместится в
направлении оси z на величину г, вызвав в слое деформацию чистого
Рис. 2.1
46 Гл. 2. Постановка контактных задач для слоя и клина
сдвига. Вне штампа поверхность у = 0 не загружена. Модуль сдвига G
слоя с глубиной изменяется по закону
G = G(y), -h^y^O. B.1)
Нижнее основание слоя предполагаем жестко защемленным. Гра-
Граничные условия для данной задачи имеют вид
ау(х, О, z) = тху(х, О, z) = О, туг(х, О, z) = О, |ж| > а, B.2)
ау(х, О, z) = тху(х, 0, z) = 0, w = е, \х\ ^ а, B.3)
г!;(ж, -h, z) = 0, B.4)
при (\х\,—у) —> оо напряжения исчезают. Здесь w(x,y,z) — пере-
перемещение по оси г; тжу, ryz, rxz — касательные напряжения; о~у —
нормальное напряжение.
Нужно определить распределение контактных касательных напря-
напряжений под штампом:
ryz(x, 0, z) = -т(х), \х\ < а, B.5)
а также связь между сдвиговым усилием Р и перемещением штампа е.
Рассмотрим сначала вспомогательную задачу, считая что
Tyz(x,O,z)=T(x), \x\ <а, B.6)
при выполнении соотношения
а
Р = I* r(x)dx. B.7)
— а
В случае чистого сдвига уравнения равновесия имеют вид
^ + ^ = 0, B.8)
ду
ох ду
так как и = v = 0, w = w(x, у), то о~х = ау = az = тху = 0.
Закон Гука в этом случае можно записать в виде
rxz = G^, ryz = G^. B.9)
дх у ду
Подставляя B.9) в B.8), получим следующее дифференциальное
уравнение равновесия в перемещениях w(x, у):
где А = —г +
92
+ G'(y)^ = O, B.10)
д2
§ 1. Чистый сдвиг полосовым штампом неоднородного слоя 47
Решение уравнения B.10) ищем в виде интеграла Фурье:
27r , W(a,y)e~iaxda. B.11)
Подставляя B.11) в B.10), получим обыкновенное дифференциаль-
дифференциальное уравнение
G(y)W" + G'(y)W - G(y)a2W = 0, B.12)
где W(a,y) — трансформанта Фурье функции w(x,y).
В случае G(y) = Gq = const общее решение B.11) имеет вид
W(a,y) = B{(a)elaly + В2(а)е~Нз/. B.13)
Из граничных условий B.4), B.5) соответственно имеем
W(a, -Л)=0, B.14)
из условия B.2)
W\a,0)=T(a)G-\0), B.15)
где Т(а) — трансформанта Фурье функции т(х), т.е.
туг(х, 0) = т(х) = i- | T(a)e-iaxda. B.16)
— СЮ
Введем вспомогательную функцию
W*{a, у) = W(a, y)G@) \a\T~\a). B.17)
Относительно W*(a, у) условия B.14), B.15) можно переписать в виде
W*(a, -h) =0, B.18)
W*f(a, 0) = \a\. B.19)
В силу однородности вид уравнения B.12) относительно вспомо-
вспомогательной функции W*(a, у) не изменится. С учетом условия B.2)
решение задачи сводится к решению интегрального уравнения относи-
относительно функции Т(а) (функции т(х))\
сю
1 f W*(a,0)T(a
2^ J G@) \a\
) i
6
Здесь функция W*(a, 0) определяется из краевой двухточечной задачи
B.18), B.19) для уравнения вида B.12).
48
Гл. 2. Постановка контактных задач для слоя и клина
1.2. Построение функции трансформанты ядра интегрального
уравнения для задачи. Введем обозначения
zi=W*(a,y), z2 = W*'{a,y).
Уравнение B.12) перепишем в матричной форме
dz
dy
= Az, -h
О,
B.21)
А =
0 1
а2 -к(у)
, z =
s
B.22)
k(y) = Gf(y)/G(y). B.23)
Краевые условия B.18), B.19) примут вид
zi(a, -h)=0, B.24)
z2(a, 0) :
= \а .
B.25)
При фиксированном а решение задачи B.21)—B.25) строим мето-
методом модулирующих функций [74]. Ищем z(y) в виде
Цу) = В,(а)а,(а, у)е^У + В2{а)к2{а,
Векторы гц (г = 1,2) определяются из задач Коши
B.26)
B.27)
где 7i = М , 72 = — М , ai(a, —К) = A, а), &2(а, —Л) = A, —а).
Неизвестные 5i(a) и Бг(а) находим из условий B.24), B.25).
Окончательно имеем
*, 0) = \а\ -
где а{ = а{(а, 0) (г, j = 1, 2).
Уравнение B.20) можно представить в виде
B.28)
B.29)
где т(х) = Ф (— ) , k(t) = 2 Г i^(u) cos utdu, t = ^г—, if (?/) = -
\aj 0 Л
г^ = а/г, Л = /га~1, L ( — J = VK* (а, 0), %х = %а~1, жх = жа~1 (в формуле
B.29) и далее штрихи опускаем).
§ 1. Чистый сдвиг полосовым штампом неоднородного слоя 49
Заметим, что в случае однородного упругого слоя функция L(a)
в интегральном уравнении B.29) имеет вид [55, 56]
L(a)=tha. B.30)
В случае многослойного основания аналогом функции L(pt) урав-
уравнения B.29) являются функции ATk(p), CTk(p), BTk(p) [193], характе-
характеризующие податливость верхней границы n-слойного основания в на-
направлении касательно к границе. Эти функции строятся с помощью
рекуррентных соотношений и обладают следующими свойствами:
Атк(р) = A - 2vk) BA - vk))~l - О (р2ке-^), рк = phk -+ сю;
() vk)-O(e-2^), р -+ 0,
если ниже fc-ro слоя расположен хотя бы один слой с гладкой границей,
то
Атк(р) = 0A), Втк(р) = О (р-1), Стк{р) = О{р-{),
в противном случае
ATfc(p) = AfcAfc+1 ...Д„A-2^+1)B(l-^+1))-'+ О (р),
Втк(р) = AfcAfc+i ... Д„ + О (р),
Стк(р) = AfcAfc+i ... Д„ A - vn+i)~l + О (р).
Для слоя на абсолютно жестком основании с номером п
л (п\ C-4и„)A -2vn) s2 -upn
ЛТП\Р) — г " " Т .
2 A - i/n) [C - 4i/n) с2 + «pi + A - 2г/пJ enj
Здесь с = 0.5A + ек), s = 0.5A - ек), рк = phk, ек = е~2рк, и =
= ркек, Ак =Ek(l- v2k+x) I (Ч+i (I - v)
1.3. Чистый сдвиг полосовым штампом неоднородного по глу-
глубине слоя специального вида. Постановка данной задачи аналогич-
аналогична п. 1.1, только условие B.1) возьмем в частном виде
G = G%y, -h^y^O, г] = const. B.31)
Тогда уравнение B.12) становится уравнением с постоянными коэффи-
коэффициентами:
W" + rjW - a2W = 0, -h^y^O. B.32)
Общее решение B.32) имеет вид
W(a, у) = Сх(а)е?хУ + С2(а)е?2У, B.33)
50 Гл. 2. Постановка контактных задач для слоя и клина
где ?i,2 = -r]/2±Q, Q = уУ/4 + ®2 - Из B.18), B.19) имеем
)г\ + С2(а)г2 = \a\,
п.
W*(a, у) = С, (а) + С2(а) = - \а\ f^Q{^, B.34)
- sh Qh — Q ch Qh
или W*{a, 0) = L{u) = ——t^-z , где V = л/и2 + /i2 , /i = 77/1/2, г^ =
= /га. Окончательно имеем
К (и) = Ц^- = (V cthV - fi)~l. B.35)
\и
Очевидно, что свойства трансформанты ядра B.35) аналогичны
свойствам трансформанты B.28). Покажем, что знаменатель подынте-
подынтегрального выражения трансформанты ядра B.35) интегрального урав-
уравнения B.29) не имеет нулей.
Рассмотрим уравнение V cthF = /i, определяющее полюса функции
W*(a, 0). Учитывая свойства гиперболических функций и разложение
г / м sh/i , ch а + (и — 1) sh/xch/i — sh2 /x 2 , гл( 4\
v л^° /i(ch/x-sh/x) 2/x2(ch/x-sh/x) V У
получим fi > V, т. е. из B.35) следует и2 < 0. Другими словами,
функция W*(a, 0) не имеет полюсов на действительной оси.
Очевидно, что при корректной постановке контактной задачи долж-
должно выполняться неравенство cthF > J\ —v?/V2. Исследование дан-
данного неравенства, обусловливающего взаимосвязь показателя при экс-
экспоненте закона неоднородности B.31) и толщины слоя h, проводится
численно и здесь не рассматривается.
§ 2. Внедрение штампа в неоднородную полосу
2.1. Постановка задачи. Недеформируемый штамп вдавливается
в верхнюю границу Г упругой неоднородной полосы силой Р. При этом
длина линии контакта между ними Fi в плане равна 2а. С полосой
связана декартова система координат (х, у) (рис. 2.2). Предполагается,
что силы трения между штампом и полосой отсутствуют. Вне штампа
полоса не загружена. Под действием силы Р штамп смещается по оси у
на величину 5.
Коэффициенты Ламе Л и М полосы с глубиной изменяются по
закону
А = А(у), M = M(j/), у 6 [-Л.0]. B.36)
Здесь А(у), M(y)eCl[-h,0}.
§ 2. Внедрение штампа в неоднородную полосу
51
У^
Рис. 2.2
Рассматриваем следующие задачи: Р1 — полоса жестко соединена
с недеформируемым основанием, Р2 — полоса без трения покоится
на недеформируемом основании. Граничные условия при сделанных
предположениях имеют вид
задача Р1:
и(х, -К) = v(x, -К) = О, B.37)
задача Р2:
и(х, —К) = 0, тху(х, —К) = О,
для задач Р1 и Р2
тху(х, 0) = 0, сгу(х, 0) = 0, \х\ > а,
v(x, 0) = f(x) = -5 + 7(ж), \х\ < а.
B.38)
B.39)
B.40)
Здесь и(х, y),v(x, у) — соответственно горизонтальное и вертикальное
перемещения, тху(х, у), ау(х, у) — касательное и нормальное напряже-
напряжения, 7(#) — форма основания штампа. Предполагаем, что при \х\ -^ оо
напряжения в полосе стремятся к нулю. Необходимо определить рас-
распределение контактных нормальных напряжений под штампом:
ay(x,0) = -
B.41)
а также связь между вдавливающей силой Р и осадкой штампа 5.
2.2. Построение интегрального уравнения, соответствующего
задаче. Используем уравнения равновесия плоской задачи теории
упругости [162]:
дох_ , дтху = q
а* ? ' B42)
дтХу { day =Q
дх ду
52 Гл. 2. Постановка контактных задач для слоя и клина
Связь между напряжениями и перемещениями определяется зако-
законом Гука:
ду'
[ду дх\
гл _ ди dv
~ ~ ~дх ду'
Представим перемещения и и v в форме интегралов Фурье:
и(х, у) = — J U(a, y)e~taxda,
^"о? _. B.44)
v(x, у) = — J V(ot, y)e iaxda.
— сю
Уравнения B.42) относительно U(a, у) и V(a, у) = — iV(a, у)
с учетом B.43), B.44) можно представить в виде
MU" + а(М + Л)УХ - а2(М + Л)С/ + М7^ + aMV = О,
Введем вспомогательные функции
U*(a,y) = -6o\a\U(a,y)/Q(a),
V*(a, у) = -00 \а\ V(a, y)/Q(a), B.46)
^о = 2М@) [Л@) + М@)] / [Л@) + 2М@)],
где Q(a) — неизвестная трансформанта Фурье искомой функции q(x).
Для сведения смешанной задачи к интегральному уравнению необ-
необходимо построить функцию V*(a, 0). После определения V*(a, 0),
используя условие B.39), придем к уравнению вида
B.47)
где
= ср (^) , k(t) = 2 f К (a) cos at dt,t =
Л '
= V*(at 0).
§ 2. Внедрение штампа в неоднородную полосу 53
Заметим, что в случае однородной или многослойной полосы функ-
функция L(a) в интегральном уравнении B.47) определяется следующим
образом.
а) Для однородной полосы [90]
задача Р1:
L(a) = fjk» , B.48)
задача Р2:
T ( ч 2>zrsh2a —4a 3M + Л /о ЛГЛ\
L(a) = = =-, x = — —; B.49)
2h2+1+>^2 + 4а2 М + Л
б) Для многослойных оснований аналогом функции L(a) для урав-
уравнения B.47) являются функции Ап(а, h\ ..., hn) [193], характеризую-
характеризующие податливость верхней границы n-слойного основания, направлен-
направленную нормально к границе. Эти функции строятся с помощью рекур-
рекуррентных соотношений и обладают следующими свойствами:
задача Р1:
Ап(а, Ль.., Лп)« 1-4^A+А1)-1а2е-2а/11, (п ^ 2), а -> оо,
B.50)
lim An(a, h\, ..., hn) = 0;
задача Р2:
Ап{а) = 1 - (o?h\ + ahi)Me-2ah[ + О (e~2a/l1) , a -> оо, B.51)
Л1 + ^ + ... + Л Afen/lnA ) + О(а2), а^О, B.52)
Ai AiA2...An-i/
где А/с = i?fc_|_i(l — ul)/(Ek(l — ^|_|_i)); h^.E^.v^ — соответственно тол-
толщина, модуль Юнга и коэффициент Пуассона fc-ro слоя; Ап(а, h\,...
..., ftfc) — функция податливости в направлении, нормальном к границе
слоя, kj = У2О — 2vj)/(\ — Vj), j = 1, 2, ...
Ниже изложим метод построения функции Ца) в общем случае
непрерывной неоднородности.
2.3. Построение функции трансформанты ядра в общем случае
непрерывно-неоднородной среды. Рассмотрим вспомогательные за-
задачи PI*, P2* со следующими граничными условиями:
@, \х\ > а,
тху(х, 0) = 0, ау(х, 0) = <^ B.53)
[— q(x), \x\ ^ а.
При у = —/г выполнены соответственно условия B.37) и B.38).
Введем обозначения:
wx =U, w2 = U', w3 = V, wA = V B.54)
54
Гл. 2. Постановка контактных задач для слоя и клина
(здесь штрих означает дифференцирование по у). Систему B.45) пере-
перепишем в матричном виде:
dm A ~
—— = Aw,
dy
B.55)
где
о
2
О
а а
М
О
м + л
2М + Л
а
О
о
о М
— OL-
0
м + л
м
2М; + Л;
2М + Л 2М + Л
W =
W2
Общее решение системы B.45) при условии Лх = М/ = О (М ф 0)
имеет вид
U(a, у) =
V(a, у) =
a
®\
к = 3 - Av = (Л + ЗМ)/(Л + M),
di (г = 1, ..., 4) — произвольные функции параметра а.
Решение w(a, у) системы B.55) строим, выделяя экспоненциаль-
экспоненциальные составляющие фундаментальных векторов решения. Представим
w(a, у) в виде
4
w(a, у) = y^di(a)?.i(a, у)еъу, B.56)
г=1
где 71,2 = -а, 7з,4 = а-
Здесь компоненты векторов аДа, у) (г = 1, ..., 4) изменяются по у
с меньшей скоростью, чем экспонента, и определяются из следующих
задач Коши:
^ = Аёц-Ъщ, ye[-h;O}, B.57)
с начальными условиями
§ц(а, -h) = (l,-a,-l, a),
а.2(а, —К) = (ay, а — а у, —к — ау, —на — а
аз(а, —/г) = A,а, 1, а),
| =_
§ 3. Чистый сдвиг полосовым штампом пространственного клина 55
Постоянные di(a) (г = 1, ..., 4) определяются из условий B.42), B.37),
B.38). В частности, для задачи Р1
4
^2di(a) [-А@)аа\(а, 0) + (Л@) +2M@))aJ(a, 0)] = в0а,
г=\
4
^ di(a) [a?(a, 0) + аа\(а, 0)] = 0,
B.58)
4
у di(a)a^(a, —/г) = 0,
г=1
4
\ 6?i(a)a^(a, —/г) = 0,
г=1
а для задачи Р2 два последних уравнения B.58) надо заменить на
следующие:
4
^ di(a)af(a, -ft) = 0, B.59)
г=1
4
^Г J ( \ Г 2 / 7_^\ i^ 3 / 7_. \ 1 /~\ /Q ?^ГЛ\
г=1
Здесь через а\ обозначена fc-я компонента вектора гц(а, у). Из B.46)
окончательно получим
_ 4
L(a) = F*(a, 0) = ^di(a)af(a, 0). B.61)
г=1
§ 3. Чистый сдвиг полосовым штампом неоднородного
пространственного клина
3.1. Постановка задачи (задача К1). Недеформируемый полосо-
полосовой штамп взаимодействует с упругой клиновидной областью с углом
раствора а @ < а < 2тг). С областью связана цилиндрическая система
координат (г, ср, z). Считаем, что грань клина ср = 0 жестко защемлена,
а на грань ср = а действует полосовой штамп. На единицу длины штам-
штампа действует сдвигающее усилие Р, вследствие чего штамп переме-
переместится в направлении оси z на величину г, вызвав в клине деформацию
чистого сдвига. При этом ширина области контакта штампа с клином
а ^ г ^ Ъ (рис. 2.3). Предполагается, что силы трения между штампом
и поверхностью клина отсутствуют, и вне штампа поверхность клина
56
Гл. 2. Постановка контактных задач для слоя и клина
(р=0
Рис. 2.3
(р = а не нагружена. Модуль сдвига клина изменяется по закону
G = G(ip), 0<ip<a. B.62)
Здесь G(ip) — произвольная гладкая функция, G(ip) > О всюду в обла-
области определения.
Граничные условия при сделанных предположениях имеют вид
w(r, 0) = 0,
Тц>г(г, а) =0, 0 < г < а, г > Ь,
w{r, а) = ?, а ^ г ^ Ь.
Здесь w(r,(p) — перемещение по оси z, т^г, '
B.63)
B.64)
B.65)
— касательные
напряжения.
Необходимо определить распределение касательных напряжений
под штампом:
т<рг(г,а)=т(г), а^г^Ъ, B.66)
а также связь между сдвиговым усилием Р и перемещением штампа е.
3.2. Построение интегрального уравнения, соответствующего
задаче К1. Используем уравнения пространственной задачи теории
упругости в цилиндрической системе координат [166]:
дг
г dip
dw
dw
B.67)
B.68)
Перемещения w(r, ф) представим в форме интеграла Меллина:
с-\-гоо
W[r, lp) = ^-. I \V(s, Lp)r~sds. B.69)
r, (р) = ^—г W(s, (p)r sds.
§ 3. Чистый сдвиг полосовым штампом пространственного клина 57
Уравнение B.67) относительно W(s,(p) с учетом B.68), B.69) мож-
можно представить в виде
$?4' + s2W = 0. B.70)
Здесь штрих означает дифференцирование по ср.
Граничное условие B.63) примет вид
W(s, 0)=0. B.71)
Представим функцию г (г) интегралом Меллина (специального вида):
с+гоо
т(г) = ^т [ t{s + l)r-{s+lUs. B.72)
c—ioo
Обратное преобразование имеет вид
p. B.73)
о
Из условия B.66) с учетом B.68) B.69), B.72) получим
W'(s, a) = Щ. B.74)
Введем вспомогательную функцию W*(s, (p):
W(8,<p) = W(8,<p)
Из условия B.65) имеем
с+гоо
2тгг
с—гоо
Учитывая B.73), придем к уравнению вида
ъ
\r(p)k(t)dp = 2iriG(a)e, a^r^b,
B.75)
C+lOO
k(t)= [ L*(s)estds, t = ln^, L*(s) = W*(s,a).
c—ioo
Для сведения смешанной задачи к интегральному уравнению необ-
необходимо построить функцию L*(s). Пределы интегрирования в зависи-
зависимостях B.69) и B.72) определяются аналогично [214].
58 Гл. 2. Постановка контактных задач для слоя и клина
Уравнение B.75) можно записать в виде
ь
r(p)k\(t)dp = 7rG(a)e, a < г ^Ь,
B.76)
L\(s,a) ,-, , л Р
—- cos stds, t = m-.
S Г
Для завершения постановки задачи к интегральному урав-
уравнению B.76) рассмотренной контактной задачи для упругого
неоднородного клина следует добавить условие равновесия штампа:
ъ
Р= \r(r)dr, B.77)
а
которое (при а = тг и а = 2тг) позволяет определить связь между
сдвигающим усилием Р и перемещением штампа е. При корректной
постановке должно выполняться условие: т(г) ^ 0 при а ^ г ^ Ъ.
Для однородного клина задача также сводится к интегральному
уравнению вида B.77), где функция L\(s,a) определяется следующим
образом:
L{(s,a) =thsa. B.78)
Изложим метод построения функции L*(s) в общем случае произ-
произвольной гладкой неоднородности.
3.3. Построение функции трансформанты ядра интегрального
уравнения. Рассмотрим вспомогательную задачу К1* со следующими
граничными условиями:
w(r, 0) = 0,
, ч /r(r)' a^r^b, B.79)
10, 0 < г < а, г > Ь,
при ip = 0 выполнено условие B.63).
Введем обозначения
zx = W*(s, ф), z2 = W*'(s, ф), ъ = (zu z2). B.80)
Уравнение B.70) перепишем в матричном виде
— = Az, A =
s2 -
§ 3. Чистый сдвиг полосовым штампом пространственного клина 59
Краевые условия:
zx(s, 0)=0, B.82)
z2(s, a) = 1. B.83)
Как видно, коэффициенты матрицы А являются переменными.
В общем случае построить решение уравнения B.81) в аналитической
форме не удается. Для данного случая решение уравнения B.81) бу-
будем строить методом, разработанным на основе метода модулирующих
функций [74], суть которого состоит в выделении существенно изме-
изменяющейся составляющей функции собственных векторов матрицы А
системы.
Известно, что решение системы дифференциальных уравнений
можно представить в виде линейной комбинации фундаментальных
решений. Фундаментальные векторы представим в виде
*f (s, <р) = (t\(s, <p)Vl(s, <p),1*(s, ^)Ф?(в, <р)), B.84)
где 4?\(s, ф) = (sinstp, scosscp), ^(s, ф) = (cosscp, — ssinscp) — соб-
собственные векторы матрицы А при х(ф) = 0, т. е. их вид обусловлен
видом решения системы для однородного клина,
W(s, (р) = В\ (s) cos sip + B2(s) sin stp,
t\(s, (p),t,2(s, (p) — некоторые модулирующие их векторы, изменяющи-
изменяющиеся по (р более плавно.
В этом случае решение системы B.81) имеет вид
z(s, ip) = ai*f(s, ф) + a2*f(s, ф). B.85)
Подставляя решение B.85) в систему B.81), сведем исходную задачу
к решению задач Коши для векторов ti(s, ф) при фиксированных
значениях s:
ji = Biii9 O^cp^a (г =1,2), B.86)
-pv / — SCtgSif S Ctg Sif
l~\ —stgscp — х(ф) + stgsip
_ ( —sXigstp —sXigstp
9' ~ — s ctg stp —н(ф) —
с начальными условиями
t,(s,O) = (l,l), B.87)
t2(s, 0) = A, 1). B.88)
60 Гл. 2. Постановка контактных задач для слоя и клина
Определив ti(s, а) (г = 1, 2), из B.85), B.80) получим
W*(s, ф) = a\t\(s, ф) sins^ + a2t\(sy ф) cos sip, B.89)
W*'(s, ф) = a\t\(s, (p)scoss(p + a2tl(s, ф)зsinscp. B.90)
Величины a\(s), d2(s) определяются из краевых условий B.82), B.83).
В частности, а\ = \t\(s, a)scossa\ , п2 = 0 и
B.91)
A(s, a) s
Окончательно получим
U (s, a) = V (is) = M^i th sa. B.92)
t\{is, a.)
3.4. Чистый сдвиг полосовым штампом неоднородного по угло-
угловой координате клина специального вида (задача К11). Поста-
Постановка задачи К11 аналогична задаче К1 из п. 3.1, только условие B.62)
возьмем в частном виде:
G((p) = G^, O^ip^a. B.93)
Тогда уравнение B.70) становится уравнением с постоянными коэффи-
коэффициентами:
W" + rjW + s2W = 0. B.94)
Общее решение B.94) имеет вид
W(s, ф) = ci(s)e^+^ + c2(s)e^-^, B.95)
где х± — собственные числа уравнения B.95), определяемые из харак-
характеристического уравнения
к2 + r)K + s2 = 0, B.96)
х± = -т)/2 ± Q, Q = ^rf/A - 52. B.97)
Из условий B.71), B.74) имеем
''ci(s)+c2(s) =0,
а + с2(з)я_е*-а = Q(s)/G(a).
Следовательно, функция
W(s, ф) = ^г1- „ ^^ .
В частности, _1
W*(s, a) = (Q cth Qa - |] . B.98)
Очевидно, что свойства трансформанты ядра B.98) аналогичны
свойствам трансформанты B.91). Покажем, что на мнимой оси плос-
§4. Внедрение штампа в неоднородный клин 61
кости комплексного переменного s знаменатель подынтегрального вы-
выражения трансформанты ядра B.98) интегрального уравнения B.75)
не имеет нулей.
Рассмотрим уравнение QcthQa = rj/2, определяющее полюса
функции W*(s, а). Учитывая свойства гиперболических функций,
получим: г]/2 > Q, т.е. из B.97) следует s2 > 0. Другими словами,
функция W*(s, а) не имеет полюсов на мнимой оси, следовательно,
можно выполнить замену переменной s на is. Тогда ядро уравнения
B.76) будет иметь вид
= щ, Q =
QcthQa — -
Очевидно, что при корректной постановке контактной задачи долж-
должно выполняться неравенство QcthQa > ^. Исследование данного нера-
неравенства, обусловливающего взаимосвязь показателя при экспоненте
закона неоднородности B.93) и угла раствора клина а, проводится
численно.
§ 4. Внедрение штампа в неоднородный клин
4.1. Постановка задачи. Жесткий штамп вдавливается в
верхнюю границу (Г) упругого клина раствора а @ < а < 2тг) силой Р
(здесь сила отнесена к единице длины штампа), приложенной на
расстоянии Н от вершины клина (рис. 2.4). Считаем, что грань клина
(р = 0 жестко защемлена. Предполагаем, что силы трения между
штампом и поверхностью клина отсутствуют и вне штампа поверхность
(р = а клина не нагружена. Ширина области контакта штампа с
клином определяется неравенством а ^ г ^ Ь, а форма основания
штампа в области контакта — функцией 7(г)- Модуль Юнга Е клина
изменяется по закону
Е(ф) = Eof(ip), 0<(p<a, B.100)
а коэффициент Пуассона v — постоянный (у = const).
Граничные условия задачи при сделанных предположениях име-
имеют вид
тГ(п(г, а) = 0, а,п(г, а) = 0 @ < г < a, b < г < оо),
B.101)
г;(г, а) = —5(г) = — [5 + /Зг — ^(г)] (а < г < Ь),
v(r,0)=0, u(r, 0) = 0. B.102)
Здесь 5 + (Зг — жесткое перемещение штампа под действием силы Р,
u(r,(p),v(r, ф) — соответственно радиальное и угловое перемещения,
тГу, о~^ — касательное и нормальное напряжения.
62
Гл. 2. Постановка контактных задач для слоя и клина
Рис. 2.4
Необходимо найти распределение контактных нормальных напря-
напряжений под штампом:
г, а) = —q(r) (а ^ г ^ Ь),
B.103)
а также связь между величинами Р, Н, 5, C.
Уравнения равновесия в цилиндрической системе координат для
плоского клина (т. е. и = u(r, (р), v = г;(г, (р), w = 0) имеют вид [162]
д(гг
1
дтГ
дг г дер
= 0,
B.104)
7\ Г 7\
or r dip
>Trip г\
r
Связь между напряжениями и перемещениями определяется соот-
соотношениями
аг = Ае + 2G-p—,
дг
- Ае + 2G- (и + —
^ г \ dip
az = Xe, B.105)
ди
du . 1
+
Tzr = T^=0,e=- + -(u+-
dv
Упругие характеристики клина:
Е
G =
А =
B.106)
§ 4. Внедрение штампа в неоднородный клин
63
Подставляя B.105) в B.106) и учитывая B.100), получим следующую
систему дифференциальных уравнений в частных производных:
1
1 de
2 dv
г2 dcp \-2v dr
G' [dv
du
v -4
r
2^du_
f dcp
1 1 de
B.107)
w2 d2 \ d \ d2
где V = —2 ^ 1—2—2*
Решение системы уравнений B.107) ищем в форме интеграла Мел-
лина:
1 с+гоо
U = ^ J V(,,^)r-^,
B.108)
v(r, у?) у ' ^ v(s>
В образах Меллина система B.107) примет вид
х- 1
s -
Е
к — 1
V" = -
(s2-\) V-%
ж+ij е
здесь штрих обозначает производную по ср, к = 3 — Аи.
Введем обозначения
= U,
= V,
тогда систему B.109) можно переписать в матричном виде
dw A ~
-р- = Aw,
где
А =
j Е v- - ^
0 0
D' 2(s-x) к-\.
B.109)
B.110)
B.111)
, w =
64 Гл. 2. Постановка контактных задач для слоя и клина
В случае однородного клина, т. е. если Е'/Е = 0, имеем
U(s, (р) = (s + к) [а\ sin (s + 1) ^ + a2cos (s + 1) ф\ +
+ E — 1) [аз Sin E — \)(p + CL4 COS E — 1) </?] ,
V(s, (p) = —E — к) [a\ cos E + \) (p — d2 sin E + 1) (p] —
— (s — 1) [аз cos E — 1) (p — CL4 sin (s — 1) tp],
где (Ц (i = 1, ..., 4) — произвольные функции 5.
Пусть ^ff (s, (p) (i = 1, ..., 4) — векторы фундаментальной системы
решений. Тогда решение уравнения B.112) будет иметь вид
4
л^ — \ Л п ¦( q)^F ( Q т) (9. 1 1 ^)
г=1
где ^f(s, v?) = Т^5, </?)ФгE, (/?), Т^5, у?) — диагональные матрицы,
на диагонали которых находятся компоненты вектор-функций ii(s, ф).
Векторы ФгE, (р) являются собственными векторами мат-
матриц А для к((р) = 0 (для однородной среды), ti(s, (p) =
= (t\(s, (p), tj(s, (p), t^(s, (p), tj(s, (p)) — векторы модулирующих
функций, связанных с неоднородностью среды, Ci(s) — некоторые
коэффициенты, не зависящие от ср и определяемые из решения
системы линейных алгебраических уравнений, выписываемой из
краевых условий. Данный прием позволяет выделить в выражении
B.113) осциллирующие составляющие ФДз, (р), затрудняющие процесс
численной реализации решения:
*1 = [sin (s + 1) (р; (s + 1) cos (s + 1) (p;
cos (s + 1) (p; — (s + 1) sin (s + 1) (p],
Ф2 = [cos (s + 1) <p; - (s + 1) sin E + 1) y?;
sin (s + 1) y?; - (s + 1) cos E + 1) <p], i ^
Ф3 = [sin E — 1) tp; (s — 1) cos E — 1) </?;
cos E — 1) tp; — (s — 1) sin (s — \)(p],
Ф4 = [cos (s — 1) (p; — (s — 1) sin (s — 1) </?;
sin E — 1) </?; E — 1) cos E — \)(p].
Векторы ti(s, (p) находим из следующих задач Коши:
^ = Вг1г (г = 1 4), О^р^а, B.115)
аср
§ 4. Внедрение штампа в неоднородный клин
65
с начальными условиями
ti(s, 0) = [s + х; s + х; —(s — х); —(s — к)},
^2E, 0) = [s + х; 5 + х; 5 — х; s — к] ,
t3(s, 0) = [5 - 1; s - 1; -E - 1); -E - 1)] ,
t4(s, 0) = [s- 1; 5- 1; 5- 1; 5- 1] ,
где матрицы В^ имеют вид
dtp '
ИЛИ
в? =
Ф1
Щ
ф3
Азз- -3-
Ф?
Алл l
^24—\
(г=1,...,4).
Чтобы завершить постановку задачи, следует найти пределы инте-
интегрирования в зависимостях B.108), т.е. значения постоянной с. Для
этого интегралы типа
оо
5, ф) = сг(р, (f)psdp,
определяющие трансформанты Меллина напряжений (<т(р, ф) — любое
из напряжений), должны быть сходящимися. Относительно поведения
напряжений при г —> 0 известно [224], что они отсутствуют при а < а*
и стремятся к бесконечности при а > а*, где а* = arcsin y/\ — v. При
этом порядок стремления к бесконечности составляет г~4 . При г -^ оо
напряжения исчезают, порядок их стремления к нулю составляет г~4.
Следовательно, Res = с находится в пределах |Res| < -.
3 СМ. Айзикович и др.
66 Гл. 2. Постановка контактных задач для слоя и клина
4.2. Решение вспомогательной задачи. Пусть граничные усло-
условия имеют вид
v(r,0)=0, u(r,0)=0, \Res\ < i,
rr(f(r, a) = 0, сгсДг, а) = -q(r), ^ {{^
fq(r), a^r^b,
air) = <
W [0, 0<r< a, b<r< ос.
Рассмотрим трансформанту Меллина функции q(r):
b c-\-ioo
Q(8)=jq(p)pedp, q(r) = ^~ J Q(s)r-s-lds. B.117)
a c—ioo
Используя зависимости B.105), B.108), B.111) и B.117), запишем
граничные условия B.116) в виде системы линейных алгебраических
уравнений для определения функций di(s) A, ..., 4):
d2(s + к) + a^s — 1) =0,
a\(s — к) + as(s — 1) = 0,
4
X—^ г99/ \ / \ ^ ^ / \
/ j г I i i^ > J v / г г V ' /J '
г=1
B.118)
При этом введены обозначения
Определив a^(s) из C.4.19) (г = 1, ...,4), получим выражение для
нахождения г;(г, а):
с+гоо
/ \ ! Г V*(s,a)Q(s) -S-, /О11п\
v(r, а) = — ГГ-—- — у ч yr as, B.119)
4 2тгг^ J s
где V*(s, а) определяется по формуле
V*(s, a) = a\t\ cos E + 1) a + a2^ sin E + 1)
- \)a. B.120)
§ 4. Внедрение штампа в неоднородный клин 67
Удовлетворив последнему условию B.116) вспомогательной задачи,
получим интегральное уравнение первого рода относительно функции
распределения контактного давления q(r):
Ъ с+гоо
\q(p)dp | V ^S' °^ (?)8 ds = 2irie5(r), a^r^b. B.121)
Пусть функция V*(s,a) такова, что на мнимой оси плоскости
комплексного переменного s она не имеет нулей, тогда можно принять
с = 0 и выполнить замену переменной s на ш. Уравнение B.121) можно
переписать в виде
ъ
q(p)ki (in ?\ dp = тгО5(г), a^r^b, B.122)
sutdu, t = ln?-, B.123)
г
где L\(u, a) = — iV*(is, а) и L\(u, a) — четная на действительной оси
функция. Вид функции L\(u, а) для однородного клина полностью
совпадает с полученным в [35, 36, 56]:
L\(u, а) = 5 г г ' ^ = 3-4za B.124)
2h2 — 2г/ cos2a-\-2u + >zr + 1
Произведем в интегральном уравнении B.122) замену переменных
и введем обозначения согласно формулам
? = \Ы(р/а)- 1, ж = Л In (г/а)- 1, Л = 2 (In (b/a))~l ,
Тогда это уравнение примет вид
1
v(Z)k(^)<% = Kg(x), ж<1, B.125)
-1
с ядром B.123).
Безразмерный параметр Л е @, оо) характеризует относительное
положение штампа на грани клина. Если параметр Л велик (мал), то
штамп расположен относительно далеко (близко) от вершины упругого
клина. Заметим, что интегральное уравнение B.122) при а —> 0 и
при фиксированном Н = tga вырождается в интегральное уравне-
уравнение соответствующий плоской контактной задачи для упругого слоя
(см. B.47)).
68 Гл. 2. Постановка контактных задач для слоя и клина
§ 5. Некоторые общие свойства трансформант ядер
интегральных уравнений контактных задач для
неоднородных полосы и клина, их аппроксимация
аналитическими выражениями
5.1. Некоторые общие свойства трансформант ядер интеграль-
интегральных уравнений контактных задач для неоднородных полосы
и клина. Структура асимптотического решения контактных задач
при больших Л, Л = Нпа~\ где а — полуширина штампа, для задач
§§1,2 определяется поведением L(a) при а —> оо [41]. Для непрерыв-
непрерывно-неоднородного слоя имеем
L(a) = Аа + Ва2 + О(а3), а -> О,
B.126)
L(a) = 1 + с\а~х + с2а~2 + О(аГ3), а —> оо,
для пакета однородных слоев [193]
L(a) = 1 + ie-2H/M + О(е-2Н/м)> а ^ оо.
Рассматриваемые контактные задачи по структуре интегральных
уравнений и свойствам их ядер можно свести к решению интегрального
уравнения Фредгольма
B-127)
k(t)= J ili^C0S5^5,
О S
где
для задач §§1,2
ср(х') = q(x)/9, х1 = х/а, X = h/a, g(xf) = 5(х)/а.
для задач §§ 3,4
~
В случае однородной среды
для Р1:
г / ч ZMshzs — As
L(s) =
2
ДляР2:
г / ч ch 2s — 1
r / ч 2>csh2sa — 2s sin 2a
1()
2h ch 2sa - 2s cos 2a + 2s
§ 5. Некоторые общие свойства трансформант ядер 69
Для всех задач при s ^ О
L(s)=As + O(s3), B.128)
где
для
для
для
Р1:
Р2:
К1:
А
А — \
А =
_ 2 Bы
= 0,
а-
~ 1
-IJ'
5,
sin 2a)
при s —> оо
L(s) = l-0(e-^s), B.129)
где для задач §§ 1, 2 /i = 2; для §§ 3,4 /i = 2а.
В случае многослойных сред свойства функций податливости, ана-
аналогичные B.128), B.129), установлены в работах [153, 154, 191, 193].
Для всех рассматриваемых задач данные свойства подтверждаются
численными примерами.
5.2. Аппроксимация трансформант ядер интегрального уравне-
уравнения функциями специального вида. Введем следующие обозначе-
обозначения:
^{и) = Ц^0. B.130)
м
*J«L B.131)
i^x +r,k
Покажем, что функцию L(u), обладающую свойствами B.128),
B.129), можно аппроксимировать выражениями вида
L(u) = th Аи [Lg(u) + L%(u)] . B.132)
Для этого, аналогично §5 гл. 1, используем лемму [68, 70].
Лемма 2.1. Пусть четная, вещественная, непрерывная на всей
действительной оси функция ip{u) обращается в нуль на беско-
бесконечности, тогда она допускает приближение в С(_оо?оо) рядами из
функций вида
<pk = (u2 + r)l)-\ B.133)
Эту лемму применим для доказательства следующего утверждения.
Теорема 2.1. При условии что функция L(u) обладает свойствами
B.128), B.129), она допускает аппроксимацию выражениями ви-
вида B.132).
70
Гл. 2. Постановка контактных задач для слоя и клина
Доказательство. Выберем постоянные 5п, 7п (п = 1, • • •, N)
N
в C.5.5) так, чтобы П 5Ъп2 = с-
п=\
Рассмотрим функцию
Ыи) =
Ци)
Из условий B.128), B.129) следует, что функция F(u) =
обладает следующим свойством:
B.134)
Ь{и)
-1
F(u) = \и\~1 +О(и
00.
thAu
B.135)
Но тогда L^(u) удовлетворяет условию леммы 2.1, т.е. имеет место
представление
«^Ц-, B.136)
или, из условий B.134), B.136):
L(u) = tYi Аи
ск \и
B.137)
При построении аппроксимации главной части L(u) выражением
вида B.130) для нахождения коэффициентов аппроксимации 5п, 7п
(п = 1, ..., N) при численной реализации метода на персональном
компьютере используем эффективный алгоритм, описанный в §5 гл. 1.
Постоянную А в B.137) можно определить с достаточной степенью
точности, вычислив значение трансформанты К (и) = L(u)/ \u\ при ма-
малых значениях аргумента (порядка 10~3).
Часть II
ДВУХСТОРОННИЙ
АСИМПТОТИЧЕСКИЙ МЕТОД
РЕШЕНИЯ ПАРНЫХ
ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
Глава 3
ДВУХСТОРОННИЕ АСИМПТОТИЧЕСКИЕ
РЕШЕНИЯ НЕКОТОРЫХ КЛАССОВ ПАРНЫХ
ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
В настоящей главе излагается приближенный аналитический двух-
двухсторонний асимптотический метод решения интегральных уравнений,
к которым сводятся контактные задачи для полуограниченных обла-
областей, эффективный для всего диапазона значений входящего в ядро
характерного безразмерного параметра Л.
Строится замкнутое решение специальных классов интегральных
уравнений, порождаемых преобразованиями Фурье, Ханкеля (с Jo (от)
и Ji(ar)) и Меллина, затем на основании теорем об аппроксимации
трансформанты ядра метод переносится на весь рассматриваемый класс
интегральных уравнений.
Показано, что построенные замкнутые приближенные решения кон-
контактных задач для полупространства являются двухсторонне асимп-
асимптотически точными решениями исходных интегральных уравнений.
Определяется форма осадки поверхности неоднородного полупростран-
полупространства для задачи из §4 гл. 1. Приводятся численные примеры рас-
распределения контактных напряжений, осадок поверхности под штампом
и вне области контакта для различных законов неоднородности.
§ 1. Классификация интегральных уравнений
контактных задач для полуограниченных областей
Введем следующие определения и обозначения.
Определение 3.1. Будем говорить, что функция L(u) принадлежит
классу AN, если L(a\) имеет вид
N о .о._о
?i?. C-D
^0 пригфк.
Здесь Ai, Bi, i = 1, 2, ..., N, — некоторые постоянные. Соответствен-
Соответственно для N = 1 функция L{u) принадлежит классу А1.
Определение 3.2. Функция L(u) принадлежит классу Ем, если
L(aX) имеет вид
ЦаХ) = L^(aX) = V ffcA"''a' ¦ C.2)
§ 2. Решение класса уравнений, порождаемых преобразованием Фурье 73
Определение 3.3. Функция L(u) принадлежит классу Sn,m> если
она имеет вид
L(aX) = L^(aX) + L%(aX). C.3)
Определение 3.4. Обозначим через Wp \a,b) соболевское простран-
пространство функций, всевозможные обобщенные производные которых, до
порядка к включительно, суммируемы на отрезке [а, Ь] со степе-
степенью р.
Определение 3.5. Обозначим через В%(а,Ь) пространство функций,
имеющих на отрезке [а, Ь] все производные до порядка к включи-
включительно, причем производные k-го порядка удовлетворяют условию
Гельдера с показателем а, с обычной нормой
к
к ^ ' ' ~ix^[a,b] x,ye[a,b]
C.4)
Определение 3.6. с\ \а, Ь) — пространство функций, k-ые произ-
производные которых непрерывны с весом (х — аI (Ь — хI, с нормой
к
I fWf \\( \ (h \i I/2+7—fc+i (о с\
г=0
Определение 3.7. Подпространство С\ \а, Ь) четных функций бу-
будем обозначать через С\ (а, Ь), нечетных — С\ (а, Ь).
§ 2. Замкнутое решение одного класса интегральных
уравнений, порождаемых преобразованием Фурье
В настоящем параграфе на основе метода работы [43] строится
замкнутое решение одного вспомогательного класса уравнений, произ-
производится обобщение метода для построения асимптотических решений
(А —> О, А —> оо) интегральных уравнений, порождаемых преобразова-
преобразованием Фурье [8, 9]. Устанавливается разрешимость рассматриваемых
задач, классы корректности.
2.1. Замкнутое решение интегральных уравнений класса А1.
Построим решение уравнений A.38), A.101) для L(u) вида
Ци) . j±Jl. ,3.6)
Подставим C.6) в A.38) или A.101), имеем
C.7)
fo(x) = ^о(О)^ (задача п.1.1 гл. 1),
/о(ж) = 6@)/(ж) (задача п. 1.3 гл. 1).
74 Гл. 3. Асимптотические решения некоторых классов уравнений
Сделаем замену переменных и = аХ. Перепишем C.7) в виде
-1
Л
или
оо
Г 1 2
1 а
J «U2
— оо
Используем
+
+
А2\~2
В2\~2
-гха
J
.-1
= 2тг/0(ж), |х| < 1. C.8)
= Т(а).
C.9)
-1
Получаем парное уравнение
2
d«
-Joc И «2 + i
оо
J T(a)e~ixada = 0,
1,
ж > 1.
C.10)
Для простоты будем считать, что /о(ж) = с, где с — постоянная. Введем
обозначение
р(х)= T(a)\a\~e-"ada.
C.11)
Используя операционное исчисление, решим первое уравнение C.10)
относительно р(х). Имеем
Общее решение C.12) имеет вид
р(х) = Dn ch A\~xx + Сп sh А\~хх + сБ2Л.
C.12)
C.13)
Так как р(х) связана с функцией C.13) соотношением C.11) и четна,
то Сп = 0, т. е.
р(х) = DnchA\-lx + cB2\-2. C.14)
Продифференцируем первое уравнение C.10) по х, имеем
оо
—i J sgnаТ(а)е~гхаda = 2тгр/(ж),
— оо
оо
J T(a)e~ixada = 0,
х\ > 1.
C.15)
§ 2. Решение класса уравнений, порождаемых преобразованием Фурье 75
Выделяем вещественную часть, имеем (домножая и интегрируя)
J T(a) sinaxda = — тгр'(х), \х\ < 1,
о
оо
J T(a) cosaxda = О,
. о
Получим
X > 1,
J
xdx
о
сю
2 р p(
6 о v?
о V t — %
°г? xdx
t vx2 — t2
, \x\ < 1,
\x > 1.
C.16)
C.17)
Обращая C.17) по Ханкелю, имеем (формула Титчмарша-Басбридж)
оо г
Т(а) = 2а J\(ar)dr УК } +7rEJo(a). C.18)
J J v т2
о о
Здесь Е — неопределенная постоянная, определяемая из условия
l
r(x)dx = Р.
-I
Подставим в C.18) значение р(х) из C.14), используя:
I. р'(х) =
2.
[112]
xshAX lxdx
l
= г
lrz)dz
\ -z1
a -
3. xZp(ax)Sp(Cx)dx =
где Zp и Sp — функции Бесселя. Получим
Т(а) = 2 Та2 _2F(a) +
где
F(a) = A\-lI0(A\-l)J{(a) - I{(A\-l)aJ0(a).
Определим постоянные ТиЕ.
C.19)
76 Гл. 3. Асимптотические решения некоторых классов уравнений
1) Используем соотношения
сю сю
Т(х) = тг~ Т(a) cos axda = - Т(a) cos axda,
2тг J тг J
О
-сю
1
r(x)dx = P;
-1 -1
Тогда
сю
,-, 2 f J J0(a) . Та j-,, хоти: i , /o OA4
P=- < тгЕ* v } sin a H—2 2~~^2"^va)^^ r ^a- C.20)
Используем интегралы
сю
a 2'
0
/'fc) sin aria = ^AA-'e"^"'/,^-1), C.21)
a + А Л ^
0
СЮ
a/ + AZX~Z 2
0
Подставляя C.21) в C.20), получим
Е = Ртг-{. C.22)
2) Выражение C.19) должно удовлетворять исходному уравнению.
Подставим C.19) в первое уравнение C.10) и продифференцируем обе
части полученного уравнения по х, получим
ггг \ • а2 + А2Х~2 л п
T(a) smra^ 5—гш = 0.
а2 + Б2Л
о
Используем следующие интегралы:
сю
Г
= 0, \х
2A-2da= m-i ко(БЛ )' N <!; C.23)
A da
2 P2A-2da m
a + i) A da
0
2 2 _2
J a + В X
0
_2 da = shBX [xKo{BX l),
§ 2. Решение класса уравнений, порождаемых преобразованием Фурье 11
Имеем
сю
|PJo(a) (a^ + А^Л z) sin a + TaF(a)} ^ ^тг = 0.
J а + Б Л
О
Используя C.21), получим
АКо^А) (А2А~2 - Б2А~2) shEA^^
¦TshBA-^fAA-^oCAA-^KiCBA-^+Zi^A-^KoCBA-1)] =0,
ГЗТ7- C-24)
Найдем выражение для т(х), используя представление
сю
т{х) = — Т(а) cos axda.
71 J
о
Для вычисления интегралов используем равенство Парсеваля
сю сю
I f(a)g(a)da = 1 \ Fc(t)Gc(t)dt, C.25)
где
ею ею
= f (a) cos atda, Gc(t) = g(a) cos atda.
о
Окончательно получим
' -) РТ
т(х) = Р
, x)
C.26)
Заметим, что функция
сю /Ал , А , , г /Ал , А , ,
г /0 - ) a ch - (а - ж) - /i - sh - (а - х)
F(a,x)= ^^ ^ Va7 ^ da C.27)
J \/1 — а2
0
выражается через линейную комбинацию неполных цилиндрических
функций в форме Пуассона, для которых в [7] построена общая теория
и имеются таблицы.
78 Гл. 3. Асимптотические решения некоторых классов уравнений
2.2. Существование и единственность решения интегрального
уравнения класса AN в антиплоской и плоской контактных зада-
задачах для неоднородного полупространства (полуплоскости). Рас-
Рассмотрим парное интегральное уравнение вида
7 Т(а) \a\~l L(aX)e~ixada = 2тг/(ж), |ж| < 1,
~™ C.28)
J T(a)e~ixada = О, \х\ > 1,
— оо
с дополнительным условием
1 оо
r(x)dx = Р, т(х) = I T(a)e~ixada. C.29)
-1 -оо
Ниже используем лемму.
Лемма 3.1. [127] Пусть функции f(x) на отрезке (—1, 1) соответ-
оо оо
ствует ряд Фурье J2 ctk^oskirx, тогда ряд J2 k\ak\ сходится, если
к=\ к=\
f(x)?Bf+s(-l,l),e>0.
Лемма 3.2. Уравнение (ЗА) с дополнительным условием C.29) од-
однозначно разрешимо при L(u) класса AN, если f(x) четна и при-
принадлежит В\ (—1, 1), г > 0, в классе функций С\ ' (—1,1), при
этом имеет место оценка 2
1|г(ж)||с(о,+(_1 п < m(AN) H/II , C.30)
Доказательство Представим правую часть первого уравнения
C.28) в виде ряда Фурье (не нарушая общности, считаем f(x) четной
функцией), имеем
/0*0 = у + 2^ ak cos к7ГХ' C-31^
к=\
Это всегда можно сделать, если выполнено условие леммы 3.1. Ис-
Используя метод работы [43], так же как и в п. 2.1, получим выражение
для напряжений [8]
N оо
г(х) = Z_ + V СгФ (ф , х) - V -p^F (кж, х). C.32)
§ 2. Решение класса уравнений, порождаемых преобразованием Фурье 79
Здесь введены следующие обозначения:
1
^—— da;
1-х2
X
1 C.33)
l x)= Jl^ I l
1 2
J
Постоянные Q определяются из системы линейных алгебраических
уравнений:
'Л/1 1 ! / г/ \ ^ \ "оп ' Л / w> /О О /I \
А / BfcA ^-^ LN(m7r) V А / C.34)
г=1 ?тг=1
fc= 1, 2, ..., JV,
где
, v mJo(m) Ki (B) + BJX (m) Ko(B)
Z (m, B) = r—-2 .
m + В
Очевидно, что система C.34) однозначно разрешима, если Ai, Bi
удовлетворяют условиям C.1).
Оценим выражение в правой части C.32). Используем асимптоти-
асимптотические свойства функции Бесселя [112]
)-^i, C.35)
где тр(х) ограничена при х -^ оо .
Рассматривая C.32), C.34), нетрудно видеть, что в случае, когда
Вк\-{) C.36)
ограничены, формула C.32) имеет смысл, если сходятся ряды вида
оо оо оо
^! = У^ аку/к , Ef = Y^ afc/c sin /стгж, Е^ = Y^ afc/c cos /стгж. C.37)
k=\ k=\ k=\
Здесь ряды C.37) выделены из C.36) с помощью асимптотических
оценок неполных цилиндрических функций в форме Пуассона [7].
На основании леммы 3.1 заключаем, что при условиях настоящей
леммы ряды C.37) являются сходящимися. Отсюда следует оценка
вида C.30) и единственность построенного решения.
Имеет место более общая лемма.
80 Гл. 3. Асимптотические решения некоторых классов уравнений
Лемма 3.3. Уравнение C.28) с дополнительным условием C.29)
однозначно разрешимо для L(u) класса AN, если f(x) четная и
принадлежит -В|+1 (—1, 1),? > 0, в классе функций С^ \ (—1, 1). При
этом имеет место оценка 2
Лемма 3.3 доказывается аналогично лемме 3.2 с помощью оценок
правых частей выражения C.32).
§ 3. Замкнутое решение класса интегральных
уравнений, порождаемых преобразованием Ханкеля J\
3.1. Некоторые вспомогательные преобразования. Рассмотрим
уравнение A.64). Приведем его к более удобному для исследований
виду [208]. Сделав замену переменных и = А7, из A.64) имеем
1 оо
(p)pdp I L(A7)Ji(r7)JiGP)^7 = G0@)re, r < 1. C.39)
о о
Используя
о
перепишем C.39) в виде парного интегрального уравнения:
= G0@)r?) r < 1,
0 C.40)
, о
Введем в рассмотрение следующие операторы [68]:
C.41)
C.42)
=sint7; C.43)
C.44)
§ 3. Решение уравнений, порождаемых преобразованием Ханкеля J\ 81
Подействуем на первое уравнение C.40) оператором C.41), а на вто-
второе — оператором C.42). Придем к парному уравнению
/оо
J TG)L(A7) sin?7d7 = g(t), 0 < t < 1,
^ ? C.45)
/ТG) sin ?7d7 = 0, ? > 1.
о
Здесь обозначено
=-. C.46)
о
3.2. Замкнутое решение интегральных уравнений класса А1.
Пусть L(u) имеет вид
C.47)
Тогда, учитывая, что Ji(r5) —> \/2г5 при 5^0, C.45) можно перепи-
переписать в виде
1г оо (оАо)
jT5G)sint7d7 = O, t > 1.
о
Введем обозначение
сю
p(t)= \T5(j)smt^.
о
Из первого уравнения C.48) имеем
A2\-2p(t) -р" = Cl(B2\-2 + 52)smt5, с, =2С0@)е<Г1,
-.2 л -2 , с-2
p(t) = D5 ch А\~11 + C5 sh A\~11 + ci Б2Л_2 + ^2 sin t5. C.49)
А Л + 5
Так как </?(?) нечетна, то р(х) нечетна и D§ = 0.
Перепишем C.48), используя C.49):
1^+^ sintS,
C-50)
82 Гл. 3. Асимптотические решения некоторых классов уравнений
Обращая преобразование Фурье, имеем
rpf ч 2В2Х~2
Т5{и) =С1--2—о
2 В X + S S sin и cos 5 — и cos и sin 5
CS-
«2 - 82
2 АХ~1 sin и ch АЛ~1 — и cos гг sh AX~1
и2 + А2 Х~2
C.51)
Определим постоянную С$ из условия, что Т$(и) из C.51) должно
удовлетворять исходному уравнению, получим
с5
АЛ ch АЛ + БЛ sh АЛ
5 cos 5 + ВХ 1 sin 5
1 А2Л + б2
Формулу для напряжений
сю
Г
т(г) = T(u)uJi(ur)du
= 0. C.52)
C.53)
приведем к более удобному виду, используя равенство Парсеваля:
1
L(XS)
sin r5 г sin 5
_
СХ5
shAA lr rshAX
cos tddt
chAA ltdt
Здесь
, г) =
/ 9^
. C.54)
C.55)
т(г) =
Ч-r2
rshAA
Co = li
'ch^A~'tdt
S(t, r)
, C.56)
После решения интегрального уравнения связь между крутящим
моментом и углом поворота г штампа может быть найдена по формуле
М = 2тга3 lT(u)J2(u)du.
о
C.57)
§ 3. Решение уравнений, порождаемых преобразованием Ханкеля J\ 83
Здесь был использован интеграл
dp = Jx(u)u-x. C.58)
Преобразуя, получим связь между приложенным к штампу момен-
моментом и углом поворота:
M=l6G0@)sa3[l/3L-\0)^C0A-2X2 (AX~l chA\-l-shA\-1)] . C.59)
3.3. Существование и единственность решения интегрального
уравнения класса AN в задаче о кручении круглым штампом
неоднородного полупространства. Напомним некоторые известные
результаты теории рядов Фурье-Бесселя [98].
Обозначим Ль Л2, ..., Апь ... занумерованные в порядке возрас-
возрастания положительные корни функции Бесселя Jp(x) (р > — 1). Пусть
f(t) — произвольная функция, заданная на интервале @, 1). Пусть
1
далее jy/if(t)dt существует (в случае, если он несобственный)
о
и абсолютно сходится.
2 { 1
Положим ат = —2 jtf(t)Jv(\mt)dt, где v + - > 0.
Ju+l(Xm) 0
Пусть х — какая-нибудь внутренняя точка интервала (а, Ь), та-
такого что 0 < а < Ъ < 1 и f(t) имеет на нем ограниченное полное
оо
изменение. Тогда ряд J2 amJv{^mx) сходится, и сумма его равна
т=\
\
Лемма 3.4. [210] Пусть функция f(x) определена и 2s раз диффе-
дифференцируема на отрезке [0, 1] (s > 1), причем
1) /@) = /'(О) = ... = /(^(О) = 0, C.60)
2) fBs\x) ограничена (эта производная может и не существо-
существовать в отдельных точках),
3) /A) = /'A) = ...=/B*-2)A) = 0. C.61)
Тогда для коэффициентов Фурье-Бесселя функции f(x) справед-
справедливо неравенство
\ап\ < B^_1} (с = const). C.62)
А
84 Гл. 3. Асимптотические решения некоторых классов уравнений
Лемма 3.5. [210]. В условиях леммы 3.3 для s ^ 1 имеем
1) р > 0, \ап Jp(AHx)K B51/2); (Я = const), Vx е [0, 1], C.63)
2) p>-i |owJp(Awo;)| < LBs); (L = const), Vx e @, 1).
C.64)
Определение З.8. Будем говорить, что абсолютно интегрируемая
на отрезке [0, 1] функция f(x) удовлетворяет условию Мо, если
имеет место разложение Фурье-Бесселя
сю сю
f(x) = 2_\anJo(^nx)uУ^&nAn ^ Mj(—1, 1) < оо. C.65)
п=1 п=1
Определение 3.9. Будем говорить, что абсолютно интегрируемая
на отрезке [0,1] функция f(x) удовлетворяет условию М\, если
имеет место разложение Фурье-Бесселя
сю сю
f(x) = y^anJ\(Xnx)uУ^ап\п < Mj(—1, 1) < оо. C.66)
п=\ п=\
Заметим, что условия леммы 3.4 при 5 = 2 являются достаточными
для того, чтобы имели место неравенства C.65) и C.66).
Рассмотрим парное интегральное уравнение вида
/ сю
I [ TG)L(A7)Мп)^ = G0@)e [г + 2/(г)], 0 < г < 1,
C.67)
Лемма 3.6. Если /(г) нечетная и удовлетворяет условию М\, то
уравнение C.67) для L{u) класса AN однозначно разрешимо в клас-
классе функций С\ (—1, 1), при этом имеет место оценка
2
lk(r)||c(o)-(_ll) <m(AN)MJ(-l, I). C.68)
||c(o)-(_lfl) <m(AN)MJ(-l, I).
Доказательство Так как /(г) удовлетворяет условию М\, то
ее можно представить в виде ряда Фурье-Бесселя:
§ 3. Решение уравнений, порождаемых преобразованием Ханкеля J\ 85
Учитывая, что J\(r5) —> \/2г5 при 5^0, уравнение C.67) посредством
операторов C.43), C.44) можно преобразовать к виду
1
оо N
-Г
sin t5 + Yl bk sin jjikt,
l, C.70)
= 0, t
Используя метод работы [39], так же как и в п. 3.2, получим
выражение для напряжений [8]
(r) =
i=,
C.71)
Здесь введены следующие обозначения:
rshA
Z(r,A) =
l -
-
sinr/i
r sin/x
Л -r2
Постоянные Q определяются из системы линейных алгебраических
уравнений:
вк\~
LN@)Bi ^
fc= 1, 2, ..., N,
где
В sin ll
C.72)
C.73)
Система C.72) однозначно разрешима, если Ai, Bi удовлетворяют
условиям C.1). Рассматривая выражения C.71) и C.72), видим, что
при выполнении оценки C.66) (условие Mi) имеет место утверждение
леммы и оценка C.68).
Гл. 3. Асимптотические решения некоторых классов уравнений
В данном случае связь между моментом и углом поворота име-
имеет вид
N . оо
M=16G0@)e<t
C.74)
г=\ j=l
Здесь введены обозначения
F (А) = А~2 (A ch A - sh A), R (/х) = /i~2 (sin /x - /х cos /x). C.75)
Запишем уравнение C.67) для L(u) класса AN через операторы
ANr = /. C.76)
Теорема 3.1 (следствие леммы 3.6). При выполнении условий
леммы 3.5 оператор AN является обратимым и имеет место оцен-
' AN |MJ(-1, 1). C.77)
в виде
§ 4. Замкнутое решение одного класса интегральных
уравнений, порождаемых преобразованием Ханкеля Jo
4.1. Вспомогательные преобразования. Используя A.116), пе-
перепишем A.119) в виде парного интегрального уравнения:
J TG)L(A7) Jo
*7 = eo(O)/(r), r^l,
г > 1.
С помощью операторов
rcp(r)dr
Jt2 - r2
rt т s \ j.
/f Jo(r7) = cost7,
t/2V(r) = f 7(
J v r2
2 — i2
= 7"' cost7
представим C.78) в виде
о
oo
J TG)
= 0,
t > 1.
Здесь
= e0@)t7f/(r), (t/fl = тг/2).
C.78)
C.79)
C.80)
C.81)
C.82)
§ 4. Решение уравнений, порождаемых преобразованием Ханкеля Jo 87
4.2. Замкнутое решение интегральных уравнений класса А1.
Пусть L(u) имеет вид
Y + bzx~z
Тогда, учитывая, что Jo(re) —> 1 при г —> 0, уравнение C.81) для
случая, соответствующего плоскому штампу, можно переписать в фор-
форме
= costs, t ^ 1,
C.84)
, о
Введем обозначение
сю
p(t) = T(j) cos tjdj. C.85)
о
Из уравнения C.84) с учетом четности pit) получим
7->2 \ —2 2
pit) = CgchA\~1t + ci 9 _9 + ?9 costs, ci =во(ОM. C.86)
АА + г
На основании C.86), C.84) можно переписать так:
сю Л 2 , Л2 л -2
О
7 + В Л
9+?9 costs, ?<1, C.87)
о
Обращая преобразование Фурье, имеем
2 В А" + ? i/sini/coss — ? sins cos i/
л-, / л 2
Ге(м)=С1- .2._2^ 2
^ АХ + ?
2 usmuch АХ~1 + AX~l cosi/sh АХ~1
2 ^Т^
Постоянную С? определим из условия, что Т?(?х) должно удовле-
удовлетворять исходному уравнению C.84). Получим
ВХ~Х dvAX~x + АХ~Х s\yAX~x ВХ~х coss- esme _ п /о оп\
в2л-2 л2л-2 +С1 л2л-2 + 2 -°- C'89)
Гл. 3. Асимптотические решения некоторых классов уравнений
Формулу для напряжений
т(г) = T?(u)uJo(ur)du
о
приведем к более удобному виду, используя равенство Парсеваля:
1
cos? , Г sin tsddt
C.90)
_
L(Xe)
'1-г2
Се_
Ч-г2
-А\~
/t2 _ r2
C.91)
( \ у ( \ 2Во(ОM Г
тут) = пт т?[т) = —^ < -
?^0 7Г (^
v-i
Ч-r2
Со = li
/t2 — г2
C.92)
Связь между приложенной силой и осадкой штампа имеет вид
а
ra(p)pdp = 2тга2 lr(pf)pfdp, т(р') = та(р'а), C.93)
или
аоо оо
Р = 2тга2 f f T(u)uJ0(up)pdudp = 2тга2 I T(u)Jx(u)du. C.94)
0 0 0
Здесь был использован интеграл
1
Jo(up)pdp = J\(u)u~x. C.95)
о
Преобразуя C.94), получим
Р = 47гаво(О){1Г1(О)+ CoA-lXshAX~l}5. C.96)
§ 4. Решение уравнений, порождаемых преобразованием Ханкеля Jo 89
4.3. Существование и единственность решения интегрального
уравнения класса AN в задаче о вдавливании штампа в неодно-
неоднородное полупространство. Рассмотрим парное интегральное урав-
уравнение вида
/оо
J тG)ь(А7)Mn)d7 = eo(oM(i + /(г)), г < 1,
{ So C.97)
/TG)J0(r7Od7 = 0, r> 1.
I о
Лемма 3.7. ?с/ш функция /(г) четная и удовлетворяет условию
Mq, то уравнение C.97) для L{u) класса AN однозначно разрешимо
в классе функций С^ +(— 1, 1), при этом имеет место оценка
-l, 1). C.98)
Доказательство Так как /(г) удовлетворяет условию Мо, то
ее можно представить в виде ряда Фурье-Бесселя:
C.99)
Учитывая, что Jo(re) -^ 1 при г —> 0, уравнение C.97) посредством
операторов C.79), C.80) можно преобразовать к виду
l, C.100)
Так же, как и в п. 4.2, используя метод работы [38], получим
выражение для напряжений [10]:
т(г) =
71 I л/ I — r'Z * *
\. C.101)
90 Гл. 3. Асимптотические решения некоторых классов уравнений
Здесь введены следующие обозначения:
1
ф(г> А) = chA - A '' shAtdt
X(r, /i) =
COS \1
1
Г sin tfidt
C.102)
Постоянные С{ определяются из системы линейных алгебраических
уравнений:
N
г=\
где
«s^> ^в^^ =
C.103)
C.104)
Система C.103) однозначно разрешима, если А^, Bk удовлетворяют
условиям C.1). Рассматривая выражения C.101) и C.103), видим, что
при выполнении оценки C.104) (условие Mq) имеет место утверждение
леммы и оценка C.98).
В данном случае связь между приложенной силой и осадкой штам-
штампа имеет вид
= 4а2(Ю0@)
N
L~\0)
sh Ai
г=\
bjLN
^- l siniij
. C.105)
Запишем уравнение C.97) для L(u) класса AN через операторы
в виде
ANr = /. C.106)
Теорема 3.2 (следствие леммы 3.7). При выполнении условий
леммы 3.5 оператор AN является обратимым и имеет место
оценка
lk(r)IU)+r-i n < lAN-^lM^-l, 1). C.107)
#5. Свойства приближенных решений задач для полупространства 91
§ 5. Двухсторонние асимптотические свойства
замкнутых приближенных решений контактных задач
для полупространства (полуплоскости)
В настоящем параграфе рассматриваются контактные задачи §§ 1-4
гл. 1. Доказывается, что интегральные уравнения, соответствующие
этим задачам, не могут иметь более одного решения в пространстве
суммируемых функций Lp(—\, 1) A <р < 2).
При построении решения двухсторонним асимптотическим мето-
методом строится замкнутое решение вспомогательного класса уравнений,
затем предлагаемый метод обобщается на случай интегральных урав-
уравнений, соответствующих задачам §§1-4; доказывается разрешимость
задач, устанавливаются классы корректности; обосновывается прибли-
приближенный метод решения при Л < Л* и Л > Л°, где Л* и Л° — некоторые
фиксированные значения Л.
5.1. Единственность решения рассматриваемых задач. Пока-
Покажем, что интегральные уравнения, соответствующие задачам §§ 1-4, не
могут иметь в пространстве суммируемых функций Lp(— 1, 1) (р > 1)
более одного решения.
Лемма 3.8. Если функции L(u) соответствуют трансформантам
ядер интегральных уравнений задач §§ 1-4, то для всех и G @, оо)
имеют место неравенства:
(задачи §§ 1-2)
О < ci = min i7(*) < L(u) < max -^Щ^ = c2 < оо;
C.108)
(задачи §§ 1-4)
0<ci= min _^> <L(u)< max -§Щ- = c2 < oo. C.109)
Справедливость леммы 3.8 нетрудно установить, используя для
рассматриваемых задач соотношения A.159) и A.160).
Теорема 3.3. Если имеют место условия леммы 3.4, то в Lp(—l, 1)
A < р < 2) интегральные уравнения, соответствующие задачам
§§ 1-4, не могут иметь более одного решения.
Доказательство следует непосредственно из результатов рабо-
работы [75].
5.2. Некоторые определения и вспомогательная теорема.
Пусть дано интегральное преобразование
ь /з
g(x) = JGG)BG, *Ш GG) = |^)МG, ОС (ЗЛЮ)
92 Гл. 3. Асимптотические решения некоторых классов уравнений
либо разложение
Y, x), Gk= \§@МAк,№, C.111)
к=о I
и пусть функция B(j, x) — решение линейного дифференциального
уравнения второго порядка по х:
)
C.112)
L7B = r(x) [s{x)Bf]' + t(x)B (a^x^ b).
Здесь s(x) > О при x G (a, b), r(x) — знакоопределенная при х G
G (a, b) функция.
Пусть также при х —> b функции В и В' ограничены, а при х =
= а имеем: а\В + а2^х = 0. Кроме того, числа 7/с составляют счетное
множество нулей некоторого трансцендентного уравнения, причем а ^
< 7/с < 7/c+i < /3.
Считаем, что уравнение C.112) удовлетворяет условиям теоремы
Фукса [112], т.е. коэффициент Рг(х) при сР~гу/с1х2~г имеет вид:
(х — а)~г Рг(х — а), где функция Pi(x — а) голоморфна в области точ-
точки а (условие теоремы Фукса необходимо и достаточно для того, чтобы
уравнение C.112) имело два независимых интеграла, правильных в об-
области точки а).
Рассмотрим парное интегральное уравнение (парный ряд-
уравнение)
h
J QG)BG, x)dh(-f) =0, a^x<c, d < x < /3,
где для C.110) функция /1G) = 7, а для C.111)
C.114)
к=0
Здесь функция ^G) такова, что при K(Xj) = 1 решение уравнения
C.113) известно.
Пусть имеют место [18] асимптотические представления
ОG
7^0;
) 7^оо
§ 5. Свойства приближенных решений задач для полупространства 93
Определение 3.10. Функция K(j) принадлежит классу AN
(Ем, Snm), если имеет вид
AN'''
г=\ а +BiX
K(Xa) = Км(Ха) = } '2Л_2> C.117)
^ а + DkX
. C.118)
Здесь Аи Bi (г= 1,2, ...,7V), Сь Dfc (fc = 1, 2, ..., M) - неко-
некоторые постоянные.
Имеет место
Теорема 3.4. [10]: При условии, что функция K(j) обладает свой-
свойствами C.115), она допускает аппроксимацию выражениями вида
К(Ха) = KN{Xa) + K^(Aa). C.119)
В соответствии с C.110) имеем
d
Q(n) =Jg@iVG, OdC, N(n, 0 = MG, 0 пРи Pin) = 1. C.120)
Подставляя C.120) в C.113), имеем
/3d
q(ZM-y)K(\>y)N(>y, 05G,
C.121)
Ниже интегральный оператор, соответствующий функции K(j),
принадлежащей классу X, будем также обозначать через X. Используя
C.119), перепишем C.111) в операторном виде:
Eoog = /. C.122)
В C.122) оператор AN соответствует в C.119) функции K(j) вида
C.116), a Eqo — функции K(j) вида C.117).
Определение 3.11. Будем говорить, что для уравнения C.113) вы-
выполнено условие А, если для него при К(^) е AN можно построить
замкнутое решение, следуя [38].
Будем обозначать это решение
q = AN/- C.123)
Иными словами, условие А означает, что для функций f(x), при-
принадлежащих некоторому классу W(c, d), существует функция q(x),
94 Гл. 3. Асимптотические решения некоторых классов уравнений
принадлежащая некоторому классу V(с, d), такая что имеет место
равенство C.123).
Из представления C.123) следует, что
\\q\\viCtd)<m(AN)\\f\\v(Ctd), m (AN) = const. C.124)
Ниже будем обозначать через т(Х) некоторую постоянную, зави-
зависящую от конкретного вида принадлежащей X функции.
5.3. Доказательство асимптотической точности решения.
На основании теоремы Хана-Банаха [129] покажем, что при вы-
выполнении некоторых условий выражение C.123) представляет собой
асимптотически точное решение уравнения C.122) при Л —> 0 и Л —> оо.
Предварительно рассмотрим вопрос о существовании и единствен-
единственности решения парного уравнения C.113) для функции K(j) класса
Sn, м; в этом случае уравнение можно записать в виде
ANg + ?Mg = /. C.125)
Определим условия, при которых оператор AN Ем уравнения
C.113) является оператором сжатия [129], для этого используем сле-
следующие утверждения.
Лемма 3.9. Для билинейной формы вида
< х) = ТРтЬьШыЬщч), C.126)
J 7 +а
если 7Р(т) — r~X(l)> M(j, x) = БG, х), и а — вещественное число,
имеет место представление
!B-(ia, ?)B+(ia, x), ? < х,
C.127)
Б( ?)В_(га, х), х < ?,
где В-{га, х) и B+{ia, x) — линейно независимые решения уравнения
C.112), такие что Б_(га, ?) —> 0, а Б+(га, ^) -^ оо при а —> оо.
Утверждение леммы 3.9 следует из леммы 28.1 работы [91], для
этого достаточно в лемме 28.1 положить 7г = ^а.
Не нарушая общности, положим в C.125) М = 1.
§ 5. Свойства приближенных решений задач для полупространства 95
Лемма 3.10. Если для уравнения C.113) выполнены условие А
и условия леммы 3.9, то оператор Si# в C.125) можно представить
в виде ряда [173] (Xlig соответствует f
к (а) =
crX
2
Ik -«
, x),
к=0
-s(c)W?(B+, B)I-+s(d)W$(B-,
C.128)
I± =
C.129)
?(A, B) = A(a, b)B'(<yk, b) - БGь b)A'(a, b).
C.130)
Здесь 7o, 7i, ..., jn, ... — совокупность всех собственных значений
задачи C.112) при соответствующих граничных условиях, .ВGь %) —
соответствующие нормированные собственные функции, С (а) некото-
некоторая фиксированная для каждого уравнения C.112) ограниченная по-
постоянная, связанная с определителем Вронского W(B+, B-) функций
В+(а,х) и В-(а, х) соотношением
W [B+(a, ж), В_(а, х)] = C(a)s-l(x).
C.131)
Доказательство Для доказательства леммы 3.10 выпишем
представление коэффициентов разложения /3k'.
C.132)
Используя лемму 3.9 и известное свойство решений дифференци-
дифференциального уравнения второго порядка [39]:
гЬ, x)-B(a, x)B'(ib, x))\ ,
p(g, x)B(ib, x)dx_
J ^(^)
C.133)
где B(a, x), B(ib, x) — любые два решения уравнения C.112), соответ-
соответствующие 7 = о* и 7 = ib, второе выражение C.132) можно переписать
96 A. 3. Асимптотические решения некоторых классов уравнений
в виде
1
{ s(x)B_(a,O[B+(a,x)B'(lk,x)-
t, x)B'{a, x)} || ,
"fk-a
\ / i\ —• • i_ \ • \ f - - /
C.134)
откуда следует утверждение леммы.
Рассмотрим уравнение C.112), положим у(х) = B(x)^/s(x). Отно-
Относительно ?/(#) получим уравнение
у" — ry2q(x)y = 0, q(x) = р(ж) — R(x)j~2, C.135)
р(х) = (rsy1 , R(x) = t (rsy1 - s"BsY + 1/4 (sfs~1J . C.136)
Лемма 3.11. Оператор AN~1EM уравнения C.113) является опе-
оператором сжатия в пространстве V(c, d) при выполнении условий
леммы 3.10 в случае, если
1. функция q"(x) непрерывна при х е (а, Ь),
2. q(x) > 0 при х е (а, Ь) для 0 < Л < Л*, где Л* — некоторое
фиксированное значение Л.
Доказательство Для доказательства оценим по Л коэффици-
коэффициенты /3k в C.128). Используем обозначения
F±(a, е) = ВТ(а, ^)Wea(B±, В) (е = с, d). C.137)
В соответствии с теоремой 2.5 из [217, с. 401] при выполнении
условий 1, 2 уравнение C.135) имеет решение вида
!/1,2(я, 7) = <Г1/4(ж)?±(ж0, х) [1 + 7ei,2(a;, 7)] , C.138)
Е±(х0, х) = exp i ±7 [ y/q(f)dt > • C.139)
\ хо )
Для функций ?i?2 справедливы оценки
\sj(x, 7I < с, хе[а,Ь], 7>7o>O, j = 1, 2, C.140)
где постоянная с не зависит от х, 7-
Асимптотику C.139) можно дифференцировать, т.е.
2/i>2(*> 7) = ±W/A(x)E±(x^x) [1 +7-Ч2ОЕ, 7)] , C.141)
где для функций е\^ имеют место оценки вида C.140). Используя
C.139), C.141) и учитывая, что в C.135) 7 = D\\~\ заключаем
следующее: так как с < ?, поведение функции ^+G» с) определяет
множитель вида Е_(с, ?) и найдется такое 7о» что ^+G> с) ^ 0 при
7 > То > 0.
§ 5. Свойства приближенных решений задач для полупространства 97
Аналогично предыдущему, так как d > ?, благодаря множите-
множителю Е-(?, d) найдется такое 7о> что ^-(т> d) ^ 0 при 7 ^ То > 0.
Таким образом, при 0 < Л < Ai (Ai = ^lT^1 )> учитывая, что коэф-
коэффициенты разложения C.128) имеют вид C.132) и функции .ВGь ж)
ортонормированы, получим оценку
/с=0
где постоянная М* не зависит от А. Отсюда следует, что А можно
выбирать таким образом, что оператор AN Ем будет оператором
сжатия при условиях данной леммы.
Исследуем, при каких условиях решение C.120) является асимпто-
асимптотически точным решением уравнения C.113) когда А —> оо G —> 0).
Для этого, следуя схеме, изложенной ранее, определим условия,
при которых оператор AN^Sm уравнения C.113) будет оператором
сжатия.
Всюду далее считаем, что решения уравнения C.112) удовлетворя-
удовлетворяют условию симметрии
В{п, х)=В{х, 7). C.143)
В соответствии с условием C.143) поведение В(п, х) при 7 ~^
—> 0 определяется поведением соответствующего решения уравнения
C.112) при х^О.
Приведем уравнение C.112) к самосопряженному виду, для этого
домножим его на функцию г~1(х). Получим из C.112):
, х) = [s{x)B']f - Q(x)B, s(x) > 0, а < х < b,
Предположим, что коэффициенты s(x) и Q(x) уравнения C.144)
аналитичны в круге \х\ < R. Тогда всякое решение В(х) уравнения
C.144) аналитично в этом круге, т.е. разлагается в степенной ряд,
сходящийся в круге \х\ < R [135].
Лемма 3.12. Оператор AN^Xm уравнения C.113) является опе-
оператором сжатия в пространстве V(c, d), если коэффициенты s(x)
и Q(x) уравнения C.144) аналитичны в круге \х\ < R для А > Аа,
где Ха — некоторое фиксированное значение А, и выполнено условие
симметрии C.143).
Доказательство Для доказательства леммы оценим по А коэф-
коэффициенты /3k в C.128). Из условия леммы и условия симметрии C.143)
следует, что найдется такое Аа, что при А > Аа решения В±(а, х)
можно представить в виде ряда по степеням А, сходящегося в круге
4 СМ. Айзикович и др.
98 Гл. 3. Асимптотические решения некоторых классов уравнений
|А| > Ла. Отсюда следует, что
k=0
где постоянная Ма не зависит от Л. Таким образом, Л можно выбирать
так, что оператор AN Ем будет оператором сжатия, если выполнено
условие данной леммы (Ла = Ма).
Отдельно рассмотрим случай, когда точка х = О для уравнения
C.144) является регулярной особой точкой, т.е.
s(x)=x<p(x), <p@)^0, C.146)
где (р(х) > 0 — функция, непрерывная на [а, Ь]. Заметим, что функция
s(x) вида C.146) удовлетворяет условиям теоремы Фукса.
Имеет место лемма ([208], с. 628).
Лемма 3.13. Пусть В+(х) и В-(х) — два линейно независимых
решения уравнения C.144), коэффициент которого s(x) удовлетво-
удовлетворяет условию C.146). Тогда, если В+@) ф 0, то В-(х) имеет при
х = 0 логарифмическую особенность. Если В+(х) имеет при х = 0
нуль п-го порядка (п > 0), то В-(х) имеет при х = 0 полюс п-го
порядка.
Лемма 3.14. Пусть коэффициент s(x) уравнения C.144) имеет вид
C.146), причем выполнено условие C.143), и, кроме того,
s{c)B{lk,c) = s{d)B{lk,d). C.147)
В этом случае оператор AN^Xm уравнения C.113) является
оператором сжатия в пространстве V(c, d) для А > Аа, где Ха —
некоторое фиксированное значение А .
Оценим коэффициенты /3k в C.128). Из леммы 3.13 и усло-
условия C.143) следует существование такого Аа, что при А > Аа, если
В+@) фО, то
vM)E A^°° (A>Aa)' C-148)
fc=0
и если В+(х) имеет при х = 0 нуль п-го порядка, то в оценке C.148)
Mi A In А заменяется на Л^А.
На основании лемм 3.11, 3.12 и 3.14, применяя к уравнению
q + ANSM^ = AN/ C.149)
принцип сжатых изображений, получаем доказательство существова-
существования и единственности решения уравнения C.125) при наложенных
ограничениях. Таким образом, доказана
§ 5. Свойства приближенных решений задач для полупространства 99
Теорема 3.5. Уравнение B.4.4) однозначно разрешимо в простран-
пространстве V(c, d) при K{pf) класса Sn,m и выполнении условий лемм 3.3,
3.4 или 3.6, причем имеет место оценка
Sm) \\f\\w(c,d) ¦ (
Более того, имеет место следующая теорема
Теорема 3.6. Уравнение C.113) однозначно разрешимо в простран-
пространстве V(c, d) для K(j), обладающих свойствами C.115) при 7Р(т) —
— r~X(l)> выполнении условия А и условий 1) и 2) леммы 3.11, если
0 < Л < Л*, а также для А > Ла при выполнении условий леммы 3.12
или 3.14 (Л*, Ла — некоторые фиксированные значения А) и имеет
место оценка C.150) при замене Ем на Еоо.
Теорема 3.6 следует из утверждений теорем 3.4 и 3.5 и доказыва-
доказывается так же, как и в работе [69], при помощи известного в теории
возмущений приема, основанного на методе последовательных прибли-
приближений.
Примеры представлений вида C.128).
1. t(x)=0, r(x) = s(x) = const в C.112)
В (а, ?) = cosa^,
B_(iD, ^) = \/2D~l exp (-D?), C.151)
В+(Ш, 0 = chDx,
где
а/ДгШ ') = -—2—-2—2 Q(€)G(€№> C.152)
(/стг) + L> A J
о
= cos /стг^ — exp ( — — ) cos /стг ch ( — ^
V A / V A
Здесь выполнены условия лемм З.П и 3.12. Пространство
V(c, d) = cfj>+(-\, I), где cfj>+(-\, I) - пространство четных
функций, непрерывных с весом (I —ж2I/2 и нормой [69]
= max f(x)(l -x2)l/2, C.153)
<«»+(
^
W(c, d) — пространство функций, имеющих на отрезке [—1, 1]
производные первого порядка, удовлетворяющие условию Гельде-
ра с показателем 1/2 -\- г с обычной нормой.
2. г(х)=х~\ s(x)=x, t(x) = -n2x~2 в C.112).
ж) = /n(i5x) (п = 0, 1).
100
Гл. 3. Асимптотические решения некоторых классов уравнений
Здесь Jn(x) — функция Бесселя, In(x), Kn(%) ~ модифициро-
модифицированные функции Бесселя. Имеем
iD
Lo
- к„ (?
n [jp)\ dP
C.155)
(n = 0, 1), причем V(c, d) = c[f2+(-l, 1) для n = 0, и
(— 1, 1) для n = 1, где Cj
c, d) =
j/2 (— 1, 1) — пространство нечет-
нечетных функций, непрерывных с весом A —ж2I/2. Соответствую-
Соответствующее пространство W(c, d) определено в [10]. Здесь при п = 0
выполнены условия леммы 3.11 и имеет место оценка C.148), со-
соответственно при п = 1 также выполняются условия леммы 3.11
и имеет место оценка C.148) при замене MiA~4nA на М2А-1.
§ 6. Замкнутое решение интегрального уравнения,
порождаемого преобразованиями Фурье и Меллина
В настоящем параграфе рассматривается класс парных интеграль-
интегральных уравнений, порождаемых контактными задачами для неодно-
неоднородных полосы и клина, лежащих на недеформируемом основании.
Решения этих уравнений строятся приближенным методом, позволяю-
позволяющим получить основные характеристики задачи в аналитическом виде.
Устанавливается разрешимость уравнений задач, классы корректно-
корректности. Доказывается, что полученные приближенные решения являются
асимптотически точными для малых и больших значений безразмерно-
безразмерного параметра задач.
Рассмотрим парное интегральное уравнение
J $(u)K(u)e-iuxdu = 2тгд{х),
J
C.156)
Пусть К (и) имеет вид
К (и) «
П2(«2
C.157)
где
(-гх2),
2) — целые функции (многочлены степени 2N, где
НУЛИ этих полиномов). Подставим аппроксимацию
§ 6. Уравнение, порождаемое преобразованиями Фурье и Меллина 101
C.157) в ядро k(t) B.127), сделаем замену переменных и = Л/3 и
введем обозначения: 5'п = 5пХ, Уп = jn, А = h/a. Тогда ядро интеграль-
интегрального уравнения B.127) примет вид
C.158)
00 N
= г th^ д
J <п — 1
п — 1 Р ~^~ 7п
Пусть функция g(x) может быть представлена в виде ряда:
оо
g(x) = ^ + Y^ (afc cos /стгж + bk sin /стгж), C.159)
k=\
где a/c, bfc — коэффициенты ряда Фурье. Выделим в функции g(x)
«четную» и «нечетную» части:
g(x)=g+(x)+g_(x),
ГД6 а °°
Я+ (ж) = у + 5^ a/c cos ^7ГЖ'
C.160)
оо
g_ (ж) = Y^ bfc sin /стгж.
fc=i
Тогда B.127) можно представить как
-?> " il2^; C.161)
J Ф(E)е~гCхAE = 0, \x\ > 1.
— оо
Аналогично [90], рассмотрим сначала случай четной функции g(x):
оо
gcos/3xci/3
(/3) C.162)
индекс «+» соответствует четной части Ф(/3), g(x). Построим решение
уравнения C.162) для правой части вида 2тгсо8?ж. Далее с помощью
суперпозиции можно построить решение для любой четной функции,
представимой рядом Фурье.
Заметим, что для дифференциального оператора L = ——»
dx
Ь(е~гРх) = /32е~гх@. Учитывая последнее и C.161), интегральное
102 Гл. 3. Асимптотические решения некоторых классов уравнений
уравнение C.156) со специальной правой частью g+(x) =
можно записать в виде
U\(L)F+(x) = 2irU2(e2)cosex, \x
где
сю
¦J
cos/tod/3,
C.163)
C.164)
U\(L), П2A/) — дифференциальные операторы по х порядка 2N.
Решение C.163) имеет вид
N
F+(x) =
C.165)
n=l
Таким образом, построение решения интегрального уравнения
C.162) сводится к решению парного интегрального уравнения
1 СЮ
— Г
оо
J
cos CxdC =
III (? ) гг=1
cosCxdC = 0, \х\>\,
C.166)
имеющего замкнутое решение. Решение уравнения C.166) содержит
неизвестные постоянные Сп, п = 1, ..., N, которые определяются из
условия удовлетворения этим решением исходного интегрального урав-
уравнения B.127).
Покажем, что для определения постоянных Сп достаточно опре-
определить не само решение (р+(х), а только его трансформанту Фурье
Воспользовавшись методом [119] и соотношениями для сфериче-
сферических функций [100, 107], получим выражение для Ф+(/3):
= GeP
eP
N
-5><
n=l
1 , -<5n
, C.167)
§ 6. Уравнение, порождаемое преобразованиями Фурье и Меллина 103
где
7rsh(9
H (u, w) =
P P1 — P1 P
-L U-L V -1 U-1 V
— присоединенные функции Лежандра.
Для определения постоянных Сп уравнение B.127) с ядром C.158)
запишем в виде эквивалентного ему парного интегрального уравнения
— оо
оо
C.168)
> 1.
Подставив в C.168) выражение для Ф+(/3) из C.167) и вычисляя
квадратуры, получим следующую систему N линейных алгебраических
уравнений для определения неизвестных постоянных Сп:
N N
\^ r _ f _|_ V^ п Т 777 — 1 N И 1 fiQ^i
/ ^п — Jm \ / атпп^п-> lib — 1, . . . , iv . ^о. iuy;
п=1 п=1
где
&т,п —
Jm
n2(?Z) ?2
Г 2
2+V 2
(гх, г;) =
^Л0
Ы+h)
Е (и, v, w) = QWT (и, v) — QVT (и, w),
Р О1 — О Р1
Т(и, v) = ^Ьр—^^ц —.
Здесь в = тг/(т4Л); i5n, i^n — нули П^г^2), Щ^2) соответственно.
104 Гл. 3. Асимптотические решения некоторых классов уравнений
Определив постоянные Сп, из B.127) получим выражение для
напряжений <р+(х) вида
2' 2
N
п=\
-
2'
где
C.170)
dr.
y/2(ch0r-ch0x)
Построим решение интегрального уравнения B.127) для нечетной
правой части g_(x). В этом случае B.127) имеет вид
C-171)
|
-1
где k(t) аналогично C.158).
С помощью дифференциальных операторов IIi(L), П2A/) инте-
интегральное уравнение C.171) можно свести, как и ранее, к уравнению
1л
= 2тг | — е
N
n sh 5nc
, \x\^l. C.172)
Решение уравнения C.172) построим, используя подход, описанный
х
в [119]. Так как в нашем случае g+ (х) = jg_(?)d? + D, a D определя-
о
ется из условия (р+ A) =0, то легко показать, что при этом условии
Тогда в нашем случае имеем
Ю-(х) = 2^ J shвх
П!(?2)
и (
где S (и, х) =
N
п=\
гл \ Л П ' *?
C.173)
, C.174)
^2 (ch в - ch (9ж) i л/2 (ch (9т - ch вх)
§ 6. Уравнение, порождаемое преобразованиями Фурье и Меллина 105
Трансформанту Фурье Ф-(/?) находим аналогично четному случаю:
n=l
. C.175)
Затем, записав C.171) в виде парного интегрального уравнения
и подставив в него C.175), после взятия квадратур получим линей-
линейную алгебраическую систему уравнений для определения коэффициен-
коэффициентов Dn:
N
ra=l,...,7V,
C.176)
п=\
где
_ т /_ 1 , Sn _ 1 7m \
П2(г2)
1,7
Здесь функция Т(и, г;) та же, что и в C.169), i5n, i^n — нули
IIi(^2), П2(^2) соответственно.
Выпишем вид решения интегрального уравнения C.156) для правой
части вида C.162):
0
п=1
фИ'4+ё4 (зл77)
Здесь функция Ф(и, г;, ж) та же, что и в C.170).
Коэффициенты Сп находятся из следующей линейной алгебраиче-
алгебраической системы уравнений:
N N
^Хп = fm^^umnXn, m=\, ...,N. C.178)
п=1 п=1
Здесь
106 Гл. 3. Асимптотические решения некоторых классов уравнений
п ,
Ш(АХктг) (/стгJ / 1 /стг _}_,Jrn _}_
: L(Afar) Q ii7mm V 2 0 ' 2 А<9' 2
А<9
, ?л_
u-v)(u + v+l)PuQv '
(гх, v, w) = QWT (и, v) - QVT (и, w),
v) -
Р О1 — О Р1
функции i?(u, г;), ?^(г^, v, w) те же, что и в C.169).
N
п=1
, C.179)
здесь ^(гх, ж) та же, что и в C.174).
Коэффициенты Dn находятся из следующей линейной алгебраиче-
алгебраической системы уравнений:
N
Z /
п=\
&тп<Еп — Jm9 ^ — А , . . . , iv .
C.180)
Здесь
к=\
k-i
' 2+ Хв)'
\ .ктг 1 jm \
2 + гТ' + Ш
Общее решение исходного интегрального уравнения C.156) име-
имеет вид
+ <р-(х). C.181)
§ 7. Свойства приближенных решений задач для полосы и клина 107
Связь между вдавливающей силой и осадкой штампа определим,
подставив выражение для <р(х) в условие равновесия штампа:
1
Р= I ф)<1х. C.182)
-1
Отсюда
N
Р=-
п=\
, C.183)
где dk (к = 0, 1, 2, ...) — коэффициенты разложения функции g(#)
в ряд Фурье, т. е.
1
ак = g(x) cos kirxdx, к = 0, 1, 2, ...
-1
В частности, для штампа с плоской подошвой формула C.183)
примет вид
^ Р 1 5П
Р= -—i+7r^Cn^i^. C.184)
§ 7. Двухсторонние асимптотические свойства
замкнутых приближенных решений контактных задач
для неоднородных полосы и клина
7.1. Существование и единственность решения парного инте-
интегрального уравнения, получаемого в контактных задачах для по-
полосы и клина, в случае трансформанты ядра класса AN. Рас-
Рассмотрим парное интегральное уравнение вида
<?>(/3)th(A\f3) ^pe-^d/3 = 2irg(x), \x\^l,
C.185)
J Ф(/3)е-^/3 = 0, |ж| > 1.
-сю
Используем лемму [120].
Лемма 3.15. Пусть функция g(x)eBf (—1,1) и g
J2
k=\
сю
Тогда ряд Y^, k\ak\ сходится, если е > 0.
/с=1
108 Гл. 3. Асимптотические решения некоторых классов уравнений
оо
Лемма 3.16. В условиях леммы 3.15 ряд J2 ^2 \ак\ сходится, если
к=\
g(x) ЕБ22 ?(— 1, 1), е > 0 (доказательство аналогично лемме 4.1
в [120]).
Лемма 3.17. Уравнение C.156) однозначно разрешимо при Ь(и)
— I г
класса AN, если g(x) — четная функция, g(x) G В^ (—1, 1), s > 0,
в классе функций С\' (—1,1). При этом имеет место оценка
2
. \\g\\ 1 , C.186)
e
1
? e
г^в т(А) — некоторая постоянная, зависящая от конкретного вида
принадлежащей классу А функции.
Доказательство Представим правую часть уравнения C.156)
в виде ряда Фурье (не нарушая общности, считаем, что g(x) — четная
функция):
g(x)=g+(x) = ^ +
k=\
Это всегда можно сделать при условиях леммы 3.15. Так же, как и в
§6, получим выражение для напряжений:
Q_iV/2(ch6»-ch6»a;)
п=1
где функция Ф (и, г;, ж) та же, что и в C.170).
Коэффициенты Сп находятся из линейной алгебраической системы
уравнений:
N N
^n = /m + ^amnxn, m= I, ...,7V, C.189)
n=l n=l
§ 7. Свойства приближенных решений задач для полосы и клина 109
где
ХП = Q1 1 Р 1 , 5гг_ Сп,
~2 ~2^Х0
&тп —
Л
^ /1 Ьг 1 7т
I 2+'T' 2+Л
g i 7m
функции R (и, v), E (u, v, w) те же, что и в C.169).
Очевидно, что система C.189) разрешима, если 5п, 7п удовлетво-
удовлетворяют УСЛОВИЮ Gг — 7/с) (^г ~~ $к) ^ 0 ПРИ i ^ k.
Оценим выражение в правой части C.188). Выражения C.188),
C.189) имеют смысл при условии сходимости входящих в них ря-
рядов. Используя асимптотические свойства функций Лежандра [100],
с помощью асимптотических оценок неполных сферических функций
в форме Пуассона [68] получим, что ряды, входящие в C.188), C.189),
сходятся, если сходятся ряды вида
оо оо . оо о
^(-l)fca^, ^(-l)fca^-2, Y,a^- (ЗЛ9°)
к=\ к=\ к=\
На основании лемм 3.15, 3.16, а также признака Лейбница сходимо-
сходимости знакопеременных рядов заключаем, что ряды вида C.190) сходятся.
Отсюда следует оценка вида C.186).
Справедлива более общая лемма.
Лемма 3.18. Уравнение C.156) однозначно разрешимо при L(u)
класса AN, если g(x) — четная функция, g(x) G В^2 (~1» 0' ? > 0,
^ (—1, 1). При этом имеет место оцен
C.191)
в классе функций С^ ^ (—1, 1). При этом имеет место оценка
<2
M)\\cin{_lA)^(y)\\g\\ l2+
Лемма 3.18 доказывается аналогично лемме 3.17 с помощью оценок
правых частей выражений C.188 ), C.189).
Обозначим интегральный оператор, соответствующий L(u) клас-
класса А, также через А.
Тогда уравнение C.156) при L(u) e AN примет вид
g. C.192)
Как следствие леммы 3.18 имеет место следующая теорема.
Теорема 3.7. В условиях леммы 3.18 имеет место оценка
k+2
С'1)
ПО Гл. 3. Асимптотические решения некоторых классов уравнений
7.2. Существование и единственность решения парного инте-
интегрального уравнения, получаемого в контактных задачах для по-
полосы и клина, в случае трансформанты ядра класса Sn,m- Урав-
Уравнение C.156) можно записать в операторном виде при L(u) G Sn, m
как
ANy? + Им^ = g- C.194)
Покажем, что верна следующая лемма.
Лемма 3.19. Оператор AN Ем задачи является оператором
сжатия в пространстве С^ j (—1, 1) при выполнении условий лем-
леммы 3.18, если 0 < А < А* или А > Ао, где А*, Ао — некоторые
фиксированные значения А.
Доказательство. Докажем лемму при к = 0. Для к > 0 дока-
доказательство аналогично.
Рассмотрим оператор Ем(^)- Не нарушая общности, полагаем М =
= 1. Имеем
20г]
^rf-ti
/=i
-l
C.195)
Представим Si(</?) в виде ряда:
Ei (ip) = со + 2_, ск cos knx.
к=\
Коэффициенты Ck находятся по следующим формулам:
ск=В\-1-{-\)
C.196)
1=\
— ti Г
VTi iv
4тг-
в\-
+ th АХктг
тг у?
C.197)
Здесь г] = г//А; 0 = -^-; tx = |B/- 1), / = 1, 2, ...; Б,т/ - некото-
некоторые постоянные.
§ 7. Свойства приближенных решений задач для полосы и клина 111
Используя C.197), получим следующие оценки:
сю
max |?i(<p+)>/ch0-ch0a;|< Y1 Ы^АМ*, А^О, Л<Л*;
же[11]' ko
| ? Ы<^-, А^оо, А>А0,
жЕ[-1,1]' /с=0 Л
C.198)
где М°, М* не зависят от Л.
Отсюда, используя оценки, аналогичные оценкам в леммах 3.17,
3.18, имеем, что Л можно выбирать таким образом, что оператор
^ будет оператором сжатия при условии леммы 3.19.
На основе леммы 3.19, применяя к уравнению
en 4- AN УЗ л * — AN" 0 (^ 199^
принцип Банаха сжатых изображений, получаем доказательство суще-
существования и единственности решения уравнения C.194) при наложен-
наложенных ограничениях.
Итак, доказана следующая теорема.
Теорема 3.8. Уравнение C.185) однозначно разрешимо в простран-
пространстве С^ 1 (—1, 1) при Ь(и) класса Sn,m, если g(x) — четная функ-
функция, g(x) е В^(-\, 1), г > 0 при 0 < А < А*, А > Ао, где А*, Ао —
некоторые фиксированные значения А, и имеет место оценка
\Ых)\\сю+(-1 1) ^ m(AN> SM, k) \\g\\ i+e . C.200)
Окончательно сформулируем следующую теорему.
Теорема 3.9. Уравнение C.185) однозначно разрешимо в простран-
пространстве С \ (—1, 1) для данной задачи, если g(x) — четная функция,
g(x) е В^(-\, 1), е > 0, при 0 < А < А*, А > Ао, где А*, Ао -
некоторые фиксированные значения А, и имеет место оценка
\\Ф)\\см+{-1 о < m(AN- soo, к) \\g\\ ,+ . C.201)
fc+j ' Вк+2 С' Ч
Эта теорема следует из утверждений теорем 3.7, 3.8 и доказывается
при помощи известного в теории возмущений приема, основанного на
методе последовательных приближений, так же, как и в работе [69].
В [90] была доказана следующая теорема.
Теорема 3.10. Если g_(x) ? Bf(—\, 1), - < а < 1 (g_(x) — нечетная
функция), (р+(х) — решение интегрального уравнения
? = 2тг?(х),
-1
112 Гл. 3. Асимптотические решения некоторых классов уравнений
X
для случая g+(x) = Jg_(t)dt + С, обращающееся в нуль при х = ±\,
о
то ф-(х) = <?+'(#) есть решение интегрального уравнения, соот-
соответствующее g_(x).
X
Условие g+(x) = Jg_(t)dt + С, где С определяется из соотношения
о
<?+A) =0, выполнено в ходе построения решения (в §6). Поэтому на
основании теорем 3.9, 3.10 может быть сформулирована следующая
теорема.
Теорема 3.11. Уравнение C.185) однозначно разрешимо в простран-
пространстве С^ 1 (—1, 1), если g_(x) — нечетная функция, g_(x) E Щ^
х
(—1, 1), ? > 0, выполняется условие g+(x) = Jg_(t)dt + C, г^в С
о
определяется из <^+A) =0 др^г 0 < Л < Л* ^тг^г Л > Ао, где А*, Ао —
некоторые фиксированные значения А, и имеет место оценка
\\Ф)\\с™-(-1 1) < m(AN' Eoo, к) \\g\\ i+ . C.202)
Таким образом, уравнение C.185) однозначно разрешимо в про-
пространстве С{к\ (-1, 1), если g(x) е В|+2е(-1, 1), ? > 0, при 0 < А < А*
/с+2
или А > Ао, и имеет место оценка
\\Ф)\\С™ (-1,1) < m(AN' Soo, Л) \\g\\ i+ _ • C.203)
fc+7> ^fc+2 ( ^' U
7.3. Примеры построения трансформант ядер интегральных
уравнений в контактных задачах для полосы и клина и их аппрок-
аппроксимаций.
7.3.1 Численное построение функций L(a) для задачи о вдавли-
вдавливании штампа в неоднородную полосу.
На рис. 3.1, 3.2 приведены графики трансформант ядер интеграль-
интегральных уравнений L(a), построенных для задачи Р1 в случае, когда
модуль Юнга полосы с глубиной изменяется по закону Е(у) = Ео(р(у),
— 1 ^ у ^ 0, а коэффициент Пуассона v = 1/3.
Рассматриваются степенные законы неоднородности:
убывающий с глубиной (рис. 3.1)
), k = 3, 6, 9;
C.204)
возрастающий с глубиной (рис. 3.2)
<рB/)=0,1 +y2ak, afc = ln0,l (к- 1)/B1п0,5), к = 3, 6, 9.
C.205)
Цифры у кривых соответствуют значениям к. Приведенные графики
подтверждают свойства C.169).
§ 7. Свойства приближенных решений задач для полосы и клина 113
0,1 1,1
<р(у)
о
ОД 1,1
-1
ч>{у)
о
0,1 1,1
\ч>{у)
-1,0
од
На рис. 3.3 приведены графики трансформант ядра L(a) для задачи
Р2 в случае однородного слоя (кривая 0) и неоднородного слоя, модуль
Юнга которого изменяется с глубиной по закону:
<р(у) = 1,1 + sin (
fc= 1, 2, 3,
C.206)
при постоянном коэффициенте Пуассона v = 1/3 (кривые /, 2, 5
соответственно). Штриховые кривые 0, 1, 2, 3 (рис. 3.3) соответ-
соответствуют разности между точными и аппроксимирующими значениями
114
Гл. 3. Асимптотические решения некоторых классов уравнений
О
-1
ОД 1,1
ч>(у)
ОД 1,1
-1
ОД
ч>(у)
2,1
<р(у)
трансформант. Погрешность аппроксимации на рис. 3.3 менее 3% для
монотонных законов и 5% для немонотонных законов.
7.3.2 Численное построение функций L(a) для задачи о чистом
сдвиге полосовым штампом неоднородного пространственного
клина.
На рис. 3.4 приведены кривые Fp = Lp(u)/Lq(u), характеризующие
вид трансформант Lp(u) (р = 0,125, 0,25, 0,5, 2, 4, 8, 0), где р —
показатель степени экспоненты в законе неоднородности клина (в зада-
задаче К1) по отношению к трансформанте Lq(u) для однородного клина с
модулем сдвига Go (см. формулу B.78)). Значения Lp(u), вычисленные
по формуле B.80), сравнивались с вычисленными по формуле B.99).
При р = 8 максимальная погрешность составила 0,14%.
7.4. Определение связи между вдавливающей силой и осадкой
штампа в контактных задачах для полосы и клина. Проанализи-
Проанализируем эффективность изложенного здесь метода. Рассмотрим в качестве
тестового примера контактную задачу для однородной полосы, сво-
свободно лежащей на недеформируемом основании. Решения этой задачи
хорошо известны по работам И. И. Воровича, Ю.А. Устинова [94],
И. И. Воровича, В.М. Александрова, В. А. Бабешко [90].
§ 7. Свойства приближенных решений задач для полосы и клина 115
10 и
Рис. 3.4
Таблица 1
А
Б
Л
4
2
1
0,5
0,25
4
2
1
0,5
х/а = 0
0,593
0,994
1,922
3,930
7,980
0,597
1,050
1,958
3,941
х/а = 0,2
0,604
1,004
1,926
3,929
7,976
0,608
1,060
1,966
3,939
х/а = 0,4
0,699
1,040
1,943
3,928
7,953
0,658
1,178
1,997
3,939
х/а = 0, 6
0,719
1,131
2,005
3,940
7,919
0,730
1,497
2,084
3,970
х/а = 0,8
0,936
1,402
2,277
4,106
7,917
0,957
1,576
2,388
4,201
В табл. 1 приведены значения контактных напряжений под плос-
плоским штампом ширины 2а, вдавливаемым в полосу толщины h, сво-
свободно лежащую на недеформируемом основании. Часть А таблицы
соответствует однородной полосе, ко-
когда Е = Ео, у = 1/3. Значение ip(x)
рассчитывали по формуле C.177)
для N = 2. В части Б таблицы
приведены результаты из моногра-
монографии [90]. Для рассматриваемого диа-
диапазона значений Л использовались
два метода: при А ^ 2 — метод
«больших Л», при Л ^ 2 — метод
типа Винера-Хопфа. Заметим, что
Л = 2 — граница применимости как
метода «больших Л», так и метода
Винера-Хопфа.
Сравнение полученного аналити-
аналитического приближенного решения с из-
0,1
116 Гл. 3. Асимптотические решения некоторых классов уравнений
Vk
0,1 1,1
0,5 x 1,0
Рис. 3.6
вестными решениями для однородной полосы из вышеупомянутой мо-
монографии показало погрешность менее 1 % при Л < 1 и А > 2. Наиболь-
Наибольшие расхождения (порядка 10%) наблюдаются при А = 2.
На рис. 3.5-3.7 приведены графики отношений ФДж) =
= (рм(х)/(ро(х), характеризующих распределение контактных нормаль-
нормальных напряжений (ры(%) П°Д штампом с плоской подошвой для неодно-
неоднородного слоя с законом неоднородности ц>(у) C.206) при разных значе-
значениях к по отношению к однородному слою. Рисунок 3.5 соответствует
к = 1, рис. 3.6 — к = 2, рис. 3.7 — к = 3. Величина <ро(х) распределения
0
-1
0,1 1,1
ОД 1,1
-1
С(Х)
0,14
0,10
2 4 6 А
Рис. 3.8
§8. Определение формы осадки поверхности 117
контактных нормальных напряжений под штампом для однородного
слоя вычислялась для Е(у) = Eq. Значения (^дг(ж) были найдены
при N = 10. Цифра / на кривых соответствует величине Л = 0, 125,
цифра 2 на кривых соответствует величине Л = 0,25, цифра 3
соответствует величине Л = 1, цифра 4 — Л = 4, цифра 5 — Л = 8.
Изменение величины С(А) = 5n/5o, характеризующей влияние
неоднородности слоя на осадку штампа 5n для задачи о вдавливании
штампа в неоднородную полосу по сравнению с однородной полосой
5о при одной и той же величине вдавливающей силы Р в зависимости
от Л показано на рис. 3.8. Значения С(А) получены двухсторонним
асимптотическим методом при j(x) = 0. Кривая / соотвутствует к = 4
для закона неоднородности C.204), кривая 2 — к = 9.
§ 8. Определение формы осадки поверхности
неоднородного по глубине полупространства для
задачи о внедрении штампа в неоднородное
полупространство
Во многих смешанных задачах решение можно получить только
приближенно. В приложениях результатов возникает необходимость
использовать это приближенное решение для определения других ха-
характеристик задач. Так, например, в задаче о вдавливании штампа в
неоднородное основание требуется определить осадку поверхности вне
штампа. Так как само решение интегрального уравнения этой зада-
задачи находится только приближенно, возникает вопрос о погрешности
величины осадки основания, определяемой с использованием этого
решения.
Известны классические результаты по определению осадки поверх-
поверхности однородного полупространства вне штампа [232]. В [168] при-
приведены формулы для значений осадок поверхности однородного полу-
полупространства в случае осесимметричного штампа произвольной формы
в плане.
В работе [29] впервые получены аналитические формулы, позволя-
позволяющие определить осадку поверхности неоднородного по глубине слоя,
сцепленного с упругим однородным полупространством, при внедрении
в него кругового штампа. Закон изменения по глубине коэффициентов
Ламе в слое произволен. Устанавливается, что полученные анали-
аналитические формулы являются асимптотически точными при больших
и малых значениях безразмерного геометрического параметра задачи.
Как было показано в §4, задача об определении контактных давле-
давлений под круговым штампом сводится к решению парного интегрального
118 Гл. 3. Асимптотические решения некоторых классов уравнений
уравнения следующего вида:
• сю
J T(a)L(Xa)J0(ar)da = 6@)/(r), 0 < г < 1,
C.207)
J T(a)J0(ar)da = 0, r > 1,
о
при выполнении условий C.109), A.120). Трансформанта L(a) облада-
обладает свойствами A.122), A.128).
На основании теоремы 1.1 L(Xa) допускает аппроксимацию выра-
выражениями вида A.170).
Если /(г) — четная функция, удовлетворяющая условию Мо
(см. C.65)), а На) принадлежит классу AN, то, используя метод из
[38], можно получить выражение для контактных давлений г (г) под
штампом:
т(г) =
{ VI -г* "
СЮ ^
" ' , C.208)
COS/X
Х(г, м) =
Постоянные Ci определяются из системы линейных алгебраических
уравнений C.103), C.104).
В общем случае, когда функция L(a) обладает свойствами A.170),
т. е. принадлежит классу Sn,m, согласно теореме 3.5 [10] решение вида
C.208) является асимптотически точным решением уравнения C.207)
при Л —> 0 и Л —> оо.
Используя аналитическое решение C.208) парного интегрального
уравнения A.166) для L(a) класса AN, найдем выражение для /(г)
при гIи L(a) e AN.
§ 8. Определение формы осадки поверхности
119
Сделав ряд преобразований, получим следующее аналитическое
выражение (с учетом того, что L(a) ? AN). Будем обозначать его
/»=2в@)тг
-1
N
п=\
arcsin - +
N
i=\
1в2п\~2
, C.209)
ldt, Dn =
?-' Ш
N
-Bj + A2
i=l,n
Возникает вопрос об использовании формулы C.209) для определе-
определения формы осадки поверхности неоднородного полупространства, т.е.
в том случае, когда трансформанта ядра L(a) обладает свойствами
A.170) и функция L(a) принадлежит классу функций Sn,m-
Согласно теореме 3.5 из предыдущего параграфа, выражение
C.208) является асимптотически точным решением уравнения C.207)
для L(a), принадлежащих классу функций Sn,m> пРи А —> 0 и
Л -^ оо. Подставив это асимптотическое решение т^(г) в C.207),
найдем приближенное выражение для формы осадки поверхности
неоднородного полупространства вне штампа $n, м в общем случае,
когда L(a) G Sn,m-
,m = (AN +
г > 1.
Здесь интегральный оператор, соответствующий функции L(a),
принадлежащей классу А, обозначим через А.
Свойства решения интегрального уравнения для L(a) ? Sn,m уста-
установлены на конечном отрезке г ? [0, 1]. Будут ли подобные свойства
сохраняться для функции /(г), определенной при г ? A;оо)? То есть
будут ли асимптотические свойства сохраняться относительно опреде-
определяемой приближенным способом правой части интегрального уравне-
уравнения C.207) вне отрезка [0, 1]? Не нарушая общности, считаем М = 1.
120 Гл. 3. Асимптотические решения некоторых классов уравнений
В этом случае
оо
= tn\P)P —9 ^-^JQ\OLr)jQ\ap)aa
J J a + D X
0 Lo
dp =
= CX Ko(rDX ) T^(p)Jo(pDX )pdp, r > 1.
0
Используя асимптотические свойства цилиндрических функций
мнимого аргумента:
Ko(z) ^ - ln(z), /o(^) - 1 при ^ -> О,
Ко(^) ^ y^rj2z exp(—z), Io(z) ~ ехр(^)/л/2тг^ при ^ ^ оо,
получим следующие оценки:
max SiTTyr(r) ^ Af* exp(—Z}A~ 5), А -^> О (А < А*), 5 = г — р > О,
max
М°Л-1+?, Л ^ оо (Л > А0), г > 0, ? -> О,
где постоянные М* и М° не зависят от А. Отсюда вытекает следующая
теорема.
Теорема 3.12. Выражение C.209) является асимптотически точ-
точным представлением осадки поверхности неоднородного по глубине
полупространства для L(a) класса Sn,m при выполнении условий
теоремы 3.5 когда 0<А<А* и А>А°, где А* и А0 — некоторые
фиксированные значения А.
Таким образом, доказано, что приближенные значения осадок по-
поверхности полупространства являются асимптотически точными при
г G A; оо) как при А —> 0, так и при А —> оо.
§ 9. Численные примеры
Считаем, что модуль Юнга верхнего неоднородного по глубине слоя
в задаче §4 гл. 1 изменяется по закону
E(z)=Eo<p(z), -H^y^O, C.210)
и коэффициент Пуассона v = 0,333.
Рассмотрим следующие виды неоднородности:
двухслойное полупространство
ip(z) = (pi = Ei/E0; <pi = 10, <р2=0,1; C.211)
степенной закон, убывающий с глубиной
§ 9. Численные примеры
121
степенной закон, возрастающий с глубиной
( \ а 1 , 2аи In 0,1 (fe- 1) п оч
Mz)=09l+z*»9 ak= 21^5 (fc = 2);
синусоидальный закон 1
( \ 1 1 i ( \ •
синусоидальный закон 2
На рис. 3.9-3.11 приведены графики относительной величины
х(г) = т(г)/то(г), характеризующей распределение контактных нор-
нормальных напряжений т(г) под штампом, вдавливаемым единичной
C.213)
C.214)
C.215)
х(
0,6
0,4
0,2
0,0
Z
0,0
я п
4 о -
—~^,
0,1 1
0
^—-^
1 0^0
z)
//
У
0,0
ОД 1,0
Х(г) -1,0
0,0
0,4 0,8 г
а
10
7,5
5,0
2,5
0,0
-2,0.
¦4,о;
^0,25^
^0,5;
0,2 0,4 0,6 0,8 г
б
Рис. 3.9
силой в неоднородное полупространство с модулем Юнга вида C.210)—
C.215) соответственно при различных значениях Л = Н/а. Величина
го(г) — распределение контактных напряжений под штампом для од-
однородного полупространства при E(z) = Eq. Рисунок 3.9 соответствует
закону C.211), причем (а) соответствует закону ср\ = 10, а (б) — ср2 =
= 0,1, рис. 3.10, а соответствует закону C.212) при к = 9, рис. 3.10, б —
C.213) при к = 2, рис. 3.11, а - C.214), рис. 3.11,6- C.215). Номер
на кривой соответствует значению Л. Значение т(г) найдены по фор-
формуле C.208) при N = 10. Для законов C.211) и C.212) при Л = 0,5 и
Л = 1 наблюдаются области \{г) < 0, что соответствует явлению отры-
отрыва поверхности полупространства от центра штампа, вызванному про-
прогибом жесткого поверхностного слоя при наличии мягкой подложки.
На рис. 3.12-3.14 приведены графики величины А(г) =
= /уу(г)тг B0(О))~ — arcsin(l/r), характеризующей изменение формы
осадки поверхности неоднородного полупространства в зависимости
от г. Рисунок 3.12 соответствует закону C.211) при (р\ = 10 (а)
122 Гл. 3. Асимптотические решения некоторых классов уравнений
X
0,7
0,4
0,0
(r)
_ -——¦
IoZ
Z
0,0
-1,0
-8,0-
-4,0-
^-2,0^
— 0,25
0,1
— —
— -—
1,0
)
J
(p(z)
W
0,0
Х(г) -1,0
12
ОД 1,0
—¦
-4,0
h—e n 1
0,25
\
\
0,0 0,5 r 1,0 0,0 °'u 0,4
Рис. 3.10
0,8 г
0,0
-0,5
Х(г) -1,0
1,2
0,
0,1 1
0
0,0
-0,5
X(r) -1,0
4,0
2,0
0,1 1,0
0,0
^4,0^
— 1вО
-0,25р*
/ 0,5
0,4
0,8 г
и (^2 = 0,1 (б). Рисунок 3.13, а соответствует закону C.212),
рис. 3.13,6 - C.213), рис. 3.14, а - C.214), рис. 3.14,6 - C.215).
Номер на кривой соответствует значению Л.
Рисунок 3.15 иллюстрирует влияние на форму осадки поверхности
вне штампа различных степеней неоднородности слоя при различных
ip(z). На каждом из рис. 3.15 а, б, в, г приведены графики величины
jfjv(r) для четырех законов неоднородности. Кривая / соответствует
двухслойному основанию, у которого значение модуля Юнга верхнего
слоя в 10 раз больше модуля Юнга подстилающего полупространства.
Кривые 2-4 соответствуют закону неоднородности вида C.212) при
§ 9. Численные примеры
123
0,0
А(г) -1,0
1,6
0,1 1,0
?>(*)
0,0
А(г) -1,0
0,00
-0,02
0,1 1
0
0,'
0,4 0,8 1/г 0,0 0,4 0,8 1/г
а б
Рис. 3.12
0,0
ОД 1,0
А(г)
1,6
1,2
0,8
0,4
0,0
ф)
/
л
/fob
А(г
0,00
-0,12
0,2 0,6 1/г 1,0 ОД)
а
Рис. 3.13
0,8 1/г
= 9, 6,4 соответственно. Рисунок 3.15,а соответствует значению Л =
0,25, рис. 3.15,6 - Л= 1, рис. 3.15, в - Л = 2, рис. 3.15, г - Л = 8.
124 Гл. 3. Асимптотические решения некоторых классов уравнений
0,0 0,4 0,8 1/г 0,0 0,4 0,8 1/г
^0,4
Рис. 3.14
0,0
-1,0
0,1 1,0
0,0
0,1 1,0
/ж(г)
1,5
1,0
0,5
л °'°
-1,0
ОД 1,0
¦ 0,0
ОД 1,0
-1,0
Л=0,25
A=l
а
ч
1,5
1,0
0,5
0,5 1,0 lnr
Г
[
б
X
0,5 1,0 lnr
1,5
1,0
0,5
I/ /
1/
1
J
^Ч
0,6
0,4
0,2
0,5 1,0 lnr 0,5 1,0 lnr
Рис. 3.15
/
ft
V
f
г
^,
Часть III
ПРИМЕНЕНИЕ АНАЛИТИЧЕСКИХ
МЕТОДОВ К РЕШЕНИЮ
НЕКОТОРЫХ ПРИКЛАДНЫХ
ЗАДАЧ
Глава 4
ИЗГИБ ПЛАСТИН НА НЕОДНОРОДНОМ
ОСНОВАНИИ
Рассматриваются следующие задачи: о цилиндрическом изгибе ко-
конечной пластины на неоднородной полосе (Р11 — полоса сцеплена
с упругой полуплоскостью; Р12 — полоса (клин) жестко соединена
с недеформируемым основанием; Р13 — полоса (клин) лежит без трения
на недеформируемом основании); Р14 — об осесимметричном изгибе
пластины, лежащей на неоднородном по глубине слое, сцепленном
с однородным упругим полупространством. Особенность этих задач
в том, что упругие свойства основания, с которым взаимодействует
пластина, изменяются по глубине, что усложняет расчет пластины, так
как для расчета необходимо определить отпор такого основания.
Возможность применения аналитических методов к решению этих
задач в случае произвольных гладких законов изменения неодно-
неоднородности по глубине основана на рассмотренном в гл.1 численном
построении трансформант ядер интегральных уравнений соответству-
соответствующих контактных задач с последующей аналитической аппрокси-
аппроксимацией трансформант ядер парных интегральных уравнений, соот-
соответствующих взаимодействию пластины с основанием, выражениями
специального вида. Для построения приближенного аналитическо-
аналитического решения соответствующих интегральных уравнений используется
двухсторонний асимптотический метод (гл.З) [2, 10, 12, 26, 31],
который здесь является эффективным как для жестких, так и для
гибких пластин, в отличие от метода ортогональных многочленов
[101, 102, 121, 122, 125, 126, 130, 161, 212, 213, 228], метода коллока-
ции [60, 226], методов малого и большого параметра [47, 57, 93].
Используется представление прогибов пластин в виде рядов по
формам их собственных колебаний [219, 222] при соответствующих
граничных условиях. Благодаря этому удается свести указанные зада-
задачи к решению систем линейных алгебраических уравнений.
Проводится анализ влияния различных законов изменения неод-
неоднородности с глубиной на распределение контактных давлений под
пластиной, ее прогибы, осадку поверхности основания вне пластины,
значения радиальных и тангенциальных моментов в пластине.
Расчету пластин на упругом основании посвящено большое число
работ. Кратко остановимся на тех, которые отражают основные этапы
развития методов расчета плитных фундаментов (с подробным обзором
публикаций по этому вопросу можно познакомиться по работам [1,
125, 126] и ряду других).
Гл. 4. Изгиб пластин на неоднородном основании 127
Задача об изгибе пластины на упругом изотропном и однородном
основании рассматривалась в работах [92, 125, 161, 228]. Решение
строилось путем представления контактных напряжений в виде степен-
степенного ряда, с последующим определением коэффициентов разложения
из бесконечной алгебраической системы уравнений.
Методом ортогональных многочленов такая задача решалась в ра-
работах [101, 108, 121, 122, 212, 213] и методом коллокации по чебышев-
ским узлам в [60, 226]. При этом возникала необходимость построе-
построения решения некоторых бесконечных систем линейных алгебраических
уравнений и ставилась проблема исследования сходимости полученного
решения к точному.
Вышеупомянутые методы эффективны для достаточно жестких
плит (пластин) и для слоя относительно большой толщины.
В работах [50, 57, 93] для решения задачи применялись асимптоти-
асимптотические методы типа «больших Л» и специальных ортогональных мно-
многочленов, что позволило получить основные характеристики решения
в нескольких формах, каждая из которых эффективна в своей области
изменения характерных параметров задачи.
Что касается решения задачи для неоднородного основания, то в
ряде работ были рассмотрены специальные виды непрерывной неодно-
неоднородности полупространства по глубине ([60, 226] — степенная, [182] —
экспоненциальная). В работах [117, 118] решение задачи строилось
методом сеток (закон изменения модуля деформации E(z) с глубиной
представлялся в виде Е = Е$ + Enzn, а отпор основания заменялся
сосредоточенными силами, приложенными в узлах сетки).
Изгиб пластин на многослойном основании рассматривался в рабо-
работах [171, 172]. Задача сводилась к интегральному уравнению Фред-
гольма второго рода относительно функции распределения контактных
давлений, решение которого строилось методом ортогональных полино-
полиномов. Впоследствии этот метод использовался в работах [121, 122, 184].
В работе [185] приведен метод решения задачи о контакте тонкой
пластинки в виде бесконечной полосы, лежащей без трения на упругом
полупространстве, в трехмерной постановке. Контактные напряжения
разыскивались в виде разложения по функциям Матье.
Иной подход к решению задачи предложен в работах [174, 222].
С помощью интегрального преобразования Ханкеля контактная задача
сводится к парному интегральному уравнению, решение которого на-
находится методом однократной и двойной ортогонализации. При этом
использовались представления контактных давлений и прогибов пла-
пластины в виде рядов по собственным функциям дифференциального
уравнения изгиба пластины при краевых условиях, совпадающих с
условиями закрепления пластины. Эти представления позволяют све-
свести задачу к нахождению решения линейной бесконечной системы
алгебраических уравнений.
128 Гл. 4. Изгиб пластин на неоднородном основании
Отметим, что большинство известных решений эффективны только
для жестких пластин. И очень немногие, в частности представленные
в [44, 57, 93], эффективны или для гибких, или для жестких пластин,
каждый в своей области.
В данной главе рассматривается изгиб пластин, лежащих на неодно-
неоднородном по глубине основании. Многочисленные способы предваритель-
предварительной подготовки оснований (силикатизация, уплотнение трамбовками,
многослойные дорожные покрытия и т. д.) приводят к тому, что упругие
свойства основания существенно изменяются с глубиной. Кроме того,
современные исследования деформируемости грунта под нагруженным
фундаментом [216] показали, что даже в литологически однородных
основаниях упругие свойства оказываются резко изменяющимися по
глубине [114]. Натурные наблюдения за осадками грунта в основании
болыиеразмерных фундаментов выявляют сильно деформируемую зону
в верхней части основания. Эффективной моделью для описания этого
явления является мягкий упругий слой, лежащий на более жестком
упругом полупространстве.
§ 1. Постановка задач
Рассмотрим изгиб пластины под действием распределенной нагруз-
нагрузки р(х). Полагаем, что пластина не отрывается от поверхности неодно-
неоднородного основания в процессе деформирования, а вне области контакта
основание не нагружено.
Дифференциальное уравнение изгиба пластины имеет вид [93, 125,
161]
L0[y(x)]=D-l\p(x)-q(x)], хе[а,Ъ], D.1)
где D — коэффициент, характеризующий ее изгибную жесткость,
q(x) — реакция основания, у(х) — прогиб пластины, Lo — дифферен-
дифференциальный оператор 4-го порядка по х.
В задачах о цилиндрическом изгибе пластины: Lo = —т, Ъ = —а =
1 * * « dx т
= 1; для задачи об осесимметричном изгибе круглой пластины: Lo =
/ d2 . 1 d V n , .
= —о + --i- , a = О, Ъ= \.
\d2 xdxj
Выбор граничных условий зависит от типа закрепления пластины
по краям. В случае свободной по краям пластины:
Задачи Р11, Р12
//() ///()О; D.2)
Задача Р13
d y b^dy_
= 0, -f
^dx2 ' xdx
Здесь v — коэффициент Пуассона пластины.
= 0. D.3)
§ 1. Постановка задач 129
Коэффициенты Ламе Л и М в слое с глубиной изменяются по
закону:
Л = Ло(г), М = М0(г), -Я < z < 0. D.4)
Кроме того, в задачах Р11, Р13
Л = Л0(-Я), М = М0(-Я), -оо<^<-Я. D.5)
Связь между контактными напряжениями под пластиной q(x) и ее
прогибом у(х) записывается в виде парного интегрального уравнения
вида (гл. 3, §5)
' d
JQ(a)p(a)L(Xa)B(a, x)da = f(x), x e [a, b],
D.6)
J Q(a)B(a, x)da = 0, x ф [a, b].
< с
В частности, в задачах о цилиндрическом изгибе пластины конеч-
конечной ширины имеем
p(a) = \a\~l, B(a, x) = e~iax, c = -d = oo, D.7)
а = —b = 1, f(x) = 2irsy(x),
X-H/a, s-Oa/D, 0(z)
_2Mo(z)[Mo(z)+Aq(z)]
2Мо(г)+Ло(г)
Q(x) = tt- Q(a)e~iaxda, \ q(?)eia4? = Q(a).
-oo -1
Связь между приложенной нагрузкой на пластину р(х) и контакт-
контактными напряжениями q(x) имеет вид
1
p(x)dx = q(x)dx. D.8)
В задаче об осесимметричном изгибе круглой пластины имеем
р(а) = а~\ В(а, х) = aJo(ax), с = 0, d = oo, D.9)
а = 0, 6=1, f(x) = sy(x),
" }-i ^ _ ЕпНп
оо 1
г г
q(x) = Q(a) J0(ax)ada, q(p)Jo(ap)pdp = Q(a).
j j
о
5 СМ. Айзикович и др.
130 Гл. 4. Изгиб пластин на неоднородном основании
Связь между нагрузкой на пластину и контактными напряжениями
имеет вид
1 1 2тг 1
f q(x)dx = I* p(x)dx = Р, I* I* q(x)xdxdy = P. D.10)
-1 -1 0-1
В случае свободной по краям пластины граничные условия для D.1)
имеют вид
d У , v_dy_
dx2 x dx
x=\
x=\
= 0, D.11)
где v — коэффициент Пуассона пластины. Требуется определить рас-
распределение контактных давлений под пластиной и ее прогибы.
§ 2. Изгиб балки на непрерывно-неоднородной
полуплоскости
Рассмотрим изгиб балки под действием распределенной нагрузки
р(х). Полагаем, что балка не отрывается от поверхности неоднородного
основания в процессе деформирования, а вне области контакта основа-
основание не нагружено. Закон изменения коэффициентов Ламе по глубине
имеет вид D.5), D.6), т.е. основание представляет собой неоднородную
упругую по глубине полуплоскость.
Представим функцию прогибов в виде ряда по формам собственных
колебаний балки:
оо
у(х) = ^2уп(рп(х), х е [а, Ъ]. D.12)
п=0
В частности, положим [219]
1 / \ COS VfiX СП VfiX io
< 1. D.13)
Здесь гп — корни характеристического уравнения tgrn = thrn, n =
= 1, 2, ..., п = 2,37, г2 = 5,49, rm = Bm - О,75)тг, m > 3.
Рассмотрим случай, когда трансформанта ядра L(u) интегрального
уравнения D.7) имеет следующий вид:
N 2 Л2 -2
а2+Х_2, (^ - В]ь)(^ -Ак)^0, г + к.
l
D.14)
Здесь Ai, Bi (г = 1, ..., N) — некоторые постоянные. Учитывая ли-
линейность задачи, контактные напряжения представим в виде линейной
§2. Изгиб балки на непрерывно-неоднородной полуплоскости
131
комбинации частных решений qm(x) с теми же коэффициентами, что
и для функций прогиба у(х) в D.12):
D.15)
га=0
Частное решение qm(x) (га = 0, 1, ...) определим из интегрального
уравнения D.7) аналогично [19]. Для этого в правую часть D.7)
вместо у(х) подставим га-ю собственную функцию (рт(х). Используя
результаты §5, гл.З, получим
qo(x) = Xs
qm(x)=Xs
Здесь обозначено:
,x) = -
- X2
п=0
D.16)
га=1, 2, ...
D.17)
1 — х2
1
A [Jq (A)a cos A(a — x) —
da
-J\(A) sin А(а - х)}
K(A) = A cos AL^\AL(A, x).
Коэффициенты G™ определяются из следующих систем линейных
алгебраических уравнений:
N
\ Bk\~l) =
п=\
N
, k= 1,2, ...,7V,
D.18)
n=\
~\ Bk\~l) = B(rm, Bk\~l) + B(irm, Bk\~l
k= 1, 2, ..., N; m= 1, 2, ...
Здесь введены следующие обозначения:
Z(a, 6) = [aJ0(a)KiF) + Ji(a)bK0(b)] (a2 + 62)
В {a, b) = aco8~\a)L^(a)Z(a, b).
D.19)
132 Гл. 4. Изгиб пластин на неоднородном основании
Считаем, что функции нагрузки р(х) и контактных напряжений q(x)
можно представить в виде ряда D.15):
р(х) = ^^Ртфт(х), Ргп— p{x)(pm(x)dx', D.20)
га=0 1
q(x) = 2^ 1тЧ>т{х), 1т = q(x)pm(x)dx. D.21)
т=0 }{
Тогда, подставив разложения D.20), D.21), D.12) в D.1), имеем
бесконечную систему линейных алгебраических уравнений для опре-
определения коэффициентов уш\
сю
rmym =pm-\s^2yjEJl, m = 0, 1, 2, ... D.22)
Здесь
N
Ej = ij - 2_^ Gnidn ,
п=\
/ /у j /v> / нч I rv* гу* \ ^_|^ нн I гь гу* гу* \ ^_1^ нн I гь гу* /j гу* \ ^_1^ нн I гу* /j гу* \ \
j — п I т \^\' т-> I j ) ~г ^\ы т, I j ) -г ^\С1 т, Li j ) -г ^\1 т, ы j )) ,
Н(а, b) = Q(a, b)T(b)x2(b), Q(a, b) = R(a, b)x(a)
х(а) = a \a\~l , l(a) = cos~1(a)L^r1(a),
R(a, b) = cos (a)r(a, b),
r(a, b) = [aJo(a) Ji(b) - Ji(a)bJ0(b)] (b2 - a2)
s~J I I и / j i fy* l—f I Г) ГУ* Г) /\ \ 1 Г) 1-е ( ГУ* Г) /\ \ 1 I
LJL A — / i f jyi J-11 LI yyi , L /1 n /\ J L±h\l jy^ , L /1 n /\ / •
В частности
fj = тгco8-\rj)L^{(r^J^rj) -
oo N
J=0 j=l
В случае равномерно распределенной нагрузки, равной р:
ро = 2р, рт = 0, m = 1,2,...
§ 3. Изгиб балки на неоднородной полосе и клине 133
Для единичной нагрузки р = 1 ограничимся в разложении D.12)
М слагаемыми. Тогда уравнение D.22) примет вид
м
, ш = 0, 1,2, ...,М. D.23)
После определения коэффициентов ут (т = 0, 1, 2, ..., М) из
D.22) определяются контактные напряжения под балкой:
м
q(x)= Y,ymQm(x), \х\ < 1, D.24)
га=0
и ее прогибы:
м
у(х) = ^Ут<рт(х), \х\ < 1. D.25)
га=0
Замечание 4.1. Используя асимптотические свойства частных ре-
решений qm(x) [1], можно показать, что при достаточно гладкой
нагрузке на балку решение вида (А.24) также будет обладать
двухсторонне асимптотическими свойствами по А и s.
§ 3. Изгиб балки на неоднородной полосе и клине
Рассмотрим изгиб балки, лежащей на неоднородном основании,
под действием распределенной нагрузки р(х). Полагаем, что балка не
отрывается от поверхности неоднородного основания в процессе дефор-
деформирования и вне области контакта основание не нагружено. В качестве
основания будем рассматривать неоднородный по глубине слой или
клин, неоднородный по угловой координате.
Такие задачи сводятся к совместному решению интегрального урав-
уравнения, исследованного в гл. 2, 3, и дифференциального уравнения из-
изгиба балки,
-fty(x)=p(x)-q(x), |ж|<1, D.26)
ах
где q(x) — реакция основания, у(х) — прогиб балки. Выбор граничных
условий зависит от типа закрепления балки по краям. В случае сво-
свободной по краям балки
у"(±1)=у'"(±1) = О. D.27)
Коэффициенты Ламе Л и М в слое, лежащем со сцеплением или
без сцепления на недеформируемом основании, изменяются по закону
B.36). Модуль Юнга Е в клине, жестко скрепленном с недефор-
мируемым основанием, изменяется по закону B.100). Считаем, что
коэффициент Пуассона основания постоянный (у = const).
134 Гл. 4. Изгиб пластин на неоднородном основании
Связь между реакцией основания q(x) и прогибом балки у(х) запи-
записывается в виде парного интегрального уравнения
- d
]Q(a)p(a)L(a\)B(a, x)da = f(x), \x\ < 1,
d D-28)
jQ(a)B(a, x)da = 0, \x\ > 1,
где р(а) = lap1, B(a,x) = е~гах, с = — d = oo, f(x) = 2irsXy(x),
G(z) = 2M(z) (A(z) + M(*)) / B№(z) + Л(^)) = 0,5E(z)/ A - z/2), 5 =
= ва3!), D — жесткость балки, Л — характерный геометрический
параметр,
q(x) = B^)-1 | Q(a)e-iaxdxx,
-оо -1
Связь между приложенной на балку нагрузкой р(х) и контактными
напряжениями q(x) имеет вид
1 1
q(x)dx= \p(x)dx = P. D.29)
-l -l
Свойства трансформант ядер интегральных уравнений вида D.28)
описаны в §5 гл. 2. В соответствии с этими свойствами функцию L(a\)
можно аппроксимировать функцией Ь^(а\) вида [26]
N
2 , г2\-2
LN(Xa) = thAAaJI. г2 -2>
где А, 5г, 7г (г = 1,... ,7V) — некоторые постоянные, причем (^—
-4)Gг-7/с) 7^0 при г ^ /с.
Необходимо определить реакцию основания #(#) и прогиб бал-
балки 2/(ж).
Представим функцию прогибов в виде ряда по формам собственных
колебаний балки:
оо
y(x)=Y,yn<Pn(x), |жК1. D.30)
п=0
В частности, положим [221]
1 / \ COS ТпХ СХТГтгЖ \ ^ л 1 о
(ро= I, (рп{х) = \- —г—, F ^ !» п=1,2, ...
v y cosrn chrn '
Здесь тп — корни характеристического уравнения tgrn = — thrn, n =
= 1, 2, ..., n = 2,37, r2 = 5,49, rm = Bm - 0,75) тг (m > 3).
§ 3. Изгиб балки на неоднородной полосе и клине 135
Коэффициенты ут определяются по формуле
1
Ут = y(x)(pm(x)dx. D.31)
-1
Учитывая линейность задачи, контактные напряжения представим
в виде линейной комбинации частных решений qm(x) с теми же коэф-
коэффициентами ут, что и для функций прогиба у(х) в D.30):
оо
q(x) = Y, УтЯт(х), |ж|<1; D.32)
га=0
га-е частное решение qm(x) (га = 0, 1, 2, ...) определим из интеграль-
интегрального уравнения аналогично [39, 45, 47, 48]. Для этого в правую часть
D.28) вместо у(х) подставим га-ю собственную функцию ipm(x). Имеем
Ь), X
N Ч
7гшФ(-1/2,-1/2 + ^/Ав, х) \
г=\ )
Здесь обозначено:
Ф (I, x)=K (-U) Ф (-1/2,-1/2 + l/в, х),
К (В) = cos"l В th (AAB) L^1 (АВ),
1
^л9 / , 1 /гк\2 ( -Рго (chr0)shr0 7
-в (г/;+1/2) -^===^^v^r'
в = тг/ (А\), Р^ = Р^ (ch в), Q^ = Q^ (ch в) — присоединенные функ-
функции Лежандра соответственно 1-го и 2-го рода.
Коэффициенты Ci определяются из системы алгебраических урав-
уравнений:
^(l-ani)xi = fm, rn= 1, 2, ..., N, D.33)
г=1
где
~2 ~2+АО
136 Гл. 4. Изгиб пластин на неоднородном основании
Q_i
атг = ~^R (-1/2 + 5г/Хв, -1/2 + 7ш
Q 1
fm = yosh l в + ^уп (E{rmijmX l) - Е [irm,
ra=l 2
Здесь
E (I, m) = 12K (-il) G (-1/2 + //6,-1/2 + т/в, -1/2) eft/,
it I Hi, U I
G (u, v, w) = QWT (u, v) — QVT (u, w),
P Ol — О Pl
(и, v) =
Положим, что функции нагрузки р(ж) и контактных напряжений
q(x) можно представить рядами вида D.30)
р(х) = 22Рп(Рп(х), рп= \ p(x)ipn(x)dx, D.34)
n=0 _J!
1
П ( rYb i/O ( rYb i fi rYb (/л. ^1
n=l _!
Подставив разложения D.30), D.34), D.35) в дифференциальное
уравнение D.26), имеем бесконечную систему линейных алгебраиче-
алгебраических уравнений:
оо
^> Ш = 0,1,2,... D.36)
Здесь
BJ = Trshe [K(rj) (h (-\ + г^, -\ + г^) +
_l h (—t -\- i7^- —i 4- ^^^ 4- K(—irA (h (— 1 4- ^
TV
Cj (h (-- 4- -^
2 ле'
г=1
§ 4. Взаимодействие круглой пластины с полупространством 137
т= 1, 2,...; j = 1, 2, ...,
l i
В частности, для т = О имеем
Бт 7Г
О = 7^Г~
т= 1, 2, ...,
В случае равномерно распределенной нагрузки, равной р, р$ = 2р,
рт = 0, т = 1, 2, ...
При численной реализации, ограничиваясь в разложении функции
прогибов конечным числом членов ряда D.30):
м
y(x) = J2ynVn(x)> \x\<h D-37)
п=0
получим, что задача определения прогиба балки, лежащей на
неоднородном основании (слое, клине), и распределения контактных
давлений под ней сводится к совместному решению уравнений
D.33) (ш = 1, 2, ..., N), D.36) (ш = 1, 2, ...,М) относительно d
(i= 1, ..., N) и уп (п = 0, 1, ..., М).
После определения этих коэффициентов контактные давления на-
находим по формуле
м
га=0
а прогибы по формуле D.37).
§ 4. Взаимодействие круглой пластины с неоднородным
полупространством
4.1. Историческая справка. Проблеме расчета круглых пластин
на упругом полупространстве посвящено большое число работ. Ниже
мы лишь кратко остановимся на некоторых из них, так как с обзором
публикаций по этой проблеме можно познакомиться по работам [1,
184] и ряду других.
Задача об изгибе круглой пластины на упругом изотропном и од-
однородном полупространстве рассматривалась в работах [92, 125, 126,
138 Гл. 4. Изгиб пластин на неоднородном основании
132, 161, 228]. Решение строилось путем использования разложения
контактных напряжений в степенной ряд с последующим определением
коэффициентов разложения из бесконечной алгебраической системы
уравнений.
Методом ортогональных многочленов с использованием полиномов
Лежандра такая задача решалась в работах [125, 161], в [132] —
с использованием полиномов Чебышева. При таком подходе возникала
проблема исследования сходимости полученного приближенного реше-
решения к точному.
В работе [125] к данной задаче применялись асимптотические ме-
методы типа «больших Л», «малых Л» и специальных ортогональных мно-
многочленов. Это позволило получить основные характеристики решения
в нескольких формах, каждая из которых эффективна в своей области
изменения характерных параметров задачи. В ряде работ задача об
изгибе круглой пластины была рассмотрена для специальных видов
непрерывной неоднородности полупространства по глубине ([231] —
степенная, [101] — экспоненциальная).
Изгибу пластин на многослойном основании посвящена работа
[184]. Задача приведена к интегральному уравнению Фредгольма вто-
второго рода относительно функции распределения контактных давлений,
решение которого находится методом ортогональных полиномов (поли-
(полиномов Чебышева). Впоследствии этот метод использовался в работах
[180, 195]. Иной подход к построению решения задачи был предло-
предложен в работах [61, 231]. С помощью интегрального преобразования
Ханкеля контактная задача сводилась к парному уравнению, которое
решается методами однократной и двойной ортогонализации. При этом
использовались разложения контактных давлений и прогибов пластины
в ряды. Членами ряда являются собственные функции дифференци-
дифференциального уравнения изгиба пластины при краевых условиях, совпадаю-
совпадающих с условиями закрепления пластины. Эти представления позволили
свести задачу к нахождению решения линейной бесконечной системы
алгебраических уравнений.
Отметим, что большинство известных методов решений, в том чис-
числе и в вышеперечисленных работах, эффективны только для жестких
пластин. И очень немногие, в частности в [93], эффективны только для
гибких.
Рассмотрим задачу об изгибе круглой пластины на упругом неодно-
неоднородном по глубине полупространстве при отсутствии сил трения между
ними. Значение анализа расчета пластин на неоднородном основании
отмечено в работе [93].
В настоящей работе предполагается, что изменение коэффициен-
коэффициентов Ламе по глубине основания носит общий характер (произвольное
непрерывно-неоднородное полупространство). Трение между пластиной
и основанием отсутствует. В случае плотного прилегания пластины к
основанию, т. е. если контакт между полупространством и пластиной
осуществляется по всей ее нижней поверхности, для построения реше-
§ 4. Взаимодействие круглой пластины с полупространством 139
ния контактной задачи применяется двухсторонний асимптотический
метод (§4 гл. 2). При отрыве пластины от основания (о чем свидетель-
свидетельствует появление при расчете отрицательных контактных давлений)
необходимо изменить постановку задачи. Зона контакта пластины с
основанием в этом случае определяется из условия обращения в нуль
контактных напряжений на ее границе. Примеры расчетов круглой
пластины с учетом ее отрыва для однородного основания приводятся
в работах [212, 213]. В данной работе случай отрыва пластины от
основания не рассматривается.
В этом пункте доказывается, что, в отличие от методов ортого-
ортогональных многочленов, асимптотических методов типа «больших Л» и
«малых Л», данный метод эффективен как для жестких, так и для
гибких пластин и является асимптотически точным при больших и
малых значениях безразмерного геометрического параметра, равного
отношению толщины неоднородного слоя к радиусу пластины. Исполь-
Использование представления прогибов пластины в виде ряда по формам
ее собственных колебаний, аналогично [66, 226], позволяет свести
указанные задачи к решению системы линейных алгебраических урав-
уравнений.
Проводится анализ влияния различных законов изменения с глуби-
глубиной коэффициентов Ламе в полупространстве на распределение кон-
контактных давлений под плитой, ее прогибы, осадку поверхности полу-
полупространства вне пластины, значения радиальных и тангенциальных
моментов в пластине.
4.2. Постановка задачи. Пластина радиуса R свободно лежит на
изотропном упругом полупространстве, коэффициенты Ламе которого
с глубиной изменяются по закону D.5)-D.6). С полупространством
связана цилиндрическая система координат (r\ (p, z), начало коорди-
координат которой совпадает с центром пластины. Пластина вдавливается
в полупространство распределенной нагрузкой р(г').
Предполагается, что контакт между полупространством и пласти-
пластиной осуществляется по всей нижней поверхности пластины, а вне
области контакта полупространство не нагружено (рис. 4.1).
Требуется определить распределение контактных напряжений под
пластиной q(rf) и ее прогибы w(rf).
В соответствии с принятыми предположениями, рассматриваемая
задача сводится к решению следующей системы уравнений:
Dw(r)=p(r)-q(r), O^r^l, D.38)
J Q(a)L(a\)J0(ar)da = s\w(r), О < г < 1,
D.39)
J Q(a)J0(ar)da = 0, r > 1,
о
где D — дифференциальный оператор изгиба пластины в цилиндриче-
цилиндрической системе координат, р(г) — нагрузка, q(r) — контактные напряже-
140
Гл. 4. Изгиб пластин на неоднородном основании
н
р(г)
R ( г
lM0(z)
AoW
МъАг
Рис. 4.1
ния под пластиной. Парное интегральное уравнение D.39) устанавли-
устанавливает связь между контактными напряжениями и прогибами пластины,
лежащей на неоднородном полупространстве [93]. Здесь
1
Q(a) = q(p)J0(ap)pdp,
q(r) = Bтг) Q(a) J0(ar)ada,
A = H/R — безразмерный геометрический параметр, s = BR3D l —
параметр, характеризующий изгибную жесткость пластины, D — из-
гибная жесткость пластины, в = 2M(z) (Л(^) + М(^)) / BМ(^) + Л(^)),
г = r'/R.
Функция w(r) должна удовлетворять на контуре пластины услови-
условиям свободного края:
d2w v dw
r=\
dr
r=\
= 0,
D.40)
где v — коэффициент Пуассона пластины, V — оператор Лапласа в
полярных координатах, и быть ограниченной в начале координат вме-
вместе с дифференциальным выражением, соответствующим изгибающему
моменту.
Построение трансформанты ядра L(u) в общем случае произволь-
произвольной непрерывной неоднородности основания подробно рассмотрено
в первой главе. При выполнении условий
min
S(z)^c\>0, max S(z)^c<oo, lim в(z) = const D.41)
?E@;) z^oo
§ 4. Взаимодействие круглой пластины с полупространством 141
L(u) обладает следующими свойствами [16, 18]:
L(u)=A + B\u\+O(\u\2), u^O; A= lim 0@)/в(г), D.42)
z—*¦ —оо
L(u) = 1 + С \u\~l + О(|гх|~2), и -> оо; Б, С = const.
4.3. Построение решения. Представим функцию прогибов в
виде ряда по формам собственных колебаний круглой пластины со
свободным краем:
w(r) = Yl ^™^m(r)> wm = w(p)(pm(p)pdp, D.43)
m=0 I
ipo(r) = л/2, ipm(r) = Am [J0(kmr) - J\(km)I^l(km)I0(kmr)] ,
значения Ат и km для m = 0, 1, ..., 10 приведены в [222].
С учетом линейности задачи контактные напряжения могут быть
представлены в виде линейной комбинации частных решений qm(r)
с теми же коэффициентами wm, что и для функции прогиба w(r)
в D.38):
q(r) = J2 wrnqm(r), (К г < 1. D.44)
га=0
Частное решение qm(r) (т = 0, 1,...) определим из интегрального
уравнения D.39) аналогично [17].
Считаем, что функция L(u) в D.39) принадлежит классу
A/V(Xm, Sat, M) , т.е. она имеет соответственно вид
L(Xa) =
П {а2 + а2Л-2)(а2 + ^А)-1 = LN(Xa) е AN,
г=\
М
а | (a
2
+ ^м(Аа) G SN, M.
Здесь di, hi (i = \,...,N), c^, dfc (fc = 1,...,M) — некоторые по-
постоянные, (a^ — ctk){bi — bk) 7^ 0, fc t^ г. Было доказано [10], что при
условии, когда функция L(u) обладает свойствами D.41), D.42), она
допускает аппроксимацию выражениями вида
L(Xa) = LN(Xa) + L^(Aa). D.45)
Используя D.45), перепишем D.39) в операторном виде:
ANq + Soog = /. D.46)
В D.46) оператор AN соответствует функции L(u) класса AN
в D.45), а Eqo — функции L(u) класса Ем, М = оо. Будем говорить,
что для уравнения D.39) выполнено условие А, если для него можно
142
Гл. 4. Изгиб пластин на неоднородном основании
построить замкнутое решение, следуя [38]. Будем обозначать это ре-
решение
qN =AN~lf. D.47)
Иными словами, условие А означает, что для функций f(x), при-
принадлежащих некоторому классу W(c,d), существует функция q(x),
принадлежащая некоторому классу V(c,d), такая что имеет место
равенство D.46). Из представления D.46) следует, что
\\qN\\v(c,d) < m(AN)\\f\\w{Cfd), m(AN) = const.
D.48)
Будем обозначать через т(Х) некоторую постоянную, зависящую
от конкретного вида принадлежащей классу X функции.
Было доказано (§5 гл. 2), что при выполнении условий D.42)
уравнение D.39) однозначно разрешимо в пространстве C\L (—1, 1)
для (рт(г) вида D.43) при 0<А<А* иЛ>Ла, где Л* и Ла — некоторые
фиксированные значения Л, при этом имеет место оценка
1к(г)||с@)+(_1Д)<ш(АЛГ,Еоо)М^(-1,1). D.49)
Таким образом, Л можно подобрать так, что оператор AN~1Y,m
будет оператором сжатия, и выражение D.47) будет представлять собой
асимптотически точное решение уравнения D.46) при Л —> 0 и Л —> оо.
Подставим в правую часть D.39) вместо w(r) га-ю собственную
функцию (рт(г). Получим замкнутое приближенное решение уравне-
уравнения D.39) вида D.47):
ф(г А) =
Постоянные Cf1 определяются из систем линейных алгебраических
уравнений:
N
bk\-l)+L-\O)\b^1 =0, к = 1, 2, ..., N,
г=\
§ 4. Взаимодействие круглой пластины с полупространством 143
N
\ кт)=0,
г=\
к = 1, 2, ..., N; т= 1, 2, ...,
а(а, 6) = (asha + bcha)(b2 -а2),
, 6) = (bcosfi — /isin/i)I/^r1(A/i)F2 + /i2),
В свою очередь контактные напряжения q^(r) можно представить
в виде ряда, аналогичного D.43):
9mW = E^^'W' у? = *%(рЫр)р*р. D.50)
i=o I
Выпишем условия, накладываемые на функцию /(г), при которых
ее можно представить в виде ряда D.50). Ниже используем следующие
определения.
Определение 4.1. Обозначим через Ск(а, Ь) пространство функций,
имеющих к непрерывных производных на интервале (а, Ь).
Определение 4.2. Обозначим через L2(a, b) пространство функ-
функций /, определенных на интервале а ^ г ^ Ь, измеримых по Лебегу
на этом интервале и таких, что
<оо,
причем интеграл берется в смысле Лебега.
Согласно [135], имеет место следующая теорема.
Теорема 4.1. Пусть функция f е С4@, 1) удовлетворяет краевым
условиям D.40). Тогда на [0, 1] имеет место представление D.43),
причем ряд сходится на [0, 1] равномерно.
Имеет место более общая теорема разложения и полноты
bL2@, 1) [135].
Теорема 4.2. Если f e L2@, 1), то имеет место равенство вида
D.43), причем оно понимается в том смысле, что
=0, fm=
144
Гл. 4. Изгиб пластин на неоднородном основании
Кроме того, имеет место равенство Парсеваля
т=0
Считаем, что функция р(г) удовлетворяет условиям теоремы 4.1 (или
4.2), т.е. может быть представлена в виде ряда:
P(r) =
га=О
), Pm =
D.51)
Тогда, подставив разложения D.43), D.44), D.51) в D.38), имеем
бесконечную систему линейных алгебраических уравнений для опре-
определения коэффициентов wm, которую запишем в каноническом виде
[129]:
wm - ak
= 0, 1, 2,...; a = -1, D.52)
E™ = 27r-
FT =
N
n=0
I l
(km)X(km,kj)],
1
s™= W(p,an)(pm(p)pdp=Am[X(an\~}km)-Ji(km)I^ \km)x(anX~}ikm)
о
Здесь j = 1, 2, ..., m = 0, 1, 2, ...,
ж(а, 6) = 6~1(cosasin6+a2~1(sin(a-6)(a-6)~1-sin(a+6)(a+6)~1)),
X(a, 6) = (a2 + 62) (ash a cos b + 6 sin 6 ch a).
В частности,
грт
E0 =
LNl@)Amkml(smkm- J\(km)Ix 1(fcm)shfcm) +
N
2
n=\
§ 4. Взаимодействие круглой пластины с полупространством 145
N
?0
Имеем
п=\
га=О
an\-x sh(anA-')- ch(anA-')).
М ^ \Рт\2 < 00
га=0
при наложенных ограничениях на р(г).
Из оценки D.49) и условия равновесия пластины
2тг 1
2тг 1
Г Г
q(r)rdrd(p = p(r)rdrd(p
оо
оо
имеем
m=0
оо.
j=0
m=0 j=0
m=0
Таким образом, на основании теоремы За ([129], С. 503), если значение
а = — 1 не является характеристическим значением для системы D.52),
то она может быть решена методом редукции (путем замены системой
из п уравнений с п неизвестными):
п-\
m = 0, 1,2,... ,п — 1, а = —
D.53)
причем при достаточно больших п система D.53) разрешима и имеет
место сходимость приближенных решений к точному.
После определения коэффициентов wm (га = 0, 1,..., п) для фикси-
фиксированного значения п из D.53) находим контактные напряжения
и прогибы пластины
m=0
п
га=0
), 0 < Г < 1.
D.54)
D.55)
Таким образом, справедлива следующая теорема.
146 Гл. 4. Изгиб пластин на неоднородном основании
Теорема 4.3. При выполнении условий D.42), если р(г) ? V^@, 1),
г = 0илиг=\ (Vi@, 1) = С4@, 1), V2@, 1) = L2@, 1)), система урав-
уравнений D.38), D.39) однозначно разрешима для w(r) ? V^@, 1) (г = О
или г = 1), g(r) e cfj>+(-\, I) при 0 < \<\* и \> Л°, где Л* и
Л° — некоторые фиксированные значения А. /7/ж этом имеет место
оценка
2
Для практических расчетов необходимо знать значения радиальных Мг
и тангенциальных М^ моментов в плите. Выпишем их выражения
через прогибы плиты:
,, / D\ fd2w , i/dw\ ,, / D\ fd2w , 1 dw\ iA ra\
Mr = к —о- Н г- , М^ = и—* —т -\ — . D.56)
V R2) \dr2 r dr) * V R2)\dr2 r dr J
Используя выражения для прогибов плиты D.43), получим
м
Мг = (^) V wmAmk2m \^P±VX (kmr) + V0(kmr)},
D.57)
^Rz
где Vi(kmr) = Ji(kmr) + BmIi(kmr), г = 0, 1.
§ 5. Определение осадки поверхности основания вне
круглой пластины
Уравнение D.39) было получено в результате использования сле-
следующего представления вертикальных перемещений поверхности про-
пространства:
f(r) = \ \ Q(a)L(Xa)J0(ar)da. D.58)
Найдем аналитическое выражение для функции /(г) в D.58), когда
L(a) ? AN, r > 1. Для L(a) ? AN функция QN(а) получена в анали-
аналитическом виде при построении решения уравнения D.39). Используя
формулу D.58), получим выражение для функции /(г), г > 1, если
L(a) ? AN; будем обозначать его fN(r). Согласно D.44) функцию
QN (а) можно записать в виде
сю
QN(a) = ? wmQ»(a).
ra=0
§5. Определение осадки поверхности основания вне круглой пластины 147
Соответствующие выражения для функций /^(г) имеют вид
G(r, km)-BmG(r, ik
N
n=\
N
, D.59)
r > 1, ra = 0, 1, 2,...,
\a)^n(a), 7n(a) = asma/(b2n\~2 + a2)
N
cos at
-dt,
Окончательно получим
м
ra=0
), Г>\,
D.60)
где wm — те же величины, что и в D.43).
Возникает вопрос об использовании формул D.59), D.60) для
определения осадки поверхности неоднородного полупространства, т. е.
в случае, когда трансформанта ядра L(a) обладает свойствами D.42)
и функция L(a) принадлежит классу функций Sat?m. Согласно теоре-
теореме 4.3 решение D.47), представленное формулами D.50) и D.44), явля-
является асимптотически точным решением уравнения D.39) для функций
L(a), принадлежащих классу Sn,m при Л —> 0 и Л —> оо. Подставив
это асимптотическое решение qN(r) в D.39) для L(a) ? Sat,m, найдем
приближенное выражение для осадки поверхности неоднородного по-
полупространства вне плиты /s(r) в общем случае, когда L(pt) ? Sn,m'-
r>\.
Асимптотические свойства решения системы уравнений D.38),
D.39) установлены на конечном отрезке г ? [0; 1]. Покажем, что подоб-
подобные асимптотические свойства сохраняются для определяемой прибли-
приближенно функции /(г) при г ? A;оо).
148 Гл. 4. Изгиб пластин на неоднородном основании
Не нарушая общности, считаем М = 1. В этом случае
1
dp =
О
2^
а + В А
1
C\-lK0(rD\-1) LN(p)I0(pD\-l)pdp,
1
г>1.
о
Используя асимптотические свойства цилиндрических функций
мнимого аргумента, получим оценки
HiqN(r)\ < М* exp(-D\-l5), А -> О (Л < Л*), 5 = г - р > О,
max
г>\
max
<М°Л-1+?, Л ^оо (Л>Л°), е>0, е -> О,
где постоянные М* и М° не зависят от Л. Отсюда вытекает следующая
теорема.
Теорема 4.4. Формулы D.59), D.60) являются асимптотически
точным представлением осадки поверхности неоднородного по глу-
глубине полупространства вне плиты при выполнении условий тео-
теоремы 4.3, когда 0<А<А* и А > Аа, где А* и Ха — некоторые
фиксированные значения А.
Замечание 4.2. Аналогичные результаты имеют место в случае
изгиба балки, лежащей на неоднородной по глубине полосе или на
неоднородной полуплоскости. Для доказательства используются
асимптотические свойства приближенных решений соответствую-
соответствующих контактных задач, установленные в [13, 14, 26].
§ 6. Примеры расчета пластин на неоднородном
основании
Рассмотрим изгиб круглой пластины под действием равномерно рас-
распределенной нагрузки единичной интенсивности. Пластина вдавлива-
вдавливается в полупространство, модуль Юнга которого с глубиной изменяется
по закону
E{z)=Ew{z), -H^z^O, D.61)
E(z)=E0<p(-l), -oo^z^-1, D.62)
а коэффициент Пуассона основания v = 1/3, —оо < z < 0. Коэффи-
Коэффициент Пуассона пластины vn =0,15. Для равномерно распределенной
нагрузки выполнены условия теоремы 4.1 (р(г) =р= 1), коэффициенты
разложения D.44) имеют вид
§ 6. Примеры расчета пластин на неоднородном основании 149
Рассмотрим следующие виды неоднородностей:
1) монотонная (степенная)
а) возрастающая с глубиной
?>,(*)= 0,1 + г2**, ак = Ы02'^- 1} (к = 2), D.63)
б) убывающая с глубиной
?*(*) = 1,1-**», afc =
2) немонотонная
<рз(я) = 1Д +sinGr^), щ(г) =0,1 -sinGT2). D.65)
На рис. 4.2, 4.3 приведены графики величины го(г) =
характеризующей распределение контактных нормальных напряжений
под пластиной на неоднородном основании по сравнению с однородным
qo(r) (для Е = Ео(р(—1)) при различных значениях Л.
Здесь и ниже рис. 4.2, 4.3, а, в, д, ж соответствуют изгибной жест-
жесткости пластины s = 0, 1; б, г, е, з —5 = 3. Цифра у кривой соответ-
соответствует значению Л, для которого производился расчет. Значения ддг(г)
найдены по формуле D.47) при N = 10, М = 10. На рис. 4.2, а, б то (г)
соответствует закону (f\(z), на рис. 4.2, в, г — ^2(^)> Рис- 4.3, д, е —
(рз(%), рис. 4.3, ж, з — (Pa(z). Можно заключить, что в случае мо-
монотонно убывающего с глубиной закона неоднородности вида <p2(z)
в окрестности края пластины наблюдается убывание коэффициента при
особенности контактных напряжений по сравнению с его значением
для однородного полупространства, вплоть до отрыва пластины от
основания (рис. 4.3, ж, з). В этом случае нужно изменить постановку
задачи. Зона контакта пластины с основанием может быть определена
из условия обращения в нуль контактных напряжений на границе
зоны. Зона отрыва расширяется при увеличении изгибной жесткости
пластины (рис. 4.3, з).
Для немонотонных законов неоднородности (fs(z) и (pi(z) в случае,
когда ip(z) возрастает с глубиной от поверхности основания ((p^(z)),
наблюдается увеличение величины то (г), характеризующей коэффи-
коэффициент у особенности контактных напряжений при приближении из-
изнутри к краю пластины. В этом случае отрыв пластины от основания
отсутствует.
Если (p(z) убывает с глубиной от поверхности основания ((p4(z)),
то наблюдается уменьшение величины то (г) при приближении изнутри
к краю пластины. Форма кривых х(г) различна для малых и боль-
больших Л, а также для малых и больших s при Л > 1.
Видно, что распределение контактных давлений существенно зави-
зависит как от толщины неоднородного слоя и вида неоднородности, так
и от изгибной жесткости пластины.
150
Гл. 4. Изгиб пластин на неоднородном основании
Рис. 4.2
На рис. 4.4, 4.5 приведены графики величины
rwN(r)/w0(r), О < г <
jN(r)/fo(r), Г > 1,
Д(г) =
1,0
характеризующей величину относительной осадки поверхности г^дг(г)
неоднородного полупространства вида D.60) по сравнению с однород-
однородным wo(r)(noR пластиной и вне ее) при различных значениях Л и s.
В случае, когда функция (p(z) монотонно возрастает (закон неод-
неоднородности (f\(z)), воронка осадки поверхности неоднородного осно-
основания вне пластины более крутая, чем для однородного основания
(рис. 4.4, а, б). Обратно, когда функция <p(z) монотонно убывает (закон
§ 6. Примеры расчета пластин на неоднородном основании
151
1,5
1,0
0,5
-16—^
-0,2»_^
0,0
1,0
0,0
~Q,2~
0,5 г 1,0 0,0 0,5 г 1,0
з
Рис. 4.3
неоднородности (p2(z)), воронка осадки более пологая, чем для одно-
однородного основания (рис. АА,в,г). Для немонотонных законов неодно-
неоднородности форма воронки существенно зависит от Л — относительной
толщины неоднородного слоя под пластиной (рис. 4.5,д,е,ж,з).
На рис. 4.6, 4.7 приведены графики обезразмеренных радиаль-
радиальных (Mj? = Mr/MQr) и тангенциальных (М^ = M^/Mq^) моментов.
Здесь и ниже рис. 4.6, 4.7, а, в, д, ж соответствуют изгибной жест-
жесткости пластины s = 0, 1; б,г,е,з — 5 = 3. Цифра у кривой со-
соответствует значению Л, для которого производился расчет. Зна-
Значения Mr, Mor, My, Mq^ найдены по формуле D.57) при N = 10,
152
Гл. 4. Изгиб пластин на неоднородном основании
М = 10. На рис. 4.6, а, б М®, М^ соответствуют закону
рис. 4.6, в, г — (f2(z), рис. 4.7, д, е — (рз(%), рис. 4.7, ж, з
), на
Д(г)
10
\
т
16
0,0
-1,0
0,1 1,0
1,U
0,5
\ \ Х
\\
ч \
Д(г)
1,0
0,5
Ч8
16
2 г 4
0,0
-1,0
ОД 1,0
А(г)
-0,5™
,2=
//
/
-0,2 __
2 г 4 0
2 г 4
г
Рис. 4.4
§ 6. Примеры расчета пластин на неоднородном основании 153
0,1 1,0
А(г)
1,0
0,5
0,0
-0,5
-1,0
0,1 1,0
ф)
1/ /
n\X
/ /
/8
^—-16"^
2 г 4 0
ж
Рис. 4.5
154
Гл. 4. Изгиб пластин на неоднородном основании
0,0
-0,2
-0,6
-1,0
-1,4
0,0
-1,0
ОД 1
о
ф)
\
0,2
\
16
¦2
-0,5-"
у
к,
/
1,0 0,6 0,2 0,2 0,6 г
а
0,00
-0,01
-0,02
-0,03
-0,04
-0,05
16
0,2
0
\
\
,5-
ч
2
и -—
/
/
1,0
0,4 0,2
б
0,8 г
0,1 1,0
12
0,2
0,0
-0,2
1,0 0,4 0,0 0,4 0,8 т 1,0 0,6 0,2 0,2 0,6 г
в г
16/
^^'
ч0,2^
2^
"^0,5^
Рис. 4.6
§ 6. Примеры расчета пластин на неоднородном основании
155
1,5
0,0
-1,5
™3,0
0,0
-0,5
-1,0
/
\
\
\
—-———.
, i '- -.
^0,2^
X
0,1 1,
0,08
0,04
0,00
-0,04
0
Ф
/
%
Ц
V
^--
0,2^
0,8 0,4 0,0 0,4 0,8 г 0,8 0,4 0,0 0,4 0,8 г
д е
0,6
0,0
-0,6
-1,2
0,0
-0,5
-1,0
\
\\
4
oi
/~
0,1 1
0,00
-0,02
0,04
0,06
0
ф)
^\
_1б
0,2
\ \
V
/
У
2 _
0,5^
0,8 0,4 0,0 0,4 0,8 г
ж
Рис. 4.7
0,8 0,4 0,0 0,4 0,8 г
з
Глава 5
НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ
СОСТОЯНИЕ НЕОДНОРОДНОГО ПО ГЛУБИНЕ
ПОЛУПРОСТРАНСТВА ПРИ ДЕЙСТВИИ
ПРОИЗВОЛЬНОЙ ОСЕСИММЕТРИЧНОЙ
НАГРУЗКИ
Глава посвящена решению граничной задачи Неймана для неодно-
неоднородного по глубине полупространства. Подробно изложены как поста-
постановка задачи, так и процесс построения фундаментального решения
(функции Грина). Описана процедура расчета полей смещений, на-
напряжений и деформации в приповерхностных слоях полупространства.
Приведены примеры для различных характерных случаев неоднород-
неоднородности.
Рис. 5.1.
§ 1. Постановка граничной задачи для
непрерывно-неоднородного по глубине
полупространства при заданных на его поверхности
усилиях
Рассмотрим (рис. 5.1) упругое полупространство О, ограниченное
поверхностью Г и нагруженное давлением р(г). Будем считать, что
упругие характеристики полупространства непрерывно меняются по
§ 1. Граничная задача при заданных на поверхности усилиях 157
глубине в пределах прилегающего к поверхности слоя, а затем ста-
стабилизируются. С полупространством свяжем цилиндрическую систему
координат г, (р, z. Обозначим через и, v, w смещения вдоль осей г, (р, z,
а через аТ, а^, az, rrip, rrz, т^г — радиальное, угловое, нормальное
и тангенциальные напряжения соответственно.
Условия равновесия неоднородного полупространства при отсут-
отсутствии массовых сил, записанные в цилиндрической системе координат,
имеют следующий вид:
д ( ч дтГш drrz г,
дгк ' дер dz *
Связь упругих напряжений с деформациями выражается законом
Гука:
ar = 2M(z)er + A(zH, a^ = 2M(z)e(p + A(zH,
az = 2M(z)ez + A(zH,
E.2)
rr(^ = 2M(z)er(p,rrz = 2M(z)erz,r(fZ = 2M(z)s(fZ,
О = ег+е^ +ez.
В качестве параметров пропорции используем коэффициенты Ламе
M(z) и A(z) и при этом полагаем, что они изменяются по глубине
в приповерхностном слое, а затем стабилизируются:
1. M(z) = M(-H)=Ms, -оо ^z^-H, A(z) = A(-H) = As;
2. M(z) = Mc(z), A(z)=Ac(z), -H^z^O;
3. MC(-H) = MS, AC(-H) = AS;
min A(z) > Л* > 0, max A(z) < Л* < oo,
ze(-oo,o) ze(-oo,o)
min M(^) > M* > 0, max M(z) < M* < oo.
zG(-oo.O) zG(-oo.O)
E.3)
Здесь Н — толщина неоднородного слоя, сцепленного с подстилаю-
подстилающим полупространством, т. е. глубина, начиная с которой упругие ха-
характеристики полупространства стабилизируются. Индекс S («space»)
соответствует подстилающему однородному полупространству,
С («coating») — неоднородному слою. Л*, Л*, М*, М* — произвольные
постоянные.
Наряду с парой коэффициентов Ламе для описания упругого пове-
поведения твердого изотропного тела используются: модуль сдвига G и ко-
158 Гл. 5. Напряженно-деформированное состояние полупространства
эффициент Пуассона v или модуль Юнга Е и коэффициент Пуассона v\
М - Г - Е Л - Ev - 2Gu
~ ~ 2A + vY ~ A + v){\ -2v) ~ 1 -2i/
E.4)
М(ЗЛ + 2М) _ Л
~ Л + М ' V ~ 2(Л + М)'
Компоненты деформации выражаются через смещения следующим
образом:
сЫ dv , и dw
_ \ , du dv v ^
-газ — 7» \ о "•" ~о~ ~J'
z гаер аг г
E.5)
\,dv dw.
л _ ^гг гг dw
dr r dz
В дальнейшем полагаем, что усилия, прилагаемые к полупростран-
полупространству, вызваны или воздействием штампа, имеющего форму выпуклого
тела вращения, или распределенной внутри круга нагрузкой, и поэтому
симметричны относительно оси координат. Таким образом, смещения,
деформации и напряжения не зависят от угловой координаты ср. В этом
случае система дифференциальных уравнений E.1) распадается на две:
-^-(го-г) + г— о-и, = 0;
дг dz E.6)
d ( N , da
дг dz
I I zr) \ I о — W'
1У'г„)+г^^. ,57)
Система E.6) описывает осесимметричное напряженное состояние,
возникающее, например, под действием нагрузки, нормальной к по-
поверхности, а уравнение E.7) описывает соответственно равновесие
полупространства, скручиваемого касательным усилием.
Выражения для компонент деформаций при этом упрощаются:
E.8)
ди
дг
Ь
7 =
dv
1
—
и
г'
(du
г
ег
dw
dw
' ~ ~dz~'
_ 1 dv
§ 1. Граничная задача при заданных на поверхности усилиях 159
Запишем на основании E.2), E.5) представления для напряжений
через смещения:
ar = 2M(z) ^ + A(z)e, а^ = 2M(z) - + ЛЫ0,
dw , д/ \л ъ/г( \/ди , dw ч
ди и dw
= Ъ—I г -^—.
or r oz
E.9)
Окончательно получаем систему дифференциальных уравнений в
частных производных второго порядка относительно перемещений. Эти
уравнения могут быть представлены в форме
, _ Ji) + (М(^) + A(z))— + Мх(^)(^^ + —) = О,
M(z)X72w + (М(^) + Л(^))^ + 2M'(z)^- + Ax(^)<9 = 0,
E.10)
dz dz
n ди . и . dw
" — т;—I r ^—•
or r oz
Нагрузка на поверхности прилагается в ограниченной области,
а именно внутри круга радиуса а ^ 0. Рассмотрим случай произвольной
нормальной к поверхности нагрузки:
az(r,0) = -p(r) O^r^a, z = 0;
az(r,0)=0 a<r<oo, z = 0; E.11)
rrz(r,0)=0 0<r<oo, 2 = 0.
На границе сцепления неоднородного слоя с однородным полупро-
полупространством, при z = —Я, должны выполняться условия сопряжения по
смещениям и напряжениям:
о-?(г, -Н) = а?(г, -Я), rg(r, -Н) = T?z(r, -Я);
E.12)
ис(г, -Я) = us(r, -Я), wc(r, -Я) = ws(r, -Я).
160 Гл. 5. Напряженно-деформированное состояние полупространства
На бесконечности, при (г, —z) —> оо, смещения, деформации и на-
напряжения исчезают:
lim {и, w, er, Sy, ez, erz, ar, a^, az, rrz} = 0;
E.13)
lim {и, w, ег, Е<р, ez, erz, ar, a^, az, rrz} = 0.
r—s-oo
Таким образом, мы сформулировали задачу Неймана для неодно-
неоднородного полупространства: найти смещения, деформации и напряжения
внутри полупространства, удовлетворяющие уравнению E.10) при за-
заданном распределении усилий на границе E.11)-E.13).
§ 2. Построение фундаментального решения для
неоднородного по глубине полупространства
Будем разыскивать решение для смещений и и w в виде интегралов
Ханкеля;
оо
u(r, z) = -
0
оо
E.14)
w(r, z) = W(j,
Подставим E.14) в систему дифференциальных уравнений в част-
частных производных E.10). Приравняв к нулю подынтегральные выраже-
выражения, получим систему обыкновенных дифференциальных уравнений:
MU" + <у(М + K)Wf - 72(М + K)U + M'U1 + jM'W = 0;
E.15)
BМ + A)W" -j(M+A)Uf -<y2MW+BMf+Af)Wf -jA'U = 0
(здесь штрих указывает на дифференцирование по z).
Граничные условия E.11), E.12) приобретают следующий вид:
BМ@) + Л@)) W'(j, 0) + 7Л@)С/G,0) = -
,0) + Uf(j, 0)) = 0,
§2. Построение фундаментального решения для полупространства 161
Используя векторное представление для трансформант:
- Х1,Х2,Х3,ХЛ , E1б)
xi = U, x2 = Uf, x3 = W, xA = W',
запишем систему E.15) в матричном виде, при этом явно выделим те
части, которые соответствуют покрытию и подложке:
О
О
2М + Л
у
7
М
О
Л'
z
о
-Я,
м
о
м + л
2М + Л Г2М + Л
О
0
м + л
м
м
^ 2М; + Л;
'2М + Л 2М + Л
> z > —оо,
E.17)
E.18)
М
О
о
1
О
О
М + Л
г
о
о
о
м
-7-
0
м + л
м
о
'2М + Л ' 2М + Л
Граничные условия при этом представляются в виде
BМ@) + Л@))ж?G, 0) - 7A@)xf G, 0) = -P(j),
Ьх<зЬ> 0) +^G» 0)) = О,
xf G, -Я) = xf G, -Я), *3СG, -Я) = ^з G, -Я),
х2сG, -Я) = xf G, -Я), х4сG, -Я) = xfG, -Я).
E.19)
Необходимо отметить, что последнее условие имеет место в силу
непрерывности изменения свойств слоя и основания E.3).
Общее решение системы E.18) для однородного полупространства
(при Лх = Мх = О, М > О, Л > 0) имеет вид
r z) =
, + G +
l+ (->€ +
+ G - 7^
ЗМ)/(Л
б СМ. Айзикович и др.
162 Гл. 5. Напряженно-деформированное состояние полупространства
где di (г = 1, 2) — произвольная функция параметра 7- Решение
хсG, z) системы E.17) строится методом модулирующих функций
[74]. Суть метода состоит в выделении в явном виде экспоненциальных
составляющих решения. Вектор хсG, z) находим в виде
E.21)
г=1
Векторы агG, z) (г = 1, 2) определяются из решения следующей
задачи Коши:
da"
dz
- 7а*, 0 > ^ > -Я, г = 1, 2,
при следующих начальных условиях для z = —Н:
E.22)
а2G, z) = (jz,
Постоянные ^G) (* = Ь
образом, мы имеем
определяются из условия E.19). Таким
i = 1
E.23)
Щ-у) = -Л(О)(Л(О) + 2M@))~ ViG> 0) +4G, 0),
Mi G) = [4 G,0)+74 G,0)],
^*G)=^РG)(Л@) + 2М@))-1,
где alk(j, z) обозначает fc-ю компоненту вектора агG, z
к = 1, 2, 3, 4. Отсюда
i = 1, 2,
d2G) = Р'G)ЛГГG), E.24)
7) - M,G)JV2G))-1.
§2. Построение фундаментального решения для полупространства 163
Окончательно получаем следующее выражение для компонент век-
вектора решения x.c(z, 7) ПРИ z = — Н:
Ъ z) = [diG)a!G. -г) +d2G)fl2G. Ф^,
WG, z) = [diG)a?G. z)+d2ALA, z)]e
Введем следующие обозначения:
E.25)
?3G, z) = Wb, z),L4G. z) = W'(-y, z),
где функции Li, согласно E.21), имеют вид
7г, г =1,2, 3,4.
V—>
^ dk GLG-
к=\
В соответствии с E.4)-E.9) выпишем выражения для радиальных
и вертикальных смещений и их частных производных по z:
00
1 - v [ -уг
ХМ J Л
О
E.26)
сю
ди(г, z) _ 1 -I/
аг ~ лм
о
сю
/ \ \ — V
°оо E-27)
dw(r, z) _ 1 -1/
dz ~ AM
0
Дифференцируя и и w по г, на основании E.26), E.27) получим
соответствующие выражения для частных производных:
ди(V Z) 1 U I T7*
$r AM J ' Л
О
сю
Н т^Г -^G)^1G» ^)^i(^")^7» E.28)
о
сю
<9u>(r, z) _ 1 — v Г
о
164 Гл. 5. Напряженно-деформированное состояние полупространства
Введем следующие обозначения
|
О
сю
о
сю
\
h =
I E-29)
1 -v
|
о
oo
0
сю
Распределение смещений, деформаций и напряжений для неодно-
неоднородного по глубине полупространства при воздействии на него с по-
поверхности произвольной осесимметричной нагрузки можно представить
в виде
u(r, z) = —I\(r, z),w(r, z) = /з(г, z),
er(r, z) = -I6(r, z) + l-h(r, z),ez(r, z) = /4(r, z),
e<p(r, z) = --/i(r, z),erz(r, z) = -I2(r, z) -/5(r, z),
e(r, z) = I4{r, z) - /6(r, z), ^ 3Q^
<rr(r, z) = -BM + Л)/б(г, 2?) + 2M-/i (r, 2?) + Л/4(г, z\
^(r, ^) = -2Mi/j(r, z)+A(I4(r, z)-I6(r, z)),
az(r, z) = BM + Л)/4(г, 2?) - Л/б(г, 2?),
rrz(r, ^) = -M(/2(r, z)+h(r, z)).
§ 3. Численный анализ фундаментального решения 165
§ 3. Численный анализ фундаментального решения
для некоторых характерных видов неоднородности
Значения компонент полей смещений, деформаций и напряжений
находятся с помощью численного интегрирования в заданных точках
(г, z) неоднородного по глубине полупространства.
Бесконечная область интегрирования по 7 разбивается на отрезки
знакопостоянства подынтегральной функции (функции Li могут ме-
менять знак в ограниченной области изменения G, z) и далее монотонно
стремятся к 0, так что корни подынтегральной функции совпадают с
корнями функций Бесселя, которые легко определяются. Расчет ве-
ведется до тех пор, пока модуль приращения функции не перестанет
превосходить заданную (достаточно малую) величину. Интегрирование
производим, отступая от границы полупространства на некоторое ма-
малое расстояние.
Рассмотрим численные примеры для некоторых характерных видов
неоднородности основания. Эти примеры описывают поведение покры-
покрытия и подложки из никеля и меди при различных их комбинациях.
Предполагаем коэффициент Пуассона v = 0,333, а модуль Юнга
в неоднородном покрытии изменяется по глубине в соответствии со
следующими соотношениями:
s трС fp^ -f'. (у\ TJ <С у <С О
kj\z) = < ~
[ Е = const, —00 < z < —Я, E.31)
i = 1,2,3,4,5,6 .
Здесь
?f = 3.5ES, Eg = l/3.5Es, E.32)
Eg = 3.5ES + 2.5Esz/H, E.33)
Eg = \/3.5Es - B.5/3.5)Esz/H, E.34)
Eg = Es(\. + 2.5sm(irz/H)), E.35)
Eg = Es(l.- B.5/3.5) sin(irz/H)). E.36)
На рис. 1.10 приведены схематичные изображения законов неодно-
неоднородности, в дальнейшем цифры 1-6 на графиках будут приводиться
в качестве меток соответствующих законов неоднородности. Кроме
того, будем также использовать словесное описание законов изменения
модуля Юнга по глубине.
В расчетах законы изменения механических свойств аппроксимиро-
аппроксимировались кусочно-линейной непрерывной функцией от z.
В случаях / и 2 мы полагаем, что с однородным полупространством
сцеплен пакет, состоящий из однородного слоя, модуль Юнга которого
больше или меньше модуля Юнга подстилающего основания (покрытие
более жесткое или более мягкое, чем подложка), и промежуточного
166 Гл. 5. Напряженно-деформированное состояние полупространства
1. Жесткий слой
Z
-0.000
-0.999
-1.000
Ес
3.500
3.500
1.000
2. Мягкий слой
Z
-0.000
-0.999
-1.000
Ес
0.285
0.285
1.000
слоя, модуль Юнга которого плавно меняется от значений в покрытии
до значения модуля в полупространстве.
3. Линейный убывающий
закон неоднородности
Z
-0.000
-1.000
Ес
3.500
1.000
5. Немонотонный закон,
жесткий слой
Z
-0.0
-0.1
-0.2
-0.3
-0.4
-0.5
-0.6
-0.7
-0.8
-0.9
-1.0
Ес
1.000
0.564
0.405
0.331
0.296
0.286
0.296
0.331
0.405
0.564
1.000
4. Линейный возрастающий
закон неоднородности
Z
-0.000
-1.000
Ес
0.285
1.000
6. Немонотонный закон,
мягкий слой
Z
-0.0
-0.1
-0.2
-0.3
-0.4
-0.5
-0.6
-0.7
-0.8
-0.9
-1.0
Ес
1.000
1.773
2.469
3.023
3.378
3.500
3.378
3.023
2.469
1.773
1.000
В случаях 5 и 6 мы рассматриваем немонотонное изменение модуля
Юнга в неоднородном покрытии. Для случая 5 характерно возрастание
значения модуля Юнга до середины слоя, а затем его убывание. Для
случая 6 значение модуля сначала убывает, а потом возрастает. При
этом мы считаем, что покрытие представлено пакетом слоев, модуль
Юнга которых линейно меняется по глубине в пределах каждого слоя
и совпадает на границах слоев, в том числе и на границе с подстилаю-
подстилающим однородным полупространством. На поверхности покрытия модуль
Юнга совпадает со значением в подложке.
§ 3. Численный анализ фундаментального решения
167
0. Модель почти однородного
полупространства
z
-0.000
-0.999
-1.000
Ес
1.0001
1.0001
1.000
Для сравнения результатов вычислений с однородным случаем мы
используем слой, свойства которого слабо отличаются от значений
в полупространстве.
Для проведения численных расчетов и визуализации их результатов
разработан программный комплекс, расчетная часть которого реали-
реализована на Fortran Powerstation 4.0, результаты расчетов сохраняются
в базе данных, которая создана и поддерживается в среде Visual-
Foxpro 7.0, а для визуализации используются пакеты Axum, Surfer,
Gnuplot, MS Excel.
В базе данных сохраняются следующие расчетные данные:
ТРАНСФОРМАНТА ЯДРА
ВЕЛИЧИНА ВНЕДРЕНИЯ
СИЛА
ЖЕСТКОСТЬ
КОНТАКТНОЕ ДАВЛЕНИЕ
СМЕЩЕНИЕ ПОВЕРХНОСТИ
АПОСТЕРИОРНАЯ ПОГРЕШНОСТЬ
ИНТЕГРАЛЬНАЯ АПОСТЕРИОРНАЯ
ПОГРЕШНОСТЬ
РАДИАЛ. СМЕЩЕНИЕ U(R,Z)
ВЕРТИК. СМЕЩЕНИЕ W(R,Z)
РАДИАЛ. ДЕФОРМАЦИЯ ER(R,Z)
ВЕРТИК. ДЕФОРМАЦИЯ EZ(R,Z)
УГЛОВ. ДЕФОРМАЦИЯ EF(R,Z)
СДВИГ. ДЕФОРМАЦИЯ ERZ(R,Z)
ИНТЕНСИВН. СДВИГ.
ДЕФОРМАЦИЙ E(R,Z)
РАДИАЛ. НАПРЯЖЕНИЯ SR(R,Z)
ВЕРТИК. НАПРЯЖЕНИЯ SZ(R,Z)
УГЛОВ. НАПРЯЖЕНИЯ SF(R,Z)
СДВИГ. НАПРЯЖЕНИЯ SRZ(R,Z)
ЭФФЕКТИВНЫЕ НАПРЯЖЕНИЯ
ЭНЕРГИЯ
МАКСИМ. КАСАТЕЛЬНЫЕ
НАПРЯЖЕНИЯ
Для визуализации компонент смещений, деформаций и напряжений
на одном рисунке строится в аксонометрической проекции трехмерное
изображение поверхности в декартовых координатах (r,z), а в нижней
части рисунка показываются линии равных значений.
и
Н/а
Н/а
Н/а
R
R
R
Н/а
R
R
R
R
R
R
R
R
R
R
R
R
R
R
L(U)
W(H/a)
Р(Н/а)
S(H/a)
T(R)
W(R)
ER(R)
IER(H/a)
Z
Z
z
z
z
z
z
z
z
z
z
z
z
z
DL(U)
T0(R)
W0(R)
U(r,z)
W(r,z)
Er(r,z)
Ez(r,z)
Er(r,z)
Erz(r,z)
E(r,z)
Sr(r,z)
Sz(r,z)
Sf(r,z)
Srz(r,z)
S(r,z)
We(r,z)
DEV(R,Z)
168 Гл. 5. Напряженно-деформированное состояние полупространства
На рис. 5.2-5.8 показаны поля вертикальных деформаций ez в
приповерхностном слое при действии равномерной нагрузки как для
однородного, так и для неоднородного полупространств при законах
неоднородности, описанных выше для Л = 1. Следует отметить, что
только в случае 4 (для линейно возрастающего изменения свойств ма-
материала) происходит монотонное изменение вертикальных деформаций.
Рисунки 5.9-5.15 показывают распределение полей вертикальных
напряжений для однородного и неоднородного полупространств при
Л = 1 в случае действия равномерной нагрузки и законов неоднородно-
неоднородности, описанных выше. Картина изменения вертикальных напряжений
однообразна для всех рассмотренных случаев изменения свойств мате-
материала покрытия.
§ 3. Численный анализ фундаментального решения 169
Ez(r,z)
0,00
0,01
-0,2
z
-1,4
0,2
0,6
1,8
1,4
1,0
r
Ez(r,z)
0,00
-0,05
-0,2" -
z ~®
,8" ¦
-1,4" 0,2
0,6
. -I
•¦¦¦'1,4
1,0
t
u'z:..:i •-.., м vv,;;— I ^o,2
-°'6 ¦ / a \--n i -се
-1:..-- ,:/./; ii\ -I -1,0
°'2 °'6 1'° X'4 r 0,2 0,6 1,0 1,4 r
1 2
1,0 3,5 0,3 1,0
Рис. 5.2 Рис. 5.3
170 Гл. 5. Напряженно-деформированное состояние полупространства
Ez(r,z) E^
0 00
0,00- .. • • U'UU ...•"*¦
0,01- . -0,05 ..•' ' "
-''I 8
-0,2 -. ...••-1,4 ^°'2 ¦.
-0,8 . Qg1'0 г'8 0,6
Z -1,4 0,2 ' Г -1'4 °'2
z . z •„,. -
™o,2 . ^0,2 ,№ ; _
™0,6^...:7Г^%^ '"¦?:'\1*^Ч-- ""* -0,6 .,„, ¦ *
.¦'¦"'¦-•. ¦ . •'¦ '"-• ¦'-¦ л»--
-1,0 v.-- -¦;•'•¦ ', ';: : v, ¦ -1,0
-1.4;---;.-'..^; / :1; -1.4
0,2 " 0J6 1,0 1,4 г 0,2 0,6 1,0 1,4
4
0,3 1,0.
Рис. 5.4 Рис. 5.5
§ 3. Численный анализ фундаментального решения 171
E?r,z) Ez(r,z)
0,00 . •.'-' • 0,00
-0,01 •-' • -0,05 • ,
-'1,8 • ¦ - ^ 1,8
-0,2-- • - ' 1,4 -0,2 . s- .--1,4
-0 8 -' • -' lj0 -0 8' - '•"" 1>0
z ' "•¦.-•¦' 0,6 r z ' ¦¦¦••..-•• 0,6 r
-1,4 " 0,2 -1,4 ' 0,2
z
-0,2
-1,0 ^¦^^-¦•¦¦¦¦y- ¦ я<* |
-1»4' " ' ,-¦'. ¦•"' 0,2 0,6 ' lfi ' 1,4 ' V
0,2 0,6 1,0 1,4 r
5 6
1,0 3,5 n n0»,3 l^
Рис. 5.6 Рис. 5.7
172 Гл. 5. Напряженно-деформированное состояние полупространства
0,00
-0,02
• . • 1,0
z ~'~ -¦• -¦ ' 0,6 r
-1»4 ' 0,2
-0,8"
1,4
1,8
0,00 I
-0,02
1,4
1,8
-1,4 0,2
Z ~
,2 ;
-0,6
-1,0
-1,4 -
0,2 0,6 1,0 1,4
z
-0,2
-0,6
-1,0
-1,4
JC*«**'...
0,2 0,6 1,0 1,4
1,0 3,5
0,0 — E{
-i,oP
z f
Рис. 5.8
Рис. 5.9
§ 3. Численный анализ фундаментального решения 173
Sz(r,z) Sz(r,z)
0,00 0,00
1,8 -°'°2
-0,2 iq1,4 -0,2 iq1,4
z ~0'8 0,6 ' r z ~ ' ' ' ¦.. 0,6 ' r
-1,4 0,2 -1.4 0,2
Z ¦ ¦ ¦ ¦•-.. ¦ Z ¦-. .щг. - — f
-0,2 ¦ -o,2- ..,,¦¦¦¦¦-¦!/;Ш\'х-, I
g L%\ % ¦ ¦' " ^ ..:¦¦.:¦¦¦'¦ ^;м|\ ¦».'¦"•¦¦, I
-0,6 V1, . ^?"-ч _o^... ^ , -^|p\^- ¦- I
¦ *" ..-•--'¦ ' .- ' •'•••• '«. 4- '']
^0,2 " O56 1,0 1,4 r ' 0,2 " 0,6 " 1,0 " 1,4 V
3
1,0 3
z
Рис. 5.10 Рис. 5.11
174 Гл. 5. Напряженно-деформированное состояние полупространства
S?r,z)
0,00
-0,02 -
-0,2 •.
z ''
-1,4'" ,2
- ¦ 1,8
•- ,4
- i,o
,6 r
Sz(rjZ)
0,00
-0,02 •
-0,2 • - .
z~°'
>8 '¦-•• .-¦ 0,6
-1,4 ' 0,2
..--1,
•",4
r
z m: ;..-' |
-W;--;; ,-"¦ 'Ч Л. I -0,6;:
-1,0 * ¦;: ¦ ¦,¦
¦M : ¦ ч -1,0 ^
-1'4' -:- ¦'¦¦¦ -1,4.
i)U LA ' 0,2 0,6 1,0 1,4
0,3 1,0,, 1>03'5
Рис. 5.12 Рис. 5.13
§ 3. Численный анализ фундаментального решения 175
0,00
-0,02
-0,2 .
Z ''
,8
-1,4 0,2
1,8
1,4
1,0
0,6 r
Sz(r,z)
0,00
-0,02
-0,2
,-0,8
-1,4
1
1,4
1,0
0,6 r
0,2
-0,6 - •••' ¦ -; " - -0,6-
>
0^2 0^6 1,0 1,4 ' V 0,2 0,6 1,0 1,4 r
0,3
0,0 -
-!,»!
Рис. 5.
1,0
N
14
0
1,0
-1,0 1
Р
Рис. 5.15
Глава 6
КОНТАКТНЫЕ ЗАДАЧИ С НЕИЗВЕСТНОЙ
ЗАРАНЕЕ ЗОНОЙ КОНТАКТА ДЛЯ
НЕОДНОРОДНЫХ ТЕЛ
Рассматривается задача о внедрении в неоднородное (слоистое или
функционально-градиентное) упругое полупространство осесимметрич-
ного выпуклого штампа. Предполагается, что штамп является телом
вращения, подошва которого имеет выпуклую форму. Задача сводится
к решению парного интегрального уравнения. Подробно изложен ме-
метод построения в аналитической форме приближенного решения этого
уравнения. На примерах изучается влияние различных законов изме-
изменения по глубине модуля сдвига в полупространстве на распределение
контактных напряжений под сферическим индентором и размер зоны
контакта индентора с основанием в зависимости от значений характер-
характерного геометрического параметра задачи и величины вдавливающей си-
силы. Анализируется изменение распределения контактных давлений для
различных законов неоднородности и зон контакта. Строятся поля на-
напряжений, возникающих в неоднородном по глубине полупространстве
при внедрении в него сферического штампа, позволяющие определить
зоны предразрушения в неоднородном полупространстве.
§ 1. Внедрение параболического индентора
в неоднородное полупространство
Осесимметричный индентор вдавливается в поверхность Г неодно-
неоднородного упругого полупространства О силой Р (рис. 6.1). С полупро-
полупространством связана цилиндрическая система координат (r,(p, z).
Предполагается, что все деформации упруги. При расчете мы будем
пренебрегать пластическими эффектами, так как исследование свойств
неоднородного покрытия на некотором удалении от контактной зоны
основано на использовании упругих свойств материала. Для органи-
организации неразрушающих испытаний материала лучше всего подходит
сферический штамп большого радиуса кривизны по сравнению с зоной
контакта, в этом случае его можно аппроксимировать параболоидом
вращения
z = ^l(r)=Cr2 F.1)
в окрестности начальной точки контакта. Также будем полагать, что
контакт гладкий, т. е. силы трения между индентором и поверхностью
полупространства отсутствуют. Вне индентора поверхность полупро-
полупространства не загружена. Под действием силы Р индентор перемещается
на расстояние \ вдоль оси z.
§ 1. Внедрение параболического индентора в полупространство 177
Рис. 6.1
Рассмотрим задачу, когда индентор не деформируем. Считаем, что
модуль сдвига G(z) и коэффициент Пуассона v[z) неоднородного слоя
являются произвольными функциями координаты z\
1. G = G0(z), v = vo(z), -H^z^O;
2. G = G(-H), v = vo(-H), -оо ^z^-H.
При вышеуказанных предположениях граничные условия имеют вид
z = 0, rrz = тГ(р = О,
' az = 0, г > а,
w — х(г) — ~Х + ^l7^)' г < а.
F.2)
F.3)
Здесь w — смещение вдоль оси z, rzr, rZ(f, az — радиальные, танген-
тангенциальные и нормальные напряжения.
При z = —Я должны выполняться условия сопряжения по напря-
напряжениям и перемещениям:
г, -Н) = abz{r, -H),T^z{r, -Н) = rrbz(r, -H),
г, -Н) = us(r, -H),wc(r, -Н) = ws(r, -Н).
F.4)
Напряжения и деформации стремятся к нулю при (г, —z) —> оо.
Требуется определить распределение нормальных контактных на-
напряжений под штампом: az(r,O) = —p(r), 0 < г ^ а, размер зоны
контакта а, связь между вдавливающей силой Р и осадкой штампа х,
а также напряженно-деформированное состояние приповерхностного
слоя неоднородного по глубине полупространства.
Так как индентор выпуклый, то его края не врезаются в поверх-
поверхность полупространства и должно выполняться соотношение р(а) = 0.
Это условие используется для определения полуширины зоны контакта
и накладывает некоторые ограничения на функцию р(г).
178 Гл. 6. Контактные задачи с неизвестной заранее зоной контакта
Заметим также, что в связи с отсутствием сцепления индентора
с поверхностью полупространства для корректной постановки задачи
должно быть выполнено соотношение р(г) > 0 для всех г < а.
Для решения поставленной задачи приведем ее к парному инте-
интегральному уравнению относительно р(г). Для этого воспользуемся ре-
результатами предыдущей главы. Запишем граничное условие на поверх-
поверхности слоя в пределах контактной зоны, при этом обозначим L^(u,0)
через L(u)\
^_ | Р(аЩХа) J0(ar)da = /(г),
Р(а) Jo(ar)ada = О, 1 < г < оо,
F.5)
г
Р(а) = p(p)J0(ap)pdp,
о
/(г) = 5 — (р(га)/а, 5 = х/а, 0
1.
Здесь Jo — функция Бесселя нулевого порядка, (р(га) = (За2г2,
C = BR)~ , R — радиус сферы, внедряемой в полупространство,
Л = Н/а — характерный геометрический параметр задачи, L(Xa) —
трансформанта ядра парного интегрального уравнения.
§ 2. Приближенное решение задачи о внедрении
выпуклого штампа в непрерывно-неоднородное
по глубине полупространство
Решение F.5) ищется следующим методом [10]: парное интеграль-
интегральное уравнение приводится к более простому виду, ядро аппроксими-
аппроксимируется дробно-рациональным выражением, с помощью операционного
исчисления находится решение, а затем обратными преобразованиями
задача сводится к решению линейной алгебраической системы.
Используя операторы
Ufa(r) = i
(p(r)dr
= a l cos a(^ 1 ,
§2. Внедрение штампа в непрерывно-неоднородное полупространство 179
представим F.5) в форме
¦ сю
J P{a)L{Xa) cosa(da = <3{0)g{(), 0< < < 1,
F.6)
I
В нашем
J P(ot) cos a(da
0
случае
Введем обозначение
;6.7), fci :
В случае
6@M@ =
= -|в@), к2 =
, когда
L(Xa) Х/дг(Л(
= 0, С
9@ = U
W
ч
k\9i{Q,
= 6в@).
Р2(А
> 1,
аг2!
^.@ = С2 + |
2а2) _ A AV + Л2
^ г
L=-\ Л2 а2 + Б2
F.7)
F-8)
используя метод работы В.М.Александрова [38], получим решение
задачи в аналитическом виде. Представим LN в виде
Здесь
LN(Xa) =
Гк (--о л-1
1 + 5^^
fc=l
) С1-^
ОкВ2кХ-2 (а2 +1
Ч^2) , L&(Aa)
ЛГ 2 2 2
| | А а +Aj
А А \2 2 _l r2
N
где Л означает отсутствие в произведении k-го множителя.
Введем функцию
сю
р(С) = т1- P(a)cosaC^- F.9)
fci J
о
Тогда, используя методы операционного исчисления, F.6) можно пред-
180 Гл. 6. Контактные задачи с неизвестной заранее зоной контакта
ставить в виде
F.10)
где полиномы Р\ и Р^ определяются, как в F.8).
Решение дифференциального уравнения F.10) может быть пред-
представлено в виде
N Г N
г=\
г=1
, F.П)
где коэффициенты Q, г = \,...,N, неизвестны и определяются в
дальнейшем при подстановке данного вида решения в интегральное
уравнение F.6).
Используя обратное преобразование Фурье в F.9), получим
х a cos a — sin a
^ + 2S{
к\ ) a J
У F.12)
N
i=\
Выражение для распределения контактных нормальных напряже-
напряжений получим обратным преобразованием:
оо
= \
(ar)da.
F.13)
Подставляя F.13) в F.12), получим
г=1
F.14)
Константу &2 определяем из условия отсутствия напряжений на
границе зоны контакта рA) =0:
L~\0) J_
N
г=1
=0.
F.15)
§2. Внедрение штампа в непрерывно-неоднородное полупространство 181
Коэффициенты С{ определяются при подстановке Р(а) из F.12)
в F.6) в случае, когда L(\ot) имеет вид F.8):
N
Р(а)
+ в1х-2
cosa(da =
О
о
F.16)
Из F.16) получим линейную алгебраическую систему уравнений
для определения коэффициентов Q:
N
г=1
-1
N
BIX'2
= 0,
F.17)
Система F.17) однозначно разрешима при А^, Б/е, удовлетворяю-
удовлетворяющих условию (Ai — Ak)(Bi — Bk) ^ 0 при г ф к. В соответствии с F.14)
выражение для нормальных контактных напряжений представляется в
виде:
Р(г) = ^в(О) J
C2-r2
1. F.18)
Значение вдавливающей силы Р определяется из условия равнове-
1
сия для индентора: Р = 2тта2 § q(r)rdr. Следовательно,
о
N
г=1
+^A-1sh(A,A-1))
F.19)
182 Гл. 6. Контактные задачи с неизвестной заранее зоной контакта
§ 3. Численный анализ решения задачи о внедрении
параболического штампа в неоднородное основание
При численном анализе построенного приближенного решения за-
задачи о внедрении выпуклого параболического штампа в неоднородное
основание мы уделим основное внимание двум вопросам:
1) оценке точности приближенного решения для разных видов неод-
неоднородности;
2) иллюстрации различий в поведении различных видов покрытий
при внедрении штампа. При этом приводится вид полей смещений,
деформаций, напряжений и т.п.
О том, как построенное прибли-
приближенное решение зависит от парамет-
параметров аппроксимации, можно судить по
рис. 6.2, на котором показано измене-
изменение контактных напряжений для зако-
закона неоднородности слоя вида 6 (немо-
(немонотонный мягкий) в зависимости от
количества членов аппроксимации N.
Как уже упоминалось в гл. 1, из
рис. 1.11 видно, что ошибка аппрок-
аппроксимации для образца неоднородности
вида 6 достигает 35 % для малого ко-
количества компонент аппроксимации, а затем плавно убывает до 10%.
Для монотонных законов ошибка аппроксимации колеблется от 2 %
до 5 %.
При построении приближенного решения поставленной задачи мы
заменили ядро уравнения L(Xa) его аппроксимацией вида
а
0,0
-0,1
-0,2
-0,3
-0,4
12
т
0,0
0,2 0
Рис.
,4 0,6
6.2
18,
J
0,8 г
= f[
f 2\~2) (a2
(а2 + А2\~2) (a2 + BfA). F.20)
i=\
Функция /(г), стоящая в правой части F.5), соответствует зна-
значениям осадки поверхности неоднородного полупространства под па-
параболоидом вращения, и, таким образом, физически значение невязки
соответствует абсолютной погрешности в задании формы штампа:
1 оо
= щ р(р)р LN(Xa)J0(ap)J0(ar)dadp,
F.21)
Здесь Jq — функция Бесселя нулевого порядка, R — радиус сферы,
внедряемой в полупространство, Л = Н/а — характерный геометриче-
геометрический параметр задачи.
§ 3. Анализ решения задачи о внедрении штампа в основание 183
На рис. 6.3 приведены графики смещений поверхности Wn(Q, г) под
штампом параболической формы, полученные численным интегриро-
интегрированием приближенного уравнения для всех 6 случаев неоднородности
слоя, и графики формы штампа Wf.
На рис. 6.4 даны те же графики смещений поверхности Wn(Q, r)
под штампом параболической формы для 3 случаев неоднородности
слоя и графики формы штампа Wf. Анализ графиков показывает хо-
хорошее совпадение приближенного решения и формы штампа во всех
случаях, за исключением немонотонных законов неоднородности слоя.
0,000
-0,004
™0,008
-0,012
-0,016
W@,r)
0,000
-0,002
-0,004
-0,006
-0,008
-0,010
°'020 0,0 0,5 1,0 1,5 2,0 2,5 г °'012 0,0 0,5 1,0 1,5 2,0 2,5
Рис. 6.3
Рис. 6.4
После определения распределения контактных давлений рп(р) под
штампом можно найти интегральную характеристику для ошибки:
1 оо
Ап(г,Л)= \pn(p)pdp (L(Xa) - Ln(\a))Jo(ap)Jo(ar)da.
F.22)
Подынтегральное выражение в F.22) отлично от нуля в ограничен-
ограниченной области, поэтому можем легко найти Дп(г,А) с помощью квад-
квадратурных формул, например формулы Гаусса. Относительное значение
погрешности определяется по формуле: sir, А) = 100 х — ,\ , где
w(r)
w(r) — перемещение поверхности полупространства под штампом.
Кроме того, можно ввести интегральную характеристику ошибки
1
e(\)=je(r,\)dr.
о
На рис. 6.5 приведены значения интегральной ошибки е(Х) для различ-
различных законов неоднородности. Значения г(г, А) показаны на рис. 6.6.
184 Гл. 6. Контактные задачи с неизвестной заранее зоной контакта
е{а/Н)
3
1
-1
-3
-5
1СГ10 2 4 5 10° а/Н
Рис. 6.5
е{г,а/Н)
Рис. б.б
§ 4. Анализ напряженно-деформированного состояния
185
§ 4. Анализ напряженно-деформированного состояния
неоднородного полупространства
При анализе напряженно-деформированного состояния неоднород-
неоднородного слоя, сцепленного с однородным полупространством, в который
внедряется параболический штамп, мы будем постоянно проводить
сравнение с однородным случаем. На рис. 6.7 приведены поверхности
выражений дДг, Л)/qo(r, Л), Л = Н/а, которые характеризуют относи-
относительное отличие в распределении нормальных контактных давлений
qi(r,\) под недеформируемым параболоидом вращения для законов
неоднородности вида Егс(г) (г = 1,...,6) в сравнении с однородным
случаем. Значения qi(r,\) были найдены по формуле F.18) при опти-
оптимальном выборе параметров аппроксимации. Для монотонных законов
неоднородности свойств слоя при фиксированных больших значени-
значениях Л и соответственно малых зонах контакта наблюдается подобие в
распределении контактных давлений по радиусу зоны контакта г в од-
однородном и неоднородном случаях. При росте зоны контакта в распре-
распределении контактных давлений наблюдается своеобразный концевой эф-
эффект. Для немонотонного случая эти эффекты выражены еще больше.
Интересная иллюстрация сжимаемости основания при внедрении
параболического штампа предложена А.Н. Динником. Развивая задачу
Герца, он проанализировал распределение упругих деформаций вдоль
оси вдавливания, просуммировал элементарные деформации вглубь от
поверхности образца и нашел дискретные значения этих сумм для
фиксированных толщин Н поверхностного слоя, нормированных на
радиус площади контакта а. Отношение такой суммарной деформации
Wh к значению W, суммирующему деформацию по всей глубине
полупространства, указано ниже:
Н/а
WH/W
0
0
1
0,500
2
0,704
3
0,794
4
0,843
5
0,870
10
0,937
20
0,970
Из этих данных видно, что на глубине z = а реализуется 50%
общего смещения, а на глубине z = 20а — 97%. На рис. 6.8 приве-
приведены графики величин (W@,0) — W(z,0))/W@,0) для законов неод-
неоднородности. Цифра возле кривой обозначает соответствующий закон
неоднородности (см. рис. A.10)). Кривая под номером 0 соответствует
данным Динника.
На рис. 6.9 приведены графики отношений значения осадок штампа
для 6 случаев неоднородности слоя к однородному случаю при соот-
соответствующих зонах контакта.
В однородном случае отношение осадки на краю штампа к осадке в
центре W@, \)/W@,0) = 0, 5. На рис. 6.10 показана зависимость удво-
удвоенной величины этого соотношения для 6 видов неоднородности слоя.
186 Гл. 6. Контактные задачи с неизвестной заранее зоной контакта
1п(а/Я)
Ы(а/Н)
Рис. 6.7
1,0
0,8
0,6
0,4
0,2
0,0
-0,2
що, о)
Из этих рисунков можно сделать вывод, что в случае градиентных сред
поведение их отлично от однородных сред при любых зонах контакта.
Для сравнения приведем отноше-
отношения приложенной к штампу силы для
неоднородных покрытий к силе для со-
соответствующего однородного покрытия
при одной и той же изменяющейся зоне
контакта (рис. 6.11).
На рис. 6.12-6.25 представлен пол-
полный набор полей компонент смеще-
смещений, деформаций, напряжений для се-
семи случаев покрытий, приведенных на
рис 1. 10. Все рис. 6.12-6.25 соответ-
0,01 1,01 2,01 3,01 4,01 z
Рис. 6.8
ствуют случаю внедрения сферического индентора при Н/а = 1.
§ 4. Анализ напряженно-деформированного состояния
187
На рис. 6.12 приведены поля радиальных смещений u(r,z), на
рис. 6.13 — поля вертикальных смещений w(r,z), на рис. 6.14 —
поля деформаций er(r,z), на рис. 6.15 — поля деформаций ez(r,z), на
рис. 6.16 — поля деформаций ?<Дг, z), на рис. 6.17 — поля сдвиговых
деформаций erz(r,z), на рис. 6.18 — поля интенсивности сдвиговых
деформаций e(r,z), на рис. 6.19 — поля напряжений ar(r,z), на
рис. 6.20 — поля напряжений az(r,z), на рис. 6.21 — поля напряжений
o~(p(r,z), на рис. 6.22 — поля касательных напряжений arz(r,z), на
рис. 6.23 — поля эффективных напряжений ae(r,z), на рис. 6.24 —
поля распределения энергии деформации W(r,z), на рис. 6.25 — поля
максимальных касательных напряжений rmax(r,z).
W@7 а/Н)
1,5
1,3
1Д
0,9
0,7
0,1 1,0
Рис. 6.9
а/Н
2W@,l)/W@,0)
1,3г
1,2
1,1
1,0
0,9
0,8
ОД 1,0
Рис. 6.10
а/Н
Для их визуализации используется трехмерное изображе-
изображение поверхности в цилиндрических координатах (г, z) в ак-
аксонометрической проекции. На каждом рисунке показан вид
поверхностей для шести неоднородных покрытий, указанных
на рис. 1. 10, в сравнении с однородным. Определяется общая
область изменения семи двумерных функций и разбивается
на 25 частей продольно-поперечными линиями. Линии уровня
проводятся на основании этой разбивки, что повышает нагляд-
наглядность при оценке диапазона изменчивости построенных функций.
7,39
2,72
1,00
0,37
ОД 1,0 а/Н
Рис. 6.11
188 Гл. 6. Контактные задачи с неизвестной заранее зоной контакта
Основной вывод, который можно сделать из приведенных графиков,
состоит в том, что поведение для четвертого случая неоднородности
слоя с линейно возрастающим модулем качественно напоминает пове-
поведение однородного слоя.
Характерной величиной для описания распределения напряжений
в упругой среде является интенсивность девиаторных напряжений,
которые мы будем также называть эффективными напряжениями:
= — /(а - а J + (а - а J + (а - а J
где ап (п = 1,2, 3) — главные напряжения на площадках. В случае
осесимметричной деформации
1
На рис. 6.26-6.31 приведены графики величин ae(r,z) для законов
неоднородности в трехмерном изображении и в виде проекций на
плоскость <те(г, z) = 0.
§ 4. Анализ напряженно-деформированного состояния
189
0,005
™0,005
—1,5
0
0,005
-0,005
-1,5
0
0,005
-0,005
190 Гл. 6. Контактные задачи с неизвестной заранее зоной контакта
-1,5
-1,5
-1,5
Рис. 6.13
§ 4. Анализ напряженно-деформированного состояния
191
0,005
0,000
0,005
Рис. 6.14
192 Гл. 6. Контактные задачи с неизвестной заранее зоной контакта
-1,0
rl.5
0,0
Рис. 6.15
§ 4. Анализ напряженно-деформированного состояния
193
-1,5
Рис. 6.16
7 СМ. Айзикович и др.
194 Гл. 6. Контактные задачи с неизвестной заранее зоной контакта
шштв&
Рис. 6.17
§ 4. Анализ напряженно-деформированного состояния
195
-1,5
-1,5
-1,0 0,00
z -0,02
-0,5
,° г
0,0
Рис. 6.18
196 Гл. 6. Контактные задачи с неизвестной заранее зоной контакта
-1,5
0,00
-0,02
Рис. 6.19
§ 4. Анализ напряженно-деформированного состояния 197
Рис. 6.20
198 Гл. 6. Контактные задачи с неизвестной заранее зоной контакта
-0,02
0,0
Рис. 6.21
§ 4. Анализ напряженно-деформированного состояния
199
Рис. 6.22
200 Гл. 6. Контактные задачи с неизвестной заранее зоной контакта
1>^
Рис. 6.23
§ 4. Анализ напряженно-деформированного состояния
201
¦л'-.^-'.^ф^Г.Г" -L
0,0005
0,0005
0,001
0,0002
Рис. 6.24
202 Гл. 6. Контактные задачи с неизвестной заранее зоной контакта
Рис. 6.25
§ 4. Анализ напряженно-деформированного состояния 203
1,8
0 2 М
' -0 8 '1'° "°'2
1Д U'^ -1,4-0,2
-о,б;--ы? г—'-"' - /
-•'•^.¦.-..Г ¦...--¦ ;• . -0,6¦
0"",2 0",6 " 1^0"' 1,4 'г 1>4- • - • ••
0,2 0,6 1,0 1,4 г
п Ь° 3'5 0,3 1,0
РОД 00+
-1,0
Z ? Z
Рис. 6.26 Рис. 6.27
204 Гл. 6. Контактные задачи с неизвестной заранее зоной контакта
0,2 ' ¦¦¦'¦-¦* ^Л^ 0,5
од
•1,8 1,8
-0,2 1,4 -0,2 -¦-¦'1,4
ПЯ- ¦¦'¦H „Я ¦¦¦¦'1>0
z ~°'8 ., 0,6 r z -°'8 .0,6 г
-1,4 0,2 -1,4 0,2
Z -—
-0,2 :: :
1'и':— -_-¦_¦::-::;*;:¦¦ ' : ; : ] -1,0. ....•¦¦¦¦¦
1-4;-:., :;:::,-¦¦•• -::.-:: . ,¦ ".. ./: -1,4
0,2 0,6 1,0 1,4 г 0J 0j6- 1H
а'03'5 0,3 1,0
Рис. 6.28 Рис. 6.29
§ 4. Анализ напряженно-деформированного состояния 205
0,4 02 /
0,2
'1,8
-0,2 , У' .1,4 -0,2 . ,-¦1,4
г "ОД Об1'0 г -0,8 / ....¦0,61'°г
-1,4 0,2 ' Г -1,4 0,2
г,,г„ >^_ГТ,._: ,; . ^0,2 ^^ЩШ^^^ще>, **
-0,2 йН:'л^;.«:^^;: -.,•¦. ...г,;ft*.:--/ •.¦•-•;/¦*•••¦•. ; ^ "
nfi-• "¦¦¦ / ' • -о,бнуу/^,;/;-/ -г ; • \
-1,0- W о.„'""" •- • ..°* } ~ ' '° ..-¦¦" 1
-1,4 -' • ¦ -1*4: ". '"
0,2 0,6 1,0 1,4 г °'2 °'6 ^ ^
0*3 1 О
Рис. 6.30 Рис. 6.31
Глава 7
ОЦЕНКА УПРУГИХ ХАРАКТЕРИСТИК
НЕОДНОРОДНЫХ ПОКРЫТИЙ МЕТОДОМ
ИНДЕНТИРОВАНИЯ
Вводится понятие функции жесткости, или эффективного модуля,
неоднородного основания при внедрении индентора. С ее помощью ана-
анализируется влияние неоднородности покрытия на поведение покрытия
при внедрении штампа.
Исследуются условия процесса индентирования реальных материа-
материалов. Определяются ограничения на величину силы, вдавливающей ин-
дентор, для того чтобы значения деформаций неоднородного полупро-
полупространства не превосходили пределов упругости. Учитывается деформи-
деформируемость штампа.
Рассматривается вопрос об экспериментальном определении меха-
механических характеристик неоднородного по глубине упругого полупро-
полупространства (толщина неоднородного слоя, значение модуля Юнга на
поверхности и в глубине).
Анализируются реальные данные. Для определения изменения по
глубине модуля упругости используется экспериментальное определе-
определение участка кривой функции жесткости поверхностного слоя.
§ 1. Определение понятия функции жесткости
неоднородного покрытия. Зависимость функции
жесткости от параметров слоя и индентора
Рассмотрим проблему определения упругих характеристик материа-
материала с неоднородным покрытием, у которого модуль упругости припо-
приповерхностного слоя отличается от модуля упругости в глубине. При этом
на практике выделяются две задачи:
1) определение физико-механических свойств подложки;
2) определение свойств приповерхностного слоя.
Для резиноподобных материалов с покрытием миллиметровой тол-
толщины существует способ испытаний на основе растяжения-сжатия,
связанный с изготовлением из материала стандартных образцов-«спут-
ников». Он трудоемок и не позволяет исследовать свойства материала
в существующих реальных конструкциях. Для более твердых и тонких
покрытий исследование упругих свойств можно проводить только при
воздействии с поверхности. Обычно эти способы определения модуля
упругости опираются на методики определения твердости поверхности.
При этом в поверхность материала некоторым усилием вдавливают
жесткий индентор (шарик, конус или пирамиду) и измеряют его осад-
§ 1. Определение функции жесткости. Ее зависимость от параметров 207
ку. Модуль упругости рассчитывают по размеру полученного отпечат-
отпечатка, величине приложенной силы и геометрическим размерам инденто-
ра по соответствующим теоретическим или эмпирическим формулам.
Также с помощью эмпирических формул пытаются учитывать влияние
покрытия и подложки.
Методы обработки результатов испытаний по вдавливанию в ма-
материал индентора, не учитывающие неоднородность материала, да-
дают низкую точность при исследовании упругости глубинного слоя,
а свойства приповерхностного слоя при этом не определяются вообще.
На основе разработанного математического аппарата появляется воз-
возможность достоверно интерпретировать данные штамповых испытаний
неоднородного материала, определить необходимый для этого набор
экспериментальных данных, повысить точность определения как моду-
модуля упругости глубинных слоев материала, так и характера изменения
модуля упругости поверхностного слоя.
Для материалов с покрытием можно, используя метод индентиро-
вания, определить модуль упругости, актуальный для некоторой зоны
контакта и в силу этого являющийся некоторой средней величиной
между модулями упругости поверхностного и глубинных слоев ма-
материала. Эту характеристику, которую будем называть эффективным
модулем или функцией жесткости неоднородного основания, можно
найти из решения контактной задачи о внедрении осесимметричного
штампа в неоднородное покрытие.
В результате ее решения определяется связь между вдавливаю-
вдавливающей силой и осадкой индентора. Однако для исследования эффекта
неоднородности материала покрытия по глубине более информативной
является производная от них величина функции жесткости.
В случае внедрения штампа с плоской подошвой функция жестко-
жесткости имеет вид
Е» = Ъ5% GЛ)
для однородного основания она является постоянной и не зависит
от размеров штампа. Здесь D — диаметр штампа, Р — величина
вдавливающей силы, 5 — перемещение штампа под действием силы Р.
Ew связана с модулем упругости Е соотношением: Ew = ^-, где
v — коэффициент Пуассона.
При внедрении параболического штампа функция жесткости имеет
следующий вид:
\1Ь
где а — радиус зоны контакта, 5 — перемещение индентора. Для неод-
неоднородного материала функция жесткости, или эффективный модуль,
является функцией безразмерного геометрического параметра а/Н.
Штамп каждого фиксированного диаметра «измеряет» некоторые
средние характеристики слоя, толщина которого пропорциональна диа-
208
Гл. 7. Оценка упругих характеристик неоднородных покрытий
метру штампа. Поэтому в результате измерений при помощи штам-
штампов разных диаметров находится информация, на основе которой, с
помощью разработанного метода расчета можно определить модуль
упругости как глубинных, так и поверхностных слоев.
Нужно отметить, что жесткость поверхностного слоя Ew (по срав-
сравнению с глубинными слоями) при постоянстве коэффициента Пуас-
Пуассона в материале не зависит от абсолютного значения коэффициента
Пуассона. Таким образом, взяв набор штампов с плоской подошвой
различного диаметра или несколько штампов с параболическим на-
наконечником, можно оценить степень неоднородности упругих свойств
поверхностного слоя и установить упругие свойства материала.
Эта задача определения упругих свойств неоднородного материа-
материала является некорректной обратной задачей математической физики.
Наиболее распространенный метод решения подобных задач — ме-
метод подбора. В нашем случае интерпретация этого метода состоит
в том, что сначала решаем прямую задачу об определении жест-
жесткости основания для некоторого набора функций изменения модуля
упругости в поверхностном слое, а затем подбираем ту функцию,
которая лучше всего согласуется с экспериментальными данными по
значениям Ew, полученным для инденторов различных диаметров.
На рис. 7.1 показаны графики функции жесткости для шести
образцов неоднородности свойств по-
171 крытия в сравнении с однородным
случаем. На рис. 7.2 приводятся
графики изменения соответствующих
трансформант ядер интегрального урав-
уравнения. Все графики даны в лога-
логарифмической шкале. Интересно от-
отметить вид трансформанты в немо-
немонотонном случае. Расположение кри-
кривых 5 и 6 обратно расположению
аналогичных кривых на рис. 7.1.
На рис. 7.3 построены графики
функции жесткости для выпуклого па-
параболического штампа G.2) (сплошные линии) и для штампа с плоской
подошвой G.1) (пунктирные линии).
На рис. 7.4, 7.5 выражения
qi(r,\)/qo(r,\)/Ew(\), A = Я/а,
приведены в виде поверхностей, которые характеризуют отличие в
распределении нормальных контактных давлений qi{r,X) под штампом
с плоской подошвой и под выпуклым индентором для законов неодно-
неоднородности вида Elc(z) (i = 1,...,6) в сравнении с однородным случаем.
Для монотонных законов неоднородности свойств слоя при фик-
фиксированных больших значениях А и соответственно малых зонах
контакта наблюдается подобие в распределении контактных давлений
3,2
1,0
0,0
од
1
Рис. 7.1
10
§ 1. Определение функции жесткости. Ее зависимость от параметров 209
2,72
1,00
0,37
2
1 10 100 и
Рис. 7.2
ОД 1,0 а/Н
Рис. 7.3
q(r)/qo(r)/E.
2,4
Ы(Н/а)
Ы(Н/а)
Рис. 7.4
по радиусу зоны контакта г в однородном и неоднородном случаях.
При росте зоны контакта в распределении контактных давлений на-
наблюдается своеобразный концевой эффект. Для немонотонного случая
210 Гл. 7. Оценка упругих характеристик неоднородных покрытий
1п(Я/о)
9(r)/qQ(r)/Ew
0,6
1п(Я/о) ~1
q(r)/qO(r)/Ew
1,5
1п(Я/а)
ln(tf/a)
q(r)/qo(r)/E
5 л
0.6
1,5
1,3
1,0
8 °'8
0,5
1п(Я/а)
Рис. 7.5
эти эффекты выражены еще больше. Для жесткого слоя при зоне кон-
контакта, сравнимой с толщиной слоя, наблюдается разгрузка под центром
штампа.
§ 2. Учет условий реального эксперимента
по индентированию
2.1. Учет деформируемости штампа. Все изложенное выше от-
относилось к абсолютно жесткому штампу. В то же время при индентиро-
вании реальных материалов, особенно металлов, упругий модуль штам-
штампа может быть вполне сопоставим с модулем исследуемого материала.
Поэтому введем в рассмотрение более общее понятие приведенного
§2. Учет условий реального эксперимента по индентированию 211
модуля при герцевском контакте сферы и полупространства:
Здесь Е\ — модуль упругости штампа, E% — модуль упругости на
поверхности неоднородного полупространства. Парное интегральное
уравнение, к которому сводится решение задачи о деформируемом
штампе, имеет вид
о
G-4)
Q(a) Jo(ar)ada = 0, г > 1.
о
Проводя, как изложено выше, построение решения уравнения, мы
получим для расчетной жесткости значение, которое будет тем ниже,
чем ближе свойства штампа к свойствам исследуемого материала.
2.2. Определение условий проведения неразрушающих испыта-
испытаний неоднородных покрытий. Пусть целью эксперимента является
контроль характера неоднородности слоя, сцепленного с однородным
упругим полупространством по зависимости сила-перемещение при
внедрении жесткого сферического индентора. Для того чтобы экспе-
эксперимент был неразрушающим при внедрении штампа в материал, на-
напряжения не должны превышать пределов упругости. Так как данные
рассуждения необходимы нам только для оценки порядка исследуемых
величин, достаточно ограничиться однородным случаем. Можно запи-
записать следующие соотношения, известные из классической задачи Герца
для сферы и полупространства [113]:
Q р п2
Е= - — , R= —. G.5)
4 aw w
Максимальное контактное напряжение при внедрении сферы в по-
полупространство имеет значение
Q р
Используя G.5), G.6), получим
а* 2Ew
~- G.6)
тга
ttR
По результатам анализа многочисленных экспериментов принято,
что предел упругости связан с твердостью по Бринеллю
а*=0.383ЯБ.
212 Гл. 7. Оценка упругих характеристик неоднородных покрытий
Введем обозначение
k Е '
тогда
сг* = k*E, G.8)
а из G.7) следует, что
2а
Таким образом, значение радиуса кривизны штампа и перемещение
связаны с зоной контакта а следующим образом:
R = 2а/тгк\ w = a2/R = тгк*а/2.
Исследование характера неоднородности слоя накладывает опреде-
определенные ограничения на размеры зоны контакта, а именно: от а = 1/4Н
до а = 4Я, где Н — толщина слоя.
Пусть перед нами стоит задача испытания покрытий толщиной от 5
до 100 мкм (микрон), причем с твердостью по Бринеллю 300-600 Мпа,
и упругим модулем подстилающего материала 210 000 Мпа. В этом
случае /с* « 2/3000, откуда
R = -ак* « 1000а *
w
а а п
W=R*W66'R =
Таким образом, R должно быть заключено в пределах от i?5 ~
~ 5/4 мм до Дюо ~ 400 мм, a w соответственно от w$ « 5/4 нм до
i 400 нм.
Так как Р = B/3)сг*тга2 , то диапазон изменения нагрузки заключен
между Ръ « 0,005 Н и Р100 -2Н.
§ 3. Определение механических характеристик
тонкого неоднородного покрытия и подстилающего
слоя по результатам экспериментального
индентирования реальных материалов
Для определения механических свойств тонких пленок использует-
используется наноиндентор, прибор, позволяющий с высокой точностью измерить
зависимость между силой, приложенной к штампу (индентору), и глу-
глубиной его внедрения в исследуемый материал.
В настоящей работе анализируются данные, которые были получе-
получены при исследовании слоя DLC (алмазоподобный углерод) толщины
250 нм с модулем Юнга 250 ГПа, нанесенного на подложку из плав-
плавленного кварца с модулем Юнга 69,6 ГПа. В ходе эксперимента был
использован индентор Hysitron, максимальная нагрузка которого —
25 мН с разрешением 100 нН. Точность при определении смеще-
§ 3. Определение механических характеристик реальных материалов 213
ния — 1 А. Данные по разгрузочному сегменту кривой сила-смещение
анализируются аналогично [264].
По результатам эксперимента была построена зависимость наблю-
наблюдаемого модуля Юнга от отношения зоны контакта к толщине слоя
Ew(a/H). При этом 0,22 < а/Н < 0,64.
Численный анализ результатов эксперимента проводился следую-
следующим образом: предполагалось, что основание является двухслойным,
требовалось определить модуль Юнга поверхностного и подстилающе-
подстилающего слоев при известной толщине покрытия. Решение находилось так,
чтобы одна из точек расчетной кривой совпадала с экспериментальным
значением, а отклонение остальных точек было минимально.
Знакопеременность функции ошибки позволяет организовать быст-
росходящийся процесс поиска параметров неоднородного основания.
При этом были получены следующие результаты:
?dlc=259 000N/mm2,
2
Таким образом, результаты наноиндентирования могут использо-
использоваться для определения параметров неоднородности основания при
известном характере неоднородности и толщине. Применение серии
штампов с различными радиусами кривизны позволит увеличить диа-
диапазон изменения Л и повысит точность определения характерных пара-
параметров неоднородности.
На рис. 7.6 сравниваются экспериментальные (ромбы) и расчетные
данные. Непрерывной линией показана функция жесткости, построен-
¦ эксперимент
- - - подбор Е0=259, Е1=50
— исходные Е0=250, Е1=70
Ew, ГПа
зоо-
250
200
150
100
50
0
0,01
ОД
Рис. 7.6
а/Н
10
ная на основе предполагаемых (до проведения эксперимента) упругих
свойств покрытия и основания. Пунктирная кривая соответствует ре-
результатам эксперимента, интерпретированным с помощью метода под-
подбора, описанного выше. Отличия от предполагаемых свойств невелики.
На рис. 7.7 представлены результаты добавочного эксперимента по
индентированию покрытия штампом радиуса 6 мкм. Из анализа этого
214 Гл. 7. Оценка упругих характеристик неоднородных покрытий
рисунка можно сделать вывод о том, что свойства кривой жесткости
определяются достаточно точно во всей области определения по отрез-
отрезку в пределах 0,22 < а/Н < 0,64.
=0,5 мкм
¦ d = 6 мкм
Я, ГПа
900
Параметры слоя
од
1 а/Н Ю 50 81 130 209 336 542 Я
Рис. 7.7
Рис. 7.8
На рис. 7.8 представлены результаты обработки экспериментальных
данных для случая, когда нам неизвестна толщина слоя. Значения
модуля упругости покрытия и подложки определялись для значений
толщины слоя от 50 нм до 1000 нм. Видно, что свойства покрытия
достаточно точно определяются при а/Н = 200 нм и более. Свойства
подложки точно определяются только при а/Н = 250 нм. Отсюда
следует, что, зная свойства подложки, мы можем оценить толщину слоя
и свойства покрытия. Для большей информативности эксперимента
нужно повысить точность определения кривой жесткости и увеличить
диапазон ее определения.
Таблица 2 позволяет провести сравнение экспериментальных и рас-
расчетных данных:
Таблица 2
Экспери-
Экспериментальные
данные Е,
[ГПа]
178,2068853
174,9839275
175,2903348
163,5181456
172,1666654
170,1402256
156,1657523
163,4591482
размер
зоны контакта,
[нм]
74,08667893
77,80391179
79,42555196
81,06043711
82,39250857
83,11300482
85,37754089
86,73016227
Л
0,296346716
0,311215647
0,317702208
0,324241748
0,329570034
0,332452019
0,341510164
0,346920649
Теоретические
значения Е,
[ГПа]
173,965213
170,965464
169,693484
168,433999
167,423541
166,882961
165,21011
164,230144
§ 3. Определение механических характеристик реальных материалов 215
Экспери-
Экспериментальные
данные Е,
[ГПа]
159,9054274
163,6266469
155,5784453
167,0463402
158,3286447
158,6768711
158,2693753
158,3886325
158,1659663
155,7275046
155,8645416
155,5282043
156,372612
156,0057148
152,268299
150,8581839
151,8765376
150,249814
145,1122533
140,696588
137,7960867
размер
зоны контакта,
[нм]
87,03602804
88,00810587
89,10613953
90,22700699
93,08661189
94,76854359
96,1777413
96,79289471
98,08263196
99,27916531
101,4941612
101,5873045
101,8815711
102,7215851
106,0761286
109,002568
109,3684182
109,7088418
118,7906526
130,027262
136,4782289
Таблица 2
Л
0,348144112
0,352032423
0,356424558
0,360908028
0,372346448
0,379074174
0,384710965
0,387171579
0,392330528
0,397116661
0,405976645
0,406349218
0,407526285
0,41088634
0,424304514
0,436010272
0,437473673
0,438835367
0,47516261
0,520109048
0,545912916
(продолжение)
Теоретические
значения Е,
[ГПа]
164,010889
163,31718
162,540633
161,758429
159,80179
158,676871
157,748892
157,348123
156,515631
155,751476
154,362515
154,30513
154,122949
153,605765
151,582382
149,869834
149,658806
149,462946
144,472209
138,844326
135,858409
Заключение
Целью исследования являлась разработка эффективного численно-
аналитического метода решения статических контактных задач теории
упругости для непрерывно-неоднородных сред. В монографии приведе-
приведены следующие новые результаты.
1. Разработан новый метод исследования краевых задач статической
теории упругости для непрерывно-неоднородных сред. Метод позволя-
позволяет с единых позиций изучить контактные задачи теории упругости для
непрерывно-неоднородных сред с фиксированной областью контакта в
антиплоской, плоской и осесимметричной постановках, изучить задачи
изгиба балок и пластин на непрерывно-неоднородных основаниях и
исследовать контактные задачи для неоднородного полупространства
с неизвестной заранее зоной контакта.
2. Разработан и обоснован численно-аналитический приближенный
метод построения интегральных уравнений контактных задач теории
упругости для непрерывно-неоднородных сред при общих законах
неоднородности, не исследованных ранее.
3. Разработан и реализован новый приближенный метод решения
парных интегральных уравнений, порождаемых контактными задачами
теории упругости для непрерывно-неоднородного слоя и полупростран-
полупространства, асимптотически точный как при больших, так и при малых
значениях характерного геометрического параметра задачи.
4. Проведен подробный численный анализ решений ряда конкрет-
конкретных контактных задач теории упругости прикладного характера, игра-
играющих важную роль в инженерных приложениях.
В основу данной работы положены исследования, выполненные
авторами в рамках исследовательского гранта РФФИ 03-01-96551-
р2003юг-а. Монография издана при финансовой поддержке РФФИ
(грант 05-01-14058-д).
ПРИЛОЖЕНИЯ
I. Фундаментальные физические константы
Гравитационная постоянная
Ускорение свободного падения
(нормальное)
Скорость света в вакууме
Магнитная постоянная
Электрическая постоянная
Масса покоя электрона
Масса покоя протона
Элементарный заряд
Отношение заряда электрона к его
массе
Постоянная Планка
Постоянная Авогадро
Постоянная Больцмана
Универсальная газовая постоянная
Постоянная Фарадея
Объем моля идеального газа при
нормальных условиях
(Ро = Ю1 325 Па, То = 273,15 К)
G = 6,6720- Ю-11 Н-м2/кг2
д = 9,80665 м/с2
с = 2,99792458 • 108 м/с
/хо = 4тг • 10~7 Гн/м =
= 12,5663706144- Ю-7 Гн/м
?0 = 8,85418782- 102 Ф/м
те = 9,109534- 101 кг
тр = 1,6726485- 10~27 кг
е= 1,6021892- 1(Г19 Кл
е/те = 1,7588047- 1011 Кл/кг
/г = 6,626176- Ю-34 Дж-с
NA = 6,022045 • 1023 моль
к= 1,380662- Ю-23 Дж/К
i^ = 8,31441 Дж/(моль-К)
F = 96,48456 • 103 Кл/моль
Vo = 22,41383 • 10 м3/моль
П. Множители и приставки для образования десятичных
кратных и дольных единиц и их наименований
Множитель
1018
1015
1012
109
106
103
102
101
Приставка
наимено-
наименование
эксо
пета
тера
гига
мега
кило
гекто
дека
обозна-
обозначение
Э
П
т
г
м
к
г
да
Множитель
ю-1
ю-2
ю-3
ю-6
ю-9
ю-12
ю-15
ю-18
Приставка
наимено-
наименование
деци
санти
МИЛЛИ
микро
нано
пико
фемто
атто
обозна-
обозначение
д
с
м
мк
н
п
ф
а
Список литературы
1. Развитие теории контактных задач в СССР. М.: Наука, 1976. 493 с.
2. Механика контактных взаимодействий / под ред. Воровича И.И., Алек-
Александрова В.М. М.: ФИЗМАТЛИТ, 2001. 672 с.
3. Абрамян Б.Л. Обзор результатов, полученных по контактным задачам
в Академии Наук Армянской ССР // В кн.: Контактные задачи и их
инженерные приложения. М. 1969. С. 3-7.
4. Абрамян Б.Л., Александров А.Я. Осесимметричные задачи теории упру-
упругости // В кн.: Труды II Всесоюзного съезда по теоретич. и прикл.
механике. М.: Наука, 1966. С. 7-37.
5. Абрамян Б.Л., Макарян B.C. Осесимметричная задача о контакте между
двумя слоями из различных материалов с учетом трения между слоями //
Изв. АН Арм. ССР. Механика. 1976. Т. 29, № 5. С. 3-14.
6. Авилкин В.И., Александров В.М., Коваленко Е.В. Об использовании
уточненных уравнений тонких покрытий в теории осесимметричных кон-
контактных задач для составных оснований // ПММ. 1985. Т. 49, вып. 6.
С. 110-117.
7. Агрест М.И., Максимов М.З. Теория неполных цилиндрических функ-
функций, их приложения. М.: Атомиздат, 1965. 351 с.
8. Айзикович СМ. Сдвиг штампом упругого неоднородного полупростран-
полупространства специального вида // Изв. АН СССР. МТТ. 1978, № 5. С. 74-80.
9. Айзикович СМ. Кручение круглым штампом неоднородного полупро-
полупространства // В кн.: Расчет оболочек и пластин. Ростов-на-Дону: РИСИ,
1978. С. 156-169.
10. Айзикович СМ. Асимптотические решения контактных задач теории
упругости для неоднородных по глубине сред // ПММ. 1982. Т. 46,
вып. 1. С. 148-158.
11. Айзикович СМ. Контактные задачи теории упругости для полупростран-
полупространства и полуплоскости, неоднородных по глубине // Статические и дина-
динамические смешанные задачи теории упругости. Ростов-на-Дону: Изд-во
РГУ, 1983. С. 121-131.
12. Айзикович СМ. Асимптотическое решение одного класса парных уравне-
уравнений // ПММ. 1990. Т. 54. С. 872-877.
13. Айзикович СМ. Асимптотическое решение одного класса парных урав-
уравнений при малых значениях параметра // Докл. АН СССР. 1990. Т. 313,
№ 1, С. 48-52.
14. Айзикович СМ. Асимптотическое решение одного класса парных уравне-
уравнений при больших значениях параметра // Докл. АН СССР. 1991. Т. 319,
№ 5. С. 1037-1041.
15. Айзикович СМ. Асимптотическое решение задачи о взаимодействии пла-
пластины с неоднородным по глубине основанием // ПММ. 1995. Т. 59, № 4.
С. 688-697.
Список литературы 219
16. Лйзикович СМ., Александров В.М. О свойствах функций податливости,
соответствующих слоистому и непрерывно-неоднородному полупростран-
полупространству // ДАН СССР. 1982. Т. 266, № 1. С. 40-43.
17. Лйзикович СМ., Александров В.М. Осесимметрическая задача о вдав-
вдавливании круглого штампа в упругое, неоднородное по глубине полупро-
полупространство // Изв.АН СССР, МТТ. 1984. Т. 39, № 2. С. 73-82.
18. Лйзикович СМ., Александров В.М. Асимптотические решения контакт-
контактных задач теории упругости для полупространства и полуплоскости,
неоднородных по глубине // Изв. АН Арм. ССР. Механика. 1986. Т. 39,
№ 3. С. 13-27.
19. Лйзикович СМ., Александров В.М. Распределение напряжений под лен-
ленточным фундаментом на неоднородном основании // В кн.: Исследование
по теории сооружений. М.: Стройиздат, 1987. Т. 25. С. 82-92.
20. Лйзикович СМ., Кренев Л.И., Серова НА. Поля напряжений и деформа-
деформаций, возникающие при взаимодействии сферы с неоднородным по глубине
покрытием упругого однородного полупространства // IV международная
конференция «Современные проблемы механики сплошной среды», 27-28
октября 1998, Ростов-на-Дону. Т. 1. С. 10-13.
21. Лйзикович СМ., Кренев Л.И., Трубчик И.С. Асимптотическое решение
задачи о внедрении сферического индентора в неоднородное по глубине
полупространство // Изв. РАН, МТТ. 2000. № 5. С. 107-117.
22. Лйзикович СМ., Кузин Б.Н. Исследование взаимодействия круглого
штампа с искусственным основанием из закрепленного химическим спо-
бом грунта // Известия СКНЦВШ. 1985. № 2. С. 87-89.
23. Лйзикович СМ., Македонов Ю.В., Герасев В.И. Авторское свидетельство
«Способ определения модуля упругости». Заявка № 4940779/28; приори-
приоритет изобретения от 29.03.91, положительное решение от 18.02.92. Патент
2002237, класс SG01#3/00, Бюллютень 39. 1993. С. 145.
24. Лйзикович СМ., Трубчик И.С. Изгиб пластин, лежащих на неоднородном
основании // Труды XIV Всесоюзной конференции по теории пластин и
оболочек. Кутаиси, 1987. Т. 1. С. 47-52.
25. Лйзикович СМ., Трубчик И.С. Асимптотические свойства приближенного
решения одного класса парных интегральных уравнений // ПММ. 1988.
Т. 52. Вып. 5. С. 850-856.
26. Лйзикович СМ., Трубчик И.С. Об асимптотических свойствах прибли-
приближенного решения одного класса парных интегральных уравнений // Докл.
АН СССР. 1989. Т. 307, № 2. С. 316-320.
27. Лйзикович СМ., Трубчик И.С. Расчет круглой плиты на неоднородном
по глубине основании // Строительная механика и расчет сооружений.
1992. № 3. С. 24-29.
28. Лйзикович СМ., Трубчик И.С. Об определении формы осадки поверх-
поверхности неоднородного по глубине полупространства при внедрении в него
кругового штампа // ДАН СССР. 1993. Т. 332, № 6. С. 702-705.
29. Лйзикович СМ., Трубчик И.С. Об асимптотическом определении фор-
формы осадки поверхности неоднородного по глубине полупространства при
внедрении в него кругового штампа // Изв. РАН, МТТ. 1995. № 2.
С. 58-63.
220 Список литературы
30. Лйзикович СМ., Трубник И.С, Шклярова Е.В. Внедрение штампа в
неоднородную по глубине полосу // Изв. АН СССР. МТТ. 1991. № 1.
С. 61-71.
31. Лйзикович СМ., Трубчик И.С, Шклярова Е.В. Расчет круглой пластины,
лежащей на неоднородном по глубине полупрстранстве // Изв. АН СССР.
МТТ. 1992. №4. С. 163-171.
32. Лкопян А.Г. О продольном сдвиге неоднородно-составного клина // Изв.
АН Армении. Мех. 1994. Т. 47, № 1-2. С. 21-26.
33. Лкопян Л.Г. О плоской деформации малонапряженного неоднородно-со-
неоднородно-составного клина // Изв. АН Армении. Мех. 1994. Т. 47, № 5-6. С. 42-48.
34. Александров В.М. О приближенном решении одного типа интегральных
уравнений // ПММ. 1962. Т. 25. вып. 5. С. 934-943.
35. Александров В.М. Контактные задачи для упругого клина // Изв. АН
СССР. МТТ. 1967. № 2. С. 120-131.
36. Александров В.М. Об одной контактной задаче для упругого клина //
Изв. АН Арм. ССР. Мех. 1967. Т. 20, № 1. С. 3-14.
37. Александров В.М. Асимптотические методы в контактных задачах теории
упругости // ПММ. 1968. Т. 32. вып. 4. С. 672-683.
38. Александров В.М. О решении одного класса парных уравнений // Докл.
АН СССР. 1973. Т. 210, № 1. С. 55-58.
39. Александров В.М. Об одном методе сведения парных интегральных урав-
уравнений и парных рядов-уравнений к бесконечным алгебраическим систе-
системам // ПММ. 1975. Т. 39. вып. 2. С. 324-332.
40. Александров В.М. Асимптотические методы в контактных задачах //
Изв. вузов. Сев.-Кавк. регион. Естеств. н. 2000. № 3. С. 12-16.
41. Александров В.М., Белоконь А.В. Асимптотическое решение одного клас-
класса интегральных уравнений и его применение к контактным задачам для
цилиндрических упругих тел // ПММ. 1967. Т. 31. вып. 4. С. 704-710.
42. Александров В.М., Ворович И.И. О действии штампа на упругий слой
конечной толщины // ПММ. 1960. Т. 24. вып. 2. С. 323-333.
43. Александров В.М., Ворович И.И. Контактные задачи теории упругости
для неклассических областей // Сб. Прочность и пластичность. М., 1971.
вып. 8. С. 19-28.
44. Александров В.М., Ворович И.И., Солодовник М.Д. Эффективное ре-
решение задачи о цилиндрическом изгибе пластинки конечной ширины
на упругом полупространстве // ИЗВ. АН СССР. МТТ. 1973. № 4.
С. 129-138.
45. Александров В.М., Гришин С.А. Напряженно-деформированное состоя-
состояние малой окрестности вершины клина при физической линейности и
различных граничных условиях // ПММ. 1987. Т. 51. вып. 4. С. 653-661.
46. Александров В.М., Калкер Д.Д., Пожарский Д.А. К расчету напряжений
в осесимметричной контактной задаче для двухслойного основания //
Изв. РАН, МТТ. 2000. № 5. С. 118-130.
47. Александров В.М., Коваленко Е.В. Метод ортогональных функций в
смешанных задачах механики сплошных сред // Прикл. мех., 1977. Т. 13,
№ 12. С. 9-17.
48. Александров В.М., Коваленко Е.В. Задачи механики сплошных сред со
смешанными граничными условиями. М.: Наука, 1986. 336 с.
Список литературы 221
49. Александров В.М., Коваленко Е.В. Задачи механики сплошных сред
со смешанными граничными условиями // ПММ. 1993. Т. 57. вып. 2.
С. 102-108.
50. Александров В.М., Коваленко Е.В., Марченко СМ. О двух контактных
задачах теории упругости для слоя с покрытием винклеровского типа //
Прикл. механика. 1983. Т. 19, № 10. С. 47-54.
51. Александров В.М., Копасенко В.В. Контактная задача для упругого кли-
клина с жестко защемленной гранью // Прикладная механика. 1968. Т. 4,
вып. 7. С. 75-82.
52. Александров В.М., Кучеров В.А. Некоторые задачи о действии двух
штампов на упругую полосу // Изв. АН СССР. МТТ. 1968. № 4.
С. 110-123.
53. Александров В.М., Кучеров В.А. О методе ортогональных полиномов в
плоских смешанных задачах теории упругости // ПММ. 1970. Т. 34.
вып. 4. С. 643-652.
54. Александров В.М., Мхитарян СМ. Контактные задачи для тел с тонки-
тонкими покрытиями и прослойками. М.: Наука, 1983. 488 с.
55. Александров В.М., Ромалис Б.Л. Контактные задачи в машиностроении.
М.: Машиностроение, 1986. 176 с.
56. Александров В.М., Сметанин Б.И. Об одном эффективном методе реше-
решения неклассических смешанных задач теории упругости // ПММ. 1971.
Т. 35, вып. 1. С. 80-87.
57. Александров В.М., Солодовник М.Д. Асимптотическое решение задачи
о цилиндрическом изгибе пластинки конечной ширины на упругом полу-
полупространстве // Прикл. мех., 1974. Т. 10, вып. 7.
58. Александров В.М., Чебаков М.И. Смешанные задачи механики сплош-
сплошных сред, связанные с интегральными преобразованиями Ханкеля и
Мелера-Фока // ПММ. 1972. Т. 36, вып. 3. С. 494-504.
59. Александров В.М., Чебаков М.И. О методе однородных решений в сме-
смешанных задачах теории упругости для усеченного клина и кольцевого
сектора // ПММ. 1983. Т. 47, вып. 5. С. 790-798.
60. Александров В.М., Шацких Л.С. Универсальная программа расчета из-
изгиба балочных плит на линейно-деформируемом основании // Труды 7-й
Всесоюзной конф. по теории оболочек и пластинок. Днепропетровск,
1969. М.: Наука, 1970. С. 46-51.
61. Александрова Г.П. Контактные задачи изгиба плит, лежащих на упругом
основании // Изв. АН СССР, МТТ. 1973, № 1. С. 97-106.
62. Александрова Г.П. О двух осесимметричных контактных задачах для
тонкого упругого слоя // В сб.: Расчет оболочек и пластин. Ростов-на-До-
Ростов-на-Дону, 1976. С. 126-135.
63. Алъперин И.Г. Напряжения в бесконечной полосе, равномерно сжатой по
половине длины // Зап. Научно-исслед. ин-та мат. и мех. Харьк. гос.
ун-та и Харьк. мат. общ. 1950. № 20. С. 107-113.
64. Ананьев И.В., Бабешко В.А. Колебания штампа на слое с переменными
по глубине характеристиками // Изв. АН СССР. МТТ. 1978. № 1.
С. 64-69.
222 Список литературы
65. Ананьев И.В., Калинчук В.В., Полякова И.Б. О возбуждении волн вибри-
вибрирующим штампом в среде с неоднородными начальными напряжениями //
ПММ. 1983. Т. 47, вып. 3. С. 483-489.
66. Андреев В.И. Обобщенные уравнения плоской задачи теории упругости
для радиально-неоднородного тела. Рук. деп. в ВИНИТИ. № 1348-85 Деп.
Моск. инж.-строит, ин-т. М., 1985.
67. Антипов Ю.А., Арутюнян Н.Х. Контактная задача для упругого слоя
с накладками при наличии трения и сцепления // ПММ. 1993. Т. 57.
вып. 1. С. 137-147.
68. Ахиезер И.И. Лекции по теории аппроксимаций. М.: Наука, 1965.
69. Бабешко В.А. Интегральные уравнения свертки первого рода на системе
отрезков, возникающие в теории упругости и математической физике //
ПММ. 1971. Т. 35. вып. 1. С. 88-99.
70. Бабешко В.А. Асимптотические свойства решений некоторых двумер-
двумерных интегральных уравнений // Докл. АН СССР. 1972. Т. 206, № 5.
С. 1074-1077.
71. Бабешко В.А. Новый эффективный метод решения динамических кон-
контактных задач // Докл. АН СССР. 1974. Т. 217, № 4. С. 777-780.
72. Бабешко В.А. Статические и динамические контактные задачи со сцеп-
сцеплением // ПММ. 1975. Т. 39, вып. 3. С. 505-512.
73. Бабешко В.А., Ворович И.И., Селезнев М.Г. Вибрация штампа на двух-
двухслойном основании // ПММ. 1977. Т. 41, вып. 1. С. 166-173.
74. Бабешко В.А., Глушков Е.В., Глушкова И.В. Методы построения мат-
матриц Грина для стратифицированного упругого полупространства // Жур-
Журнал вычислительной математики и матем. физики. 1987. Т. 27, № 1.
С. 93-101.
75. Бабешко В.А., Чепилъ М.В. О применении метода факторизации при ис-
исследовании задач гидроупругости определенного типа // Изв. АН СССР.
МТТ. 1995. № 2. С. 64-69.
76. Бабич СЮ. Контактная задача теории упругости для слоя с начальными
напряжениями // Прикл. мех., 1984. Т. 20. № 6. С. 34-40.
11. Баблоян А.А. Решение некоторых парных интегральных уравнений //
ПММ. 1964. Т. 28. вып. 6. С. 1016-1023.
78. Баблоян А.А. Плоская контактная задача для двух усеченных клиньев //
Докл. АН Арм. ССР. 1977. Т. 65. № 5.
79. Баблоян А.А., Гулканян И.О. Плоская задача теории упругости для
области, составленной из двух усеченных клиньев // Докл. АН Арм. ССР.
1976. Т. 62, № 3.
80. Беленький М.Я. Смешанная задача теории упругости для бесконечно
длинной полосы // ПММ. 1952. Т. 16. вып. 3.
81. Бирман СЕ. Об осадке жесткого штампа на упругом слое, расположенном
на несжимаемом основании // ДАН СССР. 1953. Т. 93. № 5. С. 791-794.
82. Блинова В.Г., Линьков A.M. Метод определения асимптотик в общей
вершине упругих клиньев // ПММ. 1995. Т. 59, № 2. С. 199-208.
83. Булычев СИ., Алехин В.П. Испытание материалов непрерывным вдавли-
вдавливанием индентора. М.: Машиностроение, 1990. 224 с.
Список литературы 223
84. Быркэ М.С. К решению плоской задачи теории упругости для слоистого
клина // В сб.: Вопросы механики деформируемых систем. Кишинев,
1977. вып. 1. С. 32-36.
85. Вайншлельбаум В.М., Гольдштейн Р.В. Об одном классе смешанных
осесимметричных задач теории упругости для многослойной среды //
ИПМ АН СССР, препринт № 61. М., 1975. 45 с.
86. Ватсон Г.И. Теория бесселевых функций. М., 1949. ч. 1.
87. Вигдерович И.Е., Ламзюк В.Д., Приварников А.К. Об использовании
метода функций податливости при решении граничных задач для много-
многослойных оснований сложной структуры // Докл. АН УССР. Сер. А. 1979.
№ 6. С. 434-438.
88. Вилков ИМ. Плоская контактная задача для двуслойного основания при
действии симметричной нагрузки на жесткий штамп // Изв. АН СССР.
Механика и машиностроение. 1963. № 4. С. 172-174.
89. Вилков ИМ. К вопросу определения перемещений в слоистом основании
конечной толщины // В кн.: Надежность и долговечность строит, кон-
конструкций. Волгоград, 1974. С. 91-92.
90. Ворович И.И., Александров В.М., Бабешко В.А. Неклассические сме-
смешанные задачи теории упругости. М.: Наука, 1974. 456 с.
91. Ворович И.И., Бабешко В.А. Динамические смешанные задачи теории
упругости для неклассических областей. М.: Наука, 1979. 320 с.
92. Ворович И.И., Кадомцев И.Г., Устинов Ю.А. Некоторые общие свойства
трехмерного напряженно-деформированного состояния трехслойной пли-
плиты симметричного строения // В кн.: Теория оболочек и пластин. Труды
IX Всесоюз. конф. Л., 1975. С. 36-37.
93. Ворович И.И., Солодовник М.Д. Задача об изгибе круглой пластинки,
лежащей на упругом полупространстве // Изв. СКНЦ ВШ. 1974. № 4.
С. 26-30.
94. Ворович И.И., Устинов Ю.А. О давлении штампа на слой конечной
толщины // ПММ. 1959. Т. 23. вып. 3. С. 637-646.
95. Галин Л.А. Контактные задачи теории упругости. М.: Гостехиздат, 1953.
264 с.
96. Галин Л.А. Контактные задачи теории упругости при наличии износа //
ПММ. 1976. Т. 40, вып. 6. С. 981-986.
97. Галин Л.А., Горячева И.Г. Осесимметричная контактная задача теории
упругости при наличии износа // ПММ. 1977. Т. 41, Вып. 5. С. 807-812.
98. Гахов Ф.Д. Краевые задачи. М.: Наука, 1977. 640 с.
99. Глушков Е.В., Глушкова И.В. Плоская задача о колебании штампа на
слое // Изд. СКНШ ВШ. 1969. № 1. С. 23-25.
100. Гобсон Е.В. Теория сферических и эллипсоидальных функций. М.: ГИ-
ИЛ, 1952. 476 с.
101. Голуб В.К. О расчете балочных плит на упругом основании // Изв. АН
СССР. ОТН Механика и машиностроение, 1959. № 3. С. 192-195.
102. Горбунов-Посадов И.И. Расчет балок и плит на упругом полупростран-
полупространстве // ПММ. 1940. Т. 4. вып. 3. С. 61-80.
103. Горячева И.Г., Добычин М.Н. Контактные задачи в трибологии.
М.: Машиностроение, 1988. 256 с.
224 Список литературы
104. Горячева И.Г., Торская Е.В. Анализ напряженного состояния тел с по-
покрытиями при множественном характере нагружения // Трение и износ.
1994. Т. 15, № 3. С. 349-357.
105. Горячева И.Г., Торская Е.В. Периодическая контактная задача для си-
системы штампов и упругого слоя, сцепленного с упругим основанием //
Трение и износ. 1995. Т. 16, № 4. С. 642-652.
106. Горячева И.Г., Торская Е.В. Напряженное состояние двухслойного упру-
упругого основания при неполном сцеплении слоев // Трение и износ. 1998.
Т. 19, № 3. С. 289-296.
107. Градштейн И.С, Рыжик И.М. Таблицы интегралов, сумм, рядов и
произведений. М.: Физматгиз, 1962. 1100 с.
108. Гребенщиков В.Н. Расчет круглой пластинки на упругом полупростран-
полупространстве // Сб. Теория расчета и надежность приборов. Труды II Саратовской
обл. конференции молодых ученых. 1969. С. 48-51.
109. Григорьев О.Д., Инкижинов И.С. Об упругом равновесии неоднородного
клина // В сб.: Расчеты прочности судов, конструкций и мех-мов. Ново-
Новосибирск, 1988. С. 55-62.
ПО. Грилицкий Д.В. Кручение двухслойной упругой среды // Прикл. Меха-
Механика. 1961. Т. 7. вып. 1.
111. Гудьер Дж.Н., Ходж Ф.Г. Упругость и пластичность. М.: ИИЛ, 1960.
100 с.
112. Гурса Э. Курс математического анализа М.; Л.: Гостехиздат. 1933. Т. 2.
Ч. 1. 271 с; Т. 2. Ч. 2. 287 с.
113. Джонсон К.Л. Механика контактного взаимодействия // М.: Мир, 1989.
509 с.
114. Долматов Б.И., Чикишев В.М. Определение осадок фундаментов с уче-
учетом изменения модуля деформации глинистого грунта в зависимости от
напряженного состояния // Основания, фундаменты и механика грунтов.
1984. № 1. С. 24-26.
115. Дураев А. Е. Расчет методом конечных разностей прямоугольных плит,
лежащих на грунтовом основании, модуль деформации которого меняется
с глубиной // Основания, фундаменты и механика грунтов. 1971. № 4.
116. Дураев А. Е. Расчет круглых плит на неоднородном по глубине упругом
основании // Сб. Строительные конструкции и строительная механика.
Ч. П. Саранск. 1974. С. 72-83.
117. Ефимов А. Б., Ефимов Д. Г. Сосредоточенное воздействие на упругий
несжимаемый клин // Изв. АН СССР. МТТ. 1986. № 6. С. 89-92.
118. Ефимов А. Б., Ефимов Д. Г. Действие сосредоточенной силы на ребро
несжимаемого упругого клина // Вестник Московского ун-та. Сер.1.
Математика. Механика. 1987. № 3. С. 98-101.
119. Зеленцов В. Б. О решении одного класса интегральных уравнений //
ПММ. 1982. Т. 46. вып. 5. С. 815-820.
120. Зигмунд А. Тригонометрические ряды. М.: Москва. 1965. Т. 1. 615 с;
Т. 2. 537 с.
121. Зюкин Ю. П. Изгиб балочной плиты конечной длины на линейно-дефор-
линейно-деформируемом основании общего типа // Изв. вузов, сер. Строительство и
архитектура. 1970. № 3. С. 43-48.
Список литературы 225
122. Зюкин Ю. П., Попов П. Я. Изгиб балки конечной длины на
линейно-деформируемом основании // Изв. АН СССР. МТТ. 1970. № 5.
С. 105-113.
123. Ильман В. М., Приварников А. К. Действие системы штампов на упругом
многослойном основании // Прикл. механика. 1971. Т. 7. вып. 6. С. 25-30.
124. Ильман В. М., , Ламзюк В. Д., Приварников А. К. О характере взаимо-
взаимодействия штмпа с упругим многослойным основанием // Изв. АН СССР.
МТТ. 1975. № 5. С. 134-138.
125. Ишкова А. Г. Об изгибе полосы и круглой пластины, лежащих на упругом
полупространстве // Инж. сборник. 1960. Т. 23. С. 171-181.
126. Ишкова А. Г., Коренев Б. Г. , Коренев Б. Г. Изгиб пластинок на упругом
и упругопластическом основании // Тр. 2-го Всесоюз. съезда по теорет. и
прикл. механике. М.: Наука, 1966. Т. 3. С. 157-176.
127. Каландия А.И. Математические методы двумерной упругости. М.: Наука,
1973. 393 с.
128. Калинчук В.В., Белянкова Т.П. Динамические контактные задачи для
предварительно напряженных полуограниченных тел. М.: Физматлит,
2002. 240с.
129. Канторович Л.В., Акилов Г.П. Функциональный анализ. М.: Наука,
1977. 742 с.
130. Керчман В.И. Задачи консолидации и связанной термоупругости для
деформируемого полупространства // Изв. АН ССР. МТТ. 1976. № 1.
С. 45-47.
131. Кипнис Л .А., Черепанов Г.П. Контактная задача теории упругости для
клина // ПММ. 1982. Т. 46. вып. 1. С. 141-147.
132. Клубин П.И. Расчет балочных и круглых плит на упругом основании //
Инж. сборник. 1952. Т. 12. С. 95-125.
133. Коваленко Г.П. Некоторые динамические и статические задачи теории
упругости для неоднородных сред частных видов // В кн.: Всес. конф. по
теории упругости. Тез. докл. Ереван, 1979. С. 178-180.
134. Коваленко Г.П. О контакте твердого тела с упругим полупространством
через тонкое покрытие // ПММ. 1999. Т. 63. Вып. 1. С. 119-127.
135. Коддингтон Э.А., Левинсон Н. Теория обыкновенных дифференциальных
уравнений М.: Изд-во иностр. лит., 1958. 474 с.
136. Коган Б.И. Напряжения и деформации в покрытиях с непрерывно меняю-
меняющимся модулем упругости // Труды Харьковского автомоб.-дор. инст-та.
1957. вып. 19. С. 53-66.
137. Коган Б.И., Зинченко В.Д. Напряженное состояние неоднородного слоя,
покоящегося на упругом полупространстве // Изв. ВУЗов. Строительство
и архитектура. 1969. № 3.
138. Колчин Г.Б. Плоская задача теории упругости для неоднородного кли-
клина // Изв. АН СССР. МТТ. 1971. № 3. С. 157-160.
139. Колчин Г.Б. Исследования по теории упругости неоднородных тел (основ-
(основные результаты и перспективы развития) // В кн.: X Научно-техн. конф.
Кишиневского политехи, ин-та. Тез. докл. Кишинев, 1974. С. 228-230.
140. Колчин Г.Б. Аналитические методы в теории упругости неоднородных
тел // В кн.: V Всесоюзн. съезд по теоретич. и прикл. механике. Аннот.
докл. Алма-Ата, 1981. С. 203.
8 СМ. Айзикович и др.
226 Список литературы
141. Колчин Г.Б., Лапенко В.В. Плоская задача термоупругости для неод-
неоднородного клина, жестко защемленного по одной из граней. // В кн.:
Тепловые напряжения в элементах конструкций. Респ. межвед. сб. Киев,
1978. вып. 18. С. 65-68.
142. Колчин Г.Б., Фаверман Э.А. Теория упругости неоднородного тела. Ки-
Кишинев: Штиинца, 1977. 147 с; 1987. 166 с.
143. Крагельский И.В., Михин П.М. Узлы трения машин. Справочник.
М.: Машиностроение, 1984. 280 с.
144. Кузнецов Е.А. Деформирование неоднородного полупространства при
давлении круглого цилиндрического штампа // Проблемы прочности.
1983. № 11. С. 30-37.
145. Кузнецов Е.А. О взаимосвязи некоторых контактных характеристик с
переменными упругими свойствами сопряженных тел // Трение и износ.
1983. Т. 4, № 2. С. 238-248.
146. Кузнецов Е.А. К решению контактных задач для неоднородного полу-
полупространства при давлении на него круглого цилиндрического штампа //
Прикл. мех. 1984. Т. 20, № 8. С. 24-33.
147. Кузнецов Е.А. Распределение напряжений на поверхности неоднородного
полупространства при давлении на него кругового штампа // Трение и
износ. 1984. Т. 5, № 6. С. 1085-1094.
148. Кузнецов Е.А. Давление круглого цилиндра на полупространство с пере-
переменным по глубине коэффициентом Пуассона // Изв. АН СССР. МТТ.
1985. № 1. С. 73-86.
149. Кузнецов Е.А., Гороховский Г.А. Напряженное состояние неоднородного
полупространства с переменным по глубине коэффициентом Пуассона при
действии на него сосредоточенной силы // Трение и износ. 1984. Т. 5,
№ 5. С. 806-816.
150. Лазарев М.И., Перлин П.И. О решении задач пространственной теории
упругости для кусочно-однородной среды // Докл. АН Арм. ССР. Меха-
Механика. 1978. Т. 67, № 5. С. 295-301.
151. Лазарев М.И., Перлин П.И. Решение пространственных задач теории
упругости для кусочно-однородной среды с постоянным коэффициентом
Пуассона // ПММ. 1979. Т. 43, № 6. С. 1122-1125.
152. Ламзюк В.Д. Деформация упругого слоя нормальной нагрузкой // В сб.:
Деформация упругого слоя нормальной нагрузкой. Днепропетровск, 1986.
С. 97-105.
153. Ламзюк В.Д., Приварников А.К. Упругая деформация неоднородного
многослойного пакета при неполном контакте его слоев // Докл. АН
УССР. Сер. А. 1977. № 7. С. 618-622.
154. Ламзюк В.Д., Приварников А. . Решение граничных задач теории упру-
упругости для многослойных оснований // В сб.: Устойчивость и прочность
элементов конструкций. Днепропетровск. 1978, вып. 1. 64 с, вып. 2. 68 с.
155. Ламзюк В.Д., Феденко А.И. Основные граничные задачи плоской теории
упругости для составного клина // В сб.: Устойчивость и прочность
элементов конструкций. Днепропетр. ун-т. Днепропетровск, 1979, вып. 3.
С. 64-75.
Список литературы 227
156. Лапенко В.В. Смешанная плоская задача теории упругости для неод-
неоднородного клина // В сб.: Вопросы механики деформируемых систем.
Кишинев, 1977, вып. 1. С. 12-20.
157. Лапенко В.В. Об одной задаче термоупругости для неоднородного кли-
клина // В сб.: Расчет конструкций и возведение зданий и сооружений.
Кишинев. 1986. С. 57-63.
158. Лапенко В.В., Диордиев Н.Д. Решение задачи для неоднородого клина
методом ортогонализации // В кн.: Мат. исследования. Кишинев, 1976,
вып. 40. С. 82-84.
159. Лебедев Н.Н., Уфлянд Я.С. Осесимметричная контактная задача для
упругого слоя // ПММ. 1958. Т. 22. С. 320-326.
160. Левитан Б.М., Саргсян И.С. Введение в спектральную теорию: Само-
Самосопряженные обыкновенные дифференциальные операторы. М.: Наука,
1970. 671 с.
161. Леонов М.Я. К расчету фундаментов плит // ПММ. 1940. Т. 4, вып. 3.
С. 61-98.
162. Лурье А.И. Теория упругости. М.: Наука, 1970. 824 с.
163. Лурье А.И., Брачковский Б.З. Решение плоской задачи теории упругости
для клина // Труды Ленинградского политехи, ин-та. 1941. № 3.
164. Лущик О.Н. О поведении корней уравнения, определяющего особенность
напряженного состояния в окрестности вершины составного клина // Изв.
АН СССР. МТТ. 1979. № 5. С. 82-92.
165. Марковец М.П. Определение механических свойств металлов по твердо-
твердости. М.: Машиностроение, 1979. 191 с.
166. Михлин С.Г. Интегральные уравнения. М.-Л.: ГИТТЛ, 1947. 380 с.
167. Моисеев Н.Н. Численные методы в теории оптимальных систем.
М.: Наука, 1971.
168. Моссаковский В.И., Качаловская Н.Е., Голикова С.С. Контактные задачи
математической теории упругости // Киев: Наук, думка, 1985. 175 с.
169. Мусхелишвили Н.И. Некоторые основные задачи математической теории
упругости. М.: Наука, 1966. 707 с.
170. Наумов Ю.А., Чистяк В.И. К определению напряженного состояния
упругого слоя с произвольной неоднородностью по толщине // В кн.:
Устойчивость и прочность элементов конструкций. Днепропетровск, 1979,
вып. 3. С. 97-104.
171. Наумов Ю.А., Шевляков Ю.А. К изгибу круглых плит на многослойном
основании // Изв. АН СССР, МТТ. 1967. № 1. С. 154-162.
172. Наумов Ю.А., Шевляков Ю.А. Изгиб балочных плит на упругом осно-
основании при неполном контакте // Гидроаэромеханика и теория упругости.
Научно-техн. сб. Изд-во ХГУ, 1968. вып. 9.
173. Наумов Ю.А., Шевляков Ю.А., Чистяк В.И. К решению основных задач
теории упругости для слоя с произвольной неоднородностью по тол-
толщине // Прикл. мех., 1970. Т. 6. вып. 7. С. 25-31.
174. Неустроев Э.А., Цейтлин А.И. К расчету круглых плит на упругом
основании // Основания, фундаменты и механика грунтов. 1971. № 5.
С. 7-9.
228 Список литературы
175. Никишин B.C. Осесимметричные контактные задачи теории упругости
для неоднородных сред // В сб.: Сообщения по прикладной математике.
1976, вып. 3. С. 51-103.
176. Никишин B.C. Задачи теории упругости для неоднородных сред // Со-
общ. по прикл. мат. ВЦ АН СССР. 1976, вып. 4. 60 с.
177. Никишин B.C., Шапиро Г.С. Задачи теории упругости для многослойных
сред. М.: Наука, 1973.
178. Никишин B.C., Шапиро Г.С. Задача о неполном контакте кольцевого или
кругового штампа с упругой слоистой средой // Изв. АН СССР. МТТ.
1976. № 5. С. 27-38.
179. Нуллер Б.М. Некоторые контактные задачи для упругого бесконечного
клина // ПММ. 1972. Т. 36. вып. 1. С. 157-163.
180. Нуллер Б.М. Деформация упругого клина, подкрепленного балкой //
ПММ. 1974. Т. 38. С. 876-882.
181. Плевако В.П. Распределение напряжений в зоне скачкообразного изме-
изменения упругих свойств неоднородного материала // ПММ. 1979. Т. 43,
№ 4. С. 760-764.
182. Попов Г.Я. К теории изгиба плит на упругом неоднородном полупростран-
полупространстве // Изв. вузов. Сер.Строительство и архитектура. 1959. № 11-12.
С. 11-19.
183. Попов Г.Я. Контактная задача теории упругости при наличии круговой
области контакта // ПММ. 1962. Т. 26, вып. 1. С. 207-216.
184. Попов Г.Я. Пластинки на линейно-деформируемом основании // Прикл.
механика. 1972. Т. 8, вып. 3. С. 3-17.
185. Попов Г.Я. Метод ортогональных многочленов // В кн. Развитие теории
контактных задач в СССР. М.: Наука, 1976.
186. Попов Г.Я., Ростовцев НА. Контактные (смешанные) задачи теории
упругости // В кн.: Труды II Всесоюзного съезда по теоретич. и прикл.
механике. М.: Наука, 1966. С. 235-252.
187. Попов Г.Я., Хомяк Ю.М. Изгиб круглой пластинки на линейно-деформи-
линейно-деформируемом основании // Мат. 8-й Всесоюзной конф. по теории оболочек и
пластинок. Ростов-на-Дону, 1971. М.: Наука, 1973. С. 752-756.
188. Попов Г.Я., Хомяк Ю.М. Расчет круглой пластинки, лежащей на
линейно-деформируемом основании // Строит, мех. и расчет сооружений.
1972. № 5. С. 15-19.
189. Потележко В.П., Филлипов А.П. Контактная задача для плиты, лежащей
на упругом основании // Прикл. мех., 1967. Т. 3, вып. 1. С. 87-91.
190. Приварников А.К. Действие неплоского штампа на упругий слой конеч-
конечной толщины, лежащий на жестком основании // Докл. АН УССР. 1962.
№ 8.
191. Приварников А.К. Пространственная деформация многослойного основа-
основания // В сб.: Устойчивость и прочность элементов конструкций. Днепро-
петр. ун-т. Днепропетровск, 1973. С. 27-45.
192. Приварников А.К. Решение граничных задач теории упругости для мно-
многослойных оснований. Метод. Разработка. Днепропетровск, 1976. 60 с.
193. Приварников А.К., Ламзюк В.Д. Упругие многослойные основания. 4.1.
Днепропетр. ун-т. Днепропетровск, 1985. 162 с. (рук. деп. в ВИНИТИ
23.12.85, № 8789-В).
Список литературы 229
194. Приварников А.К., Стулей В.А. О контакте растянутой полосы с ос-
основанием // Гидроаэромеханика и теория упругости. 1985. вып. 33.
С. 118-123.
195. Прокофьев Б.М. Контактная задача для составного клина // В кн.:
Взаимодействие в механике конструкций. Киев; Одесса, 1980. С. 52-59.
196. Проценко B.C., Рвачев В.Л. Пластина, имеющая форму бесконечной
полосы, на упругом полупространстве // ПММ, 1976. Т. 40, вып. 2.
С. 298-305.
197. Рвачев В.Л. Исследования ученых Украины в области контактных задач
теории упругости // Прикладная механика. 1967. Т. 3, № 10. С. 109-116.
198. Рвачев В.Л., Проценко B.C. Контактные задачи теории упругости для
неклассических областей. Киев: Наукова думка, 1977. 235 с.
199. Родзевич И.А. О расчете многослойного упругого основания // В сб.
«Вопросы механики». МГУ, 1961. вып. 193.
200. Романов В.Г. Обратные задачи математической физики. М.: Наука, 1964.
263 с.
201. Ростовцев П.А. Об одном интегральном уравнении, встречающемся в
задаче о давлении жесткого фундамента на неоднородный грунт // ПММ.
1961. Т. 25, вып. 1.
202. Ростовцев П.А. К теории упругости неоднородной среды // ПММ. 1964.
Т. 28, вып. 4.
203. Ростовцев П.А., Храневская И.Е. Решение задачи Буссинеска для полу-
полупространства при степенной зависимости модуля упругости от глубины //
ПММ. 1971. Т. 35, вып. 6.
204. Сафарян П.Б. О малонапряженности плосконапряженного составного
клина // Изв. АН Армении. Мех. 1994. Т. 47, № 5-6. С. 49-54.
205. Снеддон Я.П. Преобразования Фурье. М.: ИИЛ, 1955. 668 с.
206. Тадевосян Р.Г. Плоская задача для бесконечного составного клина //
Изв. АН Арм. ССР. Мех. 1983. Т. 36, № 6. С. 12-22.
207. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач.
М.: Наука, 1979. 288 с.
208. Тихонов А.Н., Самарский А.А. Уравнения математической физики.
М.: Наука, 1972. 735 с.
209. Титчмарш Е. Введение в теорию интегралов Фурье. М.-Л.: Гостехиздат,
1948.
210. Толстое Г.П. Ряды Фурье. М.: Физматгиз, I960. 390 с.
211. Торская Е.В. Анализ влияния трения на напряженное состояние тел с
покрытиями // Трение и износ. 2002. Т. 23, № 2. С. 130-138.
212. Триус Е.Б. Изгиб плиты на упругом основании при неполном контакте с
основанием (плоская задача) // Науч. докл. высш. школы. Сер.: Строи-
Строительство. 1958. № 3. С. 92-101.
213. Триус Е.Б. Изгиб круглой пластины на упругом основании при неполном
контакте с основанием // Научн. докл. высш. школы. Сер.: Строитель-
Строительство. 1958. № 4. С. 27-36.
214. Уфлянд Я.С. Интегральные преобразования в задачах теории упругости.
Л.: Наука, 1967. 404 с.
215. Уфлянд Я.С. Метод парных уравнений в задачах математической физики.
Л.: Наука, 1977. 220 с.
230 Список литературы
216. Федоровский В.Г., Дохнянский М.П. Осадки круглых и кольцевых фун-
фундаментов: прогноз и сопоставление с данными натурных наблюдений //
Сб. трудов II Балтийской конференции по механике грунтов и фундамен-
тостроения. Таллин, 1988. Т. 2. С. 99-106.
217. Федорюк М.В. Обыкновенные дифференциальные уравнения. М.: Наука,
1985. 350 с.
218. Фень Г.А. Нелинейная осесимметричная задача для многослойного паке-
пакета // В кн.: Устойчивость и прочность элементов конструкций. Днепро-
Днепропетровск, 1988. С. 22-30.
219. Филиппов Л.П. Колебания деформируемых систем. М.: Машиностроение.
1970. 592 с.
220. Филиппов И.А. К расчету напряженно-деформированного состояния сло-
слоистого массива горных пород // Физ.-техн. проблемы разработки полез-
полезных ископаемых. 1979. № 2. С. 3-10.
221. Цейтлин А.И. О методе парных интегральных уравнений и парных рядов
и его приложениях к задачам механики // ПММ. 1966. Т. 30, № 2.
С. 259-266.
222. Цейтлин А.И. Об изгибе круглой пластины, лежащей на линейно-дефор-
линейно-деформируемом основании // Изв. АН СССР. МТТ. 1969. № 1. С. 99-112.
223. Чебаков М.И. О дальнейшем развитии «метода больших Л» в теории
смешанных задач // ПММ. 1976, вып. 3. Т. 40. С. 561-565.
224. Чезари JI. Асимптотическое поведение и устойчивость решений обыкно-
обыкновенных дифференциальных уравнений. М.: Мир, 1964.
225. Чернышов А.Д. О деформировании сплошных сред в клиновидной обла-
области с гладкими гранями // ПММ. 1975. Т. 39. С. 1093-1099.
226. Шацких Л.С. К расчету изгиба плиты на упругом слое // Изв. АН СССР,
МТТ. 1972. № 2. С. 170-176.
227. Шевляков Ю.А. Матричные алгоритмы в теории упругости неоднородных
сред. Киев-Одесса: Вища школа, 1977. ПО с.
228. Шехтер С.Я. Расчет бесконечной плиты, лежащей на упругом основании
конечной и бесконечной мощности и нагруженной сосредоточенной си-
силой // Сб. НИС Фундаментстрой. 1939. № 10.
229. Шинджикашвили О.Н. Влияние неоднородности материала на порядок
сингулярности упругих решений вблизи вершины углов // Труды Тбилис-
Тбилисского матем. ин-та. 1979. Т. LXI. С. 60-67.
230. Ширинкулов Т.В. О расчете балочных плит на упругом основании, модуль
упругости которого является функцией глубины // ДАН УзССР. 1967.
№ 9.
231. Ширинкулов Т.В. Расчет круглых плит, лежащих на упругом полупро-
полупространстве, модуль которого есть степенная функция глубины // Сб.
Вопросы механики. Ташкент, 1970. Вып 6. С. 102-122.
232. Штаерман И.Я. Контактная задача теории упругости. М.-Л.: Гостехиз-
дат, 1949. 272 с.
233. Aizikouich S.M., Alexandrov V.M., Kalker J.J., Kreneu L.I., Trubchik I.S.
Analytical solution of the spherical indentation problem for a half-space with
gradients with the depth elastic properties. Int. J. of Solids and Structures,
2002 T. 39, № 10. P. 2745-2772.
Список литературы 231
234. Aizikovich S.M., Cells J.-P., Krenev L.I., and Serova N.A. Non-destructive
mechanical characterisation of mechanical properties of non-homogeneous
nanostructured coatings // in G.M. Chow et al. (eds.), Nanostructured Films
and Coatings, Kluwer Academic Publishers, 2000. P. 315-322.
235. Aizikovich S.M., Krenev L.I., and Serova N.A. Non-Destructive Determi-
Determination of Mechanical Properties of Non-Homogeneous Coatings. // 7-th Eu-
European Conference on Non-Destructive Testing and Exhibition. Copenhagen,
Denmark. May 26-29, 1998. P. 1063-1069
236. Aizikovich S.M., Krenev L.I., Trubchik I.S. The Analytical solution of the
Hertzian contact problem for functionally gradient materials // 19-th Int.
Congress Theor. and Appl.Mech. Kioto, Aug 25-31. 1996. Book of Abstracts.
P. 644.
237. Awojobi A.O. On the hyperbolic variation of elastic modulus in a non-homo-
non-homogeneous stratum. Intern. J. Solids Struct., 1976. V. 2, № 11, P. 639-748.
238. Brown P.T., Gibson R.E. Surface settlement of a finite elastic layer whose
modulus increases linearly with depth. Intern. J. Numer. and Anal. Meth.
Geomech., 1979. V. 3, № 1, P. 33-47.
239. Bufler H. Die Torsion der Inhomogenen Dicken Platte. ZAMM., 1963. V. 43,
№ 9. P. 389-401.
240. Burmister DM. The General Theory of Stresses and Displacements in
Layered System. J.Appl.Phys., 1945. V. 16. P. 89-94; 126-127; 296-302.
241. Chen W.T. Computation of Stresses and Displacements in a Layered Elastic
Medium. Int. J. Engng. Sci. A971). V. 9 P. 775-800.
242. Chen Dai-Heng, Nisitani Hironobu. Logarithmic singular stress field in
bonded wedges. Nihon kikai gakkai ronbunshu. A=Trans. Jap. Soc. Mech.
Eng. A., 1993. V. 59, № 567. P. 2687-2693.
243. Chen Dai-Heng. Condition for occurence of logarithmic stress singularity.
Nihon kikai gakkai ronbunshu. A=Trans. Jap. Soc. Mech. Eng. A. 1996.
V. 62, № 599. P. 1634-1642.
244. Chen Dai-Heng. Analysis of stress singularity at a vertex of bonded wedges
based on the separation of variables technique. Nihon kikai gakkai ronbun-
ronbunshu. A=Trans. Jap. Soc. Mech. Eng. A., 1999. V. 65, № 635. P. 1-8.
245. Domnich V., Gogotsi.Y. Effect of phase transformations on the shape of the
unloading curve in the nanoindentation of silicon. Applied physics letters,
V. 76, № 16, P. 2214-2216.
246. Dub. S.N. Curves of elasto-plastic deformation of thin coatings obtained in
depth-sensing indentation experiments. MRS Symposium proceedings, 1998.
V. 505. P. 223-228.
247. El-Sherbiney M.G.D., Hailing J. The Hertzian Contact of Surfaces Covered
with Metallic Films. Wear., 1996. V. 40, № 3. P. 325-337.
248. Engel P.A. Indentation debonding test for polymer coatings to a substrate.
Int.J.Adhesion and adhesives, July 1985, P. 129-132.
249. Giannakopoulos A.E., Suresh S. Indentation of solids with gradients in
elastic properties: Part I. Point force. Part II. Axisymmetric indentors. Int.
J. Solids Structures, 1997. V. 34. № 19. P. 2357-2428.
250. Gibson R.E. Some Results Concerning Displacements and Stresses in a
Nonhomogeneous Elastic Half-space. Geotechnique, 1967. V. 17. P. 58-67.
232 Список литературы
251. Gibson R.E., Brown P. Т., Andrews K.R.F. Some Results Concerning Dis-
Displacements in a Non-homogeneous Elastic Layer. Z. Angew. Math, und
Phys., 1971. V. 22, № 5, P. 855-868.
252. Gibson R.E., Kalsi G.S. The Surface Settlement of a Linearly Inhomogeneous
Cross-anisotropic Elastic Half-Space. Z. Angew. Math, und Phys., 1974.
V. 25, № 6. P. 843-847.
253. Gibson R.E., Sills Gilliane C. Settlement of a Strip Load on a
Non-homogeneous Ortotropic Incompressible Elastic Half-Space. Quart. J.
Mech. And Appl. Math., 1975. V. 28, № 2. P. 233-243.
254. Koduchi Hideo, Inoue Tadanobu, Yada Toshio. Stress singularity in
three-phase bonded structure. Trans. ASME. J. Appl. Mech., 1996. V. 63,
№ 2, P. 252-258.
255. Krai E.R., Komvopoulos K., Bogy D.B. Elastic-Plastic Finite Element Anal-
Analysis of Repeated Indentation of a Half-Space by a Rigid Sphere. ASME. J.
Appl. Mech., 1993. V. 60. P. 829-841.
256. Krai E.R., Komvopoulos K., Bogy D.B. Finite Element Analysis of Re-
Repeated Indentation of an Elastic-Plastic Layered Medium by a Rigid Sphere,
Part 1 — Surface Results, Part II — Subsurface Results. Trans. ASME. J.
Appl. Mech. V. 62. March 1995. P. 20-42.
257. Kuznetsov Ye.A. Plane contact problem for a half-space with a Poisson's
ratio that varies with depth. Wear., 1983. V. 92, № 2. P. 171-196.
258. Kuznetsov Ye.A. Stress-strain state of an inhomogeneous half-space with
Poisson's ratio that varies under the pressure of a round cylinder-shaped
indenter. Wear., 1984. V. 97. P. 213-248.
259. Lira Y. Y., Chaudhri MM., Enomoto Y. Accurate determination of the me-
mechanical properties of thin aluminum fims deposited on sapphire flats using
nanoindentations. J. Mater. Res. V. 14, № 6, June 1999, P. 2314-2327.
260. Lu C.J., Bogy D., Kaleko R. Nanoindentation Hardness Tests Using a
Point Contact Microscope. Journal of Tribology, January 1994. V. 116.
P. 175-180.
261. Mishuris G.S. Boundary value problems for Poisson's equation in a
multi-wedge - multi-layered region. Arch. Mech, 1996. V. 48, № 4,
P. 711-745.
262. Moutmitounet P., Edlinger M.L., Felder E. Finite Element Analysis of
Elastoplastic. Indentation: Part I — Homogeneous Media; Part II — Appli-
Application to Hard Coatings. Transactions of the ASME. Journal of Tribology.
V. 115. 1993. P. 10-19.
263. Mukherjee S. Torsion problem of a circular die in a non-homoeneous elastic
layer perfectly bonded to a non-homoeneous elastic layer rigidly fixed at the
other end. Indian J. of Theoretical Physics. 1984. V. 32, № 1, P. 39-46.
264. Pharr G.M., Oliver W.C. An improved technique for determining hardness
and elastic modulus using load and displacement sensing indentation experi-
experiments. J. Mater. Res. V. 7, № 6, June 1992, P. 1564-1583.
265. Pharr G.M., Oliver W.C. Measurement of Thin Film Mechanical Properties
Using Nanoindentation. MRS BULLETIN/JULY. 1992. P. 28-33.
266. Shahani A.R., Adibnazari S. Analysis of perfectly bonded wedges and
bonded wedges with an interfacial crack under antiplane shear loading. Int.
J. Solids and Struct. 2000. V. 37, № 19, P. 2639-2650.
Список литературы 233
267. Suresh S., Giannakopoulos A.E., Alcala J. Spherical indentation of composi-
tionally graded materials: theory and Experiments. Acta mater. 1997. V. 45,
№4. P. 1307-1321.
268. Suresh S., and Giannakopoulos A.E. A new method for estimating residual
stresses by instrumented sharp indentation. Acta mater. A998). V. 46, № 16.
P. 5755-5767.
269. Inoue Tadanobu, Koduchi Hideo, Yada Toshio. Effect of elastic property of
intermediate material on order of stress singularity. JSME Int. J. A. 1995.
V. 38, № 2, P. 163-170.
270. Inoue Tadanobu, Koduchi Hideo. Influence of the intermediate material on
the order of stress singularity in three-phase bonded structure. Int. J. Solids
and Struct. 1996. V. 33. № 3. P. 399-417.
271. Vetters H.R., Schulz A., Mayr P., Saunders S.R.J. Characterization and
properties of hard coatings; international standardization efforts, Surface and
Coatings Technology. 1996. V. 86-87. P. 345-350.
272. Yingzhi K.Li., Hills D.A. The Herzian Cone Crack. Transactions of the
ASME. Journal of Applied Mechnics. V. 58, March 1991. P. 120-127.
273. Zeng K., Breder K., Rowcliffe D.J. The Hertzian stress field and formation of
cone cracks: I. Theoretical approach. II. Determination of fracture toughness.
Acta metall. mater. 1992. V. 40, № 10. P. 2595-2605.
ОГЛАВЛЕНИЕ
Введение
I. Постановка контактных задач для неоднородных
полуограниченных областей
Глава 1. Контактные задачи для неоднородных по глубине полу-
полупространства и полуплоскости 12
§ 1. Чистый сдвиг полосовым штампом неоднородного полупространства 12
§ 2. Кручение жестким круглым штампом неоднородного полупростран-
полупространства 18
§ 3. Вдавливание штампа в неоднородную полуплоскость 22
§ 4. Вдавливание жесткого кругового в плане штампа в неоднородное
полупространство 29
§ 5. Некоторые общие свойства трансформант ядер интегральных урав-
уравнений контактных задач для неоднородных полупространства и
полуплоскости,
их аппроксимация 31
§ 6. Примеры построения трансформант ядер интегральных уравнений
контактных задач для неоднородного полупространства 40
Глава 2. Постановка контактных задач для непрерывно-
неоднородного по глубине слоя и клина, неоднородного по
угловой координате, в случае заданной границы контакта.
Вывод интегральных уравнений 45
§ 1. Чистый сдвиг полосовым штампом неоднородного слоя 45
§2. Внедрение штампа в неоднородную полосу 50
§ 3. Чистый сдвиг полосовым штампом неоднородного пространствен-
пространственного клина 55
§4. Внедрение штампа в неоднородный клин 61
§ 5. Некоторые общие свойства трансформант ядер интегральных урав-
уравнений контактных задач для неоднородных полосы и клина, их
аппроксимация аналитическими выражениями 68
Оглавление 235
II. Двухсторонний асимптотический метод
решения парных интегральных уравнений
Глава 3. Двухсторонние асимптотические решения некоторых
классов парных интегральных уравнений 72
§ 1. Классификация интегральных уравнений контактных задач для по-
полуограниченных областей 72
§ 2. Замкнутое решение одного класса интегральных уравнений, порож-
порождаемых преобразованием Фурье 73
§ 3. Замкнутое решение класса интегральных уравнений, порождаемых
преобразованием Ханкеля J\ 80
§ 4. Замкнутое решение одного класса интегральных уравнений, порож-
порождаемых преобразованием Ханкеля Jo 86
§ 5. Двухсторонние асимптотические свойства замкнутых приближен-
приближенных решений контактных задач для полупространства (полуплос-
(полуплоскости) 91
§ 6. Замкнутое решение интегрального уравнения, порождаемого пре-
преобразованиями Фурье и Меллина 100
§ 7. Двухсторонние асимптотические свойства замкнутых приближен-
приближенных решений контактных задач для неоднородных полосы и клина 107
§ 8. Определение формы осадки поверхности неоднородного по глубине
полупространства для задачи о внедрении штампа в неоднородное
полупространство 117
§ 9. Численные примеры 120
III. Применение аналитических методов
к решению некоторых прикладных задач
Глава 4. Изгиб пластин на неоднородном основании 126
§ 1. Постановка задач 128
§ 2. Изгиб балки на непрерывно-неоднородной полуплоскости 130
§ 3. Изгиб балки на неоднородной полосе и клине 133
§ 4. Взаимодействие круглой пластины с неоднородным полупростран-
полупространством 137
§ 5. Определение осадки поверхности основания вне круглой пластины 146
§6. Примеры расчета пластин на неоднородном основании 148
236 Оглавление
Глава 5. Напряженно-деформированное состояние неоднородного
по глубине полупространства при действии произвольной осе-
симметричной нагрузки 156
§ 1. Постановка граничной задачи для непрерывно-неоднородного по
глубине полупространства при заданных на его поверхности уси-
усилиях 156
§ 2. Построение фундаментального решения для неоднородного по глу-
глубине полупространства 160
§ 3. Численный анализ фундаментального решения для некоторых ха-
характерных видов неоднородности 165
Глава 6. Контактные задачи с неизвестной заранее зоной контак-
контакта для неоднородных тел 176
§1. Внедрение параболического индентора в неоднородное полупро-
полупространство 176
§ 2. Приближенное решение задачи о внедрении выпуклого штампа в
непрерывно-неоднородное по глубине полупространство 178
§ 3. Численный анализ решения задачи о внедрении параболического
штампа в неоднородное основание 182
§ 4. Анализ напряженно-деформированного состояния неоднородного
полупространства 185
Глава 7. Оценка упругих характеристик неоднородных покрытий
методом индентирования 206
§ 1. Определение понятия функции жесткости неоднородного покрытия.
Зависимость функции жесткости от параметров слоя и индентора 206
§ 2. Учет условий реального эксперимента по индентированию 210
§ 3. Определение механических характеристик тонкого неоднородного
покрытия и подстилающего слоя по результатам экспериментально-
экспериментального индентирования реальных материалов 212
Заключение 216
Приложения 217
Список литературы 218
Научное издание
ЛЙЗИКОВИЧ Сергей Михайлович
АЛЕКСАНДРОВ Виктор Михайлович
БЕЛОКОНЬ Александр Владимирович
КРЕНЕВ Леонид Иванович
ТРУБЧИК Ирина Степановна
КОНТАКТНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
ДЛЯ НЕОДНОРОДНЫХ СРЕД
Редактор Н.Б. Бартошевич-Жагелъ
Оригинал-макет: И.В. Шутов
Подписано в печать 12.12.05. Формат 60x90/16. Бумага офсетная.
Печать офсетная. Усл. печ. л. 15. Уч.-изд. л. 18,2. Тираж 400 экз.
Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997, Москва, ул. Профсоюзная, 90
E-mail: fizmat@maik.ru, fmlsale@maik.ru;
http://www.fml.ru
Отпечатано с готовых диапозитивов
в ППП «Типография «Наука»
121099, г. Москва, Шубинский пер., 6