Автор: Быков В.П. Силичев О.О.
Теги: применение оптики в целом физика квантовая радиотехника математическая физика теоретическая физика физматлит лазерные резонаторы
ISBN: 5-9221-0297-4
Год: 2004
УДК 535.8
ББК 22.34+32.86-5
Б95
Быков В. П., Силичев О.О. Лазерные резонаторы. — М.:
ФИЗМАТЛИТ, 2004. - 320 с. - ISBN 5-9221-0297-4.
В книге изложены основные методы анализа лазерных резонаторов —
матричный, метод интегрального уравнения, геометро-оптический метод.
Большое внимание уделено методам практического построения схем ре-
резонаторов, обеспечивающих те или иные специальные свойства лазерного
излучения — мощность, малую расходимость, стабильность и проч. с учетом
специфики активной среды, режима работы лазера. Рассмотрено большое
количество практически важных примеров.
Материал книги основан на курсах лекций, читавшихся и читаемых
авторами в МГУ и МФТИ. Он вполне доступен студентам старших курсов
технических вузов и предназначен в первую очередь лицам, специализиру-
специализирующимся в области лазерной физики и техники.
Ил. 142.
ISBN 5-9221-0297-4 © физматлит, 2003, 2004
СОДЕРЖАНИЕ
Введение 5
Глава 1. Оптика гауссовых пучков 9
§1.1. Гауссов пучок в свободном пространстве 9
§ 1.2. Лазерный резонатор, образованный сферическими зерка-
зеркалами 19
§ 1.3. Прохождение гауссова пучка через тонкую линзу и отра-
отражение его от сферического зеркала 25
§ 1.4. Потери энергии в лазерных резонаторах 30
§1.5. Матричный метод расчета лазерных резонаторов 35
§ 1.6. Астигматичный гауссов пучок, астигматичные оптиче-
оптические элементы, астигматичные резонаторы 45
§ 1.7. Эрмит-гауссов пучок и высшие моды лазерного резонато-
резонатора, образованного сферическими зеркалами 51
§ 1.8. Лагерр-гауссов пучок и вырождение мод лазерного резо-
резонатора 65
§ 1.9. Электрическое и магнитное поля гауссова пучка 70
§ 1.10. Состояние поляризации мод лазерного резонатора. Метод
Джонса 73
§1.11. Расчет резонаторов матричным методом. Резюме 81
§ 1.12. Гауссовы пучки — решения уравнений Максвелла .... 87
§ 1.13. Гауссов пучок с двумя системами главных осей 91
§ 1.14. Кольцевые резонаторы 104
Глава 2. Метод интегрального уравнения 117
§ 2.1. Преобразование параксиальных пучков гауссовыми опти-
оптическими системами 117
§ 2.2. Метод интегрального уравнения в теории резонаторов . 127
§ 2.3. Интегральное уравнение резонатора, содержащего негаус-
совые оптические элементы 134
§ 2.4. Конфокальный резонатор 140
§ 2.5. Методы решения интегрального уравнения в теории ре-
резонаторов 155
Глава 3. Сложные лазерные резонаторы 169
§3.1. Связанные лазерные резонаторы 169
§ 3.2. Селекция продольных мод 175
§ 3.3. Согласование связанных резонаторов 179
§ 3.4. Резонаторы с дисперсионными элементами 183
Содержание
Глава 4. Резонаторы твердотельных лазеров 189
§ 4.1. Термооптические искажения активных элементов твердо-
твердотельных лазеров 189
§4.2. Резонаторы с термооптически возмущенным активным
элементом 198
§ 4.3. Резонаторы одномодовых твердотельных лазеров с непре-
непрерывной накачкой 211
§ 4.4. Устойчивые резонаторы одномодовых твердотельных ла-
лазеров с импульсной накачкой 226
§ 4.5. Резонаторы одномодовых лазеров неустойчивой конфигу-
конфигурации 232
§ 4.6. Резонаторы твердотельных технологических лазеров . . 247
Глава 5. Геометрическая оптика лазерных резонаторов . . 256
§5.1. Геометрическая оптика лазерных резонаторов в парак-
параксиальном приближении 256
§ 5.2. Двумерный эллиптический резонатор 262
§ 5.3. Эллипсоидальный резонатор 267
§ 5.4. Движение короткого (фемтосекундного) волнового паке-
пакета в эллипсоидальном резонаторе 279
§ 5.5. Эллипсоидальный резонатор — волновое решение .... 283
§ 5.6. Лучевые системы в резонаторах более общего типа, чем
эллипсоидальный 293
§ 5.7. Построение волнового поля по лучевой картине 296
§ 5.8. Оптические линии задержки 303
Список-литературы 310
Светлой памяти
Александра Михайловича Прохорова
посвящается
ВВЕДЕНИЕ
Представление о волновом движении электромагнитного поля воз-
возникло после того, как Максвелл усовершенствовал существовавшие до
него уравнения электромагнетизма и в результате получил уравнения,
названные впоследствии его именем. Электромагнитные волны яви-
явились прямым следствием введенного Максвеллом в уравнения тока
смещения. С пониманием возможности волнового движения пришло и
понимание возможности использования резонаторов для наблюдения
электромагнитных волн. Действительно, первое наблюдение электро-
электромагнитных волн Герцем было связано с использованием резонатора —
так называемого вибратора Герца, который в дальнейшем широко ис-
использовался в технике и дожил до наших дней — многочисленные
телевизионные антенны, расположенные на крышах домов, представ-
представляют собой слегка модифицированный вариант вибратора Герца. От-
Отметим, что по современной терминологии вибратор Герца следовало
бы назвать открытым резонатором, поскольку часть запасенной в нем
энергии могла излучаться в свободное пространство, более того, сама
возможность наблюдения электромагнитных волн была обусловлена
именно этой особенностью вибратора Герца.
Герц работал с относительно короткими, метровыми волнами, в ра-
радиотехнике же на первых этапах использовались длинные, до несколь-
нескольких километров, волны, для которых вибратор Герца был неудобен.
Поэтому в радиотехнике тогда нашел широкое применение колеба-
колебательный контур, состоящий из соединенных последовательно конден-
конденсатора и катушки индуктивности, предложенный и исследованный
В. Томсоном. В принципе томсоновский контур также является от-
открытым резонатором, поскольку может излучать в свободное про-
пространство. Однако эта его способность в длинноволновом диапазоне
выражена крайне слабо, что обусловлено малостью его размеров по
сравнению с длиной волны.
Последующее развитие радиотехники и особенно радиолокации
было связано с тенденцией к уменьшению длины волны электромаг-
электромагнитного излучения. При этом открытость колебательного контура,
его способность излучать в свободное пространство увеличивалась, но
воспринималась исследователями как недостаток, поскольку приво-
приводила к увеличению потерь колебательного контура. Вследствие этого
существенным усовершенствованием техники генерирования электро-
Введение
магнитных волн явился переход к экранированным, закрытым со всех
сторон, иначе говоря, объемным резонаторам, не обладавшим таким
недостатком, как потери на излучение. Объемные электромагнитные
резонаторы не были чем-то абсолютно новым, так как ранее были
известны объемные акустические резонаторы.
Появление открытых резонаторов в их современной, лазерной
форме тесно связано с зарождением квантовой электроники. Как из-
известно, квантовая электроника стартовала с молекулярного генерато-
генератора или аммиачного мазера, длина волны которого близка к одному
сантиметру, т. е. является довольно короткой. При таких коротких
волнах, как сантиметровые, и особенно миллиметровые, выявились
недостатки объемных резонаторов. С уменьшением длины волны
электромагнитного поля уменьшались и размеры объемных резонато-
резонаторов. При этом возрастало отношение площади поверхности резона-
резонатора к его объему, что, в свою очередь, приводило к возрастанию роли
омических потерь резонатора. Сделать высокодобротный резонатор в
указанном диапазоне длин волн оказывалось довольно трудно, хотя
многочисленные попытки в этом направлении имели место. Делались
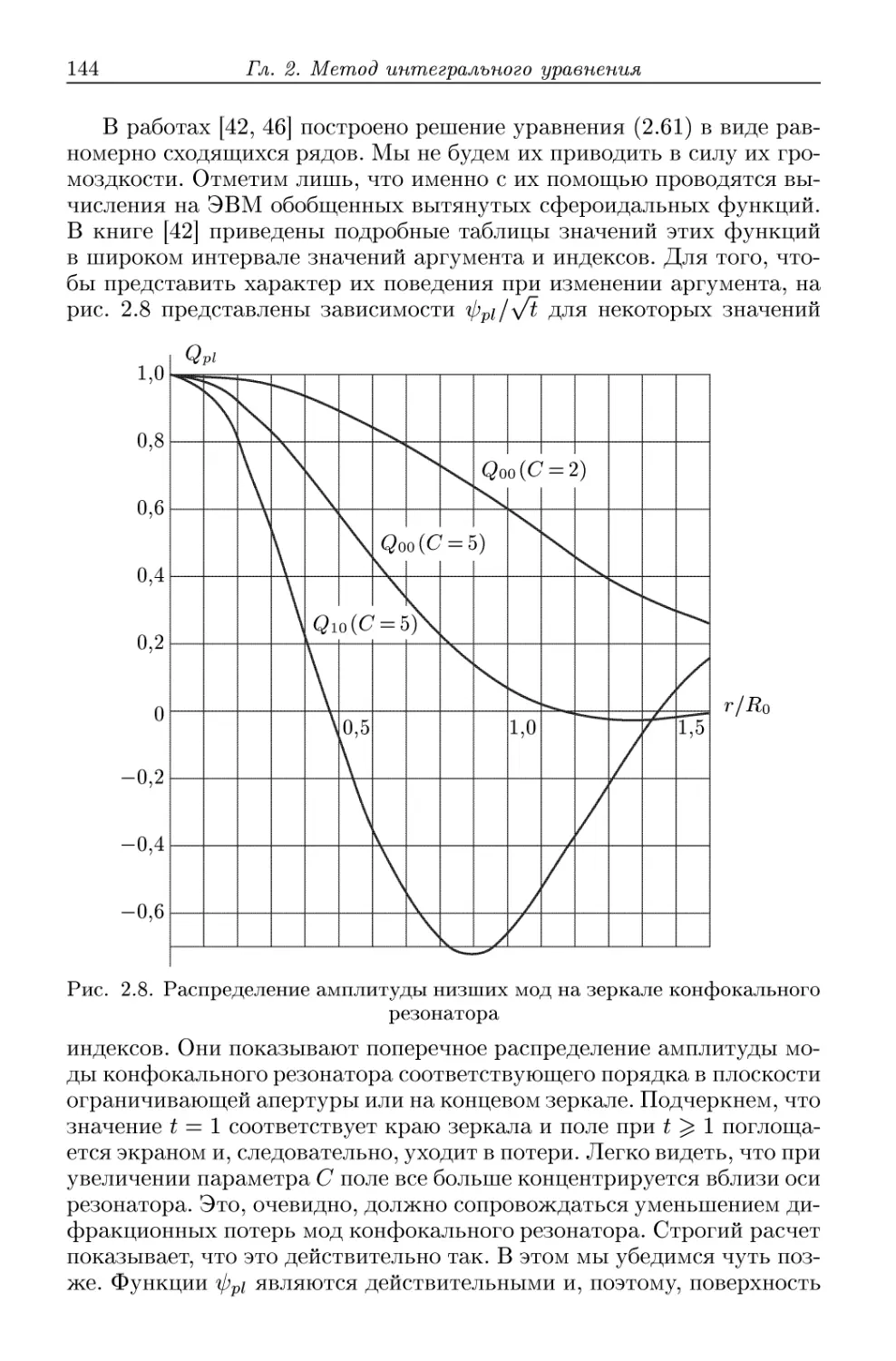
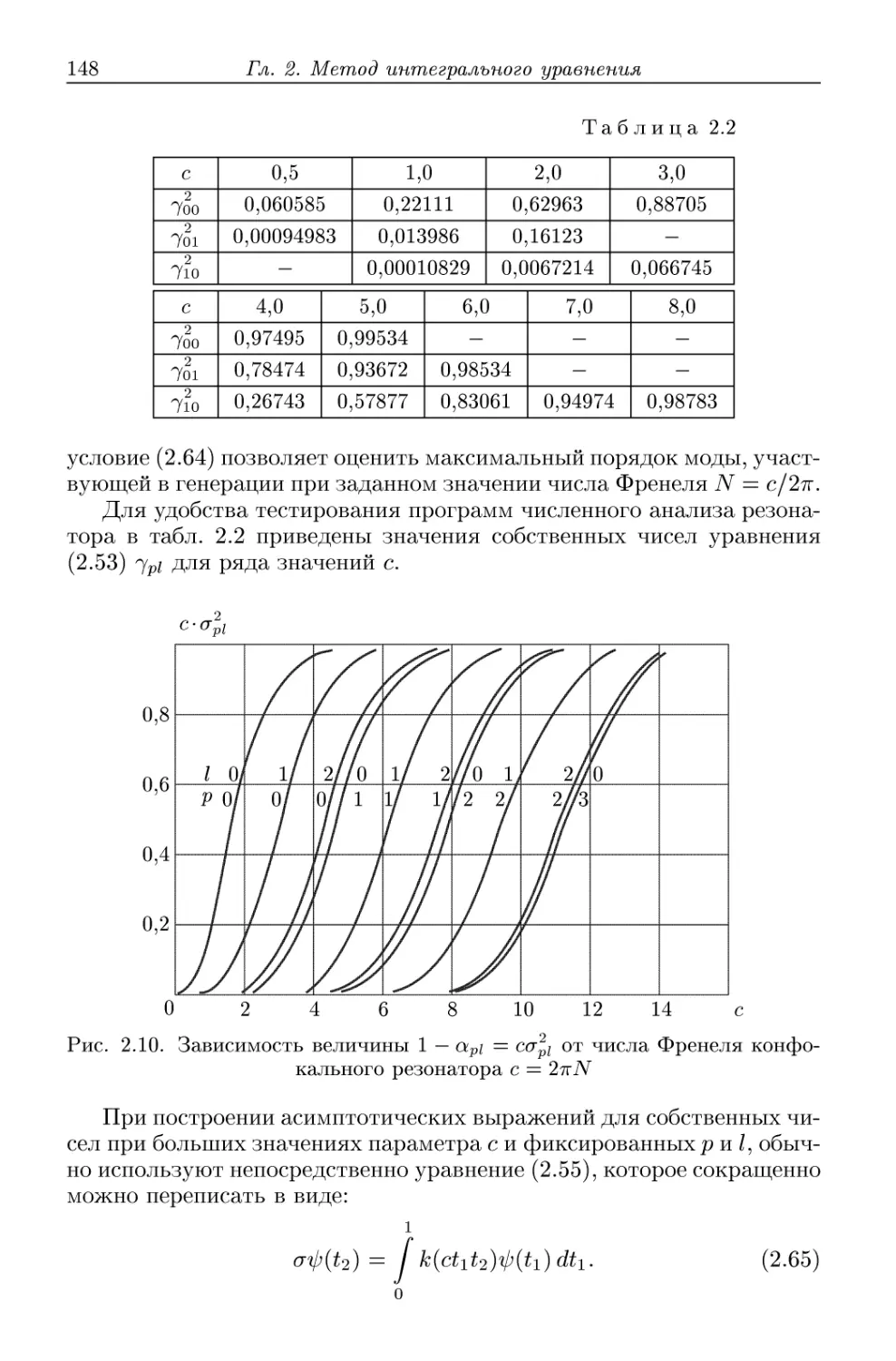
также попытки изготавливать объемные резонаторы, большие длины
волны, однако они приводили к другой трудности, а именно, к много-
модовости; с увеличением резонатора быстро возрастало число типов
колебаний (мод), способных возбуждаться в нем.
Резонатор аммиачного мазера, хотя и был типичным объемным
резонатором, имел довольно большие отверстия для впуска и выпус-
выпуска пучка молекул аммиака. При этом выяснилось, что удаление части
стенок резонатора при некоторых условиях не слишком сильно уве-
увеличивает потери резонатора. Это наталкивало на мысль о переходе к
открытым резонаторам. Главным достоинством открытого резонато-
резонатора оказалась возможность сделать его много большим длины волны.
Как выяснилось, удаление части стенок объемного резонатора слабо
влияет на распределение полей и потери лишь некоторых, достаточ-
достаточно симметричных его мод; подавляющая же часть мод оказывается
сильно деформированными и низко добротными.
Открытый резонатор впервые предложен A.M. Прохоровым [1];
первый экспериментально реализованный резонатор [2] был образо-
образован двумя параллельными соосными металлическими дисками с се-
серебряным покрытием и возбуждался петлей связи, питаемой обычным
высокочастотным клистроном на длине волны ~ 3 см.
Моды объемного резонатора можно рассматривать как стоячие
волны, имеющие узлы на стенках резонатора, а также как бегущие
волны, отражающиеся от стенок резонатора и переходящие сами в
себя при последовательных переотражениях. Рассматривая моды ци-
цилиндрического резонатора как бегущие волны, можно выделить среди
них группу мод, у которых волновой вектор почти параллелен оси ци-
цилиндра, и другую, более обширную группу мод, у которых волновой
вектор значительно наклонен по отношению к оси цилиндра. Оказа-
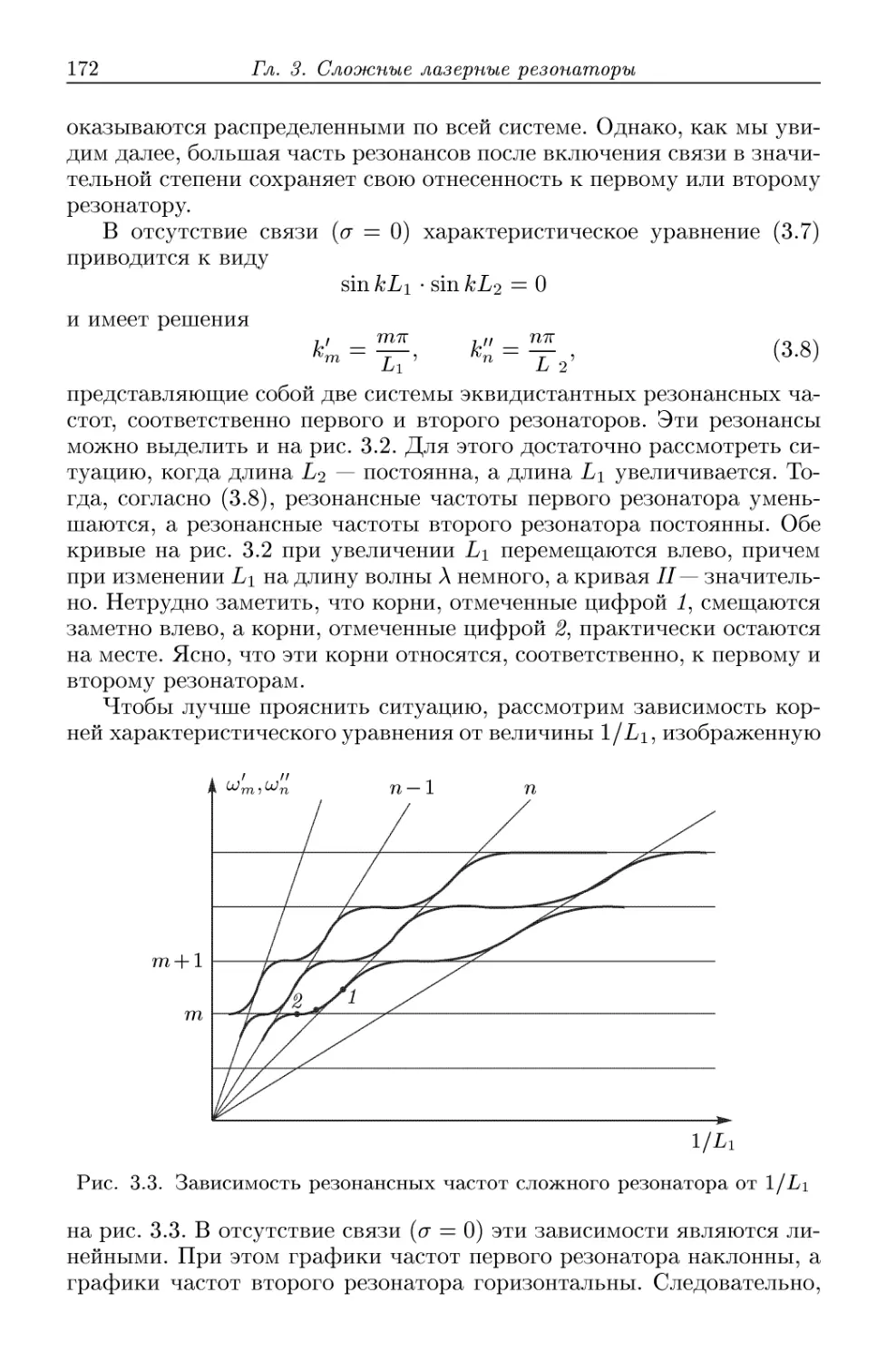
Введение
лось, что удаление боковой цилиндрической поверхности резонатора
почти не влияет на первую группу мод резонатора и в то же время
сильно деформирует и делает низкодобротными вторую группу мод.
Спектр резонатора при этом делается редким, хотя его размеры мно-
много больше длины волны; благодаря последнему обстоятельству роль
стенок оказывается незначительной и оставшиеся моды обладают вы-
высокой добротностью. Это и составляет тот полезный эффект, который
возникает при переходе от объемного резонатора к открытому. Таким
образом, открытые лазерные резонаторы возникли как усовершен-
усовершенствование объемных. В названии их — открытые резонаторы — отра-
отразилась некоторая их вторичность по отношению к объемным (закры-
(закрытым) резонаторам. Мы еще обсудим в дальнейшем вопрос о том, какие
резонаторы — открытые или объемные — следует считать первичны-
первичными, а какие вторичными, этот вопрос не только терминологический, за
ним скрыты и некоторые принципиальные обстоятельства. Сейчас же
отметим, что происхождение открытых резонаторов от объемных от-
отразилось как на постановке задачи о модах открытого резонатора, так
и на методах их исследования, постановка задачи и методы исследова-
исследования мод открытого резонатора по крайней мере на первых порах были
в значительной мере заимствованы из теории объемных резонаторов.
Напомним, что в теории объемных резонаторов постановка задачи
заключается в отыскании решений уравнений Максвелла, удовлетво-
удовлетворяющих определенным граничным условиям на стенках резонатора.
Дополнив открытый лазерный резонатор стенками так, чтобы он стал
объемным, и исследовав моды этого объемного резонатора известны-
известными методами, можно затем определить, какие моды останутся неиз-
неизменными при переходе к открытому резонатору.
Мода объемного резонатора, как уже отмечалось, может рассмат-
рассматриваться в виде волны, являющейся решением уравнений Максвелла,
которая после отражений от стенок резонатора переходит сама в себя
или совпадает сама с собой. Действительно, условие того, что вол-
волна должна отразиться от стенок резонатора, означает, что граничные
условия удовлетворяются. Условие же, что волна после отражений
должна совпадать сама с собой, есть условие стационарности. Все эти
соображения могут быть, таким образом, перенесены в теорию откры-
открытых лазерных резонаторов.
В настоящее время имеется несколько способов теоретического
описания лазерных резонаторов. Частично эти способы перекрывают-
перекрываются, важнее однако то, что каждый из этих способов имеет свою
область приложения, в которой он, так сказать, вне конкуренции.
Важнейшими такими способами являются: описание мод лазерных
резонаторов и лазерного излучения с помощью гауссова пучка, метод
интегрального уравнения, геометрическая оптика, метод разделения
переменных и некоторые другие.
Гауссов пучок пригоден для описания мод идеализированных оп-
оптических систем, а именно, оптических систем с так называемыми
Введение
квадратичными или гауссовыми элементами. Огромное число реаль-
реальных оптических элементов может быть приближенно и с высокой сте-
степенью точности отнесено к этой категории. Одним из самых универ-
универсальных методов является метод интегрального уравнения, хотя он
громоздок и в большинстве случаев требует применения вычислитель-
вычислительных машин. Информация, получаемая с его помощью, как правило,
не может быть получена другими методами. Геометрическая оптика
также является сильным методом. В параксиальном приближении она
смыкается с гауссовой оптикой. В непараксиальном же или, как иног-
иногда говорят, аберрационном приближении она вне конкуренции. Метод
разделения переменных применяется сравнительно редко и обычно
перекрывается другими методами.
В настоящее время опубликованы многие сотни работ по тео-
теории лазерных резонаторов. Первопроходцами этого направления были
Фокс и Ли [3], Бойд и Гордон [4], Сучкин [5], Вайнштейн [6], Когельник
[7], Таланов [8], Сигмен [9], Ананьев [10] и др. [11, 12]. Для матема-
математического обоснования проблемы лазерных резонаторов важны были
работы ленинградской математической школы, нашедшие отражение,
в частности, в книге В.М. Бабича и B.C. Булдырева [13].
Настоящая книга содержит пять глав. Гл. 1 посвящена оптике гаус-
гауссовых пучков. Глава 2 посвящена методу интегрального уравнения.
В ней рассматриваются методы исследования лазерных резонаторов,
содержащих негауссовы элементы — диафрагмы с резким краем, эле-
элементы с аберрациями и др. В главе 3 исследуются резонаторы, со-
содержащие несколько оптических элементов (например, вспомогатель-
вспомогательные зеркала) различного назначения. Вспомогательные зеркала могут
влиять на продольный спектр резонатора, в частности, делать его бо-
более редким. При этом важную роль играет согласование поперечных
мод лазерного резонатора. В лазерах на красителях дополнительные
оптические элементы позволяют реализовывать одномодовый режим
генерации. Глава 4 посвящена резонаторам твердотельных лазеров.
Их основной особенностью является наличие термооптически иска-
искаженного под влиянием накачки активного элемента. Отыскание ре-
зонаторных конфигураций, наименее восприимчивых к нестабильно-
стям накачки, является довольно трудным делом, читатель почерпнет
в четвертой главе много полезного для себя в этом отношении. В гла-
главе 5 излагаются геометро-оптические методы исследования резонато-
резонаторов. Введение и гл. 1, 3, 5 написаны В.П. Быковым; гл. 2, 4 — О.О. Си-
личевым.
Авторы признательны A.M. Прохорову, Ф.В. Бункину, М.Ф. Стель-
маху, П.П. Пашинину, В.И. Конову, В.В. Савранскому, Ю.Д. Голяеву,
М.И. Ананяну, А.С. Левину, Ю.И. Швецу и другим за содействие в
работе. Авторы признательны также Российскому Фонду Фундамен-
Фундаментальных исследований за поддержку издания книги (Грант № 02-02-
30055).
Глава 1
ОПТИКА ГАУССОВЫХ ПУЧКОВ
§ 1.1. Гауссов пучок в свободном пространстве
Гауссовы пучки хорошо описывают моды тех резонаторов, которые
образованы квадратичными, или гауссовыми элементами. К таким
элементам относятся (в параксиальном приближении) линзы, сфери-
сферические зеркала при нормальном и наклонном падении на них пуч-
пучка, диафрагмы с плавно (по гауссову закону) меняющимся погло-
поглощением, так называемые квадратичные среды и т. п. Подавляющее
большинство резонаторов именно такими элементами и образованы.
К негауссовым элементам относятся диафрагмы с резкими краями,
диэлектрики (в том числе активные элементы), обладающие сильны-
сильными аберрациями, т. е. неквадратичной зависимостью показателя пре-
преломления от радиуса и др.
Следует отметить огромное разнообразие резонаторов, модой ко-
которых является гауссов пучок, при том, что все эти пучки являются
разновидностями единственного астигматичного эрмит-гауссова пуч-
пучка, описанного далее в § 1.7. Если учесть еще и простоту расчета мод,
по крайней мере для резонаторов, имеющих плоскость симметрии,
(правило ABCD\ то становится ясно, что оптика гауссовых пучков
есть незаменимое и весьма мощное средство исследования лазерных
резонаторов. Даже если в резонаторе имеются негауссовы элементы,
первоначальный расчет в пределах гауссовой оптики дает хорошую
ориентировку для дальнейшего исследования.
Для того чтобы яснее оттенить свойства гауссова пучка, будем
сравнивать его с плоской волной. Волновое движение в плоской волне
описывается несколькими параметрами, такими как частота, ампли-
амплитуда, направление и скорость распространения, фаза. Считается, что
плоская волна занимает все пространство, следовательно, плоская
волна является идеализацией, реально такие объекты не существу-
существуют. Тем не менее представление о плоской волне оказывается очень
полезным. Математически плоская волна описывается простым соот-
соотношением
u(r,t) = Gexp(-iut + ikr + i(p), A.1)
где u(r,t) — величина, характеризующая волновое движение в точке г
в момент времени ?, например, смещение частиц среды в поверхност-
поверхностной или звуковой волне, одна из компонент напряженности поля в
электромагнитной волне и т. п. Частота со определяет скорость измене-
10 Гл. 1. Оптика гауссовых пучков
ния величины и со временем, волновой вектор к определяет скорость
изменения величины и в пространстве. Направление волнового векто-
вектора к определяет собой направление распространения плоской волны.
С частотой uj и волновым вектором к связаны такие величины, как
период колебаний волны Т и длина волны Л:
, Л = 2тг/|к|;
отношение
v = u/\k\
называется фазовой скоростью распространения волны.
По поводу выражения A.1) для плоской волны необходимо сде-
сделать два замечания. В природе существует много типов волнового
движения: волны на поверхности жидкости, упругие волны (в частно-
частности, звук), электромагнитные волны (в частности, радиоволны, свет),
в соответствии с гипотезой де Бройля можно говорить об электрон-
электронных волнах и вообще о волнах вещества и т. д. Несмотря на специфи-
специфику каждого типа волн, все они имеют много общих черт. Например,
для всех этих волн можно ввести представление о плоских волнах
A.1). Правда, некоторые из этих волн могут быть многокомпонент-
многокомпонентными, т. е. волна в каждой точке описывается не одной, а несколькими
величинами. Электромагнитные волны, интересующие нас в данной
книге, как раз являются многокомпонентными. Они описываются в
каждой точке пространства электрическим вектором C компоненты)
и магнитным вектором C компоненты), всего б компонент. Однако
электромагнитные поля, которые рассматриваются ниже, как прави-
правило, устроены так, что все их компоненты могут быть выражены через
одну выделенную компоненту. Тогда достаточно рассмотреть только
волну, соответствующую выделенной компоненте. Обычно в качестве
выделенной компоненты используется наибольшая поперечная (по от-
отношению к направлению распространения поля) компонента электри-
электрического поля. Более детально этот вопрос будет рассмотрен в § 1.9.
Здесь же отметим, что подобное однокомпонентное приближение (све-
(сведение к одной компоненте в общем случае может быть сделано лишь
приближенно) является очень эффективным и позволяет описать по-
подавляющую часть свойств лазерных резонаторов.
Второе замечание касается комплексного представления волны
A.1). Подобное представление или запись волновых величин широко
распространено и очень удобно. Возможность такой записи основана
на простом обстоятельстве, а именно, если некоторая комплексная ве-
величина удовлетворяет тому или иному линейному дифференциально-
дифференциальному уравнению (или даже системе таких уравнений) с вещественными
коэффициентами, то тому же уравнению удовлетворяют отдельно ве-
вещественная и мнимая части этой комплексной величины. Имеет место
и обратное положение: если некоторые две величины удовлетворяют
упомянутому выше дифференциальному уравнению, то ему же удо-
§1.1. Гауссов пучок в свободном пространстве 11
влетворяет и комплексная величина, в которой первые две величины
являются соответственно вещественной и мнимой частями.
Разумеется, всякая физически наблюдаемая величина является ве-
вещественной. Поэтому, выполнив те или иные математические преоб-
преобразования в удобной комплексной форме, для получения физически
наблюдаемых величин следует переходить к вещественным величи-
величинам. Так, взяв вещественную часть и, получим
щ(г, t) = Reu(r,t) = G cos(out - kr - ср) A.2)
— вещественное выражение, описывающее физически наблюдаемое
явление распространения плоской волны. Мнимая часть и также мо-
может быть использована в качестве вещественного выражения для вол-
волны
и2 (г, t) = — Im u(r, t) = G sm(ujt — kr — ф);
это выражение может быть получено и из выражения A.2), если в
последнем фазе ср придать новое значение, равное ср + тг/2.
В данной книге мы будем интересоваться почти исключительно
монохроматическими волнами, т. е. волнами с фиксированной часто-
частотой; описывающие такие волны выражения всегда содержат множи-
множитель
Именно из-за того, что этот множитель всегда один и тот же, он мо-
может быть опущен во всех выражениях, за исключением тех, где его
роль специально подчеркивается. Так, для плоской волны получается
выражение
и(т) =Geikr+i^. A.3)
Если вещественную часть волны A.3) умножить на cos out или si
то получится
;/ ч (cosoot „ ,, ч
и (гЛ) = Reu х < = Gcosfkr + ср) х
— выражение, описывающее стоячую волну.
Таким образом, вычисляя вещественную часть волны A.1), полу-
получаем вещественное выражение для плоской бегущей волны. Если же
вычислить вещественную часть той же волны A.1), но с опущенным
временным множителем, и умножить эту часть на cosc^t или sincjt, то
получится вещественное выражение для стоячей волны. То же прави-
правило остается справедливым и для волн более сложной конфигурации,
нежели плоская волна.
Иногда амплитуду волны G посредством соотношения
G = ea, a = lnG
переводят в показатель степени, при этом волна типа A.1) принимает
вид
u(r,t) = ea^\ A.4)
12 Гл. 1. Оптика гауссовых пучков
где anb — некоторые функции аргументов г и t. В этом случае следу-
следует понимать, что вещественная часть показателя степени описывает
амплитудное распределение волны A.4), а мнимая часть того же по-
показателя описывает зависимость фазы от г и t. В некоторых случаях
показатель степени может представлять собой выражение, в котором
вещественная и мнимая части не разделены, тогда для отыскания ам-
амплитудного и фазового распределений достаточно произвести такое
разделение известными математическими методами.
Вернемся теперь к описанию гауссова пучка. От плоской волны
он отличается прежде всего тем, что занимает не все пространство,
а некоторую ограниченную его часть, основная часть гауссова пуч-
пучка сосредоточена внутри фигурной трубки, образованной вращением
гиперболы вокруг той ее оси, которую гипербола не пересекает (выбе-
(выберем эту ось в качестве оси z координатной системы) (рис. 1.1). Вдоль
оси z гауссов пучок простирается от — оо до +оо. Поле гауссова пучка
отлично от нуля как внутри трубки, так и вне ее, но вне трубки оно
быстро убывает при удалении от оси пучка и становится ничтожно
малым по сравнению с полем внутри трубки.
Математически гауссов пучок описывается следующими двумя эк-
эквивалентными выражениями:
u[r,z) =
где г = \Jx2 + у2 — расстояние от точки наблюдения в пучке до оси z и
G — амплитудная константа. Этот пучок приближенно и с учетом дру-
других компонент поля удовлетворяет уравнениям Максвелла (см. § 1.9
и § 1.12) при зависимости от времени вида e~lujt (в выражениях A.5)
и A.6) эта зависимость, как условлено, опущена). Обратим внима-
внимание, что зависимость показателя экспоненты от поперечных коорди-
координат квадратична. Как мы увидим далее, эта квадратичность является
существенным качеством гауссова пучка. Зависимость от продольной
координаты z более сложная, кроме того, от z зависит также и пред-
экспоненциальный множитель. В выражениях для гауссова пучка фи-
фигурирует вещественный параметр 6, имеющий размерность длины и
называемый параметром гауссова пучка или чаще параметром кон-
фокальности гауссова пучка. Гауссов пучок считается заданным, если
известны его параметр Ъ и волновое число
к = со/с = 2тг/А.
Иногда в качестве основных используют параметры а и к, причем
Ь = ка2. A.7)
§1.1. Гауссов пучок в свободном пространстве 13
Нетрудно видеть, что второе выражение для гауссова пучка A.6)
отличается от первого A.5) тем, что в нем в показателе экспоненты
разделены вещественная и мнимая части. Это обстоятельство удобно
тем, что позволяет исследовать амплитудное и фазовое распределе-
распределения в гауссовом пучке и другие его характеристики. Преимущества
же первой формы выяснятся позднее. Отметим, что гауссов пучок,
поскольку он выражается лишь через г2, обладает цилиндрической
симметрией.
Рассмотрим амплитудное распределение в плоскости z = 0. Из
A.6), опуская множитель г, получаем
A.8)
Подобная зависимость в математике хорошо известна и носит назва-
название гауссовой экспоненты. От этой зависимости произошло и название
всего пучка — гауссов пучок. Как видим, параметр а характеризует
поперечный размер гауссова пучка в плоскости z = 0. В точке г = а
зависимость A.8) имеет перегиб, т.е.
д2и/дг2 = 0
при г — а. Амплитуда гауссова пучка спадает в е раз на расстоянии
г = ал/2 от оси пучка. Плотность энергии в пучке пропорциональна
квадрату модуля и:
\u(r,z = 0)\2=G2exp(-r2/a2)
и, следовательно, плотность энергии пучка спадает в е раз при г = а.
Величину а обычно называют полушириной гауссова пучка в пе-
перетяжке (см. ниже).
Отойдем теперь от плоскости z = 0 и рассмотрим распределение
плотности энергии при некотором определенном z:
Как видим, зависимость плотности энергии от радиуса качествен-
качественно такая же, как и в плоскости z = 0, т. е. остается гауссовой экспо-
нентой, однако характерный поперечный размер гауссова пучка изме-
изменился. Он стал равным
w(z) = у^+Щ/kb = y/a2+z2/k2a2, A.10)
т. е. увеличился. Очевидно, он увеличился бы и в том случае, если
бы мы положили z —> —z, т.е. пошли бы влево от плоскости z = 0
(рис. 1.1). Следовательно, в плоскости z = 0 поперечный размер гаус-
гауссова пучка минимален — это место пучка называется перетяжкой.
Отметим, что радиус пучка w и координата z связаны друг с другом,
14
Гл. 1. Оптика гауссовых пучков
согласно A.10), уравнением
w z _ л
A.П)
т.е. кривая w(z) представляет собой гиперболу, что и отмечалось вы-
выше (рис. 1.1). Поверхность, образующаяся при вращении этой гипербо-
-h
г
Ь
—а ' ~^"~~^—-^
Рис. 1.1. Гиперболические каустики, ограничивающие поле гауссова пучка
лы вокруг оси симметрии (т. е. вокруг оси z) — однополостный ги-
гиперболоид вращения — называется каустической поверхностью или
просто каустикой гауссова пучка. Это название пришло из геометри-
геометрической оптики; связь гауссова пучка с геометрической оптикой будет
обсуждаться в § 5.1.
Отметим, что в продольном направлении гауссов пучок можно
разбить на три части. В центральной части, при \z\ < 6, попереч-
поперечные размеры пучка сравнительно мало меняются с изменением z. В
двух же периферийных частях, z > b и z < — b, поперечные разме-
размеры пучка заметно растут с ростом \z\ и при больших \z\ пропорцио-
пропорциональны \z\.
Зависимость плотности энергии на оси пучка от продольной коор-
координаты z определяется предэкспоненциальным множителем в A.9).
Легко видеть, что эта плотность в центральной части пучка (\z\ <
< b) примерно постоянна, в периферийных же частях при \z\ ^> b она
обратно пропорциональна z2.
Рассмотрим теперь фазовое распределение в гауссовом пучке, т. е.
найдем фазу в различных точках, занимаемых полем гауссова пучка.
Фаза как функция г и z определяется частью показателя экспоненты
в A.6), заключенной в круглые скобки, перед которыми стоит мни-
мнимая единица г. Из этого выражения видно, что фаза квадратичным
образом зависит от расстояния г до оси z и довольно сложным обра-
образом от z. Однако эти сведения не слишком наглядны. Более интересен
другой подход, при котором отыскиваются условия постоянства фа-
фазы. Приравняв константе выражение в круглых скобках в A.6), при-
приходим к уравнению, связывающему z и г, т. е. определяющему неко-
некоторую поверхность в области, занимаемой пучком. Такая поверхность
называется поверхностью постоянной фазы или волновым фронтом.
§1.1. Гауссов пучок в свободном пространстве 15
Представление о волновом фронте играет важную роль как в теории
волн вообще, так и в теории лазерных резонаторов — в этом мы убе-
убедимся позднее.
Представим уравнение волнового фронта в виде
*(* " *о) " (axctg| - arctg^), A.12)
где zo — то значение z, при котором г = 0, т. е. координаты @, zq) яв-
являются координатами точки пересечения волнового фронта с осью z.
Придавая zo те или иные значения, будем получать различные вол-
волновые фронты данного гауссова пучка. Правую часть в A.12) можно
представить в виде
(zo_,)__arctg___
Так как угол всегда меньше своего тангенса, то вычитаемое в этом
выражении меньше, чем
Л zo — z ^ X zo — z
2^ Ъ + zzo/b ^ 2^ Ъ '
Но это последнее выражение значительно меньше, чем z$ — z, так как
А/2тг& = 1/kb < 1 (при Л ~ 1(Г4 см, Ъ ~ 10 см - kb ~ 104 > 1). Сле-
Следовательно, вторым слагаемым в A.12) всегда можно пренебречь.
Теперь из уравнения A.12) видно, что разность z$ — z по модулю
всегда меньше \z\ или \zq\. Действительно, так как множитель
r2/(z2 + Ъ2)
в левой части A.12) всегда меньше или порядка 1/kb ^C 1, что сле-
следует, например, из уравнения гиперболы A.11), то в целом из A.12)
следует, что z — zo ^C z. Полагая, вследствие этого в левой части A.12)
z = zo, получим для волнового фронта уравнение параболы
Таким образом, волновой фронт гауссова пучка имеет форму пара-
параболоида вращения. С хорошей точностью можно утверждать также,
что этот фронт является сферическим, поскольку сфера радиуса
R = zo + b2/zo A.14)
и параболоид A.13) практически совпадают при тех значениях г, где
амплитуда пучка еще заметно отлична от нуля.
Следовательно, зависимость радиуса кривизны волнового фронта
гауссова пучка от продольной координаты zq описывается соотноше-
соотношением A.14) и показана на рис. 1.2, а. Кривизна волнового фронта —
величина обратная радиусу кривизны к = 1/R — равна
и как функция zq показана на рис. 1.2, б.
16
Гл. 1. Оптика гауссовых пучков
-Ь
-Ъ
Рис. 1.2. Зависимость радиуса кривизны Я (а) и кривизны к (б) от про-
продольной координаты z
Таким образом, исследование фазового распределения позволяет
описать изменение волнового фронта гауссова пучка по мере его рас-
распространения вдоль оси z от —оо до +оо. Сначала, по мере продви-
продвижения по оси z от — оо волновой фронт все более искривляется вогну-
вогнутой стороной в направлении распространения волны. Искривленность
волнового фронта достигает максимума при zo = — Ъ после чего фронт
начинает выпрямляться и становится плоским при z$ = 0. Далее вол-
волновой фронт снова искривляется, теперь уже выпуклостью в направ-
направлении распространения волны. Наибольшая искривленность достига-
достигается при zo = 6, затем кривизна постепенно уменьшается (рис. 1.2, б).
Отметим также расположение центра кривизны волнового фронта
гауссова пучка. При zo = — оо он находится в центре перетяжки гаус-
гауссова пучка г = 0, z = 0. Затем при приближении волнового фронта к
перетяжке центр кривизны смещается в положительном направлении.
Когда волновой фронт находится в точке z$ = —b, центр кривизны
находится в симметричной точке z = Ъ. При дальнейшем смещении
волнового фронта в сторону перетяжки центр кривизны далее сме-
смещается в положительном направлении и при zq = 0 он уходит в +оо.
§1.1. Гауссов пучок в свободном пространстве 17
Далее, при удалении волнового фронта в положительную сторону от
перетяжки центр кривизны приходит из — оо и при zo = Ъ находится
в симметричной точке z = —Ъ. При z$ —У +оо центр кривизны при-
приближается к центру перетяжки. Таким образом, при z$ = =Ьоо гауссов
пучок представляет собой сферическую волну с центром при г = О
и 2 = 0.
Отметим, что как величина, так и направление фазовой скоро-
скорости зависят от поперечной координаты г поля пучка. В частности,
на каустике фазовая скорость поля направлена вдоль каустики и по
величине равна скорости света в вакууме.
Зависимость фазы гауссова пучка от продольной координаты так-
также представляет интерес. Напомним, что в плоской волне фаза в на-
направлении распространения волны линейно нарастает:
^плоск. волны — KZ ^
в гауссовом пучке зависимость фазы от z более сложна. Полагая в
выражении A.6) т = 0, получим
^гаусс. пучка — <&%
Таким образом, если в плоской волне фазовая скорость постоянная и
равна скорости света в вакууме, то в гауссовом пучке фазовая ско-
скорость равна с
1 -
Легко видеть, что в периферических частях гауссова пучка (\z\ >
> b) фазовая скорость примерно равна скорости света в вакууме, в
центральной же части пучка (\z\ < b)
с* С
^фаз — ^ '
1 ~ ~kb
фазовая скорость несколько больше с (рис. 1.3). Соответственно, в
центральной части гауссова пучка, на его оси расстояние между гор-
горбами волн несколько больше Л.
Дадим еще одну важную характеристику пучка — угол расходи-
расходимости излучения при z —У оо. Его определяют как угол между асимп-
асимптотами гиперболы A.11)
w
ol — 2 arctg —
2w
2а _ 2
b ka
Обратимся теперь к рассмотрению первой формы гауссова пуч-
пучка A.5). В ней из-за неразделенности мнимой и вещественной частей
показателя экспоненты характеристики как амплитудного, так и фа-
фазового распределений сосредоточены в одном параметре
q = z-ib, A.15)
который обычно называют комплексным параметром гауссова пучка.
Хотя мы также будем пользоваться этим общепринятым термином,
2 В.П. Быков, О.О. Силичев
18
Гл. 1. Оптика гауссовых пучков
-ь
b z
Рис. 1.3. Фазовая скорость поля гауссова пучка в разных точках оси z
отметим, что он не очень удачен, так как параметр q зависит от z и
характеризует не пучок в целом, а лишь некоторое его сечение, пра-
правильнее было бы говорить о комплексном параметре того или иного
сечения гауссова пучка. Радиус кривизны волнового фронта R и пара-
параметр kw2 = b + z2 /b, связанный с радиусом поперечного распределе-
распределения амплитуды поля гауссова пучка, можно, согласно A.10) и A.14),
выразить через параметр q
R =
и, следовательно,
kw2 =
2 , 7 2
Z + О
A.16)
A.17)
q R kw2'
где величины Л, kw2 являются функциями z, т.е. характеризуют
определенное поперечное сечение гауссова пучка с заданным z. Та-
Таким образом, один параметр q (правда, комплексный) заменяет собой
как характеристика того или иного сечения гауссова пучка два веще-
вещественных параметра, R и kw2.
При переходе от одного сечения к другому параметр q изменяется,
как это следует из A.15), по правилу
где I — расстояние, разделяющее сечения 2 и 1. Можно указать также
другое, несколько более сложное, но гораздо более общее правило пре-
преобразования q при переходе от одного сечения к другому, а именно:
Agi+B
#2 = 7^ r~Fii
A.18)
где коэффициенты А, В, С и D образуют так называемую лучевую
матрицу
М= [~ ^). A.19)
§1.2. Лазерный резонатор, образованный сферическими зеркалами 19
Соотношение A.18) выражает собой широко используемое при расче-
расчете резонаторов правило (или закон) ABCD.
При распространении гауссова пучка в свободном пространстве пе-
переход от одного сечения к другому описывается лучевой матрицей
Т =
1 I
О 1
A.20)
которая является частным случаем матрицы М и называется матри-
матрицей (или оператором) трансляции и которая в соответствии с A.18)
приводит к правилу q<± — q\ + I.
Простота преобразования параметра q при различных трансфор-
трансформациях гауссова пучка оптическими системами является основной
причиной его введения в теорию. Как мы увидим далее, на простых
правилах преобразования гауссова пучка основан метод расчета ла-
лазерных резонаторов — так называемый матричный метод.
В данном случае матрица A.20) появилась непосредственно из вы-
выражения для гауссова пучка A.5). В дальнейшем будут найдены и
другие лучевые матрицы, описывающие прохождение гауссова пуч-
пучка через различные оптические элементы. Наиболее простой вывод
лучевых матриц дает геометрическая оптика (см. §5.1); тесная связь
лучевых матриц с геометрической оптикой и породила их название.
§ 1.2. Лазерный резонатор, образованный
сферическими зеркалами
Рассмотрим лазерный резонатор, образованный двумя сфериче-
сферическими зеркалами различной кривизны, изображенный на рис. 1.4. Та-
Такой резонатор сравнительно редко используется на практике, так как
R
Рис. 1.4. Гауссов пучок — мода лазерного резонатора
внутри реальных резонаторов обычно располагаются те или иные до-
дополнительные оптические элементы, например окна Брюстера. Одна-
Однако для теории и вообще понимания роли резонатора этот резонатор
20 Гл. 1. Оптика гауссовых пучков
очень важен, в теории резонаторов этот резонатор играет такую же
роль, как атом водорода в спектроскопии.
Обращаясь к резонаторам, мы сталкиваемся с новым обстоятель-
обстоятельством, а именно с граничными условиями, которым должна удовле-
удовлетворять волна, являющаяся модой резонатора. В лазерных резона-
резонаторах конкретный вид граничных условий гораздо менее существен,
нежели в резонаторах объемных, высокочастотных. Подробное обсуж-
обсуждение их роли отложим до более подходящего случая, а пока примем
самое простое граничное условие. Будем считать, что волна и на зер-
зеркалах должна обращаться в нуль. Напомним, что в качестве вели-
величины и обычно используется одна из поперечных (по отношению к
оси пучка) компонент электрического поля. Поэтому условие и = 0
на поверхности зеркала соответствует обычному в высокочастотной
области требованию обращения в нуль касательной к поверхности ме-
металла компоненты электрического поля.
Итак, попытаемся удовлетворить граничным условиям на зерка-
зеркалах резонатора, используя гауссов пучок. Раз поле должно обращать-
обращаться в нуль, то гауссов пучок нужно использовать в форме стоячей
волны, поскольку в стоячей волне имеются узловые поверхности —
поверхности, на которых волна обращается в нуль. Идея состоит в
том, чтобы одну из таких узловых поверхностей гауссова пучка сов-
совместить, скажем, с первым зеркалом резонатора, при этом некоторую
другую узловую поверхность совместить со вторым зеркалом резона-
резонатора. Эта идея тем более привлекательна, что волновые фронты или
эквифазные поверхности гауссова пучка — а узловая поверхность сто-
стоячей волны есть частный случай такой поверхности — имеют как раз
сферическую форму. Стоячая волна, образуемая гауссовым пучком,
имеет вид
)
A.21)
Для того чтобы амплитуда этой стоячей волны обратилась в нуль,
необходимо, чтобы аргумент косинуса стал равным ттг + тг/2, а аргу-
аргумент синуса — ттт/тг, где m и тп' — целые числа. Узловые поверхности
гауссова пучка совместим с поверхностью зеркала в два приема. Во-
первых, потребуем, чтобы волна A.21) на оси z в точках ее пересече-
пересечения с зеркалами обратилась в нуль, т. е. чтобы аргументы косинуса и
синуса приняли соответствующие значения. Очевидно, в этом случае
имеем соотношения
fmiTT + тг/2,
i ,
I 777/1 7Г,
A.22)
2
:/0) + <р:
где индексы 1 и 2 указывают на отношение соответствующих величин
§1.2. Лазерный резонатор, образованный сферическими зеркалами 21
к первому и второму зеркалам. Во-вторых, потребуем, чтобы радиусы
кривизны волновых фронтов в точках z\ и z^ совпадали с радиуса-
радиусами кривизны зеркал, т.е. согласно A.14) положим
R1 = -+z1; -R2 = -+z2; A.23)
Z\ Z2
при этом волна A.21) обратится в нуль на всем зеркале, так как она
обратилась в нуль в точке пересечения зеркала с осью z. Обратим
внимание, что волновой фронт, прогиб которого направлен в сторо-
сторону возрастания z, имеет положительный радиус кривизны, фронт же
с прогибом в сторону убывания z имеет отрицательный радиус кри-
кривизны. Радиусы R\ и i?2 считаются оба положительными. Отсюда и
разница в знаках при R\ и И^ в соотношениях A.23).
Разность z\ — z^ должна равняться расстоянию d между зеркала-
Zl-z2 = d. A.24)
Таким образом, получилась система из пяти уравнений с пятью
неизвестными: z\, ?2, fr2, tp и к. Отметим, что Z\ и z^ суть расстоя-
расстояния до перетяжки пучка соответственно от первого и второго зеркал,
эти параметры практически важны, поскольку обычно бывает необ-
необходимо знать положение перетяжки относительно зеркал резонато-
резонатора. Разрешая указанную систему относительно неизвестных, можно
найти тот гауссов пучок, который является модой исследуемого резо-
резонатора.
Число уравнений и неизвестных можно уменьшить. Так, вычитая
почленно друг из друга уравнения A.22), придем к одному уравне-
уравнению
kd — arctg — = птг, A.25)
b2 + Z1Z2
где п — целое число, равное разности т\ и т^ или т[ и т2. Так
как целое число п достаточно произвольно, то проводимые вычисле-
вычисления определяют не одну моду, а целый набор мод, зависящих от п;
в связи с этим число п называют обычно продольным индексом или
номером моды. При переходе к уравнению A.25) выпала неизвестная
фаза if. Эта фаза практически несущественная величина, в частности,
она определяет, имеется ли в перетяжке гауссова пучка узел, пучность
волны или какое-либо ее промежуточное состояние. Но состояние вол-
волны в перетяжке трудно установить экспериментально, поскольку ра-
радиус пучка в области перетяжки почти не зависит от координаты z
и положение перетяжки тем самым очень плохо определено, по край-
крайней мере, в масштабе длины волны. Разумеется, при необходимости
после определения параметров пучка фаза ср может быть определена
из одного из уравнений A.22).
Из уравнений A.23) легко исключить б2, а привлекая A.24), — и
величину Z2- В результате получим уравнение, позволяющее выра-
22 Гл. 1. Оптика гауссовых пучков
зить z\ через параметры резонатора:
_ d(R2 - d) .
Zl ~ R1+R2-2d- (L26)
Тем самым положение перетяжки гауссова пучка оказывается опре-
определенным. Аналогично можно получить значение
Z2 = R+R2d- (L27)
Зная z± и используя первое из равенств A.23), находим параметр кон-
фокальности гауссова пучка
( 9
Ь ~(R1+R2-2dy' (L28)
в соответствии с A.7) радиус гауссова пучка в перетяжке оказывается
равным
„ _ Jd(R1-d)(R2-d)(R1+R2-d~j , ,
а-\/ kHR1+R2-2d) • (L29)
Дадим также поперечные радиусы моды на зеркалах резонатора.
Используя A.10), а также A.26), A.27) и A.28), получаем
d(d-R2ii)
где индексы 1 и 2 относятся соответственно к первому и второму зер-
зеркалам.
Так как параметр гауссова пучка Ъ положителен, то величина Ъ2
также должна быть положительной; условия, при которых Ъ2 > 0,
рассмотрим несколько позже. Сейчас же обратимся к условию A.25),
определяющему резонансные частоты резонатора. Вычисляя произ-
произведение z±Z2 и подставляя его в A.25), получим
d) (л О1,
-i)- (L31)
Наиболее часто это условие используют в несколько иной форме, к
которой легко прийти, вычисляя косинус арктангенса в A.31),
knd = птг + arccos yJg\Q2-> A.32)
ГД6 й й
91 = 1--?-, 92 = 1-4- (L33)
— часто используемые параметры для описания того или иного резо-
резонатора типа, изображенного на рис. 1.4. Запишем соотношение A.32)
дополнительно в форме, позволяющей непосредственно определять
резонансные частоты рассматриваемого лазерного резонатора
+
arccos у/9i 92- A.34)
§1.2. Лазерный резонатор, образованный сферическими зеркалами 23
Детальное обсуждение спектра и других свойств резонатора отложим
до того момента, как познакомимся с высшими поперечными мода-
модами. Теперь же укажем на важную частотную характеристику резона-
резонатора:
Аг/ = Yd (L35)
— частотное расстояние между соседними продольными модами (или
частота биений соседних продольных мод), не зависящее от номе-
номера моды. Следовательно, продольные моды образуют эквидистатный
спектр.
Таким образом, при выполнении условий A.28) и A.31) (или A.32),
A.34)) поле A.21) описывает собственные колебания, или моды рас-
рассматриваемого лазерного резонатора. Правда, это выражение описы-
описывает лишь продольные моды резонатора, кроме которых существу-
существуют, как мы увидим, поперечные моды. Соответственно соотношения
A.31), A.32) и A.34) определяют лишь частоты продольных мод.
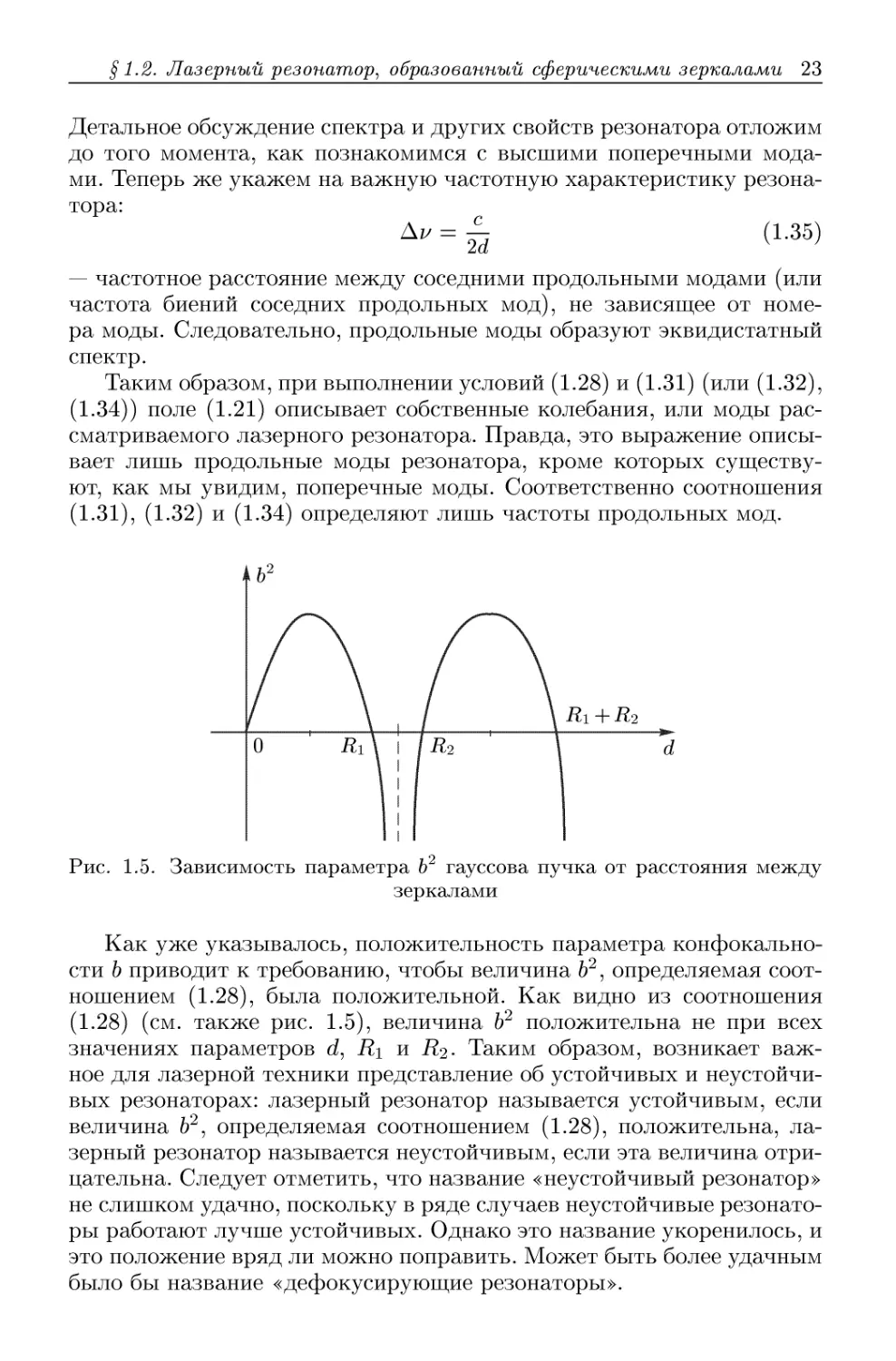
Рис. 1.5. Зависимость параметра Ъ гауссова пучка от расстояния между
зеркалами
Как уже указывалось, положительность параметра конфокально-
сти Ъ приводит к требованию, чтобы величина б2, определяемая соот-
соотношением A.28), была положительной. Как видно из соотношения
A.28) (см. также рис. 1.5), величина Ъ2 положительна не при всех
значениях параметров d, R\ и R2. Таким образом, возникает важ-
важное для лазерной техники представление об устойчивых и неустойчи-
неустойчивых резонаторах: лазерный резонатор называется устойчивым, если
величина б2, определяемая соотношением A.28), положительна, ла-
лазерный резонатор называется неустойчивым, если эта величина отри-
отрицательна. Следует отметить, что название «неустойчивый резонатор»
не слишком удачно, поскольку в ряде случаев неустойчивые резонато-
резонаторы работают лучше устойчивых. Однако это название укоренилось, и
это положение вряд ли можно поправить. Может быть более удачным
было бы название «дефокусирующие резонаторы».
24
Гл. 1. Оптика гауссовых пучков
Как видно из рис. 1.5, имеются две области устойчивости резонато-
резонатора. В первой области расстояние между зеркалами резонатора мень-
меньше меньшего радиуса кривизны, во второй области расстояние между
зеркалами резонатора больше большего радиуса кривизны, но меньше
суммы этих радиусов. Если один из радиусов кривизны отрицателен
(это означает, что соответствующее зеркало обращено к другому зер-
зеркалу выпуклостью), то имеется лишь одна область устойчивости, а
именно, когда расстояние между зеркалами меньше положительно-
положительного радиуса кривизны, но больше чем R2 + R\ = R2 - \Ri\ (R2 > 0;
Ri < 0). Если оба радиуса кривизны отрицательны, т.е. зеркала об-
обращены друг к другу выпуклыми сторонами, то область устойчивости
вообще отсутствует, резонатор в этом случае определенно неустойчив.
неуст.
неуст.
Рис. 1.6. Диаграмма устойчивости двухзеркального резонатора; штрихов-
штриховкой отмечена область устойчивости резонаторов
Различные типы резонаторов, а также области устойчивости и
неустойчивости можно изобразить на двумерной диаграмме (рис. 1.6)
в зависимости от параметров д\ и д2. Некоторые резонаторы получили
специальные названия (они указаны на диаграмме рис. 1.6):
а) плоский резонатор (д± — д2 — 1);
б) конфокальный резонатор (д\ — д2 = 0);
в) концентрический резонатор [д\ = д2 = —1);
г) симметричный резонатор [д\ = д2);
д) полу конфокальный резонатор (д± = 1, д2 = 1/2 или д\ — 1/2,
9i = 1);
е) симметричный неустойчивый;
ж) телескопический неустойчивый (д\ = 1 — d/Ri, д2 = 1 — d/Bd —
-Ri))-
Сферическое зеркало, как известно, имеет фокусное расстояние,
равное половине его радиуса кривизны, таким образом, в конфокаль-
конфокальном резонаторе фокусы зеркал совпадают — этим и объясняется его
1.3. Прохождение гауссова пучка через тонкую линзу 25
название. Концентрический резонатор назван так потому, что в нем
совпадают центры кривизны образующих его зеркал. Полу конфо-
конфокальный резонатор является как бы половиной конфокального — если
посередине между зеркалами конфокального резонатора поместить
плоское зеркало, то образуются два полуконфокальных резонатора.
Название симметричного резонатора понятно; название «телескопи-
«телескопический резонатор» станет ясно после обсуждения свойств неустойчи-
неустойчивых резонаторов.
Таким образом, использование простого гауссова пучка A.21) в ка-
качестве моды резонатора позволило нам получить обширную информа-
информацию о продольных модах рассматриваемого лазерного резонатора и о
его свойствах в целом. Как мы увидим далее, еще большая информа-
информация может быть получена, если обратиться к некоторым обобщениям
гауссова пучка.
§ 1.3. Прохождение гауссова пучка через
тонкую линзу и отражение его от сферического
зеркала
Прежде чем рассматривать прохождение гауссова пучка через тон-
тонкую линзу, познакомимся с важным понятием квадратичного фазо-
фазового корректора. Это понятие является обобщением и идеализацией
понятия тонкой линзы, оно позволяет с единой точки зрения рассмат-
рассматривать линзы, сферические зеркала и некоторые другие оптические
элементы.
Вспомним, что падающая на линзу волна проходит в диэлектри-
диэлектрике, образующем линзу, вблизи оси больший оптический путь, нежели
на краю, и, следовательно, волна в центре линзы имеет больший на-
набег фазы, чем на ее краю. Принимая во внимание симметрию линзы,
нетрудно понять, что зависимость набега фазы от расстояния до оси
линзы должна быть квадратичной. Это свойство линзы и лежит в
основе определения квадратичного фазового корректора. Квадратич-
Квадратичным фазовым корректором называется идеальный оптический эле-
элемент, который, будучи расположен на пути бегущей волны, вносит в
нее дополнительный фазовый набег, квадратично зависящий от попе-
поперечных координат. Если волна бежит в положительном направлении
оси 2:, то, проходя через квадратичный фазовый корректор, она при-
приобретает дополнительный набег фазы, равный
\ kP2 \ kPB
ж, у) = -\ kPr2 = -\ kP(x2 + у2), A.36)
где Р — оптическая сила фазового корректора — величина, обратная
26 Гл. 1. Оптика гауссовых пучков
его фокусному расстоянию
A-37)
как можно видеть, набег фазы в центре корректора (х = 0, у = 0)
больше (он равен нулю), чем на периферии (набег фазы — отрица-
отрицательная величина). Квадратичный корректор по сравнению с линзой
идеален в том отношении, что в нем не учитывается толщина линзы —
фазовый корректор бесконечно тонок, а также поперечные размеры
линзы — фазовый корректор в поперечном направлении не имеет гра-
границ. Существенно также, что пренебрегается отражением света от по-
поверхностей линзы; в результате этого фазовый корректор не облада-
обладает потерями. В реальных линзах паразитное отражение света от ее
поверхностей может быть уменьшено посредством нанесения на них
специальных покрытий — просветлением.
Покажем теперь, что плоская волна, проходя через квадратичный
корректор, превращается в сферическую волну, собирающуюся в фо-
фокусе корректора, т. е. на расстоянии F от корректора. В плоской волне,
падающей слева на фазовый корректор, расположенный при z = 0,
фаза не зависит от поперечных координат:
Ul =Aeikz+i^.
Сферическая волна, сходящаяся после фазового корректора в точ-
точке z = 2о, имеет вид
где
В параксиальном приближении, т. е. при малых г, при z = 0 (т. е. за
фазовым корректором) эту волну можно представить в виде
z + ^— ) + г<
о Zzq J
В соответствии с определением квадратичного корректора сумма
фазы волны, падающей слева на корректор, и фазы, вносимой кор-
корректором A.36), должна быть равна фазе волны, уходящей справа от
корректора, т. е.
kP2 k kl2 +
Ясно, что это соотношение может быть выполнено при
Ч>\ — ?2 = kz0 и F = zq.
Но последнее равенство как раз и означает, что сферическая волна
соберется в фокусе фазового корректора. Таким образом, квадратич-
квадратичный фазовый корректор действительно ведет себя как линза.
1.3. Прохождение гауссова пучка через тонкую линзу 27
Покажем теперь, что гауссов пучок, проходя через квадратичный
фазовый корректор, остается гауссовым пучком, хотя его параметры
изменяются. Пусть слева на фазовый корректор, расположенный в
сечении z = const, падает гауссов пучок
, ч G Г ikr2
<r> z) = V^J^b exP [2(z-z-ib)
где z — координата перетяжки пучка.
Справа же от корректора пусть отходит гауссов пучок
if \ G'
Вспоминая определение комплексного параметра гауссова пучка
A.15) и соотношение A.16), показатели экспонент гауссовых пучков
можно представить в виде
ikr2 /о 1 , .т 1\ ikr2 /о 1 , .т 1\
Re - + г Im - , Re h г Im — .
2 V q q)" 2 V ql ql)
В соответствии с определением фазового корректора следует потре-
потребовать
Re--P = Re-, 1т-=1пД. A.38)
q q' q q'
Первое из этих равенств имеет простой физический смысл; согласно
A.16), его можно представить в виде
i ~ 1 = F> (L39)
где R и Rf — радиусы кривизны волновых фронтов гауссовых пучков
в месте расположения фазового корректора. Это соотношение напо-
напоминает известную формулу линзы. Правда, в формуле линзы несколь-
несколько иные знаки, однако это следствие того, что в ней положительные
расстояния до предмета и изображения отсчитываются в разные сто-
стороны от линзы. Если эту непоследовательность в формуле линзы ис-
исправить, то она точно совпадает с соотношением A.39).
Второе из равенств A.38) также имеет простой смысл — размер пе-
перетяжки при прохождении фазового корректора не изменяется, что
впрочем ясно и из физических соображений, поскольку толщина лин-
линзы пренебрежимо мала по сравнению с ее фокусным расстоянием.
Умножим второе из равенств A.38) на г и сложим полученное со-
соотношение с первым из равенств A.38), получим соотношение
1 _ 1 _ 1
7' " q ~~f'
ИЛИ
4 F-q
28 Гл. 1. Оптика гауссовых пучков
Это и есть искомый закон преобразования комплексного параметра
гауссова пучка при его прохождении через фазовый корректор (лин-
(линзу). Этот закон можно представить в виде правила ABCD A.18), если
фазовому корректору (линзе) сопоставить лучевую матрицу
A.40)
которую называют оператором или матрицей прохождения гауссова
пучка через линзу, и Р определено согласно A.37).
Кроме равенств A.38) имеет место также равенство амплитуд
G/\q\=G'/\q'\ A.41)
и фаз
h hf
ср + arctg = ip' + arctg r, A-42)
где z — координата квадратичного корректора. Для того чтобы по-
понять роль равенства A.41), введем вместо амплитудного множителя G
величину G = G/y/b, которая так же, как и G, является константой.
Тогда равенство A.41) примет вид
„ GT?...,- A-43)
Как нетрудно видеть (см. A.10)), множители при GhG'b этом ра-
равенстве обратно пропорциональны поперечному радиусу пучка w(z),
который согласно второму из равенств A.38) не меняется при прохо-
прохождении пучка через линзу. Поэтому из A.43) следует
это равенство является математическим выражением отсутствия по-
потерь в фазовом корректоре (линзе). В § 1.4 показывается, что при
отсутствии потерь и на других элементах резонатора его собственные
частоты вещественны и затухания колебаний нет.
Равенство A.42) говорит о том, что фаза гауссова пучка на оси
пучка не изменяется при прохождении через фазовый корректор. Ес-
Если бы было необходимо учесть независимый от поперечных координат
фазовый добавок, вносимый линзой, учесть, скажем, толщину лин-
линзы таким образом, то это можно было бы сделать как раз в равен-
равенстве A.42). В этом случае в его правой части появится дополнитель-
дополнительное слагаемое Аср. Равенство A.42) важно для определения спектра
лазерного резонатора (§1.5).
Рассмотрим теперь отражение гауссова пучка от вогнутого сфе-
сферического зеркала. Удобно падающий и отраженный гауссовы пуч-
пучки рассматривать каждый в своей системе координат так, чтобы оба
1.3. Прохождение гауссова пучка через тонкую линзу 29
гауссова пучка в этих системах координат распространялись в поло-
положительном направлении оси z. Таким образом, для падающего пучка
ось z следует направить в сторону зеркала, а для отраженного пучка
ось z должна быть направлена от зеркала. Так как нами всегда ис-
используется правая система координат, то изменение направления оси
z на обратное требует, чтобы и оси х и у изменили на обратное свое
направление; однако поле гауссова пучка квадратично зависит от по-
поперечных координат и изменение их знака не играет роли. При таком
выборе координат действие сферического зеркала эквивалентно дей-
действию тонкой линзы, т. е. набег фазы в центре больше, чем на краю
зеркала. Таким образом, сферическое зеркало является квадратич-
квадратичным фазовым корректором и вносит в гауссов пучок дополнительный
набег фазы АФ A.36), где Р — оптическая сила зеркала, равная
Р = 2/Д, A.44)
где R — радиус кривизны зеркала.
Следовательно, действие сферического зеркала на гауссов пучок
может быть описано правилом ABCD, если сферическому зеркалу
сопоставить матрицу (или оператор отражения)
N = (_Хр fj , A.45)
где Р — определяется соотношением A.44).
Параметр Р в выражении A.36) может принимать и комплекс-
комплексные значения. Рассмотрим сначала, какой смысл имеют чисто мни-
мнимые значения Р = —i/F'. Легко понять, что теперь вместо равенств
A.38) имеют место равенства
Re - = Re -, Im - + iP = Im -.
q q' q qf
Они означают, что пучок, проходя через такой корректор, не изме-
изменяет кривизны своего волнового фронта, но поперечные размеры его
меняются. Поэтому устройство с такими характеристиками естествен-
естественно назвать амплитудным квадратичным корректором; его называют
также гауссовой диафрагмой. Величина F' представляет собой харак-
характерный параметр гауссовой диафрагмы с размерностью длины или ее
мнимое фокусное расстояние.
Если параметр Р — комплексный, то это означает, что на пути
пучка последовательно и рядом расположены линза и гауссова диа-
диафрагма. Такое устройство можно назвать комплексным квадратич-
квадратичным корректором. Он описывается матрицей A.40) с комплексным
параметром 1 . ,
Гауссовы диафрагмы довольно трудно реализовать практически,
хотя они представляют значительный интерес. Их преимущество пе-
перед обычными диафрагмами состоит в том, что при выделении основ-
30 Гл. 1. Оптика гауссовых пучков
ной моды они не искажают ее — основная мода сохраняет гауссов
характер поперечного распределения поля.
В некоторых случаях при расчете лазерных резонаторов необхо-
необходимо знать, как гауссов пучок распространяется в прозрачном ди-
диэлектрике. Так как в данной книге рассматриваются лишь монохро-
монохроматические пучки, то поля в свободном пространстве и в диэлектрике
различаются лишь тем, что в последнем длина волны в п раз меньше,
чем в свободном пространстве (п — показатель преломления диэлек-
диэлектрика) _ л
ЛДиэл - ".
Другими словами, поле гауссова пучка в диэлектрике получится, если
в выражении A.5) волновое число к заменить на кп:
G Г iknr2
Если комплексный параметр гауссова пучка в диэлектрике опре-
определить обычным образом
то с радиусом кривизны волнового фронта пучка в диэлектрике ЛДИЭл
и его поперечной полушириной г^диэл этот параметр будет связан, как
и прежде, соотношениями A.16), однако во втором из этих соотноше-
соотношений вместо к следует использовать кп.
§ 1.4. Потери энергии в лазерных резонаторах
Проблема потерь энергии в лазерных резонаторах весьма обширна
и трудна. В первую очередь, это касается так называемых дифракци-
дифракционных потерь, которые будут обсуждаться в гл. 2. Здесь мы коснемся
проблемы потерь лишь в рамках гауссовой оптики.
В этом плане важнейшими источниками потерь в лазерных резо-
резонаторах являются: неполное отражение излучения от зеркал, погло-
поглощение в активной среде лазера и других диэлектриках, являющихся
составными частями резонатора, паразитное отражение от торцов ди-
диэлектриков и др. В частности, для процессов, происходящих в гене-
генераторе, энергию, выводимую из лазера, также следует рассматривать
как потери, хотя термин «потери» в этом случае не вполне адекватен
сути дела.
Потери лазерных резонаторов определяют две важных, связанных
между собой характеристики резонатора. Из-за потерь энергии соб-
собственные колебания в резонаторах затухают по экспоненциальному
закону, эти потери, следовательно, определяют амплитудный пара-
параметр затухания, или декремент S. Характерное время затухания г =
= 1/5 есть время, за которое амплитуда уменьшается в е раз. (Декре-
(Декремент по мощности вдвое больше, а время затухания вдвое меньше, чем
§1-4- Потери энергии в лазерных резонаторах 31
по амплитуде.) Кроме того, благодаря потерям энергии, спектральная
ширина резонансной кривой лазерного резонатора имеет конечную
(ненулевую) ширину, равную
Аг/ = — = —. A.47)
В лазерах резонаторные потери определяют такую важную вели-
величину, как пороговое значение накачки, при котором начинается гене-
генерация, а также оказывают влияние на уровень мощности в стацио-
стационарном режиме.
Если пренебречь дифракционными потерями, т. е. потерями на
краях зеркал, а в большинстве случаев это вполне возможно, то вы-
вычисление декремента S и связанных с ним величин г и Аг/ несложно.
Как уже упоминалось, при наличии потерь колебания в резонаторах
экспоненциально затухают, это затухание математически можно опи-
описать как наличие у частоты колебаний небольшой мнимой добавки
(отрицательной при зависимости от времени вида e~ltut), т.е. можно
считать, что резонансная частота комплексна
ио = сУ — iuo".
Соответственно, волновое число также комплексно:
к = к' - ik" (к' = и1/с, к" = и"/с). A.48)
Очевидно, декремент S просто равен модулю мнимой части часто-
частоты:
6 = и".
Пренебрежем для простоты поперечной структурой поля и будем
рассматривать это поле как плоскую волну
бегущую вдоль оси z. Тогда ясно, что в промежутках, где поглощение
отсутствует, амплитуда волны возрастает как ек z, на элементах же,
где имеются потери, амплитуда уменьшается в определенное число
раз, скажем в Ni раз. Парадоксальное на первый взгляд нарастание
амплитуды волны в направлении ее распространения не связано, ко-
конечно, ни с каким усилением — во времени волна все время умень-
уменьшается, так как в резонаторе есть лишь потери. Таким образом при
обходе резонатора амплитуда возрастает в ек L раз, где L — оптиче-
оптическая длина резонатора, и уменьшается на поглощающих элементах в
целом в N раз, где N — произведение всех коэффициентов ослабле-
ослабления Ni. Следовательно, после обхода резонатора должно выполняться
равенство
Nek"L = 1
32
Гл. 1. Оптика гауссовых пучков
или к" = — (In iV)/L, и декремент равен
S = -c\nN/L A.49)
(это положительная величина, поскольку N < 1 и In TV < 0). Величи-
Величина TV практически всегда мало отличается от единицы:
где х — коэффициент потерь; в этих случаях
й ~ ск/Ь. A.50)
Приведем некоторые характерные параметры. При длине резона-
резонатора L = 15 см и коэффициентах отражения зеркал 99 и 100% время
затухания составляет т~5-10~8с. Спектральная ширина резонанс-
резонансной кривой при этом примерно в 100—1000 раз меньше, чем межмодо-
вое расстояние A.35), т.е. резонансы продольных мод не перекрыва-
перекрываются и четко выражены (рис. 1.7).
2d I
Рис. 1.7. Резонансные кривые продольных мод двухзеркального резонатора
Соотношений A.49) и A.50) достаточно для определения декре-
декремента и спектральной ширины резонанса во всех практически важ-
важных случаях. В большинстве случаев влияние потерь на поперечную
структуру пучка ничтожно мало, тем
более, что в стационарном режиме ге-
генерации эти потери компенсируются
усилением в активной среде лазера.
Однако мы рассмотрим простой при-
пример резонатора с потерями, на кото-
котором можно познакомиться с несколько
модифицированным гауссовым пуч-
пучком с комплексным значением к.
Пусть резонатор образован сфери-
сферическим зеркалом со стопроцентным
коэффициентом отражения и плоским
R1=R R2 = l
Рис. 1.8. Лазерный резона-
резонатор, в котором плоское зерка-
зеркало имеет коэффициент, мень-
меньший единицы
зеркалом с коэффициентом отражения R (рис. 1.8). Гауссов пучок, со-
составляющий моду такого резонатора и бегущий вправо, описывается
§1-4- Потери энергии в лазерных резонаторах 33
тем же выражением A.5), но теперь уже с комплексным значением к
A.48),
G Г ikr2 1
u(r, z, t) = ——:- ехр |^ _ + ikz + iip - icot\. A.51)
Разделяя в показателе экспоненты, в члене, пропорциональном г2, ве-
вещественную и мнимую части, получим выражения для радиуса кри-
кривизны волнового фронта
и квадрата поперечного радиуса пучка
w2 =
как можно убедиться, эти выражения пренебрежимо мало отличаются
от выражений A.16).
Для того чтобы найти гауссов пучок, составляющий, как и A.51),
моду резонатора, но бегущий влево, учтем, что пучок A.51) удовле-
удовлетворяет вещественному волновому уравнению (см. § 1.12), а следова-
следовательно, тому же уравнению удовлетворяет и комплексно сопряженный
с A.51) пучок
u'{r,z,t) = u*(r,z,t).
Но кроме того, в решении u'(r,z,t) можно также изменить знак при
со на обратный без изменения знака &, поскольку решение A.51) по-
получается посредством разделения пространственных и временных пе-
переменных и связь между к и со имеет вид с2к2 = со2. В результате
приходим к решению
Г ik*r2 1
Г 2(ГТ*) ~ik*z ~iip~ iu4\' (L54)
G Г ik*r
v(r> z^ = JTTb ехр
которое и является волной, бегущей влево. Нетрудно убедиться, что
для этого пучка имеют место те же самые выражения A.52) и A.53)
для радиуса кривизны волнового фронта и поперечного радиуса.
Потребовав, чтобы радиусы кривизны зеркал совпадали с ради-
радиусами кривизны волновых фронтов пучков A.51) и A.54) на них, а
также учтя, что 2" — z = L, где L — длина резонатора, можно най-
найти величины 6, 2" и z. Сумма полей на сферическом зеркале должна
быть равна нулю. Достаточно обратить в нуль сумму полей на оси
резонатора (при г = 0), поэтому получаем равенство
Qei(kz+<p-arctg(b/z)) _ _Qiег{к*Ъ-ч>' +
распадающееся на два равенства
Gek"~z = G'e-k"^, 2kfz + <р + <р' - 2 arctgF/2) = Bm + 1)тг. A.55)
3 В.П. Быков, О.О. Силичев
34 Гл. 1. Оптика гауссовых пучков
На плоском зеркале аналогично имеем равенство
Qei(kz-\-(f-arctg(b/zbar)) _ _
где R — коэффициент отражения от плоского зеркала. Из этого ра-
равенства следуют два равенства
Gek"~z = |R\G'e-k"~z, 2k'z + у? + у/ - 2 dxctg(b/z) = Bm' + 1)тг.
A.56)
Деля первое из равенств A.55) на первое из равенств A.56), получаем
\R\eM"(z-z) = 1?
ИЛИ
к" = - In \R\/2L, со" = 5 = -сIn \R\/2L,
т. е. значения к" = со"/с, полученные ранее на основе простых сообра-
соображений.
Вычитая из второго равенства A.55) второе равенство A.56), по-
получим соотношение
к'L — arctgF/z) — arctgF/z) H— argi? = птг (п = т — т'),
определяющее спектр резонатора.
Подчеркнем еще раз, что мнимая добавка в к всегда очень невели-
невелика и ее влияние на поперечные параметры пренебрежимо мало, поэто-
поэтому на практике всегда поперечные параметры определяют на основе
правила ABCD, считая к вещественной величиной, и затем декре-
декремент затухания S находят по формуле A.49) или A.50).
Рассмотрим потери, вносимые в резонатор гауссовой диафрагмой,
при этом для общности будем считать, что она совмещена с квадра-
квадратичным фазовым корректором (линзой) и их совместное действие на
пучок описывается матрицей A.40), причем величина Р принимает
комплексные значения
где F — фокусное расстояние линзы и F' — характерная длина гаус-
гауссовой диафрагмы (мнимое фокусное расстояние).
Исследуя прохождение гауссова пучка через линзу, мы отмечали,
что его поперечные размеры не изменяются, и это приводило к равен-
равенству амплитудных констант G и G пучков до и после линзы. Равен-
Равенство амплитудных констант свидетельствует об отсутствии потерь на
линзе. В случае гауссовой диафрагмы ситуация изменяется. В § 1.3,
сравнивая поля до и после корректора и приравнивая их на оси, мы
пришли к равенству A.43):
GVb GVb7
§1.5. Матричный метод расчета лазерных резонаторов 35
причем множители при G и G обратно пропорциональны поперечным
радиусам пучков до и после линзы. Легко понять, что это равенство
остается справедливым и при наличии гауссовой диафрагмы. Однако
в этом случае поперечный радиус пучка уже не остается неизменным,
поэтому множители G и G теперь не равны друг другу.
Из правила ABCD для матрицы A.40) при комплексном значении
С следует
Так как С = — Р, учитывая A.57), получаем
/2
w —
G =
kw2/F'
G
где w — поперечный радиус пучка на гауссовой диафрагме до ее про-
прохождения пучком. Эти соотношения не зависят от наличия линзы
(т.е. от величины F). Таким образом, как и при обычном ослабите-
ослабителе амплитудный множитель на гауссовой диафрагме умножается на
некоторую величину
N = mtw (L58)
меньшую единицы. Используя соотношение A.49) или A.50), можно
найти декремент, обусловленный гауссовой диафрагмой. Разумеется,
если диафрагм в резонаторе несколько, то следует взять произведение
всех множителей А^.
Существенным отличием гауссовой диафрагмы от простого осла-
ослабителя является то, что ее коэффициент ослабления N зависит от по-
поперечного радиуса пучка на входе диафрагмы. Поэтому, подбирая F'
так, чтобы потери, вносимые гауссовой диафрагмой, были заметными
лишь для высших мод, можно добиться генерации только на основной
моде.
§ 1.5. Матричный метод расчета лазерных
резонаторов
В предыдущих разделах показано, что трансформация гауссова
пучка при его распространении в свободном пространстве и при про-
прохождении через квадратичный фазовый корректор описывается пра-
правилом ABCD. Как мы увидим далее, имеется еще несколько опти-
оптических элементов, при прохождении которых гауссов пучок остается
гауссовым пучком, а изменение его комплексного параметра опи-
описывается правилом ABCD. Такие оптические элементы называют
3*
36 Гл. 1. Оптика гауссовых пучков
гауссовыми оптическими элементами или оптическими элементами
гауссовой оптики. К ним относится, в частности, отрезок свободно-
свободного пространства. В данной главе рассматриваются только гауссовы
оптические элементы и в дальнейшем это особо не оговаривается.
Правило ABCD широко используется при расчете лазерных резо-
резонаторов и составляет основу так называемого матричного метода. Ис-
Использование этого правила основано на следующем важном его свой-
свойстве. Пусть гауссов пучок проходит через некоторый оптический эле-
элемент, описываемый матрицей
(? *) A.59)
тогда его комплексный параметр q преобразуется в соответствии с
правилом ABCD
q = — —. (l.bUJ
Пусть далее гауссов пучок с параметром q' проходит через другой
оптический элемент, описываемый матрицей
мх = ' -1 Bl
и его комплексный параметр q' также преобразуется в соответствии с
правилом ABCD:
Упомянутое выше важное свойство правила ABCD заключается в
том, что параметр q" может быть выражен через параметр q также в
соответствии с правилом ABCD:
,, _ А2д + В2
q ~ C2q + D2'
причем коэффициенты А^, ??2, С<± и D^ образуют матрицу
* в
2 D
являющуюся произведением матриц М и М\, записанных последова-
последовательно справа налево в том же порядке, в каком гауссов пучок про-
проходит оптические элементы, описываемые матрицами М и М\\
М2 = М1- М.
В справедливости этого свойства нетрудно убедиться, подставляя
§1.5. Матричный метод расчета лазерных резонаторов 37
A.60) в A.61). Действительно,
Aq + B \ I ( Aq + B ,D\_
+Bl) / {ClCq-TD+DlJ-
_ {АгА + BxC)g + (АгВ + ВгР) _ A2q' + В2 ,
~ (CiA + DiC)q+ (CiB + DiD) ~ C2q' + D2'
отсюда видно, что правило перехода от q к q" соответствует правилу
ABCD, причем коэффициенты в этом правиле образованы в соответ-
соответствии с законом перемножения матриц (строка на столбец).
Из этого свойства правила ABCD следует, что сложная оптиче-
оптическая система, состоящая из многих оптических элементов (и, в част-
частности, лазерный резонатор), может быть описана некоторой одной
матрицей М, являющейся произведением матриц отдельных элемен-
элементов, Mi, M2, ..., Мдг, записанных справа налево в том порядке, в
котором гауссов пучок проходит эти элементы:
М = MN - Mtv_i • ... • М2 • Mi. A.62)
Произведение матриц зависит от их порядка, поэтому при вычис-
вычислении A.62) матрицы нельзя переставлять. Иногда при вычислении
произведения A.62) бывает удобно матрицы ассоциировать, не меняя
их порядка, в те или иные группы, например,
М = (MN • Мдг_1 • Мдг_2) • ... • (М3М2 - Mi)
— это допустимо.
Итак, если оптическая система описывается матрицей A.59), то
гауссов пучок, имевший на входе системы комплексный параметр q,
после прохождения такой системы, т. е. на ее выходе будет иметь па-
параметр q'', определяемый соотношением A.60).
У оптической системы, образующей лазерный резонатор, вход и
выход совпадают. Поэтому комплексный параметр гауссова пучка по-
после его прохода через оптическую систему резонатора должен при-
принять свое исходное значение, т.е. для лазерного резонатора в A.60)
следует положить
q' = q.
Для лазерного резонатора получаем, таким образом, правило ABCD
в форме
Aq + B , го,
q = с^Тд' (L63)
характерной для замкнутых оптических систем.
Соотношение A.63) приводит к квадратному уравнению
Cq2 + (D-A)q-B = 0, A.64)
разрешая которое, получим
38 Гл. 1. Оптика гауссовых пучков
Следует отметить, что лучевые матрицы, описывающие лазерные
резонаторы, всегда имеют детерминанты, равные единице:
AD-ВС = 1;
поэтому соотношение A.65) можно записать также в виде
q= jo [(A- D)±iy/4- (A + DJ]. A.66)
Далее имеется в виду случай (А + DJ < 4, который соответствует,
как станет ясно позднее, устойчивым резонаторам. В соответствии с
соотношениями A.16), имеем
R=-A =:, kwz = —= ' ' =, A-67)
A-DJ y/l-(A + DY
где R — радиус кривизны волнового фронта гауссова пучка, являюще-
являющегося основной модой рассматриваемого резонатора, и w — характер-
характерный поперечный размер (радиус) того же пучка. Знак модуля во вто-
втором из соотношений A.66) появляется из условия, что мнимая часть
коплексного параметра q всегда отрицательна (см. A.15)). Поэтому
при В > 0 следует выбрать тот корень уравнения A.64), который со-
соответствует верхнему знаку в A.66), а при В < 0 — нижнему. Второй
корень уравнения A.64) описывает встречный пучок — этот вопрос
обсуждается ниже.
Таким образом, расчет лазерного резонатора матричным методом
состоит из двух этапов. На первом этапе вычисляется матрица М, ха-
характеризующая оптическую систему резонатора и представляющая
собой произведение A.62) матриц отдельных оптических элементов
системы. На втором этапе по элементам матрицы М в соответствии
с соотношениями A.67) определяются радиус кривизны волнового
фронта основной моды резонатора и ее поперечный размер. Имеется
также третий этап, заключающийся в определении параметров спек-
спектра резонатора, — он будет изложен далее.
Отметим, что при вычислении матрицы М фиксируется некоторое
входное сечение резонатора (оно же — выходное сечение), поскольку
фиксируется некоторая первая матрица М\. Это сечение в дальней-
дальнейшем будем называть реперным. Величины A.67), полученные с помо-
помощью матрицы М, характеризуют основную моду резонатора именно
в этом, реперном сечении. Если необходимо знать параметры моды в
каком-то ином сечении, то они определяются матрицей, относящейся
к этому новому сечению, и связанной с прежней матрицей соотноше-
соотношением
\ A.68)
где V — матрица, описывающая распространение гауссова пучка от
старого сечения к новому, и V~x — матрица, обратная V.
§1.5. Матричный метод расчета лазерных резонаторов 39
Однако проще всего параметр qnOBJ характеризующий моду в но-
новом сечении, можно найти с помощью правила ABCD:
_ Ayq + By
Cyq + Dy '
где Ay, By, Cy, Dy — элементы матрицы V и q — параметр, харак-
характеризующий моду в исходном сечении.
Соотношение A.67) позволяет найти еще одну характеристику ре-
резонатора — положение перетяжки гауссова пучка, являющегося модой
этого резонатора. В перетяжке фронт волны плоский, т. е. R = оо, со-
согласно первому из соотношений A.67) это означает, что в матрице
резонатора, отнесенной к сечению перетяжки, диагональные элемен-
элементы должны быть равны:
A = D. A.69)
Будем предполагать, что перетяжка отстоит на расстояние I от ис-
исходного сечения в положительном направлении оси z пучка. Матрица
трансляции на расстояние I и обратная ей имеют вид
1 Л T-im _ Л -I
nil' v. / — In i
U 1 у VU 1
следовательно, матрица резонатора, отнесенная к сечению перетяж-
перетяжки, согласно A.68), равна
^перетяжки — J- \ь)М1 [I) — I ^ _>^ ^
\
Потребовав, чтобы выполнялось условие A.69), получим
/ = ^i. A.70)
Таким образом, положение перетяжки моды резонатора найдено —
перетяжка отстоит от исходного сечения на расстояние I, определяе-
определяемое соотношением A.70).
Рассмотрим два примера применения правила ABCD. Снача-
Сначала применим правило ABCD к резонатору, уже изученному в § 1.2
(рис. 1.4). Пусть вдоль оси резонатора от некоторого исходного се-
сечения, прилегающего к первому зеркалу, в сторону второго зеркала
распространяется гауссов пучок. На своем пути гауссов пучок после-
последовательно проходит отрезок свободного пространства длиной d, от-
отражается во втором зеркале, снова проходит отрезок свободного про-
пространства длиной d и, наконец, отражается в первом зеркале. Следо-
Следовательно, матрица всей оптической системы, образующей резонатор,
отнесенная к исходному сечению около первого зеркала, может быть
представлена в виде произведения четырех матриц:
M = N(P1)-T(d)-N(P2)-T(d),
40
Гл. 1. Оптика гауссовых пучков
где N(P) — оператор отражения от зеркала (см. A.45)). Перемноже-
Перемножение матриц не вызывает затруднений, и матрица М принимает сле-
следующий вид:
l-P2d 2d-P2d2
,PiP2d -Р1-Р2 1 - 2Pid - P2d + PiP2<
A.71)
Воспользовавшись теперь первым из соотношений A.16), получим для
радиуса кривизны R волнового фронта гауссова пучка значение
т. е. кривизна волнового фронта гауссова пучка около первого зер-
зеркала совпадает с кривизной первого зеркала, различие же в знаке
между R и Ri не существенно, так как оно отражает лишь то обстоя-
обстоятельство, что радиус кривизны вогнутого зеркала всегда считается
положительным, независимо от
того, куда оно обращено вогну-
вогнутостью, в то время как ради-
радиус кривизны волнового фрон-
фронта пучка положителен, если
он обращен вогнутостью в сто-
сторону убывания z. Совпадение
кривизны зеркала и волнового
фронта пучка естественно, этот
вопрос уже обсуждался в § 1.2
и там именно так подбирал-
подбирался гауссов пучок, являющийся
модой рассматриваемого резо-
резонатора.
Воспользовавшись далее вторым из соотношений A.67) и подста-
подставив в него конкретные значения матричных элементов A.71), получим
для эффективного радиуса пучка соотношение
Рис. 1.9. Лазерный резонатор с плос-
плоскими зеркалами и внутренней лин-
линзой
w =
d(d-R2)
к V (d-Ri)(Ri+R2-dY
совпадающее с A.30). Определим далее расстояние первого зеркала
от перетяжки, согласно A.70), оно равно
_ 1 , 2P1d-P1P2d2
~ 2 PiP2d-P1 -Р2
d(R2 - d)
2d-Ri-R2'
что с точностью до знака совпадает с выражением A.26).
Рассмотрим теперь резонатор, образованный двумя плоскими зер-
зеркалами, между которыми расположена тонкая линза (рис. 1.9). От-
Отражениями от поверхностей линзы будем пренебрегать, они и в обыч-
обычных условиях невелики (~ 4% по мощности), но могут быть сделаны
§1.5. Матричный метод расчета лазерных резонаторов 41
и совсем малыми посредством нанесения на них просветляющих по-
покрытий. Подобный резонатор важен практически, часто роль линзы
в нем исполняет активный элемент, оптическая сила в котором наво-
наводится в результате оптической накачки и неравномерного разогрева
элемента.
Гауссов пучок, распространяясь вправо от линзы, проходит два
отрезка свободного пространства, каждый длиной d/2; так как отра-
отражение в плоском зеркале не изменяет параметра гауссова пучка, то
эти два отрезка можно рассматривать как один отрезок свободного
пространства длиной d. Затем гауссов пучок проходит через линзу,
еще раз отрезок свободного пространствах длиной d, и еще раз линзу.
Таким образом, матрица всей оптической системы может быть пред-
представлена в виде произведения четырех матриц:
М = LT{d)LT{d)
и далее расчетов можно не делать, поскольку предыдущий рассмот-
рассмотренный нами резонатор описывался точно такой же матрицей A.71).
Положив Ri = R2 = 2F в соотношениях для Raw, получим для ра-
радиуса кривизны волнового фронта на линзе следующее значение:
а поперечный радиус пучка на линзе равен
w =
Сделаем оценку радиуса w для типичных условий. Пусть
d = 10 см, Л = 10~4 см, F = 12,5 см,
тогда
w ~ 1,4- 10~2 см.
Если радиус активного элемента г о = 0,2 см (это типичный раз-
размер активного элемента), то он примерно в 15 раз больше радиуса
основной моды резонатора и, следовательно, в таком резонаторе кро-
кроме основной будет возбуждаться большое число высших поперечных
мод. В основную моду будет излучаться лишь малая доля энергии,
запасенной в активном элементе.
Покажем теперь, что решение уравнения A.63) или A.64), получа-
получаемого из правила ABCD для резонатора, дает информацию не только
о прямом пучке, но и о встречном. Встречный пучок в линейном резо-
резонаторе получается из прямого после его частичного прохода по резо-
резонатору; поэтому его параметры можно вычислить с помощью матри-
матрицы A.68) или правила A.69). В кольцевом же резонаторе (см. § 1.14)
встречный пучок независим от прямого и для него нужно отдельно
составлять и решать уравнение A.63). Однако в обоих этих случаях,
42 Гл. 1. Оптика гауссовых пучков
как уже сказано, информацию о встречном пучке можно получить
непосредственно из уравнения A.63) или A.64) для прямого пучка.
Следует отметить, что все лучевые матрицы кроме тех, которые
описывают прохождение гауссова пучка через диэлектрическую по-
поверхность, имеют один и тот же вид, как для прямого, так и для
встречного гауссовых пучков. Можно понять, что в матрицах 10 и 11
табл. 1.2, описывающих прохождение гауссова пучка через диэлек-
диэлектрическую поверхность, при переходе к встречному пучку следует
поменять местами индексы 1 и 2 и изменить знак радиуса кривиз-
кривизны поверхности R. Следовательно, при переходе от прямого пучка к
встречному лучевая матрица изменяется в соответствии с правилом
Мпрям = ( с Dj => Мвстр = I с д) , A.72)
т. е. диагональные элементы этой матрицы меняются местами.
Таким образом, согласно изложенному в начале этого параграфа
для встречного пучка матрица, описывающая резонатор, представля-
представляет собой произведение тех же матриц М^, которые составляют матри-
матрицу М A.62) для прямого пучка, но взятых в обратном порядке:
Мвстр = Mi • М2 ..... Мдиэл ..... MN- A.73)
штрихом отмечено то, что матрица, описывающая прохождение гаус-
гауссова пучка через диэлектрическую поверхность, изменена в соответ-
соответствии с приведенным выше правилом.
Введем матрицы
Л о
а = а = \ п _^
и преобразуем Мвстр следующим образом
^встр = оГ1 аМ\оГхаМ^оГ1 • ... • аМД11Эла~г • ... • аМ]уа~1а. A.74)
Можно убедиться, что преобразование
r1 аМСГ1 = М~1
превращает г-й сомножитель в матрицу, обратную матрице, описы-
описывающей прохождение прямого пучка через соответствующий гауссов
оптический элемент. Следовательно,
= a~1(MN ..... Mi)a = a^M^a. A.75)
Таким образом, матрицы, описывающие прямой и встречный пучки
А В\ м - (D В
С D Г встр ~ V С А
§1.5. Матричный метод расчета лазерных резонаторов 43
различаются лишь переставленными диагональными элементами. Со-
Согласно A.66) переход от Мпрям к Мвстр приводит к изменению зна-
знака вещественной части комплексного параметра q. В свою очередь
это приведет к изменению знака радиуса кривизны волнового фронта
пучка. Следовательно, волновые фронты прямого и встречного пуч-
пучков совпадают — изменение знака радиуса кривизны отражает лишь
изменение направления распространения пучка. Мнимая часть пара-
параметра q не изменяется при переходе от Мпрям к Мвстр и поперечные
ширины прямого и встречного пучков одинаковы.
Следует особенно подчеркнуть, что приведенные рассуждения о
встречных пучках справедливы в случае, когда матрицы Mi веще-
вещественны, т. е. предполагается, что резонатор не содержит гауссовых
диафрагм. Если же резонатор такие диафрагмы содержит, то ком-
комплексные параметры прямого и встречного пучков, по-прежнему,
определяются соотношением A.66). Однако разделение на веществен-
вещественную и мнимую части в этих параметрах будет происходить иначе. Это
означает, что радиусы кривизны волновых фронтов и поперечные ши-
ширины встречных гауссовых пучков будут различными.
Матричный метод позволяет рассчитывать спектр лазерного резо-
резонатора. Этот спектр возникает из естественного условия, что гауссов
пучок, обходя резонатор, приобретает набег фазы, который при за-
замыкании пучка в реперной плоскости должен быть кратен 2тг. Вклад
в набег фазы дают все оптические элементы резонатора. Наибольший
вклад дают отрезки свободного пространства, которые мы рассматри-
рассматриваем как отдельные оптические элементы, а также отрезки диэлектри-
диэлектриков, например активные элементы; меньший
вклад дают тонкие линзы и совсем малый
вклад дают зеркала, но все же этот вклад,
строго говоря, не равен нулю, так как по-
поле немного проникает как в диэлектрические,
так и в металлические зеркала. При расче-
расчете продольного спектра следует все эти вкла-
вклады сложить и сумму приравнять 2тг/, где
I — целое число (продольный индекс моды).
Так как поперечная структура моды уста-
установлена выше, то приращение фазы доста- Рис. 1.10. К выводу
точно вычислить лишь на оптической оси. продольного фазового
Рассмотрим резонатор, изображенный на условия
рис. 1.10, причем пренебрежем набегами фаз на зеркалах и других
фазовых корректорах (например, линзах). Как видно из A.6), набег
фазы на оси пучка (г = 0) на отрезке свободного пространства длиной
L равен
Aip = kL - arg q' + arg q,
где д, q' — комплексные параметры пучка соответственно в начале
и конце отрезка L. Следовательно, полный набег фазы в резонаторе,
44 Гл. 1. Оптика гауссовых пучков
изображенном на рис. 1.10, равен
kLi - arg q[ + arg qx + kL2 - arg q2 + arg q2 + ...
TV TV
... + kLN - &Ygq'N + arg^ = fcL - ^ argg- +
где L — полная длина оптического пути резонатора, q[, qi — комплекс-
комплексные параметры пучка в конце и начале г-го плеча. Разность сумм в
этом выражении можно представить в виде
N N N
____ , ! ч
Покажем, что величина
является собственным значением лучевой матрицы М исследуемого
резонатора. Примем в качестве реперной плоскость сечения около ле-
левого зеркала (нулевого фазового корректора); тогда матрицу резона-
резонатора можно представить в виде
М = СnLnCn-iLn-i • • • • • C2L2C1L1,
где матрицы С\ и Li описывают, соответственно, квадратичную кор-
коррекцию и проходы (трансляции) по плечам резонатора и имеют вид
С ~ ( l °) L -
где Сi — параметр, описывающий фокусирующее действие г-го кор-
корректора (см. A.40) и A.45)). На векторы специального вида, обра-
образованные комплексным параметром пучка q, эти матрицы, согласно
правилу ABCD A.60), действуют следующим образом:
1 о\ ( 1 А ( 1 \ = / 1 \
A.76)
1 LA /дЛ _ (qi + .
х0 1 j I 1 ) ~ { 1
Вектор
(?) A-77)
является собственным вектором матрицы М, если параметр g'l опре-
определен по правилу ABCD A.63), это видно из следующего простого
1.6. А стигматичный гауссов пучок 45
вычисления:
А В\ (дЛ _ (Aqi +
С D) \1) ~ \Cqi+D
= (Cqi + D) (^ + BVV« + *>)) = (Cqi + D)
Нетрудно видеть, что в соответствии с A.76)
А (А г ? (
и, следовательно, при действии всей цепочки М на вектор A.75), по-
получим
«('¦)= л
если учесть, что qn+i = gi, так как A.77) определяет собственный
вектор матрицы М.
Таким образом, полный набег фазы в резонаторе равен
л 1 r A + D
Aip — kL- arccos —-—,
z
где А и D — диагональные элементы матрицы М резонатора, и про-
продольное фазовое условие имеет вид
kL = 2тг1 + arccos ^-^-. A.78)
§ 1.6. Астигматичный гауссов пучок, астигматичные
оптические элементы, астигматичные резонаторы
Поле астигматичного гауссова пучка описывается выражением
x,y,z) = -== exp —— +-f-+ гЬ + гу? L A.79)
где
q\ — z — Z\ — ib\ и q2 — z — z^ — ib^
— комплексные параметры пучка, имеющие размерность длины. Лег-
Легко видеть, что при q\ — q^ астигматичный гауссов пучок совпада-
совпадает с обычным, неастигматичным (стигматичным) гауссовым пучком.
Астигматизм гауссова пучка выражается в том, что он имеет теперь
различные параметры в плоскостях х и у или, иными словами, плос-
плоскостях своей симметрии. Во-первых, могут различаться z\ и z^ и, сле-
следовательно, перетяжки в плоскостях х и у будут располагаться при
z = z\ и z — Z2, т. е. у астигматичного пучка имеются две перетяжки.
46 Гл. 1. Оптика гауссовых пучков
Во-вторых, характерные поперечные размеры пучка в плоскостях х
и у различны и определяются соотношениями
wy(z) = V[(J + b2}/kb
Наконец, радиусы кривизны волновых фронтов в плоскостях х и у
также различны и определяются соотношениями
x{z) = (z-z1)+%/{z-z1),
y{z) = {z-z2)+bl/{z-z2). l -б >
Форма волнового фронта астигматичного гауссова пучка лишь в
частных случаях такая, как у обычного гауссова пучка. У последне-
последнего это всегда кусочек сферы или параболоида вращения. У астигма-
астигматичного гауссова пучка волновой фронт представляет собой кусочек
параболоида, но не вращения, а астигматичного, имеющего разные
параметры в плоскостях х и у. В перетяжках волновой фронт име-
имеет цилиндрическую форму, между перетяжками z\ < z < z^ волно-
волновой фронт имеет форму седловой поверхности. На такой поверхности
имеются, как известно, линии нулевой кривизны; в данном случае это
прямые, лежащие на волновом фронте, перпендикулярные оси z, и
составляющие с осью х угол =Ьа, где
Таким образом, у волнового фронта астигматичного гауссова пучка
наблюдается большее разнообразие форм, чем у обычного.
Учитывая эти отличия, не следует, однако, забывать, что в каждой
из плоскостей х или у астигматичный гауссов пучок ведет себя, как
обычный гауссов пучок и соотношения A.80) и A.81) есть не что иное,
как соотношения A.10) и A.14) для обычного гауссова пучка, только
переписанные в новых обозначениях и имеющие, как уже сказано,
разные параметры в разных плоскостях.
Астигматичный гауссов пучок характеризуется двумя — это ясно
из сказанного выше — комплексными параметрами
q\ = z — z\ — ibi, q2 = z — Z2 — гЬэ,
относящимися, соответственно, к плоскостям х и у.
Если оптическая система, в частности лазерный резонатор, обла-
обладает плоскостью симметрии и одна из плоскостей симметрии гауссова
пучка совпадает с плоскостью симметрии оптической системы, то с
параметрами q\ и q^ можно обращаться точно так же, как и с пара-
параметром q обычного гауссова пучка. В частности, можно пользоваться
правилом ABCD, правда, теперь уже, если оптическая система сама
астигматична, то каждый ее элемент будет описываться двумя мат-
матрицами 2x2, разными для каждой из плоскостей симметрии пучка.
1.6. А стигматичный гауссов пучок 47
Далее будут приведены примеры применения правила ABCD к астиг-
матичному гауссову пучку.
Простейшим астигматичным оптическим элементом является гра-
граница раздела свободного пространства и диэлектрика при наклонном
падении на нее гауссова пучка. Пройдя через эту границу, пучок оста-
остается гауссовым. Гауссов пучок в диэлектрике описывается следующим
выражением:
/ \ G' \iknx2 , ikny2 , ., , . ,1 (л ооЧ
^диэлО, у, z) = -== ехр —— + —f- + iknz + гср , A.82)
где штрихом отмечены параметры этого пучка. От A.79) это выра-
выражение отличается лишь тем, что везде волновое число к заменено на
произведение этого волнового числа на показатель преломления ди-
диэлектрика п.
Сравним поперечные распределения в падающем и прошедшем
пучках. Для этого введем координаты ж', у1', отсчитываемые вдоль
поверхности раздела сред:
ад = X1 COS #1, Жпрошед = X1 COS $2 ,
Упад — У 1 2/прошед — 2/ i
пад = Ж7 Sin $i, 2:прошед = ^' sin ^2 ,
Сравнение членов, пропорциональных z, приводит естественно к со-
соотношению
т. е. к обычному закону преломления. Приравнивая члены, содержа-
содержащие х и у, в показателях экспонент в выражениях A.79) и A.82),
получим
9=«П A.83)
Как легко видеть, эти соотношения получены при условии, что па-
параметры qi и #2 не сильно изменяются вдоль границы раздела сред
в области пересечения падающего пучка с этой границей. При выво-
выводе A.83) параметры q± и q^ считались постоянными в этой области.
Это означает, что падение пучка на границу раздела не должно быть
скользящим, т. е. угол $ не должен быть близок к тг/2.
Соотношения A.83) можно представить в виде правила ABCD
A.60), если ввести лучевые матрицы
COS #2 q
$ (П
(
COS$i I Д/f _
0
COS #2
описывающие изменение комплексных параметров q\ и q^ астигма-
тичного гауссова пучка при прохождении им плоской границы диэлек-
диэлектрика. Детерминанты этих матриц равны 1/п. Детерминанты матриц,
48 Гл. 1. Оптика гауссовых пучков
описывающих прохождение гауссова пучка из диэлектрика в свобод-
свободное пространство, равны п. Поэтому детерминант А??С1)-матрицы
всего резонатора при наличии в нем диэлектрика равен единице.
Типичными линейными резонаторами, моды которых — астигма-
тичные гауссовы пучки, являются резонаторы с брюстеровскими ок-
окнами или какими-то иными астигматичными элементами, а также
кольцевые резонаторы (§1.14, рис. 1.21), где астигматизм возника-
возникает из-за наклонного падения пучков на зеркала. Рассмотрим расчет
подобных резонаторов на основе правила ABCD. Такой расчет возмо-
возможен в том случае, когда резонатор обладает плоскостью симметрии,
и производится он раздельно в плоскости симметрии и в перпенди-
перпендикулярной к ней плоскости, проходящей через осевой луч резонатора.
В кольцевых резонаторах перпендикулярных плоскостей может быть
несколько в каждом его плече — своя перпендикулярная плоскость.
Однако мы для краткости будем говорить об одной такой плос-
плоскости.
Итак, в каждой из плоскостей оптическим элементам сопостав-
сопоставляются лучевые матрицы и вычисляются матрицы М\ и М2, описы-
описывающие резонатор в целом в каждой из плоскостей. Эти матрицы
определяют поперечные размеры мод и радиусы кривизны их вол-
волновых фронтов в соответствующих плоскостях (симметрии или пер-
перпендикулярной) согласно соотношениям A.67). Использование этих
соотношений вполне правомерно, поскольку, как уже сказано, астиг-
матичный пучок в плоскостях симметрии ведет себя как обычный.
Расчет продольного спектра астигматичного резонатора несколько
отличается от обычного. Набег фазы на оси пучка на отрезке длиной L
равен в этом случае
1 1 /1
+
= kL-- argft + - arg^i - - arg<?2 + - arg<?2.
z z z z
Рассмотрим для общности кольцевой резонатор (рис. 1.10), хотя те
же соображения могут быть применены и к линейному резонатору.
Полный набег фазы в таком резонаторе равен
N N , N
г=1 г=1 г=1
= kL- - argAi - - argA2,
где
N , N
г=1 г=1
и L — полная длина резонатора. Как было показано в § 1.5 (см. вывод
A.78)), Ai и Л2 — собственные значения матриц М\ и М2. Таким
1.6. А стигматичный гауссов пучок
49
образом, продольный спектр резонатора определяется условием
A2 + D2
kL = 2тг/ Н— arccos
, 1
I— arccos
A.85)
У
где / — целое.
В заключение параграфа рассмотрим изменение математической
формы гауссова пучка при повороте координатной системы вокруг
оси z. Как отмечалось выше, астиг-
матичный гауссов пучок обладает дву-
двумя взаимно перпендикулярными плос-
плоскостями симметрии, причем выражение
A.79), описывающее этот пучок, записа-
записано в координатах, у которых в качестве
координатных х- и ^-плоскостей взяты
как раз плоскости симметрии гауссова
пучка. Иногда важно знать, как выгля-
выглядит тот же самый астигматичный гаус-
гауссов пучок в более произвольно ориен-
ориентированной системе координат, в частности,
Рис. 1.11. Поворот системы
координат на угол Ф
в системе координат,
развернутой вокруг оси z на угол Ф относительно плоскостей сим-
симметрии гауссова пучка.
Пусть новые координаты выражаются через старые посредством
соотношений
где U — матрица поворота
гг — (С08 ^ ~ snl ^\
~ ys'm Ф cos Ф J
A.86)
Это преобразование означает, что новые оси развернуты относи-
относительно старых на угол Ф против часовой стрелки, если смотреть на-
навстречу положительному направлению оси z (на рис. 1.11 ось z на-
направлена на читателя, так как используется правая система коор-
координат) .
Для преобразования выражения A.79) к новым координатам до-
достаточно преобразовать в нем показатель экспоненты, так как лишь
там имеется зависимость от х и у. Для этого первые два слагаемых в
показателе (опуская множитель ik/2) представим в виде квадратич-
квадратичной формы
где
х
Р =
4 В.П. Быков, О.О. Силичев
50 Гл. 1. Оптика гауссовых пучков
Учитывая A.86), квадратичную форму W можно представить в
виде
W = (x^U^UPU^U Q = (x',y')R
где U г — матрица, обратная U, R — матрица вида
(cos2 Ф sin2 Ф /1 1 \ . _
1 ( ) sm Ф cos <;
Ql Q2 Ul q2) 2
/ 1 1 \ . л л sin2 Ф , cos2 Ф
( 1 sm Ф cos Ф 1
Таким образом, в новых переменных х' и у' астигматичный гауссов
пучок описывается выражением
г i i i\ G Г ik Г/
л/qiq^ I 2 1Л
,о-л д/1 ХА//, ^т2Ф , СО82Ф\ ,21 , -7 , • 1
+ 2 sm Ф cos Ф )х у + 1 )у \ + г/с^ + гю >,
\qi q2/ \ qi q2 J \ J
A.87)
где g'l и ^2 равны
<7i = z — z\ — ibi, #2 = z — z<i — ib2.
Может ли угол Ф принимать комплексные значения? Как выраже-
выражение A.79), так и выражение A.87), каждое в своей системе координат
удовлетворяют параболическому уравнению и приближенно — волно-
волновому. Так как угол Ф — не переменная, а параметр, не оказывающий
никакого влияния на операции дифференцирования, производимые
при подстановке выражения A.87) в уравнение, то выражение A.87)
удовлетворяет параболическому и приближенно волновому уравнени-
уравнениям независимо от того, является ли параметр Ф вещественной или
комплексной величиной. Но если параметр Ф является комплексной
величиной, то это означает, что гауссов пучок A.87) в этом случае
не может быть приведен к симметричному виду A.79) в координатах,
связанных с его плоскостями симметрии. Точнее сказать, такое при-
приведение может быть сделано, но при повороте на комплексный угол,
т. е. при выходе из реального вещественного пространства. Все это
наводит на мысль, что пучки, описываемые выражением A.87) при
комплексных значениях параметра Ф реально невозможны. Однако
это неверно.
В конце концов несущественно, откуда, из какого исходного пучка
возникает пучок A.87); важно лишь, что он является решением вол-
волнового уравнения. Мнимости же исчезнут, если при комплексном Ф
взять в качестве решений отдельно вещественную и мнимую части
A.87). Как мы увидим далее, такие пучки реально существуют и, бо-
более того, играют важную роль в приложениях.
1.7. Эрмит-гауссов пучок и высшие моды лазерного резонатора 51
§ 1.7. Эрмит-гауссов пучок и высшие моды лазерного
резонатора, образованного сферическими зеркалами
Гауссов пучок, описанный в предыдущих параграфах, играет
основную роль в теории и технике лазерных резонаторов, им опи-
описываются продольные моды простого линейного резонатора, образо-
образованного двумя сферическими зеркалами, — моды, которые называют
также основными поперечными модами. На практике обычно (за ред-
редким исключением) стремятся устроить лазерный резонатор так, что-
чтобы генерировались именно эти продольные или основные поперечные
моды, так как у них наиболее простое и равномерное поперечное рас-
распределение интенсивности, простое и равномерное распределение по-
получается также и в выходном пучке.
Кроме основных поперечных мод, в резонаторе имеются также
так называемые высшие поперечные моды (иногда основные попе-
поперечные моды называют продольными, а высшие поперечные — про-
просто поперечными). Свойства поперечных мод необходимо знать, ибо,
во-первых, довольно часто используется многомодовый режим, во-
вторых, хотя и редко, но бывают случаи, когда необходимо выделить
какую-то высшую поперечную моду и организовать генерацию на этой
высшей, а не основной моде, и, в-третьих, для выделения основной мо-
моды и предотвращения генерации на высших модах также необходимо
знать свойства этих высших мод.
Высшие поперечные моды лазерного резонатора представляют
собой обобщенные гауссовы или эрмит-гауссовы волновые пучки.
Имеется несколько обобщений гауссова пучка; вся совокупность этих
обобщений вместе с правилами преобразования пучков при их распро-
распространении в оптических системах и резонаторах составляет гауссову,
или матричную оптику. Эрмит-гауссов пучок — это одно из возмож-
возможных обобщений простого гауссова пучка.
В настоящем параграфе рассматриваются астигматичные эрмит-
гауссовы пучки, т. е. пучки, у которых распределения полей в двух
поперечных направлениях различны. Случай, когда астигматизм от-
отсутствует, имеет свои особенности и рассматривается в § 1.8.
Поле астигматичного эрмит-гауссова пучка описывается выраже-
выражением
ТТ ( х \ тт ( у \
Нп[ )Нт ( — 1 X
+ bl] \wj m\w2)
[ikx2 iky2 .( 1\ , z — z\
—— + т^-«п+- arctg —
2gi 2^2 \ 2/ oi
- i (m + i) arctg Z~Z2 + ikz + i(p\, A.88)
4*
52
Гл. 1. Оптика гауссовых пучков
Нп(?) и Нш{т]) — специальные функции — полиномы Эрмита; ком-
комплексные параметры эрмит-гауссова пучка q± и ^2, как и ранее, равны
q\ — z — Z\ — гбх, q<i — z — z<i — ibi-
Астигматизм пучка A.88) выражается в том, что параметры bi, z\ и
индекс п, описывающие распределение поля в плоскости ж, отлича-
отличаются от параметров &2, ^2 и индекса т, описывающих распределение
поля в плоскости у. Параметры z\^ и Ь\^ могут принимать не толь-
только вещественные, но и комплексные значения. При вещественных z\^
и 6i52 пучки A.88) описывают моды лазерных резонаторов, в кото-
которых нет гауссовых диафрагм. Если же такие диафрагмы в резонаторе
имеются, то его модами являются пучки A.88) с комплексными пара-
параметрами Zi52 и 6i52- Сначала мы рассмотрим пучки с вещественными
и затем — комплексными z\^ и Ъ\^-
Отметим основные свойства полиномов Эрмита. Полином (или
многочлен) Эрмита Нп является полиномом n-й степени, все кор-
корни которого вещественны и расположены симметрично относитель-
относительно начала координат приблизительно на одинаковом расстоянии друг
от друга. Как и всякий полином, полином Эрмита стремится к ±
=Ьоо, т. е. бесконечно нарастает по модулю, если независимая перемен-
переменная стремится к бесконечности по модулю. Однако амплитуда поля
эрмит-гауссова пучка u(x,y,z) не стремится к бесконечности при на-
нарастании х и у , поскольку в u(x,y,z) A.88) в качестве множителя
присутствует гауссова экспонента, которая стремится к нулю гораздо
быстрее, нежели любой полином к
бесконечности. Комбинация
также является специальной функ-
функцией, носит несколько громоздкое
название — функция параболиче-
параболического цилиндра и удовлетворяет
уравнению
п = 0
Рис. 1.12. Функции параболиче- Ясно, что нули функции Фп(?)
ского цилиндра те же^ чт0 и у полинома Эрмита
Нп(?), но эта функция затухает при ? —у =Ьоо. Несколько первых
функций Фп(?) показаны на рис. 1.12. Точки перегиба этих функ-
функций, не совпадающие с их нулями, можно видеть на том же рис. 1.12,
они расположены при
= 6» = 2
A.90)
1.7. Эрмит-гауссов пучок и высшие моды лазерного резонатора 53
В этой точке изменяется характер зависимости функции параболиче-
параболического цилиндра от ?. Из осциллирующей при |?| < ?п она переходит
в экспоненциально затухающую при |?| > ?п. Поэтому точки ? = =Ь?П
могут рассматриваться как условные границы той области, где сосре-
сосредоточено поле, описываемое функциями параболического цилиндра.
Используя функции параболического цилиндра Фп и Фш, поле
эрмит-гауссова пучка можно записать в виде
un,m(x,y,z) =
z-zi
A.91)
где
— Z\)
kb2
Как видим, фаза поля в произвольной точке пучка*) равна
ip(x, у, z) = kz- (п + -) arctg z ь Zl -
- (т
V
1) arctg
2 У &
2b2w\
A.92)
Соответственно, на оси пучка фаза поля равна
ip(z)=ip@,0,z) =
= kz - (ji + -J arctg z b Zl - [m + -J arctg ^ ^ ^2 + y?.
Отсюда видно, что фазовая скорость поля на оси пучка больше ско-
скорости света в вакууме:
дер -1
dz
--2J]}
с.
В результате на всем протяжении оси z в пучке набегает фаза на
(п + т + 1)тг меньше, чем в плоской волне.
Отметим, что набег фазы на оси пучка A.92) зависит от индексов
моды п и т, т. е. у разных поперечных мод набеги фаз различны. Это
*) Функции tyn(x/wi) и ^m,(y/w2) в зависимости от х и у могут изменять
свой знак, такое изменение знака может интерпретироваться как измене-
изменение фазы на тг. Выражение A.92) для фазы поля пучка не учитывает эту
возможность.
54 Гл. 1. Оптика гауссовых пучков
обстоятельство будет существенным, как мы увидим далее, при рас-
рассмотрении граничных условий на зеркалах, и приведет к зависимости
частотного спектра мод от поперечных индексов пит.
Найдем теперь форму и радиусы кривизны волнового фронта пуч-
пучка A.91). Для этого потребуем, чтобы фаза A.92) была постоянна и
равна фазе на оси пучка при z = zq. Тогда получим уравнение
(z - Zl)x2/2\qi\2 + (z - z2)y2/2\q22
= (z- z0) - - r^—t arctg ¦
(m + 1/2) b2(z-z0) n Q.4
— 7 dlLLgj —75 — r , yL.c/Oj
определяющее волновой фронт пучка A.91), пересекающий ось z в
точке zq. Поскольку жиув пучке малы, то на волновом фронте z — z$
и, следовательно, аргументы арктангенсов малы. Поэтому, заменяя
арктангенсы их аргументами, приводим уравнение A.93) к следую-
следующему виду:
2 2
z = Zo + ^_ +JJ_, A.94)
Д1 = |<?1|2/Фо - 2i), R2 = Ы2/?(го ~ z2)
— радиусы кривизны волнового фронта, имеющего согласно A.94)
форму астигматичного параболоида. Величина
? = 1 - ттЛ-
пренебрежимо мало отличается от единицы; действительно, добавоч-
добавочные члены в реальных ситуациях приближенно равны
(и+ 1/2) (ш + 1/2) _1П-з 1П-5
10 10
_1П-з 1
~10
Таким образом, в реальных ситуациях радиусы кривизны волновых
фронтов в точке zo для всех эрмит-гауссовых пучков вида A.91) оди-
одинаковы. Это очень существенное обстоятельство, поскольку выше бы-
было сформулировано простое правило (правило ABCD, § 1.5) для опре-
определения радиуса кривизны волнового фронта простого гауссова пучка
(основной моды); у высших поперечных мод радиусы кривизны та-
такие же, как у основной моды. Кроме того, оно показывает, что, если
какой-либо один эрмит-гауссов пучок из семейства A.91) (например,
основной с п = т = 0) удовлетворяет граничному условию на зерка-
зеркале, то и все остальные пучки этого семейства будут удовлетворять
тому же граничному условию, правда, при несколько другой частоте
и = кс.
Обратимся теперь к поперечным размерам высших мод. В качестве
поверхности, ограничивающей эрмит-гауссов пучок, т. е. в качестве
1.7. Эрмит-гауссов пучок и высшие моды лазерного резонатора 55
его каустической поверхности примем поверхность, на которой функ-
функции параболического цилиндра, входящие в A.91), имеют перегиб и
вне которой их зависимость от поперечной координаты становится
экспоненциально затухающей. Соответствующие точки определяют-
определяются условием A.90). Таким образом, каустические поверхности эрмит-
гауссова пучка A.91) описываются соотношениями
{2т
A.95)
и являются гиперболическими цилиндрами. Величины xn(z) и ym(z)
равны половинам поперечных размеров пучка соответственно вдоль
оси х и вдоль оси у. Их можно выразить через поперечные параметры
основного пучка:
xn(z) = w1(z)V2n-\-l, ym(z) = w2(z)\/2m + l. A.96)
Отсюда следует, что поперечные размеры высших поперечных мод,
так же, как и основной поперечной моды, могут быть найдены с по-
помощью правила ABCD. Действительно, согласно A.16) и A.96),
2п + 1 (Л I 2m
klm(l/qi(z)y УтК J У/ klm(l/q2(z)y
Покажем теперь, что эрмит-гауссовы пучки A.91) могут быть соб-
собственными модами резонатора, образованного сферическими зерка-
зеркалами, и выясним, при каких условиях это происходит. В таком ре-
резонаторе астигматизм отсутствует, поэтому можно положить Ъ\ = &2,
z\ — Z2 — zo, и эрмит-гауссов пучок (описывающий стоячую волну)
примет вид
, A.97)
где г = \Jх2 + у2. В § 1.2, подчиняя простой гауссов пучок граничным
условиям, мы действовали в два приема. Во-первых, требовали, что-
чтобы волна на оси z в точках ее пересечения с зеркалами обращалась в
нуль, и это приводило к уравнению A.25). Во-вторых, требовали, что-
чтобы в точках пересечения оси z с зеркалами радиусы кривизны волно-
волновых фронтов совпадали с радиусами кривизны зеркал, это приводило
к уравнениям A.23) и A.24). Действуя теперь так же по отношению к
эрмит-гауссову пучку A.97), замечаем, что второе требование вновь
приведет нас к уравнениям A.23) и A.24); поскольку кривизны волно-
волновых фронтов всех эрмит-гауссовых пучков такие же, как у основного
гауссова пучка. Так как эти уравнения определяли параметр гауссова
56 Гл. 1. Оптика гауссовых пучков
пучка Ъ и расстояния z\ и z^ от зеркал до перетяжки, то эти величины
оказываются, таким образом, общими для всех эрмит-гауссовых пуч-
пучков A.91) и по-прежнему определяются соотношениями A.26), A.27)
и A.28).
Первое же, упомянутое выше, требование об обращении в нуль по-
поля на оси z в точках ее пересечения с зеркалами приведет теперь к
другому, нежели A.25), уравнению. Для эрмит-гауссова пучка с ин-
индексами пит получаем, согласно A.97),
kimnL = Ztt + (п + т + 1) arccos л/дгд^,
или ic с
Vlmn = ТГГ + ^~F (П + Ш + 1) arCC0S л/0102, (L98)
где L — длина резонатора, I — продольный индекс, равный числу по-
полуволн поля, укладывающихся на длине резонатора L. Отметим, что в
этом соотношении учтены и частоты продольных мод, рассматривав-
рассматривавшихся в § 1.2, поскольку при п = т = 0 эрмит-гауссов пучок переходит
в простой гауссов пучок, а A.98) — в соотношение A.34).
Таким образом, мы показали, что эрмит-гауссовы пучки A.88) или
A.91) при условии A.98) являются собственными модами резонатора,
образованного сферическими зеркалами. Хотя резонатор в этом слу-
случае не обладает астигматизмом, собственная мода может быть астиг-
матичной, поскольку индексы пит могут различаться. В следующем
параграфе будут построены моды более симметричные, чем эрмит-
гауссовы пучки A.88) или A.91), и более соответствующие симметрии
рассмотренного резонатора.
Отметим некоторые особенности спектра A.98). Моды, у которых
продольные индексы отличаются на единицу (соседние, продольные),
а поперечные одинаковы, отстоят друг от друга по частоте на интер-
вал Д|/И = c/2L. A.99)
Моды, у которых только индекс п отличается на единицу или толь-
только индекс т отличается на единицу (соседние, поперечные), отстоят
друг от друга по частоте на интервал
A1 arccos Jg\g^. A.100)
Ais =
2тгЬ
Моды, у которых одинаковы суммы индексов п и т, не отличают-
отличаются по частоте. Это свойство резонатора означает вырождение его мод,
т. е. одной собственной частоте резонатора соответствуют несколько
собственных мод. Вследствие этого вырожденные моды могут обра-
образовать суперпозицию с иным, чем в A.88) или A.91), поперечным
распределением поля, которая также будет собственной модой резона-
резонатора. В частности, в следующем параграфе будут построены лагерр-
гауссовы моды, являющиеся суперпозициями мод A.88) или A.91).
Приведем соотношение, определяющее спектр произвольного ре-
резонатора, моды которого представляют собой астигматичные эрмит-
1.7. Эрмит-гауссов пучок и высшие моды лазерного резонатора 57
гауссовы пучки,
K'lmn-L/ — Z7T6 ~\
±) arccos
(m
- arccos-
' V ' о у ----- ~ 7
A.101)
где I — продольный и n, т — поперечные целочисленные индексы,
0О1тп = ckimn — резонансная частота (рад/с), L — полная длина осе-
осевого контура резонатора или длина пути, проходимого пучком до за-
замыкания, Ai52 и Di52 — диагональные элементы лучевых матриц резо-
резонатора в двух плоскостях (плоскости симметрии и перпендикулярной
к ней).
Одной из причин, приводящих к астигматичному гауссову пучку,
являются брюстеровские окна, широко используемые в лазерной тех-
технике. Как будет показано в § 5.1, совокупность сферического зеркала и
брюстеровской пластины с показателем преломление \i и толщиной D
эквивалентна астигматичному зеркалу,
у которого разность радиусов кривиз-
кривизны равна
AR =
A.102)
Рис. 1.13. Оптическая систе-
система, образованная пластиной
Брюстера и сферическим зер-
зеркалом
при этом в плоскости симметрии си-
системы (совпадающей с плоскостью
чертежа, рис. 1.13) радиус кривизны
эквивалентного зеркала больше, чем в
перпендикулярной плоскости.
Рассмотрим симметричный резона-
резонатор с двумя брюстеровскими окнами, часто встречающийся на прак-
практике. Длина такого резонатора пусть равняется 2L. Радиусы кри-
кривизны i?i52 эффективного зеркала связаны с параметрами Ъ\^ пучка
посредством соотношений
Отсюда при небольшой разности между R\ и R<± получаем
/R-L (т ^ 1 леД
Так как резонатор симметричный, то z\ — z^ — 0, и граничное усло-
условие на зеркале и@, 0, L) = 0 будет удовлетворено при
kL = /^ + (га+ - ) arctg— + (m + - ) arctg—.
Z\ Z/ Oi \ I / 02
Отсюда находим частотный спектр резонатора
cl с
A.103)
58 Гл. 1. Оптика гауссовых пучков
где I — продольный индекс, п — поперечный индекс, соответствующий
плоскости симметрии резонатора, т — также поперечный индекс, но
соответствующий плоскости, ортогональной к плоскости симметрии.
Как видно, в отличие от спектра A.98) резонатора, обладающего осью
симметрии, в резонаторе с брюстеровскими окнами отсутствует вы-
вырождение — собственные частоты щшп зависят не только от суммы
п + т, но и от разности п — т. Размеры поперечных мод различны
в двух плоскостях, так как различны параметры q\ и #2, и опреде-
определяются соотношениями A.96). Однако точность измерения попереч-
поперечных размеров мод невелика и эта разница вряд ли может быть за-
замечена. Другое дело спектр, собственные частоты резонатора могут
быть измерены с высокой точностью, и изменения в спектре, вноси-
вносимые брюстеровскими окнами, несомненно наблюдаемы. Главное же
заключается в том, что поскольку вырождение в спектре благодаря
брюстеровским окнам снято, то никаких других мод, кроме мод A.88)
или A.91), прямоугольной симметрии в резонаторе с брюстеровскими
окнами не может наблюдаться. В частности, лагерр-гауссовы моды,
исследуемые в § 1.8, не могут реализовываться в резонаторе с брюсте-
брюстеровскими окнами.
Наиболее часто встречающимся источником астигматизма в ре-
резонаторах является сферическое зеркало при наклонном падении на
него гауссова пучка. Действительно, такое зеркало (см. §5.1) при уг-
угле падения пучка, равном 7, эквивалентно астигматичному зеркалу с
радиусами кривизны R± = i^cos^1 7? гДе верхний знак соответствует
радиусу кривизны эквивалентного зеркала в плоскости падения пуч-
пучка, а нижний — радиусу кривизны в перпендикулярной к ней плоско-
плоскости. Соответственно, лучевые матрицы зеркала для этих плоскостей
имеют вид
( 1 °\
l--cosTi7 1/
\ К /
Пусть на зеркало под углом 7 падает астигматичный гауссов пу-
пучок, перетяжка которого отстоит от зеркала на расстояние L и на-
находится в точке / (рис. 1.14). Пусть также пучок после отражения
проходит расстояние X. Тогда лучевая матрица оптической системы
имеет вид
1 cos+ 7 L + X cos+ 7
— — cos+± 7 1 77 cos 7
К К
Потребуем теперь, чтобы в конечной точке F находилась перетяжка
отраженного пучка, т. е. параметр пучка в этой точке должен быть
чисто мнимым qp = —ibp. (Предполагается, что начала осей z для
падающего и отраженного пучков находятся на зеркале.) Пусть также
1.7. Эрмит-гауссов пучок и высшие моды лазерного резонатора 59
в начальной точке / находится перетяжка падающего пучка и qi =
= —гЬ/. Применяя правило ABCD, получим
qF = -ibF = (Aqi + B)/(Cqi + D) =
= [(BD + ACbj) - ib^/iD2 + C2bj).
Так как левая часть чисто мнимая, то
BD + ACbj = 0. A.105)
Отсюда получаем
_ [2b] - LjRcos^ 7 - 2L)]Rcos±1 7,
±- 4&2 + 0Rcos±17-2LJ '
Таким образом, параметры пучка #±(г) в плоскости падения и в пер-
перпендикулярной к ней существенно различны:
т. е. пучок после отражения также астигматичен.
Решим теперь небольшую задачу с астигматичным пучком, а
именно, потребуем, чтобы в рассмотренной выше системе (рис. 1.14)
расстояния X и L были равны, и найдем такой пучок, который со-
сохраняет свой параметр b при прохождении через эту оптическую
систему, т. е. найдем пучок, который в
некотором смысле является для нее соб-
собственным. Для этого нужно в матрице
A.104) положить X = L и воспользо-
воспользоваться условием A.105) также очевидно
необходимым в этом случае. Из A.105) х „
получаем
г—— — ^—- Рис. 1.14. Наклонное падение
k~VM^~^C0S 7J- гауссова пучка на сфериче-
Как мы увидим в § 1.14, это выражение ское зеРкал0
сильно облегчит нам отыскание мод кольцевых резонаторов в некото-
некоторых симметричных случаях.
Обсудим теперь одно возможное и в некоторых случаях существен-
существенное обобщение астигматичного эрмит-гауссова пучка A.88). В §1.12
показывается, что пучок A.88) удовлетворяет параболическому урав-
уравнению и, следовательно, приближенно — волновому уравнению, при
этом нетрудно видеть, и там это подчеркнуто, что все выкладки в до-
доказательстве остаются справедливыми и в том случае, когда парамет-
параметры Zi52 и 6i52 являются комплексными. При комплексных значениях
параметров х\^ и Ь\^ существенно изменяется распределение полей
высших мод. Для примера отметим, что масштабные множители w\^
60 Гл. 1. Оптика гауссовых пучков
в этом случае также комплексны, и полиномы Эрмита, поскольку их
корни обязательно вещественны, ни при каких х и у не обращаются
в нуль, т.е. при комплексных z\^ и Ъ\^ отсутствуют темные пятна в
поперечных распределениях полей пучка A.88). Такой пучок называ-
называют комплексным гауссовым пучком. Разумеется, возможны случаи,
когда пучок является комплексным лишь в одной из его плоскостей
симметрии, т. е. когда комплексны лишь z\ и bi, a z^ и Ь<± — веществен-
вещественны или комплексны z^ и &2, a z\ и Ь\ — вещественны.
Возможность комплексных значений z\^ и Ь\^ приводит к спе-
специфической проблеме определения высших мод резонатора. Пусть,
например, с помощью правила ABCD (§1.5) найдены параметры q\^
основного пучка, тогда для отыскания высших мод необходимо эти
параметры разделить на две части:
<7i,2 = (z- 21,2) - ibli2, A.106)
что при возможных комплексных значениях z±^ и Ь±^ является неод-
неоднозначной операцией — необходимы дополнительные физические со-
соображения для такого разделения. Далее эти физические соображе-
соображения приводятся и дается способ определения параметров z±^ и b±^-
Однако отметим, что, если в резонаторе отсутствуют гауссовы диа-
диафрагмы, то проблемы нет — параметры Ь±^ вещественны и просто
равны мнимым частям q±^- Соответственно, вещественны и однознач-
однозначно определяются из A.106) параметры zi^- Если же гауссовы диа-
диафрагмы в резонаторе присутствуют, то отыскание высших мод, опи-
описываемых комплексным гауссовым пучком, более сложно.
Итак, пусть в резонаторе распространяется комплексный гауссов
пучок A.88) (Imfri52 ф 0, или Imzi^ ф 0). Для того чтобы найти то
значение 6, которое, согласно A.89), определяет высшие собственные
моды лазерного резонатора, нужно проследить за его изменением при
проходе пучка по резонатору и потребовать его самовоспроизводства
после полного обхода резонатора подобно тому, как это делается с
параметром q. При этом достаточно проследить отдельно за парамет-
параметрами для каждой из плоскостей симметрии пучка.
Очевидно, что при распространении пучка между оптическими
элементами резонатора параметр b не изменяется. Изменение же b на
оптических элементах можно найти, во-первых, из известного преоб-
преобразования параметра q на этом оптическом элементе и, во-вторых, из
очевидного условия неизменности масштабного параметра w, которое
сводится к равенству
где ( = z — z (z = zip) и5- составные части параметров
q = ?-ib, q' = (' -ib'.
Легко показать, что это равенство можно представить как часть со-
соотношения, следующего из правила ABCD. Действительно, для оп-
1.7. Эрмит-гауссов пучок и высшие моды лазерного резонатора 61
тического элемента, описываемого матрицей A.40), правило ABCD
приводит к соотношению
- = --Р. A.108)
q' q
Так как q = ( — ib и q' = (' — ib', то равенство A.107) можно считать
мнимой частью соотношения A.108) в предположении, что величины
?', С, Ь'', b и Р считаются вещественными. Соответственно, действи-
действительная часть A.108) имеет вид
Два равенства A.107) и A.109) позволяют, таким образом, найти ком-
комплексные параметры (' и Ь' пучка, прошедшего через оптический эле-
элемент.
Еще раз отметим, что равенства A.107) и A.109), в которых ( и
b комплексны, вытекают из физического требования к масштабному
множителю w A.89) и из условия A.108). Лишь формально эти ра-
равенства являются, соответственно, мнимой и вещественной частями
A.108) в предположении, что С, С, b1, b и Р вещественны. Однако
это формальное обстоятельство очень удобно для вычислений. Дей-
Действительно, постоянство параметра b в свободном пространстве также
можно получить из правила ABCD, т.е. из равенства
если в нем разделить вещественную и мнимую части, предполагая ?',
?, Ь', b и Р вещественными. Естественно, что эта особенность сохра-
сохраняется и при всех последующих преобразованиях пучка.
Следовательно, параметр b резонатора, содержащего гауссовы диа-
диафрагмы, может быть определен из правила ABCD. Для этого ком-
комплексный параметр q запишем в виде q = ? — ib (? = zo — Zi, zo —
координата сечения, к которому отнесена матрица ABCD), и восполь-
воспользуемся соотношением A.63)
А((-гЪ) + В
*> C(C-ib)+D'
Предполагая в этом соотношении А, В, С, D, а также ?, b (временно)
вещественными и разделяя в нем вещественную и мнимую части, при-
приходим к уравнениям, определяющим ( и Ь. Разрешая эти уравнения,
получим соотношения
С = (А- D)/2C, b = ±v/4-(A + DJ/BC), A.110)
в которых все входящие в них величины могут быть комплексными.
Аналогично находятся параметры ? и b для другой плоскости сим-
симметрии пучка. Подставляя эти параметры в выражение A.88), нахо-
находим поле пучка в сечении, к которому отнесена матрица ABCD. Поле
62 Гл. 1. Оптика гауссовых пучков
пучка в прилегающих областях, свободных от оптических элементов,
также легко находится. Для этого величины z — zi в A.88) нужно
представить в виде z — zi — z — zq + Q (zo — координата реперного
сечения). Таким образом, соотношения A.110) полностью определя-
определяют параметры ( и Ъ лазерного резонатора, как содержащего, так и не
содержащего гауссовы диафрагмы.
Рассмотрим простой пример расчета резонатора, содержащего
гауссову диафрагму. Пусть в полуконфокальном резонаторе {R = 2L)
вблизи плоского зеркала расположена гауссова диафрагма так, что
лазерный пучок проходит ее дважды. При реперной плоскости, рас-
расположенной перед гауссовой диафрагмой, резонатор описывается мат-
матрицей
1 OWl LW 1 0\ /1 L\ _ ( 0 L \
2i/F' 1J [О 1) \-l/L 1) [О 1) ~ \-l/L 2iL/F'J '
Отсюда для параметра q получаем выражение
q = iL(a ± л/l + «2) = ±iLe±x (а = L/F' = shx).
Поскольку Reg = 0, то перетяжка моды расположена как раз в ре-
перном сечении. Для пучка, бегущего от гауссовой диафрагмы, следу-
следует выбрать нижний знак (см. с. 42), его поперечный радиус в реперном
сечении равен
Для определения параметра Ъ воспользуемся вторым из соотноше-
соотношений A.110):
Ь = =plVl + a2.
Как видим, параметр Ъ не совпадает с мнимой частью q. Таким об-
образом, для пучка, бегущего от гауссовой диафрагмы к сферическому
зеркалу, параметр q равен
q = z - z - ib,
где
z = —iaL.
Зная комплексные параметры Ъ и z, можно построить, согласно A.88),
поле комплексного эрмит-гауссова пучка, являющегося модой рас-
рассматриваемого резонатора.
Обсудим физический смысл особенностей, которыми обладает
комплексный эрмит-гауссов пучок, т.е. пучок A.88) с комплексным
параметром Ъ по сравнению с тем же пучком A.88), но с вещественным
параметром Ъ. При вещественном Ъ поперечное распределение поля,
описываемое функцией параболического цилиндра, в A.91), можно
рассматривать, как стоячую волну в пространстве между каустика-
каустиками. Для стоячей волны характерно обращение поля в нуль в ее узлах.
1.7. Эрмит-гауссов пучок и высшие моды лазерного резонатора 63
Однако могут быть волны более сложного характера, являющиеся
суперпозицией стоячей и бегущей волны, тогда наличие бегущей ком-
компоненты делает невозможным обращение поля в нуль в тех или иных
стационарных точках. Такие волны возникают, например, в тех слу-
случаях, когда имеется разное поглощение в разных точках, и в волне
происходит перераспределение запасенной энергии. Нетрудно понять,
что именно это происходит в пучке при комплексном Ъ. Действитель-
Действительно, такой пучок, как показано выше, тесно связан с наличием в резо-
резонаторе гауссовой диафрагмы, в которой поглощение на ее периферии
более интенсивно, чем в центре. Поэтому необходимо перераспреде-
перераспределение энергии в поперечном направлении, что и приводит к бегущей
составляющей в функции параболического цилиндра и исчезновению
стационарных нулей в поперечном распределении. Разумеется, ска-
сказанное следует понимать с учетом того, что волна не просто синусои-
синусоидальная или косинусоидальная, а описывается функциями параболи-
параболического цилиндра, и это несколько
усложняет картину.
Отметим также, что у комплекс-
комплексного эрмит-гауссова пучка в по-
поперечном распределении нет тех
характерных точек, определяемых
условием A.90), в которых зависи-
зависимость поля от поперечной коорди-
координаты изменяет свой характер и из
осциллирующей становится экспо-
экспоненциально затухающей. Поэтому
соотношения A.96) лишь прибли-
приближенно определяют их поперечный
размер в тех случаях, когда воздей-
воздействие гауссовой диафрагмы на пу-
пучок не слишком велико.
Для комплексного эрмит-гауссо-
эрмит-гауссова пучка понятие о волновом фрон-
фронте, как о поверхности постоянной
фазы, в значительной степени теряет свой простой смысл. Услож-
Усложнение этого понятия можно продемонстрировать на примере плоских
частично бегущих волны. Действительно, рассмотрим волну вида
U\Tj == в х fJC х . ^l.lllj
Если Р = 0, то это плоская волна, бегущая в направлении к (рис. 1.15),
с плоским волновым фронтом, перпендикулярным к. Если /3 = 1, то
7//г\ _ су- AkzZ • и „
LLyL J — Z6C- Dili 1ьх^
и волновой фронт этой волны (поверхность постоянной фазы) есть
плоскость, перпендикулярная оси z (рис. 1.15).
>
"х
l.fc
0
X
-0<Р<1
к
Рис. 1.15. Волновой фронт вол-
волны, частично бегущей и частично
стоячей в ж-направлении
64 Гл. 1. Оптика гауссовых пучков
Рассматривая случай промежуточных /3 @ < /3 < 1) нетрудно
представить, как происходит переход от одного фронта к другому.
Модуль М и фаза ср волны A.111) определяется равенствами
M2(x,z) = 1 + f32 -2f3coskxx,
ф, z) = arctg Sinjf^ + k'z\ + j ^хХ ~ k;Z\ . A.112)
^v ' ; ь cos(kxx + kzz) - /3cos(kxx-kzz) v ;
Рассмотрим поверхность нулевой фазы. Она, согласно A.112), опре-
определяется условием ip(x,z) = 0, или
(l + /3)tgkxx = -(l-/3)tgkzz.
При C = 0 имеем уравнение фронта
Гъ% X ~г rvz % ~~ V
и модуль волны постоянен вдоль фронта (М2 = 1). При малых /3
фронт немного искривляется. Заметим, что при /3 = 1 он состоит из
отдельных прямолинейных отрезков (рис. 1.15), соответствующих ус-
условиям
tgkxx = 0 и tgkzz = оо.
Но вдоль отрезков, соответствующих первому условию кхх — ттг, ам-
амплитуда равна нулю, и эти отрезки из картины выпадают. На отрез-
отрезках же, соответствующих второму условию kzz = — + ттгтг, амплитуда
волны отлична от нуля (кроме отдельных точек), и эти отрезки сли-
сливаются в единый фронт, перпендикулярный оси.
Разумеется, в комплексном эрмит-гауссовом пучке картина еще
сложнее, поскольку там не простые экспоненты, а функции парабо-
параболического цилиндра. Правда, эти рассуждения существенны для выс-
высших мод, но не для основной. Для основной моды понятие о волновом
фронте сохраняет свой простой смысл, и радиус кривизны волнового
фронта основной моды определяется формулой A.81).
При комплексном значении Ъ = Ь + ib эрмит-гауссов пучок имеет
особенности, связанные с множителем
Г
ехр
1\ , z-Zl] Г-^-^)+г6\
-) arctg НН={ (z - Zl) - гЪ \
в A.88), который при Ъ = 0 имеет чисто фазовый смысл. Выражение
в фигурных скобках нетрудно представить в виде [z\ — 1 + iz)
-Z-b-i(z-b)
где
а = arctg =, j3 = arctg
§1.8. Лагерр-гауссов пучок и вырождение мод лазерного резонатора 65
Отсюда следует, что множитель A.113) в комплексном эрмит-гауссо-
вом пучке имеет не только фазовый смысл, но и дает дополнитель-
дополнительную зависимость амплитуды пучка от z. Аналогично, множитель
[(z — Z\J + б^]/2 в комплексном эрмит-гауссовом пучке имеет не
только амплитудный смысл, но и приводит к дополнительной зави-
зависимости фазы от z.
§ 1.8. Лагерр-гауссов пучок и вырождение мод
лазерного резонатора
Поле лагерр-гауссова пучка описывается выражением
.2 N|ml/2 . / kbr2
Л I , <-> <-> I X
kbr2 ikzr2 .n . . o . .,4 , ^
^T^) + 2(^T^) " г(Н + 2n + 1) arctg -
+ ikz + irmp + iipL A.115)
где r, cp, z — цилиндрические координаты, Ln — полиномы Лагерра
(при т ф 0 — присоединенные полиномы Лагерра), ф — произволь-
произвольная фаза поля, п — радиальный и т — азимутальный поперечные
целочисленные индексы. В дальнейшем комбинацию функций
p\m\L^XP2)e-fl2, A.116)
где
2 kbr2 ,
(
будем рассматривать как единую лагерр-гауссову функцию. Тогда по-
поле лагерр-гауссова пучка можно представить в виде
¦2n + :
+ ikz + irmp + гф\, A.118)
, rAra) ( kbr2 \
из которого видно, что лагерр-гауссова функция Jz?n ( тъ г ) опи"
сывает поперечное распределение поля в сечении z.
Несколько замечаний о полиномах Лагерра и лагерр-гауссовой
функции. Полиномы Лагерра определяются соотношением
о-х п+т\.
n! dxn
5 В.П. Быков, О.О. Силичев
66 Гл. 1. Оптика гауссовых пучков
очевидно, что это именно полиномы, поскольку экспоненты после вы-
выполнения операций дифференцирования уничтожаются. Прямой под-
подстановкой можно убедиться, что они удовлетворяют уравнению
Учитывая его, можно убедиться, что лагерр-гауссова функция J^i (р)
удовлетворяет уравнению
[р4 - 2(т + 2п + 1)р2 + т2]^^ = 0.
r dp2 ' r dp
Это уравнение можно также представить в виде
где р есть функция т^ р — е~т. Отсюда видно, что характер функ-
функции <5?п различен в области между корнями уравнения (р > 0)
р4 - 2(тп + 2п + 1)р2 + тп2 = 0
и вне этой области.
Между корнями этого уравнения функция ??п (р) осциллирует —
именно здесь лежат корни полиномов Лагерра Ln , вне же этой об-
области функция <5?п (р) затухает. Поэтому значения р
2 = \/(m + 2n + 1) ± л/Bп + l)Bn + 2m TT) A.119)
мож:но принять в качестве условных границ, между которыми со-
сосредоточено поле лагерр-гауссова пучка. Учитывая A.117), получаем
уравнение каустических поверхностей, ограничивающих поле лагерр-
гауссова пучка
^4ь" i = L AЛ20)
В плоскости z = 0 поле пучка заполняет, таким образом, кольцо с
внешним и внутренним радиусами
r1>2 = Vk-4ph2 = у/к-ЧЦт + 2п + 1) ± ^{2п + 1)Bп + 2т + 1) ].
A.121)
В плоскости 2: т^ 0 размеры соответствующего кольца определяются
равенствами
(b2 + z2) [(m + 2n + 1) ± ^/Bn + l)Bn + 2m + 1) ].
A.122)
§1.8. Лагерр-гауссов пучок и вырождение мод лазерного резонатора 67
Радиусы кривизны волновых фронтов всех лагерр-гауссовых пуч-
пучков A.118) с высокой точностью совпадают и равны
где zo — координата точки пересечения волнового фронта с осью z.
Покажем теперь, что лагерр-гауссов пучок может быть представ-
представлен в виде суперпозиции эрмит-гауссовых пучков. Для этого запишем
поле эрмит-гауссова пучка для случая z\ — z<± — О, Ь\ — Ь^ — Ъ:
где также используем новые индексы s и ?, чтобы не спутать их с
индексами лагерр-гауссовапучка. Сравнивая это выражение с A.118),
убеждаемся, что зависимость от z в них одинакова при s + t = п + 2т.
Следовательно, достаточно показать, что поле лагерр-гауссова пучка
A.118) в сечении z = 0 можно представить как суперпозицию эрмит-
гауссовых полей с s + t = const = n + 2|m| том же сечении z = 0, т. е.
нужно доказать, что
eimv^imV) = J2K^i(O^N-j(v), A-123)
3
где Kj — коэффициенты, пока неизвестные, ? = pcoscp, rj = psincp —
безразмерные декартовы координаты, выраженные через полярные р
и (р, N = п + 2т. Отметим, что при N = 0 (п = т = 0) это равен-
равенство очевидно. Действительно, слева имеем Фоо = е~р ^ •> а справа
е^2/2-^2/2 = Фоо,т.е. Ко = 1.
Для доказательства равенства A.123) воспользуемся методом ин-
индукции. В связи с этим введем операторы*)
действующие на функции Ф следующим образом:
= 1).
*) Читатель, знакомый с квантовой механикой, легко узнает в этих опе-
операторах операторы рождения и уничтожения фотонов.
68 Гл. 1. Оптика гауссовых пучков
Введем также операторы
М = -i(A+B - АВ+) = -г ^-,
±
др р d
Нетрудно показать, что
MI± = I±M±I±. A.124)
Можно видеть, что функция etmip^fn (p) является собственной
для оператора М с собственным значением т. Поэтому искомую
суперпозицию функций параболического цилиндра попробуем найти
среди собственных функций оператора М.
Предположим, мы нашли собственную функцию Фту,ш операто-
оператора М с собственным значением т и с заданным N > т. Подействовав
на нее оператором 1±, получим две новых функции Ф^-т- Покажем,
что эти функции также являются собственными для оператора М.
Действительно, согласно A.124) имеем
т.е. Фдгт, действительно, есть собственная функция оператора М с
собственным значением m ± 1 и с N, на единицу большим, что следует
непосредственно из вида оператора 1±. Таким образом,
Построим теперь функцию с заданным N и m = N — 2k, где к —
целое. Очевидно, эта функция получится, если на Фоо подействовать
сначала N — к раз оператором /+ и потом к раз оператором /_
*N,N-2k = 1-к1(+М-к)У0,0- A-125)
Произведение операторов /_ и /_|_ в этом выражении можно предста-
представить в виде суммы произведений различных степеней операторов А^~
и В+. В результате действия этих операторов на распределение Фо,о
и последующего их действия на распределения Ф^ и Ф^, получается
та суперпозиция распределений, которая фигурирует в правой части
равенства A.123). При этом определяются и коэффициенты Kj.
С другой стороны выражение A.125) можно представить в виде
Шд N-k + 13-l Т^тт'гд «-1 1 -р2/2
7Г + Р\ л Р\е '
до о J J-X [^р р J
31 1
7Г
до
3=1
§1.8. Лагерр-гауссов пучок и вырождение мод лазерного резонатора 69
Операторы в квадратных скобках можно преобразовать
ди а — 1 р2/2 (а-1) д ( -о2 /2 -(а-1) \
и-ри — еР1рк > — (е ^7 о { }и)-
dp p дру
тогда для ^N,N-2k получаем следующее выражение
dp)
где к = (N — т)/2, N = s + t = const (TV = 2& + m). Таким образом,
построенная суперпозиция эрмит-гауссовых пучков A.125) как раз и
есть лагерр-гауссов пучок A.118) при z = 0.
Моды лазерного резонатора, образованного двумя сферическими
зеркалами с радиусами кривизны R\ и R^ (рис. 1.4) и обладающего
цилиндрической симметрией, описываются выражениями
A.126)
при этом параметр b и расстояния от зеркал до перетяжек по-преж-
по-прежнему определяются соотношениями A.26), A.27) и A.28), посколь-
поскольку моды A.126) представляют собой суперпозиции эрмит-гауссовых
мод. Моды A.126), соответствующие нулевому азимутальному индек-
индексу (т = 0), всегда в центре (при г = 0) имеют светлое пятно, а моды,
соответствующие ненулевым азимутальным индексам (т ф 0), всегда
в центре имеют темное пятно. Это видно из выражения A.116), по-
поскольку там имеется множитель $ш\ а полином Лагерра не обраща-
обращается в нуль при г = 0. Кроме того, согласно A.121), радиус внутренней
каустики пучка равен нулю при т = 0.
Таким образом, моды с т = 0 имеют только внешнюю каустику,
радиус которой в сечении z равен
1(Ь2+г2)Bп + 1). A.127)
В поперечном сечении эти моды представляют собой систему светлых
колец со светлым пятном в центре; радиальный индекс п равен числу
темных промежутков между светлыми кольцами.
Моды с т ф 0 имеют как внешнюю, так и внутреннюю каустики,
поперечные радиусы которых определяются соотношениями A.121).
В поперечном сечении эти моды также представляют собой систему
колец. Однако теперь в центре, как уже отмечалось, имеется темное
70 Гл. 1. Оптика гауссовых пучков
пятно, а светлые кольца обязательно имеют азимутальные разрывы
(их число равно 2т). Число светлых колец равно п + 1.
Поскольку лагерр-гауссовы моды A.115) являются линейными су-
суперпозициями эрмит-гауссовых мод A.88), то спектр рассматриваемо-
рассматриваемого резонатора по-прежнему определяется соотношением A.98) с заме-
заменой в нем в связи с новым смыслом индексов пит скобки (п + т + 1)
на скобку (\т\ + 2п + 1):
Щпт = WT + Y~J AШ1 + 2п + 1) arccos у/дпБ, A.128)
где I — продольный целочисленный индекс.
§ 1.9. Электрическое и магнитное поля
гауссова пучка
Исследуя гауссов пучок, мы пока принимали во внимание одну,
главную компоненту электрического поля, которая описывалась вы-
выражением A.5). Однако фактически в гауссовом пучке имеются и дру-
другие компоненты электрического поля, в частности продольные, а так-
также компоненты магнитного поля. Поэтому рассмотрим поля гауссова
пучка более подробно.
Для отыскания электрического и магнитного полей гауссова пуч-
пучка представим его в виде совокупности плоских волн. Одна из компо-
компонент электрического поля плоской волны может быть определена из
сопоставления с единственной компонентой пучка A.5). Остальные
же компоненты электрического и магнитного полей плоской волны
могут быть выражены через единственную известную в соответствии
с уравнениями Максвелла. Если затем найденные электромагнитные
плоские волны вновь сложить, то получится волновой пучок со всеми
компонентами полей.
Пусть ж-компонента электрического поля гауссова пучка описыва-
описывается выражением A.5)
A.129)
В плоскости z = 0 имеется, следовательно, распределение
A.130)
Представим электрическое поле пучка в виде совокупности плоских
волн
Е(х, y,z) = J dkx J dky e(kx, ky)Sk'x+kyy+k'^, A.131)
§1.9. Электрическое и магнитное поля гауссова пучка 71
где e(kXjky) — амплитуда плоской волны с волновым вектором
Так как пучок предполагается монохроматическим, т. е. имеет фик-
фиксированную частоту со, то все волновые вектора, входящие в A.131),
подчиняются соотношению
вытекающему из уравнений Максвелла. Следовательно,
kz =
и поэтому интегрирование в A.131) производится по кх и ку, но не
по kz.
Согласно A.131) в плоскости z = 0 для Д^-компоненты имеем вы-
выражение
Ех(х,у,0) = Jdkx Idkvex{kx,kv)ei{k*x+k*y\ A.132)
Зависимость ?х(кх,ку) необходимо подобрать так, чтобы компонента
Ех(х,у,0) совпала с A.130). Нетрудно догадаться, что следует поло-
положить
^[^% AЛ33)
Действительно, подставляя это выражение в A.132) и принимая во
внимание известный интеграл
+ ОО
^ -Б2/4А^ A.134)
получим как раз выражение A.130) для Ех(х,у,0). Равенство A.134)
выражает хорошо известный факт, что фурье-образ гауссовой экспо-
экспоненты есть также гауссова экспонента.
Обратимся теперь к другим компонентам электрического поля
плоских волн. Как известно, поля в плоской волне являются попе-
поперечными, т. е.
kxsx + кубу + kzez = 0. A.135)
Будем предполагать, что ^-компонента электрического поля в пуч-
пучке отсутствует (еу = 0), тогда z-компонента в соответствии с A.135)
равна
A.136)
В соответствии с уравнениями Максвелла амплитуда магнитного
поля плоской волны равна
Н = к~1[кхе]
72 Гл. 1. Оптика гауссовых пучков
и, следовательно, компоненты Н, имеют вид
Нх = -(kxky/k2)sx, Ну = [(к2х + k2z)/kkz]ex, Hz = -(ку/к)ех.
A.137)
Таким образом, все компоненты электромагнитного поля плоской вол-
волны оказались выраженными через одну компоненту электрического
поля ех. Вследствие параксиальности гауссова пучка
кх,ку^к и kz ~ к, A.138)
поэтому
т. е. в поле гауссова пучка имеются две главные, примерно равные
компоненты ех и Ну и три малых компоненты ez, Hx и Hz. Отме-
Отметим, что вследствие соотношений A.136) и A.137), существование в
гауссовом пучке продольных компонент совершенно неизбежно. В ли-
литературе можно встретить утверждение, что поля в резонаторах, на-
например описываемые гауссовыми пучками, являются ТЕМ-полями,
что расшифровывается как «поперечная электрическая и магнитная
волна». Это утверждение верно лишь приближенно в том смысле, что
продольные компоненты много меньше главных поперечных, но не
равны нулю.
Итак, для ж-компоненты электрического поля имеем, согласно
A.131) и A.133), следующее выражение:
Ех(х,у, z) = —г / / dkx dky exp ^——-—\- i(kxx + kyy +
z2 -k2x - fe^z) + гу>]; A.139)
этот интеграл довольно сложен и не поддается прямому вычислению
из-за квадратного корня в показателе экспоненты. Можно, однако,
найти его приближенное выражение, если воспользоваться условием
параксиальности A.138) и корень в показателе экспоненты предста-
представить в виде
\ X V ~ \ X ' У/ I ^^"
Тогда интегралы в A.139) приводятся к виду A.134) и для Ех полу-
получается приближенное выражение
7-1 / \ ^
т.е. гауссов пучок A.129) действительно описывает (правда, прибли-
приближенно, но с высокой точностью) главную компоненту электрического
поля.
В соотношениях A.136) и A.137) в параксиальном приближении
kz можно заменить на к. Тогда для компонент полей получаем сле-
следующие выражения:
Еу=0, Ez(x,y,z) = ^Ex(x,y,z), A.140)
1.10. Состояние поляризации мод лазерного резонатора
73
1
¦Н-х — ТТГ
1 д2
к2 дхду
Ex(x,y,z),
bh)Ex{x^z)'
A.141)
A
Рис. 1.16. Электрическое (вверху) и магнитное (внизу) поля плоской волны
и гауссова пучка; А — плоская волна, В — гауссов пучок
Поля плоской волны гауссова пучка показаны на рис. 1.16.
§ 1.10. Состояние поляризации мод лазерного
резонатора. Метод Джонса
Поляризация поля излучения, формирующегося в лазерном резо-
резонаторе, определяется теми или иными имеющимися в нем анизотроп-
анизотропными элементами. Как показано в § 1.9, гауссову пучку, являющемуся
74 Гл. 1. Оптика гауссовых пучков
модой лазерного резонатора, соответствует довольно сложная систе-
система полей, в которой, однако, одна поперечная компонента электри-
электрического поля или линейная комбинация двух поперечных компонент
значительно превосходят по величине остальные компоненты. Такой
гауссов пучок при прохождении как изотропных, так и анизотропных
оптических элементов ведет себя с высокой степенью точности как
плоская волна. Соответственно, при прохождении этих оптических
элементов достаточно учитывать лишь главные компоненты полей.
Подобный способ исследования является приближенным, но точность
такого приближения весьма высока, об этом говорит то, что этим спо-
способом рассчитаны многочисленные лазерные резонаторы и никаких
отклонений от теоретических расчетов на опыте не отмечено.
В литературе описано несколько методов расчета состояния поля-
поляризации плоских световых волн: метод сферы Пуанкаре, метод мат-
матрицы Мюллера, метод Джонса. Применительно к лазерам интерес
представляет только монохроматическое излучение, поэтому наибо-
наиболее пригодным и фактически единственно применяемым при иссле-
исследовании поляризации полей, формирующихся в лазерных резонато-
резонаторах, является матричный метод Джонса. Его изложению посвящен
настоящий параграф.
Состояние поляризации волны в методе Джонса описывается век-
вектором Джонса
е = (дА , A.142)
составленным из поперечных компонент электрического поля гауссо-
гауссова пучка (в плоской волне других компонент вообще нет); предполага-
предполагается, что пучок распространяется в положительном направлении оси z
и всюду используется правая система координат. Рассмотрим несколь-
несколько частных случаев. Пусть фазы компонент Ех и Еу совпадают. Это
соответствует линейной поляризации излучения, электрическое поле
наклонено к оси х под углом
а = B,Yctg{EvlEx). A.143)
Пусть теперь фазы компонент сдвинуты друг относительно друга
на тг/2, а амплитудные значения компонент равны друг другу Ех =
— Еу — е. В этом случае вектор Джонса можно представить в виде
е = е (Д) . A.144)
Если вспомнить, что вклад в фазу происходит также от временного
множителя e~lujt и перейти к вещественному представлению
cosut \ (СО800Л
= г ( . тг\ = s . , , A.145)
1.10. Состояние поляризации мод лазерного резонатора 75
то становится ясно, что угол, который вектор электрического поля
составляет с осью х A.143), является переменным:
, {sinout \ ,
а = arctg = cut,
V cos utJ
растущим линейно со временем. Возводя в квадрат компоненты элек-
электрического поля A.145) и складывая эти квадраты, получим
Ьх+Ьу ~?
— уравнение окружности. Таким образом, конец вектора электриче-
электрического поля при поляризации A.144) описывает окружность. По этой
причине подобная поляризация получила название круговой или цир-
циркулярной, состояние A.144) называют левой круговой поляризацией,
а состояние, отличающееся от A.144) знаком второй компоненты, на-
называется правой круговой поляризацией.
По поводу этой широко распространенной терминологии необходи-
необходимо сделать следующее замечание. Если взять небольшой отрезок луча
вблизи исследуемой точки поля и во всех точках этого отрезка постро-
построить вектор электрического поля циркулярно поляризованной волны в
тот или иной избранный момент времени, то концы этого вектора об-
образуют винтовую линию, или спираль. Поляризация по определению
считается правой, если эта винтовая линия правая, или соответству-
соответствует правому винту, если же винтовая линия левая, т. е. соответствует
левому винту, то и поляризация по определению считается левой. В
литературе состояния циркулярной и эллиптической (см. далее) по-
поляризации часто сопоставляют, таким образом, с винтом, при этом,
однако, не обращают должного внимания на существенное ограни-
ограничение подобного сопоставления, заключающееся в том, что винт при
своем движении вращается вдоль оси и отдельные его точки сами
описывают винтовые линии, в то время как поляризационная винто-
винтовая линия перемещается поступательно вдоль луча, не вращаясь, и
отдельные ее точки не описывают винтовую линию при распростра-
распространении волны. Учитывая это обстоятельство, можно убедиться, что,
если смотреть навстречу волне и определять состояние ее поляриза-
поляризации в некоторой избранной плоскости, ортогональной лучу, то вектор
электрического поля в этой плоскости при правой поляризации дви-
движется по часовой стрелке, а при левой поляризации — против часо-
часовой стрелки. Те же соображения относятся к эллиптической поляри-
поляризации.
Эллиптическая поляризация описывается вектором Джонса вида
A.146)
где А и В — амплитуды, соответственно, х- и ^-компонент электриче-
электрического поля и ? — разность фаз этих двух компонент. Угол, который
76 Гл. 1. Оптика гауссовых пучков
электрическое поле составляет с осью ж, определяемый соотношением
tga= -ф = — (cos? + sin?-tgcj?),
хотя и растет монотонно со временем, но этот его рост не равноме-
равномерен. Конец вектора электрического поля в той или иной избранной
плоскости описывает эллипс, уравнение которого имеет вид
f-^^ + §=sin4 A.147)
Этот эллипс можно привести к главным осям, поворачивая систему
координат на угол /?, называемый азимутом эллиптической поляри-
поляризации и определяемый соотношениями
Гsin2/? = 2Rcosf [A - R2J + 4R2 cos2 ?]~1/2,
[cos 2p = A - R2)[(l - R2J + 4R2 cos2 f]^
где R — BjA — отношение модуля ^-компоненты к модулю ж-ком-
поненты электрического поля. Кроме азимута эллиптическая поля-
поляризация характеризуется также отношением ? главных осей эллип-
эллипса A.147), которое называется эллиптичностью и определяется ра-
равенством
Эллиптическая поляризация A.146) представляет собой наиболее
общий вид поляризации излучения в свободном пространстве. Все
остальные поляризации — частные случаи эллиптической. Так, ли-
линейная поляризация является левой при ? > 0 (или ( > 0) и правой —
при ? < 0 (или С < 0).
Расчет поляризации мод лазерного резонатора производится, как
уже указывалось, в предположении, что этой модой является плоская
волна. При этом каждому оптическому элементу, анизотропно воз-
воздействующему на амплитуду и фазу волны, сопоставляется матри-
матрица 2 х 2. Умножение этой матрицы на вектор Джонса, описывающий
поляризацию падающей на анизотропный оптический элемент волны,
дает вектор Джонса волны, выходящей из него.
Анизотропные оптические элементы распадаются на два класса:
поляризаторы и фазовые пластинки. Поляризаторы различно воздей-
воздействуют на амплитуды волн двух возможных поляризаций. Фазовые
пластинки вносят в эти волны различные фазовые набеги. Поляриза-
Поляризатор считается идеальным, если одну из поляризаций он пропускает без
затухания, а вторую нацело поглощает. Фазовая пластинка считается
идеальной, если обе поляризации проходят через нее без затухания.
Для встречающихся на практике оптических элементов эти матрицы
известны и приведены в табл. 1.1.
Первые четыре матрицы этой таблицы описывают поляризаторы,
остальные — фазовые пластинки.
1.10. Состояние поляризации мод лазерного резонатора
77
Таблица 1.1
Матрицы, описывающие прохождение света через анизотропные
элементы
I
II
III
т\ т п
2
mri
2
П
п|2 =
1 0\ /0 0
о о или о i
1/1 ±г
2
IV
V
Pi О
О Р2
2г sin Я cos R sin - e гл
2
2г sin Я cos R sin - ег7
2
a-iS/2
VI
VII
гб/2 Q Ч ,-гб,
0 е-^2 ИЛИ { 0
0
рг<5/2
1 0
О _
-1 О
VIII
IX
5 , . 8\
COS - d= Sin -
2 2
5
cos -
2
1 / 1 П 1/1-1
—= -, -, или —= 1 1
>/2 V-1 V \/2 VI 1
X
XI
— sin $ cos $
г г
1. Идеальный эллиптический поляризатор. Волна с поляри-
поляризацией I 1 проходит через него без затухания (собственное значение
\ 77/ /
матрицы равно единице), волна с поляризацией
т*
полностью не
проходит через поляризатор (собственное значение равно нулю). Де-
Детерминант идеального поляризатора равен единице.
2. Идеальный линейный поляризатор. Этот поляризатор
представляет собой частный случай поляризатора 1 при т = 1, п = О
или т = 0, п = 1. В первом случае без затухания проходит волна, по-
поляризованная вдоль оси у, во втором — волна, поляризованная вдоль
оси х.
3. Идеальный циркулярный поляризатор представляет собой
частный случай поляризатора 1 при т = 1/л/2 и п = ±г/л/2- В пер-
первом случае (верхний знак) без затухания проходит левоциркулярно
поляризованный свет, во втором — правоциркулярно поляризованный
свет.
78 Гл. 1. Оптика гауссовых пучков
4. Частичный линейный поляризатор. Волны обеих возмож-
возможных линейных поляризаций проходят через поляризатор лишь ча-
частично, с различным ослаблением. Детерминант матрицы частично-
частичного поляризатора меньше единицы, но больше нуля. Свойствами ча-
частичного линейного поляризатора обладают, например, брюстеров-
ские окна.
5. Идеальная эллиптическая фазовая пластинка. Волна с
/COSjRe~i7//2\
поляризацией ( . г ,2 I при прохождении фазовой пластинки
\ ып ,/х с /
опережает по фазе волну с поляризацией _ • /9 на о (соо-
\ cosReZ7/z )
ственные значения матрицы равны, соответственно, ег5'2 и е
6. Идеальная линейная фазовая пластинка представляет со-
собой частный случай фазовой пластинки 5 при R = 0 или R = -к 12. В
первом случае больший набег фазы появляется у волны, поляризован-
поляризованной вдоль оси ?/, во втором — у волны, поляризованной вдоль оси х.
Свойствами линейной фазовой пластинки обладают диэлектрические
зеркала при наклонном падении на них света.
7. Полуволновая линейная фазовая пластинка представляет
собой частный случай пластинки б при 5 = =Ьтг, общий множитель i
опущен.
8. Идеальная циркулярная фазовая пластинка представляет
собой частный случай эллиптической фазовой пластинки 5 при R =
= ±тг/4 и 7 = =Ьтг/2. При верхнем знаке с опережением по фазе прохо-
проходит левоциркулярная поляризация, при нижнем — правоциркулярная
поляризация.
9. Полу волновая циркулярная фазовая пластинка представ-
представляет собой частный случай фазовой пластинки 8 при S = =Ьтг/2.
Все эти матрицы описывают анизотропные оптические элементы
в их собственной системе координат, связанной с их ортогональными
главными осями. Однако в лазерном резонаторе эти элементы могут
быть развернуты на угол $ относительно системы координат, связан-
связанной с резонатором. В этом случае анизотропный оптический элемент,
описываемый в его собственной системе координат матрицей М, в
системе координат, связанной с резонатором, описывается матрицей
М' = 5(—#)М5(#), где 5(#) — матрица поворота на угол $, приве-
приведенная в табл. 1.1 под номером X.
Сказанное выше относилось к так называемому линейному пред-
представлению. Существует и в ряде случаев оказывается более удобным
так называемое циркулярное представление. В этом представлении
базисными векторами являются векторы
1.10. Состояние поляризации мод лазерного резонатора 79
где ех и еу — единичные векторы вдоль осей х и у. Для перехода к
циркулярному представлению вектор в линейном представлении сле-
следует слева умножить на матрицу С/, приведенную в табл. 1.1 под номе-
номером XI. Все матрицы М анизотропных оптических элементов должны
быть подвергнуты при этом преобразованию М' = UMU~1.
Вся система анизотропных оптических элементов, входящих в ре-
резонатор, описывается единой матрицей, которая однозначно опреде-
определяется, если известны матрицы отдельных элементов, ориентация их
главных осей и направление распространения света. Эта единая мат-
матрица является произведением матриц отдельных элементов с учетом
их ориентации, записанных справа налево в том порядке, в котором
свет проходит эти элементы. В резонаторе вектор поляризации света,
прошедшего через все элементы, должен с точностью до постоянно-
постоянного множителя совпадать с исходным вектором поляризации. Следо-
Следовательно, в лазерном резонаторе вектор поляризации моды являет-
является собственным вектором матрицы, описывающей поляризационные
свойства всей совокупности оптических элементов, составляющих ре-
резонатор.
Пусть матрица, описывающая поляризационные свойства всей со-
совокупности анизотропных оптических элементов, входящих в резона-
резонатор, имеет вид
м = (п11 а12
Собственные значения этой матрицы равны
A [(
2 ± л/(аи
их можно записать также в виде
Ах = Aieiipi, А2 = A2ei<P2, 1 > А1, А2 > 0. A.148)
Модули этих собственных значений определяют пропускание системы
или потери за один обход резонатора, обусловленные анизотропными
элементами. Разность фаз ц>\ — (^2 определяет разность частот
резонансных мод с собственными состояниями поляризации, здесь
L — длина контура резонатора и с — скорость света. Собственные
векторы поляризации равны
и имеют в общем случае, согласно A.148), различные потери.
80
Гл. 1. Оптика гауссовых пучков
Рассмотрим для примера простейший линейный резонатор, содер-
содержащий анизотропные элементы: поляризатор и двулучепреломляю-
щую (фазовую) пластинку, главная ось которой лежит в ее плоскости
Рис. 1.17. Анизотропный резонатор с поляризатором и фазовой пластиной
(рис. 1.17). Матрица М, описывающая поляризационные свойства та-
такого резонатора и соответствующая сечению в резонаторе, отмечен-
отмеченному штриховой линией на рис. 1.17, представляет собой произве-
произведение
м = ps-^sp = (cos2ф + is™2%cos^ \
^ у г sin 2т/> sin 2<р 0J
где Р, Q, S — матрицы II, VII, X табл. 1.1, ip — угол разворота
главных осей поляризатора и двулучепреломляющей пластинки, 2ф —
разность набегов фаз обыкновенного и необыкновенного лучей в дву-
двулучепреломляющей пластинке. Матрица М имеет два собственных
значения:
\г =0, А2 = cos 2ф + г sin 2ф cos 2ip.
Потери волны, соответствующей первому собственному значению (ж-по-
ляризация), — полные, т.е. 100-процентные. У второй волны (^-поля-
(^-поляризация) потери за один полный проход резонатора равны
1 - |А2|2 = sin2 2гр sin2
Так как величина
= тгг/(пе — no)d/c
зависит от частоты световой волны v (d — толщина двулучепреломля-
двулучепреломляющей пластинки; пе, по — показатели преломления необыкновенной
и обыкновенной волн), то потери этой волны периодически изменя-
изменяются с частотой. Наибольшей глубины модуляция потерь достигает
при ip = тг/4, т. е. при sin 2ip = 1. При этом в максимуме потери равны
единице, т.е. 100%, а в минимуме — нулю, т.е. вообще отсутствуют.
Расстояние по частоте между двумя минимумами потерь равно
Av = c/2d\(ne-no)\.
Зависимость потерь, вносимых анизотропными элементами, от ча-
частоты в рассмотренном примере и других аналогичных лежит в основе
одного из возможных способов селекции продольных мод в лазерных
резонаторах.
§1.11. Расчет резонаторов матричным методом. Резюме 81
§1.11. Расчет резонаторов матричным методом.
Резюме
Матричный метод расчета резонаторов и правило ABCD весьма
эффективны и широко применяются, хотя и имеют свои ограниче-
ограничения. В предыдущих разделах и матричный метод и правило ABCD
уже описаны, но описаны на примерах и отдельные элементы этого
описания разбросаны по разным параграфам. В связи с этим пред-
представляется целесообразным дать краткое резюме этого метода, что и
сделано в настоящем параграфе.
1. Приступая к расчету резонатора матричным методом, необхо-
необходимо, в первую очередь, установить, применим ли этот метод к рас-
рассматриваемому резонатору. Матричный метод и правило ABCD при-
применимы лишь к резонаторам, обладающим плоскостью симметрии.
В частности, необходимо, чтобы осевой контур резонатора целиком
лежал в этой плоскости симметрии, а все оптические элементы, об-
образующие резонатор, должны располагаться зеркально симметрично
относительно этой плоскости. Следует иметь в виду, однако, что эта
симметрия касается только пространственного воздействия со сторо-
стороны оптического элемента на пучок, но не воздействия на поляриза-
поляризацию пучка. Воздействие на поляризацию может быть и несимметрич-
несимметричным. Например, фазовые пластинки или поляризаторы, практически
не изменяющие пространственной структуры пучка, могут несиммет-
несимметричным образом воздействовать на его поляризацию, т. е. главные оси
фазовых пластин и поляризаторов могут быть произвольным образом
развернуты относительно плоскости симметрии резонатора. Такое на-
нарушение симметрии несущественно, оно оставляет резонатор в рам-
рамках матричного метода и правила ABCD, поскольку пространствен-
пространственная структура пучка и его поляризационное состояние отыскиваются
независимо.
Другим важным ограничением как для матричного метода, так и
для гауссовой оптики в целом, является наличие в резонаторе резких
диафрагм или оптических элементов с аберрациями, т. е. элементов,
не описываемых гауссовой экспонентой. Диафрагмы могут вводиться
в резонатор специально, например, для выделения основной моды, но
ими могут быть также и те или иные конструктивные элементы резо-
резонатора. Важным источником аберраций в резонаторах твердотельных
лазеров является оптическая неоднородность, возникающая в актив-
активном элементе под действием накачки. Положение, однако, таково, что,
не проведя расчета матричным методом, нельзя сказать, сильно или
не сильно диафрагмы или элементы с аберрациями нарушают «гаус-
совость» оптики. Поэтому сначала такие негауссовы элементы можно
вообще не учитывать. Лишь определив поперечный размер моды в
месте расположения негауссова элемента, можно понять, что влия-
влияние негауссовости этого элемента пренебрежимо мало, или, что нуж-
6 В.П. Быков, О.О. Силичев
82
Гл. 1. Оптика гауссовых пучков
но учесть какие-то поправки, вносимые им, или, наконец, что нужно
произвести расчет резонатора заново, например, методом интеграль-
интегрального уравнения с существенным учетом негауссовости элемента с са-
самого начала. (Этот случай, кстати, означает, что резонатор обладает
относительно большими потерями, и поэтому, возможно, следует не
проводить дальнейшие расчеты, а просто изменить схему резонатора,
если только большие потери не являются целью.) Исходный расчет
резонатора матричным методом без учета негауссовости элементов в
любом случае дает хорошую ориентировку.
2. Расчет резонатора матричным методом производится незави-
независимо в плоскости симметрии и плоскости, перпендикулярной к ней,
проходящей через ось пучка. В кольцевых резонаторах может быть
несколько плоскостей, перпендикулярных плоскости симметрии и
проходящих через ось пучка. В этих случаях, чтобы не прибегать к
громоздким оборотам, будем говорить просто о плоскости симметрии
и перпендикулярной плоскости.
В каждой из плоскостей элементам резонатора, образующим его,
сопоставим 2x2 матрицы (табл. 1.2). Расположим эти матрицы справа
Таблица 1.2
1
2
3
4
Оптическая система
I I
1 1
I I
1 2
IAIF
I/ \l
livi2
1 [ ]i *
I Mi
11 F^l2
I L i L 1
1 ! ,
i '
i \/ \/i
11 Fi V F2vi2
Лучевая матрица
(JO
(-1/F l)
( 1 L \
\-l/F 1-L/F)
( T Li+Li- \
_J__J_+ 1-^1-^ +
Fi F2 Fi F2
| L2 LlL2
^ F1F2 FlF2J
§1.11. Расчет резонаторов матричным методом. Резюме
83
Таблица 1.2 (продолжение)
Оптическая система
Лучевая матрица
1 L/n
О 1
I
71=1 |
I
i
1
11
-*« L >
1 2
П — По П2Г
2
smb./— »
V
cosL.
г sin LaI — cos L
n°/
-1 О
2/R -1
в плоскости падения
1 О
осевой луч
в плоскости, перпендикулярной к
плоскости падения
10
в плоскости падения — = —
Sin #2 7li
COS $2
^COS^l COS $2
COS $2 J
11
в плоскости, перпендикулярной к
плоскости падения
(Г
712
711 COS$l — П2 COS $2
711
sin $2 п\
6*
84 Гл. 1. Оптика гауссовых пучков
налево в том порядке, в котором поле пучка проходит эти элементы,
начиная с некоторой исходной реперной плоскости, перпендикуляр-
перпендикулярной оптической оси резонатора. В качестве реперной следует выбрать
ту плоскость, в которой поперечное распределение поля по тем или
иным причинам наиболее интересно, хотя, в принципе, в качестве ре-
реперной можно взять любую плоскость, перпендикулярную оптической
оси резонатора. Далее перемножаем матрицы оптических элементов
в соответствии с обычным правилом и получим матрицу, описываю-
описывающую резонатор в избранной плоскости (в плоскости симметрии или
в перпендикулярной плоскости) и отнесенную к исходному реперно-
му сечению. Элементы А, В, С, D этой матрицы выражены через
параметры элементов резонатора.
Далее правило ABCD для резонатора
_ Ад + В
Q~ Cq + D
(см. A.63)) позволяет найти комплексный параметр
q= ± [-(A- D) ±i^/4- (A + D)i]
гауссова пучка, являющегося основной модой резонатора, в реперном
сечении и, пользуясь соотношениями A.16),
R = [Re(l/q)}-\ kw2 = [Imil/q)}-1 A.149)
— радиус кривизны и поперечный размер моды в том же сечении.
Если элементы матрицы М вещественны, то можно также воспользо-
воспользоваться соотношениями A.67)
2В о IBI
Л — D ^yi — (yl Ч- DJ/4
выражающими Raw непосредственно через элементы матрицы М.
Используя правило ABCD для незамкнутых оптических систем
, _ Ауд + By
Q ~ Cyq + Dv '
можно найти комплексный параметр q' в новом реперном сечении,
величины Ay, By, Су, Dy — элементы матрицы V, описывающей
переход от исходного реперного сечения к новому. Далее по тем же
правилам A.149) и A.150) можно найти R и w в новом сечении.
Положение перетяжки моды резонатора можно найти, если с помо-
помощью оператора трансляции A.20) перейти к такому реперному сече-
сечению, в котором равны друг другу диагональные матричные элементы
матрицы Мнов — Анов = DHob- Для отыскания поперечных размеров
высших мод резонатора, не содержащего гауссовых диафрагм, следу-
следует воспользоваться соотношениями A.86):
wn =
§1.11. Расчет резонаторов матричным методом. Резюме
85
где w — размер основной моды и п — поперечный индекс моды в соот-
соответствующей плоскости (симметрии или перпендикулярной) и в рас-
рассматриваемом поперечном сечении. Таким образом, поперечные ха-
характеристики полностью определены.
Обратим внимание на одну особенность матриц, приведенных в
строках 8 и 9 табл. 1.2. В падающем луче орты системы координат
расположены, как показано на рис. 1.18, при-
причем орт еу направлен за плоскость черте-
чертежа так, что система координат правая. Есте-
Естественно считать, что при отражении орт е^
не меняется, т.е. еу = е'у. Орт e'z для еди-
единообразия всегда направлен по ходу луча.
Тогда, если систему координат по-прежнему
считать правой, то орт е'х оказывается на-
направленным, как показано на рис. 1.18. Как
видим, при $ —>- О, т. е. когда падение лу-
луча приближается к нормальному, орт е'х
не переходит в орт ех. Из-за этого луче-
лучевая матрица для ж-направления не перехо-
переходит в лучевую матрицу для ^-направления
при $ —у 0, как это видно из строк 8 и
9 табл. 1.2, хотя при нормальном падении
оба направления, казалось бы, становятся
равноправными. Как видим, неравноправие
здесь обусловлено выбором системы коорди-
координат. При расчете кольцевых резонаторов это
обстоятельство нужно аккуратно учитывать.
Для линейных резонаторов (нормальное па-
падение) оно несущественно; можно пользо-
пользоваться любой матрицей — дополнительный множитель еш сократит-
сократится, так как матрица отражения от зеркал встретится в этом случае
обязательно дважды.
3. Спектр резонатора, рассчитываемого матричным методом (см.
п. 1) определяется формулой
1/2
Рис. 1.18. Орты систем
координат в падающем и
отраженном пучках
с\1 ,
v\mn = ^ [I +
arccos
arccos
A.151)
где I — продольный и m, n — поперечные целочисленные индексы мод,
L — полная оптическая длина пути, проходимого пучком в резонаторе
до замыкания, щтп — частота (Гц) моды с индексами I, m, n; Ai:2 и
?>i,2 — диагональные элементы лучевых матриц резонатора для двух
плоскостей (симметрии и перпендикулярной к ней).
4. Для многих резонаторов, в частности для кольцевых, важным
является состояние поляризации генерируемого излучения. Состояние
поляризации излучения определяется резонатором, наличием в нем
86 Гл. 1. Оптика гауссовых пучков
анизотропных элементов. В кольцевых резонаторах такие элементы
неизбежно присутствуют, так как диэлектрические зеркала при на-
наклонном падении на них излучения обладают анизотропными свой-
свойствами.
Расчет поляризационных характеристик резонатора производит-
производится с помощью метода Джонса, являющегося также матричным ме-
методом и имеющего много общего с матричным методом расчета мод.
Каждый оптический элемент резонатора описывается своей поляри-
поляризационной матрицей (сводка таких матриц дана в табл. 1.1). Поляри-
Поляризационные матрицы, описывающие оптические элементы резонатора,
располагаются справа налево в том порядке, в каком их последова-
последовательно проходит гауссов пучок, начиная с некоторого исходного сече-
сечения. Произведение этих матриц — матрица
р _ fan CL12
определяет состояние поляризации моды резонатора в исходном се-
сечении. Состояние поляризации моды в других сечениях может быть
иным. Собственные значения этой матрицы равны
Al,2 = 2 [аП + а22 ± Л/Ои +«22J +4А] ,
где А — детерминант матрицы Р. Величины
7i,2=ln(l/|Ai,2|)
— коэффициенты затухания колебаний резонатора соответственно
первой и второй поляризации, обусловленного наличием в резонаторе
поляризаторов (имеется также затухание, обусловленное изотропны-
изотропными элементами). Разность фаз
Аср = ifi — if 2 = arg Ai - arg A2
определяет разность частот Аи мод первой и второй поляризации (см.
§1.10)
где L — оптическая длина резонатора.
Собственные векторы матрицы Р определяют состояние поляри-
поляризации мод резонатора. Таких векторов два:
Если отношение компонент этих векторов представить в виде
Еу_ = Ai,a-an =/з12е<€!,2
Ех СЫ2
то эллиптическая в общем случае поляризация будет характеризо-
характеризоваться следующими параметрами: эллиптичностью, т. е. отношение (
§1.12. Гауссовы пучки — решения уравнений Максвелла 87
малой полуоси эллипса к большой его полуоси
и азимутальным углом а, определяемым соотношениями
sin 2а = 2/?cosf [A - /?2J + 4/?2 cos2 ?]~1/2,
cos 2а = A - /?2)[A - f32J + 4f32 cos2 f]^.
При ? > 0 — эллиптическая поляризация имеет правое вращение, при
С < 0 — левое. При а > 0 большая ось эллипса отклонена от оси х в
сторону оси ?/, при а < 0 — в противоположную сторону.
Таким образом, матрица Р и следующие из нее параметры 71,2,
^1,2, /^i,2, ?i,2 полностью определяют состояние поляризации моды ре-
резонатора в исходном сечении. При необходимости отыскания состоя-
состояния поляризации в другом сечении резонаторного контура матрицу Р
следует подвергнуть преобразованию
PH0B = UPU-\ A.152)
где матрица U описывает изменение состояния поляризации при пе-
переходе от старого сечения к новому, и далее действовать в соответ-
соответствии с теми же самыми соотношениями. Отметим, что величины 71,2
и ^1,2, характеризующие резонатор в целом, при этом не изменятся,
поскольку они выражаются через след и детерминант матрицы Р,
не изменяющиеся при преобразовании A.152), изменятся лишь fii^
и ?]_?2, описывающие состояние поляризации в конкретном избранном
сечении резонаторного контура. Тем самым исследование состояния
поляризации мод резонатора закончено.
На этом расчет резонатора матричным методом заканчивается.
Еще раз отметим, что расчет резонаторов с помощью правила ABCD
или, что то же самое, матричным методом чрезвычайно эффективен и
широко применяется. Резонаторы, к которым этот метод неприменим,
рассматриваются в § 1.13 и § 1.14.
§ 1.12. Гауссовы пучки — решения уравнений
Максвелла
До сих пор гауссовы пучки рассматривались нами как некоторая
данность и анализировались их свойства. Покажем теперь, что эти
пучки являются приближенными решениями уравнений Максвелла.
Уравнения Максвелла для свободного пространства имеют вид
rotE = —, rotH = — —,
с dt с dt
divE = 0, divH = 0,
Гл. 1. Оптика гауссовых пучков
Вводя, как обычно, вектор-потенциал
Е = -±2?, H = rotA
с dt
при дополнительном условии
divA = 0,
приходим к волновому уравнению
Дифференцируя его по времени и умножая на (—1/с), получим
ДЕ-1^=0 A.153)
при дополнительном условии
divE = 0.
Как неоднократно указывалось, гауссов пучок в скалярной форме,
использовавшейся в предыдущих параграфах, описывает одну, глав-
главную компоненту электрического поля. Пусть такой компонентой яв-
является Ех = ue~%ujt. Тогда для и согласно A.153) имеем уравнение
Au + k2u = 0. A.154)
В задачах, связанных с лазерными резонаторами, существует об-
обстоятельство, позволяющее сильно упростить исследование задачи.
Это обстоятельство — параксиальность лазерного получения. Как
известно из эксперимента, лазерное излучение всегда сосредоточено
вблизи оси пучка излучения и мало расходится при распростране-
распространении вдоль этой оси; это свойство лазерного пучка и определяют сло-
словом «параксиальность». В теоретических исследованиях оно находит
свое выражение в так называемом параксиальном приближении. Это
приближение позволяет перейти от уравнения Гельмгольца A.154) к
параболическому уравнению, точным решением которого и является
гауссов пучок A.88).
Из оптики известно, что, если волна ограничена в поперечном на-
направлении размером а ^> Л, то эта волна обязательно расходится, при
этом минимальная угловая расходимость, которой можно добиться,
равна
Aip ~ -.
а
Следовательно, волна увеличит свои поперечные размеры примерно
вдвое на длине
Ь = ко2;
длина 6, таким образом, является характерным размером изменения
амплитуды волны в продольном направлении. Действительно, если
§1.12. Гауссовы пучки — решения уравнений Максвелла 89
волна при распространении на расстояние Ъ расходится в двух вза-
взаимно перпендикулярных поперечных направлениях, то площадь ее
волнового фронта возрастает в четыре раза, интенсивность на этом
фронте во столько же раз уменьшится, а амплитуда уменьшится в два
раза.
Принимая во внимание медленное изменение амплитуды в про-
продольном направлении, решение волнового уравнения A.154) будем ис-
искать в виде
u = v(x,y,z)eikz; A.155)
в этом выражении основная, быстропеременная часть волны выделе-
выделена в виде экспоненциального множителя, а функция v(x,y,z) играет
роль амплитуды волны, т. е. величины, у которой характерный мас-
масштаб изменения в поперечном направлении равен а, в продольном
направлении — Ъ = ка2.
Подставляя A.155) в A.154), приходим к уравнению
d2v , d2v , о.7 dv , d2v п (Л 1K..
я~2 + !ГЧ + 2гк л" + я~2 = °' A.156)
дх2 ду2 dz dz2 v J
Учитывая то, что было сказано о поперечном и продольном масшта-
масштабах, нетрудно оценить производные v:
dv dv v dv v
~дх ~ ~ду ~ a' ~dz~ Ы2'
Так как эти оценки справедливы не в одной точке, а во всей области,
занятой волной, то для вторых производных имеют место оценки
d2v d2v v д
V
дх2 ~ ду2 ~ а2' dz2 ~ к2а4'
Соответственно четыре члена, фигурирующие в уравнении A.156)
имеют оценки
1. 1. 2ik— V •
a2' a2' ka2' k2a^
как легко видеть, третий член в этом уравнении одного порядка с пер-
первыми двумя, а четвертый член в (каJ раз меньше первых трех. Так
как в интересующих нас решениях волнового уравнения а ^> Л, т. е.
ка ^> 1, то четвертым членом в уравнении A.156) можно пренебречь.
Таким образом приходим к параболическому уравнению
pL + pL + 2ik^ = 0, A.157)
дх2 ду2 dz
или о
A±v + 2ik^- =0.
dz
Покажем теперь, что астигматичный эрмит-гауссов пучок являет-
является точным решением параболического уравнения A.157) и, соответ-
соответственно, приближенным решением волнового уравнения A.154). Как
90 Гл. 1. Оптика гауссовых пучков
указывалось выше, параболическому уравнению должна удовлетво-
удовлетворять не сама волна, а ее амплитуды, т. е. в исходной волне A.88) необ-
необходимо опустить экспоненциальный множитель elkz. Тогда получим
следующее выражение:
v(x, у, z) = Gvn(x, z)vm(y, z), A.158)
где
/ \ ! и ( x \ \ikx2 .( 1\ , z-zi]
vn(x, z) = —, Hn — exp i[n -\— arctg ,
nV ' J */(z_ZlJ + b2 n\wJ y[2qi V 2) 5 bi J'
A.159)
W* = {Z~Zk?+b21' 4i=z-Zl- ih A.160)
и vm(y,z) получается из vn(x,z) посредством замены
X —У у, Z\ —У Z2, Ъ\ —У &2, П —> ТП, W\ —У W^-
Подставив A.158) в параболическое уравнение A.157), получим
Теперь достаточно показать, что первая скобка при подстановке в
нее A.159) обращается в нуль. Полиномы Эрмита подчиняются урав-
уравнению
определяя отсюда Н"({;), получаем для второй производной vn(x,z)
по х выражение
где
' - (Ц - * + #
\wf q q
ei/ ч 1 \ikx2 .( 1\ , z-zi]
bix. z) = —, exp i\n -\— arctg — .
v ' J 4/(z_Zly + b2 pL2gi V 2) 6 bi J
b
Производная vn{x,z) no z равна
2
где
Нетрудно убедиться, что, если производную по z умнож:ить на 2ik и
сложить со второй производной по ж, то все члены сократятся. Следо-
Следовательно, эрмит-гауссов пучок A.158) удовлетворяет параболическо-
параболическому уравнению A.157).
Нетрудно убедиться также, что все вычисления останутся в силе и
в том случае, когда величины z\ и Ь\ комплексны и, соответственно,
§1.13. Гауссов пучок с двумя системами главных осей 91
комплексна величина w\ A.160). Для этого достаточно учесть, что
соотношение
X + iY = л/Х2 + Y2 ехр[г arctg(F/X)]
справедливо и при комплексных X и Y.
§ 1.13. Гауссов пучок
с двумя системами главных осей
В настоящем параграфе будет продолжено изучение астигматич-
ного гауссова пучка, начатое в § 1.6, при этом все внимание будет
уделено случаю, когда параметр Ф астигматичного гауссова пучка
является комплексной величиной. Подобные пучки обладают инте-
интересными свойствами и в ряде лазерных резонаторов именно они ока-
оказываются основными модами.
Итак, пусть имеется гауссов пучок, описываемый выражением
u(x,y,z) = ехР тг (а^2 + 2Ьху + су2) + ikz + icp , A.161)
y/qiq2 L 2 J
где коэффициенты
cos2 Ф sin2 Ф , /1 1\ . . _ sin2 Ф cos2 Ф
a— 1 , o= sin Ф cos Ф, c— 1
q\ q2 \qi q2 J q\ q2
A.162)
через параметры q± и q^ зависят от координаты z и составляют важ:-
ную для дальнейшего матрицу
параметр Ф, как уже отмечалось, считаем комплексной величиной.
Напомним, что зависимость q\ и q^ от z имеет вид
qi=z-Z!- гЬъ q2 = z - z2 - ib2-
В квадратичной форме
S(x, у) = ах2 + 2Ьху + су2, A.164)
входящей в A.161), можно произвести разделение вещественной и
мнимой частей:
S = V + iW, V = a'x2+2b'xy + c'y2, W = а"х2+2b"xy + с"у2,
причем a = a'+ia"j b = b'+ib", c = c' + ic".
Как отмечалось еще в начале главы, вещественная часть показа-
показателя экспоненты, описывающей волну A.161), определяет распреде-
распределение амплитуды в волне, а мнимая часть описывает распределение
фазы волны (т.е. форму волнового фронта). Применительно к пуч-
пучку A.161) это означает, что квадратичная форма
W(x, у) = а"х2 + 2Ъ"ху + с" у2
92 Гл. 1. Оптика гауссовых пучков
описывает амплитудное распределение в поперечном сечении пучка.
Если систему осей х и у повернуть вокруг оси z на угол
г]=- arctg д// _ d>, A.165)
т. е. перейти к координатам х" и у", связанным с х и у соотношением
) = [/(„) (Ч?) , U(r1)=(cosri ~shi11), A.166)
J \У J у sin 77 cos г) J ' v y
то выражение W(x,y) примет диагональный вид
W(x",y") = A"x + В" у, A.167)
где
А" = i [(а/;
В" = 1 [(а/; + с") - y/(a" + c"J-4(a"c" - Ъ)].
Таким образом, в осях х", 2/" амплитудное распределение принимает
симметричный вид A.167). Характерные размеры пучка, т. е. расстоя-
расстояния вдоль осей х" и у ft от продольной оси, на которых интенсивность
пучка спадает в е раз, определяются соотношениями
1 1
Обратимся теперь к поперечному фазовому распределению, опре-
определяемому вещественной частью выражения S(x, у) A.164), оно тесно
связано с формой волнового фронта, который определяется уравне-
уравнением
а'х2 + 2Ь'ху + с'у2 = 2(z0 - z). A.168)
Если подобно тому, как это делалось выше, систему осей х и у повер-
повернуть вокруг оси z на угол ?
Н8"**^, AЛ69)
то уравнение A.168) примет диагональный вид
A'x'2+B'y'2 = 2(z0-z),
где
А1 = i [(а' + с') + ч/(а' + с'J-4(а'с'-6'2)],
В' = I [(а' + с') - ч/(а' + с'J-4(а'с'-6'2)].
§1.13. Гауссов пучок с двумя системами главных осей 93
Так как величины А' и В' есть не что иное, как главные (максималь-
(максимальная и минимальная) кривизны волнового фронта и радиусы кривизны
волнового фронта есть обратные к ним величины
Rx = (A'), Ry = (ВТ1,
то оси х' и у' являются касательными к линиям главных кривизн и,
следовательно, линии главных кривизн оказываются развернутыми
на угол ? относительно исходных осей х и у.
Важным обстоятельством является то, что углы ? и г\ разные,
это означает, что главные оси амплитудного распределения в пуч-
пучке A.161) повернуты на угол rj — ? относительно линий главных кри-
кривизн волнового фронта. В гауссовых пучках, рассматривавшихся до
сих пор, главные оси амплитудного распределения и линии кривизны
волнового фронта совпадали.
Рассмотрим, к каким следствиям приводит эта особенность пучка
A.161). Сначала обсудим вопрос качественно и для этого напомним
некоторые свойства простого гауссова пучка, рассмотренного в § 1.1, а
именно, обратим внимание на влияние друг на друга амплитудного и
фазового распределения в гауссовом пучке. Волновой фронт гауссова
пучка, определяемый фазовым распределением, находясь в области
сходимости, далеко от области перетяжки, изменяется при распро-
распространении пучка в соответствии с законами геометрической оптики,
т. е. сходится к своему центру кривизны, расположенному в центре пе-
перетяжки, при этом амплитудное распределение сжимается или, ины-
иными словами, уменьшается поперечный размер пучка. Уменьшение по-
поперечного размера пучка приводит к возрастанию роли дифракции и
появлению тенденции к расходимости — в теории дифракции хоро-
хорошо известно свойство волны тем сильнее расходиться, чем меньше ее
поперечный размер.
Когда волновой фронт достигает области перетяжки, дифракция
уже играет существенную роль, кривизна волнового фронта в обла-
области перетяжки в результате дифракции или, что то же самое, в ре-
результате поперечной ограниченности амплитудного распределения не
возрастает, как в области сходимости, а уменьшается, волновой фронт
постепенно становится все менее вогнутым, в самой перетяжке стано-
становится плоским и далее делается постепенно все более выпуклым.
Таким образом, в области сходимости гауссова пучка искривлен-
искривленность волнового фронта приводит к сжатию амплитудного распреде-
распределения, иными словами, к уменьшению поперечного размера пучка, а
в области перетяжки поперечная ограниченность амплитудного рас-
распределения приводит к изменению формы волнового фронта по срав-
сравнению с той, которая диктуется законами геометрической оптики.
Применим теперь эти соображения к рассматриваемому пучку
A.161), у которого, как установлено выше, линии кривизны разверну-
развернуты на некоторый угол относительно главных осей амплитудного рас-
94
Гл. 1. Оптика гауссовых пучков
пределения. Как и у простого гауссова пучка, у пучка A.161) можно
выделить область сходимости, т. е. область, которую волновой фронт
проходит ранее области перетяжек, где лежат точки z = z\ — Ь\ и z =
= Z2 — Ъъ. Пусть для простоты фронт пучка в области сходимости бли-
близок к цилиндрическому и амплитудное распределение на этом фронте
повернуто на некоторый угол относительно оси цилиндра (рис. 1.19).
Как уже отмечалось, в области сходимости волновой фронт, распро-
распространяясь, изменяется в соответствии с законами геометрической оп-
оптики. Это означает в рассматриваемом случае, что он остается ци-
цилиндрическим и сходится к общей оси всех цилиндрических фронтов.
При таком изменении цилиндрического волнового фронта ампли-
амплитудное распределение постепенно сжимается вдоль оси х и остается
неизменным вдоль оси у. Как легко видеть из рис. 1.19, это приводит
к повороту главных осей амплитудного распределения вокруг оси z.
Рис. 1.19. Поворот амплитудного распределения при распространении
вдоль оси z гауссова пучка с двумя системами главных осей
В свою очередь, сжатие амплитудного распределения приводит к воз-
возрастанию роли дифракции и появлению тенденции к расходимости.
В первую очередь, эта тенденция проявится в направлении наиболь-
наибольшего сжатия, т. е. вдоль одной из главных осей амплитудного распре-
распределения. Так как эта ось повернута на некоторый угол относительно
линий кривизны волнового фронта, то дифракционная деформация
этого фронта наложится на уже имеющееся его искривление и эф-
эффективно это приведет к повороту линий кривизны фронта вокруг
оси z.
Таким образом, имеющейся в пучке A.161) разворот линий кри-
кривизны волнового фронта относительно главных осей амплитудного
распределения (например, при z = — оо) приводит к тому, что при рас-
§1.13. Гауссов пучок с двумя системами главных осей 95
пространении этого пучка вдоль оси z как линии кривизны волнового
фронта, так и главные оси амплитудного распределения будут испы-
испытывать поворот относительно оси z, соответственно и угол между ли-
линиями кривизны волнового фронта и главными осями амплитудного
распределения будет изменяться. Как будет видно далее, способность
амплитудного и фазового распределений к повороту относительно оси
z при распространении пучка A.161) вдоль нее представляет собой
важное свойство этого пучка, позволяющее теоретически описывать
моды некоторых резонаторов.
Обратимся теперь к количественному исследованию гауссова пуч-
пучка A.161). Как нетрудно убедиться, матрицы U A.166) обладают свой-
свойством
и(Ф1)и(Ф2) = и(Ф1 + Ф2);
поэтому, умножая A.163) слева на U(—Ф'), где
Ф' =
и справа на U~1(—Ф'), параметр Ф можно сделать чисто мнимым.
Далее, по существу без ограничения общности, можно в пучке A.161)
параметр Ф считать чисто мнимым; будем считать его равным гФ.
Тогда матрица R будет образована элементами
ch2 Ф sh2 Ф , / 1 1 \ . , Л , Л sh2 Ф , ch2 Ф
Ь\гяпФспФ с1
, / 1 1 \ .
, Ь—\ г
ch Ф sh Ф , / 1 1 \ . , Л , Л sh Ф ,
а— , Ь—\ гяпФспФ, с— 1
Ях Ц2 \qi #2 / qi
где величина Ф теперь вещественна. Так как зависимость q-± и q2 от
продольной координаты z известна, а следовательно, известна и за-
зависимость коэффициентов а, 5, с от г, то может быть найдена зави-
зависимость от z величин, характеризующих гауссов пучок A.161), его
поперечных размеров wa , wb •> главных радиусов кривизны волнового
фронта Rx, Ryj углов ?, rj. Для этого выражение
С/ \ 2 , о*, , 2 /СЬ2Ф вЬ2Ф\ 2 ,
Ь (ж, у)=ах + 2оху + су = х +
V qi Я2 /
+ ( Jг8ЪФсЪФху + 1 Ьг,
\qi Я2/ V qi q2 )
входящее в A.161), приведем к общему знаменателю:
S = — [(z + Zl sh2 Ф - z2 ch2 Ф + ih sh2 Ф - ib2 ch2 Ф)х2 +
+ 2i(zi - z2 + ibi - ib2) sh Ф ch Фху +
+ (z + z2 sh2 Ф- z1ch2Ф + ib2 sh2 Ф - ibx ch2 Ф)у2] A.170)
и, представив (qiq2)~1 в виде
96 Гл. 1. Оптика гауссовых пучков
разделим в S вещественную V и мнимую W части. Тогда, коэффици-
коэффициенты вещественной части V примут вид
а' = p[(z + 21 sh2 Ф - z2 ch2 Ф) cos С + (h sh2 Ф - b2 ch2 Ф) sin ?],
b' = p[(b2 - bi) cos С + (^i - z2) sin ?] sh Ф ch Ф,
c' = p[(z + 2:2 sh2 Ф — z\ ch2 Ф) cos ( + F2 sh2 Ф — b\ ch2 Ф) sin Q.
В соответствии с A.169) вещественную часть V можно привести к
диагональному виду, если систему поперечных координат повернуть
вокруг оси z на угол ?, определяемый соотношением
Ь ^ F2
Если ввести обозначение
^^, A.172)
Z2 — Z\
то этому выражению можно придать следующий вид:
tg2^ = -t^.tg(/? + C). A.173)
Так как величины Ф и /3 являются константами (параметрами)
пучка, то угол 2? зависит от z только через переменную ?, зависимость
которой от z будет ниже исследована.
Таким образом при распространении пучка A.161) вдоль оси z
линии кривизны волнового фронта (именно они являются главными
осями вещественной части выражения A.170)) испытывают поворот
вокруг оси z в соответствии с A.171).
Коэффициенты мнимой части W равны
а" = p[-(z + z\ sh2 Ф - z2 ch2 Ф) sin С + (Ьх sh2 Ф - b2 ch2 Ф) cos С],
Ъ" = p[-(b2 - hi) sin ( + (zi - z2) cos(] впФспФ,
с" = p[-(z + z2 sh2 Ф - Z! ch2 Ф) sin ( + (b2 sh2 Ф - bx ch2 Ф) cos Q.
В соответствии с A.165) мнимая часть W приводится к диагональ-
диагональному виду при повороте системы координат вокруг оси z на угол rj,
определяемый соотношением
Таким образом, амплитудное распределение, определяемое мнимой
частью выражения A.170), как и линии кривизны, испытывает мед-
медленный поворот вокруг оси z при распространении гауссова пучка
A.161) вдоль оси z в соответствии с A.174).
Соотношения A.173) и A.174) позволяют дать физическую интер-
интерпретацию параметра Ф. Действительно, из соотношения A.173) видно,
что при очень малых Ф, угол поворота ? будет незначителен практи-
практически на всей оси z за исключением небольших отрезков вблизи тех z,
§1.13. Гауссов пучок с двумя системами главных осей
97
где /3 + С = ^/2 и ,# + С = —7Г/2; на этих небольших отрезках ? испы-
испытывает быстрое изменение в сумме на тг. Аналогично, угол поворота г)
при очень малых Ф, согласно A.174), изменяется в сумме на — тг вблизи
тех значений z, где /? + С = Ои/? + С = тг. Таким образом, параметр Ф
определяет размеры той области на оси z, где в основном происхо-
происходит поворот линий кривизны волнового фронта и осей амплитудного
распределения пучка.
Ввиду важности величины ?, найдем ее зависимость от z. Так как
qx — z - z\ - ih\ — л/(г - z\J + b2 ехр (—г arctg —-— ),
V z — z\ J
2 = z - z2 - ib2 = \/(z - z2J + b\ exp ( —i arctg —-— ),
V \ Z — Z2 /
q2 =
TO
ИЛИ
С = arctg ¦
+ arctg ¦
i)z -
tgC
(z - zi)(z - z2) - bib2
Первое из этих соотношений показывает, что при изменении
до +00 два первых слагаемых в
его правой части монотонно убы-
убывают от тг до 0. Следовательно,
можно считать, что при измене-
изменении z от —оо до +00 величина (
монотонно убывает от тг до — тг.
Согласно A.175) tg( равен нулю
при z = —оо, z = +00 и в точке,
где равен нулю числитель в пра-
правой части A.175), т.е. при
biz2 + b2zi
A.175)
от — оо
z =
bi+b2 '
в бесконечность же tg ( обращается в точках
Рис. 1.20. Зависимость tg? от про-
продольной координаты z
z" = | [(zi + z2) - V(zi-Z2J+±b1b2],
являющихся корнями знаменателя в A.175). Следовательно, зависи-
зависимость tg? A.175) от z имеет вид, изображенный на рис. 1.20, и ве-
величина ? изменяется в следующих пределах (нетрудно показать, что
z" < z < z1):
1) при -оо < z < z", тг > С > тг/2,
2) при z" < z < z, тг/2 > С > О,
3) при z<z<z',O>(> -тг/2,
4) при z1 < z < +00, -тг/2 > С > -тг-
7 В.П. Быков, О.О. Силичев
98 Гл. 1. Оптика гауссовых пучков
Таким образом, характер изменения величины ? при распростра-
распространении пучка вдоль оси z ясен и можно проанализировать зависимости
углов ? и г) от z. Для этого обратим внимание, что согласно A.173)
нули и бесконечности тангенсов 2? и /3 + ? совпадают; поэтому ясно,
что угол ? изменится на тг, когда ( изменяется на 2тг, хотя скорость
изменения ? и ? с z различна. Аналогично, угол rj, согласно A.174),
также изменится в целом на тг, однако если ? увеличивается с г, то
г) уменьшается. Следовательно, линии главных кривизн и оси ампли-
амплитудного распределения разворачиваются в разные стороны по мере
распространения гауссова пучка вдоль оси z.
Приведем соотношения, определяющие главные радиусы кривиз-
кривизны волнового фронта в зависимости от продольной координаты z:
где
F = [-Bz - z\ - z2)cos? - (bi + fc2)sinC],
G = [(z- Zlf + (h - b2f}[sh2 2Ф + cos2(/3 + С)]-
Аналогичные соотношения имеют место для главных полуосей эл-
эллиптического поперечного распределения амплитуды гауссова пучка
A-161):
где
F' = [Bz-Z! - z2)sin(- (b± +b2)cosC],
G1 = [(z - zxf + (h - 62J][sh2 2Ф + sin2(/? + С)]-
Выясним теперь, как матрица Т, а с нею и выражения V и W
A.164), изменяются с возрастанием координаты z. Для этого напом-
напомним, что матрица Т связана с матрицей Р соотношением
Т = и(Ф)Ри-\Ф), A.178)
причем матрица Р имеет простой вид
_ /V1 о
р=- о
и матрица U является матрицей поворота A.166).
В § 1.6 преобразование A.178) так и истолковывалось — как обу-
обусловленное поворотом поперечной координатной системы на некото-
некоторый угол Ф. Однако теперь такое истолкование неправомерно, по-
поскольку величина Ф является комплексной. Преобразование A.178)
§1.13. Гауссов пучок с двумя системами главных осей 99
следует рассматривать как некоторое математическое соотношение
между матрицами Т и Р.
Важно, что соотношение A.178) и, в частности, величина Ф не за-
зависят от продольной координаты z, от которой зависят коэффициенты
матриц Т и Р; т. е. при другом значении z' = z + L будет справедливо
соотношение
T(z') = и(Ф)Р(^)и-1(Ф) A.179)
при той же, что и в A.178), величине Ф.
Переход к матрице Р в соответствии с A.178) или A.179) удобен в
том отношении, что матрица Р является простой и закон ее изменения
с увеличением z может быть легко установлен. Действительно, пусть
Pf = P(z' = z + L); тогда
O\_((q1+L)-1 О
; V ° fe + b)
о
Следовательно, при распространении пучка вдоль оси z на расстояние
L матрица Р изменяется в соответствии с матричным равенством
Р' = P(zf = z + L) = A - LP^P. A.180)
Умножая обе части этого равенства слева на С/(Ф) и справа на ?/-1(Ф),
получим согласно A.178) и A.179)
Т' = Т
=UA-
(z'=z+L)
= A - LUPU-^UPU-1 = A - LTYXT. A.181)
Таким образом, связь между матрицами Т иТ' оказывается такой
же, как и для матриц Р и Р'. Тем самым найден закон изменения мат-
матрицы Т при распространении гауссова пучка на расстояние L вдоль
оси z. Соотношение A.181) позволит нам в дальнейшем составлять
матричные уравнения для расчета лазерных резонаторов (см. § 1.14).
Рассмотрим теперь прохождение гауссова пучка вида A.161) че-
через квадратичный корректор. При прохождении пучка A.161) через
квадратичный корректор общего вида в выражении A.161) возникает
дополнительный множитель
exp [i ik(Ax2 + 2Bxy + Су2)],
при этом вещественные части коэффициентов А, В и С описывают
фазовую коррекцию, т. е. фокусирующее (или дефокусирующее) дей-
действие фазового корректора, а мнимые части тех же коэффициентов
описывают амплитудную квадратичную коррекцию, т. е. ослабление
7*
100 Гл. 1. Оптика гауссовых пучков
(или усиление) пучка. Таким образом, квадратичный корректор об-
общего вида по оказываемому на пучок действию эквивалентен суммар-
суммарному действию астигматичной линзы и астигматичной же гауссовой
диафрагмы. При этом главные оси линзы и диафрагмы развернуты
относительно осей ж, у соответственно на углы
. 1 х 2В' 1 2В"
f = - arctg А!_с„ r)=- arctg ^ _ ^ .
Если коэффициенты А, В и С расположить в виде матрицы
'А
К~\В С
то нетрудно видеть, что матрица Т гауссова пучка после прохожде-
прохождения через квадратичный корректор преобразуется в матрицу Т' по
простому закону
Если квадратичным корректором является сферическое зеркало с
радиусом кривизны R при падении на него пучка под углом $, то А =
= Rcosfi, В = R/ cos$ и С = 0. Однако, учитывая также изменение
координатной системы после отражения (рис. 1.18), необходимо после
преобразования A.182) произвести также изменение знаков недиаго-
недиагональных элементов
Т" = аТ'а, A.183)
где матрица а имеет вид
а=\0 -I)'
Рассмотрим теперь для примера симметричный пучок, у которого
z\ — Z2 = 0 и Ь\ ф &2- В этом случае параметр /3 A.172) равен тг/2 и
поворот главных осей определяется соотношениями
A.184)
Поле такого пучка описывается выражением
и(х, у, z) = ехр Г— S(x, у, z) + ikz + Щ , A.185)
yj\z - ibi)(z - ib2) L z J
- ib2)
где
ib2) ttz + i&i sh2 ф " i&2 ch2 ф)ж' -
- b2) ъЪ.ФсЪ.Фху + (z — ibi ch2 Ф + ib2 sh2 Ф)у2].
§1.13. Гауссов пучок с двумя системами главных осей 101
Согласно A.176), радиусы кривизны волнового фронта пучка в сече-
сечении с координатой z равны
Поперечные размеры пучка в том же сечении определяются соотно-
соотношением
W2A о =
' [2z sin С -
Исследуем поведение симметричного пучка A.185) при предель-
предельном переходе Ф —у 0. Естественно, что этот пучок должен переходить
при этом в обыкновенный астигматичный гауссов пучок A.79) без
вращения поля. Предельный переход Ф —у 0 не совсем тривиален, но
важен, поскольку он позволяет, как мы увидим в § 1.14, выделять фи-
физические корни при решении сложных резонаторных уравнений, когда
пучок с вращением поля является модой.
Согласно A.184), поворот осей главных кривизн пучка определя-
определяется соотношением
+ V. Orb
A.186)
При малых |Ф| ось z можно разделить на несколько участков с ха-
характерным поведением угла ?. В соответствии с A.186) и первым из
соотношений A.184) условие
определяет три области. Две для больших по модулю z:
\z\ > (h +Ь2)^2Ф A.187)
и одну для малых по модулю z:
blb2
Имеются также две промежуточные области
&1&2
Ъ\ -\- Ь2
Для предельного перехода Ф —у 0 именно последние две проме-
промежуточные области наиболее важны, так как в них при Ф —у 0 угол ?
также стремится к нулю, а в простом астигматичном пучке он должен
быть равен нулю. Так что в этих областях предельный переход проис-
происходит естественным образом. Наличие особой области для малых по
модулю z указывает как будто бы на отсутствие предельного перехо-
перехода. Действительно, согласно A.186), поворот осей главных кривизн в
102 Гл. 1. Оптика гауссовых пучков
этой области происходит при любых, даже самых малых Ф, поскольку
tg? —У 0, a tg2? —у оо при z —У 0, т.е. угол ? меняется от 0 до тг/2, у
простого же астигматичного пучка такого поворота не должно быть
вовсе. Поворот при этом сосредоточен вблизи z = 0 и происходит в
тем меньшей области изменения z, чем меньше Ф, т.е. быстро. Па-
Парадокс легко разрешается, есть учесть, что знаменатель в Ra,b мал
вблизи z = 0, он порядка [Ь\ — 62) вЬ2Ф, и, соответственно, волновой
фронт практически плоский, а его астигматизм тем менее выражен,
чем меньше 2Ф, поэтому быстрый поворот осей главных кривизн при
малых по модулю z реально не заметен.
Поворот осей амплитудного распределения как в области малых z,
так и в обеих промежуточных областях практически отсутствует, что
видно из третьего из соотношений A.184). В каждой же из областей
A.187) для больших z оси главных кривизн дополнительно поворачи-
поворачиваются на тг/4.
Имеется также симметричный пучок другого типа, у которого Ъ\ =
= &2 = Ь и z\ — —Z2 = zq. Поле такого пучка описывается выражением
С* Г1 1
u(x,y,z) = == exp\-ikS(x,y,z) + ikz + i(p\, A.188)
^/{z-ibJ-zl L2 J
где
о _ i(z ~ ib) + zo ch 2Ф]ж2 + 2iz0 sh 2Фху + [(z - ib) - z0 ch 2Ф]у2
Для такого пучка, очевидно, имеем
z = 0, г' =
Угол ( определяется соотношением
, > 2Ь
tgC =
2 ~2 U2'
— о —
Как легко видеть, угол ? изменяет знак при изменении знака 2.
В соответствии с соотношением A.176) радиусы кривизны волнового
фронта пучка в точке с координатой z равны
Rab = V[(,-,0) + 6][(,+^FTF] AЛ89)
(z cos С + b sin С) ± zq у sh2 2Ф + cos2 ?
Линии главных кривизн при этом развернуты относительно осей ж, у
на угол ?, определяемый соотношением
2 1 ,2
Легко видеть, что при изменении знака z, т.е. в симметричной точке
с координатой —z, радиусы кривизны имеют те же значения, но толь-
только другой знак, а линии главных кривизн развернуты относительно
§1.13. Гауссов пучок с двумя системами главных осей 103
осей ж, у на тот же угол ^, нов другую сторону. Поворот линий кри-
кривизны при возрастании z и есть характернейшее свойство гауссова
пучка A.161) вообще и симметричного пучка A.188), в частности.
Если в точках —z и z разместить астигматичные зеркала с радиу-
радиусами кривизны, определяемыми соотношениями A.189), то этот пучок
будет собственным для резонатора.
Поперечные размеры симметричного пучка в точке z определяют-
определяются соотношениями
2 _ ky/[(z - z0J +b*][(z + z0J + Ъ2]
^ А В — / '
z sin ( — b cos ( ± zq v sh2 2Ф + sin2 (
а его амплитудные главные оси развернуты относительно осей ж, у на
угол rj:
th2<S>
iir
Зная матрицу Т' A.182) пучка, прошедшего через квадратичный
корректор, можно найти параметры q[, q2 и Ф' этого пучка. Действи-
Действительно, параметры qi, q2 и Ф связаны с элементами матрицы Т соот-
соотношениями A.162). Поэтому из A.182) следует
cos2 Ф sin2 Ф . _ cos2 Ф7 sin2 Ф7
sin2 Ф cos2 Ф п _ sin2 Ф7 cos2 Ф'
1 НО — 1 -—,
Чх Я.2 q[ q2
( ) sin Ф cos Ф + В = ( — ) sin Ф; cos Ф;.
\qi q2J \q[ q'2 /
Вводя обозначения
-X"l,2 = ^1,2 5 ^1,2 = Ql,2 •>
приводим эти соотношения к виду
Х1 cos2 Ф + Х2 sin2 Ф + А = Х[ cos2 Ф; + Х'2 sin2 Ф;,
Х1 sin2 Ф + Х2 cos2 Ф + С = Х[ sin2 Ф; + Х'2 cos2 Ф;,
(Х1 - Х2) sin Ф cos Ф + В = (Х[ - Х'2) sin Ф; cos Ф;.
Складывая почленно первые два равенства, получим
(Хг + Х2) + {А + С) = Х[ + Х^; A.190)
вычитая почленно из первого равенства второе, получим
(Xi - Х2) cos 2Ф + (А - С) = (Х{ - Х'2) cos 2Ф;. A.191)
Третье равенство можно записать в виде
(Xi - Х2) sin 2Ф + 2В = (Х{ - Х'2) sin 2Ф;. A.192)
104 Гл. 1. Оптика гауссовых пучков
Разделив теперь последние два равенства друг на друга, получим
— соотношение, определяющее угол поворота Ф' пучка, прошедшего
через корректор. Считая теперь угол Ф' известным, из A.191) и A.192)
получаем
(Х[ -Х'2 = [(Xi - Х2) cos 2Ф + (А - С)] cos 2Ф',
\Х[ -Х'2 = [(Х1 - Х2) sin 2Ф + 2В] sin 2Ф;. ^
Комбинируя первое из этих равенств с A.190), получим
± [(Хг - Х2) соз2Ф + (А - С)] cos 2Ф'}. A.195)
Используя аналогично второе из равенств A.194), получим
± [(Х1 - Х2) эт2Ф + 2В] sin 2Ф'|. A.196)
Таким образом формулы A.195) и A.196) совместно с A.193) вы-
выражают параметры пучка, прошедшего через корректор, через пара-
параметры падающего пучка.
§ 1.14. Кольцевые резонаторы
Кольцевые резонаторы, подобные изображенным на рис. 1.21, по-
получили широкое распространение в лазерной технике. Главная осо-
особенность кольцевых резонаторов заключается в том, что их модами
являются бегущие волны, благодаря чему их называют иногда резо-
резонаторами бегущей волны. При этом все моды составляют две группы
встречных волн, практически не взаимодействующих друг с другом.
Поскольку встречные волны по-разному изменяются при вращении
кольцевого резонатора (эффект Саньяка), последние нашли широкое
применение в лазерных гирометрах.
Оптическим осевым контуром кольцевого резонатора называется
луч, который пройдя через все оптические элементы резонатора, за-
замыкается сам на себя. Существуют кольцевые резонаторы как с плос-
плоским оптическим осевым контуром (планарные резонаторы), так и с
неплоским оптическим осевым контуром (непланарные резонаторы).
Теория непланарных резонаторов существенно сложнее и менее раз-
развита, чем теория планарных резонаторов, хотя их свойства с практи-
практической точки зрения очень привлекательны.
§ 1.Ц. Кольцевые резонаторы
105
Рис. 1.21. Кольцевые резонаторы разных типов
Обычно резонаторная задача ставится следующим образом. За-
Задаются расположение и параметры зеркал и других оптических эле-
элементов, образующих резонатор. Требуется найти параметры пучка,
являющегося основной модой этого резонатора, а также в ряде слу-
случаев — близкие к основной высшие поперечные моды. Именно для
такой задачи даются ниже расчеты. Однако во многих случаях отыс-
отыскание мод не является самоцелью, а требуется лишь для оптимизации
параметров резонатора с той или иной точки зрения. В этих случаях
следует либо аналитически исследовать приводимые ниже формулы,
либо численно решать задачу об отыскании мод при разных парамет-
параметрах резонатора и затем выбирать среди полученных решений наибо-
наиболее подходящие.
Описание свойств кольцевых резонаторов распадается на две ча-
части. В рамках скалярной теории, не учитывающей поляризацию гене-
генерируемых электромагнитных волн, может быть описано поперечное
распределение мод, спектральное расстояние между продольными и
поперечными модами и геометрические параметры световых пучков,
образующих моду резонатора. Описание поляризационных свойств
резонатора завершает теорию кольцевых резонаторов.
Кольцевой резонатор всегда содержит анизотропные элементы.
Простейшим примером такого элемента является многослойное ди-
диэлектрическое зеркало при наклонном падении на него электромаг-
106 Гл. 1. Оптика гауссовых пучков
нитных волн. Поэтому поляризационные свойства кольцевых резо-
резонаторов представляют большой интерес. Их исследование позволяет
найти спектральные расстояния между модами различных поляриза-
поляризаций, встречными модами и др.
Если резонатор планарный, т. е. оптический осевой контур лежит
в одной плоскости, то моды такого резонатора описываются астиг-
матичным эрмит-гауссовым пучком с двумя плоскостями симметрии,
причем одна из этих плоскостей совпадает с плоскостью осевого кон-
контура. Для расчета собственных колебаний таких кольцевых резона-
резонаторов удобно пользоваться матричным методом, описанным в §1.11.
При этом 4 х 4-матрицы, описывающие оптические элементы резона-
резонатора, из-за наличия у него плоскости симметрии, распадаются на два
блока 2 х 2-матриц, один из которых описывает оптический элемент
в плоскости симметрии, а второй — в перпендикулярной плоскости. В
табл. 1.2 приведены 2 х 2-матрицы, описывающие простейшие опти-
оптические элементы, из которых, как правило, и составляются лазерные
резонаторы.
Резонатор в целом описывается лучевой матрицей
{А
M=\C D
которая представляет собой произведение матриц отдельных опти-
оптических элементов, взятых в порядке, обратном тому, в котором свет
проходит эти элементы. Эта матрица описывает распространение пуч-
пучка, начиная с некоторой реперной плоскости, перпендикулярной оси
пучка, и кончая той же плоскостью после обхода кольца. Вид лучевой
матрицы зависит от положения реперной плоскости в резонаторе. Со-
Соответственно и комплексный параметр пучка q, определенный по пра-
правилу ABCD, описывает пучок именно в реперной плоскости. Переход
от одной реперной плоскости к другой производится в соответствии с
соотношением
М' = ТМТ~\ A.197)
где М' — лучевая матрица в новой реперной плоскости, Т — луче-
лучевая матрица, описывающая прохождение пучка от исходной реперной
плоскости до новой реперной плоскости.
Резонансные частоты планарного кольцевого резонатора опреде-
определяются соотношением
1/2
A.198)
где L — длина осевого контура резонатора, q — продольный целочис-
целочисленный индекс, пит — поперечные целочисленные индексы (п ха-
характеризует распределение поля в плоскости контура резонатора, т —
§ 1.14- Кольцевые резонаторы 107
в перпендикулярной плоскости), величина г при четном числе зеркал
равна нулю, а при нечетном их числе отличается от нуля и равна еди-
единице лишь при нечетных п. Частота vnmq является характеристикой
резонатора в целом и не может зависеть от выбора реперной плоско-
плоскости, и такая независимость от выбора реперной плоскости действи-
действительно имеет место, поскольку vnraq выражается через следы луче-
лучевых матриц ii2 + .Di2, инвариантные относительно преобразования
A.197).
Приведем несколько формул для наиболее применяемых типов ре-
резонаторов. Спектр резонатора, образованного четырьмя одинаковы-
одинаковыми сферическими зеркалами, расположенными в вершинах квадрата
(рис. 1.21, а), определяется соотношением
, п+1/2 Л ау/2\ га+ 1/2 Л
q+ -^ arccos(l - — j + —^— arccos(l -
где а — сторона квадрата, с — скорость света в вакууме, R — радиус
кривизны зеркал, образующих резонатор, п определяет число нулей
поля в плоскости резонатора, т — число нулей поля в перпендикуляр-
перпендикулярном направлении. Перетяжки гауссовых пучков, образующих моду ре-
резонатора, расположены на серединах сторон квадрата, в поперечном
сечении поле моды представляет собой несколько деформированный
прямоугольник со сторонами
— в плоскости резонатора,
2ат = 2
— в перпендикулярной плоскости.
Спектр резонатора, образованного тремя одинаковыми зеркалами,
расположенными в вершинах правильного треугольника (рис. 1.21, б)
определяется соотношением
с Г1 /о \ , и+ 1/2 Л 2о
vnmq = - [~6 Bq - п) + ^^ arccos(l -
1/2
где а — сторона треугольника, R — радиус кривизны зеркал. Попе-
Поперечная протяженность моды в области перетяжки в плоскости резо-
резонатора
108 Гл. 1. Оптика гауссовых пучков
в перпендикулярной плоскости
причем перетяжки расположены на серединах сторон треугольника.
Спектр резонатора в форме равностороннего треугольника, у ко-
которого одно зеркало сферическое и два плоских (рис. 1.21, в), опреде-
определяется соотношением
, m + 1/2
Н -—'— arccos
V'^R
бтг V 2R
где а — сторона треугольника, R — радиус кривизны единственного
сферического зеркала. В этом резонаторе перетяжка расположена на
середине стороны треугольника, противолежащей сферическому зер-
зеркалу. Поперечная протяженность моды в области перетяжки равна
2ап = 2W ^р у За(ДV3 - За)
в плоскости резонатора и
— в перпендикулярной плоскости.
Как уж:е говорилось, поляризация электромагнитного излучения
оказывает существенное влияние на свойства кольцевых резонато-
резонаторов. Учет поляризации производится с помощью метода Джонса (см.
§1.10).
Основной проблемой при применении кольцевых резонаторов в ла-
лазерной технике является уменьшение взаимодействия между встреч-
встречными волнами. Для этого встречные волны по возможности разводят
по частоте с помощью невзаимных анизотропных элементов, а их по-
поляризации стараются сделать ортогональными.
Методом Джонса рассмотрено большое количество кольцевых ани-
анизотропных резонаторов. В качестве примера приведем результаты ис-
исследования кольцевого анизотропного резонатора (см. рис. 1.21, г),
приведенные в работе [26]. Резонатор, рассмотренный там, образо-
образован тремя зеркалами, расположенными в вершинах правильного тре-
треугольника (одно из зеркал сферическое, а два — плоские). В резонато-
резонаторе имеется 12 брюстеровских границ, ячейка Фарадея и полуволновая
пластинка, развернутая на угол ср относительно системы координат,
связанной с резонатором.
Поляризационные свойства резонатора описываются матрицей
М+ = b\
§ 1.14- Кольцевые резонаторы 109
где Рв — поляризационная матрица одной брюстеровской поверхности
(табл. 1.1, матрица IV, Р& = РA,р)), 5G) — матрица фарадеевского
вращателя (табл. 1.1, матрица V, 7 — ^/2), Q(y>) — матрица полувол-
полуволновой анизотропной пластинки (табл. 1.1, матрица VI, ср = тг/2 + 5/2),
S(+p) и S(—p) — матрицы, учитывающие разворот полуволновой пла-
пластинки на угол р, D — матрица, описывающая анизотропные свой-
свойства зеркал при наклонном падении на них электромагнитных волн
(табл. 1.1, матрица VII, р\ = — р<± = 1), п — число зеркал, к — число
брюстеровских границ.
В рассматриваемом резонаторе имелось три зеркала (п = 3) и 12
брюстеровских границ (к = 12). Для получения матрицы резонатора
М_, соответствующей обратному обходу контура, необходимо взять
произведение соответствующих матриц в порядке, обратном порядку
М_|_, заменив р на —р и 7 на —7.
В рассматриваемом случае матрица М+ имеет следующий вид:
м = ( cosBp - 7) -рк~г sinBp - j
+ \psmBp — 7) рк cosBp — 7)
Собственные значения этой матрицы равны
Ai,2 = \ [A + Рк) cosBp - 7) ±
В зависимости от знака подкоренного выражения собственные зна-
значения вещественны или комплексно сопряжены. Если угол разворота
полуволновой пластинки удовлетворяет неравенству
|2р-7|-
± ТУ
то собственные значения вещественны. В противном случае собствен-
собственные значения комплексно сопряжены.
Собственные векторы матриц М+ и М- соответствуют колебаниям
с эллиптической поляризацией, причем эллиптичность ? и азимут а
главной оси эллипса поляризации определяются соотношениями § 1.10.
Потери и фазовый сдвиг собственных колебаний определяются соот-
соотношениями
Амплитудная невзаимность резонатора представляет собой раз-
носность коэффициентов пропускания по амплитуде собственных ти-
типов колебаний, распространяющихся в противоположных направле-
направлениях: г = |А+| — |А_|. Для этих собственных типов колебаний имеет
место также невзаимный сдвиг собственных частот резонатора
где L — периметр резонатора. Результаты расчетов по этим формулам
приведены на рис. 1.22 и 1.23.
по
Гл. 1. Оптика гауссовых пучков
Найденная зависимость потерь и фазовой анизотропии от разно-
разности углов р — 7/2 приведена на рис. 1.22. Кроме этих величин найдены
также эллиптичность ( и азимуты а
главных осей поляризационного эл-
эллипса (рис. 1.23).
Из рис. 1.22 и 1.23 понятно, что в
зависимости от угла разворота фазо-
р-7/2
pt
/
Л
* х
-45
Л.
-45° У/'
1
-45° /
к
0,5 /
J
-0,5^
45°
-45°
Рис. 1.22. Зависимость потерь и фа- Рис. 1.23. Зависимость эллип-
зовой анизотропии от р — j/2 тичности Е и азимута а глав-
главных осей поля от р — 7/2
вой пластинки имеются две характерные области. При удовлетворе-
удовлетворении приведенного выше неравенства для разности 2р — 7 колебания
резонатора вырождены по частоте и линейно поляризованы, однако
различаются азимутом поляризации и потерями. При нарушении то-
того же неравенства колебания эллиптически поляризованы, вырожде-
вырождены по потерям и азимуту поляризации, но различаются по частоте и
знаку эллиптичности. При неточном изготовлении полу волновой пла-
пластинки или наличии у зеркал фазовой анизотропии полученные зави-
зависимости несколько сглаживаются и разница между двумя областями
становится менее выраженной (пунктирные линии на рис. 1.22 и 1.23).
Рассмотрим теперь кольцевые резонаторы с неплоским контуром.
Как мы увидим, модами такого резонатора являются гауссовы пучки,
описанные в § 1.13. В таких пучках по мере их распространения вдоль
продольной оси происходит поворот вокруг этой оси главных осей по-
поперечного распределения и направлений главных кривизн волнового
фронта. В связи с этим кольцевые резонаторы с неплоским контуром
называют также резонаторами с вращением поля.
В теоретическом отношении основной особенностью резонаторов с
неплоским контуром является присутствие в них некоторого допол-
§ 1.14- Кольцевые резонаторы 111
нительного по сравнению с плоским контуром поворота изображения
и поляризации на угол, получивший название угла Берри. Этот до-
дополнительный поворот возникает только от неплоскостности контура.
Даже если сами по себе отдельные элементы резонатора не поворачи-
поворачивают ни изображения, ни поляризации, то будучи расположены вдоль
неплоского контура они дадут поворот изображения и поляризации.
Важная роль угла Берри отмечена в нескольких областях физики.
Основные идеи теории кольцевых резонаторов с неплоским конту-
контуром изложим сначала в общей форме, а затем рассмотрим некоторые
простые частные случаи. Резонатор произвольного вида можно пред-
представить в виде совокупности плеч или сторон. Каждая такая сторона
состоит из свободного распространения пучка от одного зеркала до
другого и отражения в зеркале в конце стороны. Особенность резо-
резонаторов с неплоским контуром состоит в повороте плоскости падения
пучка на некоторый угол при переходе от одного зеркала к другому,
или от одного плеча к другому.
Итак рассмотрим распространение пучка по одной стороне резо-
резонатора с неплоским контуром. Преобразование матрицы пучка То при
распространении его в свободном пространстве на длину L описыва-
описывается соотношением A.180)
Г/ = A-ЬГо)-1Го;
как нетрудно убедиться, это преобразование, как впрочем и все по-
последующие, оставляет матрицу симметричной. Далее следует поворот
пучка вокруг продольной оси на угол ip, равный углу между двумя
плоскостями падения. Показатель экспоненты в выражении для поля
пучка A.161) в конце отрезка L можно представить в виде
где / • \
ф = [ cos(p sinyA
у— simp cos ipj
— матрица поворота системы координат на угол (р. Следовательно,
Т" = Ф~1Т'Ф.
Поскольку имеет место равенство
Т" = Ф^Т'Ф = A - ЬФ-1ГОФ)ФГОФ,
то преобразование при распространении на длину L и поворот на
угол ер можно делать в любой последовательности.
Преобразование матрицы Т" при отражении пучка в зеркале со-
состоит из двух операций: квадратичная коррекция A.182) и измене-
изменение знаков недиагональных элементов A.183). Квадратичная коррек-
коррекция достигается добавлением к матрице Т" симметричной матрицы
К A.182)
Г'" = Г" + К = Ф^Т'Ф + К.
112 Гл. 1. Оптика гауссовых пучков
Изменение же знаков недиагональных элементов — посредством опе-
операции гр _ rjilll
где матрица а имеет вид
а=(о -1
Объединяя все операции, получаем следующую формулу преобразо-
преобразования матрицы пучка, являющегося результатом прохождения им од-
одного плеча или одной стороны резонатора:
Ti = аф-1 A - ЬГ0)Г0Фа + аКа = W(T0, L, К, if).
На заключительном этапе составляем систему уравнений
где Wi+i (Ti) = W(Ti,Li,ki,ipi)nLi,ki,ipi — параметры плеч резонато-
резонатора; последняя матрица, как видим, совпадает с исходной, что являет-
является естественным условием замыкания пучка после обхода резонатора.
Представленная система довольно сложна, но эта сложность являет-
является отражением объективной реальности и с ней ничего не поделаешь.
Впрочем, эта система остается алгебраической и при наличии ЭВМ
вполне разрешима.
В некоторых случаях, например, когда в резонаторе с неплоским
контуром все зеркала, кроме одного, плоские, весь контур резонатора
можно рассматривать как одно плечо. Тогда
3(^/^1 нужно положить Т\ — То и для определения
2 параметров пучка получаем уравнение
То = аФ~х{\ — 1/То)-1ТоФа + аКа,
где Ф — матрица полного поворота на угол
Берри после обхода резонатора и L — длина
контура резонатора.
Рассмотрим теперь более простой четырех
Рис. 1.24. Четырех- зеркальный резонатор, зеркала которого распо-
зеркальный кольце- ложены в вершинах тетраэдра (в общем
вой лазерный резо- случае неправильного), а осевой контур со-
натор с неплоским ставляют четыре из шести ребер тетраэдра
контуром (рис. 1.24). Будем считать, что три зеркала в
этом резонаторе плоские и одно сферическое с радиусом кривизны
R; периметр резонатора пусть равен 2L. Пока, не касаясь поляриза-
поляризации, рассмотрим скалярную теорию резонатора. Как уже отмечалось,
при обходе контура резонатора изображение испытывает вращение на
угол Берри. В данном случае этот угол равен
Ziif == if\ ~\~ if2 ~\~ (Z?q ~\~ 0^4 A.199)
— сумме четырех углов, равных углам между плоскостями падения
лучей на зеркала и отсчитываемых так, чтобы резонаторный тетраэдр
лежал внутри угла.
§ 1.14- Кольцевые резонаторы 113
Воспользуемся некоторой симметрией такого резонатора. Именно,
на контуре выберем точку О, отстоящую от сферического зеркала на
расстояние L в обоих направлениях вдоль контура. Модой такого ре-
резонатора будет служить, очевидно, симметричный пучок A.185). Рас-
Распространяясь от точки О в обе стороны вдоль контура резонатора пу-
пучок будет испытывать поворот осей главных кривизн соответственно
на углы ±<р. Следовательно, угол ? во втором из соотношений A.184)
приравняем ср, координату z положим равной L и радиусы кривизны
волнового фронта пучка A.185) приравняем половинам эффективных
радиусов кривизны зеркала, в результате получим соотношения
-[2cosC + (ft + ft) sinC] ± (ft - ^1)л/8Ь22Ф + 8т2С
A.200)
A.201)
1 — P1P
где ^i,2 = h^/L, S = R/2L, R — радиус кривизны сферического зер-
зеркала и $ — угол падения пучка на сферическое зеркало. Эти соотно-
соотношения являются уравнениями, определяющими параметры основной
моды резонатора ft52 и Ф; умножая почленно друг на друга равенства
A.200) и деля их друг на друга также почленно, получаем
4(l+ft2)(l + ft2) 2
[2 cos С + (ft + ft) sin С]2 - (ft - ftJ(sh2 2Ф + sin2 C)
, A.202)
[2 cos С + (ft + ft) sin C] + (ft - ft) л/sh2 2Ф + sin2 С = cog2 ^
[2 cos С + (ft + ft) sinC] - (ft - ft)V^ 2
Из последнего равенства получаем
Подставляя это выражение в A.202), получим
— простое соотношение, связывающее между собой параметры ft и
,#2 вне зависимости от угла Берри ср или параметра Ф.
Используя теперь A.201) и A.203), получим второе соотношение
для определения ft и /?2
«^^-(tVt^J^. A-205)
где
8 В.П. Быков, О.О. Силичев
114 Гл. 1. Оптика гауссовых пучков
Разрешая уравнения A.204) и A.205) относительно Pi и /?2 и опре-
определяя параметр Ф в соответствии с A.201), находим гауссов пучок с
вращением поля, являющийся модой рассматриваемого резонатора.
Уравнения A.204) и A.205) могут иметь несколько корней. Среди
них нужно отобрать те, которые при ip —У 0 переходят в известные
корни, соответствующие пучкам без вращения. В связи с этим рас-
рассмотрим предельный переход ср —У 0. При ср = 0 уравнения A.204) и
A.205) принимают следующий вид:
1 1 sin2 ft I 1 1 + cos2 ft
3\ Scosft '
из них без труда получаем
1 + р^* = S cos $, 1 + р\ = S cos $,
где чертой сверху отмечено то, что эти решения соответствуют ip = 0.
Теперь по теории возмущения найдем решение при (р ^ 0, но ма-
малом. Замечаем, что согласно A.204)
где А означает приращение величины в скобках, обусловленное отли-
отличием ip от нуля. Кроме того из-за малости sin 2cp в а2 A.205) можно
использовать невозмущенные значения fi\ и /?| A.206). Таким обра-
образом, получаем
s-1 ft - 1)]'
8 cos3
отметим, что эти выражения переходят друг в друга при замене
cos$ —У cos $. Разумеется случай малых ср имеет и самостоятель-
самостоятельное значение.
Рассмотрим простейший тип резонатора с неплоским контуром,
свойства которого проясняют физическую картину происходящих в
подобных резонаторах явлений. Пусть резонатор образован четырь-
четырьмя плоскими зеркалами, расположенными в вершинах тетраэдра, че-
четыре ребра которого образуют оптический осевой контур кольцевого
резонатора. В одной из сторон осевого контура имеется фокусирую-
фокусирующая линза. Поскольку ни плоские зеркала (даже при наклонном паде-
падении), ни линза не обладают астигматизмом, то собственным пучком
такого резонатора будет лагерр-гауссов пучок A.115) с перетяжкой
на противоположном ребре осевого контура, при этом расстояние от
перетяжки до линзы в обоих направлениях вдоль контура одинаково
и равно L (длина контура — 2L).
§ 1.Ц. Кольцевые резонаторы 115
Полагая z = ±L в выражении для лагерр-гауссова пучка A.118),
приходим к распределениям слева и справа от линзы:
, , n G
Г ±ikLr2 -л i о 1\ ^ L , -I г • / . л 4 • /1
х ехР ~7Г9 г^т "F Ч ш + 2п + 1) arctg — =Ь г/сь + г?тг((р =Ь А(р) + ггр ,
L2(o^ + I7 ) о J
A.207)
где поворот на угол Берри распределения поля учтен как изменение
ср на Аср для двух пучков. Линза с фокусным расстоянием
2
согласовывает волновые фронты двух пучков, и в результате прихо-
приходим к равенству
qc , (|m| + 2n+l) . L тс
Таким образом, частота моды рассматриваемого резонатора имеет до-
дополнительную зависимость от азимутального индекса т, причем не
от модуля т, а от самого индекса т. Это означает, что собствен-
собственная частота моды ismnq изменяется при изменении знака т и поэтому
в рассматриваемом резонаторе модами являются волны, бегущие по
азимуту
exp[i{rmp - 27rvmnqt)\,
или в вещественной форме
[sin]
(тер- 27rjymnqt).
|_cosj
За один период поля они испытывают поворот по азимуту на угол
2тг/тп (ш/0).
Это обстоятельство многое проясняет в свойствах резонаторов с
неплоским контуром. Действительно, представим теперь, что одно из
плоских зеркал, образующих рассмотренный резонатор, немного де-
деформировано и стало сферическим; тогда из-за наклонного падения
на него пучка появится астигматизм. Ясно, что небольшая деформа-
деформация от плоского зеркала к сферическому не уничтожает полностью
вращение поля по азимуту. По существу возникнут два эффекта. Во-
первых, азимутальное движение по круговым траекториям деформи-
деформируется и сменится движением по овалам или эллипсам. Во-вторых,
поскольку теперь из-за астигматизма возникли неоднородности в ази-
азимутальном движении, волна уже не будет полностью бегущей, возник-
возникнет некоторая суперпозиция бегущей и стоячей по азимуту волн. При
большей деформации зеркал эти явления будут усиливаться. Замеча-
Замечательно, что эти довольно сложные явления описываются сравнитель-
сравнительно простыми эрмит-гауссовыми пучками A.207).
116 Гл. 1. Оптика гауссовых пучков
В заключение первой главы дадим краткий обзор литературы по
гауссовой оптике. Количество публикаций по гауссовым пучкам и их
применениям огромно; по необходимости мы ограничимся лишь глав-
главными и обзорными публикациями на эту тему.
Одной из первых работ по гауссовым пучкам являются работы Гу-
бо [14, 15]. Затем в работе Когельника и Ли [16] обсуждается правило
ABCD (см. также работу Дешана и Маета [17]). Полезен обзор Ко-
Когельника и Ли [18], переведенный впоследствии на русский язык в
качестве гл. 22 Справочника по лазерам [11]. Более поздние обзоры
можно найти в книгах Д. Маркузе [19] и A.M. Гончаренко [20]. Обоб-
Обобщение гауссова пучка — комплексный гауссов пучок (см. § 1.7) — дано
в работах Коваленко [21] и Ищенко [22]. Пучки — с вращением поля
(§ 1.13, 1.14) рассмотрены в работах Арно и Когельника [23], Панкра-
Панкратовой [24] и Савельева и Хромых [25]. Кольцевой резонатор с ани-
анизотропными элементами рассмотрен в работе В.И. Черненького [26].
Важным обобщением теории гауссовых пучков является распро-
распространение гауссовой оптики на неоднородные квадратичные среды,
из-за недостатка места лишь в малой степени затронутое нами в гл. 4.
Это обобщение дано в работах [27-30].
Глава 2
МЕТОД ИНТЕГРАЛЬНОГО УРАВНЕНИЯ
§2.1. Преобразование параксиальных пучков
гауссовыми оптическими системами
Исследование резонатора с учетом дифракционных явлений про-
проводится, в основном, методом интегрального уравнения. Суть этого
метода состоит в построении некоторого интегрального соотношения,
которое определяет поперечное распределение комплексной ампли-
амплитуды отдельных компонент вектора электрического или магнитного
поля на одном из зеркал резонатора по известному распределению
поля на другом зеркале. Этот метод наиболее удобен в случае, когда
возмущающее действие отдельных оптически неоднородных элемен-
элементов на проходящее поле можно описать путем умножения поля на
некоторую функцию от поперечных координат. В главе мы коротко
обсудим один из возможных вариантов вывода искомых интеграль-
интегральных соотношений, описывающих распространение световых пучков
через оптические системы. Обоснуем возможность и целесообразность
их использования для целей анализа резонаторов. Рассмотрим с по-
помощью метода интегрального уравнения наиболее важные частные
типы резонаторов и методы приближенного решения соответствую-
соответствующих интегральных уравнений, описывающих моды резонатора общего
вида.
Прежде чем начать изучение свойств резонаторов с помощью
метода интегрального уравнения, напомним некоторые сведения из
теории дифракции, которые нам понадобятся в дальнейшем. Рас-
Рассмотрение вопросов будем вести достаточно конспективно, поскольку
имеется большое количество книг по оптике, в которых они изложены
полно и ясно [31, 32].
Пусть имеется свободное пространство, разделенное на две части
непрозрачным, идеально поглощающим плоским экраном с отверс-
отверстием S (рис. 2.1). Рассмотрим электромагнитную монохроматическую
волну, заполняющую обе части пространства. Тогда каждая компо-
компонента вектора электрического или магнитного поля будет описывать-
описываться функцией вида
ф(т) = и (г) exp(-iujt),
где со — частота колебаний, а функция и (г) описывает пространствен-
118
Гл. 2. Метод интегрального уравнения
Рис. 2.1. К выводу дифракционного интеграла в параксиальном прибли-
приближении
ное распределение отдельных компонент электромагнитного поля и
является разной для разных компонент.
Согласно скалярной теории дифракции имеется связь, задаваемая
некоторым интегральным соотношением, между значением функции
и(Р) в плоскости отверстия S со значением и (Pi) в другой точке Pi
пространства. При этом каждая компонента электрического или маг-
магнитного поля рассматривается независимо друг от друга. В общем
случае так делать нельзя, поскольку различные компоненты векто-
векторов электрического и магнитного полей связаны уравнениями Макс-
Максвелла, и их нельзя рассматривать независимо. Однако теоретический
анализ и данные экспериментов показывают, что скалярная теория
дает очень точные результаты, если выполняются следующие усло-
условия: отверстие в экране велико по сравнению с длиной волны, а точка
наблюдения Pi расположена не слишком близко от экрана. Эти усло-
условия хорошо выполняются в задачах теории открытых резонаторов.
Поэтому использование при их решении скалярной теории дифракции
вполне оправдано. Более полное и строгое обсуждение применимости
скалярной теории в оптике можно найти в книге [31].
Существует несколько альтернативных соотношений, связываю-
связывающих и(Р) и u(Pi). В параксиальном приближении они все сводятся
к одному виду. Поэтому для целей теории открытых резонаторов, в
которой вполне уместно ограничиться параксиальной оптикой, выбор
формы дифракционного интеграла не имеет особого значения. Мы
возьмем за основу дифракционный интеграл в форме Рэлея-Зоммер-
фельда, поскольку вывод этого соотношения свободен от внутренних
противоречий, характерных для другой формы дифракционного ин-
интеграла — формулы Френеля-Кирхгофа [32].
Для того чтобы выписать искомое соотношение, введем декартову
систему координат, расположенную так, чтобы оси X и Y находились
в плоскости экрана, а начало координат лежало в плоскости отверстия
2.1. Преобразование параксиальных пучков 119
(рис. 2.1). Тогда согласно формуле Рэлея-Зоммерфельда
и(Р{) = -\ (и{Р) ехр(^р) cosOds, B.1)
A J р
где ds — элемент площади отверстия, р — расстояние между точкой
отверстия Р и точкой наблюдения Pi, k = uj/c = 2тг/А, с — скорость
света, А — длина волны излучения, в — угол между осью z и направ-
направлением от точки Р к точке Р\. Интегрирование ведется по площади
отверстия S.
Выражение B.1) можно существенно упростить, если предполо-
предположить, что расстояние между отверстием и точкой наблюдения Р\
существенно больше максимального размера отверстия S и макси-
максимального размера области наблюдения, расположенной вблизи оси z
(рис. 2.1). Эти предположения соответствуют условиям параксиально-
сти в оптике и вполне оправданы в резонаторных задачах, поскольку
в открытых резонаторах расстояние между зеркалами, как правило,
значительно превышает размеры ограничивающих излучение апер-
апертур. Из рис. 2.1 следует, что
+{x-XlJ + {y-yiJ. B.2)
В соответствии со сделанными предположениями \х — х\\ и \у —
— 2/i I ^ z- Можно разложить функцию B.2) в ряд Тейлора и огра-
ограничиться в разложении лишь величинами второго порядка малости:
С учетом этого формулу B.1) можно существенно упростить. При-
Причем в знаменателе можно ограничиться лишь первым членом раз-
разложения B.3), т.е. положить р ~ z, a cos# = z/p « 1. В экспонен-
экспоненциальном же члене нельзя ограничиться значением р — z, так как
возникающая погрешность в величине р умножается на очень боль-
большое число к = 2тг/А и неточность расчета фазы становится сравнимой
или даже большей тг. Поэтому в экспоненте следует использовать р в
виде B.3). С учетом этого, формула B.1) преобразуется к виду:
u(Pi) = -%^-Ju(P) exp{i \z [(x - х,J + (у - У1J}} ds. B.4)
s
Такое упрощение дифракционного интеграла B.1) называют при-
приближением Френеля. Очевидно, что оно должно достаточно точно
описывать ситуацию, если максимальное изменение фазы экспоненты,
вносимое членом более высокого порядка в разложении корня B.2),
много меньше тг. Это условие выполняется, если:
Z3 » max [("lJ+A("lJ]2. B.5)
120 Гл. 2. Метод интегрального уравнения
Заметим, однако, — это условие является достаточным, но не необ-
необходимым для того, чтобы вклад в интеграл B.1) от членов более
высокого порядка в разложении квадратного корня был мал. Если
условие B.5) не выполнено, то при изменении координат точки Р
экпоненциальный множитель в выражении B.1) будет очень быст-
быстро осцилировать и основной вклад в интеграл будут давать только те
точки отверстия, которые расположены вблизи точки х = xi, у = у\.
В этой области скорость изменения фазы в экспоненте минимальна. В
окрестности этих точек величиной фазового члена более высокого по-
порядка можно пренебречь. Поэтому и в этом случае приближение B.4)
вполне оправдано. Формула B.4) является основной в теории откры-
открытых резонаторов.
Подчеркнем, что мы рассматриваем лишь монохроматические вол-
волны. Это волны, амплитуда которых и в каждой точке пространства
неизменна. Следовательно, формула B.1) или B.4) не описывает про-
процесс распространения поля от отверстия до точки Р\, а устанавливает
лишь связь в один и тот же момент времени между пространствен-
пространственным распределением поля в плоскости отверстия экрана и значением
данной компоненты поля в точке наблюдения Р\. Часто, обсуждая
те или иные задачи дифракции, говорят о распространении волны, о
дифракции ее на апертуре и проч., подразумевая, что имеется некото-
некоторый немонохроматический пучок, который распространяясь по про-
пространству, встречает препятствия, например, экран с отверстием, и,
проходя через это препятствие, искажается. Причем искажения опи-
описываются формулой B.1) или B.4). Такая терминология в случае
параксиальных, квазимонохроматических пучков (амплитуда медлен-
медленно меняется по сравнению с членом ехр(—ioot)), оказывается вполне
оправданной. Это следует из рассмотрения дифракционного интегра-
интеграла для нестационарных пучков [31, 32], который в данном случае сво-
сводится к виду B.4). Более подробно с этим вопросом можно ознако-
ознакомиться в книге [31]. Здесь же лишь отметим законность терминологии,
по которой мы будем в дальнейшем, используя интеграл B.4), гово-
говорить о распространении соответствующих параксиальных пучков. Та-
Таким образом, формула B.4) описывает изменение пространственного
распределения комплексной амплитуды поля и при распространении
волны от экрана до плоскости наблюдения.
Рассмотрим теперь прохождение параксиального пучка через иде-
идеальную тонкую линзу и отражение его от сферического зеркала. Поле
после прохождения таких элементов имеет вид:
и'(х, у) = и(х, у) ехр [-г А (х* + у^, B.6)
где и(х,у) описывает распределение поля подающей волны. При от-
отражении от зеркала с радиусом кривизны R величину / в этом выра-
выражении следует заменить на R/2.
2.1. Преобразование параксиальных пучков
121
Формулы B.4) и B.6) описывают прохождение параксиального
пучка через простейшие гауссовы оптические системы, а именно уча-
участок свободного пространства B.4), тонкую линзу, сферическое зерка-
зеркало B.6). Можно построить интегральное соотношение, описывающее
распространение параксиального квазимонохроматического пучка по
гауссовой оптической системе общего вида.
Подавляющее большинство оптических элементов, используемых
в лазерной технике, с большой точностью можно рассматривать, как
гауссовы. Поэтому построение подобного интегрального соотношения
весьма важно, как для лазерной оптики вообще, так и для теории
резонаторов в частности.
Гауссовы оптические системы в геометрической оптике описы-
описываются лучевыми матрицами, с которыми нам уже приходилось встре-
встречаться при рассмотрении гауссовых пучков. Изучая преобразова-
преобразование параксиальных пучков оптической системой, изображенной на
и{Р)
. Х\
/
Рис. 2.2. К выводу интегрального соотношения, описывающего прохожде-
прохождение пар параксиального пучка через гауссову оптическую систему
рис. 2.2, путем последовательного рассмотрения изменения амплиту-
амплитуды пучка при прохождении участка свободного пространства длиной
z\, тонкой линзы и участка длиной z^ и сравнивая получающееся ито-
итоговое выражение с лучевой матрицей данной системы, можно полу-
получить интегральное соотношение, описывающее распространение пуч-
пучка через гауссову оптическую систему с геометрической длиной L:
х ехр{г А [А(х2 + у2) + D(x2 + у2) - 2{ххх + уУ1)]}, B.7)
где матрица коэффициентов
М =
А В
является лучевой матрицей данной оптической системы. Подробный
122 Гл. 2. Метод интегрального уравнения
вывод соотношения B.7) можно найти в книге [10]. Покажем, что вы-
выражение B.7) справедливо для любой гауссовой оптической системы.
Доказательство проведем методом математической индукции. Для
этого установим, что формула B.7) правильно описывает преобра-
преобразование амплитуды пучка простейшими гауссовыми элементами, та-
такими как участок свободного пространства, тонкая линза, сфериче-
сферическое зеркало. Затем покажем, что если формула B.7) справедлива
для двух оптических систем с лучевыми матрицами М\ и М^ рас-
расположенными друг за другом, то она справедлива для объединенной
системы с матрицей М равной произведению матриц М^ • М\. Тем
самым мы докажем, что формула B.7) справедлива для любой, сколь
угодно сложной, оптической системы, образованной участками сво-
свободного пространства, линзами, сферическими зеркалами.
Учитывая, что матрица участка свободного пространства длиной z
имеет вид
с.;:
легко видеть, что в этом случае формула B.7) переходит в выраже-
выражение B.4) и, следовательно, справедлива.
Для доказательства справедливости формулы B.7) в случае тон-
тонкой линзы, рассмотрим оптическую систему, изображенную на рис. 2.2,
при z\ = z^ = z. Ее лучевая матрица имеет вид:
M_(l-z/f 2z-z*/f
M-{-l/f 1-z/f
Необходимо доказать, что при z —У 0 формула B.7) переходит в B.6).
Из выражения B.7) имеем:
—уу dsu(x,y) x
s
^[А^2+у2)+D{xl+y2) ~
Учитывая, что в данном случае А = D, а также условие AD — ВС = 1,
это выражение можно преобразовать к виду:
X
2 , v 2-1 >| >|
S
Из матрицы B.8) следует, что при z —У О А —У 1 и В —У 0. Поэтому
при z —У 0 подынтегральная экспоненциальная функция будет очень
быстро осциллировать и, согласно методу стационарной фазы [31] зна-
2.1. Преобразование параксиальных пучков
123
чение интеграла будет определяться, в основном, значением подынте-
подынтегральной функции в стационарной точке х = х±/А и у = yi/A.
Это позволяет преобразовать выражение B.9) к виду
"¦<*¦•»¦> —{*
S
В нем можно расширить пределы интегрирования на всю входную
плоскость, поскольку значение интеграла определяется лишь ближай-
ближайшей окрестностью стационарной точки ( —г, ^-). После этого, исполь-
\ А А )
зуя известное интегральное соотношение [33]:
+ ОО J-
I dt exp[i(/5t + at2)] = y'l exp(-|L) B.10)
— OO
при /3 = 0 можно вычислить интеграл в последнем выражении. После
несложных преобразований получим
= 1пп{ехрBгЬ)ехр[г g (x\
Переходя в этом выражении к пределу при z —У 0 и учитывая при этом
явный вид элементов лучевой матрицы B.8), получаем формулу тож-
тождественную B.6). Следовательно, формула B.7) правильно описывает
прохождение параксиального пучка через тонкую линзу и отражение
от сферического зеркала.
и(х,у) и2(х2,У2)
(
\
о
Mi
% вЛ
(
\
Li
м2
'А2 В2\
ЧС2 D2)
Рис. 2.З. Разложение сложной оптической системы на две более простые
Рассмотрим теперь оптическую систему Mq (рис. 2.3), состоящую
из двух гауссовых подсистем Mi и М^. Предположим, что для каждой
подсистемы формула B.7) справедлива. Докажем, что в этом случае
она справедлива и для всей системы в целом. Тем самым доказатель-
доказательство справедливости формулы B.7) для гауссовой системы общего
вида будет завершено.
124 Гл. 2. Метод интегрального уравнения
Пусть и(х,у) — амплитуда поля, падающего на систему Mi,
^2(^2,2/2) — амплитуда волны на входе системы М2 и и\{х\,у\) ~
амплитуда на выходе всей системы. Тогда согласно B.7) имеем после-
последовательно:
и2(х2,У2) = -T^-eikLl dsu(x,y)x
S
х ехр{г ^- [А^х2 + у2) + D^x2 + у2) - 2{хх2 + уу2)]} B.11)
2/i) = -^-e'kL2 // dx2dy2U2(x2,y2) х
— (X)
ji ^- [A2(x^ + 2/|) + D2(x? + у2) - 2{Xlx2
х exp
где ^1,2 5 ^1,2 5 ?*i,2 — элементы лучевых матриц систем М\ и М2,
соответственно. Интегрирование в последнем выражении ведется по
всей плоскости, разделяющей подсистемы М\ и М2, так как мы по-
полагали, что общая система является гауссовой и, следовательно, не
содержит внутри себя ограничивающих апертур. Подставляя форму-
формулу B.11) в B.11а), проводя интегрирование по переменным ж2, у2 с по-
помощью B.10) и осуществляя необходимые преобразования, получаем
выражение B.7); в котором коэффициенты А, В, С, D определяются
соотношением
А В\ _ (А2 ВЛ (А,
С D) ~ \С2 D2) \Ci
и, следовательно, являются элементами лучевой матрицы системы
Mq. Тем самым справедливость формулы B.7) полностью доказана.
Ее справедливость может быть доказана и для более общих гауссо-
гауссовых систем. Например для систем содержащих участки квадратично
неоднородной среды, гауссовые апертуры, т. е. апертуры, коэффици-
коэффициент пропускания которых определяется формулой:
B.12)
и т.д. Для этого достаточно проверить справедливость формулы B.7)
для каждого нового элемента. В частности, для гауссовой апертуры
это можно сделать, не проводя никаких выкладок. Действительно,
полагая
/ = <2Г> B-13)
легко видеть, что в этом случае функция, описывающая преобразова-
преобразование поля в тонкой линзе B.6) переходит в функцию пропускания гаус-
2.1. Преобразование параксиальных пучков 125
совой апертуры B.12). Поскольку при доказательстве справедливо-
справедливости B.7) для тонкой линзы нигде не использовался факт действитель-
действительности фокусного расстояния /, то B.7) описывает действие гауссовой
апертуры B.12). Следовательно, она справедлива и для гауссовых си-
систем, содержащих произвольное число таких апертур. При расчете
лучевых матриц подобных систем, необходимо описывать гауссову
апертуру такой же матрицей, как и тонкую линзу, но с фокусным
расстоянием B.13). Лучевые матрицы таких систем содержат ком-
комплексные элементы.
Мы уже подчеркивали важность формулы B.7) для лазерной оп-
оптики. В качестве полезной иллюстрации ее использования получим с
ее помощью закон преобразования комплексного параметра гауссова
пучка, q введенного в первой главе, при прохождении произвольной
гауссовой оптической системы.
При этом, для простоты выкладок, ограничимся случаем пучка
нулевого порядка, распределение комплексной амплитуды которого в
поперечном направлении описывается функцией
и = Ао exp \i — (ж2 + у2Ц B.14)
где q — комплексный параметр пучка. Подставим B.14) в формулу
B.7). Предположим, что входная апертура гауссовой системы имеет
размер существенно больший, нежели размер пучка. Тогда в форму-
формуле B.7) интегрирование по площади входной апертуры S можно за-
заменить на интегрирование по всей входной плоскости. Проводя раз-
разделение переменных, получим выражение для функции, зависящей
только от х:
х
— оо
/ dx exp [ г — х2 \ ехр г —— {Ах2 + Dx\ — 2хх\) .
Аналогичное выражение имеется для функции Ui(y\). Амплитуда
пучка на выходе из системы в этом случае равна:
k kD
Вводя коэффициенты /3 = —x\kjB и а = \ — можно преобразо-
2q 2B
вать последний интеграл к виду:
126 Гл. 2. Метод интегрального уравнения
который может быть легко вычислен с помощью формулы B.10). Пре-
Преобразуя полученное выражение, имеем:
где
Учитывая, что для ui(yi) получается точно такое же выражение, рас-
распределение комплексной амплитуды пучка на выходе гауссовой систе-
системы можно представить в виде:
Из этого следует, что гауссов пучок после прохождения гауссовой
системы остается гауссовым. Меняется лишь его комплексный пара-
параметр q в соответствии с B.15). Соотношение B.15) подробно обсуж-
обсуждалось в первой главе. Здесь лишь подчеркнем, что формулы B.15)
и B.16) справедливы и в том случае, если оптическая система со-
содержит гауссовые апертуры. При этом элементы лучевой матрицы
являются комплексными числами.
Коэффициент ——-— в формуле B.16) описывает изменение ам-
амплитуды гауссового пучка за счет изменения его характерного попе-
поперечного размера, а также задержку по фазе по сравнению со случаем
плоской волны. Если же система содержит гауссовы апертуры, то этот
коэффициент описывает также уменьшение амплитуды пучка за счет
потерь мощности на ограничивающих гауссовых апертурах.
В заключение перепишем формулу B.7) в цилиндрической систе-
системе координат, в которой удобнее проводить анализ распространения
осесимметричных пучков. Для перехода к цилиндрическим коорди-
координатам (г, ер) достаточно в формуле B.7) провести замену переменных
х = rcostp, у = г simp, х\ — Т\ cos(pi, у\ = т\ sin(pi и положить ds =
= rdrdif. Получаем:
= -jge*kL /
s
{
x exp{^ [Ar2 + Dri ~
На этом мы закончим рассмотрение преобразования параксиальных
пучков гауссовыми оптическими системами. Отметим лишь, что если
необходимо построить уравнение, описывающее преобразование па-
параксиального пучка оптической системой, содержащей негауссовые
элементы, то следует так расчленить эту систему на составные ча-
части, чтобы негауссовые элементы располагались на входе или выходе
§2.2. Метод интегрального уравнения в теории резонаторов 127
отдельных составляющих оптических подсистем, которые бы содер-
содержали лишь гауссовые элементы. Затем для каждой подсистемы стро-
строится уравнение B.7), и зная закон преобразования амплитуды пучка
негауссовыми элементами (например, апертурой), можно составить
общее интегральное уравнение.
А
§ 2.2. Метод интегрального уравнения в теории
резонаторов
Применим теперь соотношения, описывающие преобразование па-
параксиальных световых пучков оптическими системами и введенные
в предыдущем параграфе, для ис-
исследования открытых резонато-
резонаторов.
Рассмотрим открытый резона-
резонатор общего вида (рис. 2.4). По-
Построим, согласно методике преды-
предыдущего параграфа, интегральное
соотношение, описывающее изме-
изменение пространственного распре-
распределения комплексной амплитуды
параксиального пучка при обходе
резонатора, начиная с некоторой
Рис. 2.4. Схема исследуемого резо-
резонатора
плоскости А А. Для удобства записи обозначим это интегральное соот-
соотношение в виде некоторого интегрального оператора L. Чуть позже
мы выпишем явный вид этого оператора, сейчас же выясним, как
можно использовать его для исследования свойств открытого резона-
резонатора.
Рассмотрим интегральное уравнение на собственные значения
щщ = Ь(щ) (г = 0,1,2,...).
B.18)
Коэффициенты щ, при которых это линейное уравнение имеет нетри-
нетривиальное решение, называют собственными числами интегрального
уравнения B.18). Пронумеруем их в порядке убывания абсолютной
величины
Функции щ, соответствующие данным значениям щ, называются
собственными функциями интегрального уравнения. Важной осо-
особенностью набора функции U{ является возможность представления
пучка с произвольным поперечным распределением амплитуды ф
в виде:
5>iMi. B.19)
128 Гл. 2. Метод интегрального уравнения
Здесь следует сделать небольшое замечание по поводу последнего
утверждения, так как на этот счет имеется целый ряд противоречи-
противоречивых суждений [10, 34—36]. В математике такое свойство набора функ-
функций Ui называется полнотой в некотором классе функций. Не каждый
интегральный оператор, описывающий прохождение поля по резона-
резонатору, порождает полный дискретный набор собственных функций.
При наличии дифракционных потерь дискретный спектр оператора L
должен быть дополнен системой собственных функций, собственные
значения которых образуют непрерывный спектр. В литературе уде-
уделено большое внимание проблемам, связанным с разложением по та-
такой расширенной системе собственных функций. В частности, можно
порекомендовать книгу [37]. Однако в нашем случае эти обстоятель-
обстоятельства не имеют особого значения. Известно [38], что путем сколь угодно
малого изменения вида оператора L можно добиться того, что новый
оператор уже будет обладать полным набором собственных функций.
Так как любой физический процесс мы всегда описываем приближен-
приближенно (например, используем параксиальное приближение и проч.), то
в случае, если L не обладает полным набором функций щ, его все-
всегда можно немного изменить, не нарушая точность рассмотрения так,
чтобы новый оператор обладал требуемым свойством.
Вернемся к выражению B.19). Предположим, что в резонатор за-
запущен пучок с поперечным распределением амплитуды, описываемый
функцией ф. После обхода резонатора, с учетом B.18) и B.19) имеем
После n-го обхода резонатора
^2к?щ. B.20)
Очевидно, что поперечная структура пучка меняется по мере обходов
резонатора и при п —> оо стремится к распределению, описываемому
функцией ит, для которой, с одной стороны, аш ф 0, а с другой |хт|
больше всех прочих коэффициентов в разложении B.19).
Таким образом, получаем, что первоначальное поле в резонато-
резонаторе, по мере обходов резонатора, эволюционирует, стремясь к некото-
некоторому стационарному, с точки зрения поперечной структуры, полю,
описываемому одной из собственных функций оператора L. Такие
установившиеся, стационарные структуры в резонаторе называют по-
поперечными модами резонатора. Изучение резонатора в значительной
степени сводится к изучению его модовой структуры.
Поскольку уравнение B.18) описывает поперечные моды резона-
резонатора, выясним физический смысл коэффициентов щ. Заметим, что
плотность мощности пучка пропорциональна квадрату модуля ком-
комплексной амплитуды \щ\2 [31]. Следовательно, мощность пучка Р, со-
соответствующего моде резонатора в плоскости А А, определяется соот-
§2.2. Метод интегрального уравнения в теории резонаторов 129
ношением:
Р» Ь, Лс L. I2 (О 91 "\
S
где интегрирование ведется по всей плоскости А А, а коэффициент
ко не зависит от распределения поля в пучке и является постоянной
величиной. После обхода резонатора мощность пучка составит
Dl = ко ds \L(ui
S
Из этого соотношения, с учетом B.18), получим:
Вводя величину потерь г-ой моды резонатора за время обхода резона-
резонатора oti — (Pi — Pi)/Pi имеем:
а{ = \-\щ\\ B.22)
Таким образом, модуль г-го собственного значения интегрального
уравнения B.18) характеризует потери мощности г-ой моды резона-
резонатора.
Аргумент собственного числа щ несет информацию о собствен-
собственных, резонансных частотах резонатора. Представим коэффициент в
виде щ — \щ\ exp(iSi). Для нахождения резонансных частот резонато-
резонатора достаточно, чтобы фаза волны, соответствующая моде резонатора,
менялась при обходе резонатора на величину кратную 2тг. Т. е. долж-
должно выполняться условие
Si = 27rq (<? = 0,±1,±2,...). B.23)
Условие удовлетворяется лишь при определенной длине волны Л^ или,
что эквивалентно, частоте колебаний щ = с^/2тг. Поэтому решая урав-
уравнение B.23), можно найти спектр резонансных частот исследуемого
резонатора.
Таким образом по мере эволюции поля в резонаторе устанавли-
устанавливается некоторое квазистационарное распределение поля, называе-
называемое модой резонатора. Распределение комплексной амплитуды по-
поля в поперечном сечении резонатора описывается функциями щ,
являющимися решениями интегрального уравнения B.18). Модуль
собственного числа уравнения \щ\ описывает потери г-ой моды. Зна-
Знание аргумента величины щ позволяет определить из уравнения B.23)
спектр резонансных частот. Исследование резонатора методом инте-
интегрального уравнения сводится таким образом к построению и реше-
решению уравнения B.18).
Проиллюстрируем действие данного метода на примере резонато-
резонатора, образованного лишь гауссовыми оптическими элементами и по-
подробно исследованного в гл. 1.
9 В.П. Быков, О.О. Силичев
130 Гл. 2. Метод интегрального уравнения
Рассмотрим линейный резонатор общего вида, рис. 2.4. Полагая,
что геометрия резонатора обладает осевой симметрией, расчет мод бу-
будем вести в цилиндрической системе координат. Поскольку известно,
что гауссов пучок является модой резонатора с гауссовыми элемен-
элементами, будем искать решение интегрального уравнения B.18) в виде:
= AQpl(r) ¦ {С21^ , B.24)
^)(^) B.25)
= i
q R Tvw2'
Оператор обхода резонатора L в нашем случае определяется форму-
формулой B.17), где А, В, С, D — элементы лучевой матрицы обхода ре-
резонатора, отнесенной к плоскости АА (рис. 2.4), т.е. к плоскости, где
ищется поперечное распределение амплитуды моды.
Подставляя в интегральное уравнение B.18), явный вид операто-
оператора L B.17) и искомую функцию uv\ в виде B.24), можно получить,
после проведения соответствующих преобразований, уравнение отно-
относительно Qpi:
2тг(-г)г+1 2ikLn f.kD
^rU^rr^exp^r2). B.26)
О
При выводе этого уравнения было проведено интегрирование по
углу if с помощью интегрального представления функции Бесселя 1-го
порядка: ^
i - <р)] ^/^ dip
i - <р)] ^/^
Ji(x) = ^ L ^J . B.26а)
Подставляя в уравнение функцию Qpi в виде B.25) и используя
формулу [33]
ОО
S'Llp(ar2)Ji{yr)dr =
„2
, B-27)
легко показать, что уравнение B.26) переходит в тождество, и следо-
следовательно, гауссов пучок вида B.24)-B.25) является модой резонатора
с гауссовыми элементами, при выполнении следующих условий.
§2.2. Метод интегрального уравнения в теории резонаторов 131
В случае, когда элементы лучевой матрицы обхода резонатора ве-
вещественны (т.е. гауссовые апертуры отсутствуют), р, I ^ 0 и
т. е. в случае устойчивого резонатора, должны выполняться соотно-
соотношения:
1 _ D-А _
ч2р+/+1
хР1 = expBikL0)(l - гVI - Р )zp+t+1, B.29)
где
1=Ц? B-30)
— величина, как легко показать, не зависящая от расположения ис-
исходной плоскости А А в резонаторе; Lq — длина резонатора.
Формула B.28) ранее была получена из правила ABCD преобра-
преобразования гауссового пучка и определяет величину комплексного пара-
параметра моды резонатора в плоскости АА (рис. 2.4).
Из выражения B.29), определяющего собственные числа инте-
интегрального уравнения, легко видеть, что \>cpi\ = 1. Следовательно, по-
потери энергии в таком резонаторе в рамках данной модели отсутст-
отсутствуют.
Аргумент величины xpi можно представить в виде
l + l), B.31)
где
7 = arccos(/). B.31а)
Уравнение B.23) в этом случае может быть легко решено относитель-
относительно искомых собственных частот резонатора
v* = *k9-*k&i2p+l+1)- B-32)
Легко видеть, что спектр собственных частот резонатора распа-
распадается на две части. Одна часть, описываемая первым членом в фор-
формуле B.32), эквидистантна и разница между соседними резонансными
частотами равна c/2Lq. Другая часть спектра связана с простран-
пространственной структурой моды и зависит не только от длины резонатора,
но и от его геометрии. Эта часть также эквидистантна, но расстояние
между соседними частотами иное B.32).
Заметим, что модель, рассмотренная выше, идеализирована в том
отношении, что резонатор не содержит ограничивающих апертур. По-
Поэтому лишь решения, сосредоточенные вблизи оси резонатора, ампли-
амплитуда которых в месте расположения границы апертуры мала, близки
к реальным распределениям полей мод.
9*
132 Гл. 2. Метод интегрального уравнения
Если ограничивающая апертура расположена в плоскости АА и
имеет радиус Ro, то поскольку размер р, 1-ой моды можно прибли-
приближенно представить в виде api « w^2p + l + 1, формула B.24)-B.25)
хорошо опишет моды реального резонатора, при
B.33)
Найдем следующий корень уравнения B.26). Рассмотрим случай
неустойчивого резонатора, не содержащего ограничивающих апертур.
Тогда |/| > 1 и уравнение B.26) при подстановке B.24), B.25) перехо-
переходит в тождество лишь при р = I = 0 и выполнении следующих соот-
соотношений
K00=expBikL0)(l±VP-1) . B.35)
Из выражения для комплексного параметра q и формулы B.34)
следует, что в этом случае 1/w = 0 и R\^ = qi,2- Такие значения па-
параметров со и i?i52 соответствуют двум сферическим волнам радиуса
gi52 с постоянной амплитудой поля в поперечном направлении. Одна
из этих волн является сферической волной, сходящейся к оси резо-
резонатора, вторая — расходящейся. Поскольку для обеих волн поле уже
не локализовано вблизи оси резонатора, то нельзя не учитывать ко-
конечного размера зеркал и других элементов резонатора. Поскольку
интенсивность поля на краю апертуры значительна, то дифракцион-
дифракционные эффекты могут существенно исказить полученное распределение
поля. Позже, при рассмотрении неустойчивых резонаторов, мы вер-
вернемся к этому вопросу. Сейчас же лишь заметим, что при опреде-
определенных условиях, весьма часто встречающихся на практике, расходя-
расходящаяся сферическая волна достаточно точно описывает основную моду
неустойчивого резонатора [10].
Собственные частоты основной моды неустойчивого резонатора
легко получить из уравнения B.23) и формулы B.35):
Потери основной моды, как следует из формул B.22) и B.35) рав-
равны
q/00 = 1 — [/ — sign(/)v/2 — l] . B.37)
Смысл этого соотношения легко понять, если представить сфери-
сферическую волну с радиусом R\^ в виде пучка лучей с координатами
(x^x/Ri^)- Поскольку сферическая волна является модой резонато-
резонатора, то после обхода резонаторов получим
'А В\ ( х
КС D (x/Rlt2/
2.3. Интегральное уравнение резонатора 133
Введем величины М\^ = х\/х = А + В/'R\^- С учетом B.34) имеем
Величину | Mi | > 1 называют коэффициентом увеличения неустой-
неустойчивого резонатора. Она показывает, во сколько раз возрастает попе-
поперечный размер поля после обхода резонатора. Поскольку площадь по-
поперечного сечения пучка возрастает в М2 раз, то плотность мощности
на апертуре падает в М2 раз и, следовательно, мощности пучка до и
после обхода резонатора связаны соотношением Pi = М\Ръ. Потери
моды
а00 = (Pi - P2)/Pi = 1 - Mf2 = 1 - Ml
что согласуется с формулой B.37). При приближении резонатора к
устойчивой конфигурации / —У 1, Mi52 —У 1 и потери стремятся к нулю.
Перейдем к рассмотрению последнего случая, когда резонатор со-
содержит гауссовые апертуры и поэтому лучевая матрица обхода резо-
резонатора имеет комплекснозначные элементы.
Тогда уравнение B.26) переходит в тождество для любых р, I ^ О
и выполнении условий B.28) и B.29) при
B.38)
независимо от величины /. Следовательно, в резонаторах, содержа-
содержащих лишь гауссовые элементы (в том числе и гауссовые апертуры) мо-
моды описываются соответствующими гауссовыми пучками B.24)-B.25)
с учетом B.28), B.29) и B.38). При этом, в силу комплексности эле-
элементов А и D значение w B.38) также является комплексным. По-
Поэтому структура полиномов Лагерра LlpBr2/w2), а следовательно, и
структура поперечных мод ненулевого порядка, становится достаточ-
достаточно сложной. В частности, у таких мод фазовый фронт не является в
общем случае сферическим и не совпадает с поверхностью концевых
зеркал резонатора (см. §2.1, а также [30].
Потери щр мод такого резонатора определяются выражением
B.22), которое с учетом B.29) приобретает вид,
B.39)
Резонансные частоты даются выражением B.32), при условии за-
замены величины 7 на
i = Arg(/ - л//2-1). B.40)
На этом мы закончим исследования резонатора, образованного
гауссовыми оптическими элементами. Оно не может претендовать на
полноту, однако, позволяет понять возможности и алгоритм примене-
применения метода интегрального уравнения при анализе лазерного резона-
резонатора.
134
Гл. 2. Метод интегрального уравнения
§ 2.3. Интегральное уравнение резонатора,
содержащего негауссовые оптические элементы
Из результатов первой главы и предыдущего параграфа следу-
следует, что метод гауссовых пучков дает исчерпывающую информацию
о свойствах резонатора, образованного лишь гауссовыми оптически-
оптическими элементами. Однако на практике в резонаторах часто приходится
использовать элементы, которые по своим оптическим свойствам не
являются гауссовыми. К таким элементам лазерного резонатора, как
правило, относятся ограничивающие апертуры, оптические элементы
управления, активный элемент (АЭ) и т.д. Причем наибольшие ис-
искажения вносит, в подавляющем числе случаев, АЭ, поскольку из-за
накачки, неравномерного нагрева и охлаждения, дефектов материала
оптические неоднородности в нем выражены весьма ярко.
Наиболее удобным методом расчета резонатора, содержащего не-
негауссовые оптические элементы, является метод интегрального урав-
уравнения. Он получил в таких задачах широкое распространение в силу
своей универсальности, возможности использования разнообразных
численных методов. В соответствии с этим, в настоящем параграфе
построим и обсудим интегральное уравнение, описывающее моды ре-
резонатора, содержащего негауссовый оптический элемент.
Будем полагать, что влияние оптических аберраций одного из эле-
элементов резонатора является решающим, т. е. аберрациями остальных
А А'
А2 В2\ и
С2 A2j
Ах Вх
С2 Ах
А А'
Т
Рис. 2.5. Схема линейного несимметричного резонатора с негауссовым оп-
оптическим элементом Т
элементов можно пренебречь. Тем самым мы приходим к модели ре-
резонатора, содержащего лишь один негауссов оптический элемент Т
(рис. 2.5).
Предположим далее, что помимо аберрационного элемента, все
остальные элементы резонатора обладают осевой симметрией. Поэто-
Поэтому построение соответствующего интегрального уравнения проведем
в цилиндрической системе координат.
Пусть действие негауссового элемента Т на проходящее поле опи-
-с
2.3. Интегральное уравнение резонатора 135
сывается умножением поля на функцию:
F = T0-T(r,<p), B.41)
где множитель
'1, г
[О, г
описывает действие ограничивающей круглой апертуры радиуса Ro,
а функция Т(г,ср) искажения поля, как амплитудные, так и фазо-
фазовые, вызванные оптическими неоднородностями аберрационного эле-
элемента Г.
Введем две системы цилиндрических координат (ri,(/?i) и {г 2,^2)
с общей осью z, совпадающей с геометрической осью резонато-
резонатора. Плоскость (ri,(^i) совпадает с плоскостью АА (рис. 2.5), плос-
плоскость (г2,^2) ~~ с плоскостью А!А!. Пусть распределение амплиту-
амплитуды р, /-ой моды резонатора в плоскости АА описывается функцией
upi(ri,cpi). После прохождения аберрационного элемента Т, в соот-
соответствии с B.41), имеем u'pl = F • uv\.
Изменение амплитуды моды при обходе правого плеча резонатора
описывается формулой B.17), в которой в качестве элементов луче-
лучевой матрицы следует взять элементы лучевой матрицы обхода пра-
правого плеча резонатора (рис. 2.5). Поскольку при обходе плеча имеем
оптическую систему симметричную относительно концевого зеркала,
диагональные элементы матрицы обхода должны быть равны, т. е.
D\ = A\. С учетом этого получаем выражение для поля в плоско-
плоскости А'А':
2тг оо
/ rl
О О
х ехр{-^- [Агг1 + Ахт\ - 2пг2 cosfai - y>2)]}. B.42)
В соответствии с предположением, что функция upi описывает рас-
распределение амплитуды моды резонатора, после обхода левого плеча
имеем u'lpl = icpiupi. С другой стороны, используя выражение, вполне
аналогичное B.42), легко выразить функцию и[р1 через распределе-
распределение поля в плоскости А'А' и\р\. Поэтому получаем уравнение
2тг сю
J r2 dr2 F{r2^2
0 0
-^-[A2r^ + A2r\ -2rir2cos((^i -<p2)]}, B.43)
которое совместно с выражением B.42) образует систему интеграль-
интегральных уравнений, определяющей, как структуру поперечной моды ре-
136 Гл. 2. Метод интегрального уравнения
зонатора р, 1-го порядка, так и соответствующее собственное значение
данной моды кР1.
В случае, когда функция F представлена в виде B.41) система
уравнений B.42)—B.43) может быть приведена к более удобному виду
путем перехода к безразмерным переменным t\^2 = т\^2/Ro'-
2тг 1
ulpl(t2^2) = ~iNie2ikLl Jd^ JdhhFitu^Uptih,^) x
о о
х exp{i7r7Vi[Aiti + Axt\ - 2txt2 cos(y?i - ^2)]}, B.44a)
2тг 1
,<Pi) = -iN2e2ikL2 I dif2 / d
о о
x ex-p{mN2[A2tl + A2t\ - 2txt2 cos(y?i - y?2)]}. B.446)
Параметры
JVi,2 = т^ B-45)
называют числами Френеля резонатора. L\ и L2 — геометрическая
длина правого и левого плеча резонатора.
При сколько-нибудь общем виде функции F(t,ip) решение этой си-
системы возможно лишь численными методами с помощью ЭВМ. При
этом требуются, как правило, значительные затраты машинного вре-
времени даже на мощных ЭВМ. В случае, когда неоднородности абер-
аберрационного элемента носят осесимметричный характер и функция
пропускания не зависит от азимутального угла, систему уравнений
B.44а), B.446) можно существенно упростить. Для этого будем ис-
искать решение в виде
Такое представление функций uv\ и u\v\ позволяет проинтегрировать
уравнения B.44а) и B.446) по углу и тем самым свести систему к
системе двух одномерных интегральных уравнений. Подставляя B.46)
в B.44а) и B.446) и, используя интегральное представление функции
Бесселя B.26а), преобразуем нашу систему к виду
Qlpl(t2)=27rN1(-i)l+1e2ikLlx
1
1
X
о
2.3. Интегральное уравнение резонатора 137
1
х fdt2t2T(t2)Qlpi(t2)JiB7rN2t1t2)exp[i7rN2A2(t21+t22)]. B.476)
о
Данная система, в силу одномерности интегралов, требует для сво-
своего численного решения существенно меньше машинного времени, чем
решение системы B.44). Объем расчетов можно также существенно
сократить, используя так называемые свойства подобия резонаторов.
Для этого отметим, что резонаторы, имеющие различные оптические
схемы, но характеризуемые одинаковым набором параметров (Ai, A2,
Ni, N2), описываются одной и той же системой уравнений, и сле-
следовательно, имеют одинаковые потери и структуру поперечных мод.
Поэтому система интегральных уравнений B.47а), B.476) описывает
фактически целое семейство резонаторов с одинаковым набором вели-
величин (Ai, A2, JVi, N2). Резонаторы, принадлежащие одному семейству,
называют подобными резонаторами.
В случае, когда функция Т — действительная, можно усмотреть
еще одно свойство подобия. При переходе к системе уравнений, ком-
комплексно сопряженных с уравнениями B.47а) и B.476), легко увидеть,
что полученные уравнения описывают моды резонатора, в котором
коэффициенты А\ и А2 заменены на —А\ и —А2. При этом попереч-
поперечная структура мод и соответствующие собственные значения нового
резонатора имеют вид:
QPi = Qli, Qipi = QlPi,
Kpi = -к*г exp[4zfe(Li + L2)],
где Qpi, Qipi и Kpi — моды и собственные числа резонатора с коэф-
коэффициентами А\ и А2, а звездочка означает знак комплексного сопря-
сопряжения.
Соотношения B.48), в частности, показывают, что в резонаторах,
характеризуемых наборами параметров (Ai, A2j JVi, N2) и (—Ai, —A2j
TVi, N2) потери мод одинаковы, поскольку потери моды определяются
модулем соответствующего собственного числа, a \>cpi\ = \>cpi\.
Наряду с этими свойствами подобия, можно указать еще целый
ряд менее очевидных связей [22, 39], которые позволяют иногда суще-
существенно упростить задачу расчета резонатора. Не останавливаясь на
них, переедем к рассмотрению наиболее важных частных случаев, в
которых возможно дальнейшее упрощение системы уравнений.
Когда лучевые матрицы обхода правого и левого плечей резонато-
резонатора одинаковы, имеем А\ — А2 — А и N\ — N2 = N. В этом случае ядра
интегральных уравнений B.47а) и B.476) становятся тождественны-
тождественными с точностью до несущественного, с точки зрения нашего анали-
анализа, экспоненциального множителя expBi&Li52) (в дальнейшем будем
138 Гл. 2. Метод интегрального уравнения
полагать для простоты, что L\ = L2 = Lq). Поэтому будем искать
решение системы в виде
Qipi = ipiQpi-
Подставляя его в уравнения B.47а) и B.476), проводя необходимые
преобразования, легко показать, что оно удовлетворяет системе при
условии
i
fdt1t1T(t1)Qpi(t1)JiB7rNt1t2)exp[i7rNA(t21+tl)] B.49)
B-50)
Тем самым, в случае симметрии лучевых матриц обхода плечей
резонатора, система уравнений B.47а), B.476) сводится к одному
интегральному уравнению B.49). Собственные числа этого уравне-
уравнения связаны с собственными числами мод резонатора kpi соотноше-
соотношением B.50).
Из уравнения B.49) ясен физический смысл величины 7р/- Ее мо-
модуль определяет потери р, 1-ой моды при обходе одного плеча резона-
резонатора равные 1 — |7р/|2- Из B.50) следует также, что потери моды при
обходе правого и левого плеча резонатора в рассматриваемом случае
одинаковы, а потери за обход резонатора равны 1 — |7р/|4-
Легко показать, что уравнение B.49) при Т = 1 описывает так-
также моды симметричного резонатора, образованного зеркалами рав-
равной конечной апертуры (рис. 2.6). Для этого концевое зеркало с ра-
радиусом кривизны R представим в виде плоского зеркала, вплотную к
которому расположена ограничивающая апертура, размером равным
размеру концевого зеркала, и линзы с фокусным расстоянием / = R
(рис. 26, б). Лучевая матрица
А В
С А
описывает прохождение лучей от одного плоского зеркала до другого
(рис. 2.6, б). Из рис. 2.6 очевидно, что проход резонатора (б) экви-
эквивалентен обходу резонатора (д) и обходу плеча резонатора (в). Но
обход плеча резонатора (в) описывается уравнением B.49). Поэтому
уравнение B.49) при Т = 1 связывает распределение поля на плоских
зеркалах в первоначальной схеме резонатора (б). Величина jpi опре-
определяет потери мод за проход резонатора, обусловленные дифракцией
на концевых зеркалах с конечной апертурой.
Этот же результат можно, естественно, получить и формальным
образом, записав соответствующее интегральное уравнение исходя из
формулы B.17) и проведя необходимые преобразования.
2.3. Интегральное уравнение резонатора
139
А В
С А
А В
С А
С А
С А
Рис. 2.6. Эквивалентность симметричного резонатора с зеркалами конеч-
конечного размера резонатору с внутренней диафрагмой
Рассмотрим еще один важный частный случай, когда одно из плеч
резонатора, например, левое, представляет собой плоское зеркало,
расположенное вплотную к аберрационному элементу Т (рис. 2.7).
Тогда очевидно, что поле Q'pl в плоскости А А, после обхода резона-
резонатора, связано с распределением амплитуды моды в плоскости А'А'
соотношением:
Q'pl = T(t2)Qlpl(t2).
Учитывая также, что должно выполняться условие Q'pl = /3piQpi полу-
140
Гл. 2. Метод интегрального уравнения
Q Q'
Рис. 2.7. Плоскосферический резонатор с негауссовым оптическим элемен-
элементом Т
чаем, с помощью выражения B.47а), уравнение, определяющее моды
данного резонатора
B.51)
Собственные значения данного уравнения определяют, в соответствии
с формулами B.22) и B.23), потери мод и резонансные частоты резо-
резонатора.
На этом мы закончим построение интегральных уравнений, опи-
описывающих резонаторы основных типов. Отметим, что хотя все вы-
вычисления мы вели в цилиндрической системе координат, используя
формулу B.7), легко переформулировать все полученные соотноше-
соотношения в декартовой системе координат. Выбор той или иной системы
координат, как уже отмечалось ранее, обусловлен исключительно со-
соображениями удобства и связан со спецификой симметрии, имеющих
место в анализируемом резонаторе.
§ 2.4. Конфокальный резонатор
Как мы убедились в предыдущем параграфе, уравнения, описы-
описывающие моды резонатора, достаточно сложны. Методы их анали-
аналитического решения, как правило, неизвестны. Поэтому при расчете
модовой структуры резонаторов приходится прибегать к численным
методам, использовать ЭВМ. Редким исключением из этого правила
является так называемый конфокальный резонатор, о котором уже
упоминалось в первой главе. В дальнейшем, под конфокальным мы
будем, подразумевать всякий резонатор, который описывается инте-
интегральным уравнением B.49) или B.51) при Т = 1, и в котором диаго-
диагональные элементы лучевой матрицы прохода или обхода резонатора
§2.4- Конфокальный резонатор 141
равны нулю
А = 0. B.52)
Моды такого резонатора описываются известными специальными
функциями, которые, хотя и не представимы в аналитическом виде,
но могут быть представлены в виде достаточно быстро сходящихся
рядов и для которых составлены подробные таблицы.
Знание модовой структуры конфокального резонатора позволяет,
с одной стороны, понять физические особенности поведения мод ре-
резонатора с ограничивающей апертурой, а с другой, дает возможность
провести тестирование программ численного решения уравнений в
случае резонатора общего вида, что очень важно с практической точ-
точки зрения. Кроме того, существует целый ряд приближенных методов
расчета резонаторов общего вида, базирующихся на знании модовой
структуры конфокального резонатора [40]. Эти обстоятельства опре-
определяют исключительно важную роль изучения конфокального резо-
резонатора в теории лазерных резонаторов. Поэтому уделим данному ти-
типу резонатора отдельный параграф и проведем анализ его модовой
структуры достаточно подробно. При этом, тем не менее, постараем-
постараемся избежать громоздких математических выкладок и доказательств,
отсылая интересующихся читателей к соответствующим работам по
математике [41, 42].
Прежде, чем перейти к анализу соответствующего интегрально-
интегрального уравнения, описывающего моды конфокального резонатора, при-
приведем несколько примеров конфокальных резонаторов простейшего
вида. Рассмотрим двухзеркальный симметричный резонатор, изобра-
изображенный на рис. 2.6. Он образован двумя одинаковыми сферическими
зеркалами с радиусом кривизны R. Лучевая матрица прохода такого
резонатора имеет вид
'А В\_( 1 - L/R L \
А) ~ \-2/R + L/R2 I - L/R) '
Условие B.52) выполняется при R = L, т. е. в том случае, если каж-
каждое сферическое зеркало резонатора расположено в центре кривизны
другого. Это простейший пример конфокального резонатора, кото-
который уже приводился в первой главе. Решение интегрального урав-
уравнения B.49) описывает распределение амплитуды моды на концевых
зеркалах резонатора.
Несимметричный резонатор, в котором ограничивающая апертура
расположена вблизи одного из зеркал, например, плоского, как на
рис. 2.7, может быть отнесен к конфокальному при условии, что R =
= 2L. Действительно, поскольку лучевая матрица обхода резонатора
в этом случае имеет вид
в\ - Л - 2LIR 2L - 2l2/r\
А) - \ -2/R 1 - 2L/R ) '
при R — 2L условие B.52) выполнено.
142 Гл. 2. Метод интегрального уравнения
Ранее отмечалось, что в зависимости от формы зеркал целесооб-
целесообразно применять либо декартову, либо цилиндрическую систему ко-
координат. Ограничимся подробным анализом случая, наиболее часто
встречающегося на практике, когда апертура, ограничивающая из-
излучение в резонаторе, имеет круглую форму и удобнее пользоваться
цилиндрической системой координат. Случай, когда апертура имеет
прямоугольную форму, коротко обсудим в конце параграфа.
Уравнение, описывающее моды конфокального резонатора с огра-
ограничивающей апертурой круглой формы, получим из B.49) или B.51)
положив Т = 1 и А = 0:
1
ipiQAh) = 2TrN(-i)l+1e2ikL° fdh hQpiMJtQirNhti). B.53)
О
По-видимому, уместно напомнить, что поле на зеркале (или огра-
ограничивающей апертуре) описывается функцией B.46)
/cos lip
Преобразуем уравнение B.53) к симметричному виду. Для этого
достаточно перейти к новой неизвестной функции
*l>Pi(t) = ViQpl(t), B.54)
для которой получаем уравнение
1
B.55)
И с = 2ttN. B.57)
Уравнение B.55) является уравнением с действительным симмет-
симметричным ядром, которое достаточно хорошо изучено в математике.
В частности, известно, что подобные интегральные уравнения име-
имеют систему собственных функций и собственных значений, которые
образуют бесконечное счетное множество. Все собственные значения
действительного симметричного ядра действительны. Собственные
функции взаимно ортогональны
1
B.58)
Интересной особенностью функций ippi является свойство их двойной
ортогональности, а именно ортогональность также на бесконечном ин-
§2-4- Конфокальный резонатор 143
тервале [42]:
U{° Р1фР B.58а)
Pi —P-
о v ' r'
Кроме того, система функций ippi обладает свойством полноты в клас-
классе функций с интегрируемым квадратом модуля в интервале @,1).
Это означает, что всякая такая функция может быть разложена в
абсолютно и равномерно сходящийся ряд по собственным функци-
функциям уравнения B.55). Заметим, что все сформулированные свойства
справедливы и для функций upi, так как функции cos lip и sin^ орто-
ортогональны на интервале @, 2тг) и образуют полную систему функций.
После этих общих предварительных замечаний о свойствах реше-
решений уравнения B.55), перейдем к их более тщательному анализу. Для
этого построим некоторое дифференциальное уравнение, решениями
которого являлись бы функции г/jpi. Легко показать, что собствен-
собственные функции интегрального оператора Lu, определяемого уравне-
уравнением B.55) Lu(ijjpi) = cfpi^pi будут являться собственными функциями
некоторого дифференциального оператора Lq, в том и только в том
случае, если эти операторы коммутируют, т. е.
LuLd ~ LdLu = 0. B.59)
Действительно, если Lq(iJ)pi) = cfpiippi, то равенство B.59) очевидно. С
другой стороны, из условия Lu(ippi) = (Jpi^pi и соотношения B.59) сле-
следует, что Ьи(Ьд(фр1)) = ар1Ьд(фр1) и, следовательно, функция Ld(^pi)
пропорциональна собственной функции оператора ippi, т.е.
Ldi^pi) — &pi^pi- B.60)
Таким образом, для того, чтобы построить дифференциальное
уравнение B.60) следует найти дифференциальный оператор Lg, ком-
коммутирующий с Lu. Можно показать [42], что таким оператором яв-
является
и, следовательно, для нахождения собственных функций уравнения
B.55) следует решить дифференциальное уравнение
A - х») %L - 2* ^ + [У^- - cV - Цфр1 = 0. B.61)
При значении параметра I = 1/2 уравнение B.61) переходит в извест-
известное уравнение [41], решением которого являются специальные функ-
функции, называемые вытянутыми волновыми сфероидальными функциями
нулевого порядка. В связи с этим, функции, являющиеся ограничен-
ограниченным решением уравнения B.61), при произвольном /, принято назы-
называть обобщенными вытянутыми сфероидальными функциями. Они
весьма подробно исследованы [42-46 и др.].
144
Гл. 2. Метод интегрального уравнения
В работах [42, 46] построено решение уравнения B.61) в виде рав-
равномерно сходящихся рядов. Мы не будем их приводить в силу их гро-
громоздкости. Отметим лишь, что именно с их помощью проводятся вы-
вычисления на ЭВМ обобщенных вытянутых сфероидальных функций.
В книге [42] приведены подробные таблицы значений этих функций
в широком интервале значений аргумента и индексов. Для того, что-
чтобы представить характер их поведения при изменении аргумента, на
рис. 2.8 представлены зависимости ippi/i/i для некоторых значений
1,0
0,8
0,6
0,4
0,2
0
-0,2
-0,4
-0,6
\
\
\
V
\
\
\
\
Qi
\
\
\
о (С
0,5
\
\
\
о (С
у
\
\
\
\
_ р
V
\
V
NJ
>)
\
/
N
1,0
/
/
= 2
\
/
)
/
/
/
у
/
1,5
г/До
Рис. 2.8. Распределение амплитуды низших мод на зеркале конфокального
резонатора
индексов. Они показывают поперечное распределение амплитуды мо-
моды конфокального резонатора соответствующего порядка в плоскости
ограничивающей апертуры или на концевом зеркале. Подчеркнем, что
значение t = 1 соответствует краю зеркала и поле при t ^ 1 поглоща-
поглощается экраном и, следовательно, уходит в потери. Легко видеть, что при
увеличении параметра С поле все больше концентрируется вблизи оси
резонатора. Это, очевидно, должно сопровождаться уменьшением ди-
дифракционных потерь мод конфокального резонатора. Строгий расчет
показывает, что это действительно так. В этом мы убедимся чуть поз-
позже. Функции фр1 являются действительными и, поэтому, поверхность
§2-4- Конфокальный резонатор
145
постоянной фазы моды совпадает с поверхностью зеркал, на котором
рассчитывается распределение моды.
С целью облегчения тестирования программ численного решения
резонаторных задач, в табл. 2.1 приведены значения некоторых функ-
функций Qpi.
Таблица 2.1
8
О~
о
С\
2
5
2
5
0,1
1,0
1,0
1,0
1,0
0,2
0,989
0,942
0,923
0,832
0,4
0,935
0,738
0,0626
0,272
0,6
0,850
0,476
0,0168
-0,331
0,8
0,740
0,235
-0,402
-0,692
1,0
0,613
0,0696
-1,019
-0,687
1,2
0,478
-0,00708
-1,626
-0,407
1,4
0,344
-0,0188
-2,151
-0,0649
1,6
0,263
-0,00335
-2,541
0,1436
Чтобы представить характер поведения решения в целом, очень
важно иметь приближенное аналитическое выражение для функций
фР1. Построение таких выражений проводят с помощью асимптоти-
асимптотических рядов, которые переходят в точное решение при стремлении
того или иного параметра к некоторому пределу. Асимптотические
представления функций ippi хорошо разработаны, как при больших,
так и малых значениях параметра с, аргумента ?, индексов р и I. Осо-
Особо важное значение имеют асимптотические представления функции
фР1 при фиксированных индексах ри I, и больших значениях пара-
параметра с. Т. е. такие аналитические выражения, которые стремятся к
точному значению решения уравнения B.61) при с —> оо. Важность
данной области обусловлена тем, что практическую ценность имеют
резонаторы с малыми дифракционными потерями и, следовательно,
с достаточно большой апертурой зеркал и большим значением пара-
параметра с.
Не будем останавливаться на построении приближенных выраже-
выражений для функции фр1 и приведем лишь конечный результат [42]. Вы-
Выпишем главные члены асимптотического представления функции ippi
в соответствующих областях изменения аргумента t:
с-1/4
tl+1/2ecv(l-y)p
,-1/4
-1
¦ izy+p^1
1,
У
^ t < 1 + ,
\. 1 i ^— 1
(a)
F)
(в)
(г)
(д)
B.62)
10 В.П. Быков, О.О. Силичев
146 Гл. 2. Метод интегрального уравнения
где
х = ty/c, у = л/1 — ?2,
р!
h =
и Llp(x) — обобщенный полином Лагерра, Io(x) и Jo (ж) — функции
Бесселя. Из формулы B.62) видно, что вблизи оси, т.е. в области
О ^ t ^ с/4 при больших значениях параметра с моды конфокаль-
конфокального резонатора описываются такими же функциями, как и моды ре-
резонатора с неограниченными зеркалами, образованного гауссовыми
оптическими элементами. На рис. 2.9 представлены результаты срав-
сравнения точного значения функции фР1 и ее приближенного аналитиче-
аналитического представления в виде B.62а). Видно, что при с ^ 5 расхождение
весьма значительно. Этот пример говорит о том, что использование
выражения B.62а) для описания распределения мод конфокального
резонатора при не очень больших значениях чисел Френеля N долж-
должно быть весьма осторожным, так как получаемая при этом ошибка
может быть велика.
Перейдем теперь к обсуждению характера поведения собственных
значений уравнения B.55), определяющих потери мод резонатора и
спектр резонансных частот.
Если рассматривать симметричный конфокальный резонатор, об-
образованный двумя одинаковыми сферическими зеркалами, то потери
р, /-ой моды при проходе резонатора, определяться в виде
где 7р/ — собственное значение уравнения B.53). С учетом B.56) имеем
apl = l-ca2ph B.63)
где (jpi — собственное значение уравнения B.55).
При вычислении значений api обычно исходят из представления
функции фР1 в виде абсолютно сходящегося ряда, который после под-
подстановки в интегральное уравнение B.55), позволяет найти искомое
значение api [42]. На рис. 2.10 приведены результаты соответствую-
соответствующих расчетов. Можно сказать, что при
c>cpi = 2 + 2,7Bp + Z + l) B.64)
потери мод с индексами 2pi + l\ <2р + 1 незначительны. Потери мод
более высокого порядка при этом значительны и можно утверждать,
что они не принимают участие в процессе генерации. Таким образом,
§2-4- Конфокальный резонатор
147
1,0
0,8
0,6
0,4
0,2
0
-0,2
-0,4
-0,6
-0,8
1,0
0,8
0,6
0,4
0,2
0,2
\ V,
w
\
с=10
с = 5
\
\
\\0,6
Л
0,8
л
А
V
/
4 «*- — -*
-г/Ло
^>
V
\
X
л
\
с=1(?
X
с = 2-
\
\
х
X
X
X
\
чс = 5
Х»Х
r/Ro
0 0,2 0,4 0,6 0,8 1,0
Рис. 2.9. Распределение амплитуды низших мод Qoo (а) и Qw (б) на зер-
зеркале конфокального резонатора (штриховая линия) и распределение, опи-
описываемое формулой B.62а) (сплошная линия). При с = 10 (а) обе кривые
совпадают
10*
148
Гл. 2. Метод интегрального уравнения
Таблица 2.2
с
Too
ТО2!
7ю
с
Too
ТО2!
7ю
0,5
0,060585
0,00094983
-
4,0
0,97495
0,78474
0,26743
1,0
0,22111
0,013986
0,00010829
5,0
0,99534
0,93672
0,57877
2,0
0,
0,
62963
16123
0,0067214
6,0
-
0,98534
0,83061
3,0
0,88705
-
0,066745
7,0
-
-
0,94974
8,0
-
-
0,98783
условие B.64) позволяет оценить максимальный порядок моды, участ-
участвующей в генерации при заданном значении числа Френеля N = с/2тг.
Для удобства тестирования программ численного анализа резона-
резонатора в табл. 2.2 приведены значения собственных чисел уравнения
B.53) jpi для ряда значений с.
0,8
0,6
0,4
0,2
0
1 Щ
V 0/
/
jj.
//
1/
о/
III
'0,
Г
11 1
1
ч/
/
L
B 2
1
У
Ч
Т
Ц
7
0
10 12
14
Рис. 2.10. Зависимость величины 1 — api = ca^ от числа Френеля конфо-
конфокального резонатора с = 2ttN
При построении асимптотических выражений для собственных чи-
чисел при больших значениях параметра с и фиксированных р и /, обыч-
обычно используют непосредственно уравнение B.55), которое сокращенно
можно переписать в виде:
B.65)
§2.4- Конфокальный резонатор 149
Дифференцируя его по с, получаем
1 1
^1^2^ Ф dt\ -\- I k — dt\. B.66)
о о
С другой стороны, дифференцируя B.65) по ?2, имеем
1
дф _ с
о
после чего формулу B.66) можно переписать следующим образом
1
— I 4- &Ф. -tl д^ [ д^ (jf
дс дс с dt2 J дс
о
Умножим обе части последнего выражения на ^(^2), проинтегрируем
по ^2 и используем B.65):
Интегрируя первое слагаемое в правой части по частям, используя,
условие нормировки B.58) и учитывая, что ippi@) = 0 (см. B.54)),
получим дифференциальное уравнение
которое является основным при получении приближенных выраже-
выражений для аР1 в целом ряде работ по теории резонаторов [42]. В част-
частности, используя асимптотическое представление функции фР1 B.62в)
при t = 1, из формулы B.67) легко получить приближенное выраже-
выражение для
из которого, используя B.63), получаем формулу для дифракционных
потерь /, р-ой моды конфокального резонатора
4c)J •
B-69)
На рис. 2.11 приведены точные значения величин api, рассчи-
рассчитанные численно на ЭВМ, и приближенные, полученные с помощью
B.69). Видно, что разница в значениях весьма велика. Это весьма
характерная ситуация в теории резонаторов. Обычно использование
приближенных методов позволяет получать распределение поля с
150
Гл. 2. Метод интегрального уравнения
60
40
20
10
6
4
2
1
0,6
0,4
0,2
0,1
0,06
0,04
0,02
0,01
\
\
р = &
1 = 0
X,
\
\
\°
\
\
?\
°
\
\
\
V
0\.
•
V
\
\
\
л
>
V
\°
\
\
V
\
\
V
\
\°
\
\
\
V
\
\
\
0 0,2 0,4 0,6 0,8 1,0 1,2
С/2тг
Рис. 2.11. Зависимость потерь первых низших мод конфокального резона-
резонатора с круглыми зеркалами от числа Френеля N = с/2тг (сплошные кри-
кривые). Кружком отмечены результаты, полученные из приближенной фор-
формулы B.69), точками — по формуле B.70)
достаточной точностью, в то время, как ошибка в определении потерь
может быть значительной. Объясняется это тем, что потери мод, при-
принимающих участие в генерации, невелики. Они непосредственно свя-
связаны со структурой поля на границе апертуры (см., например, уравне-
уравнение B.67)). Поскольку в этой области поле мало, то даже небольшая
неточность в вычислении распределения амплитуды моды на аперту-
апертуре в целом может приводить к существенной неточности расчета поля
на границе апертуры и порождать тем самым ошибки в вычислении
потерь. Если же установлено, что данный приближенный метод поз-
позволяет достаточно точно находить потери мод, то можно с большой
степенью уверенности утверждать, что распределение поля этот ме-
метод дает очень точно.
Вернемся к рис. 2.11. Точность приближения B.69) можно суще-
существенно повысить, если ввести эмпирическую коррекцию, проведен-
проведенную на основе сравнения точных значений api с приближенными.
Формула B.69) с учетом коррекции, принимает вид [22]:
2тгDс -
_2с
е
B.70)
§2-4- Конфокальный резонатор 151
В области api < 0,1 она обеспечивает удовлетворительную точность
расчетов для мод не слишком высокого порядка (рис. 2.11).
Спектр резонансных частот резонатора определяется уравнением
B.23). В случае симметричного конфокального резонатора, обра-
образованного двумя сферическими зеркалами, это уравнение, с уче-
учетом B.50) и B.56), принимает вид:
где q — целое число. Поскольку собственные значения ор\ действи-
действительны, то из B.71) непосредственно имеем спектр резонансных ча-
частот в виде
с
где L = 2Lo — общая длина резонатора. Эту формулу можно перепи-
переписать в эквивалентном виде
Такая форма записи позволяет увидеть тождественность данного вы-
выражения, найденного с учетом дифракционных эффектов, с форму-
формулой B.32), описывающей спектр резонатора с гауссовыми элементами.
Для этого достаточно учесть, что при А = 0 параметр в формуле B.31)
/ = —1 и 5 = тг.
На этом закончим исследование модовой структуры конфокально-
конфокального резонатора и перейдем к рассмотрению поперечного распределения
выходного излучения лазера с конфокальным резонатором. Оказыва-
Оказывается, что в случае конфокального резонатора эта задача может быть
также проанализирована аналитически достаточно полно [47].
Будем исходить, для определенности, из схемы плоско-сферическо-
плоско-сферического конфокального резонатора (рис. 2.7). Предположим, что плоское
зеркало является полупрозрачным и служит для вывода излучения
из резонатора. Исследуем дальнопольную картину излучения.
Для этого воспользуемся уравнением B.17). Распределение ампли-
амплитуды р, /-ой моды на расстоянии z от выходного зеркала имеет вид:
2тг Яо
diP
о о
\_fc_
1z
где Api — амплитуда р, 1-ой моды.
Представляя функции vpi и upi в виде B.46), проводя интегриро-
интегрирование по азимутальному углу (§2.2) и переходя в интеграле к безраз-
152 Гл. 2. Метод интегрального уравнения
мерной переменной t = г/До? получим
где
Распределение поля Fp\ будем искать в дальней зоне. Поэтому вве-
введем вместо г\ угловую переменную а = г\/z. Заметим также, что при
больших z ^> Дд/А экспоненциальным членом в подынтегральном вы-
выражении
можно пренебречь. С учетом этого имеем
1
771 / \ л rvihQ / .w_|_^ ikz ikzot /2 / j± ±гл
-Fpl\(^) — -f*-pl v 1 j вв / CLZ i\a?
0
Приводя подынтегральную функцию к виду, аналогичному подынте-
подынтегральному выражению в уравнении B.55) и преобразуя полученное
соотношение с учетом B.54) и B.55), получим:
*pi{OL) = Api——{—г)^е е ' crpiQpi\-p- I, {Z.7S)
где
в° = ik B-74)
и с = 2ttN — параметр Френеля исследуемого резонатора.
Формула B.73) дает дальнопольное распределение излучения р, 1-й
моды конфокального резонатора. Распределение плотности мощности
излучения 1(а) легко найти, учитывая, что I(a) = ko\Fpi\2 B.21). Из
B.73), с учетом B.56), B.57) и B.45), находим
I), B-75)
где В — элемент лучевой матрицы обхода резонатора, его оптическая
длина. Зная асимптотику собственных функций конфокального ре-
резонатора фР1 B.62) и учитывая B.54), с помощью выражения B.75)
легко найти приближенное распределение мощности р, /-ой моды ре-
резонатора в дальнем поле.
Исследуем расходимость излучения р, /-ой моды. Используя B.21),
имеем выражение для мощности излучения сосредоточенной внутри
§2-4- Конфокальный резонатор 153
угла а = во
2тг 60z в0
Рв0 =h d(f! / (iriri|Fp/(n)|2|cos^i|2 = к0тгг2 / da • a\Fpt\2.
0 0 0
Учитывая B.56), B.73), а также условие нормировки B.58), последнее
соотношение можно привести к виду
Рво = koTrRlAl^.
Легко показать, используя B.21), B.46) и B.58), что величина
kO7rR2A2pl
определяет мощность излучения р, 1-ой моды Pq. Поэтому доля мощ-
мощности, сосредоточенная внутри угла во равна
V=^= ll- B-76)
Поскольку дифракционные потери моды otv\ = 1 — 7^/ ? то т\ — 1 — api.
Мода только тогда возбуждается в резонаторе, когда ее потери не
слишком велики и компенсируются усилением в активной среде. По-
Поэтому, обычно, в генерации принимают участие моды, для которых
потери малы av\ С 1 и, следовательно, доля мощности таких мод в
угле #о близка к единице. Поскольку это справедливо для мод любого
порядка, то можно сделать вывод о том, что излучение конфокально-
конфокального резонатора сосредоточено в угле #0, который, с учетом B.45), B.57)
и B.74) равен
#о = Щ. B.77)
Это соотношение позволяет найти расходимость излучения лазера с
конфокальным резонатором, не детализируя модовый состав излуче-
излучения, поскольку она справедлива, как для одномодового излучения,
так и для излучения, состоящего из смеси поперечных мод, если пред-
предположить, что расходимость многомодового пучка определяется рас-
расходимостью моды максимального порядка.
До сих пор мы рассматривали резонаторы с круглой ограничи-
ограничивающей апертурой. Однако столь же подробные сведения о струк-
структуре мод конфокального резонатора можно получить и для случая
прямоугольных апертур. Мы не будем останавливаться на этом слу-
случае подробно, так как для этого пришлось бы практически слово в
слово повторить проведенный анализ. Отметим лишь, что уравнение
для мод конфокального резонатора с прямоугольной апертурой рас-
распадается на систему двух несвязанных интегральных уравнений. Од-
Одно уравнение для функции Fm(x) зависящей только от ж, другое для
функции Fn(y) зависящей от у. Поле на апертуре описывается выра-
выражением
Umn(x,y) = Fm(x) • Fn(y).
154
Гл. 2. Метод интегрального уравнения
Собственные числа резонатора кшп = jmjnj где 7ш и jn — собствен-
собственные числа интегрального уравнения для ж-й и у-й компоненты поля,
соответственно. Потери моды т, n-го порядка
атп = 1 - \lmln\2 = 1 - A - ат)A - ап),
где ат^п = 1 - |7т,п|2-
Приведем ряд выражений, являющихся аналогом формул B.69),
B.70) и B.72) для случая конфокального резонатора с прямоугольной
апертурой
ат = 4^ Л 8mcm+1/2e-2c [l + of 1I,
ml L Vc/J
m = 4^ 1- 8m(c - l,4)m+1/2e-2c,
ml
1
ml
a
Параметр с = 2т:N = 2тга2/А??, где а — размер ограничивающей апер-
апертуры вдоль оси ж, если мы ищем аш, или вдоль оси ?/, если ап.
В заключение покажем, как можно использовать полученные ре-
результаты при анализе конкретных схем. Рассмотрим резонатор твер-
твердотельного лазера (рис. 2.12, а), в котором АЭ цилиндрической
формы с радиусом Rq = 2,5 мм
расположен вблизи плоского вы-
выходного зеркала. В гл. 4, по-
посвященной рассмотрению резо-
резонаторов твердотельных лазеров,
будет показано, что индуциро-
индуцированные под действием накачки
оптические неоднородности в АЭ
могут быть описаны в виде лин-
линзы с оптической силой Р. Таким
образом, схему на рис. 2.12, б
можно рассматривать в качестве
модели исследуемого резонатора.
Для достижения стабильных про-
Рис. 2.12. Конфокальный резонатор странственных характеристик вы-
твердотельного лазера ходного излучения параметры
данной оптической схемы должны быть подобраны таким образом,
чтобы выполнялось соотношение (подробнее об этом в гл. 4):
p-jr = °- B-78)
Резонатор такого типа принадлежит к классу резонаторов с ди-
динамической стабильностью. Кроме того, он является конфокальным.
Для того чтобы убедится в этом, построим лучевую матрицу обхода
2.5. Методы решения интегрального уравнения 155
резонатора с началом на выходном зеркале:
А В\_( А,- В1Р В,
С А) ~ \d - 2Ai + BlP2 Ax - BlP
При выполнении условия B.78) А = 0.
Предположим, что данный резонатор должен обеспечивать рас-
расходимость излучения на уровне 5 мрад. Тогда, пренебрегая возмож-
возможными аберрациями линзы Р, из формулы B.77) следует, что опти-
оптическая длина резонатора В должна быть не менее 0,5 м. При этом
число Френеля N ~ 12, с ~ 75. Из формулы следует, что при таком
значении параметра с реализуется многомодовый режим генерации.
Причем в генерации будут присутствовать моды, порядок которых не
превосходит величины 2р + I < 25.
Для получения одномодового режима, необходимо уменьшить зна-
значение параметра с до величины со — 4,7 B.64). Этого можно достичь
либо удлинением схемы до величины В к, 2ttRq/cq ~ 8,3 м, что весьма
затруднительно с практической точки зрения, либо при разумном раз-
размере резонатора Б^2м уменьшить размер апертуры Rq до величины
R' « лусо\В/2тг ~ 1,5 мм. При этом расходимость излучения соста-
составит #о — 0,75 мрад., потери основной моды, согласно формуле B.70)
q/00 = 0,74%, «01 — 10%, «20 — <^io ~ 40%. Легко найти и остальные
параметры выходного излучения.
На этом закончим рассмотрение свойств конфокального резонато-
резонатора. Отметим лишь, что в процессе анализа конфокального резонатора
были весьма бегло продемонстрированы некоторые математические
приемы, которые часто используются и при анализе резонаторов об-
общего вида. Имеется в виду сведение интегрального уравнения к диф-
дифференциальному, составление и решение соответствующего уравнения
для собственного значения резонатора B.67).
§ 2.5. Методы решения интегрального уравнения
в теории резонаторов
Интегральные уравнения, встречающиеся в теории резонаторов,
относятся к классу линейных однородных уравнений второго ро-
рода. Известны многочисленные методы приближенного решения таких
уравнений [48]. В этом параграфе коротко рассмотрим те из них, кото-
которые наиболее часто применяются при расчетах резонаторов. Причем
не будем ограничиваться лишь формальным изложением сути метода,
но там, где это будет уместно, обсудим также их физический смысл
и наиболее интересные результаты, полученные с их помощью.
Начнем с метода простой итерации. Это наиболее популярный в
теории резонаторов метод решения интегральных уравнений. Суть
156 Гл. 2. Метод интегрального уравнения
метода простой итерации решения уравнения B.18)
щщ = Ь(щ) (г = 0,1, 2,...)
состоит в нахождении последовательности функций
Ф&+1) =L(^(n)), B.79)
являющихся приближением к искомому решению уравнения B.18).
Причем начальное (нулевое) приближение ф^ может быть выбра-
выбрано произвольно, что и делается, если нет каких-либо сведений о ха-
характере искомой функции. Однако, исходя из физической постановки
задачи, такие априорные данные можно определить, что позволяет
удачным выбором начального приближения, ускорить итерационный
процесс, т. е. уменьшить количество приближений в процессе реше-
решения. В качестве приближенного решения принимается функция ф(п)
при достаточно большом п. На практике признаком близости получа-
получаемых приближений к искомой функции является малость величины
разности двух следующих друг за другом итераций:
* У " B.80)
где г — малая величина, определяемая точностью решаемой задачи,
а ф — норма функции ф, соответствующая мощности пучка
= [ Aвфф\
Интегрирование проводится по площади отверстия ограничивающей
апертуры. Потери моды определяются модулем собственного числа
уравнения B.18) \щ\. Приближенное значение \щ\2 находят по фор-
формуле
при достаточно большом п, т. е. при таком п, при котором выполнено
условие B.80).
Из физических соображений очевидно, что использование метода
простой итерации должно приводить к точному решению при п —>¦
—У оо, поскольку он фактически моделирует установление попереч-
поперечной структуры поля в резонаторе по мере обходов волной резонатора.
Действительно, физический смысл соотношения B.79) состоит в том,
что оно связывает распределение поля до ф^ и после ф^п+1) обхо-
обхода резонатора. Поэтому, запуская в резонатор пучок с поперечным
распределением амплитуды ф^\ после первого обхода резонатора по-
получим ф^ = Ь(ф(°^), после второго ф^ = Ь(ф^) и т.д. Поперечная
структура пучка меняется и стремится к одной из поперечных мод
2.5. Методы решения интегрального уравнения 157
резонатора, описываемых собственными функциями оператора L, т. е.
ф(п) —У щ при п —у оо.
Количество шагов, необходимое для получения решения с задан-
заданной точностью, очевидно, должно быть связано с дифракционными
потерями поля. Чем выше потери, тем быстрее устанавливается в ре-
резонаторе модовая структура и тем меньше шагов необходимо сделать
в итерационной процедуре. Это легко видеть из выражения B.20).
Если потери мод велики, велика и разница между потерями сосед-
соседних мод. Следовательно, относительная разность членов ряда B.20)
быстро возрастает с ростом п. При достаточно большом п
В этом случае метод простой итерации эффективен и быстро при-
приводит к решению задачи. Очевидно, что итерационный процесс бу-
будет сходиться к собственной функции с максимальным собственным
значением хт, присутствующей в разложении начального приближе-
приближения B.19). Поскольку коэффициенты щ нумеруются в порядке убы-
убывания величины модуля, то kq максимален и в результате итерацион-
итерационной процедуры получается мода нулевого порядка. Для того, чтобы
получить следующую моду, необходимо так подобрать начальное при-
приближение т/>(°), чтобы «о = 0 и OL\ ф 0. Для получения моды и^ необ-
необходимо, чтобы «о = ol\ — 0, «2 ф 0 и т.д. Понятно, что построение
начальных приближений, не содержащих мод низших порядков, свя-
связано с определенными сложностями. Поэтому метод простой итера-
итерации не эффективен для расчета мод высокого порядка и реально
применяется для нахождения лишь первых двух-трех низших мод.
Таким образом, можно сделать вывод, что применение метода простой
итерации оправдано при расчете низших поперечных мод в случае
не слишком малых потерь, т. е. при сравнительно небольших числах
Френеля.
Весьма важные результаты были получена этим методом в работах
Фокса и Ли [3, 49]. В них были рассчитаны поперечные распределе-
распределения и потери низших поперечных мод симметричного резонатора, об-
образованного двумя сферическими зеркалами ограниченной апертуры.
В случае зеркал круглой формы резонатор описывается уравнением
B.49) при Т = 1. В качестве начального приближения, в случае рас-
расчета основной моды, использовалась функция ф^ = const = С. При
расчете моды первого порядка uv\ = u§\ распределение выбиралось в
виде
(о) ГС, 0 < <р < ж,
V \
ГС,
\-С,
Такое начальное приближение обеспечивало отсутствие примеси ос-
основной моды («о = 0).
158
Гл. 2. Метод интегрального уравнения
1,0
0,8
0,6
0,4
0,2
N = 1
\
л
\
N
М = о
Ni,o
\П,8
Arg(?/Oi) (град.)
20
О
-20
-40
" ¦-
——— Д
М = о
\ 0,5
Хр,^4
1,0\
о
0,2 0,4 0,6 0,7
r/Ro
Рис. 2.13, а. Распределение амплитуды и фазы первых поперечных мод г^оо
(а) и uoi (б) на зеркалах
На рис. 2.13 приведены распределения на зеркалах амплитуды и
фазы низших мод для резонаторов устойчивой конфигурации. В ка-
качестве параметров использовались число Френеля N и параметр g =
= 1 — L/R. Значение g = 0 соответствует конфокальному резонатору,
д — \ — резонатору с плоскими зеркалами. При д ф 0 фаза поля на зер-
зеркале не является постоянной и сложным образом зависит от расстоя-
расстояния от оси резонатора. Это непосредственно связано с зависимостью
потерь от параметра д (рис. 2.14). В конфокальном резонаторе при
фиксированном числе Френеля поверхность постоянной фазы совпа-
совпадает с поверхностью зеркала, потери моды минимальны. Появление
же при д ф 0 искривления фазового фронта вызывает увеличение
амплитуды поля на границе зеркала (рис. 2.13) и, как следствие
этого, увеличение дифракционных потерь. С фактом, что внесение
дифракционных потерь приводит к искривлению фазового фрон-
фронта моды относительно поверхности зеркала, мы уже сталкивались,
при рассмотрении резонатора, образованного гауссовыми оптически-
2.5. Методы решения интегрального уравнения
159
1,0
0,8
0,6
0,4
0,2
0
20
О
-20
-40
|Е/оо|
__>
~J_
7_
/
1
ЛГ = 1
\—
\
\
М = о
N0,8
\
\
Arg(C/Oi) (град.)
-^
М = о
0,5/
\\
\0,8
0,2 0,4 0,6 0,7
Рис. 2.13, б
r/Ro
ми элементами и содержащего гауссовы ограничивающие апертуры.
Зависимость потерь мод «оо и <^oi от числа Френеля Nag приве-
приведена на рис. 2.14. Видно, что потери быстро уменьшаются с ростом N.
Таблица 2.3
иоо
9
7
/5
7
0
8,4
1,84
5,1
2,69
0,2
6,9
1,66
4,3
2,46
0,4
4,9
1,38
2,84
1,91
0,5
4,4
1,34
2,46
1,83
0,6
3,9
1,34
2,18
1,84
0,7
3,5
1,27
1,86
1,81
0,8
2,9
1,16
1,5
1,58
0,85
2,6
1,08
1,34
1,46
0,9
2,3
1,01
1,18
1,35
0,95
2,0
0,86
1,05
1,12
0,99
1,83
0,59
1,02
0,835
Данные зависимости могут быть аппроксимированы функцией ви-
да I50! a = ехр(-/3№),
где параметры /3 и j зависят от g и номера моды, и приведены в
табл. 2.3. Отметим, что потери не зависят от знака параметра д, что
является проявлением свойства подобия, рассмотренного в § 2.3.
160
Гл. 2. Метод интегрального уравнения
100
60
40
20
10
8
6
0,8
0,6
\
V
\
]
\
\
А
01
\
V
X
V
\
\\\
\\
\\
\ \\
\ \
1 1
1
\
Ю,9\0
\ \
\ \
\
97
\
\
S
q\ = l
у
\
N
0,4 0,6 0,8 1,0 2 4 6 810 20
Рис. 2.14, а. Зависимость потерь низших мод резонатора, образованного
сферическими зеркалами ограниченной апертуры, от числа Френеля
При g = 1
аоо = 1 - ехр(-0,183 • TV'323),
«oi = l-exp(-0,5-7V-1'38).
На рис. 2.15 приведены зависимости Arg(x^) для двух низших мод
от числа Френеля. (Без учета набега фаз, связанного с длиной резона-
резонатора, т.е. при Z/Q = 0). При не слишком малом N аргумент собствен-
собственного числа не зависит от N и определяется лишь параметром д. Легко
показать, что значение аргумента на горизонтальном участке соответ-
соответствует формуле B.31) при Lq = 0 и / = д. Этого и следовало ожидать,
так как в резонаторе устойчивой конфигурации, при больших числах
Френеля, т. е. в том случае, когда размер апертуры существенно боль-
больше размера основной моды, можно отвлечься от эффектов, связанных
с дифракцией поля на зеркалах. Гауссовы пучки должны достаточно
точно описывать структуру мод резонатора.
Достоинством метода простой итерации является возможность ре-
решения с его помощью различного рода нелинейных задач, возникаю-
возникающих в теории резонаторов и приводящих к нелинейным интегральным
уравнениям.
В качестве примера задачи такого рода рассмотрим структуру по-
поля в резонаторе с учетом действия усиливающей среды [51]. Исходя
из простейшей модели резонатора, содержащего АЭ, будем считать,
2.5. Методы решения интегрального уравнения
161
а00
100
80
60
40
20
10
8
6
N
\
V
\
1
1
V
\ \\
\\\
\
0 |о,5
\
Д
\
0,8С
\
\
\
\
\
\
\0,9
\
\
7
\
\
1
0,4 0,6 1,0 2 3 4 6 8 10 20
Рис. 2.14, б
N
что усиление излучения происходит в двух бесконечно тонких слоях,
расположенных вблизи концевых зеркал резонатора (рис. 2.16). Для
исследования структуры поля в таком резонаторе можно воспользо-
воспользоваться уравнением B.49), в котором функцию пропускания аберраци-
аберрационного элемента Т следует заменить на функцию, описывающую рас-
распределение стационарного коэффициента усиления в активном слое.
В случае, когда усиление излучения за один проход АЭ не велико,
имеем [51, 52]
ко 1^,1, ^о
Т =
B.81)
где ко — ненасыщенный коэффициент усиления, пропорциональный
мощности накачки лазера, а член в знаменателе a|ixp/|2 описывает эф-
эффекты насыщения активной среды под действием подающего поля.
Видно, что даже в случае равномерного распределения ненасыщен-
ненасыщенного коэффициента усиления (ко = const) в процессе генерации, из-за
эффектов насыщения, усиление в слое становится неравномерным.
Решение нелинейного интегрального уравнения методом простой
итерации аналогично решению линейного уравнения. Разница лишь в
том, что в качестве критерия близости приближения ф^ к решению
берут не условие B.80), а
11 В.П. Быков, О.О. Силичев
162
Гл. 2. Метод интегрального уравнения
o) (град.)
\
UQQ
\
\
\
\
\
80
40
20
10
1
0,10,20,40,61,02 4 61020
Arg(^oo) (град.)
100 "
60
40
20
10
6
4
2
1
0,10,2 0,4 1 2 4 610 2040
ч
\
\
\
\
\
ч
\
\
\
q
0,5
0,8
0,9
0,95
1,0
N
0,5
0,8
0,9
0,95
1,0
N
Рис. 2.15. Зависимость аргумента собственного числа интегрального урав-
уравнения от числа Френеля
поскольку в силу нелинейности уравнения происходит установление
не только относительного распределения амплитуды, но и мощности
пучка. Очевидно, что при этом
щ стремится к величине, рав-
равной по модулю единице.
Решение методом простой
итерации нелинейного уравне-
уравнения B.49) с учетом B.81), для
случая осесимметричных полей
(upi(r^lP) — иро(г)) приводит к
следующим результатам.
Во-первых, поперечное рас-
распределение стационарных струк-
структур в резонаторе с усилением с очень большой точностью совпадает с
поперечными модами пустого резонатора. Этот результат позволяет
использовать решения, полученные для случая пустого резонатора,
при анализе лазерного резонатора с активной средой. Заметим, что
этот факт является проявлением общей закономерности, состоящей
в слабом искажении поперечных мод амплитудными неоднородностя-
ми, в то время, как даже сравнительно слабые, фазовые аберрации
могут приводить к весьма сильным искажениям моды [10].
Рис. 2.16. Схема симметричного ре-
зонатора с бесконечно тонким усили-
вающим слоем
2.5. Методы решения интегрального уравнения
163
Во-вторых, стационарная структура устанавливается не при всех
значениях параметров резонатора. При определенных условиях ите-
итерационный процесс сходится не к стационарному полю, а к решению,
в котором распределение поля на зеркалах периодически меняется
(например, ^(n+2) = ei6^n\ ^(n+3) = eiE>(n+1)). Легко показать, что
такое решение можно представить в виде суммы двух или более по-
поперечных мод, участвующих в генерации одновременно.
Качественно характер изменения поперечной структуры резонато-
резонатора с усилением при изменении параметров схемы, например, при уве-
увеличении числа Френеля, сводятся к следующему (рис. 2.17). Вначале,
-*ген
N
Рис. 2.17. Зависимость мощности генерации и поперечной структуры из-
излучения резонатора с усиливающей средой при изменении числа Френеля
при малых числах JV, потери мод велики, усиления недостаточно для
компенсации дифракционных потерь. В этом случае итерационный
процесс приводит к нулевому решению. Поле в резонаторе неограни-
неограниченно затухает. В области № 2 значений чисел Френеля (рис. 2.17)
реализуется одномодовый характер генерации на низшей поперечной
моде. В этом диапазоне значений N усиления достаточно, чтобы ком-
компенсировать дифракционные потери основной моды, но не хватает для
компенсации потерь первой поперечной моды. В процессе последова-
последовательных итераций B.79) мощность пучка стремится к стационарному
значению РГ. При этом поперечное распределение амплитуды пучка
приближается к распределению основной моды.
В области № 3 (рис. 2.17) стационарные решения уравнения отсут-
отсутствуют. В этой области значений N имеет место биение двух низших
поперечных мод, приводящих к периодической смене распределения
11*
164 Гл. 2. Метод интегрального уравнения
амплитуды на зеркалах. Это происходит в силу разной величины фа-
фазового набега при обходе резонатора у основной и первой поперечной
модами. По мере роста числа Френеля первая мода вытесняет ну-
нулевую, и в области № 4 (рис. 2.17) реализуется опять одномодовый
режим. При дальнейшем росте N картина будет повторяться. Одно-
Одномодовый характер генерации будет сменяться ситуацией, при которой
в генерации участвует одновременно две и более поперечных мод. Об-
Общая закономерность состоит в том, что мода более высокого порядка
вытесняет низшие моды. Это связано с тем, что мода более высокого
порядка имеет больший поперечный размер и, следовательно, более
эффективно использует энергию, запасенную в активной среде.
Естественно, все вышесказанное относится к анализу лишь уста-
установившихся модовых структур. Данная модель резонатора не описы-
описывает динамики формирования как временной, так и пространственной
структуры поля, поскольку формула B.81) справедлива лишь в ста-
стационарном режиме и не описывает динамики изменения коэффициен-
коэффициента усиления в процессе развития импульса генерации. Для описания
пространственно-временной эволюции поля в резонаторе необходимо
более тщательно описывать процессы, происходящие в активной среде
[53, 54]. Не будем более останавливаться на этих вопросах, поскольку
они далеко уходят за рамки темы данного параграфа.
Вернемся к методам решения интегрального уравнения. В случае,
когда число Френеля велико и сходимость простого итерационного
процесса медленная, часто удобно использовать другой приближен-
приближенный метод — метод моментов [48]. В этом методе приближенное ре-
решение интегрального уравнения B.18) ищется в виде линейной комби-
комбинации линейно независимых координатных функций cpi (г = 1,... ,п)
B.82)
k=i
с неопределенными коэффициентами Ск, которые можно вычислить
следующим образом: в оператор щщ — Ь(щ) вместо щ подставляется
функция B.82). Это приводит к выражению:
к=1
Исходя из требования ортогональности функции Р(ф^) ко всем
функциям ipm (m = 1,..., п) в области интегрирования в плоскости
апертуры 5, приходим к условиям
/
G71 =
S
из которых получаем систему п линейных алгебраических уравнений
2.5. Методы решения интегрального уравнения 165
относительно Ск\
^Г,Ск(ъакт-13кгп) = 0, B.83)
к=1
где г г *-
т J mi m J т
S S
Решение данной системы дает значения С&, а, следовательно, и при-
приближенное решение ф^ интегрального уравнения B.18). Нетривиаль-
Нетривиальное решение системы уравнений B.83) возможно лишь при условии,
что детерминант системы равен нулю. Поэтому имеем уравнение для
приближенного значения собственного числа щ в виде
det||^a*m-/?*m|| =0. B.84)
Оценку точности вычислений по методу моментов проводят путем
сравнения полученных приближенных значений ф^п> и f/An+1) B.80).
Отметим, что применение метода моментов равносильно замене
ядра интегрального уравнения K(t2,ti) (см. например, B.49)) вы-
вырожденным ядром Kn(t2,ti), строящимся следующим образом. Пред-
Предполагая ортонормированность системы функций срк, разлагают ядро
K(hjti)j как функцию t^ в ряд Фурье по этой ортонормированной
системе и за Kn(t2,ti) принимают п-ю частичную сумму этого ряда.
Получают п
где
1
Использование метода моментов особенно эффективно в тех случаях,
когда приблизительно известен характер возможных решений. Напри-
Например, если негауссовый оптический элемент, помещенный в резонатор,
не слишком сильно искажает поле, то моды резонатора должны быть
близки к гауссовым. Поэтому удобно в качестве координатных функ-
функций ipk взять гауссовы пучки соответствующего порядка. Очевидно,
что при слабых искажениях поля в негауссовом элементе, поле г-й мо-
моды будет близко к гауссовому пучку cpi. Следовательно, в представле-
представлении B.82) достаточно взять лишь несколько ближайших членов. Это
приводит к системе уравнений B.83) не слишком высокого порядка,
которую нетрудно решить.
Часто бывает, что при правильном выборе системы координатных
функций, достаточно взять п ~ 2-3 [55]. При этом мы получаем фак-
фактически аналитический метод приближенного решения интегрального
уравнения, позволяющий легко исследовать поведение модовой струк-
структуры от того или иного параметра.
166 Гл. 2. Метод интегрального уравнения
Очевидно, сходство метода моментов с методом теории возмуще-
возмущений, который весьма часто используется в теории резонаторов. В тео-
теории возмущений интегральный оператор, описывающий резонатор,
представляется в виде
L = Ьо + V,
где Z/Q — интегральный оператор резонатора, моды которого нам из-
известны, V — малое возмущение оператора Lq, обусловленно действием
новых элементов. Собственные функции оператора L ищутся в виде
Fi = щ + ^ацгЩк-
к
Не останавливаясь на основах метода теории возмущений, подроб-
подробно изложенных во многих руководствах [56], приведем лишь выраже-
выражения, в первом порядке малости, для коэффициентов а^& и собственных
чисел Vi оператора L:
aik ~ -^—, К~щ + Vu, B.85)
Кг — Кк
где
Vik = JdsUiV(uk) B.86)
s
— матричный элемент оператора возмущения. Обратим внимание,
что в подынтегральном выражении матричного элемента отсутствует
знак комплексного сопряжения. Такая форма записи связана с тем,
что, как было показано в работе [40], в случае, когда ядро оператора
I/O симметрично, его собственные функции ортогональны в смысле
B.86), т.е. без знака комплексного сопряжения. В общем случае во-
вопрос о целесообразности использования в формуле B.86) знака ком-
комплексного сопряжения зависит от характера ортогональности функ-
функций щ.
В качестве функций невозмущенного оператора чаще всего ис-
используют либо гауссовы пучки моды резонатора с гауссовыми эле-
элементами, либо собственные функции конфокального резонатора. По-
Последние используются особенно часто, так как позволяют построить
приближенное решение, учитывающее в нулевом порядке дифракци-
дифракционные эффекты [40].
В заключение рассмотрим квадратурный метод решения инте-
интегрального уравнения, обеспечивающий высокую точность вычисле-
вычислений при малых числах Френеля. Суть его состоит в том, что подын-
подынтегральное выражение в уравнении B.18) аппроксимируется тем или
иным образом, полиномом степени Nq [57, 58]. Для этого уравнение
B.18), путем преобразования переменных, приводят к виду, позво-
позволяющему использовать квадратурную формулу того или иного типа.
2.5. Методы решения интегрального уравнения 167
Например, в случае уравнения B.49), переход к новым переменным
#1,2 = 2??52 ~~ 1 позволяет преобразовать его к виду:
+1
= / R(x2,xi)v,i(xi) dxi, B.87)
при котором возможно использование квадратурной формулы Гаус-
Гаусса [57]:
/ R(x2,xi)ui(xi) dx\ ~ 2_j AmR(x2iXm)ui(xm). B.88)
Весовые коэффициенты
и #т — корни полинома Лежандра P/v0 JVo-ro порядка. Таблицы коэф-
коэффициентов Аш и корни хш, при различных значениях Nq , легко найти
в книгах, посвященных методам численного интегрирования [57].
Формула B.88) переходит в точное выражение в случае, если
функция R(x2,xi)ui(xi) — полином степени не выше 2Nq — 1.
Будем искать значение функции щ(хк) = У%к в узлах квадратурной
формулы Xk'-
No
щУгк = ^AmR(xk,xm)Vim (к = 1,2,..., No). B.89)
m=l
Тем самым приходим к системе линейных уравнений относительно
значений V^. Нетривиальное решение этой системы возможно лишь
при условии, что
det \\AmR(xk,xm) - 8ткщ\\ = 0, B.90)
откуда находим собственные значения щ. Из системы уравнений
B.89) получаем Vik- Значение функции Ui(x) в остальных точках апер-
апертуры находим, используя B.87) и B.88), по формуле
х No
i
m=l
Этот метод весьма эффективен в случае, когда подынтегральная
функция уравнения B.18) R{x2,x\)Ui{x\) не слишком сильно осцил-
осциллирует и хорошо аппроксимируется полиномом не очень высокой сте-
степени. Поэтому его целесообразно применять в случаях небольших чи-
чисел Френеля и для нахождения мод низшего порядка. В этой области
168 Гл. 2. Метод интегрального уравнения
он столь эффективен, что при N < 1, позволяет рассчитать достаточ-
достаточно точно потери основной моды уже при Nq = 2 [58]. Таким образом
в этой области значений чисел Френеля мы имеем фактически анали-
аналитический метод расчета резонатора.
Рассмотренные методы, естественно, не исчерпывают всего много-
многообразия способов решения интегральных уравнений, встречающихся
в теории резонаторов. В частности, при решении уравнений в декарто-
декартовых координатах методом итераций, часто удобно преобразовать ин-
интегральный оператор к виду, позволяющему использовать алгоритм
быстрого преобразования Фурье [59]. Это приводит к существенной
экономии времени вычисления на ЭВМ отдельной итерации. При ре-
решении задачи в цилиндрических координатах для этой цели можно
использовать алгоритм преобразования Ханкеля [60].
Поиск собственных чисел матриц большого размера, возникающих
при решении интегрального уравнения методом моментов B.84) или
методом квадратур B.90), возможно использование либо алгоритмов
диагонализации матриц [61], либо метода Прони [62]. Последний поз-
позволяет находить несколько первых, наибольших по абсолютной вели-
величине, собственных значений.
По-видимому, стоит отметить также метод, который, в определен-
определенной степени, объединяет метод итераций и метод Прони и в котором
проводится фурье-анализ преобразования B.79) [63].
Приступая к расчету резонатора, в каждом конкретном случае
следует внимательно изучить особенности задачи и с их учетом вы-
выбрать численный метод решения. Часто удачный выбор метода поз-
позволяет построить решение с минимальным использованием ЭВМ.
Гл а в а 3
СЛОЖНЫЕ ЛАЗЕРНЫЕ РЕЗОНАТОРЫ
§3.1. Связанные лазерные резонаторы
Третья глава посвящена описанию свойств резонаторов, содер-
содержащих различные дополнительные оптические элементы (промежу-
(промежуточные зеркала, дифракционные решетки, эталоны и др.), которые
влияют на частотный спектр резонатора, позволяя, в частности, про-
производить селекцию его продольных мод. Частотный спектр резонато-
резонатора и соответствующего лазера являются их важнейшими характери-
характеристиками. Во многих случаях исследователи стремятся к одномодовой
одночастотной генерации. Одним из возможных путей к этому как
раз и является использование сложных резонаторов.
Сначала излагается теория связанных резонаторов и описываются
методы селекции мод, основанные на этой теории. Приводятся харак-
характеристики наиболее распространенных частотных селекторов. Далее
обсуждаются вопросы согласования поперечных мод отдельных резо-
резонаторов. В заключение даются физические основы теории сложного
перестраиваемого резонатора, используемого в лазерах на красителях
и в лазерах с другими активными средами, обладающими большим
усилением.
Связанные лазерные резонаторы образуются в тех случаях, когда
в резонаторе помимо основных, составляющих его зеркал, имеются
дополнительные или промежуточные поверхности, частично отража-
отражающие и частично пропускающие излучение, так что резонатор распа-
распадается на два или большее число отдельных резонаторов, связанных
друг с другом. Такие дополнитель- ^ ^ ^ л
ные поверхности могут вводиться
в резонатор специально — так ча-
сто поступают для разрежения про-
продольного спектра — но могут воз-
возникать и естественным образом, i i i >
например, в твердотельных лазерах 2 х z
из-за наличия у активных элемен- Рис. 3.1. Волны в сложном резо-
тов отражающих торцов. Во всяком наторе с промежуточным зерка-
случае свойства связанных резона- лом
торов интересны и важны. Мы обсудим эти свойства на простом
примере резонатора, образованного тремя зеркалами (рис. 3.1), пре-
пренебрегая поперечной структурой поля; необходимые уточнения, ка-
касающиеся поперечной структуры будут даны в § 3.
170 Гл. 3. Сложные лазерные резонаторы
Итак, пусть в связанных резонаторах (рис. 3.1) распространяются
волны
Aeikz, Be~ik\ Ceikz, De~ikz,
при этом зависимость от времени всех этих волн предполагается в
виде e~ltut (со = ск). Тогда на первом зеркале имеем условие
RxAeikLl = Be~ikL\ C.1)
где R\— коэффициент отражения первого зеркала. На среднем зер-
зеркале — два условия:
A = RB + TC, D = TB + RC,
где R — коэффициент отражения, Т — коэффициент прозрачности
среднего зеркала. На втором зеркале имеем условие
R2DeikL2 =Ce~ikL2, C.2)
где R2 — коэффициент отражения второго зеркала. Исключая из этих
соотношений амплитуду В в соответствии с C.1) и амплитуду С в
соответствии с C.2), приходим к системе
- DTR2e2ikL* = 0,
- R2Re2ikL*) = 0, [ }
имеющей нетривиальное решение при равном нулю детерминанте. Это
условие приводит к характеристическому уравнению
A - i?ii?e2i*Ll)(l " RiRe2ikL2) - T2R1R2e2ik^L^L^ = 0, C.4)
определяющему резонансные частоты рассматриваемого сложного ре-
резонатора.
Если зеркала поглощают излучение или первое и второе зерка-
зеркала пропускают его наружу, то энергия, запасенная в резонаторе, со
временем уменьшается, т. е. колебания в резонаторе затухают. В этом
случае модули R\ и R2 меньше единицы и корни уравнения C.4) ком-
комплексны. Исследование уравнения C.4) в общем случае достаточно
сложно. Однако с практической точки зрения наиболее интересен слу-
случай, когда потери малы, т. е. модули R\ и R2 близки к единице. Поэто-
Поэтому вначале исследуем свойства сложного резонатора при R\ = R2 =
= — 1. Такой коэффициент отражения соответствует наиболее просто-
простому граничному условию на зеркале — обращению в нуль электриче-
электрического поля на нем. Как уже отмечалось, конкретный вид граничного
условия в лазерном резонаторе не очень существенен, поскольку его
вариация может лишь немного изменить набег фазы волны на зеркале
@ -г- 2тг), в то время как полный набег фазы в резонаторе составляет
A04 -г- 106Jтг. Приведенное выше условие соответствует дополнитель-
дополнительному набегу фазы на зеркале, равному тг.
§3.1. Связанные лазерные резонаторы
171
В отсутствие потерь характеристическое уравнение C.4) прини-
принимает вид
A + Re2ikLl)(l + Re2ikL<2) - T2e2i/e(Li+L2) = 0. C.5)
При бесконечно тонком промежуточном зеркале поля с обеих его сто-
сторон должны быть равны, поэтому для коэффициентов R и Т имеем
условие
Г = 1 + Д. C.6)
Тогда характеристическое уравнение C.5) приводится к виду
е + e + e ^ q
R R
Если теперь R и Т представить в виде
R = - cos ae~ia, Г = г sin ae~ia,
удовлетворяющем соотношению C.6), то характеристическое уравне-
уравнение примет вид
cos а • cosk(Li — L^) — cos[fc(Li + L^) — a]. C.7)
Графики обеих частей этого уравнения показаны на рис. 3.2. Их пере-
пересечения определяют корни характеристического уравнения, т. е. резо-
резонансные частоты системы связанных резонаторов. Такое графическое
cos[?;(Li + L2) — сг]
coscr • cos?;(Li — L2)
II
Рис. 3.2. Графическое решение характеристического уравнения связанных
резонаторов
решение уравнения C.7) очень удобно, получаемая с его помощью
качественная информация обычно более важна, чем точное решение
уравнения C.7).
Исследование свойств связанных резонаторов с помощью уравне-
уравнения C.7) мы начнем со случая отсутствия связи при а = 0 и затем
постепенно будем эту связь вводить. В отсутствие связи исследуемая
система представляет собой просто два отдельных резонатора, каж-
каждый со своими резонансами. При включении даже небольшой связи
все резонансы, строго говоря, становятся общими. Их поля при этом
172
Гл. 3. Сложные лазерные резонаторы
оказываются распределенными по всей системе. Однако, как мы уви-
увидим далее, большая часть резонансов после включения связи в значи-
значительной степени сохраняет свою отнесенность к первому или второму
резонатору.
В отсутствие связи (а = 0) характеристическое уравнение C.7)
приводится к виду
sin kLi • sin kL2 = 0
и имеет решения
C.8)
представляющие собой две системы эквидистантных резонансных ча-
частот, соответственно первого и второго резонаторов. Эти резонансы
можно выделить и на рис. 3.2. Для этого достаточно рассмотреть си-
ситуацию, когда длина L^ — постоянна, а длина L\ увеличивается. То-
Тогда, согласно C.8), резонансные частоты первого резонатора умень-
уменьшаются, а резонансные частоты второго резонатора постоянны. Обе
кривые на рис. 3.2 при увеличении L\ перемещаются влево, причем
при изменении L\ на длину волны Л немного, а кривая //— значитель-
значительно. Нетрудно заметить, что корни, отмеченные цифрой _/, смещаются
заметно влево, а корни, отмеченные цифрой 2, практически остаются
на месте. Ясно, что эти корни относятся, соответственно, к первому и
второму резонаторам.
Чтобы лучше прояснить ситуацию, рассмотрим зависимость кор-
корней характеристического уравнения от величины 1/Li, изображенную
п-1
Рис. 3.3. Зависимость резонансных частот сложного резонатора от 1/Li
на рис. 3.3. В отсутствие связи (а = 0) эти зависимости являются ли-
линейными. При этом графики частот первого резонатора наклонны, а
графики частот второго резонатора горизонтальны. Следовательно,
§3.1. Связанные лазерные резонаторы
173
при изменении \jL\ резонансы первого и второго резонаторов описы-
описывают отдельные, не связанные друг с другом линейные траектории.
Соответственно, корни характеристического уравнения C.7) имеют
определенную «прописку» — точное отнесение к тому или иному ре-
резонатору.
Ситуация качественно меняется, если имеется даже небольшая
связь между резонаторами, т. е. если среднее зеркало становится
немного прозрачным. Траектории корней, отнесенных к разным ре-
резонаторам, несколько деформируются и сливаются (жирные линии
на рис. 3.3). Теперь при увеличении \jL\ каждый резонанс переме-
перемещается по сложной траектории и может быть отнесен к первому или
второму резонатору в зависимости от того, близок ли он к наклонной
или горизонтальной части траектории. В промежуточном положении,
при переходе от одной части траектории к другой резонанс следует
считать принадлежащим к обоим резонаторам. Таким образом, даже
при малой связи между резонаторами с изменением L\ резонансы ме-
меняют свое отнесение к первому или второму резонатору, т. е. как бы
перемещаются из одного резонатора в другой.
Эту картину можно проиллюстрировать также отношением ам-
амплитуд полей в резонаторе, которое можно найти из первого или вто-
второго уравнения системы C.3):
А
Ъ
1 + Re2ikLi 1 - cosae2ikL2-i(T '
Вычисляя отношение квадратов модулей амплитуд, получим
sin a
1 + cos a cosB?;Li — а) + cos2 a'
C.9)
Это отношение принимает три характерных значения:
максимальное
2
D
минимальное
А 2
D min
и среднее
А 2
аах A-COSCrJ
при 2kL\ — а — 2птг,
coscrJ
при 2kL\ — а = —тг + 2птг,
D
mid
~ 1 при kL\ = птг или kL\ = а + птг.
Подставляя эти значения kL\ в характеристическое уравнение
C.7) и вычисляя соответствующие значения &Z/2, нетрудно пока-
показать, что отношение амплитуд C.9) максимально в точке 1 рис. 3.3,
174 Гл. 3. Сложные лазерные резонаторы
минимально в точке 2 и порядка единицы в промежуточном поло-
положении.
Какие практические выводы можно сделать из этого рассмотре-
рассмотрения связанных резонаторов. Первый вывод следует непосредственно
из характеристического уравнения C.7) и его графического решения
на рис. 3.2. Нетрудно видеть, что спектр такого резонатора неэквиди-
неэквидистантен. Действительно, если промежуточного зеркала нет, т. е. а =
= —, то резонансные частоты расположены эквидистантно с интер-
интервалом
2тг
Ак =
+L2
Если же а ф —, то резонансные частоты сдвигаются в разных местах
в разные стороны и спектр становится неэквидистантным.
Эквидистантность спектра важна, например, в режиме синхрони-
синхронизации продольных мод. Поэтому в этом режиме убирают все про-
промежуточные отражения, чтобы не могло образоваться отдельных
резонаторов. Это не обязательно делать путем просветления проме-
промежуточных отражающих поверхностей, достаточно их немного накло-
наклонить по отношению к пучку, так чтобы отраженный свет не попадал
в резонатор. Это, конечно, приведет к дополнительным потерям, но
во многих случаях потери — меньшее зло, чем неэквидистантность
спектра.
Второй практический вывод следует из того обстоятельства, что
при изменении длин отдельных частей резонатора резонансы не со-
сохраняют свою пространственную локализацию, т. е. как бы переме-
перемещаются из одной части резонатора в другую. При этом изменяется
резонансная частота моды и ее относительная амплитуда в месте рас-
расположения активной среды. Изменение частоты является медленным,
как говорят, адиабатическим, и генератор при возбуждении на этой
моде успевает отслеживать это изменение. Изменение же амплитуды
моды в месте расположения активной среды приводит к уменьше-
уменьшению усиления данной моды и в конечном счете к срыву ее генерации.
Заметим, что перемещение моды из одной части резонатора в дру-
другую и изменение ее амплитуды в месте расположения активной среды
происходит при удлинении или укорочении той или иной части резо-
резонатора всего лишь на полдлины волны, т. е. на доли микрона. Такое
изменение длины может быть связано с незаметной для глаза тряс-
тряской зеркала из-за его плохого закрепления. Кроме того, изменение
длины может быть связано с тепловым расширением активного эле-
элемента — лазера — в результате накачки. Таким образом, стабилиза-
стабилизация длин отдельных частей сложного резонатора должна быть очень
тщательной.
Нетрудно дать оценку изменения усиления при изменении длины
того или иного резонатора. Усиление пропорционально квадрату нор-
§3.2. Селекция продольных мод 175
мированной амплитуды поля
[L|A|2 + L|I>|2] L X
Вычислим отношение усилений при максимальном и минимальном
отношениях \D\ /\А\ . Очевидно, что имеем
I' 1 + xZmin
X=Z7
причем
mm A + COS СгJ' mX A — COS (jJ
Практически часто встречается случай, когда коэффициент отраже-
отражения от промежуточного зеркала (торца активного элемента) порядка
нескольких процентов по мощности, положим ~ 4%, по амплитуде
коэффициент отражения ~ 0,2 (а ~ тг/2 — 0,2). Полагая к — 5, что
также часто встречается на практике, получаем отношение усилений
для этих случаев
I' _ 1 + 5A + 2-0,2)
I" ~ 1 + 5A-2-0,2) ~ '
Таким образом, изменение положения того или иного зеркала на
доли микрона может привести к изменению коэффициента усиления
данной моды вдвое, что очень существенно и может привести к ее пол-
полному погасанию. Нестабильность длин отдельных парциальных резо-
резонаторов является одной из причин «пичкового» режима при свобод-
свободной генерации лазера.
§ 3.2. Селекция продольных мод
Сам по себе лазерный открытый резонатор является средством
разрежения спектра по сравнению, например, со спектром равнове-
равновеликого объемного резонатора. Однако поскольку полоса усиления ак-
активных сред, как правило, довольно велика, в эту полосу обычно
попадает большое число мод лазерного резонатора, в частности про-
продольных. Поэтому применяются некоторые средства дополнительно-
дополнительного разрежения спектра лазерных резонаторов. Такое дополнительное
разрежение спектра получило название селекции мод. Все методы се-
селекции мод основаны на увеличении потерь одних мод по сравнению
с другими, рабочими. Селекция продольных мод, отличающихся ча-
частотой, требует применения узкополосных дисперсионных элементов.
Одним из самых простых средств селекции продольного спектра
резонатора является уменьшение по возможности его длины. Дей-
L, см
100
30
10
3
Ai/, МГц
150
500
1500
5000
176 Гл. 3. Сложные лазерные резонаторы
ствительно, расстояние между продольными модами линейного ре-
резонатора равно
Аг/ = й' (ЗЛ0)
где L — его длина. При уменьшении длины L расстояние между про-
продольными модами увеличивается. В табл. 3.1 даны частотные рассто-
расстояния между продольными модами для некоторых длин. При длине
гр, г о 1 резонатора 10 см или меньше расстояние меж-
Таблица 3.1 F ^ ^ ^
ду продольными модами становится больше по-
полосы усиления некоторых газовых лазеров, т. е.
возбуждаться в них будет единственная про-
продольная мода.
Если возможности укорочения резонатора
исчерпаны, то можно прибегнуть к дополни-
дополнительным внешним зеркалам, т. е. к разрежению
спектра с помощью системы связанных резо-
резонаторов. Само по себе добавление дополнительных резонаторов не
приводит к разрежению спектра. Наоборот, спектр становится гуще,
так как к резонансам основного резонатора добавляются резонансы
дополнительных резонаторов. Разрежение спектра или селекция мод
возникает, когда имеются потери на внешних зеркалах, через которые
излучение частично выводится из резонатора. В этом случае допол-
дополнительные резонаторы играют роль устройств, согласующих большую
часть мод основного резонатора со свободным пространством, так что
их потери существенно возрастают; лишь некоторые моды основного
резонатора остаются высоко добротными. Моды дополнительных ре-
резонаторов в той части резонатора, где находится активная среда, име-
имеют малую амплитуду и, как правило, низко добротны, так что факти-
фактически они не возбуждаются.
Исследование системы связанных резонаторов можно провести,
если волны, распространяющиеся в отдельных резонаторах, связать
друг с другом с помощью коэффициентов отражения и пропускания
зеркал, подобно тому, как это делается в §3.1 для трехзеркального
резонатора. Исследуя далее качественно или с помощью ЭВМ ха-
характеристическое уравнение полученной системы, можно найти ре-
резонансные частоты, потери, отношение амплитуд полей в разных ча-
частях резонатора и вообще все характеристики сложного резонатора.
Как правило, система дополнительных зеркал не должна занимать
много места. В этом случае систему дополнительных зеркал можно
рассматривать как единое зеркало с селективными свойствами. Далее
без вывода приводятся зависимости коэффициентов отражения таких
комбинированных зеркал для четырех наиболее интересных случаев
(рис. 3.4).
Коэффициент отражения (по мощности) комбинированного зерка-
зеркала, состоящего из двух бесконечно тонких (рис. 3.4, а) зеркал, разде-
§3.2. Селекция продольных мод
177
Ri
R,T R2 i
\р\2
J
Ri
\R,T R3
i ;t/~~
с
'2L2~
Ж
Щ + l
2tt(L2+L3)
Ri
Ri
&
2(L2+L3)
\R,T
1рГ
Ir f
V~
27r(L2+L3)
2(L2+L3)
—tV-Y
"-— i -- rt2
V
к
2|L2+L3|
Рис. З.4. Четыре типа лазерных селекторов продольных мод
ленных расстоянием Z/2, равен
[\R\ ~
- Т2
A\RR2(R2 - Т2)| sin2 [^ L2
2+4|iU?2|sin2(^—L2 +
где v — частота лазерного излучения, 2ip и 2ср' — аргументы RR2 x
х (R2 — Т2) и RR2. На рис. 3.4, б эта зависимость представлена гра-
графически при R = i?2 — 1; учтено также, что для бесконечно тонких
зеркал без потерь \R\2 + \Т\2 = 1. Как можно видеть, спектр такого
12 В.П. Быков, О.О. Силичев
178 Гл. 3. Сложные лазерные резонаторы
зеркала состоит из узких полос пропускания и относительно широких
полос отражения. Нетрудно убедиться, что ширина отдельной полосы
пропускания в спектре равна
она может быть сделана порядка межмодового расстояния основного
резонатора. Расстояние между полосами пропускания равно
оно может быть сделано порядка полосы усиления активной среды.
Таким образом, характер зависимости коэффициента отражения ком-
комбинированного зеркала от частоты таков, что резонатор больше под-
подходит для подавления отдельных мод, чем для выделения в генерации
одной моды.
На рис. 3.4, в показана другая система, применяемая на практи-
практике, это так называемый резонатор Фокса-Смита. Система зеркал на
правом конце резонатора, рассматриваемая как единое зеркало, имеет
коэффициент отражения (по мощности)
- \R\2R2RsJ + 4|Я|2Я2Я3 sin2 \^- (L
где 2ср — аргумент R2R2R%. Эта зависимость показана на рис. 3.4, г
при R\ = R2 = 1 и R ~ 1. Спектр такого комбинированного зеркала
состоит из полос отражения шириной
д„=
2tt(L2 + L3)
при расстоянии между ними, равном
Л с
0
При \R\2, достаточно близком к единице, ширина полосы отражения
может быть сделана порядка межмодового расстояния для основного
резонатора. Если при этом расстояние между полосами порядка по-
полосы усиления активной среды, то в резонаторе будет возбуждаться
лишь одна продольная мода.
Аналогичными свойствами обладает Т-образный резонатор (см.
рис. 3.4, д). Коэффициент отражения (по мощности) комбинирован-
комбинированного зеркала, составленного из трех зеркал на его правом конце, сле-
следующим образом зависит от частоты:
sin2 [^ (L2 + L3)
§3.3. Согласование связанных резонаторов 179
где 2ср — аргумент T2i?2^3- На рис. 3.4, е эта зависимость показана
при условии \R2\ = |Дз| = 1 и \Т\ ~ 1. Ширина полос отражения в
этом случае равна
2
2tt(L2
а расстояние между ними
Несколько иные свойства имеет резонатор Майкельсона (рис. 3.4,
о/с), отличающийся от резонатора Фокса—Смита только поворотом
промежуточного зеркала на 90%. Коэффициент отражения (по мощ-
мощности) его комбинированного зеркала равен
И2 = (I№| + |Т2Я3|J - 4|Я2Т2Я2Я3| sin2 [^ (L2 - L3) + ip],
где 2(р — аргумент Я2Т*2Я2Щ. На рис. 3.4, з эта зависимость показана
при условии R2 = R3 = 1 и |Я|2 = |Г|2 = 1/2.
Все эти резонаторы подробно исследованы как теоретически, так и
экспериментально. В частности, резонаторы Фокса-Смита нашли эф-
эффективное применение в мощных ионных лазерах, где они позволили
осуществить генерацию на единственной продольной моде. Предло-
Предложены также различные обобщения таких резонаторов, в частности,
подобные схемы предложены для кольцевых резонаторов.
Во всех рассмотренных схемах обычно используются сферические
зеркала, и поэтому моды резонаторов имеют определенную попереч-
поперечную структуру (см. гл. 1). Применение изложенных результатов воз-
возможно только если поперечные моды отдельных частей резонатора
взаимно согласованы. Такое согласование и его условия рассмотрены
в §3.3.
§ 3.3. Согласование связанных резонаторов
Посмотрим теперь, что дает учет поперечной структуры полей в
связанных резонаторах. Как увидим, при этом оказывается важным
представление о согласованных резонаторах, к которым, строго гово-
говоря, только и применимы результаты, изложенные в §3.1 и §3.2.
Связанные резонаторы (рис. 3.5) являются согласованными, ес-
если поперечные распределения мод отдельных резонаторов и радиусы
кривизны их волновых фронтов совпадают по обе стороны от свя-
связывающего эти резонаторы зеркала. Если это условие согласования
выполнено, то пучок, являющийся модой, скажем, правого резонато-
резонатора и проходящий через среднее зеркало, попадает точно в такую же
моду левого резонатора. Аналогично, мода левого резонатора, прохо-
проходя через среднее зеркало, попадает точно в моду правого резонатора.
12*
180
Гл. 3. Сложные лазерные резонаторы
I Ri+2 *
R
Ri+2,
Рис. 3.5. Согласование поперечных распределений полей в связанных ре-
резонаторах
Никаких новых мод в этом случае не возникает. Если резонаторов не
два, а больше, то сформулированное условие согласованности должно
выполняться на каждом из промежуточных зеркал.
Если условие согласования не выполнено, то мода одного из свя-
связанных резонаторов, проходя через среднее зеркало, порождает не
одну, а несколько мод второго резонатора, среди которых могут быть
и высшие моды, обладающие большими потерями. Эти новые моды,
распространяясь в резонаторе, будут при каждом отражении от сред-
среднего зеркала порождать новые серии мод, все более широкие, под-
подходящие к краям зеркал или активных элементов и обладающие в
связи с этим большими потерями. Короче говоря, несогласованность
связанных резонаторов ведет к увеличению их потерь.
Выясним теперь, какие требования к параметрам резонатора сле-
следуют из условия согласования. Очевидно, условие согласования резо-
резонаторов будет выполнено, если комплексные параметры мод обоих ре-
резонаторов вблизи среднего зеркала будут равны. Кроме того, так как
радиусы кривизны волновых фронтов мод на зеркалах равны радиу-
радиусам кривизны зеркал, то достаточно потребовать, чтобы в связанных
резонаторах на среднем зеркале были равны величины
qt
C.11)
определяющие поперечные размеры мод, g/, qr — комплексные пара-
параметры мод левого и правого резонаторов вблизи рассматриваемого
зеркала.
Если известна А??С1)-матрица резонатора, то 1/q определяется
соотношением
1 D-A ^ yi-Q4 + ?>J/4
q = ~2B~ ± l В ' (ЗЛ2)
Для рассматриваемых резонаторов матрицы ABCD имеют вид
1 + LqPq LqB -
¦ О TDD 1 i Г D О
)Til" boioil 1 + bgio ~ ^
§3.3. Согласование связанных резонаторов 181
y _р2_ LlPlp2 х + 2L.P, - LXP2 - L\PXP2)
где
Р=|' (ЗЛ4)
и учтено, что радиус кривизны зеркала положителен, если центр его
кривизны лежит на оси z, слева от него самого.
Из C.11) с учетом C.12), C.13) и C.14) получаем
(Li - R2 + Ri)(Ri + Lx) = (Lq + До- Ri)(L0- Я1)
(L1-R2)L1 (Lo + Ro)Lo
или после упрощений
R2-Ri- 2Li = R1-Ro- 2L0 ( ,
L1(R2-L1) Lo(Ro + Lo) ' l ' }
Отсюда находим, что при заданных Rq, Ri, Lq, Li для согласования
резонаторов необходимо, чтобы радиус кривизны второго зеркала был
равен
р г ,L0(Lq + Rq)(Lq + Ri)
П2=Ь1\ —-.
Lo(Lo + Яо) + LiBLo + Яо — Hi)
Если среднее зеркало плоское, то резонатор согласован при
C.15)
C.17)
в этом случае левый резонатор устойчив, если Rq < 0 и \Rq\ >
Обозначая Rq = —До? соотношение C.17) представим в виде
— bi H
который является вариантом соотношения A.14), что, конечно, впол-
вполне естественно.
Если связанных резонаторов несколько и они последовательно рас-
расположены на оси z, то на основе C.16) можно написать рекуррентное
соотношение
о _г , ?г(Ьг + Дг)(Ьг + Дг+1) { ,
Ki+2 - bi+i + (ОТ МП П V [ОЛЬ)
которому все зеркала системы должны удовлетворять.
Возможна другая постановка задачи, а именно, может быть задан
радиус кривизны R^ и требуется найти расстояние L\, на котором зер-
зеркало нужно расположить, чтобы образовавшийся сложный резонатор
был согласованным. Тогда из C.15) получаем
L — - R + Lq(Lq + Яр) _^
2 R\ — Rq — 2Lq
7? У2
\ / Т ^9 ~1 ^ ^ ^Т г
4 2 Я1 - Яо - 2L0 (Ri -Ro- 2L0J :
182 Гл. 3. Сложные, лазерные резонаторы
при большем числе резонаторов эту формулу легко превратить в ре-
рекуррентную, подобно C.18).
Аналогичные формулы согласования имеют место для резонато-
резонаторов Фокса-Смита, Майкельсона и Т-образного
где
9i = 1- -K-iVi = Li/Lu
Hi
при этом зеркало, наклоненное под 45% к пучку, считается плоским
и перетяжка моды расположена на нем.
Важную роль согласование резонаторов играет в твердотельных
лазерах с выносными зеркалами. Из-за отражений пучков от торцов
активного элемента образуется три отдельных резонатора. Показа-
Показатель преломления активного элемента из-за разогрева накачкой зави-
зависит от радиуса
п = щA — or)
и моды, образующиеся в активном элементе, не зависят от продольной
координаты. Внешнее зеркало образует резонатор, согласованный с
активным элементом, при условии
L(R-L)(no6J = l, C.19)
где R — радиус зеркала и L — расстояние его от торца активного
элемента (рис. 3.6).
В работе [72] была исследована зависимость мощности генерации
лазера на алюмо-иттериевом гранате в зависимости от параметра со-
согласования S = L(R - L)(no?J,
который в согласованном режи-
--> ме равен единице. Основные ре-
результаты эксперимента показаны
^^ и Т на рис. 3.7. Все три кривые на
Рис. 3.6. Согласование частей ре- этом рисунке сняты при одной и
зонатора с неоднородным актив- той же мощности накачки. Кри-
ным элементом вая ]_ _ ПрИ просветленных тор-
торцах, кривая 2, когда на торцах нет покрытий (коэффициент отра-
отражения ~ 7,6%) и кривая 3, когда на торцы нанесены отражающие
покрытия (коэффициент отражения ~ 20%). Как видим, согласование
существенно влияет на выходную мощность генератора. В пределах
ошибок измерений максимум мощности приходится на согласованный
режим. Кривые 2 и 3 близки друг к другу, на этом основании можно
думать, что уже при отражении, составляющем несколько процентов,
согласование резонатора становится существенным. Отметим, что при
условии C.19) согласованными оказываются одновременно все попе-
поперечные моды резонатора.
§3-4- Резонаторы с дисперсионными элементами
183
1,0-
0,9-
0,8-
0,7-
0,6-
р
-1 max
0,5
1,0
1,5
Рис. 3.7. Зависимость выходной мощности от параметра согласования S:
1 — торцы активного элемента просветлены; 2 — торцы активного элемента
без покрытий (коэффициент отражения 7,6%); 3 — на торцах активного
элемента диэлектрические зеркала (коэффициент отражения 20%)
Таким образом, эксперименты подтверждают важность согласова-
согласования отдельных частей резонатора.
Вернемся теперь к вопросу о том, какое влияние поперечная струк-
структура поля оказывает на продольный спектр и его исследование, дан-
данное в § 3.1. Ответ прост — все выводы § 3.1, как и центральное уравне-
уравнение C.7), остаются без изменений, резонатор согласован, если длины
L\ и Z/2 заменить эквивалентными длинами
L[ = L\ — -— (m + п + 1) arccosgi,
L'2 = Z/2 — -— (m + n + 1) arccos#2,
4тш
особыми для каждой поперечной моды; здесь
2Li 2L
- i_ H^
Ri Ri+i RiRi+i
Таким образом, в согласованном режиме каждая поперечная мода
имеет свое собственное характеристическое уравнение типа C.7).
§ 3.4. Резонаторы с дисперсионными элементами
Рассмотренные в предыдущих параграфах резонаторы также со-
содержали дисперсионные элементы, которыми являлись дополнитель-
дополнительные резонаторы или комбинированные зеркала. Однако такие резона-
184 Гл. 3. Сложные лазерные резонаторы
торы полезны, лишь когда полоса усиления активной среды невелика,
например в газовых лазерах. В случаях же, когда полоса усиления
достаточно велика, например в твердотельных лазерах и особенно
в лазерах на красителях, широкое применение получили резонато-
резонаторы с традиционными дисперсионными элементами — призмами, ди-
дифракционными решетками, эталонами Фабри-Перо и т. п. Предло-
Предложенные довольно давно, эти резонаторы вначале не казались очень
перспективными, поскольку дисперсионные элементы вносят в резо-
резонатор дополнительные относительно большие потери. Однако поло-
положение изменилось с появлением оптических генераторов на красите-
красителях. Красители, как активная среда, обладают большим усилением,
так что легко компенсируют дополнительные потери, вносимые дис-
дисперсионными элементами. Вместе с тем они имеют широкую полосу
усиления; дисперсионные элементы позволяют выделить единствен-
единственную продольную моду в резонаторе такого лазера, на которой и про-
происходит генерация. Более того, они позволяют эту моду перестраивать
по частоте в широких пределах, в результате чего и лазер в целом ста-
становится перестраиваемым.
На рис. 3.8 изображена конкретная схема, часто применяемая с
теми или иными вариациями. На ее примере можно уяснить роль дис-
дисперсионных элементов в резонаторе. Изображенное на схеме устрой-
устройство состоит из зеркала _/, кюветы 2 с раствором красителя, нака-
накачиваемого через стенку кюветы, согласующего телескопа #, эталона
Фабри-Перо ^, дифракционной решетки 5, работающей в автоколли-
автоколлимационном режиме. Иногда используют не поперечную, как показано
на схеме, а продольную накачку, когда излучение накачки вводится
в активную среду примерно вдоль рабочего пучка; это, в принципе,
несущественно для исследования резонатора.
Прокачиваемая часть красителя обычно является самым узким
местом резонатора, хотя ее толщина или диаметр значительно больше
длины волны (а ^> Л). Поэтому активный элемент можно рассматри-
рассматривать как диафрагму, расположенную в резонаторе. Роль дифракци-
дифракционной решетки состоит в отклонении пучков нежелательной частоты
от оси резонатора, в результате чего они не попадают в активную
среду и их усиление уменьшается. Пучки нужной частоты дифраги-
дифрагируют строго обратно по оси резонатора (автоколлимация) и попадают
вновь в активную среду.
Однако дисперсионной силы дифракционной решетки недостаточ-
недостаточно для подавления соседних с выделенной продольных мод. Действи-
Действительно, при изменении длины волны на АЛ пучок отклоняется на угол
А<р = A\Btg<p/\) ~ 105АА рад, C.20)
где if — автоколлимационный угол падения пучка на решетку —
этот угол выбирается так, чтобы навстречу падающему пучку распро-
распространялся дифрагировавший пучок нужной частоты, он определяется
§3-4- Резонаторы с дисперсионными элементами
185
Рис. 3.8. Резонатор лазера на красителе: 1 — излучение накачки; 2 — кю-
кювета с раствором красителя; 3 — телескоп; 4 — эталон Фабри-Перо; 5 —
дифракционная решетка; 6 — отражающее зеркало
соотношением (в первом дифракционном порядке)
Л
где d — шаг решетки.
Отклонение пучков дифракционной решеткой приведет к суще-
существенному уменьшению их усиления, если эти пучки, возвращаясь к
кювете, сместятся от исходного положения на величину порядка ши-
ширины активной области, т. е. при условии
186
Гл. 3. Сложные лазерные резонаторы
где Г — увеличение телескопа, Lq = Li +Г XL + Г 2L^ — эффектив-
эффективная длина резонатора (длиной кюветы и расстоянием между ней и
зеркалом пренебрегаем). Длины волн двух соседних продольных мод
отличаются на АЛ = X2 /21, где I = L\ + L + L^ — полная длина резо-
резонатора. Таким образом, подавление соседних продольных мод требует
выполнения условия
L2T-1)
~ а.
C.21)
Обычно (LiT + L + L2F~1)/(Li + L + L2) ~ 2 - 3 и tg(p ~ 1, поэтому
выполнение этого условия затруднительно, так как а в сотни и тысячи
раз больше длины волны. Таким образом выделение одной продоль-
продольной моды с помощью дифракционной решетки невозможно. Тем более
это невозможно сделать с помощью призмы, так как ее угловая дис-
дисперсия
Aip = J ^ АЛ ~ 2,5 • 103АЛ рад,
более чем на порядок меньше, чем у решетки C.20) (Ь — ширина осно-
основания призмы, h — высота пучка, dn/dX — дисперсия показателя пре-
преломления) .
В связи с этим для выделения одной продольной моды в резона-
резонатор вводится элемент с большой дисперсией — эталон Фабри-Перо.
Он представляет собой обычно однородную стеклянную пластинку
с параллельными гранями, на которые нанесены отражающие по-
покрытия, располагается в резонаторе с небольшим наклоном к пуч-
пучку, чтобы отраженный свет не попадал обратно в резонатор, и рабо-
работает как узкополосный фильтр. Зависимость пропускания эталона от
длины волны изображе-
изображена на рис. 3.9. Расстоя-
л2
SX=—1cos6'~
2а
Л
ние между максимумами
пропускания равно
Л2
5Х = —
где $' — угол преломле-
преломления, т. е. угол, который
пучок образует с норма-
нормалью к поверхности, эта-
эталона внутри него (d —
Лт+1
Рис. 3.9. Зависимость пропускания эталона
от длины волны
толщина пластинки эталона). Угол $ и угол наклона эталона к оси
резонатора $ связаны соотношением sin^ = nsin^, где п — показа-
показатель преломления среды, заполняющей эталон. Отношение F — рас-
расстояния между максимумами пропускания к их полуширине назы-
называется резкостью, определяется качеством изготовления эталона и
обычно лежит в интервале 20-100. Ширина отдельного максимума
§3-4- Резонаторы с дисперсионными элементами 187
равна АЛ ~ Л2 /2Fdcos$' и при Fd cos $' порядка длины резонатора
она примерно равна межмодовому расстоянию.
Таким образом, эталон Фабри—Перо позволяет выделить одну про-
продольную моду. Роль решетки или призмы при этом сводится к тому,
чтобы воспрепятствовать возникновению генерации на других макси-
максимумах пропускания эталона. Требования к дисперсионным свойствам
решетки и призмы в этом случае снижаются, необходимо лишь вы-
выполнение условия
примерно в F раз более легкого, чем условие C.21).
Положение максимума пропускания эталона на шкале частот опре-
определяется соотношением т\т = 2dcosfd' и зависит, таким образом, от
угла падения плоской волны $'. Вследствие этого эффективная ра-
работа эталона возможна лишь если падающая на него волна близка к
плоской. Ее расходимость Д$ должна удовлетворять условию
Так как расходимость пучка Д$ ~ Л/тга, выходящего из активной сре-
среды, обычно в несколько десятков раз больше, то в резонаторе необхо-
необходимо иметь согласующий телескоп. Он разводит пучок по диаметру
в Г раз, во столько же раз уменьшая его угловую расходимость. Таким
образом, для увеличения телескопа Г получаем условие
r>>?=
тгапл/п2 — sin2 $
Для нормальной работы решетки также требуется широкий пучок.
Все отклонения, которые испытывают пучки нежелательной частоты,
должны быть много больше их собственной расходимости. В частно-
частности, отклонение пучка, соответствующего по частоте ближайшему к
рабочему максимуму пропускания эталона,
должно быть много больше собственной расходимости пучка. Отсюда
получаем еще одно условие на увеличение
C.23)
Разумеется, увеличение Г должно удовлетворять обоим этим усло-
условиям, C.22) и C.23), т.е. фактически наиболее жесткому из них.
Перестройка резонатора в широких пределах достигается посред-
посредством изменения угла автоколлимации ср, т.е. просто поворотом ре-
решетки вокруг оси, параллельной ее штрихам, и подстройкой осталь-
остальных элементов резонатора.
188 Гл. 3. Сложные лазерные резонаторы
Таким образом, хотя последовательная теория резонаторов, по-
подобных изображенному на рис. 3.8, отсутствует, физические явления,
происходящие в резонаторе, и роль его отдельных элементов вполне
ясны. Лазеры на красителях с такими резонаторами работают в од-
номодовом, как по продольному, так и по поперечному индексам, ре-
режиме и перестраиваются в широком диапазоне.
В заключение главы дадим несколько главных литературных ссы-
ссылок. Исследование сложных резонаторов в работах [64-67] проведено в
связи с их влиянием на пичковый режим генерации. Резонатор Фокса-
Смита предложен и исследован в работе [68], Т-образный резонатор —
в работе [69], резонатор Майкельсона — в работе [70]. Согласование
поперечных мод в сложном резонаторе обсуждалось в [71, 72].
Резонаторы с дисперсионными элементами предложены в работах
[73-76]. Их совершенствование происходило в русле развития лазеров
на красителях — см. обзор [77].
Глава 4
РЕЗОНАТОРЫ ТВЕРДОТЕЛЬНЫХ ЛАЗЕРОВ
§4.1. Термооптические искажения активных
элементов твердотельных лазеров
Лазеры на твердом теле являются в настоящее время, по-видимо-
по-видимому, наиболее популярным типом лазеров. Основная особенность ре-
резонатора твердотельного лазера состоит в том, что в процессе ра-
работы лазера он испытывает значительные изменения своих свойств
из-за появления термооптических неоднородностей в активном эле-
элементе (АЭ) при его неравномерном нагреве. Поэтому, рассматривая
в этой главе методы построения схемы резонаторов твердотельных
лазеров различного назначения, основное внимание уделим изучению
влияния наведенных в процессе накачки среды термооптических ис-
искажений АЭ на свойства резонатора. В соответствии с этим, в насто-
настоящем параграфе проведено описание характера искажений, возника-
возникающих в АЭ из наиболее популярных материалов.
В подавляющем большинстве случаев термооптический возмущен-
возмущенный АЭ можно приближенно представить в виде идеальной линзы —
термической линзы АЭ (ТЛ АЭ), оптическая сила которой зависит
от средней мощности накачки. Специфика материала АЭ, режима
накачки, конструкции осветителя и прочие особенности конструкции
твердотельных лазеров проявляются в малых аберрациях ТЛ АЭ. Ха-
Характер этих аберраций может быть весьма сложен, однако для боль-
большого числа задач их влиянием на свойства резонатора, по сравнению
с влиянием усредненной идеальной ТЛ, можно пренебречь. Поэто-
Поэтому в следующих параграфах исследование резонатора проводится в
рамках гауссовой оптики. При этом в § 4.2 исследуются общие зако-
закономерности поведения резонатора, содержащего внутрирезонаторную
линзу. Выделяются два типа резонаторов, наиболее подходящих для
использования в твердотельных лазерах. На этой основе в § 4.3—4.6
разрабатываются конкретные алгоритмы построения схем резонато-
резонаторов твердотельных лазеров как с непрерывной, так и импульсной на-
накачкой.
При накачке АЭ твердотельных лазеров газоразрядными лампа-
лампами от 3% до 10% мощности лампы накачки идет на нагрев АЭ [78].
Этот нагрев обусловлен наличием стоксовых потерь при возбуждении
190 Гл. 4- Резонаторы твердотельных лазеров
активных центров, собственным поглощением матрицей АЭ излуче-
излучения накачки, частичным поглощением в активной среде генерируемо-
генерируемого излучения и т. д. и приводит к необходимости охлаждения АЭ в
процессе работы лазера. Чрезмерный нагрев АЭ ведет к ухудшению
генерационных параметров лазера, а при достаточно высоком уровне
накачки — и к разрушению АЭ. Наличие объемного тепловыделения
и поверхностного охлаждения АЭ приводит к появлению неоднород-
неоднородного распределения температуры по сечению АЭ. Существует целый
ряд механизмов влияния температуры на оптические характеристики
АЭ. Так, нагрев материала приводит к сдвигу фундаментальных уль-
ультрафиолетовых полос поглощения, изменению плотности материала,
из-за эффекта термического расширения, к эффекту фотоупругости.
Совокупное действие этих факторов приводит к тому, что неодно-
неоднородно нагретый АЭ удлиняется; в нем возникают оптические неодно-
неоднородности, различные для излучения с разной поляризацией [79]. По-
Появившиеся в процессе накачки термооптические искажения активной
среды оказывают в ряде случаев определяющее влияние на характе-
характеристики резонатора и в конечном случае на генерационные параметры
лазера. Поэтому при разработке схем резонаторов твердотельных ла-
лазеров того или иного назначения в первую очередь приходится учиты-
учитывать, наряду со спецификой назначения лазера, величину и характер
термооптических искажений АЭ, возникающих в процессе генерации.
В данном параграфе кратко рассматриваются характер, величина и
способ описания наводимых в АЭ термооптических искажений из наи-
наиболее популярных материалов.
Рассмотрим АЭ цилиндрической формы, у которого длина I суще-
существенно больше его радиуса R. В случае стационарного, однородного
объемного нагрева такого элемента и равномерного поверхностного
охлаждения, установившееся температурное поле внутри АЭ описы-
описывается параболическим распределением [79]:
-^(R2-r2), D.1)
где Pq — полная мощность тепловыделения в АЭ, V = тгR?l — объ-
объем АЭ, Л — коэффициент теплопроводности материала. Для боль-
большинства ситуаций, при которых термооптические искажения суще-
существенны, не имеет значения, происходит ли накачка непрерывно или в
виде последовательности импульсов, следующих с высокой частотой,
так как процесс теплопроводности является сравнительно медленным.
Так характерное время установления стационарного температурного
режима г = R2Cp/\, где С — теплоемкость, а р — плотность мате-
материала, и для АЭ из АИГ: Nd3+ с R = 2,5 мм составляет 1,3 с (Л =
= 0,13 Вт-см-^К; р = 4,6 г-см, С = 0,63 джт^К). Для АЭ
того же размера из стекла это время более, чем на порядок боль-
больше, так как Л = 0,01 Вт • см К. Поэтому в случае, когда нагрев
4-1. Термооптические искажения активных элементов 191
АЭ происходит хотя и импульсно, но с достаточно высокой частотой
повторения (/ ^> 1/т), усредненное температурное поле в элементе
очень мало отличается от случая, когда нагрев АЭ происходит непре-
непрерывно. Более тщательный анализ показывает [78], что при частоте
следования импульсов накачки
где а — коэффициент теплообмена, определяемый характером и ин-
интенсивностью охлаждения АЭ, погрешность в определении темпера-
температурных перепадов, вызванная заменой импульсного источника тепла
непрерывным, будет не более 10%. Для АЭ из стекла с неодимом эта
величина составляет более 1 Гц, а для АИГ: Nd3+ не менее 5 Гц. Отме-
Отметим, что при работе лазера с меньшими частотами накачки влияние
термооптических искажений на процесс генерации существенно мень-
меньше и ими часто можно пренебречь.
На практике распределение мощности накачки в АЭ не являет-
является, как правило, равномерным и предположение, сделанное при
выводе формулы D.1), не выполняется. Однако анализ задачи с
учетом неоднородного нагрева АЭ [78] показывает, что даже при
существенной неоднородности распределения мощности тепловыде-
тепловыделения в АЭ установившееся температурное распределение близко к
параболическому.
Наличие градиента температуры в объеме АЭ приводит к выпу-
выпучиванию торцов АЭ, появлению оптических неоднородностей и на-
напряжений в нем, и как следствие этого, — анизотропии оптических
свойств элемента. В случае, когда R ^ I, влиянием прогиба торцов
АЭ на оптические свойства элемента можно пренебречь [80, 81], по-
поэтому этого аспекта мы в дальнейшем касаться не будем. Отметим
лишь, что при анализе термооптических искажений АЭ, выполнен-
выполненных в виде пластин, влияние прогиба торцов может быть сущест-
существенным [81].
В общем случае характер объемных термооптических неоднород-
неоднородностей зависит от геометрии АЭ и специфики термооптических ха-
характеристик материала. При этом исходя из особенностей термоопти-
термооптических искажений АЭ цилиндрической формы можно выделить три
характерных типа материала АЭ, используемых в твердотельных ла-
лазерах. Во-первых, аморфные материалы, например стекло с неоди-
неодимом, во-вторых, кристаллы с кубической симметрией, которые в нена-
ненагретом состоянии по своим оптическим свойствам близки к аморфным
материалам, но отличаются от последних в нагретом состоянии, и,
наконец, материалы с ярко выраженной естественной анизотропией,
например, рубин, александрит, YAIO3: Nd3+ и проч.
В АЭ с аморфной структурой параболическое распределение тем-
температуры порождает параболическое распределение показателя пре-
преломления в поперечном сечении АЭ. При этом наличие внутренних
192 Гл. 4- Резонаторы твердотельных лазеров
напряжений в АЭ, вызванных неравномерным нагревом центральной
и периферийной зон элемента, приводит к анизотропии этой зависи-
зависимости [82-84]
\§(%У, D.2)
где индексы г и (р указывают значение показателя преломления для
света, поляризованного вдоль радиуса АЭ (знак плюс) и перпенди-
перпендикулярно радиусу (знак минус) соответственно. Коэффициенты Р и
Q называют термооптическими постоянными материала. Они харак-
характеризуют суммарное влияние неравномерного нагрева АЭ на его оп-
оптические свойства. При этом величина Р характеризует усредненную
по двум поляризациям степень термооптических искажений, в то вре-
время как Q — степень анизотропии термооптических искажений. Вели-
Величины Р и Q зависят от свойств используемого материала, в частно-
частности, для АЭ из силикатного стекла ГЛС-I Р = 39 • 10~7 К, Q =
= б • 10~7 К, для элементов из фосфатного стекла ГЛС-22 Р =
= 2 • Ю-7 К, Q = 4 • Ю-7 К.
Из формулы D.2) видно, что характер наведенной анизотропии
весьма сложен и неоднороден по сечению АЭ. Величина анизотро-
анизотропии возрастает к периферии АЭ пропорционально г2, а направление
главных оптических осей в каждой точке АЭ совпадает с ортами ци-
цилиндрической системы координат.
К кристаллическим активным материалам, обладающим куби-
кубической симметрией, относятся широко распространенные в настоя-
настоящее время алюмоиттриевый гранат, активированный неодимом (АИГ:
Nd3+) [85, 87-93], щелочно- и щелочноземельно-галлоидные кристал-
кристаллы, являющиеся основой для перестраиваемых твердотельных лазе-
лазеров на центрах окраски [86]. В отсутствие механических напряжений
эти материалы оптически изотропны, однако наличие в АЭ терми-
термически индуцированных напряжений может приводить к появлению в
них анизотропии сложного вида, зависящей от взаимной ориентации
кристаллографических осей и осей АЭ. В случае, когда АЭ, например,
из АИГ: Nd3+ вырезан таким образом, что ось элемента ориентиро-
ориентирована в направлении [111] (т. е. в направлении главной диагонали куба
ячейки кристаллической решетки), относительно кристаллографиче-
кристаллографических осей, что является характерным для АЭ, производимых зару-
зарубежными фирмами, то термооптические искажения элемента вполне
аналогичны искажениям АЭ из аморфного материала. Распределе-
Распределение показателя преломления описывается выражением D.2) с Р =
= 82 • 10~7 К и Q = 17 • 10~7 К. Степень деполяризации линейно
поляризованной волны, распространяющейся вдоль оси АЭ, не зави-
зависит от ориентации плоскости поляризации.
В случае, когда ось АЭ совпадает с кристаллографической осью
[001] (рис. 4.1), что характерно для элементов из АИГ: Nd3+, произ-
производимых в России, характер термооптически наведенной анизотропии
4-1- Термооптические искажения активных элементов
193
носит более сложный вид. И, хотя зависимость показателя преломле-
преломления по-прежнему можно представить в виде D.2), величина Q уже не
[010]
У [юо]
60°
45°
о 5 ю 15 20 д-ю7(к-
Рис. 4.1. Ориентация АЭ вдоль кристаллографической оси [001] (а). Зави-
Зависимости термооптической константы Q (б) и направления локальных глав-
главных кристаллографических осей в АЭ (е) от азимутального угла при ори-
ориентации АЭ вдоль оси [001]
будет являться постоянной, а будет зависеть от значения азимуталь-
азимутального угла ip [78], рис. 4.1:
= Qo
D.3)
где ?а = 3,22, Qq = 7 • 10~7 К. При этом термооптическая постоян-
постоянная Р не зависит от азимутального угла и равна 77 • 10~7 К. На
рис. 4.1, б качественно показана зависимость величины Q от угла ср.
Видно, что минимальная анизотропия имеет место вдоль кристалло-
кристаллографических осей, максимальная величина Q = 23 • 10~7 К~ дости-
достигается при ip = 45°. Следует также отметить, что если в случае АЭ,
ориентированных вдоль оси [111], главные оптические оси в каждой
точке АЭ совпадали с ортами цилиндрической системы координат, то
в случае АЭ, вырезанного вдоль оси [001], это не так [77]. Поэтому
вместо пг^ в формуле D.2) следует писать nr/j??/, где индексы г' и cpf
13 В.П. Быков, О.О. Силичев
194 Гл. 4- Резонаторы твердотельных лазеров
говорят о том, что показатель преломления рассчитан для поля, по-
поляризованного вдоль главных оптических осей в данной точке АЭ.
При этом угол наклона cpf главной оптической оси в точке (г, ср) АЭ к
направлению ср = 0 определяется соотношением
y>' = ±axctg(fatg2y>). D.4)
Анализ выражения D.4) показывает, что имеется некоторая пре-
преимущественная ориентация наведенных главных оптических осей под
углом 45° к направлению [010] (рис. 4.1, в). Подчеркнем еще раз, что
в случае, когда ось АЭ ориентирована вдоль оси [111], ip' — (р.
Важной характеристикой термооптически искаженного АЭ с точ-
точки зрения влияния АЭ на структуру мод резонатора является степень
деполяризации им плоскополяризованного излучения. Анализ степе-
степени деполяризации, основанный на формулах D.2)-D.4), показывает,
что при ориентировке АЭ вдоль оси [001] максимальная деполяриза-
деполяризация имеет место в случае, когда направление вектора напряженности
электрического поля совпадает с кристаллографическими осями [010]
или [100]. Минимальная деполяризация достигается в случае, когда
угол между этими направлениями равен 45°. Это связано с преиму-
преимущественной ориентацией главных оптических осей, термически на-
наведенной анизотропии ср' « 45°, определяемой соотношением D.4).
При больших мощностях накачки правильная ориентировка АЭ отно-
относительно направления поляризации генерируемого излучения может
обеспечить существенный выигрыш в эффективности лазера за счет
уменьшения деполяризации излучения в АЭ.
Из материалов, обладающих существенной собственной анизо-
анизотропией, наиболее важны рубин [94], ортоалюминат иттрия YAIO3:
Nd3+ [95], александрит [96]. Характерной особенностью термоопти-
термооптических искажений АЭ в этом случае является малость наведенно-
наведенного двулучепреломления по сравнению с двулучепреломлением, обу-
обусловленным собственной анизотропией материала. Вследствие этого
направления главных оптических осей элемента во всех точках оди-
одинаковы и определяются собственной анизотропией материала. Таким
образом, в этом случае cpf = сро = const, а распределение показателя
преломления описывается формулой D.2).
После сделанных замечаний об особенностях термооптических ис-
искажений АЭ из наиболее популярных материалов получим общее вы-
выражение, приближенно описывающее действие термически возмущен-
возмущенного АЭ на проходящее поле. Для этого запишем падающую на АЭ
поляризованную волну в виде вектора Ei = (Ех, Еу) в декартовой си-
системе координат, связанной, в случае, если АЭ имеет кристалличе-
кристаллическую структуру, с главными кристаллографическими осями. Восполь-
Воспользуемся методом матриц Джонса. Для этого представим вектор Ei в
каждой точке поперечного сечения АЭ в системе координат связанной
4-1. Термооптические искажения активных элементов 195
с главными оптическими осями АЭ в данной точке:
С0У;
/ cos cp
В данной системе координат действие термооптически возмущен-
возмущенного АЭ может быть приближенно описано, в соответствии с форму-
формулой D.2), диагональной матрицей Джонса:
feiln'rk о
Используя соотношение D.2), преобразуем матрицу So к
• к 2\ /ехр
ч ,^P(-iSr2-^ О
2/>
где
Возвращаясь обратно в первоначальную декартову систему коорди-
координат, имеем окончательное выражение для поля, прошедшего через
АЭ
El) =е^ехр(-фтг2M (^ , D.6)
где
1 * Г fk \ I U(<P')- D-7)
О ехр(i - 5г2) I
Таким образом, в общем случае действие термически возмущенно-
возмущенного АЭ на поле сводится к несущественному, однородному по сечению,
изменению фазы — первый множитель в формуле D.6), к изменению
кривизны фазового фронта на величину рт — второй множитель, т. е.
действие АЭ в данном случае подобно действию идеальной линзы с
оптической силой рт, пропорциональной мощности накачки Pq D.5).
Кроме того, АЭ действует, как некоторая, неоднородная по сечению,
фазовая пластинка, описываемая матрицей Джонса S — третий мно-
множитель в формуле D.6).
В случае АЭ, выполненных из аморфных материалов или из кри-
кристаллических материалов с кубической симметрией с ориентацией оси
АЭ вдоль направления [111], ^> — ip и Q = const. При этом матрица S
описывает как деполяризующее действие АЭ, так и астигматизм тер-
термической линзы (ТЛ) АЭ. Действительно, рассмотрим фокусирующее
действие АЭ на волну поляризованную, например, вдоль оси х в на-
направлении ер = 0 и ер = тг/2. Тогда, согласно D.6), на выходе АЭ в
13*
196 Гл. 4- Резонаторы твердотельных лазеров
случае ср = 0 имеем
и, следовательно, оптическая сила ТЛ АЭ составляет величину рт\ =
= рт + 8. В направлении ip = тг/2 имеем
и оптическая сила ТЛ АЭ равна рт2 = Рт — 8. Следовательно, имеет
место астигматизм ТЛ, характеризуемый отношением
Dg)
[ }
Ц~Рт2 P-Q/2'
Легко показать, что в этом случае величина астигматизма не зависит
от направления поляризации падающей волны. Для АЭ из АИГ: Nd3+
ту = 1,2.
Если мы используем АЭ из АИГ: Nd3+ с ориентацией оси вдоль
направления [001], то значение угла if' и параметра Q в каждой точ-
точке АЭ определяются соотношениями D.3) и D.4). При этом степень
астигматизма ТЛ АЭ сложным образом зависит от ориентации поля-
поляризации падающей волны.
Наконец, использование в качестве активной среды материалов с
сильной естественной анизотропией приводит к тому, что в форму-
формуле D.7) следует положить cpf = 0, так как мы предполагаем, что де-
декартова система координат (ж, у) ориентирована вдоль кристаллогра-
кристаллографических осей АЭ. При этом матрица S переходит в диагональную
матрицу и, следовательно, деполяризующее действие АЭ в данном
приближении отсутствует. Имеющий место астигматизм ТЛ АЭ опи-
описывается выражением D.8).
Изложенная картина характера термооптических искажений твер-
твердотельных АЭ в реальной ситуации может значительно усложняться,
так как многие предположения, сделанные в процессе анализа, вы-
выполняются не всегда. Например, АЭ изначально может быть опти-
оптически неоднородным, возможно влияние напряжений, возникающих
в процессе крепления АЭ в осветителе, краевых эффектов, нестаци-
нестационарности температурного поля и проч. Однако, в первую очередь,
это относится к предположению об однородности нагрева и охлажде-
охлаждения АЭ. В реальной ситуации распределение мощности накачки по
сечению АЭ всегда в той или иной степени неравномерно. Наиболь-
Наибольшая однородность распределения накачки достигается в осветителях с
диффузным характером отражения [97]. В осветителях, выполненных
в виде отражающего кругового цилиндра или эллиптического цилин-
цилиндра, в фокусах которого расположены АЭ и лампа накачки, неравно-
неравномерность накачки может быть весьма значительной [98]. Это приводит
4-1. Термооптические искажения активных элементов 197
к усложнению характера наведенных термооптических неоднородно-
стей в АЭ. Как правило, влияние неравномерности накачки сводит-
сводится к тому, что усредненная ТЛ АЭ становится аберрационной, т. е.
величина рт начинает зависеть от г и ср. Влиянием неравномерного
нагрева на деполяризующие свойства АЭ, т.е. на матрицу 5, можно
пренебречь, как коэффициентами второго порядка.
В одноламповых осветителях, выполненных в виде кругового ци-
цилиндра, как правило, имеет место азимутальная асимметрия термооп-
термооптических искажений. В этом случае в выражение D.6), описывающее
действие термооптически возмущенного АЭ на поле, следует добавить
дополнительный множитель вида
к — exp \—i — OL\v cos ср) ехр ( — i - а^т2 cos ср). D.9)
Первый член в этом выражении описывает термооптические искаже-
искажения, эквивалентные по своему действию оптическому клину, ориен-
ориентированному в направлении ср = 0 (как правило, в направлении оси
АЭ—лампа). Появление такого рода неоднородностей влияет на по-
положение оптической оси резонатора. Второй член в выражении D.9)
апроксимирует аберрации ТЛ АЭ, возникающие в данной ситуации.
При плотной упаковке лампы накачки и оптически плотного АЭ ве-
величина «2 может достигать ~ @,2 — 0,3)рт-
В осветителях эллиптического типа термооптические искажения
АЭ в первом приближении обладают осевой симметрией. Однако из-
за сильной фокусировки излучения лампы накачки в центральную об-
область АЭ возможно наличие достаточно сильных сферических абер-
аберраций. При этом особенно сильные аберрации возникают тогда, ко-
когда радиус АЭ больше радиуса светящейся области лампы накач-
накачки. Например, в работе [92] описана ситуация, когда оптическая си-
сила ТЛ в центре АЭ в 1,8 раза больше, чем ТЛ периферийной об-
области.
В общем случае вопрос о степени аберраций ТЛ, т. е. о качестве ТЛ
АЭ, решается экспериментально путем измерения оптической силы
ТЛ в различных сечениях АЭ. Существует много экспериментальных
методов анализа характера термооптических искажений АЭ. Среди
них следует отметить интерференционный метод [90, 91], заключаю-
заключающийся в том, что изучается картина интерференции поля прошедше-
прошедшего оптически неоднородный элемент с невозмущенным полем. В тех
местах, где оптические неоднородности более ярко выражены, фазо-
фазовый фронт волны искажен сильнее и в соответствующем месте интер-
интерференционной картины будет иметь место либо сильное искривление
полос, либо их сгущение. Часто для интерференционных измерений
используют интерферометр Маха-Цендера.
Весьма просто определить величину и качество ТЛ АЭ, воспользо-
воспользовавшись установкой, изображенной на рис. 4.2. Луч газового лазера Г
расширяется телескопом Т и падает на экран с отверстием, диаметр
198
Гл. 4- Резонаторы твердотельных лазеров
АЭ
1/2п0
О
Х2
Рис. 4.2. Схема измерения величины оптической силы термической лин-
линзы АЭ
которого много меньше диаметра АЭ. Перемещая отверстие на вели-
величину х\ и измеряя зависимость положения луча газового лазера на
экране Ж2, можно легко определить оптическую силу ТЛ в данном
сечении АЭ и уровень ее аберраций.
Действительно, в случае отсутствия аберраций,
х\ + х2 = aL = xi(ptL),
где а — угол отклонения луча газового лазера (рис. 4.2). Следователь-
Следовательно, зависимость (х\ + х2) от х\ линейна и коэффициент пропорцио-
пропорциональности, равный PtL, позволяет легко найти оптическую силу ТЛ
АЭ. Нарушения линейности в этой зависимости определяют характер
и величину аберраций ТЛ АЭ.
На этом мы закончим краткий обзор характера термооптических
искажений твердотельных АЭ. Отметим лишь, что, хотя весь анализ
был проведен для АЭ цилиндрической формы, большинство полу-
полученных результатов можно использовать и в случае термооптически
возмущенных АЭ прямоугольной формы [99].
§ 4.2. Резонаторы с термооптически возмущенным
активным элементом
Анализируя характер термооптических искажений АЭ под дей-
действием накачки, мы пришли к выводу, что в первом приближении их
можно представить в виде идеальной термической линзы, оптическая
сила которой меняется при изменении накачки. В этом параграфе ис-
исследуем, как меняются свойства резонатора, содержащего ТЛ, при
изменении мощности накачки, что эквивалентно исследованию резо-
резонатора, содержащего линзу с изменяющейся оптической силой. Дан-
Данный анализ позволит выявить оптимальные виды резонаторов твер-
твердотельных лазеров и создать основу для последующего построения
алгоритмов их расчета.
4-2. Резонаторы с термооптически возмущенным элементом 199
Чтобы проанализировать с единых позиций резонаторы как устой-
устойчивой, так и неустойчивой конфигураций, будет предполагать нали-
наличие внутри резонатора одной или нескольких ограничивающих апер-
апертур с гауссовым профилем пропускания. Такой подход оправдан еще и
потому, что действие произвольной ограничивающей апертуры можно
в первом приближении рассматривать, как действие некоторой гаус-
гауссовой апертуры [100]. Особенно эффективно подобное приближение
при рассмотрении ограничивающих апертур с частично сглаженным
краем, а именно с такими апертурами обычно приходится иметь дело
на практике. Отступление свойств реальной апертуры от гауссовой
можно учесть путем введения в резонатор некоторого дополнитель-
дополнительного аберрационного элемента.
Итак, перейдем к анализу модели резонатора, содержащего лишь
гауссовые оптические элементы, в частности произвольное число гаус-
гауссовых апертур. Отметим вначале одно общее свойство таких резона-
резонаторов. Для этого рассмотрим поле основной моды резонатора в неко-
некотором поперечном сечении:
7 (-к 2\
и0 = Aoexp{i-/ior J,
где /io = 1/#о = 1/^о — гЛ/тгг^о — комплексный параметр моды. Пусть
лучевая матрица обхода резонатора, отнесенная к этому сечению, име-
имеет в общем случае комплексные элементы Aq, Bq, Со, Do- Наличие
мнимых частей у этих элементов обусловлено наличием гауссовых
апертур в резонаторе и тем обстоятельством, что, согласно изложен-
изложенному в гл. 1, действие гауссовой апертуры на гауссов пучок может
быть описано с помощью лучевой матрицы вида
1
где ра = Л/тгП2 — оптическая сила гауссовой апертуры, непосредствен-
непосредственно связанная с радиусом области пропускания апертуры П.
После обхода резонатора поле основной моды будет иметь, соглас-
согласно B.17), вид
щ = Аог-е ехр(г — Dor )
\ Г- к 1
)ехр[г-г
При выводе этого выражения было осуществлено интегрирование
в формуле B.17) по углу ср с помощью интегрального представления
функции Бесселя B.26а). Это выражение с помощью формулы B.27)
можно преобразовать к виду
к
200 Гл. 4- Резонаторы твердотельных лазеров
где
4' 4 e%kL и Со
А = А ^ =
Поскольку в исходном сечении мощность гауссового пучка пропорци-
пропорциональна величине
ОО
то потери основной моды резонатора в результате обхода резонатора
определятся величиной
Q0
Ао
где Q\ — мощность пучка после обхода резонатора. Поскольку мы
предполагали, что комплексный параметр /io соответствует моде ре-
резонатора, то \i\ = \1{л и, следовательно, с учетом формулы D.10) имеем
из последнего выражения:
7=1-,, Л ,. „¦ D-11)
Комплексный параметр моды резонатора /io определяется по правилу
ABCD:
Do-Ao, I I {Ao + 2 ~
ZBq Bq у V ^
Подставляя это соотношение в выражение D.11) и преобразуя его,
получаем
\I±^P-1\2 = ^±-, D.12)
где / = ° —-. Введем новые переменные для обозначения действи-
действительной и мнимой частей величины /:
/ = в + г/. D.13)
Если элементы лучевой матрицы обхода действительны, то резона-
резонатор называют устойчивым, если |/| < 1. Поэтому, следуя традицион-
традиционной терминологии, будем считать, что случай |s| < 1 соответствует
резонаторам устойчивой конфигурации, a |s| > 1 — неустойчивой. Ис-
Используя переменные s и /, выражение D.12) можно преобразовать к
виду
s2 f2
- + 4 = 1, D.14)
so /о
где
*§ = 1 + /2 / = DЛ5)
4-2. Резонаторы с термооптически возмущенным элементом 201
Таким образом, величины s и / полностью определяют значение
потерь основной моды резонатора. Кроме того, при произвольной
геометрии резонатора кривые, описывающие уровни одинаковых по-
потерь основной моды 7 B плоскости параметров (s, /) есть эллип-
эллипсы D.14) с главными осями, определяемыми исключительно величи-
величиной 7- На рис. 4.3 приведено семейство этих эллипсов для различных
1,5
1,0
0,5
0,8
\
7 = 0,9
о
0,25 0,5
0,75
1,0
1,25
Рис. 4.3. Уровни одинаковых потерь в пространстве параметров (/, s) (по-
(показан первый квадрант плоскости)
значений потерь 7- Этот факт, как будет следовать из дальнейшего,
позволит существенно упростить анализ свойств резонатора при ва-
варьировании оптической силы внутрирезонаторной термической лин-
линзы. Здесь лишь отметим, что произвольное малое изменение геомет-
геометрии резонатора, вызванное либо нестабильностью оптических свойств
резонаторных элементов, либо неточностью сборки схемы резонатора,
приводит к смещению точки (s, /) в плоскости этих параметров от-
относительно первоначального положения (so,/o) и изменению потерь
моды, причем тем более сильное, чем «гуще» расположены эллипсы
на рис. 4.3. В частности, из рисунка видно, что резонаторы с малым
уровнем потерь более чувствительны к изменению величины парамет-
202
Гл. 4- Резонаторы твердотельных лазеров
ров s и /. Особенно высоки требования к стабильности схемы в обла-
области s ~ 1, так как в этой области даже малое изменение параметров
s и / приводит к переходу точки (s, /) на эллипс, соответствующий
потерям, существенно отличающимся от первоначальных. Поэтому с
точки зрения стабильности, при малых потерях 7 предпочтительно
работать со схемами резонаторов, лежащими в области s ~ 0. При
большом уровне потерь, как следует из рис. 4.3, даже существенное
изменение величины параметров / и s приводит лишь к сравнитель-
сравнительно малому изменению потерь. Поэтому лазеры с такими резонаторами
отличаются повышенной стабильностью к флуктуациям оптических
свойств резонаторных элементов. Причем это характерно, как для ре-
резонаторов устойчивой конфигурации, так и неустойчивой.
А2 В,
d
С2 А2
•*— di —-
Pi
Л
V
^
Рт Р2
АЛ
V V
~^—>
** d2 >
A
р
б
Рис. 4.4. Схема исследуемого резонатора
После этих общих замечаний перейдем к анализу резонатора, изоб-
изображенного на рис. 4.4 и содержащего меняющуюся линзу рт, изобра-
изображающую термооптически возмущенный АЭ. Будем предполагать, что
плечи резонатора содержат произвольное количество оптических эле-
элементов, причем ограничивающие излучение апертуры расположены в
правом плече резонатора. Оптическая система плеча резонатора, опи-
описываемая матрицей обхода Mi [г = 1,2) (рис. 4.4) может быть пред-
представлена в эквивалентном виде, а именно, в виде линзы р^ и свободно-
свободного пространства длиной di (рис. 4.4, б), с такой же лучевой матрицей
обхода. Для этого достаточно положить:
- Ah2
51,2
D.16)
4-2. Резонаторы с термооптически возмущенным элементом 203
Таким образом, с точки зрения параметра моды /io на внутренней лин-
линзе, линейный резонатор произвольного вида эквивалентен резонатору
с плоскими зеркалами и внутренней линзой
P = Pi +РТ+Р2- D.17)
Характерной особенностью рассматриваемой нами модели является
комплексность компонент лучевой матрицы М2. Поэтому следует по-
положить:
Pi = Pf2 + ipo, d2 = d0 + id, D.18)
где все вновь введенные величины действительные. После этого вели-
величину D.17) можно представить в виде
p = p + ip0, D.19)
где
P = Pi +РТ+Р2- D.20)
Лучевая матрица обхода резонатора по часовой стрелке с началом
в плоскости АА (рис. 4.4, б) будет иметь вид
1 — 2d\p 2(d\ + d2 — 2d\d2p)
Co Do) ~ У Co 1 - 2dip - 4d2(p - dxf)
Подставим в это выражение формулы D.18), D.19) и найдем действи-
т Ао + Do
тельную и мнимую части величины 1 = :
s = и(р2 —
= v(p2 -
где
1 1 о d о, 1 о do
= -г + -г + 2-г- Ро, 2Ь2 = — - 2— р0,
do d\ do d\ d . .
-Po + ^i c2 = -'-f-p20-
2ahdo
u = 2dodu v = 2dd±. D.23)
Формулы D.21), рассматриваемые как функции параметра р, задают
кривую в плоскости (/, s), которую описывает точка (/, s) при из-
изменении оптической силы TJ1 АЭ рт- Легко видеть, что эта кривая
является параболой. Для того чтобы убедиться в этом, достаточно
перейти от координат (/, s) к координатам (/,s):
/ = Л + v] - us,
S = Si + Uf + VS,
204
Гл. 4- Резонаторы твердотельных лазеров
где
fi=v[
Si = U
G^?u*-b\ + C2\,
Тогда зависимость, задаваемая параметрически формулами D.21),
приобретает вид:
Очевидно, что это уравнение параболы в координатах (f,s). В коор-
координатах (/, s) (рис. 4.5) ее центр расположен в точке (/i,si), а ось
симметрии расположена под
, / углом ф к оси / таким, что
Таким образом, изменению
оптической силы термиче-
термической линзы рт соответствует
* движение точки N (рис. 4.5)
по параболе. При своем дви-
движении она будет пересекать
эллипсы D.14), соответству-
соответствующие различным значениям
потерь 7-
Проанализируем качест-
качественное поведение зависимо-
Рис. 4.5. Перемещение точки N в плос- сти 7(Рт), рис. 4.6, а. При
кости (/, s) по параболе при измене- больших по абсолютному зна-
знании оптической силы термической лин- чению рт величины / и s ве-
зы АЭ лики (см. формулу D.21)) и
потери основной моды 7 стремятся к единице 7 — 1- По мере умень-
уменьшения рт точка N пересекает эллипсы с меньшим размером полу-
полуосей, т. е. эллипсов, соответствующих меньшим потерям основной мо-
моды 7- Точки касания К, Л, М параболы и эллипса соответствуют
экстремумам в зависимости 7(Рт)- В этих точках, как легко видеть
из рис. 4.6, а, имеет место динамическая стабильность потерь основ-
основной моды резонатора по отношению к малым флуктуациям ТЛ АЭ.
Резонаторы именно такого типа представляют наибольший интерес,
так как обладают повышенной стабильностью к флуктуациям тер-
термооптических искажений АЭ. Подчеркнем универсальный характер
полученной нами зависимости 7(Рт)? имеющей не более трех локаль-
локальных экстремумов. При определенных условиях, т. е. при определенном
расположении параболы, эти экстремумы могут сливаться в один гло-
глобальный минимум (рис. 4.6, б).
4-2. Резонаторы с термооптически возмущенным элементом 205
N,
Рис. 4.6: а) изменение потерь основной моды j при движении точки N в
плоскости (/, s) по параболе, обусловленном изменением термической лин-
линзы АЭ; б) при указанном рисунке расположении параболы возможно слия-
слияние всех экстремумов зависимости j(p) в один глобальный минимум
Дальнейшее исследование ограничим случаем V = d = 0. Это со-
соответствует условию, когда вкладом гауссовых апертур в оптическую
длину плеча можно пренебречь D.18). Это оправдано для подавляю-
подавляющего числа практически важных случаев. В частности, если ограни-
ограничивающая апертура расположена вблизи АЭ, то d = 0.
При v = 0 парабола D.24) принимает весьма простой вид в коор-
координатах (/, s) (рис. 4.7):
s=J-
где
si =
2di
D.26)
D.27)
206
Гл. 4- Резонаторы твердотельных лазеров
При этом
/ = -pobo, D.28)
где
bo = 2d0 + 2di - 4d0dip D.29)
— оптическая длина обхода резонатора без учета гауссовых апертур.
Из рис. 4.7 видно, что в данном случае имеют место три точки каса-
Рис. 4.7. Зависимость потерь основной моды 7 от силы термической линзы
в случае, когда влиянием гауссовых апертур на оптическую длину резона-
резонатора можно пренебречь
ния параболы и эллипсов, соответствующих потерям 71 (точки К, М)
и потерям 72 (точка Л). В общем случае в этих точках имеет место
касание первого рода. В точках К и М достигаются минимальные
потери основной моды при изменении р. Точка Л соответствует ло-
локальному максимуму значения потерь. Она реализуется в резонаторах
неустойчивой конфигурации с s = so и / = 0. Из формулы D.28) сле-
следует, что это возможно лишь при Ьо = 0, т. е. когда оптическая длина
обхода резонатора равна нулю. Согласно D.29) это имеет место при
р = р' ? где
р/ = ^- + ^-. D.30)
Отметим также, что зависимость ^(р) обладает симметрией относи-
относительно точки р — р1. При определенных значениях параметров резона-
резонатора в точке Л возможно касание третьего рода (рис. 4.6, б). В этом
случае экстремумы в точках К, Л и М сливаются в один глобальный
минимум, и диапазон изменения оптической силы ТЛ АЭ, при ко-
котором потери резонатора меняются слабо, существенно расширяется
(приблизительно в два раза).
Исходя из выражений D.2б)-D.29), легко найти зависимость по-
потерь основной моды 7 от величины оптической силы ТЛ АЭ рт- Для
этого достаточно при заданном значении р найти величины s и /
4-2. Резонаторы с термооптически возмущенным элементом 207
=0,01
0,8
0,6
0,4
0,2
0,4
0,6
0,5
1,0
1,5
7
=0,1
0,8
0,6
0,4
0,2
0,4
N. 0,6
do/fa - 0,2
X/
// /
/ /
A
у
0,5
1,0
1,5
Ро
Рис. 4.8. Зависимость потерь основной моды 7 от оптической силы терми-
термической линзы АЭ (\di\ > |c?2|)- Эта зависимость симметрична относительно
р = р': a) podi = 0,01; б) podi = 0,1
D.21). Затем, учитывая, что Sq = 1 + /q , из выражения D.14) найти
/о и, воспользовавшись D.15), вычислить гу. На рис. 4.8 приведены за-
зависимости 7(р) для ряда значений параметров do/di, ^iPo- При этом
полагаем, что di > do- Это абсолютно не ограничивает общность рас-
рассмотрения, поскольку d = 0. Видно, что при касании кривых в точках
К или М зависимость 7 от р выражена весьма слабо. Форма миниму-
минимума определяется практически исключительно значением параметра
208 Гл. 4- Резонаторы твердотельных лазеров
и не меняется при изменении длины второго плеча резонатора.
Экстремум при р = р' (/ = 0) носит более локальный характер. Его
параметры определяются значением величин do/di и |di|po- Вдали от
экстремумов имеет место либо чрезвычайно резкая зависимость по-
потерь от величины оптической силы ТЛ, либо 7 — 1-
Очевидно, что резонаторы, у которых малые изменения ТЛ при-
приводят к значительным изменениям потерь, неудобны с практической
точки зрения, так как требуют либо больших усилий по стабилизации
оптических характеристик внутрирезонаторных элементов, либо до-
допустимость нестабильности выходных параметров излучения. В свя-
связи с этим подавляющее большинство схем резонаторов твердотельных
лазеров, как с непрерывной накачкой, так и с импульсной, располага-
располагается вблизи экстремумов зависимости ^(р). Поэтому, прежде чем пере-
переходить к рассмотрению алгоритмов построения конкретных схем, ис-
исследуем более подробно условия реализации и характер экстремумов.
Для этого преобразуем уравнение D.14) к виду
s = s0a^Jl - p/fl D.31)
где а = ±1. Условием касания параболы и эллипса в некоторой точке
/ = /i является равенство первых производных в точке касания. По-
Поэтому, приравнивая выражения D.26) и D.31) и дифференцируя это
равенство по /, получим систему двух уравнений, из решения кото-
которой можно найти как положение точки касания Д, так и минимальное
значение потерь, определяемое параметром /о = /оь
D.32)
Л о.. /1
/o2i VI " /iV/o2i
где si определено выражением D.27), Sqi = 1 + /qi-
Рассмотрим вначале случай минимальных потерь. Тогда /i /0 и
решение системы имеет вид
/oi = 2dipo, /i = 2dlP0^/l-s201d20/dl D.33)
Значение параметра устойчивости s = si в данной точке в соответ-
соответствии с формулами D.31)-D.33), равно
-fUSil = 4i IdoM I D.34)
и, следовательно, динамическая стабильность потерь основной моды
резонатора по отношению к флуктуациям ТЛ АЭ возможна в резо-
резонаторах как устойчивой (|si| < 1), так и неустойчивой конфигура-
конфигураций (|si| > 1). Зная /i, легко определить, используя формулы D.28),
4-2. Резонаторы с термооптически возмущенным элементом 209
D.29), значения р = р[, при которых достигается минимум потерь:
D-35)
На практике часто реализуется случай do <С di, 1/ро? тогда
Как следует из рис. 4.8, для того чтобы потери основной моды были не
слишком велики, необходимо подбирать схему резонатора, у которой
diPo <С 1. При этих условиях выражение для минимального значения
потерь 7i, в соответствии с D.15) и D.33), имеет вид
7i = 2/* [y/l + l/f[i ~ l] - 4rfiPo- D-36)
Из этого выражения следует, что минимальные потери 71 определяют-
определяются исключительно величиной апертуры ро и оптической длиной более
длинного плеча d\ и не зависят ни от величины р, ни от парамет-
параметров другого плеча резонатора. Формула D.35) или D.35а) позволяет,
используя D.20), так подобрать величины р\ и р'2, т.е. так подобрать
геометрию плечей резонатора, чтобы обеспечить минимум дифракци-
дифракционных потерь и, тем самым, максимальную стабильность выходных
параметров излучения резонатора при заданной величине оптической
силы ТЛ АЭ рт-
Если разложить в ряд зависимость 7(р) в точке р = р[ и ограни-
ограничиться первым ненулевым членом, то после несложных преобразова-
преобразований можно получить соотношение
17i(I ~7i)
( _
71 V Ро / 32 (l-7i/2)(l-7i+7i2/2)'
Оно показывает, что при данном уровне потерь 71 чувствительность
модовой структуры к флуктуациям ТЛ АЭ пропорциональна ~ р~2 и,
следовательно, ~ П45 где П — характерный размер ограничивающей
апертуры. Следовательно, переход к резонаторам с большим радиу-
радиусом ограничивающей апертуры приводит к резкому увеличению чув-
чувствительности резонатора к величине ТЛ АЭ. Именно поэтому раз-
разработка болынеапертурных стабильных лазерных систем сопряжена
со значительными трудностями. При заданном размере ограничива-
ограничивающей апертуры П переход к динамически стабильным резонаторам с
большими потерями 71 —^ 1 приводит, как это легко видеть из D.37),
к повышению стабильности характеристик. Можно также показать,
что общий размер области малых потерь Api, определяемый условием
— 1 < s < 1, приблизительно равен
±. D.38)
14 В.П. Быков, О.О. Силичев
210 Гл. 4- Резонаторы твердотельных лазеров
Перейдем теперь к изучению поведения потерь основной моды ре-
резонатора вблизи максимума при р = р'. Учитывая, что в данном слу-
случае / = 0 и решая систему уравнений D.32), найдем значение пара-
параметра /о = /02:
Потери в этой точке 72 можно найти по формуле D.36), если вместо
/oi подставить /о2- Подчеркнем еще раз, что параметр устойчивости
|s| = |sO2| = y/l + /q2 > 1 и, следовательно, резонатор соответствует
неустойчивой конфигурации. Величина р, при которой имеет место
максимум потерь, определяется выражением D.30).
Из соотношения D.39) и рис. 4.8 следует, что, варьируя оптиче-
оптическую длину правого плеча do, можно в широких пределах изменять
потери основной моды в резонаторе такого типа. Это обстоятельство,
как будет показано далее, является основой алгоритма построения
динамически стабильных неустойчивых резонаторов.
Для выяснения характерной «ширины» данного экстремума раз-
разложим зависимость ^(р) в ряд в окрестности точки р = р1'. После со-
соответствующих преобразований получим из уравнений D.14), D.15),
D.2б)-D.29) и D.39):
__ _ -4(р - р ) dodlsO2 /o42[B_72)/A72)]- D-40)
Видно, что при фиксированном уровне потерь 72, т.е. при фиксиро-
фиксированных значениях параметров /02 и sq2 •> чувствительность резонатора
к флуктуациям оптической силы ТЛ АЭ слабо зависит от величи-
величины ограничивающей апертуры и целиком определяется оптической
длиной плечей резонатора do, d\. Это коренным образом отличает
неустойчивый резонатор с динамической стабильностью, расположен-
расположенный в области / ~ 0 от резонатора, обеспечивающего минимум потерь
основной моды / ~ /i D.33) и позволяет использовать динамически
стабильные неустойчивые резонаторы в болынеапертурных лазерных
системах.
Наконец, рассмотрим последний случай, когда характер касания
параболы и эллипса таков, что происходит слияние экстремумов в
точках К, Л, М, т. е. образуется один глобальный минимум в зависи-
зависимости j(p). В этом случае, наряду с условиями D.32), вторые и третьи
производные выражений D.26) и D.31) должны быть равны:
9<n27/ ~~ U f2^ f2/f2\3/2' °и^ f4/i f2/f2\5/2 "" ^*
zPo^ JoV1- ~ J / Jo ) Jo\1-~ J / Jo )
Из последнего равенства следует, что касание подобного рода возмож-
возможно лишь при / = 0, что, впрочем, очевидно и из геометрических сооб-
соображений, изложенных ранее (рис. 4.7). Легко видеть, что выполнение
4-3. Резонаторы одномодовых твердотельных лазеров 211
равенств D.41) возможно лишь в случае, когда
si = as0, /о = -2soaplu.
Из этих соотношений получаем необходимые и достаточные условия
глобального экстремума:
J p = pf. D.42)
Потери при этом определяются соотношением D.36). Поскольку |s| =
= So > 1, то резонатор является неустойчивым. Как и резонатор, рас-
рассмотренный в предыдущем варианте, он реализуется при равенстве
нулю оптической длины обхода резонатора, рассчитанной без учета
ограничивающих апертур.
На этом мы закончим общий анализ резонатора, содержащего
внутрирезонаторную линзу. Из проведенного исследования видно, что
при построении схемы резонатора твердотельного лазера надо так
подбирать геометрию, чтобы потери основной моды находились вбли-
вблизи экстремальных значений при изменении ТЛ АЭ. В противном слу-
случае чувствительность резонатора к термооптическим искажениям АЭ
будет излишне большой. Поэтому в последующих параграфах, исхо-
исходя из особенностей режима накачки и задач, которые должен решать
лазер, проведем разработку алгоритмов расчета схем резонаторов, в
которых имеет место экстремум потерь основной моды, т. е. резонато-
резонаторов с динамической стабильностью выходных характеристик.
§ 4.3. Резонаторы одномодовых твердотельных
лазеров с непрерывной накачкой
С точки зрения построения схем резонаторов, одномодовые твер-
твердотельные лазеры целесообразно разделить на три группы. К пер-
первой группе отнесем лазеры, в которых термооптические искажения
АЭ выражены чрезвычайно сильно (рт > B -г 5) дп). Характерными
представителями этой группы являются лазеры с непрерывной на-
накачкой, а также лазеры, работающие с большей частотой следования
импульсов накачки (> 100 Гц).
Ко второй группе отнесем импульсные твердотельные лазеры, в
которых частота следования импульсов накачки не превышает 100 Гц
и рт — @,5 -г- 2) дп. Лазеры, в которых условия накачки таковы, что
Рт ;$ 0,5 дп выделим в третью группу.
Такое разделение на группы оправдано, поскольку каждая группа
лазеров характеризуется вполне определенными типами резонаторов.
В данном параграфе мы рассмотрим особенности построения схем
резонаторов при наличии сильных термооптических искажений АЭ.
Начнем рассмотрение со случая непрерывно накачиваемого лазера
14*
212
Гл. 4- Резонаторы твердотельных лазеров
на АИГ: Nd3+, характерной особенностью которого является наличие
сильного деполяризующего действия термооптически возмущенного
АЭ. Для того чтобы лучше понять влияние деполяризации излучения
на свойства основной моды резонатора, рассмотрим характер искаже-
искажения гауссова пучка, поляризованного вдоль оси х:
Ех = A0exp(-r2/w2])
при прохождении термооптически возмущенного АЭ из АИГ: Nd .
Будем считать, что ось АЭ ориентирована вдоль направления [111]
относительно кристаллографических осей. В соответствии с форму-
формулой D.6) поле после прохождения АЭ будет иметь вид
где
>ф(-фхг2) ^
и $21 — компоненты матрицы S D.7), равные:
s11 = cos ( - Sr2 J + i sin ( - Sr2 ) cos 2cp,
s2i = i sin ( - 5r2 ) sin 2cp.
D.43)
D.44)
Характер искажения гауссова пучка в АЭ иллюстрирует рис. 4.9, а.
Видно, что компонента поля с прежним направлением поляризации
АЭ
НИИ
Рис. 4.9: а) деполяризация гауссова пучка при прохождении термооптиче-
термооптически искаженного АЭ из АИГ: Nd3+
Е'х искажена, степень фокусировки пучка в плоскостях X и Y различ-
различна, т.е. имеет место, отмечаемый нами ранее, астигматизм ТЛ АЭ.
Функция Еу описывает поле с измененной поляризацией. При ра-
работе лазера в одномодовом режиме данная компонента поля почти
4-3. Резонаторы одномодовых твердотельных лазеров 213
целиком уходит в потери, как из-за наличия поляризационных эле-
элементов, так и из-за более высоких дифракционных потерь этой ком-
компоненты. Поэтому величина G = Ру/Ро, где
оо
ko27rJdrr\Ex\
О
= ko27rJdrr\Ex\2, Ру =
показывающая, какая доля мощности падающего излучения Pq деполя-
деполяризуется, приблизительно характеризует увеличение потерь основной
моды из-за деполяризующего действия термооптически возмущенного
АЭ. Используя последние соотношения, а также формулы D.43),
D.44), получаем
1+ [-г
Для АЭ из АИГ: Nd3+ с ориентацией [111], согласно формулам
D.5) S = pr(Q/2P). Поэтому
у wl = (irQ/2P)pr(wl/\) ~ 0,Зрт(^/Л).
В случае (ptWq/XJ <С 1 имеем быстрый рост потерь на деполяриза-
деполяризацию с увеличением размера основной моды в месте расположения АЭ
(~ Wq). Этот вывод, полученный на основе элементарных оценок, пол-
полностью подтверждается результатами расчетов потерь основной моды
резонатора, содержащего деполяризационный элемент, описываемый
матрицей S D.7) [101, 102], выполненных с учетом дифракционных
эффектов. Эти расчеты дают быстрый рост потерь моды с увеличе-
увеличением размера поля на АЭ, приблизительно пропорциональный ~ w$.
При этом деполяризующее действие АЭ несколько ослабляется в резо-
резонаторах, не содержащих поляризаторов, поскольку характер поляри-
поляризации основной моды искажается, становится неоднородным и как бы
подстраивается под характер наведенной неоднородной анизотропии
в АЭ [102] (рис. 4.9, б).
Потери на деполяризацию приводят к тому, что с ростом попе-
поперечного размера основной моды в АЭ происходит развитие двух кон-
конкурирующих процессов. С одной стороны, увеличение коэффициента
заполнения АЭ излучением и рост энергосъема с АЭ ~ Wq, с дру-
другой стороны, рост потерь на деполяризацию ~ Wq. Это приводит к
существованию оптимального значения размера основной моды в АЭ
wonT, при котором мощность одномодовой генерации максимальна. На
практике величина гиОПт зависит от большого количества факторов, в
частности от уровня аберраций ТЛ АЭ. Так, наличие аберраций ТЛ,
которые, как правило, растут при приближении к периферии АЭ, яв-
является дополнительным фактором роста потерь при увеличении wo и,
следовательно, приводят к уменьшению значения г^ОПт- Оценки, про-
214 Гл. 4- Резонаторы твердотельных лазеров
веденные методом теории возмущений, а также опыт практической
работы показывают, что для АЭ из АИГ: Nd3+ с ориентацией [111]
можно использовать приближенное выражение:
^ М-10-у — • D.45)
V Рт
В АЭ из АИГ: Nd3+ с ориентацией [001], как уже ранее отмечалось,
степень деполяризации прошедшего через АЭ излучения зависит от
взаимной ориентации осей АЭ и направления поляризации излучения.
При оптимальной ориентации величина г^ОПт может быть существенно
больше нежели та, что дается формулой D.45). При работе с лазером
на YAIO3: Nd3+ или с любым другим материалом с ярко выражен-
выраженным естественным двулучепреломлением, наведенная деполяризация
практически отсутствует и наличие оптимального значения заполне-
заполнения АЭ излучением основной моды обусловлено либо размером АЭ,
либо уровнем аберраций ТЛ АЭ.
Возвращаясь к формуле D.45), отметим, что величина г^ОПт не свя-
связана непосредственно с радиусом АЭ. Например, при радиусе АЭ R =
= 2,5 мм и рт = 4 дп имеем г^ОПт — 0,7 мм и, следовательно, коэффи-
коэффициент заполнения, при котором достигается максимальная мощность
генерации одномодового излучения (wonT/RJ ~ 0,08, весьма мал.
Таким образом, особенностью мощных одномодовых лазеров на
твердом теле с высоким уровнем термооптических искажений АЭ яв-
является существование оптимального значения поперечного размера
поля в АЭ, не зависящего от размера АЭ и определяемого величи-
величиной и спецификой термооптических искажений АЭ. В большинстве
случаев величина г^опт невелика и составляет не более ~ 1 мм.
Второй особенностью таких лазеров является наличие у ТЛ АЭ
аберраций, в первую очередь, астигматизма. Это приводит к необ-
необходимости либо использовать резонатор с астигматичными оптиче-
оптическими элементами, либо резонатор с такой областью динамической
стабильности, чтобы имеющийся астигматизм ТЛ не приводил к су-
существенному астигматизму характеристик моды.
Наконец, последним существенным моментом, который необхо-
необходимо учитывать при разработке мощных одномодовых лазеров, яв-
является временная нестабильность термооптических искажений АЭ.
Их приближенно можно представить в виде ТЛ с флюктуирую-
флюктуирующей оптической силой и переменного по величине термооптическо-
термооптического клина. Нестабильность искажений АЭ связана со многими фак-
факторами, среди которых можно отметить флуктуации параметров
разряда лампы накачки, турбулентный, нестационарный характер
потока охлаждающей жидкости, вибрации АЭ и проч. Нестабиль-
Нестабильности термооптических искажений носят низкочастотный характер
(< 100 Гц), их величина, как правило, не превосходит 10% от величи-
величины рт [103].
4-3. Резонаторы одномодовых твердотельных лазеров 215
Все перечисленные выше обстоятельства приводят к необходимо-
необходимости использовать в мощных одномодовых лазерах схемы резонато-
резонаторов с динамической стабильностью по отношению к флуктуациям ТЛ
[104—108]. При определенных условиях необходимо также резонатор-
ными методами нейтрализовать влияние переменного термоклина. Ре-
Резонаторы должны, кроме того, обеспечивать заданный размер основ-
основной моды в АЭ и сравнительно небольшие дифракционные потери,
поскольку коэффициент усиления в лазерах с непрерывной накачкой
обычно сравнительно невелик и для подавления мод более высоко-
высокого порядка вполне достаточно потерь в 10-20%. Этим требованиям
отвечают схемы резонаторов с динамической стабильностью и мини-
минимальным уровнем дифракционных потерь основной моды, проанали-
проанализированных в § 4.2. Динамически стабильные неустойчивые резонато-
резонаторы мало пригодны для непрерывно накачиваемых лазеров, так как в
них сложно обеспечить малые дифракционные потери с достаточно
широкой областью динамической стабильности.
Определив оптимальный тип резонатора, перейдем к построению
алгоритма расчета конкретных схем. Для этого, используя форму-
формулы D.16), D.18) и D.20), преобразуем условие образования экстре-
экстремума D.35) к виду, включающему явную связь элементов лучевых
матриц обхода плечей резонатора. Получим:
А2 „ _ , / 1 1
При малых потерях основной моды можно пренебречь влиянием
апертуры на размер основной моды в АЭ w$. В этом случае легко по-
получить приближенное выражение для потерь моды в виде 71 — %Ро/уо,
где г/о = X/ttWq. С другой стороны, согласно формуле D.36), имеем
7i = 2BiPq. Сравнивая эти соотношения, получаем
D.47)
т. е. размер основной моды в АЭ в устойчивых резонаторах с динами-
динамической стабильностью определяется исключительно оптической дли-
длиной более длинного плеча резонатора. В данном случае, в соответ-
соответствии со сделанным ранее предположением, это плечо с В\. Так как
нас интересует случай 71 ^ 15 т0 |l/-^i| ^ Ро- Поэтому в выражении
D.46) можно пренебречь величиной р$ по сравнению с 1/Bf и 1/В% и
преобразовать его к виду
+
Это соотношение было получено в работе [108] как необходимое и
достаточное условие стабильности каустики резонатора с флуктуи-
флуктуирующей линзой. В ней было показано, что при выполнении условия
216 Гл. 4- Резонаторы твердотельных лазеров
D.48) малые изменения оптической силы ТЛ АЭ не приводят к из-
изменению параметров основной моды в плече резонатора с меньшей
оптической длиной, т. е. в плече с оптической длиной 3^ - В плече с
длиной В\ параметры каустики меняются при изменении оптической
силы ТЛ. Поэтому при работе с резонатором данного типа ограни-
ограничивающие апертуры, выходное зеркало и прочие элементы следует
помещать в плечо с меньшей оптической длиной.
Используя соотношение D.37), посмотрим, как изменяется размер
моды АЭ при изменении рт- Для этого отметим, что при малых по-
потерях
7 — 7i
7i ^o
где Awo — изменение перетяжки основной моды. Переходя теперь к
пределу в формуле D.37) при 71 —>- 0 получим
Awo _ 1 / Арт \ 2 2 ( ^^о А 2
wo 4 V рт / V Л /
Из этого выражения следует, что при заданной стабильности ТЛ
(Арт/рт — const) уровень стабильности перетяжки не зависит от па-
параметров схемы динамически стабильного резонатора и определяется
лишь оптической силой ТЛ и размером перетяжки основной моды
на ней.
В лазерах, в которых параметры резонатора не удовлетворяют
условию D.48), стабильность излучения существенно хуже. Это, в
частности, видно из рис. 4.8. Используя D.49), легко также сфор-
сформулировать требования к стабильности термооптических искажений
АЭ, исходя из допустимого уровня флюктуации величины перетяжки
основной моды в АЭ. Например, если исходить из допустимого уров-
уровня флуктуации Awo/wo = 0,1, то для мощного лазера на АИГ: Nd3+
с wo = 1 мм, Л = 1,06 мкм и рт = 4 дп получим, что изменения опти-
оптической силы ТЛ в процессе работы не должны превышать 5%.
Отметим также, что поскольку ширина области устойчивости ре-
резонатора с динамической стабильностью, т. е. ширина минимума на
рис. 4.8 определяется величиной D.38), то с учетом D.47), имеем вы-
выражение для диапазона допустимого изменения Арт max, не приводя-
приводящей к выводу резонатора из области устойчивости:
АрТтах = * = -?* D.50)
\Bi\ ttWq
Это важное соотношение показывает, что чем больше размер пере-
перетяжки основной моды в АЭ, тем меньше область допустимых зна-
значений величины ТЛ АЭ и, следовательно, тем меньше допустимый
диапазон изменения мощности накачки. Оно, очевидно, справедли-
справедливо для резонатора любой устойчивой конфигурации, за исключением
случая, когда экстремумы на рис. 4.8 сливаются в один. Это имеет ме-
4-3. Резонаторы одномодовых твердотельных лазеров
217
сто при выполнении условия D.42), т. е. при \Bi\ « |#2|- В этом случае
диапазон допустимых значений Арттах удваивается.
Рис. 4.10. Преобразование резонатора со сферическими зеркалами (а) к
эквивалентному резонатору с плоскими зеркалами (б)
Рассмотрим теперь более подробно параметры каустики основной
моды в резонаторе с динамической стабильностью. Для этого найдем,
пренебрегая апертурой, лучевую матрицу обхода резонатора, изобра-
изображенного на рис. 4.10 с началом в плоскости А А:
Тогда, в соответствии с правилом нахождения значения комплекс-
комплексного параметра моды резонатора с гауссовыми элементами, найдем
значение кривизны фазового фронта моды на выходе из АЭ при рас-
распространении вправо х = (Do — Aq)/2Bq. Учитывая условие динами-
динамической стабильности D.48) и явный вид элементов матрицы обхода
резонатора можно показать, что
ж = ^1_рт. D.51)
Кривизна фазового фронта после обхода правого плеча резонатора
будет равна + рт, а после прохода АЭ
х' = -^. D.52)
218 Гл. 4- Резонаторы твердотельных лазеров
Учитывая, что поперечный размер основной моды в АЭ опреде-
определяется соотношением D.47), можно найти размер основной моды на
концевых зеркалах. Для этого преобразуем резонатор, изображенный
на рис. 4.10 к виду, в котором концевые зеркала с радиусом кри-
кривизны R заменены на эквивалентные оптические системы, состоя-
состоящие из тонкой линзы с фокусным расстоянием R и плоского зеркала
(рис. 4.10, б). В соответствии с правилом «ABCD» преобразования
гауссовых пучков, размер основной моды на концевых зеркалах опре-
определится соотношениями
w2=w2[(A'2+B'2xJ + (B'2y0J},
где элементы со штрихом обозначают элементы лучевых матриц про-
прохода соответствующих плечей резонатора от АЭ до плоского конце-
концевого зеркала (рис. 4.10, б). Учитывая условие динамической стабиль-
стабильности D.48), а также формулы D.51) и D.52), преобразуем последние
выражения к виду
w2=w2^, wl =ю*2щ[1± у/1-(Bz/Btf]. D.53)
При расчете конкретной схемы резонатора эти соотношения позволя-
позволяют контролировать размер поля на концевых зеркалах. Это важно,
поскольку чрезмерная концентрация излучения на зеркалах может
привести к их пробою.
До настоящего момента при изучении чувствительности резона-
резонатора к термооптическим искажениям АЭ внимание уделялось только
влиянию ТЛ. Однако, как уже отмечалось в §4.1, из-за неоднород-
неоднородности распределения накачки в АЭ в последнем возможно появление
термооптических искажений в виде оптического клина. Это приводит
к повороту всех геометро-оптических лучей, прошедших через АЭ,
на определенный угол /3 и, следовательно, к разъюстировке резона-
резонатора. Поэтому анализ схемы резонатора будет неполный, если мы не
исследуем чувствительность модовой структуры к разъюстировкам
резонаторных элементов.
Ограничимся рассмотрением влияния разъюстировок концевых
зеркал резонатора и термооптического клина АЭ. Для этого преоб-
преобразуем резонатор со сферическими зеркалами к эквивалентному ре-
резонатору с плоскими зеркалами (рис. 4.10, б). Пусть левое и правое
плоские концевые зеркала повернуты соответственно на углы ср± и ср2.
Пусть далее вблизи ТЛ имеется оптический клин, поворачивающий
оптическую ось резонатора на угол /?. Геометрический луч, соответ-
соответствующий оптической оси резонатора, согласно определению оптиче-
оптической оси должен переходить сам в себя при отражении от концевых
зеркал. Поэтому он перпендикулярен отражающей поверхности кон-
концевых зеркал и его координаты на левом и правом зеркалах будут
4-3. Резонаторы одномодовых твердотельных лазеров 219
иметь вид (xi,(^i) и (х2,Ц>2)- Очевидно, что эти координаты связаны
соотношением (рис. 4.10, б):
где столбец @, /3) описывает действие оптического клина. Решая си-
систему уравнений D.54) относительно неизвестных величин х\ и Ж2,
находим для х\\
xi = 1 {-^2 - MA'iD'2 + С'2В[ - D'2B[pT) - /Ш2}, D.55)
где Ъ — C[D'2 + C'2D'1 — ptD[D'2. Положение оси резонатора в месте
расположения АЭ определяется соотношением
'хо\ _ {D[ В'Л /V
) { ) [
D.56)
откуда следует, с учетом D.55), что
D[ D'2 D[Df2
о Ч2 Ч\ /
с с с
Чувствительность резонатора к разъюстировке того или иного эле-
элемента разумно характеризовать коэффициентом sr, равным отно-
отношению отклонения оптической оси резонатора к размеру перетяжки
основной моды при разъюстировке данного элемента на единичный
угол, при условии идеальной юстировки остальных элементов резо-
резонатора [109-111]. Тогда для концевых зеркал и оптического клина, в
соответствии с D.56) имеем
<Р1=C=0 С
D.57)
D[Df2
pWo (p1=(p2=0 С
Общую чувствительность резонатора к малым разъюстировкам
элементов можно характеризовать коэффициентом
Теперь у нас имеется все необходимое для перехода к построению
конкретных резонаторных схем и их сравнительного анализа. В на-
начале настоящего параграфа мы показали, что оптимальное значение
размера основной моды в АЭ составляет величину 1 мм. Как следует
из формулы D.47), это приводит к необходимости использовать схе-
схемы резонаторов, у которых оптическая длина одного плеча должна
быть достаточно велика \Bi\ = ttw^/X ^Зм. Поэтому при построе-
построении этого плеча целесообразно использовать такие оптические схемы,
которые обеспечивают повышенную оптическую длину при сохране-
220
Гл. 4- Резонаторы твердотельных лазеров
нии умеренной геометрической длины. Простейшим примером такой
схемы может служить схема левого плеча резонатора, изображенного
на рис. 4.11 [104]. В этом случае
ВЛ _ (I - 2а/R 2а - 2а2/R>
) -2/R \-2ajR
D.59)
и при R < 0 В\ может быть значительно больше а.
Плечо с меньшей оптической длиной обычно делают простейше-
простейшего вида (рис. 4.11). Напомним, что стабилизация каустики при этом
происходит в плече с меньшей оптической длиной, поэтому в качестве
выходного зеркала следует использовать правое плоское зеркало. Там
же следует располагать ограничивающую апертуру.
2W0
2W2
2Wi
R
Рис. 4.11. Одномодовый резонатор с плоским и выпуклым зеркалами. За-
Зависимость параметров динамически стабильного резонатора с выпуклым
зеркалом (рис. 4.11) от длины
Данная схема характеризуется четырьмя параметрами рт, d, аи
R. Поскольку величина рт определяется средним уровнем накачки
АЭ, то ее можно считать изначально заданной. Остается три сво-
свободных параметра. При расчете схемы следует удовлетворять двум
условиям. Первое — это условие динамической стабильности схемы
D.48), второе — обеспечение заданного размера основной моды в ме-
месте расположения АЭ, определяемого либо соотношением D.47), либо
радиусом АЭ. Поэтому в схеме, изображенной на рис. 4.11, реально
имеется лишь один свободный параметр. Возьмем в качестве такого
свободного параметра длину правого плеча резонатора d. При этом
значения остальных параметров резонатора определяются однознач-
однозначно, как функции величин <i, w$ и рт-
Из формулы D.47) имеем: 2
В, = —. D.60)
Из условия стабильности D.48), с учетом D.59) и того, что А2 = 1,
В2 = 2d, получаем выражение для
D.61)
где а = =Ы. Поскольку на практике наибольший интерес представляют
компактные схемы резонаторов, то можно предположить, что d <С
<С \Bi\. Кроме того, как выяснится чуть позже, предпочтение следует
4-3. Резонаторы одномодовых твердотельных лазеров 221
отдать схемам с а = +1. При этих условиях последнее выражение
преобразуется к виду g
а- ч , * р - D.61а)
1+рВ
Зная а и явный вид элемента лучевой матрицы D.59) ??i, легко найти
величину / пЛ \-1
* (?)
?) D.62)
которая при условии d <С |??i| равна
^ D.62а)
Формулы D.60)-D.62) позволяют рассчитать динамически ста-
стабильную схему резонатора исходя из заданных значений wq, рт и d.
Однако при расчете схемы и при решении вопроса об ее использова-
использовании в одномодовом лазере следует учитывать размер поля на зерка-
зеркалах резонатора, чтобы избежать чрезмерной фокусировки излучения
на них и их разрушения в мощном лазере. Кроме того, следует учи-
учитывать чувствительность резонатора к возможным разъюстировкам
резонаторных элементов.
Используя формулы D.53), а также явный вид лучевых матриц
прохода плечей резонатора, изображенного на рис. 4.11, имеем выра-
выражения для размера основной моды на концевых зеркалах:
wi = ——- = ^ , w2 = _ 1 + сн/1_ _ . D.63)
л/2 |^i| тг^о л/2 L V \ВХ) \
Из последнего соотношения следует, что при а — — \ ж d <^\В\\
имеется сильная фокусировка излучения на плоском выходном зер-
зеркале. Это нежелательно как с точки зрения расходимости выходного
излучения, так и с точки зрения конечной стойкости зеркал к мощно-
мощному лазерному излучению. Поэтому следует выбирать схемы с а = 1.
Тогда при условии d ^C |#i|, выражения D.63) преобразуются к виду
fe W2^W0- D-63а)
Из формулы для размера основной моды на выпуклом зеркале
D.63) следует, что, используя выпуклое зеркало вместо плоского и по-
получая выигрыш в оптической длине левого плеча резонатора по срав-
сравнению с его геометрической длиной в (\Bi\/2a) раза, мы во столько
же раз уменьшаем размер перетяжки на концевом зеркале и, следо-
следовательно, увеличиваем плотность мощности на выпуклом зеркале по
сравнению с плотностью мощности в АЭ. Из формул D.60) и D.63а)
видно, что в случае сильной TJ1 при значительном размере основной
моды в АЭ величина В\рт > 1и возможности использования данной
схемы сужаются, так как имеет место сильная фокусировка излуче-
излучения на выпуклом зеркале. Это обстоятельство следует учитывать при
выборе схемы резонатора.
222
Гл. 4- Резонаторы твердотельных лазеров
Чувствительность резонатора к возможным разъюстировкам плос-
плоского выходного зеркала sr2 и переменному термооптическому клину
в АЭ SRp определяется формулами D.57), которые для данной схемы
резонатора (рис. 4.11) преобразуются к виду
1
= -sRe = —
R-a
wo 1 -\- pt{R — a)
или, с учетом d <C B\ и В\рт >1к виду
— _ ~ ^^0
Л
D.64)
D.64а)
Чувствительность резонатора к разъюстировкам выпуклого зер-
зеркала равна
D.65)
1
R
или приближенно
1 wo I + pr(R — а)
2
sRl ~
D.65а)
На рис. 4.12 приведены зависимости параметров схем резонатора
а (м) 1/R (дп)
-10
1
0,8
0,6
0,4
0,2
^^ 1
4
X,
X
X
-----
— —
х
х
X
-----
-6
-4
-2
0 0,5 d (м)
Рис. 4.12. Зависимость параметров резонатора, изображенного на рис. 4.11,
при условии динамической стабильности его характеристик
от величины свободного параметра d — длины плеча резонатора с
плоским зеркалом. Эти зависимости позволяют более осознанно про-
производить выбор значения d.
Заканчивая рассмотрение данной схемы резонатора, приведем
пример расчета резонатора мощного лазера на АИГ: Nd3+ с опти-
4-3. Резонаторы одномодовых твердотельных лазеров
223
ческой силой ТЛ рт = 4 дп. Из D.45) имеем г^ОПт — 0,7 мм, далее
из D.60) следует, что В\ = 1,45 м. Положим d = 0,1 м, тогда из
формул D.61) (а = 1) и D.62) получаем а = 0,22 м, R = -0,1 м. В
этом случае w^ = 0,7 мм и i^i = 0,15 мм, т.е. имеет место достаточно
сильная фокусировка на заднем зеркале. Чувствительность к разъ-
юстировкам равна sr2 = — srp = 2 • 103 рад и sr± = 0,7 • 103 рад,
что, в частности, означает, что разъюстировка сферического зеркала
на 1 мрад приведет к смещению оси резонатора в АЭ на величину
sr1'Wo = 0,5 мм.
Рассмотренная схема получила достаточно широкое распростра-
распространение на практике. Однако она обладает одним недостатком, кото-
который при определенных условиях может играть весьма существенную
роль. А именно, она не обеспечивает стабилизацию выходных харак-
характеристик излучения при наличии флуктуирующего термооптического
клина в АЭ. При большой мощности накачки в АЭ может возникать
термооптический клин с /3 ~ 1 мрад. Это приводит к значительным
флуктуациям положения оптической оси резонатора и, следователь-
следовательно, к изменению мощности генерации, пространственных характе-
характеристик выходного излучения. Поэтому в таких случаях необходимо
использовать схемы резона-
r Wt Wn Wo
торов, обеспечивающие ста- VV1 ° 2
билизацию положения оп-
оптической оси резонатора в
плече, содержащем ограни-
ограничивающие апертуры и вы-
выходное зеркало [85, 108].
Из формулы D.64) сле-
следует, что это возможно при
R = а. В этом случае sr^ =
= 0 и изменение величины
рт R
Рис. 4.13. Схема резонатора, нечувстви-
нечувствительного к величине термооптического кли-
клина в АЭ
термоклина не приводит к изменению положения оптической оси в
месте расположения АЭ и, следовательно, к изменению простран-
пространственных и энергетических параметров выходного излучения. Однако
при этом оптическая длина плеча резонатора, содержащего сфериче-
сферическое зеркало, как следует из D.59), будет равна нулю. Так как мы
полагали, что \Bi\ > \B2\j то для того, чтобы сохранить прежние обо-
обозначения, будем считать, что лучевая матрица обхода левого плеча
резонатора (рис. 4.13) имеет вид
2d
0 1
а правого плеча, с учетом формулы D.59) и условия R = а:
Л
D.66)
224 Гл. 4- Резонаторы твердотельных лазеров
Тогда, в соответствии с выражением D.47), из D.66) следует, что
2
а = -^pr-j D.68)
а условие динамической стабильности принимает вид
R= Т7^7- D-69)
рт — l/2d
При этом стоит подчеркнуть, что при R = a, D'2 = 0 и, как следует
из D.55) изменение величины термооптического клина не приводит к
изменению положения оптической оси в левом плече резонатора, т. е.
в плече с большей оптической длиной, в то время как положение оси
в правом плече меняется (рис. 4.13). Стабилизация же поперечного
размера основной моды происходит, как отмечалось ранее, в плече с
меньшей оптической длиной, т. е. в данном случае в правом плече. В
плече с плоским выходным зеркалом происходит изменение попереч-
поперечного размера основной моды при флуктуациях оптической силы ТЛ
АЭ, но зато имеет место стабилизация положения оси резонатора.
Из выражений D.53) легко найти размер поля на зеркалах:
W! = ^, w2 = ол^° ,. D.70)
Чувствительность к разьюстировкам зеркал согласно формулам
D.57), определяется соотношениями
S = ° S = D71)
Приведем в качестве примера расчет схемы резонатора для случая
рт = 4 дп и wo =0,7 мм, т. е. для тех же условий, при которых рассчи-
^ тывалась предыдущая схе-
d Д a = R/2 ^ ма< Из D.68) имеем d =
= 0,73 м, из D.69) - R =
= 0,3 м. При этом из D.70) и
D.71) получаем w\ ~ 0,5 мм,
w2 = 0,15 мм, sRl = sRE =
R = 0 и sR2 = 0,3 • 103 рад.
Сравнивая эти данные с па-
параметрами схемы резонато-
Рис. 4.14 Схема одномодового динами- содержащего выпуклое
чески стабильного трехзеркального резо-
^ ^ ^ зеркало, видно, что схема с
натора „ ^
К = а обладает существенно
более низкой чувствительностью к возможным разъюстировкам эле-
элементов резонатора, но является существенно более длинной.
Весьма широкое распространение, особенно в лазерах с внутри-
резонаторной генерацией второй гармоники, получила схема резо-
резонатора, изображенная на рис. 4.14 [112]. Соответствующим подбо-
подбором элементов данной схемы добиваются ее эквивалентности схеме
4-3. Резонаторы одномодовых твердотельных лазеров 225
на рис. 4.13. Введение еще одного дополнительного свободного пара-
параметра Ъ — расстояния между сферическим и плоским зеркалами —
позволяет избавиться от однозначного определения радиуса кривиз-
кривизны сферического зеркала. Это удобно с практической точки зрения,
так как позволяет использовать сферические зеркала с имеющейся
кривизной.
Не останавливаясь подробно на анализе этой схемы, поскольку он
вполне аналогичен предыдущему, приведем лишь итоговые формулы
для расчета параметров схемы резонатора, исходя из заданного ради-
радиуса кривизны сферического зеркала R:
R , К(Л R . R\ , ttwI (л _о.
а=Г ^Т^-^Т + й)' d=lT D-72)
Размеры основной моды на концевых зеркалах определены соотноше-
соотношениями
wo R ,л ^оЧ
= sRf3 = 0, sR2 = —. D.74)
Чувствительность к разъюстировкам —
—.
Дополнительным преимуществом данной схемы по сравнению с
предыдущей является возможность простой ее перестройки к новым
значениям входных параметров р^ишо, путем изменения Ъ. Кроме то-
того, в данной схеме заложена возможность компенсации астигматизма
ТЛ АЭ за счет того, что при отражении поля от сферического зеркала
с радиусом кривизны R под углом в к нормали (рис. 4.14) эффектив-
эффективный радиус кривизны сферического зеркала в плоскости рисунка и в
перпендикулярной плоскости различен и равен соответственно Дц =
= RcosO и R± = R/ cosO. Полагая, что оптическая сила ТЛ АЭ раз-
различна в этих взаимноперпендикулярных плоскостях и равна соответ-
соответственно рц и р±, можно, путем подбора угла в, добиться того, чтобы
поперечная структура основной моды в АЭ и в левом плече резона-
резонатора была бы осесимметричной, а схема резонатора — динамически
стабильной.
Очевидно, что все многообразие схем резонаторов, используемых в
мощных одномодовых твердотельных лазерах, не исчерпывается вы-
вышеприведенными схемами. Однако проведенный анализ показал, что
какая бы конкретная реализация схемы резонатора не была бы, она
должна быть динамически стабильной или находиться вблизи точ-
точки динамической стабильности, определяемой соотношением D.48).
Следовательно, расчет схемы будет вполне аналогичен тому, как это
было сделано в данном параграфе. В каждой конкретной ситуации по-
появление тех или иных дополнительных соображений будет приводить
лишь к изменению явного вида элементов соответствующих лучевых
матриц.
15 В.П. Быков, О.О. Силичев
226 Гл. 4- Резонаторы твердотельных лазеров
В заключение данного рассмотрения отметим, что в процессе ра-
работы мощного твердотельного лазера имеет место зависимость ве-
величины оптической силы ТЛ АЭ [ИЗ] или ТЛ какого-либо другого
внутрирезонаторного элемента, например нелинейного [114], от мощ-
мощности генерации. Этот эффект может быть связан как с поглощением
доли мощности генерируемого излучения в элементе, так и с измене-
изменением теплового режима работы АЭ при наличии генерации. Подоб-
Подобные эффекты приводят к тому, что параметры резонатора, опреде-
определяющие мощность генерации, сами начинают зависеть от последней.
Такое «самовоздействие» может довольно сильно влиять, в силу высо-
высокой чувствительности резонатора одномодового лазера к термоопти-
термооптическим искажениям элементов, на параметры выходного излучения.
Приводить к эффектам гистерезисного типа в зависимости выходных
параметров излучения лазера от мощности накачки [114, 115]. При
этом следует подчеркнуть, что и в этом случае использование схем
с динамической стабильностью дает ослабление действия подобных
механизмов.
§ 4.4. Устойчивые резонаторы одномодовых
твердотельных лазеров с импульсной накачкой
Лазеры с импульсно-периодической накачкой характеризуются,
как правило, меньшей величиной термооптических искажений АЭ
(рт ^ 2 дп) и более высокой плотностью мощности излучения, нежели
лазеры с непрерывной накачкой. Эти особенности имеют существен-
существенное значение при разработке схемы резонатора. Во-первых, умерен-
умеренный уровень термооптических искажений АЭ приводит к тому, что
оптимальный размер основной моды в АЭ определяется не величиной
наведенной анизотропии или аберрациями АЭ, а поперечным разме-
размером АЭ wo ~ @,5 -г- 0,7)До- Поскольку обычно радиус АЭ До > 2,5 мм,
то оптимальный размер перетяжки основной моды wo > 1,5 мм, что
существенно больше, чем в резонаторах с высоким уровнем термо-
термооптических искажений АЭ. Таким образом, резонатор твердотельно-
твердотельного лазера с импульсной накачкой должен обеспечивать сравнительно
большой размер основной моды в АЭ. Во-вторых, необходимо избегать
сильной фокусировки излучения на внутрирезонаторных элементах, в
частности на зеркалах. Это связано с высокой пиковой мощностью из-
излучения импульсных лазеров, особенно работающих в режиме генера-
генерации гигантских импульсов и конечной лучевой стойкостью оптических
элементов. Поэтому при построении схемы резонатора, с учетом тре-
требуемых мощностных характеристик лазера, приходится вводить огра-
ограничения на предельно допустимый размер перетяжки основной моды
на элементах резонатора. Так, если предельно допустимая плотность
мощности излучения, определяемая лучевой стойкостью элементов,
44- Устойчивые резонаторы одномодовых твердотельных лазеров 227
равна РПр, а расчетная пиковая мощность импульса излучения Ри =
= Е/тИ, где Е — энергия, а ти — длительность импульса генерации, то
предельно допустимый размер поля на элементе должен быть больше:
D.75)
Например, при Рпр = 1,0 гвт/см2, Е = 0,1 Дж и ти = 20 не имеем
wnp — 0,35 мм. Если сравнить эту величину со значением перетяжки
на зеркалах в схемах, рассмотренных в § 4.3, то станет ясно, что про-
проанализированные схемы мало пригодны для импульсных лазеров, так
как характеризуются сильной фокусировкой излучения на одном из
зеркал.
С целью выделения пригодных типов резонаторов для одномодо-
одномодовых импульсных лазеров вернемся к рис. 4.8. Импульсно-периодиче-
ский характер накачки, определяющий достаточно высокий уровень
термооптических искажений АЭ, в сочетании со сравнительно боль-
большим размером основной моды в АЭ и, следовательно, с высокой чув-
чувствительностью моды к оптическим неоднородностям в АЭ приводит
к необходимости использовать схемы резонаторов, обладающих дина-
динамической стабильностью своих характеристик при малых изменениях
ТЛ АЭ. В противном случае, как видно из рис. 4.8, мы будем иметь
либо схему резонатора чрезвычайно чувствительную к различного ро-
рода флуктуациям оптических свойств внутрирезонаторных элементов,
либо потери основной моды будут очень большие. Оба эти варианта,
как правило, малопригодны.
Поэтому остановимся на схемах резонаторов с динамической ста-
стабильностью энергетических характеристик. При этом, как видно из
рис. 4.8, имеется две возможности. Во-первых, использовать неустой-
неустойчивые резонаторы (р = р', см. формулу D.30)). Во-вторых, динамиче-
динамически стабильные резонаторы, определяемые условием D.46) или D.48).
Оба эти варианта нашли широкое распространение при построе-
построении схем резонаторов импульсных одномодовых лазеров. Резонаторы
неустойчивой конфигурации, отличающиеся компактностью и просто-
простотой конструкции, мы подробно рассмотрим в §4.5.
Сейчас же проанализируем алгоритм построения резонатора им-
импульсного лазера, для которого выполняется условие D.48), и кото-
который выгодно отличается от неустойчивых схем существенно более ши-
широкой областью динамической стабильности при изменении ТЛ АЭ.
Особенно сильно это проявляется при не слишком больших потерях
основной моды 7 ;$ 0,4 (рис. 4.8). Анализ проведем с учетом вышепе-
вышеперечисленных особенностей импульсного режима работы лазера.
Как уже стало ясно из примеров, рассмотренных в § 4.3, в резо-
резонаторах подобного типа имеется противоречие между требованием
большого размера основной моды в АЭ wo и недопустимостью фо-
фокусировки излучения на резонаторных элементах. Действительно, в
15*
228 Гл. 4- Резонаторы твердотельных лазеров
соответствии с формулой D.47) значительный размер основной мо-
моды в АЭ может быть достигнут лишь за счет большой оптической
длины, по крайней мере, одного плеча резонатора (В\). Это, в свою
очередь, требует применения в данном плече оптической системы, эф-
эффективно увеличивающей оптическую длину по сравнению с геомет-
геометрической, что возможно лишь за счет соответствующей фокусиров-
фокусировки, т. е. уменьшения поперечного размера поля на концевом зеркале.
Поэтому при построении резонатора подобного типа, в случае им-
импульсного лазера, всегда приходится исходить из компромисса между
требованием эффективного заполнения излучением АЭ, т.е. большой
перетяжки основной моды в АЭ, и фокусировкой поля на зеркале в
плече с большой оптической длиной (w\ > ^Пр)- Последняя величина
определяет допустимый уровень пиковой мощности излучения лазе-
лазера D.75). В случае, когда подобный компромисс, в силу имеющихся
условий, может быть достигнут, данные схемы весьма эффективны
в лазерах с импульсной накачкой, так как обеспечивают высокое ка-
качество поперечной структуры выходного излучения, стабильность его
энергетических и пространственных характеристик. В противном слу-
случае следует применять схемы динамически стабильных неустойчивых
резонаторов.
Перейдем к рассмотрению конкретных схем резонаторов. Внача-
Вначале коротко обсудим возможность использования схемы резонатора,
содержащей одно выпуклое зеркало и изображенной на рис. 4.11.
Поскольку wo ~ i?o, то с учетом D.47), имеем обычно \Bi\ ^> d и
формулы D.61а) и D.62а) дают параметры резонатора с достаточной
точностью. Возможность использования данной схемы определяется
условием w\ > г^пр, которое, с учетом выражений D.47) и D.63а), сво-
сводится к виду \ , /к
Рт < Ртпр = 11. D.76)
При выборе длины правого плеча следует руководствоваться кон-
конструктивными соображениями и требованием, чтобы d ^ \В\\. Фор-
Формулы D.61а), D.62а) и D.63а) дают всю необходимую информацию
как для решения вопроса о целесообразности использования данной
схемы, так и для ее расчета.
Рассмотрим в качестве примера задачу построения схемы резона-
резонатора твердотельного импульсного лазера с Ro = 2,5 мм и рт = 0,5 дп,
работающего в режиме модулированной добротности с Е = 0,1 Дж.
Пусть резонатор должен обеспечивать, в соответствии с этими усло-
условиями, wo = 1,3 мм и wnp — 0,3 мм. Из выражения D.76) следует,
что в резонаторе с выпуклым зеркалом это можно обеспечить при
условии рт < 0,7 дп. Поскольку в нашем случае рт = 0,5 дп, то это
условие соблюдено и из формул D.61а) и D.62а) имеем а = 0,85 м, R =
= —0,43 м. Длину правого плеча положим равной d = 0,l м < В\. Об-
Общая геометрическая длина рассчитанного нами резонатора составляет
около 1 м.
44- Устойчивые резонаторы одномодовых твердотельных лазеров 229
-* b >
т
V A
Л f
У
/l /2
рТ
¦« ь
*¦
Ь'
>
-/2
о'-
•У
рт
Ъ'
Mo pfT=pT+p0
в
Рис. 4.15. Одномодовый динамически стабильный резонатор с внутренним
телескопом
С целью расширения диапазона применимости резонаторов данно-
данного типа часто схему плеча с большей оптической длиной делают более
сложной, например, состоящей из двух сферических зеркал, алгоритм
расчета которой изложен в работе [116], или включающей телескоп
(рис. 4.15 [117]). Схемы резонаторов, содержащих телескоп, нашли
достаточно широкое распространение, и потому мы проанализируем
их более подробно.
Выпишем лучевую матрицу телескопа Т при прохождении слева
направо (рис. 4.15)
DJ7)
где L — расстояние между линзами телескопа, а Д и /2 — фокусные
расстояния линз.
Введем коэффициент увеличения телескопа Mq = —/2//1 и пред-
представим L в виде L = /i + /2 + S. Тогда лучевую матрицу можно пре-
преобразовать к виду [117]:
Мт =
Mo
О
О W 1
1/MoJ l-P
О
-Л
1
где р0 = ?//1 • Последнее выражение означает, что телескопическую
систему Т, имеющую рассогласование ?, можно представить в виде по-
последовательно расположенного участка свободного пространства дли-
230 Гл. 4- Резонаторы твердотельных лазеров
ной —/i, линзы с фокусным расстоянием р0, тонкого преобразователя
с увеличением Mq и участка свободного пространства длиной —/2 < 0.
Тем самым первоначальная схема резонатора преобразуется к эквива-
эквивалентному виду на рис. 4.15, б. С целью упрощения последующих со-
соотношений положим a — j^- Как следует из результатов работы [117],
использование значений а ф /2 не дает преимуществ в свойствах ре-
резонатора, но усложняет его анализ.
Если а = /2, то а' = а — /2 = 0. Следовательно, исследуемый резо-
резонатор эквивалентен резонатору, изображенному на рис. 4.15, в с р'Т =
= рт + Ро • Лучевые матрицы прохода и обхода левого плеча резона-
резонатора соответственно равны:
А[ В'Л_A/М0 Ъ'М0\ (Аг ВЛ _ (\ 2&'М02\
С[ D[) '{О Мо ) ' [а А,) ~ [О 1 ) ¦ D78)
Используя данные выражения, а также формулу D.53), получаем
значение перетяжки основной моды на левом плоском зеркале
Wo
W\ = —= ,
л/2М0
реализуемое в случае, если резонатор обладает динамической стабиль-
стабильностью. Если исходить из требуемой величины размера основной мо-
моды в АЭ wo и допустимого размера поля на плоском зеркале wi, то
последнее соотношение позволяет определить требуемое увеличение
внутрирезонаторного телескопа:
Поскольку величина w$ определяется, согласно D.47), оптической
длиной левого плеча В\ — 2Ъ'М$, следовательно (рис. 4.15):
D.80)
Наконец, используя условие динамической стабильности D.48) с
а = 1 (напомним, что в данном случае следует выбрать схему резона-
резонатора, соответствующую знаку « + » перед корнем в формуле D.48), так
как в этом случае UJ2 & с^о, в случае же знака « —» имеет место силь-
сильная фокусировка излучения на правом плоском зеркале, UJ2 <С cjo)?
учитывая, что А2 = 1 и ??2 = 2d <С ??i, получаем:
JL-p'T~-A-. D.81)
Принимая во внимание, что р'т = рт + р0 и явные выражения для
р0, В\ и Ai, преобразуем выражение D.81) к виду
S = fl\^(l + ^)-pT]. D.82)
44- Устойчивые резонаторы одномодовых твердотельных лазеров 231
Последнее выражение определяет требуемое значение рассогласова-
рассогласования телескопа ?, обеспечивающее при заданных значениях wo, рт и
d <С 7twI/2X динамическую стабильность резонатора.
Используя формулы D.57) и D.78), получаем выражения для
чувствительности резонатора с внутрирезонаторным телескопом к
разъюстировкам зеркал и к появлению термоклина в АЭ:
sr9 = — srr = , sr, = — . D.83)
П2 П(В woPt г Mowopr v J
Видно, что критичность к юстировке левого плоского зеркала (рис. 4.15)
существенно понижена.
Формулы D.79), D.80) и D.82) позволяют полностью рассчитать
схему резонатора с телескопом и с динамической стабильностью па-
параметров. Проиллюстрируем данный алгоритм на примере расчета
резонатора, который должен обеспечивать wo = 2 мм и w\ = 0,4 мм.
Будем полагать, что имеется отрицательная линза телескопа с Д =
= -0,05 м. Тогда, используя D.79), находим Мо = 3,5 , из D.80) — Ъ =
= 0,46 м. Полагая d = 0,1 м и рт = 1 дп, из D.82) получаем требуемое
рассогласование телескопа S = —0,03 м. Далее, учитывая, что /2 =
— |^o/i| = 0,175 м, имеем а = /2 = 0,175 м. Чувствительность данной
схемы к разъюстировкам характеризуется величинами sr2 = — srp =
= 0,5 • 103 рад и sRl = 0,14 • 103 рад D.83). Тем самым расчет
резонатора закончен.
Схемы с внутрирезонаторным телескопом достаточно хорошо за-
зарекомендовали себя на практике и потому используются достаточно
часто. Естественно, возможно дальнейшее усложнение схемы путем
введения дополнительных линз или использования сферических зер-
зеркал, что позволяет обеспечить дополнительные возможности схемы.
Не будем останавливаться более на конкретных схемах, поскольку их
синтез и методика расчета тождественна предыдущим и достаточно
очевидна. Отметим лишь одну весьма важную деталь. Все динамиче-
динамически стабильные устойчивые резонаторы, применяемые в импульсных
лазерах, близки по своим свойствам к конфокальному. Для того что-
чтобы убедиться в этом, найдем лучевую матрицу обхода левого плеча
резонатора, включая АЭ. Легко показать, что диагональные элемен-
элементы этой матрицы с учетом D.81) равны
А = А1-РтВ1 ~-
Для d = 0,1 м и wig - 2 мм величина djB\ ~ 10~2 и, следовательно,
А ~ 0. Пренебрегая длиной правого плеча, получаем, что динамиче-
динамически стабильный резонатор с большой точностью можно считать кон-
конфокальным.
Поскольку конфокальный резонатор обладает высокой селектив-
селективностью, достаточно обеспечить сравнительно небольшие потери основ-
основной моды G < 0,1 -г- 0,2) для подавления мод более высокого порядка.
232 Гл. 4- Резонаторы твердотельных лазеров
Именно малость дифракционных потерь основной моды, необходи-
необходимых для обеспечения одномодового характера генерации, позволяет
в условии стабильности D.48) пренебрегать величиной ро? так как
PqBi ~ 7/2 и> следовательно, р0 < l/|#i| < 1/Дг.
В случае, когда ограничивающая апертура не является гауссовой и
ее края резко очерчены, для нахождения параметров модовой струк-
структуры (потери, расходимость, поперечная структура и т.д.) устойчи-
устойчивых динамически стабильных резонаторов импульсных лазеров мож-
можно использовать результаты, полученные в § 2.4 для конфокального
резонатора. При этом следует иметь в виду, что если ограничивающей
апертурой является апертура АЭ, то число Френеля Д^ф
= (RO/WO)A/7T).
§ 4.5. Резонаторы одномодовых лазеров
неустойчивой конфигурации
Основным недостатком устойчивых схем с динамической стабиль-
стабильностью, с точки зрения их использования в импульсных твердотель-
твердотельных лазерах, является необходимость иметь, по крайней мере, одно
плечо резонатора большой оптической длины
Построение же компактной оптической системы большой оптической
длины, как было показано в предыдущих параграфах, связано с опре-
определенными трудностями. В частности, в таких оптических системах
имеет место сильная фокусировка излучения на концевом зеркале.
Когда подобные явления становятся трудно преодолимыми, напри-
например, при wo > 2 мм или при работе лазера с очень высокой пиковой
мощностью, целесообразно использовать схемы резонаторов неустой-
неустойчивой конфигурации. В этом случае, как следует из рис. 4.10, воз-
возможно использование достаточно компактных схем с
Bl<\ Г'
т. е. с малой оптической длиной наиболее длинного плеча резонатора
\В\\ > |_Вз| и достаточно высокими дифракционными потерями, обес-
обеспечивающими подавление мод более высокого порядка.
Прежде чем приступить к построению алгоритма расчета схемы
неустойчивого резонатора, следует сделать одно весьма существенное
замечание. Весь ранее проведенный анализ выполнен в предположе-
предположении, что апертура, ограничивающая поперечные размеры излучения в
резонаторе, обладает идеально сглаженным краем, т. е. является гаус-
гауссовой апертурой. При этом оказывалось, что при расчете конкретных
4-5. Резонаторы одномодовых лазеров 233
резонаторов характер ограничивающей апертуру, не имеет существен-
существенного значения, так как параметры основной моды определялись почти
исключительно геометрией резонатора. Это объясняется сравнитель-
сравнительно небольшими дифракционными потерями основной моды в рассмот-
рассмотренных схемах устойчивых резонаторов.
В резонаторах неустойчивой конфигурации — ситуация иная, по-
потери основной моды должны быть существенны. В противном случае
их использование нецелесообразно (рис. 4.8). Высокие потери основ-
основной моды достигаются лишь тогда, когда амплитуда поля на грани-
границе апертуры сравнительно велика. Поэтому характер границы апер-
апертуры может играть весьма существенную роль при анализе модовой
структуры неустойчивого резонатора. Существует обширная литера-
литература [10], в которой исследовались эффекты, связанные с рассеянием
поля моды на границе апертуры в неустойчивом резонаторе, влияние
этого рассеяния на структуру и потери основной моды. Было показа-
показано, что специфика границы играет существенную роль.
В целом итог этих исследований сводится к следующему [10, 118].
В случае, когда граница ограничивающей апертуры очерчена резко и
расположена симметрично относительно оптической оси моды, рассе-
рассеивание основной моды на границе происходит на значительные углы,
волны рассеивания от различных участков границы имеют одинако-
одинаковую фазу и при интерференции усиливают друг друга. Это приводит
к тому, что структура излучения неустойчивого резонатора в этом
случае имеет весьма сложный вид. Поперечная структура излучения
изрезана, имеет место вырождение поперечных мод различного по-
порядка по потерям. Все это приводит к низкому качеству поперечной
структуры выходного излучения.
Размытие края апертуры или наличие осевой асимметрии приво-
приводят к резкому уменьшению влияния волны рассеивания. Попереч-
Поперечная структура основной моды становится сглаженной, вырождение
поперечных мод по потерям снимается, что приводит к одномодово-
му характеру выходного излучения. Качество поперечной структу-
структуры излучения резко возрастает. Особенно ярко это проявляются в
неустойчивых резонаторах с не слишком малыми дифракционными
потерями и большими числами Френеля
(как было отмечено в начале этого параграфа, именно при этих усло-
условиях разумно при разработке одномодового резонатора твердотель-
твердотельного лазера переходить от динамически стабильных устойчивых схем
резонаторов к неустойчивым). В данном случае [119, 120] необходимая
степень сглаживания имеет место на практике даже без дополнитель-
дополнительных усилий, так как имеется естественная неровность края апертуры,
небольшая разъюстировка оптических элементов резонатора, наличие
фасок на краях зеркал и проч. С целью увеличения степени сглажива-
234 Гл. 4- Резонаторы твердотельных лазеров
ния и достижения за счет этого высокого качества поперечной струк-
структуры выходного излучения предложено великое множество способов
получения апертур со сглаженным краем [121—127]. Использование
апертур с частично или полностью сглаженным краем в последнее
время нашли повсеместное распространение.
Поэтому, исходя из данной картины явления, можно сделать вы-
вывод, что с практической точки зрения интерес представляют резона-
резонаторы, в которых ограничивающая апертура имеет частично или пол-
полностью сглаженный край. В работе [100] было показано, что апертура
с частично сглаженным краем близка по своим свойствам к гаус-
гауссовой, причем разница становится чрезвычайно малой при вполне
умеренных значениях степени сглаживания. Поэтому в первом при-
приближении вполне уместно апертуры с частично сглаженным краем
рассматривать как гауссовые, а отличия учитывать в виде малых
аберраций, влияние которых на структуру мод следует учитывать во
втором порядке малости. Именно такой подход реализован в настоя-
настоящем параграфе. Читателям, которых интересует более тонкая струк-
структура мод неустойчивого резонатора, можно порекомендовать кни-
книгу [10]. В ней оптика неустойчивого резонатора рассмотрена весьма
подробно.
Для того чтобы убедиться в слабом влиянии специфики края
ограничивающей апертуры на потери основной моды, сравним за-
зависимость потерь 7 от оптической силы ТЛ АЭ в случае, когда
ограничивающая апертура является гауссовой (рис. 4.8), с той же
зависимостью, рассчитанной для резонатора с минимальной размыто-
размытостью края ограничивающей апертуры, достаточной однако для того,
чтобы при ТУф^ ^> 1 данный резонатор удовлетворительно описывался
бы геометро-оптическим приближением [10].
В геометро-оптическом приближении потери основной моды опре-
определяются соотношением (см. §2.2):
7=1-^, D-84)
где М — коэффициент увеличения неустойчивого резонатора, пока-
показывающий, во сколько раз возрастает поперечный размер моды после
обхода резонатора и равный
М = \1\ + лД2 - 1, D.85)
А' — D'
где / = ° —- — параметр устойчивости резонатора и Af0, Df0 —
элементы лучевой матрицы обхода резонатора, с началом в месте
расположения АЭ, рассчитанной без учета ограничивающих апер-
апертур. Пренебрегая влиянием апертуры, т. е. полагая ро = 0, получим
из формулы D.21) выражение для параметра / в виде
4-5. Резонаторы одномодовых лазеров
235
На рис. 4.16 и 4.17 показаны зависимости коэффициента увеличе-
увеличения М и потерь основной моды 7 от оптической силы ТЛ АЭ, рассчи-
рассчитанные по формулам D.84)-D.86). Из сравнения рис. 4.17 и рис. 4.8
М
1
^ = 0,2
0,4
0,6
—
N
----—_
о
0,25
0,5 0,75 (p-p'0)di
Рис. 4.16. Зависимость коэффициента увеличения неустойчивого резона-
резонатора от оптической силы ТЛ АЭ
7
0,8
0,6
0,4
0,2
0
do/di =
— —
оД
\0,8
1
0,2
\
\
\
X
\
\
0,25 0,5
0,75
Рис. 4.17. Зависимость потерь основной моды неустойчивого резонатора от
оптической силы ТЛ АЭ, расчитанная в геометро-оптическом приближении
видно, что геометро-оптический подход дает очень хорошую точность
при podi < 0,01. Это означает, в частности, что полученные ранее ре-
результаты для модели резонатора с гауссовой апертурой справедливы
для неустойчивых резонаторов, содержащих апертуры произвольного
вида, если только геометро-оптическое приближение хорошо описы-
описывает данный резонатор.
После того, как мы определили место настоящего рассмотрения
в общей теории неустойчивых резонаторов, коснемся коротко специ-
236
Гл. 4- Резонаторы твердотельных лазеров
АЭ
фики использования и расчета ограничивающей апертуры в неустой-
неустойчивом резонаторе. Если раньше, в случае устойчивого резонатора,
было естественно предположить,
что ограничивающей апертурой
является апертура АЭ или от-
отверстие в непрозрачном экране,
то в случае неустойчивого резо-
резонатора подобные ограничиваю-
ограничивающие апертуры практически не
используются. Дифракционные
потери в неустойчивых резона-
резонаторах слишком велики. Поэто-
Поэтому обычно в лазерах с такими резонаторами осуществляется ди-
дифракционный вывод излучения из резонатора. При этом выходным
Рис. 4.18. Неустойчивый резонатор с
зеркалом с гауссовым профилем про-
пропускания
АЭ
АЭ
Рис. 4.19. Схемы резонаторов с оптическими элементами, обеспечивающи-
обеспечивающими квазигауссов профиль коэффициента пропускания излучения
излучением лазера является та часть поля, которая обрезается огра-
ограничивающей апертурой. Особенно широкое распространение получи-
получили зеркала с переменным в радиальном направлении коэффициентом
отражения [127, 128] (рис. 4.18) и оптические элементы, обеспечиваю-
обеспечивающие квазигауссовый профиль пропускания излучения и выводящие
из резонатора периферийную часть пучка [125, 126, 129] (рис. 4.19).
Такие оптические элементы могут быть созданы на целом ряде прин-
принципов, среди которых, по-видимому, наибольшее распространение по-
получили аподизирующие элементы на основе системы линз из двулу-
чепреломляющего материала в сочетании с поляризатором [125, 126]
(рис. 4.19, а); на основе призм, в которых происходит нарушение пол-
4-5. Резонаторы одномодовых лазеров 237
ного внутреннего отражения для периферийной части пучка, [129],
(рис. 4.19, б"); элементов с переменным коэффициентом пропускания
за счет нанесения неоднородного интерференционного покрытия [127,
128] и т.д.
Очевидно, что оптическая сила данных аподизирующих апертур
должна быть существенно выше, нежели оптическая сила других
апертур, присутствующих в резонаторе, например апертуры АЭ, с
тем, чтобы подавляющая часть дифрагированного излучения была
использована в качестве выходного излучения лазера.
Рассмотрим коротко принципы, которыми следует руководство-
руководствоваться при разработке и выборе аподизирующей апертуры того или
иного типа при построении неустойчивого резонатора.
Будем исходить из заданного размера АЭ. Поскольку предполага-
предполагается одномодовый характер генерации, будем считать, что для эффек-
эффективного съема инверсной заселенности в АЭ достаточно обеспечить
размер основной моды в АЭ wo ~ @,7 -г l,0)i?o, где Ro — радиус АЭ.
Определим оптимальный уровень дифракционных потерь основ-
основной моды. Для этого рассмотрим аподизирующий элемент, пусть для
определенности это будет зеркало, с коэффициентом отражения по
мощности
где 0 ^ го ^ 1. При отражении от данного зеркала основной моды
резонатора ?/пад = Ао ехр(—г2/w2) получим
tfoxp = Аоу^ ехр [-г2 (^ + -L)]. D.87)
Поле покинувшее резонатор, описывается выражением
ивш = Аоу/1 - т0 ехР(-2г2/П2) ехр(-г2/^2). D.88)
Потери мощности основной моды при отражении от зеркала соста-
составят
/у = 1 - ^Отр
гпад
ОО
-*пад,отр — ^ ГаГ |сУПад,
отр|
— мощности падающего и отраженного излучения соответственно.
Подставляя в это выражение D.87) и проводя необходимые преоб-
преобразования, получим
7=1--о^. D-89)
Видно, что потери излучения связаны как с однородным по сечению
238
Гл. 4- Резонаторы твердотельных лазеров
пропусканием выходного зеркала, характеризуемым коэффициентом то,
так и с неоднородностью этого пропускания. Ранее, при анализе резо-
резонатора с гауссовыми апертурами, мы пренебрегли теми источниками
потерь основной моды, которые не меняют ее поперечной структу-
структуры. Поэтому целесообразно, наряду с потерями, определяемыми соот-
соотношением D.89), ввести потери 7о5 назовем их гауссовыми, которые
определяются исключительно неоднородностью коэффициента отра-
отражения. Очевидно, они совпадают с истинными потерями при то = 1,
поэтому О2
7о = 1 - -ТТШ- D-9°)
Целесообразность подобного разделения потерь связана с тем, что во
всех формулах предыдущего анализа фигурировали именно гауссо-
вые потери 7о5 ане общие потери основной моды 7, которые важны
с энергетической точки зрения. При дифракционном выводе излуче-
излучения из резонатора существует понятие оптимального уровня общих
дифракционных потерь 7опт, которое вполне аналогично понятию оп-
оптимального пропускания выходного зеркала 0ОПт, фигурирующему в
резонаторах с выводом излучения через обычное полупрозрачное зер-
зеркало. При достижении оптимального уровня дифракционных потерь,
при данном уровне накачки, мощность выходного излучения макси-
максимальна. Известно, что при росте коэффициента усиления активной
среды уровень оптимальных потерь возрастает и составляет для им-
импульсных твердотельных лазеров величину 7опт — 0,6 -г- 0,9.
1,0
0,8
0,6
0,4
0,2
'¦¦* «а.
/
/
N
\
\
о
0,2 0,4 0,6 0,8
1,0 1,2
r/w
Рис. 4.20. Поперечное распределение амплитуды внутрирезонаторного A)
и выходного излучения сто = 1(<5')ито = тОПт = 0,5 (#), Q = cjb случае
резонатора, изображенного на рис. 4.18
Вернемся к выражению D.88). На рис. 4.20 приведены профили
поперечной структуры выходного излучения при различных значе-
4-5. Резонаторы одномодовых лазеров
239
ниях го. Видно, что при го = 1 выходное излучение в ближнем по-
поле имеет кольцеобразную структуру. Дальнопольная картина такого
пучка достаточно сложна [130]. При уменьшении го поперечная струк-
структура выходного излучения становится более равномерной. Легко най-
найти такое значение топт, при котором выходной пучок будет иметь ква-
квазигауссову ю, столообразную форму. Для этого, очевидно, достаточно
потребовать, чтобы первая производная выражения D.88) по (г2) бы-
была бы равна нулю при г = 0. Как несложно показать, это достигается
при 2
гопт = 2-LO2 D.91)
или с учетом D.90) ( л
7"опт = 1 - 7о- D.92)
При подборе ограничивающей апертуры разумно стремиться к то-
тому, чтобы го = Гопт- Это обеспечивает высококачественную попереч-
поперечную структуру выходного излучения как в ближнем, так и в дальнем
поле.
Теперь мы можем сформулировать алгоритм подбора оптималь-
оптимальной аподизирующей апертуры. Исходя из рабочего значения уров-
уровня накачки определяем оптимальную полезную нагрузку резонатора,
т. е. 7опт- При условии, что то = топт из формул D.89) и D.90) находим
выражение для оптимального значения гауссовых потерь:
Из формулы D.92) имеем оптимальный уровень однородного отра-
отражения тОпт • Исходя из гауссовых потерь 7о опт и величины перетяжки
в АЭ wo = @,7 -г- 1,0)Ro легко найти, учитывая специфику конкрет-
конкретной схемы резонатора, величину Попт. Особенно просто это сделать
в случае, когда аподизирующая
апертура расположена вблизи
АЭ. Действительно, тогда из
формулы D.90) непосредствен-
непосредственно имеем
J-
D.93)
АЭ ГГ
R
рт
Ро
Рис. 4.21. Схема резонатора, в кото-
котором апподизирующая апертура распо-
расположена вблизи зеркала
70опт
Для того чтобы пояснить
алгоритм нахождения размера
апертуры в случае, когда огра-
ограничивающая апертура и АЭ
разнесены, рассмотрим вариант, в котором аподизирующая аперту-
апертура нанесена на концевое зеркало (рис. 4.21). Найдем, какой оптиче-
оптической силой должна обладать данная апертура р'о, чтобы при заданном
значении перетяжки на АЭ, гауссовые потери основной моды соста-
составили бы оптимальную величину. Для этого воспользуемся формула-
240 Гл. 4- Резонаторы твердотельных лазеров
ми D.1б)-D.19). Получаем
где Аъ и Въ — элементы лучевой матрицы обхода плеча резонатора,
содержащего зеркало с гауссовым профилем пропускания. Вычисляя
явный вид элементов А<± и ??2, а также полагая, что 1/а — 1/R^> р'о,
что, как правило, выполняется в силу небольшой геометрической дли-
длины плеча, имеем
4(b)a D94)
Учитывая, что ро = ——-—, а также соотношение D.93), из форму-
формулы D.94) легко найти искомую оптическую силу р'о и, следовательно,
оптимальный радиус области пропускания гауссовой апертуры
Здесь также уместно подчеркнуть, что хотя в рассматриваемом
случае d = а2р'о ф 0, но d/do С 1 и поэтому при анализе такого резо-
резонатора вполне пригодны все те выражения, которые были получены
в §4.2 для случая d = 0 (формулы D.26) и далее). Этот пример ил-
иллюстрирует как порядок нахождения величины апертуры в случае,
если ограничивающая апертура и АЭ разнесены, так и тот факт, что
с точки зрения алгоритма расчета остальных элементов схемы резо-
резонатора, положение апертуры в резонаторе не является существенным
и может выбираться из конструктивных соображений.
Перейдем к построению алгоритма расчета схемы неустойчивого
резонатора с динамической стабильностью. Будем исходить из то-
того, что схема должна обеспечивать заданный оптимальный уровень
гауссовых потерь и обеспечивать динамическую стабильность потерь
при заданном значении ТЛ АЭ рт и, кроме того, обеспечивать за-
заданный диапазон допустимого изменения мощности накачки, т. е.
заданный диапазон изменения ТЛ АЭ Арт- Последнее условие весьма
существенно, так как измерение оптической силы ТЛ АЭ всегда про-
проводится с конечной точностью, кроме того, на практике всегда имеют
место некоторые флуктуации рт из-за нестабильности накачки и це-
целого ряда других факторов.
Рассмотрим первое условие. Из формулы D.15) находим
Поскольку Sq2 = 1 + /025 т05 воспользовавшись выражением D.39), по-
получаем для параметра х =
х =
-4т2
4-5. Резонаторы одномодовых лазеров
241
Эта формула определяет, с учетом D.95), зависимость х = do/di от
величины 7о5 ПРИ этом величина т — d\po играет роль параметра,
рис. 4.22. Видно, что при
т < 1, в диапазоне 70 > 0,4 ве-
величина ж, при фиксированном
значении 7, практически не за-
зависит от параметра т. Если
7о ;$ 0,6 и г < 0,1, то можно
1,0
0,8
показать, что
N-l-?-|. D-97)
Воспользовавшись приближен-
приближенным выражением D.97), мож-
можно определить оптимальное
значение параметра жОПт, при
котором гауссовые потери со-
составляют оптимальную вели-
величину 70опт-
0,6
0,4
0,2
4
Л
л,
5
{
\
\
0,2 0,4 0,6 0,8
7о
Второе условие т. е. уело- Рис 4.22. Зависимость отношения оп-
вие того, что схема резонато-
резонатора обладает динамической ста-
стабильностью при заданной ТЛ
АЭ рт выполняется, если па-
параметр / (см. формулы D.13))
равен нулю. Согласно D.29) это имеет место, если оптическая длина
bo обхода резонатора с началом вблизи АЭ, рассчитанная без учета
гауссовых апертур, равна нулю:
тических длин плечей неустойчивого
резонатора с динамической стабильно-
стабильностью от потерь основной моды т =
= dlPo = 0,01 (i); 0,05 B); 0,1 E); 0,2
U);0,5E)
Ьо = 0.
D.98)
Учитывая D.29) и D.30), имеем b0 = 4:dido(p' — Ро). Поскольку \di\ ^
^ do ф 0, то условие D.98) эквивалентно требованию р — р' или, учи-
учитывая соотношения D.16)—D.20) и D.30), условию
А[ ^ А'2
РТ = "БГ + "Б7>
D.99)
где штрих означает, что соответствующие элементы лучевых матриц
вычислены без учета гауссовых апертур.
Перейдем к последнему условию. Для выяснения допустимого диа-
диапазона изменения рт воспользуемся формулой D.40), которую пере-
перепишем в виде
^ = -Kd\{ApT)\ D.100)
7о
где
К =
16 В.П. Быков, О.О. Силичев
-То)^
/о42B-7о)
D.101)
242
Гл. 4- Резонаторы твердотельных лазеров
Исходя из заданного уровня оптимальных потерь 7о опт, для фиксиро-
фиксированного значения параметра т можно найти хопт D.96), $02 D-95), /02
D.15) и, следовательно, вели-
величину коэффициента К. Резуль-
Результаты соответствующих расче-
расчетов представлены на рис. 4.23.
Видно, что при г < 1 и 7о ^
> 0,5 величина К определяет-
определяется исключительно значением
параметра 7о- Поэтому, если
предположить, что допусти-
допустимый диапазон изменения по-
потерь не должен превышать
величину А70, т.е.
+5
+3
+1
-1
-3
-5
[\
1
к
2
f
Ч
4
V
Л
V
\
0
0,2 0,4 0,6 0,8
^7о/То < V
при имеющемся уровне флук-
флуктуации оптической силы ТЛ
АЭ Арт, то из D.100) полу-
получаем условие, на допустимую
длину более длинного плеча
резонатора:
f- DЛ02)
Рис. 4.23. Зависимость чувствительно-
чувствительности неустойчивого резонатора с динами-
динамической стабильностью к флуктуациям
ТЛ от потерь основной моды т = dipo =
= 0,01 (i); 0,05 B); 0,1 E); 0,2 Ц); „ (А п_л /у1 псЛ
0 5E) Соотношения D.96), D.98)
и D.102) определяют, исходя
из заданных значений 7оопт, Рт и Арт, условия, накладываемые на
величины матричных элементов соответствующих лучевых матриц.
При построении схемы резонато-
резонатора следует так подобрать оптиче-
оптические элементы, чтобы эти усло-
условия выполнялись.
После этих предварительных
замечаний переедем к разра-
разработке конкретных резонаторных
схем. При этом ограничимся слу-
Рис. 4.24. Неустойчивый, динамиче-
динамически стабильный резонатор, образо-
образованный двумя сферическими зерка-
зеркалами
чаем, когда оптическая сила ТЛ
АЭ сравнительно невелика. Для
этого положим рт = 0, но будем
считать, что Арт ф 0. Именно этот случай наиболее часто встречает-
встречается при построении импульсных одномодовых твердотельных лазеров
с большой апертурой АЭ. В качестве базовой модели рассмотрим ре-
резонатор, образованный двумя сферическими зеркалами рис. 4.24. В
этом случае, как легко показать, элементы лучевых матриц обхода
4-5. Резонаторы одномодовых лазеров 243
левого и правого плечей резонатора соответственно равны
4 = l-2gi, B[=2Liqu
A'2 = l-2q2, B'2=2L2q2, [ " '
где
«1,2 = 1 - ^- D-104)
Подставляя выражения D.103) в условие динамической стабильности
резонатора D.99) при рт = 0, получаем
i^l = -!f2». D.105)
Рассмотрим простейший вариант этого соотношения, а именно
случай, когда
qi=q2 = 0,5. D.106)
Целесообразность выделения данного варианта в отдельный слу-
случай обусловлена тем, что резонаторы подобного типа нашли широкое
распространение. Они известны под названием SFUR-резонаторы (self
filtering unstable resonator) и достаточно подробно исследованы, как
в теоретическом, так и в экспериментальном планах [131-134]. Бы-
Было показано, что в них происходит эффективное подавление мод вы-
высокого порядка при сохранении высокой эффективности генерации и
почти дифракционной расходимости выходного излучения, они харак-
характеризуются низкой чувствительностью к малым разъюстировкам от-
отдельных элементов резонатора, отсутствием изрезанности поперечной
структуры внутрирезонаторного излучения и, как следствие этого, от-
отсутствием «горячих» точек внутри резонатора, могущих привести к
оптическому пробою внутрирезонаторных элементов. В дополнение
к этому из проведенного выше анализа следует, что они обладают
динамической стабильностью и, следовательно, сравнительно малой
чувствительностью к оптическим искажениям внутрирезонаторных
элементов. Эти обстоятельства заставляют уделить резонаторам по-
подобного типа более пристальное внимание.
Рассмотрим порядок расчета такого резонатора. Поскольку усло-
условие динамической стабильности D.105) при q\ — q2 = 1/2 выполнено,
то остается удовлетворить оставшимся двум соотношениям D.96)-
D.97) и D.102). Начнем с последнего. Из D.103) и D.106) следует,
что d\ = В[/2 = Z/i/2, поэтому необходимый диапазон допустимых
флуктуации ТЛ АЭ Арт достигается при
- DЛ07)
Для того чтобы гауссовые потери составляли оптимальную вели-
величину, необходимо, чтобы параметр х = do/di был равен оптималь-
оптимальному значению жОПт, определяемому выражениями D.96) или D.97)
16*
244 Гл. 4- Резонаторы твердотельных лазеров
при 7о = Тоопт- Из D.103) следует, что х = Ь2/Ь\, причем предпола-
предполагается, что плечо с меньшей геометрической длиной имеет индекс 2.
Поэтому
L2=xonTL1. D.108)
Поскольку р = р', то из D.85), D.86) следует, что коэффициент уве-
увеличения неустойчивого резонатора при этих условиях и х = хОПТ
м = ! .
Ж опт
Учитывая также D.84), имеем в геометро-оптическом приближении
выражение для
2
70 опт 70 опт
^опт = л/1 ~ 70 опт - 1 -
которое тождественно D.97). Поэтому можно считать, что формула
D.97) дает оптимальную величину отношения хопт = (do/di)onT в гео-
геометро-оптическом приближении.
Таким образом, алгоритм расчета SFUR-резонатора можно сфор-
сформулировать в следующем виде. Из энергетических соображений и раз-
размера АЭ находим оптимальную величину гауссовых потерь 7оопт и оп-
оптимальный радиус ограничивающей апертуры Попт. Далее, исходя из
предполагаемого диапазона изменения TJ1 АЭ Арт, Тоопт и допусти-
допустимого уровня флуктуации потерь 77, находим длину более длинного пле-
плеча D.107) (при этом величину коэффициента к находим из рис. 4.23).
По формуле D.97) находим значение хопт и, используя D.108), опре-
определяем длину более короткого плеча L2. После этого окончательно
имеем Rx = 2Lb R2 = 2L2 D.106).
Например, пусть 7оопт = 0,5, Арт = 0,5 дп, г\ = 0,1. Тогда из
рис. 4.23 имеем In К = 2, К = 7,4, из формулы D.107) Lx < 0,47 м. В
соответствии с этим положим R\ = 0,8 м, L\ — 0,4 м, из D.97) хопт =
= 0,707, L2 = 0,33 м, R2 = 0,66 м.
При расчете неустойчивого резонатора с динамической стабильно-
стабильностью общего вида, т. е. резонатора, в котором выполняется соотноше-
соотношение D.105), но gi52 ф 1/2, будем исходить из длины плечей резонатора
L\ и L2 (рис. 4.24). Тогда из условий стабильности D.105) и оптималь-
оптимальности потерь |ж| = \В[/В2\ = хопт D.96) легко найти, с учетом D.103)
и D.104), значение параметров
с х — =ЬжОпт- Эти выражения позволяют легко найти искомые ради-
радиусы кривизны зеркал резонатора R\^2 — L\^2j(\ — #1,2)- Выбор вели-
величин L\ и L2 не вполне произволен, поскольку должно выполняться
неравенство D.102), обеспечивающее заданный уровень допустимых
флуктуации ТЛ АЭ Арт. Легко показать, что для его выполнения
4-5. Резонаторы одномодовых лазеров 245
достаточно выбирать величины L\ и L^ из условий: при х = —жоп
т . 26 т
1 ^ 1 - Жопт 7
При Ж = ЖОпт
т ^ 26
D.110)
D.111)
или
г ^ 29
^l-aw' 2 ^^(Ц-ХопО-гв'
где
0= Х I *
Арт у КGоопт)'
Соотношения D.109)—D.111) определяют искомые параметры ре-
резонатора. Проиллюстрируем действие данного алгоритма на примере
расчета схемы неустойчивого резонатора с динамической стабильно-
стабильностью, в котором 7оопт = 0,5, Арт = 0,5 дп, г] = 0,1. Из рис. 4.23 имеем
К = 7,4, 0 = 0,47 м. Из формулы D.97) хопт = 0,707. Полагаем, что
х = 0,707, выбираем L\ из условия D.111): L\ — 0,5 м. При этом L^
можно взять произвольной величины, например L^ — 0,2 м. Далее с
помощью формул D.109) находим R\ = 0,76 м, R^ = 0,5 м.
На этом примере мы закончим рассмотрение схем неустойчивых
резонаторов с динамической стабильностью. Однако наш анализ ре-
резонаторов мощных твердотельных лазеров с малым уровнем термооп-
термооптических искажений был бы неполным, если бы мы не обсудили, хотя
бы коротко, возможность использования неустойчивых резонаторов
других типов. Из рис. 4.8 следует, что при высоком уровне гауссовых
потерь 7о ^ 0,8-0,9, влияние флуктуации ТЛ АЭ проявляется доста-
достаточно слабо. Поскольку такие большие потери могут соответствовать
оптимальным значениям в лазерах с достаточно большим коэффи-
коэффициентом усиления, для них допустимо использование резонаторов, не
обладающих динамической стабильностью. Среди последних наибо-
наиболее часто используются неустойчивые резонаторы телескопического
типа, в которых выполняется соотношение [10]
Д1+Д2 =2(Li+L2). D.112)
Они обладают тем преимуществом, что выходное излучение такого
резонатора в геометро-оптическом приближении имеет плоский фа-
фазовый фронт и, следовательно, минимальную расходимость. Для то-
того чтобы убедиться в этом, рассмотрим сферическую волну радиу-
радиуса Л, которая в геометро-оптическом приближении описывает моду
неустойчивого резонатора (§2.3). После обхода резонатора, согласно
правилу «ABCD», радиус кривизны фазового фронта, без учета дей-
246
Гл. 4- Резонаторы твердотельных лазеров
ствия ограничивающих апертур, определяется выражением
J_= C'q + D'o/R = 1_
R' A'o
где А'о, Bq, Cq, Df0 — элементы лучевой матрицы обхода резонатора
без учета апертур. При Cq = 0 один из корней данного уравнения
т. е. сферическая волна вырождается в плоскую. Легко видеть, что
для резонатора, изображенного на рис. 4.24, С'о = 0 при выполнении
соотношения D.112).
Наиболее часто применяется неустойчивый телескопический резо-
резонатор, изображенный на рис. 4.25. Его расчет проводят исходя из тре-
требуемого уровня дифракционных
потерь 7оопт, при которых выход-
выходная мощность максимальна, и усло-
условия D.112).
Из D.84) имеем оптимальный
коэффициент увеличения резона-
резонатора
Мопт = —
70опт
Рис. 4.25. Телескопический резо-
резонатор
Нетрудно показать, что коэффи-
коэффициент увеличения телескопическо-
телескопического резонатора М = —R1/R2. Если исходить из длины резонатора Lq,
то из условий М = Мопт и D.112), находим выражения для радиусов
кривизны зеркал резонатора
2L0 D 2L0
Ri =
1 - 1/Мопт
1 -
D.113)
Например, положим, что необходимо рассчитать резонатор, который
должен обеспечивать потери на излучение 7оопт = 0,75. Тогда
Мопт = 2.
Из конструктивных соображений выбираем длину резонатора Lq =
= 0,3 м. Из формулы D.113) имеем R\ = 1,2 м и R<± — —0,6 м. Если
АЭ радиусом Rq помещен вблизи выходного зеркала R^ (рис. 4.25), то
для полного заполнения излучением активной среды радиус апертуры
выходного зеркала должен быть, очевидно, равен ~ Rq/Motit.
В заключение отметим, что SFUR-резонаторы принадлежат к те-
телескопическому типу, поскольку при qx—q^ — 1/2 условие D.112) вы-
выполнено. Однако, в общем случае, обратное неверно, т. е. не всякий
телескопический резонатор обладает динамической стабильностью. В
частности, резонатор, изображенный на рис. 4.25, не относится к ди-
динамически стабильным резонаторам.
§4-6- Резонаторы твердотельных технологических лазеров 247
§ 4.6. Резонаторы твердотельных технологических
лазеров
Средняя мощность выходного излучения является наиболее важ-
важным параметром в лазерах, используемых в технологических процес-
процессах, таких как резка, сверление и прочие. Многомодовый режим ге-
генерации обеспечивает большую мощность генерации по сравнению
с одномодовым в силу более эффективного заполнения излучени-
излучением активной среды, поэтому в мощных твердотельных лазерах тех-
технологического назначения используются, как правило, многомодо-
вые резонаторы. Разработка таких резонаторов сопряжена с рядом
особенностей, о которых пойдет речь в данном параграфе.
Прежде чем переходить к собственно резонатору, коснемся корот-
коротко требований, которые предъявляются к поперечной структуре из-
излучения в большинстве технологических задач, решаемых с помощью
лазера. Они вытекают из необходимости фокусировать лазерное из-
излучение в фокальное пятно заданного размера и сводятся к обеспе-
обеспечению так называемого качества поперечной структуры пучка [135],
определяемого выражением
г] = ав, D.114)
где а — радиус поперечного размера пучка, 20 — расходимость пуч-
пучка. Если выходной пучок описывать в виде смеси гауссовых пучков
различного порядка с одинаковым комплексным параметром, то, по-
полагая, что поперечный размер пучка определяется поперечным раз-
размером гауссового пучка максимального порядка п, имеем (гл. 1)
а = w\/2n + 1, D.115)
где w — размер гауссового пучка нулевого порядка. Если при этом
предположить, что фазовый фронт рассматриваемого лазерного пуч-
пучка плоский, то расходимость его определяется также гауссовым пуч-
пучком максимального порядка. Поэтому
и, следовательно,
/7 = -Bп + 1). D.116)
Из этого выражения сразу следует, что если измерять качество пуч-
пучка г) до и после прохождения произвольной гауссовой оптической
системы, не меняющей модового состава пучка, то получим одну и
ту же величину при условии, что фазовый фронт плоский. Таким
образом, происходит сохранение качества лазерного пучка при его
распространении через оптические системы, не меняющие мощность
пучка. В этом плане величина качества пучка более полно характе-
характеризует структуру излучения, нежели расходимость пучка, посколь-
248
Гл. 4- Резонаторы твердотельных лазеров
ку последнюю легко изменить, пропуская излучение, например, через
телескоп.
Рассмотрим теперь объектив, который фокусирует излучение в
пятно ао (рис. 4.26). Пренебрегая сферическими аберрациями объек-
объектива, т. е. оставаясь в рамках гауссовой оптики, легко показать, что
изменение поперечного
размера пучка в районе
фокуса с учетом форму-
формулы D.115), описывается
соотношением
Рис. 4.26. Фокусировка многомодового лазер-
лазерного пучка тонкой линзой
где wo = (Joly/2n + 1 —
размер гауссового пуч-
пучка нулевого порядка в месте максимальной фокусировки. Из этого
соотношения следует, что радиус пучка возрастает в л/2 раза на рас-
расстоянии
2 2-|
~ ~Т~ ~ ~Т~ 2п+Г
Это выражение, с учетом D.115), можно переписать в виде
al = bf]. D.117)
При сильной фокусировке, т. е. в случае, когда 1// ^> X/ttw2^ легко
показать, анализируя прохождение гауссового пучка нулевого поряд-
порядка через тонкую линзу с фокусным расстоянием /, что wo = \f /irwf,
где Wf — размер пучка на линзе. Используя далее D.115) и D.116),
получаем
ao=r)(J-Y D.118)
где Of — радиус поперечного размера пучка на объективе. С учетом
D.117) имеем также
'^-V D.119)
СГ/У
Особенности технологической задачи определяют размер пятна,
характеризуемый величинами Ъ и ао, в который необходимо фокусиро-
фокусировать лазерное излучение. Например, при лазерной резке листовых ма-
материалов — это требуемая толщина 2ао и глубина 2Ъ реза. Соотноше-
Соотношения D.118) и D.119) показывают, что требуемый размер фокального
пятна однозначно определяет как параметры используемого объекти-
объектива, т. е. отношение фокусного расстояния к апертуре объектива //с/,
так и требуемое качество поперечной структуры лазерного излуче-
излучения г\. Из соотношения D.118) видно также, что при данном объекти-
объективе, возможность фокусировки излучения лазера целиком определяет-
определяется качеством пучка.
§4-6- Резонаторы твердотельных технологических лазеров 249
Проиллюстрируем сказанное примером. Предположим, технологи-
технологический лазер должен обеспечить резку листового материала толщи-
толщиной 4 мм с шириной реза не более 0,4 мм. Следовательно, Ъ = 2 мм и
сто = 0,2 мм. Из формулы D.119) получаем, что в данной задаче следу-
следует использовать объектив с (f/erf) = 10, а качество излучения лазера
(см. D.118)) не должно превосходить величину г\ ~ 20 мм • мрад.
Таким образом можно сделать вывод, что резонатор технологиче-
технологического многомодового лазера должен обеспечивать заданное качество
поперечной структуры выходного излучения rj. Легко связать вели-
величину г) с размером основной моды в АЭ w. Действительно, если пред-
предположить, что излучение заполняет весь объем активной среды, то
Ro ~ wy/2n + 1, где Ro — радиус АЭ, и согласно D.116)
J. D.120)
Качество выходного излучения определяется размером АЭ и вели-
величиной перетяжки основной моды в АЭ. Кроме того, как следует из
результатов предыдущего анализа, диапазон устойчивости резона-
резонатора при изменении оптической силы ТЛ АЭ Арттах определяет-
определяется соотношением D.50), т.е. шириной минимума в зависимости 7(р)?
изображенной на рис. 4.8. Учитывая формулу D.50), получаем, что
= ZX/ttw2 или, с использованием D.120),
2^2. D.121)
КО
Как следует из выражения D.5), Арт — х(АРн/Rq), где к — коэффи-
коэффициент, характеризующий теплофизические свойства материала АЭ.
Допустимый диапазон изменения мощности накачки, при котором ре-
резонатор остается в области устойчивости, равен
АРН = 2кг). D.122)
Это означает, что повышение качества поперечной структуры излу-
излучения неизбежно приводит к сужению диапазона допустимого изме-
изменения накачки.
В случае симметричных схем, когда экстремумы зависимости ^(р)
сливаются в один глобальный минимум (рис. 4.8), этот диапазон удва-
удваивается.
После этих предварительных замечаний перейдем к построению
конкретных резонаторных схем. Начнем с выбора типа схемы. При
построении одномодовых резонаторов мы использовали резонаторы
с динамической стабильностью параметров по отношению к малым
изменениям оптической силы ТЛ АЭ. В резонаторах многомодовых
лазеров малые флуктуации ТЛ АЭ не приводят непосредственно к
изменению выходной мощности излучения, а лишь к изменению мо-
дового состава излучения. Кроме того, в силу сравнительно малого
размера w, влияние флуктуации ТЛ АЭ на характеристики резонато-
резонатора ослаблено. Эти обстоятельства указывают на то, что использование
250 Гл. 4- Резонаторы твердотельных лазеров
резонаторов с динамической стабильностью в мощных твердотельных
технологических лазерах не является столь необходимым, как в слу-
случае одномодовых лазеров.
Однако использование динамически стабильных резонаторов и
в случае многомодовых лазеров дает целый ряд преимуществ. Во-
первых, стабильность модового состава, и следовательно, качества по-
поперечной структуры выходного пучка. Это позволяет повысить ста-
стабильность всего технологического процесса. Во-вторых, и это весьма
важно с практической точки зрения, работая в точке динамической
стабильности, мы имеем почти симметричную зависимость выходных
характеристик лазера, как при увеличении, так и при уменьшении
мощности накачки относительно расчетного значения. При этом ка-
качество пучка не ухудшается, т.е. г\ ^ 770, где щ — качество пучка в
точке динамической стабильности. Это следует из формулы D.120) и
из того факта, что при динамической стабильности имеет место мини-
минимум размера основной моды в АЭ. Вывод резонатора из состояния ди-
динамической стабильности приводит к улучшению качества излучения,
однако это сопровождается, как правило, фокусировкой излучения на
внутрирезонаторных элементах, увеличением чувствительности мо-
довой структуры к термооптическим искажениям АЭ, сужением об-
области устойчивости. Эти обстоятельства позволяют сделать вывод о
целесообразности использования при построении мощных твердотель-
твердотельных лазеров технологического назначения динамически стабильных,
как одноэлементных, так и многоэлементных схем резонаторов. При
этом динамически стабильный резонатор следует рассчитывать для
такой ТЛ АЭ рт, которая имеет место при мощности накачки, лежа-
лежащей посередине возможного рабочего диапазона.
Рассмотрение динамически стабильных многомодовых резонато-
резонаторов начнем с анализа резонатора простейшего вида, образованного
плоскими зеркалами, рис. 4.27. Поскольку максимальным диапазо-
диапазоном устойчивости обладают симметричные схемы, то для расчета
воспользуемся условиями D.42). Пренебрегая в первом выражении
членом (g?iPoJ п0 сравнению с единицей, что можно сделать в силу
многомодового характера генерации, а следовательно, малого значе-
значения размера основной моды в АЭ, получим:
^- + ^=Рт, Вг~В2. D.123)
Вычисляя явный вид элементов лучевых матриц обхода плечей резо-
резонатора (рис. 4.27), легко привести условия D.123) к виду:
а = Ъ=- . D.124)
Рт
Резонаторы, в которых выполняются эти соотношения, часто назы-
называют резонаторами типа «кошкин глаз». Они получили широкое рас-
распространение в технологических лазерах [136]. Качество поперечной
§4-6- Резонаторы твердотельных технологических лазеров 251
а
^
а | а
а
а
а | а
рт
рт
рт
рт
Рис. 4.27: а) динамически стабильный устойчивый резонатор с плоскими
зеркалами; б) двухэлементный резонатор с плоскими зеркалами; е) усили-
усилитель, согласованный с резонатором лазера
структуры излучения такого лазера определяется согласно D.121)
и D.124) выражением
D.125)
RIpt
Преимуществом данной схемы является ее простота и возможность
построения на ее основе многоэлементных схем, как резонаторов, так
и усилительных каскадов, рис. 4.27. Поперечные характеристики из-
излучения таких многоэлементных схем такие же, как и в случае резо-
резонатора с одним АЭ, а мощность генерации в соответствующее коли-
количество раз возрастает.
Недостатком резонатора с плоскими зеркалами является невоз-
невозможность обеспечить высокое качество выходного излучения при
сильной ТЛ АЭ. Действительно, согласно формуле D.125), при рт =
= 4 дп и Rq = 4 мм имеем 770 — 32 мм • мрад, что слишком много для
целого ряда технологических задач.
Для повышения качества выходного излучения необходимо, как
это видно из D.120), увеличивать размер основной моды в АЭ. Это-
Этого можно добиться увеличением оптической длины по крайней мере
одного плеча резонатора D.60). Например, переходом к несимметрич-
несимметричным схемам с плоскими зеркалами, в которых одно плечо имеет боль-
большую оптическую длину, либо к схемам, содержащим сферическое зер-
зеркало, рис. 4.28. Очевидно, что на основе таких одноэлементных схем
легко построить двухэлементный резонатор с симметричным распо-
расположением АЭ, рис. 4.29.
При расчете резонатора будем исходить из того, что он должен
обеспечивать требуемое качество излучения щ при заданной ТЛ АЭ
рт и размере АЭ Ro. Кроме того, будем контролировать размер по-
поля на концевых зеркалах. Это весьма важно, поскольку чрезмерная
252
Гл. 4- Резонаторы твердотельных лазеров
Рис. 4.28. Схема одноэлементного резонатора технологического лазера
d
Рис. 4.29. Схема двухэлементного резонатора технологического лазера
фокусировка излучения на зеркалах при высокой мощности излуче-
излучения лазера может приводить к разрушению элементов резонатора.
Проанализируем схему резонатора, изображенную на рис. 4.28. Пе-
Перейдем для этого к безразмерным переменным
1
f\i fill li /711 /1
" — аУа-> Р — аУсп Р — D •>
Уа
D.126)
где
Уа =
Введем коэффициенты
2 2
ТП\ = —т, 7712 — —о-)
показывающие, во сколько раз плотность мощности излучения на ле-
левом и правом зеркалах выше, нежели в АЭ, рис. 4.28. В новых пере-
переменных лучевые матрицы обхода плечей резонатора равны соответ-
соответственно:
Су Ах
1 - 2ар
2аA -ар)"
Уа
-2руа 1 - 2ар
А2 В2
Со А2
1 Ж-
Уа
^0 1
§4-6- Резонаторы твердотельных технологических лазеров 253
Проанализируем вначале случай, когда оптическая длина плеча
со сферическим зеркалом больше, чем плеча с плоским зеркалом, т. е.
\В\\ > 2d. В третьем параграфе мы уже обсуждали схемы подобного
типа. Было показано, что в них целесообразно использовать выпуклые
зеркала. В соответствии с этим будем считать р < 0. Если резонатор
динамически стабилен, то из D.47) следует, что \В\\ = 1/уа и поэтому
2аA - ар) = 1. D.127)
Условие динамической стабильности D.48) в новых переменных, с уче-
учетом D.127), приобретает вид
D.128)
где v = =Ы. Используя D.63) и D.127), имеем выражения для коэф-
коэффициентов TTli И 777,2:
1711 = 2^' т2 = *™?- DЛ29)
Исследуемая нами схема определяется тремя независимыми пара-
параметрами. В качестве таких параметров можно взять, например, ве-
величины а, /3 и р, или какие-либо другие. Эти параметры должны
удовлетворять двум условиям D.127) и D.128). Поэтому, если произ-
произвольно выбрать один из них, остальные будут определены однознач-
однозначно. Выберем в качестве свободного параметра величину фокусировки
излучения на плоском зеркале тэ. Тогда из D.129) имеем
V D.130)
Выразим далее, с помощью соотношений D.127) и D.129), аир че-
через mi:
Рассмотрим вначале случай 7712 = 1. Из формулы D.130) следует,
что это возможно лишь при /3 = 0. Условие динамической стабильно-
стабильности приобретает тогда вид:
1 — 2ар = р,
из которого, с учетом D.131), находим:
mi = IE±?. D.132)
Легко видеть, что при высокой мощности накачки, т. е. при силь-
сильной ТЛ рт улучшение качества выходного излучения сопровождает-
сопровождается быстрым ростом степени фокусировки на сферическом зеркале.
Действительно, при рт = 4 дп, Rq = 4 мм и 77 = 16 мм • мрад имеем
254 Гл. 4- Резонаторы твердотельных лазеров
уа = 1 дп, р = 4 и, следовательно, mi = 12,5. Такая степень фокуси-
фокусировки, как правило, неприемлема, поскольку приведет к разрушению
сферического зеркала. Поэтому в случае, когда р ^> 1, нежелательно
использовать схему резонатора, в которой плоское зеркало располо-
расположено вблизи АЭ.
Перейдем теперь к анализу случая Ш2 > 1. Преобразуем для этого
соотношение D.128), с помощью формул D.129)-D.131), к виду:
пц = I [р + 1 - Vm2-1]2, D.133)
из которого следует, что увеличение степени фокусировки на плос-
плоском зеркале т^ позволяет уменьшить фокусировку на сферическом
зеркале. Поэтому, выбирая значение свободного параметра Ш2, следу-
следует руководствоваться соотношением D.133) и исходить из некоторого
компромисса между величинами фокусировки излучения на концевых
зеркалах. Например, если в рассмотренном ранее примере положить
77i2 = 5, то 777-1 — 4,5. Такая степень фокусировки вполне приемлема.
После того, как параметр т^ выбран, значение остальных величин
легко найти с помощью формул D.130), D.131) и D.133). В нашем
примере имеем /3 = 0,4, а = 0,33, р = —0,167, или, с учетом D.126),
а = 0,33 м, d = 0,4 м и R = -6 м.
Проведенный анализ показывает, что разработка схем резонато-
резонаторов мощных твердотельных лазеров с высоким качеством поперечной
структуры сопряжена с определенными сложностями, так как при-
приходится мириться со значительной неравномерностью распределения
мощности излучения внутри резонатора.
Легко показать, что использование вогнутого зеркала с р > 0 вме-
вместо выпуклого не приводит к уменьшению фокусировки, но зато суще-
существенно увеличивает геометрическую длину левого плеча резонатора
и, следовательно, габариты всей лазерной установки.
Для того, чтобы существенно уменьшить фокусировку излучения
на концевых зеркалах, следует перейти к схеме, в которой большая
оптическая длина имеет место в плече с плоским зеркалом. В этом
случае уа = l/2d, /3 = 1/2, Ш2 = 2. Исходя из выражения для коэф-
коэффициента mi и условия динамической стабильности, можно показать,
что в данном случае имеются широкие возможности выбора степени
фокусировки на сферическом зеркале. Однако, общая длина схемы
при этом становится весьма значительной. Это обстоятельство огра-
ограничивает возможности применения подобных схем.
Однако существует ситуация, когда использование таких схем
весьма эффективно и позволяет существенно повысить выходную
мощность излучения. Это происходит в том случае, если в двухэле-
двухэлементной схеме по тем или иным причинам оптические силы ТЛ ак-
активных элементов различны. В обычных симметричных двухэлемент-
двухэлементных схемах это приводит к тому, что размер основной моды в АЭ
неодинаков и, следовательно, при равенстве размеров АЭ имеет место
§4-6- Резонаторы твердотельных технологических лазеров 255
лишь частичное заполнение излучением одного из элементов, эффек-
эффективность генерации падает.
Для того, чтобы избавиться от данного эффекта, можно использо-
использовать оптическую систему, заключенную между АЭ, оптическая длина
которой равна нулю. Если при этом диагональные элементы равны,
то легко показать, что, независимо от остальных параметров схемы
резонатора, размер поля на активных элементах будет одинаков. Дей-
Действительно, если на одном АЭ размер поля равен wi, то на другом,
согласно правилу преобразования гауссовых пучков, равен
w\ = W\[(A + B/RaJ + (BX/ttwIJ],
где Ra — радиус кривизны фазового фронта волны на выходе из пер-
первого АЭ, а А, В и D — элементы лучевой матрицы системы, располо-
расположенной между АЭ. При
B = 0hA = D = 1 имеем
w2 = w\.
Если ограничиться рас-
рассмотрением симметричных
двухэлементных схем, то
очевидно, что эквивалент-
эквивалентная ей одноэлементная схе-
схема должна иметь лучевую
матрицу обхода плеча в ви-
виде (рис. 4.30)
В2
2 А2
Схемы подобного типа
мы уже рассматривали ра-
Рис. 4.30. Схема двухэлементного резона-
резонатора нечувствительного к отличию оптиче-
оптических сил ТЛ элементов
нее в третьем параграфе. Формулы D.66)-D.70) дают всю необходи-
необходимую информацию для их расчета. Переписав их в наших переменных,
получим:
= 1/2, а=р-1,
т2 = 2. D.134)
Видно, что в данной схеме, при большом значении параметра р,
имеется довольно сильная фокусировка излучения на сферическом
зеркале. Кроме того, резонатор оказывается достаточно длинным. Од-
Однако при не слишком высоких требованиях к качеству поперечной
структуры данная схема весьма эффективна.
В качестве примера проведем расчет такой двухэлементной схемы
для лазера, качество излучения которого не должно быть хуже чем
20 мм • мрад. Предположим также, что Ro = 3 мм, рт = 4 дп. Тогда
имеем р = 1,8, уа = 2,2 дп, mi = 0,64, m2 = 2, а = р = 0,8, /3 = 0,5,
а = R = 0,36 м, Ь = 0,223 м (рис. 4.30).
Гл а в а 5
ГЕОМЕТРИЧЕСКАЯ ОПТИКА
ЛАЗЕРНЫХ РЕЗОНАТОРОВ
§5.1. Геометрическая оптика лазерных резонаторов
в параксиальном приближении
Геометрическая оптика как наука развивается примерно с первой
трети XIX столетия. Основоположниками ее были такие корифеи, как
В.Р. Гамильтон и К.Ф. Гаусс. С представлением же о лучевом харак-
характере распространения света человек сталкивался с незапамятных вре-
времен. Естественно, у людей в этом отношении имеется богатая инту-
интуиция, что и объясняет, по-видимому, поразительную эффективность
этой науки.
Появление лазеров повлекло за собой как постановку ряда новых
задач оптики, так и развитие «старых» оптических вопросов. В част-
частности, исследование лазерных резонаторов потребовало распростра-
распространения на эту область геометро-оптических методов, обладающих про-
простотой и наглядностью. Однако применение геометрической оптики
к лазерным резонаторам требует существенного изменения постанов-
постановки задачи. Действительно, в долазерных задачах (расчет объективов,
расчет прохождения радиоволн через неоднородные среды и др.) все-
всегда задается некоторая исходная волновая поверхность, как прави-
правило сферическая, и требуется определить волновую поверхность, по-
получающуюся из исходной после ее прохождения через ту или иную
оптическую систему. В резонаторных (лазерных) задачах геометри-
геометрической оптики постановка задачи иная — требуется отыскать такую
волновую поверхность, которая воспроизводится после прохождения
оптической системы, образующей резонатор. Легко понять, что лазер-
лазерные задачи сложнее прежних — прежние входят в лазерную задачу
как составная часть и притом простейшая. Даже существование са-
самовоспроизводящихся волновых поверхностей проблематично, и, как
показывает исследование, они действительно существуют не всегда.
Вместе с тем для всех практически применяемых резонаторов такие
волновые поверхности могут быть найдены, и это определяет боль-
большую значимость геометрического метода для исследований лазерных
резонаторов.
Следует отметить, что геометрический метод представляет, по
крайней мере, две уникальные возможности в теории лазерных ре-
5.1. Геометрическая оптика лазерных резонаторов
257
зонаторов. Во-первых, видимо, только геометрическая оптика предо-
предоставляет достаточно широкие возможности для выхода за пределы
параксиального приближения и, во-вторых, только геометрическая
оптика дает возможность с некоторой общей точки зрения обозреть
всю совокупность собственных колебаний того или иного резонатора
(см. §5.6).
В параксиальном приближении основное достоинство геометриче-
геометрического метода заключается в том, что он позволяет из примитивных
соображений строить лучевые матрицы оптических элементов, обра-
образующих резонатор. В частности, оказывается, что для этого нет даже
необходимости знать такое относительно сложное решение уравнений
Максвелла, как гауссов пучок.
Продемонстрируем геометрический метод сначала на простом, уже
рассматривавшемся нами примере резонатора, образованного сфери-
сферическими зеркалами с радиусами кривизны R\ и i?2, отстоящими друг
Xi
хо
0
I /
ж'
z
Рис. 5.1. Проход луча в двухзеркальном резонаторе
от друга на расстояние d. Будем считать, что центры кривизны зеркал
лежат на оси z, т.е. эта ось является осью симметрии резонатора,
пусть оси х и у касательны к первому зеркалу в точке О (рис. 5.1).
Будем рассматривать последовательные отражения от зеркал лу-
лучей, распространяющихся внутри резонатора. Собственным колеба-
колебаниям резонатора соответствуют системы лучей, которые после обхода
резонатора замыкаются на себя, при этом каждый отдельный луч не
замыкается сам на себя, он переходит в другие лучи, но из той же
системы.
Пусть луч АВ лежит в плоскости xz, будем характеризовать этот
луч двумя параметрами: расстоянием ж о его начальной точки А до
оси z и наклоном сро к той же оси z (рис. 5.1). Его конечная коорди-
координата х' определится из уравнения
х' = хо + d' tg ipo, E.1)
где d' — расстояние между проекциями точек А и В на ось z, это
расстояние приближенно можно представить в виде
17 В.П. Быков, О.О. Силичев
258 Гл. 5. Геометрическая оптика лазерных резонаторов
т. е. оно отличается от d малыми второго порядка по ж и ж7. Пренебре-
Пренебрегая в E.1) всеми членами выше первой степени по ж, х' и сро, получим
параметры
ж' = ж0 + dipo, <p' = <Л), E.2)
характеризующие рассматриваемый луч в месте его пересечения со
вторым зеркалом. Нетрудно видеть, что матрица этого преобразова-
преобразования есть не что иное, как оператор трансляции A.20).
Рассмотрим теперь отражение луча АВ во втором зеркале. Урав-
Уравнение второго зеркала вблизи оси (при малых х) можно написать в
виде
наклон нормали к зеркалу в точке ж по отношению к оси z равен
dzjdx — —x/R2.
Из простых геометрических соображений находим угол, который от-
отраженный от второго зеркала луч составляет с осью резонатора. Та-
Таким образом, на втором зеркале параметры луча испытывают преоб-
преобразование
х" = х', у" = -2xf/R2 + <p', E.3)
описываемое матрицей, которая есть просто оператор отражения
A.45).
Далее проход от второго зеркала к первому описывается преоб-
преобразованием, аналогичным E.2), и отражение от первого зеркала —
преобразованием, аналогичным E.3), в котором R2 заменено на R\.
Вычисляя произведение всех этих матриц, получаем
( I"" ™-- \ fa a
М=\ R2 Я2 = fln ai2
I _ 2 _ 2 Ы Ы _2d Ыг I \a2i a22
\ R\ R2 R1R2 Ri R2 R1R2 /
E.4)
— матрицу, описывающую прохождение лучей по всему резонато-
резонатору, которую мы уже получали ранее (см. A.71)). Естественно, что
дальнейшие вычисления можно проводить в соответствии с прави-
правилом ABCD, как это описано в § 1.5. Однако геометрическая оптика
доставляет некоторые свои возможности дальнейшего расчета.
Собственный вектор матрицы E.4) имеет, очевидно, компоненты
х0 = -Ва12, <ро = В (an - eiv), E.5)
где В — некоторый общий коэффициент и e%v — собственное значе-
значение матрицы М (cosv — (ац + а22)/2). Нетрудно видеть, что лучи с
параметрами
хп = x§elvn + x*§e~lvn', ipn = сроегип + Lp^e~lvn E.6)
5.1. Геометрическая оптика лазерных резонаторов 259
образуют некоторую совокупность, которая после прохода по резона-
резонатору, описываемому матрицей E.4), переходит сама в себя, т.е. лучи
с параметрами E.6) образуют собственную систему лучей рассматри-
рассматриваемого резонатора.
Такие системы должны удовлетворять важному фазовому усло-
условию, которое в дальнейшем нам еще понадобится, и мы его рассмот-
рассмотрим в достаточно общей форме. Рассмотрим систему лучей, опреде-
определяемых параметрами
xn = F(n), tg<pn = Ф(ra), E.7)
где Ф(п) < 1, F(n) - периодические функции непрерывного пара-
параметра п, хп — абсцисса точки пересечения n-го луча с осью х и ipn —
угол, который луч составляет с осью z. Уравнение n-го луча имеет вид
По обычным правилам дифференциальной геометрии можно постро-
построить огибающую, т. е. каустику рассматриваемого семейства лучей.
Для этого уравнение E.8) следует продифференцировать по парамет-
параметру га:
яФ'(га) = -F'(n) E.9)
и полученное уравнение E.9) разрешить совместно с E.8) относитель-
относительно х и z. В результате получаются уравнения каустики
в параметрическом виде. Как легко видеть, каустика пересекает ось х
при F'(п) = 0 , т. е. в максимумах и минимумах функции F(n).
Рассмотрим набег фазы вдоль оси абсцисс в системе лучей E.7),
когда п проходит полный период и хп пробегает все значения на оси
абсцисс от каустики до каустики и обратно. Смещение на dxn вдоль
оси х соответствует смещению волнового фронта, ортогонального к
лучам, на величину dxn sin срп и изменению фазы на k dxn sin cpn. Если
это выражение проинтегрировать по всем указанным значениям хп,
то для однозначности фазы полученный набег должен быть кратен
2тг. Точнее сказать, он должен быть равен Bт + 1)тг (т — целое),
поскольку каждое касание луча с каустикой влечет дополнительный
набег фазы тг/2 (см. [138]). Таким образом, система лучей E.7) должна
удовлетворять условию самосогласованности
к / dxn smcpn = Bm + 1)тг.
В параксиальном случае E.6) это условие дает
?/#(
= ik(xo<p*o ~ *оЫ = m + \.
17*
260
Гл. 5. Геометрическая оптика лазерных резонаторов
Учитывая E.5), получим
b = J^±111.
:
k sin v
COSZ/П,
2m + 1
ka\2 sin i/
cos z/n — cos v{n + 1)].
В ряде случаев нет даже необходимости рассматривать полно-
полностью распространение параксиального луча в резонаторе, а достаточ-
достаточно прибегнуть к некоторым простым геометрическим соображениям.
Рассмотрим примеры, которые можно объединить названием — метод
эквивалентного зеркала.
Один или несколько близко расположенных друг к другу опти-
оптических элементов можно заменить одним эквивалентным зеркалом
или линзой. Сферическое зеркало имеет выделенную точку, а имен-
именно, центр кривизны зеркала, такую, что лучи, выходящие из этой
точки, после отражения в зерка-
зеркале вновь собираются в ней, т. е.
источник и изображение нахо-
находятся на одинаковом расстоянии
от зеркала. Аналогичным свой-
свойством обладает и линза: изоб-
изображение источника, удаленного
от линзы на двойное фокусное
расстояние, также находится на
двойном фокусном расстоянии
от нее. Отыскав подобную пару
точек для той или иной оптиче-
оптической системы можно заменить ее
эквивалентными зеркалом или
линзой.
Рассмотрим для примера на-
наклонное, под углом $, падение
лучей на сферическое зеркало
(рис. 5.2). Повернем мысленно
чертеж вокруг прямой, перпен-
перпендикулярной радиусу, проведен-
проведенному из центра кривизны зеркала в точку падения осевого луча. Тогда
осевой и отраженный лучи, не нарушая закона отражения от сфериче-
сферического зеркала, опишут конические поверхности с вершинами в точках
А и В. Эти конические поверхности малыми второго порядка отлича-
отличаются от плоскостей, перпендикулярных плоскости чертежа и проходя-
Рис. 5.2. Наклонное падение лучей
на сферическое зеркало
5.1. Геометрическая оптика лазерных резонаторов
261
щих через падающий и отраженный лучи. Следовательно, выходя из
плоскости чертежа, осевой луч образует систему лучей, выходящих из
точки А, отстоящей от зеркала на расстояние R/ cos$ и собирающих-
собирающихся в точке В, отстоящей от зеркала на то же самое расстояние. Таким
образом, в плоскости, перпендикулярной плоскости чертежа, радиус
кривизны эквивалентного зеркала или двойное фокусное расстояние
эквивалентной линзы равны R/ cos$.
Поворачивая далее схему на рис. 5.2 в плоскости чертежа вокруг
точки О, можно найти лучи, соседние с осевым, и пересекающие его
в точках А' и В'. Простые рассуждения показывают, что эти точки
отстоят от зеркала на расстояние Rcosfi.
Рис. 5.3. Разность эффективных радиусов кривизны системы, образован-
образованной брюстеровской пластиной и сферическим зеркалом
Аналогичным образом рассмотрим оптическую систему, состоя-
состоящую из сферического зеркала и брюстеровской пластины (рис. 5.3).
При падении лучей на преломляющую поверхность под углом Брю-
стера ip, угол преломления равен $ = тг/2 — ip и, следовательно,
1 . п
tgip = n, cos(p =-—==, sin<p =
/п2 + Г г л/п2 + 1
при малых отклонениях от угла Брюстера имеем
На рис. 5.3 изображен осевой луч O\B'GR, падающий нормально
на зеркало и при отражении переходящий сам в себя. Поворачивая
плоскость чертежа на небольшой угол вокруг нормали АО к брюсте-
брюстеровской пластине, проходящей через центр кривизны сферического
262 Гл. 5. Геометрическая оптика лазерных резонаторов
зеркала, легко убедиться, что осевой луч образует систему лучей в
перпендикулярной к чертежу плоскости, которые все выходят из точ-
точки О]_, лежащей на пересечении осевого луча и нормали АО, и после
прохода всей системы вновь собираются в точке О\. Аналогично для
лучей, лежащих в плоскости чертежа, например, СО2, имеется точ-
точка Оъ, являющаяся для них эффективным центром оптической систе-
системы. Целью данного рассмотрения является определение расстояния
O1O2 =x.
Из чертежа нетрудно получить, что
где d — толщина брюстеровской пластины, и п — ее показатель пре-
преломления. Далее учитывая, что ВВ\ = ОО\, получаем
— = ^гс2J
tg(p п
и из треугольника АВ'О± имеем
OOi
B'Oi =
E.10)
COS if
Так как треугольники ВС О и В'С'О2 подобны, то
В'С _ В'О2
ВС ~ ВО '
Для входящих сюда длин имеем следующие выражения:
ВС = h[tg(<p + <p)- tgy>], ВО = -^-, В'О2 = В1 Ох + х,
cos ip
В1 С = htg(<p + ч>) + d[tg(<p + ч>) - tg(tf + Щ - htgip - d(tg<p- tgtf).
Подставляя эти соотношения в пропорцию E.10) и ограничиваясь чле-
членами первого порядка по ip, получим
*&> E.11)
Эта величина представляет собой разность главных радиусов кривиз-
кривизны эквивалентного зеркала, заменяющего собой брюстеровскую пла-
пластину и сферическое зеркало.
§ 5.2. Двумерный эллиптический резонатор
Далее в § 5.2-5.7 рассматриваются резонаторы без ограничения,
вносимого условием параксиальности.
Рассмотрим эллипс, изображенный на рис. 5.4. Будем считать этот
эллипс зеркальным, т. е. способным отражать лучи, лежащие в его
§5.2. Двумерный эллиптический резонатор
263
С
Рис. 5.4. Основное свойство зеркального эллипса
плоскости. После ряда отражений луч света, совпадающий с отрезком
АВ, покроет какую-то часть площади внутри зеркального эллипса, а
часть этой площади останется непокрытой. Исследуем свойства таких
лучевых потоков.
Построим внутренний эллипс, софокусный с зеркальным и каса-
касающийся луча АВ. Покажем, что луч АВ после отражения от зер-
зеркального эллипса в точке В вновь коснется внутреннего эллипса. Для
этого сделаем следующее построение: точки касания S\ и $2 и точку
отражения В соединим с фокусами эллипсов О\ и О^- Треугольник
S\O\B отразим относительно стороны S\B и получим треугольник
SiO[B. Биссектриса угла O\S\O2 между радиусами-векторами яв-
является нормалью к эллипсу, поэтому если угол O1S1O2 обозначить 27,
то ZO2S1B = 7й ^O[SiB = —Ь 7> отсюда следует, что точка О[
лежит на продолжении отрезка S\O2- Точно так же доказывается, что
при отражении треугольника S2O2B относительно отрезка BS2 вер-
вершина О2 отраженного треугольника S2O'2B лежит на продолжении
отрезка OiS^-
Можно видеть, что треугольники О[ВО2 и О±ВО2 равны. Дей-
Действительно, стороны
О[О2 = OiSi - S2O2,
S2O
2O2
равны, так как сумма радиусов-векторов в эллипсе постоянна. Сто-
Сторона О[В равна стороне О±В, так как является ее отражением, и
сторона ВО2 по той же причине равна стороне ВО2. Следовательно,
264
Гл. 5. Геометрическая оптика лазерных резонаторов
= /?ь ZS2BO2 = /?2,
равны между собой углы
ZO[BO2 =
Введем обозначения
АОХВО2 = 2а, LSXBO2
тогда
ZO[BO2 = 2а + 2/?ь АОгВО'з = 2а + 2/?2,
и из их равенства следует E\ = C2. Так как биссектриса угла 0\В02
нормальна к зеркальному эллипсу, то угол падения равен углу отра-
отражения, это означает, что касательная BS2C к внутреннему эллип-
эллипсу есть луч, возникший при отражении луча AS\B в зеркальном
эллипсе.
Естественно, что и при всех последующих отражениях луч бу-
будет касаться внутреннего эллипса. Таким образом, внутренний эл-
эллипс является огибающей или каустикой семейства лучей, касающих-
касающихся его. Это семейство при отражении в зеркальном эллипсе переходит
в себя.
Сказанное относится к случаю, когда исходный луч пересекает
большую ось эллипса правее или левее обоих фокусов. Если же ис-
исходный луч пересекает большую ось эллипса между фокусами, то ка-
каустиками будут гиперболы, софокусные зеркальному эллипсу, а лучи
после большого числа отражений покроют площадь между ветвями
Рис. 5.5. Гиперболические каустики
гиперболы (рис. 5.5). То, что луч после отражения вновь коснется ги-
гиперболы, доказывается совершенно так же, как это сделано выше для
§5.2. Двумерный эллиптический резонатор 265
эллиптической каустики, хотя следует иметь в виду, что это касание
может происходить в области вне зеркального эллипса.
Эти построения имеют непосредственное отношение к лазерным
резонаторам. В случае гиперболических каустик, как мы видели, луч,
распространяясь в зеркальном эллипсе, не выходит из области, огра-
ограниченной двумя ветвями гиперболы, поэтому отдельные части зер-
зеркального эллипса, например дуги QiN\P\ и Q2N2P2, можно удалить.
При этом зеркала не следует обрывать у самой каустики, поскольку
согласно волновой теории поле все же проникает немного за каусти-
каустику. Таким образом, получается открытый лазерный резонатор, в кото-
котором между двумя зер-
зеркалами — отрезками \~
зеркального эллипса — \у
существует система лу-
лучей, ограниченная кау-
каустиками.
Эллиптические ка-
каустики реализуются в
открытом резонаторе,
образованном дугой зер- С = С С = С
кального эллипса, если
ее ограничить по кон- Рис> 5'6' РезонатоР> образованный сектором эл-
цам зеркалами, изо- лнптнческого зеркала
гнутыми по гиперболам, софокусным зеркальному эллипсу и прости-
простирающимся от зеркального эллипса к внутреннему и немного дальше.
В таком резонаторе образуется каустика в виде отрезка эллипса, софо-
кусного зеркальному (рис. 5.6). Такие эллиптические каустики анало-
аналогичны круговым каустикам в цилиндрическом резонаторе, открытый
резонатор, изображенный на рис. 5.6, — открытому сектору такого
резонатора.
Использованные геометрические (или геометро-оптические) свой-
свойства эллипса являются следствием известных теорем геометрии; при-
приведенный вывод является наиболее простым.
Наряду с рассмотренными выше лучевыми потоками, ограничен-
ограниченными гиперболическими и эллиптическими каустиками, в зеркальном
эллипсе существуют гомоцентрические потоки, расходящиеся из фо-
фокусов эллипса и после отражения в нем снова сходящиеся к фокусам.
Лучевые потоки такого типа каустик не имеют и для лазерных резо-
резонаторов интереса не представляют.
Существенно, что кроме рассмотренных лучевых потоков, ника-
никаких других нет, в частности, нет лучевых потоков, сосредоточенных
вблизи большой оси эллипса.
Согласно сказанному, любой эллипс или гипербола, софокусные
зеркальному эллипсу, могут быть каустиками, и их множество со-
составляет континуум, в то время как множество собственных колеба-
266 Гл. 5. Геометрическая оптика лазерных резонаторов
ний счетно. Поэтому не всякая система лучей с эллиптической или
гиперболической каустикой соответствует собственному колебанию.
Собственным колебаниям соответствуют лишь те из них, которые удо-
удовлетворяют определенным фазовым условиям*).
Вследствие двумерности системы таких условий два. При написа-
написании этих условий будем исходить из следующих физических сообра-
соображений. В каждой точке каустики ее касается луч, входящий в иссле-
исследуемую систему лучей. Так как фазовая скорость волны вдоль луча
равна скорости света в вакууме, то волновой фронт вдоль каустики
также должен распространяться со скоростью света в вакууме. Если
каустика представляет собой замкнутую линию, то длина ее долж-
должна быть кратна длине волны, чтобы волновой фронт, обежав каусти-
каустику, вернулся в исходную точку с той же фазой, с которой он из нее
вышел. Если же каустика опирается на отражающие зеркала, то ее
длина должна быть кратна половине длине волны, так как она до
замыкания проходится дважды (если, конечно, волна не приобретает
дополнительной фазы при отражении от зеркала). Это и есть первое
фазовое условие.
Если длина каустики s\ есть функция некоторого параметра т, то
для эллиптической замкнутой каустики имеем
Jbsi(r) =2птг, E.12)
где к = оо/с — волновое число и п — целое. В случае гиперболической
каустики первое фазовое условие имеет вид
fesi(r) = птг. E.13)
Второе фазовое условие также имеет простой физический смысл.
В точку #2 (рис. 5.4) приходят два волновых фронта, вышедших из
точки Si — один распространяется вдоль лучей SiB и BS2, второй —
вдоль каустики Si PS2. Разность фаз этих двух фронтов должна быть
кратна 2тг, точнее сказать, если учесть дополнительный набег фазы
на каустике, равный тг/2, она должна быть равна Bт + 1/2)тг. Таким
образом, второе фазовое условие имеет вид
ks2(r) = Bт+±)тг, E.14)
где S2(t) — разность оптических путей вдоль лучей и по каустике.
Это условие должно иметь одинаковый смысл, где бы ни находилась
точка В, т.е. длина $2 не должна зависеть от положения точки В. Как
*) Иногда используется также термин «квантовые условия», по ана-
аналогии с условиями квантования, использовавшимися в ранней квантовой
механике Бора. Однако рассматриваемые вопросы только формально ма-
математически сходны с квантовомеханическими, поэтому термин «фазо-
«фазовые условия» более соответствует сути дела. Встречаются также термины
«условия стационарности» и «условия самосогласованности».
§5.3. Эллипсоидальный резонатор 267
мы увидим далее, зеркало и каустика действительно связаны таким
свойством, которое обеспечивает постоянство длины $2-
В условии E.14) предполагалось, что луч при отражении от зерка-
зеркала не испытывает никакого скачка фазы, что соответствует гранично-
ди
му условию —
= 0. Иногда скачок фазы при отражении от зеркала
дп
связан с поляризацией. При другой поляризации может реализовы-
ваться граничное условие u\s = 0, при котором скачок равен тг. Если
учитывать обе поляризации, то фазовое условие примет вид
ks2(r) = (m+^тг. E.15)
Для гиперболических каустик инвариантной является разность #2
между длиной линии P1S1BS2P2 и суммарной длиной двух каустик
PiS\R\ + i^S^it^. С учетом скачка фазы на каустике второе фазовое
условие для гиперболических каустик имеет вид
Ь2(г)=(ш+1)|.
Два фазовых условия, например E.12) и E.15), можно рассмат-
рассматривать как систему из двух уравнений с двумя неизвестными к и т.
Разрешая эту систему относительно кит, находим резонансные ча-
частоты ujmn = ckmn собственных колебаний и положения каустик (па-
(параметр ттп), соответствующих им. При этом каждому собственному
колебанию соответствуют свои целочисленные индексы пит.
Как для эллиптических, так и для гиперболических каустик мож-
можно получить явные зависимости s± и S2 от некоторого параметра т.
Однако мы сделаем это несколько позже в качестве частного случая
соответствующих трехмерных зависимостей.
Эллиптический резонатор рассмотрен в работе [140] с учетом со-
соответствующего волнового решения.
§ 5.3. Эллипсоидальный резонатор
Рассмотрим зеркальный эллипсоид с полуосями а, Ъ и с, описыва-
описываемый уравнением
где для определенности будем полагать а > Ъ > с > 0. Как известно,
такому эллипсоиду можно поставить в соответствие семейство кон-
конфокальных поверхностей второго порядка, определяемых уравнением
с одним параметром $. Это семейство конфокальных поверхностей
содержит три подсемейства: эллипсоиды — д = ?, где — оо < ? < с2,
268 Гл. 5. Геометрическая оптика лазерных резонаторов
однополостные гиперболоиды — $ = ??, где с2 < г\ < Ъ2, и двуполостные
гиперболоиды — д = ?, где б2 < ? < а2. Зеркальный эллипсоид E.16)
z Фокальная плоскость
(в плоскости ху)
Фокальный эллипс
(в плоскости ху)
Рис. 5.7. Фокальный эллипс и фокальная гипербола эллипсоидального зер-
зеркала
входит в это семейство с параметром ? = 0. В переходных случаях,
т.е. при $ = с2 или $ = Ъ2 уравнение E.17) определяет фокальные
эллипс и гиперболу (рис. 5.7)
а2 _
Если из некоторой точки зеркального эллипсоида провести каса-
касательные прямые к какой-либо поверхности из семейства E.16), то эти
прямые образуют касательный к этой поверхности конус. Известно,
что этот конус также является поверхностью второго порядка и об-
обладает тремя взаимно перпендикулярными осями симметрии второго
порядка, причем направления этих осей совпадают с тремя главными
направлениями в избранной точке зеркального эллипсоида. Главны-
Главными направлениями называются направления увеличения ?, г] и ( в
этой точке, совпадающие с направлениями нормалей к трем конфо-
конфокальным поверхностям второго порядка, проходящим через данную
точку.
Эти свойства касательного конуса позволяют утверждать, что, ес-
если некоторый луч касается какой-либо поверхности рассматриваемо-
рассматриваемого семейства, то после отражения в зеркальном эллипсоиде он вновь
§5.3. Эллипсоидальный резонатор 269
коснется той же поверхности. Действительно, первоначальный луч
является одной из образующих того конуса, вершина которого нахо-
находится в точке, где этот луч пересекает зеркальный эллипсоид. В силу
симметрии этого конуса луч, отраженный от зеркального эллипсоида
в вершине конуса, вновь станет его образующей. Но все образующие
этого конуса касаются избранной поверхности семейства и отражен-
отраженный луч также будет касаться этой поверхности.
Так как это свойство является основой дальнейшего рассмотрения,
дадим его краткий вывод [139]. Запишем уравнение E.17) в виде
Левая часть этого уравнения представляет собой квадратичную фор-
; -
где Ф — диагональная матрица 4 х 4 с элементами
-J— -J- -J-
о? - •&' Ь2 - •&' с2 - •&'
/ —
Если положить
то квадратичная форма E.19) принимает следующий вид:
F(r) = Ф(х,х) =
= A - ?JФ(ж', х') + 2t(l - ?)Ф(ж', х") + г2Ф(х", ж"), E.20)
где
Рассмотрим теперь пересечение поверхности E.18) с прямой, про-
проходящей через точки (х', з/, z;) и (х", 2/", 2:/;):
270 Гл. 5. Геометрическая оптика лазерных резонаторов
Точки пересечения этой прямой с поверхностью E.18) можно най-
найти, если параметрические уравнения прямой E.21)
х = A - t)x' + tx", y = (l- t)y' + ty", z = (l- t)z' + tz" E.22)
подставить в уравнение E.18). Учитывая E.20), получаем для t урав-
уравнение
A - ?JФ(ж', х1) + 2?A - ?)Ф(ж', х") + ?2Ф(ж", х") = 0.
Это квадратное уравнение относительно переменной A — ?)/?, имею-
имеющее единственный кратный корень при условии
Ф2(х',х") - Ф(х',х')Ф(х",х") = 0, E.23)
т.е. при этом условии прямая E.21) или E.22) является касательной
к поверхности E.18). Если зафиксировать точку х" = (жоэЗЛь^о)? a
координаты точки х' = (x,y,z) рассматривать как текущие, то урав-
уравнение E.23) описывает линейчатую поверхность с вершиной в точке
(xo,yo,zo), касающуюся поверхности E.18), т.е. касательный конус.
Это конус является поверхностью второго порядка, его уравнение со-
согласно E.23) имеет вид
^— - г) ( xl
с2 - •& Да2 -
+ + г) ( + +
- •& ^ V - •& ^ с2 - •& Да2 - •& ^ V - •& ^ с2 - •&
Поскольку этот конус будет интересовать нас в окрестности его вер-
вершины, то обозначая
уравнение E.24) приводим к виду
(хог] -
I /о г\\ / о г\\ ~Т~
Для того чтобы убедиться в симметричности этого конуса, необходи-
необходимо уравнение E.25) записать в локальной касательной ортогональной
системе координат, связанной с точкой хо, уо, zq. Декартовы коорди-
координаты связаны с эллипсоидальными Л, /i, v посредством соотношений
2 _ (а2 ~ А)(а2 - //)(а2 - у) 2 _ (Ъ2 - \)(Ъ2 - у)(Ъ2 - у)
Х ~ (а2 -Ъ2)(а2 -с2) ' У ~ (а2 -Ъ2)(Ъ2 -с2) '
2= (с2-\)(с2-у)(с2-у)
(а2 - с2)(Ъ2 - с2) '
§5.3. Эллипсоидальный резонатор 271
Дифференцируя эти соотношения по Л, /i, z/, получим
с ~ ~х° f d\ dfi diy \
- ~У° ( dX i
~ 2 U2-A
Ц ~ 2 V
2 2
c2-A с2-//
Подставляя эти выражения в E.25), получаем
fcA)fci/) V
B )(b2 )B ) $
(а2 - А)(Ь2 - А)(с2 - А) А - $ (а2 - fi)(b2 - fi)(c2 -
(i/-A)(i/-//) dv2 _
(а2 - v)(b2 - iy)(c2 -и) и-&
— уравнение конуса в локальных координатах. Отсутствие в нем пере-
перекрестных членов типа d\ d\i показывает, что касательный к поверхно-
поверхности E.17) конус E.24) симметрично расположен относительно локаль-
локальной системы координат. Это как раз и доказывает, что образующие
конуса, касающиеся поверхности E.17), отразившись в зеркальном эл-
эллипсоиде, перейдут снова в его образующие и снова будут касаться
поверхности E.17).
Очевидно, что при последующих отражениях луч будет касаться
все той же поверхности конфокального семейства. Следовательно, эта
поверхность является огибающей семейства лучей, т. е. каустической
поверхностью. К заданной прямой можно провести две касательные
поверхности из данного конфокального семейства, и обе эти поверх-
поверхности будут каустическими, т. е. будут ограничивать ту область про-
пространства, в которой, главным образом, сосредоточено волновое поле.
В зависимости от расположения исходного луча возникают четыре
топологических типа колебаний.
Назовем внутренней часть плоскости ху, ограниченную фокаль-
фокальным эллипсом и содержащую в себе его фокусы. Остальную часть
этой плоскости будем называть внешней частью. Часть плоскости xz,
в которой лежат фокусы фокальной гиперболы (состоящую из двух
частей), по аналогии назовем внутренней частью, а остальную часть —
внешней, для плоскости xz эти названия формальны.
Четыре различных типа колебаний возникают в зависимости от
того, где исходный луч пересекает плоскости ху и xz.
1. Исходный луч пересекает внешние части плоскостей ху и xz.
Касательными поверхностями к нему являются эллипсоид и двупо-
лостный гиперболоид. Область, заполненная лучами, схематически
изображена на рис. 5.8, она имеет вид тора, расположенного вблизи
плоскости yz, сечением в виде криволинейного прямоугольника.
2. Исходный луч пересекает внешнюю часть плоскости ху и внут-
внутреннюю часть плоскости xz. Касательными поверхностями являются
272 Гл. 5. Геометрическая оптика лазерных резонаторов
Рис. 5.8. Колебания первого типа в эллипсоидальном резонаторе
Рис. 5.9. Колебания второго типа в эллипсоидальном резонаторе
эллипсоид и однополостный гиперболоид. Область, заполненная лу-
лучами, имеет вид квазипрямоугольного тора, расположенного вблизи
плоскости ху (рис. 5.9).
3. Исходный луч пересекает внутреннюю часть плоскости ху и
внешнюю часть плоскости xz. Касательные поверхности — двуполост-
ный и однополостный гиперболоиды. Область, занятая лучами, имеет
§5.3. Эллипсоидальный резонатор
273
вид несколько искривленной прямоугольной призмы с плоскостями
симметрии ж = О, у = 0 и z = 0 (рис. 5.10).
Рис. 5.10. Колебания третьего типа в эллипсоидальном резонаторе
Рис. 5.11. Колебания четвертого типа в эллипсоидальном резонаторе
4. Исходный луч пересекает внутренние части плоскостей ху и xz.
Касательные поверхности — два однополостных гиперболоида. Об-
Область, занятая лучами, имеет вид полого криволинейного цилиндра,
вытянутого вдоль оси z (рис. 5.11).
Только для колебаний четвертого типа каустическими поверхно-
поверхностями являются две одноименные поверхности. Это связано с тем, что
к однополостному гиперболоиду можно провести касательные как из
внешних, так и из внутренних точек, в то время как к эллипсоиду и
18 В.П. Быков, О.О. Силичев
274 Гл. 5. Геометрическая оптика лазерных резонаторов
двуполостному гиперболоиду можно провести касательные лишь из
внешних точек.
Рассмотрим фазовые условия для эллипсоидального резонатора:
теперь таких условий три. На каустических поверхностях, ограничи-
ограничивающих то или иное колебание, есть линии, которые в каждой своей
точке касаются лучей, принадлежащих данному колебанию. Одной
из таких линий является линия пересечения каустических поверх-
поверхностей. Действительно, прямая, касающаяся линии пересечения, ка-
касается тем самым обеих каустических поверхностей и поэтому при-
принадлежит к лучам, образующим данное колебание, так как после
всех отражений эта прямая по-прежнему будет касаться избранных
каустических поверхностей. К лучам касательны также геодезиче-
геодезические линии на каустических поверхностях, которые касаются линий
пересечения каустических поверхностей. Распространение волнового
фронта вдоль этих линий происходит, очевидно, со скоростью света в
вакууме.
Набег фазы вдоль линии пересечения каустических поверхностей
по возвращении в исходную точку должен быть кратен 2тг. Следо-
Следовательно, первое фазовое условие состоит в том, что длина линии
пересечения каустических поверхностей должна быть кратна длине
волны. Аналогично, набег фазы вдоль геодезической линии, начиная
с точки касания ее с линией пересечения каустических поверхностей,
должен отличаться на величину, кратную 2тг, от набега фазы вдоль
линии пересечения каустических поверхностей между теми же точка-
точками с учетом дополнительного набега фазы на каустике. Это — второе
фазовое условие. Третье фазовое условие возникает из аналогичных
соображений, только геодезическую следует взять на второй каусти-
каустической поверхности.
Для аналитической формулировки фазовых условий приведем вы-
выражения для элементов длины различных линий в эллипсоидальных
координатах. Квадрат элемента длины в произвольном случае имеет
вид
ds2 = dx2 + dy2 + dz2 =
—Що—c' ( }
где ?, ?7, С ~~ эллипсоидальные координаты и
Элемент длины касательной к двум поверхностям $ = $i и $ = $2
равен
Л--^'Л--^ -Л. E.27)
§5.3. Эллипсоидальный резонатор 275
Элемент длины геодезической линии на поверхности ? = const, каса-
касательной к поверхности д = const, равен
Ш)—
Элемент длины линии пересечения поверхностей г\ = const, ? = const
равен
Для колебаний первого типа уравнения каустических поверхно-
поверхностей имеют вид ? = $i и ? = $2- Согласно E.29), длина линии пересе-
пересечения эллипсоида ? = $i и двуполостного гиперболоида С = $2 равна
б2 б2
*fdri±y/P(n) = 2fdriy/P(n), E.30)
с2 с2
где
и коэффициент 4 в E.30) появляется вследствие того, что при одном
обходе линии пересечения координата г) четыре раза пробегает интер-
интервал от с2 до Ъ2. Таким образом, первое фазовое условие принимает
вид
где к = со /с = 2тг/Л — волновое число, со — частота волны, с — скорость
света.
Рассмотрим теперь геодезическую линию на эллипсоидальной кау-
каустической поверхности ? = $i. Пусть она касается линии пересечения
каустических поверхностей в точке ?/. Отойдя от линии пересечения,
она в какой-то точке коснется второй линии пересечения, затем вновь
вернется к первой и коснется ее в точке г]". Согласно E.28), длина
этой геодезической равна
Согласно E.29), первое слагаемое — это длина линии пересечения
между точками ?/ и т]", при вычислении разности длин оно сокра-
сократится. Коэффициент 4 во втором слагаемом появляется вследствие
того, что интегрирование в указанных пределах соответствует лишь
четверти полной длины геодезической. Таким образом, второе фазо-
18*
276
Гл. 5. Геометрическая оптика лазерных резонаторов
вое условие имеет следующий вид:
2
Дополнительное слагаемое в правой части - тг появляется из-за двух
касаний геодезической с каустикой на рассматриваемом отрезке.
Теперь рассмотрим геодезическую на двуполостном гиперболоиде.
После касания с линией пересечения в точке ($i, ?/, $2) эта геодези-
геодезическая подойдет к зеркальному эллипсоиду, отразится от него и за-
затем вновь коснется линии пересечения в точке ($i, 77", $2)- Учитывая
E.28) и E.29), получаем третье фазовое условие в виде
E.31)
где предполагается, что отражение от зеркального эллипсоида проис-
происходит без скачка фазы, если при отражении имеет место скачок фазы
на тг, то 2N% следует заменить на 2N% + 1. В E.31) учтен также допол-
дополнительный набег фазы, обусловленный одним касанием геодезической
с каустикой.
Таким образом, колебания первого типа должны удовлетворять
трем фазовым условиям (при отражении от зеркала без скачка фазы)
Эти три условия определяют резонансные частоты с^д^д^л^ (или вол-
волновой вектор kjsf^N^N^) колебаний, а также положения каустик ? = $i
и ? = $2 этих колебаний.
Аналогично, для колебаний второго типа, когда каустиками явля-
являются эллипсоид ? = $i и однополостной гиперболоид г\ — i?2 j имеем
§5.3. Эллипсоидальный резонатор 277
Для колебаний третьего типа (каустические поверхности г\ = $i и
$2) квантовые условия имеют следующий вид:
Для колебаний четвертого типа вывод фазовых условий несколь-
несколько сложнее, поскольку линия пересечения каустических поверхностей
теперь отсутствует. Введем в точке ?, rj, ( местную декартову систему
координат <j?, av, a^, определяемую соотношениями
-С)
^ 2
Тогда, согласно E.26)
ds2 = dal + da2v + da2o E.33)
с другой стороны, согласно E.27), элемент длины луча, касающегося
поверхностей $ = $i и $ = $2, равен
as —
(f-*7)(f-C)
Равенства E.33) и E.34) могут иметь место одновременно лишь если
коэффициенты при do^, do^, do^ в E.34) являются направляющими
косинусами луча в этой системе координат:
"Г^?2 "Я сое/9 =
(ч-О(ч-С) '
(C-Ш-ч)
Если вдоль луча волна распространяется с фазовой скоростью с,
то вдоль оси о^ она будет распространяться со скоростью с/cos а,
вдоль оси оц — со скоростью с/ cos /3 и вдоль оси gq — со скоростью
278
Гл. 5. Геометрическая оптика лазерных резонаторов
с/cos 7- Приращение фазы при изменении координаты
гласно E.32) и E.35) равно
на
со-
со^ cos a = -
Изменение ? от нуля до с2 соответствует пути от зеркального эл-
эллипсоида до плоскости ху. Очевидно, если пройти до второй полови-
половины зеркального эллипсоида и затем вернуться к первой, то изменение
фазы волнового фронта для установившегося колебания должно быть
кратным 2тг. Это дает нам первое фазовое условие.
Аналогичные выкладки для других координат дадут остальные
фазовые условия. Эти условия имеют вид
Во всех квантовых условиях числа 7V?, A^, N^ считаются целыми, они
могут принимать нулевые значения в тех случаях, когда правая часть
фазового условия при этом не обращается в нуль.
Вообще говоря, по смыслу самой геометрической оптики числа,
входящие в фазовые условия, должны быть большими. Однако срав-
сравнение с точными решениями для
некоторых случаев показывает,
что и при N порядка единицы
точность определения по фазовым
условиям оказывается довольно
высокой, порядка нескольких про-
процентов.
Таким образом, на рис. 5.8-
5.11 изображены возможные типы
колебаний в эллипсоидальном ре-
резонаторе. Колебания первых двух
типов называются волнами «шеп-
Рис. 5.12. Колебания четвертого чущей галереи». Колебания тре-
типа при сильной непараксиаль- тьего и четвертого типов в парак-
ности сиальном случае, т. е. когда они
близки к короткой оси эллипсоида, представляют собой колебания,
реализуемые в линейных лазерных резонаторах.
Особое внимание следует обратить на колебания четвертого типа в
непараксиальном случае. Как явствует из рис. 5.12, эта мода способна
огибать препятствия, расположенные в точках А и В. Разумеется,
5.4- Движение короткого (фемтосекундного) волнового пакета 279
распространение волн, как обычно, происходит вдоль прямолинейных
лучей, скрещивающихся с осью резонатора, но внешне это выглядит
как огибание препятствия. Возможны случаи, когда эта особенность
четвертого типа колебаний является практически важной. Этот тип
колебаний хорошо сопрягается также с трубчатым потоком активной
среды газодинамического лазера.
§ 5.4. Движение короткого (фемтосекундного)
волнового пакета в эллипсоидальном резонаторе
В лазерной практике в последнее время широкое распространение
получили очень короткие, так называемые фемтосекундные импуль-
импульсы. Такие импульсы подчас содержат всего несколько световых волн.
Движение подобных световых волновых пакетов происходит вдоль лу-
лучей, и в некоторых задачах необходимо знать положение пакета в за-
зависимости от времени при его движении в резонаторе. Мы дадим ре-
решение этой задачи для эллипсоидального резонатора, при этом будем
считать, что световой пакет движется, как материальная точка.
Движение материальной точки единичной массы в эллипсоиде с
идеально отражающими стенками описывается функцией Лагранжа
Л=у, E.36)
где v — скорость материальной точки. В этой функции Лагранжа
учтена и возможность отражения материальной точки от стенок эл-
эллипсоида, поскольку она не зависит от знака компонент скорости. В
эллипсоидальной системе координат функция Лагранжа E.36) имеет
вид
Л = Ц2 + Mfj2 + 7VC2, E.37)
где
N =
8?>(С)
Из E.37) следуют уравнения Лагранжа
г
г <"*>-§* = о,
или в более подробной записи
280 Гл. 5. Геометрическая оптика лазерных резонаторов
дМ г дМ л (дЬ 12 , дМ .2 , dN
L & , dM -2 , dTV ^
E.39)
Умножая эти уравнения соответственно на ?7С^ С^7) и ^^С и складывая
их, получим
п)д-^ + ?Ш ~0д-щ + ?Шл - О д-щ = о. E.40)
Воспользовавшись очевидными равенствами (см. 5.38))
дМ ., (/. ч дМ
-щ- = М, {(-г])—
из E.40) получаем
Это равенство можно записать в виде
отсюда следует, что выражение в скобках есть интеграл движения
сохраняющийся, очевидно, и при отражениях материальной точки от
стенок эллипсоида.
Другой интеграл движения получим, если уравнения E.39) до-
множить соответственно на (? + rj)?, (С + Ov и (.V + ОС и сложить.
Производя после этого преобразования, подобные проделанным вы-
выше, получим
jt [(с + v)U2 + (С + OMrf + (v + 0NB} = о,
5.4- Движение короткого (фемтосекундного) волнового пакета 281
т. е. имеет место интеграл движения
?2
(С + v)l?2 + (С + OMr,2 + (v + ?Ж2 = h-
Сохраняющейся величиной, т. е. интегралом движения является так-
также функция Лагранжа E.37). Таким образом, всего имеется три ин-
интеграла движения
Ц2 + Mfi2 + NB =10,
(г,Ц2 + ({Mr,2 + rtNB = h, E.41)
(С + vM2 + (С + OMrf + (т? + 0NB = h;
это есть линейная система уравнений относительно неизвестных L?2,
Mfj2 и NB, детерминанты которой равны
Д = (С-
где
Следовательно, из E.41) получаем
^ ° (ч-ОК-С)
Из этих соотношений получаем
2ЧЪ //v> ^Vc^-o^-cMC)
Переписав эти равенства в виде
d? 2ds
у/№ ~ 00*2 -
с/т/ _ —2ds
(С - *7)(С - 0
282
Гл. 5. Геометрическая оптика лазерных резонаторов
и сложив их почленно, убеждаемся, что правая часть обратится в
нуль:
d(
= 0. E.43)
Умножая равенства E.42) соответственно на ?, г\ и ( и почленно скла-
складывая их, получим
rjdr]
= 0. E.44)
Соотношения E.43) и E.44) представляют собой дифференциаль-
дифференциальные уравнения первого порядка, определяющие траекторию матери-
материальной точки (или волнового пакета), т.е. луча в эллипсоидальной
системе координат. Умножая E.43) на г}\ и вычитая из него E.44),
получим
1 - ц х ц = н—7==== = 0;
- r,)D{r,)
аналогично, умножая E.43) на $2 и вычитая из него E.44), получим
dt; д/^2 — ? dr] <<
_n
Интегрируя эти соотношения, получим
где
E.45)
- С)
E.46)
Система E.45) представляет собой неявное уравнение прямой в эллип-
эллипсоидальных координатах, которая касается поверхностей д\ = const и
§5.5. Эллипсоидальный резонатор — волновое решение 283
$2 = const. Эти соотношения определяют зависимость двух коорди-
координат от какой-либо третьей или зависимость всех трех координат от
какого-либо независимого параметра.
При отражении материальной точки (или волнового пакета) от
поверхности эллипсоида, а также при их прохождении мимо поверх-
поверхностей $i и $2 или пересечении координатных плоскостей, одна из
скобок в подкоренных выражениях в E.46) обращается в нуль, перед
соответствующими корнями необходимо изменить знаки на обратные.
Рис. 5.13. Зависимость ? от Ф
Так как при этом одновременно меняется направление интегрирова-
интегрирования на обратное, то функции Ф и Ф либо все время убывают, либо
все время нарастают. Схематически зависимость ? от Ф1 показана на
рис. 5.13.
Таким образом, система E.45) полностью определяет движение ко-
короткого волнового пакета в эллипсоидальном резонаторе.
§ 5.5. Эллипсоидальный резонатор — волновое
решение
Рассмотрим колебания эллипсоидального резонатора, описывае-
описываемые уравнением Гельмгольца
Д^ + к2и = 0, E.47)
где к = oj/co = 2тг/А — волновое число (cj, со, А — соответственно
частота, фазовая скорость и длина волны). Будем считать, что на
поверхности S резонатора имеет место одно из граничных условий
A. u(x,y,z)\s = 0,
В. —u(x,y,z)
S
= 0.
E.48)
дп
В § 5.3 эта задача решена в рамках геометрической оптики, допол-
дополненной фазовыми условиями, сформулированными на основе простых
физических соображений.
Впервые волновое решение задачи о колебаниях эллипсоида дано в
статье Л.А. Вайнштейна [143], стимулированной геометро-оптическим
284 Гл. 5. Геометрическая оптика лазерных резонаторов
решением [141,147]*). Однако примененная там так называемая Эйри-
асимптотика не всегда удачна. Она не учитывает симметрии задачи,
требует сшивания решений на отдельных интервалах, а для колебаний
четвертого типа оставляет неясным вопрос, где следует производить
такое сшивание. Поэтому ниже дается решение этой волновой задачи,
основанное на работе [144].
Задача о колебаниях в трехосном эллипсоидальном резонаторе мо-
может быть основной для решения широкого класса прикладных задач,
в частности, в работе [145] дано решение задачи об электромагнитных
колебаниях эллипсоида в асимптотическом приближении [146], опира-
опирающееся на решение, данное ниже. Для решения уравнения Гельмголь-
ца E.47) в нем производится разделение переменных, а полученные
таким образом обыкновенные дифференциальные уравнения Ламэ ре-
решаются методом эталонных уравнений [146]. При этом широко ис-
используется информация, которую дает изложенное в § 5.3 геометро-
оптическое решение.
В эллипсоидальных координатах ?, 77, С уравнение E.47) имеет вид
где D($) = (а2 — д){Ъ2 — $)(с2 — $) и а, Ь, с — полуоси эллипсоидаль-
эллипсоидального резонатора. Вводя новые переменные Л, /i, z/, связанные с ?, Т], (
соотношениями
dv = dC/By/D(?)),
E.50)
приводим уравнение E.49) к виду
(V - О ? + к2(( - г,)(г, - 0(С - О" = 0, E.51)
где ?, ?7, С ~~ монотонные функции от Л, /i, v. Для разделения пере-
переменных положим
*) В этой статье он писал: «В работе В.П. Быкова [147] исследованы,
в рамках геометрической оптики, дополненной квантовыми условиями, —
собственные колебания трехосного эллипсоида. Данная статья является до-
дополнением к работе [147] и посвящена аналитическому решению той же
задачи».
§5.5. Эллипсоидальный резонатор — волновое решение 285
тогда уравнение E.51) можно представить в виде определителя
? 1
U2
d2us
dv2
Т] 1
v 1
= 0.
Вследствие линейной зависимости его столбцов имеем
= о,
U2
2 = 0,
,2
a us
dv2
+ к2р(()и3 = 0,
E.52)
где
- tf) = к~2{к2д2 -R&-Q)
и R, Q — константы разделения. Уравнения E.52) есть так называе-
называемые волновые уравнения Ламэ. Рассмотрим последовательно четыре
типа колебаний эллипсоида, описанные в § 5.3.
Сначала несколько слов о граничных условиях. Условия E.48)
дают краевые условия лишь для первого из уравнений E.52), и то
только для одного конца изменения ?. Краевые условия для второ-
второго конца интервала изменения ?, а также для второго и третьего
уравнений E.52) получаются из свойств симметрии эллипсоида. Так
как эллипсоид симметричен относительно трех декартовых плоско-
плоскостей, то решения уравнения E.47) должны быть симметричны или
антисимметричны относительно этих плоскостей. Следовательно, на
этих плоскостях симметрии либо сами решения, либо их производные
должны обращаться в нуль. Из этих граничных условий следует, что
корни $i и $2 функции р($) должны быть действительны и располо-
расположены одним из следующих четырех способов:
П. 0
III. с2
IV. с2
Ъ2<$2<а
<Ь2.
2-
В противном случае решение одного из уравнений E.58) на краю ин-
интервала изменения ?, г] или ? будет монотонным и не сможет удовле-
удовлетворить граничным условиям. Четыре условия E.53) соответствуют
четырем типам колебаний эллипсоида, описанным в § 5.3.
Обратимся теперь к колебаниям первого типа, у которых каусти-
каустическими поверхностями являются эллипсоид (? = $]_) и двуполостной
гиперболоид (( = $2)- На интервале изменения ? имеется одна точка
поворота д\ — корень функции р(?). Поэтому в качестве эталонного
286 Гл. 5. Геометрическая оптика лазерных резонаторов
уравнения к первому из уравнений E.52) возьмем уравнение
d24f/dt2 - k2№ = 0, E.54)
нужное нам решение которого выражается через функцию Эйри
J /l2/3j\ /г гг\
— -г± с/1 гъ 6), уО.ОО)
убывающую при t —> ±оо. Решение первого из уравнений E.52) ищем
в виде
^i(A) = д(А)Ф(?), E.56)
где д(Х) — медленно меняющаяся функция А и ?(А) — некоторая, пока
неизвестная функция А.
Подставляя E.56) в первое из уравнений E.54) и учитывая E.55),
получим
k2 (U12 +р)#Ф + Bg't' +gt"L!' + #"Ф = 0. E.57)
Третьим слагаемым здесь можно пренебречь, так как оно содержит
вторую производную медленно меняющейся функции. Второе слагае-
слагаемое можно обратить в нуль, положив
2g't' +gt" = 0,
ИЛИ
g = d/Vi. E.58)
Тогда из E.57) следует
ttt2+p = 0 E.59)
и, следовательно,
Л - 2/3
Ао
И
2/3
Учитывая E.50), эти соотношения можно записать в виде
2/3
где использовано обозначение
§5.5. Эллипсоидальный резонатор — волновое решение 287
Из E.58) и E.59) следует
и, следовательно, решение E.56) принимает следующий вид:
2/3 ¦
E.60)
E.61)
Исследование показывает, что пренебрежение третьим слагаемым
в E.57) приводит к утере в решении членов порядка /с~4'3. В реше-
решении E.60) использована лишь функция г?, убывающая с ростом ?, так
как из физических соображений ясно, что поле за каустикой убыва-
убывает. Разумеется это правильно, если каустический эллипсоид ? = $i не
слишком близок к плоскости z — 0.
Если при ? = 0 имеет место граничное условие и\ = 0, то из E.61)
следует фазовое условие
E.62)
где tjsfz — iV^-й корень функции Эйри. Если же при ? = 0 обращает-
обращается в нуль производная dui/d?, то фазовое условие также имеет вид
E.62), но t^ — теперь N^-й корень производной функции Эйри. При
больших N^ эти фазовые условия переходят в
E.63)
Обратимся теперь ко второму из уравнений E.52). В нем коэффи-
коэффициент p(rj) не обращается в нуль, оставаясь все время отрицательным.
Поэтому в качестве эталонного уравнения примем
и решение второго из уравнений E.52) будем искать в виде
288 Гл. 5. Геометрическая оптика лазерных резонаторов
Подставляя это решение в уравнение и делая обычные для метода
эталонных уравнений приближения, получаем
t = J dfi л/-рО), 9 =
МО
где /io — пока произвольно. Для и^ получаем выражение
V
E.64)
Как уже отмечалось, из симметрии эллипсоидального резонатора сле-
следует, что решение E.64) должно быть симметричным или антисим-
антисимметричным относительно плоскости z = 0, т. е. оно должно иметь вид
с*
Оно также должно быть симметричным или антисимметричным от-
относительно плоскости у = 0, и это требование приводит к фазовому
условию
ъ2
E.66)
Наконец, рассмотрим третье из уравнений E.52). При изменении (
от Ъ2 до а2 функция р(() меняет знак в точке С = $2- При ( < $2 функ-
функция р(С) < 0 и решение экспоненциального типа, при ? > $2 функция
р(С) > 0 и решение осциллирующее. В качестве эталонного примем
уравнение
ЗГГ + 7 ^о - ^2)ф = °> E-67)
с^2 4 v и ' к '
решение которого при условии
I)/h E.68)
выражается через функции параболического цилиндра
Хотя третье из уравнений E.52), подобно первому, имеет одну точ-
точку поворота на интервале изменения независимой переменной, в ка-
качестве эталонного взято уравнение E.67) с двумя точками поворо-
поворота. Это сделано с учетом геометро-оптического решения, поскольку
для колебаний первого типа условие ? = $2 определяет две каустиче-
каустические поверхности (две ветви двуполостного гиперболоида). Тем самым
учтена симметрия эллипсоида относительно плоскости х = 0.
§5.5. Эллипсоидальный резонатор — волновое решение 289
Принимая решение щ в виде
щ(р) = (?(!/)*(«), E.69)
где Ф(?) — решение уравнения E.67) и подставляя E.69) в третье
уравнение E.52), получим равенства
to
f
определяющие зависимость t от v. Поскольку изменению ( от $2 до
а2 соответствует изменение t от to до 0, то эта зависимость принимает
вид
С
\ [4 arcsin(t/t0) + t^tl-t2] =\fd( л/Р(О. E.70)
Подставляя сюда пределы и учитывая E.68), получаем третье фазо-
фазовое условие
E.71)
Решение же третьего из уравнений E.52) имеет вид
«з@ = C02BJVC + 1) - kt^}/kp(C)e-kt^4HN( (\J\t), E.72)
где t как функция ( определяется соотношением E.70).
Таким образом, решение волнового уравнения E.47) при гранич-
граничных условиях E.48) представляет собой произведение функций E.60),
E.65) и E.72), в которых к, д\ и $2 определяются фазовыми услови-
условиями E.63), E.66) и E.71).
У колебаний второго типа каустическими поверхностями являются
эллипсоид ($i) и однополостный гиперболоид ($2)- Как и для коле-
колебаний первого типа, р(^) меняет знак в точке ? = $]_. Поэтому эта-
эталонным уравнением для первого из уравнений E.52) будет уравнение
Эйри E.54). Соответственно и решение первого из уравнений E.52)
одинаково с решением для первого типа колебаний и описывается
формулой E.60) при том же фазовом условии E.63).
Во втором уравнении E.52) p(rj) изменяет знак в точке г\ — $2- Из
тех же соображений симметрии, что и раньше, в качестве эталонного
принимаем уравнение E.67) с двумя точками поворота. Соответствен-
Соответственно, решение второго из уравнений E.52) одинаково с решением щ(()
19 В.П. Быков, О.О. Силичев
290 Гл. 5. Геометрическая оптика лазерных резонаторов
для первого типа колебаний
где функция t(rf) определяется соотношением
v
arcsin(t/t0)] =
с2
Так как при г] = $2 должно быть t = to, то отсюда следует второе
фазовое условие
Решение третьего из уравнений E.52) для второго типа колебаний
аналогично и2 для первого типа, поэтому приводим его без выкладок:
Мз(С) =
C sin
Ш
k \
при этом имеет место третье фазовое условие
У колебаний третьего типа каустическими поверхностями являют-
являются однополостный гиперболоид г] = $i и двуполостный гиперболоид
( = $2- Параметр р(?) знака не меняет, поэтому решение первого из
уравнений E.52) можно написать в виде
причем синусоидальное решение относится к первому граничному
условию E.48), а косинусоидальное — ко второму граничному усло-
условию E.48). Фазовое условие имеет вид
Решение второго из уравнений E.52) имеет вид
11),
§5.5. Эллипсоидальный резонатор — волновое решение
291
где функция t(rj) определяется соотношением
ъ2
¦ tg arcsin(t/to) = /
v
tl = 2BNr, + l)/к.
Так как при г] = i?i, t = to, то из E.73) следует фазовое условие
ъ2
E.73)
Аналогично для щ (С) имеем выражение
«з@ = Ctf{tl - t^
где t(^) определяется соотношением
|t),
arcsin(t/t0)] = I d(
_ 2BNC
при фазовом условии
У колебаний четвертого типа каустическими поверхностями явля-
являются два однополостных гиперболоида. Поэтому уравнения для щ (^)
и щ(С) не имеют точек поворота. Решение для щ(?) имеет вид
МО =
sm
cos
А; [
2 у
причем синус соответствует первому граничному условию E.48), а
косинус — второму граничному условию E.48). Из симметрии задачи
вытекает первое фазовое условие
Для щ(С) получаем выражение
c sin I k
ь2
19*
292 Гл. 5. Геометрическая оптика лазерных резонаторов
при фазовом условии
а2
\k [ d( у/Р(() = I Nctt. E.74)
2 J 2
Ъ2
Интересно, что в отсутствие симметрии вращения (а2 ф Ъ2) фазо-
фазовое число Nq не может принимать малых значений. Действительно,
левая часть E.74) минимальна при $i = $2 = Ъ2. Тогда из E.74) по-
получаем
О < ^=t_ [(а2 - c2)E(s) - (Ъ2 - c2)K(s)} < \ N^n
где E(s) и K(s) — полные эллиптические интегралы второго и первого
рода. Таким образом, имеется некоторое минимальное значение N^.
Решение U2(rj) для четвертого типа колебаний несколько отлича-
отличается от предыдущих, поскольку интервал изменения г] содержит две
точки поворота. Учитывая симметрию задачи, для и^ примем следу-
следующее эталонное уравнение:
4
где
t = / dr/r.
Его решение имеет вид
Ф(?) = (y/kr) \m\L\™\(kT2/2)e-kr2/\
при
к2 А = Nc + 2NV + 1, кВ = Nv,
где п = Nv и \тп\ = |А^| — целые числа, Ln — обобщенные поли-
полиномы Лагерра. Применяя, как обычно, метод эталонных уравнений,
получим для U2 решение
и2(г]) = СУ(т± -4Ат2
где r(rj) определяется условием
[ dt л/-г4 + 4Ат2 - 4В2 = Г dr) Vp(v)- E.75)
Из E.75) вытекает фазовое условие
5.6. Лучевые системы в резонаторах более общего типа
293
Таким образом, найдены волновые функции, описывающие коле-
колебания эллипсоидального резонатора всех четырех типов, а также фа-
фазовые условия, определяющие резонансные частоты и положение ка-
каустик собственных колебаний.
§ 5.6. Лучевые системы в резонаторах более общего
типа, чем эллипсоидальный
Как можно было видеть в предыдущих параграфах, задача о дви-
движении лучей в зеркальном эллипсоиде принадлежит к классу так
называемых интегрируемых задач, т. е. задач, в которых существу-
существуют первые интегралы движения. С этой интегрируемостью связана
и возможность разделения переменных в соответствующей волновой
задаче. Хотя эллипсоидальный резонатор важен — к нему сводится
большое число различных, в том числе лазерных резонаторов, однако
далеко не все даже в параксиальном приближении. Поэтому пред-
представляет интерес рассмотреть резонаторы более общего типа, нежели
эллипсоидальный.
При этом мы сталкиваемся с той трудностью, что теория возму-
возмущений оказывается мало применимой к качественному исследованию
таких, более общих резонаторов, поскольку в рядах теории возмуще-
возмущений возникают так называемые
«малые знаменатели», делающие
эти ряды расходящимися. Есте-
Естественно поэтому обратиться к
численному решению соответст-
соответствующих уравнений.
Одним из самых простых обоб-
обобщений плоского эллиптического
резонатора является резонатор,
образованный круглым и плос-
плоским зеркалами [147] (рис. 5.14).
Действительно, такую систе-
систему зеркал можно представлять
как единую кривую, описывае-
описываемую уравнением (распадающим-
(распадающимся) третьего порядка, т. е. это ми-
Рис. 5.14. Внеосевые самовоспроиз-
самовоспроизводящиеся лучевые потоки в лазер-
лазерном резонаторе, образованном плос-
плоским и сферическим зеркалами
нимальное усложнение по сравнению с эллипсоидом. Каждый луч,
распространяющийся в таком резонаторе, можно характеризовать
двумя параметрами: углом q, который луч составляет с осью системы,
и расстоянием р от луча до центра кривизны круглого зеркала. Задав
некоторый исходный луч и приписав ему индекс п, можно вычислить
параметры (п + 1)-го луча, т. е. луча, получающегося из n-го после
его отражения от круглого и плоского зеркал. В результате такого
294 Гл. 5. Геометрическая оптика лазерных резонаторов
вычисления получаем
qn+1 = 2arcsin(-pn + ?sm<?n) - qn, E.76)
где рп = —pn-i/R, t = 2A — d/R), R — радиус кривизны круглого
зеркала и d — расстояние между зеркалами.
Условно-периодические по п решения этой системы описывают
собственные системы лучей исследуемого резонатора. Систему E.76)
можно линеаризовать вблизи значений р = q = 0. В результате она
примет вид
Pn+i = -Рп + tqn, qn+i = -2pn - A - 2t)qn. E.77)
Условно-периодическое решение этой системы очевидно:
рп = Ay/t cosz/n, qn = А(уД cosvn - у/2 — t sinz/n), cosv — t - 1.
E.78)
Однако не все решения системы E.76) имеют вид, близкий к реше-
решениям E.78) линеаризованной системы. Мы уже отмечали выше связь
этой проблемы с проблемой «малых знаменателей» в механике. Яс-
Ясно поэтому, что исследование этой проблемы лежит в круге идей
КАМ-теоремы (теоремы Колмогорова-Арнольда-Мозера). Согласно
этим идеям [148], при поворотах общего эллиптического типа, к ко-
которым принадлежит и преобразование E.76), между решениями типа
E.78) лежат резонансные зоны, где решение носит существенно иной
характер. Эти новые движения также условно периодичны, но уже с
другими центрами и с другими частотами. Более того, где-то между
ними также лежат резонансные зоны нового поколения и т. д. до бес-
бесконечности. Кроме того, области различных движений отделены друг
от друга сепаратрическими областями хаотического движения.
На рис. 5.15 представлены результаты итерационных расчетов на
ЭВМ по рекуррентным формулам E.76) при t = 0,52 и при различных
начальных условиях. Выбор этого значения t обусловлен следующи-
следующими причинами. Согласно [148] величина резонансной зоны тем боль-
больше, чем меньше период движения по п того периодического решения,
около которого расположена резонансная зона. Поэтому резонансную
зону естественно искать вблизи решения с периодом по п, равным 3.
При t = 0,5 решение с периодом по п, равным 3, имеет место уже
в линейном приближении. Следовательно, можно полагать, что при
t = 0,52 резонансная зона лежит не слишком далеко от начала коор-
координат и вместе с тем достаточно велика. Результаты, представленные
на рис. 5.15, показывают, что это действительно так. Овалы, центры
которых в начале координат, соответствуют решениям, близким к ре-
решениям линеаризованной системы E.77). Малые овалы неправильной
формы соответствуют как раз резонансным зонам. Движение изоб-
изображающих точек по малым овалам происходит с частотами, сильно
отличающимися от частот движения по овалам с центром в начале
координат.
5.6. Лучевые системы в резонаторах более общего типа
295
Рис. 5.15. Фазовая диаграмма лучевых потоков в резонаторе, образованном
плоским и сферическим зеркалами
При отражении лучей в плоском и круглом зеркалах зона 0 пе-
переходит в зону i, зона 1 — в зону 2 и зона 2 — в зону 0. Поэтому
эти три зоны представляют, по существу, одну и ту же систему лу-
лучей. Лучи, соответствующие зонам #, i, 2 после отражения в плоском
или круглом зеркалах, перейдут в лучи, соответствующие зонам 0'',
1', 2'. Таким образом, число резонансных зон равно числу лучевых
потоков на рис. 5.14, которые и образуют тип колебаний, изображен-
изображенный на этом рисунке. Центры зон соответствуют осевому лучу это-
этого типа колебаний. Они представляют собой периодическое решение
системы E.76) с периодом по п, равным 3 при начальных условиях
= f2l~tP^!~22). E-79)
Имеются также неустойчивые периодические решения, лежащие меж-
между зонами. Они, например, имеют место при начальных условиях
ро=0, COS2^0=2t*
Таким образом, фазовая картина движения систем лучей в иссле-
исследуемом резонаторе представляет собой систему резонансных зон, вло-
вложенных друг в друга, разделенных небольшими (в данном резонато-
резонаторе) зонами хаотического движения и сильно различающихся по своим
размерам. Не все эти зоны будут реально проявляться в том или ином
конкретном частотном диапазоне. Лишь достаточно большие, удовле-
удовлетворяющие фазовому условию зоны могут соответствовать реальным
модам резонатора. Остальные зоны можно назвать скрытыми, «ла-
296 Гл. 5. Геометрическая оптика лазерных резонаторов
тентными» модами, они также могут проявиться, но в более коротко-
коротковолновом диапазоне.
Фазовое условие заключается в том, что набег фазы при проходе
от каустики до каустики и обратно должен быть равен BN + 1)тг,
где N — целое число. Его можно записать в виде
k [ dxn sin qn = B7V + 1)тг, E.80)
где к = oj/c — волновое число и хп — координата точки пересечения
луча и плоского зеркала; индекс п пробегает значения, соответствую-
соответствующие одной из резонансных зон. Так как
_ рп - (l/2)tsmqn
cosqn
то, учитывая условную периодичность по п движения лучей, условие
E.80) можно преобразовать к следующему простому виду:
kR
[ dqnPn =
Таким образом, основное значение для фазового условия имеет
площадь резонансной зоны на рис. 5.15. В рассмотренном случае
эта площадь составляет примерно 10~2. Следовательно, в оптическом
диапазоне (kR ~ 106, Л ~ 10~4 см) число N может достигать значе-
значения 104.
При стремлении t к 1/2 (А = t — 1/2 —у 0) резонансная зона прижи-
прижимается к началу координат. При этом ее площадь уменьшается при-
примерно квадратично с расстоянием до начала координат, т. е. линейно
с А. Это видно из соотношения E.79), которое при малых А перехо-
переходит в ро = sin Ago — у^20А/3 и, следовательно, poqo пропорционально
А. Таким образом, первое колебание того типа, который изображен
на рис. 5.14, появится примерно при q ~ 3 • 10~3 (~ 10;) и А ~ 10~6, и
его наблюдение возможно в обычных газовых лазерах при не слишком
узкой трубке, содержащей активную среду (без брюстеровских окон).
В трехмерном случае, т. е. при сферическом верхнем зеркале и
плоском нижнем, также имеются аналогичные колебания. Представ-
Представление о них нетрудно получить, если рис. 5.14 мысленно вращать
вокруг вертикальной оси. Эти колебания ближе подходят к краям
зеркал, нежели колебания обычного типа. Следовательно, при экспе-
экспериментальном наблюдении этих колебаний необходимо тем или иным
способом подавить колебания обычного типа.
§ 5.7. Построение волнового поля по лучевой картине
Как показано в предыдущих параграфах, для многих резонаторов
могут быть построены системы лучей, переходящие в себя при отра-
отражениях в зеркалах (собственные системы лучей). В одних случаях
§ 5.7. Построение волнового поля по лучевой картине
297
(как в эллипсоиде) они могут быть построены аналитически, в дру-
других — посредством численных расчетов (см. § 5.6). Естественно поэто-
поэтому в качестве следующего шага определения мод резонатора строить
волновое поле этих мод на основе уже известной лучевой картины.
Рассмотрим систему лучей, обладающую каустикой с двумя ветвя-
ветвями (рис. 5.16) и общими асимптотами. Хотя это и не принципиально,
будем считать, что каустики симметрично расположены относитель-
относительно декартовых координат. Построим криволинейную ортогональную
биссекториальную систему координат. Координатные линии этой си-
системы делят пополам углы между лучами, при этом линии N орто-
ортогональны к каустикам и линии К ортогональны к линиям N. Коор-
Координату t будем отсчитывать вдоль линии Nq от точки пересечения ее
Рис. 5.16. Система лучей с двумя каустиками и биссекториальная система
координат
с каустикой, а координату s — от той же точки вдоль каустики Kq
(рис. 5.16). Систему лучей разобьем на две подсистемы — для первой
проекция направляющего вектора q на линии N положительна, для
второй (направляющий вектор q) — отрицательна.
298 Гл. 5. Геометрическая оптика лазерных резонаторов
Коэффициенты Ламе данной системы координат определяются из
условия rot q = rot q = 0. Так как векторы q и q равны соответственно
q = {qt(t,s),q8(t,s)}, q= {-qt(t,s),qs(t,s)},
то для коэффициентов Ламе получаем выражения
где к = >c(t) = qt(O,t) — величина проекции qt на линии Nq. Волновое
уравнение в рассматриваемой системе координат можно привести к
виду
где
t
li= I xdt, X(s,fi) = qtqj1-
о
Решение этого уравнения будем искать в виде
U = (AW + k~1/2BW')eiks, E.82)
где функция
W = W(ti) (i? = tf(/x))
является функцией параболического цилиндра, т. е. удовлетворяет
уравнению
W" + Q(d)W = 0 E.83)
при
ii
Из E.83) следует соотношение
W'" = -Ш -QW,
которое понадобится в дальнейшем.
Коэффициенты А и В будем считать медленно меняющимися
функциями s и \i. Для определения A(s,/i), 5(s,/i), а также $(/i)
подставим решение E.82) в уравнение E.81). Нетрудно убедиться,
что старшие члены, пропорциональные к2, сократятся, если положить
^'2 = § • E-84)
Отсюда следует
iV + i - i 02 dtf = Аух. E.85)
о
При интегрировании от каустики до каустики получим
§5.7. Построение волнового поля по лучевой картине 299
Это соотношение является поперечным фазовым условием. Оно пока-
показывает, что заданной системе лучей может соответствовать волновое
поле только при дискретном наборе частот. Из соотношений E.85)
и E.86) следует, что $ ~ к1!2 и Q ~ к, поэтому удобно ввести вели-
величины
т = ЛГ1/20, P = k~1Q. E.86)
Теперь выпишем полностью волновое уравнение и сгруппируем от-
отдельно члены, содержащие W и W1:
^i-X^A -ХА + Х-1 А + ХА) + kftiX^As + ^А)^ +
- 2ХР1/2В[1 -
+ (А-1)^ + ХА^ + Х
-1JB - ХВ + А-1^ + ХВ) + kfti
+ ХВ^ + Х^В^}} = 0.
Как легко видеть, члены, пропорциональные к2 и къ12 , сокращаются.
Это происходит вследствие специального выбора $(/i), определяемого
соотношением E.84). Члены, не содержащие к или пропорциональные
к~1'2, малы, и мы ими пренебрегаем. Член, пропорциональный kW,
после ряда преобразований приводит к уравнению
iX-У I- (Х-^Р-^А) - Л1/2 |- (Х^Р^В) = 0. E.87)
OS О/jL
Член, пропорциональный kxl2Wl', после аналогичных преобразований
приводит к уравнению
| Д1/2 |_
Складывая и вычитая E.87) и E.88), получим
^ 1/2 О /\ 1/2 гпч \1/2 О
А — (А .г ) — А —
-Л1/2 w-
где
F = iP~x'AА + Р1'АВ G — i\
Уравнения E.89) и E.90) являются уравнениями в частных производ-
производных первого порядка.
Выполняя дифференцирование, приводим E.89) к виду
x = +xy E.91)
д/i ds 2 \д/1 ds/
300 Гл. 5. Геометрическая оптика лазерных резонаторов
Уравнения характеристик имеют вид
1(^ 25% E.92)
dv dv dv /
Первые два уравнения E.92) являются параметрическими уравнени-
уравнениями одного из лучей. Действительно, в малой окрестности некоторой
точки имеем
ds\ = qt dp, ds2 = qs dp, E.93)
где dp — элемент длины луча. С другой стороны,
dsi = — q^1 d\i, ds2 = qj1 ds. E.94)
Подставляя E.94) в E.93) и деля соотношения E.93) друг на друга,
получим
dp _ х 2
ds
что эквивалентно первым двум характеристическим уравнениям из
E.92). Кроме того, из E.93) и E.94) следует
dp = qt dsi + qs ds2 = -d\i + ds
и, следовательно,
g = -(A + A-1). E.95)
Учитывая E.95), третье из характеристических уравнений E.92) мож-
можно привести к виду
^(A + A
dp 2 f
Это уравнение можно преобразовать к виду
d-f = -?, E-96)
dp 2p
где р — расстояние от точки поля до точки касания с каустикой того
луча, который проходит через данную точку поля и является харак-
характеристикой уравнения E.91).
Решение уравнения E.96) имеет вид
где Fq есть функция номера луча, т. е. Fq — постоянная вдоль луча —
но меняется от луча к лучу.
Решение уравнения E.90) получается аналогично и имеет вид
где J) — расстояние вдоль второго луча, проходящего через точку поля,
от точки касания его с каустикой до точки поля и Go — функция
номера второго луча.
§5.7. Построение волнового поля по лучевой картине 301
Таким образом, коэффициенты А и В имеют вид
Л - i pl/4 ( Fo G0\ „ _ 1 p-l/4 ( Fq G
A-—2P l^ + ^J' Б-2Р l^-
и, следовательно, поле между ветвями каустики в рассматриваемом
приближении оказывается равным
+
Для того чтобы поле на каустике не имело особенностей, следует по-
положить
F0(n) = G0(n).
Это соотношение эквивалентно обычному геометро-оптическому усло-
условию, состоящему в том, что набег фазы вдоль луча при прохождении
мимо каустики изменяется на —тг/2. Таким образом, окончательный
вид поля следующий:
E.97)
\П>
Нетрудно убедиться, что это поле на каустике особенностей не имеет.
Кроме решения E.97), очевидно, имеется еще комплексно-сопряжен-
комплексно-сопряженное решение.
Если исходная лучевая система является собственной для какого-
либо резонатора, то возникает вопрос об удовлетворении граничных
условий. Пусть уравнения зеркал резонатора суть s = si и s = S2- То-
Тогда для выполнения граничных условий, например U\Sl^S2 = 0, необ-
необходимо, чтобы фаза выражения E.97) не зависела от д. Положим:
V2 F0(n2) _ / da2 V2
где п — номер луча. В силу закона отражения на верхнем зеркале эти
выражения равны, и, следовательно, фаза выражения E.97) просто
равна —тг/2 и не зависит от $. В силу того же закона отражения то
же самое будет иметь место на нижнем зеркале.
Номер луча п должен обладать двумя свойствами. Во-первых, луч
с номером п после отражения от верхнего и нижнего зеркал должен
принимать номер п + 1. Во-вторых, параметры луча, такие, например,
как наклон а, должны плавно зависеть от п. Возможность введения
такого номера луча не является очевидной. Более подробно этот во-
вопрос мы обсудим ниже.
302
Гл. 5. Геометрическая оптика лазерных резонаторов
Если функцию Fo(n) выбрать в соответствии с E.98), то из гра-
граничных условий на зеркалах следует продольное фазовое условие
и поле в объеме резонатора оказывается равным
7 \ —1 /9
РУ]И)е. + к.с.
dri2 J J J
Поперечное фазовое условие E.86) имеет место даже в том случае, ко-
когда зеркала отсутствуют. Оно показывает, что заданной системе лучей
может соответствовать не произвольная частота, а лишь дискретный
набор частот. Отсюда видно, что для удовлетворения обоим фазо-
фазовым условиям необходимо знать не просто одну лучевую картину, но
систему собственных лучевых картин, зависящую от некоторого па-
параметра.
Вернемся теперь к вопросу о введении номера луча п. Систему лу-
лучей можно изобразить на своего рода фазовой диаграмме (рис. 5.17),
sin a
п = 0
п = 0
Рис. 5.17. Фазовая диаграмма лучевой картины резонатора и определение
номера луча
где по оси абсцисс отложена координата пересечения луча с одним из
зеркал, отсчитываемая вдоль зеркала, а по оси ординат отложен синус
угла, образуемого лучом с нормалью к зеркалу в точке их пересече-
пересечения. На такой фазовой диаграмме каждый луч изобразится точкой,
а вся система лучей изобразится замкнутой кривой (будем называть
эту кривую циклом). Если система лучей является собственной для
рассматриваемого резонатора, то после отражения лучей от верхнего
и нижнего зеркал этот цикл перейдет в себя, хотя каждая отдельная
§5.8. Оптические линии задержки 303
точка цикла перейдет в другую точку цикла. Будем предполагать, что
цикл не является изолированным, т. е. имеется система циклов, при-
приближающаяся к рассматриваемому, скажем, система циклов, вложен-
вложенных в рассматриваемый, или система циклов, охватывающих рассмат-
рассматриваемый. Отметим на рассматриваемом и одном из дополнительных
циклов некоторую начальную точку с номером п = 0 и точку с номе-
номером п = 1, которая получается из начальной в результате отражения
луча от верхнего и нижнего зеркал. Теперь для произвольной точки
цикла определим номер п как предел отношения площади, заключен-
заключенной между дугами циклов, ограниченными точками п = 0 и п = п,
к площади, заключенной между дугами циклов, ограниченными точ-
точками п = 0 и п = 1, при стремлении дополнительного цикла к рас-
рассматриваемому. Нетрудно убедиться, что введенный таким образом
номер луча п удовлетворяет необходимым условиям. Действительно,
точка, получающаяся из точки п = 1 после отражения луча от верх-
верхнего и нижнего зеркал, будет иметь номер п = 2, так как площадь на
фазовой диаграмме сохраняется при отражениях лучей от верхнего
и нижнего зеркал. Кроме того, все параметры луча (ж и sin а) будут
плавно зависеть от номера п.
Несколько слов о поле за каустикой, во внешней части плоскости.
Если там формально строить лучи, касающиеся каустик, то нетрудно
убедиться, что эти лучи имеют комплексные параметры. Казалось бы,
это препятствует построению там биссекториальной системы коорди-
координат. Однако можно показать, что биссектрисы между этими комплекс-
комплексными лучами вещественны и построение биссекториальной системы
координат возможно. Решение волнового уравнения после этого на-
находится так же, как это сделано выше.
Отметим, что в параксиальном приближении решение E.97) пе-
переходит в эрмит-гауссов пучок. Таким образом, соотношение E.97)
определяет волновое поле, соответствующее данной лучевой картине
с двумя каустиками с точностью до некоторой функции одного пере-
переменного Fo(n), которая может быть определена, если известны свой-
свойства источника, задающего лучевую картину. Если система лучей
является собственной для какого-либо резонатора, то волновое поле
определяется полностью.
§ 5.8. Оптические линии задержки
В лазерной технике некоторое распространение получили оптиче-
оптические линии задержки, представляющие собой прекрасный объект для
расчета с помощью геометрической оптики. Впервые они были пред-
предложены Херриотом и Шульте. В первых опытах использовался опти-
оптический резонатор с двумя одинаковыми сферическими широкоапер-
турными зеркалами. Внеосевой пучок, введенный в такой резонатор,
304
Гл. 5. Геометрическая оптика лазерных резонаторов
описывает на зеркалах фигуры Лиссажу, которые в зависимости от
начальных условий имеют вид эллипса, круга или прямой. В этом слу-
случае при небольших размерах резонатора картина, образуемая лучом
на зеркале, полностью вырисовывается за несколько проходов луча,
после чего повторяется вновь. Таким образом, времена задержки, ко-
которые могут быть получены при такой конструкции оптической ли-
линии задержки, являются незначительными. В то же время основные
части объема линии и поверхности зеркал не используются, поэтому
позже было предложено несколько деформировать одно из зеркал,
сделав тем самым его астигматичным. Внесенная таким образом раз-
разница частот колебаний луча в двух взаимно перпендикулярных плос-
плоскостях усложнила вид фигур Лиссажу, образованных на зеркалах,
и позволила значительно увеличить времена задержки, обеспечивае-
обеспечиваемые предложенным устройством. При малой величине астигматизма
движение луча по зеркалу можно считать происходящим по эллипсу,
параметры которого медленно меняются, при этом объем резонато-
резонатора и поверхность зеркала приблизительно равномерно заполняются
лучом. Это позволило увеличить времена задержки до 10 мкс.
Недостатком указанной конструкции является механический спо-
способ создания астигматизма. При деформациях зеркала форма поверх-
поверхности становится очень сложной и практически неконтролируемой.
Это не дает возможности
рассчитывать с необходи-
необходимой точностью ход луча в
резонаторе, не говоря уже
об имеющейся возможно-
возможности разрушения зеркала
под действием механиче-
механического напряжения.
Принципиально другой
способ создания астигма-
астигматизма, свободный от ука-
указанных недостатков, ре-
реализуется в конструкции
трехзеркального резонато-
резонатора с одним сферическим и
су
Рис. 5.18. Схема оптической линии задерж-
задержки с наклонным падением лучей на сфери-
сферическое зеркало
двумя плоскими зеркалами [151, 152]. Такой резонатор эквивалентен
обычному резонатору, у которого одно из зеркал плоское, а другое —
вогнутое астигматичное с главными радиусами кривизны
R
Rx = R cos 7,
Ry -
cos 7
E.99)
где R — радиус кривизны сферического зеркала, 7 ~~ угол падения
пучка на сферическое зеркало, равный половине угла между плоски-
плоскими зеркалами (рис. 5.18). Таким образом, в данной конструкции астиг-
астигматизм является легко и в широких пределах регулируемой величи-
§5.8. Оптические линии задержки 305
ной. Кроме того, отсутствует опасность разрушения зеркала. Вместе с
тем в данной конструкции форма зеркала является строго определен-
определенной и простейшей — сферической. Это позволяет точно рассчитывать
эту конструкцию при помощи ЭВМ.
Рассмотрим основные характеристики такой оптической линии за-
задержки. Радиус кривизны сферического зеркала выбирается так, что-
чтобы резонатор был близок к конфокальному (R = 21, см. рис. 5.18). Это
связано с тем, что в конфокальном резонаторе поперечный размер мод
минимален.
Точное математическое определение собственных поперечных мод
в оптической линии задержки, как и в нерегулярных оптических
линиях связи, затруднительно. Кроме того, вопрос математического
определения собственных мод при решении таких конкретных задач,
как расчет оптической линии задержки, практически несуществен.
Ясно, что для решения данной задачи достаточно найти гауссов пу-
пучок, который будет мало расплываться при большом числе после-
последовательных отражений. Такой гауссов пучок будем называть соб-
собственным пучком оптической линии задержки. Можно думать, что
собственный пучок оптической линии задержки будет близок к соб-
собственной моде конфокального резонатора. Это предположение осно-
основано на том, что хотя при каждом отражении собственный пучок
оптической линии задержки испытывает разное фокусирующее дей-
действие в зависимости от угла падения, при усреднении по всей по-
поверхности зеркала оно примерно такое же, как и в конфокальном
резонаторе.
Рассматриваемая задача является трехмерной. Решать ее удобно
в два приема. Сначала через систему пропускается один «основной»
луч. Этот луч выбирается таким образом, чтобы точки его пересече-
пересечения с зеркалами более или менее равномерно заполняли поверхность
зеркала и были достаточно далеки друг от друга. Особенно важно,
чтобы выходной луч был изолирован от соседних лучей. Один из ва-
вариантов распределения точек по зеркалу показан на рис. 5.19.
На втором этапе основной луч принимается в качестве оси оп-
оптической системы и исследуются свойства этой системы в паракси-
параксиальном приближении. Так как эта система является астигматичной,
то прежде всего нужно было выяснить положение ее главных плос-
плоскостей. Главной плоскостью называется плоскость, обладающая тем
свойством, что пучок, лежащий в этой плоскости, при последователь-
последовательных отражениях все время остается плоским. Главных плоскостей две
и они взаимно перпендикулярны. Главные плоскости являются ха-
характеристикой оптической системы и не зависят от того, какой пучок
пропускается через систему — гомоцентрический или гауссов. Для то-
того, чтобы отыскать главные плоскости, при помощи ЭВМ исследует-
исследуется прохождение гомоцентрических пучков через систему. Эти гомо-
гомоцентрические пучки представляют собой пучки образующих конуса
20 В.П. Быков, О.О. Силичев
306 Гл. 5. Геометрическая оптика лазерных резонаторов
210<
300
100
. 230
г?10А
Л/
} Veo
л
Ш90/
280
>
\
V
л
/40
{
\
>
60
\ ,
у
А
/
250
У
л
/ >
V
^ 50
\/40
гбо/узо
X У
л л
У
180А
У у
f \90/1
у
л
YJ
у150 Y4° Y
^—
220
ПО
)
200
Ьо
Рис. 5.19. Типичное распределение точек пересечения луча с зеркалом
с небольшим углом раскрыва. Сечение выходного пучка плоскостью,
перпендикулярной его оси, представляет собой эллипс, оси которого
определяют собой главные плоскости на выходе исследуемой астигма-
тичной оптической системы. Обратный пересчет на ЭВМ дает поло-
положение главных плоскостей на входе оптической системы. Результаты
расчетов показали, что главные плоскости исследуемой системы как
на входе, так и на выходе совпадают с точностью до 3-5° с плоско-
плоскостями симметрии оптической линии задержки.
В дальнейшем при исследовании гауссова пучка в качестве глав-
главных плоскостей для простоты брались плоскости симметрии оптиче-
оптической линии задержки. В оптическую систему вводился плоский гаус-
гауссов пучок, лежащий в одной из главных плоскостей и описываемый
соотношениями
1 = tg(#/2) cos Ф, \i — a sin Ф,
E.100)
где \i — смещение луча в плоскости х или плоскости у, /i — наклон
луча по отношению к оси z в этих плоскостях, Ф — параметр луча, $ —
расходимость пучка, а — размер перетяжки, причем а и $ связаны
соотношением
= 2n
п = 0,1,2,3,...
E.101)
Этот пучок при п = 0 представляет собой основную моду резонатора
со сферическими зеркалами подходящей кривизны. Придавая пара-
параметру Ф различные значения в пределах от 0 до 2тг, можно по фор-
§5.8. Оптические линии задержки 307
мулам E.100) и E.101) получить смещение и наклон различных лу-
лучей, входящих в пучок. В данном случае параметр Ф принимал 12
значений: 0, тг/6, 2тг/б, ..., соответственно через оптическую систему
при помощи ЭВМ пропускались 12 лучей и исследовалось изменение
а при последовательных отражениях. Вначале исходили из основной
моды конфокального резонатора, размер перетяжки которой дается
следующим выражением:
где Л = 0,84 • 10~4 см и R = 2 • 102 см. Оказалось, что собственная
мода конфокального резонатора не является собственным пучком оп-
оптической линии задержки, так как после ряда последовательных от-
отражений она заметно расширяется. Параметры входного пучка ва-
варьировались вблизи параметров собственного пучка конфокального
резонатора. В результате удалось найти гауссов пучок, размеры кото-
которого при последовательных отражениях практически не изменялись.
Оказалось, что в одной из главных плоскостей этот пучок шире, чем
основная мода конфокального резонатора, а в другой главной плос-
плоскости — уже. Различие размеров перетяжек найденного нерасплы-
вающегося пучка и основной моды конфокального резонатора (при-
(приблизительно в 1,5 раза) обусловлено разницей эффективных радиусов
кривизны зеркала (см. E.89)). Как и следовало ожидать, собственные
пучки оптической линии задержки оказались астигматичными.
Следует подчеркнуть, что возбуждение оптической линии задерж-
задержки необходимо производить пучком, параметры которого совпадают
с параметрами найденного нами нерасплывающегося пучка.
Как указывалось выше, важным параметром оптической линии
задержки является астигматизм. Остановимся несколько подробнее
на выборе его величины. Из конструктивных соображений ясно, что
по возможности астигматизм нужно делать небольшим, а с другой
стороны имеется некоторое минимальное значение астигматизма, при
котором оптическая линия задержки на данное время задержки будет
использоваться наиболее эффективно. Для того чтобы объем резона-
резонатора был равномерно заполнен лучами, нужно, чтобы полный пери-
период колебания лучей равнялся требуемому числу отражений. Частоты
колебаний лучей Пх, Пу во взаимно перпендикулярных направлениях
определяются соотношениями
1
где I — расстояние между плоским и сферическим зеркалами вдоль
оптической оси резонатора. Так как астигматизм предполагается ма-
малым, то
cos7^ I -72/2-
20*
308 Гл. 5. Геометрическая оптика лазерных резонаторов
Далее, учитывая, что резонатор близок к конфокальному, имеем
Пх = | + А, пу = 1-А,
где А, как указывалось выше, определяется из условия
2А • N = 2тг.
Из приведенных выражений легко находится выражение для угла па-
падения
где N — полное число проходов резонатора. При помощи ЭВМ было
просчитано несколько вариантов оптических линий задержки, рассчи-
рассчитанных приблизительно на 300 полных проходов. Типичная расчетная
картина движения лучей по плоскому зеркалу (для 7 — 8°) показана
на рис. 5.19.
Сравнение расчетных данных с линейным случаем показало, что
линейные формулы справедливы в пределах ±10%.
При помощи расчетов на ЭВМ выяснены также некоторые техни-
технические характеристики оптической линии задержки, такие, как, на-
например, устойчивость хода лучей по отношению к малым изменениям
угла 7- Оказалось, что исследованная конфигурация является весьма
устойчивой по отношению к перекосам плоских зеркал, связанным с
изменением угла 7- При перекосах вплоть до 0,5° выходной пучок ис-
испытывает смещение не более половины своего поперечного размера.
Одной из трудностей работы с оптической линией задержки яв-
является трудность ее согласования с внешним источником. Входной
пучок должен иметь сечение ~ 200 мкм при расходимости 10~3 рад.
Из приведенных данных ясно, что линия задержки может быть отно-
относительно легко согласована с газовыми лазерами и очень трудно — со
всеми остальными источниками света.
В работе Быкова, Клинкова и Сазоновой [154] описана трехзер-
кальная линия задержки сигнала на 2 км. При этом геометрическая
длина линии около 1 м. Линия образована двумя плоскими и одним
сферическим зеркалом (радиус кривизны 3 м). Коэффициент отра-
отражения зеркал составлял 99,2%, диаметр — 8 см. Угол падения осевого
луча на сферическое зеркало составляет 4,5°. Луч в линии задержки
совершает до 500 полных проходов. При увеличении коэффициента
отражения зеркал эффективная длина линии может быть еще увели-
увеличена, а геометрические размеры — уменьшены.
В заключение несколько слов о первых публикациях по геометри-
геометрической оптике резонаторных мод.
Геометрооптическая теория собственных колебаний резонаторов
впервые была развита Келлером и Рубиновым [12] вне связи с ла-
лазерными резонаторами. В дальнейшем геометрическая оптика соб-
§5.8. Оптические линии задержки 309
ственных колебаний развивалась под влиянием лазерных исследова-
исследований [140]. В частности, в работах [141, 147] дана геометро-оптическая
теория собственных колебаний эллипсоидального резонатора. Соот-
Соответствующие волновые решения даны в работах [143, 144]. Асимптоти-
Асимптотики электромагнитных полей для эллипсоидального резонатора даны
в [145]. Обобщения теории на более сложные резонаторы даны в [138]
в рамках теории возмущений и в [147] на основе численных расчетов
под воздействием идей Колмогорова-Арнольда-Мозера (КАМ теоре-
теоремы) [148]. Построение волнового поля по лучевой картине обсужда-
обсуждалось в [151, 152] в тесной связи с работами Ю.А. Кравцова [149, 150].
Оптические линии задержки исследовались в работах [153, 154].
* * *
Из-за ограниченного объема книги авторам не удалось отразить
ряд важных резонаторных вопросов. Так, вне поля зрения остались
резонаторы полупроводниковых лазеров и относительно недавно воз-
возникшие микрорезаноторы. Мало затронуты неустойчивые резонаторы
и т. д. Незатронута важная проблема резонаторов коротковолновых
лазеров и перспективы продвижения в этом направлении. По всем
этим вопросам сейчас имеются интересные публикации и, возможно,
в дальнейшем нам удастся расширить книгу в этих направлениях.
ЛИТЕРАТУРА
1. Прохоров A.M. II ЖЭТФ. 1958. Т. 34, №6. С. 1658-1659.
2. Барчуков А.И., Прохоров A.M. // Радиотехника и электроника.
1959. Т. 4, №12. С. 2094-2095.
3. Fox A.G., Li Т. // Bell Syst. Techn. J. 1961. V. 40, №2. P. 453-488.
4. Boyd G.D., Gordon J.D. // Bell. Syst. Techn. J. 1961. V. 40, №2.
P. 489-508.
5. Сучкип Г. Л. II Тезисы докладов и сообщений на IV конференции
по радиоэлектронике МВССО СССР. ХГУ, 1960. С. 106.
6. Вайнштейн Л.А. // ЖЭТФ. 1963. Т. 44, №3. С. 1050-1067.
7. Boyd G.D., Kogelnik H. // Bell. Syst. Techn. J. V. 41, №4. P. 1347-
1369.
8. Бондаренко Н.Г., Таланов В.И. О лучевых волноводах зеркаль-
зеркального типа // Доклад на II симпозиуме по дифракции волн. Горь-
Горький, июнь, 1962.
9. Siegman А.Е. // Proc. IEEE (IRE). 1965. V. 53, №3. P. 277-286.
10. Ананьев Ю.А. Оптические резонаторы и проблема расходимости
лазерного излучения. М.: Наука, 1979.— 328 с.
11. Справочник по лазерам, Т. II, гл. 22, 23. М.: Советское радио,
1978.- 400 с.
12. Keller J.B., Rubinow S.I. // Ann. of Phys. 1960. V. 9, № 1. P. 24-75.
13. Бабич В.М., Булдырев B.C. Асимптотические методы в задачах
дифракции коротких волн. М.: Наука, 1972.— 456 с.
14. Goubou С, Schwering F. // IRE Trans. 1961. V. АР-9, №3. P. 248-
256 / Пер.: Губо Г., Шверинг Ф. // Зарубежная электроника.
1961. №11. С. 3.
15. Goubou G. I/ Electromagnetic Theory and Antennas. Pt. 2. 1963.
P. 907.
16. Kogelnik H., Li T. Imaging of optical modes resonators with internal
lenses // Bell Syst. Techn. J. 1965. V. 44, №3. P. 455-493.
17. Дешан Ж., Мает П. Преобразование пучка при распростране-
распространении в системе квадратичных линз // Квазиоптика. М.: Мир,
1966.- 189 с.
311
18. Kogelnik H., Li Т. Laser beams and resonator // Appl. Opt. 1966.
V. 5, №10. P. 1550-1567.
19. Маркузе Д. Оптические волноводы. М.: Мир, 1974.— 576 с.
20. Гопчарепко A.M. Гауссовы пучки света. Минск, 1977.
21. Коваленко Е.С. Моды произвольного порядка в неоднородных
резонаторах ОКГ // Квантовая электроника. 1976. Т. 3, №2.
С. 433-438.
22. Ищенко Е.Ф. Открытые оптические резонаторы. М.: Сов. радио,
1980.
23. Arnand J.A., Kogelnik H. Gaussian light beams with general
astigmatism // Appl. Opt. 1969. V. 8, №8. P. 1687-1694.
24. Панкратова Т.Ф. Собственные частоты и поляризации объем-
объемного кольцевого резонатора. Оптика и спектроскопия // 1974.
Т. 36, №5. С. 969-974.
25. Савельев И.И., Хромых A.M. Продольные моды объемного коль-
кольцевого резонатора. Квантовая электроника // 1976. Т. 3, № 7.
С. 1517-1526.
26. Черненький В. И. Анизотропный оптический резонатор бегущей
волны // Квантовая электроника / Под ред. Н.Г. Басова. 1971.
№5. С. 53-59.
27. Kogelnik H. On the propagation of gaussian beams of light through
lenslike media including those with a loss or gain variation // Appl.
Opt. 1965. V. 4, №12. P. 1562-1569.
28. Casperson L. W. Beam modes in complex lenslike media and resona-
resonators // J. Opt. Soc. Am. 1976. V. 66, № 12. P. 1373-1379.
29. Ronchi L. Astigmatic gaussian beams in an elliptical square-law
medium // Appl. Opt. 1978. V. 17, №18. P. 2869-2871.
30. Sawa S. Propagation of light-beam through lens-like media with
complex permittivity // IEEE Trans. Microwave theory and techn.
Введение, гл. 1. 1975. V. 23, №7. P. 566-572.
31. Борн М., Вольф 3. Основы оптики. М.: Наука, 1970.— 856 с.
32. Гуд мен Д. Введение в фурье-оптику. М.: Мир, 1970.— 364 с.
33. Градштейн И.О., Рыжик И.М. Таблицы интегралов, сумм, ря-
рядов и произведений. М.: Физматгиз, 1963.— 1094 с.
34. Ананьев Ю.А., Аникичев С.Г. // Оптика и спектроскопия. 1986.
Т. 61, вып. 4. С. 856-860.
35. Силичев О.О. О полноте собственных функций интегральных
операторов в теории резонаторов // Оптика анизотропных сред.
М.: МФТИ, 1988. С. 132-137.
36. Вайнштейн Л.А. Открытые резонаторы и волноводы. М.: Сов.
радио, 1966.— 471 с.
312 Список литературы
37. Базь А.И., Зельдович Я.Б., Переломов A.M. Рассеяния, реакции
и распады в нерелятивистской квантовой механике. М.: Наука,
1971.- 534 с.
38. Беллман Р. Введение в теорию матриц. М.: Наука, 1969.— 367 с.
39. Булдырев B.C., Фрадкин Э.Е. Интегральные уравнения откры-
открытых резонаторов // Оптика и спектроскопия. 1964. Т. 17, №4.
С. 583-596.
40. Глоге Д. Расчет резонаторов Фабри-Перо для лазеров с помо-
помощью матриц рассеяния // Квазиоптика. М.: Мир, 1966. С. 264-
279; Общий метод расчета оптических резонаторов и периодиче-
периодических линзовых систем // Там же. С. 280-314.
41. Комаров И.В., Пономарев Л.П., Славянов СЮ. Сфероидальные
и кулоновские сфероидальные функции. М.: Наука, 1976.— 319 с.
42. Функции с двойной ортогональностью в радиотехнике и оптике /
Перевод и научная обработка М.К. Размахнина и В.П. Яковле-
Яковлева). М.: Сов. радио, 1971.- 256 с.
43. Бойд Д., Гордон Д. Конфокальный резонатор со многими типами
колебаний для квантовых генераторов миллиметрового и опти-
оптического диапазона // Лазеры / Пер. с англ. под ред. М.Е. Жа-
ботинского и Т.А. Шмаонова. М.: ИЛ, 1963. С. 363-381.
44. Хартли Д. Гиперсфероидальные функции и оптические резо-
резонаторы с круглыми зеркалами // Квазиоптика. М.: Мир, 1966.
С. 245-254.
45. Slepian D., Pollak. Prolate spherical wave function // Fourier
analysis and uncertainty I. BSTY. 1961. V. 40, №1. P. 43-63.
46. Flammer C. Spherical wave function. Palo Alto: Stanford univers
press. 1957. P. 220.
47. Силичев О.О. Волновая оптика стабильных резонаторов // М.:
МФТИ, 1986. С. 82-91.
48. Верлань А.Ф., Сизиков B.C. Методы решения интегральных
уравнений с программами для ЭВМ / Справочное пособие. Ки-
Киев: Наукова думка, 1978.— 290 с.
49. Ы Т. Diffraction loss and selection of modes in maser resonator with
circular mirrors // BSTY. 1965. V. 44, №5. P. 917-932.
50. Громов А.П., Трашкевичев СИ. Простые формулы для потерь
симметричных устойчивых резонаторов из круглых зеркал //
Оптика и спектроскопия. 1987. Т. 62, вып. 3. С. 618-620.
51. Fox А.С, Ы Т. Effect of gain saturation on the oscillatiag modes
of optical masers // IEEE J. QE-2. № 12. P. 771-783.
52. Пантпел Р., Путпхов Г. Основы квантовой электроники. М.: Мир,
1972. 382 с.
Список литературы 313
53. Летохов B.C., Сучков А.Ф. Динамика генерации гигантского
импульса когерентного света // ЖЭТФ. 1966. Т. 50, №4. С. 1148.
54. Летохов B.C., Сучков А.Ф. Динамика генерации гигантского
импульса когерентного света // ЖЭТФ. 1967. Т. 52, № 1. С. 282.
55. Ракчеев Д.А., Силичев О.О., Фомичев А.А. Исследование влия-
влияния наведенной анизотропии активного элемента на дифракци-
дифракционные потери одномодового лазера // Квантовая электроника.
1984. Т. II, №3. С. 4585-4591.
56. Найфе А. Введение в методы возмущений. М.: Мир, 1984.— 535 с.
57. Справочник по специальным функциям / Под редакцией М. Аб-
рамовица и И. Стиган. М.: Наука, 1979.— 832 с.
58. Силичев О.О. Аналитический расчет низшей моды устойчивого
резонатора // Квантовая электроника. 1987. Т. 14, №4. С. 842-
844.
59. Johnson M.M. I/ Appl. Opt. 1974. V. 13. P. 2326.
60. Siegman A.E. // Opt. Lett. 1972. V. 1. P. 13.
61. Sanderson R.L., Streifer W. Comparison of laser mode calcula-
calculations // Appl. Opt. 1969. V. 8. P. 131.
62. Siegman A.E., Miller N.Y. Unstable optical resonator loss calcula-
calculations using the prony method // Appl. Opt. 1970. V. 9. P. 2729.
63. Feit M.D., Fleck J.A. Spectral approach to optical resonator theory
// Appl. Opt. 1981. V. 20. P. 2843-2851.
64. Мухтаров Ч.К. О влиянии границы активной зоны на спек-
спектральный состав индуцированного излучения // ДАН СССР.
1966. Т. 171, №6. С. 1301-1304.
65. Мухтаров И.К. Влияние внутренних диэлектрических границ
на свойства оптических резонаторов и на генерацию индуциро-
индуцированного излучения в них // ЖЭТФ. 1971. Т. 60, №3. С. 929-942.
66. Голяев Ю.Д., Лантратов СВ. Пичковые режимы генерации в
лазерах на гранате с неодимом // Квантовая электроника. 1974.
Т. 1, №10. С. 2197.
67. Винокуров Г.Н., Галактионова Н.М., Егорова В.Ф., Мак А.А.,
Седов Б.М., Ханин Я.И. О пичковой структуре излучения твер-
твердотельных лазеров // ЖЭТФ. 1971. Т. 60, №2. С. 489.
68. Smith P. W. Stabilized single-frequency ontput a long laser cavity //
IEEE J. Quant. Electr. 1965. V. 1, №8. P. 343-348.
69. Петрунькин В.Ю., Высоцкий М.Г., Оку нее Р. И. Селекция про-
продольных типов колебаний в гелий-неоновом газовом ОКГ с
4-зеркальным Т-образным резонатором // ЖТФ. 1968. Т. 38,
1. С. 1983-1985.
314 Список литературы
70. Коломников Ю.А., Лисицын В.Н., Чеботаев В.П. Лазерный ин-
интерферометр Майкельсона // Оптика и спектроскопия. 1967.
Т. 22, №5. С. 828-831.
71. Авербах B.C., Власов С.Н., Таланов В.И. Методы селекции ти-
типов колебаний в открытых квазиоптических системах // Изве-
Известия вузов. Радиофизика. 1967. Т. 10, №9-10. С. 1333-1357.
72. Быков В.П., Вахитов Н.Г., Новокрещенов В.К., Шкунов Н.В.
Влияние согласования резонатора на мощность твердотельных
ОКГ // Квантовая электроника. 1971. №2. С. 53-56.
73. Bloom A.L. Observation of new visible gas laser transitions by
removal of dominance // Appl. Phys. Lett. 1963. V. 2, №5. P. 101-
102.
74. Manger H., Rothe H. Selection of axial modes in optical masers //
Phys. Lett. 1963. V. 7, №5. P. 330-331.
75. Броуде В.Л., Погорелый О.Н., Соскин СМ. Генерация R\-линии
рубина в дисперсионном резонаторе // ДАН СССР. 1965. Т. 163,
№6. С. 1342-1343.
76. Косарев Е.Л. Разрежение спектра открытого резонатора с помо-
помощью эшелеттной решетки // Письма в ЖЭТФ. 1966. Т. 3, №7.
С. 295-298.
77. Справочник по лазерам. Т. 1. М.: Сов. радио, 1978.— 360 с.
78. Лизенев А.В., Сомо Л.Н., Степанов А.И. Термооптика твердо-
твердотельных лазеров. Л.: Машиностроение. С. 1986-1999.
79. Белостоцкий Б.Р., Рубанов А.С. Тепловой режим твердотель-
твердотельных оптических квантовых генераторов. М.: Энергия, 1973.—
168 с.
80. Ананьев Ю.А., Козлов Н.А., Мак А.А., Степанов А.И. Терми-
Термическая деформация резонатора твердотельного ОКГ // ЖПС.
1966. Т. 5, вып. 1. С. 51-55.
81. Пономарев А.В., Черняк В.М. Термооптические искажения в
активном элементе прямоугольного сечения // Препринт АН
СССР. №ИАЭ-ЗС79. М., 1979. С. 17.
82. Quelle T.W. Thermal distortion of diffraction limited optical ele-
elements // Appl. Opt. 1966. V. 5, №5. P. 633-637.
83. Буэюинский И.М., Мамонов С. К. Термические эффекты в ак-
активных элементах из стекла, активированного неодимом // Тр.
МВТУ им. Н.Э. Баумана. 1974. №181, вып. 7. С. 181-190.
84. Алексеев Н.Е., Гапонцев В.П., Жаботинский М.Е. и др. Лазер-
Лазерные фосфатные стекла. М.: Наука, 1980.— 352 с.
85. Зверев P.M., Голяев Ю.Д., Шалаев Е.А., Шокин А.А. Лазеры на
алюмоиттриевом гранате с неодимом. М.: Радио и связь, 1985.—
144 с.
Список литературы 315
86. Соме Л.Н., Тарасов А. Л. Термические деформации активных
элементов на центрах окраски // Квантовая электроника. 1979.
Т. 6, №12. С. 2546-2551.
87. Koechner W. Absorbed Pump Power, thermal profile and stressis in
CW pumpa Nd:YAG crystall // Appl. Opt. 1970. V. 9, №6. P. 1429-
1434.
88. Koechner W. Thermal leusing in Nd:YAG laser rod // Appl. Opt.
1970. V. 9, №6. P. 1429-1434.
89. Foster T.D., Osternik L.M. Thermal effects in a Nd:YAG laser // J.
Appl. Phys. 1970. V. 41, №9. P. 3656-3663.
90. Koechner W., Rice D.K. Berifringence of YAG:Nd laser rods as
function of growth derection // J. Opt. Soc. Amer. 1971. V. 61,
№6. P. 758-766.
91. Дмитриев В.Г., Уманский Н.В., Шкунов Н.В. Технические на-
напряжения в активных элементах в непрерывном режиме накач-
накачки // Квантовая электроника. 1971. №2. С. 80-86.
92. Быков В.П., Горшкова Н.Н., Кушпир В.Р., Шкунов Н.В. Иска-
Искажения термически наведенной линзы активного элемента в осве-
осветителях // Электронная техника. Сер. П. 1978. №1. С. 64-68.
93. Голяев Ю.Д., Евтюхов К.Н., Капцов Л.Н. Наведенная анизо-
анизотропия в активных элементах граната с неодимом // Вестник
Моск. ун-та. Сер. физ.-астр. 1980. Т. 21. С. 29-35.
94. Желтое Г.И., Полканов Ю.А. Влияние термических искажений
на оптические свойства элементов из рубина // Квантовая элек-
электроника и лазерная спектроекппия. Минск: Наука и техника,
1974. С. 146-156.
95. Massey G.A. Measurement of device parameters for Nd: YA1O3
lasers // IEEE. J.-QE. 1970. V. QE-8, №7. P. 669-674.
96. Белоногова E.K., Шавку нов СВ. Перестраиваемые лазеры из
александрита // Обзоры по электронной технике. Сер. Лазерная
техника и оптоэлектроника. М.: ЦНИИ «Электроника», 1985.
Вып. 1. С. 1086.
97. Еременко А.С, Каленое А.А., Конский В.А. и др. Осветитель с
диффузно-отражающим слоем системы накачки твердотельного
оптического квантового генератора // Квантовая электроника.
1973. №5. С. 124-126.
98. Калинин Ю.А., Мак А.А. Системы оптической накачки твердо-
твердотельных ОКГ // Оптико-механическая промышленность. 1970.
№2. С. 61-71.
99. Дианое Е.М. Оптические искажения резонатора ОКГ в случае
стержней из граната в форме прямоугольной пластинки // Кван-
Квантовая электроника. 1971. №2. С. 80-86.
316 Список литературы
100. Силичев 0.0. Гауссова оптика резонаторов, содержащих негаус-
негауссовы оптические элементы // Квантовая электроника. 1990.
№17, №6. С. 792-796.
101. Stein A. Thermooptical distortions of resonator // IEEE. J. Quan-
Quantum Electron. 1974. V. QE-10, №4. P. 427-443.
102. Ракчеев Д.А., Силичев О. О., Фомичев А.А. Исследование влия-
влияния наведенной анизотропии активного элемента на дифракци-
дифракционные потери одномодового лазера // Квантовая электроника.
1984. Т. II, №3. С. 585-591.
103. Силичев 0.0. Ракчеев Д.А. Измерение величины нестабильно-
стей оптической силы и положения оси ТЛ АЭ лазерр на АИГ:
Nd // Физические явления в приборах электронной и лазерной
техники. М.: МФТИ, 1982. С. 44-50.
104. Chester R.B., May dan D. Convex-concavl resonators for TEMqq
operation of solid-state ion lasers // J. Appl. Phys. 1972. V. 43, № 5.
P. 2254-2257.
105. Steffen J., Lortscher J.-P., Herziger G. Fundamental mode radiation
with solid-state lasers // IEEE. J. Quant. Electr. 1972. V. QE-8.
P. 239.
106. Lortscher J.-P., Steffen J., Herziger G. Dynamic stable resonators:
a Design procedure // Opt. Quantum Electron. 1975. V. 7. P. 505.
107. Кушнир В.П. О стабильности каустики в плоскосферических ре-
резонаторах с внутренней линзой // Квантовая электроника. 1978.
Т. 5, №6. С. 1248-1256.
108. Силичев О.О. К вопросу о стабилизации параметров лазерного
излучения // Квантовая электроника. 1983. Т. 10, №2. С. 319-
326.
109. Sanderson R.L., Streifer W. Laser resonators with tilted reflectors //
Appl. Opt. 1969. V. 8. P. 224.
110. Ranch R., Kortz H.P., Weber W. Misalignment sensitivity of optical
resonators // Appl. Opt. 1980. V. 19. P. 598.
111. Magni V. Resonators for solid-state lasers with large-volume funda-
fundamental mode and high alignment stability // Appl. Opt. 1986. V. 25,
№1. P. 107-117.
112. Дмитриев В.Г., Копвисар П.Г., Люшпл И.В., Михайлов В.Ю.,
Рустамов СР., Стельмах М.Ф. // Квантовая электроника.
1981. Т. 8. С. 906.
113. Исаев А.С, Кушнир В.Р. // Квантовая электроника. 1982. №9.
С. 820.
114. Конвисар П.Г., Михайлов В.Ю., Рустамов СР. // Квантовая
электроника. 1975. Т. 2. С. 174.
Список литературы 317
115. Силичев 0.0. Особенности поведения мод нелинейного резона-
резонатора // Квантовая электроника. 1986. Т. 13, №8. С. 1560-1565.
116. Краев Е.И., Силичев О.О. Эффективный одномодовый лазер с
импульсной накачкой // Квантовая электроника. 1987. Т. 14, № 8.
С. 1653-1655.
117. Наппа D.C., Sawyers С.С, Yuratch M.A. Telscopic resonators for
large volum TEMqq mode operation // Opt. Quantum Electron.
1981. V. 13. P. 493-507.
118. Ананьев Ю.А. Оптические резонаторы и лазерные пучки. М.:
Наука, 1990.— 263 с.
119. Ананьев Ю.А., Шерстобитов В.Е. Влияние краевых эффектов
свойства неустойчивого резонатора // Квантовая электроника /
Под ред. Н.Г. Басова. 1971. №3. С. 82.
120. Шерстобитов В.Е., Винокуров Т.Н. Свойства неустойчивых ре-
резонаторов с большим эквивалентным числом Френеля // Кван-
Квантовая электроника / Под ред. Н.Г. Басова. 1972. №3. С. 36.
121. Беляев В.Н., Быковский Н.Е., Сенатский О.В., Соболев В.В.
Формирование проникающей радиацией поглощающих слоев в
оптической среде неодимового лазера // Квантовая электроника.
1976. Т. 3, №10. С. 2286-2289.
122. Емельянова Ю.В., Туркевич Л.Г., Маркова Г.В. О получении
равномерного распределения интенсивности в лазерном излуче-
излучении // Письма в ЖТФ. 1977. Т. 3, вып. 8. С. 367-369.
123. Maunders F.A., Mcallisters G.L. Streier W.H. Experiments on
improved unstable mode profile by aperture shaping // IEEE. J.
Quantum Electron. 1974. V. QE-10, №7. P. 821-822.
124. Diels J.C. Apodized aperture using frustrated total reflection //
Appl. Opt. 1975. V. 14, №12. P. 2810-2811.
125. Guilian C, Park Y.K., Byer R.L. Rodial birefringen element and
its applications to laser resonator design // Opt. Lett. 1980. V. 5.
P. 491.
126. Harter D.J., Walling T.C. Low-magnitication unstable resonators
used with ruby and alexandrite lasers // Opt. Lett. 1986. V. 11,
№11. P. 706-708.
127. Zizzo C, Arnone C, Call C, Sciortino S. Fabrication and charac-
characterization of turned gaussian mirrors for the visible and the near
inftyrared // Opt. Lett. 1988. V. 13, №5. P. 342-344.
128. Silvestri 5., Laporta P., Magni V., Svelto O. Nd: YAG laser
with multidielectrical variable reflectivity output coupler // Opt.
Commun. 1988. V. 67, №3. P. 229-232.
129. Фефелов А.П., Харьковский А.В., Хоменко СИ. Динамическая
аподизирующая диафрагма на эффекте НПВО // Физические
318 Список литературы
основы устройств обработки информации. М.: МФТИ, 1989.
С. 59-61.
130. Mecarthy Ж, Lavigned. Optical resonators with gaussian reflectivity
mirrors: output beam characteristics // Appl. Opt. 1984. V. 24, № 21.
P. 3845-3850.
131. Gobbi P.G., Reali G.C. A movel unstable resonator configuration
with a self filtering aperture // Opt. Commun. 1984. V. 52. P. 195-
198.
132. Gobbi P.G., Reali G.C. Mode analysis of a self-liltering unstable
resonators with gaussian transmissions operture // Opt. Commun.
1986. V. 57. P. 355-359.
133. Gobbi P.G., Morosi S., Reali G.C, Zarkasi A.S. Novel unstable
resonator configuration with a self-filtering aperture. Experimental
characterization of the Nd: YAG loaded cavity // Appl. Opt. 1985.
V. 24. P. 26-33.
134. Lazzaro P.D., Hernsen T.W.P.M., Zheng G. A generalization of the
self-filtering unstable resonator // IEEE. J. Quantum Electron. 1988.
V. 24, №8. P. 1543-1547.
135. Weber W., Ifflander R.M., Seiler P. High power Nd-lasers for
industrial applications // SPIE Proc. 1986. V. 650. P. 92-100.
136. Driedger K.P., Ifflander R.M., Weber W. Multirod resonators for
high Power Solid state lasers with improved beam quality // IEEE.
J. Quantum Electron. 1988. V. 24, №4. P. 665-674.
137. Быков В.П. Аберрации в геометрической оптике открытых резо-
резонаторов // Электроника больших мощностей / Под ред. П.Л. Ка-
Капицы. 1967. №5. С. 117.
138. Ландау Л.Д., Лифшиц Е.М. Теория поля. М., 1973. § 153, с. 195.
139. Мусхелишвили Н.И. Курс аналитической геометрии. М.: ГОН-
ТИ, 1938.
140. Быков В.П., Вайнштейн Л.А. Геометрическая оптика открытых
резонаторов // ЖЭТФ. 1964. Т. 47, №8. С. 508.
141. Быков В.П. Лучевые потоки и собственные колебания в откры-
открытых резонаторах // ДАН СССР. 1965. Т. 162, №1. С. 46.
142. Быков В. П. Геометрическая оптика трехмерных колебаний в от-
открытых резонаторах // Электроника больших мощностей / Под
ред. П.Л. Капицы. 1965. №4. С. 66-92.
143. Вайнштейн Л.А. Лучевые потоки в трехосном эллипсоиде //
Электроника больших мощностей. 1965. №4. С. 93-105.
144. Быков В.П., Елов В.В. Акустические колебания в эллипсоидаль-
эллипсоидальной полости // Акустический журнал. 1970. Т. 16, №3. С. 372-
382.
Список литературы 319
145. Газазян Э.Д., Иванян М.И. Коротковолновая асимптотика элек-
электромагнитного поля замкнутого эллипсоида // Радиотехника и
электроника. 1976. Т. 21, №1. С. 2052-2061.
146. Петрашенъ М.И. О полу классических методах решения волно-
волнового уравнения // Уч. зап. ЛГУ. Сер. физ. наук. 1949. Т. 120,
№7. С. 59-78.
147. Быков В.П. О некоторых колебаниях в резонаторах с круглыми
зеркалами // ДАН СССР. 1970. Т. 191, №6. С. 1257-1259.
148. Арнольд В.И. Малые знаменатели // УМН. 1963. Вып. 6 A14).
С. 91.
149. Кравцов Ю.А. Асимптотическое решение уравнений Максвелла
вблизи каустики // Изв. вузов. Радиофизика. 1964. Т. 7, №6.
С. 664.
150. Кравцов Ю.А. Об одной модификации метода геометрической
оптики // Изв. вузов. Радиофизика. 1965. Т. 7, №4. С. 659.
151. Быков В. П. Построение волнового поля по лучевой картине //
ЖТФ. 1970. Т. 40, №10. С. 2035-2042.
152. Быков В.П. Построение волнового поля по известной лучевой
картине, обладающей каустикой с двумя ветвями // Изв. вузов.
Радиофизика. 1971. Т. 14. С. 880-886.
153. Быков В.П., Сазонова З.С. Трехзеркальная оптическия линия
задержки // Радиотехника и электроника. 1972. Т. 17. С. 1953-
1956.
154. Быков В.П., Клинков В.К., Сазонова З.С. Движение лучей в
многоходовой лазерной кювете // Квантовая электроника. 1982.
Т. 9, №3. С. 462-467.
Научное издание
БЫКОВ Владимир Павлович
СИЛИЧ ЕВ Олег Олегович
ЛАЗЕРНЫЕ РЕЗОНАТОРЫ
Редактор Р.А. Бунатян
Оригинал-макет: Д.В. Горбачев
Оформление переплета: А.Ю. Алехина
ЛР №071930 от 06.07.99. Подписано в печать 20.01.03.
Формат 60x90/16. Бумага офсетная. Печать офсетная.
Усл. печ. л. 20. Уч.-изд. л. 20. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997 Москва, Профсоюзная, 90
E-mail: fizmat@maik.ru, fmlsale@maik.ru
http://www.fml.ru
Отпечатано с диапозитивов
в РГУП «Чебоксарская типография № 1».
428019 Чебоксары, пр. И. Яковлева, 15
БВМ 5 -9221 -0297 -4
9 785922 102971