Текст
А.И. Гомонова
ФИЗИКА. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ, ТЕОРИЯ
В книге представлены ответы на вопроси, входившие в экзаменационные билеты вузов России, вплоть до 1997 года.
Издание включает 200 задач по 10 основным разделам физики, подробный разбор и алгоритм их решения; основные теоретические положения, формулы, чертежи и таблицы.
Пособие адресовано преподавателям и слушателям подготовительных курсов, учащимся школ, лицеев.
СОДЕРЖАНИЕ
I. КИНЕМАТИКА 3
§ 1. Основные определения и формулы 3
§ 2. Простейшие операции с векторными величинами 7
§ 3. Равномерное прямолинейное движение 14
§ 4. Равноускоренное движение 25
§ 5. Свободное падение тел 34
§ 6. Кинематика движения материальной точки по окружности 44
§ 7. Абсолютное, относительное и переносное движения 47
II. ДИНАМИКА ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ 57
III. ЗАКОНЫ ИЗМЕНЕНИЯ И СОХРАНЕНИЯ ИМПУЛЬСА ТЕЛА И 93
ЭНЕРГИИ
§ 1. Изменение и сохранение импульса тела и системы тел 93
§ 2. Работа силы. Изменение и сохранение механической энергии тела и 95 системы тел
§ 3. Центральный удар шаров 98
IV. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ. ЗАКОН ВСЕМИРНОГО 124 ТЯГОТЕНИЯ
§ 1. Вращательное движение 124
§ 2. Закон всемирного тяготения 151
V. СТАТИКА 162
§ 1. Статика твердых тел 162
§ 2. Статика жидкостей и газов 186
VI. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕПЛОТА 199
VII. ЭЛЕКТРОСТАТИКА 240
VIII ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК 281
IX. МАГНИТНОЕ ПОЛЕ ТОКА И ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ 313 X. ОПТИКА 350
§ 1. Геометрическая оптика 350
§ 2. Элементы физической оптики 354
XI. ЗАДАЧИ, ПРЕДЛОЖЕННЫЕ В 1994-1996 гг. НА ВСТУПИТЕЛЬНЫХ 402 ЭКЗАМЕНАХ В МОСКОВСКОМ ГОСУДАРСТВЕННОМ УНИВЕРСИТЕТЕ
I. КИНЕМАТИКА
§ 1. Основные определения и формулы
п1.1 Все тела в природе движутся. Изменение положения одного тела относительно другого тела с течением времени называется механическим движением. Именно механические движения вне зависимости от сил, действующих на тела, описывает кинематика. Любое механическое движение всегда является относительным движением или перемещением относительно какого-либо другого тела.
Тело, относительно которого наблюдается движение, называется телом отсчета.
С телом отсчета связывают некоторую систему линий, пересекающихся в том месте, где находится тело отсчета. Совокупность линий, связанных с телом отсчета, называют системой координат, а точку пересечения линий — началом координат. Тело отсчета, связанная с ним система координат и часы образуют систему отсчета.
п1.2 Изучение механики начинают с изучения законов движения материальной точки. Под материальной точкой подразумевают небольшую часть тела, размеры которой достаточно малы по сравнению с размерами всего тела, или само тело, размеры которого малы по сравнению с расстоянием, проходимым телом. Движение материальной точки характеризуется траекторией, длиной пути, координатами тела, перемещением, скоростью и ускорением.
I* 3
nl.3 Траекторией называется линия, в каждой точке которой последовательно побывала движущаяся точка.
Путь - это длина участка траектории, заключенного между двумя точками, определяющими положение тела в начале и конце интересующего нас движения.
п1.4 При изучении движения тела мы пользуемся, как правило, декартовой системой координат, которая представляет собой совокупность трех прямых линий, пересекающихся под прямым углом. При движении материальной точки по одной прямой положение ее можно описать с помощью одной координаты. Положительные и отрицательные числа, определяющие положение точки, называются координатами точки, а прямая, вдоль которой отсчитывается расстояние — осью координат.
При движении точки по плоскости ее положение описывается двумя координатами (X, Y). Положение тела в пространстве задается тремя координатами (X, Y, Z) или радиусом-вектором г = f(t).
Радиус-вектор - это направленный отрезок, проведенный из начала координат в место положения материальной точки.
Перемещение - это вектор, соединяющий начальное и конечное положение точки. Обозначается: Дг = г2 - т- , где Tj и т2 — радиусы-векторы, проведенные из начала координат в начальное и конечное положение точки (рис. 1.1).
4
nl.5 Состояние движения тела характеризуется вектором средней скорости
^7 r^-rft)
v = — —-----------
ср At At
направленным в ту же
сторону, что и переме- рис j j
щение Дт, и мгновен-
ной скоростью (скоростью в данный момент времени)
Аг
направленной по касательной к траектории (рис. 1.1).
п1.6 Часто в житейской практике, например при составлении расписания поездов или при поездке в такси, важно знать путь, пройденный телом, который определить с помощью вектора средней скорости в общем случае нельзя, поэтому вводят скалярную величину средней скорости г\р. Именно эту величину показывают спидометры всех автомобилей, поездов, теплоходов и т.д. Эту скорость называют средним модулем скорости v (путевая скорость). Эта скорость по определению равна отношению полного пути (т.е. длины траектории), пройденного телом, к промежутку времени, за который этот путь пройден, т.е.
v = —.
ср At
5
nl.7 Изменение скорости co временем определяется ускорением :
Аг5 а =---
At
В школьном курсе физики рассматриваются два вида движения: а = 0 и а = const. В первом случае тело движется равномерно и прямолинейно (v = const). В этом случае положение тела в любой момент времени можно описать с помощью радиуса-вектора, который меняется по закону r(t) = r0 + v0t,
где г0 — начальное положение тела. Например, при движении тела вдоль оси ОХ его скорость vx = г>0 = const, а координата меняется по закону x(t) = х0 + vxtf где а?0 — начальная координата. При а = const движение тела — равнопеременное. В этом случае скорость тела и положение тела в пространстве описываются формулами
at2
*>(t) = v0 +at; r(t) = r0(t) + vot + —-.
При движении тела, например, вдоль оси ОХ эти формулы будут иметь вид
a t2
^(0 = vOx + M; x№ = xo + + -7-,
Zb
где vox— начальная скорость вдоль оси OX; ах — ускорение вдоль оси ОХ.
Аналогичный вид имеют формулы для скорости и координаты при движении вдоль осей 0Y и 0Z:
a t2
vy(t) = vOj/ + ayt; y(t) = y0 + vOyt + ;
Zb
6
= voz + a*t ; z(*) = z0 + vOzt+
Li
Уравнения для координаты и скорости позволяют решить любую задачу на движение точки с постоянным ускорением. Уравнение для координаты часто называют основным гфшшенгдем кинематики.
§ 2. Простейшие операции с векторными величинами
В механике часто встречаются с такими величинами, как скорость, перемещение, ускорение, сила и т. д. Для полного описания этих величин важно знать не только их числовые значения, но и направление в каждый момент времени.
Любая величина, значение которой определяется не только числом, но и направлением в пространстве, называется векторной. Мы будем обозначать любую векторную величину буквой со стрелкой наверху, а. Длина направленного отрезка, измеренная в определенном масштабе, равна абсолютной величине вектора и обозначается |а| или а.
Два вектора называются
равными, если они имеют оди- f 4 ft наковую длину и направлены а - а /-в одну сторону (рис. 1.2). / / II
Сложение и вычитание 5 = 6
векторов. Векторы складыва-ются геометрически: сумма
7
двух векторов равна диагонали параллелограмма, сторонами которого являются складываемые векторы. То есть, для того чтобы сложить два вектора а и Ь, их надо привести к одному началу, перемещая векторы параллельно самим
себе (рис. 1.3, а). При сложении этих векторов можно пользоваться правилом «треугольника». В этом случае к концу одного вектора приставляют начало второго. Тогда их суммой будет вектор, начало которого совпадает с началом первого векто
ра, а конец — с концом второго
вектора (рис. 1.3, б).
Длину вектора суммы а + b = с определяют по
теореме косинусов |с| = а + Ъ = yja2 + Ъ2 — 2ab cos а ,
где а — угол между векторами а и Ь.
Вычитание векторов можно представить как сложение с обратным вектором. Действительна, разность векторов а и b можно представить как с = a — b = d + (— Ъ), т.е. для нахождения вектора разности с нужно сложить два вектора: а и ~Ъ (рис. 1.4). _________
_ / \с = а-Ь '' \ / \с = а — Ь
/ \ '' с=а~Ь\/ \
..\С-------
ъ -ь ь
Рис. 1.4
8
Из рисунка видно: если начала векторов а и b совмещены, то вектор разности с представляет собой направленный отрезок, начало которого совпадает с концом вычитаемого вектора Ъ, а конец — с концом уменьшаемого вектора а.
Скалярной величиной называется величина, значение которой определяется числом, взятым со знаком «+» или «—». Примером таких величин могут служить: путь, время, масса, модуль любого вектора и т. д.
Если какой-либо вектор умножим или разделим на число (скалярную величину), то тем самым изменится длина взятого вектора в некоторое число раз. При этом новый вектор направлен в ту же сторону, что и умножаемый вектор, если число больше нуля, и в противоположную — если число меньше нуля.
Разложение вектора. Операция замены любого вектора несколькими называется разложение ем вектора на составляющие.
Любой вектор а, проведенный, например, из начала прямоугольной системы координат, можно представить как сумму трех векторов:
5 = ах + %+йг-
Векторы ая, 2у) а2 являются составляющими вектора а вдоль осей OX, OY, 0Z соответственно. Часто вместо составляющих вектора пользуются понятием проекций вектора на заданные направления. Для этого вводят единичные векторы i, j, к вдоль осей OX, OY, 0Z соответственно (единичным вектором называется вектор, модуль
9
ах = a cos а; ау = acosp',
Рис. 1.5
которого равен 1). В этом случае составляющие вектора можно записать в виде ах = i ах, ау = jay, az = kaz (рис. 1.5). Величины ах, ау) az — числа-скаляры. Они называются проекциями вектора на координатные оси OX, OY, 0Z. Величина проекций определяется по формулам:
az = a cos у, где а — модуль вектора а, а углы а, 0, у — это углы между положительным направлением соответствующей оси и вектором а, отсчитываемые против часовой стрелки. Другими словами, проекция вектора на выбранное направление берется со знаком «+», если направление соответствующего вектора совпадает с направлением оси, и со знаком «—», если направления противоположны.
Примеры решения задач
Задача 1.1 Определить величину и направление вектора а, лежащего в плоскости X0Y, если заданы координаты начала и конца вектора а (рис. 1.6).
10
Решение. Опустим перпендикуляры с концов вектора а на оси ОХ и 0Y. Началу вектора (точка А) соответствуют координаты хг и уи концу вектора (точка В) — координаты х2 и у2. Проекции вектора на
оси ОХ и 0Y равны разности координат концов
вектора, т. е.
ах = х2 - a?j = Дх; ау = у2 - уг = Ду.
Зная проекции вектора на оси координат, легко определить величину (модуль) вектора и направление его в пространстве.
Как видно из рисунка, длина вектора а определяется по теореме Пифагора
а = у/ах2+ау2 = 7(х2-^1)2+(У2-У1)2 = дМ^+V-
Вектор считается заданным, если известна его длина и направление в пространстве. Направление вектора определяется углом наклона его к соответствующей оси координат, т. е. углом а или р = 90° - а:
аг Дэе cos а = —— = . -.
а д/Дсс2 + ЛУ2 ’
11
cos p = — = г = sin a.
a ^x2 + Ap2
Задача 1.2 Определить проекцию вектора а на ось ОХ, полагая, что угол а задан (pttc. 1.7, 1.8).
Решение. Опустим перпендикуляры с концов, вектора а на ось ОХ. Проекция вектора а на ось ОХ равна
ах = х2 ~ xi = ~ |А^| = а cos = a cos (180°—а) = —a cos а •
Рис. 1.7
Угол 0 отсчитывается от положительного направления оси ОХ до вектора а против часовой стрелки, причем век-тгор нужно перенести параллельно самому себе так, чтобы его начало лежало на
оси ОХ (рис. 1.8).
Аналогичная операция проделывается при отыс
12
кании проекции вектора а на ось 0Y (рекоменду
ется отыскать проекцию ау самим).
Задача 1.3 Пешеход вышел из пункта А и, двигаясь строго на северо-восток, прошел расстояние АВ = ^=5 км за 1 час. Затем он повернул на восток и прошел еще расстояние ВС = S2=6 км, двигаясь 2 часа. После этого он пошел на юг и прошел расстояние CD = S3—6 км за 1 час. Определить путь, пройденный пешеходом за 4 часа, и его перемещение Дт за это время (рис. 1.9).
Решение. Полное перемёщение пешехода Дт
за 4 часа равно вектору AD. Путь, пройденный
пешеходом за это время, равен сумме отрезков АВ, ВС и CD, т.е.
S=AB+BC+CD=5 км+6 км+6 км=17 км.
Величину перемещения |Дт|=АО можно определить, пользуясь правилом сложения векторов. Воспользуемся правилом многоугольника.
Так как от перемены мест слагаемых сумма их не меня
13
ется, определим сумму векторов ВС и CD. Суммой этих векторов является вектор BD, модуль которого определяется по теореме Пифагора
BD = 7(ВС)2 + (СВ)2 = д/36 + 36 км = бд/2 км.
Модуль вектора ВС равен модулю вектора CD, поэтому угол CBD=0 =45°, следовательно, треугольник ABD — прямоугольный. Это позволяет ве-
личину вектора AD=AB + BD определить, также пользуясь правилом Пифагора:
AD = у] (АВ)2 + (BD)2 = V25 + 72 = V97 «10 км.
Таким образом, пешеход прошел путь 5=17 км, а переместился от точки А на кратчайшее расстояние |Дг|«10км.
§ 3. Равномерное прямолинейное движение
Самую большую трудность для учащихся при решении задач представляет вопрос «с чего начать?» Предлагается некоторая последовательность действий (некий алгоритм), который поможет вам.
1. Прежде всего внимательно прочтите условие задачи.
2. Нарисуйте рисунок — это позволит яснее представить задачу.
3. Условие задачи, т. е. заданные и искомые величины, следует записать в тетради в столбик
14
в той последовательности, в какой они изложены в тексте задачи.
4. Так как любое движение происходит обязательно в некоторой системе отсчета, необходимо выбрать систему координат, задать ее начало и положительное направление координатных осей и выбрать начало отсчета времени. Чаще всего выбор системы отсчета подсказывает само условие задачи.
5. Теперь нужно записать основное уравнение движения тел в этой системе отсчета. При равномерном движении — это уравнение для координат, при равноускоренном — для координат и скоростей.
6. Далее приступаем к алгебраическому решению записанных уравнений, в результате которого получаем формулы в общем виде для определения искомых в задаче величин.
7. Подставляем в полученные формулы числовые значения заданных в условии величин и выполняем арифметический расчет.
Применим предложенный алгоритм на примере решения задач на равномерное движение.
Примеры решения задач
Задача 1.4 Из городов А и В, находящихся на прямолинейном шоссе, одновременно навстречу друг другу выезжают две автомашины со скоростями г>л=100 км/ч и г?в=60 км/ч. Расстояние между городами L=120 км (рис. 1.10). Через какое время (te) и на каком расстоянии от города А (хв) встретятся автомашины? Как меняется расстояние между ними, если каждая машина, пройдя
15
120 км, остановилась? Решить зaдaчv аналитически и графически.
Решение. Изобразим условие задачи на рисунке (рис. 1.10).
Рис. 1.10
Запишем условие задачи в виде столбика:
VA =100 км/ч
vb =60 км/ч
L=120 км
*в=?
хе=?
S=?
Совместим начало координат с городом А, а ось ОХ направим от города А к В. Время будем отсчитывать с момента отправления обеих машин.
Так как автомашины движутся с постоянными скоростями, то их координаты в любой момент времени определяются формулами:
= Х0Л + VAt'> Жв(0 = ^0В + VBt-
В выбранной системе отсчета х0А = 0, хов = L,
VA = VA> VB = ~VB > ТОГДа
Xa№ = VAt> a Xb№ = L~VBt.
16
В месте встречи координаты автомашин одинаковы, т. е.
= ^в(^) или vAte =L- vBte.
Тут следует заметить, что равенство координат выполняется только в момент встречи, поэтому время t в последнем равенстве обязательно должно употребляться с каким-либо индексом (например tj.
Решая это уравнение, определим время встречи
К =---7----
va + ^b
Место встречи (координату встречи) можно получить, пользуясь любым из выражений для координаты. Подставив t = te, например, в первое из уравнений, получим
v .L x(t) = v.t =------
\ в ' Ав । ,
VA+VB
Расстояние между автомашинами S в любой момент времени равно модулю разности их координат:
£ =|xB(t)-xA(t)| = |L - vBt - vAt\ = |L - (vB +vA)t|.
Мы получили ответ на все вопросы задачи в общем (буквенном) виде. Теперь можно подставлять числовые значения:
К =120 км/(100 км/ч+60 км/ч)=3/4 ч=
va + VB
= 45 мин;
17
хв =-------= (100 км/ч-120 км)/(100 км/ч +
+ 60 км/ч) = 75 км.
Таким образом, автомобили встретятся через 3/4 часа на расстоянии 75 км справа от города А.
Эту задачу полезно решить графически. Ответы на поставленные в условии задачи вопросы мы сможем легко получить, если изобразим график зависимости координаты каждой автомашины от времени (рис. 1.11).
Прямая I представляет график зависимости координаты от времени для машины, выехавшей из города А. Строим ее таким образом: так как скорость автомобиля =100 км/ч (это расстояние, пройденное за 1 час), то из точки 3^=100 км
проводим прямую, параллельную оси времени; затем из точки tj=l час восстанавливаем перпендикуляр, который пересекает эту прямую в точке «1» (рис. 1.11). Через начало координат и точку «1» проводим прямую I. Это и есть график движения автомобиля, выехавшего из пункта А. Тангенс угла
18
наклона этой кривой к оси времени численно равен скорости vA.
Прямую II строим аналогично, однако расстояние сс2=60 км откладываем от точки В, так как автомобиль выезжает из пункта В. Проводим прямую II через точку В и точку «2» и таким образом получаем график движения автомобиля, выехавшего из пункта В.
Точка пересечения прямых I и II позволяет определить время и место встречи автомашин. Для
этого из точки пересечения прямых опустим перпендикуляр на ось времени Ot и ось координат ОХ. Точки пересечения опущенных перпендикуляров
с соответствующими осями позволяют определить
время и место встречи автомашин.
Из рис. 1.11 видно, что машины встретят-ся через 3/4 часа на расстоянии 75 км от города А.
Графически можно представить и как меняется расстояние между автомашинами, пользуясь формулой 5 = |L-(vA+vB)t| (рис. 1.12).
19
В течение времени 0 - t, обе автомашины движутся одновременно, наклон прямой 5 определяется величиной скорости (vA + vB). В момент t = te автомашины встретятся. В момент t = t, = 1,2 ч автомашина, выехавшая из города А, прибывает в город В и останавливается (рис. 1.12). Машина же, выехавшая из города В, продолжает двигаться. С этого момента времени расстояние между машинами определяется формулой 5 = |L — vBt\. Так как vA = следовательно наклон кривой на графике, изображенном на рис. 1.12, уменьшается (участок
-t2). В момент времени t = t2 =2 ч автомобиль, выехавший из города В, прибывает в город А.
Задача 1.5 Лодка переплывает реку, отправляясь из пункта А. Если она держит курс перпендикулярно берегу, то через время t} после отправления она попадает в пункт С, лежащий на расстоянии S ниже пункта В (рис. 1.13, а). Если она держит курс с той же скоростью под некоторым углом а к прямой АВ, то через время t2 лодка попадет в пункт В (рис. 1.13, б). Определить: ширину реки I, скорость лодки и, скорость течения реки v и угол а.
Решение. Приступим сразу же к выполнению 4-го пункта предложенного алгоритма, т. е. к выбору системы отсчета (полагая, что первые три пункта уже освоили). В этой задаче движение лодки в любой момент времени описывается с помощью двух координат: x(t) и y(t) (движение двумерное). Начало координат удобно совместить с пунктом А, ось 0Y направить вдоль прямой ОВ, а ось ОХ вдоль берега реки (см. рис. 1.13). В любой
20
момент времени уравнения для координат в обоих случаях запишутся:
x(t) = vxt = vt\ fx(t) — vxt = (v — и sin a)t;
V(t).- vyt - ut; y(t) = vt = ut cos a.
Для моментов времени tl и t2 эти уравнения примут вид:
1) = 5 = vtY 3) or(t2) = (v — и sin a)t2 = О
2) V(^i) = I = 4) y(t2) = I = ut2 cos a.
21
Эти 4 уравнения позволят нам определить 4 неизвестные величины, требуемые в задаче.
Скорость реки v сразу же определяется из уравнения (1)
5 v = —
Решая совместно уравнения (2) и (4), определим угол a: ut^ ut2 cosa , следовательно, cos a = —, или a = arc cos —.
t2 t2
Формула (3) позволит определить скорость лодки относительно воды и (v — и sina)t2 = 0 или v — и sin а
Ширину реки I можно определить из формулы (2) либо из формулы (4). Воспользуемся более простой формулой (2):
Таким образом, мы определили все величины, требуемые в условии задачи.
22
Задача 1.6 Человек в лодке должен попасть из точки А в точку В, находящуюся на противоположном берегу реки (рис. 1.14). Скорость течения реки г50. Прямая АВ расположена под углом а к берегу. С какой наименьшей скоростью й относительно воды должна В плыть лодка, чтобы попасть в точку В?
к Решение. Скорость
\ _ лодки относительно
а - "*•____ берега г>р (результи-
*4 рующая скорость) на-
Рис I 14 правлена по прямой
АВ и представляет собой векторную сумму скоростей и и v0> т.е. vp = й + г>0 . Решение этой задачи очень упрощается, если воспользоваться при сложении скоростей правилом треугольника (рис. 1.15). Из всех возможных значений скоростей и наименьшим будет перпендикуляр, опущенный на направление АВ. Следовательно, человеку нужно напра-
Рис. 1.15
23
вить лодку перпендикулярно направлению АВ. Величина этой скорости определяется из прямоугольного треугольника АОС:
Umin = «0Sin«-
Задача 1.7 Автомобиль проехал первую половину пути со скоростью = 40 км/ч , вторую — со скоростью v2 = 60 км/ч.
Определить среднюю скорость (средний модуль скорости) на всем пройденном пути.
Решение. Пусть первую половину пути автомобиль прошел за время двигаясь со скорос-
тью
«1
. Вторую половину пути он прошел
за время t2, двигаясь со скоростью
Тогда полное время движения равно
К
И
— + t2 — v + v . Так как весь путь, прой
денный автомобилем, равен S, то среднюю скорость легко определить:
- S ~ S _ 2viv2 _ 2-60-40
ср tj +t2 ~ S ( 1 + 1 ~ Uj + v2 ~ 100 км/4
2 v2)
= 48 км/ч.
24
. Задача 1.8 К ползуну, который может перемещаться по направляющей рейке (рис. 1.16), прикреплен нерастяжимый шнур, продетый через кольцо. Шнур выбирают со скоростью v. С какой скоростью и движется ползун в момент, когда шнур составляет с направлением оси ОХ угол а!
Рис. 1.16
Решение. Так как шнур нерастяжим, то каждая его точка перемещается со скоростью v. Именно поэтому проекция скорости и , с которой движется точка А вдоль рейки, на направление шнура, равна скорости шнура и, т.е. u cos а = v. От
сюда и = v/ „
/cos ОС
§ 4. Равноускоренное движение
При решении задач на равноускоренное движение мы будем также пользоваться ранее предложенным алгоритмом.
Задача 1.9 Ударом клюшки хоккейной шайбе сообщили скорость Vq— 20 м/с. Через время to=10 с
25
шайба, движущаяся прямолинейно, остановилась. Определить ускорение, с которым двигалась шайба, и путь 5, пройденный шайбой за это время.
Решение. Движение шайбы происходит вдоль одной прямой, поэтому координатную ось ОХ направим вдоль этой прямой. За положительное направление оси ОХ примем направление вектора начальной скорости г$0 (рис. 1-17), а начало координат совместим с точкой А — началом движения шайбы.
Рис. 1.17
При равноускоренном движении в выбранной системе отсчета надо записать два уравнения — для координаты и скорости. Эти уравнения будут иметь вид
а I2
а?(1) = х0 + vBxt + ; vx (t) = vBx + axt.
В выбранной нами системе отсчета хв = 0, ах = — a, vOx — v0. Так как шайба тормозится, то ускорение направлено в сторону, противоположную направлению вектора г50. Таким образом:
atz
x(t) = vBt - —-; vx(t) = vB - at.
26
Через время t0 = 10 с после начала движения тело остановилось. Это значит, что скорость стала равной нулю, т. е.
Vx(tQ) ~ 0 = Vo ~ ai0 ИЛИ а = —
^0
Так как тело не меняло направления своей скорости, то путь можно определить из кинематического уравнения
2
x(t0) = 5 = voto - = v0t0 -
' U' UU 2 и И 2 2
Таким образом:
а = ^=20м/с=2 5 = 2Л =100м.
t0 Юс 2 2
Задача 1.10 Автомобиль начинает двигаться из точки А со скоростью г50 и через некоторое время попадает в точку В (рис. 1.18). Какой путь прошел автомобиль, если он двигался с постоянным по величине ускорением а? Определить среднюю скорость автомобиля на всем пути движения. Расстояние между точками А и В равно I.
Рис. 1.18
27
Решение. Мы сразу же приступим к выполнению п.4 алгоритма, т.е. к выбору системы отсчета.
Давайте выберем систему координат с началом в точке А, а ось ОХ направим по направлению скорости г50 (рис. 1.18). Далее, запишем уравнения для координаты и скорости:
a t2
a?(t) = х0 + vOxt + ; vx(t) = vOx + axt.
В выбранной нами системе отсчета х0 = 0, vOx = v0 , ах = —а . В нашей задаче автомобиль может попасть в точку В только в том случае, если его ускорение а будет направлено в сторону, противоположную скорости v0. Таким образом, в выбранной нами системе отсчета уравнения для координаты и скорости в любой момент времени примут вид:
at2
= vot~~ir > = vo “ at •
В некоторый момент времени t = , скорость автомобиля обратится в нуль, он остановится (точка С) и далее начнет двигаться в сторону, противоположную направлению оси ОХ. В этот момент времени автомобиль находится на наибольшем расстоянии от точки А (рис. 1.18). Общий путь, пройденный автомобилем за время движения, равен
S = 2АС+1 = 2хтах + 1.
28
Следовательно, для нахождения пути S нам необходимо определить а?тах. В точке С скорость автомобиля обращается в нуль, т. е.
= 0 = v0 ~ ati > откуда \ .
а
Уравнение для координаты позволит получить выражение для АС = хтах, если подставить t - t}:
,2 2 •
X = =
maIt 01 2 2a
Л 2 2
C< C 2^0 17 «0 I 1
Следовательно, >S =-----F t =---F I.
2a a
Средняя скорость автомобиля за все время движения согласно определению (п1.6) равна
«ср = —, где 12 — полное время движения авто-^2
мобиля от пункта А до пункта В. Поэтому для определения средней скорости необходимо определить полное время движения автомобиля. Его легко определить. Ведь в конце движения автомобиль оказался в точке В, координата которой равна — I. Поэтому уравнение для координаты сразу же позволит определить время 12:
Это уравнение удобно переписать в виде
at2 - 2v0t2 - 21 = О-
Решение этого квадратного уравнения следующее:
29
+ ^vo± J»»2 + 2al
Г2 ~ a
Для нашей задачи пригодно только одно значение времени
, _ + 2а,1
Г2 ~ а
Отрицательное решение мы отбросим, так как согласно условию задачи t2 > 0 . Таким образом, средняя скорость автомобиля
61 г?2 + al
। = — =--------------------u ---------------.
^2 vQ + yj Vq + 2 al
Задача 1.11 График зависимости скорости автомобиля от времени изображен на рис. 1.19. Начертить график зависимости ускорения, координаты и пути, пройденного телом, от времени, полагая ссо=О.
Решение. Из приведенного рисунка видно, что движение автомобиля удобно разбить на 4 этапа: (О “ tj, ~Ч) И (Ч~Ч)- На пеРвом эта-
пе (0 — tj автомобиль движется равноускоренно с постоянным ускорением а , так как тангенс угла наклона прямой ОД, численно равный ускорению, не меняется:
At
= tga.
30
Рис. 1.19
Рис. 1.20, а
Рис. 1.20, б
Поэтому график зависимости ускорения от времени на этом этапе представляет прямую, параллельную оси времени (рис. 1.20, а) На этапе
31
(tt — tj) приращение скорости Av=0, поэтому и ускорение также равно нулю, т. е. движение равномерное.
На этапе (t2 — t4)изменение скорости Л'У<0, тангенс угла наклона участка ВС (tg а) — отрицателен, следовательно, на этом этапе автомобиль движется с постоянным по величине, но отрицательным ускорением а2. Так как |tg а| >|tgcc1|, то ах>а2.
Теперь перейдем к построению графика зависимости координаты от времени. На первом этапе уравнение для координаты в нашей задаче имеет аЛ2
вид x(t) = —, т. к. а?0 = 0 и v0 = 0.
Это — уравнение вогнутой параболы (рис. I. 20, б). На этапе —12) при равномерном движении координата меняется по закону х = я?1 + vYt — это наклонная прямая линия, которая начинается с момента В этот момент координата x(tl) = xi! а тангенс угла наклона этой прямой численно равен скорости . Следует отметить, что в момент парабола первого этапа и наклонная прямая второго этапа имеют общую касательную, так как скорость в этой точке имеет одну и ту же величину.
32
На третьем этапе (t2 — t3) автомобиль движется равнозамедленно. Его координата меняется по закону
. х a?t2
x(t) = х2 + v.t - —,
где х2 — это начальная координата на этом этапе, vY — скорость в момент времени t2, т. е. начальная скорость для этапа (t2 —13). Это — уравнение выпуклой параболы.
В момент t2 выпуклая парабола и наклонная прямая предыдущего этапа также имеют общую касательную. Другими словами, наклонная прямая второго этапа является касательной и к вогнутой параболе первого этапа в момент и к выпуклой параболе третьего этапа в момент t2. Из рис. 1.19 видно, что в момент t3 скорость автомобиля обращается в нуль. Это можно увидеть и на рис. I. 20, б, так как касательная к кривой x(t) в момент t3 параллельна оси времени Ot. Это значит, что тангенс угла наклона касательной, численно равный величине скорости, в этот момент времени равен нулю.
На этапе (f3 —14) скорость автомобиля стала отрицательной, т. е. автомобиль начал двигаться в сторону, противоположную оси ОХ, однако ускорение не изменилось ни по величине, ни по направлению. Координата автомобиля меняется на этом этапе по закону
2 Физика
33
a2t2
*(*) = хз -£
где a?3 — начальная координата на этапе (t3 - t4).
Это — уравнение выпуклой параболы.
Кривая зависимости пути от времени S(t) в интервале (0 - t3) совпадает с графиком зависимости координаты от времени x(t), так как направление скорости тела не меняется. На этапе (t3 -14) кривые расходятся, поскольку путь на этом этапе определяется формулой
2
На рис. 1.20, б изображена пунктирной линией кривая зависимости пути от времени S(t).
§ 5. Свободное падение тел
Задача 1.12 С поверхности Земли вертикально вверх со скоростью v0 выпустили сигнальную ракету. Как долго ракета будет в полете? До какой максимальной высоты Н она поднимется? Какую скорость vK будет иметь ракета при приземлении? Сопротивление воздуха не учитывать.
Решение. Поскольку сопротивление воздуха не учитывается, то движение ракеты — это свободное падение, т. е. движение с постоянным ускорением g, направленным вертикально вниз. В данной задаче векторы v0 и g направлены вдоль од
34
ной вертикали, поэтому движение ракеты является прямолинейным движением.
Направим ось 0Y вертикально вверх, а начало координат совместим с точкой бросания ракеты (рис. I. 21). В этом случае координата y(t) при движении ракеты будет описываться уравнением
at
y(t) = yo + vOyt + -^-f а £
скорость vy = vOy + ayt.
В нашей задаче
Уо = °> voy = v0, ау = - g . Тогда вышеприведенные уравнения будут иметь вид
.2 y(t)=vOt~^-,
Vy(t)= V0-gt.
В момент падения ракеты на Землю (обозначим это время t0) ее координата у обратится в нуль, т. е.
Из этого выражения легко определяется пол-
2v0 ное время движения ракеты t0 = —-.
g
35
Пользуясь выражением для скорости, мы получим скорость ракеты при приземлении ( в момент t0):
. . 2v0
Vy(fo) = vK = v0-gt0 = v0- g- = -Vo.
g
Таким образом, ракета в момент приземления будет иметь такую же по величине скорость, что и в момент бросания. Знак «—» указывает на направление движения.
Максимальная высота подъема ракеты характерна тем, что на этой высоте скорость ракеты обращается в нуль.
Обозначим время подъема tn. Уравнение для скорости в этой точке можно записать: vy(tn) =
V-
= v0~gtn = 0. Следовательно, tn= —. g
Если мы сравним выражение для t0 и tn, легко увидим, что t0=2tn, это позволяет нам утверждать, что время подъема ракеты до высоты Н равно времени падения ее от высоты Н до Земли. Максимальную высоту подъема Н вычислим из кинематического уравнения:
г,(и=я=г,А-^=г,л-?4=^ ’ 2 g 2g 2g'
Вот теперь мы ответили на все поставленные в задаче вопросы.
36
Задача 1.13 С поверхности пустого колодца вертикально вверх со скоростью vo=10 м/с бросают мяч (рис. 1.22). Определить время tn, через которое мяч упадет на дно колодца, если глубина последнего Я=7,8 м (принять g=10 м/с2).
Решение. Координатную ось 0Y направим вертикально вверх, а ее начало совместим с дном колодца. Движение мяча описывается основным кинематическим уравнением
at2 y(t) = y0 + v0yt + -^-.
В нашей задаче Уо = Н, vOy = %, ау = ~g, тогда вышеприведенное уравнение будет иметь вид
y(t) = Н + vot - —.
Из этого уравнения сразу же можно определить время tn, через которое мяч упадет на дно колодца. В момент падения мяча y(tn) = 0, т. е. у(К) = Я + ^п-^ = 0.
Перепишем его в более удобном виде:
gt2-2vot2-2H = O-
37
Это квадратное уравнение имеет два решения:
_ Уо ± д/у02 + 2gH g
Мы воспользуемся только положительным значением корня, так как по условию задачи £п>0. Подставим числовые значения:
10м / с + л/100 + 156м / с п „ t =-----------------------= 2,6 с.
п 10м/с2
Решая задачи, мы неоднократно говорили, что в кинематике все системы отсчета равноправны. Давайте проверим это на примере нашей задачи. Для этого выберем другую систему координат и получим решение. Теперь ось 0Y направим, например, вертикально вниз, а начало координат совместим с местом бросания мяча (рис. 1.23).
Запись основного кинематического уравнения останется прежней, однако в новой системе координат р0 = 0, vOy = -v0, ау = g.
Тогда это уравнение в новой системе координат будет иметь вид
р/2 p(t) = -vot + —.
В момент падения мяча на дно колодца
р/2
p(tn) = Н = -votn + , или
grn2-2votn-2H = O.
38
Если мы сравним это уравнение с аналогичным, полученным в первоначальной системе координат, то увидим, что они совершенно одинаковы, а значит, и решение будет одинаковым.
Таким образом, мы показали равноправность двух выбранных нами систем отсчета.
Задача 1.14 Снаряд выпущен под углом а к горизонту с начальной скоростью н0. Определить время полета снаряда tn, скорость снаряда в момент падения на Землю, дальность полета L, высоту максимального подъема Я.
Решение. Выберем систему координат таким образом, чтобы начало координат совпало с местом бросания снаряда, ось 0Y направим вертикально вверх, ось ОХ — горизонтально (рис. 1.24), причем плоскость X0Y выберем так, чтобы векторы и0 и g лежали в этой плоскости. Начало отсчета времени совместим с моментом выстрела. Движение снаряда описывается кинематическими уравнениями:
a t2
x(t) = х0 + vOxt + ; vx = vOx + axt,
at2
l/(t) = У0 + vOyt + ; vy = vOv + ayt.
39
Рис. 1.24
В выбранной нами системе координат х0 — О, ах = °, vox = ио c°s«; 2/о = °, % = “g, uoy = ио sin а, а уравнения для координат и скоростей запишутся:
ac(t) — vQtcosa; vx = v0 coset = const;
a/2
y(t) = vot sin a - ; vy = va sm a-gt.
В момент падения снаряда на землю координата y(t) обращается в нуль, т. е.
р/2
Ж) = uotnsina- -у- = 0.
Отсюда полное время полета
2vn sin а
40
За это же время вдоль горизонтальной оси ОХ снаряд пролетит расстояние L, т. е. дальность полета снаряда равна
,, . т vz0 sin 2а
= L = votn cos a = —-------------
g
Максимальная высота подъема снаряда определяется тем, что на этой высоте вертикальная составляющая скорости v обращается в нуль, т.е. vy(te) = v0 sinct — gte =0, где te — время подъема
vn sin a снаряда. Отсюда te = —----.
g
Сравнивая это время co временем полного движения снаряда, легко заметить, что время движения снаряда вверх равно времени его движения вниз.
Теперь легко определить высоту максимального подъема снаряда Н:
, gf vz sin2 a
У = н = vote sin a - — = .
2 2g
На рис. 1.24 изображена траектория движения снаряда, брошенного под углом к горизонту. Ее форму, т. е. уравнение траектории, легко получить из уравнений для координат. Определив время из выражения x(t) и подставив его в уравнение для координаты y(t), получим
41
v0 cos a ’
2 a? gx ,
y(t) = v0 sin a--------------— = Ax-Bx ,
v0 cos a 2vg cos a
где A = tga, В = -- —- .
2v0 cos a
Это — уравнение параболы.
Таким образом, снаряд летит по параболе.
Скорость тела в любой момент времени направлена по касательной к траектории и легко определяется как векторная сумма горизонтальной vx и вертикальной v составляющих скоростей. Вектор полной скорости
«(О = vx(t) + vy(t);
|t5(t)| = y[v2x + v2 = д/vq cos2 a + (v0 cos a - gt)2 .
В конце полета величину полной скорости г5к определим при подстановке t = tn :
|uK(t)| = д/v2 cos2 а + (v0 sin a — 2v0 sin a)2 = v0 •
Таким образом, при приземлении снаряд имеет такую же по величине скорость, что и при выстреле.
Задача 1.15 Тело брошено горизонтально со скоростью v0. Определить нормальное (an) и ка
42
сательное (тангенциальное сц) ускорения через время tQ после начала движения.
Решение. Выберем систему координат X0Y (рис. 1.25), начало которой поместим в точку бросания тела. Тело будет двигаться по параболе, а его скорость в каждый момент времени направлена по касательной к траектории.
Рис. 1.25
Полным ускорением тела является ускорение свободного падения g = аг + ап.
Тангенциальное ускорение меняет величину скорости, а нормальное меняет только направление скорости. Если обозначить угол между вертикалью и касательной к траектории через а, то ап = gsina , аг = geos а,
где, как видно из рисунка, в любой момент времени
43
V V
« _ х У
sin а = т—2-7; cosa = 7—=4-|t5(t)| |v(t)| •
В выбранной системе отсчета vx = v0,vy = gt.
Модуль мгновенной скорости в любой момент времени равен
Н*)| = + vy = Vvo + W •
Следовательно, в момент времени t = t0 нормальное и тангенциальное ускорения тела определяются:
а = g sin а = g . =
b Lj i „2.2 у + S *о
аг = gcosa = g .
^+g2t20
§ 6. Кинематика движения материальной точки по окружности
Задача 1.16 Трамвай движется со скоростью v. Радиус трамвайного колеса г, а радиус реборды R (рис. 1.26). Определить скорость и направление движения точки В.
Решение. Движение колеса можно рассматривать как его вращение вокруг неподвижной точки А в данный момент времени (точка А называется мгновенным центром вращения). При движении колеса вправо его вращение происходит по
44
V
Рис. 1.26
часовой стрелке. Поэтому линейная скорость точки В направлена влево и равна vB = (оАВ. Угло-
v
вая скорость равна о = —, следовательно
г
vB =-(R~r). г
Таким образом, выбрав точку А за мгновенный центр вращения колеса, мы сильно упростили решение задачи.
Задача 1.17 Мотоциклист въезжает на арену цирка со скоростью v0=72 км/ч. Двигаясь по окружности радиусом -R=10 м, он проходит путь jS=600 м за время t0=10 с. Определить скорость v
45
мотоциклиста и полное ускорение |а| в конце этого пути.
Решение. Рассмотрим движение мотоциклиста с того момента времени, когда он выехал на арену цирка. Скорость мотоцикла меняется по величине и по направлению, следовательно, в любой момент времени он будет иметь нормальное и тангенциальное ускорения. При этом полное ускорение равно
|а| = у]а2п+а2 .
Путь, пройденный мотоциклистом в любой момент времени, определяется по формуле о
S — vnt + ——,
0 2 ’
величина скорости
v(f) = vQ + aTt.
Для определения скорости в конце пути необходимо знать ускорение ат, которое легко определить из формулы для пути:
а
2(S ~ уо*о)
t2 ьо
= —24 м/с2.
Подставив это выражение в формулу для скорости, получим
v{t) = иГ| + art0 = Vo +-------------------2--------10
‘o
----v0 =48 м/с. 4
Полное ускорение мотоциклиста равно
а = 7^+^
V4 2 ~^ + ar
R
= 131,6 м/с2.
46
§ 7. Абсолютное, относительное и переносное движения
Говоря о движении тел, мы непременно должны указать, относительно какой системы координат происходит это движение. Действительно, пассажир, сидящий в автомобиле, неподвижен относительно машины, но в то же время он движется вместе с автомобилем в системе координат, связанной с Землей. Хотя в кинематике все системы отсчета равноправны, однако кинематические величины (координаты, траектория, путь, перемещение) в разных системах отсчета будут разными. При переходе из одной системы координат в другую указанные величины могут изменяться. В этом и состоит относительность движения.
При решении различных задач часто бывает удобно переходить от одной системы координат к другой, поэтому нужно уметь находить связи между различными кинематическими величинами в различных системах отсчета.
Представим себе две системы координат: неподвижную X0Y0Z0 и XYZ, которая движется относительно системы X0Y0Z0 со скоростью г>0.
Движение точки относительно неподвижной системы координат условно называют абсолютным.
Движение точки относительно подвижной системы координат называют относительным.
Движение самой подвижной системы координат относительно неподвижной называют переносным.
47
Соответственно скорость, ускорение, перемещение и траекторию точки в неподвижной системе координат называют абсолютными, а аналогичные физические величины в подвижной системе координат называют относительными.
Пусть по реке слева направо плывет плот, по которому перемещается человек. Одну систему координат ХоОУо (неподвижную) свяжем с берегом реки, а другую X0Y (подвижную) свяжем с плотом (рис. 1.27, вид сверху).
Человек движется по плоту равномерно и прямолинейно из точки А в точку В и тратит на это время At. За это время относительно плота человек переместился на расстояние А'В', т.е. его от-
—>
носительное перемещение А'В' = Аготн. Перемеще-ние плота за время At АА' = Атп. Это перемеще
48
ние является переносным. Перемещение человека относительно неподвижной системы Хо ОYo яв-
ляется абсолютным, т. е. АВ' = Дта.
Из рисунка видно, что абсолютное, относительное и переносное перемещения связаны между собой правилом сложения векторов
Ата = Атп + Аготн.
Если мы это равенство разделим на At, то получим
Аг Аг Аг а _ п отн
At At At
При равномерном и прямолинейном движении каждое из отношений представляет собой скорость соответствующего движения, а именно
v = v + v а п отн >
т. е. вектор абсолютной скорости равен сумме векторов относительной и переносной скоростей.
Последнее равенство устанавливает связь между скоростями тела в различных системах координат и носит название закона сложения скоростей.
Векторное сложение скоростей проводится по правилу параллелограмма или треугольника (рис. 1.28).
Рис. 1.28
49
Полученный закон сложения скоростей справедлив не только для равномерных и прямолинейных, но и для любых движений. В этом случае под va, vn , г?отн надо понимать мгновенные скорости тела (точки).
При решении задач на относительность движения прежде всего надо выбрать две системы координат. Одну из них принять условно за неподвижную. Далее нужно выяснить, какая скорость будет абсолютной, переносной и относительной. Затем записать закон сложения скоростей в векторной форме. После чего можно переходить к записи этого закона в проекциях на выбранное направление осей координат.
Следует отметить, что вовсе не принципиально, какую систему координат считать неподвижной. В ряде случаев удачный выбор неподвижной системы координат существенно упрощает решение задачи.
Задача 1.18 Два поезда движутся навстречу друг другу. Величины их скоростей соответственно равны Vj и v2. Чему равна скорость первого поезда относительно второго и ВТОРОГО от~ носительно первого
Решение. Свяжем неподвижную систему координат X0Y0Za, например, с Землей, а подвижную XYZ — со вторым поездом, движущимся со скоростью v2 (рис. 1.29). Тогда движение второго поезда относительно Земли будет переносным. Движение первого поезда относительно Земли 50
(неподвижной системы X0Y0Z0) — абсолютным. Скорость первого поезда относительно второго поезда (относительно подвижной системы XYZ) является относительной. Следовательно, при таком выборе системы координат
= V,, Т
а 1' п 2? отн 1—2
Закон сложения скоростей = vn + voth запишется так: vr = v2 + г51-2. Отсюда относительная скорость 6Х_2 = — v2. Вспомним правило вычи-
тания векторов (рис. 1.30). Из рисунка видно, что в проекциях на ось ОХо последнее уравнение запишется vL_2 = vL — (— v2) = vi + v2 - Скорость первого поезда относительно второго равна сумме величин скоростей Vi и г?2 и направлена в сторону оси ОХ. Чтобы определить скорость второго поезда относительно первого, удобно под
~V2
«1
^отн — ^1-2
Рис. 1.30
51
вижную систему координат связать с первым поездом, а неподвижную систему координат X0Y0Z0 по-прежнему оставить связанной с Землей. Тогда г?а = v2, vn = V], voTH = v2_1. При таком выборе систем координат закон сложения скоростей будет иметь вид:
= Л + ^2-1 или «отн = v2_x = v2 - .
Векторное вычитание скоростей изображено на рис. 1.31. В проекции на ось ОХ значение относительной скорости
_51 -2 запишется:
X V2-l =—^2 ~Ц =~(V2
Как видно, ско-
ОТН ~ ^9—1
z 1 рость второго поезда
Рис. 1.31 относительно первого
равна сумме скоростей v1 и v2> но направлена в сторону, противоположную оси ОХ.
Задача 1.19. По пересекающимся под углом а шоссейным дорогам движутся две автомашины со скоростями v2 и v2 (рис. 1.32). Определить вели
чину и направление скорости первого автомоби-
ля относительно второго
-Решение. Неподвижную систему координат X0YaZ0 свяжем с Землей. Подвижную XYZ — с автомашиной, движущейся со скоростью v2. Тогда движение этой автомашины будет переносным.
52
В системе координат XYZ движение первой автомашины будет относительным, а ее движение относительно Земли — абсолютным, т. е. г5а = ц,
= ”2> 4>тн = С!-2-
Пользуясь законом сложения скоростей, запишем V, = V, + V, , ИЛИ V, = V, ~ V...
Вычитание векторов показано на рис. 1.32, б.
Вектор Vj_2 является скоростью первой автомашины относительно второй.
v2 v Величина этой скорости опре-деляется по теореме косину-
—---------------- сов
«1 ___________________________________
Рис. 1.32 I*51-2! = + ~ 2U'V2 COS а
Задача 1.20 На тележке, движущейся прямолинейно с постоянной скоростью vT, установлена труба. Под каким углом к направлению движения тележки следует установить трубу, чтобы капли дождя, падающие вертикально относительно Земли со скоростью г5к, пролетали через трубу, не задевая ее стенок?
Решение. Капли дождя не будут задевать стенок трубы, если вектор скорости капель относительно тележки vKT, а следовательно, и относительно трубы будет направлен вдоль стенок трубы.
Неподвижную систему координат X0Y0Z0 свяжем с Землей, а подвижную XYZ - с тележкой. Тогда va = г5к, г5п =-г5т, г5ота = г5кт, а закон сложения скоростей можно записать в виде
53
= vT + vKT, отсюда «5КТ = vK — vT.
Векторное вычитание скоростей показано на рис. 1.33. Следовательно, трубу нужно расположить вдоль вектора vKT. Угол наклона трубы к горизонту определяется из треугольника скорос-
VK теи tga = —-.
Задача 1.21 Велосипедист едет с постоянной скоростью по прямолинейному участку дороги. Найти мгновенные скорости точек А, В, С, D, лежащих на (рис. 1.34).
ободе колеса, относительно Земли
А
Рис. 1.34
Решение. При движении колеса по Земле все его точки участвуют одновременно в двух движениях: вдоль Земли с постоянной скоростью vQ и вокруг оси, проходящей через точку 0, с линейной (касательной) скоростью г5л, направление которой меня
54
ется. Если колесо катится без проскальзывания, то ил = v0. (Попробуйте доказать это сами!)
Свяжем неподвижную систему координат X0Y0Z0 с Землей. Подвижную систему координат XYZ свяжем с центром колеса. Эта система (рис. 1.35) движется со скоростью г>0 относительно Земли. Тогда линейные скорости каждой точки обода колеса являются относительными скоростями, а мгновенные скорости точек А, В, С, D — абсолютными скоростями, которые вычисляются из закона сложения скоростей va = va + vOTH. Для нашего случая ил = v0 + vn.
Рис. 1.35
Тогда
vA = «о + «лА = v0 + «л В
vc = v0 + г5лС «d = £о + Чю
Ы = 2v0;
|vB| — г>0-\/2, |г5с| = 0;
Ы = vo^-
55
Направление скоростей точек А, В, С, D указаны на рис. 1.35.
При движении колеса без проскальзывания скорость точки касания колеса с Землей (точка С) всегда равна нулю. Поэтому движение колеса можно рассматривать как последовательность очень малых поворотов вокруг точек касания. Это легко понять, если окружность колеса представить в виде многоугольника с большим числом сторон, так как в каждый момент времени колесо (рис. 1.36) вращается вокруг точки соединения сторон многоугольника. Точка С называется мгновенным центром вращения колеса. Введение мгновенного
центра вращения часто позволяет легко решать некоторые задачи. Действительно, если считать, что колесо вращается вокруг мгновенного центра С, то радиус вращения точки А, например, равен СА=2 • ОД, следовательно, скорость точки А будет в два раза больше, чем скорость
точки 0, т.е. vA = 2vg,
ибо скорость определяется по формуле vi = 0)гг. (Угловая скорость вращения для всех точек колеса одинакова.)
56
II. ДИНАМИКА ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ
nll.l Движение любого тела вызывается или изменяется в результате его взаимодействия с другими телами. Законы динамики устанавливают связь между движением тел и причинами, которые вызвали или изменили это движение.
В начале XVII века Галилеем были проведены тщательные опыты, которые позволили сделать следующий вывод: если на тело нет внешних воздействий, то оно сохраняет покой или движется с постоянной скоростью. Это утверждение составляет основу 1-го закона динамики.
Свойство тел сохранять свою скорость при отсутствии действия на него других тел и менять ее лишь под действием других тел называется инерцией. Поэтому первый закон Ньютона получил название закона инерции. В настоящее время он формулируется так: существуют системы отсчета, называемые инерциальными, в которых изолированное тело движется прямолинейно и равномерно или находится в состоянии покоя. Изолированными называются тела, на которые не действуют другие тела.
п11.2 Второй закон Ньютона устанавливает связь между всеми действующими на тело силами и ускорением, которое получает тело в результате этого взаимодействия.
Ускорение точечного тела а пропорционально действующей на него силе F и обратно пропорционально массе тела т, т. е.
57
При наличии нескольких сил, действующих на тело, это соотношение записывается
п F / п -
5 = S/m’ или =
1=1 1=1
Последняя запись используется чаще. Она гласит: результирующая всех сил, действующих на тело, равна произведению массы тела на ускорение. Это соотношение называют вторым законом Ньютона или основным уравнением динамики.
пП.З Третий закон Ньютона указывает на тела, со стороны которых действует та или иная сила. Он формулируется так: силы, с которыми тела действуют друг на друга, равны по величине и противоположны по направлению; эти силы направлены вдоль одной прямой (2^_2 = —F2_j), т- е-силы всегда возникают попарно: всякой силе, приложенной к какому-либо телу, можно сопоставить равную ей по величине и противоположно направленную силу, приложенную к другому телу. Эти силы не могут уравновешивать друг друга, потому что приложены к разным телам.
п11.4 При упругой деформации растяжения (или сжатия) величина деформации прямо пропорциональна модулю силы упругости. Это отражается законом Гука
Гупр = -к Ах , или
IfJ = Ал? .
| УЦ>|
58
nll.5 При движении одного тела по поверхности другого возникает сопротивление движению, называемое трением. Силы трения действуют вдоль поверхности тел при их непосредственном соприкосновении. Различают два вида трения: сухое трение, возникающее между сухими поверхностями твердых тел, и вязкое трение — трение о жидкую и газообразную среду. При изучении сухого трения выделяют две его разновидности: трение покоя и трение скольжения.
Трение, действующее между двумя неподвижными друг относительно друга телами, называют трением покоя. Сила трения покоя зависит от приложенной к телу силы и меняется от нуля до максимального значения Fwmax, т. е. О < F^^ < jtN, где ji коэффициент трения, a N — сила нормального давления.
Сила трения покоя направлена в сторону, противоположную возможному движению. При достижении силой трения покоя максимального своего значения тело начинает скользить. В этом случае действует сила трения скольжения. Она равна F^ ск = fiN и не зависит от скорости движения.
п11.6 При движении тела в жидкой или газообразной среде возникает сила вязкого трения. Сила вязкого трения появляется только при относительном движении тела, т. е. сила трения покоя в жидкости или газе отсутствует. Кроме того, сила вязкого трения зависит от скорости: при малых скоростях движения эта зависимость меняется по закону
59
FTp в = — uv , где ji — коэффициент вязкого трения.
Он зависит от среды, формы и размеров тела, температуры, давления.
п11.7 Вес тела — сила, с которой тело вследствие его притяжения Землей действует на опору или растягивает подвес. Вес тела определяется совокупностью действующих на тело сил и существенно зависит от ускорения, с которым движется опора (или подвес).
Для успешного решения задач с использованием законов Ньютона предлагается следующая последовательность действий, некий алгоритм.
1. Прежде всего необходимо внимательно прочитать условие задачи, нарисовать рисунок — это позволит яснее представить задачу.
2. Поскольку движение тела определяется всеми действующими на тело силами, то необходимо на рисунке к задаче стрелочками указать все силы, действующие на тело.
Очень полезно отчетливо представить, со стороны каких тел действуют рассматриваемые силы. Это поможет сделать третий закон Ньютона.
3. Далее второй закон Ньютона небходимо записать в векторной форме
п
= Fl+F2+...+Fn = та .
i=l
4. Затем нужно выбрать направление осей ОХ и 0Y (обычно эти направления диктуются условиями задачи) и перейти к записи второго закона Ньютона для проекций на оси координат.
60
5. Если в задаче кроме сил и ускорений требуется определить координаты, расстояния или скорости, то кроме законов Ньютона нужно использовать еще и кинематические уравнения.
6. Записав систему уравнений для данной задачи, необходимо проследить за тем, чтобы общее число уравнений равнялось числу неизвестных. Решение задачи нужно получить в общем виде. Это позволит провести анализ решения, т. е. увидеть, как меняются найденные величины от условий задачи.
7. После этого в полученные формулы нужно подставить цифровые данные.
Примеры решения задач
Задача П.1 В движущемся лифте на динамометре висит груз массой т = 1 кг. При этом показания динамометра F=15H. Определить ускорение лифта и направление его движения. Чему равен вес груза Р?
Решение. На груз действуют две силы: сила тяжести mg и сила натяжения пружины F (показание динамометра). При установившемся движении груз имеет то же ускорение, что и лифт (рис. II. 1). Второй закон Ньютона для груза имеет вид (П.2)
"mg
Рис. II.1
61
mg + F = ma
Ось OX направим вверх. Запишем закон Ньютона в проекции на эту ось F — mg = та. Отсюда
o=F-2ng^l5H-9!8H=5>2M/c2 т 1 кг
Ускорение имеет положительный знак, значит, оно направлено вверх. Определить направление движения груза при заданном условии задачи мы не можем! О направлении движения тела можно судить только по направлению скорости, которая определяется формулой
v(t) = vB + at.
Поэтому лифт может в условии нашей задачи двигаться вверх ускоренно (если его начальная скорость v0 направлена вверх) либо вниз замедленно (если его начальная скорость vQ направлена вниз). И только в том случае, когда начальная скорость тела равна нулю, направление движения совпадает с направлением ускорения а.
Теперь определим вес груза Р.
Весом тела называют силу, с которой тело действует на горизонтальную опору или вертикальный подвес. При взаимодействии пружины с грузом т на него действует сила F. Тело по третьему закону Ньютона действует на пружину (вертикальный подвес) с силой Р = -F. Поэтому вес тела по величине равен силе F, но направлен вниз (рис. П.1). Таким образом, вес тела P=F=15H.
62
Как видно, вес тела в условии нашей задачи больше силы тяжести, действительно:
mg =1кг . 9,8 м/с = 9,8Я < Р = 15Я.
Задача IL2 Два груза с массами тх и т2, связанные невесомой и нерастяжимой нитью, лежат на идеально гладком столе. К телу массы т2 приложена сила F. С каким ускорением движутся тела? Каково натяжение нити Т?
Решение. Укажем стрелочками все силы, действующие на каждый из грузов.
На тело массы действуют три силы: сила тяжести m^g, сила реакции опоры Nr и сила натяжения нити Тг На тело массы т2 действуют четыре силы: сила тяжести m2g, сила реакции опоры N2, сила натяжения нити Т2 и сила F {рис. II.2, а).
Рис. 11.2
Запишем второй закон Ньютона для обоих тел: + f; = тД; m2g + N2 + f2= т2а2.
63
Направим ось ОХ вдоль направления силы F и перепишем закон Ньютона в проекциях на эту ось:
Т. — m.a,; F — Т= т9а9. А XX' & t* t*
Мы получили два уравнения с четырьмя неизвестными, поэтому нужны еще дополнительные уравнения. Одно из них мы получим из условия нерастяжимости нити. В этом случае оба конца нити за любой промежуток времени совершают равные перемещения, т. е.
так .как AXj = Дх2, то аг = а2 = а.
Условие невесомости нити позволяет найти связь между силами Т\ и Т2 . По третьему закону Ньютона на концы веревки действует сила Тг - -7j и f2 = -t2 (рис. II.2, б). В проекции на ось ОХ уравнение Ньютона для нити можно записать: f t
Т2 -Т = Дтпа > но так как нить невесома (Ат = 0) , то Т2 — TL = 0, или Т2 = TL = Т , т. е. невесомая нить действует на грузы ml и т2 с равными по величине, но противоположно направленными силами.
Таким образом, уравнения движения для грузов вдоль оси ОХ запишутся:
Т = F — Т = т2а.
Складывая эти уравнения, получим
64
F = (m, + m, )a, или a =-----, а сила на-
v 1 27 mv+m2
rr
тяжения T - mxa =----5.
m1 + m2
Задача IL3 Тело массой m движется по идеально гладкой горизонтальной плоскости под действием силы F, направленной под углом а к горизонту. Найти ускорение а тела и его вес.
Решение. На тело действуют три силы: сила тяжести mg, сила реакции опоры JV и сила F {рис. II.3). Согласно второму закону Ньютона
F + mg + N = та •
Рис. II.3
3 Физика
65
Так как тело движется вдоль горизонтальной плоскости, ось ОХ направим, как показано на рисунке, а ось 0Y — перпендикулярно к ней. Тогда закон Ньютона в проекциях на оси координат запишется соответственно
F cos а = та = та;
— mg + N + F sin а = тау = 0.
Из первого соотношения определяем ускорение
F cos а а =-------.
т
Вес тела Р (сила, с которой тело действует на плоскость) численно равен силе, с которой плоскость действует на тело (силе N) по третьему закону Ньютона, т.е. N=~ Р или |JV| = |р|. Силу N легко определить из уравнения движения, записанного вдоль оси 0Y:
N = mg — F sin а.
Следовательно, вес тела Р = mg — F sin а . Эта сила приложена к плоскости (рис. II.3). Как видно, вес тела меньше силы тяжести.
Задача IL4 На гладкой наклонной плоскости, образующей угол а с горизонтом, находится тело массой т. Определить ускорение тела а, реакцию опоры N и результирующую силу F , действующую на тело.
Решение. На тело действуют две силы: сила тяжести mg и реакция опоры N. Результирую-66
щая этих двух сил заставляет тело двигаться вдоль наклонной плоскости с ускорением а. Второй закон Ньютона запишется
N + mg = Fp = та.
Так как тело перемещается вдоль наклонной плоскости, то ось ОХ направим вдоль наклонной плоскости вниз, а ось 0Y — перпендикулярно к ней (рис. II.4, а). Тогда уравнение Ньютона в проекциях на эти оси запишется
mg sin а = тах; N — mg cos а = 0.
Следовательно, а = g sin a, N = mgcos а ,а |Кр| = |mo| = mg sin а.
Однако хочу обратить ваше внимание на то, что реакция опоры N при движении тел вдоль наклонной плоскости зависит от условия задачи.
Изменим задачу. Пусть тело массой т находится на той же плоскости, но теперь
наклонную плоскость перемещаем с ускорением а вдоль горизонтальной поверхности так, чтобы тело на ней покоилось. Вновь определим величину и направление результирующей силы Fp и реакцию опоры N.
Решение. На тело по-прежнему действуют две силы: сила тяжести mg и реакция опоры Nv Второй закон Ньютона записывается
Рис. II.4
3*
67
mg + Nt = ma
Тело массы т покоится на наклонной плоско
сти, но относительно Земли оно вместе с наклонной плоскостью перемещается с ускорением а. Следовательно, результирующая сила Fp направ
лена в ту же сторону, что и ускорение а (рис. II.4, б). Можно вновь записать уравнение движения вдоль осей ОХ и 0Y и определить силы Nx и Fpl. Но мы предложим другой способ ре-
шения. Величину результирующей силы Fpl определим из прямоугольного треугольника АВС
Fpl = mg tga.
Сила реакции опоры Nx вычисляется из того же
Рис. II.4 ,Т mg
треугольника JVj =-----.
Как видно, сила Fpl отличается и по величине, и по направлению от силы Fp, а реакция опоры N} отличается от силы Столько по величине.
Задача II.5 На тележке, скатывающейся без трения с наклонной плоскости, установлен стержень с подвешенным на нити шариком массой т. Определить силу натяжения нити Т, если плоскость образует с горизонтом угол а.
68
Решение. Предположим, что при установившемся движении (шарик и тележка движутся с ускорением а) шарик отклонился от перпендикуляра к наклонной плоскости на угол р (рис. II.5).
Второй закон Ньютона для шарика имеет вид:
Т + mg = та
Выберем ось ОХ вдоль наклонной плоскости,
а ось 0Y — перпендикулярно к ней. Тогда второй закон Ньютона в проекциях на оси координат запишется
Т sin + mg sin а = та;
Т cos/3 —mg cos а = 0.
При установившемся движении все точки тележки, нить и шарик движутся с одним и тем же ускорением а = g sin а.
Подставляя это выражение в первое уравнение,
получим Т sin /3 = 0. Так как Т Ф 0, то sin /3 = 0. Следовательно, угол (3=0. Это значит, что нить с шариком располагается Перпендикулярно наклонной плоскости.
Задача II.6 На одном конце веревки, переброшенной через невесомый блок, находится груз массой т, а на другом — человек массой М = 2т.
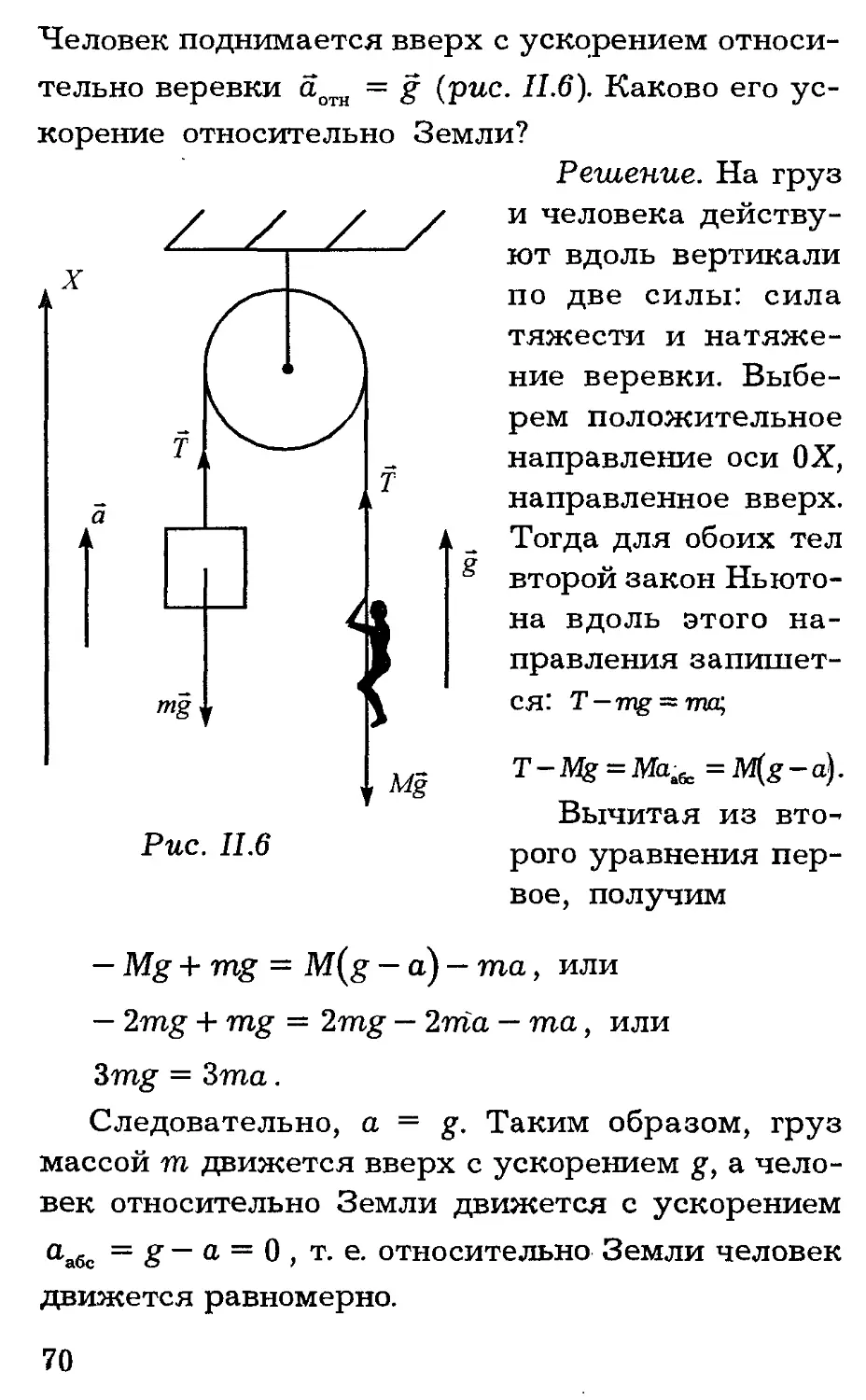
69
Человек поднимается вверх с ускорением относи
тельно веревки аотн = g (рис. II.6). Каково его ус
корение относительно Земли?
Решение. На груз и человека действуют вдоль вертикали по две силы: сила тяжести и натяжение веревки. Выберем положительное направление оси ОХ, направленное вверх. Тогда для обоих тел второй закон Ньютона вдоль этого направления запишется: T—mg — ma,
T-Mg = Ma^ =M(g-a).
Вычитая из второго уравнения пер-
вое, получим
— Mg + mg = M(g — а) — та, или
— 2mg + mg = 2mg — 2та — та, или
3mg = Зта.
Следовательно, а = g. Таким образом, груз массой т движется вверх с ускорением g, а человек относительно Земли движется с ускорением аабс = S ~ а = 0 , т. е. относительно Земли человек движется равномерно.
70
Задача II.7 На одном конце нити, перекинутой через невесомый блок, подвешен груз массой т = 1 кг. На другом ее конце осторожно подвешен груз массой М =1000 кг. Какова сила натяжения нити?
Решение. Так как масса груза М в тысячу раз больше массы груза т, то можно считать, что грузы с нитью движутся с ускорением
g. Выбрав положительное направление оси ОХ,
как показано на рис. II.7, можно записать второй
закон Ньютона вдоль этого направления для гру
за массой т: Т — mg = mg.
Следовательно, натяжение нити
Т = 2mg = 19,6Н.
Задача IL8 На невесомых блоках, изображенных на рис. IL8, подвешены грузы массой тг и т2 (mi > тг)- Определить натяжение нити Т.
Решение. На рисунке стрелочками нарисованы все силы, которые действуют на тело массой подвижный блок и тело массой т2. Выберем ось ОХ, направленную вниз. Тогда закон Ньютона для тел запишется
71
mtg - T =
T^-T-T = тбла2 = 0 (т.к. тбл = 0);
™2<? ~ Т~ = —т2а2.
Поскольку т1>т2, то тело массой движется вниз, а тело массой т2 — вверх. Из второго уравнения следует Тг = 2Т, и уравнения Ньютона запишутся
- Т = m2g — 2Т = —т2а2.
Мы имеем систему из двух уравнений с тремя неизвестными. Недостающее уравнение можно найти, используя кинематические связи. Связь
между ускорениями ах и а2 определяется из следующих соображений. Если тело массой опустится на высоту hj, то второе тело поднимется за это время на высоту , /ii
п2 = —. Так как пройденные
расстояния прямо пропорциональны ускорениям, то
ai
а2 - —. Теперь уравнения движения будут выглядеть:
nijg— Т =
72
mzg — 2T = -
m2a!
2
Решая эту систему, получим
ai
2mtg - m2g n . m7 / ’ 2mj +
или
ai
2g(2mi ~ шг).
4m, + m2 ’
T = m,g — m,a =
*m,m2g _ ' j 1*2 4mx + m2
a, (2m,-m2)
—- = g--------.
2 4m, + m2
Задача IL9 Два груза массой М связаны нитью, перекинутой через невесомый неподвижный блок. На один из грузов кладут перегрузок m (рис. II.9). С каким ускорением а движутся грузы? Каков вес перегрузка т?
Решение. Изобразим стрелочками силы, действующие на все тела. Направим ось ОХ вниз и запишем уравнение Ньютона для каждого из трех грузов:
Mg - Т = (-Ма);
Mg-T + N' = Ма;
mg — N = ma.
Отметим, что сила N — это сила, которая действует на тело массой m со стороны тела массой М
Рис. II.9
(т. е. реакция
опоры). Сила N' —это сила, которая действует на
73
тело массой М со стороны маленького тела т, т. е. это и есть вес тела массой т. По третьему закону Ньютона N = -N', а по величине эти силы равны друг другу. Из третьего уравнения системы
N = mg — та = m(g - а),
т. е. видно, что вес тела массой т меньше силы тяжести.
Решая систему из трех уравнений с тремя неизвестными, получим
а = Т = 2М(М + т)^ N = N' = 2Мт8
2М + т ’ 2М + т ’ 2М + т
Задача 11.10. Шайба, скользящая по горизонтальной поверхности, остановилась, пройдя рас
стояние S. Определить начальную скорость v0
шайбы, если коэффициент трения равен /I (рис.
11.10).
mg
Рис. 11.10
Решение. На шайбу действуют три силы: сила тяжести mg, сила реакции опоры N и сила тре
74
ния FTp. Выберем ось ОХ по направлению движения. Второй закон Ньютона вдоль этого направления запишется
— FTp = та, или — /Amg = та, т. е. а = — /Ag.
Из этого уравнения видно, что ускорение шайбы а направлено в сторону, противоположную движению. Следовательно, шайба движется замедленно. Для определения начальной скорости v0необходимо записать еще уравнение кинематики для скорости v(t) = v0 — at. Так как шайба, пройдя расстояние S остановилась, то О = v0 — atlf т. е. v0 = atr. Время движения шайбы не задано в условии задачи, но его можно определить из выражения для перемещения
д™ _ а _ х а^1 _
iXX — о — ------------------------, или
° 1 2 2 2
2S
t, = —. Подставив это выражение в уравнение vo
для скорости, получим
2S
vo = a^i = PS ~~, откуда vo
vzQ' = 2S/ag, или v0 = yj2S/ag.
Задача 11.11 На наклонной плоскости укреплен блок, через который перекинута нить. К одному концу нити привязан груз массой т^~ 1кг, лежащий на наклонной плоскости. На другом конце нити
75
висит груз с массой т2=3 кг (рис. 11.11). Наклонная плоскость образует с горизонтом угол а = 30°. Коэффициент трения между грузом и наклонной плоскостью /I = 0,1. Определить ускорение а грузов.
Рис. 11.11
Решение. На тело массой т1 действуют две силы: сила тяжести m^g и натяжение нити Т. На тело массой ш2 действуют четыре силы: сила тяжести m2g, натяжение нити Т, сила реакции опоры N и сила трения / . Закон Ньютона в векторной записи для обоих тел имеет вид
mjg + Т = mfi, m2g + Т + N + /тр = ш2а.
При переходе к записи этих уравнений для проекций на направление движения остается не
76
ясным, куда происходит движение, куда направить силу трения?
Мы должны помнить, что сила трения может замедлить движение, может его вовсе остановить, но изменить движение на обратное сила трения не может. Поэтому достаточно решить в таком случае задачу без учета силы трения, определить ускорение движения. Его знак укажет направление движения, поскольку вначале тела покоились. Затем следует вновь решить задачу, но уже с учетом силы трения.
Итак, выберем направление движения груза т, вниз. Тогда уравнения движения грузов для проекций на направление движения (без учета силы трения) запишутся
m.g — Т = m.a; Т — m,gsince = т,а.
Сложив оба уравнения, получим
mjg —m2gsince = + m2)a, или
m. — т„ since „ , ,
—-------------g = -1,25 м/с2
тг + т2
указывает на то, что ускорение сторону, противоположную той,
на-
ко-
a =
Знак «—» правлено в
торую мы выбрали, й поэтому силу трения / нужно направить вдоль наклонной плоскости вверх. Теперь запишем уравнения Ньютона вдоль истинного направления движения, но с учетом силы трения
Т1
Т - mjg = т^; - /тр - Т + m2g sin а = т2ах.
Сложим эти уравнения и, подставив значение силы трения /тр = p-N = cos a t получим
g[m2(sina- д cos a)-mJ . 2
aj = —---------------------1 = 0,6 м/с .
mr + m2
Задача 11.12 Тело начинает движение вверх по наклонной плоскости с начальной скоростью v0. С какой скоростью vl тело вернулось в начало наклонной плоскости? Коэффициент трения /л < tg а. {рис. 11.12)
Рис. 11.12
Решение. На тело действуют три силы: сила тяжести mg, сила реакции опоры N и сила трения /. При движении тела вверх и вниз сила трения направлена в разные стороны. Тело движется вверх, останавливается в некоторой точке В и возвращается в точку А. Выберем начало ко
78
ординат в точке А и ось ОХ направим вверх вдоль наклонной плоскости. Второй закон Ньютона вдоль направления оси ОХ запишется
— mg sin а — / = таг — при движении тела вверх;
— mg sin а + / = та2 — при движении тела вниз.
Ускорения а} и а2 из этих соотношений равны
а
/ - mg sin a f/N
—----------=----• - g sm a.
m m
а2 =
Выражение для силы N легко получить, записав уравнение Ньютона вдоль оси 0Y, направленной перпендикулярно к оси ОХ:
N — mg cos а = 0, или N = mg cos а.
Двигаясь вверх с ускорением ар тело достигнет точки В через некоторое время и пройдет расстояние S. В точке В его скорость обратится в нуль, поэтому
/ \ I- I «п
гл t) = v0 — a, t = 0, или tv = -гА = у----г.
aj g(sin а + /л cos а)
КН _ 2г,(А ~V0tl _ VOtl
о = vnt,--------—--------------—------.
0 1 2 2 2
После остановки в точке В тело начнет двигаться вниз с нулевой начальной скоростью и прой
79
дет до точки А то же расстояние S, но двигаться будет ускоренно, поэтому
la,\tf
S =------ или t2
2 2
ci2
Зная время движения тела вниз t2, легко определить скорость в конце движения (в точке А)
, ч i^i и2а„ [и cos a —sin а V, = v(t, = а-t, = J = vnl-----------------------
v ' v ai V Л cos a + sin a
Как видно из полученного соотношения, г?! будет меньше начальной скорости движения г>0. Это и понятно: часть начальной энергии, которую сообщили телу в точке А, тратится на работу против силы трения.
Задача 11.13 Груз массой М связан нитью с грузом та, лежащем на гладком горизонтальном столе, помещенном в лифте. Лифт движется с ускорением а (рис. 11.13). Определить натяжение нити Т. Масса та < М.
80
Решение. Изобразим стрелочками все силы, действующие на тело, и запишем второй закон Ньютона для каждого тела в отдельности:
mg + f + N = (a1+a),
где dj — ускорение, с которым перемещается тело массой т вдоль горизонтальной плоскости стола;
Mg + Т = Ма2,
где а2 — ускорение тела М относительно Земли, причем а2 = а1 - а.
Выберем ось ОХ, направленную вниз, тогда уравнение Ньютона можно записать для тела массой М вдоль этого направления
Mg — Т = М(аг — а),
а для тела массой m вдоль горизонтальной поверхности стола
Т = тах
(относительно стола груз массой М движется с тем же ускорением, что и груз массой т).
Решая эти уравнения, определим натяжение нити
т = Mm(g + а) М + т
Задача 11.14 На горизонтально расположенном стержне длиной 21 надета бусинка массой т, которая может без трения перемещаться вдоль стержня. Стержень поступательно движется с уско-
81
рением а в горизонтальной плоскости в направлении, составляющем угол а со стержнем (рис. II. 14). Определить ускорение бусинки относительно стержня, силу реакции со стороны стержня и время, через которое бусинка покинет стержень.
Решение. В горизонтальной плоскости на бусинку действует только одна сила — сила реакции стержня N, перпендикулярная стержню. Поэтому абсолютное ускорение бусинки аабс — ускорение
относительно Земли — будет в силу второго закона Ньютона направлено в ту же сторону. Относительное ускорение бусинки аотн = аабс — апер ( как видно из рисунка, направлено вдоль стержня. Из треугольника ускорений следует: аабс = а sin а'-> аотн = а cos а Согласно второму закону Ньютона
JV = шаабс = ma sin а.
Время движения бусинки вдоль стержня t0 определяется из уравнения
7 _ Артн^О 4 __
£ —” j ИЛИ Сл •“
2 V аотн V а cos а
21
21
Задача 11.15 От поезда массой М, движущегося с постоянной скоростью, отцепляется последний ва
82
гон массой т, который проходит путь S и останавливается. На каком расстоянии L находится поезд от вагона в момент остановки последнего? Сила тяги поезда остается постоянной (рис. 11.15).
Рис. 11.15
Решение. Вначале вдоль горизонтального направления на поезд действовали две силы: сила тяги FT и сила трения /, причем, так как он двигался равномерно, то F — /тр = 0, или FT = /тр = ftMg. Уравнения Ньютона для поезда и вагона после отрыва вдоль направления движения запишутся:
FT - Api = (м - ш)а1, или fiMg - ц(М - m)g = (М - т)ах,
— /тр2 = та2,или — р/тд — та2, т. е. а2 = —p,g.
После отрыва вагона поезд станет двигаться ускоренно с ускорением а вагон — замедленно с ускорением а2. Их скорости относительно Земли будут меняться по закону
83
vjt) = v0 + aj ; v2(t) = v0 - a2t.
Однако значение v0 в условии задачи не задано. Попробуем обойтись без него, выбрав удобную систему отсчета. Если мы выберем систему отсчета, которая движется со скоростью г50, то в ней поезд движется ускоренно со скоростью
v\ — vr — v0 = v0 + art — v0 = art, а вагон — co скоростью
v'z = v2 — Vg = v0 — azt — vg = — azt t т. e. вагон в этой же системе тоже движется ускоренно, но в обратную сторону. Когда его скорость в этой системе достигнет значения v0 , то относительно Земли он остановится, пройдя расстояние S (см. рис.). В системе отсчета, движущейся со скоростью v0 , вагон также пройдет расстояние 5, но в обратную сторону. Расстояние L между вагоном и поездом можно найти, если будем знать ускорение поезда относительно вагона. Это ускорение равно аотн = ai ~ (~ аг) = а1 + а2 • Расстояние между поездом и вагоном L будет так относиться к рассто-
а
янию S, пройденному вагоном, как r0T1? , т. е.
L G-] + а2
~ . Таким образом,
/zmg
г _ с (ai + аг) _ ~ М — т _ о М
JU — О ------- — О ---------- — О ------•
а2 p,g М — т
84
Задача 11.16 По бруску массой М, лежащему на гладкой горизонтальной плоскости и удержи-
ваемому нитью, скользит равномерно тело массой т под действием силы F. В некоторый момент нить пережигают. Определить силу трения между соприкас ающимися поверхностями после пережигания нити (рис. 11.16).
Решение. Запи
шем второй закон Ньютона для тела и бруска до пережигания нити
mg + fTp+N + F = 0;
Mg + f'Tp+Nl + N' + T = 0.
Вдоль горизонтального направления до пережигания нити на тело массой т действуют две силы:
сила F и сила трения / . Так как тело движется равномерно, то вдоль горизонтали можно записать
F-AP = o, (1)
причем сила трения /тр — /uN (тело скользит по поверхности бруска). После пережигания нити брусок массой М движется обязательно с некоторым ускорением а, так как на него действует
85
вдоль горизонтали единственная сила f'rp, равная по величине по третьему закону Ньютона /тр1. Это означает, что груз массой т также будет двигаться ускоренно, ибо он находится на бруске. Поэтому после пережигания нити уравнение движения для тела массой т имеет вид
F ~ /тр1 = . (2)
Если сравнить соотношения (1) и (2), то следует заметить, что сила fTpl < =JiN, поскольку
сила F не изменилась. Значит, сила трения стала меньше максимального значения силы трения покоя, равного /iN, а это значит, что сила является силой трения покоя.
Таким образом, тело массой гп после пережигания нити относительно бруска будет покоиться, а относительно Земли — двигаться вместе с бруском с ускорением а.
Запишем уравнения движения для тела массой т и бруска массой М после пережигания нити:
F - Api = /тр1 = Ма.
Решая эти уравнения, получим
F-M
Лр1 М + т'
Задача 11.17 Тележка массой М движется горизонтально без трения со скоростью v0. На пе
86
редний край тележки без начальной скорости опускают тело массой т. При какой длине тележки I тело не соскользнет с нее? Коэффициент трения между тележкой и телом и. Размерами тела можно пренебречь (рис. 11.17).
Рис. 11.17
Решение. На тело действуют три силы: сила тяжести mg, реакция опоры N и сила трения /. На тележку действуют четыре силы: сила тяжести Mg, реакция опоры R, сила давления N' со стороны тела массой т и сила трения ЛР, равная по величине по третьему закону Ньютона силе /. Запишем второй закон Ньютона в векторном виде для обоих тел:
N + mg + fTp= та^,
Mg + R + f^+N' = Ма2,
где а; и а2 — ускорения тела и тележки относительно Земли.
87
Выберем ось ОХ совпадающей по направлению со скоростью v0. Тогда второй закон Ньютона вдоль этого направления запишется
Л
/ = malt или аг = — = fig; т
- frp = Ма2, или а2 =
Таким образом, ускорения а} и а2 направлены в разные стороны, т. е. тело относительно Земли движется ускоренно, а тележка — замедленно. Скорость тела меняется по закону r>1(t) = a1t, а тележки — v2(t) = v0 — a2t. Если тележка достаточно длинная, то, очевидно, наступит такой момент времени, когда скорости тележки и тела станут равными относительно Земли. Это значит, что, начиная с этого времени, тело будет покоиться на тележке, так как его относительная скорость равна нулю. Обозначим этот момент времени t0, тогда
vi(t) = v2(fo), или а^0 = v0 - a2t0 , т. е.
а1 + а2
Как только тело остановится относительно тележки, сразу исчезает сила трения. С этого момента времени в горизонтальном направлении на тележку и тело силы не действуют, поэтому они движутся относительно Земли с постоянной скоростью.
88
За момент времени t0 тело пройдет вдоль тележки некоторое расстояние S. Поэтому минимальная длина тележки, при которой тело еще не соскользнет, должна быть равна S, т. е. I > S.
Относительно тележки в начальный момент времени тело имеет скорость - г50, а ускорение тела относительно тележки в любой момент времени равно аотн = ах + а2. Поэтому расстояние S, пройденное телом относительно тележки, равно
„ (aj + a2)tg v2 Mv2
S = -Voto + =---5------r =-------°~--r.
0 0 2 2(a1+a2) 2^ig(M + m)
Знак «—» указывает, что вдоль тележки тело перемещается влево.
Задача 11.18 Брусок массой М лежит на гладкой горизонтальной плоскости, по которой он может двигаться без трения. На бруске лежит тело массой т. Коэффициент трения между телом и бруском равен /л. При каком значении силы F, приложенной к бруску в горизонтальном направлении, тело начнет скользить по бруску?
Решений. На тело массой т действуют три силы: сила тяжести mg, реакция опоры со стороны бруска N й сила трения / . На брусок массой М действуют четыре силы: сила тяжести Mg, сила реакции опоры R, сила трения /т'р = —/тр и сила давления N' = -N (рис. 11.18). Выберем на-89
N
Рис. 11.18
правление оси ОХ, совпадающей с направлением силы F, и запишем второй закон Ньютона в проекции на это направление
/тр = та,; F - /тр = Ма2.
При малом значении силы F проскальзывания может и не быть. В этом случае тело массой т движется как единое целое с бруском, а это значит, что ускорения относительно Земли у них одинаковы, т. е. а, = а2. В этом случае сила трения / является силой трения покоя и может меняться по величине от 0 до максимального значения /тр max = ftN. В нашей задаче величину силы трения покоя можно вычислить из соотношений
Лрп = та И F - Лрп = Ма-
£ _ F
Отсюда сила трения покоя /тр п ~ т-777 •
т + М
90
Как видно из этого соотношения, с увеличением силы F увеличивается и сила трения покоя. Когда она достигнет максимального значения (в нашем случае /тр гаах = ping), то тело начнет скользить вдоль бруска. Следовательно, когда нет проскальзывания
, mF
f < pmg, или —- < pmg. v M + m
Поэтому, если F < pg (M + m), проскальзывания нет, если же F >/zg (М + т) , возникает скольжение тела массой т вдоль бруска.
Следует обратить внимание, что для скольжения тела вдоль бруска нужно приложить силу не F = pmg, как обычно утверждают учащиеся, a F > р(М + m)g.
При скольжении тела вдоль бруска их ускорения относительно Земли разные. В этом случае второй закон Ньютона для тела и бруска запишется
/тр = та1; F —/тр=Ма2,
где сила трения скольжения равна /тр = pmg.
Из этих уравнений легко определить ускорения ttj и а2:
F — pmg ai = pg, а2 =-—----.
Так как при скольжении тела F > pg(M + m),
91
то ускорение а2 > ар а это значит, что ускорение тела относительно бруска будет равно
а отн
= а, - а2 = ng -
F — nmg _ + m) ~ F
M M
Эта величина отрицательная, так как
F > ng(M + in). Это означает, что относительное
ускорение тела направлено в сторону, противоположную движению.
Задача 11.19 На горизонтальной платформе, вращающейся с угловой скоростью (У, на расстоянии I от оси вращения лежит груз массой т. Определить силу F, с которой платформа действует
на груз.
Решение. На груз массой т действуют три силы: сила тяжести mg, сила реакции опоры N и сила трения f (рис. 11.19). Сила трения направлена к центру, так как именно эта сила в горизонтальном направлении сообщает телу нормальное ускорение ап = (оЧ. При
этом сила трения /тр = теоЧ является силой трения покоя, ибо тело покоится на платформе. Со стороны платформы на тело действуют две силы: сила трения покоя f и сила
реакции опоры N. Их результирующая F = N + fTp
92
является искомой силой. Величина этой силы определяется по теореме Пифагора
F = >2 + Лр = ^(wg)2 + (ma)zl)2 .
III. ЗАКОНЫ ИЗМЕНЕНИЯ
И СОХРАНЕНИЯ ИМПУЛЬСА ТЕЛА И ЭНЕРГИИ
§ 1. Изменение и сохранение импульса тела и системы тел
пШ.1 Изменение состояния движения тела, т. е. величины и направления скорости, определяется не только величиной действующей силы F, но и длительностью ее действия. Это хорошо видно, если второй закон Ньютона записать в несколько иной форме:
V* г -
> Ft = та= т-~. или
" At
У' Fi kt = mkv = т(уг — vr),
где F. — сумма всех действующих на тело сил,
a v2 и Vj соответственно конечная и начальная скорости тела. Вводя понятие импульса тела р = mv, получим
д^У;=Ар. (1)
Таким образом, формула (1) утверждает, что
93
изменение импульса тела (или системы тел) Др за время At равно импульсу всех сил , действующих на тело за то же время.
пШ.2 Группа тел, движение которых рассматривается совместно, называется механической системой тел. Если на систему действуют только силы, которые создаются телами, принадлежащими к рассматриваемой системе, то эти силы называются внутренними, а сама система — изолированной. Силы, не принадлежащие к данной системе, называются внешними. Если сумма всех внешних сил, действующих на систему тел, равна нулю, то система называется замкнутой.
пШ.З Импульс тела (или системы тел), на которое не действуют внешние силы, остается неизменным. Другими словами, изменение импульса замкнутой системы равно нулю, т. е.
Др = 0. (2)
Это утверждение называется законом сохранения импульса. Закон сохранения импульса позволяет найти конечные скорости взаимодействующих тел, образующих изолированную систему, не вдаваясь в детали взаимодействия.
Следует отметить, что иногда этот закон можно применять и для неизолированных систем. Это можно делать в том случае, если:
1) на систему действуют внешние силы, но сумма всех внешних сил (Ft внеш ) равна нулю;
2) может случиться так, что F\ внеш 0, но вдоль какого-либо направления сумма проекций 94
этих сил обращается в нуль. Тогда только вдоль этого направления можно записать закон сохранения импульса. Например, если Z^xAt = O, то Лрх = 0;
3) в некоторых случаях начальное и конечное состояние системы тел отделены столь малым промежутком времени (например, выстрел, взрыв, удар), что импульс постоянной внешней силы (например, силы тяжести, силы трения) не может заметно изменить импульс системы тел (At -> 0). В этом случае импульс внешней силы полагают равным нулю и используют закон сохранения импульса для решения задачи.
§ 2. Работа силы. Изменение и сохранение механической энергии тела и системы тел
пШ.4 Работой постоянной силы F на перемещении Ат называется произведение проекции этой силы на направление перемещения (FT) на величину (модуль) этого перемещения (|Дт|).
А = Fr|Af | = |г||Дт| cos а, (3) где а — угол между направлениями приложенной силы и перемещения (рис. III. 1). Согласно формуле, сила, перпенди-
95
кулярная перемещению, работы не совершает (так как cos а = 0 ).
Если на тело действуют несколько сил, то под проекцией силы F на направление Дг следует понимать проекцию результирующей силы, т. е.
FP Дг = ^1Дг + F2 Дг +* • -+FnAr ' (4)
В этом случае полная работа определяется как сумма работ всех действующих сил:
А = А, + А,+...+А. 1 Z 71
F и г Если сила F меня-
Р /------s. ется во время движе-
। J/J —। ния, то полное пере-
। [х[ । мещение тела нужно
।fa1। разбить на столь ма-лые отрезки, в пределах которых силу F.
Рис. III.2 можно считать постоянной (рис. III.2). В этом случае полная работа силы F на перемещении Дг определится суммой элементарных работ А = А = У, FirДг. Эта сумма численно равна площади фигуры, расположенной под кривой графика зависимости проекции силы от перемещения.
пШ.5 Работа силы тяжести и силы упругости на любой замкнутой траектории равна нулю. Все силы, работа которых на замкнутом пути равна нулю, называются консервативными или потенциальными.
Поднимая груз или растягивая пружину, мы сообщаем телам некоторый запас работы, кото-
96
рую они могут совершить. В этом случае принято говорить, что сообщаем некоторый запас энергии, который определяется лишь положением тела, поэтому сообщенная телу энергия называется энергией положения, или потенциальной энергией. Потенциальная энергия тела, поднято-_го на высоту h, равна Еп = mgh. Потенциальная
энергия пружины, растянутой на Ах, равна
Е к(кх)2
п 2
Изменение потенциальной энергии системы равно работе внутренних консервативных сил системы, взятой с противоположным знаком:
АЕП = -^внутр ИЛИ Лнугр = -А^П- (5)
nlll.G Кинетическая энергия тела равна половине произведения его массы на квадрат скорости:
„ ти~ Ек =---
к 2
Изменение кинетической энергии равно работе внешних сил, т. е.
ДЕК = Авнеш. (7)
пШ.7 Полная механическая энергия тела (или системы тел) равна сумме потенциальной и кинетической энергий
Е = Ек + Еп. (8)
пШ.8 В замкнутой системе, в которой действуют только внутренние консервативные силы, выполняется закон сохранения механической энергии, т. е. Е = Ек + ЕП = const, или изменение пол-
97
(6)
4 Физика
ной механической энергии системы равно нулю
ДЕ = ДЕК + ДЕП = 0. (9)
пШ.9 Если на систему тел действуют внешние силы или внутренние неконсервативные силы, то изменение полной механической энергии равно работе внешних сил и внутренних неконсервативных, т. е.
ДЕ = ДЕК + ДЕП = Авнсш + Авнутрнеконс. (Ю)
§ 3. Центральный удар шаров
пШ.10 Центральным ударом называется такое взаимодействие тел, когда их скорости направлены вдоль линии, соединяющей их центры.
В механике обычно рассматривают два предельных вида взаимодействия тел: абсолютно упругое и абсолютно неупругое взаимодействия (абсолютно упругий и абсолютно неупругий удары тел). Абсолютно упругий удар — это такое взаимодействие тел, при котором механическая энергия тел сохраняется. Величина и направление скоростей после взаимодействия определяется законом сохранения механической энергии и законом сохранения импульса.
Абсолютно неупругий удар — такое взаимодействие тел, после которого тела движутся вместе (как единое целое) с одинаковой скоростью. Скорость движения тел после неупругого столкновения определяется только законом сохранения импульса. Закон сохранения механической энергии при абсолютно неупругом взаимодействии
98
не выполняется, так как часть механической энергии тел при столкновении переходит в тепловую энергию, при этом сталкивающиеся тела нагреваются.
Для успешного решения задач на законы сохранения и изменения импульса тела и энергии предлагается следующая последовательность действий:
1. Внимательно прочитайте условие задачи, нарисуйте рисунок и на нем укажите стрелочками все действующие на тела силы.
2. Далее необходимо выбрать систему тел, взаимодействие которых вы желаете рассмотреть, и определить, является ли эта система замкнутой. Если система тел замкнута, то можно применить закон сохранения импульса (2), если же на систему действуют внешние силы, то нужно применить закон изменения импульса (1). Оба эти закона часто удобно использовать вдоль какого-либо направления.
3. Может случиться так, что одного закона сохранения импульса (или закона изменения импульса) недостаточно для решения задачи. Тогда можно еще использовать закон сохранения механической энергии. Однако в этом случае мало убедиться, что система тел, выбранная вами, замкнута. Нужно еще выяснить, являются ли внутренние силы консервативными. Если силы консервативны, то можно применять и закон сохранения механической энергии (9). Если же силы неконсервативны, то нужно применить закон изменения механической энергии (10).
4*
99
4. Записав систему уравнений для задачи, нужно проследить, чтобы число уравнений равнялось числу неизвестных. Решение задачи нужно получать в общем виде и только после этого в полученные формулы подставить цифровые данные.
Задача III.1 По канатной железной дороге с углом наклона а = 30’ опускается вагонетка массой М=1000 кг. Определить натяжение каната при торможении вагонетки в конце спуска, если скорость в конце торможения м/с, а время торможения t0=10 с. Коэффициент трения принять равным и = 0,4, ускорение свободного падения g=10 м/с2.
Решение. На тележку действуют четыре силы: сила тяжести Mg, реакция опоры N, сила натяжения каната Т и сила трения / (рис. Ш.З). Для тележки эти силы внешние. Эту задачу можно решить, не прибегая к привычной записи второго закона Ньютона, а используя закон изменения импульса: изменение импульса тела Др за время At равно импульсу всех сил, действующих на тело за это время, т.е.
Рис. Ш.З
100
Направим ось ОХ вдоль наклонной плоскости, как показано на рис. Ш.З, а ось ОУ — перпендикулярно к ней.
В проекции на направление ОХ этот закон запишется в виде
(Mg sin а - Т - /тр) At = М(0 - и0), или
Mv
Т + ЛР “ sin а ~1.
Ч
Следовательно, сила натяжения каната равна
Т = —9- - /тр + Mg sin а, где /тр = /iN.
Реакция опоры N определяется из обычной записи второго закона Ньютона вдоль оси ОУ: N — Mg cos а = 0, или N — Mg cos а . Таким образом, натяжение каната Т равно
гг. п/г . Mv0
Т =----- — fiMg cos а + Mg sin а =-- +
+ Mg(sin а — /л cos a).
Подставив численные значения величин, получим
Т = 1000к1"5м/с +1000 кг-10 м/ <? (0,5 - 0,34) = 10 с
= 2100Н.
Запись второго закона Ньютона через импульс всех сил, действующих на тело, удобно использо
101
вать тогда, когда вас не интересует, как меняется скорость тела за интервал времени At, а известны начальные и конечные значения скоростей.
Задача IIL2 Шарик массой т, движущийся по идеально гладкой поверхности, упруго ударяется о преграду под углом а к горизонту (рис. IIL4, а). Величина скорости шарика до и после удара равна
v0, а угол падения равен углу отражения. Определить изменение импульса шарика Др.
Решение. Вектор скорости шарика v0, хотя и остается неизмен-(а) ным по величине, меняет свое на-
Рис. III.4
правление, а это означает, что из-
менение импульса шарика Др не
равно нулю, т. е. закон сохранения импульса для шарика не выполняется:
Ар = mAv = m(v20 — v10) О,
где 620 и v10 — конечная и начальная скорости
шарика.
Рис. III.4
Таким образом, на шарик обязательно должна действовать некоторая сила, направленная в ту же сторону, что и вектор изменения скорости Av, так как
Ар = FAt = mAv
Такой силой является сила упругости. Именно
102
она, действуя на шарик, меняет направление его скорости.
Изменение вектора импульса шарика Ар направлено в ту же сторону, что и изменение вектора его скорости Аи (рис.Ш.4, б), а по величине равно | Др| = тА« = 2mv0 cos а.
Задача Ш.3 Между двумя лодками, находящимися на поверхности озера, протянута веревка, которую человек, находящийся в одной из лодок, тянет с горизонтальной силой F=50H. Определить скорость лодки с человеком относительно берега и относительно второй лодки через время t0=5 с. Масса лодки с человеком 7^=250 кг, а лодки без человека М2=200 кг. Обе лодки движутся без трения.
Решение. На каждую из лодок вдоль горизонтального направления действует внешняя сила натяжения нити T=F (рис. III.5). За время t0 изменение импульса Ар каждой из лодок равно Ар = FAt, или
Ч(«к1 - «01) = ЛР = Fto'> ^2(«к2 -«о2) = Ар = Ft0,
Рис. III.5
103
где v01, и02 — начальные скорости лодок; ик1, г>к2 — конечные скорости лодок к моменту времени t0 относительно Земли. Так как лодки вначале покоились, то г>01 = г>02 = 0. Поэтому
«к1 =
Ft0
М.
50•5 ,
----= 1 м/с, а 250
«к2
Ft0
М2
50-5
200
= 1,25 м/с.
Скорость первой лодки относительно второй определяется из закона сложения скоростей vr_2 = г5к1 — ?5к2. Записав это уравнение в проекции на ось ОХ, получим
’->!-! = ”,1 “ ”,г) = + ”.! =
_ , «» _ «о(м. + _ 50'5 • 450
------1---—-------------—--------- — 2,25 м/с.
М, М2 МгМ2 250-200
Однако, если рассмотреть систему.тел, состоящую из двух лодок, то сила натяжения веревки является внутренней силой. Поэтому вдоль горизонтального направления для этой системы тел можно применить закон сохранения импульса. Вначале лодки покоились, т. е. г>01 = v02 = 0. Начальный импульс системы был равен
Р[ — Pi + р2 — Mrvor + M2v02 — 0 •
Этот импульс должен сохраняться и во все время движения. Через время t0 импульс системы тел равен
Рг=Р'1+Р2= М15к1 + М2«к2 = 0,
104
или MyVK1 = — M2vk2. Знак «—» означает, что лодки движутся в разных направлениях. Отношение их скоростей обратно пропорционально отношению их масс:
v
Vk2
м2
Мг-
Задача Ш.4 Человек в лодке длиной I, обращенной кормой к берегу, переходит с кормы на нос (рис. III.6). Определить скорость человека относительно берега. Как меняется расстояние между человеком и берегом? Масса человека т, лодки - М. Человек вдоль лодки передвигается со скоростью v0.
Решение. Рассмотрим систему из двух тел: человек — лодка. Для этой системы тел сумма всех внешних сил равна нулю. Поэтому выполняется закон сохранения импульса. Запишем его в системе отсчета, связанной с Землей
т(у0 + и) + Ми — 0 , где и — скорость лодки относительно Земли. В проекции вдоль оси ОХ это соотношение запишется т(у0 - и) - Ми = 0.
Это выражение позволяет вычислить скорость лодки и относительно Земли:
105
mv0 и =-------.
М + т
Скорость человека относительно берега г>чб равна
mvn Mvn v4 б= ~ и = vn---------- ~ •
0 0 М + т М + т
Скорость человека относительно берега совпадает по знаку со скоростью г>0, поэтому при любом соотношении масс т и М расстояние между человеком и берегом увеличится.
Определим на какую величину увеличится это расстояние. Так как лодка и человек движут-
I AS „ ся одновременно, то — =---- . Следовательно,
^0 ^чб
Mv0 __ М о (М + m)v0 М + т
Задача III.5 Две лодки массой М каждая идут параллельными курсами навстречу друг другу с одинаковыми скоростями г0 и с одинаковыми грузами т. Когда лодки поравнялись, с первой лодки на вторую перебрасывают груз т, а затем со второй лодки на первую перебрасывают такой же груз. Определить скорости лодок vl и v2 после перебрасывания грузов.
Решение. В этой задаче удобно рассмотреть систему тел: одна лодка и груз т другой лодки. Так как в горизонтальном направлении на систему внешние силы не действуют, то можно применить закон сохранения импульса. Для первой лодки
106
(М + m)v0 — mv0 = (M + 2m)v1, для второй лодки
— Mv0 + mv1 = (М + т)г>2, где v1 и v2 — конечные скорости лодок. Решив эту систему уравнений, получаем
vi
Mv0 = -v, =---а.
М + 2т
Таким образом, обе лодки движутся с одинаковыми по величине скоростями, но в разных направлениях.
Задача Ш.6 Навстречу платформе с песком массой М, движущейся горизонтально со скоростью и0, летит снаряд массой т со скоростью v под углом а к горизонту. Снаряд попадает в песок и застревает в нем. Определить скорость платформы й после попадания снаряда (рис. III.7).
Рис. III.7
Решение. Рассмотрим систему, состоящую из двух тел: снаряд — платформа. Вдоль горизонтального направления (оси ОХ) для этой системы тел
107
выполняется закон сохранения импульса, так как проекции всех внешних сил вдоль этого направления равны нулю, т. е. Р = Р2х. Импульс системы тел до взаимодействия Р1х равен
Р1Х = Ми(. — mv cos а .
После взаимодействия
Р2х = (М + т)и .
Таким образом, Muf. — mv cos а = (М + т)и.
Это соотношение позволяет определить скорость платформы -и после попадания снаряда
Мип — mv cos а и -----«---------.
М + т
Задача III.7 Призма массой т помещается на идеально гладкую призму массой M=3m (рис. III.8). Какое расстояние пройдет нижняя призма к мо
менту, когда верхняя коснется горизонтальной иде
ально гладкой
Рис. III.8
плоскости? Основание большой призмы а, малой — Ъ.
Решение. Рассмотрим систему, состоящую из двух тел: верхняя и нижняя призмы. Проекции внеш
них сил mg, Mg и R вдоль направления ОХ рав
108
ны нулю. Силы же N и N' являются внутренними, причем N=~N'. Поэтому можно применить закон сохранения импульса. Поскольку в начальный момент времени призмы покоились, то
О = mvx + Мих = mvx — Ми, где vx — горизонтальная составляющая скорости малой призмы вдоль оси ОХ относительно Земли; их — скорость нижней призмы вдоль горизонтальной поверхности, причем их = -и.
Отношение скоростей призм равно отношению масс
v М Зт
—— = — =----= 3.
и т т
Таким образом, vx = Зи. Это соотношение справедливо для любого момента времени.
Так как тела движутся с постоянными ускорениями и в начальный момент призмы покоились, то аналогичное соотношение справедливо и для горизонтальных перемещений призм, т. е.
А*1 -v* -з
Да?2 и
причем Ла?! = »91 = (а — Ь) — S2; Да?2 = S2, где и S2 расстояния, которые пройдут соответственно верхняя и нижняя призмы по горизонтали относительно Земли к моменту касания верхней призмы горизонтальной плоскости. Следовательно:
(а-Ь)-5г
— о .
S2
109
Отсюда расстояние S2> на которое переместится нижняя призма относительно Земли, равно
Задача III.8 На гладкой горизонтальной плоскости стоит брусок массой М, к которому на длинной нити I привязан шарик массой т. Вначале нить отклонили на некоторый угол и отпустили без начальной скорости. Определить скорость бруска в тот момент, когда нить проходит через вер-
тикальное положение, если угловая скорость шарика в этот момент равна <у (рис. III.9).
Решение. Рассмотрим систему, состоящую из двух тел: брусок — шарик. Для этой системы тел силы натяжения нитей Т и Т'являются внутренними силами, проекции сил тяжести mg и Mg и реакции опо
ры N вдоль горизонтального направления равны нулю. В начальный момент вся система покоится, следовательно, суммарный импульс тел равен нулю. Запишем закон сохранения импульса в проекции на направление ОХ для момента, когда нить
проходит через вертикальное направление:
— Ми + mv = 0, где и — скорость бруска, v — скорость шарика в
110
момент прохождения вертикального положения. Обе скорости взяты относительно Земли. Причем v = col — и • Следовательно:
— Ми + т(ы1 — и) = 0.
Отсюда скорость бруска в момент прохождения нитью вертикального положения равна
то)1 и =-------.
М + т
Задача III.9 Поезд массой М, двигавшийся со скоростью V, начинает тормозить и останавливается, пройдя путь £. Какова сила торможения F?
Решение. Сила торможения F для поезда является внешней силой, поэтому закон сохранения механической энергии не выполняется. Изменение кинетической энергии равно работе сил торможения (п.Ш.9), т. е.
А-^кин ^внеш >
2 9
0-^- = FScosl80°, или F = 2^L.
2 2S
Задача Ш.10 Тело массой т, брошенное со скоростью с высоты Н вертикально вниз, погрузилось в мягкий грунт на глубину h. Определить силу сопротивления грунта.
Решение. Тело массой т на высоте Н обладает потенциальной и кинетической энергией, которая расходуется на преодоление силы сопротивления грунта и на приобретение потенциальной энергии на глубине h.
Ill
Примем за нулевой уровень отсчета поверхность Земли. Тогда изменение механической энергии равно работе сил сопротивления, т. е.
ДЕ = ДЕК + ДЕП = Ас, или
О _ _—о. + (_ mgh — rngH) = Fch cos 180°= —Fh \ 2 /
Следовательно, сила сопротивления грунта равна
2g(H + h)m + mv2 F =----------------
2h
Задача III.ll Два абсолютно упругих шара массами га, и т2 движутся друг за другом по гладкой горизонтальной плоскости со скоростями
и v2 и соударяются. Найти скорости шаров Й, и й2 после соударения.
Решение. При соударении на шары в горизонтальном направлении действуют силы взаимодействия (силы упругости), однако они являются внутренними и консервативными, поэтому в этой задаче можно использовать закон сохранения механической энергии и закон сохранения импульса, которые запишутся в проекции на ось ОХ следующим образом (ось ОХ выберем вдоль движения шаров):
m2r2
2
TTlyV2
2
+
2 2
т.и, т7и9
- + 2.......2 ;
2 2
+ m2v2 = m1ul + m2u2.
112
Для удобства решения эту систему уравнений целесообразно переписать в виде
~и1) = тг(и1 -vl)-, (1)
wi(ui ~ui) = т2(и2 -v2). (2)
Разделив первое уравнение на второе, получим
vt + ut = и2 + v2. (3)
Далее используем уравнения (2) и (3)
Решая эту систему, получим выражение для конечных скоростей
(т, — m,}v, + 2т, v,
U. = —------г±г-----—; (4)
ту + т2
т2 ~ mi)v2 + 2т1г>1 т} + т2
Мы получили общие выражения для скоростей и и2, которые можно использовать для любого направления движения первоначальных скоростей и v2 вдоль оси ОХ. В этом случае, если какая-либо из скоростей (г^ или v2) совпадает по направлению с осью ОХ, то она берется со знаком «+» в формулах (4) и (5), если же не совпадает — то со знаком «—».
Предположим, что шар массой движется со скоростью vlt а шар массой т2 покоится (т. е. г>2=0), тогда формулы (4) и (5) примут вид
ИЗ
(т, — mAv.
1---T-----
mv + m2
2mit>1 u2 =----------
mv + m2 '
Следовательно, если ml>m2, то оба шара после взаимодействия будут двигаться в сторону, куда была направлена скорость vY. Если же то первый шар после взаимодействия отскочит в обратную сторону (и{< 0), а второй будет двигаться в направлении скорости г51.
Если же массы шаров одинаковы, то после взаимодействия первый шар остановится (Uj=0), а второй будет двигаться со скоростью vv
Задача Ш.12 Идеально гладкий шар А, дви
жущийся со скоростью vy, соударяется одновре
менно с двумя такими же соприкасающимися между собой шарами В и С (рис. III.10). Считая соударение шаров абсолютно упругими, определить их скорости после взаимодействия.
Решение. В момент соударения на шары В и С действуют силы упругости, направленные вдоль
Рис. III. 10
прямых, соединяющих их центры с центром ударяющегося шара А. Поэтому после соударения движение шаров В и С происходит вдоль этих пря
114
мых. В силу симметрии скорости шаров В и С и v2) после соударения одинаковы и направлены под углом а к оси ОХ.
Для системы тел, состоящей из трех шаров, выполняется закон сохранения импульса и закон сохранения механической энергии, так как силы упругости являются внутренними силами. Запишем эти законы:
mv0 = mv, + mv2 + тй ; (1)
mv2 mv2 mv2 mu2
v 1 । Z
2 “ 2 2
(2)
2
2
где и — скорость шара А после соударения.
Учитывая, что скорости шаров В и С после удара одинаковы по величине, т. е. |г57| = |г52| = v, уравнение (1) системы вдоль оси ОХ запишется:
тмй = mv cos а + mv cos а + mu = 2mv cos a + mu ,a систему уравнений (1) и (2) можно переписать в виде
vo ~ cos а + и> v0 — и = 2v cos а;
. . . или
v0 = 2v + и , v2 - и2 = 2v2.
Разделив второе уравнение на первое, получим v0 +и = v / cos а.
Теперь можно рассматривать систему двух уравнений, но уже первой степени:
v0 +и = v / cos а; (3)
v0 — и = 2vcosa. (4)
Сложив уравнения (3) и (4), получим
115
2t>0 = v I cos a + 2v cos a.
Откуда
_ 2г>0 _ 2u0 cosa 2v0V3 / 2 _ 2u0V3
1 / cos a + 2 cos a 1 + 2 cos2 a 1 +2’3/4 5
Скорость шарика А после удара определим из уравнения (4):
2г>„3 v и = vn —2v cos а = vn----— =-----.
° 0 5 5
Таким образом, после соударения шары В и С будут двигаться вправо (рис. III. 10), а шар А после соударения будет двигаться влево, на что указывает знак «—».
Задача Ш.13 Два абсолютно упругих шарика массами т и М подвешены на одинаковых нитях длиной I каждая (рис. III.11). Шарик массой т отклоняют от положения равновесия на 90° и отпускают. На какую высоту Н поднимется шарик массой М после соударения?
116
Решение. Рассмотрим систему двух тел: какой-либо шарик — Земля. В этой системе тел силы тяжести и натяжения нитей являются внутрен
ними и консервативными силами, поэтому для данной системы тел выполняется закон сохранения импульса и закон сохранения механической
энергии.
Однако изменение импульса Земли, так же как и изменение ее механической энергии, столь мало, что с огромной степенью точности ими можно пренебречь по сравнению с изменением импульсов шариков и изменением их механических энергий.
Если за нулевой уровень потенциальной энергии выбрать положение равновесия шариков, то
ЛЕ + ЛЕ = ЛЕ = 0. к п мех
Для первого шарика до удара
\
— О + (0 - mgl) - О /
После удара
О — '
к 2 ;
+ (mgh — О) = 0 , или
mgl = —(1) £
и mvl /ОЛ
= (2)
где Vi и v2 — скорости шарика массой т до и после удара соответственно, h — высота подъема этого шарика после удара.
117
Для большого шарика после соударения запишем
Ми2 Ми2
MgH----— = 0; MgH = ———, (3)
где и — скорость шарика массы М после соударения, а Н - высота, на которую он поднимется. При соударении шариков закон сохранения механической энергии и закон сохранения импульса запишутся
mv2 mv2 Ми2
---L =---1 +----
2 2 2
mv} = mv2 + Ми.
(4)
Уравнение (1) позволяет получить скорость шарика массой т до столкновения. Система уравнений (3) и (4) позволяет вычислить скорости обоих шариков после столкновения;
и =
2т
М + т
y[2gl; v2 =
(М — т)у['.
М + т
Знак «—» говорит о том, что в случае М > т маленький шарик после удара отскочит влево. Высота подъема шарика массой М определяется из уравнения (3)
_ и2 _ 4m2l
2g (М + т)2 ’
Именно это и требуется определить в задаче. Если бы нас интересовала высота подъема маленького шарика после удара, то мы могли бы воспользоваться уравнением (2).
118
Задача Ш.14 Пуля массой т летит со скоростью г>0 и пробивает тяжелую доску толщиной d, движущуюся навстречу пуле со скоростью и. С какой скоростью v вылетит пуля из доски? Скорость доски не меняется, а силу сопротивления Fc движению пули в доске считать постоянной.
Решение. Сила сопротивления Fc для пули является внешней силой v 7 (рис. IIL12), и она **— \ совершает работу, когда пуля движется внутри доски, т. е. на расстоянии d. Однако
пуля проходит Рис. III.12
расстояние d относительно доски, поэтому изменение механической энергии пули удобнее рассматривать относительно доски, и нужно применить формулу (10) (пШ.9), т. е.
ДЕ, = S [р _ (_ _ ”4”» - “)Г =FdQOsa= _Fdi 2 2
m(v + и)г т(г>0 + и) „ , или —>-------------= —Fd.
2 2
Перепишем это соотношение в виде
Еv 2Fd v + u = (v + и)-------т. е.
V т
119
V =
(v0 + u)2 -
2Fd m
— и.
Задача Ш.15 От поезда массой М, движущегося с постоянной скоростью, отрывается последний вагон массой т, который прходит путь S и останавливается. На каком расстоянии L находится поезд от вагона в момент остановки последнего? (рис. III.13, а).
Рис. III. 13
Решение. Сумма сил, действующих на весь состав до и после отрыва вагона, равна нулю, поэтому для системы: поезд — оторвавшийся вагон, выполняется закон сохранения импульса. Направим ось ОХ вправо. Вдоль этой оси выполняется соотношение
“ /тр = 0 > илм /тр =
120
Для простоты решения удобно выбрать систему координат, которая движется со скоростью va всего состава до отрыва вагона. В этой системе координат закон сохранения импульса имеет вид
(М - т)и
О = mv + (М — т)и, или v — —--------,
т
где v и и — соответственно скорости вагона и поезда в системе координат, движущейся со скоростью v0. По сравнению с поездом в выбранной системе координат вагон движется в обратную сторону (рис. III.13, б). Расстояния, пройденные вагоном (5В) и поездом в этой системе координат относятся как их скорости, т. е.
SB _ v _ (М — т)
Sn и т '
В условии задачи известно, что вагон остановится, пройдя расстояние 5 относительно Земли. В системе координат, движущейся со скоростью и0, вагон за время движения также пройдет расстояние S, только скорость его в движущейся системе координат станет равной ~v0 к моменту остановки относительно Земли. Действительно, йабе = ^пер + Ч™• Так как ипер = vQ, то при остановке вагона относительно Земли (иа5с = 0) скорость относительно подвижной системы координат равна
v = v . — v = 0 — vn = —vn отн абс пер О О
Следовательно,
121
S M — m _ Sm
£п т п М-т
Расстояние L между вагоном и поездом, которое нужно определить в условии задачи, равно (см. рис. III. 13, б)
L = 5 + 5n
Sm
М — т
SM
М — т
£ +
Задача IIL16 Тележка массой М движется без трения по горизонтальным рельсам со скоростью v0. На передний край тележки кладут тело массой т без начальной скорости. Тело, пройдя некоторое расстояние вдоль тележки, останавливается. Определить это расстояние I, если коэффициент трения между телом и тележкой ц.
Решение. Все силы, действующие на тело и тележку, изображены на рис. III. 14. Вдоль горизонтального направления можно применить закон сохранения импульса для системы: тело — тележка. В этом случае сумма проекций внешних
Mg
«о
Рис. III.14
122
сил равна нулю, а силы трейия являются внутренними силами (7тр1 = — /тр2). Поэтому можно записать
Mv0 = (m + M)u,
где и — скорость тележки и тела относительно Земли после остановки последнего.
Тогда
(1)
Mv0 и =------у.
(т + М)
А вот закон сохранения механической энергии для этой системы тел применить нельзя, поскольку сила трения является неконсервативной силой, поэтому изменение механической энергии равно работе сил трения, т. е.
= (Дк ~ Дн) = Лр1 + АтР2 , или
(т + М>2 Mv2 _ 2 2 Лгрз
где £ и s - расстояния, пройденные тележкой и телом относительно Земли соответственно. Решая совместно уравнения (1) и (2) и используя выражение для силы трения, получим
(m + M)(Mv0}2 , . .
--------2 ~....- = 2/zmg(s - S) = -2/zmgZ, (m + M)
(2)
( M \
или —ГТ? “1 = -2/zmgZ.
\m + M J
Таким образом, тело вдоль тележки прошло расстояние
123
2/zg(m + М)'
Следует обратить внимание на то, что работа сил трения определяется относительным перемещением тела I.
IV. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ. ЗАКОН ВСЕМИРНОГО
ТЯГОТЕНИЯ
§ 1. Вращательное движение
При вращении твердого тела вокруг неподвижной оси все его точки имеют одинаковые угловые перемещения (Аф), угловые скорости / _ Д^Л ( _ Дю\
I ы ~ и угловые ускорения I Р ~
Задачи на динамику вращательного движения по окружности, в принципе, ничем не отличаются от задач на динамику прямолинейного движения точки и также подчиняются второму закону Ньютона = та, где а — полное ускорение точки, состоящее из нормального ап и тангенциального (касательного) ат ускорений: а = ап + ах.
v2
При этом ап = — меняет только направление скорости, ах — только величину скорости.
124
Большую часть задач на динамику вращательного движения удобно решать с привлечением закона сохранения механической энергии.
Вновь предлагаем некоторую последовательность действий (некий алгоритм) при решении задач на динамику вращательного движения.
1. Аккуратно рисуем рисунок, отражающий условие задачи. На этом рисунке стрелочками изображаем все силы, действующие на тело.
2. Записываем второй закон Ньютона в векторном виде, а затем переписываем его в проекции на ось ОХ, которую направляем обычно вдоль радиуса к центру. Именно так удобно выбрать направление оси ОХ, поскольку мы знаем ускоре-
ние вдоль этой
ось 0Y
mv1
= та =------. (1)
n R k ’
обычно направляют вдоль касательной и второй закон Ньютона вдоль этой оси запишется
^Fiy = maT. (2)
Однако часто для решения задач на динамику удобнее использовать вместо уравнения (2) закон сохранения механической энергии (если это позволяет сделать условие задачи):
ЕК1 + ЕП1 = Ек! + Еп!> или Д(Ек + Е„) = 0. (3)
Закон сохранения механической энергии используется в том случае, если для решения зада
125
чи уравнения Ньютона в виде (1) нам недостаточно. Ответ получаем только в общем (буквенном) виде, так как в этом случае его удобно анализировать. И только после этого подставляем цифры в полученную формулу.
Задача IV.1 Два одинаковых шарика А и В укреплены на концах невесомой нити, продетой через трубку, как показано на рис. IV. 1. Шарик А, находящийся на поверхности диска, вращается в горизонтальной плоскости. Расстояние от оси трубки до шарика А равно г. С какой угловой скоростью должен вращаться шарик А, чтобы шарик В находился в равновесии? Будет ли равновесие устойчивым? Трением пренебречь.
Рис. IV. 1
Решение. На шарик А действуют три силы: сила тяжести mg, реакция опоры N и натяжение нити
126
Т. На шарик В действуют две силы: сила тяжести mg и натяжение нити Т. Второй закон Ньютона в векторной форме выглядит так:
для шарика A T + mg + 7V = maH, (1)
для шарика В mg + T = 0. (2)
Выберем ось ОХ, направленную вдоль нити, а ось 0Y опустим вниз. Тогда для шарика А вдоль направления ОХ уравнение (1) запишется
Т = ms>2r,
а уравнение (2) вдоль направления 0Y
mg - Т = 0.
Из этих уравнений получим
Т = ma)2r — mg. (3)
Отсюда
“ = £ • W
Очень важно теперь выяснить, будет ли это равновесие шариков устойчивым? Для того чтобы определить устойчивость равновесия, нужно сместить шарик А на Ах влево (либо вправо) и посмотреть, как изменились силы, действующие на шарик. При смещении шарика А влево сила натяжения Т уменьшается, так как теперь
Д = тш2 (г — Ат).
Но тогда сила натяжения, действующая на шарик В, тоже уменьшается, поскольку до смещения эта сила равнялась mg по формуле (3). Поэтому шарик В поедет вниз и потянет за собой шарик А. Это, в свою очередь, еще больше умень
127
шит силу натяжения и т. д. Аналогичные рассуждения можно провести и при смещении шарика А на Дж вправо. Поэтому положение равновесия шариков будет неустойчивым.
Задача IV.2 Шарик массой т прикреплен к невесомой пружине и движется по окружности в
горизонтальной плоскости с угловой скоростью (У.
Рис. TV.2
Определить силу натяжения пружины с жесткостью к (начальная длина нерастянутой пружины 10 и радиус окружности, по которой движется шарик, I (рис. IV.2).
Решение. В горизон
тальном направлении на шарик действует только сила натяжения пружины Т, которая является силой упругости и по закону Гука равна
Т = kAi = k(l — Zo). Именно эта сила сообщает ша
рику нормальное ускорение
v 27 а. = — = 0)1.
п I
Направим ось ОХ, как показано на рисунке. Второй закон Ньютона вдоль этого направления запишется
Т = mo)2l, или k(l — Zo) = mo21.
Это соотношение позволяет вычислить радиус окружности I, по которой движется шарик,
128
l(k — m<w2) = kl0, или
4
(k - met)2)
Задача IV.3 Автомобиль, масса которого М, движется с постоянной скоростью v один раз по выпуклому мосту, а другой раз по вогнутому. В обоих случаях радиус кривизны мостов одинаков и равен R. Определить вес машины Р в середине моста в обоих случаях, (рис. IV.3) Трение не учитывать.
Решение. На автомобиль действуют две силы: сила тяжести mg и сила реакции опоры N. В середине моста эти силы направлены вдоль одной прямой. Выберем ось 0Y, направленную, например, вниз. Тогда вдоль этого направления для случая а) и б) (см. рис. IV.3) второй закон Ньютона запишется соответственно
mv2
a) mg-Nr = тап = ——} откуда £t
mv2 ( v2\
N, = mg + —— = mI g + — .
Iv \ Iv I
6) mg - N2 = -man =
mv2
R
. Следовательно,
5 Физика
129
mv2 ( и2')
N2 = mg + = m g + — I
lv \ Iv /
Как видно, в обоих случаях реакции опоры Nt и N2 разные. Поскольку вес тела — это сила, с Которой тело действует на опору, то по величине вес тела в нашей задаче в обоих случаях будет разным: Ру = Nv а Р2 = N2. Таким образом, при движении автомобиля по выпуклому мосту его вес меньше силы тяжести mg, а по вогнутому — больше силы тяжести.
Задача IV.4 Грузик, имеющий массу т, прикреплен к концу невесомого стержня длиной I, который равномерно вращается в вертикальной плоскости вокруг другого конца, делая п оборотов в секунду (рис. IV.4). Каково натяжение стержня, когда грузик проходит верхнюю и нижнюю точки своей траектории?
130
Решение. На шарик действуют две силы: сила тяжести mg и сила натяжения стержня Т. В разных точках траектории сила натяжения разная. Направим ось ОХ вниз и запишем второй закон Ньютона для нижней А и верхней В точек траектории соответственно:
mg — Tj = — тап = —тш21;
mg + Т2 = тап = та>21.
Учитывая, что угловая скорость связана с числом оборотов соотношением = 2яп , получим выражение для натяжения стержня
Tl = mg + mo)2l = m(g + = m(g + 4я2п2Е) ;
T2 = mo2l - mg = m(47r2n2Z — g).
Задача IV.5 Шарик массой m подвешен на нити, длина которой I. Шарик равномерно вращается в горизонтальной плоскости,
при этом нить отклоняется на угол а от вертикали (рис. IV. 5) — конический маятник. Определить период вращения шарика Т.
Решение. На шарик действуют две силы: сила тяжести mg и натяжение нити N. Результирующая этих сил сообщает шарику нормальное ускорение Йп. Второй закон Ньютона для шарика имеет вид
131
N + mg = man
В проекциях на оси ОХ и 0Y соответственно этот закон запишется
N sin а = тм2г = mo)2l sin а ;
N cos а — mg = 0.
Решая систему двух уравнений, получим
ы21 sin а tg а =-------.
X
2 S
Отсюда , а период вращения шарика
V cos о*
2л II coset „ [h Т = — = 2л I------= 2л —
N S
где h — расстояние от точки подвеса до плоскости круга, по которому движется шарик (сравним с формулой периода для математического маятника длиной h).
Задача IV.6 По вертикально расположенному обручу радиуса R может без трения скользить колечко. Обруч вращается вокруг вертикальной оси, проходящей через его центр. Колечко находится в равновесии на высоте h от нижней точки обруча. Определить угловую скорость вращения обруча (о (раде. IV.б).
Решение. На колечко в любой момент времени действуют две силы: сила тяжести mg и сила реакции опоры N. Эти две силы сообщают кольцу нормальное ускорение ап, с которым оно движется по окружности радиуса г. Второй закон Ньютона в векторной записи имеет вид
132
N 4- mg = man
Выбрав оси OX и OY, как указано на рисунке, запишем этот закон в проекциях на эти оси соответственно
N sin а = та = таг г: п }
N cos а — mg ~ 0, или N cos а = mg.
Разделив первое уравнение на второе, получим
а> г tg« — ИЛИ б g Таким образом, ог = g tg« = g tga = g г R sin a R cos a ' 60 = J-^-. V R cos a
133
Задача IV.7 Невесомый стержень длиной I, изогнутый, как показано на рис. IV.7, вращается с угловой скоростью (У относительно оси ААг. К концу стержня прикреплен груз массой т. Определить силу, с которой стержень действует на груз.
Решение. На груз действуют три силы: сила тяжести mg, реакция опоры N и сила натяжения стержня Т. Сила F, с которой стержень действует на груз, является результирующей сил N и Т, т. е. F = л/т2 + N2 . Для отыскания сил Т и N запишем второй закон
Ньютона в проекции на оси ОХ и 0Y (см. рис. IV.7)
Т sin <р — N cos <р = man = тмЧ sin <р;
Т cos <р + N sin <р — mg = 0. Решая эту систему, получаем
Т = m(co2l sin2 <р + g cos <р};
AT = — (оЧ cos <p} sin <p.
Таким образом, результирующая сила F, с 134
которой стержень действует на тело, равна по величине
F = у1т2 + N2 = m^g2 + й)Ч2 sin2 <р .
Задача IV.8 Маленький шарик, подвешенный на нерастяжимой нити, совершает колебания в вертикальной плоскости. Когда он проходит поло
жение равновесия, нить испытывает натяжение,
равное удвоенной силе тяжести шарика (рис. IV.8). На какой максимальный угол а от вертикали отклоняется шарик? Сопротивлением воздуха пренебречь.
Решение. На шарик действуют две силы: сила тяжести
mg и сила натяжения нити t. В системе тел: шарик — Земля, эти силы явля
ются внутренними и
консервативными, поэтому можно применить закон сохранения механической энергии:
£мех1 = -Емех2) ИЛИ ЕК1 + ЕП1 = Ек2 + Еп2.
Выберем за нулевой уровень отсчета потенциальной энергии уровень 00', тогда Емех1 = Ек1, а
Емех2 = Еп2, т. е. кинетическая энергия, которую
135
имел шарик, проходя вертикальное положение, должна равняться потенциальной энергии в точке максимального подъема шарика
mi?2 v2
----= mgH, или Н = —.
2 * ’ 2g
Поскольку из рисунка очевидно, что Н = I — I cosa = Z(1 — cosa) , то максимальный угол отклонения определится из этой формулы:
COS«maX
1-Н
I
где I — длина нити.
Для определения высоты Н необходимо знать скорость шарика при прохождении положения равновесия. Это легко сделать, записав второй закон Ньютона вдоль оси ОХ в момент прохождения шариком положения равновесия (см. рис.),
т mV 2 (Т ~
Т — mg = man = —-—, или v = --—
I m
Подставив это выражение в формулу, определяющую максимальный угол отклонения шарика, получим
cos«max
Н = 1 _ Т —mg =
I ‘Z'mg 2'
Таким образом, шарик поднимется на угол
^таХ
= 60°.
Задача IV.9 Небольшое тело соскальзывает без трения с вершины полусферы радиуса R. С какой
136
скоростью v и на какой высоте Н тело оторвется от поверхности полусферы (рис. IV.9)?
Решение. На тело действуют две силы: сила тяжести и сила реакции опоры. Второй закон Ньютона в векторной записи имеет вид
N + mg = та
Следует отметить, что ускорение а — это полное ускорение тела, оно направлено в ту же сторону, что и результирующая сила Fp, равная Fp = N + mg. Поскольку полное ускорение а равно а = ап + ах, то оно лежит внутри прямого угла между векторами ап и ах, поэтому и результирующая сила Fp должна быть сонаправлена с этим ускорением. Запишем второй закон Ньютона вдоль оси ОХ, направленной вдоль радиуса, nr mv2
mg cos а — N = тап =--.
R
Посмотрим внимательно на это соотношение. При соскальзывании тела его скорость увеличивается. Это может произойти только тогда, когда
137
N уменьшается более сильно, чем mg cos а. Поэтому наступит такой момент, когда N обратится в нуль. Это означает, что тело оторвется от поверхности сферы и дальше полетит по параболе. В этот момент времени второй закон Ньютона будет иметь вид
mv2 mg cos а =---
R
Высота Н, с которой оторвется тело, определяется (см. рис.)
Н = К cos а • (2)
Подставив выражение для cos а в уравнение (1), получим
Н mv2 v2
mg—-----—, ИЛИ Н=—. (3)
R R g
Задача была бы решена, если бы мы смогли определить скорость в момент отрыва тела от сферы. Это легко сделать, воспользовавшись законом сохранения механической энергии,
mgR = —— + mgH, или v2 = 2g(R - Н). Zu
Подставим это выражение в уравнение (3), тогда
2g(R - Н) r 2R
Н = —--------, или Н = —.
g 3
_ 2
При этом cos а в момент отрыва равен cos а = —.
3
Таким образом, тело оторвется от поверхности
138
на высоте H — — R , а его скорость в момент от-О
рыва равна
/ 2 A 2
v2 =2g(R-H) = 2g[R--R\ = -gR, \ «5 / <5
ИЛИ V = л ---.
V 3
Как видно, ни высота И, ни скорость v не зависят от массы т, поэтому тело любой массы оторвется от поверхности на одинаковой высоте и с одинаковой скоростью.
Задача IV.10 Шайба массой т скользит без трения по наклонному желобу, образующему «мертвую петлю» радиусом R. На какой высоте h шайба оторвется от желоба и до какой наибольшей высоты Н после этого поднимется, если она начала спускаться по желобу без начальной скорости с высоты = 2R {рис. IV. 10)?
Решение. На шайбу действуют две силы: сила тяжести mg и сила реакции опоры N. Обе силы являются внутренними для системы тел: шайба — Земля. Поэтому можно в любой момент времени записать закон сохранения механической энергии. Запишем его в тот момент, когда тело находится в точке максимального подъема Н, тогда
, и . wvr
mghy = mgH 4-----.
2
В точке максимального подъема А у тела будет
139
только горизонтальная скорость vr, направленная по касательной к траектории. Отсюда
v2 v2
H = h.--^ = 2R--L-2g 2g •
Таким образом, задача сводится к определению горизонтальной скорости vr в точке максимального подъема. Эта скорость, как видно из рисунка, равна vT = г? cos а. Значение скорости v в точке отрыва шайбы и угол а в момент отрыва мы получили в предыдущей задаче:
2gR 2
v = J----• cos а ~ —
V 3 ’ 3
Подставив эти значения, получим
2gR 4
Н = 2R----= — R.
2g 27
140
Высоту отрыва шайбы от поверхности h также можно определить из закона сохранения механической энергии, записанного для точки отрыва В,
, , mv , , v 5
mghY = mgh + Откуда h = hl- — = -R.
Таким образом, мы ответили на вопросы, поставленные в задаче, воспользовавшись лишь законом сохранения механической энергии.
Задача IV.11 На невесомом стержне длиной I укреплены:
а) масса 2т на конце стержня,
б) две равные массы т — одна на конце стержня, другая — посередине стержня (рис. JV.11). Стержень может вращаться в вертикальной плоскости вокруг точки А. Какую горизонтальную скорость в обоих случаях нужно сообщить концу стержня, чтобы он отклонился до горизонтального положения?
Решение. В данной задаче можно применить закон сохранения механической энергии, поскольку сила тяжести и системы тел: Земля — массы, являются внутренними. Поэтому можно записать
Ек1 = К2 +Еп2-За начало отсчета потенциальной
энергии выбираем положение 00'. Для тела мас
141
сила натяжения стержня для
Рис. IV.11
сой 2т закон сохранения механической энергии имеет вид
2mv\ л 7
—= 2mgl.
Отсюда •
Для шариков с массами т
(\ 2
—
2 ) I , ,
----1------—Ь mg — = mgl + mgl, или
2 2 2
| , т. е. vz
За начало отсчета потенциальной энергии можно было бы выбрать и положение АА'. Тогда для шарика массой 2m закон сохранения запишется
— 2mgl +
2mv2
2
= 0 , или v1 = A/2gZ,
а для шариков массами т
2 7 / \2
, mv, I mv,.\
-mgl +---~mg- +— — =0, или
2 2 2 у 2 у
«2 = \/Wgl-
Таким образом, мы показали, что решение задачи не зависит от выбора начального уровня отсчета потенциальной энергии. Следует еще отметить, что шарики массами т связаны единым стержнем и в любой момент времени будут иметь одинаковую угловую скорость <у, поэтому закон сохранения механической энергии можно записать
142
только для двух шариков вместе. Линейные скорости каждого шарика определяются формулой v = cor, поэтому линейная скорость верхнего шарика в 2 раза меньше линейной скорости нижнего.
Задача IV.12 Тело соскальзывает из точки А в
точку В по двум поверхностям с одинаковой кри
визной: выпуклой и вогнутой. Коэффициент трения один и тот же. В каком случае скорость тела в точке В больше (рис. IV. 12)?
Решение. В каж
дой точке траектории на тело действуют три силы: сила тяжести mg, реакция опоры N и сила трения / .
Рис. IV.12
Второй закон Нью
тона для обоих слу
чаев вдоль радиуса запишется
mg cos а — N2
mv22
R
или TV2 = mg cos a —
mv2
R ’
nr "‘'И пси.
mg cosa - N1 =----— или = mg cos a 4---------L.
R R
Таким образом, при движении тела по выпуклой поверхности реакция опоры N2 будет меньше, чем при движении тела по вогнутой поверхности JVr А это значит, что сила трения, действующая на
143
тело в каждой точке траектории и равная fiN, при движении по выпуклой поверхности будет меньше.
Закон изменения механической энергии запишется
АЕ + АЕ = А • К п тр )
1 mvn
-mgh + —- = ATpl или
2
—~ = mgh + Атр = mgh - fTpS = mgh - /uNS.
Из этого соотношения следует, что в точке В скорость тела будет больше в том случае, когда работа, затраченная на преодоление сил трения, меньше. Поскольку сила трения при движении по
выпуклой поверхности N2 меньше, чем N, то скорость в точке В будет больше при движении тела по выпуклой поверхности.
Задача IV.13 Определить кинетическую энергию обруча массой М, движущегося с постоянной скоростью без проскальзывания (рис. IV.13).
Решение. Разобьем весь обруч на малые участки массой Дт каждый. Любой такой участок участвует в двух движениях: поступательном со скоростью v0 (скорость движения центра обруча) и вращательном со скоростью vn = (oR (линейная скорость каждой точки обруча). В отсутствие про-
_ vo скальзывания , поэтому vn = vQ.
R
144
Рис. IV.13
Рассмотрим два диаметрально противоположных участка А и В. Их результирующие скорости равны векторной сумме скоростей поступательного и вращательного движений, т. е. v = г50 + г5л, тогда
VA = v0 +v„ - 2и0ил cos а;
vb = + 2и0г?л cos а.
Суммарная кинетическая энергия обоих участков равна
Е, „ „ = + + =
К А, О 2 2 ил
= Am(u0Е, 2 + cd2R2).
Так как это выражение справедливо для любых двух симметричных участков, то для всего обруча можно записать
145
„ Vir. I 2 2r,’W Л ^V0 . M(l)2R2
~ ^kA,B ~ (^0 + W -R — n । >
т. e. энергия всего обруча состоит из кинетической Mv20 энергии поступательного движения EnocT =---
2
„ Mco2R2 и вращательного Евр = ------. Учитывая, что
обруч катится без проскальзывания, т.е. ул = г?0 = a>R , полная кинетическая энергия обруча равна
EK=Mv20.
Задача IV.14 На тонкой нити подвешен шарик. Нить приводят в горизонтальное положение и отпускают. В каких точках траектории ускорение
шарика направлено строго вертикально и строго горизонтально? В начальный момент нить не растянута (рис. IV. 14).
Решение. Из вто-
рого закона Ньютона Т + mg = та очевидно, что ускорение тела совпадает с направлением результирующей силы. Поэтому ускорение вертикально вниз направлено в край
них верхних точках
146
А и С (нить не растянута), вертикально вверх в точке В, а горизонтально в точках D и Е, положение которых определяется некоторым углом ос0 (см. рис.). Этот угол можно определить, записав второй закон Ньютона вдоль направления радиуса и по вертикали, соответственно
_ mv2
Т — mgcosa0 = mar = -у-;
Tcosa0 — mg = 0.
Решая систему уравнений, получим
mv2 _ mg(l - cos2 а0)
cos а0
(1)
Выражение для скорости можно определить из закона сохранения механической энергии.
Если начальный уровень отсчета потенциальной энергии выбрать в точке D, то
, 7 mv2
mgh = mgl costz0 = ——
или v2 = 2gl cos a0. Подста-
вим это выражение для скорости в уравнение (1), получим
g(l-cos а Л
2g cos «0 = —--------или 3cos а0 = 1.
cos«0
Отсюда cos «0 = J—. Это значение cos«0 соответ
ствует углу а0 = 5445'.
147
вость (рис. IV. 15).
Рис. IV.15
Задача IV.15 Сфера радиусом R равномерно, вращается вокруг оси симметрии с угловой скоростью СУ. Внутри сферы находится шарик массой т. Определить высоту h, соответствующую положению равновесия шарика относительно сферы. Исследовать положение равновесия на устойчи-
Решение. На шарик действуют две силы: сила тяжести mg и сила реакции опоры N. Эти силы сообщают шарику нормальное ускорение ап, заставляя шарик двигаться по окружности радиуса
г = R sin а •
Запишем второй закон Ньютона в проекции на оси ОХ и 0Y
N sin а = тап = тм2г = ma)2R sin а ; (1)
N cos а — mg = 0. (2)
Решая эту систему уравнений, получим gtga — cy2Rsin«,
или sin«|cy2R---——1 = 0. (3)
\ cos а I
Это уравнение имеет два решения:
a) sin а = 0 (Сокращать на sin а нельзя, т.к. потеряется одно решение!);
б) cos а — “2™ — это положение равновесия
148
возможно лишь при условии, что
—-— < 1, ИЛИ (О > (02R
Причем, это положение равновесия является устойчивым. Действительно, если шарик чуть-чуть опустить вниз (угол а уменьшить), то cos а увеличивается и тогда вертикальная составляющая реакции опоры Ncosa > mg, формула (2), и шарик поднимется (т. е. вернется в положение равновесия. Если же шарик поднять чуть вверх (угол а увеличить), то cos а уменьшится и N cos а < mg, т. е. шарик опустится в положение равновесия. Высота h в этом положении равна
h = R(1 — cos «) = R 1 —
g
o2rJ-
Решение sin a = 0 (a=0) возможно при любой
скорости вращения о. Однако, если о2 > —, ре-R
шение неустойчивое (см. формулу (3)), если же
,2 . g
, то решение устойчивое.
R
Задача IV.16 Определить зависимость веса тела Р от географической широты, полагая известными угловую скорость вращени Земли с) и ее радиус R.
Решение. Пусть тело находится на поверхности Земли на широте, определяемой углом <р (рис. IV. 16). При вращении Земли тело массой т дви
149
жется по окружности радиуса г. На него действуют три силы: сила тяжести mg, сила реакции опоры N и сила трения покоя f. Выберем направление осей, как показано на рисунке, и запишем второй закон Ньютона вдоль этих осей:
mg cos <р — N cos <р + f sin <p = man = nu>2r -- ma>2R cos p;
— mg sin <p + N sin <p + f cos <p = 0,
t. e. тело вдоль оси OY не перемещается.
Решая эту систему, получим
7V = mg — mco2R cos2 <р
f — mco2R sin2 tp-
Вес тела P по величине равен силе реакции опоры N и направлен в противоположную сторону.
Таким образом, вес тела зависит от географической широты и определяется формулой
Р = N = mg — ma)2R cos2
Рис. IV.16
Из этой формулы видно, что на Северном полюсе (<р = 90°) вес тела равен силе тяжести mg, а на экваторе (ср = 0°) вес тела равен
= mg — mio2R В некоторых учебни-ках вместо силы трения покоя f и
силы реакции опоры N рассматривают
150
силу Q, действующую на тело массой т со стороны Земли. Эта сила равна Q = + N2
Порой у учащихся вызывает недоумение введение силы трения покоя f. Нужно ли ее вводить? Дело в том, что если не рассматривать силу /, то N + mg = Q, и возникает вопрос: а какая же сила сообщает покоящемуся на Земле телу нормальное ускорение ап> с которым оно движется вокруг земной оси.
§ 2. Закон всемирного тяготения
nIV.l Любые два точечных тела притягиваются с силой, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними. Сила направлена вдоль прямой, соединяющей эти точечные тела.
_ т,т2 Г 2 >
Г
где G — гравитационная постоянная, равная G = 6,67 • 10"11 м3/кг с2 •
nIV.2 Ускорение свободного падения у повер-
_ GM3
хности Земли So ~ р2 . Отсюда GM3 = g0R3.
Ускорение свободного падения зависит от расстояния от Земли
151
o-(h) = - GM?_ = ^»R3__
(R3+h)I 2 (R3+h)2'
nIV.3 Тело, находящееся в поле Земли, обладает потенциальной энергией. Начальный уровень отсчета потенциальной энергии можно взять любой, поскольку изменение потенциальной энергии не зависит от выбора этого уровня.
Так как сила гравитации зависит от расстояния и, строго гово-,L ря, не является по-
р стоянной, то фор-
Ьмулу для работы А = F Аг приме-_ ‘ Г* Л
М3т _
G—— нять нельзя. Одна-
Г ко работу можно
ч. посчитать графи-
чески. Для этого ра-
I I I I I г ;. зобьем участок го т0 - г на очень ма-
Рис. IV.17 лые отрезки, в
пределах которых силу гравитации можно считать постоянной (рис. IV. 17). Тогда полная работа на участке т0 - т равна
А = у А = у GM3m|Ar|
Если Дт —> О» то предел, к которому стремится эта сумма, определяется
152
V* GM3mAr г lim > ---------= I Fdr, или
Ar-*O^ r2 J P
’b
. . „ f _ , г GMam, GMam
A = №n= fFTpdr = f—^-dr =------f-
= - GMam
где r0 и r — расстояния, отсчитываемые от центра Земли. В частности, если за начало отсчета выбрать поверхность Земли ( r0 = R3), а г = R3 + h, то изменение потенциальной энергии определится
лтр I 1 1 I GM3mh ....
АЕ = -GM3m--------= —-г-3-—-г. (1)
п 3 R3) R3(R3+h)
Для h < < R3 это уравнение запишется
. „ gnR3mh
ЛЕп = Л = ms«h-rt3
Однако часто начальный уровень отсчета выби-
рается в бесконечности, т. е. (т0 -» оо тогда
. „ , fl 1 GM3m _
АЕП = -GM3m-------=-------= -Frpr. (2)
V го/ r
Из формулы видно, что эта энергия отрицательная. Поскольку начальный уровень отсчета находится в бесконечности (т0 -* 00), то тело лежит
«ниже» нулевого уровня отсчета.
Задача IV.17 Угловая скорость вращения Земли вокруг Солнца = 1,75 • 10~2 рад/сут. Расстоя
153
ние от Солнца R3C = 1,5 • 1011 м . Определить массу Солнца.
Решение. На Землю со стороны Солнца действует сила гравитации, которая и сообщает ей центростремительное ускорение ап, т. е. второй закон Ньютона вдоль радиуса имеет вид
Gm3Mc 2 г,
^2 ~ W3an ~ ^З.С .
^з.с
Следовательно, масса Солнца равна
Z,)2!?2
м = 2-ю30 кг = 2-1027 т.
с G
Задача IV.18 Радиус Луны в п=3,7 раза меньше радиуса Земли, а ее масса в 171=81 раз меньше массы Земли. Определить ускорение свободного падения на поверхности Луны.
Решение. Для поверхности Земли можно записать
GmM3 GM3
mg° = ~R23 ИЛИ go = ~R^
Очевидно, аналогичное соотношение выполняется и для поверхности Луны, т. е.
„ =^L
ОЛ г, 2
Если поделить одно уравнение на другое, то получим
go _ М3ДЛ
К3МЛ
154
Отсюда
/(мз\ g" /[мд,
Tt
= g0 — = !>65 M/c2 •
Задача IV.19 Какой период вращения Т имел бы искусственный спутник Земли, удаленный от нее на расстояние h. Радиус Земли R3 и ускорение свободного падения на Земле g0 считать известными.
Решение. На спутник действует сила гравитации F, которая сообщает ему центростремительное ускорение ап, т. е.
GmrM4 mrv2
(K3+h)2 cn R3+h-
Таким образом, спутник вращается вокруг Земли со скоростью
I GM3 v = . ---— •
Al R3 + h I о
Так как на поверхности Земли для тела массой m можно записать
GmM3 mg0 = g-г.
rt3
то отсюда легко определить произведение GM3 = g0R3- Величины g0 и R3, стоящие в правой части уравнения, мы знаем. Тогда скорость вращения спутника вокруг Земли будет иметь вид
155
g<A _ I So R3 + h 3 у R3 + h
Период вращения спутника
2л
T = — , где (о =
<у
Следовательно,
v
R3 + h о
Т 2л(К3+7г) 2;r(R3 +
v
^зл/So
Задача IV.20 Вычислить силу тяготения, действующую на материальную точку массой т, находящуюся внутри Земли на расстоянии г от центра. Радиус Земли — R3. Плотность Земли р считать постоянной (рис. IV.18).
156
Решение. Поместим тело массой т внутри Земли в произвольной точке А. Мысленно разобьем Землю на тонкие шаровые слои толщиной Дт (Дт <<< R3) и рассмотрим один из них. Проведем конус с малым углом раствора через выбранную точку А (см. рис.). Конус вырежет из шарового слоя массы Дт, и Дт2. Тогда на точечное тело массой т действуют две силы притяжения со стороны Дт, и Дт2, т. е.
_ СтДт, GmAm?
F. —------ тл F --------2-
причем ДтП) = рб^Дт и Дт2 = рб^Дг, где Дт — толщина тонкого сферического слоя, и S2 — вырезанные конусом площадки этих слоев. Подставив выражение для Дт{, получим
_ GmpS^r _ .
Fj =---— = СтрДга и
Л
К2 = ^тР^2^Г _ Qmp^r0L)
Г2
где а — телесный угол, по определению равный
S. S2 Р
— = Таким образом, — = 1.
Г1 Г2 ^2
Силы притяжения со стороны масс Дт1 и Дт2 равны по величине и противоположны по направлению, а это значит, что результирующая сила, действующая на тело массой т, равна нулю. Так как точку А можно выбрать произвольным обра-
157
зом, то очевидно, что результирующая сила притяжения, действующая со стороны всего внешнего слоя толщиной Дг, равна нулю. Поэтому на материальную точку, помещенную на некотором расстоянии г от центра, внутри Земли действует только сила притяжения массы Земли, находящейся внутри сферы радиуса г (Мг\ Таким образом,
лгт
_GMrm _GpVrm _Gp%nr3m
Ггр 2 2 2
r r r
3
лгт _ GM3rm _ gaR3rm _ mgor ” R33 ~ R33
t. e. сила притяжения, действующая на материальную точку массой т, помещенную внутрь Земли, линейно зависит от расстояния г.
График зависимости силы гравитации от расстояния г имеет вид, показанный на рисунке IV.19.
Задача IV.21 Ракете, находящейся на поверхности Земли, сообщена вертикальная скорость v0 =6км/с. Считая, что сопротивление воздуха отсутствует, найти максимальную высоту подъема ракеты. Радиус Земли R3 = 6400 км .
Решение. На ракету действует только сила тяжести. Для системы: ракета — Земля, она является внутренней и консервативной силой, поэтому можем применить закон сохранения механической энергии, т. е. ДЕк + АЕп = 0
158
Рис. IV. 19
mv!. , \ mv!„ „ „
или---------(Екп-ЕпО)=О и —— = Еп0 -Е^а,
&
где -Екп — конечная потенциальная энергия ракеты на высоте максимального подъема Я, а Еп0 — начальная потенциальная энергия ракеты на поверхности Земли. Воспользовавшись формулой (1), nIV.3, запишем
mvo _ nzf 1 1 )
— - mgR0{- ~ , откуда
(б • 10s м/с) • 6400 10s м
Я =---2-^—- =----Ц------1 = 2500 км.
2gK3-u0 2 • 10м/с-6400 • 103 м- (б • 103 м/с)
Следует отметить, что в этой задаче нельзя пользоваться формулой для максимальной высо-
у2
ты подъема, полученной из кинематики, Я = —,
159
так как на больших расстояниях от поверхности Земли, сравнимых с ее радиусом, сила тяжести и ускорение g не являются постоянной величиной, а изменяются с высотой. Действительно,
Н = — = 1800 км (а не 2500 км!).
2g
Задача IV.22 Какую работу нужно совершить, чтобы запустить спутник массой т по круговой орбите на высоту Н = 3200 км?
Решение. Тело, находящееся в гравитационном поле Земли, обладает потенциальной энергией, которую можно отсчитывать либо от центра Земли, либо от какого-нибудь другого уровня (nIV.3). В математическом отношении наиболее удобно за начальный уровень отсчета взять т0 -» <» (расстояние г отсчитывается от центра Земли). Тогда выражение для потенциальной энергии оказывается наиболее простым — это формула (2) nIV.3
„ GM3m
Еп =-----—•
г
На высоте Н спутник должен обладать не только потенциальной энергией, но еще и кинетической, поскольку на орбите он вращается с пер-
I <?0 вой космической скоростью vK = R3—• °-- . По-
V -К3 + Н этому, чтобы запустить спутник по круговой орбите, нужно совершить работу
160
A — Aj + A2 — APn + A.EK —
GM3m о
R3+H
GM3ra\ , mv2K ----— +------ - 0 =
P3 у 2
mgRsgo ! raRko _ W0R3 2(R3 + H) 2(R3+H) R3 + H'
Мы воспользовались известным соотношением
GM3
g° = ~R*~ (nIV2)-v3
Задача IV.23 По оси вращения земного шара пробуравлена шахта и в нее падает тело. Определить максимальную скорость тела (сопротивление воздуха не учитывать).
Решение. Для тела массой та, падающего в шахту, ускорение а зависит от расстояния от цен-
„ F rag0 г г ,
тра Земли г: а = — =----------- g0-- (см. зада-
m та Rr, Rr,
о о
чу IV.20). Из этой формулы видно, что ускорение максимально при г = R3 и обращается в нуль в центре Земли (г = 0). Это означает, что скорость падающего тела максимальна именно при г = 0. После того как тело пролетит через центр Земли, его ускорение поменяет знак (будет направ-
6 Физика
161
лено противоположно скорости) и скорость начнет уменьшаться.
Для определения максимальной скорости нужно воспользоваться законом сохранения механической энергии
ЕП(г=0) + -®к(г=0) — £п(г=йз) + ^K(r=R3) •
Выбирая центр Земли за начальный уровень отсчета потенциальной энергии тела на поверхности Земли, можно записать:
Д’ — Д’ тлтттл Д’ _
•е'к(г=0) ^n(r+R3) > ИЛИ — 9
di
С другой стороны, потенциальная энергия тела на поверхности Земли равна работе, которую необходимо затратить при медленном переносе тела из центра Земли на ее поверхность. Но так как сила гравитации не остается постоянной, а меняется по линейному закону, то работу проще определить из рис. IV.19. Она численно равна площади заштрихованного треугольника, т.е.
_ mg0K3 _ m??ax
.ьп =------— = —-— . Следовательно,
Чпах = дДгЛГ-
V. СТАТИКА
§ 1. Статика твердых тел
Статика твердых тел — раздел механики, изучает условия равновесия твердых протяженных тел. 162
nV.l Абсолютно твердое тело — это тело, в котором расстояние между любыми двумя точками остается неизменным при любых условиях. В абсолютно твердом теле можно переносить точку приложения силы вдоль линии действия, при этом результат действия силы никак не изменяется.
nV.2 Момент силы относительно какой-либо оси — это произведение силы F на кратчайшее расстояние от точки закрепления тела до линии действия силы. Это расстояние называется плечом и обозначается I. Момент силы равен
M=Fl.
nV.3 Тело, закрепленное на оси, находится в равновесии, если сумма моментов всех действующих на тело сил с учетом их знака равна нулю. Для равновесия любого твердого тела необходимо, чтобы сумма всех действующих на тело внешних сил была равна нулю и сумма моментов всех внешних сил относительно любой оси была Также равна нулю, т.е.
± М-0. 1=1 1=1
nV.4 Точка приложения равнодействующей всех элементарных сил тяжести называется центром тяжести тела. Координаты центра тяжести определяются
6»
163
При решении задач на статику мы также будем пользоваться некоторой последовательностью действий (алгоритмом).
1. Прежде всего нарисуем рисунок, отражающий условие задачи (он позволяет лучше представить это условие), и стрелочками обозначим все силы, действующие на тело. В этом разделе силы, как правило, приложены к разным точкам тела.
2. Запишем условия равновесия тела
£г( = о; (1)
i=]
ХМ; = 0. (2)
»=i
Для решения некоторых задач достаточно бывает только условия (1). Это условие справедливо и для любых выбранных вами осей координат. Если же его не хватает, то используем условие (2). Так как условие (2) справедливо для любой оси вращения, то выбирать ее нужно так, чтобы облегчить решение задачи. Лучше всего поместить ось в точку приложения неизвестных сил (или на линии их действия), тогда момент этих сил обращается в нуль.
3. Когда число уравнений будет равно числу неизвестных в задаче величин, тогда можно приступать к алгебраическому их решению. Ответ получаем в буквенном виде и только после этого в полученные формулы подставляем числовые значения заданных величин.
164
В, поскольку в этом случае сумма моментов не может быть равной нулю (оба момента будут иметь одинаковый знак 0). Поэтому точка при-
ложения результирующей силы F может лежать либо слева от точки А, либо справа от точки В.
Будем отсчитывать расстояние х от точки А вправо, тогда условие для моментов сил запишется
Fr sin а - х — F2 sin а • (я? — d) = 0, или
F2d
= 2,5 м.
F - F
х 2 х 1
Если бы точка приложения силы F лежала слева от точки А, то числовое значение х было бы отрицательным.
Задача V.6 При взве-
А 4__________ шивании на неравнопле-
Лу- чих рычажных весах вес
тела на одной чаше по-
(___j лучился равным Рр а на
4--' другой — Р2. Определить
Рис. V.6 истинный вес тела Р (рис.
V.6).
Решение. Запишем условие равенства моментов для двух взвешиваний
Р]1] = Р12] Р\ = ^2»
где Р — истинный вес тела. Тогда, поделив эти соотношения друг на друга, получим
170
Как зависит сила натяжения веревки Т от угла а? При каких условиях сила натяжения на участках АВ и АС будет больше, чем на участке AD?
Решение. Так как точка А находится в равновесии, то для нее второй закон Ньютона будет иметь вид
f + т; + Т2 =0-
В проекции на ось ОХ это соотношение запишется
ex F
F -2Т cos — = 0, или Т =-------.
2 о «
2 cos —
2
С увеличением угла а натяжение нити Т увеличи-
1 сх
вается. При cosa<— (угол —>60°, а угол 2 2
а > 120°) сила натяжения Т будет больше силы F.
Задача V.3 Фонарь массой m = 20 кг подвешен
Рис. V.3
на двух одинаковых тросах, угол между которыми а =120° Определить натяжение тросов (рис. V.3).
Решение. Так как фонарь находится в равновесии, то mg — — Т3 =0, или Т3 = mg. Для равновесия фонаря необходимо, чтобы сумма всех сил, действующих на
166
точку А в горизонтальном и вертикальном направлениях была, равна нулю, т. е.
m . а . а
Т2 sm----Т. sin — = 0;
2 2 1 2
а а
Т, cos —FT, cos--То = 0.
1 2 2
Первое равенство означает, что натяжение тросов должно быть одинаковым, т. е. Tr = Т2 = Т.
Второе равенство позволяет определить это натяжение:
а
2Т cos — = Т3 = mg, следовательно
2
Т = = 20 кг-9,8 м/с = 196н
2 cos «4 2 cos 60°
Посмотрев внимательно на полученное соотношение, можно увидеть, что натянуть трос так, чтобы он не провисал, нельзя никогда! Так как в
этом случае cos0, а натяжение тросов Т должно быть бесконечным.
Задача V.4 Система, состоящая из неподвижного и подвижного невесомых блоков, находится в равновесии (рис. V.4). При каком соотношении масс это равновесие выполняется? Нарушится ли равновесие, если точку закрепления веревки А сместить вправо?
Решение. Так как система находится в равновесии, то сила натяжения нити Т, действую-
167
щая на массу т, равна mg (Т — mg = 0) - Запишем второй закон Ньютона для невесомого подвижного блока в проекции на ось ОХ 2Тг-Т = 0. Следова-
Т mg тельно, Ij - — - — .
Для тела массой М второй закон Ньютона имеет вид
— Mg — 0, или
т.е.
_ m Отсюда М - —, равновесие возможно, когда масса левого груза в 2 раза меньше массы правого груза. При перенесении веревки вправо от точки закрепления А равновесие нарушится, так как теперь по вертикали второй закон Ньютона для подвижного блока запишется
Д + Tj cos а — Т < 0, или Д + Тг cos а < Т = mg.
Таким образом, правый груз, укрепленный на подвижном блоке, опустится вниз.
Задача V.5 На стержень действуют две параллельные силы F] =10Н и F2 = 25 Н, направлен-168
ные в противоположные стороны под углом а к горизонту (рис. V.5). Определить точку приложения и величину силы F, уравновешивающей F\ и
F2) если точки приложения сил F] и F2 расположены друг от друга на расстоянии d=l,5 м.
Решение. Для равновесия стержня необходимо, чтобы:
1) сумма всех действующих на стержень сил была равна нулю,
2) сумма всех моментов сил относительно оси, проходящей че
рез любую неподвижную точку, также была рав
на нулю.
Из первого требования следует F} + F + F2 = О-Выбрав положительное направление, совпадающее с направлением силы F, получим
F, + F - F2 = 0. Следовательно, F = F2 — Fr = 15Н. Сила F > 0, это означает, что результирующая сила F сонаправлена с силой Fr Далее определим точку приложения результирующей силы F. Удоб
нее всего это сделать, если записать второе требование относительно оси, проходящей именно через точку приложения результирующей силы. В этом случае ее момент относительно этой точки равен нулю, а моменты сил F и F2 должны уравновешивать друг друга. Точка приложения силы F не может находиться между точками А и
169
В, поскольку в этом случае сумма моментов не может быть равной нулю (оба момента будут иметь одинаковый знак 0). Поэтому точка при-
ложения результирующей силы F может лежать либо слева от точки А, либо справа от точки В.
Будем отсчитывать расстояние х от точки А вправо, тогда условие для моментов сил запишется
Fr sin а - х — F2 sin а • (а? — d) = 0, или
F2d
= 2,5 м.
F — F
х 2 х 1
Если бы точка приложения силы F лежала слева от точки А, то числовое значение х было бы отрицательным.
Задача V.6 При взве-
А 4__________ шивании на неравнопле-
Лу- чих рычажных весах вес
тела на одной чаше по-
(___j лучился равным Рр а на
4--' другой — Р2. Определить
Рис. V.6 истинный вес тела Р (рис.
V.6).
Решение. Запишем условие равенства моментов для двух взвешиваний
Р]1] = Р12] Р\ = ^2»
где Р — истинный вес тела. Тогда, поделив эти соотношения друг на друга, получим
170
^ = ~, или Р =
Задача V.7 На правой чаше больших равноплечих рычажных весов стоит человек массой т, который уравновешен грузом, положенным на другую чашу. К середине правого плеча весов в точке С привязана веревка (рис. V.7). Нарушится ли равновесие, если человек, стоящий на чаше весов, начнет тянуть за веревку с силой F под углом а к вертикали? Длина коромысла весов 21.
Решение. На точку В коромысла весов действует вес тела Р, приложенный к правой чаше весов. Он равен по величине силе реакции опоры IV, но направлен в противоположную сторону. Когда человек стоит спокойно на чаше, то Р = N = mg, когда же человек тянет за веревку, то Р = N = mg — F cos а (см. рис.). Поэтому мо
171
мент силы, созданный весом тела, в первом случае будет равен Mr = mgl, а во втором случае М2 = (mg — F cos ajl. Кроме того, сила F, приложенная в точке С, также создает свой момент
I
М.. = F cos а • —.
3 2
Таким образом, когда человек стоит спокойно (не тянет веревку), на правую часть коромысла АВ действует момент силы = mgl, уравновешенный моментом сил, действующих на левую часть коромысла. Когда же человек тянет за веревку с силой F, на правую часть коромысла действует момент сил равный
I , Ft cos а М = М2 + М3 = (mg - F cos a)l + F cos a • — = mgl-.
2 2
Этот момент сил меньше момента силы тяжести (MJ груза т , т. е.
, , Ft
mgl > mgl —— cos a, поэтому равновесие нарушится, левая чаша весов перетянет.
Задача V.8 С помощью показанной на рис, V.8 системы невесомых блоков хотят поднять бревно длиной I и массой М. Какую силу F нужно приложить к концу каната А? Как нужно прикрепить концы каната В и С, чтобы бревно при подъеме было горизонтально? Нити невесомы.
172
• Решение. Так как нить невесома, то натяжение каната Т, привязанного к точке С, равно силе F. На бревно действуют три силы: сила тяжести Mg и силы натяжения и Т (см. рис.). Для того чтобы бревно находилось в равновесии,
т; + Т + Mg = 0 •
Записав этот закон в проекции на вертикальное направление, получим
T1+T — Mg = 0. (1)
Силу натяжения Т можно определить из второго закона Ньютона, записанного для правого блока. Действительно,
Рис. V.8
(2)
или Ть= F + Т - 2F. Подставив значение силы Т, в уравнение (1), получим
2F + F ~Mg = 0, или 3F = Mg .
Mg
Таким образом F =---. Следовательно, для подъе-
3
ма бревна нужно в такой системе приложить силу F в 3 раза меньшую, чем его сила тяжести. Для равновесия бревна еще необходимо, чтобы сумма моментов относительно какой-либо оси вращения была равна нулю. Выберем ось, проходящую через центр тяжести бревна. В этом случае
ТЛ-Т12 = 0,
173
где и l2 — расстояния точек В и С соответственно от центра тяжести бревна, тогда
Т \ F
Если расстояние между точками В и С равно I,
L ~
то I +1 = I, а 7- = 2.
к
Решая эту систему, получим
При этом условии точка приложения результирующей сил натяжения Тх - 2F и T=F совпадает с центром тяжести и бревно будет подниматься, оставаясь горизонтальным.
Задача V.9 Две тонкие и однородные палочки массой Мит образуют систему, изображенную на рис. V.9. Палочки могут вращаться вокруг осей, проходящих через точки А и В. Верхние концы палочек лежат один на другом под прямым углом. При каком минимальном значении коэффициента трения между палочками правая палочка не упадет? Угол а задан.
Решение. Силы, действующие на верхние концы палочек, изображены на рис. V.9: f — силы трения, 7V — силы реакции опоры со стороны каждой палочки. На нижние концы палочек в точках А и В действуют силы со стороны шарниров, однако их направление нам пока неизвестно. Имен-
174
но поэтому удобно оси вращения для моментов сил выбрать в точках А и В, проходящих через нижние концы палочек. Тогда уравнения моментов для обоих палочек запишется
I Mg
Mg — cos а — Nlx = 0, или N = —— cos а;
2 2
l2 . „ , mg .
mg — sin а = fl2, или j =--sm a ,
2 2
где Zj и l2 — длины левой и правой палочки соответственно.
Так как палочки покоятся, то сила трения f — сила трения покоя, поэтому f < fiN. Минимальное значение коэффициента трения ji, при котором палочки находятся в равновесии, равен f т ц = — = — tg а.
N М
175
Задача V.10 На земле лежат вплотную два одинаковых бревна цилиндрической формы. Сверху кладут такое же бревно. При каком коэффициенте трения между ними они раскатятся (рис. V.10)? (По земле бревна не скользят.)
Рис. V.10
Решение. Рассмотрим левое нижнее бревно. На каждое бревно действуют пять сил: сила тяжести Mg, сила
давления N, сила реакции опоры со стороны Земли R, сила трения / со стороны верхнего бревна и сила трения Ртр со стороны
Земли. Полагаем, что нижние бревна лежат вплотную, но не касаются. Второй закон Ньютона для каждого бревна имеет вид
Mg + N + R + FTp + fTp =0.
Запишем условие для моментов сил относительно оси вращения, проходящей через точку А. Тогда момент силы тяжести Mg, момент силы R
и момент силы трения FTp обратятся в нуль, поэтому условие для моментов запишется
^-/трг2 = о,
где Zj и 12 плечи соответствующих сил (см. рис.), причем
176
1. = R sin —; I, = R + R cos a , 1 2 2
где a = 60° — угол при вершине равностороннего
треугольника О,ОО2. Таким образом,
/тр
—- = —, или
N 12
—Ц= = 2-Д 2 +V3
Задача V.11 Однородная балка массой М и длиной I подвешена на концах двух пружин жесткостью к{ и к2 соответственно. Обе пружины в не-нагруженном состоянии имеют одинаковую длину. На каком расстоянии х от левого конца балки надо подвесить груз массой т, чтобы балка приняла горизонтальное положение (рис. V.11)?
Рис. V.11
177
Решение. Для того чтобы балка находилась в горизонтальном положении, удлинения обеих пружин должны быть одинаковыми, т. е. AXj = Да?2 = Да?. На балку действуют четыре силы, указанные на рисунке: силы тяжести mg и Mg и силы натяжения пружин F и F2- Поскольку все силы действуют по вертикали, запишем первое условие равновесия для балки вдоль вертикального направления
mg + Mg — J] — F2 = 0, или
mg + Mg = (к1 + к2)Да? .
(m + M)g
Отсюда Да? = —--------. Таким образом,
F = k1(m + M)g F = k2(m + M)g
1 kr + к2 ’ 2 ку + к2
Для определения расстояния х запишем момент сил относительно оси, проходящей через точку закрепления левой пружины А (второе условие равновесия балки),
I mgx + Mg— — F2l = 0.
Из этого соотношения следует
_ _ k2(m + M)gl Mgl _ I (k2(m + M) Л1)
mg mg(/c1+/c2) 2mg m( k1 + k2 2j
Задача V.12 Две невесомые пружины с коэффициентом жесткости kj и к2 соединяют один раз
178
последовательно, другой раз параллельно (рис. V.12). Какой должна быть жесткость пружины, которой можно было бы заменить эту систему из двух пружин?
Решение. При последовательном соединении пружин растягивающие их силы одинаковы и равны силе F, с которой растягивают систему пружин (в нашей задаче F = mg).
Общее удлинение системы равно сумме удлинений каждой пружины, т. е.
Да? = Axj + Да?2. (1)
Поскольку по закону Гука
F А F
= — ТО ~ 7 ,
к’ К
~ . Подставляя соответствующие выраже-
К2
ния для Да? в формулу (1), получим
F F F l.l.
ь - ь + ь > откуда к = ———.
к ki к2 ’ У к{+к2
При параллельном соединении у обеих пружин одинаковые удлинения, т. е. Да? = Да?} — Да?2, а растягивающая их сила F должна равняться сумме двух сил натяжения пружин, т. е. F = F\ + F2- Вновь воспользовавшись законом Гука для каждой из пружин, получим
179
кАх = кхАх + к2Ах, или к = к} + к2.
Задача V.13 Однородная лестница опирается на абсолютно гладкие пол и стену (рис. V.13). Каким должно быть натяжение веревки Т, привязанной к середине лестницы, чтобы удержать ее от падения?
Решение. На лестницу действуют четыре силы: сила тяжести mg, силы реакции опоры TVj и N2 и сила натяжения Т (см. рис.). Если ось вращения провести через точку А, то задача очень упростится, поскольку три силы (f, JVj И N2) будут проходить через ось и их моменты относительно этой оси
равны нулю. Останется толь
ко один момент силы тяжести mg, который ничем не компенсируется, поэтому лестница обязательно упадет, какой бы по величине ни была сила Т.
Эта задача наглядно показывает, как важно правильно выбрать ось вращения для того, чтобы облегчить решение задачи.
Если силу Т направить не в точку 0, а правее линии ОА, то лестница обязательно упадет, так как момент силы Т будет направлен в ту же сто
рону, что и момент силы тяжести mg. Если же
180
силу f направить левее линии ОА, то момент силы Т направлен в сторону, противоположную моменту силы тяжести. В этом случае лестницу можно удержать от падения.
Задача V.14 Тяжелый однородный стержень массой М упирается одним концом в угол между стеной и полом под углом а к горизонту. К другому концу привязан канат под углом р = 90’ (рис. V.14). Определить силу натяжения каната и направление силы реакции опоры со стороны стенки и пола.
Решение. На стержень действуют три силы: сила тяжести Mg, сила натяжения нити Т и реакция опоры со стороны стены и пола N, приложенная к стержню в точке 0. Так как ни направление, ни величина силы N не известны, то за ось вращения удобно выбрать
Рис. V.14
ось, проходящую через
точку 0 и перпендикулярную плоскости чертежа.
В этом случае условие равновесия для моментов
сил запишется
I Mg
Mg—cos a — IT = 0, или Т = —— cosa.
2 2
181
С увеличением угла а натяжение нити уменьшается. Для определения направления силы реакции N вспомним важное положение: если момент сил относительно какой-нибудь оси равен нулю, то это справедливо и для любой другой оси. Поэтому выберем ось, проходящую через точку пересечения линии действия силы тяжести Mg и натяжения нити Т (точка А на рисунке). Сила реакции опоры N обязательно должна проходить через эту точку, так как только в этом случае сумма моментов всех действующих сил будет равна нулю. (В этом случае плечи всех действующих сил обращаются в нуль.)
Задача V.15 К совершенно гладкой вертикальной стенке приставлена однородная лестница массой М, образующая с горизонтальной опорой угол а (рис. V.15). Определить силы, действующие на лестницу со стороны стенки и опоры. Построением определить направление силы, действующей на лестницу со стороны опоры.
Решение. На лестницу действуют четыре силы: силы реакции опоры Ny и N2, сила тяжести Mg и сила трения покоя f (она направлена в сторону, противоположную возможному движению). Первое условие равновесия для лестницы имеет вид
182
Nt + N2 +Mg + f = 0-
В проекциях на оси ОХ и 0Y это уравнение запишется соотв етственно
N2 - f = 0, или n2 = /;
Ny — Mg = 0, или Nx = Mg.
Второе условие равновесия для моментов сил удобно записать относительно оси, проходящей через точку В, т.е.
N2l sin а — Mg — cos а = 0, или
Mg
N2 = — ctg а .
Со сторрны опоры на лестницу действуют две силы: сила реакции опоры и сила трения покоя f. Величину результирующей этих сил легко определить по теореме Пифагора
Q = V/2 + Ni
Г/ \2
+ (М&У = ^>/4 +ctg2 а.
Определим направление ее. Для этого ось вращения проведем через точку пересечения линий действия сил N и Mg (рис. V.15, б) — точку С.
Для равновесия лестницы сумма моментов сил должна равняться нулю относительно любой выбранной оси. Ось, проходящая через точку С, удобна тем, что моменты сил N2 и Mg относительно этой оси равны нулю, следовательно, и резуль
183
тирующая сила Q должна быть направлена так, чтобы ее продолжение пересекало точку С.
Задача V.16 Определить положение центра масс однородного диска радиусом R, из которого вырезано отверстие радиусом г (рис. V.16), при
чем центр выреза находится от центра диска на расстоянии R/2.
Решение. Силу тяжести сплошного диска можно представить как равнодействующую двух сил: силы тяжести mg маленькой части радиусом г и силы тяжести оставшейся части (М — rn)g, каждая из которых приложена в центре масс соответствующей фигуры. Поместив ось вращения в центре масс сплошного диска (в точке 0), запишем ус-
ловие равновесия для
Рис. V.16
моментов сил
/ ч R /2
(M-m)gx = mg — , или * = (м,
184
где т = рТгтст2, М = phnR2 , р — плотность материала диска, h - его высота. Тогда
_ r2Rjtph _ r2R 2лр/г(К2—г2) 2 (К2 —г2)
Замена вырезанных частей какой-либо фигуры точно такими же частями, но из материала фигуры позволяет легко решить серию аналогичных задач с вырезанными частями куба, шара, цилиндра и других фигур.
Задача V.17 Пять шариков, масса которых соответственно равна т, 2т, 3m, 4m, 5т, расположены на столе вдоль одной прямой. Расстояние между двумя соседними шариками а. Определить центр тяжести системы (рис. V.17).
Рис. V.17
Решение. Выберем ось ОХ вдоль прямой, по которой расположены шарики. Начало отсчета этой прямой можно выбрать где угодно, например связать с положением третьего шарика (см. рис.). Координата центра тяжести системы определяется формулой (см. nV.4)
у _
Ац.т - 'V'---> ИЛИ
185
_ mlxl + т2х2 + т3х3 + т4х4 + т5х5 _ Ц т '
т4 + т2 + т3 + т4 + т5
_ т(— 2а) + 2т(— а) + Зт • 0 + 4та + 5т • 2а _ 1 Ота _ 2
15т 15т 3
Таким образом, центр тяжести системы находится на расстоянии х = справа от начала координат (от точки 0).
§ 2. Статика жидкостей и газов
Статика жидкостей и газов изучает условия равновесия жидкостей и газов.
nV.5 Давлением газа (жидкости) называется скалярная величина, измеряемая силой, действующей на единицу поверхности в направлении нормали, т. е. р = %.
nV.6 Закон Паскаля: на одном и том же уровне давление на маленькую площадку, помещенную в жидкость, не зависит от ориентации площадки.
nV.7 Давление зависит от глубины погружения в жидкость. Разность давлений др в двух точках внутри жидкости равно силе тяжести вертикального столба жидкости с площадью сечения, равной единице, и высотой, равной глубине погружения Л/г, т. е.
Лр = р2 - Pi = pgbh.
Давление жидкости, обусловленное только ее
186
силой тяжести, называется гидростатическим ( Ргидр )•
Давление жидкости на некоторой глубине h, отсчитываемой от поверхности раздела воздух — жидкость, равно:
Р = Ро +Pgh = P0 + Ргидр, где р0 — атмосферное давление. Давление в системе СИ измеряется в паскалях — Па:
Ша = = 1 кг/мс1 2 *.
1м2 '
В обыденной жизни давление измеряют в миллиметрах ртутного столба. В этом случае
РММ рт.ст. Ро мм рт.ст. ^мм рт.ст.
1 мм рт.ст. = 131,58Па.
Часто давление измеряют в технических атмосферах. Техническая атмосфера — это давление, производимое силой в 1 кгс = ЭДН на площадку в 1 см2, т. е.
1 кг • 9,8 ™/2
1 ат = 1 кгу 2 =----= 98070 Па = 105 Па.
/см 10~4 м2
nV.8 Закон Архимеда: на погруженное в жидкость тело действует выталкивающая сила, равная весу жидкости, вытесненной телом:
FA=PV£>
где р — плотность жидкости, V — ее объем.
nV.9 Итальянский физик Торричелли показал, что в стеклянной трубке, заполненной ртутью и опущенной в чашу со ртутью открытым концом, остается часть ртути высотой h=760 мм. Это os-
187
начает, что давление этого столбика ртути уравновешивается атмосферным давлением р0 у поверхности чаши, т. е.
Р0 ~ •
Это давление измеряется либо в миллиметрах ртутного столба, тогда р0 = h мм рт.ст., либо в паскалях,
Ро = PprS^p-r ~ 1Д6• 103 кг/м3 • 9,8м/с2 • 0,76м =
= 10,3 -104 Па« 105 Па.
Это давление называется физической атмосферой. Если вместо чаши и трубки со ртутью взять чашу и трубку с водой, то столб воды в трубке, уравновешивающий атмосферное давление, должен быть равен
, 1 P^h^
Ро = p^g = ps\g, ИЛИ hB = рт = 10,33 м .
Рв
Задача V.18 В двух цилиндрических сообщающихся сосудах налита ртуть. Сечение одного из сосудов Вдвое больше другого. Широкий сосуд доливают водой до края. На какую высоту h поднимается при этом уровень ртути в другом сосуде? Первоначально уровень ртути был на расстоянии I от верхнего края широкого сосуда. Плотность ртути р, воды р0 (рис. V.18).
Решение. За счет давления налитой в правый сосуд воды ртуть в этом сосуде опустится на высоту х, а в левом — поднимется на высоту h. При этом в силу несжимаемости жидкости вытеснен-
188
Рис. V.18
ные объемы будут одинаковыми, т. е. Stx = S2h,
S х
или h - где 5] и S2 — площади поперечного
S2
сечения правого и левого сосудов соответственно.
Смещение х определяется из равенства давлений жидкостей в правом и левом колене на уровне АВ
pQg(l + х) ~ Pg(x + М > или Ро 0 + сс) = р(х + 2х) > отсюда
Зр “ Ро '
Высота h, на которую поднимается ртуть в левом колене, равна:
к о 2р? h = 2х =-------.
Зр-Ро
Задача V.19 При подъеме груза массой М с помощью гидравлического пресса была затрачена работа А (только на перемещение малого поршня). При
189
этом малый поршень сделал п ходов, перемещаясь за один ход на расстояние h. Во сколько раз площадь большого поршня больше площади малого?
Решение. Гидравлический пресс представляет собой два сообщающихся сосуда различного диаметра, заполненных жидкостью и закрытых поршнями. Если к малому поршню площадью S’j приложить силу F}, то для сохранения равновесия к большому поршню площадью S2 необходимо приложить силу F2, при этом должно выполняться соотношение
S2'
Если первый поршень переместить на расстояние Ах1; часть жидкости переместится из первого сосуда во второй и поднимет второй поршень на высоту Асс2. В силу несжимаемости жидкости объем жидкости, вытесняемый поршнем из одного сосуда, равен объему, поступающему во второй, т.е.
= Ax2<S2. (2)
Используя уравнения (1) и (2), получим
F2 S2 Ах, ’
Таким образом, прикладывая малую силу к малому поршню, можно на большом поршне поднимать большие грузы.
В предложенной задаче малый поршень совершает работу А и перемещается за п ходов на рас
190
стояние Аа?1 = nh, чтобы поднять на большом поршне груз М. Для того чтобы ответить на вопрос 52/
задачи и определить , нужно воспользоваться
соотношением (3)
где F2 = Mg, a Fx можно определить из работы, совершенной малым поршнем:
д
А - FAx = F.nh, т. е. F} =-.
nh
_ S2 Mg Mgnh
Таким образом, —- = л ° = —- .
5, А/' А
Задача V.20 До какой высоты h нужно налить однородную жидкость в цилиндрический сосуд радиусом R, чтобы сила, с которой жидкость будет давить на боковую поверхность, была равна силе давления на дно сосуда?
Решение. Гидростатическое давление, обусловленное давлением только столба жидкости, изменяется с высотой от 0 до pgh. Поэтому на отдельные участки боковой поверхности в зависимости от высоты сила давления будет разная. При расчете силы давления на боковую поверхность обычно берут среднее значение давления
pgh с
рср =--- и умножают на площадь боковой по-
2
верхности.
191
Таким образом, сила давления на боковую цилиндрическую поверхность 5бок равна
ГбоК = Рср^бок = = pgTtRh2.
На дно сосуда
Ед = nR2pgh.
Из равенства этих сил следует
pgnRh2 = aR2pgh, или h=R.
Таким образом, при высоте сосуда h, равной радиусу дна сосуда, сила давления на дно и поверхность цилиндрического сосуда будут одинаковыми.
Задача V.21 Тонкая однородная палочка шарнирно укреплена за верхний конец. Нижняя часть палочки погружена в воду так, что в воде находится половина ее. Определить силу, действующую на палочку со стороны шарнира, и плотность материала р, из которого сделана палочка
192
Решение. На палочку действуют три силы: сила тяжести mg, сила Архимеда F и сила реакции со стороны шарнира N. Направление силы N легко получить из первого условия равновесия палочки (nV.3)
F\ -0, или mg + F + N = 0, или N = -(mg + Fj. В проекции на ось ОХ это соотношение запишется
N = -(mg-F). (1)
Второе условие равновесия удобно записать для моментов сил, выбрав ось вращения, проходящую через точку 0:
I ч/
mg —cos а — F cos а = 0. (2)
2
Это соотношение позволяет вычислить и выталкивающую силу
F = % mg.
Подставив это соотношение в формулу (1), можно определить величину и направление силы N, действующей на палочку со стороны шарнира, Лг ( ч/ \ mg N = -(mg- % mg\ = —.
' 'О
Таким образом, сила, действующая со стороны шарнира, направлена вертикально вверх.
Плотность материала р легко определить из выражения для силы F, воспользовавшись законом Архимеда (nV. 8)
9/ 9/ V
F = % mg = % pVng = Po^-g,
7 Физика
193
Л/ -г г
отсюда р = /3Р0, гДе Ро ~ плотность воды, Уп — объем всей палочки.
Рис. V.20
Задача V.22 На крюке динамометра висит ведерко. Изменится ли показание динамометра, если ведерко наполнить водой и погрузить в воду?
Решение. Показание динамометра уменьшится, так как воды, вытесненной ведерком, больше, чем налитой в него (рис. V.20). Показание динамометра изменится на величину веса воды, вытесняемой стенками и дном сосуда.
Задача V.23 Алюминиевый и железный сплошные шары уравновешены на рычажных весах. Нарушится ли равновесие, если шары погрузить в воду? Рассмотреть два случая:
1) шары одинаковой массы (рис. V.21, а),
2) шары одинакового объема (рис. V.21, б).
Решение.
1) Рассмотрим первый случай. Если шары имеют одинаковую массу, то они уравновешены на равноплечих весах. Однако объемы у них разные, причем VAl > VPe. Это значит, что при погруже
194
нии шаров в воду выталкивающая сила Архимеда Fx, действующая на алюминиевый шар, больше выталкивающей силы F2, действующей на железный шар. Момент силы Fj больше момента силы F2 относительно оси вращения, проведенной через точку 0. Поэтому равновесие шаров в воде нарушится: железный шар опустится вниз.
2) Если шары одинакового объема, то они должны быть
уравновешены на неравноплечих весах, так как массы у них разные, причем масса железа больше массы алюминия. При погружении обоих шаров в воду на них действуют одинаковые выталкивающие силы (Fy = F2). Однако момент силы F, больше момента силы F2 относительно оси, проведенной через точку 0. Поэтому равновесие шаров нарушится и опять железный шар опустится вниз.
Следует отметить, что в решении не рассматривались моменты сил тяжести обоих шаров, так
7«
195
как шары были уравновешены в воздухе, а это значит, что сумма моментов сил тяжести обоих шаров всегда равна нулю.
Задача V.24 Деревянная коробочка с грузом плавает на поверхности воды, налитой в сосуд. Как
изменится уровень жидкости, если груз из коро
бочки переложить на дно сосуда? Плотность гру-
за больше плотности воды (рис. '
V.22).
Решение. Когда коробочка с грузом плавает, то их сила тяжести уравновешена силой Архимеда, т.е. (m + M)g = pogVx,
где М и т - массы груза и коробочки соответ
ственно, Vj - вытесненный объем воды, р0 - плотность воды. Это соотношение позволяет вычислить первоначальный объем вытесненной воды
тг (т + М) т М
------- = — (1)
Ро Ро Ро
Во втором случае плавает одна коробочка, поэтому выполняется соотношение
mg = p0gV2 > где — объем, вытесненный только одной плавающей коробочкой. Кроме того, погруженный в жидкость груз вытесняет объем
196
V2 = —, где p2 — плотность груза. Таким обра-Р2
зом, общий вытесненный объем жидкости при погружении груза на дно сосуда равен
V2 = V2 + V2
т М
= — + —. Ро Ръ
(2)
Сравнив правые части выражений для вытесненных объемов (1) и (2), заметим, что V2 < Vn так как рг > р0.
Поскольку площадь поперечного сечения сосуда остается в обоих случаях неизменной, то уровень жидкости в сосуде понизится, т. е. Н i<H.
Задача V.25 Резиновый мяч массой т и радиусом R погружают под воду на глубину h и отпускают. На какую высоту Н от поверхности воды подпрыгнет мяч? Сопротивление воды и воздуха при движении не учитывать (рис. V.23).
Решение. На мяч действуют две силы: сила тя-
Рис. V.23
жести mg и сила Архимеда F. Изменение механической энергии мяча происходит за счет работы силы Архимеда, т. е. АЕмех = Af = Fh.
В нашей задаче
АЕ = О КИН
Если за начало отсчета потенциальной
197
энергии выбрать поверхность воды, то это соотношение будет иметь вид
ЕпВ “ £па = Fh , или mgH - (- mgh) = p0Vgh ,
отсюда Н =
Задача V.26 Сосуд, имеющий форму усеченного конуса, показанный на рис. V.24, опущен в воду. Если в сосуд налить пг=200 г воды, то дно сосуда оторвется. Отпадет ли дно, если в него на-
дно определится
лить 200 г масла, 200 г ртути, поставить на дно гирю массой 200 г?
Решение. Обозначим нижнее и верхнее сечение налитой в сосуд жидкости через и S2 соответственно. Тогда сила давления налитой в
сосуд жидкости на его
F = Pg^i = — ghSx
mghSx
— (Rl+R^+Rl)
У 1 1 <L it J
_ 3mgSi
jt^Ry + RyR2 + Rf') ’
где V - объем налитой в сосуд жидкости, a h -высота уровня жидкости в сосуде.
198
Объем жидкости V вычисляется по формуле усеченного конуса:
v = ^(r12+r,r2+r2), о
где Rj и R2 - радиусы нижнего и верхнего основания соответственно.
Для того чтобы определить, отпадет ли дно сосуда, достаточно сравнить радиусы верхних оснований R2 различных налитых жидкостей с радиусом R2 для воды, поскольку нижнее основание во всех случаях одинаково.
Таким образом, при заполнении сосуда маслом К2м < -^2в и > поэтому ДН° сосуда оторвется, при заполнении ртутью R2p > К2в (^Р < и дно сосуда не оторвется. При помещении гири на дно сосуда Fr = mg < FB и дно сосуда не оторвется.
VI. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕПЛОТА
nVI.l Моль — количество вещества, содержащего столько же молекул, сколько содержится атомов в 0,012 кг углерода, тогда число молей в веществе
N v =---
МА’
где Na — число Авогадро, равное 6,02 .1023(моль)-1,
199
т. е. число частиц, содержащихся в одном моле вещества.
nVI.2 Масса любого вещества ш = v/i , где ji — масса одного моля.
nVI.3 Основное уравнение молекулярно-кинетической теории
р = Уз nmv2 = ,
где п - концентрация, к - постоянная Больцмана, Т — температура по шкале Кельвина.
nVI.4 Связь среднекинетической энергии молекул с температурой
Е = %кТ.
nVI.5 Состояние газа определяется тремя термодинамическими параметрами: давлением р, объемом V и температурой Т (по шкале Кельвина). Связь между шкалой Кельвина и Цельсия
Т = 273 + f С.
nVI.6 Все три параметра связаны основным уравнением состояния идеального газа (объединенный газовый закон)
тп pV = vRT = — RT, Р
где R — универсальная газовая постоянная, равная R = WVA.
Для изотермического процесса (Т = const) это уравнение имеет вид
pV = const — закон Бойля — Мариотта.
Для изобарного процесса (р = const)
V
— = const, или V(t) = V0(l + at) — закон Гей-
200
1
Люссака, где Vo — объем при t = 0° С, « = .
Z I и Vx
Для изохорного процесса (у = const) р
— = const} или p(t) = р0(1 + /?t) — закон Шар
ля, где р0 — давление газа при t0 = 0° С и
273° С ‘
nVL7 «Нормальное состояние» газа определяется величинами р0, Vo, где р0 — давление, равное давлению
760мм рт. ст. = 101325Н/м2 = 105Па, при
То = 273К (о° с), Vo — объем при той же температуре.
Для количества вещества, равного 1 молю, при нормальных условиях любой газ занимает объем
р V
V0/t = 0,0224 м3/моль. Поэтому 0 0/1 = Н. — оди-Та
какова для всех газов и называется универсальной газовой постоянной R = 8,31Дж/(моль . К).
nVI.8 Закон Дальтона: давление смеси газов равно сумме их парциальных давлений, т. е. таких давлений, которые оказывал бы каждый газ, входящий в состав смеси, если бы он был один в этом сосуде:
Р= Р1 +Р2+---+Рп-
nVI.9 Внутренняя энергия одноатомного идеального газа
201
«/ т о / -э/ш
U = vNa %кТ = — 3/)RT= 3/>~RT
/2 ц /2 /2 ц
Если газ не одноатомный, то его внутренняя энер-
7П-
гия U = с — RT, где коэффициент с зависит от Ц
количества атомов в газе.
nVLIO Если внутри системы, изолированной от окружающих тел, не совершается механическая работа, то для нее справедливо уравнение теплового баланса: сумма количеств теплот AQ., полученных и отданных телами системы, равна нулю
X = AQi + AQ2+...+AQn = 0 , или
^Гс^АТ; + с2т2&Т2 + ...+сптпкТп = 0.
nVI.ll Первое начало термодинамики: количество теплоты, передаваемое телу, д<Э идет на изменение его внутренней энергии д 17 и на совершение телом работы дА, т. е.
AQ - AU + ДА, или стЛТ = уАТ + pAV,
где с — удельная теплоемкость, а у — коэффициент пропорциональности.
nVI.12 В любом газовом процессе работу, совершаемую газом, можно определить из графика зависимости давления от объема. Площадь под
202
кривой зависимости давления от объема численно равна работе, совершенной газом (рис. VI. Г).
nVI.13 Коэффициент полезного действия теплового двигателя
А - Q2
Qi Q, ’
где Q — тепло, получаемое от нагревателя, Q2 — тепло, переданное холодильнику.
nVI.14 Количество теплоты, необходимое для испарения жидкости при постоянной температуре, Q = гт, где г — удельная теплота парообразования.
nVI.15 Количество тепла, необходимое для плавления тела массой т при постоянной температуре, Q = Ат, где А — удельная теплота плавления.
nVI.16 Относительная влажность
<р = -£-100% = —100%, Р« Ря
где р и р - плотность и давление ненасыщенного пара, ря и рн — плотность и давление насыщенного пара при той же температуре.
Задача VI.1 Вычислить число N молекул, содержащихся в объеме V = 1 см3 газа при нормальных условиях.
203
Решение. При нормальных условиях 1 моль газа занимает объем Vo = 0,0224 м3/моль (nVL7). Таким образом, в обьеме V содержится количество
V
молей v —----. Поскольку в 1 моле вещества со-
держится _/VA число молекул, то общее число молекул в объеме V равно
„г v 10-6 м3- 6,1 - 1023 1/моль огт лп19
N = vNa = Na =----------:—7Г-,—'—=— = 2,7 • 1019.
Vo А 0,0224 м3/моль
Задача VI.2 Число молекул, содержащихся в единице объема идеального газа при нормальных условиях, равно п0 = 2,7 • 1025 м~3. Этот же газ при температуре t = 91° С и давлении р = 800 кПа имеет плотность р = 5,4 кг/м3. Определить массу одной молекулы этого газа.
Решение. В процессе нагревания газа его количество молей не меняется. Это значит, что выполняется соотношение
Po}i=pV То Т •
Начальный объем газа Vo легко определить из заданной концентрации
N N
п0 = —} или Vo = —, где N - общее число
Vo п0
частиц в газе. Конечный объем V легко определить из заданной плотности
204
т т
р — —, или V = —.
V р
Подставив эти соотношения в формулу (1), получим
Ро % Рт/О / по _ / Р
То Т
Отсюда легко найти массу одной молекулы неизвестного газа
_т_ раТр _ 105 Па(273 + 91) К- 5,4 кг/ м3
0 N Топор 273 2,7-10й м'3-800 кПа
Задача VL3 Сосуд объемом V = 10м3, содержащий воздух при нормальных условиях, находится в космосе, где давление можно полагать равным нулю. В сосуде пробито отверстие. Через какое время t в сосуде давление станет равным нулю, если считать, что через отверстие каждую секунду вылетает n0 = 108 молекул?
Решение. Время, через которое вылетят все молекулы, находящиеся в сосуде, определяется N
t = —, где N - число молекул в сосуде до про-по
бивания отверстия. Таким образом, задача сводится к определению числа молекул, находящихся в сосуде объемом V при нормальных условиях.
При одних и тех же условиях (р0,Т0) число молекул в сосуде пропорционально его объему, т. е.
205
N_=N±
V Vo/
где JVA - число частиц в 1 моле, a VOg - объем 1 моля. Тогда
N =
Время, через которое все молекулы вылетят
из сосуда
NaV _ 6,02 • 1023 1/моль • 10 см3 Ю81/с • 22,4 • 103 см3/моль
= 2,7 1012с =85000 лет.
Задача VI.4 На стенку площадью S налетает поток молекул со средней скоростью V. Число молекул в единице объема п0, масса каждой молекулы т. Определить силу, действующую на стен
ку, и давление, если молекулы движутся пер-
пендикулярно к стенке и удары их о стенку абсолютно упруги.
Решение. При упругом ударе о стенку каждая молекула меняет свою скорость на обратную за счет силы упругости стенки. При одном ударе молекулы, который длится очень
малое время St, на вертикальную стенку со сто
роны одной молекулы действует импульс силы fdt (рис. VI.2). По третьему закону Ньютона он равен
206
импульсу силы упругости со стороны стенки, но с обратным знаком, т. е.
fdt = —[— mv — mv] - 2mv.
За конечное время At > > <5t до стенки долетят те молекулы, которые были от нее на расстоянии I = vAt. Поэтому за время At о стенку ударится число молекул
N = n0VAt = n0SvAt.
Импульс силы этих ударившихся молекул равен
FAt = Nfdt = N2mv = 2n0mSv2 At.
Следовательно, молекулы действуют на стенку с силой
F = 2n0mv2S
Давление на стенку равно
р = — = 2nnmv2.
и s о
Задача VI.5 Как располагаются изотермы газа на графике зависимости давления от объема для случаев расширения одной и той же массы газа при низкой и высокой температурах?
Решение. На графике зависимости давления от объема нарисуем две изотермы. Проведем некоторую прямую, соответствующую изохорическому процессу (V = const). Она пересечет две изотермы в точках 1 и 2 (рис. VI.3). Для этих точек запишем объединенный газовый закон:
РЛ p2V
—— = —— = const.
Т Т
Х1 ±2
207
Из формулы видно, что темцература больше там, где больше давление, т. е. изотерма, соответствующая температуре Т2, лежит выше изотермы, соответствующей температуре Д. Другими словами, изотерма, соответ
ствующая более низкой температуре на графике p-V, располагается ближе к началу координат.
Задача VI.6 В результате некоторого процесса был получен график зависимости давления от объема, изображенный на рис. VI.4. Определить по этому графику характер изменения темпера-
туры газа.
Решение. Для определения характера изменения температуры газа следует провести на чертеже несколько изотерм, проходящих через начальную — 1, конечную — 2 и некоторую точку 3, в которой изотерма касается прямой 1-2. Тогда при движении от точки 1 до
точки 3 температура газа будет повышаться (мы идем от более низкой изотермы к более высокой), а при движении от точ
208
ки 3 до точки 2 температура газа понижается (см. задачу VI.5).
Задача VL7 В результате некоторого процесса был получен график зависимости давления от температуры газа, изображенный на рис. VI.5. В каком из положений (1 или 2) объем газа был больше?
Решение. Проведем на рисунке две изохоры, проходящие через точки 1 и 2 (пунктирные линии). Воспользуемся объединенным газовым законом для определения объема:
ц р
Так как масса газа не меняется, то обозначим тп
— R = А — это некоторая константа. Тогда М
т
V = А — = A ctg а. Р
Эта формула сразу же позволяет определить, в каком из состояний газа (1 или 2) объем больше. Там, где изохора наклонена к оси ОТ под меньшим углом, там объем будет больше. Таким образом, в состоянии 1 объем газа V меньше, чем в состоянии 2 (ctgctj < ctga2). В результате процесса 1~2 газ расширяется.
209
Задача VI.8 В узкой цилиндрической трубке, запаянной с одного конца, находится воздух, отделенный от наружного пространства столбиком ртути длиной h = 15 см. Когда трубка лежит горизонтально, воздух занимает в ней объем V\ = 240 мм3; когда трубка устанавливается вертикально, открытым концом вверх, воздух занимает объем V2 = 200 мм3. Определить атмосферное давление
Ро (Рис- VI.6).
h
( w о
Рис. VI.6
Решение. Переворачивание трубки происходит при неизменной температуре, поэтому процесс — изотермический. Для него выполняется соотношение
PiV; = p2v2-
Так как в горизонтальной трубке столбик ртути нахо
дится в равновесии, то давление воздуха в объеме VJ равно атмосферному, т. е. pj = р0. В вертикально расположенной трубке давление воздуха в объеме V2 равно давлению столбика ртути плюс атмосферное давление, т. е.
Р2 = Pgh + p0.
(1)
Подставим значение pj и р2 в уравнение Бойля — Мариотта
Povi = (Pgh+ p0)V2, отсюда р0 = •
*1 *2
Подставляя в эту формулу цифры, мы получим
210
13,6 г/см3 • 103 • 0,15 м-200 мм3 5
Ро = /„ла пааЧ-23---------“ !>02 • Ю5 Па .
(240-200) мм3
Если давление измерять в миллиметрах ртутного столба, то выражение для давления р2 по формуле (1) следует записать р2 = h + р0. Тогда атмосферное давление р0 будет измеряться в миллиметрах ртутного столба
Ро
hV2
15см- 200 мм3 (240-200) мм3
= 15 см • 5 = 75 см =
= 750 мм рт. ст.
Задача VI.9 Закрытый с обеих сторон цилиндр разделен на две равные части теплонепроницаемым поршнем. В обеих частях цилиндра находят
ся одинаковые массы газа при t0 = 27° С и давлении р0 =760 мм рт. ст. Длина цилиндра L = 40
см. На какое расстояние Да? от середины цилиндра сместится поршень, если газ в одной из частей нагреть до температуры t = 57° С? Какое давление р установится при этом в каждой из частей цилиндра (рис. V1.7)?
Решение. Так как массы
Рис. VI.7 газа не меняются и
давление после передвижения поршня остается одинаковым, объединенный газовый закон запишется
211
L A ---F Да? 2
T
До? =
, отсюда
T-To L
T + To 2
30 К • 20 см
630 К
0,95 см.
Для определения установившегося давления можно применить объединенный газовый закон для одной из частей объема. Легче записать для той части, в которой температура не менялась. В этой части сосуда процесс изотермический, т. е.
L IL ]
Ро — £ — р----До? S
2 \2 I
, отсюда
Lpn р = —5----г- =798 мм рт. ст.
2 --Дх
12 /
Задача VI.10 Два сосуда, наполненные воздухом под давлением р1 = 8 • 105 Па и р2 = 6 • 105 Па, имеют объемы У1=3л и V2 = 5 л соответственно. Сосуды соединяют трубкой пренебрежимо малого объема. Определить установившееся давление в сосудах, если температура воздуха в них была одинакова и после установления равновесия не изменилась.
Решение. Процесс, происходящий в сосудах — изотермический. После соединения сосудов находящийся в каждом из них воздух займет объем (V! + V2). Для обоих сосудов выполняется закон Бойля — Мариотта
212
P.v, = + V2); p2v2 = p2'(Vj + v2),
где р/ и p2' — парциальные давления воздуха после объединения.
Установившееся в сосудах давление по закону Дальтона равно сумме парциальных давлений, т. е. р = Pi+p2' Сложив два вышеприведенных равенства, получим
p.v, + p2v2 = (V, + v2)(p/+p2') = (V, + V2)p, откуда
ptV; + p2V2 _ 8 • 105 Па-3 л+6 • 105-5л
P-Pr+P2- V+V2 - 8
= 6,75.10’Па.
Задача VI.11 Полагая, что воздух состоит из смеси трех газов: азота массой т1 и молярной массой /ц, кислорода массой т2 и молярной массой Д2 и аргона массой т3 и молярной массой/43, определить молярную массу у, воздуха.
Решение. Для каждого газа можно записать уравнение состояния
P1V = ^RT; р2у = ^ДТ; p3V = ^RT. А*1 М-Ч А*3
Сложив эти уравнения, получим
(Pi + Рг+Рз)^- ----------RT • (1)
\ АЧ АЧ АЧ !
213
С другой стороны, для смеси газов можно записать
pV = — RT, Р
где т = т1 +т2 +т3, а и — искомая молярная масса смеси.
По закону Дальтона р = pj + р2 + р3. Таким образом, для смеси газа
(Pi + Р2 + P3)V = — RT. (2)
Р
Сравнивая соотношения (1) и (2), получим
т т, т9 т.. = -1 + -2- + —2-, Р----------Pl Р2 Рз
следовательно,
_ т} + т2 + т3 т. т. • —L + —+ —-Pi Pz Рз
Задача VI.12 Газ массой т с молярной массой J1 нагревается на ДТ = 1К в цилиндре, закрытом поршнем массой М и площадью S. Во время нагревания газ совершает работу по поднятию поршня. Выразить эту работу:
а) через давление р и изменение объема ДУ газа,
б) через универсальную газовую постоянную R.
Давлением наружного воздуха пренебречь (рис. VI. 8).
214
Решение. Газ нагревается при изобарическом процессе, поскольку
Mg
р — —— = const. Расширяясь, он со-вершает работу
А = Mgh = pSh = pAV = p(V — Vo).
Воспользовавшись объединенным газовым законом, можно записать
Mg
Рис. VI.8
т пт
до нагревания pV0 = —RT0; после ц
нагревания на АТ
pV = — R(T0 + AT).
Вычитая из второго уравнения первое, получим
p(v-4) = — КАТ. ц
Левая часть этого уравнения есть не что иное, как работа, совершаемая газом при расширении.
Таким образом, при изобарическом процессе газ совершает работу
A = p(V-V0) = —RAT
Это соотношение позволяет определить физический смысл универсальной газовой постоянной R: это работа, которую совершает 1 моль газа при изобарическом нагревании на 1К.
’215
Задача VI.13 Некоторая масса газа, занимающая вначале объем Уо при давлении р0 и температуре То, расширяется один раз изобарно, другой раз изотермически до объема V (рис. VI.9). В каком из этих случаев газ совершает большую работу?
Рис. VI.9
Решение. Изобразим эти два процесса на графике зависимости давления от объема (рУ). Работа при изобарическом процессе определяется
А, = р0ДУ = р0(У-У0).
Численно эта работа равна площади заштрихованного прямоугольника V0ABV. В случае изотермического процесса давление не остается постоянным. Но можно интервал Уо - V разбить на столь малые отрезки Ду., в пределах которых давление можно считать постоянным. И тогда элементарная работа на этом интервале равна
216
А; = PjAV,-, а полная работа при расширении объема Vo до V равна А = At. При стремлении интервалов AV; к нулю эта работа численно будет равна площади фигуры, находящейся под изотермой АС (площади V0ACV). Из рисунка видно, что при изобарическом процессе газ совершает большую работу.
Этот абзац для тех, кто хочет узнать чуть больше
Работу при изотермическом процессе тоже можно посчитать. Ведь предел, к которому стремится полная работа при стремлении к нулю, не что иное, как
V- г г г BdV vedV V
А = lim Уа. = f А = fpdV = f--= вГ — = Bln —
• v„ v0 v0 v v0 v
где значение В определяется из объединенного газового закона. Действительно,
т
pV = —RT, или р = —, R v
т. е. В = — RT. Таким образом, А = — КТ In — -/4 ц Vo
Задача VI.14 В цилиндре под поршнем находится воздух. Поршень имеет форму, указанную на рис. VI.10. Масса поршня т. Площадь сечения цилиндра So. Атмосферное давление р0. Какой груз массой М надо положить на поршень, чтобы объем
217
воздуха V в цилиндре уменьшился в п = 2 раза? Температура постоянна, трение не учитывать.
Решение. Вспомним, что давление определяется как сила, действующая на единичную площадку в направлении нормали к поверхности. Поэтому со стороны газа на поршень действуют сила Р\, направленная перпендикулярно поверхности Slt т. е.]^] = р5\, сила тяжести mg и сила давления со стороны воздуха F2 (рис. VI. 10).
Поршень находится в равновесии, если mg + F{ + F2 = 0.
Запишем закон Ньютона в проекции
на вертикальное направление оси ОХ:
mg — Fr cos а + F2 = 0 , или
mg — Pj*?! cos a + р06"0 = 0, или W-P^o +Р(А = °-
Это соотношение позволяет вычислить давление газа ри находящегося под поршнем:
Рис. VI. 10
__ mg + p0S0 _mg Pl О 0 ~ Ро.
‘-’о
Процесс происходит при постоянной температуре (изотермический), поэтому, чтобы объем воздуха уменьшился в 2 раза, давление Pj в цилиндре нужно увеличить в 2 раза (pV = const). Это можно сделать за счет добавочного груза М, т. е.
’218
2R + P.
I c* x и \ ^*0
(m + M) So
g + Po
отсюда M = + p0 — = m + .
\S0 ) g g
Задача VI.15 На рис. VI.11, a изображен график изменения состояния идеального газа в координатах V-Т. Изобразить этот график в координатах p-V и р-Т.
Решение. Процесс 1—2 является изобарическим
Рис. VI. 11
— = const (nVL6).
На рис. VI.11, б он изображается прямой, параллельной оси 0V. Поскольку при переходе от точки 1 к точке 2 объем повышается, то на рисунке этот процесс пойдет слева направо.
Процесс 2~3 на рис. VI.11, а — изотермический, причем объем его уменьшается при перехо
(б)
Рис. VI. 11
де от точки 2 к точке 3. Из закона Бойля —
Мариотта следует, что при уменьшении объема давление обязательно должно возрастать (pV = const), на что указывает кривая 2—3 на рис.
219
VI.11, б. Процесс 3-1 на рис. VI.11, а соответствует изохорическому процессу, поэтому на рис. VI. 11, б он изобразится вертикальной прямой 3-1
Р
(— = const).
Изобарический процесс 1~2 в координатах р -Т на рис. VI.11, в изобразится прямой линией, идущей слева направо, так как Т увеличивается в процессе 1~2. Изотермический процесс 2~3 изображается вертикальной прямой, идущей вверх (так как из рисунка видно, что давление в процессе 2-3 увеличивается).
Изохорический процесс 3-1 на рис. VI.11, в отразится прямой 3-1, продолжение которой обязательно должно пройти через начало коорди
нат, при этом давление должно уменьшаться, что следует из рисунка.
Задача VL16 В вертикальном цилиндре под тяжелым поршнем находится кислород массой m = 2 кг. Для повышения температуры кислорода на ДТ = 5 К ему было сообщено количество теплоты Дф = 9160 Дж. Определить удельную теплоемкость кислорода с, работу, совершаемую им при расширении, и увеличение его внутренней энергии Д17. Молярная масса кислорода = 0,032 кг/моль.
220
Решение. На поршень действуют три силы: сила тяжести, сила атмосферного давления и сила давления газа, находящегося под поршнем. Так как поршень находится в равновесии, то давление газа под поршнем остается постоянным (сила тяжести и сила атмосферного давления не меняются), поэтому процессе нагревания газа является изобарным. Количество теплоты, сообщаемое кислороду для нагревания, равно
AQ = AJ7 + AA, или cpmAT = AU + pAV, (1) где ср — удельная теплоемкость, индекс р указывает, что нагревание газа происходит при изобарном процессе. Эту теплоемкость можно определить из условия задачи
AQ = СрТпАТ, или
AQ 9160 Дж П1е Дж
р тАТ 2 кг • 5 К кг • К
Уравнения состояния газа до и после нагревания на АТ равны соответственно
7TL 77Z
pV1= — RTl; pV2=—RT2.
н- Р
Вычитая из второго уравнения первое, получим
p(V2 ~ Vi) = ~ = ”ЕЛТ •
Левая часть этого уравнения является работой при изобарном процессе, поэтому
ДА = pAV = — КАТ = -2—>3—5 = 2590 Дж.
ц 0,032
221
Зная работу, совершенную газом, и количество тепла, сообщенное ему, легко из формулы (1) подсчитать изменение его внутренней энергии
ДП = AQ - ДА = (9160 - 2590)Дж - 6570Дж.
Задача VI.17 Температура газа массой т с молярной массой р, повышается на величину ДТ один раз при постоянном давлении р, а другой раз — при постоянном объеме V. Насколько отличаются друг от друга количества сообщенных газу теплот AQp и AQv и удельные теплоемкости ср и cv в этих процессах?
Решение. При любом процессе количество тепла, сообщенное газу, идет на изменение его внутренней энергии Д[7 и на совершение газом работы, т. е.
AQ = AU + рЛУ.
При изобарном и изохорном процессах это соотношение запишется соответственно
сртДТ = Ли + рДУ; (1)
сутДТ = Ли. (2)
Ли = уЛТ в обоих процессах одинаково, так как одинаково изменение температуры ДТ. Вычитая из верхнего соотношения нижнее, имеем
AQp - AQV = тЛт(ср - cv) = pAV . (3)
Подставляя выражение для работы, полученное в предыдущей задаче для изобарного про
222
цесса ДА = — RAT, получим т AQ - AQV = —RAT.
Соотношение (3) позволяет определить, как отличаются теплоемкости при этих процессах pAV R с — с = —-----------------= —,
р v mAT д
Таким образом, теплоемкость газа при изобарном процессе ср больше его теплоемкости при изохорном процессе cv.
Известно, что для идеального газа изменение его внутренней энергии прямо пропорционально изменению его температуры, т.е. АП = у АТ.
Формула (2) позволяет вычислить коэффициент пропорциональности у. Действительно, сравнив левую и правую части этой формулы, получим
у = cvm.
Выражение для работы при изобарном процес-
се АА = — RAT позволяет выяснить физический д
смысл газовой постоянной R — это работа, которую совершает 1моль газа при изобарном процессе, нагреваясь на 1К.
Задача VI.18 На рис. VI. 12 дан график изменения состояния идеального газа. Посчитать работу, которая совершена газом за полный цикл, если
223
начальные и конечные значения давлений и объемов заданы.
Решение. Работа, совершаемая газом, определяется: А = pAV. Круговой процесс, представленный на рисунке, состоит из двух изобар (1-2, 3-4) и двух изохор (2-3, 4-1). При изохорических процессах газ работу не совершает, так как AV = 0. Поэтому А2_3 = A4_l = 0. Работа же газа при изобарических процессах определяется
А-2 = P1(V2 “ vi) и А3-4 = P4(vi “ у2)-
Таким образом, полная работа за весь цикл равна
А — Aj_2 + Д2_3 + Aj-4 + А4_4 = Aj_2 + Д3_4 — (V2 — — р4)-
Как видно из рисунка, эта работа численно равна площади заштрихованного прямоугольника 1234.
Следует отметить, что при любых замкнутых процессах, изображенных в координатах p-V, 224
полная работа равна площади фигуры, лежащей внутри этого цикла (nVL12).
Задача VI.19 Какое количество тепла AQ пе
редано одноатомному газу при переводе его из состояния 1 в состояние 2? pj = 500кПа, Vt = 2л,
V2 = 4л (рис. VI.13).
Решение. Процесс 1-2 не относится ни к одному из изопроцессов. Однако из рисунка следует, что давление прямо пропорционально объему, т.е. р - yV, где у — коэффициент пропорциональности. Из этой зависимости легко получается, что
Pl V1 V2
- = ИЛИ р2 = Р, Р2 V2 Vl
Количество тепла, переданное любому газу,
определяется первым началом термодинамики (nVLIO)
AQ = ДП + ДА.
Для одноатомного газа ДП легко определить, пользуясь выражением внутренней энергии для одноатомного газа (nVI.9):
. „ 3 т „ . т AU =-----ВАТ.
2 р,
АТ вычисляется из объединенного газового закона для двух состояний, т. е.
8 Физика
225
Р1У, — —RTt и p2V2 = —RT2. p P-
Вычитая из второго соотношения первое, имеем
— RAT = p2V2-p1V1.
Подставляя это выражение в формулу для АП, получим
ди = |(РЛ - P.V,) = V,j = - V,‘).
Работу ЛА, совершаемую газом при переходе из состояния 1 в состояние 2, можно определить по площади трапеции V112V2.
V2
, Pi + Pi
ЛА = =-----т—l(v2 - v.) =
Таким образом, количество тепла, переданное одноатомному газу:
AQ = AU + ДА = + =
= 2^-^-^).
Задача VI.20 На рис. VI.14, а изображен график изменения состояния идеального газа. Пред-
226
Р1' 1 ^2
(а)
О ______________L_>. V
Рис. VI.14
ставить этот круговой процесс в координатах р-Т и V-Т и определить, на каких участках тепло потребляется, а на каких выделяется.
Решение. Изобарический
процесс 1-2 в координатах р-Т (рис. VI.14, б) изоб
ражается прямой, параллельной оси ОТ. Однако
он может проходить слева направо (при увеличении температуры) и справа налево (при уменьшении --------------------»——температуры). Для того что-/---------бы определить, как меняет-
4/ ся температура, необходи-
/ мо воспользоваться объеди-
0 С''_________
к-----------► ненным газовым законом:
Рис. VI.14
pV = — RT
Из этого уравнения следует: при постоянном давлении с увеличением объема температура увеличивается. Поэтому изобарический процесс протекает слева направо. Процесс 2-3 изохорный, при этом давление р уменьшается: нужно соединить точку 2 с началом координат и по этой прямой опуститься вниз (так как р уменьшается). Процесс 3-4 изобарный, он проходит с уменьшением объема, поэтому и температура будет уменьшаться. Процесс 4-1 изохорный: проводим прямую через точку 1 и начало координат и поднимаемся по этой прямой вверх, так как давление в про-
8»
227
Рис. VI.14
цессе 4-1 увеличивается. Аналогичные рассуждения проводятся и для координат V-Т (рис. VI. 14, в).
Выделенное или поглощенное тепло на различных участках процесса легко по
лучить с помощью первого начала термодинамики.'
AQ = AU + pAV = уАТ + pAV.
На участке 1-2 АТ > О, AV > 0 (рис. VI.14, а), поэтому AQ1_2 > 0 , т. е. тепло поглощается газом.
На участке 2-3 АТ < О, AV = 0 (рис. VI. 14, а,б), поэтому AQ2_3 < 0, т. е. тепло выделяется.
На участке 3-4 АТ < О, AV < 0, следовательно AQ3_4 < 0 — тепло выделяется.
На участке 4-1 ДТ > О, AV = 0 (рис. VI.14, а,б), поэтому AQ4_j >0, т. е. тепло поглощается. На рис. VI.14, (в) поглощенное и выделенное тепло обозначается двойными стрелочками.
Задача VI.21 Увеличится ли энергия воздуха в обычной комнате, если в ней протопить печь?
Решение. В обычной комнате атмосферное давление не меняется, так же как не меняется ее объем (комната не является герметичной). Поэтому для двух разных температур можно записать
p0V0=-±RT\ и PqVq=^RT2, ц ц
где р0 — атмосферное давление, Vo — объем комнаты.
228
Из этих соотношений видно, что при нагревании комнаты меняется масса воздуха, находящегося в ней (часть воздуха, расширяясь, вытесняется в щели окон и дверей).
Вычитая из второго уравнения первое, получим
О = — RT,------RT2=- (тД\ - т2Т2) (п
fi р- Р-
т. е. mjT] - m2T2 = 0, или miTl - т2Т2.
Так как внутренняя энергия в газе
ст ,
U =----RT (nVI.9),
/4
то ее изменение
cR
= — (т^ - т2Т2) (2)
Из соотношения (1) следует, что изменение внутренней энергии в комнате равно нулю, т. е. энергия воздуха в обычной комнате при ее нагревании не изменится.
Задача VI.22 В запаянной U-образной трубке находится вода. Как узнать, воздух или только насыщенный пар жидкости находится над водой в трубке?
Решение. Давление насыщенного пара не зависит от изменения объема. Поэтому если трубку наклонить, то при насыщенном паре уровни воды в ее коленах будут одинаковыми; если же над водой находится воздух, то при изменении его
229
объема меняется и давление, поскольку они связаны законом Бойля — Мариотта. Поэтому уровни воды в коленах U-образной трубки будут разными.
Задача VI.23 Относительная влажность воздуха, заполняющего сосуд объемом Vo = 0,5 м3 при температуре t - 23° С, равна <р = 60%. Сколько нужно испарить в этот объем воды до полного насыщения пара? Давление насыщающих паров при этой температуре рн = 21,7 мм рт. ст. Молярная масса водяных паров р = 18 г/моль.
Решение. Пары воды при температуре t0 - 23° С не насыщенные, их давление рп = <ррн (nVI.16). Их массу можно определить из объединенного газового закона
pnV0 т _ PnV0/z <PP«V0P
То д T0R T0R
Масса насыщенных паров определяется из того же уравнения, но при насыщении
т -Н T0R
Разность этих масс и является тем количеством воды, которое нужно добавить в сосуд до полного насыщения пара
230
_ 0,0217 13,6 • 103 кг/м3 • 10 м/с • 0,5 м3- 18г/моль _
(273 + 23)К- 8,31 Нм/К " Г'
Задача VL24 Смешали Vx = 1м3 воздуха с влажностью у>1 = 20% и V2 = 2м3 с влажностью <р2 = 30%. Обе порции воздуха взяты при одинаковых температурах. Смесь занимает объем V = Vl+V2. Определить ее относительную влажность.
Решение. Давление воздуха в сосуде объемом Vj равно р1 = а в сосуде объемом V2 "* Рг = У’гРн- При смешении воздуха давление смеси определяется из закона Дальтона
Рем = P'i+Р'г.
где р\ и р'2 — парциальные давления смешиваемых газов.
Так как смешение происходит при постоянной температуре, то выполняется закон Бойля — Мариотта:
Pivi = P'l v', P2V2 = P'2V> где V = V, + V2.
Отсюда
р' =pi. р' =
Pl у , Р 2
Таким образом
= P1V, + Р2У2 = У>1РнУ1 +^2PHV2 = li^i + <ЛЛ * СМ тт т т тг Гн ’
231
Из этого соотношения легко получить относительную влажность смеси
<р = Р- = = £1 + М = о,27 = 27%
Рн V 3 3
Задача VI.25 Давление насыщающего водяного пара при температуре t = 27° С равно рн = 44,6 мм рт. ст. Какова масса при этой температуре влажного воздуха объемом Vr = 1м3 при относительной влажности <р = 80% и давлении р0 = 1 атм? fiB = 0,029 кг/моль, = 0,018 кг/моль.
Решение. Влажный воздух состоит из сухого воздуха и водяного пара. Поэтому полное давление влажного воздуха равно сумме давлений воздуха и пара, т. е.
Ро = Рв + Рп > ПРИ ЭТОМ Рп = РРн ’
Таким образом, давление воздуха
Рв = Ро “ Рп = Ро “ m = (760 - 0,8 • 44,б)мм рт. ст. = 724,3 мм рт. ст.
Масса влажного воздуха т - тв + тп. Массу сухого воздуха тв и водяного пара тп можно вычислить из объединенного газового закона:
= ,РвР?Уо . т _ f^nPnV0 _ РП<РР„У КТ п RT RT
Таким образом, масса влажного воздуха равна
_ мл + iwM = Л. („А + ) = 143 г.
В '* ВГВ Г И г А Н/
Задача VI.26 В цилиндре объемом VQ = Юл под поршнем находится влажный воздух при темпе-232
ратуре t = 20°C и относительной влажности <р = 70%. Объем цилиндра при той же температуре уменьшили в п = 10 раз таким образом, что на стенках сосуда появились капли жидкости. Каково стало давление в цилиндре, если начальное давление р0 = 100 мм. рт.ст.? Давление насыщающего пара при температуре t0 равно рн = 18 мм рт. ст.
Решение. Давление влажного воздуха складывается из давления сухого воздуха и давления паров, т. е.
Ро = Рв +Рп = Рв +<РРн-
Поскольку процесс изотермический (Т = const), то при уменьшении объема в п раз, давление воздуха увеличится в п раз, т. е.
р'в=пРв>или р'в= п(р0 -т)-
Так как на стенках цилиндра появились капельки воды, то пар стал насыщенным. Поэтому новое давление влажного воздуха в цилиндре
Р = Р'в+Рн = (Ро - <РР»)п + Рн = 892 мм рт. ст.
В задаче не учтен тот факт, что сконденсированные пары тоже могут занимать некоторый объем. Этим объемом мы пренебрегли, однако его можно оценить. Масса пара в цилиндре определяется из объединенного газового закона.
Объем всех сконденсированных паров
£L= _ = 0Псмз
рп (273 + t)Rp
233
По сравнению с V = — = 1л это пренебрежимо малый объем.
Задача VL27 В сосуде смешиваются три химически не взаимодействующие жидкости, имеющие массы TCj = 1 кг, т2 = 10 кг, т3 = 5 кг; температуры = 6°С, t2 = -40° С, t3 = 60°С и удельные теплоемкости q = 2кДж/кг-К, с2 = 4кДж/кг,К, с3 — 2 кДж/кг • К соответственно. Определить температуру смеси и количество теплоты, необходимое для последующего нагревания смеси до t=6°C.
Решение. В сосуде жидкости, нагреваясь, остаются в том же агрегатном состоянии, поэтому легко записать для них уравнение теплового баланса:
22 &Qi - О, т- е- + AQ2 + AQ3 “ или
с.тДТ. + с9т9ДТ, + с,т,ДТ, = 0.
11 1 Лл Лл Л. : J J J
c1m1(0-t1) + c2m2(0-^) + c3m3(0-t3) = 0, где 0 — температура смеси,
Q _ + C27712t2 + C3TTl3t3 _
с.т. + c,m, + XI Ct i. Ом
- 2'1'6 + 4 ‘ 1° ‘ (~ 40) + 2 •5 ’ 60 _ ~1900 = -19’ c 2-1 + 4-10 + 2-5 100
Таким образом, температура смеси 0 равна - 19° С. Далее эту смесь нужно нагреть до t = 6°С. 234
Для этого ей необходимо сообщить количество тепла
АО = с.тпЛТ + с,т,АТ + с„тчАТ =
= Al^Cj-nij + c2m2 + c3m3) = 1300 кДж
(при этом считается, что теплоемкости жидкостей при изменении температуры не меняются).
Задача VL28 В калориметре находится = =500 г воды при температуре - у С- К ней долили еще т2 ~ 200 г воды при температуре t2 = 10° С и положили т3 = 400 г льда при температуре = -60° С. Какая температура установит-
кал кал
ся в калориметре? св = 1-----; сл — 0,5-----;
г-град г-град
кал удельная теплота плавления льда Я = 80---..
г
Решение. Записать уравнение теплового баланса в этой задаче трудно, так как неизвестно, сколько льда растает и будет ли он таять вообще. Поэтому необходимо сделать предварительные оценки. Оценки проведем в системе СГС, так как в молекулярной физике это делать удобнее, поскольку удельные теплоемкости выражаются однозначными цифрами (а не четырехзначными!).
Лед находится при t3 = -60°С, поэтому при наличии воды с плюсовой Температурой он будет
235
нагреваться. Но для того чтобы его нагреть до нуля градусов, ему нужно сообщить
Qi = слтлА£ = 0,5 • 400 • 60 кал = 12500 кал.
Это тепло лед может получить за счет остывания воды. Вода же, остывая до 0°С, может выделить тепла
Q2 = cjr^A^ + cBm2At2 = (500 • 5 + 200 • 10)кал = = 4500 кал.
Но этого количества тепла мало для нагревания льда до 0°С, поэтому часть воды еще замерзнет и при этом выделит количество тепла
Q3 = тхЛ, где тх количество воды, которое должно замерзнуть, чтобы лед довести до нуля градусов.
Теперь можно записать уравнение теплового баланса:
Qi = Q2 + Q3> или Q3 = тЛ = Qi ~ Q2 = 8000 кал.
Таким образом, замерзнуть должно тх граммов воды
_ Qi ~ Q2 Л
8000 кал -------— = 100 г.
80 кал/г
После того как в калориметре установится температура 0° С, все процессы прекратятся. Следовательно, в калориметре будет смесь льда и воды при температуре t = O°C, при этом льда будет
тл =400 г + 100 г = 500 г,
а воды
236
та =500 г + 200 г - 100 г = 600 г.
Задача VL29 В калориметре с теплоемкостью С = бООДж/град находится т = 1кг льда. Какое количество тепла и Q2 нужно сообщить калориметру со льдом, чтобы нагреть его на 2 градуса: а) от температуры Т, = 270К до Т2 = 272К; б) от температуры Тх = 272К до температуры Т2 = 274К? Удельная теплоемкость воды
,„ кДж „„ кДж
св = 4,2------, а льда сл = 2,1-----. Удель-
кг-град кг-град
кДж ная теплота плавления льда Z = 330---.
кг
Решение. Если внимательно прочитать условие задачи, то можно заметить, что в первом случае лед в калориметре нагревается от t, = -3°С до t, = -ГС, т. е. он пребывает еще в твердом состоянии. В этом случае необходимо сообщить количество теплоты для нагревания калориметра и льда: Qj = CAT + тслАТ = АТ(С + тсл) = 2(0,6 +1 • 2,1) кДж = = 5,4 кДж.
Во втором случае лед в калориметре нагревается от = -ГС до t2 = +2°С, а это значит, что тепло должно сообщаться: на нагревание калориметра на 2 градуса, на нагревание льда снача-ла на 1 градус, затем на таяние льда, а затем на нагревание растаявшей воды еще на 1 градус, т. е.
АТ АТ
Q, = CAT + тс ,--1- Ат + тс„--= 337,5 кДж.
2 л 2 2
237
Как видно, во втором случае приходится тратить тепла существенно больше.
Задача VL30 Гелий массой т, заключенный в
цилиндр под поршень, очень медленно перево
дится из состояния 1 с объемом У2 и давлением рх
Рис. VI.15
в состояние 2 с объемом V] и давлением р2 (рис. VI. 15, а). Какая максимальная температура будет у газа при этом процессе, если на графике зависимости давления от объема процесс изображен прямой 1-2?
Решение. Аналогичная задача уже была рассмотрена (задача
VI.6), но только качественно. Теперь же мы по
лучим закон, по которому меняется температура, и определим ее максимальное значение. Уравнение прямой 1-2 записывается:
р = aV + b, (1)
где постоянные а, Ь определяются из начального и конечного состояний газа.
Действительно,
р, = aV, + b;
Р2 = aV2 + Ъ-
Решая эту систему уравнений, получим
= Pl ~ Р2 . b = P2V1 ~ P1V2
v,-v2’ v.-v2
238
Подставив уравнение (1) в объединенный газовый закон, получим выражение для изменения температуры:
(aV + b)V = —RT, или aV2 + bV = ~RT.
Рис. VI. 15
Как видно из уравнения, температура меняется по параболе, а график ее изменения представлен на рис. VI.15, б. Кривая эта достигает максимального значения температуры при
Ъ
Vo - - — когда совпала
дут корни квадратного уравнения (объем, при
котором температура достигает максимального значения, можно определить, исследовав параболическое уравнение на экстремум).
Давление р0, соответствующее максимальной температуре, определяется по формуле
Ро = aVo +b>
где Vo — объем, соответствующий максимальной температуре.
Объединенный газовый закон позволяет вычислить значение этой максимальной температуры:
т _ _ И + Ь)У0/г
max mR mR
где а, Ъ, Vo мы определили по ходу решения задачи.
239
VII. ЭЛЕКТРОСТАТИКА
nVII.l Все частицы имеют массу и поэтому подчиняются закону всемирного тяготения. Однако большинство из них способны взаимодействовать друт с другом с силой, которая примерно в 1О40 раз превосходит силу тяготения. Эта сила называется силой электромагнитного взаимодействия.
Если частицы способны к электромагнитным взаимодействиям, то говорят, что они имеют электрический заряд. Таким образом, заряд — это количественная мера способности тел к электрическим взаимодействиям.
Существуют два вида заряда: положительный и отрицательный. Все окружающие нас тела состоят из большого числа положительно и отрицательно заряженных частиц. И хотя электрические силы взаимодействия между зарядами очень велики, непосредственно наблюдать эти силы в любом веществе невозможно, так как сумма положительных зарядов в любом веществе равна сумме отрицательных зарядов. В целом, атомы вещества нейтральны.
nVIL2 Если каким-либо способом из атома изымается несколько электронов, то у него окажется избыток положительного заряда и он называется положительным ионом. Аналогично, если в атом попадают избыточные электроны, то получается отрицательно заряженный ион. Избыток зарядов какого-либо вида в данном теле принято называть величиной его заряда, или количеством электричества.
240
nVIL3 Важным свойством электрического заряда является тот факт, что он сохраняется: если какая-то изолированная система (система, из которой не выходят и в которую не входят заряды) обладает определенным зарядом, то его величина остается неизменной:
?! + Q2 + 9з+---+9п = c°nst.
nVIL4 Силу взаимодействия между двумя точечными зарядами можно определить с помощью закона Кулона: два неподвижных точечных заряда отталкиваются или притягивают друг друга с силой, пропорциональной произведению модулей зарядов и обратно пропорциональной квадрату расстояния между ними. Сила направлена вдоль прямой, соединяющей эти заряды:
F = k4^ = J_S&
Г 4я£о г ’
где Qj и q2 — величины зарядов, г — расстояние между ними, е0 — диэлектрическая постоянная, к — коэффициент пропорциональности. Причем
еп = = 8,85-IO"12.
В векторной форме закон Кулона записывается так:
где Fik — сила, действующая на заряд qk со стороны заряда qj , г — радиус-вектор, проведенный от заряда q, к заряду qk.
241
В среде с диэлектрической проницаемостью £ сила взаимодействия между зарядами уменьшается в £ раз:
F = 1 № 4Л££0 Г2 '
Сила взаимодействия двух зарядов не изменяется при наличии третьего, четвертого и так далее зарядов. Это свойство называется принципом суперпозиции, позволяющим определить действие целой системы зарядов на любой заряд:
F = F12 + F13+...+Fln2FH. i=2
nVII.5 Любой электрический заряд создает вок-
- _ F
руг себя электростатическое поле Е = —- Доле,
созданное точечным зарядом q0> равно Е= г
Если в пространстве есть несколько зарядов, то результирующее поле равно сумме полей каждого из зарядов:
Ер — Ег + Е2+.. .+Еп.
Заряд, помещенный на проводник, распределяется по его поверхности таким образом, чтобы поле внутри проводника было равно нулю.
Напряженность поля заряженной проводящей сферы (шара)
О
при г < Ro;
при
г > Ro,
где Ro — радиус сферы.
242
Напряженность поля, созданного проводящей заряженной бесконечной пластиной
2££0 25££о ’
nVIL6 Каждая точка пространства, в котором существует поле, характеризуется своим потенциалом <р. Потенциал — это работа, которую нужно совершить, чтобы перенести единичный положительный заряд из бесконечности в данную точку пространства.
Работа по перемещению положительного заряда из одной точки пространства в другую
А = q(<pr-<p2) = gU,
где U напряжение между точками 1 и 2.
Работа по перемещению зарядов не зависит от формы траектории и определяется только величиной заряда и его положением в электростатическом поле.
Потенциал поля точечного заряда в вакууме
<р = =
Г 4я£ог
Потенциал положительного точечного заряда положителен и убывает с расстоянием от заряда, а потенциал отрицательного заряда — отрицателен и увеличивается при удалении от заряда.
При наличии нескольких точечных зарядов общий потенциал в некоторой точке поля равен алгебраической сумме потенциалов, созданных отдельными зарядами, т. е.
243
1 i 1 i
Потенциал заряженной проводящей сферы (шара)
к — при г > Ro;
г
к~ при г < Ro
Ro
nVII.7 Связь между напряженностью Е и разностью потенциалов двух точек в однородном электростатическом поле определяется формулой
d d ’
где U — напряжение между двумя точками, d — расстояние между этими точками.
nVII.8 При помещении зарядов в диэлектрическую среду с проницаемостью £ кроме поля, создаваемого свободными зарядами, необходимо учитывать и поле связанных зарядов. Поэтому в однородном диэлектрике напряженность электростатического поля (как и сила взаимодействия и потенциал) уменьшается в £ раз по сравнению с вакуумом.
nVII.9 Коэффициент пропорциональности между зарядом, находящимся на уединенном проводнике, и его потенциалом называется емкостью этого проводника:
q = C<p.
Емкость уединенного шарика С = 4л££0К.
244
Два изолированных друг от друга проводника, заряженных равными по модулю, но противоположными по знаку зарядами, образуют конденсатор, емкость которого определяется по формуле
г _ Ч _ Ч
„ тт , или О = CU.
<P1~<PZ U 4
Емкость конденсатора с диэлектриком, заполняющим пространство между обкладками конденсатора, увеличивается в 8 раз, т. е.
С = £С0.
££„$
Емкость плоского конденсатора С = —-—.
а
4л££оаЬ
Емкость сферического конденсатора С = —--,
о —а
где а и Ъ — радиусы концентрических сфер.
nVII.10 При последовательном соединении нескольких конденсаторов общая емкость определяется формулой
£
С
При параллельном соединении конденсаторов общая емкость
п
с = с, + с, + +с = V г
12 п s j г .
г = 1
nVII.ll Энергия заряженного конденсатора w QU Q2 CU2
2 2С 2
245
nVIL12 При внесении заряда q из бесконечно удаленной точки в поле, созданное другими зарядами, совершается работа А = q <р, где <р — потенциал точки поля, куда поместили заряд q. Например, если заряд q вносится в поле, созданное точечным зарядом q0, из бесконечно удаленной точки, то совершается работа
A = q.f = ^,=kn,t
Г г
, 1
где к =--, г — расстояние между зарядами q и
4Л£
9о-
Эту работу называют потенциальной энергией взаимодействия зарядов q0 и q.
Задача VIL1 Два положительных точечных заряда q1 = 4q и q2 = q закреплены на расстоянии а друг от друга. Где нужно расположить заряд Q, чтобы он находился в равновесии? При каких условиях равновесие заряда Q будет устойчивым и неустойчивым?
Решение. Пусть за-ряд Q будет положительным и расположен на расстоянии х0 от заряда q{ (рис. VII. 1, а). На заряд Q действуют зарядов qA и q2. Условие
равновесия для заряда Q запишется:
W0-
gi=4<7
О
а
--------ч>
F„,
1о
Рис. VII.1
две силы со стороны
246
В проекциях на ось ОХ это уравнение имеет вид:
F — F = 0 или F — F (1)
Из условия равновесия (1) следует
к^ = к 92%- (2)
хо (а-*0)
Подставляя значения зарядов q} и q2, получим
4Q(a —х0)2 = Qx20, или Зх^-8ax0+4а2 = 0-(3)
Решаем уравнение (3):
4a + V16a2 — 12a2 4a + 2a
a?, , =-------------=--------;
1,2 3 3
xt = x2 = 2a.
Из этих двух решений физический смысл имеет только решение х, = так как если заряд поместить на расстоянии х2 = 2а от точки 0, то равновесия быть не может, поскольку силы, действующие со стороны зарядов q} и q2, направлены в одну сторону.
Следует отметить, что заряд Q может быть любым по величине и по знаку. Это следует из уравнения (2), в котором Q сокращается.
Для определения характера равновесия следует рассмотреть силы, возникающие при малом смещении заряда Q из положения равновесия.
Пусть Q — положительный заряд. При продольном смещении Q вправо на Да? увеличивается сила
247
отталкивания Fq (так как уменьшается расстояние между зарядами Q и д2) и уменьшается сила F (увеличивается расстояние между зарядами Q и qj. Поэтому ре-
зультирующая этих двух сил Fp будет возвращать заряд Q в первоначальное положение равновесия (puc. VII. 1, б). Это означает, что при продольном смещении положительного заряда Q положение равновесия устойчивое.
Если заряд Q сместить по вертикали от положения равновесия на величину Др, то возникает результирующая сила Fp = F + Fq^, которая удалит заряд Q еще дальше от положения равновесия (рис. VII.1, б). Следовательно, при поперечном смещении положительного заряда Q равновесие будет неустойчивым.
Пусть заряд Q — отрицательный. При продольном смещении заряда Q вправо на Да? увеличивается сила притяжения Fq> и уменьшается сила F. Результирующая этих двух сил Fp будет удалять отрицательный заряд Q еще дальше от положения равновесия (рис. VII.1, в). Это значит, что при продольном смещении отрицательного заряда Q
248
положение равновесия неустойчивое.
Если заряд Q сместить по вертикали от положения равновесия на величину Ау, то возникает результирующая сила
Рис. VII. 1
Fp = F + F^, которая возвращает заряд Q в положение равновесия. Следовательно, при поперечном смещении отрицательного заряда Q равновесие устойчивое.
Задача VII.2 На проволочное металлическое кольцо радиусом R помещен заряд Q. Определить напряженность поля в точке А, лежащей на оси кольца на расстоянии х0 от центра 0 (рис. УП.З).
Решение. Напряженность поля, созданного заряженным кольцом в точке А, является векторной суммой полей, созданных всеми отдель-
249
ними точечными зарядами Aqif которые находятся на маленьком участке кольца А1г. Заряд
(1)
ZJll
Рассмотрим два точечных заряда Aq;, находящихся на противоположных концах диаметра. Результирующее поле этих двух зарядов направлено вдоль оси ОХ и равно
Е =2£,cosa = 2k^^ = 2k^. (2)
* г г г
Подставляя выражение для заряда Aq; в уравнение (2), получим
Е = 2к^-^- = к------QAAX-0
‘ 2jlRr jzR(x20+R2)/2
Результирующее поле всего заряженного кольца
Следует отметить, что ^Alf = nR, поскольку мы рассматриваем суммарное поле Epi от двух заряженных участков А^. Следовательно:
_ Qx0 Qxn
4лЛ0Р(х2 + R2y2 4я£0(х2 + Р2)/2 Анализируя полученную формулу, можно за
250
метить, что в центре кольца (а?0 = 0) поле ЕА = 0. Оно также обращается в нуль при х0 —> <ю.
Задача VIL3 Определить напряженность поля электрического диполя в точке, отстоящей от оси диполя на расстоянии г, в двух случаях:
1) точка А лежит на прямой, проходящей через ось диполя;
2) точка В лежит на прямой, перпендикулярной оси диполя (рис. VII.3).
Решение. Электрическим диполем называется совокупность двух равных по величине и противоположных по знаку точечных зарядов, расположенных друг от друга на некотором расстоянии I, малом по сравнению с расстоянием до точек, в которых проводится измерение напряженности электрического поля. Прямая, проходящая через заряды, называется осью диполя. Электрическим моментом диполя называется вектор, направленный от отрицательного заряда к положительному и равный р = ql .
251
Каждый заряд диполя создает вокруг себя электрическое поле. Суммарное поле Е определяется по правилу сложения векторов.
Вычислим напряженность поля, создаваемую диполем вдоль его оси в некоторой точке А. Результирующее поле определяется векторной суммой полей отдельных зарядов, т. е. ЕА = Е+ + Е_ В проекции вдоль оси диполя
Е. = Е. + Е /1 т
1_______q
4Я£О (г-1/2)2
где г — расстояние от центра диполя до точки наблюдения А.
Так как I « г', то
Е _ 1 q2lr _ 2ql _ Р
А 4я£0 г4 4я£ог3 2я£0г3 ‘ (1)
Направление вектора Е определяется направлением дипольного момента р.
Для точек, лежащих на прямой, перпендикулярной оси, величина векторов Е+ и Е_ одинакова.
а результирующий вектор Ёв = Е+ + Е_ , причем
|ЁВ| = 2Е+ sin а =
1 2q(Z/2)
4Я£о (г2 +
р 4Я£оГ3
(2)
Из формул (1) и (2) видно, что напряженность
252
поля диполя убывает пропорционально /гъ т. е. быстрее, чем поле точечного заряда. Картина распределения поля электрического диполя представлена на рис VII.3.
Задач aVII.4 В центре полой проводящей незаряженной сферы помещен точечный заряд q0.
1) Где и какие электрические поля будут существовать?
2) Будут ли появляться заряды на сфере?
3) Будут ли происходить изменения электрического поля внутри и вне сферы при перемещении заряда внутри сферы?
4) Как будет меняться поле внутри и вне сферы, если заряд останется неподвижным, а внешнюю поверхность сферы заземлить на короткое время, а затем заряд осторожно вывести из полости сферы, не касаясь ее, через маленькое отверстие?
5) Где и какие заряды на сфере будут существовать, если точечный заряд поднести снаружи к незаряженной сфере?
Решение.
Внутри полой проводящей сферы будет существовать поле, определяемое по формуле для
поля точечного заряда Е = ———• На внутренней 47С80Г2
поверхности сферы наведется заряд -q0, который расположен равномерно по внутренней поверхности. Так как сфера нейтральна, на ее внеш-
253
ней поверхности равномерно расположен заряд +q0. Внутри металлического слоя поле равно нулю. Вне сферы поле определяется зарядом +q0 по формуле для поля точечного заряда (рис. VII.4, а).
При перемещении заряда внутри сферы изменяется электрическое поле внутри сферы, изменяется
распределение отрицатель-
ного заряда на внутренней поверхности сферы (рис. VII.4, б).
Однако распределение положительного заряда на внешней поверхности сферы, а следовательно, и поле вне сферы изменяться не будет. Это связано с тем, что поле внутри ме
таллического слоя равно нулю, поэтому изменение поля внут
ри сферы не влияет на распределение зарядов
на ее внешней поверхности.
При заземлении на некоторое время внешней поверхности сферы все положительные заряды «уйдут» в землю (на самом деле из поверхности
земли, которая является хорошим проводником, на внешнюю поверхность сферы придут электроны, которые компенсируют ее положительный за
254
ряд). В этом случае внутри сферы поле будет существовать, а вне ее поле равно нулю (рис. VII.4, в). После выведения заряда q0 из полости сферы отрица-
тельные заряды начнут растал- Рис. VII.4
киваться до тех пор, пока не
распределяться равномерно на внешней поверхности сферы. В этом случае поле внутри сферы равно нулю, а вне сферы су
ществует электрическое поле, подобное полю точечного заряда -q0, помещенного в центре сферы (рис. VII.4, г).
Если же заряд q0 поднести к сфере снаружи, то на внешней поверхности сферы образуется наведенный (индуцированный) заряд, который распределен, как указано на рис. VII.4, д. Вне сферы результирующее поле определяется суммой полей заряда q0 и индуцированных зарядов. Внутри сферы поле рав
Рис. VI1.4
но нулю.
Задача VII.5 Вблизи бесконечной незаряженной металлической пластины помещен заряд +q0. Будут ли появляться заряды на плоскости? Где и какие (рис. VII.5)?
Решение. При помещении бесконечной пластины в поле точечного заряда q0 в первое мгнове-
255
Рис. VII.5
ние в пластине будет существовать поле, которое стремится положительные заряды удалить в бесконечность, а отрицательные заряды приблизить к заряду q0. Перемещение зарядов внутри проводника происходит до тех пор, пока результирующее поле внутри него не обратится в нуль. После этого движение зарядов внутри проводника прекратится. Все заряды будут распределены на поверхности проводника таким образом, чтобы поле внутри него было равно нулю.
На левой стороне плоскости
возникает индуцированный отрицательный заряд, распределенный неравномерно: плотность заряда тем больше, чем ближе соответствующий участок поверхности к заряду q0. Положительные заряды ушли в бесконечно удаленные части плоскости (рис. VII.5).
Слева от плоскости поле в любой точке пространства определяется векторной суммой полей
заряда q0 и распределенного по плоскости индуцированного заряда.
Справа от плоскости поле равно нулю.
Другими словами, незаряженная бесконечная пластина экранирует часть пространства, лежащую справа от пластины, от всех полей. Если
256
пластина не закреплена, то заряд и пластина притягиваются друг к другу.
Задача VII.6 В однородное электрическое поле с напряженностью Ео перпендикулярно полю внесли большую металлическую пластину с площадью S (рис. VII.6). Какой заряд индуцируется на каждой ее стороне?
Решение. В незаряженном металлическом проводнике имеется огромное количество электронов (свободных зарядов), которые движутся хаоти-чески. Под действием электрического поля заряженные частицы начинают двигаться упорядоченно. Принято говорить, что положительные заряды перемещаются в направлении поля, а отрицательные — против поля. (На самом деле в металле при наличии поля перемещаются лишь электроны. Положительные заряды (ядра атомов) не могут перемещаться. Они образуют кристаллическую решетку. Те части проводника, откуда электроны ушли, заряжаются положительно.) Таким образом, в нашей задаче на левой стороне пластины индуцируются отрицательные заряды, а на правой — положительные. Эти заряды равны по величине, так как пластина не заряжена (рис. VII.6).
9 Физика
257
Внутри металлической пластины суммарное поле, состоящее из внешнего поля Е0) поля отрицательных зарядов Ё_ и поля положительных зарядов Ё+) равно нулю, т. е.
Ео - Е+ - Е_ = 0.
Воспользовавшись выражением для поля, созданного проводящей бесконечной заряженной пластиной (nVIL5), запишем
Q Q
Е - —*------= О
0 2S£o 2S£o
Следовательно, искомый заряд Q = E0Ss0.
Рис. VI1.7
Задача VII.7 Металлический шар радиуса R заряжен зарядом Q. Определить потенциал в любой точке внутри шара и в точке В, расположенной на расстоянии х > R от центра шара (рис. VII.7, а).
Решение. Потенциал заряженного металлического шара (или сферы) на самой поверхности и
258
вне ее определяется по формуле для потенциала точечного заряда, помещенного в центре О, поскольку поле, созданное заряженным шаром (или сферой) вне поверхности шара, в точности совпадает с полем одинакового по величине точечного заряда, помещенного в центре шара.
Определим потенциал внутри заряженного шара (сферы). Мысленно перенесем положительный заряд q0 из точки 1, лежащей на поверхности шара, в произвольную точку 2 внутри шара. При этом мы совершим работу, определяемую формулой А12 = — <р2) (см. nVIL6). С другой
стороны, А12 ~ FAl = q0EAl.
Приравнивая эти два выражения, получим
-<р2) = q0EM.
Так как поле внутри металла равно нулю (Е = 0), то <рY — (р2 = 0 , или = <р2. Поскольку точка 2 взята произвольно, то можно сделать вывод, что потенциал любой точки внутри металлического шара равен потенциалу на его поверхности.
График изменения потенциала <р заряженного шара с расстоянием г приведен на рис. VII.7, б.
Таким образом, потенциал в точке А
Q
<Ра 4л£0К’
а потенциал в точке В определяется по формуле потенциала для точечного заряда
»•
259
Q
в 4я£0Х
Задача VII.8 Металлический шар радиуса R, заряженный до потенциала <р, окружают сферической проводящей оболочкой радиуса Rv Как
изменится потенциал шара после того, как он будет на короткое время соединен проводником с
оболочкой (рис. VII.8)?
Рис. VII.8
Решение. Потенциал металли
ческого заряженного шара ради
уса R равен (см. nVIL6) <Р — к-—
R
поэтому заряд, находящийся на
<pR
шаре: Q = -—. При соединении к
шара с металлической оболочкой
радиуса R} весь заряд перетечет на внешнюю сторону оболочки, и она теперь становится заряженной зарядом Q. (Вспомним, что внутри проводящего шара (сферы) поле всегда равно нулю и заряды отсутствуют!) Теперь потенциал этой обо
лочки равен:
Этот потенциал будет таким же и в любой точке внутри оболочки, а значит, и у шара радиуса R. Таким образом, изменение потенциала шара
260
Q 1 Q ktpR fl 1) f R 1 ---fc—=——-----\ = <p - -1
RY R к R)
Задача VII.9 Сфера радиуса R заряжена зарядом Q. Ее окружают незаряженным металлическим шаровым слоем с радиусами R} и Rr Определить поле Е и потенциал (р в точках А, В, С (рис. VII.9). Расстояния от центра сферы до точек А, В, С известны: гА, тв, тс. Нарисовать график зависимости электростатического поля и потенциа
ла от расстояния г.
Решение. Поло
жительный заряд Q наводит на внутренней поверхности шарового слоя заряд -Q. Так как шаровой слой был не заряжен, то на его внешней поверхности появится положительный равномерно распределенный заряд +Q. Электростатическое поле (так же, как и потенциал) в любой точке пространства будет определяться суммой полей, созданных всеми заряжен
Рис. VII.9
261
ными поверхностями с радиусами R, Rlt R2:
Q kQ 7 1
₽л=-,где fc= —.
Поля от заряженных поверхностей радиусов R1 и R2 (как и потенциал), складываясь, дают результирующее поле в точке А, равное нулю.
В точке В поле от заряженных поверхностей шарового слоя равно нулю, и остается лишь поле, созданное зарядом Q, находящимся на сфере радиуса R, т. е.
, Q
^В ~ ^~2' ?В
Потенциал в точке В складывается из потенциала, который создает сфера радиуса R, и сферические поверхности шарового слоя с радиусами Rx и R2, т. е.
Q Q Q
<Рв = <PR + (Pr1 + <Pr2 = -+/C —.
Tb xv i R2
Поле в точке С от всех трех заряженных поверхностей равно нулю (внутри любой заряженной сферической поверхности поле равно нулю), т. е.
Ес = 0.
Потенциал в точке С равен сумме потенциалов, созданных всеми заряженными поверхностями, т.е.
Q Q Q
<Рс = <pR +<Pr2 = к —-к — + к —
XV XV 1 XV 2
262
Графики изменения электростатического поля и потенциала с расстоянием изображен на рис.VII.9.
Задача VII.10 Две параллельные металлические пластины соединены с источником напряжения с ЭДС £ (рис. VII. 10, а). Параллельно им вво-
1) Определить потенциал каждой из четырех пластин и поле во всех трех промежутках между пластинами.
2) Как изменятся потенциалы пластин и напряженности полей во всех промежутках, если пластины 2 и 3 на короткое время замкнуть?
3) Как изменятся заряды на пластинах 1 и 4?
4) Будут ли пластины 2 и 3 заряжены до и после замыкания?
Решение. Будем отсчитывать потенциалы всех пластин относительно первой пластины, т. е. ее потенциал примем за нуль = О). Тогда из схемы ясно видно, что потенциал пластины 4 равен
263
Так как все пластины одинаковы и находятся на равном расстоянии друг от друга, то падение напряжения на каждом промежутке между пластинами равны, т. е. U21 = U32 = U43 - Следовательно:
^2 ^21
-,или ^---0--;
^4 “ ^з - U43 - “, откуда ^3 - <Р1 - — - - £. О о о
Распределение зарядов на пластинах изображено на рис. VII.10, б.
Во всех трех промежутках электростатическое
поле направлено справа налево, одинаково по
величине и равно Ег =
= . Если
/3d
пластины
2 и 3 на короткое время замкнуть, то отрицательные заряды пластины 2 перейдут на пластину 3 и компенсируют положительные заряды этой пластины. Положительные заряды пластины 2 и отрицательные заряды пластины 3 останутся на мес
264
те, так как они удерживаются силами притяжения зарядов, расположенных на соседних пластинах 1 и 4. Таким образом, распределение зарядов на пластинах изменится (рис. VII. 10, в). В этом случае электрическое поле будет только между пластинами 1~2 и 3~4. Поле между пластинами 2—3 равно нулю. А это значит, что пластины 2~3 мож-
Рис. VII. 10
но мысленно (а можно и реально) соединить металлическим проводником и при этом в схеме ничего не изменится (ведь в проводнике поле всегда равно нулю!). Теперь потенциал пластины 1 равен по-прежнему нулю = О), потенциал пластины 4 <Рц = $, а потенциалы пластин 2 и 3
одинаковы и равны: (р2 = <р?> = • Следовательно,
поле Е2 между пластинами 1~2 и 3~4 увеличится, так как оно определяется формулой
Е = 4>г "li = У 4 ~Уз =
2 d d 2d
265
Однако мы знаем (nVII.6), что электрическое поле, созданное зарядами, расположенными на поверхностях металлических пластин, пропорционально величине зарядов:
Р_ ° _ Q 1L — —
2££о 25££о ’
Поэтому поле в промежутках 1~2 и 3~4 может увеличиться только за счет увеличения зарядов на пластинах 1 и 4, которые дополнительно притекают из источника ЭДС до тех пор, пока потенциалы пластин 2 и 3 не выравняются. Пластины 2 и 3 до замыкания были не заряжены, а после замыкания пдастина 2 оказалась заряженной положительно, а пластина 3 — отрицательно.
Задача VII.11 Металлическому шару радиуса Rj собщили заряд Q, а затем соединили его очень длинным и тонким проводом с металлическим незаряженным шаром радиуса R2. Как распределится заряд между шарами?
Решение. После соединения шаров начнется перемещение заряда от шара с большим потенциалом к шару с меньшим потенциалом. Это перемещение будет происходить до тех пор, пока потенциалы шаров не выравняются. Конечный потенциал шаров определяется формулой (см.пУП.6)
= = Чг.
Ri R2
где q1 и q2 установившиеся заряды шаров.
266 '
В силу закона сохранения заряда + q2 = Q. Решая совместно эти два уравнения, получим
QK1 . QR2
41 Rt+R?’ 92 R,+R2'
Задача VII.12 Точечный заряд q0 находится на расстоянии d от центра заземленной проводящей сферы радиуса R. Определить полный заряд q, индуцированный на поверхности сферы. Рассмотреть два случая: d > R и d < R (рис. VII.11, а, б).
Рис. VII. 11
Решение. Рассмотрим случай d > R. Так как сфера соединена с Землей, то ее потенциал, так
же как и потенциал всех точек внутренней полости сферы, равен потенциалу Земли, т.е. равен нулю. Электрическое поле в любой точке пространства создается зарядом q0 и зарядом q, индуцированным на поверхности сферы. При этом заряд q распределен неравномерно, но
267
таким образом, чтобы результирующая напряженность поля внутри сферы стала равной нулю.
Потенциал в любой точке пространства представляет собой сумму потенциалов полей, создаваемых точечным зарядом q0 и точечными зарядами Aqi( на которые можно разбить распределенный по внешней поверхности сферы индуцированный заряд q. Тогда для точки, расположенной в центре сферы:
, Aq. , qn „ , л
<Р0 ~ + к = 0 (так как сфера зазем-
лена),
или к — + к = 0. R d
Отсюда индуцированный заряд q = -q0 Знак «-» означает тот факт, что индуцированный заряд всегда противоположного знака по сравнению с зарядом q0. Из полученной формулы видно, что величина индуцированного заряда зависит от расстояния d. При удалении заряда q0 в бесконечность индуцированный заряд стремится к нулю, при приближении к сфере заряда q0 (d -> R) величина индуцированного заряда стремится к q0.
Рассмотрим случай d < R.
В этом случае вне сферы поле равно нулю. Внутри сферы поле есть — оно создается зарядом q0, а индуцированные заряды расположены неравномерно на внутренней поверхности сферы.
268
Определим величину этого заряда. Ее легко определить, если воспользоваться картиной силовых линий. Силовые линии электростатического поля всегда начинаются на положительных зарядах и оканчиваются на отрицательных, а число силовых линий однозначно связано с величиной заряда. Так как вне сферы поля нет, то нет и силовых линий. Следовательно, все силовые линии начались на заряде qQ и окончились на индуцированных зарядах q. Откуда следует, что полный заряд q0 + q = 0. Следовательно, q = -qQ. Величина индуцированного заряда q не зависит от расположения заряда q0 внутри сферы. При перемещении заряда q0 внутри сферы меняется лишь распределение индуцированного заряда на внутренней поверхности сферы.
Задача VII.13 Два электрона находятся на бесконечно большом расстоянии друг от друга. Один из них вначале покоится, а другой движется со скоростью 60, направленной к центру первого. На какое наименьшее расстояние они сблизятся (излучением электромагнитной энергии пренебречь)?
Решение. Электростатическое взаимодействие двух электронов тормозит движущийся электрон и ускоряет ранее покоящийся. В начальный момент потенциальная энергия взаимодействия системы из двух электронов равна нулю, а кинети-„ mv* „
ческая энергия Ек =-----. В любой момент вре-
2
мени полная энергия электронов складывается из
269
потенциальной энергии взаимодействия зарядов и их кинетической энергии, т. е. закон сохранения полной энергии имеет вид
О 9 о О
mv. mv. mv, е
L = L + 1 +-, 2-------------------------2-2-4я£от
где vr и v2 — скорости электронов, т — их масса, г — расстояние между зарядами, е — заряд электрона.
Кроме того, для электронов необходимо записать закон сохранения импульса
mv0 = mv, + mv2.
Наибольшее сближение электронов происходит тогда, когда их скорости станут одинаковыми (в этом случае скорость первого электрона относительно второго равна нулю, т. е. относительно второго электрона он останавливается). Из закона сохранения импульса следует, что в этот момент vx = v2 = , а закон сохранения энергии для
этого момента запишется так:
Ч _ 2m(voV । g2
2 2 V 2 ) 4^£ormin
е2 отсюда rmin =-----
nz^mv^
Задача VII.14 Металлический шар радиуса К, имеющий заряд q0, помещен внутри диэлектрика с диэлектрической проницаемостью £ (рис. VII. 12). Определить величину и знак поляризационного заряда qn и плотность его распределения.
270
'/-///////,
%
////////% V
•ц/////////
,/////////,
Рис. VII.12
Решение. При отсутствии диэлектрика поле, создаваемое заряженным шаром, в любой точке вне шара определяется по формуле (nVII.5)
Е = г
, 1
где к =-----•
4те0
Если же шар окружен безграничным диэлектриком, то результатирующее поле внутри диэлектрика
Уменьшение напряженности электрического поля при погружении заряженного шара или любо
271
го заряженного тела в диэлектрик объясняется появлением поляризационных зарядов qn, выступающих на границе диэлектрика у поверхности заряженного шара. Именно поле этих поляризационных зарядов приводит к уменьшению поля в диэлектрике (puc.VII.12). Вычислим поле, созданное поляризационными зарядами:
Е = Е - Еи, иля Е = Е — Е = . (1)
и Г £
Поляризационные заряды расположены равномерно по поверхности сферы, окружающей шар, поэтому поле этих зарядов Еп можно определить еще и по формуле
Еп = к^. (2)
г
Приравнивая выражения (1) и (2), получим, что поляризационный заряд
Поверхностная плотность поляризационных зарядов
_ 9п _ 9п _ (£ ~ !)<?) _ ~ 1 п 5 4яК2 £4яК2 £ °’
где g0 — плотность зарядов на шаре. Отсюда а - (£ ~
п £ 4яК2’
Задача VII.15 В заряженном плоском конденсаторе, отсоединенном от источника, напряжен-272
ность электростатического поля равна Ео. Поло-
вину пространства между пластинами конденса-
тора заполнили жидким диэлектриком с диэлектрической проницаемостью £ (рис. VII. 13, а). Чему стала равной напряженность Е электростатического поля в пространстве между пластинами, свободном от диэлектрика?
Решение. Вначале на пластинах
Рис. VII. 13
конденсатора находился заряд Q = C0U0 = CoEod, где Со — емкость пустого конденсатора, d — расстояние между пластинами, Ео — напряженность
электростатического поля в конденсаторе.
Когда половину конденсатора заполнили диэ-
лектриком, то его можно рассматривать как два параллельно включенных конденсатора и С2 (рис. VII. 13, б), так как пластины металлические и каждая из них имеет всегда один и тот же потенциал. Полная емкость конденсатора после заполнения диэлектриком
Рис. VII. 13
г рС С
С = С.+С2 + =Ч.(1 + £)
1 2 2 2 2 v
При отключенном источнике заряд на пластинах сохраняется, однако он может перераспределяться в пределах одной металлической пластины.
Новая разность потенциалов будет определяться по формуле
273
ц = Q = 2Q = 2Co£od = 2jEod ~ С ~ С0(14-е) ” Со(1 + £) l + fi' Искомая напряженность поля внутри конденсатора
г. и 2Еп d 1 + £ Следует отметить, что заряд на пластинах верхней половины конденсатора, не заполненной диэлектриком:
Su=w.
1 2 1 + £
Заряд же на пластинах нижней половины конденсатора, заполненной диэлектриком:
92 1 + £
Таким образом, при заполнении диэлектриком часть заряда переместилась с верхней половины пластин на нижнюю, хотя полный заряд
CnEnd C0E0d£ 7
Q ~ 91 + 9г — 1 1 ~ СрМ
1 + £ 1 + £
остался прежним.
Задача VII.16 Плоский конденсатор емкости С зарядили до разности потенциалов Uo и отключили от источника ЭДС. Затем пространство между пластинами заполнили жидким диэлектриком с диэлектрической проницаемостью £. В другой раз тот же конденсатор оставили подключенным к источнику ЭДС £ = 170 (рис. VII. 14). Определить
274
заряды на пластинах конденсатора и напряженность поля в нем в обоих случаях.
Решение. Рассмотрим первый случай: заряженный конденсатор отключили от источника. В этом случае заряд на пластинах остается неизменным, однако емкость при заполнении диэлектриком увеличивается в £ раз. Следовательно, согласно формуле Q = CU разность потенциалов на обкладках конденсатора должна уменьшиться в £ раз. Напряженность поля в конденсаторе Е = также должна умень
Рис. VII.14
шится в £ раз.
Во втором случае конденсатор не отключен, разность потенциалов на обкладках конденсатора не меняется и равна Uo, а емкость увеличивается в £ раз. Следовательно, заряд на конденсаторе увеличится в £ раз, т. е. Q' = sCU0.
Увеличение заряда на обкладках происходит за счет притекания дополнительного заряда из источника ЭДС. Напряженность поля Е в конденсаторе при заполнении диэлектриком не меняется, так как не меняется разность потенциалов на его обкладках:
Ь — --
d
275
Задача VII.17 Сферический воздушный конденсатор состоит из двух проводящих концентрических сфер с радиусами а и Ъ (рис. VII.15). Определить емкость сферического конденсатора.
Решение. Пусть на одной об-@ кладке сферического конденсато-ь ра (на сфере радиуса а) помещен заряд +Q, а на другой (на сфере радиуса Ъ) — заряд -Q.
В этом случае потенциал внешней заряженной сферы (относи-Рис. VII. 15 тельно бесконечно удаленной точки) определяется как алгебраическая сумма потенциалов, созданных зарядами на внутренней и внешней сферических поверхностях, т. е.
<рь —--------1--------0 .
4л£0Ъ 4л£0Ъ
Потенциал внутренней сферы
Q Q Q 1 1\
Фа = ------------- ------------ •
4я£йа 4л£0Ъ 4д£0 \а Ъ/
Разность потенциалов между обкладками сферического конденсатора
. Q /1 1\ Q (Ь-а)
\<р = Фъ~ Ф„ =-----------— 0 =------------
4л£0 \а Ъ) 4jt£0 аЪ
Таким образом, емкость сферического конденсатора
С _ Q _ 4л£оа.Ь А<р Ъ — а
276
Эта формула позволяет провести некоторые предельные переходы. Например, если Ъ » а, т. е. внешняя сфера удалена, то С = 471£оа, т. е. емкость конденсатора равна емкости уединенного шара. Следовательно, уединенный шар можно рассматривать как конденсатор, у которого роль внешних обкладок играют удаленные предметы.
Если же сферические поверхности находятся близко друг к другу, так что расстояние между ними d = (Ъ — а) намного меньше среднего ради-
, , enS m
уса сфер, т. е. d « г, то С ---н—. Ta-
ti d
ким образом, емкость сферического конденсатора, у которого расстояние между пластинами намного меньше радиуса сфер, можно вычислять по формуле плоского кондесатора.
Задача VII.18 Определить емкость батареи конденсаторов, изображенной на рис. VII. 16, а. Емкость каждого конденсатора Со.
Решение. Схема будет выглядеть проще, если ее изобразить по-другому (рис. VII. 16, б). Из этого рисунка видно, что потенциалы то-(а) чек А и В одинаковы, а это означает, что конденсатор С5 всегда не заряжен, так
как разность потенциалов между его обкладками равна нулю. Поэтому точки А и В можно соединить либо коротким проводом (эквипотенциаль-
277
Рис. VII. 16
ной поверхностью), и от этого в схеме ничего не изменится, либо конденсатор С5 вовсе выбросить. И тот и другой случай изображены на рис. VII.16, в, г.
Рис. VII.16
Полная емкость схемы (в) и (г) равна:
. 2 Сп 2 С,, ~
в) С = Со Ч--------— Со + Со = 2С0;
° 2С0+2С0 ° ° °
г) С = Со +2 -ѰѰ- = 2С0.
С + С
'“'О
Следует отметить, что в задачах подобного рода всегда нужно искать точки равного потенциала, что позволяет существенно упростить задачу.
Задача VIL19 Определить разность потенциалов между точками А и В в схеме, изображенной на рис. VII. 17. Все элементы схемы заданы.
Решение. Конденсаторы заряжаются от источника ЭДС до некоторых напряжений U,, U2> U3, U4, при этом
278
Рис. V 11.17
Так как конденсаторы Сх и С2 включены последовательно, то заряды на их обкладках одинаковые, т. е. = q2, аналогично q3 = q4.
Если конденсаторы С\ и С2 заменить одним
С С р _ ^1^2
конденсатором - q + С ’ то заРяД Qi на его обкладках определяется легко (аналогично определяется и заряд q3):
С С С С
q = q3=q =£_ЬЬ_
41 Ct+C2’ 3 4 с3+с4-
В электростатике работа по замкнутому контуру равна нулю. Выберем контур 1АВ1. При обходе контура важно правильно определить полярность обкладок конденсатора, так как при движении от большего потенциала к меньшему падение напряжения следует брать со знаком «+»,
279
а при движении от меньшего потенциала к большему — со знаком «-»:
U. + UAB — U., = 0 , или UAB = Uз — U.. 1 АО о ' ла о 1
Так как U3 = —, a U, = —, то, подставляя С3 С-1
величину зарядов q3 и q4, получим
и gctc2 _ ^дс.-дСз)
АВ с3(с3+с4) c^+q) (с1+с2)(с3 + с4)-
Можно было бы выбрать и контур АВ2А. В этом случае
UAB+U4-U2 =0 и UAB =и2-из.
Вычисления попробуйте проделать сами. Ответ получите в обоих случаях одинаковый.
Задача VII.20 В схеме, изображенной на
*3
Рис. VII. 18
рис.VII.18, потенциалы точек 1, 2, 3 равны <р2, <р3 соответственно. Емкости конденсаторов Сп С2, С3. Определить потенциал точки 0.
Решение. Обозначим потенциал точки 0 через <р. Сумма зарядов всех обкладок конденсаторов, подсоединенных к точке 0, всегда остается постоянной и равной нулю, так как до зарядки конденсаторов на всех пластинах заряд отсутствовал. Вычислим величины этих зарядов.
280
Qi =ci(p! -p); Q2 =c2(^2 -p); Q3 = c3((p3 -<p).
Тогда Qj + Q2 + Q3 = 0, или
Cl -<р) + С2(<р2 -<р) + С3(<р3-<р) = Q, __„___ ____^'1^’1 ^'^'2^2 +С3^)3 откуда ’’—с;+с;+с3
VIII. постоянный ЭЛЕКТРИЧЕСКИЙ ТОК
nVIILl Электрический ток — это направленное движение электрических зарядов.
1 ---= qnvS ,
At
где q — заряд одной частицы, п — концентрация частиц, v — средняя скорость движения частиц, S — площадь поперечного сечения проводника.
nVIII.2 Электродвижущая сила $ (ЭДС) равна работе сторонних сил по перемещению единичного положительного заряда.
„ А„
Ч nVIII.3 Закон Ома для участка цепи:
R’ где 17 — разность потенциалов на концах участка цепи, R — сопротивление участка.
281
nVIII.4 Закон Ома для замкнутой цепи: сила тока в замкнутой цепи (рис. VIII.1) равна отношению ЭДС к полному сопротивлению цепи:
R
Рис. VIII. 1
R + r’
где г — внутреннее сопротивление источника ЭДС. nVIII.5 Закон Ома для участка цепи, содержащего ЭДС: разность потенциалов на концах участка цепи, содержащего ЭДС, равна величине этой ЭДС минус произведение силы тока на внутреннее сопротивление (г) источника ЭДС (рис. VIII.2): UAB=$ — Ir.
Рис. VIII.2
nVIII.6 Для проводников, диаметр которых намного меньше их длины (d«l), существует связь между сопротивлением проводника и его размерами:
где р — удельное сопротивление.
282
nVIII.7 Зависимость удельного сопротивления от температуры:
Р = Ро(1 + at), где р0 — удельное сопротивление при 0°С, а — температурный коэффициент сопротивления. Для металлов эта зависимость часто записывается так:
* Гр '
*0
где Т — температура по шкале Кельвина, То = 213° К.
nVIII.8 При последовательном соединении проводников их сопротивления складываются, т. е.
п
Rfl = -R; + К2 + R3+- • -+Rn = 2 > i-1
где Ro — общее сопротивление.
При параллельном соединении проводников складываются их проводимости, т. е.
1 111 1 А 1
— = — + — + — +...+-----= > —.
Ro R, R2 R3 R R.
U 1 i о П iel i
nVIII.9 Для уменьшения чувствительности амперметра в п раз параллельно ему необходимо подключить шунтирующее сопротивление Rm.
где Rb — сопротивление амперметра.
Для уменьшения чувствительности вольтметра в п раз к нему последовательно необходимо подключить дополнительное сопротивление Кд.
283
Яд = RB(n-l).
nVIII.10 При расчете схем, состоящих из нескольких узлов и ветвей, пользуются двумя основными законами:
1) законом сохранения зарядов — в каждом узле количество зарядов, притекающих в единицу времени, равно количеству зарядов, утекающих за это же время, другими словами, сумма всех токов в узле с учетом знака всегда равна нулю:
п
У = i. + ц+...+ц = о-J J I Л <Ьа /1 )
i = l
2) работа по перемещению заряда по замкнутому контуру равна нулю, при этом если при обходе контура на любом элементе идем от большего потенциала к меньшему, то работа берется со знаком «+», если же идем от меньшего потенциала к большему, то со знаком «-».
В радиотехнике эти два закона используются в правилах Кирхгофа:
п __
1) 5/' = °; 2>
1=1
где I.Ri — падение напряжения на элементах, — ЭДС, входящие в контур.
nVIII.ll Закон Джоуля-Ленца: количество теплоты, выделенной протекающим током на некотором участке цепи, равно произведению квадрата силы тока, сопротивления этого участка и времени прохождения тока:
Q = I2Rt.
284
nVIII.12 Мощность — это работа, совершаемая в единицу времени:
N = —.
At
Мощность, развиваемая источником ЭДС, равна Ng = £1 .
Мощность, выделяемая при нагревании про-
2 U2
водников, N] = I R = —.
R
Если в цепи нет механических (химических) взаимодействий, то No = Nlt в противном случае No > Nv
nVIII.13 Коэффициент полезного действия — отношение полезной мощности к полной, развиваемой в цепи:
N _ полез ~ N ПОЛИ
nVIII.14 Законы электролиза: масса любого вещества, выделившегося на электроде, пропорциональна полному заряду, прошедшему через электролит, т.е.
1) т = kq = kit — первый закон Фарадея, где к — коэффициент пропорциональности, называемый электрохимическим эквивалентом данного вещества;
/alt
2) т — ~ втоРо^ закон Фарадея, где F —
постоянная Фарадея, п — валентность вещества, и — молярная масса.
285
Задача VIII.1 Определить среднюю скорость v направленного движения электронов вдоль медного проводника при плотности тока j = 11 А/мм2, если считать, что на каждый атом меди в металле имеется один свободный электрон. Молярная масса меди р = 64 г/моль, плотность меди р = 8,9 г/см3.
Решение. Часто при решении задач на постоянный ток пользуются понятием плотности тока — это ток, протекающий через единичную поверх-
. I
ность, т. е. 3 = — = nev (см. nVIII.l), где п — кон-центрация электронов, е — заряд электрона, v — средняя скорость движения электронов.
Из последнего выражения следует, что v = . Концентрация п по определению равна
_ N _ vNa _ т Na _ pNA
V V р V р ' Подставив это соотношение в выражение для скорости, получим
v = — = 8,2 • 10~4 м/с = 0,82 мм/с.
Как видно, средняя скорость направленного движения электронов весьма незначительная.
Задача VIII.2 К источнику ЭДС подключили три сопротивления, как указано на рис. VIII.3,
286
Rj = R2 = R3 — R. Определить общее сопротивление схемы и ток I протекающий через источник
Рис. VIII.3
Решение. Сопротивления R} и R2 соединены последовательно. Их общее сопротивление R' = Rt + R2 = 2R. Сопротивление R3 подсоединено параллельно сопротивлению R’, поэтому общее сопротивление цепи
RR3 _ 2R _ 2 _£_3£
° R + R3 3R 3 Ro 2R
Задача VIII.3 Оп
ределить сопротивление куба, подключенного в цепь как показано на рис. VIII.4, а. Сопротивление каждой грани куба т.
Решение. В силу симметрии схемы ясно, что потенциалы точек 2, 3, 6 одинаковы, так же как и потенциалы точек 4, 5, 7.
287
2
7
Рис. VIII.4
Точки равного потенциала можно соединить единым проводом, от этого в схеме ничего не изменится, но она будет выглядеть по другому (рис. VIII.4, б). Теперь сопротивление куба вычислить просто. Общее сопротивление между точками 1 и 3; 5 и 8 равно т/3, а сопротивление между точками 2 и 7 равно г/6 (рис. VIII.4, б). Общее сопротивление всего куба (между точками А и В) равно (рис. VIII.4, в):
г 5
RAB ~
3 6 3 6
Задача VIII.4 На рис. VIII.5 изображен мостик для измерения сопротивлений (мостик Уитстона). Неизвестное сопротивление Rx, Ro — эталонное сопротивление. Вольтметр соединен скользящим контактом с однородным проводом большого сопротивления АВ (реохорд). Расстояние контакта D от точек А и В можно измерить с помощью сан-
288
тиметра, который лежит рядом с высокоомным сопротивлением АВ. В тот момент, когда показания вольтметра равны нулю, фиксируются расстояния I] и 12. Определить неизвестное сопротивление Rx.
Рис. VIII.5
Решение. Так как разность потенциалов “ Vd ~ 0, то ток текущий через сопротивление Ro, далее потечет через сопротивление Rx, а ток 12 протекает через реохорд АВ. Через вольтметр V ток не протекает, так как <РС ~ У d = ® Поскольку потенциал точки С равен потенциалу точки D, то можно записать
~ ^2Г1! ~ ^2Г2>
где Tj — сопротивление участка проволоки АВ длиною I], г2 — сопротивление проволоки длиною 12. Разделив эти два соотношения друг на друга, получим
10 Физика
289
^0 _ Г1 г> — R0T2
------------------, или Rx -------- . RX Г2----------------Г1
Сопротивления rr и r2 связаны с длиной проводников следующим образом (см. n.VIII.6):
П = P-z; r2 = p-J.
D О
Поэтому Rx = R—
Задача VIII.5 Два одинаковых аккумулятора с ЭДС £ и внутренним сопротивлением г соединены один раз последовательно, другой — параллельно (рис. VIII.6). Определить разность потенциалов между точками А и В в обоих случаях.
Решение. При последовательном соединении ис-т 2£ £ точников по контуру течет ток Л = — =
Выберем контур А12ВА. При обходе этого контура против часовой стрелки получим
290
UAB + Цг — g = 0 , отсюда
UAB = ё - Цг = g-~r = 0.
Следовательно, при последовательном соединении источников разность потенциалов между точками А и В равна нулю.
В контуре может быть сколько угодно одина-
ковых элементов, со- единенных последова-тельно. Напряжение
S'-
& Г
между любыми элементами всегда будет равно нулю (рис. VIII.7).
При параллельном соединении источни-
Рис. VIII.7
ков ток в контуре равен 12 = —~— = 0. Вновь об
ходим верхнюю часть контура против часовой стрелки, получаем UAB + I2r — g = 0, тогда
UAB =g-I2r = g-0 = S.-
Таким образом, при параллельном соединении источников разность потенциалов между точками А и В равна £. Если параллельно включено п одинаковых источников с одинаковыми внутренними сопротивлениями, то разность между точками А и В всегда равна Если же источники разные,
то UAB * g.
Задача VIII.6 Цепь с внешним сопротивлением
R (рис. VIII.8) питается от батареи, состоящей из
10»
291
N элементов. Каждый элемент имеет сопротивление г и ЭДС £0. Батарея состоит из одинаковых последовательно соединенных элементов, которые соединены в параллельные группы. Определить число групп п и число элементов в группах т, при которых будет получена наибольшая сила тока в цепи.
Рис. VIII.8
Решение. Сопротивление каждой группы Rj=mr, а £ = £от . Групп же таких будет п = N/m. Общее сопротивление всех групп равно
R = Ri =
2 п N
Следовательно, сила тока, протекающего через сопротивление R, при любом значении т определяется
! = gom = gom = ёот
R2 + R Rj-rn / N + R rm2 / N + R'
292
Максимум этого выражения достигается при
N
Батарея из N элементов дает наибольшую силу тока тогда, когда ее внутреннее сопротивление равно сопротивлению внешней цепи, т. е. когда гт2
R2 = R, или ----= R. Таким образом:
[RN т - J, а
V г
Задача VIII.7 В схеме, изображенной на рис. VHL9, определить токи в каждой ветви. = 15 В, £, = 30 В, г. = 3 Ом , г, = 6 Ом, R = 8 Ом.
* Ct ' 4 ' (л '
Решение. Выберем направление токов, как показано на рисунке (хотя Вы можете выбрать направление токов, как пожелаете!). Применив закон Ома для участка цепи, содержащего ЭДС (nVIII.5), можно записать:
293
UAB ^1 > UАВ ^2 ^2Г2 > Uав ^3^ •
Тогда значение токов, полученных из этих выражений, будут:
Т — ~ UАВ . т _ ^2 ~ UАВ т _ Uав
г, гг 7’ - R '
Так как алгебраическая сумма токов для любого узла равна нулю, то -ь 12 — 13 = 0, или I3 = Jj +12 {рис. V1II.9, точка А) и тогда
Юв . , ga-Ю,
R3 г, тг
Перепишем это уравнение иначе:
отсюда
JJ _
АВ 1/К3 + 1/^ + 1/^'
Подставляя цифровые значения, получим Uab = 16 В, тогда
Г — ___^АВ _ 1 / л . т _ $2 АВ 2 1/ Д •
11 Г1 /3 А> 12 ~ /ъ л>
I3 = = 2А.
гз
Таким образом, направление токов 12 и 13 мы выбрали правильно, а ток на самом деле течет
294
от точки А в точку В, о чем говорит знак
Задача VIII.8 Какой ток потечет через амперметр с пренебрежимо малым внутренним сопротивлением в схеме, изображенной на рис. VIII.10?
R, = 15 Ом, R2 = R3 = R4 = R = 10 Ом, $ = 7,5 В.
Решение. Выберем направление токов в ветвях схемы, как указано на рисунке. Сопротивление амперметра равно нулю, поэтому сопротивления R3 и R4 можно считать включенными параллель-
но, а сопротивление Рис. VIII.10
участка 1~2 равно
R/2. Тогда сопротивление участка АВ
^АВ
= 7,5 Ом.
Ток I, проходящий через источник равен
I — /r — 1 А. Через сопротивление R2 течет по-
ловина этого тока, так как сопротивление участка А1-2, равное R2 + R, параллельно сопротивлению Rx и поэтому 12 - А. Токи,
текущие через сопротивления Я4 и R3, одинако
295
вы и равны половине тока J, (R3 = R4 - R), т. е.
т - т - h/ - 1/ д 24 — 1з /2 ~ /4
Поскольку ток I, проходящий через источник, равен I = 14+ Ц, где 1} — ток, протекающий через амперметр, то Ц = I - 14 = .
Задача VIIL9 В схеме, изображенной на рис. VIII.11, (а) заданы сопротивления: R, = 2 Ом, R2 = 3 Ом, R3 = 6 Ом, R4 = 7 Ом и £ = 36 В. Определить ток на участке CD. Сопротивлением подводящих проводов пренебречь.
Решение. Разность потенциалов между точками С и D равна нулю, потому что сопротивление участка CD равно нулю, но ток через этот участок протекает и он может быть любым.
296
Так как разность потенциалов <pc—<pD=G, то схему можно изобразить по-другому (рис. VIII.11, б). Общее сопротивление участков АС и СВ равны:
R = JW_ = 1)5Om;
АС R3 + R3
= R2g±...= 21Ом
+ #4
как сопротивления параллельно включенных проводников, а сопротивление участка АВ
R ,в = Rac + Rcr = 3,6 Ом.
/1О >
Рис. VIII.11
Направление токов в каждой ветви схемы мы можем выбирать произвольно. При выборе направлений токов, указанных на рис. VIII.11, (а), ток на
(f) , ~ Ч>С
участке CD I3 = 1} - 12, причем ток 1г = —--------,
Hi
а ток 12 = —----—. В свою очередь <РА ~ <РС = 11^лс ,
R2
а IRcb-
297
Таким образом, нам остается вычислить общий ток I. Он легко определяется из закона Ома для замкнутой цепи:
I=-
RaC "* ^св
---= 10 А , тогда 3,6
<рА ~ <рс — IRAC —15В, Рс Рв IRcb 21В,
Ток I = А = ^АС = &Rac
Kj Kj Rx (Rac + R-св
rp0K J _ Pc Pb _ Шсв _ Rcb
2 r2
---_ —---------- = 7 a.
^2 R^RaC 1^св)
ICD = J3 = I. — J, = 0,5 A. U» LJ О X '
В этой задаче цифровые значения сопротивлений, токов и напряжений приходилось получать по ходу решения, чтобы избежать очень громоздких выражений.
Задача VIII.10 В схеме, изображенной на рис. VIII.12, заданы все элементы. Посчитать токи, протекающие в ветвях этой схемы.
Рис. VIII.12
Решение. В этой схеме имеется три ветви: А$2В, А^В, А^В.
Направление токов в ветвях выбирается произвольно. Направим их так, как показано на рисунке. Тогда для узла А запишем
298
J1+J2-I = 0. (1)
Для определения трех неизвестных величин нужно иметь три уравнения. Два остальных уравнения мы получим, если запишем работу электрического поля по перенесению единичного положительного заряда вдоль контура. Выберем замкнутые контуры А$2{53ВА и А^В^А, причем второй контур надо выбирать так, чтобы в него вошел хотя бы один элемент, не вошедший в предыдущий контур.
Обход контура можно проводить в любом направлении (хотя удобнее — по току). Если при обходе контура на любом элементе идем от большего потенциала к меньшему, то падение напряжения берется со знаком «+», если же идем от меньшего потенциала к большему, то со знаком «-». Для контура А$2$2ВА
£2-I2r2 “£з +Iiri = °- (2)
Для контура А^В^А
IR + ^-^+I^ = 0. (3)
Теперь мы имеем три уравнения и три неизвестных тока сможем определить. Решая совместно уравнения (1), (2) и (3), получим
Л
_%(ft + ft-ft)+(ft-ft)
^2 — “
R — +
299
I = Il+I2.
Если при подстановке числовых значений величин какой-либо ток окажется положительным, значит, его направление выбрано верно, если отрицательным, значит, ток течет на самом деле противоположно тому направлению, которое мы выбрали.
Задача VIII.11 Определить падение напряжения на конденсаторе С, присоединенном к источнику с ЭДС £ = 3,9 В по схеме, изображенной на рис. VIII.13. Какой заряд будет на обкладках конденсатора, если емкость С = 2мкф, R{ = 6 Ом., R2 = 7 Ом, R3 = 3 Ом?
Решение. Источник $ заряжает конденсатор до определенного напряжения Uc. Когда потенциал правой пластины конденсатора будет равен потенциалу точки В, ток через сопротивление R3 прекратится, но он продолжает идти через сопротивления Rt и R2. Напряжение на конденсаторе равно падению напряжения на сопротивлении R2. Таким образом:
Рис. VIII.13
300
Заряд на конденсаторе определяется формулой
Q = исс = 1,8 • 2 • 1(Г6 = 3,6 • 10~6 Кл.
Задача VIII.12 Определить разность потенциалов между точками А и В в схеме, изображенной на рис. VIII.14. ЭДС источника £. Внутренним его сопротивлением пренебречь.
Решение. Источник
Рис. VIII. 14
ЭДС заряжает конденсаторы до некоторого напряжения U и Uc? до тех пор, пока сумма падений напряжений на конденсаторах не будет равна нацря-жению на участке CD.
После зарядки конденсаторов ток пойдет
только через сопротивления Rx и R2, причем этот
ток I - —;—5— .Rj + R2
Д,ля определения разности потенциалов между точками А и В достаточно выбрать контур АВСА и обойти его по замкнутому пути. Тогда 'РА-<РВ~ + ^С1 = 0, или <рА ~ <рв = IRX — UCi.
Так как конденсаторы соединены последовательно, то на их обкладках будут одинаковые заряды Q, которые определяются по формуле
301
Q = gr =ё— * p общ pc1+c2’
а напряжения равны
U =_Q= gc2 и = Q_ = gc, ' с, с. + с, •* с, с, + с.
Поэтому разность потенциалов между точками А и В
$с2
Rr+R2 Ц+С/
Тот же ответ получится, если выбрать контур ABDA.
Задача VIIL13 Определить заряд конденсатора С на схеме, указанной на рис. VIII.15. Все элементы заданы. Внутренним сопротивлением батареи пренебречь.
Решение. Потенциалы точек А, В, D будем считать относительно точки С (это равносильно
Рис. VIII.15
тому, что мы потенциал точки С положили равным нулю). Пусть потенциал точки D будет равен <р,,
тогда потенциал точ-
ки А будет tpA = $, а
потенциал точки В
tpB IR —
gR
3R + R
g
4
302
В точке соединения конденсаторов (в точке D) сумма зарядов остается постоянной и равной нулю, так как до зарядки на обкладках конденсаторов заряд отсутствовал. При зарядке конденсаторов заряды на обкладках 1, 2, 3 как-то перераспределяются, но убежать они никуда не могут, поэтому их сумма останется равной нулю. Пусть конденсаторы зарядились, как показано на рисунке, тогда -Qj + Q2 + Q3 = 0, или
— 2С(<рА — <р^ + 2>Сср + С(<р — <рв ) — 0.
Подставив значения найденных потенциалов <РА и <рВ) получим
- (£ - <р)2С + <рЗС + I <р - С = 0 .
Отсюда определим потенциал <р: <р = Заряд на конденсаторе С
Г“4 С"Т
Задача VIII.14 Железная проволока имеет сопротивление в два раза больше, чем медная. В какой из проволок выделится большее количество тепла при включении обеих проволок в цепь с постоянным напряжением: а) последовательно, б) параллельно?
Решение. При последовательном соединении проводников через них протекает один и тот же ток, поэтому
303
<ЭЖ I2R^t Rx o7 ~ ~ XT
Так как Rx > RM, то и Qx > QM.
При параллельном включении проволок напряжение на проводниках одинаковое, поэтому
Следовательно QM > <2ж.
Таким образом, при последовательном включении проволок на железной выделится в два раза тепла больше, чем на медной, а при параллельном — наоборот.
Задача VIII.15 Какое сопротивление R должно быть включено последовательно с лампой, чтобы лампа горела нормальным накалом при напряжении V = 220В, если лампа рассчитана на напряжение Vo = 120В при мощности N = 60Вт?
Решение. Лампа будет гореть нормальным накалом, если через нее будет протекать ток, на который она рассчитана. Но для этого вначале нужно рассчитать сопротивление лампы Кл. Это легко сделать, воспользовавшись формулой
N = I2Ra = Кл
(1)
Откуда
304
Кл
и2
N
14400
60
= 240 Ом.
(2)
Тогда ток I определится из уравнения (1):
т ГлГ I 60Вт' 1 .
I — I— — л------— — А
N 240 Ом 2
R
Рис. VIII.16
Схему включения лампы и сопротивления R можно представить на рис. VIII.16, причем в лампе должен протекать ток, необходимый для нормального накала лампы (I = 0,5А).
Так как лампа рассчитана на напряжение Vo - 120В, то на сопротивлении R должно падать напряжение U = V - Vo (рис. VIII.16).
Тогда сопротивление
_Д/ у-у0
I I
юов 0,5А
= 200 Ом.
Задача VIII.16 Источник тока с ЭДС 6 и внутренним сопротивлением г замкнут на реостат. Выразить мощность тока N во внешней цепи как функцию тока I.
Построить графики изменения силы тока I, напряжения U, мощности N и кпд 7] при изменении сопротивления реостата R.
При каком соотношении внешнего и внутреннего сопротивлений достигается максимальная
305
мощность во внешней цепи? Каков при этом кпд установки J] (рис. VIII.17, а,б,в,г,д)?
Решение. Мощность, развиваемая источником идет на выделение джоулева тепла как на нагрузочном сопротивлении R (в нашем случае реостат), так и на внутреннем сопротивлении источника г, т. е.
£1 = N + 1I 2г, или N = £1 - 12г-
Зависимость выделяемой мощности на нагрузке от тока представляет
Рис. VIII.17
собой параболу (рис. VIII.17, а). Каждому значению мощности соответствуют два значения тока. При токе
I = - мощность,
2т
выделяемая на нагрузке — максимальна. Это легко получить, исследуя функцию
N = $1 — 12г на экстремум: берем производную по току от выше приведенного выражения и приравниваем к нулю: (£ — 21т = 0). Таким образом
I = —. 2г
Зависимость силы тока I от сопротивления определяется по формуле
306
R + r'
(1)
Графически эта зависимость представлена на рис. VIII. 17, б. Зависимость напряжения U от сопротивления определяется формулой
U = IR = =..
R + r 1 + %’
/ £v
(2)
Рис. VIII. 17
График этой зависимости изображен на рис. VIII. 17, (в). Мощность, развиваемая на сопротивлении R (рис. VIII. 17, г), равна
307
£2R
(.R + r)2 ’
(3)
а полная мощность
R+r R+r
(4)
Максимальное значение мощности соответст-
вие. VIII.17
вует току'Д -
Это означает, что сопротивление нагрузки R должно быть равно г, что следует из формулы (4). Именно при равенстве внутреннего сопротивле-
ния и сопротивления нагрузки выделяется максимальная мощность в нагрузке.
Коэффициент полезного действия J) по опре-
делению равен Г) = —. В нашей задаче полез-
ПОЛИ
ной мощностью является мощность, выделенная на нагрузке R. Она равна: 7VnOM,3 = $I-Ir, тогда кпд
$1 - Ir Tr R
ТР Р \ /Р Г? । '
Ip $ (R + т)/0 R + г
Таким образом, при максимальной потребляе-
308
Рис. VIII. 17
Задача V1IL17 Аккумулятор подключен к сети зарядной станции с напряжением Vo - 13В. Внутреннее сопротивление аккумулятора г = 0,4 Ом, его остаточная ЭДС £ = 11 В. Какую мощность 7V0 расходует станция на зарядку аккумулятора? Какая часть п этой мощности расходуется на нагревание аккумулятора
Рис. VIII.18
ЭДС £, и определяется
(рис. VIII. 18)7
Решение. Для зарядки аккумулятор всегда включается навстречу напряжению зарядной станции (см. рисунок). Ток идет в направлении, противоположном направлению действия закона Ома:
1 = V-₽ _ 13-11 =5Д
г 0,4
309
Мощность, расходуемая зарядной станцией:
No = IVg = 65 Вт .
Мощность, расходуемая на нагревание аккумулятора:
TV, = Гг = 10Вт-
Таким образом:
N 2
" = = в ’ или 15’6%'
Задача VIII.18 Электромотор с сопротивлением г приводится в движение от сети с напряжением VQ. Мотор потребляет ток силой IQ. Какую мощность No потребляет мотор? Какая часть этой мощности превращается в механическую энергию?
Решение. Мотор потребляет мощность No = I0V0, причем эта мощность идет на механическое вращение мотора N} и на нагревание его обмоток, т. е.
NQ=I0V, = N}+I2r.
Следовательно, мощность, идущая на вращение мотора:
Ni = ^ ~ Ш ~ V) •
IQ(V, -1,г)
Эта мощность составляет п =---------часть
от полной мощности.
Задача VIIL20 Электрический чайник имеет две обмотки. При включении одной из них вода в
310
чайнике закипает через = 15 мин, при включении другой — через t2 = 30 мин. Через какое время t закипит вода в чайнике, если включить обе обмотки: а) последовательно, б) параллельно.
Решение. При любом соединении сопротивлений чайнику для закипания необходимо сообщить одно и то же количество теплоты Q = стДТ, так как с, т, ДТ остаются неизменными. Поэтому можно записать
(1)
U2 U2
Q = — t. = —t2 R, R2
(Эту формулу удобно взять потому, что всякий раз чайник включается в одну и ту же розетку.) Таким образом:
— = —, или = — = 2, т. е. R2 = 2R..
Rt R2’ R, tt ’
При последовательном включении обмоток общее сопротивление R^ = R} + R2. Применяя формулу (1) для последовательного включения обмоток, получим
U2 _ U2 р , р , или
"Г IV2 JVj
tL = 3tL = 45 мин.
Rx +-Ri + 2К
х R, 1 R,
При параллельном включении обмоток _ RtR2
Лобщ ~ r + r • Опять, воспользовавшись формулой (1), имеем
311
u2t.
---L, или
f _ f ^1^2
S ~ 4
2
. . = — t, =10 мин.
(Rt + R2)Ri 3
Задача VIII.21 Электрическую плитку, рассчи-
Рис. VIII.19
тайную на напряжение Uo = 220В, требуется переделать, не меняя и не укорачивая спирали, на U = НОВ так, чтобы ее мощность осталась прежней. Что нужно для этого сделать (рис. VIII. 19)?
Решение. Так как в условии задачи заданы напряжения, при которых должна работать плитка, то воспользуемся выражением для мощности в виде
Так как напряжение уменьшилось в два раза, то, чтобы мощность осталась прежней, новое со
противление плитки должно уменьшиться в четыре раза, действительно:
—- = —отсюда
R Rx
312
_ U*R _ R i\> т. n *
и2й 4
Так как спираль нельзя менять и укорачивать, то от центра спирали (точка 0 на рис. VIII. 19) нужно сделать отвод С, а полученные два сопротивления ОД и ОБ соединить параллельно, тогда мы имеем
+ Л/ *
/ /и
IX. МАГНИТНОЕ ПОЛЕ ТОКА И ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
nIX.1 Вокруг проводников с током, так же как и вокруг постоянных магнитов, существует магнитное поле, которое характеризуется вектором магнитной индукции В.
Магнитное поле в каждой точке пространства имеет определенное направление, зависящее от направления тока, создающего это поле, и от среды, в которой находится проводник.
Магнитное поле, созданное каждым элементом тока длиной AZ, определяется формулой Био Савар Лапласа:
4лг3
|5 । jU,uolAlsina или BJ =--------—------
1 1 4лг
313
где г — радиус-вектор, проведенный от элемента А1 в точку наблюдения, а — угол между вектора
ми AZ и т,/4 — магнитная проницаемость среды,
ц0 — магнитная постоянная (рис. IX. 1).
Эта формула позволяет посчитать вектор магнитной индукции В, созданный проводником с током любой формы. Так магнитное поле, созданное бесконечно длинным проводником с током I, определяется
igi ml
। 1 2лх
тр,е х — расстояние от проводника до точки наблюдения.
Расположение линий
магнитного поля определяется правилом буравчика. Поступательное движение буравчика направляют по току, тогда направление вращения головки буравчика указывает направление линий магнитного поля. Линии магнитного поля замкнуты (рис. IX.2).
Рис. IX.2
314
п1Х.2 Магнитное поле, созданное витками соленоида, внутри него
Вс ,
где N — число витков, I — длина соленоида.
п1Х.З При помещении в магнитное поле проводника с током на него действует сила Ампера:
F = I АIВ
, или |#| = IAJB sin а = IAI Вх,
где AZ — длина отрезка с током I, а — угол между направлением вектора магнитной индукции В и отрезком проводника АI. Направление этой силы определяется правилом буравчика или правилом левой руки. (Если левую руку расположить так, чтобы перпендикулярная к проводнику составляющая вектора магнитной индукции В входила в ладонь, а четыре вытянутых пальца были направлены по току, то отогнутый на 90° большой палец покажет направление действующей на участок проводника силы.) Правило буравчика: головку бу-
равчика вращают от вектора A I к вектору В, тогда направление его поступательного движения определяет направление силы F.
п1Х.4 На заряды, движущиеся в магнитном поле, действует сила Лоренца:
вл = д[йв] или |гл| = где q — положительный заряд.
315
Направление силы Лоренца так же определяется правилом левой руки или правилом буравчика.
п1Х.5 Потоком магнитной индукции (магнитным потоком) через некоторую поверхность с площадью S называется величина
Ф = BS cos а = BtS ,
где а — угол между вектором В и перпендикуляром к поверхности S (рис. IX.3).
Поток магнитной индукции может быть поло-
Рис. IX.3
жительным, если составляющая проекции вектора В вдоль нормали (Вп) совпадает с положительным направлением нормали п рамки с током, или отрицательным, если составляющая Вп противоположна положительному направлению нормали п (рис. IX.3).
Для любого контура условились за положительное направление нормали рамки принимать направление поступательного движения буравчика, если его головку вращать по направлению тока.
Если магнитное поле вызвано током I, протекающим по какому-либо контуру, то магнитный поток через поверхность, ограниченную этим контуром, пропорционален току, т. е. Ф = LI, где L — индуктивность контура (или коэффициент само
316
индукции), которая зависит от формы и размеров контура и магнитных свойств окружающей среды.
п1Х.6 Работа, совершаемая магнитным полем при повороте контура с током Г.
А = 1ДФ,
где ЛФ — изменение потока магнитной индукции через рамку.
п1Х.7 При изменении магнитного потока через поверхность, ограниченную некоторым контуром, в последнем возникает электродвижущая сила $ индукции, определяемая формулой
с_ АФ
где ДФ — изменение магнитного тока за некоторый интервал времени At.
Знак «-«отражает правило Лоренца, согласно которому возникающая в контуре ЭДС приводит к появлению индукционного тока такого направления, что вызванное им магнитное поле мешает изменению магнитного потока.
п1Х.8 При пересечении незамкнутого проводника линий магнитной индукции В на его концах возникает ЭДС индукции
£ИНД = ,
где В± — составляющая вектора магнитной индукции В, перпендикулярная скорости движения проводника v.
317
п1Х.9 Если магнитный поток меняется вследствие изменения тока, протекающего по этому контуру, то в контуре возникает ЭДС, которую называют ЭДС самоиндукции. Она равна
_ ДФ _ AI
^синд At L At'
nIX.10 Изменение потока, возникающее вследствие вращения рамки с частотой (О в магнитном поле, приводит к возникновению ЭДС индукции, меняющейся по гармоничному закону:
£(t) = (ЭО sin €l)t,
где (о0 — максимальное значение ЭДС индукции (амплитуда).
В свою очередь эта ЭДС приводит к появлению в контуре переменного тока
I = Io sin(cot + <р),
где 10 — максимальное значение переменного тока (амплитуда тока), а <р — сдвиг фаз между колебаниями тока в цепи и ЭДС индукции. Сдвиг фаз <р зависит от того, какие элементы (R, L, С) включены в цепь.
nIX.ll Напряжения на отдельных элементах схемы и ток, протекающий в них, колеблются с одинаковой частотой, хотя они могут быть сдвинуты по фазе: на омическом сопротивлении R ток, протекающий через этот элемент, и напряжение на нем колеблются в одинаковой фазе (т. е. <р = 0), на емкости С ток опережает напряжение на 90°
(т.е. <Р —~), на индуктивности колебания тока от
318
стают от колебаний напряжения на 90°
л
(т. е. <Р - - —) £л
(рис. IX.4). (Подробнее изложение этого материала можно прочитать в «Пособии по физике» А.И. Гомоновой. Изд-во МГУ, 1991г.)
п1Х.12 В цепи переменного тока сумма напряжений на концах цепи не равна сумме напряжений на отдельных последовательно включенных элементах, так как напряжение на
различных участ-
ках сдвинуты по фазе относительно друг друга. Амплитуду и фазу результирующего колебания
напряжения можно легко определить, пользуясь методом векторных диаграмм, который основан на том, что любое гармоническое колебание можно представить в виде проекции вектора, вращающегося с угловой частотой О). Длина вектора равна амплитуде колебаний. Сложение
319
колебаний определяется нахождением суммы векторов.
Согласно этому методу колебания переменного тока и напряжения изображают в виде векторов 10 и UQ, вращающихся с одинаковой частотой о против часовой стрелки и отличающихся амплитудой и сдвигом фаз (рис. IX.5).
Таким образом, вектор тока и напряжения при вращении не меняют своего взаимного расположения, т. е. сохраняют постоянную разность фаз. Для схемы, состоящей из последовательно включенных элементов R, L, С, векторная диаграмма изображена на рис. IX.6.
320
nIX. 13 Сдвиг фаз для этой схемы
<i)L — tg<P =-------
h
а общее сопротивление цепи
Закон Ома для цепи переменного тока имеет вид:
п1Х.14 Средняя мощность, выделяемая источником в цепи переменного тока
— цип
W =------ cos <р = 1Л17Л cos <р.
где 1Д, Ид — действующие значения тока и напряжения.
I = U = л/2’ л/2‘
Задача IX.1 Рассчитать магнитное поле В в середине кругового витка с током I радиуса R (рис. IX.7).
Решение. Каждый элемент кругового витка Д1 с током создает в центре контура поле В,., направление и величину которого легко определить с помощью формулы Био Савар Лапласа (см. nIX.1):
11 Физика
321
i-i jUjU0IAZsina
LBJ 2
1 1 4ят
По правилу буравчика это поле направлено перпендикулярно плоскости контура (рис. IX.7) и равно
' ‘I 4лг2
Результирующее элементарных полей
, (sinа = 1, г = R).
поле В равно сумме всех В,, т. е.
в = у в = У = AL
£ ' 4я:Е2 4яЕ2
У дг =
4лВ2 2R
Подобный круговой виток аналогичен магнитной стрелке. Там, где линии магнитной индукции выходят из плоскости кругового витка, расположен его северный полюс N, а где входят — южный S (рис. IX.7). Этот круговой ток является важным элементом, так как он позволяет определять наличие магнитного поля в пространстве и его направление. Во внеш
нем магнитном поле он устанавливается так, что его собственное магнитное поле всегда совпадает
322
по направлению с внешним магнитным полем {рис.
IX.8).
Рис. IX.8
Задача IX.2 Мягкая спиральная пружина подвешена так, что нижний ее конец погружен в металлическую чашечку с ртутью {рис. IX.9), а верхний подсоединен к источнику постоянного тока. Что произойдет с пружиной при замыкании ключа К?
Рис. IX.9
Решение. При замыкании ключа К по пружине потечет ток. Каждый виток пружины будет со
11»
323
здавать магнитное поле и притягивать к себе соседние витки (разноименные полюса магнитов притягиваются). Пружина сожмется, нижний конец пружины поднимется из ртути, цепь разомкнется, и ток перестанет идти. Если нет тока, нет и магнитного поля между витками и пружина расправится.
После опускания нижнего конца пружины в ртуть весь процесс начнется сначала. Таким образом, пружина совершает периодические колебания.
Эту задачу можно решить и по-другому. Отдельные участки соседних витков, лежащие друг против друга, можно рассматривать как параллельные участки проводников, по которым текут токи в одном направлении {рис. IX.9, б). Такие проводники притягиваются друг к другу. Поэтому витки пружины будут также притягиваться друг к другу и пружина сожмется, а нижний конец ее поднимется из ртути, разрывая цепь, по которой протекает ток. Исчезает магнитное поле проводников, и пружина вновь распрямляется. Конец пружины опускается в чашечку с ртутью, вновь замыкая цепь, и т. д.
Задача IX.3 Прямой проводник АС длиной I и массой т подвешен горизонтально на двух легких нитях О А и ОС в однородном магнитном поле с вектором магнитной индукции В, направленным перпендикулярно проводнику и лежащим в горизонтальной плоскости {рис. IX.10). Какой величины ток надо пропустить через проводник,
324
чтобы одна из нитей разорвалась, если каждая нить разрывается при нагрузке, большей То?
Решение. На проводник с током действуют четыре силы: сила тяжести mg, две силы натяжения нити Т и сила Ампера F, определяемая правилом левой руки, причем F = BJI.
Предположим, что ток в проводнике АС протекает слева направо. В этом случае сила Ампера F направлена вниз, в противном случае натяжение нитей при пропускании тока не возрастает, а уменьшается и нити не оборвутся.
При равновесии проводника = 0. В проекции на вертикальную ось это условие запишется
+ F
2Т - mg - F = 0 или Т = —.
Так как предельная нагрузка на нити равна То, то
m ВИ 2Тп - ms
То mg 4------, откуда I > —2-----—
2 BZ
Задача IX.4 Медный провод с сечением S, согнутый в виде трех сторон квадрата, может вращаться вокруг горизонтальной оси (рис. IX. 11). Провод находится в однородном магнитном поле, направленном вертикально вверх. При протека
325
нии тока I провод отклоняется на угол а от вертикали. Определить индукцию поля В. Плотность меди р задана.
Решение. Пусть сторона квадрата имеет длину а. На каждую из сторон рамки действует сила тяжести mg = paSg и сила Ампера F = IB^a. Момент силы F, действующий на нижнюю сторону рамки, выводит ее из вертикального положения. Этот момент при некотором угле а уравновешивается моментами сил тяжести, действующими на все стороны рамки и стремящимися вернуть ее в положение равновесия. Моменты сил Рг, действующие на боковые стороны рамки, можно не учитывать, так как их сумма в любой момент времени равна нулю. Таким образом, условие равновесия для моментов сил, действующих на рамку, можно записать:
а
Fa cos а — 2mg — sin а — mga sin a = 0 ,
2
или
326
2 O'
IBa cos a — 2paSg — sin a — paSga sin a = 0.
2
Из этого уравнения определяем индукцию магнитного поля
2pSg
В = -2—tg а.
Задача IX.5 Возле бесконечного закрепленного прямолинейного проводника с током I перпендикулярно ему и в одной плоскости с ним помещают проводник АС. Как будет вести себя этот проводник, если по нему пропустить ток i в указанном на рис. IX.12 направлении?
327
Решение. Проводник с током I создает вокруг себя магнитное поле, направление линий магнитной индукции В которого изображено на рисунке. На каждый из участков До? проводника АС действует сила Ампера, направление которой определяется правилом левой руки:
К = iAxB±.
Вектор магнитной индукции В перпендикулярен проводнику АС и в точке А больше по величине, чем в точке С, так как для бесконечно длинного проводника
В = —
2лх
Поэтому на участок Ах, прилегающий к точке А, будет действовать большая сила РА, чем на участок Ах, прилегающий к точке С. Точка приложения результирующей всех сил Ампера Fp находится левее центра тяжести проводника АС. Поэтому проводник, двигаясь вверх, одновременно будет поворачиваться по часовой стрелке до тех пор, пока не займет вертикальное положение (рис. IX. 12). Далее он будет отталкиваться от бесконечно длинного проводника с током I.
Задача IX.6 Вблизи бесконечного закрепленного прямолинейного проводника с током I перпендикулярно ему помещают проводник АС, как показано на рис. IX.13. Как будет вести себя этот проводник, если по нему пропустить ток t?
Решение. Проводник с током I создает вокруг себя магнитное поле, линии магнитной индукции 328
которого лежат в плоскости, перпендикулярной направлению тока I. Эти линии удобно рассмотреть, если на рис. IX. 13, (а) посмотреть сверху (см. рис. IX.13, б).
Рис. IX.13
На элемент Але, лежащий вблизи точки А, действует сила Ампера РА, направленная вниз 329
(согласно правилу левой руки), а на элемент лежащий вблизи точки С, действует сила Ампера Fc, направленная вверх. Эти обе силы, одинаковые по величине (FA = Fc = iAccBx), будут разворачивать проводник вокруг центра тяжести (точка 0) до тех пор, пока он не займет вертикальное положение (не станет параллельным проводнику с током J). Далее проводник АС будет притягиваться к проводнику с током I (опять же согласно правилу левой руки).
Задача IX.7 Проволочное кольцо радиуса R находится в неоднородном магнитном поле, линии индукции которого составляют в точках пересечения с кольцом угол а относительно нормали к плоскости кольца (рис. IX.14). По кольцу течет ток I. С какой силой магнитное поле действует на кольцо? Индукция магнитного поля в точках пересечения с кольцом равна В.
Решение. На каждый элемент кольца AZ действует
сила Ампера. Эту силу можно разложить на две
составляющие: Fu и Fx (рис. IX.14).
Сила Fu лежит в плоскости кольца, а
Fx = F sin a = IBAl sin a — перпендикулярна
330
плоскости кольца. Результирующая всех сил FIH равна нулю, так как на любые диаметрально расположенные элементы AZ действует одинаковая по величине, но противоположно направленная сила. Эти силы лишь растягивают кольцо, не перемещая его. Результирующая всех перпендикулярных сил
Fpi = F1; = sin а — IB sin Al. = IB sin aZntR.
i=l i=l i=l
Эта сила втягивает кольцо в сторону большего магнитного поля (магнитное поле больше там, где густота магнитных линий больше).
Задача IX.8 Определить силу, с которой действует бесконечно длинный прямой провод с током I на прямоугольный контур с током i, расположенный в плоскости провода. Стороны АВ и DC, параллельные бесконечному проводу, имеют длину а, стороны ВС и DA — дли
ну Ъ. Направления токов указаны на рисунке. Расстояние ближайшей стороны прямоугольника до бесконечного провода сс0 (рис. IX. 15).
331
Решение. Бесконечно длинный проводник с током I создает вокруг себя магнитное поле, вектор магнитной индукции которого о — —--
(п1Х.1). Поэтому на проводник АВ действует сила Ампера
= гВХ1а =
2ла?0 ’
а на проводник CD — сила
[ЩйИа
F, = гВ,?а = —7--------ч .
2я(а?0 + b)
Силы F и F2 направлены вдоль одной прямой, но в противоположные стороны, поэтому результирующая сила, действующая на контур, будет притягивать его к бесконечному проводу:
„ „ „ uuJiaf 1 1
F'= F, - F, = ®—-----------
2л х0 + Ь?
/л/л(}ИаЪ 2ла?0(а?0 + b)
На каждый участок Ab проводника ВС и AD действует сила F; = г'ДЬВ£. Эти силы разные по величине, так как разные величины В. • Однако сумма их всегда равна нулю (см. рис. IX. 15).
Задача IX.9 Положительный заряд q массой т
332
влетает со скоростью v в однородное магнитное поле, перпендикулярно линиям индукции В. По какой траектории движутся частицы в таком магнитном поле?
Решение. На заряд, движущийся в магнитном поле, действует сила Лоренца. По правилу левой руки она перпендикулярна скорости и первоначально направлена вниз, если поле В направлено на нас (рис. IX. 16, а). Эта сила может лишь изменить направление скорости, не меняя ее величины. В любой момент времени она перпендикулярна скорости V. Сила Лоренца сообщает за-
V
ряду нормальное ускорение ап = —, где г — г
радиус кривизны. Так как сила, действующая на заряд, постоянна (F = qvB), то модуль ускорения также постоянен. Это означает, что радиус кривизны г постоянен (при неизменной по величине скорости v), т. е. г = R. Таким образом, траектория должна быть окружностью. Второй закон Ньютона для движущегося заряда запишется:
„ mv2
qvB = man =-—. а.
Это соотношение позволяет определить радиус окружности R:
„ mv2 mv
R —----—----
qvB qB
При этом период вращения частицы
„ 2л: 2 л т
Т = — =-----.
(о qB
333
Как видно из этого соотношения период вращения не зависит от скорости, с которой (б) влетает частица. Это означает, что все частицы, влетевшие в магнитное поле с разными скоростями, но у
которых отношение у равны, будут иметь одина-ковый период, хотя радиусы окружностей, по ко-торым они движутся, разные. Это свойство используется для фокусировки частиц (рис. IX.16, б). Пучок одинаковых частиц, влетевших в магнитное поле в точке А, возвращается в эту точку по разным траекториям
через одно и то же время.
Задача IX.10 Северный полюс магнита со скоростью v приближается к металлическому кольцу. Определить направление индукционного тока в кольце (рис. IX.17).
Решение. Так как при приближении магнита к кольцу увеличивается магнитный поток, пронизывающий контур, то в последнем возникает ЭДС индукции, ток которой по
334
правилу Ленца должен создать свое магнитное поле В , мешающее увеличению потока.
Если поступательное движение буравчика направить по направлению В , то вращательное направление головки буравчика укажет направление индукционного тока I. Он будет направлен против часовой стрелки, если смотреть на контур сверху.
Задача IX.11 В короткозамкнутую катушку один раз быстро, другой — медленно вдвигают магнит. Определить: а) одинаковое ли количество электричества проходит через катушку в первый и во второй раз; б) одинаковую ли работу совершит рука, вдвигающая магнит.
Решение. Как мы выяснили в предыдущей задаче при помещении магнита в короткозамкнутую катушку в последней возникает индукционный ток I, обусловленный появлением в контуре ЭДС индукции, которая определяется скоростью изменения потока, т. е.
|£ I = — инд| At •
Количество электричества, проходящее через катушку:
£ АФ
Q = lAt = At = —
R R ’
определяется только изменением потока АФ и сопротивлением контура.
Эти величины в обоих случаях остаются неизменными, потому и заряд Q, прошедший через
335
катушку, будет одинаковым. При быстром вдвигании постоянного магнита £инд больше, чем при медленном вдвигании (At меньше, а АФ — одинаковое). Это значит, что работа А = <Э£ИНд при быстром вдвигании будет больше.
Задача IX.12 Небольшая проволочная прямоугольная рамка падает в пространстве между широкими полюсами сильного электромагнита так, что ее плоскость параллельна полюсам магнита (рис. IX. 18). Определить направления индукционных токов, возникающих в рамке при прохождении ею положений АА’,
ВВ', СС'. Как будет двигаться рамка на этих участках?
Решение. При падении рамки между полюсами магнита в ней возникают индукционные токи, так как меняется поток магнитной индукции через рамку. При падении сверху магнитный поток уве
336
личивается, значит, в рамке должен возникнуть такой ток, чтобы его поле Ви мешало нарастанию потока. В этом случае ток должен протекать по часовой стрелке (если смотреть на плоскость рамки справа).
При прохождении положения ВВ' — индукционный ток равен нулю, так как поток магнитной индукции постоянен. При движении рамки через положение СС' — поток магнитной индукции уменьшается и следовательно индукционный ток должен двигаться против часовой стрелки. В положении АА’ и ВВ' применяем правило буравчика: поступательное движение буравчика должно совпадать с направлением Ви, а направление вращения головки буравчика указывает на направление индукционного тока.
Как только в рамке возникнет индукционный ток, она уже не сможет падать свободно, потому что на верхнюю и нижнюю стороны рамки действует сила Ампера. В положении АА> сила, действующая на нижнюю сторону, больше силы, действующей на верхнюю сторону, так как внизу магнитное поле больше, чем вверху. Поэтому результирующая сила Fp направлена вверх, и она тормозит движение рамки (рис. IX.18).
Аналогичные рассуждения можно провести и для положения СС>, в котором рамка также будет тормозиться результирующей силой. В положении ВВ’ рамка падает свободно с ускорением g, поскольку ток в рамке отсутствует и на нее сила Ампера не действует.
337
Задача IX.13 Проводники, изображенные на
рис. IX.19, находятся в однородном магнитном
Рис. IX.19
поле, перпендикулярном плоскости чертежа. Когда поле начало уменьшаться (оставаясь однородным), в левом проводнике возникла ЭДС индукции £0. Определить ЭДС
индукции в правом проводнике, если известны площади £0, 5;, и S2. (Магнитные поля, созданные индукционными токами, не учитывать.)
Решение. С изменением магнитного поля В изменяются магнитные потоки, пронизывающие контуры, поэтому в каждом контуре возникает ЭДС индукции:
|₽»| =
АФ _ „ АВ . , , At ” At ’ |S11
АФ АВ
At 1 At
|£2| =
АФ At
AB At
В правом контуре токи индукции направлены в противоположные стороны, поэтому результирующая ЭДС индукции
₽, = ₽.-ft = -•*=)•
Скорость изменения вектора магнитной индукции ^^At легко определить из левого контура:
338
Таким образом, ЭДС индукции в правом контуре
Р о
*^0
Задача IX.14 По двум неподвижным вертикальным рейкам АВ и CD, соединенным сопротивлением R, без трения скользит проводник, длина которого I и масса т. Система находится в однородном магнитном поле, индукция которого В перпендикулярна плоскости рисунка (рис. IX.20). Как будет двигаться подвижный проводник в поле силы тяжести, если пренебречь сопротивлением самого проводника и реек?
Решение. Под действием силы тяжести рейка LK начнет двигаться вниз. Так как через контур LACK будет увеличиваться поток магнт-ной индукции, то в нем возникает индукционный ток I, мешающий увеличению потока через контур. Но на проводник с током в магнитном поле действует сила Ампера F. Таким образом, на подвижный проводник действуют две силы:
339
сила тяжести mg и сила Ампера F = Ц1ВJ. В проекции на вертикальное направление второй закон Ньютона запишется для проводника LK:
mg —ИВ —та, (1)
где ток I определяется
т £ Blv
1 = (СМ.П1Х.8).
rt К
Таким образом:
B2L2v mg------= та,
к
где v и а — это скорость и ускорение в некоторый момент времени. Легко заметить, что ускорение а по мере увеличения скорости будет уменьшаться, и в момент, когда сила Ампера станет равной силе тяжести, ускорение станет равным нулю. С этого момента проводник LK будет двигаться с постоянной скоростью ц0
„ _ mSR
° В2!2
• - А • •
. Ё .
Задача IX.15 По двум металлическим рейкам, расположенным в горизонтальной плоскости и замкнутым на конденсатор С, без трения скользит проводник АВ длиной I и массой т. Вся система находится в однородном магнитном поле, индукция которого В перпендикулярна плоскости ри
.а.
В
Рис. IX.21
340
сунка (рис. IX.21). К середине проводника приложена сила F. С каким ускорением движется проводник АВ ? Сопротивлением проводника АВ и подводящих проводов пренебречь.
Решение. Проводник АВ под действием силы F пересекает линии магнитной индукции, и на его концах возникает ЭДС индукции, равная $ = Blv (см.п!Х.8). В замкнутом контуре АВСА потечет ин-
т А<Э
дукционныи ток J где AQ — заряд на об
кладках конденсатора С, AQ = £ИНДС — BlvC. Поэтому
= В1Са
АВ кроме силы F дей-
i _ BlvC At
На проводник С током
ствует еще сила Ампера FA=IBl. Поэтому
второй закон Ньютона для проводника запишется F-FA=ma, или F — IBl = ma> или F - В212Са = та.
Отсюда ускорение, с которым движется проводник:
F а = ——-----
В212С + т
Как видно из этого соотношения, ускорение является постоянной величиной. Но тогда и ток I — тоже постоянная величина. И возникает вопрос — как может протекать постоянный ток через конденсатор? Дело в том, что по определению ток
AQ
At >
и в нашей задаче он определяется изме
341
нением заряда на конденсаторе С в единицу времени. Поэтому в нашей схеме постоянный ток через конденсатор не протекает, а скорость изменения заряда на конденсаторе остается постоянной, т. е. в цепи справа от конденсатора течет ток I.
Задача IX.16 Прямоугольный контур ABCD со сторонами а и b находится в однородном магнитном
Рис. IX.22
него сверху (рис. IX.22,
поле с индукцией В и может вращаться вокруг оси ОО' (рис. IX.22, а). По контуру течет постоянный ток. Определить работу, совершенную магнитным полем при повороте контура на 180°, если вначале плоскость контура была перпендикулярна магнитному полю и расположена так, как показано на рисунке.
Решение. Для большей наглядности изобразим puc.IX.22, а, взглянув на б). Когда рамка находится
строго перпендикулярно магнитному полю, на ее боковые стороны действуют силы Ампера F, а на верхние — f, которые уравновешивают друг друга. Рамка находится в положении равновесия, но это положение неустойчивое. Стоит рамку вывести из положения равновесия на небольшой угол а, как на нее начнет действовать пара сил, за-
342
—>-F ставляющая ее повер-
нуться на 180°. Эта пара сил совершает работу, которая равна удвоенно-,, _ ч , * t му произведению силы на
в перемещение стороны АВ
Рис 1X22 (или CD) в направлении
силы. Перемещение при повороте контура на 180° равно Ъ. Поэтому работа, совершаемая магнитным полем:
А = 2Fb = 21ВаЪ = 2IBS.
Силы f, действующие на верхние стороны рамки {рис. IX.22, а), работы не совершают, так как они перпендикулярны перемещению этих сторон.
Однако эту задачу можно решить и другим способом. Согласно п!Х.6 работа, совершаемая магнитным полем, А = 1ДФ. Поток магнитной индукции Ф = BnS. Он может быть положительным,
если Вп совпадает с положительным направлением нормали к площадке, и отрицательным, если составляющая Вп противоположна положительному направлению нормали. (За положительное направление нормали п принимают направление поступательного движения буравчика, если его головку вращать по направлению тока.) Поэтому в нашей задаче
ДФ = ф - (- ф) = 2Ф = 2ВаЪ.
Таким образом, магнитное поле совершает работу
А = 1АФ = 21ВаЪ = 2IBS.
343
Как видно, оба решения приводят к одному ответу.
Задача IX.17 В цепи, изображенной на рис. IX.23, ток меняется по закону J = at. Определить разность потенциалов между точками А и В, полагая значения элементов R и L известными.
/Решение. При изменении тока в катушке L возникает ЭДС самоиндукции. Поэтому
<Ра - 'Рв + ^.Ийд = , или
<рА - tpB = IR + L — = atR + La = a(tR + L).
Рис. IX.23
Задача IX.18 В схеме, изображенной на рис.
IX.24, течет ток, меняющийся со временем. (Сле
Рис. IX.24
дует различать ток, меняющийся со временем, и переменный ток, меняющийся по гармоническому закону!) Определить заряд на конденсаторе С в тот момент, когда
£о=5ОВ; 7 = ОДА; — = 400А/с; С = 10~5 Ф.
344
Решение. Воспользуемся замечательным условием электрического поля: работа по перемещению заряда на замкнутом пути равна нулю. Пусть ток в схеме течет слева направо, тогда
IR + L — + U-$ = 0.
At
Отсюда в любой момент времени
U =$ —IK —L —. с At
Заряд же на конденсаторе определяется по формуле Q = CUc.
В момент времени, заданный в задаче, этот заряд
Q = C[£ - 16R - L j = 10“5 Ф • (50 - 20 - 0,01 • 400) В = \ 1л1 /
= 26-10"5 Кл-
Задача IX.19 По участку АВС (рис. IX.25, а) протекает синусоидальный ток. На участке АВ амплитуда напряжения
A R В с Uas =30В’ а на Уча-
*—* *—* ' 0000 стке ВС— UBC = 40 В.
Определить ампли-
Рис IX 25 ТУДУ напРяжения на
участке АС.
Решение. Через элементы R и L протекает один и тот же ток I = IQ sin (i)t. Воспользуемся методом векторных диаграмм и отложим вектор амплитуды тока 10 по
345
Рис. IX.25
UAC горизонтали (рис. IX.25, б). Тогда напряжение на (б) сопротивлении R, совпадающее по фазе с то-Uro ком, изобразится вектором URq = I0R. Напряжение на индуктивнос-
ти опережает ток, протекающий через индуктивность, и его амплитуда изобразится вектором ULq = Амплитуда напряжения на участке АС
^АСО ^Ro Ulq > ИЛИ
Ы=А;+= Л3»)2+<4°)г = so в
напряжения станет в два раза
видно из рисунка:
_ ULo _ I0(i)L _ (i)L
Задача IX.20 На участке АС в схеме, изображенной на puc.IX.25, а, сдвиг фаз между током и напряжением ср = 30°. Как изменится эта величина, если частота больше?
Решение. Как
tg <Р
'-'Ко ‘0’“'
При увеличении частоты в два раза tg <рх = 2tg <р = 2tg30° = -i.
V 3
Следовательно:
2
<pv = arc tg—т= & arc tg 1,15 ~ 49°.
346
Задача IX.21 В схеме, изображенной на рис. IX.26, a, R ~ 20 Ом, L = 0,2 Гн, С = 100 мкф, амплитуда напряжения 170 = 75В, а частота f = 50Гц. Определить амплитуду тока, протекающего в этой схеме, разность фаз между напряжением и током и общее сопротивление цепи.
Рис. IX.26
Решение. Все элементы схемы включены последовательно, поэтому через них протекает один и тот же ток I = Io sincwt.
Для решения задачи воспользуемся методом векторных диаграмм. Отложим горизонтально амплитуду тока Jo (рис. IX.26, б). Напряжение на сопротивлении совпадает по фазе с током. Напряжение на индуктивности ULQ опережает ток на 90°, а напряжение на емкости Uco отстает от него на 90°. Результирующее напряжение определяется правилом сложения векторов. Как видно из рисунка:
347
I-------------------- I / -f \ 2
Ц, = + К - M = I« A «2 + - -7;
\ CtzV-x f
Отсюда Io = -........-—°......... = , (1)
/ 1 у Z
JR2 +1 a>L---------1
V \
где Z — JR2 + ^<yL — — общее сопротивле
ние этой схемы.
Напряжение общее меняется по закону U = UQ sin(<yt + <р).
Рис. IX.26
Сдвиг фаз между общим напряжением U и то ком легко определяется из рис. IX.26, б:
348
Ы ~ Uoc _ Io(OL соС _ _
Ц>к I0R R
(63-32) Ом +
=------------= 1,5, = arc tg 1,5 = 57 .
200 0м г
Общее сопротивление цепи
I ( 1 V
Z — л R2 + coL---------1 = 37 Ом
V \ <оС/
Амплитуда тока в этой схеме определяется из закона Ома по формуле (1):
£<,=^5В = 2а
0 Z 37 Ом
Задача IX.22 От середины катушки с большим
Рис. 1Х.27
числом витков и железным сердечником сделан отвод С (рис. IX.27). Между точками В и С подается один раз постоянное напряжение Uo, а другой раз — переменное напряжение с амплитудой UQ. Определить в обоих случаях напряжение между точками А и В.
349
Решение. В общем случае напряжение между точками А и В
С.в = UАС + UCB . /Ю /11» к» о
При подключении постоянного напряжения Uo ток протекает только по участку СВ, создавая напряжение UCB = Uo. По участку СА ток не течет, так как концы А и В разомкнуты. Поэтому
иАВ = о + ис = и0. AU l»D U
Если между точками С и В приложить переменное напряжение с амплитудой Uo, то протекающий по участку СВ переменный ток создает в сердечнике переменный магнитный поток, который на участке АС создает ЭДС индукции.
Поскольку на участке АС витков столько же, сколько и на участке ВС, то амплитуда напряжения
Uab=U0+U0=2U0.
X. ОПТИКА
§ 1. Геометрическая оптика
пХ.1 Закон отражения1, падающий луч, отраженный луч и перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Угол отражения равен углу падения (рис. Х.Г).
350
Закон преломления: падающий луч, преломленный луч и перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение синуса утла падения а к синусу угла преломления есть величина постоянная для двух данных сред, т. е.
sin а п?
——~ “ = п , где п1 =
sm р пг
абсолютные показатели преломления, которые указывают, во сколько раз скорость света в данной среде меньше скорости света с в вакууме, п — относительный показатель преломления.
пХ.2 Явление, при котором падающий на поверхность раздела двух прозрачных сред свет полностью отражается от этой поверхности, называется полным отражением. Закон преломления для этого случая имеет вид:
sm ап п?
-----= — = п, или sm а sin 90°
п2
где «о — предельный угол полного отражения.
Полное отражение наблюдается при переходе луча из более плотной среды в менее плотную.
Для границы раздела среда — воздух sina., = — п,
351
Рис. Х.2
пХ.З Для тонкой призмы (с малым преломляющим углом <р) угол между первоначальным направлением падающего луча и преломленным лучом (угол у) равен (рис. Х.2):
У = <р(п - 1) .
Различные длины волн имеют разные показатели преломления, поэтому белый свет, падающий на призму, разлагается ею на много цветов, образуя спектр, причем красный цвет отклоняется на меньший угол по сравнению с другими цветами (рис. Х.З).
пХ.4 В собирающей линзе падающие на нее лучи, параллельные главной оптической оси, сходятся по другую сторону линзы в одной точке, называемой положительным (действительным) фокусом F (рис. Х.4).
352
В рассеивающей линзе падающие на нее параллельные лучи становятся расходящимися. Воображаемое продолжение этих лучей пересекается в точке, расположенной с той же стороны линзы, с которой падают параллельные лучи. Эта точка называется отри
цательным (мнимым) фокусом (рис. Х.5).
пХ.5 Формула тонкой линзы
1 1-1
d + f ~ F’
где d — расстояние от источника до линзы, / — расстояние от линзы до изображения. Формула справедлива для рассеивающей и собирающей линзы. Однако для собирающей линзы значение F берется с положительным знаком, а для рассеивающей — с отрицательным.
Если изображение мнимое, то перед значением f всегда нужно ставить знак «~» для любой
12 Физика
353
линзы. Расстояние от источника до линзы d обычно берется положительным, однако если на любую линзу падает пучок сходящихся лучей, то расстояние d берется со знаком «-».
§ 2. Элементы физической оптики
пХ. 6 Световое излучение — это электромагнитные волны, распространяющиеся в различных средах. По теории Гюйгенса — Френеля каждую точку пространства, которой достигла волна, можно рассматривать как источник вторичных волн, распространяющихся по всем направлениям. Огибающая всех вторичных элементарных волн представляет собой новый волновой фронт в некоторый момент времени. Вторичные волны могут складываться (рис. Х.6).
Рис. Х.6
354
Сложение двух волн, вследствие которого наблюдается усиление или ослабление результирующих колебаний в различных точках пространства, называется интерференцией волн.
Устойчивую, не изменяющуюся со временем картину чередования максимумов и минимумов (интерференционную картину) можно наблюдать только в случае сложения когерентных волн, т. е. волн, имеющих одинаковую частоту и неизменный сдвиг фаз.
Если разность расстояний, прошедших волнами от источника до точки наблюдения (или разность хода А = d2 - ф двух когерентных волн), равна целому числу длин волн, то в некоторой точке пространства наблюдается максимум освещенности Д = гпЛ (точка В на рис. Х.7).
Если же эта разность хода равна полуцелому числу длин волн, то в точке наблюдения (В') находится минимум освещенности, т. е.
А = | т + — |Я \ 2/ ’
где т = 0,1,2,3,....
пХ.7 Зоны Френеля. Задачу о прямолинейном распространении света Френель решил, полагая,
Рис. Х.7
12*
355
что вторичные волны интерферируют между собой. Он применил очень наглядный прием, заменяющий сложные вычисления. Этот прием получил название «метод зон Френеля». Поскольку этот материал для абитуриентов мало известен, а задачи на вступительных экзаменах на эту тему уже предлагаются, следует немного подробнее остановиться на методе зон Френеля.
Пусть световая волна распространяется из точки А к какой-либо точке наблюдения на экране 0. На пути распространения волн находится непрозрачный экран с малым круглым отверстием. Если источник света А точечный и монохроматический, а среда изотропна, то фронт волны в любой момент времени будет иметь форму сферы радиуса г = vt, где v — скорость распространения волн. Каждая точка этой сферической поверхности является вторичным источником волн. Колебания во всех точках волновой поверхности происходят с одинаковой частотой и в одинаковой фазе. Следовательно, все эти вторичные источники волн когерентны. Для нахождения амплитуды колебаний в точке 0 необходимо произвести сложение когерентных колебаний от всех вторичных источников на волновой поверхности. Так как расстояния от точки 0 до различных участков волновой поверхности не одинаковы, то колебания от них в точку 0 будут приходить в различных фазах. Для нахождения результата интерференции колебаний от вторичных источников Френель предложил метод разбиения волнового фронта на зоны. Выделим мысленно некоторую поверхность MN.
356
Обозначим расстояние от точки 0 до ближайшей точки волновой поверхности через т0. Разбиваем поверхность NM на зоны такого размера, чтобы расстояния от точки наблюдения 0 до краев последующих зон отличались на Л/2, т. е. первая зона ограничивается точками волновой поверхности, которые находятся от точки наблюдения О
на расстоянии rt = т0 + (рис. Х.8), вторая зона расположена между краями первой зоны и точками волновой поверхности, расположенными от точки 0 на расстоянии т2 = = г0 + А и т. д.
Рис. Х.8
Построенные таким образом зоны имеют одинаковые площади и одинаковые амплитуды колебаний. Но, так как разность хода от двух соседних зон равна А/2, то колебания от них приходят в точку наблюдения в противоположных фазах, а это значит, что если в отверстии экрана укла
357
дываются две зоны, то в точке наблюдения 0 будет минимальная освещенность, так как колебания двух зон компенсируют друг друга. Таким образом, следует ожидать, что если отверстие в экране открывает четное количество зон, то результирующая освещенность в точке наблюдения О будет минимальной, а если нечетное — то максимальной. Результирующее действие световой волны в точке наблюдения 0 очень удобно оценивать, пользуясь графическим способом сложения колебаний, обладающих некоторым сдвигом фаз. Для этого каждую зону разбивают на равные участки столь малые, чтобы фаза колебаний каждого такого участка в точке наблюдения 0 практически оставалась постоянной. Тогда действие всего этого малого участка можно выразить вектором, длина которого дает суммарную амплитуду, а направление определяет фазу, обусловливаемую этим участком. Действие соседнего участка может быть выражено вторым вектором, несколько повернутым относи-
В тельно первого, так как фаза,
D определяемая действием вто-
рого участка, будет немного отличаться от фазы первого. По длине этот вектор практически не отличается от первого. Векторная диаграмма, оп-ределяющая действие ряда участков, составляющих це-А лую зону, изобразится лома-
Рис X 9 ной линией, представленной на
рис. Х.9, а. Результирующая
358
амплитуда колебаний отдельной зоны в точке наблюдения 0 выразится вектором АВ. При разбиении зоны на бесконечно большое число бесконечно малых участков ломаная линия будет стремиться к полуокружности (рис. Х.9, а),
а результирующая ампли-туда колебаний равна диаметру этой полуокружности. Для учета действия второй зоны надо продолжить векторную диаграмму. С учетом возрастающего наклона второй зоны результирующее колебание только этой зоны в
точке наблюдения 0 отразится вектором ВС. Суммарное действие двух зон определяется вектором
АС (рис. Х.9, б)
Результирующая амплитуда колебаний большого числа зон в точке наблюдения 0 изобразится
вектором AD. Легко заметить, что этот вектор равен половине вектора открытой только одной центральной зоны
АВ (рис. Х.9, в).
359
D Хорошим доказательством справед-
' ливости предложенного Френелем ме-
I тода является зональная пластинка. Эта С пластинка представляет собой экран, л 'v состоящий из последовательно череду-] ющихся прозрачных и непрозрачных
В колец, радиусы которых равны радиу-м сам соответствующих зон Френеля.
) Если пластину поместить в соответству-ющем месте сферической волны так, А чтобы она закрывала четные зоны
Рис. Х.10 Френеля, то в точке наблюдения 0 результирующая амплитуда будет намного больше, чем амплитуда одной открытой центральной зоны (рис. Х.10).
Если вместо непрозрачного экрана с отверстием на пути волны поставить экран малых размеров без отверстия, то первая зона Френеля строится от края экрана до линии пересечения волновой поверхности с конусом, образующая которо-1 / го равна го + /2 , вторая зона — до конуса с обра-i /
зующеи Л + /2 и т- Д- Причем т0 — расстояние от точки наблюдения 0 до края непрозрачного экрана (рис. Х.11). Повторяя предыдущие рассуждения при графическом способе сложения колебаний, получим, что амплитуда света в точке наблюдения 0 равна половине амплитуды, обусловленной одной открытой первой зоной. Другими словами, если в точке наблюдения 0 поставить экран перпендикулярно направлению АО, то на нем
360
будет чередование светлых и темных колец, но в точке наблюдения 0 будет всегда свет, несмотря на то, что между источником А и точкой наблюдения 0 на пути распространения волны стоит непрозрачный экран. Французс
кий физик Пуассон, изучив труды Френеля, ут
верждал, что теоретическое предсказание появления света в точке наблюдения является доказательством несостоятельной теории Френеля, однако другой французский физик Араго специально поставленным опытом доказал реальность существования светлого пятна в центре геометрической тени. Таким образом, теория Френеля была доказана.
Однако для экспериментального наблюдения этого светлого пятна (его часто называют пятном Пуассона) необходимо, чтобы размеры непрозрачного экрана были сравнимы с размерами первой зоны Френеля, а размеры шероховатостей на его краю не превышали длины световой волны.
пХ.8 Дифракционная решетка. Огромную роль в прикладной оптике играют явления дифракции на отверстиях в виде щели с параллельными краями. Рассмотрим сначала дифракцию в параллельных лучах на одной узкой щели.
361
Пусть на щель, длина которой намного больше ее ширины, падает монохроматический параллельный пучок света. Все точки волновой поверхности, достигшей щели, являются источниками вторичных волн, колеблющихся в одинаковой фазе (волновая поверхность представляет собой плоскость, перпендикулярную падающим параллельным лучам). За счет дифракции (огибания) свет после прохождения щели распространяется во всех направлениях. Для наблюдения дифракционной картины за щелью помещают собирающую линзу, а за ней в ее фокальной плоскости — экран {рис. Х.12). Рассмотрим параллельные лучи, идущие от различных точек щели под углом <р к вертикали. Эти лучи, пройдя через линзу, соберутся на экране в некоторой точке А. Однако в точку А волны приходят с неодинаковыми фазами, так как оптические пути их различны. Поскольку линза не изменяет длины оптического пути, то разность хода световых лучей от точек В и С щели определяется расстоянием ВО. Если разность хода Д = ВО = Л/2, то ВС = х является шириной зоны Френеля. Тогда в щели шириной а содержится п = зон Френеля, причем колебания от двух соседних зон, приходящих в точку А, имеют разность хода 2/2.
Поэтому если на щели укладывается четное число зон, то в точке А происходит гашение колебаний, и освещенность будет равна нулю. Если же число зон нечетное, то колебания от одной из зон останутся непогашенными и в точке А будет 362
Рис. Х.12
наблюдаться некоторая освещенность (максимум освещенности).
Из треугольника BDC видно, что
BD /4 Л
---= = sm <р, или х =-------.
ВС х 2 sin (р
Если число зон на щели четное, т. е. п — 2т, то
„ 2а sin <р . ,
п = 2т =--------- и соотношение a sm (р = тл (2)
363
является условием минимума освещенности от одной щели. При нечетном числе зон наблюдается максимум освещенности. В этом случае выполняется соотношение
. . \ 2а sin® . /п
п - (2т +1) =------, или a sm <р = (2т + 1) —. (3)
Л 2
Это условие максимума освещенности.
Таким образом, на экране будет наблюдаться
чередование максимумов и минимумов освещенности. Распределение интенсивности на экране показано на рис. Х.12, б.
Далее предположим, что имеются две одинаковых щели шириной а, разделенных непрозрачным промежутком Ъ (рис. Х.13), на которые падает плоский фронт монохроматической волны. При
Рис. Х.13
364
достижении фронтом плоскости, в которой находятся щели, все точки его можно рассматривать как источники вторичных волн. Если для какого-либо направления <р выполняется условие минимума освещенности для одной щели, то оно будет выполняться и для двух щелей. В этом направлении каждая щель в отдельности света не дает. Это условие для двух щелей называют условием прежних минимумов. Это условие справедливо и для любого числа щелей.
А вот там, где каждая щель в отдельности давала свет, при наличии двух щелей может быть и свет, и темнота. Рассмотрим две точки А и С, находящиеся на расстоянии d = а + Ъ.
Если разность хода для лучей, исходящих из этих точек равна mA, т. е.
А = d sin <р = mA, (4)
то свет от точек В и С при интерференции в точке А будет давать максимум освещенности. Соотношение (4) является условием главных максимумов. Это соотношение справедливо для любого количества щелей (как и условие для прежних минимумов).
Если же эта разность хода равна нечетному числу полуволн, то наблюдается минимум освещенности в точке А, т. е.
. \ А
d sin <р = (2m + 1) —.
2
Это условие для дополнительных минимумов, так как в случае одной щели в этом направлении на экране был свет. Распределение освещенности
(5)
365
на экране при наличии двух щелей показано на рис. Х.13, б.
а) одна щель
(б) б) две щели
Рис. Х.13
Совокупность большого числа узких щелей, разделенных непрозрачными промежутками, называется дифракционной решеткой. С увеличением числа щелей главные максимумы и прежние минимумы остаются на прежних местах, но максимумы становятся ярче, а промежутки между ними все темнее. С увеличением числа щелей увеличивается число дополнительных минимумов. Максимумы света на экране располагаются симметрично относительно центрального максимума, для которого т = 0. Максимумам присваивают номера, соответствующие значениям т. Раз
366
личают максимумы первого, второго и т. д. порядков. При освещении дифракционной решетки белым светом максимумы одного и того же порядка для различных длин волн будут наблюдаться в различных направлениях. Это значит, что дифракционная решетка разлагает свет сложного состава в спектр. Из формул (2~5) видно, чем больше длина волны А, тем на больший угол отклоняются лучи.
Дифракционная решетка позволяет очень точно определять длины волн, если известна постоянная решетки и углы отклонения лучей.
Задача Х.1 Перед зеркалом воткнуты две булавки А и В, как показано на рис. Х.14. Какое
Рис. Х.14
367
расположение изображений этих булавок увидит наблюдатель при различных положениях глаза? Как он должен расположить глаз, чтобы изображения булавок накладывались друг на друга?
Решение. Угол, в пределах которого глаз увидит ту или иную точку, определяется размерами зеркала. Чтобы найти этот угол, нужно провести лучи из точек А и В к краям зеркала и построить отраженные лучи. Эти отраженные лучи обязательно пересекутся там, где находится изображение искомой точки. Так, изображение точки А наблюдатель сможет увидеть в пределе угла АА'А, изображение точки В — в пределах угла ВВ'В. В той области пространства, где эти углы перекрываются, наблюдатель увидит две точки одновременно. Если наблюдатель смотрит вдоль линии, проходящей через изображения А' и В' булавок в зеркале, то он увидит эти изображения слившимися. Если он поместит глаз выше линии А' В’, то он увидит изображение булавки А слева от изображения булавки В. Если же он поместит глаз ниже линии А' В', то он увидит изображение булавки А справа от изображения булавки В.
Задача Х.2 На стене висит зеркало высотой h, = 1 м. Человек стоит на расстоянии а = 2 м от зеркала. Какова высота Н участка противоположной стены, который может видеть в зеркале человек, не изменяя положения головы? Стена находится на расстоянии Ъ = 4 м от зеркала (pwc. Х.15).
Решение. Максимальные размеры участка стены, которые сможет увидеть наблюдатель, опре-
368
Рис. Х.15
деляются лучами, попадающими в глаз наблюдателя, которые отразились от концов зеркала. Однако для наблюдателя эти лучи кажутся выходящими из точек А! и В'. Все остальные лучи, исходящие из точек между точками А и В, также попадают ему в глаз (см. рисунок).
Из подобия треугольников ADB и СОК видно: h _ а ~Н~ а + Ъ'
Таким образом:
h(a + b)_l(2 + 4)
н--------------------бм.
а 2
Задача Х.З Какой наименьшей высоты должно быть плоское зеркало, укрепленное вертикально на стене, чтобы человек мог видеть свое отражение в нем во весь рост, не изменяя положения
369
головы? На каком расстоянии от пола должен быть нижний край зеркала?
Решение. Для того чтобы увидеть свое изображение в полный рост, зеркало должно быть такой величины, чтобы луч от ног человека, идущий в нижний край зеркала и отраженный от него, попал в глаза человека (рис. Х.16). Луч, идущий от головы, должен при отражении от верхнего края зеркала попасть в глаз человеку. Из подобия треугольников А'АВ и CA'D видно, что CD = А В/2 = ^^2 ~ ^2’ т’ е' РазмеРЬ1 зеркала должны быть в два раза меньше роста человека. Расстояние от нижнего края зеркала до пола должно быть равно половине расстояния от глаз человека до его ступней.
Рис. Х.16
Задача Х.4 Пловец, нырнувший с открытыми глазами, рассматривает из-под воды светящуюся
370
лампочку, находящуюся над его головой на расстоянии h = 75 см от поверхности воды. Каково будет кажущееся расстояние Н от поверхности воды до лампочки? Показатель преломления воды
п = 1,33 (рис. Х.17).
Решение. Рассмотрим некоторый луч SA, падающий под малым углом а на границу раздела воздух — вода. Этот луч преломится под углом 0 и попадет в глаз человеку. Но для человека луч выходит из точки S', которая находится на пересечении двух лучей S' 0 и S' А. Любое изображение можно получить с помощью двух лучей: один
луч пускаем перпендикулярно границе раздела 50 — он отражается в обратном направлении, второй луч выбираем SA, он преломляется, и продолжение преломленного луча пересекается с лучом 0 S' в точке S'. Эта точка и является кажущимся расположением источника 5.
Рассмотрим прямоугольные треугольники А50 и А 5'0. Они имеют общую сторону 0А, которая равна 0А = h - tg а = Н • tg Таким образом,
Н tga а
— =-----~ — — п
h tgfi 0
(так как углы малы, можно считать
371
tga since a _
tg /3 sin /3 fl П
Следовательно, H = nh = 0,75 • 1,33 = 1м.
Задача X.5 На дне сосуда глубиной d, наполненного водой, лежит монета. На какой высоте h
от поверхности воды следует поместить электрическую лампочку, чтобы ее изображение, давае
мое лучами, отраженными от поверхности воды, совпадало с изображением монеты, даваемым преломленными лучами? Как можно непосредствен-
0
Рис. Х.18
ным наблюдением по вертикали установить совпадение изображений лампочки и монеты? (рис. Х.18)
Решение. Направим любой луч 0А на поверхность воды от монеты. Тогда он выйдет из воздуха под углом а (луч АВ). По этому же направлению должен пой
ти и отраженный от поверхности воды луч, падающий в точку А из источника S. Второй луч от
монеты направим перпендикулярно поверхности воды. Тогда пересечение продолжения луча 0' В с 0'5 в точке 0' даст изображение монеты и источника S одновременно. Если совпадение изображений монеты и источника S случайно, то, пе
372
ремещая глаз по вертикали, мы увидим, что изображения смещаются относительно друг друга (задача Х.1). Искомое расстояние h легко определить из треугольников SCA и О' СА, имеющих общую сторону С А:
, , , dig в d
htg а = dtg р, или h = —= — •
tga n
Задача Х.6 На дне водоема, имеющего глубину Н = 3 м, находится точечный источник света.
Какой минимальный радиус R должен иметь круг-
лый непрозрачный диск, плавающий на поверхности воды над источником, чтобы с вертолета нельзя было обнаружить этот источник света? Показатель преломления воды п = 1,33 (рис. Х.19).
Решение. Чтобы
Рис. Х.19
лучи от источника не попали в воздух, они должны падать под углом, большим угла полного отражения, т. е.
1 х R
sm а > —. Так как tga = —, отсюда
R = Н
Н sin а _ Н sin а cos a Vl — sin2 а
Н
>1п2 —1
= 8,9 м.
Задача Х.7 Луч света падает на стеклянную пластинку с показателем преломления п под уг-
373
лом а. Толщина пластины d. Определить, насколько сместился вышедший из пластины луч относительно падающего (рис. Х.20).
Решение. Луч, вышедший из плоскопараллельной пластины, параллелен падающему
Рис. 10.20 лучу. Это легко пока-
зать. Действительно, согласно закону преломления
sin a sin Д 1
—— = п, а ------= —.
sm р sm у п
Перемножив эти соотношения, получим sin a sin _ sin sin у
Следовательно, sin а = sin у и углы также равны а = у.
Таким образом, луч из плоскопараллельной пластины выходит под тем же углом, что и падает на нее. Однако он смещается на некоторое расстояние I. Определим это расстояние.
Опустим из точки D перпендикуляр DE на выходящий из пластины луч. Из треугольника CDE имеем (рис. Х.20):
DE — I = CD cos а = (BD — ВС) cos а =
= (d tga — d tgj3)cos« =
374
d sin a(-\lnz — sin2 a — Vl — sin2 a) = d(tg a - tg 0) cos a =--*----======------------L
yn —sin a
Из этого соотношения видно, чем тоньше пластина, тем на меньшее расстояние сместится луч, выходя из пластины. Если толщина пластины d стремится к нулю, то можно считать, что луч практически не смещается.
Задача Х.8 На расстоянии d = 40 см от тонкой собирающей линзы находится предмет высотой h = 10 см. Определить величину изображения И, если фокусное расстояние линзы F = 15 см (рис. Х.21).
Рис. Х.21
Решение. Любое изображение точки в линзе можно получить с помощью двух лучей. Мы воспользуемся двумя из трех «замечательных» лучей, ход которых через линзу мы всегда знаем. Таковыми лучами являются: 1) луч, идущий от источника, параллельный главной оптической оси,
375
после линзы проходит через фокус (луч АВ А<); 2) луч, идущий через оптический центр линзы, не преломляется (луч АО А'); 3) луч, идущий через фокус, после линзы выходит параллельно главной оптической оси (луч АС А' ). С помощью любых двух из этих лучей мы получаем изображение точки А. Изображение точки К получим в результате пересечения луча, проходящего через оптический центр К К' и перпендикуляра АК', опущенного на главную оптическую ось.
Воспользовавшись формулой линзы, получим расстояние, на котором находится изображение предмета А' К' от линзы (/) (см.пХ.5):
— + — = Отсюда f =----= 24см.
d f F J d-F
Из подобия треугольников АКО и А' К'О легко получить увеличение линзы к- :
_ А'К' _ Н _
“ АК _5r~d-40~5'
Следовательно, величина изображения
тт _ , 37г
Н = kh = — = 6 см .
5
Задача Х.9 На рисунке показан источник S и его изображение S'. Определить построением положение оптического центра линзы и каждого из ее фокусов в случаях, когда главной оптической осью линзы являются прямые 1 — 1', 2 — 2', 3 — 3' (рис. Х.22, а).
376
Решение. По сути дела, 1----------------1
в этом условии содержится •
три задачи. Рассмотрим их. 2 --------------2’
1. Главной оптической f
, 3 3'
осью является прямая 1 — 1.
Если внимательно посмот- (а)
реть на рисунок Х.22, (б), рис х 22 то можно заметить, что
источник и изображение всегда лежат на одной прямой .S' S', которая пересекает оптическую ось в точке, где находится оптический центр линзы. Поэтому в нашем случае, продолжив прямую S S' до пересечения с главной оптической осью 1 — Г,
получим место нахождения оптического центра линзы О. Далее из источника S проведем луч SB, параллельный главной оптической оси. Согласно рис. Х.22, (б), прямая, прошедшая через точку В и изображение S',
обязательно пройдет через фокус линзы, который находится на пересечении этой прямой с главной
оптической осью. Аналогично, если провести пря
мую S' В', параллельную главной оптической оси, а затем соединить точку В' с источником S, то прямая В' S пересечет главную оптическую ось во втором фокусе линзы.
377
Внимательно посмотрев на рисунок, заметим, что предмет находится между фокусом и линзой, поэтому изображение S' является мнимым, а линза — собирающая.
2. Главной оптической осью является прямая 2-2'. Повто
рим построения, проведенные при решении предыдущей задачи, по
лучим, что изображение S' является действительным, а линза — собирающая (рис. Х.22, в).
3. Главной оптической осью
является прямая 3-3'. Вновь проведем аналогичные построения: соединим прямой S и Sf и продолжим ее до пересечения с точкой О; из источника S проведем прямую SB, параллельную главной оптической оси 3-3'. Точку В соединим с S' и продолжим до пересечения с главной оптической осью
3-3', определяя местополо-
жение фокуса F. Из рис. Х.22, (г) мы видим, что источник находится за фокусом, его изображение
мнимое, следовательно, линза — рассеивающая.
Задача Х.10 Где следовало бы расположить предмет, чтобы собирающая линза дала его прямое изображение в натуральную величину?
378
Рис. Х.23
Решение. Все предметы, находящиеся за фокусом F, дают перевернутое изображение. Прямое изображение получается, когда предмет помещают между фокусом и линзой. В этом случае изображение будет мнимым. Проследим движение изображения при приближении предмета к линзе (рис. Х.23). Изображение будем строить по двум «замечательным» лучам: 1) луч, параллельный главной оптической оси АС, после линзы проходит через фокус; 2) луч, проходящий через центр линзы АО, нигде не преломляется. Направление луча CF при любом положении предмета остается неизменным. Луч, проходящий через оптический центр линзы О, по мере приближения предмета к линзе постепенно поворачивается вокруг точки О, составляя с оптической осью все больший угол. Поэтому, если предмет поместить в плоскости, проходящей через оптический
379
центр, то его изображение будет прямым и в натуральную величину.
Задача Х.11 Построить изображение отрезка АВ, параллельного главной оптической оси собирающей линзы с заданным положением фокусов (рис. Х.24).
Решение. Для получения изображения предмета АВ достаточно построить изображение его конечных точек А и В. Это легко сделать с помощью двух «замечательных» лучей. Один луч проведем через оптический центр О, а другой — через фокус F. Соединим точки А' и В' прямой, которая и представляет собой изображение предмета АВ.
Задача Х.12 Через круглое отверстие в экране проходит сходящийся пучок лучей. Лучи пе-
Рис. Х.24
ресекаются в точке А, лежащей на расстоянии а = 15 см от экрана. Как изменится расстояние от точки встречи лучей до экрана, если в отверстие
380
вставить собирающую линзу с фокусным расстоянием F = 30 см? Построить ход лучей после установки линзы (рис. Х.25).
Решение. Для построения изображения точки А выберем два вспомогательных луча: один луч ВА — это луч, проходящий через точку А параллельно главной оптической оси О О'; второй луч — СА, проходящий через точку А и центр отверстия (он же и будет центром линзы). Точка пересечения этих лучей после линзы определит новое положение вершины пучка А'. Эта точка является изображением точки А (рис. Х.25).
Так как на линзу падает сходящийся пучок света, то расстояние от линзы до источника А
381
следует брать со знаком «-», т.е. d = — а. Тогда положение точки А' определится из формулы линзы:
— + — ~ Отсюда — = — ч—, или
-a f F f F а
Fa _ 30-15 а + f ~ 45
= 10 см.
Таким образом, точка А' переместится на расстояние А = а — / = 5см ближе к линзе.
Задача Х.13 Точечный источник S находится на главной оптической оси за фокусом. Определить построением его изображение: а) в собираю-
щей линзе, б) в рассеивающей линзе.
Решение. Для построения изображения проведем в обоих случаях из источника любой луч в некоторую точку М
(рис. Х.26). Далее проведем побочную ось ЬЬ', параллельную проведенному лучу SM. Эта ось пересечется с фокальной плоскостью в некоторой точке /, но для собира
382
ющей линзы эта точка f лежит справа от линзы, а для рассеивающей — слева от линзы. Тогда луч Mf пересечет главную оптическую ось в точке, где находится изображение S'. Так как любое изображение можно построить по двум лучам, то второй луч выберем идущим из источника S вдоль главной оптической оси. Оба луча SM и 5 S' пересекутся в точке S', которая является изображением. Для собирающей линзы в нашем случае изображение действительное, для рассеивающей — мнимое.
Задача Х.14 Найти построением положение светящейся точки, если известен ход двух лучей после их преломления в линзе (рис. Х.27\ Один
из этих лучей (луч 2) проходит через фокус.
Решение. Лучи, выходящие из линзы, для человеческого глаза кажутся исходящими из точки S', которая является изображением источника и лежит на пе
ресечении лучей 1 и 2. Мы уже знаем (задача Х.8), что источник 5 и изображение S' лежат на одной прямой, проходящей через оптический центр, поэтому проведем луч S' О'. Так как луч 2 проходит через фокус, то до линзы он обязательно должен
383
идти параллельно главной оптической оси О О'. Поэтому, если мы проведем прямую АВ, параллельную главной оптической оси О О', то она пересечет луч S' О' в точке S, которая и является местом положения светящейся точки.
Задача Х.15 Собирающая линза положена на плоское зеркало. Где нужно поместить точечный источник, чтобы изображение его, даваемое этой системой, было действительным и совпало с самим источником (рис. Х.28)?
Решение. Чтобы изображение совпало с источником после отражения, лучи должны пройти по тому же пути, что и до отражения. Это произойдет только в том случае, если лучи на зеркало после прохождения линзы падают перпендикулярно. Это означает, что после линзы лучи выходят параллельно оптической оси О О'. Следовательно, источник должен находиться в фокусе.
Задача Х.16 Собирающая линза вставлена в круглое отверстие в непрозрачной ширме. Точечный источник света находится на главной оптической оси линзы на расстоянии d = 10 см от нее. По другую сторону линзы на таком же расстоянии d от нее поставлен перпендикулярно к этой оси экран. На экране виден светлый круг, диа-
384
метр которого в п — 2 раза меньше диаметра линзы. Определить фокусное расстояние линзы F.
Решение. В этой задаче возможны два решения: лучи падают на экран расходящимся пучком (d<f, рис. Х.29, а)
и сходящимся (d>f, рис. Х.29, б). Рассмотрим
первый случай. Из подобия треугольников AS'В
с' АВ и С S D имеем: -
CD
1 1 мулу линзы ~ + у
----= п = 2. Вспомним фор-ci-/
1
- ~ и , подставив в нее выра-
. _ nd жение для J - получим
13 Физика
385
F = nd (2n + 1) = 4 cm .
Рассмотрим второй случай. Из подобия треу-
АВ _ f гольников AS'В и CS' D имеем ~ - п,
отсюда f -
dn
п -1
. Подставив значение f в форму-
лу линзы, получим
F = dn (2п — 1) = 6,7 см.
Задача Х.17 Сходящийся пучок лучей, проходящий через отверстие радиусом г = 5 см в непрозрачной ширме, дает на экране, располо-
женном за ширмои на расстоянии Ъ = 20 см, светлое пятно радиусом R = 4 см. После того как в отверстие вставили линзу, пятно превратилось в точку. Найти фокусное расстояние F линзы (рис. Х.30).
Решение. Точка S, в которой сходятся лучи
при отсутствии линзы,
является мнимым источником, находящимся на расстоянии d от ширмы. Из подобия треугольников ASB и CSD получим
Т “ Т^ь(при ь < d}’ (1)
386
или
2r 2R
~d=b^d (при ъ > d}- <2)
Воспользуемся формулой линзы:
d Ъ~ F ‘
Значение фокуса берется со знаком «+», так как неизвестно, какая должна быть линза. Решая сначала систему уравнений (1) и (3), а затем систему (2) и (3), получим
гЪ
F = ±— = ±25 см.
R
Знак «+» соответствует случаю b < d и указывает на то, что в отверстие следует вставить собирающую линзу, знак «-»— рассеивающую.
Задача Х.18 Два когерентных источника света 51 и S2 расположены на расстоянии I друг от дру
га. На расстоянии D » I от источника помещается экран. Определить расстояние между соседними интерференционными полосами вблизи сере-
дины экрана (вблизи точки О), если источник посылает свет длины волны Л (рис.
Х.31).
Решение. Предположим, что в некоторой точке А на экране мы увидим максимум порядка т.
Рис. Х.31
13«
387
Это произойдет в том случае, когда разность хода Д = d2 - d, будет равна целому числу длин волн, т. е. d2 — d} = mA, где т = 0,1,2,.. ..Из рисунка видно, что
/ 7\2
df = D2 + \hm --
\ 2]
a d% - D2 + \hm + - , тогда \ /
(\ 2 / \ 2
hm+-] — D2—[hm——\ = 2hml
но с другой стороны
d;-< = (d2-d1XdJ + d,) = 2i„i.
Так как по условию D»l, то можно считать, что dj + d2 ® 2D. Тогда
7 7 2h Z 1
d, — d, =--= mA.
2 1 2D
Отсюда, расстояние от центра (от точки О) до светлой полосы порядка т
. mAD
hm =-----,
m г ,
а расстояние между полосами
А 7 7 7 AD
&h = hm+1-hm =—.
V
Таким образом, расстояние между соседними светлыми полосами (как и между соседними темными) остается постоянным для одной и той же длины монохроматической волны.
Задача Х.19 Собирающая линза, имеющая фокусное расстояние F = 10 см, разрезана попо-388
лам, и половинки раздвинуты на расстояние а = 0,5 мм (билинза). Оценить число интерференционных полос на экране, расположенном за линзой на расстоянии D = 60 см, если перед линзой имеется точечный источник монохроматического света (2 = 5ф 10-5 см ), находящийся на расстоянии d — 15 см от нее (рис. Х.32).
Рис. Х.32
Решение. Билинза является тем устройством, которое позволяет получить когерентные источники света. В билинзе при смещении половинок линз вместе с ними смещаются и фокусы, и оптические центры этих половинок. Поэтому каждая из половинок дает свое изображение источника S. Изображение строим по обычным зако-
389
нам: по двум из «замечательных» лучей. Один луч проведем через оптические центры половинок линзы (лучи SA и S А'), а другой — через фокусы половинок линзы (лучи и SB2S2). Пересе-
чение этих двух лучей за линзой дает изображения и 52. Все лучи, выходящие из источника и проходящие через половинки линзы, обязательно пройдут через изображения. Изображение можно видеть только в пределах угла, образованного крайними лучами, прошедшими через половинки линзы. Так, изображение можно увидеть в пределах угла ASrCv, а изображение S2 — в пределах угла A' S2C2. Экран можно поместить только в той области, где эти углы перекрываются, т. е. где встречаются лучи, идущие от когерентных источников S1 и S2, значит на экране мы сможем увидеть интерференцию в пределах MN. Таким образом, мы имеем два когерентных источника, расстояние между которыми I = S^S2, расстояние от источников до экрана равно D = L-f. Искомое число интерференционных
_ MN
полос N f где Д/г, — расстояние между соседними максимумами. Расстояние между источниками S}S2 можно легко определить из подобия треугольников S О1О2 и SStS2:
•S,S2 f + d „„ a(f + d)
-----= ;—, или ЛД, = ------------------ a d 1 1 d
390
1 1 _ 1
где / вычисляется из формулы линзы + у -
Откуда
x Fd 10-15
f =-----=------= 30 см
d-f 5
Таким образом:
( Fd a-------h d
7 cc \d-F У ad
I = о ,o, = —1------- =-----= 0,15 cm .
1 2 d d — F
Расстояние между соседними полосами Nh мы получили в предыдущей задаче. AD А, м
Расстояние MN определяется из подобия треугольников MSN и О^Ог, т. е.
MN а n,rnr a(L + d)
----г - —, или MN = —-— ---.
L + d d d
Таким образом, на экране можно увидеть число интерференционных полос.
яг MN a(L + D)l a2(L + d)
N =-----= -—-—- = 25 полос.
Nh dA(L — f) A(L-f)(d-F)
Задача Х.20 Какой минимальной толщины (d^) должна быть прозрачная тонкая пленка с показателем преломления п = 1,2, чтобы произошло усиление красного света (2 = 8-10~7 м) при отражении от верхней и нижней поверхностей пленки.
391
Свет падает на пленку под углом а = 30° (рис. Х.ЗЗ).
Решение. При падении на пленку света он частично отражается от ее поверхности (например, луч СМ), а частично проходит внутрь и вновь отражается от нижней поверхности (луч DCE). Оба эти луча
когерентные, так как они являются частями одного и того же цуга волн излучающего атома. При встрече этих двух лучей происходит их интерференция. Встретившиеся лучи проходят разные расстояния. Один из них идет по пути SCM, а другой — SADCE. Разность хода этих двух лучей
2dn
А = ADC - ВС = 2AD • п- ВС =--- - AC sin а =
cos р
=--------2d tg /3 sin а = 2dn cos fl.
cos fl
Следует отметить, что оптический путь AD . п отличается от геометрического (AD), так как световые лучи длины волны Л в воздухе, в пленке
2 с Av 2
(пластине) имеют длину 2. = — (п = — = -— = —, п 'У Arv 2Х
т. е. длина волны в пленке уменьшается в п раз
392
(n > 1), а значит, в ней укладывается большее число длин волн.
Если в разности хода А содержится целое число длин волн, то происходит усиление света (максимум освещенности).
А = 2dn cos fl = тЛ, (1)
где т = 1,2,3,....
Если А
= 2dn cos
(2)
то наблюдается ослабление света (минимум освещенности). Условия (1) и (2) записаны без учета
потери полуволны, которая происходит при отражении от более плотной среды (т. е. от верхней границы).
Минимальная толщина пленки, при которой произойдет усиление красного света, определяется из условия (1) при т = 1, т. е.
2drninn cos fl = Л, или
Л Л л
2п cos fl Г sin2 а 2у/п2 — sin2 а
2п, 1-------
V п
Столь тонкие пленки очень трудно изготовить, поэтому обычно пленки имеют толщину, превышающую dmin в целое число раз. Однако максимальная толщина пленки имеет очень ограниченный предел. Дело в том, что строго монохроматического света не существует, и длина волны
393
лежит в пределах от Л до Л 4- ДА. Поэтому может случиться так, что один край т-то максимума совпадает с краем (т+1)-го максимума, т. е.
т (Л 4- ДА) = (т 4- 1) А или ДА = . Таким обра-
зом, m не должно быть очень большим, а значит, и толщина пленки drnin — тоже. Так, например, при стеклянной пластине толщиной d = 0,1 мм наблюдение интерференционных полос уже невозможно.
Задача Х.21 Чтобы уменьшить коэффициент отражения света от оптических стекол, на их поверхности наносят тонкий । слой прозрачного вещества,
АЛ2 у которого показатель пре-
I / ломления п меньше, чем у
I I стекол. (Так называемый
I «метод просветления» опти-
1 ки.) Определить минималь-
/ ную толщину наносимого
/ слоя, считая, что световые
w лучи падают на оптическое стекло перпендикулярно. Рис. Х.34 Объяснить, почему объек-
тивы с «просветленной оптикой» имеют пурпурно-фиолетовый (сиреневый) оттенок?
Решение. Для уменьшения коэффициента отражения нужно, чтобы отраженные лучи 1 и 2 ослабили («гасили») друг друга {рис. Х.34). Это произойдет в том случае, если для двух лучей будет
394
удовлетворяться условие минимума освещенности (задача Х.18), т. е.
/ 1 /\ 2 + тп. .
2dn = + У2) > или °* == —~ л,
, 3 1
для т = 1 amin - — л. (1)
*± IV
Так как на объектив падает белый свет, то толщину наносимого слоя рассчитывают для зеленого света, поэтому зеленый свет гасится, а крайние части видимого спектра (красная и фиолетовая) отражаются. Смешение этих цветов и дает сиреневый оттенок.
Задача Х.22 Определить расстояние между со-
седними максимумами, свет с длиной волны А падает нормально на тонкую пленку в виде клина с малым углом наклона а {рис. Х.35).
Решение. Если на клин направить параллельный монохроматический пучок света, то
если монохроматический
на поверхности клина Рис. Х.35 можно наблюдать че-
редующиеся темные и светлые полосы. В этом случае наблюдается интерференция лучей, отраженных от верхней и нижней поверхностей
клина.
Если разность хода этих двух лучей равна це
395
лому числу волн А = 2dn = тЯ, то наблюдается максимум (без учета потерь при отражении).
Пусть два соседних максимума находятся на расстоянии /ij и h2 от начала клина (рис.Х.35), dj = hta и d2 = h2a соответствующие этим максимумам толщины пленок. Тогда разность хода для лучей, проходящих эти толщины:
Аг = 2d1n = -m2 и А2 = 2d2n = (m + 1)Л.
Расстояние между соседними максимумами d, d. (т + 1)Я - тЛ Л
Ah = h,—h, = —----L = -----------=-----.
а а 2па 2па
Из формулы видно, что полосы лежат на равном расстоянии друг от друга, однако, чем больше угол а, тем ближе расположены полосы.
О
143
Рис. Х.36
Задача Х.23 Почему кольца Ньютона образуются только вследствие интерференции лучей 2 и 3, отражаясь от воздушной прослойки между линзой и стеклом (рис. Х.36), а луч 4, отраженный от плоской грани линзы, не влияет на характер интерференционной картины? Полагая, что монохроматический свет падает нормально,
вычислить радиусы колец Ньютона, если известен радиус кривизны линзы (на рисунке ход лу
396
чей 4, 2, 3 несколько искажается, чтобы лучше видно было, о каких лучах идет речь).
Решение. Все три луча 2, 3, 4 являются когерентными, однако интерференционную картину можно наблюдать только в том случае, если лучи 2 и 3 отражаются от воздушной прослойки, находящейся в непосредственной близости от точки соприкосновения линзы и стекла. Вдали от точки соприкосновения наблюдать интерференционную картину невозможно, так как воздушный слой, равно как и толщина линзы, являются «толстыми» пленками (задача Х.20). При отражении лучей от воздушной прослойки разность хода лучей 2 и 3 равна Д - 2dn. Если мы будем наблюдать светлые кольца, то А = 2dn = тпХ. Из рисунка видно:
г2 = R2 - (R - d)2 = (2R - d)d « 2Rd
(так как d < 0,01мм, R~1-2m).
Отсюда r = ^2Rd« ПРИ наблюдении светлых полос
, m2 m2 d =---=-----
2п 2
Таким образом, радиус светлого кольца порядка m rm = JmAR
Расчет радиусов светлых колец был проведен без учета потери полуволны при отражении от более плотной среды.
Воздушную прослойку между поверхностью линзы и горизонтальной поверхностью можно
(для воздушного слоя п = 1).
397
рассматривать как совокупность воздушных клиньев с меняющимся углом наклона а. Согласно формуле, полученной в предыдущей задаче, расстояние между соседними максимумами будет уменьшаться (угол а увеличивается), т. е. максимумы будут сближаться при движении от центра линзы к периферии.
Задача Х.24 Вычислить радиусы зон Френеля сферической волны радиусом а для точки В, отстоящей от источника монохроматических волн длины А на расстоянии а + Ъ, полагая, что а > > Л и Ъ >> Л (рис. Х.37).
Решение. Опустим перпендикуляр из точки D на прямую SB. Радиус первой зоны (см.пХ.7) легко определяется из треугольников SDE и BDE по теореме Пифагора:
гг2 = а2 - (а - а?)2; (1)
398
= (b + /4) -(b + ac)2. (2)
Приравняв левые части уравнений (1) и (2),
/ , ч ЬЛ ЬЛ
получим: эс( а + о) = —, т. е. ас = —--- (при этом
2 2 (а + Ь)
полагаем, что — < < аЪ ).
\2/
Теперь воспользуемся первым равенством
Г]2 = а2 — (а — х)“ = 2ах + х2
и подставим выражение для х, учитывая, что х2 « ах- Тогда
I аЪ/.
г, = л----
V а + b
Для зоны Френеля номером т получим аналогично
аЪтЛ у а + Ъ
Задача Х.25 Точечный источник монохроматического света с длиной волны Л = 5 • 10-5 см находится на расстоянии а = 6,75 м от ширмы с отверстием D = 4,5 мм. На расстоянии Ъ = а от ширмы расположен экран (рис. Х.38). Как изменит
(3)
Рис. Х.38
399
ся освещенность в точке В на экране, если диаметр отверстия увеличить до Рг = 5,2 мм?
Решение. Теперь, когда мы знаем радиус любой зоны (уравнение (3), задача Х.24), можно легко определить сколько зон укладывается в отверстие диаметром D. Действительно:
D _ таЪЛ 2 \ а. + Ъ
или
Р2(а + Ь) 4аЪА
= 3.
Это значит, что отверстие открывает нечетное число зон. Следовательно, в точке В на экране будет светлое пятно. Если диаметр отверстия сделать равным Dj, то
7П!
,р;(а + ь) ,t
4оМ
т. е. теперь отверстие открывает четное число зон Френеля, значит, в точке В на экране будет темное пятно. Таким образом, увеличение отверстия приводит к уменьшению освещенности в точке В на экране.
Задача Х.26 Плоская световая волна с длиной волны Л падает нормально на узкую щель шириной Ь. Определить направления на минимум освещенности (рис. Х.39).
Решение. Чтобы дифракционная картина была видна, на конечном расстоянии за щелью помещают собирающую линзу, а в ее фокальной плоскости — экран. Тогда все лучи, идущие под углом <р, собираются в некоторой точке А на экране.
400
Рис. Х.39
Так как на щель падает плоская волна, то ее фронт совпадает с плоскостью щели и все точки этого фронта (волновой поверхности) колеблются в одинаковой фазе. Но в точку А на экране они приходят не в одинаковой фазе, так как оптические пути их различны.
Рассмотрим точки В и С щели, расположенные на расстоянии х друг от друга. Разность хода лучей, исходящих из этих точек: А = BD = х sin <р. Если эта разность хода равна ^/, то расстояние ВС = х является шириной одной зоны Френеля, т. е.
А • А
А = х sm ф = —.
2
Следовательно, если на щели укладывается четное число зон, то в точке А происходит полное гашение колебаний и освещенность равна
401
b „ _ п____ 2тЛ
нулю, т.е. — - 2 m. Тогда 0 — zm3C — , или
b sin <р = тЛ , отсюда
тЛ
sm</) =-, где т = 1,2,3,....
о
XI. ЗАДАЧИ, ПРЕДЛОЖЕННЫЕ В 1994-1996 гг. НА
ВСТУПИТЕЛЬНЫХ ЭКЗАМЕНАХ В МОСКОВСКОМ ГОСУДАРСТВЕННОМ УНИВЕРСИТЕТЕ
В этой главе разбираются задачи, предложенные в 1994—1996 гг. на вступительных экзаменах в Московском государственном университете на факультетах: геологическом, физическом, химическом, механико-математическом и факультете ВМиК.
Следует отметить, что существуют несколько способов решения задач, однако из всех возможных способов абитуриенты должны выбирать более короткий и простой способ, поскольку им нужно показать свою эрудицию, свои знания, которые были накоплены за годы обучения в школе.
Задача XI.1 С вершины горы бросили камень со скоростью -и0 под углом к горизонту. В момент падения угол между скоростью камня и горизон
402
том /?, а разность высот точек бросания и падения Ah- Определить угол а между скоростью v0 и горизонтом (pwc. XL 1).
Рис. XI. 1
Решение. Эту задачу проще всего решить, если воспользоваться законом сохранения механической энергии. Система: камень — Земля, является замкнутой, и силы, которые в ней действуют, — консервативные. Поэтому можно применить закон сохранения механической энергии.
За начальный уровень отсчета выберем горизонтальную прямую, проходящую через точку падения камня. Тогда закон сохранения механической энергии запишется
ж, mv2 mv2 mg Ah -I---- =----,
2 2
где v — скорость камня при падении.
Она легко определяется.
v = ^v20 + 2gAh
Так как на камень действует только сила тяжести, направленная вертикально, то горизон
403
тальная составляющая скорости камня не меняет своей величины, т. е.
v0 cos а = v cos fl ,
таким образом:
v о о к 2gAh
cos а — — cos fl - cos fl 1 Ч--—
«о V «о
а = arccos cos fl 11 +
2gAh
Задача XI.2 Катер, движущийся со скоростью vK — 30 км/ч, буксирует спортсмена на водных лыжах. Стальной трос, за который держится спортсмен, составляет с направлением движения катера угол а = 150°. Направление движе----------- ния спортсмена обра-зует с тросом угол
X. 0 = 60°. Определить
X. скорость спортсмена в
X. « этот момент времени
__________(puc- XL2)-
Решение. Так как
Рис XJ 2 трос стальной, а значит, нерастяжимый, то проекции скоростей спортсмена и катера на направление троса должны быть одинаковыми, т. е.
vc cos fl = vK cos (180° — a);
v cos30° /-
=------7Z7- = v V3 = 52 км/ч.
cos 60
404
Задача XI.3 Нарушитель промчался мимо поста ГАИ на автомобиле со скоростью = 108 км/ч.
Спустя = 20 с вслед за ним
ГАИ отправился на мотоцикле ин-
/>\ спектор ГАИ и, разгоняясь в
]течение t2 = 40 с, набрал ско-
0 рость v2 — 144 км/ч. На ка-
Рис. XI.3 ком расстоянии £ от поста ГАИ инспектор догонит нарушителя, если инспектор после разгона движется со скоростью v2?
Решение. Начало координат свяжем с местом расположения ГАИ (рис. XI.3). Тогда координата нарушителя, движущегося с постоянной скоростью vlt
з?н 4" t2 + t) ?
где t — время, в течение которого инспектор двигался за автомобилем с постоянной скоростью v2.
Координата инспектора
а?и „ 4- v2t.
В момент, когда инспектор догонит нарушителя, их координаты будут одинаковы, т.е.
/ >. аг
а?н = или + t2 + t) = —- + v2t.
Так как v2 = at2, то
v. (t. +t2+t) = + v2t
Отсюда
405
Через t = 100 с инспектор догонит нарушителя, при этом они оба будут находиться на расстоянии £ от ГАИ.
^1^2
2(^2 -vt)
= 1728м.
Задача XI.4 На горизонтальном столе лежат два бруска, связанные невесомой и нерастяжимой нитью. Нить расположена в вертикальной плоскости, проходящей через центры брусков, и образует с горизонтом угол а. К правому бруску массой М приложена горизонтальная сила F, проходящая через центр тяжести бруска. Определить силу натяжения Т нити при движении брусков, если коэффициент трения брусков о стол равен и. Масса второго бруска равна та (рис. XI.4).
Рис. XI.4
406
Решение. Нарисуем стрелочками все силы, действующие на оба бруска, и запишем второй закон Ньютона в проекции на ось ОХ для каждого бруска
F- А₽1 -Tcosa = Ma, (1)
где Api=/fN1.
Teas а - /тр2 = та, (2)
где = pN2.
Nt и N2 можно определить из уравнений Ньютона, записанных вдоль оси 0Y:
— Т sin а — Mg = 0, отсюда 1V1 = Mg + Т sin а
N2 + Т sin а — mg = 0, отсюда N2 = mg — Т sin а.
Сложив уравнения (1) и (2), получим
F — + m)g = (М + т)а. (3)
Следует отметить, что уравнения (1), (2) и (3) справедливы, если F > /л(М + m)g.
Из уравнения (3) видно, что оба бруска движутся с ускорением
_ F — /л(М + m)g CL — ----------->
М + т
а сила натяжения Т меняется по закону
_ Fm
rj* = . .
(М + m)(cos а + д sin а)
Задача XI.5 На идеально гладком столе находится клин массой М = 1 кг с углом наклона а — 30°. На гладкий клин кладут брусок массой т = 2
407
кг. Под каким углом $ соскользнет брусок с поверхности клина {рис. XI.5)?
Решение. Рассмотрим систему тел: клин — брусок. Для этой системы тел вдоль горизонтального направления выполняется закон сохранения импульса (силы N и N' являются внутренними). Как только брусок начнет двигаться вдоль наклонной плоскости, клин поедет влево с некоторой скоростью и. В любой момент времени выполняется закон сохранения импульса:
О = mv„ — Ми, или и =------ , (1)
г М
где -уг — горизонтальная составляющая бруска относительно Земли.
Так как клин ускользает из-под бруска, то брусок соскользнет с поверхности клина со скоростью v под углом Д, большим, чем угол а, причем
= (2)
Vr
где г>в — вертикальная составляющая скорости бруска.
Относительно клина в горизонтальном направлении (рис. XI.5, а) скорость бруска
vx о™ = - (- и) = vt + и > тогда
V
tga = -^_. (3)
vT + и
Это условие пребывания бруска на поверхности клина.
408
Рис. XI.5
Разделив числитель и знаменатель правой части уравнения (3) на vT, получим
/Р
1+% 1 + т/{
ИЛИ
п (М + т)
tg fl = tg т
Из этого соотношения следует, что tg fl > tg а.
409
Задача XI.6 Кирпич, лежащий на краю крыши
дома, толкнули вверх вдоль ската со скоростью v
— 10 м/с. После упругого
удара о конек кирпич соскользнул обратно и остановился на краю крыши. Определить коэффициент трения и между кирпичем и поверхностью крыши, если конек находится на высоте h — 2,5 м от края крыши. Угол на-
клона крыши к горизонту а = 30° (раде. XI.6).
Решение. Задача становится очень простой, если
воспользоваться законом изменения механической
энергии.
Вся кинетическая энергия, сообщенная кирпичу, пошла на работу против сил трения, т. е.
mv2 /-о mSr^lcosc£ _ 2/^mgh
2 тР sjnc£ tg a
Отсюда коэффициент трения
v2 tg a 102•1 ,
и =-----— =----------7= = 1,47.
4gh 4 9,8 • V3
Задача XI.7 К деревянному кубу массой М, лежащему на плоской горизонтальной поверхности, прикреплена невесомая пружина жесткостью к. Другой конец пружины закреплен. В куб попада-
410
M
V0
Рис. XI.7
ет пуля массой т и застревает в нем (пуля летит вдоль горизонтальной оси, проходящей через центр тяжести куба, со скоростью -у0). Определить макси
мальное смещение куба Асе, если между кубом и горизонтальной поверхностью возникает сила трения. Коэффициент трения р {рис. XI.7).
Решение. После попадания пули она движется с кубом с одинаковой скоростью и. Можно записать закон сохранения импульса
mv0 = (т + М)и, где и — скорость сразу после удара. Кинетическая энергия, которую приобрел куб сразу после удара, пошла на преодоление работы против сил трения и на сжатие пружины (сообщение ей потенциальной энергии). Поэтому можно записать:
(ш + М)и2 _
2 ~ Атр
L-Л-у2
= /л(т + M)gAcc 4-------
2
к Асе2
2
Учитывая, что
mv0
-----г, получим
и =
+ + -43L или
2(m + М) 7 2
Асе2 + — (т + M)gAcc-_ = о.
к v 7 к(т + М)
Отсюда
411
2
Дх = — у- (т + M)g + к
~-(m + M)g . к
, wo^o k(m + М)'
Физический смысл имеет только знак «+» перед корнем, так как знак «-» означает не сжатие, а расширение пружины.
Задача XI.8 В середину чаши массой М, прикрепленной снизу к вертикальной пружине жесткостью к (рис. XI.8), попадает падающий с высоты Н пластилиновый
Рис. XI.8
шарик массой т. На какую максимальную величину Дх отклонится вниз чаша в процессе колебания после попадания в нее шарика?
Решение. Непосредственно перед попаданием шарика в чашу можно при
менить закон сохранения механической энергии:
тг mV 2
mgH = —-—, отсюда v = Agn .
В момент удара выделяется некоторое количество тепла. Поэтому закон сохранения механической энергии применять уже нельзя, но можно использовать закон сохранения импульса. Чаша с шариком начнет двигаться вниз с некоторой скоростью и, которую определяем из закона сохранения импульса:
412
mv = (m + M)u, или и —-------.
v 7 m + M
При максимальном сжатии пружины на Да? кинетическая энергия чаши с шариком переходит в потенциальную энергию сжатой пружины и новую потенциальную энергию чаши с шариком, т. е.
(т + М)и2 , х . кАх2
-------— = (т + M)gAa? +-----.
2 2
Из этого уравнения следует
Л„ - (m + M)g аХ12
(т + M)g к
(m + М)и2 к
(m + M)g^ (m + M)2g2 m22gH
к у к2 к(т + М)
Следует отметить, что чаша с шариком имеет новое положение равновесия (а?0), которое определяется вторым законом Ньютона и отсчитывается от начального нулевого уровня (см. рис. XI.8).
(т + M)g — kxQ = 0.
Л т + М _
Отсюда а?0 =-----g. Около этого положения
к
равновесия будет колебаться чаша с шариком.
С другой стороны: а?0 = ^2. (см. рИС.).
Амплитуда этого колебания
А = Да?2 - а?0 = [Да?! - а?0| =
Да?. - Да?, ------------(см. рис.).
2
413
Таким образом:
(m + М)2 g2 2gHm2
к2 к(т + М)
Задача XI.9 Космический корабль движется по круговой орбите радиусом R = 4000 км вокруг неизвестной планеты. Определить ускорение свободного падения на поверхности планеты gn, если ее радиус т0 = 3500 км , а период обращения корабля Т = 2 ч.
Решение. На корабль действует единственная сила — сила гравитации. Поэтому второй закон Ньютона запишется
2п (2лг \
G —— = та = те» R = ml — R
R n {T J
(1)
где М и т — массы планеты и корабля соответственно.
Так как ускорение свободного падения у пла-
М
неты gn = G—r, то уравнение (1) можно перепило
сать
2
rom
R = Sn , отсюда rv
Sn г2т2 3,9 м/с.
'о J
414
Задача XI.10 На отрезок тонкостенной трубы симметрично намотаны две невесомые нерастяжимые нити. Труба удерживается в положении, указанном на рисунке. В некоторый момент времени трубу отпускают. Она опускается, разматывая нить. Определить ускорение осевой линии трубы (рис. XI.9), проходящей через точку А.
Рис. XI.9
Решение. Все точки трубы одновременно участвуют в двух движениях: в поступательном со скоростью центра тяжести трубы и0 и во вращательном — с линейной скоростью ил, при этом эти скорости равны по величине (катушка не проскальзывает), т. е. и0 = ил.
Кинетическая энергия тонкостенной трубы Ек = Mv^ (см. решение задачи IV. 13).
Из закона сохранения механической энергии следует
Л^мех = АЕК + АЕП = 0 .
415
Для указанной на рисунке системы координат это уравнение запишется
— Mv^ + MgAx = 0, или Mv20 = MgAx. (1)
Используя уравнение кинематики
at2 _ vot _ v2
2~~7
и уравнение (1), получим,
(2)
Искомое ускорение центра тяжести трубы а получаем с помощью уравнения (2):
2Дх
Задача XI.11 Верхний конец невесомой пружины жесткостью к с начальной длиной 10 прикреплен к опоре. На нижнем конце пружины висит грузик массой т. Пружину растянули до длины I и отклонили на угол а от вертикали, а затем грузик отпускают без начальной скорости (рис. XI.10). Какое количество тепла выделится в этой системе после затухания всех колебаний?
Решение. В положении равновесия пружина с грузом имеет длину I, которую можно определить из уравнения
— k) ~ mS, или 1Г = + .
к
Растянув пружину до длины I и отклонив ее
416
от вертикали на угол а, ей сообщили некоторый запас потенциальной энергии.
После всех колебаний пружина вернется в вертикальное положение, где запас ее потенциальной энергии станет равным
Рис. XI. 10
к 2
Рп2 = mgH + -(l1 -10) .
Начальный уровень отсчета потенциальной энергии совмещаем с горизонталью О О' (рис. XI. 10), Н — высота конечного положения грузика после всех колебаний. Разность этих энергий и будет тем количеством тепла Q, которое выделится в системе после всех колебаний, т. е.
Q = -Ещ _ -®п2-
Высоту Н можно определить из рисунка:
гт 1 11 mg + kl0
Н — I cos а — I, = I cos а-----
1 к
тогда
„ к /, , Ч2 Л , mg\ к (mg + kln , \2
Q = -mgUcosa-Z0—— -- --------------Zo =
Z \ К / Z у rC /
m2g2
2k
— mg(l cos a —10).
14 Физика
417
Задача XI.12 Над серединой большого цилиндрического сосуда площадью £ и высотой Н = 60 см закреплен маленький цилиндрический сосуд с площадью сечения s = 0,25. В верхнем сосуде находится ртуть, причем высота ее уровня над уровнем нижнего сосуда h = 1,5 м (рис, XI. 11). Через отверстие в середине дна маленького сосуда ртуть выливается в большой сосуд. Определить изменение температуры ртути At, если ее удельная теплоемкость с = 0,12 кДж/кгК. Теплоемкостью сосудов и рассеянием тепла в окружающее пространство пренебречь. Ускорение свободного падения g принять равным g = 10 м/с2.
Рис. XI.11
Решение. Центр тяжести ртути после вытекания переместится на Ах (рис. XI.11), поэтому изменение потенциальной энергии
АЕП = mgAx = т,
гт а
Н + — — mg — •
2 6 2
418
f Положение нового центра тяжести ртути (/”2) определяется из условия постоянства объема ртути, т. е.
0,257г — Sa, или а = 0,27г.
Таким образом, АЕП = mg(H + 0,47г). При падении ртути происходит неупругий удар и выделяется некоторое количество тепла AQ, которое идет на нагревание ртути, при этом ЛЕ, AQ = cmAt. Следовательно:
At = = mg(H + °’4Ч = £ (н + о,47г) = 0,1° С.
ст ст с
Задача XI.13 Ящик массой т с постоянной ско-
ростью втягивают за веревку на горку. Когда ящик
подняли на высоту 7г, совершив работу А, веревка оборвалась и ящик стал скользить вниз. Какую
скорость v будет иметь ящик, опустившись до
исходного положения? Коэффициент трения ящика о горку считать постоянным (puc. XI. 12).
Решение. Силы, действующие на ящик, изображены на рисунке. Запишем второй закон Ньютона в проекции на ось 0Х
и определим неизвестную силу F:
- mg sin а + F - /тр =0 , тогда
F = mg sin а + fimg cos а.
419
14*
Сила F для системы тел: горка — ящик, является внешней силой. Она совершает работу А, которая идет на преодоление силы трения /тр и сообщение ящику потенциальной энергии, т. е.
л , г , , cos а • h
А = Fl = mgh + fl = mgh + fx mg—:-- (1)
p smct
где I — длина пройденного ящиком пути до обрыва веревки.
При движении ящика вниз из закона сохранения механической энергии следует,
ДЕК + ДЕП - , или —----mgh = -fTpl, т.е.
mv2 , h
= mgh — [xmg cos a . (2) 2------------------------------------sin a
Сложив уравнения (1) и (2), получим
я mv2 „ , , „ , 2А
А 4----= 2mgh, отсюда v — 4gh------,
2 т
2А
или v = J4gh----
V m
Задача XI.14 Надувной шарик, заполненный гелием, удерживают на нити. Найти натяжение нити Т, если масса оболочки шарика т = 2 г, объем V = 3 л, давление гелия р = 1,04 • 105 Па, температура t = 27°. Молярная масса гелия fl = 4 г/моль, плотность воздуха р = 1,3 кг/м3, универсальная постоянная R = 8,3 Дж/моль К.
420
Решение. На шарик действуют три силы: сила тяжести (m + mr)g, сила натяжения Т и сила Архимеда FA = pgV (рис. XI.13).
Так как шарик находится в равновесии, то второй закон Ньютона в проекции на ось ОХ
запишется:
(m + mr)g + Т - Fa = 0 , отсюда Т = Fa - (m + mr)g. Массу гелия можно определить из уравнения состояния идеального газа:
m pVp
pV = —^РТ, или m = r p RT
Таким образом:
T = pgV ~ Im +
RT J
g~ 0,014 H.
Задача XI.15 В полусферический тонкостенный «колокол», плотно лежащий на столе, наливают через отверстие вверху воду. Когда вода доходит до отверстия, она приподнимает «колокол» и начинает вытекать снизу. Определить массу «колокола» М, если его радиус R = 10 см. Плотность воды р = 103кг/м3 (рис. XI.14).
Решение. Заполненный доверху водой «колокол» действует на стол с силой, равной силе тяжести
421
Рис. XI. 14
воды и самого «колокола» и направленной вниз.
2
Fr = Mg + -aR3pg.
О
С другой стороны, со стола в момент подтекания воды действует сила
F2 = pghS - pgRjtR2 = pgnR3 •
Из условия равновесия Fr - F2 =0 имеем:
2
Mg + — nR3 pg = pgnR3, т. e.
3
M = =lt)Kr
3
Задача XL16 В цилиндрический сосуд с водой опускают деревянный шар радиусом R, внутри которого помещен свинцовый грузик массой т. На какую высоту h поднимется уровень воды в сосуде, если площадь его дна S, плотность воды рв, плотность дерева рд, плотность свинца рс?
Решение. В условии задачи ничего не сказано, плавает ли шар с грузиком в воде или он 422
утонул. Поэтому необходимо рассмотреть эти два случая.
I случай: шар с грузиком плавает в воде.
Прежде всего определим массу деревянного шара со свинцовым грузиком
... t-r-r \ (4 о ТО
м = РдНш - м + ™ = Рд -лК-----------------------4-то. (1)
\3 P<J
Так как шар плавает, то Mg = pBVBbITg. (2)
Сравнив уравнения (1) и (2), получим
14
М = о — nR3 д1з
PJ
4 пЗ
+ то < рп —лЯ . в 3
Отсюда следует, что свинцовый грузик дол
жен иметь массу
4 3 Рв Рд
то < — TtR -р^ = топ
3Л Л » с и •
Ре-Рд
Теперь определим объем вытесненной воды:
выт
и высоту h,p на которую поднимется уровень
воды в сосуде
hi =
1 SpB
S
4 D3 _L 11 Pr
— jiR рп + то 1----i
L3 k Pe.
II случай: шар с грузиком утонул (то > то0).
В этом случае он вытесняет объем
423
V' , = V = — nR3 ВЫ I 7
тогда уровень воды в сосуде поднимется на высо-
ту h2:
h - _ 4^3
2 S 35
Задача XI.17 В U-образную трубку налили жидкость массой т. Определить период колебаний жидкости в трубке, возбуждаемых небольшим смещением уровней в коленах от положения равновесия. Площадь вертикальных колен трубки —S, плотность жидкости р. Трением жидкости о стенки трубки пренебречь (рис. XI. 15).
Решение. При смещении уровня жидкости из положения равновесия 0-0' на величину х возникает разность сил давления, которая за став ля-
424
ет жидкость возвращаться в первоначальное положение.
Уравнение движения запишется:
F — та, или — 2pgxS = та = тх". (1)
Как видно, уравнение (1) — это уравнение гармонических колебаний вида
х" = — 0)2х , где си2 = ,
т
а искомый период колебаний
m 2л 12т
Т = — = л-----
<у ' у pgS ‘
Задача XI.18 В теплоизолированном сосуде содержится смесь воды т^ = 500 г и льда т2 — 500 г при температуре t = 0° С. В сосуд вводится .сухой насыщенный пар массой т3 = 80 г при температуре t2 = 100° С. Какой будет температура tc после установления теплового равновесия? Удельная теплота парообразования воды г = 2,3 МДж/кг, удельная теплота плавления льда Л = 0633 МДж/кг, удельная теплоемкость воды с = 462 кДж/кг К.
Решение. Введенный в сосуд пар отдает свое тепло, сначала превращаясь в воду при t2 = 100° С, а затем охлаждаясь на At от 100° С до 0° С. При этом выделится тепла
= m2r + m3cAt = 21,76 • 104 Дж = 2,176 • 105 Дж-
425
Для того чтобы расплавить лед, нужно количество тепла
Q2 = т2Л = 500 г- 0.33 МДж/кг = 165 • 105 Дж •
Как видно из подсчетов, Q3 > Q2, т. е. выделенного паром тепла хватит для того, чтобы весь лед растаял. Количество тепла AQ = - Q2 пой-
дет на нагревание воды (mt), растаявшего льда (т2) и пара, превратившегося в воду, (тп3) до некоторой температуры смеси tc. Определим ее из уравнения теплового баланса:
п п
У, Q = У, c.m. At,. = - Qz; i=l i=l
cm{tc + cm2tc + cm3tc = - Q2,
t Q.~Q2 0,52-lP5 -115.c
c(m1+m2+m3) 4,2 • 10s • (1080) • 10 3
Задача XI.19 Сосуд содержит m = 1,28 г гелия при температуре t = 27° С. Во сколько раз (д) изменится среднеквадратичная скорость молекул гелия, если при его адиабатическом сжатии совершают работу А = 252Дж? Молярная масса гелия ц = 4г/моль. Универсальная газовая постоянная R — 8,3 Дж/моль К.
Решение. Любой идеальный газ подчиняется объединенному газовому закону. В первоначальном состоянии
426
p^-RT^
(1)
После адиабатического сжатия
p2V2=—R^ + AT), (2)
при этом АТ можно определить из первого начала термодинамики для адиабатического процесса, т. е.
AU + А = О, так как гелий одноатомный газ, то
|ДП| = - — R^T 2 р,
(см. nVL9).
Таким образом, ДТ =-------.
ЗЯ т
Поскольку в задаче требуется определить отношение среднеквадратичных скоростей, то поделим уравнение (2) на уравнение (1) и выразим давление Pj и р2 через квадраты средних скоростей:
1 _2 1 N _2
Pi = -nlmvl =--mvt (см. nvi.3); о о
1 _2 1 N _2
р, = — =-----mv,
2 3 2 2 3 2 ,
где п, и п2 - концентрации частиц, Vj и V2 — объемы гелия, и - квадраты скоростей соответственно до и после сжатия.
Т + ДТ л ДТ ------- =14----, или
427
v2 , AT , 2Ди
=X = 1 +-= 1 +----—.
v2 T SRmT uz
Следовательно:
Ё= /1+ 2Au
у v2 v 3RmT
= U.
Задача XI.20 Одноатомный идеальный газ переводится из состояния 1 (pj = 130кПа, V} = 1л) в состояние 2 (р2 = 10кПа, V2 = 2л) по прямой, указанной на рис. XI.16. Затем газ переводится в состояние 3 (р3 = 20кПа, V3 = Зл) по прямой 2~3. Какое количество теплоты AQ сообщено газу?
Рис. XI.16
Решение. Количество теплоты определяется из 1-го начала термодинамики:
AQ = АП + ДА.
428
Так как газ одноатомный, то изменение его энергии легко определяется при переводе его из состояния 1 в 3 (см. п VI.9)
Ди = и,-и,=|—R(TS-T,).
При этом температуру можно определить из объединенного газового закона:
т т
p^—RT, ; p3V3=—RT3,
Следовательно:
3
Ay = r(p.v,-p,v,).
Работа ДА = AAj_2 + ДА2_3. На каждом участке работа численно равна площади заштрихованных трапеций, расположенных под соответствующими прямыми, т. е.
A-, = i(Pi + P,)(v2-v,);
A-J = i(p> + p2)(v,-v1).
Таким образом:
3
Ae = -(p.V,-p,V,)+
+ |[(p, + p2)(v, - V>)+(p, + p2)(v3 - V,)] =
= |[P,(4 -4V.) + Рг(Ч - V,) + ft(4V, - V2)] =-200Дж.
429
Знак «-» означает, что при протекании процесса (1~2—3) тепло выделится.
Задача XI.21 В цилиндрическом сосуде 1 под поршнем массы т = 5 кг находится одноатомный газ. Сосуд 1 соединен трубкой, снабженной краном, с таким же сосудом 2, в котором под поршнем массой М — 10 кг находится такой же газ. Сосуды и трубка теплоизолированы. В начальном положении кран К закрыт, температура газа в обоих сосудах одинакова. Поршень в сосуде 2 расположен на высоте Н = 10 см от дна. На какое расстояние Ah передвинется поршень в сосуде 1 после открывания крана? Объемом трубки с краном пренебречь, атмосферное давление не учитывать (рис. XI. 17).
Решение. Внутренняя энергия газа в сосудах 1 и 2 до открывания крана:
430
ui = lviRT = |pivi = ~^fsh = lmgh, (1) Z Z Z kJ z
где pj — давление, V{ — объем сосуда, 5 — площадь его поперечного сечения, h — высота, на которой находится поршень в сосуде 1, vY — число молей в сосуде;
3 3 3 М? 3
U2 = —v2RT = -p2V2 = -~^SH = -MgH, (2) Z Z Z d z
где p2 — давление, V2 — объем сосуда, H — высота, на которой находится поршень в сосуде (2), v2 — число молей в сосуде.
Так как сосуды теплоизолированы, то работа по передвижению поршня может произойти только за счет внутренней энергии газа, т. е.
u = u1 + u2 + a, (3)
где U — внутренняя энергия газа после открывания крана.
Масса второго поршня больше массы первого, поэтому после открывания крана поршень массой М опустится на дно второго сосуда, а поршень в первом сосуде поднимется на высоту Ah, и весь газ окажется в первом сосуде. Его внутренняя энергия будет равна — см. уравнения (1) и (2),
3
U = — mg(h + Ah). (4)
2
Приравнивая уравнения (3) и (4) и учитывая, что работа по перемещению поршней А равна А = MgH — mgAh, получим
3 3 3
— mg(h + Ah) = — mgh + — MgH + MgH — mgAh,
2 2 2
mg Ah = MgH, откуда
431
ЛК МН
Ыг =---
т
Задача XI.22 Два одинаковых положительных точечных заряда величиной Q закреплены на расстоянии d друг от друга. Посередине между ними перпендикулярно отрезку, их соединяющему, расположена гладкая непроводящая штанга, по которой может скользить бусинка массой т с отрицательным зарядом -q. Определить период малых колебаний бусинки. Силой тяжести бусинки пренебречь (рис. XI. 18).
Рис. XI.18
Решение. Проведем ось ОХ перпендикулярно отрезку d, соединяющему заряды Q. На заряд q вдоль оси ОХ действует результирующая сила Кулона
Fp = 2F cos а =
2qQ cos а 4jte0R2
432
где R — расстояние между зарядами -q и Q, х — расстояние от отрезка Q — Q до заряда -q, причем
R =
cos а
х
R'
Второй закон Ньютона для заряда -q запишется
qQ х
= та, или -------— = та, или
2jI£0R^ R
2я£0 х2 4-
= тх".
(1)
Так как нас интересуют малые колебания бу
синки, то можно полагать, что
тог-
да уравнение (1) будет иметь вид
qQx
о (d\3
2Л£п1 —
°\2/
п
— тх .
Это уравнение - не что иное, как уравнение гармонических колебаний:
qQx
2лг£п — т
°Ш
433
Отсюда
2л£п — т
12/
2л , nenmd
Т = — = ndi—2-со \ qQ
Задача XI.23 Нижняя пластина конденсатора
ние. XI.19
закреплена неподвижно на изолирующей подставке, а верхняя подвешена на упругой пружине. Расстояние между незаряженными пластинами dC). При подаче на конденсатор напряжения U} — расстояние между пластинами dj, при подаче напряже-
ния U2 — расстояние d2. Определить отношение
напряжений п = (рис. XI.19).
Решение. Верхняя пластина конденсатора притягивается нижней с силой
QE _ CU2 _ s0SU2
2 ” 2d 2d2
Эта сила уравновешивается силой упругости пружины
ГупР = k(do “ d>) > т- е.
434
*(Ж2
2d2
для напряжения U{;
для напряжения U2.
2d2
Разделив одно уравнение на другое, получим
U2d2 d0 - d2 ----—, или
U^2
и2 п = —
d2
dt N do - di
d0 d2
А
2
Задача XI.24 В схеме, изображенной на рис. XI.20, (а), емкости конденсаторов С^Ыкф, С2 - 2мкф, С3 = Змкф, С4 = 4мкф. Напряжение между точками А и В равно Uo = 100В. Определить напряжение U4 на конденсаторе С4, если до подключения напряжения Uo конденсаторы были неза-ряжены.
Решение. Эту схему можно представить как два последовательно соединенных конден-сатора С] и С, где С С
С = г "г + °2 (Рис- XL20> б)-'-'3 + '-'4
Причем заряд на этих конденсаторах одинаков и равен
Рис. XI.20
435
/ с с cd—^- + с2 с,с Чс3 + с4 2
Q = U0 ! = и0-----V----------
с, + с “ f с3с4
1 с. + —+ с2
(,С3+С4 2
В свою очередь заряд Q распределяется между двумя
A
конденсаторами С2 и С3, причем Q = Qc2 + Qc3 • Заряд на конденсаторе С4 равен заряду на конденсаторе С3, т. е. QC3 = QC4, поскольку они соединены последовательно. А искомое напря-
В (б)
Рис. XI.20
жение U. = — С
Таким образом, чтобы ответить на вопрос задачи, нам необходимо определить заряд на конденсаторе С4, равный QCj.
Напряжение между точками D и В определяется по формуле
тт _ Q _ UqCi DB С С, + (
££1 С3С4
1
2
У'-'з -г ’“Ч
Заряд на емкости С3 и С4
~ =ТТ СзС4 UqC&Ci
Ct DB с3 + с4 ( с3с4 с + ———
\ С3 + С4 у
+ с2 (с3+с4)
а напряжение
436
U ^Q^^UdbCs_ и^с, _юо
4 c4 c3+c4 (C1+C2)(C3+C4) + C3C4 11
Задача XI.25 В схеме, изображенной на рис. XI.21, вначале ключ К не замкнут. На какую величину изменится заряд конденсатора, если ключ К
замкнуть? R} = 10 кОм, К2 = 15 кОм, С = 1 мкф, = 34 В, £2 = 9 В. Внутренним сопротивлением источников пренебречь.
Решение. При разомкнутом ключе конденсатор С заряжается от источника £2 и напряжение
на нем Ul = £2, а заряд Q! = С$2. После замыкания ключа К и перезарядки конденсатора ток протекает по внешней цепи (через конденсатор ток не течет!) и его легко вычислить.
-£2 + IR2 + IRX - £, = 0, отсюда I = IdJk.
R] + R2
В этом случае напряжение на конденсаторе определяется по формуле
U2 — £2 + IR2 = 0, или U2 = £2 — IR2, а новый заряд на нем
q2 =CU2 =C(£2-JK2).
Изменение заряда на конденсаторе равно
Дд = - ?! = - ж2) - С^2 = ~CIR2 =
437
= -CR2 + = -25,8 • 10"6 Кл . 2 Rt + R2
Знак означает, что заряд на конденсаторе С уменьшился.
Задача XI.26 Какое количество тепла выделится в схеме, изображенной на рис. XI.22, после замыкания ключа
Рис. 11.22
Решение. При разомкнутом ключе все конденсаторы будут заряжены до одного и того же заряда q} и одного и того же напряжения U], так как они все одинаковы и включены
последовательно, причем
Энергия всех заряженных конденсаторов
где Wo — энергия одного из конденсаторов.
После замыкания ключа К заряженными останутся только два конденсатора, лежащие слева от ключа. Конденсаторы, лежащие справа от ключа, не будут иметь зарядов, так как они разрядятся через сопротивление R. В этом случае напряжение на каждом из двух последовательно включенных левых конденсаторов
438
и2 - а заряд q2 = CU2 = —.
2
Энергия двух заряженных конденсаторов
W2=2^ = 2^ = ^,
2 о 2 4 >
где WJ — энергия одного из конденсаторов после замыкания ключа.
Перезарядку конденсаторов производит батарея с ЭДС $. Она совершает работу, которая идет на изменение энергии конденсаторов и на выделение в схеме тепла. Эта работа
£Aq = AW + AQ.
Отсюда количество выделенного тепла в схеме
AQ = £Aq-AW = $(q2 - q,) - (W2 - Wt) =
Г eg1 С£Л _ Г eg2 _ С£2Л _ eg2
" 8 ) ~ 8’
Задача XL27 Два одинаковых гальванических
элемента с внутренним сопротивлением г = 1,2 Ом каждый соединены параллельно и нагружены на внешнее сопротивление К. Если эти элемен
_1_£ JL
—I— R
_________5г
ты соединить последователь- рис xi 23 но, то мощность, выделяемая
в том же сопротивлении нагрузки, возрастет в п = 2,25 раза. Определить сопротивление нагрузки R (рис. XI.23).
439
I & I & rl H hL _____________T (6)
Рис. XI.23
Решение. Энергия, выделяемая на сопротивлении R, определяется законом Джоуля — Ленца W = I2R, где ток можно вычислить из закона Ома для полной цепи:
для 1-й схемы (рис. XI.23, а) ;
- + R 2
2£ для 2-й схемы (рис. XI.23, б) 12 = —-—.
W
По условию задачи п = т. е.
I2 1г—
*2 х2 /
п - или — = Vn , отсюда
A А
_ 2д/п — 1
R = г----т=- = 0,8 Ом
2-Vn
Задача XL28 Отрезок АВ расположен вдоль прямой, проходящей через фокус собирающей линзы под углом а = 60° к ее главной оптической оси. Расстояния от точек А и В до фокуса F равны соответственно: а = 5 см, Ъ = 10 см. Чему равно фокусное расстояние линзы F, если известно, что длина отрезка АВ равна длине его изображения (рис. XI.24, а).
Решение. Проведем один «замечательный» луч через крайние точки А и В и оптический центр 440
Рис. XI.24
линзы. Второй «замечательный» луч проведем через крайние точки А и В и фокус. Этот луч пройдет после линзы параллельно главной оптической оси и пересечет первые «замечательные» лучи в точках А' и В'. Отрезок В'А' и будет изображением отрезка АВ (рис. XI.24, б).
Теперь рассчитаем фокусное расстояние линзы. Из подобных треугольников АСА' и AFO следует
СА' CF + а
_ —-------, отсюда
441
. OF ( OF \ OF2
С А-------1-------h о. I---------h О F
а (cos а / а cos а
Из подобных треугольников BOB' и BFO следует
СВ' CF + b OF2
—— —----:--, отсюда СВ = -------h OF
OF b bcosa
лг2 /1 1
В'А' = СА' — СВ' =-----------
cos а \ а Ъ
Так как по условию задачи В'А' = В А = Ъ- а, то
, ч _ OF2 (Ь -
(Ь — а)-----— . Следовательно
cos а\ db I
OF = F = Vab cos a = 5 cm .
Задача XI.29 Точечный источник света 5 и две одинаковые собирающие линзы расположены как показано на рисунке (рис. XI.25). Определить расстояние х между изображениями источника, если известно, что фокусное расстояние линзы F = 10 см, диаметр линзы d = 4 см, а расстояние от источника света до центра каждой из линз I = 20 см.
Решение. Вначале построим изображение источника. Для этого проведем два «замечательных» луча из источника через оптические центры линз (лучи £0’5' и SO" S"). Они пройдут через линзы, не преломляясь. Следующий «замечательный» луч направим вдоль линии раздела линз (для них он
442
Рис. XI.25
будет параллельным главным оптическим осям). Он после линз пройдет через их фокусы. Точки пересечения этих замечательных лучей укажут место положения изображений S' и S”. Место положения изображений определяется формулой линзы:
111 aF
—•" Т “ > 11)111 ь ->
a b F a-F
L (d\2
где а = JI - I— I .
Из подобия треугольников S'SS" и О’^О* имеем
х а + Ъ
— =-----, следовательно:
а а
443
Рис. XI.26
Задача XI.30 Плоская монохроматическая световая волна частично проходит через стеклянную призму с малым преломляющим углом а (рис. XI.26). Длина падающей волны А, показатель преломления п. На экране волны, прошедшие через призму и мимо нее, интерферируют. Определить расстояние между соседними максимумами интерференционной картины.
Решение. В точках А и В можно наблюдать два соседних максимума, если разность хода между лучами 1 и 2 будет равна длине волны, т. е.
Л = СВ = А, или А = СВ = АВ sin у ~ Хху , где у — это угол, на который отклоняется луч при выходе из призмы (см. рис.). Он равен у = (п — 1)а. Таким образом Л = Дх(п — 1)а, отсюда расстояние между соседними максимумами * А Дх = ------——.
(п — 1)а
Задача XI.31 На непрозрачный экран, в котором сделаны две параллельные одинаковые щели, нормально падает параллельный пучек света. Длина волны света А = 0,5 мкм. Расстояние между щелями d = 50 мкм. За экраном расположена
444
собирающая линза с фокусным расстоянием f = 20см так, что ее оптическая ось перпендику
лярна плоскости экрана и проходит через середину промежутка между щелями. Определить ширину центрального дифракционного максимума, наблюдаемого в фокальной плоскости линзы (рис. XI. 27).
Решение. Все точки волновой поверхности па
дающего на щель пучка являются источником вто
ричных волн, колеблющихся в одинаковой фазе. За счет дифракции (огибания) свет после прохождения щелей распространяется во всех направлениях. Рассмотрим два параллельных луча AD и BE, идущих от симметричных точек щелей А и В под некоторым уг
лом <р к вертикали.
Причем луч AD проведем через оптический центр линзы. Луч BE после линзы также попадет в точку D на экран, который расположен в фокальной плоскости. Центральный дифракционный макси
мум лежит между двумя симметричными первыми минимумами. Это значит, что разность хода АС = Д между двумя лучами AD и BE, рассеянных от симметричных точек А и В, должна удовлетворять условию дополнительных минимумов (см. п.Х.8) :
445
л л
АС = Д = d sin <р = —, или sin <р = —.
2 2d
Для малых углов <р
Л
sin <р « <р = —.
2d
С другой стороны, из треугольника OO'D Ах
Ф = уу , таким образом :
Л Ах д А/
Р = ТГ7 = , откуда Ах = —- = 0,2см.
СОДЕРЖАНИЕ
I. КИНЕМАТИКА 3
§ 1. Основные определения и формулы......... 3
§ 2. Простейшие операции с векторными величинами.................................. 7
§ 3. Равномерное прямолинейное движение................................... 14
§ 4. Равноускоренное движение............. 25
§ 5. Свободное падение тел.............„.....34
§ 6. Кинематика движения материальной точки по окружности......... 44
§ 7. Абсолютное, относительное и переносное движения........................47
II. ДИНАМИКА ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ 57
III. ЗАКОНЫ ИЗМЕНЕНИЯ И СОХРАНЕНИЯ ИМПУЛЬСА ТЕЛА И ЭНЕРГИИ 93
§ 1. Изменение и сохранение импульса тела и системы тел......................... 93
§ 2. Работа силы. Изменение и сохранение механической энергии тела и системы тел.......................... 95
§ 3. Центральный удар шаров ............... 98
IV. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ 124
§ 1. Вращательное движение................ 124
§ 2. Закон всемирного тяготения............-.151
V. СТАТИКА 162
§ 1. Статика твердых тел...................-..162
§ 2. Статика жидкостей и газов..............186
VI . МОЛЕКУЛЯРНАЯ ФИЗИКА
И ТЕПЛОТА_________________________________—.199
VII . ЭЛЕКТРОСТАТИКА_________________________„240
VIII ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК 281
IX МАГНИТНОЕ ПОЛЕ ТОКА
И ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ-----------------313
X ОПТИКА____________________________________—350
§ 1. Геометрическая оптика..................350
§ 2. Элементы физической оптики.............354
XL ЗАДАЧИ, ПРЕДЛОЖЕННЫЕ В 1994-1996 гг. НА ВСТУПИТЕЛЬНЫХ ЭКЗАМЕНАХ В МОСКОВСКОМ
ГОСУДАРСТВЕННОМ УНИВЕРСИТЕТЕ.............. 402
447