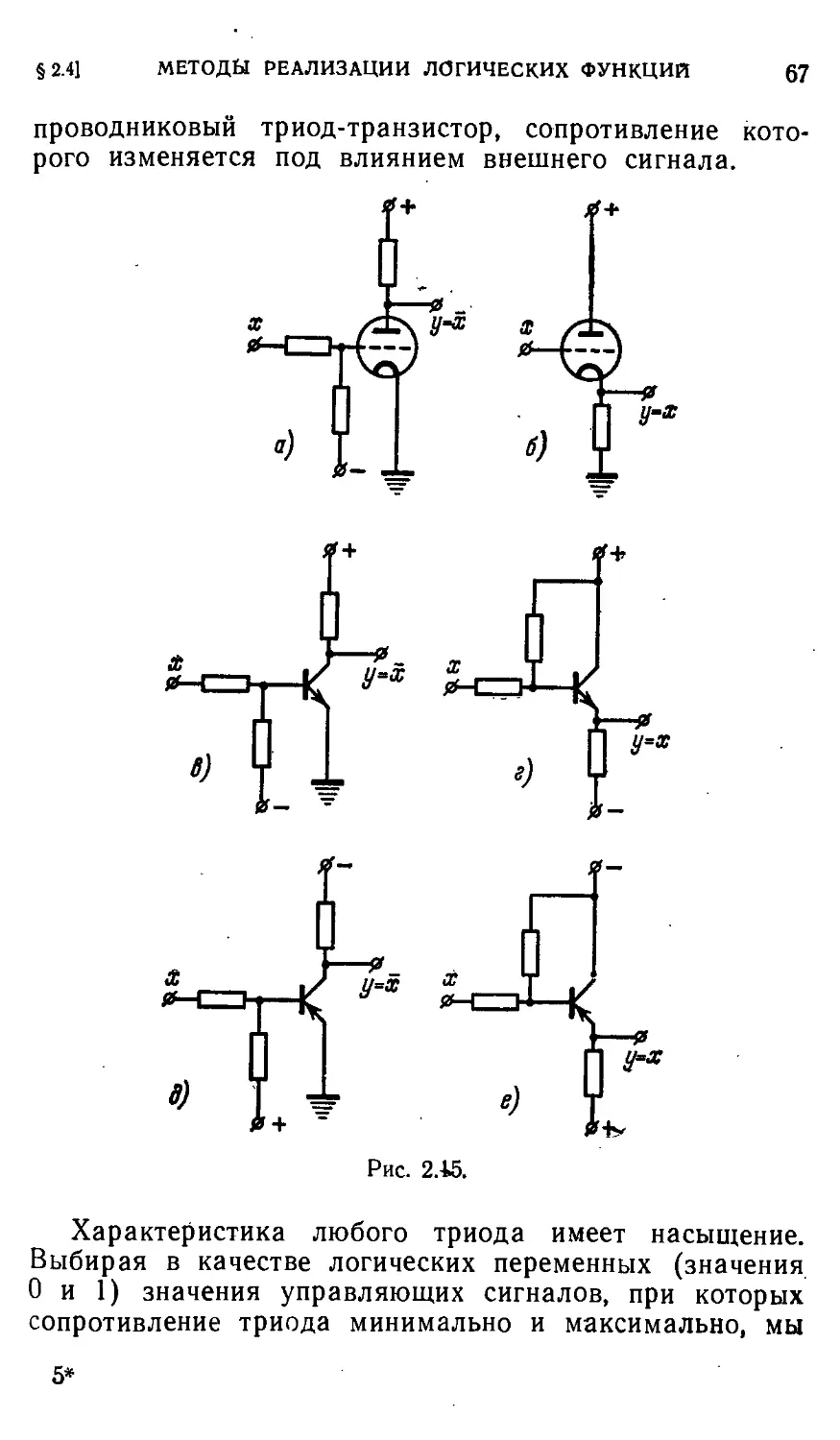
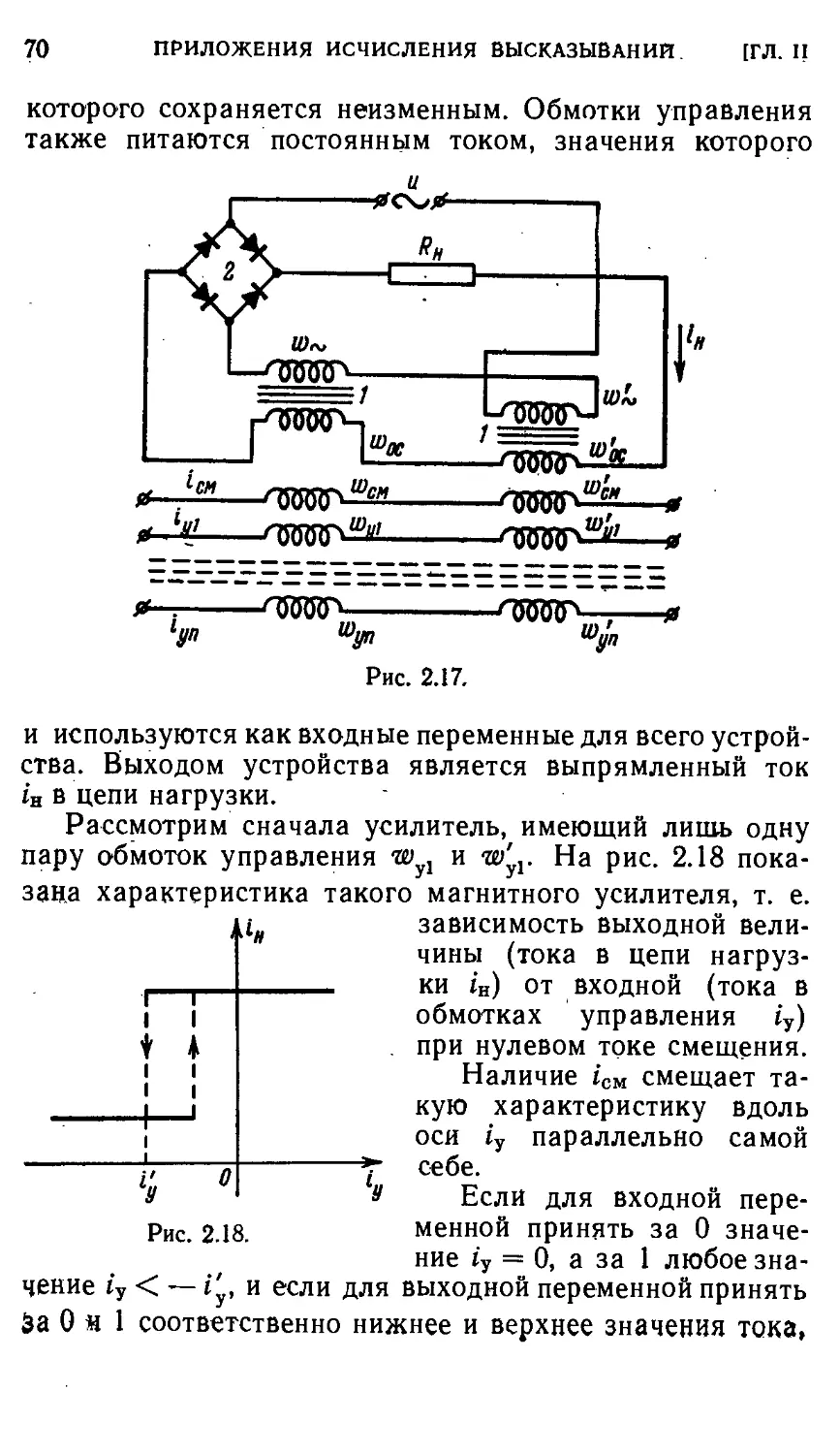
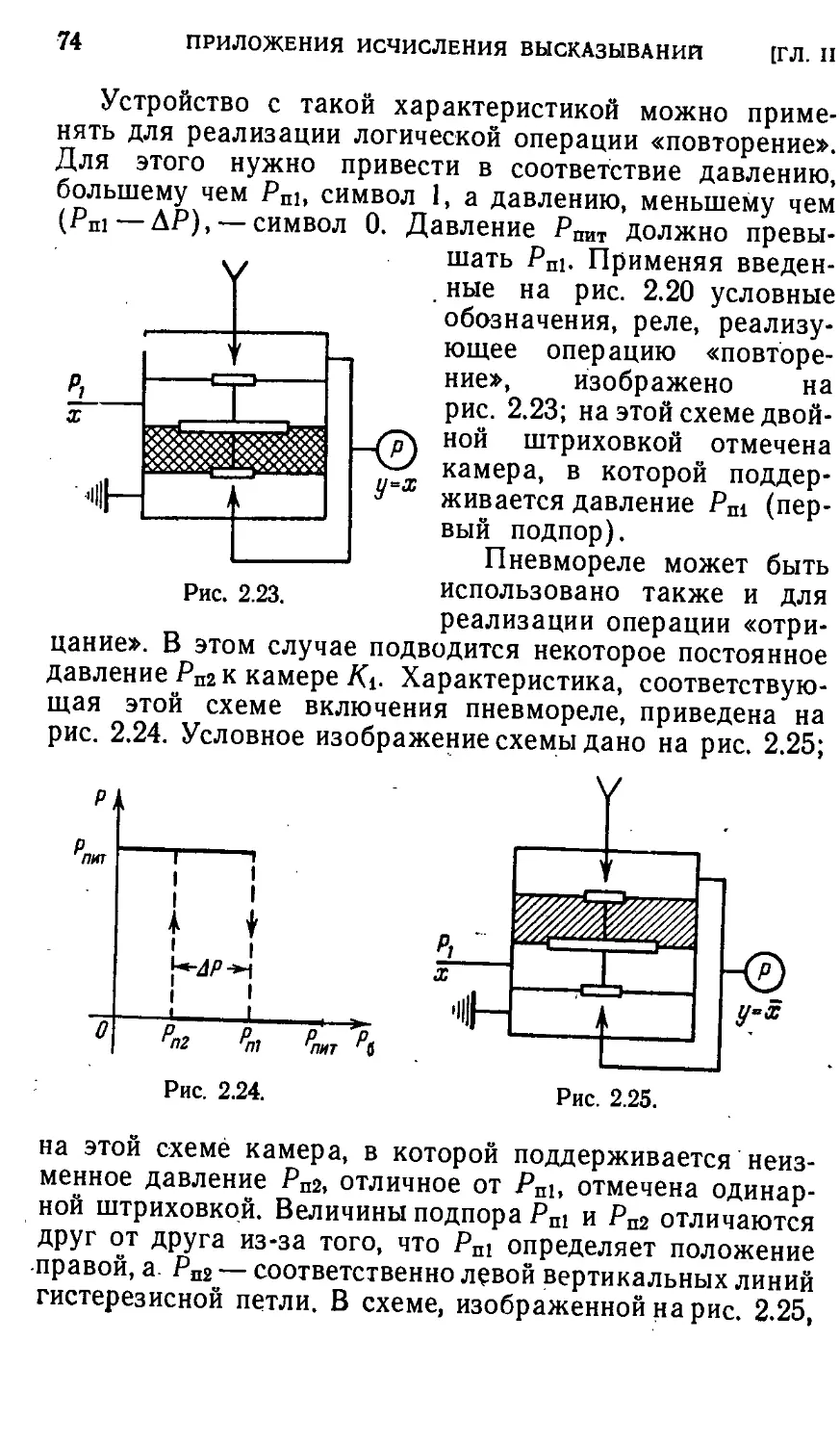
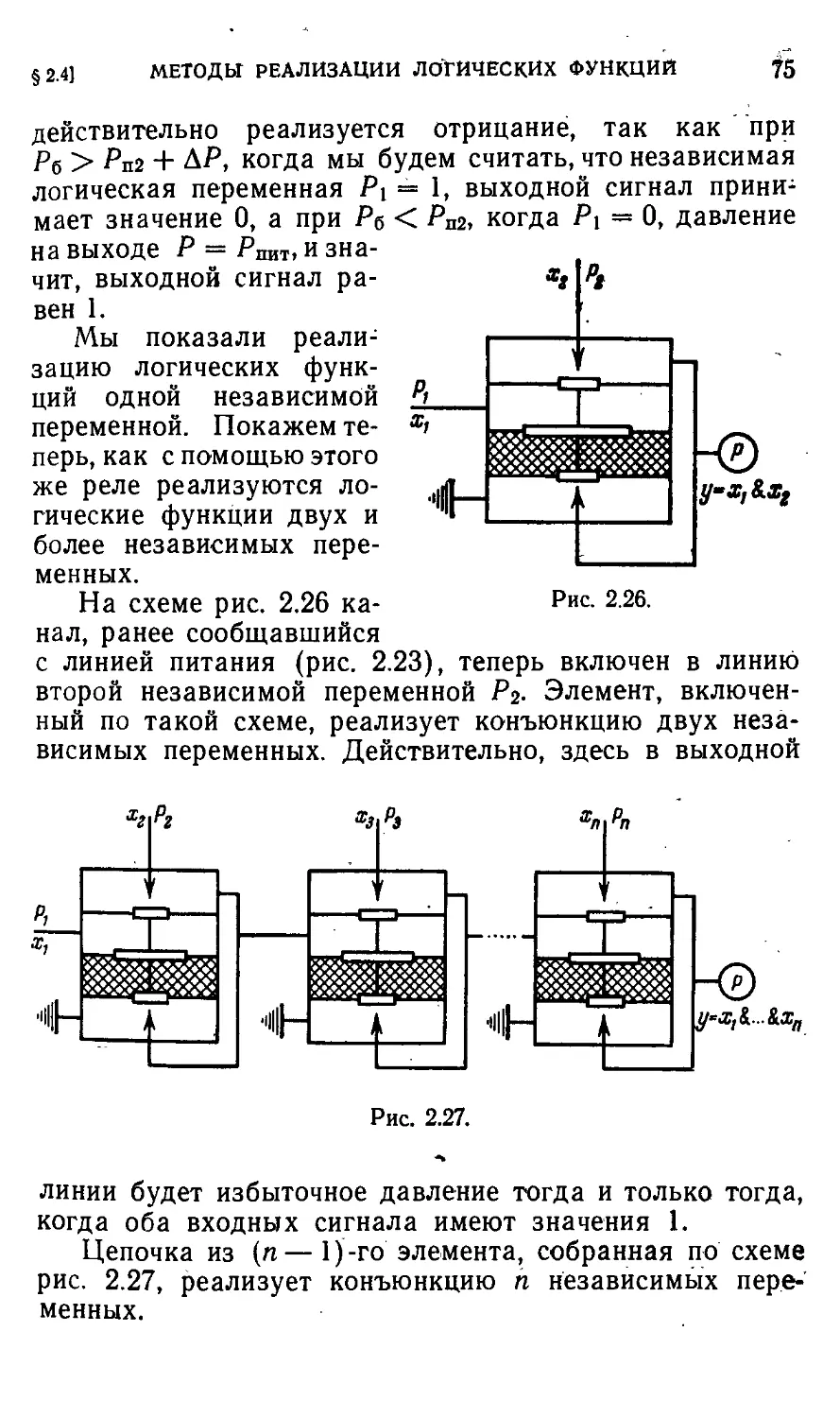
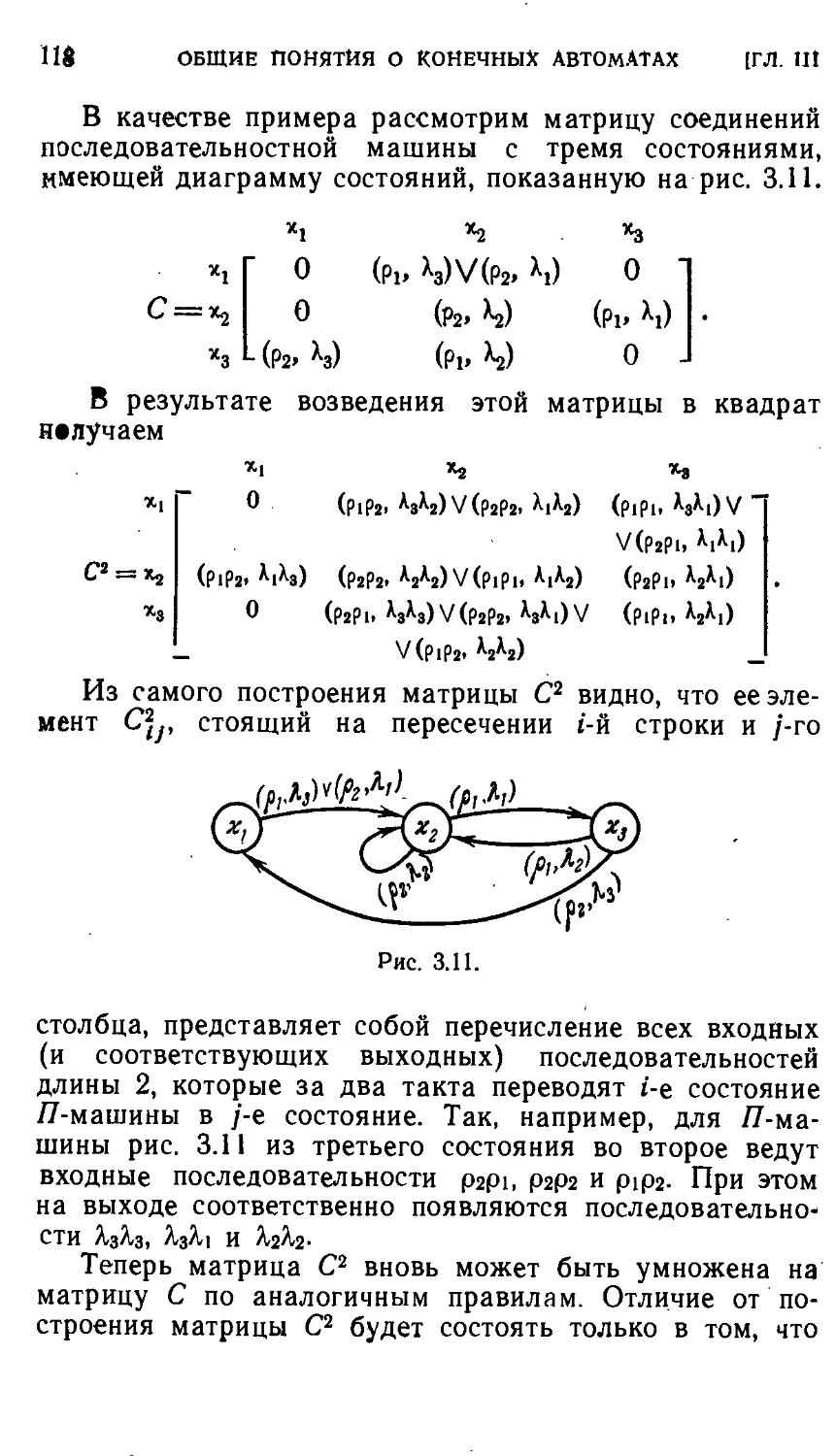
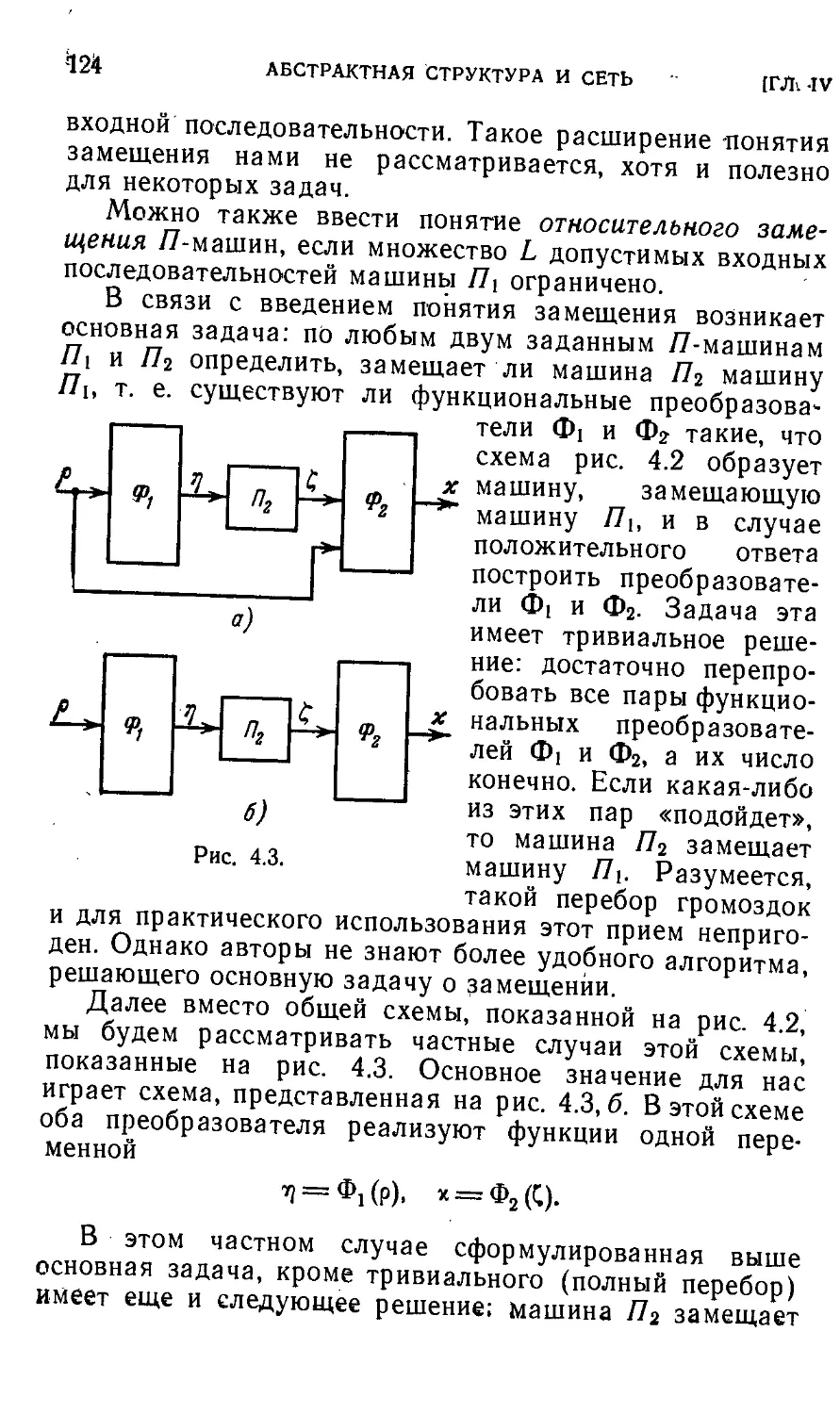
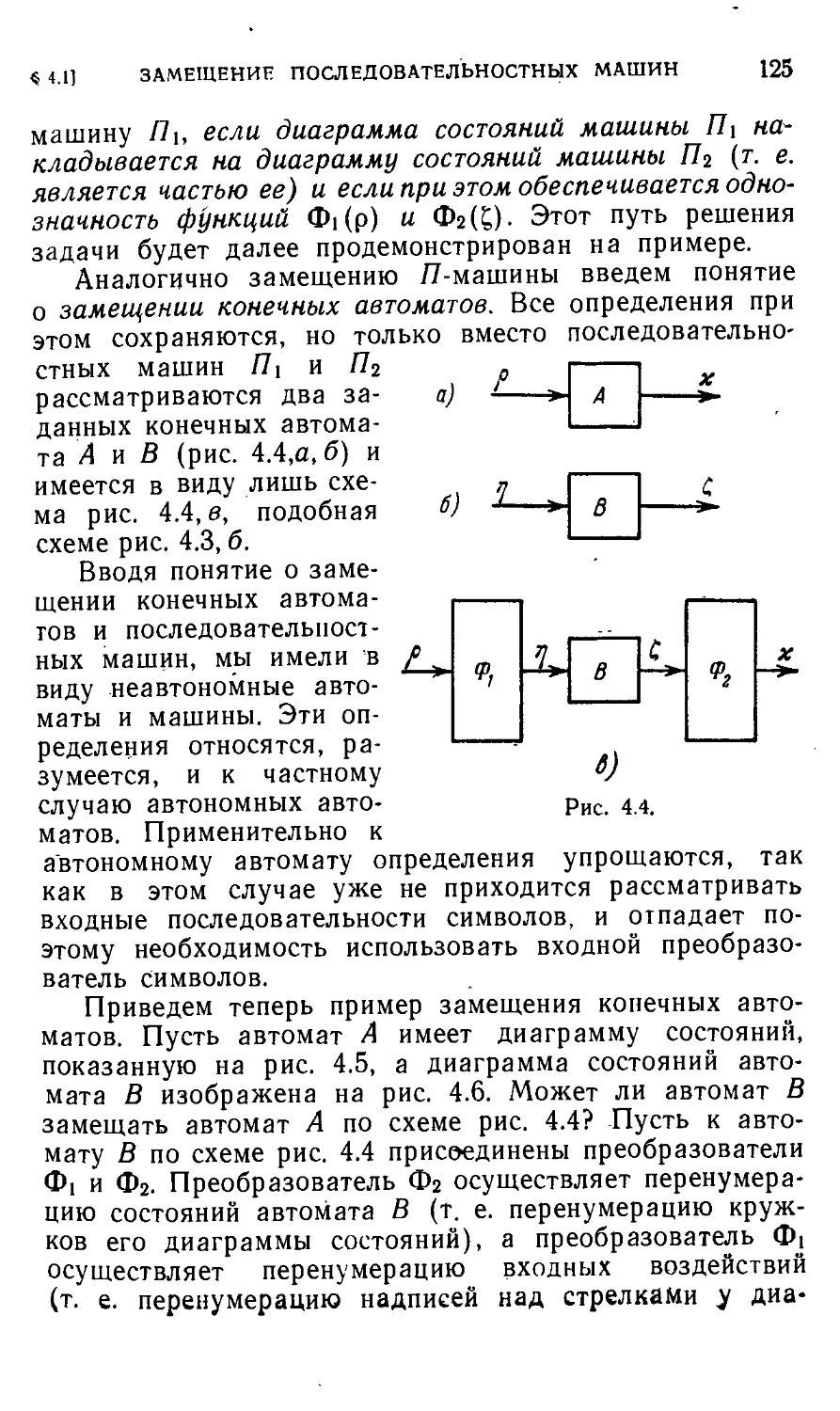
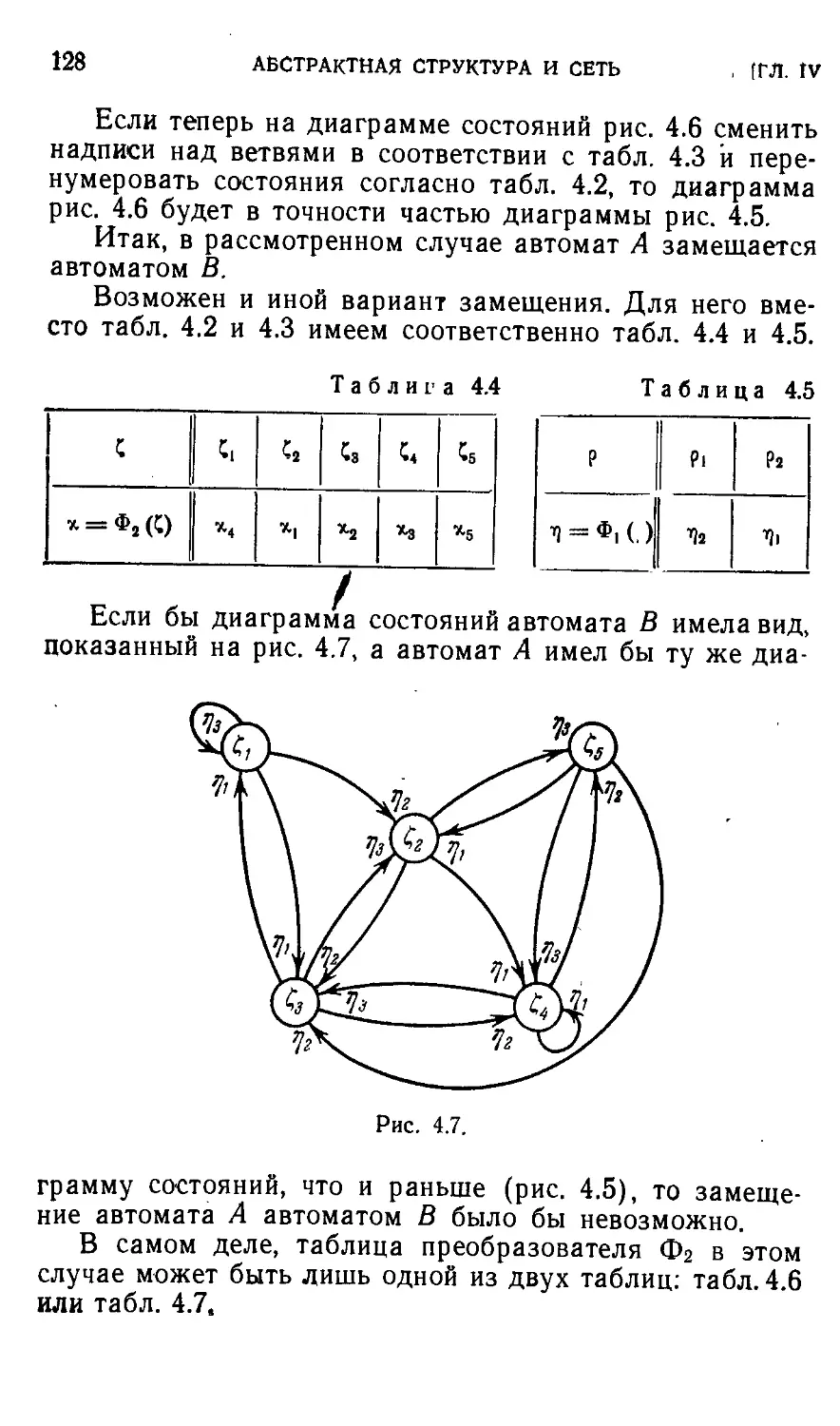
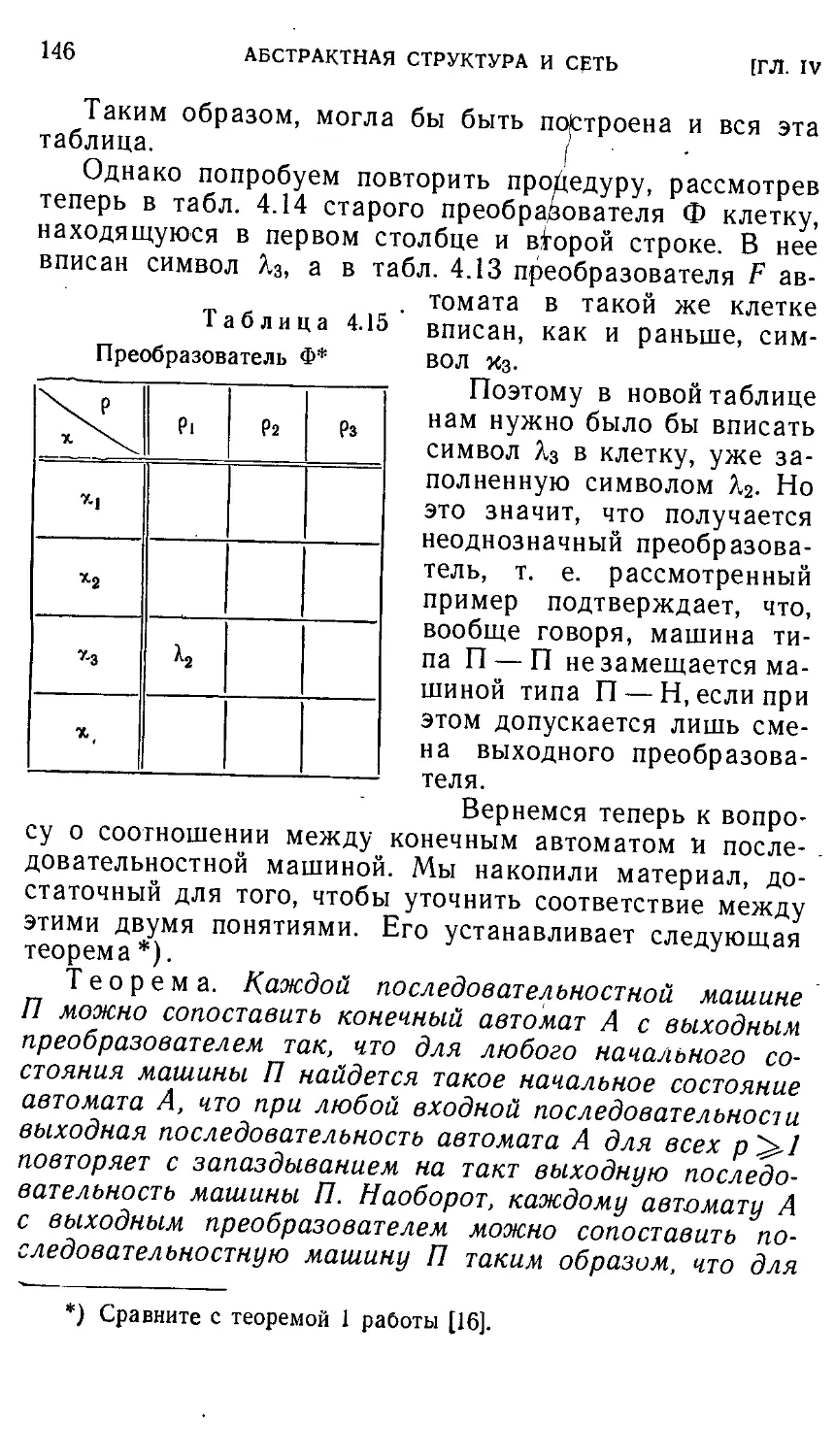
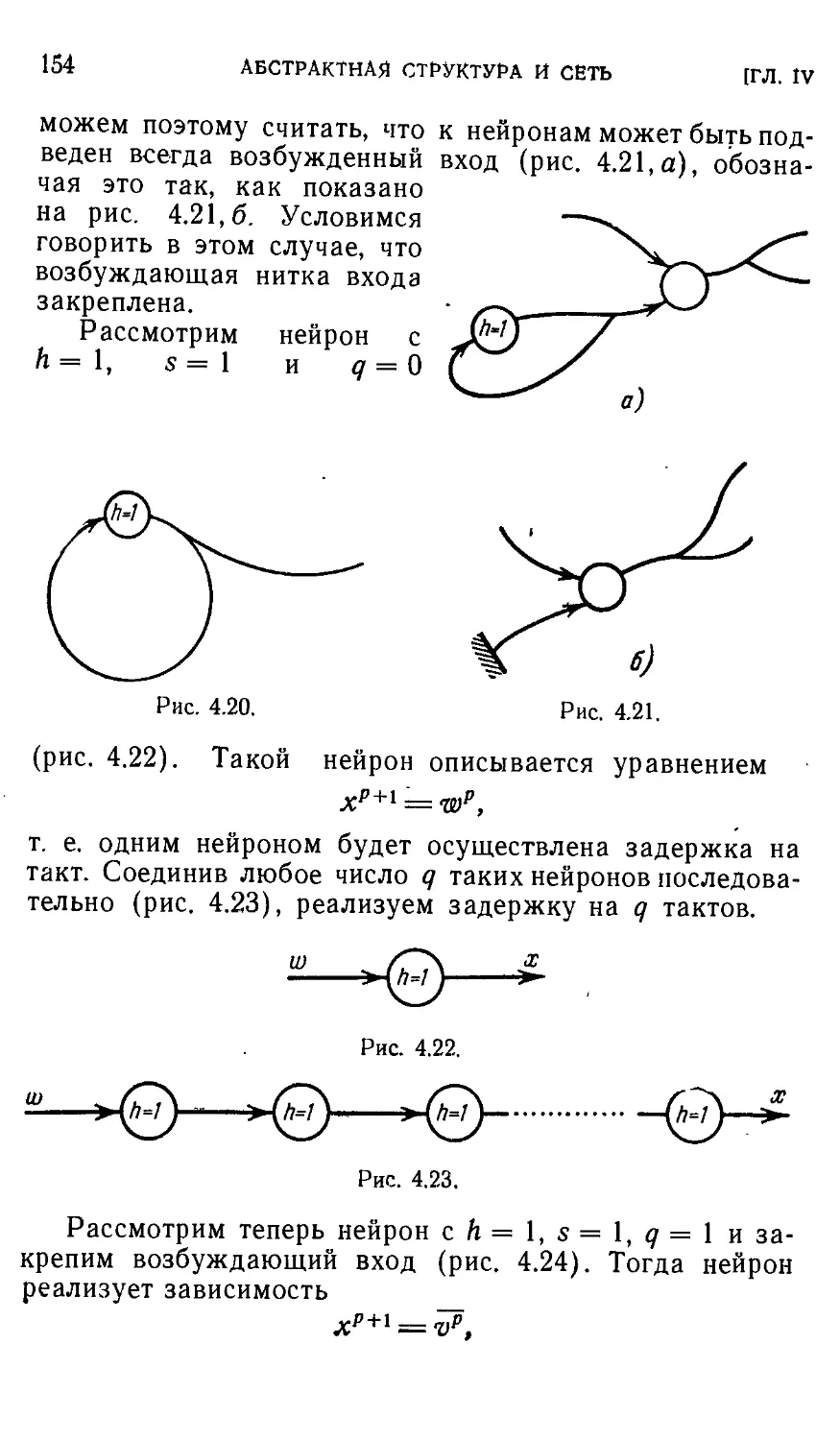
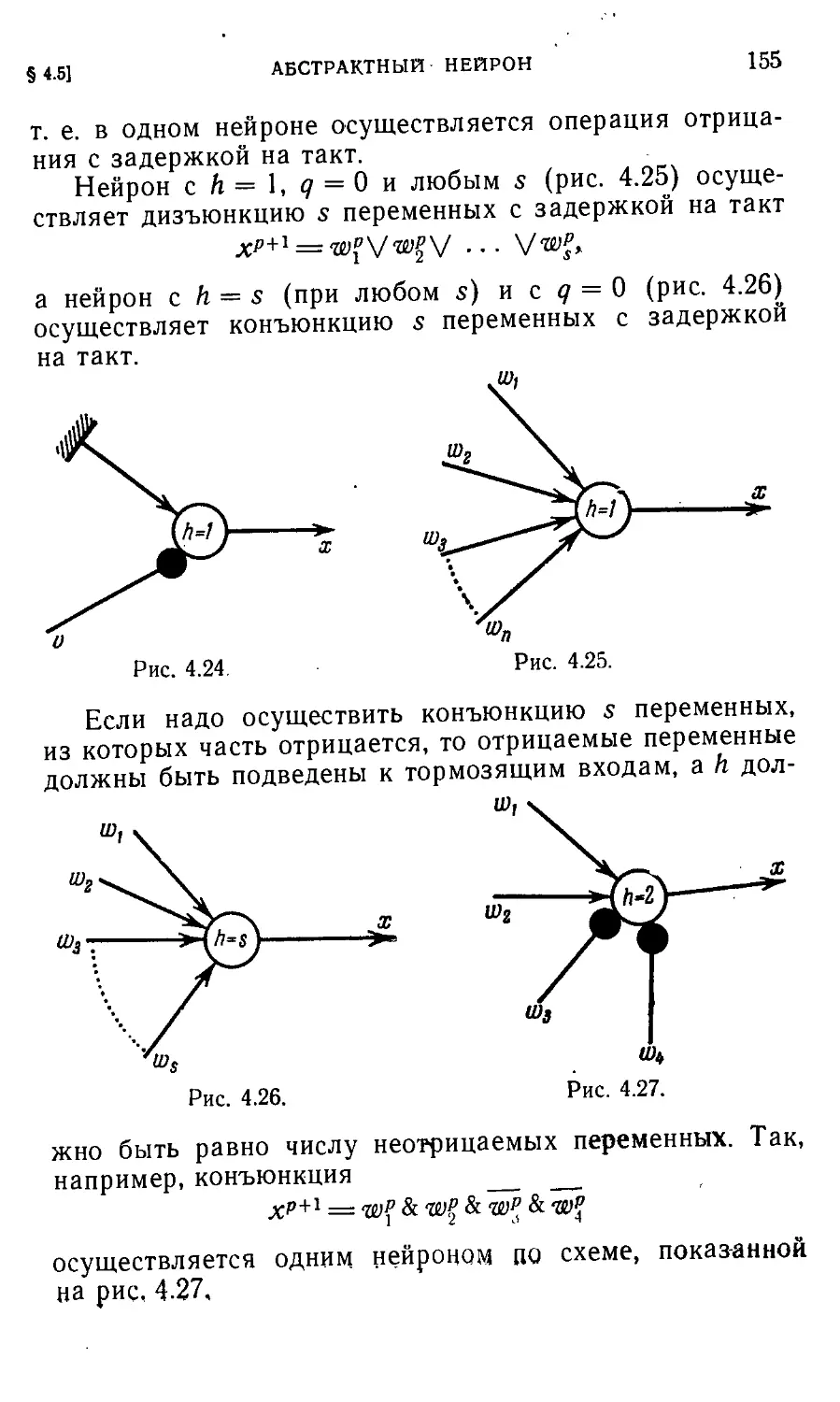
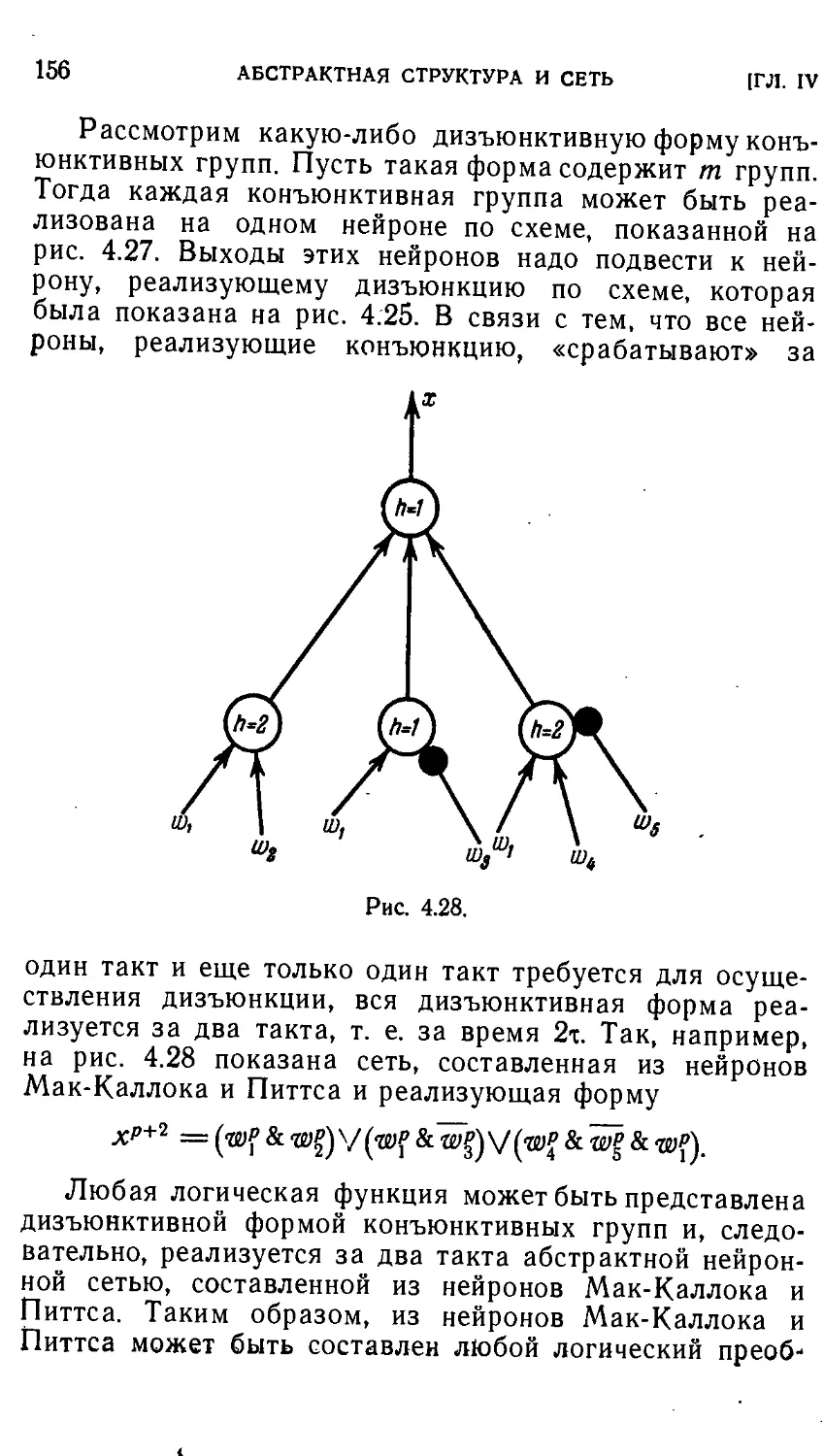
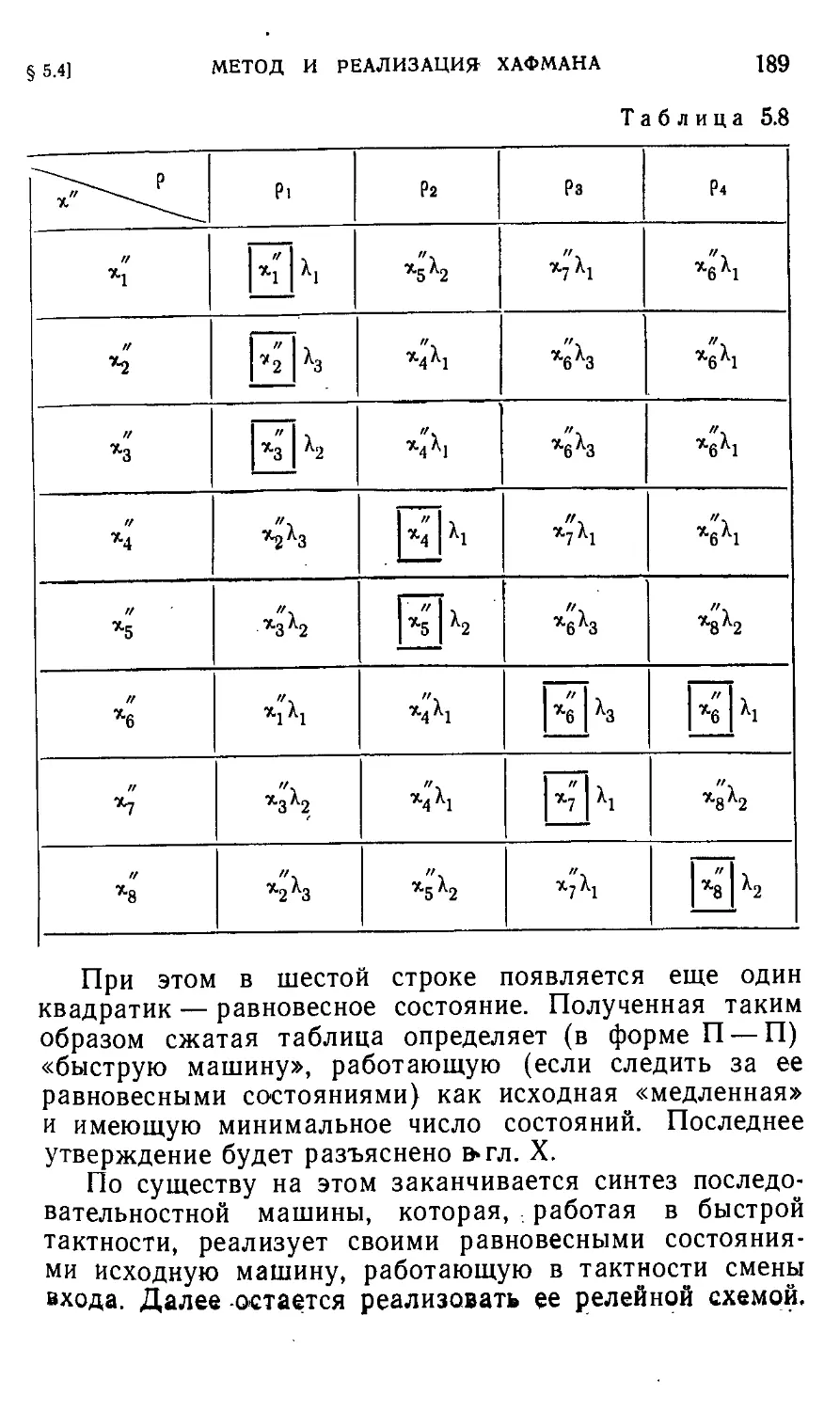
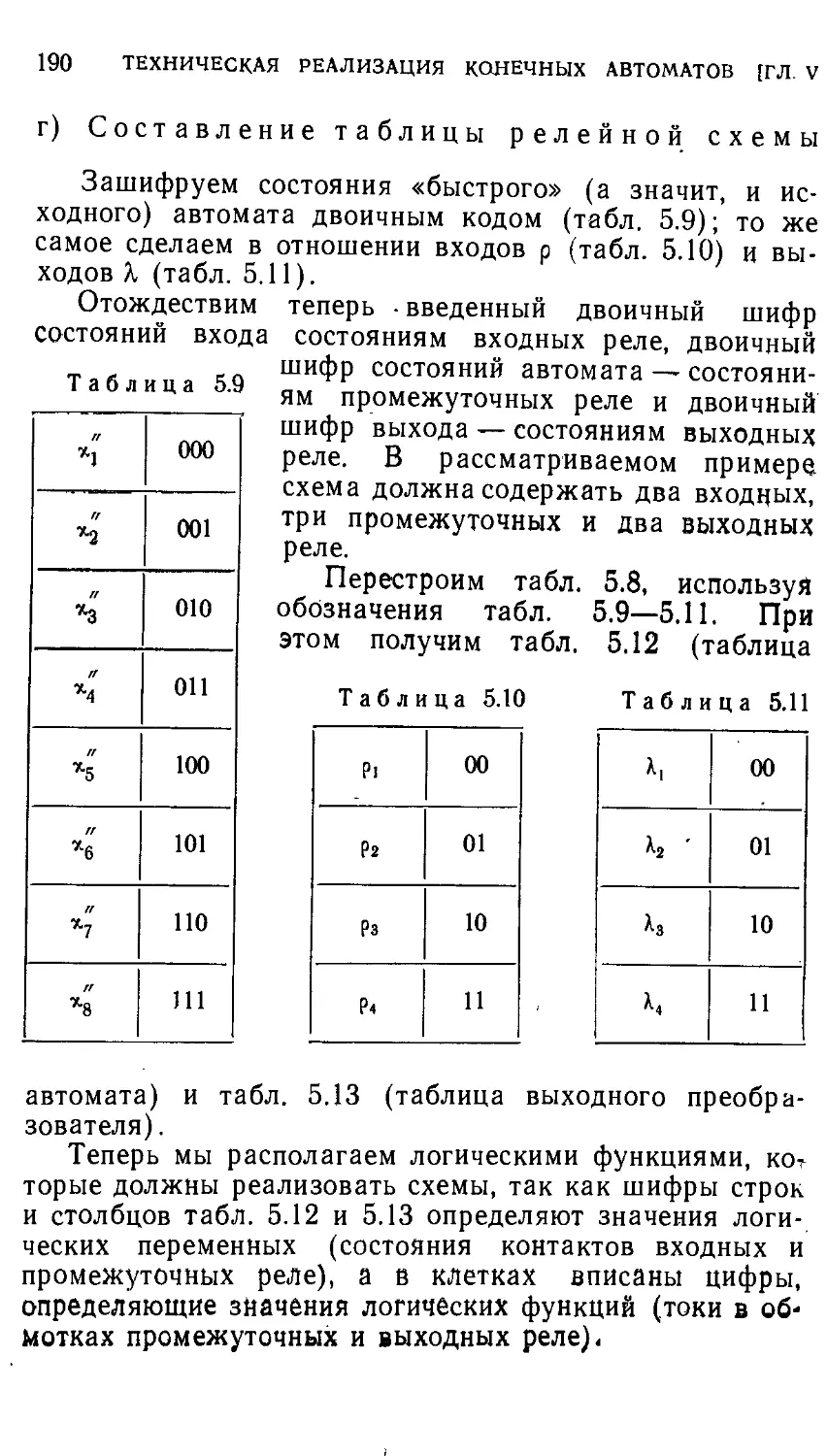
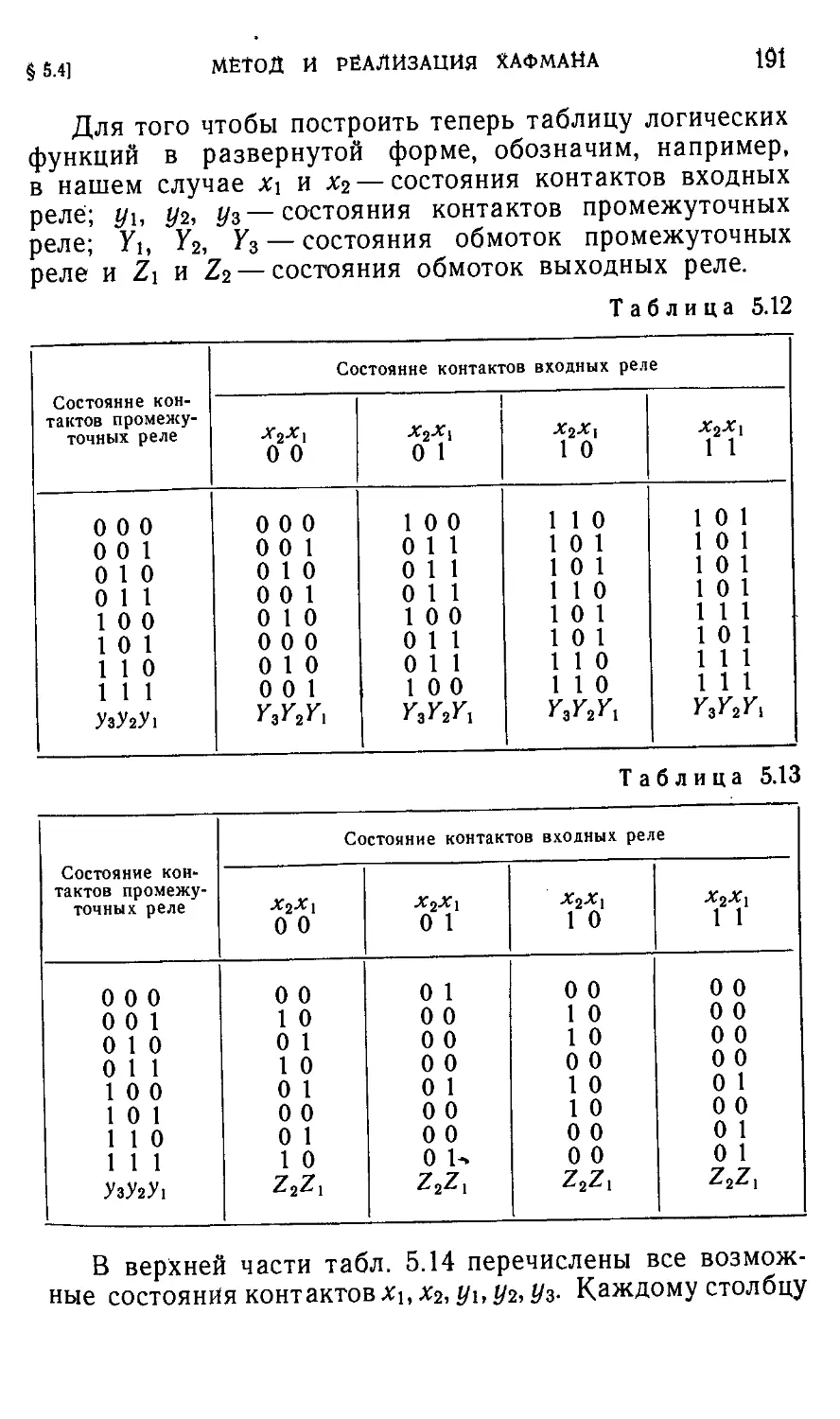
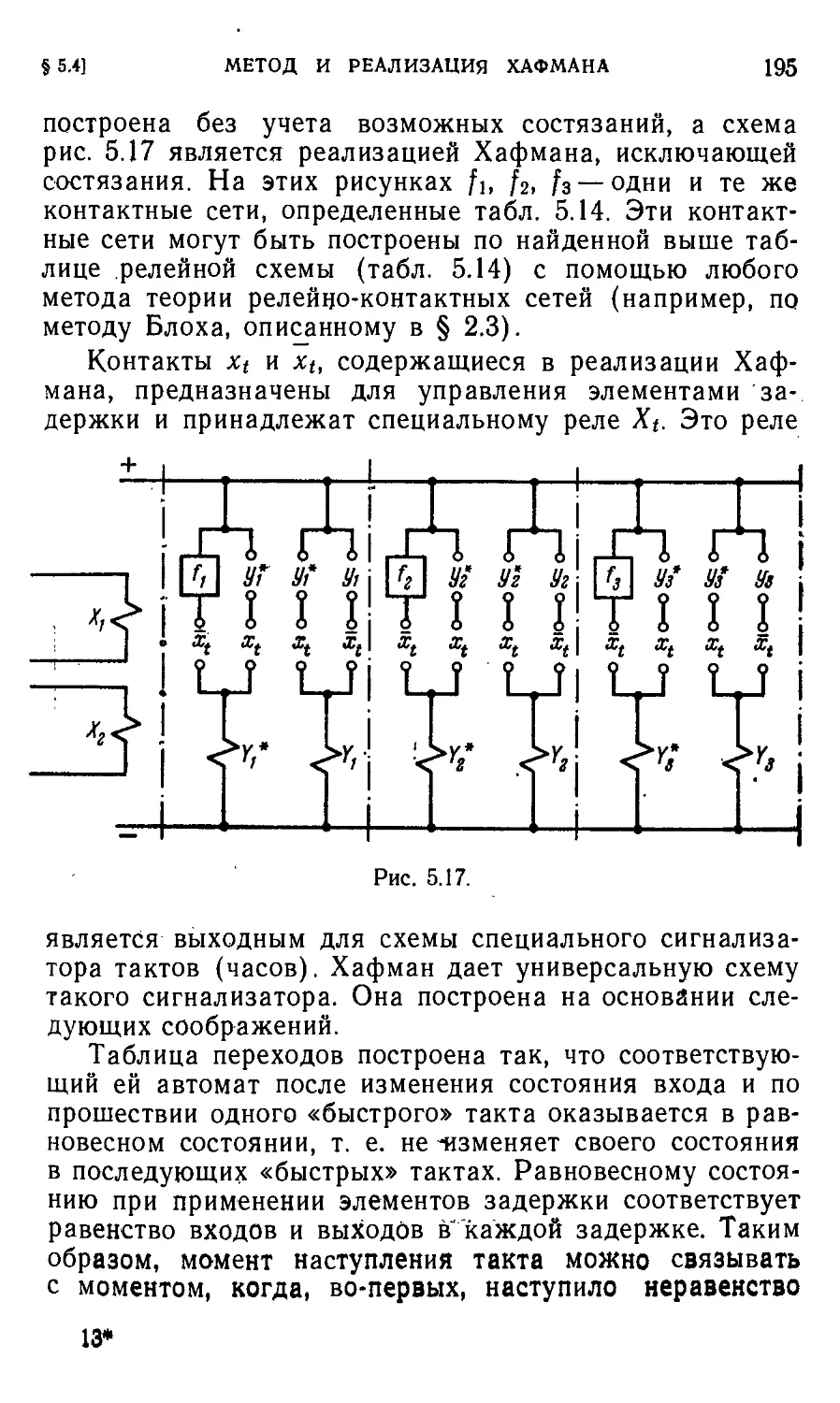
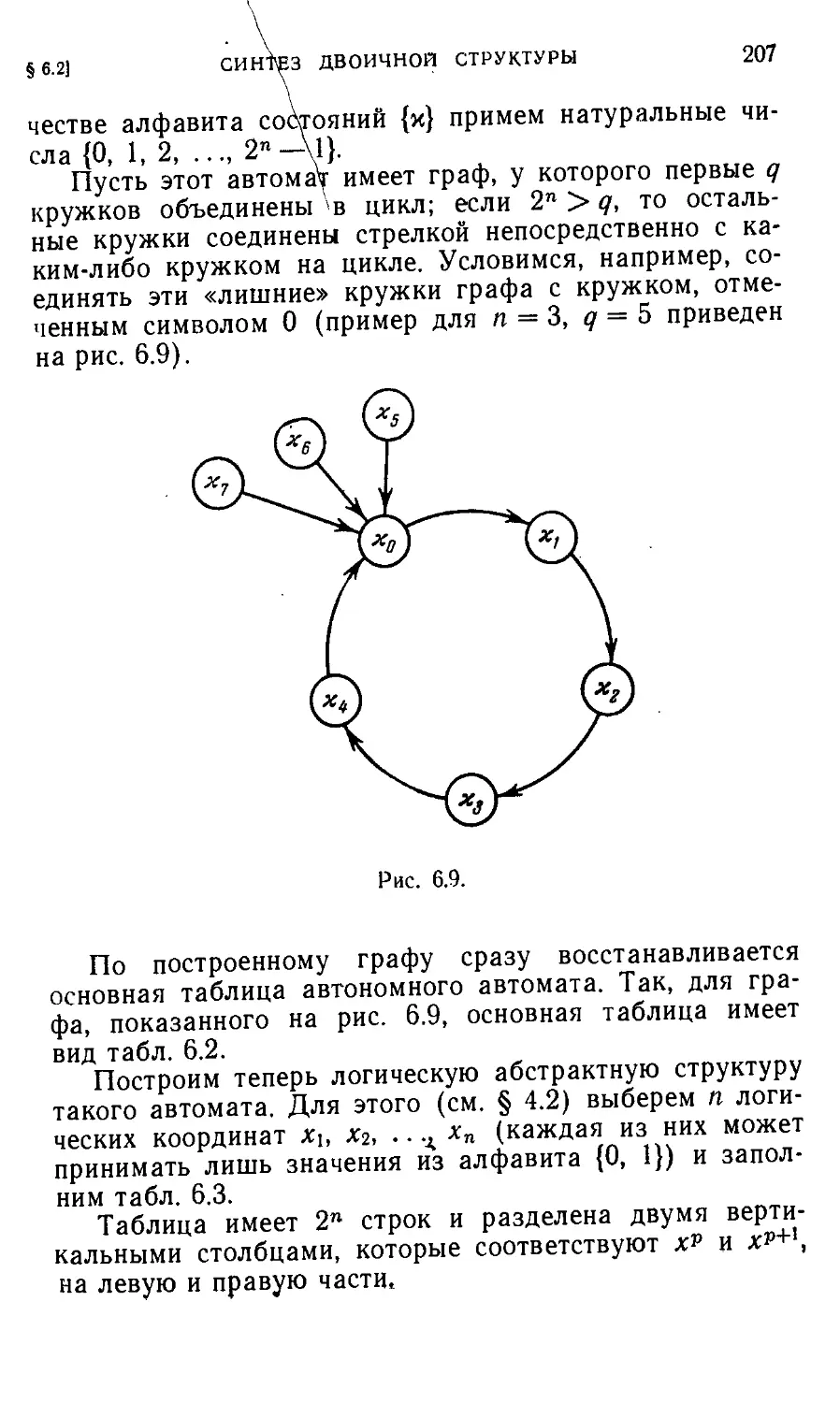
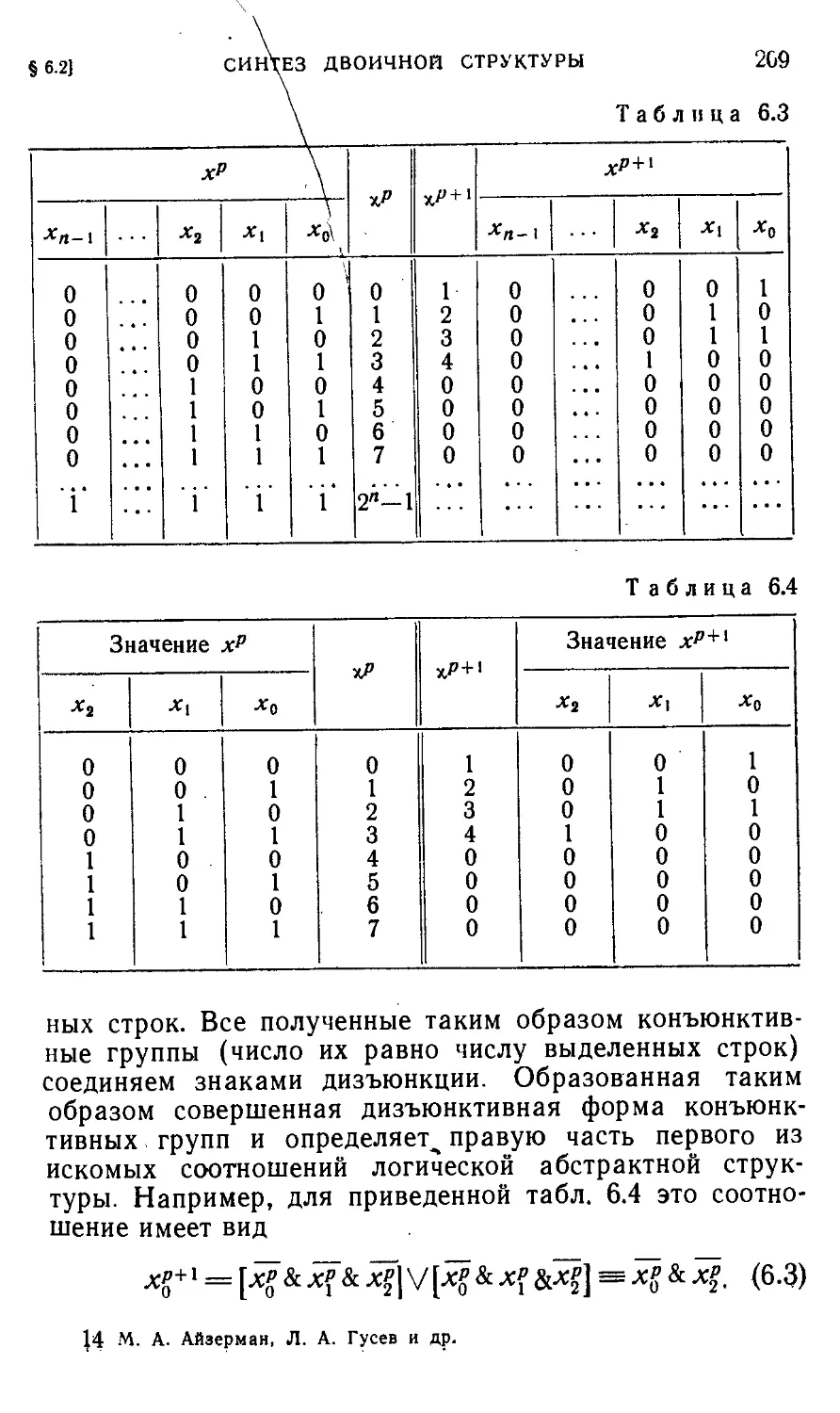
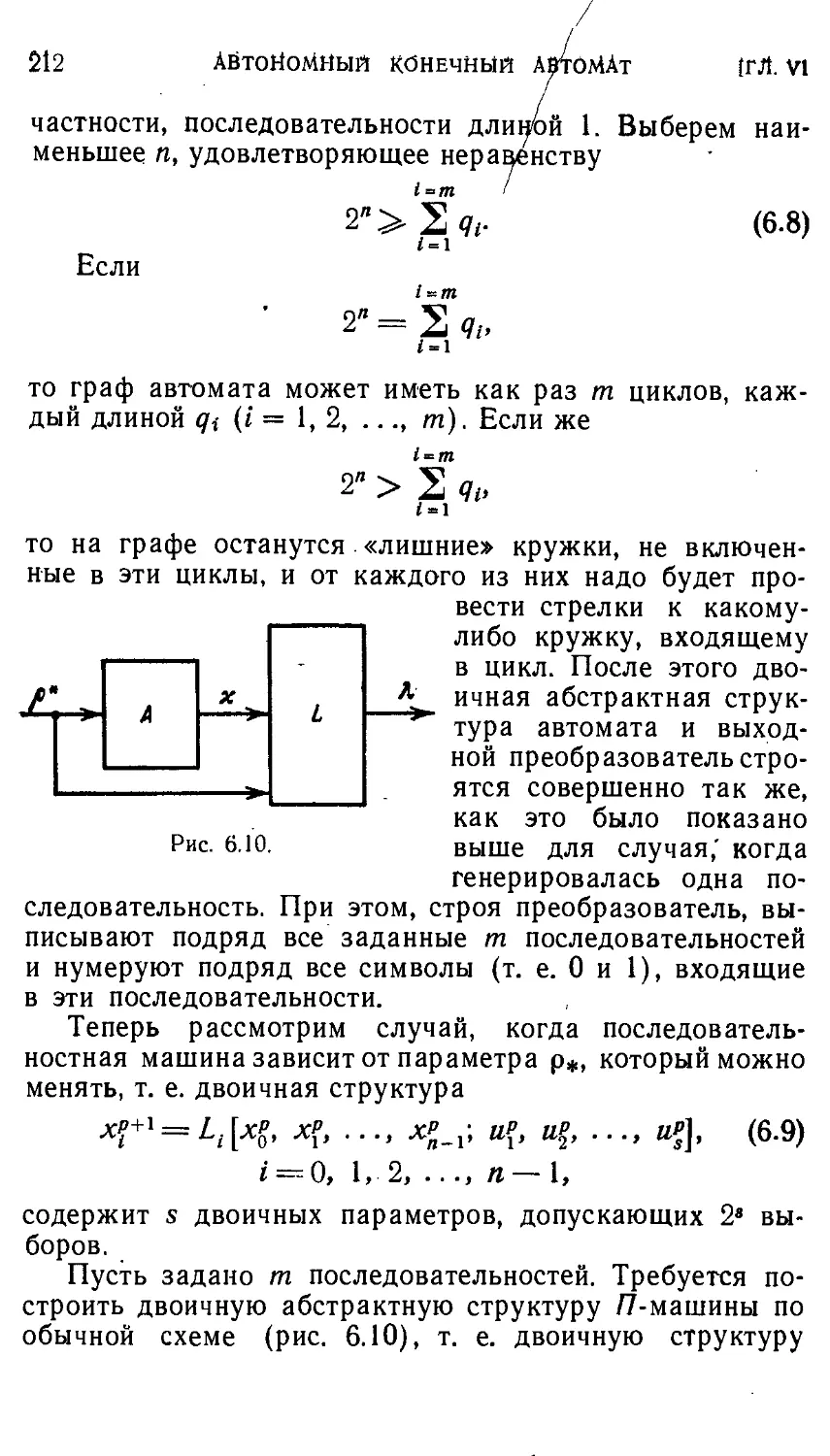
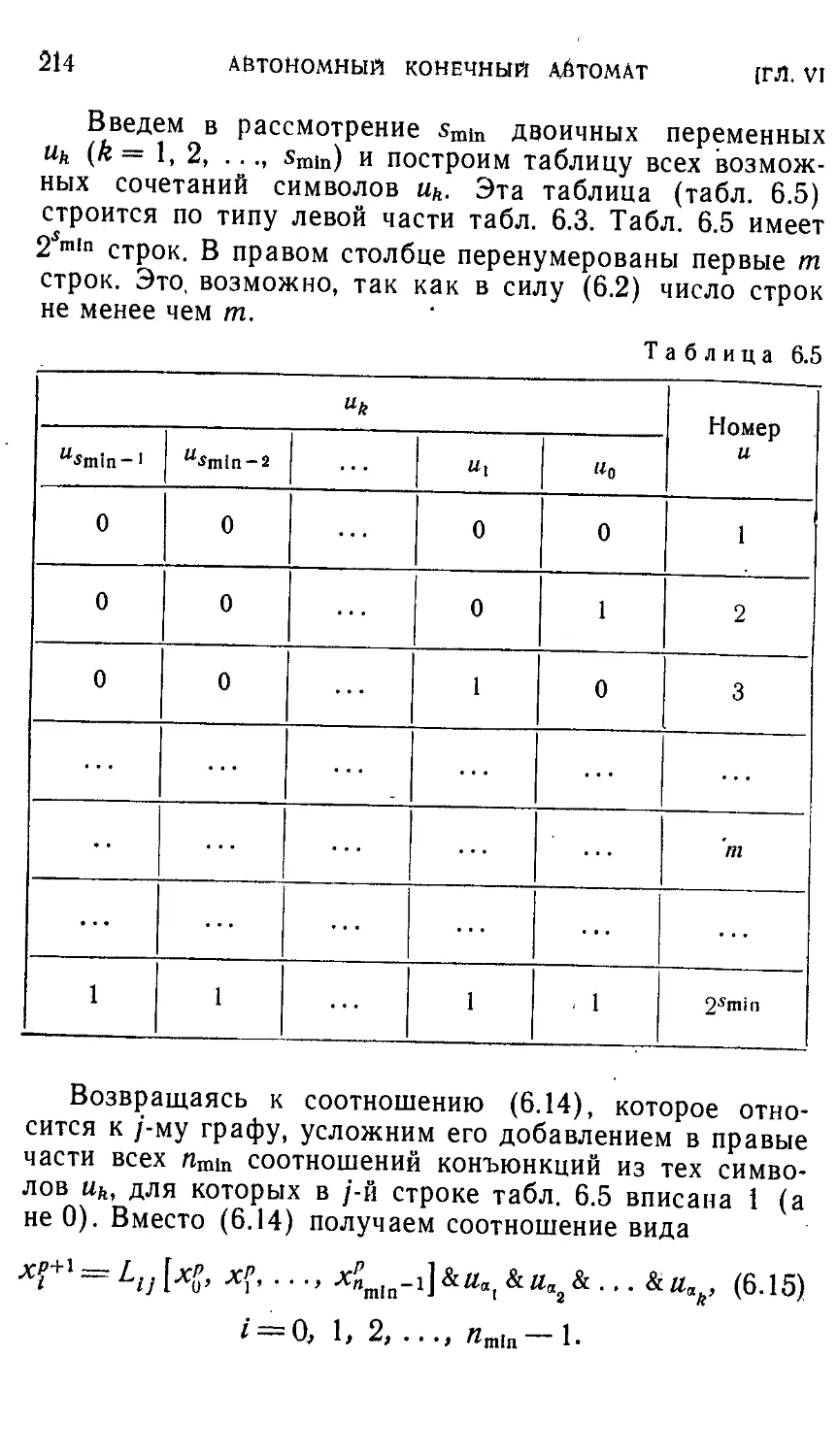
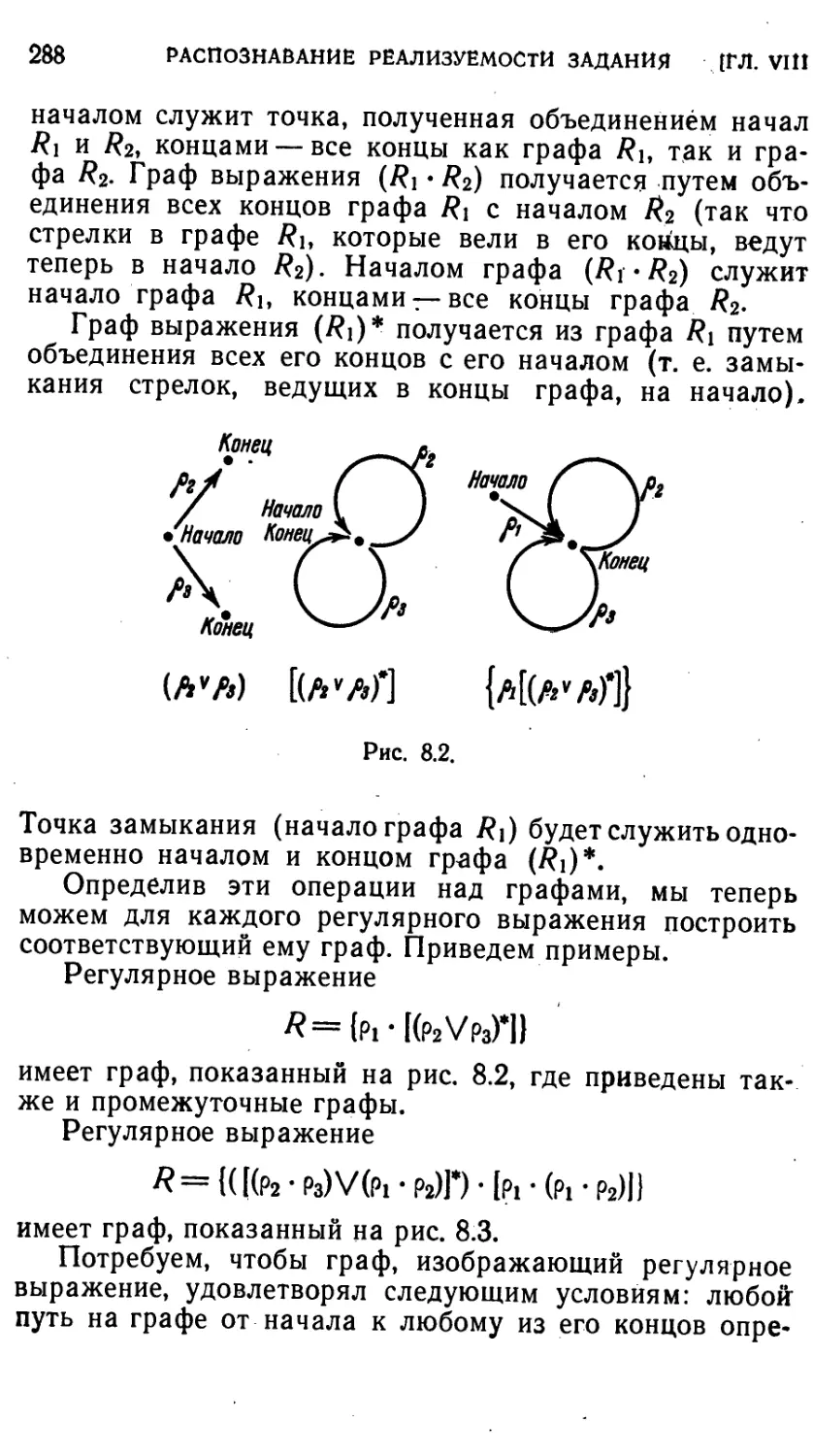
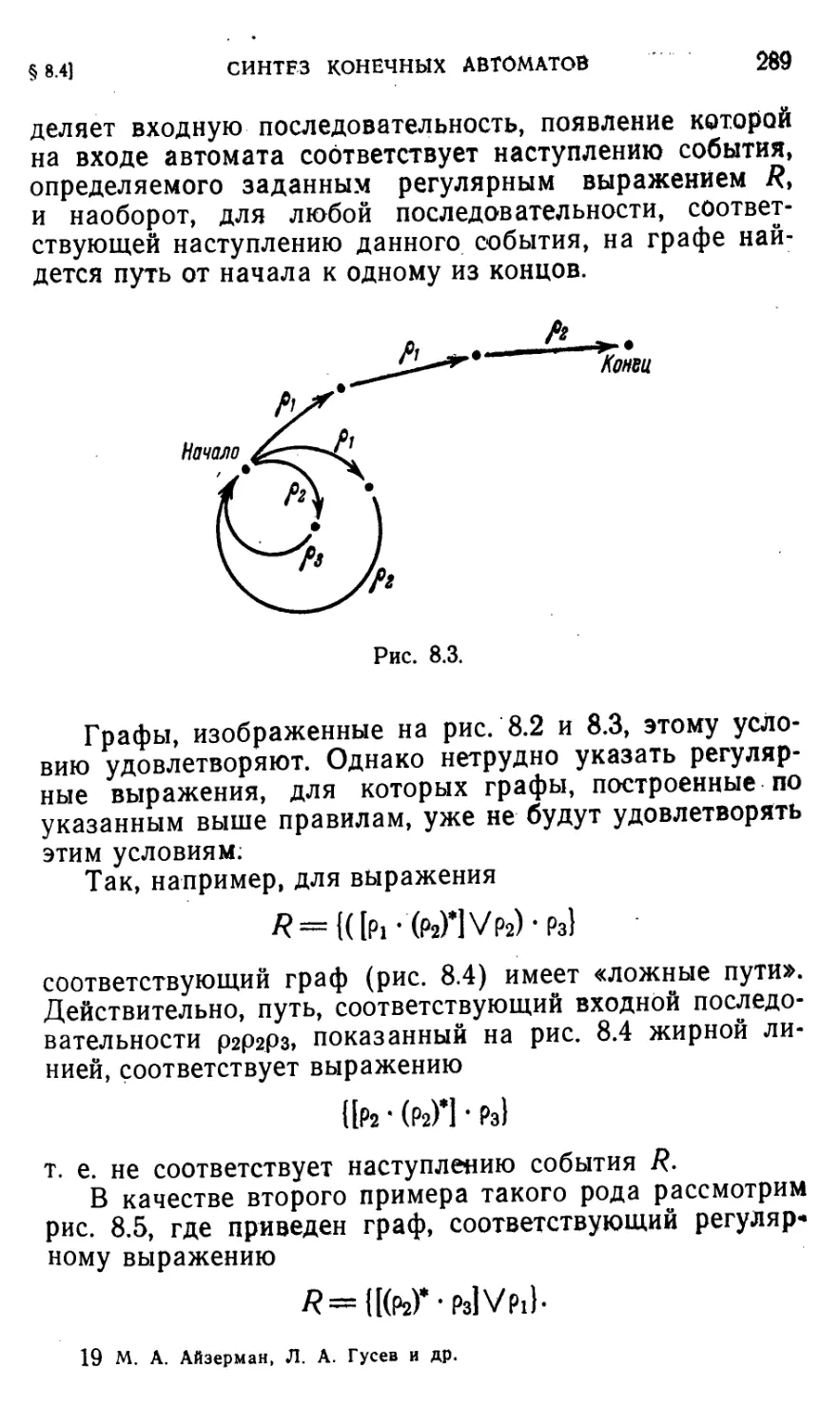
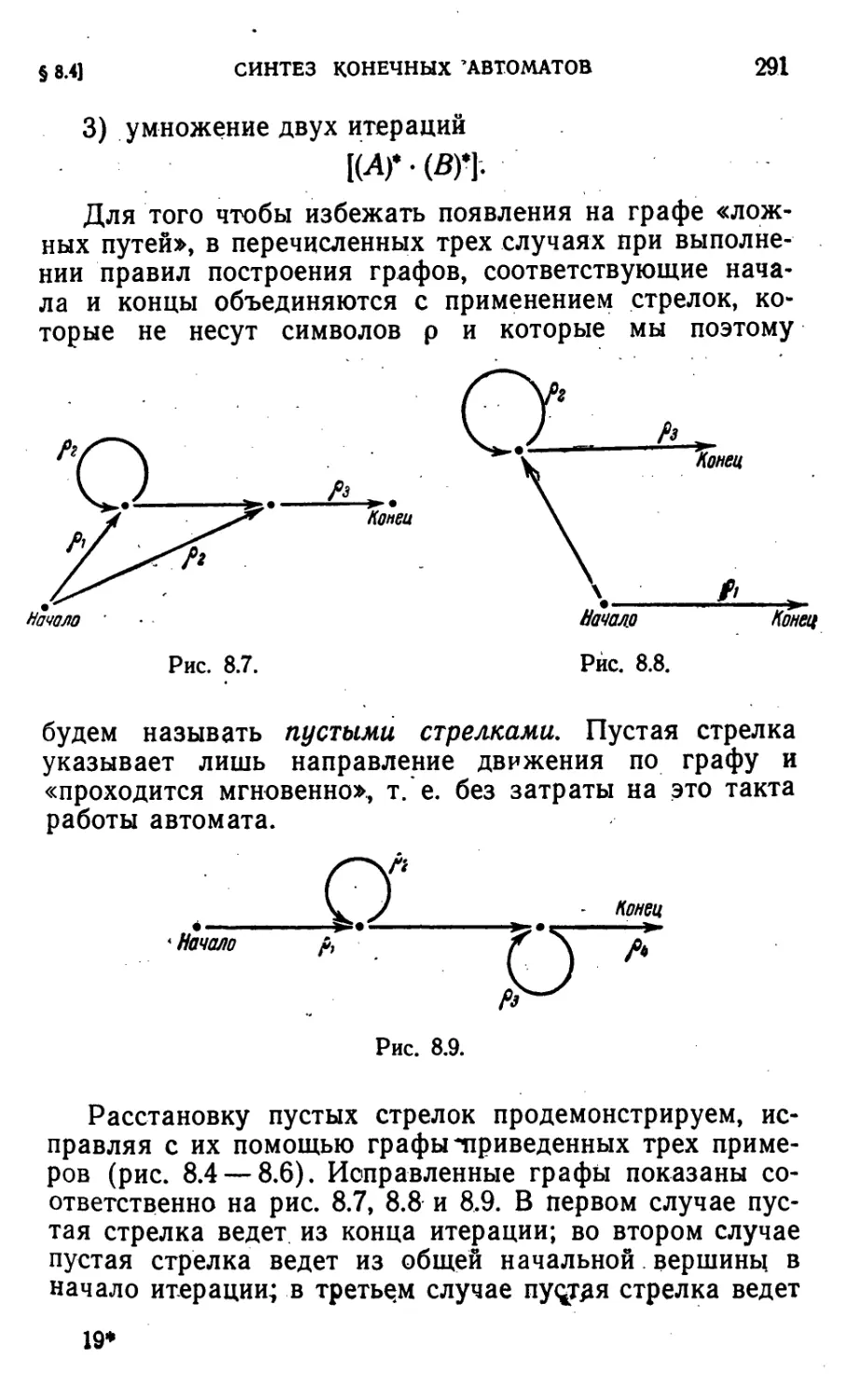
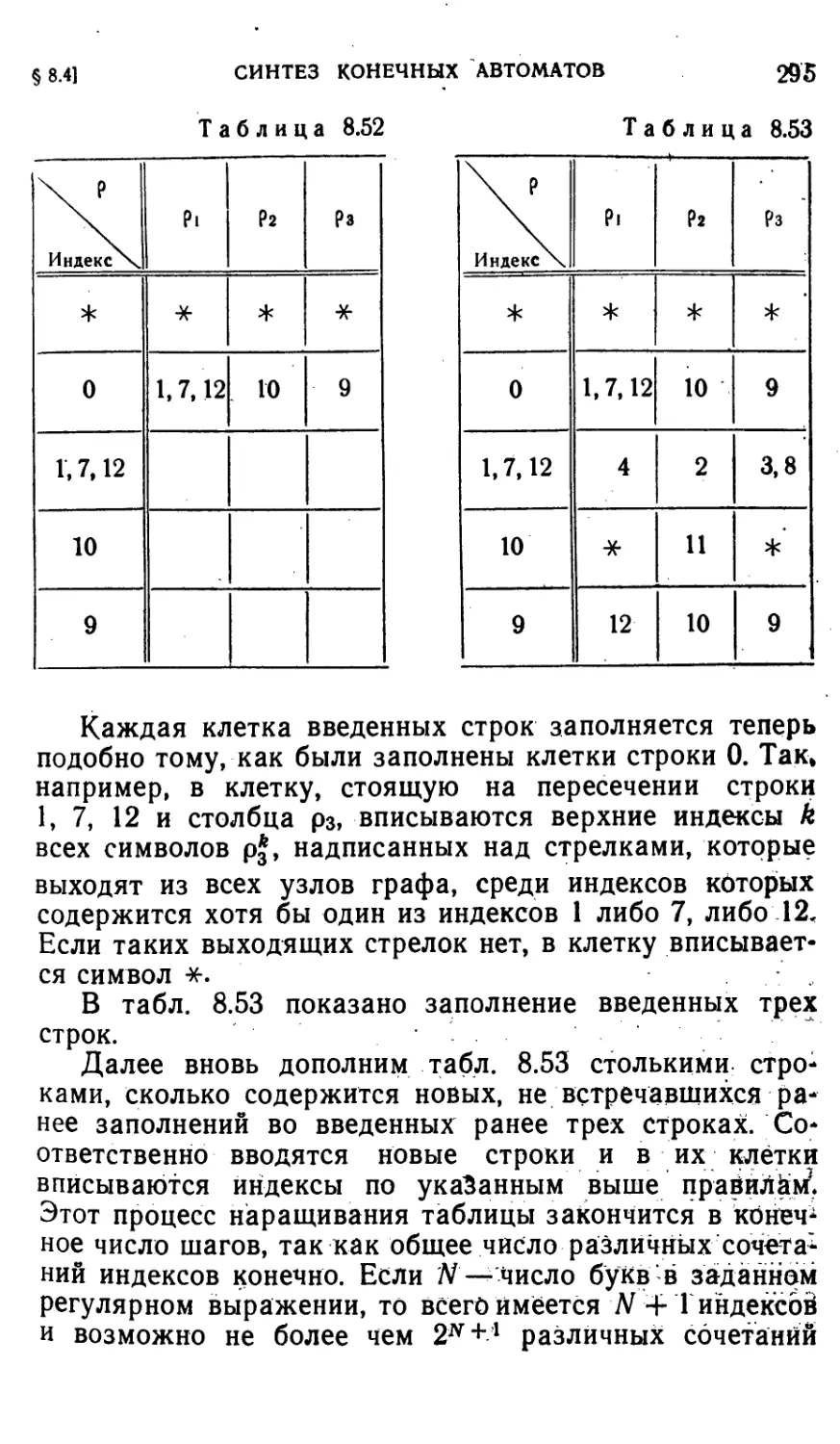
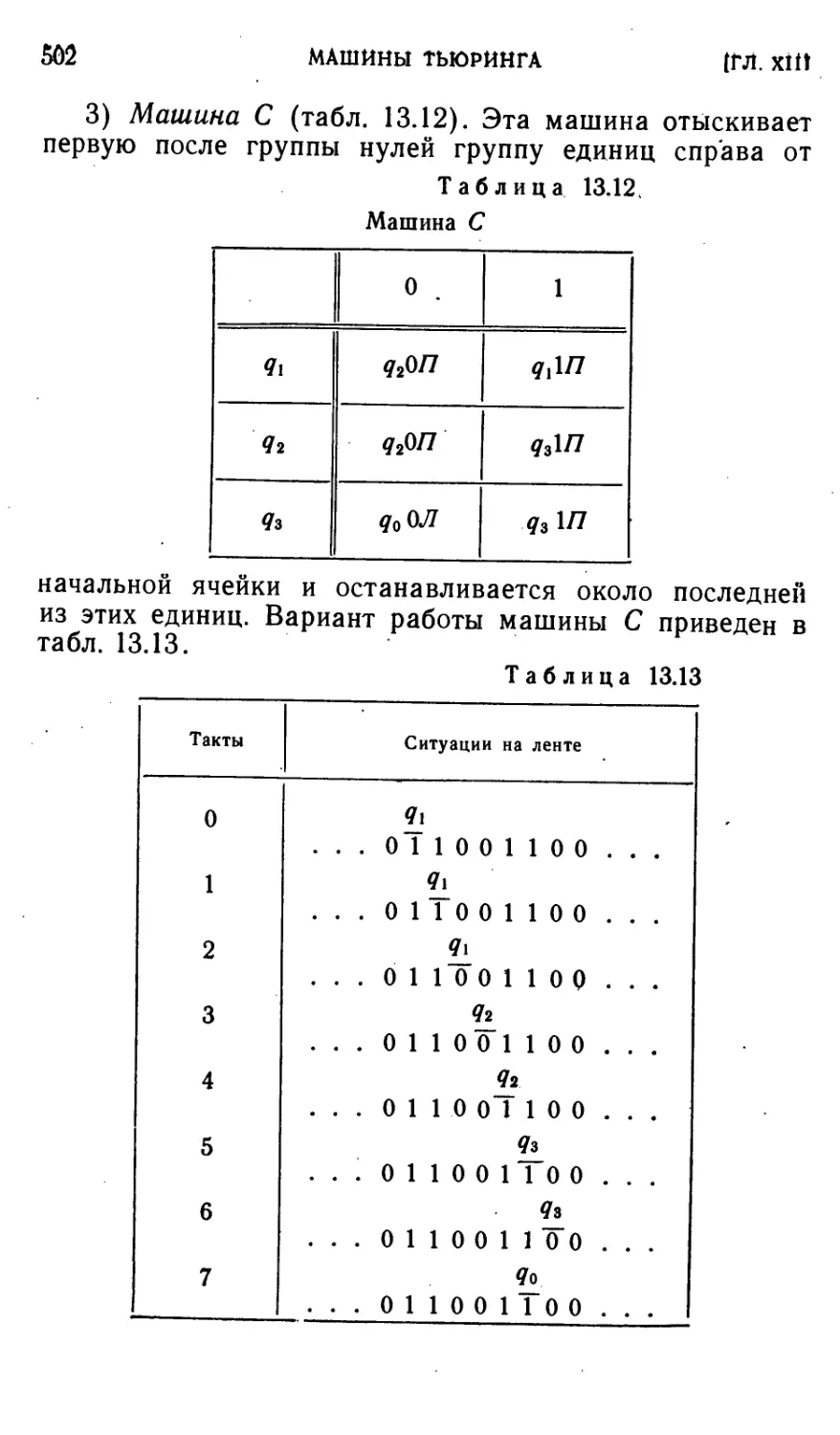
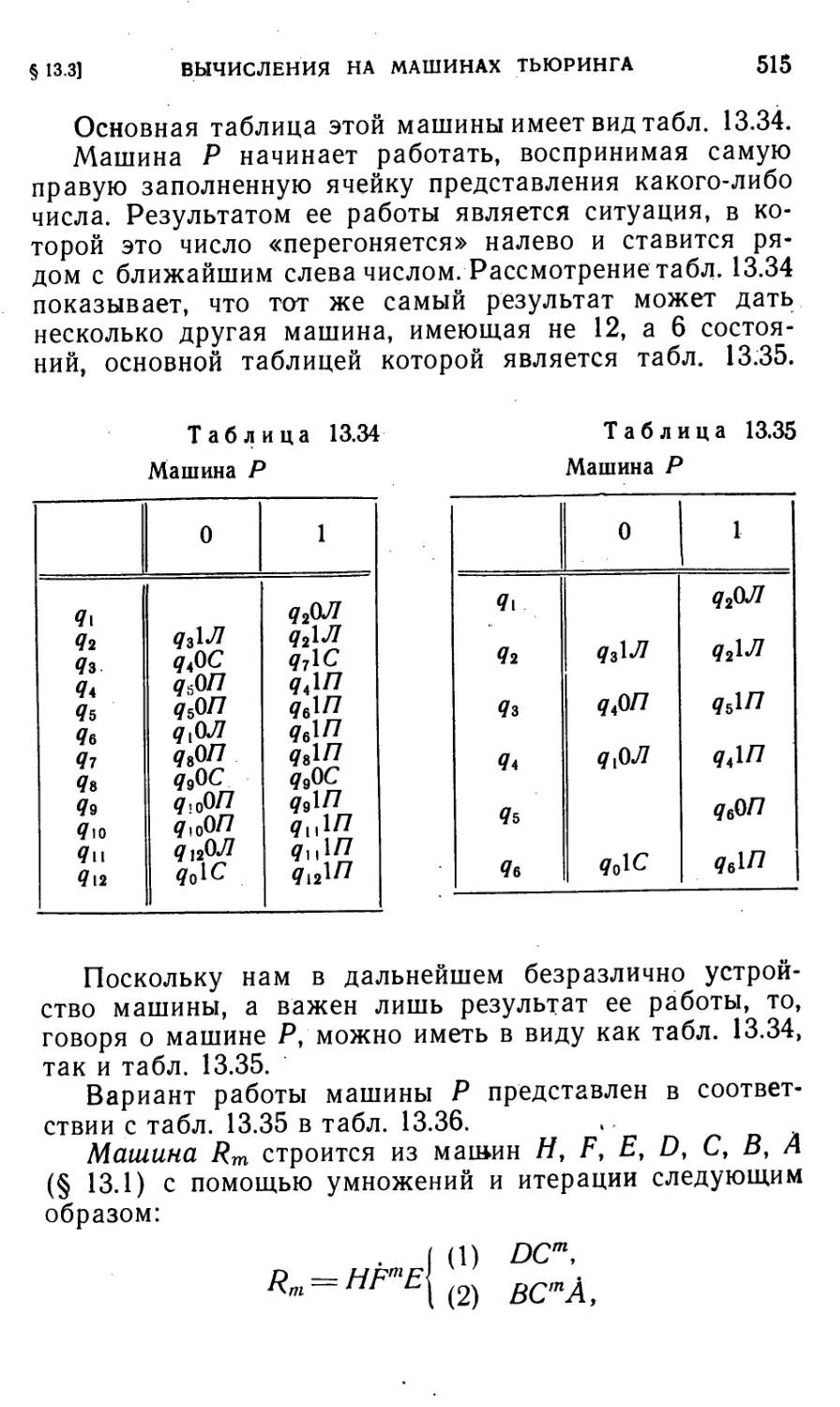
Автор: Айзерман М.А. Гусев Л.А. Розоноэр Л.И. Смирнова И.М. Таль А.А.
Теги: математика вычислительная математика
Год: 1963
Текст
М. А. АЙЗЕРМАН, Л. А. ГУСЕВ, Л. И. РОЗОНОЭР
И. М. СМИРНОВА, А. А. ТАЛЬ
ЛОГИКА
АВТОМАТЫ
АЛГОРИТМЫ
ш
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1963
6 П2.13
A 36
УДК 519-95
Айзерман Марк Аронович, Гусев Леонид Алексеевич, Розоноэр Лев Ильич,
Смирнова Ирина Михайловна, Таль Алексей Алексеевич
Логика. Автоматы. Алгоритмы.
М., Физматгиз, 1963 г., 556 стр. с илл.
Редактор Королев Н. А.
Техн. редактор Мурашова Н. Я. _ Корректор Халанская А. Д.
Сдано в набор 8/V-1963 г. Подписано к печати 19/ХМ963 г. Бумага 84х108'/м.
Физ. печ. л. 17,375. Условн. печ. л. 28,5. Уч.-изд. л. 25,96. Тираж 14 000 экз.
Т-14842. Цеиа книги 1 р. 45 к. Заказ № 1392.
Государственное издательство физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Типография № 2 им. Евг. Соколовой УЦБ и ПП Ленсовяархоза.
Ленин] рад, Измайловский пр., 29.
ОГЛАВЛЕНИЕ
Предисловие 7
Введение 9
Глава I. Элементы математической логики 11
§ 1.1. Вводные замечания 11
§ 1.2. Основные понятия 12
§ 1.3. Исчисление высказываний 20
§ 1.4. Об исчислении предикатов (двузначных) 41
Глава II. Технические приложения исчисления высказываний 46
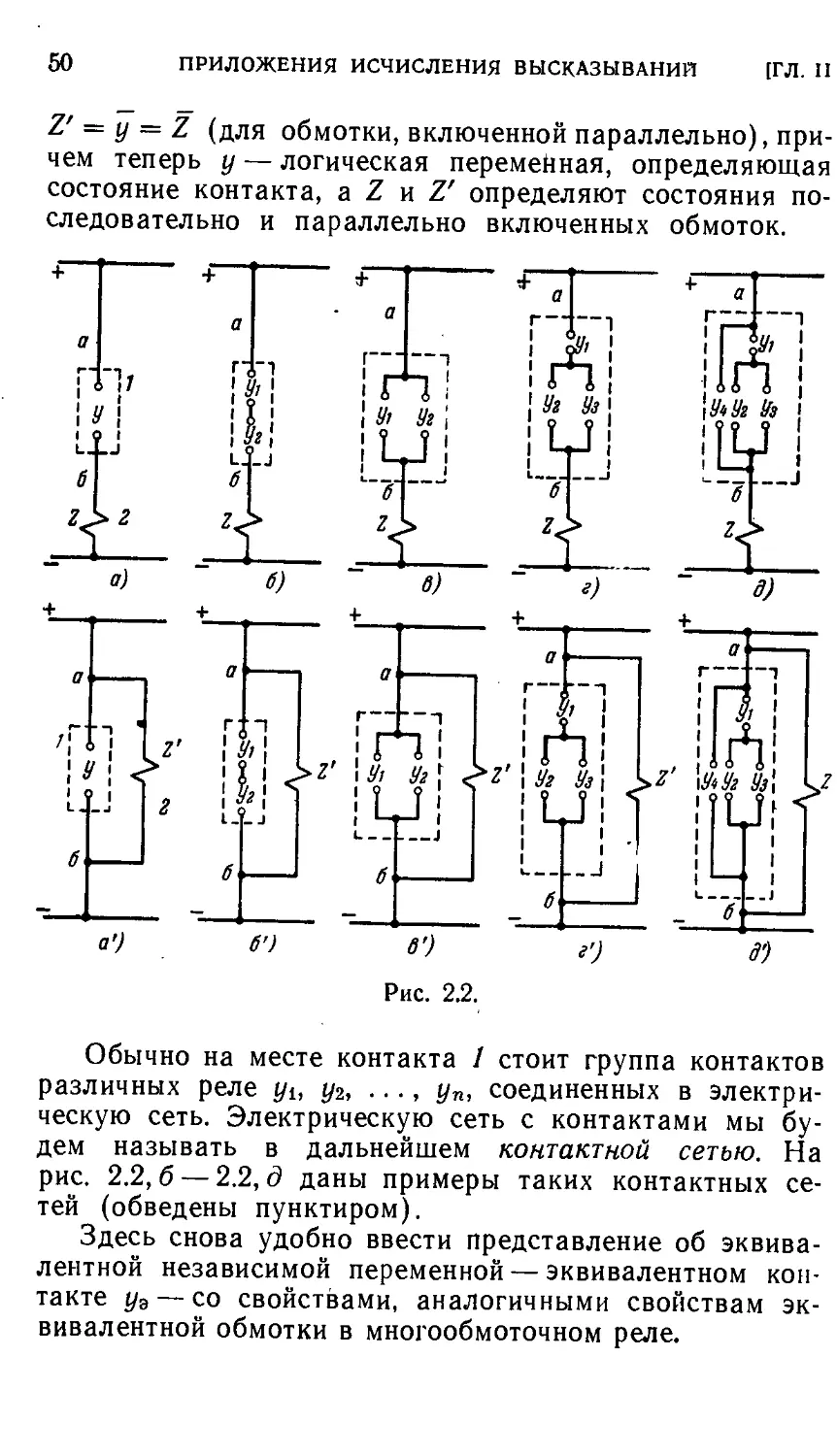
§ 2.1. Однотактные релейно-контактные схемы 46
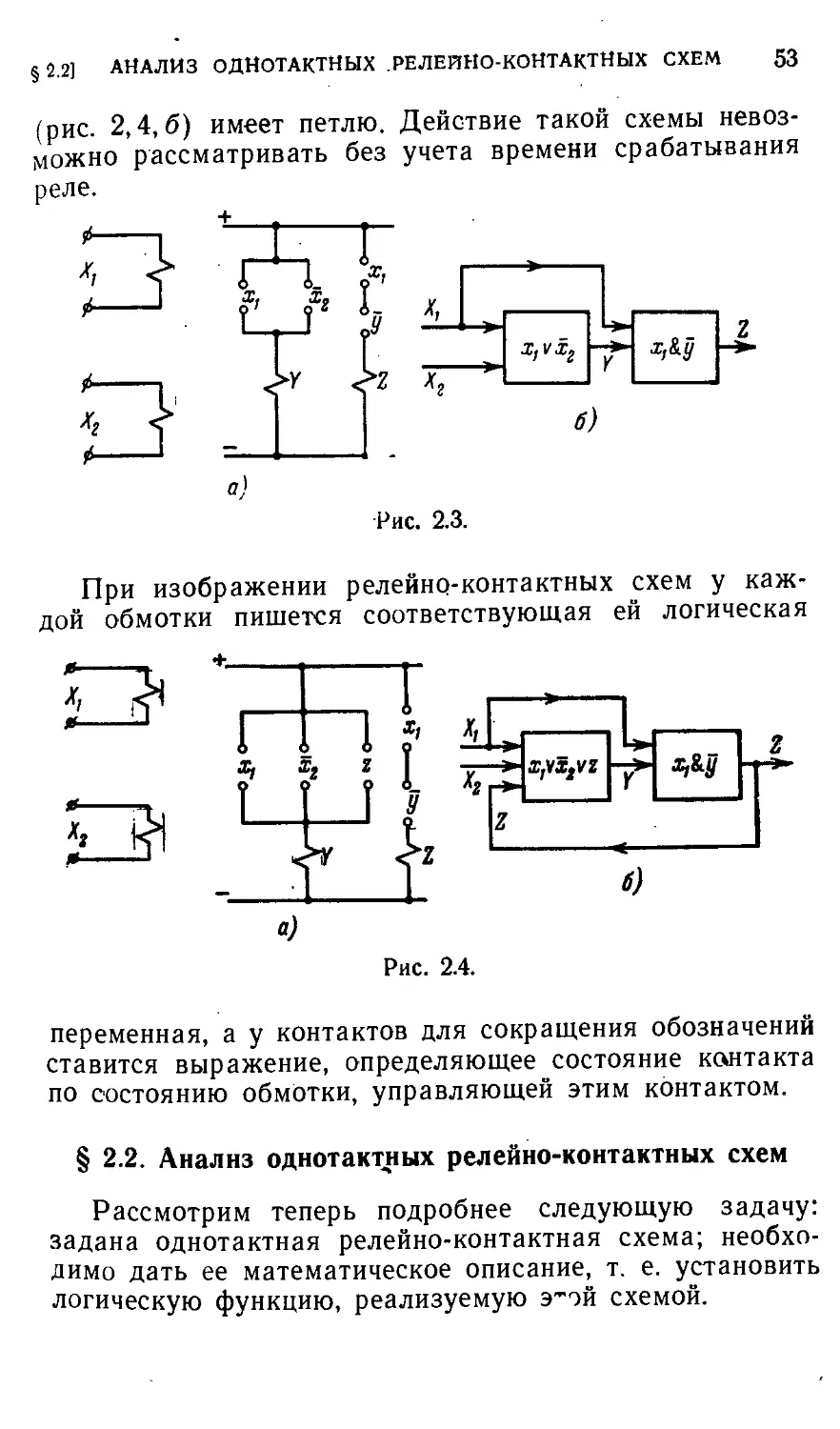
§ 2.2. Анализ однотактных релейно-контактных схем 53
§ 2.3. Синтез однотактных релейно-контактныч схем 59
§ 2.4. Иные методы технической реализации логических функций 63
§ 2.5. Проблема минимизации устройств, реализующих логиче-
логические функции 77
Глава III. Общие понятия о конечных автоматах и последова-
тельностиых машинах 86
§ 3.1. Дискретное время и такты 86
§ 3.2. О динамических системах 89
§ 3.3. Конечные автоматы 91
§ 3,4. Последовательностные машины 97
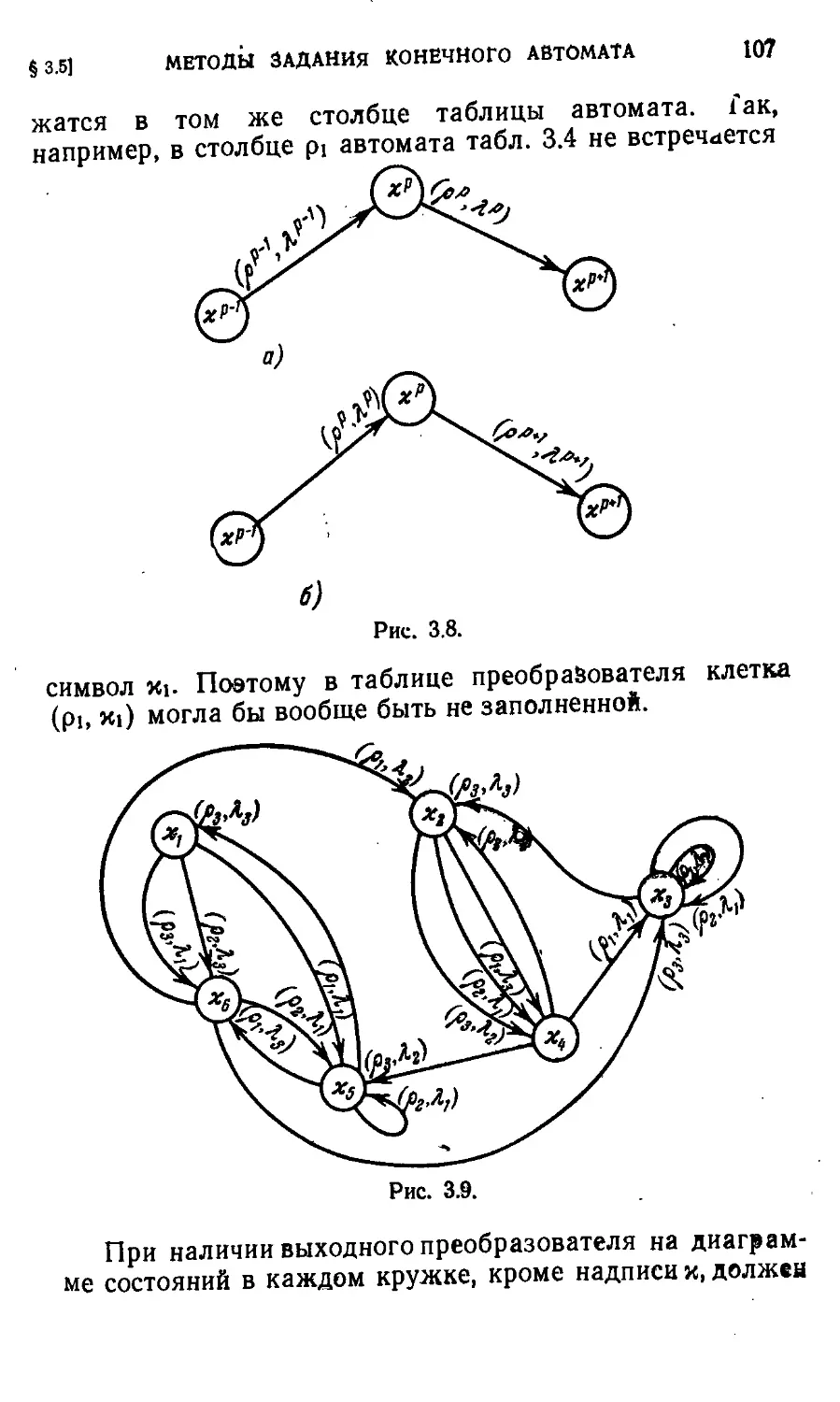
§ 3.5. Методы задания конечного автомата и последовательност-
ной машины 100
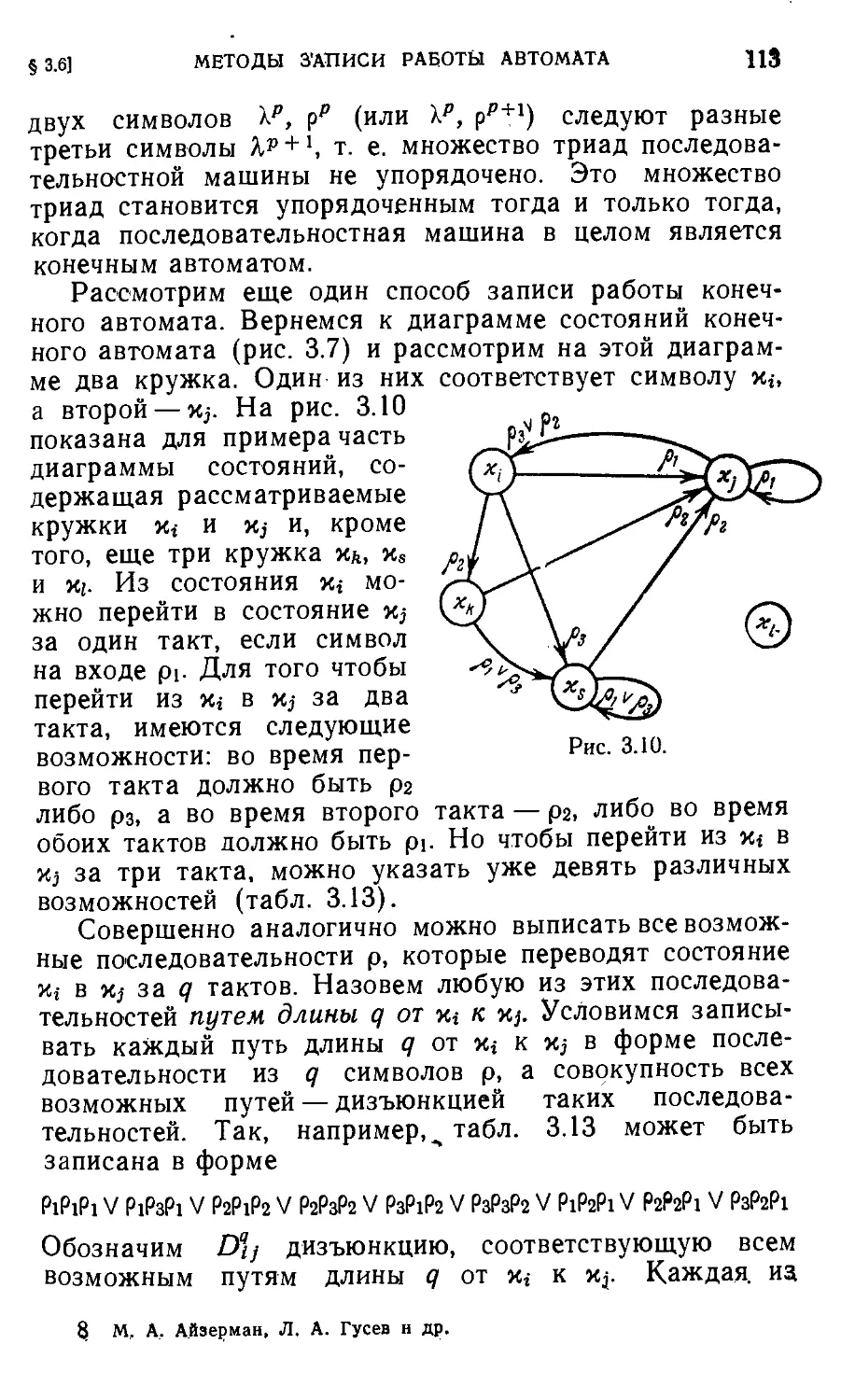
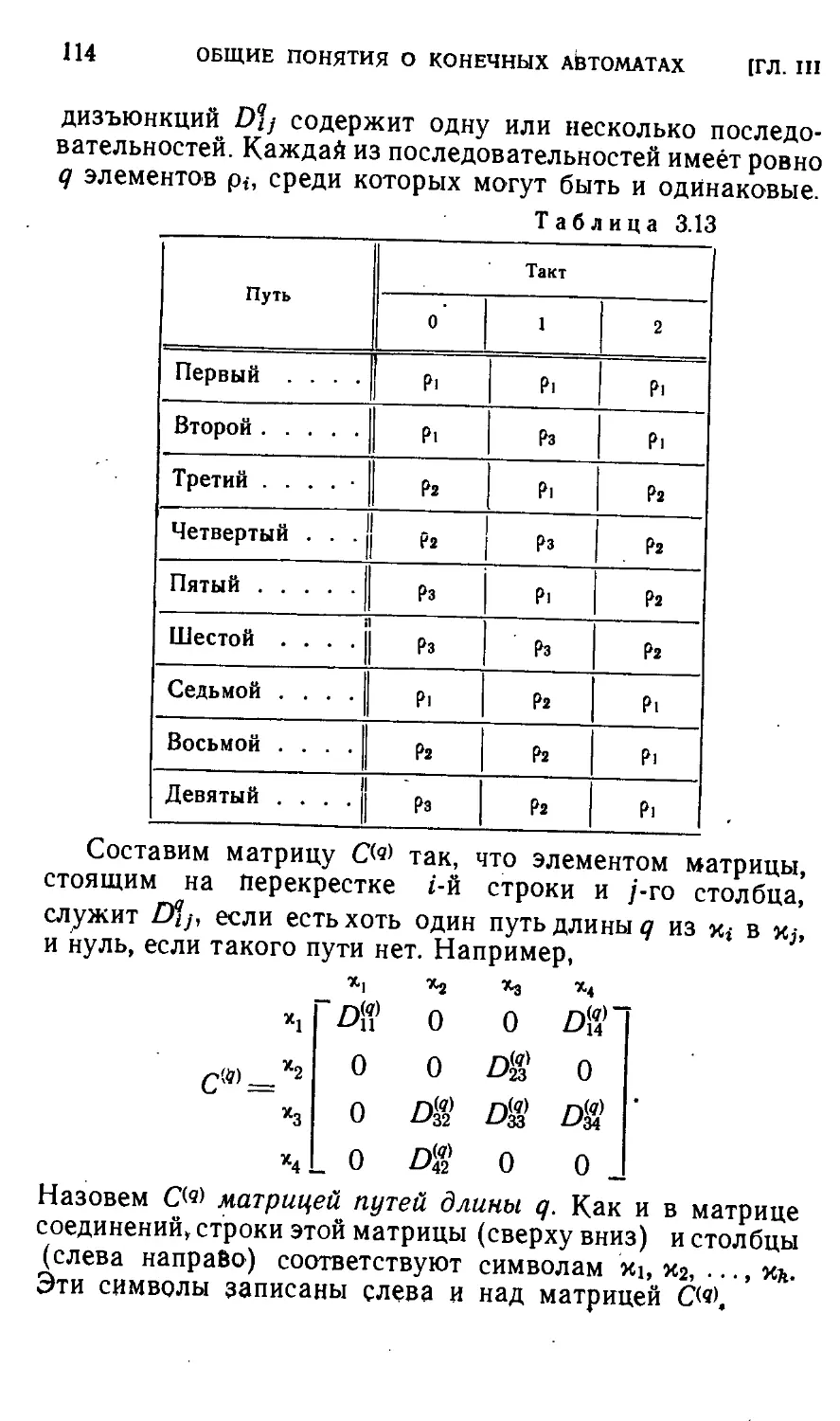
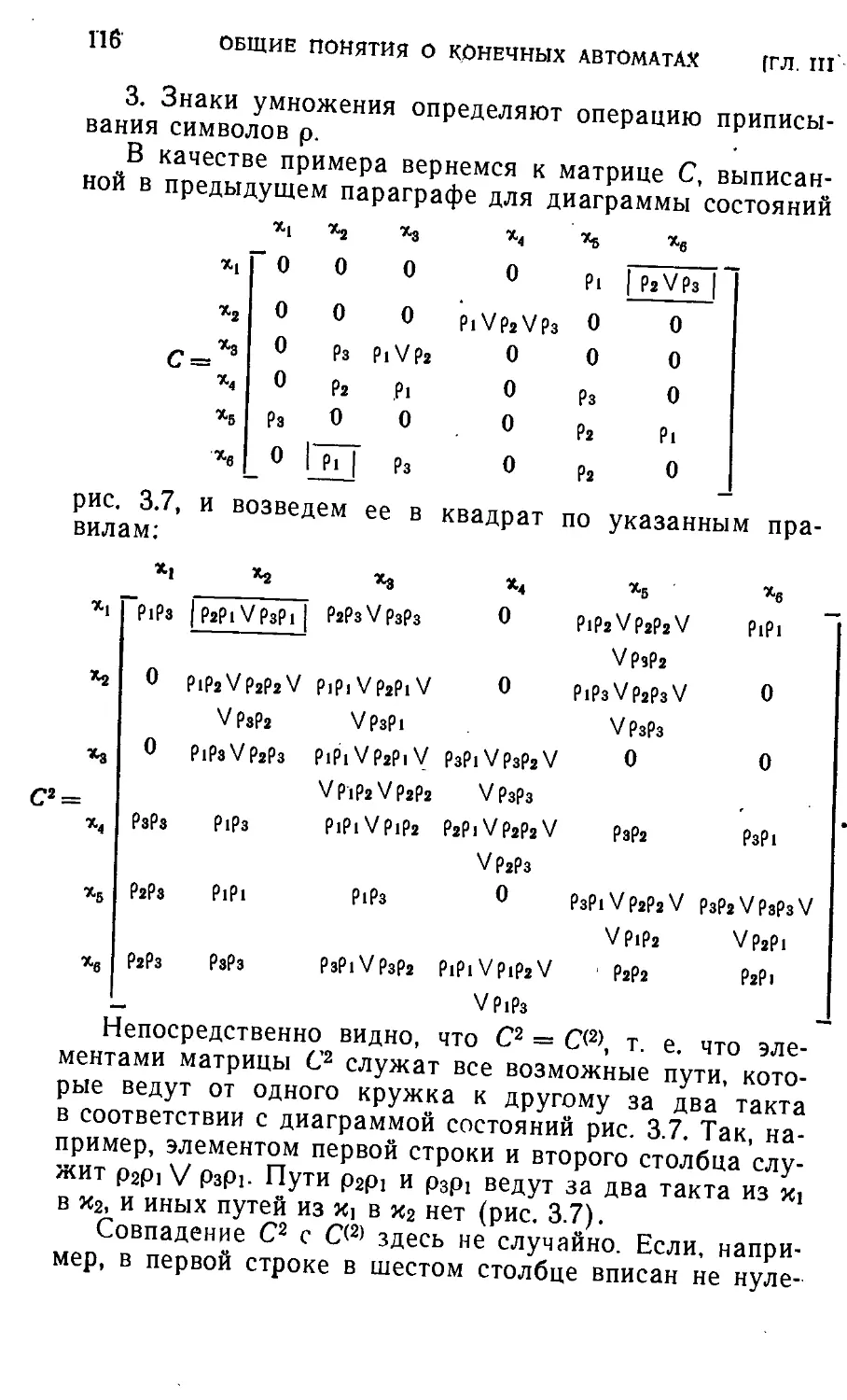
§ 3.6. Методы записи работы автомата ' ПО
§ 3.7. Замечание об ограничении входных последовательностей 119
Глава IV. Абстрактная структура и сеть 122
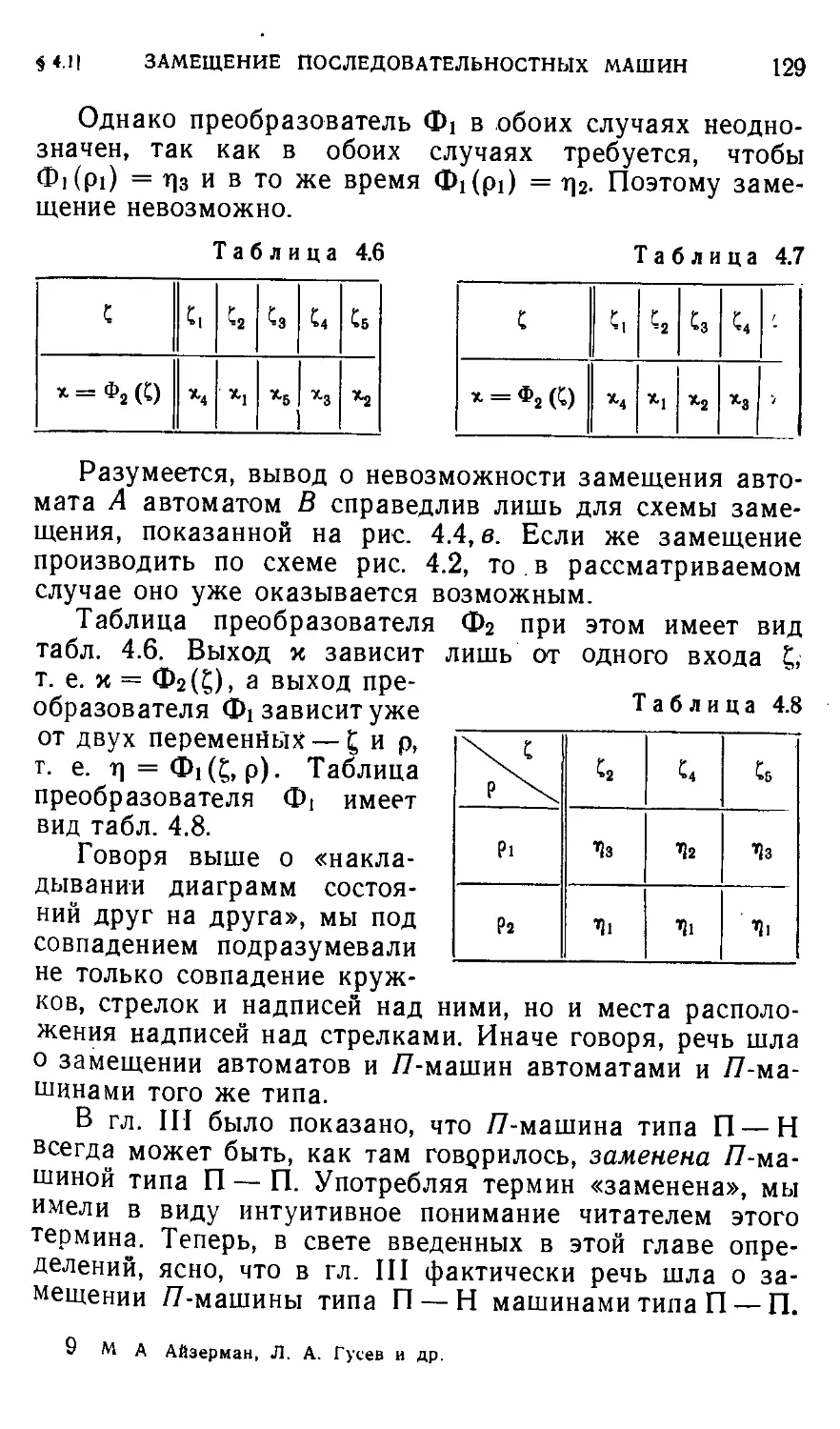
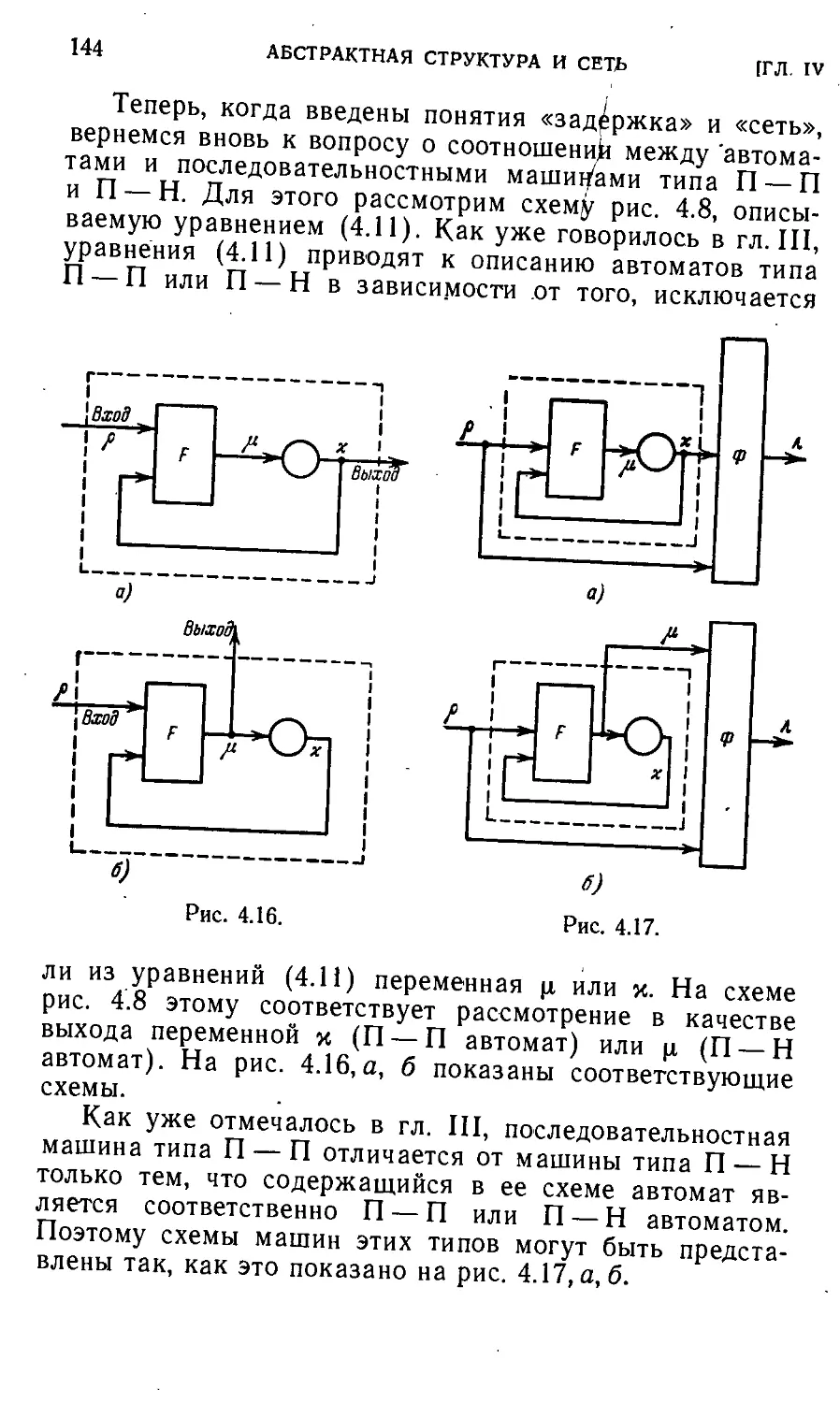
§ 4.1. Общие понятия о замещении последовательностных машин 122
§ 4.2. Абстрактная структура автомата ¦ 130
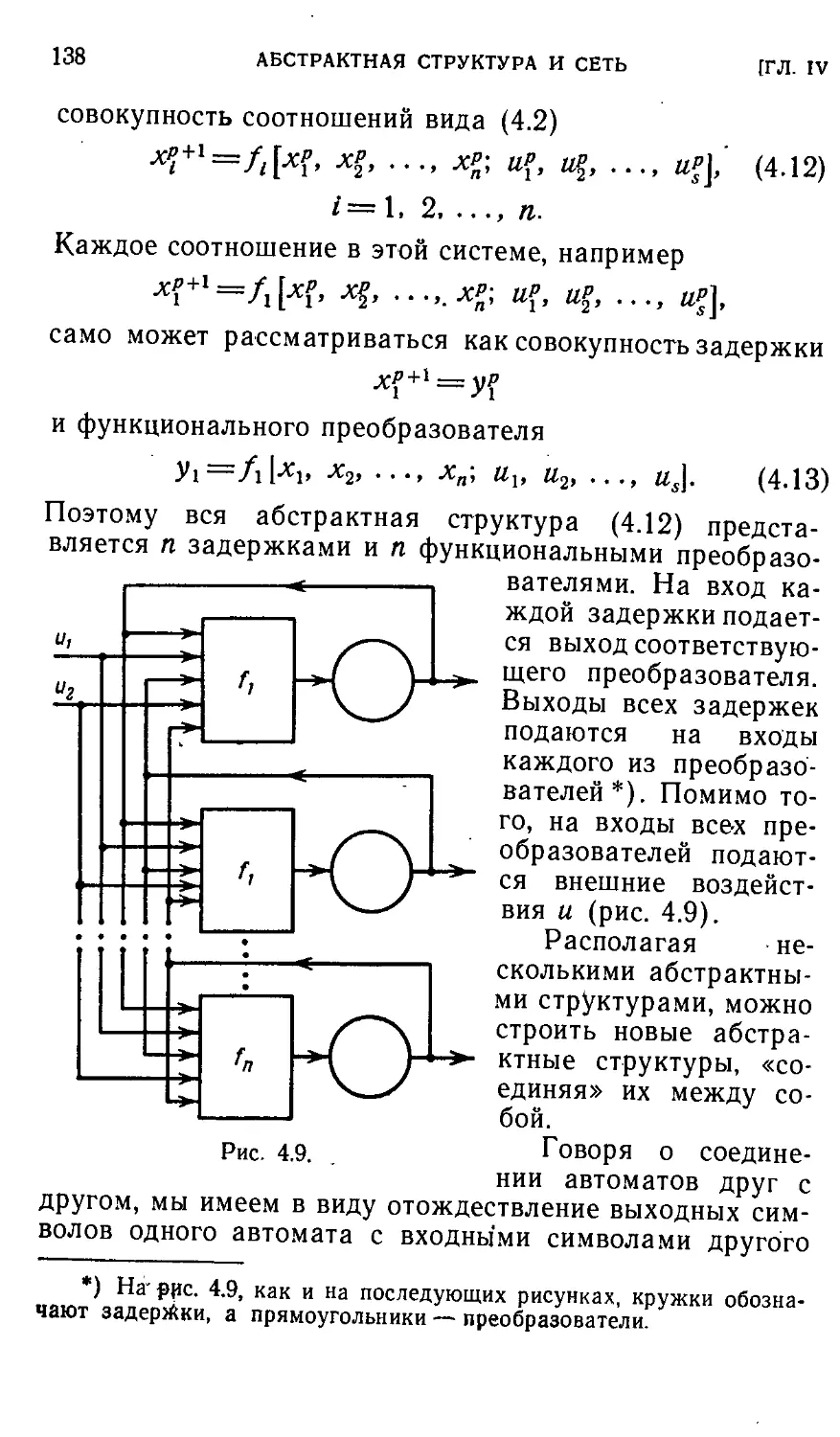
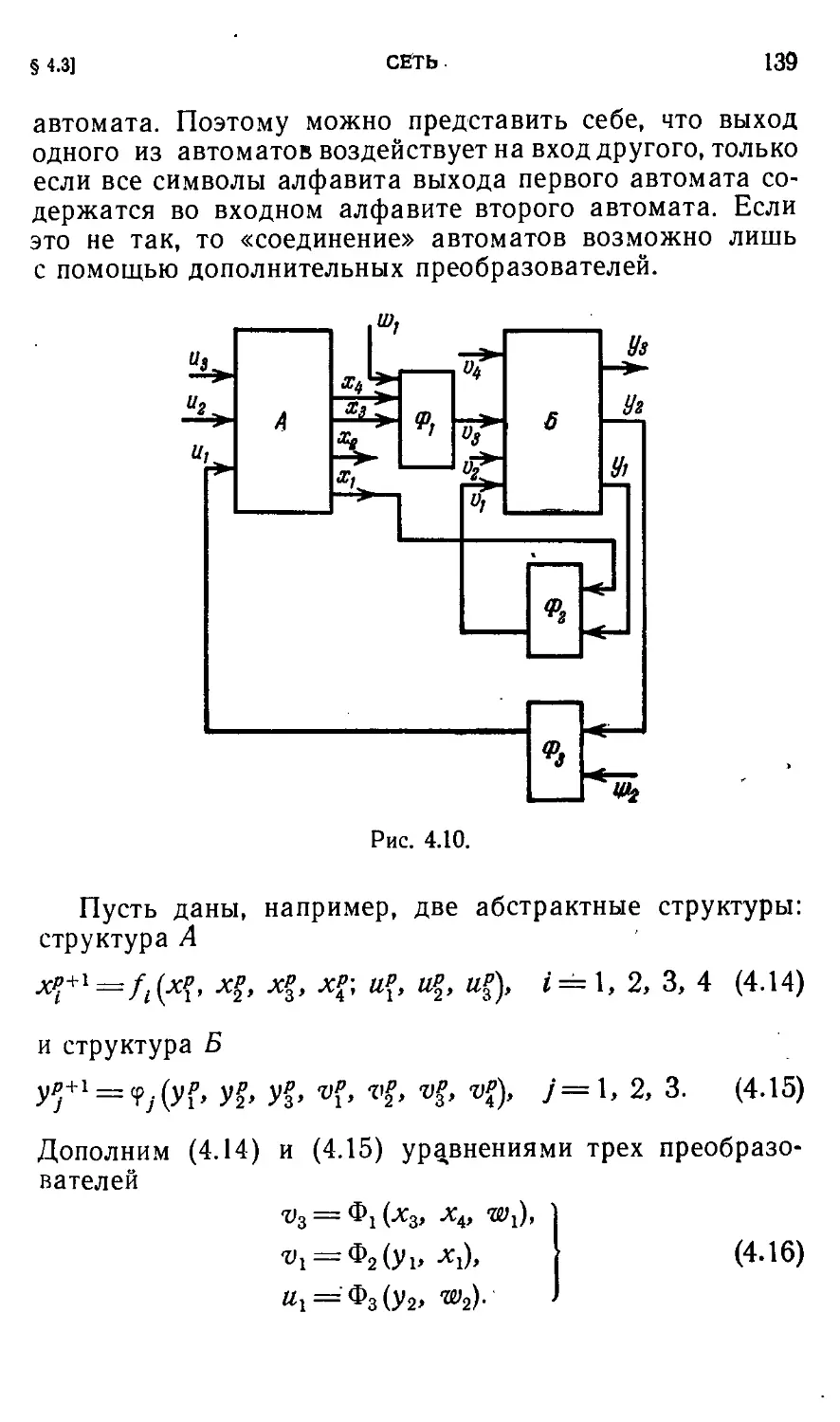
§ 4.3. Сеть 137
§ 4,4. Абстрактная агрегатизация автоматов и последователь-
последовательностных- машин 149
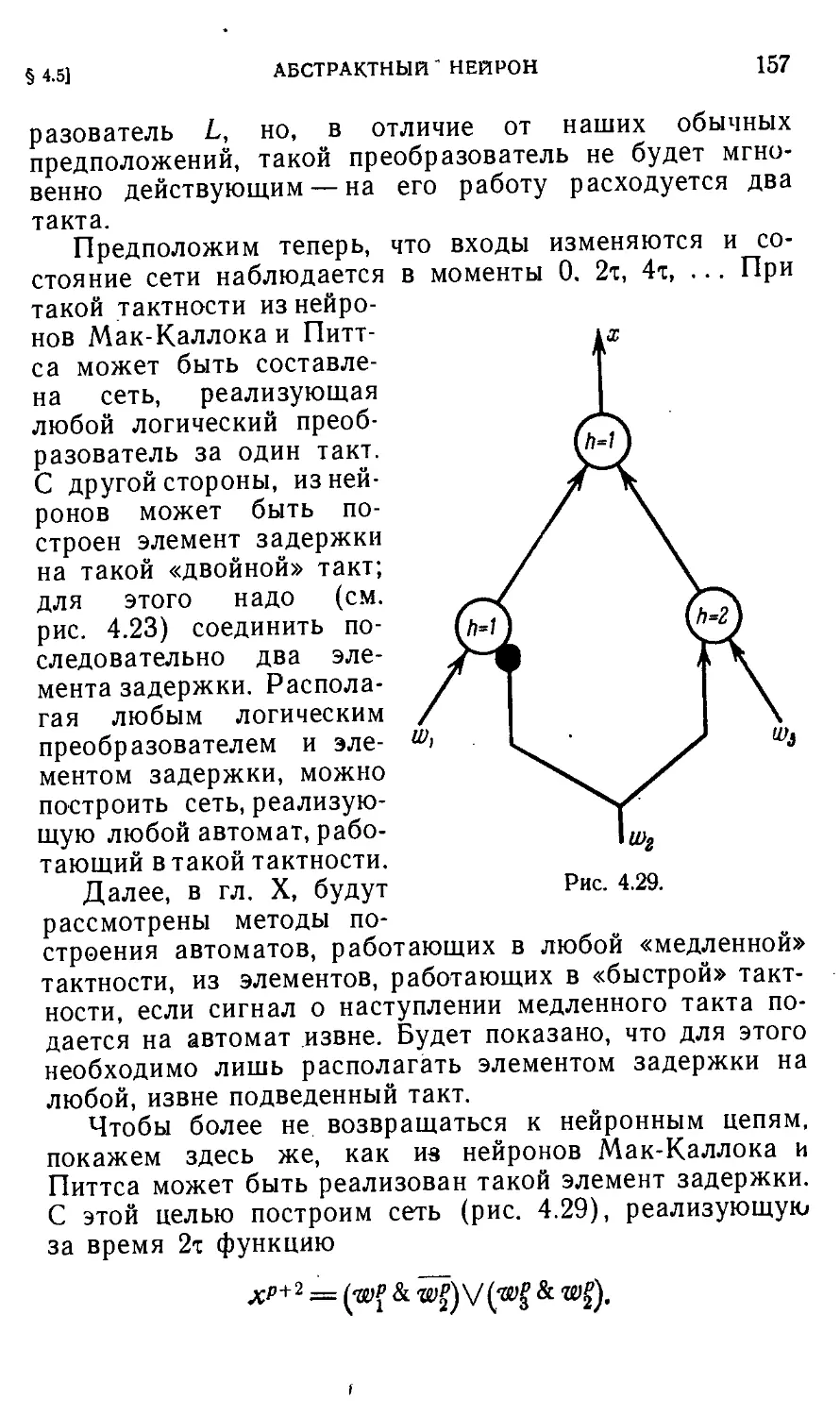
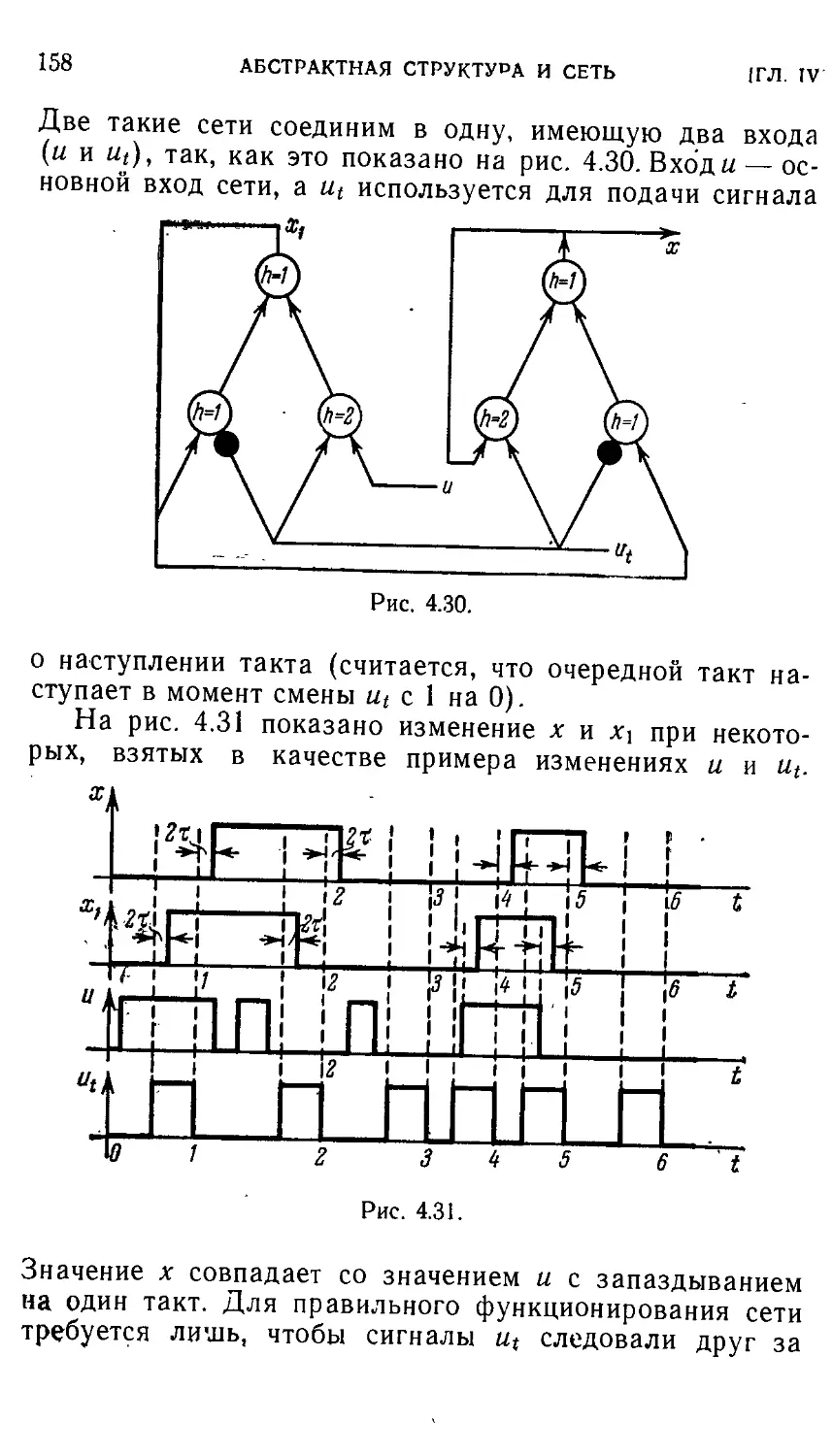
§ 4.5. Абстрактный нейрон и абстрактные модели нейронных
сетей 151
1*
4 ОГЛАВЛЕНИЕ
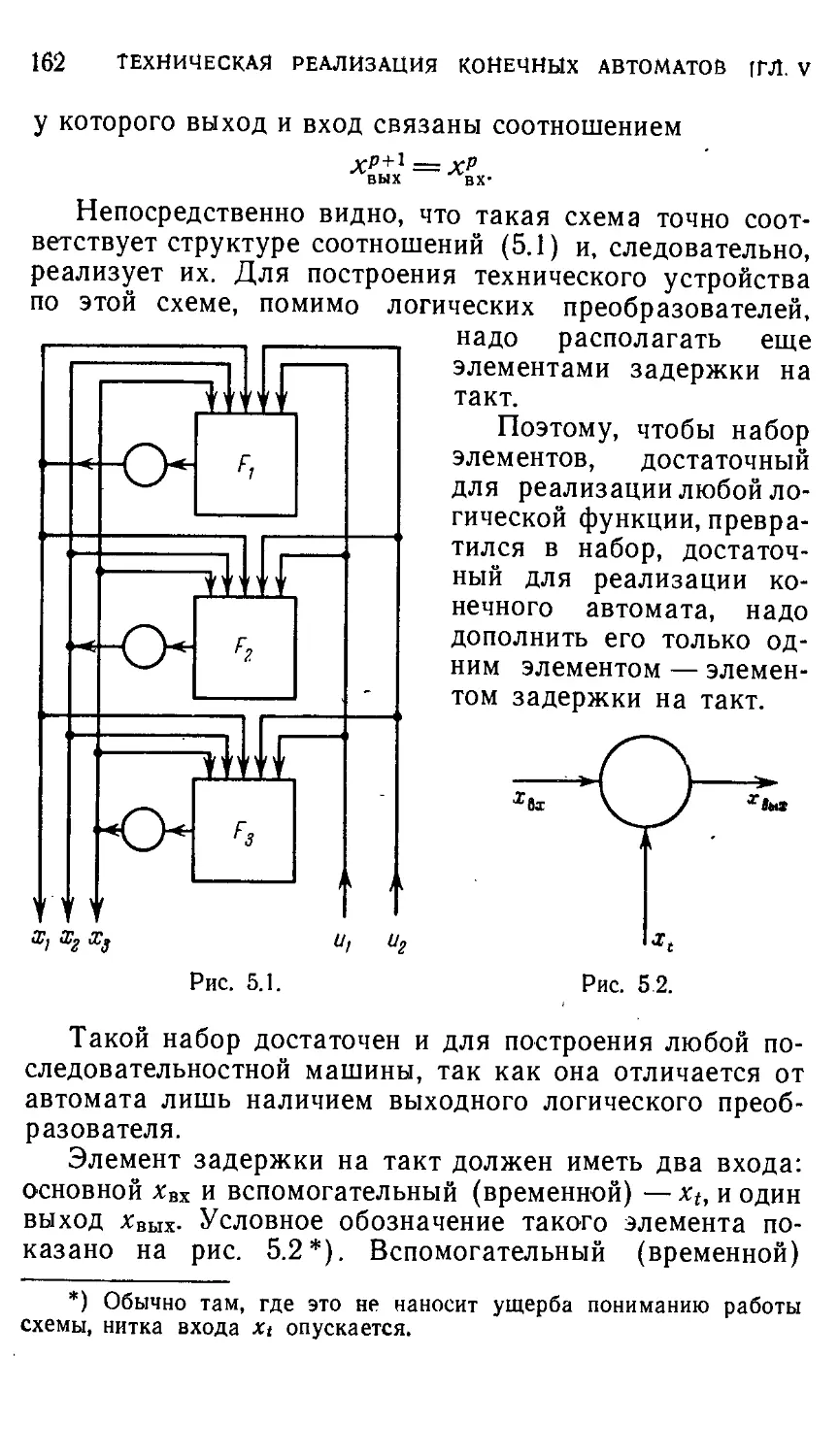
Глава V. Техническая реализация конечных автоматов и по-
следовательностных машин 160
§ 5.1. Два метода технической реализации конечных автоматов
и последовательностных машин 160
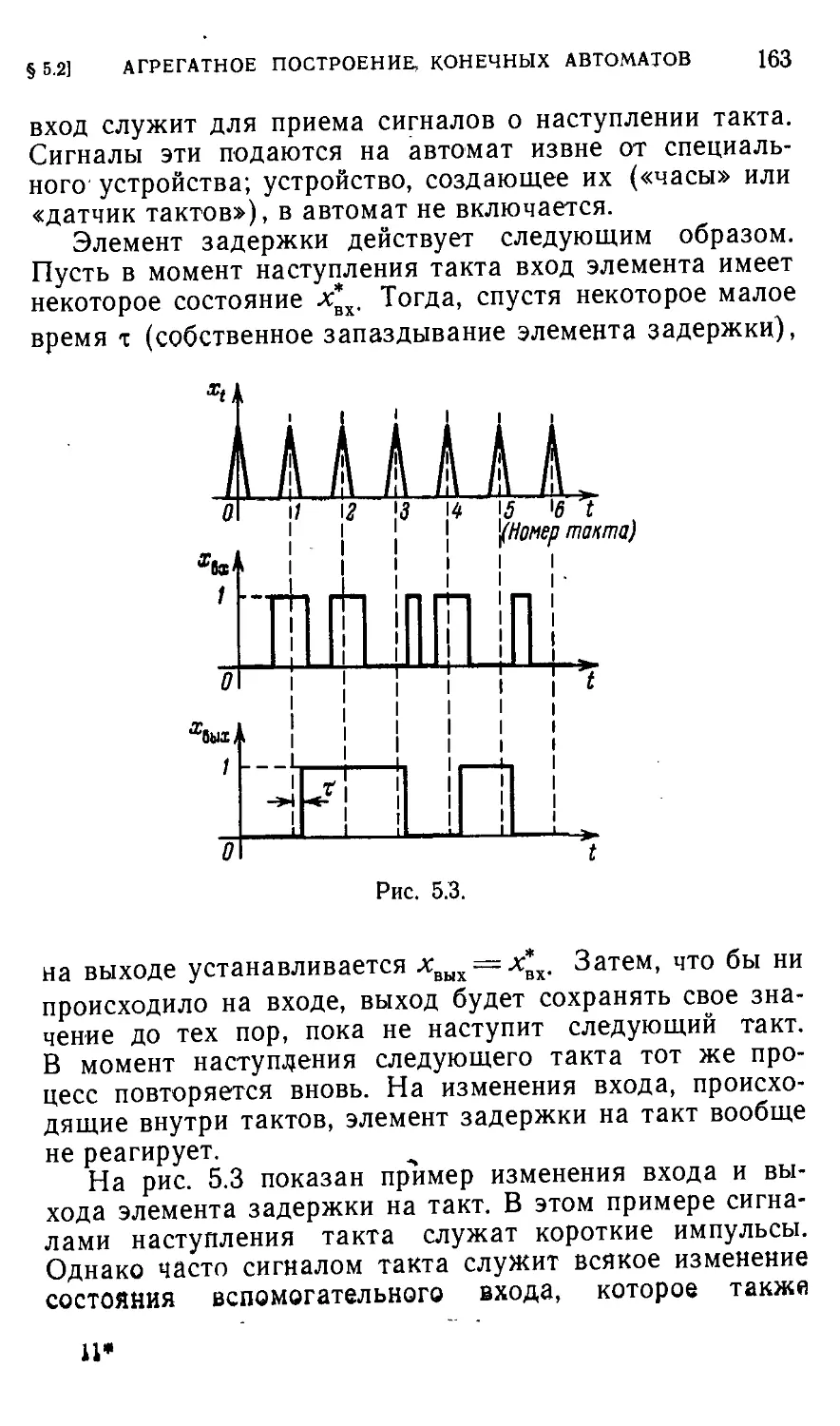
§ 5.2. Агрегатное построение конечных автоматов и последова-
последовательностных машин 161
§ 5.3. Построение конечных автоматов и последовательностных
машин с использованием естественных задержек и обрат-
обратных связей 172
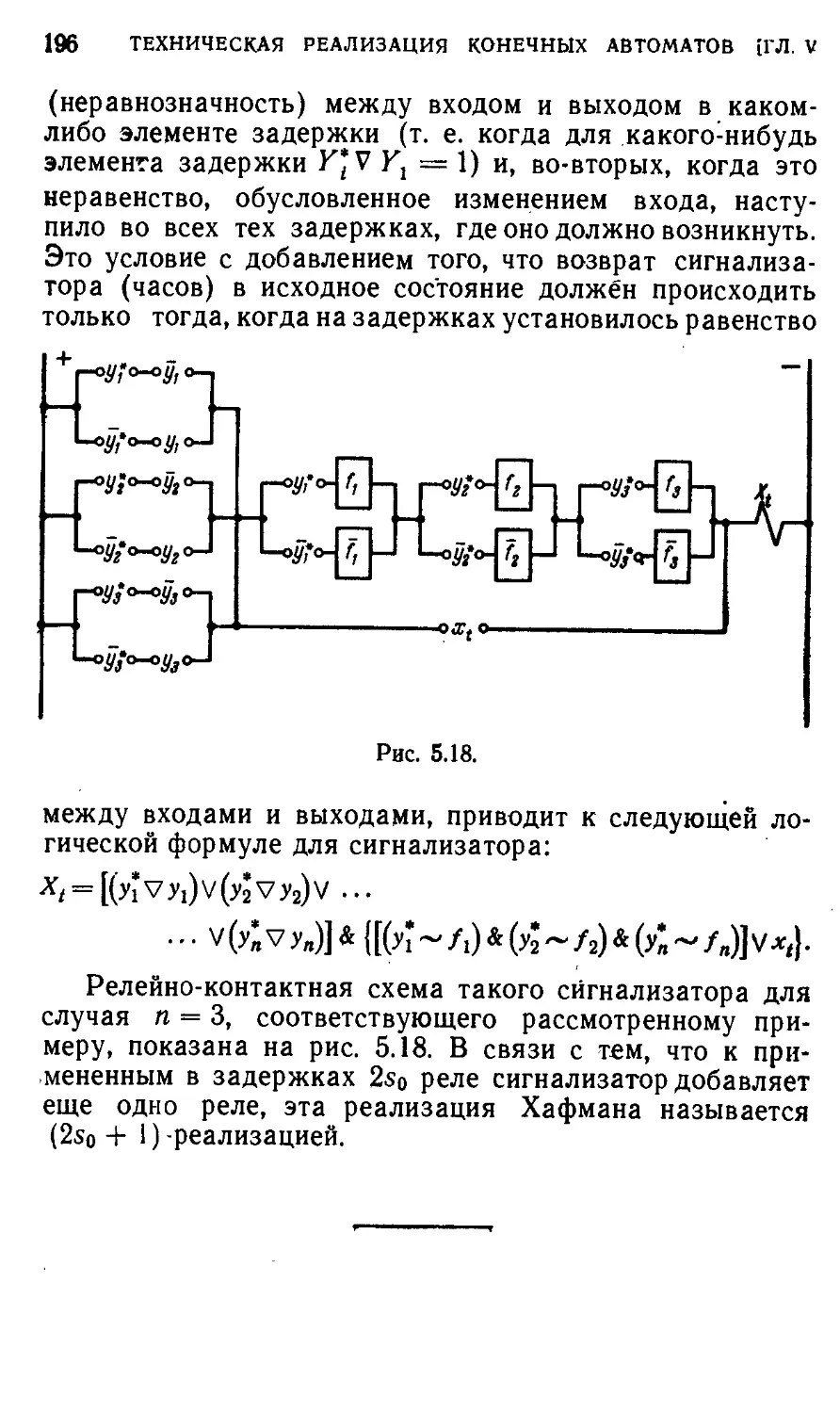
§ 5.4. Метод и реализация Хафмана 180
Глава VI. Автономный конечный автомат и автономная по-
следовательностная машина 197
§ 6.1. Что «могут делать» автономный конечный автомат и
автономная последовательностная машина 197
§ 6.2. Синтез двоичной структуры автономной последователь-
ностной машины 205
Глава VII. Представление событий в конечном автомате
и последовательностной машине ?17
§ 7.1. Постановка задачи 217
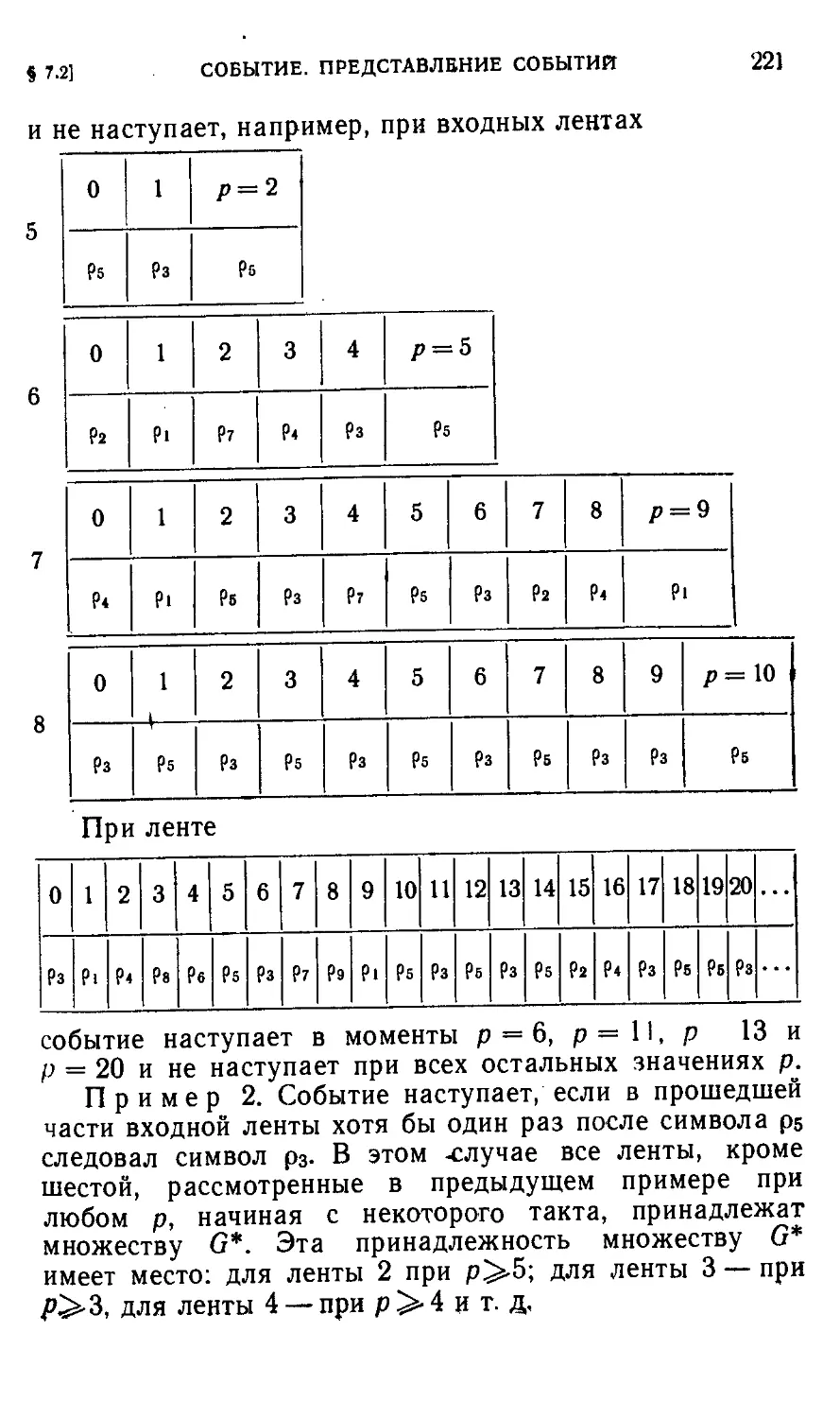
§ 7.2. Событие. Представление событий 219
§ 7.3. Действия над множествами входных последовательно-
последовательностей. Регулярные события 224
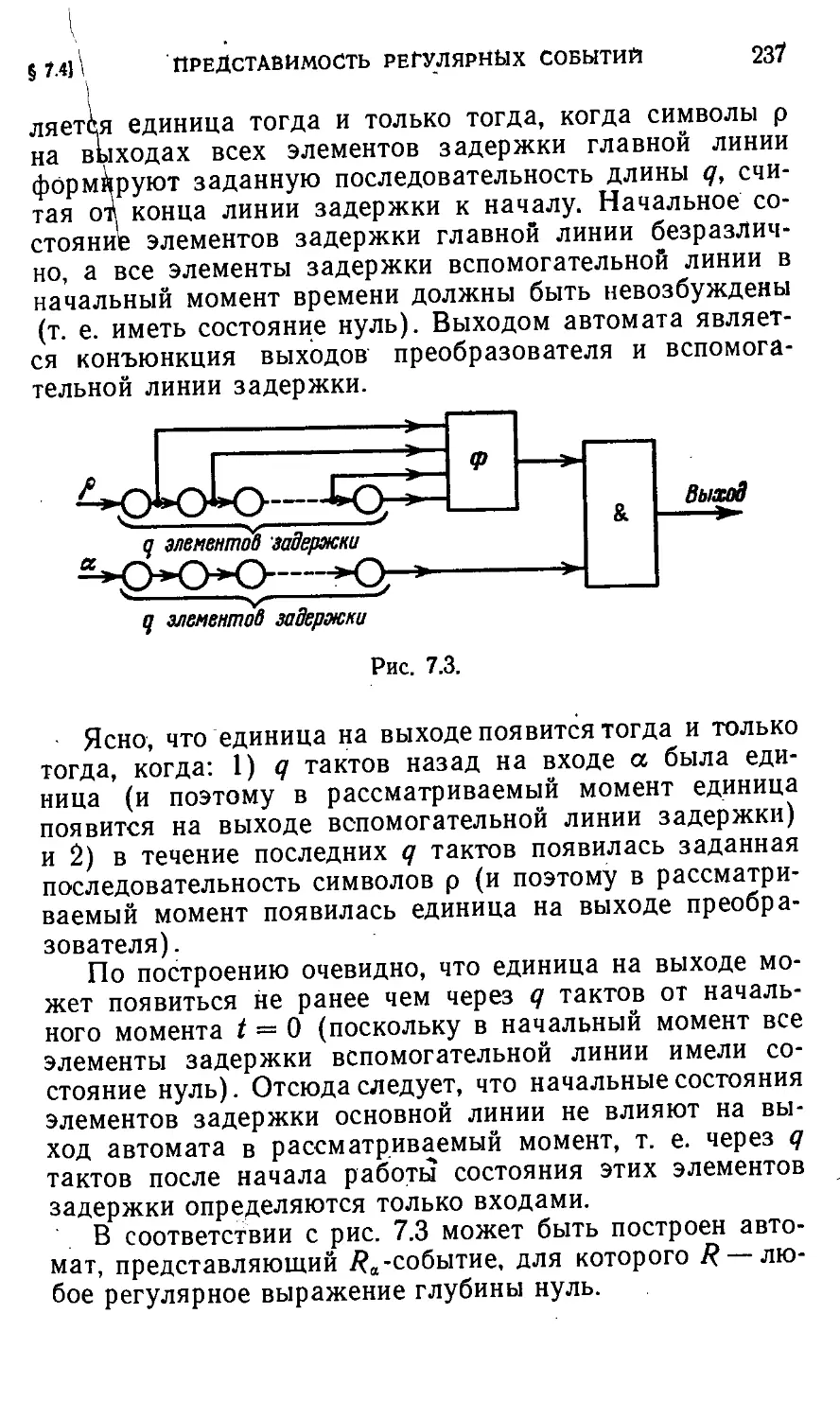
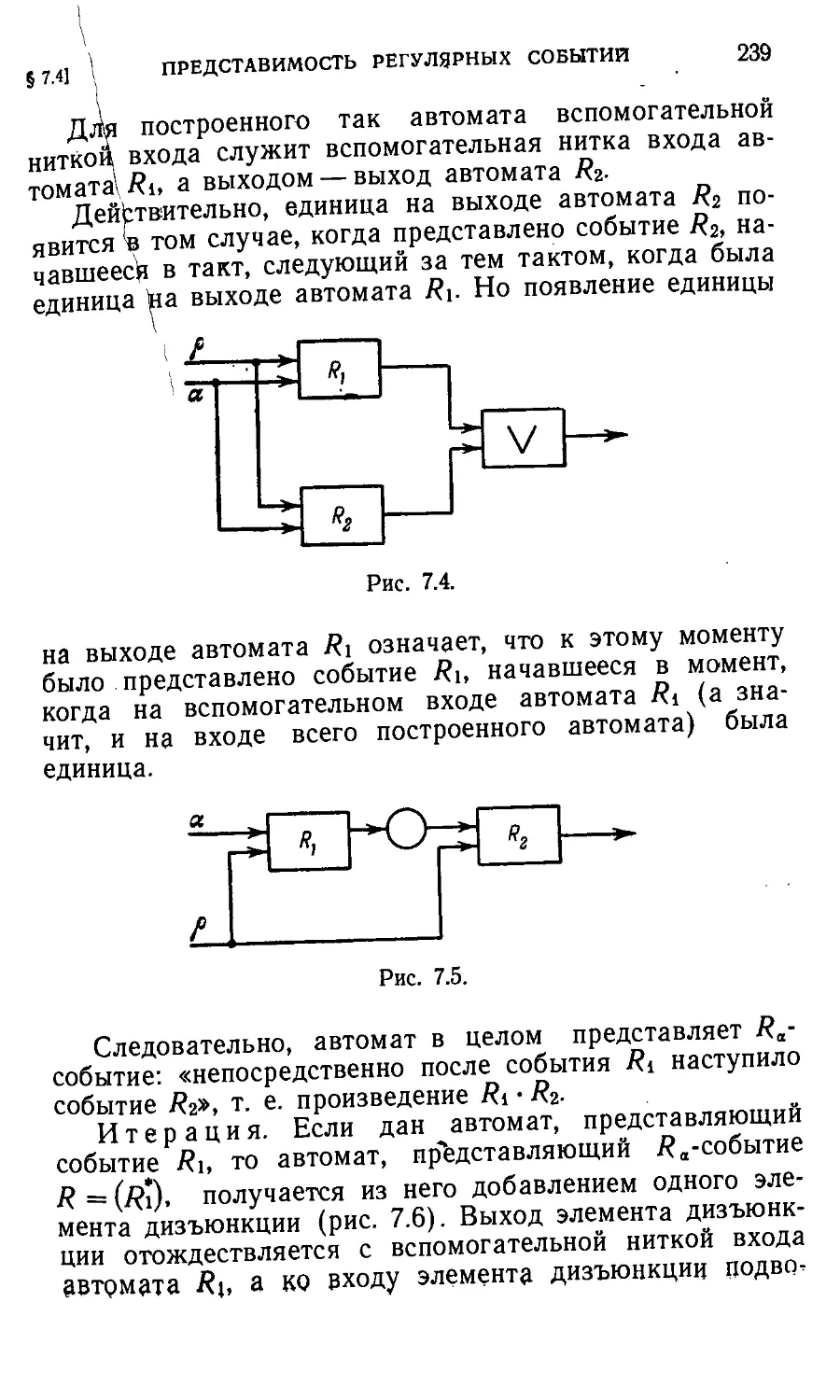
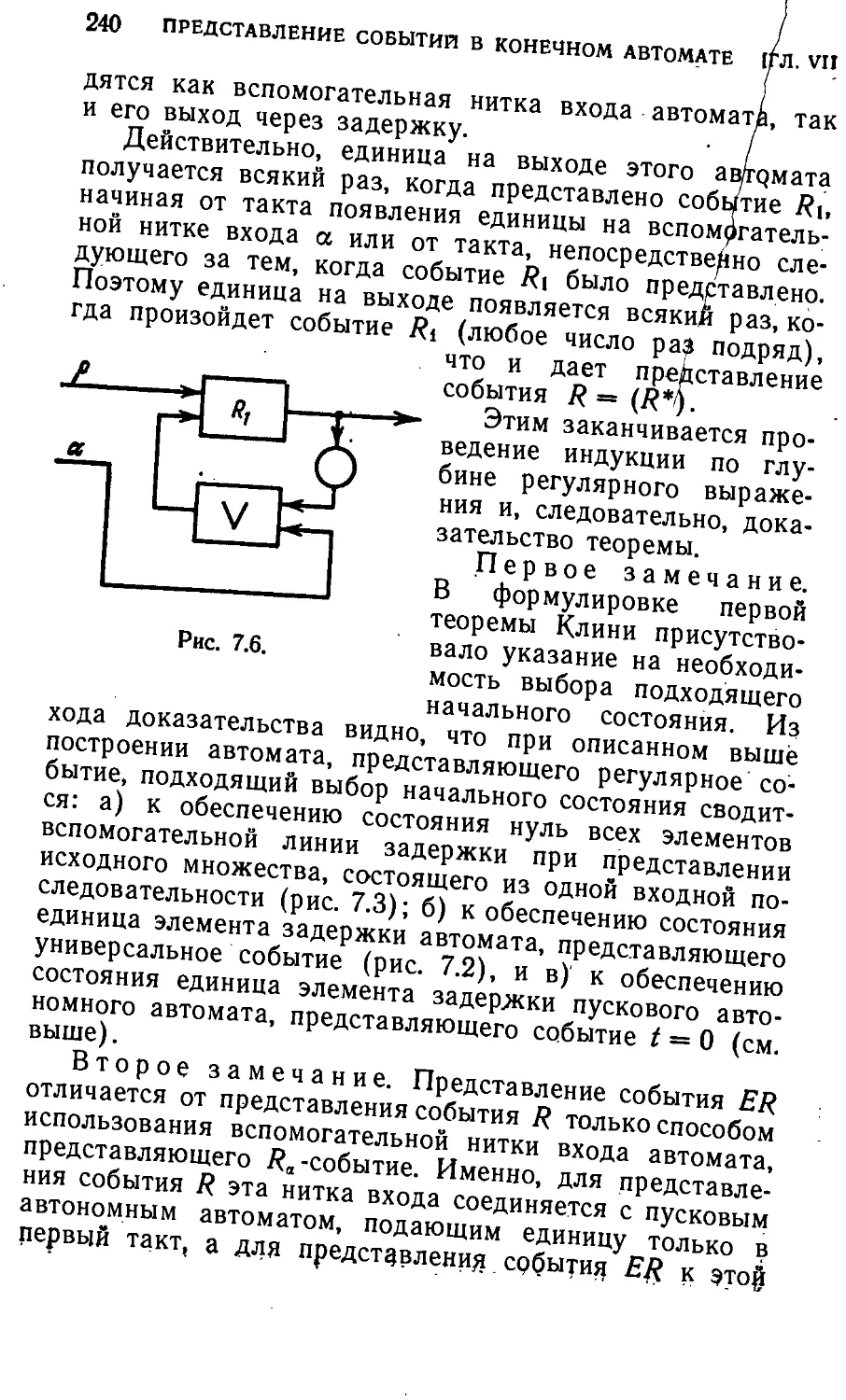
§ 7.4. Представимость регулярных событий 234
§ 7.5 Регулярность представимых событий 241
§ 7.6. Существуют ли нерегулярные (непредставимые) события? 247
§ 7.7. Что «может делать» конечный автомат -. . 253
Глава VIII. Распознавание реализуемости задания и- аб-
абстрактный синтез конечных автоматов и последователь-
последовательностных машин 255
§ 8.1. Постановка задачи 255
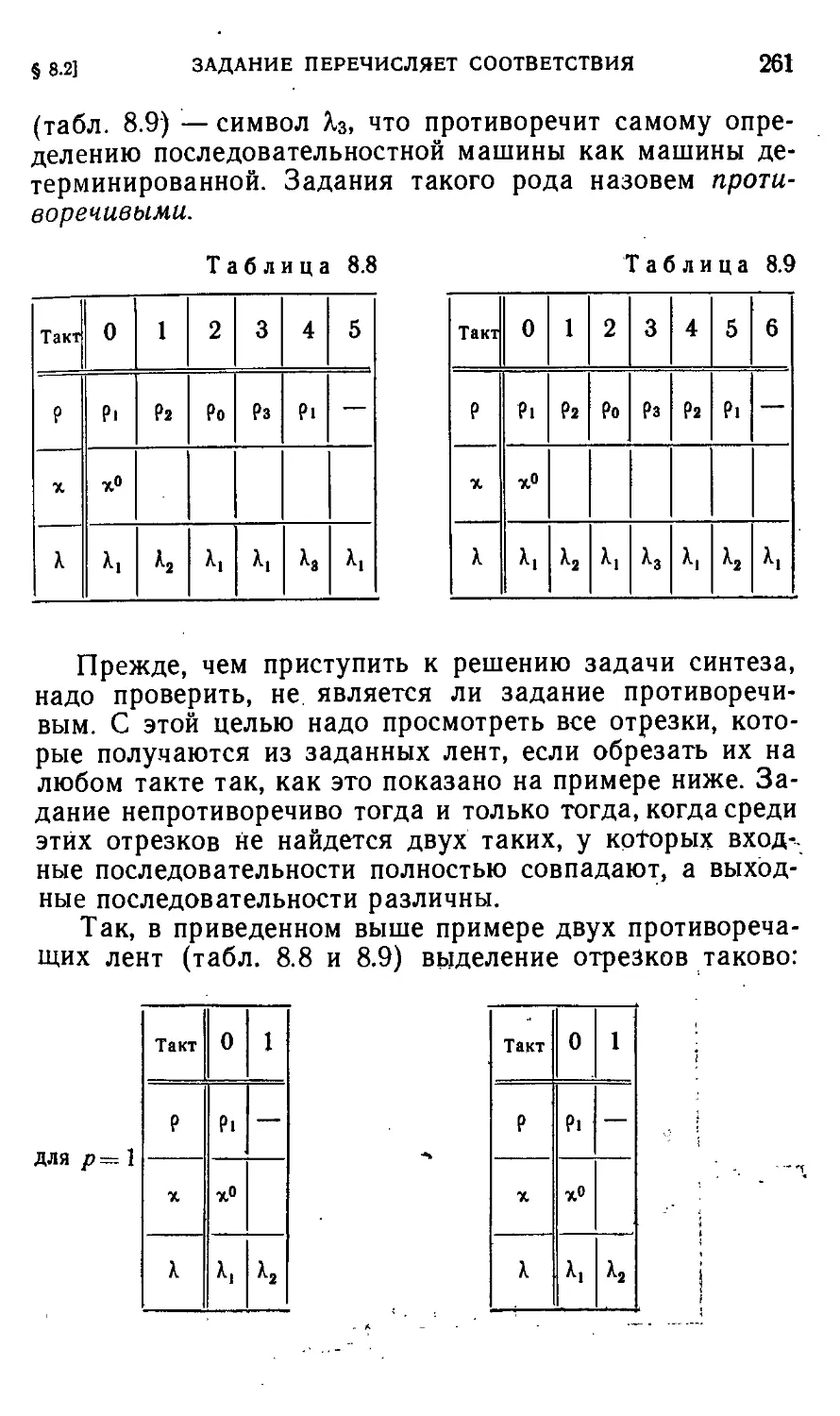
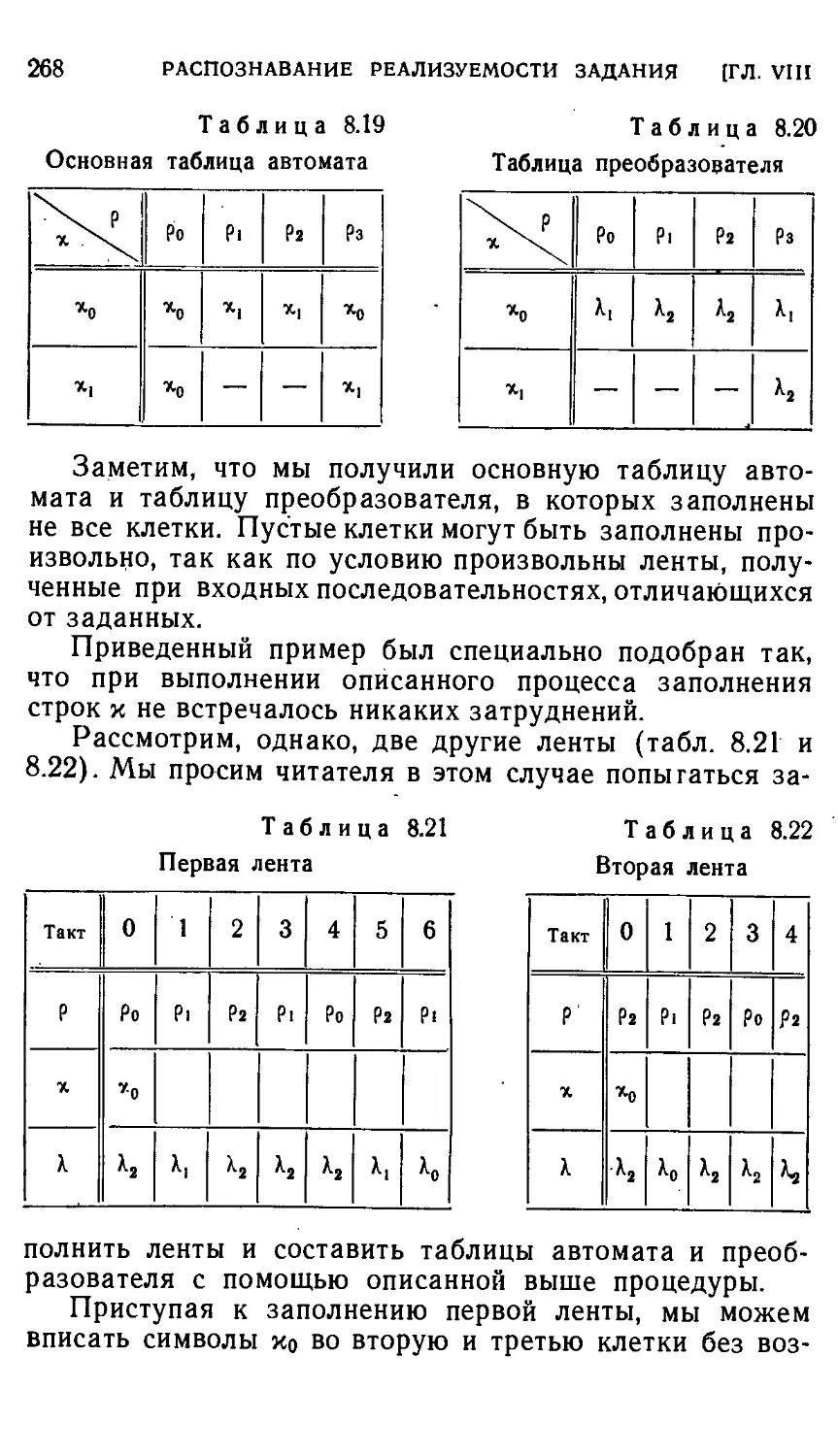
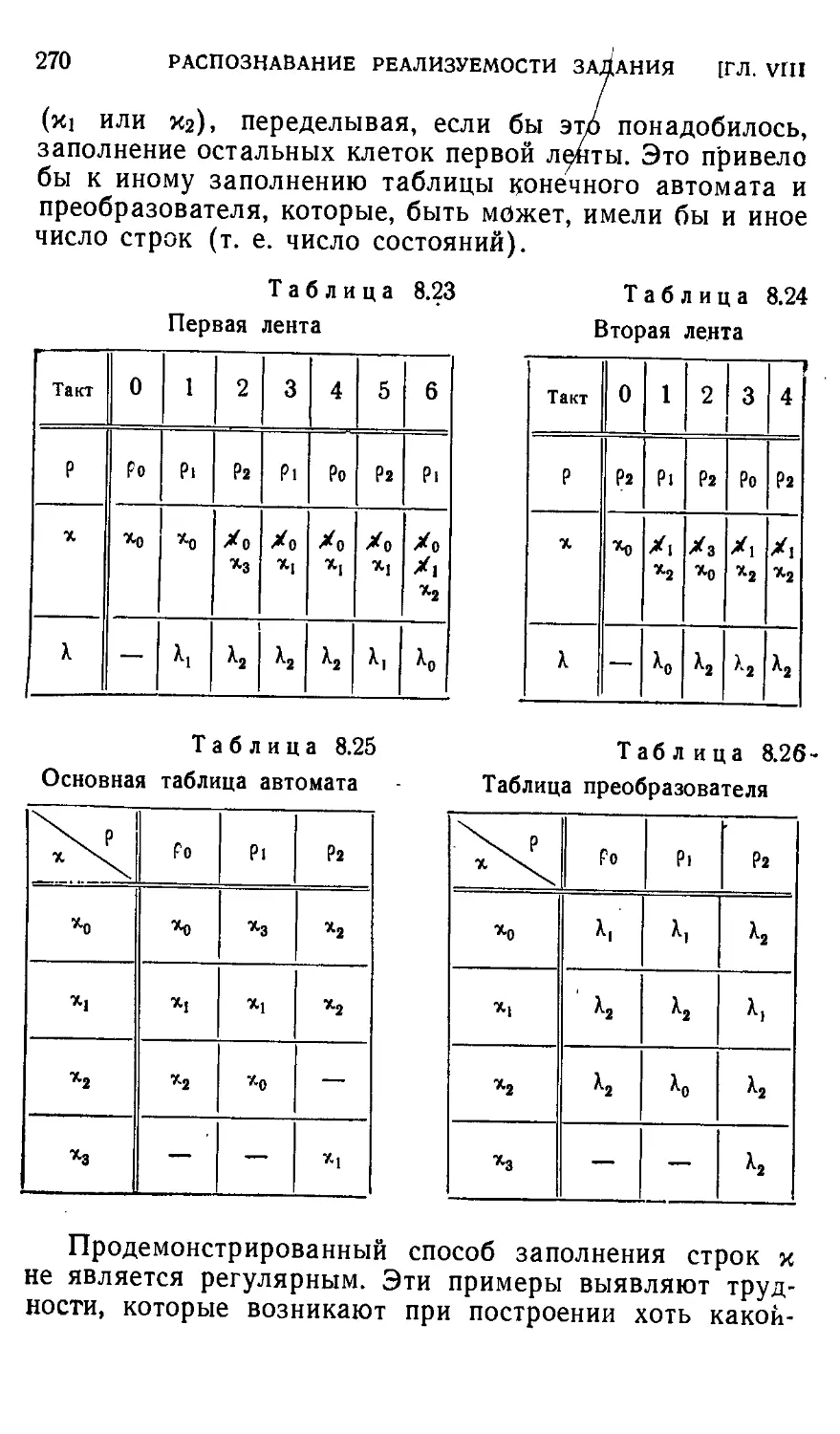
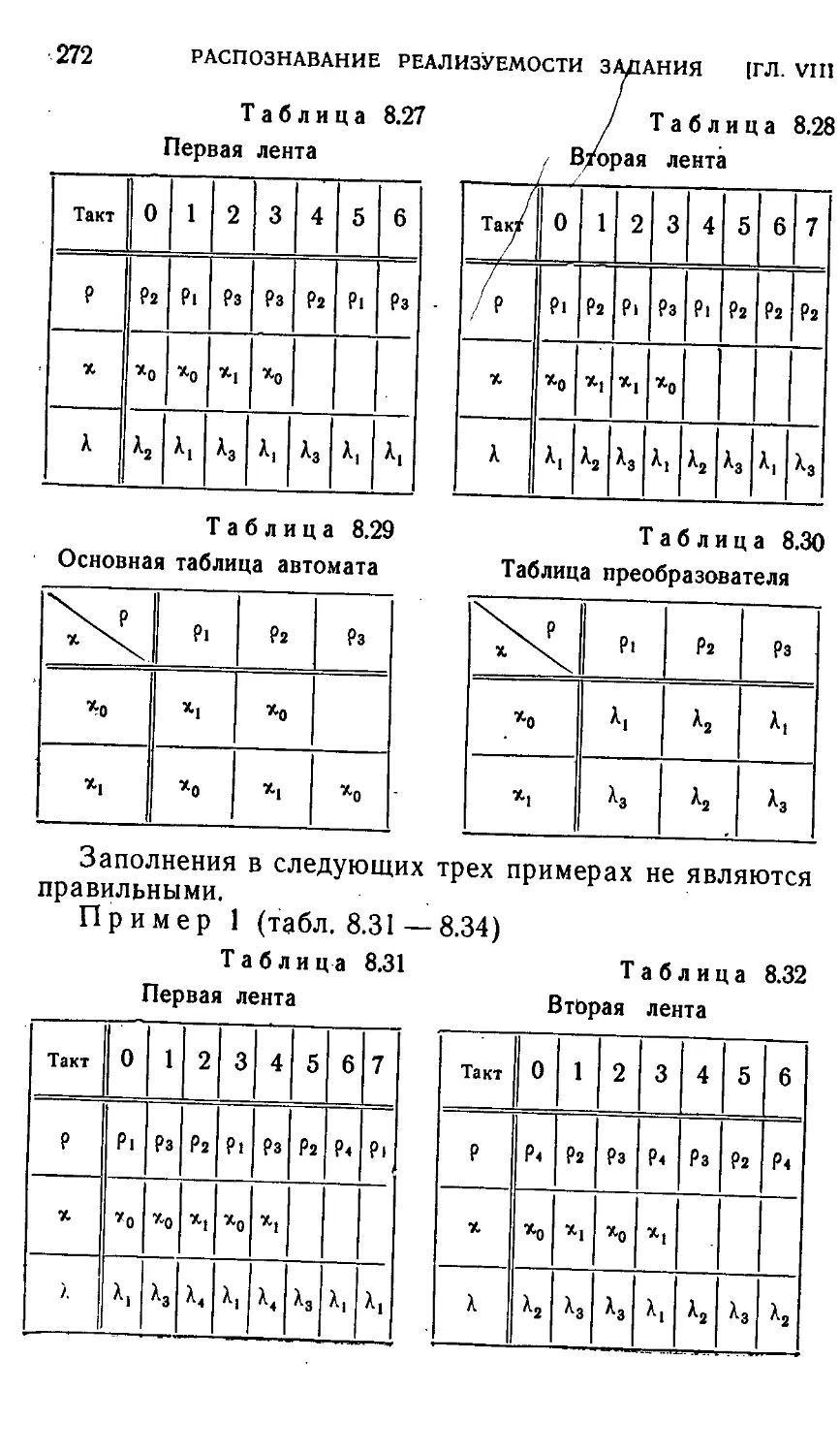
§ 8.2. Случай, когда задание перечисляет требуемые соответ-
соответствия между входными и выходными последовательно-
последовательностями 258
§ 8.3. Алгоритмическая неразрешимость проблемы распознава-
распознавания представимости рекурсивных событий 279
§ 8.4. Синтез конечных автоматов и последовательностных ма-
машин при задании, сформулированном на языке регуляр-
регулярных выражений 285
Глава IX. Эквивалентность и минимизация последователь-
последовательностных машин 301
§ 9.1. Постановка задачи о распознавании эквивалентных со-
состояний 301
§ 9.2. Алгоритмическая неразрешимость проблемы распознава-
распознавания эквивалентных состояний в общем случае 305
ОГЛАВЛЕНИЕ 5
§ 9.3. Распознавание эквивалентности состояний в случае, когда
множество входных последовательностей не ограничено . 308
§ 9.4. Распознавание эквивалентности состояний в случае, когда
ограничения наложены на длину входных последователь-
последовательностей 319
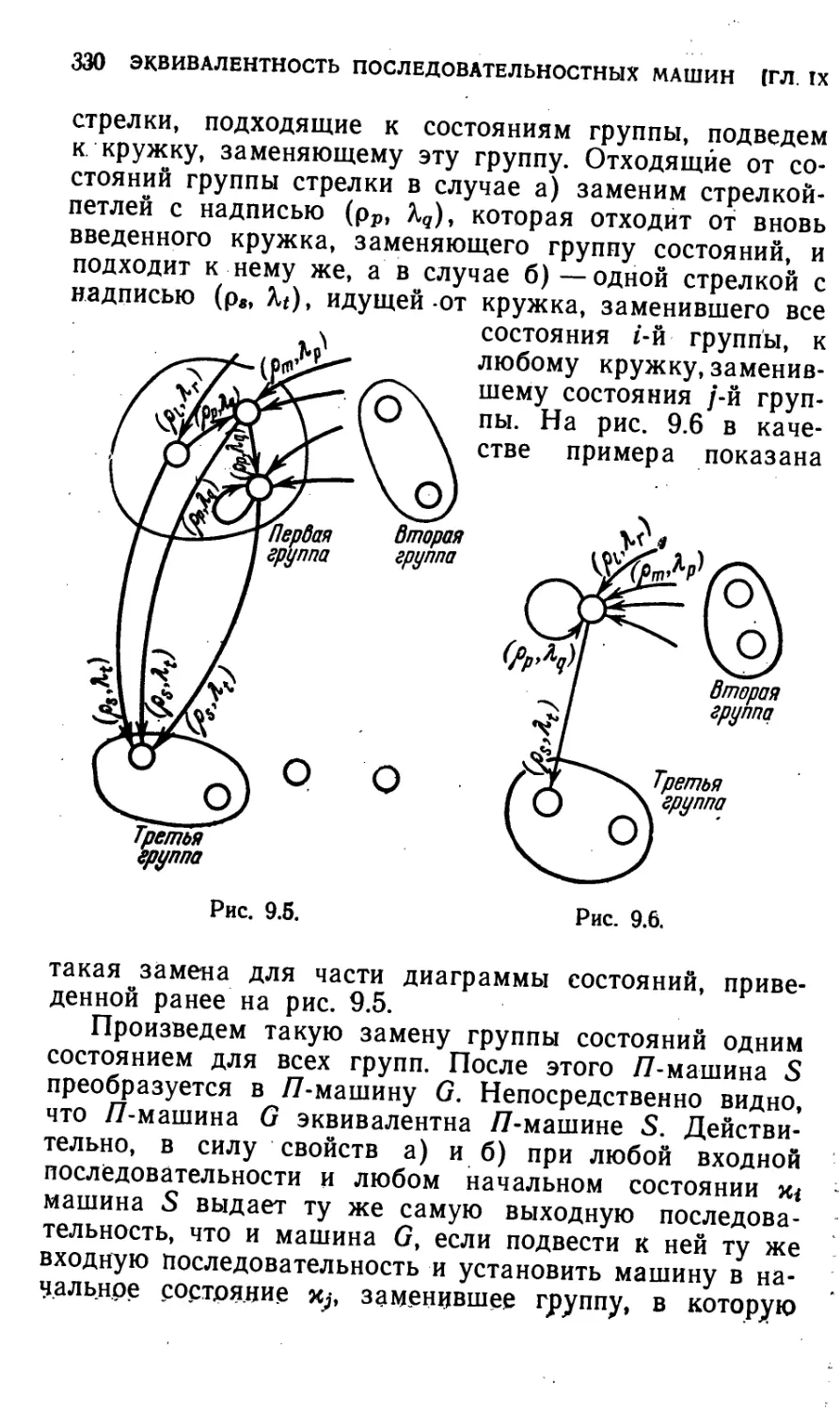
§ 9.5. Понятия об эквивалентности, отображении и минимиза-
минимизации последовательностных машин 326
§ 9.6. Минимизация последовательностной машины в случае,
когда множество входных последовательностей не огра-
ограничено 329
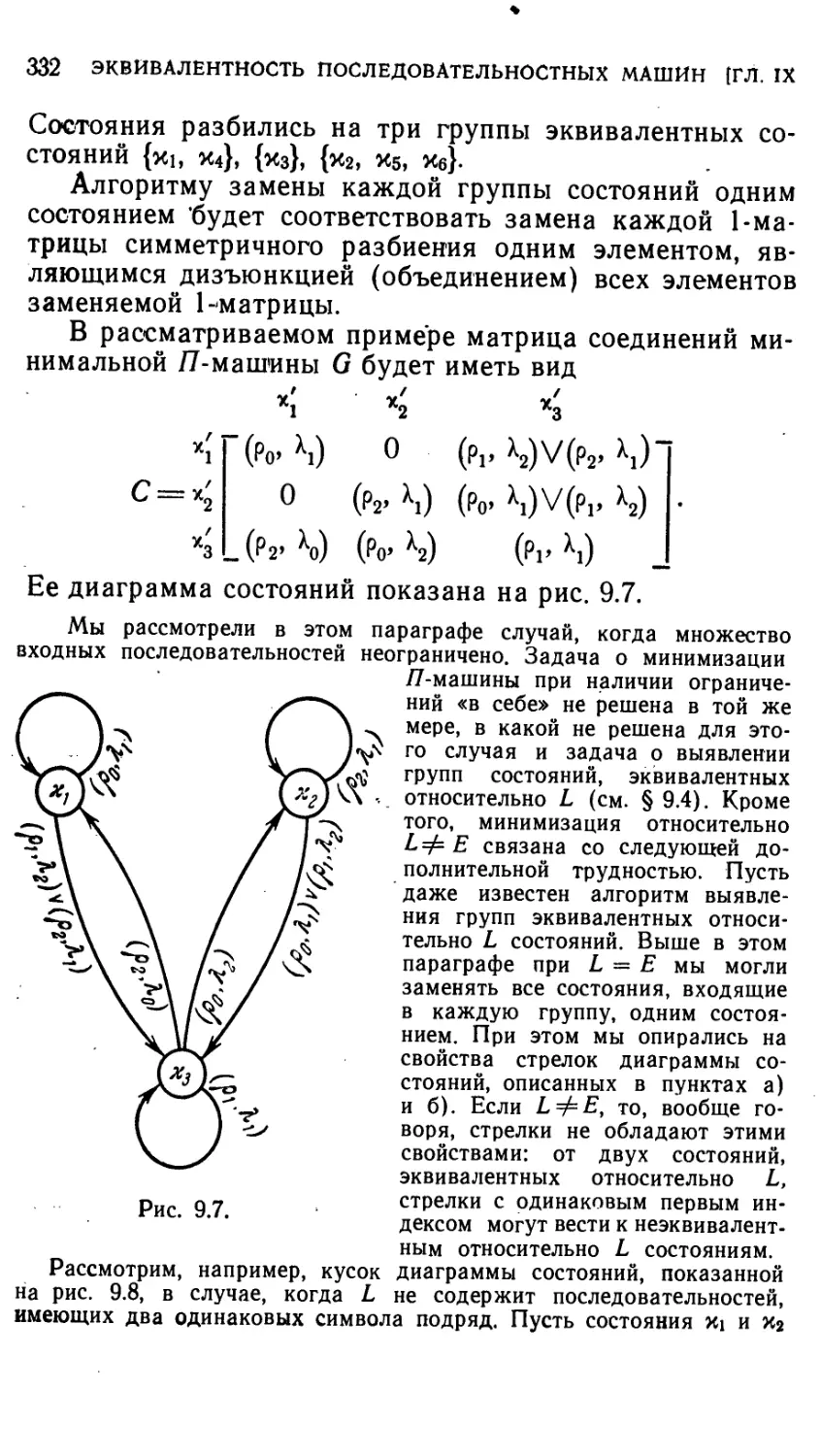
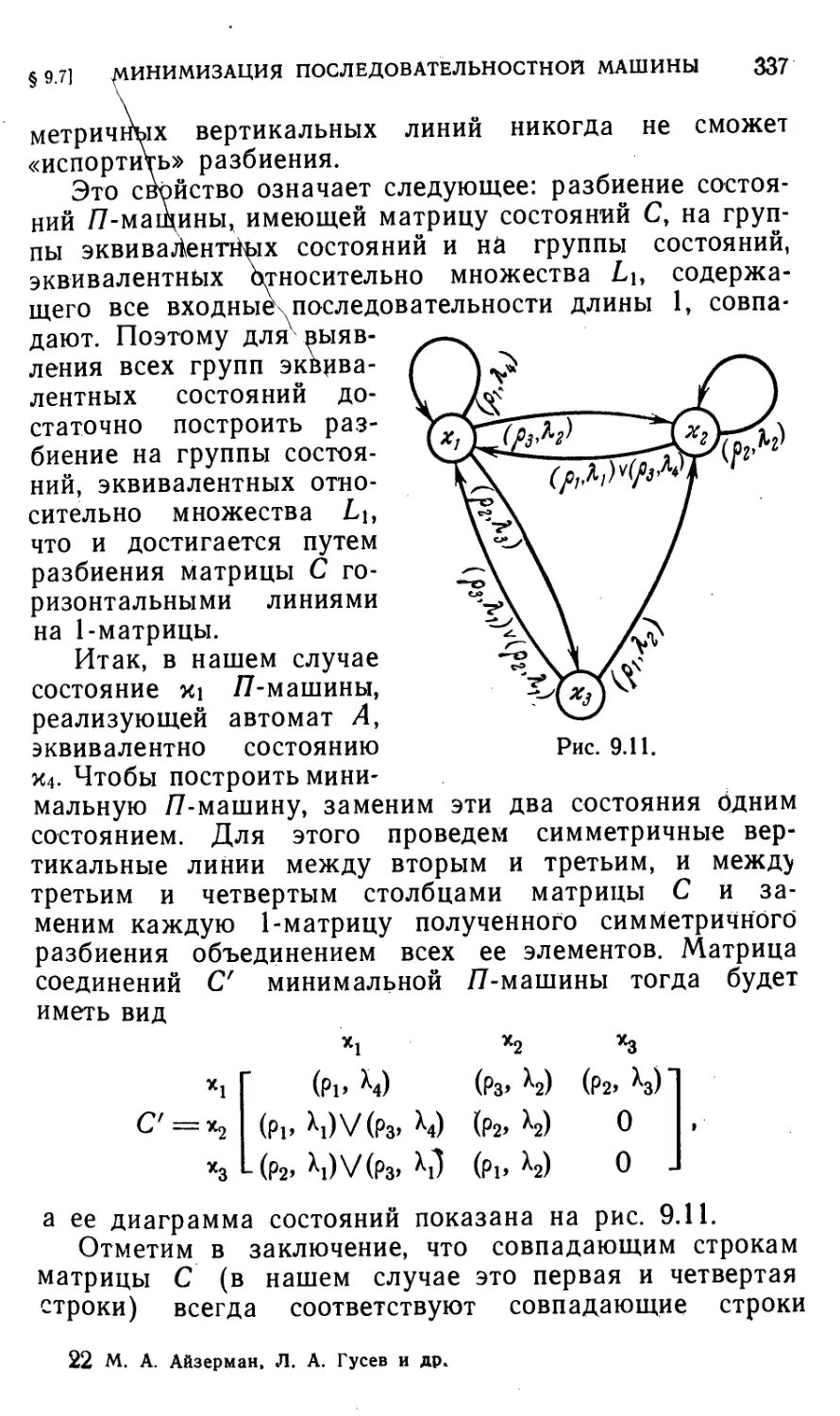
§ 9.7. Минимизация последовательностной машины в случае,
когда она работает как конечный автомат 333
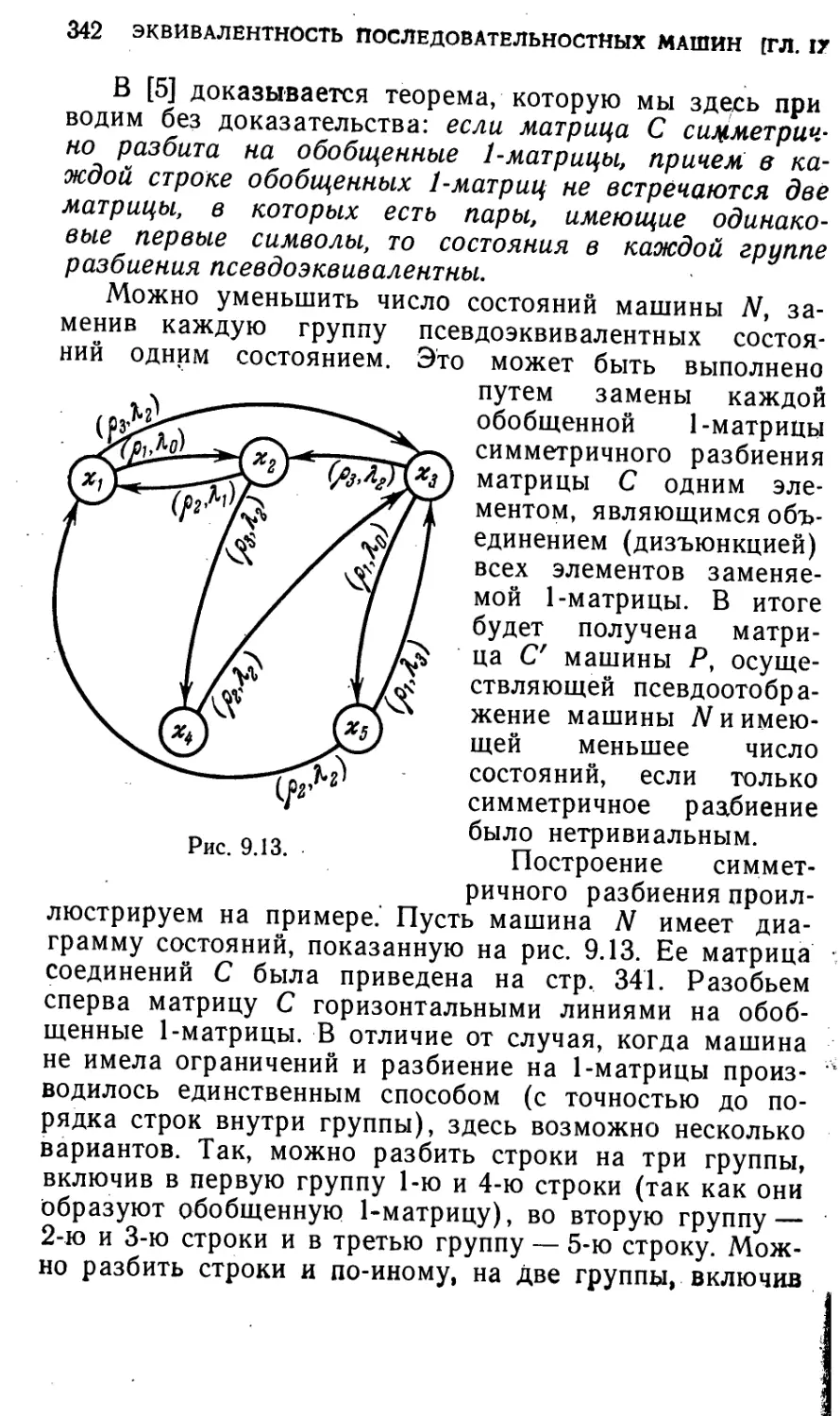
§ 9.8. Минимизация последовательностных машин в случае
ограничений типа Ауфенкампа 340
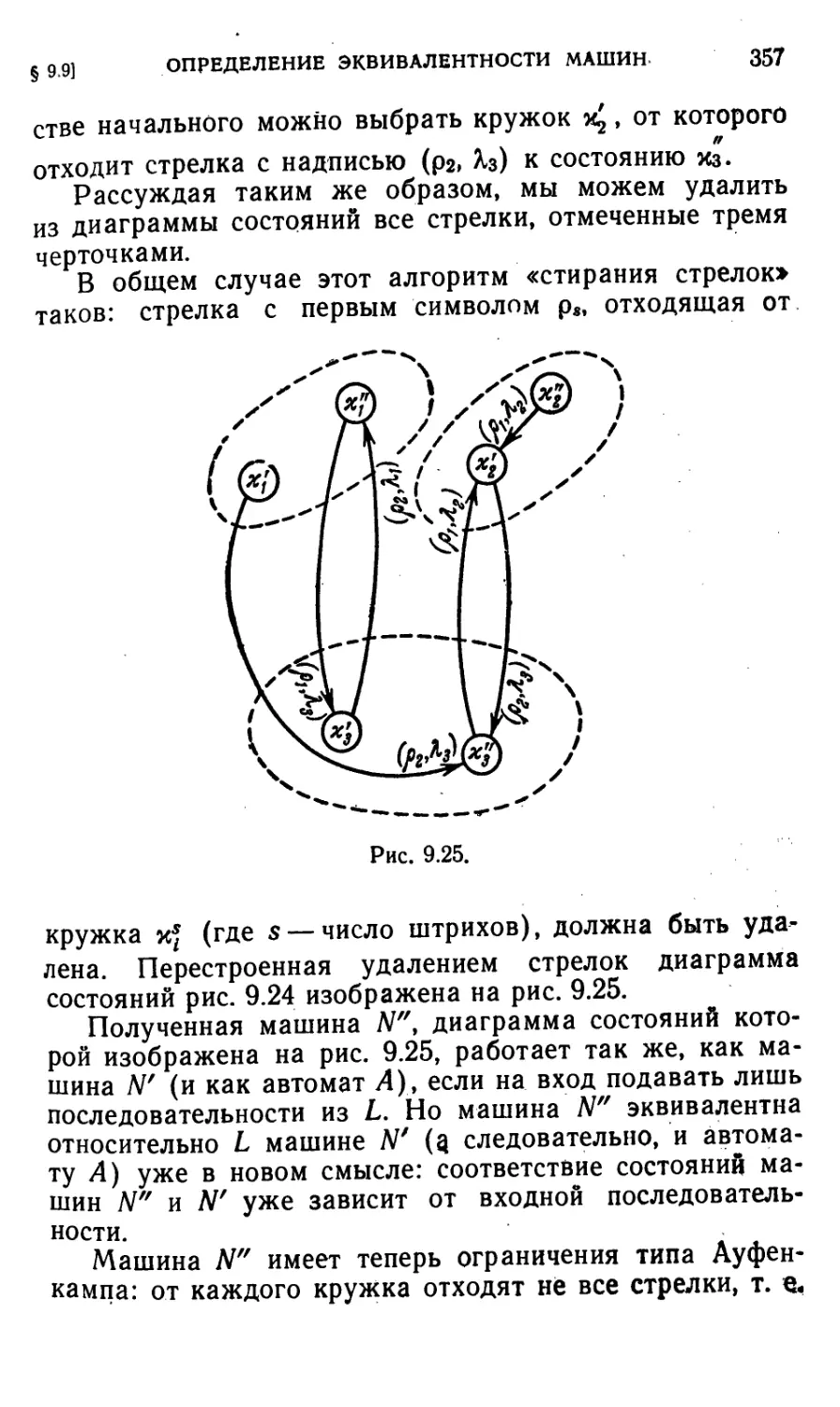
§ 9.9. Об . ином определении эквивалентности последователь-
последовательностных машин 353
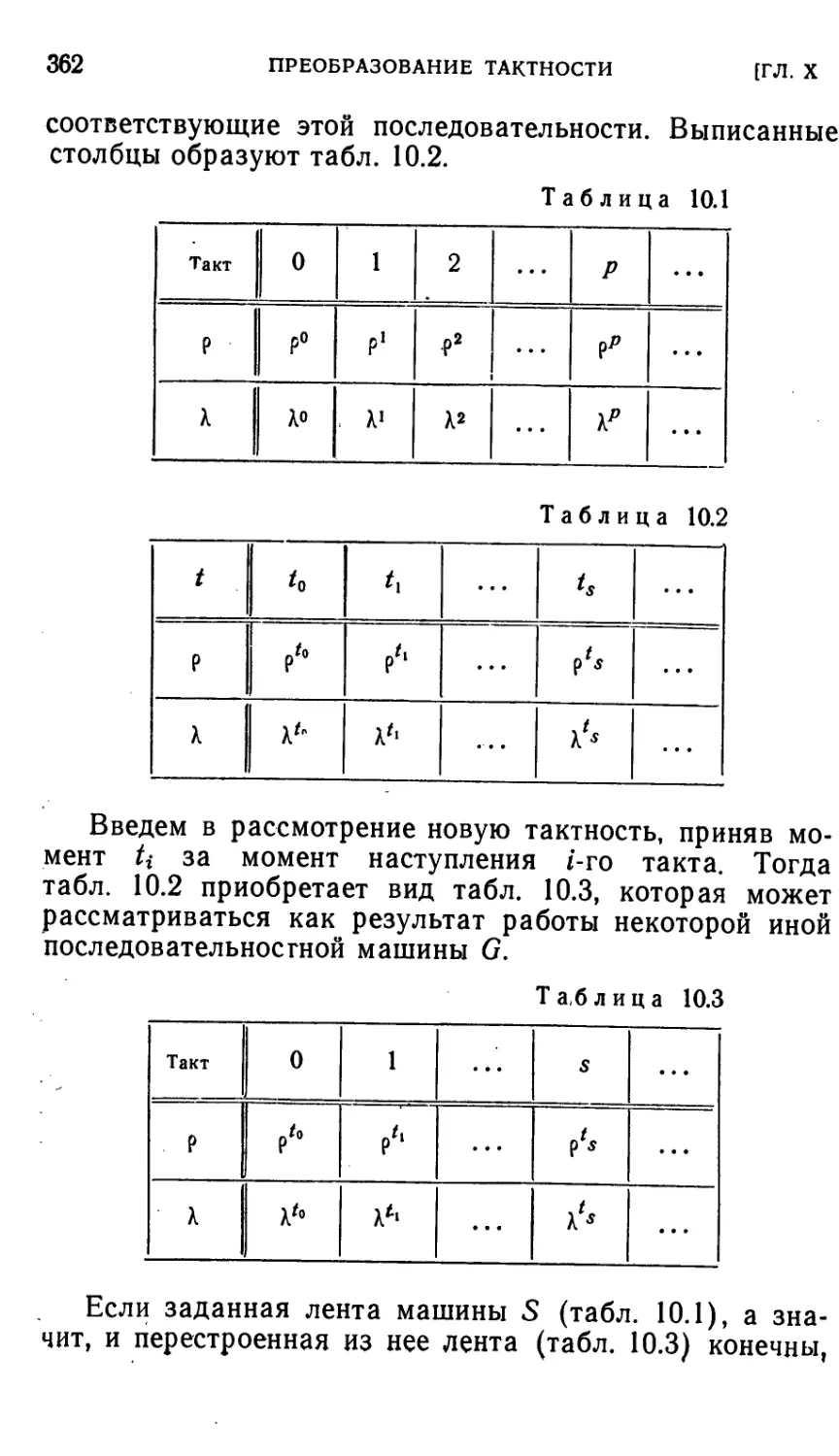
Глава X. Преобразование тактности последовательностных
машин 361
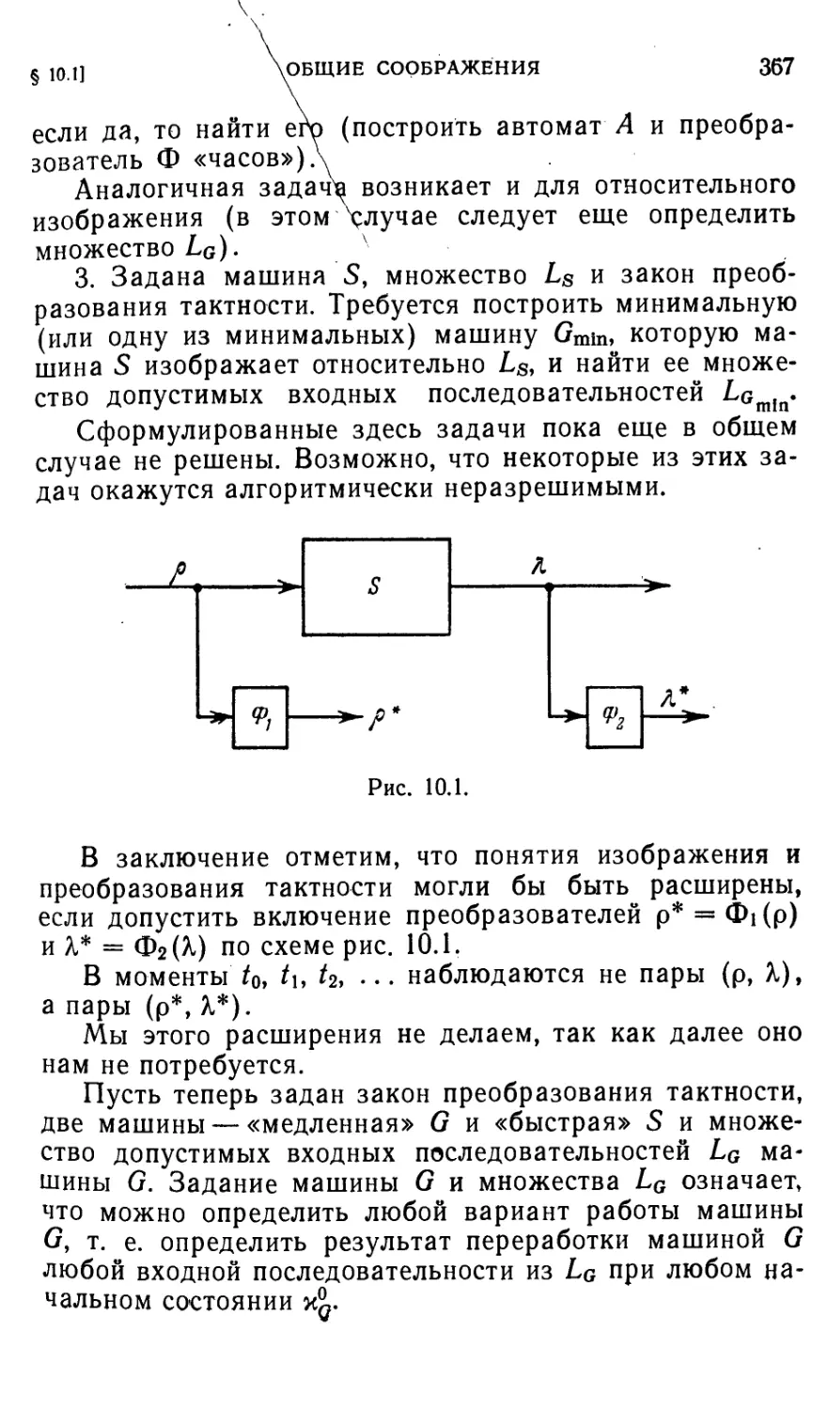
§ 10.1. Общие соображения о преобразовании тактности. Опре-
Определение понятий изображения и воспроизведения . . . 361
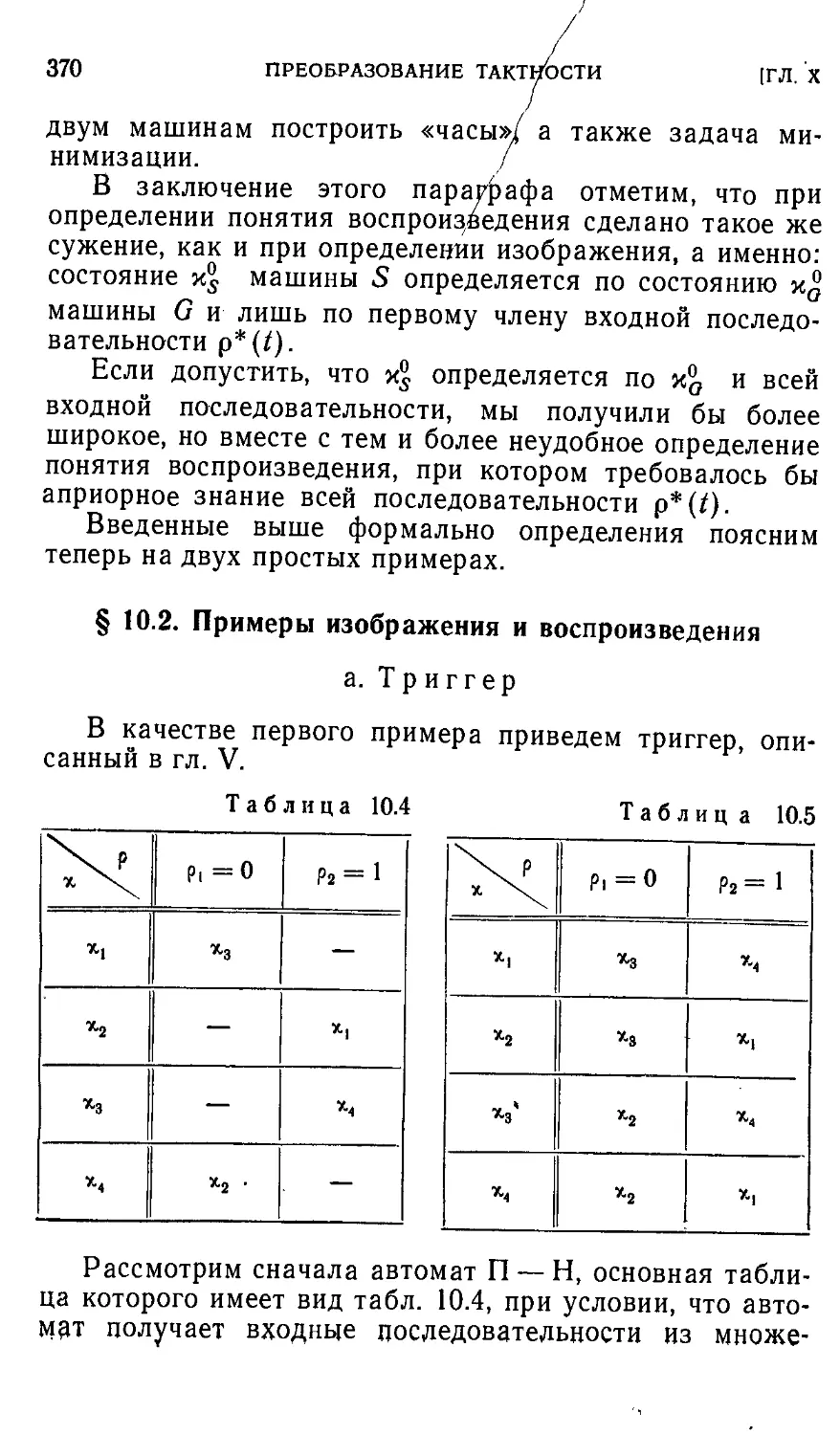
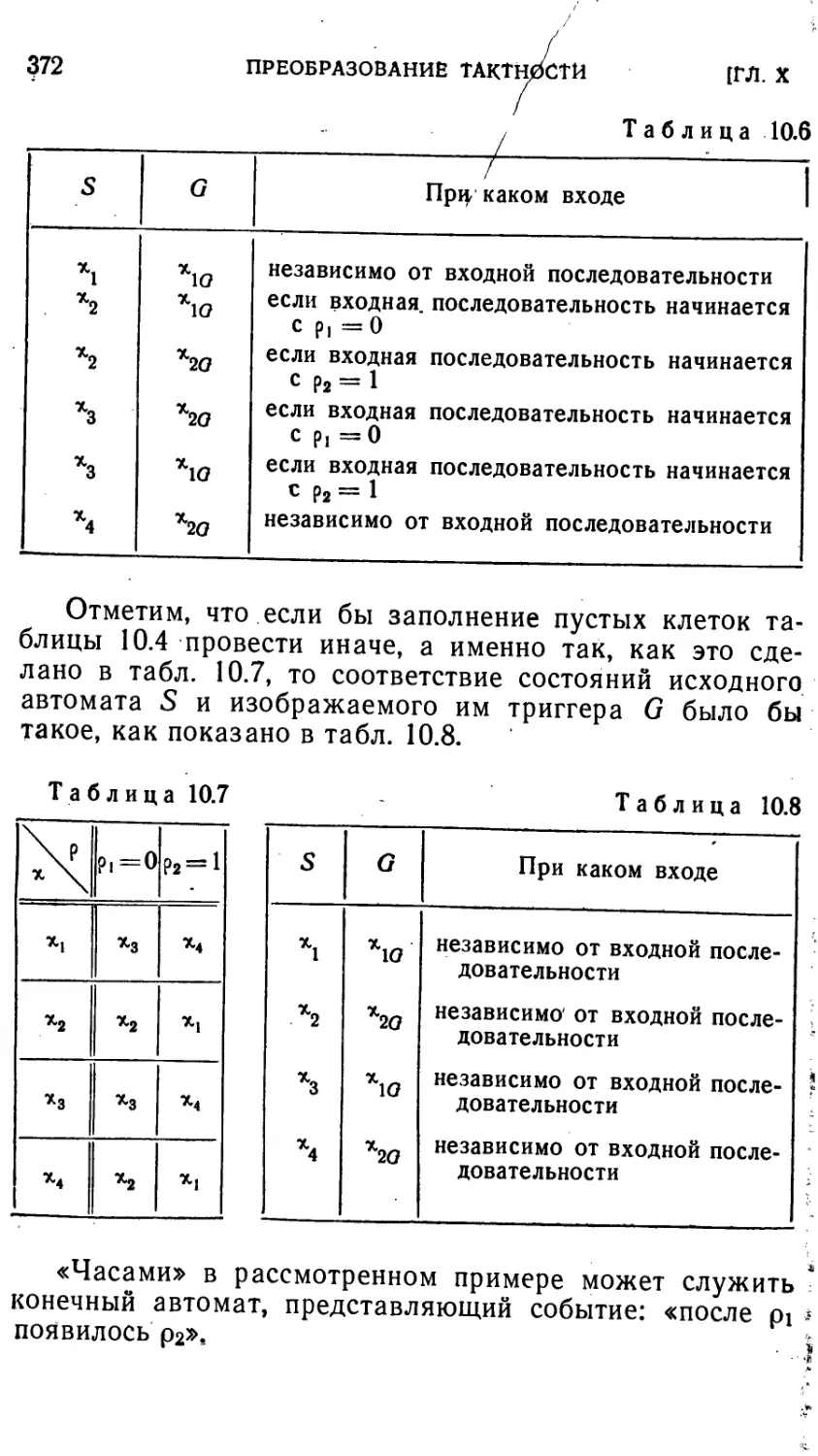
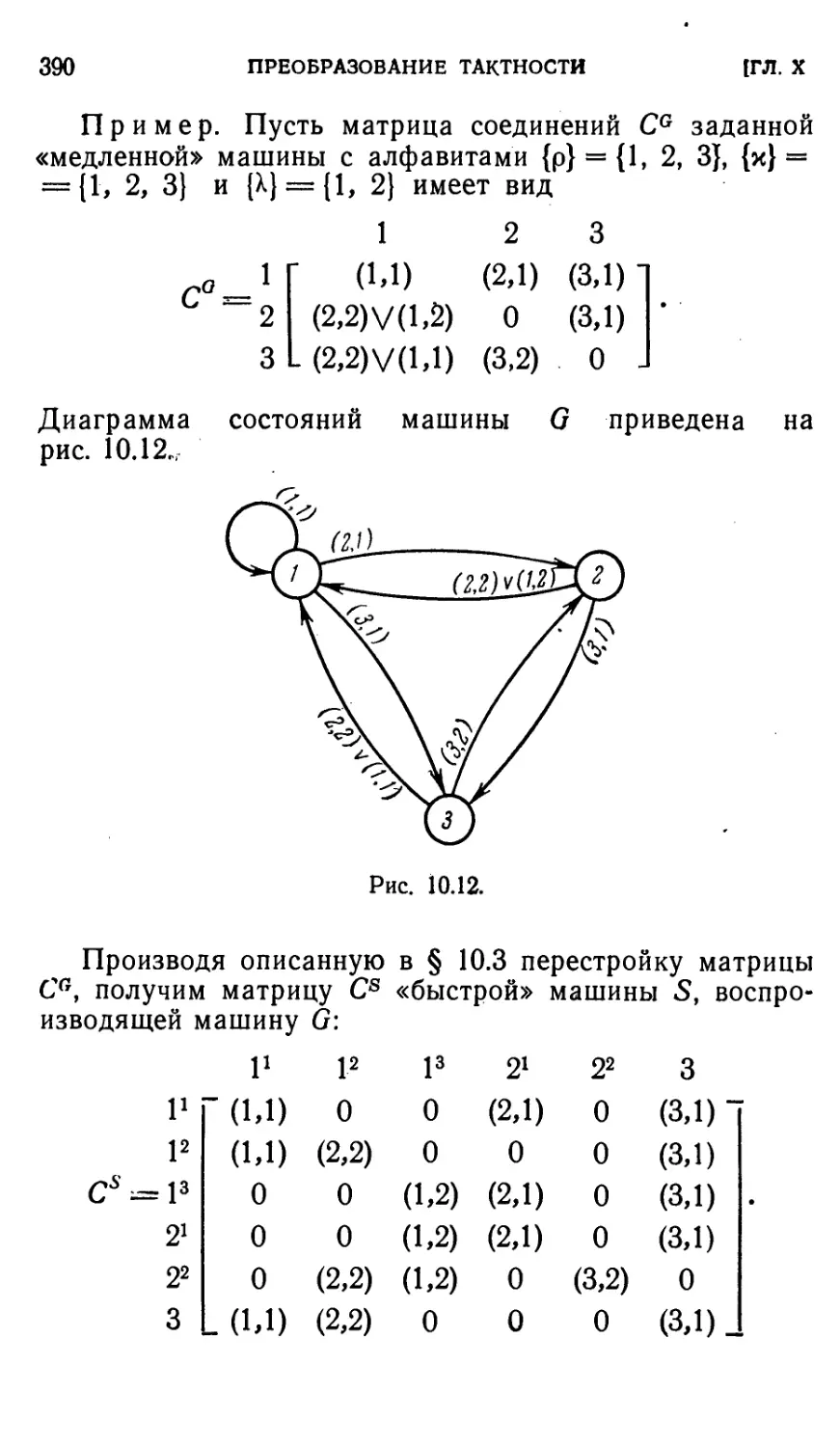
§ 10.2. Примеры изображения и воспроизведения 370
§ 10.3. Воспроизведение медленной последовательностной ма-
машины быстрой машиной в случае, когда тактность мед-
медленной машины определяется сменой состояний на
входе 376
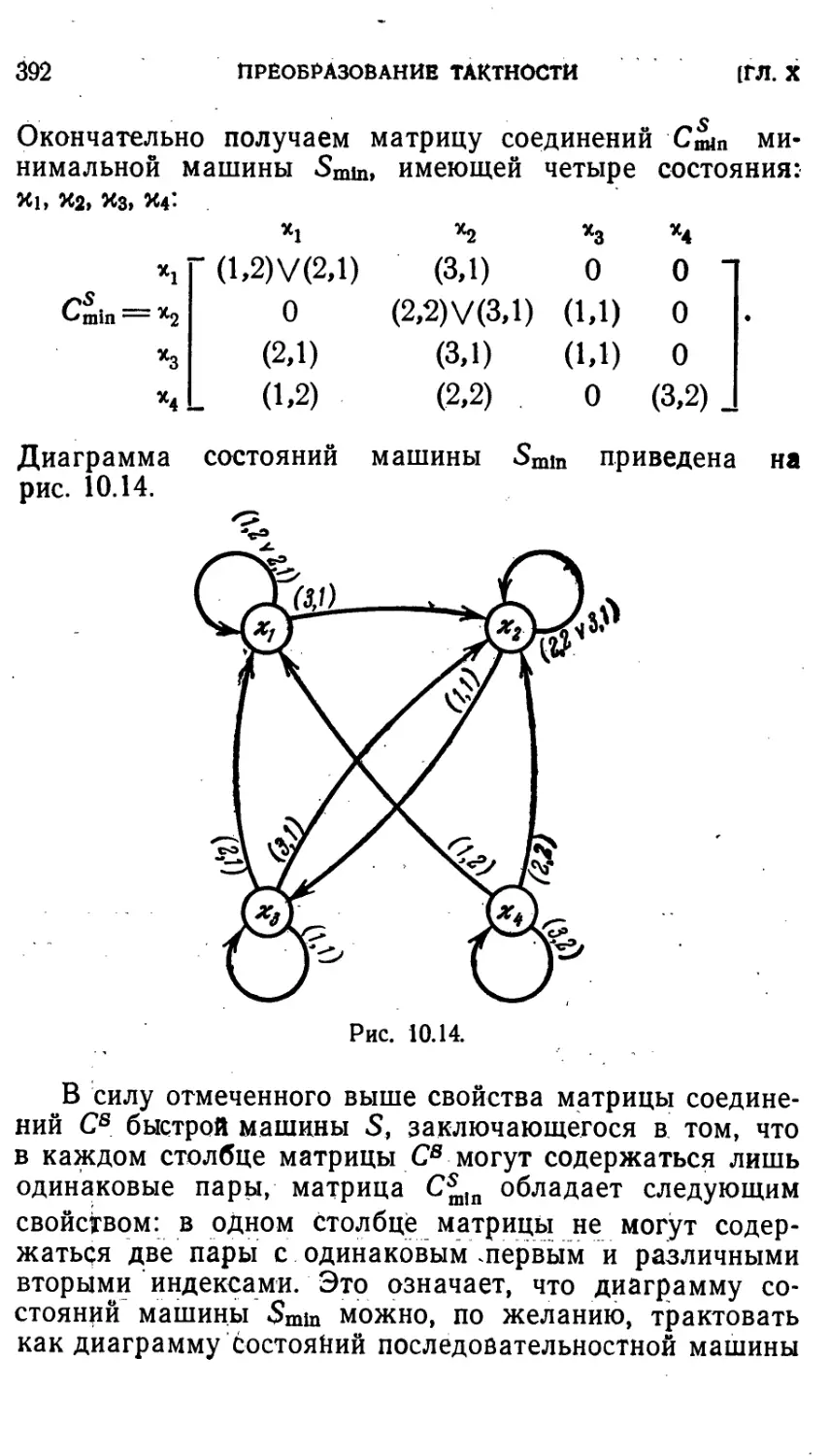
§ 10.4. Минимизация воспроизводящей последовательностной
машины, построенной в предыдущем параграфе .... 383
Глава XI. Определение свойств последовательностных машин
по их реакции на входные последовательности конечной
- длины 397
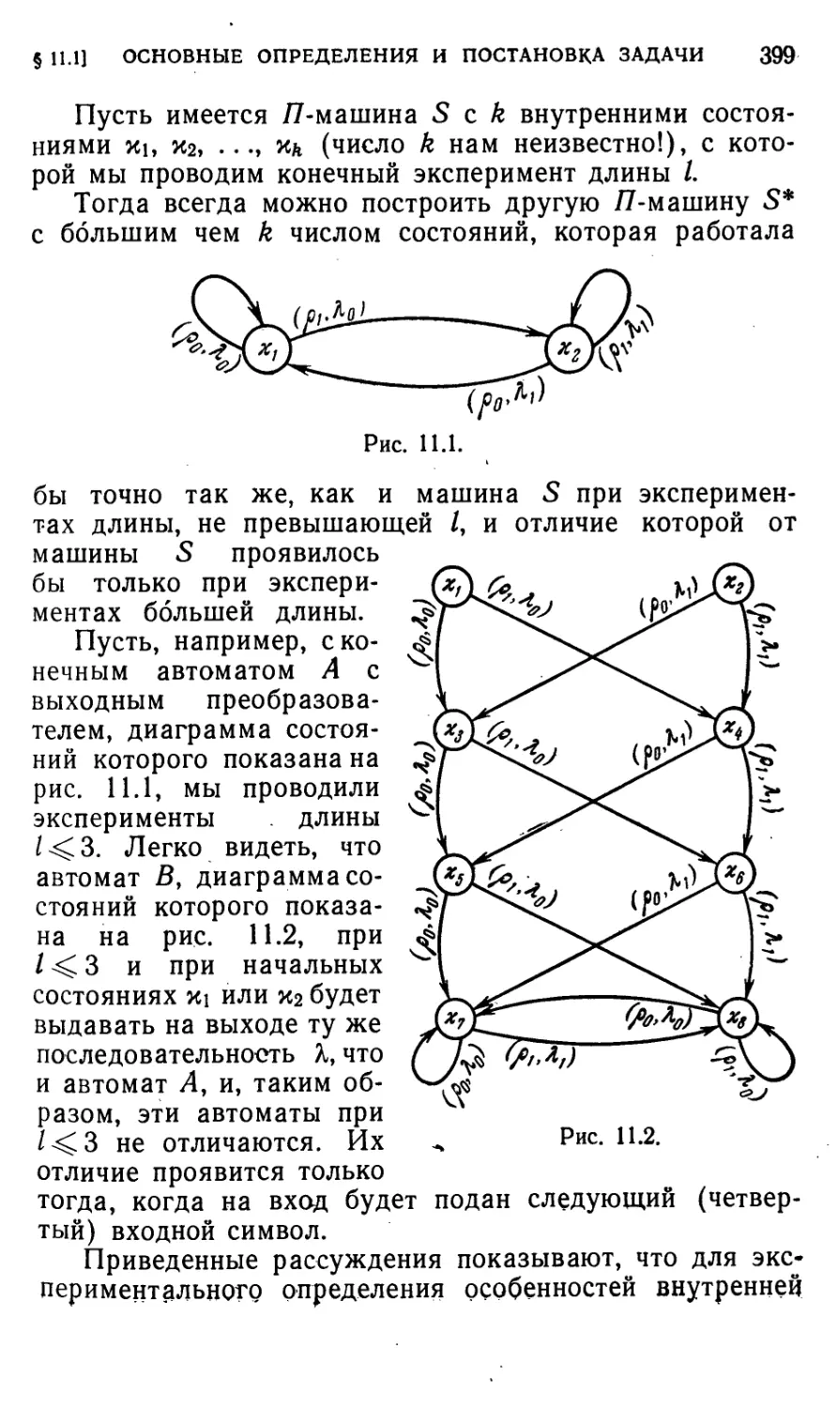
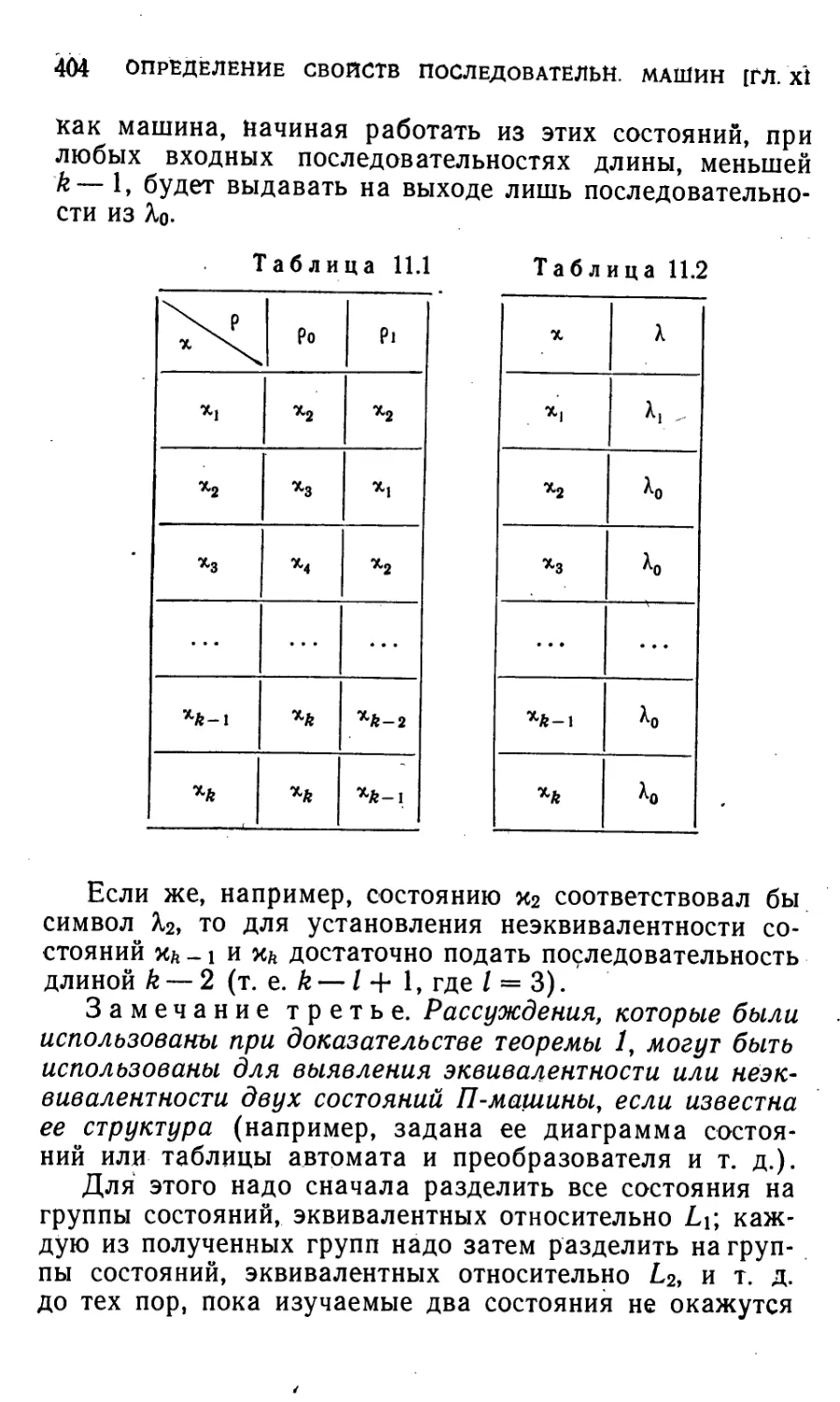
§ 11.1. Основные определения и постановка задачи 397
§ 11.2. Определение эквивалентности состояний последователь-
последовательностных машин по реакции машины на входные после-
последовательности конечной длины 400
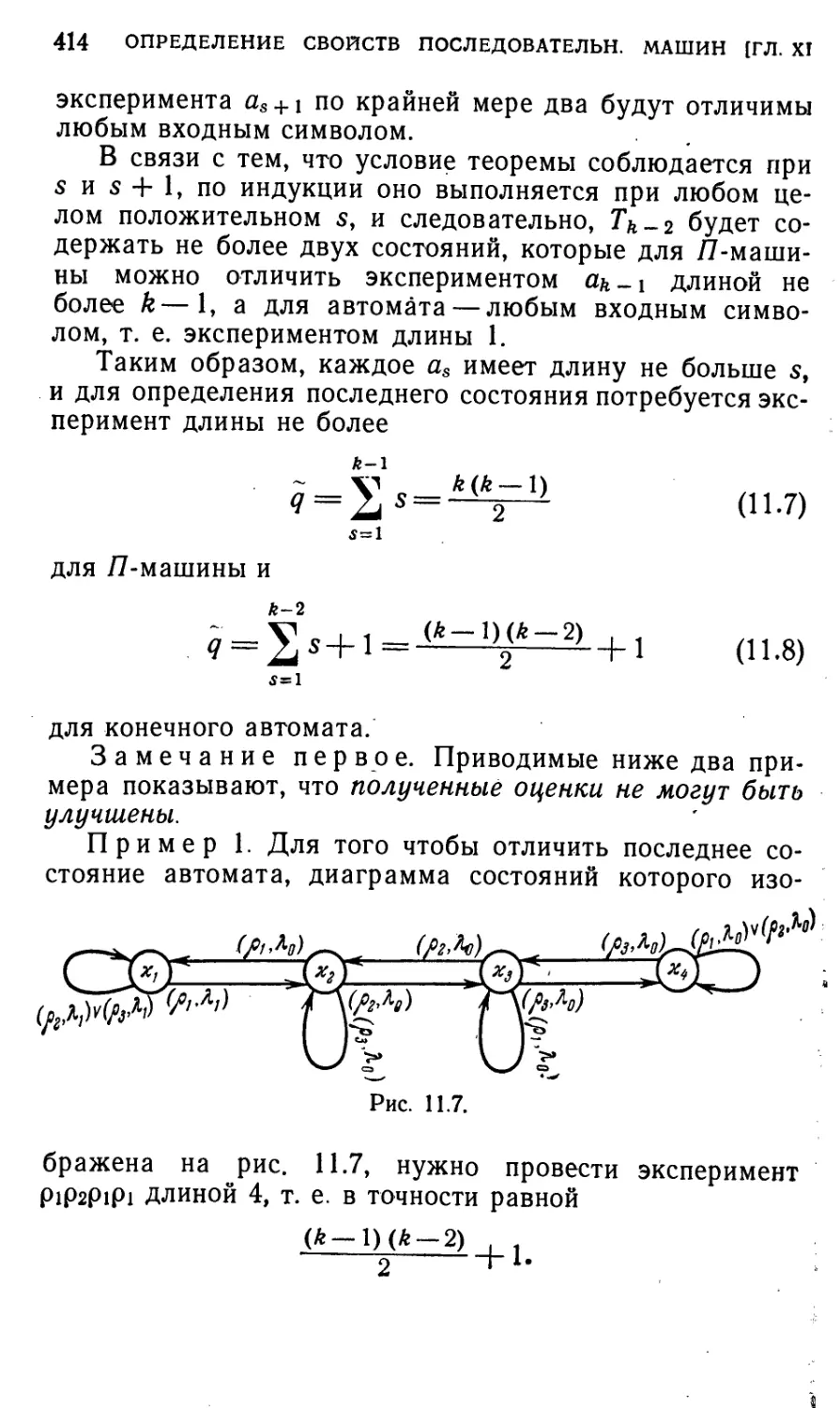
§ 12.3. Изучение последовательностных машин с помощью крат-
кратных экспериментов 407
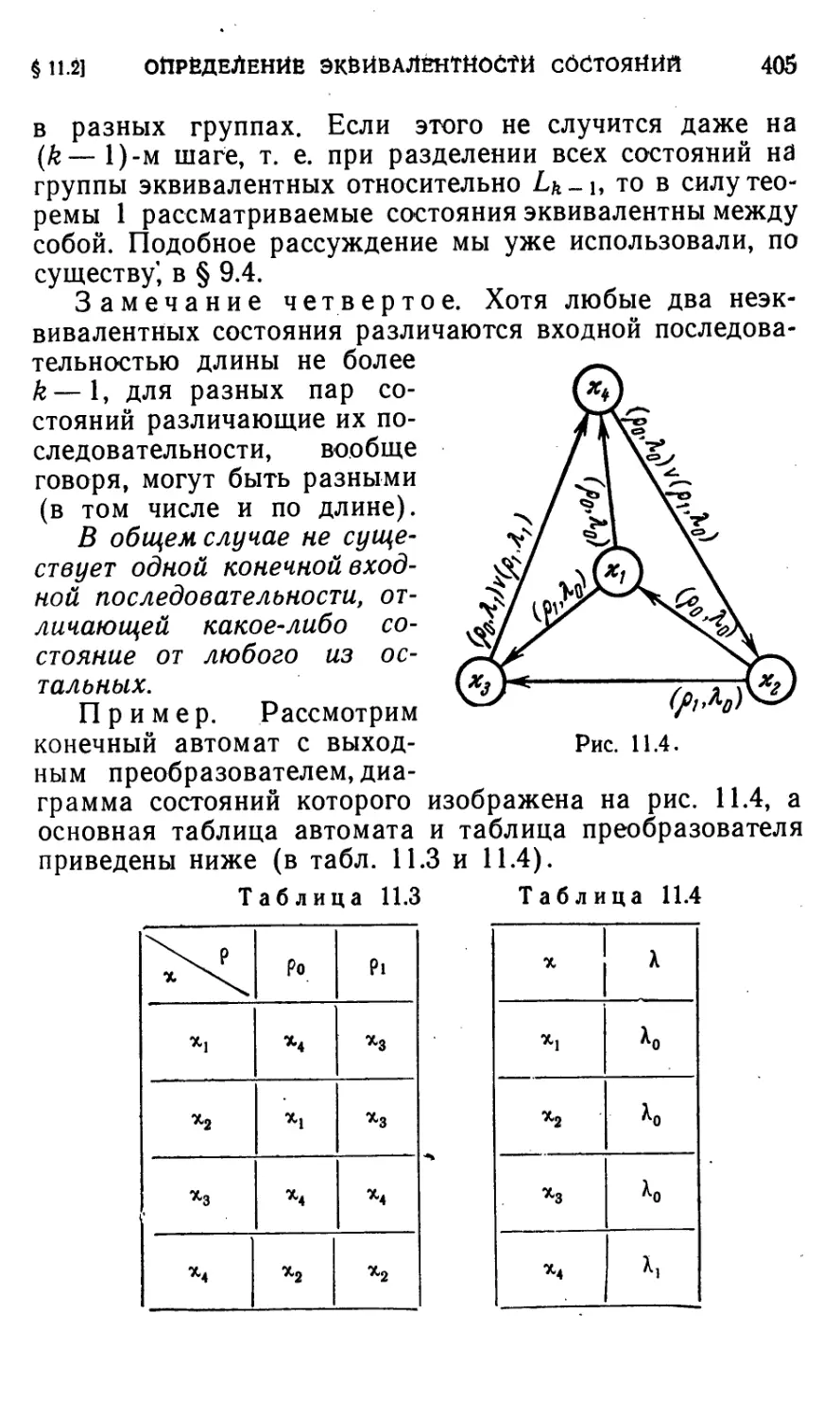
§ 11.4. Изучение последовательностных машин с помощью
простых экспериментов 411
Глава XII. Алгоритмы 425
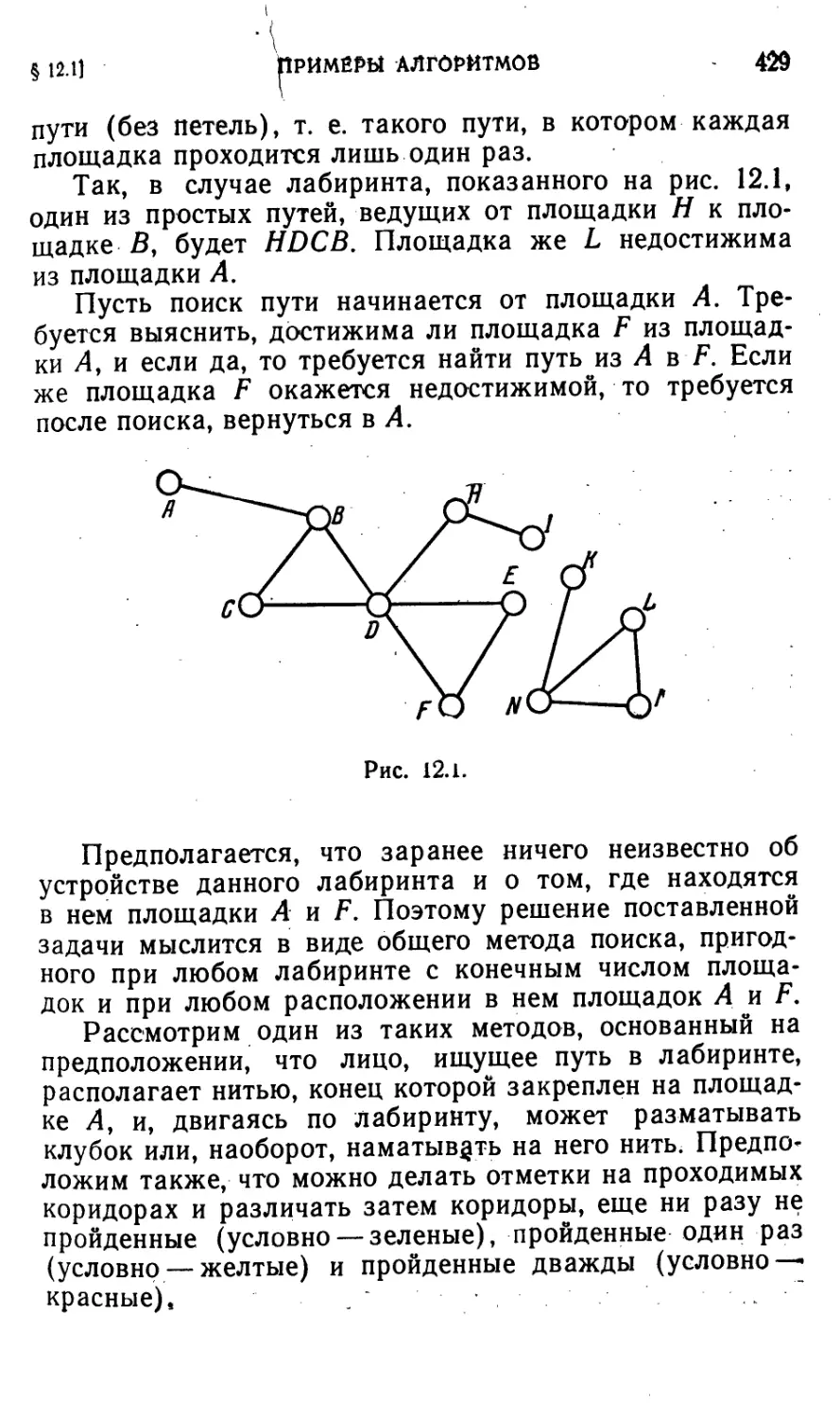
§ 12.1. Примеры алгоритмов 425
§ 12.2. Общие свойства алгоритмов 432
§ 12.3. Проблема слов в ассоциативном исчислении 435
§ 12.4. Алгоритм в некотором алфавите А. Нормальный алго-
алгоритм Маркова 441
§ 12.5. Сведение любого алгоритма к численному алгоритму.
' Гёделизация 451
6 ОГЛАВЛЕНИЕ
§ 12.6. Элементарные и примитивно-рекурсивные функции . . 455
§ 12.7. Предикаты. Ограниченный оператор наименьшего числа 466
§ 12.8. Пример построения вычислимой, но не примитивно-ре-
примитивно-рекурсивной функции 473
§ 12.9. Общерекурсивные функции. Определение Эрбрана — Гё-
деля . . 1 475
§ 12.10. Явная форма общервкурсивных функций ....... 481
§ 12.11. Тезис Чёрча 487
§ 12.12. Рекурсивные действительные числа 490
§ 12.13. Рекурсивно-перечислимые- и рекурсивные множества . 492
Глава XIII. Машины Тьюринга , 496
§ 13.1. Описание и примеры машин Тьюринга 496
§ 13.2. Композиция машин Тьюринга 506
§ 13.3. Вычисления на машинах Тьюринга 512
Заключение 524
§ 1. Что может «делать» конечный автомат и последователь-
ностная машина 524
§ 2. Последовательность синтеза технического устройства, реа-
реализующего конечный автомат или последовательностную
машину 527.
Библиография . . 536
Именной указатель 550
Предметный указатель 551
ПРЕДИСЛОВИЕ
Для инженеров, работающих в области релейно-кон-
тактной техники или техники цифровых машин, изуче-
изучение общей теории конечных автоматов и последователь-
ностных машин не связано с большими трудностями,
так как им знаком уже необходимый математический
аппарат: исчисление высказываний, общие понятия об
исчислении предикатов, основы теории алгоритмов
(теории рекурсивных функций).
В значительно худшем положении оказываются инже-
инженеры других специальностей, в том числе и инженеры;
знакомые с теорией автоматического управления. Осно-
Основой их математического образования является обычно
анализ, математическая физика, дифференциальные
уравнения. Как показал опыт, изучение проблем, в осно-
основе которых лежит математическая логика и теория
алгоритмов, представляет для них известные трудности.
Настоящая книга рассчитана «а широкий круг чи-
читателей, работающих в области автоматики, телемеха-
телемеханики и вычислительной техники и впервые знакомя-
знакомящихся с теорией конечных автоматов и последователь-
ностных машин. Авторы имели в виду также, что книга
должна быть полезна для математика (не логика),
стремящегося познакомиться с этими проблемами, а
также для физиолога и биолога, интересующихся тео-
теорией конечных автоматов и последовательностных ма-
машин применительно к созданию идеализированных мо-
моделей нервных тканей. Цель книги — ввести указанный
круг читателей в эту новую область, познакомить с ос-
основными понятиями, с постановкой некоторых задач и
результатами их решения. При этом результаты, полу-
полученные авторами, тесно переплетаются с результатами,
8 ПРЕДИСЛОВИЕ
заимствованными из литературы. Все же в основном
книга рассчитана на инженеров. Поэтому авторы при
рассмотрении некоторых вопросов логики и теории
алгоритмов вынуждены были пренебрегать строгостью
изложения.
Для каждого из упомянутых читателей была бы
удобнее своя архитектура книги, свой порядок разме-
размещения материалов. Вынужденные рассчитывать на раз-
разных читателей, авторы старались разместить материал
так, чтобы встречающиеся трудности последовательно
нарастали. Естественно поэтому, что каждый читатель
может избрать свой порядок чтения глав, руководст-
руководствуясь следующими общими советами:
1. Для инженера, не знакомого с предметом, но
стремящегося детально изучить его, рекомендуется изу-
изучение материала в той последовательности, в какой
он приведен в книге.
2. Для инженера, интересующегося предметом лишь
в общих чертах, рекомендуется прочесть последова-
последовательно первые семь глав, а затем главу XII. После
этого можно бегло просмотреть главу XIII и, наконец,
прочесть главы VIII, IX, X и XI.
3. Для инженера, знакомого с основами математи-
математической логики и ее техническими приложениями (на-
(например, для специалиста по релейно-контактной тех-
технике или вычислительным машинам), рекомендуется на-
начать чтение книги с главы III.
4. Наконец, математику, интересующемуся техниче-
техническими приложениями, можно смело опустить при чтении
книги, главы I, XII и XIII.
Параграфы 2.5 и 8.4, в которых затрагиваются спе-
специальные вопросы минимизации булевых функций и
реализации конечных автоматов, заданных на языке ре-
регулярных выражений (выходящие за рамки основ об-
общей теории конечных автоматов и последовательност-
ных машин), были по просьбе авторов написаны соот-
соответственно В. Д. Казаковым и О. П. Кузнецовым.
Авторы с благодарностью ждут замечаний и пред-
предложений от читателей.
Авторы
ВВЕДЕНИЕ
«Конечный автомат» и «последовательностная ма-
машина» — исторически сложившиеся и широко применяе-
применяемые, хотя и очень неудачные наименования некоторого,
в известном смысле простейшего класса динамических
систем. Выделение этого класса и построение его тео-
теории связано со следующими двумя обстоятельствами:
1. Динамические системы этого класса часто исполь-
используются в технике, в особенности в автоматике, теле-
телемеханике, вычислительной технике. Электронные цифро-
цифровые вычислительные машины и многотактные релейно-
контактные схемы являются примерами динамических
систем этого класса. Рассмотрение всего этого класса
динамических систем позволяет поэтому изучать их об-
общие закономерности и разрабатывать методы их ана-
анализа и оптимального синтеза.
2. С развитием техники, в особенности в связи с
созданием быстродействующих универсальных вычи-
вычислительных машин, все чаще ставятся вопросы такого
рода: Что может и что не может «делать» машина? Мо-
Может ли машина выполнять любой алгоритм? Может ли
машина принципиально делать что-либо большее, чем
выполнять алгоритм? В какой мере машина может и
в какой не может выполнять функции, свойственные
живому мозгу? Попытки в точных терминах сформу-
сформулировать подобные вопросы и тем более изыскать от-
ответы на них до сих пор оставались безрезультатными,
если термином «машина» обозначается очень широкий
класс динамических систем. Между тем для более уз-
узкого класса динамических систем, называемых «конеч-
«конечными автоматами» и «последовательностными машина-
машинами», постановка вопросов такого рода имеет смысл. Они
10 ВВЕДЕНИЕ
могут быть сформулированы в точных терминах, и на
некоторые из этих вопросов уже получены ответы.
Есть еще одно обстоятельство, на определенном
этапе развития науки поддерживающее интерес к ди-
динамическим системам этого класса. Мозг состоит из
очень большого числа нервных клеток — нейронов;
при некоторой идеализации свойств нейронов может
быть построена математическая модель мозга, разу-
разумеется, верная лишь в пределах этой идеализации. Та-
Такая модель также относится к динамическим системам
рассматриваемого здесь типа. В свете все расширяю-
расширяющихся знаний о свойствах нейрона и мозга в целом,
выяснилась неадекватность указанной идеализации и
целесообразность рассмотрения более сложных моделей
мозга. Однако тот факт, что при некоторой идеализа-
идеализации, приемлемой на определенном этапе науки, живой
мозг, с одной стороны, и универсальная цифровая ма-
машина — с другой, могли бы быть отнесены к одному и
тому же сравнительно простому классу динамических
систем, — придает изучению этих систем особый ин-
интерес.
\
\
ГЛАВА 1
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
§1.1. Вводные замечания
Математическая (символическая) логика как науч-
научная дисциплина возникла на базе так называемой тра-
традиционной формальной логики и первое время разви-
развивалась в связи со стремлением формализовать некото-
некоторые стороны интеллектуальной деятельности человека.
Дальнейшее ее развитие было в сильной степени под-
подчинено задаче создания логических основ математики.
Сюда относятся вопросы непротиворечивости и полноты
системы посылок, принятых в каком-либо разделе ма-
математики за исходные, задача об определении всех след-
следствий, вытекающих из этих исходных посылок (аксиом)
и другие подобные вопросы. Со временем математиче-
математическая логика стала мощным средством научных иссле-
исследований, но область ее применения долгое время была
ограничена чисто теоретическими проблемами. Несмотря
на то, что еще в 1910 г. П. Эренфест обратил внимание
на возможность применения математической логики для
описания работы таких технических устройств, как ре-
лейно-контактные схемы, эффективное использование
методов математической логики для решения приклад-
прикладных вопросов "рёЛёйЙо-кбнтактной техники тачалось
лишь с тридцатых годов, после того как были опуб-
опубликованы работы В. И. Шестакова [111, 112] и
К. Э. Шеннона [231]. Установленное соответствие между
математической логикой и функционированием релей-
но-контактных устройств привело к созданию самостоя-
самостоятельной технической дисциплины — теории релейно-кон-
тактных схем, впервые изложенной в монографии
12 ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ [ГЛ. 1
М. А. Гаврилова [21]. Вскоре наметилось и более ши-
широкое проникновение математической логики в приклад-
прикладные науки. Оказалось, что не только релейно-контакт-
ные схемы, но и многие другие устройства дискретного
действия нуждаются для их описания в привлечении
аппарата математической логики. Таким образом, мате-
математическая логика, сохраняя важнейшее значение для
исследований в теоретических областях, теперь уже
прочно входит в арсенал средств, применяемых при
исследовании и проектировании самых разнообразных
технических устройств. Прикладное значение математи-
математической логики в последнее время особенно сильно вы-
выросло в связи с исследованием общих законов управле-
управления, действующих как в технике, так и в природе.
В связи с двумя возможными аспектами примене-
применения методов математической логики — теоретическим
и прикладным — изложение самого предмета можно
. вести двумя способами. В соответствии с основным на-
назначением книги в этой главе принят способ изложения
математической логики, соответствующий прикладному
аспекту ее применения. Элементы математической ло-
логики приводятся в этой главе лишь в таком объеме, ко-
который необходим для понимания следующих глав книги.
§ 1.2. Основные понятия
В дальнейшем, при описании главных черт матема-
математической логики, основное значение для нас будет иметь
важнейшее математическое понятие — функциональная
зависимость.
Само понятие функциональной зависимости в наи-
наиболее общей форме связано с представлением о неко-
некоторых двух множествах и об отображении одного мно-
множества на другое. Пусть мы имеем множества X и У,
состоящие соответственно из элементов х и у, то есть
Х={х), У={у}.
Если в силу каких-нибудь условий каждому элементу х,
принадлежащему множеству X (этот факт записы-
записывается так: х ? X), оказывается приведенным в соответ-
§ 1.2] ОСНОВНЫЕ ПОНЯТИЯ 13
ствие определенный элемент у, принадлежащий множе-
множеству У (у ? У), то говорит, что эти условия определяют
у как функцию х или, иначе, говорят об отображении
множества X на множество У. Про функцию у = у(х)
говорят также, что она определена на множестве X и
принимает значения из множества У; х называют не-
независимой переменной или аргументом, а у — функ-
функцией.
Тот или иной конкретный тип функциональной за-
зависимости определяется, с одной стороны, характери-
характеристиками множеств X и У, а с другой — свойствами эле-
элементов х и у этих множеств.
Рассмотрим некоторые основные характеристики
множеств. В зависимости от того, конечно или беско-
бесконечно количество элементов, составляющих множество,
все множества делят на конечные и бесконечные. На-
Например, множество букв в русском алфавите конечно;
множество молекул в теле конечных размеров также
конечно; множества же, состоящие либо из всех целых
положительных чисел, либо из всех рациональных чи-
чисел, либо из всех вещественных чисел, служат приме-
примерами бесконечных множеств. Бесконечными являются
также множество всех точек отрезка, множество всех
точек плоской фигуры.
Множества можно сравнивать по мощности. Два
множества называются равномощными, если между
всеми элементами этих множеств может быть устано-
установлено взаимно однозначное соответствие. Среди беско-
бесконечных множеств оценка по мощности позволяет выде-
выделить два важных класса: счетные и континуальные
множества.
К счетным множествам относятся те, которые равно-
мощны множеству натурального ряда чисел, а к кон-
континуальным — такие множества, которые равномощны
множеству всех вещественных чисел.
В частности, множество всех четных чисел счетно,
так как элементы этого множества легко приводятся во
взаимно однозначное соответствие элементам множе-
множества натурального ряда. Действительно, расположив
четные числа и числа натурального ряда в порядке их
возрастания, получаем возможность установить между
14
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
[ГЛ. J
элементами рассматриваемых/ множеств следующее
взаимно однозначное соответствие:
2. 4. 6. .... 2й, ...
1, 2, 3 п, ...
Счетными множествами' являются также множество
всех алгебраических чисел, множество всех рациональ-
рациональных чисел и некоторые другие множества.
Континуальными множествами являются множество
всех иррациональных чисел, множество всех точек от-
отрезка линии, множество всех точек плоской фигуры и
многие другие. Иногда сопоставление бесконечных
множеств по их мощ-
мощности приводит к ут-
утверждениям, которые
звучат парадоксально.
Например, на пер-
первый взгляд кажется
странным, что множе-
множество точек некоторого
отрезка {АВ на
рис. 1.1) и множество
й
рис
точек некоторой части
того же отрезка (АС
на рис. 1.1) равномощны. Однако это так, в чем легко
убедиться, если сделать приведенное на рис. 1.1 вспомо-
вспомогательное построение. Из этого очевидного построения
следует, что для любой точки М отрезка АВ луч, прохо-
проходящий через эту точку и полюс О, пересекает отрезок Л С
в точке М', которую можно считать находящейся с точ-
точкой М отрезка АВ во взаимно однозначном соответствии.
Значит, оба рассматриваемых множества действительно
равномощны. Подобным же образом показывается, что
множество точек плоской фигуры или даже тела также
равномощно множеству всех точек отрезка линии, т. е.
имеет мощность континуума.
Возвратимся теперь к рассмотрению различных ти-
типов функциональных зависимостей. Как уже было от-
отмечено, они определяются особенностями элементов
§ 1.2] ОСНОВНЫЕ ПОНЯТИЯ 15
множеств, на которых ^определяется и из которых при-
принимает значения функция, и характеристиками этих
множеств. Если функциях определена на множестве X
всех вещественных чисел х и принимает значения из
множества У, также состоящего из всех вещественных
чисел у, то в этом случае мы имеем вещественную
функцию у одной вещественной переменной х или
у = у(х). Если же функция принимает значения из того
же множества вещественных чисел у, а каждый эле-
элемент множества Z = {г}, на котором она определена,
является последовательностью, состоящей из п веще-
вещественных чисел Х\, Х2, ..., хп, то в этом случае
мы имеем вещественную функцию у не одной, а п
вещественных переменных хи х2, ..., хп или
у = у(хи х2, ..., хп).
В основе построения рассмотренных функций лежит
множество вещественных чисел. По этому признаку они
объединяются в один класс. Для этого класса функций
характерно, что как сами функции, так и их аргументы
заданы на континуальных множествах.
Основная особенность функций, рассматриваемых в
математической логике, состоит в том, что здесь мно-
множества, участвующие в отображении, состоят из эле-
элементов, в общем случае не связанных с какими-нибудь
числами. Значит, для того чтобы иметь возможность
различать элементы этих множеств, не существует дру-
другой возможности, кроме приписывания им каких-либо
символов, например номеров..
Перечень всех символов, соответствующих элемен-
элементам множества, называется его алфавитом, а неопреде-
неопределенный символ, который может становиться любым
элементом множества, называют логической перемен-
ной. По отношению к логической переменной каждый
частный символ является ее значением.
Таким образом, по свойствам элементов отображае-
отображаемых множеств логические функции являются функциями
наиболее общего типа. Что же касается характеристик
отображаемых множеств, то логические функции при-
принимают значения из конечных множеств в отличие, на-
например, от функций вещественной переменной, которые
в общем случае строятся на континуальных множествах,
16
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
[ГЛ. I
В качестве примера рассм/трим два множества.
Первое из них X = {х} образуют все различные белые
клавиши рояля; обозначим вй эти клавиши слева на-
направо символами хи х% .... x50; перечень этих симво-
символов составляет алфавит множества Х= {xv х2, ¦ ¦ ¦, х50].
Второе множество Y = {у} состоит из всех нот октавы,
т. е. из семи элементов, и имеет алфавит {yv у2, ¦ ¦ ¦, у7\,
причем символами уи у2,-Уз, Уа, Уъ, Ув, и у7 обозначены
соответственно ноты до, ре, ми, фа, соль, ля и си.
Для настроенного рояля каждому символу из алфавита
{х} соответствует один определенный символ из алфа-
алфавита {у}. Это значит, что переменная у, принимающая
значения у\, у2, .... у7, является логической функцией
независимой переменной х, принимающей значения Х\,
х2, ..., #5о- Эта функция может быть задана, например,
в виде таблицы (см. табл. 1.1)
Таблица 1.1
X
У
х,
Уб
х2
У?
х%
У\
х4
Уг
Хъ
Уз
х6
У
х7
Уь
xs
Ув
х9
Ут
Хю
У1
хи
Ут
Х45
Ух
х<6
У2
х„
Уз
xAi
У*
Уа
Ув
При классификации функций, с которыми встре-
встречаются в математической логике, прежде всего следует
различать их по тому, сколько различных множеств
участвует в отображении, осуществляемом данной функ-
функцией. Если в отображении участвует всего лишь одно
множество, то есть осуществляется • отображение мно-
множества самого на себя, то соответствующую этому ото-
отображению логическую функцию мы будем называть
однородной. Неоднородной мы будем называть логиче-
логическую функцию в том случае, когда ей соответствует
отображение одного множества на другое, существенно
отличное от первого. Например, логическая функция,
заданная табл. 1.2, однородна, а логическая функция,
заданная табл. 1.3, неоднородна.
Как уже было отмечено, для всякой логической
функции множество, из которого она принимает значе-
§ 1.2]
ОСНОВНЫЕ ПОНЯТИЯ
17
ния, конечно, но вмес\е с тем любая однородная логи-
логическая функция представляет собой отображение неко-
некоторого множества самого на себя. Поэтому множество,
соответствующее однородной логической функции, обя-
обязательно конечно. Логическая переменная, относящаяся
к такому множеству, может быть двух-, трех- и вообще
т-значной.
а2
а2
а1
Таблица 1.2
«3
аз
«4
Ч
ai
а2
Р.
Таблица 1.3
аз
р.
Я4
Рэ
Каждое значение аргумента неоднородной логиче-
логической функции обычно называют предметом, а саму
функцию в этом случае принято называть предикатом.
Если множество значений аргумента неоднородной ло-
логической функции (множество предметов) может быть
и бесконечным, то сами неоднородные логические функ-
функции — предикаты, могут быть лишь двух-, трех- и вооб-
вообще m-значны, где m обязательно конечно.
/Подобно тому как в области вещественной перемен-
переменной строятся вещественные функции п вещественных
аргументов, в области логической переменной также
могут быть построены логические функции не только
одной, но и п переменных.
Функции нескольких независимых переменных мы
также будем делить на два класса. К одному из них
будем относить те функции, в которых любая из не-
независимых переменных и сама функция являются логи-
логическими переменными, принимающими значения из од-
одного и того же множества. Такие функции будем также
называть однородными. В связи с тем, что при построе-
построении математического аппарата однородных логичес-
логических функций рассматривалось множество с элемента-
элементами «истинное высказывание» и «ложное высказывание»,
весь этот аппарат обычно называют исчислением вы-
высказываний. Ко второму классу будем относить все
2 М.. А. Айзерман, Л. А. Гусев и др.
18
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
[ГЛ. I
те логические функции нескольких переменных, кото-
которые не вошли в первый класс/ и будем называть их
неоднородными.
Логические переменные, входящие в состав неодно-
неоднородных функций нескольких переменных так же, как и
в случае функций одной независимой переменной, назы-
называют предметами; сами функции в этом случае назы-
называют предикатами.
В зависимости от числа независимых переменных в
неоднородной логической функции различают одно-
одноместные, двуместные и вообще п-местные предикаты.
Иногда одноместные предикаты называют свойствами,
а многоместные — отношениями.
Для того чтобы проиллюстрировать введенные здесь
понятия и терминологию, рассмотрим несколько при-
примеров.
Пусть речь идет о событии, состоящем в том, что я
встретил знакомого мужчину. Это событие может на-
наступить или не «аступить в зависимости от того, на-
наступят или нет образующие это сложное событие про-
простые события: один из встречных оказался моим зна-
знакомым и этот же встречный был мужчина. Здесь мы
имеем дело с однородной логической функцией двух
независимых переменных;
она однородна, потому что и
независимые переменные и
сама функция являются со-
событиями, то есть логически-
логическими переменными, принимаю-
принимающими значения из одного и
того же' двухэлементного
множества с элементами
«событие наступило» и «со-
«событие не наступило». Обо-
Обозначая одну независимую
переменную (событие — встреча со знакомым) через х\,
вторую (событие — встреча с мужчиной) через Х2 и
функцию (событие—встреча со знакомым мужчиной)
через у, получаем возможность представить рассматри-
рассматриваемую функцию в виде таблицы (см. табл. 1.4). При-
Примененные при заполнении таблицы знаки 0 и 1 являются
Таблица 1.4
0
1
0
0
0
1
0
1
§ 1.2] ОСНОВНЫЕ ПОНЯТИЯ 19
символами, соответст&ующими элементам «событие не
наступило» и «событие наступило».
В рассмотренном примере с клавиатурой рояля ло-
логическая функция была неоднородной. Там мы имели
дело с семизначным одноместным предикатом, предмет-
предметная переменная которого (номер клавиши) принимала
значения из пятидесятиэлементного множества.
Оценка истинности высказывания, определяемого
алгебраическим выражением
Xi+x2> 10,
справедливым при некоторых численных значениях Х\ и
х2 и ложным при некоторых других значениях Х\ и х2,
приводит к примеру двуместного двузначного предиката;
здесь две независимые переменные, и они принимают
значения из множества вещественных чисел, которое
имеет мощность континуума.
Как известно, день недели может быть установлен,
если известны число, месяц и год. Соответствующие
этой задаче правила определяют неоднородную логи-
логическую функцию — трехместный семизначный предикат;
предметные переменные здесь принимают значения из
трех множеств: одно из них имеет 31 элемент, другое—12
и третье — счетное множество элементов.
Единого математического аппарата, пригодного для
применения ко всем разновидностям логических функ-
функций, в настоящее время не существует. Наибольшего
совершенства сейчас достиг аппарат, относящийся к
двузначным логическим функциям. Этот раздел мате-
математической логики (двузначная логика) является, с од-
одной стороны, основой, на которую опирается все по-
построение математической логики; с другой же стороны,
именно аппарат этого раздела имеет в настоящее время
наибольшее прикладное значение. Аппарат же много-
многозначной логики еще нельзя считать достаточно сфор-
сформировавшимся. В связТ* с отмеченными обстоятель-
обстоятельствами мы не будем касаться больше многозначной
логики. Основные положения двузначной логики, вклю-
включающей исчисления двузначных высказываний и преди-
предикатов, излагаются в следующих параграфах.
2*
20
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
[ГЛ. Г
§ 1.3. Исчисление высказываний
а) Общие сведения о задании
логических функций
В этом параграфе мы будем рассматривать однород-
однородные двузначные логические функции
у = у(хи -х2, ..., хп),
т. е. такие, у которых все независимые переменные
х\, х2, ..., хп и сама функция у являются логическими
переменными, принимающими значения из одного и
того же двухэлементного множества М. Обозначим два .
элемента этого множества символами 0 и 1, которые и
будут составлять алфавит любой логической перемен-
переменной, входящей в рассматриваемые логические функции.
Построим таблицу (табл. 1.5), содержащую 2П столб-
столбцов и п строк; каждой строке приведем в соответствие
одну из п независимых переменных, а столбцы прону-
пронумеруем цифрами 0, 1, 2, ..., 2П — 1.
Таблица 1.5
г = 2" столбцов
\ k
х \
Х\
х2
хп
0
0
0
0
0
1
1
0
0
0
2
0
1
0
0
3
1
1
0
0
4
0
0
1
0
5
1
0
1
0
6
0
1
1
0
7
1
1
1
0
...
...
...
...
2« —2
0
1
1
1
2я—1
1
1
1
1
Заполним каждый столбец таблицы последователь-
последовательностью символов 0 и 1 так, чтобы эта последователь-
§ 1.3] ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ 21
ность, если ее читать Снизу вверх, образовала двоич-
двоичную запись числа, равного номеру столбца. При прак-
практическом заполнении такой таблицы это удобно делать
следующим образом: в первую строку (соответствую-
(соответствующую Xi) слева направо вписываются пары @1), во
вторую — четверки (ООП), в третью — восьмерки
@0001111) и т. д.
Каждый столбец построенной таким образом таб-
таблицы определяет одну из возможных комбинаций зна-
значений п независимых переменных. Поэтому можно го-
говорить, что ему соответствует одна точка /г-мерлого
двоичного (построенного на двухэлементном множег
стве М) логического пространства. Вся таблица (сово-
(совокупность всех 2™ столбцов) содержит исчерпывающее
описание всего л-мерного двоичного логического про-
пространства, состоящего из г = 2™ точек; номер столб-
столбца k может быть принят за символ точки этого про-
пространства.
Для более наглядного представления я-мерного
двоичного логического пространства удобно рассматри-
рассматривать символы 0 и 1 как вещественные числа. Тогда,
Рис. 1.2.
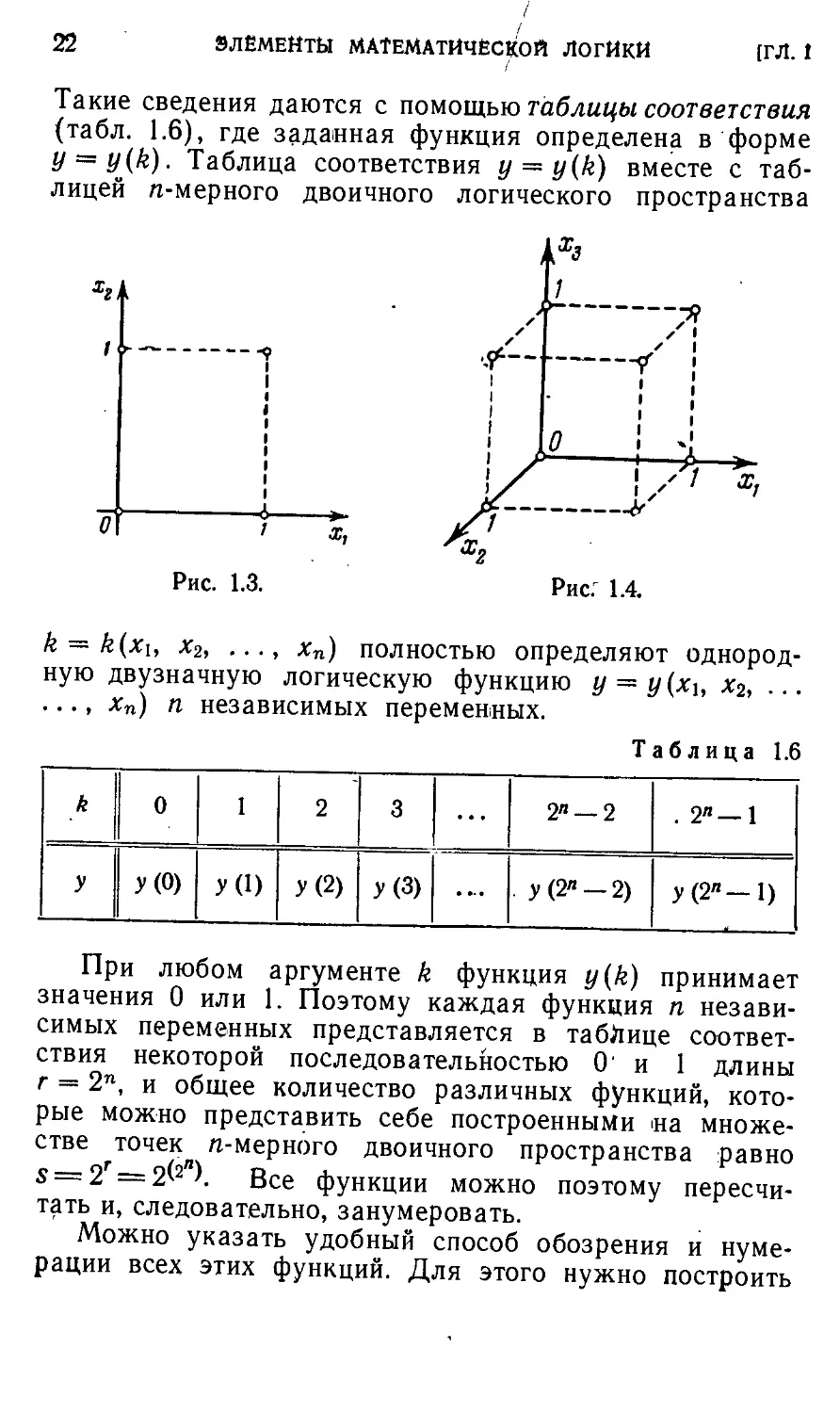
например, одномерному случаю соответствует геометри-
геометрический образ, состоящий из двух точек числовой оси
(рис. 1.2). Двумерному случаю будут соответствовать
четыре вершины единичного квадрата (рис. 1.3), трех-
трехмерному случаю — вершины единичного куба (рис. 1.4),
и вообще при таком рассмотрении я-мереое двоичное
логическое пространство представляет собой множе1
ство всех вершин я-мерного единичного куба.
Задать какую-нибудь конкретную двузначную одно-
однородную логическую функцию у = у.(хи х2, ..., хп) п
независимых переменных означает получить указание
о том, какое из двух вбзможных значений @ или 1)
принимает логическая переменная у в той или иной
точке k двоичного п мерного логического пространства
(или на той или иной вершине я-мерного куба).
22
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
[ГЛ. 1
Такие сведения даются с помощью таблицы соответствия
(табл. 1.6), где заданная функция определена в форме
У —У (к)- Таблица соответствия y — y{k) вместе с таб-
таблицей я-мерного двоичного логического пространства
-9
I
Рис. 1.3.
Рис: 1.4.
k = k(x\, х2, ..., хп) полностью определяют однород-
однородную двузначную логическую функцию у = у{х\, х2, ...
..., Хп) п независимых переменных.
Таблица 1.6
k
У
0
УФ)
1
Уп)
2
УB)
3
З-(З)
...
....
2я —2
. уB«-2)
. 2я— 1
3-B"-1)
При любом аргументе k функция y(k) принимает
значения 0 или 1. Поэтому каждая функция п незави-
независимых переменных представляется в таблице соответ-
соответствия некоторой последовательностью 0' и 1 длины
г = 2™, и общее количество различных функций, кото-
которые можно представить себе построенными «а множе-
множестве точек л-мерного двоичного пространства равно
s = 2r = 2B"). Все функции можно поэтому пересчи-
пересчитать и, следовательно, занумеровать.
Можно указать удобный способ обозрения и нуме-
нумерации всех этих функций. Для этого нужно построить
§ 1.3]
ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИИ
23
таблицу (табл. 1.7), объединяющую все возможные
таблицы соответствия и содержащую г = 2" столбцов и
s = 2Г строк.
Таблица 1.7
Уо
У\
Уг
Уг
У$-\
0
0
1
0
1
1
1
0
0
1
1
1
2
0
0
0
0
1
3
0
0
0
0
1
...
...
...
...
г — \
0
0
0
0
1
Эту таблицу удобно заполнять следующим образом: в
первый столбец вписываются пары @1), во второй —
четверки (ООП), в третий — восьмерки @0001111) и так
далее*). При этом распределение нулей и единиц в каж-
каждой строке, если ее читать справа налево, будет пред-
представлять собой двоичную запись номера функции, соот-
соответствующей этой строке. Таблицу такого типа будем
называть общей таблицей соответствия.
Наряду с изложенным табличным методом для за-
задания однородных двузначных логических функций
существует и широко применяется аналитический ап-
аппарат. Построение такого аппарата основывается на
возможности применения-в области однородных функ-
функций операции «функция от функции». В самом деле,
*) Отличие от табл I 5 состоит в том, что указанное запол-
заполнение ведется по столбцам, а не по строкам.
24
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
[ГЛ. I
ведь и сама однородная функция, и ее аргумент при-
принимают значения из одного и того же множества. Зна-
Значит, логическая переменная, выступающая в одной за-
зависимости в роли функции, в другой зависимости мо-
может быть аргументом. За счет применения операции
«функция от функции» оказывается возможным лю-
любую однородную двузначную логическую функцию вы-
выразить через некоторые элементарные функции, для
обозначения которых применяется специальная симво-
символика. Введение в употребление таких функций и связан-
связанной с «ими символики естественно влечет за собой по-
появление специфических правил — своеобразной алгебры.
б) Функции одной и двух переменных
Рассмотрение этого круга вопросов начнем с ана-
анализа простейшего случая, когда функция имеет лишь
одну независимую переменную (п = 1). Для этого слу-
случая общая таблица соответствия, совмещенная с табли-
таблицей одномерного двоичного логического пространства,
имеет вид табл. 1.8.
Таблица 1.8
к
X
З-о
3-1
3-2
З-з
0
0
0
1
0
1
1
1
0
6
1
1
Обозначение
3-0=0
У\=х
уг = х
3-3 = 1
Здесь число точек логического пространства г = 2" =
21 = 2, число различных функций, s = 2Г = 22 = 4.
§ 1.3] ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ 25
Эти четыре функции у0, у\, у2 и у3 вместе с приме-
применяемыми для них обозначениями приведены в табл. 1,8.
Других функций одного аргумента не существует.
Особенности функций у0, у\, Уг и у% состоят в сле-
следующем. Функции у0 и уз не изменяют своих значений
при изменении значений аргумента. Эти функции нал
зывают функциями-константами. Для них мы будем
применять обозначения у0 = О, у3 = 1-
Функция уг всегда имеет то же значение, что и ар-
аргумент х; для нее имеем очевидную запись у2 = х.
Функция у\ принимает значение 1, когда х = 0, и
значение 0, когда х = 1. Эту функцию называют отри-
отрицанием. Для нее применяется специальное обозначе-
яие у\ = х, которое читается «не х». Заметим, что две
из рассмотренных четырех функций всегда можно за-
записать, применяя операцию «функция от функции» и
символическую запись двух других функций. Действи-
Действительно,
Таким образом, для задания в аналитической форме
любой однородной двузначной функции одного аргу-
аргумента, достаточно применять специальную символиче-
символическую запись для двух функций: у = О и у = х.
Для случая двух независимых переменных х\ и
х2 (п = 2) общая таблица соответствия представлена
табл. 1.9.
Здесь число точек логического пространства г =
= 2П = 22 = 4, а число различных функций s = 2Г = 24 =
= 16. В этой же таблице в правом крайнем столбце
приведены применяемые способы записи функций.
Заметим, что из 16 различных функций двух неза-
независимых переменных шесть встречались среди функций
одной независимой переменной. К ним относятся две
функции-константы (у0 = 0 и ущ = 1), две функции по-
повторения (j/ю = Х\ и J/i2 = х2) и две функции отрица-
отрицания (у3 = х2 и у5 = Х\).
Из остающихся десяти функций две {уц и у и) не
являются самостоятельными, так как они отличаются
26
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ [ГЛ. I
Таблица 1.9
k
х,
х2
З-о
У\
Уч
Уг
3-4
Уь
3-е
Уч
У»
Ув
3-ю
3-и
3-12
Ун
3-й
.Vip
0
0
0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
1
1
0
0
0
1
1
0
0
1
1 .
0
0
1
1
0
0
1
1
2
0
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
3
1
1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
Обозначения
Уо = О
>*, = .*, | х2
3-2 = X, +- Х2
3-3=^2
3-4 = х2 *- х,
3-5 = *i
уь = х{ V х2
3-7 = Xi/X2
уь = х, & хг
3-9 = X, ~ Х2
3-ю = *i
3-и= х2->хх
3-12 = Х2
3-13 = х,-> х2
Уи = ххЧх2
3-15=1
§ 1.3] ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИИ 27
от соответствующих им функций у2 и г/13 лишь поряд-
порядком расположения аргументов. Для оставшихся теперь
восьми оригинальных функций двух независимых пе-
переменных применяют специальные обозначения. Осо-
Особенности этих функций состоят в следующем.
Функция ум = Х\ V *2 принимает значение 0 тогда
и только тогда, когда оба аргумента имеют значение 0.
Называют эту функцию дизъюнкцией и читают «*i
или х2».
Функцию yi3 = *i->*2 называют импликацией, она
принимает значение 0 тогда и только тогда, когда пер-
первый аргумент (*i) имеет значение 1, а второй (х2) —
значение 0; при ее чтении применяют выражение «если
хи то х2» или же «из Х\ следует х2».
Функцию у9 = Х\ ~ х2 называют эквиваленцией или
равнозначностью; она принимает значение 1 в тех слу-
случаях, когда оба аргумента имеют одинаковое значе-
значение, и значение 0, когда аргументы имеют разные зна-
значения; ее читают «*i эквивалентно (равнозначно) х2»
или «*ь если и только если х2».
Функция у8 = *1&*2 принимает значение 1 тогда и
только тогда, когда оба аргумента имеют значение 1.
Ее называют конъюнкцией и читают «*i и х2».
Функция у7 = х\\х2 носит название функции Шеф-
фера (или штриха Шеффера); она обращается в 0тогда
и только тогда, когда оба аргумента имеют значение 1.
Функцию у6 — *\ V*2 называют исключенным ИЛИ;
она обращается в 1, когда либо первый, либо второй
аргумент равен 1 (но не оба вместе).
Функцию у2 = Х\ •*- х2 в технических приложениях
называют запретом; ее значения совпадают со значе-
значениями первого аргумента (*i), когда второй аргумент
(х2) равен нулю; если же второй аргумент равен еди-
единице, то функция будет иметь значение 0, каким бы при
этом ни был первый аргумент.
Функция у\ = Х\ ], х2 называется функцией Даггера
(или стрелкой Пирса); ее особенность состоит в том,
что она обращается в 1 тогда и только тогда, когда оба
аргумента равны 0.
Отметим, что любая функция, взятая из верхней по-
половины таблицы (т. е. функций уо, у и ..., у7), является
28 ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ [ГЛ. 1
отрицанием какой-нибудь функции, принадлежащей
нижней половине таблицы (функций ys, */э, .¦ ¦ ¦, У\ъ)-
Рассмотрим, например, функции у6 и уд. Из табли-
таблицы видно, что у в = 0 тогда и только тогда, когда уд = 1,
и наоборот, J/6 = 1 для всех тех случаев, когда уд = 1.
Значит, переменная ув сама может рассматриваться как
аргумент, значения которого однозначно определяют
значения переменной у9. В соответствии с введенным
определением операции отрицания имеем: ув = Уд- Но
уь = Xi V х2, а у9 = *i ~ *2 и, следовательно, *4 V *2 =
= Xi ~ *2- Из таблицы видно также, что отмеченная за-
зависимость имеет место для всех пар функций, располо-
расположенных симметрично относительно линии, разделяющей
седьмую и восьмую строки. Это можно записать сле-
следующим образом: У1ь-г = Уй где i = 0, 1, 2, .. ., 15.
Отмеченная особенность приводит к тому, что из
восьми введенных в рассмотрение функций двух аргу-
аргументов ровно половина, т. е. еще четыре функции, не
являются самостоятельными. В самом деле,
т.
т.
т.
е.
е.
е.
xjx2 ¦¦
г V г
1 2
Хх«-Х2
= X,
= х
= х
&х2.
i — -«а
Уб=Уэ.
= у14, т.е. Xj I x2 = jfj V
A.2)
Исключив из рассмотрения операции /, v> •*- и J,,
мы придем к следующему перечню логических функций,
применение которых позволяет записать в аналитиче-
аналитической форме любую функцию одного и двух аргументов;
константа у = 0,
отрицание у = х,
КОНЪЮНКЦИЯ . угзЛ^&Х;, |
ДИЗЪЮНКЦИЯ у гз= X, V Х2, '
импликация ysf.-vr ! Ч^
эквиваленция у
§ 1.3]
ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИИ
29
Таблица 1.10
Приведенный перечень, состоящий из шести элемен-
элементарных логических функций, является достаточным, но
вовсе не необходимым для записи любой функции од-
одного и двух независимых переменных.
Для того чтобы убедиться в этом, рассмотрим функ-
функцию двух независимых переменных у = xi \/х2, полу-
полученную за счет применения функций отрицания дизъ-
дизъюнкции и операции «функция от функции». Будучи
функцией двух независимых переменных, эта функция
обязательно является одной
из шестнадцати функций,
приведенных в таблице. Для
того чтобы установить, ка-
какой именно функцией она
является, найдем ее значе-
значения во всех четырех точках
соответствующего двумер-
двумерного двоичного логического
пространства, т. е. для всех
возможных значений аргу-
аргументов Xi и x^. Процесс
отыскания этих значений от-
отражен в табл._1.10, где обо-
обозначено yi = xi и, следова-
следовательно, у — у\ V х2. Найден-
Найденные значения функции у показывают, что у = Х\ ¦
значит, имеет место тождество
k
х2
У\
У
0
0
0
1
1
1
1
0
0
0
2
0
1
1
1
3
1
1
0
1
Хх —V Х% — Хх V Х^,
Подобным же образом можно показать, что
— Хх tx Л?2,
= (хх V х2) & (хх V
¦х2 и,
A.4)
A.5)
A.6)
Приведенные тождества A.5), A.6) показывают, что
при описании функций одного и двух независимых пе-
переменных можно обойтись без применения импликации
и эквиваленции. Таким образом, комплект элементарных
30 ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ [ГЛ. I
функций может быть сокращен до следующих че-
четырех:
константа у = 0,
отрицание у=х
конъюнкция у —
ДИЗЪЮНКЦИЯ у =
A-7)
Этот комплект элементарных функций, как это бу-
будет видно из дальнейшего, наиболее удобен и чаще
всего применяется. Однако принципиально и он может
быть еще сокращен.
В самом деле, помимо установленных тождеств A.4),
A.5), A.6), освобождающих от необходимости приме-
применять импликацию и эквиваленцию, тем же приемом
можно убедиться в справедливости тождеств
Х\ V х2 =
x1&x2 = x1V х2, \ 0 -8)
0 = х&х. J
Это значит, что одна из двух последних функций ком-
комплекта A.7) и первая-функция этого комплекта также
могут быть исключены. Таким образом, мы .приходим
к системе, состоящей всего лишь из двух функций:
отрицание у = х, \
конъюнкция y = Xi&x2 (или дизъюнкция у = XiVх2), J
A.9)
применение которых позволяет записать любую функ-
функцию одного и двух аргументов.
Анализ того, сколькими элементарными функциями
можно обходиться для записи в аналитической форме
любых функций одного и двух аргументов, завершим
указанием на две особые в этом смысле функции:
«штрих Шеффера» у = xrfxz и «стрелка Пирса» у =
= Xi I x% Их особенность состоит в том, что каждая из
них в отдельности достаточна для записи любой функ-
функции одного и двух независимых переменных. Это под-
§ 1-3]
ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ
31
тверждается тем, что обе функции достаточного (в рас-
рассматриваемом смысле) комплекта A.9) могут быть вы-
выражены через какую-нибудь одну из указанных осо-
особых функций. Действительно,
х = х/х = х j. х,
V х2 = (ж, | х2) | (х, | х2).
A.10)
в) Функции п переменных.
Конъюнктивные и дизъюнктивные
нормальные формы
Символику, введенную для обозначения функций
одной и двух независимых переменных, можно приме-
применять для построения функций трех, четырех и вообще п
независимых перемен-
переменных. Так,
функция
например,
Таблица 1.11
'II
X)
х3
х»
У
0
0
0
0
1
1
0
0
0
2
0
1
0
0
3
1
1
0
1
4
0
0
1
1
5
1
0
1
0
6
0
1
1
1
7
1
1
1
1
A-11)
определяется значени-
значениями трех независимых
переменных.
Для функции п не-
независимых переменных
может быть составлена
характеризующая ее
таблица. Для заполне-
заполнения ее поочередно рас-
рассматриваются все воз-
возможные сочетания значений хи х2, ..., х„ (т. е. все точки
n-мерного логического двоичного пространства с соответ-
соответствующими номерами k) и определяются значения у
в этих точках. Так, например, в случае функции A.11)
в точке k = 2, т. е. при xi = 0, х2 = 1, х3 = 0, имеем
у@, 1, 0) = 0. Подсчитывая так же у для всех значе-
значений k (& = 0, 1, ..., 7) заполняем таблицу функции
A.11) (см. табл. 1.11).
32 ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ [ГЛ. I
Теперь покажем, что символика, введенная для
обозначения любых функций одной и двух независи-
независимых переменных, дает возможность записывать в ана-
аналитической форме также и любые функции любого ко-
количества независимых переменных.
В качестве примера обратимся снова к табл. 1.11,
построенной для функции A.11). Предполагая, что нам
задана табл. 1.11, но неизвестно ее аналитическое вы-
выражение A.11), и считая эту таблицу исходной, соста-
составим аналитическое выражение соответствующей ей
функции. При этом мы воспользуемся методикой, при-
пригодной и для любой таблицы.
Рассмотрим сначала какой-нибудь из столбцов
табл. 1.11, где у = 1; например столбец k = 3. В этом
столбце #i=l, х2 = 1, #з = 0. Построим функцию
yi = Xi&xz&x3. Эта функция, как нетрудно видеть,
принимает значение 1 тогда и только тогда, когда Х\ =
= 1, #2 = 1 и #3 = 0, то есть как раз в точке k = 3. По-
Подобным же образом построим функции
A.12)
принимающие значения 1 только в точках с номерами
k = 4, k = 6 и k = 7, т. е. во всех тех точках, где в
табл. 1.11 у = 1.
Функция у = yi V Уч V У% V Уь. принимает значение 0
тогда и только тогда, когда у\ = 0, г/2 = 0, у% = 0 и
г/4 = 0; в остальных же случаях у = 1. Так как «осталь-
«остальными случаями» являются точки k = 3, k = 4, k = 6,
k = 7, то это значит, что функция
у = (.*! & х2 & л,) V(^i & х2 & х3) V(Jci & х2 & л;3) V
\/(Х1&х2&х3) A.13)
в точности соответствует исходной табл. 1.11. Аналити-
Аналитическое выражение для функции, заданной табл. 1.11,
мы получили не в форме выражения A.11), а в неко-
§ 1.3]
исчисление высказываний
33
торой иной «стандартной» форме. Несмотря на замет-
заметное внешнее различие между A.11) и A:13), оба эти
выражения соответствуют одной и той же функции, оп-
определенной таблицей 1.11, то есть имеет место тожде-
тождество
(хг -> х2) ~ (.*! & л,) = (.*! & х2 & х3) V
. A.14)
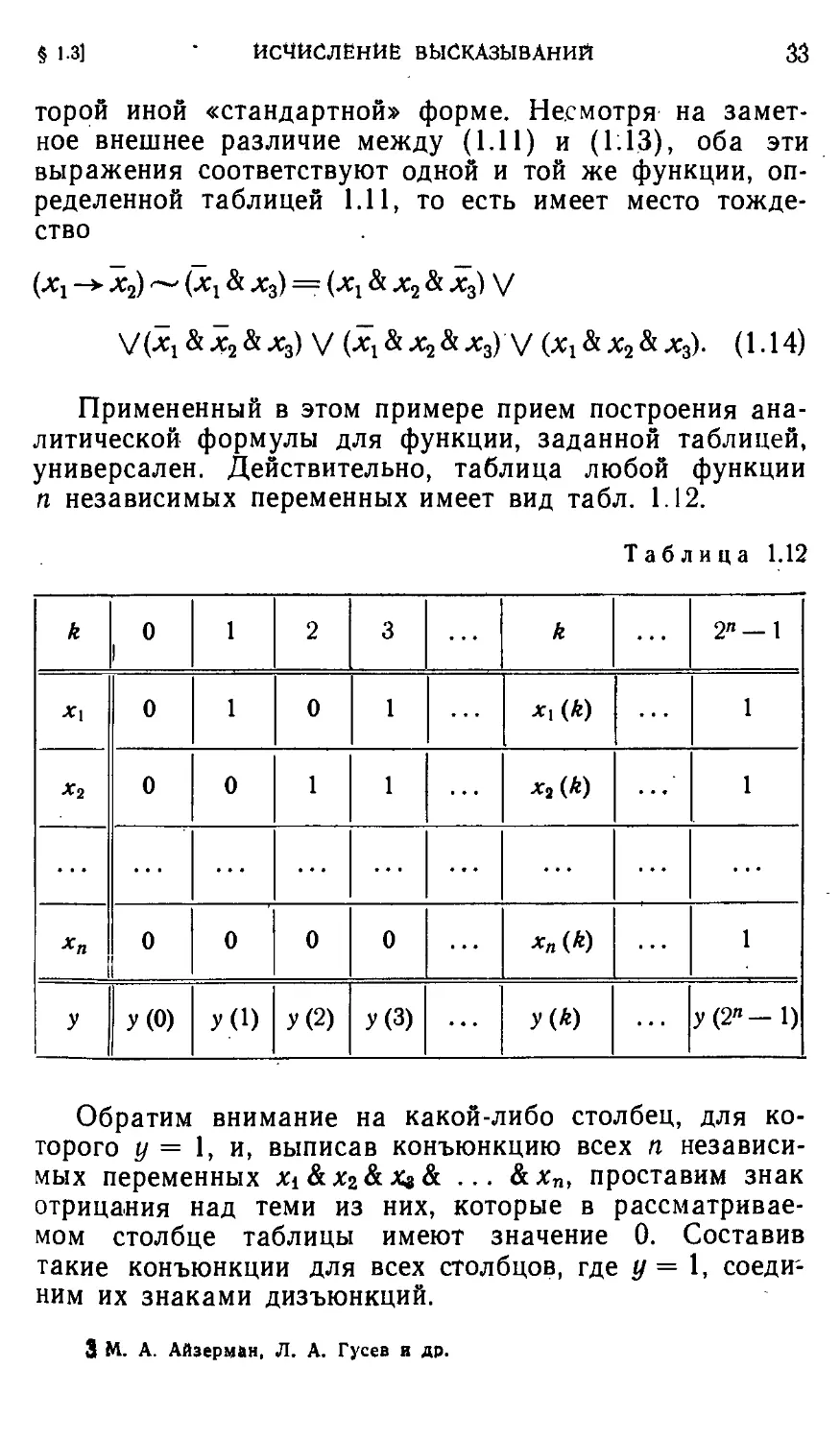
Примененный в этом примере прием построения ана-
аналитической формулы для функции, заданной таблицей,
универсален. Действительно, таблица любой функции
п независимых переменных имеет вид табл. 1.12.
Таблица 1.12
k
Х\
*2
Хп
У
0
0
0
0
У@)
1
1
0
0
УA)
2
0
1
0
У B)
3
1
1
0
УC)
...
...
...
k
xt(k)
xn(k)
У(к)
...
...
..."
...
...
...
2n—1
1
1
...
1
УB»-1)
Обратим внимание на какой-либо столбец, для ко-
которого у = 1, и, выписав конъюнкцию всех п независи-
независимых переменных *1&л:2&Ха& ••• &хп, проставим знак
отрицания над теми из них, которые в рассматривае-
рассматриваемом столбце таблицы имеют значение 0. Составив
такие конъюнкции для всех столбцов, где у=\, соеди-
соединим их знаками дизъюнкций.
3 М. А. Айзерман, Л. А. Гусев и др.
34 ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ [ГЛ. I
В результате будет получено выражение, содержа-
содержащее несколько конъюнктивных членов, соединенных зна-
знаками дизъюнкции. Каждый член имеет вид конъюнкции
всех переменных Xi, х2, ..., хп, над некоторыми из ко-
которых поставлены знаки отрицания (в частности, в вы-
выражении может присутствовать как член xt & х2 & ... & хп,
не содержащий отрицаемых переменных, так и член
Xi & х% & ... & хп, в котором все переменные отрицаются).
Различные функции, представленные в этой форме, мо-
могут отличаться друг от друга лишь числом дизъюнктив-
дизъюнктивных членов и тем, как распределены знаки отрицания
над переменными хг в конъюнкциях, образующих дизъ-
дизъюнктивные члены.
Выражения такого рода играют особо важную роль
в исчислении высказываний. Им присвоены специаль-
специальные наименования. Дизъюнкция, членами которой яв
ляются различные конъюнкции из всех независимых
переменных или их отрицаний, называется совершенной
нормальной дизъюнктивной формой.
Выше было показано, каким образом любая функ-
функция п переменных, заданная таблицей, может быть
представлена в совершенной нормальной дизъюнктив-
дизъюнктивной форме.
Совершенная нормальная конъюнктивная форма
представляет собой конъюнкцию, членами которой яв-
являются различные дизъюнкции из всех независимых
переменных или их отрицаний.
Термин «совершенная» опускают, т. е. говорят про-
просто о нормальной дизъюнктивной или конъюнктив-
конъюнктивной форме в тех случаях, когда не требуется, чтобы
каждый член этой формы обязательно содержал
конъюнкцию или соответственно дизъюнкцию всех
переменных.
Обратим внимание на следующее свойство всякой
нормальной формы записи некоторой функции. Если
какая-нибудь функция у записана в нормальной (про-
(простой или совершенной) дизъюнктивной (конъюнктив-
(конъюнктивной) форме, то замена в этой записи всех значков V
на & и значков & «а V с одновременной простановкой
над каждой независимой переменной знака отрицания
(если этот знак уже стоял над переменной, то ставится
§ 1.3] ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ 35
второй такой же знак, что равносильно снятию знака
отрицания) приводит к записи функции у в нормальной
(соответственно простой или совершенной) конъюнктив-
конъюнктивной (дизъюнктивной) форме. Это свойство является
непосредственным следствием тождеств A.8).
В отличие от просто нормальных форм совершенные
нормальные формы обладают свойством однозначности
в том смысле, что каждая функция может быть лишь
единственным образом представлена в совершенной
нормальной дизъюнктивной или конъюнктивной форме
(если при этом не обращать внимания на порядок рас-
расположения дизъюнктивных или конъюнктивных членов
и независимых переменных).
Продемонстрируем важное значение введенных по-
понятий на примерах решения двух задач.
Первая задача. Пусть требуется установить, не
является ли некоторая заданная в аналитической
форме логическая функция п независимых пере-
переменных у = y(xi, х2, . . ., хп) функцией-константой вида
у = о.
Такая задача решается приведением заданной функ-
функции к нормальной дизъюнктивной форме. Действитель-
Действительно, если после приведения функции к нормальной дизъ-
дизъюнктивной форме окажется, что в каждом дизъюнктив-
дизъюнктивном члене имеется хотя бы по одной такой переменной,
которая в этом члене встречается вместе со своим от-
отрицанием (т. е. в виде хг&х{), то это значит, что функ-
функция имеет вид у = 0. Наоборот, в противном случае
всегда можно указать значения переменных, при ко-
которых у = 1, т. е. функция не является константой
вида у = 0.
Двойственной по отношению к поставленной яв-
является задача об определении того, не сводится ли
заданная функция к виду у = 0=1. Решение можно
получить приведением заданной функции к нормальной
конъюнктивной форме. Если после приведения оказы-
оказывается, что в каждом конъюнктивном члене встречается
выражение вида х, V х{, то это значит, что в этом
(и только в этом) случае заданная функция сводится
к виду у = I.
36 ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ [ГЛ. I
Определение того, не приводится ли некоторая слож-
сложная функция у = у(хи х2; ..., хп) к виду у= 1 или
Ш = 0, называется проблемой разрешимости. В рамках
*этой проблемы функции, которые сводятся к виду
у = 1 (у = 0), называют тождественно истинными (лож-
(ложными), а функции, которые не сводятся ни к у = 1,
ни к у = 0, называют выполнимыми.
Вторая.задач а. Пусть задана в аналитической
Лорме некоторая логическая функция п независимых
переменных у = у(хи х2, .... хп). Для этой функции
гребуется найти все те наборы значений аргументов, при
которых она принимает значение 1.
Эту задачу можно было бы считать решенной, если
бы удалось заданную функцию привести к совершеиной
нормальной дизъюнктивной форме.
Наборов значений аргументов, при которых у *= 1,
ровно столько, сколько дизъюнктивных членов в совер-
совершенной нормальной дизъюнктивной форме. А конкрет-
конкретное значение всех независимых переменных в каждом
наборе определяется следующим образом. Каждой на-
набор значений Xi (t: = 1,2,..., п), обращающих функцию
в 1 и определенных по /-й скобке, имеет вид
где Xij равно 0 или 1 в зависимости or того, входит ли
соответствующая (г-я) независимая переменная в рас-
рассматриваемую (/-ю) конъюнктивную скобку со знаком
отрицания или без него.
г) Функции п переменных. Алгебра
исчисления высказываний
Подобно тому как в рассмотренном примере совер-
совершенная нормальная дизъюнктивная форма A.13) опре-
определяла функцию, для которой была возможна и более
короткая запись A.11), и в иных случаях также воз-
возможны более короткие и удобные записи функций, чем
с помощью совершенной дизъюнктивной нормальной
формы. Иначе говоря, не только в рассмотренном при-
примере, но и в иных случаях могут быть установлены тож-
тождества, подобные тождеству A.14).
§ 1.3] ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ 37
До сих пор для доказательства того или иного тож-
тождества, устанавливаемого в области функций одного,
двух или более независимых переменных, мы прове-
проверяли предполагаемое тождество подстановкой всех воз-
возможных значений независимых переменных. Этот спо-
способ имеет два существенных недостатка. Во-первых, он
не дает возможности получать новые тождества и в
этом смысле является пассивным и, во-вторых, его тру-
трудоемкость резко возрастает с ростом количества неза-
независимых переменных.
Наряду с этим существует и другая возможность,
основанная на применении некоторой системы правил
тождественных преобразований. При оперировании с
комплектом элементарных функций
— \j) у — Л| у — ^^ ' У — 1 V *
такую систему правил, обычно называемую алгеброй
логики или алгеброй Буля, образуют следующие тож-
тождества: _
х = х, A.16)
Х\ ^* Х(? — Х-у v Х<^у . ^ 1 • I / )
xl~x2 = (xl-+x2)&(x2-+x1), A.18*
(a) jc&jc =jc, (б) хух =х, A.19)
(а) х&х =0, (б) х\/х =1, A.20)
(a) jc&1 =х, (б) х\/i =\, A.21)
(a) jt&O =0, (б) jcVO =x, A.22)
(а) хх&х2 = хх V х2, (б) xlVx2 = xl&x2, A.23)
(a) xl&x2 = x2&xv (б) xxVx2 = x2Vxx, A.24)
(я\ *- & (у & г \ — (t)\ х \/(х \/ хЛ —
= (хх & х2) & хг, —{xxVx2)Vxz, A.25)
(a) xxk(x2Vx3)= " (б) хх\'(х2&хг) =
\ /v\/^-^Л/v\/v^ /1 ОА\
о ij \ V "Ч) ^^ \ 1 v *^3/' \ • ?^J}
Справедливость каждого из этих тождеств может быть
проверена прямой подстановкой всех возможны*-
38 ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ [ГЛ. I
значений переменных, входящих в левую и правую
части тождества.
Участвующие в этой алгебре операции' ИЛИ и И
имеют много общего с операциями сложения и умноже-
умножения обычной алгебры. Относительно этих операций
имеют силу первый и второй переместительные законы
(тождества A.24)), первый и второй сочетательные за-
законы (тождества A.25)). Но в отличие от обычной ал-
алгебры здесь действует не один, а два распределитель-
распределительных закона (тождества A.26)). По сравнению с обыч-
обычной алгеброй «приведение подобных членов» или «ум-
«умножение переменной самой на себя» осуществляется
здесь согласно тождествам A.19), без появления каких
бы то ни было коэффициентов или показателей степени.
Применяя приведенную систему тождеств, мы по-
получаем возможность чисто аналитическим путем решать
разнообразные задачи, причем для некоторых из них
могут быть указаны регулярные методы. Так, например,
функцию, заданную любым аналитическим выражением,
можно непосредственно преобразовать к нормальной
дизъюнктивной форме. Методику такого приведения рас-
рассмотрим на примере.
Пример. Пусть исследуемая функция задана в
форме
у = |*! -> Гх, ~ х3) & (х2 -> х3)\ V(x^x~3)- A.27)
Прежде всего необходимо исключить символы -*¦ и ~.
Применяя тождества A.17) и A.18), получаем
У = [*, V |(*i V*3) & 0*3 V*i)] & (х2 Vx3)] V(*i V-Xj,). A-28)
Далее нужно избавиться от тех знаков отрицания, ко-
которые относятся не к одной какой-нибудь независимой
переменной, а к целому комплексу. Для этого приме-
применяются тождества A.23). В нашем случае, применяя
попутно также и тождество A.16), имеем
= \x1&(x1Vx3)V(x3Vxl)&(x2\/x3)]V(xl&x3) =
{l^&xi). A.29)
§ 1.3) ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ 39
Теперь для получения нормальной дизъюнктивной
формы достаточно выражение в фигурных скобках раз-
развернуть в соответствии с тождеством A.26, а). При
этом, применяя попутно A.16) и A.19, а), получим
у = {\{хх & *! & х3)\/ (хх &х3& Xl)]& (х2 V^,)]_V(*i & Xj) =
— (хх &хх &х3&х2)\/(хх &х3&х2) V (хх &хх &х3&Хз)V
V(xl&x3&x3)V(x1&x3). A.30)
В полученной нормальной дизъюнктивной форме пер-
первый, третий и четвертый дизъюнктивные члены имеют
значение 0, так как они содержат выражения вида
х & х. Второй и последний члены такого выражения не
содержат, значит исследуемая функция не сводится к
виду у = 0 и может быть записана в форме
у = (х1&х2& Хз) V (*i & Хз)- A,31)
Таким образом, я - .:
я) & (х2 ->х3)\\/ (Хх ->х3) =
\/(xl&x3). A.32)
Для того чтобы заданную функцию привести к со-
совершенной нормальной дизъюнктивной форме, сначала
необходимо рассмотренными уже приемами привести ее
к какой-нибудь нормальной дизъюнктивной форме.
Дальнейшую процедуру удобно будет рассмотреть на
нашем примере.
Полученная нормальная форма A.32) не является
совершенной из-за того, что во втором дизъюнктивном
члене встречаются не все независимые переменные: в
нем нет *2 (или х2).
Легко видеть, что имеет место тождество
хх & х3 — хг & х3 & (x2Vx2) = (хг &х2& х3)\/(хг &х2& х3).
A.33)
Заменяя в исходной нормальной форме A.32) вто-
второй дизъюнктивный член двумя тождественными ему
дизъюнктивными членами, получаем
Ji^^ О-34)
40 ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ [ГЛ. 1
— совершенную нормальную дизъюнктивную форму за-
записи заданной функции.
Конечно, если бы в результате таких преобразований
мы пришли к выражению, содержащему несколько оди-
одинаковых дизъюнктивных членов, то в окончательной за-
записи мы сохранили бы лишь один член.
Приведение к нормальной конъюнктивной форме
отличается от рассмотренного приема приведения к нор-
нормальной дизъюнктивной форме лишь на последнем эта-
этапе, где вместо развертывания выражения, полученного
на предыдущих этапах, в соответствии с тождеством
A.26, а) применяется второй распределительный за-
закон— тождество A.26,6).
При приведении к совершенной нормальной конъ-
конъюнктивной форме также сначала приводят функцию
к какой-нибудь нормальной конъюнктивной форме, а за-
затем поступают так, как будет показано на примере.
Вр и м е р. Пусть функция трех независимых пере-
переменных, приведенная к нормальной конъюнктивной
форме, имеет вид
0-35)
Для того чтобы эту нормальную форму сделать со-
совершенной, обратимся к очевидным тождествам
хх = Xi V(x2 & х2) = (х1\/х2) & (хх Vx2),
.= xx\/x2\J{xz & x3) — (
A.36)
Пользуясь этими тождествами, получим
. С1 -37)
совершенную нормальную конъюнктивную форму пред-
представления исходной функции.
Мы продемонстрировали использование алгебры ло-
логики на примерах приведения логической функции не-
нескольких переменных к совершенной нормальной (или
просто нормальной) дизъюнктивной (или конъюнктив-
§ 1.4] ОБ ИСЧИСЛЕНИИ ПРЕДИКАТОВ 41
ной) форме. Если же функция задана таблицей и по
ней описанным приемом может быть однозначно выпи-
выписана совершенная нормальная дизъюнктивная форма,
то, подвергая затем эту форму тождественным преоб-
преобразованиям, можно для той же функции определить
иные формы аналитической записи. В таких условиях
возникают разнообразные задачи определения наиболее
выгодной с какой-нибудь точки зрения формы записи
заданной функции.
§ 1.4. Об исчислении предикатов (двузначных)
В исчислении, рассмотренном в предыдущем па-
параграфе, мы имели дело с однородными двузначными
логическими функциями. Теперь же, помимо логических
функций этого типа, мы будем рассматривать также и
такие, в которых сама функция, как и раньше, прини-
принимает значения из двухэлементного множества с сим-
символами О и 1, а независимые переменные — из множе-
множества самого общего вида. Такие логические функции
называют двузначными предикатами.
Для обозначения таких функций обычно применяют
латинские прописные буквы, что позволяет По форме
записи отличать предикат -(неоднородную логическую
функцию) от сложного высказывания (однородной ло-
логической функции). С применением такой условности
п-местный предикат можно записать в следующем виде:
у = Р(хх, .... хп),
где хх = [хп, .... х1р], .... хп = [хв1, .... xnq) — пред-
предметные переменные и их алфавиты.
В связи с тем, что двузначные предикаты прини-
принимают значения из двухэлементного множества 0 и 1,
они могут выступать в качестве аргументов в двузнач-
двузначных однородных логических функциях; по отношению к
ним имеет смысл применение символики исчисления вы-
высказываний.
Пусть мы имеем предикаты
где х1=[х1и .... х1р], )
х2== {х21, ..., x2g). J {'
42 ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ [ГЛ. I
Из этих предикатов, за счет применения какой-нибудь
операции исчисления высказываний, можно получить
новый предикат, например
# (хи х2) = Р (xjV Q (Xj). A.39)
При построении сложных функций в исчислении пре-
предикатов можно операциями исчисления высказываний
связывать предикаты -не только друг с другом, «о также
с любыми элементарными высказываниями и сложными
высказываниями, образованными из элементарных за
счет применения операций исчисления высказываний.
Из предикатов A.38) и двузначных логических пере-
переменных
х3=[0,1), х4={0, 1}
можно построить сложную функцию, например,
z= {P(x1)-+[Q(x2)\y(x3&xi)}} -x,. A.40)
В исчислении предикатов (двузначных) значения слож-
сложных функций могут быть также только двузначными.
В. сложных функциях исчисления высказываний не-
независимыми переменными были лишь элементарные вы-
высказывания. Теперь же, в исчислении предикатов, к ним
добавляются еще предметные переменные предикатов и
переменные предикаты. Последнее обстоятельство и со-
составляет главную особенность этого исчисления. С этой
особенностью связано применение в исчислении преди-
предикатов операций, качественно отличающихся от тех,
которые изменяются в исчислении высказываний. Опе-
Операторы, соответствующие этим новым операциям, на-
называют кванторами.
Применяются кванторы двух видов: квантор общ-
общности и квантор существования.
Квантор общности — это оператор, приводящий в
соответствие любому заданному одноместному преди-
предикату у = Р(х) такую двузначную логическую перемен-
переменную г, которая принимает значение 1 тогда и только то-
тогда, когда у = 1 при всех значениях х. .Символически
.это записывается формулой
§ 1.4] ОБ ИСЧИСЛЕНИИ ПРЕДИКАТОВ 43
в которой «ух» является символом квантора общности.
Запись эта читается так: «при любом х имеет место
Р(х)».
Квантор существования — это оператор, приводящий
в соответствие любому одноместному предикату
у = Р(х) такую двузначную логическую переменную z,
которая принимает значение" 0 тогда и только тогда,
когда у = 0 при всех значениях х. Символически это
записывается формулой
г = (Эх)Р(х),
в которой «Эх» является символом квантора существо-
существования. Запись эта читается так: «существует такое х,
что имеет место у = Р(х)».
Рассмотрим некоторые общие свойства введенных
операторов.
В соответствии с определениями кванторов логиче-
логическая переменная z в выражениях
= (ух)Р(х),
= (Эх)Р(х)
) A-41)
уже не является функцией предметной переменной х;
z является «интегральной» характеристикой предиката
Р(х). Для того чтобы отметить отсутствие функцио-
функциональной зависимости z от х, предметную переменную х
в таких случаях называют связанной. Не связанные
предметные переменные называют свободными. Кван-
Кванторы общности и существования можно, конечно, при-
применять и к функциям исчисления высказываний. Но
в этих случаях они вырождаются в конечные конъюнк-
конъюнкции и дизъюнкции. В самом деле, пусть мы имеем не-
некоторую функцию у = у(хи .. ., хп), в которой незави-
независимые переменные и функция являются двузначными
логическими переменными. Эта же функция может быть
задана в форме у = y(k), где k — номер точки я-мер-
ного двоичного логического пространства. В соответ-
соответствии с определениями кванторов общности и существо-
существования будем иметь
(V*)y(*) = y@)&y(l)& ... &y(k)& ... &уBл-1),
Ck) у (k) = у @)Vy A) V • • • Vy (k)V ...Уу{2п- 1).
44 ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ [ГЛ. I
Это обстоятельство позволяет считать кванторы общ-
общности и существования обобщенной конъюнкцией и об-
обобщенной дизъюнкцией. А в связи с существующей ана-
аналогией между конъюнкцией или дизъюнкцией и сумми-
суммированием вещественных чисел можно проводить анало-
аналогию между операциями, определяемыми кванторами, и
интегрированием функций * вещественной переменной.
Если квантор- (общности или существования) приме-
применяется не к одноместному, а к какому-нибудь т-местно-
му предикату, то в результате этого получается снова
предикат, но за счет связывания одной предметной пере-
переменной полученный предикат будет (т— 1)-местным.
Итак, помимо операций исчисления высказываний,
по отношению к предикатам будут применяться еще
операции связывания предметных переменных кванто-
кванторами общности и существования.
Исчисление, в котором при построении сложных
функций применяется названный перечень операций,
называется узким исчислением предикатов.
Введение операции связывания кванторами сопро-
сопровождается появлением новых тождеств, не входящих в
систему тождеств предыдущего параграфа. Такими тож-
тождествами, например, будут
= (Эх)Р(х), ¦ A.42а)
(Зх)Р(х) = (Vx) Pjx). A.426)
Эти тождества являются следствием определений кван-
кванторов общности и существования.
Система тождеств исчисления высказываний, допол-
дополненная тождествами A.42), дает возможность осуще-
осуществлять различные преобразования для решения тех
или иных конкретных задач. Так же как и в исчислении
высказываний, в исчислении предикатов на первом по
важности месте стоит проблема разрешимости, но из-за
изменения состава независимых переменных постановка
задачи в этой проблеме несколько видоизменяется.
В исчислении высказываний проблема разрешимо-
разрешимости состояла в решении вопроса, является ли данная
сложная функция тождественно истинной, выполнимой
или тождественно ложной.
§ 1.4] ' ОБ ИСЧИСЛЕНИИ ПРЕДИКАТОВ 45
Теперь же вопрос следует ставить так: является ли
данная сложная функция просто тождественно истин-
истинной, то есть принимающей значение 1 при любых пред-
предметных переменных и любых предикатах; будет ли она
тождественно истинной на некотором множестве пред-
предметных переменных, то есть принимающей значение 1
на некотором множестве предметных переменных и при
любых предикатах на этом множестве; является ли она
выполнимой, то есть принимающей значения 1 при не-
некоторых значениях предметных переменных и при не-
некоторых предикатах; и, наконец, является ли она тож-
тождественно ложной, то есть невыполнимой.
В исчислении предикатов, в отличие от исчисления
высказываний, проблема разрешимости может быть ре-
решена только для некоторых частных типов сложных
функций.
' Г Л А В А II
ТЕХНИЧЕСКИЕ ПРИЛОЖЕНИЯ ИСЧИСЛЕНИЯ
ВЫСКАЗЫВАНИИ
§ 2.1. Однотактные релейно-контактные схемы
Как уже отмечалось, впервые на возможность при-
применения символизма математической логики для опи-
описания действия технических устройств было обращено
внимание в связи с рассмотрением электрических ре-
лейно-контактных схем.
Со временем стало ясно, что математическая логика
не только применима к релейно-контактным устройст-
устройствам, но и органически им соответствует. Это привело к
возникновению технической дисциплины — теории ре-
лейно-контактных схем, опирающейся на аппарат ма-
математической логики. В дальнейшем в связи с появле-
появлением бесконтактных устройств, выполняющих те же
функции, что и релейно-контактные схемы, их теория
переросла в общую теорию релейных схем.
Теория релейно-контактных схем, ставшая в на-
настоящее время йшиь одним из разделов общей теории
релейных схем, является вместе с тем наиболее на-
наглядным примером применения, математической логики
к проблемам техники. Поэтому для иллюстрации техни-
технических приложений математической логики мы и при-
прибегнем прежде всего к этому примеру.
В этом параграфе мы будем рассматривать не лю-
любые, а лишь так называемые однотактные релейно-
контактные схемы. Именно таким схемам соответствует
рассмотренный в предыдущей главе аппарат исчисле-
исчисления высказываний.
§2.1]
ОДНОТАКТНЫЕ РЕДЕЙНОКОНТАКТНЫЕ СХЕМЫ
47
Всякая электрическая релейно-контактная схема со-
состоит из преобразователей двух типов: электромехани-
электромеханического и механико-электрического. Каждое электроме-
электромеханическое реле с принадлежащими ему контактами
преобразует электрические сигналы, поступающие на
его вход, в механическое перемещение его контактов.
А электрическая сеть, содержащая контакты и обмотки
некоторых реле, преобразует механические перемеще-
перемещения контактов в выходные для этого преобразователя
1
1
^
Рис. 2.1.
электрические сигналы (токи в обмотках реле). Объ-
Объединение выходов преобразователей одного типа со вхо-
входами преобразователей другого типа дает различные
релейно-контактные схемы.
В простейшем случае электромеханическое реле
(рис. 2.1, а) состоит из одной обмотки /, сердечника 2,
якоря 3 и двух групп контактов: нормально-замкнутых
4' и нормально-разомкнутых 4". Если по обмотке проте-
протекает ток, превосходящий по величине ток срабатывания
h (рис. 2.1,6), то якорь притягивается к сердечнику,
а это приводит к замыканию всех нормально-разомк-
нормально-разомкнутых контактов и размыканию нормально-замкнутых.
Если по обмотке течет^ток, меньший тока отпускания i\
(в частности, если обмотка обесточена), то якорь от-
отпадает от сердечника, в результате чего замыкаются
нормально-замкнутые контакты и размыкаются нор
мально-разомкнутые.
48
ПРИЛОЖЕНИЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИИ
[ГЛ. II
Мы будем рассматривать реле лишь в таких схе-
схемах, где приняты специальные меры, обеспечивающие в
равновесных состояниях значения тока i обмотки i < i\
или / > /2-
При выполнении этого условия реле имеет два рав-
равновесных состояния; значит, два состояния характерны
и для всех элементов реле. Нас будут интересовать
обмотка и контакты реле. Каждый контакт имеет два
. состояния: замкнутое и разомкнутое. Этим состояниям
приведем в соответствие символы 1 и 0 соответственно,
т. е. состояние каждого контакта будем рассматривать
как двузначную логическую переменную, принимающую
эти значения.
Первым состоянием обмотки является такое, когда
по ней протекает ток i > i2. Это состояние будем. обо-
обозначать символом 1. Во втором состоянии, которому бу-
будем приписывать символ 0, обмотка обесточена (г < ii).
Обмотке мы также будем ставить в соответствие логи-
логическую переменную, принимающую указанные два зна-
значения. Смысловое значение символов 1 и 0 отражено
в табл. 2.1.
Т а б л и ц а 2.1
Элемент
Контакт
Обмотка
Символ
1
замкнут
под током
0
разомкнут
обесточена
Состояние любого контакта реле определяется со-
состоянием обмотки следующим образом:
для нормально-разомкнутого контакта х = X,
для нормально-замкнутого контакта х' = X = х.
Здесь X, х, х' — логические переменные, определяю-
определяющие состояние соответственно обмотки, нормально-ра-
нормально-разомкнутого и нормально-замкнутого контактов.
Если реле имеет не одну, а несколько обмоток, то
удобно воспользоваться представлением об эквивалент-
§ 2.1] ОДНОТАКТНЫЕ РЕЛЕЙНО-КОНТАКТНЫЕ СХЕМЫ 49
ной обмотке. Пусть реле имеет две обмотки (Х\ и Х2L
и пусть они включены так, что срабатывание реле про-
происходит лишь тогда, когда обе они оказываются под
током, то есть при Xi&X2 = 1. Представим себе, что
реле имеет такую одну обмотку Хэ, которая именно при
условии Xi & Х2 = 1 приводит к срабатыванию реле.
Очевидно, что эта обмотка, связанная с исходными об-
обмотками соотношением
Хэ = Хг & Х2
и определяющая состояние контактов реле в соответ-
соответствии с соотношениями
х = Хэ (для нормально-разомкнутых контактов),
х' = ХЭ = х (для нормально-замкнутых контактов),
по своему действию вполне эквивалентна исходным двум
обмоткам.
Мы рассмотрели реле с двумя обмотками. Анало-
Аналогично можно представить себе реле с т обмотками,
включенными так, что срабатывание реле происходит
только при определенных сочетаниях единичных и ну-
нулевых состояний обмоток.
Применение того или иного способа включения т
исходных обмоток в схеме одного реле приводит к уста-
установлению какой-нибудь конкретной логической функции
Хэ = /И (Aj, л2, .. ., Хт),
а связь между контактами реле и его эквивалентной об-
обмоткой остается неизменной.
Рассмотрим теперь ту часть релейно-контактных
схем, где происходит механико-электрическое преобра-
преобразование, — контактную сеть с включенными в нее об-
обмотками реле.
Начнем рассмотрение со случая, когда такая сеть
(рис. 2.2, а и 2.2, а') состоит из одного контакта 1 од-
одного — входного реле и одной обмотки 2 другого реле —
выходного, которая включена либо последовательно
с контактом (рис. 2.2, а), либо параллельно ему
(рис. 2.2, а').
Сохраняя введенные обозначения состояний кон-
контакта и обмоток символами 0 и 1, для таких схем имеем
2 = у (для. обмотки, включенной последовательно),
4 М. А. Айаерман, Л. А. Гусев и др.
50
ПРИЛОЖЕНИЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ
[ГЛ. II
2' = у = Z (для обмотки, включенной параллельно), при-
причем теперь у — логическая переменная, определяющая
состояние контакта, a Z и Z' определяют состояния по-
последовательно и параллельно включенных обмоток.
а')
б')
Рис. 2.2.
Обычно на месте контакта / стоит группа контактов
различных реле уи у%, ¦ ¦ ¦, уп, соединенных в электри-
электрическую сеть. Электрическую сеть с контактами мы бу-
будем называть в дальнейшем контактной сетью. На
рис. 2.2,6 — 2.2, д даны примеры таких контактных се-
сетей (обведены пунктиром).
Здесь снова удобно ввести представление об эквива-
эквивалентной независимой переменной — эквивалентном кон-
контакте 1/э — со свойствами, аналогичными свойствам эк-
эквивалентной обмотки в многообмоточном реле.
§2.1] ОДНОТАКТНЫЁ РЕЛЕИНО-КОНТАКТНЫЕ СХЕМЫ 51
Например, для двух контактов у\ и у2 (рис. 2.2,6),
включенных последовательно, цепь на участке аб будет
замкнута только тогда, когда уу&уг — 1. Вводя
и устанавливая связь между обмоткой и эквивалент-
эквивалентным контактом
Z = y9 для последовательного включения (рис. 2.2,6)
Z' — уэ — Z для параллельного включения (рис. 2.2,6')
мы сохраняем все свойства схемы.
На рис. 2.2 даны и иные примеры включения кон-
контактов, приводящие к функциям
(Рис- 2.2, в, в'),
уэ = у1&(у2Уу3) (рис. 2.2, г, г'),
y9=[yi&(y2Vy3)]V)'4 (рис. 2.2, а, а').
В общем случае
эта логическая функция определяется конкретным спо-
способом включения контактов в • сеть, а связь между
обмотками и эквивалентным контактом остается неиз-
неизменной. Заметим, что переменной уэ здесь реально соот-
соответствует проводимость двухполюсника, содержащего
заданную контактную сеть.
Каждый из рассмотренных преобразователей обла-
обладает свойством детектирования, то есть имеет направ-
направленное действие. ¦ В электромеханическом преобразова-
преобразователе— «реле с контактами» — состояние контактов реле
определяется состоянием обмоток, а контакты не влияют
на состояние обмоток. В механико-электрическом преоб-
преобразователе «контактная сеть с обмотками» состояние
обмотки (или обмоток) определяется состояниями кон-
контактов, на которые обмбтки не оказывают обратного
воздействия. Отмеченное свойство этих преобразовате-
преобразователей позволяет рассматривать их как звенья с входными
и выходными переменными. Входными переменными
¦^ь ..., Хт для звена «реле с контактами» являются
4*
52 ПРИЛОЖЕНИЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ [ГЛ. II
состояния обмоток реле (наличие или отсутствие в них
тока); двумя выходными переменными этого звена х и
х' являются состояния двух разнотипных контактов. Как
уже отмечалось, это звено можно представлять состоя-
состоящим из двух звеньев, соединенных последовательно: в
первом из них реализуется некоторая логическая функ-
функция
Х. = М(Хи...,Хт),
а во втором — функции вида
х = Лэ, х = ла = Х-
Звено «контактная сеть с включенными в нее обмот-
обмотками выходных реле» имеет входными переменными
у и ..., уп состояния контактов входных реле, а выход-
выходными переменными Z и Z' являются состояния обмоток
двух выходных реле. Это звено тоже может быть пред-
представлено в виде цепочки из двух звеньев с реализацией
в первом из них некоторой логической функции
Уэ = М(уи ..., уп),
а во втором — функции вида
Мы видим, что звено «реле с контактами» и звено
«контактная сеть с включенными в нее обмотками вы-
выходных реле» имеют одинаковые свойства.
Всякую релейно-контактную схему можно расчленить
на звенья с описанными свойствами.
В этой главе, как уже было отмечено, мы будем рас-
рассматривать лишь однотактные релейно-контактные схе-
схемы. Для них характерно, во-первых, представлений о
мгновенно срабатывающем идеальном реле и, во>ёто-
рых, отсутствие петель — обратных связей на соответ-
соответствующих им структурных схемах, составленных из Зве-
Звеньев направленного действия.
На рис. 2.3,а приведен пример однбтёктной релейно-
контактной схемы, а на рис. 2.3,6 показана соответ-
соответствующая ей структурная схема; она не имеет петель.
.Изображенная на рис. 2.4,а схема не является одно-
тактной; соответствующая ей структурная схема
§ 2.2] АНАЛИЗ ОДНОТАКТНЫХ РЕЛЕЙНО-КОНТАКТНЫХ СХЕМ 53
(рис. 2,4,6) имеет петлю. Действие такой схемы невоз-
невозможно рассматривать без учета времени срабатывания
реле.
Рис. 2.3.
При изображении релейно-контактных схем у каж-
каждой обмотки пишется соответствующая ей логическая
Рис. 2.4.
переменная, а у контактов для сокращения обозначений
ставится выражение, определяющее состояние контакта
по состоянию обмОтки, управляющей этим контактом.
§ 2.2. Анализ однотактных релейно-контактных схем
Рассмотрим теперь подробнее следующую задачу:
задана однотактная релейно-контактная схема; необхо-
необходимо дать ее математическое описание, т. е. установить
логическую функцию, реализуемую э^ой схемой.
54 ПРИЛОЖЕНИЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ [ГЛ. И
Здесь мы ограничимся рассмотрением релейно-кон-
тактных схем, содержащих лишь однообмоточные реле,
так как такие схемы имеют наибольшее распростране-
распространение. Как уже было отмечено, действие этих реле отра-
отражает следующая запись: если X, х и х'— переменные,
определяющие соответственно состояния обмотки, нор-
нормально-разомкнутых и .нормально-замкнутых контактов
реле, то
х = X для нормально-разомкнутых контактов,
х'=Х=х для нормально-замкнутых контактов.
Это значит, что реле с одной обмоткой само по себе реа-
реализует либо повторение, либо отрицание.
Разнообразие однотактных релейно-контактных схем
связано с применением различных контактных сетей,
включающих нормально-размкнутые xt и нормально-
замкнутые Xi контакты однообмоточных реле Xi. Кон-
Контактной сети соответствует зависимость
Xэ = г (X}, X I, . • ., Хп, X „),
где xt, x'i и хэ — переменные, определяющие соответ-
соответственно состояние койтактов, принадлежащих г-му реле
и состояние эквивалентного контакта.
Какой бы сложной и запутанной ни была контакт-
контактная сеть, для нее всегда может быть получена формула
вида
-"•э=== * (Х\г Х\, ¦••, Хп, Хп)-
Для построения такой формулы можно применять спе-
специальную методику, обобщающую тот очевидный факт,
что для двух последовательно соединенных контактов х\
и х2 имеем хэ = хх &х2, а если контакты соединены па-
параллельно, то хэ = х\ V х2.
Для разъяснения существа методики рассмотрим
пример, отражающий основные ее черты.
Анализируемая контактная сеть (двухполюсник)
приведена на рис. 2.5, а. Будем осуществлять последо-
последовательное упрощение сети за счет введения вспомога-
вспомогательных эквивалентных контактов. Начнем с исключения
Шина!
Шина2
<?О Ом
3 Й
*/ *#
V
1—г 1—т
в)
•4S *1
\
г)
J7-
I*
-I
FTT 1 1 I
о о" I -n -n I III
jf i 4 ? ? ° 4 4 4
I " I I I 4Cj I I Xj X/f Xgg X\
6 A A °?oof99°
ч)
Рис. .2.5.
56 ПРИЛОЖЕНИЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ [ГЛ. II
всех цепочек последовательно включенных контактов.
Вводя
"^10 — *^2 *^5* "^11 — *^з *^2> 12 ^~ "^2 *^5>
преобразуем схему к виду рис. 2.5, б.
Теперь сделаем дальнейшее упрощение, исключая
все группы параллельно включенных контактов. Для
этого обозначим
или с учетом уже примененных обозначений,
х13 = х2\/(х3&х4); хи = хх\/х3\
х15 = (xt & х5) \/(х3&х5); х1в = хх V (х2 & х4).
При этом получим схему, изображенную на рис. 2.5, в.
В этой схеме снова исключаем цепочки последова-
последовательно включенных контактов. Для этого применим обо-
обозначения
х17 = х1& х13 = л;, & [х2 V (х3 & х4)]=(.*! & Xj) V(-*i& хз
¦«19 = *1в & -«10 = [Xl V (-«2 & -«4I & Х2 & ^5 =
= (xt &х2& х5) V (х4 &х2& х5)
и получим схему рис. 2.5, г. Ее уже больше нельзя упро-
упростить за счет исключения цепочек последовательных кон-
контактов или групп параллельных контактов.
Для дальнейшей обработки схемы пронумеруем все
ее узлы, отмечая одинаковыми номерами узлы, соеди-
соединенные проводами без контактов, как показано на
рис. 2.5, г. Получаем узлы 1, 2, ..., т. В нашем случае
т — 4. Теперь удобно представить схему в виде, изобра-
изображенном на рис. 2.5, д. Эта форма получается из рис. 2.5, г
объединением всех узлов с одинаковыми номерами.
Схему рис. 2.5, д представляем в виде «дерева»
(рис. 2.5, е), которое строится следующим образом. На-
Намечаются ярусы по числу т узлов (в данном случае
ярусы /, II, III и IV). В первом ярусе помещается узел/;
§2.2] АНАЛИЗ ОДНОТАКТНЫХ РЁЛЕЙНО-КОНТАКТНЫХ СХЕМ 57
из него проводится пучок ветвей, содержащий т — 1
ветвь, которые оканчиваются во втором ярусе. В конце
этих ветвей ставятся номера узлов схемы, составляю-
составляющих вместе с первичным узлом пучка (узлом /) полный
перечень; в рассматриваемом случае это будут узлы 2,
3 я 4, являющиеся вторичными узлами этого пучка. Да-
Далее из каждого из т — 1 узлов второго яруса, исключая
узел с номером т, т. е. из узлов 2 я 3 второго яруса,
проводятся пучки (т — 2) ветвей, заканчивающихся на
третьем ярусе. Рассмотрим сначала пучок ветвей, выхо-
выходящий из узла 2. Для этого пучка узел 2, стоящий во
втором ярусе, является первичным. В качестве номеров
окончаний ветвей этого пучка, расположенных в третьем
ярусе, берутся номера всех тех узлов, исключая номер
самого узла 2, расположенных во втором ярусе, которые
вместе с узлом 2 принадлежат окончаниям одного и
того же пучка, соединяющего первый и второй ярусы.
В нашем случае это будут номера 3 я 4. Затем анало-
аналогично нумеруются концы ветвей, образующие пучок
(т — 2) ветвей, выходящих из узла 3 и т. д. Далее
из всех полученных узлов третьего яруса, исключая
узлы с номерами т, строятся пучки (т — 3) ветвей, со-
соединяющих третий и четвертый ярусы и аналогично осу-
осуществляется нумерация. Легко проверить, что по окон-
окончании этого процесса на последнем т-ы ярусе окажутся
лишь узлы с номером т, из которых уже не выходит ни
одной ветви (тупиковые узлы).
Каждой ветви полученного «дерева», соединяющей
какие-нибудь два узла, соответствует на схеме рис. 2.5, д
провод, соединяющий эти же узлы. Этим и определяется
размещение контактов на ветвях «дерева».
Контактная сеть на рис. 2.5, е отражает процесс про-
прослеживания всех путей, ведущих из узла / в узел 4; она
эквивалентна сети рис. 2.5, д, но в отличие от нее со-
состоит из групп последовательно и параллельно вклю-
включенных контактов. Исключая теперь все группы после-
последовательно включенных контактов, получим схему
рис. 2.5, ж, где дополнительно применены обозначения
Хю = х-а & х19 = (хх & х2 & х5) V (*4 & -*2
Х^\ =z ¦"•12 "^ ¦"•le =z ¦*•! ¦"•г ¦
58 ПРИЛОЖЕНИЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ [ГЛ. П
Следующее исключение групп параллельных контактов
дает схему рис. 2.5, з, где
Х22 = Х20 V-*18 =
= (xt &х2&х5)\/(х4&х2&х5)\/(х1 &х3&х5) V (•*] &х3&jc5),
•% = -«21V -«19 = С*1 & -«2 & Х5 & *з) V (-«4 & -*2 & JC5).
После исключения в этой схеме групп последователь-
последовательно включенных контактов получим схему рис. 2.5, и.
Здесь
Хщ = JC22 ^ -^17 г== "^1 ^2 "*5»
•"•25 == -*23 -^Н :^ "•
Последняя схема дает
х9 = x2i Vx25\/x3 = (jfj & х2 & х5) V^3-
Полученная логическая функция реализуется исход-
исходной схемой рис. 2.5, а. Но, как нетрудно видеть, ей же
соответствует схема рис. 2.6, то есть
y J t схема, изображенная на рис. 2.5, а,
i эквивалентна схеме рис. 2.6.
Заметим, между прочим, что при-
присутствовавший в исходной схеме кон-
контакт Х4 отсутствует в эквивалентной
схеме рис. 2.6 и, значит, вообще не
оказывает влияния на работу схемы.
В этом можно убедиться и непосред-
непосредственно. Действительно, из схемы
рис. 2.5, а видно, что сеть не может
быть замкнутой пока разомкнуты кон-
" такты Х\ и х3; но для ее замыкания не
обязательно замыкать оба эти контак-
Рис. 2.6. та; замыкание одного контакта хл
уже влечет за собой замыкание сети;
если же х3 разомкнут, то необходимо замкнуть контакт
х\ и, кроме того, контакты х2 и х5.
Мы рассмотрели один пример, однако в любом дру-
другом случае описанный прием позволяет для заданной
схемы составить соответствующую ей логическую функ-
функцию. Построение логической функции по заданной ре-
лейно-контактной схеме называют анализом релейно-
§2.3] СИНТЕЗ ОДНОТАКТНЫХ РЕЛЕЙНО-КОНТАКТНЫХ СХЕМ
59
контактных схем. Упрощение полученной функции сред-
средствами алгебры логики позволяет указать другие схемы,
эквивалентные заданной, но более простые.
В рассмотренном примере функция упростилась до
такой степени, что соответствующая ей контактная схе-
схема могла быть непосредственно изображена. В более
сложных случаях этой цели служат специальные прие-
приемы, позволяющие каждой заданной логической функции
поставить в соответствие реализующую ее контактную
схему. Эта задача носит название задачи синтеза.
§ 2.3. Синтез однотактных релейно-контактных схем
Пусть задана произвольная логическая функция.
Требуется построить релейно-контактную схему, которая
ее реализует. Мы ограничимся при этом схемами, со-
составленными из одно-
обмоточных реле и вы- Таблица 2.2
ходного реле с обмот-
обмоткой, включенной после-
последовательно с контакт-
контактной сетью. Будем счи-
считать, что логическая
функция задана табли-
таблицей, в которой пере-
перечислены все возмож-
возможные сочетания значений
независимых перемен-
переменных и каждому сочета-
сочетанию приведено в соот-
соответствие определенное значение функции. Составление
таких таблиц было подробно описано в § 1.3.
Рассмотрим в качестве примера логическую функцию
трех независимых переменных у = L (xlt x2, х3), задан-
заданную табл. 2.2. Как было показано в § 1.3, по этой таб-
таблице непосредственно составляется совершенная нор-
нормальная дизъюнктивная форма данной логической
функции.
Так, в нашем примере рассматриваемой функции со-
соответствует совершенная дизъюнктивная нормальная
х,
х2
*3
у
0
0
0
0
1
0
0
1
0
1
0
1
1
1
0
0
0
0
1
1
1
0
1
0
0
1
1
0
1
1
1
1
60 ПРИЛОЖЕНИЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИИ [ГЛ. II
форма следующего вида:
у = (хх & х2 & jt3) V (JCj & х2 & Зс3) V (х{ & Зс2 & х3) V (х{ & х2 & ;с3).
По выписанной форме немедленно может быть по-
построена соответствующая ей контактная сеть, если вос-
воспользоваться следующими правилами.
Каждой переменной Х{ (в нашем случае i = 1, 2, 3)
соответствуют нормально разомкнутые, а Х{ — соответ-
соответственно нормально замкнутые контакты i-ro реле. Каж-
Каждой скобке в совершенной нормальной дизъюнктивной
1 II I
3*1 Xi Л*« X*
I I 1 I
X* Хл Xp Xn
i i г i
«2? л «Г* «t« «t«
1 I I I
Рис. 2.7,
форме соответствует цепочка, состоящая из последова-
последовательно соединенных контактов, определяемых перемен-
переменными, содержащимися в этой скобке. Всей форме при
этом соответствует параллельное соединение указанных
цепочек.
В нашем примере, применяя эти правила, получим
схему, изображенную на рис. 2.7.
Описанный прием ставит в соответствие любой логи-
логической функции параллельно-последовательную контакт-
контактную сеть. Разумеется, даже в классе параллельно-
последовательных сетей часто могут быть указаны сети,
эквивалентные исходным, но содержащие значительно
меньше контактов (щ, пример в § 2.2). Это тем более
возможно, если выйтй'эа рамки класса параллельно-по-
параллельно-последовательных сетей и применять так называемые мое-
тиковые схемы.
В связи с этим взамен описанного канонического
приема были предложены иные приемы, позволяющие
§ 2.3] СИНТЕЗ ОДНОТАКТНЫХ РЕЛЕЙНО-КОНТАКТНЫХ СХЕМ 61
строить по заданной логической функции более эконом-
экономные, но все-таки отнюдь не минимальные*) схемы.
Мы приведем здесь без доказательств один из таких
приемов — метод А. Ш. Блоха**). Метод Блоха описы-
описывается далее применительно к рассмотренному примеру,
так как при этом хорошо выясняются все особенности
метода, аналогичным образом применяемого и в любом
ином случае.
Обращаясь к табл. 2.2, задающей логическую функ-
функцию, выпишем отдельно только ее нижнюю строку (стро-
(строку со значениями у). В нашем примере это
01101001.
Подчеркнем попарно символы, содержащиеся в этой
строке:
01101001.
Если какая-нибудь пара состоит из двух одинаковых
цифр, то под ее чертой сниз^ пишется эта же цифра.
Под остальными парами снизу пишем цифры 2 и 3,
следя за тем, чтобы одинаковым парам приписывались
одинаковые цифры, а несовпадающим — различные:
01101001
2 3 3 2"
Выписанные цифры вновь объединяем в пары, под-
подчеркиваем их снизу и продолжаем нумеровать пары по
указанному правилу, приписывая под несовпадающими
парами следующие цифры: 4, 5, и т. д.; проставленные
номера вновь объединяем в пары и т. д. до образования
полной треугольной матрицы. Эта матрица всегда имеет
k + 1 строку, где k — число независимых переменных.
*) Вопрос о способах построения минимальных в каком-либо
смысле схем является серьезно* научной проблемой, до сих пор ие
имеющей окончательно решеюуь. По этому поводу см. § 2.6.
**) См. [17], где содержатся-к все необходимые доказательства.
Примененный автором метод» термин «канонический» ие соответ»
ствует нашему толкование эч-ofg термина,
62 ПРИЛОЖЕНИЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИИ [ГЛ. II
В нашем случае эта матрица имеет вид.
01 10 1001
2 3 3
Теперь приступаем к построению контактной сети.
Для этого проводим k + 1 горизонтальную прямую (в
нашем случае их четыре). Каждой линии ставим в со-
соответствие строку нашей матрицы. На каждой линии
проставляем точки — узлы, соответствующие элементам
матрицы, и над ними выписываем соответствующие
цифры. Узлы соединяем в «дерево», опуская лишь ветви,
ведущие к узлам, от-
• pjS^iSl меченным цифрой 0.
В нашем случае «де-
«дерево» имеет вид, изо-
изображенный на рис. 2.8.
На ветвях нижнего
яруса дерева распо-
расположим контакты треть-
третьего реле (х3 и х3), по-
помещая лг3'на левой, а хъ
на правой ветви. На
Рис- 2-8- ветвях второго яруса
аналогичным способом
размещаем_контакты х2 и х2, на ветвях третьего яруса —>
контакты х\ и х\. Если дерево содержит ветвь, соеди-
соединяющую два узла с одинаковыми номерами, то в эту
ветвь контакты не включаются, то есть узлы замы-
замыкаются накоротко. В нашем примере получаем схему
рис. 2.9.
По существу уже построена контактная сеть, реали-
реализующая заданную функцию. Ее окончательный вид по-
получается объединением одноименных узлов (узлов с оди-
одинаковыми цифрами). При этом число контактов сокра-
сокращается. В нашем случае после такого объединения узлов
получаем окончательно мостиковую схему, представлен-
представленную на рис. 2.10,
§2.4]
МЕТОДЫ РЕАЛИЗАЦИИ ЛОГИЧЕСКИХ ФУНКЦИЙ
Применение описанного приема позволяет в любом
случае по заданной логической функции получить соот-
соответствующую ей контактную сеть, а значит, и однотакт-
ную релейно-контактную схему. Построенная этим прие-
приемом схема обычно содержит значительно меньшее число
контактов по сравнению со схемой, построенной с по-
помощью канонического прием?
(использующего непосред-
непосредственно совершенную нормаль-
нормальную дизъюнктивную форму
функции).
Содержание предыдущего и
настоящего параграфов пока-
показывает, что исчисление выска-
0 110 10 0 1
' / \ ' \ • ' /—
х г,
/з з
{
6
Рис. 2.9.
зываний является математическим аппаратом, адэкват-
ным технике однотактных релейных схем, и наоборот,
однотактные релейные схемы являются естественным
техническим воплощением исчисления высказываний.
§ 2.4. Иные методы технической реализации
логических функций
Электромеханические реле не являются единствен-
единственным техническим средством, позволяющим реализовать
любую заданную логическую функцию, т. е. выполнять
операции исчисления высказываний. Существует большое
-и-
64 ПРИЛОЖЕНИЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ (ГЛ. П
разнообразие других элементов, пригодных для построе-
построения логических схем. Ниже кратко описываются не-
несколько примеров такого рода. ~
а) Диодные схемы
Диодом называется элемент, обладающий такой не-
нелинейной характеристикой, что ток (электрический,воз-
(электрический,воздушный, гидравлический и т. д.) через него в одном на-
направлении проходит почти без сопротивления, а в дру-
другом направлении встречает практически бесконечно
большое сопротивление. Это значит, что этот элемент
играет роль клапана, пропускающего ток в одном на-
направлении и запирающего в другом. На схемах он изо-
изображается так, как показано
на рис. 2.11; расположение
— треугольника, изображенного
на рис. 2.11, указывает напра-
„ П11 вление возможного тока.
Рис 2 11
¦ ¦ ¦ В отличие от релейно-кон-
тактных схем, в которых на
вход реле в виде токов подаются логические пере-
переменные Х\ и Х2 и т. д., а отрицания этих величин, если
это нужно, получаются за. счет применения нормально-
замкнутых контактов, в диодных схемах операция отри-
отрицания не может быть реализована. Поэтому входами
в диодную сеть служат не только переменные хи х2
и т. д., но, если это необходимо, и их отрицания xh х2
и т. д. Эти отрицания реализуются вне диодной схемы
на каких-либо других устройствах, например на элек-
электромеханических реле.
Покажем на примере, как при таких входах с по-
помощью только диодов и линейных сопротивлений можно
реализовать любую логическую функцию. Пусть реали-
реализуемая функция задана в совершенной нормальной
дизъюнктивной форме
y=yiVy2Vy3Vy4=
= {хг &х2 & х3) V(*i & х2 & Jc3) V(*i & *2 & -*з) V(*i & х2 & х3).
В этой функции три независимых переменных, поэтому
схема должна содержать три пары входных шин; хх их,,
§2.4]
МЕТОДЫ РЕАЛИЗАЦИИ ЛОГИЧЕСКИХ ФУНКЦИЙ
65
Х2 и х2, х3 и х3. Выходных шин должно быть столько,
сколько конъюнктивных скобок в реализуемой функции.
В нашем случае их четыре (рис. 2.12). Все выходные
шины заканчиваются диодами, выходы которых объеди-
объединяются и подключаются к выходному сопротивлению.
Это объединение обеспечивает реализацию дизъюнкции
так же, как и всякое параллельное соединение. К шинам
подведено питание через входные сопротивления.
J-
Уг
."И К-
Уг
Уз
Рис. 2.12.
Каждой шине соответствует одна из конъюнктивных
скобок рассматриваемой формы; поэтому каждая вы-
выходная шина через диоды связывается со всеми теми
входными шинами, которые соответствуют переменным,
входящим в конъюнктивную скобку этой шины. При
этом диоды располагаются так, чтобы иметь возмож-
возможность пропускать ток от выходной шины к входной.
В нашем примере первой конъюнктивной скобке
соответствует включение диодов, показанное на рис. 2.13,
а полная диодная схема, реализующая заданную ло-
логическую функцию, показана на рис. 2.14.
Аналогично может быть реализована и любая дру-
другая логическая функция.
Описанный прием исходит из представления реали-
реализуемой функции в совершенной нормальной дизъюнктив-
дизъюнктивной форме и является в такой же мере каноническим,
5 М. А. Айзерман, Л. А. Гусев и др.
66
ПРИЛОЖЕНИЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ [ГЛ. II
как и описанный в § 2.3 прием построения релейно-кон-
тактных схем. Но построенные так схемы обычно неэко-
неэкономны по числу диодов. Существуют методы построения
Выход
у,~х,&.хг&.х3
Рис. 2.13.
7
7
7
7
7
f
7
а, х,
7
7
Рис. 2.14.
-w-
У
более экономных схем (см., например, [127]), однако
описание этих методов здесь не приводится.
б) Схемы на триодах
Триодом называется элемент, в котором реализуется
переменное сопротивление, зависящее от управляющего
сигнала. Типичными примерами являются электронный
триод-лампа, в которой анодный ток при прочих равных
условиях определяется сеточным напряжением, и полу-
§2.41
МЕТОДЫ РЕАЛИЗАЦИИ ЛОГИЧЕСКИХ ФУНКЦИЙ
67
проводниковый триод-транзистор, сопротивление кото-
которого изменяется под влиянием внешнего сигнала.
а)
Рис. 2.45.
Характеристика любого триода имеет насыщение.
Выбирая в качестве логических переменных (значения
О и 1) значения управляющих сигналов, при которых
сопротивление триода минимально и максимально, мы
5*
68 ПРИЛОЖЕНИЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ [ГЛ. II
г
В)
i
x, М .у x.
у-х,/х,
« 0
_J
Рис. 2.16.
§ 2.4] МЕТОДЫ РЕАЛИЗАЦИИ ЛОГИЧЕСКИХ ФУНКЦИЙ 69
можем рассматривать сопротивление триода как выход-
выходную переменную элемента. Различно сочетая перемен-
переменные сопротивления — триоды — и постоянные пассивные
сопротивления, получаем возможность реализовать ло-
логические функции как одной независимой переменной
(рис. 2.15), так и нескольких независимых переменных
(рис. 2.16).
Имея средства для реализации отрицания, конъюнк-
конъюнкции и дизъюнкции, можно реализовать любую конъ-
конъюнктивную скобку совершенной нормальной дизъюнк-
дизъюнктивной формы любой логической функции и осуще-
осуществлять дизъюнкцию полученных конъюнктивных скобок.
Таким образом, триоды дают возможность реализовать
любую логическую функцию. И в этом случае описан-
описанный нами канонический прием не экономен по числу по-
потребных триодов и существуют методы более эконом-
экономного построения триодных схем.
в) Схемы на магнитных элементах
Особый класс логических устройств связан с исполь-
использованием в них магнитных усилителей. Существуют раз-
разные методы построения магнитных логических устройств
и систем. Мы кратко и в сильно упрощенной форме опи-
опишем один из них, имея в виду дать лишь общее пред-
представление о системах такого рода. На рис. 2.17 приве-
приведена схема магнитного усилителя с внешней положи-
положительной обратной связью. Основу усилителя составляет
магнитный сердечник 1, несущий ряд обмоток*). Усили-
Усилитель питается переменным током, который подводится
к его двум обмоткам w^ и w'^ и через диодный мост 2
и сопротивление нагрузки RH поступает на обмотки
woc и w'oc положительной обратной связи. Помимо ука-
указанных обмоток, сердечник несет обмотки смещения
wcM и w'^, а также одну или несколько управляющих
обмоток: wyl и w'yl, wy2 n~"w'y2 и т. д. К обмотка^
смещения подводится постоянный ток /см. значение
*) Применение разделенного сердечника и парных обмоток
устраняет наводки переменного тока в цепях выпрямленного и пси
стоянного тока.
70
ПРИЛОЖЕНИЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ.
[ГЛ. II
которого сохраняется неизменным. Обмотки управления
также питаются постоянным током, значения которого
s*-
ш,,
Рис. 2.17.
и используются как входные переменные для всего устрой-
устройства. Выходом устройства является выпрямленный ток
iH в цепи нагрузки.
Рассмотрим сначала усилитель, имеющий лишь одну
пару обмоток управления да j и да'г На рис. 2.18 пока-
показана характеристика такого магнитного усилителя, т. е.
зависимость выходной вели-
величины (тока в цепи нагруз-
нагрузки iH) от входной (тока в
обмотках управления iy)
при нулевом токе смещения.
Наличие iCM смещает та-
такую характеристику вдоль
оси /у параллельно самой
*г себе.
У Если для входной пере-
переменной принять за 0 значе-
значение ty = 0, а за 1 любое зна-
значение ty < — ty, и если для выходной переменной принять
Эа 0 я 1 соответственно нижнее и верхнее значения тока,
Рис. 2.18.
§ 2.4] МЕТОДЫ РЕАЛИЗАЦИИ ЛОГИЧЕСКИХ ФУНКЦИЙ 71
которые только и могут быть на выходе в соответствии
с характеристикой рис. 2.18, то при нулевом токе смещения
такой магнитный усилитель будет элементом отрицания.
Этот же магнитный усилитель может быть исполь-
использован в качестве элемента, реализующего операцию
«повторение». Для этого надо током /См сместить харак-
характеристику вправо так, как показано на рис. 2.19, и
одновременно изменить полярность управления. Теперь,
когда /у = 0, на выходе имеем наименьшее значение вы-
выпрямленного тока, т. е. вы-
выходная логическая перемен-
переменная имеет значение 0; если
же на вход подана 1, т. е. ij ~ [
достаточно большой ток i7, 1 !.
то на выходе логическая i
переменная также будет —•—
иметь значение 1, т. е. ток
в цепи нагрузки будет иметь
наибольшее значение.
Из приведенного описа- Рис 2.19.
ния видно, что магнитный
усилитель в рассмотренных схемах является бесконтакт-
бесконтактным аналогом электромеханического реле с нормально-
замкнутым либо с нормально-разомкнутым контактом.
Рассмотрим теперь этот же магнитный усилитель, но
не с одной, а с несколькими обмотками управления.
В этом случае при подаче соответствующего тока сме-
смещения характеристика рис. 2.19 остается в силе, если по
оси абсцисс отложить суммарные ампервитки всех
управляющих обмоток.
Принимая для каждой из входных переменных в ка-
качестве 0 и 1 те же самые значения тока в соответствую-
соответствующих обмотках, какие принимались раньше, когда рас-
рассматривался усилитель с одной управляющей обмоткой,
получим элемент, реализующий дизъюнкцию всех п пе-
переменных, подаваемых на входы. Действительно, доста-
достаточно иметь 1 на любой из управляющих обмоток для
того, чтобы суммарные ампервитки обеспечивали наи-
наибольшее значение выходного тока.
Если же в качестве 1 принимать значение, в п раз
меньшее прежнего (где п — число входных переменных),
72
ПРИЛОЖЕНИЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ
[ГЛ. II
то необходимые для получения 1 на выходе ампервитки
получатся только тогда, когда поданы единицы на все
входы. Магнитный элемент в этом случае реализует
конъюнкцию п переменных.
Такие магнитные усилители являются бесконтактны-
бесконтактными аналогами многообмоточного электромеханического
реле.
Магнитные усилители описанных типов могут соби-
собираться в сети, образуя, в частности, любые однотактные
релейные схемы. При этом выходы усилителей подклю-
подключаются ко входам одного или нескольких усилителей.
В связи с тем, что мы располагаем магнитными элемен-
элементами, реализующими опе-
операции отрицания, конъ-
конъюнкции и дизъюнкции,
можно, подобно тому как
это делалось на электро-
электромеханических реле, соби-
собирать их в схемы, реали-
реализующие любые логические
функции.
д) Схемы
на пневмореле
Схема пневмореле
представлена на рис.
2.20, а; на рис. 2.20,6 да-
даны принятые для такого
реле условные обозначе-
обозначения. В пневмореле имеют-
имеются четыре камеры: Ki, Kz,
/Сз. /С4; между камерами
расположены три мем-
мембраны М\, Мг, Мз, объединенные общим штоком Ш в
мембранный блок. К камерам /Ci и /С2 по каналам Л\ и Л2
подводятся управляющие давления Ра и Р^; камера /Сз
осевым каналом С3 сообщается с питающей магистралью,
а камера /С4 каналом </74 сообщается с атмосферой. Осе-
Осевой канал С4, ведущий в камеру /С4, и канал Л3 камеры
/Сз объединяются внешней коммуникацией (линией об-
Рис. 2.20.
§2.4] МЕТОДЫ РЕАЛИЗАЦИИ ЛОГИЧЕСКИХ ФУНКЦИЙ 73
ратной связи ОС), в которой устанавливается выходное,
давление Р.
Мембранный блок, если он находится в крайнем
верхнем положении, верхним торцом штока перекрывает
канал С3 и одновременно нижним торцом штока откры-
открывает канал С4; при этом на выходе элемента в линии ОС
нет избыточного давления. Если же мембранный блок
занимает крайнее нижнее положение, то он перекрывает
канал С4 и открывает канал С3, а это приводит к уста-
установлению на выходе давления, равного давлению в ли-
линии питания.
Положение мембранного блока зависит от направле-
направления усилия, действующего на его шток, а величина и
I Раит I
f I
p
Prm
0
1
1
t
1 ., A
1
1
i
i
i
¦
Л - '
P "*H
1
|
Рис. 2.21. Рис. 2.22.
направление этого усилия определяются значениями да-
давлений в камерах К\, Кг и Кг, т. е. давлениями Ра, Р&
и Р. Обратное воздействие выходного давления Р на
положение мембранного блока обусловливает положи-
положительную обратную связь.
Характеристика пневмореле, отражающая отмечен-
отмеченные его свойства, изображена на рис. 2.21.
Рассмотрим работу этого реле в условиях, когда к
камере /G подводится некоторое постоянное давление
Ръ = Рп\ (так называемый подпор, или смещение). При
этом характеристика реле ¦» координатах Р, Ра — Рб
остается, естественно, той же, но в координатах Р, Ра
(рис. 2.22) она, сохраняя свой вид, оказывается тем бо-
более смещенной вправо, чем больше величина подпора
(смещения),
74
ПРИЛОЖЕНИЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЯ
[ГЛ. II
Устройство с такой характеристикой можно приме-
применять для реализации логической операции «повторение».
Для этого нужно привести в соответствие давлению,
большему чем Рпь символ 1, а давлению, меньшему чем
{Рщ — АР), — символ 0. Давление Рпит Должно превы-
превышать Рпи Применяя введен-
введенные на рис. 2.20 условные
обозначения, реле, реализу-
реализующее операцию «повторе-
«повторение», изображено на
рис. 2.23; на этой схеме двой-
двойной штриховкой отмечена
камера, в которой поддер-
поддерживается давление Рщ (пер-
(первый подпор).
Пневмореле может быть
Рис. 2.23. использовано также и для
реализации операции «отри-
«отрицание». В этом случае подводится некоторое постоянное
давление РП2 к камере/Ci. Характеристика, соответствую-
соответствующая этой схеме включения пневмореле, приведена на
рис. 2.24. Условное изображение схемы дано на рис. 2.25;
p,
nm
V
1
1
1
1
1
Pn2
i
1
1
f
r ^~]
1
Pm
Ртт P(
Рис. 2.24.
у*
Рис. 2.25.
на этой схеме камера, в которой поддерживается неиз-
неизменное давление Рпг, отличное от Pni, отмечена одинар-
одинарной штриховкой. Величины подпора Pni и РП2 отличаются
друг от друга из-за того, что Pni определяет положение
правой, а. РП2 — соответственно левой вертикальных линий
гистерезисной петли. В схеме, изображенной на рис. 2.25,
§2.4]
МЕТОДЫ РЕАЛИЗАЦИИ ЛОГИЧЕСКИХ ФУНКЦИЙ
fs
действительно реализуется отрицание, так как ' при
Рб > Рп2 + АР, когда мы будем считать, что независимая
логическая переменная Pi = 1, выходной сигнал прини-
принимает значение 0, а при Рб < РП2, когда Р\ — 0, давление
на выходе Р = Равт, и зна-
значит, выходной сигнал ра-
равен 1.
Мы показали реали^
зацию логических функ-
функций одной независимой 0i_
переменной. Покажем те- xt
перь, как с помощью этого
же реле реализуются ло-
логические функции двух и
более независимых пере-
переменных.
На схеме рис. 2.26 ка- Рис 2.26.
нал, ранее сообщавшийся
с линией питания (рис. 2.23), теперь включен в линию
второй независимой переменной Рг. Элемент, включен-
включенный по такой схеме, реализует конъюнкцию двух неза-
независимых переменных. Действительно, здесь в выходной
*л*
щ
ш
Рис. 2.27.
линии будет избыточное давление тогда и только тогда,
когда оба входных сигнала имеют значения 1.
Цепочка из (п—1)-го элемента, собранная по схеме
рис. 2.27, реализует конъюнкцию п независимых пере-
переменных.
76
ПРИЛОЖЕНИЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ
[гл. и
На рис. 2.28 дана схема реализации дизъюнкции
двух независимых переменных, а схема на рис. 2.29, со-
содержащая цепочку из (п—1)-го пневмореле, реализует
дизъюнкцию п независимых
переменных.
Итак, имея пневматиче-
пневматические средства для реализа-
реализации логических операций от-
отрицания, конъюнкции и
дизъюнкции, мы можем
строить схемы, реализующие
любые логические функции.
Здесь также можно приме-
применить канонический способ
реализации заданной логи-
логической функции; как уже не-
Рис. 2.28.
однократно отмечалось, этот
способ основан на представлении заданной функции в со-
совершенной нормальной дизъюнктивной форме. Но так же,
как и ранее, этот универсальный способ дает схемы не
экономные по числу элементов. В этом можно убедиться
X,
ш
Рис. 2.29.
хотя бы потому, что рассмотренное пневмореле можно
применить не только как элемент отрицания, повторе-
повторения, конъюнкции и дизъюнкции двух независимых пере-
переменных, но еще и как элемент импликации (рис. 2.30)
или как элемент запрета (рис. 2.31). Указанный способ
включения реле позволяет получить импликацию с по-
помощью одного элемента, между тем канонический спо-
i 2.51
ПРОБЛЕМА МИНИМИЗАЦИИ УСТРОЙСТВ
П
соб, в соответствии с которым импликацию нужно пред-
представлять через отрицание, конъюнкцию и дизъюнкцию,
Рис. 2.31.
Рис. 2.32.
потребовал бы применения двух элементов. Это следует
ИЗ формулы D_D^D_i
Схема, реализующая импликацию каноническим спо-
способом, показана на рис. 2.32. Эта схема эквивалентна
элементу, изображенному на рис. 2.30.
§ 2.5. Проблема минимизации устройств, реализующих
логические функции*)
При построении устройств, реализующих заданные
функции, естественно возникает следующая задача: за-
задан некоторый набор блоков (элементов), реализующих
*) Настоящий параграф по просьбе авторов иаписаи В. Д. К а-
з а к о в ы м.
78 ПРИЛОЖЕНИЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ ?ГЛ. 11
элементарные логические функции; с блоком каждого
типа связано определенное положительное число, кото-
которое называют ценой (это может быть буквально цена
или какой-нибудь условный коэффициент), и задана реа-
реализуемая функция (например, в совершенной нормаль-
нормальной дизъюнктивной форме); среди схем, реализующих
заданную функцию и составленных из элементов дан-
данного набора, требуется указать схему, для которой бу-
будет наименьшей общая цена, определяемая как
г
р = 2 a.thlt
где аг- — число элементов определенного вида, hi — цена
одного элемента, а г—число различных элементов в на-
наборе.
Проблема эта — ее часто называют проблемой мини-
минимизации— является центральной для технических при-
приложений исчисления высказываний и ей посвящено боль-
большое число работ.
Предложены многочисленные алгоритмы частичного
решения этой задачи.
Все эти алгоритмы включают в себя более или ме-
менее сложные переборы (т. е. пересмотры различных
вариантов). Однако до сих пор не существует удобных
для практического использования методов минимиза-
минимизации, а разработаны лишь отдельные «тропинки», дви-
двигаясь по которым можно надеяться получить более или
менее экономичные схемы.
Для того чтобы хотя бы в самых общих чертах со-
составить представление о научной постановке этой про-
проблемы и об объеме возникающих при ее решении труд-
трудностей, мы приведем краткое изложение (опуская все
подробности) одного из алгоритмов частичного реше-
решения задачи минимизации.
Предположим, что логическая функция F задана в
совершенной нормальной дизъюнктивной форме. Если
набор блоков состоит из элементов И, ИЛИ и НЕ
(как И, так и ИЛИ имеют по два входа), а цены эле-
элементов равны, то задача минимизации сводится к отыс-
отысканию такого аналитического выражения этой функции,
§ 2.5] ПРОБЛЕМА МИНИМИЗАЦИИ УСТРОЙСТВ 79
которое содержит только знаки , &, V и общее число
этих знаков минимально.
Опишем метод Квайна [214] для решения этой задачи.
Последовательность операций в этом методе такова.
Проводятся все возможные сокращения членов совер-
совершенной формы путем использования тождества
(А&.х)\/(А&.х) = А, B.1)
где А может быть конъюнкцией нескольких переменных.
Затем эта же операция проделывается по отношению ко
всем конъюнкциям, полученным в результате первого
сокращения и т. д. до тех пор, пока дальнейшее сокра-
сокращение станет невозможным. Пары конъюнкций (из чис-
числа членов совершенной формы и полученных в резуль-
результате сокращений), к которым упрощающее тождество
B.1) нельзя применить, называются простыми импли-
кантами F. Квайном доказано, что любое минимальное
дизъюнктивное нормальное выражение F есть дизъюнк-
дизъюнкция некоторых простых импликатов F. Поэтому следую-
следующим этапом нахождения минимальных выражений F яв-
является определение комбинаций простых импликантов,
дизъюнкции которых давали бы минимальные выраже-
выражения. Для этого с помощью некоторых искусственных
приемов (см. [185]) строятся такие комбинации простых
импликантов F, дизъюнкция которых эквивалентна F и
удаление из дизъюнкции хотя бы одного простого им-
пликанта нарушило бы условие эквивалентности F. Та-
Такие дизъюнкции называются «тупиковыми» выражения-
выражениями F. Затем в каждом из_тупиковых выражении подсчи-
тывается число знаков , &, V и отбираются те из
них, у которых суммарное число этих знаков наимень-
наименьшее. Эти выражения и являются минимальными (при
принятом критерии минимальности).
Приведем пример. Пусть задана булева функция
F (xv хь х3) — (хх & х2 & хг) Vi*i & х2 & х3) V
\г(хх & .«г & xz) VUi & х\ & х3) Vfo & Xj &
В результате всех возможных попарных сокращений
членов совершенной формы (причем каждый из членов
80 ПРИЛОЖЕНИЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИИ [ГЛ. II
дизъюнктивной формы может входить более чем в одну
пару) получаем конъюнкции
х^Хз, х1&х2, х2&х3, х2&х3,
не допускающие дальнейших сокращений. Они же яв-
являются единственными конъюнкциями, не давшими ни
одного последующего сокращения. Значит все они — про-
простые импликанты F. Хотя дизъюнкция всех простых им-
импликантов эквивалентна F, непосредственной проверкой
можно установить, что вычеркивание конъюнкции *i&x3
не нарушает условия эквивалентности и нельзя вычерк-
вычеркнуть никакую конъюнкцию из числа оставшихся, не на-
нарушив эквивалентности. Следовательно,
2 & х3) V (х2 & х3)
— одно из тупиковых выражений. Можно показать так-
также, что
(х, & х3) V (х2 & х3) V (х2 & х3)
тоже тупиковое выражение. Других тупиковых выраже-
выражений у этой функции нет. Сравнение полученных тупико-
тупиковых выражений показывает, что оба они имеют одина-
одинаковое число знаков , &, V. и, следовательно, в рав-
равной степени минимальны.
Мы показали здесь на примере применение алгоритма
Квайна. В настоящее время известны десятки алгорит-
алгоритмов отыскания простых импликантов логических функций.
Некоторые из них более удобны для ручных вычисле-
вычислений, другие —для вычислений на цифровых универсаль-
универсальных машинах, третьи используются главным образом
при теоретических исследованиях, связанных с вопро-
вопросами минимизации. Различны и способы минимизации:
с этой целью пользуются специальными диаграммами
[180], построениями на n-мерных кубах [33], цифровыми
вычислениями [161], [127] и т. д.
Для построения минимальных нормальных выраже-
выражений из простых импликантов также известно несколько
алгоритмов (см., например, [33]). Поскольку нахожде-
нахождение минимальных нормальных выражений логических
функций уже сравнительно небольшого числа перемен'
§2.5] ПРОБЛЕМА МИНИМИЗАЦИИ УСТРОЙСТВ 81
ных (например, шести или семи)—весьма трудоемкий
процесс, разработан ряд упрощенных алгоритмов, по-
позволяющих получить нормальные выражения, близкие
к минимальным [216—218].
Алгоритм Квайна позволяет получать минимальные
дизъюнктивные нормальные выражения заданных функ-
функций. Однако в ряде случаев минимальные конъюнктив-
конъюнктивные нормальные выражения оказываются «меньше»
дизъюнктивных. Поэтому для получения минимальных
нормальных выражений необходимо получить как дизъ-
дизъюнктивные, так и конъюнктивные нормальные выраже-
выражения и выбрать из них наименьшие. Методы получения
минимальных конъюнктивных нормальных выражений
двойственны методам получения минимальных дизъюнк-
дизъюнктивных выражений, и поэтому мы не будем на них
останавливаться.
Получение минимального нормального выражения
некоторой функции еще не означает, что нельзя для этой
же функции найти еще более минимальное выражение.
Например, минимальное дизъюнктивное нормальное вы-
выражение некоторой функции
F(xu ..., x6) = (x2&x3&xi&x6)V(xl&x2&x5)V
V (*i & х2 & х6) V (*i & х3 & х4 & х5) B.2)
имеет 13 знаков & и V> минимальное конъюнктивное
нормальное выражение этой же функции
F(xu ..., x6) = (xl&Xj)V{Jc1&x\)V{x2&Xj)V{^2&xA)V_
V (Jc, & х2) V (Jc, & х6) V (х2 & х5) V (Зс5 & х6)
имеет 8 + 7 + 16 = 31 знак , &, V, следовательно,
B.2) есть минимальное нормальное выражение. Тем не
менее выражение этой же функции
= [хг8сх2&(х5 V *вI V{*з&*4&[(-«i&xs)V(x2&x6)]} B.3)
содержит всего 9 знаков & и Л/.
В данном случае мы получили сокращение мини-
минимального нормального выражения на основе тождества
{А&В) V (Л&С) = А&(В V С). Однако имеются функ-
функции, у которых максимальное применение распредели-
6 М. А. Айзерман, Л. А. Гусев и др.
82 ПРИЛОЖЕНИЯ ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИИ [ГЛ. II
тельного закона к минимальным нормальным выраже-
выражениям все же не дает для этой функции действительно
минимального выражения. Например, та же функция
B.2) имеет еще более минимальное выражение
F(xv ..., х6) = [(*,&х2)V(*3&xj\&[(*,&x5)V(x2&х6)],
которое можно получить из B.3), представив первый
член дизъюнкции в более развернутом виде
хг & х2 & (х5 V х6) = хг&х2& [(X! & х5) V(x2 & х6)],
а затем воспользоваться распределительным законом.
Разумеется, другие функции допускают другие со-
сокращения на основе иных тождеств, и определить, ка-
какое именно тождество нужно выбрать для сокращения
некоторого выражения (и возможно ли вообще сокра-
сокращение), представляет весьма сложную задачу.
В связи с этим была поставлена задача ^разработки
алгоритма, позволяющего находить такие выражения
заданной функции, о которых можно было бы с уверен-
уверенностью сказать, что не существует других выражений
этой же функции, минимальнее найденных [120, 121].
Такие выражения были названы абсолютно минималь-
минимальными. Алгоритмы получения абсолютно минимальных
выражений во много раз сложнее алгоритмов получе-
получения минимальных нормальных выражений, поэтому мы
не будем их здесь подробно излагать, ограничимся
лишь указанием, что каждый нетривиальный алгоритм
должен включать два момента:
1) установление границ максимальной сложности
абсолютно минимальных выражений заданной функции;
2) определение абсолютно минимальных выражений
заданной функции в границах найденной максимальной
сложности.
Например, можно установить, что функция B.2) не
может иметь минимальных выражений вида более
сложного, чем «дизъюнкция конъюнкций дизъюнкций» и
«конъюнкция дизъюнкций конъюнкций». Затем с по-
помощью специальных алгоритмов строятся некоторые вы-
выражения этой функции, подобные тупиковым, вида «дизъ-
«дизъюнкция конъюнкций дизъюнкций» и «конъюнкция дизъ-
дизъюнкций конъюнкций» и отбираются из них минималь-
§ 2.5] ПРОБЛЕМА МИНИМИЗАЦИИ УСТРОЙСТВ 83
ные. В данном случае ими будут два выражения вида
«дизъюнкция конъюнкций дизъюнкций»
F (хи ..., х6) = \х3 & (хг V *2)] V (х2 & *3).
F(xlf..., x6) = \x2&(x
и одно «вырожденное» выражение вида «конъюнкция
ДИЗЪЮНКЦИЙ КОНЪЮНКЦИЙ»
F(xv ..., х6) = (хгVx2V*3)&(-*2 V*3)-
Процесс определения абсолютно минимальных выра-
выражений имеет много общего с процессом получения ми-
минимальных нормальных выражений. Однако число вы-
выражений, сходных с тупиковыми, необычайно велико
даже у функции небольшого числа переменных, что де-
делает алгоритмы получения абсолютно минимальных
выражений практически неприемлемыми. В связи с этим
были разработаны алгоритмы с существенно меньшим
числом элементарных операций, дающие в результате
выражения более сложного вида, чем нормальные и,
следовательно, в общем случае более близкие к абсо-
абсолютно минимальным. В частности, можно построить
алгоритм, состоящий в последовательном применении
распределительного закона к простым импликантам за-
заданной функции. Получившиеся в результате импли-
канты сложного вида можно рассматривать как обыч-
обычные простые импликанты и строить из них тупиковые
выражения, а из тупиковых обычным путем выбирать
минимальные.
Но даже и в том случае, когда известно абсолютно
минимальное выражение заданной функции, соответ-
соответствующая схема, построенная на ее основе, может ока-
оказаться не минимальной.
Например, имея абсолютно минимальное выражение
функции
¦= x3 & |х5& (*! V*2) V(*2 & *4I V
}, B.4)
можно сразу же построить схему из десяти элементов.
Тем не менее схему, реализующую эту же функцию,
можно построить и на восьми элементах (рис. 2.33).
84
приложения исчисления высказываний
[гл. и
Это объясняется тем, что при синтезе устройств мы
можем в некоторых случаях использовать одну и ту же
часть структуры для реализации различных частей ми-
минимального выражения. Так, в нашем случае мы пред-
представили выражение B.4) в виде
F = {х3 & [(х5 & *,) V (х5 & х2) V (х2 & х4)]} V {х6 & [(х, & х5) V
V(x2&x4)}} = {x3&\QV(x5&x2)]}V(x6&Q)
где
B.5)
и, строя его, дважды использовали одну и ту же реали-
реализацию B.5).
В этом кратком обзоре мы бегло рассматривали за-
задачу минимизации лишь для условий, когда все элемен-
Рис. 2.33.
ты имеют одинаковую цену. Показано, однако [217], что
решение аналогичной задачи с фиксированными разными
ценами можно получить некоторыми видоизменениями
тех же приемов. Единственное отличие состоит в том,
что в этом случае используется иной критерий мини-
минимальности при отборе минимальных выражений из чи-
числа тупиковых. Мы упоминали лишь о задаче миними-
минимизации применительно к набору, состоящему из элемен-
элементов НЕ, И и ИЛИ, причем последние два имеют только
по два входа.
Аналогичные задачи рассматривались и для других
наборов, однако каждый новый набор требует решения
задачи заново.
§2.5] ПРОБЛЕМА МИНИМИЗАЦИИ УСТРОЙСТВ $5
Так, если набор состоит из элементов отрицания, а
также конъюнкции и дизъюнкции п переменных, то за-
задача сводится к отысканию таких тупиковых выражений
(или выражений, подобным тупиковым, если речь идет
о выражениях сложного вида), в которых число простых
импликантов было бы наименьшим.
Особое значение в последнее время приобретает за-
задача минимизации, когда имеются универсальные эле-
элементы, т. е. такие элементы, которые путем простой пе-
переналадки или за счет добавления не имеющих цены
внешних коммуникаций могут применяться для реали-
реализации нескольких различных функций. Типичным при-
примером элементов такого рода является описанное ранее
пневматическое реле (см. рис. 2.20).
Применительно к таким системам задачи минимиза-
минимизации остаются пока еще совсем не решенными, несмотря
па многочисленные попытки. В связи с этим примени-
применительно к таким, да и к более простым наборам разраба-
разрабатываются методы построения не минимальных, а доста-
достаточно минимизированных схем.
ГЛАВА III
ОБЩИЕ ПОНЯТИЯ О КОНЕЧНЫХ АВТОМАТАХ
И ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИНАХ
§ 3.1. Дискретное время и такты
Пусть {x}i (/=1, 2, ..., п) и {у} — алфавиты,со-
алфавиты,содержащие некоторое конечное число символов.
Тогда функциональная зависимость
У =/(*i> х2, ..., хп) C.1)
ставит в соответствие любой совокупности символов,
взятых по одному из алфавитов [x}v {x}2, ¦•-, {х}„, сим-
символ из алфавита {«/}.
Рассмотрим теперь воображаемое идеальное устрой-
устройство, реализующее функциональную зависимость C.1).
Это устройство имеет п входов и один выход. К входам
хи х2, ..., хп строго одновременно подводятся символы
из алфавитов {х}1г {х}2, ..., {х}„ соответственно. В это
же мгновение на выходе появляется символ из алфа-
алфавита {у} в соответствии с равенством C.1). Такое мгно-
мгновенно действующее идеальное устройство назовем функ-
функциональным преобразователем. В частном случае, когда
каждый из алфавитов {х}и {х}2, ..-, {х}„ и {у} содер-
содержит только по два символа, т. е. когда Х\, х2, ..., хп и
у — логические переменные, a f — логическая функция,
устройство будет называться логическим преобразова-
преобразователем.
Однотактные релейно-контактные схемы и другие
технические средства, реализующие операции исчисле-
исчисления высказываний и описанные в гл. II, если считать их
мгновенно действующими, являются техническими при-
§ 3.1] ДИСКРЕТНОЕ ВРЕМЯ И ТАКТЫ 87
мерами реализации абстрактного понятия «логический
преобразователь».
До сих пор в гл. I и II, говоря о функциональных
зависимостях, мы не вводили в рассмотрение время. По-
Поэтому и функциональный преобразователь мы предпо-
предполагали мгновенно действующим. Теперь нам предстоит
ввести в рассмотрение время.
Обычно, говоря о времени, мы предполагаем, что оно
изменяется только в одном направлении («в будущее»)
и пробегает непрерывно все возможные значения на чис-
числовой полуоси. Иными словами, время как аргумент под
знаком функции задается обычно на континууме. Этим
континуумом и служит числовая полуось (ось времени).
В отличие от этого привычного рассмотрения вре-
времени, при изучении устройств дискретного действия
1 1 1 1 ь ! 1 *•
Рис. 3.1.
удобно вводить в рассмотрение воображаемое дискрет-
дискретное время. Представим себе, что непрерывная числовая
полуось времени разбита каким-либо образом на беско-
бесконечное число конечных интервалов, не обязательно
равных между собой (рис. 3.1). Двигаясь вдоль оси от
t = 0 к t = оо, обозначим точки, разделяющие интер-
интервалы, буквами t0, tu t2, ... Эти точки образуют счетное
множество.
Условимся далее вместо t0, t\, t2, ... писать просто
ряд неотрицательных целых чисел 0, 1, 2, ... и назы-
называть дискретным временем t воображаемое время, кото-
которое принимает последовательно лишь эти целочислен-
целочисленные значения.
Моменты времени U, t\, t2, ..., обозначенные теперь
числами 0, 1, 2, ..., будем "называть тактами, а числа
О, 1, 2, ... будем рассматривать как символы, образую-
образующие алфавит {t}.
Текущий такт, т. е. такт, соответствующий настоя-
настоящему моменту, обозначим буквой р (present).. Тогда
88 ОБШИЕ ПОНЯТИЯ О КОНЕЧНЫХ АВТОМАТАХ [ГЛ. III
символы t делятся тактом р на предыдущие (р—1,
р — 2,...) и последующие (р + 1, р + 2,...) (рис. 3.2).
До сих пор, говоря о равенстве C.1), мы считали,
что переменные фиксированы. Предположим теперь, что
символы, соответствующие переменным Х\, лг2, ..., хп,
меняются в дискретном времени. Иначе говоря, в каж-
каждый такт t = 0, 1, 2, ... заданы определенные значения
р-3 р-г р-l р р*1 р*2 ,р*3 t
Рис. 3.2.
переменных и тем самым определены функции Xi(t), за-
заданные на натуральном ряде чисел t = 0, 1,2, ... и при-
принимающие значения из алфавитов [x\t (i=\, 2, ... п).
Согласно C.1) им тогда ставится в соответствие функция
y@=/I*i@. *2@. ..., *„(<)], C.2)
также заданная на натуральном ряде чисел и прини-
принимающая значения из алфавита {«/}. Система такого рода
работает в дискретном времени, но «не имеет памяти»
в том смысле, что значения «выхода» у в любой момент
t = р зависят только от значений «входов» х\ в этот же
момент t = р.
Можно, однако, представить себе системы, которые
также работают в дискретном времени и координаты
(входы и выходы) которых принимают значения симво-
символов из конечных алфавитов, но у которых осуществляет-
осуществляется более сложная зависимость между значениями вход-
входных и выходных координат. Пусть, например,
У (Р) =/[*! (Р — 1), х2 (р — 1), ..., х„ (р — 1);
Xiip), x2(p), .... х„(р)]. C.3)
Иначе говоря, символ у в любом такте t = p зависит не
только от значения всех Х{ в этот же момент р, но и от
их значений в предыдущий момент р—1. Более того,
значение координаты у в момент р может быть функ-
функцией от значений у в предыдущие такты.
Рассмотрим в качестве примера случай, когда у—ло-
у—логическая переменная и значения ее в любой момент р
§3.2] О ДИНАМИЧЕСКИХ СИСТЕМАХ 89
определяются как отрицание значения у в предыдущий
момент р— 1
У (/>) = У (/>-!)• C-4)
Хотя соотношение
У=У
противоречиво, равенство C.4) не приводит к противо-
противоречиям и определяет функцию y(t), которая принимает
последовательно значения 1 и 0, несмотря на то, что от-
отсутствуют какие-либо входные (внешние) воздействия.
По существу, устройства такого рода — своеобразные
динамические системы, но они отличаются от обычно
рассматриваемых динамических систем (например, ма-
маятника или электрического четырехполюсника) тем, что
работают в дискретном времени, и их координаты за-
заданы на конечных, множествах.
В дальнейшем нам предстоит все время иметь дело
со своеобразными динамическими системами, которые
отличаются этими двумя особенностями. Для того чтобы
яснее представить себе их место среди динамических
систем иного вида, мы в следующем параграфе подроб-
подробнее остановимся на этом вопросе.
§ 3.2. О динамических системах
Термином динамическая система обозначают обычно
системы в технике, природе, жизни и т. д., в которых
процессы развиваются во времени. Состояние динамиче-
динамической системы в каждый момент характеризуют некото-
некоторым числом (конечным или бесконечным) обобщенных
координат.
Процессы в динамической системе характеризуются
изменением обобщенных координат во времени и опи-
описываются уравнениями разных типов.
Динамические системы можно подразделять на не-
несколько классов в зависимости от следующих факторов:
а) от того, считается ли время текущим непрерывно
или дискретно, т. е. изменяется на континууме или на
счетном множестве;
90 ОБЩИЕ ПОНЯТИЯ О КОНЕЧНЫХ АВТОМАТАХ (ГЛ. lit
б) от того, имеет ли система конечное или бесконеч-
бесконечное число обобщенных координат, и, наконец,
в) от мощности множества возможных значений каж-
каждой из обобщенных координат, т. е. от того, являются
ли эти множества конечными, бесконечными счетными
или же континуальными.
С понятием «динамическая система» мы связываем
чаще всего системы, описываемые обыкновенными диффе-
дифференциальными уравнениями или уравнениями в частных
производных. В системах такого рода число обобщен-
обобщенных координат конечно (обыкновенные дифференциаль-
дифференциальные уравнения) или бесконечно (уравнения в частных
производных), но как координаты, так и время изме-
изменяются на континуумах.
В тех случаях, когда время дискретно, т. е. изме-
изменяется на счетном множестве, а каждая из конечного
или бесконечного числа обобщенных координат может
принимать значения из континуальных множеств, пове-
поведение системы описывается разностными уравнениями.
Особый класс динамических систем образуют систе-
системы, у которых время дискретно, т. е изменяется на счет-
счетном множестве, а обобщенные координаты (число их
может быть конечно или бееконечно) изменяются на ко-
конечных множествах.
Всякая динамическая система может быть подвер-
подвержена внешним воздействиям. Эти воздействия также
могут быть заданы на континууме, счетном множестве
или на конечном множестве. В динамических системах,
описываемых дифференциальными или разностными
уравнениями, обычно рассматривается конечное число
внешних воздействий, которые могут принимать любые
значения из некоторого континуума. При рассмотрении
же динамических систем, обобщенные координаты кото-
которых задаются на конечных множествах, естественно
считать, что число внешних возмущений конечно и что
каждое из них также задано на конечном множестве.
Динамические системы такого рода (время задается
на счетном множестве; координаты и внешние воздей-
воздействия задаются на конечных множествах; число внеш-
внешних воздействий и координат конечно) условимся назы-
называть конечными динамическими системами.
§ 3.3] КОНЕЧНЫЕ АВТОМАТЫ 0.1
Именно к динамическим системам такого класса при-
принадлежат конечные автоматы и последовательностные
машины, рассмотрению которых посвящена эта и по-
последующие главы.
Системы, которые отличаются от конечных лишь тем,
что число обобщенных координат может быть бесконеч-
бесконечным, составляют более общий класс динамических си-
систем. К нему принадлежат, в частности, машины Тью-
Тьюринга *) и иные аналогичные идеализированные устрой-
устройства.
Уравнения любых видов описывают не реальную си-
систему, а ее идеализированную модель. В этом смысле
динамическая система любого типа — абстракция, кото-
которой более или менее адекватны те или иные физические
процессы или технические устройства. Конечные дина-
динамические системы и системы типа машины Тьюринга —
не более чем абстракции, но абстракции эти интересны
потому, что им адекватны мног.ие технические устрой-;
ства и важные процессы в природе и в жизни.
§ 3.3. Конечные автоматы
Рассмотрим конечную динамическую систему, состоя-
состояние которой в каждый момент характеризуется конеч-
конечным числом обобщенных координат *а, *2» •¦••> **»• Си-
Система подвержена внешним воздействиям Pi{t), рг(О>---
•••» Рт@» число которых конечно. Задана шкала вре-
времени, разбитая на такты, либо заданы условия, позво-
позволяющие определить момент наступления очередного
такта. Внешние воздействия и состояния системы рас-
рассматриваются лишь в эти моменты (такты).
В рассматриваемые моменты каждая из обобщенных
координат щ может принимать значения лишь из конеч-
конечного множества, а каждый вход р, также принимает
значения лишь из своего конечного множества.
Введем в рассмотрение n-мерный вектор у, с коорди-
координатами хи х2, • • •, *п и m-мерный вектор р с координа-
координатами pi, р2, .... рт. В связи с тем, что все координаты
*) См. гл. XIII.
92 ОБЩИЕ ПОНЯТИЯ О КОНЕЧНЫХ АВТОМАТАХ [ГЛ. Ш
вектора х, т. е. xi, Хг хп заданы на конечных мно-
множествах, вектор х также задан на конечном множестве.
Если координата х, может принимать ?,- значений, то
вектор х может принимать одно из ?=Г1Л значений.
Соответственно множество, на котором задан х, состоит
из k элементов.
Совершенно аналогично вектор р с координатами
рь р2, • • •. рт задается на конечном множестве, содер-
т
жащем г элементов, где /- = JJ Tjy» a ~Ц]— число элемен-
элементов множества, на котором задана pj.
Рассмотрим какой-либо алфавит {х} = {xi, X2 ха},
состоящий из k символов, и припишем различным воз-
возможным значениям вектора х различные символы из
этого алфавита. Вектор х назовем состоянием изучаемой
конечной динамической системы.
Аналогично введем в рассмотрение алфавит
{р} = (Pi- P2 Рг},
состоящий из г символов, и припишем различным значе-
значениям вектора р различные символы из этого алфавита.
Вектор р назовем входом'ъ изучаемую конечную систему.
Теперь надо определить «движение» в рассматривае-
рассматриваемой системе, т. е. указать, как определяется состояние
системы в каждый такт. Очень важный случай такого
определения и приводит нас к понятию конечный ав-
автомат.
Определение. Конечная динамическая система
называется конечным автоматом, если состояние систе-
системы в каждый такт однозначно определяется: а) состоя-
состоянием системы в предыдущий такт и б) входом в преды-
предыдущий или в рассматриваемый такт.
Конечные автоматы, состояние которых определяется
их состоянием в предыдущий такт и входом в предыду-
предыдущий такт, назовем конечными автоматами типа П — П
(«предыдущее—предыдущее»). Автоматы же, состояние
которых определяется их состоянием в предыдущий такт
и входом в рассматриваемый такт, назовем конечными
автоматами типа П — Н («предыдущее — настоящее»).
§ 3.3) КОНЕЧНЫЕ АВТОМАТЫ 93
Далее будет показано, что термин «конечный авто-
автомат» охватывает и те конечные системы, состояние ко-
которых определяется их состояниями и входами за лю-
любое наперед заданное конечное число предыдущих так-
тактов. Термин конечный автомат не охватывает такие
конечные динамические системы, состояние которых оп-
определяется статистически или для определения состоя-
состояния которых важна вся история системы, т. е. необходимо
знание состояний и входов во все предыдущие такты.
В соответствии с определением конечного автомата
символ х, соответствующий любому такту, однозначно
определяется символом х в предыдущий такт и симво-
символами р в предыдущий или в рассматриваемый такт, т. е.
для конечного автомата типа П — П
%p+1 = F{*p, р"), Р = 0, 1, 2, ..., C.5')
а для конечного автомата типа П — Н
**+1 = F(xp, p*+1), р = о, 1, 2, ..., C.5")
где F — функция в том смысле, в каком этот термин был
разъяснен в гл. I. Она ставит символ из алфавита {х}
в соответствие символам из алфавитов {х} и {р}. Но в от-
отличие от того, что имелось в виду в гл. I, здесь уже сим-
символы-аргументы и символ-функция относятся также и
к разным моментам времени. Поэтому формулы C.5)
определяют не преобразователь, а динамическую си-
систему.
Моменты времени, к которым относятся символы х
и р, обозначены верхними индексами и соответствуют
текущим тактам: р — настоящему, р + 1 — последую-
последующему, ар — 1 — предшествующему.
Если ввести в рассмотрение символ ц, заданный на
том же алфавите {х} = {хь хг хл}, что и символ х,
то соотношения C.5') и C.5") можно рассматривать
как следствие соотношений
В первом соотношении C.6) все символы относятся к
одному и тому же моменту времени. Если отнести их
94 ОБЩИЕ ПОНЯТИЯ О КОНЕЧНЫХ АВТОМАТАХ [ГЛ. III
к моменту р, т. е. записать
и добавить второе соотношение C.6), исключив затем
JJ.P, то получим
%p+i = F(xp,pp),
т. е. соотношение C.5').
Если же отнести первое соотношение C.6) к моменту
р + 1, т. е. записать
и добавить второе соотношение C.6), исключив уже
%р + 1, то получим
т. е. соотношение вида C.5").
Рассмотрим формулу C.5'):
*P+l = F(%p, рР).
Зная р° и х° в нулевой такт, можно, положив р = 1,
найти х'. Далее, зная х1 и р1, найти х2 и т. д. Анало-
Аналогично определяются х1, х2, ... по заданному х° и по за-
заданной входной последовательности р1, р2, ... с по-
помощью формулы C.5"). В этом смысле формулы- C.5)
определяют рекуррентные соотношения, позволяющие
последовательно найти все состояния х1, х2 если
известно начальное состояние х° и входная последова-
последовательность р°, р1, р2, ...
Из определения следует, что при рассмотрении ко-
конечного автомата значения символов х и р существенны
лишь в моменты тактов. Поэтому иные моменты вре-
времени — промежутки между тактами — несущественны,
так же как и поведение рассматриваемой системы ме-
между тактами.
Если иметь в виду реальную динамическую систему
или реально протекающий процесс, то удобно предста-
представить себе, что существует устройство, которое фикси-
фиксирует значения х и р в моменты тактов*), и вопрос о
•) Или стробоскопическое устройство, освещающее наблюдае-
наблюдаемый процесс лишь в эти моменты.
5 з.3| КОНЕЧНЫЕ АВТОМАТЫ 95
принадлежности наблюдаемой системы к классу конеч-
конечных автоматов решается только по этой записи. В этом
смысле абстракция «конечный автомат» может быть ис-
использована и для описания непрерывных устройств, у
которых возможен континуум состояний, изменяющихся
в непрерывно текущем времени,— важно лишь, чтобы
в рассматриваемые дискретные моменты времени мно-
множество возможных состояний было конечным и чтобы
удовлетворялось одно из соотношений C.5). Так, на-
например, непрерывная система, имеющая несколько рав-
равновесных состояний, может рассматриваться как конеч-
конечный автомат, если моментами наступления тактов счи-
считать моменты, когда установилось равновесие, и если
выбор равновесного состояния каждый раз однозначно
определяется тем, в каком из равновесных состояний
находилась система ранее и каковы воздействия на си-
систему в моменты нарушения (или в моменты достиже-
достижения) равновесия.
В связи с тем, что любая реальная система работает
в непрерывном времени, введение в рассмотрение дис-
дискретного времени определяет необходимость в специаль-
специальном устройстве — датчике тактов, который сигнализи-
сигнализирует о наступлении очередного такта. Такой датчик тактов
мы будем называть дискретными часами (или просто
часами).
Часы не являются частью конечного автомата. Их
сигналы — внешние для автомата в такой же мере, как
и воздействия р. Но вместе с тем сигналы от часов — вре-
временной вход — отличны и от внешних входных воздей-
воздействий, так как они не шифруются символами из алфа-
алфавита {р} и не являются аргументами функции F в соотно^-
шениях C.5). В тех случаях, когда конечным автоматом
является какой-либо наблюдаемый процесс, сигналы от
часов используются лишь в устройстве, которое фикси-
фиксирует р и у, в моменты тактов. При технической реализа-
реализации конечного автомата сигналы от часов могут использо-
использоваться лишь для определения момента наступления такта.
Приведем примеры условий, определяющих разбие*
ние шкалы непрерывного времени на такты:
а) Такты наступают через равные промежутки ере*
мени. В этом случае шкала непрерывного времени
96 Общие Понятия о Конечных автоматах (гл. ш
разбита на такты равномерно и датчиком тактов могут
служить часы в обычном смысле с соответствующим об-
образом отрегулированным ходом. Тактность такого рода
будем называть равномерной.
б) Такт наступает всякий раз, когда меняется сим-
символ р, т. е. когда происходит какое-либо изменение во
входном воздействии. В этом случае шкала непрерыв-
непрерывного времени разбивается на такты, вообще говоря, не-
неравномерно. Часами может служить устройство, реаги-
реагирующее на изменение входного воздействия.
в) Такт наступает всякий раз, когда на входе появ-
появляется символ р* или pj.
г) Такт наступает, когда символ р с нечетным индек-
индексом заменяется символом р с четным индексом и т. п.
Вернемся к формулам C.5), но предположим теперь,
что входной символ р не изменяется. Тогда эти формулы
обращаются в
*'+i = FK, p.], C.7)
где р* — фиксированное неизменное значение р.
Конечный автомат такого рода будем называть авто-
автономным. Разумеется, такой автомат автономен от внеш-
внешних воздействий в обычном смысле, но сигналы от часов
о наступлении такта по-прежнему в нем используются.
Символ р = р* можно рассматривать как символ-па-
символ-параметр. Фиксировать можно любой символ из алфа-
алфавита {р}. Фиксируя разные символы из {р}, получаем г
автономных автоматов. В этом смысле каждый конеч-
конечный автомат может быть превращен в г автономных
автоматов (некоторые из этих г автономных автоматов
могут совпадать).
В заключение этого параграфа заметим, что, отвле-
отвлекаясь от содержательной стороны введенного выше по-
понятия «конечный автомат» (связанной с понятиями «ко-
«конечная динамическая система», «состояние» и «вход»),
можно это же определение понимать формально следую-
следующим образом: даны два конечных алфавита символов
{к} и {р} и переменные к и р, принимающие значения
из этих алфавитов. Конечным автоматом называются
рекуррентные соотношения C.5), связывающие эти пере-
переменные. Разумеется так определенный конечный авто-
§ 3.4)
ПОСЛЕДОВАТЁЛЬНОСТНЫЕ МАШИНЫ
97
мат — далеко идущая абстракция. Значение ее в науке
состоит в том, что, с одной стороны, многие важные
технические устройства и наблюдаемые процессы в при-
приемлемой идеализации охватываются этой абстракцией,
с другой же стороны, самые различные процессы и уст-
устройства, которым адекватна эта абстракция, управ-
управляются общими законами, которые могут изучаться с
самых общих позиций. Задача теории конечных автома-
автоматов—установить общие законы, свойственные явлениям,
процессам, системам или устройствам такого рода.
§ 3.4. Последовательностные машины
Рассмотрим систему (рис. 3.3), состоящую из: а) ко-
конечного автомата А, преобразующего символы р из ал-
алфавита {р} в символы х из алфавита {х} в соответствии
с соотношением C.50 или C.5"), с некоторой заданной
А
X
Ф
Рис. 3.3.
функцией F в правой части и б) преобразователя Ф, ко-
который мгновенно и однозначно ставит в соответствие
каждому символу х символ Я, из некоторого алфавита {Я,}:
Х" = Ф(ч"). C.8)
Символы р и Я, появляются в моменты тактов автома-
автомата. Если можно подобрать какую-либо однозначную
функцию F* (она может отличаться от функции F) так,
чтобы появляющиеся символы Я, удовлетворяли соотно-
соотношению вида C.5') или C.5"), с функцией F* в правой
части, т. е. чтобы
\P+i = F*[kP, РР\ или \P+i = F*[k", p"+1], C.9)
то рассматриваемая система, состоящая из автомата А
и преобразователя Ф, в целом вновь составит конечный
7 М. А. Айзерман Л. А. Гусев и др.
98 общие понятия о конечных автоматах П*л, ш
автомат. Такую функцию F*, разумеется, можно подо-
подобрать далеко не всегда. Ведь алфавит {%} может отли-
отличаться от алфавита {х} даже числом символов, т. е. не-
несколько разных символов х могут шифроваться одним
и тем же символом X.
Пусть, например, алфавит {%} содержит восемь сим-
символов, а алфавит {к} — два символа, и преобразователь
Ф выдает символ К\ при подводе одного из символов
Xi— щ или А,2 при %ь — ив. Рассмотрим соотношение
C.5'). Пусть функция F в его правой части такова, что
после рр = pi, %р = %\ появляется символ хр+1 = Хз, а по-
после рр = рь %р = щ появляется символ хр+1 = Хб. В пер-
первом случае считывающее устройство зафиксирует
а во втором случае
Таким образом, после одинаковых Хр и рр могут по-
появиться разные Xp + i. Но это значит, что система, со-
состоящая из автомата и преобразователя, в целом авто-
автоматом не является, так как по отношению к символам
Я, и р заведомо не существует соотношения вида C.5').
Однако система, представленная на рис 3.3, также
является конечной динамической системой. Мы будем
называть ее конечным автоматом с выходным преобра-
преобразователем или просто конечным автоматом с выходом.
Символы Я называются в этом случае выходными сим-
символами (в отличие от х — символов состояния), алфавит
{X} — выходным алфавитом, а преобразователь Ф — вы-
выходным преобразователем.
В более общем случае можно считать, что преобра-
преобразователь символов Ф имеет два входа и что к нему под-
подводятся не только символы х, но и символы р, и что он
мгновенно ставит в соответствие каждой паре символов
(х, р) символ Я, (рис. 3.4). Конечные динамические си-
системы, получающиеся соединением конечного автомата
и выходного преобразователя символов, на вход кото-
которого подводится также и р (рис. 3.4), называются после-
довательностными машинами (или сокращенно П-маши-
нами). Разумеется, при этом вся Я-машина в каждом'
§3.4]
ПОСЛЕДОВАТЕЛЬНОСТНЫЕ МАШИНЫ
99
частном случае может быть или не быть конечным авто-
автоматом. Это зависит от вида функции F в соотношениях
C.5) для автомата Л и от выбора преобразователя Ф.
Но в любом случае система, показанная на рис. 3.4, от-
относится к классу конечных динамических систем.
Последовательностная машина становится конечным
автоматом (работает как конечный автомат), если зна-
значения к на выходе однозначно определяются значением Я
f
A
x
—?-*¦
ф
Рис. 3.4.
в предыдущий такт и значением р в этот же такт,
т. е. существует зависимость
Так будет, например, всегда, когда используются тож-
тождественный преобразователь, у которого алфавит {X} со-
совпадает с алфавитом {х}, т. е. который выдает символ №,
совпадающий с подведенным символом у? независимо
от рР. В этом смысле абстракция «последовательност-
«последовательностная машина» содержит абстракцию «конечный автомат>
как частный случай.
Конечный автомат с выходным преобразователем мо-
можно рассматривать как частный случай /7-машины, у ко-
которой функция Ф не зависит от р.
На первый взгляд кажется, что абстракция «после-
«последовательностная машина» шире понятия «конечный ав-
автомат с выходом», но это нб* так. Теоремы, устанавли-
устанавливающие это, мы приведем позже, после того как будет
сформулировано понятие «сеть» (см. § 4.3).
Условимся называть последовательностную машину
машиной типа П — П или типа П — Н в зависимости от
того, какого типа автомат она содержит.
100 ОБЩИЕ ПОНЯТИЯ О КОНЕЧНЫХ АВТОМАТАХ [ГЛ ИГ
Рассмотрим произвольную последовательностную ма-
машину типа П — Н:
%p+i = F[%Pt pP+i], х" = Ф[ч", Рр]. C.10)
Исключая из уравнения преобразователя символ кр, по-
получаем
Введем в рассмотрение символ х, заданный на алфавите
{у) соотношением
После замены получим
\р = Ф \F&, ?Р), ?Р] = Ф* (**, РР).
Используя символ к в уравнении C.10) автомата,
получаем
;p+i = JFp, ppj;
т. е. в совокупности получается Я-машина типа П — П *)
**+i = F0?, р"), I" = Ф*(*р, р"). C.11)
Таким образом, любая Я-машина типа П — Н только
сменой выходного преобразователя Ф на Ф* может быть
превращена в Я-машину типа П — П. Обратное утвер-
утверждение, в общем случае, неверно. Мы вернемся к нему
позже, в § 5.4, после того как будут рассмотрены раз-
различные способы задания автомата и Я-машины и будет
введено понятие «сеть».
§ 3.5. Методы задания конечного автомата
и последовательностной машины
Любая функция
z = F(x, у),
где х и у принимают значения из конечных множеств,
может быть задана таблицей (табл. 3.1), в которую впи-
вписаны соответствующие значения г.
*) Конечный автомат с выходным преобразователем, описывае-
описываемый выражениями C.5') и C.8), в литературе часто называется ма-
машиной Мура (см. [72]), а Я-машина, которая определяется выраже-
выражениями C.11), — машиной Мили (см, [190]).
§3.5] МЕТОДЫ ЗАДАНИЯ КОНЕЧНОГО АВТОМАТА Щ
Уравнение конечного автомата типа П — П
или типа П — Н
также может быть представлено аналогичной таблицей
(табл. 3.2).
Таблица 3.1
Таблица 3.2
х \ч
•*1
х2
хп
У\
гг
гъ
Уг
гъ
...
...
...
Ут .
*в
*г
*з
\Р
*р\
*i
х2
Ч
Pi
*з
*i
Р2
*2
*б
*4
...
...
...
...
Рг
*1
ч
В каждую клетку табл. 3.2 вписываются символы
хр + 1, если строка соответствует символу ир, а столбец —
символу рр в автомате типа П — П (или рР + | в авто-
автомате типа П — Н). Такую таблицу будем называть да-
далее основной таблицей конечного автомата.
Каждый столбец основной таблицы конечного авто-
автомата сам является основной таблицей автономного ав-
автомата, который получается из заданного, если «закре-
«закрепить» соответствующее этому столбцу значение р.
Рассмотрим какой-либо один такой автономный ав-
автомат (например, табл. 3.3).
Если на плоскости изобразить k кружков, приписать
каждому кружку символ % и провести стрелки, изобра-
изображающие переходы в соответствии с основной таблицей
автономного автомата, то получим его граф. От каж-
каждого кружка графа может отходить лишь одна стрелка.
102
ОБЩИЕ ПОНЯТИЯ О КОНЕЧНЫХ АВТОМАТАХ
[ГЛ. Ш
Цодхвдить же к каждому кружку может любое число
«грелок, не превышающее k. Граф автономного авто-
автомата, показанный на рис. 3.5,
соответствует табл. 3.3. Из конеч-
конечного автомата можно построить
г автономных автоматов.и соот-
соответственно по основной таблице
конечного автомата можно опре-
определить г графов этих автоном-
автономных автоматов. На рис. 3.6
они показаны для случая
табл. 3.4.
Все эти г графов имеют оди-
одинаковое число k кружков и могут
быть теперь объединены в один
граф, если над каждой стрелкой
надписью указать значение р,
при котором эта стрелка реали-
реализуется. Надпись проставляется
у начала стрелки при автомате типа П — Пну конца
стрелки при автомате типа П — Н. На рис. 3.7 показан
Таблица 3.3 . Таблица 3.4
Рис. 3.5.
"Х р
X ^*ч_
*1
X,
*3
*4
*s
Ч
Р; = Р*
*2
*б
*3
*2
*4
*4
*|
х2
*3
*4
*5
*б
Pi
*4
*з
*з
*в
Xj
Рз
*б
*4
*3
х2
Ч
Ч
Рз
*4
х2
*5
*1
*3
( 3.5]
МЕТОДЫ ЗАДАНИЯ КОНЕЧНОГО АВТОМАТА
103
такой объединенный граф для рассмотренного выше
примера (табл. 3.4, рис. 3.6) автомата типа П — Н.
Рис. 3.6.
Рис. 3.7.
Такой объединенный граф назовем диаграммой со-
состояний конечного автомата. Из каждого кружка диа-
диаграммы состояний должна выходить уже не одна, а г
стрелок. Если несколько из них ведут к одному а тону
104 ОБЩИЕ ПОНЯТИЯ О КОНЕЧНЫХ АВТОМАТАХ [ГЛ. III
же кружку, то их можно объединить в одну стрелку, а
надписи, указывающие значения р, объединить знаком
дизъюнкции.
Диаграмма состояний полностью эквивалентна ос-
основной таблице и также задает конечный автомат. По
диаграмме состояний немедленно восстанавливается
основная таблица и тип автомата.
Составим квадратную k X k матрицу С. Припишем
ее строкам сверху вниз и столбцам слева направо сим-
символы кь кг, ..., Kft. Элементом матрицы, стоящим на
пересечении строки щ и столбца к5, служит надпись на
стрелке, которая на диаграмме состояний ведет из кру-
кружка к, в кружок Kg. Этим элементом может быть один
символ р или дизъюнкция нескольких р. Если кружок
кг на диаграмме состояний не соединен стрелкой с круж-
кружком Km, то в соответствующую клетку матрицы С впи-
вписываем 0.
В качестве примера приведем матрицу (табл. 3.5),
соответствующую диаграмме состояний, построенной на
рис. 3.7.
Таблица 3.5
о о о о р, p2vp3
0 0 0 P1VP2VP3 0 0
0 рз PiVp2 0 0 0
0 р2 р, 0 Рз 0
Рз 0 0 0 Рг Pi
0 р, рз 0 р2 . 0
Матрицу такого рода называют матрицей соедине-
соединений. Она служит еще одной формой задания конечного
автомата. Подобно заданию автомата с помощью основ-
основной таблицы, и в этом случае должно быть отдельно ого-
оговорено, рассматривается ли автомат типа П — П или
П —Н.
В каждой строке матрицы соединений обязательно
содержится любое из рг-, и при этом только один раз.
Матрица соединений может быть выписана по основной
таблице, минуя составление диаграммы состояний.
§ 3.5] МЕТОДЫ ЗАДАНИЯ КОНЕЧНОГО АВТОМАТА 105
Пусть задана основная таблица для автомата типа
П — П, т. е. для соотношения
Каждая клетка основной таблицы определяет тройку
символов
у,р йр %р+\
т. е. символ строки, символ столбца и символ, вписан-
вписанный в клетку. Назовем такую тройку символов триадой.
Каждая клетка основной таблицы определяет одну три-
триаду, а вся таблица содержит rk клеток, т. е. множество
из rk триад. Произвольное множество триад назовем
упорядоченным, если у любых двух триад из этого мно-
множества не совпадают первые два символа (ир и рр).
Любая основная таблица конечного автомата определяет
упорядоченное конечное множество триад. Наоборот,
любое упорядоченное множество из rk триад определяет
основную таблицу, т. е. задает конечный автомат.
Все изложенное распространяется и на автоматы
типа П — Н, т. е. на автоматы, задаваемые соотноше-
соотношением
xp+1 = F[*p, pp+1\.
Но в этом случае триаду образует тройка символов
и упорядоченным называется множество, не содержа-
содержащее двух триад с одинаковыми первыми двумя симво-
символами у? и рр + 1.
Переходя к заданию последовательностной машины,
приходится совместно рассматривать одно из уравнений
C.5) автомата и уравнение C.8) преобразователя. Воз-
Возвращаясь к основной таблице конечного автомата, впи-
впишем в каждую клетку не один символ, как ранее, а два:
символ хр + 1 и, в соответствии с уравнением преобразо-
преобразователя, символ № + 1. Если рассматривается автомат ти-
типа П— П (уравнение C.5')), то в каждую клетку, кроме
символа хр + 1, вписывается символ №, т. е. попросту
106
ОБЩИЕ ПОНЯТИЯ О КОНЕЧНЫХ АВТОМАТАХ (ГЛ. III
преобразователя вписывается в основную таб-
таблицу автомата. Такую объединенную таблицу автомата
и преобразрвателя назовем основной таблицей П-ма-
шины.
Так, например, если автомат типа П — П задан
табл. 3.4, а преобразователь — табл. 3.6, то основная
таблица Я-машины имеет вид табл. 3.7.
Таблица 3.6
^\ p
X \.
4
¦4
4
4
4
4
-та
x,
h
x,
Аз
I
3
P2
X2
X2
x,
X,
x,
h
Рз
Хз
Хз
Аз
Аг
Х2
>
Таблица 3.7
X >v
*i
*2
*3
Ч
ч
Ч
-та
Хд, Л]
х„Х2
хз< X]
*з,Аз
Ч, h
х2, Х3
Р2
*б. Х2
,.х2
ч, х,
*6,Хз
Рз
х6,Х3
.,Хз
Ч. Х3
Ч, h
ч, х.
Если же рассматривается автомат типа П — Н (ура-
(уравнение C.5")), то в каждую клетку вписывается символ
№ + 1, соответствующий по таблице преобразователя
символу хр + |, стоящему в этой клетке, и символу рр + |
эхогв же втвлбца. В рассмотренном примере (автомат —
>»бл. 3.4, преобразователь — табл. 3.6) основная табли-
таблица Я-машины имеет вид табл. 3.8 (стр. 108).
Заметим, что в случае автомата П—Н могут быть
заполненными не все клетки таблицы преобразователя:
в каждом столбце таблицы преобразователя заполнены
лишь клетки, соответствующие таким х, которые содер-
§3.5]
МЕТОДЫ ЗАДАНИЯ КОНЕЧНОГО АВТОМАТА
107
жатся в том же столбце таблицы автомата. Гак,
например, в столбце pi автомата табл. 3.4 не встречается
Рис. 3.8.
символ иь Поэтому в таблице преобра&ователя клетка
(pi, xi) могла бы вообще быть не заполненной.
Рис. 3.9.
При наличии выходного преобразователя на диаграм-
диаграмме состояний в каждом кружке, кроме надписи х, должен
юч
ОБЩИЕ ПОНЯТИЯ О КОНЕЧНЫХ АВТОМАТАХ
(ГЛ. III
быть надписан символ к в соответствии с таблицей
преобразователя. В /7-машине символ Я определяется не
только символом х, но и р. Поэтому диаграмма состоя-
состояний Я-машины отличается от диаграммы состояний ко-
конечного автомата с преобразователем тем, что символ к
вписывается не в кружке, а рядом с символом р
над стрелкой. Стрелка ведет от состояния хр к со-
состоянию хр + 1. При
Таблица 3.8 автомате типа П—П
(уравнение C.5')) пара
символов (р, к) над-
надписывается у начала
стрелки (вблизи круж-
кружка х? —рис. 3.8,a), a
при автомате типа
П —Н (уравнение
C,5")) — у конца
стрелки (вблизи круж-
кружка иР + 1 —рис. 3.8,6).
В первом случае сим-
символ к определяется из
таблицы выходного
преобразователя по
символу р, надписан-
надписанному над стрелкой, и
символу х, надписан-
надписанному в кружке, из ко-
которого выходит стрел-
стрелка; во втором же слу-
случае— по символу р над стрелкой и символу х в кружке,
к которому подходит стрелка.
На рис. 3.9 в качестве примера показана диаграмма
состояний, построенная по табл. 3.8.
По диаграмме состояний последовательностной ма-
машины может быть немедленно построена матрица соеди-
соединений. Она отличается от матрицы соединений конеч-
конечного автомата тем, что элементами ее служат надписи
над стрелками диаграммы состояний, т. е. пары симво-
символов (р, к). Для табл. 3.8 (см. диаграмму состояний
рис. 3.9) матрица соединений имеет вид, показанный
в табл. 3.9.
Ч
ч
*4
х.
Ч
Pi
*,А,
'4. А3
Ч.Ь
,8>А3
Х2, А2
Р2
*в. А3
Х4, Л|
„А,
,2,А2
*5. А|
Рз
»«. А,
*4. А2
7 2, А3
*5> А2
*„Аз
§3.5] " ' МЕТОДЫ ЗАДАНИЯ КОНЕЧНОГО АВТОМАТ^
со
so о о о "а о
g f f * * *
110 ОБЩИЕ ПОНЯТИЯ О КОНЕЧНЫХ АВТОМАТАХ (ГЛ. Ш
§ 3.6. Методы записи работы автомата
Символы р последовательно «сообщаются» автомату
(или Я-машине) извне и не зависят от его работы. Авто-
Автомат (или Я-машина) перерабатывает символы р в сим-
символы х (или X).
Назовем входной последовательностью любую сово-
совокупность, состоящую из конечного (но сколь угодно
большого) числа символов р, следующих подряд друг
за другом, а последовательностью состояний (соответ-
(соответственно выходной последовательностью) — аналогичную
совокупность символов х или X. Длиной последователь-
последовательности назовем число содержащихся в ней символов.
Как автомат, так и последовательностная машина
являются операторами, перерабатывающими последова-
последовательности входных символов из одного алфавита в по-
последовательности выходных символов из другого алфа-
алфавита. Описанные в предыдущем параграфе основная та-
таблица, множество триад, графы, диаграмма состояний,
матрица соединений и таблица переходов — суть различ-
различные способы задания такого оператора, так как любой
из них достаточен для того, чтобы, зная последователь-
последовательность р и начальное состояние х°, восстановить соответ-
соответствующую последовательность х (или X).
Рассмотрим теперь таблицу, состоящую из трех строк
(номер такта, символ р и символ х) и содержащую
сколь угодно большое число столбцов (табл. 3.10).
Таблица 3.10
Такт
Р
X
0
Рз
х,
1
Рз
*2
2
Pi
3
Рз
*,
4
Р4
*2
5
Рб
*12
6
Р2
7
Рз
8 ...
Pl2 j •••
Во вторую и третью строки вписываются символы р
и х, соответствующие такту, указанному в первой строке.
Таблицу такого рода назовем лентой конечного авто-
автомата.
§3.6] МЕТОДЫ Э'АПИСИ РАБОТЫ АВТОМАТА Ш
Для каждой входной последовательности p(t) может
быть составлена своя лента. Поэтому для автомата, за-
заданного, например, одной основной таблицей, может
быть составлено неограниченное число лент.
Любой начальный кусок ленты (от нулевого до про-
произвольного, &-го такта) содержит некоторую входную
последовательность и соответствующую ей последова-
последовательность состояний длины k + 1.
В любом месте любой ленты какого-либо автомата
выделим три символа так, как это показано в табл. 3.10
жирной линией, если этот автомат типа П — П, либо
пунктиром, если этот автомат типа П — Н. Ясно, что
выделенная так тройка символов является триадой и
определяет одну'клетку основной таблицы автомата.
Представим теперь себе, что вдоль ленты переме-
перемещается движок, имеющий фигурную прорезь, соответ-
соответствующую жирной линии или пунктиру табл. 3.10. Пере-
Перемещая этот движок вдоль всей ленты, выпишем подряд
все видимые сквозь него различные триады (ясно, что
число их для каждой ленты конечно). Допустим далее,
что мы могли бы поступить таким же образом со всеми
лентами данного автомата (число их уже бесконечно).
Мы выписали бы тогда множество всех триад, содержа-
содержащихся во всех лентах. Но так как все эти ленты обра-
образованы одним автоматом, все триады принадлежат ко-
конечному (содержащему rk элементов) упорядоченному
множеству триад рассматриваемого автомата.
В предыдущем параграфе мы показали, что автомат
как оператор может быть задан конечным упорядочен-
упорядоченным множеством триад. Мы видим теперь, что все лен-
ленты автомата составлены из триад этого же множества.
Выберем теперь какой-либо алфавит из rk символов,
например {-:}, и припишем символы -: всем триадам рас-
рассматриваемого автомата. Тогда лента может содержать
лишь две строки: номер такта и символ -: (табл. 3.11).
Однако в этой ленте после какой-либо триады, на-
например после -се, может следовать не любая из триад
этого же множества, а лишь «избранные». Действитель-
Действительно, пусть триадой -с5 служит
*7> Рз» *!?•
112
ОБЩИЕ ПОНЯТИЯ О КОНЕЧНЫХ АВТОМАТАХ
[ГЛ. Ш
Тогда в следующей триаде первый символ предопреде-
предопределен, а два других символа могут быть любыми, т. е. сле-
следующей триадой может быть лишь триада из этого же
множества, у которой первым символом является И12,
например Xi2, ре, хе или И12, P2, з<12 и т. д.
Такт
X
0
ч
1
Х1
2
Ч
3
Табл
4
Ч
5
ица
6
ч
3.11
...
...
Для каждой триады г,- назовем соответствующими
такие триады из рассматриваемого упорядоченного мно-
множества, у которых первый символ совпадает с послед-
последним символом рассматриваемой триады t;-. Все ленты
конечного автомата состоят из его триад, размещенных
так, что за каждой триадой следует любая из соответ-
соответствующих ей.
Для последовательностной машины также может
быть введено понятие ленты, если дополнить ленту ко-
конечного автомата строкой выходных символов Я, а за-
затем строку символов х зачеркнуть (табл. 3.12).
Таблица 3.1
Такт
t
А
0
Рз
А2
1
Ре
Аз
2
=•
Аз
3
Рз
А2
4
Р9
А,
5
Ре
А,
6
Рт
А,
7
Ps
А2
8
Р|2
Аз
...
...
...
Полученная таким образом лента (табл. 3.12) также
может быть «расщеплена» на триады типа
X", рР, X"+i или X', pp+l, Xp+K
Но среди этих триад уже могут встречаться «противо-
«противоречивые» триады, у которых после одинаковых первых
§3.6]
МЕТОДЫ ЗАПИСИ РАБОТЫ АВТОМАТА
113
двух символов ~кр, рр (или \р, рр+1) следуют разные
третьи символы Яр + 1, т. е. множество триад последова-
тельностной машины не упорядочено. Это множество
триад становится упорядоченным тогда и только тогда,
когда последовательностная машина в целом является
конечным автоматом.
Рассмотрим еще один способ записи работы конеч-
конечного автомата. Вернемся к диаграмме состояний конеч-
конечного автомата (рис. 3.7) и рассмотрим на этой диаграм-
диаграмме два кружка. Один из них соответствует символу х,-,
а второй — щ. На рис. 3.10
показана для примера часть
диаграммы состояний, со-
содержащая рассматриваемые
кружки х,- и xj и, кроме
того, еще три кружка х&, xs
Рис. 3.10.
и щ. Из состояния щ мо-
можно перейти в состояние щ
за один такт, если символ
на входе pi. Для того чтобы
перейти из х* в щ за два
такта, имеются следующие
возможности: во время пер-
первого такта должно быть рг
либо рз, а во время второго такта — рг, либо во время
обоих тактов должно быть pi. Но чтобы перейти из Xi в
щ за три такта, можно указать уже девять различных
возможностей (табл. 3.13).
Совершенно аналогично можно выписать все возмож-
возможные последовательности р, которые переводят состояние
х, в xj за q тактов. Назовем любую из этих последова-
последовательностей путем, длины q or Xi к щ. Условимся записы-
записывать каждый путь длины q от х* к щ в форме после-
последовательности из q символов р, а совокупность всех
возможных путей — дизъюнкцией таких последова-
последовательностей. Так, например,^ табл. 3.13 может быть
записана в форме
PiPiPi V Р1Р3Р1V Р2Р1Р2 V Р2Р3Р2 V Р3Р1Р2 V Р3Р3Р2 V Р1Р2Р1V Р2Р2Р1 V Р3Р2Р1
Обозначим О*1] дизъюнкцию, соответствующую всем
возможным путям длины q от х,- к Xj. Каждая, иа
М, А, Айзерман, Л. А. Гусев н др.
114
ОБЩИЕ ПОНЯТИЯ О КОНЕЧНЫХ АВТОМАТАХ
[ГЛ. III
дизъюнкций Djj содержит одну или несколько последо-
последовательностей. Каждай из последовательностей имеет ровно
q элементов р,-, среди которых могут быть и одинаковые.
Таблица 3.13
Путь
Первый ....
0
Pi
Второй pi
Третий . . . . •
Четвертый • ¦ ¦
Пятый
1
Шестой ....
Седьмой ....
Рг
н
н
ь
*
Восьмой .... pj
Девятый ....
ь
Такт
1
Pi
Рз
Pi
Рз
Pi
Рз
Рг
Рг
Рг
2
Pi
Pi
Рг
Рг
Рг
Рг
Pi
Pi
Pi
Составим матрицу №> так, что элементом матрицы,
стоящим на перекрестке i-й строки и у-го столбца,
служит Etfj, если есть хоть один путь длины q из и,- в Xj,
и нуль, если такого пути нет. Например,
Ч
'ЕЮ О
О О
о
о
О D®
о
0 0
Назовем №> матрицей путей длины q. Как и в матрице
соединений, строки этой матрицы (сверху вниз) и столбцы
(слева направо) соответствуют символам xi, хг, ..., х».
Эти символы записаны слева и над матрицей
§ 3.6] методы адписи работы автомата 115
Матрица №> содержит все пути, ведущие от любого
начального состояния к любому конечному состоянию
(оно может совпадать с начальным) за q тактов. В свя-
связи с тем, что любая последовательность из q символов
р переводит автомат из любого состояния в то же или
иное состояние, в каждой строке матрицы №> содер-
содержатся, и притом по одному разу, все возможные после-
последовательности, которые можно составить из алфавита
{р}, выбирая каждый раз по q символов. Так, например,
каждая строка матрицы О2' обязательно содержит по-
последовательности
PiPp РгРг! РзРз* Р1Р2» P2P1» Р1Р3' РзРр РзРг* РгРз-
В каждой строке матрицы №> эти группы из q симво-
символов могут быть различным образом собраны в дизъюнк-
дизъюнкции и расположены в разных столбцах. В каждом кон-
конкретном случае это определяется лишь основной табли-
таблицей рассматриваемого автомата.
Множество матриц С*1', С<2>, С<3>, ... полностью опре-
определяет работу автомата за любое число тактов. Однако
такая запись работы автомата бесполезна главным об-
образом потому, что существует простой алгоритм, позво-
позволяющий определить все это множество матриц через
исходную матрицу — матрицу соединений.
Заметим прежде всего, что СО) = С, т. е. что матрица
путей длины 1 совпадает с матрицей соединений, ибо
ее элементами, по определению, служат значения р, пе-
переводящие за один такт щ в kj.
Теперь возведем матрицу соединений в квадрат, т. е.
умножим ее саму на себя по следующим правилам:
1. Элемент Qj матрицы-произведения, стоящий на
пересечении i-й строки и /-го столбца, определяется по
общим правилам перемножения матриц как сумма про-
произведений элементов i-й строки первого сомножителя
на соответствующие элементы /-го столбца второго со-
сомножителя. При этом произведения не перестановочны,
т. е. при перемножении элементов сомножители не могут
меняться местами.
2. Знаки сложения всюду меняются на знаки дизъ-
дизъюнкций.
Пб
ОБЩИЕ ПОНЯТИЯ О КОНЕЧНЫХ АВТОМАТАХ
[ГЛ. Ш
3. Знаки умножения определяют операцию приписы-
приписывания символов р.
В качестве примера вернемся к матрице С, выписан-
выписанной в предыдущем параграфе для диаграммы состояний
ч
ч
¦ о
о
о
о
Рз
О
ч
о
о
Рз
Ps
О
О
О
PiVPs
Pi
О
Рз
О
PiVp2VP3
О
о
о
о
ч
Pi
о
о
Рз
?2
?2
ч
РаУРз
О
о
о
Pi
о
рис. 3.7, и возведем ее в квадрат по указанным пра-
правилам:
ч
'PiPs I P2P1 VPsPi I P2P3 VРзРз
0 PiPsVPsPsV PiPiVPsPiV 0 PiPsVpsPsV
Vp3ps VP3P1 VP3P3
0 P1P3VP2P3 P1P1VP2P1V P3P1VP3P2V O
VpiPsVPsPs \/рзРз
РзРз PiP3 PiPiVPips PsPiVPsPjV РзРа
О PiPsVPsPsV P1P1
О PiPaVPsPaV О
0
P3P1
РгРз PiPi
Р1Р3
P3P1VP3P2
VPiPs
' P2P2
P3P2VP3P3V
VPsPi
PsPi
xe РгРз РзРз рзк^кзрг PiPiVPiPsV
VP1P3
Непосредственно видно, что С2 = С&\ т. е. что эле-
элементами матрицы С2 служат все возможные пути, кото-
которые ведут от одного кружка к другому за два такта
в соответствии с диаграммой состояний рис. 3.7. Так, на-
например, элементом первой строки и второго столбца слу-
служит p2pi V РзРь Пути p2Pi и р3р1 ведут за два такта из х\
в з<2, и иных путей из %\ в Х2 нет (рис. 3.7).
Совпадение С2 с С<2) здесь не случайно. Если, напри-
например, в первой строке в шестом столбце вписан не нуле-
§ з.б] методы адписи работы автомата 117
вой элемент и если не нулевой элемент вписан во втором
столбце в шестой строке, то при возведении матрицы
в квадрат эти элементы перемножатся и будут вписаны
в первую строку второго столбца (соответствующие эле-
элементы обведены в матрицах Си С2). Но наличие таких
ненулевых элементов в С указывает на то, что из xi
можно за один такт попасть в Хб, а из %б за один такт —
в Х2, т. е. на существование путей, ведущих за два такта
ИЗ XI В Х2-
Таким образом, обнаруженное выше на примере со-
совпадение на самом деле представляет собой правило:
квадрат матрицы соединений есть матрица путей за два
такта: С2 = С<2>. Образуем теперь матрицу С3, т. е. ум-
умножим С2 на С. Совершенно аналогично убеждаемся,
что С3 = С<3), т. е. что куб матрицы соединений есть
матрица путей за три такта и что вообще матрица путей
за q тактов может быть получена возведением в степень
q матрицы соедин&ний
Таким образом, все возможные пути за любое число q
тактов могут быть восстановлены с помощью простой
операции — умножения матрицы соединений на себя.
Все сказанное о записи работы автомата с помощью
С'?'-матрицы и о том, что С(«> = Сч, полностью относится
и к последовательностным машинам. Надо лишь иметь
в виду, что каждая стрелка на диаграмме состояний
/7-машины несет два символа: р и К. В соответствии
с этим переход в /7-машинах характеризуется парой
(Pft, К) и «операция приписывания символов» произво-
производится по следующим правилам:
2. (Pft, XsH
Если требуется перемножить дизъюнкции пар, то надо
использовать дистрибутивность^ операции умножения
дизъюнкций, например:
V (р2, Х5)][(р8,
= (PlP8> X3Xl)V(P2P8» X5Xl)V(PlP5> Х3ХзМР2Р5> Х5Хз)«
щ
ОБЩИЕ ПОНЯТИЯ О КОНЕЧНЫХ АВТОМАТАХ
[ГЛ. tit
В качестве примера рассмотрим матрицу соединений
последовательностнои машины с тремя состояниями,
имеющей диаграмму состояний, показанную на рис. 3.11.
о (pi. x3)V(p2. xi) о
0 (р2, Х^ (puh
ЧР2. хз) (Pi. \г) О
В результате возведения этой матрицы в квадрат
н»лучаем
0
(P1P2.
<PlP2.
(P2P2.
V(p2pi,
(р2р„
(PlPl,
0 (p2Pl. Vs)V(p2P2. h4
V(pip2, *A)
Из самого построения матрицы С2 видно, что ее эле-
элемент С?,, стоящий на пересечении i-й строки и у-го
Рис. 3.11.
столбца, представляет собой перечисление всех входных
(и соответствующих выходных) последовательностей
длины 2, которые за два такта переводят i-e состояние
Я-машины в у-е состояние. Так, например, для Я-ма-
шины рис. 3.11 из третьего состояния во второе ведут
входные последовательности ргрь Р2Р2 и рфг. При этом
на выходе соответственно появляются последовательно-
последовательности Я3Я3, Я3Я1 и ЯгЯг-
Теперь матрица С2 вновь может быть умножена на
матрицу С по аналогичным правилам. Отличие от по-
построения матрицы С2 будет состоять только в том, что
§3.7] ОГРАНИЧЕНИЕ ВХОДНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 119
здесь нам придется производить операцию умножения
элементов, которые могут содержать уже не только пары
символов (ps, h), но и пары последовательностей симво-
символов типа (pipj, Khh). В этом случае под умножением
понимается операция приписывания символов, например:
(РзР5. V?) (Р4> Х2) = (РзРбР4> Х6ХЛ)-
При умножении элементов, содержащих дизъюнкции,
также используется дистрибутивный закон.
В нашем примере матрица С3 имеет вид
[(PiPsPs. MA)V(PsPsPs. biKh)\/ [(PiPsPi.
V(PsPiPs. ЫАз)] V(PiPiPi. *3*A)V(PsPiPi, МЛ)] V(PsPsPi,
(PsPiPs. MA) [(PiPsPi. Xi^3)V(PiPsPs. lWi)V [(PsPsPi.
v(PsPsPs, XsXA)V(PiPiPs, МЛ) V V(PipiPi,
V(PsPiPi- MAs)]
(PiPiPs. ^i^s) [(PsPiPs, ^3Ms)V(PsPsPs, MAs)V [(PsPiPi, X
V(PiPsPs. MA)V(PiPiPi. KhK)] V(psp2Pi,
Подобно тому как элементы матрицы С2 указывают
все возможные пути за два такта, ведущие из и» в щ,
элементы матрицы С3 указывают все входные последова-
последовательности, ведущие от одного состояния к другому за три
такта, и соответствующие выходные последовательности.
Продолжая процесс умножения матрицы С на себя,
получаем матрицу Сч и находим, таким образом, все
входные последовательности, переводящие состояние х»
в состояние щ да q тактов *).
§ 3.7. Замечание об ограничении входных
последовательностей
До сих пор мы предполагали, что последовательности
входных символов могут быть, произвольными, лишь бы
каждый из этих символов содержался в алфавите {р}.
*) В литературе встречаются и другие способы'задания работы
автомата, например, в работах Н. Е. Кобринского и Б. А. Трахтен-
брота [43] для этой цели используется «дерево» автомата. В на-
настоящей книге мы этим понятием не пользуемся.
120 ОБЩИЕ ПОНЯТИЯ О КОНЕЧНЫХ АВТОМАТАХ 1ГЛ. III
Если алфавит {р} содержит г символов, то может быть
составлено rh различных последовательностей длины k.
Часто возникают задачи, когда требуется рассматри-
рассматривать лишь последовательности символов, удовлетворяю-
удовлетворяющие каким-либо дополнительным условиям. Последова-
Последовательности, удовлетворяющие этим дополнительным усло-
условиям, назовем допустимыми.-
Примеры условий такого рода:
1. Допустимы лишь последовательности, в которых
четные и нечетные индексы у р чередуются.
Например, последовательность Р7Р2Р1Р4Р7Р6РЗ ... до-
допустима, а последовательность р7ргр4Р1Р7 • •• недопустима.
2. Допустимы лишь последовательности, в которых
два одинаковых символа р не следуют непосредствен-
непосредственно друг за другом. Например, последовательность
Р2Р7Р5РзрвР1 • • • допустима, а последовательность
Р2Р7Р5Р5рзрвР8 • • • недопустима.
3. Допустимы лишь последовательности, в которых
после pi не следует непосредственно pj и т. д.
Ограничение последовательностей часто предопреде-
предопределено особенностями разбиения оси непрерывного вре-
времени на такты. Так, например, в случае, когда такт на-
наступает всякий раз, когда происходит смена символа р,
возможные последовательности р(^) ограничены услп-
вием; два одинаковых символа не следуют непосред-
непосредственно друг за другом.
Совершенно аналогично обстоит дело и в любом ином
случае, когда тактность связана с каким-либо заранее
обусловленным «событием» на входе*). При такой такт-
ности допустимые входные последовательности всегда
ограничены.
Таким образом, ограничения на возможные входные
последовательности могут быть двух родов:
1. Они могут быть вынуждены особенностями такт-
ности — в этом случае могут возникать лишь допустимые
последовательности.
2. Они могут быть никак не связаны с тактностью,
т. е., вообще говоря, Я-машина могла бы реагировать
*) Мы употребляем здесь термин «событие», полагаясь лишь иа
интуицию читателя. К определению этого термина мы далее вернемся.
§ 3.7] ОГРАНИЧЕНИЕ ВХОДНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 121
на любые последовательности p(t), но, по условиям при-
применения, на входе Я-машины появляются лишь допусти-
допустимые последовательности.
Различие это несущественно для нас, но случаи, ко-
когда входные последовательности не произвольны, а удо-
удовлетворяют каким-либо дополнительным условиям, бу-
будет далее предметом отдельного рассмотрения. В таких
случаях основная таблица еще не задает автомата. По-
Подобно тому как она должна быть доопределена условия-
условиями наступления такта, в подобных случаях она должна
быть доопределена описанием того, какие входные по-
последовательности допустимы.
ГЛАВА IV
АБСТРАКТНАЯ СТРУКТУРА И СЕТЬ
§ 4.1. Общие понятия о замещении
последовательностных машин
Рассмотрим две последовательностные машины: ма-
машину П\ (рис. 4.1,а), преобразующую символы р из
алфавита {р} в символы и из алфавита {у), и машину П2
(рис. 4.1,6), преобразующую символы т) из алфавита {ц}
в символы ? из алфавита {?}. Рассмотрим также два
a)
л,
б)
L
T Пг 7
7 С
Г
1
<р
. X
Рис. 4.1.
Рис. 4.2.
произвольных функциональных преобразователя Ф\ и
Фг, реализующих функции
х=Ф8(С,Р).
Преобразователь G>i мгновенно и однозначно ставит в
соответствие паре символов ? и р из алфавита {?} и {р}
символ т) из алфавита (т)}; преобразователь Фг той же
паре символов ставит в соответствие символ к из алфа-
алфавита {х}.
Соединим преобразователи Ф[ и Ф2 с последователь-
ностной машиной Яг по схеме рис, 4.2, Полученная та-
§ 4.1] ЗАМЕЩЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН 133
ким способом система является новой Я-машиной, пере-
перерабатывающей последовательности из тех же алфави-
алфавитов, в которых работает машина П\.
Если машины П\ и Я2 заданы, то может оказаться
возможным подобрать функциональные преобразователи
<Di и Фг так, чтобы система, показанная на рис. 4.2, мог-
могла реализовать любой результат работы машины /7|.
Если это действительно так, то мы будем говорить, что
машина Пх замещается машиной Я2 или что машина Пг
замещает машину П\.
Для того чтобы строго определить эти термины, надо
уточнить, что, собственно, имеют в виду, когда говорят,
что некоторая система «реализует любой результат ра-
работы заданной Я-машины». Дадим точное определение
термину «замещение».
Условимся говорить, что машина Яг замещает ма-
машину П\, если можно так подобрать функциональные
преобразователи Ф\ и Ф2, что для каждого начального
состояния х° машины П\ найдется хотя бы одно началь-
начальное состояние ?° машины Я2 такое, что при любых вход-
входных последовательностях из алфавита {р} система, полу-
полученная путем соединения машины Яг и преобразовате-
преобразователей Ф\ и Ф2 по схеме рис. 4.2, отправляющаяся из ?°, и
машина Пи отправляющаяся из х°, выдадут одинаковые
выходные последовательности из алфавита {х}. Факт за-
замещения машины П\ машиной Я2 будем записывать так:
Если Я2=фЯ1, то это значит, что машина Я2 после вклю-
включения надлежащим образом подобранных преобразова-
преобразователей Ф1 и Ф2 может работать, как машина П\, заме-
заменить ее. В этом смысле схема, составленная в соответ-
соответствии с рис. 4.2, также является последовательностной
машиной.
Из факта П2=$Пи вообще говоря, не следует, что
^П2. В определении замещения существенно то, что
выбор преобразователей и начальных состояний не за-
зависит как-либо от того, какова входная последователь-
последовательность символов {р}. Можно было бы дать иное, более
широкое определение понятия замещения, связав выбор
преобразователей И начальных состояний с выбором
-124
АБСТРАКТНАЯ СТРУКТУРА И СЕТЬ
! -IV
входной последовательности. Такое расширение понятия
замещения нами не рассматривается, хотя и полезно
для некоторых задач.
Можно также ввести понятие относительного заме-
замещения Я-машин, если множество L допустимых входных
последовательностей машины Пх ограничено.
В связи с введением понятия замещения возникает
основная задача: по любым двум заданным Я-машинам
П\ и Я2 определить, замещает ли машина Я2 машину
Пи т. е. существуют ли функциональные преобразова-
преобразователи Ф! и Ф? такие, что
схема рис. 4.2 образует
х машину, замещающую
"*" машину Пи и в случае
положительного ответа
построить преобразовате-
преобразователи <Di и Ф2. Задача эта
имеет тривиальное реше-
решение: достаточно перепро-
перепробовать все пары функцио-
х нальных преобразовате-
преобразователей Ф, и Ф2, а их число
конечно. Если какая-либо
г
«j из этих пар «подойдет»,
то машина Я2 замещает
рис- 4-3- машину Пи Разумеется,
такой перебор громоздок
и для практического использования этот прием неприго-
непригоден. Однако авторы не знают более удобного алгоритма,
решающего основную задачу о замещении.
Далее вместо общей схемы, показанной на рис. 4.2,
мы будем рассматривать частные случаи этой схемы,
показанные на рис. 4.3. Основное значение для нас
играет схема, представленная на рис. 4.3,6. В этой схеме
оба преобразователя реализуют функции одной пере-
переменной
Ч = Ф,(р). * = Ф2(С).
В этом частном случае сформулированная выше
основная задача, кроме тривиального (полный перебор)
имеет еще и следующее решение; машина Я2 замещает
<S 4.1]
ЗАМЕЩЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН
125
машину Пи если диаграмма состояний машины П\ на-
накладывается на диаграмму состояний машины П2 {т. е.
является частью ее) и если при этом обеспечивается одно-
однозначность функций Ф\ (р) и Фг(?). Этот путь решения
задачи будет далее продемонстрирован на примере.
Аналогично замещению Д-машины введем понятие
о замещении конечных автоматов. Все определения при
этом сохраняются, но только вместо последовательно-
стных машин П\ и П2
рассматриваются два за- а)
данных конечных автома-
автомата А и В (рис. 4.4,а, б) и
имеется в виду лишь схе-
схема рис. 4.4,s, подобная Ю J Н В
схеме рис. 4.3, б.
Вводя понятие о заме-
замещении конечных автома-
автоматов и последовательное!-
ных машин, мы имели в р
виду неавтономные авто-
автоматы и машины. Эти оп-
определения относятся, ра-
разумеется, и к частному oj
случаю автономных авто- рис 4.4.
матов. Применительно к
автономному автомату определения упрощаются, так
как в этом случае уже не приходится рассматривать
входные последовательности символов, и отпадает по-
поэтому необходимость использовать входной преобразо-
преобразователь символов.
Приведем теперь пример замещения конечных авто-
автоматов. Пусть автомат А имеет диаграмму состояний,
показанную на рис. 4.5, а диаграмма состояний авто-
автомата В изображена на рис. 4.6. Может ли автомат В
замещать автомат А по схеме рис. 4.4? Пусть к авто-
автомату В по схеме рис. 4.4 присоединены преобразователи
Ф1 и Ф2. Преобразователь Ф2 осуществляет перенумера-
перенумерацию состояний автомата В (т. е. перенумерацию круж-
кружков его диаграммы состояний), а преобразователь Ф1
осуществляет перенумерацию входных воздействий
(т. е. перенумерацию надписей над стрелками у диа-
в
С
126
АБСТРАКТНАЯ СТРУКТУРА И СЕТЬ
ГГЛ IV
граммы состояний). Разумеется, как и всегда, при этом
еще требуется, чтобы выполнялось условие однозначно-
однозначности функциональных преобразователей Ф) и Фг — одно-
одному и тому же значению аргумента не могут соответ-
соответствовать разные значения функции. Если после такой
двойной перенумерации какая-либо часть диаграммы
состояний В будет совпадать с диаграммой состояний
автомата А, то авто-
автомат В замещает ав-
автомат А.
В рассматривае-
рассматриваемом примере вид-
видно, что диаграмма
Рис. 4.5.
Рис. 4.6.
состояний, показанная на рис. 4.5, накладывается на
часть диаграммы состояний, рис. 4.6, содержащую
кружки ?2, g4 и ^5 с относящимися к ним стрелками. По-
Поэтому преобразователь х = Фг(?) должен производить
перенумерацию состояний в соответствии с табл. 4.1.
Таблица 4.1
* = *,<:>
с,
4
ч
С
Для состояний ?i и ?з автомата В работа преобразо-
преобразователя Фг(?) не определена, так как в процессе работы
автомата В с преобразователями Ф| и Фг эти состояния
$4.1)
ЗАМЕЩЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН
127
никогда не будут проходиться. Для них работу преобра-
преобразователя Ф2 можно доопределить произвольно, напри-
например так, как это показано в табл. 4.2.
Таблица 4.2
С
с,
*4
с,
с*
Теперь преобразователь Фг(?) построен полностью.
Из табл. 4.2 видно, что он удовлетворяет условию одно-
однозначности, т. е. задание ? однозначно определяет х.
Займемся преобразователем <Di(p). Кружки xi и ха
диаграммы состояний автомата А (рис. 4.5) соединяет
стрелка с надписью pi. Кружку xi, согласно табл. 4.2,
соответствует кружок ?г диаграммы состояний автомата
В (рис. 4.6), а кружку хг диаграммы рис. 4.5 — кружок
?s диаграммы рис. 4.6. На диаграмме автомата В эти
кружки (?г и is) соединяются стрелкой с надписью т]з
(т. е. автомат В переходит из второго состояния в пятое
под воздействием входа т)з). Так как в автомате А пере-
переход от состояния Xi к состоянию Таблица 4.3
у.2 происходит под воздействием
pi, то преобразователь Ф[ дол-
должен ставить в соответствие сим-
символу pi СИМВОЛ Т)з.
Рассуждая подобным же об-
образом относительно ветви, соеди-
соединяющей, например, состояния хг и xi автомата А, при-
придем к выводу, что преобразователь Ф[ должен символу
рг ставить в соответствие символ т)[. Таким образом
строится табл. 4.3 преобразователя Ф[.
Проверяя затем аналогично все остальные ветви диа-
диаграммы состояний рис. 4.5, устанавливаем, что всегда
выполняются соотношения
р
Т) = Ф, (р)
Pi
Р2
11
т. е. условие однозначности преобразователя Ф[ выпол-
выполнено.
128
АБСТРАКТНАЯ СТРУКТУРА И СЕТЬ
(ГЛ. IV
Если теперь на диаграмме состояний рис. 4.6 сменить
надписи над ветвями в соответствии с табл. 4.3 и пере-
перенумеровать состояния согласно табл. 4.2, то диаграмма
рис. 4.6 будет в точности частью диаграммы рис. 4.5.
Итак, в рассмотренном случае автомат А замешается
автоматом В.
Возможен и иной вариант замещения. Для него вме-
вместо табл. 4.2 и 4.3 имеем соответственно табл. 4.4 и 4.5.
Т а б л и г a 4.4
Таблица 4.5
*<
Сз
Р
Pi
%
Ps
Если бы диаграмма состояний автомата В имела вид,
показанный на рис. 4.7, а автомат А имел бы ту же диа-
Рис. 4.7.
грамму состояний, что и раньше (рис. 4.5), то замеще-
замещение автомата А автоматом В было бы невозможно.
В самом деле, таблица преобразователя Фг в этом
случае может быть лишь одной из двух таблиц: табл. 4.6
или табл. 4.7,
i*.l\
ЗАМЕЩЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН
129
Однако преобразователь <I>i в обоих случаях неодно-
неоднозначен, так как в обоих случаях требуется, чтобы
<Di(pi) = т)з и в то же время <Di(pi) = тJ. Поэтому заме-
замещение невозможно.
Таблица 4.7
С
%=Ф2(?)
Таб л и
с,
*4
*1
Сз
ца
С«
хз
4.6
*2
% = Ф2 (С)
*4
Сз
*2
и
*3
'.
лишь от одного входа ?>'
Таблица 4.8
Разумеется, вывод о невозможности замещения авто-
автомата А автоматом В справедлив лишь для схемы заме-
замещения, показанной на рис. 4.4, в. Если же замещение
производить по схеме рис. 4.2, то. в рассматриваемом
случае оно уже оказывается возможным.
Таблица преобразователя Ф2 при этом имеет вид
табл. 4.6. Выход и зависит
т. е. х = Ф2(?), а выход пре-
преобразователя Ф1 зависит уже
от двух переменных — % и р,
т. е. т) = Ф1(^,р). Таблица
преобразователя Ф| имеет
вид табл. 4.8.
Говоря выше о «накла-
«накладывании диаграмм состоя-
состояний друг на друга», мы под
совпадением подразумевали
не только совпадение круж-
кружков, стрелок и надписей над ними, но и места располо-
расположения надписей над стрелками. Иначе говоря, речь шла
о замещении автоматов и Я-машин автоматами и Я-ма-
шинами того же типа.
В гл. III было показано, что Я-машина типа П — Н
всегда может быть, как там говорилось, заменена Я-ма-
шиной типа П — П. Употребляя термин «заменена», мы
имели в виду интуитивное понимание читателем этого
термина. Теперь, в свете введенных в этой главе опре-
определений, ясно, что в гл. III фактически речь шла о за-
замещении Я-машины типа П — Н машинами типа П — П.
Pi
Р2
^2
48
11
С4
12
11
к
ъ
9 М А Айзерман, Л. А. Гусев и др.
130 АБСТРАКТНАЯ СТРУКТУРА И СЕТЬ [ГЛ. IV
§ 4.2. Абстрактная структура автомата .
В гл. III было дано формальное определение конеч-
конечного автомата как оператора, который «перерабатывает»
последовательность символов р в последовательность
символов х так, чтобы эти последовательности не содер-
содержали противоречивых триад. В таких терминах абстрак-
абстракция «конечный автомат» естественно описывается рекур-
рекуррентным соотношением
xp+1 = F(%p, рр) для автомата типа П—П, 1
х'+> = /?(х", pp+1) для автомата типа П—Н, ) ^4Л^
где F — любая однозначная функция, заданная на мно-
множествах {х} и {р}.
Рассмотрим теперь подробнее на примере автомата
типа П—П, каким образом описание конечной динами-
динамической системы рассматриваемого класса сводится к со-
соотношению вида D.1).
Пусть задана конечная динамическая система, имею-
имеющая п обобщенных координат х\, х2 хп и подвер-
подверженная действию s внешних (входных) воздействий
«1, ы2, .. ., us. Каждое входное воздействие назовем нит-
ниткой входа. Каждая из обобщенных координат в рассма-
рассматриваемые моменты 0, 1, ..., р, ... может принимать
лишь одно из конечного числа значений.
Пусть координата Xi может иметь лишь одно из ki
значений (i = 1, 2 п). Аналогично каждое входное
воздействие Uj в эти же моменты может принимать лишь
одно из г, значений /= 1, 2 s. «Движение» в си-
системе подчинено условию, что значение каждой из коор-
координат в момент р + 1 однозначно определяется значени-
значениями всех координат х,- (i = 1, 2, ..., п) и всех входов Uj
(/=1, 2, .... s) в момент р. Тогда движение описы-
описывается системой рекуррентных соотношений
x"i+l=:fiК» Ч> ¦¦¦> К' «Г» Ч* ¦••> usl D-2)
/=1,2, .... л.
Введя в рассмотрение n-мерный вектор х с коорди-
координатами х\, х2 хп, s-мерный вектор и с координа-
координатами «1, ы2 us я вектор-функцию/ с координатами
§ 4.Я АБСТРАКТНАЯ СТРУКТУРА АВТОМАТА 131
fu /2. • •.. fn, систему соотношений D.2) можно пред-
представить в векторной форме
jc'+^/Ijc', »'J. D.3)
Вектор х в моменты тактов может иметь одно из
п s
k = ГГ кг значений, а вектор и — одно из г = JJr, зна-
значений. Поэтому, выбрав алфавиты {у) и {р}, содержащие
соответственно k и г символов, и приписывая различ-
различным векторам х различные символы х, а векторам и —
символы р, вместо соотношения D.3), получим соотно-
соотношение вида D.1) с конкретной функцией F в правой
части. Эта функция F строится по вектор-функции /
D.3) в соответствии с выбранной кодировкой векто-
векторов X И U.
Из изложенного ясно, что система рекуррентных со-
соотношений D.2) описывает конечный автомат
xp+i = f(xPtf>P). D.4)
Система соотношений вида D.2) по сравнению с ура-
уравнением D.4) яснее отражает такие важные черты дина-
динамической системы, как число ее степеней свободы п, а
также значения каждой из ее обобщенных координат
в зависимости от состояния каждой из ниток входа.
Условимся называть систему соотношений вида D.2)
абстрактной структурой конечного автомата D.4).
Таким образом, задание абстрактной структуры од-
нозначнр^определяет конечный автомат, т. е. по соотно-
соотношениям D.2) единственным образом восстанавливается
соотношение D.4). В этом смысле система рекуррентных
соотношений D.2) задает конечный автомат в такой же
мере, в какой он может быть задан соотношением D.4).
Поэтому на конечный автомат, заданный системой соот-
соотношений типа D.2), полностью распространяется поня-
понятие о замещении автоматов.
Покажем теперь, что по заданному конечному авто-
автомату А можно построить много абстрактных структур,
замещающих этот автомат.
Пусть задан автомат А с алфавитами {х} и {р}. Зная
k и г, выберем числа п, s, kt (i = J, 2, ..., n) и Гу
9*
132
АБСТРАКТНАЯ СТРУКТУРА И СЕТЬ
[ГЛ. IV
(/ = 1, 2, ..., s). Выбор этих чисел стеснен лишь одним
условием: должны выполняться неравенства
Введем в рассмотрение.п координат хи х2, ..., хп
(принимающих соответственно k\, k2, ..., kn значений)
и s ниток входа щ, и2, .... us (принимающих соответ-
соответственно Г\, г2, .... rs значений).
Заполним теперь таблицу (табл. 4.9) следующим об-
образом.
Таблица 4.9
хР
Xi
х2
...
х„
иР
«1
«2
...
Us
хР
Г.Р+1
хр+\
х,
Хг
...
Хп
В левые столбцы таблицы хр, up выписываются все
возможные сочетания значений хи х2,..., хп; «ь и2,..., us.
следовательно,
п s
Таких сочетаний может быть Ц kt JJ
табл. 4.9 имеет такое число строк.
Чтобы заполнить столбец у,р, обратим внимание лишь
л
на столбцы хр. В эти столбцы хр вписано J\ kt раз-
различных сочетаний из х\, х2, ..., хп. Выберем из них ка-
какие-нибудь k сочетаний, назовем их основными, припи-
припишем им символы хь х2, ..., Xh и впишем эти символы
в соответствующие строки столбца хр табл. 4.9. В связи
с тем, что в силу неравенств D.5) может быть и
п
П k, > k, часть строк столбца хр может оказаться не-
незаполненной. В этом случае остальным сочетаниям из
§ 4.2] АБСТРАКТНАЯ СТРУКТУРА АВТОМАТА 133
хи х2, ..., хп, которые не вошли в k отобранных соче-
сочетаний, припишем уже использованные символы у, в лю-
любом порядке и впишем эти символы в незаполненные
строки столбца хр. После этого столбец хр заполнен це-
целиком. Совершенно так же заполняется столбец рр, но
только рассматриваются сочетания из «ь и2, ..., us, впи-
вписанные в столбцы ыр.
В результате в столбцы хр, рр вписаны все возмож-
возможные сочетания символов х, р, но так как таких сочета-
сочетаний всего
то часть сочетаний х, р может повториться.
Обращаясь теперь к заданному автомату А, напри-
например к его основной таблице, заполняем столбец хр+1
табл. 4.9. Но с каждым символом х мы уже связали
одно из основных сочетаний из Х\, х2, *.., хп. Вписывая
теперь в столбцы хр + 1 сочетания, соответствующие
хр + 1, заканчиваем заполнение таблицы.
Построенная так таблица определяет значения всех
jc^1 по заданным xf и и^, т. е. задает п функций fi в
рекуррентных соотношениях вида D.2).
Если бы вместо неравенств D.5) имели место равен-
равенства
гу,- D.6)
го в столбцах хр, рр табл. 4.9 каждое попарное сочета-
сочетание символов х, р встречалось бы лишь один раз.
Если же
то табл. 4.9 содержит те же строки, что и в случае D.6),
и, кроме того, эта таблица" содержит также дополни-
дополнительные строки, соответствующие неосновным сочета-
сочетаниям.
Если бы мы пытались теперь от построенной в табл.
4.9 абстрактной структуры перейти к автомату, то полу-
получили бы уже не исходный автомат, а другой автомат.
134
АБСТРАКТНАЯ СТРУКТУРА И СЕТЬ
[ГЛ. IV
Таблица 4.10
Диаграмма состояний этого автомата содержала бы все
кружки и ветви диаграммы исходного автомата (их оп-
определили бы строки, содержащие основные сочетания
х и и), но, кроме того, она содержала бы дополнитель-
дополнительные кружки и ветви (соответствующие неосновным со-
сочетаниям х и и). Условия однозначности работы преоб-
преобразователей символов со-
соблюдены (по построению),
поэтому в случае D.7) аб-
абстрактная структура опреде-
определяет автомат, замещающий
заданный (исходный) авто-
автомат.
При построении абстра-
абстрактной структуры, т. е. при
построении системы соотно-
соотношений D.2) из соотношения
D.4) с помощью табл. 4.9,
мы могли распорядиться вы-
выбором чисел п, s, ki и г, раз-
различным образом, лишь бы
были соблюдены условия
D.5). Ясно, что не только
вид функций fi в прааых ча-
частях соотношений D.2), но
даже само число соотноше-
соотношений в системе D.2) зависит
от того, как мы распорядились выбором этих чисел.
Используя этот произвол, можно строить множество
абстрактных структур, замещающих заданный конечный
автомат А.
В качестве важного примера рассмотрим случай, ко-
когда все ki и tj равны двум, т. е. все х и и — логические
переменные. Абстрактная структура в этом случае имеет
вид
xP+1 = Lt[xf, хр, ..., хр\ uf, up, ..., up], D.8)
i = \, 2, ..., п.
где все Li— логические функции.
Условимся абстрактную структуру такого вида назы-
называть логической или двоичной* '
\ р
*1
Ч
н
ч
Pi
*з
*2
*6
*5
*3
*1
Р2
*4
*5
*2
*1
*1
*3
Рз
Ч
*4
ч
Ч
ч
ч
§4.2]
АБСТРАКТНАЯ СТРУКТУРА АВТОМАТА 135
Таблица 4.11
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
xp-l
х2
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
хг
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
UP
«1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
-,
«2
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
*1
ч
ч
*4
ч
ч
х,
ч
ч
*4
ч
ч
*1
ч
ч
*4
ч
ч
*1
*|
*|
X,
X,
X,
X,
X,
X,
X,
X,
X,
X,
*
рр-1
г
Pi
Pi
Pi
Pi
Pi
Pi
Р2
Р2
Р2
Р2
Р2
Р2
Рз
Рз
Рз
Рз
Рз
Рз
Pi
Pi
Pi
Pi
Pi
Pi
Pi
Pi
Pi
Pi
Pi
Pi
Pi
Pi
ч
ч
ч
ч
X,
х4
ч
ч
X,
X,
х3
ч
х4
ч
ч
х2
х2
ч
ч
ч
ч
ч
ч
ч
ч
ч
ч
ч
ч
ч
ч
Х\
0
0
1
1
0
0
0
1
0
0
0
0
1
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
хР
х2
1
0
0
0
1
0
1
0
0
0
0
1
0
1
1
0
0
0
1
• 1
1
1
1
1
1
1
1
1
1
1
1
1
х3
0
1
1
0
0
0
1
0
1
0
0
0
1
1
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
136
АБСТРАКТНАЯ СТРУКТУРА И СЕТЬ
[ГЛ. IV
В этом случае
, = 2Л и
Ш
=2*.
D.9)
Если числа k и г не являются целыми степенями двой-
двойки, т. е. не содержатся среди чисел 2, 4, 8, 16, 32, 64, 128,
256 ..., то равенства D.6) не могут быть удовлетво-
удовлетворены. Чтобы удовлетворить неравенствам D.5), надо
п и s выбирать из условий
k<2" и г<2*.
Так, например, если автомат задан основной таблицей
(табл. 4.10), то & = 6, г = 3 и можно взять, например,
п = 3, s = 2. Заполнение таблицы типа табл. 4.9 показано
в табл. 4.11.
Можно также построить иные двоичные структуры,
замещающие тот же автомат, если положить, например,
п = 4, s = 3 или п = 3, s = 3 и т. д.
Таблица 4.12
xP
Xi
0
0
0
1
1
1
0
0
0
1
1
1
0
0
0
1
1
1
x,
0
1
2
0
1
2
0
1
2
0
1
2
0
1
2
0
1
2
0
0
0
0
0
0
1
1
1
1
1
1
2
2
2
2
2
2
*p
x
*2
*3
*4
*5
*a
*i
*2
*3
y.
*5
*a
*i
*2
*S
X.
*5
Pi
Pi
Pi
Pi
Pi
Pi
?2
?2
?2
p2
P2
P2
Рз
Рз
Рз
Рз
Рз
Рз
*3
*2
*6
*5
*з-
Х1
X.
*5
*2
*1
Х1
*3
*6
х
*3
*5
*2
*2
X,
0
0
1
1
0
0
1
1
0
0
0
0
1
1
0
1
0
0
х2
2
1
2
1
2
0
0
1
1
0
0
2
2
0
2
1
1
1
§ 4.3] СЕТЬ 137
Покажем теперь, как этот же автомат может быть
заменен абстрактной структурой, не являющейся двоич-
двоичной. Положим, например, что п — 2, k\ = 2, k2 = 3, и что
по-прежнему s = 1, г\ = 3. В этом случае к = k\k2 = 6 и
г = Г] = 3, т. е. выполняются равенства D.6).
Заполняя для этого случая табл. 4.9, строим абстракт-
абстрактную структуру (табл. 4.12), но она уже не является дво-
двоичной.
§ 4.3. Сеть
Введем в рассмотрение простейший конечный авто-
автомат, для которого уравнение D.1) имеет вид
*Р+1 = РР. D.10)
Рассматривая такой автомат, мы предполагаем, что если
алфавит {х} и содержит какие-либо символы, не содер-
содержащиеся в {р}, то они могут появиться лишь в началь-
начальный момент. Символ и, «выдаваемый» таким автоматом
в момент р, тождественно совпадает с символом на
входе в предшествующий момент. Простейший автомат
такого рода' назовем задержкой на такт (или просто
задержкой).
Возвращаясь к автомату типа П — Пи вводя новую
переменную [А (алфавит {\i} совпадает с алфавитом {х}),
заменяем D.1) соотношениями
—э»
F
^/Л. х
Такое соотношение уже было
рассмотрено в § 3.3. Теперь бу-
будем считать, что первое соотно- ^|1С- 4.8.
шение в D. II) определяет мгно-
мгновенно действующий преобразователь символов х и р в
символы (х, а второе — определяет задержку. Поэтому
соотношения D.П) могут быть представлены схемой,
показанной на рис. 4.8, где, как и далее на схемах, за-
задержка обозначена кружком.
Рассмотрим теперь какую-либо абстрактную струк-
структуру автомата, например автомат типа П—П, т. е.
138 АБСТРАКТНАЯ СТРУКТУРА И СЕТЬ
совокупность соотношений вида D.2)
[ГЛ. IV
//И' *$' •••' ХРп' Ul> »%•¦••' Us\> DЛ2)
/=1. 2 , /г.
Каждое соотношение в этой системе, например
xVl=fi[xi' хР2' •••'¦К' и?> и2> •••' us]>
само может рассматриваться как совокупность задержки
к>
и функционального преобразователя
У1=/ЛХ1> х2, ..., хп; ии и2, .... us\. D.13)
Поэтому вся абстрактная структура D.12) предста-
представляется п задержками и п функциональными преобразо-
преобразователями. На вход ка-
каждой задержки подает-
подается выход соответствую-
соответствующего преобразователя.
Выходы всех задержек
подаются на входы
каждого из преобразо-
преобразователей*). Помимо то-
того, на входы все-х пре-
преобразователей подают-
подаются внешние воздейст-
воздействия и (рис. 4.9).
Располагая не-
несколькими абстрактны-
абстрактными структурами, можно
строить новые абстра-
абстрактные структуры, «со-
«соединяя» их между со-
собой.
Говоря о соедине-
соединении автоматов друг с
другом, мы имеем в виду отождествление выходных сим-
символов одного автомата с входными символами другого
т<
-О
рис 4.9.
*) Наррс. 4.9, как и на последующих рисунках, кружки обозна-
обозначают задержки, а прямоугольники — преобразователи.
§4.3]
СЕТЬ
139
автомата. Поэтому можно представить себе, что выход
одного из автоматов воздействует на вход другого, только
если все символы алфавита выхода первого автомата со-
содержатся во входном алфавите второго автомата. Если
это не так, то «соединение» автоматов возможно лишь
с помощью дополнительных преобразователей.
2»
и,
I
Рис. 4.10.
Пусть даны, например, две абстрактные структуры:
структура А
Г1=ЛК' Ч> Ч> К* ui' и2> и!)> i = Ь 2> 3> 4 DЛ4)
и структура Б
У}+1 = 9j(y?, УЬ Уръ> «f. -Ч> Ч* vp)> 1= Ь 2, 3. D.15)
Дополним D.14) и D.15) уравнениями трех преобразо-
преобразователей
D.16)
140 АБСТРАКТНАЯ СТРУКТУРА И СЕТЬ [ГЛ. IV
Здесь W\ и w2— дополнительные нитки входа преобра-
преобразователей. На рис. 4.10 показано схематически соедине-
соединение структур А и Б с помощью этих трех преобразова-
преобразователей.
Уравнения D.14), D.15) и D.16), рассмотренные со-
совместно, вновь образуют некоторую абстрактную струк-
структуру. Действительно, подставляя D.16) в D.14) и D.15),
получаем систему из семи рекуррентных соотношений
с координатами (х\, х2, х%, х^ у\, у2 и у%) и нитками вхо-
входа (и2, щ, v2, W\ и w2) того типа, который мы назвали
выше «абстрактная структура».
Любую совокупность конечного числа рекуррентных
соотношений типа D.2), дополненных уравнениями пре-
преобразователей, выражающих некоторые из входов через
координаты, назовем сетью.
Сеть сама является абстрактной структурой. Ее ко-
координатами служат все обобщенные координаты всех
абстрактных структур, составляющих сеть. Нитками вхо-
входа сети служат как нитки входа составляющих абстракт-
абстрактных сруктур, на которые не воздействуют преобразова-
преобразователи, так и нитки входа преобразователей, на которые
не воздействуют координаты абстрактных структур, со-
составляющих сеть.
Чтобы получить для сети систему соотношений типа
D.2), надо использовать уравнения преобразователей
для исключения входных переменных, на которые воз-
воздействуют преобразователи.
В связи с тем, что сеть сама является абстрактной
структурой, она замещает некоторый конечный автомат.
Поэтому, объединяя абстрактные структуры в сети с по-
помощью преобразователей, мы из одних конечных авто-
автоматов строим другие конечные автоматы.
Назовем сетью задержек сеть, содержащую только
задержки, связанные через функциональные преобразо-
преобразователи. Из изложенного выше следует, что любая
абстрактная структура и любая сеть представимы сетью
задержек. Это было показано на рис. 4.9. Такое пред-
представление не единственно в том смысле, что ъсякая сеть
задержек замещает автомат, а для каждого автомата,
как было указано в предыдущем параграфе, может быть
построено множество замещающих его абстрактных
5 4.31
СЕТЬ
141
структур. Значит, можно построить множество сетей за-
задержек, отображающих один и тот же автомат. Эти сети
>
*
о
Фз
г р
Рис. 4.11.
задержек отличаются между собой числом задержек и
алфавитами, на которых заданы задержки.
Среди сетей задержек выделим подкласс сетей без
петель. Сеть задержек называется сетью без петель,
-О
О
L
г
О
Г
Рис. 4.12.
если, перемещаясь по сети от любой из задержек вдоль
направления воздействия (вдоль стрелок на схеме типа
рис. 4.5), мы не можем достигнуть вновь исходной за-
задержки. На рис. 4.11 показан пример сети без петель,
а на рис. 4.12 —сети, содержащей петли.
142 АБСТРАКТНАЯ СТРУКТУРА И СЕТЬ 1ГЛ. IV
Важным примером сети без петель служит сеть, со-
составленная из q последовательно соединенных друг с
другом задержек (рис. 4.13). Если входы и выходы за-
задержек определены на разных алфавитах, то между
задержками включаются преобразователи (рис. 4.14).
q задержек
-Си*
Рис. 4.13.
Построенную так сеть назовем линией задержки. Линия
задержки, как и всякая сеть, есть конечный автомат. Но
если обращать внимание лишь на символы ц на ее входе
q задержек
Рис. -4.14.
и \xq на ее выходе, то символ ця будет определяться сим-
символом \х„ но не в предыдущий такт, a q тактов назад:
В том же случае, когда входные и выходные символы
всех задержек берутся из одного и того же алфавита,
символ \iq совпадает с символом ц, появляющимся q
тактов назад:
Вернемся теперь к схеме, показанной на рис. 4.8, но
заменим в этой схеме задержку на линию задержки
(рис. 4.15). Вместо соотношений D.11) получим тогда
DЛ7)
§ 4.3] СЕТЬ
Исключая ц, получаем
а исключая из D.17) не ц, а х, находим
143
DЛ8)
D.19)
Можно включить линию задержки и на входе преоб-
преобразователя. Тогда вместо соотношений D.17) получаем
D.20)
или, исключая ф и х,
у?+« = Р№, р"). D.21)
Заметим теперь, что если бы мы символы х приписы-
приписывали состоянию всей системы, учитывая выходы всех за-
задержек, то, разумеется, х в момент р + 1 зависело бы
q задержек
Рис. 4.15.
лишь от х в момент р. Поступая же так, как это было
описано выше, то есть приписывая символ х лишь вы-
выходу последней задержки, мы в этом же автомате реа-
реализуем соотношение D,19). Именно это мы имели в ви-
виду, когда, вводя в гл. III понятие о конечном автомате,
говорили, что запись автомата в форме соотноше-
соотношения C.5')
%p+\ = F{%p, f)
охватывает и тот случай, когда символ хр + ч зависит от
символов хр и рР конечное число q тактов назад.
144
АБСТРАКТНАЯ СТРУКТУРА И СЕТЬ
[ГЛ. IV
Теперь, когда введены понятия «задрржка» и «сеть»,
вернемся вновь к вопросу о соотношений между 'автома-
'автоматами и последовательностными машинами типа П — П
и П — Н. Для этого рассмотрим схему рис. 4.8, описы-
описываемую уравнением D.11). Как уже говорилось в гл. III,
уравнения D.11) приводят к описанию автоматов типа
П — П или П — Н в зависимости от того, исключается
Рис. 4.16.
ли из уравнений D.И) переменная ц или %. На схеме
рис. 4.8 этому соответствует рассмотрение в качестве
выхода переменной и (П — П автомат) или ц (П — Н
автомат). На рис. 4.16,а, б показаны соответствующие
схемы.
Как уже отмечалось в гл. III, последовательностная
машина типа П — П отличается от машины типа П — Н
только тем, что содержащийся в ее схеме автомат яв-
является соответственно П — П или П — Н автоматом.
Поэтому схемы машин этих типов могут быть предста-
представлены так, как это показано на рис. 4.17, а, б.
§4.3]
СЕТЬ
145
Напомним, ч(го машина типа П — Н всегда может
быть замещена Машиной типа П — П. Для замещения
следовало сменит^ лишь преобразователь Ф. Однако не-
неверно обратное утверждение, что одной лишь сменой
выходного преобразователя машина типа П — П может
быть замещена машиной типа П — Н. Теперь, когда мы
владеем методами задания автоматов с помощью таб-
таблиц и ввели схемы, показанные на рис. 4.16 и 4.17, мы
можем показать это на примере.
Пусть, например, задана последовательностиая ма-
машина типа П —П (рис. 4.17, а) таблицами преобразова-
преобразователя F (табл. 4.13) и преобразователя Ф (табл. 4.14).
Таблица 4.13
Преобразователь Р
Таблица 4.14
Преобразователь Ф
Ч\ р
* \.
*1
*2
*3
*4
Pi
*3
*3
*2
*2
Р2
*1
*3
*1
*4
Рз
*2
*4
*2
*3
Y. \^
*1
*2
*3
*4
Pi
h
h
Р2
^3
Рз
К2
h
Попробуем, сохранив преобразователь F, найти та-
такую новую таблицу преобразователя X = Ф* (ц, р), что-
чтобы последовательностная машина, составленная по схеме
рис. 4.17,6, замещала исходную Я-машину.
Рассмотрим, например, клетку табл. 4.14 для Ф, стоя-
стоящую на пересечении первой строки и первого столбца.
В нее вписан символ Я,2. В табл. 4.13 преобра-
преобразователя F в такой же клетке вписан символ хз. По-
Поэтому символ %ч впишем в таблицу нового преобразо-
преобразователя Ф* в клетку, стоящую на пересечении первого
столбца и третьей строки (табл. 4.15).
JO M. А. Айзерман, Л. А. Гусев и др.
146
АБСТРАКТНАЯ СТРУКТУРА И СрТЬ
[ГЛ. IV
Таблица 4.15
Преобразователь Ф*
Таким образом, могла бы быть построена и вся эта
таблица. (
Однако попробуем повторить процедуру, рассмотрев
теперь в табл. 4.14 старого преобразователя Ф клетку,
находящуюся в первом столбце и второй строке. В нее
вписан символ Яз, а в табл. 4.13 преобразователя F ав-
автомата в такой же клетке
вписан, как и раньше, сим-
символ Хз-
Поэтому в новой таблице
нам нужно было бы вписать
символ Яз в клетку, уже за-
заполненную символом Я2. Но
это значит, что получается
неоднозначный преобразова-
преобразователь, т. е. рассмотренный
пример подтверждает, что,
вообще говоря, машина ти-
типа П— П не замещается ма-
машиной типа П — Н, если при
этом допускается лишь сме-
смена выходного преобразова-
преобразователя.
Вернемся теперь к вопро-
вопросу о соотношении между конечным автоматом и после-
довательностной машиной. Мы накопили материал, до-
достаточный для того, чтобы уточнить соответствие между
этими двумя понятиями. Его устанавливает следующая
теорема *).
Теорема. Каждой последовательностей машине
П можно сопоставить конечный автомат А с выходным
преобразователем так, что для любого начального со-
состояния машины П найдется такое начальное состояние
автомата А, что при любой входной последовательное!и
выходная последовательность автомата А для всех р^>1
повторяет с запаздыванием на такт выходную последо-
последовательность машины П. Наоборот, каждому автомату А
с выходным преобразователем можно сопоставить по-
следовательностную машину П таким образом, что для
*-1
*2
*8
Pi
*2
Р2
Рз
*) Сравните с теоремой 1 работы [16].
§4 3] СЕТЬ 147
любого начального состояния автомата А найдется та-
такое начальное состояние машины П, что при любой
входной последовательности выходная последователь-
последовательность машины П для всех р*^. О повторяет с опереже-
опережением на такт выходную последовательность автомата А.
Доказательство. Докажем сначала первое
утверждение теоремы. Пусть дана последовательностная
машина, описываемая уравнениями
х"+1 = /7(х")Р"), D.22
X* = Ф (х*. р"). D.23)
Построим сеть, состоящую из двух конечных автома-
автоматов и заданную уравнениями
yp+l = Fx{yp,zp), D.24)
zp+1 = Pp, D.25)
и зададим выходной преобразователь сети
уР = ф (уР, z"), D.26)
где алфавиты {у} и {%} совпадают с алфавитами {к} и
{%} соответственно; алфавит {z} отличается от {р} доба-
добавлением одного символа z0; функция Ф в D.26) совпа-
совпадает с соответствующей функцией в D.23) на всех парах
символов из {я}, {р} и не определена (или задана как
угодно) при г = z0; функция F\ в D.24) совпадает с F
в D.22) при всех сочетаниях символов, не содержащих
2о, а при сочетаниях,содержащих z0. F\(y, z0) = у. Урав-
Уравнения D.24) и D.25) описывают конечный автомат А,
состояния которого кодируются парой символов (у, z),
а уравнение D.26) задает выходной преобразователь
этого автомата. Каждому начальному состоянию х° по-
следовательностной машины П сопоставим такое на-
начальное состояние автомата А, при котором
уо — ^ z° = z0. D.27)
При р = 0 из D.24) следует, что у1 — у0 = к0. При
1 символ z° не может появиться, и для этих момен-
моментов Fi в D.24) можно заменить на F, откуда
yP+i = f.{yPf z"), /»>1. D.28)
10*
148 АБСТРАКТНАЯ СТРУКТУРА И СЕТЬ ГГЛ. IV
Вводя новую переменную Кр=еу<р+1> (/?>0) и учиты-
учитывая D.24), можно написать
9Р)у p>j0, D.29,
причем К0 = у1 = н°. Уравнения D.22), D.29) и началь-
начальные условия х@) = х° совпадают, в силу чего для лю-
любого р >-1
Но ур = Yp-', откуда
уР = гр-\ /,>!. D.30)
Подставляя D.25) и D.30) в D.26) и сравнивая с D.23),
получаем
Х' = Ф(х', р") = *'-», />>1,
что и доказывает первое утверждение теоремы.
Докажем второе утверждение. Пусть задан конеч-
конечный автомат А
xp+1 = F(%p, Р") D.31)
с выходным преобразователем
х' = Ф(ч"). D.32)
Сопоставим этому автомату последовательностную ма-
машину П
), D.33)
p")j, D.34)
где алфавиты {у} и {и} совпадают. Каждому начальному
состоянию автомата Л поставим в соответствие началь-
начальное состояние машины П. Поскольку уравнения D.31),
D.33) и соответствующие начальные состояния совпа-
совпадают, то для всех р %¦ 0
у" = *р. D.35)
Подставляя D.35) в D.34) и учитывая D.31) и D.32),
получим для всех р>0
что и доказывает второе утверждение теоремы. Таким
образом, теорема доказана полностью.
§4.4] АБСТРАКТНАЯ АГРЕГАТИЗАЦИЯ АВТОМАТОВ 149
Если задача состоит в выяснении того, что «может
делать» последова^ельностная машина и конечный авто-
автомат, то в силу доказанной теоремы нет необходимости
рассматривать их ^орознь. Но понятия эти не эквива-
эквивалентны в том смысле, что для выполнения одного и того
же «задания» в последовательностной машине может
требоваться меньшее число состояний, чем в соответ-
соответствующем конечном автомате. Это обстоятельство суще-
существенно в тех случаях, когда рассматривается задача
минимизации числа состояний (см. гл. IX).
§ 4.4. Абстрактная агрегатизация автоматов
и последовательностных машин
Содержание предыдущих параграфов устанавливает,
что один и тот же автомат может быть замещен различ-
различными абстрактными структурами, а каждая абстрактная
структура — самыми разнообразными сетями. С другой
стороны, если каждую абстрактную структуру рассма-
рассматривать как автомат, то понятие сети показывает, что
из одних автоматов можно строить другие автоматы.
Таким образом, естественно, возникает мысль — нельзя
ли указать такой набор автоматов и преобразователей,
чтобы, используя только автоматы и преобразователи из
этого набора (каждый из них в любом числе), можно
было организовать сети, замещающие разнообразные
автоматы и последовательностные машины.
Процесс построения сетей с использованием лишь
автоматов и преобразователей из заданного набора на-
назовем агрегатизацией конечных автоматов и последова-
последовательностных машин.
Автоматы и преобразователи, входящие в набор, на-
называются элементами набора. Набор назовем полным,
если из его элементов можно построить сеть, замещаю-
замещающую любой наперед заданный конечный автомат или
любую последовательностную машину.
Выше было показано, что, имея элементы задержки
любого типа (т. е. работающие в любых алфавитах) и
любые преобразователи, можно построить сеть, заме-
замещающую любой заданный автомат.
150 АБСТРАКТНАЯ СТРУКТУРА И СЕТЬ [ГЛ. IV
Пусть мы имеем элемент задержки, работающий в
алфавите {ц}. Если бы мы располагали, кроме того,
каким-либо набором элементарных преобразователей, из
которых можно построить любой преобразователь, ра-
работающий в алфавите {ц}, то мы располагали бы пол-
полным набором.
Так, например, важный полный набор составляет: дво-
двоичный элемент задержки (т. е. элемент задержки с двумя
состояниями), дополненный элементами, выполняющи-
выполняющими операции дизъюнкции, конъюнкции и отрицания.
Действительно, любой автомат можно заместить ло-
логической абстрактной структурой, т. е. абстрактной
структурой, у которой все k{ = 2 и все г,- = 2 (i = 1,
2, ..., п; j = 1, 2, ..., s). Но такую абстрактную струк-
структуру можно представить сетью, состоящей лишь из дво-
двоичных элементов задержки и логических преобразовате-
преобразователей. Любая же логическая функция может быть пред-
представлена конъюнктивной формой дизъюнктивных групп,
и значит, любой логический преобразователь может быть
составлен из преобразователей, реализующих дизъюнк-
дизъюнкцию, конъюнкцию и отрицание (см. гл. I и II). Следова-
Следовательно, описанный набор является полным.
Разумеется, набор остался бы полным и в том слу-
случае, если бы, помимо двоичного элемента задержки, он
состоял бы из иных преобразователей, позволяющих
реализовать любую логическую функцию, например со-
содержал бы только преобразователь «штрих Шеффера».
Совершенно аналогично можно построить полные
наборы, работающие в алфавитах, содержащих более
двух, например т, символов,— задача сводится к выра-
выражению любой логической функции m-значной логики
через несколько первообразных функций. Эти первооб-
первообразные функции, дополненные элементом задержки, ра-
работающим в алфавите из т символов, составляют пол-
полный набор.
В гл. V будут описаны технические реализации раз-
различных полных наборов и методы построения из них
конечных автоматов и последовательностных машин. Но
раньше чем перейти к описанию технических реализа-
реализаций, рассмотрим кратко одну важную абстрактную мо-
модель, возникшую в связи с вопросами физиологии.
§ 4.5] АБСТРАКТНЫЙ НЕЙРОН 151
§ 4.5. Абстрактный нейрон и абстрактные модели
нейронных сетей
Изучение свойств нервных клеток (нейронов) и нерв-
нервных тканей привело на определенном этапе к рассмо-
рассмотрению абстрактных (идеализированных) нейронов и
абстрактных моделей нейронных сетей. Нервная сеть
Мак-Каллока и Питтса — одна из наиболее известных
абстракций такого рода*).
Нейроном Мак-Каллока и Питтса называется вооб-
воображаемый логический элемент, который может нахо-
находиться лишь в одном из двух возможных состояний —
Рис. 4.18.
«возбужден» и «не возбужден». Нейрон имеет любое
конечное число входов и один выход с любым конечным
числом разветвлений (рис. 4.18). Каждый из входов
может иметь окончание одного из двух видов: «тормо-
«тормозящее» (на рис. 4.18 обозначено черным кружком) и
«простое» (на рис. 4.18 — стрелка). Окончания развет-
разветвлений выхода нейрона могут воздействовать на входы
иных нейронов или на свой собственный вход. На неко-
некоторые из входов нейронов могут воздействовать внешние
возмущения. Каждое внешнее возмущение также может
иметь лишь одно из двух возможных состояний. Оно мо-
может возбуждать вход или не возбуждать его. Так обра-
образуются абстрактные нейронные сети — модели нервной
ткани (пример на рис. 4.19).
Обозначим f{t) число возбужденных в момент t
простых окончаний входа («->»), воздействующих на
*) Разработанная еще в 1943 г. (см. [62]) она, по-видимому, по-
потеряла какое-либо значение для физиологии в свете более поздних
исследований свойств нейронов.
152 АБСТРАКТНАЯ СТРУКТУРА И СЕТЬ [ГЛ. I
рассматриваемый нейрон, g{t)—число возбужденны,
тормозящих окончаний (•), воздействующих' на него
Функционирование одного нейрона (а следовательно
и сети) определяется следующим условием возбужде
ния: нейрон возбужден в момент / ¦+¦ т, если в момент t
удовлетворяются условия
?(') = 0, f(t)>h, D.36)
где h — заданное конечное число, называемое порогом
возбуждения, и нейрон не возбужден, если эти условия
не выполняются. Таким образом, тормозящее окончание
Рис. 4.19.
«обладает правом вето» — даже при выполнении нера-
неравенства D.36) возбуждения выхода нет, если к рассма-
рассматриваемому нейрону подходит хоть одно тормозящее
ответвление, отходящее от возбужденного нейрона*).
Если обозначить через ш* состояния простых ниток
входа (i = 1, 2, ..., s), через Vj состояние тормозящих
ниток входа (/ = 1, 2, ..., q), а через х состояние ней-
нейрона, то поведение нейрона Мак-Каллока и Питтса, на-
например, в случае 5 = 3, Л = 2, q = 2 описывается фор-
формулой
V [w2 (t) & w3 (t)) }&Vl(t)&v2 (t). D.37)
На оси времени отметим точки 0, т, 2т, Зт,... и бу-
будем наблюдать нейроны и нейронные сети лишь в эти
*) Часто используются и другие условия функционирования
нейронов (см., например, [73]),
5 4.5] АБСТРАКТНЫЙ НЕЙРОН 153
моменты, т. е. введем в рассмотрение такты. Обозна-
Обозначим моменты наступления этих тактов 0, 1, 2, ..., р...
соответственно. Тогда выражение D.37) можно запи-
записать так:
хр+1 = [(idp & is)P)\/(wp & w!>)\/(wp & we)] & v{ & Ц. D.38)
Рассмотрим теперь произвольную абстрактную ней-
нейронную сеть Мак-Каллока и Питтса, состоящую из п
нейронов и имеющую s «свободных» входов, к которым
могут быть подведены внешние воздействия. Перенуме-
Перенумеровав нейроны, содержащиеся в сети, номерами 1,
2, ..., п, а свободные нитки входов — номерами 1,2, ...
..., s, и обозначив Xi— состояние 1-го нейрона, а щ —
состояние j-Pi Нитки входа сети, можно выписать п ра-
равенств вида D.38). В сети на каждый вход нейрона воз-
воздействует окончание одного из нейронов или внешнее
воздействие. Поэтому каждое из w или v отождеств-
отождествляется с х или и, т. е. в правых частях выражений вида
D.38) вместо Ф? и VP вписываются соответственно
X? И №.
Из изложенного следует, что абстрактная нейронная
сеть Мак-Каллока и Питтса описывается системой со-
соотношений
хр+1 = Lt (jcf, x\, ..., х? up, up2, ..., up), D.39)
/=1, 2, ...,п,
где Li — логические функции вида D.38).
Таким образом, абстрактная нейронная сеть Мак-
Каллока и Питтса представляет собой сеть в нашем
понимании и, следовательно, является конечным ав-
автоматом. Но в связи с тем, что в правых частях выра-
выражений D.39) находятся не произвольные логические
функции, а функции специального вида (типа D.38)),
естественно возникает вопрос: можно ли для любого
заданного конечного автомата, работающего в такт-
ности 0, 1, 2, ... (т. е. О, т, 2х, ...), построить соответ-
соответствующую нейронную сеть?
Чтобы ответить на этот вопрос заметим, прежде
всего, что, замыкая на себя нейрон с h = 1, находящийся
в возбужденном состоянии (рис. 4.20), мы получаем за-
заблокированный, т, е. всегда возбужденный нейрон. Мы
154
АБСТРАКТНАЯ СТРУКТУРА И СЕТЬ
[ГЛ. IV
можем поэтому считать, что к нейронам может быть под-
подведен всегда возбужденный вход (рис. 4.21,а), обозна-
обозначая это так, как показано
на рис. 4.21,6. Условимся
говорить в этом случае, что
возбуждающая нитка входа
закреплена.
Рассмотрим нейрон с
s=
«7 = 0
Рис. 4.20.
(рис. 4.22). Такой нейрон описывается уравнением
т. е. одним нейроном будет осуществлена задержка на
такт. Соединив любое число q таких нейронов последова-
последовательно (рис. 4.23), реализуем задержку на q тактов.
ш
ш
Рис. 4.23.
Рассмотрим теперь нейрон ch=l,s=l,q=l и за-
закрепим возбуждающий вход (рис. 4.24). Тогда нейрон
реализует зависимость
§4.5]
АБСТРАКТНЫЙ НЕЙРОН
155
т. е. в одном нейроне осуществляется операция отрица-
отрицания с задержкой на такт.
Нейрон с h — 1, q = 0 и любым s (рис. 4.25) осуще-
осуществляет дизъюнкцию s переменных с задержкой на такт
Хр+1 _
а нейрон с h — s (при любом s) и с q = 0 (рис. 4.26)
осуществляет конъюнкцию s переменных с задержкой
на такт.
ш
х
а:
Рис. 4.24
Рис. 4.25.
Если надо осуществить конъюнкцию s переменных,
из которых часть отрицается, то отрицаемые переменные
должны быть подведены к тормозящим входам, a h дол-
10,
ш
Рис. 4.26.
жно быть равно числу неотрицаемых переменных. Так,
например, конъюнкция
осуществляется одним нейроном по схеме, показанной
на рис, 4-27,
156
АБСТРАКТНАЯ СТРУКТУРА И СЕТЬ
[ГЛ. IV
Рассмотрим какую-либо дизъюнктивную форму конъ-
конъюнктивных групп. Пусть такая форма содержит т групп.
Тогда каждая конъюнктивная группа может быть реа-
реализована на одном нейроне по схеме, показанной на
рис. 4.27. Выходы этих нейронов надо подвести к ней-
нейрону, реализующему дизъюнкцию по схеме, которая
была показана на рис. 4.25. В связи с тем, что все ней-
нейроны, реализующие конъюнкцию, «срабатывают» за
т.
Рис. 4.28.
один такт и еще только один такт требуется для осуще-
осуществления дизъюнкции, вся дизъюнктивная форма реа-
реализуется за два такта, т. е. за время 2т. Так, например,
на рис. 4.28 показана сеть, составленная из нейронов
Мак-Каллока и Питтса и реализующая форму
хр+2 = (wf & ii)p) V (teif & ~wp) \Z(wP&.w§& wp).
Любая логическая функция может быть представлена
дизъюнктивной формой конъюнктивных групп и, следо-
следовательно, реализуется за два такта абстрактной нейрон-
нейронной сетью, составленной из нейронов Мак-Каллока и
Питтса. Таким образом, из нейронов Мак-Каллока и
Питтса может быть составлен любой логический преоб-
§4.5)
АБСТРАКТНЫЙ" НЕЙРОН
157
разователь L, но, в отличие от наших обычных
предположений, такой преобразователь не будет мгно-
мгновенно действующим — на его работу расходуется два
такта.
Предположим теперь, что входы изменяются и со-
состояние сети наблюдается в моменты 0. 2т, 4т, ... При
такой тактности из нейро-
нейронов Мак-Каллокаи Питт-
Питтса может быть составле-
составлена сеть, реализующая
любой логический преоб-
преобразователь за один такт.
С другой стороны, из ней-
нейронов может быть по-
построен элемент задержки
на такой «двойной» такт;
для этого надо (см.
рис. 4.23) соединить по-
последовательно два эле-
элемента задержки. Распола-
Располагая любым логическим
преобразователем и эле-
элементом задержки, можно
построить сеть, реализую-
реализующую любой автомат, рабо-
работающий в такой тактности.
Далее, в гл. X, будут
рассмотрены методы по-
построения автоматов, работающих в любой «медленной»
тактности, из элементов, работающих в «быстрой» такт-
тактности, если сигнал о наступлении медленного такта по-
подается на автомат извне. Будет показано, что для этого
необходимо лишь располагать элементом задержки на
любой, извне подведенный такт.
Чтобы более не возвращаться к нейронным цепям,
покажем здесь же, как из нейронов Мак-Каллока и
Питтса может быть реализован такой элемент задержки.
С этой целью построим сеть (рис. 4.29), реализующую
за время 2т функцию
158
АБСТРАКТНАЯ СТРУКТУРА И СЕТЬ
(ГЛ. IV
Две такие сети соединим в одну, имеющую два входа
(и и щ), так, как это показано на рис. 4.30. Входи — ос-
основной вход сети, а щ используется для подачи сигнала
Рис. 4.30.
о наступлении такта (считается, что очередной такт на-
наступает в момент смены ut с 1 на 0).
На рис. 4.31 показано изменение х и хх при некото-
некоторых, взятых в качестве примера изменениях и и щ.
х
12*
i i
х,
\2
Т*
\2
ПИП]
Т» J
is
i
i.
i i
\6 t
rirliinrt
Рис. 4.31.
Значение х совпадает со значением и с запаздыванием
на один такт. Для правильного функционирования сети
требуется лишь, чтобы сигналы ut следовали друг за
§ 4.5] АБСТРАКТНЫЙ НЕЙРОН 159
другом не чаще, чем через 4т. Стрелками на рис. 4.31
отмечены интервалы времени 2т.
Располагая элементом задержки на любой извне по-
поданный такт и любым преобразователем, срабатываю-
срабатывающим за время 2т, можно по методам, изложенным да-
далее в гл. X, реализовать нейронной сетью Мак-Каллока
и Питтса любой автомат (последовательностную маши-
машину) с произвольной тактностью, удовлетворяющей лишь
одному условию: промежуток между тактами должен
быть не менее чем 4т.
ГЛАВАУ
ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ КОНЕЧНЫХ
АВТОМАТОВ И ПОСЛЕДОВАТЕЛЬНОСТНЫХ
МАШИН
§ 5.1. Два метода технической реализации конечных
автоматов и последовательностных машин
В предыдущих главах понятия «конечный автомат»,
«последовательностная машина» и «абстрактная струк-
структура» были введены формально. До сих пор эти поня-
понятия обозначали лишь уравнения или системы уравнений
определенного вида, и нам была безразлична физиче-
физическая природа динамических систем, движение которых
описывается этими уравнениями. В этой главе мы пока-
покажем, что введенным понятиям соответствуют важные
технические системы, и опишем методы технической
реализации любого заданного конечного автомата или
Я-машины.
В гл. IV было показано, что один и тот же конечный
автомат или одна и та же Я-машина могут быть пред-
представлены различными абстрактными структурами. Каж-
Каждой абстрактной структуре может быть поставлена в со-
соответствие своя техническая реализация, т. е. устройство,
процессы в котором соответствуют этой абстрактной
структуре. Поэтому один и тот же конечный автомат
может иметь различные технические реализации. Более
того, как будет далее показано, одна и та же абстракт-
абстрактная структура данного автомата может быть реализо-
реализована с помощью различных технических средств.
В настоящей главе будут рассмотрены реализации
лишь двоичных абстрактных структур, т. е. будет пред-
предполагаться, что конечный автомат задан системой соот-
§5.21 АГРЕГАТНОЕ ПОСТРОЕНИЕ КОНЕЧНЫХ АВТОМАТОВ 161
ношений
*f+1 = Ft[ХЬ Ц> ¦••> К> Щ> Ч> ¦ • ¦> «?] E-1)
(/=1, 2, ..., п),
где хг (i = 1, 2 п) и щ (/= 1, 2 s)—логиче-
s)—логические переменные, принимающие значения лишь 0 или 1,
a F{ (i = 1, 2, ..., п) —логические функции, также при-
принимающие значения лишь 0 или 1, и что задана такт-
ность автомата, т. е. условия, которыми определяются
дискретные моменты 0, 1, 2, .... р на шкале непрерыв-
непрерывного времени.
Для того чтобы техническое устройство реализо-
реализовало соотношение E.1), необходимо прежде всего рас-
располагать логическими преобразователями, реализую-
реализующими функции Fi. Подобным устройствам была посвя-
посвящена гл. П.
Теперь, однако, надо реализовать не функции Fi, a
соотношения E.1), содержащие эти функции в правых
частях. Что надо изменить в функциональных преобра-
преобразователях, описанных в гл. II, или чем надо их допол-
дополнить для того, чтобы функциональные преобразова-
преобразователи превратились в устройство, состояния которого
изменяются во времени в соответствии с абстрактной
структурой E.1)?
Ниже приводятся два существенно различных способа
решения поставленной задачи.
§ 5.2. Агрегатное построение конечных автоматов
и последовательностных машин
В гл. IV уже отмечалось, что абстрактной структуре
E.1) может быть поставлена в соответствие структур-
структурная схема. Пример такой схемы для п = 3, s = 2 пока-
показан на рис. 5.1. Схема содержит s входных шин (нитки
входов щ, «2, • • •, "s) ил выгодных шин (координаты —
состояния Х\, Хг, ..., х„). К каждому из п логических
преобразователей реализующих соответственно функции
Fu F2 г_„ подводятся сигналы от всех п + s шин;
выход t'-го преобразователя питает шину х, через эле-
элемент задержки на такт (обозначен кружком на рис. 5.1 )<,
11 М. А. Айзерман, Л. А. Гусев и др.
162
ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ КОНЕЧНЫХ АВТОМАТОВ [ГЛ. V
у которого выход и вход связаны соотношением
Непосредственно видно, что такая схема точно соот-
соответствует структуре соотношений E.1) и, следовательно,
реализует их. Для построения технического устройства
по этой схеме, помимо логических преобразователей,
надо располагать еще
элементами задержки на
такт.
Поэтому, чтобы набор
элементов, достаточный
для реализации любой ло-
логической функции, превра-
превратился в набор, достаточ-
достаточный для реализации ко-
конечного автомата, надо
дополнить его только од-
одним элементом — элемен-
элементом задержки на такт.
(м*
г \
о
о
о
1
w w \ ' \
<<
h
Рис. 5.1.
Рис. 52.
Такой набор достаточен и для построения любой по-
следовательностной машины, так как она отличается от
автомата лишь наличием выходного логического преоб-
преобразователя.
Элемент задержки на такт должен иметь два входа:
основной хвх и вспомогательный (временной) — xt, и один
выход Хвых- Условное обозначение такого элемента по-
показано на рис. 5.2*). Вспомогательный (временной)
*) Обычно там, где это не наносит ущерба пониманию работы
схемы, нитка входа Xt опускается.
§5.2]
АГРЕГАТНОЕ ПОСТРОЕНИЕ, КОНЕЧНЫХ АВТОМАТОВ
163
вход служит для приема сигналов о наступлении такта.
Сигналы эти подаются на автомат извне от специаль-
специального устройства; устройство, создающее их («часы» или
«датчик тактов»), в автомат не включается.
Элемент задержки действует следующим образом.
Пусть в момент наступления такта вход элемента имеет
некоторое состояние л:*х. Тогда, спустя некоторое малое
время т (собственное запаздывание элемента задержки),
А А А А А А
\2 \3
"me, i
!« \5 'б t
цНомер такта)
п
Рис. 5.3.
на выходе устанавливается -*Bblx = л:*х. Затем, что бы ни
происходило на входе, выход будет сохранять свое зна-
значение до тех пор, пока не наступит следующий такт.
В момент наступления следующего такта тот же про-
процесс повторяется вновь. На изменения входа, происхо-
происходящие внутри тактов, элемент задержки на такт вообще
не реагирует.
На рис. 5.3 показан пример изменения входа и вы-
выхода элемента задержки на такт. В этом примере сигна-
сигналами наступления такта служат короткие импульсы.
Однако часто сигналом такта служит всякое изменение
состояния вспомогательного входа, которое такжя
164 ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ КОНЕЧНЫХ АВТОМАТОВ [ГЛ. V
может иметь лишь два значения: 1 или 0 (рис. 5.4), или
лишь переход от состояния 0 к состоянию 1 (рис. 5.5).
В качестве примера рассмотрим устройство пневма-
пневматического элемента задержки на такт. Этот элемент
строится на базе так называемых ячеек памяти. Схемы
двух типов ячеек памяти изображены на рис. 5.6, а и
5.6,6 соответственно. Сигналом о наступлении такта в
этом элементе служит изменение состояния «временного
входа» Pt с 0 на 1.
Ячейка памяти состоит из двух пневмореле (см.
§ 2.4). Одно из них (выходное) включается по схеме «по-
«повторение» и всегда делает выходное давление ячейки Р
равным давлению Ль а второе (входное) выполняет
функцию пневмоклапана, включающего или отключаю-
отключающего камеру, где устанавливается давление Ра, с вход-
входной линией Р\. Пневмоклапан управляется давлением Ри
для ячейки первого типа (рис. 5.6, а) клапан закрыт при
Pt = 1 и открыт при Pt = 0, а для ячейки второго типа,
наоборот, закрыт при Pt = 0 и открыт при Pt = 1. Такое
устройство ячейки приводит к тому, что либо ее выход
равен входу (для ячейки первого типа при Pt = 0, а для
ячейки второго типа при Pt = 1), либо выход не связан
со входом и сохраняет неизменное значение (в ячейке
первого типа при Pt=\, а в ячейке второго типа при
Pt = 0), которое определяется величиной давления Рп
в глухой камере.
Две ячейки памяти первого и второго типа, соеди-
соединенные последовательно, образуют элемент задержки на
такт (рис. 5.6,в).
Элемент работает следующим образом. В момент /„,
когда Pt принимает значение 1 (момент начала п-го
такта), первая ячейка «запоминает» значение входа, т. е.
P*(tn) = Pi(tn); вторая ячейка памяти в этот же момент
времени (точнее, в момент времени /„ + At, где А/ обус-
обусловлено тем, что смещение в пневмоклапане второй ячей-
ячейки памяти больше, чем в первой) пропускает запом-
запомненную в первой ячейке величину на выход элемента;
на выходе устанавливается давление P(tn) =P*(tn) =
= Pi(tn). В дальнейшем, пока Pt=l, никаких измене-
изменений в элементе произойти не может, так как его состоя-
состояние определяется тем, что первая ячейка памяти все это
§ 5.2] АГРЕГАТНОЕ ПОСТРОЕНИЕ КОНЕЧНЫХ АВТОМАТОВ 165
0
01
хЬых,
1
0
I
0
1
0
ых
0
1
—»-
If
7
1
1
1
1 !
i
i
l
г
L 1
Рис
in
?
II 1
1
г
-*-
1
Рис
\з
!!
Г
II!
|
5.4.
ппп
II
1
I
I
I
ill
5.5,
¦
t
Г,
t
166 ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ КОНЕЧНЫХ АВТОМАТОВ [ГЛ. V
время «помнит» значение входа P\(tn). Значит, при
tn^t^.t'n, где tn —момент, когда Pt примет значение О,
P(t) «/>) Р()
«)
о*
1 1
1 1
т
п
1
1
1
1
1
t
t
t
Рис. 5.6.
В момент времени t'n (см. рис. 5.6, г) вторая ячейка
памяти, имея на входе величину Р* (t1^ = Я, (tn), «запо-
«запоминает» ее, а это приводит к тому, что и в этот момент
выход элемента сохраняет свое значение ^(O^^i^n)'
первая ячейка памяти в момент времени t'n + At пере-
§ 5.2! агрегатное построение конечных автоматов 167
ходит в режим повторения. В дальнейшем, пока Р( = О,
выход элемента задержки меняться не будет; он может
принять новое значение лишь тогда, когда в момент /n + i
командное давление Р< (временной вход) снова обра-
обратится в единицу.
Таким образом, рассмотренное пневматическое уст-
устройство выполняет функции элемента задержки на такт:
его выход в момент наступления такта (при Pt=\)
приравнивается ко входу и, что бы ни происходило после
этого на входе, остается неизменным до наступления
следующего такта (сравните рис. 5.6, г, с рис. 5.5).
На рис. 5.7 показана электромеханическая (релейно-
контактная) реализация элемента задержки на такт.
Схема релейно-контактного элемента задержки в зна-
значительной степени аналогична схеме рассмотренного
выше пневматического элемента задержки.
Элемент имеет два входа X и Xt\ вход Xt является
временным — момент смены Xt с 0 на 1 определяет на-
наступление нового такта. Схема элемента, так же как и
при пневматической реализации, построена на последо-
последовательном соединении двух ячеек памяти {1 и 2 на
рис. 5.7,а). Выходом элемента служит обмотка реле У.
Запоминание в ячейках осуществляется за счет при-
применения блокирующих контактов (в ячейке памяти 1 —
контакта у*, и в ячейке памяти 2— контакта у). Вре-
Временной вход Xt своими контактами xt и xt действует на
ячейки памяти так, что, когда «запоминает» первая
ячейка (это будет при Xt = 1), вторая ячейка работает
как повторитель первой (У = У*), и наоборот, когда за-
запоминает вторая ячейка (при Xt = 0), первая ячейка
повторяет вход (У* = X).
График на рис. 5.7, б иллюстрирует работу этого эле-
элемента и свидетельствует о том, что он действует точно
так же, как и описанный ранее пневматический элемент
задержки.
Для правильной работы элемента задержки, постро-
построенного на двух ячейках памяти, необходимо в каждый
момент, когда происходит смена состояний ячеек, что-
чтобы эта теоретически одновременная смена происходила
в действительности в определенной последователь
ности: сначала обе ячейки оказываются в состоянии
168 ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ КОНЕЧНЫХ АВТОМАТОВ [ГЛ. V
«запоминания», и лишь после этого одна из ячеек пере-
переходит в режим повторения.
В пневматическом элементе это достигается за счет
применения разных по величине «подпоров» Рщ и РП2.
¦- 1 -
о
x
О
Г
о
У
о
J
J L
1
—•
j
г
II
1 Z
\—
1
1 .
1
1
! /
1 м
! ,
1
Рис. 5.7.
а в релейно-контактном элементе это обеспечивается
тем, что реле У* и К имеют собственное запаздывание т.
Набор технических элементов, позволяющих реали-
реализовать любую логическую функцию, дополненный эле-
элементом задержки на такт, составляет полный агрегат-
агрегатный набор, из которого собирается любой конечный ав-
автомат. В этом смысле, например, пневматические реле
(гл. II, рис. 2.20), дополненные пневматическим элемен-
§5.2]
АГРЕГАТНОЕ ПОСТРОЕНИЕ КОНЕЧНЫХ АВТОМАТОВ
169
том задержки на такт (рис. 5.6), составляют полный на-
набор, достаточный для построения любого конечного
автомата. В пневматической системе, при применении
пневматического элемента задержки, автоматы могут
строиться в точном соответствии с рис. 5.1.
При применении релейно-контактных элементов за-
задержки любой заданный конечный автомат получается
путем включения в схемы элементов задержки (рис. 5.7)
j [гЛ У Г У* »\ Ш У! У г Уг\
\Т I I IjT I I 1
I xt xt xt xt. xt xt xt x\-
Уп Уп Уп\
iT II 1\
Рис. 5.8.
вместо входных контактов х\, ..., xs некоторых кон-
контактных цепей /ь /г, . ¦., In, содержащих входные кон-
контакты *ь .... xs и контакты Уи ¦¦¦, Уп выходных реле
элементов задержки.
Общая схема автомата в этом случае представлена
на рис. 5.8, причем здесь имеют место следующие со-
соответствия: состояниям ниток входа автомата «ь ..., us
(рис. 5.1) соответствуют состояния входных кон-
контактов Х\, ..., xs (рис. 5,8), состояниям автомата
Х\, ..., хп (рис. 5.1) соответствуют состояния обмоток
реле Yu ..., Уп (рис. 5.8) и, наконец, логическим преоб-
преобразователям Fi, ..., Fn (рис. 5.1) соответствуют кон-
контактные цепи f 1, ..., fn на рис. 5.8.
Разумеется, элемент задержки на такт сам является
простейшим конечным автоматом.
Набор, элементов, необходимый для того, чтобы из
него можно было собирать не только логические преоб:
разователи, но и автоматы, должен включать либ'
170
ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ КОНЕЧНЫХ АВТОМАТОВ [ГЛ. V
элемент задержки на такт, либо какой-нибудь иной эле-
элементарный конечный автомат (неавтономный). '
Широко применяется также дополнение логических
элементов таким элементарным автоматом, который
дает возможность строить не все, но многие практиче-
практически важные конечные автоматы. В цифровой технике
«6.4] агрегатное Построение конечных автоматов \у\
таким элементарным автоматом является триггер со
счетным входом (автономный автомат). Схема пневмо-
триггера, построенного на пневматической задержке,
изображена на рис. 5.9.
Пневмотриггер (рис. 5.9, а) получается из элемента
задержки замыканием его выхода на собственный вход
через элемент отрицания (рис. 5.9,6). Собранное по та-
такой схеме устройство является автономным конечным
автоматом, уравнение которого имеет вид хр+1 = хр,
где переменной х в данном
случае соответствует давле-
давление Р. Работу этой схемы ил-
иллюстрирует график, изобра-
изображенный на рис. 5.9, в. На
рис 5.10 показана аналогич-
аналогичная схема релейно-контакт-
ного . триггера, также образо-
образованного из элемента задержки
замыканием его выхода на
собственный вход через эле-
элемент отрицания. Рис 5 ш
Приведенные схемы триг-
триггеров построены на базе эле-
элемента задержки. В следующем параграфе будут даны
схемы триггеров иного типа.
Метод построения автоматов, описанный здесь, свя-
связан с необходимостью дополнить набор мгновенно дей-
действующих логических элементов каким-либо простей-
простейшим автоматом (например, задержкой на такт, тригге-
триггером и т. д.), и, кроме того, при применении задержек на
такт, предполагает наличие устройства (часов), выход
которого используется как временной вход в элементах
задержки.
Во многих случаях, однако, можно обойтись без до-
дополнения логического набора новыми элементами, если
учесть, что любой реальный ^элемент срабатывает с не-
некоторым запаздыванием х — включает в себя естествен-
естественную задержку на время т, т. е. является элементарным
автоматом, работающим в тактности, определяемой рав-
равномерным разбиением оси времени на интервалы дли-
длиной х. Это приводит к наиболее распространенному, но
172 ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ КОНЕЧНЫХ АВТОМАТОВ (ГЛ. V
более ограниченному по своим возможностям способу
построения автоматов. Он пригоден для применения то-
тогда, когда разбиение непрерывной шкалы времени на
дискретные моменты (такты) определяется всяким изме-
изменением состояния входа.
§ 5.3. Построение конечных автоматов
и последовательностиых машин с использованием
естественных задержек и обратных связей
Вернемся к рассмотрению простейшего электромеха-
электромеханического реле. В гл. II мы считали его мгновенно дей-
действующим. В действительности же реле срабатывает с
небольшим запаздыванием т. Это значит, что выход (со-
(состояние контактов х) и вход (наличие тока в обмотке X)
хотя и являются логическими переменными (т. е. могут
принимать лишь значения 0 и 1), но связаны временной
зависимостью
х'^ = X1.
Если разбить ось непрерывного времени равномерно
на такты 0, т, 2т, Зт, ... и считать, что вход изменяется
и выход наблюдается лишь в эти моменты, то получим
т. е. реле*) является элементарным автоматом типа
«задержка на такт», работающим в тактности т.
Если соединить контакты в сеть для получения любой
логической функции в соответствии с методами гл. II, то
такая сеть реализует в действительности не «мгновен-
«мгновенную» функцию
x = F(u1, u2, ..., us),
а автомат
= F[up, up2, ,.., up],
работающий в той же тактности 0, т, 2т, Зт, ...
*) Мы говорим о реле с нормально-разомкнутым контактом.
Реле с нормально-замкнутым контактом при учете времени сраба-
срабатывания можно рассматривать как цепочку из элемента задержки на
такт и мгновенно действующего элемента отрицания.
§5:3] ЕСТЕСТВЕННЫЕ ЗАДЕРЖКА И ОБРАТНЫЕ СВЯЗИ 173
Рассмотрим теперь цепочку, составленную из реле
так, что нормально-разомкнутый контакт каждого пре-
предыдущего реле замыкает обмотку следующего реле
(рис. 5.11). Входом всей цепочки служит ток в обмотке
Рис. 5.11.
первого реле, выходом — замыкание контакта хп послед-
последнего реле. Такая цепочка описывается соотношениями
„р+1 ур vp 4-p+i ур vp
или
„Р+П
„Р+П ур
образуя типичный автомат без петель — линию задержки
на п тактов.
Т I Г
Рис. 5.12.
Построим теперь автомат с петлей, включив обмотку
первого реле линии задержки в цепь контакта послед-
последнего реле, т. е. замкнем цепь задержки обратной связью
(рис. 5.12). Напомним, что все реле имеют нормаль-
нормально-разомкнутые контакты. После любого начального
174 ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ КОНЕЧНЫХ АВГОМАТОИ [ГЛ. V
состояния контактов этот автомат, работая в «тактно-
сти т», переходит в одно из двух возможных устойчивых
состояний (все контакты замкнуты или все контакты ра-
разомкнуты) и далее не меняет его.
Если же сделать контакт первого реле нормально-
замкнутым, а остальные оставить нормально-разомкну-
нормально-разомкнутыми, то будет происходить . непрерывное циклическое
переключение контактов. На графе такого автомата все
состояния замкнуты в цикл. В частности, именно так ра-
работает пульс-пара, схема которой изображена на
рис. 5.13. Любая релейно-контакт-
ная схема при таком рассмотрении
образует автомат, работающий в
указанной выше тактности т. Как
показывают приведенные примеры,
при этом могут быть образованы
как автоматы без петель (при-
(пример— линия задержки, показанная
на рис. 5,11), так и автоматы с
Рис. 5.13. петлями (пример на рис. 5.12 и
5.13). Имеет смысл говорить лишь
об автономных автоматах такого рода, так как пред-
предположение, что и вход меняется в тактности т,
нереально.
Заметим теперь, что у автономных автоматов без пе-
петель граф может содержать лишь одну устойчивую точ-
точку (равновесие), к которой стремится автомат при лю-
любом начальном состоянии. У автоматов же с петлями
(т. е. при наличии в схеме обратных связей) графы мо-
могут содержать замкнутые циклы, несколько равновесий
и т. д. (подробнее см. гл. VI). Хотя автоматы подобного
рода иногда используются, значение их невелико, так
как в таких автоматах тактность предопределена запаз-
запаздыванием в реле и обычно очень быстрая.
Наиболее распространены автоматы, у которых такт-
тактность должна определяться лишь моментами изменения
состояния входа, причем эти изменения происходят не
часто: интервал между двумя изменениями состояний
входа можно считать значительно большим, чем время
срабатывания реле т. Условимся такую тактность назы-
называть медленной, а тактность, определяемую равномер-
§5.3] ЕСТЕСТВЕННЫЕ ЗАДЕРЖКИ И ОБРАТНЫЕ СВЯЗ'И 175
ным разбиением оси времени на интервалы длины т —
быстрой.
Автоматы, работающие в медленной тактности, опре-
определяемой сменой состояния входа, могут быть построены
из автоматов, работающих в быстрой тактности. При
этом осуществляется преобразование тактности (подроб-
(подробнее см. гл. X). С этой целью используется возможность
строить из реле быстрые автономные автоматы, графы
которых имеют несколько устойчивых состояний.
Рассмотрим, например, простейшую релейную схему,
показанную на рис. 5.14. Эта схема содержит два реле,
обмотки которых Y\ и Y2 включены в сети, содержащие
*'
*г
\ °^° \ \ aSi° 1
Рис. 5.14.
контакты этих же реле. Следовательно, схема содер-
содержит обратные связи и представляет поэтому автомат
с петлями. Кроме того, в сеть включены контакты Х\ и х2
двух дополнительных реле Х\ и Х2. Эти контакты слу-
служат для подачи входных воздействий.
Пусть зафиксировано какое-либо положение вход-
входных контактов и далее положение их остается неизмен-
неизменным. Тогда, если задать начальное состояние остальных
контактов, схема работает как автономный автомат в
быстрой тактности в соответствии с графом этого авто-
автомата. Если этот граф не содержит замкнутых циклов и
имеет несколько равновесий, то система может только
стремиться к одному из них. Какое именно равновесие
будет достигнуто, определяется начальным состоянием.
Пусть достигнуто состояние равновесия А. Через не-
некоторое время после того, как оно достигнуто, меняется
176 ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ КОНЕЧНЫХ АВТОМАТОВ [ГЛ. V
состояние входных контактов, и затем это новое состоя-
состояние входных контактов сохраняется неизменным. При
-новом состоянии входных контактов схема образует но-
новый автономный автомат с новым графом. Этот новый
граф также может содержать несколько равновесий, но
прежнее равновесное состояние А не обязательно бу-
будет равновесным на графе нового автономного ав-
автомата. В этом случае вновь происходит «переходный
процесс», т. е. автомат начинает работать в быстрой
тактности, стремясь к новому равновесию Б, которое
определяется как графом нового автомата, так и тем,
где расположено на этом графе состояние А.
Описанный процесс повторяется каждый раз, как
только будет изменено состояние входных контактов.
Если, в частности, через некоторое время контакты вновь
будут возвращены в первоначальное состояние, система
не обязательно вернется к равновесию А. Действительно,
при этом вновь образуется старый автономный автомат
со старыми графами, но точка Б может быть распо-
расположена на этом графе на иной ветви, чем то началь-
начальное состояние, с которого мы начали рассмотрение
работы системы, и тогда будет достигнуто не равновесие
А, а иное равновесие, например, В, — ведь мы предпола-
предполагали, что граф автономного автомата содержит не одно,
а несколько состояний равновесия.
Представим себе теперь, что мы списываем состоя-
состояния входов и выходов рассматриваемой релейной систе-
системы каждый раз через а секунд после того, как произо-
произошло изменение состояния входных контактов. Величину
а мы выберем достаточно большой, чтобы все «пере-
«переходные процессы», происходящие в быстром темпе, ус-
успели закончиться, и состояние равновесия было достиг-
достигнуто, но вместе с тем не слишком большой, чтобы за
это время не изменилось состояние входа. Тогда в эти
моменты времени мы будем наблюдать только равно-
равновесные состояния; появление того или иного состояния
будет определяться предшествующим равновесным со-
состоянием и состоянием входов, т. е. схема реализует ко-
конечный автомат, работающий уже не в быстрой такт-
тактности, а в тактности, определяемой сменой входных со-
состояний. . .. .
§ 5.3] ЕСТЕСТВЕННЫЕ ЗАДЕРЖКИ И ОБРАТНЫЕ СВЯЗИ 177
Если выход и, может быть, вход этого автомата по-
поступают на логический выходной преобразователь, то
реализуется последовательностная машина медленной
тактности.
В действительности схема работает в быстрой такт-
тактности, но это не существенно для нас, если мы инте-
интересуемся состояниями лишь в указанные выше момен-
моменты,— к этим моментам переходные процессы заканчи-
заканчиваются, и мы их попросту не наблюдаем.
Описанный прием построения автомата (или Я-ма-
шины), работающего в быстрой тактности, для реализа-
реализации на его устойчивых состояниях автомата (или Я-ма-
шины), работающего в медленной тактности, определяе-
определяемой изменением состояний на входе, и лежит в основе
описываемого принципа построения конечных автоматов
и Я-машин. Так, в частности, строятся конечные авто-
автоматы и Я-машины на электромеханических реле и на
электронной аппаратуре (ламповых и полупроводнико-
полупроводниковых триодах и диодах).
Естественно возникает вопрос: любой ли наперед за-
заданный конечный автомат (или Я-машина), работающий в
тактности, определяемой изменениями состояний входа,
может быть построен с помощью указанного приема?
Положительный ответ на этот вопрос предопределен
тем, что существуют регулярные методы построения
схем, реализующих любой наперед заданный автомат
или лоследовательностную машину. Один из этих мето-
методов — метод Хафмана — описан в § 5.4.
Естественно возникает также задача о наиболее эко-
экономной сети, т. е. о сети, которая с помощью описанного
приема реализует заданный автомат и имеет вместе с
тем либо наименьшее число реле, контактов, внутрен-
внутренних состояний, либо минимизирует иные, важные для
оценки схемы, параметры. Одной из задач такого рода
в общей постановке посвящена гл. X.
Заметим теперь, что в оснрве описанного метода ле-
лежит создание сетей, у которых графы получаемых авто-
автономных автоматов имеют несколько равновесий. Но гра-
графы с несколькими равновесиями возможны только в ав-
автоматах с петлями. Значит, быстрый автомат должен
быть обязательно автоматом слетлей, что технически
12 М. А. Айзермаи, Л. А. Гусев и др.
178 ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ КОНЕЧНЫХ АВТОМАТОВ [ГЛ. V
реализуется за счет обратных связей, т. е. за счет того,
что обмотки реле включаются в цепи, содержащие кон-
контакты этих же реле. В этом смысле сети реализуют мед-
медленные автоматы только за счет обратных связей. Реле,
включенные в контуры обратных связей, называют ино-
иногда промежуточными реле, в отличие от реле, которые
служат для управления входными контактами (входные
реле) или для снятия результирующего сигнала (выход-
(выходные реле).
Сравнивая агрегатный способ построения автомата и
способ построения на устойчивых состояниях, мы видим,
что для агрегатного построения решающим является
специальный элемент, который мы назвали элементом
задержки на такт, в то время как при построении на
устойчивых состояниях не требуется никаких средств,
кроме тех же реле, которые используются для реализа-
реализации логических преобразователей, а развертывание ра-
работы во времени осуществляется за счет контуров обрат-
обратных связей и специального построения контактных се-
гей. Но зато при описанном способе непосредственно
реализуются лишь автоматы и последовательностные
машины, в которых тактность определяется моментами
изменения состояния входов.
Разумеется, все элементы агрегатного набора и, в
частности, элемент задержки на такт сами могут быть
построены на устойчивых состояниях (см. схему релей-
но-контактного элемента задержки, рис. 5.7), но для
того, чтобы элементы, построенные по этому принципу,
можно было использовать агрегатно, они должны обя-
обязательно включать выходные усилители мощности, т. е.
быть активными.
Часто релейные схемы (например, сети контактов)
строятся так, чтобы графы автономных автоматов, кото-
которые получаются при всех возможных состояниях вход-
входных контактов, имели специфический вид, показанный
на рис. 5.15; такие графы содержат несколько равно-
равновесных состояний (на графе стрелки, выходящие из этих
состояний, идут к этим же состояниям), а все остальные
неравновесные состояния непосредственно соединены
стрелкой с каким-нибудь из равновесных состояний. При
таком построении схем каждый раз для достижения
§ 5.3] ЕСТЕСТВЕННЫЕ ЗАДЕРЖКИ И ОБРАТНЫЕ СВЯйЙ 179
равновесия требуется только один такт, т. е. равновесие
достигается за время т, и поэтому время а может быть
лишь незначительно больше т. Практически это значит,
что можно наблюдать состояние медленного автомата
почти сразу после того, как произошло изменение входа.
Разумеется, за этот один такт одновременно могут пере-
переключаться несколько реле.
Если бы время т у всех реле было строго одинако-
одинаковым, факт одновременного срабатывания нескольких
реле не вызывал бы осложнений. В действительности же
в реальных реле время срабатывания т не строго оди-
одинаково. Это может привести
к тому, что система, рабо-
работая в быстрой тактности,
будет сменять состояния не
в той последовательности,
как это было бы при строго
синхронизованных реле. По-
Получающаяся смена состоя-
состояний будет зависеть от того,
какое реле срабатывает
раньше, т. е. от факторов рис 515
случайных и обычно не под-
поддающихся контролю. Пример, иллюстрирующий это яв-
явление, приведен далее, в § 5.4.
Указанное явление называют обычно критическими
состязаниями реле, подчеркивая этим термином то об-
обстоятельство, что работу схемы предопределяет то реле,
которое сработает быстрее. Работа схемы не должна
зависеть от случайных обстоятельств, и, следовательно,
критические состязания реле не должны быть допущены.
Для того чтобы избежать состязаний, схема, реали-
реализующая заданный конечный автомат или последователь-
ностную машину, должна удовлетворять еще и некото-
некоторым дополнительным требованиям: например, переход
от одного состояния к другому^ за время одного быстрого
такта должен происходить за счет срабатывания только
одного реле^ Это приводит к необходимости усложнять
схемы и увеличивать количество образующих их эле-
элементов (реле, контактов). Схемы, удовлетворяющие
этому условию, называют реализациями.
12*
180 ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ КОНЕЧНЫХ АВТОМАТОВ |ГЛ. '
Существует ряд типовых реализаций. Одна из них —
предложенная Хафманом, будет описана в следующе\
параграфе. Разумеется, проблема состязаний отпадае-
в тех случаях, когда реле строго синхронизованы. Такая
ситуация имеет место в некоторых магнитных система;,
которые строятся на магнитных усилителях и вентиль
ных элементах, так как а этих системах время т все>г
элементам навязано извне частотой питающего систем'
переменного тока.
§ 5.4. Метод и реализация Хафмана
Работа Хафмана [170] по релейно-контактным cxeMaiv
не содержит еще понятий последовательностной машинь
или конечного автомата, или каких-либо иных эквива-
эквивалентных им понятий.. Приводя ряд примеров задания нг
синтез релейно-контактной схемы, Хафман показывает,
как может быть в этих случаях построена специальная
таблица — Хафман называет ее таблицей переходов
(flow table), — которая является исходной в его методе.
Считая далее, что таблица переходов задана, Хафман
показывает, как она может быть упрощена (но не дока-
доказывает, что это упрощение предельно возможное), и раз-
разрабатывает универсальный способ построения релейно-
контактной схемы, реализующей эту таблицу переходов.
В работе Хафмана релейно-контактная схема реализует
задание своими равновесными состояниями. Однако, не
вводя понятий конечного автомата и последователь-
последовательностной машины, Хафман, естественно, не мог ска-
сказать, что по существу метод его состоит в построении
Я-Машины, работающей в быстрой тактности, которая
реализует устойчивыми состояниями заданную Я-ма-
шину, работающую в медленной тактности, определяе-
определяемой сменой состояний входа.
Используя понятия конечного автомата, последова-
последовательностной машины и преобразования тактности, мы
изложим метод Хафмана на этой основе. Будем считать
исходными данными для проектирования релейной схе-
схемы таблицу автомата и выходного преобразователя реа-
реализуемой последовательностной машины. Кроме того,
излагая метод Хафмана, мы будем иллюстрировать его
§5.4] МЕТОД И РЕАЛИЗАЦИЯ ХАФМАНА 181
на каждом этапе соответствующим преобразованием
схемы Я-машины.
Пусть задана Я-машина, т. е. две таблицы: основная
таблица конечного автомата и таблица выходного преоб-
преобразователя. Тактность работы автомата определяется
моментами смены состояний входа. Требуется построить
релейную схему, которая на устойчивых состояниях, по
принципу, изложенному в § 5.3, реализовала бы задан-
заданную Я-машину.
Решение этой задачи методом Хафмана дается на
одном простом примере, однако из дальнейшего изло-
изложения будет ясно, что метод является общим и совер-
совершенно аналогично применяется в любом другом случае.
а) Замечания о типе автомата
или п ос л е д ов ате л ь н о с т н о й машины
Напомним, что любая последовательностная машина,
и в том числе любой конечный автомат, могут быть
определены системой соотношений (см. § 3.4)
И =/="(*. Р). |
*/>+! = (Л E.2)
Х = Ф(х, р), J
где
I*. *=К • • •, ч\у Р = (Pi> • • •- РгЬ Х=\К • • •» М-
Это следует из того, что те последовательностные ма-
машины и автоматы, которые определены системой соот-
соотношений
(А = F (%, р),
*/>+! = ji", E.3)
X = Ф (\х, р),
за счет введения функции
>
всегда могут быть приведены'к форме E.2). Обратное
утверждение не имеет места, т. е. задание в виде систе-
системы E.2) без изменения числа состояний только иногда
ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ КОНЕЧНЫХ АВТОМАТОВ [ГЛ. V
может быть приведено к системе E.3). В частности,
автомат, заданный системой
E.4)
всегда может быть представлен системой
E.5)
а автомат, заданный системой
p=F(x, р),
E.6)
не может быть приведен к системе вида E.3).
Я-машины, заданные системой E.2), в § 3.4 были
названы машинами типа П — П, а Я-машины, заданные
системой E.3),—машинами типа П — Н. Далее мы бу-
будем пользоваться этой терминологией.
Универсальность системы E.2) дает основания для
того, чтобы использовать ее в качестве канонического
способа задания конечных автоматов и последователь-
ностных машин.
Системе E.2) соответствуют две таблицы, каждая с
аргументами к и р. Для того чтобы подчеркнуть общ-
общность аргументов, а также и для компактности записи,
мы в дальнейшем эти обе таблицы будем совмещать.
Итак, данные на синтезируемую релейную схему, будем
представлять в виде совмещенной таблицы автомата и
выходного преобразователя. Столбцы этой таблицы со-
соответствуют различным состояниям входа, а строки —
различным состояниям автомата; в клетки таблицы, в
соответствии с системой E.2), вписываются два сим-
символа: символ состояния автомата и символ состояния
выхода Я-машины. Совмещенную таблицу допустимо
трактовать следующим образом. Можно считать, что
§5.4]
МЕТОД И РЕАЛИЗАЦИЯ ХАФМАНА
183
строки и столбцы соответствуют настоящим состояниям
автомата и входа (состояниям в момент времени р); то-
тогда символы в клетках определяют будущее состояние
автомата (состояние в момент времени р + 1) и настоя-
настоящее состояние выхода Я-машины. Эта трактовка свя-
связана с представлением системы E.2) в виде
Х' = Ф(*', р").
Табл. 5.1 — 5.5 служат примерами представления
исходных данных совмещенными таблицами.
Табл. 5.1 задает такой автомат, который по желанию
можно трактовать как автомат типа П — П или типа
П — Н. Это можно видеть по тому, что символы Лик
во всех клетках таблицы взаимно однозначно соответ-
соответствуют друг другу.
Таблица 5.1
Таблица 5.2
\ р
7, \
*1
*2
*3
*4
?1
7.3Х2
^3 2
7.2Х,
*iX3
Р2
7.4Х4
7,4Х4
74Х4
*Л
Рз
7,3X2
7.,Х3
у.2Х,
V.3X2
Р4
7,2Х,
*4х4
7,4Х4
7,2Х,
\р
7, \^
*1
7,2
*3
*4
Pi
7,3X2
¦х-з^-з
7.2Х4
7,,Х,
Р2
7,4Х2
*4^3
7,4Х4
7,,Х,
Рз
*зХ2
7,,Х3
7,2Х4
У.3Х,
Р4
7,2Xj
Х4Х3
7,4Х4
у2Х,
Табл. 5.2 определяет автомат, который нельзя трак-
трактовать как автомат типа П — Н. Признаком этого яв-
является взаимно однозначное соответствие символов X в
каждой строке (одинаковых $о всех клетках, принадле-
принадлежащих одной и той же строке) и символов к, располо-
расположенных в левом (входном) столбце таблицы.
Табл. 5.3 определяет последовательностную машину,
приводимую к машине типа П—Н. Это следует из того,
что в клетках таблицы, относящихся к одному (любому)
184 ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ КОНЕЧНЫХ АВТОМАТОВ [ГЛ. V
столбцу, находятся взаимно однозначно соответствую-
соответствующие друг другу символы Лих.
Таблица 5.4
Таблица 5.3
\ р
у, \.
*|
*2
у.3
*4
Pi
*3*1
Vi
у.2*.3
у.|А.2
Р2
%412
%4\2
Ъ412
Рз
*3*2
*1*4
У.2А.,
*3*2
Р4
у.2Л4
у.^з
f.4l3
*2*4
\р
У. \
*1
у.2
*з
*4
а1
Pi
«3^1
*3^|
у.2^з
У,|*2
3
Р2
у4А.2
у^2
*4*3
3
Рз
*3^2
У.|*4
*2^1
*3^2
3
Р4
*2*4
у4А.3
у4А.3
у2А.4
2
Таблица 5.5
Табл. 5.4 и 5.5 определяют последовательностные
машины, не приводимые к типу П — Н, так как в таб-
ЛИцах естЬ такИе столб"
цы, в клетках которых
символы Л и х не вза-
взаимно однозначно соот-
соответствуют друг другу
(см. столбец р2). Осо-
Особенность табл. 5.4 по
сравнению с табл. 5.5
состоит в том,что в ней
во всех клетках внутри
каждого столбца со-
сохраняется однозначнос-
соответствие симв'
лов X и х, т. I.
одинаковые Л встре-
встречаются в паре с оди-
одинаковыми % (нет только взаимно однозначного соот-
соответствия). . .
\р
у, ^^^
*|
*2
*3
*4
Pi
Vi
*3*l
х2к3
*l^2
Р2
*4^2
x4l2
f.4l{
Рз
*|^4
%21,
%3к2
Р4
*2^4
*4^-3
Х413
У2А4
§S.fl
МЕТОД И РЕАЛИЗАЦИЯ ХАФМАНА
185
Табл. 5.1 — 5.4 объединяются одним общим призна-
признаком: для них будущее состояние автомата (символ и
в клетке) однозначно определяется настоящим состоя-
состоянием входа и выхода Я-машины. Только табл. 5.5 не
обладает этим свойством.
Излагаемый далее метод Хафмана пригоден для не-
непосредственного применения в тех случаях, когда зада-
задание на синтезируемую схему не относитсяктипу табл. 5.5.
Иначе говоря, этим методом можно реализовать лю-
любые автоматы (приводимые и неприводимые к типу
П — Н), последовательностные машины, приводимые к
типу П — Н, и некоторые последовательностные машины,
неприводимые к типу П — Н, но обладающие особенно-
особенностью табл. 5.4.
б) Построение таблицы переходов
по заданной таблице
последовательностной машины
Пусть требуется на устойчивых состояниях построить
последовательностную машину, заданную в форме П—П
исходной таблицей —
совмещенной таблицей Таблица 5.6
автомата и преобразо-
преобразователя (табл. 5.6).
Предполагается, что
такты определяются
сменой состояний вхо-
входа. Предполагается
также, что для синте-
синтезируемой машины бу-
будущее состояние авто-
автомата однозначно опре-
определяется настоящими
состояниями входа и
выхода Я-машины,
т. е. в одном и том же
столбце таблицы нет
клеток, заполненных одинаковыми символами К и раз-
разными х. Табл. 5.6 удовлетворяет этому требованию. Для
решения задачи в соответствии с методом Хафмана
*1
*3
ск
Pi
*2*-t
*!*3
*1*2
3
Р2
*2*1
*3^2
*2*1
2
Рз
*3А,
*1^3
2
Р4
Vi
*л
2
186 техническая Реализация конечных автоматов [гл. v
необходимо прежде всего по заданной таблице машины
построить так называемую таблицу переходов. Это пере-
перестроение таблиц продемонстрируем здесь на примере
табл. 5.6.
К таблице синтезируемой машины (табл. 5.6) доба-
добавляется нижняя строка, в которую вписываются числа а,-,
указывающие, сколько различных состояний выхода
(различных Я) может быть у машины при одном и том
же г-м входе. В нашем случае ai = 3, a2 = аз = а4 = 2.
г
Подсчитывается величина "=2аг> Где г — число
/ = i
различных состояний входа. В нашем случае г = 4,
а о = ai + аг + аз + а4 = 9. Далее заготовляется таб-
таблица (табл. 5.7), имеющая такое же количество столб-
столбцов, как и исходная, а количество строк в ней делается
равным о. Входная (верхняя) строка табл. 5.7 запол-
заполняется так же, как и исходная, символами р, а во вход-
входной (в крайний левый) столбец вписываются подряд
символы новой переменной /'={/,', ..., /). Для нашего
случая ¦*! ={/[,..., Xgj Далее начинается заполнение
клеток таблицы. В первыйстолбец вписываются подряд,
начиная с первой строки, различные символы Я (общим
числом ai), взятые из первого столбца исходной таб-
таблицы. В случае исходной табл. 5.6 это будут Яь Яз и Яг
(последовательность расположения этих символов в
столбце табл. 5.7 может быть любой). В эти же клетки
вписываются соответствующие строкам символы %'. Этим
клеткам соответствуют равновесные состояния; их отме-
отметим квадратиками. Во втором столбце таким же обра-
образом заполняется аг клеток, но заполнение идет не с пер-
первой строки таблицы, а с первой пустой строки. В нашем
случае в четвертую и пятую клетки второго столбца
вписываются пары х^ и х?Х2. Подобным же образом
заполняется по а* клеток каждого /-го столбца.
Далее, рассматривая первую строку табл. 5.7, мы
видим вписанный в клетку первого столбца символ Я
(в нашем случае Я|); отыскиваем в первом же столбце
исходной табл. 5.6 клетку, содержащую этот же символ,
i 5.4]
МЕТОД И РЕАЛИЗАЦИЯ ХАФМАНА
187
и отмечаем вписанный в эту клетку символ к (в нашем
случае это будет %2) *).
Таблица 5.7
A
A
A
f
ч
f.
f
4
4
Pi
\A\h
f
Ъ
f
4
h
h
x2X3
f
Ah
/
1
P2
f
Ah
A\h
' 1 Ti
Ah
Ah
Ah
Рз
Ah
f
f
Ah
Ah
Ah
f
h
Ah
P4
Ah
Ah
Ah
Ah
4,
Ah
4..
3
<
f
4
h
h
x"
%\
ff
*2
<
4
4
If
If
4
ft
В исходной таблице находим строку, соответствую-
соответствующую этому символу х и, сохраняя порядок, переносим
*) Отметим, что в силу принятых ограничений на вид исходной
таблицы этот вопрос всегда решается однозначно, хотя в одном
столбце исходной таблицы один и тот же символ может находиться
в нескольких клетках,
188 ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ КОНЕЧНЫХ АВТОМАТОВ [ГЛ. V
из этой строки символы Л в пустые до этого клетки пер-
первой строки табл. 5.7. В нашем случае получаем вписан-
вписанными во вторую, третью и четвертую клетки первой
строки символы Яг, A,i и Яь Точно так же поступая с каж-
каждой строкой табл. 5.7, заполним все ее клетки симво-
символами Я. Теперь в клетки (табл. 5.7), заполненные лишь
символами Я, вписываем еще и символы х' и делаем это
так, чтобы в одном столбце одним и тем же Я соответ-
соответствовали одни и те же х', иначе говоря, в каждом столбце
мы разносим в соответствии с этим условием символы х',
взятые из квадратов. Таким образом, табл. 5.7 оказы-
оказывается заполненной. Она эквивалентна так называемой
таблице переходов Хафмана. Ее следует интерпретиро-
вать как таблицу «быстрой» последовательностной ма-
машины, заданной в форме П — П. Эта «быстрая» машина,
если в ней наблюдать переменные р и Я лишь в равно-
равновесных состояниях, будет работать как исходная.
в) Сокращение (сжатие) таблицы
переходов
Если в построенной таблице «быстрого» автомата (в
таблице переходов Хафмана) имеются строки с одина-
одинаковым заполнением, то это значит, что его можно заме-
заменить другим «быстрым» автоматом с меньшим числом
состояний. Покажем, как это сделать, на примере
табл. 5.7.
Вводится новая переменная х", ее значения приво-
приводятся в соответствие значениям переменной х' и притом
так, чтобы значениям х', соответствующим строкам с
одинаковым заполнением таблицы «быстрого» автомата,
соответствовало бы одно и то же значение х". Это удоб-
удобно, сделать на таблице «быстрого» автомата, добавив
в ней справа столбец значений х". В нашем случае этот
столбец будет заполнен так, как показано на табл. 5.7,
\ где были одинаково заполнены шестая и девятая строки,
'Затем строится сжатая таблица переходов (табл. 5.8),
содержащая прежнее количество столбцов и столько
строк, сколько получилось различных символов х". За-
Заполнение таблицы ведется по табл. 5.7 с заменой
волов х' соответствующими символами х".
§5.4]
МЕТОД И РЕАЛИЗАЦИЯ ХАФМАНА 189
Таблица 5.8
<
ъ.
<
н
н
<
А
Pi
*[|xi
72 3
1*3 |Х2
//
//
*3Х2
Р2
^4 1
//
<>,
Рз
*;хз
//
*7Х1
//
±
*7
Х3
Х1
Р4
*6Х1
<х:
*6Xi
04
При этом в шестой строке появляется еще один
квадратик — равновесное состояние. Полученная таким
образом сжатая таблица определяет (в форме П — П)
«быструю машину», работающую (если следить за ее
равновесными состояниями) как исходная «медленная»
и имеющую минимальное число состояний. Последнее
утверждение будет разъяснено в>гл. X.
По существу на этом заканчивается синтез последо-
вательностной машины, которая, работая в быстрой
тактности, реализует своими равновесными состояния-
состояниями исходную машину, работающую в тактности смены
входа. Далее остается реализовать ее релейной схемой.
190 ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ КОНЕЧНЫХ АВТОМАТОВ [ГЛ. V
г) Составление таблицы релейной схемы
Зашифруем состояния «быстрого» (а значит, и ис-
исходного) автомата двоичным кодом (табл. 5.9); то же
самое сделаем в отношении входов р (табл. 5.10) и вы-
выходов X (табл. 5.11).
Отождествим теперь • введенный двоичный шифр
состояний входа состояниям входных реле, двоичный
шифр состояний автомата — состояни-
Таблица 5.9 ям промежуточных реле и двоичный
шифр выхода — состояниям выходных
реле. В рассматриваемом примере
схема должна содержать два входных,
три промежуточных и два выходных
реле.
Перестроим табл. 5.8, используя
обозначения табл. 5.9—5.11. При
этом получим табл. 5.12 (таблица
rr
*1
rr
*2
rr
*3
rr
*4
rr
*5
rr
*6
rr
*7
rr
*8
000
001
010
011
100
101
по
111
Таблица 5.10
Таблица 5.11
Pi
Р2
Рз
Р4
00
01
10
11
h ¦
h
00
01
10
11
автомата) и табл. 5.13 (таблица выходного преобра-
преобразователя).
Теперь мы располагаем логическими функциями, кот
торые должны реализовать схемы, так как шифры строк
и столбцов табл. 5.12 и 5.13 определяют значения логи-
логических переменных (состояния контактов входных и
промежуточных реле), а в клетках вписаны цифры,
определяющие значения логических функций (токи в об-
обмотках промежуточных и выходных реле).
§5.4]
МЕТОД И РЕАЛИЗАЦИЯ ХАФМАМА
191
Для того чтобы построить теперь таблицу логических
функций в развернутой форме, обозначим, например,
в нашем случае Х\ и Xi — состояния контактов входных
реле; у\, у%, уъ—состояния контактов промежуточных
реле; Yu Y2, Y3 — состояния обмоток промежуточных
реле и 1\ и Z2 — состояния обмоток выходных реле.
Таблица 5.12
Состояние кон-
контактов промежу-
промежуточных реле
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
У3У2У1
Состояние контактов входных реле
Х^Х\
0 0
0 0 0
0 0 1
0 1 0
0 0 1
0 1 0
0 0 0
0 1 0
0 0 1
YtYtYx
x2xt
0 1
1 0 0
0 1 1
0 1 1
0 1 1
1 0 0
0 1 1
0 1 1
1 00
YtYtYx
Х2Х,
1 0
1 1 0
1 0 1
1 0 1
1 1 0
1 0 1
1 0 1
1 1 0
1 1 0
Y,YtYx
1 0 1
1 0 1
1 0 1
1 0 1
1 1 1
1 0 1
1 11
1 11
YzYtYi
Таблица 5.13
Состояние кон-
контактов промежу-
промежуточных реле
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
УзУаУ,
Состояние контактов входных реле
X2Xt
00
0 0
1 0
0 1
1 0
0 1
00
0 1
1 0
Z2Z,
Х2Х\
0 1
0 1
00
00
0 0
0 1
00
00
0 Ь
Z2Z,
to1
00
1 0
1 0
00
1 0
1 0
0 0
00
Z2Z,
00
0 0
0 0
00
0 1
00
0 1
0 1
Z2Z,
В верхней части табл. 5.14 перечислены все возмож-
возможные состояния контактов хь х2, уи Уъ Уз- Каждому столбцу
192 ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ КОНЕЧНЫХ АВТОМАТОВ [ГЛ. V
га
а
Я
ч
о
га
-
о
—
о
—
о
_
о
—
о
—
о
—
о
—
о
—
о
—
о
—
о
—
о
-
о
—
о
-
о
-
о
-
—
о
о
—
о
о
-
-
о
о
-
-
о
о
-
-
о
о
-
-
о
о
-
-
о
о
-
-
о
о
- ¦
-
-
—
о
о
о
о
-
- .
-
-
о
о
о
о
-
-
-
-
о
о
о
о
-
-
-
-
о
о
о
о
-
—
—
—
-
-
-
-
о
о
о
о
о
о
о
о
-
——
-
-
-
-
- .
о
о
о
о
о
о
о
о
н
-
—
—
—
—
- •
-
-
-
-
-
-
—
-
—
—
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
-
"
о
о
—
о
—
-
о
о
^*
^*
о
—
-
о
—
о
о
о
-
о
-
о
-
-
о
—
о
о
о
о
-
-
о
о
-
о
о
—
о
-
-
о
-
—
—
о
о,
-
о
-
о
-
о
о
-
-
—
—
-
-
-
-
-
-
-
-
-
—
—
—
—
о
о
¦—
о
о
о
—
о
о
о
о
о
о
о
о
-
-
о
—
о
о
о
о
о
о
о
о
о
о
о
о
—
о
о
—
о
о
о
-
о
—
о
—
о
-
о
о
о
о
о
о
о
о
о
о
о
о
-
¦ —
о
—
—
о
о
о
о
о
о
о
о
о
—
о
о
о
—
о
-
о
5 5.4] МЕТОД И РЕАЛИЗАЦИЯ ХАФМАНА 193
этой таблицы соответствует клетка в табл. 5.12 и в
табл. 5.13.
Вписывая в строки Уь Y2, Y3, Zu Z2 нижней части
табл. 5.14 шифр, содержавшийся в соответствующей
клетке табл. 5.12 и 5.13, заполняем табл. 5.14.
Располагая такой таблицей логических функций мож-
можно восстановить соответствующую им схему любым
способом (см. § 2.3).
д) Реализация схемы по Хафману
До сих пор мы стремились построить какую-либо
схему, замещающую заданную последовательностную
машину, не следя за тем, чтобы она была реализацией,
т. е. чтобы она была защищена от критических состяза-
состязаний, например путем исключения одновременного сраба-
срабатывания нескольких реле. В частности, в примере, рас-
рассмотренном в предыдущем пункте, встречаются случаи,
когда переход из одного равновесного состояния в дру-
другое должен сопровождаться одновременным срабатыва-
срабатыванием нескольких реле. Например, если автомат нахо-
находился при входе Х\ = О, х2 = 0 в состоянии У] = О, Y2 = 1,
Уз = 0 (первый столбец, третья строка табл. 5.12), то при
действии на него входа хх = 1, х2 = 1 он должен перейти
в состояние Y\ = 1, Y2 = 0, Y3= 1. Такой переход сопро-
сопровождается одновременным переключением всех трех
реле Yu Y2 и У3. Если при этом переключении какие-ни-
какие-нибудь реле сработают быстрее, например Yi и Y3 уже
станут равными единице, a Y2 еще не переключится на
нуль, то схема может прийти в устойчивое состояние
Yi = 1, Y2 = 1, Уз = 1, т. е. осуществится неверное сра-
срабатывание автомата из-за состязаний реле.
Построение автомата на элементах задержки полно-
полностью исключает возможность критических состязаний.
Однако построить на элементах задержки исходный
автомат, по условию работающий в тактности, опреде-
определяемой моментами изменения состояний входа, трудно.
Для этого нужно было бы построить сигнализирую-
сигнализирующее устройство (часы) для управления элементами за-
задержки, реагирующее на любые изменения состояния
входа.
13 М. А. Айзерман, Л. А. Гусев н др.
ИL ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ КОНЕЧНЫХ АВТОМАТОВ [ГЛ. V
Вместе с тем таблица переходов является основной
таблицей «быстрого» автомата, соответствующего исход-
исходному в том смысле, что наблюдение за устойчивыми со-
состояниями «быстрого» автомата дает картину работы
исходного автомата, работающего в тактности, опреде-
определенной изменениями состояний входа. Можно говорить
о построении «быстрого» автомата, соответствующего
исходному, на элементах задержки, исключая, таким об-
образом, состязания. Это сделать легче, так как в этом слу-
случае проще построить сигнализирующее устройство (часы).
Реализация Хафмана состоит в том, что по таблице
переходов строится схема «быстрого» автомата с при-
применением релейно-контактных элементов задержки и
Рис. 5.16.
организуется релейно-контактное сигнализирующее уст-
устройство. Схема, являющаяся реализацией Хафмана, со-
содержит автомат на задержках (см. рис. 5.8) с контакт-
контактными сетями /i, определенными таблицей переходов.
Если в таблице переходов т строк, то эта часть схе-
схемы содержит 2s0 реле (по 2 реле в каждом элементе за-
задержки), а число элементов задержки Sq равно наимень-
наименьшему целому, удовлетворяющему неравенству т >• 2S°-
Контактные сети fi определяются теми же самыми
логическими функциями, которыми по таблице перехо-
переходов определяются состояния промежуточных реле У,-при
построении релейно-контактной сети без учета возмож-
возможных состязаний.
На рис. 5.16 и 5.17 даны структурные схемы релейно-
контактных сетей, соответствующих автомату, синтези-
синтезируемому в примере предыдущего пункта. Схема рис. 5.16
§5.4]
МЕТОД И РЕАЛИЗАЦИЯ ХАФМАНА
195
построена без учета возможных состязаний, а схема
рис. 5.17 является реализацией Хафмана, исключающей
состязания. На этих рисунках /ь /2, /з — одни и те же
контактные сети, определенные табл. 5.14. Эти контакт-
контактные сети могут быть построены по найденной выше таб-
таблице релейной схемы (табл. 5.14) с помощью любого
метода теории релейно-контактных сетей (например, по
методу Блоха, описанному в § 2.3).
Контакты xt и xt, содержащиеся в реализации Хаф-
Хафмана, предназначены для управления элементами за-
задержки и принадлежат специальному реле Xt. Это реле
1 Г
A
I
А А
. All
/1 УГ У* Vi\\U\ У г УI Уг\\и\ Уз" У? У'
Г I I IT I I IT I II
Д^ Л7л X* Л л | Л^ Ли 3Cf Xj. I Л7< Л7^ X* Х^
} i
Рис. 5.17.
является выходным для схемы специального сигнализа-
сигнализатора тактов (часов). Хафман дает универсальную схему
такого сигнализатора. Она построена на основании сле-
следующих соображений.
Таблица переходов построена так, что соответствую-
соответствующий ей автомат после изменения состояния входа и по
прошествии одного «быстрого» такта оказывается в рав-
равновесном состоянии, т. е. не -изменяет своего состояния
в последующих «быстрых» тактах. Равновесному состоя-
состоянию при применении элементов задержки соответствует
равенство входов и выходов в" каждой задержке. Таким
образом, момент наступления такта можно связывать
с моментом, когда, во-первых, наступило неравенство
13*
196
ТЕХНИЧЕСКАЯ РЕАЛИЗАЦИЯ КОНЕЧНЫХ АВТОМАТОВ [ГЛ. V
(неравнозначность) между входом и выходом в каком-
либо элементе задержки (т. е. когда для какого:нибудь
элемента задержки Y\V Yl = 1) и, во-вторых, когда это
неравенство, обусловленное изменением входа, насту-
наступило во всех тех задержках, где оно должно возникнуть.
Это условие с добавлением того, что возврат сигнализа-
сигнализатора (часов) в исходное состояние должен происходить
только тогда, когда на задержках установилось равенство
Рис. 5.18.
между входами и выходами, приводит к следующей ло-
логической формуле для сигнализатора:
Релейно-контактная схема такого сигнализатора для
случая п = 3, соответствующего рассмотренному при-
примеру, показана на рис. 5.18. В связи с тем, что к при-
примененным в задержках 2so реле сигнализатор добавляет
еще одно реле, эта реализация Хафмана называется
BsQ + 1)-реализацией.
ГЛАВА VI
АВТОНОМНЫЙ КОНЕЧНЫЙ АВТОМАТ
И АВТОНОМНАЯ ПОСЛЕДОВАТЕЛЬНОСТНАЯ
МАШИНА
§ 6.1. Что «могуть делать» автономный конечный
автомат и автономная последовательностная машина
Цель этой и последующей седьмой главы состоит в
том, чтобы определить возможности конечных автоматов
и последовательностных машин, выяснить, «что могут
они делать», отделить это от того, что принципиально
«не может быть сделано» ни в каком конечном автомате
или последовательностной машине. В настоящей главе
задача такого рода рассматривается применительно к
автономному конечному автомату. Аналогичной задаче
для неавтономного автомата (и Я-машины) посвящена
следующая глава.
Напомним, что автономным называется конечный
автомат, у которого значение переменной р под знаком
функции F фиксировано, и что из автомата, уравнение
которого (см. уравнение C.5'))
можно организовать г различных автономных автоматов
(см. 3.7)
xp+i = jj(xp,pj, F.1)
так как символ р* может совпадать с любым из г сим-
символов алфавита {р}.
Постоянный символ р* можно рассматривать как сим*
вол-параметр.
198 АВТОНОМНЫЙ КОНЕЧНЫЙ АВТОМАТ [ГЛ. VI
Если задать начальный символ х°, то в силу F.1)
найдем х1, подставляя х1 в F.1), определим х2 и т. д.
Запущенный при некотором начальном символе х° авто-
автономный конечный автомат может выдавать неограничен-
неограниченную последовательность символов х:
уО yl ,2 „Р
Число символов в алфавите {х} конечно и равно k.
Поэтому в разворачивающейся последовательности
символов х, выдаваемых автоматом, через конечное чи-
число q тактов (q^k) впервые встретится символ, кото-
который ранее уже встречался в этой же последовательно-
последовательности, например символ хв в последовательности
«2*3*6*5*4*7*6 • ' •
Тогда, начиная с (q + 1)-го такта, автомат будет лишь
периодически повторять последовательность символов,
выданных ранее. В нашем примере эта повторяющаяся
далее последовательность подчеркнута:
«2«3«6«5«4*7«6«5«4«7'>|6«5«4«7 • • ¦
Из изложенного следует, что автономный автомат,
запущенный из любого начального состояния, не позже
чем через k тактов начинает периодически повторять
одну и ту же последовательность символов х длиной не
более k.
Если этот же автомат запустить из иного начального
состояния, то он также, начиная с некоторого такта,
начнет периодически повторять некоторую последова-
последовательность символов х, причем эта последовательность
может не совпадать с последовательностью, которая
генерировалась раньше.
Особо выделим случай, когда последовательность со-
состоит лишь из одного символа. Этот случай возникнет,
если первый встретившийся в последовательности повто-
повторяющийся символ расположен непосредственно следом
за таким же символом. Например,
ИЛИ
§ 6.1] ЧТО «МОЖЕТ ДЕЛАТЬ» АВТОНОМНЫЙ КОНЕЧНЫЙ АВТОМАТ 199
Символ, появляющийся в последовательности два раза
подряд, назовем равновесным и будем говорить, что ав-
автомат достиг равновесия в тот такт, когда впервые по-
появился равновесный символ.
Условие того, что символ щ равновесный, состоит
в выполнении равенства
ху = /?(х/, р»), F.2).
т. е. в том, что при р = р* символ уц переводится урав-
уравнением F.1) в себя.
Все изложенное очень удобно иллюстрируется на
графе автономного автомата.
О
Рис. 6.1. Рис. 6.2.
Граф содержит k кружков, соответствующих всем
возможным символам х. К каждому кружку может под-
подходить несколько стрелок, но отходить может только
одна. Поэтому, двигаясь вдоль направления стрелок, мы
обязательно не более чем за k шагов попадем в один
из кружков, пройденных ранее (стрелки образуют
цикл — рис. 6.1), либо попадем в кружок, в который от-
отходящая стрелка вновь возвращается (равновесие —
рис. 6.2).
На рис. 6.3 показаны различные примеры графов для
?= 12.
В случае рис. 6.3, а цикл проходит через все кружки.
В этом случае автономный автомат генерирует периоди*
200
АВТОНОМНЫЙ КОНЕЧНЫЙ АВТОМАТ
[ГЛ. VI
ческую последовательность, состоящую из всех k сим-
символов, и начинает выдавать эту периодическую последо-
Рис. 6.3.
вательность с первого же такта, если допускать в ней
циклическую перестановку символов. От выбора началь-
начального состояния зависит лишь порядок символов.
§6.11 ЧТО «МОЖЕТ ДЕЛАТЬ» АВТОНОМНЫЙ КОНЕЧНЫЙ АВТОМАТ 201
На рис. 6.3, б показан граф, у которого цикл охваты-
охватывает лишь 5 кружков, а от всех остальных стрелки ведут
к одному из кружков цикла. В этом случае автономный
автомат генерирует последовательность длины 5 и, бу-
будучи запущен из любого начального состояния, начинает
генерировать ее (с точностью до циклической переста-
перестановки символов) не более чем через один такт.
В случае графа, показанного на рис. 6.3, в, число так-
тактов, необходимых для начала генерирования периодиче-
периодической последовательности (для выхода на цикл), не более
четырех.
На рис. б.З.г показан пример графа автономного ав-
автомата, который в зависимости от выбора начального
состояния генерирует одну из трех последовательностей
длины соответственно 2, 3 и 5.
Автомат, имеющий граф, показанный на рис. 6.3, д,
в зависимости от начального состояния не более чем за
три такта достигает равновесия, либо не более чем за
один такт переходит на генерирование периодической
последовательности длины 4.
Наконец, на рис. 6.3, е показан пример графа автог
номного автомата, имеющего три равновесия; в зависи-
зависимости от начального состояния то или иное равновесие
достигается не более чем за два такта.
Если требуется построить автономный автомат, гене-
генерирующий периодическую последовательность заданной
длины q и удовлетворяющую каким-либо дополнитель-
дополнительным условиям в отношении числа тактов, после которых
начинается ее генерирование, то задача сводится к по-
построению графа, удовлетворяющего этим условиям.
Граф однозначно задает автономный автомат, так как
по графу, как это отмечалось уже в гл. III, немедленно
восстанавливается его основная таблица.
Пусть, например, требуется генерировать периодиче-
периодические последовательности длины 2, 4 и 6. Выбор генери-
генерируемой последовательности должен определяться выбо-
выбором начального состояния, и в любом случае генериро-
генерирование последовательности должно начаться не позже
чем через один такт после запуска автомата.
В этом случае необходимо иметь k >Л2. Если k = 12
(рис. 6.4), то граф восстанавливается немедленно
202 АВТОНОМНЫЙ КОНЕЧНЫЙ АВТОМАТ [ГЛ. VI
соединением в циклы любых его двух, четырех и шести
кружков. Если же k > 12, например k — 16 (рис. 6.5), то
стрелки, отходящие от узлов, не вошедших в циклы, под-
подводятся к любым узлам циклов.
Рис. 6.4.
Аналогично могут быть поставлены задачи и с уче-
учетом возможности менять параметр р*. Каждому значе-
значению р = р* соответствует свой автономный автомат, т. е.
Рис. 6.5.
свой граф. Но все эти автоматы работают в одном и том
же алфавите {к}. Поэтому графы всех автономных авто-
автоматов, получающихся при изменении параметра р*,
имеют одно и то же число k кружков.
§ 6.1] ЧТО «МОЖЕТ ДЕЛАТЬ» АВТОНОМНЫЙ КОНЕЧНЫЙ АВТОМАТ 203
Пусть, например;, как и ранее, требуется, чтобы ав-
автомат генерировал периодические последовательности
длины 2, 4 и 6. Выбор генерируемой последовательности
должен определяться выбором уже не начального сим-
символа, а параметра р* (рь рг
или рз). Но по-прежнему при
любом р* генерирование после-
последовательности должно начать-
начаться не позже чем через один
такт после запуска.
Число k не может быть вы-
выбрано меньше, чем длина са-
самой длинной из заданных по-
последовательностей, так как в
противном случае ни при ка-
каком р нельзя было бы получить
автономный автомат, генери-
генерирующий эту последователь-
последовательность. Положив, например,
k = 6, строим граф для р* = р3 (рис. 6.6), замыкая все
шесть кружков в цикл. Граф при р* = рг также содержит
тогда шесть кружков, но в цикл надо замкнуть лишь
Рис. 6.6.
Рис. 6.7.
Рис. 6.8.
любые четыре из них. Поэтому стрелки от остальных
двух кружков подводятся к кружкам цикла (рис. 6.7).
Наконец, для р* = pi лишь два кружка замкнуты
в цикл, а стрелки от остальных кружков подведены к
ним (рис. 6.8).
204
Автономный Конечный Автомат
[гЛ. vt
Таблица 6.1
Построенные три графа (рис. 6Д 6.7 и 6.8) задают
автомат. Его основная таблица может быть немедленно
восстановлена по графам. В. случае графов, показанных
на рис. 6.6, 6.7 и 6.8, она имеет вид табл. 6.1.
Из приведенного примера ясно, как сконструировать
основную таблицу автомата, генерирующего любое ко-
конечное число последо-
последовательностей х, выби-
выбираемых как начальным
символом, так и пара-
параметром р*.
Переходя к после-
довательностной маши-
машине, надо дополнить ав-
автомат выходным пре-
преобразователем*). Но
если автомат периоди-
периодически выдает последо-
последовательность из симво-
символов х, то и преобразо-
преобразователь периодически
выдает последователь-
последовательность из символов Я
той же длины. Но в от-
отличие от последова-
последовательности из х, которая
не может содержать
двух одинаковых символов, последовательность из Я на
выходе преобразователя может содержать и одинаковые
символы. Так,- например, если автомат выдает последо-
последовательность Х1Х7Х2Х5Х3, которая потом периодически по-
повторяется, а преобразователь реализует таблицу
X,
*2
*3
*4
*5
*6
P
^2
^3
4
4
X-3
^2
Pi
*I
"-4
H
4
Рз
*2
,3
f;
•/•5
*.
% X)
X X,
*2
h
*3
Х2
х2
*) В связи с тем, что у автономного автомата символ р„ фикси-
фиксирован, в данном случае понятия «последовательностная машина» и
«конечный автомат с выходным преобразователем» совпадают.
S 6.2] СИн№з ДйоИчНой Структуры 2б5
\
то на выходе преобразователя периодически повторяется
последовательность ХХ^Х,^.
Если задана требуемая последовательность симво-
символов X, то, чтобы синтезировать Л-машину, выдающую
эту последовательность, сначала синтезируется автомат,
выдающий любую последовательность символов х, дли-
длина которой совпадает с длиной заданной последователь-
последовательности символов К. Затем, выписав эти две последова-
последовательности (из символов х и из символов К) одну иод
другой, немедленно восстанавливаем и таблицу преоб-
преобразователя. Все эти соображения имеют важные техни-
технические следствия.
Если какое-либо техническое устройство охватывает-
охватывается абстракцией «автономный конечный автомат» и если
символы х характеризуют возможные состояния устрой-
устройства, то такое устройство может либо достигать равно-
равновесия за конечное число тактов, либо периодически по-
повторять конечную последовательность состояний — и не
более того. Из изложенного следует также, что, каково
бы ни было конечное число наперед заданных последо-
последовательностей состояний любой конечной длины, всегда
можно синтезировать автомат, генерирующий любую из
этих последовательностей выбором начального состоя-
состояния либо установкой в начальный момент значения па-
параметра, который далее, во время работы автомата, не
изменяется.
Чтобы несколько конкретизировать этот вывод, важ-
важный для технической реализации автоматов, рассмотрим
этот вопрос подробнее применительно к синтезу двоич-
двоичной абстрактной структуры, замещающей автономную
последовательностную машину. Распространение рас-
рассуждений на иные абстрактные структуры потребует по-
после этого лишь кратких замечаний.
§ 6.2. Синтез двоичной структуры автономной
последовательностной машины
Рассмотрим сначала случай, когда параметр р = р*
не может быть изменен, т. е. синтезируется не однопара-
метрическое семейство конечных автоматов или после-
довательностных машин, а только одна такая машина.
206 АВТОНОМНЫЙ КОНЕЧНЫЙ АВТОМАТ [ГЛ. VI
Общую задачу синтеза двоичной/структуры автоном-
автономной Я-машины в этом случае сформулируем так: ука-
указано число начальных состоянии, которое определяет
число возможных вариантов работы машины; для каж-
каждого из них задается последовательность из 0 и 1, кото-
которую машина должна реализовать на выходе, переходя
на выдачу требуемой последовательности не более чем
за один такт работы. Требуется указать двоичную струк-
структуру конечного автомата и двоичный (логический) пре-
преобразователь, удовлетворяющие этим заданным усло-
условиям. Подлежат определению не только логические
функции в правых частях уравнений двоичной абстракт-
абстрактной структуры, но и их число п. Требуется решить за-
задачу синтеза при минимально возможном числе п. По-
Поскольку мы считаем задачу исчерпанной составлением
уравнений двоичной абстрактной структуры в наимень-
наименьшем числе, дальнейшее упрощение правых частей этих
уравнений по правилам исчисления высказываний и
исходя из какого-либо критерия оптимизации не рас-
рассматривается.
Задача синтеза автономной Я-машины, сформулиро-
сформулированная выше, может быть подразделена на четыре за-
задачи:
1. Определение минимального числа п.
2. Построение конечного автомата, на выходе- кото-
которого могут появляться последовательности заданной
длины.
3. Синтез логической абстрактной структуры, кото-
которая замещает построенный конечный автомат.
4. Синтез выходного- логического преобразователя.
Рассмотрим сначала случай, когда задана только
одна последовательность, состоящая из 0 и 1 длины q,
и требуется из любого начального состояния периодиче-
периодически генерировать ее (с точностью до циклической пере-
перестановки символов), начиная со второго такта работы
Я-машины.
Выберем наименьшее число п, удовлетворяющее не-
неравенству
Рассмотрим автомат, имеющий k = 2п состояний. В ка-
§ 6.2) СИНТЕЗ ДВОИЧНОЙ СТРУКТУРЫ 207
честве алфавита состояний {х} примем натуральные чи-
числа {0, 1,2, .... 2»-\1}.
Пусть этот автома^ имеет граф, у которого первые q
кружков объединены >в цикл; если 2n > q, то осталь-
остальные кружки соединены стрелкой непосредственно с ка-
каким-либо кружком на цикле. Условимся, например, со-
соединять эти «лишние» кружки графа с кружком, отме-
отмеченным символом 0 (пример для п = 3, q = 5 приведен
на рис. 6.9).
Рис. 6.9.
По построенному графу сразу восстанавливается
основная таблица автономного автомата. Так, для гра-
графа, показанного на рис. 6.9, основная таблица имеет
вид табл. 6.2.
Построим теперь логическую абстрактную структуру
такого автомата. Для этого (см. § 4.2) выберем п логи-
логических координат Х\, Х2, .. ч хп (каждая из них может
принимать лишь значения из алфавита {0, 1}) и запол-
заполним табл. 6.3.
Таблица имеет 2П строк и разделена двумя верти-
вертикальными столбцами, которые соответствуют х? и +1
на левую и правую части,
208
АВТОНОМНЫЙ КОНЕЧНЫЙ АВТОМАТ
[ГЛ. VI
Таблица 6.2
В столбец у? вписываются подряд сверху вниз цифры
О, 1, 2 2"—1, т. е. индексы к из левого столбца
основной таблицы построенного автомата, а в столбец
xp + i — соответствующие индексы/при х в правом столб-
столбце этой основной таблицы. В табл. 6.3 в качестве при-
примера первые 8 строк столбцов хр и
%р +' заполнены в соответствии с
табл. 6.2.
В левую часть таблицы (столбцы .
хр) вписываются в двоичной системе
счислений числа, содержащиеся в
столбце у,р. Для этого удобно восполь-
воспользоваться правилом, описанным в гл. I:
последний столбец (для лг0) запол-
заполняется попеременно 0 и 1, второй
столбец справа — парами 0 и 1, тре-
третий справа — четверками 0 и 1, пя-
пятый—восьмерками 0 и 1, так что в
каждом следующем столбце количе-
количество 0 или 1 в чередующихся группах
удваивается.
В правую часть таблицы (столб-
(столбцы хр+[) вписываются в двоичной
системе " счисления числа, содержа-
содержащиеся в столбце %р +'. Их можно вы-
выписывать непосредственно из левой
части таблицы, содержащей теперь за-
запись в двоичной системе счисления
всех чисел от 0 до k.
В качестве примера в табл. 6.4 по-
показано заполнение табл. 6.3, выпол-
выполненное для автомата, имеющего граф,
показанный на рис. 6.9, и основную таблицу, предста-
представленную табл. 6.2.
Обратимся теперь к самому правому столбцу (для*0)
правой части заполненной таблицы и выделим все те
строки, где Аг0 = 1. Возьмем какую-нибудь одну из этих
строк и выпишем конъюнкцию из всех Хи, причем над
теми из Xk, для которых в этой же строке, но в левой
части таблицы содержится 0, ставится знак отрицания.
Так же строится конъюнкция для остальных из выделен-
Ч
*1
Ч
Ч
Ч
ч
ч
ч
р*
*1
ч
ч
Ч
ч
ч
ч
ч
§ 6.2]
СИНТЕЗ ДВОИЧНОЙ СТРУКТУРЫ 209
Таблица 6.3
xp \
Xn-\
0
0
0
0
0
0
0
0
1
...
...
x2
0
0
0
0
1
1
1
1
1
0
0
1
1
0
0
1
1
1
\
¦K0\
—о—о—о—о
--
1
X."
0
1
2
3
4
5
6
7
2--1
1
2
3
4
0
0
0
0
xp+\
Xn-\
0
0
0
0
0
0
0
0
...
x2
oooo—ooo
ooooo——о
Xo
ooooo—o—
Значение хр
x2
0
0
0
0
1
1
1
1
0
0 .
1
1
0
0
1
1
Xo
0
1
0
1
0
1
0
1
0
1
2
3
4
5
6
7
1
2
3
4
0
0
0
0
T аб л
и ц а 6.4
Значение xp+i
x2
0
0
0
1
0
0
0
0
X\
0
1
1
0
0
0
0
0
¦Ко
1
0
1
0
0
0
0
0
ных строк. Все полученные таким образом конъюнктив-
конъюнктивные группы (число их равно числу выделенных строк)
соединяем знаками дизъюнкции. Образованная таким
образом совершенная дизъюнктивная форма конъюнк-
конъюнктивных групп и определяет^ правую часть первого из
искомых соотношений логической абстрактной струк-
структуры. Например, для приведенной табл. 6.4 это соотно-
соотношение имеет вид
. F.3)
М. А. Айзерман, Л. А. Гусев и др.
210 АВТОНОМНЫЙ КОНЕЧНЫЙ АВТОМАТ [ГЛ. VI
Теперь рассматриваем второй столбец правой части
таблицы (для Х\) и аналогично отроим правую часть
второго соотношения. В случае табл. 6.4 оно имеет вид
f ^ 3| /sb f jcff — jcf ] & jcf. F.4)
Для следующего столбца (для х2) аналогично полу-
получаем
x°+1 = xp&lxp&lxp F.5)
и т. д., пока не будут рассмотрены все п строк и таким
образом восстановлены все п соотношений искомой дво-
двоичной (логической) абстрактной структуры.
Построим теперь выходной логический преобразо-
преобразователь
y = L(x0, xv ..., *„_,) F.6)
следующим образом. Имея в виду, что на графе постро-
построенного автономного автомата все кружки, входящие_в
цикл (число их равно q), перенумерованы подряд @, 1,
2, .. ., д— 1), этими же числами @, 1, 2, ..., q— 1) пе-
перенумеруем подряд символы 0 и 1, содержащиеся в за-
заданной последовательности длины q.
Так, например, если задана последовательность дли-
длины 5 вида 10010, то составляются соответствия
10 0 10
0 12 3 4
Таким образом, каждому кружку, входящему на графе
автомата в цикл, ставится в соответствие символ задан-
заданной последовательности.
Выделим те номера кружков, которым соответствует
в заданной последовательности символ 1. В нашем при-
примере это кружки 0 и 3. Им соответствуют состояния
хо и хз-
Составим конъюнкцию, характеризующую значения
всех координат в каком-либо из этих выделенных со-
состояний, например х*. С этой целью составляем конь-
юнкцию из всех Х{ и ставим знак отрицания над теми из
них, для которых в строке х* левой части табл. 6.3 впи-
вписаны нули. Поступая так со всеми выделенными состоя-
6.2] СИНТЕЗ ДВОИЧНОЙ СТРУКТУРЫ
ниями., соединим получающиеся конъюнкции знаками
дизюнкции. \
Так в рассмотренном выше примере были выделены
два состояния: но и н%. Рассмотрим первое из них — со-
состояние но. В строке для но табл. 6.4 вписаны только 0.
Поэтому знак отрицания ставится над всеми тремя ко-
координатами Хо, Х\ и *2. Получаем конъюнкцию
л:0 & ЛГ) & х2.
Для второго выделенного состояния нг в соответствии
с четвертой строкой табл. 6.4 имеем конъюнкцию
л:0 & ЛГ) & х2.
В результате получаем логическую функцию
F-7)
Непосредственно видно, что построенная так логиче-
логическая функция равна 1 в тех и только в тех случаях, ко-
когда состояние Н{ совпадает с каким-либо из выделенных
выше состояний, т. е. когда должна появиться 1 на вы-
выходе преобразователя. Поэтому построенная таким об-
образом функция L (*o, xit ..., xn-i) и определяет иско-
искомый функциональный преобразователь.
Полученные дизъюнктивные формы, описывающие
работу автомата и преобразователя, могут быть упро-
упрощены методами исчисления высказываний, исходя из лю-
любого критерия оптимальности.
Построенная двоичная абстрактная структура авто-
автономной Я-машины реализует поставленную задачу. При
этом указанное число состояний п — необходимое и до-
достаточное (для двоичной абстрактной структуры). До-
Достаточность следует из того, что выше был указан спо-
способ построения автомата при этом п. Необходимость
следует из тех соображений, что при меньшем п число
кружков на графе будет меньше q и, следовательно, да-
даже если включить в цикл все кружки, число тактов в пе-
периоде будет меньше q и генерироваться может лишь
последовательность длины меньшей q.
Пусть теперь заданы т разных последовательностей
длины qt (i = 1, 2, ,,., m). Среди них могут быть, в
14*
212
АвтоНоМНый конечный АВТОМАТ
iBrtC
(гЛ. VI
частности, последовательности длиной 1. Выберем наи-
наименьшее и, удовлетворяющее неравенству
¦&¦ Zi Qi- (b-o)
Если
Ыт
то граф автомата может иметь как раз т циклов, каж-
каждый длиной qi (i = 1, 2, ..., т). Если же
2" > 5U,
то на графе останутся «лишние» кружки, не включен-
включенные в эти циклы, и от каждого из них надо будет про-
провести стрелки к какому-
либо кружку, входящему
в цикл. После этого дво-
J- ичная абстрактная струк-
структура автомата и выход-
выходной преобразователь стро-
строятся совершенно так же,
как это было показано
выше для случая,' когда
генерировалась одна по-
последовательность. При этом, строя преобразователь, вы-
выписывают подряд все заданные т последовательностей
и нумеруют подряд все символы (т. е. О и 1), входящие
в эти последовательности.
Теперь рассмотрим случай, когда последователь-
ностная машина зависит от параметра р*, который можно
менять, т. е. двоичная структура
xf+1 = l.t [xp, хр, ..., хрп_х; upv up,..., up], F.9)
j' = 0> 1,2, ..., n — 1,
содержит s двоичных параметров, допускающих 2е вы-
выборов.
Пусть задано т последовательностей. Требуется по-
построить двоичную абстрактную структуру /7-машины по
обычной схеме (рис. 6.10), т. е. двоичную структуру
г
А
X
L
Рис. 6.10.
$6.21 синтез Двоичной структуры 213
автомата А F.9) и преобразователя
y = L[xQ, xv ..., xn_{, «!, «2, .-., us\ F.10)
так, чтобы машина генерировала заданные т последо-
последовательностей. При этом числа п и s должны быть наи-
наименьшими. Выбор генерируемых последовательностей
производится за счет выбора параметров и\, и%, ..., ы.,.
Выделим среди заданных т последовательностей
самую длинную. Пусть она имеет длину <7тах, т. е. содер-
содержит <7тах символов. Найдем наименьшие значения п и s,
удовлетворяющие неравенствам
2">qmn, F.11)
2?>т. F.12)
Назовем эти значения п и s соответственно ttmin и
Smin. Построим т графов, каждый из которых содержит
2nmin кружков. Перенумеруем заданные последователь-
последовательности. На первом из графов соединим в цикл столько
кружков, сколько символов в первой последовательно-
последовательности, а стрелки от остальных кружков, не вошедших в
цикл, подведем к любому из кружков, включенных в
цикл. Аналогично построим второй граф, но на нем со-
соединим в цикл столько кружков сколько символов во
второй последовательности. Таким же образом построим
все остальные графы. Такое построение возможно, так
как в силу F.11) число кружков в каждом графе не
меньше числа символов в любой последовательности.
Методом, описанным выше, построим для каждого из
графов таблицу типа табл. 6.3, т. е. определим правые
части в соотношениях
xP+l = Li[xP,xP,...,xPnmJ, i = 0, 1,...,ли1„—1, F.13)
соответствующих каждому графу двоичной абстрактной
структуры.
Пусть для /-го графа (/=1, 2, ..., т) эти соотно-
соотношения имеют вид
LlJ[xP,xP,...,xpmJ, i = 0,\,...,nmla—l, F.14)
и, таким образом, определено т соотношений.
214
АВТОНОМНЫЙ КОНЕЧНЫЙ АВТОМАТ
[ГЛ. VI
Введем в рассмотрение smin двоичных переменных
uk (k = 1, 2, .... Sunn) и построим таблицу всех возмож-
возможных сочетаний символов ы/,. Эта таблица (табл. 6.5)
строится по типу левой части табл. 6.3. Табл. 6.5 имеет
2smia строк. В правом столбце перенумерованы первые т
строк. Это, возможно, так как в силу F.2) число строк
не менее чем т.
Таблица 6.5
«ft
0
0
0
••
1
"imIn-2
0
0
0
...
1
...
...
...
...
u,
0
0
1
...
...
1
«0
0
1
0
...
...
, 1
Номер
и
1
2
3
...
т
2*т1п
Возвращаясь к соотношению F.14), которое отно-
относится к /-му графу, усложним его добавлением в правые
части всех nmin соотношений конъюнкций из тех симво-
символов М/,, для которых в /-й строке табл. 6.5 вписана 1 (а
не 0). Вместо F.14) получаем соотношение вида
i — 0, 1, 2, ..., «min—1.
§6.2] СИНТЕЗ ДВОИЧНОЙ СТРУКТУРЫ 215
Может быть выписано т систем соотношений типа
F.15), если последовательно принимать /=1,2, ..., т.
Теперь объединим дизъюнкцией правые части всех
первых соотношений из этих т систем. Так же поступим
с правыми частями всех вторых соотношений этих си-
систем и т. д. В результате получаем одну систему соотно-
соотношений вида
[Ln[xl хр,..., x^-il&Ujv
" U2|V
F.16)
\f{Lim[xp, хр, ..., хрп
! п 1 9 и 1
где через U^ (/ = 1, 2, .... т) обозначены конъюнкции
всех элементов uh, для которых в /-й строке табл. 6.5
стоит 1.
Рассмотрим теперь все uh как параметры и выберем
их, например, в соответствии с третьей строкой табл. 6.5.
Тогда Из = 1, а все остальные U равны нулю и в каж-
каждом из соотношений F.16) останется лишь третий конъ-
конъюнктивный член. Система F.16) совпадает тогда с си-
системой F.14) при / = 3. Граф этой системы состоит из
цикла, включающего столько кружков, сколько симво-
символов (т. е. О и 1) в третьей из заданных последователь-
последовательностей.
Соотношения F.16) являются, таким образом, абст-
абстрактной структурой, замещающей конечный автомат, в
котором за счет выбора вектора U в соответствии с пер-
первыми т строками табл. 6.5 можно получить т построен-
построенных выше графов. Это обеспечивает генерирование т
последовательностей заданных длин.
Для того чтобы эти последовательности совпадали с
заданными, осталось синтезировать выходной преобра-
преобразователь. С этой целью, по описанным выше методам,
построим сначала выходной преобразователь для каж-
каждой из систем соотношений F.14) порознь так, чтобы
/¦¦е соотношение F.14) генерировало /-ю из заданных т
последовательностей.
216 АВТОНОМНЫЙ КОНЕЧНЫЙ АВТОМАТ [ГЛ. VI
Пусть эти выходные преобразователи будут
y = Lj(Xl,..., *„„,„_,).¦ ' F.17)
Тогда искомый преобразователь, который надо добавить
к F.16), описывается соотношением
y = [Ll(xQ, xv ....
(^0. xv ..., ^mIn-i)&Um].
. Непосредственно видно, что идея и ход описанного
синтеза верны не только применительно к двоичной
абстрактной структуре, но и сохраняются для любых
иных абстрактных структур.
В любом случае абстрактная структура должна обес-
обеспечить граф, у которого замкнуто в цикл столько круж-
кружков, сколько букв в заданной последовательности. Пере-
Переход от графов к структуре осуществляется таблицей
типа табл. 6.3, но ее заполнение и число строк в ней
определяются уже особенностями синтезируемой струк-
структуры, алфавитом ее символов.
ГЛАВА VII
ПРЕДСТАВЛЕНИЕ СОБЫТИИ
В КОНЕЧНОМ АВТОМАТЕ
И ПОСЛЕДОВАТЕЛЬНОСТНОЙ МАШИНЕ
§ 7.1. Постановка задачи
В гл. III было введено понятие о лентах конечного
автомата (р, х-лента, табл. 7.1) и последовательностной
машины (р, х, Х-лента, табл. 7.2).
Таблица 7.1
Такт
Р
X
0
1
2
3
4
5
...
Р
...
Таблица 7.2
Такт
Р
X
X
0
1
2
3
4
5
...
Р
218 ПРЕДСТАВЛЕНИЕ СОБЫТИЙ В КОНЕЧНОМ АВТОМАТЕ [ГЛ. VII
Лента отражает работу конечного автомата (или
Л-машины) в том случае, когда задана входная после-
последовательность символов р и начальное состояние к0.
Если рассматривать последовательности символов р
от 0-го до любого р-го такта, то такая последователь-
последовательность конечна; но поскольку время работы автомата
неограниченно, длина каждой последовательности хотя
и конечна, но может быть любой, а число возможных
последовательностей р бесконечно. Автомат (Я-маши-
на), находившийся в некотором начальном состоянии к°
ставит в соответствие каждой последовательности сим-
символов р определенную последовательность символов и
(соответственно символов К), т. е. перерабатывает по-
последовательность символов из одного алфавита в после-
последовательность иных символов из иного алфавита.
Каковы общие законы этой переработки последова-
последовательностей конечным автоматом или Я-машиной?
Пусть К—множество всех возможных последова-
последовательностей символов х, а Е—множество всех возмож-
возможных последовательностей символов р. Эти множества
имеют одинаковую мощность. Значит, каждой последо-
последовательности из К можно поставить в соответствие после-
последовательность из Е. Установим это соответствие каким-
либо произвольным образом. Можно ли создать конеч-
конечный автомат, который бы реализовал это соответствие?
Или же могут быть указаны такие соответствия между
последовательностями, которые можно реализовать в ко-
конечном автомате, и такие соответствия, которые конеч-
конечным автоматом реализовать нельзя? Если существуют
соответствия, которые не могут быть реализованы конеч-
конечным автоматом, то, естественно, возникает задача об от-
отделении соответствий между последовательностями,
которые реализуются конечным автоматом, от соответ-
соответствий, которые не могут быть реализованы никаким ко-
конечным автоматом. Аналогичные задачи возникают при-
применительно к последовательностной машине.
Эти же задачи могут быть сформулированы в иных
терминах. Рассмотрим р, х-ленту конечного автомата с
фиксированным начальным символом к°. Выделим ка-
какой-либо символ к*. Просматривая ленту, отметим все
такты, когда появлялся символ к*. Выпишем последо-
§7.21
СОБЫТИЕ. ПРЕДСТАВЛЕНИЕ СОБЫТИЙ
219
вательности символов р (начиная с 0-го такта), которые
приводили к появлению символа х*. Предположим, что
мы могли бы аналогично обработать все мыслимые
р, и-ленты этого же автомата и из множества Е всех мыс-
мыслимых входных последовательностей некоторого авто-
автомата выделить подмножество G* всех тех входных по-
последовательностей, которые в рассматриваемом автома-
автомате приводят к появлению символа и*. Будем говорить
тогда, что автомат, находящийся в начальном состоянии
к0, представляет появлением символа н* входные после-
последовательности из подмножества G*. Аналогично /7-ма-
шины представляют входные последовательности из не-
некоторого подмножества G* появлением символа К*. Лю-
Любые ли подмножества входных последовательностей мо-
могут быть представлены в автомате или /7-машине? Если
нет, то каковы условия представимости некоторого мно-
множества входных последовательностей? В каких терми-
терминах можно выделить представимые множества?
Чтобы ответить на эти вопросы, нам придется сна-
сначала сформулировать точнее задачу и с этой целью
ввести новый термин «событие» и классифицировать со-
события.
§ 7.2. Событие. Представление событий
В ленте автомата (или последовательностной маши-
машины) рассмотрим лишь ее верхнюю часть, т. е. только
последовательность символов р. Назовем ее входной
лентой (пример — табл. 7.3).
Таблица 7.3
Такт
Р '
0
Рз
1
-та
2
Р&
3
ь
4
Pi
5
Pl2
6
-та
7
-та
...
...
При фиксированном значении р (например,/? = 5 или
р — 1000) входная лента конечна. Но р может, прини-
принимать любое значение, и в этом смысле длина входной
ленты не ограничена.
220
ПРЕДСТАВЛЕНИЕ СОБЫТИЙ В КОНЕЧНОМ АВТОМАТЕ [ГЛ. VII
Пусть G — множество всех мыслимых входных лент
данного автомата. Пусть далее указан какой-либо при-
признак (критерий), позволяющий выделить из множе-
множества G входных лент подмножество G*. Каков бы ни
был этот признак, условимся говорить, что наступило
событие G* всякий раз (т. е. во всякий момент р), ко-
когда входная лента автомата, рассмотренная на длине от
0-го до р-го такта, относится к выделенному подмноже-
подмножеству G*.
С течением времени, т. е. с ростом р, факт принад-
принадлежности этой ленты к подмножеству G* может менять-
меняться, т. е. одна и та же разворачивающаяся входная лента
может принадлежать G* при одних р и не принадлежать
G* при других р.
Пример 1. Событие наступает, если в два послед-
последних такта работы автомата на входе появлялись после-
последовательно символы р5 и рз. Событие в момент р насту-
наступает, например, при появлении входных лент
0
Рз
1
Р5
р = 2
Рз
0
ь
1
-та
2
Р7
3
Р4
4
Рб
р = Ъ
Рз
0
P4
1
-та
2
-та
СП
3
Рз
4
Р7
5
Р5
6
Рз
7
Рэ
8
Р5
р = 9
Рз
0
Рз
1
Ps
2
-та
со
3
Рб
4
Рз
5
Рб
6
Рз
7
Рб
8
Рз
9
Рб
р=1О
Рз
$ 7.2] СОБЫТИЕ. ПРЕДСТАВЛЕНИЕ СОБЫТИЯ
и не наступает, например, при входных лентах
221
0
Ps
0
Ps
0
p«
0
Рз
1
Рз
1
Pi
1
Pi
1
i
Ps
p=
Ps
2
P7
2
Рб
2
Рз
3
?4
3
Рз
3
Ps
4
Рз
4
P?
4
Рз
P-
P.
5
Ps
5
Ps
..
6
Рз
6
Рз
7
Ps
7
Ps
8
?4
8
Рз
Pi
9
Рз
p=10
Ps
0
Рз
При
1
Р.
2
?4
ленте
3
Ра
4
Ре
5
Ps
6
Рз
7
Р7
8
Рэ
9
Pi
10
Ps
11
Рз
12
Рб
13
Рз
14
Ps
15
Ps
16
Р4
17
Рз
18
Ps
19
Ре
20
Рз
...
...
событие наступает в моменты р = 6, р=11, р 13 и
р = 20 и не наступает при всех остальных значениях р.
Пример 2. Событие наступает, если в прошедшей
части входной ленты хотя бы один раз после символа ps
следовал символ рз. В этом -случае все ленты, кроме
шестой, рассмотренные в предыдущем примере при
любом р, начиная с некоторого такта, принадлежат
множеству G*. Эта принадлежность множеству G*
имеет место: для ленты 2 при р!>5; для ленты 3 — при
#>3, для ленты 4 — при р >• 4 и т. д.
222 ПРЕДСТАВЛЕНИЕ СОБЫТИЙ В КОНЕЧНОМ АВТОМАТЕ [ГЛ. VII
Приведем теперь несколько формулировок событий
без дополнительных пояснений и иллюстраций.
Пример 3. Последние шесть тактов входной ленты
содержат последовательность р2 ро рь
Пример 4. За последние три такта появилась хотя
бы одна из следующих трех последовательностей: рфгрв;
р2р4Р5 или рзргрь
Пример 5. В течение последних трех тактов не
встречается символ р3.
Пример 6. В течение последних пяти тактов, если
и встречается символ рь то только после символа р3.
Пример 7. Хотя бы один раз ранее, до момента р,
встречался символ ps.
Пример 8. Хотя бы один раз ранее, до момента р,
после символа р7, следовал символ рз.
Пример 9. Ни разу за время работы автомата
(т. е. начиная с 0-го такта) не встречался символ р7.
Пример 10. Ни разу после символа р с четным ин-
индексом не появлялись три раза подряд символы р с не-
нечетными индексами.
Пример 11. В третий такт было р7.
Пример 12. В пятый такт появился какой-либо один
из трех символов: рь ре, рг-
Пример 13. В такты третий, седьмой и девятый по-
появлялись символы р с нечетным индексом.
Пример 14. В каждый такт, номер которого кратен
трем, появляется символ р5.
Пример 15. Наступил k-ft такт.
Примечание. Множеством G* в этом случае служит
множество всех лент длиной k.
Пример 16. Во всех тактах, номера которых совпа-
совпадают с квадратами целых чисел A, 4, 9, 16, 25, ...), по-
появляется символ р с четным индексом.
Пример 17. Всегда, когда номер такта — простое
число B, 3, 5, 7, 11 и т. д.), появляется символ ре или р9.
Для того чтобы разумным образом классифициро-,
вать события, нам придется предварительно подробнее
рассмотреть способы образования множеств входных
лент. Этому вопросу посвящен § 7.3.
Говоря выше о наступлении событий, мы имели в виду
человека, просматривающего входную ленту и решаю*
§ ?.2j СОБЫТИЕ. ПРЕДСТАВЛЕНИЕ СОБЫТИЙ 223
щего вопрос о том, принадлежит ли последовательность
символов р, появившаяся к моменту р, к заданному
множеству G* или нет.
Возникает вопрос: может ли эту же работу выпол-
выполнить конечный автомат или /7-машина? Для того что-
чтобы точно сформулировать этот вопрос, введем понятие
о представлении событий автоматом и последователь-
ностной машиной.
Рассмотрим множество К всех возможных состояний
конечного автомата xi, хг, ..., х&. Выделим какое-либо
непустое подмножество состояний М (в частности, М
может содержать лишь одно какое-либо состояние). Мы
будем говорить, что автомат, отправляясь от некоторого
начального состояния х°, представляет заданное событие
G* на входе состояниями из множества М, если, начав
работать в момент / = 0 при начальном состоянии х°,
автомат в момент р + 1 оказывается в одном из состоя-
состояний множества М тогда и только тогда, когда на входе
к моменту р наступает событие G*.
При включении выходного преобразователя всегда
можно сделать так, чтобы на выходе преобразователя
появлялась единица, когда х принадлежит М, и появ-
появлялся нуль при иных х. В этом случае автомат предста-
представляет событие появлением единицы на выходе, если еди-
единица появляется в момент р + 1, тогда и только тогда,
когда событие наступило к моменту р.
Аналогично последовательностная машина предста-
представляет событие появлением символа К* на выходе, если
этот символ появляется в момент р тогда и только то-
тогда, когда на входе к моменту р происходит событие.
Будем говорить, что событие G* представимо в ко-
конечном автомате, если существует такой конечный ав-
автомат А, который представляет событие G*.
Очевидно, что из представимости событий состояния-
состояниями из множеств М следует представимость событий по-
появлением единицы на выходе^при наличии преобразова-
преобразователя, и наоборот. Более того, справедливо и следующее
утверждение: из факта представимости (непредставимо-
(непредставимости) события автоматом следует представимость (не-
(непредставимость) его последовательностной машиной, и
224 ПРЕДСТАВЛЕНИЕ СОБЫТИЙ 8 КОНЕЧНОМ АВТОМАТЕ [ГЛ. Vlt
наоборот. Это следует из общей теоремы, которая дока-
доказана в § 4.3.
Поэтому при решении задачи о представлении собы-
событий мы будем рассматривать лишь конечные автоматы.
§ 7.3. Действия над множествами входных
последовательностей. Регулярные события
До сих пор, говоря о входной ленте, мы имели в виду
верхнюю часть ленты автомата, т. е. последовательность
входных символов, связанную с "последовательностью
тактов, считая от / = 0. Теперь же, в начале этого пара-
параграфа, мы будем иметь дело лишь с последовательно-
последовательностями входных символов р, не связывая как-либо начало
и конец каждой такой последовательности с определен-
определенным номером такта. Для обозначения конкретной вход-
входной последовательности конечной длины будем исполь-
использовать первые буквы латинского алфавита: а, Ь, с и т.д.
или at, а.2, а3 и т. д.
Пусть А и В — множества (конечные или бесконеч-
бесконечные) входных последовательностей, с элементами аи
а2,... и b\, b% ... соответственно. Из множеств А и В
образуем новые множества с помощью трех операций.
Первая операция.— объединение. Множе-
Множество С, содержащее все последовательности, как те, что
входят в множество А, так и те, что входят в множество
В, назовем объединением А и В и обозначим С — АуВ
Так, например, если множество А состоит из четырех
последовательностей
ас-
а2:
а3:
Pi
Ps
Рз
Р2
Pi
Pi
Рз
Ps
Р7
Pi
Pi
Pi
Ь
Pi
Pi
Ps
Pi
Рз
Ре
P2
Ре
$7.31 РЕГУЛЯРНЫЕ СОБЫТИЯ
а множество В — из двух последовательностей
225
P2
Pl2
Рз
Рв
•
то множество С в этом случае состоит из всех шести вы-
выписанных выше последовательностей, т. е.
Вторая операция — умножение. Составим
из последовательностей, входящих в множества А и В,
новое множество последовательностей по следующему
правилу, к любой последовательности из множества А,
например к а<, припишем справа любую последователь-
последовательность из множества В, например by Так образуется но-
новая последовательность сь = a,6j. Составим все возмож-
возможные последовательности такого рода, приписывая справа
к каждой последовательности из А поочередно все воз-
возможные последовательности из В. Новое множество по-
последовательностей С, элементы которых составлены по
этому правилу
назовем произведением множеств Л и В, а операцию
получения С — умножением Л на В и запишем эту опе-
операцию так
С = АВ.
Если, например, множество А состоит из четырех, а
множество В — из двух последовательностей, рассмот-
рассмотренных в предыдущем примере, то множество С = А-В
состоит из следующих восьми последовательностей:
«2 = «1*2 '
15 М. А. Айзерман, Л. А. Гусев и др.
-О
Р5
Рз
Р2
-та
Р5
Рз
Р2
Pi
Pl2
Рз Ре
>
226 ПРЕДСТАВЛЕНИЕ СОБЫТИЙ В КОНЕЧНОМ АВТОМАТЕ [ГЛ. VII
Сз = Я2*1 =
с4 = a2b2 =
C5 = a3*i =
се = аз*2 =
Pi
Pi
Pi
Pi
Pi
Pi
Pi
Pi
Рз
Рз
P2
P12
P5
P5
Рз
*
?7
P7
Pe
Pi P2
Pi Pl2
t
Рв Рв
*
P2
Pi
P4
P6
Pi
Рз
Ре
P2
РЗ ?2
Рв
Рв
P2
Pi
P4
P6
Pi
Рз
Ре
P2
Рз Pl2
= «4*1 =
C8 = «4*2
Третья операция — итерация. В отличие от
первых двух операций, которые являлись бинарными,
т. е. образовывали новое множество С из двух множеств
А и В, третья операция является унарной, т. е. образует
новое множество С из какого-либо одного множества.
Рассмотрим, например, множество В. Выберем ка-
какую-либо последовательность из множества В, припи-
припишем к ней справа любую последовательность из этого
же множества В (можно и выбранную). К полученной
последовательности вновь припишем справа любую по-
последовательность из множества В и т. д. любое (но ко-
конечное) число раз.
Этот процесс приписывания последовательностей из
множества В друг к другу может быть оборван на лю-
любом конечном шаге, в частности после первого же шага,
т. е. вообще без приписывания к первой выбранной по-
последовательности из В какой-либо иной. При этом каж-
каждый раз можно выбирать любую последовательность из
В, в том числе и такую, которая ранее уже использо-
использовалась.
i 7.3]
РЕГУЛЯРНЫЕ СОБЫТИЯ
227
Выполняя этот процесс составления новых последо-
последовательностей из последовательностей, принадлежащих
В, всеми мыслимыми путями, т. е. выбирая все возмож-
возможные комбинации приписывания к одной последователь-
последовательности из В других последовательностей и обрывая этот
процесс на всех возможных конечных шагах, образуем
новое множество последовательностей С. Если теперь к
множеству С добавить «пустую» *) последовательность Л
(не содержащую ни одного символа), то мы получим
множество С, которое называется итерацией В и обо-
обозначается так
С = В*.
Даже если множество В конечно, множество С = В*
бесконечно. Так, в нашем примере множество В состояло
из двух элементов
ье
Ра
Рз
Ре
Pis
Элементами бесконечного множества С = В* являются,
например, последовательности
с0 —А («пустая» последовательность),
н
Рз
Ре
с2 — Ь2:
= Ь\Ь\.
Р12
ь
Рз
Рб РЗ
Рз
Ре
*) «Пустая» последовательность обладает тем свойством, что
умножение любой последовательности а на Л дает снова а: а А =
= Ла= а. Введение «пустой» последовательности удобно при записи
регулярных выражений (см. ниже, пример 2).
15*
228 ПРЕДСТАВЛЕНИЕ СОБЫТИЙ В КОНЕЧНОМ АВТОМАТЕ [ГЛ. VII
c4 =
Р2
Рз
Рб Р2
Рз
Ре Рг
Рз
Рб
Р2
Рз
Ре
Р12
Pis
Р2
Рз
Рб
?12
Pis
Pis
Pl2 P2
II
Рз
Ре
Pl2
Pl2 Pl2 Pl2 ?2
Рз
Ре
Pis
Р2
Рз
Ре Pi2
Р2
Рз
Ре
f6 = b\b2:
ct =
= b2b2b2.
ce = b2btb2.
= b2b2b2bt:
= b2bib2bt:
и т. д.
Из приведенных объяснений и примера ясна связь
между операцией умножения и итерацией: итерация яв-
является результатом объединения всех множеств, полу-
получаемых умножением множества В самого на себя любое
(каждый раз конечное) число раз. Поэтому операция ите-
итерации может быть представлена «бесконечным рядом» *)
В* = А\/В\/(В • B)V((B ¦ В) ¦ B)V(((B ¦ В) • В) • B)\J ...
С помощью введения трех операций из множеств 4
и В образуются новые множества. Эти новые множества
*) Три рассмотренные операции впервые введены Клннн [42].
Наше изложение отличается от изложения Клннн в двух отношениях:
1) В работе Клннн вместо унарной операции «итерация» вводится
бинарная операция С = А*В. Эта операция может быть выражена
через введенные выше трн операции следующим образом: А * В —
— А V А • В*. 2) «Приписывание» последовательностей при опера-
операциях умножения и итерации, в отличие от Клинн, производится здесь
справа, а не слева.
|7.3] РЕГУЛЯРНЫЕ СОБЫТИЯ 229
сами могут быть приняты за исходные, и из них с по-
помощью тех же трех операций могут быть опять образо-
образованы новые множества и т. д. Даже если исходные мно-
множества конечны (более того, если каждое из них содер-
содержит только одну последовательность, состояющую из
одного символа), но если применяется хоть один раз
операция итерации, вновь образуемое множество беско-
бесконечно.
Введем в рассмотрение универсальное множество Е,
содержащее любую входную последовательность любой
(но конечной) длины.
Если в качестве множества А принять множество по-
последовательностей, содержащих только один символ р,
т. е. положить ai = pi, a2 = рг ат = рг, то универ-
универсальное множество Е может быть получено из элемен-
элементов множества А путем приписывания их друг за другом
в любом числе и в любом порядке, т. е.
Далее будем называть исходными*): а) любые мно-
множества, состоящие из одной входной последовательно-
последовательности конечной длины (а, Ь, с, ...) , и б) универсальное
множество Е.
Назовем регулярным множеством входных последо-
последовательностей:
1) любое исходное множество,
2) любое множество последовательностей, которое
можно образовать из исходных применением конечного
числа раз описанных трех операций (объединения, ум-
умножения и итерации).
*) Заметим, что было бы логично считать исходными не вход-
входные последовательности конечной длины, а последовательности
длины 1: ах = р,, а2 = р2, ..., содержащие лишь один символ. Дей-
Действительно, конечные последовательности получаются из них приме-
применением лишь операции умножения. Но далее в этой главе при дока-
доказательстве теорем Клини нам будет удобнее рассматривать в каче-
качестве исходных множества последовательностей конечной длины.
В гл. VIII будет приведено иное доказательство теорем Клини, и
там мы будем считать исходными последовательности, содержащие
только один символ.
230 ПРЕДСТАВЛЕНИЕ СОБЫТИИ В КОНЕЧНОМ АВТОМАТЕ [ГЛ. VII
Регулярные множества обозначаются далее буквой/?.
Приведем несколько примеров регулярных множеств.
Пример 1.
В этом случае регулярное множество — объединение
трех исходных последовательностей.
Пример 2.
R = [b-(aT\.
Регулярное множество — множество всех последова-
последовательностей, начинающихся с Ь и содержащих затем
лишь повторенный любое число раз элемент (последо-
(последовательность) а, например:
b, ba, baa, baaa,...
Заметим, что благодаря введению пустой последова-
последовательности Л в определение (а)*, в множество R входит
также символ b сам по себе.
Пример 3.
R={[(aVbT]c}.
Это множество содержит все последовательности, со-
состоящие из последовательностей а и Ь, повторяющихся
в любом порядке любое число раз и заканчивающихся
последовательностью с, например: с, abc, bac, aabc,
baabc, baaaabbc и т. д.
Пример 4.
/? = (?• а).
Здесь R — множество всех последовательностей, за-
заканчивающихся последовательностью а.
Пример 5.
R = \(E-a)-b].
Это множество содержит все последовательности, ко-
которые заканчиваются непосредственно следующими
друг за другом последовательностями а и Ь.
Пример 6.
R={\(a-E)-(c-E)\b\.
В этом случае R содержит все последовательности,
начинающиеся с а, заканчивающиеся последовательно-
§7.3] РЕГУЛЯРНЫЕ СОБЫТИЯ 23Г
стью Ь и содержащие где-либо внутри последователь-
последовательность с.
Выражения, подобные выписанным в приведенных
шести примерах, т. е. любые выражения, составленные
из исходных последовательностей (а, Ъ, с, ... и Е), свя-
связанных знаками объединения, умножения и итерации
(V» • и *), назовем регулярными выражениями.
Каждый знак операции в регулярном выражении мо-
может быть применен лишь к паре (для бинарных опера-
операций) или к одному (для итерации) из исходных элемен-
элементов, либо к скобкам, содержащим результат одной такой
операции. Поэтому регулярное выражение может содер-
содержать «скобки в скобках» (см. приведенные примеры).
Наибольшее число «скобок в скобках» в регулярном
выражении (с учетом наружных скобок) называется
глубиной регулярного выражения*). В приведенных
примерах глубина равна единице только в примере 4,
равна двум в примерах 1, 2, 5 и равна трем в примерах
3 и 6.
Регулярное выражение, не содержащее ни одной
операции, например: R = a, R = b, R = Е и т. п. уело-'
вимся считать регулярным выражением глубины нуль.
Заметим, что одному и тому же регулярному множе-
множеству входных последовательностей может соответство-
соответствовать несколько разных регулярных выражений. Напри-
Например, выражения
R=\{a ¦ Ь) ¦ {с ¦ d)\ и R=[\{a-b)-c\-d),
конечно, определяют одно и то же множество, но имеют
разную глубину. Поэтому понятие глубины характери-
характеризует не регулярное множество, а конкретное регулярное
выражение.
Заметим также, что подмножество регулярного мно-
множества входных последовательностей не обязательно
регулярно. Это следует, например, просто из того, что
универсальное множество регулярно по определению,
*) Операции V> •» * могли бы быть положены в основу построе-
построения алгебраических действий над множествами входных последова-
последовательностей. В частности, можно было бы получить тождества, на-
например: (Е-В)* —ЕВ (где В — произвольно заданное множество),
позволяющие упрощать регулярные выражения. В этой книге нам
подобная алгебра не понадобится.
232 ПРЕДСТАВЛЕНИЕ СОБЫТИЙ В КОНЕЧНОМ АВТОМАТЕ [ГЛ. VU
а нерегулярные множества существуют (пример нерегу-
нерегулярного множества см. далее, в § 7.6).
Напомним, что в этом параграфе рассматривались
входные последовательности, «обезличенные» в отноше-
отношении номеров тактов.
Рассмотрим теперь какое-либо множество S таких
последовательностей и к каждой последовательности из
этого множества припишем номера тактов, начиная с
нуля. Тогда из множества входных последовательностей
получается соответствующее множество входных лент.
Так, например, множество, состоящее из трех входных
последовательностей
Pi
?2
Р2
Рб
Рб
Pi
Pl2
Рз
Р2
Рз
Pi
Р4
Рб
Р5
Рб
Pi
?2
1
Pa Pi
превращается в множество, состоящее из трех входных
лент
Такт
Р
0
Pi
1
Рб
2
Pl2
3
Рз
4
Pi
5
?4
6
Ре
Такт 0
Р Р2
1
Рб
2
Рз
Такт
Р
0
Р2
1
Pi
2
Р2
3
Рб
4
Ре
5
Р.
6
Р2
7
Ре
8
Pi
§ 7.3] РЕГУЛЯРНЫЕ СОБЫТИЯ 233
Множество входных лент, которые с помощью такого
приема образуются из регулярного множества входных
последовательностей, будем называть регулярным мно-
множеством входных лент. Мы будем сопоставлять каждому
регулярному множеству входных лент то же самое
регулярное выражение, которое определяет соответ-
соответствующее регулярное множество входных последова-
последовательностей.
Теперь можно приступить к классификации событий
на входе автомата.
Событие на входе автомата называется регулярным,
если множество входных лент (рассмотренных на всей
длине от 0-го до р-го такта), определяющих наступле-
наступление события, является регулярным множеством.
Среди регулярных событий можно выделить подкласс
событий, имеющих регулярное выражение вида
где А — любое множество конечных входных последоваг
тельностей, содержащее не более чем q символов. Такое
регулярное событие называется определенным событием
длины q или просто определенным событием.
Особенность определенного события состоит в том,
что для индикации его надо рассматривать не всю вход-
входную ленту, начиная от 0-го такта и до р-го, а только ее
«хвостовую часть» длины q, соответствующую тактам
р, р — 1, р — 2, ..., р — q. Образно можно представить
себе, что вдоль, входной ленты перемещается прозрач-
прозрачный движок (устроенный подобно движку логарифми-
логарифмической линейки), сквозь который можно наблюдать
лишь определенное число q клеток ленты. Каждый такт
движок смещается вправо на одну клетку так, что са-
самая правая клетка, наблюдаемая сквозь движок, всегда
соответствует моменту р.
Определенные события отличаются тем, что для них
можно подобрать движок (для каждого определенного
события свой), так, чтобы в любой момент р факт
наступления или ненаступления события мог быть
индицирован лишь теми клетками входной ленты, ко-,
торые видны сквозь движок.
234 ПРЕДСТАВЛЕНИЕ СОБЫТИИ В КОНЕЧНОМ АВТОМАТЕ [ГЛ. VII
§ 7.4. Представимость регулярных событий
Мы можем теперь сформулировать и доказать сле-
следующие основные теоремы.
Первая теорема Клин и. Любое регулярное
событие представимо в конечном, автомате с выходным
преобразователем появлением единицы на выходе пре-
преобразователя при подходящем выборе начального со-
состояния автомата.
Мы будем доказывать теорему эффективно, т. е. ука-
укажем один из возможных способов построения автомата,
представляющего регулярное событие, заданное произ-
произвольным регулярным выражением*).
Введем в рассмотрение вспомогательные автоматы,
имеющие выходной преобразователь (на выходе преоб-
преобразователя может появиться только 0 или 1) и имеющие,
помимо входа р, вспомогательную нитку входа, к кото-
которой подводятся символы а из алфавита {0, 1}**).
Пусть задано регулярное множество входных после-
последовательностей R. Условимся говорить, что в момент р
на входе вспомогательного автомата наступило событие
Ra, если существует такой момент t (O^.t^.p), что:
1) в момент t на дополнительной нитке входа по--
явился символ а = 1 и
2) появившаяся между моментами tap последова-
последовательность символов р принадлежит R.
Пусть, например, заданное множество входных по-
последовательностей R включает, три последовательности
Р1Р2Р3» P3P2P1 и Ps-
Тогда для входной ленты нашего вспомогательного ав-
автомата (табл. 7.4) событие Ra наступает в такты 3, 5,
7, 14 и 18 и не наступает во все остальные такты.
Условимся говорить, что вспомогательный автомат
•лредставляет #„-событие появлением 1 на выходе, если
на выходе -его преобразователя появляется 1 тогда
*) Другое, также эффективное доказательство этой теоремы
будет приведено в гл. VIII в связи с изложением метода Глушкова.
**) Иначе говоря, входными символами такого автомата яв-
являются пары символов (р, 1) или (р, 0).
Представимость регулярных событий
235
и только тогда, когда на входе вспомогательного авто
мата наступает событие Ra.
Таблица 7.4
Такт
Р
Дополни-
Дополнительный
вход
0
Pi
0
1
Рз
1
2
Ра
1
3
Pi
1
4
Р2
0
5
Рз
1
6
Р5
0
7
Р5
1
8
Рз
1
9
Р<
0
10
Р5
0
11
Ра
0
12
Pi
1
13
Ра
1
14
Рз
1
15
Ps
0
16
Рз
1
17
Ра
0
18
Pi
1
Вспомогательный
автомат
Автономный
автомат
Рис. 7.1.
Представим себе теперь, что имеется автономный
автомат с выходным алфавитом {0, 1} и что выход этого
автомата отождествлен с ниткой а вспомогательного
автомата (рис. 7.1). По- (
i
лученная сеть в целом
является автоматом с
единственным входом р.
Пусть далее автоном-
автономный автомат (мы бу-
будем называть его пус-
пусковым) выбран таким
образом,что он выдает
на выходе а = 1 в ну-
нулевой такт и а = 0 во
все последующие такты. Тогда наша сеть будет пред-
представлять событие R появлением единицы на выходе.
Упомянутый выше автономный автомат, выдающий
на выходе единицу только в нулевой такт, заведомо мо-
может быть построен: таким автоматом будет, например,
двоичный элемент задержки, на вход которого всегда
подается нуль, а начальное состояние выбрано равным
единице.
Поэтому, если мы покажем, что, каково бы ни было
регулярное событие R, может быть построен вспомога-
вспомогательный автомат, представляющий R*-событие, то тем
самым будет показано существование автомата, пред-
представляющего любое регулярное событие R.
Мы докажем, что такое построение возможно, восполь-
воспользовавшись методом индукции по глубине регулярного
236 представление событий в конечном автомате [гл.
Задержка
выражения, определяющего представляемое регуляр-
регулярное Ra -событие. Покажем сначала, как может быть
представлено любое регулярное Ra -событие, для кото-
которого регулярное выражение R имеет глубину нуль. За-
Затем мы покажем, что если может быть представлено
регулярное /?„ -событие, определяемое регулярным выра-
выражением R произвольной глубины v, то может быть пред-
представлено и любое регулярное 7?в -событие, определяемое
регулярным выражением R глубины v -f 1.
Первый шаг индукции. Напомним, что регу-
регулярными выражениями глубины нуль являются просто
символы, соответствующие
I заданным входным последо-
| | 1 вательностям а, Ь, с, ..., и
^"> f~~*^ символ Е, соответствующий
универсальному множеству
входных последовательно-
последовательностей.
Представление 7?„-собы-
тия, выраженного символом
Е, означает создание автомата, на выходе которого по-
появляется и далее все время удерживается единица, на-
начиная с момента, когда впервые а = 1, независимо от
входной последовательности. Такой автомат может быть
построен, например, из элемента двоичной задержки,
находящейся в начальный момент в невозбужденном
состоянии, если на вход этого элемента через элемент
дизъюнкции подать символ а и выходной символ *)
(рис. 7.2).
Теперь построим автомат, представляющий #а-собы-
тие, когда множество Я содержит только одну входную
последовательность конечной длины q. Он состоит
(рис. 7.3) из двух линий задержки (каждая линия со-
содержит q элементов задержки) и преобразователя сим-
символов. Первая (основная) линия задержки работает
в алфавите {р}, вторая (вспомогательная)—в двоичном
алфавите {а}. На выходе преобразователя символов появ-
Рис. 7.2.
*) Для единообразия с иными рассматриваемыми автоматами
можно считать, что имеется еще и вход р, но выход автомата от
р не зависит.
7.4] \
ПРЕДСТАВИМОСТЬ РЕГУЛЯРНЫХ СОБЫТИЙ
237
ляется единица тогда и только тогда, когда символы р
на выходах всех элементов задержки главной линии
формируют заданную последовательность длины q, счи-
считая от конца линии задержки к началу. Начальное со-
состояние элементов задержки главной линии безразлич-
безразлично, а все элементы задержки вспомогательной линии в
начальный момент времени должны быть невозбуждены
(т. е. иметь состояние нуль). Выходом автомата являет-
является конъюнкция выходов преобразователя и вспомога-
вспомогательной линии задержки.
Выход
v
q элементов задержки
Рис. 7.3.
Ясно, что единица на выходе появится тогда и только
тогда, когда: 1) q тактов назад на входе а была еди-
единица (и поэтому в рассматриваемый момент единица
появится на выходе вспомогательной линии задержки)
и 2) в течение последних q тактов появилась заданная
последовательность символов р (и поэтому в рассматри-
рассматриваемый момент появилась единица на выходе преобра-
преобразователя).
По построению очевидно, что единица на выходе мо-
может появиться не ранее чем через q тактов от началь-
начального момента t — О (поскольку в начальный момент все
элементы задержки вспомогательной линии имели со-
состояние нуль). Отсюда следует, что начальные состояния
элементов задержки основной линии не влияют на вы-
выход автомата в рассматриваемый момент, т. е. через q
тактов после начала работы состояния этих элементов
задержки определяются только входами.
В соответствии с рис. 7.3 может быть построен авто-
автомат, представляющий ^„-событие, для которого R — лю-
любое регулярное выражение глубины нуль.
238 ПРЕДСТАВЛЕНИЕ СОБЫТИЙ В КОНЕЧНОМ АВТОМАТЕ [ГЛ. VII
Индукция. Покажем теперь, что если существуют
вспомогательные автоматы, представляющие /?а'робы-
тия, определяемые любыми регулярными выражениями
глубины v (v^-О), то можно построить автомат,предста-
автомат,представляющий /?„ -событие, определяемое любым регулярным
выражением глубины v + 1.
Из определения понятия «глубина регулярного вы-
выражения» следует, что любое регулярное выражение
глубины v + 1 получается из одного или двух регуляр-
регулярных выражений глубины v путем однократного примене-
применения одной из операций: объединения, умножения или
итерации.
В связи с этим для завершения индукции надо по-
показать, что если представимы /?„ -события, определяемые
регулярными выражениями /?i и R2, то представимы
Ra-события с регулярными выражениями
R = (R1VR2),
R = (R^ или R =
Рассмотрим эти три операции порознь. Для сокра-
сокращения текста всюду, где это не может привести к недо-
недоразумениям, регулярное выражение, соответствующее
ему событие и представляющий /?„ -событие автомат мы
будем обозначать одной и той же буквой /?.
Объединение. Автомат, представляющий объеди-
объединение
R = (RiVR2),
получается из автоматов, представляющих /?i и R2 по-
порознь, подводом их выходов к элементу дизъюнкции и
объединением их соответствующих входов (рис. 7.4).
Умножение. Автомат, представляющий произве-
произведение
R = (Ri-R2),
получается из автоматов, представляющих Ri и R2 по-
порознь, путем отождествления выхода автомата /?j со
вспомогательной ниткой входа автомата R2 (рис. 7.5) че-
через задержку.
§7.4]
ПРЕДСТАВИМОСТЬ РЕГУЛЯРНЫХ СОБЫТИИ
239
Для построенного так автомата вспомогательной
ниткой входа служит вспомогательная нитка входа ав-
автомата»Ri, а выходом — выход автомата Яг.
Действительно, единица на выходе автомата R2 по-
появится « том случае, когда представлено событие R2, на-
начавшееся в такт, следующий за тем тактом, когда была
единица ]на выходе автомата Rx. Но появление единицы
V
Рис. 7.4.
на выходе автомата R\ означает, что к этому моменту
было представлено событие Ru начавшееся в момент,
когда на вспомогательном входе автомата Ri (а зна-
значит, и на входе всего построенного автомата) была
единица.
Рис. 7.5.
Следовательно, автомат в целом представляет Ra-
событие: «непосредственно после события Ri наступило
событие R2», т. е. произведение Ri • R2.
Итерация. Если дан автомат, представляющий
событие Ri, то автомат, представляющий #а-событие
R = (R*i), получается из него добавлением одного эле-
элемента дизъюнкции (рис. 7.6). Выход элемента дизъюнк-
дизъюнкции отождествляется с вспомогательной ниткой входа
автомата R\, а ко входу элемента дизъюнкции подвсь
240 ПРЕДСТАВЛЕНИЕ СОБЫТИИ В КОНЕЧНОМ АВТОМАТЕ [ГЛ. VII
Рис. 7.6.
дятся как вспомогательная нитка входа автомату, так
и его выход через задержку.
Действительно, единица на выходе этого ав/го,мата
получается всякий раз, когда представлено событие Ri,
начиная от такта появления единицы на вспомогатель-
вспомогательной нитке входа а или от такта, непосредственно сле-
следующего за тем, когда событие Rt было представлено.
Поэтому единица на выходе появляется всякий раз, ко-
когда произойдет событие Ri (любое число раз подряд),
что и дает представление
события R= (R*i).
Этим заканчивается про-
проведение индукции по глу-
глубине регулярного выраже-
выражения и, следовательно, дока-
доказательство теоремы.
Первое замечание.
В формулировке первой
теоремы Клини присутство-
присутствовало указание на необходи-
необходимость выбора подходящего
начального состояния. Из
хода доказательства видно, что при описанном выше
построении автомата, представляющего регулярное со-
событие, подходящий выбор начального состояния сводит-
сводится: а) к обеспечению состояния нуль всех элементов
вспомогательной линии задержки при представлении
исходного множества, состоящего из одной входной по-
последовательности (рис. 7.3); б) к обеспечению состояния
единица элемента задержки автомата, представляющего
универсальное событие (рис. 7.2), и в) к обеспечению
состояния единица элемента задержки пускового авто-
автономного автомата, представляющего событие t — 0 (см.
выше).
Второе замечание. Представление события ER
отличается от представления события R только способом
использования вспомогательной нитки входа автомата,
представляющего Ra -событие. Именно, для представле-
представления события R эта нитка входа соединяется с пусковым
автономным автоматом, подающим единицу только в
первый такт, а для представления србытия ER к этой
§ 7.5]\
РЕГУЛЯРНОСТЬ ПРЕДСТАВИМЫХ СОБЫТИЙ
241
подводится выход автомата, представляющего со-
событие Е (рис. 7.2), т. е. подводится единица во все так-
такты. Эго относится, в частности, к представлению опре-
определенного события Е • а.
§ 7.5. Регулярность представимых событий
В настоящем параграфе будет доказана теорема, об-
обратная доказанной выше.
Вторая теорема Клин и. В конечном автомате
представицы только регулярные события.
Для того чтобы доказать эту теорему, мы сначала
введем понятие о регулярных множествах цепочек триад,
затем докажем вспомогательную лемму и, наконец, опи-
опираясь на эту лемму, докажем теорему.
.Лабиринт триад и пути в нем. В беско-
бесконечном множестве лент, которые могут быть реализованы
в каждом конкретном конечном автомате, содержится
лишь конечное число kr различных триад. Обозначим
их буквами ци \ц, • • •, Hkr и поставим в соответствие
каждой триаде ц,- точку на плоскости.
В любой из лент рассматриваемого автомата после
какой-либо триады ц* может следовать не любая иная
триада, а лишь некоторые из триад, так как у двух
смежных триад имеется один одинаковый символ. Так,
например, после триады
Pi
*4
могут следовать лишь триады, у которых в левой ниж-
нижней клетке вписан символ х4, например
Р2
*4
*6 .
Pi
*4
Р4
*4
*1
Рб
*4
*4
Ш М. А. Айзерыан, fl. А. Гусев а др,
242 ПРЕДСТАВЛЕНИЕ СОБЫТИИ В КОНЕЧНОМ АВТОМАТЕ [ГЛ. VII
и не могут следовать триады с иным символом в/ этой
клетке,.например
Pi
*4
Рз
*4
P5
*6
i
От точки, соответствующей триаде щ, / проведем
стрелки ко всем точкам, соответствующим^ триадам,
которые могут следовать после уц (рис. 7.7), и так
поступим со всеми триадами уц (/=1, 2, ..., kr).
В результате (пример на
°УИ' рис. 7.8) на плоскости будет
изображен граф, который
мы назовем лабиринтом
триад.
Выберем теперь какую-
либо триаду \ii в качестве
начальной и выпишем лю-
любую последовательность три-
триад, двигаясь любым возмож-
возможным образом, не противоре-
противоречащим направлению стре-
стрелок в лабиринте триад. Та-
Такую последовательность
триад назовем путем в лабиринте триад или просто пу-
путем. Измерять такой путь будем числом входящих в него
триад. Так, например, при лабиринте триад, показанном
на рис. 7.8, и при начальной триаде ц,2 существуют пути,
описываемые цепочкой триад
1*2 1*3 1*4 1*5 1*6 1*1 1*2»
а путь
НЗ Pi Нч \>Ъ'
Н'З 1*4 И Т-
1*2 1*3 1*6
невозможен, так как после триады ц3 не может следо-
следовать триада цв (в лабиринте триад на рис. 7.§ нет стрел-
стрелки от цз к ц6),
§7.5]
РЕГУЛЯРНОСТЬ ПРЕДСТАВИМЫХ СОБЫТИЙ
243
Рассмотрим теперь последовательности (цепочки)
триад \вне связи с каким-либо конкретным автоматом и
его лабиринтом триад. Введем понятие о регулярном
множестве цепочек триад, определив его по индукции
так: по\ определению всякое множество, содержащее
только одну триаду, регулярно; если А и В — регуляр-
регулярные множества цепочек триад, то регулярны и:
а) их объединение (А\/В), т. е. множество, содер-
содержащее как цепочки А, так и цепочки В;
Рис. 7.8.
б) произведение (А -В), т. е. множество цепочек,
которое получается приписыванием справа к каждой
цепочке из А любой цепочки из В и
в) итерация (А*), т. е. множество цепочек триад,
которое получается, если к любой цепочке из А любое
число раз приписывать справа любые цепочки из А
(включая исходную или уже приписанные).
Лемма. Множество всех путей, ведущих от триады
\х к триаде ц в лабиринте триад любого конечного авто-
автомата, является регулярным множеством цепочек триад.
Лемму докажем индукцией по q, где q — число раз-
различных триад в пути от \а к ц.
Для q = 1 лемма очевидна.„В этом случае ц совпа-
совпадает сци возможны только два подслучая:
^а) если символы х в нижней строке этой триады jx =
= ц различны, то множество путей состоит только из
одного пути, содержащего лишь эту одну триаду ц,
16*
244 ПРЕДСТАВЛЕНИЕ СОБЫТИЙ В КОНЕЧНОМ АВТОМАТЕ [ГЛ. VII
б) если ц имеет в нижней строке одинаковые
волы и, то множество путей включает все цепочки/триад
содержащие повторение одной и той же триады и, т. t
итерацию (ц)*. Следовательно, это множество регу-
регулярно.
Пусть теперь лемма верна для любого множества
путей с q ^ т. Покажем, что она верна и для любого
множества путей с q = т + 1. С этой целью рассмотрим
любой путь, имеющий q = m+ 1. Выписав явно содер-
содержащиеся в нем триады \i и последнюю триаду \х в конце
пути, заменим остальные триады (в том числе и триады
\i, которые могут встретиться не в конце пути) много-
многоточиями:
Каждое многоточие заменяет путь, который не со-
содержит триады \i. Поэтому всякий путь, замененный
многоточием, содержит по крайней мере на единицу
меньше различных триад, т. е. q^tn. По предпо-
предположению индукции, каждый путь, замененный много-
многоточием, составляет регулярное множество цепочек
триад. Обозначим эти пути соответственно г,-; r^, rg
и т. д.
Пусть_ сначала_ ц = ц. Тогда весь рассматриваемый
путь от ц к ц = ц можно представить себе состоящим
из триад \i,_между которыми расположены регулярные
множества г.
Выделим пары, составленные из двух стоящих под-
подряд путей так, как это показано выше. Каждая такая
пара — произведение двух регулярных множеств: мно-
множества, состоящего только из одного элемента ц, и со-
соответствующего множества г. Следовательно, такая
пара сама принадлежит регулярному множеству ii-R.
РЕГУЛЯРНОСТЬ ПРЕДС*А6ИМЫХ СОБЫТИИ
245
Поэтому все пути, ведущие из ц в ц = \i, являются
элементами итерации этого произведения
т. е. составляют регулярное множество цепочек триад.
Если |j, Ф ц, то аналогично множество всех путей,
ведущих из \i в ц, есть
W
т. е. также регулярно. Лемма доказана.
Лемму удобно пояснить, воспользовавшись нашим гео-
геометрическим образом—
лабиринтом триад;
Рассмотрим какой-ли-
какой-либо лабиринт триад, на- /*
пример показанный на
рис. 7.9, где для ясности
рисунка опущена часть
стрелок. Разберем воз-
возможные ПУТИ ИЗ [I В Ц.
Прежде всего, есть
выбор из двух путей:
? 1 2 3 IX
8 9 10
Рис. 7.9.
Далее, первый путь может быть удлинен обходом пе-
петель, например
jTl 2 3 57641 23?.
Петли можно обходить любое конечное число раз, на-
например
? 1 23576412357641235764123A
либо еще более усложнять путь движением по «петлям
внутри петель», например
M235764123576457645764123ilHT. д.
246 представление событий в конечном АвтбМАТЕ ttyi. vt
Ситуация такого рода имеет место не только в рас-
рассмотренном примере, но является общей. Всякое множе-
множество путей из |i в |i может содержать прежде всего не-
несколько вариантов простых путей (объединение!), при
этом оно состоит из стрелок, проходимых одна после
другой (произведение!), либо из обхода любое конеч-
конечное число раз любой встречающейся на пути в лаби-
лабиринте триад петли (итерация!). Каждый путь из ц в \i
может быть составлен из этих трех элементов. Этот
факт, почти очевидный при рассмотрении нашего гео-
геометрического образа — лабиринта триад — и утвер-
утверждается леммой. Из доказанной леммы немедленно сле-
следует и доказательство второй теоремы Клини.
Доказательство второй теоремы К л и-
н и. Рассмотрим какой-либо конечный автомат. Выпи-
Выпишем все его триады (их число конечно).
Пусть М — множество некоторых из символов х
(элемент этого множества обозначим через х), и авто-
автомат представляет событие на входе появлением какого-
либо состояния х из множества М при начальном со-
состоянии х° = х.
Выберем какую-либо триаду \а так, чтобы символ х,
вписанный в ее правой нижней клетке, принадлежал
множеству М (остальные два символа в ней 'произ-
'произвольны).
Выберем также какую-либо триаду ц, у которой
в левой нижней клетке вписан символ х, а остальные
два символа произвольны
§ 7.6] СУЩЕСТВУЮТ ЛИ НЕРЕГУЛЯРНЫЕ СОБЫТИЯ 247
В силу доказанной леммы множество всех путей,
ведущих из \i в \i, является регулярным множеством
цепочек триад.
Рассмотрим множества А и А всех возможных триад
ц и |Г. Множество всех путей, соединяющих какую-либо
триаду из Л с какой-либо триадой из А, является объ-
объединением множеств путей, ведущих от фиксированной
триады \i к фиксированной триаде \l, т. е. регулярно.
Каждой триаде соответствует символ р, вписанный
в ее верхнюю клетку, а цепочке триад соответствует
последовательность символов р.
Если некоторое множество цепочек триад является
регулярным множеством, то множество соответствую-
соответствующих последовательностей символов р является регуляр-
регулярным множеством последовательностей в том смысле,
который был определен в § 7.3.
Действительно, при составлении новых путей из за-
заданных с помощью трех операций (объединение, про-
произведение и итерация) над цепочками триад мы над по-
последовательностями р в этих цепочках совершили лишь
операции, аналогичные введенным в § 7.3, для получе-
получения регулярных множеств последовательностей.
Мы не наложили каких-либо ограничений на выбор
автомата, т. е. на число и характер его триад, или на
выбор начального состояния. Следовательно, мы дока-
доказали, что в любом автомате при любом начальном со-
состоянии множество входных последовательностей, кото-
которые ведут из любого начального состояния х° к какому-
либо состоянию из М, регулярно, т. е. доказали вторую
теорему Клини.
§ 7.6. Существуют ли нерегулярные
(непредставимые) события?
Мы доказали выше, что всякое регулярное событие
представимо в конечном автомате (§ 7.4) и что только
оно и может быть представимо (§ 7.5). Но, может быть,
любые события регулярны и, следовательно, предста-
вимы? Это предположение неверно. Нерегулярные, т. е.
непредставимые в автомате события существуют. Чтобы
248 ПРЕДСТАВЛЕНИЕ СОБЫТИЙ В КОНЕЧНОМ АВТОМАТЕ [ГЛ. VII
доказать это, мы здесь рассмотрим примеры нерегуляр-
нерегулярных событий. Более того, мы выделим целый класс за-
заведомо нерегулярных событий.
Предположим, что задана какая-либо конкретная
бесконечная последовательность символов р, например
Р5 ?2 Pi Р5 ?4 Рз Р2 Pi
Назовем ее последовательностью ?". Последователь-
Последовательность J? назовем «в конечном счете периодической»,
если, начиная с некоторого q-ro символа (считая слева
направо), последовательность состоит из периодически
повторяющегося отрезка конечной длины.
Рассмотрим событие, состоящее в том, что входная
последовательность символов р в каждый момент р сов-
совпадает с отрезком заданной бесконечной последователь-
последовательности J3?, расположенным между нулевым и р-м симво-
символом. Если такое событие представлено в автомате, то
мы будем говорить, что автомат представляет последо-
последовательность J2?-
Теорема. Заданная бесконечная последователь-
последовательность J? входных символов р представила в конечном,
автомате тогда и только тогда, когда J3? является «в
конечном счете периодической последовательностью».
Доказательство. Докажем сначала, что вся-
всякая «в конечном счете периодическая» последователь-
последовательность представима.
Пусть эта последовательность состоит из «началь-
«начального отрезка» А конечной длины h и периодически повто-
повторяющегося затем «отрезка» В, также конечной длины Т.
Рассмотрим все начальные куски Bir В2, ..., Вт _ t от-
отрезка В (В\ содержит только один первый символ от-
отрезка В, В2 — два первых символа и т. д.) и начальные
куски А\, А%,"... отрезка А. Тогда сформулированное
выше событие состоит в том, что входная последова-
последовательность должна содержать в качестве начального от-
отрезка отрезок А, затем повторенный произвольное число
раз отрезок В, а в конце последовательности должен по-
появиться один из отрезков Ви В2, ..., ВТ-и В. Поэтому
для указанного события может быть записано регуляр-
регулярное выражение
R = {[А{В)*\ -IBiVBM .., у Bt
> 7.6)
СУЩЕСТВУЮТ ЛИ НЕРЕГУЛЯРНЫЕ СОБЫТИЯ
249
Значит, согласно первой теореме Клини, это событие
представимо в конечном автомате.
Докажем теперь обратное утверждение, что всякая
представимая последовательность является «в конечном
счете периодической».
Действительно, пусть последовательность J? пред-
представляется в некотором конечном автомате с числом
внутренних состояний k. Подадим на вход этого автома-
автомата последовательность ?? и рассмотрим первые k + 1
тактов. Существует по крайней мере одно внутреннее
состояние х, которое повторится за это время по край-
крайней мере дважды. Пусть это произошло в такты ? и /"
@<*'<Г<А: + 1).
Составим последовательность ??, которая отличается
от Jg тем, что из нее выброшен отрезок от ? до t", и
подадим эту последовательность J2? на вход того же са-
самого автомата. Так, например, если при k = 8 для по-
последовательности J? мы имели ленту (табл. 7.5)л_в кото-
которой f = 3, t" = б, то для последовательности J& лента
имеет вид табл. 7.6.
t
р
у.
t
р
У.
0
Pi
...
0
Pi
...
1
Рз
...
1
Р»
...
2
Ре
2
Ps
...
t'=Z
Pi
X
3
Pl2
У.
4
P7
...
4
ho
5
Ре
...
5
Pi
Г =6
Pl2
*
6
Ps
7
Pio
7
Таблиц;
8
Pi
9
Ре
i 7.5
• • •
...
Таблица 7.6
8
9
...
250 ПРЕДСТАВЛЕНИЕ СОБЫТИИ В КОНЕЧНОМ АВТОМАТЕ [ГЛ. VII
Последовательность символов х в первой ленте, на-
начиная с момента t" (в нашем примере с 7-го такта) и
далее, точно совпадает с последовательностью х, начи-
начиная с f (в нашем примере с 4-го такта) и далее во вто-
второй ленте, так как, начиная с этих моментов, при оди-
одинаковом исходном состоянии х подаются одинаковые
входные последовательности. Поэтому из того факта,
что последовательность J3? представляется в автомате,
следует, что последовательность J3? также представляет-
представляется в этом автомате. Но это не противоречит определе-
определению термина «последовательность представляется в ав-
автомате», только если последовательности 3" и 3" совпа-
совпадают. Две бесконечные последовательности символов,
из которых вторая отличается от первой удалением всех
символов, расположенных между f и t", могут совпа-
совпадать, только если последовательность .2% начиная от f,
состоит из периодически повторяющегося отрезка, рас-
расположенного между f и t". Теорема доказана.
Доказанная теорема позволяет построить неограни-
неограниченное число примеров непредставимых событий. Приве-
Приведем два таких примера.
Пример 1. Событие наступает, если на входе авто-
автомата появляется рь в моменты t = а2 (а = 1, 2, 3, ...)
и р2 во все остальные моменты.
Пример 2. Событие наступает, если во входной
последовательности число символов рг между двумя не
стоящими подряд символами pi все время удваивается.
Так, событие имеет место, если последовательность
имеет вид
Pi Р2 Pi ?2 Р2 Pi Р2 Р2 Р2 Р2 Pi Pi Р2 Р2 Р2 Р2 Р2 ?2 ?2 ?2 Pi Pi Pi • • •...
и не имеет места при последовательности
Pi Р2 Pi Р2 Р2 Pi Р2 Р2 Р2 Р2 Pi Pi Р2 Р2 Pi • • •
В обоих этих примерах событие непредставимо, так
как соответствующая последовательность не является «в
конечном счете периодической».
Не следует, однако, думать, что все непредставимые
события охватываются этой теоремой.
Так, например, при входном алфавите р, состоящем
из двух символов {О, 1}, событие, заключающееся в том,
§7.6]
СУЩЕСТВУЮТ ЛИ НЕРЕГУЛЯРНЫЕ СОБЫТИЯ
251
что к моменту р число символов 1 во входной последо-
последовательности равно числу символов 0, не относится к рас-
рассмотренному выше классу (поскольку наступление этого
события определяется не одной конкретной входной по-
последовательностью, а целым их классом), но вместе
с тем является непредставимым. Докажем это.
Пусть задан произвольный конечный автомат А. По-
Подадим на его вход последовательность, состоящую из
одних нулей. При этом хотя бы одно состояние х ав-
автомата должно раньше или позже повториться. Пусть
состояние х появилось в моменты f и t" @<J' <t").
Рассмотрим следующие две входные последовательно-
последовательности: 1) последовательность Jg, состоящую из t" нулей,
за которыми следует t" единиц, и 2) последовательность
J2*, состоящую из ? нулей, за которыми следует t" еди-
единиц. Рассмотрим ленты автомата А при входных после-
последовательностях 3 и Jg* (табл. 7.7 и 7.8 соответственно).
t
р
X
0
0
1
0
2
0
...
t' — l
0
t'
0
...
...
t" — I
0
т
t"
1
X
аб л
...
ица 7.7
It" — 1
1
X*
Таблица 7.8
t
р
X
0
0
1
0
2
0
...
...
t' — l
0
t'
1
X
...
t'+f—l
1
X*
Последовательность состояний автомата в ленте, со-
соответствующей J?*, начинающаяся от f и кончающаяся
252 ПРЕДСТАВЛЕНИЕ СОБЫТИЙ В КОНЕЧНОМ АВТОМАТЕ [ГЛ. VII
при t' + t", совпадает с последовательностью- состоя-
состояний в ленте, соответствующей J?, начинающейся в
t" и кончающейся при It", поскольку исходные состоя-
состояния (в моменты ? и t" соответственно) и входные по-
последовательности {t" единиц подряд) совпадают. По-
Поэтому в моменты времени (' + t" при входной ленте J?*
автомат придет в состояние х*, совпадающее с состоя-
состоянием, наступающим в момент It" при входной ленте J?.
Но при появлении входной последовательности Л? со-
событие наступает (число единиц равно числу нулей),
а при входной последовательности J?* не наступает
(число единиц больше числа нулей), в то время как
состояния автомата в этих случаях окажутся одинако-
одинаковыми. Это означает, что автомат А не может предста-
представить рассматриваемое событие, что и требовалось до-
доказать.
Легко усмотреть причину, из-за которой невозможно
представление событий в этих примерах; Она состоит
в том, что конечный автомат в силу самого определе-
определения (число состояний конечно!) обладает «конечной
памятью».
Между тем в сформулированных выше приме-
примерах событий неограниченно растет с ростом номера
такта объем информации, которую должен «помнить»
автомат для того, чтобы каждый данный такт «решить»
вопрос о том, имеет место событие или нет (в первом
примере надо «знать» номер такта, т. е. «помнить»,
сколько тактов прошло, а во втором примере надо «счи-
«считать» число нулей между двумя не следующими додряд
друг за другом единицами, и это число также неогра-
неограниченно растет).
В заключение этого параграфа заметим еще раз, что
множество последовательностей, описывающих нерегу-
нерегулярное (непредставимое) событие, может содержаться
в качестве подмножества в регулярном множестве по-
последовательностей. Так, например, событие, состоящее
в том, что никогда не появляется на входе две единицы
подряд, представимо. Входные последовательности, •. от-
относящиеся к описанному выше первому примеру, яв-
являются подмножеством этого регулярного множества,
но сами они составляют нерегулярное множество.
§7.7]
ЧТО «МОЖЕТ ДЕЛАТЬ» КОНЕЧНЫЙ АВТОМАТ
253
§ 7.7. Что «может делать* конечный автомат
В предыдущей главе мы выяснили, что «может де-
делать» автономный автомат. Дополняя эти сведения тео-
теоремами о представлении событий, мы можем ответить
на вопрос о том, что «может делать» неавтономный
автомат.
Пусть мы имеем автомат А с выходным преобразова-
преобразователем или последовательностную машину, представляю-
представляющую появлением некоторого символа (для конкретно-
конкретности — единицы) на выходе регулярное событие на входе.
Пусть далее при появлении 1 на выходе айтомата А этот
- <Р
Рис. 7.10.
автомат А останавливается и пускает в ход автоном-
автономный автомат Б, который выдает на выходе заранее за-
заданную последовательность М. Выход автомата Б ото-
отождествлен с входом автомата В, который представляет
событие М.
Появление 1 на выходе автомата В используется
для того, чтобы пустить в ход автомат А и остановить
автомат Б. Это (рис. 7.10) делает автомат Ф, который
служит для представления простого события: появле-
появления заданного входного символа. Поэтому вся описан-
описанная система в целом представляет собой конечный авто-
автомат. Такой конечный автомат реагирует на любое регу-
регулярное событие, выдавая на выходе любую заранее за-
заданную конечную последовательность состояний (сим-
(символов), и после этого вновь готов к восприятию внеш-
внешнего воздействия, т. е. реагированию на событие.
При составлении автомата по схеме рис. 7.10 авто-
автомат не реагирует на часть входных символов р, которая
254 ПРЕДСТАВЛЕНИЕ СОБЫТИЙ В КОНЕЧНОМ АВТОМАТЕ [ГЛ. VII
появляется в течение тех тактов, когда работает авто-
автономный автомат Б.
Если автомат Б работает в столь быстрой тактно-
сти, что вся периодическая последовательность на вы-
выходе автомата Б укладывается за время между двумя
тактами автомата А, нет нужды включать автомат Ф,
и выход автомата А может служить входом автомата Б.
Так построенный автомат поддерживает на выходе лю-
любую заданную периодическую последовательность сим-
символов все время, пока представляется событие, и иную
наперед заданную периодическую последовательность
символов, когда событие не представляется.
Разумеется, возможны и иные сочетания автоматов.
Но уже описанные два сочетания показывают, что авто-
автомат может реагировать на регулярное событие любым,
наперед заданным циклом.
Может ли автомат сделать что-либо более этого? Что
именно? Ответы на такие вопросы связаны с тем, на
каком языке формулируются законы переработки по-
последовательностей конечным автоматом. Теоремы Кли-
ни формулируют эти законы на языке представления
событий. До сих пор не были предложены иные удобные
языки, на которых можно было бы в терминах необхо-
необходимых и достаточных условий описать, что может и что
принципиально не может «делать» конечный автомат.
В связи с этим возникает ряд новых проблем, которым
посвящена следующая глава.
ГЛАВА VIII
РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ
И АБСТРАКТНЫЙ СИНТЕЗ
КОНЕЧНЫХ АВТОМАТОВ
И ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН
§ 8.1. Постановка задачи
При проектировании конкретного автоматического
устройства можно различать несколько самостоятельных
этапов.
Проектирование начинается с анализа и идеализации
операций, которые должно выполнять автоматическое
устройство. Если эта идеализация приводит к формули-
формулировке условий работы в терминах дискретного времени
и конечного числа переменных, каждая из которых мо-
может принимать лишь конечное число значений, то возни-
возникает возможность искать проектируемое устройство в
классе конечных автоматов или последовательностных
машин. Однако такая возможность не всегда может
быть реализована, так как не всякое задание, если даже
оно и сформулировано в терминах дискретного времени
и конечного числа переменных, может быть выполнено
конечным автоматом или последовательностной ма-
машиной.
Так, например, конечный автомат и последователь-
ностная машина не могут «предсказывать» состояния вхо-
входа, т. е. выдавать на выходец момент р символ А,р в за-
зависимости от того, какой символ рр + 1 появится в после*
дующий момент времени. Но если даже задание сфор-
сформулировано так, что выход в момент р зависит лишь от
предыдущих состояний входа, то и в этом случае может
не существовать автомата или последовательностной.
256 РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ [ГЛ. VIII
машины, удовлетворяющих заданным условиям. Приме-
Примером этого явилась бы попытка создать автомат для пред-
представления нерегулярного события (см. гл. VII).
-Таким образом, следующий этап создания проекти-
проектируемого автоматического устройства, заданного в тер-
терминах дискретного времени и конечного числа координат,
состоит в том, чтобы распознать, может ли рассматри-
рассматриваемое конкретное задание быть выполнено конечным
автоматом или последовательностной машиной. Задачу,
возникающую на этом этапе проектирования дискрет-
дискретного автоматического устройства, мы назовем пробле-
мой распознавания реализуемости задания (или коротко,
просто проблемой распознавания).
После того как применительно к конкретному за-
заданию проблема распознавания решена положительно,
т. е. установлено, что это задание может быть реа-
реализовано в конечном автомате или последовательно-
последовательностной машине, то возникает задача определения
какой-либо основной таблицы автомата (и преобразова-
преобразователя, если речь идет о последовательностной машине),
выполняющей это задание. Решение этой задачи мы на-
называем абстрактным синтезом.
Абстрактным синтезом заканчивается важнейший
этап проектирования автоматического устройства, так
как до решения этой задачи проектировщик имеет дело
исключительно с заданием на проектируемый автомат,
т. е. с входными и выходными последовательностями и
заданными соответствиями между ними. После того как
абстрактный синтез завершен, в руках проектировщика
оказывается уже таблица автомата (и преобразователя),
и вся последующая работа связана с этими таблицами.
Она состоит в упрощении этих таблиц, выборе принци-
принципиальных путей для их реализации, а также в решении
ряда технических задач, связанных с конкретными осо-
особенностями технических средств, имеющихся в распоря-
распоряжении проектировщика, т. е. с реализацией заданных
таблиц.
Во всех предыдущих главах, кроме гл. VII, мы исхо-
исходили из предположения, что исходными являются таб-
таблицы автомата и преобразователя, и совершенно не
§ 8.11 ПОСТАНОВКА ЗАДАЧИ 257
интересовались вопросом о том, откуда эти таблицы по-
получены. В настоящей главе, тесно примыкающей к главе
о представлении событий, мы интересуемся именно спо-
способами получения основной таблицы автомата и табли-
таблицы преобразователя, исходя из задания на проектируе-
проектируемое устройство, т. е. кругом задач, которые выше были
названы распознаванием и абстрактным синтезом.
До сих пор, говоря о «задании на проектируемое
устройство», мы основывались на интуитивном понима-
понимании этого термина. Но теперь, приступая к рассмотрению
проблем распознавания и абстрактного синтеза, мы дол-
должны точно установить смысл термина «задание на про-
проектируемое устройство».
Всякое «задание на проектируемое устройство» под-
подразумевает установление соответствия между задан-
заданными входными и выходными последовательностями.
Наиболее просто обстоит дело в том случае, если число
заданных входных и выходных последовательностей ко-
конечно; при этом термин «задание на проектируемое уст-
устройство» приобретает точный смысл: под ним можно
понимать перечисление всех заданных последовательно-
последовательностей и соответствий между ними. Этот случай задания
рассмотрен в § 8.2.
Значительно сложнее обстоит дело в общем случае,
когда число заданных последовательностей (и, следова-
следовательно, их длина) может быть не ограничено. В этом
случае нельзя перечислить все заданные последователь-
последовательности и возникает вопрос об отыскании других способов
описания этих последовательностей и соответствий
между ними. Любой избранный способ описания беско-
бесконечных множеств входных и выходных последователь*
ностей и соответствий между ними мы назовем языком
задания.
Интересующие нас проблемы распознавания и аб-
абстрактного синтеза можно сформулировать так: избран
язык задания, и на этом я^ыке бписаны множества
входных и выходных последовательностей и соответ-
соответствия между ними. Требуется найти алгоритм распозна-
распознавания того, существует ли автомат (последовательно-
стная машина), устанавливающий эти соответствия, и
алгоритм определения основной таблицы какого-либо
17 М. А. Айзерман, Л. А. Гусев в др.
258 РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ (ГЛ. VIII
автомата (и преобразователя) в случаях, когда такой
автомат существует*).
Оказывается, однако, что сама возможность нахож-
нахождения таких алгоритмов существенно зависит от того,
каким образом выбран язык задания. Если этот язык
чрезмерно широк, то таких алгоритмов не существует,
т. е. проблемы распознавания и абстрактного синтеза
алгоритмически неразрешимы. Этому вопросу посвя-
посвящен § 8.3.
Таким образом, возникает задача о сужении языка,
на котором описывается задание на проектируемую
Я-машину. Одному из предложенных языков такого ро-
рода — языку регулярных формул — посвящен § 8.4, где
в общих чертах показано, как по заданной регулярной
формуле синтезируется относительно экономная (в смы-
смысле числа состояний) Я-машина, реализующая соответ-
соответствующее задание. Вопрос о принципиальной возмож-
возможности синтеза такой машины не возникает, так как сам
язык в этом случае позволяет описать только реализуе-
реализуемое задание.
§ 8.2. Случай, когда задание перечисляет требуемые
соответствия между входными и выходными
последовательностями
Пусть требуется синтезировать последовательност-
ную машину, условия работы которой определены сле-
следующим образом.
Задано конечное число лент (имеющих, быть может,
разные, но конечные длины) с незаполненной строкой
для «и». Так, например, могут быть заданы четыре лен-
ленты (табл. 8.1 — 8.4).
Требуется синтезировать Я-машину, которая, отпра-
отправляясь от заданного начального состояния и0, реализо-
реализовала бы указанные ленты.
*) Мы впервые использовали здесь термин «алгоритм». В даль-
дальнейшем в этой и в последующих главах нам неоднократно придется
иметь дело с этим понятием. Определение этого термина, соответ-
соответствующие разъяснения и основы теории алгоритмов (тесно связан-
связанные с теорией рекурсивных функций) изложены в гл. XII.
i 8.2]
ЗАДАНИЕ ПЕРЕЧИСЛЯЕТ СООТВЕТСТВИЯ
259
При таком задании пока остается открытым вопрос
о том, каковы остальные ленты (при других входных по-
последовательностях) этой же Я-машины. Условимся счи-
считать, что если по этому поводу нет никаких указаний,
то это значит, что другие входные последовательности
не могут появляться или, что то же самое, иные ленты
могут быть произвольными. В иных случаях задание мо-
может быть как-либо доопределено, например условием,
что любая иная лента должна содержать в строке X не-
некоторый определенный символ (например, Ко) во всех
тактах, начиная с того такта, с которого строка р этой
ленты отличается от строки р в лентах, перечисленных
в задании.
Таблица 8.1 Таблица 8.2
Такт
Р
X
1
0
Pi
1
Р2
*2
2
Ро
3
Pi
4
Рз
*3
5
—
Такт
Р
0
Ро
*2
1
Рз
*2
Таблица 8.3
Таблица 8.4
Такт
Р
X
\
0
Рз
*3
1
Pi
*|
2
—
Такт
Р
X
1
0
Р2
\2
1
Ро
2
—
В приведенном примере, когда заданы четыре ленты,
представленные в табл. 8.1—8.4, такое доопределение
17*
260
РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ [ГЛ. VIII
означало бы, что синтезируемая Я-машина должна иметь,
например, ленты, указанные в табл. 8.5, 8.6 и 8.7.'Такты,
начиная с которых появляется символ Хо, на этих табли-
таблицах отделены жирной линией.
Таблица 8.5
Таблица 8.6
Такт
Р
к
0
Pi
1
Р2
к2
2
Ро
3
Рз
*i
4
Pi
5
—
Такт
Р
к
0
Рз
*3
1
Р2
2
—
К
Таблица 8.7
Такт
Р
*
к
0
Ро
кг
1
Рз -
к2
2
Pi
*з
3
Рз
4
Pi
5
—
В связи с тем, что по условию в заданных лентах в
первом столбце в строке х должен быть вписан один и
тот же символ х°, может оказаться, что предложенное
задание невыполнимо.
Рассмотрим, например, следующие две ленты
(табл. 8.8 и 8.9). Ясно, что не существует Я-машины,
имеющей обе эти ленты, так как она должна была бы,
исходя из одного и того же начального состояния х°,
после появления входной последовательности рфгро вы-
выдать в третьем такте в соответствии с первой лентой
(табл. 8.8) символ hi, а в соответствии со второй лентой
i 8.2]
ЗАДАНИЕ ПЕРЕЧИСЛЯЕТ СООТВЕТСТВИЯ
261
(табл. 8.9) — символ Х3, что противоречит самому опре-
определению последовательностнои машины как машины де-
детерминированной. Задания такого рода назовем проти-
противоречивыми.
Таблица 8.8
Таблица 8.9
Такт
Р
X
0
-та
h
1
Рг
Кг
2
Ро
3
Рз
4
-та
h
5
—
Такт
-та
71
X
0
Pi
1
Р2
х2
2
Ро
X,
3
Рз
*з
4
Р2
5
-та
х2
6
—
Прежде, чем приступить к решению задачи синтеза,
надо проверить, не. является ли задание противоречи-
противоречивым. С этой целью надо просмотреть все отрезки, кото-
которые получаются из заданных лент, если обрезать их на
любом такте так, как это показано на примере ниже. За-
Задание непротиворечиво тогда и только тогда, когда среди
этих отрезков не найдется двух таких, у которых вход-,
ные последовательности полностью совпадают, а выход-
выходные последовательности различны.
Так, в приведенном выше примере двух противореча-
противоречащих лент (табл. 8.8 и 8.9) выделение отрезков таково:
для р— 1
Такт
-та
TV
X
0
-та
1
—
Х2
Такт
-та
71
X
0
-та
71°
1
—
х2
262
РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ (ГЛ. VIII
ДЛЯ/> =
Такт
Р
к
0
Pi
1
Р2
к,
2
—
для/>=3
Такт
Р
TV
к
0
Pi
71°
1
Р2
х2
2
Ро
К
3
—
для/> =
Такт
Pi
Ps
Po
для ^=
Такт
Р
71
0
.Pi
71°
1
Р2
к2
2
Ро
*i
3
Рз
*i
4
Pi
*3
5
—
Такт
Р
к
Такт
Р
71
К
Такт
Р
к
Такт
Р
71
0
Pi
71»
0
Pi
71°
0
Pi
TV»
*.
1»
Pi
TV»
1
P2
x2
1
P2
k,
1
P2
x2
1
P2
k2
2
—
2
Po
^1
2
Po
к
2
Po
3
—
*3
3
Рз
*3
3
Рз
^3
4
—
4
P2-
5
—
k2
§ 8.2] ЗАДАНИЕ ПЕРЕЧИСЛЯЕТ СООТВЕТСТВИЯ 263
Здесь противоречие выявляется для отрезков лент, на-
начиная с 3-го такта.
Допустим теперь, что задание непротиворечиво. То-
Тогда требуется построить соответствующую Я-машину,
т. е. указать основную таблицу ее конечного автомата
и таблицу преобразователя. Если бы в заданных лентах
были заполнены и строки х, то непосредственно по этим
лентам, выделяя триады, можно было бы выписать
заполнение по крайней мере части клеток основной таб-
таблицы автомата и таблицы преобразователя, обеспечи-
обеспечивающих реализацию заданных лент. Остальные клетки
можно было бы заполнить произвольно (в случае, если
никаких дополнительных требований на машину не на-
налагается) или иным образом, если соответствующие
дополнительные требования предъявлены. Таким обра-
образом, задача о синтезе Я-машины сводится к непротиво-
непротиворечивому заполнению строк к.
Если поставленное задание непротиворечиво и может
быть выполнено какой-либо Я-машиной А, то оно мо-
может быть выполнено и любой Я-машиной, замещающей
машину А. Если требуется построить хоть какую-либо
машину, выполняющую задание, т. е. если на синтез
Я-машины никаких дополнительных требований не на-
накладывается, то задача синтеза решается тривиально,
например одним из следующих двух способов:
а) заполнением строк к различными неповторяющи-
неповторяющимися символами щ. При этом полученное число различ-
различных состояний Хг равнялось бы сумме длин заданных
лент.
б) Построением автомата с выходным преобразова-
преобразователем, который представляет определенные события,
«записанные» в заданных лентах. Для этого надо по за-
заданным лентам выписать множество G\ всех входных
последовательностей, которые приводят к появлению на
выходе символа А,ь множество G2 входных последова-
последовательностей, приводящее к появлению символа к2, и т. д.
После этого надо по методам гл. VII построить авто-
автомат I, представляющий определенное событие G\ появ-
появлением на выходе символа 1 (из двоичного алфавита
{О, 1}, автомат II, представляющий определенное собы-
событие G2 появлением на выходе символа 1, и т, д., и
264 РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ [ГЛ. VIII
выходы этих автоматов подвести к преобразователю, ко-
который выдает на своем выходе символ К\, когда появи-
появилась 1 на первом входе в преобразователь, символ Яг,
когда появилась 1 на втором входе, и т. д.
Последовательностные машины, построенные любым
из этих двух приемов, хотя и реализуют заданные лен-
ленты, но обычно имеют чрезмерно большое число со-
состояний.
Часто ставится задача значительно более трудная:
синтезировать последовательностную машину, реализую-
реализующую поставленное задание и имеющую наименьшее чи-
число k состояний х по сравнению с любой иной машиной,
которая также выполняет это задание.
Решение такой задачи обычно разбивается на два
этапа: 1) синтез хоть какой-либо исходной машины, вы-
выполняющей задание, и 2) минимизация ее, т. е. нахож-
нахождение, исходя из этой исходной, другой Я-машины, ко-
которая также выполняет это задание, но имеет мини-
минимально возможное число состояний.
Задача, решаемая на втором этапе, носит название
задачи минимизации. Ей посвящена гл. IX. Применение
методов, которыми решается эта задача в гл. IX, сильно
осложняется, если исходная Я-машина, синтезируемая
на первом этапе, имеет много состояний. Именно по-
поэтому указанные выше два приема, тривиально решаю-
решающие задачу первого этапа, неудобны, так как часто
можно синтезировать исходную Я-машину, имеющую
хотя и не минимальное, но заведомо меньшее число
состояний.
Мы опишем один прием такого рода.
Начнем со следующего примера. Пусть требуется
синтезировать Я-машину, которая, исходя из одного и
того же начального состояния х° = х0, реализовала бы
следующие две ленты (табл. 8.10 и 8.11). Ленты, полу-
получаемые при иных входных последовательностях, про-
произвольны.
Подготовим для заполнения форму основной табли-
таблицы, автомата и таблицы преобразователя. Поскольку
число состояний нам пока неизвестно, число строк в этих
таблицах не определено и мы введем пока лишь одну.
8.2]
ЗАДАНИЕ ПЕРЕЧИСЛЯЕТ СООТВЕТСТВИЯ
265
строку — для хо (табл. 8.12 для автомата и табл. 8.13
для преобразователя).
Таблица 8.10
Такт
Р
TV
X
0
Ро
*о
*i
1
Рз
*1
2
Р2
х2
3
Рз
кг
4
Ро
*i
5
Р2
х2
6
Рз
х2
Такт
Р
71
X
0
Рз
*о
*i
1
Р2
х2
Таб л
2
Ро
*|
3
Ро
и ца
4
Pi
Х2
5
Рз
Х2
8.11
6
Ро
Вписывая далее символы xj в какую-нибудь клетку
строки х, необходимо каждый раз проверять, не проти-
противоречит ли это предыдущему заполнению этой строки,
т. е. не возникают ли противоречивые триады автомата
или несовместимые требования к преобразователю.
Таблица 8.12
Автомат
Таблица 8.13
Преобразователь
*0
Ро
Pi
Р2
»
Рз
^N. P
*0
Ро
Pi
Р2
Рз
Начнем с рассмотрения первой ленты (табл. 8.10).
В строке х первая клетка заполнена символом хо в соот-
соответствии с заданием. При-.заполнении второй клетки
строки х этой ленты ничто не препятствует вписать в нее
тот же символ хо.
Этот же символ хо вписываем также в соответствую-
соответствующую клетку таблицы автомата. В соответствующие клет-
клетки (хо, ро) и (хо, рз) таблицы преобразователя вписываем
266
РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ [ГЛ. VIII
символ Я] (в соответствии с первым и вторым столбца-
столбцами табл. 8.10). Замечаем, что ничто не мешает нам этот
же символ хо вписать теперь в третий столбец ленты
(табл. 8.10) и в соответствующие клетки табл. 8.12 и
8.13. В результате получаем заполнение ленты и таблиц,
показанное в табл. 8.14—8.16.
Лента
Таблица 8.14
Такт
Р
X
X
0
Ро
*о
h
1
Рз
V
2
Р2
*0
Х2
3
Рз
Х2
4
Ро
h
5
Р2
х2
6
Рз
Х2
Таблица 8.15
Основная таблица автомата
Таблица 8.16
Таблица преобразователя
Х^ч.
*0
Ро
*0
Pi
Р2
Рз
*0
^\ Р
X \.
*о
Ро
К
Pi
Р2
х2
Рз
До сих пор вписывание символа хо не приводило к
противоречиям. Попытаемся вписать этот же символ хо
и в следующую (четвертую) клетку ленты (табл. 8.14).
При внесении его в таблицу автомата противоречий не
возникает, так как он попадает в незаполненную ранее
клетку, но попытка вписать символ Х2 в клетку (р3, хо)
приводит к противоречию, так как эта клетка уже за-
заполнена символом Х\. У нас нет иного выхода, кроме как
§8.2)
ЗАДАНИЕ ПЕРЕЧИСЛЯЕТ бООГВЕТСТВИЯ
267
вписать в четвертую клетку ленты . (табл. 8.14) не ко,
а новый символ х\, и одновременно ввести новую строку
в заполняемых таблицах автомата и преобразователя и
вписать в них требуемые символы.
Теперь, обращаясь к следующей (пятой) клетке лен-
ленты, снова попытаемся вписать символ щ. В нашем слу-
случае это не приводит к противоречию. Если бы это при-
привело к противоречию, мы должны были бы попытаться
вписать туда символ щ, и только если бы и это привело
к противоречивому результату, мы были бы вынуж-
вынуждены ввести символ х2 и соответственно открыть новую
строку в заполняемых таблицах.
Перемещаясь так вдоль ленты (табл. 8.14), запол-
заполняем ее строку к символами щ клетка за клеткой, каж-
каждый раз вводя новые символы щ, только если попытка
вписать любой из ранее введенных символов приводит
к противоречию с заполненной ранее частью таблиц
автомата и преобразователя.
Окончив заполнение первой ленты, обращаемся ко
второй и аналогичным образом заполняем ее строку к.
При этом, проверяя непротиворечивость вписываемого
символа, мы имеем в виду все ранее произведенные (в
том числе и при обработке первой ленты) заполнения
таблиц автомата и преобразователя.
Заполненные таким образом ленты рассматриваемого
примера и соответствующие таблицы автомата и преоб-
преобразователя имеют вид табл. 8.17 — 8.20.
Таблица 8.17
Первая лента
Таблица 8.18
Вторая лента
Такт
Р
71
К
0
Ро
*о
h
1
Pj
*0
2
Р2
*0
h
3
Рз
*1
4
Ро
*0
5
Р2
*0
6
Рз
*|
Такт
Р
X
0
Рз
*о
1
Р2
*0
Х2
2
Ро
3
Ро
*0
4
Pi
*о
*2
5
Рз
*|
Х2
6
Ро
*1
268
РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ [ГЛ. VIII
Таблица 8.19
Основная таблица автомата
Таблица 8.20
Таблица преобразователя
х р
71 /Ч.
*0
*1
Ро
*0
*0
Pi
*1
—
Р2
—
Рз
*0
*|
^х р
X Ч.
*0
*|
Ро
—
Pi
х2
—
Р2
А2
—
Рз
х2
Заметим, что мы получили основную таблицу авто-
автомата и таблицу преобразователя, в которых заполнены
не все клетки. Пустые клетки могут быть заполнены про-
произвольно, так как по условию произвольны ленты, полу-
полученные при входных последовательностях, отличающихся
от заданных.
Приведенный пример был специально подобран так,
что при выполнении описанного процесса заполнения
строк х не встречалось никаких затруднений.
Рассмотрим, однако, две другие ленты (табл. 8.21 и
8.22). Мы просим читателя в этом случае попытаться за-
Таблица 8.21
Первая лента
Таблица 8.22
Вторая лента
Такт
Р
71
X
0
Ро
Ч
Х2
1
Pi
К
2
Р2
\г
3
Pi
Х2
4
Ро
Х2
5
Р2
6
Pi
*0
Такт
Р'
71
X
0
Р2
*0
Х2
1
Pi
К
2
Р2
х2
3
Ро
Х2
4
?2
К
полнить ленты и составить таблицы автомата и преоб-
преобразователя с помощью описанной выше процедуры.
Приступая к заполнению первой ленты, мы можем
вписать символы щ во вторую и третью клетки без воз-
§ 8.2] ЗАДАНИЕ ПЕРЕЧИСЛЯЕТ СООТВЕТСТВИЯ 269
никновения противоречий. Попытка вписать символ хо
в четвертую клетку приводит к противоречию в таблице
преобразователя, поэтому четвертую клетку заполняем
символом xi. Если в пятую клетку вписать символ хо, то
само по себе это к противоречию не приводит, но в ше-
шестую клетку мы вынуждены будем вписать символ хо,
чтобы не возникло противоречий в таблице автомата
(так как сочетание символов (хо, ро) уже встречалось
в первом столбце ленты и требовало вписывания в сле-
следующий столбец символа хо). Но символ хо в шестую
клетку вписан быть не может, так как это противоречит
таблице преобразователя. Мы вынуждены поэтому вер-
вернуться к пятой клетке и попробовать вписать в нее сим-
символ xi, что не приводит к противоречию. Это дает нам
возможность попытаться вписать в шестую клетку xi.
Сочетание (рг, xi) еще не встречалось, поэтому с точки
зрения заполнения таблицы автомата в седьмую клетку
ленты может быть вписан любой символ. Однако сим-
символы хо и xi исключаются в силу уже заполненных
клеток таблицы преобразователя. Мы вынуждены поэто-
поэтому в седьмую клетку вписать новый символ хг-
Теперь обращаемся ко второй ленте. Сочетание (р2,
хо) уже встречалось в третьей клетке первой ленты, по-
поэтому с точки зрения таблицы автомата мы можем впи-
вписать во вторую клетку второй ленты только xi и не что
иное. Но вместе с тем вписать xi мы не можем, так как
получаем противоречие в таблице преобразователя.
У нас нет иного выхода, кроме как вернуться к третьей
клетке первой ленты и заменить ранее вписанный сим-
символ хо на символ Хз. Это позволит нам продолжать за-
заполнение второй ленты, не меняя ничего в первой ленте.
Далее можно продолжать заполнение второй ленты, лик-
ликвидируя возникающие противоречия так, как это дела-
делалось при заполнении первой ленты. В рассматриваемом
примере новых состояний (помимо введенных ранее
to, xi, X2, Хз) вводить не придется.
Заполненные для этого примера таблицы имеют вид
табл. 8.23 — 8.26.
Возвращаясь к этому примеру, заметим, что в третью
клетку первой ленты мы могли бы попытаться вписать
вместо хо не новый символ хз, а какой-нибудь из старых
270
РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ [ГЛ. VHI
(з<1 или хг), переделывая, если бы эхо понадобилось,
заполнение остальных клеток первой ле«ты. Это привело
бы к иному заполнению таблицы конечного автомата и
преобразователя, которые, быть может, имели бы и иное
число строк (т. е. число состояний).
Таблица 8.23
Первая лента
Таблица 8.24
Вторая лента
Такт
Р
71
X
0
Ро
х.
—
1
Pi
*
2
Р2
Хо
х2
3
Pi
Хо
х2
4
Ро
Хо
Х2
5
Р2
Хо
6
Pi
Хо
X,
К
Такт
Р
71
X
О
Р2
*О
—
1
Pi
Xi
2
Ps
Хз
*2
3
Ро
X,
*2
х2
4
Р2
X,
х2
Таблица 8.25
Основная таблица автомата
Таб л ица 8.26-
Таблица преобразователя
X \.
*1
*2
*3
Ро
«0
*!
Y.2
—
Pi
*3
*1
^0
—
Р2
*2
—
*1
\. Р
71 \.
*0
*1
*2
н
Ро
h
х2
—
Pi
х2
^0
—
Р2
х2
h
х2
х2
Продемонстрированный способ заполнения строк к
не является регулярным. Эти примеры выявляют труд-
трудности, которые возникают при построении хоть какой-
§ 8.2] ЗАДАНИЕ ПЕРЕЧИСЛЯЕТ СООТВЕТСТВИЯ 271
нибудь Я-мащины, удовлетворяющей поставленным ус-
условиям и удобной для дальнейшей минимизации.
Опишем теперь вегулярный прием, который позво-
позволяет единообразно и относительно экономично (в смысле
получающегося числа,состояний) строить Я-машины,
реализующие любую заданную непротиворечивую сово-
совокупность конечного числ(а конечных лент. Ограничимся
рассмотрением случая, когда ленты, получающиеся при
входных последовательностях, не указанных в задании,
могут быть произвольными.
Заполняя в соответствии с описанным ниже алгорит-
алгоритмом пустые клетки лент, мы будем, подобно тому как
это делали раньше, одновременно постепенно заполнять
заранее заготовленные таблицы автомата и преобразо-
преобразователя, увеличивая по мере введения новых символов х
число строк в этих таблицах.
Пусть часть пустых клеток заданных лент и таблиц
автомата и преобразователя уже заполнена. Будем го-
говорить, что произведенное до сих пор заполнение лент
и таблиц является правильным, если выполнены следую-
следующие три условия:
1) Заполнение лент и таблиц согласовано между со-
собой, т. е. заполненная часть лент не содержит противо-
противоречивых триад автомата и преобразователя, а в табли-
таблицах автомата и преобразователя заполнены те и только
те клетки, которые соответствуют триадам, встречаю-
встречающимся в уже заполненной части лент.
2) Последним тактам заполненной части каждой из
лент соответствуют такие пары символов (р, х), которые
определяют в таблице автомата незаполненную еще
клетку.
3) Если среди этих, упомянутых в условии 2) пар
символов (р, х), взятых для последних заполненных так-
тактов каждой ленты, имеются одинаковые и если далее
в соответствующих лентах, в столбцах для следующих
(одного или нескольких) тактов встречаются одинаковые
символы р, то на протяжении этих же тактов следуют
одинаковые К.
Так, например, заполнение, показанное в табл. 8,27—
8.30, является правильным,
272
РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ [ГЛ. VIII
Таблица 8.27
Первая лента
Такт
Р
к
0
?2
*0
к2
1
Pi
а,
2
Рз
*i
Аз
3
Рз
А,
4
Р2
А3
5
Pi
А,
6
Рз
А,
/ Таблица 8.28
/ Вторая лента
Так/
А
к
0
pi
*о
А.
1
Р2
*1
Аг
2
Pi
*i
*3
3
Рз
*0
А,
4
Р.
А2
5
Р2
Аз
6
Р2
А,
7
Р2
Аз
Таблица 8.29
Основная таблица автомата
Таблица 8.30
Таблица преобразователя
Х\ р
*1
Pi
*1
Р2
*0
*1
Рз
\. р
X ^Ч.
*|
Pi
А,
Аз
Р2
А2
А2
Рз
А>
Аз
Заполнения в следующих трех примерах не являются
правильными.
Пример 1 (табл. 8.31 — 8.34)
Таблица 8.31 Таблица 8.32
Первая лента Вторая лента
Такт
Р
%
).
0
Pi
А,
1
Рз
*0
Аз
2
Р2
*1
А,
3
Pi
*о
А,
4
Рз
*i
А,
5
Р2
Аз
6
А,
7
Pi
А,
Такт
Р
X
X
0
Pi
*о
Х2
1
Р2
*1
Аз
2
Рз
*0
Аз
3
?4
*|
А,
4
Рз
А2
5
Р2
Аз
6
Pi
Х2
8.2]
ЗАДАНИЕ ПЕРЕЧИСЛЯЕТ СООТВЕТСТВИЯ
273
Таблица 8.33
Основная таблица авт^ата
\p
V
Pi
P2
Рз
\
\
Таблица 8.34
Таблица преобразователя
*1
Pi
x,
P2
Рз
Хз
*4
P4
x,
Пример 2 (табл. 8.35—8.38)
Т а б л и ц а 8.35
Первая лента
Такт
Р
V.
X
0
Р2
Х2
1
Pi
2
Рз
*i
*3
3
Р2
*0
Х2
4
Рз
Х2
5
Pi
Х2
6
Pi
7
Pi
Х2
Таблица 8.36
Вторая лента
Такт
Р
%
\
0
Рз
*о
*i
1
Рз
*|
^3
2
Р2
х2
3
Pi
4
Рз
^3
5
Pi
Таблица 8.37
Основная таблица автомата
Таблица 8.38
Таблица преобразователя
* ^\
*|
Pi
«1
Р2
^0
Рз
*1
^\ Р
*|
Pi
к'
Pi
х2
Рз
*3
18 М. А. Айзерман, Л. А. Гусев и др.
274
РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ [ГЛ. VIII
Пример 3 (табл. 8.39 —8.41) /
Таблица 8.39 / / Таблица 8.40
Первая лента / Вторая лента
Такт
Р
%
X
0
Рг
*о
Х2
1
Pi
*о
*i
2
Рз
*i
^3
3
Рз
4
?2
5
Pi
Х2
J
Такт
(
р
X
0
Pi
*о
X,
1
Р2
*!
х2
2
Pi
*i
Хз
3
Рз
^1
4
Ра
Хз
5
Pi
X,
Таблица 8.41
Третья лента
Неправильность заполнения в примерах 1—3 обу-
обусловлена соответственно нарушением условий 1), 2) и 3)
приведенного определения
термина «правильное запол-
заполнение».
Заметим теперь, что ис-
исходные заданные нам ленты,
у которых по условию зада-
задания в строку и вписан толь-
только символ «о в клетку так-
такта 0, в совокупности с заго-
заготовленной и совершенно не-
незаполненной формой табли-
таблицы автомата и с таблицей
преобразователя, в которой
заполнены лишь клетки, со-
соответствующие нулевому
такту всех лент, представляют собой правильное запол-
заполнение, если только задание непротиворечиво. Действи-
Действительно, в этом случае первые два условия определения
«правильное заполнение» выполняются автоматически,
а непротиворечивость задания как раз гарантирует вы-
выполнение условия 3.
Предположим, что имеется некоторое (не обязатель-
обязательно начальное) правильное заполнение. Пусть в этом за-
Такт
Р
%
X
0
Pi
1
Pi
*i
*з
2
Рз
h
3
Рг
4 .
Pi
*з
§ 8.2] ЗАДАНИЕ ПЕРЕЧИСЛЯЕТ СООТВЕТСТВИЯ 275
полнении участвуют символы хо, хь ..., xs. Дальнейшее
вписывание символов х в ленты и дальнейшее заполне-
заполнение таблиц осуществляется в соответствии с описанным
ниже алгоритмом, который после конечного числа шагов
вновь приводит к правильному заполнению и поэтому
может быть снова применен до тех пор, пока заданные
ленты не будут заполнены целиком. Задание при этом
будет выполнено, так как окончательное заполнение бу-
будет правильным и, следовательно, не будет содержать
противоречивых триад.
Опишем теперь предлагаемый алгоритм вписывания
символов х в незаполненные части ленты, исходя из
имеющегося правильного заполнения с использованными
в нем символами хо, xi, ..., xs. С этой целью предва-
предварительно перенумеруем заданные ленты в любом по-
порядке. Затем:
1. Обращаемся к первой незаполненной еще клетке
строки х первой незаполненной целиком ленты и про-
пробуем вписать в нее символ хо, проверяя при этом, не
вступаем ли мы в противоречие с уже заполненной клет-
клеткой таблицы преобразователя. Если такое противоречие
имеет место, то вместо символа хо впишем символ щ,
проверим аналогично его непротиворечивость и т. д.
Если ни один из символов хо, хь ..., xs не устраняет
противоречия, то вводим новый символ Xs+i, добавляя
новую строку в таблицы автомата и преобразователя.
Обозначим через х' выбранный нами таким образом
символ, не приводящий к противоречию в таблице пре-
преобразователя. Если им оказался вновь введенный сим-
символ, т. е. х' = Xs+ь то, заполнив соответствующую клетку
ленты и клетки во вновь введенных строках xs+i таблиц
автомата и преобразователя, переходим к третьему
пункту алгоритма. Если же х' = х& @^.k ^.s), то после
вписывания этого символа в клетку ленты и заполне-
заполнения соответствующих клеток таблиц автомата и пре-
преобразователя переходим к следующему, второму пункту
алгоритма.
2. Обращаясь к таблице автомата, дополненной те-
теперь новой клеткой в соответствии с п. 1, выясняем,
нельзя ли продвинуть далее заполнение первой ленты
(без того чтобы заполнять новые клетки таблицы
18*
276 РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ (ГЛ. VI11
автомата). Если это возможно, продолжаем заполнять
ленту, следя за тем, не вступаем ли/ мы при этом в про-
противоречие с таблицей преобразователя. Далее: а) если
таких противоречий нет, то продолжаем заполнение ленты
до тех пор, пока не попадаем в Пустую клетку таблицы
автомата или пока первая лента не заполнится цели-
целиком, после чего переходим к п. 3 алгоритма; б) если
противоречие с таблицей преобразователя получается,
то возвращаемся к клетке первой ленты, в которую мы
к концу п. 1 алгоритма вписали символ х' = хь, отка-
отказываемся от символа хй, стираем его в таблицах авто-
автомата и преобразователя, стираем также записи, которые
мы внесли согласно п. 1, и продолжаем поиск подходя-
подходящего символа в соответствии с п. 1 алгоритма, начиная
перебор символов х с символа х&+ь За конечное число
шагов мы перейдем к п. 3 алгоритма, так как, если под-
подходящий символ х' не будет найден среди символов
хо, хь ..., х8, то будет вписан новый символ xs + i.
3. Допустим, что в результате применения п. 1 и 2
алгоритма мы остановились на символе *) х" = хт
(/s<m^s+ 1).
Возвращаясь к правильному заполнению, от которо-
которого мы начали применение алгоритма, обратим внимание
на пару символов р, х в последнем заполненном столбце
первой ленты и выясним, встречаются ли такие же пары
р, х в последних заполненных столбцах каждой из
остальных лент. Если не встречаются, переходим к п. 4
алгоритма. Если же встречаются, то в каждой из лент,
где последняя пара р, х совпадает с последней парой
р, х первой ленты, надо продвинуть заполнение далее,
пользуясь таблицей автомата **) так же, как в п. 2.
При этом: а) может случиться, что заполнение всех та-
таких лент будет доведено до конца (т. е. до попадания
в незаполненную клетку таблицы автомата или до пол-
полного заполнения ленты) — тогда переходим к п. 4 алго-
алгоритма, и б) может случиться, что в процессе заполнения
этих лент мы придем в противоречие с таблицей
*) Только в этом случае, в силу пунктов 1 и 2, мы обращаемся
к п. 3 алгоритма.
**) Если был введен новый символ xt+i, то такое продвиже-
продвижение если и может быть осуществлено, то только на один шаг.
§ 8.2] ЗАДАНИЕ ПЕРЕЧИСЛЯЕТ СООТВЕТСТВИЯ 277
преобразователя^ Тогда возвращаемся к п. 1 алгоритма,
отказываемся от\символа хт, стираем все записи, вы-
вызванные этим символом, и продолжаем поиск подходя-
подходящего символа в соответствии с п. 1, но начиная с сим-
символа xm + i. За конечное число шагов мы перейдем к
п. 4 алгоритма, так как во всяком случае к нему при-
приводит вписывание символа xs + i.
4. Проверяем, является ли полученное заполнение
лент правильным с точки зрения третьего условия пра-
правильности заполнения.
В случае положительного результата проверки вновь
получено правильное заполнение и применение алго-
алгоритма может быть повторено. В случае же отрицатель-
отрицательного результата отказываемся от выбранного символа
и" = хт, стираем все заполнение лент и таблиц, внесен-
внесенное благодаря выбору этого символа, и продолжаем
поиск подходящего символа х в соответствии с п. 1,
но начиная с xm+i. Если в качестве х" был выбран сим-
символ xs+i, проверка по п. 4 всегда дает положительный
результат и поэтому проводить ее не требуется.
В качестве примера использования алгоритма
рекомендуем читателю с его помощью синтезировать
автомат, реализующий указанные ниже три ленты
(табл. 8.42—8.44).
Таблица 8.42 Таблица 8.43 Таблица 8.44
Первая лента Вторая лента. Третья лента
Такт 0
р
X
Р2
*0
1
Pi
*з
2
Pi
12
3
Рз
*i
4
Р2
Х2
5
Pi
^3
Такт
Р
X.
X "
0
Pi
*о
Х2
1
Рз
2
Р2
Х2
Такт
Р
X.
X
0
Р2
*|
1
Рз
Х2
2
Р'.
*з
3
?2
В результате шестикратного применения алгоритма
в этом примере получается заполнение лент, показанное
278
РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ [ГЛ. VIII
в табл. 8.45—8.47, и синтезируется основная таблица
автомата (табл. 8.48) и преобразователь (табл. 8.49).
Таблица 8.45 Таблица 8.46 Таблица 8.47
Первая лента Вторая лента Третья лента
Такт
Р
%
X
0
Р2
К
1
Pi
*i
*з
2
Pi
*о
Х2
3
Рз
Ч
К
4
Р2
Х2
5
Pi
*i
Хз
Такт.
Р
X
0
Pi
*о
Х2
1
Рз
h
2
Рг
*i
К
Такт
Р
X
0
?2
*0
*1
1
Рз
*1
х2
2
Pi
*2
*3
3
Р2
*1
х2
Таблица 8.48
Основная таблица автомата
Таблица 8.49
Таблица преобразователя
p
Pi
Н
?2
»,
*1
—
Рз
^2
—
»,
^2
х2
Хз
Хз
Р2
К
х2
—
Рз
.х'
Х2
—
Заметим, что этот же алгоритм решает задачу и
в том случае, когда условия синтеза более легкие: за-
задано конечное число лент конечной длины и требуется
построить Я-машину, которая реализует эти ленты, но
уже не обязательно исходя из одного и того же началь-
начального состояния. Более того, в этом случае не возникает
необходимость проверять, противоречиво ли задание, и
начальное правильное заполнение выписывается сразу
соответствующим выбором подходящих начальных со-
состояний для каждой ленты.
§ 8.3] НЕРАЗРЕШИМОСТЬ ПРОБЛЕМЫ РАСПОЗНАВАНИЯ 279
Основная идея описанного алгоритма состоит в том,
чтобы на каждом этапе заполнения лент предельно ис-
использовать уже введенные ранее состояния и лишь
в том случае, когда это невозможно, вводить новые со-
состояния. Разумеется, это, вообще говоря, не приводит
к минимальной Я-машине, так как может оказаться, что
на некотором этапе выгоднее ввести новое состояние
(хотя и можно воспользоваться каким-нибудь старым
состоянием!), чтобы уменьшить число необходимых но-
новых состояний на последующих этапах.
Все содержание настоящего параграфа жестко осно-
основывается на предположении, что число пар входных и
выходных последовательностей конечно и что в задании
все они перечислены. В следующем параграфе мы пе-
перейдем к рассмотрению общей задачи синтеза, когда
не предполагается конечность числа заданных соот-
соответствий между входными и выходными последователь-
последовательностями.
§ 8.3. Алгоритмическая неразрешимость проблемы
распознавания представимости рекурсивных событий*)
Предположим, что каким-либо образом описано со-
соответствие между входными и выходными последова-
последовательностями, которое должна реализовать синтезируе-
синтезируемая Я-машина. Мы считаем теперь, что такие соответ-
соответствия могут быть совершенно произвольными, лишь бы
их задание можно было эффективно описать, т. е.
сделать так, чтобы каждый, кому известно это описа-
описание, мог бы для любой входной последовательности
найти единственную соответствующую этому описанию
выходную последовательность.
Для ответа на вопрос о том, существует ли Я-ма-
Я-машина, способная устанавливать требуемое соответствие
между входными и выходными последовательностями,
необходимо формализовать цонятие эффективного опи-
описания таких соответствий. Это приводит нас к заданию
указанного соответствия посредством рекурсивного
*) Читателям, не знакомым с теорией алгоритмов и рекурсив-
рекурсивных функций, необходимо, приступая к чтению этого параграфа,
предварительно ознакомиться с гл. XII.
280 РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ (ГЛ. VIII
описания как единственного известного средства фор-
формализации того, что интуитивно мы выражаем словами
«все, что может быть эффективно задано на человече-
человеческом языке».
Один из способов описания соответствий входных
и выходных последовательностей основывается на ис-
использовании уже знакомого нам по гл. VII понятия
о представлении событий. Действительно, вместо того
чтобы для каждой входной последовательности указать
соответствующую выходную, можно задать множест-
множество G{ всех входных последовательностей, после про-
прохождения которых на выходе появляется заданный
символ Я*.
Если такие множества Go, G\, ..., G; заданы для всех
выходных символов Ко, К\, ..., Ki, то это и означает, что
установлено однозначное соответствие между входными
и выходными последовательностями. Так, если входной
алфавит содержит четыре символа р, а выходной алфа-
алфавит три символа К и если известно, что:
а) символ К\ появляется в такт р, если в предше-
предшествующие два такта (т. е. (р— 2)-й и (р—1)-й такты)
во входной последовательности появлялся символ pi и
за ним р4;
б) символ Яг появляется, если не выполняются усло-
условия п. а) и на протяжении предшествующих такту р
трех тактов не появлялся символ рз;
в) символ Яз появляется во всех остальных случаях,
то для любой входной последовательности, заданной
в алфавите {pi, p2, рз, р4, мы можем немедленно вы-
выписать выходную последовательность. ,
При таком способе задания соответствий между вхо-
входом и выходом задача синтеза формулируется так: за-
заданы события G\, G2, ..., Gi\ требуется создать Я-ма-
шину с выходным алфавитом {К\, Яг, ..., Kt), пред-
представляющую событие Gi появлением на выходе сим-
символа Ки
Формализация понятия эффективное задание соот-
соответствия между последовательностями, о необходимости
которой выше шла речь, сводится теперь к формализа-
формализации понятия событие, которое может быть задано эф-
эффективно.
§8.3] НЕРАЗРЕШИМОСТЬ ПРОБЛЕМЫ РАСПОЗНАВАНИЯ 281'
Поэтому и это понятие может быть формализовано
лишь в терминах рекурсивного описания, так что, го-
говоря о том, что событие G* задано, мы будем иметь
в виду, что задано рекурсивное описание множества Gi
входных последовательностей.
Используя понятие рекурсивное множество последо-
последовательностей*), условимся говорить, что событие Gi
рекурсивно, если рекурсивно множество Gi входных по-
последовательностей.
В гл. VII было доказано, что в Я-машине предста-
вимы лишь регулярные события и вместе с тем было
доказано существование нерегулярных событий. Поэтому
задача распознавания того, существует ли Л-машина,.
реализующая любое конкретное эффективно заданное
соответствие между входными и выходными последова-
последовательностями, сводится к распознаванию того, является
ли любое конкретное рекурсивное событие регулярным.
Таким образом, возникает проблема распознавания ре-
регулярности рекурсивных событий, которая формули-
формулируется так: существует ли алгоритм, позволяющий для
любого заданного рекурсивного события ответить на во-
вопрос, регулярно ли оно.
Теорема 1**). Проблема распознавания регуляр-
регулярности рекурсивных событий алгоритмически неразре-
неразрешима.
Доказательство. Сформулируем сначала более
узкую проблему, чем проблема распознавания предста-
представимости рекурсивных событий, и покажем, что уже эта
более узкая проблема алгоритмически неразрешима.
Тем самым теорема будет доказана.
*) См. гл. XIL
**) Утверждение, эквивалентное этой теореме, было высказано
впервые (без доказательства) в п. 5 работы Б. А. Трахтенброта
[101] (см. также [133] и [143]).
Теорема 1 являлась бы прямым следствием теоремы Раиса
[103], если класс рекурсивных событий считать классом событий,
«порожденных» всеми возможными рекурсивными функциями. Од-
Однако можно рассматривать рекурсивные события, «порожденные»
примитивно-рекурсивными функциями, а этот случай нуждается в
специальном рассмотрении. Приводимое же здесь доказательство
без изменения применимо и в том случае, если считать, что мы
имеем дело только с примитивно-рекурсивными функциями.
282 РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ [ГЛ. VIII
Пусть задана рекурсивная функция <p(t), определен-
определенная на множестве целых чисел и принимающая значение
из конечного множества чисел {0, 1, ..., г— 1}. Рассмот-
Рассмотрим автомат Л с входным алфавитом {р0, рь • • •» Pr-i}.
Из всех возможных входных последовательностей спе-
специально отметим последовательности
Р<р(О)>
Р<р(О) Р<рA)>
Р<р(О) Р<рA) Р<рB)>
где р <р (/)— символ из {рг}, индекс которого совпадает со
значением рекурсивной функции <р(^) при t = i.
Рассмотрим событие S9, состоящее в том, что к дан-
данному моменту на входе автомата появилась какая-либо
одна из отмеченных выше последовательностей. Иначе
говоря, событие 5Ф наступает тогда и только тогда, ко-
когда индексы у символов р входной последовательности
во всех тактах 0, 1, 2, ..., р совпадают с последователь-
последовательными значениями <р@), <рA), фB), ..., <р(/?) заданной
рекурсивной функции <р. Мы будем говорить, что авто-
автомат Л представляет рекурсивную функцию <р, если он
представляет событие 5Ф.
В соответствии с § 7.2 мы скажем, что автомат
представляет рекурсивную функцию <p(t), если в каж-
каждый момент времени р состояния автомата х(р) при-
принадлежат выбранному множеству М в том и только
в том случае, когда индексы всех входных символов,
появившихся от t = 0 до t = p, являются последователь-
последовательными значениями функции <p(t).
Совершенно очевидно, что существуют рекурсивные
функции, заведомо представимые (например, любая пе-
периодическая функция, так как для нее событие S® ре-
регулярно) и заведомо непредставимые (например, функ-
функция y(t), принимающая значение 1 при t — п2 и нуль
в остальных случаях). Поэтому возникает проблема
распознавания представимости рекурсивных функций.
Легко видеть, что эта проблема является частным слу-
случаем интересующей нас общей проблемы распознава-
распознавания рекурсивных событий.
§ 8.3] НЕРАЗРЕШИМОСТЬ ПРОБЛЕМЫ РАСПОЗНАВАНИЯ 283
В соответствии с теоремой, доказанной в § 7.6, ре-
рекурсивное событие S* регулярно тогда и только тогда,
когда рекурсивная функция <р@ является в конечном
счете периодической. Но поскольку, как известно*), за-
задача распознавания того, является ли любая заданная
рекурсивная функция в конечном счете периодической,
алгоритмически неразрешима, то алгоритмически нераз-
неразрешима и проблема распознавания регулярности собы-
события Sv, а значит, тем более, и проблема регулярности
рекурсивных событий. Теорема доказана.
Предположим теперь, что хотя алгоритма распо-
распознавания регулярности рекурсивных событий не суще-
существует, тем не менее каким-либо иным образом («твор-
(«творчески») каждый раз удается выяснить, является ли за-
заданное рекурсивное событие регулярным. Тогда воз-
возникает задача об определении алгоритма синтеза авто-
автомата, представляющего заданное рекурсивное событие.
Однако и в этом случае нет общего приема, решаю-
решающего поставленную задачу, в силу следующей теоремы,
также установленной Б. А. Трахтенбротом и приводи-
приводимой ниже без доказательства.
Теорема 2. Рассмотрим множество всех рекурсив-
рекурсивных событий, которые являются регулярными. Тогда
проблема синтеза автомата, представляющего некото-
некоторое событие из этого множества, алгоритмически нераз-
неразрешима.
Из приведенных выше теорем следует, что если не
пытаться сузить каким-либо образом допустимые спо-
способы задания на синтезируемую машину (т. е. язык, на
котором описано задание), то лишена смысла всякая
попытка найти регулярные приемы не только синтеза
Я-машины, реализующей это задание, но даже и ответа
на вопрос, существует ли такая машина. Однако можно
столь сильно сузить язык, что любое задание, выражен-
выраженное на этом языке, явится заведомо выполнимым Я-ма-
шиной, и поэтому проблема^распознавания вообще не
возникнет и останется лишь проблема синтеза.
В качестве такого языка можно принять, например,
просто язык регулярных формул, т. е. считать, что
*) См.> например, [142].
284 РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ [ГЛ. VIII
задания всегда выражаются в терминах представлений
событий, заданных регулярными формулами. Алгоритм
синтеза Я-машины, заданной таким способом, заведомо"
существует. Он, например, легко следует из рассужде^:
ний, приведенных в гл. VII при доказательстве первой;
теоремы Клини. В § 8.4 приводится другой (относи-
(относительно более удобный и экономичный по числу полу-
получающихся состояний) алгоритм синтеза машины, пред-
представляющей заданные регулярные события. '•
Другим примером языка, относительно которого <
установлено, что все выраженные на нем-задания за-
заведомо реализуемы Я-машиной, и для которого суще-
существует алгоритм синтеза, является предикатный язык
Б. А. Трахтенброта, который подробно описан в [101,
102}.
Однако практическое применение таких языков в не-
некотором смысле сводится к перенесению всех описан-
описанных выше затруднений с того, кто синтезирует автомат,
на того, кто выдает задание на синтез. Действительно,
для того чтобы воспользоваться преимуществами, кото-
которые дают языки такого типа, надо чтобы задание с са-
самого начала было сформулировано на соответствующем
языке. Поэтому лицо, выдающее задание, должно быть
обучено «мышлению» на этом языке, т. е. умению выра-
выразить непосредственно на нем свои требования к Я-ма-
шине. Однако в действительности первоначальное, ис-
исходное задание на Я-машину неизбежно выражается
словами; составление регулярного выражения по сло-
словесному описанию подразумевает, что .сначала устано-
установлена возможность этого, что вновь приводит к тем же
самым трудностям, о которых выше шла речь.
Язык, удобный для выражения задания и дальней-
дальнейшего синтеза, должен был бы поэтому удовлетворять
следующим трем требованиям:
1) Наиболее естественные и часто встречающиеся
словесные описания должны легко «переводиться» на
этот язык.
2) Язык должен быть достаточно широк, для того
чтобы этот круг «переводимых», словесных описаний,
охватывал бы также естественные и часто астречаю-
§84] СИНТЕЗ КОНЕЧНЫХ АВТОМАТОВ 285
щиеся словесные описания, которые, однако, не реали-
реализуемы Я-машиной.
3) Для всех возможных заданий, формулируемых на
этом языке, как проблема распознавания, так и проб-
проблема синтеза должны быть алгоритмически разрешимы.
Пока сделаны лишь первые шаги в направлении
поиска языков, удовлетворяющих этим условиям.
В следующем параграфе рассматривается алгоритм
синтеза в том случае, когда задание выражено на языке
регулярных формул, и поэтому проблема распознавания
не возникает.
§ 8.4. Синтез конечных автоматов
и последовательностных машин при задании,
сформулированном на языке регулярных выражений *)
Предположим теперь, что задано одно или несколько
регулярных выражений (см. § 7.3) и требуется синте-
синтезировать Я-машину, которая представляла бы события,
определяемые заданными выражениями, появлением
для каждого из этих событий своего символа на вы-
выходе**). Задача сводится к синтезу конечного автомата,
который представляет каждое из этих событий своим
множеством состояний.
Задача такого рода по существу решена уже в
гл. VII. Действительно, первая теорема Клини была до-
доказана в этой главе эффективно, т. е. доказательство
теоремы содержало метод построения автомата, пред-
представляющего любое событие, заданное регулярным вы^
ражением. Если задано несколько регулярных выраже*
ний, то этим же методом можно построить для каждого
из них свой представляющий автомат, а выходы этих
автоматов подать на вход общего преобразователя. Од-
Однако мы сталкиваемся здесь с ситуацией, подобной той,
которая встречалась нам уже в § 8.2: решение задачи
нам известно, но оно не удовлетворяет нас, так как при
*) Этот параграф по просьбе авторов написан О. П. Кузне-
Кузнецовым.
**) Как уже указывалось раньше, при этом мы полностью оста-
оставляем в стороне вопрос о тех соображениях, которыми руковод-
руководствуются при выборе этих регулйрных выражений.
286 РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ [ГЛ. VIII
этом решении синтезируемая машина имеет чрезмерно
большое число k состояний, и поэтому она неудобна
для последующей минимизации.
Ниже кратко описывается иной метод построения ко-
конечного автомата, представляющего одно или несколько
событий, заданных регулярными выражениями. Этот
метод является естественной графической интерпрета-
интерпретацией метода, предложенного В. М. Глушковым [252], и
приводит к автоматам с меньшим числом состояний,
чем метод, использованный в гл. VII при доказатель-
доказательстве первой теоремы Клини.
Начнем со случая, когда задано одно регулярное вы-
выражение. Форма записи регулярных выражений, кото-
которая удобна нам здесь, несколько отличается от формы
записи, введенной в гл. VII. Именно, исходными элемен-
элементами при составлении регулярного выражения в гл. VII
служили конечные куски входных лент (т. е. конечные
последовательности входных символов рг), которые мы
обозначали там первыми буквами латинского алфавита:
а, Ь, с, ... Здесь удобно в качестве исходных элементов
принимать сами входные символы рг-, т. е. только вход-
входные последовательности длины 1.
Для конечных последовательностей а, Ь, с,... может
быть составлено регулярное выражение в форме произ-
произведения. Например, последовательности п = рг р5 р3 р4 со-
соответствует выражение
Поэтому по регулярному выражению с исходными эле-
элементами а, Ь, с, ... немедленно составляется соответ-
соответствующее регулярное выражение с исходными элемен-
элементами— символами pi.
Так, например, регулярное выражение, которое в обо-
обозначениях гл. VII имело вид
при a = pv ? = р2-р3 и ? = Pi-p2 приобретает вид
/?= {A(Р2 • P3)V(Pi • P2)]*)V[Pi • (Pi • 92)]}-
Ясно, что глубина нового регулярного выражения может
оказаться значительно большей, чем у исходного,
§8.4] СИНТЕЗ КОНЕЧНЫХ АВТОМАТОВ 287
Следующим этапом построения автомата, предста-
представляющего соответствующее регулярное событие, является
изображение этого регулярного выражения в форме
графа.
Построение графа определим индуктивно следующим
образом:
1. Для исходных скобок, т. е. скобок
(PiVPy), (?r?j) И (р,)*,
графы представлены на рис. 8.1.
Дизъюнкция (pi V pj) изображается на графе
(рис. 8.1, а) двумя стрелками, выходящими из одной
точки и имеющими надписи рг- и pj соответственно. Граф
дизъюнкции (pi V pj) имеет одно начало и два конца.
• Конец
h/
» Начало
• Конец
¦ *
Начало
С
Рис
,. л,.
Конец
V
. 8.1.
С
Начало
Конец
Произведение (p**Pj) изображается (рис. 8.1,6)
двумя последовательно соединенными стрелками, несу-
несущими надписи рг- и pj соответственно. Граф имеет одно
начало и один конец.
Итерация (рг)* изображается (рис. 8.1, в) стрелкой,
замкнутой «на себя» и несущей надпись р*. Точка замы-
замыкания считается одновременно началом и концом этого
графа.
2. Пусть теперь для регулярных выражений R\ и #2
мы умеем строить графы. Каждый из этих графов имеет
одно начало и по крайней мере один конец (начало и
конец могут совпадать, см. рис. 8.1,б).
Тогда граф выражения (R\ V #2) получается путем
объединения начал графов R\ и /?2- В полученном графе
288 РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ ЛГЛ. VII!
началом служит точка, полученная объединением начал
Ri и /?2, концами —все концы как графа Rh так и гра-
графа R2. Граф выражения (Ri • R2) получается путем объ-
объединения всех концов графа R\ с началом #2 (так что
стрелки в графе /?ь которые вели в его концы, ведут
теперь в начало R2). Началом графа (Ri • R2) служит
начало графа Rit концами — все концы графа R2.
Граф выражения (Ri)* получается из графа Ri путем
объединения всех его концов с его началом (т. е. замы-
замыкания стрелок, ведущих в концы графа, на начало).
Конец
• •
Начало
•'Начало Коней
Конец
Рис. 8.2.
Точка замыкания (начало графа Ri) будет служить одно-
одновременно началом и концом графа (Ri)*.
Определив эти операции над графами, мы теперь
можем для каждого регулярного выражения построить
соответствующий ему граф. Приведем примеры.
Регулярное выражение
имеет граф, показанный на рис. 8.2, где приведены так-
также и промежуточные графы.
Регулярное выражение
имеет граф, показанный на рис. 8.3.
Потребуем, чтобы граф, изображающий регулярное
выражение, удовлетворял следующим условиям: любок
путь на графе от начала к любому из его концов опре-
§8.4] СИНТЕЗ КОНЕЧНЫХ АВТОМАТОВ 289
деляет входную последовательность, появление которой
на входе автомата соответствует наступлению события,
определяемого заданным регулярным выражением /?,
и наоборот, для любой последовательности, соответ-
соответствующей наступлению данного события, на графе най-
найдется путь от начала к одному из концов.
Начало
Рис. 8.3.
Графы, изображенные на рис. 8.2 и 8.3, этому усло-
условию удовлетворяют. Однако нетрудно указать регуляр-
регулярные выражения, для которых графы, построенные по
указанным выше правилам, уже не будут удовлетворять
этим условиям:
Так, например, для выражения
соответствующий граф (рис. 8.4) имеет «ложные пути».
Действительно, путь, соответствующий входной последо-
последовательности Р2Р2РЗ, показанный на рис. 8.4 жирной ли-
линией, соответствует выражению
Ita • (н)'\ • рэ)
т. е. не соответствует наступлению события R.
В качестве второго примера такого рода рассмотрим
рис. 8.5, где приведен граф, соответствующий регуляр*
ному выражению
19 М. А. Айзерман, Л. А. Гусев и др.
290
РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ [ГЛ. VIII
Путь, показанный на рис. 8:5 жирной линией, как легко
видеть, также не соответствует наступлению события R.
Рассмотрим еще один пример. Выражению
/? = {(Р. [(Рг)* - (Рз)*]) • Р*]
соответствует граф, показанный на рис. 8.6. На графе
существует путь pi p3 р2 р4 • от начала к концу, однако
событие не наступает.
Конец
Конец
Начало
Начало
Конец
Рис. 8.4.
Рис. 8.5.
Приведенные три примера (рис. 8.4 — 8.6) характе-
характеризуют все три случая, которые могут привести к появ-
появлению на графе ложных путей. Такие случаи возможны
при выполнении следующих операций:
Конец
Начало
Рис 8.6.
1) умножение слева на дизъюнкцию, если хотя бы
один из дизъюнктивных членов заканчивается итерацией
[([Л •(?)•] VC)-?>];
2) операция дизъюнкции, если хотя бы один из дизъ-
дизъюнктивных членов начинается с итерации
\WB\vcy,
§ 8.4] СИНТЕЗ КОНЕЧНЫХ 'АВТОМАТОВ 291
3) умножение двух итераций
l(Af.(BF\.
Для того чтобы избежать появления на графе «лож-
«ложных путей», в перечисленных трех случаях при выполне-
выполнении правил построения графов, соответствующие нача-
начала и концы объединяются с применением стрелок, ко-
которые не несут символов р и которые мы поэтому
Копей
Начало Конец
Рис. 8.8.
будем называть пустыми стрелками. Пустая стрелка
указывает лишь направление движения по графу и
«проходится мгновенно», т.е. без затраты на это такта
работы автомата.
- Конец
1 Начало
Рис. 8.9.
v
Расстановку пустых стрелок продемонстрируем, ис-
исправляя с их помощью графы Т1риведенных трех приме-
примеров (рис. 8.4 — 8.6). Исправленные графы показаны со-
соответственно на рис. 8.7, 8.8 и 8.9. В первом случае пус-
пустая стрелка ведет из конца итерации; во втором случае
пустая стрелка ведет из общей начальной вершинц в
начало итерации; в третьем случае пу^гдя стрелка ведет
19*
292
РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ [ГЛ. VIII
из конца первой итерации в начало второй итерации.
Этим графам соответствуют приведенные выше регуляр-
регулярные выражения, однако ложных путей графы уже не со-
содержат.
В качестве основного примера, на котором будет
демонстрироваться описываемый метод синтеза авто-
автомата, рассмотрим выражение
/?== {[(Pi • {[(Р2Г • Рз] V[Pl • (Р2Г]}) • (РзП V
V ([(Р! • Р2Г] • {[P3V(P2 • Р2)]*1 • Pi) Ь (8.1)
Граф, соответствующий регулярному выражению (8.1),
с введением пустых стрелок везде, где это необходимо,
Начало
Рйс. 8.Ю.
изображен на рис. 8Л0. На этом рисунке надписи над
стрелками имеьг и верхние индексы. Их смысл пояс-
поясняется ниже.
Предположим теперь, что нам задано регулярное вы-
выражение и по нему построен граф. Просматривая регу-
регулярное выражение, перенумеруем подряд цифрами 1, 2,
3, ... слева направо все содержащиеся в нем символы
§ 8.4] СИНТЕЗ КОНЕЧНЫХ АВТОМАТОВ 293
р, не обращая внимания на нижние индексы. Соответ-
Соответствующий номер вписывается в качестве верхнего сим-
символа у pi. При этом одинаковым р», расположенным в
разных местах регулярного выражения, будут присвоены
разные номера.
Так, например, регулярное выражение (8.1) нашего
основного примера после простановки номеров у р* пере-
перепишется так:
• (рРЛ1)
v( [(#> • Pf )•] • {[(*> v(pP" • РИП • р|I ¦ <8-2)
Обращаясь теперь к графу, проставим верхние ин-
индексы (номера) у всех символов р*, надписанных над
стрелками, в соответствий с перенумерованным регуляр-
регулярным выражением*). В нашем примере, над стрелками
графа, показанного на рис. 8.10, выписаны верхние сим-
символы в соответствии с выражением (8.2).
Выпишем теперь у каждого узла графа верхние ин-
индексы всех входящих в него стрелок, а у начального
узла, кроме того, выпишем индекс 0. Все индексы узла,
из которого выходит пустая стрелка, приписываются к
индексам узла, к которому эта пустая стрелка подходит
(но не наоборот!). Одинаковые индексы дважды у од-
одного и того же узла не выписываются. На рис. 8.11
показан граф нашего примера с выписанными индексами
у всех узлов.
Теперь приступим к составлению следующей таб-
таблицы. Столбцы таблицы соответствуют различным сим-
символам pi, содержащимся в заданном регулярном выра-
выражении. Первую строку таблицы обозначим символом ¦*
и этот же символ впишем во все ее клетки. В нашем
примере таблица с одной заполненной строкой имеет вид
табл. 8.50. Вторая строка обозначается индексом 0-
В клетку этой строки, соответствующую столбцу рг-, впи?
шем верхние индексы к всех символов pf, надписанных
*) При практическом использовании метода удобно сначада.пе-
сначада.перенумеровать символы в регулярном выражении и уже а
строить граф. ._..--¦¦-. - '
294
РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ [ГЛ. VIII
над стрелками, которые выходят из всех узлов графа,
среди индексов которых содержится 0.
Конец
7
В нашем примере таблица с залолненными двумя
строками имеет вид табл. 8.51.
Таблица 8.50
Таблица 8.51
•Индек?\
*
Pi
*•
Р2
#•
Рз
ИндексХ,!
#•
0
; р.
•х-
1,7,12
Р2
10
Рз
*
9
Теперь дополним таблицу столькими строками, сколько
содержится различных заполнений в строке 0, соответ-
соответственно обозначив введенные строки. В нашем примере
получаем табл. 8.52,
§8.4]
СИНТЕЗ КОНЕЧНЫХ АВТОМАТОВ 295
Таблица 8.52 Таблица 8.53
Индекс >ч
*
0
1.7,12
10
9
Pi
*
1.7.12
Р2
*
10
Рз
9
\ Р
Индекс \
*
0
1.7.12
10
9
Pi
*
1.7.12
4
12
Р2
*
10
2
И
10
Рз
*
9
3.8
*
9
Каждая клетка введенных строк заполняется теперь
подобно тому, как были заполнены клетки строки 0. Так»
например, в клетку, стоящую на пересечении строки
1, 7, 12 и столбца рз, вписываются верхние индексы к
всех символов pj, надписанных над стрелками, которые
выходят из всех узлов графа, среди индексов которых
содержится хотя бы один из индексов 1 либо 7, либо 12*
Если таких выходящих стрелок нет, в клетку вписывает-
вписывается символ *.
В табл. 8.53 показано заполнение введенных трех
строк. .
Далее вновь дополним табл. 8.53 столькими стро-
строками, сколько содержится новых, не встречавшихся ра-
ранее заполнений во введенных ранее трех строках. Со-
Соответственно вводятся новые строки и в их клетки
вписываются индексы по указанным выше правилам1.
Этот процесс наращивания таблицы закончится в конеч-
конечное число шагов, так как общее число различных сочета1
ний индексов конечно. Если N — число букв в заданном
регулярном выражении, то всего имеется ЛГЧ- 1 индексов1
и возможно не более чем 2^ + 1 различных сочетании
296 РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ [ГЛ. VIII
индексов, т. е. различных заполнений клеток таблицы,
и, следовательно, в таблице может быть не более чем
2N + 1 строк.
Отметим «галочками» слева все строки, содержащие
в леврм столбце индексы, которые приписаны конечным
узлам (концам графа).
Результат построения таблицы для нашего примера
приведен в табл. 8.54.
Перекодируем теперь наименования строк таблицы,
присвоив им подряд символы хо, хь ..., а затем произ-
произведем соответствующую перекодировку клеток.
Построенная так таблица (в нашем примере
табл. 8.55) представляет собой основную таблицу конеч-
конечного автомата, который, отправляясь от начального со-
состояния хь представляет множеством состояний, отме-
отмеченных галочками слева (в нашем примере это Х2, xs, X7,
ид, хю, хп, Xi2, Xi3, хн), событие, заданное исходным регу-
регулярным выражением (в нашем примере — выражением
(8.1)).
Поясним это обстоятельство, используя рассмотрен-
рассмотренный пример. Подадим на вход нашего автомата при
начальном состоянии xi входную последовательность
pipapi. Автомат придет в состояние xi3- Символом х\з
(сравните табл. 8.54 и 8.55) обозначено множество ин-
индексов 7, 12. Но тогда из самого способа построения
та($л. 8.54 следует, что на графе (рис. 8.11) существует
путь р!1 Рз2 р(* (возможно, проходящий через пустые
стрелки), ведущий из начала графа и такой, что симво-
символом р{» служит р\ и р}2, т. е. /3 = 7 или /3 = 12. Поста-
Поставим теперь вопрос: означает ли последовательность
pip3pi наступление заданного события? Применительно
к графу этот же вопрос можно сформулировать так: су-
существует ли путь рфзрь ведущий по графу из началь-
начального узла в один из конечных? Табл. 8.54 позволяет от-
ответить на этот вопрос: поскольку путь рфзР1 может за-
заканчиваться символом р}2, а стрелка с таким символом
ведет к конечному узлу (а именно, к тому, которому
приписан индекс 12), то искомый путь существует. Во-
Вообще, всякий раз, когда подача некоторой последова-
последовательности переводит автомат в состояние, отмеченное
5 8.4]
СИНТЕЗ КОНЕЧНЫХ АВТОМАТОВ 297
Таблица 8.54 Таблица 8.55
V
V
V
V
V
V
V
V
\
\ p
\
Pi
*i
x2
x2
Ч *ло
*4 *•
У-5 *0
f-7 ^13
4
^9
y.,0 ^o
^ii
^-12
*13
^14
^-15
4
*13
P2
*0
^3
^6
*8
Xg
*10
4
4
*ie
^0
^0
^0
*3
*3
P9
^7
*0
^4
*11
^12
*14
*4
*0
*ll
*M
*11
*1*
%u
*4
галочкой это означает, что соответствующий путь иа
графе заканчивается стрелков, ведущей в конечный узел
т е что этой последовательности соответствует путь из
начального узла в конечный. Но это, в свою очередь,
означает, что наступило заданное событие. C»a
тельно, построенный автомат представляет заданное
298 РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ [ГЛ. VIII
событие. В том случае, если появилась входная последо-
последовательность, которая не может служить начальным кус-
куском ни для какой последовательности, входящей в собы-
событие и, следовательно, далее событие уже не наступит,
построенный автомат попадает в состояние щ и далее
из него не выходит. В нашем примере (табл. 8.55) такая
ситуация возникает, например, при подаче последова-
последовательности pipipi или Р1Р3Р2Р1 и т. д.
В случае, когда задано несколько событий Rit
#2, •.., Rmt описанный метод применяется следующим
образом. Нумерация символов в выражениях является
общей (т. е. если символам в Ri присвоены индексы
1, 2, ..., т, то в /?2 нумерация начинается с т + 1).Для
каждого выражения строится свой граф. Начальным уз-
узлам всех графов приписывается индекс 0. Таблица со-
составляется общая, а в одной и той же клетке могут
содержаться индексы из различных графов. После по-
построения таблицы порознь выделяются строки, соответ-
соответствующие индексам конечных точек каждого из графов,
т. е. определяются множества символов, представляю-
представляющих каждое из событий R\, /?2, •.., Rm. Выходной пре-
преобразователь ставит затем в соответствие каждому из
этих множеств состояний свой символ Я. После присоеди-
присоединения такого преобразователя каждое из заданных со-
событий представится своим выходным символом. '
Пример. Задана система трех событий
Соответствующий граф изображен на рис. 8.12. Приме-
Применение описанного алгоритма приводит к построению
таблиц 8.56 и 8.57.
Состояния, представляющие события /?ь R2t /?з, вме-
вместо галочек отмечены символами Яь Яг, Я3 соответствен-
соответственно. Тот факт, что состояние кь отмечено двумя симво-
символами, свидетельствует о том, что события R\ и /?3 имеют
общую последовательность (pi • рг)» приводящую в щ.
Поэтому мы должны либо сделать Я] и Я3 одинаковыми
(т. е. не различать событий Ri и /?з), либо отметить щ
новым.символом Я4.
«Ml
СИНТЕЗ КОНЕЧНЫХ АВТОМАТОВ
Все построение представляющего автомата, которое
мы провели, перейдя от заданного регулярного выра*
жения к его графу, могло бы быть выполнено и непо-
непосредственно по регулярному выражению графа. Такой
<?•¦
путь, использованный автором описанного метода
В. М. Глушковым, может оказаться более удобным при
сложных выражениях /?, имеющих громоздкие графы.
Таблица 8.56
Таблица 8.57
\ р
¦х-
0
1,6
4
3
2,7
8
5
7
Р.
•Х-
1,6
3
*
*
*
Р2
•Х-
4
2,7
*
*
7
*
*
7
Рз
*
*
8
5
*
5
*•
К h
XI-
*."¦
-2
-3
*4
*5
*6
*7
-8
-о
7-2
*4
^0
-0
Р2
.4
-3
-8
Рз ,
ч
Ч
-7
-0
^0
*0
-7
300 РАСПОЗНАВАНИЕ РЕАЛИЗУЕМОСТИ ЗАДАНИЯ [ГЛ. V1U
Однако построение с помощью графа нагляднее .и по-
поэтому более удобно для этой книги.
Естественно, возникает вопрос об оценке «сверху»
числа состояний у автомата, который синтезирован опи-
описанным методом. Мы приведем без доказательств эту
оценку для случая, когда синтезируется автомат, пред-
представляющий определенные события*). Определенные
события составляют подкласс регулярных событий, для
которых возможна лучшая оценка числа состояний.
Пусть заданы определенные события ERh ER2, ...
..., ERm. Рассмотрим формулу
Эта формула не содержит итераций (так как события
определенные) и, следовательно, граф S не будет со-
содержать петель (т. е. ни один путь не пройдет два раза
через один и тот же узел). Формулу S можно преобра-
преобразовать к такому виду S', что: 1) граф S' будет деревом,
т. е. в каждый узел будет вести только одна стрелка и,
следовательно, разные пути всегда приведут в разные
узлы; 2) из одного узла не могут выходить две стрелки
с одной и той же буквой входного алфавита. Формула
S' эквивалентна формуле 5,- но может отличаться от нее
числом букв. Обозначим число букв в формуле S' че-
через N'. Тогда можно построить автомат, представляю-
представляющий систему событий ERU ER2, ..., ERm, число состоя-
состояний которого не превышает N' + 1.
Практически при использовании описанного метода
получаются автоматы с гораздо меньшим числом со-
состояний.
*) Верхняя оценка числа состояний в случае любого регуляр-
регулярного события предложена В. М. Глушковым [29].
ГЛАВА IX
ЭКВИВАЛЕНТНОСТЬ И МИНИМИЗАЦИЯ
ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН
§9.1. Постановка задачи о распознавании
эквивалентных состояний
В гл. III, вводя понятие о входных последователь-
последовательностях, мы говорили уже о том, что класс возможных
входных последовательностей может быть ограничен.
Затем со случаем такого рода мы встречались в гл. V.
В этой главе наряду со случаем, когда класс возмож-
возможных входных последовательностей не ограничен, мы бу-
будем рассматривать и случаи, когда на класс возможных
входных последовательностей наложены некоторые огра-
ограничения (см. § 9.7). Приведем вновь некоторые при-
примеры ограничений:
а) входная последовательность не может иметь два
одинаковых символа подряд;
б) после некоторого символа р* не может поступать
на вход некоторый другой символ ру,
в) входная последовательность не может начинаться
(или, наоборот, обязательно должна начинаться) с не-
некоторого символа pk\
г) если где-либо во входной последовательности по-
появился символ 0s или ри то pQ появляться не может.
В этих примерах множество Е всех возможных вход-
входных последовательностей (т. е. бесконечное множество,
содержащее все возможные последовательности вход-
входных символов любой конечной длины) разбивается на
два подмножества: подмножество L ? Е (конечное или
бесконечное), содержащее все допустимые для данной
/7-машины входные последовательности, и дополнение
302 ЭКВИВАЛЕНТНОСТЬ ПбСЛЁДОЙАТЕЛЬНОСТНЫХ МАШИН 1ГЛ. IX
этого подмножества L, которое образуется множеством
запрещенных входных последовательностей. В частном
случае может быть L = Е\ это означает, что для
машины допустимы любые входные последователь-
последовательности.
Рассмотренные примеры ограничений на возможные
входные последовательности не были связаны как-
либо с состояниями машины.
Возможны ограничения и иного типа, накладываемые
конструкцией Я-машины на множество входных после-
последовательностей.
Может оказаться, что на диаграмме состояний Я-ма-
Я-машины имеются такие кружки, что с отходящими от этих
кружков стрелками можно связывать не всякие входные
символы. Пусть, напри-
например, имеется три входных
символа рь р2, рз, и рас-
распределение стрелок у /-го
кружка диаграммы со-
состояний машины показа-
показано на рис. 9.1.
В этом случае, если
машина находится в со-
состоянии %и ее следующее состояние и выходная вели-
величина определены не для всякого входного воздействия.
Машина не может в нашем примере воспринять входное
воздействие рг. Тем самым О1раничения на входные воз-
воздействия накладываются свойствами рас-
рассматриваемой машины.
Подобные ограничения могут накладываться для од-
одного, для нескольких или даже для всех состояний ма-
машины. При этом ограничения для различных состояний
могут быть, вообще говоря, различными, т. е. может
быть, что машина в состоянии щ не допускает каких-
либо • одних входных воздействий, а в другом состоя-
состоянии щ запрещены уже другие входные воздействия.
Если для рассматриваемой Я-машины входная по-
последовательность не нарушает ограничений (на входные
воздействия) для состояния х* и для всех последующих
состояний, то она называется допустимой входной по-
последовательностью для состояния щ. Множество всех
Рис. 9.1.
§ 9.1] РАСПОЗНАВАНИЕ ЭКВИВАЛЕНТНЫХ СОСТОЯНИИ 303
допустимых для состояния Ki последовательностей обо-
обозначим Lxr
Ограничения такого типа впервые рассматривались
Ауфенкампом. Поэтому мы будем в дальнейшем такой
тип ограничений входных последовательностей называть
ограничениями типа Ауфенкампа.
В случае ограничений типа Ауфенкампа нет единого
множества допустимых входных последовательностей,
такого, чтобы любая последовательность, принадлежа-
принадлежащая L, могла быть введена в машину независимо
от того, в каком начальном состоянии она находится.
Для каждого из k возможных начальных состояний ма^
шины имеется свое множество допустимых входных по-
последовательностей LX/, отличное, вообще говоря, от дру-
других множеств Ц (у Ф /).
Отметим теперь, что в рассмотренном ранее случае,
когда множество L допустимых входных последователь-
последовательностей было едино, т. е. оно было независимо от состоя-
состояний Я-машины, алгоритм распознавания принадлежно-
принадлежности любой заданной последовательности множеству L
можно было формулировать в терминах, н« связанных
с выбором начального состояния машины, а иногда и
вообще не связанных с машиной. Поэтому такой тип
ограничений, когда алгоритм распознавания существует
«сам по себе», т. е, может быть выражен в терминах,
не связанных с машиной (хотя может быть он был вы-
выведен исходя из особенностей работы и конструкции ма-
машины), мы будем называть в дальнейшем типом ограни-
ограничений в себе и будем говорить, что в этом случае множе-
множество возможных входных последовательностей «ограни-
«ограничено в себе».
Рассматривая пока лишь ограничения последователь-
последовательностей «в себе», введем понятие об эквивалентности со-
состояний Я-машины (конечного автомата).
Пусть задано множество L допустимых входных по-
последовательностей и две Я-машины 5 и G (в частности,
5 может совпадать с G). Два состояния — состояние и»
машины S и состояние щ машины G — называются экви-
эквивалентными относительно множества L, если обе маши-
машины — машина S в состоянии и» и машина G в состоянии
304 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ. IX
х^, получив на вход любую (но одну и ту же) по-
последовательность из L, переработают ее в одну и ту же
выходную последовательность.
Если машины S и G совпадают, то мы получаем
определение эквивалентности относительно L двух со-
состояний одной Я-машины (автомата).
В том случае, когда L = ?, т. е. когда множество
допустимых входных последовательностей содержит все
последовательности, мы будем говорить, что два состоя-
состояния m и щ просто эквивалентны.
Отправляясь от данного выше определения эквива-
эквивалентных состояний, можно сформулировать следующую
задачу анализа Я-машины.
Задана последовательностная машина и множество
допустимых входных последовательностей L. Требуется
выработать прием, позволяющий для любых двух со-
состояний Я-машины ответить на вопрос: эквивалентны
ли эти два состояния относительно множества L?
Обладая алгоритмом распознавания эквивалентности
состояний относительно L, можно произвести разбиение
всех состояний на группы эквивалентных относительно
L состояний.
Группой эквивалентных относительно L состояний мы
здесь называем такое множество состояний Я-машины,
в котором: 1) любые два состояния эквивалентны отно-
относительно L; 2) любое из состояний внутри группы не
эквивалентно относительно L никакому состоянию вне
группы.
Такое разбиение состояний на группы, как мы уви-
увидим в дальнейшем, имеет важнейшее значение для ми-
минимизации Я*машины.
Поставленная задача анализа была бы решена пол-
полностью, если бы удалось найти такой алгоритм, который
позволял бы решать вопрос об эквивалентности состоя-
состояний для любой заданной Я-машины при любом множе-
множестве L.
Однако, как будет показано в следующем параграфе,
эта задача алгоритмически неразрешима. Поэтому мы
в §§ 9.3 и 9.4 рассмотрим несколько типичных частных
случаев, для которых алгоритм распознавания эквива-
эквивалентности может быть построен.
§ 9.2] НЕРАЗРЕШИМОСТЬ ПРОБЛЕМЫ РАСПОЗНАВАНИЯ 305
§ 9.2. Алгоритмическая неразрешимость проблемы
распознавания эквивалентных состояний
в общем случае
Говоря об ограничении множества возможных вход-
входных последовательностей, естественно требовать, чтобы
задание множества L было в определенном смысле «эф-
«эффективным». Другими словами, множество L должно
быть задано так, чтобы существовал регулярный прием
(алгоритм), позволяющий для любой последовательно-
последовательности входных символов, имеющей конечную длину, отве-
ответить на вопрос: принадлежит ли эта последовательность
множеству L.
Если множество L конечно, то оно может быть эф-
эффективно задано просто перечислением всех последо-
последовательностей, содержащихся в нем. Если же множество
L бесконечно, то оно должно быть определено каким-
либо иным способом, например заданием алгоритма рас-
распознавания того, принадлежит ли каждая конкретная
входная последовательность множеству L, или не при-
принадлежит.
Множество L может быть, например, задано следую-
следующими словесными описаниями:
1) множество L содержит все последовательности
длины, большей трех, у которых четвертым является
символ р<;
2) множество L содержит все последовательности,
оканчивающиеся символом pj и нигде не содержащие
символов рд.
Эти множества хотя и являются бесконечными, пол-
полностью охарактеризованы приведенным выше словесным
описанием, и всегда можно распознать, принадлежит ли
любая наперед заданная последовательность этим мно-
множествам. Наличие подобного словесного описания и
свидетельствует о существовании алгоритма распозна-
распознавания принадлежности любой появляющейся последова-
последовательности заданному множеству L. В этом смысле зада-
задание алгоритма такого распознавания является есте-
естественным и наиболее широким «языком» эффективного
задания бесконечных множеств L.
20 М. А. Айзерман, Л. А. Гусев и др.
306 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ. IX
Целью настоящего параграфа является выяснение
возможности определения эквивалентности двух Состоя-
Состояний относительно любого множества L «эффективно за-
заданного», т. е. заданного алгоритмом распознавания.
Для того чтобы получить ответ на этот вопрос, надо
формализовать понятие алгоритм распознавания. И мы
вновь вынуждены обратиться- к теории алгоритмов и ре-
рекурсивных функций*),
утверждающей, в частно-
ч сти, что всякое множество
rVs последовательностей, для
У которого могут быть вы-
высказаны «правила распо-
распознавания», является ре-
рекурсивным, и наоборот
(это утверждение являет-
является прямым следствием те-
тезиса Чёрча — см. стр. 487).
Пусть L — произволь-
произвольное рекурсивное множе-
множество входных последова-
последовательностей, и* и-xj — про-
произвольные состояния
Я-машин S и G соответ-
соответственно. Тогда имеет ме-
место следующая теорема.
Теорема. Проблема распознавания эквивалентно-
эквивалентности состояний Хг и щ относительно произвольного эффек-
эффективно заданного множества L алгоритмически неразре-
неразрешима.
Мы докажем теорему, показав, что алгоритмически
неразрешима даже более узкая проблема распознавания
эквивалентности состояний в некоторой специально вы-
выбранной машине относительно множеств L, принадле-
принадлежащих некоторому специальному подклассу класса всех
рекурсивных множеств.
Рассмотрим Я-машину, имеющую три состояния; ее
диаграмма состояний изображена на рис. 9.2. Для этой
машины г = 2, т. е. входной алфавит состоит лишь из
*) См. гл, XII, а также § 8.3.
§ 9.2] неразрешимость проблемы распознавания 307
двух символов {0, 1}. На выходе может появляться, Яо
либо Ki.
Рассмотрим специальный класс рекурсивных мно-
множеств, содержащих последовательности из 0 и 1, опре-
определенный следующим образом. Пусть имеется произволь-
произвольная общерекурсивная функция <р@. Определим множе-
множество L9 последовательностей нулей и единиц так: в L?
содержатся лишь последовательности*)
sg(cp(O));
sg(<p(O)), sg(cp(l));
, sg(cp(l)), sg(cpB));
, sg(cp(l)), sg(cpB)), sg(cpC));
и т. д.
Множество L9 при любой рекурсивной функции <р(/)
рекурсивно. Действительно, каждой последовательности
из 0 и 1 длины р + 1 можно поставить в соответствие
определенное значение целочисленной функции
из множества A(L9). Функция Ф(р)—возрастающая функ-
функция, и в силу рекурсивности ф(/) является также рекур-
рекурсивной**). Следовательно, множество Л(L9) перечисля-
перечисляется в порядке возрастания рекурсивной функцией Ф(р)
и потому является рекурсивным множеством. Отсюда и
следует рекурсивность множества последовательностей L9-
Легко видеть, что состояния щ и щ (i, j = 1, 2, 3;
i=hj) машины, изображенной на рис. 9.2, эквивалентны
между собой относительно L9 тогда и только тогда, ко-
когда в L9 не содержится ни одной последовательности,
в которой встречается символ "ро- Поэтому поставленная
нами проблема эквивалентности состояний и* и щ
*) Знак sg(x) означает функцию, которая равна 1 при х >• 1 и
равна 0 при х = 0. При х < 0 эта функция не определена.
**) См. § 12.6 и 12.13.
20*
Ш ЭКВИВАЛЕНТНОСТЬ ПОСЛЁДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ. IX
машины N относительно L9 алгоритмически разрешима в
том и только в том случае, если существует алгоритм
распознавания того, содержит ли L? хотя бы одну по-
последовательность, в которой встречается символ ро. Но
для построения такого алгоритма необходимо уметь для
любой рекурсивной функции <p(t) ответить на вопрос:
обращается ли эта функция при каком-либо t «* t# в
нуль? Доказано, однако, что эта задача алгоритмически
неразрешима *).
Следовательно, алгоритмически неразрешима задача
распознавания эквивалентности состояний щ и щ ма-
машины N (рис. 9.2) относительно множества Lv и, тем
более, алгоритмически неразрешима общая задача рас-
распознавания эквивалентности двух состояний любой Я-ма-
шины относительно любого рекурсивного множества L.
Теорема доказана.
Доказанная теорема устанавливает алгоритмиче-
алгоритмическую неразрешимость проблемы о распознавании со-
состояний Я-машины, эквивалентных относительно L,
если L — любое рекурсивное множество входных после-
последовательностей. Это, разумеется, не противоречит тому
факту, что для конкретных множеств входных последо-
последовательностей L* эта же проблема может быть алгорит-
алгоритмически разрешима, и алгоритмы распознавания, экви-
эквивалентных состояний могут быть построены.
§ 9.3. Распознавание эквивалентности состояний
в случае, когда множество входных последовательностей
не ограничено
Рассмотрим случай, когда на множество допустимых
входных последовательностей не наложено никаких
ограничений, т. е. L ** Е, и следовательно, требуется
просто распознавать эквивалентные состояния Я-мащи-
ны. Для этого случая имеется простой и удобный алго-
алгоритм, предложенный Ауфенкампом и Хоном**).
*) См., например, [142].
**) В работе [6] Ауфенкампом и Хоном доказана только доста-
достаточность этого алгоритма. Мы здесь дадим несколько иное дока-
доказательство достаточности алгоритма Ауфенкампа и Хона и докажем
также его необходимость.
РАСПОЗНАВАНИЕ ЭКВИВАЛЕНТНЫХ СОСТОЯНИЙ
300
Прежде чем приступить к описанию алгоритма рас-
распознавания эквивалентных состояний, отметим одно оче-
очевидное свойство эквивалентности: если какие-либо два
состояния Я-машины эквивалентны относительно мно-
множества jLi, то они будут эквивалентны и относительно
множества Li, если L% S L\. Наоборот, два состояния
могут быть эквивалентны относительно L\f L\ Э Lb
только если они эквивалентны и относительно L2. Это
свойство мы используем далее.
Пусть задана любая /7-машина. Выпишем ее матрицу
соединений. Например:
c =
*5
(Po,
(Pa,
О
О
О
о
(Pi,
(Pi.
(?2, ll)
0
(Pi
0
(Po»'
О
о о (р2,м
0 0 0
0 (p,, h) 0
(РоЛ) (Pi. h) 0
(Pa. K) (pit M 0
(Po, h) (Ps. h) 0
0
Разобьем строки этой матрицы на группы так, чтобы
строки, принадлежащие одной группе, содержали толь-
только одинаковые пары символов. В нашем случае это раз-
разбиение произойдет так: строки иь Х4, из войдут в пер-
первую группу, а строки xg, xs и Хб — во вторую.
Перепишем теперь матрицу соединений так, чтобы
строки, входящие в одну группу, стояли рядом. Для
этого в матрице нужно будет поменять порядок строк и
соответственно порядок столбцов. После этого матрица
С нашего примера будет выглядеть так;
С = —
4
" (Po, л,)
0
0
(P2, ^o)
0
_ 0
0
(Po, *j)
0
0
(p2, h)
(?2, h)
0
0
(?2. ^l)
(Po, У
(Po, *a)
> (Po, h)
(P.
(Pe
(Pi
1 (Pi
Л)
Д1)
, ^1)
0
Л)
(Pi
(Pi
(Pi
0
Л)
0
, M
0
(?2, ^l)"
0
0
0
0
0
310 ЭКВИВАЛЕНТНОСТЬ ПОСЛЁДОВАТЁЛЬНОСГНЫХ МАШИН [ГЛ. IX
Разобьем теперь матрицу С на подматрицы, проведу
горизонтальные линии между выделенными группам?,
строк. В нашем примере первая подматрица состоит из
трех верхних строк, соответствующих состояниям
иь И4, из, вошедшим в первую группу, а вторая подмат-
подматрица содержит строки, соответствующие состояниям
иг, *5 и и6, вошедшим во вторую группу.
Отметим теперь, что состояния, входящие в любую
группу, эквивалентны относительно множества L , со-
содержащего все допустимые входные последовательно-
последовательности длины единица. Действительно, при подаче любого
входного воздействия ро, pi или рг на машину появление
выходного символа не зависит от того, из какого со-
состояния данной группы начала работать Я-машина. Так,
в нашем примере при подаче ро мы получаем на выходе
Х\ независимо от того, находится ли машина в началь-
начальном СОСТОЯНИИ М\, Из ИЛИ Х4-
Поэтому при любой допустимой входной последова-
последовательности могут быть эквивалентны между собой лишь
состояния, входящие в какую-либо группу, ибо два со-
состояния, входящие в разные группы, заведомо не экви-
эквивалентны, так как они не эквивалентны даже относи-
,1
тельно множества L , содержащего последовательности
длины единица.
Однако такого разбиения матрицы недостаточно, так
как неэквивалентность каких-либо двух состояний, вхо-
входящих в группу, может проявиться в следующих тактах.
Для выявления всех эквивалентных состояний разо-
разобьем матрицу С на подматрицы симметрично вертикаль-
вертикальными и горизонтальными линиями. Линии проводятся
так, что если горизонтальная линия проведена
между k-й и (k + 1)-й строками, то k-й и (k + 1)-й
столбцы также должны быть разделены вертикальной
линией.
Назовем один-матрицей (сокращенно 1-матрицей)
такую подматрицу матрицы С, в которой все строки
содержат лишь одинаковые пары символов (если ка-
какая-либо пара встречается в какой-нибудь строке
1-матрицы, то она должна встречаться и во всех осталь-
остальных ее строках).
§9.3]
РАСПОЗНАВАНИЕ ЭКВИВАЛЕНТНЫХ СОСТОЯНИИ
311
В нашем примере симметричное разбиение полу-
получается, если кроме линии, разделяющей строки щ и
провести линию, разделяющую столбцы щ и хг.
s* __
<РоД.) О О
О (Ро. К) О
О О (р2, ?
0
(Р2.
(Ро.
(Ро. К)
\г) О (р2, /
U (Р1Д2) О
^.) (р.Д2) о
(p.. *l)
о
(р., К)
о
(pi. К)
о
о
о
о
В
две ниж-
ниж(Р2. *о)
о
о
этом примере 1-матрицами являются
ние — левая и правая — подматрицы.
Левая верхняя подматрица не является 1-матрицей,
так как в третьей ее строке есть пара (рг, fa), которой
нет в остальных строках. Аналогично обстоит дело и
с верхней правой подматрицей.
Попытаемся так симметрично разбить матрицу С,
чтобы все подматрицы этого разбиения были 1-матри-
1-матрицами. Для этого надо сначала провести наименьшее
число горизонтальных линий так, чтобы матрица С раз-
разбилась на 1-матрицы. Разбиение при этом не будет сим-
симметричным. Поэтому проведем вертикальные линии,
соответствующие проведенным горизонтальным. Если
после этого окажется, что не все матрицы являются
1-матрицами, то вновь проведем нужное число горизон-
горизонтальных линий и т. д.
В нашем примере надо провести горизонтальную
линию между строками щ и хз. При этом все подмат-
подматрицы становятся 1-матрицами, а вертикальная линия
между столбцами щ и хз не нарушает этого свойства:
г.,
-(РоД.)
0
0
(Р2» *о)
0
0
*4
0
(Ро. *i)
0
0
(р2. К)
(Р2. *0>
*3
0
0
(Р2, *.)
(РО> *2>
(Ро. *г)
(Ро. *г)
*2
(Pl. *2)
(Р2. М
(Ро. *i)
(Р.. К)
0
(р.. М
(р
(р
(р
0
.Д2)
.Д2)
0
.Д.)
0
(Р2. К) "
0
0
0
0
0
312 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ. К
В общем случае описанный процесс симметричного
разбиения на 1-матрицы закончится в конечное числе
шагов одной из двух ситуаций:
1. Разбиение тривиально, т. е. все подматрицы этого
разбиения являются матрицами порядка 1 X 1 (линии
разбиения оказываются в этом случае проведенными
между всеми строками и столбцами).
2. Имеется нетривиальное разбиение, т. е. среди всех
подматриц симметричного разбиения есть хоть одна мат-
матрица порядка тХ п, где max(m, n) > 1.
В этом случае горизонтальные линии разбиения про-
проходят не между каждыми строками матрицы С (соот-
(соответственно вертикальные — не между каждыми столб-
столбцами). Эти линии разбивают строки матрицы С и соот-
соответствующие им состояния на группы.
Так, в нашем примере состояния разбиваются на три
группы: {xi, х4}, {кз}, {иг, хв, иб}.
Теорема (Ауфенкампа и Хона). Состояния П-ма-
П-машины эквивалентны между собой тогда и только тогда,
когда они входят в одну группу симметричного разбие-
разбиения матрицы С.
Доказательство достаточности. Пусть
матрица С может быть нетривиально симметрично раз-
разбита на 1-матрицы. Рассмотрим сначала простой случай,
когда матрица имеет вид
2
k
x
Л + 2
. . •
• . .
Vr5 pi
[** kP)
c,,
(p;y;;
C12
(P<'',)
•
•
* * ."
•
-
§ 9.3] РАСПОЗНАВАНИЕ ЭКВИВАЛЕНТНЫХ СОСТОЯНИЙ 313
В этом случае имеется лишь одна группа, содержа-
содержащая к состояний {хь иг, ..., ни], а все остальные груп-
группы содержат по одному состоянию.
В верхнем левом углу матрицы С размещена 1-мат-
1-матрица порядка k X k. Обозначим ее через Си. Выпишем
все входные символы, связанные с парами, являющи-
являющимися элементами этой матрицы Си. Пусть это будут
символы рв1, раа, ..., рв/ (/</*)• Остальные символы
ра/+1, Рн+2, ", Раг в Сп не входят. Покажем теперь,
что состояния xi, X2, ..., хь эквивалентны.
Рассмотрим произвольную входную последователь-
последовательность
Ро pi ... р/ p^+i ... (9.1)
Пусть р* + 1 = ра. —первый входной символ в этой по-
последовательности, который не входит в Си.
При подаче этой входной последовательности выход-
выходная последовательность не будет зависеть от того, с ка-
какого ИЗ СОСТОЯНИЙ, ВХОДЯЩИХ В Группу {Хь Х2, • • . , Хй}»
начала работу машина. В самом деле, до момента /
входные воздействия не выведут Я-машину из множе-
множества состояний {кь Х2, ..., хй}. Но внутри этого множе-
множества состояний выходной символ Я-машины определяется
лишь входным воздействием, так как все пары матрицы
Сц одинаковы. Поэтому до момента / выходная после-
последовательность не будет зависеть от того, с какого из со-
состояний группы {иь и2, ..., хй} началась работа ма-
машины.
В момент /+ 1 будет подано воздействие pj + 1. Это
воздействие переводит любое из состояний, принадле-
принадлежащих группе {xi, кг, • •, хй), в одно и то же состояние
х/, так как все матрицы С12, С13, ..., C1(n_fe) суть 1-ма-
трицы. При этом опять выходной символ не зависит от
того, в каком из состояний группы была перед этим ма-
машина. Дальнейшая работа машины определяется тем,
что в момент j -f 1 она находится в состоянии щ и, сле-
следовательно, не зависит уже от начальных условий.
Последовательность (9.1) была взята произвольно и,
следовательно, состояния хь кг, ..., Щ эквивалентны.
314 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ. IX
Рассмотрим теперь общий случай. Пусть матрица С
симметрично разбита на 1-матрицы
?
xk+2
С = .
•
*Л-1
¦aw
с,
...
. . .
«а • • •
х*+1 xft+2 • •• Xk+S
• С|2
*••
* ' *
...
...
ч
...
^т
Покажем, что состояния, входящие в какую-либо одну
группу, эквивалентны между собой. Действительно, лю-
любое входное воздействие: 1) либо переводит машину из
состояния, принадлежащего некоторой группе, в состоя-
состояние той же группы; выход машины при этом зависит
лишь от входного воздействия и не зависит от того, в
каком из состояний группы машина находится; 2) либо
переводит машину из некоторого состояния /-й группы
в какое-либо состояние /-й группы (/ ф /). Однако в этом
случае это же воздействие, как следует из структуры
матрицы С, переводит и все остальные состояния груп-
группы / в состояния группы /'; выход машины, находящейся
в состоянии группы /, вновь не зависит от того, в ка-
каком конкретном состоянии этой группы машина нахо-
находится; 3) либо же переводит машину из некоторого со-
состояния группы / в состояние щ, не входящее ни в ка-
какую группу.
В этом случае ситуация аналогична той, что рас-
рассмотрена выше —- вновь это входное воздействие будет
§9.3]
РАСПОЗНАВАНИЕ ЭКВИВАЛЕНТНЫХ СОСТОЯНИЙ
315
переводить и все состояния группы i в состояние xj, и
дальнейшая работа машины будет определяться лишь щ.
Проведенное здесь рассуждение, естественно, приме-
применимо к любой из групп. Поэтому в каждый момент вре-
времени выход Я-машины не будет зависеть от того, с ка-
какого из состояний группы i начала машина работу.
Группы эквивалентных состояний, следовательно, ведут
себя так, что каждую группу можно рассматривать
как одно состояние. Достаточность условий теоремы
доказана.
Доказательство необходимости. Рассмо-
Рассмотрим сперва более простой случай. Пусть состояния
Xi, хг,..., Xft образуют груп-
группу эквивалентных состоя-
состояний, а состояния кл + ь
Xft + 2,..., хп не эквивалентны
как между собой, так и лю-
любому состоянию указанной
группы.
Покажем, что если от
какого-либо кружка хг- диа-
диаграммы состояний Я-маши-
Я-машины, обозначающего одно из
состояний группы хь хг, ...
..., Xft, отходит ветвь с пер-
первым индексом ps к одному
из кружков Xj вне группы,
то к этому же кружку Xj от всех остальных кружков груп-
группы подходят ветви с теми же первыми индексами ps. Так,
например (рис. 9.3), если от кружка х2 к кружку Xft + 3
отходит ветвь с первым индексом ps, то такие же ветви
должны подходить к кружку Xft + з и от всех остальных
кружков группы, т. е. от хь х3, щ, ...., Xft.
Рассмотрим в этом же примере какой-либо из круж-
кружков группы {хь хг, ..., Xft}, например кружок хз. Воз-
Возможны следующие три случая:^
1) Ветвь с первым индексом ps, отходящая от круж-
кружка Хз, ПОДХОДИТ К ОДНОМУ ИЗ КруЖКОВ {Xi, X2, ..., Xft}.
2) От кружка хз ветвь с первым индексом ps отходит
к одному из кружков Xfc + t (*'=?3), например к круж-
Рис. 9.3.
316 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ. IX
3) Ветвь с первым индексом ps идет от кружка хз
К Кружку Xft + з-
Покажем, что может иметь место только слу-
случай 3). Для этого докажем, что случаи 1) и 2) невоз-
невозможны.
Предположим, что стрелки с первым индексом ps идут
соответственно случаю 1).- Это значит, что при по-
подаче ps мы из состояния Х2 перейдем в состояние Xft + з,
а из состояния хз, эквивалентного хг, перейдем в какое-
либо состояние Xj группы {хь х, ..., X/J.
Но состояние х* + з неэквивалентно по условию ни
одному из состояний группы {хь Х2, ..., Xft}; следова-
следовательно, Xft + з неэквивалентно и Xj, и поэтому найдется
такая последовательность р р^ ря> • • •, что при подаче
на вход этой последовательности Я-мащина выдаст на
выходе различные последовательности выходных симво-
символов в зависимости от того, с какого из состояний —xj
или Xft + з — началась работа машины.
Но тогда и последовательность р5 р paj pas •.. будет
порождать на выходе различные последовательности
в зависимости от того, начинает ли машина работу
с хг или хз, что противоречит эквивалентности состоя-
состояний хг и хз. Поэтому первый случай не может иметь
места. '
Предположим, что стрелки с первым индексом ps идут
соответственно случаю 2). Тогда при подаче сим-
символа р3 состояние хг переходит в состояние Xft + з, а со-
состояние хз — в состояние Xft + i. Но хд + i не эквивалентно
Xft + з; следовательно, аналогично случаю 1) найдется по-
последовательность pPj p^ Pp. • •. такай, что выходная по-
последовательность машины при подаче на вход этой по-
последовательности будет зависеть от того, с какого из
состояний —Xft+ 1 или Xft + з—начала работу машина.
Но тогда последовательность ps pp§ pfe рРа • • • устанавли-
устанавливает неэквивалентность состояний хг и х$, что противо-
противоречит условию. Следовательно, и случай 2) не имеет
места. Итак, если, как это рассмотрено в нашем при-
примере, от кружка хг отходит ветвь с первым индексом р3
к кружку хл 4 3, то и от всех кружков хь хз, х4 ... к
кружку Xft + з также идут ветви с первым индексом р,
9.3]
РАСПОЗНАВАНИЕ ЭКВИВАЛЕНТНЫХ СОСТОЯНИЙ
317
(рис. 9.4). При этом и вторые индексы рассматриваемых
ветвей должны совпадать, так как иначе можно было бы
с помощью входного воздействия длины 1 установить
неэквивалентность некоторой пары состояний из группы
хг, ..., х&}, что противоречит условию.
Следовательно, если от какого-либо кружка группы
хг, •••» х&} отходит ветвь с надписью (pfi, Km) к од-
одному из кружков Xft+i, хь+2, ...» Хп, то к этому же
кружку подходят ветви с той же надписью (ps, Xm) и от
всех остальных кружков группы {хьхг, ..., х&} (рис. 9.4).
Рис. 9.4.
Из этого же утверждения следует, что если ветвь
с надписью (ps, Xm)r отходящая от одного из кружков
{хь ха, ..., «л), подходит к одному из кружков той же
группы {хь х2,..., хь}» т. е. не подходит ни к одному из
кружков х/н-ь х/н-2, ..., х„), ^то и отходящие от всех
остальных кружков группы ветви с надписью (pe,
подходят к кружкам той же группы {хь хг.., }
(т. е. не подходят ни к одному из кружков х*+ь х&+2» ...
..., Хп, а остаются «внутри» обведенной на рис. 9.4
группы {хь х2> ..., хл}). .
318 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ. IX
Из доказанного следует, что матрица соединений рас-
рассматриваемой машины будет иметь вид
/-»__
Си
С 21
Сгх
. . .
12
4+2
С\ (л-Л+1)
. . .
. . .
. . .
• • • в
Если провести теперь симметричное разбиение ма-
матрицы так, чтобы состояния разбились на группы
{ki, кг, •••» Kh}, {xfc+i}> {>«л+2}, ..., {хп} (см. проведенные
линии), то все подматрицы Си, Ci2, ..., Ci(n_ft + i) бу-
будут 1-матрицами на основании утверждений, набранных
выше курсивом. Остальные подматрицы Сц (i = 2, 3, ...
..., п — k + 1, /=1, 2, ..., п—-к + 1) будут также
1-матрицами, так как они все содержат лишь одну
строку (или один элемент).
В общем случае, когда имеется несколько групп по-
попарно эквивалентных состояний, проведенные выше рас-
рассуждения сохраняются, но некоторые из кружков
нн+и Kh+2, ..., Хп должны быть теперь заменены груп-
группами кружков; каждая из этих групп вполне аналогична
группе {хь кг, . • •, хл} в рассмотренном выше частном
случае. Этим замечанием завершается доказательство
теоремы.
Доказанная теорема Ауфенкампа и Хона дает про-
простой и очень удобный алгоритм определения всех групп
эквивалентных состояний заданной Я-машины. Алго-
Алгоритм этот сводится к построению симметричного раз-
бения матрицы соединений С заданной Я-машины.
§ 9.4] РАСПОЗНАВАНИЕ ЭКВИВАЛЕНТНОСТИ СОСТОЯНИЙ 319
§ 9.4. Распознавание эквивалентности состояний
в случае, когда ограничения наложены на длину
входных последовательностей
В этом параграфе рассматривается проблема экви-
эквивалентности состояний при ограничении множества L
допустимых входных последовательностей условием,
согласно которому все входные последовательности
имеют длину, не превышающую заданное число q. Мно-
Множество L может, в частности, содержать все возмож-
возможные последовательности длины, не превышающей q, или
только часть из них.
При таком ограничении считается, что на входе не-
невозможно появление последовательности, содержащей
более чем q символов, и, следовательно, рассматри-
рассматривается работа машины за q тактов. Требуется в этом
случае найти алгоритм распознавания эквивалентных
относительно L состояний /7-машины и построить раз-
разбиение всех состояний машины на группы состояний,
эквивалентных относительно L.
Поскольку число различных символов р* конечно и
длина последовательностей ограничена числом qy мно-
множество L содержит конечное число различных последо-
последовательностей.
Поэтому вопрос о существовании алгоритма здесь
не вызывает сомнений: для определения эквивалент-
эквивалентности любых двух состояний и,- и щ относительно
L достаточно перепробовать все возможности, т. е.
просмотреть, совпадают ли выходные последователь-
последовательности при подаче на вход любой последовательности
из L для машины, начинающей работу с состояния щ и
С СОСТОЯНИЯ Xj.
Такая проверка может быть проведена по. диаграмме
состояний машины либо по ее матрице соединений
и т. д., либо путем ^ эксперимента на существующей
машине. ^
Таким образом, в данном случае всегда существует
алгоритм распознавания эквивалентности—алгоритм
полного перебора. Одной из форм организации такого
перебора является «возведение в степень» матрицы со-
соединений исследуемой Я-машины, подробно рассмо-
320 ЭКВИВАЛЕНТНОСТЬ ЛОСЛЁДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ. IX
тренное в § 3.6. Напомним приведенные там свойства
матрицы Ся\
1. Элемент Cjj матрицы Сд перечисляет все после-
последовательности входных величин длины q, которые пере-
переводят машину из состояния и* в состояние щ, и соответ-
соответствующие им выходные последовательности.
2. Так как следующее- состояние машины одно-
однозначно определяется существующим состоянием и вход-
входным символом, в одной и той же строке матрицы С не
может быть двух элементов, в которых были бы члены,
содержащие одну и ту же последовательность входных
величин.
3. Любая входная последовательность длины q при-
присутствует в каждой строке матрицы С4 в одном из эле-
элементов этой строки.
Из этих свойств матрицы Ся вытекает следующий
прием определения эквивалентных относительно L со-
состояний. Расположим все входные последовательности
из L в порядке возрастания их длины. Выберем одну
из последовательностей наименьшей длины и, просма-
просматривая матрицу Ся, где q — наибольшая длина последо-
последовательности из L, обратим внимание на все входные
последовательности в ее .элементах, у которых началь-
начальный отрезок совпадает с выбранной нами последова-
последовательностью из L. Отметим как-либо эти начальные от-
отрезки, например добавляя точки над входящими в них
символами. Проделаем аналогичную операцию, выбирая
поочередно в порядке возрастания длины все последо-
последовательности из L (последовательности одинаковой дли-
длины перебираются в произвольном порядке), Если над
каким-либо символом отметка (точка) уже была ранее
проставлена, то ставить над ним новую отметку не тре-
требуется. В результате в матрице С9 часть содержащихся
в ее элементах входных последовательностей имеет от-
отметки над всеми символами, часть — над символами из
некоторых начальных отрезков, а часть последователь-
последовательностей вообще может не иметь отметок.
Например, пусть q = 3; множество L содержит сле-
следующие четыре последовательности:
Pi; P1P2; Р2Р1; Р2Р1Р2,
§9.4]
РАСПОЗНАВАНИЕ ЭКВИВАЛЕНТНОСТИ СОСТОЯНИЙ
321
а Я-машина имеет диаграмму состояний, показанную
на рис. 3.11, — матрица С3 для нее была построена
в § 3.6. При этом отметки расставляются таким образом:
С3 =
[(piPip2. *
V(p'2Pip2.
V(p2p2?2.
V(p'ipipi,
V(p2PiPi.
[(P1P2P1. ^
v(p2p2pi>
[(P2P2P1.
v(pipipi,
(PlPlp2>
V(P2P2P2>
V(piPip2»
V(p2p'iPi.
[(P2P1P2.
V(P2P2P2.
V(pip2p2,
KP2P1P1. -
V(P2P2P1.
V(pip2pi»
После того как отметки расставлены, зачеркнем в
элементах матрицы С3 те входные и соответствующие
им выходные последовательности, в которых отсутствуют
точки над символами (в приведенном примере это вход-
входные последовательности ргр2рг и p2p2pi) - В тех входных
последовательностях, в которых точки стоят лишь над
символами каких-либо начальных отрезков, зачеркнем
символы, не имеющие точек, т. е. «хвостовые» их части;
зачеркнем также соответствующие «хвостовые» части
выходных последовательностей. Полученную в резуль-
результате матрицу мы будем называть сокращенной по L
Cq-матрицей. В приведенном выше примере сокращен-
сокращенная по L С3-матрица имеет вид
(pi
(p2plp2> МЛ)
(Pi. К)
(р,р2, M3)v(pi, *
V(p2pl» Ml)
(Р2Р1Р2» Мз^-гI
V(PiP2» M2)V(Pii
i)V (Pi,
s/ (P2P1. *i
К) V(pi?2f
21 M. А. Айзерман, Л. А. Гусев и др.
322 ЭКВИВАЛЕНТНОСТЬ ПбСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ. IX
В каждой строке сокращенной по L С*-матрицы ос-
остаются лишь такие пары входных и выходных .последо-
.последовательностей, которые содержат лишь входные последо-
последовательности из L.
По виду сокращенной по L С9-матрицы можно отве-
ответить на вопрос об эквивалентности двух состояний.
Именно два состояния П-машины уц и щ эквивалентны
относительно L тогда и только тогда, когда в i-й и \-й
строках сокращенной no L С4-матрицы присутствуют
лишь одинаковые пары входных и выходных последова-
последовательностей. Так, в приведенном примере в первой строке
содержатся пары (рь Я3); (pjp2, Я3Я2); (р2рь Mi);
(Р2Р1Р2, Я1А1Я3); во второй строке — пары (рь %\)\
(pip2, Я1Я3); (р2рь Ы\); (Р2РФ2, ЫДз) в третьей стро-
строке—пары (рь Я2); (р1р2, Я2Я2); (ргрь Я3Я3); (p2pip2,
ЯзЯзЯ2). Поскольку здесь нет двух строк, содержащих
в точности одни и те же пары, в рассмотренной Я-ма-
шине нет эквивалентных относительно L состояний.
Приведенный выше алгоритм перебора очень гро-
громоздок, особенно при больших значениях q. Поэтому
важно выделить такие частные случаи задания множе-
множества L последовательностей ограниченной длины, в ко-
которых можно избежать перебора всех входных последо-
последовательностей. Рассмотрим один такой случай.
Пусть множество L содержит все последовательности
длины, меньшей или равной q. Множество L составляет
подмножество множества Е, содержащего все входные
последовательности. Поэтому всякие два состояния,
эквивалентные относительно множества Е {т. е. про-
просто эквивалентные), эквивалентны также и относи
тельно L.
Возникает такой вопрос: в каких случаях разбиение
всех состояний машины на группы эквивалентных со-
состояний совпадает с разбиением всех состояний на груп-
группы эквивалентных относительно L, т. е. когда эквива-
эквивалентные относительно L состояния являются эквива-
эквивалентными и относительно Е? Если мы будем уметь от-
отвечать на этот вопрос, то в тех случаях, когда ответ по-
положительный (т. е. когда разбиения совпадают), мы
можем применять простой алгоритм Ауфенкампа и Хона;
в тех же случаях, когда ответ отрицательный (разбие-
§ 9 4] РАСПОЗНАВАНИЕ ЭКВИВАЛЕНТНОСТИ СОСТОЯНИИ 323
ния не совпадают), придется применять описанный выше
перебор, либо искать какой-либо новый прием.
Ответ на поставленный вопрос связан с соотноше-
соотношением чисел k и q — числа состояний машины и макси-
максимальной длины допустимых входных последовательно-
последовательностей. Если длина q достаточно велика, то, как мы ниже
установим, эта длина может оказаться достаточной для
различения всех неэквивалентных состояний. Тогда вся-
всякая пара состояний, неэквивалентных относительно Е,
будет неэквивалентна и относительно L.
Пусть задана последовательностная машина 5, имею-
имеющая k состояний. Проведем симметричное разбиение ее
матрицы соединений С по методу Ауфенкампа и Хона.
Тогда состояния машины разобьются на группы экви-
эквивалентных состояний. Пусть число этих групп будет k*
(очевидно, k* <!&).
Докажем, что если q^k* — 1, то проведенное по ме-
методу Ауфенкампа и Хона разбиение состояний на груп-
группы эквивалентных состояний совпадает с разбиением
состояний машины 5 на группы эквивалентных относи-
относительно L состояний; тогда при q !> k* — 1 нашу зада-
задачу будет решать алгоритм Ауфенкампа и Хона, и число
групп будет равно k*.
Действительно, построим машину 5* с числом со-
состояний k*, удовлетворяющую следующим требованиям:
а) для каждого состояния машины 5 найдется эквива-
эквивалентное состояние машины 5* и, наоборот, для каждого
состояния машины S* найдется эквивалентное состояние
машины 5; б) в-се состояния машины 5* попарно неэк-
неэквивалентны. В § 9.7 будет показано, что машину, обла-
обладающую указанными свойствами, всегда можно по-
построить.
Воспользуемся теоремой Мура о наименьшей длине
входной последовательности (эксперимента) для раз-
различения двух заданных начальных состояний Я-машины
(см. далее § 11.2). Эта теореме утверждает, что если ма-
машина N имеет k состояний и все состояния неэквива-
неэквивалентны друг другу, то для каждой пары состояний х<
и щ всегда найдется входная последовательность дли-
длины не более k—1,-которая эти состояния позволит
различить,
21*
324 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ IX
Но в силу свойства б) машины S* последователь-
последовательности длины не более k* — 1 «различат» и все неэкви-
неэквивалентные состояния машины. Поэтому если q^>k*— 1,
то эти «различающие» последовательности содержатся
в L, откуда и следует наше утверждение.
Если же q < k*—1, то разбиение относительно L
может не совпадать с разбиением относительно Е. Тогда
разбиение относительно L приходится строить методом
перебора, например возведением матрицы С в степень q.
Кроме того, можно без труда оценить снизу число
групп эквивалентных относительно L состояний, что так-
также помогает в ряде случаев избежать перебора. Дей-
Действительно, разобьем матрицу С на 1-матрицы только
горизонтальными линиями (т. е. выделим в ней все груп-
группы строк, совпадающих с точностью до порядка элемен-
элементов). Тогда состояния машины разбиваются на т групп.
Это будут группы состояний, эквивалентных относи-
относительно множества L1 всех входных последовательностей
длины 1 (множество L1 совпадает с алфавитом
(рь рг, •••, рг}). Ясно, что число групп эквивалентных
относительно L состояний не может быть меньше чем т,
так как <?>-1 и L1 с L и, следовательно, всякие два со-
состояния, эквивалентные относительно L, эквивалентны
и относительно /Л
По той же причине k* является оценкой сверху чи-
числа групп эквивалентных относительно L состояний, таь
как Lc?( и поэтому всякие два состояния просто экви-
эквивалентные эквивалентны и относительно L.
Поэтому если окажется, что т= k*,.rot несмотря на
то, что q < k*—1, можно пользоваться алгоритмом
Ауфенкампа и Хона.
При практическом применении алгоритма Ауфенкам-
Ауфенкампа и Хона оба числа т и k* получаются на различных
этапах вычисления. Число т получается уже на первом
этапе, когда мы проводим горизонтальные линии раз
биения матрицы С. Если проведенные затем вертикаль-
вертикальные линии «испортили» разбиение, то приходится вновь
проводить горизонтальные линии и т. д., и в итоге будет
получено число k*, k* > т.
Ограничивая рассмотрение проблемы эквивалент-
эквивалентности случаями, которым посвящен этот и предыдущий
§ g.4] РАСПОЗНАВАНИЕ ЭКВИВАЛЕНТНОСТИ СОСТОЯНИЙ 325
параграфы, мы сделаем два кратких замечания, касаю-
касающихся других заданий множества L допустимых вход-
входных последовательностей.
1. Большое значение (в особенности в теории ре-
лейно-контактных схем) имеет случай, когда множество
L содержит все последовательности, в которых не встре-
встречаются два одинаковых символа подряд. Можно пока-
показать, что в этом случае существует алгоритм распозна-
распознавания эквивалентных состояний. Однако сколько-нибудь
удобных для практического использования алгоритмов
авторы не знают.
2. Для ограничений типа Ауфенкампа должна быть
изменена сама постановка проблемы эквивалентности
состояний, так как в этом случае говорить об эквива-
эквивалентности двух состояний хг- и щ не имеет смысла, по-
поскольку состояния хг- и Xj могут иметь различные множе-
множества допустимых входных последовательностей. Может
оказаться, что некоторые последовательности, допусти-
допустимые для Иг, недопустимы для Xj, и наоборот.
Однако иногда вводят понятие, близкое к эквива-
эквивалентности, а именно понятие совместимости состояний,
определяемое следующим образом:
Два состояния — состояние хг- машины S и состояние
?j машины G— называются совместимыми тогда и толь-
только тогда, когда обе машины — машина S в начальном
состоянии Хг, и машина. G в начальном состоянии ?j,
получив любую входную последовательность из пересе-
пересечения множества допустимых входных последователь^
ностей для состояния хг- с таким же множеством для
состояния ?j, выдадут одинаковые выходные последова-
последовательности. Здесь S и G могут означать одну и ту же
машину.
Состояния хг- и ?j будут, согласно данному определе-
определению, обязательно совместимы, если пересечением яв-
является пустое множество, т. е. когда состояния хг- и ?j
не имеют общих допустимых входных последовательно-
последовательностей. Если же оба множества совпадают, то совмести-
совместимость переходит в эквивалентность относительно этого
множества.
Группа состояний {xi, хг, •.., х&} называется груп-
группой псевдожвивалентных состояний тогда и тольк
326 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ. IX
тогда, когда любые два состояния щ и щ этой группы
совместимы.
Понятие совместимости часто оказывается полезным;
в частности, его можно применить для минимиза-
минимизации Я-машины, имеющей ограничения типа Ауфенкам-
па (см. §9.8).
§ 9.5. Понятия об эквивалентности, отображении
и минимизации последовательностных машин
В предыдущих параграфах рассматривался вопрос об
эквивалентности отдельных состояний; в этом и следую-
следующих параграфах рассматривается вопрос об эквивалент-
эквивалентности /7-машин.
Лее П-машины S и G называются эквивалентными
относительно L тогда и только тогда, когда для каждого
состояния Хг машины S существует по крайней мере од-
одно эквивалентное относительно L состояние ?j машины
G, и для каждого состояния ?s машины G существует по
крайней мере одно эквивалентное относительно L со-
состояние щ машины S.
Из определения видно, что в этом случае любая
входная последовательность из L должна быть допу-
допустима как для машины S, так и для машины G. Если
множество всех допустимых для машины 5 последова-
последовательностей обозначить Ls, а аналогичное множество для
машины G — через LG, то множество L должно удовле-
удовлетворять условию
L ? Ls П LQ.
В том случае, когда L = Е (т. е. L содежит все возмож-
возможные Последовательности), мы будем говорить, что ма-
машины S и G просто эквивалентны. В этом случае
Ls = LG = L = Е.
Условимся говорить, чт© машина S отображается на
машину G относительно множества L (или машина G
отображает машину S относительно множества L) тогда
и только тогда, когда для каждого состояния х< маши-
машины S существует по крайней мере одно эквивалентное
относительно I состояние ^ тшины G, Если L = Е, то
^ 9.51 эквйвалеШйость. ОтоЬМжёниё и минимизация $2?
мы будем говорить просто об отображении машины S
на машину G.
Из определения отображения и.эквивалентности лег-
легко можно вывести следующее свойство: если машина
S отображается на машину G относительно L, и машина
G отображается на машину 5 относительно того же L,
то S и G являются эквивалентными относительно L ма-
машинами.
Соотношение эквивалентности машин 5 и G обозна-
обозначается 5 ~ G, а соотношение отображения машины 5
на машину G обозначается S cz G.
В смысле переработки входных последователь-
последовательностей символов в выходные последовательности экви-
эквивалентные машины не отличаются друг от друга.
Если машина 5 отображается (или отображается
относительно L) на машину G, то это практически озна-
означает, что машина G может заменить машину 5 (но не
наоборот).
Рассмотрим две эквивалентные Я-машины S\ и 5г.
Пусть состояния этих машин разбиты на группы экви-
эквивалентных состояний. Рассмотрим какую-либо группу s\
эквивалентных состояний машины S\ и выберем произ-
произвольное состояние х< в этой группе. В машине 5г найдет-
найдется некоторое состояние xj, эквивалентное х*. Пусть со-
состояние xj принадлежит группе s\ эквивалентных со-
состояний машины 5г- Тогда любые два состояния, первое
из которых принадлежит группе s\ машины Slt а вто-
второе— группе s\~ машины 52, эквивалентны. Вместе с тем
ни одно из состояний группы sj машины Sj не эквива-
эквивалентно ни одному из состояний группы s\ машины 52
при 1Ф р. Поэтому каждой группе эквивалентных со-
состояний машины Si соответствует одна и только одна
группа эквивалентных состояний машины 5г.
В силу симметрии соотношения эквивалентности
машин (из S\ ~ S2 следует 52 ~ Si), справедливо и об-
обратное утверждение, что каждой группе эквивалентных
состояний машины 52 соответствует одна и только одна
группа эквивалентных состояний машины S\. Поэтому
число групп эквивалентных состояний в эквивалентных
328 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН (ГЛ. IX
машинах 5i и S2 одинаково, а сами машины 5i и 5г от-
отличаются лишь количеством состояний в соответствую-
соответствующих группах.
Если заданы две машины S и G, из которых вторая
отображает первую E с G), то соответствие между груп-
группами эквивалентных состояний не является взаимно
однозначным: можно утэерждать лишь, что каждой
группе эквивалентных состояний машины S соответ-
соответствует одна и только одна группа эквивалентных со-
состояний машины G, но не наоборот. Поэтому число
групп эквивалентных состояний машины G может быть ;
больше числа групп машины 5: машины 5 и G могут
отличаться, таким образом, не только количеством со-
состояний в каждой группе, но и числом групп.
Все сказанное здесь о соотношении числа групп экви-
эквивалентных состояний для эквивалентных и отображаю-
отображающихся машин остается справедливым, если рассматри-
рассматривать эквивалентность и отображение относительно мно-
множества входных последовательностей L, ограниченного
«в себе».
Введем теперь понятие о минимизации П-мащины.
Пусть задана /7-машина 5. Под процессом минимиза-
минимизации Я-машины 5 относительно множества L допусти-
допустимых последовательностей будем понимать отыскание
некоторой другой Я-машины G, удовлетворяющей еле- ;
дующим двум условиям:
1) Я-машина G отображает 5 (GzdS) относительно
множества L.
2) Не существует никакой другой Я-машины, ото-
отображающей 5 относительно L с числом состояний, мень-
меньшим числа состояний машины G.
Последов ательностная машина G, удовлетворяю-
удовлетворяющая этим требованиям, называется минимальной для
S относительно L.
Заметим, что если существует алгоритм распознава-
распознавания состояний, эквивалентных относительно множества
допустимых последовательностей L, то в принципе суще-
существует тривиальный алгоритм минимизации относитель-
относительно L. Действительно, если машина S имеет k состояний,.
то минимальная для 5 машина G имеет число состоя-
состояний, не большее чем k. В принципе возможен перебор
§9.6] МИНИМИЗАЦИЯ ПОСЛЕДОВАТЕЛЬНОСТНОЙ МАШИНЫ 329
всех машин (а их конечное число, с числом состояний,
не большим k, а наличие алгоритма распознавания экви-
эквивалентных относительно L состояний позволяет прове-
проверить, отображает ли каждая из перебираемых машин
машину S. Разумеется, такой тривиальный алгоритм не
имеет практического значения, поэтому возникает за-
задача нахождения алгоритмов минимизации, удобных
для практического использования. Такой алгоритм най-
найден пока лишь для случая, когда допустимы все вход-
входные последовательности. Рассмотрению этого случая
посвящен следующий параграф.
§ 9.6. Минимизация последовательностной машины
в случае, когда множество входных последовательностей
% не ограничено
Пусть задана последовательностная машина S, имею-
имеющая k состояний. Разобьем все состояния машины S на
группы эквивалентных состояний, например так, как
это было описано в § 9.3. На рис. 9.5 изображена часть
диаграммы состояний машины. Группы эквивалентных
состояний обведены сплошными линиями. Рассмотрим
подробнее какую-либо группу состояний, например пер-
первую группу. К состояниям первой группы подходят
стрелки от других состояний машины, имеющие надписи
(ри К), (рт, кр) и т. д. Отходящие стрелки, как это уже
было установлено в § 9.3, могут быть двух типов:
а) Если какая-либо стрелка с первым символом рр,
отходящая от одного из состояний группы, подходит
к состоянию той же группы, то и все стрелки с первыми
символами рр, отходящие от любого из состояний этой
группы, подходят также к состояниям внутри группы.
Вторые символы всех этих стрелок одинаковы.
б) Если стрелка с первым символом ps отходит от
одного из состояний i-й группы к одному из состояний
/-й группы, то и все стрелки-» с первыми символами ps,
идущие от состояний i-й группы, подходят только к со-
состояниям /-й группы. Вторые символы у всех этих стре-
стрелок совпадают.
Учитывая эти два свойства, заменим все состояния,
входящие в одну и ту же группу, одним состоянием.* Все
330 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ. IX
стрелки, подходящие к состояниям группы, подведем
к кружку, заменяющему эту группу. Отходящие от со-
состояний группы стрелки в случае а) заменим стрелкой-
петлей с надписью (рр, Яд), которая отходит от вновь
введенного кружка, заменяющего группу состояний, и
подходит к нему же, а в случае б) —одной стрелкой с
надписью (р8, Xt)t идущей-от кружка, заменившего все
состояния /-й группы, к
любому кружку, заменив-
заменившему состояния /-й груп-
группы. На рис. 9.6 в каче-
качестве примера показана
Вторая
группа
о о
Третья
группа
Вторая
группа
Третья
группа
Рис. 9.6.
Рис. 9.6.
такая замена для части диаграммы состояний, приве-
приведенной ранее на рис. 9.5.
Произведем такую замену группы состояний одним
состоянием для всех групп. После этого Я-машина S
преобразуется в Я-машину G. Непосредственно видно,
что Я-машина G эквивалентна Я-машине S. Действи-
Действительно, в силу свойств а) и б) при любой входной
последовательности и любом начальном состоянии щ
машина 5 выдает ту же самую выходную последова-
последовательность, что и машина G, если подвести к ней ту же
входную последовательность и установить машину в на-
начальное состряние xj, заменившее группу, в которую
§9.61 МИНИМИЗАЦИЯ ПОСЛеДОВАТЕЛЬНОСТНОЙ МАШИНЫ 331
входило Хг. Вместе с тем число состояний в машине G
равно числу групп эквивалентных состояний у 5, и даль-
дальнейшее объединение состояний в группы невозможно,
В § 9.5 было показано, что число групп эквивалент-
эквивалентных состояний одинаково во всех эквивалентных маши-
машинах, а в отображающих — не меньше. Минимальная
машина не может иметь меньше состояний, чем число
групп эквивалентных состояний минимизируемой ма-
машины. Поэтому машина G является минимальной для S.
Отсюда следует, что при отсутствии ограничений на
входные последовательности: 1. Минимальная машина
находится в классе эквивалентных и 2. Задача миними-
минимизации сводится к обнаружению групп эквивалентных
состояний, т. е. может быть решена алгоритмом Ауфен-
кампа и Хона (см. § 9.3).
В связи с этим удобно и замену групп состояний од-
одним состоянием осуществлять не на диаграмме состоя-
состояний, а непосредственно на матрице С.
В качестве примера вернемся к матрице С, рассмо-
рассмотренной ранее в § 9.3.
c =
ч
(Po. K)
(P2> ^o)
0
0
0
0
(p..
(Pl.
(po.
(P2.
0
(Pl.
8
*2>
*.)
M
M
K)
ч
0
(Po. *
(P2. k
0
(Po. *
(Po. *
2)
¦1)
2)
2)
*4
0
0
0
(Po. *
(P2. *l
(P2> ^
«в
0
0
(Pl. *»)
1) (Pl. ^2)
d) (Pi. ^1)
0) 0
(P2.
0
0
0
0
0
Осуществляя симметричное разбиение этой матрицы на
1-матрицы,получим
*1
г Хз
«e
*1
" (Po. *i)
0
0
(P2. ^c)
0
0
^•4
0
(Po. ^1)
0
0
(P2. *o)
(P2. ^0)
^3
0
0
(P2> ^lX
(po. ^2)
(po. ^2)
(po. ^2)
ъ
(Pl. *2>
(P2. ^l)
(Po. M
(pi. M
0
(Pi. K)
(p
(p
(p
ч
0
1. ^2)
1. ^2)
0
uK)
0
(P2. h)~
0
0
0
0
0 _
332 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН (ГЛ. IX
Состояния разбились на три группы эквивалентных со-
состояний {Xi, Х4}, {Хз}, {Х2, Х5, Хб}-
Алгоритму замены каждой группы состояний одним
состоянием будет соответствовать замена каждой 1-ма-
1-матрицы симметричного разбиения одним элементом, яв-
являющимся дизъюнкцией (объединением) всех элементов
заменяемой 1-матрицы.
В рассматриваемом примере матрица соединений ми-
минимальной Я-машины G будет иметь вид
(Po> Xi) 0 (?i>
0 (P2> Xi) (Po»
Ее диаграмма состояний показана на рис. 9.7.
Мы рассмотрели в этом параграфе случай, когда множество
входных последовательностей неограничено. Задача о минимизации
Я-машины при наличии ограниче-
ограничений «в себе» не решена в той же
мере, в какой не решена для это-
этого случая и задача о выявлении
групп состояний, эквивалентных
относительно L (см. § 9.4). Кроме
того, минимизация относительно
Ьф Е связана со следующей до-
дополнительной трудностью. Пусть
даже известен алгоритм выявле-
выявления групп эквивалентных относи-
относительно L состояний. Выше в этом
параграфе при L = Е мы могли
заменять все состояния, входящие
в каждую группу, одним состоя-
состоянием. При этом мы опирались на
свойства стрелок диаграммы со-
состояний, описанных в пунктах а)
и б). Если ЬфЕ, то, вообще го-
говоря, стрелки не обладают этими
свойствами: от двух состояний,
эквивалентных относительно L,
стрелки с одинаковым первым ин-
индексом могут вести к неэквивалент-
неэквивалентным относительно L состояниям.
Рассмотрим, например, кусок диаграммы состояний, показанной
на рис. 9.8, в случае, когда L не содержит последовательностей,
имеющих два одинаковых символа подряд. Пусть состояния щ и хг
р q7
§ 9.7] МИНИМИЗАЦИЯ ПОСЛЕДОВАТЁЛЬНОСТНОЙ МАШИНЫ 333
эквивалентны относительно L, т. е. входят в одну группу. Пусть да-
далее состояния х3 и Х4 эквивалентны относительно множества вход-
входных последовательностей L', содержащего все последовательности
из L, кроме тех, которые начинаются с символа ps, и неэквивалентны
относительно L, так как дают разные выходные символы на последо-
вательности\из L, начинающиеся с р„. Тогда расположение стрелок,
показанное на рис. 9.8, не проти-
противоречит тому факту, что состояния
xi и х2 эквивалентны относитель-
относительно L (так как в L не содержится
последовательностей, начинающих-
начинающихся с двух символов ps подряд), но
противоречит пункту б).
Из изложенного следует, что
при L ФЕ нельзя, вообще говоря,
все состояния, входящие в каж-
каждую группу эквивалентных состоя-
состояний, заменять одним состоянием,
так как при этом пришлось бы от
одного и того же нового состояния
отвести две стрелки с одинаковым
первым индексом ps к двум раз-
разным состояниям, что противоречит
самому определению Я-машкны.
В этом параграфе мы не Рис. 9.8
накладывали каких-либо
ограничений на особенности переработки последователь-
последовательностей минимизируемой Я-машиной. В следующем пара-
параграфе будет особо рассмотрен частный случай Я-маши-
ны, работающей как конечный автомат.
§ 9.7. Минимизация последовательностной машины
в случае, когда она работает как конечный автомат
Предположим, что задана основная таблица конеч-
конечного автомата с алфавитом состояний {щ, хг, .. ., х&}-
Произведем перекодировку символов, заменив щ на
А,*, и положим / = k, где / — число символов К. Тогда в
заданной основной таблице конечного автомата все сим-
символы х заменяются на символы X с сохранением индекса.
Требуется построить минимальную последовательно-
стную машину, которая реализовала бы этот автомат,
т. е. с точки зрения переработки входных последователь-
последовательностей в выходные работала бы так же, как заданный
автомат.
334 эквивалентность последовательностных машин [гл TV
Множество допустимых входных последовательностей
может быть ограничено или неограничено. /
Рассмотрим два случая — случай, когда на/входные
последовательности не наложено никаких ограничений,
и случай, когда входные последовательности (Ограничены
условием — не могут появляться последовательности,
имеющие два одинаковых символа подряд.
1. Множество L допустимых входных
последовательностей содержит все
возможные последовательности, т. е. L = Е
Построение и минимизацию Я-машины, работающей
как заданный автомат Л, рассмотрим на примере. Пусть
таблица заданного автомата А имеет вид табл. 9.1.
В § 9.6 было установлено, что при отсутствии огра-
ограничений на входные последовательности минимальная
Я-машина для заданной ма-
Таблица 9.1 шины дг находится в классе
машин, эквивалентных N, и
ни одно ее состояние не
имеет эквивалентных. Сле-
Следовательно, в рассматривае-
рассматриваемом частном случае иско-
искомая минимальная машина
должна быть эквивалентна
заданному автомату Л.
Построим сначала не ми-
минимальную, но удобную для
минимизации /7-машину,
реализующую автомат Л с
числом состояний, равным
числу строк заданного авто-
автомата (табл. 9.1). На диаграмме состояний этой машины
изобразим столько кружков, сколько имеет строк задан-
заданная таблица автомата, и перенумеруем все кружки под-
подряд числами 1, 2, ...,/. В нашем примере табл. 9.1
имеет четыре строки и на диаграмме состояний располо-
расположено четыре кружка (рис. 9.9).
Соединим кружки стрелками в соответствии с задан-
заданной таблицей автомата. Над каждой стрелкой в каче-
N\ p
х2
*з
*4
Pi
к
х2
*4
Р2
*3
А2
*3
Рз
А2
*4
§ 9.7J - МИНИМИЗАЦИЯ ПОСЛЕДОВАТЕЛЬНОСТНОЙ МАШИНЫ 335
стве первого символа указывается индекс р, соответ-
соответствующий этой стрелке по таблице автомата, а в ка-
качестве второго символа — номер кружка, к которому
подходит Стрелка. Надписи на рис. 9.9 указаны в соот-
соответствии с тгабл\ 9.1.
Будем трактовать теперь построенный граф
(рис. 9.9) как диаграмму состояний некоторой Я-ма-
Я-машины. Для этого номер t-ro кружка заменим символом
\
0,0
Рис. 9.9.
Рис. 9.10.
щ, а надпись на стрелке вида (т, п) — парой символов
(ртДп); такая замена для графа рис. 9.9 показана
на рис. 9.10.
Построим теперь матрицу соединений Я-машины,
диаграмма состояний которой изображена на рис. 9.10:
0
(Pi.
(Рз>
(P2» xi)v(p3» К) (pi
0
О
О
0
(Pi.
В соответствии с описанным способом построения диа-
диаграммы состояний в матрице соединений все ненулевые
336 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН / [ГЛ. IX
элементы любого столбца имеют одинаковые вторые ин-
индексы, совпадающие с номером столбца.
Исходя из матрицы С, можно путем симметричного
разбиения этой матрицы построить матрицу соединений
С минимальной последовательностной jtoam/шы, экви-
эквивалентной исходной и, следовательно, /являющейся ми-
минимальной последовательностной машиной, работающей
как заданный автомат А. '
Разобьем сперва матрицу С на А -матрицы лишь го-
горизонтальными линиями (т. е. сделаем первый шаг по-
построения симметричного разбиения). В нашем примере
1-Матрицу образуют строки первая и четвертая. Поста-
Поставив их рядом, будем иметь
C = —
0
0
(Pi. xl
,(P* *i)V(f
3, *,)
(Pl> X4)
(Pi, X4)
(РЗ, Х4>
0
(Рз>
(Рз>
(P2»
(p
X2)
X2)
x2)
X2)
(P2» хз)
0
0
Горизонтальные линии следует провести между второй
и третьей и между третьей и четвертой строками. После
этого матрица С оказывается разбитой на три 1-мат-
1-матрицы. Каждая 1-матрица этого разбиения обладает
следующим свойством: в каждом столбце стоят либо
нули, либо совпадающие пары. Так, в верхней 1-мат-
1-матрице (состоящей из двух строк), в первом столбце стоят
нули, во втором столбце стоят пары (рь Я4), в третьем —
(рз, ^), в четвертом — (р2, Я3). Это свойство есть след-
следствие отмеченного выше свойства матрицы С. В самом
деле, если вторые цифры пар каждого столбца во всей
матрице С одинаковы, то в строках этой матрицы, со-
содержащих лишь одинаковые пары (образующие 1-мат-
1-матрицу), будут совпадать и первые цифры пар каждого
столбца.
Но если так, то для выявления групп эквивалентных
состояний достаточно разбить матрицу С на 1-матрицы
лишь горизонтальными линиями; ввиду совпадения эле-
элементов в столбцах каждой 1-матрицы проведение сим-
§9.7]
ШНИМИЗАЦИЯ ПОСЛЕДОВАТЕЛЬНОСТНОЙ МАШИНЫ
337
метричщлх вертикальных линий никогда не сможет
«испортись» разбиения.
Это свойство означает следующее: разбиение состоя-
состояний Я-мащины^ имеющей матрицу состояний С, на груп-
группы эквивалентных состояний и на группы состояний,
эквивалентных относительно множества L\, содержа-
содержащего все входныеЧ последовательности длины 1, совпа-
совпадают. Поэтому для выяв-
выявления всех групп эквива-
эквивалентных состояний до-
достаточно построить раз-
разбиение на группы состоя-
состояний, эквивалентных отно-
относительно множества L\,
что и достигается путем
разбиения матрицы С го-
горизонтальными линиями
на 1-матрицы.
Итак, в нашем случае
состояние xi Я-машины,
реализующей автомат А,
эквивалентно состоянию
х4. Чтобы построить мини-
минимальную Я-машину, заменим эти два состояния одним
состоянием. Для этого проведем симметричные вер-
вертикальные линии между вторым и третьим, и межд>
третьим и четвертым столбцами матрицы С и за-
заменим каждую 1-матрицу полученного симметричного
разбиения объединением всех ее элементов. Матрица
соединений С минимальной Я-машины тогда будет
иметь вид
Х1 Х2 Х3
Xi)V(p3> К) (Рг> h) О
„ -(Р2> Xl)V(p3> Xll (Pl> ^2) О
а ее диаграмма состояний показана на рис. 9.11.
Отметим в заключение, что совпадающим строкам
матрицы С (в нашем случае это первая и четвертая
строки) всегда соответствуют совпадающие строки
22 М. А. Айзерман, Л. А. Гусев и др.
Рис. 9.11.
338 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН {ГЛ. IX
таблицы заданного автомата А (табл. 9.1, первая и чет-
четвертая строки), и наоборот. Поэтому, просматривая таб-
таблицу заданного автомата Л, можно сразу сказать, сколь-
сколько состояний будет иметь минимальная Я-машина, реа-
реализующая автомат А. Для этого нужной лид1Ь опреде-
определить число различных строк таблицы автомата Л.
А
А'
X
>
Рис. 9.12.
Построив диаграмму состояний, можно по ней выпи-
выписать табличы автомата А' и преобразователя Ф, кото-
которые образуют по схеме рис. 9.12 минимальную /7-маши-
ну, работающую как автомат А. В нашем примере
(рис 9.10) эти таблицы имеют вид табл. 9.2 и 9.3. Из
Таблица 9.2
Таблица 9.3
\. р
•X, X.
*1
*3
Pi
*1
*1
*2
Р2
*3
*2
Рз
*2
*1
*1
\. Р
X \.
*1
ч
Pi
*4
Р2
*з
\2
К
• Рз
*2
^4
^1
описанного на примере способа построения табл. 9.2 и
9.3 видно, что как в этом примере, так и в общем слу-
случае, таблица автомата Л'.(в нашем примере табл. 9.2)
могла бы быть получена и непосредственно по заданной
таблице автомата А (в нашем примере табл. 9.1). Для
этого в табл. 9.1 следует одну из двух совпадающих
строк (например, четвертую стррку) вычеркнуть (если
§ 9.7] МИНИМИЗАЦИЯ ПОСЛЕДОВАТЁЛЬНОСТНОЙ МАШИНЫ 339
совпадает несколько строк, то вычеркнуть следует все,
кроме одной) и всюду в оставшейся таблице символы,
совпадающие с символами, стоящими в левых частях
вычеркнутых строк (в нашем случае Х4), заменить на
символ, стоящий в левой части оставленной строки (Х4
заменить на М)\
Таблицу преобразователя также можно получить,
исходя непосредственно из таблицы заданного авто-
автомата А. Для этого\в каждой строке таблицы преобра-
преобразователя, левой частью которой является символ х*, .сле-
.следует вписать правую часть строки таблицы автомата Л,
в левой части которой стоит символ Я*.
Таким образом, в итоге имеется простой и удобный
алгоритм для построения таблицы автомата А' и преоб-
преобразователя Ф, которые по схеме рис. 9.12 образуют ми-
минимальную последовательностную машину, реализую-
реализующую автомат А. Построение же диаграммы состояний и
матрицы соединений является лишь промежуточным
этапом, необходимым для доказательства предлагае-
предлагаемого алгоритма.
2. Множество L не содержит
последовательностей, имеющих
два одинаковых символа подряд
Если через L\ обозначить множество входных после-
последовательностей длины 1, через Е — множество, содер-
содержащее все возможные входные последовательности, то,
очевидно, будет выполняться соотношение
Lx(zL(zE. (9.2)
Если число групп эквивалентных состояний обозначить
через т*, число групп состояний, эквивалентных отно-
относительно L — через т, а число групп состояний, экви-
эквивалентных относительно L\, — через т**, то из (9.2)
следует
В пункте 1 этого параграфа было показано, что
в рассматриваемом случае разбиения на группы экви-
эквивалентных состояний и на группы состояний, эквива-
340 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ. IX
лентных относительно Lu совпадают. Следовательно,
т** = т*, и из (9.2) получаем
т** = т —
Поэтому в рассматриваемом случае состояния, эквива-
эквивалентные относительно Lu будут эквивалентны и относи-
относительно Е. Минимизацию можно провести, заменив ка-
каждую группу состояний одним состоянием по способу,
изложенному выше, когда считалось, что L = Е. Итак,
в рассматриваемом случае минимальные Я-машины для
множества Е и для множества L совпадают, и миними-
минимизацию можно проводить так, как будто бы на входные
последовательности никаких ограничений не наложено.
§ 9.8. Минимизация последовательностиых машин
в случае ограничений типа Ауфенкампа
К проблеме минимизации в этом случае естественно
подойти следующим образом.
Пусть имеется Я-машина Nek состояниями, имею-
имеющая любые ограничения типа Ауфенкампа. Под выра-
выражением «минимизировать машину N» мы будем пони-
понимать, что нужно построить новую Я-машину Р, имею-
имеющую минимальное число состояний и при этом удовле-
удовлетворяющую требованию: каждому состоянию х,- машины
N должно соответствовать хоть одно состояние %. ма-
машины Р, такое, что:
а) Всякая входная последовательность, допустимая
для машины N, находящейся в состоянии хг-, была бы
допустима и для машины Р, находящейся в состоя-
состоянии хг
б) Машина N, запущенная в состоянии х*, и маши-
машина Р, запущенная в состоянии % получив на вход лю-
любую (но одну и ту же) последовательность из множества
входных последовательностей, допустимых для машины
N, находящейся в состоянии хг-, преобразуют ее в оди-
одинаковые выходные последовательности.
Условимся говорить, что машина Р (не обязательно
минимальная), для которой выполняются условия а) и
б), осуществляет псевдоотображение машины N.
§9.8] МИНИМИЗАЦИЯ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН 341
Так^м образом, машина Р, осуществляющая псевдо-
отобраз^ение машины N, «может делать» все то, что и
машина W. Она может воспринять любую входную по-
последовательность, допустимую для машины N, и перера-
переработать ее в ту же самую выходную последовательность.
Ниже описан алгоритм Ауфенкампа, позволяющий
строить машину Р, осуществляющую псевдоотображе-
псевдоотображение машины N с меньшим числом состояний, чем маши-
машина М, но не обязательно минимальную.
Ограничения типа Ауфенкампа на диаграмме со-
состояний проявляются в том, что число стрелок, отхо-
отходящих от некоторых кружков, меньше г (г—число раз-
различных входных воздействий pi, p2, ..., рг). Это озна-
означает, что машина, находящаяся в каком-либо состоя-
состоянии, не может воспринять некоторые входные воздействия.
По диаграмме состояний заданной машины N мож-
можно построить ее матрицу соединений С. Ограничения
отразятся на матрице соединений С в том, что в С мо-
могут быть строки, в которых содержится число пар, мень-
меньшее чем г, так что некоторые входные воздействия в этих
строках не присутствуют.
Рассмотрим, например, матрицу соединений
Xj %2 X3 X4 X5
Х1
0 (Pi> Xo) (Рз' Хг) О О
(р2, ^) 0 0 (р3, ^2) О
О (р3, х2) О 0 (pi, \))
^4 0 0 (р2, а2) О О
Х5 _ (Рг> Хг) 0 (р!, ^з) 0 0 _
В первой строке этой матрицы нет пары, связанной
с воздействием рг, во второй строке — с pi, а в четвер-
четвертой строке есть всего одна пара, связанная с рг.
Назовем обобщенной 1-матрицей такую подматрицу
матрицы С, которая обладает следующим свойством:
если в какой-либо строке обобщенной 1-матрицы встре-
встречается пара (рт, Хп), то в остальных строках не встре-
встречаются пары, имеющие тот же самый первый символ рт
и иной второй символ.
342 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ. \У
В [5] доказывается теорема, которую мы здесь при
водим без доказательства: если матрица С симметрич-
симметрично разбита на обобщенные 1-матрицы, причем в ка-
каждой строке обобщенных 1-матриц не встречаются две
матрицы, в которых есть пары, имеющие одинако-
одинаковые первые символы, то состояния в каждой группе
разбиения псевдоэквивалентны.
Можно уменьшить число состояний машины N, за-
заменив каждую группу псевдоэквивалентных состоя-
состояний одним состоянием. Это может быть выполнено
путем замены каждой
обобщенной 1-матрицы
симметричного разбиения
матрицы С одним эле-
элементом, являющимся объ-
объединением (дизъюнкцией)
всех элементов заменяе-
заменяемой 1-матрицы. В итоге
будет получена матри-
матрица С машины Р, осуще-
осуществляющей псевдоотобра-
псевдоотображение машины N и имею-
имеющей меньшее число
состояний, если только
симметричное раабиение
было нетривиальным.
Построение симмет-
симметричного разбиения проил-
проиллюстрируем на примере.' Пусть машина N имеет диа-
диаграмму состояний, показанную на рис. 9.13. Ее матрица
соединений С была приведена на стр. 341. Разобьем
сперва матрицу С горизонтальными линиями на обоб-
обобщенные 1-матрицы. В отличие от случая, когда машина
не имела ограничений и разбиение на 1-матрицы произ-
производилось единственным способом (с точностью до по-
порядка строк внутри группы), здесь возможно несколько
вариантов. Так, можно разбить строки на три группы,
включив в первую группу 1-ю и 4-ю строки (так как они
образуют обобщенную 1-матрицу), во вторую группу —
2-ю и 3-ю строки и в третью группу — 5-ю строку. Мож-
Можно разбить строки и по-иному, на Две группы, включив
Рис. 9.13.
§9.8] МИНИМИЗАЦИЯ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН 343
в первую группу 1-ю, 2-ю и 3-ю строки, а во вторую —
4-ю и 5-ю строки. От выбора того или иного варианта
будет зависеть и окончательный результат симметрия-,
ного разбиения.
Выберем, например, такой вариант разбиения строк
матрицы С на две группы: в первую группу войдут 1-я
и 2-я строки, а во вторую — 3-я, 4-я и 5-я. Проводим
горизонтальную линию между 2-й и 3-й строками мат-
матрицы С и разбиваем ее на две обобщенные 1-матрицы.
Теперь следует симметрично провести вертикальную
линию между 2-м и 3-м столбцами. Эта линия наше раз-
разбиение «портит», так как в нижней строке подматриц
оказались две обобщенные 1-матрицы, содержащие
пары с одинаковыми первыми символами р2. Чтобы ис-
исправить положение, проведем горизонтальную линию
между 4-й и 5-й строками (в общем случае имеется
также несколько вариантов «исправления»). Теперь уже
нет строк подматриц, содержащих пары с одинаковыми
первыми символами.
Проводим еще симметричную вертикальную линию
между 4-м и 5-м столбцами, на чем симметричное раз-
разбиение и заканчиваем.
Из разбиения мы видим, что машина N имеет три
группы псевдоэквивалентных состояний: {хь хг}, {хз, щ)
и {х5}. Псевдоотображение машины N может быть осу-
осуществлено машиной Рг с тремя состояниями, имеющей
матрицу соединений
X
(Рз>
(Р2»
(Pl.
2
Х2)
Х2)
Xg)
*з
0
(Pi. Хо)
0
(Plj
(Рз«
(Р2»
Ее диаграмма состояний приведена на рис. 9.14.
Если бы мы выбрали другой вариант разбиения строк
матрицы на группы и провели бы горизонтальную ли-
линию между 3-й и 4-й строками, то конечный результат
был бы иной. В самом деле, вертикальная линия
между 3-м и 4-м столбцами образовала бы в верхней
строке подматриц две подматрицы, содержащие пары,
344 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН |ГЛ IX
имеющие первый символ рз, и пришлось бы провести еще
две горизонтальные и вертикальные линии, чтобы ис-
исправить это положение (причем никакая перестановка
Рис. 9.14.
трех верхних строк не исправила бы его). Матрица С раз-
разбилась бы симметрично на обобщенные 1-матрицы так:
xl
" 0
(P2» К)
0
0
_(P2» Ю
4
(Pi» lo)
0
(Рз» Ю
0
0
*3
(РЗ» Х5
0
0
(P2» 2
(Pi» h
)
)
)
x4
0
(Рз» Ю
0
0
0
0 "
0
(pi» K)
0
0
Машина Р", осуществляющая псевдоотображение ма-
машины N, имела бы уже четыре состояния и матрицу С"
Xj Х2 Х3 Х4
О (pi, К) (Рз» Хг) О П
(Рг» xi) 0 0 (р3, Х2)
О (Рз»*2) О (Pl, Хо)
- (Рг. h) О (р2» x2)V(pi, Ч) Q J
§9.8] минимизация гюСлеДовАтельНостных мАшиН 345
Следовательно, для того чтобы добиться наилучшего
результата при применении этого алгоритма, нужно пе-
перепробовать все варианты симметричного разбиения
матрицы С на обобщенные 1-матрицы*).
Кроме того, этот алгоритм не обязательно дает ми-
минимальную машину Р. Известны примеры, когда ма-
машина N имеет группы псевдоэквивалентных состояний,
Рис. 9.15.
которые могут быть заменены одним состоянием (тем
самым машина N минимизируется), а условие тео-
теоремы, приведенной в этом параграфе, не выполняется.
В качестве такого примера рассмотрим диаграмму
состояний Я-машины, показанную на рис. 9.15. Огра-
Ограничение на входные последовательности здесь состоит
в том, что для машины, находящейся в состоянии хь не-
недопустимо входное воздействие рь Матрица соединений
*) Заметим, что этот алгоритм равносилен перебору всех до-
доопределений заданной машины, т. е. перебору всех возможных ва-
вариантов проведения недостающих стрелок с последующей минимиза-
минимизацией полученных машин без ограничений на входные последова-
последовательности.
346 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ. I&
Я-машины рис, 9.15 имеет вид
С =
Хо) (Рз» Хо)
- (Рз>
Матрица С может быть только двумя способами симмет-
симметрично разбита на обобщенные 1-матрицы, так что со-
состояния разбиваются на группы {иь иг},, {из} первым
способом и {иь из}, {иг} вторым способом:
С ==¦
'(Ра.
(Pi.
(Рз> хо.
(Рз.
ъЛ
a.
(Р2 Х0>
о
(Р2.
'(Р2. Хо) 0
(Рз. Хо) (Pi. }
-(Pi
(р
2»
(Pi.J
Ч
(fe. 3
(Р2. Хо)
(Рз»
Легко убедиться, что как в первом, так и во втором
случае условия последней теоремы Ауфенкампа (см.
стр. 342) не выполняются: в первом случае две верхние
обобщенные 1-матрицы разбиения имеют общую пару
(р2. ^о), связанную с входным воздействием рг; во вто-
втором случае общими оказываются пары (рг, Яо) и (рз, Яо).
В то же время исследуемая машина, (рис. 9.15) имеет
минимальную Я-машину с двумя состояниями, диаграм-
диаграмма состояний которой изображена на рис. 9.16. Соот-
Соответствие состояний при псевдоотображении таково: со-
состояниям xi и иг соответствует состояние уса, а состоя-
состоя*
нию из — состояние кв *).
*)' На рассматриваемом примере ясно видно также, что любое
доопределение заданной машины рис. 9.15 не позволяет получить
минимальную машину с двумя состояниями: при любом варианте
прохождения стрелки с первым индексом pi от состояния Xi и с лю-
любым вторым индексом эквивалентных состояний не возникает.
§9.81 МИНИМИЗАЦИЯ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН 347
Ниже описан метод Гилла, позволяющий строить ми-
минимальную машину для любой заданной Я-машины с
ограничениями типа Ауфенкампа (см. [149]). При приме-
применении этого метода следует прежде всего выписать все
пары совместимых состояний заданной машины. Для
определения совместимости состояний известно много
различных приемов. Опишем один из них.
Пусть,, например, надо определить совместимость
г-го и /-го состояний. Построим из вершины (?, /) вверх
ветви «дерева», соответствующие об-
общим для щ и щ входам.
Если при этом хотя бы при одном
входном воздействии получаются раз-
разные выходы, несовместимость состоя-
состояний уже выявлена. В противном слу-
случае на ветвях надписываются со-
соответствующие пары «вход — выход»,
а в конце ветвей указываются те со-
состояния, в которые переходят состоя-
состояния Щ И Xj.
Далее процесс повторяется, исходя
из вновь построенных узлов. В ходе
построения узлов вновь возникающие
узлы вычеркивают в следующих трех
случаях:
1. Если узел с надписью, состоя-
состоящей из тех же символов, уже встре-
встречался где-либо при построении дерева (на этом же яру-
ярусе либо на предшествующих ярусах).
2. Если обе надписи у узла совпадают, т. е. выходя
из состояний Хг и Xj на этом шаге подходим к одному
и тому же состоянию.
3. Если из этого узла нельзя провести ни одной новой
ветви, т. е. состояния, соответствующие этому узлу, не
имеют общих входных воздействий.
Построение дерева кончается, когда либо выявлена
несовместимость проверяемых состояний, либо все пути
в дереве приводят к вычеркнутым узлам. В этом послед-
последнем случае делается заключение также и о том, что сов-
совместимы все пары состояний, соответствующие всем
узлам (вычеркнутым и невычеркнутым) этого дерева.
Рис. 9.16.
348 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ. IX
В качестве примера на рис. 9.17 показано такое де-
дерево для определения совместимости состояний hi и И2
машины рис. 9.15, а для определения совместимости
состояний иг и из машины рис. 9.18 дерево имеет вид
рис. 9.19.
И в первом и во втором случаях исследуемые со-
состояния оказываются совместимыми; в первом случае,
кроме hi и иг, выявляется еще
одна пара совместимых состоя-
состояний hi и из, а во втором слу-
случае, кроме иг и из, оказываются
СОВМеСТИМЫМИ Щ И Иб, Из И И5,
Hi И Иг-
Описанный прием позво-
позволяет также оценить наиболь-
наибольшее число шагов, которые при-
придется сделать в наихудшем
рис 9 17. случае при определении совме-
совместимости двух заданных со-
состояний машины, имеющей всего п состояний. Такая
оценка имеет вид *)
Имея возможность распознавать совместимость со-
состояний, можно для всякой машины выписать все пары
совместимых состояний. Для машины рис. 9.15 таких
пар две: {иь иг} и {иь и3}, а для машины рис. 9.18 —
девять пар:
1» X3J» 1Х1»
> X3J» lX2» X4J»
» ХбЬ (Х4» ХбЬ (9.3)
Далее следует построить группы псевдоэквивалентных
состояний. Например, в списке (9.3) содержатся пары
*) Эта оценка точная, так как могут быть приведены примеры,
где она достигается. Интересно сравнить эту оценку с оценкой длины
эксперимента, распознающего неэквивалентность состояний машины
без ограничений (см. далее § 11.2); при отсутствии ограничений эта
оценка имеет вид / =? (/?— 1), т, е. не содержит членов с я2.
§9.8]
МИНИМИЗАЦИЯ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН
349
(хь иг), {иь из} и {иг, из}, поэтому состояния хь иг и
образуют группу
1, Х2, Из}-
псевдоэквивалентных состояний *)
Рис. 9.18.
Рассуждая подобным образом, можно выписать раз-
разбиение всех состояний машины на минимальное число
групп псевдоэквивалентных со-
состояний. В нашем примере та-
таких групп будет четыре:
1Х1> Х2> Х3> X5J» 1*2» X4J» lx3» X6J»
1Х4» ХбЬ
В общем случае, как и в
данном примере, эти группы
пересекаются.
Вернемся теперь к вопросу
о минимизации Я-машины с
ограничениями типа Ауфен-
кампа. Пусть задана произ- ^
вольная Я-машина Sen со-
состояниями и пусть для нее построена хотя бы одна мини-
минимальная машина Smin с k состояниями. Если k < n, то
A,3)
Рис. 9.19.
*) Напомним, что группой псевдоэквивалентных состояний назы-
называется такая группа, все состояния которой попарно совместимы.
350 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ. IX
обязательно хотя бы одному состоянию машины 5min со-
соответствует при псевдоотображении два или более состоя-
состояний машины S. Обозначим множество всех состояний
машины 5, соответствующих состоянию и* машины SmiIl>
через 2* и предположим, что построены такие множества
состояний 2Ь 22, ..., 2л машины для всех состояний
хь иг, ..., хл машины Smia- Это разбиение состояний
машины 5 обладает следующими свойствами:
1. Разбиение ?р ?2, •••» ^* охватывает все состоя-
состояния машины S, т. е. для всякого состояния машины 5
можно указать одно или несколько множеств 2, кото-
которым это состояние принадлежит.
2. Состояния, принадлежащие любому 2г-, псевдо-
эквивалентны.
3. Под действием любого входного воздействия ps
все те состояния любой группы 2г-, которые допускают
это ps, переходят в состояния одной и той же новой
группы 2j (возможно / = /).
Первые два указанных свойства очевидны. Третье
свойство нуждается в объяснении. В самом деле, пусть
состоянию и* машины 5min соответствует группа 2г-, а со-
состоянию щ, в которое переходит иг- под воздействием ps,
соответствует группа %у Допустим, что имеется такое
состояние в группе 2г-, которое под воздействием ру пе-
переходит в состояние и*, не входящее в группу 2j. Тогда
путем наблюдения поведения машин 5 и Smin при лю-
любых входных последовательностях, допустимых для со-
состояний группы 2г-, можно прийти к выводам: а) всякая
последовательность, допустимая для состояния щ ма-
машины 5, допустима и для состояния 'щ машины Smin;
б) при любой входной последовательности, допустимой
для иг, обе машины — машина S, начинающая работу
с иг, и машина 5min, начинающая работу с xj,— выдадут
одинаковые выходные последовательности.
Но это означает, что состояние и/ соответствует со-
состоянию X] при псевдоотображении и, следовательно,
должно быть, вопреки нашему допущению, включено
в группу 2j. Это и доказывает справедливость третьего
свойства.
Разбиение 2i, 22, ..., 2ft называется собственным
разбиением состояний машины S.
МИНИМИЗАЦИЯ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН
351
Из изложенного следует, что алгоритм минимизации
сводится к отысканию минимального собственного раз-
разбиения состояний машины 5 (одного или нескольких)
и последующей замены каждой группы 2* одним состоя-
состоянием. Так как все состояния каждой группы 2* псевдо-
эквивалентны, каждая группа 2* должна включаться
(или совпадать) в какую-либо из групп минимального
разбиения состояний машины 5 на группы псевдоэкви-
псевдоэквивалентных состояний.
Таким образом, этот алгоритм включает в себя пере-
переборы различных возможных собственных разбиений за-
заданной машины 5 при отыскании минимального соб-
собственного разбиения. Эти переборы могут быть весыца
громоздкими. Существуют алгоритмы, упорядочиваю-
упорядочивающие подобные переборы (см., например, [149]). Суще-
Существуют также «промежуточные» алгоритмы, которые,
уменьшая переборы, позволяют получить результат луч-
лучший, чем при применении алгоритма Ауфенкампа, хотя
и не гарантируют минимальности.
Вернемся теперь к нашим двум примерам (рис. 9.15
и 9.18).
Для машины рис. 9.15 разбиение на группы псевдо-
псевдоэквивалентных состояний {xi, хг} и {хь хз} является и
минимальным собственным разбиением. Проверим это.
Обозначим группу {xi, X2} буквой А, а группу {хь хз}
буквой В. Проследим возможные переходы:
для хг недопустимо рг, 1 группа А или
1 Xj переходит в xlt J группа В,
Группа А
I
Z }
Группа В
при
v
для
недопустимо Pl,
переходит в к3
, ]
при Р2 *> пеРех°Дит в «i. 1 группа А,
v п х3 переходит в х2, ) vl
«1 переходит в «,. j д
3, х3 переходит в xlt J r<7
352 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН (ГЛ. IX
Теперь легко построить две минимальные машины
для машины рис. 9.15, заменив состояние группы А
Рис. 9.20.
Рис. 9.21.
состоянием ха, а состояния группы В состоянием
Одна из этих минимальных машин изображена на
рис. 9.16, вторая — на рис. 9.20. Для машины рис. 9.18
(fv
Рис. 9.22,
также имеются два возможных минимальных собствен-
собственных разбиения. Это разбиение (^Xj), (х3, х5), (х4, у6) и раз-
§ 9.9] ОПРЕДЕЛЕНИЕ ЭКВИВАЛЕНТНОСТИ МАШИН 353
биение (хр х5), {х2, х4), (х3, Xg]. Диаграмма состояний ми-
минимальной машины, соответствующая первому собствен-
собственному разбиению, изображена на рис. 9.21, а соответ-
соответствующая второму — на рис. 9.22.
§ 9.9. Об ином определении эквивалентности
последовательностных машин
Иногда в литературе встречается определение экви-
эквивалентности последовательностных машин, отличное от
данного в § 9.4. Хотя это определение внешне похоже
на наше, однако они сильно различаются по существу.
Определение, о котором идет речь, может быть сфор-
сформулировано так: две Я-машины S и G называются экви-
эквивалентными, если при подаче на вход машин S и G лю-
любой входной последовательности (одинаковой для обеих
машин) каждому состоянию чц машины 5 будет соот-
соответствовать хотя бы одно состояние ij машины G и, на-
наоборот, каждому состоянию |j машины G будет соот-
соответствовать хотя бы одно состояние уц машины 5 такое,
что машины 5 и G, поставленные в состояния щ и ?j,
произведут одинаковые выходные последовательности.
Здесь соответствие состояний машин S и G зависит,
вообще говоря, от входной последовательности. Для
некоторых входных последовательностей некоторым со-
состояниям машины 5 могут соответствовать одни состоя-
состояния машины G, а для других входных последователь-
последовательностей тем же состояниям машины 5 могут соответ-
соответствовать другие состояния машины G (и наоборот).
Требуется лишь, чтобы для любой входной последова-
последовательности такое взаимно однозначное соответствие су-
существовало.
Практический недостаток этого определения состоит
в том, что для выбора эквивалентного начального со-
состояния надо заранее знать соответствующую входную
последовательность. В большинстве же практически
важных задач входная последовательность заранее не-
неизвестна.
В определении, данном в § 9.4, требуется большее, чем
в определении настоящего параграфа, а именно, чтобы
соответствие состояний машины 5 состояниям машины
23 М. А. Айзерман, Л. А. Гусев и др. ..
354 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ. IX
Таблица 9.4
\- р
к \^
л2
h
Pi
*з
К
Р2
G не зависело от подачи той или иной входной последо-
последовательности, а было бы для всех допустимых последова-
последовательностей одно и то же. Если, например, в нашем слу-
случае состояние хг- машины S соот-
соответствует состоянию |j эквива-
эквивалентной машины G, то машины
S и G, находясь соответственно в
состояниях хг- и gj, произведут
одинаковые выходные последова-
последовательности при подаче на вход
любых одинаковых допустимых
входных последовательностей*).
Требование определения § 9.4
сильнее. Поэтому, если принять
иное определение эквивалентности
последовательностных машин,
можно построить для заданной
машины 5 минимальную Я-машину G, ей эквивалентную,
с меньшим числом состояний, чем это удалось бы сде-
сделать, исходя из определения
§ 9.4. Проиллюстрируем это
на примере.
Пример. Задан автомат
Ли множество L допустимых
входных последовательностей,
в котором содержатся все
последовательности, не имею-
имеющие двух одинаковых сим-
символов подряд. Требуется по-
построить минимальную Я-маши-
Я-машину, отображающую относитель-
относительно L автомат Л, заданный ос-
основной таблицей (табл. 9.4) **).
Диаграмма состояний авто-
автомата А изображена на
рис. 9.23. Из табл. 9.4 в соответствии с § 9.7 следует, что
при определении эквивалентности по § 9.4 минимальная
Рис. 9.23.
*) В некоторых работах эквивалентность в смысле § 9.4 назы-
называется сильной эквивалентностью, а эквивалентность в смысле настоя-
настоящего параграфа слабой эквивалентностью.
**) В табл, 9.4 выполнена замена щ на Я/ (см. § 9J),
§9.9]
ОПРЕДЕЛЕНИЕ ЭКВИВАЛЕНТНОСТИ МАШИН
355
Я-машина, работающая как автомат Л, будет иметь три
состояния (так как никакие строки в табл. 9.4 не совпа-
совпадают).
Примем теперь указанное в этом параграфе опреде-
определение эквивалентности и перестроим диаграмму состоя-
состояний (рис. 9.23) автомата Л, заменив ее диаграммой[экви-
диаграммой[эквивалентной (в смысле § 9.4)
машины, которая будет
удобна для последующей
минимизации. Перест-
Перестройку произведем сле-
следующим образом. Заме-
Заменим каждый кружок щ
исходной диаграммы со-
состояний г кружками, обо-
обозначенными xj, х", х"', . . .
От каждого из г новых
кружков проведем те же
стрелки с теми же надпи-
надписями, которые отходили
от исходного кружка.
Подходящие же к круж-
кружку щ стрелки распреде-
распределим теперь следующим
образом между новыми
кружками: к кружку %\
подходят лишь те из под-
подходивших К КруЖКу Xi
стрелок, которые имеют первый символ pi, к кружку
*/ — имеющие первый символ р2 и т. д.
Перестроив по этому правилу диаграмму состояний
рис. 9.23, получим диаграмму состояний, показанную
на рис. 9.24. В этом примере кольцевую стрелку с над-
надписью (pi, Х2), идущую от кружка хг к нему же, считаем
и за отходящую и за подходящую; в качестве отходящей
она заменяется стрелками, Отходящими от кружков к'2
и *2 на диаграмме рис. 9.24, которые подходят лишь
к кружку к. Кружок к2 оказался охваченным кольцом.
Отметим, что из свойства диаграммы состояний рис. 9.23,
состоящего в том, что к кружку щ подходят лишь
23"
356 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ. IX
ветви, имеющие надписи, вторые символы которых Я* (это
следствие того, что Я-машина работает как автомат),
следует свойство диаграммы состояний рис. 9.24: к лю-
любому кружку группы %'г •*.'[, •*!" и т. д. подходят лишь
стрелки со вторым символом Я*. На рис. 9.24 эти группы
кружков обведены пунктирными линиями.
Перестроенная диаграмма состояний (рис. 9.24) со-
соответствует машине N't эквивалентной (в смысле § 9.4)
исходному автомату А (относительно множества Е всех
возможных последовательностей). Чтобы убедиться, что
диаграммы состояний рис. 9.23 и 9.24 есть диаграммы
состояний эквивалентных машин, достаточно проверить,
что состояния каждой группы, обведенной пунктирной
линией на диаграмме рис. 9.24, эквивалентны между
собой (образуют группу эквивалентных состояний). За-
Заменив каждую группу эквивалентных состояний одним
состоянием, мы возвращаемся к диаграмме рис. 9.23.
Итак, мы построили машину N', эквивалентную
(в смысле § 9.4) автомату А и имеющую гораздо боль-
большее число состояний, чем автомат А (гп состояний). Но
эта диаграмма позволяет легко перейти от ограничений
входных последовательностей «в себе» к ограничениям
типа Ауфенкампа.
Рассмотрим какое-либо состояние, например срстоя-
ние %'[ диаграммы рис. 9.24. Будем теперь подавать на
вход машины N' лишь последовательности из L (ма-
(машина N' эквивалентна в смысле § 9.4 автомату А и от-
относительно L, так как L сЕ). Так как мы к состоянию
у![ можем подойти лишь по стрелке с надписью (р2, ki),
т. е. путем подачи входного воздействия р2, отойти от
него мы можем лишь по стрелке с надписью (pi, Я3),
потому что после рг нельзя подать еще раз р2. Следова-
Следовательно, по стрелке (рг, Яз), отходящей от кружка и*, мы
никогда проходить не будем, и ее можно стереть. Исклю-
Исключение мог бы составить лишь начальный момент: если
машине, находящейся в начальном состоянии Хр было
бы дано на вход воздействие рг, она перешла бы в со-
состояние Kg. Однако, принимая теперь новое определение
эквивалентности машин (в смысле § 9.9), можно избе-
избежать этой неприятности, ибо вместо кружка щ в каче*
§9.9]
ОПРЕДЕЛЕНИЕ ЭКВИВАЛЕНТНОСТИ МАШИН
357
стве начального можно выбрать кружок %%, от которого
отходит стрелка с надписью (рг, Яз) к состоянию из.
Рассуждая таким же образом, мы можем удалить
из диаграммы состояний все стрелки, отмеченные тремя
черточками.
В общем случае этот алгоритм «стирания стрелок»
таков: стрелка с первым символом ps, отходящая от
Рис. 9.25.
кружка xf (где s — число штрихов), должна быть уда-
удалена. Перестроенная удалением стрелок диаграмма
состояний рис. 9.24 изображена на рис. 9.25.
Полученная машина N", диаграмма состояний кото-
которой изображена на рис. 9.25, работает так же, как ма-
машина N' (и как автомат А), если на вход подавать лишь
последовательности из L. Но машина N" эквивалентна
относительно L машине N' (а. следовательно, и автома-
автомату А) уже в новом смысле: соответствие состояний ма-
машин /V" и N' уже зависит от входной последователь-
последовательности.
Машина N" имеет теперь ограничения типа Ауфен-
кампа: от каждого кружка отходят не все стрелки, т. s,
358 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ. IX
от «ограничений в себе» мы перешли к машине с огра-
ограничениями типа Ауфенкампа.
Минимизируем теперь машину N" с помощью алго-
алгоритма, описанного в § 9.8. Матрица соединений машины
N" имеет вид
С"'=
О
О
О
О
О
о
1
О
О
О
О
(р2,
*2
О
о
о
>*2)
о
О
о
о
о
о
о
о
О (?2> h)
(Pv h) 0
О (р2, Х3)
о о
о
о
о
о
Матрица С" в общем случае обладает свойством, вы-
вытекающим из отмеченных выше свойств диаграммы со-
состояний: в столбце матрицы, соответствующем состоя-
состоянию у,\ (s — число штрихов), могут стоять лишь пары
(ps> К) •
Алгоритм предписывает для уменьшения числа со-
состояний машины N" построить симметричное разбиение
матрицы С" на обобщенные 1-матрицы.
В рассматриваемом случае достаточно разбить ма-
матрицу С" на обобщенные 1-матрицы только горизонталь-
горизонтальными линиями; проведение вертикальных линий никогда
не сможет «испортить» разбиения.
Разбиение матрицы С" на обобщённые 1-матрицы
горизонтальными линиями можно провести многими спо-
способами. Например, если провести горизонтальные линии
между 2-й и 3-й и между 4-й и 5-й строками, то получим
разбиение состояний машины N" на группы Ы[, *П,
%2> *2 )' 1 V Х3 | •
Заменяя каждую группу одним состоянием, возвра-
возвращаемся к исходному автомату А (рис. 9.23) с тремя со-
состояниями. Однако среди разбиений матрицы С" суще-
существуют и такие, для которых число групп минимально.
В нашем случае одно из таких разбиений получаем, про-
§ 9.9] ОПРЕДЕЛЕНИЕ ЭКВИВАЛЕНТНОСТИ МАШИН 359
ведя линию между 3-й и 4-й строками матрицы С". Все
состояния разбиваются ею на две группы:(*J, \, *'2} и
|V хз» хз1- Очевидно, разбить матрицу С" так, что-
чтобы число групп было меньше двух, невозможно, так как
1-я и 4-я строки матрицы никогда не смогут войти в одну
обобщенную 1-матрицу.
Проводя теперь симметричную вертикальную линию
между 3-м и 4-м столбцами и объединяя элементы каж-
каждой обобщенной 1-матрицы, получим матрицу соедине-
соединений С" минимальной последовательностной машины N"'
*2 L (Pi.
0 (Pi, X3)V(p2, Хз)
0
Ее диаграмма состояний изображена на рис. 9.26.
Машина N"f осуществляет псевдоотображение маши-
машины N". Но так как в этом случае множества допусти-
допустимых входных последовательностей для всех состояний
машины N" совпадают
друг с другом и с L, то
имеет место и отображе-
отображение машины Л^" относи-
тельно множества L.
Заметим, что матрица рис 926.
С" имела две пары совпа-
совпадающих строк: 1-ю и 3-ю и 4-ю и 6-ю. Первая строка со«
ответствовала состоянию и{ (рИс. 9.25), а 4-я —состоя-
—состоянию Xg. На диаграмме состояний (рис. 9.25) мы видим, что
эти состояния могут быть только начальными — к круж-
кружкам, изображающим эти состояния, не подходят никакие
стрелки. Эти состояния могут быть удалены с диаграм-
диаграммы состояний, так как состояние к[ в качестве началь-
начального может быть заменено состоянием v!2\ от кружка к'2
как и от кружка xi, идет стрелка с надписью (рг, Хз)
к кружку Из- Аналогично состояние к^ в качестве на-
начального может быть заменено состоянием xj.
Производя, когда это возможно, подобные предвари-
предварительные упрощения, мы придем к диаграмме состояний
360 ЭКВИВАЛЕНТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН [ГЛ.1*
с меньшим числом кружков, т. е. к матрице соединений
меньшего порядка. В рассматриваемом случае- в каче-
качестве исходной можно взять не матрицу С", а матрицу
с; =
н
0
0
(Р2> Х1>
0
0
0
0
(Pl> К)
(Pl>
0
0
0
О
(Р2.
О
О
в которой нет строк и столбцов, составленных из одних
нулей. Построение симметричного разбиения матрицы
С* приводит к тому же результату, который получается,
если за исходную принята матрица С".
Сравнивая теперь построенную машину N"\ диа-
диаграмма состояний которой изображена на рис. 9.26, с ис-
исходным автоматом Л, диаграмма состояний которого
изображена на рис. 9.23, мы убеждаемся, что действи-
действительно выбор соответствия состояний машин рис. 9.26
и рис. 9.23 зависит от входной последовательности.
Так, если машина рис. 9.23 начинает работать с со-
состояния щ и получает входную последовательность
Р1Р2Р1Р2Р1Р2..., то для получения той же выходной' после-
последовательности машины рис. 9.26 ее следует установить
в состояние кг*, если же машина рис. 9.23, находящаяся
в том же состоянии кг, получает входную последова-
последовательность Р2Р1Р2Р1Р2Р1 •.., то для получения той же вы- "
ходной последовательности машину рис. 9.26 следует ?
установить в начальное состояние тц.
ГЛАВАХ
ПРЕОБРАЗОВАНИЕ ТАКТНОСТИ
ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН
§ 10.1. Общие соображения о преобразовании тактности.
Определение понятий изображения и воспроизведения
В гл. V, рассматривая различные методы техниче-
технической реализации конечных автоматов и последователь-
ностных машин, мы обратили особое внимание на метод
реализации автоматов на устойчивых состояниях, ле-
лежащий в основе построения релейно-контактных схем,
диодных схем, некоторых магнитных логических систем
и т. д. При технической реализации Я-машин этим ме-
методом машина требуемой тактности создается путем
использования равновесных состояний другой Я-маши-
ны, работающей в значительно более быстрой тактности.
Мы возвращаемся к этой проблеме для того, чтобы с бо-
более общих позиций рассмотреть задачу о преобразова-
преобразовании тактности, т. е. о построении Я-машин, работающих
в некоторой тактности, используя для этого Я-машины,
работающие в иной тактности. Для этого нам придется
прежде всего вспомнить некоторые понятия и определе-
определения, введенные в гл. V.
Пусть задана Я-машина 5. Подадим на вход маши-
машины 5 какую-либо последовательность символов р, на-
например р° р1 ... рр, и рассмотрим ленту, соответствую-
соответствующую этой последовательности (табл. 10.1).
Выберем теперь каким-либо способом возрастаю-
возрастающую последовательность тактов
*о <*i < *2 <'••'• <t» (ЮЛ)
например нулевой, второй, пятый такт и т. д., и выпи-
Ш из ленты Я-машинц S (из табл. 10.1) столбцы,
362
ПРЕОБРАЗОВАНИЕ ТАКТНОСТИ
[ГЛ. X
соответствующие этой последовательности. Выписанные
столбцы образуют табл. 10.2.
Таблица 10.1
Такт
0
р | р.
X
| Хо
1
Р1
X1
2
Р2
Х2
р
9Р
\р
...
...
...
Таблица 10.2
t
Р
X
to
Р*
\'-
<¦
р'-
и
,'»
X'-
...
Введем в рассмотрение новую тактность, приняв мо-
момент U за момент наступления /-го такта. Тогда
табл. 10.2 приобретает вид табл. 10.3, которая может
рассматриваться как результат работы некоторой иной
последовательносгной машины G.
Таблица 10.3
Такт
0
р | р"
X Х'°
1
р'1
X*'
• • •
• • •
• • ш
s
t:
• • •
Ф • •
• • •
Если заданная лента машины 5 (табл. 10.1), а зна-
значит, и перестроенная из нее лента (табл. 10.3) конечны,
§ ЮЛ] ОЪЩИЕ СООБРАЖЕНИЯ 363
то Я-машина G, реализующая ее, заведомо существует
(см. §8.2).
Для наглядности представим себе работающую Я-ма-
Я-машину, освещаемую в моменты ^о, t\, • • •» is, •¦• вспыш-
вспышками стробоскопа. Тогда нам покажется, будто бы она
перерабатывает последовательность рЧ рЧ •••» 9s в п0*
следовательность ХЧ ХЧ ..., X's в соответствии с
табл. 10.3, в то время как на самом деле Я-машина 5
работает в соответствии с табл. 10.1.
Предположим теперь, что моменты to, tu •. ¦ (в на-
нашем примере со стробоскопом — моменты вспышек) вы-
выбраны столь удачно по отношению к Я-машине 5, что
какую бы входную последовательность Я-машина 5 ни
перерабатывала, начиная с какого угодно начального
состояния и$, наблюдая ее лишь в моменты tOt tit ... ,
мы видим такую переработку входной последовательно-
последовательности в выходную, которую могла бы осуществить некото-
некоторая иная Я-машина G, начинающая работать с некото-
некоторого, быть может для каждой входной последовательно-
последовательности иного, начального состояния Kq.
В этом случае мы будем говорить, что осуществляет-
осуществляется преобразование тактности — Я-машина 5, работаю-
работающая в тактности, которую мы в дальнейшем условно
будем называть быстрой, преобразуется в Я-машину G,
работающую в тактности, которую мы далее будем ус-
условно называть медленной *).
Мы будем говорить также, что Я-машина 5 изобра-
изображает в медленной тактности Я-машину G.
Приведенное определение понятий изображения и
преобразования тактности достаточно широко, однако
оно обладает одним недостатком. Дело в том, что на-
начальное состояние kqq машины G определяется не только
по начальному состоянию %°s машины 5, но и по
входной последовательности p4t). Это означает, что для
*) Удобно представлять себе, что тактность быстрой машины и
в буквальном смысле слова быстрее тактности медленной машины.
Однако это не обязательно; машины S и G, вообще говоря, никак
не связаны друг с другом, и рассмотрение далее ведется в общей
случае, когда тактности машин 5 и G любые.
364 ПРЕОБРАЗОВАНИЕ ТАКТНОСТИ [ГЛ. X
различных входных последовательностей p(t) одному и
тому же состоянию и? машинь/ 5 могут соответство-
соответствовать различные начальные состояния машины G. Для
того чтобы найти начальное состояние Kq машины G,
надо, помимо состояния к8 машины 5, наперед знать,
какая входная последовательность будет подана на вход
машины 5. Возникает ситуация, весьма похожая на ту,
с которой мы встречались в гл. IX при определении по-
понятия эквивалентности Я-машины. В гл. IX нам удалось
сузить формулировку понятия эквивалентности так, что-
чтобы выбор начального состояния не требовал априорного
знания входной последовательности.
Попытка авторов аналогично сузить понятия изобра-
изображения и преобразования тактности в нашем случае не
привела к цели, так как если бы мы потребовали, чтобы
начальному состоянию к3 машины S соответствовало
всегда одно и то же состояние уР0 машины G (незави-
(независимо от входной последовательности), мы потеряли бы
возможность рассмотреть ряд важных и часто встречаю-
встречающихся на практике случаев преобразования тактности.
Далее к этому вопросу мы вернемся и на примерах по-
поясним это утверждение.
Поэтому мы дадим иные формулировки, более узкие,
чем приведенные выше, и не требующие при определении
начального состояния априорного знания всей входной
последовательности.
Алгоритм выбора возрастающей последовательности
U, t\, t2, ... будем называть законом преобразования
тактности.
Зададим этот закон. Будем говорить, что машина S,
работающая в быстрой тактности, изображает машину
G, работающую в медленной тактности, если для лю-
любого начального состояния к°8 машины 5 и произволь-
произвольной входной последовательности р°р!р2 • • • найдется хотя
бы одно начальное состояние v?Q машины G, определяе-
определяемое по начальному состоянию и? и по первому члену
входной последовательности р°, такое, что лента ма-
машины 5, соответствующая входной последовательности
pVp2*" и начальному состоянию Ио, рассматриваемая
§ Ю.1] \ЛБЩИЕ СООБРАЖЕНИЯ 365
лишь в моменты to\ t\, t2, ..., совпадает с лентой ма-
машины G, работающей, в медленной тактности и перера-
перерабатывающей входную\ последовательность p^p'ip^ при
начальном состоянии щ.
При таком определении понятия изображения на-
начальное состояние Kq машины G определяется по на-
начальному состоянию y,°s «быстрой» машины S и лишь
по первому символу входной последовательности.
Обратим теперь внимание на то, что быстрая машина
S, воспринимающая произвольную входную последова-
последовательность, обычно изображает медленную машину G,
воспринимающую входные последовательности лишь из
ограниченного множества LG. Это означает, что любой
вариант работы машины S, рассматриваемой лишь в мо-
моменты t0, t\, t2, ..., представится нам как один из ва-
вариантов работы изображаемой машины G со входной
последовательностью из LG.
Со случаем такого рода мы столкнемся далее в
§ 10.2, где множество LG будет состоять из последова-
последовательностей, содержащих лишь один символ. Изображе-
Изображение, вообще говоря, неоднозначно: при заданном законе
преобразования тактности заданная машина 5 может
изображать много различных машин; Gu G2, G3, ...
Этот вывод верен и в том случае, когда ограничения
множества входных последовательностей машины G не
происходит, т. е. когда LG = Е.
По аналогии с понятием относительной эквивалент-
эквивалентности (см. гл. IX) можно ввести и понятие относитель-
относительного изображения. Определение относительного изобра-
изображения отличается от определения изображения лишь
тем, что быстрая машина S может получать не любую
входную последовательность, а только последователь-
последовательность, принадлежащую заданному множеству Ls допу-
допустимых входных последовательностей машины S.
Будем говорить в этом случае, что машина S изо-
изображает машину G относительно множества Ls.
При LS^E множество LG может совпадать с LSt
быть уже или шире его, пересекаться с ним и т. д.
В частности, если Ls = Е, множество LG может быть
ограниченным, и наоборот, может быть Ls с ?, я LG = Е,
366 ПРЕОБРАЗОВАНИЕ ТАКТНОСтИ [ГЛ. X
Естественно, что изображение машиной 5 какой-либо
машины G тесно связано с тем,/как выбираются мо-
моменты t0, ti, U, ... (моменты вспышек стробоскопа).
Эти моменты могут быть выбраны, вообще говоря, и так,
что машина S не изображает никакую последовательно-
стную машину.
Выбор моментов ^о, t\, t2, ... может зависеть от вход-
входной последовательности р@, выходной последователь-
последовательности МО» последовательности и@ состояний машины
5 и времени t.
«Часы», выдающие сигналы о наступлении медлен-
медленных тактов t0, ti, t2, ..., должны воспринимать время
t и символы р@» МО и х(О (или некоторые из этих
символов), которые связаны с работой быстрой маши-
машины S. «Часы» реализуют любой алгоритм*), перераба-
перерабатывающий эту последовательность символов в последо-
последовательность to, ^ь ^2»
Мы предположим, что часы сами являются конечным
автоматом с выходным преобразователем, работающим
в той же быстрой тактности, что и Я-машина 5. Вход-
Входной алфавит этого автомата получается объединением
алфавитов {р}, {и} и {А) или некоторых из них в зависи-
зависимости от того, чем определяется выбор тактов t0, t\,
t2, ... Процесс выработки сигнала о наступлении мед-
медленного такта может тогда рассматриваться как пред-
представление события на входе в автомат-часы. Можно по-
показать, что в этом случае (при таких часах) Я-машина
S всегда изображает какую-либо Я-машину G.
В связи с введением понятий изображения (относи-
(относительного изображения) и преобразования тактности
возникают следующие задачи:
1. Задана машина S, множество Ls и «часы» (т. е.
автомат Л с преобразователем Ф). Требуется найти хотя
бы одну машину G, которую машина 5 изображает от-
относительно Ls, и ее множество допустимых входных по-
последовательностей LG.
2. Заданы машина 5 и машина G. Требуется опре-
определить, существует ли такой закон преобразования такт-
тактности, при котором машина 5 изображает машину G, и
Т. е. являются машиной Тьюринга (см. далее гл. XIII).
§ 10.1]
\ОБЩИЕ СООБРАЖЕНИЯ
367
если да, то найти его (построить автомат А и преобра-
преобразователь Ф «часов»))
Аналогичная задачу возникает и для относительного
изображения (в этом Случае следует еще определить
множество LG). x
3. Задана машина S, множество Ls и закон преоб-
преобразования тактности. Требуется построить минимальную
(или одну из минимальных) машину Gmin, которую ма-
машина S изображает относительно Ls, и найти ее множе-
множество допустимых входных последовательностей LGmIn.
Сформулированные здесь задачи пока еще в общем
случае не решены. Возможно, что некоторые из этих за-
задач окажутся алгоритмически неразрешимыми.
л
s
л
Рис. 10.1.
В заключение отметим, что понятия изображения и
преобразования тактности могли бы быть расширены,
если допустить включение преобразователей р* = Ф\
и Я* = Ф2{Х) по схеме рис. 10.1.
В моменты ^о, ^ь U, • •. наблюдаются не пары (р,
а пары (р*, %*).
Мы этого расширения не делаем, так как далее оно
нам не потребуется.
Пусть теперь задан закон преобразования тактности,
две машины — «медленная» G и «быстрая» S и множе-
множество допустимых входных последовательностей Lq ма-
машины G. Задание машины G и множества LG означает,
что можно определить любой вариант работы машины
G, т. е. определить результат переработки машиной G
любой входной последовательности из LG при любом на-
начальном состоянии *&.
568 ПРЕОБРАЗОВАНИЕ ТАКТНСЖГИ [ГЛ. X
Обратимся теперь к определению понятия . относи-
относительного воспроизведения.
Пусть задан закон преобразования тактности. Будем
говорить, что машина S, работающая в быстрой такт-
тактности, воспроизводит относительно заданного множества
LG машину G, работающую в медленной тактности, если
для любого начального состояния у?0 машины G и лю-
любой входной последовательности р*@ = р°р!Р2 •••» при-
принадлежащей множеству LG, найдется хотя бы одно на-
начальное состояние xj машины S, определяемое по Kq и
по первому члену р° входной последовательности р* (t),
и хотя бы одна последовательность p(t) такая, что лен-
лента машины S, соответствующая входной последователь-
последовательности p(t) и начальному состоянию xs, рассматривае-
рассматриваемая лишь в моменты медленных тактов t0, t\, t2, ...,
совпадает с лентой машины G.
В случае, когда LG = Е, относительное воспроизве-
воспроизведение переходит в воспроизведение.
Во избежание путаницы в дальнейшем, обратим вни-
внимание на то, что понятия изображения и воспроизведе-
воспроизведения (как относительного, так и безотносительного) со-
совершенно различаются и даже в известном смысле про-
противоположны. В самом деле, при изображении требует-
требуется, чтобы любой вариант работы быстрой машины S,
рассматриваемой в моменты t0, t\, t2, ..., совпадал с од-
одним из вариантов работы медленной машины G; при
воспроизведении же требуется, чтобы для любого ва-
варианта работы медленной машины G нашелся такой ва-
вариант работы быстрой машины 5, который, будучи рас-
рассмотрен в моменты tOt t\, t2, ..., совпал бы с заданным
вариантом работы машины G.
Можно привести примеры, когда машина S изобра-
изображает машину G, но не воспроизводит ее; можно также
привести примеры, когда машина 5 воспроизводит, но
не изображает машину G.
При воспроизведении, так же как и при изображе-
изображении, имеет место неоднозначность; при ааданном законе
преобразования тактности может, существовать много
различных быстрых машин 5Ь S2, S3, ..., каждая из ко-
которых воспроизводит заданную медленную машину G.
§ юл] ОБЩИЕ СООБРАЖЕНИЯ 369
Множество допустимых входных последовательностей
Ls для быстрой машишл 5, которая воспроизводит отно-
относительно заданного Lgf) заданную машину <j, также
определяется неоднозначно**); более того, в ряде слу-
случаев множество L8 может содержать новые входные
символы, которые не появлялись в последовательностях
множества LG.
В самом деле,-согласно определению, для каждой по-
последовательности р*@ g LG и состояния хо при воспро-
воспроизведении найдется хотя бы одна соответствующая ей
последовательность р(?), подаваемая на вход машины 5.
Однако в общем случае заданным р* (t) и y?Q может со-
соответствовать не одна, а много (даже бесконечное чи-
число) различных последовательностей p(t). Из всех по-
последовательностей p(t), соответствующих всем р*@
при любых y?Q, может быть образовано много (может
быть даже бесконечное число) различных множеств
Lls, Ls, Ls> .... причем каждое из множеств Ls содер-
жит хотя бы одну последовательность p(t), соответ-
соответствующую любым заданным p*(t)?L0 и %q.
Каждое из множеств Li можно рассматривать как
множество допустимых входных последовательностей
для быстрой машины 5, воспроизводящей относительно
LG машину G. Выбор того или иного из этих множеств
определяется дополнительными соображениями практи-
практического порядка. Иногда в качестве множества допусти-
допустимых входных последовательностей для машины S удоб-
удобно брать множество Ls = [J Lls или же множество Е
i
(которое годится во всех случаях).
При воспроизведении возникают такие же задачи,
как и при изображении, — по заданным «часам» и одной
из машин построить другую машину, или по заданным
*) LG может совпадать с Е, т. е. может иметь место и безот-
безотносительное воспроизведение.
**) При изображении подобной неоднозначности не было; по
заданным L8, закону преобразования тактности и машине 5 мно-
множество LG определялось однозначно,
24 М. А. Айзерман, Л. А. Гус^в и др.
370
ПРЕОБРАЗОВАНИЕ ТАКТНОСТИ
[ГЛ. X
двум машинам построить «часы»/ а также задача ми-
минимизации. /
В заключение этого параграфа отметим, что при
определении понятия воспроизведения сделано такое же
сужение, как и при определении изображения, а именно:
состояние х? машины 5 определяется по состоянию х$
машины G и лишь по первому члену входной последо-
последовательности p*(t).
Если допустить, что х? определяется по %°а и всей
входной последовательности, мы получили бы более
широкое, но вместе с тем и более неудобное определение
понятия воспроизведения, при котором требовалось бы
априорное знание всей последовательности p*(t).
Введенные выше формально определения поясним
теперь на двух простых примерах.
§ 10.2. Примеры изображения и воспроизведения
а. Триггер
В качестве первого примера приведем триггер, опи-
описанный в гл. V.
Таблица 10.4
Таблиц а 10.5
^4 Pi=0
.3
X,
хз
—
—
X,-
P2=l
—
х,
X,
—
ч\ р
х,
¦*¦<
р, = 0
.3
.3
х,
Ч
р2 = 1
х,
*.
*|
Рассмотрим сначала автомат П — Н, основная табли-
таблица которого имеет вид табл. 10.4, при условии, что авто-
Мат получает входные последовательности из множе-
10.2]
ПРИМЕРЫ ИЗОБРАЖЕНИЯ И ВОСПРОИЗВЕДЕНИЯ
371
Рис. 10.2.
ства R, содержащего \все последовательности, не имею-
имеющие следующих подряд друг за другом одинаковых сим-
символов. Прочерки в таблице означают, что в соответствую-
соответствующие клетки при работе автомата мы никогда не попа-
попадем, и эти клетки мо-
можно заполнить произ-
произвольно.
Заполним как-либо
пустые клетки табл.
10.4, например так,
как показано в
табл. 10.5.
Диаграмма состоя-
состояний этого автомата бу-
будет тогда иметь вид
рис. 10.2. Будем на-
наблюдать теперь авто-
автомат (рис. 10.2) лишь
в моменты to, t\, t2 ... ,
когда состояние входа изменяется с pi = 0 на рг = 1, и
выясним, какую машину G изображает относитель-
относительно R этот автомат.
Прежде всего, можно определить множество LG до-
допустимых входных последовательностей машины G. Так
как мы наблюдали наш автомат лишь в те моменты, когда
р = рг = 1, то, естественно,
множество LG будет содер-
жать лишь последовательности
единиц. Иначе это означает,
что машина G будет автоном-
автономной последовательностной ма-
машиной.
Рассмотрев различные ва- Рис. 10.3.
рианты работы автомата
рис. 10.2, легко прийти к выводу, что Я-машина G (точ-
(точнее, одна из многих возможных-машин G), которую изо-
изображает наш автомат, обладает диаграммой состояний
рис. 10.3. Легко видеть, что полученная медленная ма-
машина G является триггером (см. § 5.2). Соответствие
состояний исходного автомата S и машины G (триггера)
легко проследить; оно определено табл. 10.6.
24*
372
ПРЕОБРАЗОВАНИЕ ТАКТШСТИ
[ГЛ. X
Таблица 10.6
S
Х1
*2
*2
хз
хз
*4
G
%ю
хю
%2О
%2О
хю
Х2О
/
При, каком входе
независимо от входной последовательности
если входная, последовательность начинается
с р, =0
если входная последовательность начинается
с р2 = 1
если входная последовательность начинается
с Р,=0
если входная последовательность начинается
с р2 = 1
независимо от входной последовательности
Отметим, что если бы заполнение пустых клеток та-
таблицы 10.4 провести иначе, а именно так, как это сде-
сделано в табл. 10.7, то соответствие состояний исходного
автомата 5 и изображаемого им триггера G было бы
такое, как показано в табл. 10.8.
Таблица 10.7
Таблица 10.8
\р
* \
*3
*4
Р.=0
*3
*2
*3
*2
Р2=1
*4
*1
*4
s
Л
G
V,
При каком входе
независимо от входной после-
последовательности
независимо от входной после-
последовательности
независимо от входной после-
последовательности
независимо от входной после-
последовательности
«Часами» в рассмотренном примере может служить
конечный автомат, представляющий событие: «после pi
появилось
§ Ю.2] ПРИМЕРЫ ИЗОБРАЖЕНИЯ И ВОСПРОИЗВЕДЕНИЯ 373
Отметим также, что в рассмотренном примере исход-
исходный автомат S не только изображает относительно R
триггер Gy но и воспроизводит его относительно множе-
множества Lq> содержащего входные последовательности, со-
составленные лишь из единиц. За множество L8 допусти-
допустимых входных последовательностей исходного автомата
при воспроизведении можно принять либо.множество Е,
включающее все последовательности нулей и единиц,
либо множество R, либо вообще какое-нибудь множе-
множество, включающее R.
б. Линия задержки
В качестве второго примера рассмотрим вновь (см.
гл. V) воспроизведение медленной Я-машины G с по-
помощью быстрой машины 5, реализованной на быстрых
элементах задержки.
Пусть требуется построить Я-машину G, работаю-
работающую в тактности, определяемой равномерным разбие-
разбиением оси времени на интервалы по т секунд. Множе-
Множеством допустимых входных последовательностей ?сдля
машины G пусть будет множество Е, содержащее все
последовательности входных символов. Входной алфа-
алфавит машины G содержит г различных символов р.
Если бы в нашем распоряжении имелись г-ичные
элементы задержки, работающие в заданной тактности
т, то задача реализации машины G легко решалась бы
одним из способов, описанных выше.
Но допустим, что мы такими элементами задержки
не располагаем, а в нашем распоряжении имеются толь-
только «быстрые» г-ичные элементы задержки, работающие
в тактности, определяемой равномерным разбиением оси
времени на интервалы по — (т. е. в q раз более быст-
быстрые), где <7> 2.
Попробуем из имеющихся быстрых элементов за-
задержки построить быструю Я-машину S и подобрать
такой закон преобразования тактности, чтобы эта
быстрая машина воспроизводила заданную Я-ма-
шину G.
374
преобразование тактности
[ГЛ. X
Уравнение быстрого элемента задержки (рис. 10.4)
имеет вид
A0.2)
и
а уравнение требующегося нам медленного элемента
задержки
x(t + x) = u(t). A0.3)
Рис. 10.4. Составим из q быстрых эле-
элементов задержки цепочку, как
это изображено на рис. 10.5. Полученная цепочка опи-
описывается системой рекуррентных соотношений
-i(*+ j) = *(*)•
A0.4)
Исключая из этой системы все Х\у кроме х% получаем для
цепочки в целом уравнение
*(/ + т) = «(/). A0.5)
Уравнение A0.5) совпадает с уравнением A0.3) медлен-
медленного элемента задержки; следовательно, цепочка из д
и
X
быстрых элементов равноценна одному медленному эле-
элементу.
Принимая это во внимание, построим Я-машину S
следующим образом. Предположив на время, что в на-
нашем распоряжении имеются медленные элементы за-
задержки A0.3), построим из них и мгновенно действую-
действующих логических преобразователей машину G по одному
из описанных в гл. V способов,
§ 10.2] ПРИМЕРЫ ИЗОБРАЖЕНИЯ И ВОСПРОИЗВЕДЕНИЯ 375
Заменим затем в этой машине каждый медленный
элемент задержки цепочкой из q быстрых задержек.
В результате будет получена некоторая Я-машина S,
работающая в быстрой тактности, а именно в той, в ко-
которой работают быстрые элементы задержки. Но если
смотреть на машину 5 лишь в моменты t0, tu t2, ..., со-
совпадающие с моментами 0, т, 2т, Зт, то машина 5 будет
воспроизводить Я-машину G, так как уравнение каждой
цепочки быстрых задержек A0.4) для этих моментов
совпадает с уравнением одного медленного элемента за-
задержки.
Соответствие состояний машины 5 состояниям ма-
машины G не будет зависеть от входной последовательно-
последовательности и будет определено следующим образом: каждому
состоянию KiG машины G соответствует любое такое со-
состояние всех быстрых задержек машины 5, при котором
состояние первых быстрых задержек каждой цепочки
совпадает с состоянием соответствующих медленных
задержек.
Подсчет показывает, что при воспроизведении для
каждого из гк состояний машины G имеется г^з-1) соот-
соответствующих ему состояний машины S.
За множество Ls допустимых входных последователь-
последовательностей для машины 5 при воспроизведении может быть
принято либо множество Е, либо множество R (не со-
содержащее последовательностей с повторяющимися сим-
символами), либо множество М, содержащее все последова-
последовательности вида
Ра0 Р«.Р«. ' ' ' &Ч Р«Д2 • • • Р., • • • Р. Р. • • • Ра,
S S S
q раз q раз q раз q раз
(возможно р^ =
либо какое-либо еще из многих возможных множеств
(все эти множества должны обладать следующим свой-
свойством: если из каждой последовательности, принадлежа-
принадлежащей множеству, выписать символы, стоящие на местах
0, q, 2q, 3^7, ... , то все последовательности выписанных
символов должны образовать множество Е).
«Часы» в рассмотренном случае представляют собой
кольцевую счетную схему (т. е. автономный
376 ПРЕОБРАЗОВАНИЕ ТАКТНОСТИ [ГЛ. X
автомат), собранную из быстрых элементов задержки,
и выдающую сигнал наступления медленного такта по
прошествии q быстрых тактов.
Обратим внимание, что в этом примере, так же как
и в предыдущем, построение выполнено так удачно, что
имеет место не только воспроизведение, но и изображе-
изображение: машина 5 изображает машину G (как относитель-
относительно множества Е, так и относительно любого иного мно-
множества). Соответствие состояний при изображении
остается тем же.
§ 10.3. Воспроизведение медленной
последовательностной машины быстрой машиной
в случае, когда тактность медленной машины
определяется сменой состояний на входе
Задача, упомянутая в названии этого параграфа, уже
рассматривалась в гл. V, где она была частично решена.
Здесь мы дадим другой метод решения, пригодный для
машин любого типа.
Пусть задана произвольная Я-машина G, тактность
которой определяется моментами, когда изменяются со-
состояния на ее входе. Формой задания машины G пусть
будет матрица соединений либо диаграмма состояний.
Множество LG допустимых входных последовательно-
последовательностей машины G содержит все возможные последователь-
последовательности, кроме тех, в которых имеются повторяющиеся
подряд символы.
Требуется построить быструю Я-машину S, которая
бы воспроизводила относительно LG заданную машину
G при следующем законе преобразования тактности: мо-
моментами to, U, ^2, • • •, ts, ... наступления медленных так-
тактов являются моменты прихода машины 5 в состояния
равновесия после любого изменения входа (т. е. в со-
состояния, которые в быстрых тактах переходят в себя при
неизменном входе).
Если наибольшее число быстрых тактов, нужное
для перехода машины S от одного состояния равнове-
равновесия к другому при изменении входного воздействия рав-
равно т, то мы будем считать, что множество Ls допусти-
допустимых входных последовательностей машины S при вое-
§ ю.З] ВОСПРОИЗВЕДЕНИЕ МЕДЛЕННОЙ МАШИНЫ 377
произведении содержит все последовательности вида
q0 раз ?, раз ^ раз
где qi^> m для всех i = 1,2 3, ... Это означает, что мы
запрещаем изменять входное воздействие на машину 5
до тех пор, пока она не пришла в очередное состояние
равновесия.
Множество последовательностей вида A0.6) при ус-
условии qi^q* будем обозначать символом Tq*. Множе-
Множества Tq* удовлетворяют соотношению
...,
A0.7)
причем Т\ = Е.
Итак, за множество Ls для машины 5 можно взять
любое множество Т* при условии q* >- m.
Если машины G и S должны работать синхронно, что-
чтобы машина 5 могла заменить машину G, то условие
q*^>m означает, что машина 5 должна работать на-
настолько быстро, чтобы за время между двумя смежными
тактами машины G укладывалось бы по крайней мере
m тактов работы быстрой машины.
Построение машины 5 выполним путем преобразова-
преобразования диаграммы состояний заданной машины G.
Рассмотрим кружок щ диаграммы состояний маши-
машины G. Пусть, например, этот кружок вместе с подходя-
подходящими к нему и отходящими от него стрелками имеет вид
рис. Ю.6. Заменим кружок и* несколькими кружками,
число которых будет равно числу подходящих к кружку
Иг стрелок с различными надписями (кольцевая стрелка
считается как подходящей, так и отходящей).
К каждому новому кружку подводятся от других
кружков диаграммы только стрелки с одинаковыми
надписями. Кроме того, каждый, из новых кружков охва-
охватывается петлей, несущей ту же надпись, что и у подхо*
Дящих стрелок.
В нашем случае (рис. 10.6) кружок щ следует заме-
заменить четырьмя кружками щ\, иг-2, иг-3, кц (они обведены
пунктиром на рис. 10.7).
378
ПРЕОБРАЗОВАНИЕ ТАКТНОСТИ
[ГЛ. X
От каждого из новых кружков отводятся к другим
кружкам диаграммы те же самые стрелки, которые от-
отходили на исходной диаграмме от кружка щ, за исклю-
исключением стрелок, в надписях над которыми первый сим-
символ совпадает с первым символом надписи над охваты-
охватывающими эти кружки петлями.
В нашем примере от кружка %ц следует отвести
стрелки (ррДй) и (pg,K) к кружкам щь и и,-в, от кружка
— стрелку (pg,K) к кружку куб и стрелку (ps, Яг) к
Кц, ОТ КруЖКОВ ИгЗ И Иг'4 — СТреЛКИ (ррДй) К
кружку Kj5 и стрелки с
надписью (ps, Ят) к круж-
кружку кц, охваченному пет-
петлей (ps, Ят).
Осуществим описан-
описанную перестройку для всех
кружков диаграммы со-
состояний машины G. В ре-
результате будет получена
диаграмма состояний ма- *
шины 5, которая воспро-
воспроизводит относительно LG
заданную машину (^при-
(^причем соответствие состоя-
состояний машины G и S будет
таково (рис. 10.6 и 10.7): •
состоянию щ\ машины G
при входе ps соответству-
соответствует состояние кц машины -
S, равновесное при этом
ps; это же состояние со-
соответствует и состоянию
и* машины G при ps; состоянию Xj2 при входе рр соответ- ¦
ствует состояние иг-г машины 5, равновесное при рр; со-
состоянию Xj3 при р? соответствует кг-з, равновесное при pg, t
и т. д. Аналогично устанавливается соответствие и в об-
общем случае. *
Как непосредственно видно по диаграмме состояний, \
переход машины S от одного состояния равновесия к I
другому при любом изменении входа происходит за один ;
Рис. 10.6.
§ 10.3]
ВОСПРОИЗВЕДЕНИЕ МЕДЛЕННОЙ МАШИНЫ
379
быстрый такт. Это означает, что для построенной маши-
машины введенное выше число т—\. Кроме того, непосред-
непосредственно по диаграмме видно, что машина S не имеет
неустойчивых ни при каком входе состояний; каждое со-
состояние при каком-либо определенном входном воздей-
воздействии является равновесным (все кружки охвачены
петлями).
Быстрая входная последовательность, которая при
воспроизведении соответствует входной последователь-
й
ности
Р„
(?п Ф Р
медленной машины
I № \—
Рис. 10.7.
G имеет вид A0.6), причем все q%^\. Принимая в этих
соотношениях знак равенства, находим, что одна из со-
соответствующих входных последовательностей машины 5
имеет вид р„ р„ р„ ..., т. е. совпадает со входной после-
довательностью машины G.
Моментами t0, t\, t2, ... наблюдения быстрой маши-
машины 5 будут моменты времени, наступающие спустя
один быстрый такт после любого изменения состояния
входа машины 5. Если в качестве соответствующей
входной последовательности машины 5 взята последо-
последовательность, совпадающая с входной последовательно-
последовательностью машины G, то наблюдение машины 5 должно про-
производиться во все быстрые такты.
380
ПРЕОБРАЗОВАНИЕ ТАКТНОСТИ
[ГЛ. X
Итак, описанное перестроение диаграммы состояний
решает поставленную задачу синтеза быстрой Я-маши-
ны, воспроизводящей относительно LG заданную Я-ма-
шину С/, тактность которой определяется сменой состоя-
состояний входа.
Эта задача решалась с помощью перестроения диа-
диаграммы состояний лишь для наглядности. Практически
иногда удобнее соответствующее перестроение прово-
проводить непосредственно на матрице соединений. Опи-
Опишем его.
Пусть задана матрица соединений CG машины G.
Рассмотрим i-ю строку и i-й столбец этой матрицы.
Пусть в соответствии с примером рис. 10.6 /-я строка
и i-й столбец имеют вид
Л
/2
С0
УЗ
(и
(Pp.
••"• (Pp» ^5) ••• (Pg-i *<j) '•••
Заменим i-ю строку и i-й столбец матрицы CG столь-
столькими строками и столбцами, каково число различных
пар, содержащихся в i-м столбце матрицы CG. В нашем
примере различных пар в i-м столбце четыре: это пары
<Ps, А,т), (Рр,К)> (РяДр) и (Р*. ^а). Следовательно, i-ю
строку и i-й столбец заменяем, четырьмя строками и
§ 10.3] ВОСПРОИЗВЕДЕНИЕ МЕДЛЕННОЙ МАШИНЫ 381
столбцами: П, 12, /3 и /4:
Л «2 «3 /4 ... ;5 ... ;б
«1
я.
С= 13
«4
(Pp.
> К)
(РГ
В качестве диагональных элементов построенных че-
четырех строк и столбцов напишем (в любом порядке) все
различные пары i-ro столбца матрицы С°.
Далее: в строке /1 i-ro столбца матрицы CG содер-
содержалась пара (ps, Ят); впишем ее в ту же строку Л ма-
матрицы С в тот из столбцов, в котором пара (ps, Я7) уже
содержится. В нашем примере это — столбец i\. Анало-
Аналогично поступаем с остальными парами, содержащимися
в 1-м столбце матрицы CG. После этого столбцы П, i2,
i3 и й матрицы С будут заполнены. В каждом из этих
столбцов будут содержаться только одинаковые пары.
Приступим затем к заполнению строк Л, i2, /3 и /4;
Рассмотрим i-ю строку матрицы CG. Все содержащиеся
в этой строке пары (кроме пары (ps, Я7), стоящей на диа-
диагонали матрицы CG) выпишем во всех четырех строках
382 ПРЕОБРАЗОВАНИЕ ТАКТНОСТИ [ГЛ. X
матрицы С в тех же столбцах, что и в матрице CG, за
исключением пар, у которых первый символ совпадает
с первым символом пар, уже содержащихся в строках
Л, й, /3 и *4. Пару (ps, Я7) напишем во всех четырех
строках Л, /2, *3, *4 в том столбце, в котором она уже
имеется.
В нашем примере в i-и строке содержатся пары
(ps, А7), (рр, Хь), (pg, Ae). В строке И пара (ps, Я7) уже есть;
вписываем в эту строку пару (рр, Я5) в столбце /5 и пару
(pg, К) в столбце /6. В строке 12 содержится пара (ррД в).
Дописываем в этой строке пару (ps, Я7) в столбце П и
пару (р^Дв) в столбце /6 (пару (рр, Я5) в столбце /5 пи-
писать не следует, так как в строке /2 уже содержится
пара (рр, Яа)). Аналогично заполняем строки iS и *4 ма-
матрицы С. Подобную перестройку следует осуществить
для каждой i-й строки и каждого /-го столбца матрицы
CG. В результате будет построена матрица соединений
С машины 5.
о
Отметим свойство матрицы С : в любом из столбцов
этой матрицы могут содержаться лишь одинаковые пары.
Нетрудно видеть, что процесс перестройки матрицы
соединений CG в Cs совпадает с описанным выше про-
процессом перестройки диаграммы состояний.
Сделаем в заключение два замечания.
Замечание первое. В § 10.3, так же как и в
§ 10.2, построение машины 5 выполнено столь «удачно»,
что имеет место не только воспроизведение, но и изо-
изображение. В качестве множества допустимых входных
последовательностей при изображении можно взять лю-
любое множество, в том числе и множество Е, так как
входные воздействия машины 5 могут меняться даже
с частотой быстрых тактов, ибо для машины 5 число m
равно 1. Соответствие состояний при изображении будет
тем же, что и при воспроизведении.
Замечание второе. Описанный прием дает один
из способов построения быстрой Я-машины 5, воспроиз-
воспроизводящей относительно LG заданную Я-машину G. Воз-
Возможны и иные способы решения этой задачи, так как
/7-машина 5, воспроизводящая относительно Lq машину
§ 10.4] МИНИМИЗАЦИЯ ВОСПРОИЗВОДЯЩЕЙ МАШИНЫ 383
G, не единственна. Поэтому, естественно, возникает за-
задача минимизации машины 5, т. е. построение такой
Я-машины 5, воспроизводящей относительно LG задан-
заданную машину G, которая имеет наименьшее число со-
состояний.
§ 10.4. Минимизация воспроизводящей
последовательностной машины, построенной
в предыдущем параграфе
Для рассмотренного в § 10.3 случая попытаемся ре-
решить задачу минимизации, т. е. построить такую ма-
машину Smin, воспроизводящую относительно LG заданную
машину G, которая имела бы наименьшее возможное
число состояний. Предположим заранее, что искомая
машина Smln удовлетворяет двум условиям.
Условие 1. Любое состояние машины 5min являет-
является равновесным хотя бы для одного входного воздей-
воздействия.
Условие 2. При любом изменении входного воз-
воздействия машина Smln приходит в новое равновесное
состояние за один быстрый такт (т. е. число т для этой
машины равно единице).
Рис. 10.8.
Покажем теперь, что эти условия не ограничивают общности
исследования.
Допустим, что первое условие не выполнено. Это означает, что
машина Smm имеет хотя бы одно состояние *a» которое не является
равновесным, и на диаграмме состояний машина Smin обозначается
кружком h, не охваченным петлей (рис. 10.8). Тогда это состояние
xh можно удалить, заменив подходящую и отходящую от кружка
¦х-А стрелки с первым индексом *) р* одной стрелкой с тем же пер-
*) Многоточия вместо индекса Я означают, что на этом месте
может стоять любой выходной индекс,
384 ПРЕОБРАЗОВАНИЕ ТАКТНОСТИ [ГЛ. X
вым индексом, соединяющей кружки х,- и Пц. Отходящая от кружкг
**-h стрелка с первым индексом р8, для которого не имеется соответ;
ствующей подходящей стрелки с тем же индексом, удаляете^
(рис. 10.9). Таким способом можно удалить все неравновесные со'
стояния.
Описанное преобразование, как нетрудно видеть, изменяет pat
боту машины Smm лишь в промежутке между ее двумя равновесным»
состояниями, когда мы работу этой машины все равно не наблюдаем.
Порядок же смены равновесных состояний не нарушается1 и, сле-С
доватёльно, измененная машина по-прежнему будет воспроизводить'
заданную машину G. Однако это преобразование позволяет умень-
уменьшить число состояний машины 5min, и, следовательно, машина, не
удовлетворяющая условию 1, не может быть минимальной. Таким
образом, условие 1 является необходимым для минимальной ма-
машины 6'mln.
(Sty
Рис. 10.9.
Вообще для заданной машины G может существовать несколько
различных минимальных машин Smin, воспроизводящих машину G
относительно множества Lq. Число состояний у всех этих машин
должно быть одно и то же — &min.
Мы будем считать поставленную задачу решенной, если найдем;
хотя бы одну из этих машин.
Обратимся теперь к условию 2. Докажем следующее утвержде-
утверждение. Если существует машина 5min с km\n состояниями, воспроиз-
воспроизводящая относительно Lq машину G и не удовлетворяющая уело-:
вию 2, то существует другая машина 5min с тем же числом состоя-:
ний ftmin, также воспроизводящая машину G относительно Lq и
удовлетворяющая условию 2. Тем самым будет доказано, что и-
условие 2 не является ограничением.
Для доказательства покажем, что диаграмма состояний ма-
машины Smin может быть получена из диаграммы состояний машины*
«Smin путем ее перестройки без изменения числа состояний.
Пусть машина «Smin переходит за т быстрых тактов из состоя-'
ния xit являющегося равновесным при р = рР, в состояние %/, яв-^
ляющееся состоянием равновесия при р = р^« Тогда за эти т тактов"
машина пройдет через (т—1) промежуточных состояний'
Ип, Kt2»«»», Хцт - 1) (по условиям достижимости равновесного состоя-
состояния замкнутых циклов быть не может). На рис. 10.10 показан в>
качестве примера случай т = 3.
§ 10.4]
МИНИМИЗАЦИЯ ВОСПРОИЗВОДЯЩЕЙ МАШИНЫ
385
Если соединить кружки i, П, 12, ..., 1{т—1) стрелками с над-
надписью (р*. А,р) непосредственно с кружком /, то будет получена диа-
диаграмма состояний, изображенная на рис. 10.11. Теперь переход из
состояния тч.так же как и из состояний ЩиЩг, •-•iHi.m-x) B состоя-
состояние %}, происходит под воздействием pg за один быстрый такт.
Рис. 10.10.
Если подобным способом осуществить перестройку всей диа-
диаграммы состояний машины Smin, то будет получена диаграмма ма-
машины Smin с тем же числом состояний. Работа машин 5mm и
будет отличаться лишь в промежутках между равновесными со-
Рис 10,11.
стояниями, когда мы эти фашины не наблюдаем* Смена же состоя-
состояний равновесия машины Smin под воздействием любой допустимой
входной последовательности будет происходить так же, как и у ма-
машины Smin. Следовательно, наше утверждение доказано.
Будем теперь искать минимальную машину среди
всех машин 5Ь 5г, 53, .... воспроизводящих заданную
машину G относительно множества LG и удовлетворяю-
удовлетворяющих условиям 1 и 2.
25 М. А. Айзерман, Л. А. Гусев и др.
386 ПРЕОБРАЗОВАНИЕ ТАКТНОСТИ [ГЛ. X
Как уже отмечалось в предыдущем параграфе, вход-
входной последовательности вида
р«а,р«? • • • р«, • • • ОЧ^Чм) A0*8)
машины G соответствует при воспроизведении входная
последовательность A0.6)
РаДо ' ' ' Р«о Ра, Ра, ' ' ' Р«, ' '"' Р«,Р«^ "' Р., (Рв/ ^ P./ + l)
q0 раз qx раз gg раз
машины 5 при условии qi^m (i = 1, 2, ...). Так как
для любой машины 5г- число т = 1, за множество ее до-
допустимых входных последовательностей Ls можно взять
любое множество Tq* (q* = 1, 2, 3, ...) всех последова-
последовательностей вида A0.6) при qO q* (i = 1, 2, 3, ...), в
частности множество Е = Т\.
Пусть за множество Ls при воспроизведении выбра-
выбрано множество Т-щ. Докажем следующее утверждение:
если два состояния — состояние ха, машины Sa и
состояние к» машины 5а эквивалентны относительно
множества Г-„ то они эквивалентны и относительно всех
множеств 7ь Г2, Г3, ... т. е. просто эквивалентны, так
как Т\ — Е (при этом 5а и 5р могут обозначать одну и
ту же машину).
При q > q* справедливость нашего утверждения оче-
очевидна, так как в этом случае TqcT~* (см. § 10.3, со-
соотношение A0.7)).
При q <q* справедливость утверждения следует из
того, что при любом изменении состояния входа любая из
машин 5г- переходит за один такт в состояние равновесия,
и дальнейшее как угодно долгое повторение входного
символа не меняет состояния машины.
Каждая машина Si воспроизводит относительно LG
машину G. Это означает, что для любого начального со-
состояния y?q машины G и для любой входной последова-
последовательности _2* из LG вида A0.8), начинающейся с рао, по-
поданной на вход машины, найдется начальное состояние
*°s машины Si такое, что машина 5г- при соответствую-
соответствующей входной последовательности вида A0.6) из множе-
§ 10.4] МИНИМИЗАЦИЯ ВОСПРОИЗВОДЯЩЕЙ МАШИНЫ 387
ства 71-,, наблюдаемая лишь в моменты прихода в со-
состояние равновесия после смены входного воздействия,
выдает ту же выходную последовательность, что и ма-
машина G: Без ограничения общности можно считать, что
состояние к°8 машины St равновесно при р = рао; если
бы этого не было, то за один быстрый такт машина S*
перешла бы из состояния х^ в состояние к\ , которое
при р = рао было бы уже равновесно. Это к\ и можно
было бы принять за состояние, соответствующее состоя-
состоянию к% машины G.
Рассмотрим теперь любые две машины S* и Sj из
множества Si, S2, S3, ... Пусть начальному состоянию
к°0 машины G при ра соответствует состояние xj ма-
машины Si и состояние х? машины Sj. Тогда, так как со-
состояния xj и xj соответствуют одному и тому же со-
состоянию машины G при одном и том же р^, выходные
последовательности машин Si и Sj, начинающих рабо-
работать соответственно из xj и к°3 , будут совпадать при
любой входной последовательности из Г-*, начинающей-
начинающейся с рао, в моменты, наступающие спустя один быстрый
такт после изменения состояния входа. Но так как в ос-
оставшиеся моменты при неизменном входном воздействии
машина находится в состоянии равновесия, выходные
последовательности будут совпадать и в эти моменты.
Таким образом, состояния xj и xj оказываются
эквивалентными для всех входных последовательностей
из 74, начинающихся с рао. Но эти состояния будут
эквивалентны и относительно множества Г-*, так как
они являются равновесными состояниями при р = р^.
В самом деле, если входная последовательность начи-
начинается с некоторого рРо=? р^. то можно составить после-
последовательность
G* раз
25*
"ар"ар * аргро ил п\
* "аргр
388 ПРЕОБРАЗОВАНИЕ ТАКТНОСТИ [ГЛ. X
начинающуюся уже ср^и принадлежащую Г-,. Отно-
Относительно этой последовательности состояния к? и к%
эквивалентны. По прошествии q* тактов оба этих со-
состояния переходят в себя; следовательно, начальные
условия не меняются и можно за начало отсчета вре-
времени взять (q* + 1)-й быстрый такт; последовательность
же A0.9), рассмотренная с (q* + 1)-го такта, начинает-
начинается с рр.
Итак, мы показали, что все состояния машины Si
(i — 1, 2, 3, ...), соответствующие одному и тому же со-
состоянию п°0 машины G, при р = рво эквивалентны отно-
относительно выбранного множества 7-„. Тогда в силу дока-
доказанного выше утверждения они эквивалентны и относи-
относительно Тх = ?, т. е, просто эквивалентны.
Предположим теперь, что нам удалось найти такую
быструю машину S из множества Su S2, 53, ..., которая
не только воспроизводит машину G относительно LG, но и
изображает машину G относительно Е. Это означало
бы, что каждому состоянию машины 5 при любом р = р^
можно поставить в соответствие состояние машины G
так, чтобы имело место-изображение.
Выберем произвольное состояние к- машины S.
О '
Пусть это состояние равновесно при р = рав. Тогда со-
состоянию х- при р соответствует при изображении со-
стояние к0 машины G. Подавая на вход машины S раз-
различные входные последовательности, начинающиеся
с рао, и наблюдая за работой машин S и G, нетрудно
прийти к выводу, что если состояние и0 соответствует
при р = р состоянию х- при изображении, то состояние
х_ соответствует при том же р состоянию х при вое-
произведении (машина S изображает и воспроизводит
машину G).
Так как за х_ может быть принято любое состояние
м"ашины 5, то отсюда'следует, что для каждого состоя-
§ 10.4] МИНИМИЗАЦИЯ ВОСПРОИЗВОДЯЩЕЙ МАШИНЫ 389
ния х машины S найдутся такие р„ и хп машины G,
что состояние х- может быть поставлено в соответствие
«Ь . ¦
состоянию х0 с р = рав при воспроизведении. Но отсюда
немедленно следует, что для любого состояния х- ма-
машины S найдется эквивалентное ему состояние х5 в лю-
любой машине S*. Это значит, что все машины S* отобра-
отображаются на машину S (некоторые из этих Su разумеется,
могут быть и эквивалентны S). Поэтому теперь доста-
достаточно минимизировать машину S, т. е. построить мини-
минимальную последовательностную машину Smin» эквива-
эквивалентную 5, а это можно сделать с помощью алгоритма
Ауфенкампа и Хона (см. § 9.6) *).
Найденная таким образом машина Smin и будет ми-
минимальной Я-машиной, воспроизводящей относительно
Lq машину G.
Как отмечалось в § 10.2, машина S, построенная при
помощи преобразования матрицы соединений машины
G, одновременно и воспроизводит относительно LG и изо-
изображает относительно Е машину G. В то же время эта
машина удовлетворяет условиям 1 и 2.
Следовательно, чтобы получить минимальную маши-
машину Smin (точнее, одну из минимальных машин), доста-
достаточно минимизировать машину S при помощи симмет-
симметричного разбиения ее матрицы соединений. Результат
минимизации не зависит от того, какое из множеств Г-,
выбрано в качестве множества Ls допустимых входных
последовательностей машины S при воспроизведении.
Ограничение множеств входных последовательностей в
рассмотренном случае не дает возможности дополни-
дополнительно уменьшить число состояний воспроизводящей
машины.
Приведем пример построения минимальной Я-ма-
шины Зпшъ воспроизводящей относительно LG заданную
машину G.
*) Для машины 5» разбиение всех состояний на группы, экви-
эквиентные относительно множества T-t, совпада
группы, эквивалентные относительно множества
390
ПРЕОБРАЗОВАНИЕ ТАКТНОСТИ
[ГЛ. X
Пример. Пусть матрица соединений CG заданной
«медленной» машины с алфавитами {р} = {1, 2, 3}, {х} =
= {1, 2, 3) и (Ч = {1, 2) имеет вид
1 2 3
1 Г (Ы) B,1) C,1)
B,2)V(U) 0 C,1)
L B,2)VA,1) C,2) О
Диаграмма состояний машины G приведена на
рис. 10.12,,
Рис. 10.12.
Производя описанную в § 10.3 перестройку матрицы
ССт, получим матрицу Cs «быстрой» машины S, воспро-
воспроизводящей машину G:
I1
I2
I3
21
22
3
I1
~ (Ы)
(Ы)
0
0
0
- A,1)
I2
0
B,2)
0
0
B,2)
B,2)
I3
0
0
(Ь2)
(Ь2)
(Ь2)
0
21
B,1)
0
B,1)
B,1)
0
0
22
0
0
0
0
C,2)
0
3
(зл) -
C,1)
C,1)
C,1)
0
(ЗЛ) .
§ 10.4]
МИНИМИЗАЦИЯ ВОСПРОИЗВОДЯЩЕЙ МАШИНЫ
391
Диаграмма состояний машины 5 показана на
рис. 10.13. Минимизируем теперь машину 5. В матрице
соединений С8 машины 5 2-я и б-я строки и 3-я и
Рис. 10.13.
4-я строки образуют 1-матрицы. Перепишем матрицу
С8 так, чтобы эти строки стояли рядом и осуществим
симметричное разбиение:
I3
21
3
I1
22_
I3
(Ь2)
(Ь2)
0
0
0
(Ь2)
21
B,1)
B,1)
0
0
B,1)
0
I2
0
0
B,2)
B,2)
0
B,2)
3
C,1)
C,1)
C,1)
C,1)
C,1)
0
I1
0
0
(Ы)
(Ы)
(Ы)
0
22
о -
0
0
0
0
C,2) _
392
ПРЕОБРАЗОВАНИЕ ТАКТНОСТИ
[ГЛ. X
Окончательно получаем матрицу соединений Сщш ми-
минимальной машины Smin, имеющей четыре состояния:
хь Х2, х3, х4:
A,2)VB,1) C,1)
Х3
О
О
0 B,2)VC,1) A,1) О
B.1) C,1) A,1) О
A.2) B,2) 0 C,2) _
Диаграмма состояний машины 5тт приведена на
рис. 10.14.
Рис. 10.14.
В силу отмеченного выше свойства матрицы соедине-
соединений С8 быстрой машины S, заключающегося а том, что
в каждом столбце матрицы С8 могут содержаться лишь
одинаковые пары, матрица Cj,ln обладает следующим
свойством: в одном столбце матрицы не могут содер-
содержаться две пары с одинаковым .первым и различными
вторыми индексами. Это означает, что диаграмму со-
состояний машины Smin можно, по желанию, трактовать
как диаграмму состояний последовательностнои машины
§ 10.41
МИНИМИЗАЦИЯ ВОСПРОИЗВОДЯЩЕЙ МАШИНЫ
393
типа П — П либо последовательностной машины типа
П — Н (см. об этом замечание в § 3.4).
Будем считать, например, что эта диаграмма яв-
является диаграммой состояний машины типа П —Н, и
покажем, как далее строится релейная схема, реализую-
реализующая эту машину. По диаграмме состояний можно вос-
восстановить основную таблицу автомата и таблицу преоб-
преобразователя машины Smin- В нашем примере эти таблицы
соответственно имеют вид табл. 10.9 и табл. 10.10.
Таблица 10.9
Таблица 10.10
\р
*1
*2
*3
*4
Pi
*!¦
*3
*3
>1
Р2
*1
*2
*1
*2
Рз
*2
*2
*2
*4
"Н
^3
^4
Pi
h
12
?2
К
' i2
Рз
^1
^1
>1
Таблицу 10.9 можно трактовать как таблицу пере-
переходов Хафмана; достаточно лишь обвести квадрати-
квадратиками равновесные состояния х-, т. е. те, индексы ко-
о
торых совпадают с номером строки. После этого
табл. 10.9 примет вид табл. 10.11.
Имея табл. 10.10 и 10.11, можно реализовать машину
•5mm с помощью релейной схемы способом, описанным
в § 5.4.
Для этого зашифруем сдмволы х, р и Я двоичными
числами так, как это показано в табл. 10.12—10.14.
Тогда табл. 10.9 и 10.10 можно представить в форме
табл. 10.15 и 10.16.
По табл. 10.15 и 10.16 строится объединенная
табл. 10.17.
394
ПРЕОБРАЗОВАНИЕ ТАКТНОСТИ
[ГЛ. X
Табл. 10.17 задает три логические функции Уь Y2 и Z
от четырех независимых переменных xh x2, yh y2. Рас-
Рассмотрим теперь Х\ и х2 как состояния входных контак-
контактов, а у\ и у2 как состояние контактов вторичных реле,
Таблица 10.11
н
Pi
ЕЛ
х.|
»,
Р2
-.1
Рз
«,1
и Y\ и Уг как состояния (наличие или отсутствие
токов) обмоток этих вторичных реле. Будем Z полагать
Таблица 10.12
Таблица 10.13 Та блица 10.14
\. у
*1
Ъ
«•а
^4
у2
0
0
1
1
Ух
0
1
0
1
\. х
р\^
Pi
Р2
Рз
х2
0
0
1
0
1
0
\ Z
х\^
h
z
0
1
состояниями обмотки выходного реле. Любая контактная
сеть, составленная из контактов #ь х2> Уи #2, и включен-
§ Ю.4)
МИНИМИЗАЦИЯ ВОСПРОИЗВОДЯЩЕЙ МАШИНЫ
395
ные в нее обмотки Y\, Y2 и Z, которые реализуют таб-
таблицу логических функций типа табл. 10.17, реализует и
синтезируемую машину Smtii. Такая сеть может быть
по табл. ГО. 17 построена любым приемом (см. гл. II).
Таблица 10.15
Таблица 10.16
\. х
У \^
00
01
10
11
00
00
10
10
00
01
00
01
00
01
10
01
01
01
11
У ^\
00
01
10
11
00
1
0
0
1
01
0
1
0
1
10
0
0
0
1
Теперь целесообразно сравнить изложенный выше
метод построения машины Smin, которая воспроизводит
Таблица 10.17
У\
Уг
хх
х2
Yx
Y2
Z
0
0
0
0
0
0
1
1
0
0
0
0
1
0
0
1
0
0
0
1
0
1
1
0
0
0
0
1
0
0
1
0
0
0
0
1
0
1
0
1
0
1
0
1
1
0
0
0
0
1
1
1
0
1
0
1
0
0
0
1
1
0
0
1
0
0
1
1
0
0
0
1
0
1
1
0
0
1
1
0
1
1
1
1
на состояниях равновесия заданную машину G, с мето-
методом Хафмана, предназначенным для решения этой за-
задачи и описанным в § 5.4.
Главное отличие метода ''Хафмана от метода, изло-
изложенного в этой главе, состоит в том, что область при-
применимости последнего ничем не ограничена, тогда как
метод Хафмана, как уже отмечалось в гл. V, можно
применять для построения лишь таких последователь-
ностных машин, у которых будущее состояние входящего
396 ПРЕОБРАЗОВАНИЕ ТАКТНОСТЙ [ГЛ. tf
в эти машины автомата однозначно определяется состоя-
состояниями входа и выхода машины в настоящий момент.
В тех же случаях, когда применимыми оказываются оба
метода, они приводят к совершенно одинаковым резуль-
результатам, в том числе и после минимизации.
В заключение этого параграфа заметим, что алгоритм
размножения состояний, описанный в § 10.3, применим
и в том случае, когда заданная медленная машина О
имеет ограничения типа Ауфенкампа. Построенная с по-
помощью этого алгоритма быстрая машина S, которая
воспроизводит относительно Lq машину G, также будет
иметь ограничения типа Ауфенкампа. Поэтому для ее
минимизации следует пользоваться приемом, описанным
в конце § 9.8 (или каким-либо иным способом полной
минимизации машин с ограничениями типа Ауфен-
Ауфенкампа).
Доказательство того, что минимизированная таким
образом быстрая машина 5 будет минимальной маши-
машиной, воспроизводящей заданную машину б, строится
аналогично приведенному в настоящем параграфе дока-
доказательству при отсутствии ограничений (следует лишь
дополнительно следить за множеством допустимых вход-
входных последовательностей для каждого из состояний).
Г Л А В А XI
ОПРЕДЕЛЕНИЕ СВОЙСТВ
ПОСЛЕДОВАТЕЛЬНОСТНЫХ МАШИН
ПО ИХ РЕАКЦИИ НА ВХОДНЫЕ
ПОСЛЕДОВАТЕЛЬНОСТИ КОНЕЧНОЙ ДЛИНЫ
§ 11.1. Основные определения и постановка задачи
В настоящей главе конечные автоматы и /7-машины
рассматриваются как существующие объекты, с кото-
которыми можно экспериментировать, но о внутренней струк-
структуре которых имеются лишь ограниченные сведения.
Предполагается, что исследователь может только по-
подавать последовательности конечной длины на вход ко-
конечного автомата или /7-машины и наблюдать его выход.
Задача состоит в том, чтобы на основании этих наблю-
наблюдений прийти к заключению об особенностях структуры
исследуемого .конечного автомата или /7-машины, опре-
определить состояние, в котором находится автомат или
Я-машина, определить (если возможно) диаграмму со-
состояний.
Факт подачи на вход Я-машины последовательности
конечной длины / мы будем называть экспериментом
длины I.
Пусть на вход Я-машины подается последователь-
последовательность р(/) = р°р! ... pp. Одновременно с подачей каждого
из входных символов отмечаются символы Я, появляю-
появляющиеся на выходе автомата и образующие последо-
последовательность K(t) = k°Kl ... Яр, синхронную с последо-
последовательностью входов. Последовательность К (t) мы
назовем реакцией Я-машины на входную последователь-
последовательность р(/).
398 ОПРЕДЕЛЕНИЕ СВОЙСТВ ПОСЛЕДОВАТЕЛЬН. МАШИН [ГЛ. XI
Последовательность на входе и синхронную с «ей по-
последовательность на выходе, т. е. соответствующую лен-
ленту /7-машины (без строки х), мы в этой главе будем на-
называть результатом эксперимента.
Можно представить себе различные типы экспери-
экспериментов. В случае, когда в распоряжении эксперимента-
экспериментатора имеется один экземпляр исследуемой /7-машины и
на вход ее подается заранее определенная последова-
последовательность, мы имеем дело с простым неразвет в ленным
экспериментом.
Если же последовательность входных символов та-
такова, что каждый последующий входной символ экспе-
экспериментатор выбирает в зависимости от предыдущих
выходных символов, эксперимент носит название про-
простого разветвленного (или же кратко — разветвленного).
В том случае, когда в распоряжении исследователя
имеется несколько экземпляров одной и той же /7-ма-
/7-машины, находящихся в одинаковом начальном состоянии,
можно провести кратный эксперимент, подавая одновре-
одновременно различные последовательности на входы всех этих
экземпляров. Разновидностью кратного эксперимента
можно считать эксперимент с одной /7-машиной, снаб-
снабженной «возвратной кнопкой», т. е. устройством, которое
после проведения эксперимента позволяет эксперимента-
экспериментатору возвращать /7-машину в исходное состояние.
Задачу определения тех или иных особенностей
структуры исследуемой /7-машины по результатам ко-
конечного эксперимента можно ставить лишь после того,
как точно оговорены факты, априорно известные об этой
машине. Как будет показано ниже, то новое, что можно
выяснить об изучаемой /7-машине, существенно зависит
от априорной информации, т. е. информации, которая
уже имелась в нашем распоряжении до начала экспе-
эксперимента.
С самого начала можно отметить следующее интуи-
интуитивно ясное утверждение: если о П-машине ничего не из-
известно, то никакой конечный эксперимент не позволяет
установить даже числа ее состояний. Очевидно, что для
изучения машины необходимо заранее знать характер
и число г входных символов р.
§ Ц.1] ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ПОСТАНОВКА ЗАДАЧИ
399
Пусть имеется /7-машина 5 с^ внутренними состоя-
состояниями xi, X2, • •., Xh (число k нам неизвестно!), с кото-
которой мы проводим конечный эксперимент длины /.
Тогда всегда можно построить другую /7-машину S*
с большим чем k числом состояний, которая работала
Рис. 11.1.
бы точно так же, как и машина S при эксперимен-
экспериментах длины, не превышающей /, и отличие которой от
машины S проявилось
бы только при экспери-
экспериментах большей длины.
Пусть, например, с ко-
конечным автоматом А с
выходным преобразова-
преобразователем, диаграмма состоя-
состояний которого показана на
рис. 11.1, мы проводили
эксперименты . длины
/<3. Легко видеть, что
автомат В, диаграмма со-
состояний которого показа-
показана на рис. 11.2, при
/ < 3 и при начальных
состояниях щ или Х2 будет
выдавать на выходе ту же
последовательность X, что
и автомат Л, и, таким об-
образом, эти автоматы при
/<3 не отличаются. Их
отличие проявится только
тогда, когда на вход будет подан следующий (четвер-
(четвертый) входной символ.
Приведенные рассуждения показывают, что для экс-
экспериментального определения особенностей внутренней
Рис. 11.2.
400 ОПРЕДЕЛЕНИЕ СВОЙСТВ ПОСЛЕДОВАТЕЛЬН. МАШИН [ГЛ. XI
структуры автомата или Я-машины кроме числа вход-
входных символов г во всяком случае необходимо знать
оценку числа k их состояний. В дальнейшем мы будем
предполагать, что числа k и г известны. При этом могут
быть поставлены следующие задачи эксперимента:
а) определение эквивалентности некоторых двух со-
состояний одной и той же или. двух разных Я-машин;
б) определение эквивалентности двух Я-машин;
в) определение диаграммы состояний Я-машины;
г) определение, в каком состоянии находилась Я-ма-
шина в начале эксперимента, или приведение ее в опре-
определенное состояние к концу эксперимента и т. д.
Для того, чтобы эти задачи можно было решать, не-
необходимо знать, какие эксперименты можно проводить
с Я-машинами (например, возможен ли кратный экспе-
эксперимент), а также некоторые дополнительные сведения
о множестве изучаемых машин (например, задано мно-
множество машин, число состояний которых известно, и все
состояния которых не эквивалентны друг другу).
В § 11.2 приводится решение основной задачи об
определении эквивалентности состояний Я-машины
(теорема Мура). В последующих параграфах рассмо-
рассмотрено решение задач об исследовании Я-машин в слу-
случае, когда возможно проведение кратных экспериментов
(в § 11.3), а также в случае, когда исследователь мо-
может проводить только простой эксперимент, в том числе
и разветвленный (§ 11.4).
§ 11.2. Определение эквивалентности состояний
последовательностных машин по реакции машины
на входные последовательности конечной длины
Рассмотрим два эквивалентных состояния некоторой
Я-машины. В соответствии с определением понятия «эк-
«эквивалентные состояния», при любой входной последова-
последовательности выходные последовательности совпадают, ка-
какое бы из этих эквивалентных состояний ни было при-
принято за начальное. Наоборот, если принять за начальные
неэквивалентные состояния, то найдется такая входная
последоэательность, что, начиная с некоторого ^-го так-
§ 11.2] ОПРЕДЕЛЕНИЕ ЭКВИВАЛЕНТНОСТИ СОСТОЯНИИ 401
та, выходные последовательности будут различны. Это
число q зависит как от рассматриваемой Я-машины (ее
числа состояний k и структуры), так и от «различаю-
«различающей» последовательности. Естественно, возникает задача
об оценке наименьшей длины той входной последова-
последовательности, с помощью которой может быть обнаружена
неэквивалентность двух состояний заданной Я-машины.
Оказывается, такая оценка может быть дана, если
известно лишь число k состояний Я-машины. Эту оценку
устанавливает следующая теорема.
Теорема 1 (Мура)*). Вели все k состояний П-ма-
шины N неэквивалентны, то дАя каждой пары ее состоя-
состояний существует такая входная последовательность дли-
длины не более k— 1, которая различает эти состояния.
Рассмотрим разбиения множества состояний маши-
машины N на группы состояний, эквивалентных относительно
множеств Ls всех последовательностей длины s E=1,
2, ..., п— 1).
Доказательство будем вести с помощью индукции
по s. Докажем, что если число групп состояний,
эквивалентных относительно Ls, равно /ns, то число
групп состояний, эквивалентных относительно Ls + ь не
меньше ms + 1 (т. е. ms +1 > ms + 1).
Если s = 1, т. е. рассматриваются все входные после-
последовательности длины 1, то множество состояний маши-
машины N разобьется по меньшей мере на две группы со-
состояний, эквивалентных относительно L\. Действительно,
если бы все состояния машины N были эквивалентны
относительно Li, то они были бы эквивалентны и отно-
относительно множества Е всех возможных последователь-
последовательностей (так как в этом случае выход машины опреде-
определялся бы лишь входом), а это не так — у машины N нет
эквивалентных относительно Е состояний. Следователь-
Следовательно, mi>-2.
Выберем два состояния и* и xj, эквивалентные отно-
относительно Ls. Поскольку, по определению Я-машины N,
состояния Хг и Xj неэквивалентны, то существует некото-
некоторая различающая их входная последовательность, но
*) См. [72], а также работу [98], где аналогичная теорема была
приведена независимо от Мура.
26 М. А. Айзерман, Л. А. Гусев и др.
402 ОПРЕДЕЛЕНИЕ СВОЙСТВ ПОСЛЕДОВАТЕЛЬН. МАШИН [ГЛ. XI
она не принадлежит Ls. Пусть наименьшая длина такой
различающей последовательности равна q (q ">!'). То-
Тогда под действием первых q— (s + 1) входных символов
этой последовательности состояния иг- и kj перейдут со-
соответственно в состояния xg и ил, которые также будут
эквивалентны относительно Ls. Действительно, посколь-
поскольку q — наименьшая длина различающей входной после-
последовательности, то выходные последовательности при на-
начальных состояниях Иг и Hj совпадают от (q — s—l)-ro
до (q—1)-го тактов включительно. Поэтому в течение
s тактов, начиная от момента q — 5—1 (при котором
машина находится в состояниях и# и ил соответственно),
выходные символы совпадают. Но вместе с тем состоя-
состояния xg и ил заведомо ^различаются входной последова-
последовательностью длины s у\, так как (s + 1)-й такт при на-
начальных состояниях j?g и ил является q-м тактом при на-
начальных состояниях Иг и щ, а число q было выбрано
как раз так, чтобы на этом q-м такте выходные символы
были различными. Поэтому состояния и# и ил заведомо
относятся к различным группам состояний, эквивалент-
эквивалентных относительно Ls + \.
Заметим теперь, что если два состояния и# и ил,
эквивалентные относительно Ls, неэквивалентны относи-
относительно Ls + \, то та группа состояний, эквивалентных от-
относительно Ls, к которой принадлежат xg и ил, разби-
разбивается по меньшей мере на две группы состояний, экви-
эквивалентных относительно Ls + i- Тем самым показано, что
ms +1 > ms + 1.
Как следует из этого неравенства и из доказанного
выше неравенства т\ ^-2, всегда существует число
q*^.k—1 такое, что число групп состояний, эквива-
эквивалентных относительно Lq*, в точности равно /г, т. е.
любые два состояния машины N оказываются неэкви-
неэквивалентными относительно Lq*. Но это значит, что для
каждой пары состояний машины N найдется последова-
последовательность из Lq*, имеющая длину, не большую чем
<7* = ?-1, A1.1)
при которой выходные последовательности не совпадают.
Теорема доказана.
§ 11.2
ОПРЕДЕЛЕНИЕ ЭКВИВАЛЕНТНОСТИ СОСТОЯНИЙ
403
По поводу доказанной теоремы Мура сделаем не-
несколько замечаний.
Замечание первое. Если рассматривается авто-
автомат с выходным преобразователем и известно не только
число k неэквивалентных состояний, но и число I симво-
символов в таблице выходного преобразователя, то вместо
оценки (k—1) будет оценка
$• = ? —/+1. A1.2)
Доказательство этого утверждения дословно повторяет
приведенное выше доказательство теоремы Мура, за ис-
исключением лишь того, что в этом случае вместо нера-
неравенства mi^>2 справедливо неравенство tn\^>l, т. е.
число групп состояний, эквивалентных относительно Lb
не может быть меньше /. Если же / заранее неизвестно,
то при оценке приходится исходить из «худшего» случая,
когда 1 = 2 и k — /+ 1 = k —1.
Замечание второе. Легко показать, что оценка
длины последовательности, различающей неэквивалент-
неэквивалентные состояния, которая дается теоремой 1, является точ-
точной в том смысле, что она не может быть улучшена, если
иметь в виду любые Я-машины с k неэквивалентными
состояниями. Это следует из того, что для каждого k мо-
могут быть построены примеры машин, у которых заведомо
нельзя различить два неэквивалентных состояния, если
длина входной последовательности меньше, чем k—1.
Пример. Рассмотрим конечный автомат с выход-
выходным преобразователем, диаграмма состояний которого
имеет вид, показанный на рис. 11.3. Основная таблица
Л)
Рис. 11.3.
автомата (табл. 11.1) и преобразователя (табл. 11.2)
приведены ниже.
Легко видеть, что для того, чтобы установить неэк-
неэквивалентность состояний Xft _ 1 и х/г, надо подать вход-
входную последовательность длины не менее чем k—1, так
26*
404 ОПРЕДЕЛЕНИЕ СВОЙСТВ ПОСЛЕДОВАТЁЛЬН. МАШИН [ГЛ. Х~1
как машина, начиная работать из этих состояний, при
любых входных последовательностях длины, меньшей
k— 1, будет выдавать на выходе лишь последовательно-
последовательности из Яо.
Таблица 11.1
Таблица 11.2
*з
Ч-i
Ч
Ро
-та
*|
*2
*3
• • •
Ik
К
• • •
Если же, например, состоянию иг соответствовал бы
символ А,2, то для установления неэквивалентности со-
состояний Kk -1 и кь. достаточно подать последовательность
длиной k — 2 (т. е. k — / + 1, где / = 3).
Замечание третье. Рассуждения, которые были
использованы при доказательстве теоремы 1, могут быть
использованы для выявления эквивалентности или неэк-
неэквивалентности двух состояний П-машины, если известна
ее структура (например, задана ее диаграмма состоя-
состояний или таблицы автомата и преобразователя и т. д.).
Для этого надо сначала разделить все состояния на
группы состояний, эквивалентных относительно L\\ каж-
каждую из полученных групп надо затем разделить на груп-
группы состояний, эквивалентных относительно L2, и т. д.
до тех пор, пока изучаемые два состояния не окажутся
11.2]
ОПРЕДЕЛЕНИЕ ЭКВИВАЛЕНТНОСТИ СбСТОЯМИЙ
405
в разных группах. Если этого не случится даже на
(k—1)-м шаге, т. е. при разделении всех состояний на
группы эквивалентных относительно Lk-u то в силу тео-
теоремы 1 рассматриваемые состояния эквивалентны между
собой. Подобное рассуждение мы уже использовали, по
существу', в § 9.4.
Замечание четвертое. Хотя любые два неэк-
неэквивалентных состояния различаются входной последова-
последовательностью длины не более
к—1, для разных пар со-
состояний различающие их по-
последовательности, вообще
говоря, могут быть разными
(в том числе и по длине).
В общем случае не суще-
существует одной конечной вход-
входной последовательности, от-
отличающей какое-либо со-
состояние от любого из ос-
остальных.
Пример. Рассмотрим
конечный автомат с выход-
выходным преобразователем,диа-
преобразователем,диаграмма состояний которого изображена на рис. 11.4, а
основная таблица автомата и таблица преобразователя
приведены ниже (в табл. 11.3 и 11.4).
Таблица 11.3 Таблица 11.4
Рис. 11.4.
\. р
*1
*2
*3
*4
Ро
*4
*1
*4
*2
Pi
*3
*3
*4
*2
X
*1
*2
*3
*4
\
К
к
к
406 ОПРЕДЕЛЕНИЕ СВОЙСТВ ПОСЛЁДОВАТеЛЬН. МАШИН [ГЛ. ХГ
Здесь для различения состояний щ и и2 нужно, чтобы
последовательность входных символов начиналась с ро,
для различения же состояний щ и и3 нужно, чтобы вход-
входная последовательность начиналась с рь
Замечание пятое. (Прямое следствие четвер-
четвертого замечания.) Не существует простого эксперимента,
с помощью которого можно- было бы, даже имея диа-
диаграмму состояний П-машины, установить, в каком на-
начальном состоянии она находилась.
В самом деле, как было показано, не существует ко-
конечного эксперимента, отличающего данное начальное
состояние от всех остальных. Если же мы проведем ка-
какой-либо эксперимент, отмечающий данное состояние щ
от некоторого подмножества 5 множества К всех состоя-
состояний Я-машины, то мы выведем Я-машину из состояниях*
и, следовательно, не сможем узнать, в каком из состоя-
состояний подмножества K — S была она вначале.
Легко видеть, что если нет эквивалентных состояний,
то начальное состояние всегда может быть определено
в том случае, когда есть возможность провести кратный
эксперимент (есть несколько идентичных экземпляров
Я-машины или же есть кнопка возврата).
Замечание шест о.е. Из теоремы 1 можно полу-
получить оценку длины эксперимента для определения не-
неэквивалентности состояний двух П-машин, имеющих со-
соответственно k\ и &2 внутренних состояний, если рассма-
рассматривать эти состояния как состояния одной Я-машины,
полученной простым объединением*) обеих рассматри-
рассматриваемых Я-машин. Тогда неэквивалентность этих двух со-
состояний может быть установлена экспериментом длины
не более
— 1. (Ц.З)
Неэквивалентность состояний двух различных авто-
автоматов с выходными преобразователями может быть
установлена экспериментом (см. замечание первое) дли-
длины не более
. A1.4)
*) Диаграмма состояний объединенной машины представляет со-
собой простое объединение диаграмм состояний исходных машин.
§ 11.3] КРАТНЫЕ ЭКСПЕРИМЕНТЫ 407
Если k\ = &2» то получаем соответственно оценки для
Я-машин
(И.5)
и для автоматов с преобразователями
. (И-6)
Из следующего примера видно, что эта оценка не мо-
может быть улучшена.
Пример. На рис. 11.5 показаны диаграммы состоя-
состояний двух конечных автоматов с выходными преобразо-
преобразователями, причем число выходных символов / = 2. Легко
(Mo)
(poMv(pit$
Рис. 11.5.
видеть, что для установления неэквивалентности состоя-
состояний xj и xj- этих двух автоматов нужно провести экспе-
эксперимент длиной не менее 7, например подать на вход
последовательность р(^) = popopopopipipi- Если же состоя-
состояниям >«2 и ус этих автоматов соответствовал бы новый
выходной символ Яг, т. е. если бы было / = 3, то для раз-
различения состояний щ и к\ был бы достаточен экспери-
эксперимент длины 6. Легко построить подобные примеры для
любых значений к.
§ 11.3. Изучение последовательностных машин
с помощью кратных экспериментов
Как уже указывалось, кратный эксперимент можно
провести, когда есть несколько идентичных экземпляров
исследуемой Я-машины или же когда есть кнопка, воз-
возвращающая исследуемую Я-машину всегда в одно и XQ
408 ОПРЕДЕЛЕНИЕ СВОЙСТВ ПОСЛЕДОВАТЕЛЬН. МАШИН [ГЛ. XI
же начальное состояние. При проведении такого экспе-
эксперимента рассматриваются лишь те состояния, в которые
Я-машина может прийти за конечное число шагов из
исходного состояния и0.
Последовательностная машина называется ур-связ-
ной, если диаграмма состояний ее такова, что для каж-
каждого состояния и* (/= 1, 2, ..., k) найдется входная по-
последовательность, переводящая Я-машину из заданного
начального состояния и0 в состояние щ. Очевидно, что
при изучении Я-машин с помощью кратных экспери-
экспериментов имеет смысл ограничиться рассмотрением лишь
и°-связных машин, так как, если в действительности
исследуемая Я-машина не является и°-связной, то
кратный эксперимент позволяет изучить лишь ту ее
часть, которая является и°-связной. Поэтому в настоя-
настоящем параграфе рассматриваются лишь и°-связные
машины с возвратной кнопкой.
Для и°-связной Я-машины с возвратной кнопкой от-
отпадает задача определения состояния, машины в начале
или конце эксперимента и остаются лишь задача опре-
определения эквивалентности двух Я-машин и задача опре-
определения диаграммы состояний Я-машины.
Рассмотрим сначала первую задачу. Очевидно, что
определение эквивалентности двух и°-связных Я-машин
сводится к определению эквивалентности двух соответ-
соответствующих состояний и0 в этих двух Я-машинах. В пре-
предыдущем параграфе было показано, что неэквивалент-
неэквивалентность состояний в двух Я-машинах можно установить
экспериментом длины не более 2k— 1, а для двух авто-
автоматов с преобразователями — не более 2k— /4-1.
Таким образом, с помощью кратного эксперимента
можно выделить какую-либо определенную к°-связную
Я-машину из целого класса неэквивалентных ей ^-связ-
^-связных машин, диаграммы состояний которых известны.
Отсюда вытекает способ решения второй задачи — по-
построения диаграммы состояний и°-связной Я-машины.
Алгоритм построения диаграммы состояний ^-связ-
^-связной машины следующий:
1. Проводим с машиной все возможные эксперименты
длиной 2k—1 (всего r2h~l экспериментов). Записываем
результаты их в виде таблиц (лент), оставляя без оба-
КРАТНЫЕ ЭКСПЕРИМЕНТЫ
409
значений клетки таблицы, соответствующие состояниям
Я-машины.
2. Приписываем некоторый номер i A<?</г) на-
начальному состоянию и проставляем этот номер в соот-
соответствующих строках таблиц.
3. После первого шага эксперимента будут иметь ме-
место состояния и1. Различных состояний и1 может быть
не больше чем г. Проверяем на всех последовательно-
последовательностях длины k—1, нет ли эквивалентных среди состоя-
состояний к0 и и1. Приписываем некоторые произвольные, от-
отличные друг от друга но-
номера i, / A < i, j < k)
всем состояниям х!, неэк-
неэквивалентным между собой
и неэквивалентным со-
состоянию и0. Эквивалент-
Эквивалентные состояния будем обо-
обозначать одним и тем же
номером. Пусть число
различных состояний и1
будет Г\.
4. Из каждого из обо-
обозначенных таким образом
состояний за один шаг
можно прийти не больше
чем к г новым состояниям и2; следовательно, всего
состояний и2 может быть не больше чем Г\Г. Проверяем
для всех возможных последовательностей длины k—1,
нет ли эквивалентных среди состояний х°, к1 и и2. При-
Приписываем номера состояниям к2 так же, как это было
сделано для состояний х1.
5. Продолжаем этот процесс, пока не получим k не-
неэквивалентных между собой состояний. Для этого, оче-
очевидно, может понадобиться и меньше чем 2k — 1 шагов,
т. е. не надо будет просматривать все ленты, построен-
построенные на основании проведенных экспериментов.
6. Строим диаграмму состояний, основную таблицу
или матрицу соединений в соответствии с результатами;
всех проделанных экспериментов.
Замечание. Ввиду того, что выходной символ!
конечного автомата с выходным преобразователем
Рис. 11.6*.
410 ОПРЕДЕЛЕНИЕ СВОЙСТВ ПОСЛЕДОВАТЕЛЬ!!. МАШИН [ГЛ. XI
определяется полностью его состоянием и и не зависит
от входного символа р в данный момент, при построении
диаграммы состояний такого автомата достаточно про-
провести не r2h~l+1t a r2k~l экспериментов длиной 2k— /+,
+ 1, причем последний входной символ всех экспери-
экспериментов может быть любым, в том числе он может быть
и одним и тем же для всех экспериментов.
Пример. Пусть известно число неэквивалентных
между собой состояний k = 3, число входов г = 2 и чи-
число выходных символов / = 3 некоторого автомата с вы-
выходным преобразователем. По результатам эксперимен-
экспериментов длиной 2k — /+1=4, проведенных с этим автома-
автоматом в соответствии с изложенным алгоритмом
(табл. 11.5), можно проставить в строках таблицы сим-
символы состояний (проставлены в скобках) и построить
диаграмму состояний автомата (рис. 11.6).
'I»
p
-1
X
Pi
\
1
Pi
(*,)
2
-та
(*,)
3
Pi
К
t
p
0
Pi
(*>)
1 *•
1
-та
A,
2
P2
я,
3
Pi
^2
'I-
P
•X,
X
P2
x,
Ta(
1
P2
M
x2
5 л иц
2
Ы
^3
а 11.5
3
Pi
<Ч>
х2
t
0
P2
1 / 4
X X,
l
pi
2
Pi
3
-та
я,
§ И.4]
ПРОСТЫЕ ЭКСПЕРИМЕНТЫ
411
Продолжение
t
р
X
X
0
Pi
1
Р2
2
Р2
х2
3
Pi
Ы
*3
t
Р
У,
X
0
Р2
1
Pi
х2
2
Р2
3
Pi
х2
<
p
X
0
P2
1
l
p2
x2
2
?2
Ы
к
3
Pi
Ы
X3
-
t
P
0
pi
X X,
1
P2
x,
2
Pi
Ы
x2
3
Pi
¦<«,>
§ 11.4. Изучение последовательностных машин
с помощью простых экспериментов
Изучение Я-машин с помощью простых эксперимен-
экспериментов проводится тогда, когда нет условий для проведения
кратного эксперимента.
Задача определения отличимости Я-машин и опре-
определения их внутренней структуры с помощью простых
экспериментов решена лишь для множества таких ма-
машин, все состояния которых неэквивалентны между со-
собой. Примером такого множества является множество
различных сильно связных машин. Последовательност-
ная машина называется сильно связной, если для каж-
каждой пары щ и щ состояний этой машины найдется вход-
входная последовательность, переводящая машину из состоя-
состояния щ в состояние xj.
412 ОПРЕДЕЛЕНИЕ СВОЙСТВ ПОСЛЕДОВАТЕЛЬН. МАШИН [ГЛ. XI
Ввиду того, что класс сильно связных машин являет-
является более узким, чем класс и°-связных машин, то в соот-
соответствии с предыдущим параграфом две сильно связ-
связные П-машины будут эквивалентны между собой, если
эквивалентны хотя бы два состояния этих двух машин.
Следовательно, все состояния всех машин любого мно-
множества, состоящего из различных сильно связных ма-
машин, неэквивалентны между собой.
Как указано в замечании пятом к теореме 1 (см.
§ 11.2), в общем случае не существует простого экспери-
эксперимента, отличающего начальное состояние к0 Я-машины
от всех остальных неэквивалентных ему состояний. По-
Поэтому естественно пытаться искать простой эксперимент,
приводящий машину в такое состояние, которое можег
быть однозначно определено, или, иными словами, экс-
эксперимент, для которого существует однозначное соответ-
соответствие между результатом эксперимента и последним
состоянием эксперимента кр, соответствующим послед-
последнему наблюдаемому входному символу.
Доказательство существования такого эксперимента
для всего класса Я-машин и оценку его длины дает сле-
следующая теорема.
Теорема 2 (Мура — Карацубы). Для опреде-
определения последнеф состояния заданной П-машины с k не-
неэквивалентными внутренними состояниями достаточно
провести эксперимент длиной не более ~ ' , а для ко-:
печного автомата — длиной не более — у —|- 1,
Доказательство. Пусть диаграмма состояний ма-
машины задана. Входную последовательность, отличающую
последнее состояние Я-машины, будем искать в виде
ряда следующих друг за другом последовательностей а8
(s = 1, 2, ...). Эти последовательности выбираются так,
что множество Т3 состояний*), которые могут наступить
*) В работах [72], [25], [41], [59], [60] множество Г, называется
множеством ассоциированных состояний. Подчеркнем, что множе-
множество Т8 — это множество тех состояний, которые могут наступить
после подачи последовательности as, а не тех возможных последних
состояний, которые определяют последний наблюдаемый выходной
символ и, таким образом, определяют разбиение всех состояний на
группы состояний, эквивалентных относительно аЛ.
§ и.4] ' ПРОСТЫЕ ЭКСПЕРИМЕНТЫ 413
после подачи последнего входного символа эксперимен-
эксперимента а8 и, следовательно, являются возможными началь-
начальными состояниями для последующего эксперимента а8 + и
имеет не более k — s элементов. В случае, когда Я-ма-
шина является автоматом, среди этих состояний было
бы не менее двух, отличимых любым экспериментом
длины 1, т. е. любым входным символом.
До начала эксперимента, при s = О, это условие вы-
выполнено.
Докажем, что если условие выполнено для а8у то су-
существует fls + ь для которого оно также выполнено. На-
Начальное состояние для эксперимента а8 + \ принадлежит
множеству Т8. Используя теорему 1 и рассуждения, при-
приведенные при ее доказательстве, замечаем, что элементы
множества T8t число которых по условию теоремы не
более k — s, могут принадлежать: а) не менее чем двум
группам состояний, эквивалентных относительно множе-
множества L6 +1 всех экспериментов длины не более s+1
(число таких групп не меньше s + 2, см. теорему 1) и
б) не менее чем трем группам состояний, эквивалентных
относительно множества L8 + 2 всех экспериментов длины
не более s + 2 (число таких групп не меньше s+3).
Следовательно, для любой Я-машины среди k — s со-
состояний множества Т8 всегда есть пара состояний, кото-
которые могут быть отличены экспериментом а8 + \ длины
s+1. Поэтому множество T8 + i будет содержать по
крайней мере на один элемент меньше, чем множе-
множество Ts, т. е. будет иметь не более чем k— (s+1) со-
состояний.
Если же исследуемая машина является автоматом, то
в силу б) среди состояний множества Т8 всегда есть
пара состояний, которые могут быть отличены экспери-
экспериментом длины s + 2, последовательность первых s+1
символов которого и принимаем за а8 + \. В силу того,
что по условию теоремы для автомата хотя бы два
состояния множества Т8 отличимы между собой любым
входным символом, первый же символ эксперимента
0s + i отличит эти состояния. Следовательно, множество
Ts + \ будет содержать по крайней мере на один элемент
меньше, чем множество Ts, т. е. будет содержать
^— (s + 1) состояний, и из них в силу нашего выбора
414 ОПРЕДЕЛЕНИЕ СВОЙСТВ ПОСЛЕДОВАТЕЛЬН. МАШИН [ГЛ. XI
эксперимента as + i по крайней мере два будут отличимы
любым входным символом.
В связи с тем, что условие теоремы соблюдается при
s и s + 1, по индукции оно выполняется при любом це-
целом положительном s, и следовательно, Th-2 будет со-
содержать не более двух состояний, которые для /7-маши-
ны можно отличить экспериментом аъ. - i длиной не
более k—1, а для автомата — любым входным симво-
символом, т. е. экспериментом длины 1.
Таким образом, каждое as имеет длину не больше s,
и для определения последнего состояния потребуется экс-
эксперимент длины не более
A1.7)
для Я-машины и
k-2
для конечного автомата.
Замечание первое. Приводимые ниже два при-
примера показывают, что полученные оценки не могут быть
улучшены.
Пример 1. Для того чтобы отличить последнее со-
состояние автомата, диаграмма состояний которого изо-
бражена на рис. 11.7, нужно провести эксперимент
Р1Р2Р1Р1 длиной 4, т. е. в точности равной
(*-1)(*-2)
о ~Г А»
§ 11.4] ПРОСТЫЕ ЭКСПЕРИМЕНТЫ 415
Пример 2. Чтобы отличить последнее состояние
Л-машины, диаграмма состояний которой показана на
рис. 11.8, нужно провести эксперимент Р3Р1Р3Р2Р1Р3 длиной
==6
Легко проверить, что в обоих приведенных примерах
не существует более короткого эксперимента для отли-
отличения последнего состояния. Метод построения аналогич-
аналогичных примеров для любого k очевиден.
Рис. 11.8.
Замечание второе. Если учесть, что выходной
алфавит содержит / символов, то можно с помощью по-
подобных же рассуждений прийти к следующей оценке
длины эксперимента, определяющего последнее состоя-
состояние автомата с выходным преобразователем:
Для автомата без преобразователя (k — I) получаем
очевидную оценку, равную единице.
Замечание третье. Оценка длины эксперимен-
эксперимента, определяющего последнее состояние, может быть сни-
снижена в случае, когда известно, что начальные состояния
составляют некоторое подмножество всего множества
состояний k. Если начальных состояний может быть
l<v<^& и среди них есть состояния, отличимые любым
входным символом, то, воспользовавшись рассуждения*
ми, аналогичными приведенным при доказательстве
теоремы 2, можно показать, что длина эксперимента,!
416 ОПРЕДЕЛЕНИЕ СВОЙСТВ ПОСЛЕДОВАТЕЛЬН. МАШИН [ГЛ. XI
отличающего последнее состояние, для автомата с преоб-
преобразователем будет
^ — 21 —
Для автомата с преобразователем, среди v начальных
состояний которого нет отличимых любым эксперимен-
экспериментом длиной 1, длина эксперимента будет
Пример 3. Если в первом примере (см. рис. 11.7)
начальными могут быть только состояния хз и x-t, то для
отличения последнего состояния автомата нужен экспе-
эксперимент Р2Р1Р2 длиной 3, т. е. в точности равной.
(v — 1)B? —2/ — v-f4)
Если же начальными могут быть только состояния
xi и хз, то последнее состояние автомата отличит любой
входной символ, т. е. эксперимент длиной
(v~2) Bk — 21 —
Замечание четвертое. При построении крат-
кратчайшего эксперимента следует обратить внимание на то,
что если Ts содержит не k — s элементов, а меньше, на-
например k — 5 — w, то с помощью рассуждений, анало-
аналогичных приведенным в доказательстве теоремы 2, можно
показать, что оценка длины следующей за а8 последова-
последовательности будет не 5+1, as + m+1. При этом общая
длина эксперимента, приводящего машину в определен-
определенное последнее состояние, сокращается за счет исключения
последовательностей длиной от s + 1 до s + m.
Приведем пример, иллюстрирующий регулярный спо-
способ построения кратчайшего эксперимента для опреде-
определения последнего состояния автомата с преобразовате-
преобразователем, непосредственно вытекающий из теоремы 2.
Пример 4. Рассмотрим конечный автомат с вы-
выгодным преобразователем, имеющий диаграмму состоя-
§ П.4]
ПРОСТЫЕ ЭКСПЕРИМЕНТЫ
417
ний (рис. 11.9), основную таблицу и таблицу преобразо-
преобразователя (табл. 11.6 и 11.7).
В табл. 11.8 показан процесс построения кратчай-
кратчайшего эксперимента для определения последнего состоя-
состояния автомата.
Так как в примере рассматривается автомат, то в со-
соответствии с доказательством теоремы 2 для каждого s
Рис. 11.9.
мы выбираем такие входные последовательности дли-
длиной s + 1, которые различают какие-либо два состояния
множества Т8 и берем первые s символов этих последо-
последовательностей (последние s + 1-е символы в таблице за-
зачеркнуты). Как показано в четвертом замечании к тео-
теореме 2, в этом примере можно от 5 = 1 перейти прямо
к s = 4, минуя s = 2 и s = 3. Для различения двух пред,-
последних состояний хз и щ достаточно. одного любого
входного символа. Поэтому общий эксперимент, опре-
определяющий конечное состояние рассматриваемого автома-
автомата, будет pipopopopipopopopopipo или pipopopopipopopopopipi,
и длина его равна 11.
27 М. А. Айэерман, Л. А. Гусев и др.
418 ОПРЕДЕЛЕНИЕ СВОЙСТВ ПОСЛЕДОВАТЕЛЬН. МАШИН [ГЛ. Xt
Замечание пятое. На основании теоремы 2 мо-
можно установить, что если известно некоторое множе-
множество {S} машин Si с числом внутренних состояний k{
(i = 1, 2, ..., N) (известна диаграмма состояний каж-
каждой машины этого множества), и все состояния машин
не эквивалентны между собой, то существует простой
разветвленный эксперимент, проведение которого с од-
одним экземпляром какого-либо элемента Sx множества
{S} позволяет отличить его от всех других элементов
множества.
Таблица 11.6
Таблица 11.7
х \.
X,
х2
Xg
х4
х6
х7
Ро
*5
Xg
х4
х6
х7
х2
pi
х4
х2
*з
х2
Xg
X,
X
X,
*2
Xg
х4
х6
х7
К
К
к
к
к
к
к
к
При отыскании оценки длины такого эксперимента и
при построении самого эксперимента возможны два под-
подхода.
Во-первых, можно построить разветвленный экспери-
эксперимент, состоящий из ряда последовательностей, каждая
из которых приводит каждую из машин множества в из-
известное последнее состояние. За этими последователь-
§ И.4]
ПРОСТЫЕ ЭКСПЕРИМЕНТЫ
419
Таблица 11.8
S
0
1
4
5
as
»
«4 = PoPoPoPl/l
«s =PoPoPoPoPi(/oV/i)
PoVpi
T
1 s
l^l»X2» X3> X4» X5» X6> X7 }
<X4> {X2, X8, *4, *,}
{x,> {x2, *8, x,}
{*2}{*3, *l}
Число элементов
T
1 s
k = 7
k—s—m =7-1-2=4
k—s=7—A=Z
k—s=7—5=2
ностями следуют последовательности, различающие эти
последние состояния между собой. Такой подход пред-
предложен в работе Мура [72]. Если рассматривается множе-
множество /7-машин Si с числом внутренних состояний ki
(i = 1, 2, ..., N), то оценка длины такого эксперимента
из A1.3) и A1.7) будет
N
где /Jimax и ^2тах — максимальные числа состояний.
При условии, что все k\ равны между собой, оценка
для 77-машины, очевидно, будет
— 1)Bk — 1). A1.13)
Для конечного автомата с преобразователем из A1.4)
и A1.9) получим
N
>]+
AЫ4)
или при всех ku равных между собой,
A1.15)
27*
420 ОПРЕДЕЛЕНИЕ СВОЙСТВ ПОСЛЕДОВАТЕЛЬН. МАШИН [ГЛ: XI
Наконец, если рассматривается автомат без преоб-
преобразователя или, что то же, при к = /, то любой входной
символ определит, в каком из состояний находится каж-
каждый из автоматов (см. замечание второе), и оценка экс-
эксперимента, с помощью которого можно выделить один
из N автоматов, будет
Строить такой эксперимент, имея одну реальную ма-
длину Sx из заданного множества {5} и диаграммы со-
состояний всех машин множества, можно следующим об-
образом.
1, Находим (умозрительно, по диаграммам состоя-
состояний) для данного множества машин 5Ь 5г, ..., SN все
эксперименты, определяющие последние состояния всех
машин множества. Пусть это будут эксперименты аи
#2» • • •» ям W^.N). Хотя все машины множества неэк-
неэквивалентны, но результаты каждого из этих экспе-
экспериментов (а они могут зависеть от начального состояния
соответствующей машины) могут быть одинаковыми как
для той машины, для которой этот эксперимент одно-
однозначно определяет последнее состояние, так и для дру-
других машин множества.
2. Проводим с машиной Si соответствующий экспе:
римент а\ (умозрительно) при всех ее возможных на-
начальных состояниях, и с исследуемой машиной Sx (в дей-
действительности). Если результаты этого эксперимента
совпадают для какого-либо из начальных состояний
машины Si с результатом эксперимента с машиной 5Ж,
то устанавливаем последнее состояние машины Si, соот-
соответствующее этому результату эксперимента, и тем са-
самым устанавливаем возможное последнее состояние ма-
машины Sx. Если результаты эксперимента с машиной Si
отличаются от результата эксперимента с машиной Sx
при всех возможных начальных состояниях машины Si,
то исключаем эту машину из дальнейшего рассмотрения.
Если один и тот же эксперимент п\ определяет по-
последние состояния для нескольких машин множества {S},
например для машин Sa, Sa, ..., «Sa:, то в случае, ко-
когда результаты экспериментов со всеми или с некото-
§11.4] •: ПРОСТЫЕ ЭЖСПЕРИМЕНТЫ :/ ~ ::г 421
рыми из машин $'U-,'S~,::.,S при определенных на-
12 q ¦
чальных состояниях совпадают с результатами экспе-
эксперимента с машиной Sx, устанавливаем последние состоя-
состояния этих мйщин, т. е. возможные последние состояния
машины Sx. В противном случае исключаем эти машины
из рассмотрения.
3. Проводим эксперимент а2 с соответствующей ма-
машиной $2 (или с машинами 53, 58, ..., Sa) при всех
• : ¦ ¦ V - Р1 Р2 . pft/ . .
возможных начальных состояниях (умозрительно), с ма-
машиной Sx (в действительности), а также (умозритель-
(умозрительно) с машиной 5i или с теми из машин 5а , Sa, ..., Sa »
которые не исключены в п. 1, считая начальными сек
стояниями машин Si или S . 5_,...., Sn состояния.
2 . q
определяющиеся последними их состояниями и последним,
символом эксперимента а\. Исключаем из рассмотрения
те из машин S\ и 5г (или Sa , 5w , ..., Sa и Sp,S?,..
• ••» So )> для которых результаты эксперимента а2 несо-
впадают с результатами эксперимента с машиной SXi и
устанавливаем последние состояния остальных машин.
Продолжаем так до тех пор, пока не будут прове-
проведены все эксперименты аи определяющие .последние со-
состояния всех машин заданного множества {S}. В резуль-
результате получаем, что. машина Sx может принадлежать не-
некоторому подмножеству E} S E} машин, которые при-
приведены в определенные состояния.
В случае, когда задано множество автоматов без
преобразователей, как было указанр, последние состоя-
состояния всех автоматов будут определены сразу же после
подачи любого входного символа.
4. Находим (умозрительно, по диаграммам состоя-
состояний) эксперимент b\t отличающий состояния, в которых
могут находиться любые две машины 5т: и. &п из [S}?:
Проводим этот эксперимент с машинами Sm_.и Sn (умо-
(умозрительно) .и с машиной Sx (в действительности). Йс*
ключаем, таким образом, либо обе эти машины,. либо;
одну из них. Устанавливаем последнее состояние той из.
этих двух машин, которая не исключена* :. : ,
422 ОПРЕДЕЛЕНИЕ СВОЙСТВ ПОСЛЕДОВАТЕЛЬН. МАШИН [ГЛ. XI
5. Выбираем еще одну или две машины из.множе-
из.множества {S} и проводим с ней (или с ними) тот же экспери-
эксперимент Ь\, и в случае, если результат его совпадает с ре-
результатом, полученным в п. 4 для машины Sx, то уста-
устанавливаем последнее состояние вновь выбранной маши-
машины или машин.
6. Находим эксперимент' ?2, отличающий состояние
не исключенной в п. 4 машины от состояния машины,
выбранной в п. 5. Проводим эксперимент &2 с этой па-
парой машин и с машиной S$ так, как указано в п. 4. Вы-
Выполняем далее указания п.п. 1 — 5, пока не будут исклю-
исключены все машины множества {5}, кроме одной, диаграм-
диаграмма состояний которой и будет диаграммой состояний
машины Sx.
П р и м ер 5. Пусть даны диаграммы состояний трех ав-
автоматов (рис. 11.10), и требуется установить, какая из
Рис. 11.10.
этих диаграмм соответствует некоторому реальному ав-
автомату, с которым можно проводить эксперимент.
Пусть, например, нам дан в действительности авто-
автомат 53 в начальном состоянии игз- Тогда, подав любой
первый входной символ, например символ рг, мы сразу
установим возможные начальные состояния игьигг и
§ 11.4] ПРОСТЫЕ ЭКСПЕРИМЕНТЫ 423
автомата. Подав вслед за этим последовательность из
четырех символов Р2Р1Р1Р2, мы сможем отличить друг от
друга два состояния ип и >«i2 из тех трех состояний иц,
xi2 и И1з, в которые мог бы перейти автомат после по-
подачи первого символа. Наконец, последовательность
Р2Р1Р2Р2 позволит различить состояния >«i2 И13, которые
могут наступить после подачи первых пяти входных сим-
символов. Таким образом, весь разветвленный эксперимент
Р2Р2Р1РФ2Р2Р1Р2Р2, позволяющий выделить автомат из за-
заданного множества, будет иметь длину 9, т. е. точно соот-
соответствует выражению A1.16). Легко видеть, что в этом
случае можно было бы построить более короткий экспе-
эксперимент, например Р1Р2Р1Р1Р2- Но при этом надо было бы
выбирать каждую из последовательностей, составляю-
составляющих весь эксперимент (первый шаг pi и последователь-
последовательности Р2Р1 и pip2, различающие соответствующие состоя-
состояния), просматривая предварительно для всех возмож-
возможных начальных состояний все возможные последние со-
состояния, что значительно осложнило бы алгоритм по-
построения эксперимента.
Можно также получить оценку длины простого нераз-
ветвленного эксперимента, позволяющего выделить одну
определенную машину из заданного множества {St} ма-
машин, все состояния которых неэквивалентны между со-
собой, другим способом, исходя из простого объединения
заданного множества (см. сноску на стр. 406). Экспери-
Эксперимент, определяющий последнее состояние такой объеди-
объединенной машины при всех возможных начальных состоя-
состояниях, очевидно, и позволяет выделить любую из машин
множества.
В соответствии с замечанием шестым к теореме I,
любые два состояния такой объединенной машины мо-
могут быть различены экспериментом длиной не более
kmx-\-km2— 1 (или kmi-\-km2 — /+ 1 для автоматов с пре-
преобразователями), где кщх и &т2 — наибольшие из всех k{.
Поэтому общий эксперименту определяющий последнее
состояние объединенной машины, будет складываться из
последовательностей, оценка длины которых нарастает
ОТ 1 ДО kmi-\-km2— 1 (ИЛИ kmx + km2 ~ I + 1 ДЛЯ ЭВТОМа-
тов с преобразователями), а затем остается посто-
постоянной.
424 ОПРЕДЕЛЕНИЕ СВОЙСТВ ПОСЛЁДОВАТЕЛЬН. МАШИН [ГЛ. XI
-.: Пользуясь-рассуждениями, аналогичными использо-
использованным при доказательстве теоремы 2, получим следую-
следующие оценки: для множества последовательностных ма-
машин с одинаковыми числами состояний
qun=kBk-\)(N-\)\ A1.17)
для автоматов с преобразователями
A1.18)
для автоматов без преобразователей, или же при k—i
A1.19)
Можно показать, что оценки A1.17) — A1.19) длины
неразветвленного эксперимента, полученные исходя из
объединения всех машин множества, всегда хуже оценок
A1.13), A1.15) и {11.16) длины разветвленного экспег
римента, полученных по первому способу — приэедением
каждой из машин множества в определенное состояние
и сравнением этих состояний. Кроме того, использование
-второго способа для построения самого эксперимента
значительно сложнее, чем применение первого способа,
так как при отыскании отдельных последовательностей,
составляющих этот эксперимент, приходится рассматри-
рассматривать не отдельные машины множества, а все множество
в целом.
ГЛАВА XII
АЛГОРИТМЫ
§ 12.1. Примеры алгоритмов
Начнем с рассмотрения нескольких типичных приме-
примеров алгоритмов. -
В предыдущих главах при изучении конечных авто-
автоматов нам приходилось неоднократно иметь дело с
конечными и бесконечными последовательностями раз-
различных символов, например с последовательностями, со-
составленными из нулей и единиц. Но что значит «рассмо-
«рассмотреть» бесконечную последовательность из нулей и еди-
единиц? Ведь ее нельзя непосредственно всю обозреть.
Представление, о такой последовательности можно со-
составить лишь по описанию тех или иных ее свойств.
Определение символа в бесконечной
по с л е д о в а т е л ь н о с т и. Рассмотрим последова-
последовательность, состоящую из нулей и единиц, о которой из-
известно, что символы 0 и 1 все время чередуются.
Если мы видим только изображенное ниже начало
этой бесконечной последовательности и ничего больше
0
1
0
1
1
0
1
0
1
о
1
• • •
о ней не знаем, то никакого представления о всей после-
последовательности мы создать не сможем. Однако такое
представление немедленно создается, как только мы уз-
узнаем ее свойство—нули и единицы всегда чередуются!.
Теперь мы без труда можем предсказать, какой символ^
стоит, например, на 12-м, на 87-м или на 1275642-м*
426
АЛГОРИТМЫ
ГГЛ. XII
месте: для этого надо лишь выяснить, является ли номер
места четным или нечетным.
Рассмотрим последовательность, представляющую
собой периодически повторяющуюся группу цифр 0, 7, 5,3.
0
7
5
3
0
7
5
3
0
7
5
3
• • •
Зная факт периодичности и начало последовательно-
последовательности (один период), снова можно определить, какой сим-
символ стоит в любом месте последовательности; чтобы это
сделать, надо: а) разделить номер места на длину пе-
периода (т. е. на число цифр в периоде); б) посмотреть,
какая цифра расположена в первом периоде на том
его месте, номер которого совпадает с остатком от де-
деления.
Если остаток равен нулю, то надо смотреть послед-
последнюю цифру периода.
Пусть, наконец, третья последовательность заполнена
нулями и единицами так, что единица стоит лишь на тех
местах, номера которых являются квадратами целых
чисел, а на остальных меетах стоят нули.
1
0
0
1
0
0
0
0
1
0
0
0
0
0
0
1
0
0
¦ • •
И здесь мы имеем представление о всей бесконечной
последовательности в том смысле, что по любому за-
заданному номеру места мы можем определить, какой сим-
символ стоит на этом месте. Это определение сведется к рас-
распознаванию того, является ли заданный номер места
квадратом целого числа, что связано с процедурой из-
извлечения квадратного корня.
Во всех этих трех примерах «свойство», благодаря
которому мы могли составить представление о всей бес-
бесконечной последовательности, состояло в том, что име-
имелась процедура, позволяющая «предсказывать» — узна-
узнавать по любому номеру места ту цифру, которая на
§ 12.1] ПРИМЕРЫ АЛГОРИТМОВ 427
этом месте стоит. Точнее можно сказать, что в этих
примерах имелся алгоритм распознавания символа по
номеру места.
Вообще под алгоритмом мы интуитивно понимаем
некоторое формальное предписание, действуя согласно
которому можно получить нужное решение задачи. Та-
Такая формулировка, разумеется, не претендует на точ-
точность, а скорее выражает то интуитивное воззрение на
алгоритм, которое сложилось еще в древности*).
Для более полного уяснения основных свойств, кото-
которыми должен обладать алгоритм, рассмотрим несколько
типичных примеров и сделаем из них соответствующие
выводы.
Алгоритм Евклида. Рассмотрим алгоритм Ев-
Евклида для нахождения наибольшего общего делителя
двух заданных целых положительных чисел а и Ъ. Этот
алгоритм может быть записан в виде следующей систе-
системы последовательных указаний:
1. Обозревай данные числа а и Ь. Переходи к сле-
следующему указанию.
2. Сравни обозреваемые числа (а = Ь, или а<Ь, или
а > Ь). Переходи к следующему указанию.
3. Если обозреваемые числа равны, то каждое из них
дает искомый результат. Процесс вычисления остано-
остановить. Если нет, переходи к следующему указанию.
4. Если первое обозреваемое число меньше второго,
то переставь их местами. Переходи к следующему ука-
указанию.
5. Вычитай второе число из первого и обозревай два
числа: вычитаемое и остаток. Переходи к указанию 2.
Итак, после того как выполнено последнее пятое ука-
указание, надо вновь возвратиться ко второму указанию
и т. д. до тех пор, пока не окажется выполненным усло-
условие, содержащееся в третьем указании. Тогда процесс
прекращается.
*) Термин «алгоритм» происходит от имени средневекового узбек-
узбекского математика Аль-Хорезми, который еще в IX веке дал правила
выполнения четырех арифметических действий в десятичной системе
счисления. Ясно, что на арифметические правила можно смотреть
как на формальные предписания, которые всеми и всегда выпол-
выполняются одинаково и, если нужно, могут быть автоматизированы.
428 АЛГОРИТМЫ UV
:: Алгоритм Евклида представлен здесь в виде доста-
достаточно детализированного предписания. В качестве эле-
элементарных операций фигурируют простейшие арифме-
арифметические действия (вычитание, сравнение), которые,
естественно, могли бы быть разложены на еще более
элементарные операции; мы такого разложения не де-
делаем лишь в силу простоты и привычности арифмети-
арифметических правил.
Алгоритмы, в соответствии с которыми решение по-
поставленных задач сводится к арифметическим действиям,
называются численными алгоритмами. Рассмотренные
выше примеры были примерами численных алгоритмов.
Численными алгоритмами также являются любые фор-
формулы и схемы, служащие для решения некоторого клас-
класса задач, если этими формулами полностью выражен
как состав действий (умножение, вычитание, деление),
так и порядок, в котором они должны выполняться.
Пример логического алгоритма. Приве-
Приведём теперь пример алгоритма, где предписание о спо-
способе действия будет относиться уже не к цифровым объ-
объектам, Этот алгоритм служит для решения одной логи-
логической задачи—поиска пути в конечном лабиринте.
"Представим себе лабиринт в виде конечной системы
площадок, от которых расходятся коридоры, причем
каждый коридор соединяет две площадки (назовем их
¦смежными площадками), но возможно существование и
таких площадок, из которых можно пройти только в
один коридор (такие площадки будем называть тупи-
тупиками). Геометрически лабиринт можно представить в
виде системы кружков Л, В, С, ..., изображающих пло-
площадки, соединенные отрезками прямых линий, изобра-
изображающих" коридоры (рис. 12.1). .-¦
Будем говорить, что площадка У достижима из пло-
площадки X, если существует путь, ведущий от X к Y через
промежуточные коридоры и площадки. Это означает,
что либо X и Y— смежные площадки, либо существует
-последовательность смежных площадок ¦¦;-.=
X, X^f Xyj X& ..., Xn, Y. •
Очевидно, что если площадка Y вообще достижима с
площадки X, то она достижима и посредством простого
§ 12.1]
РИМЁРЫ АЛГОРИТМОВ
429
пути (без петель), т. е. такого пути, в котором каждая
площадка проходится лишь один раз.
Так, в случае лабиринта, показанного на рис. 12.1,
один из простых путей, ведущих от площадки Н к пло-
площадке В, будет HDCB. Площадка же L недостижима
из площадки Л.
Пусть поиск пути начинается от площадки Л. Тре-
Требуется выяснить, достижима ли площадка F из площад-
площадки Л, и если да, то требуется найти путь из Л в F. Если
же площадка F окажется недостижимой, то требуется
после поиска, вернуться в Л.
Предполагается, что заранее ничего неизвестно об
устройстве данного лабиринта и о том, где находятся
в нем площадки Л и F. Поэтому решение поставленной
задачи мыслится в виде общего метода поиска, пригод-
пригодного при любом лабиринте с конечным числом площа-
площадок и при любом расположении в нем площадок Л и F.
Рассмотрим один из таких методов, основанный на
предположении, что лицо, ищущее путь в лабиринте,
располагает нитью, конец которой закреплен на площад-
площадке Л, и, двигаясь по лабиринту, может разматывать
клубок или, наоборот, наматывать на него нить. Предпо*
ложим также, что можно делать отметки на проходимых
коридорах и различать затем коридоры, еще ни разу не
пройденные (условно —зеленые), пройденные один раз
(условно — желтые) и пройденные дважды (условно—•
красные),
430 АЛГОРИТМЫ I [ГЛ. XI f
Находясь на какой-либо из площадок, можно попасть
на смежную площадку посредством одного из двух
ходов:
а) Разматывание нити. Прохождение от данной пло-
площадки по любому зеленому коридору до смежной пло-
площадки. Пройденный коридор после этого считается жел-
желтым, и по нему протянута разматываемая нить.
б) Наматывание нити. Возвращение от данной пло-
площадки по последнему пройденному желтому коридору
до смежной площадки. При этом нить наматывается, а
коридор объявляется красным.
Отметим, что необходимо различать лишь зеленые и
красные коридоры; желтые различимы тем, что по ним
протянута нить.
Находясь на какой-либо площадке, можно различать
обстановку, характеризуемую одним из пяти признаков:
1) Это площадка F — цель достигнута.
2) Петля: от данной площадки расходятся по край-
крайней мере два желтых коридора, т. е. через данную пло-
площадку уже протянута нить.
3) Зеленая улица: от данной площадки отходит по
крайней мере один зеленый коридор.
4) Это исходная площадка Л.
5) Пятый случай. Отсутствие всех предыдущих при-
признаков.
Метод поиска теперь может быть задан следующей
схемой:
Признак. Ход
1) Площадка F Остановка
2) Петля Наматывание нити
3) Зеленая улица Разматывание нити
4) Площадка А Остановка
5) Пятый случай Наматывание нити
Находять на какой-либо площадке, следует делать
очередной ход так: нужно проверить по порядку номе-
номеров в соответствии с левым столбцом схемы, какой из
перечисленных признаков имеет место. Обнаружив при-
признак, следует, не проверяя более последующих призна-
признаков, делать соответствующий ход. Такие ходы делаются
до тех пор, пока не наступит остановка.
§ 12.1]
ПРИМЕРЫ АЛГОРИТМОВ
431
Относительно предложенного метода поиска можно
доказать справедливость следующих трех утверждений:
Первое. При любом взаимном расположении А и F
после конечного числа ходов наступит остановка либо
на площадке А, либо- на площадке F.
Второе. Если остановка наступит на площадке F, то
цель достигнута и нить протянута по простому пути, ве-
ведущему от А к F.
Третье. Если остановка наступила на площадке А, то
площадка F недостижима.
Покажем на примере лабиринта (рис. 12.1), как дей-
действует предложенный метод.
Процесс поиска удобно изобразить в виде табл. 12.1.
Порядко-
Порядковый номер
хода
1
2
3
4
5
6
7
8
9
10
11
Признак, которым
руководствуются
Зеленая улица
Пятый случай
Зеленая улица
Петля
Зеленая улица
Площадка F
Ход
Разматывание
Наматывание
Разматывание
Наматывание
Разматывание
Остановка
Та
Пройден-
Пройденный
коридор
АВ
ВС
CD
DH
HI
IH
HD
DB
BD
DF
блица 12.1
Цвет коридора
после его
прохождения
Желтый
Красный
Желтый
Красный
Желтый
В данном случае площадка F достижима. Выделив
в предпоследнем столбце те коридоры, которые оста-
остались желтыми, получим простой путь от А к F.
Заметим, что описанный метод поиска в произволь-
произвольном конечном лабиринте содержит элемент произвола,
которого не было в ранее рассмотренных примерах.
Так, при нахождении наибольшего общего делителя
двух заданных чисел с помощью алгоритма Евклида
операции, которые будут сделаны разными вычисли-
вычислителями, руководствующимися указаниями 1—5 этого ал-
алгоритма, совпадут во всех своих деталях, и никогда не
432 алгоритмы / [гл. хп
встретится такой ситуации, когда вычислителю придется
что-либо выбирать по своему усмотрению.
Здесь же, если от некоторой площадки отходит не-
несколько зеленых коридоров, искателю предоставлена
возможность выбрать любой из них. Разные искатели
могут прийти от площадки А к площадке F по-разному.
Алгоритмом традиционно называют лишь строго де-
детерминированную систему правил, и мы сохраним эту
традицию. Поэтому, чтобы иметь право называть пред-
предписания поиска алгоритмом, нужно указания 1—5 до-
дополнить точным указанием, какой коридор выбирать
при наличии нескольких зеленых коридоров (например,
первый по часовой стрелке).
§ 12.2. Общие свойства алгоритмов
Из рассмотренных примеров отчетливо выступают
общие свойства, которые естественно считать свойства-
свойствами, присущими любому алгоритму:
а) Д етер м иниров а н но с ть а л гор ит м а. Тре-
Требуется, чтобы метод действия (вычисления) был на-
настолько точен и общепонятен, чтобы не оставалось ме-
места произволу. Этот метод можно сообщить другому
лицу в виде конечного числа указаний о том, как над-
надлежит поступать на отдельных этапах действия. При
этом действия, согласно этим указаниям, не зависят от.
произвола действующего лица и представляют собою
детерминированный процесс, который может быть в лю-
любое время повторен с тем же успехом другим лицом.
б) Массовость алгоритма. Алгоритм служит не для
решения какой-либо одной конкретной задачи, а для ре-
решения целого класса задач. Указания о методе действия
применимы к начальным данным, которые могут варьи-,
роваться.
Так, алгоритм Евклида применим к любой паре це-
целых чисел а > О, Ь > 0; формулы для решения системы
двух уравнений определяют решение при любых значе-
значениях коэффициентов уравнений; арифметические пра-
правила применимы к любым числам; правила поиска при-
применимы к любому, как угодно сложному конечному ла-
лабиринту и т. дг .. , . '
§ 12.2] ОБЩИЕ СВОЙСТВА АЛГОРИТМОВ 433
В математике\серия задач определенного типа счи-
считается решенной, когда для ее решения установлен ал-
алгоритм; нахождение таких алгоритмов является есте-
естественной целью математики. Если же мы не обладаем
алгоритмом для решения всех задач данного типа, то в
отдельных случаях приходится придумывать специаль-
специальную процедуру, которая для других случаев будет не-
непригодна.
Процедуру для решения одной индивидуальной за-
задачи не называют алгоритмом. Так, например, неизве-
неизвестен алгоритм, позволяющий для любого п = 1, 2, 3,
4, ... определить, имеет ли уравнение
= zn A2.1)
целочисленное решение.
Тем не менее для конкретных значений п эта задача
может быть решена. Так, для п = 2 можно легко подо-
подобрать тройку чисел (х = 3, у = 4, z = 5), удовлетво-
удовлетворяющую A2.1). Для п = 3 удалось доказать, что урав-
уравнение A2.1) не имеет целочисленных решений. Но это
доказательство уже не годится для иных п.
в) Результативность алгоритма. Это свой-
свойство, называемое иногда еще направленностью алгорит-
алгоритма, требует, чтобы алгоритмическая процедура, приме-
примененная к любой задаче данного типа, через конечное
число шагов останавливалась и после остановки можно
было бы вычитать искомый результат.
Так, при применении алгоритма поиска к любому как
угодно сложному (но конечному!) лабиринту, после ко-
конечного числа шагов обязательно наступит остановка
либо на площадке F, либо на площадке А. По тому, где
наступила остановка, мы делаем вывод о достижимости
площадки F.
При применении алгоритма Евклида к любым двум
числам а>-1, 6>Л также, как нетрудно доказать,
обязательно рано или поздно^наступит остановка, и мы
получим возможность определить значение наиболь-
наибольшего общего делителя. При применении алгоритма
арифметического сложения остановка наступает после
того, как произведено суммирование чисел старшего
разряда. : •. . ;.._.'¦
?8 М. А. Айэерман, Л. А. Гусев и др,
434 алгоритмы I [гл. хн
Однако ничто не препятствует формально применить
указания 1—5 алгоритма Евклида к/числам а>-0 и
b >- О или же к любым целым (положительным " или
отрицательным) числам. На любом этапе при выполне-
выполнении любого указания не может возникнуть никаких не-
недоразумений, но может случиться так, что остановка
алгоритмической процедуры никогда не наступит. На-
Например, если а = О, Ь — 4 (наибольший общий делитель
равен 4), то, применяя указания 1—5, последовательно
получаем пары
0,4
0,4
0,4
0,4
и так до бесконечности. Подобная картина будет на-
наблюдаться и для пары а = —2, Ь — 6.
Из свойства результативности алгоритма естествен-
естественно вытекает понятие области применимости алгоритма:
областью применимости алгоритма называется такая
наибольшая область начальных данных, на которой ал-
алгоритм результативен; иначе говоря, если условия за-
задачи взяты из области применимости, то алгоритм пере-
перерабатывает условия в решение задачи и наступает оста-
остановка; если же условия взяты не из этой области, то
либо никогда не наступает остановка, либо же оста-
остановка наступает, но мы не можем вычитать результат.
Так, областью применимости алгоритма Евклида
служит множество целых чисел {1, 2, -3, 4, ...}; обла-
областью применимости алгоритма поиска является множе-
множество всех конечных лабиринтов; область применимости
десятичного алгоритма суммирования — все числа в де-
десятичной записи с конечным числом разрядов, и т. д.
Следует подчеркнуть, что число операций, которые
нужно сделать, следуя той или иной алгоритмической
процедуре, заранее неизвестно и зависит от выбора ис-
исходных данных. Поэтому осуществимость алгоритмиче-
алгоритмической процедуры следует понимать как потенциально воз-
возможный процесс, так как для некоторых конкретных за-
задач из области применимости алгоритма при практиче-
§ 12.3] ПРОБЛЕМА (СЛОВ В АССОЦИАТИВНОМ ИСЧИСЛЕНИЙ 435
ском осуществлении может не хватить бумаги, чернил
или времени вычислителю, или памяти, реализующей
этот алгоритм вычислительной машине.
Свойства детерминированности, массовости и резуль-
результативности — свойства эмпирические; это те общие
свойства, которые подмечены во всех до сих пор по-
построенных алгоритмах. Выводы о них сделаны на осно-
основании богатого опыта.
Однако сами по себе эти свойства не могут являться
точной математической формулировкой понятия «алго-
«алгоритм» в силу их неточности, расплывчатости, и потому
они не могут быть положены в основу математической
теории алгоритмов.
§ 12.3. Проблема слов в ассоциативном исчислении
Далеко идущим обобщением проблемы поиска в ла-
лабиринте является проблема слов. Если описанный выше
поиск мог происходить в произвольном конечном лаби-
лабиринте, то проблема слов является в определенном смы-
смысле проблемой поиска в бесконечном лабиринте.
Впервые эта проблема возникла в алгебре, в теории
ассоциативных систем и теории групп, но затем ее зна-
значение вышло далеко за рамки этих специальных теорий *).
Назовем алфавитом любую конечную систему раз-
различных символов. Символы, составляющие алфавит, бу-
будем называть буквами. Например, {а, ъ, ?, 7, *} — алфа-
алфавит, а, ъ, ?, 7, *—буквы.
Любая конечная последовательность букв некото-
некоторого алфавита называется словом в этом алфавите.
Так, в алфавите из трех букв {а, Ъ, с] словами бу-
будут последовательности ас, a, abbca, ЬЬЬЬЬ, ЬЬасаЬ и т. д.
Пустое слово, не содержащее ни одной буквы, обозна-
обозначим символом Л.
Рассмотрим два слова: слово L и слово М в некото-
некотором алфавите А. Если слово" L является частью слова
*) Большой вклад в решение этой проблемы внесен А. А. Мар-
Марковым, П. С. Новиковым и их учениками. Знание этого круга во-
вопросов поможет нам в дальнейшем глубже понять элементы теории
рекурсивных функций.
28*
436 АЛГОРИТМЫ / . ГГЛ. XI!
М, то говорят, что слово L входит в /слово М или что
имеется вхождение слова L в М. В качестве примера
можно привести два слова: L = ас; М = bbacab.
В общем случае слово L может входить в слово М
несколько раз; так слово bcb два раза входит в слово
abcbcbab.
Опишем теперь процесс преобразования слов, по-
позволяющий из заданного слова получать новые слова.
Зададим в некотором алфавите конечную систему допу-
допустимых подстановок
где Р, Q, L, М, ..., 5, Т — слова в том же алфавите.
Любую подстановку вида L—М можно применять к
некоторому слову R этого алфавита следующим спосо-
способом: если в слове R имеется одно или несколько вхо-
вхождений слова L, то любое из этих вхождений может
быть заменено словом М, и наоборот, если имеется вхо-
вхождение слова М, то его можно заменить словом L.
Например, подстановка ab — bcb применима четырьмя
способами к слову abcbcbab. Замена каждого из двух
вхождений bcb дает слова aabcbab, abcabab, а замена
каждого из двух вхождений ab дает слова bcbcbcbab,
abcbcbbcb.
Подстановка же ab—bcb неприменима к слову bacb,
так как в это слово не входят ни слово ab, ни сло-
слово bcb.
К полученным с помощью допустимых подстановок
словам можно снова применить допустимые подстанов-
подстановки: так будут получены новые слова и т. д.
Совокупность всех слов в данном алфавите вместе с
системой допустимых подстановок называется ассоциа-
ассоциативным исчислением. Чтобы задать ассоциативное
исчисление, достаточно задать алфавит и систему под-
подстановок.
Два слова Pi и Рг в некотором ассоциативном исчи-
исчислений называются смежными, если одно из них может
быть преобразовано в другое при помощи однократного
применения некоторой допустимой подстановки.
§12.3] ПРОБЛЕМА СЛОВ В АССОЦИАТИВНОМ ИСЧИСЛЕНИИ 37
Последовательность слов Р, P\r Рг, Рз, • •., Q назы-
называется дедуктивной цепочкой, ведущей от слова Р к
слову Q, если каждые из двух рядом стоящих слов этой
цепочки являются смежными.
Два слова Р и Q называются эквивалентными, если
существует дедуктивная цепочка, ведущая от слова Р к
слову Q. Отношение эквивалентности обозначается так:
Р ~ Q. Очевидно, что если Р ~ Q, то Q ~ Р, так
как допустимые подстановки можно применять в обе
стороны.
Пример. Зададим следующее ассоциативное исчи-
исчисление: .
{а, Ь, с, d, e) — алфавит,
ас — са)
ad— da
be— cb
bd — db
— допустимые
подстановки.
abac — abacc
eca — ae
edb — be
Слова abede и acbde в этом исчислении являются
смежными, так как слово abode может быть преобразо-
преобразовано в слово acbde с помощью применения подстановки
bc—cb.
Слово aaabb.ue имеет смежных слов, так как к нему
неприменима ни одна подстановка.
Слово abode эквивалентно слову cadedb, так как су-
существует дедуктивная цепочка смежных слов:
abede, acbde, cabde, cadbe, cadedb.
Здесь последовательно применены 3-я, 1-я, 4-я, 5-я под-
подстановки.
Ассоциативному исчислению можно поставить в со-
соответствие бесконечный лабиринт следующим способом:
каждому слову данного алфавита: ставится в соответ-
соответствие определенная площадка лабиринта. Так как чис-
число слов, которые могут быть. составлен^ из букв
438 АЛГОРИТМЫ [ГЛ. Xlf
данного алфавита, как угодно велико, то и лабиринт
будет иметь бесконечное число площадок. ' :
Любые две площадки этого лабиринта, соответствую-
соответствующие смежным словам, соединяются коридором.
Если теперь два слова Р и Q эквивалентны, то в
построенном лабиринте это означает, что площадка, со-
соответствующая слову Q, достижима с площадки, соот-
соответствующей слову Р, т. е. что в этом лабиринте суще-
существует путь, ведущий от площадки Р к площадке Q.
Иногда рассматривается специальный вид ассоциа-
ассоциативного исчисления, которое задается алфавитом и си-
системой ориентированных подстановок вида P-+Q.'
Стрелка здесь означает, что подстановку разрешается
производить лишь слева направо, т. е. заменять вхо-
вхождение слова Р на слово Q, но не наоборот. Такое ас-
ассоциативное исчисление может быть изображено бес-
бесконечным лабиринтом, по каждому из коридоров
которого разрешается двигаться только в одном на-
направлении.
Ясно, что в таком ассоциативном исчислении из эк-
эквивалентности Р ~ Q ни в коей мере не следует, что
Q ~ Р. Мы не будем рассматривать проблемы, связан-
связанные с таким особым ассоциативным исчислением.
Для каждого ассоциативного исчисления возникает
своя специальная проблема слов. Она заключается в
следующем: Для любых двух слов в данном исчисле-
исчислении требуется узнать, эквивалентны они или нет.
Это та же проблема достижимости, которая была
рассмотрена в примере с лабиринтом, однако лабиринт
теперь стал бесконечным. Поэтому естественно, что раз-
разработанный раньше метод поиска становится теперь не-
непригодным, так как уже нельзя в конечное время обсле-
обследовать весь бесконечный лабиринт.
Поскольку в любом ассоциативном исчислении со-
содержится бесчисленное множество различных слов, про-
проблема эквивалентности представляет собой бесконечную
серию однотипных задач, а решение мыслится в виде
алгоритма, распознающего эквивалентность или неэкви-
неэквивалентность любой пары слов.
Зная алгоритм поиска в конечном лабиринте, можно
легко построить алгоритм, решающий так называемую
§ 12.3] ПРОБЛЕМА СЛОВ В АССОЦИАТИВНОМ ИСЧИСЛЕНИИ 439
ограниченную проблему слов: требуется установить, мож-
можно ли одно из заданных слов преобразовать в другое
применением допустимых подстановок не более чем к раз,
где k — произвольное, но фиксированное число. Если в
случае поиска в конечном лабиринте ограничение было
наложено на сам лабиринт — лабиринт имел конечное
число коридоров и площадок, что давало возможность
обследовать его целиком, то здесь ограничено число
ходов: мы должны обследовать все площадки бесконеч-
бесконечного лабиринта, которые отделены от заданной не более
чем k коридорами; остальная часть лабиринта нас не
интересует.
Применительно к подстановкам это означает, что
сперва надо построить все слова, смежные с одним из
заданных слов, затем для каждого из полученных слов
построить все слова, смежные с ним, и т. д., всего к раз.
В итоге мы получим список всех слов, которые можно
получить из заданного с помощью применения допу-
допустимых подстановок не более k раз. Если второе задан-
заданное слово окажется в этом списке, то, следовательно,
ответ на поставленный вопрос будет положительным,
если его в списке нет, ответ будет отрицательным.
Разумеется, описанный здесь алгоритм переборки
можно усовершенствовать, избавившись от излишних
повторений (т. е. от петель в лабиринте).
Однако успешное решение ограниченной проблемы
слов ни в коей мере не приближает нас к решению ос-
основной, «неограниченной» проблемы. Поскольку длина
дедуктивной цепочки, ведущей от слова Р к слову Q
(если такая цепочка существует), может оказаться
сколь угодно большой, то вообще говоря, неизвестно,
когда следует считать законченным процесс переборки.
Для получения желаемых результатов здесь прихо-
приходится отказатьсяот простой переборки, необходимо при-
привлекать иные идеи и строить иные алгоритмы.
Из изложенного следует, что логическая задача о
поиске пути в лабиринте может быть сформулирована
на языке ассоциативного исчисления. Иные дедуктив-
дедуктивные логические процессы также можно трактовать как
ассоциативное исчисление. Так, например, любую логи-
логическую формулу можно трактовать как Э&пись слова в
440 АЛГОРИТМЫ ; [ГЛ. XII
некотором алфавите, содержащем знаки логических
символов V, &, ~, -*• (, ) и т. д., логических переменных
и логических функций.
Процесс вывода следствия может быть записан в
виде формально-логического преобразования слов, схо-
схожего с подстановками в ассоциативном исчислении, при-
причем однократному применению каждой подстановки со-
соответствует элементарный акт логического умозаклю-
умозаключения.
Сами подстановки имеют вид логических правил или
тождеств, например х—х (двойное отрицание можно
снять) или
(yx)ftAlVx)&:(A2\/x)] — Al8iA2 | правило исключения
i3x)[(Axyx)k(A2yx)) — Al\/A2 } и т. д.
Применяя какие-либо из подстановок к данной по-
посылке, т. е. к слову, изображающему эту посылку, мы
будем последовательно получать все новые и новые вы-
выводы (следствия).
В простейшем случае, в рамках'исчисления высказы-
высказываний существуют методы получения всех следствий из
данной системы аксиом. _
Существует и алгоритм распознавания выводимости,
то есть может быть проверено, является ли любое
утверждение следствием аксиом или нет.
Однако исчисление высказываний не может охватить
всего, так как оно не в силах выразить отношения од-
одного предмета к другому в пределах одного высказыва-
высказывания; для этого требуется исчисление предикатов, кото-
которое аналогично можно трактовать как ассоциативное
исчисление.
Итак, в итоге мы имеем вариант ассоциативного ис-
исчисления— логическое исчисление с указанной систе-
,мой допустимых подстановок. Вопрос о распознавании
выводимости становится вопросом существования де-
дедуктивной цепочки, ведущей от слова, изображающего
посылку, к слову, изображающему следствие..
Таким образом, и в этом случае мы пришли к
проблеме эквивалентности слов в ассоциативном ис-
исчислении, / .
§ 12.4] НОРМАЛЬНЫЙ АЛГОРИТМ МАРКОВА '441
¦" В этом же смысле любой процесс вывода формул,
математические выкладки и преобразования также яв-
являются дедуктивными цепочками в подходящем обра-
образом выбранном ассоциативном исчислении.
В следующем параграфе мы приведем примеры, по-
показывающие, что арифметические процессы также мо-
могут трактоваться как ассоциативное исчисление.
Естественно предположить, что построение ассоциа-
ассоциативных исчислений может быть универсальным методом
для задания детерминированного процесса «переработ-
«переработки» исходных данных, т. е. для задания алгоритма. Но
чтобы сделать такое предположение, надо прежде всего
уточнить, что мы имеем в виду, говоря об алгоритме в
некотором алфавите.
§ 12.4. Алгоритм в некотором алфавите А.
Нормальный алгоритм Маркова
По аналогии с интуитивным определением алгоритма
вообще (см. выше), мы могли бы и здесь интуитивно опре-
определить понятие «алгоритм в алфавите Л» примерно так:
I. Алгоритмом в алфавите Л называется всякое обще-
понятное, точное предписание, определяющее потенциаль-
потенциально осуществимый процесс над словами из Л, допускаю-
допускающий любое слово в качестве исходного и последова-
последовательно определяющий новые слова в этом алфавите.
Алгоритм применим к некоторому слову Р, если, от-
отправляясь от этого слова и действуя согласно предписа-
предписанию, мы получим в конце концов некоторое новое сло-
слово Q, на котором процесс оборвется. Будем тогда гово-
говорить, что алгоритм перерабатывает Р в Q.
Например, следующее предписание удовлетворяет
нашему определению. Перепиши заданное слово
начиная с конца. Полученное слово есть
результат. Остановка. Этот алгоритм предстат
вляет собой совершенно точцое предписание, примени-
применимое к любому слову.
Однако определение I слишком широко: уточнение
понятия «алгоритм в алфавите Л» связано .с использо-
использованием аппарата подстановок, т. е. с построением ас-
ассоциативного исчисления.
442 АЛГОРИТМЫ (ГЛ. Xlt
II. Будем считать, что алгоритм в алфавите А за-
задается в виде некоторой системы допустимых подстано-
подстановок, дополненной общепонятным точным предписанием
о том, в каком порядке и как нужно применять допу-
допустимые подстановки, и когда наступает остановка.
Так как алфавит и система допустимых подстановок
задают ассоциативное исчисление, которому, как мы
знаем, можно поставить в соответствие бесконечный ла-
лабиринт, то вторую составную часть этого определения
алгоритма (т. е. общепонятное и точное предписание о
том, как пользоваться подстановками) можно понимать
как точное предписание о способе движения в беско-
бесконечном лабиринте.
Приведем пример алгоритма в алфавите А в смыс-
смысле II.
Пусть алфавит А содержит три буквы: А = {а, Ь, с],
а алгоритм определен с помощью системы подстановок
cb — ее, \
сса — пЬ,
ab — Ьса
и следующего указания о способе применения этих под-
подстановок: исходя из произвольного слова Р, следует про-
просмотреть схему подстановок в том порядке, в каком они
выписаны, разыскивая первую формулу, левая часть ко-
которой входит в Р. Если такой формулы не найдется, то
процесс обрывается сразу же. В противном случае бе-
берется первая из найденных формул и делается подста-
подстановка ее правой части вместо первого вхождения ее ле-
левой части в слово Р, что дает новое слово Pi в алфа-
алфавите А. Затем слово Pi играет роль Р, т. е. вновь берется
в качестве исходного, и процесс повторяется. Остановка
наступает в том случае, если на п-и шаге получено сло-
слово Рп, в которое не входит ни одна из левых частей
формул схемы подстановок.
Итак, схема подстановок вместе с указанием, как
ими пользоваться, определяет алгоритм в алфавите А.
Этот алгоритм перерабатывает слово babaac в слово
bbcaaac (применена 3-я формула), слово cbacacb — по-
§ 12.4] НОРМАЛЬНЫЙ АЛГОРИТМ МАРКОВА 443
следовательно в слова ccacacb, ссасасс, abcacc и, наконец,
в Ьсасасс, на котором процесс обрывается; слово bcacabc
порождает бесконечно повторяющуюся последователь-
последовательность слов bcacabc, bcacbcac, bcacccac, bcacabc и т. д.,
т. е. остановка никогда не наступит, и следовательно,
к слову bcacabc наш алгоритм неприменим.
Наш алгоритм несколько напоминает такой способ
задания движения в бесконечном лабиринте: выйдя на
какую-либо площадку, иди в первый коридор направо
и т. д. Остановка наступит, когда придешь в тупик.
Ясно, что здесь также может быть три случая: отходя
от данной площадки, мы можем либо попасть в тупик
(сравни слово cbacacb), либо бесконечно кружиться по
циклу (сравни слово bcacabc), либо двигаться беско-
бесконечно долго, не попадая в циклы.
С первого взгляда можно решить, что определение
алгоритма в смысле II уже, чем определение в смысле L
Однако оказывается, что на деле такого сужения нет*
ибо для любого известного алгоритма в смысле I может
быть построен эквивалентный ему алгоритм в смысле II.
Это, конечно, не доказательство того, что определения I
и II равносильны; такого доказательства не может су-
существовать вообще в силу неточности и расплывчатости
обоих определений (и там, и там фигурируют слова
«общепонятное точное предписание»).
Во всяком случае очевидно, что определение II —
шаг вперед по пути уточнения понятия «алгоритм».
Определим теперь понятие эквивалентности алгорит-
алгоритмов: два алгоритма Ах и А2 в некотором алфавите на-
называются эквивалентными, если области их примени-
применимости совпадают и результаты переработки ими любого
слова из их общей области применимости также совпа-
совпадают. Иначе говоря, если алгоритм А\ применим к не-
некоторому слову Р, то и А2 должен быть применим к
этому слову, и наоборот; оба алгоритма должны пере-
перерабатывать слово Р в некоторое слово Q. Если же один
из алгоритмов неприменим к некоторому слову В, то и
Другой алгоритм должен быть неприменим к нему.
Для того чтобы дать точное математическое опреде-
определение алгоритма, потребовалось сделать еще один шаг
444 алгоритмы . [глухи
по пути дальнейшего уточнения. Этот шаг был сделан
А. А. Марковым. Построенный им нормальный алго\
ритм, так же как и алгоритм в смысле определения .II,
выражен в терминах системы подстановок; однако вме-
вместо расплывчатого «общепонятного указания» о том, как,
пользоваться подстановками, Марков дал стандартные^
раз и навсегда определенные точные указания о поряд-
порядке использования подстановок. Определение нормаль-
нормального алгоритма Маркова таково:
Задается алфавит А и фиксируется схема подстано-
подстановок. Алгоритм предписывает, исходя из произвольного,
слова Р.в алфавите Л, просмотреть формулы подстано-
подстановок в том порядке, в каком они заданы в схеме, разыт
скивая формулу с левой частью, входящей в Р. Если*
такой формулы не найдется, то процесс обрывается.,
В противном случае берется первая из таких формул iti
делается подстановка ее правой части вместо первого
вхождения ее левой части в Р, что дает новое слово Р\>
в алфавите А. После только что выполненного первого*,
шага процесса приступают ко второму его шагу, отли-i
чающемуся от первого только тем, что роль Р играет-
Pi. Далее делают аналогичный третий шаг и т. д. до;
тех пор, пока не придется оборвать процесс. Оборвать*
ся же он может лишь двумя способами: во-первых, когда ?
мы получим такое слово Рп, что ни одна из левых ча-
частей формул схемы подстановок не будет в него вхо^
дить; во-вторых, когда при получении слова Рп нам при-
придется применить последнюю формулу. В обоих этих
случаях мы считаем, что наш алгоритм перерабатывает--
слово Р в слово Рп-
Как мы видим, приведенный в определении II при-t
мер является примером «почти нормального» алгорит-
алгоритма. Вся разница состоит в том, что там остановка на-
наступает лишь в одном случае, когда ни одна из подста-'"
новок неприменима, а здесь остановка может наступать
в двух случаях.
Различные нормальные алгоритмы отличаются друг
от друга лишь алфавитами и системами допустимых
подстановок. Чтобы задать какой-либо нормальный ал-
алгоритм, достаточно задать алфавит и систему подста-
подстановок. .
§ 12.4] НОРМАЛЬНЫЙ АЛГОРИТМ МАРКОВА 445
Примеры нормальных алгоритмов
Пусть алфавит А и система подстановок имеют вид
-л={1, -н i
4- 1 -> 1 ¦
1¦ -> 1
(стрелками общепринято обозначать тот факт, что за-
задано не ассоциативное исчисление обычного вида, а нор-
нормальный алгоритм Маркова).
Посмотрим, во что переработает этот алгоритм
слово 1 1 1 1 —|— 1 1 + 11 1. Последовательно получаем
слова:
1111 + 11 + 111
111 + 111 + 111
11 + 1111 + 111
1 + 11111 + 111
111111 + 111
II 11 1 + 1 1 1. 1 .
1111 + 11111
III + 111111
11+1111111
1 + 11 111111
111111111
111111111
111111111
11 Г. l l l l l l
Процедура оканчивается применением заключитель-
заключительной подстановки 1->1, которая перерабатывает слово
111111111 в себя. v
Пусть теперь система подстановок в том же алфа-
алфавите, имеет вид . .
446 алгоритмы [гл. хн
(Л — пустое слово). Слово 11 + 111 + 1 + 11 этот алго-
алгоритм переработает так:
11 + 111+1+11
11111+1 + 11
111111 + 11
11111111
111111 1 1.
Мы видим, что оба алгоритма суммируют количество
единиц, т. е. осуществляют сложение. Нетрудно пока-
показать, что эти два нормальных алгоритма эквивалентны.
Третий эквивалентный им обоим нормальный алго-
алгоритм можно было бы задать с помощью системы под-
подстановок
1 + -> + 1,
+ -> Л.
Читателю предлагается убедиться, что следующий
нормальный алгоритм А={\, *, V, ?)
перерабатывает всякое слово вида
- 1111 ... 11*111 ... 111 в слово 111 ... 111,
т раз п раз т-п раз
т. е. осуществляет умножение.
§ 12.4] НОРМАЛЬНЫЙ АЛГОРИТМ МАРКОВА 447
Понятие алгоритма в некотором алфавите было уточ-
уточнено Марковым следующим образом: Марков предпо-
предположил, что всякий алгоритм в алфавите А эквивален-
эквивалентен некоторому нормальному алгоритму в этом же
алфавите.
'¦ Это утверждение является гипотезой; оно не может
быть строго доказано, так как, с одной стороны, здесь
фигурирует расплывчатое понятие «всякий алгоритм»,
а с другой стороны — точное понятие «нормальный ал-
алгоритм». На это утверждение можно смотреть как на
закон, который не доказан, но который проверен и под-
подтвержден всем нашим опытом.
В пользу высказанной гипотезы говорит и тот факт,
что никому еще не удалось сформулировать пример та-
такого алгоритма в алфавите А, для которого нельзя было
бы построить эквивалентный ему нормальный алгоритм.
Возвращаясь к содержанию последних абзацев пре-
предыдущего параграфа, естественно рассматривать нор-
нормальный алгоритм Маркова как удобную «стандартную
форму» для задания любого алгоритма, т. е. предполо-
предположить, что вообще любой алгоритм может быть задан
в форме нормального алгоритма Маркова. Разумеется,
это не более чем гипотеза, и притом значительно менее
ясная, чем гипотеза Маркова, о которой выше шла речь,
так как она не может быть даже высказана в точных
терминах, но интуитивный смысл ее очевиден.
Как только мы примем эту гипотезу, сразу стано-
становится ясным один из путей, каким можно строго про-
проводить доказательство алгоритмической неразрешимости
того или иного круга проблем.
Например, чтобы доказать алгоритмическую не-
неразрешимость проблемы слов, т. е. доказать, что не су-
существует алгоритма, позволяющего для любого ассо-
ассоциативного исчисления и для произвольных заданных
слов Р и Q ответить на вопрос: эквивалентны ли эти
два слова, достаточно было построить пример ассоциа-
ассоциативного исчисления и доказать, что для этого исчисле-
исчисления не существует нормального алгоритма, распознаю-
распознающего эквивалентность слов.
Впервые такие примеры были построены А. А. Мар-
Марковым в 1946 г. и Э, Постом в 1947 г.
448 > АЛГОРИТМЫ {ГЛ. XII
"'¦ После того стало ясно, что и подавно не существует
алгоритма для распознавания эквивалентности слов в
любом ассоциативном исчислении.
Примеры ассоциативных исчислений, приведенные
Марковым и Постом, были весьма громоздкими, насчи-
насчитывали сотни допустимых подстановок. Позже ленин-
ленинградский математик Г. С. Цейтин привел пример ассо-
ассоциативного исчисления, насчитывающего всего лишь семь
допустимых подстановок, в котором проблема эквива-
эквивалентности слов также алгоритмически неразрешима.
В качестве иллюстрации приведем одну схему дока-
доказательства алгоритмической неразрешимости.
Пусть б некотором алфавите А — {аи а2, ..., ап}
задан с помощью системы подстановок нормальный ал-
алгоритм U. В записи этого алгоритма, кроме букв алфа-
алфавита Л, содержатся символы -> и ,. Приписав этим сим-
символам новые буквы ап+1 и ата+2, мы получим возмож-
возможность изображать алгоритм U словом в расширенном
алфавите A={alt a2, ..., ап+2}- Применим теперь ал-
алгоритм U к слову, которое его изображает.
Если алгоритм U перерабатывает это слово в неко-
некоторое иное слово, после чего наступает остановка, то
это означает, что алгоритм U применим к собственной
записи. Такой алгоритм назовем самоприменимым.
В противном случае алгоритм будем называть несамо-
применимым. Естественно, возникает задача распозна-
распознавания самоприменимости: по записи данного алгоритма
определить, самоприменим этот алгоритм или нет.
Решение этой задачи мыслится в виде построения
некоторого нормального алгоритма V, который, будучи
применен ко всякой записи самоприменимого алгоритма
и, перерабатывает эту запись в некоторое слово М, а
примененный ко всякой записи несамоприменимого ал-
алгоритма U, перерабатывает эту запись в некоторое
иное слово L. В этом случае по результату примене-
применения распознающего алгоритма V мы могли бы узнать,
является ли заданный алгоритм U самоприменимым
или нет.
Доказано, что такого нормального алгоритма V не
существует (см. [64]); тем самым доказано, что пробле-
проблема распознавания самоприменимости алгоритмически
§ 12.4] НОРМАЛЬНЫЙ АЛГ0РИТМ МАРКОВА 449
неразрешима. Доказательство проводится от противного.
Допустим, что нормальный алгоритм V распознавания
построен и перерабатывает всякую запись самопримени-
самоприменимого алгоритма в слово М, а всякую запись несамопри-
менимого алгоритма в слово L.
Тогда, путем некоторого изменения системы подста-
новок алгоритма V можно построить иной алгоритм V,
который всякую запись несамоприменимого алгоритма
по-прежнему перерабатывает в слово X, а ко всякой за-
записи самоприменимого алгоритма неприменим (оста-
(остановка никогда не наступает).
Итак, V применим ко всякой записи несамопримени-
несамоприменимого алгоритма (перерабатывая ее в слово L) и не-
неприменим к записи самоприменимых алгоритмов (оста-
(остановка не наступает). Однако это приводит к противоре-
противоречию. Действительно:
1. Пусть V самоприменим, т. е. он применим к соб-
собственной записи в виде слова (остановка наступает). Но
это свидетельствует как раз о том, что V несамопри-
меним.
2. Пусть V несамоприменим, тогда он применим к
своей записи (так как он применим к любой записи не-
несамоприменимого алгоритма); но это означает как раз,
что V самоприменим.
Полученное противоречие доказывает алгоритмиче-
алгоритмическую неразрешимость проблемы распознавания само-
самоприменимости.
Итак, решая какую-либо задачу, приходится счи-
считаться с тем, что алгоритм для ее решения может суще-
существовать, а может и не существовать. Поэтому одновре-
одновременно с поиском нужного алгоритма приходится направ-
направлять усилия и на доказательство его несуществования.
Отметим еще, что несуществование алгоритма для
решения того или иного класса задач не означает не-
неразрешимости вообще; это означает лишь, что рассма-
рассматриваемый класс задач настолько широк, что единого
эффективного метода для решения всех задач не суще-
существует. Так, хотя в ассоциативном исчислении Г. С. Цей-
тина общая проблема распознавания эквивалентности
29 М. А. Айзерман, Л. А. Гусев в др.
450 алгоритмы [гл. xii
слов алгоритмически неразрешима, тем не менее для
конкретных пар слов мы обычно тем или иным способом
можем сделать вывод об их эквивалентности или неэк-
неэквивалентности.
До уточнения понятия «алгоритм» в математике было
две точки зрения:
1) Все проблемы, для решения которых пока не уда-
удалось найти алгоритм, алгоритмически разрешимы, но
искомый алгоритм еще не найден, потому что не хва-
хватает средств в современной математике для его построе-
построения. Иначе говоря, в наше время ситуация в ряде проблем
похожа на ситуацию, когда пытались найти площадь
круга с помощью циркуля и линейки или решить урав-
уравнение п-й степени в радикалах. Естественно, что реше-
решения найдено не было, так как для этого использовались
недостаточные средства. Может быть и нам для решения
проблем, которые мы называем алгоритмически неразре-
неразрешимыми, просто не хватает средств современной матема-
математики, и построение искомых алгоритмов — дело завт-
завтрашнего дня?
2) Существуют классы задач, для решения которых
не существует алгоритма вообще. Иначе говоря, есть та-
такие проблемы, которые нельзя решать механически с
помощью формальных рассуждений и вычислений и ко-
которые требуют творческого мышления.
Утверждение это тем более сильно, что оно имеет
характер прогноза на все будущие времена, примени-
применительно ко всем будущим средствам. Не тратьте сил зря
на поиски несуществующих алгоритмов!
Но как могли бы сторонники второго взгляда дока-
доказывать несуществование какого-либо алгоритма? До тех
пор, пока в определении алгоритма так или иначе фигу-
фигурируют слова «общепонятное точное предписание», о
таком доказательстве нельзя и думать, так как невоз-
невозможно вести доказательство путем перебора всех «об-
«общепонятных точных предписаний» и показа того, что ни
одно из них не годится.
Поэтому само существование второй точки зрения
возможно только благодаря наличию смелых гипотез
о существовании «стандартных форм» для любого ал-
§ 12.51 СВЕДЕНИЕ ЛЮБОГО АЛГОРИТМА К ЧИСЛЕННОМУ 451
горитма, например, нормального алгоритма Маркова,
т. е. гипотез, делающих возможным сформулировать по-
понятия «алгоритм» и «алгоритмически неразрешимая
проблема» в точных терминах.
§ 12.5. Сведение любого алгоритма к численному
алгоритму. Гёделизация
Мы рассмотрели в этой главе несколько примеров
численных и логических алгоритмов. Интуитивное опре-
определение как численных, так и логических алгоритмов
схоже: в обоих случаях алгоритм определяется как си-
система правил для решения определенного класса задач,
которая обладает свойствами детерминированности, мас-
массовости, результативности.
Уточняя понятие алгоритма, мы ввели в рассмотре-
рассмотрение нормальный алгоритм Маркова. Эта форма алго-
алгоритма удобна для специалиста логика. Для тех же спе-
специалистов, которые имеют дело преимущественно с вы-
вычислительными машинами, безусловно важнее иметь
разработанный стандартный аппарат, более близкий к
естественной форме численных алгоритмов.
В процессе построения теории численных алгоритмов
было выяснено, что любой логический алгоритм можно
простыми методами свести к численному алгоритму. По
мере усовершенствования этих методов стало ясно, что
вообще любой алгоритм может быть всегда сведен к
численному алгоритму.
Таким образом, теория численных алгоритмов (да-
(далее мы отождествим это понятие с понятием «теория
вычислимых функций») стала универсальным аппаратом
для исследования всех алгоритмических проблем.
В этом параграфе будет показано, каким способом
любую алгоритмическую проблему можно свести к вы-
вычислению значений некоторой целочисленной функции
при целочисленных значениях аргументов.
Включим все условия задачи, доступные для перера-
переработки данным алгоритмом А, в занумерованную неот-
неотрицательными целыми числами последовательность
i^2» . . •» •**/}» • • •
29*
452 алгоритмы [гл. хи
Совершенно аналогично записи возможных решений
также включим в занумерованную последовательность
Как только проведена нумерация, становится оче-
очевидным, что любой алгоритм, перерабатывающий запись
условий Ап в запись решения Вт, можно свести к вы-
вычислению значений некоторой числовой функции
так как после введения нумерации мы можем иметь
дело уже только с соответствующими номерами записей
условий и решений, а не с самыми записями, и можем
говорить об алгоритме, перерабатывающем номер за-
записи условий в номер записи решения. Этот алгоритм
будет численным алгоритмом.
Очевидно также, что если есть алгоритм, решающий
исходную задачу, то есть и алгоритм вычисления зна-
значений соответствующей функции. Действительно, чтобы
найти значение <р(/г) при п = /г*, можно ,по п* восста-
восстановить запись условий задачи, затем с помощью имею-
имеющегося алгоритма найти запись решения и по записи
решения определить номер т*. Следовательно,
Обратно, если есть алгоритм вычисления функции
ф(/г), то, стало быть, имеется и алгоритм решения ис-
исходной задачи. Действительно, по записи условий за-
задачи можно найти соответствующий ей номер /г*, затем
вычислить т*=<р(/г*) и по т* определить запись ре-
решения.
Приведем теперь один широко применяющийся ме-
метод нумерации — метод Гёделя.
. Рассмотрим запись некоторого числа п в форме
где ро = 2, р\ = 3, р2 = 5 и вообще рт — т-е простое
число.
Из этой записи видно (в силу теоремы о единствен-
единственности разложения любого числа на простые множите-
§ 12.5] СВЕДЕНИЕ ЛЮБОГО АЛГОРИТМА К ЧИСЛЕННОМУ 453
ли), что каждому числу л однозначно соответствует на-
набор аи U2,*.., ат и, наоборот, каждому набору аи
#2, • • •> а-т однозначно соответствует число п. Например,
если п = 60, имеем
60 = 223151, т. е. ах = % а2=\, а3=\.
С помощью этого способа мы можем нумеровать те-
теперь любые упорядоченные последовательности, состоя-
состоящие из т чисел. Рассмотрим несколько примеров.
1) Каждой паре чисел а\ и аг, для которой мы
ищем ее наибольший общий делитель q, может быть
поставлен в соответствие гёделевский номер этой пары
п = 2fll • 3fll.
Алгоритм Евклида сведется тогда к вычислению функ-
функции q = ф(/г).
2) Требуется найти символ, расположенный на г-м
месте чисто периодической последовательности, состоя-
состоящей из бесконечно повторяющейся последовательности
чисел аи #2, • •., о,т. Условию задачи можно поставить
в соответствие гёделевский номер
Алгоритм распознавания числа, стоящего на г-м месте,
сведется тогда к вычислению значений функции
Я = <Р in),
причем q может принимать лишь значения из множе-
множества {аи а2> ..., ат).
3) Уравнению /г-й степени, записанному в общем
виде (bi — буквы, но не конкретные числа)
можно приписать номер /г; по /г, очевидно, легко вос-
восстановить запись уравнения.
При п = 2 уравнение имеет^вид
Его решение выражается через коэффициенты так*
-V A2.2)
454 алгоритмы [гл. хп
Перепишем A2.2) в виде строки
считая, что радикал действует, на соответствующие
скобки. Предположим, что мы намереваемся найти выра-
выражение решения уравнения п-й степени в радикалах. Оче-
Очевидно, как бы это решение ни выглядело, оно может
быть составлено лишь из следующих символов:
2 3 г
"К —> X, '• > (, )> Ь bv b2, • •., bn, у, V , .-.., у .
Наличие среди этих символов символа 1 и символа сло-
сложения + позволяет записать с помощью этих символов
любое число в виде 1 + 1 + 1 + .. .+1. Припишем этим
символам числа:
г
у соответствует число 2г ) соответствует число 13
-f- » » 3 1 » » 15
— » » 5 bx » » 17
X » » 7 b2 y> » 19
( » » 11
bn » » Bл-f 15).
Тогда всякому выражению, составленному из пере-
перечисленных символов, соответствует определенный набор
чисел. Например, выражению
соответствует набор чисел
6, 11, 17, 3, 19, 13.
Набору чисел, как мы знаем, может быть поставлен
в соответствие его гёделевский номер, равный
2б-Зп-517-73- И19- 1313. _"г.
Обратно, по заданному геделевскому номеру всегда
можно восстановить набор чисел, затем каждое число,
заменить на тот символ, который ему приписан, и та^1
ким образом по геделевскому номеру будет восстанов-
восстановлена запись любой формулы.
§ 12.6] ЭЛЕМЕНТАРНЫЕ И ПРИМИТИВНО-РЕКУРСИВН. ФУНКЦИИ 455
Следовательно, мы имеем способ нумеровать любые
выражения, составленные как из цифр, так из иных
символов — букв, символов различных операций и т. д.
4) Пусть требуется перенумеровать все слова в не-
некотором алфавите А. Это легко сделать, поставив в со-
соответствие каждой букве алфавита какое-либо число.
Тогда каждому слову в алфавите А будет соответство-
соответствовать последовательность чисел. Проводя затем обыч-
обычным способом гёделизацию, получим гёделевский номер
этой последовательности. Разумеется, гёделевский но-
номер слова зависит от выбранной системы соответствий
букв и чисел. Теперь легко пронумеровать все последо-
последовательности слов (например, все дедуктивные цепочки).
Действительно, последовательности самих слов одно-
однозначно может быть поставлена в соответствие последо-
последовательность гёделевских номеров этих слов; проводя
гёделизацию вторично, мы можем определить гёделев-
гёделевский номер самой последовательности гёделевских но-
номеров отдельных слов.
Таким образом, не только арифметические алгорит-
алгоритмы сводятся к вычислению значений целочисленных
функций. Любой нормальный алгоритм Маркова с по-
помощью гёделизации может быть также сведен к вычис-
вычислению значений целочисленных функций. Поэтому алго-
алгоритм вычисления значений целочисленных функций
можно считать универсальной формой алгоритма.
Раньше чем перейти к изучению целочисленных
функций, сделаем лишь следующее замечание: все из-
изложенное выше предполагало, что всех исходных усло-
условий задачи, которые могут быть переработаны алгорит-
алгоритмом, хотя и может быть бесконечно много, но множе-
множество это все же счетно. Только такого рода условия мы
имеем в виду, говоря здесь и далее об алгоритме.
§ 12.6. Элементарные и примитивно-рекурсивные
функции-
Функции вида у = <р(*ь *2, ..., хп) называются ариф-
арифметическими функциями, если как аргументы, так
и сами функции могут принимать значения лишь из
множества {0,1, 2, ...}. В дальнейшем мы будем рассмат-
456 АЛГОРИТМЫ [ГЛ. XII
ривать только арифметические функции. Логические
функции (см. гл. I) являются частным случаем ариф-
арифметических функций. '
Далее мы будем придерживаться следующей систе-
системы обозначений.
Переменные обозначаются малыми латинскими бук-
буквами:
a, Ь, с, ..., т, п х, у, z либо хг, х2 и т. д.
Значками функций будут служить малые греческие
буквы:
Ь Ф» Ъ t, • • •, а, р, Т либо <р„ cp2, ср3 и т. д.
Предикаты будем обозначать большими латинскими
буквами:
А, В, Р, Q, R, S и т. д.
Фиксированные числа будем обозначать теми же
буквами, что приняты для обозначения переменных, до-
добавляя сверху звездочку
а*, Ь*у х*, у* и т. д.
Дадим теперь определение вычислимой арифметиче-
арифметической функции и разрешимого предиката.
Функция у — ф(*ь Х2 хп) называется алгоритми-
алгоритмически вычислимой или просто вычислимой, если суще-
существует алгоритм, позволяющий определить значение
функции при любых значениях переменных Х\, х^, ...
Предикат Р(хи х2 хп), определенный на множе-
множестве целых чисел, называется алгоритмически разреши-
разрешимым или просто разрешимым, если существует алгоритм
для определения значения предиката Р при любых зна-
значениях переменных хи х2, ..., хп.
Данные определения являются интуитивными, иеточ-,
ными определениями, поскольку еще не было сформу-
сформулировано точно определение вычисляющего алгоритма.
Для того чтобы эти определения уточнить, мы по-
попробуем построить класс вычислимых функций, начав
это построение с самых простейших элементарных
функций.
§ 12.6] ЭЛЕМЕНТАРНЫЕ И ПРИМИТИВНО-РЕКУРСИВН. ФУНКЦИИ 457
Элементарными будем называть арифметические
функции, получающиеся из неотрицательных целых чи-
чисел и переменных с помощью конечного числа сложе-
сложений, арифметических вычитаний (под арифметическим
вычитанием здесь понимается абсолютная величина
Iх—#D» умножений, арифметических делений (под
арифметическим делением понимается целая часть
частного |у| при ЬфО) и построений сумм и произ-
произведений.
Вычислимость элементарных функций не вызывает
сомнений, поскольку хорошо известны алгоритмы для
выполнения всех действий, допустимых при построении
элементарных функций.
В качестве исходного числа для построения элемен-
элементарных функций можно было бы взять лишь число 1,
ибо
О = 11 — 11, 2=1 + 1, 3 = A + D+1 -и т. д.
Приведем примеры элементарных функций:
1) Элементарными функциями являются все простые
функции вида
<р(л:)==л:+1, <р(у)==12у, ty(a, b, c) =
^b2 (так как Ь2 = Ь-Ь) и т. д.
2) Многие из часто употребляемых функций эле-
элементарной теории чисел являются элементарными. На-
Например:
1 при х^\,
О при х = О. '"*
Функция sg(x) может быть выражена через функцию
min(*, у):
sg (x) = min (x, 1).
458 алгоритмы [гл. хп
С помощью sg(x) легко строится sg(x):
__ f 1 при х = 0,
sg(x) = 1 — sg(x)\ = \ _
BV ' 6V ' 10 при j
в) Неравенство *<;*/ эквивалентно равенству
min (х, у). г= х или |min (дс, у) — х\ = 0.
Тогда предикат «х меньше или равен у» можно за-
записать в виде
Р(х, y) = sg(\m\n(x, y) — x\).
Действительно, если **<*/*, Р(х*, у*) = 1, т. е. соот-
соответствует истинному высказыванию; в противном слу-
случае Р'=0.
г) Впоследствии нам пригодится функция
( \У — х\> если У ^-х>
V * X {
у 10, если у < х.
Это элементарная функция, ибо ее можно представить
в виде
y-*-x=\y—x\sg(\m\n(x, y) — x\).
д) Остаток от деления а на п
res (а, п)= а — п ^] I.
Возникает вопрос: шире ли класс всех вычислимых
функций класса элементарных функций? Можно ли по-
построить вычислимую функцию, не являющуюся элемен-
элементарной?
Из всех элементарных функций быстрее всего, оче-
очевидно, растет произведение. Произведение an есть п
раз повторенное сложение а + а + а + ... + а или,
как говорят, умножение есть итерация сложения.
Возведение в степень, в свою очередь, есть итерация
умножения:
п
ап — а • а • а
Эта функция является еще элементарной, так как она
выражается через произведение. Растет эта функция
с ростом а и п весьма быстро.
§ 12.6] ЭЛЕМЕНТАРНЫЕ И ПРИМИТИВНО-РЕКУРСИВН. ФУНКЦИИ 459
Построим еще более быстро растущую функцию,
являющуюся итерацией возведения в степень:
ф@, а) = а, <|>A, а) = а\ фB,а) = а<аа)
и вообще
<|>(я+Ь а) = Ф («.«). A2.3)
Эта функция растет чрезвычайно быстро. Можно дока-
доказать (см. [77]), что с помощью построения элементар-
элементарных функций уже невозможно «угнаться» за ростом
функции ф(д, а), точнее, что эта функция, начиная с не-
некоторого а = а*, мажорирует все элементарные функ-
функции, т. е. для любой элементарной функции <р(а)
найдется такое число т*, что будет выполняться не-
неравенство
()(*, а)
для всех а^-а*. Но тогда легко показать, что функ-
функция i(n) = ф(/г, п) не является элементарной.
Действительно, если бы ф(/г, п) была элементарной
функцией, то нашлось бы число т* (можно считать
т* !> 2 в силу монотонности функции ф(/г,а)) такое,
что ф(/г, п) < ф(т*, п) при я!>2. Это неравенство
должно, в частности, выполняться и при п = т*, так
какт*>2. Получаем при этом ф(т*, т*) <ф(т*,-т*),
что невозможно.
Таким образом, итерация возведения в степень по-
позволяет получить неэлементарную функцию. В то же
время ф(/г, а) заведомо вычислима. Действительно,
пусть мы хотим вычислить значение ф(/г, а) при любых
п = /г*, а = а*. Общую формулу для определения функ-
функции ф(/г, а) мы записали так A2.3):
= а*:
или при а = а
Обозначим (а*)т = x(m)i x(m)—элементарная, всюду
однозначная вычислимая функция. Алгоритм ее вычис-
вычисления сводится к повторенному т раз умножению на а*.
Запись
02.4)
460 АЛГОРИТМЫ [ГЛ. XII
связывает значение функции ф в следующей точке е ее
значением в предыдущей точке. Достаточно задать те-
теперь начальное значение ф@, а*) = а*, чтобы получить
вычислительную .процедуру, дающую последовательно
значения
ФC, а*) =
Этот процесс следует продолжить до тех пор, пока не
будет достигнуто значение ф(л*, а*). Очевидно, этим
способом функция ф определена всюду и однозначно,
так как вычисление ее значений сводится к вычислению
значений функции х(т)> которая является всюду опре-
определенной и однозначной.
Из построенного примера мы делаем вывод, что
для построения всех вычислимых функций класс эле-
элементарных функций нуждается в расширении. Рассмо-
Рассмотрим с этой целью подробнее способ определения функ-
функции ф(д, а). Эта функция была задана по индукции:
было задано начальное значение функции ф@, а) —ба-
—базис, и был указан способ подсчета последующих ее значе-
значений по предыдущим с помощью допустимых операций.
Попробуем положить метод математической индук-
индукции в основу определения вычислимой функции. Для
этого сперва несколько уточним и расширим схему оп-
определения по индукции.
Определение по индукции можно,' вообще говоря,
ввести на любом упорядоченном множестве, где опре-
определены понятия «предыдущий» и «следующий».
Обозначим через хг функцию «следования за», кото-
которая означает переход к следующему элементу задан-
заданного множества. Если заданное множество — множе-
множество натуральных чисел
{0, 1, 2, ...}, то 0'=1, Г = 2, 2' = 3 и т. д.
Здесь функция следования х' совпадает с функцией
х+ 1.
§ 12.6] ЭЛЕМЕНТАРНЫЕ И ПРИМИТИВНО-РЕКУРСИВН. ФУНКЦИИ 461
Если же в качестве исходного множества задано
упорядоченное множество четных чисел {0, 2, 4, .. .},
то О7 = 2, 2' = 4 и т. д. и вообще х' =* + 2.
Мы, как правило, будем применять функцию следо-
следования для множества натуральных чисел, и поэтому
всюду в дальнейшем можно операцию «штрих» пони-
понимать как прибавление единицы: х' = х 4- 1.
Общую схему определения функции <р{х) теперь
можно уточнить следующим образом:
1) Задано <р@).
2) Для любого х указывается, каким образом зна-
значение <р(*') выражается в терминах х и ()
<Р @) = q,
В более общем случае могут присутствовать еще и
неизменяемые в процессе индукции параметры х2, *з.
..., хп. Схема тогда будет иметь вид
<f\0,X2,X^,...,Xn)=::ff{X2t Х%, -.., Хп), \
? (У »«^2» "^3» * * * *Хп) == X (У» ? (У» Х2> XZ> • • • >*п)> Х2> Х3> • • • >Хп)')
A2.6)
Если функции фи/ известны и вычислимы, то с
помощью этой схемы может быть организована про-
процедура вычисления последовательно <рA, х*2, ..., х*пу
<рB, х*2, ..., .*;*) и т. д. Следовательно, схема, заданная
выражениями A2.6), действительно определяет вычис-
вычислимую функцию.
Посмотрим теперь, какие арифметические функции
могут быть определены по индукции и насколько широк
класс таких функций.
Для точной постановки этого вопроса мы должны
условиться, какие функции считаются известными пер-
первоначально и какие операции, кроме схемы индукции,
допустимы при определении функций.
Первоначально известными или просто первоначаль-
первоначальными будем считать следующие функции:
I. ф(лг) = х' — описанная выше функция следования,
примененная для множества натуральных чисел. Сокра-
Сокращенно обозначается буквой S.
462 АЛГОРИТМЫ [ГЛ. XII
II. <p(*i, *2, ..., хп) = <7, где q = const — функция-
константа. Сокращенно обозначается Cj.
III. ф(*ь х2, ..., *„) = Xi — функция тождества *).
Сокращенно обозначается U".
Кроме схемы определения по индукции A2.5) или
A2.6), в число допустимых операций включим схему
подстановки IV.
IV. фС*Ь *2. .-.. -^п)=ф(Х1(^Ь *2. ..., *л),Х2(*Ь *2. •••
• • •» Хп) 1 • • •» Хт\^Ь ^2» • • ¦» Хп)).
Выпишем теперь все схемы в одну колонку, друг
под другом:
И. <p(*i> х2,
III. <p(*i, д:2,
IV. <pUi» ^2>
Х2 v^l» "^2
• l
ср(О,
V.6.
Здесь схемы I—III задают первоначальные функ-
функции и как бы играют роль аксиом, а IV и V — правил
вывода.
Определение. .Функция <р(*ь *2, ..., хп) назы-
называется примитивно-рекурсивной, если она может быть
определена с помощью конечного числа применений
схем I—V.
*) Вместо функции тождества можно было бы считать перво-
первоначально известными просто переменные, как это делалось при оп-
определении элементарных функций. Функция тождества вводится
здесь лишь для большего единообразия изложения.
В качестве первоначальных функций вместо функции-константы
можно было бы взять функцию-нуль ф(*ь *2, ..., хп)ЕЕ 0, так как
с помощью повторного применения функции следования можно полу-
получить 1 = 0', 2 = 1' и т. д. все константы,
§ 12.6] ЭЛЕМЕНТАРНЫЕ И ПРИМИТИВНО-РЕКУРСИВН. ФУНКЦИИ 463
Будем говорить, что некоторая функция <р непо-
непосредственно зависит от других функций, если она удо-
удовлетворяет схеме IV при каких-нибудь типе какими-
нибудь ф, хь Х2> • • -»Xm (в этом случае <р непосредствен-
непосредственно зависит от ф, xi> X2> •••¦Xm), или V, а или V, б при
каком-нибудь q с какими-нибудь ф, х (в этом случае <р
непосредственно зависит от ф и %).
Определение. Примитивно-рекурсивным описа-
описанием примитивно-рекурсивной функции q>(xh хч, ..., хп)
называется такая последовательность функций <pi, 92, ...
..., <рь, что каждая функция этой последовательности
является или первоначальной, или непосредственно за-
зависящей от предыдущих функций последовательности,
а последняя функция <р& есть <р. Число k назовем глуби-
глубиной примитивно-рекурсивного описания функции <р.
Примитивно-рекурсивное описание — это, по сути
дела, выписанный ряд функций, последовательно полу-
получаемых в результате применения схем I—V при выводе
функции ф. Действительно, мы отправляемся от первона-
первоначальных функций, которые должны стоять в начале по-
последовательности, и дальше, шаг за шагом, движемся
к функции ф.
Приведем теперь примеры построения некоторых
примитивно-рекурсивных функций. При этом мы вве-
введем условные обозначения для некоторых функций, ко-
которые нам понадобятся далее.
1) Определим функцию ф(*, ?/) так:
<р@, х) = х,
Согласно этой схеме имеем
= [срB,
и вообще
Составим теперь примитивно-рекурсивное описание
этой функции. Для этого полностью выпишем схему
464 алгоритмы [гл. хи
V, б, которой мы пользуемся при определении ф (у, х) —
« х + у:
?(/, х) = х(у, ср(у, х), х). I
В рассматриваемом примере функция ф(*) имеет
вид ф(х)==х, т. е. является первоначальной функ-
функцией тождества ф (х) = U\ (x).
Функция %(у, z, x) =z' может быть получена из пер-
первоначальной функции U\(у, z, x)^=z с помощью при-
применения схемы IV, где в качестве ф взята функция сле-
следования S(z)zz=zr. Поэтому можно записать
Х(у, z, х) = 5 [U\ (у, z, х)].
Примитивно-рекурсивным описанием функции % бу-
будет последовательность U2, S, х- Добавляя к этой по-
последовательности функцию. <|> (х) 2= U\ (х), от которой
непосредственно зависит функция ф(г/, х) по схеме A2.7),
получим примитивно-рекурсивное описание у(у,х):
u\, s, х> и\* ?•
2) Для определения следующей примитивно-рекур-
примитивно-рекурсивной функции воспользуемся тем, что сумма х + у
определена уже как примитивно-рекурсивная функция.
Зададим
<Р(О, х) = 0,
Последовательно имеем
срA, л:) = ср@,
срB, л:)==срA, х)-\-х
срC, л:) =
и вообще
Следовательно, произведение также является прими
тивно-рекурсивной функцией.
§ 12.6] ЭЛЕМЕНТАРНЫЕ И ПРИМИТИВНО-РЕКУРСИВН. ФУНКЦИИ 465
3) Используя результаты примера 2), определим
ср(О, х)=\,
Нетрудно проверить, что определенная так функция
будет представлять собой возведение в степень:
у {у, х) = ху.
4) <р@) =1. <р(л:') = у{х)х'. Легко видеть, что
ср(х) = х\.
5) Определим функцию «предшественника х»
0 при х = 0,
|Л_!| при л:>0.
Это — примитивно-рекурсивная функция, так как она
определяется по схеме V, а
pd(O) = O
pd (xr) = х.
6) Встречавшаяся раньше функция х— у опреде-
определяется так:
7) Функция min(x, у) может быть теперь определе-
определена с помощью применения схемы IV:
^, у) = у — (у -*- х).
8) max (л:, у) = (х-\-у)~т1п(х, у).
9) sg (x) = min (x, 1).
10) sg(x)=\-^-x.
11) \х-
12) Остаток от деления у на х (эту функцию обо-
обозначают через res (у, х)) определяется так:
res(O, л:) = 0,
res (у', x) = (res(y, х))' •
30 М. А. Айзерман, Л. А. Гусев и др.
466
АЛГОРИТМЫ
[ГЛ. XII
13) Г—1 определяется так:
14) С помощью примитивной рекурсии могут быть
определены конечные суммы и произведения вида
у у
2 <Р(*\ х) и. H<?(i, х).
i=0 i=0
Действительно,
о
У'
== ср (О, X),
У
', х)
П 9 С -«) =
/=0
В числе определенных нами примитивно-рекурсив-
примитивно-рекурсивных функций оказались сумма х + у, модуль разности
\х — у\, произведение «п/, частное -j L а также конечные
суммы и произведения. Следовательно, все элементар-
элементарные функции, о которых говорилось в начале параграфа,
примитивно-рекурсивные. Это значит, что класс элемен-
элементарных функций является подклассом класса прими-
примитивно-рекурсивных функций.
§ 12.7. Предикаты. Ограниченный оператор
наименьшего числа
Предикаты (см. гл. I) вводятся в логике там, где
необходимо символически отобразить соотношение ме-
между несколькими предметами. В общем случае преди-
предикат определен на некотором множестве предметов (ко-
§ 12.7] ПРЕДИКАТЫ 467
нечном или бесконечном) и может принимать два зна-
значения: истинно или ложно A или 0).
Мы рассматриваем здесь лишь арифметические пре-
предикаты, определенные на множестве натуральных чи-
чисел {0, 1, 2, ...}.
Предикат Р(х\у х2, ..., хп) зависит вообще от п пе-
переменных (л-местный предикат). Если некоторые пере-
переменные входят под знаки кванторов, стоящих перед
предикатом, то они называются связанными перемен-
переменными; остальные переменные свободные.
Например, предикат Р(х, у, z, t) зависит от четырех
переменных. Предикат же*) (Vx)Cy)P(x, у, z, t)
имеет связанные переменные х и у и зависит от сво-
свободных переменных z и /. Поэтому выражение
(Vjc) (Зу) Р (х, у, z, t) является по сути дела предикатом
Q(z, t)
(Чх)(ЩР(х, у, z, t)^Q(z, f).
Действительно, эта запись означает следующее:
в зависимости от выбранных значений z* и t* может
для всех х существовать такое у, что Р(х, у, z*, t*),
либо этого может не быть. В первом случае Q истинно
(или Q = 1), во втором — Q ложно (или Q = 0).
Предикат, как и функция, может быть определен по
индукции. Например, по схеме
Е@) (или Е@)=1),
определяется предикат Е(а)~ «а четно».
Поэтому открывается возможность построения схе-
схемы определения предикатов по аналогии со схемой
определения примитивно-рекурсивных функций и введе-
введения понятия «примитивно-рекурсивный предикат».
Мы, однако, не пойдем по этому пути и приведем
иное определение примитивно-рекурсивного предиката,
предложенное Гёделем в 1931 г. Назовем представляю-
*) Читается: «для всех х существует такое у, что P(x,y,z,t)
истинно». Часто слово «истинно» опускается.
30*
468 АЛГОРИТМЫ [ГЛ. XII
щей функцией предиката Р(хи х2, ..., хп) такую функ-
функцию ф(*ь л'2, ..., хп), которая обращается в нуль 'лишь
для тех и только тех хи х2 ,.., хп, для которых Р(хи
*2, • •., хп) истинно. Тогда истинность Р(хи х2у ..., хп)
соответствует равенству
Очевидно, что один и тот же предикат может иметь
несколько представляющих функций, нули которых дол-
должны совпадать.
Определение. Предикат называется примитивно-
рекурсивным, если существует примитивно-рекурсивная
функция, представляющая этот предикат.
При рассмотрении рекурсивных предикатов часто
вводятся ограниченные кванторы всеобщности и суще-
существования, и ограниченный оператор наименьшего числа.
Предположим, что предикат Q{xu x2, ..., хп) опре-
определен через примитивно-рекурсивный предикат Р{хи
*2, •.., хп, у) с помощью применения ограниченного
квантора всеобщности
Q(xlf х2, ..., xn) = (Yy)y^zP(xv x2, ...,хп,у) A2.8)
или, подробнее,
Q(xv х2, ..., xn)=(Vy)[y <Cz->P(xv x2, ..., хп, у)].
Предикат Q(xu x2, ..., хп) соответствует высказы-
высказыванию, что при данных х\% х2, ..., хп для всех */<z
значение P(xh x2, ..., хп, у) истинно. Определенный так
предикат Q(*i, x2, ..., хп) будет примитивно-рекурсив-
примитивно-рекурсивным, так как его представляющая функция <р(*ь х2, ...
..., хп) может быть выражена через представляющую
функцию ф(*ь х2, ..., хп, у) предиката Р:
2, ..., xn) = 2j <?(xlf x2, ..., хп, у).
Отметим, что 2, вообще говоря, может зависеть от Х\,
*2, •. •, хп\ для того, чтобы все выводы остались в силе,
эта зависимость должна быть примитивно-рекурсивной.
§ 12.7] ПРЕДИКАТЫ 469
Аналогичный вывод можно сделать для преди-
предиката Q, определенного с помощью применения ограни-
ограниченного квантора существования
Q(xv х2, ..., хп)= (Щу<г P(xv х2, ..., хп> у) A2.9)
или, подробнее,
Q(xv х2, ..., хп)= (З.у)\у <г&Я(л:1, х2, ..., хп, у)].
Здесь представляющая функция предиката Q опре-
определяется через произведение
г
<?(хх, х2, ..., *„) = П ? (-*i> *2» •••> -*я> У)-
у=о
Введем в рассмотрение ограниченный оператор наи-
наименьшего числа.
Пусть дан некоторый примитивно-рекурсивный пре-
предикат Р(хи х2, ..., хп, у) и заранее известно, что вы-
выполняется условие
(V^HVx,) ... {Vxn)(Vy)y<,P{xlt х2У ..., х„, у), A2.10)
т. е. при любом наборе xh jc2, ..., хп найдется хоть
одно у <z такое, что Р(хи х2у ..., х„, у) будет истинно.
Тогда с помощью предиката Р можно определить
функцию ф(хь *2, ..., хп) следующим образом: за зна-
значение функции ty(x*, х*2, ..., х*^при заданных х\, х\,
...,х*пбудем принимать то наименьшее число у*, при
котором Р(х\, х*2у ..., х*п, у*) истинно. Обозначим это
так:
2, ..., xn) = ^yy<zP(xv x2, ..., хп, у). A2.11)
В силу условия A2.10), при любых хи х2, ..., хп, такое
у найдется; следовательно, ф(хь х2, ..., хп) будет всюду
определена.
Если вместо предиката Р(хи х2> ..., хп, у) рассмат-
рассматривать его представляющую функцию <p(*i, *2, ..., хп>у)>
то A2.11) можно записать в виде
lt x2, ..., хп,
470 АЛГОРИТМЫ [ГЛ. XII
т. е. в качестве значения ф(*1, х2, ..., хп) нужно взять
то наименьшее */, при котором <p(*i, х2у ..., хп% у) об-
обращается в нуль.
Таким образом, ограниченный оператор наименьше-
наименьшего числа позволяет, отправляясь от примитивно-рекур-
примитивно-рекурсивных функций, получать новые функции. •
Покажем, что определенная с помощью ограничен-
ограниченного оператора наименьшего числа функция ф(*ь х2, ...
..., хп) является примитивно-рекурсивной. Для этого
выразим явно функцию ф(хь х2у ..., хп) через предста-
представляющую функцию <р(*1, х2у ..., хп, у) предиката Р
ty(xl9 х2, ..., л:л) = 2 sg( П
k-Q \У-О
В том, что A2.12) действительно выражает ф(*1,ж2, ...,
хп), можно убедиться следующим образом: развернем
запись A2.12):
2, ..., xn) = sgl<?(xlf х2, ..., хп, 0)|-f
(!, х2, ..., хп, 0)- <?(xv х2, ..., хп,
Каждое слагаемое остается равным единице до тех
пор, пока в произведение не войдет значение <p(*i, x2, ...
• • •, хп, у) = 0; все дальнейшие слагаемые равны нулю.
Таким образом, число единиц суммируется столько раз,
каково число у, т. е. в результате суммирования и по-
получается это число у.
Так как ф(хь х2, ..., хп) определена с помощью по-
построения сумм, произведений и функции sg(jc), она яв-
является примитивно-рекурсивной.
В § 12.6 была приведена в качестве примера прими-
примитивно-рекурсивная функция res (а, п)—остаток от де-
деления а на я. С помощью этой функции легко подсчи-
подсчитать число делителей числа а.
Будем последовательно делить а на 1, 2, 3, 4, ... и
считать, сколько раз деление произошло без остатка. Та-
Таким образом мы определим число делителей числа а.
§ 12.7] ПРЕДИКАТЫ 471
Обозначим это число р(а). Функция р(а) —примитивно-
рекурсивная, так как
а
Р (а) = 2 sg (res (a, i)).
Если а — простое число, то р(а) =2, так как про-
простое число делится лишь на 1 и на самого себя. Тогда
1, если а простое число,
Э в остальных случаях.
Теперь легко подсчитать число простых чисел, не
превосходящих у. Обозначим его через ъ(у):
у
Здесь суммирование начинается с а = 2, так как 0 и 1
мы за простые числа считать не будем. За нулевое про-
простое число примем 2, за первое — 3 и т. д.:
Ро = 2, р\ = 3, р2 = 5, ръ = 7, ...
Приведем несколько значений функции и
•«D) = 2,
«G) = 4,
«(8) = 4,
«(9) = 4,
и A0) = 4,
тс(П)==5 и т. д.
Определим теперь функцию рп = ф(я) как функцию,
которая по п позволяет найти простое число, обладаю-
обладающее номером п.
Из теории чисел известно, что л-е простое число не пре-
превосходит 22"+ • Поэтому можно записать
472 АЛГОРИТМЫ (ГЛ. ХИ
ибо п-е простое число есть наименьшее число, обладаю-
обладающее тем свойством, что среди не превосходящих его чи-
чисел есть ровно п + 1 простых.
Например,
ср B) = /?2 = jxy [У < 256 & тг (у) = 3] = 5.
Функция Рп = ф(л) является примитивно-рекурсив-
примитивно-рекурсивной, так как определена с помощью ограниченного опе-
оператора наименьшего числа (роль границы z(n) здесь
играет примитивно-рекурсивная функция z(n) = 22"+1)
и примитивно-рекурсивного отношения равенства
ъ(у) = п + 1.
Определим еще одну функцию, которая позволяет
узнать показатель, с которым простое число ра входит
в разложение числа п на множители. Эта функция обо-
обозначается ехра(л).
Очевидно, что значение ехра(п) есть такое наиболь-
наибольшее число у, что руа делит п, или, иначе, такое наимень-
наименьшее у, что руал1 уже не делит п. Тогда можно записать
ех/*в(л) = ру[у <я&/*2+1 не делит п]
или
ех/>в(л)=>у[у<я&ге8(я, р*а+1)ФО]. A2.13)
Из A2.13) делаем вывод, что ехра(п)—примитивно-
рекурсивная функция.
Вспомним теперь, что гёделизация связана с разло-
разложением заданного числа на простые множители и оп-
определением показателя, с которым простое число ра
входит в это разложение. Следовательно, процесс гёде-
лизации связан лишь с примитивно-рекурсивными функ-
функциями.
Выпишем в заключение еще две примитивно-рекур-
примитивно-рекурсивные функции (без вывода).
Пусть имеется набор чисел /пь /п2, ..., /пг, гёделев-
ский номер которого равен а, и набор Ль п2, ..., ns, гё-
делевский номер которого равен Ь. Образуем теперь
строку mh m2, ..., mr, n\, n2, ..., ns путем приписыва-
приписывания последовательности nh n2, ..., ns к последователь-
§ 12.8] ПРИМЕР ПОСТРОЕНИЯ ВЫЧИСЛИМОЙ ФУНКЦИИ 473
ности rtii, 1П2, • • •» tnr. Требуется по известным гёделев-
ским номерам а и Ъ определить гёделевский номер у со-
составной строки. Функция, которая позволяет провести
это вычисление, сокращенно обозначается у = а ° Ь и
оказывается примитивно-рекурсивной.
Пусть теперь имеется последовательность чисел ти
т2, ..-., /Пг, тг+ь ..., nt], nij+i, ..., пгп, которая имеет
гёделевский номер а. Вырежем из этой последователь-
последовательности «кусок», начинающийся с т* и кончающийся nij
(этот кусок подчеркнут снизу), и на его место вставим
другую последовательность чисел с гёделевским номе-
номером Ь. Требуется определить гёделевский номер у по-
полученной последовательности.
Функция, которая дает этот номер в зависимости от
а, г, /' и 6, называется функцией включения и обозна-
обозначается
Эта функция также оказывается примитивно-рекур-
примитивно-рекурсивной.
Вспомним теперь преобразование слов в ассоциатив-
ассоциативном исчислении. Операция подстановки после гёдели-
зации ассоциативного исчисления сводится к описанной
выше операции включения. Следовательно, преобразо-
преобразование слов в ассоциативном исчислении связано лишь
с примитивно-рекурсивными функциями.
Эти выводы будут полезны нам в дальнейшем при
изучении общерекурсивных функций.
§ 12.8. Пример построения вычислимой, но не
примитивно-рекурсивной функции
Выше был описан класс примитивно-рекурсивных
функций. Как было видно из самого построения, ка-
каждая примитивно-рекурсивная функция вычислима.
Верно ли обратное утверждение? Всякая ли вычис-
вычислимая функция примитивно-рекурсивна?
Отрицательный ответ на эти вопросы был дан поч-
почти одновременно Петер и Аккерманом, которые, идя
совершенно различными путями, построили примеры
474 АЛГОРИТМЫ 1ГЛ. XII
вычислимой, но не примитивно-рекурсивной функции. По-
Познакомимся с идеей примера Петер.
Р. Петер впервые обратила внимание на то, что
множество примитивно-рекурсивных функций является
счетным множеством.
Действительно, класс первоначальных функций сче-
тен (так как число различных переменных Xi и кон-
констант q счетно). Следовательно, счетен класс прими-
примитивно-рекурсивных функций, определенных с помощью
одного применения схем IV или V, потому что счетно
множество наборов ф, хь %2, •.., Хт для схемы IV или
пар ф, х Для схемы V, образованных из элементов счет-
счетного класса.
Далее, счетно множество примитивно-рекурсивных
функций, образованных с помощью двух применений
схем IV или V и т. д. Поэтому и вообще счетно множе-
множество примитивно-рекурсивных функций. В частности,
счетно множество примитивно-рекурсивных функций од-
одной переменной (как часть всего счетного множества).
Петер удалось все примитивно-рекурсивные функ-
функции одной переменной эффективно перенумеровать, т. е.
расположить их в последовательность
••• О2-
так, что по виду функции можно определить ее номер
и по номеру определить вид той функции, которая этим
номером обладает. Коль скоро удалось эффективно
перенумеровать все примитивно-рекурсивные функции
одной переменной, немедленно оказалось возможным
построить пример вычислимой, но не примитивно-рекур-
примитивно-рекурсивной функции.
Введем функцию ф(*/, х)==уу(х)\ функция ф(у, х)
вычислима (так как по значению у = у* можно оты-
отыскать соответствующую функцию <ру* (х) и вычислить
ее значение при заданном х = х*\ тем самым будет вы-
вычислено значение ф(*/*, **)). Но она не примитивно-ре-
примитивно-рекурсивна. Действительно, если бы ф(*/, х) была прими-
примитивно-рекурсивна, то была бы примитивно-рекурсивна
и функция ф(я, х) как функция одной переменной. То-
Тогда была бы примитивно-рекурсивна и функция
, х) + 1, так как прибавление единицы есть допустимая
§ 12.9] ОБЩЕРЕКУРСИВНЫЕ ФУНКЦИИ 475
операция «следования за». Но так как в ряду A2.14)
содержатся все примитивно-рекурсивные функции од-
одной переменной, то нашелся бы такой номер */*, что
ty(x, х)-f-1 н= сру#(х) для всех х. Иначе
ф(л:, л:)+1^ф(/, л;).
Так как это равенство должно выполняться для всех
х, то, в частности, оно должно выполняться и для х =
= у*. Но тогда
¦ (У*. /)+!-¦ (У*. У')>
что невозможно. Значит, перечисляющая функция ф(у, х)
не примитивно-рекурсивна. Вместе с тем она заведомо
вычислима. Следовательно, класс примитивно-рекурсив-
примитивно-рекурсивных функций не охватывает всех вычислимых функций
и нуждается в расширении.
Если в классе элементарных функций ограничение
состояло в том, что с помощью допустимых операций
невозможно было строить очень быстро растущие функ-
функции, то теперь в классе примитивно-рекурсивных функ-
функций нас ограничивает принятая форма индукции. Вся
беда в том, что мы заранее фиксировали ту схему
(схема V), в которой должна проявиться индукция.
Расширение класса примитивно-рекурсивных функ-
функций было предложено Гёделем в 1934 г. и основано на
одной смелой идее Эрбрана.
§ 12.9. Общерекурсивные функции. Определение
Эрбрана — Гёделя
Схема примитивно-рекурсивной функции определяла
некоторую функцию <р через некоторое число функций
X и ф, которые считались уже известными. Рассмотрим
два примера вычисления с одной вспомогательной
функцией х-
Пример 1. Пусть задана система равенств
Х@, 4)= 7, A2.15)
ХП> 7) = 7, A2.16)
9@) = 4, A2.17)
02.18)
476 АЛГОРИТМЫ [ГЛ. XII
Просмотрим цепочку формальных выкладок, позво-
позволяющих из системы A2.15) — A2.18) вычислить<рB) = 7.
J) В A2.18) подставим у = 0:
<РA) = Х(О, ср(О)). A2.19)
2) В A2.19) вместо <р@) подставим 4 согласно
A2.17):
( = х@, 4). A2.20)
3) Воспользуемся A2.15):
Поступая далее аналогично, последовательно полу-
получаем:
4) <рB) =
5) <рB) = хО> 7),
6)<рB) = 7.
Пример 2. Пусть задана некоторая функция
ф(я, а) с помощью схемы
ср(О, а) = а, A2.21)
ср(/гН-1, а) = сР(/г) а)-hi, A2.22)
и пусть нас интересует значение <рC,5). Попробуем
формально проанализировать, какие операции нам
нужно совершить, чтобы, пользуясь схемой A2.21),
A2.22), вычислить <рC, 5):
1) Подставим в A2.22) вместо переменных числа
п = 2, а = 5. Имеем
ср C,5) = ср B,5)+1.
2) Подставим в A2.22) п = 1, а = 5 и опреде-
определим ф B,5) :
ср B,5) = ?(l,5)-f 1.
3) Аналогично
<? A,5) =
12.9] ОБЩЕРЕКУРСИВНЫЕ ФУНКЦИИ 477
4) Подставим в A2.21) а = 5. Имеем
9@,5) = 5.'
5) Заменим в C) <р @,5) на 5, согласно D),
6) Подставляя <рA,5) из E) в B), имеем
7) Наконец, подставляя <р B,5) из F) в A), полу-
получаем
ср C,5) = 7+1=8.
В рассмотренных двух примерах нам для производ-
производства вычислений понадобились лишь две операции:
1) подстановка чисел на место переменных; 2) замена
вхождений, т. е. замена в одном из равенств входящей
в него левой части другого равенства на его правую
часть (или наоборот).
Если некоторое равенство может быть выведено с
помощью этих двух операций из заданной системы ра-
равенств ?, то говорят, что это равенство выводимо в си-
системе Е.
В теории общерекурсивных функций проблема выво-
выводимости занимает центральное место. Поэтому нам
сейчас необходимо более детально рассмотреть эту
проблему.
Прежде всего дадим более широкое и точное опре-
определение понятия «выводимость». Для этого сперва опре-
определим понятие «терм», а затем понятия «равенство» и
«вывод».
Назовем буквы, которые мы раньше обычно приме-
применяли для обозначений функций
?» Х> *> а> ?i» Ъ> Ъ> ?4» • • •
функциональными буквами. Список функциональных
букв неограничен.
Переменные, как и раньше, будем обозначать
буквами
<%) у t z, t, пъ, и, a, t?t с, х^,
4Td алгоритмы [гл. хп
Понятие «терм» определим индуктивно:
1) 0 есть терм.
2) Каждая переменная есть терм.
3) R' есть терм, если R— терм.
4) ф(/?ь /?2, ..., Rn) есть терм, если <р — функцио-
функциональная буква, a Ru /?2> • • •> Rn — термы.
5) Иных термов нет.
Приведем примеры выражений, которые являются
термами:
1. Цифра 3 есть терм, так как 0 есть терм, 0' = 1 —
терм, V = 2 есть терм и 2' = 3 тоже терм.
2. Любая постоянная есть терм. Постоянные в даль-
дальнейшем будем обозначать теми же буквами, которые
приняты для обозначения переменных, но со звездоч-
звездочками:
х*> у*у 2?, t*, m*, rf, ...
3. ф B) есть терм. Термами являются также
4. <р(х, у).
5. Ф(*, Xi (8,*/),Х2C,5), хз(#,*)).
6. X(*'></).
7. «K/.J/foWn и т. д.
Примеры выражений, которые не являются термами:
1. ср(ф); 2. 5(*); 3. у (ср); 4. <?(z, ф) .
и т. д.
Таким образом, с помощью понятия «терм» четко вы-
выделен определенный класс выражений, которые могут
быть составлены из символов переменных, констант и
функциональных букв при помощи скобок и штрихов.
Теперь можно точно определить понятие «равенство».
Выражение R = S, где R и 5 — термы, назовем ра-
равенством.
Осталось точно определить правила вывода новых
равенств из заданной системы равенств Е. Будем счи-
считать, что разрешается:
Операция 1. Подставлять числа на место пере-
переменных.
Операция 2. Переходить от выражений вида R =»
= 5 и Я = Р, не содержащих переменных (/?, 5, Я, Р —
термы), к выражению, получающемуся из R == 5 путем
§ 12.9] ОБЩЕРЕКУРСИВНЫЕ ФУНКЦИИ 479
замены в одном или нескольких местах одновременно
вхождений Н на Р.
Возвращаясь теперь к рассмотренным в начале этого
параграфа двум примерам, мы видим, что при выводе
интересовавших нас значений функций мы пользовались
лишь операциями 1 и 2, т. е. подстановкой чисел и за-
заменой вхождений.
Обратим внимание на то, что схема определения
примитивно-рекурсивных функций наделена следующи-
следующими двумя свойствами:
а) Значения функций выводятся из равенств спосо-
способом, который формально был проанализирован.
б) Схема является определением с помощью мате-
математической индукции.
Мы уже выяснили, что класс примитивно-рекурсив-
примитивно-рекурсивных функций оказался ограниченным потому, что мы
заранее фиксировали схему индукции, заранее опреде-
определили, в какой форме должна проявиться индукция.
Если бы мы, стремясь расширить класс примитивно-
рекурсивных функций, фиксировали бы иную, может
быть в некотором смысле более широкую схему индук-
индукции, то у нас вновь не было бы гарантии, что и эта но-
новая схема не будет нас ограничивать.
Поэтому Эрбран предложил вообще не фиксировать
заранее схему индукции, а принять само свойство а) за
определение. Эрбран-гёделевское определение общере-
общерекурсивной функции таково:
Функция <р (*ь Х2, •-, хп) называется общерекурсив-
общерекурсивной, если существует такая конечная система равенств Е,
что для любого набора чисел х*ъ х\ х*п найдется
такое одно и только одно число у*, что равенство
<р (х*, х\, ..., л;*) = у* может быть выведено из Е с
помощью конечного числа применений операций 1 и 2
(т. е. подстановок чисел на место переменных и заменой
вхождений).
Система Е называется определяющей системой ра-
равенств; говорят также, что Е рекурсивно определяет
функцию ф.
Здесь не требуется, чтобы значения функции вычис-
вычислялись с помощью ее значений в предыдущих точках;
480 АЛГОРИТМЫ (ГЛ. XII
не требуется, чтобы входящие в систему Е вспомогатель-
вспомогательные функции были всюду вычислимы; не фиксируется
никакая схема индукции. Требуется только, чтобы си-
система равенств Е так определяла данное значение ф
с помощью других значений <р и некоторых значений
вспомогательных функций, чтобы ф во всех точках можно
было однозначно вычислять на основании системы Е.
Однозначность здесь означает, что нельзя одновре-
одновременно вывести из системы Е два противоречивых ра-
равенства.
Приведенное определение общерекурсивной функции
само по себе не дает вычислительной процедуры. В са-
самом деле, из определения мы узнаем, что если данная
система равенств Е рекурсивно определяет некоторую
функцию ф, то для любых х*, x*v ..., х*п найдется такое
у*, что из Е может быть выведено равенство
j, x^t • • •» ^о)== У •
Но как организовать этот вывод? Как найти это чи-
число */*? Можно, конечно, попробовать выводить из ? все
возможные равенства до тех пор, пока не встретится
равенство, интересующее нас. Однако при таком подходе
нет никакой гарантии, что этот процесс не продлится не-
неопределенно долго. Ведь даже в конечном лабиринте,
если неразумно организован поиск, можно как угодно
долго ходить по коридорам и площадкам и все-таки не
найти нужной площадки (в связи с тем, что конечный
лабиринт может содержать коридоры, замкнутые в
цикл).
Процессу перебора можно придать определенную ре-
регулярность так, чтобы этот процесс годился и для вы-
вывода равенства <р(л;*, х*2, ..., **) = У* в конечное, но не
ограниченное заранее число шагов.
Мы не будем приводить здесь описания этого про-
процесса. Оказывается, что путем гёделизации процесс пе-
перебора всех выводов сводится к применению оператора
наименьшего числа.
Введение в рассмотрение этого оператора приво-
приводит к иному способу определения класса рекурсивных
функций.
§12.101 ЯВНАЯ ФОРМА ОБЩЕРЕКУРСИВНЫХ ФУНКЦИЙ 481
§ 12.10. Явная форма общерекурсивных функций
В § 12.8 мы ввели понятие ограниченного оператора
наименьшего числа, который ставит в соответствие при-
примитивно-рекурсивному предикату Р(хи х2,,..,, хп, у) (или
примитивно-рекурсивной функции <р(*ь xi> • •¦ **•>, У),
представляющей предикат Р) примитивно-рекурсивную
функцию ф(*ь Х2, •.., хп) следующим образом:
Х2, ..., Xn) = \*.yy<zP{xv Х2, .. ., Хп,
— Wy<*I<P(*i> *2> •••> хп, у) = 0] .'A*2.23)
при условии
y< x2, ..., л:я,
ИЛИ • ..-•¦¦:.. •.¦..-•¦ ¦. / ¦
(Ухд (Vxj)...; (Гха) (Зу)у < е fcpUi, х2,-. •., дс., У)
где 2 в общем случае может быть примитивно-рекурсив-
примитивно-рекурсивной функцией хх; х2у ...Ухп'. .. : • ¦
Z=. Z\X\, X
2> ."i «^ ^
Рассмотрим теперь случай, когда ограничение опера-
оператора снято.
Пусть ф(*ь *2, ..., Д^п, 1/)—примитивнофекурсйвная
функция такая, что ¦
..., xnf y) = 0]. A2.24)
Здесь уже не указана верхняя граница для у, а гово-
говорится лишь, что для всех хи х2, ..., хп существует та-
такой у, что .
( x2t ..., хп,
В этом случае функция ф(*ь JC2, ..., хп), определенная
с помощью применения оператора наименьшего числа
, ..., хп) = jxy[<p(xv х2, ..., ^л, у)*-01, A2.25)
оказывается заведомо вычислимой. Действительно, для
вычисления ее значения в любой точке х\, х\, ..., х*п
31 М. А. Айзерман, Л. А. Гусев и др.
482 АЛГОРИТМЫ [ГЛ. Xff
достаточно последовательно вычислять
т (Х^ > «*2* * * *' п* )
и т. д. до тех пор, пока не будет достигнуто такое у*,
для которого <р(х[, х*, ..., х*п, у*) =0. Это у* должно
быть принято за значение функции ф в рассматриваемой
точке.
Описанный процесс должен обязательно через конеч-
конечное число шагов окончиться, так как, согласно A2.24),
существует y*t обращающий функцию <р в нуль. Будет
ли определенная согласно A2.25) при условии A2.24)
вычислимая функция ф(хи x2l.,.txn) общерекур-
общерекурсивной?
Оказалось, что в этом случае можно построить си-
систему равенств Е, которая бы рекурсивно определяла
функцию ф, т. е. функция ф оказывается общерекур-
общерекурсивной.
Чтобы упростить выкладки, рассмотрим функцию од-
одного переменного
¦ (х) = w |<р (х, у) = 01 )
и A2.26)
<Ух)<ЯуI?(х, у) = OJ. J
Система Е, рекурсивно определяющая ф(*), в этом
случае будет такова:
(Е)
х> Я = У,
3. ф(л:) = в[<р(х, 0), x, 0).
Покажем, что Е рекурсивно определяет ф(*). Пусть
х* — некоторое число, и мы хотим определить ф(**).
Согласно 3, Е (равенству 3 системы Е)
<Н**) = °|<РС**» 0), х*, 0J.
Дальше возможны два случая. Либо у{х*г 0) = 0,
и тогда можно применить лишь первое определяющее
равенство
сг(О, х\ 0) = 0, т. е.
§ 12.10] ЯВНАЯ ФОРМА ОБЩЕРЕКУРСИВНЫХ ФУНКЦИЙ 483
Но нуль в этом случае и должен быть значением функ-
функции ф согласно A2.26).
Если же ф(**, 0) Ф 0, то ее значение можно предста-
представить как z + 1 и воспользоваться вторым определяю-
определяющим равенством
о[<р(л*, 0), х\ 0] = а [ср (л:*, 1), х*, 1|.
Теперь опять возможно два случая. Либоф(л:*, 1) =0,
и тогда можно пользоваться лишь равенством 1,?
о[0, *М]=1
и, следовательно, ф(**) = 1. Но в этом случае 1,? и
должно давать значение функции ф согласно A2.26).
Если же <р(**, 1) Ф 0, то ее представляем в виде z + 1
и опять пользуемся равенством 2, Е:
*, 1), х\ l]=rol<p(x*, 2), х\ 2),
и так до тех пор, пока впервые не встретится у* такое,
что <р(**, У*) = 0. Это у* и будет значением ф(**).
Таким образом, система Е действительно рекурсивно
определяет функцию
. У) = 0]
и, следовательно, ф(я) является общерекурсивной
функцией. . >
В приведенном доказательстве мы нигде не исполь-
использовали тот факт, что функция <p(*i, x2, .... хП1 у) в
A2.25) есть примитивно-рекурсивная. Все рассуждения
остаются справедливыми, если считать функцию
Ф(*ь *2» •••» хп, у) общерекурсивной.
Итак, оператор наименьшего числа \ху при выполне-
выполнении условия A2.24) позволяет из примитивно-рекурсив-
примитивно-рекурсивных функций (предикатов) конструировать общерекур-
общерекурсивные функции. Более того, было выяснено, что всё
отличие примитивно-рекурсивных функций от общерекур-
общерекурсивных охватывается оператором цу. Доказано следую-
следующее утверждение:
Любая общерекурсивная функция у{хи х2,». ,txn) мо-
может быть представлена в виде
?(*!, х2, ..., xn) = ty{v.y[x(xlf х2, ..*, хп, у) = 0|),
A2.27)
31*
484 АЛГОРИТМЫ [ГЛ. XII
где ф и т — примитивно-рекурсивные функции, причем.
для функции т справедливо утверждение ¦ ¦
(VX|) (Yicj)... (V*e) (Эу) [х (xlf х2, ..., хп, у) = 0J.
Форма A2.27) носит название явной формы общере-
общерекурсивных функций. Приведем идею - доказательства
этого утверждения. Пусть имеется система равенств
Е — {е0, ей ..., es] рекурсивно определяющая функцию
Ф(*ь Х2, .... хп)- Каждому равенству е{ соответствует
его гёделевский номер тг-. За гёделевский номер всей си-
системы Е тогда следует принять число .
Будем теперь как-либо выводить из системы Е новые
равенства. Это значит, что мы будем последовательно
получать равенства
О' 1*
2*
Если П{ — гёделевский номер равенства е<, то каждому
выводу (т. е. каждой цепочке вида A2.28)) можно по-
поставить в соответствие гёделевский номер вывода
Пусть мы интересуемся значением функции <р в точке
х*, xv ..., х*п% т. е. мы хотим вывести из системы Е ра-
равенство вида
J, x\, ..., х*п) = у*. A2.29)
Какими свойствами должен обладать гёделевский номер
z этого вывода?
1. Переход от одних равенств к другим, как мы
знаем, может совершаться с помощью подстановки чисел
на место переменных и замены вхождений. При этом
гёделевские номера новых равенств оказываются прими-
примитивно-рекурсивными функциями гёделевских номеров
исходных равенств, так как операции замены вхожде-
вхождения, подстановки, определения гёделевского номера свя-
связаны лишь с примитивно-рекурсивными функциями. Не-
§ 12.10] ЯВНАЯ ФОРМА ОБЩЕРЕКУРСИВНЫХ ФУНКЦИЙ 485
которые из этих функций рассмотрены нами выше — это
функции вида ¦ ',
ex pt (х), а о b, subste (hbJ), рп =у (п) х -'; ;;
и некоторые другие.
-Поэтому первое свойство, которому должно удовле-
удовлетворять число 2, таково: любой из показателей п0, пи
м2, ... разложения числа z на простые множители есть
либо гёделевский номер одного из определяющих ра-
равенств ви либо он представляет собой значение опреде-
определенной примитивно-рекурсивной функции от этих но-
номеров.
2) Последний показатель пг разложения числа z дол-
должен быть гёделевским номером равенства вида A2.29).
В итоге оказывается, что предикат
Т (х\, х*2, ..., х*п, z) s: jz есть гёделевский
номер вывода значения у(х*, x*v ..., х*\\
является примитивно-рекурсивным предикатом. Следова-
Следовательно, его представляющая функция ^{x*v х*2, ..., х*п, z}
также примитивно-рекурсивна, и она равна нулю лишь
для тех и только тех z, которые являются гёделевскими
номерами выводов, заканчивающихся равенством
j, x*2, ..., х
Поэтому задача нахождения нужного вывода может
быть теперь сформулирована так: найти хоть одно
число z* такое, чтобы
*
*v х*2, ..., х*п, z*) = 0. A2.30)
Так как вывод в любой точке существует (Е по уело*
вию рекурсивно определяет <р), то функция t обладает
свойством
j) (V.*2)... (Vxn) Cz) [x (xv x2, ..., xn, z) = 0]. A2.31)
Найдя такое z*, для которого выполняется A2.30),
мы можем расшифровать этот гёделевский номер и по-
получить
У* = Ф (**)>
32 М. А. Айзерман, Л. А. Гусев и др.
486 - алгоритмы [гл.
причем ф оказывается также примитивно-рекурсивной'
функцией, так как расшифровка сводится к примитив-
но-рекурсивным операциям: определению последнего по-
показателя пг разложения числа z* и последующей расшиф-
расшифровке числа пг, которое является гёделевским номером
выводимого нами равенства A2.29). Более того, ф(г)
оказывается универсальной примитивно-рекурсивной
функцией, одинаковой для всех систем Е (т. е. для всех
общекурсивных функций <р), так как расшифровка геде-
левского номера вывода во всех случаях производится
стандартно.
Если, как мы установили, любое г, для которого
*^ VI' 2' * * *» п* ) —' ^'
есть гёделевский номер искомого вывода, то и
\, ..., х*п, г) =
есть также гёделевский номер вывода. Поэтому оконча-
окончательно получим
{xXi x2, ..., хп, z) =
где ф и т—примитивно-рекурсивные функции и для т
выполняется условие A2.31).
Отметим, что из формы записи A2.30) сразу следует
вывод о том, что все общерекурсивные функции обра-
образуют счетное множество*), так как счетно число раз-
различных примитивно-рекурсивных функций т, с помощью
которых определяются общерекурсивные функции по
схеме A2.30).
Однако, в отличие от примитивно-рекурсивных функ-
функций, множество общерекурсивных функций не является
эффективно-счетным (подробнее см. в § 12.12) и, следо-
следовательно, невозможно методом Петер построить пример
вычислимой функции более общей, чем общерекур-
общерекурсивная.
*) Вообще говоря, этот вывод можно было бы сделать и ра-
ранее, обратив внимание на то, что различных систем Е, рекурсивно
определяющих функции <р , счетное число, так как все системы Е
можно перенумеровать, поставив им в соответствие их гёделевские
номера.
§ 12.11] ТЕЗИС ЧЁРЧА 487
В заключение этого параграфа выпишем схемы, опре-
определяющие общерекурсивные функции. Здесь схемы
I — V — уже знакомые нам схемы определения прими-
примитивно-рекурсивных функций, а схема VI представляет
собой явную форму общерекурсивной функции:
11. 9
111. СС \Х\, Х^ • . • > Хп) = Х[,
IV. <p(*i, х2, ..., xn) = ty{xl(xl, x2, .
• • •» -^п/» Х2 v-^l» -^2» • • •» •^п/» • • •» Z/и
Va. <р@) = ?, <р(у/) = х(у, <р(у)),
V6. ср @, х2, . •., ^„) = ф (л:2, ..., хп),
9(у', д:2, ..., ха) = х(У> ?(У» -^2» ••¦»
VI. <p(^i» *2. •••» ^J^tll^y Iх(^р
причем
xv) (vxa)^^, x2
Теперь можно дать такое определение общерекурсив-
общерекурсивной функции. Функция ф(*ь #2, ..., хп) называется об-
общерекурсивной, если она может быть определена с по-
помощью конечного числа применений схем I — VI.
Отметим еще, что так как схемы I—V, определяю-
определяющие примитивно-рекурсивные функции, являются частью
схем I—VI, определяющих общерекурсивные функции,
примитивно-рекурсивные функции являются частным
случаем общерекурсивных функций; всякая примитивно-
рекурсивная функция есть общерекурсивная функция,
но не наоборот.
§ 12.11. Тезис Чёрча
Вернемся к поставленной нами задаче — построить
класс вычислимых функций. Решая эту задачу, мы по-
последовательно построили класс элементарных функций,
затем класс примитивно-рекурсивных функций и, нако-
наконец, класс общерекурсивных функций. Решили ли мы
поставленную задачу? Потребуется ли нам расширять
и класс общерекурсивных функций?
32*
488 алгоритмы [гл. хп
Многочисленные попытки расширения класса обще-
общерекурсивных функций не привели к успеху. В 1936 г.
Чёрч выдвинул тезис, согласно которому всякая эффек-
эффективно вычислимая функция (эффектно разрешимый пре-
предикат) является общерекурсивной (см. [ПО]).
В силу этого тезиса класс вычислимых функций со-
совпадает с классом общерекурсивных функций.
Тезис Чёрча нельзя доказать, так как в нем, с одной
стороны, фигурирует расплывчатое понятие вычислимой
функции, а с другой стороны — точное математическое
понятие общерекурсивной функции. Этот тезис является
научной гипотезой, в пользу которой высказан ряд важ-
важных доводов и которую не удалось опровергнуть. Одним
из таких доводов является то, что различные уточнения
понятия «алгоритм», сделанные разными авторами, ока-
оказались равносильными. Так, например, описанный в
§ 12.4 нормальный алгоритм Маркова оказался сводимым
к общерекурсивным функциям.
Выше мы отождествили понятия «алгоритм» и «вы-
«вычисление значений арифметической функции».
. В свете тезиса Чёрча задача оказывается алгоритми-
алгоритмически разрешимой лишь тогда, когда арифметическая
функция, к вычислению которой мы сводим нашу «за-
«задачу, оказывается общерекурсивной.
Резюмируя, можно сказать коротко: алгоритм суще-
существует лишь тогда, когда может быть построена соответ-
соответствующая общерекурсивная функция.
Наоборот, в силу тезиса Чёрча, алгоритмическая не-
неразрешимость проблемы означает, что арифметическая
функция, к вычислению которой сводится задача, не яв-
является общерекурсивной.
Часто доказательство алгоритмической неразрешимо-
неразрешимости оказывается не легче, чем поиск нужного алгоритма.
Однако в некоторых случаях удается доказать алгорит-
алгоритмическую неразрешимость. Мы приведем без доказа-
доказательства два примера такого рода.
Первый пример. Мы могли бы получить полное
представление о том, какие системы равенств Е опреде-
определяют общерекурсивные функции, и смогли бы эффектив-
эффективно перенумеровать все общерекурсивные функции, если
бы имелся алгоритм, позволяющий по гёделевскому но-
§ 12.11] ТЕЗИС Ч6РЧА 489
меру w системы равенств Е узнать, определяет ли си-
система Е общерекурсивную функцию.
Иначе говоря, проблема была бы решена, если бы
существовала, например, такая общерекурсивная функ-
функция ф(до):
О, если w есть гёделевский номер системы Е,
определяющей общерекурсивную функцию,
> 0 в иных случаях.
Удалось доказать [42], что подобной общерекурсив-
общерекурсивной функции ф(ау) не существует. Поэтому оказывается
алгоритмически неразрешимой проблема распознавания
того, какие системы Е определяют общерекурсивные
функции. Множество общерекурсивных функций оказа-
оказалось счетным, но не эффективно.
Второй пример. Оказалась алгоритмически не-
неразрешимой следующая проблема: требуется найти алго-
алгоритм, позволяющий для любой примитивно-рекурсивной
функции t(x, у) (любого примитивно-рекурсивного пре-
предиката Т{х, у)) узнать, обладает ли эта функция свой-
свойством
(Чх) (Зу) [т (х, у) = 0] A2.32)
(для предиката, соответственно (Чх)(Зу)Т(х, у)).
Так как примитивно-рекурсивные функции могут
быть эффективно перенумерованы, то задача может
быть сведена к нахождению такой вычислимой функ-
функции ф(г):
О, если г есть номер примитивно-рекурсивной
функции, обладающей свойством A2.32).
> 0 в иных случаях.
Эта функция оказалась не общерекурсивной и, следова-
следовательно, невычислимой.
Условие A2.32) можно несколько ослабить, и все-
таки задача остается алгоритмически неразрешимой.
Именно, было доказано, что алгоритмически неразре-
неразрешима даже такая простая задача: при заданной при-
примитивно-рекурсивной функции <р(х, у) для любого х*
33 М. А. Айзерман, Л. А. Гусев и др.
490 алгоритмы Ггл. хи
требуется узнать, справедливо ли для этого х* условие
Алгоритмически неразрешима также следующая за-
задача: для любого примитивно-рекурсивного предиката
Р(у) узнать, справедливо ли
(Ну) Я (у).
Во всех случаях доказательство свелось к доказа-
доказательству того, что соответствующая распознающая функ-
функция оказывалась не общерекурсивной.
Часто доказательство алгоритмической неразреши-
неразрешимости проводят следующим образом: показывают, что
рассматриваемая проблема сводится к другой проблеме,
алгоритмическая неразрешимость которой доказана.
Иногда достаточно показать, что этим свойством обла-
обладает даже более узкая проблема, являющаяся частным
случаем рассматриваемой.
В гл. VIII и IX таким методом доказана алгоритми-
алгоритмическая неразрешимость двух основных проблем теории
конечных автоматов и последовательностных машин.
§ 12.12. Рекурсивные действительные числа
Понятие о рекурсивном действительном числе вво-
вводится в конструктивной математике.
Конструктивное направление в математике возникло
в связи со стремлением избежать противоречий («анти-
(«антиномий»). Оно связано с требованием считать доказа-
доказательство исчерпывающим, когда не только установлен
какой-либо математический факт, но и показано, что со-
соответствующие математические объекты могут быть фак-
фактически подсчитаны.
В конструкивной математике важное значение имеет
аппарат рекурсивных функций. В терминах рекурсивных
функций обычно даются алгоритмы для эффективного
построения нужных объектов.
Рассмотрим в качестве примера конструктивную фор-
формулировку одной часто встречающейся схемы.
В анализе часто встречается высказывание вида «для
всякого малого е > 0 существует такое число N, что не-
§ 1212] РЕКУРСИВНЫЕ ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА 491
которая величина, зависящая от п, при п !> /V становит-
становится меньше е».
Каков будет конструктивный вариант этой схемы?
Для его построения необходимо:
1) Уточнить, что мы будем понимать под «всяким
малым е». Примем, например, е = —,где т — как угод-
угодно большое целое положительное число.
2) Надо, чтобы по е (т. е. по т) существовал способ
эффективно определять число /V.
Поэтому эффективная формулировка рассматривае-
рассматриваемой схемы будет такова: «существует такая общерекур-
общерекурсивная функция v (m), что некоторая величина, завися-
зависящая от п, становится при п !>v(m) меньше —».
Формулировку такого вида можно отнести к сходи-
сходимости последовательности рациональных чисел.
Назовем последовательность рациональных чисел
рекурсивной, если существуют такие общерекурсивные
функции а (я), р(м) и i(n) G (л) > 1), что
Будем говорить, что эта последовательность сходится
рекурсивно (или эффективно), если существует общере-
общерекурсивная функция v(m) такая, что для любого как
угодно большого m > 0
\а>п — а>п*\ <-^> если л, w*!>v(m).
Число г, которое определяет эта эффективно сходящаяся
последовательность, называется рекурсивным действи-
действительным числом.
Можно доказать, что из того, что число г рекурсив-
рекурсивно, т. е. что существует рекурсивная последовательность
рациональных чисел, рекурсивно к нему сходящаяся, ни
в коей мере не следует, что это число можно разложить
в рекурсивную десятичную дробь, т. е. что существует
33*
492 алгоритмы [гл. хп
общерекурсивная функция ф(/г) <!9 такая, что
ю
Однако есть одна специальная последовательность,
из рекурсивной сходимости которой можно сделать вы-
вывод о рекурсивном разложении г в любой системе счис-
счисления.
Такой специальной последовательностью является
факториальное разложение
~ 1! "f" 2! •" 3!
2! •" 3! ¦" * * ' "^ л!
причем для больших п число ап^.п—1. Если сущест-
существует общерекурсивная функция %(п) такая, что
ап — %(п), то этот ряд сходится всегда рекурсивно и
определяет рекурсивное действительное число, которое
может быть разложено в рекурсивную дробь в любой
системе счисления.
Обратим внимание также на то, что рекурсивных
действительных чисел не больше, чем общерекурсивных
функций, т. е. счетное множество; всех же действитель-
действительных чисел — континуум. В этом смысле лишь незначи-
незначительная часть действительных чисел рекурсивна.
Рекурсивное действительное число — это фактически
такое число, для вычисления которого с любой степенью
точности имеется алгоритм. Все обычно рассматривае-
рассматриваемые в анализе числа (например е, тс, У и т. д.) яв-
являются рекурсивными действительными' числами.
§ 12.13. Рекурсивно-перечислимые и рекурсивные
множества
Имеется несколько эквивалентных формулировок,
определяющих понятие рекурсивного и рекурсивно-пере-
рекурсивно-перечислимого множества целых чисел. Для удобства мы со-
соберем их в таблицу так, что в левой половине этой та-
таблицы будут находиться определения рекурсивно-пере-
рекурсивно-перечислимого множества, а в правой — определения рекур-
рекурсивного множества.
§ 12.13]
РЕКУРСИВНО-ПЕРЕЧИСЛИМЫЕ МНОЖЕСТВА
493
Рекурсивно-перечислимое
множество чисел
1А. Множество называется
рекурсивно-перечислимым,
если оно есть множество
значений некоторой обще-
общерекурсивной функции; иначе,
если существует пересчиты-
пересчитывающая его, может быть
с повторениями, общерекур-
общерекурсивная функция. Пустое
множество считается реку о-
сивно-перечислимым.
2А. Множество С, имеющее
хотя бы один элемент, ре-
курсивно-перечислимо тогда
и только тогда, когда пре-
предикат «у ? С» выразим
в форме (Зх) Р (х, у) с
общерекурсивным Р (х, у).
Рекурсивное множество чисел
1Б. Множество С называется
рекурсивным, если существует
алгоритм, позволяющий узнать,
принадлежит ли данное число у
множеству С.
2Б. Множество С называется
рекурсивным, если предикат
«у ? С» выразим в виде Р (у)
с общерекурсивным Р.
ЗБ. Множество С называется
рекурсивным, если оно и его
дополнение С рекурсивно-пе-
речислимы.
4Б. Бесконечное множество С
рекурсивно тогда и только
тогда, когда оно может быть
пересчитано общерекурсивной
функцией без повторений и
в порядке возрастания его эле-
элементов (т. е. <р @), <р A), <р B), ...
дают в порядке возрастания
элементы множества С).
Сделаем теперь относительно этих определений не-
несколько замечаний:
Замечание относительной. Доказано, что
если некоторое множество можно пересчитать общере-
общерекурсивной функцией с повторениями, то оно может быть
пересчитано и без повторений (некоторой другой обще-
общерекурсивной функцией).
Замечание относительно 2А. Покажем, как
определение 2А вытекает из 1А. Пусть С—множество
значений некоторой общерекурсивной функции <р(*). То-
Тогда тот факт, что некоторое число у принадлежит мно-
множеству С, означает, что существует такое х, что
У = ?(*)»
иначе
Равенство у = у{х) может рассматриваться как общере-
общерекурсивное отношение равенства двух общерекурсивных
494 алгоритмы [гл. хи
функций:
> У)ЩХ\(х* У) = ъ(х, У)],
где
Х\(Х, У)е*У, J
Замечание относительно 2Б. Определение
2Б является лишь уточнением определения 1Б.
Замечание относительно ЗБ. Из выполне-
выполнения условия ЗБ следует выполнение условия 1Б. Дей-
Действительно, пусть множество С перечисляется общере-
общерекурсивной функцией cpi(x), а С — функцией фг(*).
Для того чтобы узнать, принадлежит ли данное число
множеству С, будем параллельно вычислять последова-
последовательности
... (I)
... .(II)
Так как число у принадлежит либо С, либо С, то
оно рано или поздно должно встретиться или в ряду I,
или в ряду II. Если оно встретилось в ряду I, тоу?С,
если в II — у ? С. Поэтому имеется алгоритм распозна-
распознавания принадлежности любого у множеству С.
Замечание относительно 4Б. При условии
4Б также имеется алгоритм распознавания принадлеж-
принадлежности любого у множеству С. Действительно, будем вы-
вычислять последовательность <р@), <рA), <рB), ... Если
при некотором п <р(п) > у, то процесс^ вычисления можно
остановить и сделать вывод, что у ? С; если же встретится
т^.п такое, что <р(т) = у, то у ?С.
Приведем примеры рекурсивных множеств:
1) Двухэлементное множество {0, 1} рекурсивно в
силу условий 1Б или 2Б.
2) Любое конечное множество рекурсивно в силу
условий 1Б или 2Б.
3) Множество четных чисел {0, 2, 4, 6, 8, ...} рекур-
рекурсивно. Здесь у?С = [res (у, 2) = 0], и множество рекур-
рекурсивно в силу условия 2Б; или <p(x) = 2x, и множество
рекурсивно в силу условия 4Б.
§ 12.13] РЕКУРСИВНО-ПЕРЕЧИСЛИМЫЕ МНОЖЕСТВА 495
Приведем теперь примеры рекурсивно-перечислимых
и не рекурсивно-перечислимых множеств.
Согласно определению 2А рекурсивно-перечислимым
множеством будет множество тех у, для которых
(ilx)P(x, у) при некотором общерекурсивном Р(х, у).
Можно так подобрать Р(х, у), что множество {у} будет
рекурсивно-перечислимым, но не рекурсивным; его до-
дополнение {у} будет множеством тех у, для которых
(ЩР(х, у) = (Yx) Р (х, у) = (Yx) Q (х, у)
(где Q — общерекурсивный предикат); это множество
{у} будет не рекурсивно и не рекурсивно-перечислимо.
Множество гёделевских номеров z тех систем Е, ко-
которые определяют общерекурсивную функцию, не рекур-
рекурсивно и не рекурсивно-перечислимо.
В заключение заметим, что из сравнения 1А и 4Б и
из того факта, что любое конечное множество как ре-
рекурсивно, так и рекурсивно-перечислимо, следует, что
любое рекурсивное множество есть рекурсивно-перечис-
рекурсивно-перечислимое множество. Обратное утверждение неверно.
Понятие о рекурсивных действительных числах и о
рекурсивно-перечислимых множествах важно при вы-
выяснении того, может ли машина «делать» что-либо боль-
большее, чем реализовывать заданный алгоритм. Выше было
показано, что любой алгоритм сводится к подсчету зна-
значений вычислимой целочисленной функции.
Если какое-либо устройство «выдает» на выходе мно-
множество чисел, и если это множество не является рекур-
рекурсивно-перечислимым, то это свидетельствует о том, что
процесс работы этого устройства не может быть алго-
алгоритмизирован, т. е. что устройство «делает больше, чем
реализует алгоритм».
ГЛАВА XIII
МАШИНЫ ТЬЮРИНГА
§ 13.1. Описание и примеры машин Тьюринга
В гл. XII были разъяснены основные интуитивно оче-
очевидные требования, которые предъявляются к алгорит-
алгоритмам. Это требования детерминированности, массовости
и применимости («целенаправленности») алгоритмов.
Важно, что результат применения алгоритма совершен-
совершенно не зависит от того, кто его использует. Человек, вы-
выполняющий алгоритм, должен действовать, «как маши-
машина», заботясь лишь о том, чтобы правильно выполнить
предписания. Поэтому, естественно, возникает мысль:
нельзя ли действ'ительно поручить выполнение алго-
алгоритма машине?
Из упомянутых свойств алгоритмов вытекают общие
требования к машине, выполняющей алгоритм. Во-пер-
Во-первых, машина должна быть полностью детерминирован-
детерминированной и действовать в соответствии с заданной системой
правил! Во-вторых, она должна допускать ввод различ-
различных «начальных данных» (соответствующих различным
задачам из данного класса задач). В-третьих, заданная
система правил работы машины и класс решаемых за-
задач должны быть согласованы так, чтобы всегда было
можно «прочитать» результат работы машины.
Можно предложить различные «конструкции» ма-
машин, способных выполнять алгоритмы. Наиболее нагляд-
наглядна схема, предложенная в 1936 г. английским матема-
математиком Тьюрингом. Ниже приводится описание одного из
возможных вариантов функционирования таких машин
Рассмотрим бесконечную одномерную ленту, которая
разделена на ячейки. Мы будем считать, что лента бес-
§ 13.1] ОПИСАНИЕ И ПРИМЕРЫ МАШИН ТЬЮРИНГА 497
конечна лишь в одном направлении — направо, так что
существует самая левая ячейка. В каждой ячейке мо-
может быть записан лишь один символ S* из конечного
алфавита {sQ, ..., sn]. Символ s0 мы выделим специально
и будем говорить, что если в некоторой ячейке записан
So, то эта ячейка «пустая». В дальнейшем всегда будем
считать, что непустых символов на ленте каждый раз
имеется лишь конечное (но сколь угодно большое) чи-
число, остальные же ячейки пустые.
Представим себе также специальное устройство —
считывающую и записывающую головку, которая может
располагаться напротив каждой из ячеек ленты и по
команде извне «стереть» записанный в этой ячейке сим-
символ и записать новый. Считывающая и записывающая
головка может также по команде перемещаться на одну
ячейку вправо или влево (если она не находится в са-
самой левой ячейке). Команды на считывающую и запи-
записывающую головку подаются от управляющего устрой-
устройства, которое в свою очередь получает от головки сигнал
о наличии того или иного символа в ячейке ленты, рас-
расположенной против головки.
Управляющее устройство имеет конечное число m + 1
внутренних состояний qo, ..., qm и работает в дискрет-
дискретном времени ^ = 0, 1, 2, ... Входом управляющего уст-
устройства являются символы Si, выдаваемые считывающей
и записывающей головкой, выходом — команды на дей-
действия головки: какой символ головка должна записать
в соответствующей ячейке и куда передвинуться. Пусть
в момент времени t считывающая и записывающая го-
головка находилась напротив /-й (считая слева) ячейки,
в которой был записан символ «г, а управляющее устрой-
устройство находилось в состоянии qj. Управляющее устрой-
устройство в зависимости от состояния qj и входа st- выдает
символ sft (в соответствии с которым головка стирает
старый символ S* и печатает новый sft), а затем один из
символов П, Л или С («право»? «лево», «стоп»), в соот-
соответствии с которым головка передвигается на одну клет-
клетку вправо или влево, или остается на месте. После этого
управляющее устройство переходит в новое состояние qr
(также определяемое однозначно символами q^ и sf).
Тем самым в момент времени t + 1 в 1-й ячейке будет
498
МАШИНЫ ТЬЮРИНГА
[ГЛ. XIII
записан символ sh, управляющее устройство будет нахо-
находиться в состоянии qr, а считывающая и записывающая
головка расположится напротив / + 1, /— 1 или 1-й ячей-
ячейки (в зависимости от того, появился ли символ Я, Л
или С). Таким образом, управляющее устройство яв-
является последовательностной машиной с двумя выход-
выходными преобразователями: вход машины — воспринимае-
воспринимаемый символ с головки (алфавит входа {s0, .. -, sn})\ со-
состояния—символы из алфавита \q0, ..., qm}; первый
выход — сигнал на запись из алфавита {s0, ..., sn}', вто-
второй выход — сигнал на перемещение головки из алфа-
алфавита {Я, Л, С}. Работу этой последовательностной ма-
машины можно задать тремя таблицами: таблицей авто-
автомата и двумя таблицами преобразователей. При описа-
описании работы машины Тьюринга принято совмещать эти
таблицы в одну основную таблицу.
Например, если таблица автомата есть табл. 13.1,
Таблица 13.1
Таблица 13.2
Таблица 13.3
Яо
Я\
So
Яо
Яо
Sx
Я\
Яо
s2
Яо
Ях
Яо
Я\
So
s*
Si
Si
So
Si
s2
Si
s2
Яо
Я1
So
П
С
Si
П
•
Л
s%
Л
П
таблица первого преобразователя — табл. 13.2, второго—
табл. 13.3, то совмещенная таблица, целиком описываю-
описывающая работу машины Тьюринга, имеет вид табл. 13.4.
Таблица 13.4
Яо
Я1
So
q0s2n
*..л
§ 13.1]
Й ЙРЙМЁРЫ МАШИН ТЬ10РЙНГА
В клетках этой таблицы первым записан символ из {q},
вторым —из {s}, третьим--из {Я, Л, С}. Если основная
таблица машины Тьюринга задана, то при каждом за-
заполнении ленты работа машины однозначно определена.
Далее будем считать, что символ qo состояния упра-
управляющего устройства означает состояние покоя машины
Тьюринга, т. е. строка qo основной таблицы имеет сле-
следующие свойства: 1) первым символом в каждой клетке
этой строки всегда является <7о (и никогда qj при / ф 0);
2) вторым символом в клетке столбца Si этой строки яв-
является тот же символ 5г- (и никогда Sk при k Ф i)\
3) третьим символом в каждой клетке этой строки яв-
является символ С (и никогда Л или Л) (см. пример
табл. 13.5).
Таблица 13.5
So
qoSoC
q{s2jl
Si
qos{C
qxsQn
s2
q0s2C
4oS\C
Поэтому, если управляющее устройство в какой-то
момент времени имеет состояние qo, то где бы ни нахо-
находилась считывающая и записывающая головка и каким
бы ни было заполнение ленты, в последующие моменты
времени управляющее устройство будет оставаться в том
же состоянии, головка также не двинется, и заполнение
ленты останется прежним. Для упрощения записи основ-
основной таблицы мы будем опускать в ней строку qo (см.
табл. 13.6).
Таблица 13.6 Таблица 13.7
Машина А
So
qxs^
S\
q{son
s2
QoS\C
0
q0 1С
1
Ч\ 1Я
500
МАШИНЫ ТЬЮРИНГА
[ГЛ. XIII
В дальнейшем для простоты будем предполагать, что
алфавит символов [st} состоит всего лишь из двух сим-
символов: «пустого» 0 и «непустого» 1.
Приведем несколько простых примеров машин Тью-
Тьюринга. Начальное состояние машины мы будем назы-
называть состоянием q\.
1) Машина А (табл. 13.7). Если в начальный момент
машина А находится в состоянии q\ и воспринимает за-
заполненную клетку, то она «отыскивает» на ленте пер-
первую пустую (т. е. заполненную символом 0) клетку
справа от той, на которой находится головка, «печа-
«печатает» там символ 1 и останавливается. Если же вна-
вначале головка находилась напротив пустой клетки, то
машина ее «заполняет» и останавливается, не передви-
передвигая головку.
В табл. 13.8 и 13.9 приведены два варианта работы
машины.
Таблица 13.8
Моменты
времени
О
1
2
3
4
5
Ситуации на ленте
_?
1111100..
111110 0. .
Я\
1111100..
?!
1111100..
111110 0 . .
1°
1111110..
Черта над соответствующей ячейкой ленты означает,
что считывающая и записывающая головка находится в
данный момент как раз напротив этой ячейки. Символ
над чертой — состояние управляющего устройства в этот
§ 13.1]
ОПИСАНИЕ И ПРИМЕРЫ МАШИН ТЬЮРИНГА
501
Таблица 13.9
Моменты
времени
0
1
Ситуации на ленте
Я\
... 10001 ...
Я\
... 1 оТо1 ...
момент. Многоточия означают те ячейки ленты, запол-
заполнение которых заведомо не меняется в рассматриваемые
такты работы машины
(поскольку головка не Таблица 13.10
достигает этих ячеек). Машина В
2) Машина В (табл.
13.10). Эта машина
имеет также лишь одно
состояние (не считая
состояния покоя). Она
«стирает» единицу в
той ячейке, где нахо-
находится головка (если эта ячейка непуста), или в первой
слева непустой ячейке, передвигает головку еще левее
на ячейку и останавливается. Один вариант работы
машины В приведен в табл. 13.11.
Таблица 13.11
Ях
0
qx0JI
1
ЯоОД
Такты
0
1
2
3
Ситуации на ленте
... 0 1 1 1 0"о ...
Ях
...011100...
9\
... 011100 ...
Яо
... 011000 ...
502
МАШИНЫ ТЬЮРИНГА
[ГЛ. ХШ
3) Машина С (табл. 13.12). Эта машина отыскивает
первую после группы нулей группу единиц справа от
Таблица 13.12.
Машина С
Я\
Яг
Яъ
0
Я20П
q20fI
ЧоОЛ
1
Чх\П
q3W
q3W
начальной ячейки и останавливается около последней
из этих единиц. Вариант работы машины С приведен в
табл. 13.13.
Таблица 13.13
Такты
0
1
2
3
4
5
6
7
Ситуации на ленте
Ч\
...011001100...
Я\
...011001100...
Ях
...011001100...
Чг
...011001100...
4%
... 0 1 1 0 0 1 1 0 0 ...
Яз
...011001100...
Яз
... о 1 1 о о 1 1 "(Го ...
Яо
...011001100...
§ 13.1]
ОПИСАНИЕ И ПРИМЕРЫ МАШИН ТЬЮРИНГА
503
В некоторых случаях машина Тьюринга может быть
недоопределенной в том смысле, что не все клетки ее
основной таблицы заполнены. Это допускается в тех
случаях, когда по\тем или иным причинам можно зара-
заранее сказать, что соответствующие сочетания состояний
машины и символов на ленте никогда не встретятся.
Рассмотрим пример.
Таблица 13.14
Машина D
Ч\
Яг
Яз
Як
0
Чг\П
q3W
1
qtW
д2\П
ЧЛЛ
ЯоОЛ
4) Машина D (табл. 13.14). Эта машина заполняет
первый промежуток справа между двумя группами еди-
единиц, оставляя всего одну незаполненную ячейку. Если
головку машины в нулевой такт не помещать напротив
пустой ячейки в состоянии Ц\ и q^ то сочетания q\y 0
и qAy 0 никогда не встретятся и в дальнейшем: состоя-
состояние q\ вообще никогда не повторится, а в q^ машина
может прийти лишь тогда, когда единица уже напечата-
напечатана. Вариант работы машины приведен в табл. 13.15.
Иногда нам придется рассматривать машины, имею-
имеющие не одно, а два или несколько состояний покоя
(я'о> Яо и т- Д-)- Рассмотрим ^соответствующий пример.
5) Машина Е (табл. 13.16). Эта машина, находясь
в начальном состоянии всегда напротив заполненной
ячейки, обнаруживает, что записано в соседней ячейке
слева — 0 или 1. В зависимости от этого она переходит
в состояние q'o или q и останавливается в исходной
504
МАШИНЫ ТЬЮРИНГА
[ГЛ. XIIГ
ячейке. Два варианта работы машины Е приведены
в табл. 13.17 и 13.18. ,
Таблица 13.15
У
Такты
0
1
2
3
4
5
6
7
8
. . . 0
. . . 0
. . . 0
. . . 0
. . . 0
. . . 0
. . . 0
... 0
. . . 0
Ситуации на
Ях
1
1
1
1
1
1
1
1
1
1
Яг
1
1
1
1
1
1
1
1
1
1
Яг
1
1
1
1
1
-
1
1
0 0 0
0 0 0
0 0 0
Яг
0 0 0
Яг
1 0 0
Яг
1 1 0
1 1 1
Яа
1 1 1
Яо
1 1 0
леьт.з
1
1
1
1
1
1
Яг
1
1
1
i
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
0 ...
0 ...
0 ...
0 ...
0 ...
0 . . .
0 . . .
0 ...
0
В заключение параграфа без особых пояснений при-
приведем еще несколько примеров машин Тьюринга. Эти
машины понадобятся нам в дальнейшем.
Таблица 13.16
Машина Е
Я\
Я2
0
1
q2\Jl
п¦ __
до\П
§ i3.ii
ОПИСАНИЕ И ПРИМЕРЫ МАШИН ТЬЮРИНГА
505
Такты
0
1
2
Та
б
Ситуации
... 0
... 0
... 0
0
0
0
л
иц
на л\
1
Чг
1
1
Чх
1
1
/•/
Т
а
ште
\
\
V)
1 .
1 .
13.17
V
• •
• •
Такты
0
1
2
Табли
Ситуации
... 0 0
Чг
... 0 0
... 0 0
на
Чх
1
1
Чо
ца 13.18
ленте
1 ...
1 ...
1 ...
6) Машина F (табл. 13.19). Эта машина отыскивает
ближайшую слева группу единиц после группы нулей.
Таблица 13.19
Машина F
Таблица 13.20
Машина G
Таблица 13.21
Машина Н
Чх
Чг
0
Я20Л
q2OJI
1
ЧЛЛ
?о1С
Ч\
0
ЧоОС
1
дх0Л
Чх
42
0
qo\C
ЧхОП
1
qtW
д2\П
7) Машина G (табл. 13.20). Машина G стирает все
единицы слева (если они есть) до ближайшего слева
нуля.
8) Машина Н (табл. 13.21). Печатает единицу спра-
справа после группы единиц через одну пустую ячейку. От-
Отличается от машины А (пример 1) только тем, что печа-
печатает единицу не на первой справа пустой ячейке, а на
второй.
9) Машина I (табл. 13.22). Отправляясь от заполнен-
заполненной ячейки, стирает в ней единицу и «переносит» ее в
ближайшую пустую ячейку слева (другими словами,
«сдвигает» группу единиц левее исходной ячейки на одну
ячейку влево).
34 М. Л- Айзерман, Л. А. Гусев и др.
506
МАШИНЫ ТЬЮРИНГА
[ГЛ. XIII
10) Машина К (табл. 13.23). «Стирает» одну еди-
единицу в ячейке, расположенной правее исходной (если
там есть единица). / ^ыш
Таблица 13.22 /Таблица 13.23
Машина ' Аашина К
Я\
0
Яо\Л
1
q2OJI
д2\Л
/
/
Ч\
Чг
0
Я20П
qQ0C
1
q2W
qQ0C
11) Машина L (табл. 13.24). Отправляясь от запол-
заполненной ячейки, идет налево и останавливается левее
группы единиц на две ячейки.
Таблица 13.24 Таблица 13.25
Машина L Машина М
0
qQ0M
1
12) Машина М (табл. 13.25). Имея два состояния
покоя, «распознает», напротив какой ячейки находится-
пустои или заполненной. В зависимости от этого пеое-
ходит в первое или второе состояние покоя.
§ 13.2. Композиция машин Тьюринга
Как мы убедились в предыдущем параграфе работа
машины Тьюринга однозначно определяется функцио
нированием управляющего устройства в соответствии с
основной таблицей. Здесь и далее всегда будем пред-
предполагать, что машина начинает работу от определенного
начального состояния, обозначаемого символом Г и
еТрабоТ ИмСе°яТГИе П°К°Я "* К0Т°РЫМ оканчивайся
ее работа. Имея в виду такое соглашение, можно опое
делить операции над машинами Тьюринга Позволяю
§ 13.2J КОМПОЗИЦИЯ МАШИН ТЬЮРИНГ А 50?
щие по заданным основным таблицам получать новые.
Представим себе, что имеются две машины: Т\ и Т2.
Пусть в начальными момент времени U — 0 имеется не-
некоторая ситуация _на ленте, которую начинает перера-
перерабатывать машина А, отправляясь от начального состоя-
состояния q\, причем считывающая и записывающая головка
машины находится при t — О напротив некоторой /0-й
ячейки ленты. Тогда к некоторому моменту t\ машина
Т\ перейдет в состояние покоя ql0, а головка машины
остановится напротив некоторой /J-й ячейки. В момент
t\ «отключим» машину Т\ и представим себе, что с это-
этого момента начинает работать машина Гг, отправляясь
от начального состояния q\, причем головка машины
Т2 находится в момент t\ напротив той самой ячейки /J,
около которой закончила работу машина Т\. К какому-
то моменту времени t\ машина Т2 закончит работу, пе-
перейдя в состояние покоя q\, причем головка машины
остановится напротив некоторой ячейки 1\. Легко по-
понять, что результат такой последовательной работы ма-
машин Т\ и Т2 при любом начальном (при t = to = 0) за-
заполнении ленты и положении головки /0 эквивалентен
работе одной машины Тьюринга Г, основная таблица
которой строится по следующему правилу: если управ-
управляющие устройства машин Т\ и Т2 имеют k\ и k2 состоя-
состояний*) соответственно, то управляющее устройство ма-
машины Т имеет kx + k2 состояний, причем, начальным со-
состоянием машины Т является q\, а состоянием покоя —
q2Q. Основная таблица Т состоит из двух частей: верх-
верхняя часть описывает машину Т\, нижняя — Г2, причем
состояние Покоя q*Q машины 7\ отождествляется с на-
начальным состоянием q\ машины Г2. Пусть, например,
Тг—это машина F из предыдущего параграфа, а Г2 —
машина G (табл. 13.19 и 13.2Q соответственно). Тогда
машина Т имеет таблицу с 2 + 1 = 3 состояниями —
табл. 13.26, где qo = ql — состояние покоя машины G.
*) Говоря о числе состояний, мы договоримся не включать в
это число состояния покоя (которых может быть, как в машине М
из предыдущего параграфа, несколько).
34*
508
МАШИНЫ ТЬЮРИНГА
(ГЛ. XIII
Если перенумеровать подряд состояния машины Т,
то табл. 13.26 примет вид табл. 13.27.
Таблица 13.26
Таблица 13.27/
Таблица 13.58
Я\
ь
Я\
0
д2ОЛ
q'fiJI
ЯоОС
1
д[\л
qx\C
д^ОЛ
Я\
Яг
Яг
0
д2ОЛ
д2ОЛ
доОС
\/
дх\Л
дъ\С
д3ол
Ях
Яг
Яг
0
д2ОС
д3ОЛ
д3ол
1
дк0Л
д2\Л
до\С
Машину Т, получаемую описанным выше способом
из Тг и Г2, назовем произведением машин Т\ и Т : Т =
— Т\ • Т2, а саму операцию получения по двум заданным
машинам третьей будем называть умножением машин.
В этих обозначениях табл. 13.26 и 13.27 представляют
собой таблицы машины F>G. Очевидно, умножение ма-
машин — некоммутативная операция, т. е. Т\'Т2фТ2' Т\.
Например, произведение G-F представлено табл. 13.28,
отличающейся от табл. 13.27.
Вместе с тем, как легко понять, умножение ассоциа-
ассоциативно, т. е. если имеются три машины Гь Т2 и Г3, то
(Т\ • Т2) • Тъ = Т\ • (Г2« Г3). Поэтому при записи произве-
произведения нескольких машин можно не употреблять скобок.
Обычным образом определяется операция возведения
в степень: п-й степенью машины Т называется произве-
произведение Т ... Т с п сомножителями *).
До сих пор в этом параграфе шла речь об умножении
машин, имеющих одно состояние покоя. В том случае,
когда одна из перемножаемых машин имеет два или не-
несколько состояний покоя (например, машины Е и М из
предыдущего параграфа), умножение определяется со-
совершенно аналогично, но только обязательно должно
присутствовать указание, какое из состояний покоя пре-
*) В дальнейшем изложении точки в произведении машин опу-
опускаются.
§ 13.21 КОМПОЗИЦИЯ МАШИН ТЬЮРИНГА 509
дыдущего сомножителя отождествляется с начальным
состоянием последующего. Так, например, если маши-
машина Ti имеет два состояния покоя, то произведение Т\ и Т2
мы будем обозначать через Т—Тх | ' или через
т т I М'
' == 1 1 /о\ т в зависимости от того, отождествляется
ли начальное состояние машины Г2 с первым или вто-
вторым состоянием покоя машины Т\. Машина Т в этом
случае также имеет два состояния покоя: первое — одно
из состояний покоя Т\, второе — состояние покоя Т%
Из предыдущих определений ясен также смысл та-
такой, например, записи:
т==т {A) т2тъ,
МB) Г4.
Здесь умножение производится независимо по двум
«каналам», связанным с первым и вторым состояниями
покоя машины Т\. Наряду с операцией умножения двух
или нескольких машин введем также операцию итерации,
применяемую к одной машине. Пусть машина Т\ имеет s
состояний покоя. Выберем какое-либо г-е состояние по-
покоя и отождествим его в основной таблице машины Т\
с начальным состоянием. Полученная машина, обозна-
обозначаемая через
A),
Т— Т
1 — / г
(г),
и является результатом итерации машины Т. Здесь точки
указывают на отождествление r-го состояния покоя с
начальным состоянием машины Т\. Если Т\ имеет лишь
одно состояние покоя, то после применения итерации по-
получается машина, не имеющая состояний покоя вовсе.
510
МАШИНЫ ТЫОРЙНГА
(ГЛ. Xttl
В дальнейшем будут использованы следующие обо-
обозначения. Если итерация производится над машиной,
которая сама является результатом умножения и ите-
итераций других машин, то соответствующее число точек
ставится над теми машинами, чьи состояния (покоя и
начальные) отождествляются. Например, запись
A) К
B) Т4Т5,
C) Т6
означает, что состояние покоя машины Г3 отождествляет-
отождествляется с начальным состоянием машины Ти а состояние по-
покоя 7*5 — с начальным состоянием Т2.
Приведем пример построения машины с помощью
операций умножения и итерации. Пусть С, G, L и М —
машины, описанные в пре-
Таблица 13.29 дыдущем параграфе. Тогда
машина N машина
Я\
Яг
Яъ
Яа
Яь
Яв
0
q2OJI
яФС
q50n
q,0C
ЯьОП
ЯоОЛ
1
чЛЛ
q<\C
Чг\П
?40Л
q6m
имеет в качестве основной
таблицы табл. 13.29, по-
построенную по описанным вы-
выше правилам из табл. 13.12,
13.20, 13.23 и 13.25. Маши-
Машина N, находясь в начальный
момент времени в состоянии
q\ напротив заполненной
ячейки, стирает, все единицы
слева от начального поло-
положения до того1 места, где
впервые встречаются две пустые ячейки подряд, пбсле
этого головка машины возвращается наза'д и остана-
останавливается у крайней правой заполненной ячейки той
группы расположенных подряд единиц, из которой ма-
машина начинала работать.
В табл. 13.30 показан один вариант работы маши-
машины N. Приведены лишь те ситуации на ленте, при кото-
которых машина переходит из одного состояния в другое,
§ 13.2]
КОМПОЗИЦИЯ МАШИН ТЬЮРИНГА
511
Такты
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
0
2
0
3
0
0
0
0
0
0
0
0
0
0
0
0
0
0
4
0
1
0
0
0
5
0
0
0
0
0
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
Ситуации
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
2
1
4
Т
0
0
0
0
0
0
0
0
0
0
0
0
0
4
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
на
1
1
2
1
4
1
0
0
0
0
0
0
0
0
0
0
0
0
0
т
аб
ленте
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
5
1
1
1
1
л и
1 '
1
1
1
1
1
1
1
1
1
1
1
1
1
6
1
1
1
ц
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
а
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
1
13.30
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
6
0
' 0
512 МАШИНЫ ТЬЮРИНГА [ГЛ. XIII
Для сокращения вместо символов состояний qi в т.абли-
це записаны их номера /.
Таким образом, применение итерации позволяет со-
составлять машины, повторяющие определенную последо-
последовательность операций на ленте (в приведенном примере
машина N повторяет операцию «стирания» групп единиц
до тех пор, пока левее некоторой группы единиц не ока-
окажутся две пустые ячейки).
§ 13.3. Вычисления на машинах Тьюринга
Покажем, что, каков бы ни был алгоритм, всегда
существует машина Тьюринга, выполняющая этот алго-
алгоритм. Для того чтобы это утверждение точно сформули-
сформулировать, необходимо воспользоваться какой-либо форма-
формализацией понятия алгоритма. Мы воспользуемся тези-
тезисом Чёрча, сводящим каждый алгоритм к вычислению
рекурсивной функции. Поэтому нам придется сначала
дать определение того, что означает «вычислять» ариф-
арифметические функции на машине Тьюринга.
Условимся, как мы будем представлять натуральные
числа и нуль на ленте машины Тьюринга. Воспользуемся
кодом, согласно которому числа записываются в нату-
натуральной («единичной») системе счисления и число п
представляется п + 1 расположенными подряд симво-
символами 1 в ячейках ленты, так что нуль — один символ 1,
единица — два символа 1 и т. д.*).
Будем говорить, что два числа расположены рядом,
если между записями кодов этих двух чисел имеется
ровно одна пустая ячейка. В табл. 13.31 рядом с числом
3 справа расположено число 0, а рядом с числом 0 спра-
справа — число 2.
Таблица 13.31
0011110101110
В этом случае мы скажем, что числа 3, 0 и 2 распо-
расположены подряд.
*) Казалось бы более естественным представлять число п та-
таким же числом расположенных подряд символов 1, но тогда пред-
представление нуля совпадало бы с пустой ячейкой, а пустые ячейки
нужны нам для разделения записи чисел и производства вычислений.
§ 13.3] ВЫЧИСЛЕНИЯ НА МАШИНАХ ТЬЮРИНГА 513
Условимся теперь, как будут записываться и считы-
ваться с ленты аргументы и значения вычисляемых функ-
функций. Пусть машина Т должна вычислить значение функ-
функции у(х\, ..., хп) п переменных х\, ..., хп при значе-
значениях аргументов х\ = а\, .. ., хп = ап.
Вспомним, что в нашей «конструкции» машины Тью-
Тьюринга имеется самая левая (первая) ячейка ленты.
Оставим пустыми первые две ячейки ленты, а начиная
с третьей ячейки, запишем в принятом нами коде п чи-
чисел аи ..., ап подряд в том же порядке, в котором про-
пронумерованы независимые переменные. В табл. 13.32 при-
приведен пример подобной записи при п = 3: х\ = 2, х2 = 1,
Xz — 3.
Таблица 13.32
?1
00111011011110
В тех случаях, когда это не будет приводить к недо-
недоразумениям, мы в дальнейшем одними и теми же бук-
буквами х\, ..., хп будем обозначать как независимые пе-
переменные (аргументы), так и конкретные численные
значения, принимаемые этими переменными.
Будем говорить, что считывающая и записывающая
головка воспринимает систему чисел (хи ..., хп) в стан-
стандартном положении, если, во-первых, эти числа запи-
записаны на ленте подряд и, во-вторых, головка расположена
напротив самой правой ячейки в представлении послед-
последнего из чисел (хп) (см. пример в табл. 13.32; положение
головки, как обычно, обозначено чертой). Теперь можно
дать определение того, что означает вычисление на
машине Тьюринга. Пусть задана машина Т, и пусть
в начальный момент времени выполнены следующие
условия:
а0) машина Т находится в начальном состоянии q\\
б) на ленте представлена система п чисел
(*i, • •., хп), которую головка машины воспринимает в
стандартном положении;
в°) все ячейки, расположенные правее той, напротив
которой находится головка, пусты.
Пусть Т начинает работать, отправляясь от описан-
описанной начальной ситуации. Мы скажем, что Т вычисляет
514 МАШИНЫ ТЬЮРИНГА [ГЛ. XIII
функцию х = ф(*ь .-.., хп) п переменных, если, каковы
бы ни были числа хи ..., хп, существует такой момент
времени, в который
а) машина Т достигнет состояния покоя qo\
б) на ленте будет представлена система п + 1 чисел
*ь • •., хп, х, где х = ф(хь ..., хп), которую головка
машины воспринимает в стандартном положении;
в) все ячейки, расположенные правее той, напротив
которой находится головка, пусты.
Если же для какой-либо системы чисел (х\, ..., хп)
машина никогда не останавливается или останавли-
останавливается, но при этом не выполнено условие б) или в), то
такая машина не вычисляет значения функции <р при
этих значениях аргументов.
Приведем пример, поясняющий определение вычис-
вычислений на машине Тьюринга. Пусть п = 3 и ф(*ь *2, *з) =
= хх + х2 + *з- Тогда при хх = 2, х2 = 1, хъ = 3 на-
начальная ситуация на ленте должна быть такой, как в
табл. 13.32; ситуация после остановки машины представ-
представлена табл. 13.33.
Таблица 13.33
00111011011110111111100
Теперь мы в состоянии показать, что, какова бы ни
была рекурсивная функция, можно построить машину
Тьюринга, вычисляющую эту функцию. Для того, чтобы
подобное доказательство провести, достаточно показать,
что существуют машины Тьюринга, способные вычислять
функцию следования, функции-константы и функции-
тождества, а также машины, производящие операцию
суперпозиции, вычисление по индукции и взятие опера-
оператора наименьшего числа (см. § 12.10).
Предварительно нам понадобится ввести в рассмо-
рассмотрение еще несколько специальных машин Тьюринга.
Машина Р строится с помощью умножения и итера-
итерации из машин /, М, С, /С, Л, описанных в § 13.1, следую-
следующим образом:
B) КСА.
§ 13.3]
ВЫЧИСЛЕНИЯ НА МАШИНАХ ТЬЮРИНГА
515
Основная таблица этой машины имеет вид табл. 13.34.
Машина Р начинает работать, воспринимая самую
правую заполненную ячейку представления какого-либо
числа. Результатом ее работы является ситуация, в ко-
которой это число «перегоняется» налево и ставится ря-
рядом с ближайшим слева числом. Рассмотрение табл. 13.34
показывает, что тот же самый результат может дать
несколько другая машина, имеющая не 12, а 6 состоя-
состояний, основной таблицей которой является табл. 13.35.
Таблица 13.34
Машина Р
Таблица 13.35
Машина Р
Ч\
Чч
Чъ
Ча
Чь
Чб
Ч?
Чь
49
Чч
Ч\2
0
Ч31Л
q4OC
q&0f7
q50f7
qy0Jl
q60n
qa0C
^°fi/7
q\20Jl
qo[C
1
q\\JI
q7\C
^41/7
^6l/7
^6l/7
^gl/7
qa0C
q\\w
ql2W
4\
Чч
Чъ
Ча
Чь
Ч*
0
^з1Л
q$n
q\OJl
qo\C
1
q2OJI
q2\JI
q^\n
q\\n
q^On
q^lfl
Поскольку нам в дальнейшем безразлично устрой-
устройство машины, а важен лишь результат ее работы, то,
говоря о машине Р, можно иметь в виду как табл. 13.34,
так и табл. 13.35.
Вариант работы машины Р представлен в соответ-
соответствии с табл. 13.35 в табл. 13.36.
Машина Rm строится из машин Я, F, E, D, С, В, А
(§ 13.1) с помощью умножений и итерации следующим
образом:
A) DCm,
встА,
516
МАШИНЫ ТЬЮРИНГА
Таблица 13.36
[ГЛ. XI11
Таблица 13.37
Такты
0
1
• •
¦ * •
• • •
Ситуации на ленте
1
0 1 1 1 0 0 0 1 1 1 ТО
2
О111ООО11ТО 0
2
0 1 1 1 0 0 О" 1 1 1 0 0
3
oiiioFiliioo
4
0 1110 ОТ 11 10 0
4
0 1 1 1 0 0 1 1 1 1 "б" 0
1
0 1110 0 11 lTO 0
1
0 1110 11 lTO 0 0
2
0 1 1 1 0 1 lTO 0 0 0
2
0 1 1 1 1 1 1 0 0 0 0
3
0 1 lTi 1 1 1 0 0 0 0
5
0 1 1 lTi 1 1 0 0 0 0
6
0 1 1 1 oTl 1 0 0 0 0
6
0 1110 11 l~0 0 0
0
0 1 1 1 0 1 1 1 To 0 0
Такты
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Ситуации
1
1
1
1
1
1
1
1
т
о
1
1
1
г
1
г
\'
1
1
1
0
0
0
1
1
1
т
1
т
02
1
0
0
0
0
0
0
т
1
0
0
0
0
0
0
0
0
0
0
0
0
на
0
т
1
1
1
г
1
1
1
1
1
1
ленте
0
0
0
0
0
0
1
1
1
1
1
1
0
0
0
0
0
0
0
т
1
'
1
1
0
т
0
0
0
0
0
0
0
0
0
0
0
0
н
F
Е
в
с
А
F
Е
п
г
§ 13.3]
ВЫЧИСЛЕНИЯ НА МАШИНАХ ТЬЮРИНГА
517
где индекс т наверху обозначает степень соответствую-
соответствующей машины. В частности,
A) DC,'
B) ВСА.
Воспринимая в начальный момент времени систему чи-
чисел {х\, ..., хт) в стандартном положении, машина Rm
печатает справа от представления чисел х\, ..., хт пер-
первое из этих чисел (т. е. х\) и останавливается, воспри-
воспринимая в стандартном положении систему т + 1 чисел
(хи • • м хт, х\). Если же машина Rm воспринимает в
начальный момент времени в стандартном положении
систему чисел х\, ..., хп, где п > т, то она отпечатает
справа от этой системы чисел число хп-т + \ и остано-
остановится, воспринимая систему (х\, х2, ..., хп, xn_m + 1).
В качестве примера вариант работы машины R\ изобра-
изображен в табл. 13.37. Буквы справа здесь означают, какие
из машин, «составляющих» R\, ответственны за переход
от одной ситуации на ленте к другой. Символы Oi и Ог
означают состояния покоя машины Е.
Можно показать, что т-я степень Rm машины Rm
копирует систему чисел (х\, ..., хт), воспринятую в
стандартном положении, справа, так что результатом
работы будет система 2т чисел {х\, ..., хту хи ..., хт),
воспринимаемая в стандартном положении. Начальная
и конечная ситуации работы машины R1^ при т — 3,
xi = 1, Х2 = 0, xz = 2 изображены в табл. 13.38.
Таблица 13.38
Такты
0
0
0
0
0
1
1
1
1
0
0
1
1
Ситуации
0
0
1
1
1
1
1
Т
1
на
0
0
0
1
ленте
0
1
0
0
0
1
0
0
0
1
0
1
0
0
т
0
0
0
0
518 МАШИНЫ ТЬЮРИНГА [ГЛ. XIII
Машина Sm делает «почти то же самое», что и ма-
машина ЯЩ, т. е. копирует систему (хи ..., хт) справа, но
не рядом, а с одним промежутком (т. е. между числами
хт и Х\ расположена не одна, а две пустые ячейки). Ма-
Машина Sm строится по формуле
m
Начальная и конечная ситуации работы машины Sm при
т = 3, х\ = 1, х2 = 0, хъ = 2 изображены в табл. 13.39.
Таблица 13.39
Такты
0
• • •
0
0
0
0
1
1
1
1
0
0
1
1
Ситуации на
0
0
1
1
1
1
1
То
1 0
0
0
ленте
0
1
0
1
0
0
0
1
0
0
0
1
0
1
0
0
т
0
0
Перейдем теперь непосредственно к доказательству
того, что для любой рекурсивной функции найдется ма-
машина Тьюринга, ее вычисляющая. Покажем это сначала
для «исходных» рекурсивных функций — следования,
константы и тождества.
I. Функцию следования <р(х) = х' вычисляет маши-
машина R\A. Действительно, воспринимая в начальный мо-
момент число х в стандартном положении, машина напе-
напечатает ф(л:) = х + 1 правее числа х и остановится в стан-
стандартном положении системы чисел (х, х + 1), т. е., по
определению понятия «вычисление», вычислит у{х) = х'.
Работа машины при х = 3 изображена в табл. 13.40.
II. Функцию-константу <p(JCi, .. ., хп) = q вычисляет
машина HAq. Пример работы машины для п = 3, хх = 1,
*2 = 0, хъ = 0, q = 2 приведен в табл. 13.41.
III. Функцию тождества у(хи ..., хп) = xt вычисляет
машина Rn-i + \. Действительно, эта машина правее си-
системы чисел (хь ..., хп) печатает (п — i + 1)-е чи-
число справа, т. е. xt.
§ 13.3]
ВЫЧИСЛЕНИЯ НА МАШИНАХ ТЬЮРИНГА
519
Дальнейшее доказательство ведем по индукции по
глубине рекурсивного описания рекурсивной функции.
Функции I, II, III имеют по определению глубину нуль.
Таблица 13.40
Такты
0
• • •
Ситуации на ленте
1
0 0 11 lTO 0 0 0 0 0 0
/?,.
0 0 11110 11 lTO 0
0 А
ooiiiioiii 1~Г о
Применение операций суперпозиции, индукции и опера-
оператора наименьшего числа приводит к функциям, глубина
которых на единицу больше, чем наибольшая глубина
функций, к которым эти операции применяются. Посколь-
Поскольку каждая из рекурсивных функций может быть получена
из исходных применением конечного числа этих опера-
операций, то остается только доказать существование машин
Тьюринга, способных эти операции совершать.
Таблица 13.41
Такты
0
• • •
Ситуации на ленте
1
0 0 110 1 ОТО 0 0 0 0
н
0 0 110 10 1*оТо 0 0
0 0 110 10 10 1Т0 0
? А
0011010101110
520 МАШИНЫ ТЬЮРИНГА [ГЛ. XIII
Для простоты изложения мы не будем давать точных
конструкций машин Тьюринга, выполняющих эти" опера-
операции, а ограничимся рассмотрением более простых част-
частных случаев; например, вместо суперпозиции по п пере-
переменным рассмотрим суперпозицию только по одной пе-
переменной*).
IV. Операция суперпозиции. Пусть заданы машины
Тьюринга М^ и Mv вычисляющие рекурсивные функции
ФМ и хМ' глубина которых равна соответственно
аир. Построим машину Тьюринга М , вычисляющую
функцию у(х) ^^(ФМ) глубины max (а, р) + 1. Такой
машиной будет
V. Операция индукции. Пусть задана машина Mv
вычисляющая рекурсивную функцию %(х) глубины а.
Построим машину М9, вычисляющую рекурсивную функ-
функцию у(х) глубины а + 1, задаваемую схемой индукции
9@) = q, <Р (*') = X (<Р W )•
Такой машиной является
f(l) ВСР,
1 B) BCMtNP.
VI. Оператор наименьшего числа. Пусть задана ма-
машина Мх, вычисляющая функцию %(ху у) глубины а.
Построим машину М , вычисляющую функцию
у(х) = \ху[%(х, у) =0] глубины а+ 1. Такой машиной
является
JO) GFP,
' \ B) QFA.
Машина М9 останавливается только в том случае, когда
х таково, что выполнено требование (Зу)[%(х, у) = 0].
Приведем примеры вычисления по индукции и взя-
взятия оператора наименьшего числа, поясняющие схемы
машин V и VI.
*) Точное описание машин Тьюринга, выполняющих эти опера-
операции в общем случае, см. в [42].
§ 13.3] ВЫЧИСЛЕНИЯ НА МАШИНАХ ТЬЮРИНГА 521
Таблица 13.42
Такты Ситуации на ленте
1
О О О 1 1ТОО О О О О О О О О О О О О О О О О О О
._. 5,
ОО111ОО111ООООООООООООООО ц
0011 1001 1101 ТО 00000000000
FE
о,
0011100111011ООООООООООООВ
00111001Т0011000000000000
._. с
0 011100110011000000000000
_...... м,
0011100110011011111000000
N
001 1 1001 1000001 1 1 1Т000000
р
001 1 1001 101 1 1 ITО 000000000
FE
о,
00111001 101 1 1 1 100 0 0 0 ОООООд
0011100ТО 0111110000000000
._. с
0011100100111110000000000
• •__• м,
0011100100111110111111110
._ N
0011100100000000111111110
._ р
0011100101111111100000000
FE
о,
001 1 100101 1 1 1 1 11 1ООООООООВ
0011100 "СТО 1111111100000000
^ . ._. с
0011100001111111100000000
р
о
001 1 101 1 I 1 1 1 1TV0 0 00000000
522
МАШИНЫ ТЬЮРИНГА
[ГЛ. XIII
Такты
0
• • •
*
• ¦ •
• • •
• • •
• • •
« • •
• • •
• • •
4 • •
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
т
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
Ситуации
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0"
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
т
1
1
г
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
г
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
н.
0
0
1
0
0
0
0
0
f
1
1
т
1-
ь
1
1
1
1
1
1
1
1
* ленте
0
0
1
0
0
0
1
0
0
0
0
~0
0
f
1
1
1
1
1
1
1
1
0
т
0
0
1
0
0
0
1
0
0
0
1
0
0
0
0
0
1
1
1
1
1
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
0
0
0
0
0
0
0
02
1
0
0
0
02
0
0
0
02
1"
0
0
0
02
1
0
0
0
т
0,
т
0
0
0
т
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
а б л и ц а 13.43
S,GA
<J 1 VJ Л Л
МгЕ
G
р
ж
¦
А
М Е
G
р
ж
¦
А
МуЕ
G
р
I
ш
А
М Е
G
Р
ж
¦
А
М-,
А
Е
G
F
Р
§ 13.3] ВЫЧИСЛЕНИЯ НА МАШИНАХ ТЬЮРИНГА 523'
Пример вычисления по индукции. Пусть
Х(У) = У + 3, q=\,
так что
В табл. 13.42 машина М вычисляет значение <рB).
Индексы Oi и 02 означают состояния машины Е.
Идея вычисления заключается в повторном вычисле-
вычислении функции %(у) при соответствующем контроле того,
сколько раз это вычисление проведено.
Результат вычисления: <рB) = 7. г
Пример взятия оператора наименьшего
числа. Пусть х(х, у) =[х2 — у\, так что
и надо вычислить <рB). Работа машины представлена
в табл. 1.3.43.
Идея вычисления заключается в определении после-
последовательных значений i(xy 0), %(х, 1) и т. д. до тех пор,-
пока %(х, у) = 0. Результат вычисления: <рB) = 4.
Заметим еще, что все машины, выполняющие I — VI,
сконструированы так, что они никогда не заходят за ле-
левый край ленты. ¦
Таким образом, мы показали, что любая рекурсивная:
функция может быть вычислена на машине Тьюринга.
Можно показать, что на машинах Тьюринга вычисляют-
вычисляются только рекурсивные функции. Этот факт доказывает-
доказывается при помощи гёделизации ситуаций налёнте и провер-
проверки того обстоятельства, что любое изменение ситуации
может быть описано с помощью рекурсивных функций
(см. доказательство в [42]).
В силу эквивалентности понятий «рекурсивная функ-
функция» и «функция, вычислимая на машине Тьюринга»,
а также в силу тезиса Чёрча можно дать и следующее
определение понятия алгоритм: алгоритмом называется
любая процедура, сводящаяся *>с вычислению значений
целочисленной функции на соответствующей машине
Тьюринга. :.
*.' VV .
ЗАКЛЮЧЕНИЕ
Во введении было указано, что в теории конечных
автоматов и последовательностных машин ставятся две
'основные задачи: 1) выяснение того, что могут и что
принципиально не могут «делать» динамические систе-
системы этого класса, и 2) разработка методов синтеза уст-
устройств, являющихся динамическими системами этого
•класса и выполняющих конкретные задания.
Материал излагался в такой последовательности и
форме, которые, с нашей точки зрения, были удобны для
разъяснения основных понятий и методов теории ко-
конечных автоматов. Решения двух поставленных задач
накапливались при этом постепенно и оказались раз-
разбросанными по разным главам. Не излагая нового ма-
материала, мы здесь постараемся систематизировать
разрозненные факты, относящиеся к названным выше
двум основным задачам теории конечных автоматов.
l § 1. Что может «делать» конечный автомат
и последовательностная машина
Ответ дается в различных терминах в зависимости от
того, является ли автомат (соответственно Я-машина)
автономным или нет.
Автономный конечный автомат, начиная с некоторого
такта, может лишь генерировать периодическую по-
последовательность состояний к (соответственно Я-ма-
Я-машина— последовательность выходных символов X).
Если эта последовательность состоит лишь из одного
символа, то это означает, что за конечное число тактов
автомат достигает равновесного состояния. Если же эта
последовательность содержит несколько символов, то
§ П ЧТО МОЖЕТ «ДЕЛАТЬ» КОНЕЧНЫЙ АВТОМАТ 525
это означает, что автомат последовательно проходит со-
состояния, соответствующие этим символам, а затем ра-
работа автомата неограниченно долго периодически по-
повторяется.
Более того, какова бы ни была периодическая после-
последовательность состояний конечной длины, всегда может
быть построен автономный конечный автомат, который,
начиная уже со второго такта, генерирует эту последо-
последовательность. Ничего иного, кроме периодического повто-
повторения одного и того же состояния или конечной после-
последовательности состояний, автономный автомат «делать»
не может.
Однако в связи с тем, что последовательное выпол-
выполнение заданного цикла операций типично для многих
областей современной техники, динамические системы,
которые в приемлемой идеализации можно рассматри-
рассматривать как автономный автомат, имеют широкое при-
применение.
Старинным примером могут служить автоматы-
куклы, выполнявшие сложные последовательности дей-
действий, например: пишущие на бумаге определенный
текст, играющие На рояле заранее установленные пьесы
и т. д. Современным примером служат многие станки-
автоматы, автоматические линии и системы автоматиче-
автоматического управления циклическими производствами.
Если автомат не автономен, т. е. состояние входа
изменяется от такта к такту, то ответ на вопрос, что
может «делать» и что не может «делать» конечный
автомат, можно дать в разных терминах. Например,
ответ можно сформулировать на языке представления
событий.
Действительно, неавтономный конечный автомат или
последовательностная машина лишь преобразуют вход-
входные последовательности символов в последовательности
состояний или выходных символов, и сказать, что мо-
может и что не может «делать» конечный автомат, значит
выяснить, какие преобразования последовательностей
возможны в конечном автомате, а какие невозможны.
Но так как количество состояний (соответственно выход-
выходных символов) конечно, этот вопрос эквивалентен такому
вопросу: при каких входных последовательностях
35 М. А Айзерман, Л. А. Гусев и др.
526 ЗАКЛЮЧЕНИЕ
возникает каждое из возможных состояний (или каж-
каждый из выходных символов). Этот последний вопрос
в терминах, принятых в теории конечных автоматов,
формулируется так: какие события могут и какие не
могут быть представлены в конечном автомате каждым
из возможных состояний (или каждым из выходных сим-
символов). Ответ дается теоремами Клини. Этот ответ точ-
точный, так как теоремы Клини устанавливают необходи-
необходимые и достаточные условия представимости событий в
автомате, а именно: выделяются особые множества по-
последовательностей входных символов — регулярные мно-
множества. Факт появления входной последовательности из
такого множества называется соответствующим регуляр-
регулярным событием. Теоремы Клини устанавливают, что в ко-
конечном автомате могут быть представлены регулярные
события и только они. Таким образом, на языке пред-
представления событий ответ на вопрос, что может «делать»
конечный автомат, дается однозначно: конечный авто-
автомат может представлять только регулярные события.
Ряд важных множеств входных последовательностей,
с которыми часто приходится иметь дело на практике,
заведомо регулярны. Так, например, заведомо регуляр-
регулярно множество, состоящее из любого конечного числа
входных последовательностей конечной длины; множе-
множество любых периодических входных последовательно-
последовательностей; множество бесконечных последовательностей, ко-
которое содержит заданные конечные последовательно-
последовательности на протяжении нескольких последних тактов, и т. д.
В общем случае, если каким-либо произвольным спосо-
способом задано бесконечное множество входных последова-
последовательностей, то остается открытым вопрос о том, регу-
регулярно ли это множество. Дело в том, что понятие
регулярного множества вводится индуктивно, т. е. уста-
устанавливается прием построения любых регулярных мно-
множеств. Однако не существует достаточно эффективного
способа решения обратной задачи, т. е. установления
того, является ли каждое заданное множество регуляр-
регулярным. Хотя теоремы Клини и отвечают на вопрос о том,
что может делать конечный автомат, но отвечают они
на этот вопрос не эффективно. Сделаны первые попыт-
попытки построения иных языков, на которых ответ может
§ 2] РЕАЛИЗАЦИЯ КОНЕЧНОГО АВТОМАТА 527,
быть дан эффективно. Эта проблема языка, играющая
кардинальную роль в получении эффективного ответа
на вопрос, что может и что не может «делать» конечный
автомат, имеет решающее значение и для первых этапов
синтеза автомата, т. е. для ответа на второй из сформу-
сформулированных выше вопросов.
Если расширить класс динамических систем, которые
мы определили терминами «конечный автомат» и «по-
следовательностная машина», включением бесконечной
памяти (ее образом может быть, например, бесконечная
лента или бесконечное число состояний), то для дина-
динамических систем этого более широкого класса (абстракт-
(абстрактные системы этого класса называют машинами Тьюрин-
Тьюринга) ответ на вопрос «что они могут делать?» значитель-
значительно более прост —они могут реализовать любой наперед
заданный алгоритм. При этом само понятие алгоритма
трактуется в современной математике как реализация
вычисления значений какой-либо рекурсивной функции.
Столь однозначный и четкий ответ на вопрос «что может
делать машина Тьюринга?» дает возможность положить
понятие о машине Тьюринга в основу определения поня-
понятия алгоритма: алгоритмом называется любой процесс,
который может быть осуществлен на конечном автомате,
дополненном бесконечной памятью, т. е. на машине Тью-
Тьюринга.
§ 2. Последовательность синтеза технического
устройства, реализующего конечный автомат или
последовательностную машину
В том случае, когда существенны состояния входов
и выходов системы лишь в определенные дискретные мо-
моменты времени (эти моменты могут быть заданы зара-
заранее или могут определяться работой проектируемого
устройства) и когда число таких состояний заведомо
конечно, есть основания предполагать, что устройство
может быть найдено в классе конечных автоматов или
Я-машин. Поскольку цель состоит в том, чтобы обеспе-
обеспечить получение нужных последовательностей на выходах
при поступлении на входы определенных заданных
последовательностей, в задании на проектируемое
35*
#28 ЗАКЛЮЧЕНИЕ
устройство было бы естественно перечислить все воз-
возможные входные последовательности и соответствую-
соответствующие им выходные последовательности. Если при этом
Задание содержит лишь перечисление конечного числа
непротиворечивых последовательностей конечной дли-
длины*), то оно может быть реализовано конечным
автоматом или Я-машиной. При этом, непосредственно
по заданным входным и соответствующим им выходным
последовательностям можно построить основную таб-
таблицу конечного автомата и таблицу выходного преобра-
преобразователя, которые в совокупности образуют одну из
возможных Я-машин, реализующих задание. Алгоритм
построения этих таблиц описан в § 8.2 **).
Значительно сложнее' обеспечить определенные вы-
выходные последовательности при задании входных после-
последовательностей бесконечной длины. Такие случаи часто
встречаются на практике, когда заранее нельзя устано-
установить длительность работы проектируемого устройства и
когда выходы должны индицировать некоторые общие
свойства входных последовательностей, начинающихся
с первого такта работы машины. В таких случаях воз-
возникает основной вопрос: каким образом задать соответ-
соответствие между бесконечными, входными и выходными по-
последовательностями, так как прямое перечисление после-
последовательностей здесь уже невозможно. Как бы ни было
задано это соответствие, оно означает в конечном итоге
задание алгоритма, позволяющего установить для каж-
каждого такта, каковы входной и выходной символы в этот
такт.
Если способ задания соответствий между бесконеч-
бесконечными последовательностями не ограничен как-либо, то
мы с самого начала сталкиваемся опять с такой же труд-
*) При этом априорно предполагается, что других входных по-
последовательностей появиться не может, либо они могут появляться,
но в этих случаях безразлична выходная . последовательность,
либо наконец, что при появлении любой иной последователь-
последовательности на выходе появляется какой-либо символ, индицирующий
этот факт.
**) Именно задания такого рода часто рассматриваются при
проектировании релейных схем, где перечисление входных и соответ-
соответствующих им выходных последовательностей выполняется, напри-
например, с помощью так называемых таблиц включений.
§ 2J РЕАЛИЗАЦИЯ КОНЕЧНОГО АВТОМАТА 529
ностью, о которой шла речь в конце предыдущего пара-
параграфа. Именно: не существует эффективного способа
установить, регулярно ли событие, которое должен пред-
представлять автомат; а это значит, что если не ограничен
как-либо язык, на котором сформулировано задание, то
нельзя даже установить, может ли какой-либо конечный
автомат или Я-машина выполнить это задание. Значит,
бессмысленно говорить о способе синтеза автомата или
Я-машины, выполняющих это задание. Вновь в качестве
центральной проблемы возникает проблема нахождения
языка, достаточно широкого, для того чтобы на нем мо-
могли быть выражены важные для техники задания на
автомат или Я-машину, и вместе с тем такого, чтобы
имелись алгоритмы распознавания, существует ли авто-
автомат или Я-машина, способные выполнить это задание, и
в случае положительного ответа дающие возможность
построить нужную Я-машину.
Поэтому при формулировке заданий на автомат (в
случае бесконечных последовательностей) используются
специальные приемы (или, иначе говоря, специальные
языки), обходящие это затруднение. Один из этих прие-
приемов— запись задания не с помощью описаний соответ-
соответствий между входными и выходными последовательно-
последовательностями, а непосредственно с помощью описания регуляр-
регулярных событий, которые автомат должен представлять.
Этот прием изложен в § 8.4, где указан и эффективный
способ построения основной таблицы автомата и табли-
таблицы преобразователя, которые в совокупности образуют
Я-машину, представляющую заданные события.
Другой значительно менее экономный (по требуе-
требуемому числу состояний автомата) способ решения этой
задачи был описан в § 7.4 в ходе доказательства теорем
Клини.
Известны и другие языки, характерные тем, что лю-
любое задание, которое удалось выразить на этом языке,
заведомо выполнимо Я-машиной, и соответствующая
Я-машина (т. е. ее таблицы) по этому выражению эф-
эффективно строится. Примером может служить предикат-
предикатный язык Трахтенброта, который в этой книге лишь
упомянут. Использование этих языков по существу осно-
основывается на предположении, что человек способен не
530 ЗАКЛЮЧЕНИЕ
алгоритмически (творчески) решать указанную выше за-
задачу, переводя задания с обычного общего языка, на
котором человек мыслит, на специальный язык, в котором
не возникает проблемы распознавания представимости
событий. Если человек не смог выразить задание на по-
подобном языке, то остается открытым вопрос, произошло
ли это потому, что задание не .может быть переведено на
этот язык и, значит, реализовано Я-машиной, либо по-
потому, что человек не сумел «творчески» это сделать.
Из изложенного следует, что первый этап синтеза
в одних случаях выполняется по стандартным правилам,
а в других случаях принципиально требует творческого
акта; но в любом случае, если только задание выпол-
выполнимо, результатом первого этапа синтеза являются та-
таблицы автомата и преобразователя, которые образуют
одну из Я-машин, реализующих задание. Построенная
так Я-машина не единственна; вообще говоря, сущест-
существует множество иных Я-машин, выполняющих это же
самое задание, т. е. эквивалентных построенной нами
либо отображающих ее. Эти Я-машины могут отличать-
отличаться числом п символов в алфавите состояний {к}, т. е. чис-
числом строк основной таблицы автомата. Чем меньше п,
тем более простой получается далее конструкция или
схема реальной машины. Поэтому следующим, вторым,
этапом синтеза является минимизация полученной' ма-
машины, т. е. построение Я-машины, эквивалентной най-
найденной на первом этапе синтеза и имеющей вместе с тем
наименьшее возможное число состояний п.
Решение задачи о минимизации существенно зависит
от множества последовательностей, которые могут по-
появиться на входе в автомат при его работе. Это множе-
множество, естественно, указывается в исходном задании.
Наиболее простой случай имеет место, если множе-
множество входных последовательностей никак не ограничено,
т. е. если на входе автомата может появиться любая
последовательность. В этом случае задача о построении
минимальной в указанном смысле Я-машины полностью
решена, т. е. найдены необходимые и достаточные усло-
условия минимизации. Метод, осуществляющий построение
минимальной Я-машины, связан с разбиением матрицы
соединений на определенные подматрицы и указан в § 9.6.
§ 2] РЕАЛИЗАЦИЯ КОНЕЧНОГО АВТОМАТА 531
Значительно сложнее обстоит дело тогда, когда мно-
множество возможных входных последовательностей как-
либо ограничено. Если предположить, что эти ограничения
произвольны, то есть что задан некоторый произволь-
произвольный алгоритм, позволяющий установить, удовлетво-
удовлетворяет ли какая-либо последовательность заданным огра-
ограничениям, то проблема минимизации оказывается алго-
алгоритмически неразрешимой (см. § 9.2). Поэтому нельзя
найти метод минимизации, пригодный при любых огра-
ограничениях, и можно пытаться лишь искать необходимые
и достаточные условия минимизации для заданного ча-
частного вида ограничений. Однако, если исключить пол-
полный перебор, то даже для наиболее часто встречающихся
видов ограничений (например, когда ограничение со-
состоит в том, что на входе могут появляться лишь после-
последовательности заданной длины, либо последовательности
любой длины, но не содержащие нескольких одинаковых
символов подряд, и др.) такие необходимые и достаточ-
достаточные условия до сих пор не найдены. Некоторые сооб-
соображения о минимизации в этих случаях приведены в
§§ 9.4 и 9.7.
Нам известны лишь две задачи при наличии огра-
ограничений на входные последовательности, имеющие пол-
полное решение. Это задача о построении минимальной
Я-машины в случае, когда она должна работать как ко-
конечный автомат, а входные последовательности не со-
содержат нескольких одинаковых символов подряд и за-
задача о построении минимальной Я-машины в случае ог-
ограничений типа Ауфенкампа (§ 9.8).
Итак, в результате второго этапа синтеза, если он
оказался выполнимым, строятся основная таблица авто-
автомата и таблица преобразователя, которые в совокупно-
совокупности определяют Я-машину, выполняющую указанное
задание, и вместе с тем имеют наименьшее возможное
число состояний. В общем случае на этом заканчивается
формирование основной таблицы автомата и таблицы
преобразователя и оказывается возможным перейти к
третьему этапу синтеза, который должен состоять в по-
построении абстрактной структуры проектируемой Я-ма-
Я-машины. Однако существует часто встречающийся на прак-
практике частный случай, в котором входные последователь-*
532 ЗАКЛЮЧЕНИЕ
ности ограничены, и требуется еще дальнейшая работа
по формированию минимальной Я-машины. Мы имеем
в виду случай, когда тактность работы проектируемой
машины определяется сменой состояний на входе, и по-
поэтому всегда отсутствуют входные последовательности,
содержащие подряд несколько одинаковых символов.
В этом случае дальнейшая работа по формированию
таблиц Я-машины существенно зависит от того, какими
техническими средствами и приемами предполагается
в дальнейшем пользоваться для реализации этих та-
таблиц. Именно, существенно заранее установить, какой
из двух возможных путей мы будем в дальнейшем ис-
использовать. Первый путь — применение элементов за-
задержки на извне подведенный сигнал такта и специаль-
специальных устройств, сигнализирующих о наступлении такта
(т. е. о смене состояния входа). Второй путь не требует
применения специальных элементов задержки, а опи-
опирается на то, что реальные технические элементы всегда
обладают некоторым запаздыванием в срабатывании и
допускают построение машины с использованием устой-
устойчивых состояний.
На первом пути описанный выше второй этап синтеза
в той мере, в какой он может быть доведен до конца при
указанных ограничениях на входные последовательности,
заканчивает формирование таблиц Я-машины и далее
непосредственно следует третий этап синтеза — переход
к абстрактной структуре (см. далее).
На втором же пути необходима дальнейшая обра-
обработка таблиц автомата и преобразователя. Она сводит-
сводится к построению таблиц другой Я-машины, работающей
в быстрой тактности (которая определяется временем
задержки в элементах, используемых для построения
Я-машины) и воспроизводящей на устойчивых состоя-
состояниях проектируемую Я-машину, работающую в «мед-
«медленной» тактности, определяемой моментами смены со-
состояний входа.
С этой целью проводится сначала построение какой-
либо «быстрой» машины, удовлетворяющей этому усло-
условию, а затем минимизация этой полученной машины,
т. е. повторяется второй этап синтеза (подробнее см.
§§ 10.2 и 10.3). В конечном итоге и на этом втором пути
§ 2] РЕАЛИЗАЦИЯ КОНЕЧНОГО АВТОМАТА 533
мы получаем таблицы минимальной Я-машины и тоже
можем перейти к третьему этапу синтеза.
Третий этап синтеза состоит в построении абстракт-
абстрактной структуры, т. е. в том, чтобы по полученным на пре-
предыдущем этапе таблицам Я-машины построить логиче-
логические уравнения абстрактной структуры, отображающей
эту Я-машину, т. е. найти логические функции F{ и
в уравнениях вида *)
/=1, 2,...
рп\ и?,
7=1, 2, ..., /.
В зависимости от количества состояний у элементов,
которыми мы располагаем для построения машины, эти
функции будут функциями двух-, трех- или вообще
m-значной логики. Метод кодировки и построения этих
функций изложен в § 4.2.
В случае построения автомата на устойчивых состоя-
состояниях кодировка и построение функций Т7,- и (Dj даны
в § 5.4.
В результате третьего этапа синтеза задача оказы-
оказывается уже сведенной к значительно более обычной для
инженера-проектировщика задаче — реализовать имею-
имеющимися в его распоряжении техническими средствами
систему логических соотношений. На этом, по существу,
заканчиваются задачи абстрактного синтеза, а значит, и
задачи общей теории конечных автоматов и последова-
тельностных машин. Начиная с этого момента, задача
переходит в область технической реализации полученной
абстрактной структуры.
Возникающие здесь задачи изучаются уже в теории
релейных схем и теории логических систем в узком по-
понимании этих терминов. Проблемы, решаемые этими тео-
теориями, в книге почти не рассматриваются или упоми-
упоминаются вскользь.
Если построение схемы ведется далее на элементах
задержки, то число этих элементов предопределено
*) Уравнения выписаны для машины типа.П—П,
534 ЗАКЛЮЧЕНИЕ "I
числом уравнений в абстрактной структуре, а оно -заве-
-заведомо минимально, если доведен до конца второй этап
синтеза. Именно в этом — в получении схемы с наимень-
наименьшим числом элементов задержки — и состояла цель вто-
второго этапа синтеза. Задача технической реализации сво-
сводится тогда к построению логических преобразователей,
реализующих функции Ft и Ф;, содержащиеся в правых
частях уравнений абстрактной структуры. Из одного и
того же набора логических элементов эти преобразова-
преобразователи могут быть построены различными способами. Здесь
возникают свои проблемы минимизации, но они касают-
касаются уже собственно не последовательностных машин, а
преобразователей, т. е. относятся не к динамике, а к ста-
статике, и поэтому упоминаются лишь кратко в § 2.6.
Если располагаемый набор логических элементов не
содержит готового элемента задержки, то это не исклю-
исключает возможности построения схем, так как сам элемент
задержки, будучи простейшим автоматом, может быть
построен из элементов этого набора, например на устой-
устойчивых состояниях равновесия.
Если вся машина строится на устойчивых состояниях,
т. е. без специальных элементов задержки на извне под-
подведенный сигнал такта, то это означает, что должна
быть построена быстрая машина, для которой была по-
получена абстрактная структура в конце третьего этапа,
а задержками служат элементы (например, повторите-
повторители), имеющие собственное запаздывание. В частности,
в распространенном случае, когда схемы собираются
из реле, элементом задержки для «быстрой» Я-машины
служат промежуточные реле, а преобразователи Fi и со-
сообразуются цепями контактов приемных и промежуточ-
промежуточных реле.
При таком построении схем (на устойчивых состоя-
состояниях) возникают дополнительные технические затрудне-
затруднения, связанные с тем, что в несинхронизованных системах
времена запаздывания элементов не строго одинаковы.
Это приводит к угрозе возникновения «состязаний»
реле, следствием чего иногда может быть непра-
неправильная работа схемы. Опасность состязаний в таких
случаях устраняется применением специальных схем —
их называют реализациями, — в которых либо в каждом
§2] РЕАЛИЗАЦИЯ КОНЕЧНОГО АВТОМАТА 535
такте срабатывает не более одного реле, либо же в мо-
моменты переключений искусственно разрываются цепи об-
обратных связей.
Существуют различные способы построения реализа-
реализаций, из которых лишь одна кратко описана в § 5.4, так
как вопросы реализации не относятся к общей теории
конечных автоматов и последовательностных машин.
При построении схем на элементах задержки с подведе-
подведением к ним извне сигнала такта, угрозы возникновений
состязаний нет, и поэтому проблема реализации не воз-
возникает.
БИБЛИОГРАФИЯ
1. А й з е р м а н М. А., Гусев Л. А., .Р о з о н о э р Л. И., Смир-
Смирнова И. М., Таль А. А., Конечные автоматы. 1. Автоматика
и телемеханика, т. XXI, № 2, 1960.
2. Айзерман М. А. и др., Конечные автоматы. 2. Автоматика и
телемеханика, т. XXI, № 3, 1960.
3. Айзерман М. А. л др., О методах реализации конечного ав-
автомата, тактность которого определяется изменением состояния
входа. Автоматика и телемеханика, т. XXI, № 12, 1960.
4. Айзерман М. А. и др., Алгоритмическая неразрешимость
проблемы распознавания представимости рекурсивных событий
в конечных автоматах. Автоматика и телемеханика, т. XXII,
№ 6, 1961
5. Ауфенкамп Д. Д., Анализ последовательностных машин, II.
Математика, периодический сборник переводов иностр. статей,
3 :6, 1959.
6. Ауфенкамп Д. Д., Хон Ф. Е., Анализ последовательност-
последовательностных машин, I. Математика, периодический сборник переводов
иностр. статей, 3 : 3, 1959.
7. Ауфенкамп Д. Д., Хон Ф. Е., С е ш у С, Теория сетей. Ма-
Математика, периодический сборник переводов иностр. статей, 3 : 3,
1959.
8. Б а з и л е в с к и й Ю. Я., Вопросы теории временных логических
функций. Сб. «Вопросы теории математических машин» № I,
Физматгиз, 1958.
9. Базилевский Ю. Я., О некоторых преобразованиях конеч-
конечных автоматов. Сб «Теория и применение дискретных автома-
автоматических систем», под ред. Я. 3. Цыпкина, Изд. АН СССР, М.,
1960.
10. Базилевский Ю. Я-, Решение временных логических урав-
уравнений методом редукции. Сб. трудов конференции по теории и
применению дискретных автоматических систем, Изд. АН СССР,
М., 1960
11. Беркли Э., Символическая логика и разумные машины. ИЛ,
М., 1960.
12. Б е р е н д с Т. К., Т а л ь А. А., Пневматические релейные схемы.
Автоматика и телемеханика, т. XX, № Ц, 1959.
13. Блох А. Ш., Синтез многотактных схем. Сб. трудов Ин-та ма-
машиноведения и автоматизации АН БССР, № 1, 1961,
БИБЛИОГРАФИЯ 537
14. Блох А. Ш., Канонический метод синтеза электронных схем.
Сборник трудов Института машиноведения и автоматизации
АН БССР, № 1, 1961.
15. Блох А. Ш., Синтез релейно-контактных схем. ДАН СССР,
т. 117, №4, 1957.
16. Блох А. Ш., О задачах, решаемых последовательностными ма-
машинами. Сб. «Проблемы кибернетики», вып. 3, Физматгиз, М.,
1960.
17. Б л о х А. Ш., Канонический метод синтеза контактных схем.
Автоматика и телемеханика, т. XXII, № 6, 1961.
18. В а н X а о, М а к - Н о т о н Р., Аксиоматические системы тео-
теории множеств. ИЛ, М., 1963.
19. Вавилов Е. Н., О с и н с к и й Л. М., Об одном методе струк-
структурного синтеза конечных автоматов. Автоматика, № 2, 1963.
20. Г а в р и л о в М. А., Современное состояние и основные напра-
направления развития теории релейных схем. Сб. «Тезисы докладов
на Всесоюзном совещании по теории устройств релейного дей-
действия», Изд. АН СССР, М., 1957.
21. Га ври лов М. А., Теория релейно-контактных схем. Изд. АН
СССР, М.—Л., 1950.
22. Га в рилов М. А., Структурная теория релейных устройств.
Лекция. ВЗЭИ, ч. 1, 1959; ч. 2, I960; ч. 3, 1961, Изд. ВЗЭИ.
23. Г а в р и л о в М. А., Минимизация булевых функций, характери-
характеризующих релейные цепи. Автоматика и телемеханика, т. XX, №9,
1959.
24. Гильберт Д., Аккерман В., Основы теоретической Логики,
ИЛ, М., 1947.
25. Гинзбург С, О длине кратчайшего эксперимента, устанавли-
устанавливающего конечные состояния машины. Кибернетический сбор-
сборник, № 3, ИЛ, М., 1961.
26. Г л е б с к и й Ю. В., Кодирование с помощью автоматов с ко-
конечной внутренней памятью. Сб. «Проблемы кибернетики», № 7,
Физматгиз, М., 1962.
27. Г л ушков В. М., Абстрактная теория автоматов. Успехи ма-
тем. наук, т. 16, вып. 5 A0), 1961; т. 17, вып. 2 A04), 1962.
28. Г л у ш к о в В. М., Некоторые проблемы синтеза цифровых ав-
автоматов. Журнал вычислительной математики и матем. физики,
т. 1, № 3, май—июнь, 1961.
29. Г л у ш к о в В. М., Абстрактные автоматы и разбиение свобод-
свободных полугрупп, ДАН СССР, т. 136, № 4, 1961.
30. Гудстейн Р. Л., Математическая логика. Сб. под ред. и с
предисл. С. А. Яновской, ИЛ, М., 1961.
31. Дэви с М. Д., Замечание об универсальных машинах Тьюрин-
Тьюринга. Сб. «Автоматы», под ред. К. Э. Шеннона и Дж. Маккарти,
ИЛ, М„ 1956.
32. Ж у р а в л е в Ю. И., О различных понятиях минимальности
дизъюнктивных нормальных форм. Сибирский матем. журнал,
т. 1, № 4, ноябрь — декабрь, 1960.
33. Ж у р а в л е в Ю. И., Об отделимости подмножеств вершин
я-мерного единичного куба. Труды матем. ин-та им. В. А. Стек-
лова, т. 51. Изд. АН СССР, 1958,
538 библиография
34. 3 а в о л о к и н а 3. И., Магнитные элементы в цифровых вычис-
вычислительных устройствах. Госэнергоиздат, М.—Л., 1958.
35. Закревский А. Д., Минимизация структурных формул мно-
готактных схем. Труды Сибирского физико-технического ин-та
при Томском Гос. университете им. Куйбышева, вып. 40, 1961.
36. Закревский А. Д., К синтезу последовательностных автома-
автоматов. Труды Сибирского физико-технического ин-та, вып. 40,
1961.
37. Казаков В. Д., Кузнецов D. П., Список иностранных ра-
работ по теории устройств релейного действия и конечных автома-
автоматов за 1958 год. Автоматика и телемеханика, т. XXI, № 9, 1960.
Список отечественных работ по теории релейных схем и конеч-
конечных автоматов за 1959 год. Автоматика и телемеханика, т. XXII,
№ 2, 1961, т. XXIV, № 5, 1963.
38. К о л ь м а н Э., Значение символической логики. Сб. «Логиче-
«Логические исследования», под ред. Э. Кольмана и др., Изд. АН СССР,
М., 1959.
39. Калбертсон Дж. Т., Некоторые неэкономичные роботы. Сб.
«Автоматы», под ред. К. Э. Шеннона и Дж. Маккарти, ИЛ, М.,
1956.
40. К а р а ц у б а А. А., Решение одной задачи из теории конечных
автоматов. Успехи матем. наук, т. 15, вып. 3, 1960.
41. Клин и С. К., Представление событий в нервных сетях и ко-
конечных автоматах. Сб. «Автоматы», под ред. К. Э. Шеннона и
Дж. Маккарти, ИЛ, М., 1956.
42. К л и н и С. К., Введение в метаматематику, ИЛ, М., 1957.
43. Кобринский Н. Е., Трахтенброт Б. А., О построении
общей теории логических сетей. Сб. «Логические исследования»,
под ред. Э. Кольмана и др., Изд. АН СССР, М., 1959.
44. Кобринский Н. Е., Трахтенброт Б. А., Введение в тео-
теорию конечных автоматов. Физматгиз, М., 1961.
45. Колдуэлл С, Логический синтез релейных устройств, ИЛ,
М., 1961.
46. Копи И. М., Э л г о т К. С, Р а и т Д. Б., Реализация событий
логическими сетями. Кибернетический сборник, №3, ИЛ,М., 1961.
47. Кудрявцев В. Б., Теорема полноты для одного класса ав-
автоматов без обратных связей. ДАН СССР, т. 132, № 2, 1960.
48. К у д р я в ц е в В. Б., Вопросы полноты для систем автоматов.
ДАН СССР, т. 130, № 6, 1960.
49. Л а з а р е в В. Г., П и й л ь Е. И., Метод синтеза конечных ав-
автоматов. Автоматика и телемеханика, т. XXII, № 9, 1961.
50. Лазарев В. Г., Методика определения числа реле, необходи-
необходимого для построения релейных схем по заданным условиям ра-
работы. Сб. «Проблемы передачи информации», вып. 1, изд. АН
СССР, 1959.
51. Лазарев В. Г., Определение минимального числа промежу-
промежуточных реле при синтезе многотактных схем. Сб. работ по про-
проводной связи, вып. 5, Изд. АН СССР, 1956.
52. Лазарев В. Г., П и й л ь Е. И., Уменьшение числа состояний
одного класса конечных автоматов. ДАН СССР, т. 143, № 5,
1962.
БИБЛИОГРАФИЯ 539
53. Л е т и ч е в с к и й А. А., О синтезе конечных автоматов. ДАН
УССР (на укр. языке), т. 11, № 2, 1961.
54. Л е т и ч е в с к и й А. А., Условия полноты для конечных автома-
автоматов. Журнал вычислительной математики и матем. физики, т. 1,
№ 4, 1961.
55. Лунц А. Г., Приложение матричной булевой алгебры к ана-
анализу и синтезу релейно-контактных схем. ДАН СССР, т. 70,
№ 3, 1950.
56. Л у п а н о в О. Б., Об асимптотических оценках числа графов и
сетей с п ребрами. Сб. «Проблемы кибернетики», вып. 4, Физ-
матгиз, М., 1960.
57. Л у п а н о в О. Б., Об одном методе синтеза схем. Изв. высших
учебных заведений, Радиофизика, Ш 1, 1958.
58. Л у п а н о в О. Б,. О возможностях синтеза схем из произволь-
произвольных элементов. Труды матем. ин-та им. В. А. Стеклова, т. 51,
Изд. АН СССР, 1958.
59. Л у п а н о в О. Б., О возможностях синтеза схем из разнооб-
разнообразных элементов. ДАН СССР, т. 103, № 4, 1955.
60. Лупанов О. Б., О реализации функций алгебры логики фор-
формулами из конечных классов (формулами огранич. глубины в
базисе &, V, —"). Сб. «Проблемы кибернетики», № 6, 1961.
61. Лупанов О. Б., О принципе локального кодирования и реа-
реализации функций из некоторых классов схемами из функцио-
функциональных элементов. ДАН СССР, т. 140, № 2, 1961.
62. М а к - К а л л о к У. С., П и т т с В., Логическое исчисление идей,
относящихся к нервной активности. Сб. «Автоматы», под ред.
К. Э. Шеннона и Дж. Маккарти, ИЛ, М., 1956..
63. М а к к а р т и Д ж., Обращение функций, определяемых маши-
машинами Тьюринга. Сб. «Автоматы», под ред. К. Э. Шеннона и
Дж. Маккарти, ИЛ, М., 1956.
64. М а р к о в А. А., Теория алгорифмов. Труды матем. ин-та
им. В. А. Стеклова, т. 42, 1954.
65. Марков А. А., Математическая логика и вычислительная ма-
математика. Вестник АН СССР, № 8, 1957.
66. М а р т ы н ю к В. В., Соотношение между памятью и некоторы-
некоторыми возможностями конечного автомата. Сб. «Проблемы кибер-
кибернетики», вып. 5, Физматгиз, М., 1961.
67. Медведев Ю. Т., О классе событий, допускающих представ-
представление в конечном автомате. В прилож. к сб. «Автоматы», под
ред. К. Э. Шеннона и Дж. Маккарти, ИЛ, М., 1956.
68. М е к л е р Я. И., Упрощение алгебраического синтеза релейных
схем. Автоматика и телемеханика, т. XIX, № 12, 1958.
69. Минский М. Л., Некоторые универсальные элементы для ко-
конечных автоматов. В прилож. к сб. «Автоматы» под ред.
К. Э. Шеннона и Дж. Маккарти,44Л, М., 1956.
70. М о и с и л Г. К., Алгебраическая теория работы реальных релей-
релейно-контактных схем. В сб. «Тезисы докладов на Всесоюзном со-
совещании по теории устройств релейного действия», Изд. АН
СССР, М., 1957.
71. М о и с и л Г. К., И о а н и н Г., Синтез релейно-контактных схем
при данных условиях срабатывания исполнительных элементов,,
540 библиография
Журнал чистой и прикладной математики, Акад. РНР, т. 1,
№ 2, 1956.
72. М у р Э. Ф., Умозрительные эксперименты с последовательност-
ными машинами. Сб. «Автоматы», под ред. К. Э. Шеннона и
Дж. Маккарти, ИЛ, М., 1956.
73. Нейман Дж., Вероятностная логика и синтез надежных орга-
организмов из ненадежных компонент. Сб. «Автоматы» под ред.
К. Э. Шеннона и Дж. Маккарти, ИЛ, М., 1956.
74. Нечипорук Э. И., О синтезе #-схем. ДАН СССР, т. 137,
№ б, 1961.
75. Н о в и к о в П. С, Элементы математической логики. Физмат-
гиз, М., 1959.
76. Ости а ну В. М., Томфельд Ю. Л., Об одном применении
математической логики. Уч. записки Кишиневского Гос. ун-та,
т. 29, 1957.
77. Петер Р., Рекурсивные функции. ИЛ, М., 1954.
78. Поваров Г. Н., О логическом синтезе электронных вычисли-
вычислительных и управляющих схем. Сб «Логические исследования»,
под ред. Э. Кольмана и др., Изд. АН СССР, М., 1959.
79. Поваров Г. Н., О симметрии булевых функций. Труды Все-
Всесоюзного математического съезда, т. IV, Краткое содержание
докладов, Изд. АН СССР, М„ 1959.
80. П о в а р о в Г. Н., О функциональной разделимости булевых
функций. ДАН СССР, т. 94, № 5, 1954.
81. Поваров Г. Н., К изучению симметричных булевых функций
с точки зрения релейно-контактных схем. ДАН СССР, т. 104,
№ 2, 1955.
82. Поваров Г. Н., О структурной теории сетей связи. Сб.
«Проблемы передачи информации» вып. 1, Изд. АН СССР, М.,
1959.
83. П а р х о м е н к о П. П., Блочный анализатор релейных схем.
В сб. «Технические средства автоматизации и телемеханизации»,
вып. 14, М., 1961.
84. П о п о в и ч К., Минимальная дизъюнктивная форма булевых
функций. В сб. «Тезисы докладов на Всесоюзном совещании по
теории устройств релейного действия». Изд. АН СССР, М., 1957.
85. Поспелов Д. А., Арифметические и логические основы вы-
вычислительных машин дискретного действия, ч. I. Арифметиче-
: ские основы вычислительных машин дискретного действия, ч. II.
Функции алгебры логики, синтез и анализ схем, работа которых
не зависит от времени, Изд. МЭИ, М., 1960.
86. Сб. «Применение логики в науке и технике», под ред. П. В. Та-
ванец и др., Изд. АН СССР, М., 1960.
87. Р о г и н с к и й В. Н., Элементы структурного синтеза релейных
схем управления. Изд. АН СССР, М., 1959.
88. Рог и некий В. Н., Равносильные преобразования релейных
схем. Сб. научных работ по проводной связи, № 6, 1957.
89. Р о г и не к и й В. Н., Графический метод построения контакт-
контактных схем. Электросвязь, № И, 1957.
90. Р э н и Д ж. Н., Последователыгостные функции. Кибернетиче-
Кибернетический сборник, № 3, ИЛ, Мм 1961,
БИБЛИОГРАФИЯ 541
91. Сборник статей по математической логике и ее применениям к
некоторым вопросам кибернетики. Труды матем. ин-та им.
В. А. Стеклова, т. 51, Изд. АН СССР, М., 1958.
92. С к о р н я к о в Л. А., Об одном классе автоматов (нервные
сети). Сб. «Проблемы кибернетики», вып. 4, Физматгиз, М., 1960.
93. Соколов О. Б., К построению функционально-устойчивых ав-
автоматов. Итоговая научная конференция Казанского гос. ун-та
за 1960 г., Казань, 1960.
94. Соркин Ю. И., Алгоритмическая разрешимость проблемы изо-
изоморфизма для автоматов. ДАН СССР, т. 137, № 4, 1961.
95. С т о г н и й А. А., Синтез абстрактного автомата по представ-
представляемому им событию. Журнал вычислительной математики и
матем. физики, т. 1, № 3, 1961.
96. Т а р с к и й А., Введение в логику и методологию дедуктивных
наук. ИЛ, М., 1948.
97. Трахтенброт Б. А., Алгоритмы и машинное решение задач.
Физматгиз, М., 1957.
98. Т р а х т е н б р о т Б. А., Об операторах, реализуемых в логиче-
логических сетях, ДАН СССР, т. 112, № 6, 1957.
99. Т р а х т е н б р о т Б. А., Синтез логических сетей, операторы ко-
которых описаны средствами исчисления одноместных предикатов.
ДАН СССР, т. 118, №4, 1958.
100. Трахтенброт Б. А., Асимптотическая оценка сложности ло-
логических сетей с памятью. ДАН СССР, т. 127, № 2, 1959.
101. Трахтенброт Б. А., Некоторые построения в логике одно-
одноместных предикатов. ДАН СССР, т. 138, № 2, 1961.
102. Трахтенброт Б. А., Конечные автоматы и логика одномест-
одноместных предикатов. ДАН СССР, т. 140, № 2, 1961.
103. Успенский В. А., Лекции о вычислимых функциях. Физмат-
Физматгиз, М., 1960.
104. Фельдбаум А. А., Вычислительные устройства в автомати-
автоматических системах. Физматгиз, М., 1959.
105. X а р к е в и ч А. Д., О коммутационных схемах и их логической
сущности. Сб. «Логические исследования», Изд. АН СССР, 1959.
106. Цейтин Г. С, Алгорифмические операторы в конструктив-
конструктивных метрических пространствах, Труды матем. ин-та им.
В. А. Стеклова. т. 67, 1962.
107. Цетлин М. Л., О непримитивных схемах. Сб. «Проблемы ки-
кибернетики», № 1, Физматгиз, 1958.
108. Цетлин М. Л., Некоторые задачи о поведении конечных ав-
автоматов. ДАН СССР, т. 139, № 4, 1961.
109. Ч ё р ч А., Введение в математическую логику. ИЛ, М., 1960.
ПО. Шеннон К. Э., Универсальная машина Тьюринга с двумя
внутренними состояниями. Сб. «Автоматы», под ред. К. Э. Шен-
Шеннона и Дж. Маккарти, ИЛ, М., 1956.
111. Шест а ко в В. И., Алгебраический метод анализа автономных
систем двухпозиционных реле. Автоматика и телемеханика,
т. XV, № 2, 1954; т. XV, № 4, 1954.
112. Шест а ко в В. И., Векторно-алгебраический метод анализа и
синтеза многотактных релейных схем. Труды III Всесоюзного
математического съезда, т. I, 1956.
3@ ДО. А Айзерман, Л. А. Гусев и др.
542 библиография
113. Ш рейдер Ю. А., Задача динамического планирования и ав-
автоматы. Сб. «Проблемы кибернетики», № 5, Физматгиз, М., 1961.
114. Эшби У. Р., Введение в кибернетику. ИЛ, М., 1959.
115. Яблонский С. В., Функциональные построения в многознач-
многозначных логиках. Труды III Всесоюзного математического съезда,
т. II, Изд. АН СССР, М., 1956.
116. Яблонский С. В., О предельных логиках. ДАН СССР, т. 118,
№ 4, 1958.
117. Яблонский. С. В., Об алгоритмических трудностях синтеза
минимальных контактных схем. Сб. «Проблемы кибернетики»,
№ 2, Физматгиз, М., 1959.
118. Яновская С. А., О некоторых чертах математической логики
и отношении ее к техническим приложениям. Сб. «Применение
логики в науке и технике», Изд. АН СССР, М., 1960.
119. Яновская С. А., Математическая логика и основания мате-
математики. Сб. «Математика в СССР за 40 лет» A917—1957), т. I,
Физматгиз, М., 1959.
120. A bh yank а г S., Minimal «sum of products of sum» expression
of Boolean functions. IRE Trans., vol. EC-7, № 4, 1958.
121. Abhyankar S., Absolute minimal expressions of Boolean func-
functions. IRE Trans., voL EC-8, № 1, 1959.
122. Arant G. W., A time-sequential tabular analysis of flip-flop lo-
logical operation. IRE Trans., vol. EC-6, June, 1957.
123. Arbib M., Turing machines, finite automata and neural nets.
JACM, vol. 8, № 4, 1961.
124. A r d e n D., Delayed logic and finite state machines. Symposium
on Switching Circuit Theory and Logical Design, AIEE, Detroit,
Michigan, October, 1961.
125. Auf encamp D. D., Hohn F. E., Oriented graphs and sequen-
sequential machines. Bell Laboratories Reports, 30, 1954.
126. В aid a M.,Klasifikace automatu. Automatizace, t. IV, №2, 1961.
127. В eat son T. J., Minimization of components in electronic swit-
switching circuits. Communication and Electronics, № 4, July, 1958.
128. Bellman R., Sequential machines ambiguity and dynamic pro-
programming. JACM, vol. 7, № 1, 1960.
129. Bellman R., Adaptive control processes. A guided tour. Prin-
Princeton, New Jersey, 1961.
130. Bellman R., Holland J., Kalaba R., On an application
of dynamic programming to the synthesis of logical systems.
JACM, vol. 6. № 4, 1959.
131. Bianchini R., Freiman C, On internal variable assign-
assignment for sequential switching circuits. IRE Trans., vol. EC-10,
№ 1, March, 1961.
132. В u с h i J. R., Weak second-order arithmetic and finite automata.
Zeitschrift fur Mathematische Logik und Grundlagen der Math.,
Band 6, Heft 1, 1960.
133. Buchi J. R., El got С. С, Wright J. В., The non-existence
of certain algorithms of finite automata theory (Abstracts).
Notices Amer. Math. Soc, vol. 5, 1958.
134. Burks A. W., Wang H., The logic of automata, part I—II.
JACM, vol. 4, 1957,
БИБЛИОГРАФИЯ 543
135. Burks A. W., The logic of fixed and growing automata. Intern.
Symp. on the Theory of Switching, vol. 29, part 1, 1959.
136. Cad den W. J., Equivalent sequential circuits. IRE Trans., vol.
CT-6, № 1, 1959.
137. Church A., Application of recursive arithmetic in the theory
of computers and automata. Lecture Notes, Summer Conference,
University of Michigan, June, 1958.
138. С h u J. Т., Some methods for simplifying switching circuits using
don't care conditions. JACM, vol. 8, № 4, 1961.
139. Culbertson J. Т., Robots and automata; a short history. Part
I—II. Computers and Automation, vol. 6, № 3—4, 1957.
140. Culbertson J. Т., Mathematics and logic for digital devices.
Princeton, 1958.
141. Culik K-, Some notes on finite-state languages and events re-
represented by finite automata using labelled graphs. Casopis pro
pest. Mot., vol. 86, № 1, 1961.
142. Davis M. D.. Computability and unsolvability, N.-Y., 1957.
143. E 1 g о t С. С, Decision problems of finite automata design and
related arithmetics. Trans. Amer. Math. Soc, vol. 98, № 4, 1961.
144. E 1 g о t С. С, Lectures on switching and automata theory. The
University of Michigan Research Institute, Technical Report, Janu-
January, 1959.
145. E 1 g о t С. С, RutledgeJ. D., Operations on finite automata.
Symposium on Switching Circuit Theory and Logical Design,
AIEE, Detroit, Michigan, October, 1961.
146. E1 s p a s В., The theory of autonomous linear sequential net-
networks. IRE Trans., vol. CT-6, № 1, 1959.
147. Fitch F. В., Representation of sequential circuit in combinatory
logic. Philosophy, vol. 25, № 4, October, 1958.
148. George F. H., Behaviour network systems for finite automata.
Methodos, vol. 9, № 35—37, 1957.
149. Gill A., Introduction to the theory of finite-state machines.
N.-Y., McGraw-Hill, 1962.
150. Gill A., Comparison of finite-state models. IRE Trans., vol.
CT-7, № 2, June, 1960.
151. Gill A., State-indentification experiments in finite automata. In-
Information and Control, vol. 4, № 23. Sept., 1961.
152. Gill A., Cascaded finite state machines. IRE Trans., vol. EC-10,
№ 3, Sept., 1961.
153. G i n s b u r g S., Compatibility of states of input independent
machines. JACM, vol. 8, № 3, July, 1961.
154. G i n s b u r g S., On the reduction of superfluous states in a se-
sequential machine. JACM, vol. 6, April, 1959.
155. G i n s b u r g S., Connective properties preserved in minimal sta-
state machines. JACM, vol. 7, № 4, 1960.
156. Ginsburg S., A technique for the reduction of a given machi-
machine to a minimal state machine. IRE Trans., EC-8, № 3, 1959.
157. G i n s b u r g S., Sets of tapes accepted by different types of
automata. JACM, vol. 8, № 1, January, 1961.
158. G i n s b u r g S., Some remarks on abstract machines. Trans,
Amer. Math. Soc, vol. 96, № 3, 1960.
16*
544 библиография
159. Н а к i m i S. L., On readability of a set of trees. IRE Trans.,
CT-8, № 1, March, 1961.
160. H a r i n g D. R., The sequential transmission expression for flow-
-graphs. MIT Electronics Systems Laboratory Technical Memo-
Memorandum, № 7848-T-14-3, November, 1960.
161. Harris В., An algorithm for determining minimal representa-
representation of a logic function. IRE Trans., EC-6, № 2, 1957.
162. Hibbard Th. N., Least upper bound on minimal terminal state
experiments for two classes of sequential machines. JACM, vol. 8,
№ 4, October, 1961.
163. H i g о n n e t R. A., G r e a R. A., Logical design of electrical
circuits. McGraw-Hill, N. Y., 1958.
164. Hilton A. M., Logic and switching circuits. Electric Manufac-
Manufacturing, April, 1960.
165. Hoffman A. J., Singleton'R. P., On Moore graphs with dia-
diameter 2 & 3. IBM Journ. of Research and Develop., vol. 4, № 5,1960.
166. Hohn F. E., Some mathematical aspects of switching. Amer.
Mathem. Monthly, vol. 62, 1955.
167. Hohn F. E., Applied boolean algebra. An elementary introduc-
introduction. N. Y. McMillan, 1960.
168. Hoi brook E. L., Pneumatic logic. I—II. Control Engineering,
vol. 8, № 7—8, 1961.
169. Holland L., Cycles and automata behaviour. Preliminary re-
report. Session on Advanced Theory of Logical Design of Digital
Computers, Univ. of Michigan, June, 1958.
170. Huffman D. A., The synthesis of sequential switching circuits.
Journ. Franklin Inst., vol. 257, № 3—4, 1954.
171. Huffman D. A., The design and use of hazard-free switching
networks. JACM, vol 4, January, 1957.
172. Huffman D. A., Sequential tranbducer. Papers Buyer's Guide.
IRE Trans., vol. CT-6, № 1, March, 1959.
173. Humphrey W. S., Switching circuits with computer applica-
applications, John Wiley & Sons, N. Y., 1958.
174. Huzino S., On some sequential machines and experiments.
Mem. Fac. Sci. Kyusyu University, vol. A12, № 2, 1958.
175. Huzino S.,. Reduction theorems on sequential machines. Mem.
Fac. Sci. Kyusyu Univ., vol. A12, № 2, 1958. ,
176. Huzino S., On the existence of Scheffer stroke class in the se-
sequential machines. Mem. Fac. Sci. Kyusyu Univ., vol. A13, № 2,
1959.
177. Huzino S., Theory of finite automata. Mem. Fac. Sci. Kyusyu
Univ., vol. A16, № 2, 1962.
178. Huzino S., Turing transformation and strong computability of
Turing computers. Mem. Fac. Sci Kyusyu Univ., vol. A13, Mb 2,
1959.
179. Huzino S., On some sequential equations. Mem. Fac. Sci. Kyu-
Kyusyu Univ., vol. A14, № 1, 1960.
180. Karnaugh M., The map method for synthesis of combinatorial
logic circuits. AIEE Trans., vol. 72, 1953.
181. Keller H. В., Finite automata, pattern recognition and per*
ceptrons. JACM, vol. 8, № 1, 1961.
БИБЛИОГРАФИЯ 545
182. Lee С. I., Automata and finite automata. Bell Syst. Techn,
Journal, vol. 39, № 5, 1960.
183. Lee C. I., Categorizing automata by W-machine programs.
JACM, vol. 8, № 3, 1961.
184. L о w P. R., M a 1 e у G. A., Flow table logic. Proc. IRE, vol. 49,
№ 1, 1961.
185. McC lu skey E. J., Minimization of Boolean functions. Bell.
Syst. Techn. Journ., vol. 35, 1956.
186. M с С 1 u s к е у E. J., Minimal sums for Boolean functions having
many unspecified fundamental products. Communication and
Electronics, № 63, November, 1962.
187. McNaughton R. F., Yamada H., Regular expressions and
state graphs for automata. IRE Trans., vol. EC-9, N° 1, 1960.
188. McHaughton R. F., The theory of automata, a survey.
Advances in Computers, vol. 2, ed. by Franz L. Alt, 1962.
189. Ma у е d a W., Synthesis of switching functions by linear graph
theory. IBM Journ. of Research and Develop., vol. 4, № 3, 1960.
190. Mealy G. E, A method of synthesizing sequential circuits.
Bell. Syst. Techn. Journ., vol. 34, Sept., 1955.
191. Mezei J. E., Minimal characterizing experiments for finite me-
memory automata, IRE Trans., vol. EC-10, N° 2, June, 1961.
192. Mleziva M., К teorii konecnych automatu (neuronovych siti).
Rokvoky matematiky, fysiky a astronomie, vol. 5, № 6, 1960.
193. M о i s i 1 G r. C. Logica matematica si tehnica modern^. Acad.
RPR, Inst. de Stud. Romino — Sovietica, 1960.
194. M о i s i 1 G r. C, Rapport sur le developpement dans la R. P. R.
de la theorie des mecanismes automatiques, Analele Universitatu
С I. Parhon, Bucure§ti, Seria Acta Logica, № 1, 1959.
195. M о i s i 1 G r. C, Functionarea in mai multi timpi a schemelor
cu relee ideale. Bucure§ti, Acad. R. P. R., 1960.
196. Moore E. F., A simplified universal Turing machine. Proc.
Assoc. Сотр. Mach., 1953.
197. M о 11 Т. Н. Jr., An algorithm for determining minimal normal
forms of an incomplete truth function. Commun. and Electronics,
№ 3, March, 1961.
198. M u 11 e r D. E., В a r t к у W. S., A theory of asynchronous circu-
circuits. Intern. Symp. on the Theory of Switching. Part I, The Annals
of the Сотр. Lab. Harvard Univers., vol. 29, 1959.
199. M у h i 11 J., Finite automata and the representation of events.
WADC Technical Report, № 57—624, 1957.
200. M у h i 11 J., Linear bounded automata. US Govt Research Re-
Reports., vol. 35, 10 March 1961.
201. N a s 1 i n P., Introduction a l'etude des automatismes a sequen-
sequences. 1-е partie, Les fonctions logiques et les circuits combinatoi-
res. Automatisme, vol. 3, № 1, 1938.
202. N a s 1 i n P., Circuits a relais et automatismes a sequences. Du-
nod, Paris, 1958.
203. N a s 1 i n P., A note on the simplification of boolean functions.
Process Control and Automation, vol. 8, № 6, 1961.
204. Nedelcu M., Teoria algebrica a schemelor cu functionare dis«
creta, Automatica si electronica, vol, 4, № 6, 1960.
546 БИБЛИОГРАФИЯ
205. N е г о d e A., Linear automaton transformations. Proc. Amer.
Math. Society, vol. 9. 1958.
206. Netherwood D. В., Minimal sequential machines. IRE Trans.,
vol. EC-8, № 3, 1959.
207. Neumann J. von, The general and logical theory of automata.
В сборнике Cerebral Mechanisms in Behaviour, N.-Y., 1951.
208. О 11 G., F e i n s t e i n N. H., Design of sequential machines from
their regular expressions, JACM., vol. 8, № 4, 1961.
209. P a u 11 M. C, U n g e r S. H., Minimising the number of states
in incompletely specified sequential switching functions. IRE
Trans., vol. EC-8, № 3, 1959.
210. Percus J. K-, Matrix analysis of oriented graphs with irredu-
irreducible feedback loops. IRE Trans., vol. CT-2, № 2, 1956.
211. Pfeifer J. E., Symbolic logic. Scientific American., vol. 183,
№ 6, 1950.
212. Phister M. Jr., Logical design of digital computers. N.Y.John
Wiley & Sons, 1959.
213. Putnam H., Decidability and essential undecidability. Journ.
Symb. Logic, vol. 22, 1957.
214. Quine W. V., Way to simplify truth functions. Amer. Math.
Monthly, vol. 62, 1955.
215. R i e g e г, О teorii neuronovych siti. Aplikace matematiky, vol. 3,
№ 4, 1958.
216. Roth J. P., Minimization of nonsingular boolean trees. IBM of
Research of Journ., vol. 3, № 4, 1959.
217. Roth J. P., Minimization over boolean trees. IBM Journ. of Re-
Research and Develop., vol. 4, № 5, 1960.
218. Roth J. P., Algebraic topological methods for the synthesis of
switching systems, I. Trans. Amer. Math. Soc, vol. 88, July, 1958.
219. Rubin off M., Remarks on the design of sequential circuits.
International Symp. on the Theory of Switching, Part II. Annals
of the Сотр. Lab. Harvard University, vol. 30, 1959.
220. Schubert E. J., Matrix algebra of sequential logic. Communic.
and Electronics, vol. 46, № 1, 1960.
221. Schubert E. J., Simultaneous logical equations. Communic.
and Electronics, vol. 46, № 1, 1960.
222. Schubert E. J., Symmetric switching functions. Communic. and
Electronics, vol. 46, № 1, 1960.
223. Schutzenberger M. P., A remark on finite transducers. In-
Information and Control, vol. 4, № 2—3, 1961.
224. Schutzenberger M. P., On the definition of a family of
automata. Information and Control, vol. 4, № 2—3, 1961.
225. S e с h u S., On electric circuits and switching circuits. IRE
Trans., vol. CT-3, № 3, 1956; vol. CT 4, № 3, 1957.
226. S e с h u S., Mathematical models for sequential machines. IRE
Convent. Record, vol. 7, part 2, 1959.
227. Sechu S., Miller R. E., Metze G., Transition matrices of
sequential machines IRE Trans., vol. CT-6, № 1, 1959.
228. Semon W., Matrix methods in the theory of switching. Inter-
International Symposium on the Theory of Switching, Part. II, Annals
Сотр. Lab. Harvard Univ., vol. 30, 1959.
БИБЛИОГРАФИЯ 547
229. Shannon С. Е., Von Neumann's contributions to automata
theory. Bull. Amer. Math. Soc, vol. 64, part 2, 1958.
230. Shannon С. Е., Computers and automata. Proc. IRE, vol. 43,
1953.
231. Shannon C. E., A symbolic analysis of relay and switching
circuits. Trans. AIEE, vol. 57, 1938.
232. Simon J. M., A note on the memory aspect of sequence trans-
transducers. IRE Trans., vol. CT-6, № I, 1959.
233. Simon J. M. Some aspects of the network analysis of sequence
transducers. Journ. Franklin Inst., vol. 65, June, 1958.
234. S r i n i v a s a n С F., N a r a s i m h a n R., On the synthesis of
finite sequential machines. Proc. Indian Acad. Sci., vol. A50, № 1,
1959.
235. S r i n i v a s a n С V., State diagram of linear sequential machi-
machines. Journ. Franklin Inst., vol. 273, 1962.
236. Sucheston L., Note on mixing sequences of events. Acta
Mathematica, Acad. Sci. Hung., vol. 11, fasc. 3—4, 1960.
237. S u t о S., W a t a n a b e Т., The theory of analysis of sequential
time switching circuits. Journ. Inst. Electr. Communic. Engrs.
(Japan), vol. 42, № 6, 1959.
238. Tang D. Т., Analysis and synthesis techniques of oriented com-
communications nets. IRE Trans., vol. CT-8, № 1, 1961.
239. Turing A. M., On computable numbers with an application to
the entscheidungsproblem. Proc. London Math. Soc, vol. 42,
1936—1937. With a correction, vol. 43, 1947.
240. U n g e r S. H., Hazards and delays in asynchronous sequential
switching circuits. IRE Trans., vol. CT-6, № 1, 1959.
241. Urbano R. H., Mueller R. K. A topological method for the
determination of minimal forms of boolean functions. IRE Trans.,
vol. EC-5, № 3, 1956.
242. W a 1 d A. Sequential analysis. John Wiley & Sons, N.-Y., 1947.
243. Wang H a b, Circuit synthesis by solving sequential boolean
equations. Zeitschrift fur Mathematische Logik und Grundlagen
der Math., vol. 5, 1959.
244. Wang Hao, A variant to Turing's theory of computing machi-
machines. JACM, vol. 4, Jan., 1957.
245. Watanabe Sh., 5-symbol 8-state and 5-symbol 6-state univer,
sal Turing machines. JACM, vol. 8, № 4, 1961.
246. Watanabe Sh., On a minimum universal Turing machine.
MCB Report, Tokyo, 1960.
247. W h i t e s i 11 J. E., Boolean algebra and its applications. Addison
Wesley Pub. Co. Inc., 1961.
ДОПОЛНЕНИЕ К БИБЛИОГРАФИИ
248. Айзерман М. А. и др., Преобразование тактности последо-
вательностных машин и синтез релейных схем. Автоматика и
телемеханика, т. XXIII, № 11, 1962.
249. Б е л я к и н Н. В., Об одком классе машин Тьюринга. ДАН
СССР, т. 148, М 1, 1963.
548 библиография
250. Б е р ж К., Теория графов и ее применение. ИЛ, М., 1962.
251. Беркс А., Райт Дж., Теория логических сетей. Кибернетиче-
Кибернетический сборник, № 4, ИЛ, М., 1962.
252. Глушков В. М., Синтез цифровых автоматов. Физматгиз,
М., 1962.
253. Козмидиади В. А., Чернявский В. С, Об упорядоче-
упорядочении множества автоматов. В сб. «Вопросы теории матем. ма-
машин», № 2, 1962.
254. Корпелевич Г. М., О соотношении понятий разрешимости
и перечислимости для конечных автоматов. ДАН СССР, т. 149,
№ 5, 1963.
255. Л е в е н ш т е й н В. И., Об обращении конечных автоматов.
ДАН СССР, т. 147, № 6, 1962.
256. Летичевский А. А., Условия полноты в классе автоматов
Мура. Материалы научных семинаров по теорет. и прикл. вопро-
вопросам кибернетики, т. 1, № 2, 1963.
257. Л у н ц А. Г., Конечные р-адические автоматы. ДАН СССР,
т. 150, № 4, 1963.
258. М о и с и л Г р. К., Алгебраическая теория дискретных автома-
автоматических устройств. ИЛ, М., 1963.
259. Р а б и н М. О., С к о т Д., Конечные автоматы и задачи на раз-
разрешение. Кибернетический сборник, № 4, ИЛ, М., 1962.
260. Сивински Е., Синтез многотактных систем с элементами за-
задержки. Archiwum automatyki i Telemechaniki, torn VII, Zeszyt
1—2, 1962.
261. Спивак М. А., Новый алгоритм абстрактного синтеза автома-
автоматов. Материалы научных семинаров по теорет. и прикл. вопро-
вопросам кибернетики, т. 1, № 3, 1963.
262. Шепердсон Дж. К., Сведение двусторонних автоматов
к односторонним автоматам. Кибернетический сборник, № 4,
ИЛ, М., 1962.
263. Янов Ю. И., О тождественных преобразованиях регулярных
выражений. ДАН СССР, т. 147, № 2, 1962.
264. Arthur M. E., Geometric mapping of switching functions. IRE
Trans., vol. EC-10, № 4, December, 1961.
265. В a r - H i 11 e 1 J., Shamir E., Finite-state .languages: formal
representations and adequacy problems. Bull. Res. Concil Israel,
vol. 8F, 1960.
266. В e a 11 у J., Miller R. E., Some theorems for incompletely
specified sequential machines with application to state minimiza-
minimization. Switching Circuits Theory and Logical Design (Proc. of
the Third Annual AIEE Symposium), September, 1962.
267. Brzozowski J. A., McCluskey E. J., Signal flow graph
techniques for sequential circuit state diagrams. U. S. Govern-
Government Research Reports, vol. 37, 20 May, 1962.
268. Burks A. W., Wright J. В., Sequence generators graphs and
formal languages. Inform, and Control, vol. 5, № 3, September,
1962.
269. E 1 g о t С. С, R u 11 e d g e J. D., Machine properties preserved
under state minitnization. Switching Circuits Theory and Logical
БИБЛИОГРАФИЯ 549
Design. (Ргос. of the Third Annual AIEE Symposium), Septem-
September, 1962.
270. G i n s b u r g S., Rose G. F., A comparison of the work done by
generalized sequential machines and Turing machines. Trans.
Amer. Math. Soc, vol. 103, № 3, 1962.
271. Gr zegorczy к A., Zaris logiki matematycznei, Warszawa,
1961.
272. Hartmanis J., Maximal autonomous clocks of sequential ma-
machines. IRE Trans., vol. EC-11, № 1, 1962.
273. Hartmanis J., Loop-free structure of sequential machines.
Information and Control, vol. 5, № 1, March, 1962.
274. Hartmanis J., The equivalence of sequential machine models.
IEEE Trans., vol. EC-12, № I, February, 1963.
275. Hartmanis J., Stearns R. E., Some dangers is state re-
reduction of sequential machines. Information and Control, vol. 5,
№ 3, September, 1962.
276. J a m a d a H., Disjunctively linear logic nets. IRE Trans., vol.
EC-11, №5, October, 1962.
277. К a u t z W. H., Some unsolved problems in switching theory.
«Switching Circuits Theory and Logical Design» conference paper,
Detroit, October, 1962.
278. Me С luskey E. J. Jr., Minimum state sequential circuits for
a restricted class of incompletely specified flow tables. Bell Sys-
System Technical Journal, vol. 41, № 6, November, 1962.
279. Narasimhan R., Minimizing incompletely specified sequential
switching functions. IRE Trans., vol. EC-10, № 3, September,
1961.
280. N e m i t z W., Reeves R., A mathematical theory of switching
circuits. Mathematical Magazine, vol. 33, № 1, 1959.
281. Shepherdson J. C, Sturgis H. E., Computability of re-
recursive functions. JACM, vol. 10, № 2, April, 1963.
282. W e e g G. P., Finite automata and connection matrices. Commu-
Communications of the ACM, vol. 3, № 7, 1960.
283. W e e g G. P., К a t e 1 e у J., Some properties of strongly connec-
connected machines. Communications of the ACM, vol. 3, № 7, 1960.
284. Z e m a n e к Н., Sequentielle asynchrone logik. Elektronische Re-
chenanlagen, vol. 4, № 6, 1962.
ИМЕННОЙ УКАЗАТЕЛЬ
Аккерман 473
Аль Хорезми 427
Ауфенкамп 302, 308, 318, 322
и д., 340 и д., 389
Блох А. Ш. 61, 195
Гаврилов М. А. 12
Гедель 467, 475, 479
Гилл 347
Глушков В. М. 234, 286, 299, 300
Евклид 427, 431 ид.
Казаков В. Д. 77
Карацуба 412
Квайн 79, 81
Клини 228 и д., 284 и д., 526,
529
Кабринский Н. Е. 119
Кузнецов О. П. 285
Мак-Каллок 151, 152
Марков А. А. 435, 441, 444 и д.,
488
Мили 100
Мур 100, 323, 400, 401, 403, 412,
418
Новиков П. С. 435
Петер Р. 437, 474, 486
Питтс 151» 152
Пост Э. 447, 448
Райе 281
Трахтенброт Б. А 119, 281 и д.,
529
Тьюринг 366, 497 и д., 527
Хафмен Д. 177, 180 и д., 393 и д.
Хон 308, 322 и д., 389
Цейтин Г. С. 448, 449
Чёрч А. 306, 487, 523
Шестаков В. И. И
Шэннон К- Э. 11
Эрбран 475, 479
Эренфест П. 11
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абстрактная агрегатизация 149
— нейронная сеть 151
— структура конечного автома-
автомата 131
логическая 134
Я-машины 211
Абстрактный синтез 256
Агрегатное построение конечных
автоматов 161, 178
Я-машины 161
Алгебра логики 37
Алгоритм 432, 450, 488, 496, 523
— Ауфенкампа (построение псев-
псевдоотображения) 341, 342, 351
— Ауфенкампа и Хона (миними-
(минимизации) 308, 324, 389
.достаточность 312
.необходимость 315
— в алфавите А 441
эквивалентный 443
— воспроизведения Я-машины в
тактности смены входа (алго-
(алгоритм размножения состояний)
377, 380
— Гилла (минимизации) 347
— Евклида 427, 453
— замены группы эквивалентных
состояний 329
— Квайна 81
— логический 428, 451
— минимизации Я-машины 329,
334, 339
— несуществования 449
— нормальный 444
— перебора подстановок 439
— полного перебора (распозна-
(распознавание эквивалентности) 319
— построения диаграммы со-
состояний 408
Алгоритм построения экспери-
эксперимента, отличающего одну ма-
машину из множества 420
— распознавания 306, 453
выводимости 440
— самоприменимый 448
— «стирания стрелок» в диа-
диаграмме состояний 357
— численный 428, 451
Алгоритма детерминированность
432
— массовость 432
— целенаправленность (примени-
(применимость) 433
Алгоритмическая неразрешимость
448, 488
проблемы распознавания
самоприменимости 449
Алфавит 15, 435
— выходной 98
Ассоциативное исчисление 436 "
Буквы 435
— функциональные 477
Возвратная кнопка 398
Воспроизведение Я-машины 368
в тактности смены входа
376
, пример 373
Временная зависимость 172
Временной вход 95
Вхождение слов 436
Вывод 477, 478
Выводимость 477
Выходной преобразователь 98
Вычисление на машинах Тьюрин-
Тьюринга 512
552
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Вычислимость
функций 457
элементарных
Гёделизация 451 472
Генерирование периодических по-
последовательностей 198
Граф автономного автомата 101
— регулярного выражения 287
, входящие стрелки 293
, ложные пути 289
, пустые стрелки 291
Дерево контактной сети 62
Диаграмма состояний 103
объединенной Я-машины
406
и°-связной машины 408
эквивалентной машины 356
Дизъюнктивная нормальная фор-
форма 34
— минимальная 79
совершенная 34
Дизъюнкция 27
Дискретное время 87
Естественная задержка 171
Задание на проектируемое уст-
устройство 257, 528
— на языке регулярных выраже-
выражений 285
— противоречивое 261
— соответствий между последо-
последовательностями 258
Задержка на такт 137, 162
пневматическая 164
Замещение конечных автоматов
125
— относительное 124
-г- Я-машин 123
Записывающая головка 497
.стандартное положение513
Запрет 27
Изображение Я-машин 363, 364
, пример 370
Импликанты простые 79
Импликация 27
Исключенное ИЛИ 27
Исчисление высказываний 20,
440
Исчисление высказываний, алге-
алгебра 36
— предикатов 41, 440
узкое 44
Квантор 42
— общности 42
ограниченный 468
*— существования 42
ограниченный 468
Конечная динамическая система
91
Конечные автоматы 92
автономные 96, 197
, агрегатное построение 161
, входы 92
,итерация 239
, объединение 238, 406
с выходным преобразова-
преобразователем (с выходом) 98
, синтез 527
, состояния 92
Типа П—Н 92, 183
типа П—П 92, 183
, умножение 238
Конструктивная математика 490
Контактная сегь 50
Контакты нормально-замкнутые
47
— нормально-разомкнутые 47
— эквивалентные 50
Конъюнктивная нормальная фор-
форма 34
минимальная 81
:— совершенная 34
Конъюнкция 27
Критические состязания в ре-
лейно-контактных схемах 179
Лабиринт 429
— бесконечный 437
Лента входная 219
—.заполнение правильное 271
— конечного автомата ПО
— машины Тьюринга 496
— Я-машины 112
Линия задержки 142, 173, 373
Логическая функция 15, 456
абсолютно минимальная 82
выполнимая 36
неоднородная 41
предметный указатель
553
Логическая функция однород-
однородная 16
тождественно истинная 36
тождественно ложная 36
Логический преобразователь 86
Логическое пространство 21
Математическая логика 11
Матрица путей длины q 114
— соединений, возведение в сте-
степень 115, 319
конечного автомата 104
/7-машины 108
— —, симметричное разбиение
310
— сокращенная по L 321
Машины Тьюринга 91, 366, 496
, внутреннее состояние 497
— —..возведение в степень 508
, итерация 509
, композиция 506
, состояние покоя 492
, умножение 508
, управляющее устройство
497
Мгновенная функция 172
Метод Гёделя 452
— Глушкоза 286
, графическая интерпретация
285
— Хафмана 177, 180, 394
Минимизация 264, 530
— воспроизводящей /7-машины
383
— /7-машины 328, 329
при ограничениях типа
Ауфенкампа 340, 347
, работающей как автомат
333
г— устройств, реализующих ло-
логические функции 77
Множества 12
— исходные 229
—,итерация 226
—, объединение 224
— регулярные 229
входных лент 233
— рекурсивно-перечислимые 493
— рекурсивные 493
—, умножение 224
— универсальные 229
Набор полный 149, Л68
Нейрон 151
— Мак-Каллока и Питтса 151
, возбуждающее оконча-
окончание 151
, возбуждающий вход
151
, тормозящее окончание
151
, тормозящий вход 151
, условия функционирот.
— вания 152
Нейронная сеть 151
Нитка входа 130
Номер 452
— записи решений 452
условий 452
Нормальный алгоритм (Марко-
(Маркова) 444, 455
, примеры 445
Обратная связь 52, 173
Объединенная /7-машина 406
Ограничения на входные после-
последовательности 301
в себе 303
типа Ауфенкампа
302, 325, 341, 395
, переход от одного
типа к другому 356
Один-матрица 310
—.обобщенная 341
—, объединение элементов 332
Однотактные схемы на диодах
64
на магнитных элементах 68
на пневмореле 72
на триодах 66
Оператор наименьшего числа 480,
520
ограниченный, 466, 469
Операция индукции 520
— приписывания символов 117
— суперпозиции 520
Основная таблица конечного ав-
автомата 101
Я-машины 106
Относительная эквивалентность
304
Относительное воспроизведение
368
554
Лредметный указатель
Относительное изображение
365
Отношения 18
Отображение Я-машин 326
Отрицание 25
Оценка длины эксперимента, оп-
определяющего последнее со-
состояние 412, 414
, отличающего одну ма-
машину из множества 418
• , устанавливающего не-
неэквивалентность состояний
401, 403, 406
Переменная независимая 12
— свободная 467
— связанная 467
Переходный процесс 176
Подстановки, допустимая систе-
система 442
— ориентированные 438
—, схема 462
Последовательностная машина
(Я-машяна) 97, 98
автономная 197
, синтез двоичной струк-
структуры 205
, агрегатное построение 161
• минимальная относительно
L 328
, преобразование 363
сильно связная 411
, синтез 527
х°-связная 408
типа П—Н 99, 182
типа П—П 99, 182
Последовательность в конечном
счете периодическая 249
— входная 110
.переработка 218
— выходная 110
—, длина 110
— допустимая 120, 302, 326
— ограниченная 301
— пустая 227
— рекурсивная 491
— состояний 110
—, сходящаяся рекурсивно 491
Построение машины на устойчи-
устойчивых (равновесных) состояни-
состояниях 177, 178, 180, 185
Предикаты 17, 466
— арифметические 467 •
— двузначные 41
я-местные 41, 467
— двуместные 18
— одноместные 18
— примитивно-рекурсивные 467
— разрешимые 456
Предмет 17
Представимость регулярных со-
событий 234
Представление событий 223
Представляющая функция преди-
предиката 467
Преобразование тактности 175,
363, 364
Примитивно-рекурсивное описа-
описание 463
Проблема анализа Я-машин 304
— разрешимости 36
— распознавания 256
, алгоритмическая неразре-
неразрешимость 281, 283
эквивалентности состояний
305
— слов (проблема достижимо-
достижимости) 438
ограниченная 439
Псевдоотображение Я-машин
340
Псевдоэквивалентные состояния
325, 342
группы 325, 349
Равенства 477, 478
—, определяющая система 479,
482
Равнозначность 27
Разбиение множества состояний
на группы эквивалентных от-
относительно эксперимента дли-
длины q 401
Реакция Я-машины 398
Реализация релейно-контактных
схем 179
по Хафману 193
Регулярность представимых со-
событий 241
Регулярные выражения 231
, глубина 231
предметный указатель
555
Результат эксперимента 398
Рекурсивная функция 281, 282
, представление 282
Рекурсивные действительные чис-
числа 491
— последовательности 281
Реле промежуточное 178
— электрическое многообмоточ-
многообмоточное 49
Релейно-контактные схемы 11
однотактные 47
, анализ 53
, минимизация 79
, синтез 59
, устойчивые (равновесные)
состояния 176
Свойства 18
Сеть 140
— без петель 141
— задержек 140
Символ равновесный 199
Синтез конечных автоматов 527
при задании регуляр-
регулярных выражений 285
соответствий ме-
между последовательностями
258
— технических устройств, реали-
реализующих машину 160, 527
Следствие 441
Слова 435
—, дедуктивная цепочка 437
—, преобразование 436
— смежные 436
— эквивалентные 437, 440
Собственное разбиение состоя-
кий 350
минимальное 351
, перебор 351
Событие 219
— нерегулярное (непредстави-
(непредставимое) 247
— определенное 233
—, порожденное рекурсивной
функцией 281
— регулярное 233
— рекурсивное 281
Совместимые состояния 325
Состояние 92
Состояние начальное 146
— последнее 412
Стрелка Пирса (функция Даг-
гера) 27
Считывающая головка 497
, стандартное положение
513
Таблица быстрой Я-машины 188
— исходная 185
— переходов 186, 393
.сжатие (сокращение) 188
— преобразователя 106
— релейной схемы 190
— соответствия 22
общая 23
Такт 87, 95
Тактность быстрая 157, 175,
363
— медленная 157, 174, 363
—,определяемая сменой входов
174
—,преобразование 175
Тезис Чёрча 306, 487, 488
Теорема Ауфенкампа 342, 346
— Клини первая 234
вторая 241
— Мура 323, 400, 401, 403
— Мура—Карацубы 412
— Трахтенброта 283
Теория численных
130
Терм 477, 478
Техническая реализация 160
Триады 105
—, лабиринт 241
— противоречивые 112
—, путь в лабиринте 242
—, регулярное множество цепо-
цепочек 243
— соответствующие 112
—.упорядоченное множество 105
Триггер 370
— пневматический 171
¦«»
Функциональная зависимость 12
Функциональный преобразова-
преобразователь 86
Функция 12
— арифметическая 455
вычислимая 456
алгоритмов
556
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Функция арифметическая вычис-
вычислимая, пример построения 473
элементарная 457
—. включения 473
— общерекурсивная 475, 479, 483
явная форма 481
— первоначальная 461
— «-переменных 15, 31
— примитивно-рекурсивная 462,
470.
— рекурсивная 281, 282
— следования 460, 518
— тождества 462, 518
— Шеффера 27
Функция-константа 25, 462, 518
Цикл 199
Часы (датчик тактов, сигнализа-
сигнализатор тактов) 95, 195, 366
Штрих Шеффера 27
Эквивалентность Я-машин 326,
353
сильная 326, 354
сильно связных 412
— — слабая 353, 354
— состояний 303
Эквивалентность состояний, ал-
алгоритм распознавания при ог-
ограничениях' на входные по-
последовательности 308
, алгоритмическая неразре-
неразрешимость проблемы распозна-
распознавания 305
начальных 353
, определение по реакции на
эксперименты 400
относительно множества L
последовательностей 305
при ограничениях на дли-
длину входных последовательно-
последовательностей 319
Эквивалендия 27
Эксперимент 397
— кратный 398, 407
— простой неразветвлённый 398,
411, 423
разветвленный 398, 418
Элемент агрегатного набора 149
— задержки 137, 162
Эффективное задание событий
280
Язык задания 257
— предикатный 284
— регулярных выражений 285
Ячейка памяти пневматическая
164