Вычислительные методы. Том 2 - Крылов В.И., Бобков В.В., Монастырный П.И.

Автор: Крылов В.И. Бобков В.В. Монастырный П.И.
Теги: математика вычислительная математика
Год: 1977
Похожие
Вычислительные методы высшей математике Т.1
Численные методы
Линейная алгебра
Динамическое программирование
Текст
                    В. И. КРЫЛОВ, В. В. БОБКОВ,
П. И. МОНАСТЫРНЫЙ
ВЫЧИСЛИТЕЛЬНЫЕ
МЕТОДЫ
ТОМ II
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебного пособия
для студентов высших учебных заведений
4)
ш
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1977

518
К 85
УДК 519.95
Вычислительные методы, том II. В. И. Крылов,
В. В. Бобков, П. PL M о н а с т ы р н ы и. Главная
редакция физико-математической литературы изд-ва
«Наука», М., 1977.
Книга является второй частью пособия,
предназначенного для студентов высших технических учебных
заведений, физических и механико-магематических
факультетов университетов. Она может служить
справочником для всех лиц, которым приходится иметь дело
с научными и техническими расчетами.
В книге содержится изложение методов решения
обыкновенных дифференциальных уравнений,
дифференциальных уравнений с частными производными и
интегральных уравнений. Приведены также наиболее часто
применяемые методы ускорения сходимости рядов и
последовательностей. Кроме того, дано краткое
изложение некоторых вопросов общей теории
вычислительных методов на основе функционального анализа.
20204—068 © Главная редакция
К ~ 10-77 физико-математической литературы
053@2)-77 издательства «Наука», 1977

ОГЛАВЛЕНИЕ
Предисловие 7
Глава 6. Решение обыкновенных дифференциальных
уравнений
§ 1, Методы решения задачи Коти. Вводные замечания ... 10
§ 2. Построение одношаговых методов способом разложения
решения в ряд Тейлора 14
1. Пошаговый вариант метода рядов A4), 2.
Видоизменение метода рядов, не требующее вычисления
производных правой части уравнения A5).
§ 3. Способ Рунге — Кутта построения одношаговых методов 21
§ 4. Построение вычислительных правил на основе принципа
последовательного повышения порядка точности
результата ... 32
1. Случай уравнений первого порядка C2). 2. Случай
уравнений высших порядков C8).
§ 5. Сходимость одношаговых методов 42
§ 6. Главный член погрешности. Правило Рунге 53
§ 7. Методы типа двусторонних . ; 59
§ 8. Многошаговые методы 72
1. Экстраполяционные методы Адамса G4). 2.
Интерполяционные методы Адамса G9). 3. Методы с забеганием
вперед (85).
§ 9. Решение линейных граничных задач 93
1. Постановка задачи. Понятие о многоточечных и
граничных задачах (93). 2. Метод дифференциальной
прогонки (95).
§ 10. Решение нелинейных граничных задач 100
1. Метод редукции к задачам Коши A01). 2. Метод
линеаризации A04).
§ 11. Метод сеток для решения линейных граничных задач . . 107
1. Постановка задачи. Идея метода сеток A07). 2. Методы
замены обыкновенных дифференциальных уравнений и
граничных условий системой алгебраических уравнений
A08). 3. О разрешимости систем разностных уравнений
A11). 4. Метод ортогональной прогонки (ИЗ). 5. Оценка
погрешности и сходимость метода сеток A17).
§ 12. Метод Галеркина и метод моментов 120
§ 13. Метод наименьших квадратов и метод Ритца 129
Литература 140
1*

4
ОГЛАВЛЕНИЕ
Глава 7. Решение дифференциальных уравнений
в частных производных
§ 1. Разностные схемы, основные понятия 141
1. Сходимость и аппроксимация разностных схем A42).
2. Связь аппроксимации и устойчивости со сходимостью A45),
§ 2. Разностные схемы для уравнений параболического типа . . 146
1. Решение задачи Коши A46). 2. Об устойчивости
двухслойных разностных схем A51). 3. О разностных схемах
расщепления A55). 4. Решение смешанных граничных
задач A59). 5. Необходимое спектральное условие
устойчивости Неймана A62). 6. Экономичные разностные
схемы A65).
§ 3. Разностные схемы для уравнений эллиптического типа . . 175
1. Построение разностных аппроксимаций для уравнений '
A76). 2. Аппроксимация граничных условий A80). 3.
Построение разностной схемы в случае задачи Дирихле для
уравнения Пуассона A83). 4. Об устойчивости разностной
схемы B0) A84). 5. Метод матричной прогонки A88).
6. Правило Рунге A91). 7. Метод итераций для разностной
задачи Дирихле A92).
§ 4. Разностные схемы для уравнений гиперболического типа . . 201
1. Решение задачи Коши B03). 2. Решение смешанной
задачи B08). 3. Об устойчивости явной трехслойной
разностной схемы B10).
§ 5. Метод характеристик , 215
1. Характеристики дифференциального уравнения B15).
2. Построение сетки характеристик B21). 3. Нахождение
характеристических полосок B24).
§ 6. Метод прямых 228
1. Поперечные схемы метода прямых для уравнений
параболического типа B29). 2. Продольные схемы метода
прямых для параболических уравнений B34). 3. Метод
прямых для уравнений гиперболического типа B38). 4. Метод
прямых для эллиптических уравнений B41).
§ 7. Метод интегральных соотношений 244
§ 8. Понятие о методе моментов и методе Галёркина 248
Литература 251
Глава 8. Численное решение интегральных уравнений
§ 1. Введение 252
§ 2. Уравнения вольтеррова вида второго рода 258
1. Вид вычислительного правила и теорема о сходимости
вычислительного процесса B58). 2. Правила вычислений,
основанные на формуле Эйлера—Маклорена B64).
§ 3. Уравнения Фредгольма второго рода. Метод квадратур . . 266
1. Метод квадратур B67). 2. Сходимость метода квадратур
B73). 3. Интерполяционный квадратурный метод B75).
§4. Метод замены ядра уравнения на вырожденное ядро . . . 278
1. Некоторые сведения об уравнениях с вырожденным ядром
B78). 2. Замечания о методах построения вырожденного

ОГЛАВЛЕНИЕ
5
ядра, близкого к ядру уравнения B80). Оценка близости
между решениями уравнений в зависимости от близости
самих уравнений B82).
Литература 285
Глава 9. Улучшение сходимости рядов
и последовательностей
§ 1. Введение 286
1. О задаче улучшения сходимости B86). 2. Связь с
проблемой суммирования расходящихся рядов и определения
пределов расходящихся последовательностей B89).
§ 2. Интерполяционные методы преобразования
последовательности ; 297
1. Некоторые общие сведения B97). 2. Интерполирование
при помощи многочленов от 1/я. Случай постоянного числа
узлов C01). 3. Некоторые типы сходимости C08). 4.
Вспомогательная лемма C09). 5. Некоторые теоремы об
ускорении сходимости C12). 6. Интерполяционные методы
преобразования с возрастающим числом узлов C14). 7.
Обращение преобразования C16). 8. Теорема об ускорении
сходимости C20).
§ 3. Улучшение сходимости последовательностей, для которых
погрешность приближения к пределу близка к
показательной функции или линейной комбинации таких функций . . 325
1. Простейшее правило преобразования и некоторые его
свойства C25). 2. Об улучшении сходимости C27). 3.
Применение 62-преобразования к улучшению сходимости и
аналитическому продолжению степенного ряда C29).
4. Связь с методом интерполирования предельного
значения C31). 5. О пути уточнения 62-преобразования C33).
6. Правило ускорения сходимости последовательности, для
которой погрешность приближения к пределу близка к
линейной комбинации показательных функций C35). 7.
Теорема об ускорении сходимости C42). 8. Об улучшении
сходимости и аналитическом продолжении степенного ряда
мероморфной функции C49).
§ 4. Улучшение сходимости ряда с помощью выделения медленно
сходящейся части 351
1. Введение C51). 2. Числовые ряды. Случай убывания
членов ряда по степенному закону C52). 3. Улучшение
сходимости тригонометрического ряда C55).
Литература 357
Глава 10. Применение функционального анализа к построению
теории некоторых разделов вычислительной математики
§ 1. Необходимые сведения из функционального анализа . . , 358
1. Метрические пространства. Сходимость и полнота C58).
2. Линейные нормированные пространства. Линейные
операторы C61). 3. Дифференцирование нелинейных
операторов C65).

6
ОГЛАВЛЕНИЕ
§ 2. Метод итерации для решения операторных уравнений . . 371
1. Метод итерации для операторных уравнений C72). 2.
Теоремы о сходимости и единственности C73). 3. Приложение
к системам уравнений с числовыми неизвестными C76).
§ 3. Метод Ньютона для операторных уравнений 380
1. Правило построения приближений к решению C80).
2. Теорема о сходимости последовательности
приближений C81).
§ 4. Задача упрощения уравнений 387
1. Введение C87). 2. О разрешимости приближенного
уравнения C89). 3. Оценка погрешности приближения и
условия сходимости C92).
Литература 394
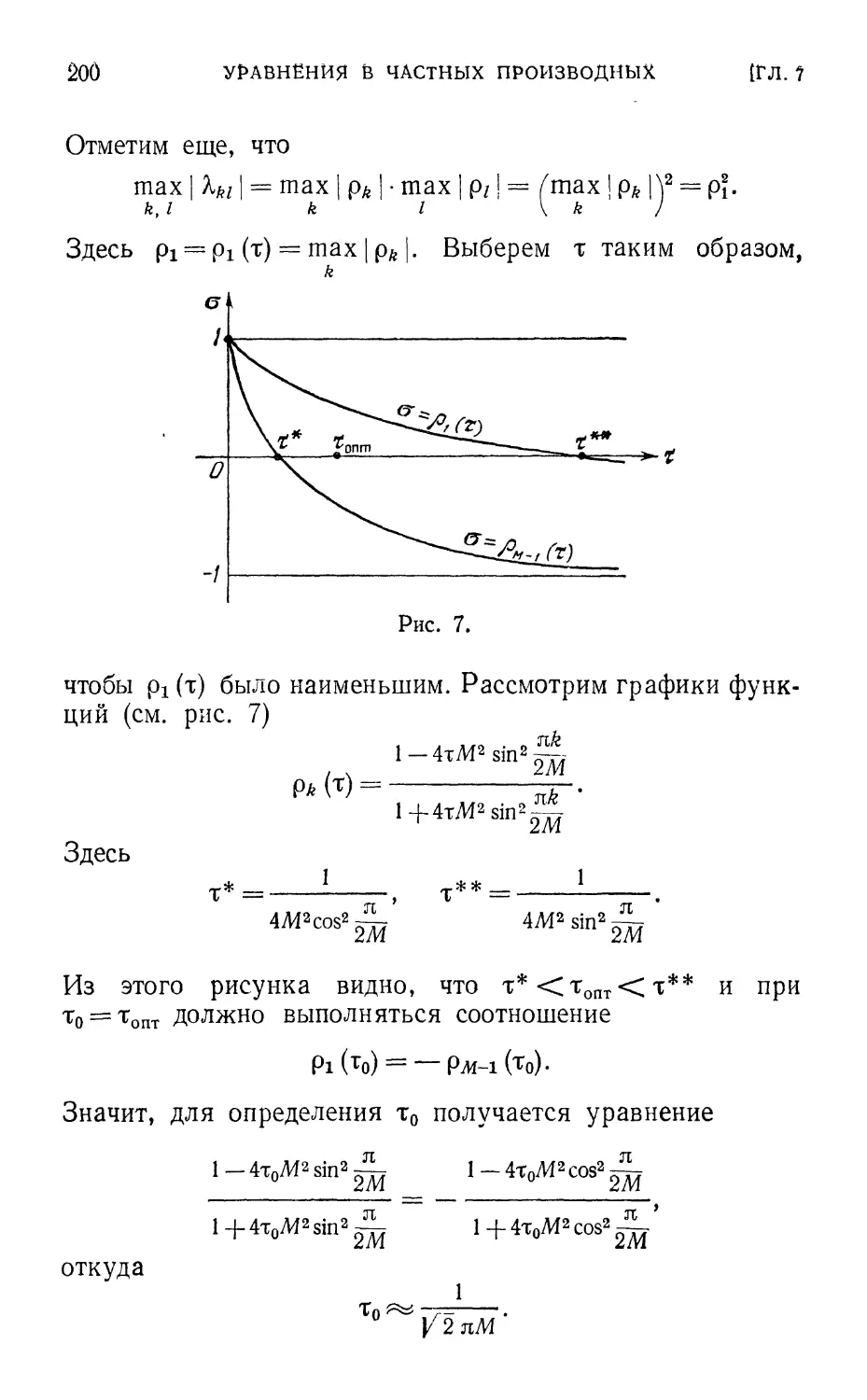
Указатель обозначений 395
Предметный указатель 396

ПРЕДИСЛОВИЕ
Главы 6 и 7, занимающие большую часть книги,
посвящены изложению основных сведений из теории численного
решения дифференциальных уравнений. Такие уравнения
имеют очень широкую область применения и лежат в
основании многих разделов теоретической и, особенно,
прикладной науки. Вид дифференциального уравнения тесно
связан с природой исследуемого явления, и уравнения
могут различаться между собой по их порядкам, по числу
переменных, по типам, зависящим от того, будет ли процесс
установившимся или развивающимся, по дополнительным
условиям — будут ли они начальными, граничными или
смешанными, по особенностям, вид которых зависит от
характерных свойств процесса и т. д. Этот перечень
приведен, чтобы пояснить, насколько многообразными могут
быть дифференциальные уравнения, встречающиеся в
приложениях. Для задачи каждого вида должны быть развиты,
как правило, свои методы решения, и поэтому проблема
численного решения уравнений является весьма
разветвленной.
Учебная книга обязана быть в какой-то мере
универсальной и должна содержать изложение всех основных
и наиболее часто применяемых методов. Добиться же
этого на небольшом числе страниц можно, если только
отказаться от полного изложения и ограничиться
описанием лишь идей методов и начал их теории. Чтобы не
увеличивать принятый объем книги, авторы вынуждены
были опустить или изложить очень кратко многие важные
вопросы. Например, в проблеме сходимости
последовательности приближенных решений к точному авторы могли
рассмотреть только простейшие случаи.. Теория конечно-
разностных методов решения уравнений с частными
производными, ввиду очень большого значения их в
приложениях математики, за последние два десятилетия разраба-

а
ПРЕДИСЛОВИЕ
тывалась особенно интенсивно, и здесь были получены
многие важные результаты, авторы же имели возможность
включить в книгу лишь основные понятия и некоторые
простейшие факты. В очень сжатом виде изложены также
вопросы приближенного решения интегральных уравнений.
Для уравнений, содержащих интегралы с переменной
границей, дано описание общей вычислительной схемы
и приведена только одна конкретная вычислительная
схема, основанная на формуле Эйлера — Маклорена.
Несколько более подробно рассмотрены уравнения
с интегралами, имеющими фиксированные границы
интегрирования. Для них были избраны два метода: метод
квадратур и метод замены ядра уравнения К(х, s) на
так называемое вырожденное ядро.
В книгу включены также вопросы ускорения
сходимости рядов и последовательностей. Авторы избрали здесь
три следующие задачи.
1. Методы ускорения сходимости последовательностей,
основанные на алгебраическом интерполировании
предельного значения.
2. Методы, предназначенные для ускорения сходимости
последовательностей, стремящихся к пределу по закону,
близкому к изменению показательных функций или их
линейных комбинаций.
3. Ускорение сходимости рядов при помощи выделения
медленно сходящейся части.
Наконец, авторы считали полезным хотя бы кратко
описать, как может быть применена теория операторов
к построению общей теории приближенных и, в частности,
численных методов математики.
Параграфы 1 — 8 главы 6 и §§ 5 — 7 главы 7 написаны
В. В. Бобковым, §§ 9— 13 главы 6 и §§ 1 —4, 8 главы 7
написаны П. И. Монастырным. Весь остальной текст
книги принадлежит В. И. Крылову.
Авторы

ГЛАВА 6
РЕШЕНИЕ ОБЫКНОВЕННЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Среди задач, с которыми приходится иметь дело
в вычислительной практике, значительную часть
составляют различные задачи для обыкновенных
дифференциальных уравнений. Такие задачи возникают как
непосредственно при математическом моделировании многих
реальных явлений, так и в качестве промежуточных при
решении ряда более сложных математических задач.
При этом, как правило, точное решение рассматриваемой
задачи не удается выразить через элементарные функции.
Доля задач, решаемых в явном виде, в случае
обыкновенных дифференциальных уравнений ничтожно мала.
Обычно приходится прибегать к помощи приближенных
методов решения подобных задач. Такие методы в
зависимости от того, ищется ли приближенное решение
в аналитическом виде или в виде таблицы чисел, часто
разделяют на аналитические и численные. Подобное
разбиение методов на две группы основано на достаточно
грубых признаках и носит общий характер. Конкретный
вид метода существенно зависит прежде всего от типа
решаемой дифференциальной задачи. В случае
обыкновенных дифференциальных уравнений в зависимости от
того, ставятся ли дополнительные условия в одной
или в нескольких точках отрезка изменения
независимой переменной, задачи обычно подразделяют на
одноточечные (задачи с начальными условиями, или задачи
Коти) и многоточечные. Среди многоточечных задач
наиболее часто в прикладных b вопросах встречаются
так называемые граничные задачи, когда
дополнительные условия ставятся на концах рассматриваемого
отрезка.

10 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
Наиболее простой из указанных выше задач является,
вообще говоря, задача Коши. Заметим, что нередко
решение многоточечных и, в частности, граничных задач
сводят к решению задач с начальными условиями. Задачи
Коши очень важны для приложений и в книге им уделено
много внимания.
Рассмотрение методов решения обыкновенных
дифференциальных уравнений мы начнем со случая задачи
Коши для уравнений первого порядка.
§ 1. Методы решения задачи Коши.
Вводные замечания
Для простоты изложения основных идей
вычислительных методов решения задач с начальными условиями
будем рассматривать, как правило, случай одного
обыкновенного дифференциального уравнения первого порядка.
Обычно эти идеи легко переносятся на системы
уравнений первого порядка и сравнительно просто обобщаются
на случай уравнений высших порядков.
Пусть на отрезке х0^х^Х требуется найти
решение у(х) дифференциального уравнения
y'=f(x,y), A)
удовлетворяющее при х = х0 начальному условию
У(*о) = Уо- B)
Условия существования и единственности решения
поставленной задачи Коши будем считать выполненными. Будем
предполагать также, что функция / (х, у) в некоторой
области изменения ее аргументов обладает необходимой
по ходу изложения дополнительной гладкостью.
Основной нашей целью на данном этапе будет построение
вычислительных правил нахождения приближенного
решения рассматриваемой задачи.
Из общего курса обыкновенных дифференциальных
уравнений хорошо известен метод последовательных
приближений, или метод Пикара приближенного решения
задачи A), B). Этот метод позволяет получать в
аналитическом виде последовательность приближений ут(х),
т=1, 2, ..., к решению у(х) рассматриваемой задачи

§п
МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ КОШИ
11
Коши по следующему итерационному правилу:
х
Ут (X) = Уо + \ f [/, Ут-i (t)] dt, Xo < X < X,
0о(О=#о> *<></<*, т=*1, 2, ...
Метод Пикара, однако, редко используется в практике
вычислений. Одним из его существенных недостатков,
препятствующих широкому практическому применению
метода, является необходимость выполнения операции
интегрирования при осуществлении каждой итерации.
Несколько более широкое распространение в
вычислительной практике получил другой аналитический
метод, основанный на идее разложения в ряд решения
рассматриваемой задачи Коши. Особенно часто для этих
целей используют ряд Тейлора. В этом случае
вычислительные правила строятся особенно просто.
Приближенное решение ут (х) исходной задачи ищут в виде
т
Ут (X) = 2 "^ТГ^ У[{) М- Х° < Х < Х> W
t = 0
где
У{0) (х0) = у (х0) = у0, у[1) (х0) = у' (х0) = / (х0, Уо),
а значения у{п (х0), / = 2, 3, ..., т, находят по
формулам, полученным последовательным дифференцированием
уравнения A):
У{2) (х0) = у" (х0) = fx (х0, у о) + / (х0, у о) fy (х09 у о),
У{3)(Хо)-У'"(Хо)-!хЛхо, Уо) +
+ 2/ (Х0, Уо) fXy (Хо, Уо) + /а (*о, Уо) /> (*о> У о) +
+ fy (Xo, Уо)\[х(Хо, yo)+f(x0f yo)fy(Xof УьI D)
У{т) (Хо) =
= Рщ (У; fx, fy\ /x2, /^, //,...; /^-i, ..., fym-i)x==:XQt у^Уо
(конкретный вид многочлена Fm не приведен из-за
громоздкой записи). Для значений х, близких к х0, метод
рядов C) при достаточно большом т дает обычно
хорошее приближение к точному решению у(х) задачи A),

12 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
B). Однако с увеличением расстояния \х — х0\
погрешность приближенного равенства у (х) я^ ут (л:), вообще
говоря, возрастает по абсолютной величине и правило C)
становится вовсе неприемлемым, когда х выходит
из области сходимости соответствующего C) ряда
Тейлора.
Предпочтительными в таких случаях будут,
например, численные методы решения задачи Коши,
позволяющие в некоторых попарно близких друг другу
фиксированных точках (узлах)
*о < *i < *2 < • • • < *n = X E)
последовательно находить значения уп^у(Хл), п =
= 1,2,...,//, приближенного решения. Сходимость методов
подобного типа не так жестко связана с длиной отрезка
[х0, X], и их чаще кладут в основу стандартных
программ для ЭВМ. Таким методам ниже будет уделено
основное внимание.
Большинство численных методов решения
рассматриваемой задачи Коши можно привести к виду
Уп+1 — F (Уп-qj Уп-д+Ъ • • • » Уп> Уп+Ъ • • • » Уп+sjy F)
где У7 —некоторая известная функция указанных
аргументов, определяемая способом построения метода и
зависящая от вида уравнения A) и избранной сетки E).
При g = 0, O^s^l такие вычислительные правила
обычно называют одношаговыми, а при q^ 1 или s> 1 —
многошаговыми. Как одношаговые, так и многошаговые
методы вида F) называют явными в случае s = 0 и
неявными при s=l. В случае s>l многошаговые правила
часто называют методами с забеганием вперед. С
примерами правил указанных типов, особенностями их
использования и основными способами построения мы
познакомимся несколько позже, а сейчас сделаем лишь несколько
замечаний общего характера.
Если правило F) является одношаговым, то
вычисления по этому правилу можно начинать со значения п = 0
и проводить до значения n = N—l включительно. В
случае же многошаговых методов указанного вида
дискретный аргумент п может пробегать значения лишь от n = q
по n = N — s, что, вообще говоря, влечет за собой
нарушение однородности вычислительного процесса и требует

§13
МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ КОШИ
13
применения специальных вычислительных правил для
нахождения первых q значений уъ у2, ..., yq
приближенного решения и последних его s — 1 значений г/лг-5+2>
yN-s+3> . ••, Уы- Одношаговые методы в этом отношении
являются предпочтительными. Удобнее пользоваться ими
и в том случае, когда шаг сетки hn = xn+i — xn не
является постоянным для всех значений п (скажем, величина
шага интегрирования выбирается ЭВМ автоматически
по результатам вычислений). Вид одношаговых правил
не связан с величиной шага на предыдущем этапе
вычислительного процесса и поэтому эти правила легко
допускают изменение шага численного интегрирования,
в то время как многошаговые методы нужно
специальным образом приспосабливать для этих целей. Полезно
также иметь в виду, что при построении многошаговых
методов (в силу их вида) должна использоваться
информация об исходной задаче Коши на отрезке [xn-gi xn+s],
в то время как в случае одношаговых правил подобную
информацию нельзя привлекать за пределами отрезка
[хп, хп+1]. Это предопределяет концентрирование такой
информации на малом отрезке в случае одношаговых
методов и рассредоточение ее на отрезке длиной в
несколько шагов интегрирования в случае многошаговых
правил. Последние соображения дают основания
ожидать, что в областях резкого изменения поведения
функций предпочтительнее будут методы, при построении
которых информация о таких функциях (при сохранении
ее количества) привлекалась бы более концентрировано.
Эти же соображения поясняют и основной недостаток
одношаговых методов (в сравнении с многошаговыми),
связанный с их трудоемкостью. Так как в случае одно-
шаговых правил информация о решаемой задаче
используется лишь в пределах одного шага, то при переходе
от шага к шагу ее, вообще говоря, нужно каждый раз
заново получать, в то время как в случае многошаговых
методов предоставляется возможность повторного
использования части такой информации на нескольких
соседних этапах вычислений, что позволяет уменьшить затраты
вычислительного труда на каждый шаг численного
интегрирования. Трудоемкость одношаговых методов долгое
время была основным препятствием на пути их
широкого практического применения. До появления вычисли-

14 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
тельных машин такие методы чаще использовались лишь
для построения начала таблицы, а основной счет
выполнялся обычно с помощью многошаговых методов. С
ростом быстродействия ЭВМ область применения одноша-
говых правил быстро расширяется. С рассмотрения таких
правил мы и начнем изложение основных численных
методов решения задачи Коши.
§ 2. Построение одношаговых методов способом
. разложения решения в ряд Тейлора
1. Пошаговый вариант метода рядов. Будем считать,
что процесс решения задачи A.1), A.2) доведен до
точки хп @^n<.N), и известно (точно или приближенно)
соответствующее значение у(хп) искомого решения.
Построим вычислительное правило для нахождения значения
решения в очередной узловой точке xn+1 = xn + hn сетки
A.5). Поскольку при построении одношаговых методов
используется информация о решаемой задаче лишь в
пределах одного шага интегрирования, то можно без ущерба
для понимания не писать индекс, означающий номер
шага процесса.
Чтобы по известному значению у (х) соответствующего
решения дифференциального уравнения A.1) в узловой
точке х^х0 найти значение этого решения в очередной
точке x + h сетки A.5), можно, очевидно,
воспользоваться вычислительным правилом типа A.3), положив
там х0 = х и взяв вместо текущей точки х отрезка [х0, X]
узловую точку x + h. Это позволит записать
приближенное равенство т
ym(x + h)^ 2li У(,)М' W
которое может быть положено в основу
соответствующего одношагового метода, если для вычисления
значений y{i) (х), / = 2, 3, ..., т, использовать формулы типа
A.4). При условии, что данное решение уравнения A.1)
имеет на рассматриваемом отрезке непрерывную
производную порядка т+1> погрешность приближенного
равенства A) будет, очевидно, величиной порядка hm+x
и при малых /i>0 и больших т построенный
пошаговый вариант метода рядов будет давать, как правило,

§2]
РАЗЛОЖЕНИЕ РЕШЕНИЯ В РЯД ТЕЙЛОРА
15
достаточно хорошее приближение к искомому значению
решения. Привлекательной чертой полученного
вычислительного метода является то обстоятельство, что искомое
значение приближенного решения (см. A)) разложено
по последовательным главным частям, что позволяет
в процессе решения задачи без дополнительных
вычислительных затрат по величине последних слагаемых суммы
A) составить представление о локальной погрешности
приближенного решения (погрешности нахождения
значения y(x~\-h) в предположении, что значение у (х) известно
точно). Однако такой одношаговый метод интегрирования
дифференциальных уравнений при т > 1 все же редко
используется в практике вычислений, так как его
применение требует на каждом шаге нахождения значений
^Ltll раЗЛИЧНЫХ фуНКЦИЙ /, fx% fy, fjt, fxy, ..., fym~i
(см. A.4)). При использовании ЭВМ это сопряжено
с написанием большого числа блоков вычисления
значений указанных функций, что осложняет связь
пользователя с машиной и увеличивает, как правило, время
решения задачи. Поэтому данный метод редко кладут
в основу стандартных программ решения задач Коши,
хотя в специальных частных случаях (например, когда
приходится многократно решать задачи, отличающиеся
лишь начальными данцыми или мало отличающиеся
правыми частями уравнений) использование метода может
быть оправданным. В общем случае стандартные
программы чаще строятся с использованием вычислительных
методов, не требующих нахождения значений
производных от правых частей уравнений. Ниже будут
рассмотрены основные способы построения таких методов.
2. Видоизменение метода рядов, не требующее
вычисления производных правой части уравнения. Естественно
поставить задачу о таком усовершенствовании
приведенного выше одношагозого метода, которое сохраняло бы
основные его достоинства, но не было связано с
нахождением значений производных правой части уравнения
A.1). Чтобы выполнить последнее условие, производные
y{i) (x), t = 2, 3, ..., m, входящие в правую часть
равенства A), можно заменить по формулам численного
дифференцирования (см. § 6 гл. 1) их приближенными

16 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
выражениями через значения функции у' и учесть, что
у' (х) =f[Xy у (х)]. Требование одношаговости
конструируемых правил накладывает при этом свои условия
на такую замену. Ниже на конкретных примерах будет
рассмотрен один из возможных подходов к решению
поставленной задачи.
В случае т=1 приближенное равенство A) не
требует вычисления производных правой части уравнения
A.1) и позволяет с погрешностью порядка h2 находить
значение, у (xn + h) решения этого уравнения по
известному его значению у(хп). Соответствующее одношаговое
правило можно записать в виде
[2] [2] [2]
Уп+1 = Уп+Ь[п, B)
использовав широко применяемое ниже обозначение
f[xn + ah, уя+а) = Ын1> C)
[*]
где Уп+а — найденное с локальной ошибкой порядка hk
приближенное значение решения в точке хл
+отправило B) впервые было построено Эйлером и
носит его имя. Иногда его называют также правилом
ломаных или методом касательных, чем подчеркивают
простой геометрический смысл формулы. Погрешность гп+1
этой формулы можно, очевидно, записать в виде
Гп+1 = %!Г(Хп + Щ, 0<8<1.
При т = 2 равенство A) требует вычисления
производной у" (хп) и дает возможность находить значение
y(Xn + h) с локальной ошибкой порядка /i3. Чтобы не
понизить порядок погрешности приближенного равенства
у (хп + h)^y (хя) + hy' (хп) + \ у" (хп), D)
значение производной у" (хп) необходимо найти по
крайней мере не хуже, чем с ошибкой порядка Л, для чего,
очевидно, достаточно иметь два значения функции у' (х) =
= f[x, у(х)] из отрезка xn^x^xn + h @</i<l).
[3]
В точке хп значением fn этой функции мы уже
располагаем, так как, по предположению, на предыдущем

§ 2] РАЗЛОЖЕНИЕ РЕШЕНИЯ В РЯД ТЕЙЛОРА 17
[3]
шаге процесса было найдено уп. Заметим, что в силу
[3]
локального характера наших рассуждений значение уп
можно рассматривать как точное значение у (хп) того
решения уравнения A.1), значение которого в точке xn + h
интересует нас на данном этапе вычислений.
Найдем теперь еще значение функции у' в точке *)
xn-\-hl (/^1). Для этого с учетом уравнения A.1)
достаточно указать правило вычисления y(xn-\-hl).
Очевидно, у (хп + hl) = у (хп) + К у' (хп) + О (h2i). Поэтому
справедлива следующая расчетная формула
[2t] [3] [3]
Уп + ^=Уп+Ь%. E)
Так как
У'(Хп + Г1*) = Пхя + Н*, у(хп + к1)]у
то на основании D) можно записать
[3] [3] [3] h2-i f[2i] [3]\
Уп+1 = Уп + tfn+—\fn + hi-l-fn) =
Формулы E), F) можно рассматривать как семейство
(зависящих от параметра i^\) одношаговых методов
решения задачи Коши A.1), A.2) с локальной
погрешностью порядка /i3.
При i=l эти формулы принимают вид
[2] [3J [3]
У л+1= Уп+ hfn, G)
[3] [3] h /[3] [2] \
Уп+1 =*Уп + -о\!п+ /W . (8)
Они имеют предсказывающе-исправляющий характер:
формула G) служит для получения грубого приближения
искомой величины y(xn-\-h), а по формуле (8) произво-
*) Здесь и ниже величины хп и h считаются безразмерными.

18 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
Г21
дится уточнение полученного значения. Сравнение уп+1
с уп+1 дает возможность высказать суждение о локальной
погрешности результата.
Заметим, что иногда на основе формулы (8) бывает
полезным сделать одну итерацию. Это может (при
сохранении порядка погрешности) несколько повысить точность
приближения величины у(хп + 1г). К существенному
увеличению объема вычислений эта итерация не приведет,
[3J
так как значение fn+l9 которое при этом необходимо бу-
[3]
дет вычислить, можно использовать в качестве fn на
следующем этапе вычислений. И наоборот, если вместо
формул G), (8) применить формулы
[2] [3] [21
tjn+i = yn+hfn, (9)
ГЗ] [3] h /[2] [2] \
Уп+1 = Уп +  \ fn + fn+l) , A0)
[2] [2]
то значение fn+i можно будет использовать в качестве fn
на следующем этапе счета. Погрешность приближенного
решения в случае метода (9), A0), вообще говоря,
несколько возрастет (при сохранении порядка), но это
позволит почти вдвое уменьшить общий объем вычислений
в сравнении с методом G), (8). Подобное специфичное
использование информации о решении, полученной на
предыдущем этапе вычислений, не является, вообще
говоря, характерным для одиошаговых методов. При этом,
в частности, несколько нарушается однородность
вычислительного процесса, так как первый его этап будет
сопряжен с нахождением двух значений функции f(x9y)9
а каждый последующий будет требовать лишь одного
обращения к блоку вычисления значений этой функции.
В случае i = 2 формулы E), F) имеют вид
[41 [3] ГЗ]
Уп+г1 = Уп + Ь%, A1)
[3] ГЗ] ГЗ] ! /[41 [31 \ [31 ( п ГЗ] i Г4]
Уп+1 = У я + Щп + ~9: [ fn+h - fn) = Уп + \h - 2"; fn +  f"
n+h •
A2)

§2]
РАЗЛОЖЕНИЕ РЕШЕНИЯ В РЯД ТЕЙЛОРА
19
Увеличение значения i на единицу позволило, вообще
говоря, несколько улучшить структуру остаточного члена
вычислительного правила. Если в случае правила G),
(8) погрешность складывалась из одного слагаемого вида
~-#'" (хп + Щу 0 < б <С 1, представляющего собой ошибку
приближенного равенства D), и еще двух слагаемых
также порядка А3, порождаемых соответственно
неточностью замены производной у" и ошибкой формулы
Эйлера E), то в случае A1), A2) два последних
слагаемых остаточного члена будут уже, очевидно, величинами
порядка А4. При i = 3 соответствующие слагаемые остатка
станут величинами порядка А5 и т. д. Однако увеличение
значения i, улучшая структурные свойства остаточного
члена вычислительного правила, предъявляет повышенные
требования к выполнению вычислений, так как в этом
случае в силу ограниченности разрядной сетки ЭВМ
возможна потеря точности результата за счет операций
вычитания близких величин и деления на малые по
абсолютному значению числа (см. F)).
Рассмотрим далее случай т = 3. Соответствующее
разложение решения по формуле Тейлора будет сейчас
обрываться на члене, содержащем вторую производную
функции у'. Чтобы построить приближенное выражение
для этой производной через значения функции, нужно иметь
по меньшей мере три таких значения. Возьмем в качестве
них у'(хп), y'ixn + h1) и у'{хп + 2М), где /^2 при 0<
<А^1/2. Чтобы воспользоваться простейшими
симметричными приближенными выражениями для первой и
второй производных функции у' через эти значения,
будем исходить из разложения решения по формуле
Тейлора не около точки хп, а около точки xn + hf:
У (хп + h)=y [хп + Ы + А A - Л'-1)] =
= У {хп + АО + А A - ft-1) у' (хп + АО +
Опираясь на это представление, можно записать
следующее семейство вычислительных правил (подобно

20 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
изложенному в случае т = 2):
[2*] [4] [4]
Ц . J-i = if + hlf
[Щ [4] hi /[4] [2/] \
Уя + л* = #л + 2 \ fn + In + h1'1) >
[3/] [3f] # / [30 [4]\
Уп + 2/Г1 = #я + Л1' + У 1 3At + Л1'~~ W '
[4] [3i] [3*]
Ла-1-A-Л'-1)а/^ Щ\ ,
Н  \in + 2/Г1"" In) "*"
ЙЗ»/ A-^-1)8/[34 [34 [4]\
^ _ ^ ^ + 2^_х _ Ц^ + ^ _|_ ^у =:
__ [3l'] . h24 A - Л*-*)* М1"* - 1 1 \ [\] ,
- 0Л + л*-1 Н ~2 ^ § 27 'п +
+ *A-»»)[1-Й^]^ +
, /l2-/A_^-lJ Ml-»-l J \ [34
"Г 2 \ 3 + 2/ '/г + 2/»1"
При t = 2, например, имеем расчетное правило
[4] Г4] [4]
*/л+А = Уя +^2//г,
[6] [4] да Л4] [4] \
Уп+h = Уп + -£ \fn + /л+ft/ ,
[6] [6] h2 ( [6] [4] \
#л+2л — J/я+А + у ^/л+л ~~ /л/ '
[4] [6] n^_n_h п[4]
Уи+1 — Уп+лi 2 \~ЗЛ 2"/ '" '
+ A—Л)[Л 3^-J /»+* + —T~iS" + '2"j '
Л+2Л»
Полезно иметь в виду, что многие из предлагаемых
выше одношаговых методов позволяют, кроме
приближенного значения y(xn + h), попутно находить также
приближенные значения решения и в некоторых других
точках отрезка [хп, xn + h].
Описанным способом можно строить вычислительные
методы и более высокого порядка точности. Следует,

§3]
МЕТОД РУНГЕ—КУТТА
21
однако, заметить, что при больших значениях т
построение таких методов связано с приближенной заменой
производных высоких порядков по интерполяционным
формулам численного дифференцирования, а эта процедура,
как известно, сопряжена обычно с повышенными
требованиями к точности выполнения вычислений. Ниже мы
рассмотрим другие способы получения одношаговых
правил, которые непосредственно не связаны с подобной
аппроксимацией производных.
§ 3. Способ Рунге— Кутта построения
одношаговых методов
Изложим основную идею этого способа на примере
задачи A.1), A.2).
Интегрируя уравнение A.1) в пределах от х до x + h
@</г < 1), получим равенство
У(х + Н) = у(х)+Х\ f[t, y(t)]dU A)
х
которое посредством последнего интеграла связывает
значения решения рассматриваемого уравнения в двух
точках, удаленных друг от друга на расстояние шага h.
Указав эффективный метод приближенного вычисления
интеграла в A), мы получим тем самым одно из правил
численного интегрирования уравнения A.1). В силу
требования одношаговости конструируемых вычислительных
правил при нахождении значения указанного интеграла
мы можем использовать информацию об интегрируемой
функции у'{f)=f[t, y(t)] лишь на отрезке [х> х + А].
По постановке задачи значение этой функции в точке х
нам известно. Поэтому для вычисления интеграла можно
применить, например, одноточечную формулу левых
прямоугольников ь
5ф@Л^(Ь-а)ф(а).
а
В результате мы получим, очевидно, известный метод
Эйлера B.2). Погрешность формулы B.2), как мы уже
отмечали, является величиной порядка /г2.
По формулам типа A.4) в точке х можно найти и
значения производных y{i)f i = 2, 3, ..., m, интегрируемой

22 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
функции у'. Использовав для наших целей
квадратурную формулу с единственным кратным узлом на
левом конце отрезка интегрирования Дмы придем к пошаговому
варианту типа B.1) метода рядов.
Если же интеграл в A) приближенно заменить
квадратурной суммой двухточечной формулы трапеций E.3.2),
получим приближенное равенство
y(x + h)^y(x)+h2[f(xy y(x))+f{x + h, y(x + h))]9
которое позволяет записать так называемый метод
трапеций численного интегрирования уравнения A.1):
Уп+i = Уп + j U (хп, Уп) + / (хп + h, yn+i)l B)
Погрешность последней формулы (см. E.3.3)) будет
величиной порядка №.
Равенство B) дает нам пример неявного одношагового
метода. Неизвестное значение уп+1 здесь приходится
находить путем решения численного уравнения B). Обычно
для этих целей используют итерационные методы.
Подробнее на неявных методах решения дифференциальных
уравнений мы остановимся несколько позже,.а сейчас
отметим лишь, что на основе равенства B) с
использованием формулы Эйлера B.2) можно очевидным образом
построить известное уже нам явное вычислительное
правило B.7), B.8) типа предиктор-корректор того же
порядка точности.
Более сложный пример неявного метода можно
получить, если и на правом конце отрезка [х, x-\-h] через
значение функции y(x + h) при помощи формул типа A.4)
выразить значения производныхy{i) (x + h), i' = 2, 3, ..., ш,
и применить для вычисления интеграла в A)
соответствующую квадратурную формулу с двумя кратными
узлами х и x-\-h. Однако использование такого неявного
метода потребует на каждом шаге итераций вычисления
значений производных правой части уравнения, что, как
мы отмечали ранее, является существенным недостатком
вычислительного правила. Чтобы построить методы более
высокого порядка точности, не связанные с вычислением
производных функции f[x, у (х)]у нужно привлечь
дополнительную информацию по значениям интегрируемой

§3]
МЕТОД РУНГЕ-КУТТА
23
функции. Поскольку эта функция, как функция одного
аргумента х, в случае задачи Коши A.1), A.2), в
отличие от ее частного случая — рассмотренной уже нами
ранее задачи вычисления неопределенного интеграла
E.10.1), — вообще говоря, неизвестна внутри отрезка
интегрирования [х, x-\-h], то использовать
непосредственно квадратурные формулы с числом узлов N>2
не удается. Поэтому в способе Рунге — Кутта применяют
следующий специальный метод приближенного
вычисления интеграла в A).
Для удобства записи используем обозначение Ду =
~ y(x + h) — y(x) и равенству A) придадим новый вид,
произведя замену переменной интегрирования t = x + ah:
1
Ay = h^f[x-\-ah, y(x + ah)]da. C)
б
Чтобы на основе C) построить одношаговый метод
численного интегрирования уравнения A.1), введем три
набора параметров:
ось ос2, ..., ад\ (а)
Рю,
Р20> Н2Ь
(Р)
PqQi Pqli • • • i Pq, q -1»
Л0, Ль ..., Aq, (А)
выбором которых распорядимся в дальнейшем. При
помощи двух первых наборов составим величины
q>i = /i/(x + ai/i, у + рюфо).
42 = hf{x + <*2h, У + Р20Ф0 + Р21Ф1),
% = lif(x + aqfi, у + р?0фо + Р?1ф1 + .-- + Р?,?-1ф?-1),
которые при заданных (а) и (Р) могут быть вычислены
последовательно,

24 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
Хотя
Ф/ = Щ (х + ЩК У + РгоФо + • • • + Р/, i-1%-1),
1 = 1, 2, ..., q,
вообще говоря, не равны значениям
hf[x + atK y(x + <Xih)l
однако при соответствующем выборе параметров ф) их
можно трактовать как приближенные значения
интегрируемой функции f[x-\-ah, y(x-\-ah)]y умноженные на h.
Это дает основание надеяться при помощи параметров
(А) составить такую линейную комбинацию величин фЬ
*' = 0, 1, ..., q, которая будет являться аналогом
квадратурной суммы и позволит вычислить приближенное
значение приращения &у (см. C)):
Ауъ^Ам. D)
1 = 0
Тем самым параметрам (а), (C) и (А) можно придать
некоторый квадратурный смысл.
Рассмотрим теперь задачу выбора этих параметров.
Введем величину q
rq(h) = Ay- J] Aw, E)
t = 0
представляющую собой погрешность приближенного
равенства D). В предположении, что правая часть
уравнения A.1) является достаточно гладкой функцией,
запишем следующее разложение этой величины:]
k
rq (A) = ^ 7Г ^ (°) + -(ЙЖ- Г?+ " ^> ° < 9 < * •
На основании этого разложения можно утверждать, что
если параметры (а), ф) и (А) подобрать так, чтобы
выполнялись условия
гуЧ0) = 0, / = 0, 1, ..., k9 F)
то погрешность E) приближенного равенства D) будет
величиной порядка не ниже hkJrl:
M^iiSWr1'^)- en

§3]
МЕТОД РУНГЕ-КУТТА
25
Число k при этом обычно называют порядком точности
соответствующего метода. Такому определению порядка
точности метода можно дать следующее объяснение.
В случае рассматриваемой задачи Коши A.1), A.2), как
и в случае изученной ранее задачи неопределенного
интегрирования E.10.1), оказывается, что если погрешность
типа E) расчетной формулы данного метода является
величиной порядка hk+1 в достаточно широкой
окрестности решения, то погрешность метода (та часть
погрешности приближенного решения, которая определяется
лишь неточностью самой формулы) для случая конечного
отрезка интегрирования будет величиной порядка hk.
Доказательство этого факта будет приведено несколько
позже, а сейчас продолжим рассмотрение вопроса о
построении вычислительных правил по способу Рунге—Кутта.
Для выполнения условий F) при возможно большем
значении k величины /^(О), / = 0, 1, ..., k, выражают
через значения функции f (x, у) и ее частных
производных и требуют обращения в нуль возможно большего
числа этих величин для любой достаточно гладкой
функции /. Иными словами, выбор параметров (а), ф) и (А)
осуществляют на основании требования, чтобы разложение
by = y(x + h)-y(x)=ty'(x) + ^y"(x) + ^y'"(x) + ...
(8)
и разложение по степеням h линейной комбинации
я
2 Ai% совпадали до членов с возможно более высо-
кими степенями h в случае любой правой части
уравнения A.1).
При произвольном q систему уравнений для
определения параметров (а), ф) и (А) записать очень трудно.
Поэтому мы ограничимся здесь рассмотрением лишь
нескольких конкретных примеров построения одношаговых
правил указанным способом.
Метод первого порядка точности. Зададимся
минимальным значением д = 0, что равнозначно введению
лишь одного параметра AQ. Приближенное равенство D)
в этом случае принимает вид
Ду^Л0фо = ЛЛ0/(х, у)

26 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
и погрешность E) может быть записана следующим
образом:
r0 (h) = у (x + h) - у (х) - hA0f (х, у).
Тогда
>*о (A) = y'(x + h)- А о/ (*, у),
r'o(h)=y"(x + h).
Так как rj (h) не зависит от Л0, то уже при / = 2
условие F) в случае произвольной функции / удовлетворено
быть не может. Поэтому Ы1 и система F) принимает
вид
A-A0)f(x, у) = 0.
Отсюда находим, что А0=\. Следовательно (см. D)),
Ay^hf(x, у)
и (см. G))
ro(h)=h^r:(dh)==^yf,(x + bh)y 0<G<1.
В простейшем случае q — О, таким образом, способ
Рунге — Кутта приводит к известному методу Эйлера B.2).
Квадратурный смысл этого вычислительного правила был
уже выяснен.
Методы второго порядка точности. При
q = 1 имеем
= hA0f{x, y) + hAif[x + axh, y + h$10f(xy у)].
С целью выбора введенных параметров аъ р10, Л0,
А± разложим Ау и Лофо + Лхфх по степеням h.
Разложение (8) для Ау с учетом A.1) можно
записать в виде
АУ = У (x + h)-y(x) = fif + ^- (fx+ffy) +
+ 4L U** + 2ff*y + f'fyy + fy (/.v + ffy)] + О (/i4) • (9)
Используя формулу Тейлора, для линейной комбинации
^4офоЧ-^1ф1 можно дать следующее представление:
А0фо + Л1ф1 = h (Ло + А0 / + AMi К/л- + Puffy) +
+ ^А, (a\fxx + 2a$ltffxll + pi Ли,) + О (¥). A0)

§3]
МЕТОД РУНГЕ—КУТТА
27
Сравним в разложениях (9), A0) коэффициенты при
Л/, Щх и h2ffy. Тем самым на выбор четырех
параметров «1, C10, AQ, Ax будут наложены три условия:
Ло + Лх-1, Л ^=1/2, AiPi0=l/2.
Непосредственно из (9), A0) следует, что в случае q = 1
для произвольных / нельзя добиться совпадения всех
членов с множителем /i3 за счет выбора введенных
параметров. Поэтому при q=l вычислительные правила типа
Рунге — Кутта будут иметь лишь второй порядок
точности. Параметры аъ р10, Л0 могут быть выражены через
коэффициент Ai по формулам
ai = Pio = -2j-> ^o=l —Аг.
В качестве Лх может быть взято, вообще говоря,
произвольное отличное от нуля число. Например, при Лх =1/2
будем иметь
Ay=-g-fao + <Pi) + 0(ft8j, (И)
Фо = А/(х, у), ф1==А/(х + А, У + фо).
Вычислительное правило, построенное на основе
равенства A1), имеет следующий квадратурный смысл. Так как
4>i = hf(x + h, y + hy')^hf[x + h, y(x + h)]y
то линейная комбинация тг(Фо + ф1) является аналогом
квадратурной суммы формулы трапеций E.3.2) при
вычислении интеграла в правой части равенства A).
Выбрав j4i = 1, получим еще одно из широко
известных вычислительных правил типа Рунге —Кутта второго
порядка точности:
Д^ф1, A2)
<Po = hf(x, у), Ф1 = й/(х + у, 0 + -у-).
Формула A2) является, очевидно, аналогом
одноточечной квадратурной формулы средних прямоугольников.
Локальная погрешность любого из методов типа
Рунге —Кутта второго порядка точности, как следует из

28 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
разложений (9), A0), может быть представлена в виде
гЛЩ = -f- \} хх A - 3aMi) + 2ffxy A - За^юЛ^ +
+ Pfyy(l - Зр!„Л х) +f»(fx + ffy)] + О (А*). A3)
Иногда свободный параметр Л1 выбирают так, чтобы
в этом представлении можно было обратить в нуль хотя
бы часть членов. Например, если учесть, что ах = [510 =
= 7гт-, и положить Л1 = 3/4, то правая часть равенства
A3) существенно упростится:
ri(h) = ~fy(fx + ffy) + 0(¥).
При таком выборе Ах будем иметь
Л#^4(Фо + Зф1), A4)
Фо = А/(*. У)> <Pi = tf(x + jh9 y+ з"Фо).
Методы третьего порядка точности. С
повышением требований к точности вычислительных
правил типа Рунге—-Кутта очень быстро возрастает
громоздкость необходимых построений, хотя общая схема
таких построений и не претерпевает существенных
изменений. Поэтому в случае q = 2 мы не станем здесь
воспроизводить все выкладки и выпишем лишь ту систему
уравнений, которым должны удовлетворять параметры
(а), (р) и (А) в методах типа Рунге—Кутта третьего
порядка точности:
A0 + A1 + A2=l9 i4iai + i4aaa= у, А&1 + A2al= 1/3,
i43CXiPai= 1/6, P20+P21 = a2, Pl0 = «l-
Одно из решений этой системы шести уравнений с восемью
неизвестными приводит к следующим формулам:
Фо = /№ у), <Pi = A/(* + 4, */ + -|-)> A5)
Фа = Л/(л: + /г, у-ф„ + 2ф1).
Это вычислительное правило является, очевидно,
аналогом трехточечной квадратурной формулы Симлсона E.3.5).

§3]
МЕТОД РУНГЕ—КУТТА
29
Часто встречается в практике вычислений и такой
метод типа Рунге—Кутта третьего порядка точности:
Ьу^-j (Фо + Зф2),
Фо = /*/(*, у), Ф1 = А/^ +у, 0 + -^п/,
<Pa = Af (я + уй, »+3"9i).
По квадратурному смыслу приведенное вычислительное
правило сходно с методом A4) второго порядка точности
и еще раз косвенно подчеркивает достоинства последнего.
Методы четвертого порядка точности.
В случае q = 3 система ограничений на выбор
параметров (а), (Р) и (А) вычислительных правил типа Рунге —
Кутта четвертого порядка точности может быть
приведена к виду
А о + Аг + А2 + ^з = 1, А1а1 + Л2а2 + Л3а3 = -^,
AvA + A2al + A3al = у, ^aj + A2al + Л3а| = ■ ^,
А2^21^1 + A3$3i<Xi + А$32а2 = ^,
i42p2i^2ai + ЛзРзгаза! + А3$д2а3а2 = -g ,
^2p2icti + ^sPsiaf + Аф32щ = -й-,
Лзр32Р21<*1 ^"^Г' Рз0+Рз1+р32 = ^3,
Рго + Ргг^^» Pio = ai-
Одним из методов, удовлетворяющих этим требованиям,
является следующий аналог четырехточечной
квадратурной формулы «трех восьмых» E.3.10):
Ау я« -8- (ф0 + Зфх + Зф2 + фз),
Фо = А/(х, У), Ф1 = А/(* + у, # + -?-),
42 = hf(x + -jh, у-^+щ),
фз = Й/(^+А, ^ + Фо~ф1 + ф2)-

30 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
Особенно широко известно другое вычислительное
правило типа Рунге —Кутта четвертого порядка точности:
&У ^ 6 (Фо + 2ф! + 2ф2 + ф3),
4o = hf(x, у), <p1 = hf(x + -j, y + J2~)> A6)
ф2 = Л/(^ + -2", У + ^[)> ^s = hf(x + K у + ъ)-
Так как' справедливы приближенные равенства
2ф1 + 2Ф2 ъ 4ft/ [ х + -|, у (х + у;],
то формулу A6), как и A5), тоже можно считать
аналогом квадратурного правила Симпсона E.3.5), хотя и не
столь естественным, как A5). Однако если сопоставить
порядки остаточных членов квадратурного правила
Симпсона (см. E.3.7)) и формул A5), A6), то можно сделать
вывод, что вычислительное правило A6) является более
точным аналогом формулы Симпсона. Это одношаговое
правило наиболее часто служило основой стандартных
программ решения задач с начальными условиями для
уравнений вида A.1) и систем таких уравнений.
Чтобы построить вычислительные правила типа Рунге —
Кутта пятого и более высоких порядков точности,
придется брать значения д>3. В рассмотренных выше
случаях увеличение q на единицу, как мы видели,
позволяло повышать на порядок точность правила. Однако
при <7 = 4 поднять порядок точности вычислительных
правил по отношению к случаю q=^3 не удается, так как
параметров (а), ф) и (А) при этом значении q еще не
хватает для того, чтобы их выбором можно было для
любой функции f (х9 у) обеспечить совпадение разложе-
4
ний ку и 2 АьЪ по степеням h до членов с множите-
1=0
лем /г5 включительно. В этом нетрудно убедиться
непосредственно. Необходимые условия можно выполнить
лишь при q^5.

§ti
МЕТОД РУНГЕ-КУТТА
31
В качестве примера правилатипаРунге — Кутта
пятого порядка точности можно привести
следующий одношаговый метод:
Ау ^ 192" B3фо + 125ф2 —81ф4+ 125ф5),
Фо = А/(*, у), ф1=А/(^ + у, » + ■§■)'
Фз^А/(* + А, г/ + Ф°~12ф41+15ф2),
Ut( I 2 А . 6Фо + 90Ф1-5°Ф2 + 8Фз\
Ъ?( 1 4 Ь , Ч + 36Ф1+10Ф2 + 8ФЗ \
ф5 = А/^+уА, у + -2 ^—1- j.
Дальнейшее повышение порядка точности методов
типа Рунге —Кутта также связано, как правило, с
быстрым возрастанием их трудоемкости, которую можно
характеризовать, скажем, числом обращений на одном
шаге процесса к вычислению значений правой части
уравнения. Однако нужно учесть, что методы более
высокого порядка точности обычно допускают использование
большего шага А, что может снизить общие
вычислительные затраты.
С примерами правил типа Рунге —Кутта при
значениях q > 5 можно познакомиться в рекомендованной
к данной главе литературе.
Одношаговые методы, построенные способом Рунге —
Кутта, в отличие от вычислительных правил,
полученных на основе разложения решения в ряд по
последовательным главным частям, непосредственно не
представляют простой возможности судить о локальной точности
найденного значения приближенного решения по
результатам промежуточных вычислений. Обычно в практике
вычислений для этих целей используют следующий
простой прием. Исходя из yn^y{xn)i приближение
к y(xn-\-h) вычисляют по-разному: сначала данное
вычислительное правило типа Рунге —Кутта применяют с
избранным шагом А, а затем заново используют его дважды
с шагом А/2. Сравнение так найденных двух приближен-

32 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
ных значений величины y(xnJrl) позволяет, во-первых,
вынести суждение о локальной точности полученного
приближения и, во-вторых, высказать мнение об удаче
выбора шага интегрирования. Однако такая организация
вычислений требует больших дополнительных затрат
вычислительного труда: объем работы на один узел сетки
возрастает почти втрое. Рассмотрим сейчас способ
построения правил численного интегрирования
дифференциальных уравнений, который позволяет во многих случаях
полнее использовать результаты промежуточных
вычислений и, в частности, получать одношаговые методы
предсказывающе-исправляющего характера, что дает
возможность практически без дополнительных вычислений
судить о локальной погрешности полученного значения
приближенного решения и об удаче выбора шага
численного интегрирования. Заметим, что здесь и всюду, где
речь идет о построении вычислительных правил, мы
рассматриваем обычно приближенное решение без учета
погрешностей, обусловленных ошибками округлений и
неточным заданием исходных данных, тем самым понятие
погрешности приближенного решения используется в более
узком смысле погрешности метода.
§ 4. Построение вычислительных правил
на основе принципа последовательного
повышения порядка точности результата*)
1. Случай уравнений первого порядка. Для простоты
изложения основной идеи предполагаемого способа
построения методов численного решения дифференциальных
уравнений будем сначала иметь в виду задачу Коши A.1),
A.2). Как и в случае способа Рунге —Кутта, при
построении вычислительных правил будем исходить из
равенства типа C.1), которое, подобно C.3), для наших целей
удобнее записать в виде
У (xn + h) = y(xn)+h \ zn (ayda, (l)
о
*) В. В. Бобков, Об одном способе построения одношаговых
правил приближенного решения дифференциальных уравнений. Изв.
АН БССР, сер. физ.-матем., № 4, 1967.

§4}
ПОВЫШЕНИЕ ПОРЯДКА ТОЧНОСТИ
33
где 2Л (а) = / [хп + аЛ, у (*л + «А)]. Заменим интеграл
квадратурной суммой
1 = 0
Тогда вместо A) получим
tj(xn + h)^y (хп) + h У] Л/2Л (а,) -
i = 0
= У (хп) +h%Atf [хп + а Д У (хп + сф)]. B)
t = 0
Выбор параметров Aiy a/, i = 0, 1, ... , ^» в этом
приближенном равенстве будем осуществлять, например,
на основании требования, чтобы квадратурная формула
1 Я
\zn(a)da^ 2 At*n(<*d C)
0 t=-0
была точной для всевозможных алгебраических
многочленов до степени k — 1 @ <С k <; 2q-f-2) включительно.
Это приводит к следующей системе А уравнений с 2q + 2
неизвестными Aiy ah i = 0> 1, ... , q:
2Ai==]> i^=yTr; i==u 2'-" *~l ^
* = 0 1=0
Заметим, что последняя система может быть получена
и из требования, чтобы разложения по степеням h обеих
частей приближенного равенства
1
у (хп + h)-y (xn) ъ h 2] A{yr (xtl + a-h)
1 = 0
совпадали до членов с № включительно. Такой способ
получения системы D) позволяет, в частности, записать
следующее представление для погрешности
я
rn+i = y(xn + h)-y(xn)-h >] AtflXn + cLih, y(xn + aLh)]
t' = 0
2 В. И. Крылов и др., т. II

34 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
приближенного равенства B)
1 * ^а^
(k+l)\ k\
t = 0
+ 0(A*+2). E)
Так как весовая функция в случае интеграла \ zn (a) da
о
равна единице, то квадратурная формула вида C),
имеющая наивысшую алгебраическую степень точности
2*7+1, может быть построена и притом единственным
образом для любого д^О. Поэтому при k = 2q-{-2
система D) имеет единственное решение, при этом 0<
<Д-< 1, 0<а/<1, i = 0, 1, ..., q (см. пп. 5.4.1, 5.4.2).
Следовательно, при 1 ^k^2q-\-2 у этой системы
существует хотя бы одно решение, и приближенное равенство B)
может быть построено.
Если бы в B) все значения y(xn-\-a,ih), i' = 0, l, ... , qy
были известны точно, то это приближенное равенство
позволяло бы найти искомое значение y(xn-\-h)
соответствующего решения уравнения A.1) по известному значению
у(хп) этого решения с ошибкой порядка hk+1 (см. Ej).
Хотя точными значениями величин y(xn-{-a,ih)9 i =
= 0, 1, ... , q, мы не располагаем, но, подобно B), заменив
там h на аД нетрудно указать правила их
приближенного вычисления через значения y{xn-\-a$jh)9 для
нахождения которых, в свою очередь, можно построить
подобные же рекурсивные формулы. При этом следует иметь
в виду, что наличие множителя h перед суммой в B)
позволяет находить значения у(хл + а//г) с локальной
ошибкой порядка hk, а значения у (хл + ^/Р//г) — с
ошибкой порядка №~г и т. д. Параметры соответствующих
приближенных равенств должны удовлетворять системе
уравнений типа D), в которой с понижением требований
к точности на порядок следует отбрасывать последнее
уравнение. При этом часто бывает целесообразным
уменьшать и число #> определяющее количество подлежащих
выбору параметров. Следуя такой схеме построений,
мы придем, наконец, к приближенным равенствам
у (хп + (*$/...ykh) pv у (хп) + агР/... ykhf (xn, уп)У
на которых процесс замыкается. Погрешность таких
равенств будет, очевидно, величиной порядка /г2. Они

§4]
ПОВЫШЕНИЕ ПОРЯДКА ТОЧНОСТИ
35
получаются из равенств типа B) в случае, когда
квадратурная формула C) является простейшей формулой левых
прямоугольников.
Проиллюстрируем предлагаемый способ построения
вычислительных правил на нескольких простых примерах.
Методы первого порядка точности.
Система D) в этом случае вырождается в единственное
требование
tAi=L F)
Параметры ah i = 0, l, ... , q, могут принимать при
этом, вообще говоря, любые фиксированные значения.
Однако для случая одношаговых методов выбор этих
параметров должен быть подчинен ограничению
0<(Х;< 1.
Взяв, например, q = 0, найдем, что А0=\. Полагая
а0 = 0, получим исходную формулу известного метода
Эйлера B.2)
у (xn+1)^y(xn)+hf[xn, у {хп)] + 0 (h2).
При а0=1 получим простейший неявный метод
[2] [2] [2]
yn+i = yn + hfn+i.
При записи последнего вычислительного правила
использованы обозначения типа B.3).
Методы второго порядка точности. В этом
случае требование F) нужно дополнить условием
2^=-2- G)
1 = 0
При q = 0 система F), G) имеет единственное
решение Л0=1, ac=l/2f что приводит к следующему
вычислительному правилу:
[2] [3] h [3]
Z/n+1/2 = Уп + ~^ fn>
(8)
13] [3] [2]
У п+1 = У n~{~hfn-г 1/2-
о*

36 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
При q^\ система F), G) принимает вид
Л0 + Лх= 1, Лоссо + Лхосх^ 2~.
Выбрав, скажем, а0 = 0, ах=1, найдем, что А0 = А1= 1/2,
и получим неявный метод трапеций C.2)
[3] [3] д /[3] [3] \
У/г+1 = ^л + у1/я+ /я+1/ •
Используя формулу Эйлера B.2), это вычислительное
правило можно преобразовать в известное уже нам явное
правило B.7), B.8).
Методы третьего порядка точности.
Требования F), G) здесь необходимо пополнить уравнением
1 = 0
Этим условиям удовлетворяют, например,
вычислительные правила
[2] [4] h [i]
yn+ij4 = yn + jfn, (9)
[3] [4] h [2]
Уп + ЦЪ — УпЛ"~2 /л+ 1/4» (Ю)
[3] [4] [3]
yn+i = yn + hfn+i/2, A1)
[4] [4] h f\i] [3] [3] \
Уп+i = Уп+ e \fn + 4/я+1/а + //i+i/, A2)
где i может принимать значения 3 или 4. При i = 4
построенное правило на один узел сетки A.5) требует
четырехкратного обращения к блоку нахождения
значений правой части уравнения A.1). В случае же i = 3
точность результата, вообще говоря, несколько понижается
(при сохранении порядка), однако в основном счете число
обращений к блоку вычисления значений функции / (х, у)
сокращается до трех на узел сетки.
Заметим, что построенные численные методы, как и
вычислительное правило B.7), B.8), имеют предсказы-
вающе-исправляющий характер. Приближенное значение
величины у{хп+д> найденное по формуле A1) с локаль-

§43
ПОВЫШЕНИЕ ПОРЯДКА ТОЧНОСТИ
37
ной погрешностью порядка /i3, уточняется затем по фор-
[3] [4]
муле A2). Сравнение значений уп+1 и уп^ дает
практическую возможность по ходу вычислений без
дополнительных затрат составить представление о локальной
точности полученного приближения к у {xn±i). Такое
сравнение, в частности, может быть положено в основу
правила автоматического выбора шага интегрирования.
На примере приведенных вычислительных правил
легко видеть, что предлагаемый выше способ построения
методов численного интегрирования дифференциальных
уравнений, как и способ, изложенный в п. 2.2,
удовлетворяет принципу модульности, когда сложные
вычислительные алгоритмы компонуются на основе более простых
типовых расчетных формул. Так, например, в случае
последнего вычислительного правила формула (9)
записана на основе метода Эйлера B.2), для равенств A0),
A1) базовой является формула средних прямоугольников
типа (8), а равенство A2) непосредственно связано с
формулой Симпсона E.3.5).
Методы четвертого порядка точности.
Система требований к построению таких методов получается
из D) при & = 4. В качестве примера приведем здесь
лишь одно семейство вычислительных правил четвертого
порядка точности, имеющих предсказывающе-исправляю-
щий характер:
[2] [5] h M
Уп 4- 1,'т == Уп\ J£ /я»
И [5] и .'6-тф, т Ф
Уп+i з — Уп ~г ~з~ v б 'п ' ' ' п + 1,!т
W [51 k ЯП [3] ^
*/л+1/2 = #л+-з" ^я+ З/п + 1/3/. A3)
[4] [5J h /[*] [3] [4]
Уп-rl = Уп + 2 V fn — 3/д +1/3 + 4/я + 1/2.
[5] [5{ h /[/] [4] [4]
Уп-rl = Уп+^ \ fn + 4ftt+l/2 + fn+1,
Здесь т>0, a i может принимать значения 4 или 5.
При / = 4, в частности, соответствующий метод сопряжен

38 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
в основном счете лишь с четырехкратным обращением
к блоку вычисления значений правой части уравнения
A.1) на один узел сетки A.5). Следует отметить также,
что значение т = & является наибольшим, при котором
[3]
в, правой части равенства для уп+1/3 нет отрицательных
коэффициентов, а при т = 9/2 обращается в нуль одно
из слагаемых с h3 в остаточном члене этой формулы.
Подобным же образом могут быть построены
численные методы и более высокого порядка точности, при этом
увеличения точности вычислительных правил можно
достигать как за счет привлечения новых значений
функции у\ так и за счет использования значений
последующих производных.
Все сказанное выше применительно к задаче A.1),
A.2) без существенных затруднений может быть
перенесено на случай задачи Коши для системы обыкновенных
дифференциальных уравнений первого порядка. Это,
в частности, дает возможность использовать построенные
методы при решении уравнений высших порядков, сводя
предварительно последние к системам уравнений первого
порядка. Вычислительные правила можно строить и
специально для случая уравнений высших порядков, при
этом часто удается получить более приемлемые алгоритмы.
2. Случай уравнений высших порядков. Изложенные
выше способы построения вычислительных методов
решения задачи Коши A.1), A.2) легко могут быть обобщены
на случай уравнений высших порядков. Проведем такое
обобщение только для последнего способа. Для простоты
рассмотрим задачу Коши для уравнения второго порядка:
y" = f(x, У, у')> (И)
У(х0)=Уо> y'(xQ)=yl A5)
Подобно A), B), здесь можно записать, что
1
У' (Xn+h) = У' (хп) + h\y" {Хп + оЛ) da ъ*
о
** у' (хп) + h 2] Atf [хп + а,А, у (хп + а,А), у' (х„+лЩ A6)

§ 4]
ПОВЫШЕНИЕ ПОРЯДКА ТОЧНОСТИ
39
И аналогично
у{хя + Ь) = У (хя) + W {хп) +
Подберем параметры Л/, ah i = 0, l, ..., <7ъ и 5,, р/,
f = 0, 1, ..., <7о» этих приближенных равенств так, чтобы
их погрешности были величинами порядка hk+1 A<&<^
^min{2^ + 2, 2^0 + 3}). Эти требования, подобно
изложенному в предыдущем пункте, приводят к следующим
системам, вообще говоря, нелинейных уравнений
относительно искомых значений параметров:
2^=1, 2Л/а( = тгг. /=1,2,...,й-1, A8)
/=0 1 = 0
Ж
<7о
2*<
*=0
Уо
2 в&
/-1
1
i = 0
'/(/ + !)'
/=2,3,..., А-1. A9)
Разрешимость системы A8) была изучена ранее
(см. D)). Подобным же образом выясняется этот вопрос
и для системы A9).
Подобрав, согласно указанным требованиям,
подходящие значения параметров, мы построим приближенные
формулы A6), A7), погрешности которых, подобно E),
могут быть записаны соответственно в виде
гп+\
ftA+yft+2) (Xn)
r^l==h^y^V{xn)
1
2 AflU
i=0
1
+ 0(h*+%
(A+1I (*- 1I
l ^?-'
* = 0
+ 0(/i*+2).
Процесс дальнейшего построения вычислительных
правил для задачи A4), A5) совершенно аналогичен случаю
задачи A.1), A.2). При этом полезно отметить, что
наличие множителя h2 перед суммой в A7) позволяет
находить значения у(хп + ^Н)9 у' (*Л + М)» i = 0, 1, ..., q0f

40 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
по отношению к требуемой точности значения y(xn-\-h)
грубее не только на порядок, как это было в случае
приближенного равенства B), а даже на два порядка.
Это позволяет, в частности, быстрее уменьшать число
точек, привлекаемых при построении промежуточных
формул, и упрощает вид вычислительных правил.
В качестве примера для задачи A4), A5) приведем
здесь лишь одно семейство вычислительных правил
четвертого порядка точности, тесно связанных с
вычислительными правилами из семейства A3):
[2] [5] h [5, i]
Уп + 1/т= Уп-\~~ /п у
[3] _[5] 1 h [5-. h% [У]
Уп-\-\Jtn— Уп~Т m Уп + 2^2 In у
Щ W, . h /б-т^<] , ™[У]
Уп+113 = Уп + -$ ^—-Q- In -T-q fn + h'm
Уп + i/з = Уп + у Уп + -g \ 18 /л > Is h+i/mj, )
[4] [5] А /[5, О [4, 3] \
y'n + l,2=yn + j[ U +3 fn+lfl), B0)
[4] [5] h [5] д2 /[5, i] [4, 3] \
#я + 1/2 = Уп + ~2 У'пЛ- JgV /л + /я+ 1/3/,
14] [5] л /[5,/] [4,3] [4,4]
#я + 1 = Уп + -2 \ fn —3 /л + 1/3 + 4 /л+ 1/2.
[5] [5] [5] ла/[5, I] [4,4] \
Уп+1= Уп + Ьу'п + ^К fn +2 /я + 1/2/,
[5] [5] л /[5,1] [4,4] [5,4]
0п + 1=0Л+еЧ /я +4 /я+ 1/2+ /яг1.
Как и в случае вычислительных правил A3), здесь т>0,
a i может принимать значения 4 или 5. Смысл
обозначений также аналогичен используемым в случае
формул A3):
и* я / m щ \
[п+а~1 \#л + оЛ» Уп+ау Уп + a/t
М [/]
где уп+а и y'nVQt есть приближенные значения величин
y(xn~{-ah) и у' {xn-\-ah)y найденные с локальными
ошибками порядка Ы и hJ соответственно.

§4]
ПОВЫШЕНИЕ ПОРЯДКА ТОЧНОСТИ
41
К приведенному набору формул B0) можно
присоединить формулу
[4] [5] [5] h2 [4, 3]
Уп+1 = Уп + hy'n + у fn + 1/з
или формулу
[5] [5] [5] h2 ( [5, П [4,3] [5. Я \
Уп%\= Уп+Ьу'п + ^[2 fn +9 /„+1/8+ fn+l),
где /, как и i, также может принимать значения 4 или 5.
Это дает возможность (при / = 4 — без дополнительных
обращений к блоку вычисления значений правой части
уравнения A4)) сравнить между собой не только при-
[4] [5]
ближенные значения у'п+1, у'п+г величины y'(xn-\-h), но
[41 [5] [5]
и приближенные значения уп+1, уп+ъ уТ+\ величины
y(xn~{-h)y что позволит высказать более достоверные
суждения о локальной точности полученных результатов и
удаче выбора шага h.
При необходимости, присоединив к B0) формулу
[5] [5] [5] /2 2 [ [5,«]
Уп+у = Уп + Нууп + ^- {[3-7C-7I h +
[4, 4] [5,/] \
+ 2?B-Т) fn+i/2 + y(y-l) fn+i), B1)
можно с локальной ошибкой порядка hb найти значение
решения и в любой внутренней точке xn-\-yh @<у<1)
отрезка [хп, xn + h] (в случае / = 4 —без дополнительных
вычислений значений функции /).
В заключение заметим, что если бы мы предварительно
задачу A4), A5) свели к соответствующей задаче для
системы двух уравнений первого порядка и стали решать
ее численно методом типа A3), то мы использовали бы
приближенные значения функции у(х) в точках xn + h/tn
и xn + h/3 соответственно с локальной ошибкой порядка h2
и h3y в то время как в случае вычислительного правила
B0), построенного специально для уравнений второго
порядка, в указанных точках используются
приближенные значения функции у(х), точность которых на порядок
выше. В этом направлении можно, очевидно, достичь и
большего. Например, если к равенствам B0), предвари-

42 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
[5] [6]
тельно заменив в их правых частях слагаемое уп на уп,
присоединить формулу
[6] [6] [51 h2 / [5, i] [5, 4] [5, 4] \
Уп+1 = Уп + Ьуп + п[$ \п +25 /я+2/5 + 2 /я+1//,
[5] [4]
где Уп+2/ь находится из B1) при 7 = 2/5, / = 4, а у'п+2/ъ
вычисляется по правилу
[4] [5] 2h ( [5 /] [4,4] [5,4] \
Уп+2/5 = Уп + 375Ч 38 /л + 44 fn+1/2 - 7 fn+1) ,
то получим возможность ценой вычисления одного
дополнительного значения функции / повысить на порядок
локальную точность нахождения y{xn-\-h) (при
сохранении порядка скорости сходимости метода). В случае
уравнений высших порядков появляются еще более широкие
возможности для построения подобных вариантов
вычислительных правил.
§ 5. Сходимость одношаговых методов
Для простоты записи и большей наглядности снова
будем иметь в виду задачу A.1), A.2). Как и раньше,
основные результаты этого параграфа могут быть
перенесены на случай систем уравнений первого порядка и
обобщены на уравнения высших порядков.
Будем считать, что уравнение A.1) на отрезке [л:0, X]
имеет единственное решение не только при начальных
данных A.2), но и в случае любых начальных условий
вида
У(Ъ) = *1>
где
у[%, X, у(Х, х0, ?o)-8]<4<JfR, X, у(Х, х0, #о) + е],
в>0,
а через у (х, |, г|) обозначено значение в точке х
решения у{х) уравнения A.1) при начальном условии уA)^ц.
Величина е при этом может быть истолкована, например,
как верхняя граница допустимой абсолютной погрешности
в нахождении интересующего нас значения у(Х> х0у у0).

§5]
СХОДИМОСТЬ ОДНОШАГОВЫХ МЕТОДОВ
43
Поедположим также, что при любых значениях аргументов
из указанной выше области их изменения решение
y(xf l> ч) непрерывно дифференцируемо по начальному
данному tj. Для такой производной, как известно из
теории обыкновенных дифференциальных уравнений,
справедливо равенство
Это равенство может быть просто получено путем
интегрирования однородного линейного дифференциального
уравнения первого порядка
относительно неизвестной функции z(t)= \*' ^ с на-
чальным значением г (£•) = у \ ^ = 1. При условии
непрерывной дифференцируемости функции / (/, у) по у,
достаточном для существования непрерывной производной
*v *——, последнее уравнение может быть получено
непосредственно дифференцированием по г) очевидного
равенства
-щ-УУ* %> ^Wfr У& £» 4I
с последующей перестановкой порядка дифференцирования.
Пусть, скажем, константа М>0 ограничивает сверху
„ дц (х, £, т]) ^
значения производной д~—- для любых значении
переменных х, g, г) из указанной выше области их
изменения при естественном дополнительном условии £ ^ х.
Будем предполагать также, что решение у(х, |, ц) имеет
непрерывные производные по х достаточно высокого
порядка, определяемого точностью избранного для
исследования одношагового метода вида
yn+i = F(yn), л = 0, 1, ..., ;V-1, A)
где заданная функция F зависит, естественно, от правой
части уравнения A.1), шага /г, который сейчас будем
считать постоянным, и точки хп отрезка [*0, X] (xt = x0 + ih.

44 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
* = 0, 1, .... N, Nh = X-x0). Через &(f=l, 2,..., ЛГ)
в A) обозначено приближенное значение величины
y(xiy х0, уо)у получаемое рассматриваемым методом.
В действительности вследствие наличия ошибок
округления вычисления по формуле A) выполняются, как
правило, неточно. Фактически найденные по этой формуле
значения уъ у2, ..., Уы не будут точно удовлетворять A),
а будут связаны соотношениями вида
Уп+1 = F (уп) - бл+1, п = О, 1, ..., N - 1, B)
где через у0 для единообразия записи обозначена
величина реально участвующего в вычислениях начального
значения у0~у(х0).
Разность 80 = yQ — у0 будем называть погрешностью
начального условия, а величину — бл+1, определяемую
формулой B), —погрешностью округления на (я+1)-м
шаге вычислительного процесса.
Пользователя интересует непосредственно величина
погрешности приближенного решения в точке хп (п =
= 1,2, ..., N), задаваемая разностью
Ъп = У(Хп, Х0, Уо)-Уп = У(Хп, Х0, Уо)-У(хп, Хп, уп).
При условии отсутствия ошибок начальных данных и
округлений эту погрешность называют обычно погрешностью
метода. Последняя задается разностью
£п = У(хп, х0, Уо)-Уп = У(хп, х0, Уо)-у(хп, х„, уп)
и для данной задачи зависит лишь от точности избранного
метода. В действительности же погрешность приближенного
решения зависит, очевидно, от погрешности начального
условия, ошибок округлений и точности самой расчетной
формулы. Погрешность формулы A) на каждом шаге
реального вычислительного процесса можно задать,
скажем, посредством равенства
У(хп+19 хп, yn) = F[y(xn, хп, Уп)] + гп+1 = Р(Уп) + гп+1. C)
Величина г/1+1 этой погрешности характеризует, насколько
хорошо точное решение дифференциального
уравнения A.1), на которое мы вышли на предыдущем/г-м шаге
рассматриваемого вычислительного процесса,
удовлетворяет на данном этапе вычислений аппроксимирующему
разностному уравнению A). Она отражает точность замены

§ 5J СХОДИМОСТЬ ОДНОШАГОБЫХ МЕТОДОВ 45
на отрезке [хп, хп-\-Н\ дифференциального уравнения A.1)
разностным уравнением A) и представляет собой локальную
погрешность избранного метода или ошибку приближенного
решения на одном шаге вычислений без учета погрешности
округления на данном шаге. С учетом же погрешности
округления локальная ошибка приближенного решения
может быть задана формулой
У(*п+ъ хп, Уп)~Уп+1^гп+1 + 8п+1. D)
Эту формулу можно получить путем почленного вычитания
равенства B) из C).
Обычно, как мы видим на примерах вычислительных
правил, рассмотренных в предыдущих параграфах, при
построении одношаговых методов добиваются того, чтобы
погрешность формулы была малой величиной некоторого
порядка k+l (k>0) в сравнении с шагом h. Что
касается погрешности округлений, то любая ее малость, как
и малость погрешности начального условия, принципиально
говоря, всегда может быть обеспечена. В реальных же
условиях уменьшения абсолютного значения погрешности
округлений обычно достигают повышением значности счета
и уровня рациональности его организации. Практические
возможности такого уменьшения ограничены.
Если бы мы располагали эффективными оценками
погрешностей формулы и округлений, то на основании
равенства D) можно было бы дать оценку и локальной
погрешности приближенного решения на каждом шаге
вычислительного процесса, что позволило бы оценить,
насколько сильно на данном этапе вычислений мы можем
отклониться от того решения уравнения A.1), которое
получено на предыдущем этапе. Нас же больше интересует
оценка итогового отклонения от искомого решения. Такое
отклонение не равно, вообще говоря, сумме локальных
ошибок, допущенных на каждом из выполненных этапов
процесса. Оно существенно зависит и от характера
поведения интегральных кривых уравнения A.1). Предположив,
например, что мы допустили ошибку лишь на первом
этапе процесса, а все остальные шаги его не уводили нас
с того решения, на которое вышли вначале, мы будем
иметь принципиально разную качественную оценку
итогового отклонения в сравнении с начальным в зависимости
от того, сближаются или расходятся интегральные кривые

46 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
уравнения A.1) при изменении х в направлении
численного интегрирования. Оценка итогового отклонения и
будет нашей ближайшей задачей.
Отклонение от искомого решения мы допускаем, вообще
говоря, как на каждом этапе вычислений по формуле A),
так и в случае неточного задания начального условия.
Организуя вычислительный процесс при оговоренных
ранее условиях, мы должны прежде всего позаботиться
о том, чтобы ни одно из этих отклонений не вывело нас
за пределы области G8, ограниченной прямыми х = х0,
х = Х и кривыми у = у[х, X, у(Х, х0, Уо)—&], У =
= у[х, X, у(Х, х0, у0) + г]. Для данной задачи при
избранном методе типа A) это требование можно
обеспечить лишь за счет выбора величины шага интегрирования
и уменьшения погрешности начального условия и
округлений. Сформулировать условия, достаточные для
обеспечения указанного требования, можно на основании разных
принципов. Например, в рассматриваемом случае
постоянного шага h можно поставить условие, чтобы допустимое
итоговое отклонение от точного решения было в каком-то
смысле равномерно распределено по всем этапам
вычислений. Можно потребовать, скажем, чтобы влияние
каждого из N-\-\ возможных отклонений на итоговую
ошибку в интересующей нас точке X не превышало по
абсолютному значению величины N . Тогда абсолютная
величина погрешности приближенного решения в точке X
заведомо не превысит е, что. и будет свидетельством
выполнения исходного требования.
Первое отклонение от искомого решения может быть
допущено за счет погрешности начального условия. На
основе сформулированного выше принципа для этого
отклонения должно быть выдвинуто требование
\у(Х, х0, у0)-у(Х, х0, #о)!<д^фр
Если воспользоваться теоремой Лагранжа о конечном
приращении, то левую часть последнего неравенства
можно представить в виде
\у(Х, х0, у0)-у(Х, х0, у о)
(и и \ ду (Х) х°> Чо)
\Уо — У о) щ

СХОДИМОСТЬ ОДНОШАГОВЫХ МЕТОДОВ 47
% = У о + % (Уо-Уо), 0 < в0 < 1.
В силу этого указанное требование будет заведомо
выполняться, если
или
где величина е0 удовлетворяет неравенству
I е01 < е0. F)
При заданном шаге /г, ограничения на выбор которого мы
сформулируем ниже, условие E), принципиально говоря,
всегда может быть выполнено за счет уменьшения
абсолютной величины погрешности начального значения.
Дальнейшие отклонения от искомого решения связаны
с локальными ошибками приближенного решения, которые
задаются равенствами вида D). В силу сформулированного
принципа при этом должно быть обеспечено выполнение
требований
\у(Х, хп, уп)-у(Ху хп+ъ yn+i)\^jf~j,n^0, l,...,iV—!.
G)
Но
у(Х, хп, дп)-у(Х, хя+1, £„+i) =
-=у[Х, хп+и У(*п+ь *п, Уп)]-у(Х, *л+1, yn+i) =
— [У \*п+1г Хп, уп) ~ Уя+lJ ~gz >
где
Чп+1 = Упп + ®пп[у(хп+ъ хп} y„)-gn+i], о<ел+1<1.
Поэтому требования G) с учетом D) принимают вид
(у 1 я \ дУ (х> *я+г» *b+i) 1 - 8
V п+1 + 0п+1) д-
дц
N + 1 '
л = 0, 1, ..., N— 1,
и будут заведомо выполняться, если

4$ ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
ИЛИ r_j_g е
~h~~ ^ M(X — x0 + h) ' ^
где гиб удовлетворяют неравенствам
к,|<л, |б,|<б, i = l, 2, ..., #. (9)
Условие (8) накладывает ограничения и на погрешность
формулы и на погрешность округлений. Так как обычно
г = О (hM), где k > О, то выбором достаточно малого шага
/z>0 всегда можно гарантировать необходимую малость
величины г. При фиксированном же h соответствующая
малость.величины б, принципиально говоря, также всегда
может быть обеспечена.
Будем считать выполненными указанные выше
требования и получим интересующую нас оценку погрешности
приближенного решения, для чего дадим сначала
выражение этой ошибки через погрешность начального
условия, погрешности формулы и округлений.
Ошибка
£п = У(хп, х0, Уо)-Уп = у(Хп, *о> Уо)—у(хп> хп, уп)
очевидным образом может быть записана в форме
%п=У(Хп, х0, Уо)-у(хп, х0у у0) +
п
+ 2 [у{хп, хь-ъ yi-i)-y(xn, xh у()]. A0)
Так как
У(Хп, Xt i, yi-i)=y[Xn, Xh y(xh Xi-ъ УгЛ)\
то равенству A0) можно придать следующий вид:
8/г = У (Хп> X0j У о) — У (ХПУ Х0У у 0) +
п
+ 1] {У[хп, xh y(xh х^ъ yi~i)]-y(x^ xh &)},
1=1
откуда на основании теоремы Лагранжа о конечном
приращении получаем
гп = (Уо-Уо)ду{Х'%0'"Ь) +
П

§ 5]
СХОДИМОСТЬ ОДНОШАГОВЫХ МЕТОДОВ
49
где, как и выше,
% = Уо + % (Уо ~ 17с)» 0 < 80 < 1,
4i = St + % \у (xt, х-, -ъ yt~i) - h\ o <ef. < l.
Поэтому, учитывая D) и определение погрешности
начального условия, можно записать
п
вя-в0 щ + £(П+Ъ£) щ , A1)
1 = 1
/1=1, 2, ..., N.
Формула A1) дает искомое представление погрешности
приближенного решения в точке хп через погрешность
начального условия, погрешности формулы и округлений
на всех выполненных этапах вычислительного процесса.
Из этой формулы хорошо видна также зависимость
характера накопления ошибок при счете на большое число
шагов от индивидуальных свойств решаемого
дифференциального уравнения. Такая зависимость может быть
наглядно пояснена, скажем, с помощью приводимого
в начале этого параграфа равенства
^^ = eXp\\fy[t,y(t,l, „)]*}.
В случае, когда при £<#, например,
ду(*. I, т]) { fdfjx, у) '
дг| \ ду
и интегральные кривые уравнения A.1) при изменении х
в направлении численного интегрирования расходятся,
влияние погрешности начального условия и каждой из
локальных ошибок приближенного решения, допущенных
на предыдущих шагах вычислительного процесса,
возрастает. Если же, скажем,
ду (дг,JL г}) j Ш(х, у) 0
дц \ ду
и интегральные кривые уравнения A.1) сближаются, то
влияние каждой из ошибок, наоборот, ослабевает.

50 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
Заметим, что, опираясь на формулу A1), можно
получить вместо E), (8) другое достаточное условие того,
что значения приближенного решения ни на одном шаге
вычислительного процесса не выходят за пределы
указанной ранее области Ge. Для этого в силу A1) с
учетом F), (9) достаточно, чтобы было выполнено неравенство
[г0 + (г + б)АГ|М<е,
или
Это условие, в отличие от E), (8), не основано на
принципе равномерной малости местных ошибок, отнесенных
к интересующей нас точке (роль X может играть и любая
другая фиксированная точка отрезка [х0, X]), а имеет
суммарный характер. 1<ж и условия E), (8), последнее
условие является, конечно, завышенным, хотя, вообще
говоря, и менее жестким. Оно заведомо выполняется,
если удовлетворены ограничения E), (8). Действительно,
г° + ~1Г(А~~Хо}^ M(X-xQ + h) +
8 F
На основании формулы A1) можно получать также
различные оценки погрешности приближенного решения.
Для целей выяснения условий и скорости сходимости
рассматриваемого вычислительного процесса можно
ограничиться лишь следующей достаточно грубой
равномерной оценкой, которая непосредственно вытекает из A1)
с учетом неравенств F), (9):
\h\^[zo + r-^(X-xQ)~\M, я=1, 2, .... N. A2)
В силу этой оценки можно утверждать, что если при
ео->0, |->0, -£-*0, A3)
то в любой точке отрезка [д:0, X] приближенное решение
задачи A.1), A.2), полученное одношаговым
методом типа A), будет сходиться к точному решению этой
задачи.

§51
СХОДИМОСТЬ ОДНОШАГОВЫХ МЕТОДОВ
51
В частности, когда ё0 = 0, 6^ = 0, t = l, 2, ..., N,
л речь идет лишь об оценке погрешности метода A),
неравенства A2) принимают вид
|eJ<-£(X-*o)M, /2 = 1, 2, ...f N, A4)
а условия A3) переходят в следующее условие
сходимости метода:
~-->0 при й->0. A5)
Так как обычно при построении одношаговых методов
добиваются выполнения требования
r = 0{h^)f /г>0,
то условие A5) в этом случае заведомо выполняется
и оценка A4) гарантирует в любой точке отрезка [х0, X]
сходимость одношагового метода A) со скоростью
порядка hk. По этой причине соответствующий метод
называют обычно методом k-го порядка точности.
Чтобы в условиях реального вычислительного
процесса в любой точке отрезка [х0, X] приближенное
решение, полученное данным одношаговым методом k-vo
порядка точности, сходилось к точному решению
исходной задачи Коши со скоростью порядка hk, достаточно
потребовать (см. A2)), чтобы выполнялись условия
е0 = О(А*), 6 = 0(A*+1).
Хотя эти требования, принципиально говоря, и
выполнимы, однако в реальных условиях, когда значность
вычислительных машин ограничена, с уменьшением шага
/г>0 практически трудно бывает столь быстро повышать
точность выполнения вычислений. Обычно для реальных
ЭВМ погрешности е0 и 8if i=\, 2, ..., N, при
изменении h остаются ограниченными снизу по абсолютному
значению величинами. При сохранении значности ЭВМ
погрешность ё0, как правило, вообще не изменяется.
Следовательно (см. (И)), с уменьшением шага
практически не изменяется и неустранимая погрешность — часть
погрешности приближенного решения, зависящая только
от ошибки начального условия. Вычислительная же
погрешность (часть погрешности приближенного решения,

52 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
источником которой являются лишь ошибки округлений)
в силу оценки A2) из-за наличия множителя б/А при
А->0 может возрастать со скоростью порядка А. Что
же касается погрешности метода, то она, как мы уже
отмечали, при этом обычно убывает со скоростью
порядка А*. Поэтому главную часть полной погрешности
приближенного решения в зависимости от величины
шага А составляют, как правило, либо погрешность метода
(при относительно больших значениях А), либо
вычислительная погрешность (при очень малых значениях шага).
В случае грубого задания начального условия может,
конечно, оказаться доминирующей и неустранимая
погрешность, однако при сильном изменении шага в
сторону его увеличения или уменьшения на первый план,
особенно при счете на большое число шагов, выходят,
как правило, погрешность метода или вычислительная
погрешность, при этом результат вычислений может
оказаться неприемлемым по точности как при больших, так
и при очень малых значениях шага. Естественно
поставить задачу о нахождении такого значения А, при
котором величина правой части оценки погрешности
приближенного решения в данной точке была бы наименьшей.
Это значение шага приведет, грубо говоря, к равным
долям погрешности метода и вычислительной
погрешности. Доля неустранимой погрешности при этом должна
бьпь также не больше. Тогда вычислительный процесс
будет сбалансирован. В практике вычислений обычно
стараются добиться того, чтобы неустранимая и
вычислительная погрешности не влияли на результат в пределах
погрешности метода.
Многие из только что приведенных наводящих
рассуждений основаны на оценке A2), которая является
явно завышенной. Ошибки округлений, например, могут
иметь разные знаки и частично компенсировать друг
друга, не обязательно должна сохранять знак на каждом
шаге процесса и погрешность формулы; составляющие
части полной погрешности по шагам также, вообще
говоря, могут давать отклонения не в одну сторону от
решения. В действительности же все это, однако, вносит
лишь незначительные искажения в нарисованную
асимптотическую картину. Практикой вычислений
правильность сделанных выводов обычно подтверждается.

§ 5] ГЛАВНЫЙ ЧЛЕН ПОГРЕШНОСТИ. ПРАВИЛО РУНГЕ 53
Изложенное выше позволяет утверждать, что при
организации вычислительного процесса необходимо
следить за взаимным согласованием метода вычислений,
величины шага hy требуемой точности результата, точности
задания входных данных и точности вычислений. Иногда
для такого согласования прибегают к помощи модельных
задач. Частичное согласование этих факторов можно
проводить, например, и на основании полученной оценки
A2). Правда, использование этой оценки затруднено
тем, что практически пригодные значения входящих
в нее констант для большинства задач получить очень
трудно. Величина г, например, обычно оценивается через
максимумы абсолютных значений достаточно высоких
производных от решения исходного уравнения. В редких
случаях удается получить удовлетворительные оценки ее.
По той же причине априорная оценка A2) не часто
используется и для суждения о точности окончательного
результата. Для этих целей чаще применяют более
простые в употреблении апостериорные оценки, пользоваться
которыми можно лишь после проведения вычислений.
При рассмотрении основных способов построения одно-
шаговых методов мы иногда касались вопроса
апостериорной оценки погрешности, особенно в тех случаях,
когда сам метод был хорошо приспособлен для этих
целей. Сейчас мы еще раз затронем эту проблему.
§ 6. Главный член погрешности. Правило Рунге
Будем иметь в виду по-прежнему задачу Коши A.1),
A.2), предполагая выполненными требования к ней,
сформулированные в предыдущем параграфе. Сейчас нас
будет интересовать преимущественно лишь погрешность
метода, т. е. та часть погрешности приближенного
решения, которая зависит лишь от неточностей формулы.
Считая равными нулю погрешности начального условия
и округлений, подобно E.11), можно записать
е„=ф^(у Ч »-l,2,...,JV, A)
1=1
где
% = У1 + в/ [У (Ь, **-i, yi-i) — yi]t 0 < 6/ < 1.

54 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
Пусть погрешность формулы (см. E.4))
П = у(ъ, */-i, У1~\)-Уь *"=1, 2, ..., л,
представима в виде
#(*„ хн, |//-1)-^ = Л*+1Ф(х/.1, #-i) + 0(ft*+2), B)
где £>0, при этом известная функция ср(х, у) в области
G£, введенной в предыдущем параграфе, ограничена по
абсолютному значению вместе со своими частными
производными первого порядка.
Для. большинства вычислительных методов типа E.1)
при естественных требованиях к гладкости правой части
уравнения A.1) представление остаточного члена в виде B)
получить нетрудно. Первое слагаемое такого
представления при малых значениях шага /г>0 дает главную часть
погрешности формулы. Во многих случаях бывает
достаточным вместо учета всей погрешности г/, t= 1, 2, ..., N,
ограничиться рассмотрением лишь ее главной части.
Поставим перед собой задачу, опираясь на
представление B) для локальной погрешности метода, выделить
главную часть также и из суммарной погрешности A)
рассматриваемого метода. Использование главной части
погрешности метода вместо всей погрешности более удобно
для целей практики вычислений и часто бывает
достаточным.
В силу B) и оценки E.14)
y(Xh *o> yo)-yi^O(hk).
Поэтому, если предполагать решение у(х, g, tj)
уравнения A.1) в описанной ранее области изменения
переменных ху £, т) дважды непрерывно дифференцируемым по
начальному данному ц, то, опираясь на теорему Лаг-
ранжа о конечном приращении, значение
дц
в A) можно- заменить на
ду [хп, хь у fa, *0, г/о)] . q „к.
дц "т \ /•
И аналогично ф(х*-1, yi-i) можно заменить на
ф[*ы. y(xi-b x0f y0)] + O(hk) = (p[xiy y{xi9 xQ9 y0)] + O{h)f

§ 6] ГЛАВНЫЙ ЧЛЕН ПОГРЕШНОСТИ. ПРАВИЛО РУНГЕ 55
что позволяет записать B) иначе:
П = /г*+1Ф [xh у (xh х0, ус)] + О (hk^).
Тем самым, принимая во внимание, кроме того, что
nh<,X—x0, формуле A) можно придать вид
п
i=i
X ^^^У(^^УоI + о (А**), C)
п=1, 2, ..., N.
Если теперь на основании квадратурной формулы
правых прямоугольников
хп п
х0 i = l
где Xi~x0-\-ih, /i>0, записать равенство
п
i= 1
Xq
to C) можно переписать в виде
£n=*hk \ y[t, y(t, х0, Уо)]х
Ха
ду[хя, U УУ, х0) уо)] dt + Q ^ш^^ ^
Так как
то в D)
0У[*п> *>
дц
ду(х, %,
А
_Л1
дц
п=1, 2, ...,
= ехрП/Дт,
ду [хп, U у (t, x0
N.
у(ъ
.0оI.

56 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
можно заменить на
(хп )
exp j \ fy{r, у [г, U y(t, x09 y0)]}d%}
или, что то же самое, на
ехР j! /Лт> #(т> *о. Уо)№-
Тогда будем иметь, что
гп=hkp (хя) + О (/ife+1), /г = 1, 2, ..., JV, E)
где
Р(*)= $Ф[^» #(*> *о. Уо)]ехрП/Лт, г/(т, лг0, #0)]<*Ч<#.
Если р (хл) Ф 0, то величина /ifep (xn) при достаточно
малых значениях шага /iX) будет давать неплохое
представление о значении погрешности метода в точке хп.
Поэтому величину hkp (xn) называют обычно главным
членом погрешности метода или просто главным членом
погрешности. Она не дает, конечно, полной
характеристики погрешности метода и, тем более, погрешности
приближенного решения, однако нередко посредством ее
можно получить достаточно хорошее представление об
истинной величине ошибки. Это будет в том случае,
когда неустранимая погрешность невелика по
абсолютному значению в сравнении с погрешностью метода,
а шаг h выбран настолько малым, чтобы величина hkp (xn)
достаточно хорошо представляла собой погрешность
метода, но все же и не очень малым, чтобы
вычислительная погрешность оставалась еще небольшой по
абсолютному значению по отношению к погрешности метода.
Практика вычислений показывает, что для данного класса
задач и фиксированного типа ЭВМ существует
ограниченная сверху и снизу область значений шагов, в
которой главный член погрешности избранного метода дает
хорошее представление о величине полной погрешности
приближенного решения, при этом, конечно, имеется
в виду, что требования к точности результата
согласованы с величиной неустранимой погрешности, которая

§ 61 ГЛАВНЫЙ ЧЛЕН ПОГРЕШНОСТИ. ПРАВИЛО РУНГЕ 57
от шага h не зависит, либо заранее обеспечена
необходимая малость этой погрешности. При значениях h из
этой области члены высших порядков в асимптотическом
разложении погрешности метода вместе с вычислительной
погрешностью малы по абсолютному значению в
сравнении с главным членом погрешности. Такую область
изменения h назовем реальной областью асимптотики. При
подходе к границе этой области в сторону увеличения
значений шагов наблюдается обычно постепенное
ухудшение асимптотики, поскольку при этом в правой части E)
возрастает роль членов, содержащих высшие степени h.
Ухудшение же асимптотики на выходе из этой области
в сторону уменьшения значений шагов связано с
возрастанием относительной доли вычислительной погрешности.
Нижняя граница реальной области асимптотики
существенно зависит от разрядной сетки вычислительной
машины. Для машин с более широкой разрядной сеткой
эта граница, вообще говоря, меньше, так как в этом
случае обычно меньше величина 6 (см., например, оценку
E.12)) и отношение 8/h достигает критических значений
при меньших h.
На основании формулы E) легко указать простое
апостериорное правило оценки главного члена
погрешности, известное под названием правила Рунге, которое
часто используется в вычислительной практике.
Предположим, что в некоторой фиксированной точке х
отрезка [х0, X] при двух достаточно малых значениях
шага h = hx и h = h2 данным одношаговым методом &-го
порядка точности найдены соответственно два
приближенных значения у\ч и yhz решения у (х) задачи Коши A.1),
A.2). Тогда в силу E) можно ожидать, что будут малы
по абсолютному значению погрешности приближенных
равенств y(x)-yhi~hfr{x),
y(x)-yh2^h*p(x).
Исключая из этих равенств неизвестное значение у(х),
hi-
щ
точки х с шагами h = h1 и A==/i.a получить приближенные
находим / > **.-**.
Это дает возможность после проведения вычислений до

53 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
значения каждой из величин А?р(*), /=1, 2, и
составить представление в погрешностях значений унх и ун2.
Кроме того, при заданной границе е допустимой ошибки
на основании приближенного равенства
е*Чр(*)|йе
по результатам этих вычислений можно будет выбрать
практически более приемлемое при данных требованиях
к точности значение шага
■Ук2
G)
В практике вычислений наиболее часто в качестве
значений шагов h\ и /г2 избирают h и /г/2. В этом случае
формулы F), G) принимают соответственно вид
2к(У1Ч2-Уь)
Р(х)~
/V
А»B»-1) '
h_ k /~ B*-1)8 У '
2 I/ \Ун>2-Уц\'
Используя (8), в частности, можно записать, что
Эта простая формула, как и все приближенные равенства,
основанные на представлении E) для погрешности метода,
имеет асимптотический характер и при конкретных
значениях шага h не играет роли гарантированной оценки.
Заметим, что, записав равенство (9) в виде
можно истолковать его как правило увеличения точности
приближенного решения. Правило A0) является частным
случаем более общего метода Ричардсона ускорения
сходимости последовательности. Подробнее о методах
улучшения сходимости речь пойдет в гл. 9.
Отметим в заключение, что правило Рунге может быть
использовано не только при решении обыкновенных
дифференциальных уравнений одношаговыми методами. Это

§7]
МЕТОДЫ ТИПА ДВУСТОРОННИХ
59
правило можно применять всякий раз, когда
асимптотическое поведение погрешности избранного метода имеет
указанный выше характер. Широко пользуются этим
правилом, например, в практике вычисления интегралов,
при численном решении различных задач для
дифференциальных уравнений с частными производными и в
других вычислительных задачах.
§ 7. Методы типа двусторонних
Во многих практических задачах, приводящих к
решению обыкновенных дифференциальных уравнений с
начальными условиями, на первом плане стоит проблема
получения результата с гарантированной точностью. Объем
вычислений при этом учитывается не как первостепенный
фактор. Решение этой проблемы значительно
упрощалось бы, если бы были построены вычислительные методы,
которые позволяют одновременно находить два
приближенных решения данной задачи Коши, соответствующие
значения которых в рассматриваемых точках расположены
по разные стороны от истинного значения искомого
решения. Задача о построении таких методов издавна
привлекала внимание математиков. Еще в начале этого
столетия С. А. Чаплыгиным, например, были разработаны
основные принципы построения одного из двусторонних
методов. Метод Чаплыгина принадлежит к группе
аналитических методов и позволяет строить на каждом отрезке
интегрирования две последовательности кривых,
приближающих сверху и снизу искомую интегральную кривую
данного уравнения. Правда, этот метод накладывает
довольно сильные ограничения на правую часть др1фферен-
циального уравнения и, кроме того, он трудно
реализуется при работе на ЭВМ. Достаточное полное
изложение метода Чаплыгина дано, например, в [2]. Мы
остановимся здесь на рассмотрении методов несколько
иного типа, которые не являются строго двусторонними
и обеспечивают приближение к искомому значению
точного решения с разных сторон лишь в смысле главного
члена погрешности. Однако, в отличие от метода
Чаплыгина, эти методы принадлежат к группе численных
методов, легко реализуются на ЭВМ и являются более
универсальными,

60 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
Предположим, что в случае задачи A.1), A.2)
построено семейство таких методов типа E.1), для которых
выражение F.2) погрешности формулы имеет вид
ri = y(xh xi-ъ №-i)-^-/**+>|>(*/-i> yi-i) + Q(hk+2), A)
где у — свободный числовой параметр семейства, а ty (х, у) ~
известная функция указанных аргументов. Тогда,
согласно F.5), для погрешности гп каждого из этих
методов будет справедливо представление
вл = 0(*я, *о, Уо) - Уп = hkp (хп) +0 (hk + 1), n=l,2,...,N,
B)
где
p(x) = y\q[t> У(*> *о> ^o)]6xpK/t/[r, у(т, х0, y0)]dT\dt.
Если теперь среди вычислительных правил данного
семейства избрать два таких метода, для которых соответствую-
[f] [-] [+J
щие значения у и у параметра у удовлетворяют у х
X у < 0 (скажем, у = — у), то в точке хп (п = 1, 2, ..., N)
в силу B) главные части погрешностей избранных
методов будут иметь противоположные знаки. Это дает
основание надеяться на получение по избранным
вычислительным правилам приближений к значению у(хп, х0,
у0) с избытком и с недостатком, если, конечно,
неустранимая погрешность мала по абсолютному значению
в сравнении с погрешностью метода, а шаг h > 0 взят
настолько малым, что величина hkp (xn) в B) достаточно
хорошо представляет собой всю погрешность метода;
при этом вычислительная погрешность еще не настолько
велика, чтобы исказить результат вычислений в пределах
принятой точности.
Семейства вычислительных правил, для которых
локальная погрешность представима в виде A), можно получать
по-разному. За основу может быть взят, например,
способ Рунге —Кутта построения одношаговых методов.
Однако более просто такие методы строятся способом,
указанным в § 4. Поэтому мы остановимся здесь лишь
на последнем подходе к построению подобных
вычислительных правил.

§7]
МЕТОДЫ ТИПА ДВУСТОРОННИХ
61
В п. 4.1 было показано, что погрешность
приближенного равенства D.2) при выполнении условий D.4) может
быть представлена в виде D.5)
'л + 1-
zhk+ly{k+l)(Xnj
1 1
№+1I k\
i = 0
i a^
+ 0(/i*+2).
В этом представлении, как и всюду в § 4, в силу
локального характера построений значение в точке хп
соответствующего решения уравнения A.1) считается
известным точно. При этом для упрощения записи зависимость
решения от начальных данных в обозначениях не
указывается (необходимые значения производных решения
по формулам типа A.4) могут быть точно выражены
через это значение).
Если выбор параметров Aif aiy i = 0, 1, ..., qy в D.2)
дополнительно к условиям D.4) ограничить требованием
где у —произвольное вещественное число, то тем самым
будет описано семейство приближенных равенств типа
D.2), погрешность которых представима в виде A):
rn+1=zh^yy^+V(xn) + 0(hk + *). D)
Конкретный вид функции г|) (х, у) при этом может быть
получен последовательным дифференцированием правой
части уравнения A.1). Для того чтобы на основании
этих приближенных равенств можно было построить
соответствующее семейство вычислительных методов,
достаточно указать такие правила эффективного вычисления
значений у(хп + at-/i), i = 0, l, ..., qy чтобы вносимая ими
в D.2) погрешность не изменяла главного члена ошибки
D). Для этого, очевидно, достаточно обеспечить
нахождение значений #(хл + а;/г), * = 0, 1, ..., qy с локальной
погрешностью порядка hkrl. Соответствующие
вычислительные правила легко могут быть построены способом,
изложенным в § 4.
Выделив из построенного так семейства
вычислительна
ных правил два метода, отвечающие значениям у и

62 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
Y vY * V <0/ параметра у> мы получим два набора
расчетных формул, позволяющих при выполнении
оговоренных выше требований находить приближения с
избытком и с недостатком к значениям искомого решения
задачи A.1), A.2) в фиксированных точках отрезка [х0, X],
Наиболее существенным из упомянутых требований
является условие, чтобы величина hkp(xn) в B), знаком
которой мы можем управлять за счет выбора знака
параметра у> действительно являлась главной частью
погрешности метода. Последнее существенно зависит от
того, будет ли действительно главным первый член в
правой части равенства D), иными словами, будет ли при
выполнении условий D.4), C) слагаемое
Л*+у*+1>(*л)
№+1)!
-»■ I *<*
i = 0
E)
играть определяющую роль в асимптотическом разложении
гя+1= 2hl'+lyU+1){Xn)
1 = 0
1
(/+1I
2Aia{
i = 0
F)
погрешности приближенного равенства D.2). Чтобы
повысить роль слагаемого E) в сумме F), можно, кроме
выполнения условий D.4), C), выбором параметров Ah
<xh i = 0, 1, ..., q (при соответствующем значении q),
обеспечить также обращение в нуль нескольких
следующих за слагаемым E) членов разложения F). Система
ограничений на выбор Ah ah i = 0, 1, ..., q, в этом
случае может быть записана в виде
я
У А--
1, ^АМП
1
t = 0
+ 1
р.уЫ, /=1, 2, ..., р,
G)
где б£ — символ Кронекера, а заданием p(p^k)
определяется число p — k слагаемых в F), следующих за E),
которые будут обращены в нуль. При p = k требования
G) эквивалентны условиям D.4), C). Если выбор
параметров в D.2) осуществляется на основе этих требований,

§7]
МЕТОДЫ ТИПА ДВУСТОРОННИХ
63
то, чтобы не нарушить оговоренной выше структуры
локальной погрешности при вычислении значений у (хп +
+ а/А), 1 = 0, 1, ..., <7, соответствующие расчетные
формулы необходимо выбрать так, чтобы обеспечить
нахождение этих значений с погрешностями по крайней мере
порядка Ар+1. Построение таких формул может быть просто
осуществлено способом, изложенным в § 4.
С увеличением р возрастает, естественно, и
громоздкость вычислительных правил. Поэтому значение р
желательно брать не сильно превышающим &, а дальнейшего
повышения роли главных членов погрешности формулы
и погрешности метода можно добиваться за счет
уменьшения шага А>0 численного интегрирования. При этом
удачу выбора А (и р) можно контролировать, сопоставляя,
например, величину главного члена погрешности метода
с величиной погрешности полученного приближения к
решению и следя за согласованием этих погрешностей с
требованиями к точности результата.
Описанный выше вычислительный процесс
предполагает получение в каждой узловой точке хп двух прибли-
Н-] [-]
женных значений уп и уп величины у(хп), отвечающих
Ж [-1
соответственно значениям у и у параметра у. При
выполнении условий G) в силу B) главные члены
погрешностей метода в каждом из этих случаев являются
величинами порядка А*; при этом их знаки будут
противоположными. Очевидно (см. B)), что приближенное значение
уп величины у(хп), вычисленное по формуле
У - У
будет (без учета ошибок начального условия и
округлений) характеризоваться погрешностью уже по крайней
мере порядка hk+1. Можно показать, что погрешностью
порядка hk+1 обладает и следующий метод получения
приближений к искомому решению, не связанный с
предварительным нахождением в каждой узловой точке хп
[+] I-]
двух приближений уп и уп. В этом методе значение уп
вычисляется не по формуле (8), а находится
непосредственно по одному из двух вычислительных правил

64 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
[+]
построенного выше семейства, отвечающих значениям у
[-]
или у параметра у. При этом избранные правила
используются не одновременно, как ранее, а применяются
поочередно, так что в каждой узловой точке вычисления
производятся лишь по одному из них. При такой
организации вычислительного процесса не ставится задача
о получении двусторонних приближений, а построенный
вычислительный метод будет характеризоваться лишь тем
обстоятельством, что на каждом шаге процесса главная
часть локальной погрешности, как правило, меняет знак
на противоположный. Этим и объясняется утверждаемое
выше благоприятное поведение суммарной погрешности
метода.
Только что описанный вычислительный процесс
поочередного использования каждой из двусторонних формул
требует приблизительно вдвое меньшего объема
вычислений на узел сетки в сравнении с рассмотренным выше
двусторонним методом, который предполагает независимое
построение верхних и нижних приближений. Если же
отказаться от принципа независимого нахождения верхних
и нижних приближений, то на основании изложенного
в § 4 способа построения вычислительных методов можно
сконструировать и более экономичный процесс
двусторонних приближений. Надежность двусторонности при этом
не будет сильно ослаблена.
В описанном ранее методе основные расчетные
формулы двусторонних приближений имели вид
[+] [+] * Ш / [+] [+] \
Уп+г= Уп + h 2j Aif[xn+ath, у [+] ,
[-] [-] « [-] / [-] [-] \ v ;
Уп + 1= Уп + h 2j Aif[xn+a>ih, у \-]);
i - 0 \ п + «. /
при этом одношаговые вычислительные правила нахожде-
[+] 1-1
ния у [+] и у [_], f = 0, 1, ..., q, предполагали
использование в качестве исходной информации значений
Ш [-] Г+] Ш [-] [-]
уп и уп соответственно. Здесь под Ai9 щ и Ah a£,
* = 0, 1, ..., q} следует понимать значения параметров
Ai, a/, i = 0, 1, ..., q, удовлетворяющие системе G) при

§71
МЕТОДЫ ТИПА ДВУСТОРОННИХ
65
у= Y и 7= У соответственно. Смысл других
обозначений в (9) также вполне аналогичен используемым ранее.
Сейчас будем считать, что на каждом шаге процесса
величина уп предварительно вычислена по формулам
типа (8), а основные расчетные формулы двусторонних
приближений имеют вид
[+] Ж , « [+1 / [+] \
0*+1= Уп + п Zj Aif\xn+ &ih> У ж ,
'-° \ я+а'/ A0)
0/1+1= f/« + A Zj Aif\xn+ а*Л, г/ м ,
при этом для нахождения у [+] и У г—]» t = 0, 1, ...
..., #» применяются одношаговые правила, использующие
в качестве исходной информации лишь одно вычисленное
ранее значение уп. Если (при достаточно большом q) поло-
!+■] [~]
жить at= at для всех (или почти всех) значений / = 0,
1, ..., qy то построенный метод двусторонних
приближений будет почти вдвое экономичнее соответствующего
двустороннего метода типа (9). Ив случае такого
вычислительного процесса, подобно B), для верхних и нижних
приближений можно получить выражения главных членов
погрешности метода, которые также будут различаться
[+] [-1
между собой лишь множителями у или у .
В последнем методе получения двусторонних
приближений можно сравнительно просто проследить за
переменой знака множителя y[k + l)(xn) в представлении типа
D) главного члена локальной погрешности. О перемене
знака этого множителя при оговоренных ранее
предположениях можно с достаточно высокой достоверностью
сделать заключение на основании сравнения знаков величин
h 2 Aif[xn+ ath9 у ж - ft ^ Aif[xn+ осД у м
(и)
И
[+3 [-]
Уп- Уп (п>0). A2)
3 В. И. Крылов и др., т. II

66 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
Если знак разности A1) окажется противоположным
знаку разности A2), естественно формулы A0) заменить
на формулы
Ш [+] f ^ Н / [-1 \
Уя+1= Уп + h 2j Aif\Xn+ а/Л, у [.,],
1 = 0 \ п+ aii
Е-] [-] . * [+] / [+] \
Уп + г= Уп + h Zi Aif\xn+ щК У г-Ч !-
/ = о \ п+<*ч/
[-] Г-Н
Заметим, что разность A2) равна еЛ— е,„ где
[+] [+1 [-] [-1
£п = У (Хп) ~ #я, 8л = У (Хп) - уя.
Так как в случае достаточно малого шага h>0 ошибки
[+] [-]
гп и еп должны иметь противоположные знаки, то
абсолютное значение этой разности должно давать хорошее
представление о сумме абсолютных значений главных
членов погрешностей двусторонних приближений. И
аналогично абсолютное значение разности A1) при малых h
должно хорошо представлять сумму абсолютных
значений локальных погрешностей соответствующих методов.
Сопоставляя значения величин A1) и A2), вычисленных
при соблюдении условий малости абсолютных значений
ошибок начального условия и округлений, с
соответствующими величинами главных членов погрешностей и
требуемой точностью результата, можно, в частности,
высказать суждение об удаче выбора шага h с большей
достоверностью, чем в случае двусторонних
приближений (9), когда мы не имели непосредственно по ходу
вычислений информации типа (И) о локальной
погрешности метода. При этом, конечно, приходится считаться
с тем, что даже грубое вычисление главных членов
погрешностей является очень трудоемкой задачей. Поэтому
при выборе шага часто руководствуются и другими
соображениями.
Чтобы не загромождать изложение, не станем все
сказанное выше иллюстрировать примерами конкретных
вычислительных правил, а приведем только некоторые
из простейших примеров.

§7]
МЕТОДЫ ТИПА ДВУСТОРОННИХ
67
Рассмотрим сначала случай, когда fe = p=l. Тогда
система G) принимает вид
При 9 = 0 находим
л 1 I
Л0=1, «о^у-Т-
Требование одношаговости 0 ^ а0 ^ 1 приводит к
следующим ограничениям на выбор параметра у:
-2Uv«4.
Выбрав два значения у = 1/2, у =— 1/2 параметра у,
удовлетворяющие этим ограничениям, найдем
соответственно
[+] м [+] [-]
а0 = 0, а0=1, А0=А0=1.
Метод двусторонних приближений вида (9) в этом
случае может быть записан в форме
[2] [2-] [2-]
j/nu= Уп+h fn,
[2-] [2-] [2 J ,nv
^л+1= Уп + hfn+i, \l6>
[2+J [2+] [2+J
*/л+1= */л + ^ /я-
Верхние индексы здесь, как и ранее, дают указание на
порядок локальной погрешности метода, с которой было
найдено данное значение приближенного решения, а также,
где это существенно, определяют знак соответствующего
значения параметра Y-
Погрешности основных формул двусторонних
приближений (см. D)) будут при этом иметь вид
[rL = ±yftV(^) + 0(A8)-
Метод A3) требует на каждый узел сетки трех
обращений к блоку вычисления значений правой части
уравнения.
3*

68 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
Более экономичным, наверное, будет следующий
процесс получения двусторонних приближений:
[2] гз] m
УпП ~ УпЛ-"*]п,
[2-] [2-] Щ
У mi— Уп-r h fn+ъ
12 +] [2+J [l] О4)
Упп= Уп + hfn,
13] i /[2+] [2-3 \
^/л+1 = 2 V уп+1-\- Уп+iJ-
Здесь i может принимать значения 2 или 3. Для случая
/ = 2 формулы A4) в основном счете сопряжены с
нахождением лишь одного значения функции f(x, у) на
каждый узел сетки, при этом будут вычислены четыре, вообще
говоря, разных приближенных значения интересующей
нас величины у(хп+1), сопоставление которых также может
дать полезную информацию. В этом случае, правда,
проявляются некоторые особенности конструкции
вычислительных правил A4), не характерные, вообще говоря,
для одношаговых методов. На первом этапе, например,
придется вычислять не одно, как всюду далее, а два
значения функции f (х, у). При этом каждый из
последующих шагов вычислительного процесса будет связан
со специфичны^ использованием информации разного
уровня точности об искомом значении решения,
полученной на предыдущем шаге. При £ = 3 однородность
вычислений будет восстановлена; при этом окажется несколько
улучшенной, вообще говоря, и точность результата,
однако при таком значении i вычислительный процесс
будет требовать двух обращений к блоку вычисления
значений функции / (х, у) на каждый узел сетки.
Положим теперь в системе G) k=lf p = 2. Тогда
будем иметь
я я я
t' = 0 i = 0 i = 0
Приближенные равенства типа D.2), подчиненные таким
ограничениям, будут характеризоваться погрешностью
следующего вида (см. F)):
rn+i = h*yy"(xn) + 0(h*). A5)

§73
МЕТОДЫ ТИПА ДВУСТОРОННИХ
69
При q=\ и а0 = 0 полученные ограничения
значительно упрощаются:
i40 + i4i=l, Л^^у-у* 41*1=3-.
Отсюда находим, что
*1-Щ^Щ> А^\{\-2у)\ Л0=1 —-|-A—2Y)».
Из условия 0<ос1<с1 получаем следующее
ограничение на область изменения параметра у:
В частности, при 7 =1/6 и у =—1/6 соответственно
находим
[+] [+1 2 М f+1 1
а0 = 0, Ло=з> а!=1, 4i = y,
[-] М 1 [-1 1 М 4
а0 = 0, Л0 = —з, ai=2"» ^1="з"-
По этому набору параметров можно построить следующее
вычислительное правило:
[2] Г4] h К]
[3] М д [21
Уп+\,2 = Уп~{- 7f fn+\/49
[3] [4J [3]
Уп+1— yn + hfn+l.V,
12+] [2+] Л / Щ [3]
#/i+i = S//1 + -3 W* + ^+1
[2-3 [2-] h( [С] [3] \
УпП = У* + у V— /л + 4 /W 1/2У >
[4] J /12+1 [2-3 \
У/1+i = ' V Уя+1 ~Ь Уя+1/ •
Здесь индекс i может принимать значения 3 или 4.
На основании этих расчетных формул нетрудно
записать и двусторонний метод вида (9), в котором верхние
и нижние приближения находятся уже независимо.
Погрешность подобных двусторонних формул
характеризуется равенствами (см. A5))
[?M = ±\h*y"{xn) + 0(W).

70 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
Построим пример двусторонних методов при k = p==2.
В этом случае система G) принимает вид
24=i, 2><Ч> 2^4~2v-
1 У л _, 1
2 ' Am'
Возьмем q—l и положим сс0 = 0. Тогда будем иметь
Тем самым будет описано однопараметрическое семейство
приближенных равенств типа D.2), погрешность которых
(см. D)) представима в виде
rn+i = h*yy"f(xn) + 0(h*).
Из условия 0<ai<cl получаем следующие ограничения
на выбор параметра у этого семейства:
найдем
-и<т<|.
[+] 1 [-]
Положив, например, у =^-- у =
Г+] [+! [+] !
[-] [-1 1 Н
а0 = 0, А0= -о-, ai=l,
1
~" 12* ]
Г-Н
Аг=\-
что позволит записать следующий метод двусторонних
приближений вида A0):
[2] f4] h Щ
Уп+1/*= Уп+ 4 /л,
[3J [■*] h [2]
Уп+1,2= Уп-\- //г+1'4,
[3] [•!] [3]
#/i+l = yn + hfn+\'2,
[3+] [3+] [3]
Уп+1 = IJn + hfn+lV,
f3~] _[3"], */"? . I?] \
У/г+1 ~ У/г "Г ~2 \ Г п ~Т / л+1/ »
[4] ! /[3-] [3+J
Уп+1 = т1 */л+1 + 2 Уя+1

§71
МЕТОДЫ ТИПА ДВУСТОРОННИХ
71
Индекс i здесь может принимать значения 3 или 4. При
1^3 процесс нахождения двусторонних приближений
в каждом (кроме первого) узле сетки сопряжен с
вычислением трех новых значений функции / (х, у).
Очевидным образом может быть записан и
соответствующий двусторонний метод вида (9). Он, правда, будет
требовать на каждый узел сетки уже семи обращений
к блоку нахождения значений правой части
уравнения A.1).
Погрешности основных двусторонних формул при
избранных значениях у имеют вид
Приведем без вывода еще один набор двусторонних
формул вида A0), отвечающий случаю k==p = 3:
[2] [5] h [С]
Уп+\/9= Уп + ~д fn>
[3] И 2Л[2]
*/rt-f 2/9 = Уп+~д /л+1/9,
[4] И h (U\ [31
Уп+ 1/3 = Уп + ] V fn + 3 //1 + 2..9.
[4] Г5] ^ f\i} ГЗ] [4]
Ул + 2/3 = #я + "з" V /^ — 3/rt + 2/9 + 4fn-f 1/3/»
[4] [5] h ([i] [4] \
Уп+1 ^Уп+jKfn + 3/л + 2/зЛ
[4+] [4+] - л /[<] [4] \
Уп+1= У/г+-4Л/я + 3/« + 2зЛ
[4~1 [4-] h / [4] [4J
Уя+1 = У/1 + J W fn+ 1/3 + /я+1/.
[5] J /[4+] [4-]
#я+1 — ~2 \ Уп+1 + Угс+1
Здесь i может принимать значения 4 или 5; при этом
в случае / = 4 использование указанных формул связано
лишь с пятикратным обращением к блоку вычисления

72 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
значений функции / (*, у) на каждый узел сетки (кроме
узла Хх).
Соответствующие формулы типа (9) теперь легко могут
быть выписаны.
Погрешности подобных формул двусторонних
приближений задаются равенствами
I?L = ±2i6AV4,(^) + 0(A5).
Заметим, что при использовании указанных выше
расчетных формул, как и в случае приведенных ранее
двусторонних методов вида A0), в каждом узле хп+г
сетки будут получены четыре приближенных значения
величины у{хп+х), сопоставление которых может дать
полезную информацию, в частности, в вопросе выбора
шага h или при оценке точности результата.
§ 8. Многошаговый методы
В предыдущих параграфах этой главы мы
рассматривали, как правило, лишь одношаговые методы решения
задач с начальными условиями. Такие методы, обладая
рядом удобных для практики вычислений особенностей,
страдают одним существенным недостатком. При
построении этих методов предполагается привлекать информацию
о решаемой задаче только на отрезке длиной в один шаг,
поэтому подобная информация на каждом этапе процесса
должна быть, вообще говоря, получена заново, что
предопределяет большую трудоемкость соответствующих
вычислительных правил. Отказавшись от требования одно-
шаговости, можно вычислительные методы строить так,
чтобы часть полученной информации могла быть
использована повторно на нескольких соседних шагах
вычислительного процесса. При этом иногда оказывается
целесообразным привлекать также и информацию с забеганием
вперед за ту точку, значение решения в которой в
настоящий момент мы вычисляем. Подобные методы,
использующие информацию о решаемой задаче на отрезке длиной
более одного шага, и будут основным объектом нашего
изучения в этом параграфе.
Для простоты и большей наглядности изложения будем
рассматривать сейчас, как и ранее, задачу Коши A.1),

§3]
МНОГОШАГОВЫЕ МЕТОДЫ
73
A.2), имея в виду, что все основные результаты,
полученные в этом случае, могут быть перенесены без больших
затруднений на задачи с начальными условиями для
дифференциальных уравнений любого порядка и систем таких
уравнений.
Мы не станем здесь подробно останавливаться на
вычислительных правилах достаточно общего вида A.6),
а ограничимся лишь методами типа
р я
Уп+1=%сцУпч + Ь 2 А${хпЧ, упЧ)9 A)
t = 0 / = — s
позволяющими искать приближенное значение уп±г
решения рассматриваемой задачи в точке хп+г сетки A.5) в виде
линейной комбинации нескольких известных, вообще
говоря, приближенных значений уп^ решения в точках xn-i
этой сетки с коэффициентами ah i = 0, l, ..., р, и
нескольких приближенных значений f(xn-/, yn~j)
производной y'(x) = f[x, у(х)] искомого решения в точках лся_у
с коэффициентами Л Л/, / = —s, —s+1, ..., q. При этом
среди указанных значений производной могут быть и
неизвестные (npns^l). Вычислительные правила A)
очевидным образом могут быть обобщены, например, на тот
случай, когда при разыскании уп+1 привлекается
информация и о значениях производных более высокого порядка
от решения.
Если s< 1, то вычислительные методы вида A) обычно
называют явными, при s=l —неявными (если, конечно,
Л_!=^=0), а в случае s>l при естественном условии
— 2
2 Л/>0 такие правила вычислений часто называют
/ = —S
методами с забеганием вперед.
Коэффициенты вычислительных правил вида A) в общем
случае неравномерных сеток A.5) должны, вообще говоря,
зависеть от избранной сетки. Как мы уже отмечали
в § 1, в случае неравномерных сеток использование
многошаговых методов усложняется. Здесь сетку A.5) мы будем
предполагать равномерной:
Xi = x0-{-ili, i = 0, 1, ..., Л/, Nh = X — x0.
В § 10 гл. 5 при рассмотрении задачи
неопределенного интегрирования E.10.1), являющейся частным

74 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
случаем задачи A.1), A.2), были изучены вычислительные
правила вида E.10.2), сходные с методами A) численного
решения задачи Коши. Там было выяснено, что поведение
погрешности рассматриваемого метода существенно зависит
от корней характеристического уравнения E.10.11),
определяемого коэффициентами при значениях приближенного
решения. Подобная зависимость имеет место и в более
общем случае задачи Коши A.1), A.2). Опираясь на
результаты этих исследований, положим р = 0 в
формулах A). Тем самым будут заведомо исключены из
рассмотрения все вычислительные правила указанного вида,
по упомянутому признаку мало пригодные для вычислений
(при этом, правда, будет отброшено также и значительное
число приемлемых вычислительных методов). Ограничив
себя рассмотрением вычислительных правил вида
я
Уп±1 = Уп + 1г ^ Aif(xn-i, Уп-д, B)
i = — s
мы тем не менее сохраним для изучения все наиболее
часто встречающиеся в вычислительной практике
многошаговые методы.
Среди вычислительных правил вида B) особенно широко
известны экстраполяционные (при s = 0) и
интерполяционные (при s = l, Л_х#0) методы Адамса, к рассмотрению
которых мы и приступаем.
1. Экстраполяционные методы Адамса. Построение
многошаговых методов вида
Я
Уп+i = Уп + h 2 A if (xn-h yn- i) C)
t = 0
можно осуществлять, например, способом, изложенным
в § 4.
Как и в случае одношаговых методов, будем исходить
при этом из равенства D.1). На его основе построим
приближенное равенство D.2), где параметрам аг, i = 0,
1, ..., q, заранее придадим нужные для C) значения
«/ = — i, i = 0, 1, ..., q. D)
Соответствующие значения параметров Ah i == 0, 1, ..., q9

§8]
МНОГОШАГОВЫЕ МЕТОДЫ
75
могут быть найдены из следующей системы (см. D.4), D))
линейных алгебраических уравнений:
2^ = 1, 2А|(-'")/==7ТГ' /=1.2,...,?. E)
Так как определитель этой системы есть определитель
Вандермонда, а все а* =— /, / = 0, 1, ..., q, различны,
то значения параметров Л/, i = 0, 1, ..., <?,
удовлетворяющие ограничениям E), могут быть выбраны для любого
^0 и притом единственным образом. При заданном q
тем самым будет построен соответствующий экстраполя-
ционный метод Адамса C). В силу D.5) погрешность
формулы C) при этом может быть записана в виде
г,»1 = А*+У*+2)(*л)
+
i = 0 J
+ 0(/i*+3). F)
Нетрудно непосредственно проверить, что те же
вычислительные правила экстраполяционного метода Адамса
C) можно получить и следующим способом.
Для приближенного вычисления интеграла в D.1)
предварительно подынтегральную функцию у' (хп-\-аК) на
отрезке интегрирования аппроксимируем алгебраическим
интерполяционным многочленом степени q, построенным
по ее значениям в точках xn-~ih, i = 0, l, ..., q,
предшествующих отрезку интегрирования. Такое
интерполирование за пределы таблицы значений интерполируемой
функции обычно называют экстраполированием, с чем и
связано название метода C). Осуществив затем простую
операцию интегрирования алгебраического
интерполяционного многочлена, мы придем к приближенному
равенству D.2) при ct/ = — /, / = 0, 1, ..., q, которое является
основой формулы C). Эта формула может быть записана
по-разному в зависимости от того, в каком виде
предварительно был представлен соответствующий
интерполяционный многочлен. Если его взять, скажем, в форме
Лагранжа (см. A.3.5)), то экстраполяционный метод Адамса
окажется записанным непосредственно в виде C). Для
коэффициентов Ah t = 0, I, ..., q, в этом случае можно
получить явные выражения, не прибегая к решению

76 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 3
системы E). Эти коэффициенты выразятся через интегралы
по отрезку [хп, хп+1] от соответствующих коэффициентов
Лагранжа и после простых преобразований могут быть
записаны в виде
Л,. = -1^- ( «i«±2b^±2lda, i = 0, I, .... д.
1 i\ (q — i)\ J a + * ^
0
Если же соответствующий интерполяционный
многочлен для функции у' (x)=f[x, y(x)] представить в форме
Ньютона для интерполирования в конце таблицы (см.
A.4.3)), то экстраполяционный метод Адамса может быть
записан через конечные разности функции / (х, у). Такая
форма записи метода позволяет получить интересующее
нас значение приближенного решения в виде разложения
по последовательным главным частям, что может быть
использовано, например, для практической оценки
локальной погрешности. Правда, оперирование с таблицами
конечных разностей вызывает очевидные затруднения при
работе на ЭВМ. Нужно иметь в виду также, что
составление таких таблиц обычно сопряжено с быстрым
накоплением вычислительной погрешности, особенно при
высоких порядках разностей. Это предъявляет повышенные
требования к точности выполнения вычислений. Поэтому
в настоящее время в практике работы на ЭВМ часто
отдают предпочтение форме записи C) экстраполяцион-
ного метода Адамса.
Замена уравнения A.1) разностным уравнением C)
при начальных условиях A.2) приводит, вообще говоря,
к некорректной задаче, так как задание лишь одного
начального данного у0 при q*>0 не выделяет
единственного решения этого разностного уравнения порядка q-\-l.
Чтобы построенное вычислительное правило позволяло
находить единственное решение, достаточно задать
дополнительно к у0 значения уъ уъ ..., уд. Эти начальные
значения приближенного решения могут быть получены по-
разному. Для их нахождения можно использовать любой
из рассмотренных выше одношаговых методов. Часто,
чтобы не так сильно нарушать однородность
вычислительного процесса, для построения начала таблицы
значений приближенного решения конструируют специальные
вычислительные алгоритмы, стараясь по возможности более

§SJ
МНОГОШАГОВЫЕ МЕТОДЫ
77
тесно привязать их к методу основного счета. Не
останавливаясь здесь подробно на таких алгоритмах, заметим
лишь, что точность построения начала таблицы должна
быть согласована с точностью нахождения последующих
значений решения исходной задачи. Как и в случае одно-
шаговых методов, для метода C), в частности, также
может быть получена оценка погрешности приближенного
решения, сходная с оценкой E.12), где роль е0 будет
играть соответствующая граница неточностей начальных
данных. Основные выводы, которые были сделаны на
основании E.12) в отношении одиошаговых методов,
остаются справедливыми и для многошаговых
вычислительных правил указанного вида. Очевидно также, что
в случае рассматриваемых многошаговых методов можно
получить и многие другие результаты, сходные с
приведенными ранее для одношаговых правил. Повторно на
этом мы не будем здесь останавливаться, а ограничимся
лишь конкретными примерами экстраполяционных методов
Адамса.
Возьмем д = 0. Тогда, очевидно, из C) получаем
известный метод Эйлера
Уп+i^yn + hfn G)
где fn4(*n, Уп).
Формула F) для локальной погрешности методов в этом
случае также приводит к известному результату
^i=y/»VW+0(ft8).
При q = 1 система E) имеет вид
Ло + ^i-l, Лх = —1/2,
откуда находим
Л0-3/2, Лх 1/2.
Метод Адамса C) при таком значении q принимает вид
Упп = Уп+Н2-(УпЧп-1). (8)
Погрешность последней формулы в силу F) задается
равенством с

78 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
В отличие от метода Эйлера G), который не требует
предварительного построения начала таблицы значений
приближенного решения, экстраполяционный метод Адамса
(8) уже предполагает предварительно нахождение
величины уг.
В случае q = 2 имеем
Ао + Аг + A^U Лх + 2Ла = -1/2, Л! + 4Ла=1/3,
откуда находим
А0 = 23/12, Аг = — 4/3, Ла = 5/12,
что позволяет записать следующий метод:
Уп-vi = Уп + -^ B3/я - 16/^i + 5/„-2). (9)
Его локальная погрешность задается формулой (см. F))
r„+1 = yAV4)(^) + 0(A5).
Вычислительное правило (9), очевидно, может применяться,
начиная со значения п = 2.
При q = 3y как легко проверить непосредственно, C)
будет иметь вид
Уп+1 = Уп + ~ E5/я - 59/w + 37/„_2 - 9/л_3). A0)
Погрешность формулы A0) задается равенством
^+1 = ЖАб*E)(^) + 0(Лв).
В заключение без подробного вывода дадим другой
вид экстраполяционных методов Адамса, запись которого
связана с использованием конечных разностей функции
y'(x)=ftx, У(х)]:
Уп+i = Уп + Фя + ~2 Афл-i + 72" Д2Ф"-2 + -g- Д3Ф«-з +
, 251 А4 . 95 А- . 19 087 Afi , 5275 А7
+ 720-А V* + 288"А Ч""* + WW А Ф-6 + 7280- А ^ +
, 1 070 017 А о . 1082 753 А q . , п А „ /11ч
+ 3 628 800 А^-8+ У257600"А Ф-9+ - + C«AW (И)

§81
МНОГОШАГОВЫЕ МЕТОДЫ
79
Здесь
1
4>i = hh> Cq = -^^a(a+l) ... (a + q-l)da,
б
a AJ'(pi — конечная разность порядка /, составленная для
функции Ц)(х) по ее значениям в точках xh х^ъ ..., xi+J
(см. § 2 гл. 1).
Погрешность формулы A1), как следует из описанного
ранее способа ее построения, может быть представлена
в виде
'»+i = Т^Ж у(д+2) ® J «<« + 0 • • ■ (« + <7) da,
б
или
rn+1 = h^y^) (Хя) С,+1 + 0 (А™>). A2)
Формулы A1), A2), как мы уже отмечали,
эквивалентны формулам C), F) соответственно. Однако в
реальных условиях из-за наличия ошибок округлений
вычислительные правила C), A1), отвечающие одним и тем же
значениям q, на одной и той же ЭВМ могут дать разные-
результаты при решении одной и той же задачи, так как
они существенно отличаются организацией вычислений.
2. Интерполяционные методы Адамса. При s~\
формула B) принимает вид
ц
Уп+1 = Уп + Ь> 2 Atf(xn49 упЧ). A3)
t = —1
Построение таких вычислительных методов может быть
осуществлено совершенно аналогично случаю экстраполя-
ционных формул C).
Положив
«/ = — i, i = — l, 0, 1, ..., q,
для нахождения соответствующих значений параметров Ah

80 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
i = — 1, 0, 1, ..., q, получим систему линейных
алгебраических уравнений
2 Ai = l, J M-iy = -j^T, /=1,2,...,?+1,
t = -l t = —1
которая однозначно разрешима при любом q^~\.
Для коэффициентов А и i = —1» 0, 1, ..., q,
вычислительных методов вида A3), подобно случаю экстраполя-
нионных методов Адамса, можно дать следующие явные
выражения:
А (~ 0й1 С («—!)«(«+!) ... (a + g) ^
A,-"(i^ 1IG-0! 3 oc + i Ш*
о
*=—1, 0, 1, ..., q.
Погрешность формулы A3), аналогично F), может
быть записана в виде
гя+1 = А"Ум)(*л)
(<7 + 3I G + 2)!
t = —1
2 ^п-ом
+
+ 0(^+4). A4)
Приведем несколько примеров интерполяционных
методов Адамса A3).
При q = — 1 будем иметь
В случае G = 0 находим
/г
'2
12
Уп+1 — #л + "9 (fn+1 + /л)»
Гл+1 = — 4о- №f (Хя) + О (/24).
A5)
A6)
При q= 1 получаем
Уп-rl = У/г +
^i = -^AV4)W + 0(/i6).
Уя-rl = Уп + То" E/я+1 + Щп " /л-l)»
A7)

§ S]
МНОГОШАГОВЫЕ МЕТОДЫ
81
Взяв q — 2, найдем
h
4
Уп+i = Уп + 4г (9/„+i + Щл - 5/л -1 + /л_2),
19 <18>
r»+i = -jlbh*^(xn) + 0(h*).
Перечень подобных правил нетрудно продолжить. Не
станем здесь выписывать другие вычислительные правила
вида A3), а приведем без предварительных выкладок лишь
иную форму записи интерполяционных методов Адамса,
использующую конечные разности функции f (х, у):
Уп+i = Уп + фл+1 - 2 ДФ* ~ у1 Л2фл л ~ 24" ДЗ(Р«-2 -
№ Л4 3 А5 863 лб 275 А7
- 720 AV-з-Тео А5Ф«-4—60480 Л ^ 5~Ш% АV-e-
Здесь
о
<Pi = hfh Cq+l= ( 2I ^ а(а+0 ••• (a + ?)da.
— 1
Погрешность A4) при этом может быть записана в виде
/*+i = А*+У м> (*я) С,+2 + О (А™). B0)
Формулы A9), B0) могут быть получены совершенно
аналогично случаю экстраполяционных методов Адамса.
Для этого достаточно в очевидном равенстве
xn+i о
У(Хп+г)=У(х*)+ \ y'(x)dx = y(xn) + h \ у' (хя+1 + ah) da
X — 1
п
заменить функцию у' по интерполяционной формуле
Ньютона для интерполирования в конце таблицы при
узлах интерполирования хп+ъ хпу ... , хп-д и выполнить
операцию интегрирования. В этом случае для q^0
точки отрезка [хпу хп+1], на котором производится замена
функции у' по интерполяционной формуле, принадлежат
наименьшему отрезку [хп.я% хп+1], содержащему все узлы
интерполирования. Таким образом, здесь выполняется
не экстраполирование за пределы используемой таблицы

82 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
значений приближаемой функции, как это было в
предыдущем пункте, а производится интерполирование в
собственном смысле слова, чем и объясняется название
методов A3), A9). Подобное расположение узлов
интерполирования является, очевидно, более благоприятным,
чем в экстраполяционном случае (см. представление
A.3.11) для остаточного члена интерполирования). Этим,
в частности, объясняется тот факт, что абсолютные
значения коэффициентов при конечных разностях в A9)
убывают с ростом порядка разности быстрее, чем в
случае метода A1), что предопределяет и более быстрое
убывание абсолютных значений слагаемых в разложении
A9) в сравнении с A1). По той же причине константа
при hky{k) (xn) в главном члене погрешности формулы A9)
интерполяционного метода Адамса для k>2 по
абсолютной величине меньше соответствующей константы
в случае экстраполяционного метода того же порядка
точности. Заметим, что указанные константы, кроме того,
имеют противоположные знаки (см., например, вид
остаточных членов формул G) и A5), (8) и A6), (9) и A7),
A0) и A8)). В общем случае это непосредственно следует
из вида коэффициентов в разложениях (И), A9).
Поэтому при достаточно малых значениях /z>0 локальные
ошибки экстраполяционного и интерполяционного
методов Адамса одного и того же порядка точности также
должны иметь противоположные знаки. В силу этого
соответствующая линейная комбинация так полученных
двух приближений к у(хп+1) может дать результат на
порядок точнее, если, конечно, ошибками округлений
в пределах требуемой точности можно пренебречь.
Как по экстраполяционным, так и в случае
интерполяционных методов Адамса приведенного выше вида
вычисления можно начинать со значения n — q. При этом
предварительно должно быть заготовлено начало таблицы
значений приближенного решения до значения yq
включительно. Для одинаковых значений q при этом порядок
малости относительно h погрешности B0) в случае
интерполяционного метода Адамса будет на единицу выше
соответствующего порядка малости погрешности A2) для
экстраполяционного метода Адамса. Это обстоятельство
является очевидным следствием того, что
интерполяционный метод A3) по отношению к экстраполяционному C)

§ sj
МНОГОШАГОВЫЕ МЕТОДЫ
83
строится с использованием одного дополнительного
приближенного значения f {хп±ъ уп+1) производной у', При
<7 = 0, например, когда начало таблицы приближенных
значений решения предварительно строить нет
необходимости, методы C) и A3) переходят в одношаговые методы
Эйлера B.2) и трапеций C.2) с локальными ошибками
порядка /г2 и /г3 соответственно (см. G) и A6)).
Заметим, что построенные интерполяционные методы
Адамса не дают явных выражений для нахождения уп±ъ
а представляют собой лишь уравнения относительно этой
неизвестной. Это значительно осложняет процесс
вычисления уп+г и является существенным недостатком метода.
Обычно значение г/я+1 находят лишь приближенно,
пользуясь, как правило, каким-либо методом
последовательных приближений. Как в форме A3), так и в форме A9)
интерполяционный метод Адамса уже приведен к виду,
удобному для итераций. Кроме того, заданием достаточно
малого Л>0 при удачном выборе начального
приближения можно обеспечить сходимость соответствующего
итерационного процесса. В самом деле, уравнение
относительно уп+1 можно (см. A3), A9)) записать в виде
Уп+1 = Ч>(Уп+г),
где
Ф (Уп+i) = А A + £ CAf (xn+ly уп+1) +
+ F(hy хпу уп, уп.ъ ... , уп_д),
а через F (h> хп> уп> уп1, ..., уп-д) обозначена известная
функция указанных аргументов. Если при х^[х01Х]
f(xy у) в достаточно широкой окрестности решения имеет
непрерывную производную ■ ' , то при удачном
выборе исходного приближения Уп + i за счет уменьшения
шага /z>0 можно заведомо обеспечить выполнение
условий сходимости процесса итераций Уп^1) = Ч {Уп'+г)*
* = 0, 1, ... (см. § 2 гл. 4, теорема 1).
Начальное приближение к уп+г можно выбирать по-
разному. В случае интерполяционного метода Адамса
в форме A9) вместо выбора исходного приближения y'n + i
к уп+1 можно выбрать соответствующее приближение
д?+1ф(о_^ к д?+1фл_^# Так как конечная разность A?+1cp„_^

84 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
является малой величиной по крайней мере порядка hq+%
в сравнении с шагом h (см. A.2.10)), то при малых h и
больших q она станет настолько малой по абсолютному
значению, что нетрудно будет подобрать начальное
приближение к ней с небольшой абсолютной погрешностью.
Особенно просто это сделать в том случае, когда
последняя участвующая в вычислениях конечная разность
в пределах принятой точности является практически
постоянной. Тогда в качестве начального приближения
&v+1(p'nLq можно взять известную величину Д9+1фл_9_!,
после чего по простым формулам составления конечных
разностей найти соответствующие приближения
Д*Ф„%+1, A*-V*%+o, ..., AqC, ф^ь
Теперь уже по правилу (см. A9))
yV±l) = y +ф<2') - I Дф('">_
-™Д2Ф<° -...+С , Д* + У° B1)
при i = 0 легко вычислить значение y'n + i* Затем, исходя
из Уп+1У можно по формуле
при / = 1 и по простым правилам составления конечных
разностей последовательно найти
Ф^1, АФ^, Aaq>5i-i. .... Д^%,
после чего из B1) при i=\ получить у1п-\-\ и т.д.
Если же последняя конечная разность не является
практически постоянной, то в силу малости ее
абсолютного значения начальное приближение к ней с
небольшой абсолютной погрешностью можно выбрать,
экстраполируя значение Д9+1Фл q по нескольким
предшествующим значениям конечной разности того же порядка.
При использовании интерполяционного метода Адамса
в форме A3) обычно в качестве начального приближения
к Уп+i берут соответствующее значение, полученное экстра-

§ ь]
МНОГОШАГОВЫЕ МЕТОДЫ
85
поляционным методом C). При этом часто ограничиваются
лишь одной итерацией. В этом случае вычислительный
процесс приобретает предсказывающе-исправляющий
характер: по формуле C) находится приближенное
значение величины у (xn+i) с локальной погрешностью порядка
hqAr2y которое затем уточняется на порядок на основании
формулы типа A3). Такая организация вычислений при
использовании ЭВМ применяется наиболее часто.
Можно подобный процесс организовать и так, чтобы
формула C) применялась при значении q на единицу
большем, чем в формуле A3). Тогда предсказывающая
и исправляющая формулы будут характеризоваться
погрешностями одного порядка малости относительно шага А,
правда, первая из них все же будет давать более
грубый, вообще говоря, результат, так как расположение
узлов интерполирования, положенное в ее основу, как
мы уже отмечали ранее, является менее удачным для
минимизации остатка интерполирования в точках отрезка
интегрирования [хп, xn+i], чем в случае
интерполяционного метода Адамса A3) с таким же числом узлов.
Привлекательным, при такой организации вычислений
является то обстоятельство, что погрешность, вносимая
теперь за счет неточности формулы типа C) в остаток
A4) формулы A3), не изменяет вида его главного члена.
Поэтому, если шаг /z>0 достаточно мал и ошибки
округлений не влияют на результат в пределах принятой
точности, то локальные погрешности приближенных
значений величины y(xn+i), полученные в рассматриваемом
вычислительном процессе по формулам экстраполяцион-
ного и интерполяционного методов Адамса, будут иметь
противоположные знаки, что позволяет составить такую
линейную комбинацию этих приближенных значений,
которая будет на порядок точнее приближать искомое
значение у(хп+1). Коэффициенты этой линейной
комбинации очевидным образом определяются через известные
множители при hg+3y{q+z) (xn) в главных членах
погрешностей соответствующих формул экстраполяционного и
интерполяционного методов Адамса.
3. Методы с забеганием вперед. Выше мы уже
отмечали, что при построении вычислительных методов
решения задачи A.1), A.2) существенно, как расположена

86 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
относительно отрезка, где производится аппроксимация
дифференциального уравнения A.1), используемая для
этого информация. В этом отношении при одном и том
же числе привлекаемых значений функции /(,t, у)
интерполяционный метод Адамса, например, оказывается
предпочтительнее экстраполяционного. Еще более
благоприятные по точности результаты можно ожидать в том
случае, когда используемая информация будет
расположена симметрично (или почти симметрично) относительно
рассматриваемого отрезка. Если при построении
многошаговых .методов решения задачи A.1), A.2) исходить,
скажем, из равенства C.1)
хп+1
y(xn+i)=y(Xn)+ I f[x,y(x)]dx9
хп
то в указанном смысле значения функции у' (x) = f[x, у (х)]
естественно привлекать парами в следующих точках:
В этом случае получим вычислительное правило вида B)
при s = q-\-1:
я
yn+i = yn + h 2' Atf(Xn-h Уп-i). B3)
Формулы указанного вида называют обычно методами
типа Коуэлла.
Строя такие методы способом, описанным в п. 1,
следует вместо D) задать
at = — i, i = — q—l, —q,...,q.
Тогда для определения значений параметров Ah i =
= — q~ 1, — q, ..., q, вместо E) получим следующую
систему линейных алгебраических уравнений:
i=—g—\ i=—q—\
/ = 1, 2, ..., 2<?+1.

§81
МНОГОШАГОВЫЕ МЕТОДЫ
87
Можно указать и другой способ нахождения
коэффициентов А-п t = — q—\, — q, ... , q, вычислительных
правил типа Коуэлла. Совершенно аналогично случаю
методов Адамса для этих коэффициентов можно получить
следующие явные выражения:
Л Ы)***1 С («-?-!)(«-?) ... (а + д) <
О
i = — q— 1, — q, ... , q.
Погрешность формулы B3) в силу D.5) может быть
записана в виде
^ 1 + 0 (/г2^4). B4)
с/
1 1
BG+3)! Bg + 2)! Zj Л^ 1)
При ^==1, например, соответствующая формула типа
Коуэлла будет иметь вид
Уп+i = Уп + -gf (— /*+2 + 13/л+1 + 13/„ - ^_х). B5)
Ее погрешность задается равенством (см. B4))
rn+i = ^h^>(xn) + 0(h«).
Заметим, что коэффициент при /т5уE) (хп) в главной части
остатка формулы B5), как и следовало ожидать,
оказался меньше по абсолютному значению
соответствующих коэффициентов в остаточных членах формул A0)
и A8) экстраполяционного и интерполяционного методов
Адамса.
Подобно случаю методов Адамса, формулы типа
Коуэлла также могут быть записаны через конечные
разности функции f (х, у). При узлах B2) для
интерполирования функции y'(x)=f[xy y(x)] на отрезке [хп> хп+1]
естественно использовать формулу Ньютона— Бесселя
вида A.4.6). После выполнения в C.1) простой операции

88 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
интегрирования алгебраического многочлена вместо B3)
получим тогда следующую формулу:
„ _ и J- Фк-^ + Фл L Д2Ф* + А2Ф/*-1 I
Уп+1 — У п. \ 2 12 2
, 11 А4фч_1 + Д4фя_2 1Ц_ Д6фД-2 + А6ФЯ-з ,
Здесь
720 2 60 480 2
...+С,/"*'"'--+А"*-'. B6)
ф/ = &/<,
c^ = W)rS(a_9)(a~'G+1) ••• (a~1)a(«+1) •••
о
... (a + q—l) da.
Коэффициенты С2; в формуле B6) разностного метода
Коуэлла с ростом i убывают быстрее соответствующих
коэффициентов и экстраполяционного, и
интерполяционного методов Адамса (см. A1), A9)). Погрешность этой
формулы может быть записана в виде
гп+1 = №**у**^ (хп) С2д+2 + О (№+*).
В случае методов типа Коуэлла разыскиваемое
значение уп+1 по формулам вида B3) или B6) выражается
не только через известные величины уп_д, уп-д+ъ ..., уп>
но и через неизвестные значения уп+ъ уп+2, ..., yn+q+i-
Тем самым при каждом значении п равенства B3) или
B6) дают нам не расчетные формулы для нахождения
Уп+ъ а уравнения, связывающие неизвестные значения
Уп+ъ Уп+21 • ••> Уп+д+ъ Эти равенства можно записать,
вообще говоря, лишь при n=^q, q+U • ••> N — q—l.
Поэтому в случае методов типа Коуэлла однородность
вычислительного процесса может нарушаться не только
при нахождении начальных значений уъ у2, ... , yq
таблицы значений приближенного решения, но и при
вычислении последних значений уы-д+ъ Ум-Я\ъ • • • » Уы этой
таблицы. Кроме того, использование самих формул типа
Коуэлла также требует специальной организации
вычислений; при этом в зависимости от формы записи B3)
или B6) этих формул можно поступать по-разному.
Поясним, как можно вести вычисления на основе,
скажем, формулы B3). Для определенности и простоты

§8]
МНОГОШАГОВЫЕ МЕТОДЫ
89
записи будем считать q=l. Тогда B3) принимает вид
B5). Эта формула представляет собой уравнение с двумя
неизвестными уп+ъ уп+2. Вычисления в этом случае можно
начинать со значения п=1. Один из возможных вариантов
организации таких вычислений может быть следующим:
B7)
[3]
02 =
[4]
Уг =
Уп+2
[5J
Уп+1
[5]
[5J
Ух +
14]
-У пи
h
2
h
2
.+
,5j , <
'3/i-foj,
/ [31 \i\
45/2 + 8/i
h ( f4J
ill /я+2
-/oj,
[«'1 M \
-16/„ + 5/„J,
[4]
+-13/л+1
+ 13/„-
In
Здесь j может принимать значения 4 или 5.
Для построения такого алгоритма использованы
формулы (8), A7), (9) и B5); при этом в целях большей
наглядности применены обозначения типа B.3).
Явное вычислительное правило B7) можно заменить
другим, если, например, вместо двух первых его формул
использовать неявную формулу (см. A7))
[4] 1.5] и ( [4] [i\ \i)\
02= 01 + ^E/2 + 8/, -/J.
. При записи метода типа Коуэлла в форме B6)
вычисления можно организовать и по-другому. Поясним это,
например, для случая q=l. Тогда формула B6)
принимает вид
и _1_ Ф/М-1 + Фи 1 А2фп + А2ф»-1 /OQ\
Уп+г = Уп-\ g ' ~ 12" 2 * ^ '
Из этого уравнения с двумя неизвестными уп+1, уп+2
интересующее нас значение #л+1 будем находить
итерационно.
Предположим, что, кроме дополнительного начального
значения уъ предварительно найдено также значение у2.
Будем вести вычисления с помощью формулы B8),
начиная с п = 2. Тогда наряду с уП9 фя нам будут известны
также значения Aqvi и Д2ф„-2- По Д2<ря-2 выберем
начальные приближения Д-ф;?^1 и Д2ф„' к Д2фд_! и Д2ф„.

90 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
Проще это сделать в том случае, когда при выбранном
шаге h вторые конечные разности практически постоянны
в пределах принятой точности вычислений. В противном
случае приходится прибегать к экстраполированию
в столбце вторых разностей. По Д2ф^°1_1 посредством
простых формул составления конечных разностей
последовательно вычислим Афд; и фп+i, что позволит на
основе B8) найти значение tjn+\ по формуле
Ф^ = „ + ч&. + Ч _ JL АЧ0 + Д^-,
Уп + i Уп^ 2 12 2 [ }
при i-—0. Затем, исходя из у'п + и по правилу
при i=l можно найти ф^ и, следовательно, вычислить
Дф^ и А2ф„-1. Пользуясь полученным значением A^Lj,
можно найти уточненное приближение А2ф^ к Д2ф„,
после чего из B1) при 1 = 1 получим уТ+i и т. д.
При численном решении задачи Коши A.1), A.2)
для сравнительной характеристики методов можно
рассматривать различные показатели. О трудоемкости метода
естественно судить по числу обращений к блоку
вычисления значений правой части уравнения на каждый узел
сетки. Однородность вычислений можно характеризовать,
в частности, числом дополнительных начальных значений
приближенного решения, которые предварительно находят
каким-то другим методом. Полезную дополнительную
информацию о методах одного порядка точности можно
получить, сравнив длины отрезков оси х, на которых
при одном шаге вычислительного процесса
рассматривается решение исходного дифференциального уравнения;
при этом важным является также и расположение этих
отрезков относительно отрезка интегрирования в C.1).
Построенные методы типа Коуэлла по этим показателям
можно сравнить с другими численными методами
соответствующего порядка точности. Например, вычислительное
правило B7) при t = 4 характеризуется длиной 3/г
указанного выше отрезка с симметричным расположением его
относительно [хпу хя+1], одним дополнительным начальным
значением и двумя обращениями на каждый узел сетки
к блоку вычисления значений функции f (х, у). В случае

§8]
МНОГОШАГОВЫЕ МЕТОДЫ
91
соответствующего по порядку точности экстраполяцион-
ного метода Адамса длина рассматриваемого отрезка
возрастает до 4ft, сильно нарушается симметрия его
расположения относительно отрезка [хП1 хп+1\, число
дополнительных начальных значений увеличивается до трех,
но зато этот метод требует нахождения лишь одного
значения функции f(x, у) на узел сетки. С другой стороны,
одношаговые методы с локальной ошибкой порядка ft5
сопряжены уже с четырьмя обращениями к блоку
вычисления значений функции / (х, у) на узел сетки, но не
требуют нахождения дополнительных начальных значений
и характеризуются минимальной длиной ft упомянутого
выше отрезка.
Подобное положение методов типа Коуэлла, а также
крайние позиции в отношении рассматриваемых
показателей одношаговых методов и явных многошаговых
вычислительных правил изучаемого выше вида наводят
на мысль о разыскании таких методов с забеганием
вперед, которые в указанном смысле носили бы еще более
компромиссный характер. Ниже способом, указанным
в § 4, мы построим простейшие примеры подобных
вычислительных правил.
Положим, например, q = 4 и k = b в системе D.4).
Это дает возможность строить вычислительные правила
с локальной ошибкой порядка ft6, свободно распоряжаясь
выбором пяти параметров.
Выберем по своему усмотрению параметры ah 1 = 0,
1, ..., 4, имея намерение за счет удачного расположения
точек Xn + oiih9 i = 0, l, ..., 4, построить на основе D.2)
такие вычислительные правила с локальной ошибкой
порядка ft6, которые, во-первых, требовали бы в
сравнении с соответствующими по порядку точности одношаго-
выми методами меньшего числа обращений к блоку
вычисления значений функции f (x, у) и, во-вторых,
характеризовались бы в сравнении с экстраполяционным методом
Адамса указанного порядка точности меньшим числом
дополнительных начальных значений, лучшим
расположением и меньшей длиной отрезка, на котором при
одном шаге вычислительного процесса рассматривается
решение исходного дифференциального уравнения. С этой
целью при выборе ah 1 = 0, 1, ..., 4, не будем строго
придерживаться требования одношаговости 0 ^ at <; 1 и

92 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
в то же время будем задавать числа at не обязательно
целыми.
Возьмем, например,
а0 = —1/2, ах = 0, а2=1/2, а3=1, а4 = 3/2,
что позволит из D.4) найти соответствующие значения
Л0 = Л4 = —1/180, Лх = Лз-34/180, Ла= 114/180.
Используя методику построения вычислительных методов,
предложенную в § 4, на основе приведенных значений
параметров можно получить следующие расчетные
формулы:
[4] [6] h f[5] m [51 ^
Уп+1 ^УпЛ- 6 V fn - 1/2 — Щп + Vn -f 1/2,/ »
[5] [6] h m [5] [41 \
Уп+1 = Уп+ б I /л + Цп + 1 /2 + fnvl) '
С5] Г6] . Ы( [Р ,Jf № . 7^ ^ C0)
У/1 + 3 2 = ^л + jg i -/я-1/2 +5/л--^я+1.2 + 7^+1;» К J
[6] [6] д
Уп+1 ~ УпЛ~ JgQ X
/ [5] М [5] [51 [51 \
X [-fn- 1 2+ Щп+ 144/я + ,/2 + 34/л+1 -fn + ш).
Здесь / может принимать значения 5 или 6.
При i = 5 построенный вычислительный метод требует
в основном счете лишь трех обращений к блоку
нахождения значений функции / на узел сетки (одношаговые
правила соответствующего порядка точности связаны
с вычислением не менее шести таких значений). Этот
метод, кроме того, характеризуется симметричным
расположением относительно [хпу хп^] и длиной 2h отрезка,
на котором при одном шаге вычислительного процесса
рассматривается решение исходного уравнения A.1).
При этом он предполагает нахождение лишь двух
дополнительных начальных значений, для получения которых
можно в случае /1 = 0 использовать вычислительные
правила D.13) при шагах —h/2 и /г/2. Для экстраполяцион-
ного метода Адамса такого порядка точности длина
упомянутого отрезка равна 5/г, при этом предполагается
предварительное нахождение четырех дополнительных
начальных значений. Метод C0) является удобным и

§9]
РЕШЕНИЕ ЛИНЕЙНЫХ ГРАНИЧНЫХ ЗАДАЧ
93
в том отношении, что без дополнительных
вычислительных затрат он дает возможность на каждом шаге процесса
Ш 151 [6]
сопоставить три приближенных значения уп+ъ упп, уп+г
искомой величины у(хп+1).
При выбранном выше исходном наборе параметров ah
i = 0, l, ..., 4, можно построить и другие варианты
вычислительных правил типа C0). Например, в
последнем методе вместо двух первых формул для нахожде-
[5]
ния Уп+i можно использовать вычислительное правило
[5] [6] h / [5] [5] \i\ [5] \
Уп+1 = Уп + у \— fn-1 + 4/гг - 1/2 ~ bfn + 8fn+ 1/2/ >
что позволит сократить до двух число вычисляемых
значений функции / на каждый узел сетки в основном счете,
однако при этом возрастет до трех число дополнительных
начальных значений, несколько нарушится симметрия
расположения относительно [хпу хп+1] и увеличится до 2,5/г
длина отрезка, на котором при одном шаге процесса
рассматривается решение исходного дифференциального
уравнения.
§ 9. Решение линейных граничных задач
Наряду с задачами Коши для обыкновенных
дифференциальных уравнений рассматриваются также граничные
задачи. В этих задачах дополнительные условия,
присоединяемые к дифференциальным уравнениям, задаются
в виде уравнений, содержащих комбинации значений
решения и его производных, взятых в нескольких точках
отрезка, на котором разыскивается решение. Примером
подобных задач может служить задача о нахождении
средней линии нагруженной строительной балки,
лежащей на нескольких точках опоры, задача о
провисании нагруженной цепи, закрепленной в двух точках, и др.
Рассмотрим некоторые методы решения граничных
задач.
1. Постановка задачи. Понятие о многоточечных и
граничных задачах. Пусть на отрезке а <; ж; 6 задана система
линейных обыкновенных дифференциальных уравнений

94 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
первого порядка
У[ + Яп (*) Ух + 0-12 (х) У-2 + • • • + tfi/i (х) Уп = /i (*),
*У* + «21 (X) Ул. + «22 (X) У2 + . . • + «2л (*) У* = h (*)»
Уп + ап1 (х) ух + ап2 (х) у2+ ...+ апп (х)уп = fn (х)у
которую мы в дальнейшем будем записывать в векторном
виде
? + A(x)y=f(x), A)
где А (х) = {ач (я))?, f(x) = (/_ (х), ..., fn (x))T - известные
матрица и вектор, a{f(x), ft (х) ~ непрерывные на [а, Ь]
функции, Т — знак транспонирования; у (х) = (уг (х), ...
• • • , Уп (х))т — вектор-функция, подлежащая определению.
Будем считать, что к уравнению A) присоединены
граничные условия в форме
9sr.y (*_) = «_, l<s<m, B)
где
т
% =
as = (a(.
фЙ'
5)
, . . .
ФЙ -
ф2 -
Ф^2 •••
ФЙ1
ФЙ
ф^
— изве<
— известная матрица,
__*.
:А1,
известный вектор, т^2,
a < *i < х2 <... < ;cm_i < хт < Ь.
Линейные комбинации B) при всех s должны быть
невырожденными для того, чтобы можно было надеяться
на однозначную разрешимость граничной задачи A), B).
Поэтому мы будем предполагать, что ранг матрицы cpj
равен ks. Заменим это условие эквивалентным:
(let q>fcps ф 0, s = 1, 2, ..., т. C)
Если т = 2, то в задаче A), B) граничное условие
принимает вид
Ц>1у (xi) = a_, ф[.У (х2) = а2, D)
где, как правило, полагают х1 = а, х2 = Ь. В этом случае
граничную задачу A), D) называют двухточечной.

§ 9]
РЕШЕНИЕ ЛИНЕЙНЫХ ГРАНИЧНЫХ ЗАДАЧ
95
Если т>2, то граничная задача A), B) называется
многоточечной или m-точечной задачей.
Отметим, что граничные задачи для линейных
обыкновенных дифференциальных уравнений некоторого
порядка п путем введения новых неизвестных функций
могут быть записаны в виде A), B).
2. Метод дифференциальной прогонки. Пусть
рассматривается граничная задача A), B). Решение этой
задачи можно было бы найти как решение задачи Коши для
уравнения A), когда нам станет известным значение у (t)
в некоторой точке отрезка [а, Ь]. Если бы такое
значение удалось как-либо определить, то тогда для
нахождения у(х) можно было бы применять метод Рунге —Кутта
или метод Адамса, описанные нами выше. Идея метода
прогонки как раз и состоит в том, что, используя
уравнение A) и граничное условие B), находят значение
искомого решения задачи A), B) в некоторой точке
отрезка [а, 6], затем на всем отрезке [а, Ь] вычисляют у (t)
как решение задачи Коши.
Рассмотрим функциональное соотношение вида
иТ (х)у{х) = у{х), E)
где
ит (х)
run(x) ип(х) .
«21 W «22 W •
_ип(х) щ2{х) .
.. uin(x)-
•• и2п(х)
•• tiin(x)_
, У(х) =
Yi (*)
Y2 (*)
Y/M
1</</2,
функции щ(х), yj(x) дифференцируемы, у (х) — решение
уравнения A), Т — знак транспонирования. Пусть при
хг = а известно, что u(a) = ul9 Y(a) = Yi> гДе ui и Yi —
заданные матрица и вектор. Предположим еще, что
det(w1T«i)=#0. Поставим задачу: определить и(х) и у (х)
таким образом, чтобы у (х) удовлетворяло при а^х^Ь
уравнению A). Продифференцировав E) и
воспользовавшись формулой A), получим
(ит* - итА (х))у = yf - uTf(x). F)
Выберем теперь и(х) и у(х) так, чтобы F) выполнялось
при любых у(х). Для этого достаточно положить
ит'-итА{х) = 0

%
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
ИЛИ
и' — Ат (х) н = 0,
V'=uT(x)f(x).
G)
(8)
Поскольку и (а) и у (а) известны, то, используя G), (8),
можно определить и (х) и у (х) на всем отрезке [я, 6].
Если бы при этом матрица и (х) обладала свойством
det (ит (х) и (х)) ФО при всех а^х^Ъ, то с помощью
соотношения E) и граничных условий B) можно было бы
определить значение у{х), например, в точке х = Ь.
Однако условие det (uT (х) и (%)) Ф О часто не выполняется,
если уравнение G) решается приближенно.
Усовершенствуем уравнения G), (8), Представим
матрицу и (х) в виде
и (х) -=^v (х) о (х),
(9)
где
v (х) =
о(х) =
vn (х)
V12 (X)
vm (х)
Оц (X)
о21 (х)
V22(x) •
012 (.V) .
о22 (х) .
• У/1 (X)
- v In (х)
• ог2/ (л)
0П(Х) <5Н(Х) ... Оц(х)
Функции Vij (x), Оц (х) дифференцируемы. Предположим
также, что на отрезке а-^x^b матрица о (х) не
вырождена, причем а(а) = Е, где Е — единичная матрица.
Получим для матрицы v (x) дифференциальное
уравнение. В силу формулы (9) и условия на матрицу о (х)
имеем
1ф) = И1. A0)
Используя формулы G) и (9), получим
v'-AT(x)v + vS(x) = Q, A1)
где
S(x) = o'(x)-o-l(x).
Матрицу S (х) выберем таким образом, чтобы
выполнялось условие
{vT (х) • v (х))' = vr (х) v (x) + vT (x) v' {х) = 0. A2)

§ 9] РЕШЕНИЕ ЛИНЕЙНЫХ ГРАНИЧНЫХ ЗАДАЧ 97
Для этого нужно положить
S (х) - (vT (х) v (х))-1 vT (x) A (x) v (х).
Таким образом, искомым для v (x) будет уравнение
v'-AT (x) v + v(x) (vT (x) v (х)У1 vT (x) A (x) v (*) = 0. A3)
Отметим, что матрицу v (x) теперь можно найти по
уравнению A3) и начальному условию A0). При этом в силу
свойства A2) матрицы v (x) будем иметь
vT (x) -v(x) = vT (a) - v (а) = и[и
и, значит, det (vT (x) v (х)) Ф 0 при всех а ^ х ^ Ь.
Получим уравнение для вектор-функции о> (*),
определяемой в соответствии с формулами E) и (9) по правилу
vT(x)y(x) = ®(x)9 A4)
где <o(x) = (<Oi(x), ..., со/(а')O. Продифференцировав A4)
и заменив в полученном выражении v' (x) и у' (х) по
формулам A) и A3), придем к уравнению вида
о)' + vT (x) AT(x)v (x) (vT (x) v (х))-1 <d-^vT (x)f(x). A5)
Вектор-функцию со (x) можно вычислить как решение
задачи Коши для уравнения A5) с начальным условием
в точке х = а:
<o(a) = Yi.
Построенная здесь схема вычислений позволяет с
помощью соотношения A4) переносить любое из граничных
условий B) в произвольную точку отрезка [а, Ь]. Это
может быть использовано для определения значения у (х)
в точке х = Ь следующим образом.
1. Полагаем / = &х и находим матрицу vT (х)
размерности (ki х п) по уравнению A3) и начальному условию
v (хх) == v (а) = фх; при этом а<,х^х2. Соответствующий
вектор со (х) определяем на отрезке [хъ х2], решая
уравнение A5) с начальным условием ш (xi) = (o(a)^=ai.
В точке х = *2 получим vT (х2)у (х2) = о> (х2). Объединим
это условие с условием B), заданным в точке х2, и
запишем их в виде
4 В. И. Крылов и др., т. II

98 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. C
где \|xj = г **2' — матрица размерности (/ х л), / = &х -f
+ k2l P2 = J — вектор-столбец размерности kx + й2.
Предполагаем, что det (^Ji|J) ^ 0.
2. Полагаем / = £i + £2 и находим на отрезке [х2у х3]
матрицу vT (x) размерности Aхп) по уравнению A3) и
начальному условию u(x2)=ijV, вектор о> (х) на этом же
отрезке определяем по уравнению A5) с начальным
условием со (х2) = р2. В точке х = х3 получим vr (xs)y (x3) = о> (*3),
кроме того, в этой точке, согласно граничному условию
B), имеем соотношение ц>^у (хз)-=а3. Объединив их,
получим ^(JC8) = Ps,
T==z\vT (хз)]
I Фз J
где я|э3
+ k2 + kB, Рз-
+ k2-\-k3.
— матрица размерности (lxn)> l = kx -f
ю **3' — вектор-столбец размерности kt -f
#3 J
Полагаем, что det (ipjops) ф 0 и по аналогии
продолжаем прогонку решения на отрезках [х3у х4], ...
••• » [^/n-2»^m-i]- В точке х = jcm_х имеем
Я|Эт-1.У (*m -l)"=Pm-l»
где i|)m-i — известная матрица размерности (Ixri), 1 =
ш— 1
= 2 ^ь Pm-i — известный вектор-столбец той же размер-
т—\
ности. При /=2 ^ решаем на отрезке [xm~i> *,„],
*„, = &, задачу Коши для уравнения A3) с начальным
условием у (*/72.-i) =^m-i и для уравнения A5) с
начальным условием co(xm_i) = pw-i. В точке х = хт получим
vT (хт)у(хт) = (д(хт). A6)
В этой же точке в силу граничного условия B) имеем
еще соотношение
Ч?пу(хт)=ат. A7)
Формулы A6) и A7) представляют в совокупности
систему п линейных алгебраических уравнений с п неиз-

§ g] РЕШЕНИЕ ЛИНЕЙНЫХ ГРАНИЧНЫХ ЗАДАЧ 99
вестными уг(хт), у2(хт)> • , Уп(Хт)- Предположим, что
ранг этой системы п и, решив ее, например, по методу
Гаусса, найдем
J>(*m) = Pm. A8)
где Рт = (Рг1т). Р'Л •••» Рпт))г~ известный вектор.
Искомое решение граничной задачи A), B)
вычисляется теперь как решение задачи Коши для уравнения A)
с начальным условием A8) в точке хт = Ь. Эту задачу
приходится решать в направлении от точки Ь к началу
отрезка— точке а. Для этой цели, как мы уже отмечали,
могут быть использованы какие-либо методы численного
решения задач Коши, например, методы Эйлера, Адамса,
Рунге — Кутта и др.
Теория изложенного здесь метода разработана
советским математиком А. А. Абрамовым.
Укажем на преимущества этого метода перед такими
известными методами решения линейных граничных задач,
как метод дополнительных функций и метод
сопряженных уравнений (см. [4], §§ 8—10 гл. 3). Указанные
методы основаны на использовании структуры общего
решения для целей переноса граничных условий. Однако
часто фундаментальная система решений однородного
уравнения имеет тенденцию к вырождению, когда часть
векторов в ней становится почти линейно зависимой. Это
приводит к тому, что граничное условие, обладающее
свойством невырожденности, скажем, в точке xs> теряет
это свойство при своем переносе в точку xs+i из-за
быстрого накопления погрешностей. В методе Абрамова
этого не происходит. Действительно, пусть мы в точке
x = xs имеем граничное условие
<ply{xs)=as- A9)
Свойство невырожденности этой линейной комбинации
характеризуется величиной det(cpsr(p5), по условию
det (ф5 ф5) Ф 0. В методе Абрамова перенос этого
граничного условия из xs в avi осуществляется с помощью
функционального отношения A4). Значит, при переносе
граничного условия A9) из xs в xs г1 мы получим в точке
x==:xs+1 новое граничное условие
vT (xs+1)y (xs+1) = о (xs+1). B0)
4*

100 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
Свойство невырожденности линейной комбинации B0)
характеризуется величиной det (vT (xs+1) v (xs+1)), но в силу
свойства A2) det (vт (х) -и (х)) = const при х3<,х^х5+ъ
и потому
det (vT (xs + 1) v (x5+i)) = det (vT (xs) v (xs)).
Значит, линейные комбинации A9) и B0) в смысле
невырожденности обладают одинаковыми свойствами.
§ 10. Решение нелинейных граничных задач
Рассмотрим при а^х^Ь систему нелинейных
дифференциальных уравнений
A)
y' = F{*> У)
с граничным условием
«ГОФ). J>(&)) = A. B)
где у (х) = (уг (л:), ... , уп (х))т — вектор-функция,
подлежащая определению, F=(Fl9 ..., Fn)T — известная
вектор-функция,
Fi = Fi{x, у), g=(gi, ..., gn)T, gi = gi(y(a), yib)),
g-—известная вектор-функция, Н = Aгъ ..., hn)T —
заданный числовой вектор, у (а), у (Ь) — значения искомого
решения граничной задачи A), B) соответственно в
точках х = а и х = 6.
Требуется найти вектор-функцию у(х), которая при
a<ix<ib удовлетворяла бы A), а при х = а и х = Ь —
граничному условию B).
В приложениях граничное условие B) часто задается
в упрощенном виде, а именно:
C)
By(a) = d, Су(Ь) = е,
где
£ =
ь21 ыл
"in
?ki
?k2
Ll2
Too
LC-pi
k + p = n,
B,C nd, e — соответственно известные матрицы и векторы и
rang В = ky rangC = p, d = (dx, ... , dk)Tf e = {еъ ..., ep)T.

§ ю] РЕШЕНИЕ НЕЛИНЕЙНЫХ ГРАНИЧНЫХ ЗАДАЧ \Q\
Предположим, что граничная задача A), B) имеет
единственное на [а, Ь] решение.
1. Метод редукции к задачам Коши. Будем считать
уравнение A) таким, что для него задача Коши с
начальным условием у (а) = г, где г — некоторый вектор из
я-мерного евклидова пространства Еп, имеет
единственное решение.
Рассмотрим задачу Коши
zr=F(xy z), a<x<b,
*(а) = гЧ z{VzEEnf ( }
где z(x) = (z1(x)9 ..., гя(х))т, z^ = (z\«\ ..., г?у.
Решение задачи D) можно записать в виде
z(x)=Z(x,z<*% E)
где Z= (Zj, .,., Zn)T — некоторая вектор-функция, Zt =
— Zi(x> z{0)). Положим в E) x = b и полученное
значение z (Ь) подставим в B) вместо у F), а вместо у (а)
подставим z (а) = £@), получим
Q(zio>) = g(zi°\ Z(b, z{G))).
Если бы было G (г@)) = Л, то это означало бы, что £(о) =
= <у(а), где у (а) — значение решения граничной задачи
A), B) в точке х = а, и £ (х) — решение задачи Коши D)
тождественно совпадало бы с у(х).
Если z°=f=y(a), то и G(z°)=£h. Таким образом,
вычисление искомого значения j/ (#) можно выполнить,
решая систему нелинейных численных уравнений
G{z{»]) = h F)
или в развернутом виде:
G1(z\()\ га0', ..., z'£')=hl9
G2(z{\ z?, ..., 2л°)=А2,*
Будем считать, что система уравнений F) имеет
единственное решение z[0)=y(a).
Отметим здесь, что вид функций G* нам неизвестен,
однако мы можем вычислить значение О (z{k)) для любого

102 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
z{k) e Еп. Этого можно добиться путем решения задачи
Коши , . _, ч _ _,
z=F(x,z)9 Жх<&,
г (а) = *<*>, г^еЯ*. ()
Пусть £(fe) (х) — решение задачи G), тогда
Теперь можно сформулировать алгоритм метода
редукции к задачам Коши. Он состоит в следующем:
1) решаем систему нелинейных численных уравнений
F) и находим ее решение z{0)~y(a);
2) искомое решение граничной задачи A), B) находим
как решение задачи Коши:
z' = F(x, z), a^x^b,
z{a)^y{a).
Как мы уже отмечали, будет выполняться тождество
Z(x)=y(x).
Для решения упоминавшихся здесь задач Коши могут
быть использованы многие методы, в том числе меюды
Эйлера, Адамса, Рунге — Кутта и др.
Остановимся на вопросе численного решения системы
уравнений F). Для решения этой системы целесообразно
избрать какой-либо итерационный метод, обладающий
быстрой сходимостью. Покажем, как для этого можег
быть применен метод Ньютона.
Пусть z{k)—k-e приближение к решению у (а)
системы уравнений F), тогда в методе Ньютона (£+1)-е
приближение может быть вычислено по формуле
z{k+v = z[k)-v(k\ (8)
где v[h) =(v[k\ v(o\ ... , v^y — вектор-столбец,
определяемый как решение системы линейных алгебраических
уравнений,
G(^vik} = G(z(k])-hy (9)
G<*> =
"дгГ
ди)р
dzL
dGih;
dG(>)
(JG ,7
dzn
1
Gf=Gi(z(k)),

§ 10J РЕШЕНИЕ НЕЛИНЕЙНЫХ ГРАНИЧНЫХ ЗАДАЧ ЮЗ
k = 0, 1, 2, ...; /=1, 2, ..., п. Мы предполагаем, что
det G<,fe) Ф 0. Точно вычислить элементы матрицы G^ мы
не можем, ибо неизвестен вид функций Gi(z{k)). Однако
эти элементы могут быть вычислены приближенно,
например, по формулам
где Ik > 0 — достаточно малое число, выбираемое
вычислением
*,■=((), ..., 0, 1, 0, ..., ОO, f, /=1, 2, ..., л.
(у)
Обозначим через G^ матрицу, элементы которой
вычисляются по формуле A0). Реально мы можем вместо
последовательности z{k) вычислить последовательность
z{k\ определяемую по правилу
51*н) = 5<*)_.£1*)э (И)
где v{k) — решение системы уравнений
Gfi(*> = G (£<*>)-*. A2)
5(о) = *Ч * = 0f 1, 2, ...
Чтобы полностью уяснить вычислительную схему метода
редукции к задаче Коши, покажем, как по z(Q) = £(о)
(г{0) — некоторый вектор из Еп) вычислить z{1).
1. Решаем задачу Коши G) при z{a)=zio),
вычисляем значение решения этой задачи в точке х = Ь
(обозначим его черезz{0) (b)\ вычисляем Q(z{o))~g{z{0\ z{G){b))>
2. Решаем п задач Коши G) при начальных условиях
z(а) = z{0) + /0#у, / = 1, 2, ..., п\ значения решений этих
задач в точке х = Ь обозначим соответственно
Вычисляем G(i@) + /0^/) по правилу
О(*@4/о*у) = £(*"". z{0'i](b)), /=1, 2, ..., п.
По формуле A0) вычисляем элементы матрицы G'z'.

104 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
3. При k = 0 решаем систему уравнений A2) и
находим v[0). Первое приближение к у (а) вычисляем по
формуле A1) при k = 0. Имеем: z{1) = z{0) — v{0).
4. Аналогично по z{1) вычисляется z{2) и т. д.
Пусть при некотором s мы с удовлетворительной
точностью получили значение ~z{s)^y(a). Тогда
приближенное решение граничной задачи A), B) вычисляется как
решение задачи Коши для уравнения A) с начальным
условием у (а) = J(s).
Сходимость метода редукции к задачам Коши
обусловливается сходимостью метода Ньютона A1), A2) с
приближенной матрицей Якоби Ъ{гк). Условия сходимости
такого метода сходны с условиями сходимости основного
метода Ньютона, определяемого формулами (8), (9).
Отметим еще, что если на каждом номере итераций
величину lk выбирать из неравенства
/*< max \Gl{z^)-hi\, A = 0, 1, 2, ...,
1 < / ^ п
то метод Ньютона, определяемый формулами A1), A2),
может иметь квадратичную сходимость.
Укажем на некоторые особенности в выборе
величины 1к. Если мы хотим, чтобы формула A0) была
возможно более точной, мы должны по смыслу производной
величину 1к выбирать возможно меньшей. Но тогда
в выражении A0) в числителе будет результат
вычитания двух близких по абсолютной величине чисел, и если
эти числа были большими, то произойдет сильная потеря
значащих цифр. Это приведет к тому, что производная
в формуле A0) будет вычислена с большой погрешностью.
Если же 1к будет выбрано недостаточно малым, то тогда
по смыслу определения производной формула A0) не
может дать хорошего по точности результата. По этим
причинам вопрос оптимального выбора величины lk
требует в каждом конкретном случае специального
рассмотрения.
2. Метод линеаризации. Задачу A), B) можно
линеаризовать, используя идею метода Ньютона. Пусть
у{0) (х) = (у\0> (х)у ..., у'п {х))т —нулевое приближение к
искомому решению граничной задачи A), B). В предпо-

РЕШЕНИЕ НЕЛИНЕЙНЫХ ГРАНИЧНЫХ ЗАДАЧ Ю5
ложении, что функции F; и gt дважды непрерывно
дифференцируемы по своим аргументам, можно записать
следующие соотношения:
Fi (х, У (х)) **
п
^Ft (х, У°> (*)) + У ^,f'M) (У; (х)~У'Г М). A3)
/=1
s, (у ("). у (<>)) ~ft (У" (о). У01 (»)) +
+ 2 *,(УТ;»Г(-<*F) -™» -}- 2,..., п.
A4)
Покажем теперь, как, используя формулы A3), A4),
на основании задачи A), B) вычислить первое
приближение у{1) (х) Гт& решению у(х) по нулевому
приближению у0) (х). Введем обозначения:
f,tey"w>-(df"'^w>);.
Ся»(У°Ч°).У№)) = (%''у;у(>)));;
это известные матрицы размерности (пхп). Теперь для
определения у[Х) (х) можно записать линейную граничную
задачу:
ybY(x) = Fy(x, y{0)(x))(y^(x)-y^(x)) + F(x, у™ (х))9
Сум (У0) (a), У0) (Ь)) (У« (а) ~У0) (а)) + A5)
+ Gy(b) (У0) (a), У°> (Ь)) {у™ (b) ~У<» F)) +
+г(У0,(А), У0) (*)) = *•
В некоторых случаях для решения задачи A5) может
быть использован метод дополнительных функций в такой

106 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
форме. Вычисляем фундаментальную систему решений
г{1) (х), г{2) (.г), ..., zKn] {х) по правилу
-^W- = Fy (х, у °> (х)) zw (х), Ы,2 п,
г™(а) = ек, ek = @, ..., 0, 1, 0, ..., ОO", а^х^Ь.
k
Находим на [я, Ь] функцию Y (х) как решение задачи
Коши:
Y'(x) = Fy(x, y{0)(x))(Y(x)-^(x))+F(x, у™ (х))9
У(д) = 0.
Искомое решение задачи A5) определяем по формуле
у{1) (х) = Y(x) +c^l] (х)+... + спгМ (х). A6)
В этой формуле параметры съ съ ..., сп вычисляются
из условия, что функция уA) (х), определяемая по A6)
при x='(i и х = Ь, удовлетворяет граничному условию
в A5), т. е. из системы уравнений
[Gy{a)(y{0)(a), y{0)(b)) + Gy{b)(y@)(a), у{0) (Ы) Z (b)]C ^d,
где Z(b)=[z{l) (b), z{2) (b), ..., z{n) (b)]-~матрица
размерности nxn,
С = (с1у с2» ..., сп) ,
d = h + Gy(a)(yw(a), уМ(Ь))-у"Ча)-
-ОуФ)(У{0)(а), y{04b))(Y(b)-y^(b))-g(y^(a), yw (&)).
После вычисления параметров си с2, ..., сп решение
задачи A5) можно вычислять по формуле A6). Но можно
поступать и по-другому. Используя A6), вычисляем
значение уп) (х) при х = а или х = Ь, а затем вычисляем на
всем отрезке [а, Ь] функцию у[Х) (х) как решение задачи
Коши для дифференциального уравнения A5) с
начальным условием в точке х = а или в точке х = Ь.
Аналогично по уп) (х) вычисляется у{2) (х) и т. д.
Обычно вычисления ведутся до тех пор, пока не будет
достигнут такой номер k итерации, что будет
выполняться условие
max max \tAk + l)(x) — t/V(x)\^e9 A7)
где 8 —некоторое положительное число, характеризующее

§ И] ° МЕТОД СЕТОК. ДЛЯ РЕШЕНИИ ГРАНИЧНЫХ ЗАДАЧ Ц)?
точность вычисления у(х). Если у{к) (х) — такая вектор-
функция, что для нее выполняется условие A7), то ее
принимают за приближенное решение граничной задачи
A), B).
Метф* линеаризации, при обычных для метода
Ньютона условиях, в частности при достаточно хорошем
начальном приближении у10) (л), имеет квадратичную
сходимость.
Отметим еще, что если среди фундаментальных
решений дифференциального уравнения A5) есть быстро
растущие решения, то от метода дополнительных функций как
средства решения задачи A5) следует отказаться из-за
его неустойчивости к ошибкам округлений. Здесь
целесообразно будет воспользоваться методом С. К. Годунова,
описанным в [1].
§ 11. Метод сеток для решения линейных
граничных задач
Этот метод является одним из наиболее
универсальных как для обыкновенных дифференциальных
уравнений, так и для уравнений в частных производных. Мы
проведем изложение метода сеток на примере простейших
линейных граничных задач для дифференциальных
уравнений второго порядка.
1. Постановка задачи. Идея метода сеток. Пусть при
а^х^Ь рассматривается граничная задача для
дифференциального уравнения
Hy)^!f + p{x)y' + q(x)y = f{x) A)
с условиями
1а (у) == аьу (а) 4- ауу' (а) - А, B)
1ьЬ)^оУ{Ь) + №(Ь) = В. C)
Будем считать, что граничная задача A)—C) имеет
единственное решение, это решение непрерывно на [а, Ь] и
имеет непрерывные производные на этом отрезке до
четвертого порядка включительно.
Метод сеток для решения граничной задачи A)—C),
равно как и для многих других задач, состоит в
следующем.

108 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
1. Область задания дифференциального уравнения
A) — отрезок [а, Ь] — заменяется некоторой дискретной
(сеточной) областью. Это означает, что на отрезке [а, Ь]
выбирается некоторая система точек. Совокупность этих
точек называется сеткой. Если положение каждой точки
определяется по правилу xk==a + khf k = 0f 1, ..., N,
/i=-^-, N — целое число, то сетку называют
разномерной. Точки xk называют узлами сетки.
2. Граничная задача A)—C) на множестве узлов,
принадлежащих сетке, заменяется некоторой сеточной
задачей. Под термином сеточная задача мы будем
понимать некоторые соотношения между приближенными
значениями решения граничной задачи A)—C) в узлах сетки.
В рассматриваемом случае это будет система линейных
алгебраических уравнений.
3. Полученная сеточная задача решается по какому-
либо численному методу и тем самым находятся
приближенные значения решения граничной задачи в узлах
сетки. Это и является конечной целью метода сеток.
Можно указать как на основные в методе сеток на
следующие вопросы.
1. Как заменить область задания дифференциальных
уравнений, а в случае дифференциальных уравнений
в частных производных еще и границу области
некоторой сеточной областью?
2. Как заменить дифференциальное уравнение и
граничные условия некоторыми сеточными соотношениями?
3. Будет ли полученная сеточная задача однозначно
разрешимой, будет ли она устойчивой, сходящейся?
Смысл последних двух понятий будет пояснен позже,
в частности в § 1 гл. 7.
2. Методы замены обыкновенных дифференциальных
уравнений и граничных условий системой алгебраических
уравнений. Возвратимся к граничной задаче A)—C).
Выберем равномерную сетку: xk^a-\-kh, k = 0> l, ..., N,
/i=—rf-. Дифференциальное уравнение A) будем
рассматривать только во внутренних узлах сетки, т. е. будем
полагать, что x — xkf k= 1, 2, ..., N — 1. Граничные
условия B), C) рассмотрим при xQ = a и х^ = Ь.

§ 11] МЕТОД СЕТОК ДЛЯ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ \QQ
Положим в A) х = хк:
L (у) !* = *л = у" (хк) + р (хк) if (xk) + q (xk) у (xk) = f (xk), D)
ft=l, 2, .... N-l.
Выразим у' (хь), у" (хь) через значения функции у(х)
в узлах xk-l9 xk% xk+1, т. е. через значения у (лг^), у {хк)у
y(Xk+i)- Для этой цели мы воспользуемся
интерполированием и численным дифференцированием на основе
интерполяционных полиномов (см. т. I, § 6 гл. Г).
Имеем
'*" (Л) =|/(**"). хк.1<хГ<х„;
у'{хк)=у{х^]-у(н) Л-rTih),
rf (h) = — j у" (x'i'), xk < xf < хк+ъ
y'ix^^^-v^ + rTih),
rf Ф) = -%y"' (Af), xk-x< x? < xk+1;
У \Щ — -g. rrk (n)>
rf (ft) = — ~ yiv D4'), x*-! < 44' < xk+1.
E)
F)
G)
(8)
Подставив в формулу D) выражения G) и (8) для у' (хк)
и у" (xk), получим
L (У) U = *k-Lh (У (**)) + Rk (h) = / (xk), (9)
где
Rk{h) = r't{h) + p{xk)-rT{h).
Выражение Lh (у (хк)) называется разностным оператором
второго порядка, а величина Rk (ft) — погрешностью
аппроксимации дифференциального оператора L (у) разностным

110 обыкновенный дифференциальные уравнения [гл. о
оператором Lk (у (xk)) на решении. Если для Rk (h)
выполняется условие
\Rk(h)\^Mh\ й=1, 2, ..., W-1,
где М = const, не зависящая от /z, то говорят, что
разностный оператор Lh аппроксимирует на решении
дифференциальный оператор L с погрешностью второго
порядка относительно h.
Пусть h достаточно мало, тогда в формуле (9)
величиной Rk (h) можно пренебречь и мы получим
"iAW=/W, A=l, 2, ..., N-1 A0)
где при выполнении некоторых условий молено
предположить, что Ui^yiXi), / = 0, 1, 2, ..., N. Вообще говоря,
всегда yL Ф у (*,-), и только при Rk (h) ~= 0 можно ожидать,
что будет У1 = у(х/), i = 0, l, 2, ..., N. Равенство A0)
мы будем называть разностной схемой,
аппроксимирующей уравнение L(y)=f(x).
Отметим еще, что A0) есть система линейных
алгебраических уравнений, число таких уравнений N — 1,
а матрица этой системы — трехдиагональная.
Неизвестными являются у0, уъ ..., yN. Число этих неизвестных
в системе равно Л/"+1.
Обратимся к граничным условиям B), C). Используя
F) при & = 0, из B) получим
la(y)^l^l)(y(Xo)) + Ro(h)-A1 A1)
где
^(У^^ауЫ + а^^^),
/?o(A) = cziri"(/i).
Аналогично, используя E) при k — N, из C) получим
1„ (у) s l[h) (у (xN)) + RN (h) =B, A2)
где
If (У Ы) = № (хк) + Рх (^iZ^Lll),
RN(h) = $irN'(h).
При достаточно малом h величинами R0(h) и Rx(h),
имеющими первый порядок малости относительно h, в выра-

§ П] МЕТОД СЕТОК ДЛЯ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ Ш
жениях A1) и A2) можно пренебречь. Тогда вместо A1)
и A2) будем иметь
#°Ы = Л, A3)
Операторы 1(а] (у0) и 4А) (ух) аппроксимируют
соответственно граничные операторы 1а (у) и 1Ъ (у) с
погрешностью 0(h). Формулы A0), A3), A4) образуют в
совокупности систему N + 1 линейных алгебраических
уравнений с неизвестными у0, уъ ..,, yN. В методе сеток эту
систему решают по какому-либо численному алгоритму
и после этого полагают у{хк)^ук, fe = 0, 1, ..., N.
Обратим внимание на то, что граничные условия B),
C) при необходимости можно аппроксимировать
разностными условиями с погрешностью второго порядка малости
относительно h. Для этого достаточно, например,
воспользоваться вместо E) и F) следующими формулами:
3. О разрешимости систем разностных уравнений. Как
мы видели, в методе сеток приближенное решение
граничной задачи A)—C) вычисляется как решение системы
линейных алгебраических уравнений, образуемых
формулами A0), A3), A4). Выясним условия, при которых
такая система уравнений будет однозначно разрешимой.
С целью упрощения доказательств будем считать, что
в граничных условиях B), C) а0 = р0=1, cti = p1 = 0.
В этом случае сеточная задача A0), A3), A4) может быть
записана в таком виде:
• МЫ =fr&h(yk)=fk> *=1, 2, ..., N-l,
Уо = А, Ух = В,
где
Л?г Ы = Акукп + 2Вкук + Скук.ъ
ЛА=1 + -$Р*, 2Bk = -2 + h*qk, Ск=\-\рк,
Pk^P (xk), qk = q (xk), fk = / (xk).

112 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
Перепишем систему уравнений A5) в ином виде,
нормировав уравнения для внутренних точек сетки. Получим
ЛнШ=Щк, й=1, 2, ..., tf-1,
Уо = А, yN = B.
Чтобы доказать однозначную разрешимость системы
уравнений A6), достаточно показать, чю соответствующая
однородная система уравнений
ЛлЫ = 0, Л=1, 2, ..., JV-1,
20 = 0, 2^ = 0 * }
имеет только нулевое решение, т. е. zk~0. Тогда
определитель системы уравнений A7) отличен от нуля, и так
как он совпадает с определителем системы уравнений A6),
то последняя будет однозначно разрешимой в силу
правила Крамера.
Доказательство разрешимости системы уравнений A6)
будем вести при двух предположениях относительно шага
сетки h и коэффициента q (х) уравнения A).
Будем считать, что выполняются условия:
1) -\- max \p{x)\<\, A8)
2) <7(*)<0 при а^х^Ь. A9)
Предположим, что заданы некоторые числа У0, Ylt...
..., YNy среди которых есть неравные. Имеет место
Лемма 1. Пусть выполняются условия A8), A9) и
А,(П)^0 (Лл(У*)<0) B0)
при k=\, 2, ..., N—l. Среди чисел Y0, Yly ..., YN
наибольшее положительное значение (наименьшее
отрицательное значение) принимает или У0, или YN.
Отметим, что эту лемму часто именуют принципом
максимума.
Доказательство. Будем доказывать только
первое утверждение при условии, что имеет место
неравенство
ЛА(ПK*0, А=1, 2, ..., N-\.
Предположим противное и будем считать, что
наибольшее положительное значение числа Yk принимают при

§ 11] МЕТОД СЕТОК ДЛЯ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ ЦЗ
некотором k A <; k <: N — 1), и пусть Ys = М > 0 есть
одно из таких значений, для которого К5+1 или F5l
строго меньше М. Тогда
Лл(У5)^ЛЛ75+1 + 2В5У5 + С5Г5-1<(Л5 + С5)Л1 + 2В5М,
ибо As и С5 строго положительны в силу условия A8).
В силу условия A9)
ЛЛ (Ys) <(AS + CS + 2BS) M = h%M < 0.
Таким образом, имеем Л^У5)<0. Но это противоречит
условию B0). Значит, наше предположение неверно и
наибольшее положительное значение будет иметь или Y0f
или YN. Аналогично доказывается утверждение леммы и
в случае условия Ah(Yk)^0.
Теорема 1. Пусть выполняются условия A8), A9).
Тогда система уравнений A7) имеет только нулевое
решение.
Доказательство. В силу формулы A7) Ah(zk) = Q1
А=1, 2, ..., Л"—1. Поэтому можно считать, что
выполняются оба условия B0) леммы 1, т. е. Ah(zk)^0 и
Ah(zk)^0. В этом случае по лемме 1 наибольшее
положительное значение и наименьшее отрицательное
значение среди чисел z0, гъ ..., zN будут иметь числа z0
или zNf но в уравнениях A7) 20 = zA' = 0, значит, все
числа zk = 0. Теорема доказана.
Из теоремы 1 сразу следует однозначная разрешимость
системы уравнений A6).
4. Метод ортогональной прогонки. Мы уже отмечали,
что системы алгебраических уравнений, возникающие
в методе сеток, имеют специальный вид. Так, например,
система уравнений A6) имеет трехдиагональную матрицу,
т. е. матрицу, у которой отличными от нуля являются
только элементы главной диагонали и элементы двух
соседних диагоналей, все же другие элементы матрицы
равны нулю. В настоящее время разработан ряд
численных алгоритмов, приспособленных к нахождению
решений подобных систем. Одним из таких методов является
метод ортогональной прогонки. Мы изложим этот метод
на примере системы уравнений, подобной системе A6),
но более общей.

114 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ.6
Пусть задана система линейных алгебраических
уравнений
адж + %+адн=Мь а=1, 2, ..., jV-i,
где ^, &ь cfe, dft, a0> (гх, у, т0, ть б —известные числа
и ol + a'l = 1, тй + т{ = 1, ак-скФ0, k= 1, 2, ..., Л/- 1.
Предположим, что система уравнений B1) имеет
единственное решение. Легко видеть, что система уравнений
A0), A3), A4) и A6) является частным случаем
системы B1).
Дадим вывод алгоритма метода ортогональной
прогонки. Пусть yk, k = 0, 1, ..., N, — искомое решение
системы B1). Введем в рассмотрение новые неизвестные
величины a*, uk, vk, определяемые соотношениями
uk = £/ft sin ak + ykl cos a*, B2)
Vk = Uk cos ak - yk x sin a* B3)
и системой уравнений B1). Очевидно, что
yk = и* sin afe + a* cos a*, B4)
f/fe-i = ^* cos afe — ofe sin a*. B5)
Используя формулы B1)—B5), запишем разностные
уравнения для сеточных функций ak и ил:
И*+1 = ^ • J "л + ^ ^ ' Sin a*+i' B6)
^-=n--^i + f-Jsina*+i-sinaife +
Р/? 9k L
+ cos ал+1 (■* cos a, + ^ ■ sin a*)] ak - ^J±i • /i2 d*f B7)
где
Г о , ■'<* • 26* \2-|I/2
P* = [cos2ak + ^sin^k~~cosa* j J .
Величины sinobA+i» cosa*+i определяются из условия
cosa^-cosaft+i + U" sinaft— -^cosa*) sin ал+х = 0. B8)
Это условие выводится из требования, чтобы правая
часть уравнения B6) не содержала значений сеточной

§ 11] МЕТОД СЕТОК ДЛЯ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ Ц5
функции vk> Из B8) выводятся следующие рекурре'нтные
формулы:
COS Cifc
sina*+i =
9k
Ck • %bk B9)
- --- sin ak — cos ak ^ >
CLh Clh
cosa^ + 1 = ~ .
* + 1 Pk
Заметим, что р*^0 при всех значениях k, ибо в
противном случае нулю должен был бы равняться
коэффициент ck/ak. Но это невозможно из-за предположения ak-
•скфО.
Чтобы можно было вести вычисления по формулам B6),
B7) и B9), надо вычислить начальные значения sinab
cosai, иг и vk. С этой целью подставим в условие о0у0 +
-\-°1У1^2У значение yQ, определяемое по формуле B5)
при &=1, и уъ определяемое по формуле B4) при k = \.
Получим
(сх0 sin ax -f ai cos <Xi) u1 + (au cos ax — o± sin ax) v± = y. C0)
Поскольку мы намерены определить их и vNy то в
формуле C0) Vi можно считать произвольным. Чтобы
исключить влияние Vi на иъ положим в формуле C0)
аэ cos аг — Gi sin ax = 0.
Можно считать, что
с in r/. -— а*.
C1)
sin ax = a0,
cosai^ax.
Теперь из C0) получим
«i = Y. C2)
ибо по предположению стЗ + ai = 1.
Таким образом, используя формулы B9), C1) и B6),
C2), можно последовательно вычислить
sinab sina2, ... , sinav,
cos ax, cos a2, ... ; cos a,v,
иъ иъ .. . , Ujs;.
Положим в формуле B2) k = N:
(sin aN) yx + (cos aiV) yN-1 = «jV. C3)

116 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ.6
Кроме соотношения C3), мы еще имеем второе
граничное условие
Ti#A' + To&V-l = S. C4)
Пусть
Д = т0 sin a,v — Ti cos aiV Ф 0;
тогда из системы уравнений C3), C4) получим
Ук~ 1 = д- F sin aN — wA-Ti),
#w = д- ("*то — б cos ал-).
Подставим эти значения в формулу B3), положив в ней
k — N. Получим
Vn = д (— б + (т0 cos av + Tj sin a#) и#). C5)
Значения vN, vN^lt ... , v1 могут быть вычислены теперь
по формулам B7) и C5) при k^N—\, N — 2, ... , 1.
Все изложенное выше позволяет сформулировать
алгоритм метода ортогональной прогонки.
1. Вначале, используя формулы B9), C1) и B6), C2),
последовательно вычисляем sina^, cos a*, uk, k=lt
2, ...,N.
2. Затем проверяем, выполняется ли условие Д^=0,
и если оно выполняется, то по формулам B7), C5)
вычисляем значения vNl vN...u ... , vx.
3. По формуле B4) при k~N и по формуле B5)
при k=l вычисляем соответственно yN и у0. Другие
значения уъ у2, ..., Уы-i искомого решения
системы уравнений B1) можно вычислять по любой из
формул B4), B5).
Непосредственной проверкой можно убедиться, что
определяемые таким образом значения у0, уъ ... , yN
удовлетворяют системе уравнений B1).
Укажем на следующие свойства метода ортогональной
прогонки, важные в вычислительном смысле. Все
формулы, по которым ведутся вычисления, являются
рекуррентными, и потому они просто программируются.
Вычисление величин sin a*, cosa^ благоприятно в смысле
медленного накопления погрешностей округления из-за
свойства | sin ak j ^ 1, | cos ak j ^ 1. Благоприятным в смысле

§ И] МЕТОД СЕТОК ДЛЯ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ 117
накопления погрешностей округления является и процесс
вычисления величин uk и vk, так как при Д Ф 0 имеем
4 + 4 = у£ + у!-ь
Значит, сеточные функции uk и vk по своей величине
такие же, как и искомое решение системы уравнений B1).
5. Оценка погрешности и сходимость метода сеток.
Эти вопросы мы будем изучать на примере упрощенной
задачи A) — C). Будем считать, что граничные условия B),
C) заданы в форме
у(а) = А, у(Ь) = В.
Учитывая (9) и A5), запишем сеточную задачу для
точных значений граничной задачи A)—C) в следующем
виде:
jFA«{y(Xk)) + Rk(lt)=f(xk), k=l, 2, ..., N~l
у(х0) = А, y(xN) = B.
Отметим, что в случае, когда решение граничной задачи
A) —C) непрерывно и имеет непрерывные на [а, Ь]
производные до четвертого порядка включительно, для
погрешности аппроксимации Rk (И) верна оценка
\Rk{h)\^Mh\ fe-1, 2, ..., tf-1, C7)
где М — постоянная, не зависящая от h.
Реально из-за наличия погрешностей округления
сеточные значения будут вычисляться как решение
системы линейных алгебраических уравнений, сходной
с системой A5):
рЛАЫ=/*-в*, k=l, 2,..., ЛГ-1,
00 = Л, ljN = B,
где через 6^ обозначены погрешности округлений. Будем
считать, что для б^ указана некоторая оценка сверху:
}6*!^6, *=1, 2, ..., N-1. C9)

11в ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ.6
Введем следующие обозначения:
£* = #(**)-#*.
е (Л) = max \ek\.
О ^ к < N
Метод сеток, определяемый формулой C8), называется
равномерно сходящимся, если при п-~>0 выполняется
условие: а (Л)->0.
Дадим оценку для | ek \ и установим условия
сходимости метода сеток.
Используя формулы C6) и C8), получим
ЛЛ(еЛ)=А2(-^(Л) + в*). *=1, 2,..., ЛГ-1, мо
е0 = 0, е^ = 0. l '
Метод получения оценки для ' гк ! будет заключаться
в построении некоторой функции и(х), которая будет
мажорантой для \ek\, т. е. будет выполняться условие
|ел|<и(х*), u(x)^0, k = Q, 1, ..., ЛЛ
Для построения мажоранты нам понадобится
следующая лемма.
Пусть /0, tu ... , tN и s0, Si, ... , Stv — некоторые числа,
причем Sfc^O, k = 0, 1, ... , N.
Л е м м а 2. Пусть выполняются неравенства A8), A9) и
1) ЛАЫ<-|ЛА(Ь)|, *=1, 2, ..., tf-1,
2) Uol<s0, \tN\<,sN.
Тогда
Ua|<sa> £=1, 2, ... , iV— 1.
Доказательство. Рассмотрим сумму sk-\-tk. В силу
первого условия леммы имеем
Л* (sk + tk) = ЛЛ (s*) + Лл (**) < 0.
По лемме 1 среди чисел s* + /* наименьшее
отрицательное значение могут иметь или s0-\-t0i или su\r-\~tN.
Но по второму условию леммы эти числа неотрицательны,
значит, все sk-\-tk^0. Аналогично можно показать, что
также и sk — tk^0. Последние два неравенства означают,
что — sk^tk^sk или \tu\^sk. Лемма доказана.

§ И] МЕТОД СЕТОК ДЛЯ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ Ц9
Рассмотрим вспомогательную задачу
L(v)^u" + p(x)v' + q(x)v^-U
1ф)-0, v (Ь) = О, ( '
где q(x)<C0. Ее решение обозначим через v
(^.Покажем, что у(л*)>0 для всех а<х<6. Действительно,
если бы функция v (х) принимала на [а, Ь]
отрицательные значения, то существовала бы точка х такая,
что y(x)<0, v'(x) = 0 и v (х)^0. Но тогда
L (v) \х=1 = v" (х) + р (х) v' (х) + q (х). v (x) > О,
что противоречит D1), ибо L(v(x))= — 1 при всех а<
<х<Ь.
Определим и(х) по формуле u(x) = a-v(x), где а —
положительное число, правило выбора которого мы укажем
позже.
Имеем
АлИ^)) = Л2(-1~^(^ А)).
где через R (v, А) мы обозначили погрешность
аппроксимации дифференциального оператора L (v) разностным
Lh{v(xk)). Очевидно, что
\Rh(v9 /z)KM*/z2, D2)
где М* — постоянная, не зависящая от h.
Запишем сеточную задачу для и (х):
Ah(u(xk))=-ah*(l+Rk(v, /z)), А=1, 2,..., iV-1,
и(*о) = 0, u{xN) = 0. D3)
Сравним задачи D0) и ^43). Если нам удастся
определить а так, чтобы было
ЛЛ (и (хк)) < -! Ля (е*) | D4)
при k= 1, 2, ... , /V— 1, то тогда в силу леммы 2 будет
выполняться неравенство \гк\^и(хк). Используя оценку
C7), имеем
!ЛЛ(8,)!</12(М/12 + б). D5)
Пусть h настолько мало, что 1— М*/г2>0. Очевидно,
что
Ah (и (хк)) < - ос/г2 A - М */г3). D6)

120 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ГГЛ. 6
Из D5^ D6) следует, что неравенство D4) будет
выполняться, если а выбрано из условия
- а/г2 A - М*/г2) < - /г2 (М/г2 + б).
Положим
а—1-Л4*/12'
Тогда
I Ч I < и (xk) = ою (xk) = j^Af^ • я (**)>
£ = 0, 1, ... , N. D7)
Оценка D7) является искомой оценкой погрешности
метода сеток, определяемого формулой C8).
Пусть 1/з? max v(x), тогда на основании D7) можно
записать, что
8 (Л) < 1_Л^да • У- D8)
Из этого неравенства видно, что e(/i)->0 при /г->0 со
скоростью О (А2), если 6 <: 60 • /i2. Таким образом,
установлена оценка погрешности D7), равномерная сходимость
и скорость сходимости метода сеток.
Теорема 2. Пусть решение граничной задачи A)—C)
с условиями частного вида у(а) = А, у(Ь) = В,-
единственно и непрерывно дифференцируемо на [а, Ь] до
четвертого порядка включительно. Если выполняются условия
A8), A9), то метод сеток для рассматриваемой задачи
будет равномерно сходящимся со скоростью 0(/i2), если
Теорема 2 имеет место для граничной задачи A)—C)
и при более общих граничных условиях, в частности,
она верна в случае, когда
1а (у) = а0у (а) + аху' (а) = Л, 1Ь (у) = М Ф) + (W Ф) = В
и oc0ai^0, PoPi^O.
§ 12. Метод Галерккна и метод моментов
Решение ряда задач физики и механики иногда более
выгодно находить в аналитической форме. Этим
свойством обладают методы Галеркина, моментов, наименьших
квадратов и др. По универсальности и простоте реал и-

§ 12] МЕТОД ГАЛЕРКИНА И МЕТОД МОМЕНТОВ 121
зации упомянутые методы часто уступают методу сеток
и некоторым другим подобным методам. Вместе с тем
они имеют и определенное преимущество перед методом
сеток, поскольку позволяют находить решение в
аналитической форме.
Рассмотрим методы Галеркина и моментов на
примере граничной задачи для нелинейного
дифференциального уравнения второго порядка.
Пусть при а^х^Ь задано дифференциальное
уравнение
F(x, у, у\ у") = 0 A)
с граничными условиями
la (У) = ад (а) + аху' (а) = А, B)
1Ь(У)^№Ф) + №(Ь) = В. C)
Будем считать, что граничная задача A)—C) имеет на
[а, Ь] единственное решение и это решение непрерывно
дифференцируемо до Еторого порядка включительно.
В методе моментов применительно к граничной задаче
A)—C) рассматриваются две системы функций:
1) система функций {ф*(#)}, подчиненная условиям:
а) Цк(х)е=С[а, Н * = 0, Ь 2, ...;
б) функции tyk (x) образуют замкнутую на [а, Ь]
систему;
2) система функций {фП*)Ь удовлетворяющая
условиям:
а) (pfe(x)£C2[fl, b\ * = 0, 1, 2, ...;
б) при любом конечном п функции <рх (х), <р2 (х), ...
•••> Фл(*) линейно независимы на [а, Ь];
в) функция ф0 (х) удовлетворяет граничным условиям
B), C), а функции щ{х) удовлетворяют требованиям
МФ*) = 0, М<Ра) = 0, fe=l, 2, ...;
г) функции q)k{x) образуют в классе функций С2[а, Ь]у
удовлетворяющих условиям B), C), полную систему.
Сделаем некоторые пояснения. Систему функций
{tyk {x)} мы будем называть замкнутой на множестве
интегрируемых на [ау Ь] функций, если не существует
такой непрерывной функции, кроме тождественного нуля,
которая была бы ортогональной на [а, Ь] ко всем

122 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ 'УРАВНЕНИЯ [ГЛ. $
функциям г|>*(*). Таким образом, если система функций
{% (*)} замкнута, то из условия
ь
$/(*)•**(*)<& = 0, * = 0, 1, 2, ...,
а
где / (х) — непрерывная на [а, Ь] функция, следует, что
/ (х) = 0. Свойство полноты, о котором говорится в
условии г), понимается так. Обозначим через G класс
функций у{х), принадлежащих С2[а, Ь] и удовлетворяющих
граничным условиям B), C). Говорят, что система
функций {ф* (*)} полна в классе G, если для любого в>0и
любой функции у (х) ge G можно указать такое п и такие
параметры аъ аъ ... у апу что имеет место неравенство
\У{()(х)-У%Чх)\<е> / = 0, 1, 2, а^х^Ь,
п
где уп (х) = ф0 (*)+ 2 akyk (x). Это означает, что для
любой допустимой функции (/(х)е6 найдется такая
функция уп(х), которая на [а, Ь] будет сколь угодно
точно приближать функцию у(х) вместе с ее
производными у' (х) и у" (х).
Перейдем к построению приближенного решения
граничной задачи A)—C) методом моментов.
Будем считать функцию F (х, у, г, /) непрерывной
по всем аргументам в области
£2 = {а^х^6, — оо<*/, г, ^< + соЬ
Составим линейную комбинацию из п-\-\ первых
функций yk(x):
п
Уп (х) = Фо (х) + 2 akyk (х), D)
k = i
где ак — некоторые численные параметры, выбор которых
будет указан ниже. Отметим, что функция уп (х)
удовлетворяет граничным условиям B), C) при любых
значениях ak. Действительно, в силу условия в) и
линейности граничных условий имеем
п
L (Уп) = la (фо) + 2 Qkl» (Ф*) = А>

§ 123 МЕТОД ГАЛЕРКИНА II МЕТОД МОМЕНТОВ 123
ибо /а(фо) —Л, а /л(ф£) = 0 при всех k~ 1, 2, ...
Аналогично можно показать, что и 1ь(Уп) = В при любых
av a2y ..., ап.
Мы будем выбирать параметры аъ а2, ..., #я таким
образом, чтобы функция уп (х) в указываемом ниже
смысле возможно лучше удовлетворяла
дифференциальному уравнению A). Подставив в F (х, уу у', у") вместо
у, у\ У" соответственно выражения уп(х)% у'п(х), Уп(х),
получим
F(x, Уп, Уп, yn)^Fn(x).
Образуем обобщенные моменты функции Fn(x):
ь
^k=\Fn{x)'iik(x)dxt fe = 0, 1, ...
а
По своему смыслу момент \ik является некоторой
функцией параметров аъ a2i ..., ап. Выберем их так, чтобы
первые п моментов обратились в нуль:
щ = 0 при Дг==0, 1, .•., дг — 1. E)
Эти равенства образуют систему п уравнений, из
которой должны быть найдены коэффициенты аъ аъ ..., ап.
Пусть мы решили систему E) и нашли значения я*,
at, ..., а%. В методе моментов в качестве n-го
приближения к решению граничной задачи A)—C) принимают
функцию
п
Уп (х) = фо (х) + 2 fl^* (*)•
Почему функцию у%(х) можно рассматривать как
приближенное решение задачи A)—C)? Поясним это
наглядными соображениями. Если бы оказалось, что
равенства /ы^ = 0 выполняются при всяких fe = 0, 1, 2, ...,
то ввиду замкнутости системы функций {ф& (х)) отсюда
следовало бы, что
F% (х) 5~ Fn {х, у?и Уп , Уп) = О
и функция у* {х) была бы точным решением граничной
задачи A)—C). Но в нашем распоряжении имеется
только конечное число параметров аъ аъ ..., ап и
выполнить бесконечное число условий ([ift = 0, 6 = 0, 1, 2, ...)

124 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
при помощи их выбора можно только в
исключительных случаях. Например, в тех случаях, когда решение
граничной задачи A)—C) является линейной
комбинацией вида D). Можно надеяться, вообще говоря, на
выполнение лишь п условий [а* = 0, ft = 0, 1, ..., /г —1.
При этом можно ожидать, что если л —достаточно
большое число, то функция F% (х) будет близкой к нулю:
F%(x) = en(x), max |ел(*)|<е и е>0 —достаточно
а ^ х ^ b
малое число. В этом случае функция у%(х) будет
удовлетворять дифференциальному уравнению
F(x, у%, у%\ у%) = еп(х), F)
которое мало отличается от заданного уравнения A).
Можно ожидать, что для широкого класса функций F
из условия F) будет следовать достаточная малость на
[а, Ь] разности \ у (х) — у* (х)!, где у (х) — решение
граничной задачи A) —C).
Изложим алгоритм метода моментов применительно
к граничной задаче A)—C):
1) в начале вычислений выбираем системы функций
{% (x)} и {ф*(*)}» подчиняя их выбор сформулированным
выше условиям;
2) затем решаем систему нелинейных численных
уравнений E) и выписываем ее решение а*, а*, ..., а£;
3) значения параметров at подставляем в формулу D)
и полученную функцию у% (х) принимаем за п-е
приближение к искомому решению у (х).
Как мы уже отмечали, о близости у\ (х) к у (х) во
многих случаях можно судить по величине max \еп(х)\,
а^х^Ь
а иногда по абсолютной величине нескольких последних
параметров: а*, а*+\, ..., а?г.
Если уравнение A) линейно, то запись системы
уравнений для определения параметров ak упростится.
Рассмотрим, например, уравнение
F(x, у, у\ y")=L(y)-f(x) = 09
где d
1 &) = -&(р W у') ~~q W * У' р W ^Ро > о,
р(х)^С1[а1 b], q(x)^0, a^xb,
с граничными условиями у(а) = А, у(Ь) = В. В этом
случае мы получим систему линейных алгебраических

§ 12] МЕТОД ГЛЛЕРКИНА И МЕТОД МОМЕНТОВ 125
уравнений вида
п
2 Сыа*-Д. = 0, г = 0, 1, ..., п-19 G)
* = i
где ^
Сл/ = J L (cfk) ■ i|)/ (х) dx,
G
A = $[/(x)-L(9o)]M*)^.
В методе Галеркина обе системы функций {tyk (х)} и
{щ (х)} совпадают, поэтому система уравнений E)
примет следующую форму:
ь
\F(x> Уп> Уп, ynL>k{x)dx = 0, k= 1, 2, ..., п. (8)
а
Здесь мы считаем, что свойством замкнутости обладает
система функций {ф&(х)}, ft = l, 2, ... Если исходное
дифференциальное уравнение было линейным
самосопряженным, то в методе Галеркина система уравнений G)
в силу (8) примет вид
п
£ Ckflk-Dt = 0, t=l, 2, ..., п, (9)
где ь
Сы = \ L Ы • ф, (х) dx,
а
b
Di = \[f(x)~L(^0)]%(x)dx.
а
Запись коэффициентов Ск1 можно упростить следующим
образом:
ь
Сы = J (J- (Р (х) ф*) - q (х) щ (х)) ф, (х) dx =
а
]Ь Ь
\ (р (х) щ (х) Ф,- (х) +
= Р (х) Ф* (х) Ф/ (х)
\а а
ъ
+ q (х) фА (х) ф, (х)) dx^ — \(p (х) Ф^ (х) ф^ (х) +
а
+ Ч (х) ф* (*) ф,- (х)) dx,

126 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
ибо
Ф* (a) q>i (а) = 0 и ф£ (b) <pi (b) = 0.
Отметим, что Cki = Cik и матрица системы уравнений (9)
симметричная. Аналогично для Д получим
ь
Д = $ (р (*) Фо (х) % (х) + q (х) Фо W Фг (*) + / (*) ф; (х)) dx.
а
Покажем, что система уравнений (9) однозначно
разрешима. Для этого мы установим, что соответствующая
однородная система имеет только нулевое решение.
Предположим противное и будем считать, что система
уравнений
2 Cfcibk = Q9 * = 1, 2, ..., п, A0)
имеет ненулевое решение, т. е. &*=£0. Обозначим через
гп(х) = Ьхфх (х) + 62ф2 (*)+.. . + Ьпуп (х).
Отметим, что гп (х) ^е 0, ибо функции ф* (х) линейно
независимы и, по предположению, bk^0. Используя
выражение для Cki из A0), получим
ъ
\ (р {х) г'п (х) & (х) + q [х) гп (х) % (х)) dx «= 0, A1)
а
i= 1, 2, п.
Умножим обе части соотношения (И) на bt и
просуммируем по i от 1 до п:
ъ
\[p{x){z'n{x)f-Yq(x)zl{x)]dx=-Q.
а
Поскольку р (х) ^ Ро > 0, то отсюда следует, что z'n (x) s= 0
и, значит, г„ (х) == const, но in (a) = zn (b) = 0, поэтому
zn(x)=Q. Мы пришли к противоречию. Наше
предположение о том, что Ьк^Е0 неверно. Значит, bk===0> и,
следовательно, система (9) однозначно разрешима.
Мы говорили, что функция фо(х) должна
удовлетворять условиям /,,(ф0) = Л, 1Ь (ф0) = 5. Для этого можно
ф0 (х) определить как многочлен первой степени ф0 (х) =

§ 12J МЕТОД ГАЛЕРКИНА И МЕТОД МОМЕНТОВ 12?
= а -\- Рх и коэффициенты аир выбрать как решение
системы уравнений
a0(a + pa) + cxiP = ^
Po(oc + pfr) + PiP = £.
Другие функции фА (х) можно, например, в случае,
когда a1 = Pi = 0, a0 = p0=l, вычислять по правилу
4>k(x) = (x — a)k{x — b), *=1, 2, ..., п,
или
Ф* (а-) = (х — а) (х — b)k, £—1, 2, ..., /г.
Чтобы иметь представление о скорости сходимости
метода Галеркина хотя бы для некоторых частных задач,
приведем известный результат для следующей граничной
задачи: у-q{x)y = f{x)i o^x^l,
r/@) = y(l) = 0. ( '
П
Пусть фА (а) = sin knx. Обозначим через у% (х) = ^ я$Фл (а)
приближенное решение, полученное по методу
Галеркина. Если
0<<7(*)<?; /(а), ?(А), ^LeEL2[0, 1],
то имеет место оценка
L4 (л + 1 J
/2
(л + 1)* (я +1/2)
>/2
К<7 II /(*)
/Зл- ||У~<?(лс)
= О (Я" 3/2),
где через у (х) обозначено решение граничной задачи A2)
и
1 \1/2
f{x) " ■'"■■
J Я(х)
Vq{x)\\ V(f
Выше было дано изложение методов моментов и
Галеркина, применительно к задаче A)—C) некоторого
конкретного вида. Приведем краткое изложение схем
методов моментов и Галеркина в общем случае для
операторов, заданных в гильбертовом пространстве Н.
Пусть линейный оператор А задан на множестве D (Л),
всюду плотном в Я со значениями, принадлежащими тому

128 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
же пространству Я. Предположим, что пространство Н
обладает счетной и полной системой линейно
независимых элементов.
Рассмотрим уравнение
Ay = f, A3)
где у — искомый элемент из D (Л), подлежащий
определению, / — некоторый элемент из Н.
Выберем последовательность элементов {ф^}, ф^еО (А),
Предположим, что любой элемент у из D (А) однозначно
представим сходящимся рядом
со
у = 2 °Wb
где ak — некоторые коэффициенты, зависящие от у.
Обозначим через уп п-е приближение к решению уравнения
A3) и будем разыскивать это приближение в виде
п
Уп= £ад>А, A4)
Aj = 1
где ak — параметры, которые мы определим из условия
ортогональности выражения Ауп — [к элементам фь ф2, ...
..., фл. Будем считать, что имеют место соотношения
(Ayn-f, Ф*)=0, *=1, 2, ..., п. A5)
Подставляя сюда вместо уп его выражение A4),
получим систему линейных алгебраических уравнений
п
2] Akiak-Bi = 0, i = l, 2, ...,/i, A6)
где
Лл; = (Лфл, фО, i5/ = (/:, <tt).
Пусть система уравнений A6) однозначно разрешима
и а*, а*, ..., а% — ее решение. Тогда n-е приближение
к элементу г/ —решению уравнения A3) в методе Галер-
п
кина вычисляют по формуле у% = ^ а*Ф*. Если бы вы-
/fe = 1
ражение Ay% — f оказалось ортогональным ко всем
элементам щ (k=l, 2, ..., п, ...), то это бы означало, что

§ 13] МЕТОД НАИМЕНЬШИХ КВАДРАТОВ И МЕТОД РИТЦА 129
Ay% — f = 0 и у% было бы точным решением уравнения A3).
Если же условие ортогональности A5) выполнено для
достаточно больших пу то можно надеяться, что и у% близко
к точному решению уравнения A3).
В методе моментов параметры ak определяются по-
иному. Требуют выполнения условий ортогональности
элемента Ayn — f к элементам последовательности (фА}
(Ayn-f, *Ы=0, *=1, 2, ..., п. A7)
При этом предполагается, что элементы а|)ь г|J, ..., i|>„
линейно независимы при любом конечном п и
последовательность {tyk} полна в Н. Формула A7) есть система
линейных алгебраических уравнений вида
п
^ Cwaft-D, = 0, 1 = 1, 2, ..., п, A8)
г*е С^(Лф*, %), D* = (M>i).
Пусть а*, а*,..., а„ — единственное решение системы
уравнений A8). В методе моментов, как и в методе Галер-
кина, п-е приближение к решению уравнения A3)
вычисляется по формуле
п
У'п= 2 a%<pk.
Легко видеть, что при я|>л == фл метод моментов
совпадает с методом Галеркина. Отметим еще, что оба эти
метода применимы и к решению нелинейных уравнений.
§ 13. Метод наименьших квадратов и метод Ритца
Рассмотрим алгоритм метода наименьших квадратов
применительно к операторным уравнениям.
Пусть L2 [a, b] — пространство вещественных функций,
интегрируемых с квадратом на [а, Ь]> и Л—линейный
оператор со значениями из L2[a> Ь]. Пусть А определен
на множестве D(A), всюду плотном в L2[a, b].
Предположим, что требуется найти решение уравнения
Ay = U 0)
где/^Я, уеО(Л). Будем считать, что уравнение A)
имеет единственное решение.
5 В. И. Крылов и др., т. II

130 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. б
Поставим в соответствие уравнению A) функционал
J(y)=\\Ay-ff- B)
Здесь знаком || || помечена норма в пространстве L2 [я, b].
Если в L2 определено скалярнсе произведение и г —
некоторый элемент из L2, то
'Ъ 1/2
\ г2 (х) dx
г|) = 1/(г, г):
Задачу отыскания решения уравнения A) заменим
эквивалентной задачей об определении элемента,
минимизирующего в D (А) функционал B). Очевидно, что
min J(y) = J(y*)=0
и элемент #* является решением уравнения Ay — f.
Метод решения уравнения A), основанный на минимизации
функционала B), получил название метода наименьших
квадратов.
Функционал / (у) можно минимизировать различными
способами. Можно это выполнить так. Выбираем
последовательность линейно независимых элементов {ф^,},
q>k^D(A). Определяем элемент уп — п-е приближение
к решению уравнения A) по формуле
п
Уп= 2 а^ C)
k = l
где ^ — некоторые параметры. Они определяются из
условия, чтобы функционал J (уп) = \Ауп — /|2 принимал
минимальное значение на подпространстве Ол(Д)еО(Л),
натянутом на элементы фь ф2, ..., ф„. Это требование
приводит к системе линейных алгебраических уравнений
для определения аъ а2, ..., ап:
^ = 0, £ = 1,2,...,«. D)
Если а*, а*, ..., а* —решение системы уравнений D), то
/г-е приближение к решению у дается формулой C) при
подстановке в нее вместо ak величин а%.

§ 13] МЕТОД НАИМЕНЬШИХ КВАДРАТОВ И МЕТОД РИТЦА 131
Дадим более подробное описание метода наименьших
квадратов на примере линейной граничной задачи для
дифференциального уравнения второго порядка
Hy)=y* + p(x)y' + q(x)y = f(x). E)
с граничными условиями
1а (У) = <ЗД (а) + (*&' (а) = А, F)
Ш^$оУФ) + М(Ь) = В. G)
Будем считать, что задача E)—G) имеет единственное
решение и это решение вместе со своими производными
до второго порядка включительно непрерывно на [а, Ь].
В методе наименьших квадратов применительно к
граничной задаче E)—G) рассматривается система функций
{ф* (Л')Ь которая выбирается так же, как это мы делали
в методе моментов (см. стр. 121).
Приближенное решение задачи E)—G) ищется в виде
п
Уп (х) = Ф0 (х) + 2 ад* (х), (8)
где аЛ —некоторые параметры. Функция уп(х)
удовлетворяет граничным условиям F), G) при любых значениях
параметров ak. Выберем их так, чтобы уп(х) возможно
лучше удовлетворяла уравнению E). Подставим уп(х)
в уравнение E), получим
L(yn)-f(x) = en(x).
Почти всегда гп(х)^0. Мы заинтересованы в том, чтобы
погрешность еп (х) по абсолютной величине была возможно
меньшей. Введем в рассмотрение величину бд, определив
ее по правилу ь
бя = \ e.i (x) dx.
а
Параметры аъ а2, ..., ап выберем так, чтобы величина б„
принимала наименьшее значение.
Заметим, что б„ = J (уп), если J (у) определять по
правилу J(y)=\Hy)-ff = (Liy)-U L(y)'-f). Здесь
скалярное произведение имеет следующий смысл:
ъ
(g> h) = \g{x)h(x)dx
а
Для любых функций g(x) и h (x)f принадлежащих L2[a, b].
5*

132 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
Имеем
L(yn) = L(<p0)+ 2 akL(<fk)9
«i = S
2 akL($k)—fQ
k = \
dx,
где f0 = f-L (cpo).
Для определения искомых значений параметров ал
записываем систему линейных алгебраических уравнений
1. 00* f V
А=1
£(ф*) dx = 0,
f=l, 2, ..., /г.
Зту запись можно упростить. Имеем
п
2 Aikak-Bt = 0, /=1, 2, .... п,
(9)
Jfe=l
где
Л/л = ^« = 5 L (фл) • L (ф/) dx,
а
Ь
Bi=\fQ(x)-L(%)dx.
а
Отметим, что матрица системы уравнений (9) симметрична
и ее определитель есть определитель Грама для
функций Liipi), Ь(ф2), ..., L(q>„). Предположим, что система
уравнений (9) однозначно разрешима и а*, #|, ..., а% —
ее решение. Тогда п-е приближение к решению у(х)
задачи E)—G) вычисляется по формуле (8), если в нее
вместо ak подставлены значения а%.
Выясним, когда можно надеяться на однозначную
разрешимость системы уравнений (9). Ответ на этот
вопрос зависит не только от свойств системы функций
{ФаМЬ но также и от природы рассматриваемой
граничной задачи E)—G), в частности от того, имеет ли
однородная граничная задача
L(z) = 0, Uz) = 0, M*) = 0 (Ю)
только нулевое решение. Будем далее предполагать, что

§ 13] МЕТОД НАИМЕНЬШИХ КВАДРАТОВ И МЕТОД РИТЦА 133
а1 = рх = 0, а0 = р0 = 1. Пусть D = (Л^)? — матрица системы
уравнений (9), a |Dj —ее определитель.
Теорема 1. Если граничная задача A0) имеет только
нулевое решение z(jc)==0, mo |Z) ф0 и система
уравнений (9) имеет единственное решение.
Доказательство. Рассмотрим однородную систему
уравнений
п
2 Aikbk = 0, f=l, 2, ..., п.
k = \
Докажем, что эта система имеет только нулевое решение
bk==0. Умножим уравнение номера i на bt и
просуммируем полученные выражения по i от 1 до п. Имеем
t bi 2 ^***= \ t t ^(Ф/)-6*Ь(Ф*)Лс = 0. A1)
г = 1 Л = 1 а I = 1 6 = 1
Введем обозначение
/г
k= l
Теперь из соотношения (И) получим
ь
]L2(zn)dx = 0.
а
Отсюда следует, что L(z„)e==0. В силу выбора функций
Ф/г (х) имеем: zrt (а) = гл F) = 0. Следовательно, /^(z„) = 0,
^BЛ) = 0. Таким образом, функция гп(х) удовлетворяет
граничной задаче A0) и по условию теоремы должно быть
п
гп (х) == 0 или ^] bk(fk (х) = 0. Поскольку функции фх (х)>
k = \
Фг(*), ...» Ф«М линейно независимы, то из условия
гл(*) = 0 следует, что bk^=0. Значит, D;^0 и система
уравнений (9) имеет единственное решение. Теорема
доказана.
Изучим вопрос о сходимости метода наименьших
квадратов на примере граничной задачи E)—G) в частном
случае, когда
1а(у)^у(а) = 0, 1ь{у)=у(Ь)=0. A2)

134 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
Пусть у* (х) — точное решение задачи E), A2), а у%(х)
п-е приближение к у* (х), получаемое по методу
наименьших квадратов. Заметим, что в случае граничных
условий A2) п
Ф0 (х) 5= 0 и у% (х) = 2 а%Щ (х).
k = \
Теорема 2. Последовательность функций {у% (х)}у
получаемых по методу наименьших квадратов, сходится
в метрике L2 к точному решению у* (х), если выполняются
следующие условия:
1) граничная задача E), A2) имеет единственное ре-
шение у* (х);
2) существует такая постоянная М, что для любой
дважды непрерывно дифференцируемой функции у(х)>
обращающейся в нуль на концах отрезка [а, Ь], имеет место
неравенство >ь \i/2
\\L(y)\\^-}i{\y^x)dxj .
Доказательство. В силу условия 1) и теоремы 1
последовательность решений {yl (х)) может быть построена.
Последовательность {yk (x)} полна в классе С2 [а, 6],
поэтому для любого е>0 можно указать такое N и такие
параметры аъ а2, ..., aN, что
I N I
Это неравенство можно переписать в виде
1/-1Ы||<м-. 03)
так как
N I N \
L (#*) = /, 2 ^Мф*) = М 2 а*Ф* r:LЫ•
Неравенство A3) тем более будет выполняться, если в нем
функцию yN (x) заменить на функцию у% (х), ибо
последняя строится из условия минимизации квадратичной
формы J {ум) = || L (ум) — /1|2 на множестве пар аметров
аи а2, ..., aN. Значит,
\Uy*)-L№)\<k-

§ 133 МЕТОД НАИМЕНЬШИХ КВАДРАТОВ И МЕТОД РИТЦА 135
Очевидно неравенство
Отсюда, используя условие 2) теоремы 2, получим
[у'-уЦ^МЪЦуЬ-МК*. A4)
Поскольку е может быть любым сколь угодно малым
числом, то из A4) следует, что
Пт\у*-уЦ = 0.
Теорема доказана.
Неравенство A4) можно переписать в виде
\\y*-y%\\^M\\f-L(y*)\\.
По этому неравенству можно судить о том, с какой
скоростью у% (х) сходится при п->оэ к точному
решению г/* (х).
Изложим теперь вычислительную схему метода Ритца
на частном примере граничной задачи для уравнения
(p(x)yy-q(x)y = f(x) A5)
с условиями
у(а) = А, 1/F) = В, A6)
где р (х) ^ ро > 0, р (х) е d [a, b], q (х) ^ 0, q(x) и / (х)
принадлежат классу С [а, 6]. Будем предполагать, что
задача A5), A6) имеет единственное решение.
Рассмотрим функционал
J (У) - \[Р {х) f + q (x) if + 2/ (х) у] dx A7)
а
и попытаемся найти его минимальное значение на классе
допустимых функций, т. е. функций, удовлетворяющих
двум условиям:
1) эти функции непрерывно дифференцируемы на [а, Ь]\
2) они удовлетворяют граничным условиям A6).
Теорема 3. Если функция у* (х) доставляет
минимальное значение функционалу J (у) среди всех
допустимых функций, то она является решением граничной задачи
A5), A6).

136 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ {ГЛ. 6
Доказательство. Так как функция у* (х)
является допустимой, то она удовлетворяет граничному
условию A6) и остается доказать, что она удовлетворяет
уравнению A5). Для этой цели воспользуемся одной из
теорем вариационного исчисления. Пусть рассматривается
ь
функционал вида G (у) = ^ F (х, у, у') dx и требуется в
а
упомянутом выше классе допустимых функций найти
наименьшее значение G(y). Доказывается, что при
достаточной гладкости F минимизирующая функция должна
удовлетворять дифференциальному уравнению Эйлера
В вариационной задаче F = p (x) уу -}-q (х) у2 + 2f (х) у.
Для нее Fy> = 2р (х) у> Fy = 2q (х)у-\-Щ (*)• Поэтому
уравнение Эйлера для минимизирующей функции у* (х) будет
иметь вид
2{p(x)y*')'-2q(x)y*-2f(x)=09
или
(р(х)у*У-яШ*=!(х)>
что и требовалось доказать.
Таким образом, задачу вычисления решения #* (х)
граничной задачи A5), A6) можно заменить задачей
отыскания минимума функционала A7) в классе непрерывно
дифференцируемых на [а, Ь] функций, принимающих
заданные значения у(а) = А и уф) —В на концах отрезка.
Эта вторая задача в вычислительном смысле во многих
случаях оказывается предпочтительнее первой.
В методе Ритца я-е приближение к минимизирующей
функции у* (х) вычисляется в виде
п
Уп (X) = Фо (X) + 2 акЩ (X), A8)
где ак — численные параметры, ц>к (х) — некоторые
известные функции. Выбор этих функций подчиняют условиям
1) <рй (х) е= d [а, Ь], k = 0, 1, 2,...;
2) ф0(а) = Л, ф0F) = В, фА(а) = фАF)=0, k=l, 2,...;

§ 13] МЕТОД НАИМЕНЬШИХ КВАДРАТОВ И МЕТОД РИТЦА 137
3) при любом конечном п функции q>i(#), cpa (#),...
.. • , Фл Iх) линейно независимы;
4) образованное по функциям yk (x) семейство функций
{уп{х)} обладает свойством Сгполноты.
Отметим, что при любом выборе параметров ak функция
Уп (х) <= Сг [а, 6], уп (а) = А, уп ф) = В. Подставив уп (х)
в функционал / (у), получим
где
ЦУп) = А0+2 J£ Акак+ 2] 2 Л/*ОДк.
* = i t=lЛ=1
^о = \[Р (х) Фо2 + q М Фо + 2/ (х) ф0]dx,
Ak=\[p (х) Фо'ф* + <7(а:) Ф0ф* + / (*) Фа]dx,
B
&
-4/Л = Aki = ^ [Р (*) Ф*Ф' + </ (*) Ф*Ф*]rf*'
/, fe = 1, 2, ..., я.
Параметры а1у а2> ... у ап определяем из системы
линейных алгебраических уравнений
1 dJ (уп)
2 dak ~ La
У^й + ^ = 0, £=1, 2, ..., /г. A9)
Система уравнений A9) имеет единственное решение, это
можно показать подобно тому, как доказывалась
однозначная разрешимость системы уравнений (9).
Пусть а*, а*у .,., а%— решение системы уравнений A9),
тогда вычисляемая в методе Ритца функция у% (х) =
п
= Фо (х) + 2 а*Ф* (*) будет /2-м приближением к реше-
нию у* (х) граничной задачи A5), A6).
Введем следующее обозначение:
lim J (y%) = m= J {у*). B0)
л-*оо
Последовательность функций {у%} называется минимизи-

138 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
рующей, если она удовлетворяет условию B0). Отметим,
что из B0) не всегда следует, что
lim yt(x) = y* (x).
То есть из того, что последовательность является
минимизирующей, не всегда следует ее сходимость. Сходимость
имеет место только при выполнении определенных условий.
Теорема 4. Пусть выполняются условия:
1) р(х)^ро>0, р{х)<=Сг[а, Ь],
2) g(x)S*0 и q(x)t f{x)EEC[a, b\
3) последовательность функций {у?г(х)} является
минимизирующей. Тогда эта последовательность функций
будет сходящейся равномерно на [а, Ь] к у* (х) — решению
граничной задачи A5) —A6).
Доказательство. Имеем
ь
W' (*)-У*п' {t)]dt
\\У*'{t)-yl'{t)\dt. B1)
Используя неравенство Буняковского, получим
\\У*' {t)-yt (/) | dt < Vb=~a \\ {у*' (t) - у%' (ОJ dt\ ".
B2)
Для интеграла в правой части неравенства B2)
очевидным образом можно продолжить следующую цепочку
неравенств:
b -Л/2
\{у*' {t)-y*'{t)ydt\
а \
г Ь
fb-a\U2
УЬ-а
Ро
b — aV/2
Ро
[pit) {у*' (t)-yl' {t)fdt
- b
\[p{t){y*' {t)-yt' {t)f+
_ a
+ q(x)(y*(t)-y%(t)r\dt]'
B3)

§ 13] МЕТОД НАИМЕНЬШИХ КВАДРАТОВ И МЕТОД РИТЦА 139
Установим связь между последним интегралом из B3) и
разностью J {yt) — J (у*). Имеем
J{yl)-J{y*) =
^2 2
= \[р(х)Уп + q(x)y%2 + 2f{x)y%-p(x)y*' -q(x)y*2-
a
b
-2f{x)y*]dx = \[p{x){yt' -y*'J + q(x)(y*n-y*y]dx +
a
Ь ,2
+ 2\[p (x) y*'y*' + q (x) yty*-p(x) y*' - qy*2 +
a
b
+ f№- У*)] dx = \ [p (x) {yt' - y*ef + q (x) {yt - y*f\ dx +
a
b
+ 2\[p{x)y*' {yt' ~y*') + q{x)y*{yt~y*) + f{yt-y*)]dx.
a
Здесь второй интеграл равен нулю в силу уравнения A5).
Чтобы в этом убедиться, достаточно воспользоваться
интегрированием по частям и учесть, что yt(a)—y* (а) =
= Уп (Ь) — у* (Ь) = 0. Таким образом,
ь
J № - J (У*) = ] [Р (х) {yt' ~y*'J + q (x) {yt - Л2] dx.
B4)
Теперь на основании неравенств B1) —B3) и равенства
B4) получим
I У* (х) - yt (х) | < i^j'2 ■ (J {yt) - J (У*))  • B5)
В оценке B5) правая часть от х не зависит. Так как по
условию теоремы J {yt) — J {у*) ->• 0 при п -> оо, то из
неравенства B5) следует, что минимизирующая
последовательность функций {yt {x)} сходится равномерно
относительно х к функции у* {х) на отрезке [а, Ь]. Теорема
Доказана.

140 ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. 6
ЛИТЕРАТУРА
1. Бахвалов Н. С, Численные методы, т. I, М.» «Наука», 1973.
2. Берез и н И. С, Жидков Н. П., Методы вычислений, т. 2,
М., «Наука», 1962.
3. Крылов В. И., Бобков В. В., Монастырный П. И.,
Вычислительные методы высшей математики, т. 2, Минск, «Вышэй-
шая школа», 1975.
4. Л а н с Д. Н., Численные методы для быстродействующих
вычислительных машин, М., «Наука», 1962.
5. Мыс о век их И. П., Лекции по методам вычислений, М.,
«Наука», 1962.

ГЛАВА 7
РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
В ЧАСТНЫХ ПРОИЗВОДНЫХ
§ 1. Разностные схемы, основные понятия
Дифференциальные уравнения в частных производных
имеют широкие приложения в математической физике,
гидродинамике, акустике и других областях знаний.
В большинстве своем такие уравнения в явном виде не
решаются. Поэтому широкое распространение получили
методы приближенного их решения, в частности метод
сеток.
Мы уделим основное внимание вопросу решения
линейных дифференциальных уравнений второго порядка.
Построение различных схем метода сеток в случае
уравнений в частных производных зависит от типа
уравнений и вида граничных условий, присоединяемых
к уравнениям.
В связи с этим сделаем несколько замечаний о
классификации линейных дифференциальных уравнений второго
порядка.
Пусть D —некоторая область изменения независимых
переменных х, у> ограниченная контуром Г. Говорят, что
в области D задано линейное дифференциальное уравнение
второго порядка для функции и (х, у), если для любой
точки из области D имеет место соотношение
г / \ / v д2и , г»/ / \ д*и , , ч д2и ,
L(u)==a (х, sO-g^r + 26 (х, у) -q^- + c{x, у) -^ +
+ 2d(x, у)^- + 2е(х, y)^L + g(x, y)u = f{x, у), A)
где а (х, у), Ь (х, у),... — коэффициенты, f (x, у) — свободный
член уравнения. Эти функции известны и их обычно считают

142
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
определенными в замкнутой области D = D~\-Т. Обозначим:
8(х, у) = Ь2(х, у)—а(х, у)с(х, у). Уравнение L(u) = f
называют эллиптическим, параболическим или
гиперболическим в области D, если соответственно выполняются
условия
6(*, у)<0, 6(х, 0) = О, 6(х, у)>0
для всех (х, у) из области D.
В зависимости от типа дифференциального уравнения
по-разному ставятся граничные и начальные условия,
связанные с этим уравнением. Конкретно вид граничных
и начальных условий мы рассмотрим при изучении схем
метода сеток для соответствующих уравнений.
Выше мы привели общее линейное дифференциальное
уравнение второго порядка. Построение и исследование
разностных схем непосредственно на примере этого
уравнения связано с большими записями и вычислениями.
Поэтому далее мы будем рассматривать некоторые частные
случаи:
1) уравнение Пуассона (эллиптическое уравнение)
д2и . д2и £,
-5pr + -W=f(*>y)>
2) уравнение теплопроводности (параболическое
уравнение)
ди д2и . * , ,х
3) волновое уравнение (гиперболическое уравнение)
дх* ду2 --/v*> У)-
Дадим некоторые основные понятия и определения,
необходимые для изучения элементов теории разностных
схем.
1. Сходимость и аппроксимация разностных схем.
Пусть и есть решение дифференциального уравнения
L.{u) = f, B)
заданного в некоторой области D, ограниченной контуром Г.
Рассмотрим некоторое множество Dh = {Mh)y состоящее
из изолированных точек Mh> принадлежащих области

§ i] РАЗНОСТНЫЕ СХЕМЫ, ОСНОВНЫЕ ПОНЯТИЯ 143
2? = /?-ЬГ. Число точек в множестве Dh будем
характеризовать величиной /г, чем меньше й, тем большим будет
число точек в Dh. Множество Dh называется сеткой, а
точки Mh из этого множества — узлами сетки. Функция,
определенная в узлах сетки, называется сеточной функцией.
Обозначим через U пространство непрерывных в D
функций v(xf у). Через Uh обозначим пространство,
образованное совокупностью сеточных функций vh(x, у),
определенных на Dh. В методе сеток осуществляется замена
пространства U на пространство Uh.
Пусть и (лг, у) — точное решение уравнения B) и
и (х, у) е U. Поставим задачу: вычислить значения uh (x, у).
Эти значения в совокупности образуют таблицу, в которой
число значений равно числу точек в Dh. Точно
поставленную задачу удается решить лишь в немногих случаях.
Как правило, можно вычислить некоторые сеточные
значения u{h\ относительно которых при выполнении
дополнительных условий (о которых мы еще скажем) можно
утверждать, что
uWp**uh{x, у).
Величины u{h) называются приближенными сеточными
значениями решения и(х, у). Для их вычисления строят
систему численных уравнений, которую мы будем
записывать в виде
Lh{uW)==f(H)y C)
где Lh есть разностный оператор, соответствующий
оператору L, f{h) e Fh. Если / (х, у) е F, то Fh образуется по F
аналогично тому, как Uh образовывалось по U.
Формулу C) будем называть разностной схемой.
Пусть в линейных пространствах Uh и Fh введены
соответственно нормы \-\ик и ll'lkA» которые являются
сеточными аналогами норм \-\и и \-\? в исходных
пространствах U и F.
Будем говорить, что разностная схема C) является
сходящейся, если при /г-^0 выполняется условие
ИМ*» У)-и(л)||с/л->0.
Если выполняется условие
\uh{x, y)-u^\\Vh^Chs,

144 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
где С —постоянная, не зависящая от A, s>0, то говорят,
что сходимость имеет место со скоростью порядка s
относительно А.
Говорят, что разностная схема C) аппроксимирует
задачу B) на решении и(х, у), если
Lh(uh(x, у))=/<АЧв/(л)
ЩшК~+° при А-*0.
Величина б/(/г) называется погрешностью аппроксимации.
Если ||6/(л) \\Fh^Mha, гдеМ — постоянная, не зависящая
от А, а>0, то говорят, что разностная схема C)
аппроксимирует задачу B) на решении и (х, у) с
погрешностью порядка а относительно А.
Отметим, что смысл понятий сходимости и
аппроксимации разностной схемы в случае линейных обыкновенных
дифференциальных уравнений второго порядка нами уже
частично обсуждался в § 11 гл. 6.
Введем важное понятие устойчивости разностной
схемы C).
Пусть LA — линейный разностный оператор.
Разностная схема C) называется устойчивой, если
существует такое А0>0, что для всех А<А0 и любых
fW^ph выполняются условия:
1) разностная схема C) имеет единственное решение;
2) \\u{h)hh^M\\f{h)\\fh, где М — постоянная,
независящая от А и /(л).
Из этого определения видно, что устойчивость
разностной схемы существенным образом связывается с понятием
норм, вводимых в пространствах Uh и Fh. Возможны
такие случаи, когда условие 2) будет выполняться для
некоторых норм и не будет выполняться для других норм.
В каждом отдельном случае важно выяснить, по какой
причине для рассматриваемой разностной схемы условие 2)
не выполняется. Если оно не выполняется из-за того, что
мы неудачно ввели определение норм в пространствах Uh
и Fh, то следует испробовать другие способы введения
норм в Uh и Fh с тем, чтобы добиться выполнения
условия 2). Но если 2) не выполняется ни при каком (!)
разумном выборе норм, то это будет означать, что
разностная схема неустойчива.

§ Ц РАЗНОСТНЫЕ СХЕМЫ, ОСНОВНЫЕ ПОНЯТИЯ 145
Отметим, что устойчивость является внутренним
свойством разностной схемы, и поэтому на устойчивость можно
влиять, изменяя некоторые параметры, входящие в
разностную схему, или вообще видоизменяя всю разностную
схему.
2. Связь аппроксимации и устойчивости со сходимостью.
Между введенными выше понятиями сходимости,
аппроксимации и устойчивости существует связь. Она состоит
в том, что из аппроксимации и устойчивости следует
сходимость,
Теорема 1. Пусть разностная схема Lh(u^h))=f{h)
аппроксимирует задачу L(u)—f на решение и (х, у) с
порядком s > О относительно h и устойчива. Тогда эта
схема будет сходящейся и порядок ее сходимости будет
совпадать с порядком аппроксимации, т. е. будет
справедлива оценка
\\uh(x, y)-u^\\Uh^Khsy D)
где К — постоянная, не зависящая от h.
Доказательство. По определению аппроксимации
имеем
|| 6/<Л> \\Fh < Chs, где б/<Л> = Lh (uh (x, у)) - /<*>.
Обозначим: гн (х, y)~uh{x, y)—u{h). Легко видеть, что
в силу линейности Lh для ел (хг у) имеет место формула
ЬнЫх, у))=в/<л>.
Отсюда, используя определение устойчивости, получим
II Ыг (*, у) \\uh ^М || 6/<*> \\Fh < М (СЛ*) = Kh\
где К,=МС. Таким образом, оценка D) установлена
и теорема доказана.
Теперь можно высказать некоторые общие замечания,
показывающие, как следует поступать при изучении
вопросов построения и исследования разностных схем.
1. Вначале указывается правило выбора сетки, т. е.
указывается правило замены области D и контура Г
некоторой сеточной областью. Чаще всего сетка
выбирается прямоугольной и равномерной.
2. Потом указывается и строится конкретно одна или
несколько разностных схем. Проверяется условие аппрок-

146
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
симации разностных схем и устанавливается порядок
аппроксимации.
3. Доказывается устойчивость построенных разностных
схем. Это один из наиболее важных и сложных вопросов.
Если разностные схемы обладают аппроксимацией и
устойчивостью, то о сходимости разностных схем судят
по доказанной выше теореме.
4. Рассматривается вопрос численного решения
разностных схем. В случае линейных разностных схем это
будет система линейных алгебраических уравнений. Уже
в двумерном случае порядок таких систем может быть
очень большим. Это делает задачу численного решения
упомянутых систем во многих случаях весьма трудной.
Поэтому для решения систем уравнений, возникающих в
методе сеток, разработаны и разрабатываются специальные
методы решения, учитывающие особенности таких задач.
Ниже при рассмотрении вопросов численного решения
параболических, эллиптических, гиперболических
уравнений мы раскроем конкретное содержание введенных
понятий и определений. При этом мы всюду будем
стремиться следовать при изучении вопросов построения и
исследования разностных схем по пути, указанному
в пп. 1 —4.
§. 2. Разностные схемы для уравнений
параболического типа
В этом параграфе мы рассмотрим вопросы построения
и исследования разностных схем, возникающих при
численном решении параболических уравнений по методу сеток.
1. Решение задачи Коши. Рассмотрим задачу Коши
для уравнения теплопроводности
ди д^и
"ar:=="a^~ + (p^ *)• -оо<*< + оо, />о, A)
с условием на прямой / = 0
и(х, 0)=г|ф), —oo<x< + oo. B)
Требуется найти функцию и(х, /), которая при />0 и
— со<х<С-\-оо удовлетворяла бы уравнению A), а при
/ = 0 выполняла бы условие B). Будем считать, что за-

§21
УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
147
дача A)» B) имеет в верхней полуплоскости единственное
решение и(х, /), непрерывное вместе со своими
производными -щГ /=1, 2, и ~к-, k=\, 2, 3, 4. Запишем задачу
A), B) в виде L(u)=f. Для этого достаточно положить
ди
■со <Ca:<C + cx), />>0,
и(х, 0), — оо<х<; + сх),
|ф(л', t), — оо<х< + оо, ^>0,
I * (*),
-co<x< + co, tf = 0.
Будем далее считать, что t изменяется в пределах
В рассматриваемом случае D = {—оо<<х<< + оо,
0<t^T\, Г —объединение прямых t = 0 и t = T.
Выберем прямоугольную сетку и заменим область
D = D-\-Y сеточной областью Dh. К области Dh отнесем
совокупность точек (узлов) (хт, tn), координаты которых
определяются по правилу
xm = mh, m = 0, ± 1, ±2, ..., А>0, /я = ят,
/i = 0, 1, ..., N, т>0, Nx^T<(N+l)%.
Заменим задачу L(u)=f разностной схемой вида
Lh(u{h)) = f{h). Обозначим через и (хту tn) точное значение
решения задачи L(u)=f в узле (хт, tn), через ^ —
соответствующее приближенное сеточное значение. Имеем
L(uy
(хт> 'я) ;
ди
д°-и
дх*
m = 0, ±1, ±2, .
(*m. '»)'
1, 2, .... Л/,
т = 0, ±1, ±2,
■Ф (*) 1'ж П.
я-«1, 2,
дн
Для замены выражений ^
а2ц
Cm. 'л)
/V,
разност-

148
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. ?
ными отношениями воспользуемся формулами численного
дифференцирования. Имеем
ди
Ж
ди
~Ж
ди
Ж
д2и
дх2
u(xmt tn+1)-u{xm, tn) т dhi_
(хт>*п) т 2 dt2
in <С tn <C tn+i>
^ ti{xm, tn) — u{xm, tn__x) . т д2и
(*m. *п) т Т2 dt2
*п-1 ^ *п <С */г»
"(*m» tn+1)—u(xm, tn_t) Т2 fftt
6 д/»
(*т» 'я)
2Т
tn-i<Ltn <С tn+ъ
(*■».#'), D)
(W)f), E)
) h2 дЧ
h2 12 " d*
Я/я -i < %m <C! #/я+1 •
D', '„), F>
Назовем некоторую совокупность узлов, привлекаемых
для замены задачи L(u)=f в узле (хт, tn) разностной
схемой Lh(u{h))=f{h\ шаблоном. Приведем наиболее
употребляемые для параболических уравнений шаблоны:
(/77, П f/)
(т-1,п) (т,п) (т+1,п)
— явный двухслойный шаблон,
(m-f,n+t) (m,n+f) (m+f,n+f)
О q О
— неявный двухслойный шаблон.
(т,п)
Явный трехслойный шаблон
(т,п+1) п
(т-/,п)
о—
\(т,п) (гп+!,п)
L о
(/77, /7-/) 6
некоторое время применялся в вычислительной практике.

УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
149
Однако в настоящее время он не используется, так как
оказалось, что соответствующая ему разностная схема
неустойчива при любом выборе шага h~ по пространству
и шага т —по времени.
Рассмотрим явный двухслойный шаблон. Имеем
^(")к,у-
a(*m> tn+1)~u(xmttn) __
т
—2и(хт, tn) + u(xm_lt tn)
Л2
[и(хт, 0) + 0.
+ r'Xn(h),
G)
Здесь мы воспользовались формулами C) и F) и обозначили
Д2 d*U
■ (А) = -
2 dt2
(*т, #')
12 дх*
\хт у *п)»
Введем следующее обозначение:
:(Л) =
(8)
Теперь на основании формул G), (8) можно записать
разностную схему для задачи L(u)=f:
Lp{u{H))ssfih)t (9)
где разностный оператор Lft* определяется по правилу
[ u!+l-ul
тиш)->
*т+\'
-*<+<-
т~Тит-\
Т №
Мщу
т = 0, ± 1, ib 2
л = 0, 1, .... /V-1.
Аналогично, если использовать неявный двухслойный
шаблон, можно получить такую разностную схему:
Д2'("(Л))=/(Л),
A0)

150 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ {ГЛ. 7
где
um-\-l Zum -Гит~\
h2
Д2Ул))Н
m = 0, ±1, ±2, ...,
л = 0, 1, ..., N~\y
ф(*т> tn)9
f(h) =
l|>(*m).
На основании формул G) и (9) можно записать:
где
0.
^(Df(h)
Аналогично, используя формулы D), F), A0), можно
получить
где
ftB)f(h) -_ ,
.(h)-
2" Ж
0.
Выясним порядок аппроксимации разностных схем (9)
и A0). В качестве Fh возьмем линейное множество всех
пар ограниченных функций gUl) = { m Норму в Fh опре-
делим по правилу
|g<A>|| = max|a» | + max,ipmj.
т, п т
Если тах|а^| или maxj|3mj не достигается, то будем
т, п т
под нормой понимать величину \g{h)|| = sup \апт\ + sup \$m\.
ту п т
Пусть x — rh\ r, s — некоторые положительные числа.
__ д2и д*и
Предположим, что для -^ и ^-4- верны оценки:
max
д2и
dt2
М2у max
\МА.

§2]
УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
151
Тогда легко получить
|| 6ii)fW \\Fh = max ! r'£n (A) \ < (~ M2 + ^ M4) • A*, A1)
|| b^f^ 1 = max | /iSi W |< (| M2 + ^J Al4) • h*. A2)
Для параболических уравнений, как мы увидим далее,
в случае схемы (9) можно взять s = 2, в случае схемы
A0) s можно взять равным единице.
Из формул A1), A2) следует, что разностные схемы
(9), A0) аппроксимируют задачу L(u)=f на и(х9 у)
с погрешностью порядка s (l<;s<;2) относительно ft.
Разностная схема (9) позволяет по значениям
решения на нулевом слое, т.е. по значениям и0ту т = 0, ±1,
±2, ..., вычислить значения на первом слое и1т, /п = 0,
±1, ±2, ... Для этого достаточно в (9) положить я = 0
и произвести вычисления, носящие рекурсионный
характер. Потом по значениям и1т можно аналогично при м= 1
вычислить значения и2т и т. д. В силу таких
вычислительных свойств разностную схему (9) называют явной.
Разностная схема A0) упомянутыми выше свойствами
не обладает. Действительно, если мы в A0) положим
п = 0у то в левой части полученной формулы будет
линейная комбинация из значений и1т^ъ ulmi и1т+ъ и°т, в
правой части будут значения известной функции <р (хт, 0) и
ty(xm). Для вычисления значений на первом слое ..., и12,
uLl9 Uq, u\, u\, ... в этом случае необходимо решать
бесконечную систему линейных уравнений. По этой причине
разностную схему A0) называют неявной.
2. Об устойчивости двухслойных разностных схем.
Определим норму в пространстве Uh по правилу
\uMhh = max\u»m\.
т, п
Рассмотрим разностную схему (9). Выясним при каких
значениях г, т = М2, возможна устойчивость этой схемы.
Для доказательства устойчивости надо показать, что
разностная схема однозначно разрешима и при любых
gih) __ I vm> g(A) e p^ имеет место оценка
I Pro,

152
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
где М — постоянная, не зависящая от h и g^h) и
Разностная схема (9) явная и ее однозначная
разрешимость очевидна.
Перепишем формулу L(h] (z{h)) = g{h) в виде
znm+l = r(z?n+l + z«m_l) + (l-2r)z"m + xa"m, z«m = $m, A3)
m = 0, ±1, ±2, ..., и = 0, 1, 2, ..., N-l.
Пусть выполнено условие
l-2r^0 или r = J<-i. A4)
Тогда из A3) получим
max | z£+ 1\<:Г /'max j z^ j + max | znm j \ -f-
m \ m m J
+ (l-2/-)max|z» | + ттах|с£|,
m m, n
или
max 12^+! |^max|z£j + Tmax jaJJJ. A5)
m m m, я
Неравенство A5) означает, что при ct^==0, тах^^+Н
не превосходит maxjzM, т. е. max i znm j не возрастает
m m
с увеличением /г. Это свойство однородной (а^п == 0)
разностной схемы принято называть принципом максимума.
Иногда так называют все неравенство A5).
Положим в A5) /г = 0, 1, ..., N— 1, получим
max | zlm I <: max | z°m | + т max ! a^ j,
m m m, n
max j 4г j ^ max | zlm \ +t max j a^ |,
m m m, n
max | z% | < max | z^~ * | -}- т max | a^ |.
m tn m, n
Заметим, что maxja^J есть число, не зависящее от т
т, п
п. Просуммировав эти неравенства, получим
max | г^ | ^ max | pm | + N% max | апт | ^
т т т, п
< max | pm | + Т max j an j <
max(l, T)/maxia-H-max|pmj\ = M.||^i|F/i, A6)
\ m, n m J

§2]
УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
153
где обозначено M = max(l, T); Л1 = 1, если Т<1, и
М = Т, если Т ^ 1.
На основании A6) можно записать
max\zl\^M.\\g^\\Fll или \г™ \\Uh^M -\8^W
m, n
Таким образом, разностная схема (9) при выполнении
условия A4) на т и h устойчива. Отметим, что условие
A4) налагает жесткие ограничения на выбор т, а именно,
должно быть t^y/i2. Это приводит к тому, что если мы
желаем сохранить устойчивость, то при вычислениях по
схеме (9) шаг по времени т приходится выбирать очень
малым. Если бы мы рассматривали уравнение
теплопроводности с переменным коэффициентом
^ = <Ф> 0"а? + Ф(*. 0. fl(*. <)>0,
то достаточное условие устойчивости, даваемое
формулой A4), видоизменилось бы и, как это легко видеть,
приняло бы форму
Г = ¥^2 max \a(x, t)\ ' ' 7)
(X, t)E£D
Обратимся теперь к разностной схеме A0) и
перепишем ее в виде
т = 0, ±1, ±2, ..., /i = 0, 1, ..., ЛГ-1.
Посмотрим, какие надо проделать вычисления, чтобы,
используя формулы A8), можно было вычислить,
например, значения ulm на первом временном слое по
значениям u°m (m = 0, ±1, ±2, ...) на нулевом временном
слое. Положив в формулах A8) п = 0, получим
- Г (u^ + UJn^ + il +2r) UJn^U^ + XCp (Хту 0),
и°т = ур(хт), т = 0, ±1, ±2, ... l j
Формулы A9) представляют собой бесконечную систему
линейных уравнений относительно неизвестных ... uL\,

154 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
и\, и\, ... Решение таких систем является сложной и
трудоемкой задачей, поэтому разностные схемы A0) неудобны
для задач Коши на бесконечных отрезках и применяются
редко. Однако если отрезок оси х, на котором
рассматривается задача Коши, конечен: а^х^Ь, Ь — а^/С,
а на прямых х = а и х = Ь дополнительно заданы
некоторые ограничения на решение и (х, /), то разностные
схемы вида A0) оказываются весьма эффективными. В
частности, как это будет показано в п. 4, такие схемы
являются абсолютно устойчивыми, т. е. устойчивыми при
любых значениях r = T//i2>0.
Если, например, на отрезках прямых х = а и х = Ь
заданы условия и (a, f)=yQ(f), u(b, t) = yi(t), то вид
системы A9) существенно изменится:
-г{и1тл.1 + и1т.1) + {\+2г)ихт = ^{хт) + щ{хту 0),
Ио = Yo(*i)» uSil = Yi(*i)»
m=l, 2, ..., M-l, й = ^р.
Формулы B0) представляют собой систему М +1
линейных алгебраических уравнений относительно и\, и\, ...
..., и1м. Эту систему можно решить по методу прогонки
(см. § 11 гл. 6).
Проведенные рассуждения показывают, что
реализация неявных разностных схем требует больших
вычислительных затрат для вычисления решения на одном
временном слое, но таких временных слоев может быть
немного из-за того, что в этом случае отсутствуют
ограничения на соотношение т/Л2. Если пользоваться явной
разностной схемой, то вычисление решения на следующем
слое осуществляется по рекурсионному правилу и
связано с минимальными вычислительными затратами, однако
из-за ограничения т/Я2 <; 1/2 число временных слоев
в случае явных схем может быть существенно большим по
сравнению с числом временных слоев для неявных схем.
Выскажем здесь еще суждение о сходимости
разностной схемы (9).-Эта схема аппроксимирует задачу A), B)
на решении и(х, t) с погрешностью порядка 0(т + Л2) и
устойчива при г ^1/2. Поэтому схема (9) будет
сходящейся в силу теоремы 1 из § 1; при этом погрешность
для приближенного решения будет величиной порядка
0(T + h2).

§2]
УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
155
3. О разностных схемах расщепления. В тех случаях,
когда число пространственных переменных в задачах
теплопроводности больше или равно двум, сильно
возрастает объем вычислительной работы, которую необходимо
выполнить при численной реализации разностных схем.
Были предприняты попытки поиска таких схем, которые
специально предназначены для решения многомерных
задач и которые наряду со свойством устойчивости
обладают свойством минимальности объема вычислений.
Такими схемами являются, в частности, схемы расщепления.
Рассмотрим правило построения схемы расщепления в
случае двумерного уравнения теплопроводности.
Рассмотрим задачу Коши
да _ д?и , д2и ~ . . j,
u(x, y, 0) = (p{x, y), — oo<x, y<oo,
где ф(х, #) —известная функция.
Обозначим Аи == v" -f ^4 • Выберем квадратную сетку
по пространству с шагом /z>0 по направлению х и по
направлению у. По времени выберем шаг т из условия
N%^T<C {N ~\- 1)т. Таким образом, координаты
некоторого узла (хт, Уп> tp) будут определяться по формулам
xm = mh, yn = nh, tp = px,
т, л = 0, ±1, ±2, ...; р = 0, 1, ..., N.
Предположим, что нам известно решение задачи B1)
в момент времени t = tp, т.е. известны значения функции
и(х, у, tp).
В дальнейшем значения функции и (х, у, t) при
некотором t = tk будем обозначать через uk.
Поставим задачу: выразить значение ир+1 через ир и
значение оператора А.
Имеем
и(х> У, tp+1) = u(x, у, /р + т) =
= и(х, у, tp) + ~Au(x, у, tp) + 0(T2) =
= (Е + тА)и{х, у, tp) + 0(x2).

156 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
д2 д2
Положим 4i = -a-a, Ла=^-, тогда А=А1 + А2.
Наряду с задачей B1) рассмотрим две
вспомогательные задачи
Ж = дх? ' tp<.t^ tp+1, B2)
f(x, У» tp) = u(x, у, tp), — оо<х, J/< + oo;
Ж ^ду2' tP<t<: tp+i, B3)
w(*, г/, /p) = t>(x, у, /р+1), ~оо<х, #< + оо.
Заметим, что задачи B2) и B3), в отличие от задачи B1),
одномерные. Их можно решать последовательно, сначала
задачу B2) (это позволит вычислить функцию v (x, у, tp+1)),
затем задачу B3) (это позволит вычислить функцию
w(x, у, tp+1)). Какова связь между значением и(х, у, tp+1)
и значением w (x, у, /p+i)?
Имеем
v(x, у, tp+1) = (E + TA1)u(x, у, tp) + 0(%2)y
w(x, у, tp+1) = {E + %A2)w{x, у, tp) + 0(T2) =
= (Е + %А2)(х, у, /p+i)+0(xa) =
= (£ + тЛ2)'[(£ + тЛ1)и(^> у, У + 0(т*)] =
= (Е + %А)и(х, у, tp) + 0(T2) = u(x, у, /р+1) + 0(т2).
Таким образом, если мы последовательно решим задачи
B2) и B3), то при t = tp+1 получим значения функции
w (х, у, /p+i), которые отличаются от истинных значений
и(х, у, tp+i) — решения задачи B1) лишь на величину
0(т2). Но при этом нам удалось заменить процесс
решения двумерной задачи B1) процессом решения двух
одномерных задач B2) и B3). В смысле объема вычислений
второй процесс имеет преимущества перед первым и это
делает изложенную здесь операцию расщепления
выгодной.
Построим теперь две схемы расщепления для задачи
B1), заменяя задачи B2) и B3) подходящими
разностными аппроксимациями.

§2]
УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
157
(/"//,/7,/7 У-/)
О
Возьмем два явных двухслойных шаблона видов
(т,п,р+!)
> (/77+ /, п, р) (т, n+f,p) <
f(m,n,p) (m,n,pjt
<{т-1,п7р) (м,л-/,р)>
и, используя их соответственно для задач B2) и B3),
запишем разностные схемы:
р+1 к
"тп тп
:Л~Ю.
C = iC' m> я = 0- ±!' •••• р = 0' *•
тя тп
= A^KJ.
f УУ \ тп'
Wmn = Vmt^ Ш> " = 0> ±1> •'- Р = °» *•
где приняты следующие обозначения:
у т + 1 /г ~~ 2 У m/г + и т — 1 п
ЛГ-
N-
B4)
1,
B5)
-1,
I
^Уу(Кп)--
h2
h2
Формулы B4), B5) образуют в совокупности явную
разностную схему расщепления для задачи B1). Численная
реализация этой схемы осуществляется так. При р = 0
значения итп известны, поэтому в B4) при р = 0 имеем
Vmn--=umn = q){xm, tjn). Значения vpmp при р = 0 вычисляем
по явной формуле
Vim = ф (*m, Уп) + 1&хх iPmn) •
Полагаем в B5) р = 0 и вычисляем значение Wmn по
правилу
Wmn = Vmn -f- tAyy (Vmti)-
Таким образом, мы вычислим значения wmn (m, n = 0,
±1, ...) на первом временном слое. Далее полагаем

158 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ.?
umH^wmtu и это означает, что нами определены
приближенные значения решения задачи B1) на первом
временном слое. Аналогично по итп вычисляем итп и т. д., пока
не вычислим значения и%п на последнем временном слое.
Как мы видели, для устойчивости вычислений схемы
B4) и B5) требуют жестких ограничений на шаг т: т^
<>.
Рассмотрим теперь два неявных двухслойных шаблона
видов
(т+/,п% p+f) (т, п+t, р+!)
(тп-1,п,р+1)
'гл,п,р+/)
(гл,п,р+!)
(пл,п-1,р+1)
(гп,л,р) (т,п,р)
и по ним запишем для задач B2) и B3) разностные схемы
итп тп
уР =UP ,
тп тп»
+ц
-КАК
/и, /i = 0, ±1, ..., р —0, 1, ..., N — 1,
B6)
B7)
w^n = vPmV> m,/i = 0,±l,..., р = 0, 1, ..., АГ-1.
Формулы B6) и B7) образуют в совокупности неявную
разностную схему расщепления для задачи B1).
Численная реализация этой схемы расщепления осуществляется
следующим образом. Полагаем в B6) р = 0 и вычисляем
значение vmn как решение системы линейных
алгебраических уравнений
vlmn — xAxx(vlmn) = <p(xm, уп), т, /г = 0, ±1, ...,
ибо vmn = итп = Ф{хт, уп)- Затем полагаем в B6) р = 0 и
находим wmn как решение системы линейных
алгебраических уравнений
wlnn — tAyy(w}nn)=vlnvl9 m, /г = 0, ±1, ...,

§ 2] УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА 159
где vim уже вычислено на первом этапе. Полагаем ихтп ^
f^Wmn- Значит, мы вычислили приближенные значения timn
решения задачи B1) на первом временном слое. Далее
по аналогии вычисляем irmny timn, •••, и%п. Решение
упомянутых выше систем линейных алгебраических
уравнений после их усечения *) можно осуществить по какому-
либо алгоритму разностной прогонки.
Для устойчивости схем B6) и B7) никаких
ограничений на шаги т и h не требуется.
4. Решение смешанных граничных задач. Наряду с
задачами Коши вида B1) для уравнений параболического
типа рассматриваются также и смешанные граничные
задачи, состоящие в том, что требуется определить
функцию и (х, t), которая в области D = {0 <: х <; 1, 0 < t <: Т}
удовлетворяет уравнению
W = 5?+ Ч> <*•<>. - B8)
на начальной прямой при / = 0 условию
и(х, 0)=$(х), 0<*<1, B9)
а на границе области D при # = 0 и х=\ условиям
[ао@-а- + Ро@«]Жв0 = То@. C0)
[aAt)'%+h(t)u\x=si=y1(f). C1)
Здесь предполагаются известными функции ф(я, f), ty(x)
и а,(*), Р/ @. Y*@. ' = 0, Ь причем a}(t) + $i(t)>0.
Будем считать, что задача B8)—C1) имеет единственное
решение и это решение непрерывно в D вместе со своими
производными —, £ = 1, 2, —г, 1=1, 2, 3, 4.
Выберем прямоугольную равномерную сетку,
определив в ней узлы по правилу
xm = mh, m = 0, 1, ..., М, /i=l/Af>0,
*« = пт, п = 0, 1, ..., #, т>0, #т<Г<(Л^+1)т.
*) С. Г. М и х л и н, Прямые методы в математической физике,
М.—Л., 1950, § 51, стр. 303.

160 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ^Л. 7
Способы замены уравнения B8) и начального
условия B9) мы рассматривали выше (см. разностные схемы (9)
и A0)). Укажем замену граничных условий C0) и C1)
сеточными условиями. Используя формулы, аналогичные
формулам C) и D), при /п = 0 и т = М:
» %о <С #о "^ %ъ
ди
дх~
ди
дх\
| __и(хъ tn) — u(xQ, tn) h д2и 1
l(*0. tn) h 2 дх* \(хт,
U(XM> *п)~и(*М-1' *п) . h д*и
(*М.*п) h 2дх"\
%М-1 <С ХМ < %Mi
(*м'
получим на основании условий C0) и C1) при t = tn
выражения
«0/1 '
u(xi, tn) — u(x0, tn)
' h
" Po/i^ (■£<)» *n) —
C&i/i ^ h pin" WW» In) —
_ v Vinu d2u
К^пУ
№'*)'
C2)
C3)
где ain = a,- (*Л), р/Л = p* D), Ъп = Y* ('«)> * = 0,1.
Отбрасывая в выражениях C24) и C3) члены, имеющие
первый порядок относительно Л, построим сеточные
граничные условия
а0л '
«1/1-
ИЛ1 — м
М-1
•Роя^о = Yon»
■Pin^M =Yi/i-
C4)
C5)
Далее в целях упрощений будем полагать, что
а,(/)-0, М0^1. '' = 0,1.
Используя формулы (9), A0) и C4), C5), запишем
две разностные схемы, аппроксимирующие задачу B8) —
C1) с погрешностью порядка 0(т + Л2).
Имеем
Liiwr. C6)

§2]
УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
161
где
( ,," + I ,. П П су П i П
Um um Um+\ lUm-TUm-\
LV(u{h))
т=1,2,...,М-1, л = 0, 1,
т = 0, 1, ..., М,
., N-1,
., N-1,
.,N-
UJ+1, n = 0, 1,
/(«==
где
Фт-
Ycw + b
?1л+Ь
т=1, 2, ..., М-1, /г = 0, 1,
т = 0, 1, ..., М,
п = 0, 1, ..., tf-1,
п = 0, 1, ..., jV — 1,
., iV — 1,
Д** («<*>) =
г /г2
/п=1, 2Э...» Л4— 1, /z = 0, 1,
«Si, m = 0, 1, ..., М,
ajf+i, п = 0, 1, ..., #-1,
C7)
JV-1,
В схеме C7) правая часть /(л) определяется так же,
как и в схеме C6).
Разностная схема C6) явная, она, как и схема (9),
устойчива при т ^ у Л2; разностная схема C7) неявная,
она устойчива при любых отношениях т и h. Как
мы отмечали раньше, схема A0) тоже устойчива при
любых ти Л,
Очевидно, что разностные схемы C6) и C7)
аппроксимируют задачу B8)—C1) (при условии, чтоа/(/) = 0,
Pi-(/)==l, i = 0t 1) с погрешностью 0(т + /*2). В силу
теоремы 1 из п. 2 § 1 разностная схема C7) сходится
при любых значениях г = ^ > 0, разностная же схема C6)
будет сходящейся при г= р-^у-
6 В, И. Крылов и др., т. II

162
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
Для многих задач несложным путем могут быть
указаны необходимые условия устойчивости. Такие условия
позволяют сразу отбрасывать те схемы, для которых
они не выполняются, и не проводить для этих схем
доказательств устойчивости (поскольку в случае нарушения
необходимого условия устойчивости быть не может).
5. Необходимое спектральное условие устойчивости
Неймана. Вывод этого условия дадим на примере задачи
Коши для уравнения теплопроводности
ди
—/>2
,д2и
df-a*'l№+(f(x' *)' -схэ<х< + схэ, 0<*<7\ C8)
и (х, 0) = г|э (х), а2 = const.
По аналогии с (9) и A0) напишем две разностные схемы
для задачи C8):
1Й>(и(а>) =/(*>, C9)
где
и
п-\-\_
-И"
Ц»(и(л)) =
т
/72 = 0,
>ит + 1~~~ ^tlmJrum — \
/i2
1, ±2,
/г-0, 1, ..., АГ-1,
ф(*т» tn), '
fW = \ m = 0, ±1,±2,..., n = 0, 1,..., tf-1,
ЦЯ)("(Л)Н/(Л). D0)
где
Г ия + 1вИл
Г B)
■а'
. m + i z"m *um— 1
Т " /г2
/и = 0, ±1, ±2, ...,
/2 = 0, 1, 2, ..., tf-1,
I ^m»
/i/l) определяется так же, как и в формуле C9).
Очевидно, что разностные схемы C9) и D0)
аппроксимируют задачу C8) с погрешностью 0(т + /*2).
Получим необходимое условие устойчивости
разностной схемы C9).

§ 2] УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА 163
Пусть эта схема устойчива, тогда по определению
устойчивости существует такое h0 > 0, что для всех h <. h0
и любых /(л) е Fh выполняется условие
где М — постоянная, независящая от /ги/(л). Перепишем
неравенство D1), раскрывая содержание понятия
норма. Получим
max | и»т К М (max |Ф» | + max | ярт |\ D2)
Отметим, что в D1) /(л) есть любой элемент из Fh и
Так что, в частности, может быть ф^==ф(л;т, /л), tym =
= \f(A:m) и, следовательно, /(л) будет совпадать с правой
частью разностной схемы C9). Поскольку неравенство D2)
должно иметь место для любых fih)^Fh, положим
Тогда D2) примет вид
тах|аЧ<Мтах|а° I, п = 0, 1, ..., N, D3)
ибо здесь ипт есть решение разностной схемы со
специальной правой частью
15{>(иЮ) = /о»-@, D4)
Говорят, что разностная схема C9) устойчива по
начальным данным, если для нее имеет место оценка D3).
Оценка D3) должна иметь место при некоторых
частных значениях и°т. Положим
и*т=ут = <*ат, D5)
где а — численный параметр, — оо < а < + оо.
Выпишем решение задачи D4) при условии D5).
Сделать это можно, используя метод разделения
переменных. Положим
«; = Wam. D6)
6*

164
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
Подберем здесь численный параметр А, так, чтобы
выполнялось однородное разностное уравнение из схемы D4).
Подставляя ипт% определяемое по формуле D6), в зто
однородное уравнение, получим
\ n+ieiam \iiQiam %neia (.m+D 2) neiam_L.^neia im-1)
a2 *—_L = 0.
% n2
Сокращая на Хпе1(Ут и преобразовывая оставшуюся часть,
получим п т
^=l-4aVsin2-J, r = ~. D7)
На основании D6) можно записать:
тах!^|<|Я|я, п = 0, 1, ..., N, D8)
так как \eiam\= 1.
Теперь видно, что правая часть D8) может быть
ограниченной при любых сколь угодно больших
значениях п, например, в случае, когда
|Г|<1+Ст, D9)
где С —постоянная, не зависящая от т. Действительно,
L
|Я|Л = A+Ст)л<A+Ст)^<A+Ст)^<гсг.
Из формулы D7) следует, что неравенство D9) будет
выполняться при 1
Условие D9) называется необходимым спектральным уело-
выем устойчивости Неймана. Для разностной схемы C9)
эти условия будут выполняться только для значений г,
удовлетворяющих неравенству E0), т. е. при r^^-^h2.
Если проделать аналогичные выкладки в случае
разностной схемы D0), то для Я мы получим
х= \ .
l+4ra2sin2y
Из этого выражения видно, что для разностной схемы D0)
необходимое спектральное условие Неймана будет
выполняться при любых /*>0.

§2]
УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
165
Отметим здесь, что при r>iy^ разностная схема C9)
перестает быть устойчивой. Действительно, в этом случае
при а = я из D7) имеем
Я=1-4а2г.
И, значит, |А,|>1, ибо 2а2г>1. Еще получим
и"т = A - Аа2г)п • ёлт = A - 4а2г)п • (—1)л,
Поэтому
|а^|-> + оо при д->4-°°
и устойчивости не может быть.
Если в уравнении C8) коэффициент а2 зависит от х, t,
т. е. a2 = a2(xf t)9 то в этом случае для исследования
устойчивости разностных схем вида C9) и D0), в
которых а2 заменено на а2 (хт, tn), может быть применен
принцип замороженных коэффициентов (см. [3], § 26).
Отметим, что разностная схема D0) опять будет
удовлетворять необходимому спектральному условию
устойчивости Неймана при любых г>0, а разностная
схема C9)-при г< 2тах *2 .
(x,t)
6. Экономичные разностные схемы. Построение таких
разностных схем мы рассмотрим на примере смешанной
граничной задачи для уравнения теплопроводности
E1)
где Г —боковые грани прямоугольного параллелепипеда
D = {0<x, y^l, 0<^<Г}. Будем предполагать, что
задача E1) имеет единственное решение и(х, у, t) и это
решение непрерывно в D = D-\-T вместе со своими про-
dhi , о dku dku , Q
изводными-^-, 1=1, 2, ^, ^, £ = 3,4.
ди
и(х,
и(х,
У.
</>
+
0)
0
дЧ
= ty(x,
|г = 0,
0^
У).

166 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
Выберем квадратную сетку по пространству и
координаты узлов (хт, уп, tp) определим по правилу
(хт> Уп, tp) = (mh, nh, рт), m, /г = 0, 1, ..., Af, h = -^y
т>0, р = 0, 1, ..., N, Nx^T<(N+l)%.
Рассмотрим явный шаблон
(т,П+/,р)
(т,г7,р+/)
о
(т+(,п,р)
(m-f,n,p)
(m,n-f,p)
и по аналогии, например, с B4), B5) запишем
разностную схему для задачи E1)
где
L£> («<*>) = р>,
1 ™ mn—A (up )__л № )
хх \ тп) 1Хуу\ tnnjy
E2)
Ш («<*>):
% хх \" /пл/ XJL#i/ 1
т, /г=1, 2, ..., Af-rl, р = 0, 1, ..., JV—1,
"тп, т, я = 0, 1, ..., М,
MJ+1, (т/г, n/i, (р+1)т)е=ГА.
Через Th мы обозначили узлы сетки, принадлежащие Г,
(О,
/W = 1|>(*я» #я), т, /i = 0, 1, ..., М,
I 0.
Очевидно, что разностная схема E2) явная и что она
аппроксимирует задачу E1) с погрешностью порядка
О (%-{-№). С помощью принципа максимума можно
установить, что при т^ ~^h2 разностная схема E2)
устойчива.

§2]
УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
167
Возьмем «неявный» шаблон
(/77, П+1, р+ 0 (/77*/, П, р+1)
(т,п,р+1)
(m-i,n,p+l) (m,n-Itp+i)
6
(т,п,р)
и, используя формулы, подобные B6), B7), запишем
разностную схему для задачи E1):
wo-г.
где
E3)
( ир+х-иР
■А (иР+1)-А (иР+1)
хх \ тп ) у у \ тп /у
£,д(и(А))=з{ т, п=1, 2, ..., Af-1, /i = 0, 1, ..., tf-1,
4я, т, я = 0, 1, ..., М,
и**1, (m/i, лА, (р+1)т)еГа,
О,
У{хт, Уп), т, л = 0, 1, ..., М,
/W =
0.
Разностная схема E3) неявная, она аппроксимирует
задачу E1) с погрешностью порядка 0(т + /*2) и
устойчива при любых значениях r>0, r = x/h2.
Обозначим через ик совокупность значений сеточной
функции на слое номера k, т. е. uk = {u^n, m, п =
-0, 1, ..., М}9 ft = 0, 1, ..., N.
Пусть нам известны значения ир. Для того чтобы
вычислить значения ирп по явной разностной схеме E2),
мы должны выполнить число арифметических операций,
пропорциональное числу неизвестных и%+{. Этих
неизвестных будет (М — IJ, так как значения на Th известны:
^+1 = 0, если узел принадлежит ГЛ.
Введем понятие экономичной разностной схемы. Будем
говорить, что двумерная разностная схема экономична,

168
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
если для вычисления значений ир+1 по значениям ир
эта схема требует выполнения числа арифметических
операций, пропорционального числу неизвестных
значений на слое р+ 1.
Очевидно, что разностная схема E2) экономична, но,
как мы уже отмечали, вычисления по этой схеме будут
устойчивыми только при выполнении условия %-
■\ь\
которое является весьма жестким ограничением на шаг т.
Если мы будем использовать разностную схему E2),
то для вычисления ир+1 по иР нужно будет решать
систему линейных алгебраических уравнений, в которой
число уравнений есть (М — IJ и этих уравнений
столько же, сколько неизвестных. Даже при условии,
что эта система уравнений будет решаться по
методу Гаусса, одному из наиболее быстродействующих
методов, число операций, необходимых для вычисления
ир+1 по ир, будет приблизительно пропорционально
[(М — IJ]3. И, следовательно, схему E3) отнести к
экономичным схемам нельзя. Однако при. этом следует
отметить еще раз, что важным положительным свойством
этой схемы является ее абсолютная устойчивость.
Поставим задачу построить, разностную схему,
которая аппроксимировала бы задачу E1) и обладала
свойствами:
1) экономичности; 2) абсолютной устойчивости.
Искомую разностную схему можно записать,
используя идею расщепления (см. п. 3) и формулы B6), B7).
Получим Lh(uW)=fW, E4)
где
М"(Л,)«
итп итп
УУ
KV),
N-l,
fW —
т, п=1, 2, ..., М—1, р = 0, 1, .
иР+К (mh, nh, (р+1)т)€ЕГл,
WL> m,n = 0,l,...,M, p = 0,l,...,N-l;
fO, m, n=l, 2, ..., M-l, p = 0, 1, ..., N-l,
0, (mh, nh, (p-f 1)т) ёГ»,
m, n = 0, 1, ..., M, p = 0, 1, .... N-l.
йр+]

§ 2] УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА 169
Сеточная функция й%£1} фигурирующая в
определении /(/г), вычисляется как решение вспомогательной
разностной схемы
йР+1—ир
т, я=1, 2, ..., М-1, р = 0, 1, ..., Л^ — I, E5)
£mtl=0, (mft, nh, (р+1)т)еГА.
Доказано, что разностная схема E4) аппроксимирует
задачу E1) с погрешностью порядка 0(т + Л2)> абсолютно
устойчива (об этом подробно написано в [3], § 32) и
экономична. Здесь мы уделим большее внимание вопросу
реализации разностной схемы E4) и установлению
свойства ее экономичности. Проследим, как по значениям
u<}nn = 'tymn вычислить значения и1тп на первом слое и затем
по значениям Umn — значения Umn и т. д.
Положив в E5) р = 0, получим
Umn— Umn Um-\- \п — Штп-YUm— \п 10 Л/Г 1
т " ¥ ' m-^ z> •••> т" Ь E6)
^ = 0, й^Л = 0, л=1, 2, ..., М-1.
Формулы E6) представляют собой при фиксированном п
линейную граничную задачу для разностного уравнения
второго порядка.
Опишем одну из возможных реализаций метода
разностной прогонки применительно к задаче E6). Пусть п
фиксировано (l^n^M — 1). Перепишем E6) в виде
Гй1т + 1Л — A + 2Г) Ufnn + Гй\п- \п = tymn,
т=1, 2 ..., М-1, E7)
йол = 0, й1мп = 0, r = T/h2>0.
Пусть й£„ @^k^M) — искомое решение задачи E7).
Предположим, что между двумя соседними значениями
этого решения существует связь
uln = ainul+in + $in, * = 0, h ..., М-1, E8)
где а/л, §in — некоторые числовые коэффициенты. При
£ = 0 определим а0п и р0л таким образом, чтобы выпол-

170 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
нялось левое граничное условие uj/i = 0. Для этого
достаточно положить
а0л = 0, E9)
Рол = 0. F0)
Возьмем i = m—l. Значение й\п, определяемое по
формуле E8), подставим в E7) и затем выполним
элементарные преобразования. Получим
Umn-{1+ 2r) _ ramin ■ Un+ , „ - (, + 2r) _ гатш . <bl)
Выберем. ос,„ и §,-„ так, чтобы выражения E8) при i = m
и F1) совпадали. Это дает формулы
am* = (\+2r)-ra.m_x ' F2)
Теперь можно указать алгоритм вычисления значений
й\т й12п> ...» й1м-\п по методу разностной прогонки:
1) по формулам F2), E9) и F3), F0) при т=1, 2, ...
..., М — 1 последовательно вычисляем а1п, а2п> ..., а>м-т
и $in, $2п> • ••> Рж-1«; этот процесс называют прямым
ходом метода прогонки;
2) искомые значения й\П9 ..., йм-ы вычисляем по
формуле E8) при i = M—l, М — 2, ..., 1, 0. Отметим,
что в силу E7) ймп = 0. Процесс вычисления значений
й1м — \п9 й1м~2п, ..., й{п называют обратным ходом метода
прогонки.
Легко видеть, что 0^ат/г<1, и потому метод
прогонки устойчив к ошибкам округлений.
Такие вычисления надо проделать для каждого /г,
т. е. надо вычислить таблицы значений
all> а21> •••> аМ-1Ъ Р.11> Н21> •••> Рж-11>
йм — М* UM-2U -.., й\и
CXi2, 0С22, . . . , 0ЬЖ-12» Pl2> P22» • • • » HM-12J
^!д1— 12» UlM — 22> •••> Й}2,
0&Ш-1» а2М-1> ••«> &М-1М-1> Hl/И 1т Р-2Л1-1» •••> Рм-Ш-Ъ

§ 2] УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА 171
Для дальнейших вычислений потребуется только таблица
нз значений йтп\ ее и следует хранить в памяти ЭВМ.
Обратимся теперь к задаче E4). Положив р = 0,
получим
umn umn umn+l *umniumn—l
T "" /l2
mU = 0, wU = 0, n=l, 2, ..., M-l, F4)
m=l, 2, ..., M-l.
Пусть в F4) m фиксировано, тогда эту задачу можно
записать в виде
rUmn+l — A ~Ь 2r) Umn -f- ttlmn-\ = Й/пя>
/1=1, 2, ..., Af-1, F5)
*4о = 0, h}„ai = 0, г = т/А2 > 0.
Метод прогонки для задачи F5) полностью аналогичен
методу прогонки для задачи E7). Укажем только на
порядок вычислений.
1) По формулам
Чтп- A+2A)_rWi> Y™o = 0,
с г^тп-1 итп с гч
ВЫЧИСЛЯеМ ywl, ут2, . . . , Утм-Х и Swl> Sm2> • • • > 8/яЛ*-1.
2) Приближенные значения а?™ на первом слое
вычисляем по формуле:
Umi^ymlUml+l + bmU "JnAf = 0, I = М - 1, М - 2, ... , 1, 0.
Вычисления, указанные в 1) и 2), надо проделать для
каждого т, 1 ^т^М — 1. Таким образом, и здесь надо
вычислить три таблицы.
7ш 7i2> • • • > 7ш-ъ бц, б12, ..., 6x^i-i;
^11» ^12> • • ♦ > ^Ш-1>
?21i 722» • • • > 72М~Ь S2l, 622, . . . , S2iM+l'>
^21» Щ%1 • • • » #2М-1»
7л1-и> 7^1-12» • ••> 7ж-1Л1-1> бм-ц, б^_12; ..., S^-iAf-il
ИМ-1Ъ UM-Пу . • • » UM-IM-Ъ

172
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
Отметим, что как при вычислении таблиц для атпу $тпу
йтп> так и для вычисления таблиц для утт Ьтп, ulnn,
необходимо было выполнить число арифметических
операций, которое пропорционально (М—IJ, т. е.
пропорционально числу неизвестных и]пП- Поэтому схема E4)
экономична.
Далее вычисления аналогичны. А именно, при
вычислении йт„ поступаем так же, как и при вычислении й1тп,
только и0тп = ^)тп заменяем на и1тп, при вычислении ufnn
правую часть й1тп заменяем на й2тп и т. д. Конечным
итогом вычислений будет получение значений иРтп при т,
/1=1, 2, ..., М-1, р=1, 2, ..., N.
В заключение параграфа о разностных схемах для
уравнений параболического типа мы приведем несколько
разностных аппроксимаций для уравнения
L(u) =
ди
д2и А
где a = const>0. Эти схемы часто использовались в
вычислительной практике и их полезность и хорошие
свойства были многократно подтверждены.
1. Схема Дж. Кранка и Р. Николсона. Она строится
по шеститочечному двухслойному шаблону
(т~ U л+ f) (т,п+П (т+1,п+0
(т-1,п) (/л, п) (m+f,n)
и имеет вид
U (и***) -
ит т
Эта схема неявная, она абсолютно устойчива и для
погрешности аппроксимации rmn (h) верно представление
rmn(h) = 0(T* + h*).

§2]
УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
173
2. Неявная двухслойная шеститочечная разностная
аппроксимация. Эта схема строится по тому же шаблону
точек, что и схема Дж. Кранка и Р. Николсона, и имеет
вид
— а
тК+1+2С+<^0+A-т)КУ1-К+1+с±11),
/I2
= 0,
где у = const, 0 ^ у ^ 1.
При O^y<у схема устойчива, если
а -гр- = const =
2A—2y) e
При у<у<^\ схема абсолютно устойчива.
Для погрешности аппроксимации в обоих случаях
верно представление rmn (А) = О (т + Л2). Если положить
Y = T~
Л2
12ат '
то схема будет устойчивой, но порядок ее аппроксимации
по сравнению с двумя предыдущими случаями будет более
высокий, а именно
rmn(h)=0(T*)=0(h*).
3. Схема Е. Дюфорпга и С. Франкела. Она строится
по четырехточечному трехслойному шаблону вида
(т,п+!)
(m-f,n)
4 О
А- —I
(m+1,n)
и имеет форму
Ы"(Л)):
ит ит
2т
(т,п-1)
а ^2 —и.

174 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
Эта схема явная, абсолютно устойчивая. Для
погрешности аппроксимации верно представление
,(/0 = o(t+/*2)+o[(:lJ]
при условии, что -г-->0, когда т, А->0.
4. Неявная пятиточечная трехслойная схема. Здесь
рассматривается шаблон вида
(/77-/,/7*/) (/77,/7+/) (/77-/,/7*/)
о <■
(/77,/7)(
L J
> о
> 1
(т,п-1)
Имеем
з <+1-«"
1А(ц1*))^т_»__Л
1 <-
-,я —1
Н2 ~~
Схема абсолютно устойчива,
Л™(Л) = 0(т» + Л»).
Отметим еще, что при изучении устойчивости
разностных схем мы рассмотрели только простейшие приемы
и методы исследования устойчивости так называемых
модельных задач. Мы рассмотрели принцип максимума,
метод разделения переменных (которым мы
воспользовались при выводе необходимого спектрального условия
устойчивости Неймана) и частично принцип
замороженных коэффициентов.
Другие методы исследования устойчивости разностных
схем, а также подробное рассмотрение современной теории
и состояния этого вопроса даны в работах А. А.
Самарского, в частности в его монографии [6].

§3]
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
175
§ 3. Разностные схемы для уравнений эллиптического типа
Как мы уже отмечали (см. § 1), уравнение
/ ч / \ д2и . аи , ч д2и , . \ д2и .
I(и) ^а(х, у)-шг + 2Ь (*, У)ш^Л-с (х, у) -щ-2 +
+ 2d{x, у)~ + 2е(ху y)~- + g{x, у)-u = f (x, у) A)
называется эллиптическим в области D, если
6(х, у)==Ь2(х, у)—а(х^у)-с(х, у)<0 B)
для всех (я, у) из D. К уравнениям эллиптического типа
на границе Г области D присоединяются граничные
условия трех видов:
1) граничные условия первого рода
и|г = Ф(М), C)
где ф —известная функция, М — точка контура Г;
2) граничные условия второго рода
да
дп
,= Ф(А«), D)
где ф —известная функция, М — точка контура Г, -~—
производная по внешней нормали;
3) граничные условия третьего рода
[а(х, У)|£ + Р(*, y)-u]F = <p(M), E)
где а, E, ф —известные функции, М— точка контура Г,
да
-g производная по внешней нормали.
Требуется определить функцию и(х, у), которая
в области D удовлетворяла бы уравнению A), а на
границе Г области D — одному из трех условий.
Задача A), C) называется задачей Дирихле, задача
A), D) называется задачей Неймана и задача A), E)
называется смешанной граничной задачей.
Рассмотрим элементы теории разностных схем для
эллиптических уравнений. Область D будем считать
ограниченной и ее границу Г —простой (без кратных
точек) кусочно-гладкой линией.

176
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
1. Построение разностных аппроксимации для уравне-
ний. Пусть в уравнении A) смешанная производная ^--г-
отсутствует, т. е. Ъ (х, у) = 0. Построим разностную
аппроксимацию для такого уравнения в предположении,
что оно имеет наиболее простой вид
ЖГ+^г = /(*. У). F)
Уравнение F) называют уравнением Пуассона.
Выберем прямоугольную сетку, определив положение
узлов (хт, уп) по правилу
хт = т/г, т = 0, ± 1, ±2, ...;
#л = л/, п = 0, ±1, ±2, ...; А>0, />0.
К сеточной области Dh отнесем все узлы, принадлежащие
области D = D + Г (рис. 1).
Рис. 1.
Возьмем пятиточечный шаблон
(m}n+f)Q
(т-/,п)
о <>
(/77, п) (т+1,п)
о
(гп,п-1)о
Пользуясь расположением точек в этом шаблоне, разобьем

§3]
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
177
узлы области на две категории: внутренние и граничные.
Некоторый узел (т, п) будем считать внутренним, если
он сам и четыре соседних точки шаблона принадлежат
области Dh (такие узлы помечены на рис. 1 знаком •),
и множество их мы обозначим через Dn. Остальные узлы
назовем граничными (они помечены на рис. 1 знаком *),
и множество этих узлов обозначим через Тп: таким
образом, Dn = Dn + Th.
Из сказанного здесь следует, что разбиение узлов
области Dh на внутренние и граничные зависит от того,
какой шаблон выбран для аппроксимации
дифференциального уравнения.
Пусть узел (m, п) <=D°n. Замену дифференциального
уравнения F) разностным будем осуществлять только
во внутренних узлах.
Имеем
дх2
д*и
(*т' Уп) °У2
>»п)
= /(*«. Уп).
G)
Воспользовавшись формулой, подобной F.11.8), и анало-
гичнои формулой для-g-a", получим на основании G)
Ц (*т+1> Уп) — 2" (*/я. Уп) + и (Хт-й Уп) h2 д*и
№ 12 ' дх*
(*%.Уп)
+
"(Хт> Упи) — 2и(хт> Уп) + и(*
/2
Т2 ^
■•f(xm> Уп), (т, п)ееО°п, (8)
Ы Ук")
Хщ-1 < %т <С Х/п+1 » Уп-1 <^Уп' < Уп-Ъ
Пусть функции
д*и(х, у) дЧь (х, у)
дх*
дУ*
ограничены по
абсолютной величине в области D; тогда в формуле (8)
при достаточно малых h и I можно пренебречь членами,
содержащими в качестве множителей /г2 и /2, и мы
получим искомое разностное уравнение
mi(uW)=fM9
(9)

178 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
где
га) /fAh)\ um+in ^ilmn\um-in i amn+i ^umn~rumn-i
(m, n) <= £>л,
/<*> = / (xm, #„), (m, n) <= £>£•
Здесь через ^тя мы обозначаем приближенное сеточное
значение решения уравнения F), так что итп я^ и (хт, уп)
и и(х, у) — решение уравнения F). В отличие от
уравнений параболического типа, в обозначении сеточного
значения итп мы оба индекса ставим внизу; в силу их
равноправности, они указывают на изменения положения
узла на плоскости. В случае уравнения параболического
типа аналогичное значение обозначалось через ип и
различной постановкой индексов подчеркивалась в сущности
различная роль, которую играют в нестационарных
задачах переменные по времени и пространству.
В силу определений и понятий, введенных в § 1,
можно из формул (8), (9) получить
ДПМ*. y))=r + 8f
p(h)
A0)
где
дх*
/2
(*т> Уп) + 12" '
ду*
(*т.ЯУ (т'л>е^
Следовательно, при сделанных выше предположениях
относи д*и
сительно
дх*
ду*
имеет место оценка
Цб/С'Ц^Ш*
A1)
где М — постоянная, не зависящая от h. Считаем, что
l = ahy а —некоторое положительное число.
Оценка A1) означает, что разностное уравнение (9)
аппроксимирует дифференциальное уравнение F) на
решении и(х, у) с погрешностью порядка О (Л2).
Рассмотрим теперь случай, когда в уравнение A)
д2и
входит смешанная производная ■ - и это уравнение

§ 3] УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА 179
имеет, например, такой вид:
д2и . п, д2и ,
а^ + 26-
дх2
дхду
ду2
= f(*> У)*
A2)
где a, Ъ, с — постоянные и Ь2 — ас<0.
Для замены дифференциального уравнения A2)
разностным выберем шаблон
(m-f,n+/) (m,n+f) (m+1,n+f)
g <р -Q
(m-ltri)
(т-1,п~Г)\
(т,п)
ш, л-/)
>
(m+f,n-f)
Используя этот шаблон, выделим в области Dh множество
внутренних узлов Z% и множество граничных узлов Гл.
Будем считать узел (/и, п) внутренним и помечать его
знаком • (рис. 2), если этот узел и восемь соседних узлов,
Рис. 2.
содержащихся в шаблоне, принадлежат Dh. Оставшиеся
узлы области Dh отнесем к числу граничных, они
помечены знаком *; множество таких узлов обозначим через Yh.
о д2и
Запишем разностное выражение для замены д д .
Чтобы не загромождать записи, остатки записывать не
будем, ограничимся только указанием на порядок остатков.

180
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ
[ГЛ. 7
Используя формулу, аналогичную формуле E), получим
д2и
дхду
__д__(ди
(хт> Уп)~ д* \dyJ\(xm> yn)
ди\ I да
W) (хт+ъ Уп) ~~ \ду
2/i
(*m-i- *п) + Q щ =
1 Г и (хт+1, уп+1) — и (хпн1, уп_г)
~ 2/i L 2/ ~*~
+ 0A2)- ~Ит-ь ^+^2/"^-1' **-" - о (/2I + О (Л2) =
u(xm_l9 yn+i) — u(xm-i, Уп-л)
21
и(хт+1> Уп+1)~~и (хт+ъ У/г .л) — и {Хт-Ъ Уn+l) ~\~ и (хт-Ъ Уп-i)
Ш
+
+ 0(А2 + /а),
где предполагается, что //А = const.
Теперь, подобно тому, как было построено разностное
уравнение (9), можно построить для уравнения A2)
разностное уравнение, обладающее аппроксимацией порядка
0{h2 + l2). Имеем
ит+1п *итп "г ит-1п
/I2
■2fti
'm+i/n-l um+in -l — um-in+i 4" итЛп-Л
Ahl
+
i p umn+i ^m/i t Umn_i г / ч
" ^ /2 — / \лгт Уп)
для всех узлов (m, л) из области D£.
2. Аппроксимация граничных условий. Рассмотрим,
как можно заменить граничные условия вида C) и D)
разностными условиями.
Отметим, что условия C) и
D) заменяются разностными
условиями на множестве граничных
узлов Yh.
Пусть (т, п) — некоторый узел
"я? из Гл, обозначим его буквой 5;
(т+1, п) — внутренний узел,
ближайший к В по направлению х,
Рис.3, обозначим его буквой А.
Буквой М обозначим точку
контура Г, ближайшую к В по направлению х (рис. 3) *).
</<
п
!
\
1
h
My
/в]
.1.
—>■
//
А
Г
В
X
*) Аналогично можно поступать в том случае, когда ближайшая
к В точка Г будет лежать в направлении оси у.

§3]
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
181
Координаты этих точек такие: М (хт — б, уп), 0 < б < Л,
В(Хт> Уп)> A(xm+lt yn). По условию C) имеем
и ;г = ф(М).
Значит, можно положить
Umn = ф (М)
A3)
для узлов (т, я) е ГА. Какова погрешность формулы A3)?
Имеем
<р (Af) = и (*« - 6, уп) = и{хт, Уп)-~^-^\
(*%.УпУ
хт — 8<х'т<хт. Отсюда получим
б ди
и{хту Уп)-ц(М)-=и(хт Уп)-11тп = —-ТГ-Ту
11 д*
(*£.*.)'
Из этой формулы следует, что погрешность формулы A3)
будет иметь первый порядок относительно h в
предположении, что б == ah, a — некоторое положительное число. Если
точки М и В совпадают, то формула A3) будет точной.
Точность вычисления ипш при (m, n) e Гл можно
повысить, если воспользоваться еще значением а (х, у) в точке А.
Имеем
б2д%
и(М) = и(хт—6, 4/я) = W (S) jn-
(В)
+ 21 дх2
1! дх
где В —некоторая средняя точка между М и В,
u(A) = u(xm + hy yл) = и(B) + -тг^--,
(В) ~*~ 2! д*2
где Л —некоторая средняя точка между В и А Исклю-
и с помощью формулы A5), получим
чив из A4)
дх
U (В):
hq>(M) + &u(A)
/г + б
+ 0(/i2).
Отбросив здесь величину О (Л2), получим разностное
граничное условие, аппроксимирующее граничное условие C)
в узле (т, п)еГА с погрешностью порядка 0(h2):
Umri —
A6)
Формулы вида A3) или A6) могут быть записаны для
любого узла (т, /г), принадлежащего Th.

182 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
Теперь обратимся к задаче замены граничного
условия D) разностным. Рассмотрим рис. 4.
Поясним обозначения на этом рисунке: В — граничный
узел с координатами (хт, уп),
М — ближайшая к В точка
контура Г, А — внутренний
узел с координатами (xm-l9 yn),
С — граничный узел с
координатами (хт, yn-i), я
—внешняя нормаль к Г в точке М.
Обозначим угол между п
и Ох через а, между п и
х Оу — через C. Легко видеть,
з
что р=уя + а. Поставим
задачу. Заменить граничное
Рис 4.
= ф(М) разностным в граничном узле В.
ди
условие -р
По определению имеем
да да . ди Q ди . ди .
_ = _cosa + -¥cosp = ^-cosa + -^-sina.
Далее мы предполагаем, что в точке В направление
нормали п сохраняется таким же, как и в М. Поскольку
расстояние между В и М есть величина порядка О (К),
то это предположение связано с внесением погрешности
того же порядка 0(h). Значит,
ди
дп
(М)
ди
дп
(В)
Поэтому окончательно получим
U(xm, Уа)-и{хт_Ь уп) . cos ^ | и(хт>Уп)-и(Хт>Уп-1) . s jn a I
+ 0(А + /) = Ф(М)
или, используя приближенные сеточные значения,
-cosa-
[-sina = y(M). A7)
Формула A7) представляет собой искомое разностное
условие, аппроксимирующее в узле (т, п) е= Гл граничное

§3]
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
183
условие D) с погрешностью порядка 0(h-\-l).
Выражения вида A7) должны быть записаны для всех граничных
узлов (m, n) e Гл, после чего будут получены разностные
граничные условия, аппроксимирующие граничное
условие D). Как видим, процедура замены граничных
условий разностными может оказаться громоздкой и сложной,
особенно если контур Г имеет непростую форму.
Замена граничных условий вида E) может быть
осуществлена с помощью формул вида A3), A6), A7).
Рассмотрим вопросы сходимости и устойчивости
разностных схем для уравнений эллиптического типа на
примере задачи Дирихле для уравнения Пуассона.
3. Построение разностной схемы в случае задачи
Дирихле для уравнения Пуассона. Пусть в области D =
= {0<х<а, 0<у<Ь} задано уравнение Пуассона
!?- + $ = /<*. У)> A8)
а на границе Г области D — условие Дирихле
и|г = ср(Л1), A9)
где ф —известная функция, М — точка контура Г. Будем
считать, что задача A8), A9) имеет единственное решение
и(ху у) в области D = D-{-T и это решение имеет непре-
рывные в и производные -г-j- и -^-г.
Возьмем прямоугольную сетку, положив
xm = m/z, m = 0, 1, ..., My h = a/M;
yn~nl, n = 0, 1, ..., N, l = b/N.
Для аппроксимации уравнения A8) выберем пятиточечный
шаблон (см. п. 1) и к множеству внутренних узлов D°h
отнесем все узлы, лежащие в D, а к множеству граничных
узлов Th отнесем узлы, лежащие на Г.
Используя формулы вида (9) и A3), запишем разностную
схему, аппроксимирующую задачу A8), A9) с
погрешностью порядка 0(/г2 + /2):
М"(Л)Н/(Л).
B0)

184 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
где
| ит + 1п 2итп ~\~ит-1п \ итп + 1 — *итп "Ь итп ~ i
Lh(uM)*s
m=l, 2, ..., М-1, д=1, 2, ..., N-l,
иля, (nth, nl) ge Гл,
М —1, п=1, 2, ..., Л^ — 1,
Разностная схема B0) представляет собой систему
линейных алгебраических уравнений, число уравнений
этой системы равно (М — \) x(N — 1), столько.же и
неизвестных, это — значения итп при т = 1, 2, ..., М — 1,
/1 = 1, 2, ..., ЛГ-1.
4. Об устойчивости разностной схемы B0).
Доказательство устойчивости разностной схемы B0) сводится
к выявлению двух свойств.
1. Разностная схема Lh (z{h))=g{h\ где g{h) = №mn ,
gift) — произвольный элемент из гЛ, однозначно разрешима.
2. Имеет место оценка
\*(h)W^c-\\6(h)W
где С —постоянная, не зависящая от h и g(/*j. Напомним,
что, как и прежде, нормы определяются по правилу
lz(%h = max\zmn\,
т, п
llg(Wk = max |am„j + тах| рт„|.
т, п т, п
Введем следующее обозначение:
Ah(u^)^Axx(u{h)) + Ayy(u^).
Лемма 1. Пусть v{h) = {vmn}, vmn^Ёconst, —
некоторая сеточная функция, определенная на Dh = D°h-\-Yh. Если
выполняется условие
AA(^)!(^f „я>^0, B1)
где (*т, Уп) ^ £^# то ^(л) достигает своего наибольшего
значения на DKh) в граничных точках, т. е. на Гл,

§31
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
185
Доказательство. Предположим противное. Пусть
vKh) имеет свое наибольшее значение vy в области D\.
Мы можем считать, что хотя бы одно из значений vi + 1jy
Vi-u> vi;+i> vij-i строго меньше Vif. Тогда получим
Aft (*%,. „,, = A,v (v^%v yj)\ + Ayy (rfi*%tt yj) < 0, B2)
ибо
AxX \V ) Ц. Vf) Д2
_ (Pi + 1/ — Vij) + (Vi - 3J - Vjj)
/i2
д {v{h))\. .-VtJ + l-toiJ + ViJ-l.
ЛууУУ )Щ,У;) — 12
_ (Vij+i ~ Vij) + (vy -1 - уц)
;o,
при этом хотя бы одна из этих величин строго
отрицательна в силу предположения о значении vy. Но B2)
противоречит условию B1) леммы, и потому наше
предположение неверно. Лемма доказана.
Лемма 2. Пусть v{h) = {vmn}, vmn =fcconst,—
некоторая сеточная функция, определенная на Dh = D°h + Гл. Если
выполняется условие
Mv{h))\(Xm.Vn)^0, B3)
где (хт, уп) е DI, то v{h) достигает своего наименьшего
значения на Dh в граничных точках, т. е. на Тп.
Доказательство аналогично предыдущему.
Теорема (принцип максимума). Каждое решение
разностного уравнения
Лл (v{h))\ <*m, yn) = 0, (хт, уп) е= Da,
принимает свое наибольшее и наименьшее значение в
некоторых точках границы Th.
Доказательство следует из лемм 1, 2.
Применим эту теорему к доказательству однозначной
разрешимости разностной схемы
Ы*(Л)Н£(/г) B4)
при любых £(Л) е Fh. С этой целью рассмотрим однород-
ную разностную схему Lh(z{h)) = 0 и покажем, что она

186 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
имеет только нулевое решение z{h) s= 0. Отсюда будет
следовать однозначная разрешимость схемы B4).
Подробно разностную схему Lh (г(Л)) = 0 можно
записать в виде
Lizih)){Kh(z{h))\{Xm,yn) = ^ (Xm Уп)<=01
l^k^V^0' (*т,Уп)^Тн.
Если бы г(/г)^0, то тогда свое наибольшее значение и
свое наименьшее значение величина 2(Л) в силу принципа
максимума могла бы иметь в точках Гл; но на Th г(Л) = 0,
значит; и всюду в Dh = D°h-\-Th будет г(Л) = 0. Поэтому
разностная схема B4) однозначно разрешима.
Теперь покажем, что разностная схема B4) обладает
свойством
max Jz^KС/ max \атп\ + max \$mn\\9 B5)
т>"> \{m,n)^D°h (т,л)е=Гл J
где С —постоянная, не зависящая от h и g{h) = { ^тп*
v Ртп-
Если мы это установим, то тем самым будет доказана
устойчивость разностной схемы B0).
Оценку B5) мы получим путем построения мажоранты
для функции | г(Л) | по правилу С. Гершгорина.
Обратим внимание на следующий факт. Если
Р(х, У)= 2 aijrftj
есть некоторый многочлен второй степени от двух
аргументов X И Г/, ТО
Л* (р{Н))! (*т. уп) - [S + ЩХт, Уп) - 2 («*» + ««)• B6)
Действительно,
Кроме того, имеем
= 2а20)
Лл.л (Р(Л)) '(*т, „я) = ш<
dk+lP
иб° 5F^ = ° ПРИ /s + /^s3-
.. . = 2°02,

§3]
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
187
b
0
>
D
Г
Л
а х
Мажоранту Z (х, у) определим по правилу
Z(x, У) =
= ]r[(a2 + b2)-(x2 + y2)] max \атп\ + max \$mn\.
Поясним геометрический смысл функции S (х, у) = (а2+&2)—
— (х2 + У2). Рассмотрим рис. 5, на котором изображена
область D с контуром Г.
Длина диагонали О А
равна l/^ + b2, поэтому
уравнение кривой S(x, y) = 0
есть уравнение
окружности с центром в начале
координат и радиусом,
равным О А = ]/а2 + б2.
Таким образом, если (х, у) е Рис- 5-
еО = 0 + Г, то S(x9y)^
^0, причем S (х, у)==0 только для одной точки из D,
когда х = а9 у = Ь. Отметим, что эта точка не
принадлежит Dh, и потому
Покажем, что
|2^)|<ZW. B7)
Рассмотрим сумму z{h)-{-Z{hK На множестве Yh имеем
Vh) + Z(h)hm- *№ = ^ К + ^ К = Р- кЫ' №н +
+ \S(x,y)\(x У)(=Т max |am„|+ max |ртя>0. B8)
Кроме того,
Лл Bi*> + z<*> |D. = Ah (*<*>) \D]i + Ah (Z<*>) |Do =
= ccmn o + (— max o | amn j) < 0. B9)
{tn,n)^D°h (m,/i)e4
Из B9) в силу леммы 2 следует, что функция z[h)-{-Z{h)
принимает свое наименьшее значение в точках Г/г, но
по B8) на Th выполнено неравенство г^ + Z^^O.
Значит, всюду в Dh
г<Л> + #Л>5*0. C0)

188
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
Если рассмотреть разность z{h) — Z{h) и воспользоваться
леммой 1, то всюду в Dh получим неравенство
2i*>-Z^><0. C1)
Из C0) и C1) следует, что
|2<л>|<#л> C2)
для всех (хт yn)^Dh. Из оценки C2) получим, что
I *тп I < х s (хт> Уп) max | атп | + max | §тп | <
<т(а2 + 62) max \ccmn\+ max |pwrtj<
<maxi-|(a2 + 62), l} • Г max \amn\+ max | pm/2II =
1 j \_{m,n)<=D°h (mtn)^Vh J
:•[" max \amn\+ max |рдал|]
[(m.n)eD; (т,л)€=Гл J'
где C=max{4(a2 + 62), l}.
Таким образом, имеем
тах|гтл|<СГ max \amn\+ max | p„
и, значит, оценка B5) установлена. Тем самым доказана
устойчивость разностной схемы B0).
Разностная схема B0) аппроксимирует задачу A8),
A9) с погрешностью порядка О (/г2) (мы предполагаем,
что h/l = const) и устойчива. В силу теоремы 1 из § 1
эта схема будет сходящейся со скоростью 0{№).
Для решения систем линейных алгебраических
уравнений, определяемых формулой B0), разработан
специальный метод —метод матричной прогонки.
5. Метод матричной прогонки. Перепишем разностную
схему B0) в ином виде:
Um+lTi £Umn "T" ^m-ln ~T"
+ a {Umn+1 - 2итп + Umn-l) = Щ (Хт, Уп) C3)
т=1, 2, ,.., М-1, я=1, 2, ..., ЛГ-1,
"оя = ф@, #я), "ш = ф(^ Уп), я=1, 2, ..., /V—1,
т=1, 2, ..., М-1, А// = а>0.

§ 3] УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА 189
Пусть М ^> N. Введем обозначение
I uml
\ ит2
Um —
mN-1
m = 0, 1, ..., М.
C4)
Положим в формулах C3) л=1, 2, ..., N—1 и,
используя C4), запишем систему уравнений C3) в векторной
'форме:
Ит+1 + 4Ит + «т-1 = /т, /71=1, 2, ..., М-1, g
где Л — трехдиагональная матрица порядка N — 1 вида
г_B + 2а) а 0 ... О О О
а — B + 2а) а ... О О О
А
fm =
О 0 ... а — B + 2а) а
О 0 ... О а — B +2а).
Л2/(*«. #1)-аф(*т> 0)
/*7 (*т. #2)
/i2/ (xm, yN_2)
h*f (xm> yN-l)—a(P(Xm> b)
Фо =
ф@, Уд
ф@, #2)
ф @, Удг-l)
. Фа =
ф(я. #i)
ф (а, #2)
Ф (а> %-i)
Задача C5) аналогична задаче E7) из § 2 и ее
отличие состоит лишь в том, что она имеет векторную форму.
Формулы метода матричной прогонки подобны формулам
E8) —F0), F2), F3), поэтому мы не будем приводить
здесь их вывод и сразу изложим алгоритм метода
прогонки в векторном виде.
1. По формуле
Rm+i^-iA+Rm)-1, m-1, 2, ..., M-l,
(m)\N-l
полагая £?i = 0, вычисляем матрицы Rm=(Ri/Jl))^
= 1, 2, ..., Af, затем по формуле
Sm+l = Rm+l(Sm-fm), /И = 1, 2, ..., М - 1,
, т =

190 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
полагая Sj. = <Po, вычисляем векторы sm=(s\m\ sf>m), ...
..., s^ljO, Г —знак транспонирования, т= 1, 2, ..., М.
2. По формуле
ит-г = Rmum +sm, т = М, М —1, ..., 1,
полагая им = сра, вычисляем последовательно искомые
значения решения задачи C5): им, uM-i9 • •, Щ, и0.
Устойчивость описанного здесь алгоритма метода
матричной прогонки зависит от свойств матриц Rm. Если
окажется, что ||/?т|ш^1 для всех т, то устойчивость
к ошибкам округлений метода матричной прогонки будет
очевидной. Пусть %t (i = 1, 2, ..., Л^ — 1) — собственные
значения матрицы А; известно (см., например, [4]), что
Яг<-2, i=l, 2, ..., ЛГ-1. C6)
Мы рассматриваем евклидову норму матриц, понимая
под нормой матрицы ЦЛЦш корень квадратный из
наибольшего собственного значения матрицы Л*Л, где *
помечен переход к комплексно сопряженной и
транспонированной матрице. В нашем случае А —вещественная
матрица, поэтому Л*Л =А'А. Пусть а — ненулевой (N—1)-
мерный вектор-столбец. В силу свойств евклидовой нормы
и неравенства C6) имеем
iAo\lu^mm\Xi\-\\o\\lu^2\\o\\nu ' C7)
i
ибо | %i | ^ 2.
Предположим, что при некотором k ||/?й||ш<[ 1, и
покажем, что \Rk\-i\w\ <11. Тогда это будет означать,
что все ||/?m|iii< 1, m=l, 2, ..., М, так как |/?i||ni = 0.
Наряду с вектором а рассмотрим вектор т, определяемый
по формуле
т = — {A + Rk)G = Rk+1G.
Имеем
lTliii = Ha + /?AaIiii^li4a|iii-||/?Aa|ni>
^21ali,i-lal„i=|a|in.
Таким образом,
lx|ni^i|a||iii, lTliii = |/?AflaJin.
Значит, |/?ft+i|ni ^ 1, что и требовалось установить.
Мы описали метод матричной прогонки для случая,
когда направление прогонки выбирается совпадающим

§3]
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
191
с направлением оси Ох. Такое направление особенно
выгодно брать при условии M^N, так как основной
объем вычислений в методе прогонки падает на
определение матриц jRm+г по формуле Ят+1 = — (А + Ят)'г;
этот объем будет тем меньше, чем меньше порядок
матриц A-\-Rm. При условии, что M^N, выгоднее
обратить М матриц порядка N—1, чем N матриц порядка
Л1 — 1. Если задача C3) такова, что N^>M, то алгоритм
метода прогонки следует видоизменить, взяв за
направление прогонки ось Оу.
6. Правило Рунге. Укажем здесь один практический
прием, позволяющий на основе вычислений судить о том,
с какой точностью получены приближенные сеточные
значения решения.
Пусть и(х, у) — точное решение некоторой граничной
задачи, a uh(x, #) —приближенное решение этой задачи,
полученное по методу сеток с шагами h и /, l/h = const.
В методе сеток часто известен порядок относительно h
погрешности
Eh (х, у) = и (х, у) - uh (х, у). C8)
Предположим, что для гн (х, у) имеет место
представление г/г (х, у) = К (х, у) • hp, верное с точностью до величин
порядка 0(/ip+1), где К (х, у) —некоторая положительная,
ограниченная в области задания граничной задачи
функция, р — положительное число. При шаге, в два раза
большем h, получим
е2И*> У) = и(х, y)-u2h(x, у), C9)
е2Л (х, У) ^ К (х, у) • BА)" = 24h (х, у). D0)
Из формул C8)—D0) можно вывести правило для
определения 8Л (х, у) через сеточные значения uh (х, у) и
и*н(х, у)
*н(х, У) = "*(*' *£**<*'й. D1)
Формула D1) носит приближенный характер, ибо
приближенной была формула гн (х, у) = К (х, у) hp, на основе
которой получено выражение D1). Достоинство такого

192
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
выражения для гн (х, у) состоит в том, что эту величину
можно реально вычислить. Можно ожидать, что значение
будет более точным, чем uh(x, у). В этом и состоит
правило Рунге для уточнения сеточных значений ип(х, у).
В реальных вычислениях часто поступают следующим
образом. Находят решение при шаге /г, потом
вычисляют решение при шаге 2Д и сравнивают
значения ип(х, у) и иън(х, у) в одинаковых узлах. Если
эти значения совпадают на заданном числе знаков, то
решение uh (x, у) принимают за искомое. Если такого
совпадения нет, то шаг h делят пополам и вычисляют
решение ин/2(х, у). Далее контроль точности в
вычислении значений ин/2 {х> У) осуществляют аналогично
предыдущему.
7. Метод итераций для разностной задачи Дирихле.
Здесь мы рассмотрим итерационные методы,
приспособленные для решения разностных схем вида B0).
Основное внимание будет уделено наиболее простым вариантам
метода установления [3, 6].
Как мы видели, разностная схема B0), которую мы
перепишем в виде
Ахх (Цтп) ~Г Л-уу \Цтп) = [ \Хт, уп),
т=1, 2, ..., М-1, п=1, 2, ..., 7V — 1, D2)
итп = Ф {хт, уп), {mhy nh) e Гл,
где
Л-хх (Umn) — /,2 \Цт+\п ^тп "г ^т-1п)у
**УУ \Цтп) — /2 \Цтп\-1 £Umn -\- Umn-i),
аппроксимирует задачу Дирихле для уравнения Пуассона
di-hd^ = f(x,y)Ax,y)^D={0<x<a,Q<y<b},
u]r = (p(Q), Q —точка контура Г.

§3]
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
193
Сопоставим задачу D3) с родственной ей
нестационарной задачей о распространении тепла
pjr = q>(Q), Q — точка контура Г, '44/
v(x, у, 0)=г|)(х, у), (х, у)еД
где тр(х, г/) —произвольная функция, выбираемая так,
чтобы она возможно мало отличалась от решения
задачи D3).
В задаче D4) источник тепла f (х, у) и температура
на границе ф (Q) не зависят от времени t. Естественно
ожидать поэтому, что при /->- со будет выполняться
соотношение у->0, откуда
lim v (/, х, у) = и(х1 у),
t-+oo
поскольку в этом случае задачи D3) и D4) совпадают.
Можно предположить, что для достаточно больших
значений t, например для />7\ будет с необходимой
точностью верно приближенное равенство
и(/, х, у)?&и(х, у).
На этой закономерности основана идея метода решения
стационарных задач, состоящая в замене их подходящими
нестационарными задачами. Этот метод и ряд его
модификаций принято называть методом установления.
Запишем для задачи D4) простейшую двухслойную
разностную схему (см., например, B.52)):
<iх - «fun=Ахх ^+л^ ^ __f{Xmi уп) 9
т=1, 2, .... М —1, /г=1, 2, .... Л/-1,
р = 0, 1, 2, .... D5)
<а' = ф(хт, г/„), (mh, п/)еГл,
v°mn = q{xm, уп), т=1, 2, ..., М-1,
л=1, 2, ..., N-1,
7 В. И Крылов и др., т. И

194 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
и двухслойную разностную схему переменных
направлений (см., например, разностную схему B.54))
Wmn~vPmn = i [Ахх (wmn) + Ауу (vpmn) -/ (xm yn)l
V™A~Wmn = J [A^ (vmn) + Л„„ fe+ 0 - / (xm yn)]f
/?7=1, 2, ..., Af-1, /i=l, 2, ..., tf-l, D6)
p-0, 1, 2, ...,
t>m2" * = Wmn = ф (A'm, #/i), <M,  ^ Гл,
l>m/i = lK*m, Уп), /П=1, 2, ..., УИ-1,
л=1, 2, ..., W-1.
Доопределим функцию \|?(х, #) так, чтобы при (mft, n/) e
е Гл выполнялось условие
Обратим внимание на преимущества, которые имеют
разностные схемы D5) и D6) перед разностной схемой D2).
Последняя представляет собой систему линейных
алгебраических уравнений с числом неизвестных (М —l)(N— 1).
При больших М и N решение таких систем на ЭВМ
представляет собой довольно трудную задачу. В то же
время вычисления по формуле D5) весьма просты и носят
несложный рекурсионный характер. Вычисления по
формуле D6) сложнее, чем вычисления по формуле D5), но и
они намного проще вычислений, которые необходимо
проделать в задаче D2). Это станет очевидным, если мы
при решении задачи D6) воспользуемся методом
разностной прогонки по направлению переменной х для
вычисления значений {wmn} и методом разностной прогонки
по направлению переменной у для вычисления значений
{vmn}- Схему D5) будем называть простейшим явным
методом установления, а схему D6) — методом переменных
направлений.
Остановимся на выявлении условий сходимости явного
метода установления D5).
Пусть итп — решение разностной схемы D2), a vpmn —
решение разностной схемы D5) при некотором фиксиро-

§3]
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
195
ванном р. Положим ^n = ^n — timn и определим норму
по правилу
I* И 21 KIT-
Отметим, что по условию гР1П т, = 0 при всех р == 0, 1, 2, ...
Выясним, когда и с какой скоростью ||8р||->0 при р->оэ.
Если в разностной схеме D2) уравнение записать
в эквивалентном виде
О = и™-и™ = Ахх (итп) + Л^ (итл) - f [xm уп),
то на основании этой формулы и формул D2) и D5)
можно получить разностную схему для погрешности гртп\
США2 ГПП __ К ( р \ , Д / 0 \
— -< 4v* \Ътп) \ l vyy \bmn)i
Т
/л=1, 2, ..., М~1, /i=l, 2, ..., W-1,
р = 0, 1, 2, ..., D7)
eSxt* = 0, (mh, nt)£EThJ
т=1, 2, ..., Л4-1, /i=l, 2, ..., ЛГ-1.
В целях упрощения анализа задачи D7) будем
считать, что а = &=1, Л = / и, следовательно, M = N.
Решение разностной схемы D7) можно выписать
в явном виде, если воспользоваться собственными
значениями %ы и собственными функциями ^'п1) разностного
оператора.
Известно ([3], § 27), что
^=l-J(sin»|?- + sina^), Л=1 ЛГ, /=1 М,
ib^^sin^sin^ m = 0, 1, ..., М, /i = 0, 1, ..., М,
з функции г]/^ образуют ортонормированный базис.
Решение схемы D7) на слое номера р обозначим через гр
и там, где в этом не будет особой необходимости, далее
7*

196
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
не будем указывать зависимость этой величины от т, п,
аналогично будем писать г|зи/) вместо г|)^. Имеем
еР='Ё CkK4kJ\ D8)
k, i = \
где с*/ —некоторые постоянные.
Функции г|)<*'Z) выбраны таким образом, чтобы
выполнялось условие ^mkl)\vh = 0. Поэтому будет е£„!Гл = 0 и,
значит, решение е^, определяемое по формуле D8),
удовлетворяет разностному уравнению и граничному условию,
фигурирующим в D7). Чтобы выполнялось еще и
начальное условие в0тп = Ц{хт, уп) — итпу т. е.
М—1
kl
нужно в качестве постоянных сы взять разностные
коэффициенты Фурье для функции ty [хт, уп) — итп. Таким
образом, получим
м
cki = h* 2 (Ф(*ш Уп) - итп) 2 sin^-sin j£. D9)
m, я = 0
Формулу D8) можно записать в виде
м — \
где l^i^Cki-X^. Из этой записи видно, что числа \\Pkl
являются коэффициентами Фурье при разложении
погрешности 8^ по функциям г|)^' 1К Поэтому
М — 1
(еР, 8^)= 2] | <*,*,& |2
/г, / = 1
и, значит,
/М — 1 \ 1/2
'k, l = 1
/ М —
м—1
2
E0)
Обозначим max | %ы | через %\ тогда I А,^ | ^ Я.

§3J
УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
197
На основании E0) получим
\вЦ^Ще*\. E1)
Если А,<1, то из формулы E1) следует, что|;ер||->0
при р->оо; это стремление |)epj) к нулю тем быстрее,
чем меньше X. По определению Я —функция от т, т. е.
Я = Х(т), так как
max ! Xkl | = max
kA k,l
1
4т
2М
sin2^-f sin2
2M
= Цт).
Выберем т таким образом, чтобы К (т) имело наименьшее
значение. Обозначим
р(£, 0 = s^22^ + sin2^,
Очевидно, что
1<£, /^Af-1.
2 sin2
2ЛГ
;p(fe, 0<2cos2
2АГ
E2)
Рассмотрим семейство функций
aw(x)=l-gsp(fe, От
при 1^&, /^М — 1 и т>0. Все графики функций
этого семейства расположены в области Р, заключенной
Рис. 6.
между двумя прямыми, проходящими через точки С, D
и С, £ (рис. 6). Здесь С@, 1), £>(т*, 0),

198 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
Из рис. 6 видно, что подходящие значения т
расположены в интервале 0<т<т0. Если т^т0, то возможны
значения | а (т) | ^ 1. Оптимальное значение т должно
находиться в интервале т* •< т < т0, так как на этом интер-
вале функция а (т) = 1 — j-2- % sin2— убывает и а (т) < 1,
а функция | (Т (т) | = 1 — р- т cos2 ~ возрастает и | а (т) | <
< 1. Поэтому оптимальное значение топт может быть
определено из условия равенства
л О . 9 Я
1-A*TSin2M:
1 8 0 Я I
l-/?TC0S 2Ж|
на отрезке т*<т<т0. Простые вычисления дают
Из формулы Xki=l — r2-p(ky l)x при т = топт получим
я
^maxl %ы\\ = 1 —2 sin2
Л,/ т = топт
Если теперь мы захотим, чтобы \\гр\\ была меньше
некоторого наперед заданного числа б>0 F<j]e°|), то мы
должны число р определить из условия
|^K(l-2sin»^r.|Ie»]<e-
Отсюда получим
или, в частности,
InS-
ln(l-2sin^
р^?^-2Aп||е0|1-1пб) = О(М2).
Исследуем теперь сходимость метода переменных
направлений, определяемого формулами D6). Как и ранее,
в целях упрощения будем считать, что а = 6 = 1, h = l и
M = N.
ПОЛОЖИМ Втп = VPmn ~ Umn, Ьтп = Wmn — Umn. Подобно
формулам D7), на основании схем D2) и D6) можно

§ 3J УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА 199
записать задачу для определения погрешностей ъртп и б„
' = Аххфтп)-{-АуУ^ртп1
- — **-xx\Vmn) Л^ ^уу \ьтп )>
т E3;
б/л л |гл = £тп \rh = °>
^m^ == Y \^m» Уп) " Umn,
т, /i=l, 2, ..., М —1, р = 0, 1, 2, ...
Для погрешности е^ в этом случае имеет место
прежнее представление, даваемое формулой D8), с той лишь
разницей, что теперь собственные значения %н
вычисляются по другому правилу:
[\ -4тМ2 sin2 ~\ (\ -4тМ2 sin2 ~)
Я« = А ^2) Ж. . E4)
(l+4TM2sin2gj(l+4TM2sin2^j
Обозначим j = max|^/| и по аналогии с E1) получим
k,i
1^Ц<^||8°||. E5)
В силу формулы E4) должно быть |Я^|<<1. Значит,
<7<1. Поэтому из E5) следует, что lim |ер(|=:0. Сходи-
р -*оо
мость метода переменных направлений установлена. Как
видно, скорость этой сходимости зависит от величины q
и особенно от того, насколько q меньше 1. В связи с этим
вновь встает задача выбора т таким образом, чтобы
max j ЯЛ/1 был возможно меньшим. Обозначим
l_4xM2sin2||
l+4xM2sin2^
Тогда A^/^pfcP/. Поскольку
sm227w<sin 2Ж^С08 Ш'
то
Рм-1 < 9k < Pi.

200 УРАВНЕНИЯ Ё ЧАСТНЫХ ПРОИЗВОДНЫХ (ГЛ. 1
Отметим еще, что
max | %kl | = max | pk \ • max | Р/1 = /max I р* П2 = pf.
/г, / ^ / v k J
Здесь pi = pi (т) = max \pk |. Выберем т таким образом,
k
«■— >-t
Рис. 7.
чтобы рх(т) было наименьшим. Рассмотрим графики
функций (см. рис. 7)
1-4тМ28т2~;
Pk (т) =
l+4TM2sin'
Здесь
Ш
тчо&~
AM2 sin2 —
*м sin 2Af
Из этого рисунка видно, что т*<топт<х** и при
^о = топт должно выполняться соотношение
Pi(t0) = — Рм-гЫ-
Значит, для определения т0 получается уравнение
l_-4T0M2sin2^
l+4T0M2sin2~
1-4т0М2
Gossip-4т0М2 cos2 ^'
откуда
\r2 nM '

§ 41
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА 201
При т = т0 имеем
тах!А,| = 1-1^ + 0Ц2).
Если теперь мы захотим, используя метод
переменных направлений D6), добиться того, чтобы норма \\ер\\
не превосходила наперед заданного б (б << ||e°j|), то
необходимое для этого число итераций р определяется из условия
Ki=(i-^)Vi<e.
Отсюда получим оценку для р
р ^2 V " ,- х ^ —г- A11 8° — 1П б) = О (М).
н . L V2n\ V2nK |J u ' v ;
Отметим, что в методе установления при применении
явной схемы для достижения такой точности требовалось
выполнение О (М2) итераций. Поэтому, если М велико,
то метод с применением переменных направлений будет
выгоднее метода установления с явной схемой.
Искомое решение задачи D3) с помощью разностной
схемы D2) может быть вычислено с точностью О (h2) =
= OiM~2). Поэтому и число б следует задавать
согласованным с этой точностью. Во всяком случае брать его
по порядку меньшим величины О(тр) бессмысленно.
Если шаг т периодически менять, чтобы удерживать
вблизи нулевой точки значения Xkh то можно добиться
ускорения сходимости метода установления. На этой идее
основано несколько модификаций метода установления;
со многими из них можно ознакомиться по книгам [3, 6].
§ 4. Разностные схемы для уравнений
гиперболического типа
Будем рассматривать линейные дифференциальные
уравнения 2-го порядка гиперболического типа. Такие
уравнения часто встречаются в физических задачах,
связанных с переносом энергии и с процессами
колебаний. Метод сеток для уравнений гиперболического типа
по своей структуре имеет много общего с методом сеток
Для уравнений эллиптического и параболического типов.

202 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
Мы уделим основное внимание типичному и наиболее
простому по виду уравнению с постоянными
коэффициентами гиперболического типа — волновому уравнению
д2и д2и с / \ /14
l^~W = nx'y)' A)
где f (х, у) — известная функция, которую мы будем
считать дважды непрерывно дифференцируемой в некоторой
нижеуказываемой области D.
В связи с уравнением A) будем рассматривать
следующие задачи.
Задача Кош и. В области D={y>Q, — сю<<
<Cx<-f °°} найти дважды непрерывно
дифференцируемую функцию и (х, у)у которая в этой области
удовлетворяла бы уравнению A), а на прямой у = 0 —
начальным условиям
и(х, 0) = ср(х), ~|^о=г|ф), B)
где ф и я|) — заданные функции.
Смешанная граничная задача. В области
D = {y>0, a<x<f}} найти дважды непрерывно
дифференцируемую функцию и (х, у), которая в этой области
удовлетворяла бы уравнению A), а на границе Г
области D при у = 0 — начальным условиям B) и при х = а,
х = р~ одному из трех граничных условий:
а) (условиям первого рода)
и (a, y) = \ii(y), и(р, y)=ii2(y); C)
б) (условиям второго рода)
в) (условиям третьего рода)
■■Oi(y)\ D)
[fi(i/)^- + T2(i/)w| _=©i(y),
ж_р = и.ДО;
E)
дх
где \ii(y), Oi(y), %i(y)9 6i(y), <Oi(y), i'=l, 2,—известные
функции. Коэффициенты т* (у) и 8((у) подчинены
естественным условиям
Ы(У)\ + Ы(У)\>0, \^(У)\ + \8АУ)\>0.
Отметим, что условия C) и D) являются частным
случаем условий E).

§ 4] УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА 203
1. Решение задачи Коши. Рассмотрим метод сеток
решения задачи Коши для дифференциального
уравнения A) с начальными условиями B).
Выберем прямоугольную сетку, положив
xm = mh, /п = 0, ±1, ±2, ...,
yn = nl, n = 0, 1, 2, ..., А>0, />0.
Рассмотрим трехслойный пятиточечный шаблон
(т-!,п)
о—
(>77, Л-/) А
(/77, п) (ГЛ+/,П)
: о
и в соответствии с этим шаблоном определим
множество Uh внутренних узлов и множество Yh граничных
узлов. К множеству D\ отнесем узлы (хт, yn) gD, к
множеству Th отнесем узлы, лежащие на прямой у = 0. Вся
сеточная область Dh==D°h-\-Th будет состоять из узлов
(*да, yn)^D==D + T.
Используя взятый шаблон и формулу B.6), а также
аналогичную формулу для замены -^-у, получим
разностную схему
Ми<А>Н/<л>, (б)
где
Г „1 9//л Л-1,п unJr 1 __ О//п Л-пп — 1
U(u™)
(*Л =
fW=EE<
h2
Umi
и«-"т
/
m = 0, ±1,
/ \Xmi Уп)ч
ф(*/я),
1|> (*/я),
m = 0, ±1,
±2, ..
±2, ..
/2
., n=l, 2, ...,
., n= 1, 2, ...,

204 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ {ГЛ. 7
Эта схема аппроксимирует уравнение A) с погрешностью
порядка 0(/г2 + /2), а начальные условия —с
погрешностью порядка 0A). Действительно, на основании
формул B.3) и B.6) и по определению аппроксимации по-
лучим ЫМ*. у))=/<*> + ^*>,
где через ин (х, у) обозначены значения точного решения
задачи A), B) на сетке Dh, а для 8[{h) имеет место
представление:
6/lft>ss
h2 д*и
12 дх*
/2 д*и
Ы *Л
U*X. уп) 12 ^
%т-1 < %т < Хт+Ъ Уп-1 <С JZ/г <С Уп+Ъ
о,
2 дФ I/ мл' Уо<У1о<Уъ
\ /71 = 0, ± 1, ±2, ..., л=1, 2,
Порядок аппроксимации начальных условий можно
повысить. Для этой цели заменим -ч~
(хт> °)
"(*m> yi) — u(xm> У-i)
21
6 ' &/3
«•°)
по формуле
G)
(*«• "о1')
где r/-i = — /, —/<#о2)</. При этом мы предполагаем,
что решение задачи A), B) продолжимо в область G =
= {—l^y^O, — оо<х< + оо}. Из формулы G)
получим сеточное условие, аппроксимирующее начальное
условие ~^-\ =ty(x) с погрешностью порядка 0(/2):
2/
■ = *(U т = 0, ±1, ±2,
(8)
Значение £*„/ (8) можно исключить с помощью
разностного уравнения из (8) при п = 0. Имеем
h*
— / (*m> Уо)>
и потому (8) можно преобразовать к виду
: Ф (*т) + у /Л^д, (и°т) -Tlf (xm, у о),
(9)

§ 4] УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА 205
где л (ц.)-нЬ + '-2<+вЬ-'
**-хх Щт) — Jj2
Таким образом, вместо разностной схемы F) можно
записать другую разностную схему, аппроксимирующую
задачу A), B) с погрешностью порядка 0(h2-\-l2):
1А(и(А>) = /(А), A0)
где оператор Lk вычисляется так же, как и в формуле
F), а
{ / \%гт Уп)>
ф (Хт)>
f{h)^\
"Ф (*т) + о /A-v.v (Um) - 2 If (Xm, 0),
/и = 0, ± 1, ±2, ..., /2-1, 2, ...
Остановимся на вопросе численной реализации
схемы A0). Покажем, как по значениям и1)т и ихт
вычислить значения и2т.
В силу F) и A0) имеем
и]п = Ф Ы +1 (г|) (х,„) + -J /Л- (Ф (*«)) - | # (х™> °)) > (!!)
т = 0, ±1, ±2, ....
Разностное уравнение в схеме A0) перепишем в виде
и
= 2ипт+ 12АХХ (и?п)- ипм-l - l2f (xm, уп), A2)
т = 0, ±1, ±2, ..., /i=l, 2, ...
При /2=1 по формуле A2) вычислим значения и2т, т =
= 0, ± 1, ± 2, ...; значения и£, и и1т известны в силу A1).
Затем по A2) при /г = 2 вычисляем значения uzm через
уже известные значения и{ту игт и т. д.
В случае параболических уравнений мы видели, что
численная реализация явных разностных схем связана
с жестким ограничением на шаг т по времени. Можно
ожидать, что и численная реализация явной разностной
схемы A0) возможна лишь при определенных
ограничениях на к и /. Покажем, каким может быть отношение
l/h = y^>0 в случае гиперболического уравнения.

206
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
Рассмотрим однородное уравнение, соответствующее
уравнению A), &и д2и а
Aо)
дх2
ду2
= 0.
Присоединим к этому уравнению начальные условия B).
Разностную схему F) применительно к задаче A3), B)
можно записать в виде
. /я = 0, ±1, ±2, ..., л=1, 2, ....
Предположим, что в узле S с координатами (xh y(), где
/ — любое целое число, /^?2, нужно вычислить
значение uly пользуясь формулами A4). Положим в A4)
n = j—\, тогда мы видим, что и* определяется значе-
и\-2. Если ]' — 2>1, то зна-
Щ ~ly u[Zlp и(~~2 в свою очередь по
формуле A4) могут быть выражены через значения на
низших слоях
— 2 „/ — 2 ///-2 /,/—3 ///—3 ///-3 /!/ —4
ниями w{t}, w/_1
чения «/-} "' _1
Ui-\-2> ui-\-V ui
w~2
W/
-2 /i/-3 /,/-3 ///-3
-2' i+P / ' Ui—V
w.-
B конечном счете значение и[ может быть выражено
через значения и°т (m = i-\-s, s = 0, ± 1, ..., ± / — 2) и
^ (/72 == t-|-s, s = 0, ±1, ..., ±/—1). Все эти значения
Рис. 8.
находятся внутри треугольника (рис. 8), вершина
которого лежит в точке S, одна сторона лежит на прямой Ох,
две другие стороны проходят через точку S и образуют с
осью Ох углы SDC и SCD, равные соответственно arctg (—у)

§ 4] УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА 207
и arctgYi 7 = ^/^ = const >- 0. Треугольник SCD называют
треугольником определенности разностной схемы A4).
Таким образом, значение и[ в точке 5 определяется
разностным уравнением A4) и начальными значениями и*т
и ихт> лежащими на отрезках CD и EF.
Пусть теперь мы хотим вычислить в этой же точке 5
точное значение решения и(х, у) задачи A3), B). Из
теории уравнений математической физики известно, что
значение решения и (х, у) в точке 5 определяется
уравнением A3) и начальными условиями, содержащимися
на отрезке, высекаемом характеристиками, проходящими
через точку S, на прямой у — О, т. е. начальными
условиями на отрезке АВ. Характеристики уравнения A3)
перпендикулярны друг другу и образуют с осью Ох
углы, равные я/4 и Зя/4. Это —углы SAB и SBx.
Треугольник SAB называют треугольником определенности
дифференциального уравнения A3).
На рис. 8 изображен случай, когда ^ SAB<C L SCD
и tg B SCD) = у = l/h > 1. Такой выбор соотношения
шагов (l/h — у = const > 1) оказывается неудачным по
следующей причине. В этом случае треугольник
определенности разностного уравнения содержится внутри
треугольника определенности дифференциального уравнения,
поэтому начальных условий, задаваемых на отрезке CD,
будет недостаточно для определения решения в точке 5.
Если мы, например, изменим как-то начальные условия
на отрезках АС и DS, то это может изменить решение
задачи A3), B) во всей области D, в том числе и
в точке S. Однако сеточное значение и\ в точке S от
таких изменений не будет зависеть и остается прежним.
Значит, при l/h = y = const > 1 нельзя надеяться на
сходимость решения разностной схемы A4) к решению
задачи Коши для уравнения A3). Поскольку разностная
схема A4) аппроксимирует задачу A3), B), то она не
может быть устойчивой, ибо в противном случае из
аппроксимации и устойчивости следовала бы сходимость. Мы
показали, что при у > 1 сходимости быть не может,
значит, не может быть и устойчивости. Можно надеяться
на устойчивость при условии, что Д ASB содержится
внутри Д CSD. В нашем случае это будет при l/h = y^l.
Итак, в разностной схеме A4) для устойчивости
необходимо наложить условие v^l.

208 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
Если уравнение гиперболического типа имеет более
общий вид, чем A3), то для него, как правило,
треугольник определенности будет криволинейным,
криволинейным может быть также и треугольник
определенности соответствующего разностного уравнения. Однако
упомянутая закономерность (она впервые была высказана
Курантом, Фридрихсом и Леви), что треугольник
определенности дифференциального уравнения содержится в
треугольнике определенности разностного уравнения, должна
сохраниться, если мы хотим надеяться на устойчивость.
Достаточные условия устойчивости будут рассмотрены
ниже.
2. Решение смешанной задачи. Пусть уравнение
iw-W = f{x'y) A5)
задано в области
D = {0<#<y< + oo, a<x<p}.
Будем считать, что к уравнению A5) присоединены
начальные условия
и(х, 0) = ф(х), -ду\у„0 = У№' «<*<Р. A6)
и граничные условия третьего рода
К (у) -£+т2 (у) «L =<°i(y)»
ь
[fil (У) gx + б2 (У) и] = С02 (у).
A7)
Предположим, что смешанная граничная задача A5) — A7)
имеет единственное решение в области D = D-\-T, Г —
контур области D, и это решение вместе с производными
до 4-го порядка по х и по у включительно непрерывно в D.
Выберем прямоугольную равномерную сетку, положив
xm = mh, m = 0, 1, ...,М, Л = *~^, Уп= nl,
л = 0, 1, ..., Л/, Nl^Y<(N+l)l, />0.
Для замены уравнения A5) разностным воспользуемся,
как и в случае задачи Коши, пятиточечным явным
трехслойным шаблоном. По этому шаблону сеточную область
Dh разобьем на два множества: множество D\ внутрен-

§ 4] УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА 209
них узлов, Dh = {(xm% Уп), т=1, 2, ..., /V-l, я=1, 2,
,.., /V— 1}, и множество Гл граничних узлов, ГА =
= {(Хт, Уп), т = 0, 1, ..., М, я = 0; т = 0, /г = 0, 1,
..., N; т = М, /г = 0, 1, ..., #}.
На множестве D\ уравнение A5) и начальные
условия A6) аппроксимируются разностной схемой вида A0)
(далее будет приведена ее подробная запись). Для замены
граничных условий на прямых х = а и х = |5
воспользуемся формулами типа формул B3) и B4). Получим
и.,—и
М - 1
J\n-
Tln h
■ Т2/2^0
: СО.
'2/1»
©in, A8)
п = 0, 1, ..., N,
где rVl = Tl(yn)i т2ч = т2(#„) и т. д.
Легко видеть, что разностные граничные условия A8)
аппроксимируют граничные условия A7) с погрешностью
порядка 0(h).
Теперь на основании формул A0) и A8) запишем
разностную схему, аппроксимирующую граничную задачу
A5) —A7) с погрешностью 0(h + l2):
Lh(^h))=j'h\ A9)
где (
Lh{uh)^{
/г2 Р
m=l, 2, ..., М- 1, я=1, 2,
u°„u m = 0, 1, ..., M,
//1 -_//">
/
fin'
m = 0, 1, ..., /VI,
, N-l,
/V,
*m-i
f(A)
б2лим> " = 0, 1, ..., Af,
/V-l,
f(xm, #„), m = l,2, .... M-l, n=\, 2, .
ц>(хт), m = 0, 1, ..., M,
согп, и = 0, 1, ... ,
«).,„, n = 0, 1, ... ,
- /(*m. °)>  = 0, 1,
/V,
/v.
, M,

210
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
Отметим, что если хг (у) = 6i (у) = 0 и т2 (у) = 82 (у) = 1,
то разностная схема A9) аппроксимирует граничную
задачу A5) —A7) с погрешностью О (/г2-И2).
Численная реализация разностной схемы A9)
осуществляется почти так же, как и численная реализация схемы
A0). Вначале, используя формулы вида A1), вычисляем
значения на нулевом слое Um, потом значения на
первом слое и\п\ в обоих случаях т изменяется в пределах
О^т^М. Далее по уравнению A2) при лг = 1
вычисляем значения и\, и\, ..., им-\* Для вычисления на
втором слое значений и% и и% воспользуемся разностными
граничными условиями A8) при п = 2. Получим
Tl2 „2 to12
иь =
и"м =-
Tl-2-
$12
-/rr2<>
U\
U>M-
t12
1 +
-flT22'
Нщ2
612 + /1б22 Ж~1^б12+/1б22>
в предположении, что т12 — Ат22#0 и 6i2 + /i622 '^О.
Таким образом, мы указали, как по значениям а^ и а^,
/я = 0, 1, ..., М, вычислить зачения м^. Аналогично
по значениям и)п, и2т, т = 0, 1, ..., М, вычисляются
значения w?n и т. д.
3. Об устойчивости явной трехслойной разностной
схемы. Исследование устойчивости приведем на примере
смешанной граничной задачи A5) — A7) при условии,
что а = 0, р = 1, хг (у) = 6i (у) = 0, т2 (у) = б2 (у) si. В этом
случае для разностной схемы A9) правая часть будет
прежней, а оператор Lh примет вид
Ш%
<+i-2< + <
т— 1
r,«+l.
•к+<
/г2 /2
/и=1, 2, ..., М-1, л=1, 2,
и?и, ш = 0, 1, ... , /W,
и,1,, —и?,
tf-1,
/
[ им,
т = 0, 1, ... , М,
/г-0, 1, ..., Л7,
/г = 0, 1, ..., N.
Будем исследовать устойчивость разностной схемы
lfi [и^1)) = fW по начальным условиям. Для этого мы
должны установить два свойства:

§ 43 УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА 211
1) разностная схема Lh (z{h)) =g{h\ где
[О,
ah, m = 0, 1, ... , М,
у(Л):
{ Рт+^ЛххШ, т = 0, 1, ..., М,
о,
Ю,
однозначно разрешима;
2) верна оценка
где С —постоянная, не зависящая от ft и g(h). Правило
выбора норм в пространствах Uh и Fh будет оговорено
позже. При доказательстве устойчивости разностной
схемы Lh (u{h)) = f{h) мы будем следовать доказательству,
приведенному в [6].
Прежде всего отметим, что рассматриваемая
разностная схема явная, и поэтому свойство 1) очевидно.
Для установления свойства 2) разностную схему
Lh (z{h)) =g{h) запишем в развернутом и
преобразованном виде:
АуУ{гпт) = Ахх^т\ т=1, 2, ..., М-1,
/z=l, 2, ..., tf-1, B0)
г'т = а°т, *^ = о& + %, т = 0, 1, ..., М, B1)
где
2^ = 0, 4*=0, л = 0, 1, ..., N. B2)
Решение задачи B0) — B2) будем искать методом
разделения переменных. Найдем частные решения уравнения
B0) в виде
znm(k) = Xm(k).Y"(k)=£0.
После подстановки гпт (k) в уравнение B0) и некоторых
преобразований получим
Axx{XM(k)) АуУ(У"№
Xm{k) Yn(k)
= — h, B3)

212 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
где Xk — некоторое число. Из B3) и граничных условий
B2) получаем для Хт (k) задачу на собственные значения
Axx(Xm(k)) + XkXm(k) = 0,
X0(k) = XM(k)=0, Хт(к)=£0.
Она имеет решения
%k =T2sin2^-, Xm (k) = )/sin nkmh.
Для Yn (k) получим разностное уравнение второго порядка
или
Yn+1 (k) - B - l2Xk) Yn (k) + Yn~l (k) = 0. B4)
Для него характеристическое уравнение имеет вид
q*-B-2ak)q+l=0,
где ak = — l2Xk. Корни этого уравнения q12-=\— a±
± У di — 2ak. Если 0<а#<2, то корни 91,2 = 1 — °^ ±
— i Vak B — ock) комплексные и |^Jf2J = l. Введем новую
переменную ок1 полагая
cos ok = 1 — akl sin ok = Vak B — ock)*
Тогда
qi(k)=eia*, q2{k)=e-iQk.
Общее решение уравнения B4) имеет вид
Yn (k) = Ck (qx (k))» + Dk (q, (k))n = Ak cos nak + Bk sin nakt
где Ak и Bk — произвольные постоянные.
Теперь решение задачи B0) — B4) может быть
записано в форме (см., например, п. 3.7)
м — 1
гпт = S (А* cos nGk + Bk sin nok)-Xm(k). B5)
Пусть #£ и feft — коэффициенты разложений
Af-l М —1
/e=l fe=l
Потребуем, чтобы г,*, определяемое по формулам B5),

§4]
УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
213
удовлетворяло начальным условиям B1). Это возможно
при следующих значениях Ak и Вк:
Л гч* R 1 — COS Gfe 0
/ /P^+|a„(^)). B7)
Подставим эти значения Ak и fi* в B5) и, выполнив
преобразования, получим
a"+L^?b")Xm(k). B8)
COS [ ft - у ) 0Л
Af — I
A- 1,
ft=l \ COS -Oft
Оценим величину р (zn) =
rAf—1
2 W
m=l
Имеем
l
cosa*=l — аЛ, 8таЛ = 1ЛхЛB — аЛ), cck= ^l2Kk.
Наложим на шаги /г и / ограничение
/2
где е> 0 —любое число. Тогда
2
a<k'
Значит,
1+8*
Л=1, 2, ..., Л4- 1.
cosya*=]/ 1 -ya*Ss ]/
1 + e-
B9)
C0)
C1)
sin ok
Оценим величину —~~ снизу. Имеем
/
Но так как
2 sin -К оь , 2 sin -^ ok
-n_q*__£jcos|ffik^_X_*
/
/it:-
2 Sin 2 °* /2A-cos a,) /2aft l/T-
TO
^)Л*
8
T+T
Из B8) следует неравенство
рИ<рИ+рИ,
C2)
C3)

214 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ.7
где
тЬ
м — \
i
k = \ cosy0/?
akXm(k),
Sm —
k = \
Воспользовавшись формулами B6) и оценками C1), C2),
получим
-М —1 /М-1 \2у/а
_т=1 \/г = 1
гМ-1 -,1/г
2
.т = 1
^/Ч1 2
Lm==l
1/2
Таким образом, оценка C3) окончательно может быть
записана в виде
- м-\
р(г^/~ 21 <а*J
т=\
11/2
+
[Af-l 2 1
Lm=\ J
1/21
>, C4)
где л = 2, 3, ... , N.
В оценке C4) правая часть от п не зависит и может
быть истолкована как некоторая норма в пространстве Fh.
Это означает, что для схемы Lh(u{h))=f^ выполняется
и свойство 2).
Следовательно, достаточным для устойчивости по
начальным данным разностной схемы Lh(u{h))=f{h) является
условие B9), налагающее на шаги h и / ограничение
T^rh' где8>°-
Отметим, что для уравнений гиперболического типа
рассматриваются также и неявные разностные схемы;
об этом подробно сказано в [6].

§5]
МЕТОД ХАРАКТЕРИСТИК
215
§ 5. Метод характеристик
Для каждой точки Р из области D определения
решения исходной дифференциальной задачи существует,
очевидно, такая наибольшая область G(P)^D, что
значение искомого решения в точке Р зависит от
соответствующей информации об этом решении во всех точках
области G(P). При построении сходящихся сеточных
схем необходимо позаботиться о том, чтобы в сколь
угодно малой окрестности любой точки области G (Р)
при достаточно малых значениях шагов сетки имелась
хотя бы одна точка сеточной области, от информации
о разностном решении в которой зависит значение этого
решения в точке Р. В случае уравнений гиперболического
типа подобная область может быть описана с
использованием характеристик исходного уравнения. Последние
часто имеют достаточно сложный вид и, кроме того,
могут зависеть от искомого решения. Поэтому при
использовании простейших разностных схем, рассматриваемых
ранее, не всегда оказывается учтенным высказанное выше
требование. Более подходящим в таких случаях может
быть численное интегрирование здоль характеристик,
которое и лежит в основе одноименного метода. При
этом обычно используется сетка характеристик или
аппроксимирующая ее сетка. В тех случаях, когда
характеристики зависят от искомого решения,
построение такой сетки приходится проводить одновременно
с нахождением решения. Подобная организация
вычислений позволяет достаточно точно определять область
влияния исходных данных и, следовательно, строго учитывать
распространение возмущений, что придает методу
характеристик четкий физический смысл. Ниже мы изложим
основную идею этого метода на примере задачи Коши
для квазилинейного уравнения второго порядка
гиперболического типа.
i. Характеристики дифференциального уравнения.
Рассмотрим относительно неизвестной функции и = и(х, у)
дифференциальное уравнение второго порядка
ar + 2bs + ct + f = 0, A)
где
Г = ЫХху S = Uxyt t = Uyy9

216 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ.7
а функции
а = а{х, у, и, р, q), b = b(x, г/, и, р, <?),
с = с(х, у, а, р, 9). / = /(*» У» "» Р. <7)
являются известными функциями переменных л\ у, и,
р = иХ1 q = uy.
Такое уравнение обычно называют квазилинейным.
В частном случае, когда
а = а(х,у), b = b(x,y), с = с(х, у), f = f(x, у, и, р, q),
уравнение A) будем называть почти линейным. Линейным
же это уравнение будем называть в случае, когда
неизвестная функция а и ее частные производные входят
в A) линейно.
Если линейность уравнения не оговаривается особо,
будем иметь в виду более общий квазилинейный случай.
При этом функции а, 6, с, f будем считать достаточно
гладкими в некоторой области изменения их аргументов.
Присоединим к уравнению A), скажем, начальные
условия (условия Коши)
и!* = ф№). Р|/ = Ы<2). ?!/ = Ы<Э> B)
где / есть некоторая регулярная кривая в плоскости
переменных х, у, а ср, ^ъ г|?а — известные достаточно
гладкие функции точки Q этой кривой. Функции ф, уръ
г|>2 при этом не могут задаваться независимо. Вдоль
линии I они должны быть подчинены условию
согласования
du = pdx-\-q dy. C)
Поставленную дифференциальную задачу более
наглядно можно пояснить геометрически.
Уравнение A) задает в трехмерном пространстве
переменных х% у, и множество поверхностей, которые
обычно называют интегральными поверхностями данного
уравнения. Дополнительные же условия B), C)
геометрически означают следующее. Равенство а |г = ф (Q) задает
в указанном пространстве над линией / некоторую
линию /0. Задание же на / производных р = их и q = uy,
согласованных с и посредством условия C), определяет
в каждой точке линии /0 касательную плоскость. В сово-

§5]
МЕТОД ХАРАКТЕРИСТИК
21?
купности это равносильно заданию бесконечно узкой
полоски интегральной поверхности. Будем называть эту
полоску полоской первого порядка /^ Поставленная задача
Коши, таким образом, состоит в том, чтобы полоску
первого порядка /х, заданную условиями B), C), с помощью
уравнения A) расширить до интегральной поверхности
и — и{х, у).
Возникает вопрос, всегда ли можно осуществить такое
расширение и единственно ли оно. Выясним сначала,
можно ли с помощью уравнения A) расширить полоску 1г
хотя бы до полоски второго порядка /2, т. е. можно
ли по условиям B), C) с учетом A) найти на линии /
значения вторых производных г, s, t (если подобное
расширение понимать в буквальном смысле слова,
то после нахождения на линии / значений г, s, t его
можно приближенно осуществить, например, с помощью
формулы Тейлора).
Поскольку задание некоторой функции на линии
предполагает выполнение условий согласования типа C),
то применительно к функциям р, q на линии / будем
иметь
dp = r dx-\~s dy,
dq = sdx-\-t dy.
С учетом A) это позволяет для неизвестных значений г,
s, / на линии I указать следующую систему трех
линейных алгебраических уравнений
ar + 2bs + ct = — /,
rdx + sdy = dp, D)
s dx-\-t dy = dq.
Если для данной полоски 1Х определитель
I a 2b с I
А = \dx dy Q\ = ady2-2bdxdy + cdx2 E)
I 0 dx dy\
системы D) отличен от нуля, то г, s, / на / могут быть
найдены единственным образом. Тем самым полоска /х
может быть однозначно расширена до полоски /2.
Подобным же образом нетрудно убедиться, что в случае Д^О
однозначно определяются и полоски более высоких

218 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
порядков, что дает возможность однозначно осуществить
требуемое расширение.
Если же определитель E) равен нулю на 1Ъ то система
уравнений D) либо не имеет решения, либо имеет
бесчисленное множество решений. Условие
& = ady*-2b dxdy + cdx2 = 0 F)
может выполняться и не для всей полоски 1Ъ В
дальнейшем для нас особый интерес будет представлять
именно та полоска, для которой условие F) выполняется
всюду, при этом система D) остается совместной. Такую
полоску /х станем называть характеристической полоской.
Соответствующую линию /0 будем называть
характеристической кривой (характеристикой) в пространстве
переменных х, у, и, а ее проекцию I — проекцией
характеристической кривой (характеристикой) на плоскости
переменных х, у.
В случае характеристических полосок значения
вторых производных решения на / определяются с помощью
исходного дифференциального уравнения лишь с
точностью до слагаемого, являющегося произвольным
решением однородной системы линейных алгебраических
уравнений, соответствующей системе D). Такие полоски
допускают неоднозначное расширение до полосок второго
порядка, и по ним возможно ветвление интегральных
поверхностей.
Так как в случае характеристических полосок
выполняется условие А = 0, но система D) при этом разрешима,
то уравнения этой системы линейно зависимы. Выяснив
эту зависимость, мы найдем для элементов таких полосок
дополнительно к C), F) новые соотношения.
Требование совместности системы D) означает, что
ранг матрицы коэффициентов этой системы должен
совпадать с рангом ее расширенной матрицы. Так как на
линии / определитель матрицы коэффициентов системы D)
равен нулю, а по крайней мере один из ее миноров
второго порядка
dx dy
0 dx
>
dy 0
dx dy
отличен от нуля, то ранг этой матрицы, а следовательно

§5)
МЕТОД ХАРАКТЕРИСТИК
219
и ранг расширенной матрицы системы D), равен двум.
Отсюда вытекает равенство нулю всех миноров третьего
порядка у последней матрицы, что дает возможность
записать:
а 2Ь —£
dx dy dp
О dx dq
а с —/
dx 0 dp
0 dy dq
\ = a(dxdp — dy dq) + 2Ь dxdq-\-f dx2 = 0,
= a dy dp -f с dx dq -f f dx dy = 0,
2bdydp + c (dy dq - dxdp) + fdy2 = 0.
Получив из F) выражение
2b
dy
dx
с
0
dy
~/|
dp
[dq
dy--
Vb*-
■dx
G)
и использовав его в каждом из трех полученных выше
равенств, во всех случаях после простых преобразований
приходим к соотношению
(adp + fdx){b±Vb2-ac) + acdq = 0.
(8)
Итак, в случае характеристических полосок
дополнительно к условиям согласования C) и требованию F),
из которого следуют соотношения G), должны
выполняться также равенства (8). В совокупности все эти
соотношения
ady-(b±Vb2-ac)dx = 0,
(a dp + fdx) 0 ± Vb2-ac) + acdq = 0,
du = pdx-\-qdy
(9)
называют обычно уравнениями характеристических
полосок или уравнениями характеристик. Два уравнения,
получающиеся из первого равенства (9) при выборе
знака у корня, называют уравнениями направления
характеристик, а остальные — дифференциальными
соотношениями вдоль характеристик.

220
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
Уравнения направления характеристик, записанные
dy _ Ь±УЬ2-ас пп
dx ~ a ' {lV>
можно рассматривать как обыкновенные
дифференциальные уравнения первого порядка относительно
неизвестной функции у = у(х). Правые части уравнений A0)
содержат дискриминант ас — Ь2 исходного уравнения A).
Если в некоторой точке данной интегральной
поверхности выполнено условие ас — Ь2< 0, то через эту точку
будут проходить две разные характеристики с разными
проекциями на плоскость переменных х, у. Подобные
точки обычно называют гиперболическими точками
интегральной поверхности. В случае, если условие ас — Ь2 <0
выполняется для всех точек интегральной поверхности,
эту поверхность называют гиперболической. Если же все
интегральные поверхности данного дифференциального
уравнения вида A) в некоторой области изменения
переменных х, у удовлетворяет условию гиперболичности, то
в этой области рассматриваемое уравнение относят к
гиперболическому типу. Подобным же образом через
условия ас — Ь2 = 0 и ас — Ь2>0 вводят соответственно
параболические и эллиптические уравнения. Для
параболических уравнений обе характеристики сливаются в
одну, а в эллиптическом случае вещественных
характеристик нет.
В дальнейшем мы будем рассматривать лишь
гиперболические уравнения. Для таких уравнений можно
говорить о двух семействах характеристических полосок.
Вдоль каждой из двух характеристик, выходящих из
данной точки интегральной поверхности, в силу (8)
выполняются разные дифференциальные соотношения. Если
ввести обозначения
}и)== Ъ-VW-ac ^ }j2)=b+\fb*
то после умножения (8) на b±Yb2 — ас уравнения
характеристических полосок можно привести к виду
dy-Wdx^O,
a(dp + K2)dq)+fdx = 0, A1)
du = р dx + q dy

§ 5]
МЕТОД ХАРАКТЕРИСТИК
221
для характеристических полосок первого семейства или
кввду du-№dx = 0,
a{dp + №dq)+fdx = 0, A2)
du = pdx + qdy
для характеристических полосок второго семейства.
Уравнения A1), A2) позволяют для каждого решения
исходного уравнения A) находить как характеристики
обоих семейств, так и само решение вдоль этих
характеристик вместе с его первыми производными. При этом
интересующие нас величины не могут, вообще говоря,
находиться независимо, так как в случае квазилинейного
уравнения A) величины X{i\ i=\, 2, являются
функциями переменных х, у, и, р, q. В частных случаях
линейного или почти линейного уравнений вида A),
когда коэффициенты а, Ь, с и Яц), ЯB), а значит, и
проекции характеристик на плоскость переменных х, у> не
зависят от значений и> р, q, указанные проекции могут
быть найдены как решения обыкновенных
дифференциальных уравнений
% = №Цх,у), A3)
§ = №(х,у) A4)
соответственно для характеристик первого и второго
семейств. В таких случаях уравнения A1), A2) можно
решать в два этапа: сначала с помощью уравнений
направления характеристик A3), A4) строится сетка
характеристик, а затем из дифференциальных соотношений на
построенных характеристиках находятся величины и> р, q.
Рассмотрение численных методов решения уравнений
характеристических полосок мы и начнем со случая,
когда возможно подобное упрощение процесса решения.
2. Построение сетки характеристик. Будем считать,
что коэффициенты а, Ь, с в уравнении A) не зависят от
и, р, q\ при этом в некоторой достаточно широкой
области изменения переменных ,т, у выполняется условие
гиперболичности ас — Ь2<0. Условия Коши B), C) будем
предполагать заданными на некоторой линии I, не

222
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
принимающей ни в одной точке характеристических
направлений этого уравнения.
Через крайние точки М0, Мм этой линии проведем
характеристики обоих семейств исходного
гиперболического уравнения A). Тем самым будет построена область,
состоящая из двух криволинейных треугольников, в
которой существует единственное решение поставленной
задачи Коши. Будем решать эту задачу численно лишь
в одном из таких треугольников MGPMN (рис. 9). Для
точки Р этот треугольник будет
играть роль области G (Р), о
которой шла речь в начале
этого параграфа.
Аппроксимируем эту область сеточной
областью следующим образом.
Выберем на линии /, несущей
начальные данные, в
дополнение к точкам Л!о, MN еще N — 1
(не обязательно равноотстоя-
, Мдг_1 и проведем через каждую
из этих точек обе характеристики исходного уравнения.
Точки пересечения этих характеристик, принадлежащие
треугольнику M0PMN, примем, за узлы
аппроксимирующей сеточной области. Будем находить эти точки
последовательно по слоям, принимая за нулевой слой точки
Л40, Мь ... , MN линии /.
Допустим, что все узлы n-го слоя (п^О) сетки
характеристик построены. Тогда любая точка 3 с
координатами Хз, Уз слоя номера я+1 может быть найдена как
точка пересечения характеристик первого и второго
семейств исходного уравнения, проведенных соответственно
через точки 1 {хъ ух) и 2 (х2у у2) я-го слоя сетки. Такие
характеристики могут быть построены как решения задач
Коши для уравнений A3) и A4) при начальных данных
y(Xi)=yi Для *'=1 и i = 2. Интегрируя последние
уравнения соответственно в пределах от х1 до х3 и от х2 до
х3, получим Хз
У* = У1 + \ Kl)(x, y)d*>
Уз = у2+\ Л<а>(х, y)dx.
хг
Рис. 9.
щих) точек Мъ М2> ...

§5]
МЕТОД ХАРАКТЕРИСТИК
223
Так как на рассматриваемых участках характеристик
зависимость у от х, вообще говоря, неизвестна, то
координаты хз, Уз точки пересечения избранных характеристик
обычно приходится находить из A5) приближенно.
Рассмотрим простейшие вычислительные правила,
применяемые для этих целей.
Аналог метода Эйлера. Если интегралы в
правых частях равенств A5) заменить приближенно
соответствующими квадратурными суммами простейшей
формулы левых прямоугольников, то можно записать
Уз ^ У\ + Ц1) (Хз - *i), Уз ъ* Уг + К* (*з - х2), A6)
где
Погрешность каждого из приближенных равенств A6)
будет, очевидно, величиной порядка /г2 (см. выражение
для остаточного члена формулы Эйлера F.2.2)), где
h=--max{ \х3 — хг\, \х3 — х2\}.
Равенства A6) дают нам систему двух приближенных
линейных алгебраических уравнений относительно
неизвестных значений Хз, уз-
Аналог метода трапеций. Чтобы получить
более точные, чем A6), равенства, связывающие
координаты точек У, 2, 3, заменим интегралы в A5) по
двухточечной квадратурной формуле трапеций (см. E.3.2)).
Тогда можно записать
Уз ^ Ух Л—д g 3 (*з - ХХ),
Уз^Уг+ " g (хв — Х2).
Погрешность каждого из таких приближенных равенств
будет уже величиной порядка h3 (см. выражение E.3.3)
для остаточного члена формулы трапеций).
Система A7) является аналогом метода трапеций
F.3.2) численного интегрирования обыкновенных
дифференциальных уравнений вида F.1.1). Она, вообще говоря,
нелинейна. Неизвестные значения х3, Уз из этой системы,
как правило, находят итерациями. Начальные прибли-

224 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 1
жения л'зо» Узо к этим значениям можно получить из
линейной системы типа A6)
#зо = Ух + К1} (*зо - Xi)> Узо = У г + >ч} (А'зо - х2).
Уточнение же исходных значений можно осуществлять,
например, посредством последовательного решения
линейных систем
#з/+1 — #2 i 2 \*з/+1 — л2;, г — и, i, z, ... ,
которые очезидным образом строятся на основе формул
A7). Обычно при этом ограничиваются одной-двумя
итерациями.
Еще более точные вычислительные правила
построения сетки характеристик можно получить, если
сконструировать соответствующие аналоги более точных
методов (как одношаговых, так и многошаговых) численного
интегрирования уравнения вида F.1.1). Достаточно
удобные расчетные формулы можно построить, например, по
аналогии с одношаговыми методами, рассматриваемыми
в § 4 гл. 6. Для каждого уровня точности
использование таких формул сводится к последовательному
решению фиксированного числа систем двух линейных
алгебраических уравнений с двумя неизвестными. Аналоги
многошаговых методов менее удобны для этих целей,
так как они предполагают привлечение на каждой
характеристике не одного, а нескольких найденных ранее
узлов сетки, которые расположены, вообще говоря,
неравномерно. Все это предопределяет громоздкость и
неоднородность соответствующих вычислительных правил.
3. Нахождение характеристических полосок. . Сначала
будем иметь в виду случай, когда сетка характеристик
предварительно построена. Значения величин и, р, q
в узлах этой сетки будем искать последовательно по
слоям (см. рис. 9). В простейшем случае эта задача
сводится к нахождению величин и3 = и (x3l */з), рз =
= Р (*з> Уз), q3 = q{x3i Уз) по известным значениям щ =
= и (xh yt), pi = р (xh y>), qi = q (xh yt), i = 1, 2. Для
нахождения этих величин используем из уравнений ха-

§ 5]
МЕТОД ХАРАКТЕРИСТИК
225
рактеристических полосок A1), A2) лишь
дифференциальные соотношения
a(dp + №dq)+fdx = 0,
du = pdx+qdy,
a(dp + №dq)+fdx = 0,
du = p dx + q du
вдоль характеристик первого и второго семейств
соответственно. Подобно изложенному в предыдущем пункте,
на основании A8), A9) можно записать точные равенства
\[a(dp + № dq)+fdx] = 0,
1
][a(dp + №dq) + fdx] = 0, B0)
2
3
«1 + «2 | 1
Us- 2 , 2
J (pdx + qdy)+^ (pdx + q dy)
Прибегая, как и ранее, к различным способам
приближенной замены интегралов в этих равенствах, получим
различные вычислительные методы нахождения величин и3, Рз, <7з-
Аналог метода Эйлера. Использование
простейших квадратурных формул левых прямоугольников
позволяет на основании B0) записать приближенные
равенства
fli (Рз - Pi) + аг%? (q3 - ft) + /i (х3 - хг) ъ* 0,
^2 (Рз - р2) + О^*1' (^з ~ Яг) + h (*в - Х2) ъ* 0,
W3^i^:^ + y[pi^3-^i) + 9i(y3~yi) +
+ Р2(^3-Л'2) + 92(УЗ~У2I,
гДе at = a(xh yt), fi = f(xh yh uh ph q().
Тем самым относительно неизвестных значений ws» Рз, <7з
получим приближенную систему трех линейных
алгебраических уравнений, которая может быть решена
последовательно: сначала из первых двух ее уравнений находят
приближенные значения величин р3у q3y после чего из
последнего в системе B1) уравнения можно непосредственно
вычислить приближенное значение функции и в точке 3.
8 В. И. Крылов и др., т. II

226 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
Аналог метода трапеций. Замена интегралов
в B0) квадратурными суммами двухточечной формулы
трапеций позволяет указать для приближенного нахождения
величин и3, рз, Яз следующую систему численных уравнений:
+ Цк(х3-х1)^0,
4*-1р,-рл+а^+9а*? (*-*) +
и3.
"l + «2
+ Щк(х3-х2)ъО,
{Ц^(х3-х1)+Ц^(у3-у1) +
B2)
В отличие от B1), первые два уравнения системы B2)
уже, вообще говоря, нелинейны; при этом неизвестные
^з, Рзу Яз входят в каждое уравнение системы.
Систему B2) можно решать итерационно. Исходные
значения и3о, Рзо» <7зо ПРИ этом обычно находят из
линейной системы типа B1), а процесс их уточнения проводят
также на основании линейных систем вида
—2 Фзг+1 — Pi) ~\ 2 W3/+1 ~" ™ *
i /i + /(*a» #з> Ц3г, Рзп ^з/) /^ _ х \ __ о
—2— vPa/+i — Рг/ i § W3*+i — <7г/ ~г
1 /8 + /(*з» Уз> "зЬ Psh йзд /„ v\_n
-j 2 \Х3 —■ л 2) — U ,
«3,4, = ^ + 2 РЧг^ <*» - *> + iiIT^ <* - Л) +
+ _^31±L(X3_X2)+ii±|2£±L(^-y2)]) f = 0,.l, 2, ...
При каждом фиксированном значении i процесс решения
таких систем, как и в случае аналога метода Эйлера,
распадается на два более простых этапа.
Подобно изложенному в § 4 гл. 6, могут быть
построены и более точные вычислительные методы
нахождения характеристических полосок. Не останавливаясь

§ 3]
МЕТОД ХАРАКТЕРИСТИК
227
здесь на рассмотрении таких методов, сделаем лишь
несколько замечаний относительно нахождения
характеристических полосок для более общего случая
квазилинейного уравнения A), когда характеристики зависят от
решения поставленной задачи Коши. В этом случае
сетка характеристик должна строиться одновременно
с нахождением значений функций и, р, q в ее узлах.
Равенства типа A5) сейчас не могут рассматриваться
независимо от B0). В квазилинейном случае, очевидно,
необходимо одновременно рассматривать все пять равенств:
з
Уз — У1 = \№1] (*, У, и, р, q)dx,
1
з
Уъ -Уъ=\ ^{2) (х, У у и, р, q) dx,
2
3
\{а(х, #, и, р, q)[dp + №(x, у, и, р, q)dq] +
1
+ f(x, у, и, р, q)dx} = 0,
з
^ {а(х, у, иу р, q) [dp + X(i) (*, у, и, р, q) dq] +
2
+ f(x, у, а, р, q)dx} = 0,
иг + и2 . 1
w8 = —2 hy
з
^ (pd.v+<7^)+J (pdx + qdy)
A 2
Ha основании этих равенств, подобно изложенному выше,
можно построить, например, следующий [^аналог
метода Эйлера:
Уз-У1^(хз — Х1)Ь{1)(хъ уъ иъ рх, <7i),
i/з — //2 ^^ (^з — Х2) Л^2) (Х2, у2, и2, р2, ?2),
а (*ь #ь иь рь 0i) x
x[(p8-Pi)+^2)(*b Л, «ь Pi. <7j)(<73-<7i)] +
+ /(*i> 0i. «i, Ръ <7i) (*з--*i)-^ 0,
a{x2l y2f u2J p2, q2) X
X[(p3-P2) + ^A)(^ #2, u2, p2, ^(^-^J-f
+ /(x2, y2, u2y p2, <?2) (x8 - x2) ъ 6,
+ 2" iPi (a;3 ~ *i) + qi (Уз - </i) + p2 (*з ~ *2) + q2 (y3 - y2)].
8*

228 уравнения в частных производных [гл. 7
Решение этой линейной системы может быть
расчленено на три простых этапа: приближенные координаты
точки 3 находятся из системы двух ее первых уравнений,
значения р3, <7з вычисляются приближенно с помощью
двух следующих уравнений, после чего из последнего
уравнения непосредственно находится приближенное
значение функции и в точке 3. При этом, очевидно,
координаты узлов следующего слоя сетки характеристик
могут быть приближенно вычислены лишь в том случае,
если известны не только координаты узлов предыдущего
слоя, но и значения функций «, р, q в этих узлах.
Аналог метода трапеций в квазилинейном
случае приведет, как и ранее, к нелинейной системе
пяти численных уравнений, однако каждое уравнение
системы будет содержать уже все пять неизвестных
величин Х3, {/з, И3, рз, Яз.
В процессе итераций решение этой нелинейной
системы, подобно изложенному выше, можно свести к
последовательному решению линейных систем; при этом
решение каждой из них может быть расчленено на три более
простых этапа.
При некоторых дополнительных ограничениях с
использованием, скажем, способа построения
вычислительных правил, основанных на принципе последовательного
повышения порядка точности результата (см. § 4 гл. 6),
могут быть построены и более точные методы решения
уравнений характеристик.
§ 6. Метод прямых
В методе прямых, в отличие от метода сеток,
операцию дифференцирования аппроксимируют не по всем, а
только по некоторым избранным переменным, тем самым
дифференциальные уравнения приближенно заменяют
дифференциально-разностными с меньшим числом
непрерывных независимых переменных. Этот метод можно
рассматривать как предельный случай метода сеток, когда
шаги разбиения по части независимых переменных
стремятся к нулю. Метод прямых, таким образом, позволяет
понизить размерность дифференциальной задачи. Подобное
понижение размерности бывает особенно оправданным
в тех случаях, когда роли независимых переменных ока-

§6]
МЕТОД ПРЯМЫХ
229
зываются неравнозначными. Такие задачи нередко
встречаются в приложениях.
С основными вариантами метода мы познакомимся
ниже на примере линейных дифференциальных уравнений
в частных производных второго порядка, хотя метод
применим и в случае нелинейных уравнений любых
порядков и систем таких уравнений.
1. Поперечные схемы метода прямых для уравнений
параболического типа. Пусть в полуполосе 0 <; х ^ 1,
t^O поставлена следующая граничная задача:
ut = L(u) + f(x9 t), (l)
и(х, 0) = <р(*), B)
и (О, /)=Ы0> > 0=Ы0. C)
Здесь
L(u)~a(x, t)uxx + b(x, t)ux + c(x, t)u.
Существование и единственность достаточно гладкого
решения рассматриваемой задачи предполагаются. Будем
искать его приближенно методом прямых в
прямоугольнике П{0^л:^1, 0^/^Т<сх>}. В зависимости от
того, будем ли мы при этом аппроксимировать производные
по х или по /, получим продольный или поперечный
вариант метода. В соответствии с историческим развитием
вопроса рассмотрим сначала поперечный его вариант.
Обозначим через Их решеточную область 0<л:<;1,
t = tnr=nx, n=ly 2, ..., N (Nx = T)y а под ее границей
Гт будем понимать множество, состоящее из отрезка
O^jc^I прямой / = 0 и точек @, tn), A, tn), n =
-1, 2, ..., N.
Рассмотрим задачу A) —C) на Пх-\-Тх. Производную
щ{х, t) в A) при t = tn, n=l, 2, ..., Ny заменим
приближенно левосторонним разностным отношением
щ{х> tn)^uJ^uzphJjtA. D)
Тогда для решеточной функции, задаваемой системой
функций ип=ип(х), А1 = 0, 1, ..., N, приближенно
представляющих функцию и(ху t) на отрезках O^x^l
прямых t = tn> n = 0, 1, ..., N, в IIt 4- Гт можно поставить

230 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
следующую дифференциально-разностную граничную
задачу:
Un{x)~-xUn-l{X) = Lfl(un) + fn(x), E)
и0(х) = ч>(х), F)
М0)=Ы'я)> М1) = Ы<д)- G)
Здесь
Ln {ип) = а„ (л:) и£ (х) + Ъп (х) и'п (х) + сп (х) ип (х),
ап(х) = а(х, tn), bn{x) = b(x, tn),
сп(х)=с(х, tn), fn{x)=f{xy tn).
Задача E) — G) распадается на N граничных задач
для обыкновенных дифференциальных уравнений второго
порядка. Действительно, так как функция и0 (х) известна
из начального условия F), то неизвестные функции
и« (х)^и(х, tn), /г = 1, 2, ..., Ny можно находить
последовательно, решая при каждом значении п=\, 2,..., N
одно обыкновенное дифференциальное уравнение второго
порядка вида E) с соответствующими граничными
условиями G).
Построенная вычислительная схема метода прямых
достаточно четко поясняет геометрический смысл
названия метода. В силу этого в многомерном случае
рассматриваемый метод часто называют методом плоскостей или
методом гиперплоскостей.
На примере вычислительной схемы E) — G) можно
проследить связь между методом прямых и методом сеток.
Если дополнительно к прямым t = tn = nT, /г = 0, 1, ..., N,
в прямоугольнике П провести прямые x = xm = mh, m —
= 0, 1, ..., М (М/г—1) и во всех внутренних точках
(хт, /„), т=1, 2, ..., M—U п=1, 2, ..., N,
полученной сеточной области, кроме замены типа D), произвести
также приближенную замену производных иХХ1 их их
простейшими симметричными выражениями через значения
функции и, то, с учетом дополнительных условий B), C),
получим широко распространенную в практике вычислений
двухслойную трехстолбцовую неявную схему метода
сеток. В пределе при й->0 эта схема, очевидно,
переходит в схему E) — G) метода прямых. В § 2 для
случая уравнения теплопроводности было показано, что

§ 61
МЕТОД ПРЯМЫХ
231
подобная неявная схема метода сеток может применяться
при любом отношении шагов т и /г. Поэтому предельный
переход при Л->0 в ней оправдан, и можно надеяться,
что схема E) — G) метода прямых будет вполне
приемлемой для вычислений.
Параллельно с этой схемой можно построить и
другую поперечную схему метода, заменив производную щ
не левосторонним, а правосторонним разностным
отношением. Однако следует ожидать, что такая схема метода
прямых будет уже мало пригодной для вычислений.
Действительно, в § 2 было выяснено, что явная схема
метода сеток для уравнения теплопроводности,
построенная с использованием правосторонней замены
производной щ, может применяться для счета на большое число
шагов по / при условии типа x^O(h2). Последняя же
вычислительная схема метода прямых получается из
подобной явной схемы метода сеток предельным переходом,
когда /г->0. При этом неизбежно будет нарушено
упомянутое выше соотношение между /гит.
По построению очевидно, что погрешность
аппроксимации вычислительной схемы метода прямых будет, вообще
говоря, меньше соответствующей погрешности связанной
с ней разностной схемы метода сеток. В схеме E) —G),
например, эта погрешность возникает лишь за счет
приближенной замены D) и имеет вид
гп{х) = \ии(х, /л-еЛт), 0<ея<1, /2 = 1, 2, ..., N. (8)
При построении соответствующей вычислительной схемы
метода сеток дополнительно к (8) будут внесены ошибки
и за счет приближенной замены производных ихх, их.
Правда, в последнем случае аппроксимирующая задача
будет, как правило, более простой с точки зрения ее
реализации. Однако в ряде частных случаев метод
прямых может оказаться предпочтительнее и в этом
отношении. Например, поперечная схема E)—G) особенно удобна
в том случае, когда коэффициенты уравнения A) не
зависят от х. Соответствующая аппроксимирующая
задача приводит тогда к последовательному решению
граничных задач для обыкновенных дифференциальных
Уравнений второго порядка с постоянными
коэффициентами.

232 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
Если в прямоугольнике П производная utt ограничена
по абсолютному значению, то погрешность (8) будет
величиной порядка т. Для задач с более гладким решением
можно ставить вопрос о построении более точных
вычислительных схем. Повысить порядок погрешности
аппроксимации можно следующим простым приемом.
Рассмотрим уравнение A) при / = /л и t = tn^1.
Производную щ в первом случае заменим левосторонним
разностным отношением, а во втором —правосторонним.
Тогда можно записать
ц(*. tn)-u(x, ;я-г) =L(u)\Mn + fn(x) + }uti(xf /л-вят),
o<e;<i,
откуда
и(х9 tn) — u{xt tn^) =
т
Ч»)|,-,в+М») !,.,„_, ;„(*)+/„-!(*)
где
= ^ (е; ~ 6> "<« <*' '" ~ ^ ° < ^ < 1 • (9)
Соответствующая схема метода прямых принимает вид
»П (*) — "л-1 (*) ^ ^Я («я) + *-Я-1 ("я-l) | //I (*) + /я-1 (*) /|qv
0<*<1,
и0(*) = ф(*)» 0<дг<1, (И)
ия@)=Ч>0(/л), Ml)=*i('*). /i=l, 2, ..., ЛГ. A2)
Поперечная схема A0) —A2) точнее схемы E) —G)
в том смысле, что порядок малости в сравнении с т ее
погрешности аппроксимации на единицу выше, чем в
случае схемы E) —G) (см. остаточные члены (8) и (9)).

§63
МЕТОД ПРЯМЫХ
233
Каждое дифференциальное уравнение в рассмотренных
выше поперечных схемах метода прямых связывает
приближенные значения неизвестной функции и (х, t) на двух
соседних прямых. Такие двухслойные схемы метода
особенно часто используются в практике вычислений.
Дальнейшего повышения порядка точности поперечных
схем можно добиваться, например, на пути построения
многослойных схем метода. Заменив в уравнении A)
производную щ на прямой t = tn {n = q, q-\-\> ..., N)
приближенным выражением через значения функции и
при t = tn, t = tn~ly ..., t = tn-.q, нетрудно по аналогии
с рассмотренным выше построить пример (q-\- 1)-слойной
поперечной схемы метода прямых. Если приближенные
значения функции и на начальных прямых 1 = 1Ъ t = t2, ...
..., t = tg-1 были как-то найдены предварительно, то
построенная (q-\- 1)-слойная схема дает возможность
находить приближенные значения функции и на
очередных прямых t = tq, t = tg+l9 ..., t = tN последовательно
как решения соответствующих обыкновенных уравнений
второго порядка с граничными условиями вида G).
Через значения функции и при t = tn, 1 = 1п-Ъ ...
..., t = tn-g можно приближенно выразить производную^
не только при t — tny но и на любой из прямых t = tn^lf
t = tn-2, •••> t = tn-g. Соответственно этому получим
различные варианты (q-\- 1)-слойных поперечных схем метода.
Необходимо отметить, что полученные так схемы не
всегда пригодны для вычислений, так как они могут
оказаться неустойчивыми. Комбинируя их, как и в
случае двухслойных схем, можно построить (<7+ 1)-слойные
схемы повышенной точности аппроксимации. В этом
случае вместо A0) будем иметь более общие уравнения
Я о
~ У Atu^t (х) =JiBi [Ln-t («„_,) + /„-/ (а-)], A3)
n = <7, q+h ..., N.
Аппроксимацию уравнения A) можно и непосредственно
искать в виде A3) с неопределенными коэффициентами
Ai и Bh i=^0, l, ..., q. Выбор этих параметров можно
подчинить, например, требованиям максимального порядка
аппроксимации и устойчивости вычислений.

234 УРАВНЕНИЯ 6 ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
2. Продольные схемы метода прямых для
параболических уравнений. Будем иметь в виду, как и ранее,
первую граничную задачу A) —C). Однако сейчас при
построении вычислительных схем метода прямых будем
аппроксимировать операцию дифференцирования не по
времени /, а по пространственной переменной х. Для
этого, подобно случаю поперечных схем, предварительно
исходную область приближенно заменим решеточной
областью, проведя прямые x = xn = nh, я = 0, 1, ..., N
(Nh= 1). На каждой из внутренних прямых х = х„, п= 1,
2, ..., JV—1, производные ихх и их аппроксимируем
через значения функции и на нескольких соседних
прямых. Если для этих целей использовать, скажем,
простейшие симметричные выражения, то, подобно случаю
поперечных схем метода, можно записать:
и' li\—n N\Uii+l(t) — 2^nit) + Un_1(t) . b ,^ Un+1(t) — Un^(t) .
+ Cn(f)Un(t)+fn(t), *>0, A4)
Фо@э МО = яМ/), ^°> (Щ
<р(хл), /1=1, 2, ..., #-1. A6)
un(t)?^u{xn, t),
an(t)=a(xn, t),
bn(t) = b(xn,.t),
cn(t) = c(xn, /),
fn(t)=f(Xn, t).
Тем самым нахождение приближенных значений ип (f)
решения и(х, t) на прямых х = хп, п=1, 2, ..., N— 1,
сводится к решению задачи Коши для системы N — 1
линейных обыкновенных дифференциальных уравнений
первого порядка.
Погрешность аппроксимации задачи A) —C) задачей
A4) —A6) предопределяется неточностью замены
производных ихх, их соответствующими простейшими
симметричными выражениями через значения функции и и будет,
очевидно, величиной порядка /i2, если решение и (х, t)
обладает достаточной гладкостью (скажем, функция и
■п v/
<*п w
«о @ =
и» @) =
Здесь

§ 61
МЕТОД ПРЯМЫХ
235
имеет в рассматриваемой области ограниченную по
абсолютному значению четвертую производную по х). В тех
случаях, когда решение будет более гладким, можно
ставить вопрос о построении вычислительных схем,
характеризующихся более высоким порядком погрешности
аппроксимации. Подобно случаю поперечных схем,
повышать точность аппроксимации можно по-разному.
Остановимся здесь лишь на некоторых из простейших
подходов к решению этой проблемы.
Прежде всего обратим внимание на то, что в случае
аппроксимирующей задачи A4) —A6) при каждом из
значений /i=l, 2, ..., N— 1 соответствующее обыкновенное
дифференциальное уравнение первого порядка связывает
три функции ww.i@» w« @» un±i(t), но при этом каждое
отдельно взятое уравнение содержит производную лишь
одной из них. Можно записать несколько схем типа
A4) —A6), для которых соответствующие обыкновенные
дифференциальные уравнения, как и выше, будут
связывать три соседних по номеру функции, но при этом
схемы могут отличаться друг от друга, в частности, тем,
что будут содержать производные разных функций (из
указанных выше). Линейным комбинированием таких
схем можно построить новые вычислительные схемы, для
которых каждое обыкновенное дифференциальное
уравнение первого порядка будет связывать не только три
соседних по номеру функции, но и производные каждой
из них. Удачным выбором соответствующей линейной
комбинации, подобно случаю поперечных схем, можно
получить схему с более высоким порядком погрешности
аппроксимации.
При построении подобных вычислительных схем
исходную задачу в рассматриваемой области удобнее записать
в виде
р(х, t)iit = uxx + c(x, t)u + f(x, t), A7)
и(х, 0) = <р(*), A8)
и (О, 0 = Ы0. и0> 0 = %('). О9)
Такая форма записи может быть легко получена из
прежней, если в уравнении A) заменой неизвестной функции
исключить слагаемое с первой производной по х.

236
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
Рассмотрев уравнение A7) на трех соседних прямых
х = хп±1, х = хп, x = xn-i, можно составить линейную
комбинацию соответствующих равенств с произвольными
коэффициентами Л, В, С. При этом, в частности, будет
образована следующая комбинация значений второй
производной:
Аихх(хп+1, t) + Buxx{xn, t) + Cuxx(xn„ly t). B0)
Представив эту комбинацию по возможности более точно
через значения функции иу скажем, в форме
цц(хя+1> 0 + Ри(*я, 0+уц(*я-ь 0 BD
очевидным образом можем построить интересующую нас
аппроксимацию задачи A7) —A9) (заметим, что
уравнение A7) не содержит производной их).
Коэффициенты Л, В, С и а, C, у подберем так, чтобы
в разложениях по степеням h выражений B0) и B1)
совпадали слагаемые до членов с возможно более высокими
степенями h. Указанные разложения легко могут быть
выписаны, если предварительно с помощью формулы
Тейлора составить разложения около точки (хп, t)
значений и (хп ±hy t) и ихх (хп ± А, /) функций и и ихх.
Простыми вычислениями можно проверить, что выбором
параметров Л, В, С и а, C, у удается добиться
совпадения таких разложений, вообще говоря, лишь до членов
с /г3 включительно; при этом указанные параметры должны
быть подчинены ограничениям
1 5
Y = a, Р = — 2а, Л = С=^а, B=ga.
Тем самым непосредственно может быть проверена
справедливость равенства
гп @. B2)
«+1- B3)
ихх \хп+1>
где
f) + mxx(xn
=
rn(t) =
12
, t) + u
и(Хп+ь 0-
40
дх*
XX (ХП-1
2и(хп,
h?
А
, 0
t)+
хп.
и (хл-ъ
-1<1п
01
1
.<*/

§61
МЕТОД ПРЯМЫХ
237
Теперь уже, используя B2), нетрудно записать
следующую вычислительную схему продольного варианта
метода прямых:
Рд+i @ и'п+1 @ + 10РЯ @ и'п @ + Ря-1 @ "п-1 W
12
- /Z2 i~
д ^i-i (*> ц^+1 @+ 10g« @ "/i (Q+fii-i @ иЛ.! (Q ,
"*" 12 "^
+ /^(о+у+/^(од />0> B4)
М'НЫО. ^ (/)=%(/), /5*0, B5)
М0) = Ф(*„), /z=l, 2, ..., tf-1. B6)
Смысл используемых в этой записи обозначений вполне
аналогичен применяемым ранее.
Если решение исходной задачи имеет ограниченную
по абсолютному значению производную ^ 6' > то в силу
B3) порядок погрешности аппроксимации в случае схемы
B4) — B6) будет на две единицы выше, чем в случае
схемы типа A4) —A6).
Дальнейшего повышения точности аппроксимации при
построении продольных схем метода прямых можно
добиваться за счет привлечения информации более чем на
трех соседних прямых. При этом, как и в случае
поперечных схем, аппроксимирующие уравнения можно искать
непосредственно в виде равенств, аналогичных A3),
с произвольными коэффициентами, подчиняя выбор
последних соответствующим требованиям. Следует, однако,
заметить, что в случае продольных многослойных схем при
аппроксимации дифференциального уравнения на прямых,
близких к граничным, обычно возникают трудности,
связанные с нарушением однородности процесса
приближения. В некоторых частных случаях, правда, эти
трудности удается существенно ослабить за счет использования
граничных данные.

238 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
3. Метод прямых для уравнений гиперболического типа.
Пусть в полуполосе 0^ж;1, t^O поставлена
следующая граничная задача:
utt + g(x, f)ut = L(u)+f{x, t), B7)
и{х, 0) = q>(*), щ(х, 0)=Ф(*), B8)
"(О, 0=Ы0. . 0=Ы0- B9)
Здесь L (и) имеет такой же вид, как и в A). Будем
считать, что а(х, /)^а>0. Существование и единственность
достаточно гладкого решения задачи B7) — B9)
предполагаются. Будем искать это решение методом прямых
в прямоугольнике П{0^я<;1, 0^:/^Т<со}.
Как и в случае параболических уравнений, здесь
также можно говорить о продольном и поперечном
вариантах метода. Приведем сначала пример поперечной
схемы.
Прямоугольник П аппроксимируем решеточной
областью Пт + 1\; при этом, в отличие от параболического
случая (см. п. 1), к границе 1\ рассматриваемой области
отнесем также и интервал 0<;с<;1 прямой t = t1 = T.
На каждой прямой t = tn+1 для л=1, 2, ..., N—1
производные щ и ии заменим следующими левосторонними
разностными отношениями первого и второго порядков
соответственно:
Щ (*, tn+1) ъ *<*' ^-Ц(*,_Ь) f C0)
и lv i \^U^ tn+l) — 2u(X> *п) + и(Х, /я„г) п],
ии (х, гп+1) я^ -^ • к61)
Кроме того, на прямой / = 0 для аппроксимации
производной ut используем правостороннюю замену
Ut{Xt 0)^и(х,,)-и(Х,0)^ C2)
Это позволит для решеточной функции, задаваемой
системой функций ип (х) ^и (я, Q, м = 0, 1, ..., Af, поставить

§6]
МЕТОД ПРЯМЫХ
239
в области Пг + 1\ следующую
дифференциально-разностную граничную задачу:
ил+1(х)—2ип(х) + ип^(х) , „ /^и^М-ЦдМ
—: ~2 Г gn+l \Х) =
= Ln+i{un+1)+fn+1(x), C3)
«оМ = фМ, и*(х)-и°{х)=Ф(х), C4)
. ип+1 @) = % (tn+1) мЛ+1A)=г|I(/я+1). C5)
Здесь использованы обозначения, совершенно
аналогичные применяемым в параболическом случае.
Процесс решения аппроксимирующей задачи C3) — C5)
очевидным образом может быть расчленен на следующие
этапы. Сначала по заданной функции и0(х) = <р(х) из
C4) непосредственно получаем
иг (х) = ф (х) + тФ (х).
После этого последовательно находим функции и2(х),
и3(х), ..., uN(x); при этом нахождение каждой из них
сводится к решению одного обыкновенного
дифференциального уравнения второго порядка вида C3) с
граничными условиями первого рода C5).
Так как ошибки приближенных равенств C0)— C2)
являются малыми величинами, вообще говоря, лишь
порядка т, то построенная вычислительная схема
характеризуется только первым порядком погрешности
аппроксимации. Если при аппроксимации дифференциального
уравнения B7) для замены производной щ вместо C0)
использовать более точное равенство *)
„ и i \~,3"(*> W —4ц(*» *я) + Ц(*, */i-i) (осл
Щ \х-> 1п+1) ^ ^ » ' ^
то при малых значениях т>0, как правило, удается
уменьшить часть погрешности аппроксимации исходного
уравнения, зависящую от неточности замены первой
производной по времени. При некоторых дополнительных
предположениях более точно можно заменить первую
*) Разлагая значения и (х, tn_1)t и (х, tn) функции и(х, t) по
формуле Тейлора около точки (х, ?ft4-i)» нетрудно показать, что
погрешность приближенного равенства C6) будет величиной порядка т2.

240 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
производную и при аппроксимации начального условия.
Предположив, например, что решение исходной задачи
продолжимо хотя бы на один шаг т вниз под прямую
t = 0, можно вместо C2) использовать более точное
симметричное представление первой производной:
„,(*, 0)я,"(^х)-и(х, -х)_ C?)
Введенную при этом новую неизвестную функцию u.x (x)
можно исключить, рассмотрев уравнение C3)
дополнительно и при м = 0.
Использование приближенных равенств вида C6),
C7) позволит, как правило, несколько уменьшить
погрешность замены исходной задачи, однако порядок этой
погрешности, вообще говоря, не возрастет, так как при
аппроксимации уравнения B7) была использована
грубая левосторонняя замена второй производной. Если же
для замены производной ии использовать более точное
симметричное представление через значения функции и
на трех соседних прямых, то соответствующая
вычислительная схема, следует ожидать, будет мало пригодной
для вычислений. К такому выводу можно прийти с
помощью рассуждений, подобных проведенным в п. 1 и
основанных на связи метода прямых с методом сеток.
Заметим, что последнее еще в большей мере относится,
очевидно, к вычислительной схеме, основанной на
правосторонней замене второй производной.
Чтобы построить поперечную схему метода прямых,
характеризующуюся более высоким порядком погрешности
аппроксимации в сравнении с C3) —C5), можно, подобно
параболическому случаю, составить, скажем, полусумму
C3) и сходного уравнения, основанного на
правосторонних заменах производных щ, utt> Аппроксимацию
начального условия при этом естественно проводить с помощью
приближенного равенства C7). Погрешность
аппроксимации такой вычислительной схемы будет, очевидно,
величиной порядка т2.
Если воспользоваться формулой типа B2), то можно
построить и более точную трехслойную аппроксимацию
исходного уравнения, в котором предварительно с
помощью соответствующей замены искомой функции
исключен член с первой производной по времени. Подобно
параболическому случаю, дальнейшего повышения порядка

§61
МЕТОД ПРЯМЫХ
241
точности замены исходного уравнения можно ожидать
на пути построения многослойных аппроксимаций,
сходных с A3).
Процесс построения поперечных схем метода прямых
для гиперболических уравнений, как мы видели, во
многом схож со случаем уравнений параболического типа.
Подобные аналогии еще более сильно проявляются в
случае продольных схем метода. Если, например, в
рассматриваемой области вместо прямых, параллельных
оси х, провести прямые
x=zxn = nh, я = 0, 1, ..., N (#А=1),
то, поступая аналогично изложенному в п. 2, для задачи
B7) — B9) можно построить следующую продольную схему
метода прямых:
*п (t) +gn (t) un (l)=an (t) ""+' @У + Ц-1 @ +
+ bn (t) Um^~hUn~l(t) +cn (t) un (t)+fn (/), *>0, C8)
Щ (t) = Ь @> ^N (t) - Ь @, t ^ 0, C9)
M0) = <P(*„), и'п@) = Ф(хп), n==l, 2, ..., tf-1. D0)
При записи этой схемы использованы обозначения, вполне
аналогичные принятым ранее.
Аппроксимирующая задача C8) — D0) может быть
истолкована как задача Коши для системы N—1
линейных обыкновенных дифференциальных уравнений
второго порядка относительно неизвестных функций ип (/),
/7=1, 2, ..., Л/—1, приближенно представляющих
искомую функцию и (х, t) на прямых х = хпл п=\, 2, ..., N — 1.
По способу построения схема C8) — D0) совершенно
аналогична схеме A4) —A6). Подобное можно наблюдать
и при построении продольных схем более высокого порядка
аппроксимации.
4. Метод прямых для эллиптических уравнений. Пусть
в прямоугольнике П {0 <: х <; X, 0 <: у <; У) существует
и единственно решение задачи Дирихле
uyy + L(u)=f(x, у), D1)
и(х1 0) = cp(*), и(х, У) = Ф(х),
и@, у)=Ц(у), и(Ху у) = Ч(у), ^ )

242 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
где
L(u) = a(x, y)uxx + b(x, у)их + с(ху у) и, а(х, у) >я>0.
Будем предполагать решение достаточно гладким и станем
искать его приближенно методом прямых.
Для задачи D1), D2), в отличие от рассмотренных
ранее эволюционных задач, исчезает принципиальное
различие между поперечным и продольным вариантами метода:
в обоих случаях мы получаем в качестве
аппроксимирующей граничную задачу для системы обыкновенных
дифференциальных уравнений второго порядка.
В качестве примера построим здесь применительно
к рассматриваемой задаче Дирихле одну из простейших
вычислительных схем метода.
Прямоугольник П аппроксимируем решеточной
областью, проведя, скажем, прямые у = #л = пА, п = 0, 1, ..., N
(Nh= Y). Производную иуу при # = #я, /i= 1, 2, ..., W — 1,
выразим приближенно через значения функции и>
опираясь на известную формулу
и (у „ ^ "(*> Ум) — 2и(х> Уп) + и(*, Уп-i)
иУУ\л> Уп) — JJ2
~ 12 W ' -К9<1. D3)
Тогда, используя обозначения, совершенно аналогичные
применяемым ранее, можно записать
им (х)-2и^х) + ип_г(х) + Ln (Un)=fn (jc)> 0<х<Х, D4)
u0(x) = q>(x), uN(x) = (D(x), 0<ЖХ, D5)
М0) = Ч>Ы. un(X) = W(yn), /г= 1, 2, ..., iV- 1. D6)
В силу D3) дифференциально-разностная задача D4) —
D6) аппроксимирует исходную задачу Дирихле с
погрешностью порядка /i2. Она сводится к решению системы
обыкновенных дифференциальных уравнений второго
порядка с граничными условиями первого рода.
Опираясь, например, на формулу типа B2), можно
построить и более точную трехслойную аппроксимацию
дифференциального уравнения D1). Соответствующая
вычислительная схема метода прямых в случае достаточно

§ 6]
МЕТОД ПРЯМЫХ
243
гладкого решения исходной задачи (см. B3)) будет
характеризоваться погрешностью аппроксимации порядка Л4.
Как и в случае эволюционных задач, дальнейшего
повышения порядка погрешности аппроксимации можно
ожидать, например, на пути построения многослойных
схем метода. Способы построения таких схем и основные
трудности, которые могут возникнуть при этом, очень
близки рассмотренному ранее случаю продольных схем
для уравнений параболического и гиперболического типов.
Вопрос построения вычислительных схем метода
прямых обсуждался выше на примере ориентированных по
осям прямоугольных областей. В случае областей более
сложной формы применение этого метода может быть
сопряжено с определенными осложнениями. В самом деле,
проекции gn> п = 0, 1, ..., N, на ось координат
внутренних сечений области избранными прямыми совпадут при
любом числе прямых только для соответствующим образом
ориентированного прямоугольника. В общем же случае
п-е уравнение рассматриваемой вычислительной схемы
метода, связывающее приближенные значения искомого
решения на соседних прямых номеров от п — р до n-\-q,
без дополнительных предположений определено лишь на
пересечении
Gn = П gn+i-
— р ^ i ^ q
Если же считать такие уравнения выполняющимися и
вне Gn, то даже для очень простых областей
аппроксимирующая задача при некоторых N может оказаться
неразрешимой. Чтобы преодолеть подобные затруднения,
иногда предпочитают продолжать непрерывно внутрь
области функцию, задающую граничные условия, а
уравнения аппроксимирующей системы рассматривают лишь
на соответствующих пересечениях Gny при этом
вычислительный алгоритм приходится строить специальным
образом (подробнее об этом см., например, в [2], гл. 10,
§ 8, п. 2).
Часто удается избежать подобных затруднений,
разбивая рассматриваемую область на полосы не прямыми,
а кривыми линиями, избранными с учетом формы области.
Один из методов понижения размерности задач,
допускающих подобное разбиение, мы сейчас и рассмотрим.

244
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
§ 7. Метод интегральных соотношений
Пусть в области D с границами х = а, х = Ь> у —О,
уг=д = Ь(х)>0 рассматривается следующая система т
дифференциальных уравнений в частных производных
дивергентного вида:
-foPi(x, У у "ъ и2у ..., um)-\--0-Qi(x, у у иъ и2, ..., ит) =
= Fi(x, у, иъ и2, ..., ит), i'=l, 2, ..., /я. A)
Здесь ulJt u2y ..., ит — искомые функции независимых
переменных х, у у а Р/, Q/, Fi — известные достаточно гладкие
функции переменных х, у, иь иъ ..., um. Будем считать
также, что имеется в общей сложности т дополнительных
условий на прямых х = а, х = Ь и т условий на границах
0 = 0, у = 8(х).
Предполагая существование и единственность
достаточно гладкого решения поставленной задачи, зададимся
целью свести приближенно решение этой задачи для
дифференциальных уравнений в частных производных к
решению некоторой аппроксимирующей задачи для
обыкновенных дифференциальных уравнений. Для этого от системы
дифференциальных уравнений A) перейдем к системе
интегральных соотношений следующего вида: .
6(х) б(х) 6(х)
J ^-fi(y)dy+ J *°LU{y)dy= j FfiMdy* B)
0 0 0
i=l, 2, ..., т.
Такой переход заключается в интегрировании по у от 0
до б (х) каждого уравнения исходной системы,
умноженного предварительно на некоторую известную функцию
fi(y), * = 1, 2, ..., т. Функции/* (#), i = l, 2, ..., m, при
этом играют роль сглаживающих функций. Для различных
значений i эти функции мргут и совпадать между собой.
Соотношения B) легко могут быть приведены к виду
б<*)
£ J Pifi(y)dy-8f(x)Pi{6)fl(8) + Qi{6)fi(b)^
о
6 {х) 6 (х)
-Qmft(fi)- \ Qif'i(y)dy= \ Fih(y)dy,
0 0
1=1, 2, ..., т9 C)

§7]
МЕТОД ИНТЕГРАЛЬНЫХ СООТНОШЕНИЙ
245
где для сокращения записей введены обозначения типа
М8(*)] = Ы6),
Si{a) = Si[xy уу иг{х, У), U2(X, у), ..., Um(x, уI,-а{х).
Отметим, что за счет умножения исходных уравнений
на сглаживающие функции и последующего
интегрирования часто удается построить интегральные соотношения
вида C), более благоприятные для приближенной замены,
чем дифференциальные уравнения A). При аппроксимации
соотношений C) можно поступить, например, следующим
образом.
Область D разобьем на N, вообще говоря,
криволинейных полос линиями
У = Уп(х) = ±6(х), п = 0, 1, ..., N, D)
и каждую из функций Ph Qh Fiy i = 1, 2, ..., m,
представим тогда интерполяционно через ее значения на
границах всех полос. Например, для функции Pi получим
приближенное равенство
N
Pi (х, у, щ, и2, ..., ит)ъ £ шл (у) РЦп), E)
где через (оп(у)у п = 0, 1, ..., N, обозначены
интерполяционные коэффициенты, конкретный вид которых зависит
от выбора базисных функций, положенных в основу
интерполирования (в случае алгебраического интерполирования
в качестве соп(у), п = 0, 1, ...,#, могут быть взяты
интерполяционные множители Лагранжа (см. п. 1.3.1)).
Будем искать сейчас лишь значения ицп)(х) =
= Щ[х, Уп(хI f=l, 2, ..., т; л = 0, 1, ..., А/, функций
Ui{x> У)* i= if 2, ..., ш, на линиях D). С целью
согласования числа интегральных соотношений с числом
подлежащих разысканию функций uiw{x)y запишем
равенства вида C) для каждой из функций fij(y), i = l, 2, ...
..., /n; / = 1, 2, ..., Л/, где //;- (у) выбираются заранее
с учетом имеющейся информации об исходной задаче; при
этом для каждого значения / = 1, 2, ..., т функции
/ii» /i2> • • • у fiN должны быть линейно независимыми (для

246 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
различных значений i избираемые функции могут
совпадать). Тогда будем иметь
6(Х)
£ j Pit и (У) dy - б' (х) Р1 {rfif (б) + Q, F)/,7 (б) -
О
- Qi {0)fif @) - f Qif'n (У) dy = \ Ffa (y) dy9
о о
f=l, 2, ..., m; /= 1, 2, ..., N.
Заменив в этих соотношениях функции Ph Qiy Fh i —
= 1, 2, ..., m, их приближенными выражениями типа E),
получим для m(N-\-\) приближенных значений uin(x),
i= 1, 2, ..., m; n = 0, 1, ..., N, функций ui{n) (x) получим
систему mN обыкновенных дифференциальных уравнений
первого порядка
N
i 2 а-> w Рг" -б' w Putt, (б)+Qisfa (б) -
JV N
t = l, 2, ..., т; / = 1, 2, ..., tf, F)
где
«//*(*) = \ <*n(y)fu(y)dy,
о
б (ж)
Pi/*(*) = J <*п (У) Гч (У) dy,
о
Ля^ЛО» J//.W. я W. ^W. • ••> Ит«М]
(аналогично определяются Qin и /^Л). Используя условия
на границе области D, часто удается поставить для
системы F) граничную задачу, которая позволяет
единственным образом найти интересующие нас функции uin (х),
t = l, 2, ..., т\ п = 0, 1, ..., N.
Описанный выше метод понижения размерности
исходной дифференциальной задачи обычно называют
обобщенным методом интегральных соотношений, в отличие от
простого метода интегральных соотношений, в котором
сглаживающие функции не вводятся, но, с целью согла-

§ 7]
МЕТОД ИНТЕГРАЛЬНЫХ СООТНОШЕНИЙ
247
сования числа интегральных соотношений с числом
неизвестных функций, интегрирование выполняется не поперек
всей области D, а лишь от нижней до верхней границы
каждой полосы, на которые исходная область разбивается
линиями D). В этом случае вместо соотношений C) будем
иметь следующую систему интегральных соотношений:
~ ^ Pidy- y'n {X) Pi {П) + Уп-1 (X) Р( {п-1) +
+ Qi(n)-Qi{n-i)= \ Ftdyy G)
Уп-lM
i = 1, 2, ..., т; п= 1, 2, ..., N.
Как и в случае обобщенного метода интегральных
соотношений, функции Ph Fiy t = l, 2, ..., m, стоящие под
знаком интеграла в равенствах G), заменяются
приближенными, например, интерполяционными выражениями
через их значения на границах полос; при этом может
быть использована как сквозная интерполяция вида E),
так и кусочная интерполяция, когда приближение
осуществляется по значениям рассматриваемой функции лишь
на части из линий разбиения D), что позволяет обычно
упростить вид аппроксимирующей задачи (удобные и
достаточно точные двухслойные схемы метода можно
получить, пользуясь линейным интерполированием по
значениям функции на границах полосы, поперек которой
выполняется интегрирование).
Простой метод интегральных соотношений можно
трактовать как частный случай обобщенного. Он, например,
получается из последнего, если в качестве функций fi/(y),
i = l, 2, ..., m; / = 1, 2, ..., N, взять «ступенчатые»
функции
(О, y<yf-u
fi/(y)= U У;~1^У^У/,
10, у,<у.
В свою очередь простой метод интегральных соотношений
можно рассматривать, очевидно, как обобщение метода
прямых.

248
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
§ 8. Понятие о методе моментов
и методе Галёркина
Применительно к обыкновенным дифференциальным
уравнениям эти методы были рассмотрены нами в § 12
гл. 6. Здесь мы изложим вычислительные схемы метода
моментов и метода Галёркина на примере линейного
уравнения
L{u) = a{x, y)^- + 2b(x, y)J^L- + c{x, у)^т +
; ду -Г - \ У} ду2
дх ' "" ^' у/ ду
+ 2d {х, у) -~ + 2е (х, у) -~ + g (x, y)u = f(x, у). A)
Будем предполагать, что коэффициенты этого уравнения
и свободный член f(x, у) есть функции, непрерывные
в области D, ограниченной контуром Г. Предположим
также, что это уравнение имеет в области D —D + Г
эллиптический вид, т. е. всюду в этой области
выполняется неравенство
Ь2 (х, у)-а (х, у) • с (х, у) <0.
Присоединим к уравнению A) условие на границе Г
в виде
a|r = q>(Q), B)
где ф —известная функция, Q — точка на контуре Г.
Поставим задачу: найти функцию и (х, у), которая
в области D удовлетворяла бы уравнению A), а на
контуре Г —граничному условию B).
Для построения вычислительной схемы метода
моментов рассмотрим две системы функций
К(*> »)}, {Ун(х, У)}, k = 0, 1, 2, ...
Выбор функций фа (х, у) и tyk (xy у) связывается с видом
уравнения A) и видом граничного условия B). В
рассматриваемом случае на функции <р*(я, у), фл (х, у)
накладываются следующие условия:
1) функции г[>л (jc, у), й = 0, 1, 2,..., непрерывны
в области D\

§ si
МЕТОД МОМЕНТОВ. МЕТОД ГАЛЕРКИНА
249
2) функции %(х, у), & = 0, 1, 2,..., образуют на
классе непрерывных в области D функций замкнутую
систему в том смысле, что из выполнения условия
Цр(х> У)'Ь(х> y)dxdy = 0} k = 0, 1,2,...,
где F (х, у) — некоторая непрерывная в D функция,
следует, что F (ху у) н£ 0;
3) функции фЛ (х, у), k = Q, 1, 2, ..., дважды
непрерывно дифференцируемы в D\
4) при любом конечном п функции фх (х, у), ..., уп (х, у)
линейно независимы в D;
5) функция ф0(х, у) удовлетворяет граничному
условию B), т. е. Фо|г = ф(<2), а ф*!г = 0, k=l, 2, ...;
6) для любой дважды непрерывно дифференцируемой
в D функции и (ху у)у удовлетворяющей условию B), и
любого е > 0, найдутся такие п и аъ аъ ..., аП9 что
выполняются условия:
1 = 0, 1, 2,
д*и (х, у) ___
дх1
д1и (х, у)
ду1
1 д2и (х, у)
\ дхду
д'ип (*, у)
дх1
д1ип (х, у)
ду1
д2ип(х, у)
дхду
<е,
<е,
<е,
где ип (ху у) = ф0 {Ху у) + 2j я*Ф* (х> У)> 0ь аъ ..., ап —
k=\
некоторые числовые параметры.
В методе моментов функция ип(х, у) принимается за
/1-е приближение к решению граничной задачи A,2), если
параметры afc9 fc=l, 2, ..., п, определяются по
следующему правилу. Подставим в L(u) вместо и линейную
комбинацию ип- Точное выполнение уравнения L (ип) — f = 0
равносильно условию
ll[L(un)-f]yk{x,y)dxdy = 0 при £ = 0, I, 2, ...
Отметим, что, имея в своем распоряжении п
произвольных числовых параметров ak(k = 1, 2, ..., п), нельзя

250 УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ [ГЛ. 7
рассчитывать за счет их выбора удовлетворить
бесконечному числу условий.
Определима* из условий ортогональности L(un)—f
к первым п функциям хрл (л:, у):
№(«„)-/] %(*> y)dxdy = Q. Л = 0, 1, ..., /i-l. C)
D
Формулы C) представляют собой систему линейных
алгебраических уравнений, которую мы запишем в виде
п
2 Akiai + Ak = 0, £ = 0, 1, ..., n-l. D)
где
Ли = $ $ MTi) ^* d* d#,
D
Пусть a*, a*, ..., a% есть решение системы уравнений D),
тогда n-е приближение к искомому решению граничной
задачи A), B) в методе моментов вычисляется по формуле
п
"£(*» у) = ч>о(х, у) +2 я2ф*(*» у).
Метод Галёркина является частным случаем метода
моментов. В нем система функций {ср^ (#, у)} выбирается так же,
как в методе моментов, а функции -фл (х, #) определяются
по правилу
%(*> у) = Фл+i (х, #), * = 0, 1, 2, ...
Отметим, что если оператор L имеет вид
L М = - Ж (р &' у) ж) "" ~а7 (Р (*' у) д£~) + q (х> у) и E)
и р (х, у) ^ро > 0, q (х, у) ^ 0, р (,t, у) — непрерывно
дифференцируемая функция, q(x, г/) — непрерывная функция
в области Д то метод Галёркина для задачи A), B)
с оператором E) обладает сходимостью в среднем *).
*) Говорят, что последовательность {ип(х, у)} сходится в
среднем к и (х, у) в области D, если выполнено условие
lim \\(un(x, y) — u(x, y)Jdxdy==0.
n-+coJDJ

ЛИТЕРАТУРА
251
В монографии [5] читатель может найти достаточно
полное изложение теории метода Галёркина и вопросов,
связанных с его численной реализацией.
ЛИТЕРАТУРА
1. Бахвалов Н. С, Численные методы, т. 1, М., «Наука», 1973.
2. Берез и н И, С, Жидков Н. П., Методы вычислений, т. 2,
М., «Наука», 1962.
3. Годунов С. К., Рябенький В. С, Разностные схемы,
М., «Наука», 1973.
4. Крылов В. И., Бобков В. В., Монастырный П. И.,
Вычислительные методы высшей математики, т. 2, Минск, «Вышэй-
шая школа», 1975.
5. Михлин С. Г., Численная реализация вариационных методов,
М., «Наука», 1966.
6. Самарский А. А., Введение в теорию разностных схем, М.,
«Наука», 1971.

ГЛАВА 8
ЧИСЛЕННОЕ РЕШЕНИЕ
ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
§ 1. Введение
Идеи методов численного решения интегральных
уравнений мы постараемся выяснить на примере простого
случая, когда неизвестная функция зависит от одного
аргумента и интегралы, в которых она содержится,
являются однократными и неособенными. Такие
уравнения не исчерпывают всех видов интегральных уравнений,
встречающихся в приложениях, но с ними приходится
сталкиваться достаточно часто; кроме того, методы их
решения являются типичными для других случаев и
знание этих методов полезно для решения более сложных
уравнений.
В виде, достаточно общем для нашей цели, эти
уравнения можно записать в форме
F(x, ср(х), г) -0, A)
где ф(я) есть искомая функция, а буквой г обозначен
один из следующих интегралов:
Ь х
г = $ / (Ху s, ф (s)) ds или г = \ f (х> s, <p (s)) ds. B)
а а
С формальной точки зрения второй из интегралов является
частным случаем первого, когда функция / такова, что
f (xy s, ф) = 0 при s > х и любых значениях ф. Но это
свойство функции f имеет настолько глубокие следствия,
что делает теории уравнений с интегралами первого или
второго видов B) принципиально различными.

§1]
ВВЕДЕНИЕ
253
Уравнения, содержащие интегралы первого из видов
B), называются уравнениями Фредгольма, а уравнения
с интегралами второго вида —уравнениями Вольтерра.
Остановим внимание на отличительных особенностях
каждого из видов уравнений и укажем на то, какое
влияние они оказывают на методы приближенного их решения.
В уравнениях вольтеррова вида значения функции ф
в точке х определяются ее значениями в предшествующих
точках t<.xf значения же в последующих точках t>x
не влияют на ф(л:). Для приближенного решения
уравнения на отрезке а^х^Ь> где разыскивается ф, берут
сетку точек а^х0<*!<;. ..<х^^6 и находят
приближенно значения ф (xk) = ф^ только в точках сетки. Для
этого интегральное уравнение заменяют близкой к нему
в каком-то смысле системой N+ 1 численных уравнений
между величинами q)k. Эта система строится так, чтобы
по известным значениям ф0, ..., ф^_2 могло быть
построено уравнение для нахождения ф^
Ф*(фо. фь ...> Щ-ъ ф*) = 0. C)
Часто такое уравнение строят в форме
Фа^ЫФо» •••' Фа-ь Ф^)» D)
позволяющей удобно применять метод итерации. В
частных случаях уравнение D) может иметь форму рекурсион-
ного правила, позволяющего вычислять yk по
предшествующим значениям ф без решения уравнения
Фо = ао> Фа = £*(Фо1 Фь ..., Фл-i) (й=1, 2, ..., N).
Для уравнений Фредгольма система для нахождения
щ должна иметь иную форму, чем C). Интеграл z первого
из видов B) зависит от значений ф (х) на всем отрезке
а^х^Ь. Поэтому система должна быть такой, чтобы
в каждое ее уравнение входили значения фд, во всех
точках xk сетки и система должна решаться «в целом»,
а не последовательно.
Ниже мы ограничимся рассмотрением линейных
уравнений. В фредгольмовом случае линейные уравнения
имеют вид
ь
А (х) ф (х) + \К (х, s) ф (s) ds = F (x), E)
а

254 ЧИСЛЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИИ [ГЛ. 8
а для случая Вольтерра —
а:
А(х)ц>(х) + \К{х, s)<p(s)ds = F(x). F)
а
Когда коэффициент А (х) тождественно равен кулю,
уравнения E) и F) называют уравнениями первого рода.
Они имеют вид
для случая Фредгольма
ь
$К(х, s)q(s)ds = F(x), (*)
а
для случая Вольтерра
х
§ К (х> s) ф (s) ds = F (х). (**)
а
Если же коэффициент Л (х) отличен от нуля всюду
на отрезке [а, 6], уравнения E) и F) называются
уравнениями второго рода. Они, очевидно, могут быть
приведены к следующим каноническим формам:
в случае уравнения Фредгольма
ь
Ф (х) + \К {х, s) ф (s) ds — f{x)9 a < * < 6, G)
а
в случае уравнения Вольтерра
л:
Ф (х) + \К (х, s) ф (s) ds = / (jc), u < х < 6. (8)
а
В дальнейшем будут рассматриваться только эти
уравнения. Функции f (х) и К (ху s) предполагаются
непрерывными в областях соответственно а^х^Ь, а^
^s^x^b для уравнений Вольтерра ис<х<й, а^
^s, x^b для уравнений Фредгольма.
Прежде чем перейти к изложению методов численного
решения таких уравнений, мы объясним причины,
побудившие нас отказаться от рассмотрения уравнений
первого рода. Это даст нам возможность на их примере

§11
ВВЕДЕНИЕ
255
ознакомиться с классом задач, которые получили
название некорректных. Содержание приведенного термина
требует пояснения. Рассмотрим какую-либо задачу. Все
величины, определяющие решение, называются входными
данными задачи. Например, для уравнения G) входными
данными являются свободный член / (х)> ядро К (х, s) и
отрезок интегрирования [а, Ь]. Для решения уравнений
с частными производными входными данными будут: само
уравнение или, точнее говоря, параметры, определяющие
уравнение (его коэффициенты, свободные члены и т. д.),
затем присоединяемые к уравнению начальные или
граничные условия, или и те и другие.
Очень часто входные данные зависят от измерений и,
стало быть, известны только приближенно. Поэтому
особый интерес имеют задачи, для которых выполняются
следующие два условия: 1) решение существует при любых
входных данных, когда они изменяются в некоторых
допустимых границах; 2) решение задачи мало изменяется
при малом изменении входных данных, т. е. является
устойчивым относительно изменений этих данных. Такие
задачи называются корректными или корректно
поставленными.
Но среди прикладных задач встречаются такие,
изучение которых имеет большое значение, но которые
не обладают каким-либо из указанных свойств.
Задачи, которые не имеют решения или решения
которых неустойчивы относительно входных данных,
называется некорректными (некорректно поставленными).
Уравнение первого рода вида Фредгольма (*) является
примером такой задачи. По существу, равенство (*) дает
интегральное преобразование функции <p(s) в F (х). В нем
Ф является оригиналом и F — изображением.
Для простоты будем считать ядро К {х> s)
непрерывной функцией в квадрате a^s, x^b и оригинал cp(s) —
принадлежащим множеству 10 абсолютно интегрируемых
на [а, Ь] функций. При этих предположениях интеграл,
стоящий слева в равенстве (*), будет непрерывной на [а, Ь)
функцией х. Преобразование будет отображать множество
/0 во множество непрерывных на [а, Ь] функций С0.
Может оказаться, что множество изображений
составит только часть С0. Тогда, если в качестве F (х) мы
возьмем непрерывную функцию, не входящую в эту часть,

256 ЧИСЛЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [ГЛ. $
уравнение (*) не будет иметь решения ф (s) в множестве
/0 и задача (*) будет неразрешимой. Например, пусть
ядро К (х, s) непрерывно и имеет непрерывную частную
производную по аргументу х в квадрате a^s, x^b.
Интеграл в (#) будет непрерывно дифференцируемой
функцией х на [а, Ь] и преобразование (*) отображает /0
в множество непрерывно дифференцируемых на [а, Ь]
функций. Поэтому, если в уравнении (*) F (х) есть
непрерывная, но не дифференцируемая на [а, Ь] функция,
уравнение не разрешимо в /0.
Приведенные рассуждения показывают, что
уравнение (*) разрешимо не при всяких входных данных и,
стало быть, не обладает первым из указанных свойств
корректных задач.
Проверим также, что оно не обладает и свойством
устойчивости решения. Пусть ф (s) удовлетворяет
уравнению (*). Изменим значительно ф на очень коротком
частичном отрезке [а, р] и вновь полученную функцию
обозначим фх. После изменения (#) перейдет в новое
равенство ъ
§ К (х, s) фх (s) ds = Fi (x). (***)
а
Если длина р~ а частичного отрезка взята достаточно
малой, то новая функция F± (x) будет при всех х мало
отличаться от F(x). Мы могли бы добиться близости Fx
к F, изменяя значительно ф не на одном частичном
отрезке, а на многих отрезках, сумма длин которых будет
достаточно малой, и также получили бы два
интегральных уравнения (*) и (***) с одним и тем же ядром К и
с близкими свободными членами F и Flt но с решениями
Ф и фь значительно различающимися между собой. Это
показывает неустойчивость решения ф относительно
изменений свободного члена F.
Несколько иначе обстоит дело с уравнением первого
рода вольтеррова вида (**). Допустим, что ядро К (х9 s)
и свободный член F (х) имеют непрерывные производные
по х в областях a^s^x^b и а^х^Ь
соответственно.
Отметим предварительно, что при х = а левая часть
уравнения (**) обращается в нуль, и поэтому
необходимым условием существования решения будет F(a)=0.

§11
ВВЕДЕНИЕ
257
Вычислим производную от обеих частей уравнения (**):
х
К (х, х) ф (х) + J Kx (x9 s) ф (s) ds = F' (x). (****)
Здесь возможны три следующих случая.
1) Когда
это уравнение путем деления на К (х, х) приводится
к уравнению второго рода (8), задача решения
которого является корректной. /Методы решения изложены в
§ 2, но можно применить аналогичные методы
непосредственно к (**).
2) Пусть
К(х, х)==0, а^х^Ь.
Тогда получится однородное уравнение, аналогичное (**):
х
$ Кх (х, s) ф (s) ds = F (x).
а
К нему можно применить предыдущие рассуждения:
проверить, будет ли выполняться необходимое условие
разрешимости F' (а) = 0, вычислить производные от обеих
частей уравнения и т. д.
Особенным здесь будет случай, когда правая или левая
части уравнения не имеют производной или производная
от интеграла не может быть вычислена по обычному
правилу. Такой случай требует дополнительного изучения.
3) Исключительным является случай, когда функция
К {х> х) не есть тождественный нуль, но обращается
в нуль на некотором множестве точек на [а, Ь]. Тогда
интегральное уравнение (****) имеет особые точки и должно
быть исследовано, так как общие методы решения здесь
могут оказаться неприменимыми.
8 предыдущих главах книги рассматривались методы
решения только корректных и неособенных задач. Такие
методы для решения некорректных задач или задач
с особенностями могут оказаться неприменимыми. Для
решения задач такого типа создаются свои методы,
которые в книге не излагаются. Все это и заставило авторов
отказаться от рассмотрения уравнений первого рода.
9 В. И. Крылов и др., т, II

258 ЧИСЛЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [ГЛ. 8
§ 2. Уравнения вольтеррова вида второго рода
1. Вид вычислительного правила и теорема о
сходимости вычислительною процесса. Допустим, что для
решения уравнения (8) на конечном отрезке а^х^Ь взята
сетка равноотстоящих точек с шагом h: xk = a-\-kh[k =
= 0,1, ..., N; a + Nh^b<a + (N+l)h].
Положим в интегральном уравнении x = xk и
рассмотрим систему равенств
Ф(х0)=/(а),
*п (!)
Ф (хп) + $ К (хп, s) ф (s) ds = f{xn) (n= 1, ..., N).
а
Пусть для вычисления интегрального члена последнего
равенства взята квадратурная формула с узлами в
точках Xq, Xi, . . . , Хп
хп п
\ К (хя, s) ф (s) ds = h 2 AniKni<P (xt) + rn. B)
a i = 0
Здесь Kni = K(xn, xi) и гп — остаток квадратурного
правила. Множитель h перед суммой выделен для того,
чтобы коэффициенты Ani были безразмерными величинами.
Внеся это представление интеграла в равенства A),
приведем их к виду
ф(*о)=/о>
п
Ф (Хп) + Л £ Лл//С/Ф (*,) + ГЯ = /л, /я - / (ХЯ) C)
(л=1, .... /V).
Отбрасывая остаток /*я, получим уравнения для
приближенных значений функции ф в узлах хп. Зти значения
обозначим через фл. При вычислениях уравнения для фл
будут выполняться неточно. Если погрешность, с
которой они выполняются, обозначить через 8„, то точное
правило вычисления фл может быть записано так:
Фл + А |] Лл,/Ся*Ф/=/л + бл (л=1, 2, ..., tf). D)

§ 2] УРАВНЕНИЯ ВОЛЬТЕРРОВА ВИДА ВТОРОГО РОДА 259
Рассмотрим погрешность приближенных значений гп =
= ФЛ — <р(хя) (п = 0, 1, ...); при этом ф (*<>)=/(*<>), а ф0
есть приближенное значение, полученное при вычислении
f(x0). Уравнение для погрешности при п^1 получится,
если из D) вычесть почленно уравнение C)
п
tn + h 2 АщКп&^Гп + бп (л=1, 2, ..., АО. E)
1 = 0
Для получения оценки ел, гарантирующей равномерную
сходимость приближенного решения ц)п к точному
решению ф(я), предположим, что при всех значениях я= 1, ...
..., N выполняются неравенства
1гя|<г = г(А), |бл|<б = б(/1).
Введем числа Л, /С, определив их неравенствами
|Ля,КЛ<оо (*<л, л=1, 2, ...), j/C(*, s); </С.
В качестве Л и /С могут быть взяты, например,
Л = тах|Лш-| и К = тах | К {х, s) |.
t/x xs
Выделим в сумме, стоящей слева в C), слагаемое с гп
и перепишем равенство в виде
«—I
A+АЛлл/Сля)ея = гя + дл-А2 AniKnfii (/i^l). F)
t = i
Предположим, что при всех достаточно малых h и
п=1, 2, ..., Л/" выполняется неравенство
А|Лял/Сяя|<(/<1 (/г-1, ..., #). G)
Тогда из F) получается рекурсионное неравенство для
погрешностей гп
Введем величины Еп {п = 0, 1, ...), определив их
начальным условием £0=|е0| и рекурсионным соотношением
En=T~(r + 8 + hAK J £,l * = 1, 2, ... (9)
9*

260 ЧИСЛЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [ГЛ. 8
Легко проверяется, что \еп\^Еп. Для этого
воспользуемся индукцией. При п==0 неравенство, очевидно,
верно, так как |е0| = £0- Пусть |ел|^££при i' = 0, 1, ...
..., п — 1. Тогда из (8) и (9) следует
/ п~~* \
\e»\^T=rq[r + 6 + hAK % Ei) = En-
Для упрощения последующих записей введем
обозначения:
^(/- + 6) = а, Л-11АК = $.
Соотношение (9) примет вид
п-\
£* = ot + P ££,. A0)
1 = 0
Убедимся в том, что величина
£л = (а + рЯо)A + Р)я-1 ("=1, 2, ...) (И)
является решением этого уравнения. Для этого
подставим в правую часть A0) значение Et (i^l). Получим
а+р£ Я/ = а + Р£о + Р(а + РЯо) 2 О+Р)'":1^
= (cc + p£0){l + p. I [(l+p)-i_l3\ =
Ha + PSoMl+P)*-1^,,.
Этот результат показывает, что величина A1)
действительно удовлетворяет уравнению A0).
Изложенное выше позволяет утверждать, что при
всяких значениях л=1, 2, ... для погрешности е/г верна
оценка
|ея|<(а + Р|в0|)A + Р)»-1 =
= j^{r + b+ hAK\e0^[l +J^hAKf'1.
Получим равномерную относительно п оценку
погрешности. Воспользуемся очевидными неравенствами п^
^iV^-^ и заменим показатель степени п—1 большей
^ h

§ 2] УРАВНЕНИЯ ВОЛЬТЕРРОВА ВИДА ВТОРОГО РОДА 261
величиной т- (Ь — а). Воспользуемся также тем, что при
/-> + 0 величина (\-\~t){t возрастает и стремится к е.
Все указанное позволит записать систему неравенств
Ь — а
(л , 1 l о>1 'i , If, ЛЬЛ~1Г
■АЛ/С J <fl Ч-у^АЛК
L(i+^M/cVi*-*
6_ллк
1-7 <е\-<
что дает следующую равномерную относительно п
оценку ел:
Ы^т~е^АК (г + Ь + АК\г0\к). A2)
Полученная оценка погрешности позволяет высказать
заключение о сходимости приближенного решения ф^
(/г = 0, 1, ..., N) к точному решению ф(х) (a<x^6).
Предположим, что число узлов JV+1 сетки
неограниченно возрастает; при этом для определенности допустим,
что шаг сетки всегда берется равным ^ (b — a) =/i. Если
окажется, что для избранного квадратурного правила (9)
верхняя граница г (h) погрешности может быть взята
стремящейся к нулю и если точность вычислений выбрать
так, чтобы граница б погрешностей бя вычислений
стремилась к нулю, то правая часть неравенства A2) будет
стремиться к нулю. Поэтому можно утверждать, что
приближенное решение Ц)п (/г = 0, 1, ..., N) будет
равномерно сходиться к точному решению ср(х). Последнее
означает, что для любого е>0 существует такое
значение /г0, что при всяких /г</г0 будут выполняться
неравенства
|Ф*-фЫ1<г (я = 0, 1, ...,ЛГ). A3)
Заметим, что в неравенстве A2) справа в скобках
стоят слагаемые, зависящие от различных факторов.
Первое из них г определяется свойствами интегрального
уравнения и избранным для вычислений квадратурным

262 ЧИСЛЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИИ [ГЛ. 8
правилом; второе — 6 учитывает погрешности, которые
совершаются при нахождении приближенных значений фл,
и, наконец, третье связано с погрешностью е0
вычисления начального значения ср (х0) решения. Величиной
двух последних членов можно, при вычислениях
распорядиться, увеличивая или уменьшая точность
вычислений. Этой возможностью обычно пользуются так, чтобы
соответствующие всем членам доли погрешности были
сравнимы по величине или по меньшей мере имели
одинаковый порядок малости.
Сформулируем теперь теорему о сходимости,
вытекающую' из проделанных исследований. .
Будем считать отрезок [а, Ь] произвольным отрезком
конечной длины, ядро К (х, s) непрерывной функцией
в области a^s^x^b (следовательно, ограниченной)
и свободный член f (x) непрерывным на отрезке а^х^Ь.
При этих условиях уравнение A.8) имеет и притом
единственное решение ц>{х).
Теорема 1. Пусть для вычислительного процесса D)
выполняются условия:
1) погрешность гп квадратурной формулы B)
стремится к нулю равномерно относительно п, когда /г-^0;
2) существует число А такое, что при всех значениях
i, ny h выполняется неравенство
\АЫ\<, А <со\
3) погрешность 8п вычислительного правила стремится
к нулю равномерно относительно п при /г->0.
Тогда при всяких достаточно малых h приближенное
решение уп может быть построено по правилу D) и для
него будет выполняться неравенство A3) при любом
заданном положительном е, если h будет достаточно
малым.
Закончим настоящий пункт указанием на
необходимость составления начала расчетной таблицы при
применении правила D). Коэффициенты Ani обычно
выбирают так, чтобы локальная погрешность гп правила
имела во всех узлах один и тот же порядок малости
относительно h> т. е. чтобы погрешность гп при всяких п
имела представление вида
rn = hkCn(h), Сп{Н)-*СпфО при ft->0.

§ 2] УРАВНЕНИЯ ВОЛЬТКРРОВА ВИДА ВТОРОГО РОДА 263
Предположим теперь, что нам необходимо вычислить фА.
Для этого рассмотрим квадратурную формулу B) при
п= 1:
a+h
\ К(хи s)<?(s)ds = h[AlQKiQ<p(a) + AllKn<?(a + h)] + r1,
а
xQ = a, Xi = a-{-h.
Она содержит два численных параметра Aw и А1Ъ кото*
рые мы можем выбрать так, чтобы формула имела
возможно более высокую степень точности. Максимум, что
мы можем получить в этом отношении — это сделать
формулу точной для многочленов первой степени. Тогда
формула станет известным правилом трапеций, для
которого Лю == Лц = у:
a+h
£ К (*i, s) ф (s) ds - 2- [/СюФ {а) + /(пф (а + А)] + гх.
а
Остаточный член гх этого правила приведен в
равенстве E.3.3), которое для рассматриваемого интеграла
имеет вид
1 Г Я2 1
12
^КФ
S = T|
Отсюда видно, что гг имеет относительно h третий
порядок малости. Если окажется, что принятый в
вычислениях порядок k малости гп больше трех, то формулу D)
нельзя применять к нахождению фх. Тогда эта величина
должна быть найдена с необходимой точностью
предварительно, до применения вычислительного правила D).
Аналогично, чтобы воспользоваться правилом D) для
нахождения ф2, нужно положить в B) п = 2 и
рассмотреть квадратурную формулу
a+2/t
$ K{x2j s)q>(s)ds =
а
= h [ Л20К2оФ {а) + А 21КолЧ> (a + h) + А2гК*& {а + Щ] + г*.
Наивысшая степень алгебраической точности, которую
можно достичь при помощи выбора коэффициентов A2Qi

264 ЧИСЛЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [ГЛ. 8
Л2ъ А2о, равна 3 и достигается она в правиле парабол,
ДЛЯ КОТОрОГО ^20 = ^22 = -3"> ^21==~:
а + 2/1
$ К (х2, s) Ф (s) ds =
а
= | [К20Ф (а) + 4/С21ф (а + А) + К22Ф (а + 2й)] + г2.
Форма остаточного члена правила парабол указана
в равенстве E.3.7):
Остаток г2 имеет пятый порядок малости относительно hf
и если окажется, что &>5, то правило вычислений D)
нецелесообразно применять для вычисления ф2, и это
значение, так же как и фь необходимо найти заранее,
до применения D) и т. д.
Значения ф„, которые должны быть найдены
предварительно, составят начало расчетной таблицы. Оно
зависит от порядка k малости гп. Если принять во внимание
степени точности интерполяционных квадратурных
правил, о которых говорилось в § 3 гл. 5, то можно
сказать, что в начало таблицы должны войти значения уп
по меньшей мере с индексами /г, для которых
выполняются неравенства
n<ik — 3, когда п — четное число,
n<k — 2, когда л —нечетное число.
Значения фл, входящие в начало таблицы, можно
находить, например, решая интегральное уравнение
в окрестности точки а при помощи степенного ряда, если
функция / (х) и ядро К (х, s) являются аналитическими
функциями, или применяя для вычисления значений
решения формулу трапеций с уменьшенным шагом h.
2. Правила вычислений, основанные на формуле
Эйлера — Маклорена. В качестве примера построения
вычислительного правила вида D) рассмотрим задачу
использования для этой цели разностного варианта

§ 2] УРАВНЕНИЯ ВОЛЬТЕРРОВА ВИДА ВТОРОГО РОДА 265
формулы Эйлера —Маклорена*)
aj-nh
J y(x)dx = h\-2-yb + yi + ...+ yn-i + 'jyn\-
а
- f2 (&Уп i - Д#о) - 24 (Д2Уя- 2 + &%) -
~ 720 №Уп~в ~ А'^о) "" Шб (Л^ 4 + А^°) ~" '' *
... - АС2ГЯ [А2туп-2т + &2тУо] + гл, 2т A4)
где rn2m = 0 (ft2m+1), если функция у имеет на [а, а + яЛ]
непрерывную производную порядка 2т +1 и 2т < д.
Если, как и выше, рассмотреть сетку равноотстоящих
точек хл = а + nhy h = у (& ~ а), положить в
уравнении A.8) х = хп, применить к вычислению интеграла
правило Грегори A4) и, наконец, отбросить остаточный
член гПч2гп1 то Для нахождения приближенных значений ц>п
функции ф получим систему уравнений
фл + А 2 КяоФо + /СЛ1ф1 + • •. + Кпп-гУп г + 2 #/шфлJ —
- т^ [Д5 (/Слл-1фя-1) - As (*Г«оФо)] -
24
[As {Knn 2Ф/1-2) + As (К"/гоФо) ] - • • •
... - АС2т [ДГ (/Сяя- 2«ФЯ -2«) + ДГ (/СпоФо)] = /«• A5)
Знаком Д5 обозначен оператор конечной разности по
аргументу s:
Д5 (Кл/Ф*) = КпмУм - КтЧь
Дз (Kni%) = Кл/+2ф/+2 — 2/С/+1Ф/+1 + Кя/Ф/, ...
Применять к вычислениям правило A5) можно при
п^2т, при этом необходимо составить начало
расчетной таблицы, которое содержало бы предварительно
найденные значения ф0, ..., tp2m-i- Кроме того, конечная
разность высшего порядка 2т, применяемая в
вычислениях, должна при принятой точности вычислений сохра-
*) Том I, E.8.5).

266 ЧИСЛЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [ГЛ. 8
нять постоянное значение или, что равносильно, разности
порядка, большего 2га, должны обращаться в нуль при
этой точности.
Остановимся более подробно на простейшем и
типичном случае т=1, когда в вычислениях применяются
конечные разности по s до второго порядка:
фл + h \j КпоЪ + KnlVl + ••• + Knn~l<Pn~l + 2 Л'/шфл] -
- ~ [А5 (Knn-lVn-l) ~ ^5 (КяоФо)] -
12 ■
-I
24 I
- ¥а [М {Кпп 2фд 2) + Д5 (/СяоФо)] =
фя + 1гТл + ]9 Ап + птS* + о hKnnVn = /я,
12 Л ' 24
/1—1
7\i = >, KnWi - -9 ^лоФо. ^л = Кпч~1Ч>п-1 + As (КлоФо)»
t = 0
Вп = Ап + Д5 (КлЛ-2фл 2) - А, (/Ся1ф1).
Отсюда получаются следующие расчетные формулы
для фя:
Ф2 = (l ~ ^^22) (/2 - 3 Л^21ф1 ~ з Л#Зффо),
Ф„ = A --1А/СлдУ1 (>я-hTn-%Ап- * Вп),
12 л 24 J
л = 3, 4, 5, ...
Для применения их к вычислениям шаг h должен быть
взят настолько малым, чтобы для принятой точности
вторые разности &i(Kni%) (J = 0, 1, ..., л —2) сохраняли
постоянные значения. Чтобы начать вычисления,
необходимо предвар ительно найти значения ф0 = /0 == / (х0) и ф1в
§ 3. Уравнения Фредгольма второго рода.
Метод квадратур
Задача численного решения уравнений Фредгольма
является более сложной, чем для уравнений Вольтерра,
и имеет значительно более развитую теорию. В книге
будут рассмотрены только два метода: метод квадратур
и метод замены ядра уравнения на вырожденное ядро.

§ 3] УРАВНЕНИЯ ФРЕДГОЛЬМА. МЕТОД КВАДРАТУР 267
1. Метод квадратур. Пусть дано интегральное
уравнение второго рода вида Фредгольма
ъ
<р (*)=/(*)+*.$*(*, s)<p(s)ds. A)
а
На отрезке интегрирования [а, Ь] возьмем
произвольно п точек а^х1<х2<...<.хп^Ь и для
нахождения приближенных значений функции ф в них построим
систему уравнений. Такую систему можно получить, если
к вычислению интеграла, входящего в уравнение,
применить какое-либо правило приближенного интегрирования.
Интеграл зависит от параметра х, поэтому коэффициенты
правила и его остаточный член будут, вообще говоря,
некоторыми функциями от х:
\ К (х, s) Ф (s) ds=}]Ck (х) Ф (xk) + p (х). B)
а к=\
Подставив это выражение интеграла в уравнение A)
и положив там последовательно
X = A'i, Л'2» • • • > Хп,
получим для точных значений <р (х) систему уравнений
Ф (*/) = h + %j]Ck (Xi) Ф (xk) + ^p (Xi). C)
Остаток р (а:) в квадратурном правиле B) по сравнению
с квадратурной суммой имеет обычно малую величину.
Поэтому, если в равенствах C) пренебречь малыми
величинами %р (xj), можно рассчитывать на то, что получится
алгебраическая система уравнений, решение которой ф*
(i=l, ..., п) будет близким к значениям ср(#/) точного
решения интегрального уравнения
Ф,-Я V Ск(х1)щ = !( (/=1, 2, ..., п). D)
Определитель системы
Д(А,) = 0(£-ХС), E)

268 ЧИСЛЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИИ [ГЛ. 8
где
с =
1.Сг(хп) ... Ся (д:л) J
есть многочлен от Я степени п.
Предположим, что X не есть собственное значение
уравнения A) и уравнение, следовательно, имеет только
одно решение. Тогда можно ожидать, что определитель
А (X) системы будет отличен от нуля и система D) также
имеет единственное решение. Но это надлежит проверять
в каждой частной задаче.
Будем считать, что А(Х)фО. При численном решении
системы каждое уравнение удовлетворяется с некоторым
округлением чисел, и если погрешности округлений
обозначить через — б/, то для % будут выполняться
равенства
Ф* - ^ 2 ci (**) 4k = fi - б/ F)
и, следовательно,
Ф/ = ЛЩ bktUk-6k]f G)
1_
У
где Aki есть алгебраическое дополнение элемента
определителя А (Я) с индексами k> i.
Теперь рассмотрим погрешность приближенного
решения ej = cp(#/) —<pj и получим ее оценку. Точные
значения ф (Xi) решения удовлетворяют уравнениям C),
которые отличаются от уравнений D) для % только заменой
— б* на Яр(Х/), и поэтому для ф(л:/) верны выражения
вида G) с такой же заменой:
^^=щ2^^+1р^ <8>
Если теперь отсюда вычесть почленно G), получится
представление для е*:
п
El = джг 2 Aki ^ ^+б^- (9)
4)
*=1
Оно дает возможность получить оценку г,-.

§ 3] УРАВНЕНИЯ ФРЕДГОЛЬМА. МЕТОД КВАДРАТУР 2G9
Пусть для погрешности р (х) квадратурного правила (8)
верно неравенство ' р (х) | ^ р = р (п). В качестве р (п)
может быть взята величина р (п) = max) p(x)\. Предполо-
х
жим также, что для погрешности бь вызванной
округлениями, выполняется неравенство | 8k | ^ б = б (п) (k =
= 1, ... , п). Величина б (я) определяется принятым
вычислительным процессом.
Из представления (9) вытекает следующая оценка
для ef.
|в,!<В[;А,|р + 6], A0)
где п
в^ГШт21А«!-
" /е = 1
Отметим попутно, что значения А (Я) и kkl находятся
в процессе вычислений и поэтому В является
вычислимой величиной. В оценке A0) остается еще найти
величину р. С этой целью возвратимся к остаточному члену р(х)
квадратурного правила B) при произвольном значении х:
ь п
р(х) = \К (х, s) ф (s) ds- У] Ck (х) ф (xk).
Внесем в него вместо ф(х) выражение, стоящее в правой
части уравнения A):
р (*) = $*(*, в)
ds-
f(s)+K\K(s, u)<p{u)du
а
b
f{Xk)+h\K(xk, u)y(u)du
a
= \K(x, s)f(s)ds-yiCk(x)f{xl!) +
- %Ck(x)
b
k=l
+ к
b b
\\K {x, s) К (s, и) ф (u) du ds —
a a
n b
2 Ck (x) \ К {xk, и) ф (w) du
a ~i
b
= Pf(x)+h\pK(x, u)<p(u)dut A1)
£ = 1

270 ЧИСЛЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [ГЛ. 8
где
Ь п
Р/ (х) = $ К (х, s) / (s) ds-%Ck (x) f (xk),
a k=\
b n
pK (xy u) = [K (x, s) К (s, u) ds - ^ Си (д:) /С (*a, и).
Очевидно, pj (x) есть остаток приближенного
интегрирования по правилу B) свободного члена / заданного
уравнения, а рк{х, а) —остаток интегрирования по тому
же правилу функции К(s, и). Обе эти функции известны
и поэтому две следующие величины: pf = max I pj (x) I и
x
b ■
Pk= niax \! pK (Xy и) \ du мы вправе считать также извест-
х а
ными.
Из представления A1) получается следующая оценка
для р:
IP fa) | ^ р < max j р (х) | < pf +1 к | рКН,
и */м A2)
Н = max | ф(х) |.
X
Полученное неравенство совместно с соотношением A0)
приводит к выписанной ниже оценке погрешности е(:
\*i\^BlM(pf + \X\pKH) + 8] (i = l,..., n). A3)
Эта оценка во многих случаях позволяет сделать
заключение о сходимости вычислительного процесса и о порядке
малости погрешности е,-. Для этой цели ниже мы
воспользуемся ею, а сейчас отметим недостаток, не
позволяющий без оговорок применять ее в численных
расчетах: она содержит число Я, являющееся наибольшим
абсолютным значением неизвестной функции *). Этот
недостаток можно устранить и оценить Н через
вычислимые величины (см. A6)).
*) Для нестрогих ориентировочных расчетов число Н можно
часто заменить на тах;ф;|, основываясь на том, что если сетка
i
точек Xi достаточно густо заполняет отрезок [а, Ь\ и на сетке
значения <p(xi) и ер,- (* = 1, ... , п) близки между собой, то max ( ф (х) | и
X
max | ф/1 должны мало отличаться друг от друга.

§ 3J УРАВНЕНИЯ ФРЕДГОЛЬМА. МЕТОД КВАДРАТУР 271
Для этого потребуется определить приближенное
решение не только в точках xh но и на всем отрезке
[а, Ь]. Такую интерполяцию приближенного решения
с сетки на отрезок можно выполнить многими способами,
например, при помощи алгебраического
интерполирования или какого-нибудь другого.
Мы воспользуемся «естественным» в рассматриваемой
задаче интерполированием через квадратурное правило.
Возвратимся к уравнению A) и вычислим в нем интеграл
при помощи квадратурного правила B):
п
Ф (x)=f(x) + K £ Ck (x) Ф (xk)+Kp (х). A4)
Заменим в правой части точные значения ф (хк) функции ф
в узлах xk на вычисленные приближенные значения ф*
и отбросим «малый» остаток Хр(х):
ф (*)=/(*) + * %Ск(х)ъ. A5)
/г=1
Полученную так функцию ф (х) примем за
приближенное решение' на всем отрезке [а> Ь]. Ввиду уравнений D)
ясно, что ф (х) в узлах x-t принимает значения ф^
соответственно. Поэтому ф (х) выполняет интерполирование
в обычном смысле сеточной функции ф*(г = 1, ... , п)
на весь отрезок [а, Ь]. В основу интерполирования здесь
положены функции Ck(x), Так как они определяются
ядром К (х, s) интегрального уравнения, то A5) есть
интерполирование ф^ через ядро К (х, s), что в нашей
задаче является естественным.
Получаемая погрешность имеет значение
е (х) — ф (х) — ф (х) = А,
п
%Ck(x)8k + p(x)
-k = l
Отсюда, если ввести обозначение max ^] I Ck (x) \ = С,
k=i
то для в(х) с помощью оценок A2) и A3) получится
неравенство

272 ЧИСЛЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИИ [ГЛ. 8
Введем, наконец, величину # = max j ф (я) |. Она может
X
быть вычислена, так как ф (х) выражается только через
величины, находимые в процессе вычислений.
Из равенства ф (х) = ф (л:) + 8 (х) следует # ^ Я +
+ тах| г(х)\.
X
Если воспользоваться полученной выше оценкой для
|в(*)|, то будем иметь неравенство
H^H + \k\{BC[\X\(pf + \X\pKH) + 8] + (pf+'X\pKH)}.
Отсюда при условии, что | X |2р^A +;Я| ВС) < 1 вытекает
неравенство для Я:
H + \X\lpf(\ + \%iBC) + bBC]
М"^ 1-!Х|2р^A + \l\BC) ' (и>
Оно дополняет оценку A3) погрешности е, для тех
случаев, когда необходимо знать границу для численного
значения величины Я.
В предыдущем изложении узлы xk считались
произвольными. Сделаем сейчас несколько замечаний об их
выборе и соответствующих им квадратурных правилах.
Когда необходимо составить таблицу значений решения ф,
то наибольший интерес представляет случай
равноотстоящих значений аргумента sk = a-\-hk (k = 0, l,..., n),
h = ~-(b — a). Тогда для вычисления интеграла могут
быть применены, например, правила трапеций, парабол,
трех восьмых и т. д.
В случае трапеций формула B) будет иметь вид
ъ
[К(х, s)(p(s)ds = h^jK(x9 sQ) ф (s0) + К (х, s1)<p(s1)+...
а
... + К(Х, S/,_i)q>(s„_1)+2-/C(*, 6)фF)]-
{Ь-йK\д* (Кп)]

§ 3] УРАВНЕНИЯ ФРЕДГОЛЬМА. МЕТОД КВАДРАТУР 273
В случае парабол
{ К {х, s)=h || \К (х, s0) ф (s0) + К (х, sn) ф (sn) ] +
а
+ у 2 К (Х> S*m^ ф (S2m +1) + з 2 ^ ^' ^ ф (S*«)} ~~
m m
н т, д. Правила приближенного интегрирования этого
вида имеют невысокую степень точности и для получения
малой погрешности часто бывает необходимо брать малое
значение Лив соответствии с этим большое число узлов xk.
Тогда система вида D) будет иметь большое число
уравнений и ее решение потребует большое количество
вычислений. Ввиду этого часто предпочитают применять
квадратурные правила, имеющие высокую степень
точности, например правило Гаусса или его аналоги.
2. Сходимость метода квадратур. Вычислительный
процесс метода квадратур определяется двумя таблицами:
бесконечной таблицей узлов квадратурных правил
X
ДГ|, Х%
A7)
и таблицей коэффициентов С\(х) этих правил
-С\(х)
СЦх) СЦх)
А
СЦх) С(х) ... С»(х)
A8)
Таблицы составлены так, что в строке номера п
помещены узлы и коэффициенты квадратурного правила
вида B), которое применяется для приближенного
вычисления интеграла на шаге номера п процесса:
Ь п
\ К (х, s) Ф (s) ds^^Ct (x) Ф D) + р* (х). A9)

274 ЧИСЛЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [ГЛ. 8
В вычислительном процессе все величины, зависящие
от См и xl, будут некоторыми функциями от я,
например остаточный член рп (х) квадратурного правила будет
зависеть как от х, так и от п. В оценке A3) от номера п
шага будут зависеть как сама погрешность е,-, так и
величины 5, р/, р^. От п будет зависеть и погрешность б,
так как, если мы хотим сделать процесс сходящимся
к точному решению, то с ростом п должны
неограниченно увеличивать точность решения системы вида D).
Указанная зависимость от п отмечена при помощи
приписки'величине верхнего индекса п.
Для процесса оценка вида A3) запишется в следующей
форме:
\г?\<:Вя1{К(р" + \Ь\р'кН) + Ьп] (*=1, .... п). B0)
Такая оценка погрешности позволяет считать
доказанной приводимую ниже теорему о сходимости
вычислительного процесса метода квадратур.
Теорема 1. Предположим, что X не есть
собственное значение ядра К (х, s) и уравнение A) имеету
следовательно, единственное решение.
Пусть для вычислительного процесса метода квадратур,
определяемого равенством A9), выполняются условия:
1) погрешности Pfis)(x) и Р\{х s)(x) квадратурного
правила A9) для функций ф (s)=f(s) и ф (s) = /C (s, и) таковы,
что при неограниченном росте п будет соответственно
вяР?<я>(*)-*° B1)
равномерно относительно х и
BnpnK(s,u)(x)-+0 B2)
равномерно относительно х и и;
2) погрешности — б? решения уравнений систем вида D)
уменьшаются настолько быстро при увеличении п, что
имеет место соотношение
Вп8п -> 0, б* = шах 16? |. B3)
i
Тогда для всякого положительного г существует N (г)
такое у что при п> N (г) будут выполняться неравенства
|Ф(*?)-Ф?|<е {i===l> 2> •••> ")• B4)

§ 3] УРАВНЕНИЯ ФРЕДГОЛЬМА. МЕТОД КВАДРАТУР 275
Приведенная теорема имеет ту особенность, что ее
условия B1) и B2) должны проверяться в процессе
вычислений, а условие B3) должно учитываться при
определении точности решения системы уравнений для
нахождения ср£ (i = l, ..., п).
3. Интерполяционный квадратурный метод. Этот метод
является частным случаем общего квадратурного метода
и основан на интерполировании неизвестной функции ф.
Для определенности изложения будем иметь в виду
алгебраическое интерполирование.
Выберем на отрезке [a, b] n различных точек а<,хх<.
<х2<- -.<хп^Ь и выполним интерполирование
функции ф по ее значениям в этих точках. Воспользуемся
лагранжевым представлением интерполяционного
многочлена
п
п
= 2 М*)ФЫ+ >"(*)• B5)
Внесем это представление ф в интегральный член
уравнения A):
п
Ф (х) =/(x) + ^L, (х) Ф (xk) + Хр (х),
ь /;==1 ь B6)
Lk {х) =\К (х, s) lk (s) ds, p (x) = $ К (х, s) r (s) ds.
a a
Чтобы получить систему уравнений для ф (хп), отбросим
в B6) остаточный член Хр(х) и в полученном
приближенном равенстве положим х равным хъ х2, ..., хп:
ф| = /* + *2] М**)Ф* (i = l, ..., п). B7)
Эта система является частным случаем более общей
системы D), когда Ck(xi) = Lk(Xi),
После решения системы B7) мы будем знать
приближенные значения ф^ решения ф в точках x-t (i = l, ..., ri).

276 ЧИСЛЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [ГЛ. 8
Чтобы найти приближенные значения ф всюду на [а, Ь\
можно выполнить алгебраическое интерполирование ф
по значениям фг, как было сделано выше для получения
уравнений B7). Но можно ожидать, что лучшая точность
будет достигнута, если воспользоваться «естественным»
интерполированием ф через ядро К (х9 s). Оно получится,
если в раЕенстЕе B6) отбросить остаточный член Хр(х):
Ъ(х)=Нх) + Х%Ьк(х)ч(хк). B8)
Остановимся еще на вопросе выбора узлов xk в
интерполяционном методе. Если точное решение ф (х) является
многочленом от х степени не выше п— 1, то
интерполирование ф (х) будет точным и остаточный член г (х) в B5) —
тождественно равным нулю. В соответствии с этим
остаточный член Яр (х) в представлении B6) также будет
тождественным нулем и системе B7) будут удовлетворять
точные значения решения Ф/ = ф(#,-). Эти значения могут
быть найдены из системы и по ним построено точное
решение ф (х).
Это верно при всяких узлах хк (k=\, ..., п)9 лишь
бы они были различными. Поэтому говорят, что
интерполяционный метод при любых узлах xk имеет степень
точности не меньше п — 1. Естественно попытаться
выяснить, можно ли путем выбора узлов сделать
интерполяционный метод точным для любых многочленов ф(^)
степени п или, может быть, для всяких многочленов
некоторой степени т>п.
Остановимся на требовании точности метода для
многочленов степени п. Это требование эквивалентно тому,
чтобы выполнялись точно равенства
ь п
\K(xh s)y(s)ds= 2 М**)ф(*а) (i = 1. •••> п) B9)
a k=l
для любых многочленов <p(s) степени п.
Теорема 2. Для того чтобы равенства B9) были
точными для всякого многочлена y(s) степени п,
необходимо и достаточно выполнение условий:
1) коэффициенты Lk(Xi) должны быть значениями при
x = Xi функции Lk(x)t указанной в равенствах B6);

§ 3} УРАВНЕНИЯ ФРЕДГОЛЬМА. МЕТОД КВАДРАТУР 277
2) многочлен со (s) = (s — хг)... (s — хп) должен
удовлетворять следующим условиям ортогональности:
ъ
\К{хь s)a)(s)ds = Oy i=\, 2, ..., п. C0)
а
Сделаем замечание по поводу этой теоремы.
Равенства C0) дают систему п уравнений, из которой должны
быть найдены узлы x-t (i=l, ..., п). Уравнения
определяются ядром К (х, s), и поэтому для каждого ядра
узлы Х[ будут, вообще говоря, своими. Последнее очень
затрудняет практическое использование указанного
способа повышения степени точности интерполяционного
метода.
Доказательство. Проверим необходимость
условий теоремы. Предположим, что равенство B9) верно
для всякого многочлена cp(s) степени п. Рассмотрим
коэффициент Лагранжа lm(s), отвечающий узлу хт:
/m(S)r=>-*m)<0'(*m)'
Это есть многочлен степени п— 1, поэтому для него
равенство B9) должно быть точным. С другой стороны,
1т (хд ^0 (ьфк) и 1т (хт) = 1 ив сумме соотношения B9)
сохранится только слагаемое, отвечающее k = m. Тогда
равенство B9) примет вид
ъ
\К(хь s)lm(s)ds = Lm{Xi)y
а
что доказывает необходимость первого условия.
Положим теперь ф (s) = co(s). Многочлен co(s) имеет
степень м, и для него B9) выполняется точно. Но так
как (x)(xk) = Q (k=l, ..., /г), то равенство B9) совпадает
с C0). Этим доказывается необходимость второго условия
теоремы.
Проверим достаточность условий. Пусть ф (х) есть
произвольный многочлен степени п. Разделим его на со (s).
В частном получится постоянная величина, которую
обозначим через а, а в остатке — некоторый многочлен Q (s)
степени не больше п — 1:
q>(s) = aa)(s) + Q(s).

278 ЧИСЛЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [ГЛ. 8
Ввиду соотношения a(xk) = 0, очевидно, будет Q (xk) =
= Ф <Л) и
ь ъ ь
\ К (xh s) ф (s) = а \К (xh s) о> (s) ds + \ К (xh s) Q (s) ds.
a a a
По второму условию теоремы первый из интегралов,
стоящих справа, равен нулю. Так как Q (s) имеет степень
<я- 1, то для него интерполяционное правило
интегрирования
\ К (*, s) ф (s) ds = 2 L* (*) ф (хА) + Р (*),
а /г=1
6
£*(*) = $#(*» s)lk(s)ds
выполняется при всяких х точно (без остатка р{х));
в частности, при x = xt имеем
b n n
\ К (xh s) Q (s) ds = V Lk (Xi) Q (xk) = £ L* (*<) Ф (**)•
Поэтому
6 n
l К (xh s) ф (s) ds - 2 L* (*') Ф (**)
и равенства B9) действительно точны для всякого
многочлена ф (s) степени п.
§ 4. Метод замены ядра уравнения на вырожденное ядро
1. Некоторые сведения об уравнениях с вырожденным
ядром. Ядро уравнения К (х, s) называют вырожденным,
если оно представимо в виде
К(х, s)=£at(x)h{s). A)
Функции at (/ = 1, ..., п) можно, очевидно, считать
линейно независимыми. Аналогичное можно сказать
о функциях р/ (t = l, ..., п).

§ 4] ЗАМЕНА ЯДРА УРАВНЕНИЯ НА ВЫРОЖДЕННОЕ 279
Когда в интегральном уравнении A) ядро К (х, s)
имеет форму A), то его решение, если оно существует,
представ и мо в следующем виде:
^(х) = [(х)+У^А^(х), B)
где коэффициенты Aj есть некоторые неизвестные
постоянные
ъ
Aj=X\$j(s)q>{s)ds.
а
Для нахождения этих коэффициентов может быть просто
построена линейная система уравнений. Введем
следующие обозначения:
ь ъ
P/y=$Ms)ay(s)ds, fi = \f(s)h(s)ds.
Подставим в уравнение C.1) вместо ср представление B):
f[x)+j]Aiai(x) =
Ъ п •- п
Ids.
i = \
= f to + Ч S ai W Pi (s)I/(s) + I] V/ (s)
o/=i l_ /— i
Ввиду линейной независимости функций a-t (x)
коэффициенты при них в левой и правой частях равенства
должны быть одинаковыми и после сравнения их мы
получим систему уравнений для At:
п
^ = Vi+^UM/ (i = 1» •••> п). C)
Если ввести векторы А = (АЪ ..., Ап), / = (/ъ ..., fn) и
матрицу
В:
LP/21 ••• $ППЛ
то систему C) можно записать в виде
A = %f + XBA.
D)

280 ЧИСЛЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [ГЛ. 8
Будем считать, что определитель этой системы отличен
от нуля:
l — lfiu —^Pi2 ••• — ^р1л|
— А,р21 1—^22 ••• — ^р2я =7^0.
— ^Ря1 — ^Рл2 ••• 1 — ^Эдя I
AX = D(E-XB) =
Решением системы D) является следующий вектор:
А = {Е-Щ-^. E)
Чтобы дать явное выражение для его составляющих,
обозначим А/у (X) алгебраическое дополнение элемента
определителя А (X), стоящего в строке номера i и столбце
номера /. Тогда составляющая At вектора А может быть
записана в виде
п
Внося эти значения коэффициентов At в равенство B),
получим представление решения через известные величины
п п Ь
Ф (х)=f (х)+1 ~Т) 2 2 А^а'{х) Sf (s) e(s) ds=
i = 1 у = l а
6
:/W + ^^A)/(s)ds. F)
Резольвента интегрального уравнения здесь имеет
простое явное выражение
п п
1 = 1 /=i
Построение решения ср (х) приводится в случае
вырожденного ядра К (х9 s) к вычислению величин Д-, $tj и к
решению линейной системы C).
2. Замечания о методах построения вырожденного
ядра, близкого к ядру уравнения. Метод приближенного
решения, который рассматривается в настоящем
параграфе, основан на простом соображении: если в заданном

§ 4] ЗАМЕНА ЯДРА УРАВНЕНИИ НА ВЫРОЖДЕННОЕ 281
интегральном уравнении ядро заменить на близкое к нему
вырожденное ядро, то решение нового вспомогательного
уравнения, как следует ожидать, будет близким к
решению заданного уравнения. Построение же решения
вспомогательного уравнения будет намного проще ввиду
вырожденности ядра. В следующем пункте будет доказана
теорема, подтверждающая такое ожидание: решение
вспомогательного уравнения может быть сделано сколь угодно
близким к решению заданного уравнения, если, во-первых,
число X не есть собственное значение заданного уравнения
и, во-вторых, вырожденное ядро вспомогательного
уравнения взято достаточно близким к заданному ядру. Сейчас
мы укажем некоторые приемы построения вырожденных
ядер.
Применение степенного ряда. Этот метод,
наверно, применим в случае, когда ядро К {х, s) есть
аналитическая функция от х или 5, регулярная в
достаточно широкой окрестности отрезка [а, Ь]. Пусть К' (х, s)
есть аналитическая функция от s в области \s — c\<.R,
где с есть середина отрезка [а, Ь] и R > -^ (Ь — а). В этом
случае К{х, s) можно разложить в степенной ряд по
степеням s— с, сходящийся в круге \s — c\<.R;
коэффициенты этого рода будут зависеть от х:
К(х, s)=C0{x) + C1{x)(s-c)+ ... +Cn{x){s-c)»+ ...,
Cn(x) = ±grK(x,c).
В качестве вырожденного ядра К(х9 s) здесь может
быть взят отрезок степенного ряда
R(x, s) = C0(x) + C1{x)(s — c)+ ... + Cn(x)(s — c)*.
Аналогично можно поступить и в тех случаях, когда
ядро есть аналитическая функция от х или от обоих
аргументов.
Использование ортогональных
разложений. Пояснение этого способа сделаем на примере
ряда Фурье. Для упрощения записи будем считать, что
ядро К (х, s) задано в квадрате 0 <; х, s ^ 1.
Предположим, что К (х, s) может быть разложено по переменной s

282 ЧИСЛЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [ГЛ. 8
в равномерно сходящийся относительно х и s ряд Фурье,
коэффициенты которого будут зависеть от х:
оо
К {х, s) = а0 (х) + 2 lUn (x) cos 2 я fe + bn (x) sin 2 я kx],
k=\
i i
а0 (х) = J /С (х, s) ds, Cft = 2 J /С(jc, s) cos 2л^ dsf
о о
l
Ьл = 2 $ /((*, s)sin2n;fes rfs.
о
В качестве вырожденного ядра К(х, s) может быть
взят отрезок этого ряда. Очевидно, подобным же образом
можно использовать ряд Фурье по аргументу х или
кратный ряд Фурье по обоим аргументам х и s.
Тригонометрические ряды были взяты лишь для
определенности записи и, очевидно, можно воспользоваться
любыми другими ортогональными разложениями.
Интерполяционные методы. Выберем на
отрезке [а, Ь] п узлов 5Ъ 52, ..., sn и проинтерполируем
по аргументу s функцию К{х, $) по ее значениям ео
взятых точках. При этом будет получено приводимое
ниже приближенное представление К (х, s), которое может
быть принято за вырожденное ядро:
ю (s) = (s — sl) ... (s — sn).
3. Оценка близости между решениями уравнений в
зависимости от близости самих уравнений. Пусть задано
интегральное уравнение
ь
<P(*WM + 4 *(*• s)<fls)ds G)
а
и одновременно с ним рассматривается измененное
уравнение
ь
Ч{х)=}{х)+Ь \ К(Х; 5)фE) ds. (8)

§ 4] ЗАМЕНА ЯДРА УРАВНЕНИЯ НА ВЫРОЖДЕННОЕ 283
В рассматриваемом сейчас методе роль измененного
уравнения играет уравнение с вырожденным ядром.
Нас будут интересовать два следующих основных
вопроса:
1) если известна разрешимость измененного
уравнения, то при каких условиях близости можно быть
уверенным в разрешимости заданного уравнения и как может
быть оценена разность между решениями;
2) что можно сказать о сходных вопросах для
измененного уравнения по известной разрешимости заданного
уравнения.
Так как уравнения G) и (8) в этих вопросах играют
сходные роли, то достаточно получить ответы на первый
из вопросов.
Теорема 1. Предположим, что для уравнений G) и
(8) выполняются условия:
1) для ядер К (х, s) и К (х, s) при всяких х из [а, Ь]
выполняется неравенство
ъ
\\К(х, s)-R(x, s)|ds<ft; (9)
а
2) при всяких х и s из отрезка [а, Ь] для резольвенты
f (x, s; Я) уравнения (8) верна оценка
|Г (х, s; Я)|<£; A0)
3) для свободных членов f и f уравнений верно
неравенство
1/W-fWKl. хе[а,Ь]] A1)
4) числа Я, А, г|, В удовлетворяют условию
l-\X\h(\ + \l\B)>0. A2)
Тогда можно утверждать, что уравнение G) имеет
единственное решение -ф (х) и для решений уравнений G) и (8)
верна оценка
\г(х)\ = \ч(х)-$(х)\^(г\ + \ЩМ)A+\Х\В)9 A3)
где М = max j ф (х) j, при этом для М выполняется нера-
X
венство A* I ' /1 1  I оч
М^-^ЩЩЩ' ^ = -ax iф(х) |. A4)

284 ЧИСЛЕННОЕ РЕШЕНИЕ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ [ГЛ. §
Доказательство. По условию A0) резольвента
уравнения (8) ограничена, поэтому К не является
собственным значением уравнения и уравнение имеет
единственное решение. Предположим, что уравнение G) имеет
решение <р (х). Ниже увидим, что в условиях теоремы это
предположение будет оправдано. Рассмотрим разность
г(х) = ф (х) — ф (х) между решениями и построим для нее
уравнение. С этой целью из G) вычтем почленно (8)
е (х) = ф (х) - ф (х) =
ь ь
= [(х)-1(х) + ^\К{х, s)q>(s)ds-X\K{x, s)q>(s)ds =
а а
b
= /(*)-7(*) + Ч[/С(*, s)-^(*> s)]9(s)rfs +
а
Ъ
+ ЦК(х, s)[v(s)-$(s)]ds =
а
Ь
= /*(*)+*$£(*, S)[q>(s)-q)(s)]ds.
а
Полученное равенство является интегральным
уравнением для г (х) = ф (х) — ф (х) со свободным членом f* (х)
и ядром К (х, s). Из него с помощью резольвенты Г
получается явное выражение ф — ф:
ъ
Ф (х) - Ф (*)=/* W + Я J f (х, s; Я) /* (s) ds. A5)
а
Ввиду неравенства
\f*(x)\^\f(x)-f*(x)\ +
\ь
+ IM-
;ti + IMAM
$[/£(*, S)-/((*, s)]<p(s)dS
|а I
из A4) вытекает следующая оценка:
= (TJ+1 г. | лл1) A +1 х i в). A6)
В правую часть неравенства входит неизвестная
величина М. Если К и К, так же как f и f, «близки» между
собой, то, как правило, <р и ф будут также мало отли-

ЛИТЕРАТУРА
285
чаться и при нестрогих оценках М в A6) часто бывает
можно заменить на М и получить нестрогую оценку
ф — ф, имеющую только ориентировочное значение и
применимую не во всех случаях. Однако в условиях теоремы
для М можно получить строгую оценку. В самом деле,
\4(x)\ = \9 + (V-®\^M + (r\ + \b\hM)(l+\X\B),
и так как это неравенство верно при всяких х, то
М^М + (ц + \Х\кМ)A + \Х\В).
Отсюда и на основании условия (И) следует
М^ М + ц(\ + \%\В)
m~-l-\X\h(\ + \l\B)'
Этот результат показывает, что все решения
уравнения G) в условиях теоремы ограничены одним числом.
Но тогда к не может быть собственным значением ядра *)
К (х, s) и уравнение G) имеет решение и только одно.
ЛИТЕРАТУРА
1. Бе резин И. С, Жидков Н. П., Методы вычислений, т. 2,
Физматгиз, М., 1959, гл. 10, § 10.
2. Канторович Л. В., Крылов В. И., Приближенные методы
высшего анализа, Физматгиз, М.—Л., 1962, гл. 2.
3. Крылов В. И., Бобков В. В., Монастырный П. И.,
Вычислительные методы высшей математики, т. 2, Минск, «Вы-
шэйшая школа», 1975, гл. 8.
*) Если К есть собственное значение ядра К (х, s), то к
решению неоднородного уравнения можно прибавить решение однородного
уравнения, умноженное на любую постоянную, и решения
неоднородного уравнения поэтому не могут быть ограничены в
совокупности.

ГЛАВА 9
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
И ПОСЛЕДОВАТЕЛЬНОСТЕЙ
§ 1. Введение
1. О задаче улучшения сходимости. Ряды и
последовательности очень часто и успешно применяются для
решения большого числа практически важных задач и
исследования многих вопросов теории. Но нередко
оказывается, что получающиеся ряды или
последовательности сходятся настолько медленно, что хотя они в принципе
и решают стоящую перед исследователем задачу, но ими
невозможно реально пользоваться, так как для
нахождения суммы ряда с нужной точностью необходимо было
бы взять чрезмерно много членов ряда или найти очень
много членов последовательности, чтобы последний из
найденных членов с хорошей точностью давал предел
последовательности.
В этих случаях естественно поставить задачу об
ускорении сходимости, т. е. о таком преобразовании
заданного ряда в другой ряд, который имел бы такую же сумму,
но сходился бы быстрее. Аналогично для
последовательности: ее нужно преобразовать в новую
последовательность, имеющую тот же предел, но сходящуюся к нему
более быстро, чем заданная.
Ускорение сходимости есть только одна из задач,
которые рассматриваются в проблеме улучшения
сходимости. Иногда полезно рассмотреть иные задачи,
например задачу преобразования произвольно сходящейся
последовательности в монотонную или колеблющуюся около
предела последовательность и т. п.
Ниже мы будем заниматься преимущественно задачей
ускорения сходимости.

§ и
ВВЕДЕНИЕ
287
С целью сокращения изложения напомним, что
сходимости ряда и последовательности равносильны между
собой: сходимость ряда и1-\-и2-\-.. --\-ип-\-... к сумме s,
по определению, есть сходимость последовательности
частичных сумм su s2, ..., sn, ... (sn = ах + .. . + ая) к
пределу s; наоборот, сходимость последовательности sn
(п = 1, 2, ...) к s равносильна сходимости ряда Si + (s2—
— Si) + -..+ (s„ — s,2_]) + - •• к сумме s. Поэтому ясно, что
каждый результат, установленный для
последовательности, может быть с необходимыми изменениями
преобразован в равносильный результат для ряда, и наоборот.
Это позволит доказывать утверждения только для одного
из объектов — ряда или последовательности,— избирая его,
как будет удобнее или нагляднее.
Пусть дана сходящаяся последовательность sn
(/2—1, 2,...; sn ->-s). Рассмотрим погрешность приближения
rn = s — sn. Ускорить сходимость snK s означает, что из гп
нужно выделить главную часть, т. е. представить гп
в виде суммы двух слагаемых гЛ = со^ + гА, из которых г,}
стремится к нулю быстрее, чем со,! [гД = о (соД)], и затем
главную часть (о„ прибавить к sn:
5л == $л ~Г ^п * $ — Sn ~г Гп •
Новая последовательность sn будет, очевидно, более
быстро сходиться к s, чем sn.
Если одного шага преобразования недостаточно для
получения нужного ускорения сходимости, мы должны
такие же преобразования выполнить с sn и гп' из г\
выделить главную часть, представив гп в форме суммы гп =
= <*>2п + гПу где гп = о (соп) (п -> со), прибавить сап к sA и т. д.
В общем случае для всякого к нужно разложить гл
на &+1 слагаемых так, чтобы выполнялись условия
^ = Ч + ^ + ... + со* + ^, К+1=°Н) 0)
(s=l, .... А-1), /^ = о(со*).
Чтобы выполнить такое разложение, необходимо иметь
некоторые достаточно полные сведения о законе, по
которому гп стремится к нулю при возрастании п.
Приведем из предыдущих глав примеры выделения из
погрешности главной части и разложений вида A).

288 УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ |ТЛ. 9
I. В § 2 гл. 4 говорилось о том, что метод одноша-
говой итерации хп+г = ф(хп) (/2 = 0, 1, ...) для
нахождения решения х* уравнения х = ср(х), наверное, сходится
к х* при выполнении двух условий: 1) функция <р имеет
непрерывную производную ф' (л:) в окрестности л:* и
притом j фг (х*) !< 1; 2) начальное приближение х0 взято
достаточно близким к решению х*. Когда приближение #л
близко к х*, то для его погрешности еп = хп — х* с
нужной точностью выполняется приближенное равенство
б/г+1 ^ ф' (**) ея. Можно считать, что это равенство
выполняется, начиная с п = 0. Из него следует явное
выражение для ея:
ея^[ф/(^*)]яео = 8о9я, B)
показывающее, что с ростом п погрешность гп убывает
приблизительно по закону геометрической прогрессии.
Приближенное же значение B) для гп дает главную часть
погрешности.
Эти факты были использованы в п. 4.3.3 для
ускорения сходимости метода простой итерации и построения
правила преобразования D.3.9) такого, что для новой
последовательности погрешность убывает по
квадратичному закону вида D.3.11).
II. Напомним, что погрешность квадратурного
правила трапеций, если функция / имеет достаточно высокий
порядок дифференцируемое™, представима в виде (см.
п. 5.8.2, E.8.4))
ь
Rn=\f(x)dx-Tn =
а
k
= - 2 ■щс3»^'"{b)~ps'1] (a)]+p2s+2 (/)> C)
где
Тя = л[4-/(а)+/(а + А) + ... + у/(&)],
ft = 1F-а), р25+2-0(/*25+2).
Когда п неограниченно возрастает, это равенство дает
представление погрешности Rfl в форме суммы бесконечно
малых величин относительно 1/п возрастающих порядков

§ i]
ВВЕДЕНИЕ
289
и имеет вид A)э Главным членом в Rn является величина
-й[/'(*)-/'(а)] и т. д.
В общем виде проблема улучшения сходимости
последовательности имеет следующий смысл: по заданной
сходящейся последовательности sk (k = 1, 2,...; sk ->• s) нужно
построить новую последовательность
<*n = fn{si, s2, ...) (я=1, 2, ...), D)
удовлетворяющую условиям:
1) новая последовательность сходится к тому же
пределу s, что и sn;
2) сходимость ап к s «лучше» в каком-то смысле
сходимости S„KS.
Критерий сравнения сходимостей должен быть при
этом точно указан.
В преобразовании D) можно воспользоваться выбором
функций fm и если мы хотим добиться «улучшения»
сходимости, например ее ускорения, то выбор fn должен
быть как-то согласован с законом сходимости sn->s.
Обычно, чтобы избежать чрезмерной специализации
правил для такого согласования, избирают некоторое
множество S сходящихся последовательностей sn, близких
между собой по характеру стремления к пределу. В
качестве таких множеств берут в первую очередь множества
последовательностей с особенно часто встречающимися
в приложениях видами сходимости. .Примерами таких
множеств могут служить последовательности sn,
сходящиеся ло закону, близкому к тому, как стремятся к
пределу рациональные функции, или же показательные
функции s-\-Ae~an и их линейные комбинации и т. д.
Преобразование D) выбирают так, чтобы оно ускоряло
сходимость не одной фиксированной последовательности sn9
а всех последовательностей взятого множества S.
Некоторые способы такого выбора fn будут рассмотрены ниже.
2. Связь с проблемой суммирования расходящихся
рядов и определения пределов расходящихся
последовательностей. Задача улучшения сходимости
последовательностей и рядов в некоторых сторонах своих связана
с другой классической задачей, имеющей почти столь
же длительную историю. Ее содержание указано в назва-
10 В. И. Крылов и др., т. II

290
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
нии пункта. Поясним смысл этой задачи двумя
примерами.
1. Первый из них возьмем из области гармонического
анализа. Пусть f есть 2я —периодическая функция,
абсолютно интегрируемая*) на (—я, тс]. Для нее могут быть
вычислены коэффициенты Фурье
л л
ап = — \ f (x) cos nx dx, bn = ~ \ f (x) sinnx dx, E)
—я —л
П = 0, 1, ...
Рассмотрим обратную задачу, которую часто называют
гармоническим синтезом: по известным коэффициентам
Фурье ап и Ъп функции / нужно найти саму функцию /.
Напомним некоторые факты, связанные с такой
задачей. Предположим, что мы изменили функцию / на
множестве точек, имеющем меру нуль **), и получили новую
функцию /\, которая пусть также является абсолютно
интегрируемой. При таком изменении коэффициенты ап
и bni очевидно, сохранят свои значения, так что
функции f я fi будут иметь одинаковые коэффициенты Фурье.
Верно и обратное: если две абсолютно интегрируемые
функции / и /1э имеют одинаковые коэффициенты Фурье,
то они могут отличаться между собой только на
множестве меры нуль.
Поэтому коэффициенты Фурье определяют функцию f
лишь с точностью до ее значений на множестве
нулевой меры.
Пусть даны числа ап и Ьп и известно, что они
являются коэффициентами Фурье некоторой функции /, но
ее значения нам неизвестны и мы должны найти их по ап
и Ьп. Для этого обычно составляют ряд Фурье,
отвечающий /,
1 °°
/W^yflo+I] (an cos nx + bn sin nx). F)
*) Имеется в виду абсолютная интегрируемость по Риману. Для
функций, интегрируемых по Лебегу, некоторые оговорки, которые
делаются в дальнейшем изложении, будут излишними и могут быть
опущены.
**) Говорят, что множество точек имеет меру нуль, если оно
может быть покрыто счетным множеством интервалов, сумма длин
которых может быть сделана меньше любого положительного числа 8.

§ 1]
ВВЕДЕНИЕ
291
Известен следующий простой результат: если ряд F)
равномерно на [—я, я] сходится, то сумма его s (х) будет
иметь ап и Ьп своими коэффициентами Фурье и будет,
следовательно, одной из разыскиваемых функций f.
Но может оказаться, что этот ряд будет расходиться
на некотором множестве точек отрезка [— я, я] или даже
всюду на этом отрезке*). В этих случаях мы
сталкиваемся со следующим: ряд F) содержит достаточно полную
информацию о функции /, определяющую ее всюду на
[— я, я], кроме множества точек меры нуль, но обычное
понимание суммы ряда здесь не приводит к цели и не
дает возможности найти функцию /. Чтобы получить
правило для вычисления / по ап и Ьп, нужно каким-то
целесообразным образом изменить понятие суммы ряда. Такие
правила указываются в теории рядов Фурье. Простейшим
из них является метод средних арифметических: нужно
составить частичные суммы ряда F)
1 п
s« (*) = у До + 2 (unZOsnx-\-bnsinnx)
и образовать из них средние арифметические величин
оп (х) = — [si(x) + ... + sn (х)].
Доказывается, что если / есть непрерывная на [—я, я]
функция **), то lim on (х) = / (х); при этом сходимость будет
п
равномерной на [—я, я].
*) Существуют, например, непрерывные 2л-периодические
функции, для которых соответствующий им ряд Фурье расходится
на всюду плотном на [— л, л] множестве точек и такие
функции /, абсолютно интегрируемые по Лебегу, для которых этот ряд
расходится всюду на [— я, я]. (Примеры можно найти в книге:
Н. К.Бари, Тригонометрические ряды, М., Гостехиздат, 1961,
гл. V, §§ 17, 20)/
**> В общем случае, когда / есть любая абсолютно
интегрируемая функция, она может быть найдена по ряду F) при помощи
следующего предельного перехода;
lim
r-*i— о
ао + / rn (an cos nx-\-bn sin nx)
л=1
= /(*)
всюду, кроме множества меры нуль,
10*

292
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
2. В качестве второго примера рассмотрим задачу
аналитического продолжения степенного ряда. Пусть
аналитическая функция f (z) комплексной переменной г
задана степенным рядом
оо
m=2Cv2V = *o + *12+..., G)
v = 0
сходящимся в круге \z\<R. Ряд представляет f и дает
возможность вычислить ее значения только внутри круга
и, может быть, в некоторых точках граничной
окружности, там, где он сходится. Но область существования
функции/ может быть значительно шире, чем круг \z\<R.
Степенной ряд определяет функцию / во всей области
ее существования, но если взять любую точку z в этой
области, лежащую вне круга lz|</?» то вычислить
там значение f (z) при обычном понимании суммы ряда G)
мы не сможем, так как в этой точке ряд расходится.
Значение f(z) естественно считать обобщенной суммой
расходящегося ряда G). Вычислить же его через
коэффициенты ряда cv и координату z можно только в том
случае, если отказаться от обычного понятия суммы
ряда G), подвергнуть его предварительно
целесообразному преобразованию и лишь потом воспользоваться
классическим понятием предела. Некоторые правила
преобразования степенного ряда, применяемые для
аналитического продолжения его суммы за круг сходимости,
указываются в курсах теории функций комплексной
переменной и книгах по теории расходящихся рядов.
Пусть дана произвольная последовательность sn (п= 1,
2, ...). Применим к ней преобразование D), которое
кратко запишем в виде
o = f(s). (8)
Если окажется, что новая последовательность ап
сходится и limcr„ = G, то ее предел а называют /-пределом
или обобщенным /-пределом заданной последовательности
и пишут
а = / — lims„.
п
Величина сг зависит, очевидно, не только от
последовательности S/i, но и от выбора преобразования,, т. е. от

§13
ВВЕДЕНИЕ
293
выбора функций fn. Такой выбор не должен, очевидно,
противоречить обычному пределу последовательности:
если заданная последовательность sn сходится к пределу s
и если к sn применимо преобразование D) и обобщенный
предел а существует, то должно быть cr = s. Это требование
оставляет еще достаточно большой произвол в выборе fn.
Кроме того, в каждой конкретной задаче к
преобразованию предъявляется свое требование, зависящее от
цели задачи: если строится преобразование для
обобщенного суммирования ряда Фурье и если обобщенный предел
существует, то он обязан быть одной из функций /, для
которой числа ап и Ьп будут коэффициентами Фурье;
когда строится преобразование для обобщенного
суммирования степенного ряда в точке z, лежащей вне круга
сходимости | z | < #, то обобщенный предел должен давать
одно из аналитических продолжений / в точке z (или
избранную ветвь продолжения) и т. д.
Для более полной характеристики преобразований,
которые будут рассматриваться в последующем
изложении, полезно ознакомиться с некоторыми понятиями,
относящимися к обобщенным пределам.
Рассмотрим некоторое множество S сходящихся
последовательностей sn. Говорят, что преобразование D)
сохраняет сходимость на 5, если преобразование
применимо ко всякой последовательности sn e S и новая
последовательность ап сходится: ал-хх, при этом не
обязательно предел ап совпадает с пределом sn.
Если S есть множество всех сходящихся
последовательностей и из sn->s следует ап -> о-, то говорят просто,
что преобразование сохраняет сходимость.
Когда из sn -> s (sn <= S) следует оп -> s, то говорят,
что преобразование сохраняет предел на 5, или просто
сохраняет предел, если sn есть любая сходящаяся
последовательность. В последнем случае, когда из sn -> s всегда
следует an->sf преобразование D) часто называют
регулярным.
Признаки сохранения сходимости или предела при
преобразовании изучены с достаточной полнотой лишь
в случае линейных преобразований
со
<Уп= У! anmsm (n=l, 2, ...). (9)

294
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
Теорема 1 (о сохранении сходимости). Для того
чтобы преобразование (9) было применимо ко всякой
сходящейся последовательности sn (sn-+s) и сохраняло
сходимость, необходимо и достаточно выполнение условий:
1) существует число М такое, что при всяких
п = 1, 2, ... выполняется неравенство
оо
Ап= 2 \апт\^М<сю; A0)
2) при п->оо
оо
5/1= 2 а™->а; (И)
3) (Зля каждого фиксированного значения т при п->оо
выполнено соотношение
аПт~>^т (т= 1, 2, ...). A2)
Лрг/ выполнении этих условий предельное значение ап
дается равенством
I ОО \ ОО
а = lim ая = I а - 2 а™)s + 2 а**л- A3)
\ m = l / /1 = 1
Доказательство теоремы мы. опускаем и сделаем лишь
некоторые пояснения ее условий. Первое из них не имеет
простого и наглядного истолкования. Но можно показать,
что если оно не выполняется и числа Ап не будут
ограничены в совокупности, то существует такая сходящаяся
последовательность sn, для которой соответствующая
последовательность ап будет неограниченной и,
следовательно, расходящейся.
Если мы возьмем стационарную последовательность
51 = s2=. • .= 1, ей будет отвечать последовательность оп = В
и условие 2) означает, что она должна сходиться к
некоторому пределу а.
Наконец, условие 3) имеет следующий смысл. Возьмем
т
последовательность sn вида 0, ..., 0, 1, 0, 0, ...,
состоящую из нулей, и только на месте номера т стоит
единица. Она, очевидно, сходится к нулю. Соответствующая
ей последовательность оп есть оп = апт (т фиксировано,
м=1, 2,/..). Условие 3) является записью требования
сходимости такой последовательности ап.

§ 1]
ВВЕДЕНИЕ
295
Сделаем еще два простых замечания. Рассмотрим
бесконечную матрицу линейного преобразования
| Яц 012 ••• <hm •••[
^21 022 • • • 02m • • • I
a/ii 0^2 ••• апт •••
Числа Вп суть суммы элементов этой матрицы по
строкам. Условие 2) требует, чтобы суммы Вп имели
конечный предел при п->со. Элементы апт, где т
фиксировано, стоят в столбце номера т матрицы. Условие 3)
требует, чтобы последовательности элементов, стоящих
в каждом столбце матрицы, имели конечный предел.
Отметим также, что условия 2) и 3) могут быть
объединены в одно более простое и наглядное.
Последовательности вида sl9 s2, ..., sm, 5, s> s, ..., у которых
все значения, начиная с некоторого места, являются
одинаковыми, называются почти —или
квазистационарными. При помощи таких последовательностей условия 2)
и 3) могут быть заменены одним: всякая почти
стационарная последовательность sb ..., smt s, s, ...
преобразуется в сходящуюся последовательность ап.
Теорема о сохранении предела является простым
следствием высказанной выше теоремы 1.
Теорема 2. Для того чтобы преобразование (9)
сохраняло предел, т. е. чтобы из sn-+s следовало on-*sy
необходимо и достаточно выполнение условий:
1) существует число М такое, что при п=\9 2, ...
выполняется неравенство
оо
Ап= 2 \аят\<!М <оо; A4)
2) при /г-*-оо
3) для каждого фиксированного тип-+оо выполняется
соотношение
ая«-*0 (т=1, 2, ...). A6)

296
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
Первые условия теорем 1 и 2 совпадают. Второе
условие теоремы 2 означает сохранение предела для всякой
стационарной последовательности sn = s.
Коэффициент апт стоит множителем при sm и
соответствующий член в сумме (9) есть anmsm. Поэтому
условие A6) означает уничтожение влияния на предел оп
(п->-сю) любого значения sm с фиксированным номером т.
Полезно обратить внимание на то, что в теореме 1,
в которой не требуется сохранение предела, на предельное
значение новой последовательности а = \imon может
а
оказывать влияние любое значение sn заданной
последовательности, как это видно в равенстве A3). В теореме 2
о сохранении предела влияние отдельных значений s,
естественно, должно быть исключено.
Две рассмотренные задачи — об улучшении сходимости
и о суммировании расходящихся рядов или пределах
расходящихся последовательностей — связаны между собой.
Во-первых, для решения их применяется один и тот же
аппарат преобразований D), и хотя эта связь является
формальной, но она иногда позволяет дополнять
исследования одной из задач результатами из другой. Во-вторых,
задачи имеют некоторую внутреннюю связь, объяснить
которую можно наиболее просто на частном случае.
Причиной расходимости ряда ]>]ап часто является недоста-
п
точно быстрое убывание модулей членов ап. Для введения
«обобщенной суммы» заданный ряд преобразуют в другой
^\Ьп [&л==ф(а1, а2, ...)], и если он сходится, то его сумму
принимают за обобщенную сумму данного ряда. Так как
2^я сходится, его члены Ьп будут убывать, вообще го-
п
воря, более быстро, чем ап> и преобразование 2 #/*-* 2^*
п п
ускоряет убывание модулей членов ряда.
Поэтому можно ожидать, что каждое преобразование
последовательности или ряда, позволяющее ввести понятие
обобщенных сумм или пределов, должно, по крайней мере
в некоторых случаях, улучшать сходимость. Можно также
ожидать, что преобразования, построенные для улучшения
сходимости, иногда будут применимы к определению
обобщенных пределов и сумм. Примеры этого можно найти ниже.

§2] ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ ПРЕОБРАЗОВАНИЯ 297
§ 2. Интерполяционные методы
преобразования последовательности
1. Некоторые общие сведения. Задача интерполирования
предельного значения последовательности в общей форме
будет рассматриваться только для пояснения содержания
некоторых понятий, полезных в дальнейшем изложении.
Для этой цели достаточно ограничиться случаем
интерполирования при помощи линейных комбинаций.
Пусть дана сходящаяся последовательность sn (п =
= 1, 2, ...; sn ->s). Ее можно рассматривать как функцию
целочисленного аргумента п, область определения которой
есть множество натуральных чисел плюс бесконечно
далекая точка, где функция имеет некоторое значение
s = Sco> подлежащее разысканию.
Допустим, что выбрана система функций со0(/г),
Ох (п),... целочисленного аргумента п (п= 1, 2,...), которая
будет лежать в основе интерполирования: из функций Ш; (п)
'будут составляться линейные комбинации, служащие для
интерполирования s„,
Pk (ft) = а0щ (ft) + <*!©! (ft) +... + акщ (ft). A)
Выбор со/ (ft) естественно подчинить следующим условиям:
1) никакая из функций со£ (ft) не есть линейная
комбинация конечного числа других функций o);(ft) (]Ф1)',
2) каждая функция со£ (ft) (t=l, 2, ...) имеет конечное
предельное значение при /i-»-oo
C0;(ft)->(D;; B)
3) при всех k и для любых k+l различных значений
ft0, fti, ..., nk аргумента п выполняется неравенство*)
|©о(«о) <М"о) .♦. ©л («о)
U>o(%) <*i(ni) ... Щ(п{)
Dk = Dk(n0l ft^ ..., nk) =
®o{nk) <M%) ••• Щ{пк)
ФО.
C)
Ниже будет ясно, что третье условие равносильно
требованию возможности и единственности интерполиро-
*) Вместо этого часто говорят, что функции щ{п) (я=0, 1, ...)
образуют систему Чебышева.

298
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
вания любой последовательности sn по значениям sn в узлах
/г0, ..., nk.
Четвертое условие будет указано ниже.
Комбинация A) содержит k-\-\ параметров а,- (/=
= 0, 1, ..., k). Выберем их так, чтобы Pk (n) в узлах щ
принимала значения, равные значениям sn:
Pk(n;)=snf (/ = 0, 1, ...,*). D)
Эти условия для нахождения а;- дают систему
линейных уравнений
аоЩ (Щ) + tficoi (nf) + ...+ акЩ (nf) = snj9 E)
определитель которой совпадает с Dk (п0, пъ ..., nk) и,
по третьему условию, отличен от нуля. Поэтому система E)
имеет решение и только одно. Будем считать, что af
найдены и их значения внесены в линейную комбинацию A),
так что Рк (n) выполняет требования интерполирования D).
Комбинацию Pk (n) примем за приближенное
представление sn при всех значениях п. Устремляя п к
бесконечности, найдем предел Pk (/г), существующий ввиду второго
условия. Этот предел (гудем считать приближенным
значением для limsn = s:
G = Pk (oo) = а0щ + %% +... + акщ ^ s. F)
Можно просто записать явное выражение а через, значения
®t(nj) (*» / = 0» 1, ..., я) и snj. Для этого присоединим
равенство A) к уравнениям E) и полученную систему
запишем в виде
- Pk (я) + воЩ (п) +... + акщ (п) = 0,
- sno + aQco0 (n0) + • • • + акщ (п0) - 0,
- snk + а0щ (nk) +... + с*кЩ (nk) - 0.
Ее можно рассматривать как однородную систему k + 2
уравнений с неизвестными — 1, а0, ..., ал, и так как они
образуют ненулевое решение системы, то ее определитель
должен равняться нулю при всех п:
\Pk(n) ©о(л) ... <ок(п)
3ло
Vnk
Dk (n0,
пк)
= 0.

§ 2] ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ ПРЕОБРАЗОВАНИЯ 299
Отсюда сразу получается
ад)--5Г
О CD0(rt) ... U>k(n)
Jno
*nk
Db
G)
Предельный переход при ft~>oo дает следующее выра
жение для а:
10 ®0 ... щ
1 • п / \ — М Sn0
hm/>ik(n) = a = 1T '
°Л£
Oft
(8)
Необходимо отметить, что погрешность s — g
приближенного равенства s я^ о зависит от выбора функций щ (ft)
и узлов rij (/ = 0, 1, ..., ft). Обратим внимание на одну
сторону этой зависимости: чтобы можно было сделать
погрешность s — о сколь угодно малой, необходимо
функции со/ (ft) взять такими, чтобы sn можно было приблизить
при помощи Pk (я) сколь угодно точно, выбирая
надлежащим образом k и коэффициенты а;- (/ = 0, 1, ..., k).
Это приводит к следующему понятию полноты.
Пусть рассматривается некоторое множество S
сходящихся последовательностей sn.
Множество линейных комбинаций Pk (n) называется
полным в S, если для каждого е>0 и всякой
последовательности sna S существуют такое k и такие
коэффициенты а, (/ = 0, 1, ..., k), что при всех значениях п =
== 1, 2, ... выполняется неравенство
\sn-Pk(n)\<E.
В качестве четвертого условия, которому подчиняют
выбора со; (д), берут обычно следующее:
4) функции со/ (/г) таковы, что множество линейных
комбинаций Pk (ft) является полным в множестве S всех
сходящихся последовательностей sn.
Равенство (8) дает интерполяционное правило
преобразования последовательности sn в число а. Чтобы
получить преобразование последовательности sn в последова-

300 УЛУЧШЕНИЕ СХОДИМ6СТИ РЯДОВ ГГЛ. $
тельность gp (р=1, 2, ...), нужно указать бесконечную
матрицу узлов
N =
"J
"о
<
п\ .
п\ .
«? •
•• к
■■ 4
•• <
"р
(9)
которая записана так, что в ее строке номера р стоят
узлы, используемые для получения значения ср:
lim PkAn)
■■ар~
-1
d*p (»!
0 оH
i\"
k
... <*п
Dh
A0)
(P=l, 2,...).
Применяя полученное правило преобразования F) при
р = 1, 2,..., построим новую последовательность 0!,
а2, ..., (тр, ...
Естественно поставить вопрос ее сходимости.
Оказывается, что сделанных предположений для этого, вообще
говоря, недостаточно. Дело в том, что свойство полноты
гарантирует существование для всякой сходящейся
последовательности sn такой последовательности Pk (/z), которая
сходится к sn равномерно относительно я=1, 2, ... Для
такой последовательности Pk (со) ->s (k -> со по некоторым
значениям). При этом на выбор линейных комбинаций
Pk (n) не налагается ограничений: величины k и Яу могут
быть любыми. В нашей проблеме построение Pk (n)
определяется равенством G) и все значения со/ (nj) находятся
по таблице узлов (9). Если функции о); (п) и таблица (9)
заданы, то комбинации Pk (n) (&=1, 2, ...) вполне
определены, и мы не имеем права ничего выбирать, а тогда
сходимости (Ур-KS может не быть.
Если функции со; (п) таковы, что соответствующая им
система Pk (n) не обладает свойством полноты в
рассматриваемом семействе S, то, по-видимому, следует считать
выбор функций а>/ (п) неудачным, так как невозможно
рассчитывать на сходимость op->s для всех sn из
семейства S.

§ 2] ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ ПРЕОБРАЗОВАНИЯ 301
Если же система Ри (п) обладает полнотой в S, то это
еще не может гарантировать сходимость ep-+s при любых
sn cz S. Проблема сходимости должна быть исследована
дополнительно. В ней мы имеем дело со следующими
объектами: множеством S последовательностей, функциями
со/ (п) (/ = 0, 1, ...), лежащими в основе интерполирования,
и таблицей Л^ узлов интерполирования (9). Необходимо
выяснить, как должны быть связаны между собой эти
объекты, чтобы можно было ответить на следующие
основные вопросы.
1. Для какого множества S последовательностей sn
новая последовательность оп будет сходящейся?
2. В каком случае из sn-*s и оп-^а следует cr = s,
т. е. когда преобразование A0) будет сохранять предел?
3. Для каких сходящихся последовательностей sn
преобразование A0) ускоряет (или улучшает) сходимость?
4. Как может быть оценена погрешность on — s новой
последовательности?
2. Интерполирование при помощи многочленов от 1/п.
Случай постоянного числа узлов. В качестве функций 0/ (л)
возьмем отрицательные степени п:
со0(я) = 1, щ(п) = -, ..., щ(п)^--г, ...
Их линейными комбинациями будут многочлены от 1/п:
Полнота всех Pk(l/n) на множестве сходящихся
последовательностей sn является следствием теоремы Вейершт-
расса о возможности равномерного приближения
непрерывной функции алгебраическим многочленом.
Пусть sn-+s (п-+сю). Введем новую переменную х,
положив х — п1, п = х'1. Рассмотрим функцию v(x)~sn.
Она определена в точках я=1, у, у, ... Доопределим
ее всюду на отрезе [0, 1], интерполируя ее линейно на
отрезках у, . { (А=1, 2,...) и положив t;@) = s.
Так построенная функция v (x) будет непрерывной всюду
на [0, 1J. Для любого е> 0 существует многочлен Pk (x) =
~ а0-{-а1х + . ..-\-akxk некоторой степени k> такой, что при

302
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
всякихх <=[0, 1] будет верно неравенство \v(x)—Pk(x)\<.e.
В точках же x—\jn будет выполняться неравенство
1
*.-Ч.т)
<е
(л=1, 2, ...),
доказывающее полноту Pk(l/n).
Для интерполирования на шаге номера р и
построения ар возьмем k-\-\ узлов я = р, р+1, ..., Р + &.
Матрица (9) узлов интерполирования для всех шагов при
р*= 1, 2, ... имеет вид
II 2 ... * I
||2 3 ... k + V
N-.
р р + 1
р + £
Возможность и единственность интерполирования
посредством Pk(l/n) любой последовательности sn по
значениям ее в этих узлах вытекает из аналогичных
результатов для интерполирования обычными алгебраическими
многочленами, полученных в первой части книги
(см. п. 1.1.1).
Выражение интерполирующего многочлена Pk(l/n)
может быть построено при помощи формулы Лагранжа
и будет следующим:
1
(Л I
У = о
1
Р + 1
P+iJ
эр+/>
(П)
где
со
© -г =
/ 1
(--
\п
1 \/1
У К»
р+1
р+1
_j
p+i
i
= /.
~\p+i
i
р+/—i Л р+/
1
/ 1
Р-И
L1
р+/-ЫУ'"\р+у
P + fc,
(P + /)*P(P+1) ••• (р + /-1)(Р + /+1) ••• (Р + А)'
Предел Pk(\/n) при /г->со принимается за 0р:
(-l)*-j(p+/)*
Л (А-/)!
а/>+У'
:L(Sp) (p=l, 2, ...). A2)

§ 2] ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ ПРЕОБРАЗОВАНИЯ 303
Это равенство является записью линейного
преобразования последовательности sn в последовательность ар.
Оно применимо ко всякой последовательности sn
независимо от сходимости или расходимости ее и является
частным случаем общего линейного преобразования A.9),
К0ГДа ( п ^
0, т<р,
рт | (т—р)\ (k + p — т)\ * г ^ '
0, m>p + k.
Формула A2) показывает, что при возрастании р
коэффициенты преобразования растут как pky поэтому для
них не выполняется первое условие теорем 1 и 2 и
преобразование может, следовательно, переводить
сходящуюся последовательность sn в расходящуюся
последовательность ор.
Обратим еще внимание на некоторые свойства
коэффициентов преобразования A2). Функции s„e== 1, sn = --, ...
..., s„ = —£- интерполируются многочленом Pk(l/n) точно
и преобразование A2) должно - при всяких р точно
давать их предельные значения, что приводит к следующим
соотношениям:
/=о
k
A3)
т
l(-LW У (~ i)k-fJE±JrL . _1_
Ь\рт ^[ } Ж*-/)! (Р + П
1 = 0
(р= 1, 2, ...; т= 1, 2, ..., k).
Чтобы ответить на некоторые из вопросов,
поставленных в конце предыдущего пункта применительно к
преобразованию A2), обратим это преобразование. Для этого
перепишем его подробнее:
г /,ч_ (P+W* (P + k-Dk , .f-lV^-a
L\Sp) — £| S/>+* J! (£—1)! SP+k-l-\-----T{— L) 'tfSp — Op.
A4)
Примем прежде всего во внимание то, что это преобра-

304
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
зование относительно sp является линейным конечнораз-
ностным уравнением порядка k со свободным членом ор.
Когда gp тождественно равно нулю и L (sp) = 0,
оно называется однородным. Существенно заметить
следующее: из второго равенства A3) следует, что функции
1 1 1
sp = — ,sp = —, ..., sp = —£ являются решениями
однородного уравнения L(sp) = 0.
Полагая в A4) р=1, получим равенство
Ь (Si) = Xl S*+1 ~~~ ll(fe-l)! s* + ••• + (— !) Ж Sl = ai»
из которого можно найти s^+1, выразив его линейно через
Si, ..., S* и ах. При £ = 2 формула A4) даст
, , ч (£ + 2)* F + 1)* , , / и* 2й
VS2/ = £j S/e+2 и (^_l)t S^+l + * * * + i~~ V ~£Г S2 = ^2»
откуда найдем sk+2 как линейную функцию от s2, ..., sM
и а2, и так как раньше sk+1 было выражено через sx, ...
..., Sft, ax, то окончательно найдем sft+2 как линейную
функцию от sb ..., s*, аъ а2 и т. д.
Продолжая такие вычисления, мы представим sP в виде
линейной комбинации от sly ..., sk, аг, ..., ар_л,
коэффициенты которой зависят от р:
5/>=2гЯ'+1] G^ (P = k+l, k + 2, ...). A5)
Величины Si, ..., sk, называемые начальными значениями
решения, остаются произвольными и могут иметь любые
значения. Когда они заданы, все дальнейшие значения
sp (Р > k) решения уравнения определяются единственным
образом.
Коэффициент Тр учитывает влияние, которое оказывает
на sp начальное значение Sj. Аналогично коэффициент Glp
учитывает влияние значения о*/ свободного члена. Ввиду
такой роли Тр и Gp их называют функциями влияния или
функциями Грина соответствующих начальных значений
и значений правой части.
Для нахождения Гр заметим прежде. всего, что когда
все at (*'=1, 2, ...) равны нулю и уравнение A4)
однородно L (sp) = 0, в представлении A5) для sp останется

§ 2] ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ ПРЕОБРАЗОВАНИЯ 305
только сумма с sj. Если, кроме того, все начальные
значения, кроме s,, равны нулю, a s, = l, то sp = rj>.
Поэтому можно сказать, что Гл есть решение однородного
уравнения L(sp) = 0 с начальными значениями Гр = 0
(р = и ..., k, РФ1), г;=1.
Гр имеет следующее выражение:
r^^-.T..-lfi-iVi-i
Р- (}-\)\{k-j)\ p\p 1)\р 2,
7=г)("?~7Тт)-G""т)- <16>
Проверим это. Правая часть равенства A6) есть многочлен
от 1/р степени k без свободного члена и является линейной
комбинацией функций sp = —, sp = -^, ..., sp = —ft-. Но
каждая из них есть решение однородного уравнения
L(sp) = 0, поэтому и Г£ также есть решение этого
уравнения. То, что правая часть имеет нулевые начальные
значения при р=1, ..., k, рф], является очевидным,
численный же множитель (— \У~Х\{] — 1)! (k — /)!] х в правой
части выбран так," чтобы она была равна единице при р = /.
Рассмотрим теперь коэффициент Gp4. Он совпадает
с решением sp, если считать, что все Sj (/ = 1, ..., k)
равны нулю и аг=0 (ьфт), crw=l. Таким образом, Gp
есть решение неоднородного уравнения
L(sp) = 8pn A7)
с нулевыми начальными значениями.
Когда р<т, указанное уравнение будет однородным,
так как 6^ = 0, и ввиду нулевых начальных значений
его решение будет тождественным нулем для p<im-\-k,
так что
Gp=0, p=l, 2, ..., m + ft-1. A8)
При р = т уравнение A7) дает равенства
Для p>m, так как 6™ = 0, уравнение A7) вновь
становится однородным. Можно, следовательно, сказать,

306
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
что G™ для р>т есть решение однородного уравнения
с следующими начальными значениями:
Покажем, что при p^m-\-k функция G™ представима
в форме
p ~P \ p J\ P )"'[ P J
(p^m + k). A9)
Действительно, правая часть есть многочлен от 1/р
степени k без свободного члена, она является линейной
комбинацией решений sp = —, sp = ~¥, ..., sp = --■■£■
однородного уравнения L(s/7) = 0 и является поэтому
решением однородного уравнения. Начальные же значения
правой части при p = m-\-U m + 2, ..., m-\-k совпадают
с начальными значениями G™.
Таким образом, в равенстве A5), обращающем
рассматриваемое преобразование A2), найдены все
коэффициенты. Правило обращения можно считать известным.
Оно позволяет дать ответ на два первых вопроса,
сформулированных в конце предыдущего пункта. Если в этом
равенстве считать величины Sj (/ = 1, ..., k) и at (i =
= 1, 2, ...) произвольными численными параметрами, то
можно сказать, что множество всех
последовательностей sn, которые при преобразовании A2) переходят
в сходящиеся последовательности aiy имеет
параметрическое представление A5), где параметры s, могут иметь
произвольные значения, параметры же ot должны
образовать сходящуюся последовательность, которая может
быть любой.
Но если дана последовательность sn, то проверить,
что она может быть представлена в форме A5) со
сходящейся последовательностью at (* = 1, 2, ...) можно,
вероятно, в очень редких случаях. Поэтому возможность
указанного представления sn нельзя считать
эффективным признаком того, что sn при преобразовании A2)
перейдет в сходящуюся последовательность.
Более простой и интересный ответ представление A5)
позволяет дать на второй вопрос.

§ 2] ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ ПРЕОБРАЗОВАНИЯ 307
Теорема 1. Если последовательность ап сходится
и lima„ = <7, то всякая последовательность sn>
переходящая при преобразовании A2) в ал, также будет
сходящейся и при этом Нт5„ = а.
Теорема может быть сформулирована более кратко:
если преобразование A2) сохраняет сходимость, то оно
сохраняет и предел.
Доказательство. Рассмотрим отдельно суммы,
входящие в A5):
k > p — k
sp = s'p + Sp, Sp=^ r'psj, srp = 2 tfpOi.
/ = 1 i=\
Формула A6) позволяет сказать, что Г^->0 при
р->оо, и поэтому при всяких Sj сумма Sp-^0 (р->оо).
Рассмотрим частный случай стационарной
последовательности sn== 1. Для нее правило обращения A5), ввиду
того, что при всех значениях р L(l)=ap, имеет вид
k p—k
у = 1 i = 1
При р~>оо первая из сумм правой части стремится
к нулю и, следовательно,
P-k
JG^I, p->oo. B0)
i= l
Рассмотрим теперь вторую сумму
^Ё ^. B1)
* = 1
Равенство можно рассматривать как линейное
преобразование сходящейся последовательности g( '(Нто^ = а)
в последовательность зр*. Это есть частный случай линей-
оо
ного преобразования sfp= 2 apt°i- Покажем, что преоб-
i= 1
разование B1) сохраняет предел. Применим к нему
теорему 1 п. 1.2 о сохранении предела и убедимся в том,
что для B1) условия теоремы выполняются. В самом
деле, заметим прежде всего, что из A8) и A9) следует
неотрицательность Gp при всех р.

308
. УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
Так как
/ =1 1 = 1
то множество чисел Ар ограничено: АР^М<со и
первое условие теоремы выполнено.
Ввиду того же соотношения B0)
BP=P%(fp-*l IP-***)
i= l
и второе условие теоремы также выполняется.
Наконец, из представления A9) следует, что если т
фиксировано и р->оо, то G^->0. Поэтому выполнено
третье условие теоремы. Все сказанное убеждает в том,
что преобразование B1) действительно сохраняет предел,
и, стало быть, \\mSp = o.
р
Из равенства sp = sp + Sp вытекает, что sp-*0-f а==сг
при р~>оо, что доказывает теорему.
3. Некоторые типы сходимости. Выше мы обращали
внимание на то, что методы улучшения сходимости должны
быть тесно связаны с законами стремления
последовательностей к их пределам. В этом пункте будут указаны
некоторые виды сходимостей, когда правила
преобразований, основанные на алгебраическом интерполировании,
могут ускорить сходимость.
Сходимость почти алгебраического типа.
Говорят, что последовательность sn имеет почти
алгебраический тип сходимости к пределу степени г, если
она представима в форме
sn = c0 + ^+^ + ..-+Cr+2rAn),yr(n)-+0(n-><x,), B2)
где с0, ..., ^ — постоянные числа, причем свободный
член с0 здесь есть предельное значение sn.
Асимптотический степенной тип
сходимости. Переменную sn называют обладающей
асимптотическим степенным типом сходимости, если существует

§ 2] ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ ПРЕОБРАЗОВАНИЯ 309
степенной ряд а0 + ~ + -?- + ••• такой, что при любом
/=1, 2, ... верно соотношение
[s^(fl0+^ + ...+-J-)]/i^0 (/i-оо). B3)
Это равносильно представлению sn в виде B2) при
любом г. Поэтому принадлежность sn асимптотическому
степенному типу сходимости равносильна
принадлежности sn типу почти алгебраической сходимости сколь
угодно высокой степени.
Аналитический тип сходимости.
Последовательность sn называют обладающей аналитическим типом
сходимости, если существует число N такое, что при
всяком п> N переменная sn является суммой степенного
ряда вида
*п = с0+% + ... + •£ + ... - B4)
Введем комплексную переменную г и рассмотрим
аналитическую функцию F(z), определенную степенным рядом
^(г) = с„ + -Н... + £ + ...
Ряд сходится по меньшей мере в области | z | > N.
В целых точках г = п функция F (z) принимает такие
же значения, как и sn.
Внутри области регулярности аналитическая
функция изменяется очень плавно и принадлежность sn
аналитическому типу сходимости означает, что sn
приближается к предельному значению особенно «гладко».
Указанные три типа сходимости часто встречаются
в прикладных задачах и выработка правил ускорения
сходимости для них имеет не только теоретическое, но и
практическое значение.
4. Вспомогательная лемма. Выше мы указывали на
значения, которые принимает оператор L(sp) на
нескольких первых отрицательных степенях р [см. A3)]:
L(l) = l, L(pr™) = 0, m=l, 2, ..., k.
Нам потребуются значения этого оператора при m>k.

310
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. %
Лемма 1. Если т>&, то
Lip-m)=y(P+iL(P+b)a>^ B5)
Доказательство. Введем новую переменную / =
= -- и выполним интерполирование функции sn = —w =
=^ tm по ее значениям в узлах t = —, —r-r, .... —гт-
J Р P+l Р + &
/е
^(■~) = пА@=2 л ia\\( 1 \ 'таг'
Cu(/) = f^--M...f/ -J-Л
w \ P/ \ P+k j
Возьмем представление остатка интерполирования
tm — Uk(i) в форме контурного интеграла (см. п. 1.3.2,
A.3.13))
im_Uk{f ^sir «™ du.
* v ' 2л^ J (w — /) со (и)
Здесь / есть произвольная замкнутая линия,
охватывающая отрезок 0, - . Напомним, что значение
Lf—^)==сгр получается из Pk\-~) = Uk(t) в пределе при
п—>со или t-+Q. Перейдем в представлении остатка
к пределу при ^-^0:
0_n,@) = ap = -^f-4-d«
R v ; р 2ш J ш (и)
l
( 1 )/г+1
или ввиду того, что (й@)= р{р+ху'Лр+к) »
v/^ ; р p(p-f-i)... (р + /г) 2ш J ыш (w) v '
Интеграл может быть легко вычислен просто. Будем
считать контур интегрирования / линией, охватывающей

§2] ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ ПРЕОБРАЗОВАНИЯ 311
О, — , например окружностью с центром в начале
координат и достаточно большого радиуса. Тогда \и\ на /
будет большой величиной и будут возможны проводимые
ниже разложения в степенные ряды по степеням 1/и,
при этом ряды будут сходиться равномерно относительно
и на / и допустимым будет почленное интегрирование
ряда, которое выполняется ниже. Подынтегральная
функция в соотношении B6) представляется в виде
\ ир}\ u(p+\)j \ и{р + к),
оо оо
= ит~^~2
/г Г* ГУ / I Г/ ГУ. * * • / I
1 ^ 1
«« «о AJ
а^0 «V0 а^о « Mp + D с^о « *(/>+*)
При вычислении интеграла \ , .■ da заменим интегри-
/
руемую функцию полученным для нее степенным рядом
и выполним почленное интегрирование. Если принять
во внимание равенства
/ Bш, s = — 1,
то будет ясно, что
J
du =
иы («)
оо
:2m
+ ... + <Г=т-А-1 p°(p+1) 1...(P+^)
Для завершения доказательства леммы осталось
внести полученное значение интеграла в равенство B6).
Необходимо сделать одно замечание, полезное для
дальнейшего изложения. Когда р неограниченно возра-

312
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
{ГЛ. 9
стает, величина av при v ^ 1 стремится к нулю, при
этом порядок малости av будет следующим: av = 0(p~v),
и этот порядок является точным, так как в сумме,
которой определяется av, все слагаемые положительны.
Из равенства B5) следует, что при возрастании /?,
в силу соотношений p{p+xy{p+k) = 0(p~k~l) иат.н=
= О (p~m+*+1), значение оператора L(p~m) будет малой
величиной следующего точно указанного порядка:
4tW-0(tW- <27>
5. Некоторые теоремы об ускорении сходимости.
Нашей целью будет выяснение условий, при которых
преобразование A2) будет ускорять сходимость
последовательностей, принадлежащих трем типам, определенным
в п. 3.
Пусть sn принадлежит почти алгебраическому типу
сходимости степени г и имеет следующее представление:
** = * + % + № + '-- + % + ^. B8)
где Уг{п)-*0 (я->оо), сдФ0.
Скорость сходимости sn-*s определяется, очевидно,
членом Cgit'9; q называют порядком сходимости.
Применим к sn преобразование A2)
L (sn) = s + cqL Ш + cq+1L (-lp) +
+... + crL (-L) + L (n-ryr (n)). B9)
Оценим последнее слагаемое. Если считать уг(п)
произвольной величиной, стремящейся к нулю при я->оо, то
будет верна следующая неулучшаемая оценка:
\L{nr'yr(n))\ =
У ( \\k-f ln + j)k. Уг(п + 1)
ь.
1
j\(k-j)\ (n + jY
k
raax|Y,(n + /)!2 T(k=W ■ -jfj^
j=o
maxJY^" + /)io(-^r)-

§ 2] ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ ПРЕОБРАЗОВАНИЯ 313
Так как max \ yr{n + j)! -*0 (/г-^оо), то L (гггуг (п)) =
Рассмотрим сначала случай k<Cq. Тогда, в
соответствии с леммой, L\-q\ отлично от нуля и будет иметь
значение, указанное в B5) при m = q. Остальные члены
в правой части равенства B9), имеющие вид L\ -у] (i>q)>
обладают более высоким порядком малости.
Главным членом разности on — s может быть либо L (п~9),
имеющий порядок 0{ггд), либо последний член, порядок
которого о(пк'г). Поэтому в рассматриваемом случае &<
<iq ускорения сходимости при преобразовании, вообще
говоря, не произойдет и не исключено даже замедление
сходимости, когда L (п~гуг (п)) стремится к нулю менее
быстро, чем п q.
Указанные результаты можно было предвидеть заранее,
так как если степень точности интерполирования k взять
меньше порядка сходимости, то при такой несогласованности
между k и q невозможно ожидать ускорения сходимости.
Положим теперь k^q. При такой степени точности
интерполирования L (п~д) ==..,= L (п~к) — 0, несколько
первых членов в представлении B9) для L (sn) исчезнут
и L (sn) примет вид
Остающиеся справа члены вида L (пг() (i^k+l>q)
будут иметь порядок малости более высокий, чем L(rrq).
Вопрос об ускорении сходимости решится последним
членом L(n-ryr(n)) = o(-y=jf)- Чтобы он стремился к нулю
быстрее L(n~q)j достаточно выполнить неравенство г —
— k^q или kr^r — q.
Изложенное позволяет считать доказанной следующую
теорему.
Теорема 2. Для того чтобы преобразование A2)
увеличивало скорость сходимости последовательности
вида B8), достаточно степень точности k
преобразования A2) взять так, чтобы выполнялись неравенства
q^ck^r-q. C0)

314
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
Более просто формулируется правило ускорения
сходимости для последовательностей, принадлежащих
асимптотическому и аналитическому типу сходимости. Для них
показатель степени г может быть взят как угодно
большим, и поэтому вторая часть k^r — q условия C0)
всегда выполняется. Поэтому верна
Теорема 3. Для того чтобы преобразование A2)
увеличивало скорость сходимости последовательностей
асимптотического степенного и аналитического типа
сходимостей достаточно степень точности
интерполяционного .преобразования k взять не меньше, чем порядок
сходимости q последовательности sn:
k^q.
6. Интерполяционные методы преобразования с
возрастающим числом узлов. По поводу преобразования A2),
построенного в п. 2, можно сделать замечание,
побуждающее изменить постановку задачи интерполирования
предельного значения s и построения ар, а именно:
на шаге номера р интерполирование sn выполнялось
по значениям sn в узлах р, р+1, ..., p + k, что же
касается предшествующих узлов 1, 2, ..., р— 1, то
значения sn в них не использовались. Поэтому естественно
построить интерполяционные методы, которые используют
все предшествующие значения sn: при интерполирований
предельного значения s и построении оп на шаге номера п
пользуются узлами 1, 2, ..., п.
Соответствующая такому процессу преобразований
таблица N узлов будет треугольной:
1
2
И 2 3
N'-
1 2 3 ... п
Правило построения приближения ап к предельному
значению s здесь может быть получено из A2), если
положить там р = 1, k = п — 1:
ай =
п — 1
V.
-Р"-1-; A + /У-1
ъп+/-

§2] ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ ПРЕОБРАЗОВАНИЯ 315
После изменения индекса /+ 1 =/' и отбрасывания штриха
у нового индекса преобразование запишется в следующей
более удобной форме:
/=i
Отметим некоторые свойства этого преобразования.
1. Степень точности преобразования. Напомним, что
для получения ап должно быть выполнено
интерполирование переменной sn по ее значениям в п точках 1, 2, ...
1 / l'N
..., п с помощью многочлена от — степени п—\ Pn^i\—-).
Такое интерполирование будет точным для случаев sp==
■== 1, sp = ~, ..., sp=-1£=T. Поэтому преобразование C1)
должно при всяких п давать точно предельные значения
этих последовательностей и, стало быть, должны точно
выполняться равенства
LMl)=l(-l)-'/R£iyi=l) C2)
1=1
Ь \лда/ Lk К ' /Ц/г-/')! jm
(m=l, 2, ..., /г-1). C3)
2. Преобразование C1) применимо ко всякой
переменной srt, сходящейся или расходящейся. Представляет
интерес (по крайней мере теоретический) выяснение
вопроса, может ли преобразование C1) переводить
расходящиеся последовательности в сходящиеся. Несколько
позже будет доказано, что это не так и что из
предположения о сходимости оп вытекает сходимость sn.
Можно проверить, что преобразование C1) не всегда
сохраняет сходимость и может сходящуюся
последовательность sn переводить в расходящуюся последовательность ап.
Для этого достаточно проверить, что для коэффициентов
преобразования не выполняется первое условие теоремы 1
из п. 1.1. Действительно, рассмотрим коэффициент, соот-
пп
ветствующий значению j^-n: опп=-^. Так как п\ =
= м^К2ялA+ея) (ея->()), то аяя = ел Bлл)-1'2 A+6Я)

316
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
1ГЛ. 9
(б«->0) и при /г~>оо этот коэффициент будет быстро и
неограниченно возрастать. Поэтому для преобразова-
оо
ния C1) величины Ап = ^] \ап;-\ не могут быть ограни-
/ = i
ченными в совокупности.
3. В сумме C1) при больших п будут присутствовать
большие по абсолютной величине коэффициенты, при этом
соседние будут иметь противоположные знаки. Ввиду
этого преобразование C1) при больших п очень часто
связано с большой потерей значащих цифр, а это
затрудняет применение преобразования.
7. Обращение преобразования. Полагая р=1, 2, ...,
запишем преобразование C1) подробно
— ф1 + 22ф2 = 2!(Т2,
фх — 23ф2 + 33c<;;s3 = 3!(Т3,
Задача обращения преобразования есть задача решения
бесконечной системы уравнений с треугольной матрицей.
Она, очевидно, имеет единственное решение. Первое
уравнение дает значение Si> пользуясь им, из второго
уравнения находим s2, выражая его через аг и а2. Из третьего
уравнения, используя уже полученные sx и s2, находим s3,
выразив его через сг1э а2, а3 и т. д. Все эти вычисления
могут быть проделаны и будет найдено явное выражение
sn с любым номером п через оъ ..., ап. Оно оказывается
очень простым:
n(n-l)...(n-l±lHi (/|elf 2f ^ (М)
п1^
/=1
Убедиться в его правильности можно путем подстановки
приведенных выражений sn в уравнения C1)
= 1
/=1 1-Х

§ 2] ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ ПРЕОБРАЗОВАНИЯ 317
Если изменить порядок суммирования по индексам / и /,
то получим
L* (Sn) = У lat У (— 1)»-/ —£ 'i
^ /Г/ Л (я-/)!
yf+i
Можно заменить нижнюю границу изменения индекса /
и суммировать в границах 1^/^/г; при этом сумма
не изменится, так как все добавленные слагаемые равны
нулю, например при ./= 1 обратится в нуль скобка (/ — 1)
и так далее до значения /'==/—1, когда в нуль
обращается скобка (/ — /+1).
Внутренняя сумма при этом станет результатом
преобразования A2) переменной
Sn=n(n-l)...(n-l + D^ C5)
В самом деле,
fn{n-\)...{n-l + \)\ _
[ т )
= У(-1)*-/—]1 't/-U-(/-'+UB (зб)
/=i
Если в r/_1 [/(/"" !)..-(/ — /+ 1)] раскрыть скобки и
расположить слагаемые по степеням /-1, то получим
многочлен от г1 вида —+ — + ...+(— I)' (/ — 1)! 4 • По"
/' Р г
этому правая часть C6) является суммой нескольких
выражений вида C3), для которых т=1, 2, ..., /, и
при 1^п— I все такие суммы, как указано в C3), равны
нулю. Поэтому в выражении для L* (sn) при
суммировании по / может быть отличным от нуля только слагаемое
для t = n:
L*{Sn) = non2(-ir>j£^/.
/(/-!)..(/-/*+1)
Так как
/—Ч/ (/-1).••(/-«+ 1)]==

318
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
то среди сумм по индексу / ввиду C3) отличной от нуля
может быть лишь сумма с последним членом (—1)л_1х
Х(я-1)!1:
П
L*(sn) = non(-\Y~4n-\)\ J (-I)"' /!(,/ly), -;4- C7)
Последняя сумма есть значение оператора L* для
последовательности st = j£ и легко вычисляется*). Проинтер-
полируем st по значениям в узлах /=1, 2, ..., п с по-
мощью многочлена Р^А-) степени п— 1 от - и рас-
смотрим остаток интерполирования Пу) = tn—Pn-i[j )•
Это есть многочлен от у степени п со старшим
коэффициентом, равным единице. Корни г (у ] известны: это есть
1111 11
г = у, т = 2, ..., т=-, поэтому
'(fH-Mi)-(f-T)e-;)-a-.L)-_
При неограниченном увеличении t РпЛ (y]->L* l~).
л!"
Правая часть стремится к (—1)лу. Поэтому в пределе
получится равенство
\/_1У^ ..,/" ... . ' /*Щ
= ПтРл._1(}) = -(-1г1.
Из C7) найдем выражение для L* (s„):
L* Ы = /иг» (-1)"-1 (л- 1)! [- (-1)*1] = сгл
*) Индекс п последовательности заменен на t, чтобы отличить
его от обозначения п точки, в которой вычисляется значение
оператора L*.

§ 21 ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ ПРЕОБРАЗОВАНИЯ 319
и значения snj указанные в равенстве C4), действительно
удовлетворяют уравнениям C1) и обращают,
следовательно, это преобразование.
Сделаем несколько замечаний об обратном
преобразовании C4). Оно является частным случаем общего линей-
со
ного преобразования sn= ^ ctni^h когда его коэффи-
/ = i
циенты имеют значения
Ал/ = { nlx C8)
I 0, 1>п.
Отметим некоторые свойства коэффициентов:
1. ani^0 при любых пу I.
2. При фиксированном значении / и п-^со
коэффициент ап1 является, как видно из верхнего равенства C8),
величиной порядка См —
3. Можно просто проверить, что сумма
коэффициентов в преобразовании C4) равна единице при любых п.
Действительно, если s„e==1, to, так как постоянная
величина интерполируется многочленом от 1/п всегда точно,
из C1) следует, что сг„=1. Ввиду же однозначной
обратимости этого преобразования для C4) можно
утверждать, что из ап === 1 вытекает sn = 1 и, следовательно,
Bn-2anl=ltn-%l+1) = l (n=I, 2,...).
Покажем, теперь, что преобразование C4) сохраняет
предел. Для этого достаточно проверить выполнение
условий теоремы 2 § 1 для C4).
Так как коэффициенты преобразования неотрицательны,
то сумма их модулей Ап совпадает с суммой Вп;
последняя по третьему из указанных свойств равна единице:
Ап = 2| йщ\ = Y,ат = вп = 1.
Первое из условий теоремы 2 действительно выполнено.
Ввиду Вп=1 (п=1, 2, ...) второе условие также
выполняется.

320
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
Второе из отмеченных свойств говорит о том, что для
преобразования C4) выполняется и третье условие
теоремы 2 § 1.
Этот результат позволяет для преобразования C1)
сформулировать следующую теорему.
Теорема 4.. Если последовательность опу полученная
в результате преобразования C1), сходится и Нт0л==а,
то исходная последовательность sn также будет
сходящейся и при этом Umsn = limGn = o.
Скажем еще несколько слов о природе обратного
преобразования C4). Так как его коэффициенты
положительны и их сумма равна единице, то sn есть не что
иное, как среднее взвешенное значение *), составленное
, ч 1 п(п— I) ... (п —1+1)
из Oi, ..., ал с весами тг (п) = / — —щ —-.
Выше мы обращали внимание на то, что
преобразование C1) может переводить сходящиеся
последовательности sn в расходящиеся последовательности ап.
Представляет интерес (главным образом теоретический)
выяснить, какое множество составляют сходящиеся
последовательности sn, переходящие при преобразовании C1)
в сходящиеся последовательности ап. Обратное преобра-.
зование и теорема 4 позволяют высказать приводимый
ниже результат.
Теорема 5. Если ко всем сходящимся последователь-
ностям ап применить преобразования средних взвешенных
C4), то получится множество последовательностей sn,
которые при преобразовании C1) переходят в сходящиеся
последовательности.
Последовательности sn этого множества будут
сходящимися, и для них преобразование C1) сохраняет
не только сходимость, но и предел.
8. Теорема об ускорении сходимости. Укажем теперь
класс последовательностей sn, применительно к которым
преобразование C1) дает ускорение сходимости. Как
будет видно ниже, это ускорение будет сильным, но при
*) Среднее взвешенное величин хъ ..., хп с весами mv ..., тп
есть |= , -—'±-2-, Если xi есть координаты масс ти то $
Щ + • • • + тп
есть координата центра инерции системы масс.

§ 2] ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ ПРЕОБРАЗОВАНИЯ 321
преобразовании будет, как правило, происходить
значительная потеря точности.
Пусть sn имеет аналитический тип сходимости и при
больших п представляется сходящимся степенным рядом
s* = c0 + -J + ^ + ... + ^ + ..., n-^N. C9)
Здесь с0 есть предельное значение sn при /г->оо: c0 = s.
Параллельно с sn будем рассматривать аналитическую
функцию комплексной переменной г, определив ее рядом
F(z) = c0 + % + ±+...
Она регулярна по меньшей мере в круге | г \ > N и
значения ее в целых точках п совпадают с sn:
F(n)=sn, n^N. D0)
Напомним, что для построения ап мы
интерполировали функцию st (t=l, 2, ...) по значениям sb ...,sn
посредством многочлена Pn-i(-f) степени п— 1 от \/t и
полагали вп= lim Pn-ivjX что привело нас к
правилу C1).
Нам нужно оценить погрешность оп — s. Чтобы
воспользоваться аппаратом контурных интегралов в
привычной форме, заменим переменную t, положив t=l/u,
u=\/t, и введем функцию y(u)=F^)==F(z)==c0-{-c1u+
+ с2и2-\~... Она регулярна в круге \u\<.l/N и связана
с последовательностью sn равенствами
Интерполирование sn многочленом /Vily) по
значениям st в узлах 1, 2, ..., п совпадает с
интерполированием ф(^) по значениям в узлах 1, у, ..., —с помощью
многочлена Pn-i(u). В частности, очевидно, ап =
- lim/VxfaH/V^O).
11 В. И. Крылов и др., т. II

322
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
Рассмотрим точки 1, у, у, ..., они сгущаются к
началу координат а = 0, и лишь конечное число их может
лежать вне круга \u\<.l/N. Пусть это будут точки
, 1 1 11
1» -о-» •••» —» так что все следующие точки ——г,—го*...
принадлежат открытому кругу | и \ <С 1/N.
Возьмем произвольную достаточно гладкую замкнутую
линию/, лежащую в круге |u|<l/JV и содержащую
отрезок О, jfp-Л внутри себя.
Составим интеграл *)
2т J шо (и) f
1 D1)
(">-<«-!)(« -у) -("-!)
(О
и вычислим его, считая п>т. Он равен сумме вычетов
интегрируемой функции в особых точках, лежащих внутри
контура /. Числитель у (и) не имеет особенностей ни на
самом контуре, ни внутри его. Поэтому особыми точками
интегрируемой функции будут нули знаменателя и® (и),
находящиеся внутри /. Это будут точки и = 0, и =
= —, ..., и = —гт- Все они будут простыми полюсами
функции -2-, и вычеты в них, найденные с помощью
известных простых правил, имеют следующие значения:
Res Гф(цI
Ф@)
@@)
Далее, так как со( — ) = 0,
п<Л Ф(ц) 1 _
KesL«co(u) Jw=i//"-
1
/
/
ф(
со'
'! \
TI
1 * \
—•
\1
*) Он связан с интегральным представлением остатка
интерполирования (см. п. 1.3.18), но эта связь сейчас несущественна.

§ 2] ИНТЕРПОЛЯЦИОННЫЕ МЕТОДЫ ПРЕОБРАЗОВАНИЯ 323
Следовательно,
2т
С ф(ц)
i J wco (и
du--
,Ф@)
+ 2
■<в@)
1
!ю@)
ш@) '" i- 1 ,/ 1 \ "
ф@)+ | w@)
1 „< / '
/ = m + l J Ш ^у
ф@)+2
<в@)
' 1 \1
•>-!
оэ@)
1 , /1 \ J
1 \J
Приведенные ниже вычисления не требуют пояснений:
1
Ф@)=с0 = 5, о@) = (-1)*/гГ,
«Чт =,
\/
1 \/1
1
1 1
1 iV±_±
— \ Ч jn~ini •
Формула Лагранжа для интерполяционного
многочлена Рп-г (и) имеет вид
Рп-Х(и)=2
он (и)
Она показывает, что первая из сумм в выражении,
полученном для интеграла, есть значение Рп-Х @) = апу взятое
со знаком минус. Таким образом для интеграла будем
иметь соотношение
г т п
/
отсюда
/=1
*-*-- 2 (-1)л-/7Г^5/+W 1
(-1)" f Ф(«)
/-1
/г! 2ж J и© (а)
dtf.
11*

324
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
Оценим сначала первое слагаемое в правой части.
Очевидна оценка
]п jn(n—j+i) • •• п jnnf тппт
"^ j\n\ ^ л!
j\(n-j)\
Если для /= 1, 2,
/In!
,, т верно неравенство \sf\^M> то
1 1-1Г'ц
1п
/=1
/I (*-/)!
Mm
тппт
тппт
Для нашей цели достаточной является грубая оценка
интеграла. Так как ни одна из точек — (/=1, 2, ...)
не лежит на линии / и эти точки сгущаются к и — О, то
существует такое положительное число б, что при вся-
\и—Н^=6 и \и\^8. Поэтому
ком / будет
|ю(и)
(и-1) и--« .
и
ввиду ограниченности v(u) на / существует число В
такое, что
2т J wo (u)
Таким образом, для разности s — on верна оценка
I s — сгл
п\
п\Ьп
D2)
Из проведенных рассуждений вытекает
Теорема 6. Если последовательность sn имеет
аналитический тип сходимости и sn-^s, то существуют
положительные числа А> С и б такие, что для
последовательности оп, получающейся из sn при преобразовании
C1), верна оценка D2).
Заметим теперь, что если sn не приводится при
больших п к постоянной величине, то в ряде C9) среди
коэффициентов cr (r S* 1) существуют отличные от нуля. Пусть
первый из них есть cq и разложение C9) имеет вид
в» = Со + % + % + ..., с9ФО.

§ 3] УЛУЧШЕНИЕ СХОДИМОСТИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 325
В этом случае, очевидно, для погрешности приближения
s — sn = c0 — sn верно точное соотношение
|s-s«| = 0(/r*).
Правая же часть оценки D2) ввиду быстрого
возрастания п\ (п-^оэ) убывает быстрее, чем любая
отрицательная степень п. Поэтому сходимость an->-s будет много
быстрее, чем sn-+s.
§ 3. Улучшение сходимости последовательностей,
для которых погрешность приближения
к пределу близка к показательной функции
или линейной комбинации таких функций
1. Простейшее правило преобразования и некоторые
его свойства. Сначала рассмотрим самый простой случай,
когда последовательность sn мало отличается от
показательной функции и представима в виде
sn = s + Aqn(\ + sn), где ел->0 при д->оо. A)
С такими последовательностями мы встречались в первой
части книги, например при рассмотрении задачи
ускорения сходимости при решении системы линейных
уравнений или нахождения собственных значений и векторов
методом итерации, при решении нелинейных уравнений
тем же методом и в других вопросах.
Правила ускорения сходимости этих
последовательностей указывались в весьма краткой форме, часто без
достаточного выяснения наглядной стороны Еопроса и без
изучения свойств этих правил. Сейчас мы остановимся более
подробно на правиле улучшения сходимости
последовательностей вида A). Начнем с рассмотрения
показательной функции
sn = s + Aq", Aq=£Oy цф\, л=1, 2, ... B)
Величину s назовем постоянной частью показательной
функции и Aqn — переменной ее частью. Если \q\<\y
то, очевидно, sn-+s при п->оо. Когда же \q\~^ 1 и q=£\,
последовательность sn будет расходиться.
Независимо от значения q и, следовательно,
независимо от сходимости или расходимости s„, найдем
выражение s через значения sn. Для этого потребуется исклю-

326
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
чить из равенств B) А и q и получить соотношение только
между s и значениями sn. Возьмем равенства B),
отвечающие трем смежным значениям п— 1, пу /z+'l
аргумента п:
sn-i -- s = Aq"-1, sn-s = Aqn, sn+1 - s = Aqn+1.
Если второе из них разделить почленно на первое и
третье —на второе, получатся два выражения для qf
а приравнивание их даст уравнение для s
sn-i s sn s
Из него находим
sn+l *sn ~T sn
Это равенство позволяет при всяком п найти точно
постоянную часть показательной функции B), а, стало быть,
и ее предел s, если он существует, по трем значениям sn
смежных номеров. Оно было положено в основу правила
преобразования последовательностей: по любой заданной
последовательности sn (л=1, 2, ...) составляют новую
последовательность
„ sn+lsn-l~~sn / 0 о \ /о\
g" = sn+1-2s, + sn_x <я = 2. 3> -)• О)
Это преобразование часто называют преобразованием
Эйткена или ^-преобразованием.
Говорят, что преобразование C) применимо к
последовательности s„, если для всех достаточно больших
значений п знаменатель A2sn-1 = sn+1 — 2sn-\-sn-1 отличен от
нуля.
Условия, при которых преобразование C) сохраняет
предел, указываются в следующей простой теореме,
дающей эти условия в форме, доступной для применения.
Теорема 1. Пусть последовательность sn сходится
к пределу s и к ней применимо преобразование C). Для
того чтобы при преобразовании сохранялся предел, т. е.
чтобы on-+s, необходимо и достаточно выполнение
условия
fa+i-^)fa-^-i) = As As^ ^Q /Лв>00ч /4ч
Sn+l-2Sn + Sn-l AV-1- V / W

§ 3] УЛУЧШЕНИЕ СХОДИМОСТИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 327
Доказательство. Легко проверяется, что
преобразование C) может быть записано в виде
„ (sn + l sn) (sn — sn-l) /c\
sn+i *snrSn + i
Если sn-+s, то для сходимости on-+s необходимо и
достаточно выполнения условия D).
Укажем еще, какую форму будет иметь 82-преобра-
зование для рядов. Пусть задан ряд
cti + a2+ ... +ап+ ... F)
Возьмем последовательность его частичных сумм sn = a1-\-
-\-а2+ ... +ап (л = 1, 2, ...) и применим к ней
преобразование C). Если принять во внимание, что sn+1 = sn-\-
-\-ап+г и sn-i = sn — an, для оп получим
°n = sn-^^=ai+a2 + ... + an+^^^ G)
ап + 1 ап ап ал-Ы
Преобразование возможно, если ап — ап+1фОу начиная
с некоторого места в ряде.
Как показывают равенства E) и G), преобразование C)
сводится к тому, что к sn добавляются дополнительные
члены, имеющие простое строение: в случае
последовательности такой член указан в E), в случае же ряда —
в G), где он имеет тот же смысл, но более простую запись.
2. Об улучшении сходимости. Правила C) и E)
построены так, что если переменная sn имеет форму B) и
сходится к 5, то эти преобразования при всяком п дают
предельное значение s. Аналогично правило G) при
всяком п дает сумму ряда F), если он есть сходящаяся
геометрическая прогрессия A-\-Aq-\-Aq2-\-... Простота
дополнительных членов в F) и G) заставляет ожидать,
что эти правила позволят ускорить сходимость
последовательности и ряда, если они достаточно близки к B)
или к прогрессии соответственно. Поясним это более
подробно на случае ряда.
Предположим, что ряд F) сходится и имеет сумму s.
Если ввести остаток ряда r„ = a„+1-fa„+2-f... и
заменить sn на s — rni правило преобразования G) можно
записать в форме
on = s — гп +
anan+i
ип+1

328 УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ [ГЛ. 9
Так как гл-^0 (/г->оо), условием сходимости оп к s будет
следующее: апйп^1—^о (п-+со). Если окажется, что
ап ап+1
величина рп = гп g*g/t+i стремится к нулю при п ->
аП аГ1 4 1
->оо быстрее, чем гп, то новая последовательность оп
будет сходится к s быстрее, чем sn. Это означает, что
дробь —п пп должна быть главной частью остатка гп.
Но гп есть бесконечный ряд, указанный выше, а
бесконечным рядом для дроби будет, вообще говоря,
геометрическая прогрессия
ап ап + 1 1 Чп ап
и чем больше л, тем меньшим должно быть различие
между этими двумя рядами.
Получим теперь количественные признаки улучшения
сходимости. Рассмотрим последовательность sn, представи-
мую в форме A). Преобразование C) для нее даст
следующий результат
Так как е„->0 (д->оо), то знаменатель дроби будет
стремиться к величине A — qJ> отличной от нуля ввиду
цф 1, и при всех достаточно больших п будет отличным
от нуля.
1. Когда |<7|<1, переменная sn стремится к s, при
этом разность sn — s будет величиной порядка 0 (qn). Новая
последовательность ал, как вытекает из (8), также
сходится к s и разность on — s имеет порядок малости О (g^).
Это верно для любого закона стремления гп к нулю.
Преобразование C) в этом случае даст ускорение
сходимости; при этом ускорение будет тем сильнее, чем
быстрее гп стремится к нулю.
2. При |?| = 1 и цф\ переменная sn, оставаясь
ограниченной, не имеет предела, тогда как оп будет
ввиду еп-*0 сходиться к s и сходимость здесь будет
не медленнее, чем при стремлении гп к нулю.
3. Если |<7|> 1, АфО, то модуль sn будет
неограниченно возрастать, когда и->оо, поведение же оп зависит
от свойств ел, в частности, если для гп выполняется

§ 3] УЛУЧШЕНИЕ СХОДИМОСТИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 329
условие q4n-+0 (n-^oo), то ап сходится к s, причем
погрешность приближения имеет порядок on — s = 0(qnen).
Приведенные рассуждения позволяют сформулировать
следующую теорему.
Теорема 2. Преобразование C) применимо к
последовательности A) при всяких достаточно больших п и
верны следующие утверждения:
1) При |<7!<1 полученная после преобразования
последовательность оп сходится к s и преобразование
ускоряет сходимость, так как sn — s = 0 {qn)> тогда как
an-s^O(qnen);
2) Когда | q\ = 1, q-фХ, последовательность sn не имеет
предела, последовательность же оп сходится к s и ап —
— s = 0(en);
3) Пусть | q \ > 1 и переменная s„, следовательно,
неограниченно возрастает по модулю при п-+оо. Если
выполняется условие
?%г->0 (л-*оо), (9)
то новая последовательность ап будет сходиться к s и
при этом
Gn-s = 0(qnen).
Теорема показывает, что для последовательностей
вида A) преобразование C) позволяет не только ускорять
сходимость, когда sn сходится, но и ввести обобщенный
предел для sn в случае расходимости sn, если выполняется
условие (9).
3. Применение 82-преобразования к улучшению
сходимости и аналитическому продолжению степенного ряда.
Пусть функция / (г) задана степенным рядом, сходящимся
в круге радиуса R:
f(z) = c0 + c1z + c&* + ... + w" + ..., \z\<R, A0)
и пусть известно также, что на окружности круга
сходимости / (г) имеет единственную особую точку,
являющуюся полюсом первого порядка.
В этом случае f (г) представима в следующем виде:
/(*) = -£ГГ + ф(*). * = ***. (»)

330
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
где функция cp(z) регулярна в круге радиуса р большего,
чем Rf и может быть там разложена в степенной ряд
<р(г) = Ь0 + Ь1г + Ь2?* + ..., \г\<р. A2)
Ряд A0) для / есть сумма ряда A2) и геометрической
прогрессии
аа
а~2 l~a v=°
aa-v2v:
v = 0 v=0
A3)
Рассмотрим конечную сумму последнего ряда, считая z Фа
И |*|<р
п—\
5л=2 (aa-v + &v)^ =
v = 0
аа
a — z \a J ' hA Ad
a — z
•Ф(*)-
v = 0
аа ( z\n
a — z \ a
a — z a\n
aa \ z
2^v
Она имеет форму A) при s=. + ф(з)=/(г)>
Л =
aa _ z
a —2
aa
f Г 2 **■
Оценим ел. Для этой цели воспользуемся известной
теоремой о коэффициентах степенного ряда: так как
ряд A1) сходится в круге |г|<р, то для всякого б>0
существует такое число М, что верно неравенство | bv | ^
<; М (р — 6)~v. Будем считать б настолько малой
величиной, что |z|<p — б. Для гп получим следующее
неравенство:
a—z
аа
*. 2A!(p-6)-*|Z|v =

§ 3] УЛУЧШЕНИЕ СХОДИМОСТИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 331
Применим теперь к последовательности частичных
сумм sn б2-преобразование. В результате получим новую
последовательность оп вида (8) с указанными несколькими
строками выше значениями s, Л, q и гп. Произведение цпгп
в рассматриваемом вопросе имеет следующую оценку:
г
1<7%И
а
I е„ | < М
аа
Р-8 \*1" (И)
р-6-|2| (р-6)«
Отсюда ввиду того, что |г|<р —б, сразу же следует
соотношение | цпъп | -> О, а из теоремы 2 и из
выражения (8) для оп вытекает, что дополнительный к s член
в правой части (8) стремится к нулю не медленнее, чем
I z Iя (Р — 6)~л- Поэтому оп при всяком значении г из круга
|z|<P и г Ф а сходится к s = f(z). При этом, если
проследить оценки, можно без труда увидеть, что
сходимость on->f (z) будет равномерной относительно z в любой
замкнутой области, лежащей в круге | z | <р и не
содержащей точку z = a.
Когда точка z принадлежит кругу \z\<R, ряд A0)
00
сходится. Главной частью его остатка г„= 2 (aa_vzv-|-
v = n
оо
-f- bvzv) будет более медленно сходящаяся часть ^ aa~vzv =
= °^ f —) . Вторая группа слагаемых имеет больший
радиус сходимости и, следовательно, члены ее убывают
быстрее с ростом п, чем в главной части. При п->оо
остаток стремится к нулю и имеет порядок малости
0[fWl. Разность a„-/(z) имеет, как видно из
U ' r/\z\\ni
оценки A4), порядок малости О (^ztr) более высокий
чем /"я, и применение преобразования C) к sn дает
значительное ускорение сходимости. Когда же точка г
принадлежит кольцу |7?^[z|<p, z=£a], то ряд A0)
расходится и последовательность оп сходится к аналитическому
продолжению степенного ряда A0).
4. Связь с методом интерполирования предельного
значения. Пусть дана произвольная последовательность
sn (n=l, 2, ...). Рассмотрим показательную
функцию f(n) = B + Aqn9 содержащую три параметра В, Л, q.

332
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
Выберем их так, чтобы в трех узлах п — р—\, р, р+1
функция / принимала такие же значения, как и sn:
f(p - 1) = sp-i, f (p)=sp, f (p+ 1) =spfl.
Для нахождения значений параметров будем иметь
следующую систему уравнений:
B + Aq*-*=sp-l9 B + AqP = sp, B + ;V+1 = sp+1.
При ее решении за неизвестные проще принять 5, Aqp = u,
q. Система примет вид: В-\—u = sp-ly B-\-u = sp, B + qu ==
ч
= sp+1. Она решается просто. Значения параметров,
найденные из нее, зависят от значения р (это отмечено
индексом (р), поставленным около них):
fiip)=-J^£±=£i_, u^ = (AqP)^JSp+1~Sp}{Sp~Sp-1\
sp+l *sp-T~sp -1 sp + l ^sp~T sp~l
SP SP ~ 1
Подстановка этих выражений в f (n) приводит к
следующему выражению для интерполирующей функции:
!р{П) =sp+1-2sp+sp^X
X [sp+1sp ^-sl + isp+i-sp) (sp-s^g^^y2 /]. A5)
Построение /р возможно при выполнении условий
Sp+1-2sp + Sp_!^0, Sp-Sp^^O. A6)
Будем считать, что неравенства соблюдаются для
всех достаточно больших р.
Устремим теперь п к со. Предельное значение у fp (n)
существует лишь при условии
sp+i~
|s-sD,i<1- A7)
I йр ар * •
Считая условие A7) выполненным, примем lim fp(h) за
п
элемент новой последовательности и обозначим его через ар:
oP = llmf,(n) = B*=/>+*Zl7*> ■
Это правило преобразования такое же, как C), но
получение его потребовало больших условий, чем для C).

§ 3] УЛУЧШЕНИЕ СХОДИМОСТИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 333
5. О пути уточнения 82-преобразования. В
рассмотренном выше множестве последовательностей A)
погрешность приближения sn к пределу s изменялась по закону,
близкому к геометрической прогрессии или
показательному закону
sn-s = Aq*(l+en).
При построении преобразования C), предназначенного
для улучшения сходимости sn к 5, считалась известной
структура только главной части Aqn погрешности; при
этом параметры ее А и q предполагались любыми.
В некоторых случаях бывает известной структура
не только главных частей, но и нескольких следующих
по порядку малости частей погрешности. Тогда
естественно изменить преобразование C) так, чтобы
учесть не только главные, но и следующие известные
части.
Законы изменения погрешностей, строение их и,
в частности, разложение их на слагаемые с
последовательно возрастающими скоростями убывания, зависят от
вида задачи и метода ее решения. Последние могут быть
многообразными и уточнять методы ускорения их
сходимости можно в многих отношениях. На примере мы
поясним причины, лежащие в основе обобщения метода C),
которое будет излагаться ниже. Этот пример связан
с переходом от метода итерации для одного
численного уравнения к применению его для решения систем
уравнений и с переходом от одной последовательности
к системе последовательностей.
Предварительно рассмотрим простую задачу о
решении методом итерации линейной системы. Запишем систему
где х и b есть ^-мерные векторы и А есть квадратная
kx ^-матрица. После выбора начального приближения
х° к решению, все дальнейшие приближения находятся
по правилу
xt^b + Ax"-1, n=U 2, ... A8)
Пусть jc* есть точное решение системы
х*=Ъ + Ах*. A9)

334
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
Рассмотрим погрешность приближения номера п:
6п = хп — х*. Для нее верно соотношение, получающееся
при почленном вычитании двух предшествующих
равенств:
6Я = Л8Я.
Если это соотношение применить п раз, то для 8;г
получится выражение через погрешность 6° начального
значения
8" = Л "8°.
Предположим, что матрица А может быть подобным
преобразованием приведена к диагональному виду
A = S[kl9 К ..., h]S~\
Тогда *)
и
Поэтому для приближения хп к решению х* верно
представление
xn = x* + fr = x*+S[Xt, XI ..., k%]S-4°.
Отсюда вытекает, что каждая составляющая xnt (/=1,
..., k) вектора хп является функцией следующего вида:
x»==xf + ailXnl+... + aiX (/=1,2,...,*). B0)
Параметры xf, ап, ..., aik, Яь ..., Kk таких
представлений нам неизвестны, так как они либо зависят от л:*,
либо требуют вычислений, превосходящих по сложности
решение линейной системы, и в последующих
рассуждениях их нужно считать произвольными.
Для простоты будем считать, что собственные
значения Ъ* матрицы Л различных по модулю и занумерованы
в порядке убывания модулей
|Аа|>|Ха|>...>|ЯА|.
*) Здесь и ниже запись Х^ означает степень числа \

§ 3] УЛУЧШЕНИЕ СХОДИМОСТИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 335
В правой части равенства B0) главным членом при
больших п будет сумма хТ + ацХп{1 если только ааф0, и
равенство может быть записано так, как указано в A):
х?=х?+ааХ1A+г?), в?=^(^)Ч... B1)
Преобразование C) учитывало только постоянный член
х* переменной xf и первый член апХп переменной части,
все остальные считались произвольными. В
рассматриваемой задаче нам известно строение не только первого
члена погрешности, но и строение всех остальных ее
членов. Этим можно воспользоваться при создании
правила улучшения сходимости, применяя для этого все
члены с известной структурой или часть их. К каким
уточнениям это приводит, будет выяснено в следующем
пункте.
Выше был приведен очень простой пример,
показывающий возможность и желательность уточнения 62-преоб-
разования. Но существуют другие задачи, в которых
главный и дополнительные члены погрешности имеют
сходное строение и где построенные ниже правила
ускорения сходимости будут иметь применения.
6. Правило ускорения сходимости последовательности,
для которой погрешность приближения к пределу близка
к линейной комбинации показательных функций. Сначала
определим само преобразование. Пусть sn (п = 1, 2, ...)
есть произвольная последовательность. Введем два
связанных с ней определителя
1 1 ... 1
As„.
As„.
As*.
Sn-
As/i-
As/i-
As/i-
-fe
-k+i
-i
-k
-k
-k+i
-1
As„-
Д*л-
Д*л
Sn-
Asrt_
ten-
As/i
-k+i •
-k+2 •«
•
-k+i ••
-k + i •
-k+2 ••
,,
. A%
. As„+1
. ten+k-i
. Sn
.. As„
. ten+i
. &Sn+k-i

336
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
С их помощью построим преобразование
последовательности sn в новую последовательность аП1 положив
On = <*kn
Dkn (snV
= *+!, k + 2,
B2)
Ниже это правило будем называть 5^-преобразованием
или преобразованием Шенкса порядка k. Условием его
применимости является неравенство Dkn =£ 0. Будем
говорить, что преобразование B.2) применимо к
последовательности sn, если для всяких достаточно больших п
Для k = 1 правило B2) совпадает с б2-преобразованием:
вы-
S/l-l Stl
As/Z_! А^
1
sn + lsn-i s"n
64.
AS/l-1 Д5Л|
При k = 2 преобразование B2) имеет вид:
<?2/г =
. S/i-2 [Ag/i-iAs„+i — (AsJ2] + ^-i [As^^ — As^As^]
S/l-2
As^_2
As^_!
1
As„_2
lAs,^!
sn -1 s/i
A^/i-i As„
As„ As„ + 1 |
1 1 1
As^i As„
As„ As„+1|
A^_2A^-(A2Srt_1J
A^A^-^^J
"Г Л2с -Л2С _М2с Л2 ' \ZO/
Оно является простейшим уточнением б2-преобразования.
Выясним теперь, для какого множества сходящихся
последовательностей можно наверное при применении,
преобразования B2) ожидать ускорения сходимости. Для
этого предварительно рассмотрим следующую комбинацию
показательных функций:
sn = s + c1(fl + c2ql + ... + ckql (n=l, 2, ...). B4)
Основания qt (i = 1, ..., k) показательных функций
предполагаются различными, отличными от нуля и единицы.
Коэффициенты ct можно считать отличными от нуля.
Если все <7* будут по модулю меньше единицы,
величина sn при п -> оо будет стремиться к своей постоянной

§ 3] УЛУЧШЕНИЕ СХОДИМОСТИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 337
части s. Если же |<7,-!>1 (/=1, ..., &), то sn-+s при
я-> — оо. В случае, когда среди оснований qt будут как
меньшие, так и большие единицы по модулю, \sn\ будет
неограниченно возрастать при м->оо и п-*—со.
Наконец, когда J qi \ = 1 при всех iy то sn будет ограничена,
но не будет иметь предела.
Функция sn зависит от 2&+1 параметров s, ch q{
(t = l, ..., k). Первый из них имеет для нас особое
значение. Найдем его выражение через значения sn. Для
этого необходимо исключить параметры ch qh число
которых равно 2&, и получить соотношение между s и
значениями sn. Чтобы выполнить операцию исключения,
нужно построить 2&+1 уравнений. Для этого возьмем
2fe + l значений аргумента п — k, n — k-\-l, ..., n-\-k и
рассмотрим уравнения
k
sn-k = s+ Д] ctf ?"""*,
i = 1
k
l~l B5)
b + > = 8+Z Ciqrk.
i = l
Исключим сначала параметры ct. Рассмотрим многочлен
степени ky для которого qt будут корнями:
Р (q) = (q~qi) •.•(<!-4k) = qk + aiqk-1 + ... + ak.
Коэффициенты аь ..., ak зависят от qh и их
исключение равносильно исключению qh как будет видно из
дальнейшего.
Возьмем первые k+l равенств B5), умножим их
последовательно на а*, а>к~ъ ..., #i, 1 и сложим почленно:
akSn-k + ak-1sn-k+i+ • •• +sn =
= *(аА + я*-1 + ...+ 1) + 2 Qi~kCiP(qi). B6)
Но Р(^)=0, так как qt являются корнями P(q), и
члены с Р (q^ справа в равенстве исчезнут:
akSn-k + ctk-iSn-k+i+ ... + sn = s(ak + ak+1+ ... +1). B7)
12 В. И. Крылов и др., т. II

338
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
Если взять k+l равенств B5), начиная с второго
и проделать такие же преобразования, получим уравнение,
сходное с найденным и получающееся из него заменой п
на я+1 и т. д. В результате получатся k+ 1 уравнений,
в которых параметры с{ будут отсутствовать. Перепишем
эти равенства, перенося все члены в левые части равенств:
я* (sn-k - s) + a*_i (s„_*+1 _ S) + ... + (sfl - s) = О,
Q-k (Sn-k+l — s) + Clk-l \Sn-k+2 — S) + • • • + E/г+1 — S) =0. /gg\
%
ak (sn s) + ak.x (s+1 - s) + ... + (sn+k - s) = 0.
Удобнее преобразовать уравнения, вычитая почленно из
каждого уравнения предшествующее. При этом первое
уравнение останется без изменения и система примет вид
Ctk {Sn-k — S) + Я*-1 (S/i-*+l ~ S) + . . . + (S„ - S) = 0,
akAsn.k + a^As^+j + ... + Asn = 0,
B9)
cibAsn-г + ak^Asn + ... + Asn+-k-i = 0,
Для исключения коэффициентов аъ ..., а* и
построения уравнения, связывающего s и sn„b, • ••» S/i+ъ
достаточно обратить внимание на то, что полученные выше
равенства можно рассматривать как линейную однородную
систему относительно ак, ак-ъ ...,аъ 1. Так как они
образуют ненулевое решение системы, то ввиду
присутствия среди них единицы определитель системы должен
быть равен нулю. Если определитель приравнять нулю,
получится уравнение, связывающее $ со значениями sn.
При его записи мы разложили определитель на разность
двух определителей по хорошо известной теореме
sn-k s sn-k+l s ••• sn s
As,, , As» ... As,
n+k-l
= D%n(sn)-sDkn = 0. C0)
Убедимся теперь в том, что для последовательности B4),
при принятых предположениях о параметрах ct и qh
определитель Dkn отличен от нуля. Преобразуем Dkn%
вычитая из каждого следующего столбца, начиная с
последнего, предыдущий столбец. При этом первый столбец
останется без изменения, а во всех остальных столбцах

§ 3] УЛУЧШЕНИЕ СХОДИМОСТИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 339
появятся вторые разности, в первой же строке всюду,
кроме первого места, получатся нули:
1 о ... О
Dkn=*
A2S,t-fe ••• Д%г-1
&2sn„i ... A2s„+*_2
Asn_t Л25/г_х ,.. Да5я+*-2
Так как последовательность sn имеет форму B4), то для
нее справедливо равенство
k k
A2s, = sn+2 - 2s„+1 + sn = 2 W fa - }J ~ 2 <#?,
Воспользуемся правилом умножения определителей
«строка на строку»:
D
kn:
k
n— 6
s ^r*
1=1
,n-\
r'nn~~l
С\Я\
wr1
1
Й1
1
*?~!
rf
Если из столбцов первого из перемножаемых
определителей вынести множители соответственно c\qnL-k =
= сх (qx -\Jq«-k... ckqnk~k == сл (qk - lJ ?£-*, то получится
определитель Вандермонда Wk (<?i, ...» ?/г) такой же, как
второй множитель и
C1)
По предположению, ct Ф О, qt Ф0> qt^l, qi¥= q/ [i Ф j)
и, следовательно, ЬкпфО.
Поэтому из B6) для s получим
—все- <32>
Сравнение найденного значения s с преобразованием B2)
12*

340
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
позволяет сказать, что если последовательность sn имеет
вид B4), то при всяком значении п = k+ 1, £ + 2, ...
преобразование дает постоянную часть s переменной B4),
каковы бы ни были ch qh удовлетворяющие указанным
выше условиям.
Напомним, что при доказательстве этого результата
мы предполагали основания qt показательных функций
в B4) различными между собой. Если же среди qt будут
одинаковые, то определитель Вандермонда Wk (qu ..., qk)
в C1), а вместе с ним и Dkn обратятся в нуль, и
преобразование B2) к такой последовательности sn будет
неприменимым. В этом случае для получения результата,
аналогичного указанному выше, необходимо изменить вид
последовательности B4). Сейчас мы сделаем краткое
замечание о том, какой должна быть она взята в случае
совпадения некоторых qt.
Рассмотрим последовательность вида
где функции z^ оставим на время произвольными линейно
независимыми. Выясним, каким условиям они должны
удовлетворять, чтобы в линейных комбинациях вида
L (sm~k) = akSm-k + (Ik-lSm-k+l + • • • + ^l^m-l +.S/n>
m = ny ..., n~\-ky
стоящих слева в равенствах B6) и аналогичных ему,
получающихся при замене п над+1, ..., n-\-k,
коэффициенты при параметрах ct обращались в нуль и эти
параметры в L (sm_k) не входили. Так как
L (sm-k) = s(ak + ak„x + ...+!) +
то для исключения с. достаточно выбрать функции z% так,
чтобы L(z%_k) = 0 (/=1, ..., k\ m = k+l, k + 2, ...).
Последнее говорит о том, что г$ должны быть решениями

§ 3] УЛУЧШЕНИЕ СХОДИМОСТИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 341
однородного линейного разностного уравнения порядка k
с постоянными коэффициентами
Его решения, как известно*), определяются
характеристическим уравнением, .имеющим в нашем случае вид
ak + ctk-tf + ak_2q2 + ... + а^*-1 + qk = 0.
Пусть оно имеет / различных корней цъ ... у qt кратностей
соответственно къ ..., kt. Для кратностей, очевидно,
выполняется соотношение kL+ ... -\-ki~k- Корню qt
отвечает ki независимых частных решений
<£,. nq% .... n'i-'q? (/=1, ..., I).
Общее число таких решений равно kx+ ... + kt = k,
и они образуют полную систему линейно независимых
решений уравнения. Примем их за z^K Соответствующая
им последовательность sn будет иметь вид
/
sn = s+ S (ci + с* п+-..+скп * )q(, C3)
С = 1
Если коэффициенты аъ а2, ...» а* определить равенством
(q-qtfi ... {д-д1)к1 = дк + а1дк-1+ ... +а\
то в линейных комбинациях L (sm-k) будут отсутствовать
члены с коэффициентами c{p(j=l, ..., k.\ i = 1, ..., /) и
будут верны соотношения
^ (З/я-fc) ~ ak$m-k + ttk-lSm-k+l + •• • + #lSm-l + $m =
= s(aft+ ... +ai+l), m — д, л+ 1, ..., /i + 6,
из которых сразу же следуют системы B8) и B9). Из них
в свою очередь путем исключения коэффициентов аь ..., ак,
зависящих от ^(t = l, ..., /), получится равенство C0)
для нахождения s через значения s„_A, ..., sn+k.
Выше для переменной sn, имеющей вид B4), было
найдено простое явное выражение C1) для Dkny
позволившее убедиться в том, что Dkn Ф 0. Когда sn имеет вид
C3), явное выражение для Dkn является значительно
*) С таким уравнением мы встречались в п. 5.10.1 (см.
уравнение E.10.9)).

342
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
более сложным, и его получение потребовало бы
громоздких вычислений. Убедиться в выполнении неравенства
можно было бы сравнительно просто, если воспользоваться
некоторыми результатами теории конечноразностных
уравнений, но изложение их также потребовало бы
некоторого места и отвлекло бы от основной темы. Примем без
доказательства, что для последовательности C3) будет
Dkn¥=0.
Тогда из C0) для s следует выражение C2). Это
приводит к формулируемой ниже теореме, частным случаем
которой является утверждение, высказанное раньше для
последовательности B4).
Теорема 3. К последовательности sn вида C3)
преобразование B2) применимо при любом n — k-\-l, ft+ 2, ...
й для каждого п дает постоянную часть s
последовательности sn.
Отметим, что если дана последовательность sn, имеющая
вид C3), то для определения преобразования B2),
обладающего указанным в теореме 3 свойством, необходимо
знать только число ft = kx + ... + kh и не нужно знания qt,
kt и других параметров формулы C3).
7. Теорема об ускорении сходимости. Если
последовательности B4) или C3) сходятся, то s для них является
предельным значением и преобразование B2) при всех
значениях п дает это предельное значение, так как тогда
по теореме 3 on = s (n = k+l9 ft+ 2, ...). Это есть
крайний случай ускорения сходимости при преобразовании,
когда предельное значение получается сразу.
Если последовательность sn не совпадает с C3),
а в каком-то смысле близка к такому виду, то
преобразование B2) даст величину а„, не совпадающую с s,
а мало отличающуюся от s, и можно ожидать, что новая
последовательность оп будет сходиться быстрее к пределу s,
чем к нему сходится sn. Нам надлежит выяснить, какого
рода «близость» sn к C3) для этого достаточна. Начнем
с выяснения достаточных условий сходимости ап и
ограничимся простым случаем, когда последовательность sn
близка к B2). Рассмотрим последовательность вида
*n = s + ci4i+--"+c& + *n = s + zn + *n, C4)
ciФ0, Цьф0; 1 (* = !,.,., ft), ciФс,- (iФ/).

§ 3] УЛУЧШЕНИЕ СХОДИМОСТИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 343
Будем предполагать, что величина ед является «малой»
сравнительно с показательными функциями и для нее
выполняются условия
■со
(*=!....,*).
C5)
Выделим в определителях Dktn(sn) и D%in(sn) главные
части. Возьмем Dkjn и преобразуем его, вычитая из
последнего столбца предпоследний и т. д. и первый столбец
из второго. Это позволит привести Dkn к виду,
содержащему только вторые разности
1 о ... о
Я*я =
As/i-i А%л_! ... A2s„^„2
A2s*-i
A2%-i
Ввиду
/-1
справедлива формула
A*« =
/=1
<7 = С/(9/-1)в' Чт-ДЧ
2 ^Г1+!!„_,
S^r'+^-i- 2^/я+*-я+ч
/*i
/=i
1/14-Ai—2
Каждый столбец в D*n можно рассматривать как
сумму k столбцов с элементами (eft}-1, ..., с^7?~'+*),
которые будем называть столбцами первого вида, и одного
столбца второго вида с элементами 01л~,-» •••» Tl«-«+*-i)*
Поэтому Dkn можно представить как сумму (А+1)*
определителей того же порядка к, в каждом из которых
столбцами будут отдельные слагаемые столбцы этих сумм.
Приведем запись суммы к простейшей форме. Возьмем
один из слагаемых определителей. В нем будет несколько
столбцов первого вида. Их всегда можно переставить на

344
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
1ГЛ. 9
первые места; при этом может измениться знак
определителя, и если такие перестановки выполнить во всех
слагаемых определителях, получим для Dkn разложение
следующего вида:
Д
'knz
-2±
' п-а,
саЯа
сУа Чч
саЯ
n-a+k-1
a4d
n-y+k-1,
%-l+k-i
Пп-т
Из столбцов первого вида можно вынести общие
множители с'Ап~а,
qna> ..., qnd, зависящие от я,
стоянный множитель с'\
1
Яа
Отделим в них множители
а остальные объединим в по-
Dkn = z±cYa
<а
1
Ял
Цп-т
Цп-т+г
Яа
••• Я а
lin-l+k-i
hi-m+k-l
Если среди индексов а, ..., d есть одинаковые, то
соответствующий определитель равен нулю, так как в нем
будут два одинаковых столбца, и при суммировании
следует принимать во внимание лишь слагаемые с разными
индексами я, ..., d.
Разделим Dkn на произведение q\ ... q\. При почленном
делении суммы множитель qna...qnd сократится.
Оставшееся после сокращения произведение обозначим через
Япе • • • Я%- Число оставшихся множителей будет равно числу
столбцов второго вида в соответствующем слагаемом
определителе. Внесем множители q~ni ..., q~^n под знак
определителя и присоединим их по одному к элементам
каждого столбца второго вида:
— п —
k
= S±c'
1
Яа
Id
Яе Пх\п-1
я7ппп-м
ЯН %-т
Я^\1-т+1
Яа''
я,'1
Як ^n-m+k-l
C6)
Выясним, какое значение имеет сумма, стоящая справа
при больших п. Для определенности будем считать, что
основания qt перенумерованы в порядке убывания модулей:
\Яг\
■ \ Чч I
ш

§ 3] УЛУЧШЕНИЕ СХОДИМОСТИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 345
Для Беличий гп выполняются условия C5), и так как
г\п = гп+2 — 2гп+1-\-&ПУ то для i}n будут выполнены
аналогичные условия:
07п\^° (п->со).
Каждый определитель, стоящий под знаком суммы и
имеющий хотя бы один столбец второго вида, будет
стремиться к нулю при /1->оои является величиной порядка
о(а^пепу Число таких определителей не зависит от /г, и
их сумма с коэффициентами с' будет малой величиной
такого же порядка.
Рассмотрим теперь сумму членов в C6), в которых
определители не содержат столбцов второго вида.
Это будет разложение определителя, получающегося из
DknQTn ••• 4Jny если в Dkn заменить гп тождественным
нулем. Такой определитель без множителя (fi~n...qjn
рассмотрен в предыдущем пункте перед равенством C1)
и его значение указано в C1). Все изложенное
позволяет сказать, что равенство C6) при больших п имеет
форму
^VT"...^^^ ... с,^-1)«...(</,-1)»^*...
и, следовательно, при больших п
л*.=«1-'*(?.-1>'-(**-1),Я-*-
•••?Г^Ц?р •••.<)[1 + °(<7ГЧ1I- C7)
Сходные вычисления проделаем для определителя Dln:
D%n (sn) =
S + 2„ +
As„
= sDkn +
ДBя-1 + вл-1) •"•• ^(zn+k-l + ^ri+k-l)
±=sDkn + Dtn(zk + Bn),

346
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
1ГЛ. 9
Последний из определителей — D%n (гп + вп) — приведем к
более удобной для преобразований форме. Первую строку
прибавим ко второй, после чего на месте второй строки
получим гя-Л+1 + C/i-ft+i ... гя+1 + ея+1. Новую вторую строку
прибавим к третьей и т. д. После этого получим
Dtn(Zn + Zn)-
2п~к~^гп-к
гп + *п
Zn + En
*n+k
+ «
л+fe
Л <14Г* + *;
/=1
tl-k
к
/=1
cfl1+zn
2 *tf + *n
/ = 1
.2 с/*/+* + е„.
+/г
Каждый столбец последнего определителя есть сумма &+ 1
столбцов, и подобно тому, как это сделано выше для Dkny
Dkn(zn + en) можно представить в форме суммы (k+l)^1
определителей порядка k+l следующего вида:
Dtn (г„ + ел) =
саЧа
cd4d
В 8
п—ш Ti—p
с an-a+k
саЧа
cdQd
Если из столбцов определителей, стоящих под знаком
суммы, вынести множители caq%-a .. , cdq«-v, отделить в них
части qna, ..., qnd, зависящие от /г, а остальные множители
объединить в один, не зависящий от п, и обозначить его
через С, то получим следующее представление:
Dtn (гл + ел) =
«2±С<й...л
1 ••• 1 ««-/
7а •;• 7rf 8д-/+1
ъц-тРя—р
e/t-m-f 18/г-р+1
</а ••• Яй
°n-l+k
En-m+kEn~p+k
Рассмотрим сначала определители, в которых нет
столбцов со значениями гп. В них будет k+l столбцов с
величинами qa ... qd, и так как среди этих величин может
быть только k различных, то все такие определители равны
нулю ввиду того, что в них обязательно будут одинако-

§ 3] УЛУЧШЕНИЕ СХОДИМОСТИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 347
вые столбцы. Отличными от нуля могут быть только
определители, имеющие столбцы со значениями гп. Кроме
того, если в таких определителях некоторые из чисел
<7а> •••>?</ окажутся равными, определитель обратится
в нуль, и мы вправе считать qa, ..., qd различными.
Обе части последнего равенства разделим на
произведение q^ ... qnk. При почленном делении суммы множители
qnay ..., qnd сократятся нацело, при этом оставшихся
степеней q, которые назовем qf, ..., q^ будет на единицу
меньше числа столбцов со значениями величины е. Внесем
множители qjn, ..., q~n под знак определителя и
присоединим по одному к столбцам с е, кроме последнего,
который останется свободным:
чтп ■
~<KnDL(zn+%)
= £±С
1 .
Ча ■
<?*•
• 1 CV* •
• Id Ч~ ел-т •
• Чл ЧТ\-м •
" 4h гп-тп еп-р
•• Qh s/i-m+l 8л-р+1
• 4h e'n-m+kEn-p+k
Среди определителей, стоящих под знаком суммы,
наиболее низкую по порядку малости оценку будут иметь те,
где значения е стоят только в одном столбце (последнем
в нашей записи), и такие определители должны быть
оценены величиной 0(ея). Если в определителе будет
несколько столбцов со значениями е, то порядок малости
их оценок будет не ниже чем О (ел) (~). Поэтому правая
часть последнего равенства при больших п будет
величиной О (е„) и для Dkn(zn-\-en) получится соотношение
Я;й(гп + ел) = Я ...ЯО(еп). C8)
Возвратимся к преобразованию B2)
„ _ DLfa) _ P&, (»+»„+*„) _„ , P&, (»„+«„)
Ha основании равенств C7) и C8) можно сказать, что
a„ = s + 0(en), C9)
и верна

348 УЛУЧШЕНИЕ.СХОДИМОСТИ РЯДОВ [ГЛ.9
Теорема4. Если последовательность имеет форму C4)
и. для нее выполняется условие C5), то при всяких
достаточно больших п к ней применимо преобразование B2);
при этом новая последовательность оПУ полученная из sn
после преобразования, сходится к значению s, если гп -> О,
когда п-+оо} причем Gn — s = 0(en)-
Допустим вновь, что i последовательность sn имеет
вид C4) и для нее выполняются условия C5). Пусть,
кроме того, sn сходится. Последнее может, очевидно,
быть лишь в том случае, когда все основания qt по
модулю меньше единицы: 1 > I qx | Ss | q2 \ ^... ^ | qk \ > 0.
Пределом последовательности является число s. Скорость
стремления к нулю погрешности sn — s = с$1 + ... + скЯ1 +
Н- &п определяется наиболее медленно убывающей
показательной функцией, так что sn — s = 0(qfy Применим
к sn теорему 4. Условие еп-^0 (п-^сю) в
рассматриваемом случае выполнено, так как из -п ->■ 0 следует, что
Як
Соотношение C9) здесь имеет вид
ап-* = 0(г^ = о(д$. D0)
Преобразование sn в оп может дать сильное увеличение
скорости сходимости.
Изложенное позволяет сформулировать приводимую
ниже теорему.
Теорема 5. Пусть для последовательности sn вида
C4) выполнены условия C5) и 1 > | q1 | ^ | q2 | ^... ^ | qk I >
>> 0., Тогда верны утверждения:
1) sn сходится к s и скорость сходимости
характеризуется равенством
sn-s = 0(qfy
2) к sn при всех достаточно больших п применимо
преобразование B2), новая последовательность оп также
сходится к s и ускорение сходимости, получающееся при
преобразовании, характеризуется равенством D0).
Аналоги теорем 4 и 5 могут быть доказаны для
последовательностей вида C3), но они требуют более
громоздких вычислений и по этой причине опущены.

§ 3] УЛУЧШЕНИЕ СХОДИМОСТИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 349
8. Об улучшении сходимости и аналитическом
продолжении степенного ряда мероморфной функции. Пусть
аналитическая функция f(z) комплексной переменной г
задана степенным рядом
f{z)=cQ + c1z + ... + cnz» + ..., D1)
сходящемся в круге \z\<cR. Пусть, кроме того, известно,
что f (г) в круге большего радиуса jz|<p(p>#) имеет
конечное число особых точек, которые являются
полюсами функции f. Рассмотрим первоначально простейший
случай, когда все полюсы имеют первый порядок. Тогда
/ (г) представима в форме
fto-2-^+чы <42>
а1фа] AФ\), /?<|а/!<р (/= 1, ..., £)>
где ф(г) регулярна в круге |zj<p и может быть,
следовательно, разложена в степенной ряд
оо
«P(z)=l>vzv, |z|<p. D3)
v==0
Ряд D2) является суммой k степенных рядов для
элементарных функций ajdjicij — z)-1 и ряда D3)
оо k оо оо
2«-2«*2®'+2^-
v = 0 /=1 v = 0 v = 0
В этом представлении функции / нам известны лишь
коэффициенты cv, число k и то, что ряд D2) сходится
в круге | г \ < р. Считая | z | < р, рассмотрим частичную
сумму заданного ряда
v = 0 /=1 v = 0 v = 0
= 24^-^1+2^-2^-
/=1 v == О v ~ л

350
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
Величина sn имеет форму C4) при
k
s= У _!i~f<p(z), c, = '-L.
£d а; —г ' T v n ' a; — z *
oo
v — n
Проверим выполнение условия C5). Так как ряд D2)
сходится в круге jzj<p, то для всякого 6>0
существует такое число М, что выполняется неравенство jfcv|^
^Л1|р — б i_v. Будем считать б настолько малым, что
|г|<р —б, |tf/j<p — б,
1м
(р-б)
г = М
р-б
р-б-
р-6
Поэтому
:М
Р-(
9-6-
Р-
г J р-б-|г|
р-б
Отсюда ввиду ! а;- \ < р — б следует соотношение C5).
Наконец, последнее условие теоремы 4 ел->0 (я->оо),
очевидно, выполняется, так как ряд D3) в точке г сходится.
Теорема 4 применима к последовательности
частичных сумм sn ряда D1), и новая последовательность ая,
полученная из sn преобразованием B2)» сходится к
k
а/Я/
^Г7 + ФЮ
у=1
при всяких г из круга |г|<р, отличных от я (/—1, ...
..., &), и предел оп дает аналитическое продолжение
суммы степенного ряда D1) в этом круге.
Если г лежит в круге | г \ <£?, то последовательность оп
по теореме 5 будет сходиться к s, причем скорость
сходимости характеризуется соотношением ofl — s = 0 (ел) =
= 0 2 ^v!» и, так как ряд D3) сходится в круге
\v = п J
|г|<р (р>>#), будет больше, чем у заданного ряда D1).
Случаем простых полюсов функции / (г) мы
ограничились для облегчения записи. Без доказательства
отметим, что справедлива более общая теорема.

§ 4] ВЫДЕЛЕНИЕ МЕДЛЕННО СХОДЯЩЕЙСЯ ЧАСТИ 351
Теорема 6. Пусть функция f (z), заданная
степенным рядом D1), имеет внутри круга |z|<p (p>^)
конечное число особых точек аъ ..., ah являющихся полю-
сами, и известно, что сумма порядков этих полюсов
равна k. Тогда преобразование B2) применимо к
последовательности частичных сумм sn степенного ряда D1).
Новая последовательность ап будет сходиться к f (г) всюду
в круге | z | < р, кроме точек at (i = 1,..., /); при этом
сходимость ап к f (г) в круге \z\<R будет более быстрой,
чем сходимость sn к f(z).
§ 4. Улучшение сходимости ряда с помощью
выделения медленно сходящейся части
1. Введение. Пусть рассматривается сходящийся
численный или функциональный ряд
иг + и2 + ... + ия + ... A)
Если сходимость является недостаточно быстрой, можно
пытаться ускорить ее с помощью выделения из ряда
медленно сходящейся части. Достигают этого обычно
путем разложения заданного ряда на сумму двух
сходящихся рядов
со со со
2>»=2>«+2>». B)
п — \ п— 1 п — 1
Эти ряды выбирают, чтобы первый из них имел
известную сумму или легко находимую, второй же ряд должен
быть более быстро сходящимся, чем A).
Члены рядов связаны между собой очевидным
соотношением: un — vn-\-wn. Так как третий ряд с членами wn
должен сходиться быстрее ряда A), то его члены wn
должны стремиться к нулю быстрее ип и величина vn
при неограниченном росте п должна быть главной
частью ип. Разложение B) есть в первую очередь
операция выделения из членов ип главных частей при
условии п-*оо. Такое выделение может быть сделано
многими способами и разные значения vn могут отличаться
между собой лишь малыми величинами более высокого
порядка малости, чем они сами. Произволом в выборе vn
пользуются обычно для того, чтобы сумма ряда ^vn

352
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
была известной или могла быть найдена достаточно
просто. Удовлетворить это последнее требование не
всегда возможно, и поэтому метод выделения медленно
сходящихся частей рядов не является универсальным.
Однако существует много случаев, когда он применим
и может быть полезен в вычислениях.
Ниже будут рассмотрены два таких случая.
2. Числовые ряды. Случай убывания членов ряда по
степенному закону. Рассмотрим ряд вида
со
2 n^F(n), |i>l, C)
П= 1
и предположим, что функция F (п) имеет следующее
разложение по обратным степеням п:
F(„)=flo + «L + ... + ?* + ?*£>, Yft(n)-*0(rt-oo). D)
Параметры at и yk (n) такого представления F могут
быть найдены последовательно при помощи правил:
a0 = limF(/z),
п
аг = limn[F (п) — а0],
п
Tik(/i) = /i*^(/i)-(a0 + ... + ^].
При помощи D) рассматриваемый ряд разлагается на
две части
со со
п—\ /г = 1
СО °° , •
/г—1 '• л=1
со со
= 2^ + 2^-

§ 4] ВЫДЕЛЕНИЕ МЕДЛЕННО СХОДЯЩЕЙСЯ ЧАСТИ 353
Второй из рядов сходится тем быстрее, чем больше k.
Что же касается первого ряда, то его сумма выражается
точно через значения дзета-функции Римана
2*-2 E +
Я*
= aoS(M') + «iS(H' + 1)+-.-+^£(m.+*).
Численные значения этого выражения могут быть во
многих случаях найдены с помощью известных таблиц
функций *) £ (я).
В случае, когда \х есть целое число, большее единицы,
вычисления упрощаются и могут быть выполнены без
обращения к функции. £ (я).
Заменим разложение по отрицательным степеням п
другим разложением —по обратным величинам фактори-
альных многочленов.
Напомним, что факториальным многочленом степени р
называют следующую функцию:
Пр(х)=х(х+1)...(х + р-1). E)
Присоединяя множитель п~^ к F(n)9 можно считать,
что рассматривается ряд
2 F («), F)
/1=1
где функция F (п) имеет представление
р /п\ = Вг г El 4- 4-^4-yk ^
w Ф ^ пз ^'" л* ^ п* '
Такое разложение может быть заменено близким к нему
разложением
р^^ п{п+\) +n(n+l)(n + 2) "*"•'•
-•• + n{n+lhb!?(n+k„l) + bk(n), G)
fi/г (п) -* 0 (/г -> со).
*) См., например, А. В. Лебедев, Р. М. Федорова,
Справочник по математическим таблицам, М., Ияд-во АН СССР,
1956, гл. XI; Н. М. Брунова, Справочник... Добавление Ns I,
М., Изд-во АН СССР, 1959,

354
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
Его параметры bt и 8k(n) определяются равенствами
&2 = Нт л(я+ l)F(n),
п
h = Пт n (n + 1) (п + 2) [f (п) - ^^j,
йА —lim n(n+1)...
..■(»+^-i)[f(n)-(^^+...+w(,+1),6:g+fe_2))].
в* СО
и(я+1)...(п+й—1)
P i v / b<i . . bk \
-r W""\n(n+i)+--'+n(rt+i)...(/i+fe-.i);-
Равенство G) позволяет разделить ряд F) на две
части
2 «„= Vf(n) =
£i \n(n+l) ^ n(n+l)(n+2) ^-"
••*+n(rt+l)...(n+ft-l)j+ 2i n(n
e*(«)
+ l)...(n + *-l)*
Если число ft достаточно велико, то второй из рядов
правой части будет быстро сходящимся. Сумма первого
ряда вычисляется точно. Если обратить внимание на
то, что
п(п+\) ...(п + т— 1)
Г ! ! 1.J-
1п(п-{-\)...(п + т — 2) (n-fl)(/i + 2)...(/i + m—l)Jm—1
и, следовательно,
00
1
У
^ rt(rt+l)...(rt + /7l—1)
оо
JL.y Г 1 ! "U
т—1 ^j Lrt(/l+1)---(^ + m —2) (л+1)...(л + /п — 1)J
n = l
1
(т-1)(/л-1)! '

§ 4] ВЫДЕЛЕНИЕ МЕДЛЕННО СХОДЯЩЕЙСЯ ЧАСТИ 355
то можно сказать, что сумма первого ряда равна
' I 9.91 » * " ' (Ь— \\(Ь—. \\\ * W
Ml "^ 2-2!'r,,,"r (£-l)(£-l)t
3. Улучшение сходимости тригонометрического ряда.
Как пример задачи ускорения сходимости
функциональных рядов будет рассмотрена задача для сходящегося
тригонометрического ряда
оо
5 (х) = а0 + 2 (а« cos пх + &л §in пх) (— оо < х < со). (9)
п = \
Ввиду сходимости ряда его коэффициенты ап и Ъп
стремятся к нулю при я->со. Предположим, что при
больших значениях п коэффициенты имеют следующие
представления:
ап = ~п + -J + • • • + Ч + "Г е* (п)» е* (п) -* °»
/2 ' /I'
&/i = Pi + b+...+ P*_ + ±6,(«), б*(«)ч-о.
A0)
Если эти выражения для ап и Ьп внести в ряд (9),
то его можно разложить на сумму нескольких слагаемых
рядов
S(x) = ao +
2 cos пх , о \Ч sin п
л?=1
л=1
+
оо
оо
+
«2
COSH*
"IT"
о V sin r
■р*2 ~^
Л=1 Я=1
cos лх
+.
а*
2cosnx , о \J sii
sm пх
/i*l
«=l
л*
+
+ У — [в/? (/2) COS ПХ + 6* (л) sin fix].
П^\
Последний из них будет сходиться тем быстрее, чем
больше число k. Что же касается всех других рядов

356
УЛУЧШЕНИЕ СХОДИМОСТИ РЯДОВ
[ГЛ. 9
правой части равенства, то суммы их известны в теории
рядов Фурье и значения сумм приводятся ниже*).
00
2 sin пх я — х л - ^ с\
оо
2 ^ = -lnBsin|) = ^(^), 0<х<2л,
?~1
yi COStlX _(Х-Л)* Л2 O^y^Orr
X X
ИГ
л 00
ПК»
Vn=l О О
{ оо
V sin л* *3 — Зл*2 + 2л2* А . ^0
2l?- = ПГ • 0^х<2я,
Л«1
п=1 0 л«1
оо
^ l = gC) = 1,202 056903 ....
п=1
оо
2 cos яд: г1 — 4ях3 + 4 я2*2 . я4 г\ ^ ^ о
Т = if—+ 90' 0<*<2я,
ОО * 00
\rt=l 0 /2=1
Выше был рассмотрен основной случай, когда в
тригонометрическом ряду могут содержаться гармоники
IV
*) Первую пару равенств можно найти, например, в книге:
Г. М. Фихтенгольц, Курс дифференциального и интегрального
исчисления, т. Ill, M , «Наука», 1970, гл. XIX, § 2. Каждая
следующая пара равенств может быть получена из предыдущей при
помощи почленного интегрирования по переменному отрезку [0, х].
Последовательность равенств этим путем может быть продолжена
сколь угодно далеко.

ЛИТЕРАТУРА
357
любых кратных частот. В частных случаях, когда,
например, тригонометрический ряд содержит гармоники только
нечетных кратностей, вычисления могут, очевидно, быть
упрощены путем построения равенств, аналогичных
приведенным выше, но содержащим только нечетные
значения п.
ЛИТЕРАТУРА
L Крылов В. И., Бобков В. В., Мо настырный П. И.,
Вычислительные методы высшей математики, т. 2, Минск, «Выш^й-
шая школа», 1975, гл. 9.
2, Харди Г.7 Расходящиеся ряды, AL, ИЛ, 1951.

ГЛАВА 10
ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНОГО АНАЛИЗА
К ПОСТРОЕНИЮ ТЕОРИИ НЕКОТОРЫХ РАЗДЕЛОВ
ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ
В вычислительных методах математики к середине
текущего столетия было накоплено обширное количество
знаний и построен большой арсенал методов численного
решения научных и технических задач. После появления
быстродействующих вычислительных машин количество
задач, поддающихся численному, решению, увеличилось
во много раз. Было создано много новых методов,
учитывающих свойства новых задач и свойства машин.
Вычислительной математике грозила опасность стать собранием
большого числа частных приемов вычислений,
недостаточно объединенных по идеям и не всегда теоретически
полно обоснованных.
Потребность в упорядочении и идейном объединении
методов вычислений стала настоятельно ощущаться. Такую
возможность объединить и получать из общего источника
много частных, родственных по своему характеру
результатов, дал функциональный анализ, в частности общая
теория операторов. К настоящему времени в этом
направлении сделано очень многое. Из большого числа
полученных здесь результатов авторы избрали только три
вопроса, считая, что их достаточно для того, чтобы сделать
понятной полезность абстрактных разделов математики в
задаче объединения и упрощения разрозненных знаний.
§ 1. Необходимые сведения из функционального анализа
1. Метрические пространства. Сходимость и полнота.
Множество X произвольных элементов х называется
метрическим пространством, если каждой паре элементов х,
у из X соответствует число р(;с, у), которое называют

§ 1] НЕОБХОДИМЫЕ СВЕДЕНИЯ ОБ ОПЕРАТОРАХ 359
расстоянием между х и у и которое удовлетворяет
следующим условиям, называемым аксиомами метрики:
1) р(х, у)^0 и р(х> у) = 0 в том и только в том
случае, когда х=у;
2) р(х9 у) = р (у9 х);
3) р(х, ^)<р(х, У) + Р(>% г).
Первое из условий называется аксиомой различения,
второе — аксиомой симметрии и третье — аксиомой
треугольника.
Говорят, что последовательность элементов хп (я=1,
2,...) сходится к элементу х*9 если р(д:я, х*)-+0 (я-*-оо).
Это записывается либо в форме лгя-^л:*, либо в форме
Нтлгя = д:*.
1. Если Хп-+х* и уп-+у*, то р(лгя, ^)->pU*, у*).
Действительно, двукратное применение аксиомы
треугольника позволяет написать:
р(Хп, УпХр(Хп, Х*)+р(Х*, уп)^
<р(*«, х*) + р{х*> у*) + р(у*> Уп).
Поэтому
р(Хп, Уп)-Р(Х*9 У*)<:Р(Хп, Х*)+р(у*9 уя).
Если переменить местами нары элементов хП9 уп и лс*,
у*, то получится неравенство с другим знаком левой
части и, стало быть,
|р(**, jy*)-p(x„y ^я)|<р(а:я, **) + р(У, уп).
Поэтому из того, что р(хпу х*)-+0 и р(уп, у*)->09
следует р(хя, _уя)-^р(л;*, 5>*).
Таким образом, расстояние р (х, у) есть непрерывная
функция своих аргументов х и j>.
2. Если дгя->л:* и хп-*у*, то jc*=j;*, т. е.
сходящаяся последовательность не может иметь два различных
предела.
В самом деле, 0 = р(л;я, хп) ->р (х*9 у*).
Следовательно, р(х*9 j;*) = 0 и х*=у*.
Нам потребуется еще понятие полноты пространства.
Всякая сходящаяся последовательность хп выполняет
условие Больцано —Коши, так как, если хп-+х, то для

360 ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНОГО АНАЛИЗА [ГЛ. 10
всякого е>0 существует номер п0 такой, что при п^п0
будет р (хп> х)<-g е. Возьмем п>щ и m>n0. Тогда
р(хп, Xmj^piXn, x) + p(x, хт)^^в + -^е = е.
Обратное утверждение, вообще говоря, не всегда верно,
так как можно указать такое метрическое пространство,
для которого из выполнения признака Больцано — Коши
для последовательности хп не следует существование
элемента х, к которому сходится последовательность хп.
Метрическое пространство называется полным, если
для любой последовательности хп, выполняющей условие
Больцано —Коши, в X будет существовать предельный
элемент.
Рассмотрим числовое пространство Rnj элементами
которого являются упорядоченные совокупности п
действительных (комплексных) чисел х = (хъ х2, ..., хп).
Определить в нем расстояние между элементами можно
многими способами. Приведем три наиболее
употребительных метрики.
1. Кубическая или m-метрика. Здесь
Pi (х, У) = 9т (*, у) = max | xt - щ |.
i
2. Октаэдрическая или s-метрика:
п
Рп (х, у) = ps (X, y)=2±\xt-y,\.
1 = 1
3. Сферическая или /-метрика
п -,1/2
Рш(х, y) = pt(x, у)
1 = 1
Легко проверить, что для каждого из этих
расстояний выполняются аксиомы метрики. Во всех указанных
метриках сходимость последовательности элементов
х(т)-+х* (т->оо) равносильна сходимостям по
координатам и в каждой из метрик Rn является полным
метрическим пространством.

§ I] НЕОБХОДИМЫЕ СВЕДЕНИЯ ОБ ОПЕРАТОРАХ 361
2. Линейные нормированные пространства. Линейные
операторы. Множество X называется линейным *), если
для каждых двух его элементов определена сумма х-\-у,
являющаяся элементм из X, и для любого элемента х
и числа Я определено произведение %х, также являющееся
элементом X, и обе эти операции подчинены условиям:
1) коммутативность сложения х-\-у=у-\-х;
2) ассоциативность сложения (x+yj + Z^x + iy + Z);
3) существует элемент 0, который называют нулевым,
такой, что при всяком хеХ будет х + 0 = х;
4) для всякого х существует такой элемент —х,
называемый противоположным, что х + (— х) = 0;
5) умножение — ассоциативно: Я (\ix) = (Яр) х\
6) верны два распределительных закона:
(Я + р) х = %х + pjc, Я (х +у) = Ял: + Яу;
7) 1 • х = л:;
8) 0 • jc = 0;
9) если Ял:-0 и л:=^0, то Я = 0.
Линейное множество X называется нормированным,
если каждому л'еХ соответствует число |лг||, называемое
нормой Ху для которого выполняются условия:
1) |jc||^0, и |л:!| = 0, только когда л: = 0;
2) \\х+у1^\\х\\ + 1у\\;
3) ||Ял;||НЯ|-||л;||.
Линейное нормированное пространство всегда может
быть метризовано, и для этого достаточно за расстояние
между элементами х и у взять норму разности х—у:
р(х, у)=\\х-у\\.
Линейное нормированное и полное пространство часто
называют пространством типа Банаха или, сокращенно,
В-пространством. Ниже приведены примеры таких
пространств.
1. Пространство С [а, Ь\ Рассмотрим множество
функций x(t)% непрерывных на конечном отрезке [а, Ь]. Под
сложением элементов этого множества понимают обычное
сложение функции и под умножением элемента на число —
*) Линейные множества часто называют векторными
пространствами.

362 ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНОГО АНАЛИЗА [ГЛ. 10
обычное умножение функции на число. Под нормой
функции понимают максимум ее абсолютного значения
|| *(/)! = max \x(f) |.
t
Сходимость последовательности элементов есть
равномерная на [а, Ь] сходимость последовательности
непрерывных функций.
Пространство С [а, Ь] является полным.
2. Пространство Lp[a, b]. Возьмем множество
функций x(t), измеримых и суммируемых со степенью р (р^ 1)
на конечном отрезке [а, Ь]. Норма функции определяется,
следующим интегралом:
ь
||х(/)||р = $|х@|рЛ.
а
Две функции, отличающиеся между собой на
множестве меры нуль, считаются совпадающими.
Пространство Lp[ay b] является полным.
Пусть X и Y есть два линейных нормированных
пространства и Л есть оператор, определенный на X и со
значениями в пространстве Y: у = А (х). Оператор А
называется непрерывным на элементе х, если из
сходимости хп-*х в X следует сходимость А (хя)-> А(х) в У.
Говорят, что оператор А непрерывен в X, если А
непрерывен *) на каждом элементе х е X.
А называют аддитивным оператором, если для всяких
двух элементов хх и х2 из X верно равенство A (jci.+jc2) =
— АХг + АХг.
Укажем некоторые свойства аддитивных операторов:
1. А @) = 0. Действительно, А @) = А @ + 0) = Л (б) +
+ А@) и Л@) = 0.
2. А (— х) = — А (х). В самом деле, 0 = А @) = А [х +
+ (—х)] = А(х) + А{—х) и Л(—*) = —Л(х).
3. Пусть Л есть аддитивный и непрерывный оператор,
тогда он однородный, т. е. для любого действительного
числа К верно равенство
А(Ьх) = КА(х).
*) Приведенное определение непрерывности оператора сохраняет
свой смысл, если X и У есть два любых пространства, в которых
определено понятие предела.

§ 1] НЕОБХОДИМЫЕ СВЕДЕНИЯ ОБ ОПЕРАТОРАХ 363
Ввиду аддитивности А при всяком целом значении р
будет А.(рх) = рА (х).
Далее, при целых q А (х) = A (q — -x) = qA i — x) и
А \~х) = —А (х). Следовательно, при всяких целых р
и q a(£x) = £A(x).
Возьмем произвольное действительное число К и
рассмотрим последовательность рациональных чисел гп,
сходящуюся к X. Ввиду непрерывности оператора А
А (Хх) = lim А (гпх) = lim rnA (х) = Ы (х).
Оператор А называется ограниченным, если
существует число М такое, что при всяких х из X верно
неравенство
\\А(х)\\^М\\х\\. ■ A)
Аддитивный оператор А называют линейным, если он
непрерывен.
Теорема 1. Для того чтобы аддитивный оператор
был линейным, необходимо и достаточно, чтобы он был
ограниченным.
Доказательство. Необходимость.
Предположим, что оператор А неограничен. Тогда существует
последовательность элементов хп такая, что будет *
\А{хп)\^п\хп\-
Возьмем элемент
Хп~ п
При п-*со х'п->0. Но
и оказывается, что при х'п->0 значение А(х'п) не
стремится к нулевому элементу и А не является
непрерывным на нулевом элементе. Сделанное выше
предположение о неограниченности А противоречит его
непрерывности.
Достаточность. Пусть \х — хп\-+0.
\A(x) — A(x^\ = \A(x-xnyi<iM\x--Xn\-*'0 (л-^оо),

364 ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНОГО АНАЛИЗА [ГЛ. 10
и поэтому
А(Хп)-+А(х).
Нормой оператора А называют наименьшее число М,
для которого при всяких х выполняется неравенство A).
Норму обозначают |) А |].
Теорема 2. Норма линейного оператора А равна
верхней грани значений || А (х) | в единичном шаре \\ х ||^ 1:
И|= sup И Л (jc) 1. B)
II X [|< 1
В самом-деле, при |jc|=^1
||Л(л:)||<||Л|Ц|л:||<1Л|1. C)
С другой стороны, по определению нормы оператора для
всякого е> 0 существует элемент х' такой, что \ А (х') || >
>(||Л||-е)[л:'|. Положим x=j^j.
И WHifjIA (*') \>jLj (IА||-е) Цх'ИИ 1-е.
Так как |je||=l, отсюда получится
sup ||Л(л:)||>||Л-е|.
Ввиду произвольности е это неравенство совместно с C)
доказывает справедливость B).
Оператор У, определенный в пространстве Y и
имеющий значения в X, называется обратным для
оператора А и обозначается Л-1, если он удовлетворяет двум
следующим условиям:
1) при всяких х е X VA (х) = х,
D)
2) при всех j/e=F AV(y)=y.
Отметим, что если оператор Л имеет обратный У = Л-1,
то Л осуществляет взаимно однозначное отображение X
на Y. Действительно, по второму условию каждый
элемент у есть результат преобразования некоторого jceX,
например в качестве такого элемента может быть взят
X = А (у). Остается проверить, если хх Фхг, то Л (Xi) Ф
фА(х2)- Действительно, если A(Xi) = A(x2)> то по
первому условию будет Xi = VA (Xi) = VA (x2) = x2.

§ 1] НЕОБХОДИМЫЕ СВЕДЕНИЯ ОБ ОПЕРАТОРАХ 365
В качестве примера рассмотрим линейное
преобразование v-мерного векторного пространства Xv с
элементами х (хъ ..., *v) в A-мерное векторное пространство Yvl
с элементами у {уъ ..., у^:
у = А(х).
При линейном преобразовании Xy^Y^
составляющие yt вектора у будут линейными функциями
составляющих Xj вектора х и само преобразование определится
системой равенств
v
yi= 2 avxJ> i = i> 2> •••> Iх-
Это есть обычное линейное преобразование с
прямоугольной матрицей переменных X/ (/=1, ..., v) в
переменные yt (i = l, ..., (л).
3. Дифференцирование нелинейных операторов. Нам
потребуются некоторые факты теории линейных и
билинейных операторов.
Пусть X и Y — линейные нормированные
пространства. Возьмем множество всех линейных операторов,
переводящих X в Y. Обозначим его [X-+Y]. Это
множество можно при надлежащем определении операций
сложения элементов, умножения их на число и выборе
нормы сделать линейным нормированным пространством.
Если Л—линейный оператор, принадлежащий [X-+YJ
и X — произвольное число, то под произведением ХА=А
понимают оператор, определенный равенством А (х) =
- Ы (х).
Пусть AL и А* два любых элемента из [X-+-Y].
Сумму А =Аг + А2 определяют равенством
А(х)=А1(х)+А2(х).
Так как А± и А2 — аддитивные операторы, то А также
аддитивный оператор. Далее
11А{х)ЫА1(х)-\-А,(хЦ<1
<|^1(*)!+ll^(*)!l<(IHill+M»IDI*l-
Поэтому А — ограниченный и, следовательно, линейный
оператор со следующей оценкой нормы:

366 ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНОГО АНАЛИЗА [ГЛ. 10
За нулевой элемент в [X -+■ Y] примем нулевой опера-
Р °* А0(х)=0 при всех х&Х.
Все аксиомы линейного множества, как можно легко
проверить, при выбранном определении умножения на
число и сложения для [X -v Y] будут выполняться.
За норму А, как элемента из [Х->К], принимают
норму оператора А (х):
ИН sup \\A(x)l
U*li<r
Введем понятие билинейного оператора. Пусть
каждой паре элементов х, х' е X ставится в соответствие
некоторый элемент у е Y:
у = В(х\ х).
Оператор В (х\ х) называется билинейным, когда
выполняются следующие условия:
1) при всяких элементах хУ х', х, х'еХ и
числах а, а верны равенства
В (ах'+ ах', х)^аВ\х\ х) + аВ(х'у х)>
В{х\ ах + ах) = аВ(х', х) + аВ(х\ х)'9
2) существует число М такое, что при любых х\
х ^ X верно неравенство
\\В(х', х)\^М\\х'\-\\х\\. F)
Нормой оператора В(х'у х) называют наименьшее
значение М, при котором выполняется F).
Пример. Пусть Xv есть v-мерное векторное
пространство с элементами х (хъ х2, ...» *v) и Y^ есть (Li-мер-
ное векторное пространство, элементы которого —у (уь
Уъ, •••> У\х)- Предположим, что у = В(х\ х) есть
билинейный оператор из Xv в Y^. Каждая составляющая yt
элемента у является, очевидно, билинейной формой
от составляющих элементов х' (х[9 ..., x'v) их (хъ ..., xv)
v
#=2 a)kx'jxk (* = 1 Н)- G)

§ 1] НЕОБХОДИМЫЕ СВЕДЕНИЯ ОБ ОПЕРАТОРАХ 367
у = В(х\ х) — fx-мерный вектор, Есе составляющие
которого есть билинейные формы вида G).
Норма оператора В (х\ х) зависит от выбора норм
в пространствах Xv и Y^. Пусть в них приняты
кубические (или т-) нормы
\х\т = max | xt |, I.уIk = max \yt |.
i i
Тогда
1у\\тЧВ(х',х)\\ = тах%
1 l k
a)kX)*k
\^^J!1Wik\\x'\m\xll
1 /. *
и, следовательно,
]£b<max2|a/*|
1 ik
При определении второй производной от оператора
мы встретимся с отображением пространства X на
множество операторов [X-+Y]. Обозначим [X-*-[X-+Y]]
множество таких отображений. Существует тесная связь
между ними и билинейными операторами.
Пусть U есть оператор, отображающий X в [X~>F].
Возьмем элемент х' из X и рассмотрим U (х') = Ах>. Это
есть оператор m[X-+Y], поэтому у = Ax>x = U(x') x =
= В (х\ х) является элементом из Y. Оператор В(х\ х)
удовлетворяет второму из условий E), так как
оператор Ах*х линеен относительно х и удовлетворяет
первому условию E) ввиду того, что Ах> =U (xf) является
линейным относительно х'.
Неравенство F) также выполняется при некотором М,
так как
\В(х\ x)\<,\A^\\x\^]Uxfi\x\<\U\\xf\\xl
и можно положить M = ||t/|L Таким образом, В{х', х)
действительно есть билинейный оператор и
151KB ^ И- (8)
Указанным выше способом каждому оператору U
из [X -*[Х -> Y]] ставится в соответствие билинейный
оператор В(х', х). Убедимся теперь в том, что при
указанном законе соответствия каждый билинейный опера-

368 ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНОГО АНАЛИЗА [ГЛ. 10
тор В(х\ х) есть отображение некоторого оператора U
из [X-+[X+Y]].
Фиксируем элемент х'. Оператор В{х\ -) = U(x') =
= Ах> принадлежит множеству [X-^F], и ввиду
неравенств
1 £/(*') И sup 11 £/(лг') (лг)I = sup \В(х',х)\<ь\В\\х'\
оператор U ограничен, а следовательно, линеен и
принадлежит множеству [X-*-[X-*~Y]]. Из неравенств
вытекает также, что ||£/|^||5||. Сравнение последнего
результата с неравенством (8) позволяет утверждать, что
ЦВЫ£/||. О)
Определим производную первого порядка от
оператора. Как и раньше, будем считать X и Y линейными
нормированными пространствами и предположим, что
дан оператор
y = f(x), A0)
преобразующий X в Y. Оператор / называют
дифференцируемым на элементе х, если существует линейный
оператор Я, принадлежащий [X -> F], такой, что верно
неравенство
«/ (х + Ах) -f(x)-H (Ax) J < |Л*« е (j| Ax ||), A1)
где е(8)->-0 F-vO). Линейный оператор Н называют
производной от оператора f на элементе х:
Н = Г(Х). A2)
Заметим, что Я (Ад:) имеет смысл дифференциала
оператора *) и является аналогом известного в курсах
анализа дифференциала функции.
Для примера рассмотрим преобразование v-мерного
векторного пространства Xv в ^-мерное векторное
пространство Уд. Такое преобразование y = f(x)
равносильно заданию (х функций
yi = fi(Xi> *2, ..., *v)> t = l, 2, ..., ц. A3)
*) f (x + Ax) — / (jc) есть изменение оператора при переходе
от элемента х к элементу jc + Ajc и Н (Ах) есть главная линейная
часть этого изменения.

§ 1] НЕОБХОДИМЫЕ СВЕДЕНИЯ ОБ ОПЕРАТОРАХ 369
Для вычисления производной от оператора / нужно
из его изменения f (х + Ах) — / (х) выделить главную
часть, линейно зависящую от hx = (Axlt ..., A*v):
f {x + Ах) -f (x) = H {Ax) + 8 (jc, Ал:),
где
*^Uo (||Дл;|КО).
Возьмем одну из составляющих изменения оператора
fi(x + Ax)-fi(x) =
= fi(x1 + Axlf ..., xv + &Xv)—fi{xi, ..., xv)=Afi.
Главной частью приращения функции fh линейной
относительно А*!, ..., Axv, является полный дифференциал
функции fh так что
{Н(Ах)}^2Щ^ Axh A4)
Это говорит о том, что производная /' есть линейное
преобразование Ху->Уц9 матрица которого есть vxjx
матрица Якоби с элементами, вычисленными для точки х:
Определим теперь вторую производную от оператора f.
Первая производная H = f'(x) есть линейный оператор,
принадлежащий [X ->- Y]. Он зависит от элемента х,
на котором вычисляется /', как от своего аргумента, и
каждому элементу х отвечает свой линейный оператор.
Может оказаться, что оператор /' имеет производную
на элементе х. Производную от /' называют второй
производной от оператора / и обозначают /". Она
принадлежит множеству [X-+[X-*Y]].
Выше было показано, что рассмотрение множества
операторов [X -> [X ->- У]] равносильно рассмотрению
множества билинейных операторов В(х\ х) при выборе
определенного, указанного выше закона соответствия
между элементами этих множеств. Такой
равносильностью пользуются в вычислениях, так как билинейные
формы часто бывают удобнее.
13 В. И. Крылов и др., т. II

370 ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНОГО АНАЛИЗА [ГЛ. 10
В качестве примера вычислим вторую производную
от рассмотренного выше оператора, преобразующего
векторное пространство Xv> имеющего размерность v,
в векторное пространство Уй размерности \i. Выберем
произвольный элемент х0 из Xv и вычислим f на х0.
По определению производной A1) нужно иайти такой
линейный оператор U из множества [X ->- [X ->- F]], для
которого выполняется неравенство
\\Г(х0 + Ах)(х)^Г(х0)(х)^и(Ах)\\^\\Ах\МАх\\). A5).
Полезно, преобразовать это условие к другой форме,
более удобной для вычислений. Зафиксируем какой-либо
элемент xf <^XV и положим kx = tx'. Разделив A5) на t
и перейдя к пределу при ^->0, получим равенство
lim }[Г (Хо + tx') (х) -/' (Хо) (х)] =
= U(x')(x) = Ax,(x). A6)
Или, так как Ах> (x) = U(xf) (x) = В(х\ х),
lim]rU'(Xo + tx')(x)-r(Xo)(x)] = B(x\ х). A7)
Значение В (х\ х) принадлежит пространству Y^ и
является вектором у (уъ ..., у^). Его составляющие yt
есть билинейные формы от (х'1у ..., *v) и (хъ ..., xv) и
их значения записываются в виде G)
v
{В(х\ x)}i= 21 aiikx'i*k* (I8)
jk = \
Векторное равенство A7) равносильно v численным
равенствам
Hm-V
*--о г
Отсюда получается
v
21 1^М*о) */** = {£(*'> x)}i
= {В{х> x)}t.
/a=i

§2]
МЕТОД ИТЕРАЦИИ
371
и, следовательно,
Для § 3 нам потребуются теоремы об изменении
оператора и о главной части изменения. Мы ограничились
тем, что сформулировали эти теоремы, но для краткости
опустили их доказательства, которые можно найти в
статье [2] (с. 166—168) или в [1] гл. 9 (с. 252—253).
Теорема 2. Пусть f есть дифференцируемый
оператор. Для его изменения верна оценка .
1/(*+д*)-/(*)]<: sup 1П*+ел*I11Д*11
@<е<1). A9)
Теорема 3. Если f есть дважды дифференцируемый
оператор, то для разницы между изменением
функционала f и главной линейной частью его верна оценка
\\f(x + Ax)-f(x)-f'(x)Ax\\^
^ 1 max 1 /" (х + в Ад:) Ц - Ц Да: f. B0)
8
§ 2. Метод итерации для решения операторных уравнений
Метод итерации применялся в гл. 2 первого тома
для решения систем линейных уравнений и в гл. 4 для
решения любых уравнений или их систем, и в обоих
случаях речь шла о нахождении значений неизвестных
чисел. Но совершенно очевидно, что идея метода
итерации может быть применена для решения уравнений с
неизвестными любой природы. Им пользуются, в частности,
для решения многообразных задач, где неизвестными
являются функции одного или многих аргументов; при
этом в уравнения могут входить не только сами функции,
но и некоторые операторы от них, такие, как операторы
дифференцирования, интегрирования, смещения аргумента
и т. д.
Было бы целесообразно не рассматривать отдельно
применение метода итерации к большому числу
различных видов уравнений, а построить общую теорию метода
итерации, не зависящую от вида уравнений, и из нее
13*

372 ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНОГО АНАЛИЗА [ГЛ. 10
как частные случаи получать необходимые результаты
для отдельных конкретных задач.
Простейший результат общей теории метода1
итерации — принцип сжатых изображений — будет изложен
в настоящем параграфе.
1. Метод итерации для операторных уравнений.
Предположим, что рассматривается множество X элементов х
произвольной природы: это могут быть числа или их
системы, функции или их системы и т. д. Пусть на этом
множестве задан оператор у = (р(х), значения которого
принадлежат тому же множеству. Этот оператор ставит
в соответствие каждому элементу х из X некоторый
элемент из того же множества. Действие такого
оператора может быть истолковано как преобразование
множества X в себя. Рассмотрим уравнение
х = (р(х). A)
Решить его —значит найти такие элементы X, которые
при преобразовании X оператором ф переходят в себя,
иначе говоря, остаются неподвижными при таком
преобразовании.
Будем считать, что такие неподвижные элементы
существуют, и рассмотрим итерационный метод построения
последовательных приближений для их нахождения. Пусть
каким-то способом найдено исходное приближение х°
к неподвижному элементу. Все остальные приближения
находятся по следующему закону:
x*+i = <p(xn) (п==о, 1, ...). B)
Заметим, что при принятом выше предположении о том,
что значения ср (х) принадлежат области определения X
оператора ср, приближения хп могут быть построены для
всех значений п. В некоторых задачах такое
предположение не будет выполняться, и тогда может возникнуть
проблема выяснения условий о возможности построения
бесконечной последовательности хп.
Пусть последовательность хп построена. Для нее мы
должны выяснить следующие вопросы: 1) будет ли она
сходиться в каком-то принятом нами смысле? 2) если х*
есть элемент, к которому сходится хп, то какова
скорость сходимости?

§2]
МЕТОД ИТЕРАЦИИ
373
2. Теоремы о сходимости и единственности.
Рассмотрим случай, когда X есть полное метрическое
пространство. Обозначим его метрику через р(лг, у).
Теорема 1. Предположим, что выполняются условия:
1) оператор ср (х) определен в замкнутом шаре S
радиуса 8 с центром в х°:
р(х, лг0)<6; C)
2) для всяких элементов х и у из шара S верно
соотношение
Р[ф(*). ф(У)]<де(*. J>). 0<?<1, D)
где q — постоянная величина;
3) для начального элемента х° выполнено неравенство
р[ф(лг°), *°]<т; E)
4) для чисел б, q, т, соблюдается условие
Тогда верны следующие утверждения:
1) итерационные приближения хп, вычисляемые по
правилу B), могут быть найдены при всяком значении п, и
все они принадлежат шару S;
2) последовательность хп сходится к некоторому
элементу jc* из S:
\im'xn = x* (a;*<=S);
п
3) предельный элемент х* есть решение заданного
уравнения A);
4) для приближения хп верна следующая оценка
близости к решению л;*:
р[х\ а:*]<т^9». G)
Перед доказательством сделаем пояснительные
замечания относительно условий теоремы. Начнем со второго
условия и запишем его в виде
р[ф(*). Ч>(уI ^
9{х>У) ^у*
Здесь знаменатель есть расстояние между элементами х
и у до преобразования, числитель р[ф(л:), ср (у)] — рассто-

374 ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНОГО АНАЛИЗА [ГЛ. 10
яние между теми же элементами после преобразования
шара S при помощи оператора <р. Отношение имеет смысл
коэффициента изменения расстояния между элементами
при преобразовании. Он не больше числа q, и так как
<7<1, то при преобразовании происходит уменьшение
всех расстояний между элементами шара.
Если исходное приближение х° случайно окажется
решением уравнения A), то ф(л:0)=л:0 и будет p[(p(jc°),
х°] = 0. Если же х° не будет совпадать с решением, но
будет близким к нему элементом, то расстояние р[ф(#°),
х°] будет малой величиной и число т может быть взято
малым. 'Когда х° лежит на большом расстояний от
решения уравнения, то трудно ожидать, что т будет иметь
малое значение. Ввиду этого число т в условии E)
тесно связано с близостью х° к точному решению
уравнения.
Условия теоремы означают следующее. Когда в
некотором шаре S достаточно большого радиуса 6 с центром
в х° при преобразовании оператором у = ф (х)
происходит достаточно сильное сжатие (q не близко к единице)
и х° взято достаточно близко к решению (т есть
достаточно малая величина), то уравнение имеет решение в шаре
S и к нему сходятся итерационные последовательные
приближения хп. Численная же характеристика всех
этих условий дается в неравенстве F).
Теорему 1 ввиду указанного наглядного содержания
часто называют принципом сжатых отображений.
Доказательство аналогично доказательству сходной
теоремы в гл. 4. т. I.
Убедимся сначала в том, что приближения хп могут
быть построены при всяких п, принадлежат шару S и
выполняется неравенство
р(хп, xn^l)<zmqn. (8)
Для п = 0 это очевидно ввиду того, что л:0 есть центр
шара, и значение хг = ц>(х°) может быть найдено,
так как оператор ср на элементе х° определен и,
кроме того,
р(лг°, х1) = р (л:0, фМ)<ш<р<«,
поэтому х1 принадлежит S,

§2]
МЕТОД ИТЕРАЦИИ
375
Предположим теперь, что л;0, х1, ..., хп построены,
принадлежат 5 и для них выполнены неравенства
р(х\ xk+1X;tnqk (£ = 0, 1, ..., я-1). (9)
Приближение хп+1 = у{хп) может быть вычислено, так
как xn^S. По второму условию теоремы и по
индуктивному предположению
р(хп, xn+1) = p[q>(xn-1), Ф(л^)]<до(л^-1, *")<
^ q • mqn~г = mqn
и неравенство (9) для k — n действительно выполнено.
Осталось проверить, что хп+1 принадлежит шару S. Если
применить несколько раз аксиому треугольника, получим
р(лг°, хп+1)^р(х°, хп) + р(хп, л;л+1)^...
...<P(jc°, хг) + р(хг9 х2)+... + р(хп, хп+1)^
^m + mq + ... + mqn<Y^r<:b.
Отсюда видно, что р (л:0, хп+1)^6 и ^+1gS.
Проверим, что для последовательности хп выполняется
признак Больцано — Коши
р (xnt хп+р)^р {хп, хп+1) + р (хп+1, хп+2) + ...
... +р(лгл+*>-\ xn+p)^mqn + mqn+1+ ... +т^р=:
Так как 0^^<1, из неравенства р{хп, хп+р)<.~гйп
вытекает, что для любого е>0 при всяких достаточно
больших п и всех р будет р (хп, хп+р)^е.
Из признака Больцано — Коши ввиду полноты
пространства следует существование элемента л;*, к
которому сходятся хп:
хп-+х* (п-+оо).
Переходя в неравенстве р (л;0, хп) ^ б к пределу при
/г->оо, получим р(л:°, л;*)^8, что доказывает
принадлежность л:* шару S.
Наконец, переходя в неравенстве р[ф(л?л), ф(**)]=^
<,qp{x'\ л;*) к пределу при я->оо, ввиду р (хп, #*)->■
->0 получим, что р[ф(*л), ф(#*)]-*-(), т. е. ф(л;л)-*

376 ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНОГО АНАЛИЗА [ГЛ. 10
->ср(л:*). Увеличивая же в рекурсионном соотношении
хп+1 = <р(хп) неограниченно п, получим в пределе л;* =
= ф(л;*). Таким образом, л:* есть решение заданного
уравнения.
Осталось еще проверить правильность оценки
приближения G). Для этого воспользуемся вспомогательным
неравенством, полученным по ходу доказательства
р(хп, *Л+Р)<Г^-<7Я.
Оно выполняется при всяких р. Увеличивая в нем
неограниченно р, получим в пределе G),
Дополним теорему 1 доказательством единственности
решения. Во втором условии теоремы число q считалось
независимым от х и у и меньшим единицы. Для
доказательства единственности это требование может быть
ослаблено и верна
Теорема 2. Во всяком множестве элементов, где
для двух любых элементов х> у верно неравенство р(ф (х),
Ф 00) < Р (•*> У) Уравнение A) не может иметь больше
одного решения.
Доказательство. Допустим противоположное:
пусть х = (р{х), у = у(у) и р(лг, у)>0.
Тогда верно неравенство
Р (х, у) = Р [Ф (х), Ф (у)] < р (х9 у).
Но это невозможно, и допущение р(х> у)>0 является
ошибочным.
3. Приложение к системам уравнений с числовыми
неизвестными. Предположим, что система приведена
к канонической для метода итерации форме:
%1 — ф1 \%Ь *2> • • • > Xm)i
Х2 = ф2 (#1, Л?2, • • • > Хт/9 /1 л\
Для записи ее в /я-мерном числовом пространстве Rm
введем два вектора: один из них х для изображения
совокупности неизвестных (хг, х29..., хт), второй ф будет

§2]
МЕТОД ИТЕРАЦИИ
377
обозначать совокупность значений функций (<plf cp2, ...
...t фт)- Система запишется в краткой векторной
форме
х = (р(х).
Пусть как-то выбрано начальное приближение к
решению x° = (x°i, х\, ..., х°т). Все следующие приближения
будут находиться по правилу итераций
хп+1 = <р(хп).
Для выяснения условий, достаточных для сходимости
последовательности приближений хп (д = 0, 1, ...),
применим теорему 1. Для этого мы должны в Rn ввести
метрику. Сделать это можно многими способами, и мы
остановимся на трех классических метриках.
1. Случай кубической метрики р(х, у) =
= max\Xi — yi\. В шаре р(х, х°)^8 возьмем две
произвольные точки х = {хъ лг2, ..., хт) и у = (уъ y2f
Оценим изменение функции ф^:
\<Pi(x) — <ti(y)\ = \<9i{xi>x*
(xj-yj)
Хщ) - ф« (Уъ Уз, • •
... Ут).
Ут)\ =
1
1 т
dxj
max I Xj -
/ т

дх/
•У/
р(х, у).
Звездочкой у скобок отмечено то, что значение
функции, стоящей в скобках, должно быть взято в некоторой
точке отрезка прямой, соединяющего хну. Чтобы найти
оценку изменения, не зависящую от i и положения точек
jc, у, заменим последнюю из скобок ее максимальным
значением по х и i. Тогда получим
1ф/(*)-ф;0>I
;тах|ф,(*)-ф,О0|=р[ф(л0, фОО]
к
т
[ дх/
/ = 1
max max
i x
р (х, у).

378 ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНОГО АНАЛИЗА [ГЛ. 10
Отсюда видно, что в качестве числа q в неравенстве D)
может быть взята величина
q = max max 7
i x f*x
dq>i
dxf
Все это позволяет сформулировать теорему о сходимости
итерационной последовательности в случае кубической
метрики.
Теорема 3. Пусть:
1) функции %(хъ ..., хт) определены и непрерывно
дифференцируемы в области
|**-*?|<а A=1 ..., т)\ (ПО
2) в этой области
max
д9А
дх/
\q<l (/ = 1, ..., т); A2х)
3) начальные приближения неизвестных удовлетворяют
неравенствам
|4-Ф*(*ь ..., х°т)\^М (/=1, ..., т)\ A3х)
4) для чисел б, q и М выполняется условие
Тогда:
1) система A0) в области A1х) имеет решение (rf,
#*> ..., #m) ^ /с нему сходится итерационная
последовательность Приближений (#ь ..., Хт)\
2) скорость сходимости может быть охарактеризована
неравенствами
2. Сл учай октаэдрической метрики р(д:,ву) =
= 2 \xj~~yj\' Аналогично теореме 3 для октаэдричес-
кой метрики в Rn может быть доказана

§2]
МЕТОД ИТЕРАЦИЙ
379
Теорема 4. Пусть:
1) функции %{хъ ..., хт) (/=1, ..., т) определены
и непрерывны в области
т
2) удовлетворяют в этой области условию
7 пи
max max
X
dq>i
dxj
1; A2*)
3) Зля начальных приближений неизвестных х\, • • •» *т
выполняется неравенство
2 |4-Ф;(*!, .... 4)КМ; A32)
4) для чисел б, <?, М соблюдается условие
Т^<б- A42)
Тогда:
1) система A0) в области A12) аж^т решение (*?,...
..., Хт) « /с #£Ш/ сходится итерационная
последовательность приближений (х\, ..., Хт);
2) скорость сходимости характеризуется неравенством
т
к~*<Т^<Л A52)
3. Случай шаровой метрики р(х, у) =
/ m - \I/2
= Bl^""^la) • Аналогично теоремам 3 и 4 может
быть доказана следующая теорема о сходимости
итерационного процесса.
Теорема 5. Пусть:
1) функции Ф/(хь ..., хт) определены и непрерывны
в области
т
21*|-х5|2<62; A13)
i=l

380 ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНОГО АНАЛИЗА [ГЛ. 10
2) удовлетворяют в этой области условию
2"™21£Г<«<1! <12->
i =1 * /= 1
3) для начальных приближений (х°и ..., х*т) верно
неравенство
т
Ц |4-ф;D, .... 4г)|2^М2; A3,)
1=1
4) для чисел 6, q и М соблюдается условие
ё-,^- сад
Тогда:
1) система A0) в области A13) имеет решение
(х*> ..., л:т) а /с «елеу сходится итерационная
последовательность приближений (xf, ..., л:^);
2) скорость сходимости можно характеризовать
неравенством
( т U/2
§ 3. Метод Ньютона для операторных уравнений
В гл. 4 т. I рассматривался метод Ньютона для
решения уравнений с численными неизвестными и для
систем таких уравнений. Но ясно, что основная мысль
этого метода — приведение решения нелинейного
уравнения к решению последовательности линейных
уравнений—может применяться к уравнениям других видов:
к многочисленным нелинейным задачам для
дифференциальных уравнений обыкновенных и с частными
производными, для нелинейных интегральных уравнений и
т. д. В настоящем параграфе будут рассмотрены начала
общей теории метода Ньютона для операторных
уравнений достаточно общего вида.
1. Правило построения приближений к решению.
Предположим, что X и Y являются полными, линейными,
нормированными пространствами.

§3]
МЕТОД НЬЮТОНА
381
Пусть в некоторой области D пространства X задан
нелинейный оператор y = f(x) со значениями в Y.
Будем рассматривать уравнение
/(*) = 0. A)
В правой части его стоит нулевой элемент
пространства Y. Допустим, что каким-либо способом найдено
исходное приближение х0 к решению. Для выделения
из уравнения главной линейной части положим f (x) =
= /(■*<>) + [/(x)—f(x0)] и рассмотрим изменение оператора
f(x) — f(Xo). Так как х0 берется обычно близким
неточному решению х и норма их разности \\х — х0\\ будет
малой величиной, изменение оператора / (x) — f(x0) будет
отличаться, как показывает неравенство A.17) от/' (х0)х
х(х — Хо) «весьма мало», и поэтому заданное
уравнение A) будет «близким» к следующему приближенному
линейному уравнению:
/ (*W С*о) + /' (Хо) (X - ДГо) = 0. B)
Можно ожидать, что его решение, которое мы
обозначим через хъ ближе к точному решению, чем х0.
Когда для /' (х0) существует обратный оператор [/' (jc0)]_1,
х± получим в форме
X1 = Xo-[f'(X0)]-1f(Xo)>
Для Хг можно повторить проделанные рассуждения и
по хл построить второе улучшенное приближение лг2 и
так далее. Правило Ньютона для нахождения
следующего приближения по предыдущему имеет вид
Хп+1 = ХЯ-[Г (Хп)]-Ч(Хп). C)
Построение последовательности приближений хп (п =
= 0, 1, ...) возможно при выполнении двух условий:
1) все приближения хп принадлежат области D; 2) при
всяком значении п существует обратный оператор [/' (хп)]~г.
2. Теорема о сходимости последовательности
приближений. Докажем теорему о разрешимости уравнения,
о возможности построения последовательности
приближений хп и о сходимости ее к решению. Известно несколько
теорем такого содержания, мы приведем одну из них,

382 ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНОГО АНАЛИЗА [ГЛ. 10
аналогичную теореме о сходимости процесса Ньютона
для численных уравнений, доказанную в гл. 4.
Теорема 1. Предположим, что выполняются условия:
1) оператор f (х) определен в замкнутом шаре
!*-*o!<e, D)
дважды дифференцируем там, при этом вторая
производная от него ограничена по норме числом К:
|П*)||</С, 1*-*о||<в; E)
2) оператор f (х0) имеет обратный Г0 = [/' (х0)]~г9
для нормы которого выполнена оценка
II Го 1<В; F)
3) для начального приближения х0 к решению верно
неравенство
11У(*оI<т); G)
(8)
(9)
Тогда:
1) в шаре D) уравнение f(x) = 0 имеет решение;
2) в вычислительном процессе Ньютона C)
приближение хп может быть построено при любом значении п,
все хп принадлежат шару D) и последовательность хп
сходится к решению х* уравнения;
3) для приближения хп верно следующее неравенство,
характеризующее скорость сходимости:
1**-*я| </*-/*, (Ю)
где t* есть меньший корень уравнения
и tn есть приближение к нему, построенное по методу
Ньютона при начальном значении t0 = 0.
4)
5)
величины
для
числа
К,
: 6
В, у] удовлетворяют
А = /С5т,<1;
верно неравенство
г Л^б.
условию

§3]
МЕТОД НЬЮТОНА
383
Доказательство. Предварительно необходимо
напомнить *) некоторые факты, касающиеся уравнения
р (t) = 0 и последовательности tn. Если для параметров
К у By г] уравнения выполнено условие (8), то корни
уравнения действительны и положительны, при этом
меньший из них есть t* =/r1 [l — "|/"l — 2/i]. Ньютонова
последовательность приближений tn к /*, начатая с 10 = 0,
является монотонно возрастающей и скорость
приближения tn к t* достаточно наглядно характеризуется
неравенством
В ходе доказательства нам потребуется простая лемма
0 существовании обратного оператора.
Лемма 1. Предположим, Что в полном
нормированном линейном пространстве X задан линейный
оператор Я, преобразующий X в себя. Если ||Я||^#<1, то
для оператора I — H существует обратный ему (/ —Я)-1
и при этом || (/ — Я)-11| <; г-—.
Доказательство. Рассмотрим в пространстве X
ряд Ах = х + Нх + Н2х +... и покажем, что он сходится.
Применим к нему признак Больцано — Коши. Возьмем
отрезок ряда и оценим его норму
1 Нпх + Нп+1х +. .. + Нп+Рх |] ^
^\\H\\»-\\x\\ + ...+ \\H\\"+P\\x\\^(q" + ... + ?"*) |*| =
= 1"^fl«lJCl<^
- 1_<7' Ч \\X\\<^l_qq •
Для всякого е >> 0 последняя часть системы неравенств
будет меньше 8 при всех достаточно больших п и
любых р, поэтому для рассматриваемого ряда признак
Больцано—Коши выполняется. Ввиду же полноты
пространства X ряд будет сходящимся и сумма его Ах будет
некоторым элементом пространства X. Кроме того, || Лл:||^
<jzr^!«*I и» стало быть» 1И11<т^-
*) См. п. 4.5.1, т. I

384 ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНОГО АНАЛИЗА [ГЛ. 10
Приведенные ниже равенства являются очевидными:
A-Н)Ах = (х + Нх + Н2х + ...)-(Нх + Н2х + ...) = х,
АA-Н)х = (х-Нх) + (Нх-Н2х) + ... = х.
Они позволяют утверждать, что Л = G —Я)-1 и, значит,
|(/-я)-Ч = М1<т^-
Докажем, что при принятых в теореме условиях
приближения хп могут быть построены для любых пу все хп
принадлежат шару D) и для хп выполняются неравенства
\\xn+i-xn\\^tn+1-tn (л = 0, 1, ...)• (И)
Для этого прибегнем к индукции. Начальное
приближение xQ принадлежит шару D), и по второму условию
существует обратный оператор Г0 = [/' (^о)]- Поэтому
может быть построено первое приближение х± = х0 —
— iy(*o). Далее ввиду A7) || *i - л;0 |Н1 го/(*о) || < Л-
Из соотношения t1 — t0 = —р/\"\ = — р,)' = ц вытекает
г {10) г (и)
ll^i — хо 1 ^h — to, и неравенство A1) при л = 0
выполняется.
Предположим, что приближения х0, хъ ..., хп
построены, все принадлежат шару D) и для них
выполняются неравенства
||^i-^N4+i-4 (А = 0, 1, ..., л-1). A2)
Приближение хп+1 должно быть найдено по правилу
C). Мы убедимся в возможности его построения, если
докажем существование оператора [/' (Хп)]'1. Для этой
цели воспользуемся леммой и предположением о
существовании обратного оператора Г0 = [/' (Xq)]'1.
Рассмотрим оператор H = T0[f (xn)—f' (х0)]. Он
отображает X на себя. Оценим его норму. Разность /' (хп) —
— Г (Хо) есть изменение оператора /' при переходе от
элемента Хо к хп. Здесь может быть применено неравенство
A.19), где / должно быть заменено на /', х на х0 и Ах
на хп — х0:
и'(**)Ч'(Х0Ц<:
< sup 1Г[Хо + 9(ха-х0)]1-1хп-Хо1<:К1хп-Хо1

§3]
МЕТОД НЬЮТОНА
385
Воспользовавшись неравенствами A2), получим для
lxn-xQ\:
I) *п - *о 1 = || (Хя - Xn-i) + (Хп-1 — Хп-*) +.--+(Х1 — Х0)\<1
^ (tn — tn-i) + (tn-i — ^л-г) + • • • + h — to — tn — ^o = ^;
отсюда
1П*я)-П*о)Л<*/я.
Для |Я| из цепочки неравенств
\Щ<>\ТМГ (хя)-Г (x*)\<>BKtn<BKt* =
= BK4l~Vlh~2h= l-VT^2h^l
получается оценка
\\H\\^BKtn<\.
По лемме оператор / + # имеет обратный
(/ + Я)-1 = {/ + Г0[/'(^)-/'(^о)]}-1
и верна оценка его нормы
||(/ + Я)-К—^-.
Положим ГЛ = (/ + Я)_1Г0 и проверим, что это есть
нужный нам оператор [/' (Хп)]-1:
Гя = (/ + Я)-1 Г0 = [/ + Го (/' (хя) - f (Хо))]-1 Гс =
= {T?[I + T0tf' (ха)-Г (Хо))]}-1-
= {/' (*<>) + (/' (*„)-/' (лго))}-1 = {// (*„)}-!.
Этим доказано существование оператора {/' (хп)}'1 = Тп.
Получим оценку его нормы
I {Г(хп)}-ц = || г. | < т=^щ- в=(^ - юпу=- ^.
Найдем еще оценку нормы f{xn). Приближение хп
находится по правилу Ньютона C)
хп = хя-1-[/' (Xni)]-1 f (xn-i)
или
/ (Xn-l) + f (Xn-l) (Xn - *i»-i) = 0.
Поэтому для f(xn) верно представление
/ (Xn) = [f (Хп) - f (Xn-l)] - Г (Xni) (Хп - ЛГ.-х).

386 ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНОГО АНАЛИЗА [ГЛ. 10
К полученной разности между изменением оператора /
и главной линейной частью изменения могут быть
применены теорема 3 из § 1 и неравенство A.20). Это
приводит к следующему результату:
f(xn)\\^~ max ЪПХп-г + ЧХп-Хп-МИХп-Хп-гГ^
Заметим, что если бы рассматривалось не операторное
уравнение /(л:) = 0, а численное уравнение P(t) = 0 и
мы хотели бы оценить Р (/„), то на этом пути для Р (tn)
нашли бы точное значение
P(tn) - Р (tn) - [Р (tn-l) + P' (tn-l) (tn ~ tn г)] =
= ~ Р* ft,-,) (tn ~ tn-l? = 1 К (tn - tn-lJ.
Для f(Xn) будем иметь оценку
\\f(Xn)\\^P(tn).
Все полученное дает возможность оценить |) хп+1 — хп ||:
Неравенство A1) для хп+1 действительно верно.
Принадлежность xn+i шару D) проверяется просто:
| Хп+1 — Хо || ^ || Хп+1 — Хп || + || Хп — Хп -11 +... +1| Х± — Х0 |] ^
^ (tn+1 — tn) + (tn — tn-l) + • • •+ (^1 ~ ^o) = tn+l — to =
= *л+1<** = -J T|<6.
Для доказательства сходимости хп (п->оо) применим
признак Больцано — Коши
^ 1 Хп+р — Xn+p-i || + J Хп^р-1 — Хп+р-г I! + • • • +|| Xn+i — Хп || ^
^ifn+p *n+p-i) "I ('/г+p-J tn+p-ъ) ~Г • • • + (*я+1 */i) = f/i+p — tn>
\\Xn+p-Xnl^tn+p-tn. A3)
Так как последовательность ttl сходится, для нее
признак Больцано — Коши выполняется. Из последнего

§4]
ЗАДАЧА УПРОЩЕНИЯ УРАВНЕНИЙ
387
неравенства следует, что признак выполняется и для
последовательности хп- Ввиду полноты пространства X
последовательность хп является также сходящейся:
\imxn = x*. Все хп принадлежат шару Цд: — jc0|| ^S,
поэтому л;* также принадлежит ему.
Утверждение о скорости сходимости получится из A3),
если там фиксировать п и увеличивать неограниченно р.
В пределе получится неравенство A0).
Утверждение о том, что предельный элемент х* есть
решение уравнения f(x)=Q, можно доказать,
воспользовавшись правилом Ньютона C). Запишем его в виде
/ (хп+д + Г {хп) (хп+1 -хп) = 0.
Будем считать п неограниченно возрастающим. Так как
хп-^х* и хп+г-+х*, то ||л:л+1-л:л||->0. f (х) и f (x)
предполагались дифференцируемыми всюду в шаре, в
частности на элементе je*. Поэтому они будут
непрерывными на jc* и в пределе последнее равенство даст
/(л;*) = 0, что доказывает утверждение.
Замечание. Если воспользоваться оценкой/* — ^,
указанной в начале доказательства теоремы, можно
неравенство A0) для оценки скорости сходимости заменить
другим, более грубым, но более наглядным:
\\х*-хп\\^^=гBкГ-^ц. A4)
§ 4. Задача упрощения уравнений
Умение заменять сложную задачу на «близкую» к ней
более простую позволяет в многих случаях очень сильно
расширить круг разрешимых проблем. Возможность
такой замены особенно важна при использовании
вычислительных машин, так как тогда всякая задача должна
быть приведена только к операциям с числами, в
частности уравнение любого вида должно быть приведено
к численному уравнению или к конечной системе таких
уравнений.
1. Введение. Предположим, что X и У есть два
любых множества, элементы которых будем обозначать
соответственно х и у. Пусть на X задан оператор у =

388 ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНОГО АНАЛИЗА [ГЛ. 10
= f(x)> значения которого принадлежат У. Возьмем на
У произвольный элемент _у* и рассмотрим уравнение
f(x)=y*. A)
Ниже его мы будем называть точным уравнением.
Допустим теперь, что с целью упрощения уравнения
множества X и У заменены на Хп и У„, при этом
преобразования Х-+Хп и Y-*Yn выполняются операторами
фл и г|)л, которые часто называют операторами сноса.
Наконец, предположим, что точное уравнение A)
заменяется, «близким» в каком-то смысле к нему
приближенным уравнением
fn(Xn)=y* = yny*. B)
Здесь Хп е Хя, y*^Yn и оператор fn выполняет
преобразования Хп в Yn.
После того, как найдено решение х% приближенного
уравнения B), необходимо по нему построить элемент х{п)
во множестве X, который будет принят за приближение
©к решению je* точного уравнения.
Пусть необходимое преобразование
Хп в X выполняется оператором <рл.
Принято называть х% каркасом или
скелетом приближения хКп\ а ф„-
оператором восполнения.
v-ч /^ Схема действий операторов и
\Хп) j— \^) множеств указана на рис. 10.
" Нас будут интересовать следую-
Рис. 10. щие основные вопросы. Известно, что
точное уравнение A) имеет на
некоторой части множества X единственное решение х*. При
каких условиях приближенное уравнение B) будет иметь
решение х%? В каких случаях последовательность
приближений х^п) будет сходиться к точному решению л;*
уравнения A), и если сходимость имеет место, то как
может быть оценена погрешность #* — х{п) приближений?
Результаты исследований здесь могут быть получены
только при некоторых предположениях о множествах X,
У, Х„, Yn и об операторах /, /л, срл, -фл, фл.
Ниже всюду будем считать множества X, У, Хл, Yn
линейными, нормированными и полными пространствами,
а операторы /, fn, фл, я|зл, фл — линейными.
®
%
% %

§4]
ЗАДАЧА УПРОЩЕНИЯ УРАВНЕНИЙ
389
2. О разрешимости приближенного уравнения.
Предварительно докажем следующую лемму о разрешимости
уравнения.
Лемма 1. Пусть X и Y есть пространства типа
Банаха и А — линейный оператор из X в Y.
Если для каждого у е F существует элемент х е X
такой у что
И*-.у11<?1.у11. 1!*1Клад C)
где q и N есть некоторые числа, не зависящие от у,
причем q < 1, то уравнение
Ах=у D)
имеет при всяком у <= Y решение х е X и выполняется
неравенство
II^K-I^IJ'II- E)
Перед доказательством заметим, что лемме может
быть придано следующее истолкование. Элемент х можно
рассматривать как приближенное решение уравнения D).
В лемме утверждается, что если при каждом у е Y
уравнение D) имеет приближенное решение, для
которого выполняются неравенства C), то уравнение D) при
любом у ^Y имеет точное решение и для него
выполняется неравенство E).
Доказательство. Пусть у — элемент из Y.
Положим Уг=у и построим последовательность элементов
уп по следующему правилу. По предположению, для yL
существует элемент х± такой, что
\\Ax1-y1\\^q\\y1\\, l^l^iVI^I.
Положим y2=yi — Ах\. В силу предположения,
сделанного в лемме, для уг существует элемент х2, для
которого будут верны неравенства
IА х2 -yt I < q \уг | < <?2 \Уг \, || xt\^N \yt \\ < Nq \\yx \\
и т. д. В результате получим две последовательности
элементов Xk, yh таких, что
Уш=Уи — АХь,
Ш^Ф-ЧУА \хЛ^ Nq^\yi\.

390 ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНОГО АНАЛИЗА [ГЛ. 10
Если просуммировать почленно равенства у^1=Ук—
— Axk (k=l, 2, ..., п), получим следующее
представление уп+1:
Уп+1 =Уг -А(хг+ ... +ХЯ). F)
РЯД Хг + ... +Хп+ ... СХОДИТСЯ ВВИДУ ОЦеНКИ ||jCft||^
=^ Nqt*-1 \\уг || и полноты пространства X. Обозначим его
сумму через х. Левая часть равенства уп+1 будет
стремиться к нулевому элементу, так как [jVul^^lLyil-
В пределе из F) получится
0=у — Ах.
Поэтому х есть точное решение уравнения D). Кроме
того, очевидно,
ОО 00
Лемма доказана.
Будем, как указано выше, считать, что точное
уравнение
Ах=у G)
и приближенное
Апхп=уп (8)
являются линейными. Оба оператора сноса фл, tyn и
оператор восполнения фя также предположим
линейными, пространства же X, У, Хп, Yn — линейными,
нормированными и полными.
Допустим, что оператор А точного уравнения имеет
обратный Л-1 и х = А~гу. Надеяться на разрешимость
приближенного уравнения (8) можно только в том
случае, если оно окажется близким в каком-то смысле (еще
подлежащем уточнению) к точному уравнению. Близость
зависит от операторов срл, tyn сноса и уравнения (8).
За локальную погрешность, порождаемую этими
операторами при обработке элемента х, может быть принята
величина
е„ (х) = || Апц>пх - ЦпАх \\у . (9)
Схема ее получения указана на рис. 11.

§43
ЗАДАЧА УПРОЩЕНИЯ УРАВНЕНИЙ
391
Нам потребуется также предположение о характере
сноса Y->Yn оператором tyn. Будем считать, что для
каждого уп е Yn существует элемент
у из Y такой, что выполняются
неравенства
1%у-УпЬ
\\у\\у~~
'^п\Уп\\уп,
'М\Уп\\у,
A0)
где ап и рл есть некоторые числа,
не зависящие от элемента уп. рис 11в
Теорема 1. Если для точного
и приближенного уравнений G) и (8) выполняются условия:
1) для оператора А существует обратный А~г;
2) существует число уп, не зависящее от элемента х>
такое, что для погрешности гп (х) выполняется нера-
венство гп(х)^уп\\х\\х; A1)
3) для оператора г|)я, выполняющего снос Y-*Yn, верно
предположение A0);
4) для чисел апу р„, уп и ЦЛ] справедливо неравен-
с™° q = *n + №AA-l\<b A2)
тогда приближенное уравнение (8) имеет решение хп при
всяком элементе уп из Yn и для нормы хп верна оценка
\Хп\хп^^~\\УпЬп, Х-ШпА-Ц. A3)
Доказательство. Покажем, что для уравнения (8)
выполняются условия леммы 1. Возьмем любой
элемент уПу принадлежащий Yn. По третьему
предположению теоремы существует элемент у <=Y, для которого
выполнены неравенства A0). По у построим элемент
х = А~ху, затем положим хп = Ч>пХ = Ч)пА~1у. Проверим
для пары элементов хп> уп первое неравенство условия C)
леммы 1:
1 Апхп -Уп 1 = |] (АпЧпХ - %Ах) + ($пУ -Уп) \\уп <
^\Ап^пХ-^пАх^я + \^пУ-Уп17я<:ея(х) + ап1уя1г^
Ввиду того, что гп(х)^Уп1х\\х и
lxU = lA^yk^\A4№\r^iA-4finly*k>

392 ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНОГО АНАЛИЗА [ГЛ. 10
для \АпХп—уп\уп получим оценку
|] Апхп -уп \\гп < ФпУп || Л-11| + ап) \\уп \\уп = q\\yn Jv
Так как q<Cl по условию A2), первое из неравенств C)
действительно выполняется.
Второе неравенство C) проверяется так же просто.
Ввиду хп = фяА: = фяЛ-1^ получим
II Хп \\Хп < J ФяЛ-i ||. ||j; ||r < рл || ф.Л-11| • \ул \уп.
Отсюда сяедует, что второе неравенство C) выполняется
при
^ = рл|ФяЛ-1|.
Утверждения теоремы 1 получаются, если к
уравнению (8) применить лемму 1.
3. Оценка погрешности приближения и условия
сходимости. Предположим, что точное уравнение
Ах=у* A4)
имеет решение л;*, что же касается приближенного
уравнения
Апхя=уЪ = 1рпУ*, A5)
то будем считать, что оператор Ап при всех я=1, 2, ...
имеет обратный Ап1. Решением приближенного уравнения
является
v* — А~* 11*
По нему на шаге номера п с помощью оператора
восполнения фя строится приближение номера п к
точному решению
x{h)==ynXn==4nAnlyt
Нас интересует погрешность приближения х* — Xм.
Ниже мы оценим ее норму рл = || jc* — л:и)||х и получим
условия, при которых имеет место сходимость х[п)~>х*
в норме пространства X:
Рп = \\Х*-хМ\\Х = \\х*-упХ*п\\х =
= ](**- ФяФяЛГ*) + (фяфл** - ЧпХ*п \\х <
<1^-ФЯФ^*к+11ф»1-1ф|^*-^Ь. A6)

§41
ЗАДАЧА УПРОЩЕНИЯ УРАВНЕНИЙ
393
Первая из величин, стоящая в последней части
системы соотношений, имеет наглядный смысл: разность
.#* —Ф/гфл#* есть, очевидно, несогласованность операций
сноса фя и восполнения ф„ на решении. Норма разности
есть мера этой несогласованности. Она зависит от
точного решения x*f нам неизвестного, и должна быть
оценена в каждой частной задаче на основании
дополнительных сведений. Нередко бывает известен порядок
малости этой величины.
Во второй член входит разность <p„x* — х%, которая
характеризует несогласованность на точном решении л;*
между операцией сноса фя и приближенным уравнением
A5). Она может быть оценена через величину еп(х),
введенную раньше в (9). Ввиду Апх* = ^пу* = ^пАх*
будем иметь
[] ЧпХ* - Xt ||х = [| An" (Ап<(пХ* - АпХ%) ||x„ =
= || A~n' (АпЧпХ* -я|>яЛ**) кя <
В силу A6) это приводит к следующей оценке нормы
погрешности:
|^*-^М1х<1^*~Ф,Ф^^|х + ||ф,||-1^М|-еЛ^*)^ A7)
Величина гп. (#*) также зависит от неизвестного
точного решения л:* и должна быть оценена для каждого
конкретного типа задач. Порядок ее малости часто может
быть указан.
Оценка A7) позволяет сформулировать теорему о
сходимости.
Теорема 2. Если для приближенного уравнения A5)
и операторов сноса и восполнения фл, tyn, фЛ выполняются
условия:
1) мера несогласованности на точном решении х*
операторов сноса ц>п и восполнения <рп стремится к нулю
при п->оо _
1**-фяфл**|х->0;
2) для погрешности еп(х*) верно соотношение

394 ПРИМЕНЕНИЕ ФУНКЦИОНАЛЬНОГО АНАЛИЗА [ГЛ. 10
тогда имеет место сходимость в норме пространства X
приближенного решения х{п) к точному решению л;*:
||**-л;(л)||-^0, п-^оо.
Значение оценки A7) и теоремы 2 состоит
преимущественно в том, что они выясняют строение
погрешности и указывают направление исследований, которые
должны быть проведены в конкретных задачах.
ЛИТЕРАТУРА
1. Гавурин М. К., Лекции по методам вычислений, М., «Наука»,
1971.
2. Канторович Л. В., Функциональный анализ и прикладная
математика, М., УМН 3, вып. 6B8), 1948.
3. Коллатц Л., Функциональный анализ и вычислительная
математика, М., ИЛ, 1971.

УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
в» 14
Уп+а 1б
т
fn + a 16
Ш
Е*±]
Уд 67
1*±]
/я 67
ут 95
Lh 109
Дл(Л) 109
Ад 1П
С [а, 6] 121,
С2[а, Ь] 121
12[а, 6] 129
Dh 143
*/д 143
Fh 143
361
lit/,
143
143
^L„ .,147
а">
143
/<л> 143
ди
~дх~
(*/»•"
Ахх 157
Ауу 157
1д («<*>)
Лл(
а(Л))
'я)
160
184
> 189
И 11ш 190
— 290
Res (/ (ы)) 322
р (х, у) 359
Pi (*» £/) 360
Pm (*» У) 360
Рц (*. У) 360
р5 (л:, у) 360
рш (х, у) 360
Р/ (х, У) 360
Lp [а, Ь] 362
[X ->- Г] 365
И || 366
И* 367
[X-»[X-+Y]] 367

ПРЕДМЕТНЫЙ
УКАЗАТЕЛЬ
Аддитивный оператор 362
Аксиома различения 359
— симметрии 359
— треугольника 359
Аксиомы линейного пространства
361
— метрики 359
— нормы 361
Аналитический метод 9
— тип сходимости 309
Асимптотический степенной тип
сходимости 308
Аппроксимация граничных
условий 180
— оператора 142
— разностной схемы 142, 176
Гармонический синтез 290
Главный член погрешности
метода 56
Двухточечная граничная задача 94
Задача граничная линейная
107
многоточечная 95
нелинейная 100
смешанная 159, 202
— корректно поставленная 255
— Коши 146
— многоточечная 95
— некорректно поставленная
255
Интегральные уравнения
Вольтер р а 253
второго рода 254
первого рода 254
Фредгольма 253
второго рода 254
: первого рода 254
Интерполяционное
преобразование с возрастающим числом
узлов 314
постоянным числом
узлов 301
Интерполяционный
квадратурный метод 275
Каркас приближенного решения
388
Квазистационарная
последовательность 295
Корректно поставленная задача
255
Кубическая метрика 360
Метод аналитический 9
— Галеркина 120, 248
— гиперплоскостей 230
— дифференциальной прогонки
95
— замены ядра интегрального
уравнения на вырожденное 278
— интегральных соотношений
обобщенный 246
— касательных 16
— k-го порядка точности 51
— линеаризации 104

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
397
Метод ломаных 16
— матричной прогонки 188
— многошаговый 12, 72
— моментов 122, 248
— наименьших квадратов 129
— неявный 12, 73
— Ньютона для операторных
уравнений 380
— одношаговый 12
— ортогональной прогонки ИЗ
— Пикара 10
— плоскостей 230
— последовательных
приближений 10
— прямых 228
для гиперболических
уравнений 238
параболических
уравнений 229
эллиптических
уравнений 244
— Ритца 136
— рядов 11
— сеток для решения линейной
граничной задачи 107
— трапеций 22, 36
— установления 192
— характеристик 215
— Чаплыгина 59
— явный 12, 73
Методы Адамса
интерполяционные 74, 79
экстраполяционные 74
— с забеганием вперед 12, 73, 85
— типа двусторонних 59
Коуэлла 86
Метрика 359
— кубическая 360, 377
— октаэдрическая 360, 378
— сферическая 360
— шаровая 379
Метрическое пространство 358
Минимизирующая
последовательность функций 137
Многоточечная задача 95
Некорректно поставленные
задачи 255
Необходимое спектральное
условие устойчивости Неймана 164
Несогласованность операторов
сноса и восполнения 393
Неявная двухслойная
шеститочечная разностная
аппроксимация 173
— пятиточечная трехслойная
схема 174
— разностная схема 151
Неявный метод установления
194
Норма 361
— оператора 364
билинейного 366
Нормированное линейное
пространство 361
Обобщенный метод
интегральных соотношений 246
Обратный метод прогонки 170
— оператор 364
Октаэдрическая метрика 360
Оператор аддитивный 362
— билинейный 366
— восполнения 388
— дифференцируемый на
элементе пространства 368
— линейный 363
— непрерывный 362
— обратный 364
— ограниченный 362
— однородный 362
— разностный 109
— сноса 388
Оператора норма 364
Оценка апостериорная 53
— априорная 53
— погрешности метода 51
приближенного решения
51
Погрешность аппроксимации
144
дифференциального
оператора 109
— вычислительная 51
— локальная 15
— метода 25, 52
— начального условия 44

398
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Погрешность неустранимая
51
— округлений 44
— приближенного решения 44
— формулы 44
Полное метрическое пространство
360
Полоска первого порядка 217
Поперечная схема метода
прямых 229
Порядок точности метода 25
Правило ломаных 16
*— Ньютона для операторных
уравнений 380
— Рунге 57, 191
— Рунге — Кутта 31
Преобразование
последовательности регулярное 289, 293
, сохраняющее предел 293
сходимость 293
— Ценкса 336
— Эйткена 326
Принцип максимума 112
— сжатых отображений 374
Продольная схема метода
прямых 234
Производная от оператора 368
Простой метод интегральных
соотношений 246
Пространство линейное 361
— линейных операторов 365
— полное 360
— типа Банаха 361
Прямой метод прогонки 170
Разностная схема ПО, 143
неявная 151
расщепления 155
устойчивая 144
экономичная 167
явная 151
Разностный оператор 109
Реальная область асимптотики
57
Регулярное преобразование 293
Сетка 108, 143
— равномерная 108
Сеточная функция 143
Система Чебышева 297
Скелет приближения 388
Смешанная граничная задача
202
Сферическая метрика 360
Схема Дюфорта и Франкела 173
— Кранка и Николсона 172
— разностная ПО, 143
Схемы расщепления 155
Сходимость аналитического
типа 309
— асимптотического степенного
типа 308
— метода Ритца 138
сеток 117
— одношаговых методов 42
— почти алгебраического типа
308
*— разностных схем 144
Теорема о сохранении предела
295
сходимости 294
Треугольник определенности диф-
феоенциального уравнения
207
— — разностной схемы 207
Узел внутренний 177
— граничный 177
— сетки 108, 142
Уравнения направления
характеристик 219
— характеристик 219
— характеристических полосок
219
Устойчивость разностных схем
144
— схемы по начальным данным
163
Факториальный многочлен 353
Функция влияния значения
свободного члена 304
начального значения 304
— Грина 304

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
399
Характеристика 218
Характеристическая кривая 218
s— полоска 218
Шаблон 148
Экономичные разностные схемы
167
Экстраполирование 75
Экстерполяционные методы
Адамса 74
Экстерполяция 75
Явная разностная схема 151
Явные вычислительные методы 73
Явный метод установления 194
Ядро 255
— вырожденное 278
В-пространство 361
б2-преобразование 326

Владимир Иванович Крылов
Владимир Васильевич Бобков
Петр Ильич Монастырный
ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ
Том II
М., 1977 г., 400 стр. с илл.
Редакторы Е. Ю. Ходан, Е. В. Шикин.
Техн. редактор С. #. Шкляр.
Корректор Е. В. Сидоркина.
Сдано в набор 01.11. 1976 г.' Подписано к печати
19.04. 1977 г. Бумага 84Xl08Vs2 тип. № 3. Физ. печ.
л. 12,5. Условн. печ. л. 21. Уч.-изд. л. 20,74.
Тираж 37 000 экз. Цена книги 99 коп. Заказ № 947.
Издательство «Наука»
Главная редакция
физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени
Ленинградское производственно-техническое объединение
«Печатный Двор» имени А. М. Горького Союзпо-
лиграфпрома при Государственном комитете
Совета Министров СССР по делам издательств,
полиграфии и книжной торговли. 197136, Ленинград,
П-136, Гатчинская ул., 26.