СБОРНИК ЗАДАЧ И УПРАЖНЕНИЙ ПО ТЕОРЕТИЧЕСКИМ ОСНОВАМ ЭЛЕКТРОТЕХНИКИ
Для студентов вузов
ББК 31.21
С 23
УДК 621.3.01 (076.1)
КЬК- I ис .ли
ТОЭ ОТЦ ТЛЭЦ Электротехника
Рецензенты: Кафедра Московского авиационного института им. Серго Орджоникидзе, зав. кафедрой проф. С. П. Колосов; проф. Ю. Г. Толстов
Авторы: Г. П. Андреев, С. Н. Андреев, И. И. Баранов, Б. А. Болдов, С. И. Ващенко, Г. Г. Гусев, А. И. Донской, Ф. П. Жарков, Б. Я. Жуховицкий, П. А. Ионкин, Е. И. Калугин, В. В. Каратаев, В. А. Киселева, Я. Н. Колли, Н. К. Круг, В. Н. Кудин, В. А. Кузовкин, Е. С. Кухаркин, С. А. Левитан, В. А. Майбога, В. Г. Миронов, В. И. Паротькин, М. Д. Пирогова, Л. П. Соболева, Б. М. Фрадкин, Ф. Н. Шакирзянов, В. М. Юркевич
Сборник задач и упражнений по теоретиче-С23 ским основам электротехники: Учеб, пособие для вузов/Под ред. проф. П. А. Ионкина.— М.: Энергоиздат, 1982.— 768 с., ил.
В пер.: 1 р. 50 к.
Содержание задачника охватывает все разделы теории линейных и нелинейных цепей и теории электромагнитного поля курса теоретических основ электротехники и соответствует утвержденной программе.
В сборнике приведены задачи, как иллюстрирующие тот или иной метод расчета, так и возникающие при исследовании реальных электротехнических устройств. Все задачи имеют ответы, многие задачи даны с подробными решениями.
Предназначен в качестве учебного- пособия для студентов электротехнических и энергетических специальностей вузов
2302000000-254	ББК 31.21
С-----------------144-82.
051 (01)-82	6П2.1
ПРЕДИСЛОВИЕ
Настоящий сборник задач и упражнений по теоретическим основам электротехники составлен коллективами кафедр теоретических основ электротехники (ТОЭ) и электрофизики (ЭФ) Московского энергетического института как учебное пособие для студентов инженерно-технических специальностей вузов. Задачи и упражнения, включенные в сборник, охватывают все разделы курса ТОЭ в соответствии с программой курса «Теоретические основы электротехники», утвержденной Учебно-методическим управлением по высшему образованию 28 декабря 1977 г.
Помещенные в сборнике задачи предназначены как для решения в аудитории с помощью преподавателя, так и для самостоятельного решения, в том числе и студентами заочных отделений вузов; поэтому в каждой главе для типовых.задач и задач повышенной трудности приведены подробные решения с необходимыми методическими указаниями. У таких задач после номера поставлена буква Р. Для всех задач даны ответы, причем в случаях, koi да ответ прямо соответствует поставленным вопросам, в ответе приведены только числа, формулы или слова, служащие прямым ответом.
Принятый порядок расположения глав и задач в каждой главе не определяет желательную или необходимую последовательность их самостоятельного решения студентами и решения в аудитории преподавателем или студентами совместно с преподавателем.
При составлении задач авторы стремились по возможности связать их с электротехнической практикой и дать параметры, характерные для реальных технических устройств. Некоторые задачи появились в результате обобщения и идеализации практиче
ских вопросов, с которыми представители промышленности обращались на кафедры. Но, конечно, в сборнике есть и достаточное число учебных задач, подобранных так, чтобы в решении можно было подчеркнуть особенности того или иного метода расчета электрических цепей или электромагнитного поля.
В списке литературы указаны основные учебники и учебные пособия, вышедшие за последние годы и предназначенные для студентов как дневных, так и вечерних отделений вузов.
Отзывы, критические замечания и пожелания просьба посылать в адрес Энергоиздата: 113114, Москва, М-114, Шлюзовая наб., 10.
Авторы
Глава первая
ЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ ПОСТОЯННЫХ ЭДС И токов
Введение к гл. 1
К простейшим двухполюсным пассивным элементам схемы линейной электрической цепи относятся резистивный, индуктивный и емкостный элементы.
Резистивный элемент — это элемент, в котором напряжение и и ток i связаны соотношением (закон Ома)
ur - rir или ir = диг,	(1.1)
где г — сопротивление; д == 1/г - проводимость.
Мощность преобразования электромагнитной энергии в тепловую (закон Джоуля — Ленца)
p = ri2r.	(1.2)
Индуктивный элемент — это элемент, в котором напряжение и ток связаны законом электромагнитной индукции:
uL= LdiL/dt,	(1.3)
где L— индуктивность; t — время.
Энергия, запасаемая в магнитном поле индуктивного элемента, равна:
w = Li\/2.	(1.4)
Емкостный элемент — это элемент, в котором напряжение и ток связаны соотношением
ic = Cduc/dt,	(1.5)
где С — емкость.
Энергия, запасаемая в электрическом поле емкостного элемента, равна:
w = Си2с/2.	(1.6)
В установившемся режиме цепи постоянного тока ток I и напряжение U постоянны (не изменяются во времени). Из (1-3) и (1.5) следует, что в таком режиме отсутствуют напряжение на индуктивности и ток в емкости: uLy — 0; iCy — 0.
Источник энергии (активный элемент) линейной электрической цепи постоянного тока можно представить любой из двух схем замещения: последовательной, состоящей из идеального источника ЭДС Е и внутреннего сопротивления гвт (рис. 1.А,а), и параллельной, состоящей из идеального источ-
Рис. 1.А
ника тока J и внутренней проводимости (рис. 1.А, б). У идеального источника ЭДС гвт = 0; он развивает мощность Р = ЕЦ	(1.7)
а у идеального источника тока двт = 0; он развивает мощность
Р = UJ.	(1.8)
Для последовательной схемы (рис. 1.А,я)
С/ = Е-гвт/,	(1.9)
а для параллельной схемы (рис. 1.А,б)
l = J-g„Uy	(1.10)
причем у одного и того же источника энергии
Е =	гвт</ и дъх — 1/гвт.	(1.11)
Основные уравнения	цепи (уравнения состояния). Первый
закон Кирхгофа: алгебраическая сумма токов ветвей, соединенных в узле, равна нулю, т. е.
£i*=o,	(1.12)
к
где с положительным знаком учитываются токи, направленные от узла.
Второй закон Кирхгофа: алгебраическая сумма напряжений на ветвях любого замкнутого контура равна нулю, т. е.
E«»=o,	(in)
к где с положительным знаком учитываются напряжения, направления которых совпадают с направлением обхода контура.
В установившемся режиме постоянный ток на участке цепи, схема которой показана на рис. 1.Б,ц (с последовательными схемами замещения источников), можно определить из выражения (обобщенный закон Ома)
где £ Е — алгебраическая сумма ЭДС в ветви; гаЬ — сумма ab
сопротивлений в ветви и gab - 1/гаЬ.
Алгебраические методы расчета цепей. При записи уравнений на основании законов Ома и Кирхгофа в матричной форме пользуются понятием обобщенной ветви (рис. 1.Б,б).
Рис. 1.Б
Закон Ома для обобщенной ветви:
U = r(I + J) — Е.	(1.15а)
Записав это соотношение для всех b ветвей, получим матричную форму закона Ома:
U<8> = R(B) [1(B) + j(B)j _ Е(в)5	(1.156)
где RW — диагональная матрица сопротивлений ветвей:
R(B) = diag |[Г1Г2...гь||;	(1.16)
ц(в), j(B), j(B)^ g(B) _ векТ0рЫ напряжений и токов ветвей, токов И ЭДС источников:
LW=	(1.17)
!»•>= i|/iZ2	(1.18)
(1.19)
E<?>= || EjEj ... £ь||т.	(1.20)
Закон Ома можно записать в другой форме:
J(B) = Q(b) [U(b) + Е(в)] _ J(B)>	(1.21)
где
G(B’ = diag||gIg2...sl,||.	(1.22)
Первое уравнение Кирхгофа в матричной форме имеет вид: А1(в) = 0,	(1.23)
где А = ||	|| - матрица соединений (узловая), у которой
строки соответствуют узлам, а столбцы — ветвям, причем ац = 4-1, если ветвь j присоединена к узлу i и направлена от узла; = — 1, если ветвь j присоединена к узлу i и направлена к узлу; = 0, если ветвь j к узлу i не присоединена; число строк матрицы А равно числу независимых узлов. Если матрица соединений записана для всех узлов (неопределенная), то она обозначена Ан.
Первое уравнение Кирхгофа можно представить в виде
Qp)==0,	(1.24)
где Q = || Qij || — матрица главных сечений, у которой строки соответствуют сечениям, а столбцы — ветвям, причем = = 4-1, если ветвь j содержится в сечении i и направления у них одинаковые (направлением главного сечения считается направление ветви дерева этого сечения); q^ = — 1, если ветвь j содержится в сечении i и направления их противоположны; qij = 0, если ветвь j не содержится в сечении i.
Второе уравнение Кирхгофа в матричной форме имеет вид:
BUB) = 0,	(1.25)
где В = || bij || — матрица главных контуров, у которых строки соответствуют контурам, а столбцы — ветвям, причем =4-1, если ветвь j содержится в контуре i и ее направление совпадает с направлением обхода контура; = — 1, если ветвь j содержится в контуре i и ее направление противоположно направлению обхода; Ьц = 0, если ветвь j не содержится в контуре z.
Соотношения (1.23) и (1.25) можно представить в виде
А1Г = А№)1Л = AJ<B>;
(1.26)
BU, = BR(S)I, = ВЕ(в);
(1.27)
здесь Ir и Ur — векторы токов и напряжений на сопротивлениях, причем их элементы связаны соотношением Urk = в ПДгк*
Получить независимые уравнения по первому и второму законам Кирхгофа, т. е. выбрать независимую систему контуров и сечений, можно при помощи дерева графа (схемы), содержащего все узлы графа, но ни одного контура, и ветвей связи, дополняющих дерево до исходного графа. Если граф содержит b ветвей и у узлов, то число ветвей дерева d = у — 1, а число ветвей связи к = b — (у — 1). Для дерева образуется d главных сечений, каждое из которых состоит из ветвей связи и одной ветви дерева, и к главных контуров, каждый из которых состоит из ветвей дерева и только одной ветви связи. Уравнения, составленные по законам Кирхгофа для главных сечений и главных контуров, линейно независимы.
Если ветвям дерева присвоены первые номера, то матрица главных сечений может быть разделена на две подматрицы:
Q = [1F],	(1.28)
где 1 — единичная подматрица порядка у — 1; F — подматрица, столбцы которой соответствуют ветвям связи.
Матрицы A, Q и В, составленные для одного и того же графа (схемы), удовлетворяют соотношениям
АВТ = 0, или ВАТ = 0,	(1.29)
QBT = 0, или BQT = 0.	(1.30)
Применение узловых уравнений позволяет уменьшить число совместно решаемых уравнений, так как в качестве независимых переменных выбираются потенциалы узлов (метод узловых потенциалов)
G(y)cp = J(y),	(1.31)
где ф — вектор потенциалов узлов; G(y), J'y) — матрицы узловых проводимостей и узловых токов:
GM = AG<B)AT;	(1.32)
j(y) = AJ(b) _ AG(b)E(b).	(1.33)
Напряжения ветвей определяются через узловые потенциалы:
ув) = ДТф
(1.34)
В развернутой форме (1.31) имеет вид:
9иФ1 -0i2<₽2	- gi.1Ф,.-1 = J/*’;
~ 021Ф1 + 022Ф2 — • • • — вг, у- 1Фу-1 =	(1-35)
•••••• • • • • •
~ 9у-1, 1Ф1 ~0у-1,2ф2 — ... + ду- 1,у- 1фу_ 1 =
здесь дц — сумма проводимостей ветвей, присоединенных к узлу i (собственная узловая проводимость); д^ — сумма проводимостей ветвей, соединяющих узлы i и j (общая узловая проводимость); — алгебраическая сумма токов источников тока и произведений ЭДС на соответствующие проводимости для всех ветвей, присоединенных к узлу i, при этом с положительным знаком записывают токи и ЭДС, направленные к узлу. Матрица G(y) симметричная, так как д^ = д^.
В качестве независимых переменных можно выбрать напряжения ветвей дерева (узловых пар) LM:
С(с)С(д) = J<c\	(1.36)
где G(c), J<c) — матрицы проводимостей и токов сечений:
№ = QG(B)QT;	(1.37)
J(c)	= QJ(b) __	(1.38)
Напряжения ветвей	определяются	через напряжения ветвей
дерева:
и(в) = <уи(Ч	(1.39)
Контурные уравнения получаются, если в качестве независимых переменных выбрать контурные токи Гк\ связанные с токами ветвей соотношением
1(в) = вт1<к>	(1.40)
и записать для них выражение (метод контурных токов)
R(K)p) = №,	(1.41)
где R(*\ Е(к) - матрицы контурных сопротивлений и контурных ЭДС:
RW = BRHBT;
Е(К) = ВЕ(в) _ BR(b)J(b).
(1.42)
(1.43)
В развернутой форме (1.41) имеет вид:
Гц/?1 +	+ ... + г1кЦ* = £/«>;
г21//'> + г211^ +  + 'гЛ"’ = Ь?’;	(1.44)
rk	+ • •  + га1^> = £?>;
здесь Гн — сумма сопротивлений ветвей соответствующего контура с положительным знаком (собственное контурное сопротивление); r,j - сопротивление ветви, общей для контуров i и j (общее контурное сопротивление) с положительным знаком при условии, что токи 7(к) и в общей ветви направлены одинаково; Е!к) — алгебраическая сумма ЭДС источников контура I, включая ЭДС источников, эквивалентных источникам тока, с положительным знаком следует записать ЭДС, направления которых совпадают с направлением контура.
Матрица R(k) симметричная, так как гу = rjf.
Основные свойства и преобразования электрических цепей. Суммарная мощность, генерируемая источниками электрической энергии, равна суммарной мощности, потребляемой в цепи (баланс мощностей): b	b	ь
£Ekh+ Yukjk =	О-45)
k=l	Л=1	k=1
или в матричной форме
IrTR<4 = [Е<вф1, + [U<B>]T J<B).	(1.46)
По методу наложения ток и напряжение любой ветви могут быть представлены как алгебраические суммы составляющих, обусловленных действием каждого источника в отдельности:
ь	ь
/»=	й = 1,.2, .... fe; (1.47)
f=l	/=1
b	ь
+	h= 1,2, ..., b, (1.48)
I= 1	1= 1
или в матричной форме
1(в) = ge<b> + K(i)J<B>;	(1.49)
ув) = rj(b) + K(u)E(B);	(i.50)
здесь
при действии в цепи только источника ЭДС Ef.
Гы = Uh/J,; к® =	(1.52)
при действии в цепи только источника тока Jt. Матрицы G, K(l), R и К(и) удовлетворяют соотношениям
AG = 0; AK(i) = 0; BR = 0; ВК<“> = 0.	(1.53)
При изменении какого-либо параметра одной из ветвей (ЭДС, тока источника или сопротивления) напряжения и токи
Рис. 1.В
любой пары ветвей связаны линейнььми соотношениями
вида
у — ах + Ь,
(1.54)
где х, у — напряжения или токи; а, b — постоянные коэффициенты.
На основании теоремы о компенсации любое сопротивление схемы rh с током Ih (рис. 1.В,а) можно заменить источником ЭДС Eh = rhIh (рис. 1.В,б); любую ветвь с током Ih можно заменить источником тока Jh (рис. 1.В,в).
Ток в одной из ветвей можно определить на основании теоремы об эквивалентном источнике (активном двухполюснике). Активную часть цепи, к которой присоединена пассивная ветвь с сопротивлением г (рис. 1.Г, а), можно заменить источником с ЭДС, равной напряжению Ux на выводах разомкнутой пассивной ветви, и сопротивлением, равным входному сопротивлению гвх активной части цепи (рис. 1.Г, б), или источником тока, значение которого /к равно току в короткозамкнутой пассивной ветви, и проводимостью, равной входной проводимости дъх активной части цепи (рис. 1.Г,в). Ток и напряжения ветви
/ = Ux/(r3X + г), U = IJ(gw + д),	(1.55)
где
7*ВХ = ^х/^к>	~ 1/^ВХ-	(1.56)
При взаимном преобразовании пассивной трехлучевой звезды (рис. 1.Д,л) и треугольника (рис. 1.Д, б) сопротивлений имеем:
r12Г31
r12r23

Гз
Рис. 1.Г
Топологические методы анализа цепей применяются для определения входных и взаимных сопротивлений и проводимостей, передаточных функций (токов и напряжений) непосредственно по схеме без записи уравнений.
По топологической формуле (формуле Мэзона) передаточная функция или передача, т. е. отношение показания измерительного прибора (вольтметра или амперметра) к параметру источника (Е или J), имеет вид:
(1.59) к
где Щ — путь передачи, т. е. произведение проводимостей ветвей пути, включающего выводы источника и измерительный
Рис. 1.Д
прибор (проводимость прибора принимается равной единице); Ак — минор пути передачи или узловой определитель схемы, получающейся при замыкании к-ro пути; А - узловой опреде
литель схемы, получаемой после исключения вольтметра и источника тока и замыкания амперметра и источника ЭДС:
л
А= £Gj1G,.2...G№_1,;	(1.60)
J=1
здесь Gji — проводимость ветви i дерева j; п — число деревьев схемы. Определитель может быть вычислен разложением по путям между парой узлов:
Д = £ПА,	(1.61)
к •
где Пк - произведение проводимостей ветвей fc-ro пути; Ак — определитель схемы, которая получается при замыкании /с-го пути исходной схемы.
Если схема состоит из двух подсхем, имеющих общий узел, то
А = AiA2,	(1.62)
где Ai и А2 — узловые определители подсхем.
Миноры пути передачи Ак вычисляются аналогично.
Ток и напряжение любой ветви схемы с несколькими источниками могут быть найдены при помощи топологической формулы с применением метода наложения.
Сигнальные (направленные) графы. Для построения сигнального графа узловые или контурные уравнения цепи надо записать в форме причина — следствие, т. е. каждое уравнение разрешить относительно переменной, отличной для каждого уравнения.
Узлы графа х< и х,-, соответствующие зависимым (потенциалы, токи) и независимым переменным, соединяются направленными ветвями с передачами а^ (рис. 1.Е):
х, = atjXj.	(1.63)
К узлу — истоку сигнального графа присоединены только исходящие ветви, к узлу — стоку — только входящие ветви.
Xj	xi-
о------>— о
Рис. 1.Е
Графы узловых и контурных уравнений могут быть построены без записи • уравнений. Для построения графа узловые уравнения (1.35) записываются в форме причина —
следствие:
021	.	02,у-1, Л	1 J (vb
(р2 - ---Ф1 + ... ч---- Фу-1 + — Jiy\
022	022	022
(1.64)
Фг-i =	<Р1 + ••• + ------ty-t-
9у- 1, у- 1	0у- 1, у- 1
Потенциалам всех узлов схемы ставятся в соответствие узлы графа. Каждая пара узлов графа ф7 и срк соединяется ветвью с передачей д^дц, направленной от узла ф;- к узлу фь и ветвью с передачей дц/дьк от узла фк к узлу ср? Узел графа соединяется с узлом cpj ветвью с передачей 1/0jj. Вместо узлов можно ввести узлы Jj и Ej.
Передача сигнального графа (формула Мэзона) имеет вид:
£п;дк	£пкд'к
ц = ~— --------------------:-----------------, (1.65)
д i -	+ --
к	к	к
где Пк — произведение передач ветвей пути, начинающегося в истоке и заканчивающегося в стоке; Дк — определитель графа, получающегося из исходного при исключении ветвей, принадлежащих к-му пути; Д — определитель графа (системы уравнений, отображаемых графом); X-Pk1) = X^k — сУмма пе-к	к
редач всех контуров графа; = £LklLk2 ... Lkm — сумма к	к
передач всех возможных комбинации из т некасающихся контуров (т = 2, 3 ...).
Во всех задачах этой главы, кроме особо оговоренных случаев, надо считать, что сопротивление вольтметра бесконечно велико, а сопротивление амперметра равно нулю.
1.1.	Простейшие электрические цепи
1.1.	Для электрической цепи рис. 1.1 заданы сопротивления Tj = 30 Ом; г2 = 60 Ом и напряжение на входе U = = 120 В.
Найти показания амперметров.
1.2.	Для цепи рис. 1.1 вывести формулу распределения общего тока I по двум параллельным ветвям с сопротивлениями Г], и г2.
1.3.	В цепи рис. 1.1 выразить входное сопротивление rBX -V/I через сопротивления т{ и г2 двух параллельных ветвей.
Рис. 1.1
1.4.	В цепь рис. 1.1 дополнительно включено сопротивление г последовательно с амперметром, измеряющим общий ток I.
Выразить входное сопротивление rBX = U/I через сопротивления г, гг и г2.
1.5.	Показать, что распределение общего тока I по двум параллельным ветвям с сопротивлениями и г2 в цепи задачи 1.4 такое же, как и в цепи задачи 1.2.
1.6.	Написать необходимое для определения всех токов число уравнений по законам Кирхгофа (в общем виде) для схем рис. 1.7, а и 1.8—1.10 при замкнутом ключе.
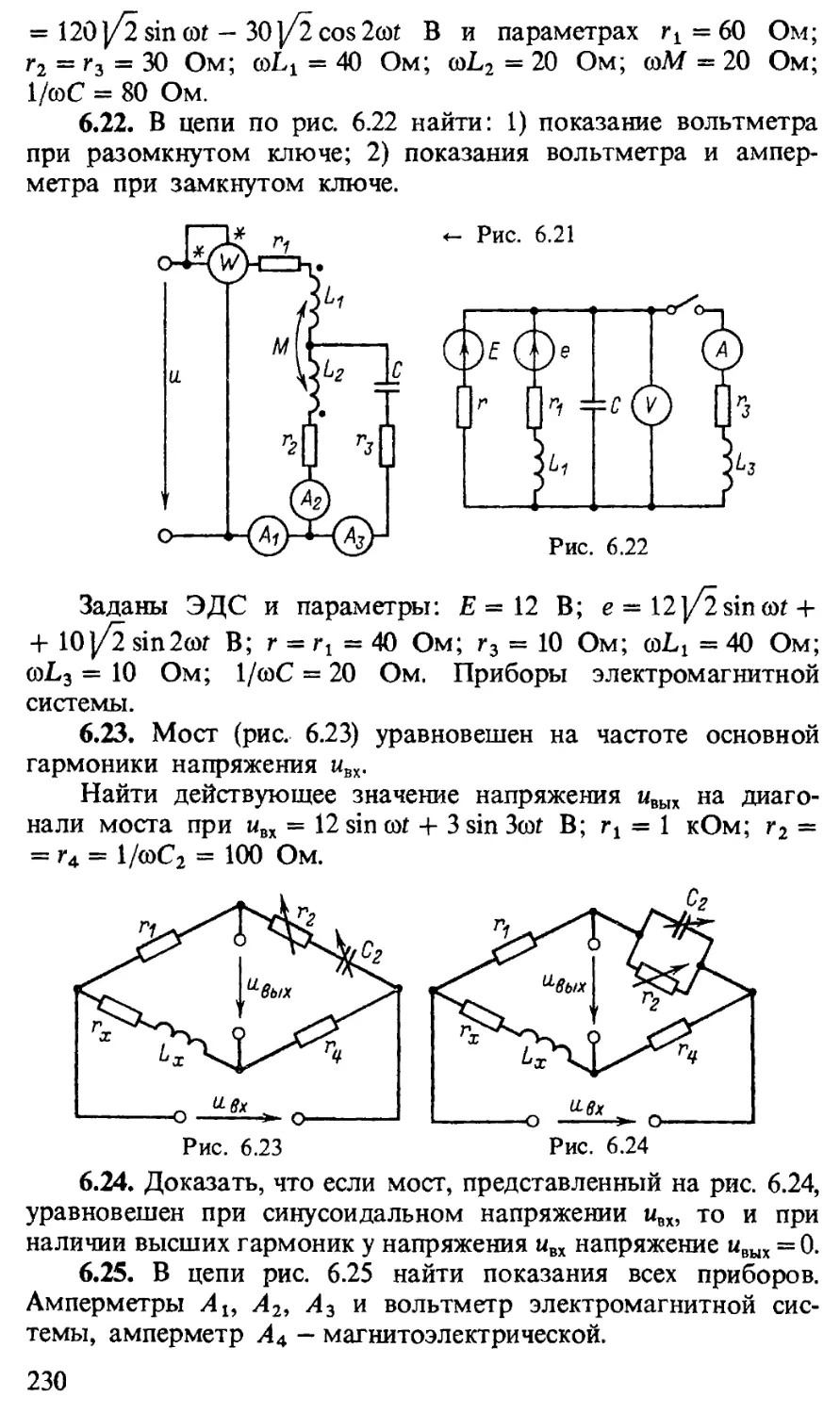
1.7(	Р). В цепи рис. 1.7,а включены: источник синусоидального напряжения u„(t), которое изменяется, как показано на рис. 1.7,6, источник постоянной ЭДС Е = 80 В, линейный резистор с сопротивлением г = 1 кОм и нелинейный резистор, несимметричная вольт-амперная характеристика которого представлена на рис. 1.7, в.
Найти напряжения на резисторах: 1) в момент времени когда напряжение uK(t) положительно и равно амплитуде Um; 2) в момент времени г2, когда напряжение ыи(г) отрицательно и равно - Um.
Рис. 1.8
Решение. Обходя контур по направлению движения часовой стрелки, запишем по второму закону Кирхгофа уравнение
и (t) -I- ur (f) - ик (г) = - Е или w (f) = ми (t) - ur (г) - Е.
1) Дано: ии(г1) = 400 В. По вольт-амперной характеристике определим, что при этом ток i — 10 мА =10-10“3 А. Следовательно, ur = ri = 10 В; и = 400 — 10 — 80 = 310 В.
2) Дано: иИ (г2) = — 400 В. По вольт-амперной характеристике найдем, что i = 0. Следовательно, иР = 0; и — — 400 — 80 = = - 480 В.
1.8(Р). Для цепи рис. 1.8 дано: гх = г2 = 10 Ом; L— 5 мГн; С = 10 мкФ; Е = 100 В.
Найти все токи, напряжения на емкости С и индуктивности Ев момент замыкания ключа (t = 0), если известно, что у тока в индуктивности и напряжения на емкости в момент включения остаются те же значения, которые были непосредственно перед замыканием ключа (перед коммутацией).
Решение. До коммутации в цепи был установившийся режим* (токи и напряжения не изменялись), в котором согласно (1.3) напряжение на индуктивности uL = 0; ток ц = = Е/(г! + г2) = 100/(10 + 10) = 5 А; ис = 0 (на емкости не было заряда). После коммутации по условию ток и напряжение ис в первый момент времени (t = 0) имеют те же значения. Остальные параметры найдем из уравнений, составленных по законам Кирхгофа:
1)	по второму закону Кирхгофа для внешнего контура ri4 + uL+ ис = Е, или 5-10 + uL + 0 = 100, откуда uL= 50 В;
2)	по второму закону Кирхгофа для правого контура — hh + ис = 0, или — 10i2 = 0, откуда i2 = 0;
3)	по первому закону Кирхгофа для верхнего узла а: — Е + + *2 + h == 0, откуда i3 = 5 А.
1.9.	Для цепи рис. 1.9 дано: г = 10 Ом; L= 40 мГн; С = 100 мкФ; Е = 100 В.
Задание то же, что и в задаче 1.8.
1.10.	Для цепи рис. 1.10 задано: г = 100 Ом; С = 2 мкФ;
J(t) = 2j/2sin(104t + 135°)A; e(r) - 100]/2sin(10‘t + 45°)В.
Задание то же, что и в задаче 1.8.
Рис. 1.9
Рис. 1.10
1.11.	В цепи рис. 1.11 ключ в момент времени Г = 0 переводится (мгновенно) из положения а в положение Ь.
Дано: L= 10 мГн; С = 100 мкФ; г = г2 = 10 Ом; Е = = 30 В; е = 5|/2sin(103? + 135°) В.
Задание то же, что и в задаче 1.8.
1.12.	Для источника энергии (рис. 1.12) с ЭДС £ = 2 В и внутренним сопротивлением гвт = 0,02 Ом найти напряжение Uab на выводах при токе, равном 2 А и направленном: 1) по направлению действия ЭДС; 2) противоположно направлению действия ЭДС.
1.13.	Для схемы рис. 1.13 дано: Е = 2 В; г — 0,02 Ом; Uab = 1,6 В.
Найти ток Z: 1) при направлении ЭДС, указанном на схеме; 2) при обратном направлении ЭДС.
Рис. 1.11
Рис. 1.13
Рис. 1.12
1.14.	Пользуясь законом Ома для участка цепи с ЭДС, найти токи в ветвях и проверить вычисления по первому закону Кирхгофа для следующих цепей:
1) токи Jlt 12, /3, /4» Ц в цепи рис. 1.20 при потенциалах узлов: фв = 46 В; (рь = - 32 В; фс = 24 В; = — 8 В;
2) токи /ь /2, h, Л, Ц в цепи рис. 1.32 при потенциалах: фа = 2 В; фь = - 36 В; фс = 8 В; фй = - 28 В.
1.15.	Составить балансы мощностей для цепей рис. 1.20 и 1.32 при данных задачи 1.14.
1.16.	Пользуясь законом Ома для участка цепи с ЭДС и первым законом Кирхгофа, найти токи в ветвях и проверить вычисления, составляя уравнения по второму закону Кирхгофа: 1) для цепи рис. 1.28 при токе /1=8 А; 2) для цепи рис. 1.32 при токе Ц = 1 А.
Рис. 1.17
Рис. 1.18 ->
1.17.	Для цепи рис. 1.17 дано: 7^=0; г2 = 2 Ом; г3 = 2*Ом;	— 2 Ом; г5 = 4 Ом; Е2 = 6 В; Е3 = 4 В;
Е^ — 1 В; Е5 = 3 В; £6 = 3 В, ток /2 = 2 А. Найти все токи, применив закон Ома для участка цепи с ЭДС и первый закон Кирхгофа. Составить баланс мощностей.
1.18(	Р). Для схемы рис. 1.18 дано:
Номер ветви . .	1	2	3	4	5	6	7	8
Е, В .	?	7	14	14	?	28	28	10
ЛА	. - 1	2,2	0,8	-1,4		1,2	- 1	0
г, Ом	0	10	8	4	4	3	2	2
1)	Не определяя ЭДС Е2 и Е5, найти показания вольтметров.
2)	Определив потенциалы узлов, найти ЭДС Еь Е2 и Е5; проверить вычисления, составив уравнения по второму закону Кирхгофа.
3)	Построить потенциальную диаграмму вдоль контура /, d, b, a, приняв потенциал заземленной точки равным нулю.
Решение. 1) Для определения показаний вольтметров найдем потенциалы узлов и точек д, d, а и с: фд = Ев — = 10 В; cpz =	- гвЦ = срд; cpd = ср, + Е7 + г7/7 = 36 В; фа =
= ф, - Е6 + гб/6 - г4/4 + Е4 « 31,2 В; фс = фЛ + Е3 - г313 = 38,8 В. Показания вольтметров: Ui = (рс — cpd = 2,8 В; Й2 = cpd — - Фй = 4,8 В; U3 = фс - фд = 28,8 В; С/4 = фс = 38,8 В.
Рис. 1.18Р
2) Определим значения ЭДС: Ei = Фс — Ф/ + т. е. Ei = 28,8 В; аналогично Е2 = 17,2 В; Е5 = 28 В. Проверим выполнение второго закона Кирхгофа по контуру dacbd: r2I2 + r3I3 -г515 4- г6Ц = £2 + Е3 - Е5 + Еб, что после подстановки численных значений дает 31,2 В = 31,2 В.
По полученным значениям потенциалов узлов строим потенциальную диаграмму (рис. 1.18Р).
1.19.	Для схемы рис. 1.17 построить потенциальную диаграмму вдоль контура acdba, приняв потенциал точки 1 равным нулю (ф! = 0).
1.20.	В цепи рис. 1.20 амперметр показывает ток 8 А. Определить остальные токи в ветвях, пользуясь законом Ома для участка цепи с ЭДС и первым законом Кирхгофа.
1.21.	Указать 1) параллельно и 2) последовательно соединенные сопротивления в схемах, приведенных на рис. 1.71 и 1.72.
1.22(	Р). Найти входные сопротивления для схемы рис. 1.17 при Г1 = 2 Ом относительно: 1) выводов источника ЭДС Е6; 2) точек Ь, с; 3) точек с, d; 4) точек 1, 3.
Решение. 1) Эквивалентная схема для определения гвх относительно выводов Е6 приведена на рис. 1.22Р. Входное сопротивление гвх = г5гзк/(г5 + гэк), где гэк — эквивалентное сопротивление: гэк = Tj + г4 + г2г3/(г2 + г3). Подставив численные значения, получим: гэк = 5 Ом; гвх = 2,22 Ом.
Рис. 1.20	Рис. 1.22Р
1.23.	Для схемы рис. 1.23, где сопротивления указаны в омах, найти входные сопротивления относительно выводов: 1) источника тока; 2) источника ЭДС.
1.24.	На рис. 1.24 значения ЭДС указаны в вольтах, сопротивлений — в омах, тока — в амперах.
Найти входное сопротивление относительно выводов источника тока, применив преобразования: 1) треугольника сопротивлений в звезду; 2) звезды сопротивлений в треугольник. Рассчитать мощность источника тока.
Рис. 1.23
1.25.	1) Заменив треугольник сопротивлений эквивалентной звездой, найти входное сопротивление относительно выводов источника ЭДС в схеме рис. 1.25 при гаЬ = гЬс = гса — 3 Ом, ГаЬ = гса = 30 Ом, == 40 Ом.
2)	Найти сопротивления эквивалентного треугольника для звезды сопротивлений с общей точкой лучей а при гаЬ = гсс = = 30 Ом и гЬс = 40 Ом.
1.26.	Для схемы рис. 1.18 найти: 1) сопротивления эквивалентной звезды для треугольника abc; 2) входные сопротивления относительно точек с, f и a, d.
Рис. 1.28
1.27.	Для схемы рис. 1.18 найти сопротивления эквивалентных треугольников: 1) для звезды с общей точкой лучей Ь; 2) для звезды с общей точкой лучей а.
1.28.	Определить токи Ц и 12 в схеме рис. 1.28, предварительно преобразовав источник с ЭДС Е и внутренним сопротивлением 2 Ом в источник тока.
1.29.	Найти токи Ц и 12 в схеме рис. 1.28, предварительно преобразовав источник с током J и внутренним сопротивлением 3 Ом в источник ЭДС.
Рис. 1.31
Рис. 1.32
1.30.	Определить: 1) мощность, развиваемую источником с ЭДС Е в схеме на рис. 1.28; 2) мощность, развиваемую источником тока, который эквивалентен источнику ЭДС рис. 1.28. Сравнить эти мощности.
1.31.	В схеме рис. 1.31 заменить источник с напряжением (73 идеальным источником ЭДС Е3. Преобразовать источники Ез, г2 и Е3, г3 в эквивалентные источники тока.
1) Найти токи в ветвях заданной (не преобразованной) схемы.
2) Составить баланс мощности?а) до преобразования схемы;
б) после преобразования.
Дано: = 10 Ом; г2 = 20 Ом; г3 = 10 Ом; Е2 = 100 В; U3 = 20 В. .
1.32. Заменить двумя источниками ЭДС узловой ток 2 А в схеме на рис. 1.32. Найти токи в заданной схеме.
1.33. Для схемы рис. 1.32 составить баланс мощностей:
1)	до преобразования узлового тока; 2) после преобразования.
1.2.	Переходные и установившиеся процессы в простейших цепях
1.34(	Р). Определить ток iL в индуктивности и напряжение uL на индуктивности в схеме рис. 1.34 после размыкания ключа. Построить зависимости iL (?) и uL (t).
JJ&hg: J = 0,1 A; R = 30 Ом; r = 20 Ом; L = 0,1 Гн.
Решение. При выбранных на рис. 1.34 положительных направлениях токов в ветвях составим уравнения Кирхгофа для схемы после коммутации:
J	;	1	z. ч
RiR — Ldijdt — riL = 0. J
Исключив ток iRi получим дифференциальное уравнение первого порядка с постоянными коэффициентами:
Рис. 1.34
(2)
Решение для тока запишем в виде суммы:
= J'l = iy "Ь &СВ»	(3)
здесь iy = RJ/(r + R) = 0,06 А — составляющая тока, соответствующая установившемуся режиму (г -► оо). В этом режиме diijdt — 0, т. е. напряжение на индуктивности uL=LdiJdt~0.
Поэтому установившийся ток iy найден в схеме рис. 1.34Р,а (без индуктивности). Свободная составляющая тока iCB представляет собой решение соответствующего уравнению (2) однородного уравнения:
=	(4)
В решении (4) постоянная времени цепи т = L/rBX = = L/(R + г) = 0,002 с; гвх — входное сопротивление заданной схемы рис. 1.34Р,б относительно выводов индуктивности.
г
Постоянная интегрирования А определяется из условия неизменности тока в индуктивности в момент коммутации
Рис. 1.34Р
t — 0, т. е. условия iL(0 +) = iL(0 —), где iJO —) — ток в индуктивности непосредственно перед размыканием ключа. Ток iL(0 —) = 0, так как до коммутации весь ток источника проходил через ветвь с ключом. Подставим это значение в решение (3) для тока iL при t = 0:
0 = RJ/(R +г) + А,
откуда А = — RJ/(R + г).
Следовательно, ток
iL(t) = —У(1 - е-"’) = 0,06(1 - е~50°') А.
к + г
Напряжение на индуктивности
^ = £> = 47Тя^ = 3е’5О°'в-
Зависимости iL(t) и uL(t) приведены на рис. 1.34Р,в и г. 24
1,35.	Для схемы рис. 1.35 определить время t, в течение которого ток i достигнет значения, равного половине установившегося. Для рассчитанного момента времени определить напряжение на индуктивности.
Дано: Е = 12 В; г = 10 Ом; £=20 мГн.
1.36.	Определить ток после замыкания ключа в цепи рис. 1.36 при Г! = г2 = г3 = 10 Ом; L = 1 Гн; £ = 60 В.
Рис. 1.35
Рис. 1.36
1.37.	В схеме рис. 1.37 определить ток в индуктивности iL и напряжение uL после замыкания ключа.
Дано: J = 2 А; г = 4 Ом; £=0,1 Гн.
1.38.	Для цепи рис. 1.38, в которой = г2 = 5 Ом; г3 = г4 = 2,5 Ом; L— 10 мГн; £ = 30 В, размыкается ключ.
Определить ток в индуктивности и напряжение на ней после коммутации.
Рис. 1.37
Рис. 1.38
1.39(	Р). Определить напряжение и ток конденсатора в цепи рис. 1.39 после замыкания ключа.
Дано £ = 2 В; R = 10 Ом; г = 40 Ом; С = 10“6 Ф.
Решение. Уравнения Кирхгофа для заданной цепи после коммутации следующие:
i = ir + ic; Ri 4“ Uc = E.
С учетом соотношений ir = ис/г и ic = Cduc/dt получим дифференциальное уравнение для напряжения
+ Uf = Е
г
г + R
(1)
Напряжение на конденсаторе ис запишем в виде суммы:
ис = иу + uCB
+ Ае г/т;
(2)
здесь иу — составляющая, соответствующая установившемуся режиму (t = оо). В этом режиме Cduc/dt = 0 (ток в емкости отсутствует). Поэтому напряжение иу найдено из схемы рис. 1.39Р,
Рис. 1.39
Рис. 1.39Р
на которой ветвь с емкостью отключена. Постоянная времени цепи т = Сгвх, где гвх — входное сопротивление заданной цепи относительно выводов конденсатора: rBX = Rr/(R + г) = 8 Ом и т = 8  10~6 с = 8 мкс.
Напряжение на конденсаторе не изменяется скачком в момент коммутации ис (0 4-) = ис (0 -). До коммутации ис(0 —) = 0 (конденсатор не был заряжен). Поэтому для момента времени t = 0 согласно (2) получим:
О = Er/(r + R) + 4,
откуда А - - Er/{r + R).
Следовательно, напряжение
uc(t) = Е-4-(1 -е‘"*)= 1,6(1 — е"125°00') В. к + г
Ток
Ic(t) = С	= С-Е —Г—е~^ = -е'"’ = ОЛ’125 °00' А.
dt т г + R г
1.40.	Цепь рис. 1.40, где г = 10 Ом; С = 100 мкФ, подключается к источнику с постоянным напряжением U = 10 В.
Найти напряжение на конденсаторе и ток; построить их зависимости от времени. Определить напряжение на конденсаторе и ток через 10 мс после замыкания ключа.
1.41.	При переводе ключа в положение 1 (рис. 1.41) конденсатор С заряжается через резистор с сопротивлением г = 12 Ом от источника с постоянной ЭДС Е = 12 В. Затем ключ переводится в положение 2 и конденсатор разряжается через такой же резистор.
Найти наибольшие значения тока при зарядке и при разрядке конденсатора.
1.42.	Определить напряжение ис на конденсаторе С и ток ic в цепи рис. 1.42 после замыкания ключа. Дано: =
Рис. 1.40
Рис. 1.41
Рис. 1.42	Рис. 1.43
Рис. 1.44
= 5 Ом; г2 = г3 = 10 Ом; С = 100 мкФ; Е = 15 В. Построить зависимости uc(t) и
1.43.	Для цепи рис. 1.43 определить напряжение ис и ток ic после размыкания ключа.
Дано: J — 20 мА; г = 100 кОм; С — 2000 пФ.
1.44.	В цепи рис. 1.44 определить ток и напряжение на конденсаторе после замыкания ключа.
Дано: = г2 = г3 = г4 — 10 Ом; С = 1 мкФ; Е = 60 В.
1.3.	Применение уравнении Кирхгофа
1.45(	Р). Определить токи в ветвях схемы рис. 1.45, применяя матричную запись уравнений Кирхгофа.
Дано: Ei - 3 В; Е2 = 2 В; Е3 — 2 В; Е5 = 1 В; J3 — 1 А; J4 = 0,5 A; i'i = 4 Ом; г2 = 6 Ом; г3 — 2 Ом; г4 = 8 Ом; г5 = 10 Ом.
Решение. Граф схемы, в которой каждая обобщенная ветвь (см. рис. 1.Б, б) представлена отрезком линии, изображен на рис. 1.45Р.
Рис. 1.45
Рис. 1.45Р
Выберем дерево графа — ветви 1 и 5 и запишем топологические матрицы А и В графа. Матрицу соединений А составим определенную, приняв ср3 = 0. Для составления матрицы главных контуров В образуем эти контуры, каждый из которых состоит из ветвей дерева и одной ветви связи. За направление обхода контура принимаем направление ветви связи, входящей в его состав.
Матрицы:
-11-1	00
00	1-11
А =
110 0 о
-1010-1 0 0 0 1	1
Столбцовые матрицы параметров источников и диагональная матрица сопротивлений ветвей:
№ = || 3 2 2 0 1 ||т; J<B’ = ||0 0 - 1 - 0,5 0||т;
R(b) = diag \\rir2r3rs51|.
Перемножая матрицы в соответствии с (1.26) и (1.27), получаем :
—11—1	00
00	1-11
г2	О	О	О
"*^10	/*з	0	—	Г5
О 0	0	г4	г5
М
7,2
7,з
7,4
7,5
М
Л-2
Лз
7,4
7,5
-11-1	00
0 0	1-11
110 0 о
-10 10 - 1
0 0 0 1	1
о
о
-1
-0,5
О
3
2
2 О
1
В развернутом виде:
~~ Л14- ^2 — 1гз — 1Д
Лз ~ ^4 + 7,5 = — 1,0 4- 0,5;
r i7ri + Г2^г2 = 3 + 2;
“	+ гз7,з “ rs^r5 = — 3 + 2 — 1;
Г47,4 + Г5^г5 — !•
После подстановки численных значений решение этих уравнений дает следующие токи: 7Г1 = 0,2 А; 1г2 = 0,7 А; 7,з = — 0,5 А; 7г4 = 0,1 А; 7,5 =0,1 А.
Рис. 1.46
Рис. 1.47
1.46.	Составить уравнения Кирхгофа для схемы рис. 1.46, где стрелками показаны положительные направления токов, применяя топологические матрицы.
Дано:	=	12 Ом; r2 = 5 Ом; r3 = 2 Ом; r4 = 4 Ом;
r5 = 4 Ом; г6 = 1 Ом; r7 = 24 Ом; Ех = 4 В; Е2 = 1 В; Е6 = 5 В; Е7 = 2 В; J2 = 0,7 А.
Определить токи.
• 1.47. Для схемы рис. 1.47, где стрелками показаны положительные направления токов, записать уравнения Кирхгофа в матричной форме и определить токи.
Дано: Ji = 1,2 А; Е8 = 1 В; rL = 20 Ом; г2 = 20 Ом; г3 = 8 Ом; г4 = 4 Ом; г5 = 7,5 Ом; г6 = 8 Ом; г7 — 4 Ом; г8 = 2 Ом.
Рис. 1.49
1.48.	По заданной узловой матрице А составить граф электрической цепи	и для него записать матрицу	главных контуров В, выбрав	в	качестве ветвей	дерева	ветви	2-3-5-6:
1 0	0	0	1	0	1	0
0 1-1	0-1	1	0	0
А “ 0 0	0	1	0-1-1	0’
00	1-1	0	0	0-1
где столбцы соответствуют узлам 1 — 4, а строки — ветвям 1 —8.
1.49.	На рис. 1.49 изображен граф электрической схемы.
Составить матрицу главных сечений при ветвях дерева /-2-4-6.
1.50.	Для графа на рис. 1.50 составить матрицу главных контуров при ветвях дерева 4-6-7S-9.
1.51.	На примере графов рис. 1.49 и 1.50 проиллюстрировать матричные соотношения (1.23) — (1.25), (1.34).
1.52.	Для графа, изображенного на рис. 1.52, составить матрицы А, В при дереве 4-5-6 и проверить выполнение соотношений (1.29).
1.53.	На рис. 1.53 приведен граф электрической схемы.
1)	При указанной нумерации ветвей записать матрицу А, выбрав за базисный узел 5.
2)	Выбрать дерево графа, состоящее из ветвей 2-5-6-7, и изменить нумерацию ветвей таким образом, чтобы можно было представить матрицу сечений разделенной на две подматрицы: Q = || 1F ||; составить матрицу Q.
3)	Составить матрицу В.
4)	Проверить выполнение соотношений (1.29) и (1.30).
8
9
Рис. 1.53
I
Рис. 1.54
Рис. 1.54Р
1.54(Р). Для схемы рис. 1.54 составить уравнения Кирхгофа в матричной форме, приняв за базисный узел 4.
Решение. Схема имеет особенность в виде ветви, содержа-
щей только идеальный источник тока J. Для устранения особенности заменим источник тока двумя источниками тока J (рис. 1.54 Р), при этом уравнения Кирхгофа для токов в узлах Л 2, 3 не изменятся. Запишем уравнения Кирхгофа (1.26) и (1.27) для полученной схемы, выбрав в качестве ветвей дерева
ветви 3-4-5:
- 1	0 10 0
1 -10 0 1
0	10 10
Л Л h Л
—1	0 10 0
1 -10 0 1
0	10 10
J о о о
ri 0 г3 0 - г5 0 г2 о -г4 г5
010-1	1
0 о Ез Еа 0
Рис. 1.55
1.55	. Составить уравнения Кирхгофа в матричной форме для схемы, изображенной на рис. 1.55. На схеме стрелками показаны выбранные положительные направления токов.
Дано: гх = 40 Ом; г2 = 40 Ом; г3 = 20 Ом; г4 — 20 Ом; г5 = 20 Ом; г6 — 30 Ом; г7 = 16 Ом; г8 = 80 Ом; г9 = 75 Ом; г10 = 20Ом;£\ = 2,5В;Ег = 6 В; Е5 = 2,5 В; Е8 = 0,5 В; J = 0,4 А.
Определить токи.
1.56	(Р). Для цепи рис. 1.56 составить уравнения Кирхгофа с применением топологических матриц, приняв (р4 = 0.
Решение. Схема имеет особенность в виде ветви, содержащей только идеальный источник ЭДС. Для ее устранения перенесем ЭДС через узел 1 и получим схему (рис. 1.56Р), в которой на один узел меньше, чем в исходной. Составим матрицы А и В и запишем уравнения Кирхгофа (1.26) и (1.27):
-11	00	1
0 0-1 1 - 1
Л
rt г2 0 0 0
0 0 г3 г4 0
Г1 0 - г3 0 г5
Рис. 1.56Р
Рис. 1.56
Рис. 1.57
1.57	, Составить уравнения Кирхгофа в матричной форме для схемы рис. 1.57, на которой положительные направления токов показаны стрелками.
Дано: Е = 7,5 В; гг—2 Ом; г2 = 5 Ом; г3 = 10 Ом; г4 = 2 Ом; г5 — 10 Ом; г6 = 2 Ом; r7 = 1 Ом.
Определить токи.
1.4.	Применение узловых уравнений и уравнении с напряжениями ветвей дерева
1.58	(Р). В цепи рис. 1.58 определить токи во всех ветвях, пользуясь методом узловых потенциалов.
Дацо: Ei = 4 В; Е3 = 2 В; Е5 — 12 В; J3 = 2 А; г\ = 4 Ом; г\ = 4 Ом; г2 = 2 Ом; г3 = 2 Ом; г4 = 8 Ом; r5 = 1 Ом. Положительные направления токов указаны на рис. 1.58 стрелками.
Решение. Примем ср t = 0 и запишем уравнения согласно (1.35) для узлов 2 и 3:
toi +#2 + 0з)ф2 -0зФз = -д3Ез + ^з;
— 03ф2 + (03 + 04 + 0$)фз = — ^3 + 03^3 + 05^5-
Подставив значения ЭДС, тока источника и проводимостей, т. е. gr = l/(rz! + 4) = 0,125 См, д2 = 1/г2 =0,5 См и т. д., получим:
1,125ср2 — 0,5Фз = - 0,5 — 1 + 2;
— 0,5 ср2 4" 1,625 срз = — 2+14- 12.
2 п/р Ионкина П. А.	33
Решение этих уравнений дает: ф2 = 4 В; Фз = 8 В.
Токи в ветвях определим по закону Ома для участка цепи (1.14):
Л = (ф2 + Е1)^1 = 1 А; 12 = ср202 = 2 А; /3 =-(Фз - <р2 -
- Е3)д3 = 1 А;
•^4 ~ Фз$4 = 1 А; 15 = (— ф3 + Е^д3 = 4 А.
Рис. 1.58
Рис. 1.59
1.59.	Методом узловых потенциалов определить токи в схеме рис. 1.59.
Дано:	= 8 В; Е2 = 2 В; J3=0,5 А; гг — 20 Ом;
г2 = 80 Ом; г3 = 50 Ом; г4 = 20 Ом; г5 = 10 Ом.
Положительные направления токов показаны на схеме стрелками.
Рис. 1.60
Рис. 1.61
1.60.	Для схемы рис. 1.60 определить все токи методом узловых потенциалов.
Дано: rl=r2=r3 = 5 Ом; г4 = г5 — 10 Ом; Ej = 8 В;
Е2 = 6 В; Е4 = 4 В; J3 = 2 A; J5 = 1 А.
Положительные направления токов показаны на схеме стрелками.
1.61.	Определить токи в цепи рис 1.61 методом узловых потенциалов.
Дано: Ej =0,4 В; Е2 = 1,0 В; J3 =0,03 А; г{ — 10 Ом; г2 = 40 Ом; г3 = 20 Ом.
Положительные направления токов показаны на схеме стрелками.
1.62.	Определить ток /4 в цепи рис. 1.62 методом узловых потенциалов.
Дано: Ei — 25 В; Е2 = 30 В; Е3 = 15 В; гг = г2 — 100 Ом; г3 = 200 Ом; г4 — 150 Ом.
1.63.	Для схемы рис. 1.63 определить методом узловых потенциалов показание вольтметра, считая его сопротивление бесконечно большим.
Дано: Ei = 80 В; Е2 = 30 В; Е3 =20 В; = г3 = 4 кОм; г2 = 2 кОм.
b
Рис. 1.65
1.64.	Определить показание вольтметра рис. 1.63, если его сопротивление конечно и равно 10 кОм.
1.65.	Определить потенциалы точек а и b в схеме рис. 1.65, приняв <р0 = 0.
Дано: Ei =220 В; Е2 = 100 В; Е3 = 120 В; = 40 Ом; г2 = 200 Ом; г3 = 100 Ом; г4 = 50 Ом; г5 = 20 Ом; г6 = 100 Ом.
1.66.	Вычислить показание вольтметра с внутренним сопротивлением 500 Ом, если вольтметр включить между точками а и b на схеме рис. 1.65 (плюс вольтметра подключен к точке а).
1.67(	Р). Определить токи в схеме рис. 1.67 при помощи узловых уравнений, записанных в матричной форме. Все сопротивления указаны в омах.
Решение. Для графа рис. 1.67Р, у которого выбрана нумерация ветвей, составим матрицу соединений, приняв ф4 = 0:
А =
1-1	00001
- 1 О 1110 0
0	1-10010
Матрица узловых проводимостей по (1.32) запишется так: G(y) = AG^AT =
1-1	00001
- 1	0	1110 0
0	1-10 0 10
(91 + 92 + 91)	~~ 91	~ 92
“ 91	(91 + 9з + 9а + 9s)	— 9з
— 92	~ 9з (92 + 9з + 9б)
1,25 -0,05 -0,20
-0,05	0,45	-0,10
-0,20 -0,10	0,80
Запишем правую часть узловых уравнений (1.31) согласно (1.33): JM = AJ<B> - AG<B>E<B> при Е(в) = || E1E20E40E6Er ||т;	=
= II Ji 0 0 0 0 0 0 IIт.
После перемножения и суммирования матриц получим:
J(y) = II68 5 - 351|т.
Запишем (1.31) в развернутом виде:
1,25 -0,05 -0,20
-0,05	0,45	-0,10
-0,20 -0,10	0,80
Ф1
Ф2
Фз
68
5
-35
откуда определим потенциалы узлов: (рх = 50 В, <р2 = 10 В, ф3 = — 30 В. Токи найдем, например, по закону Ома для обобщенной ветви (1.21):	= 12 А; 12 - 4 А; 13 = 4 А;
/4 = 4 А; 15 - 10 А; /6 = 0;/?=2 А.
Рис. 1.67
Рис. 1.68
Рис. 1.69Р
1.68.	Составить узловые уравнения для схемы рис. 1.68 в матричной форме. Определить токи, положительные направления которых указаны стрелками.
Дано: Ej=6 В; Е2 = 1 В; Е6 = 5 В; J3 = 0,025 А; ri == 80 Ом; г2 = 20 Ом; г3 — 20 Ом; г4 = 16 Ом; г5 = = 20 Ом; гб = 10 Ом.
1.69(	Р). Составить узловые уравнения для схемы рис. 1.59, применяя неопределенную матрицу соединений Ан.
Решение. Составим неопределенную матрицу соединений для графа рис. 1.69Р, соответствующего схеме рис. 1.59:
-10101
Ан —
1 - 1 - 1 - 1 о
0	1	0	1-1
Неопределенная матрица узловых проводимостей аналогична (1.32)
GH(y) = AhG^AJ =
-10101
1 - 1 - 1 - 1	0
0	1	0	1-1
01
02
03
04
05
- 1	10
0-1	1
1-1 о
0-1	1
1	0 -1
(01 + 03 + 05)	(“01 -0з)	“05
(—01 —0з) (01 + 02 + 03 + 04) (— 02 —04)
“05	(“02“ 04)	(02 + 04 + 05)
Полученная матрица дает возможность произвести контроль правильности составляемых уравнений, так как суммы проводимостей как по строкам, так и по столбцам равны нулю.
Для получения определенной матрицы проводимостей нужно вычеркнуть из GH(y) одну (любую) строку и один (любой) столбец. Вычеркнем, например, третий столбец, что соответствует схеме, в которой принято ср3 = 0, и третью строку, т. е. уравнения составим для узлов 1 и 2. Узловые уравнения для этих узлов:
(31 + Зз + 9s)	(-01-дз)
(-91 ~9з) (91 +92 +Эз + 9t)
<?i
Фз
Можно, например, вместо уравнения уравнение для базисного узла 3:
для узла 2 записать
(01 + 0з + 0s) (— 01 — 0з)
- 05	(- 02 - 04)
Ф1
Ф2
«Л + -Е101 — ^202
Узловой определитель в этом случае содержит 8 слагаемых:
Д(У) = - (gig2 4- д2д3 + д2д5 + д^ + д3д* + д^д5 + д^ + 0305), а в случае уравнений для узлов 1 и 2 — 15 слагаемых:
д(у) = gl + gvg3 + gig5 4- 0102 + 020з + 0205 + 0103 + + 03 + 0305 + 0104 + 0304 + 0405 “ 01 “ 2 0103 ~ 03-
Таким образом, после приведения подобных членов определители совпадают с точностью до знака и при применении уравнения для узла, потенциал которого принят равным нулю, уменьшается число слагаемых в узловом определителе.
1.70.	Составить неопределенную матрицу узловых проводимостей схемы рис. 1.60.
1.71(	F). Рассчитать токи в цепи рис. 1.71, приняв в качестве независимых переменных напряжения ветвей дерева.
Дано: rj » r3 = 1 Ом; г2 ~ г4 = 0,5 Ом; г5 = г6 = 2 Ом;
= 10 В; Е2 = 1 В; 0 = 8 А.
Решение. Составим граф схемы рис. 1.71 Р, выберем дерево (ветви 2-3-4) и сечения (Sb S2, S3). Сначала рассчитаем по (1.36) напряжения ветвей дерева. Запишем матрицы Q, №, J(b) и Е(в):
Q =
0 10 0-1-1
-1001	1	1
-1010 о о
G^ = diag 11010203040506 h — ||00J000||T;
Е(в)== ||Е;Е20000Г.
Матрица проводимостей сечений по (1.37):
Gc = QG(B)QT =
0 10 0 -1 - 1
-1001 I 1
-1010 о о
0-1-1
1	о	о
0	О	1
0	1	о
-	1	10
-	1	1	о
(02 +05 +0б)	~(05+0б) О
“ (05 + 0б) (01 + 04 + 05 + 0б)	01
О	01	(01 + 0з)
Правая часть уравнения (1.36) по (1.38) JC = QJ(B) _ QG<b)№ =
Поэтому уравнения (1.36) можно записать в виде
3-10
- 1	4 1
0	1 2
3-10
- 1	4 1
О	1 2
- 8
10
2
с напряжениями
ветвей дерева
V2 у*
Уз
- 8
10
2
откуда U2 = — 2 В; U3 - 0; С74 — 2 В.
Напряжения остальных ветвей можно выразить через найденные напряжения ветвей дерева согласно (1.39):	— — 2 В;
С75 = U6 = 4 В. Токи в ветвях: Ц — gY (Vх	— 8 А; /2 =
= 02 (У2 + Е2) = 4 A; I3 = g3U3 — 0; Z4 = g4U4 = 4 А; /5 = ~ У$У5 — 2 А; — 9вУ6 — 2 А.
Рис. 1.72
Рис. 1.73
1.72.	Для заданной схемы рис. 1.72 определить все токи, положительные направления которых показаны стрелками, применив уравнения с напряжениями ветвей дерева.
Дано: 7=1 А; Е2 = 10 В; Е3 = 200 В; £4 = 56 В; г\ = 20 Ом; г'( = 10 Ом; г2 = 30 Ом; г3 = 6 Ом; г4 = 8 Ом; г5 = 15 Ом; г6 — 40 Ом.
1.73.	Определить токи в ветвях цепи рис. 1.73, применив уравнения с напряжениями ветвей дерева.
Дано: = 0,05 A; J2 = 0,25 A; J3 = 0,25 A; = 80 Ом; г2 = 80 Ом; г3 = 30 Ом; г4 = 20 Ом; г5 = 20 Ом; г6 = 40 Ом. Положительные направления токов указаны на схеме стрелками.
1.5.	Применение контурных уравнений
1.74(	Р). В схеме рис. 1.74 определить все токи методом контурных токов.
Дано: г! = 20 Ом; г2 — 30 Ом; г3 = 40 Ом; г4 = 80 Ом; г5 = 20 Ом; г6 = 20 Ом; Е3 = 16 В; J = 0,3 А.
Решение. Выберем контуры для получения независимых уравнений таким образом, чтобы в каждом была по крайней мере одна новая ветвь (показаны на рис. 1.74 штриховой линией). Контурными будут токи 12 и 73.
Запишем уравнения для выбранных токов в соответствии с (1.44):
0*1 + г4 + г6)Ц - rj2 — r4I3 — r4J;
— Гб11 + 0*2 + Г5 + Гб) Ъ ~ г5^3 ~
~ rJi - Г512 + (r3 + r4 + r5)I3 = E3 — (r4 + r5) J, откуда при заданных параметрах находим =0,3 А; 12 = = 0,2 А; /3 =0,1 А.
Рис. 1.74
Токи в ветвях: J4 = -	+ I3 + J = 0,1 A; I5 = - I2 + I3 +
+ </ = 0,2 А; /6 = Л - J2=0,l A.
1.75.	Определить токи в схеме рис. 1.75 методом контурных токов.
Дано: £=12 В; <7=2 А; гг = 1 Ом; г2 = 2 Ом; г3 = = 4 Ом; г4 = 2 Ом; г5 = 2 Ом; г6 = 0,5 Ом. Положительные направления токов указаны на схеме стрелками.
1.76.	Методом контурных токов определить токи в ветвях цепи рис. 1.76.
Дано: £=11 В; <7=0,3 A; = 10 Ом; г2 = 20 Ом; г3 = 5 Ом; г4 = 40 Ом; г5 = 10 Ом. Положительные направления токов указаны на схеме стрелками.
Рис. 1.78
Рис. 1.78Р
1.77.	Для схемы рис. 1.77 определить токи, применив
контурные уравнения.
Дано: Et = 3 В; Е2 = 12 В; J =0,2 А; гх = 30 Ом; г2 = 20 Ом; г3 = 20 Ом; г4 = 40 Ом; г5 = 5 Ом. Положительные направления токов указаны на схеме стрелками.
1.78(	Р). Определить токи цепи рис. 1.78 методом контурных уравнений, записанных в матричной форме.
Дано: гх = 30 Ом; г2 = 20 Ом; г3 = 20 Ом; г4 = 40 Ом; г5 = 60 Ом; г6 = 40 Ом; г7 = 10 Ом; Е3 = 3 В; Е4 — 4 В; Е6 = 18 В; J7 =0,4 А.
Решение. Для графа схемы рис. 1.78Р выбираем дерево (ветви 2-5-3-7). Образуем главные контуры, присоединив к ветвям дерева по одной ветви связи. Составим матрицы В, R(B), Е(в), Гв):
В =
1-1-10 00 о
0 О 10	11-1
0 1 01-10 о
= diag || rlr2r3r4r5r6r1 ||;
Е<-> = ||00Е3Е40Е60||т;
J<’> = ||

Матрица контурных сопротивлений по (1.42)
r(k) = BR(°)BT =
1-1-10 00 о
0 О 10	11-1
0 1 01-10 о
1 о о
- 1	0	1
- 1	10
0 О 1
0	1-1
0 1 о
0-1 о
?7

г3
?5

70 - 20 - 20 - 20 130 -60 - 20 - 60 120
Для контурных уравнений (1.41) определим правую часть:
ЕЮ =
-3 18+3 + 4
4
Токи в обобщенных
ветвях
схемы найдем из (1.40):
О 1 О
1
- 1 О О
Токи в сопротивлениях совпадают с токами в обобщенных ветвях для всех ветвей, кроме седьмой, в которой имеется источник тока, поэтому /г7 = /7 + J7 = 0,1 А.
1.79.	Составить контурные уравнения для схемы рис. 1.74 в матричной форме, выбрав ветви 4-5-6 в качестве ветвей дерева. Записать в общем виде выражение для токов в ветвях схемы через контурные токи.
1.80.	Для схемы рис. 1.75 записать контурные уравнения в матричной форме, выбрав в качестве ветвей дерева ветви 2-3-5.
1.81.	Составить контурные уравнения для цепи рис. 1.77 в матричной форме, выбрав в качестве ветвей связи ветви 1 и 2.
1.6.	Метод наложения. Свойство взаимности
1.82(	Р). Для цепи рис. 1.82 заданы параметры: Ei = 25 В; J2 = 125 мА; rj = 100 Ом; гн = 500 Ом; г2 = 2 кОм.
Рис. 1.82
Определить токи во всех ветвях, применив метод наложения. Рассчитать мощность сопротивления нагрузки гн.
Решение. При расчете цепи с применением метода наложения рассматриваем отдельно действие источника ЭДС Ei и источника тока J2- Эквивалентные схемы для частичных токов изображены на рис. 1.82Р.
При действии источника ЭДС Et токи в ветвях схемы рис. 1.82Р,а равны: Г2 = 0,01 А; 1\ - 0,05 А; Гн = 0,04 А. При действии источника тока J2 токи в ветвях схемы рис. 1.82Р,б равны: = 0,005 А; Ц = -0,10 А; Г' = 0,02 А.
Искомые токи:	+ Г{ = - 0,05 А - - 50 мА; 12 —
= /' + Г' = 0,015 А = 15 мА; 7Н = Гн 4- Г' = 0,06 А = 60 мА.
Мощность сопротивления нагрузки Рн = гн7„ = 1,8 Вт.
Рис. 1.82Р
1.83.	Для схемы рис. 1.83 определить все токи, применив метод наложения.
1.84.	Для схемы рис. 1.84 с параметрами Ei —2 В; £3 = 3 В; Е4 — 9 В; тх = 6 Ом; г2 = 6 Ом; г3 — 3 Ом; г4 = 6 Ом; г5 = 3 Ом; г6 = 2 Ом. Определить ток 15, применив метод наложения и свойство взаимности.
Указание. При решении учесть, что взаимные проводимости 051 = д15; д53 = д35;	= проводимости ^i5, д35 и
#45 рекомендуется рассчитывать, включив источник ЭДС в пятую ветвь и исключив остальные источники ЭДС
Рис. 1.83
Рис. 1.84
1.85.	В цепи рис. 1.85 были выполнены два опыта: О при действии только источника ЭДС Et = 40 В ток амперметра оказался равным 4 А; 2) при действии только источника тока J2 = 5 А ток амперметра оказался равным - 1 А.
Определить показание прибора при одновременном действии источника ЭДС Ех = 20 В и источника тока J2 = 6 А.
1.86.	Определить ток I в схеме рис. 1.86, применив метод наложения.
1.87.	В схеме рис. 1.87 определить ток I, применив метод наложения.
Рис. 1.85
Рис. 1.86
1.88.	В схеме рис. 1.87 определить напряжение U между выводами источника тока, применив метод наложения.
1.89.	Проверить выполнение свойства взаимности между первой и пятой ветвями схемы рис. 1.89.
Дано:	= 5 Ом; г2 = 8 Ом; = 2 Ом; г4 = 3 Ом;
г5 = 6 Ом.
Рис. 1.89
Рис. 1.87
Рис. 1.91
1.90.	Для цепи рис. 1.90 с параметрами г1 = 40 Ом; г2 = 10 Ом; г3 = 50 Ом; г4 = г5 — 20 Ом; Ei = 50 В; J2 = — 2,5 А вычислить: 1) коэффициенты
2) взаимное сопротивление г42; 3) напряжение Us, применив метод наложения.
1.91.	Найти токи /7 и /8 в схеме рис. 1.91, применив метод наложения.
Дано: ri — г3 = 10 Ом; г2 = 10 Ом; г4 = г5 = г6 = 40 Ом;
Е7 = 54 В; Е8 =48 В.
1.7.	Линейные соотношения между напряжениями и токами
1.92(	Р). Для цепи рис. 1.92 известны показания амперметров Ai и А2 в двух режимах: 1) г = 0; Zj = 5 А; 12 = 2 А; 2) г = rH; Zi = 4 A; I2 = 1 А.
Определить показание первого амперметра при г = ос.
Решение. Для линейной цепи справедливо соотношение вида (1.54) Ц = а.4- Ы2. По данным двух режимов находим коэффициенты а и b из уравнений
5 = а + 6-2; 4 = а 4- b-1,
откуда а = 3 A; b = 1.
При г = оо ток 12 — 0 и /i=a4-b-0 = 3 А.
Рис. 1.92
Рис. 1.93
1.93.	Для схемы рис. 1.93 с параметрами ri = г3 = г4 = 5 Ом; г2 = 10 Ом; г5 = 0 -г оо; = 20 составить уравнение линейной связи между напряжением U5 и током 13.
1.94,	В цепи рис. 1.94 выделены две ветви. При разомкнутых ключах Ki и К2 токи Zt = 1 А; 12 =0. При замкнутом ключе и разомкнутом ключе К2 токи Ц = 2 А; 12 =0,5 А.
Определить ток Ц при замкнутых ключах и К2, если в этом режиме /2 = 1 А.
1.95.	Составить уравнение линейной зависимости Ц = ДЛя схемы на рис. 1.95, если гг = 1 Ом, г2 = 2 Ом, г3 = 3 Ом, г<- = 4 Ом, гп = 0 -г оо, J = 1 А.
1.96.	Для схемы рис. 1.96 записать уравнение линейной зависимости между напряжениями 1712 и IZ34.
1.97(	Р). В цепи рис. 1.97 определить все токи при Е = 124 мВ. Сопротивления указаны в омах
Рис. 1.94
Рис. 1.96
Рис. 1.95
Рис. 1.97
12	5	2	1
Рис. 1.98
Решение. Схема содержит один источник ЭДС. Применим один из простых методов расчета режима такой линейной цепи — метод пропорциональных величин. Выберем точку нулевого потенциала — точку а, т. е. положим сра — 0. Найдем значение ЭДС Е\ при действии которой ток /7 будет равен выбранному значению, например Г7 = 1 А. Для определения Е' нужно вычислить значения других токов при = что можно сделать в следующем порядке: <р'д = (24+16) /7 = = 40 В; 7^ = 40/40 = 1 А; Г5 = Г7 + Г6 = 2 А; <р'г = ф'а + + 10-2 = 60 В; /; = 60/40 = 1,5 А; Г3 = Г5 + Г4 = 3,5 A; tp'rt =
ф'г + 4Q.з,5 = 200 В; Г2 = 200/80 = 2,5 А; 1\ = Г3 + Г2 = 6 А; ф'$ = Фе + 8 • 6 = 248 В.
Эти значения токов получатся при ЭДС Е' = ф'б - ср'я = = 248 В. В силу линейности токи при Е =0,124 В отличаются от полученных в к = Е/Е' = 0,5-10“3 раз, т. е., например, /7 = кГ7 - 0,5 • 10“3 А = 0,5 мА. Аналогично /6 =0,5 мА и т. д.
1.98.	Определить токи в схеме рис. 1.98, применив метод пропорциональных величин. Значения сопротивлений указаны на схеме в омах.
Указание. При решении учесть, что у схемы на рис. 1.98 могут быть независимо рассчитаны режимы правой и левой частей (относительно источника ЭДС).
Рис. 1.99
1.99.	В схеме рис. 1.99 рассчитать все токи методом пропорциональных величин. Значения сопротивлений указаны на схеме в омах.
1.8.	Преобразования электрических схем
1.100(	Р). Для цепи рис. 1.100 найти	мощность,
потерь в резисторе с сопротивлением г3 = 3 Ом.
Дано: Г! = 10 Ом; г4 = 2 Ом; г5 = 5 Ом; = 20 A; J2 = = 20 А.
Рис. 1.100Р
Рис. 1.100
Решение. Преобразуем источники тока Ji и J2 в эквивалентные источники ЭДС (рис. 1.100Р), чтобы уменьшить число узлов расчетной схемы и упростить расчет. Значения
ЭДС эквивалентных источников: Е{ = r4Ji — 40 В; Е2 = г5J2 = = 100 В. Ток /3 = (Ei - Е2)/(г3 + г4 + г5) — —6 А; мощность Р3 = г3/2 = юз Вт.
1.101.	На рис. 1.101 изображена электрическая цепь, в которой необходимо определить токи во всех ветвях, выполнив предварительно преобразование источников ЭДС в источники тока.
Дано:	= 2 Ом; г2 — 12 Ом; г3 = 5 Ом; г4 = 5 Ом;
г5 = 10 Ом; Ег = 16 В; Е2 = 12 В.
Рис. 1.101	Рис. 1.102
1.102.	Определить токи и составить баланс мощностей для схемы рис. 1.102 при Е = 10 В; J = 3 А; г2 = 2 Ом; г2 = 3 Ом.
1.103,	Три генератора с ЭДС Ег = 155 В; Е2 = 130 В; Е3 = 95 В и внутренними сопротивлениями = 0,5 Ом; г2 — 0,2 Ом; г3=0,5 Ом работают параллельно (рис. 1.103). Найти ЭДС, внутреннее сопротивление эквивалентного генератора и мощности, потребляемые в резисторах с сопротивлениями гн1 = 4 Ом и гн2 = 3 Ом.
Рис. 1.103	Рис. 1.104
1.104(	Р). Определить токи в схеме рис. 1.104, положительные направления которых выбраны, при = 5 Ом; г2 = = 9 Ом; г3 = 300 Ом; г4 = 20 Ом; г5 = 60 Ом; г6 = 30 Ом; г7 = 20 Ом; г8 = 20 Ом; EY = 15 В; Е2 = 105 В.
Решение. Для сокращения числа совместно решаемых уравнений звезду сопротивлений г7 — г8 — г4 заменим экви-50
валентным треугольником (рис. 1.104Р,а):
г78 = Г7 + г8 + г7г8/г4 = 60 Ом; г47 = r4 + r7 + г4г7/г8 = 60 Ом; r48 = r4 + r8 + iWblri = 60 Ом.
В полученной схеме заменим параллельно соединенные сопротивления эквивалентными (рис. 1.104Р,б):
гЭК1 = г3г^/(г3 + г47); гэк2 = г5г48/(г5 + г48); гэк3 = г6г78/(гб + г78).
Рис. 1.104Р
Наконец, треугольник эквивалентных сопротивлений гэк1 — - гэк2 — гэк3 заменим эквивалентной звездой (рис. 1.104Р,в):
7*12 = Гэк1Гэк2/0эк1 4" 7*эк2 4” 7*экз) в 1^ Ом, Г±3 — ^эк 1^”экз/С^*эк1 4" Гэк2 +
+ гэк3) = 10 Ом; г23 = ГжгГжз/^эк! + Гж2 + т*эк3) = 6 Ом.
Полученная схема содержит два узла, и токи в ней легко определяются методом узловых потенциалов. Отметим, что при выполненных эквивалентных преобразованиях потенциалы узлов а, Ь, с не изменяются, т. е. токи Ц и /2 участков, не затронутых преобразованиями, также не изменились.
Напряжение между узлами d и с
тт _	~ -^i/(ri 4- г13) + Е2/(г2 + г2з) _ 3Q р
dC l/(ri 4" Пз) 4" 1/г12 4" 1/0*2 4" г2з)
и токи по (1.14)
Л =	~ £1)/(т*1 4- г13) = - 3 A; I2 = (Ucd + £2)/(г2 + г23) = 5 А.
Выбрав, например, <рс = 0, найдем потенциалы узлов:
(ра = - Ei - rJi =0; Фь = Е2 - г212 = 60 В.
В заданной схеме (рис. 1.104) токи
/3 = (<рв - Фс)/г3 =0; /5 = (фь - фс)/г5 = 1 А; /6 = = (Фй - фв)/т*б = 2 А.
Остальные токи определим по первому закону Кирхгофа:
/7 = Л + 16 - 13 = - 1 А; /8 =/2 -/5 -]6 = 2 А.
1.105.	В схеме рис. 1.105 найти ток 13.
Дано: Ei — 16 В; Е2 — 8 В; rt = г2 = г3 = г4 = г5 = ге~ 3 Ом.
Рис. 1.105
Рис. 1.106
1.106.	Определить ток 15 в диагонали четырехплечевого моста (рис. 1.106).
Дано: rt = 120 Ом; г2 = 180 Ом; г3 = 120 Ом; г4 = 80 Ом; г5 = 80 Ом; Е = 30 В.
1.9.	Эквивалентные источники
(активные двухполюсники)
1.107(	Р). В цепи рис. 1.107 определить ток 16, применив теорему об эквивалентном источнике (активном двухполюснике).
Дано: rt = 45 Ом; г2 = 30 Ом; г3 = 15 Ом; г4 = 36 Ом; г5 — 18 Ом; г6 = 3 Ом; г7 = 5 Ом; Ег = 225 В; Е4 = 180 В.
Рис. 1.107
Решение. Разомкнем ветвь с резистором г6 (рис. 1.107Р, а) и найдем напряжение Ux между точками б и а. Для этого в схеме рис. 1.107Р,а определим токи
= Е1/О2 + г3) = 5 А; 12р = Е4/г5 = 10 А
и напряжение
— ГзЛр + г5^2р — 225 В.
Входное сопротивление, измеренное между точками а и б при отключенном резисторе с сопротивлением г6 (рис. 1.107Р, б), гвх = r7 + г2г3/(г2 + г3) = 15 Ом.
По (1.55) ток
/6 = UJ(rM + г6) ~ 15 А.
Рис. 1.107Р
Рис. 1.110
Рис. 1.Ш
1.108.	Определить методом эквивалентного источника ток в сопротивлении г2 (рис. 1.108).
Дано:	— 4 Ом; г2 = 2 Ом; г3=6 Ом; г4 = 5 Ом;
г5 = 8 Ом; Е2 = 22 В; Е4 = 13 В; J = 3 А.
1.109.	В схеме на рис. 1.109 определить ток 7, применив теорему об эквивалентном источнике.
1.110.	Применив теорему об эквивалентном источнике, определить ток в сопротивлении R = 10 Ом схемы рис. 1.110.
1.111.	В цепи рис. 1.111 при разомкнутых ключах Кг и К 2 амперметр показывает 1,2 А. При разомкнутом втором ключе и замкнутом первом амперметр показывает 3 А.
Найти показание амперметра для режима, при котором первый ключ разомкнут, а второй замкнут.
1.112.	Применив теорему об эквивалентном источнике и условие передачи максимальной мощности, определить сопротивление резистора г3 (рис. 1-.112), при котором в нем выделяется максимальная мощность, и вычислить значение этой мощности.
Дано: = 5 кОм; г2 — 3 кОм; г4 = 2 кОм; г5 = 20 кОм; гб = 4 кОм; £6 = 40 В ; J = 10 мА.
1.113.	В схеме рис. 1.113 найти ток /4, применив теорему об эквивалентном источнике.
Дано: = 2 Ом; г2 = 3 Ом; r3 = 1 Ом; г'4 - = 2 Ом; г6 = 4 Ом; £j=4 В; £^ = 10 В; ££ = 2 В; £5 = 10 В; £6 = 6 В.
Рис. 1.114
1.114.	Определить ток 13 в схеме рис. 1.114 при действии источников ЭДС Ei — 110 В и £4 = 200 В.
Дано:	= 1 Ом; г2 = 10 Ом; г3 — 5 Ом; г5 = 5 Ом;
г6 = 10 Ом.
1.10.	Топологические методы расчета передаточных функций
1.115.	Вычислить узловой определитель схемы, граф которой показан на рис. 1.115, применив разложение определителя ПО узлу.
Дано: £1 = 02 = 0з = 04 = 05 = 06 = 07 = 0,5 См.
1.116.	Вычислить узловой определитель схемы, граф которой приведен на рис. 1.116, применив разложение определителя по ветви.
Дано:0! = 02 = 0з = 2 См;04 = gs = 1 См; д6 = 07 = 0,5 См.
1.117.	Для схем, графы которых приведены на рис. 1.115 и 1.116, вычислить узловые определители разложением их по путям между двумя узлами.
1.118(	Р). Топологическим методом вычислить передаточную проводимость 041 для схемы рис. 1.118.
Рис. 1.118
Дано: 0! = 1 См; д2 =0,1 См; 03 =0,2 См; 04 = 0,5 См; 05 = 0,2 См; 06 = 0,1 См.
Решение По топологической формуле (1.59) взаимная ПРОВОДИМОСТЬ 041 = £ П'ЛД'*/Д.
к
Для графа рис. 1.118Р, а существует два пути передачи через источник и измерительный прибор в направлении,
указанном стрелкой. Значение первого пути: П\ = д^д^; минор Д1 = 1, так как при коротком замыкании первого пути граф вырождается в узел. Аналогично найдем П2 = — 919з9495\ Д'2 = 1. Узловой определитель Д схемы рис. 1.118Р, б найдем
разложением по путям (1.61) между узлами 3 — 4, между которыми есть пять путей передачи. Определим значения путей и их миноры:
П, = 929з>	— 91 + 9s + 9б1 П2 = д^дв', Д2 = gi + g2 + 9з>
Пз == 91919б1 Дз = 11 П4 = 9s9i93> Дд = П5 = д4;
А5 = Я1 (91 + 9з + 95 + 9б) + (91 + 9 з) fos + 9б)-
Графы, полученные при замыкании путей Пь П2 и П5, изображены на рис. 1.118Р, в — д. Минор Д5 может быть найден разложением по путям между узлами 1—2.
Подставляя все значения, получаем:
д41 = (0,005 - 0,02)/0,447 = - 0,0336 См.
1.119(	Р). Для схемы рис. 1.118 топологическим методом определить ток Г. 1) при действии только источника ЭДС Ei; 2) при действии источников ЭДС Ei — 140 В и Е4 — 200 В.
Решение. 1) Ток при действии источника ЭДС Е{ Г = ~ 94iEi — -0,0336-140 = -4,7 А (значение д41 найдено в решении задачи 1.118).
2) Ток I при действии двух источников ЭДС определим методом наложения: I = g^t Ег + д44Е4.
Найдем ^44 по топологической формуле (1.59) для схемы рис. 1.119Р:
040302 (01 + 05 + 0б) + 040506(01 + 02 + 0з) +
п = .____________+ 9.939195 +9.9б9192-------------0,114 См;
044	Д	’	’
здесь узловой определитель А = 0,447 См3 тот же, что и в задаче 1.118.
Подставив численные значения, получим I = 18,1 А.
1.120.	Вычислить напряжение Uab в схеме рис. 1.120 топологическим методом по формуле Мэзона.
Дано: Ei = 4 В; J5 — 0,4 А; = г2 = 10 Ом; г3 = 25 Ом; г4 = 40 Ом.
1.121.	Для цепи рис. 1.121, применяя формулу Мэзона, определить коэффициент передачи тока коэффициент передачи напряжения и напряжение 17б.
Дано: = 0,05 Ом; г2 = ОД Ом; г3 = 0,2 Ом; г4 = 0,1 Ом; г5 - 0,1 Ом; г6 = 0,2 Ом; Ei =0,2 В; J3 = 0,5 А.
Рис. 1.122
1.122.	Определить ток I в схеме рис. 1.122 топологическим Методом по формуле Мэзона. На схеме указаны значения проводимостей в сименсах.
1.123(	1*). Определить входное сопротивление схемы рис. 1.123 относительно узлов 1 и 2 по формуле Мэзона.
Дано: ri = 1 Ом; т2 = Ю Ом; г3 = г4 = 5 Ом; г5 — 10 Ом.
Рис. 1.123
Рис. 1.123Р
Решение. Для определения входного сопротивления источник тока J и измерительный прибор включим, как показано на рис. 1.123Р,а. По формуле Мэзона (1-59): ги = £ЩДк/А. Через источник и измерительный прибор к
имеется единственный путь с передачей П{ = 1. Минор этого пути определим из графа рис. 1.123Р, б:
М — 01 (02 + 0з) + 01 (05 + 0д) + (02 + 0з)(05 + 04) ~ 0,69 См2.
Узловой определитель схемы находим из графа рис. 1.123Р, в: А — 0203 (01 + 05 + 04) + 020105 + 040103 + 0504(02 + 01 + 0з) ~ = 0,102 См3.
Входное сопротивление гЕх = 6,76 Ом.
П ©
Рис. 1.124
Рис. 1.125->
1.124.	Рассчитать входное сопротивление схемы рис. 1.124 относительно узлов 2-4, применив топологическую формулу (Мэзона) для расчета передаточных функций, если rt = г2 == г3 == = Г4 = Г5 = Г6 = 1 Ом.
1.125.	Определить по формуле Мэзона ток I в диагонали моста (рис. 1.125). Сопротивления указаны в омах.
1.11.	Применение сигнальных графов
1.126(Р). Определить передачу сигнального графа рис. 1.126 между истоком х4 и стоком xj методом последовательного преобразования.
Решение. Исключим петлю с передачей е в узле х2, при этом передача всех остальных входящих в узел х2 ветвей умножается на 1/(1 —е). Полученный граф приведен на рис. 1.126Р, а.
Исключим узел х2. При устранении узла х2 образуется петля с передачей cd/(l - е) в узле х3 (рис. 1.126Р, б). После исключения этой петли получается граф рис. 1.126Р, в, состоящий из последовательно и параллельно соединенных ветвей. Его передача равна сумме передач всех ветвей из узла 4 в узел 1:
Xi _ ab	ас /(1 — е) + db
Хд.	е^~1—e-cd 1-е
1.127.	Для сигнального графа рис. 1.127 определить xt при заданном х0, применив преобразование графа.
1.128.	Определить передачу от истока х0 к узлу х3 графа рис. 1.128 методом последовательного преобразования.
1.129.	Определить передачи от истока х0 к узлам х2 и х3 графа рис. 1.128, применив формулу Мэзона.
1,130.	Составить систему уравнений, которой соответствует граф, приведенный на рис. 1.128.
1.131(	Р). При помощи сигнальных графов решить систему уравнений:
2хг + Зх2 — 0; — 3Xi + 4х2 + 2х3 = 0; Xi + х3 — х0 - 0, где х0 =
Решение. Приведем систему уравнений к причинно-следственной форме:
Xi — — 1,5 х2; х2 = 0,75 Xj — 0,5 х3; х3 = — xt + х0.
По полученной системе уравнений строим граф (рис. 1.131Р). Передачу Н10 — xi/x0 сигнального графа определим по формуле Мэзона (1.65):
1 “ 2_^к Т	— • • •
к	к
У построенного графа можно выделить только два контура с передачами:	- 1,5-0,75 =- 1,125; L2 = (-1)(-0,5) х
х ( — 1,5) = — 0,75. При этих значениях А = 2,875. Из истока х0 в узел х: имеется один путь с произведением передач ветвей Щ = 1(-0,5)(- 1,5) -0,75, и минор этого пути A't = 1. Таким образом,
Х1 = х0Н10 == 10’0,75/2,875 = 2,61.
Аналогично получим х2 = — 1,74.
При определении Нзо = х3/х0 учтем, что существует один путь между истоком х0 и узлом х3 с передачей П1 = 1 и есть ОДИН контур не соприкасающийся с этим путем, т. е. Al = 1 - Следовательно,
Язо = 1 (1 - LJ/& = 1 • 2,125/2,875 = 0,73 и х3 = 7,3.
Рис. I.131P
Рис. 1.133
1.132.	Применив сигнальный граф, решить систему уравнений:
Зхх -I- 2х2 — Зх3 -I- 4х4 — 0;
Зхг — х2 + 4х3 + 2х4 = 0;
— 5xj + 2х2 — х3 = 0,
при х4 = 29.
1.133.	Построить сигнальный граф по уравнениям Кирхгофа для схемы, приведенной на рис. 1.133.
1.134(	Р). Определить напряжение 176 в схеме рис. 1.134 при помощи сигнального графа узловых уравнений.
Дано: ^71=2 См; д2 = 5 См; д3 = 5 См; #4 = 10 См; д5 = 10 См; дб = 5 См; Ех - 0,2 В; J3 « 0,5 А.
Рис. 1.134Р
Рис. 1.134
Решение. Примем <р4 = 0, тогда U6 = ср3. Построим сигнальный граф узловых уравнений (1.64), который имеет узлы Фь Ф2» Фз и истоки Ei и J3 (рис. 1.134Р), где дг1 =
= 01 + 02 + 04 = 17 См; g22 = 02 + 05 + 0з = 20 См; д33 = д5 + + 04 + 06 = 25 См.
Искомый потенциал
Фз — ^ЗЕ^1 + H3jJ3i
где передачи графа равны:
= 1,157;
и _ 1 0t
“ЗЕ ~ "7-----
А 011
0205
022033
04
033
н _ 1 1 “ А 922	05	0204 033	011033_	= 0,069 Ом,
так как определитель графа
02
011022
022033
04
011033
__040s02_ \ = 0 734
011022033 J
Следовательно, U6 = (р3 = 0,2 • 1,157 + 0,5-0,069 = 0,066 В.
1.135.	Определить ток I в схеме рис. 1.135, применив: 1) сигнальный граф узловых уравнений: 2) сигнальный граф контурных уравнений.
Дано: = г2 = г3 = г4 == г5 = г6 = 10 Ом; Et = 12 В; Е2 = = 18 В; J = 3 А.
Глава вторая
ЛИНЕЙНЫЕ ЦЕПИ С ИСТОЧНИКАМИ ГАРМОНИЧЕСКИХ ЭДС И ТОКОВ
Введение к гл. 2
Мгновенное значение синусоидального тока
i = i (t) = Im sin (cot + ф),	(2.1)
где Im — амплитуда; co = 2л/- угловая частота; / — частота; ф - начальная фаза.
Действующее значение тока
I =	(2.2)
Переходные и установившиеся проиессы в электрических цепях. Процессы в цепи, содержащей сопротивление г, индуктивность L, емкость С и источники гармонических ЭДС и токов, описываются неоднородными линейными дифференциальными уравнениями. Решением дифференциального уравнения, полученного, например, для тока, будет функция
i = "Ь J*cb>	(2.3)
где iy — установившаяся составляющая тока, частное решение неоднородного дифференциального уравнения:
iy = Im sin (cot + ф);	(2.4)
iCB - свободная составляющая тока, общее решение соответствующего однородного дифференциального уравнения.
Для цепей, содержащих один накопитель энергии (Лили С),
iC8 = Аер\	(2.5)
где р — корень характеристического уравнения.
Постоянная А определяется независимыми начальными условиями — начальным значением тока в индуктивности или начальным значением напряжения на емкости (см. также гл. 1 и гл. 8). По «законам коммутации» ток в индуктивности и напряжение на емкости не могут изменяться скачкообразно.
Значения 1т и ф определяются при подстановке решения (2.4) в неоднородное дифференциальное уравнение для больших значений t, при которых 0.
Изображение синусоидальных величин комплексами. На-пример, для тока
i == Im sin (cor + ф) = Im [7m cos (cor + ф) + j7m sin (cor + ф)] ==
= Im	= Im [/„ г. (cot + ф)],	(2.6)
где Im — мнимая часть, 1т = Im z. ф — комплексная амплитуда; I = I z. ф - комплексное действующее значение тока.
Законы электрической цепи в комплексной форме. Мгновенные значения:
иг == ri; uL= L^~ ; ис = (1/C) f idt; Hl
комплексные действующие значения:
U = г/; UL = j($Lt = jxLt = ZL/;
и с =	= - jxci = Zci,
jmC
где г — активное сопротивление; xL = coL — индуктивное (реактивное) сопротивление, хс = 1/соС — емкостное (реактивное) сопротивление.
Комплексные сопротивления и проводимости. Пассивный двухполюсник. Для ветви рис. 2.А,я комплексное сопротивление
Z = г + jx = г + j (xL - хс) ~	= г z. ср, (2.7)
где z = уг2 + х2 — модуль комплексного сопротивления или полное сопротивление; ф = arctg(x/r) — угол сдвига фаз между напряжением и и током i.
Рис. 2.А
Комплексное сопротивление может быть представлено на комплексной плоскости (±1; ±Д — рис. 2,А,б.
Комплексная проводимость
У= 4- = g ~ jb = уе~™ ^ул. - ф,	(2.8)
где g — активная проводимость; b — реактивная проводимость; 64
i/z = уд2 + b“ - полная проводимость; ср - arctg(fe/gf). Например, для схемы рис. 2.А, а
Y=g - jb = у г. - = i/Z =l/[r + j(xL - хе)].
где у = 1/г; tg<р = (xL-xc)/r; д = r/z2; b = (xL-xc)/z2.
Для схемы рис. 2.Б,а
Х = д -jb = 1/r + 1/>£+/(оС = д -j(bL-bc), где д = 1/r; bL= 1/coL— индуктивная и Ьс = соС — емкостная (реактивные) проводимости.
На рис. 2.Б,б проводимости изображены на комплексной плоскости.
У пассивного двухполюсника две схемы замещения.
Переход от последовательной схемы замещения (рис.-2.В,а) к параллельной (рис. 2.В,б)
т. е.
д = г/(г2 + х2); b = х/(г2 + х2).	(2.9)
Обратный переход ~	.	11 д . b
Z = ZZ.(p = — = -------— = ~5-----ту- + J —i--пг = г +
X д - jb д + ь д + ь2 J т. е.
г = д/(д2 + ь2); X = Ь/(д2 4- Ь2).	(2.10)
Мощность, Мгновенная мощность пассивного двухполюсника (рис. 2.В,д,б)
р = ui « Um sin (cot + \|/u) • Im sin (cot +	=
“ у COS ф - у COS (2 COt + l|/M + \|/Д гДе ф ==	и определяется параметрами пассивного двух-
полюсника (х и г или д и Ь).
3 п/р Ионкина П. А.	65
Средняя за период (активная) мощность, Вт, т
р = у = у cymcos(p - ШсоБф. (2.11) о
Полная мощность, В А,
S = UL	(2.12)
Реактивная мощность, вар,
6 = Wsin(p.	(2.13)
Знак угла (р определяет характер реактивной мощности — емкостной (2 < 0) или индуктивной (Q > 0).
Рис. 2. Г	Рис. 2.Д
Комплексная мощность
S = Ui = Р + jQ = SeJ^ где f * ~ сопряженный комплекс тока /;
S = |/Р2 + е2;
(2.14)
(2.15)
tg ср = 2/Л cos Ф = Р/S ~ коэффициент мощности.
Мощность может быть изображена на комплексной плоскости в виде треугольника мощностей (рис. 2.Г).
Баланс мощностей: сумма комплексных мощностей, по- ' требляемых электрической цепью, равна нулю. Например, для схемы рис. 2.Д
ЛЛ - Ё21$ + VJ* =	+ 122Z2 +
+ ^з2з —	1 + ^2r2 + ^3r3 + j+ ^2X2 + 1зхз)-
Взаимная индуктивность. Одноименные выводы у индуктивных катушек на рис. 2.Е, а обозначены точками. Магнитные
потоки (а также напряжения) самоиндукции и взаимной индукции складываются, если положительные направления токов / и /2 одинаковы относительно одноименных выводов (согласное включение), или вычитаются в противном случае (встречное включение).
В)
Рис. 2.Е
Напряжение взаимной индукции им = + Mdi/dt,	(2.16)
где М — взаимная индуктивность.
В комплексной форме
UM = ±	= ± jxMt = ± ZJ,	(2.17)
где хм = х12 = wM — сопротивление взаимной индукции.
На рис. 2.Е,а показано встречное включение, поэтому
Ui	-7<вМ/2; U2 = j^L2i2 jcoM/p
Для схемы рис. 2.Е,б
Ui — А1Л — А12Л — АпА + А2Л — А12Л +А23Л;
U3 ~jX3l3 — jXi3I! +jX23/2 +jx2i2 + A'23^3 ~jx12^L>
Коэффициент связи
k = M/|/L1L2.	(2.18)
Возможна эквивалентная замена схем со взаимными индуктивностями схемами, не содержащими магнитных связей. В случае трех ветвей, соединенных в общем узле, две из которых имеют индуктивную связь, в эквивалентной схеме добавляются сопротивления + Zw в индуктивно связанные
Рис. 2.Ж
ветви и ± Zm — в общую ветвь (верхний знак берется для индуктивностей, присоединенных к узлу одноименными выводами и наоборот). Этот прием применяется последовательно к каждой паре индуктивностей до полного устранения всех связей.
Например, для схемы рис. 2.Е,б получим эквивалентную схему рис. 2.Е,в. Потенциал (pi узла Г схемы рис. 2.Е,в не равен потенциалу (pi узла 1 схемы рис. 2.Е,б.
Уравнения линейного двухобмоточного трансформатора (рис. 2.Ж)
О = /2^2 ~~
где Zj. = + jxi; Z2 = r2 + jx2; ZH = rH +№•
Первичный и вторичный токи трансформатора равны:
/ —	/9
11 ~ 7	7	» 12 ”
^1 “Г £±ВН	А 2 "Г Z/
Ж»	" " ' П
где вносимое сопротивление
хм __ о2М2 , со2М2
“ВН J?2 + Zh г22 + х22 22	Г22 + Х22	22’
г22 =Г2 + Гн; х22 == х2 + хп.
Коэффициент трансформации п == Ut/U2.
(2.21)
Для идеального трансформатора (ri=r2 = 0; к = 1; w2->oo)
иг/и2 = wt/w2 = и; t1/l2 = 1/и,	(2.22)
где и>!, и w2 — числа витков первичной и вторичной обмоток соответственно.
Входное сопротивление идеального трансформатора
Z1BX == U1/I1 = h2Zh.	(2.23)
Резонанс. Условие резонанса в двухполюснике: реактивная мощность двухполюсника равна нулю.
Для двухполюсника (рис. 2.В) при последовательном резонансе — резонансе напряжений х = 0 (рис. 2.В, а), при параллельном резонансе — резонансе токов b = 0 (рис. 2.В, б).
Для последовательного контура г, L, С (рис. 2.А,а) угловая резонансная частота
со0 = 1/0LC.	(2.24)
Добротность контура
Q = a>0L/r = 1/сооСг = ]/b/C/r.	(2.25)
Резонансная кривая тока
/(®) =	-	,	(2.26)
]Л + <2 (оо/(00 - С0о/со)2
где /0 = U/г — ток при резонансе.
Полоса пропускания контура (coi - <о2) определяется из соотношения
м2/соо - ео1/сп0 = V2,	(2.27)
где (Dj и о)2 — частоты, при которых ток в ]/2 раз меньше резонансного.
Условие передачи максимальной мощности от активного Двухполюсника к пассивному
Z* = Z*,
(2.28)
где 7^ — внутреннее сопротивление пассивного двухполюсника; Z* — сопряженное значение внутреннего сопротивления активного двухполюсника.
2.1. Переходные и установившиеся процессы в простейших цепях
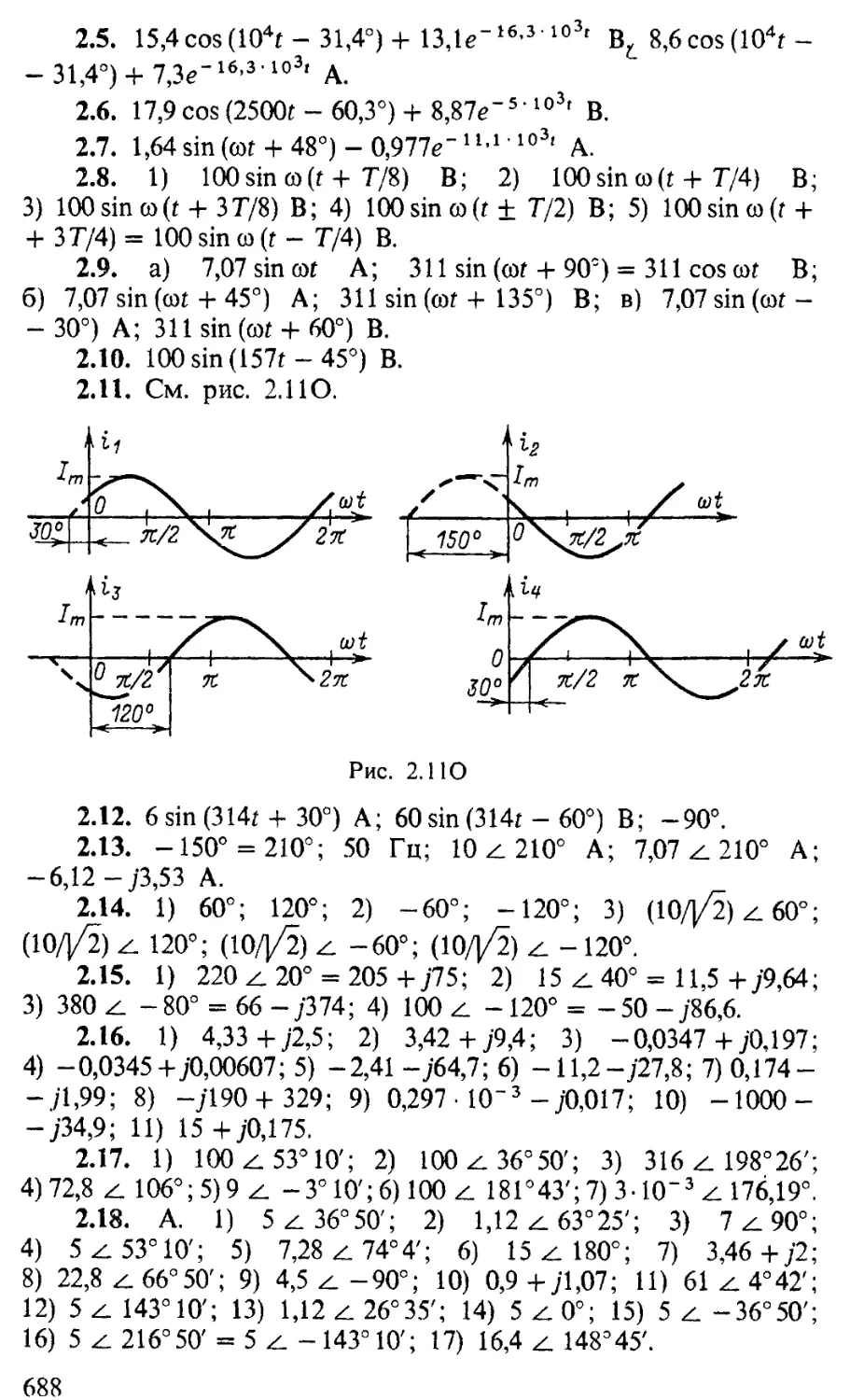
2.1(Р). Для схемы рис. 2.1 найти ток i после замыкания (t = 0) ключа.
Дано: г=1 Ом; R — 2 Ом; L=0,01 Гн; e = Emsincot = = 10 sin 200t В.
Решение. На * основании законов Кирхгофа составим
уравнения:
(1)
ri 4- Ri2 = е или г 4- R at
di2 _ de dt dt '
Исключив из системы уравнений (1) токи ц, i2 изводные токов dijdt, di2/dt, получим неоднородное ренциальное уравнение первого порядка для тока i: г Л r\ di . L de LI 4- — — 4- п = e 4- —-г-.
\ R J dt	R dt
и npo-диффе-
(2)
Запишем его решение по (2.3) — (2.5):
i — iy 4- iCB = sin (f')f + Ф) + Aept,	(3)
Определим частное решение iy (t велико и iCB -> 0). Для этого подставим решение (3) при iCB = 0 в (2):
LI 1 + Ъ" )®7mcos(cot 4- ф) 4- Imr sin (cot 4- ф) =
= Ет sin cot 4-
СО-Г£т R
COS tot.
(4)
Из и синус миру ем cos cot):
(4) найдем 1т и ф. Для этого разложим косинус суммы двух углов cos (tot 4- ф) и sin (cot 4- ф) и просум-коэффициенты при одинаковых функциях (sin cot и
тЛ г \ - coL 1 4--^-
sin ф + rl„ cos ф = Ет;
(5)
toL
lm cos ф 4- rlm sin ф =
R
(6)
Возведя в квадрат (5) и (6), суммируя и учтя соотно
шение sin2 ф 4- соз2ф — 1, получим уравнение для определения амплитуды тока 1т
(®L)2 (1 + r/R)212 + (rlm)2 = E2 + (vLEJR)2. (7)
Рис. 2.1
Рис. 2.1P->
Разделив (6) на (5), получим уравнение для начальной фазы (ф)
+ r/R) + г tg ф _ coL - cdL(1 4- r/K)tg\|/ 4- г R
Из (7)
найдем
(8)
т
г = 4>47 А,
а из (8)
(f)LR2
= - 0,5,
т. е. ф = - 26° 30'.
Для определения постоянной А в решении (3) рассмотрим момент времени t = 0:
i(0) = sin ф + А.
(9)
Начальное значение тока после коммутации г(0 4-) определим из системы (1) при t = 0:
— i(0 4") 4" G (0 4") 4" (0 4") = 0; ri (0 4") 4~ Ri2 (0 4-) = e (0 4-).
(10)
Ток ц в индуктивности не может изменяться скачкообразно, т. е. 1'1(0 4-) равен току до коммутации ц(0—) = 0.
Из системы (10) находим
i(0 +) = i2 (0 +) = е (0 + )/(r + R) и из (9)
А = - Im sin ф = 2 А.
Из характеристического уравнения для уравнения (2), 4* r/R) + г = 0, находим корень
rR	с -1
р —----------=гг~ — — 66,6 С .
Общее решение уравнения (2):
i = 4,47 sin(2001 - 26°30') + 2е'66’6г А.
На рис. 2.1Р представлена кривая тока i(t).
2.2.	Резистор с сопротивлением г2 — 30 Ом (рис. 2.2) клю чается к источнику с параметрами = 10 Ом;
= 0,005 Гн; е = 200 sin 600t В в момент времени гь когда е (ц) = — Ет/2 и de > 0.
Определить напряжение и на резисторе.
т. е.
под-
Рис. 2.3
Рис. 2.2
Рис. 2.4
Рис. 2.5
2.3.	Источник тока J(t) = 20 sin (3141 4- 90°) А с внутренним сопротивлением г = 20 Ом подключается к двухполюснику (рис. 2.3) с параметрами R = 20 Ом; L= 0,0318 Гн.
Найти ток i после замыкания ключа. Построить график изменения тока.
2.4.	В схеме рис. 2.4 замыкается ключ.
Дано: е - 30sin(1001 4- 45°) В; г = 30 Ом; R = 10 Ом; £ = 0,3 Гн.
Найти закон изменения тока i.
Рис. 2.7
Рис. 2.6
2.5.	Незаряженный конденсатор емкостью С подключается к цепи (рис. 2.5).
Определить uc(t) и i(t).
Дано: е = 36coscot В; со » 104 рад/с; г1 — г2 = 1,8 кОм; С = 68 пФ.
2.6.	К цепи, состоящей из параллельно соединенных источника тока J(t), резистора гг и конденсатора С, подключается резистор г2 (рис. 2.6).
Найти узловое напряжение u(t) при J(t) = 10 cos (cot — - 33,7°) мА; со = 2500 рад/с; С = 10“7 Ф; = 6 кОм; г2 = = 3 кОм.
2.7.	Для схемы на рис. 2.7 заданы параметры: С = 1 мкФ; гj == 1 кОм; г2 — 0,1 кОм; ЭДС е = 220 sin cot В; со — 104 рад/с.
Найти закон изменения тока i источника.
2.2. Мгновенные значения синусоидальных величин. Простейшие операции с комплексными числами. Последовательное и параллельное соединение элементов цепи
2.8.	Синусоидальное напряжение u(t) с амплитудой 100 В и периодом Т изображено на рис. 2.8 при начале отсчета времени в точке 0.
Записать напряжение w,(t) при других началах отсчета времени в точках: 1)	2) О2', 3) О3; 4) 04; 5) О5.
2.9.	На рис. 2.9, а—в показаны кривые мгновенных значений гармонических токов и напряжений.
Записать аналитические выражения мгновенных значений этих токов и напряжений при амплитудах Im = 51/2 A; Um =
2.10.	При t = 0 мгновенное значение синусоидального напряжения и(0) = —100/2 В, а при Т/8 = 1/200 с напряжение и (Т/8) = Um = 100 В.
Записать мгновенное значение напряжения.
2.11.	Заданы токи: = Imsin(314t + 30°); i2 = sin(314t + + 150°); i3 = 7msin(314t - 120°); i4 = 7wsin(314r + 330°).
Построить графики этих токов.
2.12.	На рис. 2.12 построены мгновенные значения тока и напряжения.
Записать их аналитические выражения. Определить сдвиг фаз ф между напряжением и током.
2.13.	Мгновенное значение тока i — 10 sin (314г 4- ф) при t = (7/6) 10“2 с равно -5 А и di/dt < 0.
Найти значение ф. Определить частоту. Записать комплексную амплитуду и комплексное действующее значение в полярной и алгебраической формах.
2.14.	Для тока i = 10 sin (314t 4- ф) А известно при f = 0 мгновенное значение: i(0) = 8,66 А.
1)	Найти возможные значения ф.
2)	Определить, как изменятся значения ф, если i (0) = = -8,66 А.
3)	Записать комплексные действующие значения токов при найденных значениях ф.
2.15.	Записать в полярной и алгебраической формах комплексные амплитуды напряжений и токов, мгновенные значения которых: 1) и = 220 sin (cot + 20°); 2) i = 15 cos (cot - 50°); 3) и = ss -380 sin (cot + 100°); 4) i - 100 sin (<ot - 120°).
2.16.	Разложить на действительную и мнимую составляющие следующие комплексные числа: 1) 5 z. 30°; 2) 10	70°;
3)	0,2 а 100°; 4) 0,035 а 170°; 5)-250 а 195°; 6) 30 а -112°; 7) 2 а 275°; 8) 380 а -30°; 9) 0,017 а 269°; 10) 1000 а -178°; И) 15 а 40°.
2.17.	Найти модуль и аргумент следующих комплексов: I) 60 4- J80; 2) 80 + /60; 3) -300 -J100; 4) -20 + J70; 5) 9 -Д5; 6) -lOO-j’3; 7) -0,003 +7’0,0002.
2.18.	А. Представить следующие комплексные числа, которые заданы в алгебраической форме, в полярной форме и наоборот: 1) 4 + 7З; 2) 5 + 7; 3) J7; 4) 3 + 7’4; 5) 2 + J7; 6) -15; 7) 4 а 30°; 8) 9+J21; 9) —/4,5; 10) 1,4 а 50°; 11) 61 +/5; 12) -4+7’3; 13) 1+Д5; 14) 5; 15) 4-/3; 16) -4-7’3; 17) -14+7’8,5.
Б. Вычислить комплекс 10"5 (76 + 7’52) ( — 4,3 + 7'15)( —4,75 — — /7,8) (14 — 7’3,49), представив его в полярной и алгебраической формах.
В. Вычислить комплекс
(4,36 -Д02) (-7’4,37) + 73 а -205°
54 а 180° + 7’0,437 (Д5) (1 а 90° + 5,07 - 7’2,5) ’ представив его в полярной и алгебраической формах.
2.19. В последовательном контуре с индуктивной катушкой (^ = 20 мГн; г = 50 Ом) и конденсатором (С = 1 мкФ) задан ток i = 0,5 cos 104t А.
Определить мгновенные значения напряжений на катушке и на входе цепи.
2.20.	Цепь рис. 2.20 подключена к источнику тока J (t) = = 2 sin (cot + 30°) А с частотой / = 200 Гц. Параметры цепи: г = 10 Ом; L — 0,01 Гн; С = 80 мкФ.
Найти мгновенные значения напряжений на всех участках и мгновенную мощность источника.
Рис. 2.20
Рис. 2.21
Рис. 2.23
2.21.	В цепи г, L (рис. 2.21) известны показания первого и второго вольтметров: Щ - 100 В; U2 = 150 В и сопротивление г = 10 Ом.
Определить показание третьего вольтметра и индуктивность, если частота тока / = 50 Гц.
2.22.	Определить, при каком значении угловой частоты тока в цепи, схема которой показана на рис. 2.22, напряжение Ui будет в 2 раза больше U2.
Дано: г — 50 Ом; С = 3,18 мкФ; L = 0,1 Гн.
2.23.	Определить показание приборов в цепи рис. 2.23, если известно показание первого амперметра Л = 1 А и заданы параметры: Ti = 100 Ом; L — 0,276 Гн; г2 — 200 Ом;/ = 100 Гц.
2.24.	При замкнутом ключе сдвиг фаз между напряжением и током в цепи (рис. 2.24) составил 45°.
Определить сдвиг фаз при разомкнутом ключе, если частота тока не изменяется.
2.25.	В цепи, состоящей из двух последовательно соединенных индуктивных катушек (рис. 2.25), напряжение на входе и — 120 sin cot В.
Определить мгновенные значения напряжений и и2 на катушках и показания приборов. Параметры катушек: = 5=4 мГн; Г! = 50 Ом; L2 = 20 мГн; г2 = 10 Ом; частота f = 400 Гп.
2.26.	1) Определить показание вольтметра в схеме рис. 2.26 при U = 100 Z. 30° В; = 5 Ом; г2 = 25 Ом; L= 0,159 Гн; С — 127 мкФ; со = 314 рад/с. Построить топографическую диаграмму, приняв равным нулю потенциал точки 0.
2)	Найти показание вольтметра в той же схеме, но после того как элементы и L поменяли местами.
2.27.	В цепи рис. 2.27 известны показания трех амперметров: 71а=2|/з А; /2 = 73 = 2 А и сопротивление резистора г = 50 Ом,
Найти значения хс и R. Определить coscp цепи.
2.3.	Разветвленные электрические цепи.
Векторные и топографические диаграммы.
Энергетические соотношения
2.28.	Для схемы двухполюсника рис. 2.28 заданы параметры: Li = 5 мГн; = 150 Ом; Ci = 0,667 мкФ; L2 = 10 мГн; ^2 = 200 Ом; С2 = 1 мкФ; напряжение на входе и — = 10 ]/2 sin 104t В.
Найти напряжение uC2(t) на конденсаторе С2, построить топографическую диаграмму, приняв равным нулю потенциал точки 1.
Рис. 2.28
2.29.	На схеме рис. 2.29 указаны (в омах) сопротивления элементов, входное напряжение и = 100 sin cot В.
Определить токи ветвей. Построить векторную диаграмму токов и топографическую диаграмму, приняв равным нулю потенциал точки 1.
J4-0
-j80
Рис. 2.29
2.30.	На схеме рис. 2.30 ЭДС £ = 10 В, сопротивления xL = хс = г = 10 Ом.
1)	Построить векторную диаграмму токов.
2)	Построить векторную диаграмму токов при увеличенной в 2 раза частоте ЭДС.
Рис. 230
2.31.	Цепь рис. 2.31 преобразует однофазное напряжение U в трехфазное, т. е. потенциалы фа, ф& и фс образуют на комплексной плоскости равносторонний треугольник.
Построив качественно топографическую диаграмму, определить, при каких соотношениях параметров возможно такое преобразование.
Рис. 2.31
2.32(	Р). Для цепи рис. 2.32 известны показания амперметров: Ii = 12 — 1з — 5 А и вольтметров: Ui — U2 = 100 В.
Определить параметры цепи и показание вольтметра на входе, если входные напряжение Uae и ток совпадают по фазе.
Рис. 2.32Р
Указание. Построить векторную диаграмму токов и топографическую диаграмму.
Решение. Построим диаграмму (рис. 2.32Р). Для узла б запишем уравнение, составленное по первому закону Кирхгофа: Л —12 + Л- Изображаем векторы этих токов на комплексной плоскости, отсчитывая их начальные фазы от узлового напряжения U6e = U2 = 100 В, начальную фазу которого выберем равной нулю.
Ток /3 отстает от напряжения U2 по фазе на 90°, ток 12 опережает на неизвестный угол а < 90°, а ток Д равен их сумме. Ввиду равенства модулей (Ц = 12 = /з) углы между векторами пары токов /2, Л и пары токов Д, Д равны 60°, т. е. а = р = = 30°. Напряжения Ur2 =г212 и С/я2 — (“АсзМг образуют катеты прямоугольного треугольника с гипотенузой = U2l значит, U2e = Ur2 = U, cos а = 1001/3/2 и = Ux2 = U2 sin а = == 50 В.
Далее строим векторы напряжений для элементов первой ветви: йх1 — (—ДсОЛ.и Uri = При этом согласно условию входное напряжение йав и ток Ц должны иметь одинаковые фазы. Следовательно, векторы — йхг и Uai = Url совместно с вектором Ua6 образуют прямоугольный треугольник, катет I7fll которого составляет часть входного напряжения Uae.
Ввиду равенства треугольников 1вб, 1аб и 2вб находим, что (7le = Ua{ — U2e и входное напряжение Uae = 2L72g = 2 •100 j/3/2 =
Рис. 2.35
Рис. 2.34
Рис. 2.36
Параметры определим по закону Ома: х£ = (72//3 = = 100/5 = 20 Ом; хс2 = хс1 = ^62/Л — 50/5 = 10 Ом; = г2 — =	= 86,5/5 = 17,3 Ом.
2.33.	Для схемы рис. 2.33 построить векторную диаграмму токов при 1 = 1 А и топографическую диаграмму, приняв потенциал фе = 0. Параметры: п - xL = xcl = r3 = xL4 = r/2 = = XL2 ~ хсз — 1 Ом.
Определить ЭДС Ё.
2.34.	В схеме рис. 2.34 ЭДС е = 150|/2 sin со/ В и значения сопротивлений элементов даны в омах.
Определить мгновенные значения токов и напряжений иаЬ, иас и uad. Построить векторную диаграмму токов и топографическую диаграмму, приняв равным нулю потенциал точки Ь.
2.35.	Применив преобразование треугольника сопротивлений в звезду, определить ток I источника в схеме рис. 2.35, если хс = xL = г = 10 Ом и Ё = 100 В.
2.36.	В цепи рис. 2.36 действуют источник ЭДС Ё -= 250 х_ 90° В и источник тока J = 51/2 х. 45° А.
Дано: rt — 25 Ом; г2 = 50 Ом; г3 = 20 Ом; хс = 20 Ом и — 50 Ом.
Определить показания амперметров.
2.37	(Р). Определить ток 1 в сопротивлении Z мостовой схемы рис. 2.37Р.
Дано: хс = 104 Ом; xL=0,8 103 Ом; п = 5103 Ом; r2 = 103 Ом; г3=0,32 103 Ом; Z=192-j41 Ом; Ё = = 290	—21° 50' В.
Рис. 2.37Р
Решение. Вычислим предварительно комплексное сопротивление первой ветви:
Zi = n (-Ac)/(fi - Ас) = (4 - J2)' Ю3 Ом.
Решим задачу методом активного двухполюсника (эквивалентного источника) по (1.55):
/ = ^(Zbx + Z)-	(1)
Определим напряжение Ux при разомкнутой ветви с сопротивлением Z (рис. 2.37Р, л). Предварительно рассчитаем токи:
+ г2) == 53,85 • IO’3 х. 0° А;
/Р2 = Ё/(г3 + Al) = 03366 х. -90° А.
Напряжение
= -Al/P2 +	= 215’4	180° А-
Определим входное сопротивление двухполюсника относительно выводов а, б разомкнутой ветви (рис. 2.37Р, б), учтя, что внутреннее сопротивление идеального источника ЭДС
равно нулю:
+ 1Х1Гз
J*l+ гз
= 1104+J41 Ом.
Искомый ток по (1) i = 0,1662 х. 180° А.
2.38.	Для схемы рис. 2.38 заданы параметры: xL = хс = = 0,5г = 10 кОм; Ё = 10 В
Определить ток /.
Рис. 2.39
Рис. 2.38
Рис. 2.41
Рис. 2.40
2.39.	Определить, применив метод наложения, токи в цепи рис. 2.39.
Дано: Ё = 10J/z В; j = 1 z. 45° мА; coL= 1 кОм; 1/соС = = 2 кОм и г = 1 кОм.
2.40.	Определить ток ветви с источником э. д. с. (рис. 2.40)
методом эквивалентного источника.
Дано: Ё = 32 В; j = 40 z. — 22°36' мА; — 500 Ом; г2 — = хс = 200 Ом; г3 — 400 Ом; xL = 600 Ом.
2.41.	Для схемы рис. 2.41 дано: Ё —10 В; j = 1 А; 2xL1 = xL2 = 10 Ом; хс — г = 5 Ом.
Рис. 2.42
1)	Определить токи ветвей методом контурных токов, найти напряжение на выводах источника тока.
2)	Решить задачу методом узловых потенциалов, выбрав ф2 = 0.
2.42.	Определить комплексные мощности источников в схеме рис. 2.42.
Дано: xL = 5,48 Ом; хс— = 4 Ом; и = 10 Ом; г2 = 50 Ом, Ё{ = 100 В; Ё2 = — J50 В.
2,43.	Определить токи в ветвях схем рис. 2.43, а —г при е = 220 j/2sin(cot + 45°) В; n = r2 = 200 Ом; xL = xC2 = 200 Ом и xci = 100 Ом.
Рис. 2.43
2.44.	Даны: векторная диаграмма токов и топографическая диаграмма (рис. 2.44) двухконтурной схемы.
Составить схему и определить ее параметры.
2.45.	Для цепи рис. 2.45 задано: входное напряжение и= 100cos(dt В и сопротивления г — 20 Ом; coL=2O Ом; 1/(йС = 10 Ом.
Определить показания амперметра и ваттметра для двух положений ключа: 1 и 2.
Рис. 2.45
Рис. 2.46
2.46.	Для цепи рис. 2.46, а известна векторная диаграмма (рис. 2.46,6), на которой показаны ЭДС Ё2, напряжения
U и ток / трех режимов: /а, 1б, /в.
Записать комплексные мощности источников и двухполюсников Л и Б; определить в указанных режимах, отдаются или потребляются ими активная и реактивная мощности.
2.47.	В схеме рис. 2.47 известны параметры = 20 Ом; r2 — xL — хс = 40 Ом и показание ваттметра Р — 600 Вт.
Определить ток и ЭДС источника, приняв 1—1.
Рис. 2.47
Рис. 2.48
2.48.	В цепи рис. 2.48 известны напряжения иаЬ — — 8 sin ((dt 4- 30°) В и иас = 2 ]/2 sin art В. Значения сопротивлений (в омах) указаны на схеме.
Определить показание ваттметра и сопротивление Z.
2.49.	Для цепей рис. 2.49, а и б J (г) - 10 sin cor А; г1 = хс = « 40 Ом; г2 = хы = 20 Ом и xL2 = 80 Ом.
Определить все токи и найти показание ваттметра.
2.50.	В цепи рис. 2.50 были произведены измерения напряжения и тока: 1) при отключенном элементе Z6; 2) при корот-84
ком замыкании точек а и б. В первом опыте получено U& = = 200 j/5 z. 30° В, во втором опыте / = 10 л. —150° А.
Найти сопротивление эквивалентного источника для элемента Z6 и определить ток / при z6 == 10 х. 60° Ом.
Рис. 2.49
2.51.	Для схемы рис. 2.51 дано: /а = ]/2 х. 135° A; ib = = 4|/2zl45° А; Ёг = 4 В; £2 = 4 z. -90° В; = 2 + ;4 Ом; Z3 = 2 Ом.
Определить токи 1Ъ i2i Ц и 1С.
Рис. 2.50
Рис. 2.51
2.52Q	P). Определить токи в схеме рис. 2.52, применив ме
тод контурных токов.
Дано: == 20 Ом; хС2 — 120 Ом; г2 = 30 Ом; г3 = 70 Ом; xL3 = *ci = 50 Ом; хЛ2 = Ом: = J200 В; Ё2 — — jlOO В; £3=(1-у 1)100 В.
Решение. Для схемы, изображенной на рис. 2.52, выбираем положительное направление контурного тока (по часовой стрелке) в каждом из трех контуров-ячеек 1, 2, 3. Составляем уравнения:
Zltill> + Zl2t<21 + Zl3i(3) = Ёа>;
Z21/(l> + z22tw + Z23/(3) = £(2);
z3J<l> + z32im + z33i(3> = ft3',
где tw, iw, /(3) - контурные токи; Z2l = rt + r2 + jxL2+jxL3 =
= 50+yl50 Ом; Zl2 — — (r2 + jx^i) — —(30+/100) Ом; Z13 —
“ ~jxL3 ~ “J 50 Ом ; Z2 1 — Zj2 j Z.22 — r2 + jxL2 + r3 ~ JXC1 ~ = 100 +J50 Ом; Z23 = -r3 = -70 Ом; Z31 = Z13; Z32 = Z23; Z33 - JXL3 + гз —jxc2 = 70 - j70 Ом, а контурные ЭДС Ё(1) = = E1=j200 В; Ё(2) = -Ё3= -100+jl00 В; Ё<3) == Ё3 - Ё2 = = 100 в.
Рис. 2.52
Вычислим определитель матрицы Z:
211 212 213
2г 1 2з2 213
= (19,72 — ;4,77) • 105 Ом3,
2з1 2зг 2зз
а также следующие определители:
	£(1) z12 Z13	
Ai =	£<2) z22 z23	= (—1,09 + j'2,39)  106 B Om2;
*	Ё™ Z32 Z33	
	Zn F z13	
а2 =	Z21 e<2) z23	= (- 4,18 + /3,97)  106 В  Ом2;
	z31 E<3) Z33	
	z1( z12 £<J>	
А3 =	Z21 Z22 £<2>	= (-2,79 -/0,28) • 106 В • Ом2.
	Z31 Z32 £(3>	
Находим контурные токи (решим систему уравнений): /(1) = А^А = 1,296 z_ 128,1° А = (-0,799 + jl,02) А;
1(2) = А2/А = 2,837 z. 150,1° А = (-2,46 + ;1,41) А;
/<3) = А3/А = 1,379 z. -160,7° А = ( - 1,3 - Д456) А.
Токи ветвей:
Л =	/2 = /<2>; /, = -/<’>; /4 = -/<»> + /<’> =
= -0,5 -Д476 = 1,56 zl -108,7° А; /5 = -1т + /(3> = = 1,16 —у1,866 = 2,2 z. -58,1° А; /6 = /(1’ - 1т = 1,66 -/0,39 = = 1,69 г. -10,2° А.
Для того чтобы убедиться в правильности вычислений, составим баланс мощностей.
Мощность, развиваемая источниками,
£ ВД* =	+ Ё21* + Ё3Ц* - 200/(-0,799 -./1,02) -
I
- 100/(1,3 -Д456) + 100(1 - J) (1,16 + 71,866) =
= (461 —/219,2) В-А.
Мощность потребляемая: активная
X Рпотр = г + г3Ц + r2ll = 20  1,2962 + 70  2,22 + 30 • 1,692 = = 458 Вт;
реактивная
X 2потр = (~xCl) ^2 + ( — Хсг) ^3 + XL3^4 +	=
= (-50) 2,8372 + (-120) 1,3792 + 50 • 1,562 + 100 • 1,692 = = -223,3 вар.
Относительная ошибка вычислений:
Sp% =
461 -458 0,5(461 + 458)
100 % = 0,65 %;
я °/ = 223,3 219,2	_
Q /о 0,5 (223,3 + 219,2) /о ’ /о'
2.53(Р). Определить потенциалы узлов и записать по закону Ома токи в схеме рис. 2.53.
Дано: = г3 = г4 = г5 = хС1 = хс2 = 10 Ом; r2 = r6 = xL2 = = 5 Ом; = 20 Ом; Ei=j20Q В; Ё2 = 50 В; Ё3 = (100 + + J200) В; J = 10 А.
Решение. Для решения задачи применим метод узловых потенциалов. Приняв ф4 = 0, запишем уравнения по методу
узловых потенциалов:
+ ТиФ1 — У12Ф2 ~ ТхзФз =^1>
~ Т21Ф1 + Х22Ф2 ~ УгзФз = А;
“Уз1Ф1 ~ У32Ф2 + УззФз — А,
где Уц = —+-у^—+ J —+ — = (0,2 + )0,05) См; Г1 JxLi хС2 г5
у22 = — + -Д~+ —+ —Д = (0,4 -Д15) См; rl JXL1 r2 ?6+JXl2
------:----= (0,45 + Д15) См;
r4 — JXC1
I12 = —+ -4-= (0,1 -J0,05) См;
Г 1	JXL1
У13 — F j = (0,1 + j0,l) См; У2з =	= 0,2 См;
г 5 хС2	г 2
Jt = - -Д- + J =0; j2 =-Д-+— = 20 А;
JXLi	JxLt г2
J3= -2J	= -20(2+JI) А.
r2 r3
Решим систему уравнений для потенциалов. Определитель системы:
0,2 + ;0,05	- (0,1 - Д05) - 0,1 (1 + J1)
- (0,1 -J0,05)0,4-70,15	-0,2
-0,1 (1 + J1) -0,2	0,45 + J0,15
= 0,0364 0,0045° См3.
Определитель, в котором элементы первого столбца заменены свободными
членами
Д, = 2,121 z. 57,73 А-См2.
Потенциал узла 1
Ф1 = Д,/Д = 58,128 л. 57,723° В.
Аналогично для определения потенциалов узлов 2 и 3 вычислим:
Д2 = 0,9656 z. 63,566° А См2;
Д3 = 3,917z. - 166,93° А-См2.
Следовательно,
ф2 = Д2/Д = 26,46 z. 63,56° В; ф3 = Д3/Д = 107,37 z. - 166,94° В.
Рис. 2.53
Токи ветвей запишем по обобщенному закону Ома (1.14): . Ui2 + £1 . /	&2 “ ^23 . / _ ^34 + £з .
11 — --------, — -------------, 13 —----------,
J*L1	г2	Тз
j #34	. j _ l>13 . /	U2<	. i U12 .
14 = ----;---» 15------9 л 6 =	; --> 17 — ----,
4-JXC\	Г5	r6+jxL2	rt
j ^3 is —	:	•
-JXC2
2.4.	Эквивалентные схемы двухполюсников
2.54.	Для последовательной схемы (рис. 2.54) при г = = 100 Ом; С == 10“5 Ф найти параметры параллельной эквивалентной схемы. Вычисления провести для двух случаев: 1) со = 103 рад/с; 2) со = 2 * 103 рад/с.
2.55(	Р). Полная проводимость конденсатора у = 0,01 См, его добротность Qc = 5.
Определить параметры параллельной и последовательной схем замещения.
Решение. В конденсаторе с потерями разность фаз ср приложенного напряжения и тока по абсолютному значению меньше тс/2 на угол потерь 5.
Представим конденсатор эквивалентной схемой, содержащей емкость и параллельно включенное сопротивление (рис. 2.55Р, а). Для этой схемы tg 8 = 1/QC - xc/R = 0,2 и 5 = 11° 20'
г
Рис. 2.54
Рис. 2.55Р-►
Значения хс и R определим из соотношений sin 8 = IR/I = U/(RUy) = l/(Ry); cos 8 = Ic/I = U/(xcUy) = l/(xcy), откуда R = l/(y sin 8) = 508 Ом; xc = I/O cos 8) = 102 Ом.
Для последовательной схемы замещения (рис. 2.55Р, б)
tg 8 = \/Qc = r/x'c = 0,2; sin 8 = Ur/U = Ir/Iz — r/z\ cos 8 = Uc/U = Ix'c/Iz = x'c/z\
здесь z — \Jy — полное сопротивление конденсатора. Следовательно, г = z sin 8 = (1/у) sin 8 = 19,6 Ом; x'c = zcos8 = = (l/y)cos 8 = 98 Ом.
Те же значения можно получить из выражения для комплексной проводимости, вычислив предварительно угол | ф | = — п/2 — 8 = 78° 40' и ф = —78° 40' (схема замещения конденсатора), при этом
Y = у а. -q>=g-jb=-^+j—= 0,01 г. 78°4О' См, К Хс
и для последовательной схемы замещения
Z = z z. ф = 1/У= г -jx'c = 100 z. -78°40' Ом.
Отметим, что поскольку угол 8 мал, то cos 8 близок к единице и, следовательно, С « С', а г R. Это следует из соотношений r/R = zsin 8(уsin 8) = sin2 8 1 ;х'с/хс = zcos8(ycos8) = = cos2 8 « 1. Поэтому основными параметрами конденсатора считают его емкость и угол потерь.
2.56.	На входе двухполюсника (рис. 2.56), содержащего резисторы и индуктивные катушки, измерены: мощность Р = = 110 Вт, напряжение U = 220 В и ток / = 5 А.
Определить параметры: а) последовательной и б) параллельной схем замещения двухполюсника.
2.57.	Для реального конденсатора известны потребляемая мощность Р = 10 мВт и тангенс угла диэлектрических потерь tg 6 = 0,316 при напряжении U = 220 В.
Определить параметры последовательной схемы замещения.
Рис. 2.59
Рис. 2.56
2.58.	Конденсатор емкостью С = 1 мкФ с реальным диэлектриком имеет tg 8 = 0,15 на частоте f = 50 Гц.
Определить полное сопротивление конденсатора.
2.59.	Электродвигатель с номинальными параметрами L7H0M = 127 В, Рном = 2 кВт и cos фном = 0,8 включается в сеть с напряжением U = 220 В по схеме рис. 2.59.
Найти сопротивление резистора R, при котором двигатель будет работать в номинальном режиме, и параметры х и г последовательной схемы замещения двигателя, а также полную, активную и реактивную мощности всей установки.
2.60.	Для определения неизвестных параметров катушки (х, г) ее соединили последовательно с резистором, сопротивление которого R = 2 кОм (рис. 2.60), и измерили напряжения U! = 45 В, U2 = 20 В и и3 = 30 В.
Определить х и г.
Рис. 2.60
2.61.	Сопротивление R конденсатора постоянному току равно 10 кОм. При переменном токе частотой — 1600 Гц tg 8 = 0,05.
Для параллельной схемы замещения конденсатора определить tg 8, S, Р и Q при частоте f2 = 3200 Гц и напряжении питания U = 380 В, считая постоянным и равным R активное сопротивление в схеме замещения.
2.5* Резонанс. Режим согласованной нагрузки
2.62.	К последовательному rLC-контуру, параметры индуктивной катушки которого известны: L = 2,26 мГн, г = 10,6 Ом, приложено напряжение (7 — 50 мкВ с частотой, соответствующей длине волны радиостанции X = 2000 м.
Найти емкость С конденсатора, при которой контур настроен в резонанс, добротность контура и напряжение на катушке.
2.63.	Источник тока J (г) = 10 sin cot А, частота которого может изменяться, подключен к схеме (рис. 2.63) с параметрами г = 10 Ом и С = 1 мкФ. Напряжение на емкости в режиме резонанса равно 10 В.
Определить резонансную частоту и индуктивность.
Рис. 2.63
Рис. 2.64
2.64.	Найти ток 1 в схеме рис. 2.64 при £ = 10 В. Решение провести двумя методами — путем преобразования источника с ЭДС Ё в эквивалентный источник тока и применения свойства взаимности.
2.65.	На рис. 2.65 показан параллельный контур, в котором индуктивная катушка представлена параллельной схемой замещения, а конденсатор можно считать идеальным.
Рис. 2.65
Рис. 2.66
Дано: ток источника J (t) = 10 sin 103t А, индуктивность L = 1 мГн и добротность контура 2 = 5.
Определить показание амперметра, емкость С и сопротивление г, если в цепи наблюдается резонанс.
2.66.	Параллельный контур (рис. 2.66) настроен в резонанс.
Дано: 12 = 14,1 A; U = 100 В и Ц
Определить показания первого и третьего амперметров и параметры контура.
2.67.	Для цепи рис. 2.67 в режиме резонанса известны показания приборов Р = 4 Вт, U — 4 В и индуктивное сопротивление xL= 2 Ом.
Определить сопротивления г и хс.
Рис. 2.68
2.68.	В цепи рис. 2.68 определить показания приборов при г = 10 Ом, xL = хс = 40 Ом, Ё = 220 В.
2.69.	У электродвигателя при напряжении U = 220 В и cos ф = 0,4 мощность Р = 1,76 кВт.
1)	Найти ток двигателя.
2)	Вычислить емкость конденсатора, при включении которого (рис. 2.69) cos ф повысится до 0,8.
3)	Определить ток сети при включении такого конденсатора.
Рис. 2.69	Рис. 2.70
2.70.	В схеме рис. 2.70 определить сопротивление г и токи, если в режиме резонанса xL = 14,4 Ом, хс = 40 Ом, U == 384 В.
2.71.	На рис. 2.71 показана резонансная кривая последовательного rLC-контура при напряжении питания, равном 100 В.
Определить полосу пропускания (coi—со2) и добротность контура, параметры rLC-контура и комплексные мощности при граничных частотах полосы пропускания.
2.72.	В схеме рис. 2.72 известны параметры: С£ = 3 мкФ; С2 = 1 мкФ; L=4 Гн; г = 100 Ом и напряжение питания U = 200 В.
Определить резонансные угловые частоты и токи при резонансных частотах.
«—Рис. 2.71
Рис. 2.72
2.73(	Р). Двухполюсник (рис. 2.73) настроен в резонанс, причем /1 = 12. Известны показания вольтметров: Ui = 100 В; U2 = 40 В.
Определить показания вольтметров U3, U4, Us и U6.
Рис. 2.73	Рис. 2.73Р
Решение. Построим векторную диаграмму токов и топографическую диаграмму (рис. 2.7 ЗР). Начнем с вектора напряжения Uба = ^4 на разветвленной части цепи, отложив его по действительной оси и приняв потенциал точки а равным нулю.
Ток Л в активном сопротивлении г совпадает по фазе с напряжением ток /2 опережает по фазе напряжение йба на 90°, а общий ток 7 равен их геометрической сумме и опережает по фазе напряжение йба на 45° (Ц = 12).
Из точки б параллельно току i откладываем вектор напряжения Ue6 на активном сопротивлении R и из точки в — вектор напряжения на индуктивности иге, опережающий по фазе ток / на 90°. Получаем точку г. Сумма векторов U6ai Ue6 и ^гв равна вектору напряжения питания йга — которое совпадает по фазе с током 1 (резонанс). Из диаграммы следует, что иге - U3 = Uv - U2 = 60 В; U6a = U4r = (U1--U2)\/i = S5 В;	= ]/Vl + Uj = 72 B; Um = U6 =
=	+ 1/1/1/2)2 + (У1/|/2)2 = 117 B.
2.74.	Для цепи рис. 2.74 дано: угловая частота ЭДС со = = 104 рад/с, индуктивность катушки L=0,l Гн.
Найти емкость С конденсатора, при которой действующее значение тока I не зависит от сопротивления резистора г. Определить, как изменится этот ток, если катушку и конденсатор поменять местами.
2.75.	Определить индуктивное xL и активное г сопротивления двухполюсника (рис. 2.67), при которых его входное сопротивление ZBX = 20 Ом, если хс = 40 Ом.
2.76.	Электрическая схема замещения магнитострикционного преобразователя без потерь представлена на рис. 2.76, где Lq = 677 мкГн — индуктивность обмотки преобразователя с магнитопроводом, индуктивность L—2,6 мкГн и емкость
Lo
Рис. 2.76
Рис. 2.74
С — 0,584 мкФ отражают механические свойства магнитной цепи.
Построить (качественно) частотную характеристику х(со) преобразователя и указать на ней частоты резонансов токов и напряжений.
2.77.	Для пьезоэлектрического преобразователя составлена электрическая схема замещения, приведенная на рис. 2.77, где Со = 5,2 пФ — статическая емкость электродной пары, индуктивность Lj = 0,0557 Гн и емкость Ct = 0,01334 пФ учитывают механические свойства пьезокерамики (потери в диэлектрике не учитываются).
Построить (качественно) частотную характеристику Ь(со) преобразователя. Записать условия резонанса напряжений и резонанса токов. Найти частоты резонансов и отметить их на характеристике.
о——-------
о
Рис. 2.77
2.78(	Р). Для схемы рис. 2.78 в области частот, близких к резонансу, построить (качественно) резонансную кривую выходного напряжения U = F (Q), где Q = со/(оо — соо/со — относительная расстройка, соо — резонансная частота каждого контура, причем контуры образуются закорачиванием соответствующих узлов (при закорачивании узлов 2 и 3 оставшиеся элементы Llf Li2 и Ci образуют первый контур, при закорачивании узлов 1 и 3 элементы Ll2, L2 и С2 образуют второй контур).
Рис. 2.78
hU
Рис. 2.78Р
У Казани е. Рекомендуется применить метод узловых потенциалов, так как схема содержит параллельно включенные элементы.
Решение. Выбрав ф3 = О, запишем уравнения
OG 4- l/jo^Li + 1/joL12) Ф1 - (1/>L12) ф2 = J; (1)
~~ (1/Л°^12)Ф1 + ОС2 4- 1/jcoL2 4- 1//coL12) ф2 = 0.	(2)
Определитель системы
А == (>С1 4- l/JcoLi 4- 1/>L12)(JcdC2 4- 1/jcoL2 4- 1//®Ь12) 4-
4- (1/coLi2)2.
Алгебраическое дополнение при замене второго столбца свободными членами
А2 = J (1//giL12).
Напряжение на выходе схемы
т'т А ^2 Г УУ^12	/-5\
С/=ф2=—=J—.	(3)
Выражение (3) можно упростить, если ввести резонансные
частоты контуров =<в2 = (£>0, т.е.
и коэффициент связи как отношение индуктивной проводимости 1/(dL12, общей для рассмотренных контуров, к геометрическому среднему индуктивных проводимостей, получающихся при закорачивании соответственно узлов 2 и 3 и узлов 1 и 3, т.е.
_ ________________УЮ-^12	_____ _
12 ” ]/(Ц + L12)(L2 + L12)/(oL1L12a)L2L12
1/EIZ7
= ? И •	  	(5)
|/(Li 4- Li2)(L2 4- L12)
Выражение (3) с учетом (4) и (5) приводится к виду . == ।______________________(соо/со)/с12____________
2 /coJCtCz [(юр/ю2) Мг “	“ ^о»2]
В области частот, близких к резонансной, сооА° « 1 и выражение (6) упрощается:
U = ф2 = kl2J/jalC^ (k2i2 - О2).	(7)
Функция претерпевает разрывы в точках, где к22 — О2 =0, т.е. О1>2 = + fci2. В действительности элементы цепи имеют потери, и функция будет ограниченной. В точке св = го0, т. е. 0 = 0, знаменатель выражения (7) максимален, и функция имеет минимум: Umin — 31<£%СхС2к12. Качественно амплитудно-частотная характеристика напряжения представлена на рис. 2.78Р.
Данная методика может быть распространена на большее число контуров.
2.79.	У источника ЭДС (рис. 2.79) амплитуда неизменна, а частота изменяется.
4 п/р Нонкина П. А.
97
Составить выражение для тока 1 в функции относительной расстройки Q = со/соо — соо/со и коэффициента связи к12 контуров Li, Ci и L2, С2, т. е. для резонансной кривой при С0/С0о, близком к 1.
Рис. 2.79
Рис. 2.80
Указания: 1) При последовательном включении элементов для анализа проще применять метод контурных токов.
2)	Резонансная частота контуров определяется элементами, остающимися в контуре при размыкании контуров слева и справа от рассматриваемого:
LiCiCi2/(Ci + С12)	-^2С2С12/(С2 + С12)
3)	Коэффициент связи равен отношению сопротивления, общего для двух контуров, к геометрическому среднему сопротивлений, получающихся при разрыве соответственно второго и первого контуров:
&12 = CiC2/(Ci + С12)(С2 + С12).
2.80.	К точкам а и б цепи (рис. 2.80) подключен приемник с комплексным сопротивлением Z^.
Определить, при каком активная мощность приемника Рн максимальна; найти при этом сопротивлении Рн.
Дано: Rx = 500 Ом; xLJ — 3,9 кОм; хС] = 3,4 кОм; xL2 = = 12,2 кОм; Хс2 = 12,7 кОм; et = 40 sin (cot — 15°) В; е2 = = 14,1 sin (cot 4- 30°) В.
2.81.	Определить реактивные сопротивления Xj и х2 (рис. 2.81), при которых в сопротивлении нагрузки гн = 100 Ом будет максимальная мощность; параметры последовательной схемы замещения двухполюсника: Z = г = 10 Ом и Ё = 40 В.
Определить максимальную мощность и найти, во сколько раз эта максимальная мощность отличается от мощности в сопротивлении нагрузки гн при его непосредственном подключении к активному двухполюснику.
2.82.	Определить сопротивления xt и х2, при включении которых между активным двухполюсником (рис. 2.82) и приемником с сопротивлением га = 10 Ом мощность приемника максимальна. Эквивалентные параметры последовательной
^2
Рис. 2.82
схемы замещения активного двухполюсника: Z = r = 100 Ом и Ё = 40 В. Найти, какую часть этой максимальной мощности получит приемник при его непосредственном подключении к активному двухполюснику.
2.6.	Электрические цепи с взаимной индукцией
2.83. Для катушек (рис. 2.83, а—г), имеющих индуктивную связь, произвести разметку выводов с указанием знака взаимной индуктивности.
б)	S)	г)
Рис. 2.83
2.84.	Определить показание вольтметра в цепи рис. 2.84, если известны магнитные индукции: Bj = 0,5 Тл; В2 = = 0,41/2 л. 45° Тл; числа витков катушек: = 100; vv2 = 200; w3 = 300; сечения магнитопровода: Sj = 10 см2; S2 = 6 см2; S3 = 7,62 см2; частота со = 103 рад/с.
2.85.	Разметить выводы трех катушек и найти показания вольтметров в схеме рис. 2.85.
Дано: / = 2 zi 40° А; со = 1000 рад/с; М13 = ЗЮ"3 Гн; М23=7-10"3 Гн; L=310’3 Гн.
2.86.	В схемах рис. 2.86, а — в определить показания вольтметров: 1) при указанной разметке выводов; 2) при перемене местами выводов одной из катушек в каждой схеме.
Параметры схем: = 20 Ом; х2 = 10 Ом; хс = 10 Ом; г = 40 Ом; хм = 10 Ом; Е = 200 В.
Рис. 2.84
Рис. 2.86
Рис. 2.88
2.87.	Для двух последовательно включенных индуктивно связанных катушек (рис. 2.87) получено: 1) при встречном включении ток 7В = 1 А, мощность Ръ = 30 Вт; 2) при согласном включении ток 1С = 0,6 А. Напряжение питания U = 100 В, в обоих случаях частота f = 400 Гц.
Определить взаимную индуктивность М.
2.88.	Одна из двух одинаковых последовательно соединенных индуктивных катушек с сопротивлением coL = 2 кОм закорочена (рис. 2.88). Катушки имеют индуктивную связь с коэффициентом к =0,8.
Найти входное сопротивление цепи. Определить входное сопротивление при соединении катушек в узле одноименными
выводами. Выяснить, можно ли подобрать коэффициент к и соединение так, чтобы сопротивление получалось емкостным.
2.89.	Определить показания ваттметра и вольтметра в схеме рис. 2.89, если известны показания амперметра и параметры схемы: 1 = 4 A; хг = = 10 Ом; х2 = 15 Ом; ri = г2 = = 4 Ом; хм = 5 Ом; г = 2 Ом, одноименные выводы катушек в общем узле.
Рис. 2.89
2.90.	В цепи рис. 2.90 определить показание амперметра.
Дано: Xi = 40 Ом; х2 = 10 Ом; хс = 50 Ом; к = 1;	=
= (80 -/60) В; Е2 = (40 + /30) В
Рис. 2.90
Рис. 2.91
2.91.	Определить входные сопротивления для цепей рис. 2.91, а и б при хс = 40 Ом; xt = 50 Ом; х2 = 40 Ом; хм = 10 Ом; г = 30 Ом.
Указание. Рекомендуется предварительно цепи преобразовать в эквивалентные схемы, не содержащие взаимной индуктивности.
2.92.	Для цепи рис. 2.92 заданы ток /3 = 1 А и сопротивления хС1 = 35 Ом; xLl = 20 Ом; г2 = 20 Ом; xL3 = 60 Ом; Х/и = 10 Ом.
Определить токи и построить топографическую диаграмму при: 1) указанной разметке выводов; 2) соединении индуктивных катушек в узле б разноименными выводами; принять фа = 0.
Рис. 2.92
Рис. 2.93
2.93.	Для двухполюсника (рис. 2.93) дано: г = coL= 2 кОм; 1/соС = I кОм; к = 0,5.
1)	Найти входное сопротивление двухполюсника.
2)	Определить входное сопротивление при соединении индуктивных катушек в узле разноименными выводами.
2.94.	Для двухполюсника (рис. 2.94) дано: xL1 = 80 Ом; xL2 = 240 Ом; xL3 = 160 Ом; х12 = х23 = 80 Ом; х13 = 40 Ом. Частота напряжения питания со = 105 рад/с.
Определить, при каком значении емкости С в двухполюснике будет наблюдаться резонанс.
Рис. 2.94
Рис. 2.95 -♦
2.95.	Для двухполюсника (рис. 2.95) дано: = 20 мГн; L2 = 40 мГн; М = 20 мГн; г3 = 1 кОм; напряжение питания U = 20 В с частотой со = 105 рад/с. Емкость подобрана так, чю вся цепь настроена в резонанс.
Определить при возможных резонансах показания приборов. Рассмотреть два варианта соединения катушек в узле а: 1) одноименными (рис. 2.95) и 2) разноименными выводами. 102
2.96.	Найти, при каком сопротивлении конденсатора источник ЭДС (рис. 2.96) развивает максимальную мощность и определить эту мощность.
Дано: Ё = 100 В; = 20 Ом; х2 - 30 Ом; хм — г - 10 Ом.
jxi
Рис. 2.96
2.97.	Рассчитать токи в схемах рис. 2.97, а — г и найти показания приборов.
Дано: E=J180 В; j = j‘15 А; ^ = 10 Ом; х2 = 20 Ом; хм - 10 Ом; хс = 20 Ом; г = 15 Ом.
2.98.	Найти токи и построить топографическую диаграмму для схемы рис. 2.98, приняв <ра = 0.
Дано: Ёг — 100 В; Е2 — 100 zl 90° В; — 20 Ом; coLj = = 20 Ом; cdL2 = 60 Ом; 1/соС2 = 30 Ом; г3 = 30 Ом; coL3 = = 40 Ом; G)M = 20 Ом.
2.99.	Определить емкостное сопротивление хс, при котором в схеме рис. 2.99 мощность, отдаваемая источником с напряжением U = 100 В, чисто активная; найти эту мощность.
Дано: rt = 100 Ом; — 10 Ом; х2 — 20 Ом; = 10 Ом.
Определить, если возможно, значение хс, при котором полная мощность источника равна нулю.
а.
Рис. 2.98
Рис. 2.99
U
А
Рис. 2.100
2.100(	F). Для двухполюсника рис. 2.100 дано: г = 10 Ом; Li = 17 мГн; L2 = 4,75 мГн; L3 = 6,34 мГн; М12 = М23 = = М31 = 1 мГн; угловая частота напряжения питания со = = 104 рад/с.
Пользуясь эквивалентными схемами без взаимных индуктивностей, найти: значения емкости, при которых будет резонанс; число возможных резонансов; входные сопротивления при резонансах.
Решение. Исключим индуктивную связь первой и второй катушек. Индуктивности Lj и L2 подключены к узлу а разноименными выводами. Поэтому в ветви, содержащие и L2, включаем дополнительные индуктивности, равные М12, а в третью ветвь аг — такую же индуктивность, но отрицательную. Для устранения ой и третьей катушек необходимо
в ветви, содержащие L2 и L3, включить отрицательные индуктивности, численно равные М23, так как ветви подключены к узлу б одноименными выводами, а в третью ветвь б — д — такую же положительную индуктивность. Проведя аналогичные рассуждения для узла в, получим эквивалентную схему рис. 2.1 OOP, а.
Определим значения результирующих индуктивностей ветвей:
индуктивной связи
ЬАБ = L2 + М12 - М23 = 4,75 +	1	-	1	=	4,75 мГн;
Гбв = Г3 + Mj3 — М23 = 6,34 4-	1	—	1	=	6,34 мГн;
Lba =	4“ Mj3 4- Mj2 = 17 -|-	1	4“	1	=	19 мГн.
Преобразуем треугольник АБВ, состоящий из однородных элементов, в эквивалентную звезду (рис. 2.100Р, б):
ЬА = LABLBA/(LAB 4- LSB 4- Lba) = 3,0 мГн
и аналогично ЬБ — 1,0 мГн; LB — 4,0 мГн.
Как видно из рис. 2.100Р,б, в схеме возможны два резонанса: параллельный, когда проводимость параллельно включенных ветвей чисто активная, а в данном случае должна быть равна нулю, и последовательный, когда мнимая часть входного сопротивления двухполюсника равна нулю.
Запишем условие, при котором в цепи будет параллельный резонанс:
оуБв 4- соЛ/ 2з	j з — 1/соС
откуда найдем значение емкости: С = 2-10 9 Ф.
Рис. 2.100Р
Входное сопротивление двухполюсника
ZBX — г + j G)La — ОЭЛ/12 4-
(coLB - (oM13 - 1/соС) (coLg + coM23) (dLB - ®M13 - l/юС 4- (f)LB 4- coM23
Приравняв нулю мнимую часть, найдем значение емкости, при которой в цепи будет последовательный резонанс: С — = 40-10'6 Ф.
Определим входные сопротивления при резонансах. При параллельном резонансе проводимости ветвей, включенных между точками О и д (рис. 2.100Р,б), равны и противоположны по знаку и, следовательно, суммарная проводимость равна нулю, т. е. входное сопротивление бесконечно большое.
При последовательном резонансе входное сопротивление равно г = 10 Ом, так как его мнимая часть равна нулю.
2.101.	Две индуктивно связанные катушки включены по схеме, показанной на рис. 2.101.
Дано: Li = 1 Гн; L2 = 1 Гн; М=0,5 Гн; Cj = 1 мкФ;
С2 = 2 мкФ; ток источника J = 0,1 А; ю — 103 рад/с.
Определить показания приборов (не применяя преобразования схемы).
Рис. 2.101
Рис. 2.102
2.102.	Для цепи рис. 2.102 дано: coLi = qjL2 = 20 Ом; к = = 0,5; rj =2 кОм и напряжение питания и = 14,1 sin (104Г + 34°) В.
Определить емкость С, при которой вся цепь будет настроена в резонанс, и ток i2 при резонансе. Выяснить, изменится ли значение емкости С, если разметку выводов у одной из катушек изменить на противоположную.
Рис. 2.103
Рис. 2.104
2.103.	Для трансформатора (рис. 2.103) дано: со^ = 1 кОм;
<вЬ2 = 4 кОм; к = 0,6;	= 200 Ом; г2 — 800 Ом и rH = 1 кОм.
Определить комплексные сопротивления: вносимое из вторичной цепи трансформатора в первичную и входное.
2.104.	В цепи рис. 2.104 определить показания вольтметров.
Дано: Xj = 10 Ом; х2 = 40 Ом; х3 = 30 Ом; х4 = 60 Ом; х — 10 Ом; — 20 Ом; х^2 ~ 40 Ом; j = 5 А.
2.105(	Р). С двухобмоточным трансформатором, подключенным к источнику с напряжением =200 В (рис. 2.105), производятся опыты короткого замыкания и холостого хода на
вторичных выводах. В режиме короткого замыкания 7iK — = 60,6 z. - 54°50' А, в режиме холостого хода /1х = 20(1 — J3) А, ^2х = 60(3+Л) В.
Определить парамегры трансформатора.
Решение. Для трансформатора нужно определить величины гь хь г2, х2 и хм.
В режиме холостого хода:
входное сопротивление
Zx = Zi = ri 4- jxx = L\/7lx = 1 + j3 Ом,
т. е. гх = 1 Ом; — 3 Ом;
сопротивление взаимной индуктивности
Z/j ~ ^2х/Ах = Л Ом,
т. е. хм = 3 Ом.
В режиме короткого замыкания при выбранных положительных направлениях токов справедливы следующие уравнения для первичного и вторичного контуров:
AkZi —	= ^15 Лю?2 ~ Лк2м = 0,
откуда
Ъ = r2 + jx2 =  	_ = 3 (3 + jl) Ом,
и 1/7 1к ” ^.1
т. е. г2 = 9 Ом; х2 = 3 Ом.
Рис. 2.105
Рис. 2.106
2.106.	Понижающий трансформатор мощностью S = = 60 МВ-А с номинальными напряжениями = 36 кВ, U2 = = 5 кВ в режиме холостого хода потребляет мощность Рх = 50 кВт при токе 71х = 0,05 715 а в режиме короткого замыкания — ток 71х = Ц при 171к = 0,09 Щ и Рк = 150 кВт.
Определить параметры Zlx и Z2v эквивалентной схемы рис. 2.106.
2.7.	Диаграммы для цепей с изменяющимися параметрами
2.107.	Каждый из двухполюсников, представленных на рис. 2.107, <2 —з, присоединен к источнику синусоидального напряжения U — 10 В. Неизменяющиеся элементы цепи имеют сопротивления по 100 Ом, сопротивление изменяющегося элемента принимает значения от 0 до оо.
Рис. 2.107
Построить круговую или линейную диаграммы входного тока для каждого из двухполюсников.
2.108.	Для схемы рис. 2.108 определить, как изменяются значение и фаза Р напряжения Ua6 при изменении емкостного сопротивления хс от 0 до оо, если U = l7z_0°, г2 — 5гР
Что изменится, если сопротивления увеличить в 5 раз?
Рис. 2.108
2.109.	При помощи круговой диаграммы показать, как изменяется показание вольтметра при изменении индуктивного сопротивления xL от 0 до оо, если цепь рис. 2.109 подключена к источнику синусоидального напряжения U — 100 В. 108
2	.119, Построить круговые диаграммы токов /, 1С и напряжения йаб схемы рис. 2.110 при изменении емкое! и С в пределах от 0 до оо и известных сопротивлениях rL — = 10 Ом; г с — 12,5 Ом; xL = 30 Ом и напряжении U = 200 В.
Определить из диаграмм: 1) значения тока при которых общий ток I совпадает по фазе с напряжением U, и соответствующие сопротивления хс; 2) значение тока /, при котором Ua6- — 0, и соответствующее сопротивление хс.
Рис. 2.110
Рис. 2.111
2	.Ш. При изменении частоты напряжения питания двухполюсника (рис. 2.111) в пределах 0 ю оо годографом тока / на комплексной плоскости является дуга окружности.
Найти: 1) значение xL, при котором токи
2) значение хь при котором ток I — ]/512; 3) токи /ь 12 и I при xL = 2,5 Ом, если U — 200 В, rL = 10 Ом и г = 20 Ом.
2.112.	В схеме рис. 1.112 сопротивление нагрузки г изменяется в пределах от 0 до оо.
Дано:	= — 20 Ом; х2 = — 20 Ом; х3 = 40 Ом;
Ё = 120 В.
При помощи круговой диаграммы тока 1 найти: 1) при каком значении сопротивления г реактивная мощность источника
Рис. 2.112
Рис. 2.113
равна нулю и активную мощность источника в этом режиме; 2) при каких значениях сопротивления г угол сдвига фаз между ЭДС Ё и током 1 равен: а) + 45° и б) — 45°.
2.113.	Построить круговую диаграмму для тока j схемы рис. 2.113 при изменении сопротивления г в пределах 0 < г < оо.
Дано: xL = — 20 Ом; х2 = — 20 Ом; х3 = 40 Ом; Ё = 120 В.
При помощи диаграммы: 1) определить, при каком сопротивлении г активная Р и реактивная Q мощности источника численно одинаковы; найти их значения, а также ток I и напряжение Ur в этом режиме; 2) найти значения 1, U„ Р, Q и полной мощности источника S при г = 10 Ом.
2.114.	В схеме рис. 2.114 индуктивность изменяется в пределах 0 оо.
Дано: Ё = 100 В; г — 25 Ом; гс = 45 Ом; хс = 70 Ом.
Построить круговую диаграмму тока /. При помощи диаграммы определить значение тока I и сопротивление xL: 1) в режиме, при котором реактивная мощность источника равна нулю; 2) в режиме, при котором сдвиг фаз между ЭДС Ё и током максимален, найти значение этого сдвига фаз.
2.115.	Для схемы рис. 2.115 дано: — 400 В; Ё2 =J40 В; j = 10|/2 z. — 45° A; xLl = 40 Ом; хс = 20 Ом; г — 20 Ом.
При помощи круговой диаграммы тока 12 определить: 1) при каком сопротивлении xL источник ЭДС Ё2 отдает или потребляет максимальную активную мощность, значение этой мощности и угол сдвига фаз тока /2 в этом режиме относительно этого же тока в режиме короткого замыкания (xL = 0); 2) при каком сопротивлении xL потребляемая источником ЭДС Ё2 мощность чисто активная и ее значение.
Рис. 2.114
Рис. 2.115->
2.116.	По круговой диаграмме тока Ц трансформатора (рис. 2.116) определить его значение при сопротивлении г = 75 Ом; вычислить полную, активную и реактивную мощности источника в этом режиме.
Дано: Xi = 200 Ом; х2 = хм = 100 Ом; г2 — 100 Ом; Ё = = 100 В.
2.117(	Р). Для трансформатора (рис. 2.117) построить круговую диаграмму тока Д.
Определить по диаграмме: 1) сопротивление хс, при котором ток Ц совпадает по фазе с ЭДС Ё, и ток Д в этом режиме;
2)	сопротивления хс, при которых полная мощность трансформатора максимальна и минимальна, и значения этих мощностей;
3)	сопротивление хс, при котором максимальна активная составляющая тока Л, и комплексную мощность источника в этом
режиме.
Рис. 2.116
jsu
Рис. 2.117
Дано: Ё — 100 В; = 500 Ом; х2 = 30 Ом; хм = 100 Ом; г2 = 100 Ом.
Решение. Определим токи Лк(хс = 0) и /1х(хс->оо).
Из системы уравнений трансформатора при хс — 0
Jxj/jк	— Е,
0*2 +А2)Лк =0
получим
JX1 + х$/(г2 + Jx2)
= 0,2-70,4 А;
при хс-> оо находим 7ix = Ё/jxi = - JO,2 А.
Из опыта обратного короткого замыкания определим Z2K (короткозамкнуты выводы 1-1' и определяется сопротивление со стороны выводов 2-2'). Подключив источник ЭДС Ё' между выводами 2-2', запишем уравнения
JX1/; -jxMi2 = 0; (r2 +jx2)i2 -jxMi\ = Ё',
откуда
Z2k = z2k z. ф2к = Ё'/1'2 == г2 + jx2 -jx^/x^ = 10]/2 z. 45° Ом.
На комплексной плоскости (рис. 2.117Р) построим в выбранном масштабе векторы JlK и /1Х (на рисунке показаны только точки к и х). Соединим точки к и х и проведем перпендикуляр аб через середину отрезка хк. Из точки х на отрезке отложим в некотором масштабе сопротивление z2k = = 10J/2 Ом (точка д).
Из точки д под углом - ф = ср2к — ср2 = 45° — (- 90°) = = 135° проведем линию переменного параметра (ЛПП). На
ЛПП от точки д откладываем модуль сопротивления нагрузки хс в том же масштабе сопротивлений, что и для z2k.
Из точки х проведем перпендикуляр к ЛПП до пересечения с перпендикуляром аб в точке б — центре круговой диаграммы тока Рабочая часть окружности находится с той же стороны отрезка хк, что и ЛПП. Векторы, соединяющие начало координат (точка 0) с точками окружности, изображают ток /Р
0	0,1	0,2	0,3	0,4 А
Рис. 2.117Р
Из диаграммы рис. 2.117Р следует:
1)	Режим, при котором совпадают по фазе ток i\ = 0,2 А и ЭДС Ё, получается при х'с = 20 Ом (точка в). Для определения этого значения х'с соединяем прямой рабочую точку 1 дуги окружности с точкой х. Точка пересечения в прямой и ЛПП определяет искомое сопротивление.
2)	Максимальная полная мощность получается при максимальном токе (точка 2 на дуге окружности) Цтах = — 0,487 z. — 45° А. При этом хс = 6 Ом (точка г) и полная мощность Smax = EIlmax = 48,7 В • А.
Минимальная полная мощность получается при токе = = 0,0835 z. — 45° А (точка 2'); ПРИ этом хс = 34,5 Ом и Smin — Ell „in = 8,35 В • А.
3)	Режиму с максимальной активной составляющей тока /р равной 0,4 А, соответствует рабочая точка 3, т. е. ток /'(=0,4— j0,2 А при хс = 10,5 Ом; комплексная мощность S = Ё (/f)" = 40 + J20 В-А.
2.8. Топологические методы анализа. Расчет схемных функции
2Л18(Р). По топологической формуле (Мэзона) определить ток 1 в цепи рис. 2.118 и найти сопротивление цепи для источника тока j = 5 z. 90° А при г = xL = хс = 5 Ом.
Решение. По топологический формуле (1.59) вычислим передачу Н = I/J, где I — искомый ток, j — источник тока.
Рис. 2.1J8
Ток I можно рассматривать как показание прибора — амперметра, условно вводимого в цепь (рис. 2.118Р, а).
Записываем проводимости всех ветвей:
11 =Ь = l/JxL= — ./0,2 См; У3 = 1/( -jxc) =/0,2 См; У4 = = 1/г = 0,2 См.
Передача = £ ПЖ/А, гДе Дл и А£ — соответственно к
произведение проводимостей ветвей всех путей от источника через прибор и миноры этих путей; А — узловой определитель схемы.
В рассматриваемой схеме рис. 2.118Р, а только один такой путь, для которого Hi - _У2_1з; Д1 = !•
При определении определителя А замыкаем накоротко амперметр, размыкаем ветвь с источником тока (рис. 2.118Р, б) и находим, что
А = (_У3 + _У4)СУ1 + У2) + li У2 = 0,04 — /0,008 См2.
Следовательно, гг	-Гг^з
= 0,447 л. 63°20'.
2
Ток i = Hj = 2,235	153°2О' А.
Сопротивление цепи для источника тока рассмотрим как передачу
н2 = UU,
где U — показание прибора — вольтметра (рис. 2.118Р,в).
По топологической формуле (1.59) передача
я2 = Х1КЛ1/4 к
причем имеется только один путь, для которого IJi == 1. Определяя минор, закорачиваем этот путь; получается граф, показанный на рис. 2.118Р, г. Следовательно, минор Ai = = Y2 + Y3 + Y^
Для вычисления определителя А размыкаем ветви с вольтметром и источником тока; получаем граф рис. 2.118Р,б, для которого определитель был уже найден.
Таким образом,
Z., = И, = - +	- 2,24 z. 63°25 Ом.
Рис. 2.119
2.119.	Определить ток 15 в схеме рис. 2.119 по топологической формуле (Мэзона) при = г4 — 5 Ом; ®L2 = = ю£б = 1/соС3 = 1/соС5 = 2 Ом; ЭДС е — 20}/2 sin (со? + 45°) В.
Найти напряжение U 5 при разомкнутой ветви ab.
2.120.	Определить входное сопротивление цепи рис. 2.120 для источника ЭДС е = 24]/2sinto£ В и найти показание вольтметра, применяя формулу Мэзона.
Дано: п = xt = 2 Ом; г2 — гб = х5 = — х3 = — х4 = 5 Ом.
Рис. 2.120
Рис. 2.121
2.121.	Применяя топологическую формулу (Мэзона), определить коэффициенты Л, В, С, D четырехполюсника (рис. 2.121) и найти напряжение U2 при заданном напряжении (Д = 20 В и параметрах четырехполюсника: г = 2 Ом; coL= 1/соС = 5 Ом.
2.9. Применение сигнальных графов
2.122(Р). Для схемы рис. 2.122 составить систему уравнений методом узловых потенциалов. По системе уравнений построить сигнальный граф. При помощи сигнального графа найти по формуле Мэзона (1.65) ток /2:
Дано: Ei=24z_0o В; Ё2 = 12 z. 90° В; х2 — — хх = = — х3 = 2 Ом; rj = г2 = 5 Ом.
Решение. Запишем уравнения для узловых потенциалов узлов 1 и 2 при ф3 =0:
1Ф1 + .У12Ф2 —	_У21ф1 4- _У22ф2 = В2_У2,
где
уп = 1//Х1 + 1/п + 1/г2 = 0,64 z. 51°20' См; У22 = 1/г2 +
+ 1//х3 + 1//х2 = 0,2 См; _У12 = _У21 = - 0,2 См; X =
= 1/JXi = j0,5 См; _У2 = l/jx2 = -J0,5 См.
Кроме того, по обобщенному закону Ома
/2 = (В2 — фг)/^2,
где Z2 =Jx2.
Приведем эти три уравнения в причинно-следственной форме:
Yi •	У12	У2 •	У21
Ф1 =	- -#^Ф2; Ф2 = -~-я2 ~ v Ф1;
_111	-Ill	.122	J.22
А — ё2 —^~Ф2-112	£.2
Последней системе уравнений соответствует сигнальный граф, показанный на рис. 2.122Р. Граф имеет только один замкнутый контур, поэтому его определитель
(	Vi2W	У21\
Д = 1 -	1 = 0,836 z. 17°5'.
\	У и / \ х22)
Рис. 2.122
Рис. 2.122Р
Для вычисления тока /2 От источника Ёх к столу /2 с передачей
применим принцип наложения, есть только один прямой путь
— = 0,39 z. 128°4О' См, _2 J
который касается замкнутого контура; поэтому минор этого пути A'i = 1.
При помощи формулы (1.65) находим составляющую тока /2, обусловленную источником ЭДС
1'2 =	£ = 11,1^ 11Г35' А.
2 А
От источника Ё2 к стоку /2 есть два прямых пути: первый путь с передачей П'2 = 1/Z2 = - j 0,5 См и минором Д2 = Д, второй путь с передачей П'3 = (У2/У22)( — 1/Z2) = = 1,25 См и минором Д'3 = 1. Поэтому составляющая тока
12, обусловленная источником ЭДС Ё2, . = (ЩД'г + П'зЛз) £ = 2	д	2
Ток /2 = 1'2 4- i'l = 29,2 z. 68°55' А.
2.123. Для схемы рис. 2.123 составить систему уравнений методом контурных токов. Построить сигнальный граф, соответствующий этой системе уравнений. При помощи сигнального графа определить напряжение 1/2.
Дано: г = xL = хс = 5 Ом; хм = 2 Ом; ЭДС и ток источников: = 6 z. 0° В; Ё2 = 6 z. 90° В; J = 2 z. 45° А.
Рис. 2.123
2.124. Для схемы рис. 2.124 построить сигнальный граф, который соответствует системе уравнений, составленной методом контурных токов. Определить передачу H~UjE графа. Найти показание вольтметра электродинамической системы.
Дано: е — 100]/2 sin (юг + 45°) В; г = 4 Ом; юД = 2юМ = = 4 Ом; 1/юС = 8 Ом.
Глава-третья
ТРЕХФАЗНЫЕ ЦЕПИ
Введение к гл. 3
Соединение обмотор трехфазных источников. При соединении обмоток источника звездой (рис. З.А,а) линейные напряжения определяются через разности фазных напряжений:
Uab =Ua~ Ub'Vbc = Ub- Uc\ Uca = UC- Ua-	(3.1)
Для источника с симметричными напряжениями при правильном соединении обмоток фазные напряжения
UA = Пф z. 0°; UB = Пф z. - 120°; Uc = Пф z. 120°, (3.2) линейные напряжения
UAB = Unz_ 30°; UBC = илг_- 90°; UCA =	150°	(3.3)
(рис. З.А, б). По модулю линейные напряжения ил больше фазных Г7ф в |/3 раз:
U„ = ]/з С7ф.	(3.4)
При соединении обмоток источника треугольником (рис. З.Б,я) линейные напряжения равны фазным (рис. З.Б,б).
Рис, З.А	Рис. З.Б
Симметричный режим. Для симметричного приемника, соединенного звездой (рис. З.В,<я), Za - ZB — Zc = Z; напряжение смещения нейтрали Un^ равно нулю, и токи в фазах
Л = Va/(Z + ^); iB = UB/(Z + ZJ; 1С = UC/(Z + Z^ (3.5)
где Zu — сопротивление симметричной линии на фазу. По модулю токи одинаковы и имеют сдвиг по фазе относительно друг друга, равный 120° (рис. З.В,б):
Ъ=/в = /с = 1>ф/|2 + гл|.	(3.6)
Рис. З.В
Для симметричного приемника, соединенного треугольником (рис. З.Г, a), Z^b = Zjk = Zra = Z. Если = 0, то фазные токи приемника
Ль = IHb/Z; 4 = Ubc/Z; /„ = <7cVZ.	(3.7)
По модулю токи одинаковы и имеют сдвиг по фазе относительно друг друга, равный 120° (рис. З.Г, б):
4ь = ^ = /св=/ф = ^л/|2|.	(3.8)
Линейные токи приемника определяются через разности фазных:
= ^ab	% В ~ ^bc ^ab* ~ ^са %Ьс‘	(3«9)
Рис. З.Г
Как видно из векторной диаграммы (рис. З.Г, б),
1А = /зй - 30°; 1в=1Ал- 120°; ic = tA± 120°. (3.10)
По модулю линейные токи больше фазных в ]/3 раз:
Л=1/3/Ф.	(3.11)
Если Zn Ф 0, то (после преобразования треугольника сопротивлений в эквивалентную звезду) линейные токи
или
/ =/ =/ =/	(3.13)
л в с л iz/3 + ^l	'
Фазные токи определяются через линейные:
1Л = -^^°-ibc = z. - 120°; /«, = 4 z. 120°. (3.14) 1/з
Активная, реактивная и полная мощности симметричного приемника независимо от вида соединения
Р = 317ф/фСозф = ]/з ип/лсо8ф;	(3.15)
Q = 3 1/ф/ф5т<р = |/31/л/л81пф;	(3.16)
S = 3 иф/ф = |/з их	(3.17)
где <р — сдвиг по фазе между фазными напряжением и током.
Несимметричный режим. При соединении приемника звездой с нейтральным проводом (рис. З.Д) напряжение смещения нейтрали
(3.18)
где Ха = 1/(2л + 2J; Ув = 1/(2^ + 2J; Хс = 1/(2с + ZJ; Xn = — 1/2jv; линейные токи и ток в нейтральном проводе
_ Uа “ UnN	, j _UВ ~ 0nN . f __	UС ~ UnN	.	i _	0nN
+	’ в~ Z^ + Zj ’ с~	Zc + Z»	’ N~	Zfi
По первому закону Кирхгофа iN = iA + I в + 4-	(3.20)
Если сопротивление Zv = 0, то Xn = 00» UnN — 0 и iA =	+ Z,); 1В = (4/(2я + ZJ; /с = c/(Zc + ZJ, (3.21)
а ток iN определяется по (3.20).
Если в цепи рис. З.Д Zjv = оо, т. е. Xn~<X т° получается схема соединения звездой без нейтрального провода (рис. З.В, а), для которой
• Uл Ya + UB YB + Uc Yc
U„N = у у" v-~,	(3.22)
+ JLb + J.c линейные токи определяются по (3.19). По первому закону Кирхгофа
iA + h + I с = 0.	(3.23)
Для приемника, соединенного звездой без нейтрального провода, токи можно определить без предварительного расчета напряжения смещения нейтрали:
... _ УлвХв - UcaIc . ... _ йвЛс - УлвХл .
UAn	v 1 V । у ’ U Bn	V -L. V -L V
Xa+.1b + J_C
у _ VcaXa - и вс Хв . Сп Ха+Хв+Хс ’
(3.24)
(3.25)
З.Г,а) и
(3.26)
При соединении приемника треугольником (рис. Zt = 0 фазные токи
Ль ~ UАв/Xab'i he ” $BcIXbc'') 1 са ~ UСл/Хю
линейные токи определяются по (3.9).
Если Z„ / 0, то треугольник сопротивлений можно преобразовать в эквивалентную звезду и для этого соединения рассчитать линейные токи, как показано выше. Фазные токи определяются по предварительно найденным фазным напряжениям приемника:
иаЬ = zAiA - zBiB- = zBiB - z'cic; uea = Xch - zjAiA; (3.27)
hb = Uab/Zab, L = Uhc/Xhc', L « Uca/Xa, (3.28)
где Z'A, Z'c — сопротивления лучей звезды, эквивалентной треугольнику.
Активная и реактивная мощности приемника равны суммам соответствующих мощностей трех фаз.
Измерение мощностей. Для измерения активной мощности, передаваемой от источника к приемнику, в трехфазной цепи с нейтральным проводом при несимметричном режиме включают ваттметры в каждую фазу (рис. З.Е). Активная мощность равна сумме показаний ваттметров:
Р =	+ Р и/2 + Р^з-	(3.29)
В случае симметричного режима достаточно одного ваттметра, включенного в какую-либо фазу, при этом измеряемая мощность
Р = ЗРиг.	(3.30)
При отсутствии нейтрального провода активную мощность измеряют двумя ваттметрами, включенными по схеме, пока
занной на рис. З.Ж (и при симметричном, и при несимметричном режимах). Активная мощность равна • алгебраической сумме показаний ваттметров:
Р =	+ Р wi-	(3.31)
Для измерения реактивной мощности той же трехфазной системы применяют схему включения ваттметров, показанную на рис. З.И. Реактивная мощность
е = 1/3(Ри-1 + Ри,2).	(3.32)
Рис. З.Ж
Рис. З.И
При симметричном режиме реактивную мощность можно измерить одним ваттметром, включенным по схеме рис. З.К. В этом случае
е = 1/зр,,.	(з.зз)
Симметрии ные составляющие. Любая несимметричная трехфазная система синусоидальных величин (токов, напряжений, ЭДС, магнитных потоков) может быть представлена в виде суммы трех симмегричных систем (прямой, обратной и
нулевой последовательностей) соответствующих величин. Например, для фазных напряжений (рис. З.Л)
Ua =	+ По; j
. С78 =а2П1 +aU2 + По; |	(3.34)
Vc = aUi+a2V2 + 1>о. I
где <7Ь U2, й0 — векторы соответственно прямой, обратной
и нулевой последовательностей; а — фазный множитель:
а = 1 z. 120° = - 71 +} /3/2; / = lz- 120° = - 1/2 -/|/з/2,
причем 1 + а +' а2 = 0.
Векторы UA, Uв, йс раскладываются на симметричные составляющие по формулам
(7j =-у((7л+ а(7в + я2(7с);
Сопротивления элементов цепи для токов различных последовательностей могут быть различными:
Zi = (71/7’1; Z2 = (72/72; Zo = (7О/7О,	(3.36)
где (7Ь (72, (70 — напряжения прямой, обратной и нулевой последовательностей на элементе; /2, /0 — токи прямой, обратной и нулевой последовательностей, вызванные в элементе напряжением соответствующей последовательности.
3.1.	Соединение обмоток и разметка выводов трехфазных источников
3.1(	Р). Для показанного на рис. 3.1 соединения обмоток трехфазного источника определить напряжение между выводами А и В, если фазная ЭДС равна 220 В.
Решение. Учитывая векторную диаграмму фазных напряжений источника (рис. 3.1Р, а), строим топографическую диаграмму для заданного соединения (рис. 3.1Р,б), из которой видно, что искомое напряжение UAB = 2 U$ = 440 В.
3.2(	Р). Обмотки I, II, III симметричного трехфазного генератора имеют выводы 1-6 (рис. 3.2). Выводы 2, 4, 6 объединены. Показания вольтметров: Ui = 220 В; U2 = 380 В; U3 = 220 В.
Определить, какие выводы обмоток II и III соответствуют началам Н и какие - концам К, если у обмотки I вывод 1 принят за начало Н, а вывод 2 — за конец К.
Решение. Примем, что обмотка I является фазой А. Так как по данным задачи нельзя определить, какая из обмоток — II и III — является фазой В и какая фазой С, предположим, например, что обмотка II — фаза В, а обмотка III — фаза С, и по показаниям приборов построим топографическую диаграмму (рис. 3.2Р). Из диаграммы видно, что началам соответствуют выводы 3 и 6, а концам — 4 и 5.
Если принять, что обмотка II является фазой С, а обмотка III — фазой В, то топографическая диаграмма изменится, но
ответ останется тем же.
3.3.	На щитке трехфазного генератора (рис. 3.3) указана разметка выводов его обмоток.
Определить, как нужно соединить выводы, чтобы получить соединение обмоток; 1) звездой; 2) треугольником.
N
Рис. 3.4
АВС
ООО
о
X
Рис. 3.3
3.4.	Обмотки трехфазного генератора, соединенные звездой (рис. 3.4), образуют симметричную систему напряжений. Показания вольтметров: Ui = 220 В; U2 - 380 В; U3 = 380 В.
Определить показания вольтметров после обратного присоединения выводов обмотки: 1) в фазе А; 2) в фазе В.
3.5.	Определить напряжения между свободными концами вторичных обмоток трехфазного трансформатора для указанных на рис. 3.5, а —в их соединений при напряжениях на обмотках, равных 127 В.
а)	t)	В)
Рис. 3.5
3.6.	Вторичные обмотки двух одинаковых трехфазных трансформаторов, соединенные звездой (рис. 3.6), имеют еще соединение между выводами Cj и В2. Напряжения одноименных обмоток совпадают по фазе и численно равны 220 В.
Определить напряжения между выводами и Л2, и С2.
Рис. 3.7
Рис, 3.6
Рис. 3.8
Рис. 3.9
3.7.	Вторичные обмотки двух одинаковых трехфазных трансформаторов, соединенные треугольником, имеют еще соединение между выводами Q и С2 (рис. 3.7). Напряжения одноименных обмоток совпадают по фазе и численно равны 127 В.
Определить напряжения между выводами и Л2, и В2.
3.8.	Обмотки 7, 17, III симметричного трехфазного генератора имеют выводы 1—6 (рис. 3.8). Выводы I, 3, 5 объединены. Показания вольтметров: = 127 В; U2 = 127 В; U3 = 127 В.
Определить, какие выводы обмоток II и III соответствуют началам и какие — концам, если у обмотки I вывод 2 принят за начало Н, а вывод 1 — за конец К.
3.9.	Вольтметр, присоединенный к выводам трехфазного генератора 1 и 4, или 2 и 5, или 3 и 6 (рис. 3.9), показал 380 В. После соединения выводов 4, 5 и 6 вольтметр показал: между выводами 1 и 2 напряжение равно 380 В и между выводами 2 и 3 напряжение равно 380 В.
Определить, как надо соединить выводы, чтобы получить симметричную систему с линейным напряжением: 1) 660 В; 2) 380 В.
3.2.	Симметричная нагрузка
3.10(	Р). Найти токи в приемниках и линий цепи рис. 3.10, построить векторную диаграмму токов и топографическую диаграмму при Un — 380 В в начале линии.
Дано: coL= 5 Ом; г = 10 Ом; 1/соС = 30 Ом.
Рис. 3.10
Решение. Для симметричного источника, соединенного звездой, фазные ЭДС ЕА = Ев = Ес = 38О/|/з = 220 В. Примем ЁА = 220 0° В, тогда аналогично (3.2) Ёв — 220	—120° В;
Ёс = 220 /_ 120° В.
Преобразуем треугольник сопротивлений 1/соС в эквивалентную звезду с сопротивлением 1/соС' = (1/3) (1/соС) = 10 Ом.
Объединив нейтральные точки приемников с нейтралью источника (можно соединить, так как потенциалы одинако-।
вые), получим расчетную схему для одной фазы (фазы А), показанную на рис. ЗДОР, а Для этой схемы
Z9K = jcoL +
Г( 4”-^- = 5 Ом; Л = EA/Z„ = 44 z. 0° А; г — j/cdC
/а1 = Л J^C', = 31,1 z - 45° А;
Г -]/®С
г
Ial = ‘А г - j/e>C =
= 31,1 г. 45° А.
Соответствующие токи в фазах В и С: Ig = = 44z —120° А; /c = 44zl20° A; = 31,1 г. - 165° А; 1Ь2 - 31,1 z. -75° А; 7с1 = 31,1	75° А; 1с2 - 31,1 z 165° А.
Фазные токи приемника, соединенного треугольником, по (3.14)
1аЬ =	- 17,95 z 75° А; - 17,95 - 45° А;
/з
1са = 17,95 z. 195° А.
Для построения топографической диаграммы примем <p,v = = <р„ = 0, тогда <р,1 = ЁА - 220 z. 0° В; фв = Ёв = 220z_ -120° В; Фс- Ёс = 220 z. 120° В; фа = ф„ + riai = 10-31,1 z. -45е = = 311 z. —45е В; фь=.311 z. -165° В; фс = 311 z. 75° В.
Векторная диаграмма токов и топографическая диаюзмма п°казаны на рис. 3.10Р,б.
3.11.	Три одинаковые индуктивные катушки, каждая из которых имеет сопротивление a>L= 20 Ом, присоединены звездой к трехфазной линии с линейным напряжением 380 В.
Определить токи катушек.
3.12.	От трехфазной линии с линейным напряжением 380 В получают питание три одинаковых приемника, соединенных звездой. Сопротивление каждого приемника Z = 8 + ;6 Ом.
Найти токи приемников.
Рис. 3.13
Рис. 3.16
3.13.	К трехфазному трансформатору, обмотки которого соединены звездой, подключены соединенные треугольником три одинаковые индуктивные катушки (рис. 3.13). Фазное напряжение трансформатора равно 127 В, сопротивление катушки coL — 22 Ом.
Определить токи в катушках и в обмотках трансформатора.
3.14.	Три одинаковые группы ламп соединены треугольником. и получают питание от трехфазного трансформатора, обмотки которого соединены звездой. Сопротивление каждой группы ламп 11 Ом, фазное напряжение трансформатора 127 В.
Определить токи в обмотках трансформатора и фазах приемника.
3.15.	К трехфазному трансформатору присоединены треугольником три одинаковых приемника, сопротивление каждого из них Z = 16 + j 12 Ом. Обмотки трансформатора соединены звездой с фазным напряжением 127 В.
Найти фазные и линейные токи.
3.16.	На рис. 3.16 представлена симметричная трехфазная система с параметрами хс = 90 Ом, г = 40 Ом.
Определить показания приборов и ток i при UA = « 120 z. 0° В.
3.17.	На рис. 3.17 представлена симметричная трехфазная система.
Определить показания приборов и ток i, если г = 76 Ом; coL= 44 Ом, UAB = 380 z. 30° В.
3.18.	Трехфазная линия с линейным напряжением 380 В питает цепь, показанную на рис. 3.18, с параметрами г = 1/соС = 6 Ом, coL = 2 Ом.
Определить показания приборов, активную и реактивную мощности источника. Построить топографическую диаграмму.
3.19.	К выводам генератора с линейным напряжением 6600 В через реакторы сопротивление каждого из которых 75 Ом, присоединен электродвигатель с сопротивлениями фаз r = coL=50 Ом (рис. 3.19). Сопротивление каждого из конденсаторов, соединенных треугольником, хс = 300 Ом.
Определить показание ваттметра и активную мощность цепи. Построить топографическую диаграмму.
п
Рис. 3.20
3.20.	К выводам генератора с линейным напряжением 380 В через реакторы 10 (xL = 23 Ом) подключены (рис. 3.20) треугольник сопротивлений 7 = 60+/60 Ом и три конденсатора 40 Ом), соединенных звездой.
Определить токи IAh 1А2, 1аь, построить топографическую диаграмму.
5 П/p Ионки на П. А.	129
3.21.	Для цепи рис. 3.21 дано: Un = 380 В; cdLj = 10 Ом; coL3 = 5 Ом; (f)L- 15 Ом; г = 30 Ом; 1/соС = 30 Ом.
Определить показания приборов и активную1 мощность цепи: 1) при включенной конденсаторной батарее; 2) при отключенной конденсаторной батарее.
3.22.	В трехфазную сеть с линейным напряжением 380 В включен электродвигатель, фазы которого соединены звездой. Двигатель работает с cos ср = 0,8 при активной мощности 50 кВт.
Определить сопротивление Z — г + jxL каждой фазы звезды, эквивалентной двигателю.
3.23,	Трехфазный электродвигатель работает с cos ср = 0,8 при активной мощности 50 кВт; обмотки двигателя соединены треугольником и включены на линейное напряжение 220 В.
Определить токи в подводящих проводах и обмотках двигателя.
3.24.	В цепь электродвигателя Д (рис. 3.24) с линейным напряжением 380 В включены два ваттметра, показания которых соответственно равны 398 и 2670 Вт.
Определить активное и реактивное сопротивления каждой фазы звезды, эквивалентной двигателю.
3.25.	К трехфазному генератору (17 л =10 5 кВ; f = 50 Гц) подключен через сопротивления г = 6 Ом симметричный при-130
емник (cos ф = 0,707; ф > 0; z = 700 Ом), фазы которого соединены звездой.
Определить емкости конденсаторов, которые нужно включить параллельно каждой фазе приемника для полной компенсации реактивной мощности. Сравнить мощности потерь в сопротивлениях г до и после компенсации.
3.26.	К трехфазному генератору подключен симметричный приемник, фазы которого соединены звездой. Полное сопротивление фазы z — 100 Ом при индуктивном cos ф — 0,8.
Определить показания ваттметров (рис. 3.26) при Un = 220 В.
3.27.	Решить задачу 3.26 при условии, что фазы приемника соединены треугольником.
3.3.	Несимметричная нагрузка
3.28(	Р). Цепь рис. 3.28. получает питание от симметричного источника с линейным напряжением 660 В.
Дано: г = coL= 1/соС = 10 Ом; rt =	— 5 Ом.
Найти токи в фазах приемников, соединенных звездой и треугольником, а также активную мощность цепи.
Решение. Предположим, что фазы источника соединены звездой с фазными напряжениями UA = UB = Uc — 660/]/3 = Т 380 В и 1^ = 380^0° В, при этом по (3.2) напряжения vb == 380 z. - 120° В, йс = 380 z. 120° В.
Преобразуем звезду сопротивлений в эквивалентный треугольник (рис. 3.28Р,а):
Zeb=>L+r +
j($Lr
-j(VcoC)
=Д0
Ом;
„	. 1	. r [ - j (1/coC)] jatL
Zj.a — ~ J—^ + k Л --------------------—------ = 10 ОМ.
cdC	r
Поскольку соответствующие фазы треугольников соединены параллельно, объединим сопротивления параллельно вклю-
Рис. 3.28Р
ченных фаз и получим схему, представленную на рис. 3.28Р,б, для которой
z^-j/coC) _ до(-до)
Z^b-jMC до-до
_ Z^r +j(£>L)
-* Z^ + r+jwL 10 710 ° ’
Zea = Zear/fZ,.,, + r) = 5 Ом.
Сопротивление Zi» = оо вследствие резонанса токов в контуре из двух параллельных ветвей (на схеме рис. 3.28Р,б фаза ab разомкнута).
Полученную схему можно рассматривать как соединение звездой с нейтральной точкой с. Сопротивления фаз звезды Za — Г1 + Z'ca = 10 Ом; 7Д = j(f)L+ Z^ = 10 Ом; Zc = foLi =
= jS Ом.
Проводимости фаз 1л = 4- = 0,1 См; Ув =
= — j'0,2 См.
Напряжение смещения нейтрали по (3,22)
. Va Y^r Ub Yb + U с Ус
cN YA+YB+YC
= 301 z 48°25' В.
Линейные токи по (3.19)
IA = (UA - UcN)/ZA = 28,8 z — 5Г20' A;
iB = (UB - UcN}/ZB = 67,8 z -125° 10' A; ic = Wc~ UCN)/Zc = 80,7 z 75° A.
Проверка: 1A + IB + ic~G-
Напряжения на фазах приемника, соединенного треугольником, Uса — -Z'catA = 144 z 128°40' В; Ubc — Z^C1B = = 956z —170° 10' В; U~ab = - Uca - Ubc = 1033 z 2°50' B.
Токи в фазах приемника
= 67,8 г. - 215°10' А; /„ =--^- = 14,4 z. 128О4(У А. Г
Напряжения Uab, йса для приемника, соединенного звездой, — линейные. По (3.24) фазные напряжения приемника йт = Z°b~--v	= И52 z 7° В
.141 + _£В1 + _1С1
и аналогично йь„ = 144 z 38°45' В; Uc„ = 1084z 13°30' В,
где Yai = J- = -уо,1 См; YBl = - = 0,1 См; Ycl = jwL
= ~^=/0,! См.
Токи /Л1 = УЛ1С7Я„ = 115,2 z — 83° A; IBi - YBXUhn = = 14,4 z 38°45' A; ia = YCjUcn = 108,4 z 103°30' A.
Проверка: iA{ + tBi + icl £ 0.
Активная мощность цепи равна суммарной мощности потерь в резисторах:
р = rjЛ + r/2Bi + rl2bc + rl2ca = 54,2 кВт.
Эту мощность можно определить и как развиваемую источником:
Р = Ке(йА1*А + йв1% + Uci&
3.29.	На выходных выводах трансформатора линейное напряжение равно 220 В. Трансформатор питает катушку с индуктивностью L и две лампы с сопротивлениями г, соединенные звездой с нейтральным проводом.
Найти ток в нейтральном проводе при coL=r=25,4 Ом.
3.30.	В трехфазной цепи рис. 3.30 известны фазные токи: 1А = 3 А; /в = 4 А; /с = 4 А.
Определить показание амперметра в нейтральном проводе.
3.31.	В трехфазной цепи рис. 3.31 известны фазные токи: 1А = 5 А; 1В = 2 А; 1С = 2 А.
Определить показание амперметра в нейтральном проводе.
3.32.	Найти показание ваттметра в схеме, показанной на рис. 3.32, при L/ф = 100 В, г = ®L = 1/соС = 10 Ом.
Определить, как нужно изменить активное сопротивление в фазе Л, чтобы показание ваттметра равнялось нулю.
3.33.	К выводам трехфазного генератора с линейным напряжением 380 В присоединены звездой два приемника (рис. 3.33), у каждого из которых г — mL= 1/соС = 11 Ом.
Определить токи на участках нейтрального провода.
3.34.	Линейное напряжение трехфазного трансформатора, обмотки которого соединены звездой с нейтральным проводом, равно 220 В. В фазе А включено 30 одинаковых ламп, в фазе В — 20 ламп, в фазе С — 10 ламп (40 Вт и 127 В каждая).
Определить: 1) ток в нейтральном проводе; 2) напряжение на каждой группе ламп при обрыве нейтрального провода.
3.35.	Определить токи в цепи рис. 3.35, если источник питания симметричен и г = coL= 1/соС = 2 Ом, UAN = 20z_0° В.
Рис. 3.35
Рис. 3 39
3.36.	Три группы ламп, имеющих сопротивления 2; 2,5 и 10 Ом, соединены звездой с нейтральным проводом, сопротивление которого 1 Ом, и подключены соответственно к фазам А,В и С трехфазного источника с линейным напряжением 380 В.
Пренебрегая сопротивлениями линейных проводов, найти напряжения на каждой группе ламп.
3.37.	Найти напряжения на группах ламп задачи 3.36 при обрыве нейтрального провода.
3.38.	К трехфазной линии без нейтрального провода с линейным напряжением 220 В подключены звездой: в фазе А — индуктивная катушка с малым активным сопротивлением, в фазах Jj и С — лампы с сопротивлением в каждой фазе, равным индуктивному сопротивлению катушки.
Найти напряжения на катушке и лампах. Построить топографическую диаграмму.
3.39.	На рис. 3.39 изображена трехфазная цепь, соединенная звездой, с фазным напряжением генератора, равным 173 В.
Определить токи, если г = coL= 1/соС = 30 Ом.
3.40.	К трехпроводной трехфазной линии с линейным напряжением 220 В присоединены звездой без нейтрального провода: в фазе А — лампы, в фазе В — реактор, в фазе С — конденсатор. Реактивные сопротивления конденсатора и реактора Равны каждое сопротивлению ламп.
Найти напряжения на приемниках и смещение нейтрали, Достроить топографическую диаграмму.
3.41.	Определить показания ваттметров в цепи рис. 3.41. Линейное напряжение генератора 380 В. Сопротивления г = = o)L= 1/<оС — 76 Ом.
3.42.	Трехфазная линия с линейным напряжением 380 В питает соединенные звездой два приемника (рис. 3.42), у каждого из которых г = coL = 1/соС = 20 Ом.
Определить показание вольтметра, включенного между нейтралями приемников.
3.43.	В цепи рис. 3.43 с линейным напряжением 10J/3 В определить показание амперметра, если г = coL= 1/юС = 1 Ом.
Рис. 3.44
Рис. 3.43
3.44.	В конце трехпроводной линии из-за неравномерной нагрузки линейные напряжения образуют равнобедренный треугольник: 1) рис. 3.44, а; 2) рис. 3.44,6. К линии подключен симметричный приемник, фазы которого с сопротивлениями г = 10 Ом соединены звездой. '
Определить токи в фазах приемника.
3.45.	К выводам сети с линейными напряжениями: а) по рис. 3.44, а; б) по рис. 3.44,6 присоединен приемник, сопротивления фаз которого (звезда) Z^ = г; ZB = jxL; Zc= — jxc, причем г = xL = хс.
Определить: 1) напряжения на фазах приемника; 2) те же напряжения после перемены местами сопротивлений в фазах В и С.
3.46.	Три амперметра включены в рассечку проводов, соединяющих выводы А, В и С трехфазного генератора с выводами приемника, фазы которого соединены звездой (без нейтрали). При равномерной нагрузке амперметры показывают по 20 А.
Определить их показания после короткого замыкания фазы А приемника.
Х47. В схеме рис. 3.47 линейное напряжение равно 100 ]/з В, г = 10 Ом.
Определить токи lA, IBy 1Су IN при следующих положениях переключателей: 1) ключи К2 замкнуты, К3 разомкнут; 2) ключи К3 замкнуты, К2 разомкнут; 3) ключи К1у К2, К3 разомкнуты.
3.48.	Фазоуказатель, состоящий из двух одинаковых ламп (40 Вт; 220 В) и конденсатора хс = г, подключен к линии с линейным напряжением 220 В.
Определить: 1) ток в фазе В, если конденсатор подключен к фазе А, а лампа в фазе В замкнута накоротко; 2) напряжения на конденсаторе и на лампах фазоуказателя после обрыва линейного провода фазы В.
Рис. 3.47
Рис. 3.49
3.49.	В цепи рис. 3.49 определить токи в линии и в фазах приемника при коротком замыкании между точками b с, если Un = 380 В; coL=2 Ом; Z^ — 10 Ом; ZB — = ДО Ом; Zc = — ДО Ом.
3.50.	В цепи рис. 3.49 определить токи в линии и фазах приемника при коротком замыкании между точками b и с, если (7Л == 380 В; coL=2 Ом; ZA=j3. Ом; ZR = Zc = ®= — ДО Ом.
3.51.	В цепи рис. 3.49 определить токи в линии и фазах приемника при коротком замыкании между точками b и с, если ил = 380 В; o>L== 2 Ом; Z« = jS Ом; ZR = Zc = -ДО Ом.
3.52.	Для схемы рис. 3.52 построить геометрическое место нейтральной точки п при изменении индуктивности Lx в фазе В от 0 до оо и определить наибольшее и наименьшее значения напряжения, измеряемого вольтметром. Фазное напряжение симметричного источника, соединенного звездой, равно 220 В.
Рис. 3.52
Рис. 3.53
3.53.	Для схемы рис. 3.53 построить геометрическое место нейтральной точки п при изменении емкости в фазе В от 0 до оо и определить наибольшее и наименьшее значения напряжения, измеряемого вольтметром. Линейное напряжение симметричного источника равно 220 В.
3.54.	Для схемы рис. 3.54 определить фазные и линейные токи, построить векторную диаграмму токов, если известны: фазное напряжение источника, соединенного звездой, 220 В, сопротивления г = caL= 38 Ом.
3.55.	К симметричному трехфазному генератору с линейным напряжением 220 В подключен несимметричный приемник, фазы которого соединены треугольником с сопротивлениями = — 10 Ом; 'Zrc = 10 —jlO Ом; Т^с.а ~ 5 Ом.
Определить фазные и линейные токи.
3.56.	Определить показания приборов, включенных в цепь по рис. 3.56, и построить топографическую диаграмму, если ил = 220 В; г{ = 22 Ом; г = 19 Ом; xL = хс = 11 Ом.
3.57.	Определить показания приборов в цепи рис. 3.57.
Дано: ил = 220 В; xL = хс — 11 Ом; г — 19 Ом.
3.58.	У трехфазного генератора, обмотки которого соединены звездой, линейное напряжение равно 220 В. Между его выводами А и В включена катушка, а между выводами
Рис. 3.57
Рис. 3.58
В и С — другая (рис. 3.58). К серединам обеих катушек присоединен вольтметр. Заданы параметры: г = coL = 22 Ом.
Определить показания приборов. Сравнить сумму показаний ваттметров с реактивной мощностью.
3.59.	Определить комплексные линейные напряжения в схеме рис. 3.59.
Дано: г = 57 Ом; coL= 1/соС = 78 Ом и токи 1А = = 20]/2 А; 1В = 20 z. - 135° А; 1С = 20 z. 135° А.
До-
5о-
Со
Рис. 3.59
АО
Во
Со
Рис. 3.60
3.60.	К трехпроводной трехфазной лийии с линейным напряжением 220 В присоединен приемник (рис. 3.60), параметры которого: (йЬ= 100 Ом; = 50 Ом; г = 100 Ом; 1/соС = = 100 Ом.
Определить линейные и фазные токи.
3.61,	В схеме рис. 3.61 известно, что 17л — 380 В; г = = coL= l/ос = 10 Ом.
Определить линейные и фазные токи.
3.62.	В конце трехпроводной линии линейные напряжения образуют равнобедренный треугольник: а) по рис. 3.44,а; б) по рис. 3.44,6. К линии подключен симметричный приемник, фазы которого с сопротивлениями г = 10 Ом - соединены треугольником.
Рис. 3.61	Рис. 3.64
Определить фазные и линейные токи приемника.
3.63.	К выводам сети с линейными напряжениями, показанными: а) на рис. 3.44, а и б) на рис. 3.44,6, подключен приемник, фазы которого с сопротивлениями	= j 10 Ом,
Zjgc = 10 Ом, ZCA = — j 10 Ом соединены треугольником.
Найти фазные и линейные токи приемника.
3.64.	В цепи рис. 3.64 амперметры, включенные в фазах приемника, показывают по 10 А, амперметры в линейных проводах — по 17,3 А.
Найти показания амперметров: 1) после отключения фазы ВС приемника; 2) при обрыве линейного провода В.
Рис. 3.66
3.65.	Напряжение на вводе в дом трехфазной трехпроводной сети равно 120 В. На первом этаже 10 ламп по 50 Вт подключены к выводам Л и В, на втором этаже 2 лампы по 25 Вт — к выводам В и С, на третьем этаже 18 ламп по 25 Вт — к выводам А и С.
Определить напряжения на лампах каждого этажа после обрыва провода фазы С, считая сопротивления ламп неизменными.
3.66.	Для приемников по рис. 3.66,а —в известно: 1/л = = 220 В; г = 1/соС.
Найти напряжения на резисторах до и после обрыва линейного провода фазы С.
Рис. 3.67
Рис. 3.69
3.67.	В схеме рис. 3.67 определить токи в линии и фазах приемника при коротком замыкании между точками b и с, если ил = 380 В; coL=2 Ом; Z„h — jlO Ом; = 20 Ом; Zca = - j 10 Ом.
3.68.	В схеме рис. 3.67 определить токи в линии и фазах приемника при коротком замыкании между точками b и с, если ил = 380 В; coL=2 Ом; = Zca = -j'4 Ом; Zj,c = = 20 Ом.
3.69.	В схеме рис. 3.69 найти фазные токи приемников 1 и 2 при линейном напряжении на входе, равном 380 В.
3.4.	Симметричные составляющие
3.70	(Р). Найти симметричные составляющие линейных напряжений, показанных на рис. 3.70.
Решение. Примем UAB= 220^.0° В, при этом йзс = == 220 z. -90° В; UCA = 311 z 135° В. По формулам разложения
= -^(йлв + айвс + а2йСА) = 4(220 г. 0° + 220 z. 30° +
+ 311 z 15°) = 245z 15° В; й2 =	+ a2UBc + <МСА) =
= 65,7 z - 105° В; !70 =	+ #вс + Уел) = 0.
Таким образом, напряжения UAB> UBC, UCA можно представить следующими симметричными составляющими:
UABl = 245	15° В; UAB2 = 65,7 z. -105° В; UAB0 = 0;
UBCl = 245	-105° В; UBC2 = 65,7 z. 15° В; UBCQ = 0
UCAi = 245 z. 135° В; UCA2 = 65,7 z. -225° B; UCAQ = 0.
На рис. 3.7OP показаны диаграммы найденных симметричных составляющих, а также построенный по ним треугольник заданных напряжений.
3.71	. Линейные напряжения в конце трехфазных трехпроводных линий вследствие неравномерной нагрузки образуют треугольники, показанные на рис. 3.71,а—г.
Для каждого случая определить коэффициент несимметрии напряжений
3.72	. На рис. 3.72, а — д показаны векторы токов в несимметричных трехфазных системах.
Найти их симметричные составляющие Ц, I2, 1о-
3.73	(Р). Для схемы рис. 3.73 определить сопротивления токам прямой Zb обратной Z2 и нулевой Zo последовательностей, если известно: coL= 10 Ом; соМ = 2 Ом; г = 1 Ом.
Решение. Пусть к рассматриваемой цепи приложены симметричные фазные напряжения С7Л1, UBi, Ucl прямой после-142
довательности, которые вызовут в фазах токи /В1, ZC1. Вследствие симметрии цепи ток в нейтральном проводе равен нулю. Составим по второму закону Кирхгофа уравнение для контура фаза А — нейтральный провод:
UAi =j®LlAX + jaMtBl +>Af/cl =
=+>м (iBi + /С1) =jatiAi
По (3.36)
Zi = &a\/Iai =j(f)L-j($M = j$> Ом.
Аналогично напряжения UA2, UB2i Uc2 обратной последовательности вызовут токи 1А2, i&b ici' Уравнение для того же контура:
и А2 —j^^Al + jwMiB2 + j(f)MlC2 =
— ja)LiA2 + j(f>M (IB2 + Л2) = №Ь1А2 — j(f)MlA2 и
?2 = Стл2Дл2 =j®L-j®M =;8 Ом.
Если к цепи приложить напряжения нулевой последовательности UAQ — UBq = Uсо — то они вызовут в фазах токи ^40 == /до = /со = /о- В нейтральном проводе ток будет равен 3/0.
Уравнение для того же контура:
UG = ja)Li0 + JcoM/o + jcoM/o + г • 3/0 = (3r + jcoL + ;2coM) /0
и
ZQ — Uq/Iq = 3r -b;wL4- j2($M = 3 + j'14 Ом.
3,74. Определить сопротивления прямой, обратной и нулевой последовательностей для схемы рис. 3.74, если сопротивления взаимной индуктивности Z^ = Z!ir = ZCA ZAN = = Zbw = Zcx —
Рис. 3.73
Ao
Bo-
Co-
No-
Рис. 3.74
3.75. Трехфазная машина при расчете режима может быть представлена схемой рис. 3.75, в которой взаимная индуктивность между фазами Z^ = — Zbc = Zca — Zm '> Zba = Zcb ~ = Za c = Z^, причем ZM Zn-
Полагая известными сопротивления Z, ZM и Z/n, выразить
рис 3 75	через них сопротивления схемы
для токов прямой, обратной и нулевой последовательностей.
3.76(Р). Трехфазный двигатель, фазы которого соединены звездой, подключен к сети с линейными напряжениями, показанными на рис. 3.70. Сопротивления фаз двигателя в рассматриваемом режиме для токов прямой последовательности Zt = 2,82 + J2,82 Ом, для токов обратной последовательности Z2 = 1 + 7*1,73 Ом.
Найти токи в фазах двигателя.
Решение. Для определения токов разложим фазные напряжения источника на симметричные составляющие. В данном случае фазные напряжения можно взять любыми при
условии, что их разности равны заданным линейным напряжениям. Например, приняв нейтраль источника совпадающей с точкой В на рис. 3.70 и UAB = 220 z. 0° В, получим UA = = UAb’, йв = Ъис=-Uвс = 220 z. 90° В.
Симметричные составляющие прямой и обратной последовательностей этих напряжений по (3.35)
U, = 141,5 л -15° В; U2 = 38,0 zi -75° В.
Напряжение й0 можно не находить, так как при любом его значении ток /0 = 0 из-за отсутствия нейтрального провода.
Отметим, что найденные фазные напряжения Ui и U2 можно рассчитать по линейным напряжениям (Ц и й2, полученным в задаче 3.70:
тт	245 / 15°
и., =	-----= 141>5 л _ 15° В;
]/3	|/Э
U&2 =	= 65,7	= 38,0 z. -75° В.
]/3	j/3
По (3.36) находим составляющие токов:
Л =	= 35,4	-60° А; /2 = U2/Z2 = 19 zl -135° А.
По найденным симметричным составляющим определим фазные токи двигателя аналогично (3.34):
Л = Л + /2 + /о = 44,3 z. — 84°25' А;
1В = а21х + al2 + /0 = 17,7 л. -163°55' А;
/с = а!1 + а212 + /0 = 50,7 z. 75° 25' А.
3.77. Трехфазный двигатель, обмотки которого соединены звездой, подключен к сети с линейными напряжениями, показанными на рис. 3.71, а —г. В рассматриваемом режиме сопротивление каждой фазы двигателя для токов прямой последовательности равно j‘5 Ом и для токов обратной последовательности равно ;3 Ом.
Определить токи в фазах двигателя.
3.7§(Р). В конце трехфазной линии (рис. 3.78) произошло замыкание фазы А на землю через сопротивление Z = ;0,5 Ом.
Определить напряжения и токи фаз генератора, ток в сопротивлении заземления нейтрали Z# и напряжения между точками а, Ь, с линии и землей.
Дано: фазная ЭДС генератора £ = 220 В; сопротивления различных последовательностей: генератора = J12 Ом;
Zf2 Ом; Zr0 = JI Ом; линии Z^ - Z,12 = JI Ом; - j2 Ом и Zjv = JO, 5 Ом.
Решение. Заменим сопротивления несимметричного приемника в конце линии (рис. 3.78Р, л) источниками ЭДС
Рис. 3.78
(рис. 3.78Р,б), которые можно представить состоящими из источников ЭДС прямой, обратной и нулевой последовательностей (рис. 3.78Р,*?).
Рассматривая каждую из последовательностей, получаем расчетные схемы для фазы А (рис. 3.78Р, г — е). Так как генератор симметричный, то Ё{ = = ЁА = 220 z. 0° В; Ё2 = £0 = 0.
(Если бы ЭДС генератора были несимметричными, то их необходимо было бы предварительно разложить на симметричные составляющие ЭДС в схеме.)
Основные уравнения для схем прямой, обратной и нулевой последовательностей:
(Zri + Znt) /i 4- U i = £ j;
(1)
(Zr2 4-Zn2)Z2 4-IJ2 = 0;	(2)
(Zro + ?ло + 3Zn) /0 + Uq ~ 0.	(3)
Дополнительные уравнения:
ZJa =	=0;	= 0,
t. e.
Z(il+i2 + io)^Ul + V2 + U();	(4)
a2ii 4- ai2 4- Io = 0;	(5)
al i 4" (X~i2 4" Zo =0.	(6)
Из (5) и (6) следует, что Z\ = Z2 = io-
Складывая соответственно левые и правые части уравнений (1)—(3) и учитывая (4) и полученное равенство токов, имеем:
(Zr. 4- Z_ii 4- Zj-2 4- Zjx2 4" Zj-o 4" Z.iO 4“	4" 3Z)Zj = Ёь
откуда Zj = -J 10 A = Z2 = Zo.
Из (1) —(3) определим составляющие: Ui—90 В; U2 = = -30 В; UQ = -45 В.
Симметричные составляющие напряжений на фазах генератора
(jrl =	- Zri/1 = 100 В; Ur2 «	= -20 В;
йа =	= - ю в.
77/777777777/7777777/7>
^77777777777/77777777777/7
Рис. 3.78Р
Напряжения на фазах генератора по (3.34) и А =	+ й<2 + 1% = 70 В;
UB — a2Vri + а0г2 +	= -U5,3zl 64° 18' В;
Uc = aUrl + a2lJr2 + йл= -115,3z_ -64° 18' В.
Ток фазы А генератора 1А = Л + /2 + Л) = 30 zi —90° А.
Для проверки найдем токи в фазах В и С:
1В — и211 + ai2 + /0 = —jlO (fl2 + a + 1) = 0;
ic = ui i + a2i2 + /q = —j io (д + a2 + i) = o.
В сопротивлении Zln ток iN = 3/0 = 30 zl —90° A.
Напряжения между точками a, b, с и землей Пвй = СЛ + #2 + #о = 15 В;
Vbn = a2V^ aU2 + UQ= -128,1 z. 54° 10' В;
Ucn =а1Ц + fl2l)2 + l70 = -128,1 z. -54° 10' B.
Проверка: Van = ZIA = JO,5 (— J30) - 15 B.
3.79.	Определить ток фазы А и показания вольтметров в цепи рис. 3.79 (при однофазном коротком замыкании генератора), если сопротивления генератора прямой, обратной и нулевой последовательностей соответственно равны: jl2; j'3; J1 Ом; фазная ЭДС равна 160 В.
3.80.	Определить показания вольтметров и ток в фазе, В при двухфазном коротком замыкании генератора (рис. 3.80).
Сопротивления генератора прямой и обратной последовательностей: J8 и J2 Ом; фазная ЭДС равна 100 В.
3.81.	Трехфазный симметричный генератор питает линию, разомкнутую на конце (рис. 3.81).
Дано: фазная ЭДС генератора Е = 280 В; сопротивления различных последовательностей: генератора Z^ — /7 Ом; Zj-2 — = J1 Ом; Zro — jQ,5 Ом и линии Z^ — Z^2 = j'l Ом; Z^ = j2 6м; сопротивление заземления нейтрали генератора Z^ ~ j‘0,5 Ом.
Рис. 3.79
Рис. 3.80
Найти напряжения и токи фаз А и В генератора, ток в сопротивлении Z#, а также напряжения между точками а, с и землей, если в конце линии: 1) фаза А замкнута на землю; 2) фазы В и С замкнуты на землю; 3) между фазами В и С короткое замыкание; 4) между фазами В и С включен приемник с сопротивлением Z = ;4 Ом.
3.82.	В конце линии (рис. 3.82) произошло замыкание фазы А на землю.
Дано: фазная ЭДС генератора Е — 200 В; сопротивления различных последовательностей: генератора = J9 Ом; Zj.2 =
Ом; Zro = JO,5 Ом, линии Z^i = Z& = Л Ом; Zjio = J2 Ом и приемника ZHi = J10 Ом; Z^2 = J2 Ом. Сопротивление заземления нейтральной точки генератора ZN = J0,5 Ом.
Определить токи во всех фазах генератора и приемника.
3.83.	К генератору с фазной ЭДС 220 В подключен приемник, фазы которого соединены звездой. На шинах генератора произошло однофазное замыкание фазы А на землю через сопротивление Z = 4,65 Ом. Сопротивления различных последовательностей генератора: ZTi - J10 Ом; Z& - JI Ом; Zro = = J10 Ом; сопротивление фаз приемника Zj, = J100 Ом; сопротивление заземления нейтрали генератора ZN = 2 Ом.
Определить токи во всех фазах генератора и приемника.
3.84	Трехфазный двигатель получает питание по линии передачи от источника с линейным напряжением 380 В. Сопротивления различных последовательностей: линии Zjh = Z^ = = JO,5 Ом и двигателя ZHi — jA Ом; Z^2 = J0,5 Ом. На линии произошел обрыв провода фазы А.
Определить напряжения и токи фаз А и С двигателя и напряжение между точками обрыва, если сопротивления различных последовательностей остаются неизменными.
3.85.	Для ограничения пусковых токов двигателя, обмотки которого соединены звездой, во все его фазы включают пусковые сопротивления Z, которые после пуска отключают. Вследствие неисправности выключателя одно из сопротивлений после пуска осталось включенным (рис. 3.85).
Гене-	Дви'га-
Рис. 3.85
Рис. 3.86
Определить: 1) отношение токов обратной 12 и прямой последовательностей; 2) напряжение на выводах пускового сопротивления, если сопротивления прямой и обратной последовательностей двигателя равны соответственно Zx и Z2, фаз-110е напряжение симметричного источника питания равно V.
3,86.	Трехфазный двигатель получает питание от генератора по линии передачи (рис. 3.86).
Дано: фазная ЭДС генератора Е = 210 В; сопротивления различных последовательностей: генератора = J3 Ом; Zr2 = = jl Ом; Zj-o = j'0,5 Ом, линии Z^ = J0,5 Ом; Z^ = Ом; Zno = j‘O»75 Ом и двигателя Z^ — J4 Ом; Z^2 = jl Ом; ZI{0 = = ;0,5 Ом; сопротивление заземления нейтрали генератора Zv = у 0,2 5 Ом. Вследствие неисправности пусковой аппаратуры произошло отключение фазы А и одновременно короткое замыкание нейтрали двигателя на землю.
Определить напряжение между разомкнутыми контактами выключателя и ток короткого замыкания, если сопротивления различных последовательностей остаются неизменными.
3.5. Вращающееся магнитное поле
3.87(Р). Катушки 1 и 2 с синусоидальными токами ц = = Im sin cot и i2 = Im sin (cot + л/2) расположены в плоскостях, пересекающихся под углом 60° (рис. 3.87).
Рис. 3.87
Рис. 3.87Р
Определить вектор индукции магнитного поля в точке 0, находящейся в центре катушек, и его угловую скорость при указанных на рисунке положительных направлениях векторов магнитной индукции Bi и В2, создаваемых соответственно токами ц и i2.
Решение. Индукции Bi и В2 магнитного поля в точке 0 пропорциональны токам, т. е. Вг = klm sin cot; В2 = klm sin (cot + + я/2) == klm cos cot, где к — коэффициент пропорциональности.
Для определения результирующего вектора магнитной индукции вычислим его составляющие по осям х и у как 150
сумму проекций векторов Вj и В2 на эти оси (рис. 3.87Р): 1/3
Вх - В2 cos 30° — klm cos cot;
Ву -	4- В2 cos 60° = klm sin cot + — klm cos cot.
Значение результирующего вектора
Из полученного выражения видно, что результирующий вектор магнитной индукции за период изменения тока дважды достигает максимального значения Втах = klm ]/з/2 и дважды имеет минимальное значение Bmin = к!„/]/2. Направление вектора В в плоскости ху можно характеризовать, например, углом а, отсчитываемым от положительного направления оси х (рис. 3.87Р):
а = arctg-^- = arctg
Из этого выражения следует, что угол а с течением времени увеличивается, т. е. вектор В вращается вокруг точки 0 против направления движения часовой (^грелки.
Угловая скорость вектора
da/dt = ]/3 й>/(2 + sin 2 cot),
т. е. не постоянная и за период изменения тока дважды достигает максимального значения (Ja/cZt)^ = |/з со и дважды имеет минимальное значение (da/dt)^ = со/|/з.
Если перейти к системе координатных осей х' и у', повернутой по отношению к осям х и у на угол 30° по направлению движения часовой стрелки (рис. 3.87 и 3.87Р), то получим:
Вх> = -Bi cos 60° -I- В2 cos 60° = —klm cos (cot +	);
By’ = Bt cos 30° + В 2 cos 30°
Следовательно,
т. е. годографом вектора В является эллипс, большая ось которого, равная ЗВтах, находится на оси /, а малая ось, равная 2B„in, — на оси х'.
Таким образом, в рассматриваемой точке 0 получается эллиптическое вращающееся магнитное поле. Направление вращения — против направления движения часовой стрелки. Угловая скорость периодически изменяется с частотой, вдвое большей частоты тока.
Рис. 3.89
Рис. 3.88
3.88.	По катушкам 1 и 2, которые расположены во взаимно перпендикулярных плоскостях (рис. 3.88), проходят синусоидальные токи и i2, создающие магнитные индукции с указанными на рисунке положительными направлениями векторов.
Определить характер вращающегося магнитного поля в точке 0, находящейся в центре катушек. Найти значение результирующего вектора магнитной индукции и его угловую скорость для случаев:
1)	z’i	— Im sin cot;	i2	— Im	sin (cot — n/2);
2)	h	= Im sin cot;	i2	= Im	sin (cot + k/2);
3)	h	= Im sin cot;	i2	= 21	m sin (cot — k/2);
4)	ii	= Im sin cot;	i2	=	1m sin (cot + k/2).
3.89.	Катушки 1 и 2 с синусоидальными токами = = Im sin cot и i2 = Im sin (cot — к/2) расположены в плоскостях, пересекающихся под углом 60° (рис. 3.89).
Определить характер вращающегося магнитного поля в центре катушек (точка 0). Найти значение суммарного век-152
тора магнитной индукции и его угловую скорость для случаев, когда угол между положительными направлениями векторов магнитной индукции Вх и В2, создаваемых токами и г2, равен: 1) 60°; 2) 120°.
3.90.	Катушки 1—3 с синусоидальными токами ib i2, ?з расположены в плоскостях, пересекающихся под углом 60° (рис. 3.90). В центре катушек указаны положительные направления соответствующих векторов индукции В2, В3.
Определить характер вращающегося магнитного поля в центре катушек (точка 0). Найти значение суммарного вектора магнитной индукции и угловую скорость его для случаев:
1)	= Im sin cot;
i2 — sin (wt - 120°); i3 = Im sin (cot + 120°);
2)	ij = sin cor; h = /„sin (cor + 120°);
Рис. 3.90 i3 = Im sin (cot — 120°).
3.91.	У катушек задачи 3.90 вектор В3 имеет обратное положительное направление.
Определить характер вращающегося магнитного поля в центре катушек (точка 0). Найти результирующий вектор магнитной индукции и скорость его вращения для случаев:
1)	ц = Im sin cot; i2 = i3 = Im sin (cot + n/2);
2)	h = Im sin	h = h = —-Д-sin (cot — я/2).
/3
Глава четвертая
ЧЕТЫРЕХПОЛЮСНИКИ
Введение к гл. 4
Несимметричные пассивные четырехполюсники. Режим пассивного взаимного (проходного) четырехполюсника задается напряжением U2 — z \|/Mi и током = Ц z на первичных 1-1' и напряжением U2 = Г2 z \|си2 и током /2 —I2 z \|ci2 на вторичных 2-2' выводах (рис. 4.А).
Напряжения и токи можно связать уравнениями с коэффициентами различного типа:
Ul ”411^2 + 412^2»
Л ~ 4г 1	+ 422^2 >
или
(4.1)
1/1
й2
1г
— матрицы-столбцы напряжений и токов;
411 412
4г 1 412
— квадратная матрица коэффициентов;
и
Из четырех коэффициентов каждой системы уравнений только три независимых; справедливы уравнения связи
411422 — 412-421 = U Т21 = ~Т12» Z2I = — Z12»
(4.6)
£112 ~ £121, ”12 — ”21-	J
В табл. 4.1 дана связь коэффициентов уравнений различного типа при указанных на рис. 4.А положительных направлениях напряжений и токов.
Рис. 4.А
Входные сопротивления со стороны первичных выводов Z1BX при сопротивлении нагрузки на вторичных и со стороны вторичных Z2BX при сопротивлении нагрузки ZHl на пер-
Таблица 4.1. Коэффициенты уравнений четырехполюсника
Типы		Коэффициенты		
уравнений	А	У	Z	H
А	411 <4-12 — 21	—22	|	е-i	~ г» <4	<N 1х,| 5^|	<J| >н| 1	1	IN _	IN	IN t-J	l-J	•— |N IN	|N	|> Li Й	LN	1 to	1^	I?	II> -	к	* 15:	_	15;	15; IO	lo	—
Y	1^ __ 1—	— to tO	ЮМ 1	1 I-U	1^1	_ ю —	1	In In 2г 1 Х22	1	|> IN |> IN N й	! Sj Li 1 |> |N	|[> IN N _	N	t _^J2 ^11 £11 £21 £h £n
Z	1^ и	(О	— ь—	•—* 1^. |tb. Ю	Ю	Ю «—К>	—	Г 22 _Ij2 А у	А у _ - 21	- 11 А у	А у	IN	IN w	•— 1—• IN	IN ю	>-»	01 Ot	ГЧ « сч	гч 5:1 й;1 ~ 5ql 5 3 Г, Й <11 Й51	5:1 151
Н	— 12	1 — 22	— 22 1	_ -21 <4.22	—22	J	112 Y и	1ц У 21	At Гц	Гц	1	IN |> IN IN й N ro K> K> — IN IN IN _ Й 5 to	£11 £12 £21 £22
G	•4.21 J_ 4ц 4ц 1	_ — 12 4ц 4ц	Ду 112 г 22 Г 22 _Ь1 1 Г 22	г 22	IN |N IN —«to	— 1 |N||> IN IN C |N — w	£ 22 __ £ 12 Ая Дя .^21 £п Дя Дя
Примечание. Д у ~ L11X22 ~ У 12X21» A.Z = ? л422 “ 4 12?2г ^Н~^ц^22~ " -12Ц21 
винных:
(4.8)
В частности, входные сопротивления при короткозамкнут тых соответственно вторичных (U2 = 0) и первичных (Ui = 0) выводах
41к = 4.12/А22 =	22к = 412/411 = ~^1Х12->	(4-9)
входные сопротивления при разомкнутых соответственно вторичных (Z2 =0) и первичных (/\ = 0) выводах
41х = 411/421 = Zlb — ^22/^21 = — Zl22 (4.10)
И
41х/21к = 22х/^2к-	(4.11)
При известных Zlx, Z1K, Z2<, Z2K
All = ]/Z1xAZ2x “ Z2k); 412 = Al 121^	)
All = All/X.lxi A22 — A21A2X ~ А11А.2х/А1х- J
Уравнения с характеристическими (вторичными) параметрами (характеристические сопротивления Zcl, Zc2 и постоянная передачи 0:
V 1 = Б’г ch Г + |/Z^ i2 sh г; )
h = u2 sh ry/z^z^ + j/z^/z^ i2 ch r, J
где	_____________ __________
Zci = VA11A12/42142 2 = ]/AikAix', 1
-------------.---------- (4.14)
Zc2 — 1/422^12/^12 1411 — ]/ZjxZlx J
ch Г — ]/4114г2 j sh Г = |/t1i	1; 'j
Г = In (|/411422 + 1412421);	(	(4.15)
th Г = l/zjzlx = J/Z2./Z2, j
При питании co стороны первичных выводов и согласованной нагрузке Zjl2 = Zc2 на вторичных
г = а+7в=4-1п?гт-; а=41птгт~ Нп; 2	С/212	»>2/2
ТТ Т	|	1	(4.16)
А = 10 lg -lyl- дБ; В = ^-(фи1 - ф„2) + -у (фп - ф(2), О 2* 2	"
где А — постоянная ослабления; В — постоянная фазы. 156
Симметричные пассивные четырехполюсники. Для пассивного взаимного симметричного четырехполюсника справедливы все приведенные выше уравнения и расчетные формулы (4.1)—(4.12), причем
Уи= -I22; Zu= — Z22; Лц-422; |Я| = |С|--1, (4.17) где | И | и | G | - определители.
Уравнения с вторичными параметрами (характеристическим сопротивлением и постоянной передачи):
и2
Ui = U2 chr + 72Zcshr; Ц = -у-sh Г +/2 ch Г, (4.18)
где
Zr —	9 — А-^/А2\ j ch Г — A11;	1
sh Г = ]/л12Л21; Г = In (4 ц -I- ]/a12A2i\ j
Входное сопротивление при сопротивлении нагрузки 7^
7 _ 4uZh + d.i2 _ 7 Zj, + Zc th Г _ Zh + Zy
421^ + 4.!! “-c Z, 4-ZHthr Zh + Z/
В частности, в режимах короткого замыкания и холостого хода
Zg - Zc th Г; Zx = Zc/th С
откуда
Zc = ]/z,Z,; th Г = Те1' = j/z^;
г Л ,n 1.1+Г^Т	1	,,
Г = А + уВ = — In ----= vtn we >
2	1 — T z. т 2
(4.21)
(4.22)
A=2-lnw; B1 = ^/2; B2 =(^2)±л;
w =
1 "h T Z_ X
1 — T z. x
= arg
1 + Tz.x
1 — T z. т ’
(4.23)
В табл. 4.2 приведены значения коэффициентов, вторичных параметров и сопротивлений Т-, П-образных и Х-образного (мостового) симметричных четырехполюсников. Для Т- и П-образных четырехполюсников следует всегда считать, что суммарное продольное сопротивление равно Z15 а суммарное поперечное равно Z2. В табл. 4.2 характеристическое сопротивление Т-образного четырехполюсника обозначено Z?, а П-°бразного обозначено Zn. Т- и П-образные четырехполюсники
Таблица 4.2. Коэффициенты и параметры симметричных четырехпо
Схема	Коэффициенты		
	А	Y	
	|>U. К	м	z II	II	и	II -	~	IN	- + |N	+ KJ	м	>—	м |N IN	4-	|N |N K> *“	Ю ** IN IN IQ	11 = “ - 22 ~	
Н-?2 о	1	о		-Zl(Zl+4i2)’ ~ -12 = -	4~2	
о—г—CZ3—-f—о h2Z,	А U ггг[\ 0—1	1—0	Nl 2? 4-	-	- Nl	N1 Й1 i	м	-Ini	i II	II	II	II —.	e)	_	<4 «	7 Tqf	-^j	^1	II	..	II Cl	1	Cl Ini m l Л7 -In7 Nl	II	Nl	II	
о	о Ч	J' WOi /  Г Nil \ О	О	|йк	Ik.	|k. У	£	— II	l>	II IN	IN	к,	IN	IN M	.	IN	M	M 1 bJ	IK)	1	+ |N	IN	M	|N	IN 1 |k. M Ю	II	II <N	,	ГЧ Г4	_ V	Nl M ?	Nl n7 1	।	CN	1	|	<N II	Cl Nl	II	«N M - Nl	a Ni Nl	II	Nl	II	
можно рассматривать как составленные из двух Г-образных. Коэффициенты и параметры Г-образного четырехполюсника приведены в табл. 4.3.
ЛЮС ников
При согласованной нагрузке Z* = Zc уравнения (4.18) упрощаются :
Л=/2^,	(4.24)
откуда при согласованной нагрузке
Г = 1п((71/1/2) = In (Л//2);	(4.25)
.	, 1Л , Ц 1 , S2 1 , Г, „
А = In —- = In — = — In — = —In — Нп; )
О 2	Ч	' 2	I
U	I	S	Pi (4.26)
A = 201g -T = 201g	= 101g ^-= 101g -j- дБ,
*2	^2	*2 У
где Si — U Ji; S2 — ^2^2» ^1 ~ U17 1 cos 0; P2 ~ U2^2 cos 0;
В = Ф«1 - \|/u2 = i - ^12-	(4.27)
Для цепочки симметричных четырехполюсников характеристическое сопротивление Z„ равно характеристическому сопротивлению одного звена Zc. Постоянная передачи цепочки
Гц = пГ,	(4.28)
где Г — постоянная передачи одного звена; п — число звеньев.
Рис. 4.Б
Рис. 4.В
При каскадном соединении любых пассивных четырехполюсников перемножаются матрицы || А ||, при параллельном соединении суммируются матрицы || У||, при последовательном — матрицы || Z ||, если соединения регулярные.
Активные четырехполюсники. Для активных четырехполюсников с зависимыми источниками (неавтономных) справедливы уравнения (4.1)—(4.5), но все четыре коэффициента каждого типа уравнений независимы, т. е. уравнения связи (4.6) не выполняются.
Для активных четырехполюсников с независимыми источниками (автономных) можно применять эквивалентные схемы, представленные на рис. 4.Б и 4.В. Уравнения типа А для схемы по рис. 4.Б:
= 411^2 + 412 (Л ~ Лк) 5 Л “ Лк — 4.21 ^2 + А.22 (Л “ ЛкЛ
(4.29) где ilK = Jj и /2к — J2 равны токам /1 и / при одновременном коротком замыкании первичных выводов и коротком замыка-
Таблица. 4.3. Коэффициенты и параметры Г-образного четырехполюсника
Схема	К оэф фициенты			Параметры
	А	Y	Z	
;	2 о	у	Г~~1	О fbz2 1'	М	2' о	4	-О	4П = 1; 4.12 = —1/2; 4.21 = 1/2Z2; 4-22 = 1 4* Z 1/42^2	Y = —1 + — 2 • -11	2ZjZ2 ’ Г21 = - Г12 = 2/^Р У 22= -2/Zi	^n=2Z2; Z 2i — — Z i2 = 2Z-,; — 22 = = _(^“+2-2) \	£»	i	Zci=Zn; Zc2 = Zt(cm. табл. 4.2);
нии вторичных выводов. Эти уравнения отличаются от уравнений (4.1) тем, что токи и /2 заменены токами — /1к и /2 — Ък- Такую же замену нужно сделать и в (4.2)—(4.5). Уравнения связи (4.6) выполняются, так что четырехполюсник характеризуется пятью независимыми параметрами.
Уравнения типа А для схемы рис. 4.В:
Ul ~~ U1Х = (U2 — ЬГ2х) + d.12^2 5 Л• = 4.21 (^2 ~~ U2х) + 422-G» (4.30)
где С71Х=Ё1 и и2х=Ё2 равны напряжениям йг и Я2, когда одновременно разомкнуты первичные и вторичные выводы. В (4.2)—(4.5) напряжения и U2 также нужно заменить напряжениями 171 — и V2 — Ё2х.
Передаточные функции четырехполюсников. Передаточная функция четырехполюсника = Я (со) е^(<а), как и для других цепей, делится на амплитудно-частотную Я (со) и фазочастотную ф(со). Для безразмерных передаточных функций логарифмическая амплитудно-фазовая характеристика (JIAX)
In Я (jco) = In Я (со) + /\|/ (со).	(4.31)
4.1. Уравнения и коэффициенты пассивных четырехполюсников
4.1 (Р). Составить матрицу А для четырехполюсника по рис. 4.1 при coL=2/coC = 20 Ом; 1) записывая уравнения типа А в режимах холостого хода и короткого замыкания; 2) выражая коэффициенты через предварительно вычисленные
Рис. 4.1
Рис. 4.1Р ->	О
сопротивления холостого хода и короткого замыкания. Убедиться, что коэффициенты удовлетворяют уравнению связи. При напряжении на первичных выводах 1-Г, равном 20 В, найти напряжение на разомкнутых выводах 2-2'.
Решение. 1) При разомкнутых вторичных выводах (12 =0) из уравнений типа А (4.1) получается:
= 4.11	Лх=421^Т2х-
По схеме рис. 4.1
йц = (-Д/«>С + /wL)/lx = (—/10 + /20) Лх =Д0/1к;
U2x = /гоЬ71х или /1х = С2х//20 и 6т1х = ДОС72х//2О = 0,5[/2х.
Следовательно, Ац =0,5; Л21 = 1//20,.= -/0,05 См.
При короткозамкнутых вторичных выводах (U2 = 0) из уравнений типа А (4.1) получается:
^Лк = 4.1 гЛк 5 Лк = 422^2к-
По схеме (рис. 4.1)
£Лк ~ ~ /1/®О Лк = — ДОЛК, Лк = Лк-
Следовательно, Л12 = -ДО Ом, Л22 = 1 и уравнение связи выполняется.
2) Сопротивления со стороны выводов 1-1' при соответственно короткозамкнутых и разомкнутых выводах 2-2'
ZlK = -ji/ayC = -ДО Ом;
Zlx = -Д/соС 4- jcoL = —ДО + /20 = ДО Ом.
Аналогично со стороны выводов 2-2'
Z2K =	= -J20 Ом; =j®L = J20 Ом.
JCOL — J 1/соС
По (4.12)
4и = l/Zlx/(Z2x - Z2K) = l/jlO/0'20 +J-20) = ±0,5.
Из (4.1) Ли = lrix/tr2x» а из векторной диаграммы (рис. 4.1Р), построенной для четырехполюсника по рис. 4.1 при разомкнутых вторичных выводах, следует, что при заданных значениях фЬ и 1/соС напряжение й2х совпадает по фазе с напряжением й т. е. Ац = + 0,5.
По (4.12) Л12 = А1 iZ2g = —/Ю Ом; Л21 == А\\/Z\x = —/0,05 См; 4.22 = 421Z2x = 1. Напряжение Ц2к = U1JA.1 t = 20/0,5 = 40 В.
4.2(Р). Найти коэффициенты матрицы А для четырехполюсника по рис. 4.2 при 1/соС = 35 Ом, coLj = 20 Ом, = 60 Ом, соМ = 10 Ом, сравнивая уравнения типа А с Уравнениями, составленными по законам Кирхгофа.
Решение. Для четырехполюсника по рис. 4.2 по второму закону Кирхгофа для левого и правого контуров
^-/^+/®L1^/1 -/соМ(Д — Л) 4-/соЬ2 (Z\ -/2)-
-jwMii = U ь
-/соЬ2 (Д - /2) + /О)М/j + U2 = 0.
После подстановки тока 11 из второго уравнения в первое и приведения уравнений к виду (4.1) при заданных числовых значениях сопротивлений получаем:
= 0,5[>2 -J20/2; Z, = ^-+
т. е. 4П = 0,5; Л12 = —>20 Ом; A2l = -j'0,02 См; А22 = 1,2.
Рис. 4.2
Рис. 4.3
4.3.	Найти элементы матриц A, Z, Y, Н симметричного Т-образного четырехполюсника (рис. 4.3) при = гг — 10 Ом, Z2 = г2 — 5 Ом. Проверить выполнение уравнений связи коэффициентов.
4.4.	Найти элементы матриц A, Z и Y простейших четырехполюсников по рис. 4.4, а и б.
4.5.	Составить матрицы Y и Н для П-образного симметричного четырехполюсника по рис. 4.5 при — rv = 20 Ом, 2Z2 = 2r2 — 100 Ом. Проверить выполнение уравнений связи коэффициентов.
4.6.	Определить элементы матрицы Z «разорванного» четырехполюсника (рис. 4.6). Записать матрицу для частных случаев: 1) Zt = 0; 2) Z2 = 0.
4.7.	Определить элементы матрицы А идеального трансформатора, имеющего витков первичной обмотки и w2 — вторичной.
4.8(	Р). Найти коэффициенты матрицы А несимметричного Т-образного четырехполюсника (рис. 4.8), предварительно вычислив сопротивления короткого замыкания и холостого хода со стороны первичных и со стороны вторичных выводов.
Решение. По схеме рис. 4.8 находим:
После подстановки найденных величин в (4.12) получаем:
4.9.	Выразить коэффициенты системы уравнений четырехполюсника в форме Z через известные сопротивления холос
того хода и короткого замыкания.
4.10.	Определить коэффициенты матрицы А для четырехполюсников, представленных на рис. 4.10, а —в: 1) записывая для рассматриваемой схемы уравнения типа А, 2) по предва-
рительно вычисленным сопротивлениям короткого замыкания и холостого хода. Проверить выполнение уравнения связи коэффициентов.
Рис. 4.10
Параметры четырехполюсника на рис. 4.10,6: г = ю£ = = 20 Ом; 1/соС = 40 Ом; на рис. 4.10, в: г = xL = хс = 10 Ом.
При заданном напряжении на первичных выводах, равном В, найти напряжение на разомкнутых вторичных.
4.11(	Р). Измерены первичный и вторичный токи симметричного аттенюатора при замкнутом рубильнике Р (рис. 4.11): *1* = 3,2 мА, /2к - 1,6 мА.
Определить токи при разомкнутом рубильнике, если Ё = 55 48 В, гн = 5 кОм.
Решение. При замкнутом рубильнике (режим короткого замыкания на вторичных выводах) = 02 = 0. Следовательно, по (4.1) Ui = Л12/2к; Лк ~ 4пЛк, где учтено, что для симметричного четырехполюсника Л22 =ЛП. Токи и напряжения совпадают по фазе, так как аттенюатор состоит из резисторов, т. е. Ац = Дк/Лк = 2 = Л22; Л12 = 17д/Лк ~ £/Лк = 30 -103 Ом = = 30 кОм. Коэффициент А21 = 10"4 См определяется из уравнения связи (4.6).
При разомкнутом рубильнике Р напряжение на сопротивлении нагрузки СУ2=гн/2 и по (4.1)	= (Лпгн + Л12)/2;
Л — (4з1гн + 4.2 2) Л» откуда при Ui — Ё = 48 В и гн = 5 кОм получается /2 = 1,2 мА; Л = 3 мА.
4.12.	Аттенюатор собран по Т-образной схеме рис. 4.3 с сопротивлениями Zr =	= 8 кОм и Z2 = г2 = 4 кОм.
Определить ток источника питания Ц и напряжение на сопротивлении нагрузки U2 при напряжении источника питания Ui = 48 В и сопротивлении нагрузки гн, равном: 1) оо; 2) 6 кОм; 3) 0.
4.13(	Р). Для трансформатора (рис. 4.13) определить коэффициент У21,
Решение. Из (4.2) следует, что У21 = /2к/^1- По схеме рис. 4.13 при коротком замыкании вторичных выводов
21Лк ~	~	— 0,
где Zt = +>1!,' Z2 = г2 + jcoL2; Zw
Рис. 4.11
Рис. 4.13
Исключив ток /1К из этих уравнений, получим:
= (212г/2м — 2м) Лк» т. е. У21 = Zv/(Z1;Z2 — Z^).
4.14.	Для четырехполюсника по рис. 4.14 (Г-образного) известны сопротивления ZJ2 = 2Z2 = 10 + ;20 Ом.
Определить: 1) коэффициенты матрицы А; 2) напряжение источника питания, при подключении которого напряжение на активном сопротивлении нагрузки 10 Ом составит 20 В;
3) ток источника при питании четырехполюсника со стороны вторичных выводов и коротком замыкании первичных, если напряжение источника питания равно 100 мВ; 4) показание ваттметра, через токовую обмотку	1	Z^2 2
которого проходит первичный ток,	о ? —-L_j  --о
а вольтметровая обмотка подклю-	п
чена к вторичным выводам, если	t LI -г	.
последние разомкнуты, а к первич-	о |	о
ным подключен источник с напря-	Рис 4Д4
жением ut = 80 sin (cot + 45°) В.
4.15(Р). 1) Составить матрицы Y и Z для симметричного мостового (Х-образного) четырехполюсника (рис. 4.15) при Zt = у 10 Ом; Z2 = Ю - ДО Ом.
2) Рассчитать режим четырехполюсника (определить
/2, U2) при напряжении источника питания Ux = 100 мВ: а) при короткозамкнутых и б) при разомкнутых вторичных выводах.
Рис. 4.15
Рис. 4.15Р ->
Решение. 1) При коротком замыкании вторичных выводов (U2 = 0) из уравнений типа У (4.2) получаем 1{к = Уц171к, т. е. УГ1 — величина, обратная входному сопротивлению со стороны первичных выводов при коротком замыкании вторичных: -и = 1/Z1K. При коротком замыкании схему рис. 4.15 можно изобразить так, как показано на рис. 4.15Р, а. Следовательно,
ZjK = 2ZyZ2/(Zi + Z2) и Уп = (Zj 4- Zi)/2ZiZ? =
= (2,5 — j‘2,5)-10"2 Cm.
При разомкнутых вторичных выводах (I2 = 0) из уравнении У получаем: 0 = У21Й1х + Xit^iw и так как для симметричного четырехполюсника У22 = — У1Ь то У21 = УцП2х/С71х. то же время при разомкнутых вторичных выводах (рис. 4.15Р,б)
trix=(Z2 + Z1)/lx/2; U2x=(Z2-Zi)iiJ2, (1)
или
1>2хДЛх = (Z2 ~ ZX)/(Z2 + ZJ, поэтому
bl = (Z2 - ZJ^ZiZ, = -(2,5 + Д5). IO’2 См = - У12.
Коэффициенты уравнений типа Z определяются проще. При разомкнутых вторичных выводах (12 = 0) из уравнений типа Z (4.3) получаем:
^ix = Zn/lx; t^2x = Z2i^ix-
Для заданного четырехполюсника при разомкнутых вторичных выводах (рис. 4.15Р, б) выше записаны уравнения (1). Сопоставляя их с последними уравнениями, находим:
Zu = (Z2 + ZJ/2 — 5 Ом = ~Z22;
Z2i = (Z2 ~ Zi)/2 = 5 — j 10 Ом — — Z12.
Составить матрицу Z по уже известной матрице Y или наоборот можно и при помощи общих формул связи коэффициентов (табл. 4.1).
2а) При короткозамкнутых вторичных выводах (Lr2=0) по (4.2)
Л. =111^1.= 2.51/2^ -45° • 10"2 •100 = 3,53 л -45° мА;
4 =12|С'1к = 7,91 zi —108°25'• 10*2  100 = 7,91 z. -108°25'мА.
26) При разомкнутых вторичных выводах (12 — 0) по (4.3) == Zn/ix, т.е. Лх “ t>ix/Zn = 100/5 = 20 мА;
^2x = Z21/1x и 172x = 11,2z. — 63° 30'• 20 = 224 z. -63° 30' мВ.
Рис. 4.16	Рис. 4.17
4.16. Показать эквивалентность мостовой (рис. 4.15) и дифференциально-мостовой (рис. 4.16) схем при отношении чисел витков первичной и вторичной обмоток трансформатора Wi/w2 = 1/2.
4.17. Для изменения уровня сигнала в аппаратуре связи часто применяется Т-образный мостовой аттенюатор (рис. 4.17), 168
так как в такой схеме необходимы только два переменных резистора.
Определить коэффициенты матрицы А аттенюатора при г п = 100 Ом, г2 = 10 Ом, r3 = 1 кОм.
1 4.18. Известны сопротивления двух четырехполюсников (рис. 4.8): первого Zi = Д1 Ом; Z2 = jTO Ом; Z3 = ~;6 Ом; второго Zi = — J1 Ом; Z2 = — j2 Ом; Z3 — j6 Ом.
Выяснить, можно ли отличить четырехполюсники: 1) после измерения сопротивлений холостого хода и короткого замыкания на частоте, для которой даны значения Zn Z2, Z3; 2) после повторного измерения, увеличив частоту на 10%.
Рис. 4.19	Рис. 4.21
4.19.	Схема четырехполюсника для уменьшения амплитудных искажений сигналов показана на рис. 4.19. Сопротивление нагрузки Zh = R.
Показать, что при любых Zj и Z2, удовлетворяющих условию ZjZ2 — R2 (обратные двухполюсники), входное сопротивление со стороны первичных выводов также равно R.
4.20.	В схеме четырехполюсника рис. 4.19 элементы Zj и Z2 - обратные двухполюсники. Элемент состоит из параллельно соединенных резистора с сопротивлением = = 1,6 кОм и конденсатора емкостью С, элемент Z2 = г2 + + JcdL2 — индуктивная катушка. Сопротивление нагрузки — резистор Zh = R =*= 400 Ом.
Найти значения параметров С, L, г2, если на частоте 1 кГц отношение напряжений и отношение токов на входе и выходе равны 2,23.
4.21.	Состоящие из реактивных элементов четырехполюсники включают между генератором и потребителем для получения максимальной потребляемой мощности. Так, в установках Диэлектрического нагрева применяют, например, Г-образ-«УЮ схему (рис. 4.21).
Определить, как следует выбрать емкость С подстроечного конденсатора и частоту генератора, чтобы входное сопротивление четырехполюсника было активным и равным 2,85 кОм, если в эквивалентной последовательной схеме сопротивление ^Рузки гн = 80 Ом и Сн = 50 пФ. Индуктивность L — 5 мкГн.
Найти активную мощность в сопротивлении нагрузки при напряжении на входе четырехполюсника 3,1 кВ.
Указание. Емкость С и частоту f следует выбирать так, чтобы входная проводимость контура (на выводах 1-Г) была чисто активной, т. е. Увх = дв*.
4.2	. Характеристические (вторичные) параметры
4.22	(Р). Для П-образного четырехполюсника (рис. 4.5) известны сопротивления: = /50 Ом; Z2 = —/10 Ом.
Определить характеристическое сопротивление и постоянную передачи. Найти напряжение на сопротивлении согласованной нагрузки при напряжении питания 10 В.
Решение. Определим характеристическое сопротивление
по сопротивлениям короткого замыкания и холостого хода (4.22). Для схемы рис. 4.5
= 2Z2Zt _. 100	2Z2 (2Z2 + Zt) =
2Z1 + Z1 } 3	’ -K 2Z2 + 2Z2 + Zi
—/60 Ом;
z. = Zn = \/z.Z. = /2000 (-180° + 360°) = +/44,8 Ом (два значения согласованной нагрузки). Постоянная передачи по (4.19)
ch Г = ch (А + /В) = ch A cos В + j sh A sin В = t = t/i/(72x.
По схеме рис. 4.5 при отсутствии сопротивления нагрузки на вторичных выводах
t\/(?2x = (Zi + 2Z2)/2Z2 — - 1,5 (действительное),
поэтому sh A sin В = 0. Если принять В = 0, то cos В — 1 и ch А = —1,5, чего не может быть. Значит, В = тг; cos В = — 1; ch А = 1,5 и два значения постоянной ослабления: А = = ±0,96 Нп.
Если выбрать Z^ = Zr = — /44,8 Ом, то по схеме четырехполюсника рис. 4.5 с - емкостной согласованной нагрузкой (Zh = —/44,8 Ом) получаем U2 = 0,38317 j = 3,83 В, т. е. U2 < что соответствует А = +0,96 Нп, так как по (4.26) 17i/H2 = = ек = е + 0,96, и также получаем U2 = 0,383 . При Z^ = Zc — = +/44,8 Ом соответственно А = —0,96 Нп, так как получаем U2 =2,6Ш! =26,1 В.
4.23	. В трактах телефонных сигналов аппаратуры телемеханики установлены симметричные уравновешенные аттенюаторы, схема которых показана на рис. 4.23.
Определить характеристическое сопротивление и постоянную передачи аттенюатора.
4.24	(Р). Для Т-образного симметричного четырехполюсника (рис. 4.3) при Zi=Z2=5 Ом определить: 1) характеристические параметры; 2) ток и мощность приемника в режиме согласованной нагрузки, мощность источника питания, если напряжение источника питания равно 10 В.
решение. 1) Характеристические (вторичные) параметры
можно найти по (4.19), предварительно вычислив коэффициенты матрицы А, или по (4.22), предварительно вычислив сопротив-
Рис. 4.23	Рис. 4.26
ления Z* и Zx. Так как схема рис. 4.3 типовая, то для нее расчетные формулы даны в табл. 4.2:
Zf. = ZT = ]/Z1Z2 (1 + Zi/4Z2) = 5,58 Ом (активное);
ch Г = ch (А 4- /В) = 1 4- Zt/2Z2 = 1,5.
Так как схема состоит из активных сопротивлений, то постоянная фазы В = 0 и при ch А = 1,5 постоянная ослабления А = +0,96 Нп. Второе решение А = —0,96 Нп нужно отбросить, так как у четырехполюсника, состоящего из активных сопротивлений, напряжение на выходе должно быть меньше, чем на входе.
2)	При согласованной нагрузке симметричного четырехполюсника ZbX — Zc = ZH по (4.26) напряжение приемника U2 = = Uх/еА *= ю. 0,383 = 3,83 В. При активном характеристическом сопротивлении Zc = га = гвх ток приемника I2 = Uг/гн — 0,686 А.
Мощность приемника Р2 = (72АН = 2,62 Вт. Мощность источника Рг = П?/гвх = 17,9 Вт.
4.25.	Определить характеристические параметры для Т- и П-образных симметричных четырехполюсников по рис. 4.3 и 4.5 при = -/200 Ом и Z2 = /50 Ом.
4.26.	Найти зависимость от частоты характеристического сопротивления, постоянных ослабления и фазы для четырехполюсника по рис. 4.26.
4*27. Для четырехполюсника по рис. 4.1 найти входные сопротивления со стороны первичных и со стороны вторичных плодов при согласованных нагрузках соответственно на вто-ных и первичных выводах.
Указание. Учесть, что при Z^2 = Za получается Z1BX =а = Z^; при обратном питании и — Zcl получается Z?RX —
4.28.	Найти характеристические сопротивления четырехполюсника по рис. 4.10, а.
4.29.	Определить, при каком сопротивлении нагрузки входное сопротивление четырехполюсника по рис. 4.10,6 равно этому сопротивлению.
4.30(	Р). Из трех резисторов с сопротивлениями 100, 100 и 50 Ом составлен: 1) симметричный Т-образный, четырехполюсник, 2) симметричный П-образный четырехполюсник.
Найти характеристические сопротивления и постоянные ослабления этих четырехполюсников.
Решение. Схема четырехполюсника показана на рис. 4.3, где Zi/2 = Ti/2 — 100 Ом и Z2 = г2 = 50 Ом. Вторичные параметры определяются, например, по (4.19) или (4.22). В первом случае коэффициенты матрицы А даны в табл. 4.2:
411 = 4.22 = 1 + ri/2r2 « 3; Л12 = n (1 + ri/4r2) - 400 Ом;
4г 1 = 1/г2 — 0,02 См.
Во втором случае по схеме рис. 4.3 Z* = гх = 150 Ом; Zv = гк = 133,3 Ом.
По (4.19) или (4.22) получаем Zf = 141 Ом, А = 1,76 Нп.
4.31.	В приемнике одноканальной системы телемеханики для получения ослабления сигналов на 2 Нп применяется Т-образный аттенюатор (рис. 4.3) с характеристическим сопротивлением 100 Ом.
Найти мощность в сопротивлении согласованной нагрузки, если мощность источника питания равна 200 мВт. Рассчитать сопротивления схемы.
4.32.	Определить характеристическое сопротивление и постоянную ослабления аттенюатора задачи 4.17.
4.3.	Схемы замещения
4.33(	Р). У симметричного четырехполюсника известны коэффициенты: Ац =0,8; Л12 = jl,8 Ом.
Определить сопротивления Т-образной схемы замещения и характеристическое сопротивление. Построить топографическую диаграмму напряжений при согласованной нагрузке, приняв /2 = I2 = 1 А.
Решение. Для симметричного четырехполюсника Л22 — = 4п> коэффициент Л21 определяется из уравнения связи
411 — 412421 = 1, т-е. 411 =(4ii — 0/412 =j0,2 См.
Сопротивления Т-образной схемы замещения (см. табл. 4.2) Z1/2 = (All - 1)/421 =jl Ом; Z2 = 1/Л21 = —jS Ом.
Характеристическое сопротивление (см. табл. 4.2) Zc = в]/Л12/421=3 Ом. Полученная схема и топографическая диаграмма показаны на рис. 4.33Р, а и б. При построении учтено, что постоянная ослабления А = 0; это следует из соотношения ch (А + /В) = 411 = 0,8 или ch A cos В- + J sh A sin В = = 0,8. Если sin В = 0, то cos В = + 1 и | ch А | < 1, чего не может быть. Значит, shA=O и А = 0. Следовательно, Л=/2 и Ui 02-
Рис. 4.33Р
4.34.	Для составления Т-образной схемы замещения четырехполюсника, схема которого неизвестна, были измерены сопротивления холостого хода и короткого замыкания: Zlx = = г1х = 40 Ом; Z2x = г2х = 20 Ом; Z^ = г2к = 10 Ом.
При помощи схемы замещения найти отношение первичного и вторичного токов при питании со стороны первичных выводов и коротком замыкании вторичных.
4.35.	Чтобы составить схему замещения линии передачи электроэнергии (симметричный четырехполюсник), были проведены опыты холостого хода и короткого замыкания. Опыты дали: иЛх = 30 кВ; 71х = 6 А; Р1х = 27 кВт; ср1х <0; UlK = 4,5 кВ; Лк = 30 А; Р1к = 69 кВт; <р1к > 0.
Определить входное сопротивление П-образной схемы замещения, если сопротивление нагрузки ZH = гн — 80 Ом.
4.36.	Для симметричного четырехполюсника заданы коэф-Фициенты Лп = А22 = 1,18 z. -135°; Л12 =7,10zl -8О°5О' Ом; 411 =0,235 z. -135° См.
Составить: 1) Т-образную (рис. 4.3) и 2) мостовую (рис. 4.15) схемы замещения четырехполюсника.
4.37.	В цепь включен трансформатор (рис. 4.13) как согласующий четырехполюсник.
Составить Т-образную схему замещения, предварительно вычислив элементы матрицы А. Определить входное сопро-Ивление трансформатора при активном сопротивлении на-
грузки rH = 10 Ом на вторичных выводах, если: 1) Xj = х2 = = rj = г2 = 10 Ом; коэффициент связи к = 0,5 и 2) х2 — 4^ = = 40 Ом; г2 = 4ri = 40 Ом; к = 0,5. Найти напряжение на сопротивлении нагрузки при напряжении источника питания 184 В.
4.38(	Р). Для согласования воздушной и кабельной линий связи в месте их соединения включены автотрансформатор и конденсатор (рис. 4.38). На расчетной частоте сопротивления coLi = 100 Ом; 1/соС = 700 Ом; coL2 = 900 Ом; коэффициент связи к = 0,667. Потерями в трансформаторе и конденсаторе можно пренебречь.
Рис. 4.38
j300 0v	-jZOOOm
Рис. 4.38Р
Составить Т-образную схему замещения этого четырехполюсника. По схеме замещения вычислить входное сопротивление со стороны первичных выводов при сопротивлении нагрузки Zh = гн = 75,7 Ом.
Решение. Для несимметричного Т-образного четырехполюсника (рис. 4.8) можно вычислить значения сопротивлений Zb Z2 и Z3, если, например, известны коэффициенты матрицы А.
Коэффициенты Ли и Л21 определяются из уравнений, составленных для схемы рис. 4.38 при разомкнутых вторичных выводах (12 = 0):
Ulx = Ах ОМ +	+ 2j0)M - jl/a>C);
l?2x = Лх (j®t2 + j«>M -
откуда An = Vix/Uj, = 1.75;	Л21 =/lx/U2x = Ли/1х/(71х =
= —/2,5-10 3 См. Коэффициент Л22 найдем из уравнений, составленных для схемы по рис. 4.38 при обратном питании и разомкнутых первичных выводах (Л =0):
= Г2х ОЬ2 - /1/соС); U'1K = Й'2х 4- Г2х>М, откуда U2JU\X - А22 = 0,5. Сопротивления Zt = /300 Ом; Z2 = = —/200 Ом; Z3 = /400 Ом.
Входное сопротивление можно найти по схеме рис. 4.38Р: Zibx = 265 Ом. Эту схему можно составить и сразу для авто-174
трансформатора как эквивалентную, не содержащую индуктивных связей.
4.39.	У несимметричного четырехполюсника известна мат-
рица А.
Определить сопротивления Т-образнои схемы замещения (рис. 4.8).
4.40(	Р). Составить П-образную схему замещения (рис. 4.5) для мостового четырехполюсника (рис. 4.15) при Zj = п = = 20 Ом; Z2 = г2 = 60 Ом. Опре-
делить, во сколько раз напряжение Q	| Q
на выходных выводах меньше, чем °	°
на входных, при согласованной нагрузке.
Решение.У П-образнойсхе-мы замещения должны быть такие же коэффициенты и параметры,	Рис. 4.41
как и у заданного четырехполюсника. Например, по табл. 4.2 для Х-образного (мостового)
четырехполюсника
4и —	= 2; А12 = -------= 60 Ом;
Г 2 - П	~	Г2~ Г1
Л21 = 2/(г2 - Г1) = 0,05 См.
Для П-образной схемы по табл. 4.2 Z1==412 = 60 Ом; 2Z2 = Л12/(Л11~1) = 60 Ом.
Расчет может быть выполнен и с применением сопротивлений короткого замыкания и холостого хода или вторичных параметров.
При согласованной нагрузке U JU 2 = е*, где А — постоянная ослабления, которая одинакова у мостового четырехполюсника и его П-образной схемы замещения.
4.41.	Составить Т-образную схему замещения (рис. 4.8) для несимметричного мостового четырехполюсника (рис. 4.41) при ri == г2 = 8 Ом; г3 = 4 Ом; г4 = 12 Ом.
4.4.	Соединения четырехполюсников
4.42(	Р). Симметричная мостовая схема (рис. 4.15) с Zr = и Z2 = г2 либо цепочка, состоящая из звеньев мостового типа, применяются в различной аппаратуре связи. Для таких четырехполюсников часто необходимо знать зависимость входного еопротивления от сопротивления нагрузки га.
1)	Составить эту зависимость для одного звена: а) при Помощи уравнений четырехполюсника типа Л; б) при помощи Вт°Ричных параметров.
2)	Составить зависимость входного сопротивления от сопротивления нагрузки для цепочки, состоящей из трех звеньев, применив уравнения с гиперболическими функциями.
Дано: Г1 = 20 Ом; г2 = 60 Ом.
Решение. 1) По (4.20) входное сопротивление
411Гн + 412 _ гн + Zc*h Г
4.21гн + А.22 “^Zc + ^^T
Коэффициенты Ац = Л22, 412> 4г i и вторичные параметры заданного симметричного четырехполюсника можно выразить, например, через сопротивления короткого замыкания Zv и холостого хода Zx. Для схемы рис. 4.15
Zx = 2-rir^~ =30 Ом; Z, =	= эд ом.
о + г2	-х 2
По (4.12) и (4.22)
Лц = ]/Z,Z(Z, — Z.) = 2; Л12 = Л-iiZx = 60 Ом;
411 = 411/Z, = 1/20 См; Z, = ]/Z^ = 34,7 Ом; th Г = th (А + /В) = j/Z^Zx = 0.865,
откуда А = | Г | = 1,31 Нп (В = 0).
Входное сопротивление одного звена
7 = 2Г" + 60 =34 7 Г" + 34,7'0,865 = 40 г" + 30
0,05г„ + 2	’ 34,7 + ги • 0,865 г„ + 40
2)	Для цепочки из трех звеньев постоянная ослабления Ац = ЗА = 3,93 и th Ац = 0,999 та 1, характеристическое сопротивление Zu = Zc-
По определению (4.20) входное сопротивление цепочки
Zbx = (гн + Zu 1Ь AJ/(Za + rH th Ац),
и при th Ац та 1 практически при любом г„ получается Zbx == = Z„ = 37,4 Ом.
4.43(	Р). Цепная схема состоит из трех одинаковых симметричных звеньев — аттенюаторов, для каждого из которых известны коэффициенты: Ац =3; А21 =0,2 См.
1)	Найти характеристическое сопротивление Z„ и постоянную ослабления Ац цепочки.
2)	При напряжении питания 17 2 = 120 В определить ток в сопротивлении согласованной нагрузки.
Решение. 1) Характеристическое сопротивление цепочки, состоящей из одинаковых симметричных звеньев, равно харак-176
туристическому сопротивлению одного звена, т. е. Z„ - Z,. == ==	— 1М Ом, где из уравнения связи (4.6) для сим-
метричного четырехполюсника имеем Л12 = (Л?! - 1)/Л21 = -=40 Ом.
Постоянная ослабления одного звена — аттенюатора по (4.19) ch Г - ch А = 41! = 3, откуда А = 1,76 Нп. Постоянная ослабления цепочки равна сумме постоянных ослабления трех звеньев, т. е. Ац ЗА 5,28 Нп,
2)	Напряжение на сопротивлении согласованной нагрузки
у2 = Uге Ац = 0,61 В. Ток в сопротивлении согласованной нагрузки /2 == L72/zu = 43,2 мА.
шЬ/2 шЬ/2 2
Рис. 4.45	Рис. 4.46
4.44.	Из двух одинаковых четырехполюсников по рис. 4.1 составлена Т-образная симметричная схема.
Определить вторичные параметры полученного четырехполюсника.
4.45.	К входным выводам симметричного четырехполюсника, составленного из реактивных элементов coL/2 = 2,5 Ом, 1/соС = 5 Ом (рис. 4.45), присоединен резистор с сопротивлением г - 100 Ом.
Составить матрицу А полученного четырехполюсника, рассматривая этот четырехполюсник как каскадное соединение простейшего четырехполюсника (рис. 4.4,6) и симметричного Т-образного (рис. 4.3).
4.46.	Составить матрицу А для Г-образного аттенюатора (рис. 4.46): 1) рассматривая схему рис. 4.46 как каскадное соединение простейших четырехполюсников (рис. 4.4,6 и а); 2) предварительно составив матрицу Z для двух последовательно соединенных четырехполюсников — «разорванного» (рис. 4.6) при Zj = 0 и простейшего (рис. 4.4,6). Проверить Регулярность соединения.
4.47(	Р). Двойной Т-образный четырехполюсник (рис. 4.47) применяется в аппаратуре телемеханики и связи для изменения Фазы напряжения.
Определить сдвиг фаз между напряжениями иг и й2 ПРИ 1/соС = г и Z,, = г.
Решение. Рассматривая четырехполюсник по рис. 4.47 Как параллельное соединение двух Т-образных схем, сначала
составим матрицу этого четырехполюсника Y = Y' + Y", где
Y' и Y" — матрицы Т-образных схем. По табл. 4.2
у __у	2Z1 + 4Z2 .	__	4Z2
-n -22 Zj(Z,+4Zj)’ -21	-12	Z1(Zi+4Z2)’
где для первой схемы Zi = г; Z2 — —j\/^C — —jr, для второй
Zt = — jr; Z2 — г, поэтому для первой схемы Уц = — -—
2 — /2	2 -2 + /1	2 -2
вт°р°й
и для четырехполюсника по рис. 4.47
111=111+111
„	, лч л 112 Уц 11+J11 л 1
По табл. 4.1 Аи -	-	- ——- - , , ; 412- у —
_£21	221 О +JO	2.21
_ 8’5г
6 + J6 *
Из (4.1) после подстановки 12 = V2/Zn = U2/r получим 171/&2 = 411 + 41г/г = 2,62 z. — 15°3 j, т. е. напряжение U2 опережает по фазе напряжение на угол 15° 30'.
4.48.	Параллельно соединены два Т-образных симметричных четырехполюсника (рис. 4.48, а и б). Их матрицы А' и А" заданы: Лп = 1 + Л; 412 = 10+ j5 Ом; Я'21 = Д2 См; Л'22 = = 1 + Л; 411 = 1 - Л; 412 = -5 -;10 Ом; = 0,2 См; А$2 = = 1 - л.
Составить матрицу А для их параллельного соединения и проверить его регулярность.
4.49.	Два одинаковых четырехполюсника по рис. 4.14 с параметрами Zi/2 = г и 2Z2 = г соединены: 1) каскадно; 2) параллельно с соблюдением регулярности; 3) последовательно с соблюдением регулярности.
Определить коэффициенты матрицы А для трех полученных несимметричных четырехполюсников.
4.50.	Рассматривая аттенюатор по рис. 4.17 как параллель-ное соединение простейшего по рис. 4.4, а и симметричного Т-образного по рис. 4.3, составить матрицу Y аттенюатора, если rt/2 = г2 = г3 = 100 Ом.
4.5.	Активные четырехполюсники
4.51	(Р). У электронной лампы — триода известны параметры : н — 50 — статический коэффициент усиления, S = =: 10 мА/B — крутизна анодно-сеточной характеристики, = - 5 кОм — внутреннее сопротивление.
Составить матрицы А и Z для триода - активного четырехполюсника (рис. 4.51) при сопротивлении в цепи сетки г = 0,2 МОм. Межэлектродные емкости лампы не учитывать.
Решение. При работе триода (рис. 4.51) в линейном режиме для определения синусоидальных составляющих напряжений и токов можно пользоваться любой из схем замещения, представленных на рис. 4.51Р, а и б, где учтено, что параметры триода связаны соотношением ц = SR(.
Рис. 4.51Р
Из рис. 4.51Р, а следует, что
ri^ = U RJ2 + 1^2 = —
Эти уравнения легко приводятся к уравнениям типа А (4.1) и типа Z (4.3), которые справедливы и для активных четырехполюсников с зависимыми источниками (но все четыре коэффициента каждого типа уравнений независимы):
(7, =	Л;
И н -1/и -1/S - 1/цг - i/Sr
-0,02	-100 Ом
-10’7 См —5’ 10-4 ’
1Ц = rii; U2 = -|Wi - Rii2y
г О
-цг -Rt |
т. е.
2 • 1О5 Ом О
-107 Ом —5-103 Ом
4.52.	Для триода задачи 4.51 составить матрицу Y при сопротивлении в цепи сетки г = оо.
4.53(	Р). Для простого каскада усиления по рис. 4.53 составить матрицу Y, считая известными параметры триода ц, S, Ri (см. задачу 4.51) и учитывая емкость С между анодом и сеткой (емкости между сеткой и катодом и между анодом и катодом отнесены соответственно к источнику питания и сопротивлению нагрузки).
Рис. 4.53	Рис. 4.53Р
Решение. Эквивалентная схема каскада с источником напряжения для синусоидальных составляющих напряжений и токов показана на рис. 4.53Р. Для этой схемы
Z/j + U2 - гДе I = 1//соС;
Rt(iI-i1) + u2= -nUi,
откуда Л	it = -	+ Л.
Z/	Z/	К; /\,
т. е.
Ill = 1/Z; 112 = ” 1/Z; У21 = 1/Z -	Y22 = - 1/Z - 1/Kf.
4.54.	Для каскада усиления предыдущей задачи найти численное значение определителя = АПА22 — А12А21 при заданных параметрах: ц = 50; S = 10 мА/B; - 5 кОм; 1/шС = = 100 Ом.
Рис. 4.55
4.55.	Одна из схем замещения транзистора типа р-п-р представлена на рис. 4.55. Параметры схемы: гэ = 50 Ом; гк = 2 МОм; гб = 500 Ом; гт = = 1,9 МОм.
Составить матрицу А и найти численное значение ее определителя Ал.
4.56.	Для транзистора задачи 4.55 составить матрицу Н.
4.57(	Р). На рис. 4.57 представлена схема замещения активного четырехполюсника с зависимыми источниками, где = -= 200 Ом; г2 = 400 Ом; г3 = 300 Ом; = 0,Ш2; Ё2 = бО^.
Найти элементы матрицы Н, предварительно построив сигнальный граф.
Решение. Если выбрать структуру сигнального графа так, чтобы ток и напряжение U2 были представлены в нем узлами-истоками, то коэффициенты Я1Ь Н12, H2i, Н22 системы уравнений (4.4) определятся прямо по топологической формуле (Мэзона).
Запишем уравнения Кирхгофа в виде
йг = 0,Ш2 + 200Д + ЗОО/3; Л = /1 - Л,
где 13 = Ua6/r3 = 4/2/3 - O,2l7 i 4- С/2/300.
Сигнальный граф, построенный по этим уравнениям, приведен на рис. 4.57Р. Граф имеет два контура, передачи которых: Lj = -4/3 = -1,333 и L2 — —60. Определитель графа
При U2 = 0
по топологической формуле определяем
где П1. == 200; логично
«-±—— -1-1; -2-2 ~ 1з,9 ом, д	д
П2 = 1 (4/3) 300; А! == 1 - (-1,333); Д2 = 1;
ана-
= 1,620.
-21	62,33
При = 0 по топологической формуле определяем
И Н^22-
0,1 (1 + 1,333) + 0,0033 300	. ,...
62,33	°’1802’
-0,1 (-0,2)- 0,0033 = 2>679.10- 4 См.
62,33
4.58	(Р). Определить матрицу Y четырехполюсника с зависимым источником тока J = SUt (рис. 4.58).
ю
о?1
Рис. 4.58Р
Дано: Ci = 4 пФ; С2 = 0,14 пФ; С3 = 3,3 пФ; 5 = 6 мА/В; двт — IO"4 См; f = 50 МГц.
Решение. Из (4.2) следует, что параметры Уц и У21 определяют режим короткого замыкания на выходных выводах четырехполюсника (2-2'), т. е. режим при й2 = 0 (рис. 4.58Р, а), а параметры yi2 и У22 — режим короткого замыкания на входных выводах (1-Г), т.е. режим при Ci=0 (рис. 4.58Р,б):
1 ио ш-4
£
г
2
'1
=	= —60 -10~4 z. -0,42° См;
и 2 =0
1
1
Г2
= -jcoC2 = —/0,4398 • 10"4 См;
Ui =о
1Л =0
У = —— й2 = -10,86-10"4z 84,71° См.
4.59(	Р). Определить матрицу Y четырехполюсника с зависимыми источниками тока p/t и напряжения цС73 (рис. 4.59) при Г1 = 500 Ом, г2 = 2 кОм, г3 — 100 Ом, р — 20, ц - 0,2 при помощи предварительно построенного сигнального графа.
Решение. Из (4.2) видно, что структура сигнального графа должна быть такой, при которой переменные и U2 представлены узлами-истоками.
Рис. 4.59
Рис. 4.59Р ->
Систему уравнений Кирхгофа представим в виде
Л =	+	и3 =
Г]	Pi	rt	1 — Ц 1 — Ц
Л = -РЛ-— й3-, i3=il-i2.
Сигнальный граф, построенный по этим уравнениям (рис. 4.59Р), имеет пять контуров, передачи которых
Определитель графа Д = 1 - (Lt 4- L2 + L3 + L4 + L5) = = 6,252.
По топологической формуле (Мэзона) определяем:
У ЦД*
In =	= 3,399 • 10'4 См,
ui й2=о Q
Hi — 1/^!; Д! — 1 — L5 = 1 + r3/r2 (1 — ц).
Аналогично
= —1,719-10“3 См.
4.60. Составить сигнальный граф для четырехполюсника по рис. 4.60 с зависимыми источниками тока и ЭДС и, применив топологическую формулу (Мэзона), определить элементы матрицы Н четырехполюсника.
4.61.	Определить элементы матрицы Z четырехполюсника с зависимым источником тока (рис. 4.61) при Г1 = 400 Ом; г2 = 50 кОм; г3 = 25 Ом; р = 50.
4.62.	Для четырехполюсника с зависимым источником тока (рис. 4.61) известны коэффициенты: Иц = 1400 Ом; Н12 = = 5 • 10"4; Н21 = -40; Н22 = -20 мкСм.
Определить параметры схемы гь г2, г3, р.
4.63.	Определить коэффициенты матрицы Н четырехполюсника с зависимым источником тока (рис. 4.63) при параметрах: = 375 Ом; г2 — 50 кОм; г3 = 25 Ом; Р = 40.
4.6.	Передаточные функции
4.64(	Р). Для симметричного Т-образного четырехполюсника (рис. 4.3) определить передаточные функции: по напряжению в режиме холостого хода и по току в режиме короткого замыкания.
Параметры четырехполюсника: Zj = j’40 Ом; Z2 = — jlO Ом.
Решение. По определению передаточная функция по напряжению в режиме холостого хода Ну = П2х/Й1х. Для цепи по рис. 4.3
Н	~Л°	1
~U Zi/2 + Zi /20-ДО
Аналогично передаточная функция по току в режиме короткого замыкания
Рис. 4.63
Рис 4.66
4.65.	Решить задачу 4.64 для симметричного П-образного четырехполюсника (рис. 4.5).
4.66.	Определить передаточную функцию по напряжению для не нагруженного четырехполюсника по рис. 4.66.
4.67.	Определить модуль и аргумент передаточной функции по напряжению Ни = U2/Ui для четырехполюсника по рис. 4.66 при сопротивлении нагрузки = г.
4.68.	Решить задачу 4.66 для четырехполюсников по рис. 4.68, а и б.
а-)	«9
Рис. 4.68
4.69(	Р). Составить передаточную функцию по напряжению пРи разомкнутых вторичных выводах для двойной Т-образной CXeMbI по рис. 4.69. Такой четырехполюсник применяется в технике связи.
Решение. Двойную Т-образную схему можно рассматри-Ть как регулярное параллельное соединение двух Т-образных
четырехполюсников. Матрицу Y такой схемы найдем суммированием матриц Y отдельных четырехполюсников.
Для первого четырехполюсника с сопротивлениями Zt/2 =
— г и Z2 = jx/2 коэффициенты
у/ __ _ у/ _ 2Zj + 4Z2	_ 2 + jX/r .
~22 Z1 (Zi + 4Z2) “ 2(r + jx) ’
Г = — У' =	4-2	= }x!r
~21	~12	Z1(Z1+4Z2)	2(r + jx)
(см., например, табл. 4.2).
Для второго четырехполюсника с сопротивлениями Zt/2 = = Jx и Z2 = г/2
v„ v„ 2 - jr/x ' v„ v„ -jr/x
In - -I22- 2(r + )x)’ 121 " -12 ~ 2(r + jx) •
Коэффициенты уравнений типа Y для заданной схемы
V - V -V л. V" _ 4 + ЛХ/Г - Г/Х) .
In - -I22 - In + Ill -	2(r+jx)	’
I21 - -112 - I21 + I21 - 2(r+jx) 
Из (4.2) при разомкнутых вторичных выводах (/2 = 0) находим передаточную функцию:
„ = £гх_ = _ I21 = j (х/г - г/х)
~U Uix I22	4 + j (х/г - г/х) ’
4.70.	На рис. 4.70 представлена схема замещения воспроизводящей головки магнитофона.
Рис. 4.69
Рис. 4.70
Составить частотную характеристику передаточной функции H(co) = /2/U1 головки. Параметры схемы: L = 0,04 мГн; г = 0,3 Ом; Li = 8 мГн; L2 = 0,06 мГн; г2 = 30 Ом.
4.71	(Р). Напряжение на выходе дифференцирующей схемы должно быть пропорционально напряжению на входе, умно-186
ценному на Jco, т. е. U2=-JnxUi, где т = гС - постоянная времени. Схема собрана по рис. 4.71 с усилителем, для которого U2 = —KU™ ПРИ данном сопротивлении нагрузки гн.
Рис. 4.71Р
Составить для этой схемы передаточную функцию по напряжению в виде
-;сот[1+/((о)],
где f (со) — некоторая функция частоты; т — гС.
Решение. Составим эквивалентную расчетную схему с заданным источником ЭДС Ё{ = и источником неизвестной ЭДС Ё2—г„1п=и2 (рис. 4.71Р). Для схемы рис. 4.71Р по методу узловых потенциалов
U3K = (EJaC + £2/</соС + 1/r)
или после подстановки значений U1=Ei; U2 = E2 и Сви которое по условию равно — (J2/K,
U2/K + С2/(1 +>Сг) = -t\/coCr/(l + jcoCr),
откуда следует, что
Hu = U2/U1 = -дот [1 + /(со)], где f (со) = -(1 + jcot)/(K + 1 + усот).
Рис. 4.72
Рис. 4.73
4.72.	Напряжение на выходе интегрирующей схемы должно быть пропорционально напряжению на входе, деленному на т. е. U2 = —U i/farr, где т = гС — постоянная времени. Схема собрана по рис. 4.72 с усилителем, для которого U2= —KUm.
Составить для этой схемы передаточную функцию по напряжению в виде
Ни = UJlh = - 1/Jcot [1 4- f (со)],
где f (со) — некоторая функция частоты.
4.73.	Для транзисторного усилителя (рис. 4.73) определить передаточную функцию по напряжению при сопротивлении нагрузки гп = 2 кОм и конденсаторе емкостью С — 1,5 мкФ.
Параметры транзистора (схема замещения рис. 4.55): гэ = 20 Ом; гб = 100 Ом; rK = 1 МОм; rJrK = 0,98.
4.74(	Р). Активный четырехполюсник, заданный коэффициентами Яи = 1500 Ом; Н12 = Ю~3; Н21 = —50; Н22 = = — 250 мкСм, имеет сопротивление нагрузки RH — 5 кОм и подключен к источнику с ЭДС Ё и внутренним сопротивлением гвт - 500 Ом (рис. 4.74).
Определить ЭДС Ё, если напряжение на сопротивлении нагрузки должно быть равно 3 В, и выходное сопротивление четырехполюсника.
Рис. 4.74Р
Решение. Для схемы рис. 4.74 запишем систему уравнений (4.4):
= НиЛ + Н^12и2', Л = Й21Л 4- Н.21П2.
Кроме того,
Л = —Ci/rBT 4- Ё/гвт; и2 — RJ1'
На рис. 4.74Р, а показан сигнальный граф, соответствующий этой системе уравнений и содержащий три контура, передачи которых
Ln — “iL j/Гвт = — 3; L2 — Н22Кн = ~ 1,25;
Ьз = —ЦцНцК-н/Гтя = 0,5.
Определитель графа Д = 1 — (Lt + L2 + /з) + L1L2 = 8,5.
Передаточную функцию = (72/Ё рассчитаем по топологической формуле (Мэзона):
Приняв для напряжения U2 — V2% получим Ё = 51 z. 180° мВ. Выходное сопротивление 7вЬ1Х = — Z/2/Z2 определим по схеме рис. 4.74Р, б. Это отношение найдем как передачу сигнального графа (рис. 4.74Р, в), построенного по системе уравнений (4.4) и при Zj = - Ui/rBT.
Сигнальный граф содержит один контур с передачей Li = —Нц/гат. Определитель графа Д = 1 + Иц/гвт =? 4.
Так как 12 = — £Л/2вых> то по топологической формуле
_ _±_ = = _225.10-« CMj
^вых	А
откуда = 4444 Ом.
4.75.	Активный четырехполюсник задан коэффициентами: Ни = 1500 Ом; Н12 = 10"3; H2i = -50; Н22 = -250 мкСм.
Определить входное сопротивление четырехполюсника и передаточную функцию тока Hi = /2/Л ПРИ сопротивлении нагрузки RH = 5 кОм.
4.76(	Р). Четырехполюсник (рис. 4.74) с зависимыми источниками задан коэффициентами (в сименсах): Уп =>26,01 • 10“12/; Ii2=-Д8796-10-12/; У21 = = -6 • 10~3 + >0,8796 • 10“12/; У22 = - IO-* ->21,61 • 10“12/, где f — частота, Гц.
Определить напряжение на сопротивлении нагрузки RH = = 5 кОм, если у источника ЭДС Ё = 1 В, внутреннее сопротивление гвт = 10 кОм и частота: 1) /= 10 кГц, 2) /= 200 МГц.
Решение. Для схемы рис. уравнений (4.2)
Л = Уц^1+112^2; Л =	+ Угз^.
Рис. 4.76Р
4.74 справедлива система
Кроме того,
[71 = Ё — гвт/1; Й 2 = Кн/2.
Сигнальный граф, построенный по этой системе уравнений, показан на рис. 4.76Р. Передачи контуров графа: =
= -ГвтХи; = RaY22; L3 = -гвтХ2i^hZi2- Определитель графа А = 1 — (L± + L<2 + Г3) 4~ ^1^2 = 1 4- /26,01 • 10 $ f 4" 0,5 (1 4-4- /26,61 • 10"8/) 4- 5 - 10"5 Г/26,01 (10-4 4- /26,61 • 10’12/) -— /0,8796 ( — 6  10“3 4-/0,8796 - 10"12/)]/.
По топологической формуле (Мэзона) находим передаточную функцию:
5 (-6 4-/0,8796- IO"9f) А
При частоте f = 104 Гц получим U2 = — 20 z. —0,3° В, и
при частоте/ = 2-108 Гц й2 I---------------1 <J—“ ^О,с
Рис. 4.78
= — 2,159-10"2 Z. -175,2° В.
Четырехполюсник этой задачи может быть представлен принципиальной схемой рис. 4.58. С увеличением час-н* тоты емкостные сопротивления хС1 и %сз уменьшаются, в то время как сопротивления гвт и jRh остаются неизменными (хС1 = 3,979 х
Рис. 4.78Р
х 10б Ом при частоте / = 104 Гц и хС1 = 198,9 Ом при частоте / = 2 • 108 Гц). Именно поэтому получается существенное изменение модуля и аргумента передаточной функции при изменении частоты.
4.77.	Для четырехполюсника предыдущей задачи определить передаточную функцию Hv = U2/E при частоте / = = 200 МГц, внутреннем сопротивлении гвт = 100 Ом и прежнем сопротивлении нагрузки.
4.78(	Р). Четырехполюсник задачи 4.74 с сопротивлением обратной связи Zo> с представлен на рис. 4.78. Определить передаточную функцию напряжения = У2/Ё при RH = 5 кОм;
== 500 Ом и следующих значениях сопротивления обратной связи: a) Zo, „ = 100 кОм; б) Zo, с = 40 кОм; в) Z», с = -jxc (С= 10" 9 Ф).
Решение. Для схемы рис. 4.78 запишем систему урав
нений (4.4)
Ui = HiJi + H12U2‘
^2 — ZfllA + Н.22^2-
Кроме того,
/ =—Ё-—ui; и2 = + z„,Л«;
^ВТ	7*ВТ
i 1	Л. с 4"	4 с ^2 ~п U2‘
^н
Сигнальный граф, построенный по этой системе уравнений, приведен на рис. 4.78Р, а. Упростим его, исключив узел /2 (рис. 4.78Р, б). У графа, полученного после упрощения, передачи контуров,
Ь1--Нц/гвт; — #215	— ZOi с (—1 + Н22Ян)/Ян;
= Н12 j ^5 = Н.1 1 (”* 1 + ^22^н)/^н> — 6 = — H^lZfllZo, с/гвт.
Определитель графа
А = 1 — (П1 4“ — 2 4“ £±3 4" £14 4" £±5 4" £;б) "Ь
+ (Ь1Ь3 + L2LJ = l/rBT [0,85ZOi с + 27312].
По топологической формуле (Мэзона)
ЕП/Л ПЛ+ПЛ — [££n + Zo, сЯн]
LT к	±£1“1 ’ 1 *2^?. ^вт
1U = ------= -----7-----= --------7--------
А	А	А
_ tLii + tLnZo, с
“ 0,85Zo. с + 27312 ’
Где Й! = Яп/Гвт; п2 = H21Z0> лт; At = А2 = 1.
При Zo, с = 100 кОм получаем Hv — — 44,5; при ZOi с = 55 40 кОм получаем Ну = - 32,6. При Zo, с = — Jxc результаты Расчета сведены в таблицу:
Рад/с
Ни
о
- 58,82
104
-56 г. -17,83°
105	106
- 17,48 Z. - 72,9° - 1,831 z. - 89,9°
Глава пятая
ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Введение к гл. 5
Для расчета режима однородной двухпроводной линии задаются ее первичные параметры: индуктивность Lo> активное сопротивление г0, емкость Со и активная проводимость д0 на единицу длины, т. е. при заданной частоте тока продольное сопротивление
ZQ=rQ+j®LQ	(5.1)
и поперечная проводимость
Го ~ 0о + Jo)Co	(5.2)
на единицу длины. Значения первичных параметров зависят от конструкции линии и материалов, из которых она изготовлена.
При известных первичных параметрах мгновенные значения напряжения и — и (х, t) между проводами и тока i = i (х, t) в любом поперечном сечении (точке) линии связаны телеграфными уравнениями:
—	ди/дх = roi + L^di/dt', )
>	(5.3)
—	di/dx — дои + C^u/dt, J
где координата х поперечного сечения отсчитывается от начала линии (рис. 5.А).
В комплексной форме
—	dU/dx = rQl + jd)LQi = Zo/; 1
-	di/dx = gQU + j(£)CQU = YQU. J	<
Вместо первичных параметров могут быть заданы вторичные: волновое (характеристическое) сопротивление
Z, = zBe>e = ]/z0/y0	(5.5)
и коэффициент распространения
у = а + /Р = j/zoyo,	(5.6)
где а — коэффициент ослабления; р — коэффициент фазы.
Решение уравнений (5.4):
Г>(х) = (7 = {7пр + 17встр = 41е-^ + Л2е+^;	(5.7)
i (x) = i = /пр - /встр =	(5.8)
где Ai = Ai z.	и Л2 = Л2 ф2 - постоянные	интегрирова-
ния, которые определяются по заданным граничным условиям в начале х = 0 и	в конце х = I	линии длиною	/; (Упр,	/пр —
напряжение и ток	прямой волны	(движется от начала к	концу
линии); С/встр, Астр ~ напряжение и ток встречной волны (движется от конца к началу линии).
Рис. 5.А
Мгновенные значения:
«пр = «пР (х, 0 =	sin (cot -	+ фО;
«всгр = «встр (х, t) = Л2те+ах sin (юг + рх + ф2);
*пР = inp (х, 0 = ^-е~ах sin (юг - рх + ^ - 0);
ZB
iflcrp = гвстр (х, о = е+*х sin (юг + рх + ф2 - 0).
Фазовая скорость волны с = dx/dt = ю/р.	(5.9)
В воздушной линии без потерь (г0 = 0, gQ = 0) фазовая скорость наибольшая: с = с0 = 3 • 108 м/с. В кабеле без потерь, изоляция которого имеет относительные диэлектрическую ег
и магнитную цг проницаемости, c = c0/[/sr|x,.	(5.10)
Длина волны в линии
Х = с// = 2тг/р,	(5.11)
где / = 1/Т— частота тока; Т — период.
При отсчете расстояния х от конца линии
!> = (>„„ + и^р = В,е+*х + В1е^х; (5.12)
/ = Ар - 4СТр =	- ^е-^\	(5.13)
7 п/р Ионкина П. А.
193
где Bi = А^'11 и В2 = Л2е+11 — постоянные интегрирования. При заданном режиме — напряжении U2 и токе 12 в конце (х = 0) линии
В1 = и2пр = 4-(1>2 + гвЛ); в2 = 1>2встр = 4(*>2 - 2Л)- (5.14)
Напряжение и ток в любой точке линии
U = Ue*" = U2 ch ух + /2Z, sh ух;
1 = ZeJ*' = -^-sh ух + i2 ch ух.
(5.15)
В частности, при х = I получается U — йг и Z =
Уравнения, связывающие режим в начале и конце линии, аналогичны уравнениям пассивного симметричного четырехполюсника, причем
у/ = а/ +./₽/ = Г = А + JB;	(5.16)
где а измеряется в неперах (Нп) на единицу длины, £ — в радианах (рад) на единицу длины.
Если источник питания (генератор) присоединен в начале линии, а приемник с сопротивлением ZH — в конце, то мощности генератора и приемника соответственно
=Pi +jQi = UiH; S2 = P2 +jQ2 = U2i*2.	(5.17)
Входное сопротивление линии
U i _ ZH + Zn th у I
Z^ + Z^hyr
В частности, для короткозамкнутой линии Zk = Zj th у/ = Zj th (а/ + уЭД
(5.18)
(5.19)
и для ненагруженной — разомкнутой линии (холостой ход)
Zx = ZH cth yl = Zn cth (а/ + 7 p/),
(5.20)
откуда следует, что
Z, = ]/zX; th yl = ]/zJz*;	(5.21)
Z»x = Z< +	(5.22)
При согласованной нагрузке, т. e. ZH — ZB и Z*x = Zg, встречная волна отсутствует, при несогласованной — зависит от коэффициента отражения
и
(5.23)
^1-ре-2уГ
При согласованной нагрузке U = С7пр; / = /пр; U/I = = [71Д1 = Й2Д2 =	б; Р — UI cos 9; Q= UI sin 0;
а/ = A = In = In U2 I2
Р/=В = фи1 -фи2 = фп -t|/f2;
у I = Г = In -ИЗ- = In ^2 I2
Для неискажающей линии (а = const, выполняться соотношение — Qq/Cq. В
а = |/ro0o = 0о*в; Р = ^- = со ]/LoCo:
(5.25)
(5.26)
(5-27)
с = const) должно этом случае
О
о-
(5.28)
— ^в
У линии без потерь (г0 =0, д0 = 0) ZR = zB — ]/Lq/C0 — активное сопротивление; 0 = 0; а = 0 п 2л: со В =	= — = 0)
(5.29)
с
с о >
U — U2 c°s Рх + j72zb sin рх;
[Л
/ = j-----sin рх + I2 cos Рх;
В
1 + ре“72₽/ = z« 1 _ pe-J2P/ 
(5.30)
(5.31)
При согласованной нагрузке (Z^ = rH = Zj, = z0 = ZBX = rBX, P == 0) нет встречной волны:
U = U2e^x'	U = U2; I = 12;
U/1 = U/I = zB; w = t/2msin(ci)f + рх); (	(532)
и2т
i ------sin (cot + рх).
При разомкнутой линии, т. е. в режиме холостого хода (Рх = 1),
U — Uj cos рх; 1 = j —-^-sin Рх;	(5.33)
Zn
Umin — ® в узлах напряжения; Umax = U2—k пучностях напряжения, I min О, I max U> ^пр ^встр ^2/2» Aip ~~ ^встр = = LZ2/2zB;
и = U2т cos рх sin (ot; i = ——sin px sin (cot + 90°); (5.34)
Zx = -jzB ctg p/.
В режиме короткого замыкания (рк = — 1) U = ji2z3 sin рх; Z = /2cosPx;
(5.35)
(5.36)
Imin = 0 в узлах тока; 1тах = 12 — в пучностях тока; Umin ~ 0; U тах ~ ^2^В’ ^пр ~ ^встр ~ ^z/2»
С/пр
^встр
— ^2гв/25
и ~ hmzn sin Р-х sin (art + 90°); i = I2m cos ₽* sin cot; (5.37) Zx^Atgp/.	(5.38)
При произвольной нагрузке
J max = ^np 4“ ^встр = ^в-^max, U mjn — U np	U Встр = % Barnin, 1
max ~ ^np 4“ ZBCTp — Umax/Z^^ ^min ~ ^пр ^встр	Umin/z^-	J
Коэффициенты бегущей и стоячей волн
[Л  Zw{ 1 ~ IРI 1 г   mtn   •* mtn   __1 £_ 1 , к    
6"	~ 1^ ~ 1 + 1рГ с“ V
(5.40)
При расчете симметричных трехфазных линий в уравнения длинной линии входят фазные напряжения и токи, т. е. U = — I = Л}>, и параметры r0, Lo> 0о, Со> отнесенные к одной фазе.
Для линий постоянного тока во всех расчетных формулах следует считать со = 0.
5.1.	Параметры линии
5.1 (Р). Диспетчерская связь осуществляется по воздушной линии на частоте 100 кГц. На этой частоте были измерены сопротивления холостого хода и короткого замыкания линии: Zx = 767 z. 4° 30' Ом и Zk — 735 z. —4° 30' Ом. Передающий и приемный аппараты находятся на расстоянии 20 км.
Определить первичные и вторичные параметры линии связи, фазовую скорость и длину волны.
Решение. При заданных сопротивлениях и ZK вторичные параметры определяются по (5.21):
ZR = zB ZL 0 = ]/z~Zy = 750 z. 0° Ом;
где Y — коэффициент распространения; I — длина линии.
Второе возможное значение угла т = 175° 30' не подходит, так как при дальнейших расчетах приводит к отрицательному значению коэффициента ослабления.
Коэффициенты ослабления а и фазы р можно найти по номограммам гиперболического тангенса или выразить через Ти т:
у/ = а/ + = 4- In -1 + ?ЛТ = 4 In We\
откуда а/ - -^-ln W = 1,6 Нп; р/ = -^-(^ + 2кп)- (к — 0,2) л, рад, где /с = 0, 1, 2...—целое число полуволн, укладывающихся вдоль линии.
В воздушной линии с потерями фазовая скорость с меньше скорости света в вакууме, т. е. длина волны X меньше длины волны в вакууме Хо = cQ/f = 3 км, соответствующей частоте f = 100 кГц.
Если принять X = Хо, то Z/(X/2) = 13,3, и получаем kt — 13, при X < Хо число к может быть и более 13 (к2 = 14; к3 = 15 и т. д.). Соответственно PJ = 12,8л рад; р2/ = 13,8л рад; р3/ = = 14,8л рад и т. д.
Каждому значению р/ соответствуют определенные значения фазовой скорости с и длины волны X: с1=<о/р1 = = 3,13 • 105 км/с; с2 = 2,90 • 105 км/с; с3 = 2,71 • 105 км/с и т. д.; Хх = ci/f = 3,13 км; Х2 = 2,90 км; Х3 = 2,71 км и т.д.
Первое решение, конечно, следует отбросить. Сделать выбор среди остальных решений, основываясь только на данных измерений сопротивлений холостого хода и короткого замыкания, нельзя.
Первичные параметры рассчитываются по (5.5), (5.6), откуда
Zo = г0 4- j(oLo = ZbY и Уо = 0о + 7«С0 = y/Z^.
Для второго решения г0 = 60 Ом/км; Lo = 2,60 мГн/км; 0о = Ю6 мкСм/км; Со = 4,60 нФ/км; для третьего решения rQ — 60 Ом/км; Lq = 2,79 мкГн/км; gQ — 106 мкСм/км; Со = = 4,94 нФ/км и т. д.
5,2.	Для определения первичных параметров линии были измерены сопротивления короткого замыкания и холостого хода при частоте 800 Гц. Измерения дали: Zy = 900 z. 63° Ом;
= 360 z ~ 78° Ом. Длина линии 59 км.
Рассчитать первичные параметры.
5.3.	Воздушная линия связи имеет следующие параметры: г0 = 2,84 Ом/км; Lo = 1,94 мГн/км; д0 = 0,70 мкСм/км; Со = = 6,25 нФ/км. Увеличения дальности передачи сигналов по линии с заданными г0 и д0 можно добиться, если отношение индуктивности к емкости будет удовлетворять требованию Ьо/Со = го/0о- Это условие совпадает с условием отсутствия искажений, так как в этом случае ZR = |/l0/C0, а = с = 1/{/ь0С0 не зависят от частоты.
1)	Найти индуктивность каждой из катушек, которые необходимо включить через каждые 0,5 км, чтобы линия стала неискажающей.
2)	Выяснить, как изменится индуктивность, если учесть потери в катушках. На расчетной частоте 800 Гц добротность катушки Q = 200.
3)	Определить фазовую скорость волны в неискажающей
линии.
4)	Найти, какую наибольшую длину могла бы иметь неискажающая линия при допустимом затухании 11,3 дБ.
5.4.	Для определения параметров трехфазного кабеля длиной 100 км, работающего на частоте 50 Гц, были проведены опыты холостого хода и короткого замыкания. Данные опытов: 1/1х>л = 10 кВ; /1х = 32 А (ф1Х<0); Р1х = 54 кВт; Г71кл = = 3 кВ; Цк = 32,4 A ((pjK > 0); Р1к = 167 кВт.
Определить первичные и вторичные параметры кабеля.
5.5(	Р). Определить первичные параметры воздушной линии без потерь, волновое сопротивление которой равно 600 Ом
Решение. По (5.29) ZR - 600 Ом = \/bJC0 и с0 — = •3 • 105 км/с = 1/]/ь0С0, поэтому т _ .	600
Lo = ZbAo = 30Q- ~10з = 2>° мГн/км;
с° ZbCo 600-3-105	180 мкф/км	5,5 нФ/км.
5.6.	Для определения первичных параметров воздушной линии без потерь длиной 3 м было измерено при частоте 10 МГц входное сопротивление в режиме короткого замыкания: zK = 290 Ом.
Определить первичные и вторичные параметры линии.
5.7(	Р). Определить волновое сопротивление кабеля без потерь, если входное сопротивление отрезка кабеля в режиме короткого замыкания в конце Z* — /90 Ом, а в режиме холостого хода Zx = — /40 Ом. 
Решение. По (5.21) ZR =	= 60 Ом.
5.2	. Линия с потерями
5.8	(Р). Известны первичные параметры воздушной линии связи: г0 = 2,84 Ом/км; Lo = 1,94 мГн/км; gQ =0,70 мкСм/км; Со = 6,25 нФ/км.
1)	Определить, при каком сопротивлении приемника в линии отсутствует отраженная волна на средней расчетной частоте 800 Гц.
2)	При этом приемнике найти напряжение, активную мощность источника и КПД линии длиной 59 км, если напряжение приемника равно 20 В.
3)	Выяснить, можно ли рассчитать коэффициент ослабления как для линии с малыми потерями, если допустима погрешность не более 5 %.
Решение. 1) Отраженная волна отсутствует при сопротивлении нагрузки, равном волновому (характеристическому) сопротивлению линии, т. е. при Z^ — Z^.
Для линии с потерями по (5.5)
Zn — j/Zo/Уо = j/(ro + jft)L0)/(^0 + JcoCo),
где to = 2nf = 2тг • 800 = 5,03 • 103 рад/с; wL0 — 5,03 • 103 • 1,94 x x 10"3=9,75 Ом/км; coCo = 5,03 • 103 • 6,25 • 10“ 9 = 31,4• 10" 6 См/км; Zo = ro + J(oLo = 2,84 + j'9,75 = 10,15 z. 73°45' Ом/км; Уо = gQ + + JfoCo - 0,70- 10“6 + ;31,4-10"6 « 31,4- 10"6 См/км.
Волновое сопротивление ZR = 568 z. —7° 30' Ом.
2) По (5.25)
<7i = U^',
где U2 = 20 В.
Коэффициент ослабления а — действительная часть коэффициента распространения (5.6)
у = а + /р = ]/z0Y0 = 17,9• КГ3 z. 81° 15' =
= 2,72 • 10~3 + /17,5 КГ3,
т. е. а = 2,72 • 10“3 Нп/км; а.1 = 2,72 • 10-3.• 59 = 0,16 Нп; Ut = = 20е0,16 = 20 • 1,17 = 23,4 В.
Активная мощность источника по (5.17) тт2	ГТ2
Р< = и.ц cos 0 = —-cosO = —^-e2aZcosG =
202
= -7- 1,38 cos (- 7° 30') = 0,96 Вт.
568
3) Для линии с малыми потерями коэффициент ослабления
определяется по приближенной формуле
= 2,74 • 10“3 Нп/км,
т. е. погрешность менее 1%.
5.9	(Р). Определить, какую наибольшую длину может иметь линия задачи 5.8, если считать допустимым ослабление сигнала 11,3 дБ, и какое напряжение должно быть в начале линии, чтобы напряжение приемника осталось прежним.
Решение. При допустимом ослаблении сигнала в линии а/ = 11,3-0,115 = 1,30 Нп наибольшая длина линии 1тах — 1,30/а, где а = 2,72-10“3 Нп/км (см. решение задачи 5.8).
Необходимое напряжение в начале линии при U2 = 20 В и I = /гах по (5.25) Ui =	= 20 • 3,68 = 73,5 В.
5.10	(Р). Для линии задачи 5.8 найти фазовую скорость волны и коэффициент отражения в случае чисто активного сопротивления приемника, равного zB.
Решение. По (5.9) фазовая скорость при частоте тока f — 800 Гц, т. е. со — 2тг/ — 5,03 • 103 рад/с, и коэффициенте фазы Р= 17,5 > 10“3 рад/км (см. решение задачи 5.8)
с = со/Р = 286 • 103 км/с.
При активном сопротивлении нагрузки Z,, — ги = zB = = 568 Ом и волновом сопротивлении ZB = 568 z — 7° 30' Ом коэффициент отражения по формуле (5.23)
Р =Фв - ZJ/fe + Zb) = 0,065 z 90°40', т. е. р = 6,5 %.
5Л1(Р). Для линии задачи 5.8 длиной 59 км найти напряжения прямой и встречной волн в конце и в начале линии при сопротивлении нагрузки = rH = zB и напряжении в конце линии 20 В. Вторичные параметры линии известны: ZR = = 568 z —7°ЗО' Ом; у = 17,9 • 10“3 z 81° 15'. км“\
Решение. Из (5.12) и (5,23) й2 = 02пр + С/2встР и р = = ^2встр/^72пр ПРИ U2 = U2 = 20 В и £ = 0,065 z 90° 40' (см. решение задачи 5.10) находим:
(У2пр = Вх = 19,91 z —3°47' В; (У2встр = В2 = 1,31 z 86° 13' В,
или, иначе, при ZH = zB по (5.14)
Ui 2
(1 ± 1 z 0)
и получаем тот же ответ.
В начале линии по (5.12) при х = I
U1 = ^1пр 4* ^1встр = ^2пр^ 4* ^2встр^ » ^Лпр = ^2пр^ , ^Лвстр = ^2встр^ ,
где С/2пр = 19,91 В; eal = 1 ,17 (см. решение задачи 5.8), С72встр = = 1,31 В; е~" = 1/1,17; С/1пр = 23,3 В; <71встр = 1,1 В.
5.12	(Р). В конце линии задачи 5.8 отсоединили приемник. Напряжение в начале линии осталось прежним: 23,4 В. Определить, на сколько процентов изменится напряжение в конце
линии.
Решение. При Z2 — 0 по (5.15) Щ — U2 ch у/, где ch у/ = = у(еа,еда + е'“'е"да); а/= 0,16 Нп; е” = 1,17; р = 17,5 х х 10"3 рад/км (см. решение задачи 5.8); 0/ = 59°15' и chy/ = = 0,55 л 14°.
Напряжение в конце линии U2 = Ui/| ch у/1 = 23,4/0,55 = =42,6 В. Напряжение в конце линии при подключенном приемнике было равно 20 В (см. задачу 5.8), т. е. изменилось более чем в 2 раза, или на
42,6 - 20
20
100= 113%.
5.13(Р). Определить, каким двухполюсником можно заменить линию задачи 5.8, чтобы режим источника питания не
изменился. Сопротивление нагрузки: 1)	= гн = 568 Ом;
2) ZH = 568 X- 7° 30' Ом. Вторичные параметры линии известны; Zb = 568 z.-7° 30' Ом; у = 17,9 • 10~3 z 81° 15' км"1.
Решение. 1) Сопротивление двухполюсника должно рав
няться входному сопротивлению линии. При ZH
Ом
= гн = 568
по (5.24)
1 + ре~211 1-ре~2^
где ZB = 568 z-7°3O' Ом; а/= 0,16 Нп; р/ = 59°15'; р = « 0,065 z 90° 40' (см. решения предыдущих задач) и Z^x = = 620 z —10° Ом, т. е. активно-емкостное сопротивление.
5.14(Р). Определить, какая ошибка получится при определении длины волны в линии задачи 5.8, если не принимать во внимание потери в линии. Вторичные параметры линии известны: Z, = 568 z -7°30' Ом; у = 17,9 «10"3 z 81°15' км"1.
Решение. При учете потерь фазовая скорость волны (см. решение задачи 5.10) с = 286-103 км/с и частоте f = 800 Гц соответствует длина волны X = с/f = 357 км.
Для линии без потерь фазовая скорость с = с0 = 300 х х Ю3 км/с и Хо = с0// = 374 км.
Погрешность 374 — 357 л пп,
~"357	100 = 4’8
5Л5(Р). В аппаратуре телеграфирования «постоянным током» все буквы алфавита передаются кодами Морзе или Бодо (комбинации посылок тока и пауз). Один из простейших испытательных сигналов — периодическая последовательность прямоугольных импульсов.
Найти сигнал в конце неискажающей линии с параметрами Lo = 32,1 мГн/км, Со = 6,25 нФ/км, gQ = 0,7 мкСм/км при согласованной нагрузке, считая, что фильтр в конце линии пропускает только постоянную составляющую, 1-ю и 3-ю гармоники этого сигнала. Высота импульсов 20 В; длительность посылки равна длительности паузы и составляет 12,5 мс. Передача идет на расстояние 818 км.
Решение. Заданный сигнал, если отбросить гармоники выше 3-й, записывается в виде (см. разложение в ряд прямоугольных импульсов)
у 2	/	1	\
м - __-------итах sincojt + — sin Зое»!? -
2 л	у	3	у
= 10 + 12,7 sin cotГ + 4,25 sin Зсо^ В.
Для неискажающей линии по формулам (5.28) находим параметры Zb = |/ь0/С0 = 2265 Ом; а = gQZ^ = 1,585 мНп/км; с = 1/]/£оСо = 7,07-10* км/с. Они не зависят от частоты, поэтому постоянная составляющая, 1-я и 3-я гармоники уменьшаются в одинаковое число раз (eal = 3,67). Сдвиг по фазе в конце линии для каждой гармоники пропорционален частоте: р/ = со ]/lqC0 /, поэтому сигнал в конце линии имеет ту же форму, что и в начале, и запаздывает на = 1/с = 11,6 мс.
5Л6(Р). Сигналы телемеханики передаются по линии электропередачи.
Найти напряжение сигнала на вводах приемного устройства, если в линии длиной 50 км удалось создать режим бегущей волны. Коэффициент ослабления линии на частоте сигнала равен 96 мНп/км, волновое сопротивление равно 640 z. —10° Ом и уровень сигнала в начале линии (по мощности) равен 4,6 Нп.
Решение. Уровень сигнала на вводах приемника меньше, чем в начале линии, на а/ = 96 • 10"3 • 50 = 4,8 Нп, т. е. равен -0,2 Нп.
Уровень сигнала а (по мощности) определяется по формуле 1 1 р а = — In -=—*
где Ро = 1 мВт; р = е2я - мощность сигнала, мВт. При уровне д == —0,2 Нп получается Р = е-0,4 — 0,67 мВт.
5.17.	Для трехфазной сталеалюминиевой воздушной линии электропередачи сечением 400 мм2 и длиной 900 км известны первичные параметры: г0 =0,08 Ом/км; gQ = 3,75-10”8 См/км; Хо = 0,42 Ом/км; bQ = 2,7 мкСм/км.
Найти фазное напряжение, ток и активную мощность в начале линии (на станции), если на приемном конце линейное напряжение 330 кВ, активная мощность всех приемников 300 МВт и коэффициент мощности нагрузки равен 1.
5.18.	Определить фазовую скорость волны, длину волны и КПД для линии задачи 5.17.
5.19.	В конце линии задачи 5.17 произошел сброс нагрузки.
Определить линейное напряжение в конце линии и ток в начале, считая, что фазное напряжение на станции осталось неизменным и равным 229 кВ.
5.20.	Определить естественную мощность в конце линии задачи 5.17. Для этого же режима найти линейное напряжение и ток в начале линии. Линейное напряжение в конце линии равно 330 кВ.
5.21	(Р). Найти напряжения прямой и встречной волн в конце и в начале линии задачи 5.17, а также коэффициент отражения, считая, что фазное напряжение в конце линии ^2ф = й2= 190,5 кВ. Вторичные параметры линии известны: Zb = 397 z. —5°23' Ом; у= 1,073 • 10”3 84° 37' км”1.
Решение. При активной нагрузке, фазном напряжении U2 — 190,5 кВ и мощности Р2 = 300 МВт фазный ток /2 = = P2/3U2 = 525 А = /2.
Напряжения прямой и встречной волн в конце линии (при отсчете координаты х от конца) по (5.14) равны:
’ t>2nP = (t>2 + Zb/2)/2 = 199,2	- 2° 50' кВ;
t>2Bcrp = (U2 - ZJ2)/2 = 13,1 z. 131° ЗУ кВ.
В начале линии
l>inp = tW1' = 218 z. 52° 10' кВ;
lAserp = ^встрв'1' = 12,0	76° 35' кВ.
Коэффициент отражения по (5.23)
P = С>2всф/^2пр = 0,066 z. 134° 25'.
5.22.	При сбросе нагрузки фазное напряжение в конце линии задачи 5.17 равно 394 кВ при напряжении в начале 229 кВ.
Определить напряжение в конце линии при расчете по упрощенным эквивалентным схемам: 1) П-образной с продольным сопротивлением (r0 + ;coLo) I и поперечными проводимостями (д0 + j(oC0) 1/2, включенными на входе и на выходе; 2) без учета проводимостей.
5.23.	Последовательно соединенные воздушная линия (1г — = 20 км; го1=4,О Ом/км; д01 = 1 мкСм/км) и кабель (12 = = 40 км; г02 = 0,5 Ом/км; gQ2 = 0,5 мкСм/км) подключены к генератору постоянного тока с напряжением 10 кВ. Кабель имеет согласованную нагрузку.
Определить мощности приемника и генератора; вычислить мощность по приближенным формулам, пренебрегая утечкой; сравнить КПД передачи в обоих случаях.
5.24.	Определить мощность генератора задачи 5.23 при условии, что кабель на конце разомкнут.
5.3. Линия без потерь
5.25(Р). Измерено напряжение U2 = 120 В в конце воздушной линии без потерь с волновым сопротивлением 600 Ом при сопротивлении нагрузки 2Н = гн = 300 Ом.
Определить, на каких расстояниях от конца линии напряжение: 1) минимально, 2) максимально. Вычислить значения этих напряжений. Построить график распределения действующего значения напряжения вдоль линии, откладывая расстояния в относительных единицах х/Х, где X — длина волны.
Решение. Напряжение минимально в тех точках линии, где фазы напряжений прямой (7пр и встречной [?встр волн отличаются на 180°, а максимально при одинаковой фазе Ппр И в стр-
Коэффициент отражения в конце линии (5.23)
Р = (Гн ZB)/(rH "Ь 2В) =	1/3 ,
т. е. П2встр=£^2пр в конце линии находится в противофазе с [72пр- Значит, и2 =	= С7пр “ ^встр = 2С7пр/3, и так как
U2 = 120 В, то 17пр = 180 В и 17встр = 60 В. Следующие минимумы напряжения будут на расстояниях иХ/2 от конца линии, где п — целое число.
Максимумы напряжения сдвинуты вдоль линии относительно минимумов на Х/4 и Umax = С7пр 4- UBcrp = 240 В.
5.26	(Р). В середине линии без потерь с волновым сопротивлением 400 Ом подключен генератор с ЭДС 12 В и активным внутренним сопротивлением гвт = 300 Ом. Длина линии равна Х/2.
Найти напряжения и токи на левом и правом концах >1нии, а также в точке подключения генератора, если на обоих концах линии произошло короткое замыкание. Построить графики распределения действующих значений напряжения и тока вдоль линии.
Решение. Длины левого и правого участков линии 1л = /п = Х/4 (рис. 5.26Р), поэтому по (5.38) входные сопротивления участков
. П1 2л: А, ^ВХ, Л = ^ВХ, П J?B Ш Р‘ J^B 1g д" О® ,
ток 1Т генератора равен 0, а напряжение иг равно ЭДС.
При коротком замыкании линии наблюдается стоячая
волна и напряжение в конце U жения). Пучность напряжения находится на расстоянии Х/4 от
узла, т. е. Ur = Umax — 12 В. Узлы и пучности тока совпадают соответственно с пучностями и узлами напряжения, т. е. в точке подключения генератора у зел тока lmin = 1Г = 0, а на обоих концах линии — пучности тока. По (5.36) 1тах = 1я2 = 1п2 = = UmaJzB = 30 мА.
л2 =	= Umi„ = 0 (узел напря-
!“* *Л 7"*“I Р?"	&П “"S—I
“Вх,л £вх,п
Рис. 5.26Р
Графики распределения действующих значений напряжения и тока вдоль обоих участков линии одинаковы и строятся по (5.36):
U — zj21	0* I; I = /21 cos px |.
5.27	. Повторить расчет режима и построение графиков для линии задачи 5.26, если длина линии равна X и линия на обоих концах разомкнута.
5.28	(Р). Рассчитать режим и построить графики распределения действующих значений Uni для линии задачи 5.26, если длина линии слева от генератора равна Х/4, а справа Х/8.
Решение. Входные сопротивления участков линии (рис. 5.26Р) различны. По (5.38)
2п X
Z»X, п = Л, tg P<n = Jz, tg — -g = jzB tg 45° = jz, = J400 Ом;
л = JZB tg р/л — 00,
В конце каждого короткозамкнутого участка линии имеют место узел напряжения, т. е. ил2 = С/п2 = и пучность тока.
Для построения графиков распределения напряжения и тока необходимо определить напряжение в начале каждого участка линии, т.е. напряжение генератора. Ток и напряжение генератора
£	.	. Ё
 (у r _ lrZ^,n = -	- jzw
rWT T" £иэх, П	'ВТ Т J^B
ИЛИ
иг = ,	= 9,6 В; 1Т =	= 24 мА.
]/dT + z»	Zbx-"
Для левого участка линии Ur — Unmax и по (5.36) 1л2 — = Л max = тах/^ъ = 24 мА. Для правого участка напряжение в начале линии С7п1 = (7Г = 9,6 В — не пучность, и ток Ini = = 1Г — 24 мА, так как /л1 = 0. Ток в конце правого участка линии по (5.36) Znl = In21 cos р/п |, откуда /п2 = 34 мА.
Построение графиков распределения действующих значений напряжений и токов см. в решении задачи 5.26.
5.29.	Измерен ток 12 = 0,1 А в конце воздушной линии без потерь с волновым сопротивлением 600 Ом при сопротивлении нагрузки Zh = гн = 1200 Ом.
Определить, на каких расстояних от конца линии напряжение 1) максимально и 2) минимально. Вычислить значения этих напряжений. Построить график распределения действующего значения напряжения вдоль линии, откладывая расстояния от конца линии в относительных единицах х/Х, где X — длина волны.
5.30.	Измерено напряжение U i = 120 В генератора, включенного в начале линии задачи 5.25; частота равна 15 МГц.
Построить график распределения действующего значения тока вдоль линии, если ее длина равна 30 м.
5.31.	На концах двух одинаковых кабелей длиной 100 см с волновым сопротивлением 200 Ом и полиэтиленовой изоляцией (ег = 2,4) включены приемники с сопротивлениями соответственно — rHi = 200 Ом и 7^1 — гн2 = 100 Ом. Напряжение на вводах каждого приемника должно быть равно 20 мВ.
Определить необходимые напряжения двух генераторов, работающих на частоте 75 МГц. Найти, какое минимальное напряжение генератора можно получить при Z^2 = гн2 = 100 Ом, если изменять длину кабеля, и наименьшую длину кабеля, при которой получится это напряжение.
5.32.	Определить, при какой длине линии без потерь значение напряжения в конце линии остается неизменным независимо от подключения и отключения согласованной нагрузки. Напряжение генератора поддерживается постоянным.
5.33.	Генератор с внутренним сопротивлением должен отдать максимальную мощность приемнику с сопротивлением г2. Для согласования сопротивлений между генератором и приемником включена воздушная линия, потерями в которой можно пренебречь.
Найти наименьшую длину линии, а также ее индуктивность и емкость на единицу длины.
5.34(	Р). В линии, соединяющей источник питания с приемником, сопротивление которого Z* = 800 + /450 Ом, должна быть бегущая волна. Для согласования применяется схема, показанная на рис. 5.34.
Определить наименьшую длину короткозамкнутой линии (шлейфа) у ~ У1 и волновое сопротивление четвертьволнового трансформатора zTp. Волновое сопротивление линии и шлейфа 600 Ом. Длина волны генератора 20 м.
Решение. Линия будет работать в режиме согласован-‘ ной нагрузки, если входное сопротивление трансформатора 2вх,тр равно волновому сопротивлению линии zB (активное сопротивление, так как линия без потерь). По (5.31) входное сопротивление трансформатора
JZTp tg |3/Тр _зх,тр-2тр 2Tp+7Z3tg₽/Tp’
где Z3 — сопротивление нагрузки трансформатора, которое состоит из параллельно включенных сопротивления Z^ и входного сопротивления шлейфа ZK = /zBtgPyi.
Длина трансформатора = Х/4, т. е. р/^ = я/2. Поэтому получается
гу ___ z3 ctg л/2 4- /zTp _ zTp
-вх’ТР"2тр z.rp ctg л/2 + JZ3 ” Z3
и должно быть ZBX>Tp = 2B, т. e. необходимо выбрать 2тр = = У zaZ3. Волновое сопротивление трансформатора z^ — актив
ное (линия без потерь), поэтому и Z3 должно быть активным сопротивлением. Так как 1/Z3 — 1/7^ + l/Z^ = д3 - jb3, то должно быть Ь3 — 0, т. е. при заданных условиях
j60Q tg Pyi
или -0,535 • 10 3 -	- * Q— = 0, откуда tg рух = -3,12; £ух =
600 tg ру J
= ЗбОуi/X — 107,5° и у! = 5,96 м. При этой длине шлейфа
Z3 9з Re V 800 + /450
и 2з = гз = 1/0 з ~ Ю50 Ом.
Волновое сопротивление трансформатора 2тр = |/v3 s 795 Ом.
5.35.	Линия задачи 5.34 подключена к генератору с напряжением 200 В. Определить ток в сопротивлении нагрузки.
5.36.	Для согласования нагрузки воздушной линии, соединяющей передатчик с антенной, применяется отрезок короткозамкнутой линии (шлейф) длиной у (рис. 5.36), подвешенный на расстоянии х от конца.
Определить необходимые минимальные длины х ~ xt и у = уР Волновое сопротивление шлейфа и линии равно 600 Ом; входное сопротивление антенны Z# = гн = 800 Ом. Длина волны генератора 20 м.
5.37.	Длина линии задачи 5.36 равна 8 м.
Найти мощность, которую отдает передатчик с напряжением 200 В до согласования нагрузки и после согласования. Определить, во сколько раз напряжение падающей волны больше напряжения отраженной волны до согласования нагрузки и на каком расстоянии от конца линии находится ближайший минимум напряжения.
5.38.	Для согласования нагрузки линии задачи 5.36 вместо короткозамкнутого отрезка применяется: 1) разомкнутый отрезок; 2) четвертьволновый трансформатор.
Определить: 1) наименьшую длину разомкнутого отрезка при длине = 2,72 м, полученной в задаче 5.36; 2) волновое сопротивление трансформатора.
5.39.	Длина линии задачи 5.36 равна 8 м.
Определить напряжение на сопротивлении нагрузки до ее согласования (шлейфа нет) и после согласования, если напряжение генератора остается неизменным и равным 200 В. Известно, что х = xt = 2,72 м и у = ух — 4,12 м.
5.40(	Р). После согласования нагрузки линии задачи 5.36 длиной 8 м произошло короткое замыкание в конце.
Определить, как изменится входное сопротивление линии. Считая, что напряжение генератора равно 200 В, найти напряжение Ua6 (рис. 5.36), ток в короткозамыкающей перемычке шлейфа и ток короткого замыкания в конце линии. Известно, что х = *1 = 2,72 м и у = ух = 4,12 м.
Решение. Проводимость параллельно соединенных шлейфа и короткозамкнутого участка длиной xt
1	1	1,15
у =-----------1_ -------=—’—
Atgp^i jzetgPxi yz.
Такую же входную проводимость или сопротивление имеет эквивалентный двум параллельно соединенным участкам короткозамкнутый отрезок линии длиной х0 (рис. 5.4ОР), определяемый из уравнения = jz9 tg рх0, откуда х0 — 2,28 м.
Следовательно, линия с шлейфом длиной I = 8 м может быть заменена эквивалентной без шлейфа длиной = (/ — Xj) 4-+ х0 = 7,56 м. Входное сопротивление этой линии Z^ = = JzBtg p/i = -J58O Ом.
Ток в конце эквивалентной линии определяется по (5.36)
= jzj2 sin	откуда при 17х = Ui = 200 В получается
12 = —J0,48 А. Напряжение [7fl6 = jzj2 sin ₽хо = 189 В. Такое же напряжение Ua6 будет и у заданной линии при 2^ = 0 (см. рис. 5.36). Ток в перемычке шлейфа /ш и ток короткого замыкания в конце линии /н определяются по (5.36): й?б = ==Д7Ш8Ш pyt; иаб = JzB7Hsin рхь откуда /ш =-Д328 А; ZH = = -/0,418 А.
5.41.	Для согласования с воздушной линией приемника, сопротивление которого Z# = 800 + J450 Ом, выбрана схема, показанная на рис. 5.41.
Определить наименьшую длину отрезка у = ух и волновое сопротивление четвертьволнового трансформатора z.rp. Волновое сопротивление линии и отрезка zB = 600 Ом. Длина волны генератора 20 м.
5.42(	Р). Определить ток генератора, питающего воздушную линию с индуктивностью Lo = 5/3 мГн/км, длиной I =
= 100 м. Сопротивление нагрузки линии 7^ = гн = 380 Ом; напряжение генератора — 1,2 кВ, длина волны X = 60 м.
Решение. Для воздушной линии без потерь волновое сопротивление ZB = zB = ]/L0/C0, фазовая скорость с = = 1/]/ь0С0 = с0 = 300 •103 км/с. Из этих двух формул получаем zB = 504 Ом. Ток генератора Ц = Г\/гвх, где zBX — входное сопротивление линии. По (5.31) имеем 2^х = 553 z. 12°4О' Ом (р/ = 600°, tg р/ = 1,74) и ток Л = 2,16 А.
5.43.	Линия без потерь длиной 1/4 закорочена на обоих
концах.
Найти зависимость сопротивления Z(x), нагружающего
генератор, при изменении места присоединения генератора к линии. Здесь х — расстояние от левого конца линии до точки
присоединения генератора.
5.44(	Р). Для измерения емкости конденсатора при высокой частоте найдено положение узлов напряжения вдоль линии без потерь, в конце которой включен конденсатор, а в начале — генератор заданной частоты.
Определить емкость конденсатора, если расстояние от конца воздушной линии с волновым сопротивлением zB = = 550 Ом до ближайшего узла напряжения xt = 10 см, частота тока в линии 150 МГц.
Решение. Входное сопротивление участка линии относительно сечения хь в котором напряжение равно нулю (узел напряжения), также равно нулю. Следовательно, по (5.31) ^ = 0 :₽х!	’
2л
-т-Xi =0, Л
в
где Zj, = -/1/соС, или -j —г; ши
откуда определяется емкость С = 5,9 пФ.
Возможен и другой путь решения. Конденсатор можно заменить отрезком разомкнутой линии, входное сопротивление которой по (5.35) Zx = — jzB ctg р/0, где /0 ~ длина отрезка, которую нужно выбрать такой, чтобы в сечении Xi по-прежнему был узел напряжения. Ближайшее расстояние между узлами и пучностями напряжения равно 1/4, поэтому длину отрезка следует выбрать равной lQ = Х/4 - Из уравнения —jzB ctg р/0 = —Jl/toC находим емкость.
5.45.	Определить расстояние от конца линии задачи 5.44 до ближайшей пучности напряжения, если емкостное сопротивление конденсатора равно волновому сопротивлению линии.
5.46.	При измерении емкости методом, указанным в задаче 5.44, не учитывалось влияние краевого эффекта в конце линии
(электрическое поле распространяется и за пределы линии, что эквивалентно некоторой включенной в конце линии емкости). Для определения этой емкости было измерено расстояние от конца линии до ближайшего узла напряжения при отключенном конденсаторе. Оказалось, что оно равно 45 см.
Определить поправку, которую следует внести в найденное в задаче 5.44 значение емкости конденсатора, если учесть краевой эффект (считая, что краевой эффект нагруженной и разомкнутой линий одинаков).
5.47(	Р). Коаксиальный кабель с полиэтиленовой изоляцией (ег = 2,4) имеет волновое сопротивление ZR = гв — 75 Ом. Известно, что при частоте 70 МГц сопротивление нагрузки кабеля = 100 z. 20° Ом.
Найти первые две точки от конца, относительно которых входное сопротивление чисто активное. 4
Решение. Входное сопротивление линии в общем случае комплексное и определяется по (5.31):
_	1 + р ( —2р/ + у)
Z“ 1 — р z. (—2р< + v) ’
где v - аргумент комплексного коэффициента отражения р = = р z. у. Входное сопротивление будет активным, если угол -2рГ+ v равен целому числу л, т. е. 2р/ — v = кп и
I = (v + /ся)/2р.
При указанных в задаче значениях параметров по (5.23) р = 0,266 zi49c30' и v = 0,86 рад; по (5.29) р — 2280 рад/км.
Первая точка находится на расстоянии = v/2[3 = O,19 м, вторая - на расстоянии /2 = (v + л)/2р = 0,88 м.
5.48.	У воздушной линии без потерь с волновым сопротивлением 400 Ом было исследовано распределение напряжения вдоль линии. Оказалось, что первый минимум напряжения 12 В находится на расстоянии 0,4 м от конца линии, а первый максимум напряжения 16 В — на расстоянии 0,9 м.
Определить сопротивление нагрузки.
5.49.	Воздушная линия без потерь имеет волновое сопротивление, равное 400 Ом. Измерения показали, что первый от конца минимум напряжения находится на расстоянии 2 м, а второй — на расстоянии 7 м и отношение ^min/Uinax = 0,5.
Определить сопротивление нагрузки.
5.50(	Р). У генератора метровых волн, работающего с частотой 150 МГц, контур состоит из отрезка короткозамкнутой линии, которая служит индуктивностью. Линия выполнена из медных трубок с внешним диаметром 6 мм, находящихся на расстоянии 90 мм друг от друга. Короткозамы кающее у строй-
ство может перемещаться. Емкость контура 40 пФ состоит из межэлектродной емкости лампы и емкости монтажа.
Определить, на каком наименьшем расстоянии от начала линии должен находиться короткозамыкатель, чтобы контур был настроен на генерируемую частоту.
Решение. Входное сопротивление короткозамкнутой линии без потерь длиной / меньше четверти длины волны X индуктивное, заменяет индуктивность контура и может быть найдено по (5.38):
где L - необходимая индуктивность, значение которой определяется условиями резонанса: coL = 1/соС.
Индуктивность и емкость воздушной линии на единицу длины
Lo = — In —rS Со = яе0/1п л a	d
где D — расстояние между осями проводов (трубок); d — диаметр провода.
После вычисления значений L, zB и р находим, что I = — 38 см.
5.51	(Р). Определить входное сопротивление короткозамкнутого отрезка линии длиной Х/4 на частоте 10 МГц, учитывая активное сопротивление проводов г0 == 0,087 Ом/м (такое сопротивление имеет двухпроводная воздушная линия с диаметром медных проводов 3 мм и расстоянием между проводами 20 мм). Проводимостью gG пренебречь, волновое сопротивление считать чисто активным и равным 585 Ом (линия с малыми потерями).
Решение. Входное сопротивление короткозамкнутой линии с потерями определяется по (5.19), где для линии с малыми потерями можно считать, как и для линии без потерь, zB — ]/Lq/Cq; P = co]/loCo, а коэффициент ослабления (при 0о = 0) « = (го/2) ]/Cq/Lq.
Индуктивность Lq и емкость Со рассчитываются по формулам, приведенным в решении задачи 5.50.
5.4.	Схемы замещения линии
5.52(	Р). Составить П-образную схему замещения для линии задачи 5.8; при помощи этой схемы определить напряжения в конце разомкнутой линии при напряжении в начале линии 23,4 В. Вторичные параметры линии: Zn = 568 z. —7,5° Ом; 2 == 17,9 -10"3zl 81° 15' км”1.
Решение. При известных вторичных параметрах линии и частоте тока сопротивления схемы замещения рассчитываются так же, как и у пассивного симметричного четырехполюсника. В частности, для П-образной схемы (см. рис. 4.5 и табл. 4.2)
Zi =ZnshF; 2Z2 = Zn sh £/(ch Г - 1) = Z^ cth (Г/2), где в случае линии Zn = 2^; Г — у/ = а/ + jfil.
Для вычисления гиперболических функций комплексного аргумента можно пользоваться формулами
sh у/ = у И - е’1'); ch у/ = у (е* + е~гУ,
sh yl = sh а/ cos PZ + j ch а/ sin pf;
ch yl = ch aZ cos pZ + j sh aZ sin PZ;
th (y//2) = (sh aZ + j sin pZ)/(ch a/ + cos p/) или номограммами этих функций.
При заданных параметрах а/= 0,16 Нп; pZ = 1,03 рад = = 59°15'; shyZ = 0,87 z. 84°30'; chyZ = 0,55 z. 14°; Zt = = 495 z. 77° Ом; 2Z2 = 1020 z. -87° Ом.
Напряжение в конце линии
С/2х = ZZzUJtZi + 2Z2.) = t/i/ch yl.
При заданных параметрах (72х = 42,6 В.
5.53.	Диспетчерская связь осуществляется по линии электропередачи на частоте 100 кГц. Передающий и приемный аппараты находятся на расстоянии 20 км друг от друга и присоединяются между одной из фаз линии и землей. Параметры такой линии связи равны: Zn « гв = 750 Ом; a = 0,08 Нп/км; фазовая скорость 2,9  105 км/с.
Составить Т-образную схему замещения линии связи и сравнить напряжения на приемном конце при подключенном и отключенном приемнике с сопротивлением Z^ = гн = 750 Ом. Напряжение передающего аппарата в обоих случаях равно 200 В.
5.54.	При составлении Т- или П-образной схемы замещения линии небольшой длины Z можно пользоваться приближенными формулами Zi = Z0Z; Z2 = 1/У0/, где Zo = r0 + To = 9o + j®C0.
1)	По приближенным формулам составить П-образную схему замещения линии задачи 5.17, для которой Zo = = 0,427	79° 15' Ом/км; Уо ® 2,7  10"6 z. 90° См/км. Вычислить
в процентах ошибку при определении напряжения холостого хода в конце линии по приближенной схеме. Напряжение
в начале линии Uj = 229 кВ, напряжение в конце линии при холостом ходе, вычисленное по уравнениям длинной линии U2x =*394 кВ.
2)	Повторить расчет для линии задачи 5.8, для которой известно Zo = 10,15 z. 73°45' Ом/км; Уо = 31,4 z. 88°45' Ом/км; Ui = 23,4 В; U2K = 42,6 В.
3)	Повторить расчет для линии задачи 5.53, для которой Zb = 750 Ом; yl = 43,4 z. 88°30'; Ux = 200 В; U2x = 80 В. Объяснить, почему для этой линии ошибка так велика.
5.55.	Для согласования нагрузки линии без потерь можно применить четвертьволновый трансформатор. Если длина линии-трансформатора меньше 1/4, то недостающий участок I можно заменить цепочкой из Т- или П-образных звеньев, а иногда даже одним звеном.
Определить элементы Т-образной схемы, если длина волны X = 30 м, волновое сопротивление трансформатора 600 Ом, I — 1,5 м.
5.56.	Телевизионная антенна соединена с телевизором коаксиальным кабелем без потерь с полиэтиленовой изоляцией (ег = 2,4) и волновым сопротивлением 75 Ом, так что в кабеле нет отраженной волны. Ввиду слишком большого уровня сигнала между кабелем и телевизором включили Т-образный аттенюатор.
Определить элементы аттенюатора, включение которого позволит снизить напряжение сигнала в 4 раза, причем в кабеле по-прежнему не должно быть отраженной волны.
5.57.	Составить: 1) Т-, 2) П- и 3) Х-образные схемы замещения четвертьволнового трансформатора задачи 5.34.
5,58.	Для определения вторичных параметров кабеля без потерь с полиэтиленовой изоляцией (ег = 2,4) было измерено на частоте 75 МГц сопротивление короткого замыкания Zr — — —;171 Ом отрезка длиной 1 м.
Рассчитать вторичные параметры и составить эквивалентную Т-образную схему замещения отрезка.
5.59.	П-образный симметричный четырехполюсник работает на частоте 500 Гц и состоит из элементов: L= 10 мГн; Ci = С2 = 2 мкФ.
Определить длину и волновое сопротивление воздушной линии, эквивалентной четырехполюснику. Выяснить, при любо.й ли частоте этот четырехполюсник может быть заменен эквивалентной линией.
5.60(	Р). Воздушная линия без потерь длиной I = 24 м с волновым сопротивлением zB = 552 Ом соединяет передатчик 214
с антенной (согласованная нагрузка). Длина волны передатчика X == 36 м.
Сравнить распределение напряжения вдоль линии и эквивалентной цепочки, состоящей из п = 10 одинаковых Т-образ-ных симметричных звеньев. Найти параметры звена. Вычислить напряжение на входе восьмого звена при согласованной нагрузке и в режиме холостого хода, если напряжение источника питания цепочки и линии 20 В. Определить, на каком расстоянии от передатчика будет такое же напряжение в линии.
Решение. Для линии р/ = (2я/Х) I = 240°. Так как цепочка состоит из п = 10 звеньев, то постоянная фазы звена В = 24°. По известным zB и В четырехполюсника (А = 0) находим элементы Т-образного звена (см. табл. 4.2): Zi/2 = tg (В/2) = =jll7 Ом — индуктивное сопротивление; индуктивность каждой катушки L/2 = 2,23 мкГн; l/Z? — J sin B/zB —	• 10-4 См —
емкостная проводимость; емкость конденсатора С = 14,1 пФ.
При согласованной нагрузке напряжение на входе и выходе любого звена одинаково и равно напряжению на входе цепочки — 20 В.
При холостом ходе по (5.33) Ur = L^cosnB и аналогично Uк = ^2 cos (и — к + 1) В, где к — номер звена; Uk — напряжение на входе к-го звена. Исключая напряжение на выходе цепочки U2, при к = 8 находим 178 - 12,35 В.
Распределение напряжения вдоль цепочки и линии одинаково. Напряжение на входе восьмого звена соответствует напряжению на расстоянии 31/п = 7,2 м от конца линии.
5.61.	Для измерения возможных режимов кабеля с согласованной нагрузкой собрана цепочка из десяти Т-образных четырехполюсников. Каждый четырехполюсник состоит из двух катушек и конденсатора. Индуктивность катушки 1 мГн, добротность 200, емкость конденсатора 1 мкФ, потерями в конденсаторе можно пренебречь.
Определить напряжение и активную и реактивную мощности источника питания цепочки, работающего на частоте 800 Гц, если напряжение в конце должно быть равно 100 мВ. Выяснить, какая часть активной мощности источника теряется в активных сопротивлениях катушек.
Указание. При заданной добротности сопротивление катушки г/2 = 0,025 Ом много меньше индуктивного сопротивления coL/2 = 5 Ом. Поэтому при расчете режима каждое звено можно рассматривать как четырехполюсник без потерь. После расчета режима потери в каждой катушке определяются по формуле 12г/2, где I — ток в катушке.
Глава шестая
ЛИНЕЙНЫЕ ЦЕПИ С НЕГАРМОНИЧЕСКИМИ ПЕРИОДИЧЕСКИМИ ИСТОЧНИКАМИ
Введение к гл. 6
Источник несинусоидальной периодической ЭДС можно представить в виде последовательного соединения ряда источников с гармоническими ЭДС и источника постоянной ЭДС, источник несинусоидального периодического тока - параллельным соединением источников гармонических тока и источника постоянного тока. Примеры подобного представления приведены в решении задач 6.1 и 6.2. Такое представление основано на том, что любую периодическую функцию времени f (г) с периодом Т, удовлетворяющую условиям Дирихле, можно представить рядом Фурье:
/ (г) = Ао + f Ак„ sin (k<ot + ф6) =
оо
= Л0 + д (Лsin Ын Лcos W).	(6.1)
к= 1
Т
1 f
где со = 271/7’ — частота основной гармоники; Ао = — f (t)dt =
о
2п
=	/ (cot) d&t — постоянная составляющая; Акт и \|/ft —
J V I
о
амплитуда и начальная фаза /с-й гармоники;
т
^кт р
о
f (t) sin ком dt = -^7
о
*
f (a>t) sin k(ot dwt ;

T	2n
•	if
f (rt cos ktnt dt = — f (cor) cos k®t dat. it
Примеры разложения некоторых простейших функций приведены в приложении 1.
Приведенные выше интегралы могут быть вычислены численными методами. Например, применение формулы прямоугольников приводит к следующим приближенным выраже-
ниям:
2л- 1
2л—1
i=0
i = 0
ft кт
fi cos (kin/n\
/=о
(6.2)
где предполагается, что период Т разделен на 2п равных частей, а — значение функции f (Z) при t = Ti/2n.
При указанном представлении источников периодических ЭДС и токов можно для анализа линейных цепей применять принцип наложения, т. е. отдельно рассматривать цепь при действии источников постоянных ЭДС и токов и при действии каждого из гармонических источников или группы источников с одинаковой частотой. .
При применении комплексного метода необходимо учесть, что индуктивное сопротивление для тока к-й гармоники xLk в к раз больше, чем для тока первой (основной) гармоники xL — (лЬ, так как xLk = k&L = kxLi а емкостное сопротивление хск в к раз меньше, чем хс = 1/соС, так как хск = 1//доС = = хс/к.
Результирующее мгновенное значение тока (напряжения) равно сумме постоянной составляющей и мгновенных значений токов (напряжений) всех учтенных при расчете гармоник:
i & /0 + h + *2 +  • • + h + • • • +
где ik = Ikfn sin (kot 4- фк) — мгновенное значение /с-й гармоники тока.
Действующие значения тюка и напряжения
где 10 и U0 — постоянные составляющие тока и напряжения;. 1к и Uk — действующие значения тока и напряжения fc-й гармоники.
Мощность, потребляемая двухполюсником при негармонщ ческих периодических токе и напряжении,
Г	оо
„ 1
ui dt — UqIq У cos (pk, о
(6.4)
ft = 1
где срк — угол сдвига по фазе тока относительно напряжения для k-й гармоники.
Периодические функции, симметричные относительно оси абсцисс, т.е. f (?) = —/ (? + Т/2), либо такие, которые смещением по оси абсцисс могут быть приведены к функциям, симметричным относительно начала координат, т. е. f (?) — = —/( — ?), характеризуют следующими коэффициентами: к$ = - F/Fср - коэффициентом формы, /са = FmaJF - коэффициентом амплитуды, киск = FJF — коэффициентом искажения, где F — действующее значение; Ft - действующее значение первой (основной) гармоники; Fcp — среднее по модулю значение функции; F,^ — максимальное значение функции.
При измерениях негармонических периодических токов и напряжений следует иметь в виду, что показания приборов в зависимости от их устройства определяются различными параметрами измеряемой величины. Магнитоэлектрические приборы показывают постоянную составляющую измеряемой величины, а электромагнитные, электродинамические, электростатические и тепловые — ее действующее значение. Показания электронных приборов в зависимости от устройства входного преобразователя могут определяться: действующим значением измеряемой величины; средним по модулю значением; усредненным за период положительным (или отрицательным) зна-
I-	т .
чением измеряемой величины
kf (?) dt, где к = 1 (или 0),
о
если f (?) 0 и к — 0 (или 1), если f (?) < 0 ; максимальным
(^max > 0) или минимальным (Fmin < 0) значениями измеряемой величины.
На входе электронного прибора может быть включен конденсатор, который не пропускает на вход преобразователя постоянную составляющую измеряемой величины. В этом случае показание прибора определяется соответствующим параметром переменной составляющей измеряемой величины.
Группа электронных приборов, которая предназначена для измерений в цепях синусоидальных токов и напряжений, вне зависимости от того, на какой параметр периодической кривой прибор реагирует, градуируется так, что при синусоидальной измеряемой величине выходное устройство (стрелка или цифровой индикатор) показывает действующее значение этой величины.
В задачах этой главы требуется рассчитывать показания электронных вольтметров трех типов:
1)	вольтметра В 3-40, предназначенного для измерения синусоидального напряжения; показание прибора пропорционально действующему значению, но на входе прибора включен конденсатор, поэтому при измерении негармонических напряжений прибор показывает
[w(t) - Uo]2dt;
(6.5)
2)	вольтметра B3-38, предназначенного для измерения синусоидального напряжения; на входе этого прибора включен конденсатор, не пропускающий постоянной составляющей напряжения на преобразователь, который устроен так, что показание прибора пропорционально среднему по модулю значению напряжения, приложенному ко входу преобразователя, и при измерении негармонических напряжений прибор показывает
17пр = 1,11 у
|u(0- Vo \dt ;
(6.6)
3)	комбинированного вольтметра ВК7-15, который при соответствующем положении переключателя предназначен для измерения синусоидального напряжения; так как при этом положении переключателя на входе прибора включен конденсатор, а преобразователь реагирует на амплитуду отрицательной полуволны приложенного к нему напряжения, то прибор при измерении негармонического периодического напряжения показывает
iz„p = 0,7071 umin- L70|.	(6.7)
В последовательном резонансном контуре г, L, С при изменении частоты основной гармоники со резонанс напряжения на /с-й гармонике наступает при выполнении условия
k(i)L= 1//ссоС,
(6.8)
т. е. при частоте
<о = 1/fc уТс.	(6.9)
Если резонанс на /с-й гармонике достигается изменением емкости (индуктивности), то резонансная емкость Ск (индуктивность Lk) в к раз меньше емкости (индуктивности), при которой наблюдается резонанс на частоте основной гармоники.
При параллельном соединении ветвей Ги г2, С условие резонанса токов на /с-й гармонике имеет вид:
= 1/fccoC
(/ccoL)2 + rf (1/АхоС)2 + ?2 '
Если при указанном соединении = г2 = ]/£/С, то резонанс токов наблюдается на частотах всех гармоник приложенного напряжения и форма кривой тока повторяет форму кривой напряжения.
В трехфазных симметричных цепях при анализе периодических процессов следует иметь в виду, что сдвиг по фазе на 120° между фазными напряжениями (токами) основной гармоники приводит к сдвигу на к -120° для гармоник с номером к. Вследствие этого все гармоники, кратные трем (3, 6, 9 ...), образуют систему нулевой последовательности фаз:
£/4(3, 6, 9..-) = £в (3,6.9...) “ £с (3, 6, 9 .. .)•	(6-11)
Гармоники 1, 4, 7 ... образуют прямую последовательность фаз, т. е.
£#(1,4, 7...) = а2^А (1, 4, 7...)’	£f(l, 4, 7 ...) = а&А (1, 4, 7 .. .)> (6.12)
а гармоники 2, 5, 8 ... - обратную последовательность фаз, т. е.
£fi(2, 5, 8...) = а^А(2, 5, 8...)> £(? (2, 5, 8 ...) = fl2£/4 (2, 5, 8 .. .)> (6.13) где а = е7120" и а2 = е"7120°.
Так как гармоники фазных ЭДС, кратные трем, совпадают по фазе, то при соединении фаз источника треугольником в линейных напряжениях нет гармоник, кратных трем. При соединении звезда — звезда в симметричной системе без нейтрального провода отсутствуют токи гармоник, кратных трем, а в системе с нейтральным проводом ток в этом проводе содержит только гармоники, кратные трем.
6.1.	Разложение периодических функций в ряд Фурье
6.1(	Р). На рис. 6.1 изображена кривая напряжения u(t). Записать четыре первые гармоники разложения этого напряжения в ряд Фурье. Составить схему замещения источника, учитывающую эти четыре гармоники.
Решение. Воспользуемся разложением, приведенным в приложении 1:
и = ^т- ( sin a sin юг + -~ sin За sin Зюг +-— sin 5а sin 5юг + ...). ал у	-9	25	/
После подстановки значений Um — t В и а = л/4 получим:
и = иг + и3 + и5 + м7 = 6,88 sin юГ 4- 0,764 sin ЗюГ +
+ 0,275 sin (5юг - 180°) + 0,140 sin(7cof - 180°) В.
Схема замещения представлена на рис. 6.1Р.
Рис. 6.1	Рис. 6.1Р
6.2(	Р). Ток J (f) источника тока является периодической функцией времени, представленной на pre. 6.2. Составить схему замещения этого источника, учитывающую постоянную составляющую и три первые гармоники тока
Рис. 6.2Р
Рис. 6.2
Решение. При смещении начала координат на 60 мА вверх и на Т/4 влево получим кривую, разложение в ряд которой приведено в приложении 1. В соответствии с таблицей 4Г /	1 .	1	\
j' (f) = —2L sin юг' + — sm Зюг' + — sin 5юг'), л \	3	5	/
подставив Гт = 60 мА, получим:
J' = 76,4 sin юг' + 25,5 sin Зюг' +15,3 sin 5юг' мА.
Учитывая, что t' — t + Т/4 и кривая J'(r') получена смещением кривой J (t) на 60 мА, найдем ток источника:
J (Г) = Jq 4- Ji (t) +	(t) 4- J5 (t) =
= 60 4- 76,4 cos cor — 25,5 cos 3cor 4- 15,3 cos 5cor mA,
где частота основной гармоники со = 2я/Т = 628 рад/с.
Схема замещения представлена на рис. 6.2Р.
6.3.	Определить постоянную составляющую и три первые гармоники напряжения, представленного на рис. 6.3.
Указание. Если для кривой 2 в приложении 1 положить а = я/2, сдвинуть ее вверх на AJ2 и вправо на л/2, то получим кривую, заданную в условии задачи.
Рис. 6.5
6.4.	Вычислить постоянную составляющую и три первые гармоники напряжения, изображенного: а) на рис. 6.4,а и б) на рис. 6.4,6. Каждый из импульсов напряжения представляет собой полуволну синусоиды.
Указание. Воспользоваться разложением в ряд функции, представленной в пятой строке приложения 1.
6.5.	Постоянная составляющая напряжения, представленного на рис. 6.5, равна 100 В.
Определить амплитуды и начальные фазы трех первых гармоник.
6.6	(Р). На рис. 6.6 показана осциллограмма периодического напряжения на участке цепи.
Вычислить постоянную составляющую и две первые гармоники.
Решение. Делим период Т на 2п = 12 равных частей. Составляем расчетную таблицу (табл. 6.6), в которой во втором столбце записываем значения щ напряжения при = хТ/12, где
Таблица 6.6
	i	Щ	1-я гармоника »				2-я гармоника			
			. in Sin — n	in cos	 n	. in U/Sin — ‘ n	in UjCOS — 1 n	. 2ztt sin	 n	2zn cos — n	- 2in on — n	2in U/COS	 1	n
	1	2	3	4	5	6	7	8	9	10
	0	0	0,000	1,000	0,00	0,00	0,000	1,000	0,00	0,00
	1	10	0,500	0,866	5,00	8,66	0,866	0,500	8,66	5,00
	2	14	0,866	0,500	12,12	7,00	0,866	-0,500	12,12	-7,00
	3	16	1,000	0,000	16,00	0,00	-1,000	-1,000	0,00	-16,00
	4	18	0,866	-0,500	15,59	-9,00	-0,866	-0,500	— 15,59	-9,00
	5	24	0,500	-0,866	12,00	-20,78	-0,866	0,500	-20,78	12,00
	6	44	0,000	-1,000	0,00	-40,00	0,000	1,000	0,00	44.00
	7	60	r- 0,500	-0,866	-30,00	-51,96	0,866	0,500	51,96	30,00
	8	0	-0,866	-0,500	0,00	0,00	0,866	-0,500	0,00	0,00
	9	-6	-1,000	0,000	6,00	0,00	0,000	-1,000	0,00	6,00
	10	-8	-0,866	0,500	6,93	-4,00	-0,866	-0,500	6,93	4,00
	11	—6	-0,500	0,866	3,00	-5,20	-0,866 ’	0,500	5,20	-3,00
NJ NJ LU	E	166	—	—	46,64	-119,28		—	48,50	66,00
i — номер отсчета. Сумма строк этого столбца дает сумму, стоящую в первом выражении (6.2). Следовательно, постоянная составляющая напряжения Uo = 166/12 = 13,8 В.
После деления на п = 6 суммы чисел в пятом и шестом столбцах таблицы в соответствии с (6.2) получим амплитуды синусной и косинусной составляющих 1-й гармоники. Таким образом,
Ui = 3,89 sin coi - 9,94 cos art — 10,67 sin (art - 68° 40') В
Аналогично после суммирования чисел в девятом и десятом столбцах и деления результатов на п = 6 получим 2-ю гармонику напряжения:
и2 = 4,04 sin 2art + 5,50 cos 2art — 6,82 sin (2co? + 53°40') B.
Частота основной гармоники f — l/T = 200 Гц (co = — 1256 рад/с).
6.7.	Периодически изменяющийся (Т = 0,02 с) ток i содержит только 1-ю и 2-ю гармоники.
Найти амплитуды и начальные фазы этих гармоник по известным мгновенным значениям тока (в амперах) в 24 точках, заданных через каждую 1/24 часть периода: —0,10; +2,04; + 4,33; +6,33; +7,60; +7,83; +6,93; +5,04; +2,50; —2,06; —2,60; -4,29; -5,10; -5,04; -4,33; -3,33; -2,40; -1,83; -1,73; -2,04; -2,50; -2,79; -2,60; -1,71.
Построить зависимость i(t) как сумму двух гармоник и сопоставить значение тока, полученного в результате суммирования гармоник, со значениями, заданными в условии задачи.
6.2.	Периодические процессы в линейных цепях
6.8(	Р). Определить мгновенные значения токов i в схемах рис. 6.8, а и б.
Дано: г = 100 Ом; L=0,l Гн; С — 10 мкФ и ЭДС е~
100 sin cor + 100 sin 2соГ В, где со = 1000 рад/с. Сравнить отношения амплитуд 12тЩт Для схем Рис- 6.8, а и б.
Решение. В схеме рис. 6.8,а для 1-й гармоники комплексное сопротивление = г + j(aL= 100 4- j 100 = 141 z. 45° Ом, комплексная амплитуда ЭДС Ё1т = 100 z. 0° В, комплексная амплитуда тока iim = E^JZ^ = 0,707 z. —45° А. Для второй гармоники Z2 = г -I- j2(&L — 100 + J200 = 224 z. 63° 20' Ом и Ё2т = 100 0° В, следовательно, /2т = 0,446	—63° 20' А. Мгно-
венное значение тока i = 0,707 sin (cor — 45°) + 0,446 sin (2cor — - 63° 20') A.
Для схемы рис. 6.8,6
Zj = r -jl/®C = 100 - jlOO = 141 z. -45° Ом;
/1Ж = 0,707 z +45° A;
Z2 = r -jl/2aC = 100 — j'50 = 112 z. -26° 35' Ом; t2m = 0,893 z. + 26° 35' A.
Мгновенное значение тока
i = 0,707 sin (cor + 45°) + 0,893 sin (2cor + 26° 35') A.
Отношение амплитуд тока для схемы 6.8, а равно 0,63, а для схемы 6,8,6 равно 1,26 (индуктивность подавляет высшие гармоники в кривой тока).
Г	г	г	г
Рис. 6.9 -► cl)	б)
6.9.	Вычислить мгновенные значения напряжений и на выводах источников тока в схемах рис. 6.9, а и б.
Дано: J (Г) = 2 sin соГ 4- 1 sin ЗсоГ А; г = 12 Ом; coL = 12 Ом; 1/соС = 12 Ом.
6.10.	В цепи рис. 6.10 действует источник ЭДС е = 20 + + 12 sin cor — 3 sin 2сог В.
Найти мгновенное значение тока i при г = 50 Ом, 1/соС = = 100 Ом, coL = 50 Ом.
6.11(	Р). На вход цепи рис. 6.11, а с параметрами г — 10 Ом, L=31,8 мГн, С = 318 мкФ подается напряжение wBX в виде прямоугольных импульсов (рис. 6.11,6).
Определить мгновенное и действующее значения напряжения на выходе, учитывая гармоники до 7-й включительно. Найти действующее значение напряжения на входе и сравнить
8 п/р Иоикина П. А.
225
его с действующим значением, рассчитанным по постоянной составляющей и трем первым гармоникам.
Решение. Записываем ивх в виде ряда (см. приложение Ц учитывая, что заданная кривая смещена по сравнению с табличной на 50 В вверх:
мвх = 50,0 4- 63,7 sin cor -b- 21,2 sin ЗюГ 4- 12,7 sin 5cot 4- 9,1 sin 7<ot B,
где частота основной гармоники cd = 2 л/Т = 2я/0,02 = 314 рад/с; сопротивление <oL= 10 Ом; проводимость (дС — 0,10 См.
Рис. 6.10
._____________________t
10	~20	30 мс
б)
Рис. 6 11
Отношение напряжений /с-й гармоники
м =_3k.=s_____________Г________________	1
к ^вых	г (1 — /c2coLcoC) -I- jkatL	(1 — к2) 4- jk ’
Отметим, что полученное выражение справедливо и для вычисления отношения постоянных составляющих (/с = 0).
Дальнейший расчет целесообразно вести в табличной форме (табл. 6.11).
Напряжение на выходе
ивых = 50,0 4- 63,7 sin (cor - 90°) + 2,48 sin (Зсог - 159° 25') 4-
4- 0,518 sin (5соГ - 168° 15') 4- 0,188 sin (7cor - 171°4O') + ... B;
1/.ЫХ = ]/50,02 + (63,7/j/2)2+(2,48/01)2 + (0,518//2)2 + (0,18 8/|/2)2 = = 67,3 В.
Таблица 6.11
к	^вхет	(1 - Л2) + jk	Мк	^выхт
0	50,0	1	1	50,0
1	63,7 z. 0°	0 + yl	1 z. -90°	63,7 z. -90°
3	21,2^0°	— 8+у’З	0,117 z. - 159°25'	2,48 z. —159°25'
5	12,7 г. 0°	— 24 + j5	0,0408 z. - 168° 15'	0,518 z. -168°15'
7	9,1 z. 0°	-48 + у’7	0,0206 z. —171°40'	0,188 z. - 171°40'
Действующее значение напряжения на входе
1Лх =
7/2
1002 dt = 70,7 В,
о
а при учете только трех первых гармоник
V'a = |/50,02 + (63,7/]/2)2 + (21,2/|/2)2 + (12,7/]/2)2 = 69,5 В.
Рис. 6.12
6.12.	Напряжение на входе схемы рис. 6.12, а имеет форму периодических треугольных импульсов (рис. 6.12,6) с действующим значением 100 В.
Дано: г = 20 Ом; 1/соС = 90 Ом; ®L= 10 Ом.
Определить действующее значение выходного напряжения, учитывая первые три гармоники напряжения на входе.
6.13.	Найти ток i в цепи, представленной на рис. 6.13.
Дано: = 100 В; е2 = 100 sin or + 50 sin (ЗсоГ + 30°) В; co = = 500 рад/с; г = 100 Ом; = 1 Гн; Cj = 4 мкФ; С2 = 20 мкФ.
Рис. 6.14
6.14.	Для схемы рис. 6.14 рассчитать мощность тепловых потерь в сопротивлении г3.
Дано: gj = 26 В; е2 = 18 sincof + 6 sin Зсог В; = 160 Ом; г3 = 20 Ом; coLi = 160 Ом; соЬ2 — Ю Ом; 1/соС2 = 90 Ом.
6.15.	На вход фазовращателя, изображенного на рис. 6.15, подается напряжение
мвх = 20 sin cot -I- 10 sin 3ort + 6 sin 5cot B.
Рассчитать напряжение на выходе ивых при г = 1/<оС = = 1 кОм.
6.16.	При разомкнутых выходных выводах фазовращатель (рис. 6.16) с параметрами г = 1/соС = 1 кОм дает сдвиг по фазе первой гармоники приложенного напряжения на я/2.
1)	Найти мгновенное значение напряжения на выходе ивых при напряжении на входе ивх = 20 sin cot 4- 20 sin 2cot В.
2)	Найти мгновенное значение напряжения на выходе
при том же напряжении на входе при сопротивлении нагрузки фазовращателя гн = 10 кОм.
6.17.	На входе трансформатора (рис. 6.17) ток znx = = 2 sin cot 4- 1 sin 3cot А. Сопротивление нагрузки трансформатора rH = 100 Ом.
Рассчитать напряжения на входе и выходе при двух вариантах параметров трансформатора: 1)	= r2 = a>Li = coL2 =
= 10 Ом; коэффициент связи к = 0,5; 2) 74 = г2 = 10 Ом; coLj = coLj = 1 кОм; к = 1. Убедиться, что при параметрах варианта 2 у трансформатора, близкого к идеальному, форма кривой напряжения почти не искажается: tAm вх/^im вх ~ Л ^Зт вых/^lm вых И Ф1вых Ф1вх 3 (\|/3вых Фзвх)*
6.3.	Мощность. Коэффициенты, характеризующие формы периодических кривых. Измерения в цепях несинусоидального тока
6.18(	Р). Задано напряжение на входе двухполюсника (рис. 6.18) и = 20 4- 50 sin cot 4- 25 sin (ЗсоГ 4- 90°) В и параметры г = 11,2 Ом; Г1 = 7 Ом; coL = 10 Ом; 1/соС = 90 Ом.
Найти мгновенные значения тока i и напряжения на емкости, активную мощность двухполюсника и показания магнитоэлектрических приборов Лх и и электромагнитных приборов Л2 и ^2-
Решение. Применив принцип наложения, вычислим общий ток
i = 2,86 4- 3,62 sin (cot - 24°) + 1,37 sin (ЗоГ + 90°) A
и напряжение на емкости
ис = 28,8 sin (coz 4- 66°) 4- 16,3 sin (Зсог -I- 90°) В.
Активная мощность по (6.4)
к= 1
UknJkm COS ф^
157,0
Вт.
Показания амперметров:
At = 2,86 А; А2 = |/2,862 + (3.62/J/2)2 + (1.37Д/2)2 = 3,96 А.
Показания вольтметров:
=0; V2= ]/(28,8/|/2)2 + (16,3/|/2)2 = 23,1 В.
Мощность потерь можно найти по закону Джоу ля-Ленца: Pr = rj2 4- U2c/r = 7 • 3,962 4- 23,12/11,2 = 156,4 Вт, и проверить баланс активной мощности (Р = Рг): 157,0 ® 156,4.
Г1
Рис. 6.18
6.19.	’ Определить показания приборов электромагнитной системы в цепи рис. 6.19 при м = 20 j/5 sin cot 4-6,5 ]/1 sin 2cof В; (дЬг - 1/coCi = r; 2coL2 = 1/2cdC2.
6.20.	Напряжение на входе двухполюсника (рис. 6.20) и — = 100]/2 sin (dt 4- 70 ]/5 sin (3cof 4-+120°) В.
Найти показания приборов электромагнитной системы при
г = 10 Ом; rt = 20 Ом; г2 — 30 Ом; asL— 10 Ом; 1/соС = 60 Ом.
6.21.	В цепи рис. 6.21 найти показания ваттметра и амперметров электромагнитной системы при напряжении и =
= 1201/2 sin cot — 30|/2 cos 2cot В и параметрах 74=60 Ом; r2 = r3 = 30 Ом; coLi = 40 Ом; coL2 = 20 Ом; coM = 20 Ом; 1/соС = 80 Ом.
6.22.	В цепи по рис. 6.22 найти: 1) показание вольтметра при разомкнутом ключе; 2) показания вольтметра и амперметра при замкнутом ключе.
- Рис. 6.21
Рис. 6.22
Заданы ЭДС и параметры: Е = 12 В; е = 12]/2sin cot + 4- 10]/2 sin2cot В; г =	= 40 Ом; г3 = 10 Ом; coLt = 40 Ом;
coL3 = 10 Ом; 1/соС = 20 Ом. Приборы электромагнитной системы.
6.23.	Мост (рис. 6.23) уравновешен на частоте основной гармоники напряжения wBX.
Найти действующее значение напряжения мвых на диагонали моста при ивх = 12 sin cot 4- 3 sin 3cot В; rx = 1 кОм; r2 — = = l/coC2 = 100 Ом.
Рис. 6.23	Рис. 6.24
6.24.	Доказать, что если мост, представленный на рис. 6.24, уравновешен при синусоидальном напряжении ивх, то и при наличии высших гармоник у напряжения ивх напряжение ивых = 0.
6.25.	В цепи рис. 6.25 найти показания всех приборов. Амперметры А19 Л2, А3 и вольтметр электромагнитной системы, амперметр Л4 — магнитоэлектрической.
Дано: м = 180 + 220]/2sin(tot—10o) + 40]/2sin(3tot + 20°) В;
Е = 60 В; г = 20 Ом; юЬ= 10 Ом; шЦ = 8,75 Ом; 1/соС = 90 Ом.
6.26(	Р). При измерении индуктивности по схеме рис. 6.26 применяются приборы электромагнитной системы. Известно, что напряжение источника питания содержит основную и третью гармоники; коэффициент искажения равен 0,92.
Рис. 6.25	Рис. 6.26
Рассчитать методическую погрешность измерения, обусловленную искажением формы кривой приложенного напряжения.
Решение. Истинное значение индуктивности L= U измеренное значение
Обозначив U3/Ui = а, найдем, что
/3/Zi = а/3 и U = L ]/(1 + ос2)/(1 + а2/9).
Для’ заданного напряжения /сиск = U 1/|/(72 +' U% — 1/J/1 + а2, т.е. а = |/( 1ДИСК)2 — 1 = 0,426, и, следовательно, L'/L— 1,076. Методическая погрешность измерения равна 7,6%.
6.27.	При измерении емкости кон-
денсатора по схеме рис. 6.27 приме- °	I
няются приборы электромагнитной	/у\
системы. Питание цепи: 1) от источ-
ника напряжения или 2) от источника о----------------1
тока, которые кроме основной содер-	Рис. 6.27
жат еще 3-ю гармонику.
Определить максимально допустимое значение коэффици
ента искажения соответственно напряжения или тока источника,
при котором методическая погрешность измерения не превышает 5 %.
6.28	(Р). Измеряются напряжения:
и' = 70 4- 100 sin cot 4- 50 sin 3cot В;
и" = 70 + 100 sin cot — 50 sin 3cot B.
Найти показания: а) магнитоэлектрического вольтметра; б) электромагнитного вольтметра; в) вольтметра действующего значения (ВЗ-40); г) вольтметра среднего по модулю значения (B3-38); д) вольтметра ВК7-15 с амплитудным детектором. При решении задачи учесть (6.5)—(6.7).
Решение, а) Магнитоэлектрический вольтметр в обоих случаях покажет постоянную составляющую . Uq = 70 В.
б)	Электромагнитный прибор в обоих случаях покажет действующее значение U = [/702 4- (1001/2)2 4- (50 ]/2)2 = 105,6 В.
в)	Конденсатор, включенный во входную цепь прибора, не пропустит постоянной составляющей. Следовательно, вольтметр ВЗ-40 в обоих случаях покажет действующее значение переменной составляющей U~ = ]/(100 ]/2)2 4- (50/]/2)2 = 79,1 В.
г)	Конденсатор, включенный во входную цепь прибора, не пропустит постоянной составляющей. Следовательно, на входе преобразователя действуют напряжения или и'С, которые содержат только 1-ю и 3-ю гармоники (рис. 6.28Р). Прибор покажет среднее по модулю значение указанных напряжений и'~ и и", умноженное на коэффициент 1,11.
Напряжение и'~ не изменяется по знаку в течение полупериода, следовательно,
Т/2
2 f
^ср~ (100 sin (tit 4- 50 sin (3cot))dt =
0
п
1 г
: — (100 sin cot + 50 sin 3cot) d (cot) =
71 J
0
=(100• 2/tc) + (3 • 50 • 2/k) = 74,3 B.
Показание прибора U'np = 1,11 -74,3 = 82,4 В.
Напряжение u'L в пределах каждого полу периода изменяется по знаку, следовательно,
т
| 100 sin cot — 50 sin 3cot | dt =
о
a	n/2
(* (*
(50 sin 3cot — 100 sin cot) dcot +	(100 sin cot —
V	%
0	a
— 50 sin 3cot) cicot
100(2 cos a - 1) +
50 „	_	„ .
— (1—2 cos 3a)
Угол a найдем из условия 100 sin a — 50 sin 3a = 0. Учитывая, что sin 3a = 3 sin a — 4 sin3 a, получаем sin a = 0,5; a = 30° и = 57,2 В. Показание прибора [7"p = 1,1 ШсР~ = 63,5 В.
д) Конденсатор на входе прибора не пропускает постоянной составляющей. У кривых на рис. 6.28Р (симметричных относительно начала координат) = | u~min |. Поэтому далее вычислим
Для напряжения и'~ из условия du'~/dt = 100 cos cot + + 50-3 cos 3cot = 0 при cot = 0 и, учитывая, что cos 3cot = = 4 cos3 cot — 3 cos cot, находим угол 0 — 40° 15', при котором у напряжения первый максимум
и'~тах = 100 sin 40° 15' + 50 sin 120°45' = 107,6 В.
Показание прибора 17'пр = 0,7071/L^ = 76,1 В.
Для напряжения и", как видно из рис. 6.28Р,б, u" = = 100 + 50 = 150 В. Следовательно, С7"р = 0,707w'£mdX = 106 В.
6.29.	Найти показания вольтметров задачи 6.28 при измерении напряжений, представленных на рис. 6.29.
6.30.	Найти показания вольтметров задачи 6.28 при измерении напряжений:
1)	и' = 10 sin cot + 5 sin 2cot В; 2) u" = 10 sin cot — 5 sin 2cot B.
6.31.	Вольтметр электромагнитной системы при измерении напряжений (рис. 6.31) показывает 10 В. Найти показания вольтметров других систем, указанных в -задаче 6.28.
6.32.	Рассчитать мощность потерь в резисторе с сопротивлением 1 МОм при токах, осциллограммы которых приведены на рис. 6.32, а — е. На рис. 6.32, г длительность положительного импульса равна */з периода.
6.33.	К резистору с сопротивлением 2 кОм приложено периодическое напряжение, изменяющееся по закону
( 120 — 90е В при 0 С f < G = 11,78 мс;
“ ~ 1 70е"<1*'1)/’2 В при < t < Т= 20,23 мс.
a.)	б)
Найти мощность потерь в резисторе, если ij = 0,02 с; т2 = 0,01 с.
6.34.	Определить коэффициенты формы, амплитуды и искажения для напряжений, представленных на рис. 6.34, а —в.
6.4.	Резонанс в цепях несинусоидального тока
6.35(	Р). Определить, при каких значениях параметров С15 С2 и L2 в двухполюснике (рис. 6.35) будут резонансы токов на частотах 1-й и 5-й гармоник и резонанс напряжений на частоте 3-й гармоники, если индуктивность =0,1 Гн, частота основной гармоники f = 1 кГц и L2 < Lx.
Найти ток в сопротивлении г = 200 Ом при напряжении питания и = 100 sin cot + 50 sin ЗооГ + 30 sin 5сог В и полученных значениях параметров.
Решение. Из условий резонансов токов на частотах 1 -й и 5-й гармоник следует, что
l/LiC^co2;	(1)
1/L2C2 = 25со2.	(2)
Из условия резонанса напряжений на частоте 3-й гармоники следует, что
Зсо^/ЗсоС^ 3coL2/3coC2
3<oL! - 1/ЗгоС! + 3wL2 - 1/ЗсоС2 " ’ или после преобразований
_______I_____^2____ _ Q
- 1 9co2L2C2 - 1	V '
После подстановки в (3)	= со'2 из (1) и L2C2 = со“2/25
из (2) получим L2 — Li/12,5 = 0,008 Гн. Если предположить, что 1/LjCi = 25со2 и 1/Ь2С2 = со2, т. е. что резонанс тока на частоте 1-й гармоники будет в контуре L2, С2, а на частоте 5-й — в контуре Li, Ci, то условие задачи L2 < не выполняется. Из (1) и (2) найдем =0,253 мкФ и С2 = 0,127 мкФ.
Сопротивление контура Lb Ci бесконечно большое при частоте 1-й гармоники, а контура Ь2, С2 — при частоте 5-й, поэтому в сопротивлении г нет токов с частотами 1-й и 5-й гармоник. Общее сопротивление контуров L15 Ct и L2, С2 имеет нулевое сопротивление для 3-й гармоники тока, поэтому i = и 3/г = 0,25 sin 3cot А.
6.36.	Показанный на рис. 6.36 электрический фильтр не пропускает в сопротивление нагрузки 5-й гармоники тока и не создает сопротивления 3-й гармонике тока.
Найти напряжение на сопротивлении rH = 1 кОм при Lt = L2 = 10 мГн, f=2 кГц и и = 120 sin соГ + 60 sin ЗсоГ + + 30 sin 5cot В.
6.37.	В двухполюснике, изображенном на рис. 6.37, имеет место резонанс напряжений на частотах 1-й и 3-й гармоник и резонанс тока на частоте 2-й гармоники.
Определить параметры Сь С2 и Ь2, если = 10 Гн, со = 1000 рад/с и известно, что Ci > С2.
6.38. Рассчитать, при каких значениях емкостей и С2 двухполюсника (рис. 6.38) на сопротивлении гн напряжение ия — 100 sin cot В и не зависит от значения сопротивления гн.
Дано: Lt — 2,5 Гн; и = 100 sin art +
Рис. 6.38
Рис. 6.37
Рис. 6.39
6.39.	Найти общий ток двухполюсника (рис. 6.39) при резонансе на частоте 1-й гармоники.
Дано: a)L= 10 Ом; 1/соС = 40 Ом; г — 200 Ом; и = = 120 sin cot + 100 cos 2cot + 50 sin 3cot B.
6.40.	Для двухполюсника (рис. 6.40, a) с параметрами г = 100 Ом, L=15,9 Гн задано напряжение питания в виде треугольных импульсов (рис. 6.40,6).
Рис. 6.41
*- Рис. 6.40
Найти мгновенное и действующее значения тока при условии, что контур настроен в резонанс: 1) на частоте 1-й гармоники; 2) на частоте 3-й гармоники и 3) на частоте 5-й гармоники. При расчете учитывать три первые гармоники разложения в ряд Фурье напряжения питания.
6.41.	Рассчитать напряжение иг и токи iLi ic в цепи по рис. 6.41. При определении токов учесть три первые гармоники разложения в ряд Фурье напряжения и на входе (рис. 6.40,6).
Дано: L= 0,1 Гн; гг — r2 « |/1/С = 1 кОм; г — 2 кОм.
6.5. Несинусоидальные режимы симметричных трехфазных цепей
6.42(Р). Обмотки симметричного трехфазного генератора соединены звездой. Задано напряжение фазы А : иА = 100 sin cof 4-4- 20 sin 3art + 15 sin 5cot B.
Найти мгновенные значения всех фазных и линейных напряжений и действующие значения фазного и линейного напряжений.
Решение. В симметричной цепи 1-е гармоники напряжения образуют систему прямой последовательности (6.12), 3-и — нулевой (6.11), а 5-е — обратной (6.13), следовательно,
ив = 100 sin (cot — 120°) 4- 20 sin 3cot 4- 15 sin (5ort 4- 120°) B;
uc — 100 sin (cot 4- 120°) 4- 20 sin 3cot 4- 15 sin (Scot — 120°) B.
Линейные напряжения найдем как разность фазных:
VABl = (100Д/2) л 0° - (100/|/2) Z. -120° =
= (100Д/2)|/з л + 30° В;
= (20/|/2) z 0° - (20Д/2) z 0° = 0;
= (15/J/2) z 0° - (15/1/2) z + 120° = (15/|/2)]/з z -30° В.
Следовательно,
илв = 173 sin (art 4- 30°) 4- 26 sin (5cot - 30°) В;
uBC = 173 sin (cot - 90°) + 26 sin (5cot + 90°) B;
мсл = 173 sin (cot 4- 150°) 4- 26 sin (5art - 150°) B.
Действующие значения по (6.3):
l/ф = (l/|/2)]/1002 + 202 + 152 = 72,9 В;
U, = (l/J/2) j/1732 + 262 = 123,1 В.
6.43.	Три обмотки трехфазного симметричного генератора соединены треугольником.
Найти показание электромагнитного вольтметра, включенного в рассечку треугольника. Известна ЭДС одной из фаз: е = 120 sin art — 10 sin 3art 4- 5 sin 5cot + 4 sin 7art 4- 3 sin 9art B.
6.44.	Вторичные обмотки трансформатора соединены треугольником (рис. 6.44). Фазное напряжение иф = 1201/2 sin art — — 50]/2 sin 3cot 4- 40 ]/2 sin 5cot — 30]/2 sin 7art 4- 201/2 sin 9cot B.
Найти показания вольтметров электромагнитной системы при 1) замкнутом и 2) разомкнутом ключе.
6.45.	Вторичные обмотки трех одинаковых однофазных трансформаторов соединены треугольником (рис. 6.45). Активное сопротивление каждой обмотки г = 5 Ом, индуктивность L = 15,92 мГн. Фазная ЭДС еф = 2201/2 sin cof 4- 50j/5 sin Зсог 4-4- 40 ]/2 sin Scof — 30 ]/2 sin 7го? + 25 J/2 sin 9соГ В; f — 50 Гц.
Найти показание амперметра электромагнитной системы.
6.46(	Р), Электродвижущая сила фазы А трехфазного симметричного генератора (рис. 6.46)
еА = 120 sin cot 4- 30 sin 3cot 4- 20 sin 5cot B.
Пренебрегая внутренним сопротивлением генератора, найти мгновенные значения линейных и фазных токов, показания ваттметров и показания вольтметров и амперметров электромагнитной системы.
Рис. 6.46
Дано: г = 60 Ом; ooL=30 Ом; сопротивление проводов линии = 10 Ом.
Решение. Так как 3-и гармоники образуют систему нулевой последовательности, то в схеме рис. 6.46 3-х гармоник токов не будет. Поэтому расчет выполним для 1-й и 5-й гармоник.
Преобразуем сопротивления нагрузки, соединенные треугольником в эквивалентную звезду:
zA1 = ^д1/3 = (20 + л°) =22’4 26°35' Ом;
2д5 = 2д5/3 = (20 4- /50) = 53,9 л. 68° 10' Ом.
Линейные токи
Л1 = EaiI(Zj^ + г„) = 120 z. 07/2(30 + ДО) = 2,68 ± -18’20' А; /л5 = £л5/(2а5 + Гл) = 20 z. 0“/|/2 (30 + ДО) = 0,243 z. -59°0' А.
Амперметр 4t показывает действующее значение линейного тока Ц = ]/2,682 + 0,2432 = 2,69 А. Мгновенное значение тока в линейном проводе фазы А
iA = 3,79 sin (cot - 18° 20') + 0,343 sin (5cot - 59° O') A.
Учитывая, что /в1=а2/л1; iCt=aiA1 и iB5 = aiA5; lC5 = = a2iAi, где a = 1 z. 120°, получаем:
iB = 3,79 sin(<ot - 138° 20') + 0,343 sin(5wt + 61 ° O') A;
ic = 3,79 sin (cot + 101 ’40') + 0,343 sin (5wt - 179’0') A.
Так как iA = iab - i*, to IAt = /oM (1 - o)= /«n ]/3	-30°,
следовательно, = (Л1//3) z. 30° = 1,55 a. 11’40' А. Аналогично iAi = iab5 (1 - a2) = iabs ]/3 z. +30°, следовательно, iabs = = (/xs//3) z -30’ = 0,140 z. -89’0' A.
Амперметр A2 показывает действующее значение фазного тока 12 = ]/1,552 + 0,142 = 1,56 А. Мгновенные значения токов в сопротивлении нагрузки
iab = 2,19 sin (cot + 11°40') + 0,198 sin (5tot - 89°O') A;
ibc = 2,19 sin (cot — 108°20') + 0,198 sin (5cot + 31°O') A;
ica = 2,19 sin (cot 4-131° 40') + 0,198 sin (Scot + 151° O') A.
Показания ваттметров:
?W1 ~ Rt(UacJAl) + Re (^5^*5);
P w2 = Re + Re (Ubcsf%\
где Cflcl = -Z^lcai = 104 z. — 21°45' B; Uac5 = -ZA5/ca5 = = 22,6 4 40° 10' B; Ubcl = Uaci -60° = 104 z. -81°45' В и Ubcs = Uacs 60° = 22,6 z. 100° 10' В, следовательно,
PWi = 104 • 2,68 cos 3°25' + 22,6 • 0,243 cos 99°10' = 277 Вт;
PW2 = Ю4 • 2,68 cos 56° 35' + 22,6 • 0,243 cos 43° 10' = 157 Вт.
Баланс активных мощностей: Ppvl + Pw2 — Pa Pwi + Pw2-= 434 Вт; Pr = 3 (ri?) = 3  1,562 • 60 = 432 Вт.
Погрешность расчета меньше 0,5%.
6.47.	Симметричный трехфазный генератор с фазной ЭДС еА = 120 sin cot + 80 sin (3cot — 45°) 4- 30 sin (Scot — 90°) В соединен звездой (рис. 6.47).
Найти мгновенные значения токов ic, напряжения иВп и показания приборов электромагнитной системы при г = 3 Ом, d)LN = 1 Ом, 1/соС = 9 Ом.
6.48.	Вторичные обмотки трансформатора симметричной трехфазной системы соединены треугольником, фазы приемника — звездой (рис. 6.48). Известен ток iAB = 12 sin cof + + 0,5 sin 3atf 4- 3 sin 5cof A.
Определить мгновенное значение тока iB и показания амперметра электромагнитной системы.
6.49.	Найти показания приборов электромагнитной системы в цепи рис. 6.49 при фазном напряжении генератора иАВ = 220 sin cor + 80 sin 5cof В и сопротивлениях г = 60 Ом; coL = 1 Ом; 1/соС = 75 Ом.
6.50.	Найти показание вольтметра (при разомкнутом ключе) и показание амперметра (при замкнутом ключе) в схеме рис. 6.50, а с параметрами г = 48 Ом, со£ = 4 Ом, (£)Ln = 4 Ом.
Фазная ЭДС симметричного трехфазного генератора представлена на рис. 6.50,6. Приборы электромагнитной системы. Учесть все гармоники ЭДС до девятой включительно.
Глава седьмая
ФИЛЬТРЫ
Введение к гл. 7
Для фильтров-четырехполюсников, собранных из катушек и конденсаторов, потерями в которых можно пренебречь, т. е. для фильтров из реактивных элементов, полоса пропускания (прозрачности) определяется условием
А = 0	(7.1)
(постоянная ослабления равна нулю).
У симметричных Т-образных (см. рис. 4.3) и П-образных (см. рис. 4.5) фильтров в полосе пропускания продольное Zi = и поперечное Z2 = ±jz2 сопротивления должны быть разного характера (одно — индуктивное, другое — емкостное) и удовлетворять уравнению
(7.2)
откуда определяются граничные частоты полосы пропускания при
Zi — 0 или z2 = оо и Zi = 4z2.	(7.3)
В этой полосе постоянная фазы В удовлетворяет условию cos В = 1 — zJ2z2 или sin(B/2) = zj^z2. (7.4)
В полосе задерживания (непропускания) А 0 и 1) cos В = +1 (В = 0) для полосы частот, в которой Zx и Z2 одинакового характера, или 2) cos В = — 1 (В = ± я) для полосы частот, в которой Zj и Z2 разного характера.
В случае 1 постоянная ослабления удовлетворяет условию
ch А = 1 + z2/2z2 и sh (А/2) — ]/z1/4z2,	(7.5)
в случае 2 — условию	_____
ch А = — 1 + Zj/2z2 и ch (А/2) = ]/zJ^z2,	(7.6)
Характеристическое сопротивление рассчитывается по формулам для ZT и Zn, приведенным в табл. 4.2.
В частности, для фильтров типа к
ZiZi = к2,	(7.7)
где к — действительное число, т. е. Zj и Z2 — обратные двухполюсники, и, следовательно, они разного характера. Схемы, граничные частоты, частотные зависимости постоянных ослабления и фазы, рассчитанные по (7.3)—(7.6), и параметры фильтров типа к приведены в табл. 7.1.
Таблица 7.1
Фильтры типа к
м
Продолжение табл. 7.1
Полосовой (полосный) 2Ci 2Ci
Li Ci
fl	f 1,2 —/о(|/и2 + 1 + и);
/о= 077=1/2^1/^;
L2[Lx = Сх!Сг = и2;
М = fc/jt(f2 -/j); cx = (f2 -W/2k;
Ь2 = *(/-2-ЛУ4ЛЛЛ;
C2 = -fi)k, где к = ]/L2ICx
2n2
2n2
7	(Г/Л - /о//)2 .
~T	/	4n2
7 ,AL V'/fo -f„/A2
2" = V p-------------------
Заграждающий
Li/2	L^/2
fi co;
Л.2 = ^(l/i6n2 + 1 + 1);
4n
fo= 077=l/2n]/I^c;;
Li
~ ^l/^l ~~ n » bi =(/2 -/i)Wi/2; Ci = \/{f2 -/L)4nA-;
c2 = W2-/i)4n;
c2 = «2 -Л)М/1/2, где к = ]/lJC~2
ph A — _____- ______________ — I "
2n2 iflfo-fjf)2- ’
1 1
COS B. 1	~ - / /•\7 >
2n2 (Г//о-/о//)2
1/ 1 1
2t = * p - 4^r	_ fo//)2 ;
, / i	i
Zn-V / 1 “ ^2- (///o _ /o//)2
Простейшие несимметричные фильтры собираются по Г-образной схеме (рис. 4.14), у которой два характеристических сопротивления: Zd = Zn и Zc2 = ZT (см. табл. 4.3), а постоянные ослабления и фазы вдвое меньше, чем у Т- и П-образных схем.
Для последовательно-производных фильтров типа т _	Z2 (1 —m2)Zj	ft.
Zim = wZij Z2m — H	>	(7-8)
где m — действительный коэффициент, удовлетворяющий условию 0 < tn < 1.
Для параллельно-производных фильтров типа т
Z2m = —;		(7.9)
т Zlm	2mZ2
Характеристические сопротивления фильтра типа т
Zjlm ~ у 21т2гт /----------- ’ I
у 1 “h 21т/422т	>	(7.10)
2тт = ]/21т2гт jA + 21т/42гт,
причем у последовательно-производного фильтра ZTm = ZT, а у параллельно-производного Znm = Zn.
Полоса пропускания совпадает с полосой пропускания соответствующего фильтра типа к. В полосе задерживания постоянная ослабления может быть вычислена по (7.5) и (7.6) после замены zt и z2 на zlm и z2m.
Для мостового фильтра-четырехполюсника (см. рис. 4.15), собранного из реактивных элементов Zj и Z2, полоса пропускания, определяемая по (7,1), получается в диапазоне частот, для которых сопротивления Zt и Z2 разного характера. Граничные частоты задаются условиями
Z1=0hz2 = 0.	(7.11)
Постоянная фазы удовлетворяет условию
cos В = (±z2 + zt)/(±z2 ± Zi).	(7.12)
В полосе задерживания сопротивления Zj и Z2 одинакового характера. Постоянная ослабления удовлетворяет условию
ch А = | (z2 + zMz2 - zj I,	(7.13)
а постоянная фазы — условию cos В = +1. Характеристическое сопротивление
Z, = /ZiZj.
(7.14)
7.1.	Фильтры типа к
7.1	(Р). Составить Т-образную схему низкочастотного фильтра типа к, у которого номинальное значение характеристического сопротивления в полосе пропускания равно 600 Ом и постоянная ослабления на частоте 100 Гц равна 40 дБ. При этой же частоте определить постоянные фазы и передачи, отношение напряжений на входе и выходе при согласованной нагрузке и граничные частоты.
Решение. За номинальное значение характеристического сопротивления фильтров типа к принято считать характеристическое сопротивление, равное параметру к, т.е. определяемое по (7.7): к = j/Z^. Такое активное характеристическое сопротивление фильтр имеет при одной из частот полосы пропускания.
Для низкочастотного фильтра Zi =jwL и Z2 = —Jl/o)C, т.е. k = ]/L/C, и по условию задачи
боо = ]/Т/с.	(1)
Постоянная ослабления для фильтров типа к определяется по (7.6), т.е. при = coL и z2 = 1/соС имеем:
ch А = - 1 + <o2LC/2,	(2)
где А = 40 дБ = 4,6 Нп; ch А = 49,75; со = 2л/ = 628 рад/с.
Из двух уравнений (1) и (2) получается L/2 = 4,8 Гн и С = 26,6 мкФ. Схема фильтра показана в табл. 7.1.
Постоянная ослабления задана (4,6 Нп), постоянная фазы р в полосе пропускания для низкочастотных фильтров типа к равна я. Поэтому постоянная передачи Г = А + JB = 4,6 +/3,14.
При согласованной нагрузке по (4.26) А = 201g (C7i/tJ2), т.е. при А = 40 дБ UJU2 — 100 (полоса задерживания).
Фильтр низкочастотный, поэтому первая граничная частота /i=0 (zi = 0 и z2 = оо), вторая граничная частота по (7.3) определяется из уравнения 2л/2Ь = 4/2л/2С, откуда /2 =20 Гц.
Пользуясь табл. 7.1, можно сначала определить граничную частоту /2 из формулы ch(A/2) = ///2, где А = 4,6 Нп и /2 = = 20 Гц, затем индуктивность и емкость по формулам L — = k/nf2 и С = \/nf2k.
7.2(	Р). Известны параметры Т-образного низкочастотного фильтра типа к: индуктивность L = 9,6 Гн и емкость С — = 26,6 мкФ. Сопротивление нагрузки фильтра гн = у L/C = = 600 Ом (постоянное), так что режим согласованной нагрузки получается только на одной частоте полосы пропускания.
Определить отношение напряжений на входе и выходе фильтра на граничной частоте 20 Гц и на частоте 100 Гц и сравнить их с отношением напряжений при согласованной нагрузке.
Построить график зависимости отношения UJU2 от частоты при постоянном сопротивлении нагрузки гн. По графику определить полосу пропускания, считая, что фильтр пропускает при условии U2 >	На этом же графике по-
строить зависимость отношения Ui/U2 от частоты при согласованной нагрузке. Какое заключение о фильтрующих свойствах схемы при постоянном сопротивлении нагрузки по сравнению со случаем согласованной нагрузки можно сделать, сравнивая построенные кривые?
Решение. При согласованной нагрузке четырехполюсника и, в частности, фильтра отношение напряжений на входе и на выходе определяется постоянной ослабления по (4.26).
Для Т-образного низкочастотного фильтра типа к характеристическое сопротивление ZT (согласованная нагрузка) может быть найдено, как и для любого симметричного Т-об-разного четырехполюсника, по формуле (см. табл. 4.2)
Zt = j/Z2Z2(l + Zt/4Z2),
которая получена из (4.22) и в которой Zt = jwLn Z2 = —Jl/coC.
Характеристическое сопротивление можно вычислить и по формуле (табл. 7.1)
zT = 1/Е/с|/1-/Ж
где /2 = 1/л ]/Ес = 20 Гц — граничная частота. При этой часто-те Zt = 0; при частоте 100 Гц (в полосе задерживания) ZT — реактивное сопротивление. Следовательно, при заданном активном сопротивлении нагрузки гн = 600 Ом фильтр на частотах 20 и 100 Гц не работает в режиме согласованной нагрузки и отношение напряжений на входе и выходе не определяется по формулам (4.26).
Отношение напряжений можно найти, как и для всякого четырехполюсника при заданном сопротивлении нагрузки, при помощи уравнений четырехполюсника, справедливых при любом сопротивлении нагрузки. Например, по первому уравнению (4.1)
U1 = Ацй2 + 412^2 = G411 + 412/Гн) U1-
Для Т-образного симметричного четырехполюсника коэф
фициенты (см. табл. 4.2) равны:
л	+	<	<o2LC .	_ f2
4ц — 1 + Zi/2Z2 = 1------z— =1—2 ~~2— действительный;
Xf	/ 2
(	z \	(	f2 \
412 =41(1+ -Г—-1 =j2nfL[ 1 - _-2 ) - мнимый;
\	4Z2 /	\	J 2 /
412/гн ~ мнимая величина, поэтому
L11 / V2 =	+ (1412 1/гн)2 •	(1)
При/ = /2 = 20 Гц получаем Ли = —1; Л12 = 0, т.е. = = 1/2- Приf ~ 100 Гц получаем 4tl = —49; Л12 = — /14,5 • 104 Ом и UJV2 = 246.
При согласованной нагрузке на граничной частоте, как и во всей полосе пропускания, А = 0, т.е. Ui = U2 (теорети-
чески, так как при этой частоте сопротивление согласованной нагрузки ZT = 0 и ZnT = 0). При
частоте 100 Гц из формулы (табл. 7.1) ch (А/2) = f/f2 = 5 получаем А = 4,6 Нп = 4,6 • 8,7 = = 40 дБ, и так как по (4.26) А = 20 lg (UJUJ дБ, то UJU2 = = 100.
График зависимости отношения UJU2 от частоты при
ZH = гн = 600 Ом, построенный по (1), и график этой же зависимости при ZH = ZT, построенный по (4.26), представлены на рис. 7.2Р. Из графиков следует, что при гн = 600 Ом и поставленном условии 172 > x/j/2, т.е. UJU2 ]/2, граничная частота равна 22 Гц и в полосе задерживания фильтрующие свойства хуже, чем при согласованной нагрузке (UJU2 меньше).
7.3.	Решить задачу 7.1, заменив Т-образную схему низкочастотного фильтра П-образной.
7.4.	Для разделения входной и выходной цепей в аппаратуре высокочастотного телефонирования применяется низкочастотный П-образный фильтр типа к.
Определить индуктивность катушки и емкость каждого конденсатора фильтра с нижней граничной частотой 25 кГц, если входное сопротивление фильтра в полосе пропускания при согласованной нагрузке должно быть не менее 800 Ом. Вычислить постоянную ослабления фильтра при частоте 50 кГц.
7.5.	Низкочастотный П-образный фильтр типа к с номинальным значением характеристического сопротивления в по
лосе пропускания 600 Ом и постоянной ослабления на частоте 100 Гц, равной 40 дБ, работает в режиме холостого хода.
Найти отношение напряжений на входе и выходе при частотах f — 0; 0,4/2; 0,8/2; /г? 1,2/2, где /2 — верхняя граничная частота. Построить график зависимости отношения напряжений на входе и выходе иг/и2 от частоты в режиме холостого хода. По графику определить полосу пропускания, считая, что фильтр пропускает при L72 > l/i/|/2.
7.6(	Р). Высокочастотный П-образный фильтр состоит из двух звеньев типа k с параметрами L=20 мГн, С = 2 мкФ.
Определить полосу пропускания фильтра и постоянную передачи при угловой частоте со = 1250 рад/с. При частоте (О = 5000 рад/с, напряжении на входе 100 В и согласованной нагрузке найти ток на входе.
Решение. Полоса пропускания фильтра совпадает с полосой пропускания одного звена, схема которого приведена в табл. 7.1, причем продольное сопротивление Zt — —jl/mC и поперечное Z2 = jcoL.
Граничные частоты определяются по (7.3) или по формулам табл. 7.1:	= 2nfi — 1/2 j/Ec = 2500 рад/с, ®2 = 00 •
В полосе задерживания при частоте со = 1250 рад/с постоянная ослабления одного звена определяется по (7.6) или по формулам табл. 7.1: ch(A/2) - fjf = «н/со = 2, откуда А = = 2,64 Нп, а постоянная фазы В= + л. Для фильтра из двух звеньев постоянные в 2 раза больше.
При согласованной нагрузке симметричного четырехполюсника входное сопротивление равно характеристическому. Для фильтра, состоящего из двух одинаковых звеньев, характеристическое сопротивление равно характеристическому сопротивлению одного звена, поэтому = l/i/zn, где характеристическое сопротивление находится по формулам табл. 4.2 или 7.1: Zn = zn = 100/(]/з/2) Ом и Л = ]/3/2 А.
7.7.	У фильтра задачи 7.6 известен выходной ток первого звена ilt2 — 1 А. При частоте со = 5000 рад/с и согласованной нагрузке фильтра найти напряжение Ult2 между звеньями, отношение напряжений на входе и выходе звена и сдвиг по фазе между ними.
7.8.	Сопротивление нагрузки фильтра задачи 7.6 постоянно: Zh = гн = 100 Ом. Напряжение на входе равно 100 В. Определить напряжение на выходе при частотах 1000 и 5000 рад/с.
7.9.	Из двух конденсаторов емкостью 4 нФ каждый и катушки с индуктивностью 0,34 мГн, потерями в которых можно пренебречь, сначала собрали низкочастотный фильтр, а затем высокочастотный.
Сравнить полосы пропускания этих фильтров, а также постоянные ослабления на двух частотах: 1) 120 кГц. 2) 240 кГц (при согласованной нагрузке).
7.10.	Высокочастотный Т-образный фильтр типа к собран из двух конденсаторов емкостью 4 нФ каждый и катушки с индуктивностью 0,34 мГн, потерями в которых можно пренебречь.
Определить, при какой частоте сопротивление согласованной нагрузки активное и равно 300 Ом.
7.11.	Высокочастотный П-образный фильтр типа к с граничной частотой 96 кГц применяется для подавления мешающего сигнала на частоте 64 кГц и пропускания сигналов более высоких частот. Емкость конденсатора фильтра равна 4 • 103 пФ.
2С1 Ы/2 Li/2 2С1
Рис. 7.12Р	Рис. 7.I4
Найти индуктивность каждой катушки фильтра. Определить, достаточно ли одного звена для уменьшения уровня мешающего сигнала на 40 дБ, а если нет, то из скольких звеньев должен быть собран фильтр.
7.12(	Р). Полосовой Т-образный фильтр типа к имеет следующие параметры: = 10 мГн; С] =0,2 мкФ; L2 = 10 мГн; С2=0,2 мкФ. При сборке фильтра конденсатор С2 не был присоединен.
Определить, как при этом изменилась полоса пропускания фильтра.
Решение. Для полосового фильтра типа к граничные частоты рассчитываются по (7.3) или по формулам табл. 7.1:
fl. 2 = /о (|/«2 + 1 + 4
где /0 = 1/2я |/Цс\ = 1/2я]/Цс2; n2 = L2/L1 = G/C,.
При заданных параметрах /0 — 3,55 кГц; и2 = 1;	=
= 1,45 кГц; f2 = 8,55 кГц.
Схема фильтра без конденсатора С2 показана на рис. 7.12Р. Продольное сопротивление — j (coL — Jl/coC), поперечное Z2 = = j(&L, где обозначено L = Lx = L2; C =
Из условия (7.3) находим граничные частоты: = coL — — 1/соС | = 0, откуда f = f2— fQ = 3,55 кГц; = 4z2 или o)L-
- 1/соС | = 4<oL, откуда f = J\ = /о/]/5 = h58 кГц. Условие z2 = оо, т. e. co2 = 00 не подходит, так как дает значение, большее 3,55 кГц.
7.13.	Заграждающий Т-образный фильтр типа к содержит три катушки и три конденсатора, потерями в которых можно пренебречь. Индуктивности двух катушек равны по 18 мГн, емкости двух конденсаторов — по 0,04 мкФ, параметр к = = 600 Ом.
Найти индуктивность третьей катушки и емкость третьего конденсатора, а также ширину полосы задерживания.
7.14(	Р). Найти полосу пропускания и зависимость постоянной ослабления Аг от частоты для Г-образного высокочастотного фильтра (рис. 7.14). Сравнить Аг с постоянной ослабления высокочастотного П- или Т-образного фильтра типа к.
Решение. Из двух Г-образных четырехполюсников (рис. 4.14) каскадным соединением можно составить Т-образную схему (рис. 4.3) или П-образную (рис. 4.5). Полоса пропускания Т- или П-образного фильтра получается такой же, как и у Г-образного, так как соединение выполняется с соблюдением согласования, т. е. для высокочастотного фильтра (табл. 7.1) j\ = 1/4тг|/Ес; /2 = Постоянная ослабления Г-образного фильтра (полузвена) вдвое меньше, чем у Т- или П-образного (звена), т. е. определяется (см. табл. 7.1) по формуле ch Аг = /1//.
7.15.	У П-образного высокочастотного фильтра с параметрами L= 2 мГн, С = 2 мкФ отпаялся провод, присоединяющий одну из катушек.
Определить, как изменится граничная частота фильтра.
7.16.	Для Т-образного низкочастотного фильтра типа к определить, при какой частоте полосы задерживания характеристическое сопротивление по модулю равно параметру к = = ]/l/C. Найти постоянную ослабления фильтра при этой частоте и частоту, начиная с которой постоянная ослабления больше 2,2 Нп.
7.17.	В системе связи по распределительным электрическим сетям передающую и приемную аппаратуру защищают
от напряжения сети 500 В уравновешенным Т-образным высокочастотным фильтром типа к (рис. 7.17). Емкость каждого конденсатора фильтра 0,15 мкФ, характеристическое сопротивление с увеличением частоты приближается к значению 600 Ом.
о
о
Рис. 7.17
Найти граничную частоту фильтра, постоянную ослабления на частоте сети и напряжение сети на выходе фильтра, считая нагрузку согласованной.
7.18(	Р). На вход П-образного низкочастотного фильтра типа к с параметрами L = 0,956 мГн, С = 26,6- 102 пФ (граничная частота 200 кГц, к — 600 Ом) подается сигнал, модулированный по амплитуде: и = Uim (1 -I- т cos cos coz, где C7lw = = 1 В и коэффициент модуляции т — 1.
Найти напряжение на выходе фильтра при модулирующей частоте F = П/2л = 10 кГц и несущих частотах 1) /н1 = Ю|/2л = = 150 кГц; 2) /н2 = 200 кГц и 3) /н3 = 250 кГц, считая сопротивление нагрузки согласованным на каждой из частот.
Решение. Напряжение на входе можно представить в виде суммы трех гармоник: нижней боковой, несущей и верхней боковой:
и у — (1 + cos Qf) cos cof = 0,5 cos (co - Q) t +
4- 1 cos cof + 0,5 cos (св + Q) t.
1)	При согласованной нагрузке и /Hi = 150 кГц все три гармоники попадают в полосу пропускания фильтра, поэтому постоянная ослабления А = 0, т. е. амплитудных искажений нет. Сдвиг по фазе любой гармоники определяется постоянной фазы В. Для низкочастотного фильтра (см. табл. 7.1) в полосе пропускания sin (В/2) = //f2 и при частотах f =	- F =
= 140 кГц, f = /Н1 = 150 кГц и f — /Н1 + F = 160 кГц постоянная фазы соответственно равна 89, 97 и 106°, поэтому
и2 = 0,5 cos (2л • 140 • 103z - 89°) + 1 cos (2л • 150 • 103г - 97°) +
+ 0,5 cos (2л • 160 • 103г — 106°) В.
Так как постоянная фазы не пропорциональна частоте, то фазовые искажения есть.
2)	При /Н2 = 200 кГц нижняя боковая и несущая находятся в полосе пропускания; для них А = 0. Верхняя боковая попадает в полосу задерживания. Постоянную ослабления на этой частоте найдем по формуле ch(A/2) == flf2. При f = /н2 + F = = 210 кГц получаем А = In(t7i/Cr2) = 0,66 Нп и Uy = 1,95С72-Постоянная фазы при частоте f = fn2 — F = 190 кГц равна 144°, а при граничной частоте f = /н2 = 200 кГц и в полосе задерживания при частоте f = /н2 + F = 210 кГц не изменяется и равна 180°, следовательно,
и2 = 0,5 cos (2л • 190  103£ - 144°) + 1 cos (2л • 200 • 103f - 180°) +
+ 0,26 cos (2л • 210 - 103f - 180°) В
3)	Для третьего сигнала, спектр которого целиком находится в полосе задерживания (подавляемый сигнал), проводим расчет так же, как и для верхней боковой в случае 2:
f.................................  •	/нЗ ~ F /нЗ /нЗ + F
А, Нп.................................. 1,24	1,38	1,51
UJV2 ..............-	. .	.	3,47	3,98	4,54
7.2. Другие типы фильтров
7Л9(Р). Заданы параметры последовательно-производного полузвена типа т высокочастотного фильтра: к = 400 Ом, т — 0,6.
Составить схему фильтра и найти индуктивности и емкости его катушек и конденсаторов, если необходимо иметь постоянную ослабления, равную оо, на частоте 50 кГц.
Решение. Схема Г-образного полузвена типа т показана на рис. 7.19Р, а, где Zim и Z2m рассчитываются по (7.8), причем для высокочастотного фильтра (см. табл. 7.1) Zt = — Jl/coC, Z2 = jcoL и
к = ]/Е/С.	(1)
Постоянная ослабления А для Т- или П-образного звена, т. е. А/2 для Г-образного, как и для фильтров типа к, определяется по (7.5) или (7.6) после замены zx и z2 на zim и ^2т, т. е.
z2m = 0 или по (7.8) 4coooL= (1 - т2)/о)даС,
В обоих случаях А == оо при 4Z2 4- (1 — т2) Zi = 0 или
откуда
Л = /1 - т2 Л,	(2)
где/i = 1/4тг]/Ес — граничная частота, одинаковая для фильтров типов к и т. Из (1) и (2) при к = 400 и = 50 кГц получаем: L= 50,7 мкГн; С = 31,7 нФ.
Продольное сопротивление последовательно-производного фильтра
7	~	. т .1
Z|m — mZ\ — —j ~—— — —j ———, _lm _1 J	J	,
где Cim = С/т — 31,7/0,6 = 52,8 нФ.
Поперечное сопротивление по (7.8)
_ jcoL 1 — т2 / . 1 \
-2т ~ ~ + )’
т. е. состоит из последовательно соединенных Ь2ш = L/m = = 84,5 мкГн и С2т = 4тС/(1 - т2) = 119 нФ. Схема фильтра показана на рис. 7.19Р, б.
7.20*	Для П-образного низкочастотного последовательнопроизводного фильтра типа т при L= 31,8 мкГн; С = 200 пФ и «1=0,5 найти: 1) граничные частоты; 2) частоту, при которой постоянная ослабления бесконечно велика; 3) частоты, при которых гПт = у L/C.
Рис. 7.21
7.21.	Определить постоянную ослабления каскадного соединения Г-образных полузвеньев типа т и типа к, выполненного по принципу согласования (рис. 7.21), на частоте 4,4 МГц, если L=31,8 мкГн; С = 200 пФ; т = 0,5. Найти, во сколько раз при этой частоте и согласованной нагрузке напряжение на выходе соединения меньше, чем на входе.
7.22.	Г-образные полузвенья задачи 7.21 поменяли местами (к вторичным выводам полузвена типа к присоединили первичные полузвенья типа т).
Определить, останется ли постоянная ослабления соединения прежней.
7.23.	Для П-образного низкочастотного фильтра типа к с параметрами L = 0,2 Гн и С =0,1 мкФ составить параллельнопроизводное Г-образное полузвено типа т. Найти индуктивности и емкости составляющих его катушек и конденсаторов при т = 0,5.
7.24.	Для Г-образного высокочастотного параллельно-производного полузвена типа т известны параметры: к = 400 Ом и т = 0,6.
Составить схему фильтра и найти индуктивности и емкости его катушек и конденсаторов, если необходимо получить бесконечно большую постоянную ослабления на частоте 50 кГц.
7.25.	Для мостового фильтра по рис. 7.25 с параметрами Li = 40 мГн; L2 = 20 мГн; Ci = 0,04 мкФ найти полосу пропускания. Определить, при какой частоте постоянная ослабления фильтра бесконечно велика и как изменится полоса про
пускания, если поменять местами ветви с сопротивлениями ZiA И ^2-
7.26.	Для мостового фильтра задачи 7.25 найти характеристическое сопротивление: 1) на средней частоте полосы пропускания, 2) на частоте, при которой постоянная ослабления бесконечно велика.
7.27.	У мостового фильтра задачи 7.25 закоротили индуктивности Как изменится полоса пропускания?
Рис. 7.25	Рис. 7.28
7.28(	Р). Схема полосового фильтра, состоящего из двух индуктивно связанных контуров, потерями в которых можно пренебречь, показана на рис. 7.28. Известны параметры фильтра: L/2 = 5 мкГн; 2С = 40 пФ; М = 1 мкГн.
Определить полосу пропускания фильтра и характеристическое сопротивление при частоте /0 = 1/2tt|/Zc = 11,25 МГц.
Решение. Запишем уравнения цепи при отсутствии сопротивления нагрузки:
= AxZi/2; о = [)2х ~ AxZm,
где Zt = j (coL — 1/соС); Zw = jcoM.
По определению для симметричного четырехполюсника и, в частности, фильтра по рис. 7.28
• ch Г = ch(A 4-JB) = 4ц = UiJU2x *
или с учетом уравнений цепи ch A cos В + j sh A sin В = ZJ2Zm = = (coL — 1/соС)/2соМ — действительная величина.
В полосе пропускания А = 0, т. е. ch А = 1 и sh А = 0. Следовательно,
cos В = (coL — 1/coQ/2coM.	(1)
Граничные значения cosB = +1 определяют полосу пропускания. При cos В = — 1 из (1) находим, что
со = СО] = 1/]/LC (1 4- ксв) = 64,5 • 106 рад/с, где ксъ = M/J/LjLj = 2M/L = 0,2. При cos В = +1 получаем:
со = со2 = 1/]/ЬС (1 — fcCB) = 78,7 • 106 рад/с,
откуда граничные частоты полосы пропускания // = 10,25 МГц; /2 = 12,55 МГц.
Характеристическое сопротивление симметричного четырехполюсника определяется по (4.22). Входное сопротивление фильтра при разомкнутых вторичных выводах Z* = Zt/2, а при короткозамкнутых определяется из уравнений ~ Лк^1/2 — /2к^лт>	= Ък^1/2 “
откуда Z* = U iJi 1к = Zj/2 - IZ^/Zp
Подставив Zj и Zx в (4.22), получим: Zc = ]/Zi/4 — Zl,. При частоте соо — i/l/Zc сопротивление Zx = 0 и Z^ = = <а0М =	= 70,7 Ом.
Задачу можно также решить, составив эквивалентную схему фильтра без индуктивной связи.
7.29. На рис. 7.29 показан фильтр присоединения с конденсатором связи Ск. При помощи такого фильтра высокочастотную аппаратуру подключают к линии электропередачи, по которой передаются сигналы телемеханики и связи. Известны параметры фильтра: Ск = С2 = 1100 пФ;
= L2 = 4,84 мГн.
Определить коэффициент связи катушек, при котором полоса пропускания фильтра равна 55-110 кГц.
7.30	(Р), Для П-образного фильтра по рис. 7.30 определить граничные частоты и постоянную ослабления при двух частотах полосы непропускания, отличающихся от граничных на 0,9 кГц.
Параметры фильтра: = 10 мГн; = С2«0,25 мкФ.
Рис. 7.29
Решение. Для всех симметричных Т- и П-образных фильтров в полосе пропускания продольное ZY и поперечное Z2 сопротивления должны быть разного характера и удовлет-
ворять уравнению (7.2). Следовательно, полоса пропускания определяется как интервал частот, в котором Xj и х2 различны по знаку и | Xi | < 14х2 |.
Найдем этот интервал частот графически. На рис. 7.ЗОР построены зависимости хг (со) и 4х2 (со). Из рис. 7.ЗОР видно, что граничная частота coj определяется равенством Xi = О или o1L1 - 1/cOiCi = 0, т. е. cojl =	= 2,0 • 104 рад/с, а гранич-
ная частота со2 — равенством | хд | = | 4х21 или | co2Lt — - 1/со2С! | = 4/со2С2, т. е. со2 = j/cof + 4/ЬгС2 = 4,48 • 104 рад/с, или /i = 3,19 кГц; f2 = 7,14 кГц.
Постоянную ослабления нужно найти на частотах /3 = - 3,19 — 0,9 = 2,29 кГц и/4 = 7,14 + 0,9 = 8,04 кГц. При частоте /з < fi сопротивления Zr и Z2 емкостные (рис. 7.30Р) и постоянная ослабления определяется по (7.5):
sh (А/2) = ]/z. (/3)/4z2 (Л) = 0,347 и А = 0,68 Нп.
При частоте /4 сопротивления Zv и Z2 имеют разный характер (рис. 7. ЗОР) и постоянная ослабления определяется по (7.6): ch(А/2) = ]/Z1 (Л)/4г2 (/4) = 1,15 и А = 1,08 Нп.
7.31	(Р). Найти характеристическое сопротивление Т-образного низкочастотного фильтра гС (рис. 7.31, а) на верхней граничной частоте полосы пропускания, если параметры фильтра г = 2 кОм; С = 500 пФ.
Решение. Верхняя граничная частота фильтра определяется из условия равенства активного и реактивного сопротивлений соответствующего Г-образного полузвена (рис. 7.31,6), т. е.
2/со2С = г/2, откуда f2 = со2/2я — 637 кГц.
Для симметричного четырехполюсника характеристическое сопротивление можно определить по (4.22): Zr = ]/zyZy, где для фильтра по рис. 7.31, а на граничной частоте
г ... r/2(-jX/(n2C)
2	г/2 — ;1/со2С ’
Zx = 4-fl/^гС
hZc = 1,19	-22° 30' кОм.
9 п/р Ионкина П. A.
257
7.32	. Для фильтра предыдущей задачи определить постоянную ослабления на верхней граничной частоте.
7.33	. Из резисторов и конденсатора задачи 7.31 собрали симметричный высокочастотный фильтр.
Найти граничную частоту этого фильтра.
Рис. 7.34Р
7.34	(Р). Схема замещения четырехполюсника с зависимым источником напряжения KU^ обладающего бесконечно большим входным сопротивлением и нулевым выходным сопротивлением, приведена на рис. 7.34, а. Подключив к этому четырехполюснику резисторы и конденсаторы, как показано на рис. 7.34,6, получим схему активного RC-фильтра низкой частоты.
Составить выражение для модуля передаточной функции этой схемы Н = | UJU | в относительных единицах и в децибелах: HflE = 201gH. Построить амплитудно-частотную характеристику /7дБ(у), если R = 1 МОм; С = 1,417 нФ; п = 4; К = 1,166; v = cdRC.
Решение, В более удобном для анализа виде схема фильтра показана на рис. 7.34Р, а. Систему уравнений, описывающих режим этой схемы, запишем в виде
/ = U/R - yJR; фа = Ui 4- Rl3;
Ui ==/3/>С; /OjC =jd)nCKUl —](дпСфа;
/3 = / + /0,с.
Передачи контуров сигнального графа (рис. 7.34Р,б), построенного по этим уравнениям, = пК; L2 = — и; L3 = —Jvn; L4 = -1; Ls = — 1/jv. Определитель графа
A = 1 — (Lj + L-2 + Ь3 + L4 + L5) —
= (l//v) [(1 - v2n) + jv(2 + n - nK)].
Рис, 7.35
Передаточная функция по. топологической формуле (Мэзона)
К У ПА
=	=_2__ =_____________*_________
- U г U А (1 -nv2)+jv[2 + n(l - К)] ’
Модуль передаточной функции: в относительных единицах
2
(1 - nv2)2 + v2 [2 + п (1 — К)]2 ’
в децибелах
ЯдБ = 201g К - 101g [(1 + nv2)2 + n2v2 (1 - К)2 + 4v2 (1 - иК)].
Результаты расчета амплитудно-частотной характеристики приведены:
V . . .	0	0,1	0,3	0,44	0,5	0,6	0,9	5.0
НдБ	...	1,33	1,61	3,77	5,35	4,84	2,11	-6,77 -38,6
График амплитудно-частотной характеристики показан на рис. 7.34Р, в.
135, Получить выражение для модуля передаточной функции в относительных единицах Н = | UJU | и в децибелах //4B = 201gH активного высокочастотного КС-фильтра (рис 7.35). Построить амплитудно-частотную характеристику фильтра ЯдбМ при Я =0,1 МОм; С = 2 нФ; п = 0,25; К = = 1,1; v = соКС.
Г лава восьмая
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЦЕПЯХ С СОСРЕДОТОЧЕННЫМИ
ПАРАМЕТРАМИ
Введение к гл. 8
При анализе переходного процесса в электрической цепи классическим методом можно рекомендовать, например, следующий порядок расчета искомой величины:
1)	Из'расчета цепи до коммутации найти токи в индуктивностях i’l(O-) и напряжения на емкостях ис(0 —) в момент коммутации t = 0, т. е. независимые начальные условия.
2)	Получить дифференциальное уравнение цепи после коммутации и представить искомую величину в виде суммы установившихся и свободных составляющих.
3)	Рассчитать установившийся режим в цепи после коммутации.
4)	Составить характеристическое уравнение и определить его корни.
5)	В зависимости от вида корней характеристического уравнения записать решения для свободных составляющих.
6)	Составить систему уравнений для определения постоянных интегрирования.
7)	Найти начальные значения свободных токов в индуктивностях iLc3 (0 + ) и свободных напряжений на емкостях иссв (0 + ) после коммутации.
8)	Записать уравнения Кирхгофа для свободных составляющих.
9)	Определить начальные условия для свободной составляющей искомой величины.
10)	Вычислить постоянные интегрирования.
11)	Искомую величину записать в виде суммы установившейся и свободной составляющих.
Составление характеристического уравнения. 1) Для цепи после коммутации записать систему уравнений Кирхгофа для мгновенных значений. Разрешив систему уравнений Кирхгофа относительно искомой величины (или какой-либо другой переменной), получить дифференциальное уравнение относительно этой величины. Характеристическое уравнение получится после замены символов дифференцирования d/dt символами р в соответствующем однородном дифференциальном уравнении и приравнивания полученного алгебраического уравнения к нулю. Примеры приведены в задачах 8.8 — 8.10, 8.22, 8.36, 8.37,
2) В цепи после коммутации разорвать ветвь с искомой величиной (или какую-либо другую ветвь). Найти комплексное входное сопротивление цепи Z(jco) относительно точек разрыва. Характеристическое уравнение получится после замены символов /со на р и приравнивания входного сопротивления к нулю:
Z(p)=0.	(8.1)
Примеры приведены в задачах 8.55, 8.56, 8.63, 8.64, 8.70.
3) Для цепи после коммутации записать комплексные уравнения методом контурных токов (при синусоидальном токе). Символы усо заменить на р и составить главный определитель системы уравнений, который для получения характеристического уравнения приравнять к нулю. Пример приведен в задаче 8.87.
Решение для свободных составляющих, например тока, записывается различно в зависимости от вида корней характеристического уравнения.
Если корни pi, р2 ... действительные и различные, то
*св — AiePl 4- А2еР2 4-...	(8.2)
Если корни pi, р2 ... действительные и равные, т.е.
Pi = Р2 = Рз = • • • = Р, то iCB = Aiept +'A2tept + Л3Г2ер' 4-...	(8.3)
Для каждой пары комплексных сопряженных корней рг = = а+ /сосв и pi = а — ;сосв свободная составляющая
iCB - Aieat sin coCBt 4- cos аМ = Beat sin (coCBt 4- p). (8.4)
Начальные значения (при t = 0 4-) свободных составляющих тока в индуктивности и напряжения на емкости после коммутации (независимые начальные условия) находятся из
iicB (0+) = i’l (0 4-) — Q,y (0 4-);	(8.5)
мСсв (0 + ) = UC (° + ) - мСу (0 + )	(8.6)
В (8.5) и (8.6) начальные значения тока в индуктивности и напряжения на емкости находятся из законов коммутации:
/L(0 + )=’iL(0-) = iL(0);	(8.7)
uc(0+) = uc(0-)=-uc(0).	(8.8)
Все остальные начальные значения — завйсимые начальные условия — находятся из уравнений Кирхгофа для момента времени t=0+ (см. решения задач 8.63 — 8.65).
При анализе переходного процесса в электрической цепи операторным методом рекомендуется следующий порядок расчета :
1)	Из расчета цепи до коммутации найти токи в индуктивностях i’l(0 —) и напряжения на емкостях ис(0—).
2)	По виду исследуемой электрической цепи после коммутации составить эквивалентную операторную схему (если целесообразно, то для свободных составляющих). По эквивалентной операторной .схеме известными методами расчета цепей найти изображение искомой величины.
Изображение искомой величины можно получить и другим способом. Для цепи после коммутации записать систему уравнений Кирхгофа для мгновенных значений, затем все величины представить их изображениями и полученную систему уравнений разрешить относительно изображения искомой величины.
3)	По изображению искомой величины найти оригинал, т. е. искомую функцию времени.
Если задана функция действительного переменного f (г) (оригинал), то соответствующая функция комплексного переменного Г(р) (изображение) — прямое преобразование Лапласа:
F(p) = J f dt.	(8.9)
О
Эквивалентные операторные схемы элементов цепи представлены на рис. 8.А. Операторная схема для индуктивности L содержит операторное сопротивление pL и источник с ЭДС Li (0), направленной по току i, а операторная схема для емкости С содержит операторное сопротивление 1/рС и источник с ЭДС ис (0)/р, направленной против напряжения на емкости ис.
Способы перехода от изображения к оригиналу
1.	Применение теоремы разложения. Если изображение искомой величины имеет вид рациональной дроби:
_ атРт + ат-1Рт~' + ... + akp*+... + fliP + fl0 _
Flip) b„pn + Vip"-1 + ... + bkpk + ... + biP + b0
атрт + вт-1Рт 1 +    + atP* + •   + а,р + g0 b„(p - Pi) (p - Pi) • • • (P - Pt)- • • (p - p„)
(8.10)
где ak и bk — действительные числа; р1э p2... — действительные и различные корни характеристического уравнения F2 (р) = 0, то
и
(р)	Fl (Рк) Pkf	/о 1 1\
Г1(рГ/(г)~Лг1(рУ •	(811)
k= 1
Рис. 8.А
Если многочлен F2 (р) имеет один нулевой корень, т. е. F 2 (р) = pF з (р), то
4И-,7М.Щ® + У-£Л> A. (S..2)
pFз (р)	F3 (0)	/, ркР3 (рк)
Если многочлен F2 (р) имеет п пар комплексных сопряженных корней, то
к=1
и при одном нулевом корне. и
W =	+ У 2 Re ( УУГеП,\ (8.14)
(р)	F3(0)	/ J \Рк^з(Рк) /
k= 1
Примеры применения теоремы разложения приведены в задачах 8.94, 8.96, 8.97.
2. Применение метода неопределенных коэффициентов. Пример дан в решении задачи 8.92.
3. Применение таблицы соответствия оригиналов и изображений (см. приложение 2).
Для расчета переходного процесса при воздействии на электрическую цепь источников напряжения или тока произвольной формы можно применить формулы Дюамеля. Ниже приведены четыре наиболее часто применяемые формы интеграла Дюамеля, где h (t) — переходная функция, т. е. реакция цепи на единичный скачок входного воздействия, х (г) — входная величина (воздействие), у (г) — искомая величина (реакция цепи на воздействие).
Первая форма записи интеграла Дюамеля при непрерывном воздействии x(t):	(
у (t) — х (0) h (t) -I- j x' (x) h (t - x) dx,
о
где x'(T) = dx/dt\tsi^ при различных законах воздействия Xi (г) и х2 (0 в интервалах времени 0 t и t >
у (0 = xt (0)h (t) + f Xi (x)/i (t - x)dx; (8.15a) о
!i
у (t) = Xi (0) h (t) + j x'i (x) h (t - x) dx + о
+ [x2(ti)-x1(t1)]/i(t- h)+ $x'2(x)h(t-x)dx (8.156) ч
и аналогично при большем числе интервалов.
Вторая форма записи интеграла Дюамеля:
У (t) = Xi (0) h (t) + J x'i (t - x) h (x)	(8.16a)
о
У (0 =	(0) h(t)+ f xi (t - x) h (x) dx +
t-ti
r-:i
+ [x2 (ti) - Xi (tj)]/z(t - ti) + f x2 (t - x) h (x) dx. (8.166)
0
Третья форма записи интеграла Дюамеля:
у (г) = *1 (г) h(0) + f Xi (т) h' (t — т) б/т; (8.17а) о
'1	г
у (t) = х2 (0 h (0) + f Xi (т) h' (t - т) dx + J х2 (т) К (t - т) dx. (8.176) о	»1
Четвертая форма записи интеграла Дюамеля:
У (0 = xi W h (0) + f xt (t - т) h' (т) dx; (8.18а) о t
У (О - х2 (0 h (0) + f хх (t — т) h1 (т) dx +
r-q
'-*1
+ f x2 (t — T) h' (t) dx.	(8.186)
0
При переходе от электрической цепи к расчетной схеме в последней могут в результате коммутации две (или более) емкости с разными начальными напряжениями оказаться соединенными параллельно или две (или более) индуктивности с разными начальными токами оказаться соединенными последовательно. В этих случаях независимые начальные условия определяются из соотношений:
для двух параллельно соединенных емкостей
(Сг + С2) и (0) = ClM1 (0_) + С2и2 (0_);	(8.19)
для двух последовательно соединенных индуктивностей
(М + L2)i(0) = L1i1(0_) + L2i2(0_).	(8.20)
При решении задач методом переменных состояния уравнение состояния записывается в виде
х = AiX + Bi.v,	(8.21)
где х и х — столбцовые матрицы размера п х 1 переменных состояния, в качестве которых выбираются напряжения на емкостях и токи в индуктивностях и их производные; Ai — квадратная матрица порядка и; Bi — матрица размера п х q, причем q равно общему числу источников ЭДС и тока; v — столбцовая матрица размера q х 1 напряжений источников ЭДС и токов источников тока.
Элементы матриц Ai и Bi определяются только параметрами схемы и ее топологией.
К (8.21) необходимо добавить еще уравнение для выходных
переменных:
у = А2х + B2v,
(8.22)
где у — столбцовая матрица выходных переменных размера т х 1, причем т — число выходных переменных; Аг и В2 -матрицы, имеющие размеры т х п и т х q соответственно, элементы которых определяются параметрами и топологией схемы.
Решение (8.21) имеет вид:
х = еА1'х (0) 4- еАк f е~AlTBiV (т) dz	(8.23)
о
или, если v не зависит от времени,
х = еА,'х (0) + (еА,! - 1) АГ ‘BjV,	(8.24)
еА1'= а01 + aiAi + “2А1 + •  • +	*.	(8.25)
Коэффициенты oro, at, ..., an-i определяются из уравне-
НИЯ	а0		1	Х1...ХГ1	-1	хц е	
	«1		1 х2 xi ...г?-*		е1'	
	«2	=	3"^ « * 1	•	гз*	(8.26)
	аи-1		1 К		е "	
где различные коэффициенты Х2, ...,	— собственные зна-
чения матрицы Ai, т. е. корни уравнения
А (X) = det (V 1 - At) = 0.	(8.27)
Матрицы Ai, Bi, А2 и В2 могут быть определены из уравнений:
(8.28)
где
С
о
; п' + п" = и,
а матрицы H — это входные и взаимные проводимости или сопротивления, или передаточные функции по току или напря-
жению, которые определяются по методу
наложения из урав-
нений:
где
Нсс Hcl
HLC HLL
Uc k
HCe He hLc He
e
i i
u2
Uc
H1C
H2c
= x;
H1L
H2L
1
*•
(8.29)
e
J

ic, uL — столбцовые матрицы токов в емкостях и напряжений на индуктивностях; ib u2 — столбцовые матрицы выходных токов, и напряжений.
8.1.	Переходные процессы в цепях rL (классический метод расчета)
Свободные процессы в цепях rL
8.1	(Р). Обмотка возбуждения электрической машины отключается от источника с ЭДС Е = 200 В и внутренним сопротивлением = 20 Ом и закорачивается без разрыва цепи (рис. 8.1). Индуктивность обмотки L = 0,2 Гн, сопротивление обмотки г = 20 Ом.
Найти ток в обмотке и построить график зависимости i (t).
Решение. Находим ток в обмотке до коммутации
i(0_) = £/(r + r1) = 5 А.
Дифференциальное уравнение для тока после коммутации
однородное:
L di/dt + ri = 0.
Характеристическое уравнение
Lp 4- г = О
имеет один корень pt = —rfL=- -100 с’1.
Установившегося тока после коммутации нет (дифференциальное уравнение для тока однородное), поэтому решение уравнения (1) представим в виде
i = Ае"1'.	(2)
Для вычисления постоянной интегрирования А запишем решение (2) при t = 0, т. е. начальное значение: i (0) = А. По закону коммутации ток в индуктивности не изменяется скачком, следовательно, i(0) = Ц0_) = 5 А и А = ЦО) = 5 А.
Таким образом, ток в обмотке возбуждения
i = 5е“100* А.
График тока представлен на рис. 8.1Р.
Рис. 8.2
8.2(	Р). Для ускорения процесса спада тока в обмотке возбуждения электрической машины с параметрами L, г ее присоединяют без разрыва цепи к резистору с сопротивлением rt (рис. 8.2).
Найти ток i и напряжение и на обмотке. Вычислить время ti спада тока до значения, равного 5% начального; сравнить его с временем t2 спада в случае ri = 0.
Дано: Е = 40 В; L = 1 Гн; г = 1 Ом; Г! = 10 Ом.
Решение. Ток в индуктивности до коммутации
Ц0_) = £/г = 40 А.
Дифференциальное уравнение для тока после коммутации однородное:
_ di j	\ • t\
L-5-+ (г + Г1) I = 0.
at
Характеристическое уравнение
Lp + (г + rj = 0
имеет корень
Pt = ~(r + rt)/L= -11 с"1.
Решение однородного дифференциального уравнения запишем в виде
i — АеР1\
Постоянную интегрирования А находим из начальных условий (t = 0). По закону коммутации для тока в индуктивности начальное значение
' i(0) = Л = i(O-) = 40 А.
Ток в обмотке возбуждения
i = 40е-1 п А.
Напряжение на обмотке возбуждения
u = — rri = — 400е-1П В.
Время спада тока до значения, равного 5% начального, найдем из уравнения
0,05.40 = аде'11'1,
откуда	tt = In 0,05/( — 11) = 0,272 с.
При = 0 корень Pi — — 1 с"1 и ток i = 40е"1г А. Время спада тока получим из уравненйя 0,05 • 40 = 40е~ П2, откуда t2 = — In 0,05 = 2,99 с.
Таким образом, чем больше сопротивление тем быстрее спадает ток. Однако чрезмерно увеличивать это сопротивление нельзя, поскольку начальное напряжение на обмотке ц (0) = = — >*!? (0) может быть больше допустимого напряжения и произойдет пробой изоляции обмотки.
г?	г	г
Рис. 8.4	Рис. 8.5
8.3.	В схеме рис. 8.3 происходит замыкание ключа. Параметры схемы: £ = 90 В; = 30 Ом; г = 15 Ом; L = = 0,1 Гн.
Найти и построить зависимость i(t).
8.4.	Для схемы рис. 8.4 дано: е = 50j/2 sin(100£ + 30°) В; = 20 Ом; г = 30 Ом; L = 0,5 Гн.
Найти ток i после замыкания ключа.
8.5.	Определить ток i в схеме рис. 8.5 после замыкания ключа.
Дано: J = 6 А; г = 10 Ом; L — 0,25 Гн.
8.6.	Заданы параметры схемы рис. 8.6: J (t) = 0,5 sin (1000: + + 53,13°) А; г = 120 Ом; L= 0,1 Гн.
Найти ток i после коммутации.
Рис. 8.7
8.7.	Для измерения сопротивления обмотки индуктивной катушки постоянному току собрана цепь по рис. 8.7. Показание амперметра 2 А, показание вольтметра 5 В, сопротивление вольтметра rv = 1500 Ом.
Определить начальное напряжение на вольтметре Wjz(O) при размыкании ключа.
Переходные процессы в цепях rL при воздействии источников постоянных напряжения и тока
8.8(Р). Для ускорения процесса гашения тока в обмотке
возбуждения электрической машины ее отключили от источ-
ника ЭДС Ei в момент
Рис. 8.8
времени, который принят за t — 0, и подключили к источнику ЭДС Е обратной полярности (рис. 8.8). В момент времени :х, когда ток спадет до нуля, обмотка возбуждения отключится от источника ЭДС £.
1) Определить ток i в обмотке возбуждения и момент времени :Р
2) Сравнить время с временем спада тока t2 при Е — 0
(короткое замыкание обмотки), где t2 — время, в течение которого значение тока уменьшается до 3% начального.
Параметры цепи: £г=20 В; £ = 120 В; г =0,5 Ом; rj =0,5 Ом; L = 0,5 Гн.
Решение. 1) Ток в индуктивности до коммутации
f(0-) = £1/(r + r1) = 20 A.
Дифференциальное уравнение цепи после коммутации: r di	_
L~ + п = — Е.
dt
Решение этого неоднородного уравнения найдем в виде суммы частного решения неоднородного уравнения — тока установившегося режима iy и общего решения соответствующего однородного уравнения — свободной составляющей тока
$ = iy + iCB.
Ток iy находим либо расчетом цепи постоянного тока, которая получается (рис. 8.8) после первой коммутации, либо из дифференциального уравнения при diidt—Q'.
iy — —E/r = —240 А.
Характеристическое уравнение Lp + г — 0 имеет один корень pi = —r/L = —1 с-1.
Поэтому свободная составляющая тока iCB = AePlt — Ае~ u и ток
i = iy + iCB = — 240 + Ае~1г.
Постоянную интегрирования А находим, учитывая начальные условия (при t = 0) для тока в индуктивности i (0) = = i(0—) = 20 А, т.е. из уравнения 20 =—240 + 4, откуда А = 260. Следовательно, ток
i= — 240 + 260e"n А.
Время ti определим, приняв в решении согласно условию i(Zi) = 0,’T.e.
0= - 240 + 260е +
откуда = —In (240/260) =0,08 с.
2	) При Е = 0 (короткое замыкание обмотки) после коммутации существует только свободный процесс и ток
i = 20е”1г А.
Время t2 спада тока получим из уравнения
0,03 • 20 = 20е" *'2,
откуда t2 = —In0,03 = 3,50 с.
Таким образом, в заданной цепи введение форсирующего источника ЭДС Е ускоряет процесс спада тока в t2/tY « % 44 раза.
8	.9(Р). Найти токи во всех ветвях схемы рис. 8.9 при замыкании ключа во второй в£тви-
Дано: Е = 150 В; — г2 — гз = 100 Ом; L= 0,1 Гн.
Решение. Находим независимое начальное условие — ток в индуктивности i2 (0—) = 0.
Рис. 8.9	Рис. 8.9Р
Уравнения Кирхгофа для схемы после коммутации:
-G + i2 + Ь = 0;	(1)
rih + г^з = Я;	(2)
r2i2 + L “ г*'3 = °’	(3)
at
Преобразуем систему уравнений Кирхгофа в уравнение относительно одной переменной» например тока i2. Для этого исключим переменные ц и i3. Получим дифференциальное уравнение для тока i2:
Аналогичные уравнения мс>жно записать и для других переменных (ц и ?3), но в этом нет необходимости, поскольку характеристическое уравнение схемы (при отсутствии в ней особенностей) для всех переменных одинаково (особенностью может быть, например, короткое замыкание параллельных ветвей).
Решение будем искать в виде
Ч = Йу + Йсв! Й — Йу + Йсв, г'3 = by + Йсв-
В установившемся режиме токи:
Характеристическое уравнение
Ьр + (г2 + 'j = О у ”i т ”з J
имеет один корень
r2 + r1r3/(r1+r3) = _1500
L
т.е. свободные составляющие токов:
i1C8 = Л/1'; 12., = Be”1'; i^ = CePl<.
При этом токи:
h = 1 + Я/1'; i2 = 0,5 + Be"1'; i3 = 0,5 + Се"1'.
В частности, при t = 0 токи:
;1(0) = 1 + Я; i2 (0) = 0,5 + В; i3 (0) = 0,5 + С. (5) а
Для определения постоянных интегрирования найдем начальные значения токов. По закону коммутации независимое начальное условие — ток в индуктивности i2 (0) = i2 (0—) = 0.
Начальные значения остальных токов ц (0) и i3 (0) — зависимые начальные условия определим из двух первых уравнений Кирхгофа, записанных для момента времени Г =0:
-Й (0) + i2 (0) + h (0) = 0;
'•1'1 (0) + rj/j (0) = Е, откуда
Ч (0) = i3(0) = E/(r1 + r3) = 0,75 А.
Из уравнений (5) находим постоянные- интегрирования
А = -0,25 А; В = -0,5 А; С = 0,25 А.
Таким образом, токи;
= 1 - О,25е-1500' A; i2 = 0,5 - О,5е‘ 1500' А;
z3 =0,5 +0,25с’1500‘ А.
Соответствующие зависимости представлены на рис. ,8.9Р. До коммутации = z3 = E/(rt + r3) = 0,75 A.
8.10(	P). Определить токи во второй и третьей ветвях при размыкании ключа в первой ветви (рис. 8.10) при параметрах: Е = 120 В; J = 6 A; = г2 — г3 = 10 Ом; L = 0,05 Гн.
Решение. Ток в индуктивности до коммутации (постоянный ток) найдем, например, методом наложения от действия источника ЭДС Е и источника тока J:
G (0-) = z"3 (0-) + z3'(0~) = 4 А+ 2 А = 6 А.
Уравнения Кирхгофа для схемы после коммутации:
—J — 1*2 + Ь = 0;	(1)
?2h. + ^"5“ + гз*з = Е-	(2)
at
Исключив из уравнений (1) и (2) ток i2, получим дифференциальное уравнение для тока г3:
+ гз) Ь = Е +	(3)
at
Искомые токи:
1*2 = Ьу + *2св» h = i3y i3cB.
Токи установившегося режима найдем методом наложения: by = Е/(г2 + r3) - Jr3/(r2 + г3) = ЗА;
ijy = Б/(г2 + r3) + Jr2/(r2 + гэ) = 9 А.
Характеристическое уравнение
Ер + (г 2 + г3) = 0
имеет корень pj — — (г2 + r3)/L== — 400 с-1, и свободные составляющие токов:
i2cB = AeP[t; i3cB = BePi\
Следовательно, токи:
i2 = 3 + Ае”1' A; i3 = 9 + Be”1' А.	(4)
Уравнения для определения постоянных интегрирования получим из (4) при г = 0:
|2(0) = 3 + Л; i3(0)=9 + B.
Независимое начальное условие — ток в индуктивности 1*з (0) находим по закону коммутации: г*3 (0) = z*3 (0—) — 6 А.
Зависимое начальное условие i2 (0), т. е. начальное значение, определим из уравнения (1) для момента времени t — 0, откуда i2 (0) = i3 (0) — J = 0 и постоянные интегрирования: А = 12 (0) -- 3 = -ЗА; В = i3 (0) — 9 = -ЗА.
Токи:
i2 = 3 - Зе’400' A; i3 = 9 - Зе’400г А.
Эти зависимости представлены на рис. 8.ЮР.
8.11.	Найти ток первичной цепи и напряжение на вторичной разомкнутой обмотке и2 трансформатора (рис. 8.11) после замыкания ключа при параметрах: Е = 30 В; гг — 150 Ом; Li = 0,2 Гн; М = 0,4 Гн.
Рис. 8.14
Рис. 8.13
8.12.	Найти ток i в цепи рис. 8.12 после замыкания ключа при параметрах: Е — 80 В; гх = 30 Ом; г = 10 Ом; L = 0,02 Гн.
8.13.	’ Для ускорения процесса нарастания тока i в обмотке возбуждения (L, г) электрической машины (рис. 8.13) в момент t = 0 замыкается первый ключ. При этом последовательно с основным источником ЭДС Е включается дополнительный источник с ЭДС Ei и внутренним сопротивлением В момент времени когда ток i достигнет номинального значения iHOM = Е/r, замыкается второй ключ, т. е. дополнительный источник отключается.
Определить ток i и время t2 его нарастания до номинального значения. Сравнить время с временем t2 нарастания тока до значения, равного 95 % номинального, при отсутствии дополнительного источника (ri =0; Ег =0).
Параметры цепи: г ~ 50 Ом; - 10 Ом; L = 0,l Гн; Е = 100 В; Ei = 260 В.
8.14.	В цепь синусоидального тока (рис. 8.14) с параметрами. е = 100]/2 sin (1000г + 75°) В; rj — 75 Ом; г2 = 25 Ом; L = 0,l Гн включается источник постоянной ЭДС Е = 50 В.
Определить ток i2.
Рис. 8.16 У
Рис. 8.15у
Рис. 8.18
Рис. 8.17 '
Рис. 8.19
Рис. 8.20
8.15.	Определить ток i2 в схеме рис. 8.15 после размыкания ключа в третьей ветви.
Заданы параметры: Е = 24 В; — 6 Ом; г2 = 12 Ом; г3 = 6 Ом; L = 0,05 Гн.
8.16.	Найти токи во всех ветвях схемы рис. 8.16 после коммутации при Е = 36 В; гх = 12 Ом; г2 = 24 Ом; L = 0,02 Гн.
8.17.	Определить токи и i3 в схеме рис. 8.17 при замыкании ключа в третьей ветви.
Дано: Е = 50 В; = 20 Ом; г2 = 30 Ом; L — 0,01 Гн.
8.18.	В схеме рис. 8.18 найти токи ц и i5 во время переходного процесса при Е = 80 В; = г4 = 20 Ом; г2 = = г3 = 80 Ом; L = 0,02 Гн.
8.19.	Определить ток i5 в схеме рис. 8.19 при замыкании ключа.
Параметры схемы: J = 2 А; = Гл = 80 Ом; г, == г, = = 20 Ом; L = 0,01 Гн.
8.20.	Рассчитать токи во всех ветвях схемы рис. 8.20 после коммутации при Е = 90 В; = 10 Ом; г2 = 30 Ом; г3 = 15 Ом; L = 0,04 Г н.
Переходные процессы в цепях rL при гармоническом воздействии и при воздействии нескольких источников
8.21	(Р). Найти ток переходного процесса i в индуктивной катушке (рис. 8.21) при е = 100 sin(2500? + 30°) В; = 30 Ом; г = 20 Ом; С = 4 мкФ; L = 0,04 Гн.
Решение. Находим ток в индуктивности до коммутации. Его комплексная амплитуда
f __________Ёт_________100 30°	— ? / ЗП° А
т~	1 “ 20 + 30 +/100 -j 100
r + rl+jaL-j-^-
и мгновенное значение
i = 2 sin (2500г + 30°) А.
Следовательно, при t = 0 ток i (0 —) — 2 sin 30° = 1 А.
Уравнение Кирхгофа для схемы после коммутации
г М
L— + п = е.
at
Решение для тока ищем в виде
i — iy + iCB
Комплексная амплитуда тока установившегося режима
Ёт 100 z, 30°
г + j(f)L ~ 20 + j 100
= 0,980 z. —48,7°
А,
мгновенное значение тока
iy = 0,980 sin (2500t - 48,7°) А.
Характеристическое уравнение цепи Lp + г = 0 имеет корень р! = —r/L= —500 с-1, т. е. свободная составляющая тока iCB = Ле₽1Г = Ле-500'
и ток
i = 0,980 sin (2500г - 48,7°) + Ае'500'.
Для определения постоянной интегрирования А запишем при t = 0 ток
i(0) = 0,980 sin ( — 48,7°) + А, где начальное значение тока в индуктивности по закону коммутации i (0) = i (0 -) = 1 А, т. е. А = 1,74 А.
Таким образом, ток
i = 0,980sin(2500г - 48,7°) + l,74e"5OOf А.
График тока представлен на рис. 8.21Р.
8.22(	Р). Найти токи ix и i2 в схеме рис. 8.22 при размыкании ключа.
Дано: е — 100sin (1000г + 90°) В; J = 2 A; r2 ='г2 - 50 Ом; L = 0,l Гн.
Решение. До коммутации ветвь r2L была закорочена. Следовательно, непосредственно перед коммутацией ток в индуктивности i2 (0 —) = 0.
Уравнения Кирхгофа для схемы после коммутации:
— J — G + i2 = 0;	(1)
ь ~-Г~ + г2*2 + rlzl = С.	(2)
at
Преобразуем систему уравнений Кирхгофа в дифференциальное уравнение относительно одной переменной, например тока i2, исключив из уравнений (1) и (2) ток тогда получим:
Ь —£- + (ri + гг) l2 = е + Jrt.	(3)
Решение будем искать в виде
Z1 zly z1cb, z2 = z2y "Ь z2cb*
Найдем токи установившегося режима, применив метод наложения. От действия источника синусоидальной ЭДС е токи j' — j> _ __________90 Q	ДГО А
lm 2т ri + r2 +	100 + J100	’ °7	45 А’
т. е.
Г1у = Г2у = 0,707 sin (1000г + 45°) А.
От действия источника постоянного тока J токи
-зу = J 7-Т7- = 1 >
*’Гу =
Таким образом,
ily = Gy + Gy = 0,707 sin (1000t + 45°) - 1 A;
Gy = Gy + Gy = 0,707 sin(1000t + 45°) + 1 A.
Рис. 8.22
Для дифференциального уравнения (3) записываем характеристическое уравнение и находим его корень:
Lp + (ri + г2) = 0; Pi = -(гх +г2)/^= -1000 с-1.
Свободные составляющие токов:
lice = Л/1'; Gcb = BePit и токи
= 0,707 sin (1000г + 45°) - 1 + Ле"1’;	(4)
i2 = 0,707 sin (1000г + 45°) + 1 + Be'’1'.	(5)
Для определения постоянных интегрирования запишем при t = 0 токи:
G (0) = 0,707 sin 45° — 1 + 4; 1
i2 (0) = 0,707 sin 45° + 1 + В. J	(6>
Определим начальные значения токов (0) и i2 (0). Независимое начальное условие — ток в индуктивности i2 (0) находим по закону коммутации: i2(0) = /2(0 —) =0.
Начальное значение тока i1 (0) найдем из уравнения Кирхгофа (1); для момента времени t = 0 имеем: iY (0) = i2 (0) - J — = —2 А и из (6) постоянные интегрирования А = —1,5 А; В = -1,5 А.
Токи переходного процесса:
G = 0,707 sin(1000г -F 45°)- 1 - l,5e"loo0t А;
i2 = 0,707 sin(1000Г + 45°) + 1 - l,5e“1000' A.
8.23.	В схеме рис. 8.23 с параметрами г = 5 Ом; L = = 0,1 Гн происходит замыкание ключа в момент, который принят за t = 0.
Найти: 1) ток i при ЭДС е — 50sin(314г + 30°) В; 2) начальную фазу at ЭДС е = 50 sin (314г + at) В, при которой переходный процесс отсутствует, и ток i в этом режиме; 3) начальную фазу а2 ЭДС е = 50 sin (314г + а2) В, при которой максимальное значение тока во время переходного процесса получается наибольшим, и это максимальное значение тока.
Рис. 8.24
Рис. 8.25
Рис. 8.27
Рис. 8.26
8.24.	Найти ток и напряжение и2 трансформатора (рис. 8.24) во время переходного процесса при ЭДС е = = 100sin(1000г - 30°) В и параметрах: г = 100 Ом; LY = 0,1 Гн; М = 0,2 Гн.
8.25.	В схеме рис. 8.25 до замыкания ключа протекал постоянный ток.
Определить ток i2 после коммутации при параметрах: Ft = 50 Ом; г2 = 50 Ом; Е=0,1 Гн; Е = 100 В; е = = 80 sin (2500г + 15°) В.
8.26.	Найти ток I в схеме рис. 8.26 после замыкания ключа.
Дано: Г] = 80 Ом; г2 — 20 Ом; Lr =0,1 Гн; L2 =0,2 Гн; е = 100 sin (314г + 120°) В.
8.27.	Определить токи i и i2 в цепи рис. 8.27 с источником тока J (г) = 1 sin (1000г 4- 30°) А после размыкания ключа при = г = г2 = 100 Ом; L = 0,1 Гн; С = 10 мкФ.
8.2. Переходные процессы в цепях гС (классический метод расчета)
Свободные процессы в цепях гС
8.28(Р). В цепи рис. 8.28 отключается источник с ЭДС Е — 120 В и внутренним сопротивлением п = 10 Ом.
Рассчитать и построить зависимости напряжения ис на конденсаторе С = 20 мкФ и тока i в резисторе г = 50 Ом.
Решение. Напряжение на конденсаторе до коммутации мс(0-) = £г/(г + г1)= 100 В.
Записываем дифференциальное уравнение цепи после коммутации, принимая во внимание, что i = — ic = —Cduc/dt: dur ис + гС —т— = 0.
at
Так как уравнение однородное, то установившееся значение напряжения на конденсаторе равно нулю.
Характеристическое уравнение
1 4- гСр — 0 имеет один корень
Р1 = -1/гС= -ЮОО с"1, т. е. решение однородного дифференциального уравнения можно записать в виде
A Plf ис = «Сев = Ае \ Для определения постоянной интегрирования А положим t = 0 и получим: wc(0) = А, где мс(0) — независимое начальное условие, которое определим по закону коммутации (напряжение на емкости не изменяется скачком): мс(0) = мс(0 —) = = 100 В, т. е. А = 100 В.
Таким образом, напряжение на конденсаторе ис = 100е”10001 В.
Ток резистора
i — uc/r — 2е 1000г А.
Зависимости uc(t) и i(t) представлены на рис. 8.28Р.
8.29(Р). К заряженному до напряжения = 120 В конденсатору емкостью Ci = 4 мкФ подключаются последовательно соединенные резистор с сопротивлением г = 1 кОм и конденсатор емкостью С2 = 2 мкФ (рис. 8.29).
Определить напряжения и и2 на конденсаторах и ток i в цепи во время переходного процесса.
Решение. Напряжения на конденсаторах до коммутации:
МО-) =	= 120 В; u2(0—) = 0,
Дифференциальное уравнение цепи после коммутации
-Ui + и2 + ri - 0,
(1)
Исключив из (1) и например w2, получим:
(2) все переменные, кроме одной,
du2 _ тг
2 dt ~U1'
Напряжения и ток запишем в виде
= "1У 4- MjCB, и2 — и2у + w2cB, i = iCB,
где учтено, что в установившемся режиме тока в цепи нет. Установившиеся напряжения на конденсаторах найдем из закона сохранения заряда: суммарный заряд до коммутации равен суммарному заряду в любой момент после коммутации и, в частности, в установившемся режиме:
CjWi (0 — ) 4- С2и2 (0—) = CiUiy 4- С2и2у,
Кроме того, ясно, что в установившемся режиме uiy — и2у. Из этих двух уравнений находим: и1у = м2у = 80 В.
Для дифференциального уравнения (3) характеристическое уравнение
1 4- "тг-4) 4- гС2р = 0 С1 /
имеет один корень = —750 с-1.
Таким образом,
щ = 80 4- АеР1‘; и2 = 80 4- Be*1'; i = CePl\
и при t = О
Wj (0) — 80 4- Л j U-2 (0) — 80 4~ В', г(0) = С, где начальные значения напряжений на конденсаторах находим по закону коммутации: ”
Ui (0) = Ui (0 — ) = 120 В; w2 (0) — u2 (0—) = 0
и начальное значение тока
/(0) = [М1(0)-«2(0)]/г = 0,12 А.
Следовательно, Л = 40 В; В = — 80 В; С=0,12Аи
М1 = 80 + 40е’750г В; w2 = 80 - 80e-75Ot В; i = 0,12e’75Ot А.
Рис. 8.29	Рис. 8.30
8.30.	В цепи рис. 8.30 заряженный до напряжения UQ = = 100 В конденсатор емкостью С = 1 мкФ подключается к резистору с сопротивлением г = 2 кОм.
Рассчитать зависимости uc(t) и i(r).
8.31.	В схеме рис. 8.31 с параметрами: J = 0,3 А; г1 = = 500 Ом; С = 10 мкФ; г = 250 Ом происходит размыкание ключа.
Найти зависимости uc(t) и i(t).
Рис. 8.31
Рис. 8.32
8.32.	Определить напряжения u2 на конденсаторах и ток i в цепи рис. 8.32 после коммутации.
Конденсаторы емкостью = 8 мкФ и С2 = 2 мкФ предварительно заряжены соответственно до напряжений (0) = = UlQ = 120 В и w2(0) = U2Q — —180 В. Сопротивление резистора г = 250 Ом.
8.33.	В схеме рис. 8.33 с синусоидальной ЭДС е = == 100 sin (250(к — 30°) В происходит размыкание ключа.
Параметры схемы: = 100 Ом; г — 500 Ом; С — 2 мкФ.
Найти напряжение на емкости ис.

м )е
Рис. 8.33
Рис. 8.34
8.34.	В схеме рис. .8.34 найти напряжение на емкости ис и ток i после коммутации.
Дано: J (г) = 0,4 sin (314г + 90°) А; = 800 Ом; г = 800 Ом; С — 10 мкФ.
Переходные процессы в цепях гС при воздействии источников постоянных напряжения и тока
8.35(	Р). В цепи рис. 8.35 два предварительно заряженных конденсатора емкостью Ct = 6 мкФ и С2 = 4 мкФ подключаются через резистор с сопротивлением г = 250 Ом к источнику ЭДС Е = 100 В.
Определить напряжения и м2 и ток i при 1^(0 — ) = = 20 В и м2 (0 —) = 10 В.
Решение. В данной задаче независимые начальные условия «1(0—) и и2(0 —) заданы.
Дифференциальное уравнение цепи после коммутации
«1 + и2 + ri — Е,
где
_ du2 dt ~ 2 dt
(1)
(2)
Исключив из (1) и (2) все переменные, кроме одной, например тока i, получим однородное дифференциальное уравнение
Цепь содержит предварительно заряженные конденсаторы и источник ЭДС Е, поэтому решения для напряжений будем искать в виде суммы установившейся и свободной составляющих:
«1	«1у 4“ «1св, U2 «2у “Ь «2св'
Тока в установившемся режиме нет, т. е. i — iC3.
Найдем установившиеся напряжения на конденсаторах. По второму закону Кирхгофа для установившегося режима и1у + и2у + Пу = и1у + w2y = Е,	(4)
так как iy = 0.
Для точки а по закону сохранения заряда “^iy + Qiy —	(0“) + $2 (0—),
или
— CiUly + C2w2y = — Ci«i (0 —) + 62w2 (0 -).	(5)
Решив совместно уравнения (4) и (5), получим: и1у = 48 В; и2у = 52 В.
Для дифференциального уравнения (3) характеристическое уравнение гр + (1/Cj + 1/С2) = 0 имеет один корень рг = —1666 с"1.
Таким образом, напряжения и ток можно представить в виде
U1 = 48 + Ае"1'; и2 = 52 + ВеР1‘; i = Се"1'.
В частности, при t = 0 получим:
М1 (0) = 48 + A; w2(0) = 52+B; u(0) = C. (6)
Начальные напряжения (0) и w2(0) определим по независимым начальным условиям: (0) = их (0—) = 20 В; и2 (0) = = и2 (0-) = ,10 В.	*
Начальное значение тока найдем из уравнения (1) при t — 0, откуда i (0) = 0,28 А.
Постоянные интегрирования находим из (6): А = — 28 В;
В= —42 В; С = 0,28 А.
Таким образом,
«1 =48 - 28e’1666t В; и2 = 52 - 42е~1б66г В; i = 0,28е"166б: А.
8.36(	Р). В схеме рис. 8.36 с параметрами: Е = 120 В; г 1 = 250 Ом; г2 = 250 Ом; г3 = 500 Ом; С = 10 мкФ происходит замыкание ключа.
Найти напряжение на емкости и все токи.
Решение. Напряжение на емкости до коммутации
“с (0 -) = Ег2/(г3 +	+ г2) = 30 В.
Уравнения Кирхгофа для схемы после коммутации:
—и + G + ь = 0;	(1)
fiii + r2i2 = Е;	(2)
Wc - r2i2 = о,	(3)
где !3 = С duc/dt.
Рис. 8.36Р ->
Разрешив систему уравнении (1) —(3) относительно одной переменной, например wc, получим дифференциальное уравнение
+ (1 + 7г)“с = £-	(4)
Напряжение и токи представим в виде сумм установившейся и свободной составляющих:
>	^Су ^Ссв,
11	1\у + licBJ ^2	^*2у	^2св, Ъ Цу GcB'
В установившемся режиме токи и напряжение постоянны: iiy = h? = Е/(Г1 + гг) = 0,24 A; i3y = 0; иСу = r2i2y = 60 В.
Для дифференциального уравнения (4) характеристическое уравнение
riCp + (l + пЛ2)=о
имеет один корень рх = —800 с"1, т.е. свободные составляющие иСсв = AePl‘; i1CB = ВеР1'; ьсв = CePl‘i i3ca = DePit.
Следовательно,
uc = 60 + Ле'’1'; G = 0,24 + Be'’1'; i2 = 0,24 + Ce₽I'; i3 = De'’1', и при t = 0 начальные значения:
uc (0) = 60 + Л; it (0) = 0,24 + В; i2 (0) = 0,24 + C; i3 (0) = D.
Независимое начальное условие — напряжение на емкости находим из закона коммутации ис(0) = мс(0 —) = 30 В.
Зависимые начальные условия — начальные значения токов определим из системы уравнений Кирхгофа (1)-(3), записанных для момента времени г = 0:
-ii (0) + i2 (0) + i3 (0) = 0;	(0) + r2i2 (0) = Е;
«с (0) - r2i2 (0) = 0,
откуда i2 (0) = 0,12 A; G (0) = 0,36 A; i3 (0) = 0,24 А, и постоянные интегрирования А =—30 В; В =0,12 А; С =—0,12 А; D = 0,24 А.
Записываем искомые величины:
ис = 60 - 30e'8OOf В; = 0,24 + 0,12г"800: А;
i2 = 0,24 - 0,12е“800' A; i3 = 0,24e"800r А.
Эти зависимости представлены на рис. 8.36Р.
8.37(Р). В схеме рис. 8.37 с источниками ЭДС Е = 50 В и тока J.— 0,5 А определить токи ц и i2 и напряжение ис после коммутации, если гг = 200 Ом; г2 = 300 Ом; г3 = 200 Ом; С = 4 мкФ.
Решение. Напряжение на емкости до коммутации определим, например, методом узловых потенциалов:
«с(0-) =	(0-) =	+	+ J = 75 В.
L Я	чг1 + 1/гз
Уравнения Кирхгофа для схемы после коммутации:
h + h =	(1)
«с + r2i2 - rYiY = E,	(2)
где i2 = C duc/dt.
Разрешив систему уравнений (1) и (2) относительно одной переменной, например ис, получим:
С(Г!+r2)-~- + uc = Е +(3) Ctl
Напряжение и токи запишем в виде двух составляющих: ~ ^Су 4" ^Ссв» Ч = Чу 4“ Чсв» Ч = Чу 4" Чсв»
В установившемся режиме
Чу = J = 0,5Л; i2y = 0; иСу = Е + Jr{ — 150 В.
Характеристическое уравнение
С (г 1 + г2) р + 1 = 0
имеет один корень pi = -500 с^1; поэтому свободные составляющие
wCcB = AePl‘; ilCB = ВеР1‘, i2cB = СеР1‘
и искомые величины
ис = 150 + АеР1‘; i, = 0,5 + BePl‘; i2 = Сер<
В частности, при t = 0 имеем: ис(0) = 150 + Л; (0) = = 0,5+В; i2(0) = C,
Для вычисления постоянных интегрирования определим начальные значения. По закону коммутации независимое начальное условие — напряжение на емкости мс(0) = мс(0—) = = 75 В. Начальные значения токов в ветвях, найдем из уравнений Кирхгофа (1), (2), записанных для момента времени Г = 0:
J = ii (0) + i2 (0); ис (0) + r2i2 (0) - г212 (0) = Е, откуда i2(0)=0,15 А; ч(О) = О,35 А, и постоянные интегрирования А = —75 В; В = —0,15 А; С =0,15 А.
Записываем искомые величины:
мс= 150 — 75е"5001 В;
Ч = 0,5 - 0,15e"500r A; i2 = O,15e’5OOt А.
Соответствующие зависимости представлены на рис. 8.37Р.
Рис. 8.38	Рис. 8.39
838. В цепи рис. 8.38 конденсатор емкостью С = 1 мкФ подключается через резистор г = 2500 Ом к источнику ЭДС Е = 100 В.
Рассчитать зависимости ис(0 и i(t) для трех случаев: 1) Мс(0-) = 0 В; 2) wc(0 —) = 50'В; 3) ис(0-) = -50 В.
8.39.	В схеме рис. 8.39 при размыкании ключа параллельно включенные емкость и сопротивление подключаются к источнику тока. Параметры схемы: 7 = 0,2 А; г = 1000 Ом; С — = 2 мкФ.
Найти зависимости ис(г) и ic (г).
Рис. 8.40
Рис. 8.41
8.40.	В цепи рис. 8.40 последовательно включенные конденсатор емкостью С = 1 мкФ и резистор с сопротивлением гi = 250 Ом подключаются к источнику постоянной ЭДС Е = 80 В. До замыкания ключа цепь питается от источника с гармонической ЭДС е = 100 j/2 sin (2500t — 45°) В и внутренним сопротивлением г2 — 150 Ом.
Определить ис и ix после коммутации.
8.41.	В схеме рис. 8.41 происходит замыкание ключа. Параметры схемы J = 0,5 А; гг = 200 Ом; г2 = 300 Ом; С = = 10 мкФ.
Найти зависимости wc(t), il(t) и i2 (t).
8.42.	Определить напряжение ис и токи i2 в схеме рис. 8.42 после коммутации.
Дано: Е = 180 В; = 240 Ом; г2 = 120 Ом; С = 25 мкФ.
Рис. 8.42
Рис. 8.43
8.43.	В схеме рис. 8.43 происходит замыкание ключа. Параметры схемы: Е — 120 В; г< = 20 Ом; г2 = 80 Ом; г* = = 120 Ом; С = 15 мкФ.
Рассчитать зависимости uc(t) и :2(г).
8.44.	Определить ис и в схеме рис. 8.44 после коммутации при J = 1 A; rt = 100 Ом; г2 - 150 Ом; г3 = 50 Ом; С = 16 мкФ.
8.45.	Найти напряжение ис и ток it в схеме рис. 8.45 после коммутации.
Дано: Е = 100 В; =г4 = 20 Ом; г2 = г3 = 80 Ом; С = = 50 мкФ.
Рис. 8.44
Рис. 8.45
8.46.	В результате увеличения сопротивления в одной из ветвей цепи рис. 8.46 возникает переходный процесс.
Определить напряжение ис и токи ix, i2 при заданных параметрах: Е = 180 В; = 60 Ом; г2 = 20 Ом; г3 = 100 Ом; С - 25 мкФ.
Рис. 8.48
мыкания ключа при J = 2
8.47.	В схеме рис. 8.47 размыкается ключ. Параметры схемы: Е = 80 В; = г3 = = 100 Ом; г2 = 50 Ом; С = = 12,5 мкФ.
Найти зависимости uc (0 и i3(t).
8.48.	Определить токи i1} i2, напряжение на емкости ис и напряжение источника тока и в схеме рис. 8.48 после раз-А; Г! = 40 Ом; г2 = 60 Ом;
г3 = 20 Ом; С = 25 мкФ.
Переходные процессы в цепях гС при гармоническом воздействии и при воздействии нескольких источников
8.49(Р). Участок с параметрами г2 = 30 Ом; L=0,04 Гн неразветвленной цепи переменного тока, в которой действует ЭДС е = 100 sin (25OOt 4- 60°) В, замыкается накоротко (рис. 8.49).
Определить ток i в участке цепи с параметрами rt = 20 Ом; С — 4 мкФ и напряжение ис на конденсаторе.
Решение. Из режима цепи до коммутации определим начальное напряжение нс(0 —). Комплексная амплитуда напряжения ис до коммутаций
а =	£m[-j(l/<oO]	=
°" И + r2 + ja>L - j (1/<оС)
_ 100 z. 60’(-ЛОО) _
" 20 + 30 + ДОО-J100	В-
Мгновенное значение напряжения
ис = 200 sin (2500Г - 30°) В.
Следовательно, при t = 0 напряжение
ис(0-) = 200sin(-30°) = -100 В.
Рис. 8.49
Уравнение Кирхгофа для цепи после коммутации
rtC duc/dt + ис = е. (1)
Решения для искомых величин запишем в виде
Z 1у + Wf ^Су 4” ^Ссв'
Рассчитаем ток и напряжение установившегося режима:
100 zl 60°
20 -ДОО
= 0,98 z. 138,7° А;
1У = 0,98 sin (2500г + 138,7°) А;
UCmy =Jmy(-j • 1/соС) = 0,98 z. 138,7° • 100 ZL -90° = 98 z. 48,7°В; иСу = 98 sin (2500Г + 48,7°) В.
Характеристическое уравнение
ггСр + 1 = 0
имеет один корень Pi = —12 500 с-1. Поэтому свободные составляющие
иСсз = AePl‘; iCB = BePi‘t и
ис = 98 sin (25001 + 48,7°) + Ае"1';
i = 0,98 sin (25001 + 138,7°) + Be'’1'.
При t = О
ис (0) = 98 sin 48,7° 4- А; 1
i (0) = 0,98 sin 138,7° + В. J	®
Начальное напряжение на емкости находим из закона коммутации:
uc(0) = uc(0-)= -100 В.
Начальное значение тока найдем из уравнения (1), записанного для момента времени t = 0:
uc(0) + n(0) = e(0),
откуда i (0) = 9,33 А и из (2) постоянные интегрирования А = —173,6 В; В = 8,68 А. Следовательно,
ис = 98 sin (2500? + 48,7°) - 173,бе"12 500t В;
i = 0,98 sin (2500? + 138,7°) + 8,68е"12 500‘ А.
8.50(Р). В схеме рис. 8.50 происходит размыкание ключа. Параметры схемы: J = 2 А; е = 120sin(1000t + 30°) В; гх -= г2 = 50 Ом; С = 10 мкФ.
Найти зависимости ис (t) и ij (?).
Решение. Определим напряжение на емкости до коммутации «с(0 —). Поскольку в этом режиме ветвь г2С закорочена, то ис(0-) = 0.
Уравнения Кирхгофа для схемы после коммутации:
—J +	+ /*2 “	(1)
r2i2 + ис - г Jt = е.	(2)
Решение будем искать в виде
иС = иСу + «Саи l'l = l'ly + ZlcB*
Найдем установившийся режим после коммутации, применяя метод наложения. От действия источника постоянного тока J имеем:
fly = J = 2 А; и'Су — r^iy = 100 В.
От действия гармонической ЭДС е имеем
Кт = -Кт----------~> = -0,848 л 75° А;
lm 2" rt + r2 - у/юС
&ст = Кт (-у/а>С) = 84,8 z. -15° В,
т. е.
ify = -0,848 sin (1000г + 75°) A; u'cy = 84,8 sin(1000t — 15°) B.
Таким образом,
мсу ~ и'су + wcy = 100 4- 84,8 sin (lOOOt — 15°) B; hy = *iy +	= 2 — 0,848 sin (1000г 4- 75°) A.
0	2	4	6	8	10 mc
Методом входного сопротивления (8.1) составим характеристическое уравнение
Z (р) = r2 + 1/рС +	= 0,
корень которого = -1000 с-1.
Следовательно,
wCcB = АеР1‘; i’1CB = ВеР1\
Искомые величины:
ис = 100 4- 84,8 sin (1000г - 15°) 4- 4е₽1';
И == 2 - 0,848 sin (1000t + 75°) + Вер< и, в частности, при t = 0 имеем;
ис(0) = 100 4- 84,8sin(-15°) + А; |
h (0) = 2 - 0,848 sin 75° + В. J
Начальное значение напряжения на емкости найдем из закона коммутации: wc(0) = ыс(0—) = 0. Начальное значение тока ч (0) найдем из уравнений Кирхгофа (1) и (2). При t = 0 из уравнений
—J 4- ii (0) 4- i2 (0) = 0;
r2ii (0) + ис (0) -	(0) = е (0)
получим ii (0) =0,4 А и из (3) постоянные интегрирования А = -78 В; В = -0,78 А.
Записываем искомые зависимости:
ис (0 = 100 + 84,8 sin (1000г - 15°) - 78е-1О°°‘ В; ц (t) = 2- 0,848 sin (1000г + 75°) - О,78е"1000' А.
Эти зависимости представлены на рис. 8.5ОР.
Рис. 8.51	Рис. 8.52
8.51.	Цепь гС (рис. 8.51) с параметрами г = 250 Ом, С = 100 мкФ подключается к источнику синусоидальной ЭДС е.
Найти: 1) напряжение и ток i при ЭДС е = 312 (sin 314г-Ь + 30°) В; 2) начальную фазу ott ЭДС е == 312 sin (314г + В, при которой отсутствуют переходный процесс и напряжение ис в этом режиме; 3) начальную фазу а2 ЭДС е = = 312 sin (314г + а2) В, при которой напряжение ис во время переходного процесса получается наибольшим, и максимальное значение этого напряжения.
8.52.	В цепи рис. 8.52 до коммутации начальный режим определялся источником с постоянной ЭДС Е = 30 В и внутренним сопротивлением — 75 Ом. После замыкания ключа цепь гС с параметрами г = 125 Ом, С = 80 мкФ подключается к источнику гармонической ЭДС е = 180 sin (3141 + + 30°) В.
Рассчитать зависимости uc(t) и i(t).
Рис. 8.53
Рис. 8.54
8.53.	Определить напряжение ис в цепи гС (рис. 8.53) при уменьшении сопротивления от значения rj + г2 до значения г2, где Г} = 400 Ом; г2 — 200 Ом. Электродвижущая сила источника е — 200 sin (3141 + 30°) В, емкость конденсатора С — 10 мкФ. 294
8.54.	В схеме рис. 8.54 происходит размыкание ключа. Параметры схемы: е = 250sin(314г + 10°) В; = 400 Ом; г2 = = 100 Ом; Ci = 60 мкФ; С2 = 20 мкФ.
Найти напряжения на емкостях исл и ис2.
8.3.	Переходные процессы в цепях с несколькими реактивными элементами (классический метод расчета)
Свободные процессы в цепях с несколькими реактивными элементами
8.55(	Р). После замыкания ключа источник тока J = 1 А отключается от цепи (рис. 8.55) с параметрами: г = 100 Ом; L= 2,083 Гн; С = 50 мкФ.
Определить напряжение ис и токи и i2.
Решение. Рассчитаем сначала напряжение на емкости мс, после чего токи найдем из соотношений
i2 = uc/r\ ij = i2 + С dujdt.
Находим ток в индуктивности и напряжение на емкости до коммутации:
q (0-) = J = 1 A; uc(0—) = Jr = 100 В.
Так как источник отключается, то составляющие установившегося режима отсутствуют:
= 0, i2y = 0, Ucy 0.
Характеристическое уравнение составим методом входного сопротивления (8.1). Например, при разрыве ветви с индук
тивностью получим
 ’	71п\ п! 4. Г<1Л’С') _(V
Z(p) = pL + г+~/рС -°,
и характеристическое уравнение 2	1	1 А
р + 7ср + LC =0
имеет корни
Pi,2 = -1/2гС ± ]/l/4r2C2 - 1/LC, т.е. р, = -80 с-1;
р2 = —120 с-1.
В случае двух различных действительных корней решение для свободной составляющей запишем по (8.2) в виде
Мс = Мссв = AiePlt + А2еР2\
Составим систему уравнении для определения постоянных интегрирования. Поскольку для определения двух постоянных интегрирования необходимо иметь два уравнения, то дополнительно запишем производную искомого напряжения
duc/dt = duCcJdt =	4- р2А2еР2*.
Запишем систему уравнений для определения постоянных интегрирования (t =0):
мс(0) =	+ ^2> duc/dt |0 = pMj 4- р2А2.	(1)
Для вычисления постоянных интегрирования из (1) необходимо найти начальные условия — искомую величину и ее первую производную при t = 0.
Начальные значения тока в индуктивности и напряжения на емкости — это независимые начальные условия, которые находим из законов коммутации (8.7) и (8.8): ц (0) = (О-) = — 1 А; ис(0) = «с(О-) = 100 В. Все остальные начальные условия являются зависимыми. Они находятся из уравнений Кирхгофа для мгновенных значений:
4- i2 4- i3 — 0;	(2)
Ldi\/dt + ri2 = 0;	(3)
~ ri2 = 0,	(4)
причем напряжение uc и ток i3 связаны соотношением
i3 = С duc/dt.	(5)
В частности, для момента времени t = 0 — h (0) 4-i2 (0) 4-/3 (0) == 0;	(2а)
Ldii/dt\o-^ ri2(0) = 0;	(За)
wc (0) - rit (0) = 0.	(4a)
Это три уравнения с тремя неизвестными величинами. Из этих уравнений находим:
i2 (0) ~ uc(0)/r = 1 A; i3 (0) = G (0) - i2 (0) = 0
и из (5) при t — 0 имеем:
duc/dt |о = ii (0)/С = 0.
При найденных значениях Uc(0) и duc/dt\0 из системы (1) получим: At = 300 В; А2 = -200 В.
Записываем искомое решение для напряжения на емкости:
ис = 300e‘80t - 200е“12<* В.
Находим токи
i2 — uc/r = Зе 80r — 2е~l20t А;
it = i2 + C duc/dt = l,8e-80' - 0,8e'120' A.
8.56(P). В схеме рис. 8.56 происходит замыкание ключа.
Найти ток i и напряжение на емкости ис в двух случаях: 1) параметры схемы: г — 80 Ом; L = 0,5 Гн; С — 122 мкФ; 2) параметры схемы: г — 200 Ом; L = 0,2 Гн; С = 20 мкФ. Ток источника J (О = 2 sin (250г + 90°) А.
Рис. 8.56Р
Реш’ение (для случая 1). Из схемы до коммутации находим ток в индуктивности и напряжение на емкости при t =0:
i(0 —) = 2sin90° = 2 А;
Ucm = Л (“Ac) = 2 90° (->32,79) = 65,58 0° В,
т.е. ис = 65,58sin250г В и, в частности, ис(0—) = 0.
Поскольку после замыкания ключа схема отключается от источника тока, установившиеся значения равны нулю, т. е. ток и напряжение равны свободным составляющим: i = iCB, ис = Wccb-
Характеристическое уравнение составим методом входного сопротивления (8.1) для схемы после коммутации:
Z (р) = г + pL + 1/рС = 0,
откуда после элементарных преобразований получим: , г	1
Р +-J-P+ Тг = °-Li	LL
Корни характеристического уравнения
Pi, 2 = -r/ZL±	- 1/LC
получаются комплексные сопряженные:
Pi == ( —80+J100) с”1; р2 = (-80 — J100) с"1.
В этом случае свободные составляющие можно записать по (8.4) в виде
iCB = i = 4e"80tsin(100t + a);
uCcB = uc = Be"80* sin (lOOt + P).
где A, a, В, p — постоянные интегрирования.
Для отыскания двух постоянных интегрирования каждой из величин вычислим производные тока и напряжения: 4s- =	= -804e'8°'sm(100t + a) + 100A«>-80‘cos(100t + a);
at at
= _ 8oBe- so. sin (ioot + ₽) + at dt	v
+ 100Be~8°*cos(100f + p).
Для определения постоянных интегрирования запишем значения каждой из величин и их производных при t = 0:
iCB (0) = i (0) = A sin a;
^'св dt
UccAty = uc(0) =Bsinp;
^Ccb dt
(1)
— — 804 sin а + 1004 cos а; о
о $t
_ duc о
= — 80B sin P + 100B cos p. ( v ' о	J
В данной задаче свободные составляющие равны искомым величинам, поэтому далее их будем сразу записывать.
Независимые начальные условия - ток в индуктивности и напряжение на емкости найдем из законов коммутации: i(0) = i(0-) = 2 А; ис(0) = ис(0-) = 0.
Уравнение Кирхгофа для цепи после коммутации
ri + Ldi/dt + ис = 0,	(3)
i — С duc/dt,
(4)
и, в частности, при t = О
ri (0) + L di/dt |0 + ис (0) = 0.
(За)
г, ч	di
Из (За) находим — dt
= - 320 А/с. о
Начальное значение производной напряжения на емкости получим из (4): duc dt
= Д91 = 16,39 • 103 —. о С	с
При найденных начальных значениях из системы уравнений (1) и (2) определим постоянные интегрирования:
Л =-2,56 А; а =-51,34°; В = 163,9 В; р = 0°.
Записываем искомые величины:
i= -2,56еГ80'sin(100г-51,34°) А;
ис= 163,9е"80г sin (100г) В.
Эти величины представлены на рис. 8.56Р, а.
Решение (для случая 2). В этом случае корни характеристического уравнения получаются действительными и равными: pY — р2 ~ —500 с-1.
В случае двух равных корней решение для свободных составляющих записывается по (8.3) в виде
ice = i = AtePlt + A2teP2t;
. «сев = uc = BiePlt + B2teP2*.
Производные искомых величин
.	^p^' + A^' + p2A2tePi‘;
at at
=^ = plBIePl' + B2eP2’ + p2B2teP2t. at at
При t = 0 получим системы уравнений для определения п осто янных интегрирования:
1’св (0) = i(0) = Л^
(5)
мссв (0) — «с (0) — Bi;
duC св dt
duc
— piBi + в2. о
(6)
Независимые начальные условия те же, что и в случае 1: i(0) = i(0—) = 2 А; Мс(0) = мс(0-) = 0.
Зависимые начальные условия находим опять из (3) и (4):
di dt
-2000 А/с;
duc
,	= 105 В/с.
dt о
Постоянные интегрирования находим из (5) и (6):
= 2 А; Л2 = -1000 А/с; =0; В2 = 105 В/с.
Следовательно, искомые величины i = 2е 500г — - lOOOte"500' А; ис = КРгеГ500' В.
Эти зависимости представлены на рис. 8.56Р, б.
8.57(Р). Параллельный колебательный контур с параметрами £=10~3 См; С = 5 мкФ; L = 0,2 Гн при нулевых начальных условиях подключается к источнику тока J = 0,1 А (рис. 8.57).
Рис. 8.57
Рис. 8.57Р
Найти зависимости от времени напряжения на контуре и и тока в индуктивности iL.
Решение. Для отыскания напряжения и тока применим свойство дуальности. На рис. 8.57Р представлена схема последовательного колебательного контура, дуального заданному контуру. Решения для тока i и напряжения на емкости ис последовательного контура полагаем известными:
Е .
i	———е	smcoot;
cooL
г /
—•	t I
ис = Е - Ее 2L I cos coof +
г .	\
—-----sincB0t ,
2Ixo0 J
где соо = |/ 1/LC — r2/4L2.
Для обоих контуров дуальны величины i и и, ис и iL, Е и J, г и д, Ln С, С и L. Чтобы получить искомые решения, заменим в известных решениях электрические величины и параметры соответствующими дуальными величинами, т. е.

J - — I и=а^Се *
,	_ т — t [	Q	<	\
iL	— J — Je cos co0/ +	— sm a>ot ,
у	2Ccoo /
где <o0 = j/l/CL - 32/4C2.
При заданных параметрах контура имеем: и = 20,le-100'sin995г В;
iL = 0,1 - 0,k" 100t(cos995f + 0,1005 sin 995f) =
= 0,1 - O,lOO5e“loot sin(995t + 84,26°) A.
8.58.	Предварительно заряженный до напряжения Ыс(0“*) = s= 40 В конденсатор емкостью С = 200 мкФ подключается к цепи гЦрис. 8.58) с параметрами: г = 20 Ом; L = 0,2 Гн.
Рассчитать зависимости wc(t) и *(0-
Рис. 8.60
Рис. 8.59
Рис. 8.61

Рис. 8.62
8.59.	От цепи, состоящей из двух параллельных ветвей с параметрами rt = 10 Ом; С = 80 мкФ и г2 — 40 Ом; L = = 0,25 Гн, отключается источник ЭДС Е = 50 В (рис. 8.59).
Определить напряжение на конденсаторе ис и ток в катушке i2.
8.60.	В схеме рис. 8.60 происходит размыкание ключа. Параметры схемы: Е — 100 В; г = 500 Ом; L = 0,l Гн; С = = 10 мкФ.
Найти зависимости uc(t) и i(t).
8.61.	Определить напряжение uCi и ток i2 в схеме рис. 8.61 после коммутации.
Дано: иС1(0-) = 100 В; Сх = 10 мкФ; С2 = 5 мкФ; гг = = 100 Ом; г2 = 250 Ом.
8.62.	В схеме рис. 8.62 происходит замыкание ключа.
Рассчитать зависимости (t) и i2 (t) при J — 1,4 A; rj = — 20 Ом; r2 — 50 Ом; = 0,05 Гн; L2 = 0,1 Гн.
Переходные процессы в цепях с несколькими реактивными элементами при воздействии постоянных и гармонических источников напряжения и тока
8.63(	Р). В схеме рис. 8.63 происходит замыкание ключа. Параметры схемы: Е — 200 В; J = 1 A; ri = 100 Ом; г2 = = 100 Ом; L — 0,5 Гн; С = 400 мкФ. Найти зависимости токов ветвей от времени: (t), i2(t), i3(t).
Решение. Порядок решения примем следующим. Сначала найдем напряжение на емкости ис. Затем ток ц определим по закону Ома ij — (Е — ис)/г15 ток в емкости i3 — = С duc/dt, а ток i2 найдем по первому закону Кирхгофа
Ток в индуктивности и напряжение на емкости до коммутации: г2 (0—) = J = 1 А; ис (0-) = Е = 200 В.
Применяя метод наложения, вычисляем токи и напряжение установившегося режима в схеме после коммутации:
Г , г2 Л. .
z _----------j--------_ 05 д.
12у -
Г1
i3y = 0; иСу = r2i2y =150 В.
Для составления характеристического уравнения по (8.1) составим входное сопротивление относительно точек разрыва ветви с индуктивностью и приравняем его нулю:
= 0,
откуда при заданных параметрах схемы получим характеристическое уравнение
р2 + 225р + 104 = 0,
корни которого Pi = —61 с"1, р2 = —164 с’1. Следовательно, по (8.2) свободная составляющая напряжения
мссв = А1вР1 4- А2еР2 .
Напряжение на емкости представим в виде суммы установившейся и свободной составляющих: ис = wCy + иСсв-
Для определения двух постоянных интегрирования А{ и Л2 дополнительно запишем производную напряжения:
duc/dt = duCcJdt =	4- р2А2еР2‘.
„	~	Рис. 8.63Р
Это система уравнении для определения постоянных интегрирования.
Для вычисления постоянных интегрирования необходимо найти начальные условия — начальное значение свободной составляющей напряжения на емкости и ее производной.
По законам коммутации ток в индуктивности и напряжение на емкости не изменяются скачком, т. е. i2 (0) — i2 (0—) = = 1 A; u^(0) = пс(0-) = 200 В.
Начальные значения свободных составляющих тока в индуктивности и напряжения на емкости:
*2св (0) = i2 (0) - 12у (0) = 1 — 1,5 = -0,5 А;
«сев (0) = ис (0) - иСу (0) = 200 - 150 - 50 В.
Запишем уравнения Кирхгофа для свободных составляющих схемы после коммутации. При этом идеальный источник ЭДС Е заменяем короткозамкнутым участком, а ветвь с идеальным источником тока J разрываем:
j'icB “Ь ^2св "Ь ^Зсв 0»
П*1св "Ь ^Ссв = 0, di2c&! dt + ис св
(3)
(4)
(5)
В частности, для момента времени t = О
“ *1св (В) 4- ^2св (0) + *3св (0) — 0»	(За)
Ш’1св(0) + иСсв(0) = 0.	(4а)
В двух последних уравнениях две известные величины: i2c3(0) и иссв(0); две другие находим:
Чсв(О) = -мСсв(0)/Г1 = -0,5 А;
Ъсв (0) = 11СВ (0) - i2cB (0) = 0.
Производная свободной составляющей напряжения на емкости duCcB/dt — i3cB/C в момент времени t = 0 равна нулю:
d^C св __ 1*3св (0) _q
dt о С
При найденных значениях иСсв(0) и duCcB/dt |0 из (1) и (2) определим постоянные: Ai — 79,6 В; А2 = —29,6 В.
Таким образом, решение для напряжения на емкости подучено:
ис = 150 + 79,бе"61' - 29,бе"164f В.
Находим токи:
ц = (Е - uc)/ri = 0,5 - 0,79бе"61' 4- 0,29бе"164* А;
i3 = Cduc/dt = -1,942е"61' 4- l,942e'l64t А;
i2 = j + i, - j3 = 1,5+ 1,14бе"61'- 1,64бе‘164г А.
Эти зависимости представлены на рис. 8.63Р.
8.64(Р). В схеме рис. 8.64 размыкается ключ. Параметры схемы: J (t) = 2 sin (2500t + 30°) А; г = 100 Ом; С = 1 мкФ; L = = 0,2 Гн.
Найти зависимости ис (t) и i2 (t).
Решение. Напряжение на емкости и ток в индуктивности в момент t = 0 до коммутации: ис(0-) = 0,	(0—) = 0.
Искомые величины представим в виде суммы установившейся и свободной составляющих: ис — иСу + иссв; i2 — i2y + г2св-
Найдем комплексные амплитуды и мгновенные значения токов и напряжения на конденсаторе для установившегося режима после коммутации:
i _ j г_______________	100
””	" г + jxL - jxc	100 + J500 - j400
= ]/2 z. -15° А;
*2т
jXL - jxc r + jxL-jxc
= ]/2 ZL 75° А;
Uc„ = iim(~jxc) = |/2 z. -15° (-J400) = 400]/2 z. -105° B;
ily = |/2 sin (2500г - 15°) A;
i2y = ]/2 sin (25ООГ + 75°) A;
uCy = 400 ]/2 sin (2500г - 105°) B.
Рис. 8.64
Методом входного сопротивления (8.1) составим характеристическое уравнение
Z(p) = r + pL+ 1/рС=0.
Рис. 8.64Р
Это характеристическое уравнение р2 4- 500р + 5  10б = 0 имеет корни комплексные сопряженные Pi, 2 = — 250 + J2220 с “1.
Следовательно, свободные составляющие можно по (8.4) записать в виде
иСсв = Ле"250' sin (2220t + а);
i2cB ~ Be~25Ot sin (2220t + p).
Найдем свободные составляющие. Составим системы уравнений для определения постоянных интегрирования А, а, В, р. Для определения двух постоянных интегрирования каждой из искомых величин вычислим производные:
-^2- = —25ОЛе*250' sin (2220f + а) +
+ 222ОЛ«Г 2501 cos (2220г + а);
= -25ОВе-250' sin (2220г + 0) + at
+ 2220Ве_ 2501 cos (2220г + р).
Уравнения для определения постоянных интегрирования (момент времени t — 0) имеют следующий вид:
Ыссв (0) = 4 sin а;
св
dt
^2св dt
= —2504 sin а + 22204 cos а; о
^2св (0) = Bsinp;
= — 250В sin Р 4- 2220В cos р. о
Для вычисления постоянных интегрирования найдем начальные условия для свободных составляющих. Из законов коммутации следует, что ис (0) = ис (0-) = 0; h (0) = ц (0-) = 0. Поэтому начальные значения свободных составляющих тока в индуктивности и напряжения на емкости
1'10» (0) = 1] (0) - !1у (0) = -|/2 sin (—15°) = 0,366 А;
«сев (0) = ис (0) - иСу (0) = -400 ]/2 sin (-105°) = 546 В.
Запишем уравнения Кирхгофа для свободных составляющих, отключив ветвь с идеальным источником тока:
*2св Чсв = 0»	(0
^Ссв di{CB/dt ^2св = 0,	(^)
где
Ijcb С duc CB/dt
(3)
и, в частности, для момента времени t = 0
*2св (0) — i 1св (0) — 0;
мСсв (0) + £
^1св dt
- п’2св (0) = 0;
^"1св (0) ~~ С du£CB/dt\o,
(la)
(2а)
(За)
причем в этих уравнениях известны иСсв(0) и iiCB (0).
Из (1а), (2а) и (За) находим i2cB (0) = —0,366 A; di{cB/dt |0 = = -2913 А/с; ducJdt |0 = 366- 103 В/с.
Для определения производной второго тока дифференцируем уравнение (1): di2cB/dt - -diicB/dt, откуда следует, что для момента времени t = 0 производная di2cB/dt\Q = — dilCB/dt\Q = = 2913 А/с.
Из уравнений для определения постоянных интегрирования находим: 4 = 591 В; а = 67,5°; В - 1,321 А; р = -16,08°.
Записываем искомые величины:
Uc (t) = 400 ]/z sin (2500t - 105°) + 59le~2501 sin (2220t + 67,5°) В; i2 (0 = |/2 sin (2500Г + 75°) + 1,321е"2501 sin (2220f - 16,08°) A.
Эти зависимости представлены на рис. 8.64Р.
8.65(Р). Определить ток ц источника ЭДС (рис. 8.65) с па
раметрами Е = 80 В и гг = 200 Ом после коммутации при
г2 — ; С = 40 мкФ; L = 0,1 Гн.
Решение. Напряжение на емкости и ток в индуктивности до коммутации: wc(0—) — Е = = 80 В; i3(0 —) = 0.
Искомый ток представим в виде суммы двух составляющих:
Il Ijy 4“ ilCB,
Рис. 8.65
где после коммутации
ily = £/(rj. + г2) = 0,2 А.
Кроме того, 13у = 0 и иСу = Ег2/(гх + г2) = 40 В.
Приравняв нулю входное сопротивление относительно точек разрыва первой ветви
Z (р) = ri +
r2 (pL 4- 1/рС)
r2 4- pL 4- 1/рС ’
получим по (8.1) характеристическое уравнение р2 + 1000р 4- 250 • 103 = 0,
корни которого равные действительные: рг = р2 = —500 с-1.
Поэтому свободную составляющую искомого тока запишем по (8.3) в виде
Чсв = Л1в"500г 4- A2te~500t.
Чтобы определить две постоянные интегрирования и Л2, дополнительно вычислим производную свободной составляющей:
dhJdt = -SOOAie’500* + A2e"500f - 500A2te-500'.
В частности, при t = 0 имеем:
Чсв(О) = 41 и ^i'icb/^Io = — 500А1 4-А2.	(1)
Для вычисления Aj^ и А2 из этой системы найдем начальные значения свободного тока и его производной.
По законам коммутации (8.7) и (8.8) напряжение на емкости и ток в индуктивности не изменяются скачком, т. е. ис (0) — = ыс(0—) = 80 В; i3(0) = f3(0-) = 0.
Найдем еще начальные значения свободных составляющих напряжения на емкости и тока в индуктивности:
«сев (0) = «с (0) - ису (0) = 40 В; i3cB (0) = i3 (0) - i3y (0) = 0.
Уравнения Кирхгофа для свободных составляющих цепи после коммутации (в ветви с источником оставляем только
сопротивление rj:
~*1св + *2св + z3cb =	(2)
ПЧсв + г2/2св =0;	(3)
L diteJdt + иСсъ- r2i2cB = 0	(4)
и, в частности, для момента времени t — 0
— h св (0) + *2св (0) + Ьсв (0) = 0;	(2а)
ПЧсв(0) 4- г212св(0) = 0;	(За)
Ldi3cB/dt|0 4- ис св (0) — r2i2cB (0) == 0.	(4а)
В этих уравнениях уже известны иСсв(0) и z3cB(0); находим: Лев (0) = 0; i2cB(0) = 0; $3cB/dt|0 = -400 А/с.
Для определения производной первого тока дифференци-
руем уравнения (2) и (3):
-di{Jdt + di^/dt + di3c3/dt = 0;	(5)
П di^Jdt + r2 di2cJdt = 0	(6)
и, в частности, для момента времени t — 0 ^zicb/^ Io 4- ^z2cb/^Io 4* ^'зсв/^1о =	(5a)
Г1 di{C3/dt Io 4- r2 di2c3/dt |0 = 0.	(6a)
Из двух уравнений (5a) и (6a), в которых di3cB/efr]0 известно, находим diiC3/dt\0 = —200 А/с. Теперь из системы уравнений (1) находим Ai =0, А2 = —200 А.
Искомое решение
ii = Gy + г’1св = 0,2 — 2OOte'500' A.
8.66.	В схеме рис. 8.66 происходит замыкание ключа. Параметры схемы: Е = 100 В; = г2 — 100 Ом; L = 0,1 Гн; С = = 10 мкФ.
Найти начальные значения: /1Св(0), *2св(0), *зсв(0), иссв(0), ^lcb (0), di\CB/dt |о, di2c3/dt |o, di3c3/dt |o, ,du^c^/dt [q, du^ C3/dt |q.
8.67.	В схеме рис. 8.67 замыкается ключ. Параметры схемы: Е = 80 В; = г2 = 40 Ом; L == 0,05 Гн; С = 5 мкФ.
Найти начальные значения: Чсв(0), г2св(О), *зсв(О), Асв(О), ^Ссв (0), св (®), ^IcbA^Io* ^2св/^|о? ^'зсв/^ l(h ^4св/^ l(b ^^Ссв/^1о> св/^ 1о*
Рис. 8.67
8.68.	Определить токи переходного процесса i и i2 в схеме рис. 8.68 при Е = 60 В; г = 80 Ом; г2 = 100 Ом; = 0,2 Гн; Ь2 = 0,1 Гн.
Рис. 8.68
8.69.	В схеме рис. 8.69 параллельно ветви с сопротивлением — 30 Ом подключается ветвь с сопротивлением г2 = 60 Ом и индуктивностью Ь2 — 0,5 Гн.
Рассчитать ток ц и напряжение uL2 после коммутации при Е = 85 В; L = 0,6 Гн.
Рис. 8.70
Рис. 8.71
8.70.	В цепи рис. 8.70 с параметрами Е = 80 В; г = 40 Ом; г2 = 50 Ом; - 50 мкФ; С2 — 10 мкФ происходит замыкание ключа.
Найти зависимости i(t) и uc2(t).
8.71,	Параллельно ветви с емкостью Ci = 500 мкФ (рис. 8.71) подключается ветвь с параметрами г2 = 10 Ом; С2 = 150 мкФ. Известны параметры источника постоянной ЭДС: Е = 50 В; г = 7 Ом.
Определить ток i2 и напряжение иС1.
Рис. 8.72
Рис. 8.73
8.72.	Последовательный контур rLC подключается к источнику постоянной ЭДС Е (рис. 8.72).
Определить ток i и напряжение ис, а также их максимальные значения во время переходного процесса, если Е = = 120 В; г = 20 Ом; L — 0,1 Гн; С = 2,49 мкФ.
8.73.	Параллельно ветви rLL подключается ветвь г2С (рис. 8.73).
Рассчитать зависимости ii (t) и uc(t) при параметрах ветвей:	= 300 Ом; L=l,25 Гн; г2 — 200 Ом; С = 10 мкФ
и токе источника J = 0,125 А.
Рис. 8.75
Рис. 8.74
8.74.	К источнику с постоянной ЭДС Е = 100 В и внутренним сопротивлением г = 20 Ом (рис. 8.74) дополнительно подключается катушка с индуктивностью L = 0,05 Гн и сопротивлением г2 = 30 Ом.
Определить токи i, i2 и напряжение ис на емкости конденсатора С = 50 мкФ.
8.75.	Определить ток i и напряжение ис в схеме рис. 8.75 после коммутации. Параметры схемы: Е = 150 В; г = 50 Ом; г2 = 30 Ом; L = 0,05 Гн; С = 100 мкФ.
8.76.	В схеме рис. 8.76 параллельно ветви г2С подключается ветвь с сопротивлением rt.
Найти зависимости (г) и мс(Г) при Е = 10 В; = г2 — = 100 Ом; L= 1,0 Гн; С = 10 мкФ.
8.77.	Определить ток i2 и напряжение ил в цепи рис. 8.77.
Дано: Е = 10 В; г{ = г2 = 100 Ом; L= 1,0 Гн; С = 10 мкФ.
Рис. 8.76
Рис. 8.77
8.78.	К параллельному контуру с параметрами L— 1,0 Гн; С = 100 мкФ; rj = 80 Ом; г2 = 120 Ом подключается источник тока J = 1 А (рис. 8.78).
Найти зависимости ц (г) и u2(t).
8.79.	Определить ток i и напряжение uL в схеме рис. 8.79 после коммутации. Параметры схемы: Е = 100 В; г —5 Ом; г2 — 3 Ом; L = 0,1 Гн; С = 200 мкФ.
Рис. 8.78
Рис. 8.80
Рис. 8.81
8.80.	В цепи рис. 8.80 параллельно конденсатору емкостью С — 200 мкФ подключается резистор с сопротивлением г2 = — 5 Ом.
Определить ток i и напряжение и2 на резисторе при Е = 100 В; г = 3 Ом; L = 0,1 Гн.
8.81. В схеме рис. 8.81 Параметры схемы: Е = 100 L = 0,l Гн; С — 1000 мкФ.
Найти зависимости ц (t)
происходит размыкание ключа. В; J = 1 A; fi = г2 — Ю Ом;
Рис. 8.82
Рис. 8.83
и uc(t).
8.82.	В цепь рис. 8.82 включается дополнительный источник тока J2. При известных параметрах Ji — \ А; Л = 2 А;
= 80 Ом; г2 = 120 Ом; L = 1,0 Гн; С — 100 мкФ определить токи ц и i2 в резисторах.
8.83.	Найти токи i и напряжение ис в схеме рис. 8.83 после коммутации при параметрах: Е = 100 В; J = 1 A; = = г2 = 200 Ом; L = 0,5 Гн; С ~ 10 мкФ.
Рис. 8.84
Рис. 8.85 -
8.84.	Последовательный контур rLC при нулевых начальных условиях подключается к источнику гармонической ЭДС е (рис. 8.84).
Рассчитать ток контура i и напряжение на конденсаторе ис для трех режимов:
1)	Резонансный режим, когда частоты ЭДС источника е — 5 sin 104t В и собственных колебаний контура совпадают. Параметры контура: г — 10 Ом; L= 50 мГн; С =0,2 мкФ.
2)	Режим сверхтока, когда частота ЭДС источника е — = 5 sin (104t - 90°) В значительно меньше частоты собственных колебаний контура и установившаяся составляющая тока в момент включения близка к нулю. Параметры контура: г = 10 Ом; L= 10 мГн; С = 0,01 мкФ. Для этого режима вычислить отношение максимального тока переходного процесса к амплитуде тока установившегося режима.
3)	Режим перенапряжения на конденсаторе, когда частота ЭДС источника е = 5 sin 105t В значительно больше частоты собственных колебаний контура и установившаяся составляю-
щая напряжения на конденсаторе в момент включения близка к нулю. Параметры контура: г = 10 Ом;
50 мГн; С ~ 0,2 мкФ. Для этого режима найти также отношение максимального напряжения на конденсаторе к амплитуде напряжения установившегося режима.
8.85.	Определить ток г\ и напряжение ис в схеме рис. 8.85 после
Рис. 8.86
коммутации.
Дано: е = 100 sin 105t В; = r2 = 20 Ом; L = 0,l Гн; С = = 0,25 мкФ.
8.86.	В цепи рис. 8.86 к выводам резистора с сопротивлением = 30 Ом подключается конденсатор емкостью С = = 10 мкФ.
Найти зависимости ц (г) и i (t) при е = 127 sin (104г 4- 60°) В; г ~ 8 Ом; L= 6,35 мГн.
Переходные процессы в цепях с взаимной индукцией
8.87(	Р). Определить токи и i2 в индуктивностях (рис. 8.87) после коммутации при заданных параметрах: Е — — 60 В; = 50 Ом; г2 = г3 — 20 Ом; = 0,6 Гн; Ь2 = 0,5 Гн; М = 0,45 Гн.
Р е ш е н и е. До коммутации токи отсутствуют, т. е. ц (0—) = = 0; 1*2(0 —) = 0. Поэтому по закону коммутации (0) = 0; G (0) = 0.
После ‘коммутации
~ hy "Ь Чсв» ^2 — hy "Ь ^2св>
где
—	—.	__ । A; i
Г1 + Г2г3/(г2 4- г3)
= ilv —V— = °,5 А. г2 + г3
Чтобы получить характеристическое уравнение, составим главный определитель, выбрав контуры 1 и II, как показано на рис. 8.87, и заменив оператор на р:
т*1 4“ ^2 + р(Е14- Ь2 4- 2Af) т*2 4- р (L2 4- Af)
7*2 4- р (L2 4- Af)	7*2 4- т*з 4- pL2
Приравняв определитель нулю, получим характеристическое уравнение
р2 4- 790^4- 24 615 = 0,
корни которого действительные: = — 33 с-1, р2 = -757 с-1. Поэтому свободные составляющие токов запишем по (8.2) в виде
Чсв = Л1С“33г + л2е"7571;
*2св = B1e~33r + B2e~757t.
Найдем начальные значения свободных составляющих токов в индуктивностях:
i1CB (0) = ц (0) - fly (0) = -1 A; i2cB (0) = i2 (0) - i2y (0) == -0,5 A.
ГИС. б.56
Составим систему уравнений для определения постоянных интегрирования
iicB (0) — А + Л2;
^'1св/^1о = — ЗЗЛ t — 757/42;
^2св/^1о — -ЗЗВ1 — 757В2. j
Уравнения Кирхгофа для свободных составляющих имеют вид:
и, в
’ I т ^11СВ	. 1Ж ^2св	.	Л
ПЧсв + Ц —h М 	+ r3z3cB — 0;
—	v г	R	*	—
	1"	' At + Г212св ~ Г 3^св = 0 at----------at
частности, для начального момента времени (t = 0)
“*1св (0) + 72св (0) + Gcb (0) = 0; at
dt
о
о
+ м^-
о dt
^2св dt
о
+ Г2*2сВ (0) — г3г3св (0) = 0,
откуда находим зависимые начальные условия: dilc3/dt |о = 308 А/с;	= -277 А/с.
Из систем уравнений (1) и (2) находим: Аг = —0,620 А; А2 = —0,380 А; Вх = -0,905 А; В2 = 0,405 А. Искомые величины: й = 1 - 0,620е“33' - 0,380е' 757' A; i2 = 0,5 - 0,905е’33' + + 0,405е'757' А.
Рис. 8.89
Рис. 8.90
8.88.	Воздушный трансформатор (рис. 8.88) подключается к источнику постоянной ЭДС Е = 100 В. Известны параметры трансформатора: Lx =0,1 Гн; rj = 10 Ом; Ь2 =0,18 Гн; М = 0,107 Гн (к = 0,8) и сопротивление нагрузки г2 = 30 Ом.
Найти токи ц и i2.
8.89.	Определить токи ix и i2 в цепи рис. 8.89 после замыкания ключа, если Е = 200 В; гх = 10 Ом; г2 = 20 Ом; Lj = 0,1 Гн; Ь2 = 0,2 Гн; М = 0,12 Гн (к = 0,85).
8.90.	Нагруженный трансформатор (рис. 8.90) с параметрами Lx = 0,5 Гн; = 20 Ом; L2=0fi Гн; М = 0,5 Гн подключается к источнику гармонической ЭДС е = 100 sin 100г В. Сопротивление нагрузки г2 = 100 Ом.
Определить токи ц и i2.
8.91.	В цепи рис. 8.91 к трансформатору*, который питается от источника гармонической ЭДС е= 100 sin 100г В, подключается резистор с сопротивлением г2 = = 50 Ом. Параметры трансформатора: Li = 0,5 Гн; ri = 20 Ом; L2 = 0,6 Гн; М = 0,5 Гн.
Рассчитать зависимости fj (t) и i2(t).
8.4.	Операторный метод расчета переходных процессов
8.92(Р). Цепь гС с незаряженным конденсатором (рис. 8.92) подключается (при t = 0) к источнику линейно изменяющегося
напряжения и (t) = kt, где к — 1000 В/с. Параметры цепи: г == = 100 Ом, С = 100 мкФ.
Определить ток i в цепи и напряжение на конденсаторе ис.
Решение. До коммутации конденсатор не был заряжен, т. е. ис (0-) = 0; следовательно, ис (0) = ис (0—) = 0.
Рис. 8.92
Рис. 8.92Р
Дифференциальное уравнение цепи после коммутации
ri + ис = и (£).
Операторная форма этого уравнения:
rI(p)+Uc(p) = U(p)
или
П (р) + -^1 (р) +	= и (р),	(1)
где по закону коммутации ис (0) = 0. Операторная схема, соответствующая уравнению (1), представлена на рис. 8.92Р, где U (р) — к/р2 — изображение линейно изменяющегося напряжения и (t) = kt.
Из (1) находим изображение искомого тока:
/(р)= pCp/l/rC)-	(2)
Для определения оригинала тока применим метод неопределенных коэффициентов. Изображение представим в виде суммы
, ьл - — х В - л (Р + УгС) + ВР т {Р) р + р + l/гС р (р + 1/гС)	'	(3)
Сравнивая числители уравнений (2) и (3), запишем:
к/г = Ар + Air С + Вр,
откуда, приравняв коэффициенты при одинаковых степенях р, получим: 0 = А + В и k/r = А)гС.
Из этой системы уравнений находим постоянные А — кС; В = —кС. Таким образом, 316

кС
кС
р 4- 1/гС ’
Первое слагаемое является изображением постоянной величины, второе — экспоненты, т. е. ток
i = кС - kCe~t/rC.
Напряжение на емкости
1
Л
i dt = kt + krCe~^rC 4- D.
Постоянную интегрирования D найдем из начальных условий. Так как ис (0) = кгС 4- D — 0, то D = ~кгС и
ис = —кгС 4- kt 4- krCe~t/rC.
С учетом заданных параметров схемы имеем:
i = 0,1 - 0,1е~i00t, А; ис - -10 + 1000г 4- 10е“ 100\ В.
8.93(Р). Последовательная цепь rL (рис. 8.93) при нулевых начальных условиях подключается (t = 0) к экспоненциально затухающему напряжению u(t) = Uoe~at. Параметры цепи: UQ = 100 В; а = 2000 1/с; г = 100 Ом; L = 0,l Гн.
Найти ток цепи i(t).
Рис. 8.93Р
Решение. Из режима цепи до коммутации имеем 1(0 — ) = 0; следовательно, i (0) = i (0 —) = 0.
Дифференциальное уравнение цепи после коммутации ri 4- Ldi/dt = иое~^.
Операторная запись этого уравнения:
ri (р) + рЫ (р) - Ы (0) = U0/(p 4- а),	(1)
где по закону коммутации Li (0) = 0.
Операторная схема, соответствующая уравнению (1), представлена на рис. 8.93Р, где учтено, что изображением напряжения Uoe~at является функция Ud(p 4- а) (см. приложение 2).
Из (1) находим изображение искомого тока:
гм = U°/L W (р + а) (р + r/L) ’
Для перехода к оригиналу выпишем соотношение из таблицы оригиналов и изображений (приложение 2):
1	1
-------------= —-— (е " ы - е ~ (р + а)(р + Ь)’ а-Ь{	’
Следовательно, ток
и при заданных параметрах цепи
i(t) =e-iooot _е-'2000Г д
8.94	(Р). Определить, применяя операторный метод расчета, напряжение на емкости ис в схеме рис. 8.36 при параметрах, приведенных в задаче 8.36.
Решение. До коммутации напряжение на емкости ис (0~) = ^r2/(ri + г 2 + г3) = 30 В; следовательно, ис(0) = = мс(0-) = 30 В.
Составим эквивалентную операторную схему (рис. 8.94Р). В этой схеме учтено, что изображение постоянной величины Е равно Е/р.
Найдем изображение напряжения на емкости, например, методом узловых потенциалов (по формуле для схемы с двумя узлами):
, (гЛ _ (E/p)(l/ri) + (uc(O)/p)pC _
°b W 1/r, + l/r2 + pC 120 + 0,075p Fj (p)
p (2,5 • 10- 3p + 2) “ pF3 (p) •
Корень характеристического уравнения определим из уравнения F3 (р) = 0, т.е. 2,5 • 10“Зр + 2 = 0, откуда р3 = —800 с“’.
Оригинал искомого напряжения найдем по теореме разложения (8.12):
ис-и°>- F3(0) + PlFM
120
120 + 0,075 (-800) _800f ( — 800)’2,5* 10’3 е
= 60 - ЗОе"800', В.
8.95	(Р). Решить задачу 8.21 операторным методом.
Решение. Электродвижущая сила е = 100 sin (2500t + 4- 30°) В имеет достаточно сложное изображение:
п .	100 (р sin 30° + 2500 cos 30°)
Е(Р) =--------р2 + 25002------’
поэтому целесообразно применить операторный метод к расчету свободной составляющей тока.
Рис. 8.94Р	Рис. 8.95Р
Составим эквивалентную операторную схему для свободных составляющих (рис. 8.95Р), которая не содержит источника ЭДС Е (р).
Для расчета тока 7св(р) необходимо определить iCB (0) = i (0) - iy (0),
где по закону коммутации i(0) = i(0 — ) = 1 A, a iy = = 0,980 sin (2500г — 48,7°) А (см. решение задачи 8.21), т. е. iy(0) = -0,736 А и iCB (0) =1,736 А.
Из схемы (рис. 8.95Р) следует, что изображение свободной составляющей тока
т AM0) _ U0) _ 1,736 cbW (r + pL) p + r/L р+500
и оригинал
iCB = 1,736е-500', А.
Следовательно, искомый ток
i = iy + iCB = 0,980sin (2500t - 48,7°) + l,736e"5OOr, A.
8.96	(P). Определить операторным методом ток i3 в схеме рис. 8.63 при параметрах, приведенных в задаче 8.63.
Решение. Применим операторный метод для определения свободной составляющей. Начальные значения свободных составляющих тока в индуктивности и напряжения на емкости найдены в решении задачи 8.63: i2cB(0)=—0,5 А; иссв(0) = = 50 В.
Составим эквивалентную операторную схему для свободных составляющих (рис. 8.96Р). Для этой схемы, применяя любой из методов расчета линейных цепей, находим операторное изображение искомого тока:
, ,,	- Р [г^а2д, (0) + LCuCa (0)] - (п + г2) СиСсв (0)
3“	р2Г1ЬС + р OViC + L) + (П + г2)
=__________^4___________Ft(p)
р2  0,02 + р • 4,5 + 200 F2 (р) '
Рис. 8.96Р
Рис. 8.97Р
Корни характеристического уравнения определим из уравнения F2 (р) — 0, т. е.
р2 • 0,02 + р • 4,5 + 200 = 0,
откуда Pi = -61 с"1; р2 = —164 с“1.
Оригинал искомого тока найдем по теореме разложения (8.11):
. F1 (Pi) pi* , Ft (Рг) Р21
l3cB — “73—в 4“	,
F'2(pi)	F'2(p2)
где Ff2 (р) = 0,04р + 4,5.
Подставив значения корней, получим:
i3cB = -l,942e’61f+ 1,942е“164', А.
Поскольку при постоянных ЭДС Е и токе J в установившемся режиме ток в емкости i3y равен нулю, то ток переходного процесса i3 равен свободной составляющей тока i3cB.
8.97	(Р). Найти ток i2 задачи 8.64 операторным методом.
Решение. Применим операторный метод к расчету свободных составляющих. Эквивалентная операторная схема представлена на рис. 8.97Р, для которой йсв (0) =0,366 А, иСсв(0) = = 546 В (см. решение задачи 8.64). Как следует из операторной схемы,
Ьсв (p) =
^ccb(Q)/p b\CB(0) r + pL + 1/pC
—0,0732 • 10“ 6p + 546 - 10"6	Fi(p)
0,2-10-6p2 + 10’4p + 1	~ F2(p)'
Из уравнения Г2(р) = 0, т. e. 0,2 • 10“6р2 + 10"4р + 1 = О, вычислим корни характеристического уравнения: plt 2 = —250 ± + J2220 с"* 1 11.
Оригинал тока 12св найдем по теореме разложения в случае двух комплексных сопряженных корней (8.13):
i —1	гр^
^2св £ ке , , . с , Г 2 \Р1)
где F'2(p) =0,4' 10"6р+ 10~4; при этом имеем:
—0,0732 • 10~6 (—250+72220)+546 • 10~6 2S0tl2210,
2св	0,4-10"6 (-250 +72220)+ 10’4
— 2 Re0,660e"JI06'08’e~250te/2220' = 2 НеО^бОс’250*^22201-106,080) —
= 1,32 te-2S0t cos (22201 - 106,08°) = 1,32 le “250г sin (22201 - 16,08°) А.
Ток установившегося режима i2y = |/5 sin (2500? + 75°) А был найден в решении задачи 8.64.
Следовательно, ток
h — Gy + Gcb =
= ]/2 sin (25001 + 75°) + 1,321е"250‘ sin (2220t - 16,08°) А. ч
8.98(Р). Решить задачу 8.65 операторным методом.
Решение. В задаче 8.65 найдены следующие величины:
ily = 0,2 А; ёзсв (0) = 0; иссв (0) = 40 В.
Операторная схема для свободных составляющих представлена на рис. 8.98Р, где ток
I In) = [~“Ce.(0)/P][^/(rl +>7)] =
1cbW Г1Г2/(Г1 + r2) + pL+1/рС
__________-200	_ Fx(p)
р2 + 1000р + 250 • 103 F2 (р)'
11 п/р Ионкина П. А.
321
Из уравнения F2 (р) = 0 корни характеристического уравнения pi=p2=p—— 500 с-1. Таким образом, изображение тока /1св(р) можно записать в виде
Zta(p)= -200/(р + 500)2.
Рис. 8.98Р
Обратившись к таблице приложения 2, Запишем оригинал* f1CB = — 2ОО?е"500*, А.
Искомый ток
h = г1У + *1св = 0,2 — 200te“5OOt, А.
8.99(Р). Для цепи задачи 8.88 найти зависимость ц (?) операторным методом.
Решение. Запишем уравнения Кирхгофа для трансформатора
ri4 + Lj dijdt — М di2/dt == £;
r2i2 4- L2 di2/dt - M dijdt — 0
Рис. 8.99P
и перейдем к операторным изображениям:
г J1 (р) + РШ1 (р) - pMI2 (р) - LJi (0) + Mi2 (0) = Е/р\ r2?2 (Р) + pb2/2 (р) - pM/t (р) - L2i2 (0) + Мц (0) = 0. •
Операторная схема, соответствующая этим уравнениям, приведена на рис. 8.99Р. Для цепи данной задачи G (0) ~ 0, i (0) = 0, т. е. начальные условия нулевые, и дополнительный источников в эквивалентной схеме нет.
Из системы уравнений найдем:
Е (г 2 + рЬ2)______________
Р [р2	- М2) + р (г 2L2 + г2Ь1) + Г1Г2]
18р + 3000	_	(р)
р (6,55 • 10* Зр2 + 4,8р + 300) ~ pF3 (р)
и два корня характеристического уравнения F3 (р) — 0, которые получаются действительными: pi = —69,5 с-1, р2 — — 672 с“\ По теореме разложения (8.12) найдем оригинал:
. _ Fj (0) Fj (р^ P1t Fj (p2) P2r
1	F3(0) + P1F'3 (pj +p2F'3(p2)
где Fj (p) = 13,1  10-3p + 4,8.
После подстановки численных значений получим:
h = 10 - 6,17e-69,5t - 3,83е’672', А.
8.100. Решить задачу 8.3 операторным методом. 8.101. Решить задачу 8.6 операторным методом.
8.102. Решить задачу 8.9 операторным методом.
8.103. Решить задачу 8.10 операторным методом.
8.104. Решить задачу 8.11 операторным методом.
8.105. Решить задачу 8.12 операторным методом.
8.Г06. Решить задачу 8.15 операторным методом.
8.107. Решить задачу 8.16 операторным методом.
8.108г Решить задачу 8.17 операторным методом.
8.109. Решить задачу 8.19 операторным методом.
8.110. Решить задачу 8.22 операторным методом.
8.111. Решить задачу 8.25 операторным методом.
8.112. Решить задачу 8.26 операторным методом.
8.113. Решить задачу 8.27 операторным методом.
8.114. Решить задачу 8.28 операторным методом.
8.115. Решить задачу 8.31 операторным методом.
8.116. Решить задачу 8.37 операторным методом.
8.117. Решить задачу 8.38 операторным методом.
8.118. Решить задачу 8.41 операторным методом.
8.119. Решить задачу 8.42 операторным методом.
8.120. Решить задачу 8.43 операторным методом.
8.121. Решить задачу 8.44 операторным методом.
8.122. Решить задачу 8.46 операторным методом.
8.123.	Решить	задачу 8.47	операторным методом.
8.124. Решить		задачу 8.48	операторным методом.
8.125.	Решить	задачу 8.49	операторным методом.
8.126.	Решить	задачу 8.50	операторным методом.
8.127.	Решить	задачу 8.51	операторным методом.
8.128.	Решить	задачу 8.53	операторным методом.
8.129.	Решить	задачу 8.54	операторным методом.
8.130.	Решить	задачу 8.55	операторным методом.
8.131.	Решить	задачу 8.56	операторным методом.
8.132.	Решить	задачу 8.60	операторным методом.
8.133.	Решить	задачу 8.68	операторным методом.
8.134.	Решить	задачу 8.69	операторным методом.
8.135.	Решить	задачу 8.70	операторным методом.
8.136.	Решить	задачу 8.71	операторным методом.
8.137.	Решить	задачу 8.72	операторным методом.
8.138.	Решить	задачу 8.73	операторным методом.
8.139.	Решить	задачу 8.74	операторным методом.
8.140.	Решить	задачу 8.75	операторным методом.
8.141.	Решить	задачу 8.76	операторным методом.
8.142.	Решить	задачу 8.77	операторным методом.
8.143.	Решить	задачу 8.78	операторным методом.
8.144.	Решить	задачу 8.79	операторным методом.
8.145.	Решить	задачу 8.80	операторным методом.
8.146.	Решить	задачу 8.81	операторным методом.
8.147.	Решить	задачу 8.82	операторным методом.
8.148.	Решить	задачу 8.83	операторным методом.
8.149.	Решить	задачу 8.84	операторным методом.
8.150.	Решить	задачу 8.85	операторным методом.
8.151.	Решить	задачу 8.86	операторным методом.
8.152.	Решить	задачу 8.87	операторным методом.
8.153.	Решить	задачу 8.89	операторным методом.
8.154.	Решить	задачу 8.90	операторным методом.
8.155.	Решить	задачу 8.91	операторным методом.
8.5. Переходные процессы при действии источников напряжения или тока произвольной формы
8Л56(Р). Для цепи рис. 8.156,а определить uL(t) и u2(t) в общем виде.
Вычислить значения uL и w2 в моменты времени tx = Т/2 и t2 = ЗТ/2 при действии на входе цепи импульса напряжения (рис. 8.156,6), у которого Т = 1 мс; U = 10 В, и параметрах г —1 кОм; L = 0,l Гн. Построить зависимости uL(t) и u2(t).
Решение. Как следует из рис. 8.156,6, {О при t <О;
Ut/T при О t < Г;
О при t > Т.
Для решения задачи определим сначала передаточные функции напряжения yL (г) и у2 (0, численно равные напряжениям на индуктивности и на выходных выводах при действии
на входе единичного скачка напряжения. Применив классический или операторный метод, получим:’
Уь(0 = е1*; у2(0 = 1
где —r/L= —104 с'1.
Для интервала времени 0 t Т, применив вторую форму интеграла Дюамеля (8.16а), запишем:
uL(0 = Ui (0) yL (0 + f wi (t - T)yL(T)tfc;
о
t
W2 (t) = Kj (0) у 2 (t) + f u'i (t - т) у2 (т) dT 0
Для интервала времени t > Т согласно (8.166)
“lW = «1 (0)к(0 + J «1 (t - т)у/.(т) dt + t-T
+ [И1 (T+)-Ul(T-)]yL(t-T) =
= IO4 j e^dt - 10e’<'-r>=	10^<'-T> =
t-T
= -198 200e-,0\ B;
w2 (t) = Uj (0)y2 (t) + f и, (t - т)y2 (t) dt + t-T
+ [«1 (T+ ) - «I (T - )] У1 (t-T)= 198 200e- lo4‘, B.
Как и должно быть для t > Т, когда uL + и2 = 0, получили ML(t) = -и2 (Г).
							
							
				Л и-2			
		«к*	7				
			2			' *ч	t
О',2	0,4	0,6	0,8	1',0' 1,2	мс							
							
					/ /		
							
							
Рис. 8.156Р
Результаты расчета uL(t) и и2 (t) представлены в табл. 8.156а
8.1566 соответственно для интервалов времени О С t < Т
Таблица 8.156а
/, мс	0	0,2	0,4	0,5	0,8	1,0
«L, В	0	0,865	0,982	0,993	0,9996	1,0
м2’ В	0	1,135	3,018	4,007	7,0	9,0
Таблица 8.1566
f, мс	1,0	1,1	1,2	13	1,5
В	-9,0	-3,311	-1,218	-0,448	-0,006
И2, В	9,0	3,311	1,218	0,448	0,006
На рис. 8.156Р приведены зависимости ur (t), uL(r) и и2 (t).
8.157(Р). 1) Выяснить, при каких соотношениях между параметрами цепи rL (рис. 8.156, а) и длительностью импульса Т(рис. 8.156,6) выходное напряжение и2 будет пропорционально интегралу от входного напряжения ut.
2) Рассчитать значение и2 (t = Г) при L = 10 Гн; г = 0,1 кОм и сравнить с значением интеграла от входного напряжения для этого же момента времени.
Решение. 1) Выходное напряжение при t Т найдено в решении задачи 8.156:
Представив функцию е1* в виде ряда, получим:
Если можно пренебречь слагаемыми ряда, начиная с (r2/L2) UP/6T, то выходное напряжение и2 будет пропорционально интегралу от входного напряжения иь так как
t	t
f	f
«1(0Л= —tdt =
о	о
Ut2
IT ‘
Это допустимо для начальной стадии переходного процесса [см. зависимость и2 (г) на рис. 8.156Р], когда t с т = = L/r. Следовательно, для того, чтобы на всем промежутке времени действия входного сигнала их выходное напряжение и2 было пропорционально интегралу от входного, необходимо выполнение неравенства Т т = L/r.
2) При t = Т = 1 мс =10 3 с 10	-л
к2(Т)= ^^[Ю-3- 0,1(1 - е'10'10 3)] = 4,983 ЦТ2 В,
т
a f wt (t) dt = 5 • 10"3 В • с. о
Если и2 (0 разделить на r/L = 10, то полученный результат с некоторой погрешностью представляет интеграл от иг:
U1<f = Т) = 4,983 • 10" 3 В • с,
г. е. при t = Т выходное напряжение отличается от точного значения интеграла от на 0,33%.
8.158.	Для электрической цепи, представленной на рис. 8.156, а, определить ток i при Mj = U (1 - В.
Рис. 8.161
8.159.	Для четырехполюсника (рис. 8.159, а) с параметрами г = 1 кОм; С = 0,5 мкФ определить ток и напряжение и2 при входном напряжении ut, представленном на рис. 8.159,6, где Tj = 1 мс; Т2 = 2 мс; U = 10 В. Построить зависимости ц (Г) и «2 (0 на одном графике с зависимостью (t).
8.160.	Для четырехполюсника (рис. 8.159, а) определить при = С7е"л В,
8.161.	Для четырехполюсника, схема которого представлена на рис. 8.161, а, с параметрами ц = 2 кОм; г2 — 3 кОм; г = 2 кОм; С— 0,25 мкФ определить ток i и напряжение и2. 328
На входе четырехполюсника задано напряжение щ (рис. 8.161, б), где Т = 1 мс; U — 1 В.
Найти ток i и напряжение м2 при = 0£5Т; t2 = О,75Т и = 1,25 т.
8.162.	Форма импульса напряжения и на входе цепи (рис. 8.162, а) показана на рис. 8.162,6.
Определить ток i2 при r — rt=2 кОм; г2 = 3 кОм; L = = 0,8 мГн; Um = 10 В; Т — 0,5 мс. Вычислить значение тока i2 при = 0,5Т и t = 1,5Т.
8.163.	Для электрической схемы рис. 8.162, а определить ток в индуктивности, если напряжение и на входе соответственно равно: 0 при t < 0; U (1 — t/T) при 0 < t < Т; 0 при t > Т.
Рис. 8.162
AU.
Рис. 8.164
8.164.	Определить напряжение на сопротивлении нагрузки rn = 1 кОм четырехполюсника (рис. 8.164, а) при заданном напряжении на входе их — и по рис. 8.164, б, где показаны два импульса синусоидального напряжения с Um = 100 В; Т з= 0,02 с, действующие с момента t = 0. Построить зависимость мн (t) совместно с заданной зависимостью (t).
Параметры четырехполюсника: г — 250 Ом; С = 50 мкФ.
8.165.	Для четырехполюсника (рис. 8.164, а) определить напряжение ив при напряжении иь соответственно равном: 0 при Г < 0; Ut при 0 < t < Т; — U при Т < t < 2Т; 0 при t > 2Т.
8.166.	Определить ток i и напряжение ulb цепи (рис. 8.166), если г 1 — г = 2 кОм; L=1 мГн и напряжение и на входе равно: 0 при t < 0; Юе-0,5 1о6г В при Г > 0.
Построить зависимости i(t) и uL(t) на одном графике с u(t).
Г1
Рис. 8.166
Рис. 8.167
8.167.	В схеме рис. 8.167 ток J (г) источника равен: 0 при t < 0; Jo при 0 t С То; 2J0 — (J0/TQ) t при TQ < t С 2T0; 0 при t > 2Т0, где Jo - 100 мА; То = 0,01 с.
Определить ток i при параметрах п = 5 кОм; г — 10 кОм; С = 1 мкФ. Построить на одном графике зависимости i (г) и J (г).
8.168.	Определить ток iL в цепи рис. 8.168 с параметрами L==0,l Гн; г = 10 Ом при действии на входе источника тока J (г), который равен: 0 мА при t < 0; -100 + 200Г мА при 0 t Т; 0 мА при t > Т, где Т — 100 мс.
Построить на одном графике зависимости iL(t) и J (t).
Рис. 8.168
Рис. 8.169
8.169(	Р). Для схемы рис. 8.169 определить напряжение w2.
Дано: г = 1 кОм; = 4 кОм; г2 — 10 кОм; Ct = 1 мкФ; С2 — 1 мкФ. Ток J (t) источника равен: 0 при t < 0; 1е~* при t > 0, где I — 100 мА; а = 200 с“ \
Построить на одном графике зависимости J (г) и u2(t).
Решение. Определим, применяя, например, классический метод расчета, переходное сопротивление, которое численно равно искомому напряжению и2 при действии не заданного источника тока J (г), а единичного скачка тока Jo — 1 А (рис. 8.169, я). Обозначим его w0. Записав входное сопротивле-330
ние, например, относительно точек разрыва ветви с сопро-
тивлением г2, т.е.
Z (?) = г2 +
rid/pCQ
+ 1/рС!
и приравняв его нулю, получим по (8.1) характеристическое уравнение, корни которого = —403,7 с-1, р2 = —28,15 с-1. В установившемся режиме после коммутации иОу ~ 0; поэтому по (8.2) м0 =	+ А2еР2‘.
Рис. 8.169Р	б)
Независимые начальные условия для рассматриваемой схемы:
иС1 (0) — иС2 (0) — 0.
Постоянные интегрирования Ai и А2 определим из системы
уравнений:
и0 (0) = Ai 4- А2;	(1)
du0/dt|0 = PiAi + р242.	(2)
Найдем начальные значения и0(0) и du^/dt |0.
Запишем систему уравнений Кирхгофа для схемы рис. 8.169Р, а:
— Jq + i? + i2 = 0;	(3)
— i 4- ir], 4- i‘ci = 0;	(4)
Wei “ riiri = 0;	(5)
«С2 + Ц) -	- и = 0.	(6)
Из этой системы уравнений с учетом независимых начальных условий (см. решения задач классическим методом) найдем:
/ЛЧ г r'r2 . duQ r r2(C2r2-Cir) ”o(0)-Jo7T^-> ~dT 0~Jq CjC2(r 4-r2)2 '
Теперь при заданных параметрах из системы уравнений (1) и (2) определим постоянные интегрирования:	= —2049;
А2 = 2958, т. е. переходное сопротивление
г (г) = -2О49е"403’7' + 2958е“28’15', Ом.
Таблица 8.169
/, С	0	10~5	Ю-4	10“3	10-2	0,02	0,1
м2(/), В	90,91	91,47	96,31	128,3	30,08	-17,7	-2,902
J(t), мА	100	99,8	98,02	81,87	13,53	1,832	2 • 10“7
Применяя первую форму интеграла Дюамеля (8.15а). записываем искомое напряжение:
и2 (0 = J(0)г(t) + J	- т)Л,
О
где 7(0) = I = 0,1 A; J' (t) = —aZe at = — 20е 200t, А/с. С учетом этих соотношений получим:
u2(t)=7(^1Z1' + 42Z2')-
= 0,1 (5455е"200' - 4061е“403’7' -484,6е’28’15'), В.
Для построения зависимостей составим табл, 8.169.
Эти зависимости построены на рис. 8.169Р, б.
Рис. 8.170
8.170.	Для схемы рис. 8.170 с параметрами г = 10 Ом; L= 10 мГн; С = 400 мкФ определить напряжение м, если ток J (t) источника равен: 0 при t < 0; 70(1 — е~Л) при t > 0, где JQ =0,1 A; a = 200 с"1. Построить зависимость и (г).
8.6. Переходные процессы при скачкообразных изменениях токов в индуктивностях и напряжении на емкостях
8.171(Р). Определить напряжения иС2 и иС1 после замыкания ключа в схеме рис. 8.171 при иС1(0—)= 100 В; г = 1 Ом; R — 100 Ом; Ci =0,5 мкФ; С2 = 1 мкФ. Найти момент вре-
Рис. 8.171
мени Т, в который напряжение достигает максимального значения. Для этого момента времени определить суммарный заряд на емкостях и сравнить его с зарядом первой емкости до коммутации.
Решение. Приравняв нулю входное сопротивление
ч 1 Л(1/рС2)
получим по (8.1) характеристическое уравнение
р2 + 3- 106р + 2 • Ю10 = 0,
корни которого pi = -5-Ю3 с"1; р2 = -2995-103 с-1.
Искомое напряжение запишем в виде
ис2 = иСу + мссв — AieP1 + А2еР2 ,
так как иСу = 0. Отметим, что вторая составляющая напряжения Uc2 затухает существенно быстрее первой.
Для определения постоянных интегрирования Ai и А2 запишем напряжение и его первую производную для момента времени t = 0:
мсз(0) — Ai + А2;	(1)
ducjdt |о = PiAi + р2А2.	(2)
По закону коммутации иС1 (0) = uCi (0—) = 100 В и ^(0) = = wC2(0-) = 0 В. Чтобы найти начальное значение производной, запишем уравнения Кирхгофа для схемы после комму-
тации:
h - h ~ 1'3 = 0;
—wCi 4- uc2 + i\r = 0; i3R — uc2 — 0,
(3)
(4)
(5)
где	ducl/dt и i2 = C2 du^/dt, откуда найдем при t = 0
dt*C2 dt
ill® = h(0)-Uc2(0)/K	ЦС1(0)
Теперь из (1) и (2) определим = -А2 = 33,44 В и напряжение
ис2 = 33,44 (г>~3 1о3< - е~2993 ' 1°3'), В.
Продифференцировав последнее выражение по времени и приравняв производную нулю, получим уравнение для определения момента времени Т, когда напряжение ис2 достигнет максимального значения:
duc2Jdt = 0 = -5 • 103е~5 ШЗТ+ 2995 • 103e“29951о3т, откуда Т = 2,14 • 10" 6 с.
При t = Т получим иС2 (Т) = 33,03 В и заряд Яс2 (Л = С2иС2 (Л = 33,03 мкКл.
Определим напряжение ис1. Аналогично предыдущему
иС1 = ВУ1' + В2еР2'; иС1 (0) = 100 = В, + В2;	(6)
duCi/dt\0 = pjBj + р2В2.
(7)
Переписав уравнение (3) в виде
~С| ducJdt — С2 duC2jdt —	= 0,
получим из него при t = 0
dua/dt |о = — (С2/С1) duC2/dt\Q = — 2-108 В/с.
Теперь из (6) и (7) находим: = 33,28 В; В2 — 66,72 В и напряжение
uci = 33,28е’5 1о3' + 66,72е'2993 '1о3', В.
Для t = Т — 2,14 • 10" 6 с получим ucl (t == Т) = 33,04 В и заряд qci (t = Т) — CiUcl (t = Т) = 16,52 мкКл.
При t — Т суммарный заряд на первой и второй емкостях
Qci (^ = Л + Qci (t = Т) = 49,55 мкКл. •
Заряд на первой емкости до коммутации qCi (0) = = CiUd (0-) = 0,5 • 10“6 • 100 = 50 мкКл.
Результаты расчета позволяют сделать следующие выводы:
1)	к моменту, когда напряжение на второй емкости достигнет максимального значения, напряжения на обеих емкостях становятся почти одинаковыми (при условии, что сопротивление г мало);
2)	к этому моменту времени суммарный заряд на первой и второй емкостях почти равен заряду на первой емкости до коммутации;
3)	указанные «равенства» выполняются более точно при уменьшении г, что приводит к формулировке обобщенного закона коммутации в виде (8.19);
4)	показанная на рис. 8.171Р зависимость uC2(t) содержит две фазы переходного процесса: фаза быстрого изменения при О t < Г, фаза медленного изменения при t > Т; в тех случаях, когда фаза быстрого изменения интереса не представляет, можно считать г = 0 и пользоваться обобщенным законом коммутации.
8.172(	Р). Для схемы рис. 8.171 предыдущей задачи определить ис2, считая г = 0, а остальные данные прежними.
Решение. Для расчетной схемы рис. 8.172Р можно записать обобщенный закон коммутации (8.19) в виде
С1иС1(0-) = (С1 + С2)ис(0),
где ис (0) — напряжение на параллельно включенных емкостях Cj и С2 после коммутации при t = 0.
Из этого равенства определим напряжение ис (0) = 33,33 В.
Находим корень характеристического уравнения для расчетной схемы: р = — l/R(Ct + С2) = -6,67-103 с-1. Заметим, что в предыдущей задаче переходный процесс после момента времени t = Т = 2,14-10“6 с почти целиком определялся первым корнем Pi = — 5-103 с-1, который при г->0 стремится к значению 6,67 • 103 с"
Искомое напряжение записываем в виде
иС2 — иС — иСу + иС св = иС св = Ав**-
Постоянную интегрирования определим по начальному значению: uc2(0) = ис(0) = 33,33 В.
Таким образом, = 33,33е"6,6’ 1о3<, В.
Рис. 8.172Р
Рис. 8.173
8.173(	Р). В цепи рис. 8.173 практически мгновенно происходит разрыв быстродействующим выключателем ветви с током гв.
Определить ток после коммутации, если Е == 120 В; = = 10 Ом; г2 — 30 Ом; Lj = 0,1 Гн; Ь2 — 0,4 Гн.
Решение. Находим ток и потокосцепление индуктивности Lj до коммутации:
G (0-) = E/ri = 12 А; 4х! (0—) = Liil (0-) = 1,2 Вб.
По обобщенному закону коммутации (8.20)
^(О-О-ЧМОНЧМО) или Ь1ч(0-) = (Ь1-ЬЬ2)Г(О),
где i (0) = (0) = i2 (0) — общий ток первой и второй индуктивностей.
Следовательно,
i(0) Ь . 1,(0-) = 2,4 А.
bj + ь2
Корень характеристического уравнения р = — (rj + г2)/(М + + L2)=-80 с"1.
Решение задачи ищем в виде
Постоянную интегрирования находим из уравнения z(0) = 2,4 = E/(r1 +г2) + Л,
откуда А = —0,6. Следовательно,
i = 3 -0,бе"80‘, А.
8.174.	Определить ток i2 второго конденсатора (рис. 8.174)
после коммутации.
В цепи действует источник синусоидальной ЭДС е = z= 100sin(103t + 30°) В. Заданы параметры: г = 100 Ом; — 10 мкФ; С2 = 30 мкФ.
8.175.	Найти закон изменения тока после размыкания ключа в схеме рис. 8.175, если = 500 Ом; = 40 мГн; L2 = 10 мГн; С = 1 мкФ; е — 200 sin 104t, В.
8.176(	Р). Для трансформатора (рис. 8.176) с параметрами Li =0,1 Гн; L2 =0,2 Гн; = 10 Ом; г2 = 5 Ом и коэффициентом связи к = 1 найти токи и i2 после коммутации. Источник ЭДС - постоянный с Е = 50 В.
Решение. Сначала заметим, что практически коэффициент связи не может быть равен единице из-за потоков рассеяния (т. е. практически всегда к < 1).
Чтобы получить характеристическое уравнение, составим главный определитель цепи
ri + pLi рМ
рМ	г 2 + рЬ2
и приравняем его нулю. Получим характеристическое уравнение
* P2LiL2 (1 - к2) + p(Ltr2 + L2ri) +	= 0,
где учтено, что к = М/|/LiL2.
При к = 1 характеристическое уравнение имеет один корень, а не два, как было бы при к < 1, а именно рг — =	+ L2Ti) = -20 с"1.
Искомые токи запишем в виде
	<	• Е . _ 2 л.
Ч ~ Чу "Ь Чсв = ~ Ае , r 1
h. = hy + *2cb = Be 2 % где учтено, что i2y = 0.
Если теперь для определения постоянных интегрирования А и В применить закон коммутации в формулировке: потоко-337
сцепление в индуктивности не может изменяться скачкообразно, то получится система уравнений:
L.i. (0) + Mf2(0) = Мн (0—) 4- Mi2(0-) = 0;
Mli (0) + L2i2 (0) = Mi. (0—) + L2i2 (0—) = 0,
где учтено, что i. (0—) = i2 (0—) = 0.
Главный определитель системы
= L.L2 -М2 = L.L2 (1 - /с2) = 0.
Lt М м l2
Поэтому из этой системы уравнений нельзя определить значения i. (0) и i2 (0). При решении задач, в которых принято
к = 1, нужно сначала определить зависимости Ч^ (t) и Ч*2 (г), применив тот же закон коммутации для потокосцепления, а затем, подставив эти зависимости в уравнения Кирхгофа, найти токи.
Запишем решение для потокосцепления в индуктивности Lt:
¥1 ~ Ч^у 4-Ч^св = Т1у 4-Ре*
где Т1У = Ltily 4- Mi2y = L.E/r. = 0,5 Вб.
По закону коммутации Ч^ (0) = Ч^ (0 —) = 0; следовательно, D = 'Pt (0) - 'Pty(0) = -0,5 Вб и ?t = 0,5(1 - е-20г).
Теперь из уравнения Кирхгофа i.r. 4- с№./dt = Е определим ток
й =	=	А.
г. г. dt
Аналогично
= Ч*2У +	= %у + Ge*,
Е /----- г
где = L2i2y 4- Mi.y = —yL.L2 = 0,5 [/2 Вб.
ri
При t — 0 потокосцепление Ч*2 (0) = Ч*2 (0—) = 0 = 0,5 ]/1 4-+ G, откуда G= -O,5j/2 Вб и Ч>2 =0,5j/2(l -е-20') Вб.
Из уравнения Кирхгофа i2r2 + d^¥2/dt = 0 получим:
1 <М2 ч dt
8.177.	Определить ток i2 трансформатора (рис. 8.177) после коммутации при Е — 1 В; Li = 4 мГн; = 1 Ом; Ь2 = 2 мГн; С = 103 мкФ; коэффициент связи к = 1 и ис(0-) = = 100 В.
8.178.	В схеме рис. 8.178 определить ток it после коммутации.
Дано: е = 100sm(104г + 60°) В;, г =100 Ом; Ci = 4 мкФ; С2 = 1 мкФ; Ь2 = 10 мГн.
Рис. 8.178
8.179.	Определить ток ij трансформатора (рис. 8.179) после замыкания ключа, если е — 50sin(103t + 30°) В; = 0,1 Гн; л*! = 100 Ом; Ь2 = 0,2 Гн; г2 = 50 Ом; коэффициент связи к = 1.
8.7.	Расчет переходных процессов методом переменных состояния
8.180(	Р). Для схемы рис. 8.180 определить напряжение ис
и токи i, ii методом переменных состояния.
Решение. Начальное значение напряжения на емкости (рис. 8.180) мс(0) = Е/2.
Уравнение состояния (8.21) е( j получим из системы уравнений Кирхгофа, составленной для схемы рис. 8.180 после замыка
Рис. 8.180
ния ключа:
— ii + ic “1“ i2 4" i — 0; rii + ис = Е\
(1)
(2)
«с - ^2 = 0;
ис — ri — О,
(4)
подставив в (1) выражения для i, i2f полученные из (2) —(4) соответственно, и ic = Сduc/dt. В результате получим:
duc/dt =йс= - (З/rQ ис + (1/гС) Е.	(5)
Согласно обозначениям (8.21) имеем:
Вх
; v = ||E||.
Выходные переменные it и
х = || «с II;	=
х ~ II ис ||;
i находим из (2) и (4):
i = uc/r; ?! » -uJr + E/r
или в матричной форме
1
В соответствии с (8.22) имеем:
Поскольку порядок квадратной матрицы At равен единице, то согласно (8.25)
eAlf = «о II 1 II.	(9)
Коэффициент а0 определим по (8.26) из уравнения
II а» 11 = 1И Г1-Не4'||,	(10)
где собственное значение Xj матрицы Ai находим из (8.27): A (X) = det (X • || 1 II -Ai)=0, или % - (~3/гС) = 0, откуда Xi = ~3/гС.
Подставляя Xj в (10), получаем: _2_t «о = е тС , Таким образом, матричная экспоненциальная функция (9)
имеет вид:
_ _L
=е гС ' || 1 || =
_ JL е гС
(И)
С учетом соотношений (6), (И) и wc(0) = Е/2 запишем решение (8.24):
начального условия
X
II «с II = II еХ1' || •
+ (II еХ1' || - 1) х
Подставив это решение в (7), получим уравнение в матричной форме для выходных переменных i и ц:
2Е	Е
-------— е	гС
Зг	6г
т. е.
2Е	Е
*1 =	--~7~е
Зг	6г
з
гС 1
8.181(Р). В схеме рис. 8.181 определить все токи методом переменных состояния при Е = 30 В; г= 100 Ом; = г2 = = 200 Ом; С — 100 мкФ; L-0,1 Гн.
Решение. Начальные значения напряжения на емкости и тока в индивидуальности (рис. 8.181) равны:
ис(0) = Ег2/(г + г2) = 20 В; iL(0) « Е/(г + г2) = 0,1 А. (1)
Запишем для схемы рис. 8.181 систему уравнений Кирхгофа:
i - ic - k = 0;	(2)
ri + rjc + ис = Е;	(3)
+ uc — Ldijdt = 0,	(4)
где ic = C duc/dt.
Решив совместно уравнения (2) и (3), найдем:
Подставив в (4) ток ic == Cduc/dt и (5), получим:
Система уравнений (5) и (6) в матричной форме записи — это система уравнений переменных состояния (8.21):
Для составления системы уравнений выходных переменных ic и i решим совместно (2) и (3), в результате получим:
и, решив совместно (2) и (8), найдем, что
1 ~ ~ у л г Uc + ». Zu?” IjL	г г	(9)
? + ?!	Г + ?!	Г + ?!
Запишем теперь уравнения (8) и (9) в матричной форме, т.е. систему уравнений выходных переменных (8.22):
где по (8.22)
Аг =
1
? + ?!
1	_2
зоо	з
1	2
300	3
• II Е ||, (10)
1 300
1 300
Матрицы Ai, Bi, А2, В2 можно определить и иначе, применяя метод наложения. Сначала находим матрицы уравнений (8,29), которые для схемы рис. 8.181 имеют вид:
ic — Hcc'Uc + Hciit + uL = HLCUc 4- HlJl + H/ee; 1
ic = Hlcuc + H1LiL + Hlee; i = H2cuc + H2LiL + H2ce, J
где ic = || ic ||; uc = || uc ||; iL = II iL II; uL = || uL ||; i = || i ||; e = = \\E\\.
Заменив в схеме рис. 8.181 емкость источником ЭДС и индуктивность источником тока, получим схему рис. 8.181Р, при помощи которой методом наложения определим матрицы Н с различными индексами.
При ис = 0, iL = 0 (рис. 8.181Р)
i = ic = E/(r + ?i); uL = ?iE/(? + ?i),
т. е.
Но Н1е Н?^
(12)
При Е = 0 ток iL источника тока равен нулю (рис. 8.181Р) j =zjc=: - Wc/(r + Г1); Ul = _ if = rUc/(r + Г1)? T< e<
При E = 0, uc — 0 (рис. 8.181P) i = r^/fr + r5); ic = e -~riL/(r + rj; uL = rxic ==	+ rt), t. e.
Уравнения состояния (8.21) и уравнения выходных переменных (8.22) для схемы рис. 8.181 с учетом (8.28), (12)-(14) запишем в виде
что, конечно, совпадает с (7) и (10).
Определим собственные значения матрицы Ах из (8.27)
A(X) = det(X-l - AJ =
104
3
. 2 • 103
3
откуда Xj = -51,39 и X2 = -648,6.
Для определения матричной экспоненциальной функции eA,f необходимо из (8.26), которое для квадратной матрицы второго порядка Ах имеет вид:
«о 1 Xj -1
1 Х2
Х2 Хх
Х2 —Хх
-I 1
xir е
«1
определить коэффициенты а0 и Подставив в (15) найденные значения Хх и Х2, получим:
а0	1,086?*'- 8,605- 10'2?2'
«1
1,674- 10’3?1' - 1,674-10" 3?2'
Следовательно, матричная экспоненциальная функция (8 25) имеет вид:
?' = а01 + aiAj = (1,086?*' - 8,605  10’2?2') х
X
+ (1,674-10-3?*' - 1,674-10"3?2') х
102	10“
3	3
х 10	2-103	=
3	3
1,03?*' - 3,023 • 10~2?2'	-5,581?*' + 5,581?2'
5,581 • 10’3?*' - 5,581 • 10‘3?2' -3,023 • 10’2?*' + 1,03?2' ’
Учитывая, что v = || Е || от времени не зависит, решение уравнения состояния (8.21) можно записать в виде (8.24), в котором
х(0) =
ис(0)
it(0)
20
0,1
-2-10’2	10’1
-10'4	-10’3 ’
(17)
Подставив (16) и (17) в (8.24), получим: ис 21,72с4'- 1,721с12'
Х“ iL ~ 0,1177с4' - 0,3177с4'+ 0,3
т. е.
ис = 21,72е’51’39' - 1,721с"648-6', В;
iL = 0,3 + 0,1177е'51’39' - 0,3177е"648’6', А.
Теперь по (10) определим выходные переменные:
ic= -0,1116с"51’39' + 1,116е’648’6', А;
i = 0,3 + 6,047 • 10’3с"51’39' - 0,206е"648’6', А.
8Л82(Р). Решить задачу 8.63 методом переменных состояния.
Решение. Начальные значения напряжения на емкости и тока в индуктивности (рис. 8.63):
uc(0) = Е == 200 В; i2 (0) = J = 1 А.	(1)
Запишем для схемы рис. 8.63 после коммутации систему уравнений Кирхгофа:
— ii — J + 7’3 + 12 = 0;,	(2)
г171+нс=Е;	(3)
L di2/dt + r2i2 -ис = 0,	(4)
где 1*з = С duc/dt.
Решив совместно (2) и (3), найдем, иго duc 1	1  , 1 F I 1 ,
~dT= ~7^cc~ cl2 + ~^cE+cJ- (5)
Уравнение (4), разрешенное относительно производной di^jdty и уравнение (5) образуют систему уравнений переменных 346
состояния, которые запишем в матричной форме:
т.е. согласно (8.21)
E
J
(6)
(7)
-25 -25- 102
2 -200	’
>
(8)
Выразив из (3) ток
h = -uc/ri + ЕД1
и подставив его в (2), получим:
Ь = -«cAi “ h + E/rt + J.
Эти два уравнения, т. е. систему уравнений менных, запишем в матричной форме:
выходных
т.е. согласно (8 22)
Г1
10'2 0
10"2 1
пере-
да
(Ю)
Определяем собственные значения матрицы Ai из (8.27) А (%) = det{X  1 - Ai} =
= det
— 25 -25-Ю2
2 -200
X О
О X
= (X + 25) (X + 200) + 5 • 103 = О,
откуда kj = -61; Х2 = -164.
Коэффициенты а0 и матричной экспоненциальной функции eAt\ у которой Ai — квадратная матрица второго порядка, находим так же, как и в решении задачи 8.181Р:
а0 1,592?’'	- 0,5922г’2'
«1
9,709 • 10“ V1’ - 9,709 • 10* V2'
Аналогично вычислим и матричную экспоненциальную функцию (8.25):
1,35е4' - 0,3495/2'	- 24,27?1’ + 24,27?2'
е ‘ = 1,942  10*2еч‘ - 1,942  10* V2' - 0,3495г'1' + 1,35?2' ’
(И)
Решение уравнения состояния запишем по (8.24), в котором
х(0) =
«с(0)
«2(0>
200
1
-2-10*2 25-10*2
-2- 10*4 -25-10**
Ai"lBiV =
-150
-1,5
(12)
Подставив (11) и (12) в (8.24), получим: 150 + 79,61г4' - 29,61?2'
*= 1,5 + 1,146?1'-1,646е’‘2' ’
т. е.
ис = 150 + 79,61е*6" - 29,61е"164', В;
i2 = 1,5 + 1,146е*61' - 1,646е*164', А.
Теперь, подставив (13) в (9), получим выходные переменные:
i, =0,5 — 0,7961е*61' + 0,2961г*164<, А;
i3 = — 1,942е*61' + 1,942е*164', А.
8.183. Решить задачу 8.10 методом	переменных состояния.
8.184. Решить задачу 8.15 методом	переменных состояния.
8.185. Решить задачу 8.18 методом	переменных состояния.
8.186. Решить задачу 8.37 методом	переменных состояния.
8.187. Решить задачу 8.41 методом	переменных состояния.
8.188. Решить задачу 8.42 методом	переменных состояния.
8.189. Решить задачу 8.65 методом	переменных состояния.
8.190. Решить задачу 8.68 методом	переменных состояния.
8.191. Решить задачу 8.71 методом	переменных состояния.
8.192. Решить задачу 8.72 методом	переменных состояния.
8.193. Решить задачу 8.78 методом	переменных состояния.
8.194. Решить задачу 8.81 методом	переменных состояния.
Глава девятая
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Введение к гл. 9
Ввиду относительно быстрого протекания переходных процессов в реальных цепях с распределенными параметрами ЭДС синусоидальных источников промышленной частоты за рассматриваемые интервалы времени мало изменяются, так что их можно считать постоянными. Поэтому в этой главе надо считать, что заданы источники с постоянными ЭДС, кроме задач, в которых по условию заданы другие источники.
Напряжение и ток переходного процесса можно представить наложением соответственно напряжений и токов прямой и обратной волн, т. е. в виде
w ~ Нпр “Ь ^обр> i ~ $'пр ^обр»	(9*1)
где «пр, inp - напряжение и ток прямой волны, движущейся слева направо; м^р, - напряжение и ток обратной волны, движущейся справа налево.
При заданном на левом конце - в начале линии (х = 0) -напряжении их = (0, t) в интервале времени, когда отсутствует обратная волна, напряжение и ток прямой волны
^пр = ^пр (^» 0 =	^/^)» j'np Wnp/zB,	(9*2)
где с == 1/J/LoCo - скорость движения волны в линии без потерь или без искажений (если нет указаний, то считать в воздушной линии без потерь с = 3 • 10s км/с, в кабеле без потерь
с = 1,5 • 105 км/с); zB = ]/ь0/С0 — волновое сопротивление линии без потерь или без искажений; Lo и - индуктивность и емкость на единицу длины; время t отсчитывается с момента включения источника с напряжением в начале линии. В случае источника с постоянным напряжением = V по линии распространяется волна с прямоугольным фронтом.
Рис. 9.А
Рис. 9. Б
Распределение напряжения вдоль линии в заданный момент времени t =
«пр (х, «1) = U • 1 (X - ctj).	(9.3)
Напряжение в заданной точке линии с координатой х = иПр(*ь 0= U-Ht-tJ,	(9.4)
где ti = х t/с — время распространения волны до заданной точки линии; 1 (х) или 1 (г) — единичные функции.
Для определения напряжения и2 и тока i2 в конце линии длиной I с сопротивлением нагрузки — пассивным двухполюсником П можно составить расчетную схему (рис. 9.А), в которой ключ замыкается в момент прихода волны к концу линии, т. е. при t — l/с и 9 = t — 1/с — 0.
Напряжение обратной волны в конце линии
«2о6р = М2 (0) - м2пр (6)	(9.5)
и в любой точке
/ 2Z — х \	/	/ — х \
^обр (-^, 0 = ^2обр I	j = ^2обр I ®	~	)>	(9*6)
\	С* J	\	v J
ток обратной волны
^обр ^обр/^в*	(9»7)
При t > 2//с для расчета напряжений и токов применяется метод наложения всех последующих прямых и обратных волн. -
Если в конце линии с волновым сопротивлением zB1 включен пассивный четырехполюсник П с сосредоточенными параметрами, к выходу которого присоединена линия с волновым сопротивлением zb2, то для определения токов и напряжении четырехполюсника до момента времени, когда волна, отра
зившись от конца второй линии, дойдет до места соединения линий, можно пользоваться расчетной схемой рис. 9.Б. На схеме и в расчетных соотношениях одним штрихом обозначены величины, относящиеся к первой линии, а двумя штрихами — ко второй линии.
Если конец первой линии непосредственно соединен с началом второй линии (четырехполюсник отсутствует), то в месте соединения коэффициент преломления волны равен:
П = и'[/и'2„р = 2zb2/(zb1 + zb2),	(9.8)
и для первой линии коэффициент отражения волны
Р ~ ^2обр/^2пр = (^в2	^в1)/(^в1 “1“ ^в2)*	(9.9)
В этом случае
М'6р(х', 6') = pul (б* -	^р(х", п = пи'. ft" - £-\ (9.10)
где расстояние х" отсчитывается от начала второй линии, а время г" = 0' — от момента прихода волны к месту соединения линий.
Если на выходе четырехполюсника присоединено несколько линий, то в расчетной схеме для определения волн, возникающих в этих линиях, каждая из них заменяется волновым сопротивлением, присоединенным к выходу четырехполюсника.
Режим в линии при включении новой ветви рассчитывается методом наложения. Токи и напряжения в линии равны суммам соответственно токов и напряжений до коммутации и токов и напряжений, возникающих после включения в эту ветвь источника с напряжением, равным напряжению на разомкнутом ключе, при отсутствии других источников питания.
Режим в линии при отключении ветви определяется наложением на токи и напряжения линии до коммутации токов и напряжений, которые возникают при включении в коммутируемую ветвь источника с током, равным по значению, но противоположным по направлению току в ветви до ее отключения, при отсутствии других источников питания.
Формирование импульсов получают подбором линий (волновых сопротивлений и длин), а также параметров присоединенных к ним цепей с сосредоточенными постоянными (в общем случае — многополюсников! При расчете токов и напряжений можно применить наложение последовательно возникающих волн, как прямых, так и обратных.
При расчете операторным методом, кроме теоремы разложения (с решением в виде ряда Фурье), применяют и ре
шение Даламбера (в виде последовательности единичных функций). В линии без искажений волна распространяется без изменения формы, но с экспоненциально уменьшающимися
значениями напряжения и тока.
В операторной форме напряжение и ток в линии длиной I при сопротивлении нагрузки Z2 (р) и напряжении в начале
Z2 (р) ch f7(p) = t7i(p)-----------
с
Z2 (р) ch
Z2 (р) sh
%в
Z2 (р) ch
с
с
где zB = ]/l0/C0 - волновое сопротивление; а == г0/д0 — коэффициент ослабления; с = 1/1/ЕоСо — скорость волны.
Рис. 9.IP
9.1. Формирование прямой и обратной волн в линии без потерь
9.1(Р). Найти распределение напряжения и тока вдоль воздушной линии без потерь длиной 180 км с волновым сопротивлением 400 Ом через интервал времени tj = 1 мс после выключения в начале линии источника с напряжением щ = = Uoe~at = 100e“2‘103', кВ. В конце линии присоединена батарея конденсаторов общей емкостью С = 0,5 мкФ. .
Р е ш е н и е. За время = 1 мс волна проходит путь, равный 300 км. Следовательно, на участке линии х = 0 ч- 60 км наблюдается только прямая волна. Для прямой волны согласно (9.2) напряжение, кВ, и ток, А,
unp = 100c~21°3(t“x/c);
inp = MnpAB = 250e-2-^(r-/c) линии найдем по расчетной схеме
(рис. 9.1Р) классическим методом. Ток i2 равен сумме установившейся и свободной составляющих.
h = z2y + *2св-	П)
Напряжение в конце
Корни характеристического уравнения цепи определим из
уравнения	„ , .	, ,, с = 0
откуда после подстановки данных находим корень (один) р{ = - l/zBC = -5 * 103 с-1, т. е. /2св = ВеР1&, где В — постоянная. Ток i2y определим как частное решение дифференциального
уравнения схемы рис. 9.1Р:
где i2y = Ае~ав.
Для определения постоянной А подставим частное решение в дифференциальное уравнение:
Л z,-e0
-aO
5
откуда после интегрирования находим:
А = -2UoaC/(l - aCzB) = -333,33 А, т.е. i2r = — 333,33е"2'1о3в А и решение (1) для тока
|2 = -ЗЗЗ.ЗЗе-2103® + Бе-5’1®3’ А.
Для определения коэффициента В учтем начальное условие: конденсаторы не были заряжены, т. е. при 0=0 напряжение м2 (0) = 0 и ток
i2 (0) - 2U0/zB = 500 = -333,33 + В,
т.е. В = 833,33 А и ток
. i2 = — 333,33г"2'1о3® + 833,33е—5 ‘1о3®, А.
Ток обратной волны в конце линии найдем по (9.1):
'2обр = i2np - h = — - h = [583,33е~2'1о3в - 833,33г"5 ’1о3в], А. гв
Напряжение обратной волны по (9.7) «2обР = «2овр2« = 233,33г"2•1о3’ - 333,33е"5'10’9 кВ.
При х < 60 км 1 = 1пр и и = ипр, при х > 60 км
.„j,	, ,	- 2,"х'
-2-Ю (П-х/е) _ 583(33е
21 — х\~
с
j'np ^обр — 250e
-5- 10э	-
+ 833,ЗЗе V
12 п/р Ионкина П. А.
353
^пр “Ь Иобр —
„ ,л3,	, г	— 2  103 (г3 -
lOOe"210 (tl"x/c) + 233,33е	\
-5 - IO3 (h - 3L_L\ - 333,33е	' с '
кВ.
Ток i2 можно определить и операторным методом. По>рас-четной схеме рис. 9.1Р находим изображение тока
I ы = 2С7о/<Р + °) s 5 • 1Q2P == Fi (Р)
2[Р) zB + 1/рС p2 + 7-103p+ 107	F2(p)'
По теореме разложения (8.11) находим оригинал
;	(Р1) лхе , F1 (р2) р2е
,2 = К(К)е + W =
= -333,33г'2'1о3’ + 833,ЗЗе’5103’ А;
здесь корни Pi и р2 определяются из уравнения F2 (р) = О, откуда Pi = -2 • 103 с"1, р2 = -5 • 103 с“ \
Зная ток i2, находим все остальные величины.
9.2.	В конце воздушной линии (рис. 9.2) длиной I - 120 км с волновым сопротивлением zB = 500 Ом присоединен приемник с сопротивлением г = 100 Ом. Линия подключается к источнику постоянной ЭДС с параметрами Е = 100 кВ; гвт = 100 Ом.
Построить зависимость напряжения в конце линии от времени и2 (г) в интервале 0— 1500 мкс после коммутации.
9.3.	На катушку с индуктивностью Ь2 = 0,2 Гн падает волна, напряжение Uj которой изменяется в начале линии по закону, изображенному на рис. 9.3. Волновое сопротивление линии zB = 400 Ом; длина линии / = 300 км.
Построить распределение тока вдоль линии через время ti = 1,75 мс после начала движения волны от начала линии.
9.4.	В конце воздушной линии (/ = 150 км; zB = 500 Ом) включены параллельно соединенные конденсатор емкостью С = 1 мкФ и резистор с сопротивлением г = 1000 Ом. Линия
присоединяется к источнику с постоянным напряжением U = 300 кВ.
Построить кривые изменения напряжения и тока в зависимости от времени в интервале 0 — 1,4 мс в точке Л, находящейся на расстояний — 60 км от конца линии, считая за начало отсчета времени момент присоединения линии к источнику.
9.5.	К воздушной линии (/ = 30 км; z3 = 400 Ом) в конце присоединен двухполюсник, параметры которого в последовательной схеме замещения заданы: г2 = 100 Ом; L2 = 100 мГн. Линия подключается к источнику с постоянным напряжением U = 20,2 кВ.
Записать выражения для построения графиков распределения напряжения и тока вдоль линии для момента времени, когда волна, отразившись от конца, дойдет до середины линии. Найти напряжение на активном сопротивлении двухполюсника в этот момент времени.
9.6.	У коаксиального кабеля длиной / = 10 м с волновым сопротивлением zB = 50 Ом сопротивление нагрузки активное и равно г2 = 150 Ом. Кабель подключается к источнику синусоидального напряжения и = 100 sin (art + л/6) В с частотой f = 10 мГц. Скорость волны в кабеле с = 1,5-105 км/с.
Построить графики распределения напряжения и тока вдоль линии через интервал времени =0,1 мкс после подключения.
9.2.	Переход волны с одной линии на другую
9.7(	Р). Между концом первой воздушной линии = 120 км; zB1 = 500 Ом) и началом второй (/2 ~ 30 км; zb2 = 400 Ом) включены реактор с индуктивностью L = 0,135 Гн и реостат с сопротивлением г = 600 Ом (рис. 9.7).
В конце второй линии емкость шин приемной подстанции С = 0,125 мкФ. В начале первой линии включается источник с постоянным напряжением U = 100 кВ.
Найти распределение напряжения вдоль линий в мо
Рис. 9.7
мент, когда волна, отразившись от конца второй линии, дойдет До ее начала.
Решение. Напряжение и ток прямых волн в первой линии постоянные: и^р = U = 100 кВ; i'ip = u^p/zB = 200 А.
Через время tj — ljc = 0,4 мс прямая волна достигнет конца первой линии (точка а на рис. 9.7). Расчетная схема для определения тока и напряжения в месте перехода волны с одной линии в другую дана на рис. 9.7Р, а, где 0' — время,
Рис. 9.7Р
отсчитываемое с момента прихода волны к концу первой линии.
Ток i'2 представим в виде суммы установившейся и свободной составляющих:
^2 ~ *2 у + *2св>
где !2у-----7-Г = 270’27 А-
2,1 + Ггв2/(Г + ZB2)
Корень характеристического уравнения найдем из уравне-
ния
Z13X (р) ZBl +
r(pL+z,2) г + z,2 + pL
откуда рх — — 5 • 103 с"1 и, следовательно, i2 = (270,27 + AeP1V) А.
Начальные условия: при 0'=0 ток if (0) = 0, т.е. по рис. 9.7Р, а
Г2 (0) = 2l7/(zB1 + г) = 181,818 = 270,27 + Л,
откуда А — —88,45 А и ток
Гг = (270,27 - 88,45е-5 ’1о3в') А.
Ток обратной волны в первой линии = ^ - ii = (-ТО,27 + 88,45е-5 • 1О’в') А.
Напряжение обратной волны в первой линии «;6р = 2B1i;6p = (-35,135 + 44,225е"5' 1о3«') кВ.
Напряжение в конце первой линии (рис. 9.7Р, а) и'2 = 2V - z,if2 =(64,86 + 44,22е’5 1о3’') кВ.
Ток в сопротивлении
ir = и'2/г = (108,1 + 73,7е-5' 1О’в) А.
Ток прямой волны в начале второй линии
'inp = 1'2 - ir = 162,17(1 - е’5 •1о3"') А.
Напряжение прямой волны в начале второй линии
M'i„P =	= 64,87 (1 - е-5 •1о3’ ) кВ.
За время 02 = li/c = 0,1 • 10“3 с прямая волна достигнет конца второй линии. Расчетная схема для определения тока и напряжения в конце второй линии дана на рис. 9.7Р, б, где 9" - время, отсчитываемое с момента прихода волны к концу второй линии, и напряжение
и'{ (0") = 64,87(1 - е’5 •1о3’' ) кВ.
Для определения тока i2 в схеме рис. 9.7Р,б применим интеграл Дюамеля:
i'i = 2и'{ (0) д (О") + 2 f [>? (0")/d0"]e..=t д (0" - т) dx, о
где и'{ (0) = 0 — напряжение прямой волны в начале второй линии при 0" = 0, и переходная проводимость
0(0") = — е-2 Ю4«"=	’ е-210«." См
z„2	400
(у характеристического уравнения схемы рис. 9.7Р, б один корень р2 = — 2 • 104 с~1).
После интегрирования находим ток
i'i = 108 (е“5'1о3’е'2',о4’") А.
То.к обратной волны в конце второй линии
>2обР = Ппр - i'l = (162,17 - 270, 17е~5' 1°3’" + Юве"2 1°4в") А.
Напряжение обратной волны в конце второй линии
и'мр = Z»2<2o6p = (64,87 - 108,06е-5 -1о3в" + 43,2е"2 ’1о4е") кВ.
Для рассматриваемого (по условию задачи) момента времени, когда обратная волна пройдет всю вторую линию, в формулу для и2обР следует вместо 9" подставить 92 = 12/с, т. е.
/	-5  ю3
Мо'бр = 1 64,87 - 108,Обе	с ' +
Искомое напряжение во второй линии и" = и'пР + и"бр.
В первой линии при х' С 60 км и' = и£р = 100 кВ, а при х' > 60 км
-5 1О3 292 - — и'= 1<р + и'бр = 64,865 + 44,225?
кВ.
9.8.	Между двумя кабельными линиями (zBi = 100 Ом; zb2 = 50 Ом) включена четвертьволновая согласующая линия с волновым сопротивлением zB = ]/zb]zb2 = 70,7 Ом- Длины кабельных линий много больше согласующей.
Найти распределение напряжения и тока вдоль согласующей линии после трех отражений от точки соединения согласующей линии со вторым кабелем при движений вдоль первого кабеля волны прямоугольной формы с напряжением и = 100 кВ.
9.9.	В месте соединения воздушной (1г =90 км; zB1 = = 400 Ом) и кабельной (12 =40 км; zb2 = 50 Ом) линий последовательно включен конденсатор емкостью С — 0,1 мкФ.
Найти напряжения и токи прямых и обратных волн в линиях через интервал времени =0,5 мс после подключения воздушной линии к генератору постоянного напряжения V = = 63,5 кВ.
9.10.	Волна в виде прямоугольного импульса длительностью 40 мкс с напряжением U = 100 кВ переходит из воздушной линии (li = 120 км; zB1 = 400 Ом) через катушку с индуктивностью L = 90 мГн (последовательное включение) в кабельную линию (12 = 30 км; гв2 = 50 Ом).
Построить график распределения напряжения и тока вдоль линий через интервал времени = 200 мкс после того, как волна достигла места соединения линий.
9.11.	Построить график _z 62'^2	распределения напряжения и
I	S	тока вдоль воздушных линий
Р	^5	(рис. 9.11) через 400 мкс после
„L	-L	подхода прямой волны в пер-
вой линии к узлу А.
рис. 9.Ц	Дано: U = 127 кВ; /1 = ^ =
= 150 км; zB1 = zb2 =®= 400 Ом; г = 200 Ом; С = 1 мкФ; L = 20 мГн.
9.12.	Построить график распределения напряжения и тока вдоль линий (рис. 9.12) для момента времени t2, когда прямая волна достигнет конца второй линии.
Напряжение источника питания U = 5,8 кВ. Параметры цепи: /j = 20 км; zB1 = 50 Ом (кабельная линия); 12 = 9 км; Zb2 = 400 Ом (воздушная линия); г = 100 Ом; L= 5 мГн.
Рис. 9.12
9.13.	Волна прямоугольной формы с напряжением U = = 10 кВ движется по кабелю длиной 1Л = 30 км с волновым сопротивлением zB1 — 50 Ом, который соединен с воздушной линией длиной 12 ~ 30 км с волновым сопротивлением
zb2 = 300 Ом (рис. 9.13).	- гв2,<'2
В месте соединения линий
включен последовательно ре- у I	£ = =
зистор с сопротивлением __ *	„
г = 50 Ом и в конце воздуш-
ной линии конденсатор ем-	рис 9^3
костью С = 0,1 мкФ.
Найти распределения напряжения и тока вдоль линий для момента времени t2 = 50 мкс после отражения волны от конца воздушной линии.
9.3. Волны в линиях при подключении и отключении ветвей
9.Н(Р). В начале воздушной линии с волновым сопротивлением zB = 500 Ом длиной / — 400 м присоединен генератор с постоянной ЭДС Е = 2000 В и внутренним сопротивлением гвт = 100 Ом, а в конце линии — приемник с сопротивлением г = 300 Ом.
Найти распределение тока и напряжения вдоль линии через время fi = l мкс после включения в середине линии реактора с индуктивностью L= 125 мкГн (рис. 9.14).
Решение. Ток и напряжение линии до коммутации
10 = £/(гвт + г) = 5 A; UQ = 10г = 1500 В.
Дополнительные токи и напряжения найдем при помощи расчетной схемы (9.14Р, а), где uab = UQ = 1500 В, применяя операторный метод.
Ток в индуктивности
Г м =	=	12 •106	= К
pL+zJl р(р + 2-106)	pF3(p)'
Из характеристического уравнения цепи Г3 (р) = О находим корень pt = — 2-106 с"1. Оригинал i'L определим по теореме разложения (8.12):
/МО)
Ft (0) +
— е-21°6') А.
Ц--
2-~
Рис. 9.14
Дополнительные токи в середине линии i’i = if2 = — ifL /2, которым соответствуют токи и напряжения волн
Ьобр = ^2пр ~
= -3(1 -е~2-1о6<'-х'с)), А;
^1обр ~ ^вЧобр = = -1500[1 -е-21°6(,-х/й] В;
^2пр = ^в^2пр = = —1500 [1 -в-2 ‘о6»-»«] В,
движущихся от середины линии
х
м
•i______
^2о^р
1оо 2§Рм цк 1/2 ^2пр
20.0^ 100 _2 1/2
к ее началу и концу, причем
здесь х отсчитывается от се-	рис 9.1 др
редины линии вправо для пра-
вой половины линии и влево — для левой половины линии.
Коэффициенты отражения от начала и конца линии соот-
ветственно равны:
Гвт 2В
Р1 =Т----ГТ-
^1лр
X
Л Г “ 2в
Р2 — “ Т " "
в
в
Токи и напряжения волн
„	/ I — х
-2-106! Г---
*1пр = Р1Чобр =	1 в
А, ^1пр ^вЧпр»
А, ^2обр ^в^2обр-
/ I — Y -2. 10*4/ -1—1 ^2обр Рз^2пр 0,75 1 а
Дополнительные напряжения и токи в линии после включения индуктивности получаются суммированием прямых и обратных волн:
U = ^1пр 4“ ^1обр> i Чпр ~~ Чобр»
U ~ ^2пр 4" ^2обр, i = 1*2пр	1*2обр*
На рис. 9.14Р, б и в показано распределение результирующих напряжения и тока вдоль
линий в момент времени tt:
a zg
“2
Гвт
Рис. 9.15
9.15(	Р). У воздушной линии длиной I = 400 м с волновым сопротивлением zB = 400 Ом в конце присоединен реактор с индуктивностью L=10 мГн (рис. 9.15). Линия отключается от' генератора с постоянной ЭДС Е = 5 кВ и внутренним сопротивлением гвт = 100 Ом.
Построить кривые распределения тока и напряжения вдоль линии через время ti = 1 мкс после отключения.
Решение. До коммутации напряжение и ток в линии Uо = 0; 10 = Е/гвт = 50
В расчетную схему (рис. 9.15Р, а) включается источник тока J = /0 = 50 А. Поэтому в начале линии f = -J = -50 А,
Рис. 9.15Р
напряжение и' — zBi’ — -20 кВ. Соответствующая волна за время ti пройдет путь Xj =	= 300 м. Распределение тока и напря-
жения показано на рис. 9.15Р, б и в.
9.16,	Воздушная линия (/ = 70 км; zB = 400 Ом), присоединенная к источнику постоянного напряжения U = 63,5 кВ, длительное время работала с разомкнутым концом.
Построить график распределения напряжения и тока вдоль линии через время tj — 0,2 мс после подключения к концу линии двухполюсника, который можно представить в виде последовательного соединения индуктивности L = 1 мГн и сопротивления г — 200 Ом.	Рис 9 17
9.17.	К концу воздушной линии (/± — 120 км; zBi = 400 Ом) с сопротивлением нагрузки — 200 Ом (рис. 9.17) подключается кабель (12 = 60 км; zb2 — 50 Ом), параметры двухполюсника в конце которого г2 = 150 Ом, С2 =0,5 мкФ. Параметры источника питания: ЭДС Е = 500 кВ, внутреннее сопротивление гвт = 800 Ом.
Построить график распределения напряжения, и тока вдоль линий для момента времени = 600 мкс после коммутации.
9.18.	В воздушных линиях без потерь, длительное время находившихся под напряжением U — 100 кВ, произошел обрыв в точке В (рис. 9.18).
Построить график распределения напряжения и тока вдоль линий для момента времени Г] = 140 мкс после коммутации. Параметры цепи: Ц =48 км; 12 = 13 = 24 км; zBt = zb2 = zb3 = = zB = 400 Ом; С = 0,5 мкФ; г = 600 Ом.
9.4.	Формирование импульсов
9.19(	Р). Определить зависимость тока от времени в середине разомкнутой линии без потерь длиною /, подключаемой в момент времени t = 0 к источнику постоянной ЭДС Е.
Решение. Общее решение Даламбера для напряжения и тока запишем в виде
U(p) = Ale^x + А2е^х;	(1)
1(р) = — (А1е-^-А2е^	(2)
2в
где у = y(p) = ]/pLQpCo=p]/LQCQ~p/c; At и Л2-постоянные, которые можно определить, если, например, известно напряжение в начале линии Uj = Е и сопротивление в конце линии z2.
Как следует из (1) и (2), при х = 0
(р) —	+ А2
и при х - I
U2 (р) =	+ 4^'; 12 (р) =	- A2eyI).
"в
Кроме того, U2 (р) = Z2 (р) 12 &)•
Рис. 9.19Р
Исключив из этой системы неизвестные U2 (р) и 12 (р), определим постоянные Ai и Л2. После подстановки постоянных в общее решение (1) и (2) получим:
UW - и. м	t ‘к7"О>
Z2 (р) ch yl + zB sh yl •
I(n\ = U1^ Z2(p)shy(l - x) + zBchy(l - x)
W z„	Z2 (p) ch yl + zB sh yl ’ U
где для рассматриваемой задачи Z2 (р) = оо; С/! (р) = Е/р.
При х = 1/2 по (4) получим:
Z/2	//2
Е/р е с - е Р с _ Е/р е-рх - е-3рт _ pplSc + е~р1!с ~~	1 + «?"4/п“
= —(е-Р' - е-3^) (1	+	+ ...) =
Р^В
=	_ е-5рт + е-7рт + е-9рт _ е-Ирт _ е-1Эрт +
Р^в
где т = (1/2)/с; выражение 1/(1 4- е-4рт) представлено как сумма убывающей геометрической прогрессии.
Искомый ток (рис. 9.19Р) представляет собой оригинал полученного изображения тока:
i (t) = — [1 (t — т) — 1 (t — Зт) — 1 (t — 5т) + 1 (t - 7т) + Zb
+ 1 (t - 9т) - 1 (t - 11Т) - 1 (t - 13т) +
Здесь учтено, что — е~рт.= 1 (t — Т).
Р
9.20.	Для формирования импульсов напряжения одной полярности применяется линия без потерь длиной /, в середине которой включен резистор с сопротивлением г = 2zB, а конец ее разомкнут (рис. 9.20). В момент времени t = 0 линия подключается к источнику постоянной ЭДС Е.
Определить импульсное напряжение иг и построить его зависимость от т =
9.21.	На рис. 9.21 представлена схема для формирования прямоугольных импульсов тока в сопротивлении нагрузки г. Схема состоит из трех линий без потерь одинаковой длины I с одинаковой скоростью движения волн.
Определить ток в сопротивлении нагрузки г.
9.5.	Волны в линии без искажении
9.22 ((Р). Получить выражение для напряжения и тока линии длиною I без искажений при включении ее к источнику постоянного напряжения U i = const. На конце линии сопротивление нагрузки активное и равно г2«
Решение. Обозначим: т = l/с; тх = х/с. При UY = const вместо (9.11) и (9.12) получим:

(р + я)(т-тх) , +
(р + «) (Т-Тх)
- (р + я) (т-тх)-— е	л
[е(р+а) (Т-Тх) — е~ (^+a)(T"Tx)j
U2	+гв[е«’^Н’-’х) + с-<р^Х’-ч)-|
~ РЪ Г2 [е(р+а) ’ + е~ "’+а) ’] + z„ [е(<’+’)’ - е~,<’+” ’] или, введя обозначение т = (r2 — zB)/(r2 + zB),
Ui е~(р+а)Тх + те’(р+а)(2г~Тх)
(Р)~ р	1 + ^-2(₽+а)т
„ 1
Представляя выражение ^_2(Р+а)Т в виде суммы ряда убывающей геометрической прогрессии, окончательно получаем:
тг/ \	Г “(Р + «)тх	- (р + я) (2т —тх)	-(р + я)(2т + т )
U (р) =---- I е + те	— те	—
Р
2 - (р + «) (4т-тх)	2 “ (р + «) (4т + тх)	з - (р + я) (6т-тх)
—	те	+ тге	4- те	х
Принимая во внимание, что ~е .= 1 (t — тх), находим оригинал полученного изображения:
и = Ui[e а’х • 1 (Г — тх) + те “(2т *х) • 1 (Г — 2т 4- тх) —
—	те а (2т+’х). I (г — 2т — тх) — т2е а (4т ’х) • 1 (t — 4т 4- тх) 4-
4- т2е Я(4т+Ьс). 2 (г — 4т — тх) 4-..
Аналогично
i = [е аТх • 1 (t - тх) - те “(2т ’х)  1 (t - 2т 4- тх) -
— те- а (2т+Тх). 1 (j — 2т — тх) 4- т2е а (4т tx) • 1 (t — 4т 4- тх) 4-
4-	т2е а(4т+Тх). / _ 4Т _
9.23.	Получить выражения для установившихся значений напряжения и тока задачи 9.22 в точке х,
9.24.	Получить выражения для напряжения и тока в точке с координатой х при подключении линии без искажений к источнику постоянного напряжения Ut = const и согласованной нагрузке на ее конце.
9.25.	Для короткозамкнутой линии длиною I без искажений, подключаемой к источнику постоянного напряжения Щ — = const, получить выражения для напряжения и тока в точке с координатой х.
Глава десятая
ЭЛЕМЕНТЫ СИНТЕЗА ЛИНЕЙНЫХ ЦЕПЕЙ
Введение к гл. 10
Двухполюсники без потерь. Частотная характеристика любого пассивного двухполюсника без потерь (реактивного) — зависимость реактивного сопротивления от частоты х(со) удовлетворяет условию dx/dw > 0, т. е. нули и полюсы характеристики чередуются. В частности, при со = 0 и при со -> оо получается либо нуль, либо полюс. В операторной форме входные сопротивление Z (р) и проводимость Y (р) должны быть реактансными функциями, например
Z(p)=W(p)/V(p),	(10.1)
где W (р) и К(р) — полиномы с вещественными положительными коэффициентами, степени которых отличаются на 1, причем один из полиномов содержит только четные степени р, а другой — нечетные, нули и полюсы попарно сопряженные, простые, расположены на мнимой оси плоскости р и чередуются.
По заданной частотной характеристике или реактансной функции двухполюсник можно реализовать любой из четырех типовых схем с минимально необходимым числом элементов (L и С).
Первая типовая (первая каноническая) схема (Фостера) состоит из параллельных контуров LC, соединенных последовательно; реализуется разложением реактансной функции Z(p) на простейшие дроби:
(1”л
i
где KQ - вычет в полюсе р = 0, соответствующем значению х (со) = — оо при (0 = 0,
KQ = lim pZ(p) при р -> 0;	(10.3)
2Kf — удвоенный вычет в полюсе р = ;соь соответствующем полюсу характеристики при резонансе токов в контуре на частоте со,,
2Ki = lim —Z (р) при р2 —со2;	(10.4)
Р
— вычет в полюсе р = оо, соответствующем значению 366
X (co) = ОО При co = co,
KT = lim Z(p}/p при p —> oo.	(Ю.5)
Каждая дробь суммы реализуется параллельным контуром с емкостью С( = 1/2К{ и индуктивностью Lf = 2Kf/co?, первое слагаемое — емкостью Со = 1/К0 и последнее — индуктивностью = К да (неполные контуры).
Вторая типовая (вторая каноническая) схема (Фостера) состоит из последовательных контуров LC, соединенных параллельно; реализуется разложением реактансной функции У (р) = 1 /Z (р) на простейшие дроби так же, как Z (р) первой канонической схемы. Но в этом случае каждая дробь суммы реализуется контуром с индуктивностью L{ = l/2Kt и емкостью С{ = 2Xf/co?, первое слагаемое — индуктивностью Lo = 1/К0 и последнее — емкостью Сда = Кх.
Третья типовая (первая цепная) схема (Кауэра) состоит из продольно включаемых индуктивностей и поперечно включаемых емкостей; реализуется разложением Z(p) в цепную дробь с последовательным выделением полюсов при р = оо:
Z(P)=^ = PM +-----------1
(10.6)
где полиномы W (р) и V (р) нужно расположить по убывающим степеням р. Если у Z(p) нет полюса при р = оо, то индуктивность отсутствует и разложение нужно начинать с выделения емкости С2 у У (р) (полюс при р = оо).
Четвертая типовая (вторая) схема (Кауэра) состоит из продольно включаемых емкостей и поперечно включаемых индуктивностей’; реализуется разложением Z (р) в цепную дробь с последовательным выделением полюсов при р = 0:
(Ю.7)
где полиномы IV (р) и V (р) нужно расположить по возрастающим степеням р. Если у Z (р) нет полюса при р = 0, то продольная емкость Ci отсутствует и разложение нужно начинать с выделения индуктивности L'2 у У (р) (полюс при р = 0).
Двухполюсники с потерями. Входные функции пассивного двухполюсника с потерями Z(p) = W (p)/V(p) и y(p) = l/Z(p) должны быть положительными вещественными функциями (ПВФ).
Если полюсы входной функции расположены только на отрицательной действительной полуоси плоскости р, то ее можно разложить на простейшие дроби. В частности, для rC-двухполюсника (содержащего только элементы г и С) сопротивление
z(p}=^+y^+Kxt	(ш)
т
где
Ко = Нт Р% (р) при р -* 0;
Кт = lim (р + ат) Z (р) при р-»-ат;
K^-VimZip) при р —> оо.
(Ю.9) (10.10) (10.11)
Каждая дробь суммы реализуется параллельным гС-кон-туром с элементами Ст = 1/Km; rm = К„/ат, первое слагаемое — емкостью Со = 1/К0, последнее — активным сопротивлением = Кю (неполные контуры). Все контуры соединены последовательно (первая каноническая схема). Проводимость гС-двухполюсника
у (р) = ко + У + к„р,	(10.12)
/ J р +
п где
Ко = Ит У (р) при р —> 0;	(10.13)
Кп = Нт У (р) при р->-ап;	(10.14)
р
Кда = lim У (р)/р при р —> оо.	(10.15)
Каждая дробь суммы реализуется последовательным гС-контуром с элементами rn = 1/К„; Сп — первое слагаемое — сопротивлением г0 = 1/К0, последнее — емкостью Сед = = Кда (неполные контуры). Все контуры соединены параллельно (вторая каноническая схема).
Нули входной функции гС-двухполюсника также лежат на отрицательной действительной полуоси и чередуются с полюсами, причем у Z (р), ближайший к началу координат - полюс, а У У (р) - нуль.
Разложением входной функции Z (р) в цепную дробь реализуются цепные схемы, аналогичные схемам двухполюсников без потерь (в которых индуктивности заменяются сопротивлениями).
Для rL-двухполюсника Z(p) записывается по (10.12). Каждая дробь реализуется параллельным rL-контуром с элементами r„ = Кп; Ln = К.п/&„ первое слагаемое — сопротивлением Го = Ко и последнее — индуктивностью	(неполные
контуры). Все контуры соединены последовательно.
Проводимость rL-двухполюсника записывается по (10.8). Каждая дробь реализуется последовательным rL-контуром с элементами Lm = \/Кт; rm = первое слагаемое — сопротивлением гда = 1/Коо, последнее — индуктивностью Lo = 1/К0 (неполные контуры). Все контуры соединены параллельно.
Если Z (р) имеет еще простые полюсы на мнимой оси, то сначала можно выделить слагаемые (10.2), т.е. реактансную функцию Zp (р), и реализовать часть двухполюсника из LC-элементов. Разность Z (р) - Zp (р) = Zx (р) будет ПВФ, и можно приступать к ее реализации. Если У (р) имеет простые полюсы на мнимой оси [т. е. Z (р) — нули], то разложением на простейшие дроби аналогично (10.2) можно выделить реактансную функцию Ур (р). Разность У (р) — Ур (р) = yj (р) будет ПВФ.
Мостовая схема четырехполюсника. У мостовой (Х-образ-ной) симметричной схемы четырехполюсника (см. табл. 4.2) с согласованной нагрузкой — активным сопротивлением гн передаточные функции по напряжению Ни(р) = U2 (р)/1/1 (р) и току Hi(p) = h (Р)Д1 (р) одинаковы и равны:
Ни (р) = Н{ (р) =
М(р) _ 1 - |/Zt (p)/Z2 (р)
N(p} ~ 1 + ]/zt (p)/Z2 (р) ’
(10.16)
Если четырехполюсник состоит из обратных двухполюсников, т. е. ’Zi (р) Z2 (р) = k2 = const и гн = к, то
„ , 1	1 - Z1 (р)/к
Hv W = ~1 + w	(10Л7)
и функция
(10.18)
должна быть ПВФ. В частности, у четырехполюсника без потерь М (р) = У(-р) и Zi (р) - реактансная функция.
У мостового симметричного четырехполюсника без потерь с активным сопротивлением нагрузки г„ (не обязательно согласованной) передаточное сопротивление
(Р) _ М(р) Z21(p)
Л(Р) N(p) 1 + Zu(p)Ah’
(10.19)
где М(р) — четный или нечетный полином; Z21 и - коэффициенты уравнений типа Z, и для мостовой симметричной схемы (см. табл. 4.2)
Zi^VHZz + ZJ; Z21 = 1/2(Z2-Z1), откуда сопротивления схемы
Zi (р) = Zu (р) - Z21 (р); Z2 (р) = Zn (р) + Z21 (р) (10.20) должны быть реактансными функциями.
Для реализации нужно заданную функцию Hz (р) привести к виду (10.19), разделив полином N (р) на четную и нечетную части и поделив М (р) и N (р) на четную часть N (р), если М (р) — нечетный, или на нечетную часть N (р), если М (р) -четный.
В задачах данной главы все сопротивления заданы в омах, а проводимости в сименсах.
10.1.	Двухполюсники без потерь
10.1	(Р). Найти параметры двухполюсника (рис. 10.1), резонансные частоты которого =650 Гц, /2 = 1130 Гц и на частоте /'=950 Гц входное сопротивление индуктивное и
Решение. Двухполюсник (рис. 10.1) составлен как вторая каноническая схема. Построим частотную характеристику х (со) этой схемы (рис. 10.1Р), которая имеет две заданные точки резонанса, т.е. заданные нуль и полюс. Так как при частоте со' реактивное сопротивление х' > 0 (индуктивное) и характеристика должна удовлетворять условию dx/dw > 0, то при частоте сох =2^ =4080 рад/с у характеристики нуль, а при частоте со2 = 2тт/2 = 7100 рад/с - полюс и в начале координат —
полюс.
Комплексное сопротивление двухполюсника следует запи
сать в виде
К со? - со2 Z (усо) = ----------=------г,
v /со со 2 — со2
(1)
соответствующем характеристике рис. 10.1Р (обеспечивает показанные на рисунке нули при частотах cot; со = оо и полюсы при частотах со = 0; со2).
При частоте со7 = 2nf — 5990 рад/с задано сопротивление 2 (/оУ) — jx' = /2300 Ом и из формулы (1) определяется коэффициент К = 107.
В операторной форме после замены /со = р и — со2 = р2 сопротивление, Ом, и проводимость, См, равны:
_ 107 Р2 + 408°2	у Р Р2 + 71002
ZW~ р р2 + 71002; У (Р) - Ю7 р2 + 40802 ’
Параметры второй канонической схемы определим разложением проводимости на простейшие дроби (10.2):
У = р2 + 40802 +Кя,Р	(2>
[у проводимости У (р) полюсы в бесконечности и при частоте со! =4080 рад/с]. Вычеты: при р -► J4O8O и р2 -> -40802
2К! = lim
р2 + 40802 Р
Y (р) = lim
р2 + 71002
107
= 3,4 =
1
т. е. Lj =0,294 Гн; = l/co2/^ =0,204 мкФ; при р-► оо = = lim У (р)/р = 1/107 = С3 и С3 = 0,1 мкФ.
10.2(Р). По заданной частотной характеристике х (со) реак-
10.2) составить четыре типовые
тивного двухполюсника (рис. схемы. Известны частоты по-люсов/! = 100 кГц,/3 = 250 кГц, частоты нулей fQ = 0, f2 = = 180 кГц, /ж = оо и сопротивление x't = 4 кОм при частоте Г = 50 кГц.
Решение Составим сначала по частотной характеристике входное сопротивление в комплексной форме:
Z(Jco) -JcaK
Рис. 10.2
(col ~ Ц2)
(со? - со2) (со2 - со2) ’
где coi = 628 • 103 рад/с, со2 = 1130 • 103 рад/с, со3 = 1570-103 рад/с и коэффициент К = 7,7 • 109 определяется из (1) при со = со' = = 2л/' и Z(jco') = ;х'.
В операторной форме
Z(p)= FF(p)/K(p),	(2)
где W (р) = 7,7 • 109р (р2 4- со!) = 7,7 • 109 р (р2 + 1276 • 109) = 7,7 х х 109р3 4- 9,8 • 1021р; V (р) - (р2 + со2) (р2 4- со2) = (р2 4- 395 х х 109)(р2 4- 28,6- 109) = р4 4- 28,6- 101 У 4- 9,75 • 1023.
Так как характеристика х (со) и функция Z (р) не имеют полюсов в начале координат и в бесконечности, то Z (р) раскладывается на две простейшие дроби вида 2Kf (р)/(р2 + «?) и первая каноническая схема состоит из двух параллельных
Рис. 10.2Р
контуров с резонансными частотами (полюсами) а>! и со3 (рис. 10.2Р, а). По (10.4) при р2 —со2 — -395- 109
1 r Р2 4-0)? Ж(р) ..	109(р2 + 1276-109)
G	p V (p)	0,13 (p2 4- 2462 • 109)
и Cj = 0,30 нФ; Li = 27<i/o)2 = I/gJiG = 8,22 мГн при p2 — co2 = —2462 • 109
аналогично
W(p)
V(P)
и C3 = 0,23 нФ; L3 = l/co?C3 = 1,75 мГн.
Для составления второй канонической схемы нужно разложить на простейшие дроби входную проводимость У (р) = = 1/Z (р), полюсы которой совпадают с нулями входного сопротивления, т.е. будут при частотах со = 0, со2 и со — оо. Следовательно, по (10.2)
Г(р) =
_ Ко 2К2р W(p)~ Р + p2 + wf
т. е. схема состоит из параллельно соединенных индуктивности Lq = 1/К05 последовательного контура Ь2С2 и емкости
= (рис. 10.2Р, б). По (10.3)-(10.5):
при р ->• 0 Ко = -Д-= lim р и Lo = 10,0 мГн;
W \р)
lim р2 + ®2 V W = hm -р- W
при
Ь2 = 9,4 при
Р2 -> -coi 2К2 = — ь2 мГн, С2 = 1/(0г^2 =0,084 нФ;
р -» со К„ = С„ = lim = 0,13 нФ.
и
Первая цепная схема начинается с поперечной емкости С2, так как характеристика х (со) и сопротивление Z (р) не имеют полюса в бесконечности. Для выделения емкости С2 (рис. 10.2Р, в) представим входную проводимость в виде У (р) = V {p)/W (р) = = рС2 + У1 (р). Чтобы выделить слагаемое рС2 [целая часть У(р)], разделим V(р) на W (р):
р4 + 28,6 • 101 * * * * * 7 * * * * * * * * У + 9,75 • 1023 |7,7- 109р3 + 9,8» 1021р
р4 + 12,7 • 1011р2	0,13 • 10 р = рС2.
15,9 • 10Х1р2 + 9,75 • 1023
Остаток
15,9 •1011р2 +9,75  1023 = У,(р)
7,7-109р3 + 9,8-1021р	W(p)'
Из обратной величины остатка, т.е. Z{ (р), выделим продольную индуктивность L'3. Для этого представим сопротивление в виде Zj (р) = W (p)/V], (р) = pL3 + Z2 (р). Чтобы выделить слагаемое pL'3, разделим W(p) на V\ (р):
7,7 • 109р3 + 9,8 • 1021р 115,9- 10ир2 + 9,75-1023
>~7,7»109р3 + 4,7»102^р	4,85 - 10" Зр = pL'3.
5,1 • 10я р
Остаток
7 . , 5,1-1021р_________________W2(p)
2lP> 15,9 • 10“р2 + 9,75 • 1023	^(р) ’
Аналогично ИЗ проводимости У2 (р) = 1/^2 (р) —	(Р)/^2 (р)
выделяем слагаемое pQ:
15,9 • 10* 1р2 + 9,75  1023 |5,1 • 1021р
15,9 -101 У	0,31 • 10 -9p = pQ.
9,75 • 1023
Остаток
У3 (р) = 9,75 • 1023/5,1 • 1021р = V3 (p)/W2 (р).
Делением 1Г2 (р) на V3 (р) находим, что L's = 5,25 мГн. Остатка нет, т, е. реализация цепной схемы закончена.
Вторая цепная схема начинается с поперечной индуктивности L2, так как характеристика х(со) и сопротивление Z (р) не имеют полюса в начале координат. Для выделения индуктивности L'2 представим Y (р) в виде У (р) = V (p)/W (р) = = l/pZ-2 + У1 (р). Чтобы выделить 1/рГ2, разделим V (р) на И7 (р), записав полиномы по возрастающим степеням р:
9,75  1023 + 28,6- 10пр2 + р4 [9,8- 1021р + 7,7 > 109р3 “9,75 • 1023 + 7,7 * 10пр2	99,5/р = 1/рГ2,
20,9- 101гр2 +р4
т.е. Ь2 % 10,0 мГн (рис. 10.2Р,г).
Заменяя остаток У1 (р) = V\ (p)/W(p) обратной функцией Zi (Р) = 1/Vi (Р) = ^(р)/^ (р) = 1/рС'3 + Z2 (р), выделяем 1/рС3, где С3 — 0,22 нФ, делением W (р) на VY (р) и находим остаток Z2 (р) = И'г (р)/И1 (р). У обратной функции У2 (р) = 1/Z2 (р) = =	(р)/^2 (р) = Vp^-4 + Уз (р) выделяем 1/pZi, где 14 = 1,4 мГн,
делением V\ (р) на W2 (р) и находим остаток У3(р) = = V3 (p)/W2 (р). Обратная функция Z3 = 1/рС'5 дает значение емкости С5 = 0,33 нФ.
10.3.	Составить вторую цепную схему для двухполюсника рис. 10.3 при Lt = 8 мГн, Cj =0,05 мкФ, L3 = 15 мГн, С3 = = 0,08 мкФ.
10.4.	Составить первую каноническую схему для двухполюсника задачи 10.1.
10.5.	Задана частотная характеристика реактивного двухполюсника: резонансные частоты j\ =0,5 МГц, f2 — 2 МГц; при частоте/' = 1 МГц сопротивление емкостное и численно равно 20 кОм.
Реализовать двухполюсник первой канонической схемой.
10.6.	Частотная характеристика двухполюсника рис. 10.1 построена на рис. 10.1Р.
Построить качественно характеристику х(о)) этого двухполюсника после включения между точками а и б: 1) индуктивности; 2) емкости; 3) последовательного контура LC; 4) параллельного контура LC с резонансной частотой, большей со2.
10.7.	Двухполюсник без потерь задан входной реактансной функцией (в омах) . 1Q_ 13р3 +	. w- 5р
1,6-10~17р4 + 17,7  10-9р + 2,0 ’
Составить две канонические и две цепные схемы, реализующие двухполюсник по заданной входной функции.
10.8.	По заданной входной проводимости двухполюсника без потерь (в сименсах)
_ lnn (р2 + 106)(р2 + 9  106) W р(р2+4-106)(р2 + 25-106)
найти элементы первой и второй кононических схем.
10.9.	Проверить, относится ли к реактансным функция входной проводимости
ч Р4+ 10V+9-1012
" р5 + 29 • 106р3 + 1014р ’
Рис. 10.10Р
Рис. 10.3
10.10(	Р). Для заданного двухполюсника (рис. 10.1) с параметрами Li =0,3 Гн; Ci =0,2 мкФ; С3 =0,1 мкФ составить схему и найти значения элементов обратного двухполюсника; произведение входных сопротивлений обоих двухполюсников должно равняться 2 кОм2 на частоте 950 Гц.
Решение. При составлении обратного двухполюсника последовательно включенные элементы и участки заменяются параллельно включенными элементами и участками и наоборот. Для цепи рис. 10.1 последовательно соединенные элементы Li и Ci с сопротивлениями Z{ = jtoLi и Z2 = —yl/coCi заменяются параллельно включенными Z\ и Z2 (рис. 10.ЮР). Элемент С3 с сопротивлением Z3 = —Jl/coC3, соединенный параллельно 'с участком Zi 4- Z2, заменяется сопротивлением Z3, включенным последовательно с параллельно соединенными Z'i и Z'2. Произведение сопротивлений ZiZi; Z2Z'2; Z3Z3 должно равняться одному и тому же значению к2 = 2 кОм2 = = 2 • 106 Ом2.
По известному значению Li находим Z\ = k2/Zr — = H/jcoLi = 1/jcoC'i, т. e. Ci = Lj//c2 = 0,15 мкФ. Аналогично Z2 = k2/Z2 = k^coCi = >L'2, t. e. L'2 = k2C{ — 0,4 Гн, и Z3 = = k2/Z3 = k2j(t)C3 = JcoL3, т.е. L'3 = k2C3 = 0,2 Гн.
10.11.	Для двухполюсника задачи 10.1 составить первую цепную схему.
10.12.	Для двухполюсника задачи 10.3 составить первую цепную схему.
10.2.	Двухполюсники с потерями. Мостовые четырех» полюсники
10.13(	Р). Задана входная функция двухполюсника с поте-
рями (ПВФ)
Z(p) =
р2 + 4р + 1
Р2 + Р
Составить первую каноническую и первую цепную схемы двухполюсника.
Решение. Нули входной функции: -0,28; —3,72 и полюсы: 0; —1 лежат на отрицательной действительной полуоси. Ближайший к началу координат — полюс. Следовательно, задана входная функция гС-двухполюсника.
Для составления первой канонической схемы раскладываем Z (р) на простейшие дроби (10.8), причем сумма состоит из одной дроби с а! = 1:
Z(p) = K0/p + K1/(p+l)+K00,
По (10.9)-(10.11) находим Ко = 1;	= 2;	= 1, т.е.
Со = 1/К0 =1 Ф; С1 = 1/Ki = 0,5 Ф;	= 2 Ом; =
— Кх — 1 Ом. Схема дана на рис. 10.13Р, а.
Для составления первой цепной схемы, состоящей из продольно включенных активных сопротивлений и поперечно включенных емкостей, раскладываем входную функцию в цепную дробь. Так как степень полинома числителя не меньше, чем знаменателя, то схема начинается с продольного сопротивления :	_	,
_Р2 + 4р + 1 |р2 + р
Р2 +Р 1 = ri
_р2 + р | Зр + 1
Р2 + Р/З p/3=pCi
Зр 4- 1 | 2р/3
9/2 = г'3
2р/3 = pCi.
Схема приведена на рис. 10.13Р, б, где г\ - 1 Ом; С> = = 1/3 Ф; г'з = 4,5 Ом; С\ = 2/3 Ф.
10.14.	Для входной функции задачи 10.13 составить вторую каноническую схему.
10.15.	По заданной входной функции гС-двухполюсника с потерями (ПВФ)
У(р)
р(р+ 1) р2 + 4р + 1
составить вторую цепную схему (с продольными емкостями и поперечными сопротивлениями).
Рис. 10.13Р
10.16.	Полиномы W (р) полюсника с потерями
и V (р) входной функции двух-
7( а -	_ 4р2 + 24р + 32
И(р) " р2 + 4р + 3
имеют нули: —2; —4, и —1; -3, т.е. находятся на отрицательной действительной полуоси и чередуются.
Выполнить реализацию четырех типовых схем двухполюсника.
10.17.	Выяснить, относится ли к ПВФ функция входного сопротивления
Z(p) =
10.18.	Определить, относится ли к ПВФ функция входной
проводимости »
2р2 4- 2р 4- 8 р2 + р 4- 1
10.19(	Р). По заданной ПВФ
W(p) 10"16р3 + 10’1Ор2+ 2-10”4р+100
Г(р) “	10"12р2 + 1
реализовать двухполюсник разложением входного сопротивления на простейшие дроби.
Решение. Полином V(р) имеет корни Pi = Jah = J106 и р\ = —ytOi = — J106 — два сопряженных полюса функции Z(p), расположенных на мнимой оси. Степень полинома W (р) выше, чем полинома V (р), т. е. функция Z (р) имеет полюс в оо. Следовательно, можно выделить из функции Z (р) слагаемые,
соответствующие реактансной функции (10.2)
7р W " р2 + <of к“р’
По (10.4) и (10.5) находим 2Kt = 108; Кх = Г4, т.е функцию Zp(p) можно реализовать параллельным контуром Ci — \/2Ki — 10"8 Ф; Li — 2К1/со2 = 10"4 Гн и последователь-HO С контуром включенной индуктивностью	= Ю“4 Гц.
Остается реализовать функцию Zj (р) = Z (р) — Zp (р) = 100. Это активное сопротивление г = 100 Ом, которое включается последовательно с контуром и индуктивностью Ьда.
10.20.	По заданной ПВФ
ч 10"2Ор3 + 10" 14р2 + 2 • 10"8р + 10“2
У(р) =------------1б~ V +1--------------
реализовать двухполюсник разложением входной проводимости на простейшие дроби.
10.21.	По заданной ПВФ
10"4р3 + 102p2 + 2-104p+ Ю10 2•10"2р2 + 104р
составить цепную схему двухполюсника, которая начинается с продольной емкости.
10.22.	Задана входная функция пассивного двухполюсника с потерями
_ 16р4 + 20р3 + 24р2 + 7р + 3 16р3 + 4р2 + 4р + 1
Реализовать двухполюсник при помощи разложения входной функции на простейшие дроби.
10.23(	Р). По заданной передаточной функции мостового симметричного четырехполюсника
2<10"3р + 200
2-10‘3р + 600
при сопротивлении согласованной нагрузки rH = 1 кОм состД* вить схему и определить ее параметры.
Решение. По (10.18) при к = гн получаем:
Z‘ = 10‘8р + 2 -10-3 ’
т.е. параллельное соединение емкости = 10“8 Ф и сопр£' тивления rt = 0,5 кОм. По формуле Z2 = k2/Zi находи*4
ч , ю' 2р + 2 • 103, т. е. последовательное соединение ин-тивности Ь2 = 0,01 Гн и сопротивления г2 = 2 кОм.
10.24.	Известна передаточная функция мостового симметричного четырехполюсника
„ . . _ 3-105-р
Ну (р) j _ 1о5 +
при сопротивлении согласованной нагрузки rH = 1 кОм.
Составить схему четырехполюсника и определить ее параметры.
10.25.	Для мостового симметричного четырехполюсника с согласованной нагрузкой заданы передаточная функция
104
Hv = 2р + 104
и сопротивление нагрузки гн — 100 Ом.
Составить схему четырехполюсника и найти значения ее элементов.
10.26(	F). Составить мостовую схему четырехполюсника без потерь и найти значения ее элементов, если сопротивление нагрузки гн = 400 Ом и передаточная функция
и гм = М(р) =	0.8р2 -4 -1011
zP> Nip) 2 • 10~3р2 + 400р + 109 '
Решение. Преобразуем передаточную функцию к виду (10.19). Так как М (р) — четный полином, то делим числитель и знаменатель на нечетную часть N(р), т.е. 400р:
нм- 2  10~3р — 109/р
z{P> 1 + 5 • 10-6р + 2,5 • 106/Р
Значит, Z21 (р) = 2 • 10'3р - 107р; Zu (р) = 2 • 10"Зр + 109/р.
По (10.20) Zl (р) = 2 • 1О?/Р = 1/рС,; Z2 (р) = 4 • 10“ Зр = pLs, т. е.
Г1 — 500 пФ; L2 = 4 мГн.
W.27. Задана передаточная функция
___________1Q12
- 4	|Q- Зр2 + |Q3p IQ9
Мостового симметричного четырехполюсника без потерь при сопротивлении нагрузки rH = 1 кОм.
Составить схему четырехполюсника и найти значения ее элементов.
ГЛАВА ОДИННАДЦАТАЯ
НЕЛИНЕЙНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКд
Введение к гл. И
Для расчета нелинейных цепей постоянного тока применяются графические, аналитические, графо-аналитические и численные методы. При расчете целесообразно предварительно провести преобразование схемы таким образом, чтобы упростить уравнения цепи. В частности, для цепи с одним нелинейным элементом можно преобразовать линейную часть схемы, применяя теорему об активном двухполюснике.
Для графического расчета цепи нужно характеристики всех ветвей записать в функции одного и того же аргумента. В этом случае система уравнений цепи приводится к одному уравнению с одним неизвестным. Решение часто целесообразно проводить методом пересечений, при котором нелинейное уравнение разбивается на две части
Л W=/2(4
после чего строятся характеристики (х) и f 2 (х) и решение определяется точкой их пересечения.
При аналитическом методе расчета можно рекомендовать аппроксимацию характеристик нелинейных элементов полиномами второй и третьей степени. В этом случае расчет сводится к решению квадратного или кубического уравнения.
Для численного расчета нелинейных цепей широко применяются итерационные методы: метод простой итерации и метод Ньютона.
При решении задачи методом простой итерации нелинейное
уравнение цепи	.
/(х) = О,
(11.1)
где х — искомая величина, частично разрешается относительно
этой величины:
X = <р (х).
(11.2)
расчет проводится по алгоритму Х»+1 = ф(хД
(11.3)
где к = 0, 1, 2 номер шага итерации.
При k — 0 начальное приближение х0 обычно находится оешением уравнения (11.1), в котором отброшены нелинейные члены. Условие сходимости метода
Метод простой итерации применяется и к расчету систем нелинейных уравнений. В этом случае аналитическая проверка условий сходимости весьма сложна, поэтому чаще всего сходимость проверяется непосредственно в процессе итераций.
		А пц.	I	
				
		-П ?	1	
				и
-10	Г	Г	0 5	В 10
				
		-оу -0.6		
				
Рис. 11.Г
При решении задачи методом Ньютона нелинейное уравнение (11.1) линеаризуется в окрестности каждого к-го приближения хк и решается линейное уравнение
f (хк) + f (хк) &хк = Q,	(11.5)
где f (хк) = df (x)/dx при х = xt. Из (11.5) поправка Дхк = = ~ f (xk)/f (хк). Расчет проводится по алгоритму
хк+1 = хк -f(xk)/f' (xk),	(11.6)
где к = 0,- 1, 2 ...-номер шага итерации. Начальное приближение х0 находится так же, как и в методе простой итерации. Условия сходимости метода Ньютона
df{x}/dx 0 0; d2f(x)/dx2 * 0.	(11.7)
Метод Ньютона может применяться и к системе нелинейных уравнений. В частности, когда цепь описывается двумя Уравнениями с двумя неизвестными
алгоритм
Л(х,у) = 0;/2 (х,у) = 0, расчета:
хк + 1 — Хк —
fi (хь Л) 3/1 (х*, ук)/ду
Л) c/2(xt, ук)/8у
J (х*, Л)
(11.8)
(И.9)
где
Ук + l Ук ~
J (xk, yk) =
8f i (**, yk)/8x Л (xk, yk)
Ук)/8х f2(xk, Ук)
j (xt, Ук)
Sf i (xk, yk)/8x 8f2(xk, yk)/8x
Sf i (xk, Ук)/ду 8fi(Xk, yk)/8y
(11.10)
(11.11)
9
— якобиан системы уравнений (11.8). Ввиду сложности аналитической проверки условий сходимости в этом случае целесообразно проверять сходимость в процессе итераций. Первое приближение метода Ньютона является графо-аналитическим методом линеаризации нелинейных характеристик.
В задачах данной главы итерационный процесс можно считать законченным в том случае, когда значения искомой величины на двух соседних шагах итерации отличаются не более чем на 3-4%.
Характеристики нелинейных элементов (резисторов), рассматриваемых в задачах § 11.1, приведены на рис. 11.А — Ц.Г, причем характеристики рис. 11.А, 11.Б симметричные.
11.1. Графический метод расчета
11.КР). Нелинейный двухполюсник (рис. 11.1) состоит из
последовательно включенных линейного резистора с сопротивлением г = 80 Ом и нелинейного резистора, характеристика
которого приведена
на рис. 11.А (кривая 1).
Построить: 1) вольт-амперную характеристику двухполюсника I(U 2) зависимость напряжения V на нелинейном элементе от входного напряжения Uv Определить ток I при ЭДС Е = 40 В.
Решение. 1) Цепь описывается уравнением, составленным по второму закону Кирхгофа,
Рис.11.1	Vi (/) = rl + и (I) = Ur (/) + V (I), (1)
т. е. алгебраическим выражением вольт-амперной характеристики пассивного двухполюсника. Построение этой характеристики приведено на рис. 11.1Р, а. Здесь 1 - характеристика Ur(l) линейного резистора; 2 - характеристика нелинейного резистора U (7); 3 — характеристика, полученная суммированием характеристик согласно уравнению (1), которая является иско-
- вольт-амперной характеристикой двухполюсника
Отмечая напряжения на входе цепи Щ (кривая 3) н3 нелинейном элементе U (кривая 2) при одинаковых значениях тока, строим зависимость U(U^ показанную на рис. б.
A
Рис. 11.1Р
При Е = U1 = 40 В ток I = 0,25 А определим непосредственно по построенной вольт-амперной характеристике двухполюсника-кривой 3 на рис. 11.1, а.
Если вольт-амперная характеристика двухполюсника не строится, то ток может быть найден методом пересечений. Запишем уравнение цепи в виде
U (I) = Е - г!
и построим (рис. 11.1Р, в) характеристики левой (кривая 2) и правой (прямая 4) частей этого уравнения. Равенство левой и правой частей соответствует точке их пересечения. В точке пересечения I = 0,25 A (U = 20 В).
Рис. 11.2	Рис. 11.3
И»2. В схеме рис. 11.2 г = 100 Ом, характеристика нелинейного элемента (симметричная) дана на рис. 11.Б (кривая 5).
Построить зависимость напряжения на выходе цепи 17а от вводного напряжения U Р
И«3. В схеме рис. 11.3	= 25 Ом, г2 = 75 Ом, характе-
ристика нелинейного элемента (симметричная) дана на рис. И.Б
(кривая 5). Построить зависимость выходного напряжения от входного Ui.

Определить, в каких пределах изменяется выходное напря. жение при изменении входного от 30 до 60 В.
Рис. 11.6
11.4.	Характеристики нелинейных элементов НЭ1 и НЭ2 (симметричные) схемы рис. 11.4 показаны на рис. 11.А (кривые 1 и 2 соответственно).
Определить при ЭДС Е = 35 В ток Z, напряжения Ui, U2 и мощность источника. Построить вольт-амперную характеристику цепи I(U) и зависимость напряжения U2 от напряжения источника U.
11.5.	В схеме рис. 11.5 ток источника J = O,35 А, характеристики нелинейных элементов НЭ1 и НЭ2 (симметричные) приведены на рис. 11.А — соответственно кривые 1 и 2.
Определить токи Ц, 12 нелинейных элементов и мощность источника. Построить вольт-амперную характеристику цепи I (и)'
11.6(	Р). В схемах двухполюсников рис. 11.6, а — е Е = 25 В и J = 0,2 А. Характеристика нелинейного элемента (симметричная) изображена на рис. И.Б (кривая 4).
Построить вольт-амперные характеристики для этих двух
полюсников.
решение. Для двухполюсника рис. 11.6,а по второму закону Кирхгофа и(1) = Е (/), где U (Л ” алгебраическое выражение вольт-амперной характеристики двухполюсника. Характеристика, построенная в соответствии с этим уравнением, показана на рис. 11.6Р.
Рис. 11.7
<- Рис. 11.6Р
11.7. К активным двухполюсникам задачи 11.6 (рис. 11.6, а и д) подключены пассивные двухполюсники: 1) задачи 11.4; 2) задачи 11.5.
Найти токи I и напряжения U двухполюсников (рис. 11.7).
11.8(Р). В схеме рис. 11.8 г — 200 Ом, Е = 20 В, диод Д
Построить вольт-амперную характеристику I(U) и зависимость выходного напряжения Ui от входного U.
Решение. Характеристика идеального диода (рис. 11.8Р,я) описывается выражениями: при /д > 0 напряжение UA = 0; при < 0 ток /д = 0.
13 п/р Ионкина П. А.
385
Запишем уравнение цепи (рис. 11.8) по второму закош, Кирхгофа
и(/) = г/ + сл(П, где УДГ) = Е — ил(Г).
При U > Е тока в цепи нет, поэтому = U. При U < £ диод проводит ток, напряжение на диоде (7д = 0 и = £ / = (U - Е)/г.
Вольт-амперная характеристика I (17) и зависимость (у) изображены на рис. 11.8Р, б и в.
Рис. 11.9
11.9,	В схеме (рис. 11.9) г = 200 Ом, диод Д идеальный.
Построить вольт-амперную характеристику двухполюсника Z (С7) и зависимость Ui (U) при: 1) Е = 0; 2) Е = 20 В.
11.10(	Р). в схеме рис. 11.10	=
= 1 кОм, г2 — 0,4 кОм, Е2 = 10 В. диоды идеальные.
Построить вольт-амперную харак
теристику двухполюсника I (U).
Решение. При U < Е2 диод Д t открыт, диод Д2 заперт, т.е. ток 12 = 0. Поэтому / — 119 где Ц = С7/гь так как в проводящем направлении напряжение [7j на диоде Д1 равно нулю.
Рис. 11.10
о
При U > Е2 оба диода открыты, напряжения 1/1=0 и и2 =0, ток I = Ц + /2, где л = (7/n; 12 = (17 - Е2)/г2.
Построение вольт-амперной характеристики показано на рис. 11. ЮР.
11.11,	В схеме рис. 11.11	= г2 = г3 — 2 кОм; Е2 = Ю
Е3 = 20 В; диоды идеальные.
Построить вольт-амперную характеристику двухполюсника.
11.12(Р). В схеме (рис. 11.12)	= 10 Ом; г2 = 20 Ом.
Характеристика опорного диода (стабилитрона Ст) приведена на рис. И.В.
Построить зависимость выходного напряжения U2 от вход-71 Найти токи при напряжении на входе: 1)	= 18 В;
НОГО
U = 6 в.
" решение. Уравнение цепи (по второму закону Кирхгофа) U. = г.Ц - U = гЛ + С/2,	(1)
где U ~~	&2‘
Чтобы построить характеристику U2(Ui), нужно получить для уравнения (1) все величины в зависимости от одного
параметра, например тока Ц. Сначала построим характеристи-ку
по уравнению (первый закон Кирхгофа)
Л (U) = /2 (U) - I (U) = - U/r2 - I (17),	(2)
которая показана на рис. 11.12Р, а. На рис. 11.12Р, б та же характеристика построена в координатах — С7(Л), т- е- ^(Л)-/ п Т°М Же РисУнке выполнено графическое решение уравнения U)> т.е. получена зависимость
Зависимость U2 (U показанная на рис. 11.12Р, в, построена по характеристикам и2(Ц) и (Ц) рис. 11.12Р,б. Из Рис- 1112Р, в следует, что при Ui > 16 В в цепи наблюдается режим стабилизации напряжения.
При известном напряжении U i на входе ток Ц определим По характеристике ^(/J на рис. 11.12Р,б; ток I2 = U2/r2, где 13*	387
U2 находим при известном напряжении Ui по зависимости построенной на рис. 11.12Р,в, и ток I диода вычислим по первому закону Кирхгофа: I =12 — Ц.
1)	При 171 = 18 В получим: ^=0,8 A; U2 = 10 в-/2 = 10/20 = 0,5 А; I = 0,5 - 0,8 = - 0,3 А; 2) при	= 6 в
находим: Zt = 0,2 A; U2 = 4 В; Z2 = 0,2 А; I = 0.
Рис. 11.13
Рис. 11.14
ПЛЗ. В схеме рис. 11.13	— 50 Ом; г2 = 200 Ом, Е = 30 В;
характеристика нелинейного элемента (симметричная) приведена на рис. И.А (кривая 2).
Определить токи.
Построить вольт-амперную характеристику Zx (Ц\) и зависимость U (Ui).
Рис. 11.14Р
11Л4(Р). На схеме рис. 11.14 сопротивления линейных резисторов указаны в омах; ток J = 0,4 А; характеристика нелинейного элемента дана на рис. 11.Г.
Найти напряжение и ток нелинейного элемента.
Решение. Для линейной части цепи составим эквивалентную схему, применяя теорему об активном двухполюснике (рис. 11.14Р, а, где Е = 0,8 В; гвх = 10 Ом).
Для эквивалентной схемы запишем уравнение
U(I)=E
е решим методом пересечений (рис. 11.14Р,б).
К°Т Абсцисса и ордината точки пересечения определяют искомые величины U = 0,5 В, / = 0,03 А.
11.15.	На схеме рис. 11.15 сопротивления линейных резисто-даны в омах; ЭДС Е - 100 В; характеристика нелинейного лемента (симметричная) приведена на рис. 11.А (кривая 2).
Найти токи /, /1, /2 и напряжение U на нелинейном элементе.
Рис. 11.15
Рис. 11.16-
Рис. 11.17
11.16.	В схеме рис. 11.16	=25 Ом; г2 = 25 Ом; г3 =
= 50 Ом; характеристика нелинейного резистора (симметричная) приведена на рис. 11.А (кривая 3).
Определить ток нелинейного резистора и мощность источника тока J = 3,2 А.
11.17.	В схеме рис. 11.17 J = 2,5 А; Е = 60 В. Нелинейный резистор имеет характеристику, изображенную на рис. 11.А (кривая 1), сопротивления линейных резисторов даны в омах.
Найти напряжение и ток нелинейного резистора.
11.18(	Р). В схеме рис. 11.18
=40 В; Е3 = 20 В; характе-
ристики нелинейных элементов (симметричные) приведены на Рис- И.А: НЭ1 - кривая 1; НЭ2 — кривая 2; НЭЗ — кривая 3.
Найти токи и напряжения нелинейных элементов.
Решение. Решение задачи целесообразно разделить на этапа. Сначала построим зависимости токов всех ветвей от одного и того же напряжения — в рассматриваемой схеме Двумя узлами от узлового напряжения Uab. Эти вольт-амперные характеристики
Uab	(Л); Uab = U2 (/2); Uab = U3 (/3) - Е3
изображены на рис. 11.18Р (кривые /, 2, 3 соответственно).
При построении учтена симметричность характеристик, осле этого графически решим уравнение, составленное по
первому закону Кирхгофа,
h (Uab) = 12 (Uab) + I3 (Uab), где все токи являются функциями одного и того же напряжения Uab.
Рис. 11.18
Рис. 11.18Р
Решение определяется точкой, в которой ток Ц (кривая 1) равен сумме токов 12 + /3 (кривая 4 на рис. 11.18Р). Для этой точки Uab = 15 В; Ц = 0,26 А; 12 = 0,06 А; 13 = 0,2 А. Напряжения на нелинейных элементах находим по характеристикам рис. 11.А: Ux =25 В; U2 = 15 В; U3 = 35 В.
Рис. 11.19
Рис. 11.20
11.19.	В схеме рис. 11.19 нелинейные элементы имеют характеристики (симметричные), приведенные на рис. И.А: НЭ1 и НЭЗ — кривая 1; НЭ2 — кривая 2; Е = 50 В.
Определить токи и напряжения нелинейных элементов; вычислить мощность источника ЭДС.
11.20.	В схеме рис. 11.20 г2 = 100 Ом; Е^ = 30 В; Е2 =40 В; нелинейные резисторы имеют характеристики (симметричные), изображенные на рис. 11.А: НЭ1 — кривая 1; НЭЗ - кривая 2.
Найти токи и напряжения на резисторах.
11.21.	Характеристики нелинейных элементов (симметричные) в схеме 11.21 приведены на рис. 11.А и 11.Б: НЭ1 — 390
кривая 1; НЭ2 — кривая 2; НЭЗ — кривая 5; ЭДС источников: £1 = 10 В; Е2 = 10 В; Е3 =40 В.
Определить суммарную мощность нелинейных резисторов.
11.22(	F). В схеме рис. 11.22 Е = я= 40 В; 7 = 0,2 А; характеристики нелинейных элементов (симметричные) изображены на рис. 11.А: НЭ1 — кривая I; НЭ2 - кривая 2.
Определить токи и напряжения нелинейных элементов.
Рис. 11.21
Решение. Характеристики ветвей 1 и 2 запишем в функции общего
узлового напряжения Uabi
= £-<?! (Л);	(О
иаЬ = и 2 (М	(2)
после чего графически решим уравнение, составленное по первому закону Кирхгофа,
Ii(Uab)=I2 (Uab)-J
(рис. 1L22P). Точка пересечения определяет напряжение Uab = = U2 = 30 В и ток Zi = 0,2 А.
’ Рис. 11.22
Рис. 1I.22P -
На основании уравнений (1), (2) и характеристик нелинейных элементов находим: = 10 В; /2 =0,4 А.
11.23.	В схеме рис. 11.23 характеристики нелинейных элементов НЭ1Ч НЭ2, НЭЗ (симметричные) приведены на рис. 11.А (кривая /, 2, 3 соответственно); Ei = 40 В; Е3 = 30 В; J = 0,2 А.
Найти токи и напряжения нелинейных элементов.
И.24(Р). Характеристики нелинейных элементов (симметричные) схемы рис. 11.24 изображены на рис. И.А: НЭ1 и НЭЗ - кривая 1; НЭ2 — кривая 3; г = 50 Ом; Е{ — 40 В; Е2 = = 15 В; 7 = 0,2 А.
Определить напряжение U и ток I нелинейного элемента НЭЗ, если: а) Е = 30 В; б) Е = - 30 В; в) Е = 0.
Решение, а). Для решения задачи преобразуем схему в неразветвленную, заменив две параллельные ветви с НЭ1 и НЭ2 эквивалентным нелинейным двухполюсником. Эквива
Рис. 11.23	Рис. 11.24,
Рис. 11.24Р
лентная схема показана на рис. 11.24Р, а и подробнее на рис. 11.24Р,б, причем источник тока заменен эквивалентным источником ЭДС с Е32 = rJ = 10 В.
Характеристику нелинейного двухполюсника Аг определим на основании	уравнений, составленных по законам	Кирхгофа:
1/12 = Е1 -1УЛЛ);	(1)
с12 = с2(/2)-е2;	(2)
7(С12) = 71((712)-/2([/12).	(3)
Характеристики (1), (2) и графическое решение уравнения (3) показаны	на	рис. 11.24Р,в (кривые 1, 2, 3	соответственно).
При построении учитывалась симметричность характеристик. 192
Рис. 11.25
После построения характеристики I (1712), или, что то же самое, U12 (Д находим ток в неразветвленной схеме рис. 11.24Р, б, ппя которой Л	Ui2(l) = U(I)+U32(I)-E.
Это уравнение решим методом пересечений (рис. 11.24Р,г). Точка пересечения определяет напряжение U = 8 В и ток / = 0,17 А.
11.25.	В схеме рис. 11.25 нелинейные элементы имеют характеристики (симметричные), приведенные на рис. 11.А: НЭ1, И ЭЗ - кривая 7; НЭ4, НЭ5 — кривая 2; НЭ 2 — кривая 3; Ei— = 40 В; Е2 = 15 В; Е3 = = 10 В; Е4 = 20 В.
Определить напряжение
НЭ5 при: а) Е = 0; б) Е = 30 В.
11.26	(Р). Транзистор Г включен по схеме с общим эмиттером (рис. 11.26, а). Дано: Ег = 1 В; Е2 = 20 В; — 500 Ом. Входная характеристика /б (1/бэ) и семейство выходных характеристик /к (икэ) изображены на рис. 11.26,6 и в.
U и ток I нелинейного элемента
Предполагая, что входная характеристика не зависит от напряжения Uкэ, построить зависимости тока /к и напряжения U2 от сопротивления г2.
Решение. По входной характеристике определим ток базы 7б из уравнения
^бэ (М = Ei —	(1)
Графическое решение методом пересечений приведено на рис. 11.26Р,а: ток базы /б = 600 мкА.
По выходной характеристике определим ток коллектора ZK и напряжение U2 = r2IK. Для коллекторной цепи транзистора (РИС. 11.26,47)
(ZK) = Е2 - г21к,	(2)
где характеристика UK3 (ZK), т. е. выходная характеристика ZK(O должна быть выбрана при найденном токе базы
Рис. 11.26Р
Z6 = 600 мкА. Графическое решение последнего уравнения методом пересечений приведено на рис. 11.26Р,б, где цифрами п = 1, 2, ..., 10 обозначены прямые, удовлетворяющие уравнению (2) при различных значениях г2 (табл. 11.26). В той же
Таблица 11.26
п	1	2	3	4	5	6	7	8	9	10
г2, Ом	0	50	100	200	300	400	500	600	800	1000
/к, мА	65	62	60	60	58	47	38	32	24	19
В	0	зл	6	12	17,5	19	19	19	19	19
таблице приведены результаты графического решения, т. е. даны значения тока ZK и напряжения t/2 = r2ZK.
Зависимости ZK(r2) и П2(г2) построены на рис. 11.26Р,в.
11.27.	Транзистор включен по схеме с общим эмиттером (рис. 11.27, а). Входная характеристика транзистора Z6(L736) дана на рис. 11.27,6 и семейство выходных характеристик ZK(Zr3K)~ на рис. 11.27,в. ЭДС Ег=0,3 В; Е2 = 20 В; сопротивление г х = 10 кОм.
Считая, что входная характеристика не зависит от напряжения Uж определить напряжение U2 на сопротивлении нагрузки при: а) г2 = 10 кОм; б) г2 = 20 кОм.
11.28.	Для схемы предыдущей задачи построить зависимость выходного напряжения U2 от ЭДС
11.29.	.Усилитель на ламповом триоде собран по схеме рис. 11.29, а. Семейство анодных характеристик триода приведено на рис. 11.29,6; ЭДС Е = 250 В; сопротивление нагрузки г = 5 кОм.
Определить анодный ток I и напряжение на сопротивлении нагрузки U„ при напряжении на сетке 1/с = - 4 В. Построить зависимость UH(UC).
11.2.	Аналитический метод расчета
11.30	(Р). Цепь состоит из последовательно соединенных линейного резистора с сопротивлением г = 10 Ом и нелинейного резистора, подключенных к источнику ЭДС Е = 18 В (см. рис. 11.1). Вольт-амперная характеристика нелинейного резистора при положительных значениях тока и напряжения I 0,
U > 0 может быть аппроксимирована зависимостью:
a)	U = al + Ы2, где а = 6 В/А; b = 2 В/А2;
б)	I = а<7 + ₽1/2, где а = 0,05 A/В, р = 0,003 А/В2.
Определить ток в цепи^
Решение, а). Запишем уравнение цепи по второму закону Кирхгофа
rl + U (/) = Е.
После подстановки зависимости U (I) получим квадратное уравнение
Ы2 + (г + a)I-E = Q или при заданных числовых значениях 2/2 + 16/- 18 = 0, откуда находим I = 1А.
Решение I = - 9 А не удовлетворяет условиям аппроксимации и потому не имеет смысла.
11.31	. В схеме рис. 11.13 rj =4 Ом; г2 — 1,33 Ом; Е = 6 В. Вольт-амперная характеристика нелинейного резистора может быть при U > 0, />0 аппроксимирована зависимостью:
а)	I — aU2, где а = 0,5 А/В2;
б)	U = W2, где b = 4 В/А2.
Определить все токи и напряжение на нелинейном резисторе U.
Рис. 11.32Р
Рис. 11.33
11*32(Р). На схеме рис. 11.16	= г2 = 40 Ом; г3 = 80 Ом;
J = 0,6 А. Характеристика нелинейного элемента при (7 > 0, I > 0 аппроксимирована зависимостью:
a)	U (I) = al + W2, где а = 30 В/А, b = 500 В/А2;
б)	/(17) = аС7 +pH2, где а = 2-10“3 А/В, р = 3-10'* А/В2.
Определить напряжение U и ток I нелинейного резистора.
Решение, а) При решении задачи целесообразно линейную часть цепи представить эквивалентной схемой (рис. 11.32Р). Применяя теорему об активном двухполюснике, получаем Е = 12 В; гвх = 40 Ом. Для схемы рис. 11.32Р по второму 396
закону Кирхгофа составим уравнение U (Z) + rBXZ = Е или после подстановки аппроксимирующей зависимости и числовых данных: 500Z2 + 70/ — 12 = 0, откуда ток I = 0,1 А (решение I s= — 0,24 А отброшено, поскольку аппроксимация справедлива только при положительных значениях тока). По заданной зависимости (а) находим напряжение U = 8 В.
11.33.	В диагональ моста (рис. 11.33) включен источник ЭДС Е = 18 В; сопротивления линейных резисторов указаны на схеме в омах. Характеристика нелинейного элемента при положительных значениях напряжения и тока задана выражением:
a)	Z = aC72, где а = 0,25 А/В2;.
б)	U = Ы2, где b = 2 В/А2.
Определить мощность нелинейного резистора.
11.34.	Определить показание вольтметра в цепи рис. 11.34, где ЭДС источника Е = 9 В, сопротивления линейных резисторов указаны на схеме в омах, характеристика нелинейного элемента аппроксимирована выражением: а) I = aU2, где а — 0,25 A/В2, или б) U = Ы\ где b = 2 В/A2, причем I > 0,
Рис. 11.35
11.35(	Р). В схеме рис. 11.35 £ = 30 В, г = 20 Ом, характеристики нелинейных элементов НЭ1 и НЭ2 соответственно заданы зависимостями Zt = a^U + a2U2, где = 0,01 A/В; а2 = 0,003 A/В2, и I2 = btU + b2U2, где Ьг = 0,04 A/В; Ь2 = = 0,002 A/В2, при U > 0.
Определить токи и напряжения нелинейных элементов.
Решение. Для схемы рис. 11.35 по законам Ома и Кирхгофа:
Z = (E-U)/r;	(1)
Z=Z1+Z2.	(2)
После подстановки заданных зависимостей Zj (17), h (tZ) и совместного решения уравнений (1) и (2) получим квадратное
Ц = 0,4 А; 12 = 0,6 А.
Рис. 11.36
1137.
уравнение
(Е - U)/r = (а2 + b2) U2 + (at 4- hi) V или при заданных числовых значениях
0,005 (72+О,Ш - 1,5 = 0,
откуда U = 10 В. По заданным зависимостям находим токи
11.36.	Определить ЭДС источника Е и токи уравновешенного моста (рис. 1136, где 1А — 0), если сопротивление линейных резисторов г = 40 Ом, характеристики нелинейных резисторов одинаковы и представлены уравнением U* — = 304 + Ю/J, где к = 1; 2, напряжение в вольтах, ток в амперах.
нелинейных элементов схемы
рис. 11.19 аппроксимированы уравнениями (токи в амперах, напряжения в вольтах):
Ц = 0,0Ш1 + 0,002 U2; 12 = 0,0Ш2 + 0,003Ul; I3 = 0,04 U3 + + 0,002VI (аппроксимация справедлива при положительных значениях напряжений).
Определить токи и напряжения нелинейных элементов при ЭДС Е = 30 В.
11.38(Р). В схеме рис. 1138 Ei = 40 В; Е2 = 10 В; Е3 = 20 В; характеристики нелинейных элементов аппроксимированы уравнениями (токи в амперах, напряжения в вольтах):
Л =0,01СЛ 4-0,002(7?;	(1)
12=0,0Ш2 + 0,001 U22,	(2)
13 = 0,0Ш3 + 2,5 • 10-4(73,	(3)
причем аппроксимация имеет смысл только при положительных значениях напряжений и токов.
Определить напряжения и токи нелинейных элементов. Решение. По первому закону Кирхгофа
Л=/2 + /3.	(4)
Для решения этого уравнения выразим все токи через общее напряжение V между узлами. Из рис. 1138 следует, 398
что
l/j = £1 - и = 40 - и- U2 = и - Е2 = и - 10; U3 = U + Е3 =
= U + 20.	(5)
После подстановки равенств (5) в уравнения (1), (2), (3) и токов 71? 72, h в (4) получим уравнение
001 (40 - U) + 0,002(40 - U)2 = 0,01 (U - 10) + 0,001 (U - 10)2 + + 0,01 (U + 20) + 2,5 • 10’4 (U + 20)2
и (после алгебраических преобразований) квадратное уравнение
U2 - 240(7 + 4400 = 0,
откуда U — 20 В. Второе решение U = 220 В не удовлетворяет условиям аппроксимации, так как получается Zi < 0.
Рис. 11.38	Рис. 11.39
Подставив найденное значение U = 20 В в равенства (5), определим напряжения: (7j=20 В; (72 = Ю В; (73 = 40 В. По уравнениям (1), (2), (3) находим токи: Л = 1 А; 12 = 0,2 А; 13 = 0,8 А.
11.39. В схеме рис. 11.39 нелинейные элементы имеют следующие характеристики (токи в амперах, напряжения в вольтах):
Ц =0,01^! + 0,002(7?;
12 = 0,0Ш2 4- 0,003(7?; 13 = 0,04(73 + 0,002(7? (аналитическая аппроксимация справедлива только при положительных значениях напряжений и токов). ЭДС источников: Ei = 40 В; Е2 = 10 В; Е3 = 10 В.
Определить суммарную мощность источников.
11.3. Численные методы расчета
11.40(Р). В схеме рис. 11.4 характеристики нелинейных элементов заданы уравнениями (токи в амперах, напряжения в вольтах): = 1000/ + 101/7; (72 = 500/ + 20	; ЭДС источ-
ника £ = 18 В.
Определить ток и напряжения на нелинейных элементах методом простой итерации.
Решение. По второму закону Кирхгофа
(Л + U2 = Е.
После подстановки заданных зависимостей напряжений и U2 от тока получим уравнение (11.1):
1500/ + 30^7- 18 = 0.
Разрешим уравнение частично относительно тока (11.2):
/ = 0,012 - 0,02	= ф (/).	(1)
Проверим сходимость по условию (11.4), для чего вычислим производную
I dq>/dl | = 0,02/3	< 1.
Условие (11.4) выполняется, если ток 1> 5,45-10“4 А.
Выберем начальное приближение /0 = 0,012 А. Применяя алгоритм (11.3), находим по (1) значения тока:
1)	I = 0,012 - 0,02^0,012 = 0,0074 А;
2)	I = 0,012 - 0,02^0,0074 = 0,0081 А;
3)	/ = 0,012 - 0,02^ 0,0081 = 0,0080 А.
Последние два значения отличаются друг от друга менее чем на 2%, поэтому итерационный процесс можно закончить.
Подставив полученное значение тока I в уравнения характеристик нелинейных элементов, определим напряжения Ut = 10 В; U2 = 8 В.
11.41.	В схеме рис. 11.4 характеристики нелинейных элементов аппроксимированы уравнениями (ток в амперах, напряжения в вольтах):
I = 1,5-+ 2-10“3C7f;
I = 2,5-10"3и2 + 1.10’3l7i;
ЭДС источника £ = 3 В.
Определить ток и напряжения на нелинейных элементах методом простой итерации.
11.42.	В схеме рис. 11.13	= г2 = 8 Ом; ЭДС источника
Е = 16 В, характеристика нелинейного элемента задана уравнением (ток в амперах, напряжение в вольтах): U (/) = 2 In (14-1).
Определить ток нелинейного элемента методом простой итерации.
11.43.	Методом простой итерации определить напряжение U и ток 1 нелинейного элемента, а также мощность источника 400
9 ПС Е - 36 В в схеме рис. 11.43. Задана характеристика нелинейного резистора: I = aU2, где а = 2,5• 10"4 А/В2; сопротивления линейных резисторов указаны на схеме в омах.
Рис. 11.43	Рис. 11.44
11.44	(Р). На рис. 11.44 представлена схема нелинейной цепи, для которой заданы характеристики нелинейных элементов (токи в амперах, напряжения в вольтах):
h = ]//0,011/1;	(1)
Л =|^0,005С2;	(2)
/3=0,0Шэ3;	(3)
ЭДС источников Е{ = 8 В; Е2 ~ 7 В.
Определить напряжения и токи нелинейных элементов методом простой итерации.
Решение. Запишем уравнения цепи по законам Кирхгофа: С/1(/1) = Е1-1/3(/3) = 8-173(Л);	(4)
U2 (h) = E2-U3 (73) = 7 - U3 (73);	(5)
Л = Л + Л	(6)
и выберем начальные значения напряжений: V Y = 8 В, U2 = 7 В. .
1)	На первом шаге вычислений, подставив начальные значения l/j и U2 в (1) и (2), определим токи 11 = 0,431 А; Л =0,327 А и по (6) Iз =0,758 А. В соответствии с (3) напря-
жение U3 =]/10073 - 4,23 В.
2)	На втором шаге процесс вычислений повторяется. По (4) и (5) находим напряжения Ui =3,77 В; 172=2,77 В. Затем по (1) и (2) определим токи Ц = 0,335 А; 12 = 0,240 А и по (6) и (3) ток и напряжение Z3 =0,575 А и U3 = 3,86 В.
Аналогично вычислим значения токов и напряжений на следующих шагах итерации: 3) 6^= 4,14 В; U2 — 3,IA В; Ц =0,346 А; 12 =0,250 А; 13 =0,596 A; U3 = 3,90 В; 4)	=
= 4,10 В; U2 = 3,10 В; Ц = 0,345 А; 12 = 0,250 А; 13 = 0,595 А; Уз = 3,90 В.
Значения, полученные на третьем и четвертом шагах итерации, отличаются друг от друга менее чем на 2%; поэтому можно закончить вычислительный процесс и считать значения напряжений и токов, полученные на четвертом шаге итерации, ответом задачи.
11.45.	Методом простой итерации определить в цепи рис. 11.45 токи Z2, h и напряжения U2. Характеристики нелинейных резисторов заданы (токи в амперах, напряжения в вольтах): Ц =1/0,011'!; /2 = |/0,005(72; сопротивление линейного резистора г = 10 Ом; ЭДС источников: Ej = 11 В;Е2=12В.
Рис. 11.46
11.46.	Схема нелинейной цепи изображена на рис. 11.46.
Методом простой итерации определить напряжения U^ U2, U3 и токи /1, J2, Z3, считая, что характеристики нелинейных элементов аппроксимированы зависимостями (токи в амперах, напряжения в вольтах) Ц = {/ДОШь 12 — ]/0,005172, 13 — = 0,01 U3 и известны ЭДС источников: a) Ei = 6 В; Е2 = 5 В; Е3 = 2 В или б) Ег = 10 В; Е2 = 9 В; Е3 = -2 В.
Рис. 11.47
Рис. 11.48
11.47.	В схеме рис. 11.47 Ej = 9 В; Е2 = 14 В, г = 3 Ом; характеристики нелинейных элементов приведены в задаче 11.46.
Определить токи Zb Z2,13 и напряжения Ul9 U2, U3 методом простой итерации.
11.48.	В схеме рис. 11.48	= 8 В; Е2 = 7 В; гг — 2 Ом;
Г2 = 3,5 Ом; г3 = 2 Ом; характеристики нелинейных элементов приведены в задаче 11.46.
Определить напряжения и токи нелинейных элементов методом простой итерации.
П.49(Р). Последовасельпо соединенные линейный резистор, сопротивление которого г = 10 Ом, и нелинейный резистор с характеристикой U = я/3, где а = 1000 В/А3, присоединены к источнику ЭДС Е = 10 В (рис. 11.1).
Определить ток I и напряжение U на нелинейном элементе методом Ньютона, найти мощность Р источника.
Решение. Запишем уравнение цепи по второму закону Кирхгофа
rl + U = Е
или после подстановки численных значений
10 - 10/ - 1000/3 = /(/) = 0.
Первая и вторая производные функции/(/):
f (/) = - Ю - 3000/2; /" (/) = - 6000/.
Проверим условия сходимости по формулам (11.7). Подстановка значений производных в (11.7) дает всегда выполняемое неравенство I2 / —1/3000 и условие / / 0.
Начальное значение тока /0 определим из приближенного уравнения: 10 — 10/о =0, откуда /0 = 1 А.
Итерационный процесс проведем по формуле (11.6):
4+1=Л-Я4)//'(4)-
Итерации:
1)
2)
10-10- 1000 ~-пГ-^зоосГ
= 0,67 А;
10- 10’0,67— 1000-0,673 — 10 — 3000  0,672
= 0,45
А.
Следующие шаги итерации выполняются аналогично.
Ответ: 1 = 0,2 A; U = 8 В; Р = г/2 4- UI = 2 Вт.
11.50.	Параллельно соединенные линейный резистор, сопротивление которого г = 10 Ом, и нелинейный резистор с характеристикой U = а!3, где а = 1000 В/А3, присоединены к источнику тока J = 1 А (рис. 11.50).
Определить напряжение и ток нелинейного элемента методом Ньютона; вычислить мощность источника.
11.51.	В схеме рис. 11.13 Е = 25 В; = 50 Ом; г2 = 100 Ом; характеристика нелинейного резистора аппроксимирована полиномом / = aU 4- bU3, где а = 0,01 А/В; b = 10-4 А/В3.
Определить методом Ньютона напряжение и ток нелинейного резистора, а также токи в линейных резисторах.
11.52.	В схеме рис. 11.52 ток J = 0,7 А; = 100 Ом; г2 — 20 Ом; характеристика нелинейного резистора U = al + Ы3, где а = 30 В/A; b = 5000 В/А3.
Определить напряжение на нелинейном элементе и токи 1, Ц методом Ньютона.
Рис. 11.50
Рис. 11.52
11.53.	В схеме рис. 11.53 Е = 15 В; J = 0,5 А; = 30 Ом; г2 = 15 Ом; характеристика нелинейного элемента U = а!3, где а = 1000 В/А3.
Определить методом Ньютона напряжение и ток нелинейного элемента.
Рис. 11.53
Рис. 11.54
11.54(	Р). В схеме рис. 11.54 г = 10 Ом; = 15 В; Е2 = 8 В; характеристики нелинейных элементов аппроксимированы зависимостями (токи в амперах, напряжения в вольтах):	=
= 201 i + 1000Z1; U 2 = 3012 + 200011.
Определить все токи и напряжения на нелинейных элементах методом Ньютона.
Решение. Запишем уравнения цепи по первому закону Кирхгофа
— h + 1г	(1)
и с учетом (1) по второму закону Кирхгофа
Et - U, (/,) - г (Л + I2) = /L = 0;
Е2 - v2 (12) - г (Ц + /2) = /2 (/1,12) = 0 или после подстановки числовых значений
15 - 30/х - 100071 - 1072	(Л,/2) = 0;	(2)
8 - 4072 - 200071 - 1071 = f2 (Ц,12) = 0.	(3)
Вычислим производные	l2)/dli — ~ 30 — 30007?;
гд (/ь hM = -10; df2 (л, i^/di, = - ю; df2(Л, i2)/ai2 = - 40 - 6000/1.
Решение задачи выполним по алгоритму (11.9), (11.10), где х = /р у = 12. Сходимость проверяем в процессе итераций.
Выберем начальные приближения по уравнениям (2) и (3), отбросив третий и четвертый члены: /10 = 0,5 А; /20 = 0,2 А.
Итерации: 1) вычислим по (2) и (3) функции /ЛЛо, /20) = = -127; f2 (710, /20) = -21 и производные a/i(/10, /20W1 = = -780;	аЛ(/10, /20)Ж2= -10;	а/2(71О, 1^/дЦ = -10;
а/2(/ю, 72oW2 = -280.
Якобиан (11.11) системы уравнений (2) и (3):
J (Л0Д20) —
- 780
- 10
- 10
-280
== 2,18 • 105.
Токи первого приближения по (11.9), (11.10):
/и =0,5-
-127 - 10
- 21 -280
2,18-105
= 0,336 А;
I21 =0,2-
-780 -127
-10 - 21
2,18-105
= 0,130
А.
Далее процесс вычислений повторяется: 2) f i(/n,/2i) = = -34,3; f2(In, I2i)= -5;	а.Л(Л1,	= -370;
^1(/ц, /21)/а/2= -Ю;	a/2(/n, I2l)/dlt = -10;
^/2(^11, /2i)/a/2 = “142; 7(7ц, /21) = 5,25 • 104. Токи второго приближения /12 = 0,244 А; 122 = 0,101 А.
Следующие шаги итерации выполняются аналогично. В результате получим: 1Х — 0,2 А; 12 — = 0,1 А. По формуле (1) и характеристикам элементов находим: 13 = 0,3 A; U{ = 12 В; U2 = 5 В.
11.55. Методом Ньютона определить токи /1} /2, 73 и напряжения U U2 на нелинейных элементах в цепи по рис. 11.55. ЭДС
источников и сопротивления линейных резисторов (в омах)
указаны на схеме; заданы характеристики нелинейных элементов (токи в амперах, напряжения в вольтах): = 511 + 10007?; U2 = 107 2 + 200072.
Глава двенадцатая
МАГНИТНЫЕ ЦЕПИ ПРИ ПОСТОЯННЫХ ПОТОКАХ
Введение к гл. 12
Для участка магнитной цепи магнитная индукция
В = Ф/$,	(12.1)
где Ф — магнитный поток; S — поперечное сечение участка; магнитное напряжение
[7М = Н/ = ФЯМ,	(12.2)
где Н — напряженность магнитного поля; I — средняя длина участка; магнитное сопротивление участка
= //HrlA)S,	(12.3)
где — относительная магнитная проницаемость материала участка; р,0 = 4я-10“7 — магнитная постоянная, Гн/м.
Магнитная индукция и напряженность магнитного поля участка связаны соотношением
В = цгц0Н.	(12.4)
При расчете магнитных цепей при постоянных потоках зависимость между В и Н для ферромагнитных участков задается кривой намагничивания (приложение 3). Для воздуха и для воздушных зазоров ц, = 1, следовательно,
И = В/ц0 = 0,8-106В,	(12.5)
где Н в амперах на метр, а В в теслах.
Если Н измеряется в кратных единицах, А/см, то
Н = 8-1О3В.	(12.6)
Магнитодвижущая сила (МДС)
F = In,	(12.7)
где I — ток в обмотке; w — число витков обмотки.
Между величинами, характеризующими магнитные и электрические цепи, существует формальная аналогия:
Электрические цепи	Магнитные цепи
Ток 1, А	Поток Ф. Вб
ЭДС Е, В	МДС F, А
Сопротивление г, Ом	Магнитное сопротивление RM, 1/Гн
Проводимость д, См	Магнитная проводимость дм, Гн
Напряжение U, В	Магнитное напряжение См, А
Эта формальная аналогия распространяется и на методы расчета магнитных цепей.
Первый закон Кирхгофа для магнитной цепи
£Ф=О	(12.8)
и второй закон
=	=	=	(12.9)
В большинстве случаев магнитные цепи — нелинейные, и их расчет аналогичен расчету нелинейных электрических цепей.
Аналогом вольт-амперной характеристики U (/) является вебер-амперная характеристика Ф((7М), которая рассчитывается по заданным кривым намагничивания В (И) и геометрическим размерам участков магнитной цепи.
Вебер-амперная характеристика (часто называют магнитной характеристикой) рассчитывается в следующем порядке: задают индукцию В, вычисляют поток Ф = BS, по кривой В(Н) определяют Н и находят 17 м = Hl.
В слабых полях цг % const, следовательно, и RM = const, поэтому магнитная цепь рассчитывается как линейная.
Для наглядности можно составить эквивалентную электрическую схему (см. рис. 12.15Р), при помощи которой выполняется расчет.
12.1.	Линейная магнитная цепь
12.1(Р). П-образный магнитопровод прямоугольного поперечного сечения замкнут якорем, имеющим такое же сечение S = 0,25 см1 2, но вдвое меньшую проницаемость (рис. 12.1). Средняя длина магнитных линий в магнитопроводе /1=4 см, в якоре 1^ — 0,9 см, в каждом разделяющем их воздушном зазоре /в = 0,02 мм. Относительная магнитная проницаемость материала магнитопровода р1г = 500.
Определить МДС обмотки, при которой индукция в магнитной цепи В — 0,02 Тл. Вычислить магнитное сопротивление цепи.
Решение. Так как задано = const, то цепь считаем линейной. Магнитное сопротивление'цепи равно сумме магнитных сопротивлений участков (12.3):
о G h 2/0	1 / /1	4	\
RM = -----~	~	~ I-----------h-----h 2/B ) =
PlrPoS	p2rPo*^ Po-S	\Plr	|^2r	/
1	/409	X
= ~л—a-. / tut +	+ 2 • 2 • 10“3 = 4,95 • 106 1/Гн.
4тг • 10“9-0,25 \ 500	250	/
По закону Ома для магнитной цепи
F = Iw = ФЯ = BSR„ = 2,48 А.
*1	М	'
12.2.	Магнитопровод состоит из двух П-образных частей (рис. 12.2), разделенных двумя зазорами длиной /в = 0,4 мм каждый. Средняя длина магнитных линий в ферромагнетике 8 см, сечение магнитопровода 0,25 см2. Относительная магнит*
ная проницаемость материала цг
Рис. 12.1
Рис. 12.2
= 200.
Рассчитать магнитное сопротивление магнитной цепи и его изменение при увеличении и уменьшении длины воздушного зазора на 50%.
Выразить магнитный поток, который сцеплен с обмоткой, охватывающей магнитопровод, через число ее витков и ток, пользуясь понятием магнитного сопротивления.
12.3.	Дужка из пермаллоя (рис. 12.3), выполненная в виде полуокружности радиуса R = 1,25 см, имеет равномерно распределенную обмотку с числом витков w = 250 и расположена
над плоской поверхностью продольно намагниченного тела Каждый воздушный зазор между поверхностями тела и краями дужки равен 0,1 мм.
Напряженность поля Н на-
магниченного тела параллельна его поверхности и равна 4 А/см.
Определить, при каком токе в обмотке дужки магнитный поток внутри нее равен нулю.
Рис. 12.4
Рис. 12.3
12.4.	Магнитопровод собран из двух Ш-образных частей, разделенных воздушными зазорами. Обмотки с токами, направления которых показаны на рис. 12.4, расположены на всех трех стержнях.
расчетные длины участков магнитной цепи /j = 1\ + Г[ = 13 == /з + /з = 9,0 см; /2 = lf2 + 1'1 = 4,4 см; /в = 0,01 см (каждый); расчетные сечения участков: — S3 = S2/2 = 1,6 см2.
Относительная магнитная проницаемость ферромагнетика в области слабых полей, на которые и рассчитана система, постоянна и равна 1000.
Найти потоки Фь Ф2, Ф3, если МДС и токи в обмотках равны:
a)	?2w2	=	1	A;	/j = /3 — 0.
б)	ZiWj	=	1	А;	72 = /3 = 0.
в)	=	1	А;	12 = 0; I3w3	—	+0,5	А.
г)	IiW!	—	—0,5	A; 72w2 = 1	А;	13	=	0.
12.5.	Определить изменение потока Ф2 в магнитопроводе предыдущей задачи при увеличении в 2 раза каждого воздушного зазора при следующих значениях проницаемости: а) = 1000; б) = 50; в) = 10000.
12.2.	Нелинейная магнитная цепь без гистерезиса
12.6.	На рис. 12.6, а изображена симметричная магнитная система, выполненная из электротехнической стали 1211. Внешняя часть магнитной цепи (включая крайние стержни) имеет по всей длине постоянное поперечное сечение. Сечение среднего стержня в 2 раза больше сечения крайних стержней и равно 8 см2. В среднем участке магнитной цепи индукция равна 1,2 Тл, если в каждой из катушек, содержащих по 100 витков, проходит ток 2,5 А.
Определить магнитный поток в среднем стержне, если при том же токе обе катушки расположить на среднем стержне (рис. 12.6,6).
Рис. 12.6	Рис. 12.7
12.7.	На рис. 12.7 схематически изображены две магнитные системы машин постоянного тока. Соответствующие участки этих систем выполнены из одного и того же ферромагнитного материала и имеют одинаковые геометрические размеры.
Определить, при каком расположении катушек требуете^ для создания одинаковых магнитных потоков в воздушных зазорах меньше витков при равных токах.
12.8.	Для ферромагнитного тороида с воздушным зазором длиной /в = 0,2 мм и средней длиной ферромагнитного Мате> риала /ф = 30 см на баллистической установке снята зависимость В — f (7и’//)> представленная в табл. 12.8, где I = /ф + / Таблица 12.8
Iwjl, А см	5	10	13	17	20	24	30	40	50	60
В, Тл	0,4	0,8	1	1,2	1,29	1,4	1.48	1,56	1,59	1,6
Рассчитать зависимость В(Н) для ферромагнитного материала.
12.9.	Два магнитопровода из стали 1512 (рис. 12.9) имеют общую обмотку. Магнитный поток в воздушном зазоре второго магнитопровода равен 6,36-10“4 Вб. Поперечное сечение каждого магнитопровода постоянно по всей длине и равно 6 см2. Средние длины участков = 12 + /зв = 60 см и 12ъ = 0,11 см.
Определить поток в первом магнитопроводе.
12.10.	В воздушном зазоре электромагнита, выполненного из стали 1411 (рис. 12.10), необходимо создать индукцию В = 1,05 Тл.
Определить МДС, необходимую для создания магнитного потока с заданной индукцией, если 1С + 1Я = 100 см, суммарный воздушный зазор 2/в = 1 мм, сечение магнитопровода одинаково по всей длине электромагнита и равно 16 см2.
12.11.	У электромагнита предыдущей задачи МДС равна 3000 А.
Найти магнитный поток в магнитопроводе.
12.12(	F)- Магнитная цепь, изображенная на рис. 12.12, выполнена из электротехнической стали 1211 и имеет следующие размеры: =60 см; 12 = 20 см; /в =0,1 см; /3 = 80 см; с	= см2. Магнитные потоки в крайних стержнях
ф = 0,25-10"3 Вб и Фэ = 1,31 IO’3 Вб.
Найти МДС Fx — ZiWi и F3 — Z3w3; указать направления токов в обмотках.
Решение. По первому закону Кирхгофа для магнитной цепи
ф2 =0! + ф3 = 1,56 - 10"3 Вб.
Индукция в стержнях
Bj = ф1/51 = 0,25 Тл; В2 = Ф2/$2 = 1,56 Тл;
В, = Ф3/53 = 1,31 Тл.
По кривой намагничивания для стали 1211 (см. приложение 3) находим: Нх =0,6 А/см; Н2 = 20 А/см; Н3 = 6 А/см. По второму закону Кирхгофа определяем МДС:
F. = IiWi = и Ji + H2l2 + Z/B/B « 1680 А;
F 3 = ?3W3 = H3I3 + н212 + ZZB/B « 2130 А,
где напряженность поля в воздухе вычислена по (12.6).
12.13.	Для магнитной цепи задачи 12.12 определить МДС и F3 при обратном направлении потока Ф3.
12.14.	Магнитная цепь (рис. 12.14) выполнена из электротехнической стали 1561 и имеет следующие размеры: = = 40 см; /2 = 12 см; 13 = 30 см; = S3 = 4 см2; S2 = 2 см2. Магнитодвижущая сила F — 1800 А, поток в первом стержне Ф1 =5,94-10"4 Вб.
Определить длину воздушного зазора /в.
12.15(	F). Магнитопровод (рис. 12.15) выполнен из электротехнической стали 1512 и имеет следующие размеры: Ц =
= 30 см; l2 = 12 см; /3 — 30 см; 5, = S2 = S3 = 15 см2; F, = = Iiwt = 100 A; F2 = I2w2 = 470 А.
Определить магнитную
Рис 12.15
индукцию в каждом стержне.
Решение. Выберем положительные направления потоков: в левом и среднем стержнях -вверх, в правом — вниз — и составим эквивалентную схему (рис. 12.15Р, а\
Магнитные напряжения на участках запишем на основании второго закона Кирхгофа для магнитной цепи:
С/маб = ^-17м1;	(1)
^Ma6 = F2-l/M2;	(2)
<4 аб ~ ^мЗ,	(3)
По первому закону Кирхгофа
Рис. 12.15Р
^м2
Аналитическое решение
Аналитически задача может быть решена, например, итерационным методом. Для схемы (рис. 12.15Р, а) с двумя узлами запишем расчетную формулу
ТТ	______тт	/с\
^маб ($+1) = ~	----'	- ^мЗ (> +1),	Р)
Ум1 (s) Т вы! (s) т УмЗ(л)
где магнитные проводимости соответствующих участков маг-412
$	Ци.аб’ &	Я3, А/см	В	3, Тл	Ф,-10’ Вб	-4 5	SmS-IO-4, Гн		А
0 1 2 3 4 5 6	150 130,36 120 115,9 114,7 114,1 114,1	5 4,35 4,0 3,86 3,83 3,8 Итерация	1,2 1,175 1,16 1,15 1,15 1,15 закончена		18 17,625 17,4 17,25 17,25 17,25		0,12 0,135 0,145 0,149 0,150 0,151		-50 -30,36 -20 -15,9 -14,7 -14,1
									
5	Яр А/см	5р Тл		Фг10	"4, Вб	£м1	•10-4, Гн		UM?, А
0 1 2 3 4 5 6	-1,66 -1,01 -0,67 -0,53 -0,49 -0,47 Итерация зак	-0,93 -0,725 -0,55 -0,43 -0,42 -0,38 ончена		-13,95 -10,875 -8,25 -6,45 -6,3 -5,7		0,279 0,358 0,412 0,406 0,429 0,404		320 339,6 350 354,1 355,3 355,9	
$	Н2, А/см	В2, Тл		Ф<10	“4, Вб	гм2-10-4, Гн		Цл,аб($+1)> А	
0 1 2 3 4 5 6	26,66 28,3 29,16 29,5 29,6 29,65 1	1,52 1,525 1,53 1,53 1,53 1,53 Итерация зак		22,8 22,875 22,95 22,95 22,95 22,95 ончена		0,071 0,067 0,066 0,065 0,065 0,0645		130,36 120 115,9 114,7 114,1 114,1	
нитной цепи определяются по формулам 0Mi = Ф1 (s)>* ^2(5) = Ф2(5)/^м2(ф ^мЗ(5) = Фз(5)/^мЗ(5), а индекс S соответствует номеру приближения.
Расчет ведем в следующей последовательности. Задаемся (нулевое приближение) UMa6{Gi, вычисляем Н3 (0) = аб (оА, по кривой В (Н) находим В3 (0), подсчитываем Ф3 (0) = В3 (0)53 и определяем 0м3(О) = Фз(О)/^мЗ(О)« Из (1) и (2) находим 17м1(0) и ^м2(0) и подобно предыдущему определяем дм1(0) и 0м2(о), по (5) подсчитываем значение С7МОб(1) ДЛЯ следующего приближения и т. д.
Результаты расчета сведены в табл. 12.15а.
Таблица 12.156
Ф, = ф, = ф? мВб	0	1,095		1,50		1,875	
5° и to 'll	0	0,73		1,0			 1,25	
= И2 = н3, А см	0	1,0		2,0		6.0	
Ct । =	А	0	30		60		180	
Сг2, А	0	12		24		72	
Ф1 = ф, = ф,. мВб	1,98	2.06	2,10		2,16		2,25
= В2 = By Тл	1,32	1,36	1,4		1.44		1,5
Н} = н2 = А/см	8,0	10	12		14		20
= С(3> А	240	300	360		420		600
Ctb А	96	120	144		168		240
Г рафическое решение
Для графического решения задачи рассчитаем магнитные (вебер-амперные) характеристики участков Фм (Г7М). Задав поток Ф, определим индукцию В = Ф/S, по кривой намагничивания (приложение 3) найдем Н и вычислим UM = Hl (табл. 12.156).
По уравнениям (1)—(3) строим зависимости Фь Ф2 и Ф3 от UMa6 (кривые 1, 2, 3 рис. 12.15Р, б). Согласно уравнению (4) складываем ординаты кривых 1 и 2, получаем суммарную кривую 4. Точка пересечения кривых 3 и 4 дает решение системы уравнений (1)—(4): Фт = —0,57 мВб; Ф2 = 2,3 мВб; Ф3 = 1,73 мВб. Соответственно индукции Вг = -0,38 Тл; В2 = = 1,53 Тл; В3 = 1,15 Тл. Отрицательные знаки у Фх и Bt показывают, что действительное направление потока Ф! обратно выбранному.
12.16.	На рис. 12.16 изображен магнитопровод толщиной 100 мм, выполненный из стали 1411. Остальные размеры 414
указаны в миллиметрах на рисунке. Число витков каждой обмотки w = 500, токи в обмотках = 10 А; 12 = 1,6 А.
Определить магнитную индукцию в тех стержнях, на которых находятся обмотки.
Рис. 12.17
Рис. 12.16
12.17.	Во втором стержне магнитной системы (рис. 12.17), выполненной из электротехнической стали 1211, индукция равна 0,8 Тл. Магнитопровод имеет следующие размеры: /1=20 см; /1 = 10 см; /в = 0,1 см; 12 = 15 см; /3 = 30 см; S{ = S3 = 4 см2; S2 = 6 см2.
Определить ток в обмотке с числом витков w = 200.
12.1&,	В среднем стержне разветвленной магнитной цепи (рис. 12.18) магнитный поток равен 1 мВб. Магнитопровод выполнен из электротехнической стали 1211 и имеет следующие размеры: ^=40 см; /2 = 20 см; /3 = 40 см, S1—S3 = = 4 см2 и S2 = 8 см2.
Определить длину воздушного зазора /в, при которой магнитный поток в зазоре равен 40 % потока в среднем стержне; найти число витков обмотки w, если ток I = 5 А.
12.19.	Участки магнитной цепи (рис. 12.19) выполнены из различных материалов. Материалы участков и их геометрические размеры указаны в табл. 12.19. Магнитодвижущая сила = 1580 А, поток Ф3 = 1,3 мВб.
Определить F2 = /2w2, Ф1 и Фа-
№ участка	Материал	S, см2	1, см	№ участка	Материал	S, см2	/, см
1	Сталь 1512	20	26,0	3	Сталь 1211	10	8,5
2	Сталь 1411	8	50,0	4	Воздух	10	0,135
12.20.	Для магнитной цепи (рис. 12.19) известны: ItWi = = 1580 А и Ф2 = 1,1 мВб (направлен вниз), материалы участков и размеры указаны в табл. 12.19.
Определить F2 = Ф1 и Фз-
12.3.	Расчет магнитной цепи с учетом гистерезиса.
Постоянные магниты
12.21.	Тороид с круглым сечением изготовлен из магнитотвердой стали, магнитная характеристика которой, имеющая форму петли, задана (табл. 12.21).
Построить петлю гистерезиса, выражающую зависимость индукции от тока в обмотке для тороида, в котором сделан воздушный зазор 0,5 мм. Средняя длина тороида 25 см, число витков равно 100. При расчете считать, что средняя длина тороида значительно превышает диаметр его сечения.
Таблица 12.21
В, Тл	0	0,25		0,50		0,75		1,00		1,25	
Я, А/см	77	78		84,5		92,5		115		175	
В, Тл	1,50	1,25	1,00		0,75		0,50		0,25		0
И, А/см	369	92,5	0,0		-54		-61,5		-70		-77
12.22.	Ячейка (матрица) магнитного запоминающего устройства (рис. 12.22) состоит из 16 кольцевых ферритовых тороидов размерами D х d х h — 3,1 х 2,0 х 1,3 мм (наружный и внутренний диаметры, высота). Характеристика феррита прямоугольная с индукцией насыщения Bs = 0,3 Тл и коэрцитивной силой Нс = 1,6 А/см.
Через каждый тороид проходит два провода, один из вторых принадлежит ряду х (7Х1, 1х2 ...), другой - ряду у (lyu lyi ' • •)• В исходном положении все тороиды имели отрицательную остаточную индукцию —Ва.
Определить: а) как изменится магнитное состояние тороидов (и каких именно) после включения токов 1у1 — /у3 = 1х2 = ix3 = 0,85 А; 1у2 = 1у4. = 7х1 = 1х4 = 0; б) как изменятся магнитные состояния тороидов, если при новом состоянии включить ТОКИ 1у1 = у4 ~ Iх1 ” хЗ 0,85 А, 1у2 уЗ ““ ^х2 ~~ в Лс4 = 0.
Рис. 12.22
Рис. 12.23
12.23.	Определить магнитную индукцию в воздушном зазоре магнитной системы гальванометра (рис. 12.23) в случае, когда эта система была намагничена до насыщения в собранном виде. Магнитным рассеянием, а также магнитным сопротивлением сердечника С и наконечников Н пренебречь. Расчетная длина и сечение магнита и воздушных зазоров: 1М = 24 см, SM = 3 см2; Гв = 2 • 0,6 — 1,2 см; SB = 7,5 см2. Кривая размагничивания кобальтовой стали (из которбй изготовлен магнит) задана (табл. 12.23).
Таблица 12.23
В, Тл	0	0,28	0,54	0,70	0,90
Н, А/см	-190	-160	-120	-80	0
12.24.	Для магнитной цепи предыдущей задачи определить магнитную индукцию в воздушном зазоре, если намагничивание до насыщения производилось при вынутом цилиндрическом
14	п/р Ионкина П. А.	417
сердечнике, после чего сердечник был вновь помещен между полюсами. Расчетную длину воздушного промежутка при вынутом сердечнике принять равной 3,25 см, кривую возврата считать прямой с наклоном 12,5-10“ 4 Тл/(А/см).
Глава тринадцатая
НЕЛИНЕЙНЫЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА
Введение к гл. 13
Установившиеся процессы в нелинейных цепях переменного тока рассчитываются графическими, аналитическими и графоаналитическими методами. Численные методы, применяемые при расчете установившихся процессов в цепях переменного тока и при расчете переходных процессов в нелинейных цепях (гл. 14), по существу одни и те же.
Графические и графо-аналитические методы целесообразно применять для решения задач, в которых характеристики нелинейных элементов могут быть приближенно представлены в виде кусочно-линейных функций. При этом на каждом из линейных участков характеристики задача решается как линейная, и определяются координаты точек перехода с одного линейного участка на другой (углы отсечки).
Применение аналитических методов расчета требует аппроксимации характеристики нелинейного элемента какой-либо достаточно простой функцией — чаще всего полиномом. Простейший аналитический метод состоит в непосредственном решении уравнения цепи (когда это возможно). Широко применяются метод гармонического баланса, метод гармонической линеаризации, а также итерационный метод.
При решении задачи методом гармонического баланса искомая величина представляется в виде периодической функции с неизвестными коэффициентами и подставляется в уравнение цепи. Неизвестные определяются приравниванием коэффициентов при одинаковых гармонических составляющих в левой и правой частях уравнения.
Сущность метода гармонической линеаризации заключается в том, что при воздействии на нелинейный элемент гармонического сигнала в отклике учитывается только основная гармоника, а высшие гармоники отбрасываются, и для расчета можно применять комплексный метод. Нелинейный элемент характеризуется нелинейным комплексным сопротивлением —
птношением комплексов первых гармоник напряжения и тока нСЛЙцейн°го элемента, причем в общем случае нелинейное комплексное сопротивление зависит от амплитуды и частоты тока. Например, при вольт-амперной характеристике нелиней
ного резистора
и (0 == ai + Ы3
(Ш)
нелинейное комплексное сопротивление (активное)
Z* = Ки = а + Ы*,	(13.2)
где 1т ~ амплитуда синусоидального тока. После определения сопротивления нелинейного элемента уравнения цепи решаются алгебраическими методами.
Итерационный метод применяется для решения задачи, если уравнения цепи имеют достаточно малые члены, которыми в первом приближении можно пренебречь. Уравнение цепи относительно неизвестного x(t)
/(х, dx/dt, d2x/dt2, ...) = 0	(13.3)
предварительно разделяется на две части, причем в правую часть выносятся достаточно малые члены:
fi (х, dx/dt, ...) = е/2 (*, dx/dt, ...),	(13.4)
где £ — малый параметр. Нулевое приближение х0 (г) находится решением уравнения, в котором отброшены малые члены (параметр е принят равным нулю):
/i(x, dx/dt, ...) = 0.	(13,5)
Полученное решение х0 (t) подставляется в правую часть уравнения (13.4), отбрасываются члены второго порядка малости (если они есть), и находится решение х(?) уравнения
/i (х, dx/dt, ...) = е/2 (х0, dx^/dt, ...),	(13.6)
которое является уточненным решением — первым приближением. Для получения дальнейших, более точных приближений процедуру следует повторить. В задачах данной главы достаточно ограничиться получением первого приближения.
Расчет нелинейных цепей переменного тока по действующим значениям токов и напряжений дает возможность приближенно учесть гистерезис и вихревые токи в магнитопроводах. Несинусоидальные токи и напряжения заменяются эквивалентными синусоидами. Потери на гистерезис и вихревые токи определяются по экспериментальным данным — либо непосредственно по показаниям ваттметра, либо по экспериментально полученным кривым удельных потерь в стали (кривые приве
дены в задаче 13.40). Для эквивалентных синусоид тока ц напряжения уравнения цепи можно записать и решать в комп-лексной форме и пользоваться векторными диаграммами.
При ювестном амплитудном значении потока в магнитопроводе Фот действующее значение соответствующего напря-жения рассчитывается по формуле
(13.7) где f — частота; w — число витков.
В ряде задач настоящей главы для определения искомых величин нужно решить кубическое уравнение. Уравнение
х3 + Зрх + 2q = 0	(13.8)
имеет один действительный корень
х = ]/-д 4- ]/q2 + р3 + ]/ - 4 - ]/<?2 + р3.	(13.9)
Уравнение
у3 4- ay2 4- by 4- с = 0	(13.10)
введением новой переменной
х = у + а/3	(13.11)
приводится к виду (13.8), где
2q~~~a3~ ~ab + c; Зр = b	(13.12)
/	«Л	v
Примечание. При решении задач § 13.1 и 13.2 потерями в реактивных элементах следует пренебречь.
13.1.	Графические и графо-аналитические методы расчета
13.1 (Р). Резистор с сопротивлением r = 1 кОм подключен к источнику синусоидальной ЭДС € = 150 sin cof, В (рис. 13.1, а) через диод Д, вольт-амперная характеристика которого дана на рис. 13.1,6.
Построить график тока i(t)» определить среднее /0 и действующее I значения тока в цепи; найти мощность Р источника и мощность Рг потерь в резисторе.
Решение. При расчете диод может быть представлен резистором, эквивалентное сопротивление гэк которого различно при прямом и обратном направлении тока. Эквивалентная схема цепи приведена на рис. 13.1Р, а.
Эквивалентное сопротивление диода определяется по характеристике рис. 13.1,6 и равно в прямом направлении 420
100/0,2 - 500 Ом и в обратном направлении 200/0,05 = 4000 Ом. Ток в цепи в ПРЯМ<>М h и обратном i2 направлениях представляет собой отрезки синусоид, амплитуды которых 1т = s= Е„/(г + гэк) и равны соответственно 0,1 А в прямом и 0,03 А в обратном направлении. Зависимость i (t) показана на рис. 13.1Р, б.
Среднее значение тока /0=Лн-Л)2, где
;02 =* 1т2/п. Таким образом, 10 = (0,1 - 0,03)/п = 0,0222 А. Действующее значение тока
к
*
sin2 at dot 4-
* о
2я
а
/2 2 sin2 cot dat
я
=4 +&=т /°>12+°>°32=°-°52 а-
Мощность источника
=~(/я1 + 42) = -^-(0,1 + 0,03) = 4^ Вт.
Мощность пЪтерь в резисторе
Рг = г!2 = 1000 • 0,0522 = 2,7 Вт.
Примечание. Мощность источника нельзя определить как произведение действующих значений напряжения и тока, поскольку ток несинусоидален.
13.2.	На входе цепи, состоящей из резистора с сопротивлением г 1 кОм и идеального диода (рис. 13.2), напряжение и = 200 sin cot, В.
Определить среднее и действующее значения тока и мощность потерь в резисторе.
Рис. 13.2
Рис. 13.3
13.3.	Аккумуляторная батарея, ЭДС которой Е = 12 В и внутреннее сопротивление гвт = 6 Ом, подключена через идеальный диод к источнику синусоидального напряжения с амплитудой 24 В (рис. 13.3).
Рис. 13.4
Рис. 13.6
Определить максимальное и среднее значения тока и максимальное обратное напряжение на диоде.
13.4.	У выпрямителя, собранного по схеме со средней точкой (рис. 13.4), сопротивление нагрузки г = 1 кОм. Диоды можно считать идеальными. Напряжение и на вторичной обмотке трансформатора синусоидальное с амплитудой 400 В.
Определить постоянную составляющую тока в резисторе г, мощность потерь в резисторе и максимальное обратное напряжение на диоде.
13.5.	У выпрямителя, собранного по мостовой схеме с диодами, которые можно считать идеальными, сопротивление нагрузки — резистор с г = 180 Ом.
Определить действующее и среднее значения тока в сопротивлении нагрузки, мощность потерь в резисторе, максималь
ное обратное напряжение и среднее значение тока диода. Цепь питается от источника синусоидального напряжения, действующее значение которого 380 В.
13.6.	Для цепи, схема которой приведена на рис. 13.6, заданы сопротивление г = 100 Ом и ЭДС е = 20 sin 1000t, В;
т= 5 В; Е2 = Ю В. Диоды идеальные.
Определить длительность фронтов положительного и отрицательного импульсов напряжения и.
13.7.	В цепи по рис. 13.7 известны сопротивления резисторов: ri = 100 Ом; г2 = 400 Ом и ЭДС источников е = = 100sin 1000г, В; £ - 20 В. Диоды идеальные.
Определить длительность фронтов импульсов напряже-
13.8.	Параметры элементов цепи по рис. 13.8 указаны в задаче 13.7.
Построить график напряжения w(t) на резисторе г2.
13.9(	Р). Выпрямитель, собранный по трехфазной мостовой схеме (рис. 13.9) с сопротивлением нагрузки г = 20 Ом — резистором, получает питание от источника трехфазного напряжения. Диоды можно считать идеальными. Действующее значение линейного напряжения ил = 380 В.
Определить среднее и действующее значения тока резистора, мощность потерь в резисторе, а также средний ток и максимальное обратное напряжение диода.
Решение. На рис. 13.9Р,а и б показаны линейные и фазные напряжения цепи.
Ток резистора идет через те фазы, напряжение между которыми в данный момент наибольшее. График тока представлен на рис. 13.9Р, в. Максимальное значение тока
1„ = U„.Jr = 3801/2/20 = 27 А.
Среднее значение рис. 13.9Р,в:
2я/3
I г
° л/3 J
тока резистора определяется
Im sin cot d<at = 31 Jn = 25,8 A.
из
я/э
Действующее значение тока
ТяТЗ---------------
ф
Im sin2 cot d($t — 0,9587 m = 25,9 A.
n/3
Рис. 13.9
Мощность потерь в резисторе Р = гI2 = 13,4 кВт.
Для определения среднего тока диода 7Д0 рассмотрим графики токов диодов (рис. 13.9Р,г —м). Ток через каждый диод протекает в течение 7з периода, поэтому /» « IQ/3 = 8,6 А.
Для определения напряжения на диоде рассмотрим, например, диод 1 (рис. 13.9). При открытом диоде 1 напряжение мд1 = 0. Чтобы определить напряжение на закрытом диоде, запишем уравнение по второму закону Кирхгофа для любого из контуров, включающих диод 7, например:
илв + “дЗ - Ид1 = °-
Если диод 3 открыт, то Идз = 0 и “д! = иАВ = т-е’ максимальное обратное напряже-
ние на диоде равно С7лт=	Рис 13 9р
= 380 у 2 = 540 В.
13.10.	Выпрямитель собран по трехфазной схеме со сред-
ней точкой (рис. 13.10). Сопротивление нагрузки г = 20 Ом; вторичное фазное напряжение 220 В. Диоды считать идеальными.
Определить среднее и действующее значения тока и мощность потерь в резисторе, а также средний ток и максимальное обратное напряжение диода.
13.11.	В цепи по рис. 13.11, а два опорных диода (стабилитрона) включены навстречу друг другу. Идеализированная характеристика диода изображена на рис. 13.11,6; сопротивление резистора г = 500 Ом; ЭДС источника е = 20sin314г, В.
Определить длительность фронта импульсов напряжения и.
Рис. 13.10	Рис. 13.11
13.12.	В цепи предыдущей задачи определить амплитудные значения ЭДС источника, необходимые для получения фронтов импульсов длительностью: а) Т/12; б) Т/16; в) Т/24, где Т - период ЭДС.
0 , 0,1 0,2 0,3 0;¥ В
• 0	0,2 Ofl В
0
2К
2
bojcM

Рис. 13.13Р
13,13(Р). На входе усилителя, схема характеристики которого приведены 11.27, а — в, действует сигнал

И на рис.
= 0,2 + 0,1 sin 314t, В.
Построить зависимость выходного напряжения м2 от времени при сопротивлениях нагрузки: а) г2 = 10 кОм; б) г2 — 20 кОм.
Указание. Рекомендуется вос-
пользоваться результатами решения задачи 11.28.
Решение. По результатам решения задачи 11.28 на рис. 13.13Р, а построены зависимости u2(ei) при г2 — 10 кОм (кривая а) и г2 = 20 кОм (кривая б). Зависимость ЭДС (cot) дана на рис. 13.13Р, б. Графическое решение задачи представлено на рис. 13.13Р, в.
13.14.	На выходе усилителя, схема и характеристики которого приведены на рис. 11.26, а — в, включен резистор, сопротивление которого зависит от времени: а) г2 =200 + + 100 sin 104t, Ом; б) г2 ~ 300 + 150 sin 104t, Ом.
Построить зависимость выходного напряжения м2 от времени.
Указание. Рекомендуется воспользоваться результатами решения задачи 11.26.
13.15.	На сетку лампового усилителя, схема и характеристики которого приведены на рис. 11.29, а и б, подведено напряжение: а) ис — — 4 + 2 sin Cot, В; б) мс = -8 + 4 sin cot, В.
Построить зависимость выходного напряжения wH от времени.
Указание. Рекомендуется воспользоваться результатами решения задачи 11.29.
13.16(	Р). Две катушки с числами витков = 2000 и w2 = 400 намотаны на магнитопровод, сечение которого S = = 0,2 см2 и средняя длина магнитной линии / — 10 см (рис. 13.16, а). Кривая намагничивания материала дана на рис. 13.16,6.
Построить зависимости потока Ф в магнитопроводе и напряжения м на вторичной обмотке от времени при питании цепи от источника синусоидального тока i = 0,6 sin 1000t, А.
Решение. Построим кривую намагничивания в координатах Ф и i (рис. 13.16Р, а), учитывая, что поток (в веберах) Ф = BS = В • 0,2 • 10" 4 и ток (в амперах) i = Hl/w{ = Н • 5 • 10“ 5 (закон полного тока).
Построение зависимости потока от времени (от cot) приведено на рис. 13.16Р,а— в.	'
Напряжение на вторичной Обмотке
u = w2 dtydt = w2 (бФ/di) di/dt.	(1)
Зависимость магнитного потока от тока получена в виде кусочно-линейной функции (рис. 13.16Р, а), поэтому можно рассчитать напряжения на отдельных участках. На первом участке (0<Ф^0,03 мВб), как следует из рис. 13.16Р,а, производная дФ/di = 3* 10“4 Вб/А и напряжение
и = 400 • 3 • 10" 4 • 0,6 • 1000 cos 1000г = 72 cos 1000t, В. (2)
и = 72 cos 0,17 = 71 В.
угол отсечки 9, соответствующий точке перелома кривой гничивания при токе i = 0,1 А, определяется из соотно-Йа ния 0,1 = 0,6 sin 9, откуда 9 = 0,17 и t - 9/со = 0,17 • 10“3 с. пС момент t = 0 по (2) напряжение и = 72 В и в момент _ 0 17.10"3 с напряжение
Рис. 13.16
р На втором участке (0,03 < Ф < 0,04 мВб) производная Ф/dz = 0,2 • 10"4 Вб/А и напряжение
« = 400• 0,2 • 10"4 • 0,6• 1000cos 1000г = 4,8 cos 1000г В. (3)
В момент t = 0,17 • 10" 3 с по (3) напряжение и = 4,8 cos 0,17 = ”4,7 В и в момент t = (я/2) • 10"3 с напряжение и = 0. Зависимость w(oot) показана на рис. 13.16Р, г.
13.17.	На магнитопроводе, кривая намагничивания и геометрические размеры которого приведены в задаче 13.16, намотана катушка, имеющая 2000 витков. Катушка подключена к источнику синусоидальной ЭДС е = 80 cos 1000t, В.
Построить график тока в катушке.
13.18.	Для материала магнитопровода трансформатора (рис. 13.18, а) задана кривая намагничивания (рис. 13.18,6), Размеры магнитопровода: сечение $ = 0,2 см2; средняя длина магнитной линии I = 10 см; числа витков обмоток: Wj = 2000, w2 = 500; сопротивление резистора г == 1 кОм. Цепь получает питание от источника тока J (г) — 0,08 sin 1000t, А.
Построить зависимости от времени тока ij в первичной обмотке и напряжения и2 на вторичной обмотке, полагая, что при t = 0 индукция магнитопровода В — —1,5 Тл.
13.2. Аналитические методы расчета
13.19.	Катушка, имеющая 500 витков, намотана на стальной магнитопровод, кривая намагничивания которого может быть аппроксимирована полиномом Н — 100В + 200В3, где напряженность магнитного поля в амперах на метр, магнитная индукция в теслах. Сечение магнитопровода S = 10"3 м2, средняя длина магнитной линии I = 0,5 м. Катушка подключена к источнику гармонического напряжения u = 1101/2 cos cot, В.
Определить мгновенное и действующее значения тока в катушке при частотах напряжения: а) 50 Гц; б) 100 Гц.
13.20(	Р). В цепи по рис. 13.20 катушка, параметры которой приведены в задаче 13.19, соединена параллельно с конденсатором емкостью 4 мкФ и подключена к источнику синусоидального напряжения и с частотой 50 Гц.
Определить, при каком действующем значении напряжения в цепи возможен резонанс токов на частоте первой гармоники; найти действующие значения всех токов в этом режиме.
Решение. Составляем по заданной кривой Н (В) зависимость /ь('Г)» где 'Г — потокосцепление, учитывая, что
wS 500-10"3
wi,	500 . 4ЛЛЛ.
~l	6J!'- = 1000'L
Рис. 13.20
(закон полного тока).
Подставив эти зависимости в заданное в задаче 13.19 выражение кривой намагничивания, получим:
tL= 0,24х + 1,64х3,	(1)
где ток в амперах, потокосцепление в веберах.
При резонансе токов в контуре
1-я гармоника it общего тока I должна равняться нулю:
’1 = ’ы + 'ci = °-	(2)	=
При синусоидальном напряжении и потокосцепление катушки также сину- рис социальное, так как и — cM/dt, и может быть выбрано с нулевой начальной фазой
4х = 4х» sin ©t.	(3)
Ток катушки найдем по (1):
iL — ( 0,24х" + ~1,64х3 ) sin ©t - 1,64х3 sin ЗсоГ =
= (0,24х" + 1,24х 3) sin cot - 0,44х3 sin 3©t.	(4)
Ток конденсатора
ic = С du/dt = Cd24/dt2 = - со2 С4Х„, sin ©t - - 0,3944х" sin ©t. (5)
Из условия резонанса (2) получим:
, (0,24х" + 1,24х3) sin ©t - 0,3944х,, sin ©t = 0, откуда:1 a) 4*m = 0 — тривиальное решение или б) 1,24х"+ + 0,2 - 0,394 = 0 и 4х" = 0,402 Вб.
Напряжение и = dW/dt - ©4х" cos ©t. Поэтому в режиме резонанса токов действующее значение напряжения
и = CO4V1/2 = 314 • 0,402/]/2 = 89 В.
Мгновенное значение тока в катушке по (4)
iL = 0,1584 sin ®t — 0,026 sin 3©t, A.
Действующее значение тока в катушке
4 = |/0,15842/2 + 0,0262/2 = 0,114 А.
Действующее значение тока в конденсаторе по (5)
1С = 0,3944хт/|Л == 0,394 • 0,402/]/2 = 0,112 А.
Мгновенное значение тока источника
i = L+ ic = -0,44*^ sin 3cot = -0,026 sin 3cot, A,
Действующее значение тока источника
I = 0,026/1/5 = 0,0184 А.
13.21. Цепь состоит из катушки со стальным магнитопроводом, имеющей 100 витков, соединенной последовательно с конденсатором емкостью 8 мкФ и подключенной к источнику синусоидального тока i — Im sin 1000t А. Зависимость магнитного потока от тока катушки аппроксимирована полиномом Ф = 2-10“3i — 10 “3i3, где поток в веберах, ток в амперах.
Цепь настроена в резонанс на частоте первой гармоники изменением амплитуды тока.
Определить, при какой амплитуде тока наблюдается резонанс, найти действующие значения напряжений на входе цепи, на катушке и на конденсаторе в режиме резонанса.
13.22(Р). Катушка со стальным магнитопроводом имеет постоянное подмагничивание и подключена к источнику ЭДС е — Ет cos cot, где Ет — 40 В, со = 2 • 104 рад/с. Вебер-амперная характеристика катушки с учетом подмагничивания задана зависимостью iL = ЗОЯ* + 1044*2 + 4- 10б4*3, где ток в амперах, потокосцепление в веберах.
Определить ток в катушке.
Решение. Для определения тока в катушке предварительно вычислим потокосцепление
f	f	Е
4* = edt= Emcosatdt = 4*0 + —— sin cot — ¥0 + 4*m sin cot, (1)
J	J
где 4*m = EJd) — 2 • 10“3 Вб.
Постоянная интегрирования 4*0 определяется из условия отсутствия постоянной составляющей у тока катушки. Подставив 4* по (1) в заданную зависимость тока, получим:
iL = (4. Юб4*о + 1044*о + 544*0 + 2 • 10“2) +
+ (2,4  1044*g + 404*0 + 8,4 • 10“ 2) sin cot -
— (244*0 + 2 • 10“2) cos 2cot - 8 • 10“3 sin 3cot, (2) откуда из условия отсутствия постоянной составляющей тока следует, что
4 • 10б4*о + 1О44*о + 544*о + 2 • 10“2 = 0, или
4*В + 2,5 • 10“34*о + 13,5 • 1О"64*о + 5 • 10“9 = 0	(3)
- кубическое уравнение вида (13.10).
Подстановкой (13.11)
X = ?0 + 2,5 -10“ 3/3 = Ч*о + 0,833 • 10“3	(4)
приводим уравнение (3) к виду (13.8), где в соответствии с (13.12) р == 3,81 • 10“6; q = -2,55 • 10 “9. Таким образом, получили уравнение
х3 + 11,42 • 10“6х — 5,1 • 10“9 = 0
и по (13.9) находим х = 0,44-10“3.
По (4) искомое значение постоянной интегрирования То = = х — 0,833-10“3 = —0,393 • 10“ 3 Вб. Подставив 4х0 в выражение (2), найдем- ток iL = 72 • 10“3 sin cot - 10,6 • 10“ 3 cos 2cot — — 8 -10"3 sin 3<ot, A.
13.23. Параллельно катушке, параметры которой приведены в задаче 13.22, включен конденсатор емкостью 0,09 мкФ (рис. 13.23), ЭДС источника е = 40 cos 2 • 104t, В.
Определить ток источника i(t).
13.24(Р). Цепь состоит из последовательно соединенных линейного и нелинейного НЭ резисторов и источника ЭДС е = Ет sin cot, где Ет = 120 В; со = 314 рад/с (рис. 13.24). Сопротивление линейного резистора г — 40 Ом, вольт-амперная характеристика нелинейного резистора аппроксимирована зависимостью
и (z) = ai + bi3,	(1)
где а = 50 Ом; b = 40 В/А3.
Определить первую гармонику тока в цепи методами: 1) гармонического баланса; 2) гармонической линеаризации.
Решение. 1) Метод гармонического баланса. Уравнение цепи по второму закону Кирхгофа:
(г + a) i + bi3 = е.	(2)
Представим ток гармонической функцией i = Im sin (cot — ср). Требуется определить амплитуду тока 1т и сдвиг по фазе ср относительно ЭДС.
Для удобства последующих преобразований обозначим cot — ср — 0; тогда заданная ЭДС е = Ет sin(9 4- ср).
Подставим искомое решение для тока в уравнение цепи (2) и выделим синусную и косинусную составляющие в выражении ЭДС:
(г + a) Im sin 0 4- Ы% (3 sin 9 — sin 30) =
= Ет cos ф • sin 0 4- sin ф  cos 0.
Приравняв коэффициенты при одноименных тригонометрических функциях в левой и правой частях равенства, получим:
0 = Еш8Шф;	(3)
3 (г 4- а) 1т 4- — bl* = Ет cos ф.	(4)
Из уравнения (3) следует, что 8Шф = 0; ф = 0; созф = 1.
Уравнение (4) при заданных численных значениях величин
(40 + 50) 1т + ~ 40/ ’ = 120
приведем к виду
/’ + З1и-4=О и решим по формуле (13.9), где р = 1; q = —2;
1„ = ^2 + ]/4 + 1 + ]/1 - /4 + 1 = 1,62 - 0,62 = 1 А, т. е.
i = 1 sin cot, А.
2)	Метод гармонической линеаризации. При i = Im sin (cot -— ф) = Im sin 0 нужно определить 1т и ф.
Определим сопротивление нелинейного резистора по 1-й гармонике Rn(Im) -	где в соответствии с (1) Uim =
= (50Zm 4- 30Z„) — амплитуда 1-й гармоники напряжения на нелинейном элементе. Сопротивление в комплексной форме
(ZJ = RH (Im) = 50 + 30/да,
так как у резистора первые гармоники напряжения и тока совпадают по фазе.
Составим уравнение цепи по второму закону Кирхгофа в комплексной форме
[r + zH(U]/w = Ew,
где комплексные величины Ёт ~ Ет; tm = Im z. — ф.
После подстановки численных значений получим:
(40 4- 50 4- 30/2)^'^=120.
Рис. 13.26
Поскольку правая часть уравнения действительная, то <р « 0 и уравнение приводится к виду 4- 3/т - 4 = 0. откуда 1„ - 1 А.
13.25.	Для цепи рис. 13.24 заданы сопротивление резистора г s= 40 Ом и ЭДС е = 300 sin rot, В; вольт-амперная характеристика нелинейного элемента НЭ аппроксимирована полиномом i(u) = 0,02u 4- 4-10“ 6w3, где ток в амперах, напряжение в вольтах.
Определить первую гармонику напряжения на нелинейном элементе методами гармонического баланса и гармонической линеаризации.
13.26.	Для цепи рис. 13.26 дано: ri = 600 Ом; г2 = 300 Ом; г3 « 300 Ом; ЭДС источников ei « е2 = 240 sin 314t, В; вольт-амперная характеристика нелинейного резистора и (i) = 400i 4-4- 8000i3, где напряжение в вольтах, ток в амперах.
Определить первую гармонику тока i методами гармо
нического баланса и гармонической линеаризации.
13.27.	Цепь состоит из последовательно соединенных линейного резистора с сопротивлением г = 200 Ом, катушки, характеристика которой аппроксимирована полиномом i = =	4- &Т3, где а = 50 А/Вб, b = 4 • 107 А/Вб3, и источника
ЭДС е = 19 sin cot, В, где со — 104 рад/с.
Полагая потокосцепление в катушке синусоидальным 4х = = 'Em sin (cot — Г|), определить амплитуду потокосцепления начальную, фазу т| и найти ток i (t) методами гармонического баланса и гармонической линеаризации.
13.28.	Последовательно соединены: нелинейный резистор с вольт-амперной характеристикой, которая аппроксимирована зависимостью и (i) = ai 4- bi3, где а = 40 Ом, Ъ « 1400 В/А3, катушка без потерь с индуктивностью L = 23 мГн и источник ЭДС e=17sin 1000t, В.
Полагая ток в цепи синусоидальным i = Im sin (1000t — ср), методами гармонического баланса и гармонической линеаризации определить амплитуду тока 1т и сдвиг фаз ср.
13.29.	Последовательно соединенные катушка, характеристика которой аппроксимирована полиномом i (4х) = 304х 4-+ 4 • 106vP3, где ток в амперах, потокосцепление в веберах, и конденсатор емкостью 0,1 мкФ подключены к источнику ЭДС е = Ет sin cot.
Полагая потокосцепление 4х = 4xm sin (cot — т|), методами гармонического баланса и гармонической линеаризации рассчитать и построить амплитудную характеристику — зависимость амплитуды Um 1-й гармоники напряжения на катушке от амплитуды Ет ЭДС источника при частоте со = 2 • 104 рад/с, а также амплитудно-частотную характеристику Um (со) при амплитуде ЭДС Ет = 5 В.
Рис. 13.30
Рис. 13.31
13.30.	Характеристика катушки без потерь в схеме рис. 13.30 аппроксимирована выражением i (4х) = 304х + 4 • 10бгР3, где ток в амперах, потокосцепление в веберах; емкость конденсатора 0,1 мкФ, сопротивление резистора 5 кОм, ЭДС источника е = Ет sin cor, где со = 2 • 104 рад/с.
Полагая потокосцепление синусоидальным 4х = 4х w sin (cor — — т|), методами гармонического баланса и гармонической линеаризации рассчитать и построить амплитудную характеристику - зависимость амплитуды первой гармоники напряжения на катушке Um от амплитуды ЭДС Ет.
13.31.	В схеме рис. 13.31 емкость конденсатора 0,1 мкФ, сопротивление резистора 5 кОм, характеристика катушки аппроксимирована полиномом i (4х) = 304х + 4 • 1064х3, где ток в амперах, потокосцепление в веберах, ЭДС е = Ет sin cot с частотой со = 2 • 104 рад/с.
Методами гармонического баланса и гармонической линеаризации рассчитать и построить зависимость амплитуды первой гармоники напряжения на резисторе Um от амплитуды ЭДС Ет (амплитудную характеристику), полагая 4х = = 4XW sin (cot - ц).
13.32(	F). Последовательно соединенные катушка, характеристика которой аппроксимирована зависимостью i (4х) = = «4х -Ь Ь4х3, где а = 50 А/Вб, b = 107 А/Вб3, и резистор с сопротивлением г = 200 Ом подключены к источнику ЭДС е = Ет sin cot = 10 ]/2 sin 104t, В.
Полагая Ь4х3 04х, итерационным методом определить мгновенные значения потокосцепления, напряжения на катушке и тока в цепи.
Решение Запишем уравнение цепи по второму закону Кирхгофа:
dV/dt + П (49 = е,	(1)
Подставим в (1) заданную зависимость ip?) и в правую часть уравнения вынесем малый член:
е - d4/dt - агТ = ЬгЧ3.	(2)
Определим нулевое (линейное) приближение. Отбросив малый член ЬгТ3, решим полученное линейное дифференциальное уравнение комплексным методом. Запишем уравнение (2) в комплексной форме:
(аг + » откуда
101/2	1
= Е^аг +» = (50-200 4-ДбД = 10 " "45 Вб>
и мгновенное значение потокосцепления в нулевом приближении
То “ ^om sin (cot — ос) - 10“ 3 sin (104t — 45°) Вб.
Чтобы получить первое приближение, подставим нулевое приближение в правую часть уравнения (2). После перегруппировки членов получим:
cM/dt + arT = Ет sin cot —
3	1
— — brTom sin (cot - a) 4- — sin 3 (cot - a).	(3)
4	4
Уравнение (3) можно считать уравнением линейной цепи при несинусоидальном внешнем воздействии (правая часть). Каждую гармонику потокосцепления рассчитаем комплексным методом.
Запишем уравнение (3) в комплексной форме для 1-й гармоники:
(аг + » Ф1т = Ё„ - ~ z. -a,
откуда после подстановки численных значений находим потокосцепление Ч'ы = 0,925 • 10“3 z.—40° 20' Вб и напряжение
= 9,25 z. 49° 40' В.
Уравнение (3) в комплексной форме для 3-й гармоники
(аг + уЗю)	= -у fer'P’o zi - За
имеет решение:	= 0,0162 • 10"3 zl+153° 30' Вб и напряже-
ние &зт == /ЗсоФ3м = 0,486 z. -116° 30' В.
Мгновенные значения потокосцепления ¥ (г) = 0,925 • 10"3 sin (104t - 40° 20') + + 0,0162 • 10"3 sin (3 • 104t + 153°30') Вб;
напряжения на катушке
и = 9,25 sin (104t + 49° 40') + 0,486 sin (3 • 104t - 116° 30') В.
По закону Ома ток в цепи
i (t) = (<? - u)/r.
Каждую из гармонических составляющих тока определим комплексным методом. Для 1-й гармоники /1М — (Ёт — Uim)/r= = 0,054 z. ~ 40° 50' А; для 3-й гармоники 1зт=—йзт/г = = - 0,0024 z. -116° 30' А.
Мгновенное значение тока
i (?) = 0,054 sin (104t - 40° 50') - 0,0024 sin (3 • 104t - 116° 30') A.
Рис. 13.35
Рис. 13.36
13.33.	Цепь состоит из последовательно соединенных источника ЭДС е = 100 sin 104t, В, катушки без потерь с индуктивностью 40 мГн и нелинейного резистора, вольт-амперная характеристика которого аппроксимирована выражением и (i) = = ri + bi3, где г = 300 Ом, b = 2500 В/А3.
Полагая bi3 с ri, определить мгновенное значение тока в цепи итерационным методом.
13.34.	Последовательно соединенные резистор с сопротивлением 7,5 кОм и конденсатор с сегнетоэлектриком, вольт-кулоновая характеристика которого аппроксимирована зависимостью u(q) = aq + bq3, где а = 109 В/Кл, b = 5 • 1021 В/Кл3, получают питание от источника ЭДС е — 250 sin 105t, В.
Полагая bq3 aq, определить мгновенные значения тока и напряжения на конденсаторе итерационным методом.
13.35.	Для схемы рис. 13.35 заданы параметры: г = 400 Ом; L — 4O мГн и вольт-амперная характеристика нелинейного резистора i (и) — аи + bu3 = 0,002и + 2 • 10"7ы3, где ток в амперах, напряжение в вольтах; ЭДС источника е « 100sin 104t, В.
Полагая bu3 ащ определить итерационным методом мгновенные значения тока и напряжения нелинейного резистора, а также тока источника.
13.36.	Параметры элементов схемы рис. 13.36 указаны в задаче 13.35.
Итерационным методом определить ток и напряжение нелинейного резистора.
13.3.	Расчет по действующим значениям токов
и напряжении
13.37(	Р). Катушка с числом витков w = 500 и магнитопроводом из трансформаторной стали включена в сеть с напряжением U = 220 В (частота 50 Гц). Ток катушки I = 10 А, активная мощность Р — 1500 Вт. Сопротивление обмотки из медного провода постоянному току гм = 10 Ом. Амплитуда потока в магнитопроводе Фт = 10”3 Вб.
Рис. 13.37Р
Составить схему замещения катушки и построить векторную диаграмму.
Решение. Схема замещения катушки представлена на рис. 13.37Р, а, где Ьэк — эквивалентная индуктивность катушки, обусловленная потоком в магнитопроводе; Lpac — индуктивность рассеяния; гэк — эквивалентное активное сопротивление, учитывающее потери в магнитопроводе; гм — сопротивление обмотки.
Для определения параметров схемы замещения предварительно вычислим по (13.7), приняв Фт = Фт, составляющую напряжения, связанную с потоком в магнитопроводе йф = ^Я,44/)4Фт=Л11 В.
Определим эквивалентное сопротивление потерь в магнитопроводе гэк, записав по закону Джоуля —Ленца активную мощность (потерь) Р « гы12 + t/®/r3K, откуда гэк = 24,5 Ом.
Составляющая тока, обусловленная потерями в магнитопроводе, /г = 17Ф/гэк = )4,53 А.
Для определения эквивалентного индуктивного сопротивления хэк = соЬэк находим ток IL = ]/l2 — /2 = 8,9 А, и хэк == = U*/IL = 12,5 Ом.
Индуктивное сопротивление рассеяния храс = а>£рас определим, вычислив комплексное сопротивление катушки по схеме замещения (рис. 13.37Р, а):
~ "Ь 7-^рас "l" 7^эк^*эк/(^эк + Лэк) = 15,05 4- j (храс + 9,9)
и полное сопротивление по закону Ома z = U/I = 22 Ом. Таким образом, 222 = 15,05 2 4- (храс + 9,9)2, откуда храс = 6,2 Ом.
Векторная диаграмма для схемы замещения построена на рис. 13.37Р, б.
13.38.	У катушки со стальным магнитопроводом при напряжении питания U = 220 В ток I — 10 А, активная мощность Р = 1500 Вт. Сопротивление обмотки постоянному току гм = 10 Ом.
Пренебрегая потоком рассеяния, составить параллельную схему замещения катушки и построить для нее векторную диаграмму, приняв 1 = 1.
13.39.	Дроссель, включенный в сеть с напряжением 380 В, частотой 50 Гц, имеет стальной магнитопровод сечением 6 см2, массой 2 кг.
Определить необходимое число витков и действующее значение тока обмотки для получения амплитуды индукции
в магнитопроводе Вт = 1,5 Тл, при которой удельные потери
в стали Pq = 4 Вт/кг, удельная реактивная мощность намагни-
чивания Qq = 32 вар/кг.
Активным сопротивлением обмотки и потоком рассеяния
можно пренебречь.
13.40.	Трансформатор, работающий в режиме холостого хода, имеет стальной магнитопровод сечением 20 см2, массой 20 кг; числа витков обмоток Wi = 600; w2 = 360; активное сопротивление первичной обмотки гм = 10 Ом; сопротивление рассеяния храс = 12 Ом. Напряжение питания первичной обмотки 380 В, частота 50 Гц.
Пользуясь графиком удельных потерь в стали Ро и удельной реактивной мощности намагничивания Qq (рис. 13.40),
определить ток первичной и напряжение вторичной обмоток трансформатора.
13.41.	Характеристика катушки со стальным магнитопроводом для действующих значений токов и напряжений может быть аппроксимирована выражением U = 200/ — 10Z3, где напряжение в вольтах, ток в амперах. Катушка соединена последовательно с конденсатором емкостью 29 мкФ и получает питание от источника синусоидального тока частотой 50 Гц.
Определить действующее значение тока, при котором в цепи будет резонанс напряжений.
Глава четырнадцатая
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ ЦЕПЯХ. АВТОКОЛЕБАНИЯ
Введение к гл. 14
Для расчета переходных процессов в нелинейных цепях в общем случае нельзя применять метод наложения и определять переходный процесс, как это делается в линейных цепях, в виде суммы установившейся и свободной составляющих. Но, как и в линейных цепях, дифференциальные уравнения цепи составляются на основе законов Кирхгофа и постоянные интегрирования определяются с применением законов коммутации.
Применение при расчете только рабочего участка — участка нелинейной характеристики элемента, представляющего интерес с точки зрения поставленной задачи, увеличивает точность решения.
Для расчета переходных процессов в простейших нелинейных цепях применяют метод интегрируемой аппроксимации, метод условной линеаризации, метод кусочно-линейной аппроксимации, метод последовательных интервалов.
Устойчивость состояния равновесия
Состояние равновесия в электрической цепи постоянного тока определяется отсутствием изменений во времени токов и напряжений. Для нелинейной цепи переменного тока в состоянии равновесия не должны изменяться амплитуды и фазы гармонических составляющих.
Математически состояния равновесия х0 либо могут быть определены из дифференциальных уравнений приравниванием нулю первой и высших производных, либо найдены в результате расчета установившегося режима. В линейной цепи с независимыми источниками может быть только одно состояние равновесия, и оно всегда устойчиво. Исследования устойчивости необходимы в нелинейных цепях и цепях с обратной связью (с зависимыми источниками), где устойчивых состояний равновесия может быть несколько.
При исследовании устойчивых состояний в цепях с источниками постоянных ЭДС и токов предварительно рассчитывается установившийся режим и определяется положение рабочих точек на характеристиках нелинейных элементов. Далее с учетом характеристик нелинейных элементов рассматривается изменение переменных составляющих. В условиях многих задач этой главы приводятся уже найденные параметры нелинейных элементов относительно рабочих точек и рассматриваются сразу переменные составляющие.
Для определения устойчивости состояния равновесия, заданного некоторым значением переменной х = х0, следует величине х дать малое приращение Дх. Из-за малости приращения нелинейность характеристики проявляется слабо, и цепь можно считать линейной. Поэтому при аналитическом исследовании функциональную зависимость у = f (х), определяющую характеристику нелинейного элемента относительно состояния равновесия y^—f (х0), можно представить рядом Тейлора, полагая у — у0 + Ду и х = х0 + Дх, т. е. в виде
(14.1а)
dx
2! dx2
х = х0
Дх2
х = х0
Учитывая, что	и опуская величины второго
порядка малости, можно (14.1а) упростить и записать для приращений соотношение
by = df/dx\x=X(j &х.	(14.16)
Таким образом, для приращений нелинейный элемент может быть заменен линейным с постоянным параметром, равным дифференциальному в точке равновесия х0, т.е.
d//rfx|XSX0 = Ду/Дх.	(14.2)
Поскольку при анализе устойчивости «в малом» нелинейная цепь сводится к линейной, то изменение приращений во времени определяется изменением свободных составляю-440
щих процесса, т. е. слагаемыми вида Aept. Поэтому состояние равновесия устойчиво «в малом» в том случае, если все действительные корни и действительные части комплексно-сопряженных корней отрицательны, т. е. все свободные составляющие с течением времени затухают. В частности, в цепях первого и второго порядков состояния равновесия устойчивы, если все коэффициенты характеристического уравнения положительны (одного знака).
Рис. 14. А
Рис. 14.Б
Для цепи третьего порядка с характеристическим уравнением
«зР3 + «2Р2 + flip + а0 =0
состояние равновесия устойчиво, если все коэффициенты положительны и дополнительно выполняется условие > а3а0.
Для сравнительно простых цепей характеристические уравнения проще составлять по методу входного сопротивления [ZBX (р) = 0]. В частности, для цепей с обратной связью или зависимыми источниками входное сопротивление можно найти, включив в одну из ветвей цепи независимый источник ЭДС Е(Р) и вычислив входное сопротивление по формуле
ZBX (р) = Е (р)/1 (р),	(14.3)
где I (р) — ток этого источника.
Для упрощения вычислений источник Е(р) рекомендуется включать последовательно с зависимым источником.
Если цепь содержит только резистивные элементы, среди которых есть элементы с N- (рис. 14.А) или S-образной (рис. 14.Б) вольт-амперной характеристикой, то при анализе устойчивости необходимо учесть емкость С, включенную параллельно элементу с N-образной характеристикой (рис. 14.А), и индуктивность L, включенную последовательно с элементом, имеющим S-образную характеристику (рис. 14.Б). Спадающий
участок характеристик, соответствующий отрицательному дифференциальному сопротивлению, приводит к неоднозначности по напряжению (рис. 14.Б) и току (рис. 14.А).
Изображение переходных процессов на фазовой плоскости
На фазовой плоскости, координатами которой являются некоторая переменная х и ее производная dx/dt — у (рис. 14.В), состояние цепи определяется изображающей точкой и линиями, вдоль которых движутся изображающие точки, — фазовыми траекториями и их совокупностями — фазовыми портретами.
Через каждую регулярную точку плоскости может проходить только одна траектория, пересекаться фазовые траектории могут только в особых точках, которым соответствуют устойчивые и неустойчивые состояния равновесия. Периодическим процессам в электрических цепях на плоскости соответствуют замкнутые фазовые траектории — предельные циклы.
Основные свойства фазовой плоскости: 1) Движение изображающей точки в верхней полуплоскости, где dx/dt > О, может происходить только в направлении увеличения переменной х, а в нижней полуплоскости, где dx/dt < 0, только в направлении уменьшения х. По замкнутой траектории — предельному циклу — движение возможно только в направлении движения часовой стрелки.
2) Изображающая точка может пересекать ось абсцисс х только под углом я/2.
3) Особые точки могут находиться только на оси абсцисс как точки состояния равновесия, определяемые из условия dx/dt = 0.
Для построения фазовых портретов часто сначала определяют положения особых точек и находят фазовые траектории в окрестности этих точек. При этом фазовые траектории нелинейных цепей рассматривают по малым отклонениям от 442
состояний равновесия, полагая, что цепь линейна. Вид фазовой траектории в окрестности состояния равновесия определяется типом особых точек, т. е. корнями характеристического уравнения.
Для цепи с одним независимым накопителем (характеристическое уравнение первой степени) возможна особая точка типа узел. Узел может быть устойчивым, когда корень р < О, и неустойчивым, когда р > 0.
Для цепи с характеристическим уравнением второй степени возможны особые точки: 1) Узел при действительных корнях pi, р2 одного знака; если Pi<0 и р2 ~ устойчивый узел, а если pt >0 и р2 >0 - неустойчивый. 2) Фокус при комплексно-сопряженных корнях Pi, 2 = а ± если а < 0 — устойчивый фокус (колебания затухают), а если а > 0 — неустойчивый (колебания нарастают). 3) Седло при действительных корнях Pi и ₽2 разного знака (неустойчивая особая точка). 4) Центр при мнимых корнях Pi,2 = ±jcoo (незатухающие колебания).
Переход от полученного решения на фазовой плоскости у (х) к зависимости х (Г) с учетом зависимости у — dx/dt выполняется при помощи соотношения
t= f dx/y(x).
х(0)
Существует взаимное соответствие между прямыми линиями на фазовой плоскости и экспоненциальными временными зависимостями. Изменению переменной во времени по гармоническому закону соответствует движение изображающей точки по эллипсу или окружности на фазовой плоскости.
Зависимость искомой переменной от времени может быть получена с применением приближенных вычислений по интервалам. При этом фазовую траекторию у(х) на /с-м интервале между-точками хк и xfc+i заменяют отрезком прямой у = = а + Ьх (рис. 14.Г) и находят интервал времени, необходимый для движения изображающей точки на /с-м интервале,
хк+1
* Яу	1
=	----— = ™ In (а + Ьх) |**+1
к a + Ьх h V хк
или, учитывая значения ординат на границах к-го интервала Ук и Ук+i (рис. 14.Г) и значения Ь = (ук+1 -ук)/(хк+1 -
ДГ» =	л+1	(144)
Ук+1 ~ Ук Ук
и tk+1 —	+ Atfc.
Выражение (14.4) целесообразно применять, когда движение изображающей точки определяется отрезками прямых, например, в случае релаксационных колебаний. Временная зависимость при этом определяется отрезками экспонент.
Метод усреднения
Метод усреднения при решении многих задач по существу совпадает с методом медленно меняющихся амплитуд. Он применяется при расчете переходных и установившихся процессов в электрических цепях, обладающих фильтрующими и резонансными свойствами для основной гармоники, причем часто достаточно рассмотреть только основную гармонику, а высшими гармониками пренебречь.
Дифференциальное уравнение неавтономной цепи с источниками ЭДС или токов и двумя реактивными элементами можно свести относительно некоторой переменной х к виду d2x/dt2 + со2х = е/(х, dx/dt,
где е — малый параметр, определяющий близость закона изменения переменной х к гармоническому; f — функция, определяемая нелинейными характеристиками элементов цепи. Точность метода тем выше, чем меньше параметр в, т.е. чем ближе колебания к гармоническим.
При решении конкретных задач часто параметр s не выносится, а близость к гармоническому закону определяется малостью значений коэффициентов правой части или другими соображениями, например данными эксперимента.
Решение дифференциального уравнения ищется в виде
х = a (t) cos ф; dx/dt = - a (t) со sin ф,	(14.5)
где ф = со? — ф (?) — полная фаза. При этом уравнения установления амплитуды а = а (?) и фазы ф = ср (?) переменной х, или
укороченные уравнения, имеют вид:
da ~dt
Е
2лсо
2л
*
/(о cos ф,
— асозтф, r)sin ф<2ф;
2я
= — f/(a cos ф, dt 2лсоа J о
-ясоэтф, ?)созф^ф.
(14.6а)
(14.66)
о
Малый параметр е в правой части указывает на медленные изменения амплитуды а и фазы ф. Поэтому при интегри-.
ровании в течение периода (усреднении) амплитуда и фаза в подынтегральных выражениях принимаются постоянными.
При решении задач можно вместо времени t ввести безразмерное время т = cot
Автоколебания
Релаксационные или почти гармонические автоколебания могут возникнуть в нелинейной цепи с элементами, имеющими спадающий участок вольт-амперной характеристики, или в цепях с обратной связью.
Расчет генераторов релаксационных колебаний часто выполняется методом кусочно-линейной аппроксимации.
При расчете генераторов почти гармонических колебаний достаточно учесть основную гармонику. На первом этапе исследования таких генераторов полагают, что амплитуды (относительно состояния равновесия) малы и цепь можно считать линейной. В линейном приближении находится условие возбуждения колебаний из условий устойчивости и определяется частота по мнимым составляющим корней характеристического уравнения.
При линейном приближении нельзя определить амплитуду колебаний. Для определения амплитуды в установившемся режиме необходимо учесть нелинейности характеристик элементов, у которых нелинейность проявляется наиболее сильно.
Расчет амплитуды и частоты автоколебаний может быть выполнен методом усреднения или методом гармонической линеаризации. При расчете методом гармонической линеаризации учитывается только основная гармоника и возможно применение комплексного метода. При этом принимается во внимание зависимость эквивалентных параметров нелинейных элементов от амплитуд переменных величин, определяющих нелинейность характеристики.
Составив характеристическое уравнение [ZBX (р) = 0] для цепи с эквивалентными параметрами, можно определить частоту и амплитуду установившихся колебаний, решив совместно два уравнения:
Re [ZBX ОМ] = 0; Im [ZBX ОМ] = 0.	(14.7)
Численные методы интегрирования
При расчете нелинейной цепи с применением метода переменных состояния составляется система, например, п дифференциальных уравнений, каждое из которых имеет вид:
dxj/dt fj (xb x2,..., x„),	(14.8)
где Xj (j = 1, 2, ...» и) — переменные состояния, в качестве которых часто выбирают токи в индуктивностях или потокосцепления, напряжения на емкостях или заряды.
При численном интегрировании уравнений состояния (14.8) все переменные, включая и время г, рассматриваются как дискретные величины и выбирается шаг интегрирования h = = Af. На каждом шаге по известному состоянию в момент времени tk (к = 0, 1, 2, ..., N), т. е. xt (rk), х2 (tk\ ..., х„ (tfc), находится состояние при tk+1 = tk + h.
Наиболее простым методом численного интегрирования является метод Эйлера. Так, для цепи первого порядка с одним реактивным элементом в соответствии с уравнением состояния dx/dt — f (х, t)	(14.9)
значение переменной при t = tk+1
tk + h
xfc+1 = xfc + Axk = xk 4- f /(x, Г) dt, (14.10)
где xk — известное значение переменной при t = tk; Axk — приращение переменной на fc-м шаге.
Предполагается, что известно начальное условие при t = t0, т.е. x(t0)=x0.
При численном интегрировании значение интеграла (14.10) находится приближенно. В соответствии с явной (прямой) формулой Эйлера подынтегральная функция на интервале полагается постоянной и равной производной в начале интервала, т. е. f(*k, h) = dx/dt \t=tk.
При этом по (14.10)
x*+i “ хк + hf (xk, tk).	(14.11)
Если выбирается значение производной в конце интервала /(Xk+i, tk+1) = dx/dt\t=tk+1, то получается неявная (обратная) формула Эйлера:
= xfc + /i/(xk+1, Гк+1).	(14.12)
Искомое значение хк+1 входит в (14.12) неявно и может быть найдено как решение этого нелинейного алгебраического уравнения. Неявный метод применяется с целью получения устойчивого процесса.
Для цепи второго порядка уравнения состояния имеют вид: dxjdt == (xt, х2, 0; dx2/dt = f2 (xb .x2, t).	(14.13)
(14.14)
Предполагается, что известны начальные условия при t —10, т.е. Xi (*о) = х10 и х2 (t0) = х20- В этом случае явные формулы Эйлера:
*1 (к+1) =	+ Vl [xlfc> х2к> tjJj
х2 (к + 1) = х2к + hf2 [xifc, Х2к, tfc].
Если характеристики нелинейных элементов задаются в виде таблицы, то при вычислениях выполняют интерполяцию. При линейной интерполяции зависимости у(х) между двумя точками i и j применяется формула
У = У1 (х - x;)/(Xi - Xj) + уj (х - Xi)/(xj - xj, (14.15) где j == i + 1; i — порядковый номер точки в таблице.
14.1. Аналитические и графические методы расчета
14.1 (Р). Ключ в цепи по рис. 14.1, а размыкается. Заданы ЭДС Е = 250 В, сопротивления резисторов: гх — 120 Ом; г2 = = 5 Ом; г3 = 0,2 Ом; характеристика Т (i) катушки (рис. 14.1, б).
Определить ток катушки методами: 1) аналитической 2) условной линеаризации;
3) кусочно-линейной аппрок-
во время переходного процесса аппроксимации вида i *= /сТ2;
Рис. 14.1
симации с двумя отрезками прямых, проходящих через точку b с координатами 0,5 А; 1 Вб (рис. 14.1,6); 4) последовательных интервалов при аппроксимации вида i — fc1?2, где к — 0,5 А/Вб2.
Решение. Составим дифференциальное уравнение цепи после коммутации
d^/dt + ri (Т) = Е,	(1)
где г =	г2.
Определим рабочий участок характеристики ¥ (i). В момент коммутации (г = 0) ток в катушке не изменяется скачком,
т.е. i(0) = £r3/p = 0,08 А, где p = rtr2 + r2r3 4- r3r19 в установившемся режиме i(oo) = E/(rr 4- r2) = 2 A.
Таким образом, начальная точка а на рабочем участке (рис. 14.1,6) имеет координаты: i(0)—0,08 А; Ч/(0) = 0,4 Вб; конечная точка с — координаты i(oo) = 2 А; 4х (оо) = 2 Вб. Во время переходного процесса 0,08 А < i (t) < 2 А и 0,4 Вб < <T(t) <2 Вб.
1) Метод аналитической аппроксимации. Предварительно для принятой аппроксимации i (*Р) = kW2 определим, рассматривая начальную точку а, коэффициент аппроксимации к = = i (0)/Т2 (0) = 0,08/0,42 = 0,5 А/Вб2.
Метод аналитической аппроксимации предполагает возможность интегрирования нелинейного дифференциального уравнения цепи (1) с учетом выбранной аппроксимации:
dV/dt + rW2 = Е.	(2)
Разделяя переменные в (2) dt = d4/(E - rW2), вычислим ¥ t-----------------------------------------
_1_ f	_	1 fin + V
r/t . (E/rk — Ч'2) j \/rkE \ VE/rk — 'P/vm T (0)
откуда
e-2рШ, = V^k-'P ]/£M + 4>(0) ]/Е/йс + 'Р ]/Ё/гк - T (0)
или после подстановки значений параметров
е'25°'= TPF1,5'	(4)
Из (4) находим потокосцепление
3 - 2e~25Ot
* = 1,5+ е-250’’ Вб’
И ток
/ 3 _ Эр-25ОГ \2
i = /c^2=0,5	, А.
у 1,э 4- е j
Полученное аналитическое решение позволяет анализировать в общем виде влияние отдельных параметров цепи на зависимости тока и потокосцепления от времени.
2) Метод условной линеаризации. В методе условной линеаризации нелинейная характеристика заменяется на рабо-
чем участке прямой, т. е. рассчитывается переходный процесс в линейной цепи.
Заменим характеристику Т (i) на рабочем участке (рис. 14.1,6) отрезком ас прямой (не проходящей через начало координат), уравнение которой
i(T) = (T-'Po)/Lo,	(5)
где Lq — индуктивность. Эту индуктивность определим по
приращениям:
= Т (оо) - Т (0) _ 2-0,4 °- i(со) —1(0) “2-0,08
= 0,833 Гн,
и из (5) при i (оо) = 2 А и Т (оо) = 2 Вб вычислим Фо = 0,33 Вб. Подставив (5) в дифференциальное уравнение цепи (1),
получим:
(6)
Найдем его решение в виде
= Фу + Aept,
где, как следует из (6) при cFV/dt — 0, т. е. для установившегося режима,
Ч» = — Е + То = 1,98 Вб.
у г
Корень характеристического уравнения р=—г/Ь^~ ® —150 с-1. Таким образом, Т = 1,98 + Ас"150*.
Из условия Т (0+) = 'Р (0_) = 0,4 находим А = 0,4 — 1,98 = = -1,58 иТ = 1,98 - 1,58с"150*, Вб.
По тдривой i(T) ток i(t) может быть найден графически. При заданной зависимости i = №, где к — 0,5, получим аналитическое решение
i = 0,5 (1,98 - 1,58с"150*)2, А.
3) Метод кусочно-линейной аппроксимации. Для повышения точности расчета рабочий участок характеристики заменим отрезками нескольких прямых, в рассматриваемой задаче по условию отрезками ab и Ьс (рис. 14.1,6). Расчет для каждого участка выполним так же, как для линейной цепи. Постоянные интегрирования найдем из условия непрерывности изменения рассматриваемой величины при переходе с одного участка на Другой. Для каждого участка определим момент времени, соответствующий переходу на следующий участок.
ние
Для расчета тока i(t) исходное дифференциальное уравне-(1) представим в виде
Ж di di dt
(7)
где на каждом участке
¥ = Lki +	(/< = 1, 2),	(8)
т.е. вместо (7) получим:
Ц^-+П = Е.	(9)
III1
Рассмотрим решение на каждом участке.
а)	Первый участок ab (к = 1). На этом участке в интервале времени 0 t < tj ток и потокосцепление изменяются в пределах 0,08 А i 0,5 А; 0,4 Вб < 4х 1 Вб, т. е. индуктивность
Li = A'Pi/Aij = (1 - 0,4)/(0,5 - 0,08) = 1,43 Гн.
Ток
.	.	.	я	j pi*
i — iy 4“ iCB —	~ ”Ь A j с ,
П + г2
где iy = 2 A; Pi = -(^ + r2)/Lt = -87,4 с’1.
Из условия i(0+) = Ц0_) = 0,08 А находим постоянную Ai = —1,92. Следовательно, ток на первом участке
i = 2 — 1,92е“87’% А.
Время гь соответствующее моменту перехода на второй участок, определим из условия i (tj = 0,5 А, т. е.
0,5 = 2 — 1,92г"87’4*1,
откуда

б)	Второй участок Ьс (к = 2). На этом участке в интервале времени < t оо ток и потокосцепление изменяются в пределах 0,5 А < i 2 А; 1 Вб < Т 2 Вб, т.е. индуктивность L2 = М2/&2 = 0,67 Гн.
Ток
i = + *св = —;-----1" А2с ,
где zy = 2 А; р2 = - (^ +r2)/L2= -186,6 с”1. Учитывая, что i fo) = 0,5 А, находим постоянную А2 = -1,5.
Таким образом, на втором участке ток
1- = 2-1,5е-186-6,'-‘1’, А.
На втором участке вследствие насыщения (L2 < М) постоянная времени меньше, чем на первом.
Таблица 14.1
Г 10 3, с	% Вб	/, А	1-10“3, с	Вб	i, А
0,0	0,40000	0,08000	10,0	1,87635	1,76035
2,0	0,88000	0,38720	12,0	1,93626	1,87456
4,0	1,28320	0,82330	14,0	1,96762	1,93577
6,0	1,57737	1,24405	16.0	1,98368	1,96749
8,0	1,76636	1,56001	18,0	1,99180	1,98364
4) Метод последовательных интервалов. При решении задачи этим методом интервал времени, в течение которого рассчитывается переходный процесс, делим на п интервалов — шагов At — h.
В фиксированный момент времени tk = kh на к-м интервале потокосцепление равно Через интервал времени Аг, т.е. момент tk+1 = (к + 1)/1, потокосцепление изменится на ДФк, т. е.
4'k+1=Tk + A'P = Tk + f <№.
Представив уравнение цепи (1) в виде
d^/dt = E-ri^	(10)
получим:
rk+ 1
'Pk+1=T/t+ f	(11)
Интеграл вычислим приближенно, полагая подынтегральную функцию на малом интервале времени постоянной при токе i fP) = i 0?к) в начале интервала. В результате получим явную формулу Эйлера:
Ч\+ х=Фк+[Е -П (Ч\)] h.	(12)
Выбрав шаг h = 2 • 10"3 с при заданной аппроксимации i = ~ W2, где к = 0,5 А/Вб2, запишем расчетную формулу (12)
в виде
Ч\+1 =^ + 0,5-0,125^, Вб.
Рис. 14.2
Результаты расчета сводим в табл. 14.1.
14.2(Р). Для схемы рис. 14.2 методом условной линеаризации найти наибольшее возможное отношение максимального тока переходного процесса к амплитуде тока в установившемся режиме.
Дано: 17=1200 В; / = 400 Гц; г = 500 Ом; вебер-амперная характеристика катушки аппроксимирована зависимостью i = &*Р5, где к = - 1,5 А/Вб5.
Решение. При мгновенном значении напряжения питания и = = Um sin (tor + а) запишем дифференциальное уравнение цепи для потокосцепления
d'V/dt + г/сФ5 = Um sin (cot + а).	(1)
Вычислим эквивалентную индуктивность катушки Ьэк, заменяя заданную вебер-амперную характеристику линейной зависимостью i = 'Р/Ьэк. При определении рабочего участка характеристики будем считать, что г = 0, т. е. uL — и. Тогда рабочий участок задается пределами изменения потокосцепления и тока — Т < 'Pn,;	i < причем по (13.7)
= t^/4,44/ = 0,676 Вб и по характеристике катушки = = кТ5 = 0,21 А.
Эквивалентная индуктивность Ьэк =	= 3,19 Гн.
Принятое допущение (г = 0) при определении Ьэк и допустимо, так как <в£эк = 8000 Ом » г = 500 Ом.
Применяя метод условной линеаризации, решаем вместо уравнения цепи первого порядка (1) линейное дифференциальное уравнение яф г
+ -—¥ = Um sin (cot + а).	(2)
dt
Запишем решение в виде
Ч» = Ч»у + 4»^ = Ч*у + Ле”, где Ч\ = Ч'уи sin (rot + а - <р); Ч»^ = L,Jm = L3KL/,„//(®LJ2+r2 = 5= 0,675 Вб; ф = arctg(wL^Jr) = 86°25'; р = —гЩ* = —157 с“*. Учитывая, что Ф (0) = Tym sin (а — ф) + А = 0, находим: А = = — 4'ymsin(a - ф); следовательно,
4х = 0,675 sin (cot + а — ф) — 0,675 sin (а — ф) е~157t Вб.
Значение угла а, определяющего начальную фазу напряжения, т.е. момент замыкания ключа, найдем из условия получения наибольших значений потокосцепления Т и тока i во время переходного процесса в линеаризованной цепи г, Ьэк. Очевидно, этому будет соответствовать условие а — (р — п/2, при выполнении которого свободная составляющая наибольшая, т. е. а = я/2 + ср == 176° 25'.
Таким образом, потокосцепление
= 0,675 cos	- 0,675е"157(, Вб.
Определим возможное наибольшее значение потокосцеп* ления во время переходного процесса которое получится в некоторый момент времени г'. Сопоставляя постоянную времени линеаризованной цепи т = — 1/р = 6,38  10“3 с и период Т -\/f = 2,5 • 10-3 с, замечаем, что т > Т. Поэтому, не анализируя трансцендентное уравнение, считаем t' — Т/2 — 1,25 • 10"3 с. В этот момент
| «Р | =	= | -0,675 - 0,675е-157 '1'25'10’31 = 1,23 Вб
И соответствующий ТОК iinax — Ъ^тах = 4,34 А.
Искомое отношение i'max/imax = 4,34/0,21 = 20,6.
14.3.	В цепи рис. 14.1, а после размыкания ключа наступил практически установившийся режим. В момент времени, который принят за t = 0, произошло короткое замыкание между точками 1 и 2. Параметры цепи и кривая намагничивания Т (/) приведены в условии задачи 14.1.
Применяя методы: 1) аналитической аппроксимации; 2) кусочно-линейной аппроксимации, определить ток катушки /(Г) во время’ переходного процесса и найти зависимость дифференциальной индуктивности катушки La от времени, учитывая связь
Указание. При расчете методом кусочно-линейной аппроксимации принять, что характеристика катушки 'P(i) задается двумя отрезками прямых cb и ЬО с координатами точки с: 2 А, 2 Вб; точки Ь: 0,5 А, 1 Вб (рис. 14.1,6).
14.4.	Пренебрегая потерями в магнитопроводе и потоком рассеяния, определить во вре1МЯ переходного процесса напряжение и2 на выходе трансформатора (рис. 14.4).
Дано: Ei = 6 В; = 4 Ом; vv2 = 2wt. Зависимость ¥(/) для первичной обмотки трансформатора аппроксимирована отрезками двух прямых Ф = 0,8/ при 0 i < 0,5 и Т = 0,35 4- 0,1/ при 0,5 < / 1,5, где Ч* - в веберах, / — в амперах.
Сопоставить полученный результат с зависимостью u2(t) в случае, если магнитопровод не будет насыщаться,
14.5.	Конденсатор емкостью С = 12 мкФ заряжен до напряжения (70 = 1 В. С момента t = 0 конденсатор разряжается через диод, вольт-амперная характеристика которого аппроксимирована зависимостью i = ки2, где к — 10 мА/В2.
Определить методом аналитической аппроксимации время разрядки конденсатора до напряжения, равного 0,5 В. Найти это же время методом условной линеаризации.
Рис. 14.4
Рис. 14.6 -*
14.6.	Определить ток i во время переходного процесса в цепи рис. 14.6, а.
Дано: ток источника J = 10 мА, емкость конденсатора С = 5 мкФ и вольт-амперная характеристика диода (рис. 14.6,6). Задачу решить методами: а) аналитической аппроксимации вольт-амперной характеристики диода параболой i = ки2; б) условной линеаризации. Методом последовательных интервалов найти время, в течение которого напряжение на конденсаторе достигнет значения 0,8 В.
а.)	0 0,5 1,0 В
б)
Рис. 14.8
14.7.	Определить время переходного процесса в цепи рис. 14.7, считая, что переходный процесс заканчивается, когда ток диода составит 0,1г (0+), где г(0+) —ток в момент коммутации.
Характеристика диода приведена на рис. 14.6,6; Е = 1 В; г = 2 кОм; С = 4 мкФ.
Задачу решить методами: а) аналитической аппроксимации характеристики диода зависимостью i(u) = кги 4- к2и2, коэффициенты kt и к2 выбрать, считая, что значения тока и напряжения диода, найденные по его характеристике, совпадают со значениями, определяемыми зависимостью i — кги 4- к2и2 в крайних точках рабочего участка; б) условной линеаризации; в) последовательных интервалов при шаге Аг = т/4, где т — постоянная времени цепи при линеаризации.
Рис. 14.9
Рис. 14.10
14.8.	Заданы ЭДС Е = 1,5 В и параметры схемы рис. 14.8, а: г = Ю Ом; С = 20 мкФ; вольт-амперная характеристика диода приведена на рис. 14.8,6.
Определить напряжение на диоде во время переходного процесса (после замыкания ключа) методом кусочно-линейной аппроксимации.
14.9.	Методом условной линеаризации определить время, за которое напряжение на индуктивной катушке (рис. 14.9) после коммутации уменьшится на 80%.
Дано: Ё = 1 В; L=0,5 Гн; г = 0,7 кОм; характеристика диода приведена на рис. 14.6,6.
мкКл
Рис. 14.11
14.10.	Найти время, в течение которого ток ir в цепи рис. 14.10 достигнет значения 0,9/г, где 1Г — ток установившегося режима после коммутации. Задачу решить методами
аналитической аппроксимации характеристики диода, полагая i (и) = ди2, где а = 100 мА/B2, и условной линеаризации.
Дано: С = 50 мкФ; г = 40 Ом; ЭДС е = Е = 1 В.
14.11.	Определить в схеме рис. 14.11, о напряжение ис на емкости после коммутации при Е — 150 В; Tj = 56 Ом; г2 = = 4 Ом; вольт-кулонная характеристика конденсатора приведена на рис. 14.11,6.
Задачу решить методами: а) кусочно-линейной аппроксимации двумя отрезками прямых, пересекающимися при и — 50 В; б) условной линеаризации.
7л В
Рис. 14.12
14.12.	Определить методом условной линеаризации наибольшее возможное значение тока в индуктивной катушке (рис. 14.12, а) во время переходного процесса.
Напряжение питания 17 = 220 В; f = 50 Гц; параметры схемы = 50 Ом; г2 — 800 Ом; у катушки сечение стали магнитопровода S = 16,5 см2; средняя длина магнитопровода I = 390 см; число витков w = 600; кривая намагничивания задана отрезками трех прямых (рис. 14.12,-6).
Указание. См. решение задачи 14.2.
14.2. Устойчивость состояния равновесия
14.13(F). Вольт-амперная характеристика газоразрядного нелинейного элемента имеет S-образную форму (см. рис. 14.Б). Рабочий участок на спадающей части этой характеристики, соответствующей разряду, аппроксимирован зависимостью и = = fcj 4- k2/i, где kt = 20 В; к2 = 25 В - А.
Нелинейный элемент включен в цепь по рис. 14.13, где сопротивление резистора г = 8 Ом, постоянная ЭДС источника Е = 50 В.
Найти состояния равновесия и определить условия их устойчивости. На плоскости параметров Е, г построить область устойчивого разряда.
Решение. Найдем ток, определяющий состояния равновесия, аналитически. Запишем уравнение цепи (рис. 14.13)
ri + и = ri +	+ k2/i = Е	(1а)
или
,2 _ к±-Е . +	= о
Г	г
(16)
откуда	______________________
ioi, 02 = (£ - fci)/2r + |/[(£ - fcx)/2r]2 - k2/r,
т.е. на рассматриваемом рабочем участке возможны два состояния равновесия: г01 =2,5 А и i02 — 1,25 А.
Рис. 14.13
Рис. 14.13Р -
Для исследования их устойчивости в резистивную цепь (рис. 14.13) последовательно с нелинейным элементом, имеющим S-образную характеристику, необходимо включить индуктивность L (значение ее может быть очень малым). При этом процессы в цепи будут описываться дифференциальным уравнением
Ldi/dt + ri + ki 4- к2/i = Е.	(2)
Рассмотрим малые отклонения относительно равновесий гоп (п = 1, 2). Записав ток в виде i = iOn + подставим его в Дифференциальное уравнение (2) и получим:
Ldtjdt + г (iQn + £) + к. + k2/(iQn + Q = Е.
Последнее слагаемое в левой части равенства представим в виде ряда Тейлора, ограничиваясь слагаемым с линейной зависимостью, т.е.
^2
ki _ к2 „ ^*0п
При этом, учитывая, что в соответствии с (1а)
rion + fci + k2/iQn = Е,	(3)
получаем линейное дифференциальное уравнение для отклоне
НИИ
+ (г - k2/&) ij = 0. at
Состояния равновесия будут устойчивыми, если коэффи-циенты этого уравнения будут положительными (корень характеристического уравнения — отрицательным), т. е. если (г -- k2/io„) > 0.
Для состояния равновесия i01 = 2,5 А находим (8 — 25/2,52) == = 4 > 0, т. е. оно устойчиво, а при i02 = 1,25 А получим (8 — 25/1,252) <0, т.е. это состояние равновесия неустойчиво.
Для определения области устойчивого разряда на плоскости параметров Е, г запишем условие границы устойчивости (г - кг/ifa = 0,
откуда, определив iOn = ]/к2/г и подставив это значение в (3), получим уравнение для построения границы рассматриваемой области	—	г
Е = кг +1ук2г = 20+ 10]/г.
На рис. 14.13Р построена кривая Е(г), разделяющая первый квадрант на две области: верхнюю (заштрихованную) и нижнюю. Точка Е = 50 В и г = 8 Ом (заданные значения) находится в верхней области. Поэтому приходим к выводу, что эта область соответствует устойчивому разряду при токе iOi. Эта же область параметров соответствует возможному появлению и неустойчивых состояний, так как при токе i02 состояние равновесия неустойчивое.
В нижней области при заданной аппроксимации вольт-амперной характеристики состояния равновесия существовать не могут. В действительности, если учесть нарастающий участок вольт-амперной характеристики нелинейного элемента, эта область будет соответствовать устойчивым режимам в отсутствие разряда.
14.14(	Р). Коэффициент усиления к = и2/иг усилителя с обратной связью (рис. 14.14) не зависит от амплитуды и частоты напряжения щ на входе. Усилитель имеет бесконечно большое входное сопротивление и равное г выходное.
Определить условие устойчивости состояния равновесия. На плоскости параметров кМ и построить область возбуждения колебаний.
Решение. Представим схему с обратной связью (рис. 14.14) эквивалентной схемой (рис. 14.14Р, а) с зависимым 458
источником, ЭДС которого равна kut и внутреннее сопротив-1ение г равно выходному сопротивлению усилителя.
Так как независимых источников в линейной схеме
оис. 14.14Р, а нет, то должно быть нулевое состояние равновесия. Для исследования его
устойчивости составим характеристическое уравнение методом входного сопротивления (14.3), для чего последовательно с зависимым источником ЭДС включим источник ЭДС Е (р) и найдем ток I (р) (рис. 14.14Р, а). Обозначим сопротивление параллельного соединения элементов Г1 и С
Рис. 14.14
Z = Оч/рСЖ + 1/рС)
и запишем ток
Е (р) + kVi (р) = E(p)(Z + pL) W г + ZpLKZ + pL) r(Z + pL) + pZ(L — kM) ’
“ U t (p) = pMIL (p) = pMI (p) Z/(Z + pL).
Входное сопротивление
у <	- r(Z + pL) + pZ(L-kM)
BX I (p)	Z + pL
т.е. характеристическое уравнение
r(Z + pL) + pZ (L-Ш) = 0
ИЛИ (если подставить Z)
p2 +
L(r + rt) — цкМ rr^LC
1
LC
= 0.
P +
Для устойчивости состояния равновесия необходимо, чтобы все коэффициенты характеристического уравнения второго порядка были положительными, т.е. должно быть [L(r + rx) —
Tj/cM] > 0. Граничное значение этого условия определяет границу области возбуждения
kM = L + rL/rv.
Зависимость /cM(rj) приведена на рис. 14.14Р, б. При значениях кМ и соответствующих верхней (заштрихованной) области, когда коэффициент при р характеристического урав-
нения отрицателен, так как кМ > L(1 + г/гД и корни харак, теристического уравнения положительны, условие устойчивости не выполняется, т. е. происходит возбуждение колебаний. Коле* бания возбуждаются только при положительных значениях kfy
Рис. 14.14Р
(рис. 14.14Р, б), т.е. к и М должны быть одного знака. При инвертирующем усилителе, у которого коэффициент усиления к < 0, необходимо М < 0, т. е. при тех же уравнениях цепи нужно поменять местами выводы одной из катушек трансформатора.
С уменьшением сопротивления rj добротность резонансного контура уменьшается и для возбуждения колебаний нужно выбрать большее значение к, чтобы компенсировать потери.
Рис. 14.16
Рис. 14.17
14.15.	Для амплитуды колебаний я(т) в автогенераторе известно дифференциальное уравнение da/dx = Еа(1 — а2/4), где е — обобщенный параметр цепи; т — безразмерное время.
Определить состояния равновесия аОп и условия их устойчивости.
14.16.	Вольт-амперная характеристика туннельного диода в схеме рис. 14,16 аппроксимирована для переменных состав' ляющих тока и напряжения относительно рабочей точки зависимостью i = — кги + к2и3.
Составить для напряжения на диоде дифференциальное уравнение и привести его к виду
d2x/dT,2 + е (1 — х2) dx/dx + х = 0.
Определить состояние равновесия х0 и получить условие его устойчивости.
Указание. Учесть обозначение и нормировки:
14.17.	Для схемы рис. 14.17, а при аппроксимации вольт-амперной характеристики туннельного диода отрезками прямых, как показано на рис. 14.17,6, определить условие устойчивости состояния равновесия. В плоскости параметров Е, г построить область, для которой возможны неустойчивые
состояния равновесия.
14.18.	Определить емкость конденсатора из условия возбуждения колебаний в схеме рис. 14.18, если в рабочей точке характеристики нелинейного элемента его дифференциальное сопротивление равно гд и отрицательно.
14.19.	Схема автогенератора с индуктивной обратной связью и полевым транзистором представлена на
рис. 14.19,а. На рис. 14.19,6 приведена схема замещения транзистора в линейном режиме при тех же обозначениях выводов
Рис. 14.18
транзистора: с - сток, и — исток, з — затвор.
Определить в общем виде условие возбуждения колебаний. Построить на плоскости параметров цЛ1 и г область возбуждения.
14.20. В схеме с обратной связью (рис. 14.20) усилитель имеет коэффициент усиления к = u2/wi» не зависящий от частоты и значения напряжения на входе, входное сопротивление гвх = °°5 выходное сопротивление квых = 0.
Определить в общем виде условие устойчивости и построить область возбуждения на плоскости параметров: а) к, г б) к, С.
Рис. 14.20
Рис. 14.21
14.21. В схеме рис. 14.21 усилитель идеальный (с постоянным коэффициентом усиления к = и2/и^ бесконечно большим входным сопротивлением и равным нулю выходным).
Определить условия устойчивости.
14.3. Изображение переходных процессов на фазовой плоскости
14.22(Р). Для схемы рис. 14.22, а заданы: ЭДС Е = 9 В и параметры г-9 кОм; С = 0,1 мкФ; вольт-амперная характеристика нелинейного элемента i(u) аппроксимирована тремя отрезками прямых (рис. 14.22,6): jb; bd; de.
а) Построить фазовые траектории для напряжения на конденсаторе; б) установить устойчивость состояния равновесия; в) найти период колебаний; г) по фазовой траектории определить зависимость wc(t).
Решение. Ответы на поставленные вопросы найдем, применяя метод фазовой плоскости и учитывая особенности фазовых траекторий, определяемых отрезками прямых.
а)	Для построения фазовых траекторий у(х), где х=ис; у = duc/dt, составим дифференциальные уравнения схемы по законам Кирхгофа:
h = *с + 1 (м) = С duc/dt + i;
rij + и = Е; и — ис = 0.
Исключив ток и напряжение и, получим для напряжения на емкости зависимость — прямую (Е — uc)/r == f (ис). Чтобы 462
пОлучить траектории у (х), вычтем из ординат этой зависимости ординаты характеристики i (ис) = i (и) при одних и тех же значениях и = ис. Получим отрезки fab, bd и de на рис. 14.22Р, а.
Рис. 14.22
Рис. 14.22Р
Дифференциальное уравнение для напряжения на конденсаторе
duc/dt =-![(£- wc)/r - i (ис)] = 10* [(£ - uc)/r - i (и)], В/с,
V/
где учтено, что на рис. 14.22,6 ток задан в миллиамперах.
Свойства фазовой плоскости позволяют указать стрелками на рис. 14.22Р, а возможные направления движения изображающей точки. Моменту времени t = 0 соответствует точка /, так как i (0) = 0. Состояние равновесия (duddt =* 0) определяется точкой р. Первоначально с увеличением напряжения ис изображающая точка перемещается от точки f к точке Ь. Из точки b Движение изображающей точки к точке р невозможно (в соответствии с указанным направлением движения). Но изображающая точка не может остаться и в точке Ь, поскольку точка b
не определяет состояния равновесия. Поэтому изображающая точка из точки b скачкообразно (при неизменном напряжении ис) переходит в точку с (показано пунктиром). Далее аналогично из точки d происходит скачок в точку а, откуда изображающая точка снова движется к точке Ь, и т. д., полу, чается непрерывное движение по замкнутой фазовой траекто. рии abcda — предельному циклу, т. е. происходят периодические незатухающие колебания. На рис. 14.22Р, б сплошными лини* ми показана зависимость uc(t). Наклонные участки фазовой траектории ab и cd соответствуют отрезкам экспонент на рис. 14.22Р, б,
б)	Устойчивость равновесия, определяемого точкой р, можно установить, рассматривая малые отклонения относительно этой точки. Как следует из указанных на рис. 14.22Р,а возможных направлении движения изображающей точки, равновесие в точке р неустойчивое.
в)	Период колебаний Т = t3 4- tp, где г3 — время зарядки, tp - разрядки конденсатора (рис. 14.22Р, б). Зарядке соответствует участок фазовой траектории ab, разрядке — cd. Интервалы времени, необходимые для движения изображающей точки на этих участках, найдем по (14.4):
=	Л±1_ = 5 1 tn 44&= 2>775'1О’“ с;
Л+1-А Л (1-2)-10	2-10*
1-5	1 • 104
tp" (-1 +5)-104 1П 5-10*
= 1,609  10"4 с.
Период Т = r3 + tp = 4,384 • 10“ 4 с.
г)	Для определения периодически изменяющегося напряжения ис (г) учт ем соответствие прямолинейного участка фазовой траектории и экспоненциальной зависимости. Так, для участка ab uCab — uy + А{е tlxi = Е + Ate t/T1 = 9 - 8е </ч, так как в точке а (рис. 14.22Р,а) при t=0 напряжение иСяЬ(0) — = 1 и Л1 = 1- 9=-8. Аналогично для участка cd uCcd — ~ uy + А2е г1'2 = -5е */Т2, так как здесь иу - 0.
Постоянная времени т экспоненциальной зависимости равна тангенсу угла наклона прямой на фазовой плоскости к оси ординат, т.е. (рис. 14.22Р,а)
Zl = tga‘ = д (duc/dt) = (2 - 1) • 104 = 4‘10 4 с;
Ъ = tga2 = (5 _ у. 104 = 1-10 4 с-
Получилось Ti > т2, т. е. процесс зарядки происходит медленнее, чем процесс разрядки (см. кривые на рис. 14.22Р, б).
14.23.	По кривым мгновенных значений напряжения, приведенным на рис. 14.23, а—г, построить качественно фазовые траектории на плоскости du/dt4 и. Указать стрелками направления движения изображающей точки.
Рис. 14.24
14.24.	По фазовым траекториям, приведенным на рис. 14.24, а, б, построить качественно кривые мгновенных значений u(t),	(г).
14.25.	Характеристика диода при прямом включении (рис. 14.25) аппроксимирована зависимостью i = аи2.
Полагая, что параметры элементов схемы Е = const, г и С известны, получить уравнение фазовой траектории тока [di/dt » =/(«)]
14*26. Для потокосцепления катушки в задаче 14.1 при аналитической аппроксимации найти уравнение фазовой траектории dW /dt = f (Т).
14.27.	Вольт-амперная характеристика газоразрядного элемента, включенного в цепь по рис. 14.27, а, где J — 5 мА, С = 0,1 мкФ, приведена на рис. 14.27,6.
Построить фазовый портрет в координатах duc/dt, ис.
Определить устойчивость состояния и найти период Т возможных колебаний.
Рис 14.27
Рис. 14.28
14.28.	Заданы параметры элементов в схеме рис. 14.28, а: Е = 200 В; г = 2 Ом; С — 100 мкФ; характеристика индуктивной катушки Т (0 приведена на рис. 14.28, б,
а) Найти уравнения фазовой траектории и построить фазовый портрет на плоскости х = Ф, у = dW/dt\ б) определить
Рис. 14.29
период колебаний Т; в) найти период при уменьшении ЭДС £ до 20 В.
14,29.	Полагая в схеме рис. 14.29 начальные условия нулевыми, J = const и диод идеальным, составить уравнение фазовой траектории тока iL[y = /(x), где х = ’1; У = dijdt],
14.30,	Для схемы задачи 14.20 установить типы особых точек при изменении коэффициента усиления к от 0 до оо: а) в случае неинвертирующего усилителя (к > 0, положительная обратная связь); б) в случае инвертирующего усилителя (к < 0, отрицательная обратная связь).
14.31.	Для автогенератора задачи 14.19 определить возможные типы особых точек и соответствующие соотношения параметров элементов.
14.4. Метод усреднения
14,32(Р). В схеме рис. 14.32 получен колебательный характер переходного процесса. Начальное напряжение на конденсаторе wc(0) = Uq. При известных значениях г, С и заданной вебер-амперной характеристике в виде i (4х) = (1/LO) (Т + /сТ3) методом усреднения определить зависимости амплитуды потокосцепления, фазы и частоты собственных колебаний от времени.
Решение. Запишем уравнения по законам Кирхгофа для схемы рис. 14.32:
ic »ir +	wL-uc==0; uL-ur = 0.
Учитывая, что ic ——C duc/dt =—C dujdt — —C d2x¥/dt2, так как uL = dW/dt и ir = ur/r = uL/r — <№/г dt, уравнения сведем к однородному нелинейному дифференциальному уравнению второго порядка для потокосцепления
^. + _L^._LT+ _^ = о
dt2 гС dt L0C L0C
Введя обозначения 2S = 1/rC, <i>o = 1/LOC, К -- k/L0C, по-лучим:
d24/dt2 + ogT = -25 M/dt - КТ3.
Предположим, что затухание 25 и коэффициент аппрокси-
мации к малы; решение будем искать в виде (14.5): 4х = a cos 9; c№/dt = — асоо sin 0,
где 0 = wQt — cp.
Уравнения установления амплитуды a — a (t) и фазы ср = — ср (г) найдем по (14.6):
2я
/•
(26дсоо sin 0 — Ka3 cos3 0) sin 0 dQ;
________1 2л(оо
о
In
1 f
= x-------- (26aco0 sin 0 — Ka3 cos3 0) cos 0 dQ.
2тг(00а J
о
da dt
dtp dt
Рис. 14.32
Операция усреднения определяется интегрированием за период, например, 2п
1 f	1
—— sin2 0d0 = ~v
2к J	2
о
Приведенное усреднение условно обозначим чертой сверху sin2 0 = 1/2.
Так как cos3 0 • sin 0 = 0; sin 0 • cos 0 = 0; cos4 0 = 3/8, то получим уравнения в виде
3
da/dt = — да; dip/dt =—— Ка2.	(1)
о
Для определения постоянных интегрирования вычислим предварительно значения а(0) и ср (0). Учитывая начальные условия для схемы рис. 14.32 и принимаемый вид решения, найдем, что
4х (0) = 0 = а (0) * cos [®0 • 0 — ср (0)];
-jr = «l(0) = UC (0) = и0 - -а (0) • ®о sin [и0 • 0 - <р(0)],
т. е.
а (0) • cos <р (0) = 0;
а (0) - sin ф (0) = Uo/coq-
(2)
(3)
Так как а (0) Ф 0, то из (2) ф (0) = ± я/2. Поскольку а (0) > >0, то из (3) имеем ф(0) = я/2 и а(0) = По/соо. Интегрируем уравнение установления амплитуды (1) da/а — —§dt и получаем: _	,	,	1	, а
- or = In а + In = in Ct	Ci
т. е.
a(t) = C!e-s<,
откуда, учитывая начальное значение а(0), определим постоянную Ci = Uq/cdq. Следовательно, искомое решение
a(t) =	e~5t.
CD0
Подставив его в уравнение установления фазы, получим:
-25,
dt Sg)q
и после интегрирования находим:
q(t) =
ЗКЦ -25, 16о2>о5
Так как ф(0) = л/2, то С2 = л/2 — 3KGq/16(DoS и, следова-
тельно,
/ ч Я
Ф(0 = Т-
зки20
16сОо^
е 2&t).
Полная фаза колебаний
0 (г) = (Dot - <Р (t) = <00t - 4 +	- е~ 28Г)-
Z JLOCOqO
Частота свободных колебаний во время переходного про-
цесса
co(t) =
dO(t) dt
3 KVl
= C0° +
О COq
e~25r.
Зависимость co (t) приведена на рис. 14.32P, где со (0) -3 KUl „
= coo + -Q--С течением времени при уменьшении ампли-
о соо
туды колебаний a(t) насыщение магнитопровода катушки ска
зывается все меньше и меньше, индуктивность увеличивается и, как видно из графика, частота уменьшается, асимптотически приближаясь к значению соо = IfyL^C. При и амплитуда колебаний мала и катушку можно считать линейной с наибольшей индуктивностью L « Lq.
14.33.	В схеме рис. 14.28, а известны значения (0) = Ч'о, г, С и задана характеристика i (40 = к^ + к3Ч3. При размыкании ключа возникают затухающие колебания.
Найти зависимость (г) методом усреднения. Потери в контуре учесть включением параллельно индуктивности сопротивления rL.
Рис. 14.35
Рис. 14.34
14.34.	Начальный заряд на конденсаторе (рис. 14.34) q (0) = = Go- Кулон-вольтная характеристика аппроксимирована полиномом и (q) = kiq + k3q3.
При известных параметрах г и L рассчитать зависимость q(t) во время переходного процесса методом усреднения.
14.35.	Вольт-амперная характеристика нелинейного резистора (рис. 14.35) аппроксимирована зависимостью i = ки3, где к = 10“10 A/В3. Полагая, что после коммутации в цепи возникают затухающие колебания, найти время, за которое амплитуда колебаний напряжения ис уменьшится в 2 раза.
Дано: L= 0,01 Гн; С = 20 пФ; uc(ty = 100 В.
14.36.	Методом усреднения определить период свободных колебаний в схеме задачи 14.28.
14.37.	Дифференциальные уравнения цепи по рис. 14.37, подключенной к источнику синусоидального напряжения и = = Um sin cd£, преобразованы относительно потокосцепления к уравнению Дуффинга:
d2x/di2 + х = £,х — 6 dx/dx — кх3 4- Р cos т.
Вебер-амперная характеристика индуктивной катушки аппроксимирована полиномом z(4/) = к^Ф + к-^3', здесь приняты обозначения: х = 'P/'Pg, где Тб — заданное базисное значение потокосцепления; т = cot; 8 = 1/согС; £ - 1 — со§/со2; ©о = kJC\ * = /с3Ч>2С; Р =
а) Методом усреднения составить уравнения установления амплитуды а и фазы (р; б) получить выражение амплитудной характеристики Р(п); в) получить выражение амплитудно-частотной характеристики £(а).
14.38.	В последовательном контуре (рис. 14.38) частота напряжения питания и = Um sin cot равна собственной частоте контура соо = 1/|/Ес при малых амплитудах колебания потокосцепления катушки.
Считая, что потери в контуре отсутствуют (г = 0), найти при известной емкости С и заданной характеристике катушки
Рис. 14.37
Рис. 14.38
/(Ф) = (1/L)(1 + &Т2)*Р амплитуду установившихся колебаний а методом усреднения.
14.39.	Нелинейная характеристика катушки последовательного контура (рис. 14.38) аппроксимирована зависимостью ¥ == LqIq arctg(?/j0), где Lo и 10 — коэффициенты аппроксимации; известны параметры г, С и напряжение питания и = = Um sin cot.
Методом усреднения составить уравнения установления амплитуды а и фазы <р напряжения на конденсаторе.
14.5. Автоколебания
14.40(F). Для генератора почти гармонических колебаний (рис. 14.14) при заданной характеристике усилителя i2 = к^ -- къи\ составить дифференциальное уравнение цепи и определить амплитуду и частоту автоколебаний во время переходного процесса и в установившемся режиме методом усреднения. Входное и выходное сопротивления усилителя считать бесконечно большими.
Решение. При заданной характеристике i2 fai) заменим усилитель зависимым источником тока. Дифференциальное уравнение цепи составим относительно напряжения пропорционального напряжению на резонансном контуре, которое наиболее близко к синусоидальному по сравнению с другими
переменными цепи. Дифференциальное уравнение составим по предварительно записанным уравнениям в операторной форме. Обозначив
получим:
17, (р) = pMIL(p) = рМ12 (р) pL + Z{p)
откуда
П(р) =
pL + Z (р)	= p2rjLC + pL + rt
pMZ (р)	1W	pMrt
2r, , .	1	„ . .	1 „ , . M , , .
I?Ui (p) + —7г pUi (p) + 77 Ui (p) = 77 pl2 (p)-г i Cz	Lt V
Учитывая, что p и p2 — операторы дифференцирования
и что
di2 dui dt dur dt
= (kt - 3k3ul)
du i IT9
записываем дифференциальное
dt2
уравнение цепи в виде
1 \ dux Зк3М dux ~~l~dt LC~U1~dT'
(1)
Введем обозначения и нормировки
После их подстановки в (1) получим приведенное дифференциальное уравнение цепи (уравнение Ван дер Поля): d2x/dx2 + х = 8 (1 — х2) dx/dx.	(2)
Полагая, что параметр 8 мал, т.е. колебания почти гармонические, решение записываем в виде
х = a cos ф; dx/dx — — a sin ф,
где ф = т - ср.
Применив метод усреднения (14.6), находим уравнения установления амплитуды п(т) и фазы ф(т):
2л
« - -- (1 - a2 cos2 ф) (- a sin ф) sin ф <2ф;
О
dtp s
dx 2na
2n
(»
(1
0
- a2 cos2 ф) (- a sin ф) cos ф </ф.
Учитывая, что sin2 ф = 1/2; sin2 ф • cos2 ф = 1/8; sin ф • cos ф = _ 0; cos3 ф • sin ф = 0, получаем:
da/dx = (&a/2)(l-a2/4); d<p/dx = Q.	(3)
Из уравнения (3) установления фазы следует, что частота автоколебаний
(й = dty/dt = d ((f)Qt — <p)/dt — coo = l/]/Ec,	(4)
т. e. равна резонансной частоте контура и остается постоянной (во время переходного процесса и в установившемся режиме).
Уравнение (3) установления амплитуды после разделения переменных можно интегрировать, предполагая, что начальное значение амплитуды а (0) — а0:
da dX “ га (4 — я2)/8 ’	__ 8	da _	1 f «2	4 - ао \ Т £ J а (4 — а2) б П у 4 - а2 а$ / ао
ИЛИ	Н * II счо « но 1 <3 М* гЧ <3 гч « 1 ХГ
откуда амплитуда
(Т) =	.	-----:	..
|/(4 - а§)	+ а?
(5)
Из решения (5) видно, что для возникновения автоколебаний необходима некоторая (сколь угодно малая) начальная амплитуда а (0) = а0 # 0. Практически всегда существуют случайные малые отклонения - флюктуации, которые приводят к возбуждению автоколебаний.
При т —> со независимо от начальных условий в генераторе Устанавливаются колебания с амплитудой — 2, т. е. с учетом принятых ранее обозначений для искомого напряжения щ амплитуда	__________
и1т = 2 |/|/LC/3/c3M.
14.41 (Р). Для генератора задачи 14.14 при характеристике Усилителя и2 = fciWj — k3uj методом гармонической линеариза
ции найти общие выражения для частоты и амплитуды уст^, повившихся колебаний.
Решение. При решении задачи методом гармонической линеаризации учитывается только основная гармоника. По. этому предварительно определим эквивалентный коэффициент усиления К по первой гармонике.
Пусть напряжение на входе усилителя синусоидальное: Mi = У im sin tot. Тог да при заданной характеристике u2(uj имеем:
«2 =/c1Uimsincot -k3U3im
-г sin cot —- sin 3cot
4	4
или, отпуская третью гармонику, /	з \
u2 = I кхи1т - —Isincot = l/2msincot.
Эквивалентный
U.m ЛЯ _
Uim
коэффициент усиления 3
klV{m Y^^Vim	з
~ ki rk3Ulm,
Vim
т. e. с ростом амплитуды Uim напряжения на входе коэффициент усиления уменьшается (вследствие насыщения усилителя).
Далее применим условие баланса фаз и баланса амплитуд для определения амплитуды и частоты автоколебаний. Рассмотрим характеристическое уравнение генератора, полученное в решении задачи 14.14:
„2
= o.
rrYLC
Учитывая нелинейность характеристики усилителя, полагаем к = К и при р = jco получим уравнение
Ь(Г + rt) - j fcx -|
— co2 + ;co
rrtLC
LC °
Применим условия (14.7):
Re {ZBX (Jco)} = — со2 + 1/LC = 0;
Цг + г^-^М^-^к^Л
Im {ZBX (»} = co----------------- = 0.
Из первого условия находим частоту автоколебаний со = i/j/LC, а из второго - амплитуду:
vlm = ^/Ук^^-Цг + г^/Мг^.
14.42.	Для автогенератора задачи 14.19 из линейного приближения определить условие возбуждения и частоту автоколебаний.
14.43.	Для схемы задачи 14.16 методом усреднения: а) определить амплитуду Um (t) автоколебаний напряжения на диоде во время переходного процесса, полагая, что Ст(0) = С7о; б) найти частоту и амплитуду колебаний в установившемся режиме.
14.44.	Зависимость напряжения на выходе усилителя от напряжения на входе (рис. 14.20) аппроксимирована уравнением и2 =:	- fc3Ui, входное сопротивление усилителя равно беско-
нечности, выходное — нулю.
Преобразовать дифференциальное уравнение схемы рис. 14.20 относительно напряжения Wj к уравнению Ван дер Поля:
d2x/dx2 — е (1 — х2) dx/dx + х = 0,
где обозначено:
х —	]/Зк3/(к1 — 3); т = coot; соо = l/гС; с = к^ — 3.
14.45.	Методом гармонической линеаризации определить амплитуду напряжения на входе усилителя и частоту автоколебаний в цепи генератора по рис. 14.20.
Учесть, что входное сопротивление усилителя бесконечно большое, а выходное равно нулю. Характеристика усилителя аппроксимирована зависимостью и2 =
14.46.	‘Определить в цепи Рис. 14.46 частоту со и амплитуду установившихся колебаний тока i методом гармонической линеаризации. Значение тока J источника выбрано таким, что характеристика нелинейного элемента относительно рабочей точки для переменных составляющих может °Ь1ть аппроксимирована полиномом Условие существования колебаний.
14.47.	Считая параметры элементов г, R и С на схеме Рис. 14.21 известными, определить в линейном приближении Частоту колебаний о. Усилитель идеальный.
Рис. 14.46
i = —ajU + а3и3. Найти
14.6. Численные методы интегрирования
14.48(Р). В цепи задачи 14.1 принята ап Проксима характеристики катушки i СР) = 0,5Т2.
На основе явной формулы Эйлера при шаге й = 1О“3с вычислить длительность переходного процесса гп, приняв, что переходный процесс заканчивается, когда приращение потоке, сцепления на шаге получается менее 0,01 %.
Решение. В соответствии с явной формулой (12) реше. ния задачи 14.1 получим расчетную формулу при h = 10“3 с
+1 =	+ 0,25 - 0,0625Т|.
Время установления tn находим из выражения tn == tk+1 = = tk + Л, когда
ф _ ш
Д = ——- 100 < 0,01, * к
где Тс = Т*+1.
Алгоритм вычислений можно представить в следующем виде: 1) вводим значения (см. табл. 14.1) t0 = 0; Т(0) = 0,4; Тс(0) = 0,4; h; 2) вычисляем Tk+1, tfc+1, А; 3) полагаем Тс = = Tfc+1; 4) если А 0,01, идти на 2; 5) выводим значения
Результаты вычислений на ЭВМ: гп = 27 мс; Т = 1,9998 Вб.
14.49(Р). Для схемы рис. 14.37 заданы напряжение и == - Um sin (DZ, где Um — 100 В; / = 50 Гц, и параметры С = 7 мкФ; г - 2 кОм; ЦТ) = /сТ5, где к = 1,5 А/Вб5.
а)	Составить уравнения состояния для Т и ис.
б)	Получить явные расчетные формулы Эйлера.
в)	Принимая шаг h = Т/50, по формулам п. «б» вычислить ис (0 и i (г) в установившемся режиме при t > 107 в течение периода для двух случаев: 1) Т (0) = 0; ыс(0) = 0; 2) Т (0) = 0; ис (0) == 250 В.
Найти максимальные значения иСтах и Пояснить полученные результаты.
Решение, а) Запишем в общем виде уравнения состояния
</Т/Л = /1 р (40, ис, t]; duc/dt = f2 р (49, uc, г].
Из схемы рис. 14.37 найдем значения производных для переменных Т и ис:
c№/dt = u — ис; duc/dt = ic/C = [i (T) + Ц/С.
По второму закону Кирхгофа rir + ис — и, откуда
Um • ис
1Г = —— Sin CDt--.
Г	Г
С учетом характеристики ?(Ф) получим уравнения состоя-
ния:
d>V/dt = Um sin cot - ис;
<fac dt С
Um .	ис
rC Sm	rC
б)	Перейдя к конечным приращениям, получим явные расчетные формулы:
Ч\+1 = Tit + h(U„sin 2лЛ - ua);
uC(k+l) = uCk +	---
в)	Вычисления можно выполнить согласно следующему алгоритму:
1)	вводим значения г0 =0; Ч'(О); wc(0); ит; С; г; к; h;
2)	вычисляем Ч^+1, uc(k+l}, tk+1 -tk + h, ik+1 = kWsk+l;
3)	если t 10T = 10// = 0,2, идти на 2;
4)	выводим значения f, wc, i;
5)	если t 0,22, идти на 2.
Результаты вычислений на ЭВМ: а) wCwox = 23,042 В; Uc = 7,251 мА; б) иСтах = 330,897 В; imax = 1,636 А.
Для указанных параметров феррорезонансной цепи при нулевых начальных условиях а) устанавливаются нерезонансные колебания. При заданных начальных условиях в случае б) устанавливаются резонансные колебания с большими максимальными значениями. Феррорезонансная цепь в зависимости от начальных условий имеет одно из двух возможных устойчивых состояний равновесия; ее можно применить в устройствах, обеспечивающих функции памяти.
14.50(	Р), Для цепи задачи 14.1 на основе неявной формулы Эйлера для потокосцепления катушки Т рассчитать во время переходного процесса Т (t) и i (£) в интервале времени от *о = 0 до t„ = 18-10-3 с. Характеристика катушки аппроксимирована зависимостью = 0,5Т2; шаг h = 2 • 10~3 с.
Решение. В соответствии с уравнением (12) решения задачи 14.1 запишем неявную формулу (14.12)
^+1=^ + Л[Е-п(Т*+1)]
или, подставляя численные значения,
¥»+j =	+ 2 • 10~ 3 [250 - 125 • 0,5Ч<Ь 1],
т.е.
¥ft+1=T* + 0,5-0,125T2k+1.
Из этого квадратного уравнения находим расчетную формулу
1 + )/1.25 + 0,5^1
Результаты расчета сведены в табл. 14.50.
Таблица 14.50
1’ 10~3, с	Вб	г, А	МО-3, с	Ф, Вб	/, А
0,0	0,4000	0,0800	10,0	1,7194	1,4781
2,0	0,8166	0,3334	12,0	1,8099	1,6379
4,0	1,1510	0,6624	14,0	1,8719	1,7520
6,0	1,4045	0,9863	16,0	1,9140	1,8317
8,0	1,5889	1,2623	18,0	1,9424	1,8864
14.51.	Для задачи 14.2, принимая шаг h = Т/50, составить расчетные формулы для потокосцепления и тока на основе явной формулы Эйлера.
По расчетным формулам вычислить наибольшие возможные значения потокосцепления и тока после коммутации в зависимости от начальной фазы приложенного напряжения а.
Указание. Значение начальной фазы а выбрать по результатам решения задачи 14.2.
14.52.	В схеме рис. 14.10 ЭДС источника е = 12 sin cot, В, при f = 50 Гц. Параметры: С = 1 мкФ, г = 120 кОм; вольт-амперная характеристика диода i(u) задана: i(u) = 3,5x х 10"5 [exp (41,8м) - 1].
По явной формуле Эйлера с шагом h — Т/100 вычислить постоянную составляющую напряжения на конденсаторе в установившемся режиме. Считать, что режим устанавливается в течение времени, после которого среднее значение напряжения за период изменяется менее чем на 2%.
14.53.	Решить задачу 14.49, считая, что характеристика катушки i (4х) симметрична и определяется данными табл. 14.53.
Применить формулу линейной интерполяции.
14.54.	Для цепи задачи 14.5 вычислить по неявной формуле Эйлера время разрядки конденсатора до напряжения, равного 0,2 В. Принять шаг h = 0,1 мс.
Таблица 14.53
i, А	0	0,1		0,2	0,4	0,6	0,8	1,0
% Вб	0	0,58		0,66	0,769	0,83	0,88	0,92
i, А	1,2		1,4		1,6	1,8	2,0	2,2
Т. Вб	0,956		0,985		1,00	1,04	1,06	1,08
14.55.	Вычислить амплитуду напряжения UCm установившихся автоколебаний в схеме рис. 14.16.
Дано: Е = 120 мВ; г = 10 Ом; L = 0,2 мГн; С = 1 мкФ. Вольт-амперная характеристика туннельного диода задана табл. 14.55.
Таблица 14.55
м, мВ	40	60	80	100	140	160	180	200	220	240	260	300	320	340	360	380
г, мА	6	9,5	10	9,5	4,5	3,5	2,5	2,3	2	1,9	1,8	1,85	2,0	2,3	3	4
Расчет выполнить на основе явных формул Эйлера с шагом h = Т/24 для iL и мс. Применяя формулу линейной интерполяции, считать, что при нулевых начальных условиях режим устанавливается, когда приращение амплитуды за период меньше 10%.
Глава пятнадцатая
ВВОДНЫЕ ЗАДАЧИ ТЕОРИИ ПОЛЯ
Введение к гл. 15
Электромагнитное поле характеризуется двумя основными векторами: напряженностью электрического поля Е и индукцией магнитного поля В,
Напряженность электрического поля определяется по силе Р, действующей на неподвижный точечный заряд q:
F = qE.	(15.1)
Индукцию магнитного поля можно определить по силе действующей на заряд q, движущийся с постоянной ростью v:
г = Я [”В]»	(15.2)
или по силе, действующей на линейный элемент длиной/ с током /:
F « №°)В] I,	(15.3)
где /° - единичный вектор, направление которого совпадает с направлением тока.
Для диэлектрика
D = е0Е + Р,	(15.4)
где D и Р — векторы электрического смещения и поляризации; е0 — электрическая постоянная.
Для линейного диэлектрика
Р = EoXr# = Ео - 1) Е;	(15.5)
D == ег£оЕ,	(15 6)
где %г — относительная диэлектрическая восприимчивость; ег -относительная диэлектрическая проницаемость.
Для магнитной среды
В = ЦоЯ + М,	(15.7)
где Н и М — векторы напряженности магнитного поля и намагниченности; Цо _ магнитная постоянная.
В случае линейной магнитной среды
М = хН,	(15.8)
где и — магнитная восприимчивость, и
В =	(15.9)
где цг — относительная магнитная проницаемость среды.
Сила взаимодействия точечных зарядов и q2 в электростатическом поле определяется по закону Кулона
<11(12
47С£гЕ0В2 *
где R — расстояние между зарядами.
Напряженность поля точечного заряда q
г_
4яеге0Е2 ’
(15.10)
(15.И)
где Я0 — единичный вектор, направленный от заряда q в точку наблюдения; R - расстояние от заряда q до точки наблюдения. Для потенциального электрического поля разность потенциалов между точками А и В
Фд - Фв =f Edl,	(15.12а)
А
потенциал
(р = — j Edl + С,
(15.126)
где dl - элемент пути интегрирования; С — постоянная.
Сила, действующая на отрезок длиной I любого из двух бесконечно длинных параллельных тонких проводов с токами и i2:	/ ; /
=	(15.13)
где г — расстояние между проводами.
Индукция магнитного поля, бес-конечно длинного тонкого провода	//
с током i:
(15.14)	Г----o'
где г — расстояние от оси провода y/z	1
с током до точки наблюдения М (у
(рис. 15.А); /° - единичный вектор,	рис 15д
совпадающий по направлению с током; г° — единичный вектор, направ-
ленный от оси провода с током в точку наблюдения по кратчайшему расстоянию.
Уравнения электромагнитного поля в интегральной форме
Теорема Гаусса $DdS = Y<l	(15.15)
или fe0E£/S = X(« + fe,3).	(15.16)
Для однородной среды (s, = const)
jEdS = ^q/^r.	(15.17)
Связь между вектором поляризации Р и связанным зарядом (/свяЗ •
(15.18)
В формулах (15.15)-(15.18)	и £ дсвяз - алгебраические
суммы свободных и связанных зарядов, находящихся внутри поверхности S.
Закон полного тока
$ЯЛ = £/ = рПОлН«	(15.19)
где i — полный ток, охваченный контуром интегрирования;
Лолн = j + dD/dt	(15.20)
— плотность полного тока; J — плотность тока проводимости.
Закон электромагнитной индукции (Фарадея)
(15.21)
в комплексной форме
(15.22)
где е и ^-ЭДС; Ф - магнитный поток.
Уравнение непрерывности магнитного потока
=	(15.23)
Уравнение непрерывности полного тока
рполн^ = 0	(15.24)
р dS = - 8 (Sq)/at.	(15.25)
Уравнения электромагнитного поля в дифференциальной форме
Теорема Гаусса
(15.26)
(15.27)
divD = р;
div е0£ = р + ргаяз, для однородной среды
div Е - р/егЕ0.
(15.28)
Связь между вектором поляризации Р и объемной плотностью связанного заряда рсвяз:
div Р = - рсвяз,
(15.29)
где р — объемная плотность заряда. Закон полного тока
rot Н = 7П0ЛН = J + dDjdt.
(15.30)
Закон электромагнитной индукции rot Е = — dB/dt.
(15.31)
Уравнение непрерывности магнитного потока divB = 0	(15.32)
и для однородной среды div И = 0.	(15.33)
Уравнение непрерывности полного тока
div (J + dD/dt) = 0.	(15.34)
Энергия электрического поля ^-dV.

Энергия магнитного поля
Для потенциального электрического поля £ = —grad (р.
(15.35)
(15.36)
(15.37)
15.1.	Симметричные поля
При расчете симметричных полей можно и рационально пользоваться уравнениями электромагнитного поля в интегральной форме.
15.1	(Р). Определить силу, которая действует в вакууме на каждый из точечных зарядов системы, изображенной на рис. 15.1* где да = 4-10“12 Кл, qb=15-10"12 Кл, qc = = 15-10'12 Кл.
Решение. Действующая на заряд qa сила по (15.1) Fa = qaEa, где Еа — напряженность электрического поля в точке расположения заряда qa (рис. 15.1 Р), создаваемая всеми зарядами, кроме qa, т.е.
к* — F j. г — са I W 
° Еса + ЕЬа	,
где г % - единичный радиус-вектор, направленный из точки с в точку а; г°Ьа — единичный радиус-вектор, направленный из точки b в точку а.
В декартовой системе координат _ /gccosai qb \	<?с sin
а \ 4яе0г2о 47tsor2baJ 4яеог2са
где cos а, = rba/rca = 0,3/0,5 = 0,6; sin otj = rcb/rca = 0,4/0,5 = 0,8. При этом Fa = (-7,25i + 1,72/), мкН, Аналогично Fb = (6,0i + 14,3/), мкН; Fc = (1,2/ — 14,52/), мкН.
15.2	* Три точечных заряда расположены вдоль прямой линии на равных расстояниях друг от друга, причем крайние заряды одинаковые.
Определить соотношение между значениями среднего и крайнего зарядов, если вся система находится в состоянии равновесия.
15.3	. Две одинаковые заряженные частицы находятся в вакууме на расстоянии 5 см друг от друга. Заряд каждой частицы равен 2-10"10 Кл, масса - 1 мг.
Найти конечную скорость, которую приобретут частицы, разлетаясь под влиянием сил отталкивания.
15.4	. Два одинаково заряженных бузиновых шарика подвешены в воздухе на нитях, закрепленных в общей точке.
Определить угол между нитями, если заряд каждого шарика равен 5-10”8 Кл, масса — 16 мг, длина каждой нити равна 50 см.
15.5	(Р). Определить напряженность поля Е и потенциал (р в вакууме над плоской металлической пластиной вдали от ее краев, на одной стороне которой равномерно распределен поверхностный заряд qs = 10“10 Кл/м2. Рассчитать силу, действующую на положительный пробный заряд д=10”12 Кл, находящийся на расстоянии а от пластины.
Решение. В полупространстве, ограниченном заряженной стороной бесконечной металлической пластины, существует однородное электрическое поле, напряженность которого перпендикулярна ее плоскости. По другую сторону пластины поля нет.
Выбрав в качестве гауссовой поверхности прямоугольный параллелепипед, который пересекает пластину и боковые грани 484
оторого перпендикулярны плоскости пластины, по теореме Гаусса (15.16) получим:
s0E&S = qs&S,
где AS — торцевая поверхность параллелепипеда.
Поток через все остальные грани параллелепипеда равен нулю.
Выбрав начало координат на поверхности, где распределен заряд qs, и ось у, перпендикулярную этой поверхности, получим Е =ЕУ = qs/&0 = 11,3 В/м.
Сила, действующая на пробный заряд, по (15.1) F = qE — = 11,3* 10"12 Н, и по (15.12) потенциал <р= - f Еу dy + const -== - 11,3у, В, если выбрать на пластине (у = 0) потенциал (р = 0.
15.6	(Р). Определить распределения потенциала и напряженности поля в пространстве около тонкого плоского слоя зарядов (простой слой), плотность qs которых постоянна.
Построить зависимости потенциала <p(z) и напряженности
Рис. 15.6Р
Решение. Будем считать слой зарядов бесконечно тонким и бесконечно протяженным. Тогда вследствие симметрии: 1) вектор напряженности поля по обе стороны слоя будет численно одинаковым, но противоположным по направлению; 2) поле будет иметь только нормальную составляющую; 3) поле не будет зависеть от координат.
Выделив прямоугольный параллелепипед, включающий часть слоя, и применив теорему Гаусса (15.16), получим:
е0Еи AS + еоЕи AS = Qs
откуда
Е. = I I = 9s/2e0-
Напряженность Ег (рис. 15.6Р, а) в каждом полупространстве постоянна, а при переходе через слой изменяется скачком на qs/E0.
Потенциал (по 15.126)
ср = - Ez dz + С — z 4- Ci при z > 0; 2еп
Ф = - Ez dz + С = —— z + С2 при z < 0. 2£а
Выбрав ф = 0, при z — 0 получим Ci = С2 = 0; ф — -qszP^ при z > 0; ф — qsz/2zQ при z < 0 (рис. 15.6Р, б).
15.7	(Р). Найти напряженность поля, электрическое смещение, поляризацию, свободный и связанный заряды и емкость для плоского конденсатора с площадью пластин S = 25 см2 и расстоянием между обкладками-пластинами d = 2 мм в двух случаях: а) диэлектрик — воздух; б) диэлектрик — текстолит с £г = 4. Постоянное напряжение U на конденсаторе равно 1 кВ.
Решение, а) В плоском конденсаторе, заполненном однородной средой, напряженность поля всюду одинакова (краевой эффект не учитываем), направлена перпендикулярно плоскости пластины и при заданном напряжении
Е = U/d = 5 • 105 В/м.
При заполнении воздухом (er = 1) по (15.6) и (15.5) электрическое смещение D = &0Е = 4,43 • 10"6 Кл/м2, а поляризация Р =0. Поверхностный свободный заряд по (15.15) равномерно распределен по металлической пластине с плотностью qs = — D = 4,43 мкКл/м2. Весь свободный заряд пластины q = — qsS = 11,1 • 10”9 Кл. Связанный заряд равен нулю. Емкость
С = q/U = qsS/U = DS/U = s0&rS/d = 11,1 пФ.
б) При заданном напряжении напряженность поля остается прежней при любом однородном диэлектрике, поэтому
Е = U/d = 5 • 105 В/м; D = е08гЕ = 17,7• 10”6 Кл/м2;
Р = (er - l)s0E = 13,3 • 10"6 Кл/м2;
q =qsS = DS = 44,4-10’9 Кл.
Связанный заряд и его плотность найдем по (15.18). В диэлектрике у положительно заряженной пластины конден-Сатора	= - PS = - 35 • 10' 9 Кл.
Емкость С — q/U = -'у = 44,4• 10"12 = 44,4 пФ.
Отметим, что при внесении диэлектрика емкость увеличилась в ег раз и при заданном напряжении на пластинах накопился в раз больший заряд.
15.8	(Р). Воздушный конденсатор задачи 15.7 отключен от источника, а затем в него вставлена текстолитовая пластина.
Определить свободный заряд, электрическое смещение, напряженность поля, поляризацию и связанный заряд: а) до внесения пластины; б) после внесения пластины.
Решение. После отключения источника в конденсаторе остаются неизменными заряды на пластинах.
а)	После отключения источника напряженность поля, а значит, и все другие величины остаются теми же, что и в варианте «а» задачи 15.7.
б)	После внесения текстолитовой пластины при том же заряде д = 11,1-10"9 Кл получим: D = q/S = 4,43 мкКл/м2; £ = />/ег80 = 125 кВ/м, т.е. в £г раз меньше, чем до внесения текстолитовой пластины: Р — (sr - 1) е0Е = 3,32 мкКл/м2; <?5связ = PS = 8,3 нКл.
15.9	. Определить зависимость емкости конденсатора (рис. 15.9) от угла поворота а подвижных пластин относительно неподвижных. На рис. 15.9 размеры даны в миллиметрах. Краевым эффектом пренебречь.
15.10	(Р). Рассчитать напряженность поля Е и потенциал ф: внутри ,(1) и вне (2) шарообразного электронного облачка
радиусом Rq = 0,5 см. Построить зависимости Е и ф от координат в двух случаях: а) объемная плотность заряда р постоянна и равна —2,5-10“9 Кл/см3; б) объемная плотность заряда .изменяется по закону — 2,5 • 10-9а/(а + Я), Кл/см3, где R — расстояние от центра облачка, коэффициент а = 0,2 см.
Решение. Из шаровой симметрии поля следует, что напряженность поля имеет радиальную составляющую (Е = = Ед), зависящую только от радиуса Е, и, следовательно, ее значение постоянно на сфере данного радиуса и вектор напряженности нормален к поверхности сферы. Поэтому задачу можно решить, применив теорему Гаусса (15.16) и выбрав в качестве поверхности интегрирования сферу.
При R < Ro в сферической системе координат
,	4
е0Е • 4лЕ2 = — лЕ3р,
Неподвижная Подвижная пластины
Рис. 15.9
откуда Е = рЕ/Зе0 = —9,4' 103Е, В/см.
Потенциал по (15.126)
<p=-f£d« + C1 = -pR2/6e0 + Ci = (4,7• 103R2 + СД B.
Выбрав ср = 0 при R = 0, получим: Cj = 0.
При R > Ro имеем:
4 £0E-4tcR2 = —ttRqP,
откуда E = pRo/3soR2 = —11,8-10 2/R2, В/см, потенциал
\	pKo / 11,8 -102	\ Л
ср = — E dR + C2 =	+ C2 = (-------„-----Ь Cz )’
J	jSqA.	у	л	/
npH-R=R0 должно быть равенство потенциалов, откуда постоянная С2 = - pRo/2eo = 3,52 • 103 В.
15.11	(F). Рассчитать напряженность поля и потенциал: 1) внутри металлического шара; 2) вне (в воздухе). На поверхности шара равномерно распределен заряд q = 20 мкКл; радиус шара Ro = 25 см. Построить зависимости Е и ср от координат, считая потенциал равным нулю в бесконечно удаленной точке.
Решение. Как и в предыдущей задаче, применим теорему Гаусса.
При R < Ro (внутри шара), где R - расстояние от центра шара, по (15.15) D • 4rcR2 =0, т. е. D = 0 и Е = 0.
При R > Rq (вне шара) £qE • 4nR2 = q и Е = ER = q/4itz0R2 = = 18- 106/R2, В/см.
Потенциал
’ n 18-IO6
(р = — Е dR + С =----—----Ь С.
К
Так как принято ср = 0 при R -> оо, то С = 0, и при R = Rq потенциал <р0 = 720 кВ.
15Л2(Р). Определить, какой радиус Ro должен иметь уединенный металлический шар, находящийся в воздухе, чтобы на нем можно было разместить заряд q — 1 Кл, если пробивная напряженность воздуха Епр = 30 кВ/см.
Решение. Приравняв Епр наибольшей напряженности поля (на поверхности шара), получим: Епр = д/4тс£оКо> откуда Rq — 54,7 м.
15.13(	F). Рассчитать напряженность поля Е и потенциал (р и построить зависимости Е (г)и ср (г): 1) внутри; 2) вне электронного луча цилиндрической формы с объемной плотностью заряда -2-10"15 Кл/см3.
Радиус луча r0 = 1 мм. Длина луча много больше его
радиуса- Расчет провести для области, удаленной от концов луча. Принять потенциал равным нулю на оси.
Решение. Из цилиндрической симметрии поля следуем что напряженность поля имеет только радиальную составляю' тую (Е = Ег), зависящую только от радиуса г. Следовательнб ее значение постоянно на цилиндре данного радиуса и векто? напряженности нормален ' к поверхности цилиндра. Задач/ можно решить, применив теорему Гаусса (15.16) и выбра^ в качестве поверхности интегрирования цилиндр, соосный лучу и единичной длины.
При г < г0 в цилиндрической системе координат e0Ei • 2лт=? = лг2р, откуда Ei = рг/2е0; потенциал
(Pi = -fEt^r + Ci = — рг2/4г0 + СР
Выбрав ср = 0 при г — 0, получим С] = 0.
При г > г0 имеехМ &0Е2  2пг = лгор, откуда Е2 = рг§/2е0*'; потенциал	*	2
(р2 = — Е2 dr + С2 — —In г 4- С2.
При г = rQ должно быть равенство потенциалов, откуда постоянная	пг2
C2 = f^(21nr0-l).
4во
Численные результаты даны в ответах.
15.14.	Рассчитать напряженность поля и потенциал 1) внутри; 2) вне бесконечного цилиндрического проводник! с коаксиальным отверстием, находящегося в воздухе, есл!1 линейный заряд проводника 2-10"10 Кл/м, радиус проводник! г0 = 3 мм. Выяснить, изменится ли распределение потенциала если отверстие некоаксиально. Принять (р = 0 при г — г0.
15.15.	На бесконечно длинную прово-
локу с радиусом гг и зарядом +т на	/X
единицу длины коаксиально надета метал-	.Z /z )
лическая труба (рис. 15.15).	уХ / У
Определить электрическое смещение	/
Di в воздухе внутри и D2 вне трубы, Х/Д / а также поверхностный заряд на проволоке, на внутренней и наружной поверхностях трубы в случаях: а) труба изолирована; 3
б)	труба заземлена; в) проволоку соединили Рис. 15.15 с изолированной трубой.
15.16.	Рассчитать напряженность поля Е, распределений потенциала ср (приняв ср = 0 на оболочке) и емкость на еди ницу длины для воздушного цилиндрического конденсатор*1
(рис. 15.15), находящегося под напряжением U = 1 кВ, есл = 2 мм; г2 — 6 мм; г3 = 7 мм.
15.17.	Определить, при каком отношении радиусов г2 и г наибольшая напряженность поля в цилиндрическом конденса* торе (рис. 15.15) минимальна. Заданы радиус г2 и напряжение на конденсаторе.
Рис. 15.18	Рис. 15.19
15.18(	Р). Рассчитать силу, действующую на каждый из электронов луча, при их движении со скоростью v = 3 • 109 см/с через магнитную отклоняющую систему осциллографа, которая состоит из двух катушек (рис. 15.18), в области, где индукция равна 10"3 Тл. Заряд электронов равен -1,6-10"19 Кл.
Определить, как изменится сила, если электронный луч проходит под углом 45° к оси катушек.
Р е ш е н и е. По формуле Лоренца (15.2) при v 1 В получим: F = gvB = 4,8 • 10"15 Н.
Если луч проходит под углом 45° к оси катушек, то F = = qvB sin 45° = 4,8 • 10' 15/]/2 Н.
15.19.	Рамка магнитоэлектрического прибора находится в воздушном зазоре постоянного магнита. Поле в зазоре однородное с индукцией 0,8 Тл. Размеры рамки, имеющей 100 витков, даны на рис. 15.19 (толщиной катушки пренебречь). Ток в рамке равен 10 мА.
Определить вращающий момент, действующий на рамку, и объяснить, чем определяется равномерность шкалы этого прибора.
15.20.	Отклоняющая система электродинамического прибора состоит из подвижной и неподвижной катушек (рйс. 15.20).
Каков характер шкал амперметра, вольтметра и ваттметра?
15.21.	Определить магнитную индукцию в точках Mi (& 12; 0 см) и М2 (8; 12; 10 см) поля тока 1= 100 А в бесконечном проводе, который изогнут под прямым углом (рис. 15.21)-Выяснить, целесообразно ли для решения этой задачи применить закон полного тока.
1Я.22(Р). Рассчитать магнитное поле в медных жиле, обо-ке коаксиального кабеля и между ними (см. рис. 15.15), если жиле и оболочке кабеля ток постоянный и равен 10 А; радиусы: п = 3 мм; г2 = 9 мм; г3 = 10 мм.
Р Вычислить внешнюю и внутреннюю индуктивности кабеля на единицу длины. Получить формулу для внутренней индук-
тивности для случая г2 -> г3.
Решение. Поле обладает цилиндрической симметрией, так что в цилиндрической системе координат В = Ва, Н — На и зависят только от радиуса г.
Применив закон полного тока (15.19), при г < получим: H'i’lnr — (I/nrj)пг2, откуда Н[ = 1г/2пг2 = 17,7г, А/см; при < <r <г 2 напряженность Не = 7/2яг — 1,59/г, А/см; при г2 < г < г3 получим: Н- • 2nr = I - In (г2 — г2)/я (г3 — г2), откуда
Т j.2 _ „2	1 __ „2
Щ = л------I---т = 8Л------". А/см;
2пг г3 - г2	г
при г > г3 (вне кабеля) Нё • 2пг = 0 и Н'ё = 0. Внешняя индуктивность
= Фс = ^oH'edS I I
где I — длина кабеля.
Внутренняя индуктивность Lf наиболее просто вычисляется
из соотношения (15.36) WM = Ц12/2, где
wu=4-м 2
BiHidV-
энергия магнитного поля в жиле и оболочке кабеля.
Следовательно, = J В^ dV/I2, где В,- и Hi — индукция и напряженность поля внутри жилы и оболочки коаксиального кабеля.
Вычислим:
^BiHidv= f в;н;<?г + f В'ЖЛУ, у yt	y2
где — объем жилы; V2 - объем оболочки на единицу длины Получим:
ri	гз
2nrl dr =
О	гэ
yl2l 1
2л | 4
2	-2	„4	„4 Л

Внутренняя индуктивность г __ fl, гз ,2\2
In———
2л
На единицу длины после подстановки числовых значений получим:
£е0 = 0,22 мкГн/м; Li0 = 0,052 мкГн/м.
При г3 -> г2 раскрытие неопределенности дает: Li = ц0//8л.
Рис. 15.24 ->
Рис. 15.23

— 0 W мм-и
15.23. На тороид заданных размеров (рис. 15.23) из ферромагнитного материала с цг = 1000 нанесены равномерно две однослойные обмотки с числами витков = 20 и w2 == 200.
Определить собственную индуктивность каждой обмотки, взаимную индуктивность между обмотками и коэффициент связи (для однослойных обмоток тороида при большой относительной магнитной проницаемости потоком рассеяния можно пренебречь).
15.24. Трехфазный ток трехпроводной системы шин (рис. 15.24) имеет амплитуду 20000 А.
Определить средние значения сил, действующих на изоляторы; найти законы изменения этих сил во времени.
1*,25(Р). Между проводами двухпроводной линии симмет-чно и в одиой плоскости с ними расположена рамка током 1Р = Ю sin 500t, А, имеющая w = 100 витков (рис. 15.25). С Получить формулу для взаимной индуктивности. Определи, ЭДС, наводимую в линии, при размерах: а = 40 мм, b == 25 мм, I = 50 мм.
решение. Взаимная индуктивность между рамкой и линией равна взаимной индуктивности между линией и рамкой: М = wO/i,
где Ф — магнитный поток поля тока в линии, пронизывающий
рамку; i — ток в проводах линии.
Индукцию В поля тока в линии в любой точке внутри рамки вычислим по закону полного тока (15.19):
i	i
В = Ll0Я = Цо —---F ~—7----г ,
и 2лх	2тс (а — х)
где х — расстояние от оси одного из проводов до рассматриваемой точки.
Поток
(в-Ь)/2
i
2л (п — х)
dx = . л а — b
Взаимная индуктивность
w|i0/ а + b	„
М = —-—In-------- = 2,93 мкГн.
л а — b
Амплитуда ЭДС в линии при заданном токе в рамке
= -Д0147 В, т.е. е = -0,0147 cos 500г, В
15.26. Определить взаимную индуктивность между дВух< проводной линией передачи энергии и линией связи (рис. 15.2б) Провода линии проходят параллельно; длина линии I = 7 км
Рис. 15.27	Рис. 15.28
15.27.	Плоская проволочная петля расположена вблизи провода с током i = 100 sin 314г, А (рис. 15.27). Ось провода находится в той же плоскости, что и петля.
Вычислить ЭДС, наводимую в петле.
15.28.	Переменный ток в контактном проводе электрифицированной железной дороги равен 100 А, частота 50 Гц.
Определить ЭДС, наводимые (на единицу длины) в проводах двух линий связи 1 и 2, проходящих параллельно полотну железной дороги (рис. 15.28). Расстояние между проводами каждой линии связи 50 см. Влиянием земли на распределение поля пренебречь.
Решить задачу: а) считая, что ток в рельсах распределен поровну; б) заменяя рельсы одним эквивалентным проводником, расположенным посередине между рельсами. Сопоставить решения.
15.29.	Для измерения магнитного поля применили плоскую катушку (все витки расположены в одной плоскости), содержащую w витков; площадь, ограничиваемая витками (в плоскости витков), равна <5. Провода катушки образуют контур, замкнутый на прибор, измеряющий протекающий заряд (кулонметр). Катушку поместили в область поля, подлежащего измерению (например, у полюсных наконечников электрической машины), быстро повернули на 180° и отсчитали показание кулонметра.
Дано: w = 100, 5 = 0,2 см2, сопротивление всей измерительной цепи (включая катушку) R = 250 Ом, отсчет по кулон-метру q = 8,8- 10“7 Кл.
Что можно определить при таком измерении? Каких данных недостает и какие еще измерения нужно произвести для определения вектора магнитной индукции в заданной точке (полагая, что в плоскости катушки поле изменяется мало).
15.30.	При измерении остаточной магнитной индукции постоянных магнитов (рис. 15.30) применяют следующий ме-
обычно служит
Рис. 15.30
на среднюю часть магнита надевают плотно прилегающую однослойную катушку, цепь которой замкнута на прибор «ля измерения заряда (таким кулонметром i ' баллистический гальванометр БГ); маг-лит выдергивают или сбрасывают катушку и фиксируют показание прибора.
Определить остаточную индукцию магнита сечением 2 см2, если измеренный заряд равен 6 мкКл; число витков катушки 20; сопротивление цепи (катушки, соединительных проводов лонметра) 400 Ом.
15.31.	Изменится ли значение репного заряда в задаче 15.30, если в результате повреждения изоляции между двумя соседними витками один из витков измерительной катушки окажется замкнутым накоротко?
15.32.	Изменится ли значение измеренного заряда в за
и ку-
изме-
даче 15.30 при наличии дополнительной короткозамкнутой обмоткй (ключ К на рис. 15.30 замкнут).
15.33(	Р). Плоский конденсатор с круглыми электродами диаметром 500 мм и расстоянием между электродами 2 мм (рис. 15.33), у диэлектрика которого ег = 5,5, подключается к источнику постоянного напряжения U — 1000 В через резистор с сопротивлением R — 100 кОм.
Определить закон изменения напряженности магнитного
поля от координат и времени.
Решение. По закону полного тока (15.19) для любого контура I в диэлектрике

где Лм — плотность тока смещения в диэлектрике.
Вследствие симметрии в цилиндрической системе координат Н = На— f (г), a JCM = JCmz и от координат не зависит.
Поэтому, выбрав контур I в виде окружности с центром в начале координат, получим:
Н  2яг = Усмяг2,
откуда Н = По определению плотность тока смещения Лм = dD/dt, rj\e D = Dz = &r&0E - zrzQucld, а напряжение на конденсаторе uc = U(i - e“t/T), где т = RC = Rs&S/d.
Следовательно,
r z ij\ duc U —tit
~ (Br^o/d)	— • e
IXlJ
и напряженность поля
Ur 2RS
= 6,36 • 10“3ге 522\ А/м.
е
15.34.	Проволочное кольцо (короткозамкнутый виток) охватывает длинную катушку (соленоид) с переменным током, намотанную на фарфоровый цилиндр (цг = 1). К диаметрально противоположным точкам кольца ник присоединены три прибора для измерения напряжения — вольтметры V2, Г3 (рис. 15.34).
Рис. 15.33	Рис. 15.34
Провода, присоединяющие вольтметр проходят с одной стороны соленоида, а провода, присоединяющие вольтметр У2, проходят с другой стороны соленоида, причем ни один из этих проводов внутрь соленоида не заходит. Один из проводов, присоединенных к вольтметру V3, проходит по диаметральному каналу внутри соленоида. Сопротивление всех вольтметров бесконечно велико. Кольцо выполнено из однородной манганиновой проволоки с удельной проводимостью о = — 2 • 104 См/см. Показание первого вольтметра 0,01 В.
Определить показания второго и третьего вольтметров.
15.35(	Р). Измерительные устройства - «вольтметры» — предыдущей задачи позволяют определять как модуль, так и фазу напряжения (в качестве таких «вольтметров» могут служить вектормерные схемы, компенсаторы переменного тока, осциллографы). Показания приборов зависят от порядка присоединения выводов (фаза изменяется на 180°). Один из выводов каждого вольтметра (рис. 15.34) считаем началом ( + ), а другой — концом (—). Вольтметр Fj показывает 0,01 В. Радиус кольца а = 2 см, частота тока f = 50 Гц, удельная проводимость манганина, из которого выполнено кольцо, о =2 • 104 См/см.
Определить показания вольтметров V2 и V3, полагая, что все начала обмоток вольтметров присоединены к точке н проволочного кольца, а все концы — к точке к.
Вычислить магнитный поток в соленоиде, напряженность дектрического поля и плотность тока в манганиновом кольце.
решение. По закону электромагнитной индукции (15.22) в кольце возникает напряженность поля Е и течет ток плотностью J (при указанном на рис. 15.34 положительном направлении магнитного потока положительные направления напряженности поля и плотности тока следует выбрать по направлению движения часовой стрелки).
Из уравнения закона электромагнитной индукции для гармонического процесса (15.22)
§Edl = — ;®Ф
найдем напряженность электрического поля и плотность тока в кольце:
Ё = -jo&/2itcr, J = <зЁ - -/соФа/2тга.
Для определения показаний вольтметра обходим любой контур, содержащий этот вольтметр. Направление обхода должно быть согласовано с направлением магнитного потока, который пронизывает площадь, ограниченную контуром, по правилу правоходового винта. Так, для контура, который обходим через вольтметр от вывода « + » к выводу « —» и верхнее полукольцо от точки к к точке н, получим: U! - Ёла = 0 (контур не охватывает потока), т. е. U i = Ёла — = — усоФ/2, откуда <Ь =	= 0,0636/, мВб; Ё = IJJna —
= 1,59 мВ/см; J = сЁ = 31,8 А/см2. Здесь принято Ul = UY-
Аналогично U2 + Ела — 0 или U2 7 Ела = ;<оФ/2, т. е. U2 = = -Ul = -0,01 В; U3 + Ёла = —j($®/2 или U3 = — Ёла — - >Ф/2 = 0.
15.36.	Определить показания вольтметров задачи 15.35 при условии, что точка к, к которой присоединены концы всех вольтметров, передвинута на У4 окружности по направлению движения часовой стрелки. Соединительный провод вольтметра V3 остается внутри диаметрального канала. Магнитный поток ф = /0,0636 мВб тот же, что и в задаче 15.35.
15.37.	То же, что в задаче 15.36, но после перемещения точки к вдоль кольца еще на */4 окружности (т.е. до совмещения с точкой н).
15.38(	Р). Определить показания вольтметров V2 и V3 (рис. 15.34) задачи 15.35 при неоднородном кольце: верхняя половина кольца выполнена из манганиновой (qj = 2 • 104 См/см), а нижняя из нихромовой (а2 = Ю4 См/см) проволок. Сечения обеих проволок одинаковые. Показание первого вольтметра Vl =0,01 В.
Вычислить магнитный поток, напряженность поля и ПЛОт ность тока в кольце.
Решение. Ток и плотность тока в обеих половинах кольца одинаковы, а напряженности поля Ё1>2 = «М?х,2 - различны.
Обходя кольцо по направлению движения часовой стрелки на основании закона электромагнитной индукции (15.22) получаем Ё1Па + Ё2па = —/соФ. Так как плотность тока вдоль кольца не изменяется, т.е. = о2Ё2, то Ё2 — 2Ё^
Из двух уравнений находим:	= —/соФ/Зтга; Ё2 ==
== — 2;соФ/Зла.
Для определения показаний вольтметра обходим любой контур, содержащий этот вольтметр, согласуй направление-обхода с направлением потока по правилу правоходового винта. Выбирая те же контуры, что и в решении задачи 15.35, получаем:
17 х - Ё^па = 0, т.е. Ё{ - UJna = 1,59 мВ/см; Ё2 = 3,18 мВ/см; й2 4- Ё2па = 0, т. е. й2 = — Ё2ка = — 2Ё{па = — 2(7х = —0,02 В; U2 + Ё2ка = -)<оФ/2, т.е. U2 = — 0,25тш£2 или 173 = -0,5171 =
= -0,005 В.
Поток Ф = — Ё2 • 1,5тш//а) = — Ё± • Зтш/jo) = 0,0955/, мВб.
Плотность тока j — с^Ёх = о2Ё2 = 31,8 А/см2.
15.39.	Определить показания вольтметров задачи 15 38 (рис. 15.34) после перемещения точки к по направлению движения часовой стрелки на 1/4 окружности. Магнитный поток Ф = /0,0955 мВб тот же, что и в задаче 15.38.
15.40.	То же, что в задаче 15.39, но после смещения точки к на х/2 окружности (точки присоединения концов и начал вольтметров совпали).
15.41.	Определить, как нужно расположить точку присоединения конца вольтметра У2 задачи 15.38, чтобы он показывал нуль.
15.42(	Р). По бесконечно длинному ферритовому стержню радиусом а проходит магнитный поток, равномерно распределенный по сечению и изменяющийся во времени по закону
Ф =Ф0(1 -e"at).
Определить напряженность электрического поля внутри и вне стержня. При решении пренебречь процессом распространения волн и токами смещения.
Решение. Для решения применим закон электромагнитной индукции (15.21). Направим ось z вдоль оси цилиндра 498
г2
-2-Ф0ае“иг, а .
dt
выберем положительное направление индукции по оси z. Вследствие симметрии поля Е = Еа.
При г < а получим:
г2 5Ф
Е  2яг =--ч-
а
откуда Е = - 2^ф°ае'М-
При г > а получим:
Е •2яг = —
дФ dt
= —Фоае"®*,
откуда Е = -Фоае”а727сг.
15.2.	Анализ полей
В этом параграфе собраны задачи, в которых требуется проанализировать решение для заданного поля, т. е. определить характер поля, его вихри и истоки и сделать предположения о возможном способе его возбуждения. Для анализа рационально пользоваться уравнениями поля в дифференциальной форме.
15.43(Р). Определить характер поля, его вихри и истоки и сделать предположения о способе его возбуждения при заданной зависимости вектора поля N от координат в цилиндрической системе:
a)	N = eaNa; Na = cr, 0 <r < а;
б)	N = erNr; Nr — cr, 0 <r < a;
в)	N = eaNa; Na = c/r, a < r< co;
r) N = erNr; Nr — c/r, a <r < oo.
Решение.. а) Вычислим rot и div заданного вектора в цилиндрической системе координат: rot N = ez- 2с; div N = О, т.е. задано вихревое поле без истоков.
1.	Таким вектором может характеризоваться, например, магнитное поле внутри провода с постоянным током. Дей-' ствительно, по уравнениям (15.30) и (15.32) для постоянного магнитного поля в области, где протекают токи, rot Н = J и div В = 0, откуда при ц, = const по (15.33) получим div Н = 0. Например, в решении задачи 15.22 было найдено, что внутри бесконечно длинного проводника радиуса с током I напряженность Н = Нл = Ir/2nrl = Jr/2, т. е. с = J/2 и rot N = ezJ.
2.	Рассматриваемым вектором может характеризоваться также переменное электрическое поле в однородной среде при отсутствии объемного заряда. Для такого поля по уравнениям (15.31) и (15.28) rotE = — dB/dt и div Е = 0; такое поле
существует, например, в бесконечно длинном соленоиде, виткам которого протекает переменный ток.
3.	Рассматриваемым вектором не может характеризоваться постоянное электрическое поле, поскольку для него rot £ == о
б) В этом случае rot N = 0 и div N = 2с, т. е. это безвих-ревое поле с истоками.
1. Поскольку div N / 0, то вектор N не может описывать магнитное поле в однородной среде, для которого справед. ливы уравнения (15.30) и (15.33).
2. Таким вектором может характеризоваться, например, постоянное электрическое поле в вакууме при наличии объемного заряда. Действительно, для постоянного электрического поля в вакууме по уравнениям (15.31) и (15.28) имеем rot£ = 0 и div £ = р/е0.
Из решения задачи 15.13 следует, что внутри электронного луча цилиндрической формы с объемной плотностью заряда р электрическое поле Е{ = Ег = рг/2£0, т.е. с = р/2е0.
15.44.	Определить характер поля, его вихри и истоки и сделать предположения о способе его возбуждения для заданных выражений вектора поля в декартовой системе координат:
a)	N — i с/х, а < х < Ь;
б)	N су, 0 <у < Ь;
15.45.	Определить истоки поля (заряды) в следующих случаях:
1)	в области а < х < b напряженность электрического поля изменяется по закону: Ех — EQa/x; Еу = £г = 0;
2)	в области а2 < х2 4- у2 напряженность электрического поля изменяется по закону:
ах
О v2 . „2 ’
аУ . £ =0
2 I ,,2 ’
15.46.	Определить характер поля (вихри и истоки), если:
1)	Ех — —су; Еу = сх; Ег = 0;
2)	Ех = су; Еу — сх; Es = 0.
Для потенциального поля написать уравнения линий поля и эквипотенциалей.
15.47(	Р). Определить способ возбуждения поля, если из-
2 ПУ .
вестно, что ср = к Ini
, TIX cos — а' а
Построить картину поля (линии поля и эквипотенциал и).
решение. Определим напряженность поля в декартовой системе координат:
Е = кп__________sin (2пх/а)
х a cos (2пх/а) + ch (2пу/а) ’
„ кп	sh (2тс у/а)
— —...... .......... ~ —
у a cos (2пх/а) + ch (2пу/а)'
по (15.37)
Вычислив rot и div в декартовой системе координат (см, приложение 4), получим: rotE = 0; divE = 0, т.е. потенциальное поле без объемного заряда.
WIWI7
< > О X?" -<» а/2 За/2 5а/2
Силы
б)
Рис. 15.47Р
При у — 0 имеем Ех = (Zcrc/a) tg (тсх/а); Еу — 0; при у = а/2п получим:
Е __ кп sin (2тсх/а) _ кп 1,18 a cos (2пх/а) 4- 1,54 ’ у a cos (2пх/а) + 1,54 ’
при у -> оо соответственно Ех -> 0; Еу -> — кпа.
На рис. 15.47Р, а представлены зависимости напряженности поля от координат. На рис. 15.47Р, б дана качественная карена распределения сил, действующих на положительный пробный заряд, на основании которой можно утверждать, что такое поле создается системой одноименно заряженных осей,
расположенных на расстоянии а друг от друга; линейный заряд осей т = клг0. По уравнению линий поля [Е df] == q получим: tg (их/а) — с th (ну/а).
Уравнение эквипотенциален ср = const, т. е. е^/к = = cos2 (пх/а) + sh2 (пу/а), причем ф = О при sh (тсу/я) = ±sin (ях/а). На рис. 15.47Р, в представлена качественная картина экви-потенциалей и линий поля.
15.48.	Между двумя плоскими электродами (рис. 15.48) напряженность электрического поля изменяется по закону Ех = = Ео (1 - x2/2d2); Ey — Ez = 0. Расстояние между электродами d много меньше размеров электродов а и Ь,
Определить объемный заряд и разность потенциалов U между электродами. Выяснить, как изменится напряженность поля, если электроды подключены к источнику постоянного напряжения Uo, которое отличается от найденной разности потенциалов.
15.49.	Определить закон распределения плотности свободных зарядов, который обеспечил бы постоянство модуля напряженности электрического поля Е = Ег = 100 В/см во всех точках между обкладками цилиндрического конденсатора с параметрами Г1 = 1 мм, г2 — 3 мм, £г = 1.
15.50.	Определить характер поля, его вихри и истоки, сделать предположения о способе его возбуждения, если в декартовой системе координат внутри прямоугольника 0 < х < а, 0 < у < b задано поле:
_	—	. / Л1Я \	. ,	, .	_
Ех = Ет sin —г— у • sin (cot - kz); Ey = Ez = 0;
во всем остальном пространстве поле равно нулю.
15.51.	Найти divE и rotE внутри (1) и вне (2) шарообразного электронного облачка, поле которого рассчитано в задаче 15.10.
15.52.	Найти div Е и rot Е внутри и вне электронного луча цилиндрической формы, поле которого рассчитано в задаче 15.13.
Глава шестнадцатая
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
Введение к гл. 16
Для статических, стационарных и квазистатических электрических полей справедливы уравнения
rot£ = 0;	(16.1а)
§Edl = 0;	(16.16)
divD = p;	(16.2а)
$DdS = ^q,	(16.26)
где I — контур интегрирования; S — поверхность интегрирования; р — объемная плотность свободных зарядов; £<? — сумма свободных зарядов.
Скалярный потенциал ф определяется
E=-grad9,	(16.3)
В однородной среде (с постоянной относительной диэлектрической проницаемостью £r = const) для потенциала справедливо уравнение Пуассона
V29=-p/er£0	(16.4)
и, в частности, уравнение Лапласа
72ф = 0.	(16.5)
Граничные условия
Для всех электрических полей
Eu = E2t или Ф1=ф2;	(16.6)
^2п ~ Din =	(16.7)
Для статических полей на границе раздела двух диэлектриков
Din = D2n или £Г1Е1И = £г2£2и;	(16.8а)
?2п ~ Din = —	(16.86)
При этом
D = е0Е + Р	(16.9)
Для стационарных полей на границе раздела двух про-водников
Jin = J 2п ИЛИ CiEin = <32Е2п.	(16.10)
Для квазистатических полей на границе раздела двух диэлектриков с проводимостью
Jln + 8Dln/ct = J2„ + 8D2„/Bt,	(16.11)
на границе раздела двух диэлектриков с вязкостью
= &2п,	(16.12)
причем Е, D и Р связаны соотношением (16.9).
В приведенных выше формулах Et — составляющая вектора напряженности поля, касательная к границе раздела сред; Ь Рп и Jn — составляющие векторов смещения, поляризации и плотности тока проводимости, нормальные к границе раздела, при условии, что нормаль направлена из первой среды во вторую; qs и qs Связ — поверхностные плотности свободных и свя* занных зарядов; аг1 и ер2 — относительные диэлектрические проницаемости; О) и о2 — удельные проводимости.
Электростатическое поле
Для линейной среды по методу наложения
Е — Е^ + Е2 + •.. = Еп",	(16.13а)
л
q> = <р, + ф2 + ...=£ <р„.	(16.136)
Для системы заряженных проводов формулы Максвелла
с потенциальными коэффициентами имеют вид:
Ф1 — ^n<?i + a12g2 + а13д3 + ...; '
Ф2 — а21Q1 + а22<?2 + а23<2з + • • 4 фз — а31<?1 + а32<?2 '+ &33<7з + • • •;
(16.14)

где <рк и qk — потенциалы и заряды проводов, причем собственный потенциальный коэффициент ам„ — <pn/qn при всех остальных qk (кроме qn), равных нулю, взаимный потенциальный коэффициент аит = q>n/qm при всех остальных qk (кроме qm\ равных нулю.
Формулы Максвелла с емкостными коэффициентами:
Qi в РиФ1 + Р12Ф2 + Р1зФз + • • •;
= Р21Ф1 + Р22Ф2 + РгзФз + ...;
4з = Р31Ф1 + Р32Ф2 + РззФз + • • 4 ................................. *
(16.15)
где собственный емкостный коэффициент рин = д„/срм при всех остальных ср*; (кроме ср„), равных нулю, взаимный емкостный коэффициент рпш = ди/(рт при всех остальных <рк (кроме срД равных нулю.
Формулы с частичными емкостями:
qi = Сц (Ф1 “	Фо) + С12 (Ф1	—	Фг) + С\з (фi — Фз)	+ •  •>
q2 = С21 (Ф2 —	Ф1) + ^22 (Фг	—	Фо) + С23 (Фг “ Фз)	+ • •цб
q2 = С31 (фз —	Ф1) 4- С32 (фз	—	Ф2) + 6*33 (срз + фо)	+ ...;
’.............. * ’ >
где собственная частичная емкость Сп„ — qnKtyn — ф0) при <pt = я <р2 = ...	<р0, взаимная частичная емкость Спт = д„/(фя ~ Ф™)
при ф! = ф2 = ... = фо = 0 (кроме фи ф фт).
Потенциал поля диполя
Ф = р cos 0/4лег£оЯ2,	(16.17)
где р — дипольный момент; R и 0 — сферические координаты. Потенциал поля двухпроводной линии в вакууме
<р = ^—In—,	(16.18)
2яе0	г +
где т — заряд на единицу длины линии; г_ и г+ — расстояния от точки наблюдения до отрицательно и положительно заряженных проводов соответственно.
Для расчета электростатического поля заряда вблизи плоской границы раздела диэлектрика и проводника или двух диэлектриков можно применить метод отражений. При отражении точечного заряда q у плоской границы проводника отраженный заряд qr — -q. При отражении у границы двух диэлектриков (рис. 16.А, и) поле в той среде, где задан точечный заряд q (рис. 16.А, б), определяется зарядом q и зарядом
41 = q (г,1 - e.2)/(s>-i + 6,2) = ktq; (16.19а)
поле по другую сторону границы (рис. 16.А, в) определяется зарядом
q2 = q * 2£г2/(ем + Егг) =	(16.196)
где £Г1 — относительная диэлектрическая проницаемость среды, в которой находится заряд q; гг2 — относительная диэлектрическая проницаемость среды по другую сторону границы.
Дополнительные заряды должны находиться на том же расстоянии от границы, что и заданный.
Для неоднородного диэлектрика (ег const)
div Е = _Р_ _ £ 8^1^- = -р-+-р^-,	(16.20а)
£r£o	£г	^0	7
div Р = -рсвяз,	(16.206)
где рсвяз — объемная плотность связанных зарядов.
"У
у'П
Рис. 16. А
Стационарное поле
В стационарном поле основные уравнения и соотношения (16.1)-(16.7) дополняются следующими:
div J = 0;	(16.21а)
pdS = 0;	(16.216)
J = сЕ,	(16.22)
где J — плотность тока проводимости; ст — удельная проводимость среды.
Мощность потерь в единице объема
р = JE = aE2 = J2/g.	(16.23)
Для расчета поля провода с током / вблизи плоской границы двух проводящих сред можно применить метод отражений (см. расчет поля точечного заряда у границы раздела диэлектриков и рис. 16.А). Дополнительные токи
Л =/(ог -CT2)/(CTi + CT2) = nJ; 12 =	+ o2) = n2Z.
(16.24)
Для неоднородной (с const) проводящей среды
_ grad а	.
div Е = — Е--------.	(16.25)
с
Существует аналогия между электростатическим полем без объемного заряда и стационарным полем в области, где нет сторонних сил, при этом аналогичны параметры:
Электростатическое поле . . Е ср D q s,Eq С Стационарное поле ... Е <р J 1 о G
Проводимость G между двумя электродами в проводящей среде определяется через емкость С между теми же электродами в диэлектрике (или наоборот).
G = — С.	(16.26)
£г£о
Квазистатическое поле
Основные уравнения и соотношения (16.1) —(16.7) допол
няются следующими:
di v (J + dD/dt) = 0;	(16.27а)
§ (J + dD/dt) dS = $ /полн dS = 0,	(16.276)
где плотность полного тока
Лолн = J + dD/dt = п£ + Er£0 dE/dt. (16.28) Для вязкого диэлектрика справедливо уравнение вязкости т dP/dt = £0 (£г - 1) Е - Р = £оХгЕ - Р, (16.29)
где т - постоянная времени вязкости и векторы £, Р и D связаны соотношением (16.9).
Для гармонического поля с напряженностью
£ = iExm sin (wr -I- фх) + jEym sin (со? + фу) + kEzni sin (cot + фг);
(16.30а) комплексный вектор
Ёт = iExm + jEym + kEzm,	(16.306)
где = Ekme , k = х, у, z.
Уравнения поля	в	комплексной	форме:
rot£ = 0;	(16.31)
divA = p;	(16.32)
div (j + jcoD) = div jnojlH = 0,	(16.33)
где	7ПОЛН	=	j+;coD = c£+;a)£r£0£;	(16.34)
£=-gradcp,	(16.35)
причем
V2cp = - p/£r£0 или V2<p = 0.	(16.36)
Для вязкого диэлектрика в гармоническом поле уравнение вязкости следующее:
JcdtP = £о (£г - 1) £ - Р.	(16.37)
Комплексная относительная электрическая восприимчив вость
Хг = £, - 1 = ter - 1)/(1 + Лот).	(16.38)
Комплексная относительная диэлектрическая проницаемость
&=Е;_К = ^±Ж = 1+^_.	(16.39)
-г j 1 + JCOT 1 + JCDT	’
На границе раздела двух диэлектриков с проводимостями di ^0 и сг2 7^0
£lf = E2t или фг == ф2;	’ (16.40)
2лЁ1п = ^2^2»,	(16.41)
где <т ~ о + jcoer£o-
На границе раздела двух вязких диэлектриков
Elt = E2t или ф1 = ф2;	(16.42)
t>in = Ь2п или = гг2Ё2п.	(16.43)
Удельная комплексная мощность в диэлектрике с проводимостью
So = Ро + JQo = ъЕ2 - ;жг£0Е2,	(16.44)
в вязком диэлектрике
So == Ро + JQo = (ы&оЕ2 - }(йф0Е2.	(16.45)
Комплексная мощность
S = fSorfK	(16.46)
Энергия и силы
Силы поля можно определить на основе закона сохранения энергии: энергия, отданная источником АЖИ, равна сумме приращения энергии поля АЖи произведенной работы АЛ, т.е.
АЖИ = AW + АЛ. '	(16.47)
Если работа происходит за счет энергии, отдаваемой источником при заданном напряжении, то приращение энергии поля и произведенная работа равны: А И7 = ЛА - AWJ2. Если источники отсутствуют, то работа происходит при постоянстве суммы зарядов за счет убыли энергии поля АЛ == — АЖ.
Энергию, электрического поля можно определить:
1) через объемный интеграл от скалярного произведения
векторов Е и D по всему объему V поля:
1 f W = — EDdV;
2 .
(16.48)
2) через потенциалы проводников, и заряды на них:
W =
(16.49)
i
16.1. Электростатическое поле в вакууме
16.ЦР). Точечные заряды +2д и — q находятся на расстоянии I = 10 см (рис. 16.1) в вакууме.
1) Считая потенциал бесконечно удаленной точки равным нулю, найти положение, размеры и потенциал эквипотенциальной поверхности, имеющей сферическую форму.
Рис. 16.1Р
Рис. 16.1
2) Доказать, что заряд —q лежит в плоскости, которая проходит через точки касания лучей, проведенных к сфере из точки расположения заряда 2q.
Решение. 1) При выбранных осях координат (рис. 16.1) для любой точки, находящейся в плоскости, где находятся заряды, потенциал
4ле0 j/x2 + у2 4яе0 ]/(х — /)2 + у2
Уравнение окружности
экви-
потенциаль в плоскости ху, получится, если положить потенциал <р = 0. Следовательно, форму окружности (рис. 16.1Р) имеет эквипотенциаль, потенциал которой равен потенциалу
бесконечно удаленной точки. Радиус окружности R — 21/3 — 6,7 см, центр ее лежит на оси х на расстоянии а = 4Z/3 = 13,3 см от начала координат. Отметим, что остальные эквипотенциали имеют более сложную форму.
2) Проведем касательные из точки расположения заряда 2q (начала координат) к сфере и плоскость через точки касания фис. 16.1Р). Так как треугольник OBD подобен треугольнику BCD, то b/R = R/a или b = R2/a; кроме того, b — а — ОС, откуда ОС = а — R2/a — 4//3 — 1/3 = 1; таким образом, заряд -q находится в точке С и действительно лежит в плоскости.
проходящей через точки касания.
16.2(Р). Точечный заряд Q = 10 7. Кл находится в воздухе
на расстоянии а = 1 м от центра проводящего заземленного шара, радиус которого R = 0,2 м (рис. 16.2).
Определить плотность заряда, индуктированного на поверхности шара, в точках 1, 2, 3 и 4.
Решение. Поверхность шара — эквипотенциаль (р = 0. Поэтому для расчета проводящий заземленный шар и точечный заряд Q можно заменить двумя точечными зарядами с разными знаками (см. решение задачи 16.1). Один из заря-
дов Q задан, значение и расположение второго можно
найти, приравняв потенциал заземленного шара нулю. Из двух уравнений для двух любых точек на поверхности шара по
лучим:
Qi = ~QR/a = — 0,2Q; (/ — а) = b = R2/a = 0,04 м,
где I — расстояние между зарядами Q и Qi (рис. 16.2Р). Далее решаем задачу при уже известных значениях и расположении двух точечных зарядов.
Плотность поверхностного заряда на шаре по (16.7)
г 2	,21
<7s = Et>£„ = -^j-cosa! + -^ycos7.,.
Выразив rit r2, cosot! и cosa2 через переменные R и 9 сферической системы координат, получим:
_ Q R — a cos 0	R — b cos 0
4л _ (R2 + а2 — 2aR cos G)3/2	’ (R2 + b2 — 2bR cos G)3/2 _
л при заданных числовых значениях
_ 9 J 0,2 — cos 9	0,04 — 0,008 cos 9	1	2
^₽8-Ю	— 0,4 cos 9]3/2 [0,0416— 0,016 cos 9]3/2 j лм-
Для точки 1 (cos 9 = l)qs = —74,6 нКл/м2; для точек 2 и 3 (cos 9 = 0) qs~ -36,1 нКл/м2; для точки 4 (cos 9 = -1) qs = -= -22,2 нКл/м2.
16.3.	Решить предыдущую задачу в предположении, что шар не заземлен. Определить потенциал шара, считая равным нулю потенциал бесконечно удаленной точки.
16.4.	Определить силу, с которой точечный заряд задачи 16.2 притягивается к шару в случае а) заземленного и б) незаземленного шара.
16.5(	Р). Проводящая сфера радиусом R находится в поле точечного заряда расположенного на расстоянии а от ее центра (см. рис. 16.2).
Показать, что для заземленной сферы отношение заряда на части поверхности сферы, видимой из точки располо-жения заряда Q, к остальному заряду qH сферы равно
+ R)/(a - R).
Решение. Из решений задач 16.1 и 16.2 следует, что при расчетах проводящую сферу можно заменить точечным зарядом Qi = — QR/a, лежащим внутри сферы в плоскости, которая проходит через точки касания сферы лучами, проведенными к сфере из точки расположения заряда Q. Отсюда по теореме Гаусса (16.26) поток Ч7 вектора D через видимую часть сферы, равный заряду на ней дв, и поток через невидимую часть сферы, равный заряду на ней qH, соответственно равны:
Зв = Ув = Qt/2 - 2со/4я; qu =	= QJ2 + б<о/4л,
где со = 2тг < 1 - ---->.
I а
Отношение qJqK = ]/а + R/f/a — R
16.6.	Определить потенциал и напряженность электрического поля диполя р = ql = 12 • 10“9 Кл • см (рис. 16.6) в точках, достаточно удаленных от него, т. е. при R » /, где R — расстояние от центра диполя до точки наблюдения М.
Рассчитать зависимости составляющих напряженности поля от R при 9 = 0 и 0 = я/2; сравнить их с соответствующими зависимостями для поля точечного заряда.
16.7(	Р). Определить потенциал и напряженность поля двойного слоя зарядов, равномерно распределенных на плоскости ху (двойным слоем называют распределенные по поверхности диполи). Слой характеризуется плотностью дипольных моментов ps.
Решение. Запишем потенциал поля элементарного дипольного момента Psdxjdyi (рис. 16.7Р) для произвольной точки М: d<p = Psdxi dyx cos 91/4яе0.К2. Учитывая, что cosO^ = z/R, получаем dtp — pszdxi dyJ^n&QR3 и
_ * ff Ps dxx dyt
471e0 R3 ’
где R2 = (x - Xi)2 + (y - yi)2 + z2.
Если ps — const, to
zps ff____________dxt dyy____________
47t£0 JJ [(л - *i)2 + O' ~ У1)2 + Z2]3'2 
При бесконечно протяженном слое + 00	+ оо
ф = _Р«£_ f dx f__________________01______________
4ле0 J 1 J [(* - xj2 + O' - >'i)2 + Z213/2 '
— co — 00
Обозначим (х — Xj)2 + z2 — а; у — yi = t; dyt = — dt, тогда
4-оо	У" оо
______________^У1____________ = - f________d*____-Ila
J [(x - х,)2 + (у - У1)2 + z2]3'2 J (a + t2)*2 Z/a
- oo	y+ 00
И
Полученное решение показывает, что потенциал двойного
слоя в каждом из полупространств остается постоянным и изменяется скачком на Дер = Ps/^o при переходе через двойной слой. Напряженность поля всюду равна нулю. Последний результат можно получить, суммируя поля от двух простых заряженных слоев с зарядами разного знака.
16.8(	Р). Предположив, что отрезок нити длиной I равномерно заряжен с линейной плотностью т, найти составляю
щие вектора напряженности электрического поля и написать уравнение эквипотенциален.
Решение. Выберем начало декартовой системы координат в середине заданного отрезка (рис. 16.8Р). Введем, кроме того, переменную Xi - координату элементарного заряда dq = — Tdxi, при этом
dq> =
т dxi
4ле0 ]/(х - xj2 + у2 + z2
и
После интегрирования находим, что
Далее, положив К = е4пе°ф/т = const, получим уравнение эквипотенциалей в виде
_________х2_________
17 (1 4- К)/2(1 - К)]2
_______у2_________(_______z^________
[/ |/К/(1 - К)]2	[/ |/к/(1 - К)]2~ ’
из которого видно, что эквипотенциальные поверхности имеют форму эллипсоидов вращения.
Составляющие вектора напряженности поля по (16.3)
16.9.	Рассчитать напряженность поля и потенциал в точках М2, М3, М4 (рис. 16.9) вблизи двухпроводной линии с радиусом проводов г0 = 2,5 мм, находящейся под постоянным напряжением U = 10 кВ. Определить емкость линии. Найти зависимости Е(х, 0)/Е (0, 0) и <р (х, О)/(17/2).
16.10.	Для двухпроводной линии, изображенной на рис. 16.9, построить (определить положение центра и радиус) эквипотен-циаль <р = 0,4[7/2 и силовую линию, так чтобы между этой линией и линией, соединяющей оси проводов, проходила 75 часть всего электрического потока.
16.11(	F). Двухпроводная линия (рис. 16.11, где 2s = 25 мм; г0 — 10 мм) находится под постоянным напряжением 1 кВ.
Найти распределение заряда по поверхности провода и определить емкость системы на единицу длины. Получить зависимость напряженности поля от координаты х в плоскости, проходящей через оси проводов.
Решение. Два металлических провода заменим двумя заряженными осями (рис. 16.11Р), положение которых определим по выражению а = ]/s2 - Гд = 7,5 мм. Здесь 2а — расстояние между электрическими осями проводов.
Емкость между проводами на единицу длины Со = т/(Ф1 " — <р2), где т — заряд на единицу длины провода; cpi и ср2 ~ потенциалы левого и правого проводов соответственно.
Как видно из рис. 16.11Р, для точек 1 и 2 по (16.18)
Ф1 =
т . а 4- s - rQ
— {п---------------•
2яе0 а — s 4- г0
т . а - s 4- г0 ф -	-----1П------------'
2яе0 л 4- s - г0
Емкость и заряд
Со = ле0/1п	—— = о,4 пФ/см; т = C0U — 0,4 • 10 9 Кл/см.
<2 — S + Гд
Поверхностный заряд на проводе (рис. 16.11Р) по (16.7)
qs = Е°£" = Е° C0S “* + 2^TCOSC4
где
г2 = rQ + (s ~ д)2 ~ 2г0 ($ - a) cos 0;. rj = rg + (s 4- a)2 - 2r0 (s + + a) cos 9;
r0 — (s — a) cos 9	(s + a) cos 0 — r0
cos	---------5 cos a2 — 1---------------
f'l
или
т j r0 — (s — a) cos 9
2я | го 4- (s — a)2 — 2r0 (s — a) cos 0
r0 — (s + a) cos 9	[
Гд 4- (s + a)2 — 2r0 (s 4- a) cos 9 J ’
Напряженность поля в плоскости, проходящей через оси проводов, имеет одну составляющую:
е = _— {_____!___|____!__
х 2те0 [ 0,75 4-х	0,75 - х
В/см,
где х-в сантиметрах.
16.12.	Двухпроводная линия состоит из двух медных цц. линдров с радиусами 6 и 10 мм, находящихся на расстоянии 25 мм друг от друга.
Определить емкость системы.
16.13.	Определить емкость и пробивное напряжение в системе двух некоаксиальных цилиндров (рис. 16.13), между которыми находится воздух. Пробивная прочность воздуха Япроб == 30 кВ/см.
Рис. 16.13
Рис. 16.14
16.14(	Р). Для каждого из двухпроводных экранированных кабелей (рис. 16.14, а—в) определить емкость, рассчитать поле и найти распределение плотности заряда на внутренней поверхности оболочки.
Дано: R — 10 мм; I— 10 мм; /1 = 3 мм; диаметр жилы <2 = 0,5 мм; £r = 1. Между жилами кабеля приложено напряжение U = 100 В.
Решение, а) Заменим кабель (рис. 16.14,а) системой четырех заряженных осей так, чтобы оболочка кабеля осталась эквипотенциальной поверхностью (рис. 16.14Р, а). Для этого должны быть s — а = 2/2 и s2 = а2 4- R2, откуда а = R2/I - 2/4 = = 7,5 мм; s = R2/l -I- 2/4 = 12,5 мм; s 4- а = 2R2/l = 20 мм.
Запишем потенциал любой точки поля двух двухпроводных линий (7-2 и Г-2') по (16.18), принимая ср = 0 при х = 0:
(х - 0,5)2 4- у2 (х 4- 2)2 4- у2 (х + 0,5)2 4- у2 П (х - 2)2 4- у2
По (16.3)
х 4- 0,5	х - 0,5
(х + 0,5)2 4- у2 (х - 0,5)2 4- у2
х — 2	х 4- 2
(х - 2)2 4- у2 (х + 2)2 + у2
В/см;
6)
Рис. 16.14Р
Как следует из граничного условия (16.7), плотность заряда на оболочке кабеля
Qs — -с0Ег = £0а<р/аг|г=я,
где
4s = 1,4
Er = Ех cos а + Еу sin а; 1 —0,5 cos а 1,25 — cos а
1 + 2 cos а 1—2 cos а 5 + 4 cos а 5 — 4 cos а
1 4- 0,5 cos а -----’—р 1,25 + cos а
2,1 cos а _ , , —г? —j— пКл/см2. 1,56 — cos а
б) Для кабеля (рис. 16.14,6), для которого схема замещения показана на рис. 16.14Р, б, потенциал
ср = 8,05 In
(х - 0,5)1 2 + (у - 0,3)2 (х + 0,5)2 + (у - 0,3)2
1
(х + 1,47)2 + (у - 0,884)2 1 (х - 1,47)2 + (у - О,884)2
х + 0,5	х — 0,5
(х + 0,5)2 + (у - 0,3)2 " (х - 0,5)2 + (у - 0,3)2
х - 1,47
(х - 1,47)2 + (у - 0,884)2
х + 1,47
(х + 1,47)2 + (у - 0,884)2
Еу = 16,1
_________У - 0,3______________________у - 0,3__________ (х + 0,5)2 + (у - 0,3)2 (х - 0,5)2 + (у - 0,3)2
у - 0,884
(х - 1,47)2 + (у - 0,884)2
у - 0,884
(х + 1,47)2 + (у - 0,884)2
В/см;
qS = 1,43
0,3 sin а — 0,5 cos а — 1
1,34 + cos а + 0,6 sin а
0,3 sin а + 0,5 cos а - 1	0,884 sin а + 1,47 cos а - 1
1,34 — cos а + 0,6 sin а 3,93 + 2,94 cos а — 1,76 sin а
0,884 sin а — 1,47 cos а — 1
3,93 - 2,94 cos а - 1,76 sin а
пКл/см2.
в) Для кабеля (рис. 16.14, в), для которого схема замещения показана на рис. 16.14Р, в
Qs = 1,43
1 — 0,3 cos а 1+0,7 cos а
1,09 — 0,6 cos а 1,49 + 1,4 cos а
1-г 1,43 cos а 1—3,33 cos а
3,05 + 2,86 cos а 12 — 6,66 cos а
пКл/см2.
16Л5(Р). Определить потенциалы и заряды системы проводов, изображенной на рис. 16.15, если рубильники проводов 1 и 2 замкнуть, а рубильник провода 3 оставить разомкнутым. Выяснить, как изменится решение, если сначала провод 2 отключить от земли, затем провод 1 отключить от источника и, наконец, провод 3 соединить с землей.
Дано: U = 10 кВ; радиус проводов г0 = 10 мм; hr = /?3 = - 3 м; h2 = 4,5 м; d = 2 м.
2
Рис. 16.15
Рис. 16.15Р ->
Решение. Заданную систему проводов по методу зеркальных изображений заменим системой шести проводов (рис. 16.15Р).
Потенциалы проводов 1 и 2 заданы условиями задачи: Ф1 = 10 кВ; (р2 = 0; заряд т3 — 0.
Остальные потенциалы и заряды определим из системы трех	уравнений	с	потенциальными коэффициентами (16.14)
после замены	q	на	т, причем при заданных	условиях
104 = ЯцТ1 + a12t2;	(1)
0 = a2iTi + а22т2;	(2)
<р3 =а31Т1+а32г2,	(3)
где «!! = а33 = -г-— In— = ——— In 600 = 115-109 м/Ф; а22 = 2 71 Eq	Vq ZTCEq
=	ln^-= ^2_1п900= 123-ю9 м/Ф; а12 = а21 = а23 =
2тгг0 го 2ле0
= аз2 ~ %-с	~~ ~ 20' Ю9 м/Ф; 0С1з = а31 == In. =
Z7lEo	г i2	ZTlEo Г13
== 10,6 • 109 м/Ф записаны в соответствии с (16.14) с учетом (16.18).
Рис. 16.16
Решив совместно (1) и (2), получим: xj = 80,0 мкКл/км; х2 = —12,0 мкКл/км. Из (3) находим ф3 == 605 В.
После переключений xi = хь х2 = х2, ф2 = 0. Далее из системы уравнений с потенциальными коэффициентами определим: <р\ - 9950 В; (р2 = -88,0 В; т'3 = -4,76 мкКл/км.
16.16.	Определить заряды проводов 7, 2, 3 радиусом г0 = 5 мм системы, изображенной на рис. 16.16, при заданных потенциалах проводов относительно земли ф! = 10 кВ, ф2 = —20 кВ, Фз = 10 кВ.
16.17(	F). Двухпроводная линия 1-2 (рис. 16.17) находится в однородном поле грозовой тучи с напряженностью £0, направленной вертикально.
Рассчитать и построить распределение потенциала вдоль оси у и распределение плотности заряда на поверхности земли для случаев рис. 16.17,а и б, если U — 100 кВ; £0 = 2 кВ/м; h = 5 м; d = 3 м; радиус проводов г0 = 2,5 мм.
Решение. Применив метод зеркальных изображений, заменим заданную систему проводов четырьмя осями.
Запишем формулы Максвелла с потенциальными коэффициентами (16.14) с учетом поля тучи:
Ф1 = ацХ! + a12x2 ±E0(h + d);
Ф2 =a2iTi +a22x2 ±Eoh,
(1)
где йц = -т-5—in —— = 15,8-1010 м/Ф; 2tT8q Kq
a12 — a21 “
1 , 2h 4- d * . 1П	1 , 2/i	_
=  ---In —-—= 2,65 • IO10 м/Ф; a22 =  -In— = 14,9 x
2ле0 d	/ »	2k80 rQ
x 1010 м/Ф записаны по формулам (16.14) с учетом (16.18).
Для случая рис. 16.17, а. Из решения системы (1) при ф! = 0, ф2 = -100 кВ и Ео = 2 кВ/м найдем Xj « 22,1 • 10-9 Кл/м и х2 — -736-10"9 Кл/м. По формуле (16.18) получим:
Ф = 1981п k±g±4 - 6610 In 4Ц44 + 2.103у (у - В)2 + х2	(у - 5)2 + х2
и, в частности, при х = 0
Ф (0, у) = 396 In
у + 8 у-8
- 13 220 In
У + 5 у- 5
+ 2 • 103у,
где ф — в вольтах, х и у — в метрах.
Плотность заряда
qs = £0Еу (0, х) =
Кл/м2,
где х-в метрах; с0 — в фарадах на метр.
Зависимости ф(у) (сплошная линия) и qs(x) (пунктир) построены на рис. 16.17Р.
16.18(	Р). Рассчитать поле и построить эквипотенциали и линии поля (последние — качественно) для бесконечного заряженного провода диаметром d, проходящего в воздухе между заземленными (ф = 0) бесконечными металлическими пластинами (рис. 16.18), при 1/2 = 50 мм, d = 4 мм. Потенциал провода ф0 = U — 100 В.
Определить емкость на единицу длины системы.
Решение. Заменим провод между двумя проводящими заземленными пластинами (по методу -зеркальных изображений) бесконечной решеткой знакопеременных осей, расположенных на расстоянии I друг от друга.
Потенциал поля осей по (16.18)
Ф = In z,
27C£q
где
]/(3Z 4- х)2 4- у2 |/(5Z — х)2 4- у2 ~ cos2 (тгх/2/) 4- sh2 (пу/21) р(4/ _ Х)2 +	+	“ sin2 (ях/20 4- sh2 (тсу/2/) ‘
Приравняв потенциал точки х = d/2, у = 0 на поверхности провода к (р0, получим:
4/	4/
Т = 71Е0ф0/1п—Г’ т- е- Со — 7tSo/in—Т= 8 пФ/м, nd	па
и
cos2 (ях/2/) 4- sh2 (пу/21) sin2 (пх/21) 4- sh2 (пу/21)
Уравнение эквипотенциалей ф = фк
(еЛа + 1) sjn2	_ 1) sft2 =
где Л = 2 In (4l/nd), а = фк/ф0, получим, приравняв выражение потенциала к осф0. На рис. 16Л8Р построены эквипотенциали и качественно изображены (пунктиром) линии поля.
16.19.	Рассчитать и построить эквипотенциаль ф = 0,Ш для бесконечного заряженного провода диаметром d, проходящего в воздухе параллельно ребру угла, который образован проводящими пластинами (рис. 16.19), при Ц = 10 мм, 12 = 20 мм, d = 5 мм, т — 2-10“10 Кл/м.
Определить емкость системы на единицу длины и распределение заряда по поверхности проводящих пластин.
Указание. Провод, проходящий параллельно ребру угла, по методу зеркальных изображений следует заменить четырьмя проводами, образующими две двухпроводные линии с равными и противоположными зарядами. Необходимость четырех проводов определяется граничными условиями (16.6) и (16.7) на проводящих пластинах, образующих прямой угол.
16.20(	Р). Определить частичные емкости системы проводов задачи 16.15 (рис. 16.15).
Решение. По определению (16.15) и (16.16) Clt = (Рц + 4- Р12 + Р1з);	С12 = С21 = —Р12 = —р21 ;	С22 — (Р22 + Р21 +
+ Р23); С1з = С31 = — Р1з = — 0з 1; С33 = (Рзз + Р31 + Рзг); С2з = = С32 ~ ~ р23 = *~Рз2*
Емкостные коэффициенты р можно выразить через потенциальные коэффициенты а, как следует из (16.14) и (16.15):
«12	«13
«32	«33
«12	«13
«22	«23
Д
«11	«13
«31	«33
Д
«11	«12
«21	«22
Д
где Д =
«31
«12	«13
«22	«23
«32	«33
Вычисление потенциальных коэффициентов дано в решении задачи 16.15.
При заданных размерах системы Сц =7,05 пФ/м; С22 = = 5,8 пФ/м; С33 = 7,05 пФ/м; С12 = 1,38 пФ/м; С13 =0,59 пФ/м; С23 = 1,38 пФ/м.
16.21.	Определить частичные емкости экранированных кабелей задачи 16.14.
16.22.	Известны частичные емкости трехжильного кабеля Сц = С22 = Сзз =0,064 мкФ/км; Ci2 = С13 = С23 = 0,076 мкФ/км.
При испытании кабеля в лаборатории одна из жил была заземлена, другая имела потенциал <р2 = 2 кВ, третья <р3 = = — 3 кВ. Оболочка кабеля не заземлена.
Найти потенциал оболочки и заряды жил.
16.23.	Между металлическими пластинами 1 и 3 (рис. 16.23) площадью S = 10/ib, находящимися в воздухе, параллельно им вставлена металлическая пластина 2; ее толщина d = 0,5 мм,
высота h — 40 мм и ширина b = 50 мм. Расстояние I между пластинами 1 и 3 равно 4,5 мм. Расстояние f между пластинами 1 и 2 равно 3,0 мм.
Найти частичные емкости системы, пренебрегая краевыми эффектами.
16.24.	Потенциалы наружных пластин 1 и 3 в задаче 16.23 (рис. 16.23) соответственно фх = +50 В и <р3 = -100 В.
Найти потенциал внутренней пластины.
16.25.	Найти заряд внутренней пластины в задаче 16.23 (рис. 16.23), если ее потенциал ср2 = 0, а потенциалы наружных пластин 1 и 3 равны: срх = 100 В и <р3 = — 50 В.
16.26.	Найти максимально допустимое значение точечного (пробного) заряда, при котором погрешность в определении напряженности поля по силе, действующей на пробный заряд, не будет превосходить 1 %. Истинная напряженность поля (т.е. напряженность поля в рассматриваемой точке при отсутствии пробного заряда) равна 5 кВ/см.
Определить силу, испытываемую пробным зарядом, в случае определения поля протяженной плоской пластины на расстоянии 5 мм от ее поверхности.
Примечание. Напряженность электрического поля определяют как отношение силы, действующей на пробный заряд, к численному значению этого заряда. При таком определении дополнительно требуется: 1) чтобы в пределах области, в которой распределен пробный заряд, изменение напряженности поля было ничтожно малым («точечный заряд») и 2) чтобы не происходило перераспределение зарядов, создающих поле, из-за внесения пробного заряда. Последнее требование всегда выполняется, если значение пробного заряда достаточно мало.
16.27.	То же, что и в задаче 16.26, но для поля, определяемого в центре плоского конденсатора.
Расстояние до каждой пластины 5 мм, истинная напряженность поля Е = 5 кВ/см.
16.2. Электростатическое поле в диэлектрике
16.28(Р). Плоский конденсатор с двумя слоями диэлектрика (рис. 16.28) зарядили до напряжения U и отключили от источника.
Дано: U = 100 В; di — d2 = 1 см; ег1 — 3; ег2 = 6.
Найти электрическое смещение, напряженность поля и распределение потенциала в обоих диэлектриках.
Определить: 1) как изменятся эти величины и емкость конденсатора, если из конденсатора вынуть пластину второго диэлектрика; 2) каковы будут эти величины, если конденсатор
останется подключенным к источнику.
Решение. По определению напряжение между пластинами конденсатора (разность потенциалов)
(rfl + d2) (7= f Edx. о
В пределах каждого диэлектрика напряженность поля постоянна, поэтому
U = Е^ + E2d2.	(1)
На границе двух диэлектриков свободный Рис. 16.28 заряд отсутствует и, следовательно, по (16.8а)
еГ1Е1 = гг2Е2.	(2)
Из (1) и (2) находим:
Е, = -—~—-= 66,7 В/см; Е2 = -—-----33,3 В/см.
«1£г2 + “2£г1	“1£г2 + d2&ri
Электрическое смещение
Dj = D2 = D = sP1s0E = 200eo = 17,72 • 10"12 Кл/см2.
Потенциал по (16.3) <р=—fEdx + C, и, следовательно, <Pi =s (100 — 66,7х) В и (р2 = (66,7 - 33,Зх) В, где х-в сантиметрах.
1)	Если вынуть вторую пластину при отключенном источнике, то останется неизменным заряд на пластинах, поверхностная плотность которого по (16.7) равна смещению D, г. е. останется прежним: D = 17,72-10”12 Кл/см2.
Напряженность поля по (15.6)
Ei = D/ep1£0 = 66,7 В/см; Е2 =	= 200 В/см.
Напряжение на конденсаторе увеличится: U = Ejdi + E2d2 = 266,6 В.
Распределение потенциала: <р! = (266,6 — 66,7х); ср2 = (400 — - 200х) В.
2)	Если вынуть пластину второго диэлектрика при включенном источнике, то напряжение останется прежним, и при
er2 = 1 получим:
E, = -—5^1----= 25 В/см; E2 = -—------- 75 В/см.
“Isr2 + #2ег1	«1ег2 + “2£rl
Электрическое смещение D = s,i£o^i = £о^2 = 6,65 х х 10“12 Кл/см2, т.е. плотность заряда на пластинах умень
шится.
Распределение потенциала: срл = (100 — 25х) В; ф2 = (150 — - 75х) В.
В обоих случаях емкость конденсатора на единицу поверхности электродов Со = qs/U = D/U - £ri£r2£o/Wi£r2 + ^2£п) уменьшится.
16.29.	При сборке плоского конденсатора между электродами и диэлектриком (ег = 4) образовался воздушный зазор. Расстояние между электродами 0,5 см. Толщина воздушного зазора 0,01 см.
Определить, как изменится его пробивное напряжение, если пробивная прочность воздуха 30 кВ/см, диэлектрика 200 кВ/см.
16.30.	Между пластинами плоского конденсатора симметрично расположен диэлектрический слой (^ = 7), занимающий по толщине половину межэлектродного пространства. Расстояние между пластинами 2 см.
Определить электрическое смещение, напряженность поля,
поляризацию и распределение потенциала в воздухе и диэлектрике, если: 1) к пластинам присоединен источник с постоянным напряжением 10 кВ; 2) пластины замкнуты накоротко, но поляризация в диэлектрике осталась прежней.
16.31.	В поле плоского конденсатора потенциал изменяется, как показано на рис. 16.31 (ломаная линия а), где х -
Рис. 16.31
координата, перпендикулярная плоскости пластин конденсатора.
1)	Что можно сказать о диэлектрических свойствах изоляции конденсатора?
2)	Как изменится Трафик, если диэлектрик однородный при том же приложенном напряжении ?
3)	При каких условиях график потенциала в плоском конденсаторе имеет вид ломаной b на рис. 16.31? Чему соответствует угол наклона отрезка ломаной?
16.32(Р). К цилиндрическому конденсатору дважды подво-
дится напряжение, доводящее конденсатор до пробоя: первый
раз, когда диэлектриком был воздух, пробивная напряженность которого Епр = Е1 =30 кВ/см, и второй раз, когда диэлектриком было масло (ег = 2,4) с Епр = Е2 = 54 кВ/см.
Определить соотношение между напряжениями, прикладываемыми к конденсатору в первом и во втором случаях, и между зарядами конденсаторов в тех же случаях.
Решение. По теореме Гаусса (16.26) напряженность поля в цилиндрическом конденсаторе Е = т/2л£г£ог. Учитывая, что г2 по (16.3) разность потенциалов или напряжение U - J Е dr, ri
получим Е — и/\ г In — ), где гг — радиус внутреннего провод-V ri 7
ника (жилы) и г2 — внутренний радиус внешнего проводника (оболочки).
Максимальная напряженность поля
тах	rjnfo/ri)’
откуда допустимое напряжение
U = (п In — ]Епр \ ri /
и заряд на единицу длины
Т = 27Г£г£0Г1ЕПр-
Следовательно, отношение допустимых напряжений равно отношению пробивных напряженностей: UJU2 = EJE2 = 0,556, а отношение зарядов
Т1/т2 = Е1/ег2Е2 = 0,232.
16.33	(Р). Цилиндрический конденсатор (рис. 16.33, где = 1 мм, г2 = 2 мм, г3 = 4 мм) заполнен двухслойным диэлектриком: 1) гга = 1; £гЬ = 3 или 2) гга = 3; £гЬ = 1.
Определить в обоих случаях пробивное напряжение и построить зависимости напряженности поля от радиуса. Сравнить со случаем однородного диэлектрика, имеющего свойства слоя а или Ь.
Пробивная напряженность воздуха 30 кВ/см, пробивная напряженность диэлектрика 60 кВ/см.
Решение. Из теоремы Гаусса (16.26) следует, что
Е — Т Е — Т а ~ 2я£гя£0Г ’ b 2пЕгЬ^Г ’
Напряжение между жилой и оболочкой
гз
V = Е dr =

В случае 1, если допустить Етах = Еатах при г = т.е. 30 = т/2лс0 - ОД, то т = 6яе0, если Е^ - ЕЬтах при г = г2, т. е. 60 = т/2ле0 • 3 • 0,2, то т = 72тсе0.
Во избежание пробоя надо взять меньшее значение заряда, т. е. т = 6л£0, при этом пробивное напряжение
Unpo6= 5—^-(1п2 +-|-1п2) = 2,76 кВ. 2я$>о \	3 J
В случае 2 меньшее значение т = 12ле0 и пробивное напря-
жение
4 Л	Гл	\
^проб =	 (-Z- In 2 + In 2 ) = 5,52 кВ.
н 2тс£0 \ 3	J
Рис. 16.33
Из зависимостей Е(г), приведенных на рис. 16.33Р, а и б, видно, что в случае 2 поле в конденсаторе меньше изменяется, что приводит к повышению пробивного напряжения.
Если имеется только диэлектрик а, то Еа тах — 30 кВ/см = т/2л£0^1 и Т = 6я£о, при ЭТОМ [/проб = (т/2л£гд£0) X х In (гз/rj = 4,14 кВ. Если имеется только диэлектрик Ь, то Еь тах ==
= 60 кВ/CM = т/2пЗе0Гt И Т = 36л£о, ПрИ ЭТОМ Gnpo6 = - (т/2л£гг,£0) In (г3/Г1) = 8,28 кВ.
16.34	. На плоской границе раздела двух диэлектриков (би - 6, £г2 = 2) отсутствует свободный заряд. В первом диэлектрике в некоторой точке на границе раздела составляющие напряженности поля: Е1Х = 100 В/см, Е1у = 50. В/см (ось х лежит в плоскости раздела, ось у ей перпендикулярна).
Найти составляющие векторов Е2, Di, D2, а также qsсвяз на границе в той же точке.
16.35	(Р). На высоте h — 1 см над плоской границей раздела двух диэлектриков (рис. 16.А, о) расположен точечный заряд q = 50 пКл.
Определить значение и направление силы, действующей на заряд, и распределение поверхностного заряда вдоль границы раздела в двух случаях: 1) £rl = 1; &г2 = 4; 2) £г1 = 4; &г2 = 1. Нарисовать качественную картину линий поля в обоих случаях.
Решение. По методу зеркальных отражений (16.19) для расчета поля в диэлектрике с £г = £Г1 введем кроме заданного заряда q еще и фиктивный заряд qi =krq (рис. 16.А, б); для расчета поля в диэлектрике с £г = £г2 введем фиктивный заряд q2 = k2q (рис. 16.А, в).
Сила взаимодействия заряда q с нижним диэлектриком F = Eqi9 причем Е - д/4тг£г1е0 (2А)2 - напряженность поля заряда q в однородной среде с относительной диэлектрической проницаемостью в точке, где находится заряд qv Следовательно, сила зависит от fcb т.е. от соотношения £Г1 и ег2; при £ri > £г2 заряды и q одинакового знака (kL > 0), т.е. заряд q отталкивается от диэлектрика.
Распределение потенциала в первой и второй средах запишем соответственно от двух и одного точечного заряда:
4Л£г1£0 L |/(у — ft)2 х
2	/(У + ^)2 + *2 -
при у > 0;
(р2 = ^2^/4л£г2£0 ]/(у - к)2 + х2 при у < 0.
Связанный заряд на границе диэлектриков найдем по (16.86) как разность нормальных составляющих поляризаций или с учетом (16.9) и (16.8а) по формуле -з$связ = £0 [Ein - Е2и], где Е1п = -Ely = 6cpi/6y; Е2п = -Е2у = dq>2/dy при у = 0.
Окончательно
qh 1 - £r2/Eri 1
<?Sce’0 " 2rt е,2 + s,! (й2 + х2)3/2
Знак связанного заряда на границе, конечно, зависит от соотношения £ri и ег2 и совпадает со знаком фиктивного заряда
1)	При erl = 1, sr2 = 4 заряд q притягивается ко второму ди, электрику с силой 3,37-10~8 Н и qScM3 = -4,78/(1 + х)3/2 пКл/см2.
2)	При srl = 4 и ег2 = 1 заряд q отталкивается от диэлектрика с силой 0,842-10"8 Ни д5связ = 1,2/(1 + х2)3/2 пКл/см2.
Качественная картина линий поля для случаев 1 и 2 показана на рис. 16.35Р, а и б соответственно.
16.36(Р). Рассчитать поле и построить эквипотенциали и
линии поля (последние - качественно) внутри диэлектрического уголка (рис. 16.36) с е,-! = 20 » 1, если в нем параллельно его
ребру проходит бесконечно длин-
ный заряженный провод диаметром d.
Дано: h = I = 20 мм; d = 5 мм; т = 0,2 мкКл/км. Внешняя среда -вакуум (sr2 = 1).
Решение. По методу зеркальных отражений (см. решение задачи 16.35) при ег1 » ег2 имеем « 1, к2 « 0. В этом случае поле внутри уголка рассчитывается от четырех одинаково заряженных
осей с линейным зарядом т = = 0,2 мкКл/км (рис. 16.36Р, а).
По (16.18)
2я£г1£0	4/l4
= -0,18 In
Г1Г2Г3Г4
4/i4
В,
где п = ]/(х - 2)2 + (у - 2)2; г2 = ]/(х + 2)2 4- (у - 2)2; г3 = = ]/(х — 2)2 + (у 4- 2)2; г4, = ]/(х 4- 2)2 4- (у 4- 2)2; напряженность поля
F - а<р - л i<J * ~ 2		* + 2 I
дх -и’1Ъ|(х-2)24-(у-2)2 + (х 4- 2)2 + (у - 2)2 +
Потенциал ср = 0 при х = у = 0. Поле вне уголка практически отсутствует. Картина поля изображена на рис. 16.36Р, 6.
16.37	(Р). В центре сферы из диэлектрика (ег1 = 4) расположен точечный заряд q = 1,2-10”8 Кл (рис. 16.37). Окружающая среда имеет относительную диэлектрическую проницаемость ег2 = 1.
Найти поток вектора напряженности поля через поверхность симметрично расположенного эллипсоида вращения, вырезающего на сфере два участка поверхности, каждый из них видим из центра сферы под телесным углом со = л/2.
Решение. Электрический поток, пронизывающий поверх-
ность эллипсоида, частично проходит по первому диэлектрику,
частично — по
OEdS —
второму, .поэтому по теореме Гаусса (16.26)
— ------(4л - 2со) + -г—----2со = 59 кВ  см.
4л£г1е0	4лег2Е0
16.38.	То же, что и в задаче 16.37, но при ег1 = 4,5 и ^г2 — 1,5.
16.39(	Р). То же, что и в задаче 16.37, но эллипсоид пересекает сферу так, что заряд q лежит вне эллипсоида (рис. 16.39). Эллипсоид вырезает на сфере два участка поверхности, каждый из них видим из центра сферы под углом со = я/4.
Решение По теореме Гаусса (16.26)
OEdS =
—3—2со — 4лег2£0
-— ------2со = 12,7 кВ • см
4Я£г1£о
(см. также решение задачи 16.37).
Рис. 16.37
Рис. 16.39
16.40.	То же, что и в задаче 16.39, но при ег1 = 1 и ег2 = 4.
16.41.	Найти поток вектора смещения через поверхность эллипсоида задачи 16.37.
16.42.	Найти поток вектора смещения через поверхность эллипсоида задачи 16.38.
16.43.	Найти поток вектора смещения через поверхность эллипсоида задачи 16.39.
16.44.	Два точечных заряда = — q2 — 1,2-10“8 Кл расположены симметрично по обе стороны плоскости раздела двух сред с относительными диэлектрическими проницае-мостями ег1 =2, £г2 = 5 (рис. 16.44).
Найти поток вектора напряженности поля через замкнутую поверхность, охватывающую оба заряда и вырезающую на пограничной плоскости площадку S, видимую из точек расположения зарядов под углами ©! = о2 = к.
16.45.	То же, что и в задаче 16.44, но углы = со2 = = 1,5л.
16.46(	Р). Найти поток вектора напряженности поля зарядов задачи 16.44, если заряды qt и q2 расположены несимметрично, причем телесные углы (Di и со2, под которыми площадка S видна из точек расположения зарядов qi и q2, соответственно равны: (Oj = л и со2 — 1,5л.
Дано: qi = 1,2 • 10“8 Кл; q2 = -2 • 10~8 Кл; ег1 == 2; е^ = 5.
Решение. По методу зеркальных отражений (16.19) поле в диэлектрике с проницаемостью ег1 можно рассчитать как поле трех точечных зарядов в первой среде (рис. 16.46Р, а): 3
qi; q'i = Uri - er2)<?i/(£ri + ег2) = - ~q^ который расположен зеркально относительно заряда q^ и q2 = 2e71g2/(£rl + ег2) =* 532
4
_ — q24 который находится там, где в действительности рас-
положен заряд q2.
Поле в диэлектрике с проницаемостью &г2 можно рассчитать как поле трех точечных зарядов во второй среде
зеркально относительно заряда q2, и q'[ =
10
— который
находится там, где в действительности расположен заряд qr.
Поток от трех зарядов через левую поверхность (рис. 16.46Р, а)
'EdS = _Л1_(4я - «>,) + -^-+
* 4тсвг18о	4л8Г1£о 4тсеГ1£о
Поток через правую поверхность (рис. 16.46Р, б)
EdS = -r^—(4л-ю2) + 4лбг280
л------~	+ ~~л-----
4Л8г28о	4Л8г28о
Поток через замкнутую поверхность
f_ <21/3	3	1 \ q2 / 1,5	2,5	4,5
J£ S~	+14 )+ёг(“14“+^0“+140
= — 6450 В • см.
16.47.	В рассматриваемой области цилиндрического конденсатора 1 см < г < 2 см с неоднородным диэлектриком sP — f (г) поляризация Р = Рг — (а + Ьг2} Ро, где а = 1, b = == 0,05 см“2, Ро = 3,5 • 10"10 Кл/см2.
Найти плотность связанного заряда.
16.48.	В рассматриваемой области плоского конденсатора с неоднородным диэлектриком sr = f (х) поляризация Р = Рх = (а + bx2) Pq9 где а = 1, b = 0,05 см-2, Ро = 3,5 • 10"10 Кл/см2.
Найти плотность связанного заряда.
16.49.	Плоский конденсатор заполнен неоднородным диэлектриком с er — 4d/(d + х) (рис. 16.49). Пластины конденсатора подключены к источнику постоянного напряжения U = 1 кВ.
Определить зависимость от координаты х напряженности поля, поляризации, связанного объемного заряда. Рассчитать емкость системы. Расстояние между пластинами d = 2 мм, площадь 5 = 4 см2.
Рис. 16.50
16.50(	Р). Между жилой и оболочкой цилиндрического конденсатора заданных размеров = 1 см, г2 = 4 см, г3 — 4,5 см (рис. 16.50) относительная диэлектрическая проницаемость изменяется по закону £г = Аг, где А = 1 см"1.
При постоянном напряжении 1 кВ определить напряженность поля, смещение, поляризацию и связанный объемный заряд.
Решение. По теореме Гаусса (16.26) напряженность поля в диэлектрике
Е==_L_ = _Е_.
2легвог 2л£0‘Лг2
Напряжение или разность потенциалов между обкладками конденсатора
г2
ГГ	17 Л	т / 1	1 \
U = Edr = ------------------,
. J 2лс04 г2 )
Г1
откуда при заданном напряжении U находим заряд т — = 740 мк Кл/см.
Следовательно, Е = 1.33/г2 В/см; D = ers0E = 118/г пКл/см2; по (15.5) Р = е0(ег - 1)Е = 118 (1/г - 1/г2) пКл/см2 и по (16.206)
I В , „ч 118 „ , 3
Рсвяз = - — 77 (гР,) = —-у- и Кл/см , г от	т
где г - в сантиметрах.
16.51.	То же, что и в задаче 16.50, но при ег = Л/r2, где А - 16 см2.
16.52.	Определить, при каком законе изменений ег в цилиндрическом конденсаторе задачи 16.50 получится Е — Ег — = const.
16.3. Стационарное электрическое поле в проводящей среде
16.53(Р). Плоский конденсатор с двухслойным диэлектриком (d{ = d2 = 1 см; £Г1 = 2; ег2 = 4; сд = 2 • 10”10 См/см; сг2 = = 10”10 См/см) подключен к источнику постоянного напряжения 3 кВ.
Определить: 1) напряженность поля, сопротивление конденсатора и мощность, выделяющуюся в единице объема диэлектрика, а также свободный и связанный поверхностные заряды на границе слоев; 2) как изменится решение задачи, если диэлектрики будут идеальными (од = сг2 = 0).
d
Решение. 1) По определению напряжение U = [ Е dx — о
= Ut + U2 = Е^ + E2d2, граничное условие (16.10) сд/д = = ъ2Е2. Из двух уравнений находим Et = 1 кВ/см; Е2 = == 2 кВ/см; J} = J2 = QiEi = о2Е2 = 0,2 мкА/см2; = Zr^oEi = = 2ОООео, Кл/см2; D2 = ег2е0Е2 = 8О00ео Кл/см2; по (15.5) = Со te-i - l)£i = 1000е0 Кл/см2; Р2 = е0 (ер2 - 1) Е2 =
= 6000е0 Кл/см2; по (16.7) qs = D2 — Dy = 6000е0 Кл/см2; по (16.86) <7$связ = Р{ -Р2 = -50О0ео Кл/см2, где е0 - в фарадах на сантиметр.
Активная мощность в единице объема по (16.23)
р! = сдЕ2 = 0,2 мВт/см3 и р2 — о2Е2 = 0,4 мВт/см3.
Сопротивление конденсатора на единицу площади пластин Ro = U/J = 1,5- 1010 Ом/см2.
2) При од — сд = 0 по-прежнему V =	+ U2 — Exdx +
+ E2J2; (по 16.8a) eP1Ei = ег2Е2- Из двух уравнений получим Ei = 2 кВ/см; Е2 = 1 кВ/см; — D2 = 4ОООео Кл/см2; = = 20О0ео Кл/см2; Р2 = ЗОООе0 Кл/см2; qs = 0; <7$Связ == = — IOOOsq Кл/см2, где е0 - в фарадах на сантиметр.
16.54. Изоляция коаксиального кабеля имеет удельную проводимость о — 10"9 См/м. Радиус жилы 4 мм, внутренний радиус оболочки 8 мм. Напряжение между жилой и оболочкой 600 В.
Определить проводимость и ток утечки на единицу длины кабеля, плотность тока утечки у поверхностей жилы и оболочки, удельную мощность, выделяющуюся в тех же точках, и мощность потерь в изоляции кабеля на единицу длины.
16.55. Определить ток утечки на единицу длины коаксиального кабеля с двухслойной изоляцией (задача 16.33), если Era = 1; Од = 2 • IO"10 См/см; &гЬ = 3; — 10”10 См/см.
Кабель подключен к источнику постоянного напряжения 10 кВ.
______	16.56(Р). К плоской проводящей
1 шайбе (рис. 16.56) подводится посчо-гт \	& янное напряжение U = 1,57 В при по-
/ /	\	мощи двух медных радиально рас-
I f	]	// положенных пластин, врезанных в
\	у	шайбу. Проводимость материала шай-
\	[ 2 у	бы о = 2 • 106 См/м. Размеры шайбы:
У	rr — 50 мм; г2 = 80 мм; толщина
Д	I а — I мм.
Рис 16 56	Определить наибольшее и наи-
меньшее значения плотности тока в шайбе и ток источника питания. Потенциал каждой медной пластины считать во всех ее точках постоянным.
Решение. Считая, что линии плотности тока и напряженности поля совпадают с полуокружностями и напряженность поля зависит только от радиуса, из уравнения 17 = 2
= f Е dlполучим: Е — U/nr и по (16.22) J = a U/nr, следовательно, 1
Jmax —	- 2  107 А/м2; Jmin = aU/nr2 = 1,25 • 107 А/м2;
r2
С	(*
ток 1 = 2 J dS = 2 <зЕа dr -
J •
2Uaa , r2
----In —== 940 n
A.
ri
16.57	. Два параллельных цилиндрических провода проходят через мраморный щит, толщина которого а = 3 см. Расстояние между осями отверстий для проводов 20 см. Диаметр проводов 0,4 см.
Считая плоскость щита неограниченно большой, найти ток утечки через мрамор между проводами при напряжении между ними 240 В. Удельная проводимость мрамора 10”10 См/м.
16.58	(Р). Сферический заземлитель радиусом Ro = 2 м находится в земле (crj = 2 • 10"4 См/см) на расстоянии h = 10 м от ее поверхности (рис. 16.58). Ток заземлителя I = 1000 А.
Определить распределение шагового напряжения и поверх
ностного заряда на границе.
Решение. Для расчета поля в земле (первая среда) введем по (16.24) фиктивный ток (рис. 16.58Р, а) ц = щ! = I = 1000 А (считая удельную проводимость воздуха сг2 = 0); для расчета поля в воздухе (вторая среда) введем фиктивный заряд (рис. 16.58Р, б) q2 = 2/Cq/q! = 0,886 х х 10"6 Кл [выражение заряда q2 через ток I получается из граничных условий (16.6) и (16.10)].
Рис. 16.58
В однородной проводящей среде при растекании тока I
напряженность поля Е = J/c = I/4naR2 и <р =
I
EdR + C-
если принять ф = 0 при R со.
Шаговое напряжение (разность потенциалов на поверхности земли между точками, находящимися на расстоянии 0,8 м) с учетом токов 1 иЦ
U - j L 1________________________1_______К
2яст I ]/х2 + й2	|/(х + 0,8)2 + й2 J
= 8 • 10э | . 'X - - . .... 1 Д В,
(j/x2 + 100	|/(х + 0,8)2 + 100 J
где х — в метрах.
По (16.7) поверхностный заряд qs = е0^2л» так как по (16.10) «Ля = Аи = 0 (тока во 2-й среде нет) и в первой среде (земле) £1И = ЛПМ =0.
Выразив во второй среде Е2п через д2, получим:
_ Qih________________21&oh_______0J
Qs 4n(h2 + x2)3/2 4ТГСГ! (h2 + x2)3/2	(x2 + 100)3/2 MK л'м ’
где x — в метрах.
16.59	. Ток короткого замыкания 1000 А проходит в землю через фундамент опоры, который можно рассматривать как полусферический заземлитель. Удельная проводимость земли 2- 10" 4 См/см.
Найти шаговое напряжение на расстоянии 5 м от центра
16.60	(Р). Полусферический заземлитель диаметром 4 м находится в земле с удельной проводимостью Qi = 5 • 10" 4 См/см (рис. 16.60). На расстоянии h — 50 м от заземлителя проходит плоская граница раздела, за которой земля имеет удельную проводимость сг2 = 10”4 См/см. С заземлителя растекается ток I = 2000 А.
1) Построить зависимость шагового напряжения (длина шага 0,8 м) от координаты х.
2) Построить ту же зависимость при о2 — Ю”3 См/см.
Решение. 1) По методу зеркальных изображений ток от полусферического заземлителя, расположенного в земле на границе с воздухом, растекается так же, как и двойной ток в однородной среде с параметрами земли.
Для учета границы, разделяющей земли с разными проводимостями, по формулам (16.24) введем фиктивные токи: для расчета поля в первой среде ток I и фиктивный ток Ц — nil, для расчета поля во второй среде — фиктивный ток ^2 =
в первой среде шаговое напряжение (см. решение задачи 16.58)
°,87 (1	Hi	1 _
С'ш1 ~ 2»^ ( х (х + 0,8)	(2/1 - х - 0,8) (2/г - х) J “
— 0 51 104 ______1__________________0>66__________ _
’	|_х(х + 0,8)	(100 - х — 0,8)(100 - х) J ’
во второй среде
----;	= 0,85 • 104 - *- В
2п<52 х (х 4- 0,8)	х (х + 0,8)
(кривая 1 на рис. 16.60Р). При х — h получим [7Ш1 = 0,67 В и иШ2 = 3,35 В.
2) На рис. 16.60Р построена пунктиром та же зависимость (кривая 2) для случая сг2 — 10“3 См/см.
16	.61. Определить проводимость утечки на единицу длины двухпроводной линии, провода которой расположены в средах с различной удельной проводимостью (рис. 16.61).
Дано: ai = 2 • 10"10 См/см; сг2 = 10"10 См/см; а = 40 м; b = 60 м; радиус проводов г0 = Ю см.
Указание. По методу зеркальных отражений (16.24) поле I в первой среде (рис. 16.61Р, й) определяется токами 7; 7i =пг1 и 72 = 7 • 2ст1/(ст1 + ог2); поле во второй среде (рис. 16.61Р, б) определяется токами 7; Ц = —п11 и Г2 = п21.
16	.62(Р). 1) Составить схемы для определения частичных емкостей трехфазной линии над землей (рис. 16.15) при помощи электролитической ванны.
2)	Подобрать приборы с необходимыми пределами измерений, если удельная проводимость электролита с = *2*10"2 См/см и при моделировании размеры линии уменьшены в 10 раз. В распоряжении экспериментатора имеется источник постоянного напряжения 50 В, глубина ванны h = = 20 мм.
3)	Определить необходимую удельную проводимость электролита, если в распоряжении экспериментатора имеются приборы: вольтметр на 50 В и миллиамперметр на 300 мА.
Решение. По определению (16.16) частичные емкости G1 = ^1/(<Р1 ~ <Po)i С22 = Тг/(ф2 “ Фо); £зЗ = *з/(фз ” фо) При Ф1 = Фг = Фз; С12 = C2i =т2/(Ф1 - Фг) при ф2 = фз = ф0; С13 « = С31 = Т1/(Ф1 - Фз) при Ф1 = ф2 = ф0; С23 = С32 = т2/(ф2 - ф3) при ф! = ф2 — ф0, где фо — потенциал земли.
7777^7777777777777777777	77777^77777777777777^7
9п	д,г
а)	б)
Рис. 16.62Р
1)	Вместо частичных емкостей измеряются частичные проводимости д; емкости рассчитываются по формуле (16.26).
Схемы для.измерения проводимостей glt и gi2 приведены на рис. 16.62Р, а и б.
2)	Наибольшие из частичных емкостей данной схемы Сц = ~ С33 = 7,05 пФ/м (см. задачу 16.20). Следовательно, наибольшая проводимость = Сцст/eo == IJhV. Отсюда наибольший ток (рис. 16.62Р, а) при заданном напряжении источника = = иЛСцп/eo = 1,59 А.
3)	При заданном максимальном токе = 300 мА проводимость электролита находится из того же соотношения о = 3,77-10’3 См/см.
16	.63(Р). Рассчитать поле (найти напряженность и потенциал) двухпроводного экранированного кабеля (рис. 16.14), изоляция которого имеет удельную проводимость о. Найти сопротивление утечки г между жилами. Определить, какая часть тока утечки протекает по изоляции кабеля, минуя оболочку.
Задачу решить для конструкций кабеля, изображенных на рис. 16.14,а —в. Дано: R = 10 мм; диаметр жилы d — 0,5 мм: / = 10 мм; h = 3 мм; ст — 10’12 См/см.
Решение, а) Заменим кабель системой четырех линейных токов (рис. 16.14Р), где заряды т надо заменить токами утечки между жилами на единицу длины /0 так, чтобы оболочка кабеля была эквипотенциальной поверхностью. Для этого должно быть: s — а = 1/2 и s2 = а2 + R2, откуда а — R2/l — Z/4 = — 7,5 мм; s = R2/l + //4 = 12,5 мм; s 4- а = 2R2/1 — 20 мм (см. решение задачи 16.14).
Учитывая аналогию электростатических и стационарных полей и принимая во внимание формулу (16.18), рассчитываем потенциал любой точки от двух линий (1 и 2), выбрав <р = О при х = 0:	_________________
10 , ]/(х + 2R2/l)2 + у2 10 , |/(х - 1/2)2 + у2 ~—.  .	+ —----1П	-----4^ =
2тш	]/(х - 2R2/l)2 + у2	271(7	]/(х + 1/2)2 + у2
О,159/о . Ю- {in	+ Щ
I ]/(х - 2)2 + у2 |/(х + 0,5)2 + у2 J
В,
при этом получается (р = 0 также и на оболочке кабеля. По (16.3)
(х - 0,5)2 + у2
где х и у - в сантиметрах.
Сопротивление утечки на единицу длины г = U/1Q = = 1012 Ом • см, где U = ф1 — (р2 “ напряжение между жилами.
Ток, протекающий по изоляции кабеля, минуя оболочку,
+R
Го = j <зЕх (0, у) dy = 0,637/о (arctg 2 — arctg 0,5) = O,413/o
-k
,, f l/(x - 0,5)2 + (y - 0,3)2 6) q> = O,159/o • 1012 <In V,
I ]/(x + 0,5)2 + (y - 0,3)2
j/(x + 1,47)2 + (y - 0,884)2 )
+ In	——r.-..т ..............>	B;
|/(x - 1,47)2 + (y - 0,884)2 J
Ex - 0,1597o • 1012 | (x + ад2 + _ 0 3)2 x ~ 0,5	x + 1,47
(x - 0,5)2 + (у - 0,3)2 “ (x + 1,47)2 + (y - 0,884)2 +
x - 1,47	]
+ (x - 1,47)2 + (y - 0,884)2 J B/CM’
’	’ u ((x + o,5)2 + (y - 0,3)2
У - 0,3	у- 0,884
(x - 0,5)2 + (y - 0,3)2 + (x - 1,47)2 + (y - 0,884)2
у-0,884 I
(x + 1,47)2 + (y - 0,884)2 J B/CM;
r = 0,98 • IO12 Ом  см; I'o = 0,3637o.
f l/(x — O,3)2 + y2
в) ф = 0,159/o • 1012 -Un ",	y
I y(x + 0,7)2 + y2
l/(x + 1,43)2 + y2 ]
+ In y;--------,^=- + 1,69 J- B;
]/(x - 3,33)2 + y2 J
. _ f x + 0,7	x — 0,3
£- - M!W" 10 1(7+ 0,7>‘ t / - (x - .ДЧ? +
x “ 3,33	X 4- 1,43	)
+ (x - 3,33)2 + y2 (x + 1,43)2 + y2 J B/CM;
Ev == 0,159/O * 1012y <-----------------у--------------------у +
y ’	0	((x + 0,7)2 + y2 (x - 0,3)2 + y2
1	1 I R/
+ (x - 3,33)2 + y2 (x + 1,43)2 + y2 J /CM’
r = 0,995 • 1012 Ом  см; Го = 0,42/o.
16.64(P). Плоский конденсатор (рис. 16.49) заполнен неидеальным диэлектриком с ег = 5 и о = ст0 — кх, где сг0 = = 10"10 См/см, к = 0,5 • 10“10 См/см2, х — в сантиметрах. Расстояние между пластинами d = 1 см, конденсатор подключен к источнику постоянного напряжения U = 1 кВ.
Определить распределение свободных и связанных объем
ных зарядов.
Решение. В постоянном поле по (16.21а) в декартовой системе координат (при J = Jx) dJ/dx = 0 и, следовательно, J — const. Выразим напряжение на конденсаторе через напря-d
женность поля: U = f Edx, или, так как Е — J/c, то о
d
J dx
J о0 — кх о
J |, gp к о0 “ kd
= J/Go,
где проводимость конденсатора на единицу площади пластин G = кЛп —а°-, , = 0,5 • 10“1 °/1п 2 и, следовательно, J = 0,722 х и° ' о 0 — ка.
722
х 10"7 А/см2, при этом Е - J/& = -—г-?— В/см; D = гг^Е =
361Оео	тг j 2 п ( о г 2900ео	„ . 2
= -—Кл/см2; Р	= б0 (е, - 1) Е	= -——-	Кл/см2;	по
1 — 0,5х	1 — 0,5х
(16.2а) р = dD/dx = 1805ео/(1 — 0,5х)2 Кл/см3; по (16.206) рсвяз = = -dP/dx = -1450со/(1 - 0,5х)2 Кл/см3, где г0 - в фарадах на сантиметр, х — в сантиметрах.
16.65.	Решить предыдущую задачу при условии = 5 — Зх и о - 10"10 См/см.
16.66.	У конденсатора задачи 16.49 диэлектрик обладает постоянной проводимостью ст = 10”10 См/см.
Определить объемную плотность свободного заряда и мощность потерь в диэлектрике.
16.67.	В цилиндрическом конденсаторе задачи 16.50 (рис. 16.50) диэлектрик с ег = 4 имеет удельную проводимость: 1) ст = 10"10 См/см; 2) ст = В/r, где В = 10"10 См; 3) о = С/г2, где С = 10"10 См-см; 4) и = Кг, где К = 10"10 См/см2. Здесь г - в сантиметрах.
При постоянном напряжении 1 кВ определить напряженность поля, смещение, связанный и свободный заряды, проводимость конденсатора и ток утечки на единицу длины.
16.4.	Квазистатическое электрическое поле в реальной среде
16.68(	Р). Плоский конденсатор заполнен вязким диэлектриком, у которого электрическая восприимчивость = 6, постоянная времени вязкости т = 5 мс, расстояние между пластинами d = 0,5 см. Конденсатор подключен к источнику синусоидального напряжения с U = 1 кВ.
Построить зависимости от частоты действительной (е') и мнимой (е?) частей относительной комплексной проницаемости. Найти напряженность поля, смещение, поляризацию, плотности тока и поверхностных свободных и связанных зарядов у пластин при частотах: 1) со = 0; 2) со -* оо и 3) частоте, при которой е'г = г/. Для последнего случая построить векторную Диаграмму и определить активную мощность конденсатора. При расчете пренебречь излучением и неоднородностью поля в диэлектрике.
Решение. По определению комплексной проницаемости вязкого диэлектрика (16.39)
„ _	.•„« (Xr + 1) + (<ОТ)2	. х,<ат
'	г 1 ' ~	1 + (сот)2	1 1 + (сот)2 '
Зависимости 8, (сот) и е, (сот) показаны на рис. 16.68Р, а.
При со = 0 получим г, - Хг + 1 = 7; б" = 0; 8, = 7, а при соответственно е, = 1; el' — 0;	= 1.
СО -> ОО
Из уравнения d&r/d (сот) = = 0 находим, что с/ == 8" тах при со = 1/т = 200 рад/с, при этом е, = 4; е/ = 3 и е, = = 5zl—36°50'.
При любой частоте Ё == — U/d — 2 кВ/см.
1)	При со —► 0 получим Ь — г^Ё = 14OOso К л/см2 =
= — 12ООбо
Кл/CM2 = -сЬсвяз, ) при	со —► оо
соответственно	D -
= 2О00ео Кл/см2 = qs; Р = 0; <lscw3 = 0; j-*oo; 3) при
со = 1/т = 200 рад/с получим D = 10000s0 z. -36° 50' Кл/см2 -— qs[ Р = 80 (3 - 3/) Ё = 8500ео z. -45° Кл/см2 = -&связ; J = =j(f)D = 80 • 2 • 106 zl 53° 10' А/см2, где 80 - в фарадах на сантиметр.
Векторная диаграмма построена на рис. 16.68Р, 6.
Комплексная мощность на единицу поверхности пластины So = Ul$ = 103 • е0 • 2 • 106 zi -53° 10' = 2 • 109e0 z. -53° 10',
или иначе: So = Ёdj* = E2d($&Q (&'' - js') = Po + JQ0, откуда Po = = Е2с/соео8^ = 1,2* 1O98o Bt/cm3, где e0 — в фарадах на сантиметр.
16.69	. Плоский конденсатор (d = 1 мм, S = 10 см2), заполненный вязким диэлектриком (%г = 4, т = 5 мс), подключается к источнику постоянного напряжения 100 В через резистор с сопротивлением г = 1 МОм.
Получить зависимости от времени напряженности поля, смещения, поляризации и тока. Составить баланс энергий.
Указание. При т — 5 мс » т0 = rzQS/d = 8,86 мкс корни Pi = - 1/(егТ0 + т) - 1/т, р2 = - (Бг/т + 1/т0) « - 1/т0. В этом случае
Р = РУ(1 -«"'+ —е“М;
т
16.70	(Р). Плоский конденсатор (5=4 см2) с двухслойным диэлектриком подключается к источнику постоянного напряжения U = 1 кВ. Слой а — диэлектрик (егд = 2), толщина а = г 1 см; слой b — вязкий диэлектрик: %г = 4, т = 5 мс, толщина b = 1 см.
Рассчитать зависимости от времени плотности свободных и плотности связанных зарядов на границе диэлектриков, напряженности поля, смещения, поляризации и плотности тока смещения. Определить потери энергии на вязкость.
Решение. Напряжение U = Ua + Ub = Еаа 4- ЕЬЬ. Из граничных условий (16.8а) Da = erfle0Pfl =	- &0Eb + Pb.
Дополнив эти соотношения уравнением вязкости (16.29) т dPb/dt = Ео/гЕь — Рь, получим систему трех дифференциальных уравнений с тремя неизвестными.
Любую из искомых величин представим как сумму установившейся и свободной составляющей, например Pb = Pby + 4* PbcR‘
В установившемся режиме Рь>, = и ®ьу — ео (Хг + 4- 1) ЕЪу = Day = &ya&oEayi т. е. 5ЕЬу = 2Еау, откуда Еау = 712 В/см; ЕЬу = 285 В/см; РЬу = 114Оео Кл/см2 и т. д.
Корень характеристического уравнения получим, приравняв нулю определитель системы уравнений
Р = - [я(%г + 1) + terj/(a + bsra) т = -466 с“\
Следовательно, Рь = 114Оео + Аер\ и так как при Г=0 должно быть Рь = 0, то А = — РЬу и Pb = 114Oso (1 — е1*) Кл/см2.
Из уравнения вязкости получим: Еь — 285(1 4- 1,3^) В/см. По (16.9) и (16.8а) Db = &ОЕЬ 4- Pb = Da = &ге£оЕа - 1425е0 -- 77Огоерг Кл/см2, т.е. Еа = Da/zrazQ = 712 — 385e₽t В/см; Ра = = Da - е0Еа =(712 - 385ер')£о Кл/см2; JaCM = dDjdt = JbcM = = dDb/dt = JCM = 317 • 10“1ОерГ, А/см2; i = JCMS = 0,127^ мкА.
Плотности зарядов по (16.7) и (16.86)	= £)ь — £>а=0;
связ — Ра — Рь — -427е0 — 755еоер/ Кл/см2. Здесь е0 — в фарадах на сантиметр.
Энергия источника, отданная за время переходного процесса, = J Ui dt = 2,72 • 10“7 Дж. Энергия, запасенная в о +
электрическом поле, в установившемся режиме по (16.48)
И'у = Way + Wby = Sd
яу^ау । ^by^by
IT T
= 2,52 -10“7 Дж.
18 п/р Ионкина П. A.
545
Энергия электрического поля в начале процесса
W (0) = Sd [Еа (0) Da (0)/2 + Еь (0) Db (0)/2] = 1,16 - 10 ~7 Дж.
За время переходного процесса энергия электрического поля увеличилась на ДНИ = Wy - W(0) = 1,36 • 10"7 Дж. Энергия потерь в вязком диэлектрике
W, = МИи -	1,36 • 10“ 7 Дж = Жи/2.
16.71	. Удельная проводимость реального диэлектрика равна 1 См/см; относительная диэлектрическая проницаемость 80.
Определить, при какой частоте амплитуда тока смещения равна амплитуде тока проводимости.
16.72	. Плоский конденсатор заполнен реальным диэлектриком (ег = 5,5; о = 10~9 См/см). Толщина диэлектрика d = 1 см. Конденсатор подключен к источнику синусоидального напряжения с действующим значением U = 100 В.
а) Получить зависимости от частоты действительной о' и мнимой о" частей комплексной удельной проводимости и действительной е'г и мнимой е, частей эквивалентной комплексной диэлектрической проницаемости.
Найти напряженность поля, смещение, поляризацию, плотности тока проводимости и смещения для трех частот: 1) /ь при которой о' = о"; 2) /2 = 0; 3) /3 -* оо, не учитывая излучения и неоднородности поля внутри диэлектрика.
16.73	(Р). Плоский конденсатор заполнен реальным диэлектриком (ег = 3, о = 10"10 См/см). Толщина диэлектрика d = 1 см, площадь пластины S = 10 см2. Конденсатор подключается к источнику постоянного напряжения 17 = 1 кВ через резистор с сопротивлением 1 МОм (рис. 16.73).
Рассчитать зависимости от времени напряженности электрического поля, зарядного тока, свободного заряда на пластинах и связанного заряда у пластин в диэлектрике.
Решение. По второму закону Кирхгофа
ir + ис = U.	(1)
Полный ток по (16.28)
i = Лолн-S =	+ £r£oS dE/dt.	(2)
Подставив (2) в (1), получим уравнение
£ег£ог dE/dt + (d + Sor) Е = 17,
где напряженность поля Е = Еу + Есъ.
В установившемся режиме dE/dt = 0 и, следовательно, Еу = U/(d 4- Sor) = 500 В/см.
Из характеристического уравнения 8ггг0гр + Sor + d = О найдем один корень р=-7,5-105 с-1, т.е. Е = 500 + Aept. Так как ис(0) =0, то и £(0) = 0; следовательно,
Е = 500(1 - 1е?₽‘) В/см.
Из (2) получим i = 0,5(1 + le^) мА и по формулам (16.7) и (16.86)
qs = D = £ге0Е = 133 • 10'12 (1 - lept) Кл/см2
И -9sMln = ^=eo(s, - l)£ = 88,6 10*12(l - le”) Кл/см2.
Рис. 16.73
Н~
Рис. 16.74
16.74(	Р). Плоский конденсатор заполнен двухслойным диэлектриком (рис. 16.74). Слой а — идеальный диэлектрик (его = = 7; сга = 0; а- 1 мм). Слой b - реальный диэлектрик (£г6 = 3; оь = 10“10 См/см; b = 1 мм). Площадь пластины S = 100 см2. Конденсатор подключается к источнику постоянного напряжения U = 1 кВ через резистор с сопротивлением г = 1 МОм.
Рассчитать зависимости от времени напряженности электрического поля в слоях, связанного и свободного зарядов на границе слоев и тока i в зарядной цепи. Вычислить энергию, выделяющуюся в реальном диэлектрике, энергию, запасенную в электрическом поле конденсатора, и энергию, отданную источником. Составить баланс энергий.
Решение. По второму закону Кирхгофа
ir + иа^иь~ ir + Еаа 4- Ebb = U,	(1)
причем полный ток равен току в зарядной цепи: /полн5 = ’ По граничному условию (16.11)
Jа полн = ^ra^O dEjdt — полн = &Ь&Ь 4" ^rb^O dE^/dt.	(2)
Получены два дифференциальных уравнения с двумя неизвестными: Еа и Еь. Определив обычным путем корни характеристического уравнения pi = -110 с-1 и р2 =-5650 с“1, запишем напряженности поля:
Еа = Еау + А^"110' + А2е“5650'; Еь = ЕЬу +	+ В2е’5650'.
В установившемся режиме тока нет, так как = О, ц по (1) Еауа + Ebyb = U, где ЕЬу = 0, так как <зь # 0, т. е. Е = U/а = 10 кВ/см.
Начальные условия: ufl(0) = ий(0) = 0; i(0) — U/r = 1 мА-J„(0) = Jb(0) = i(0)/S=0,01 мА/см2; dEa/dt |,=0 = Л(О)/е,<.£о = = 1615 • 104 В/(с • см); dEt/dt |,.0 = Л (0)/erteo = 3760 • 10* В/(с • см).
Определив постоянные, получим: Е„ = 10* - 7280е-110' -— 2720е-5650' В/см; Еь = 6790g-1101 - 6790g'56501 В/см; i = dFu	dF
= <sSEb + && a-± = Seros0 =0,0496g-“°* + 0,951g-565«' mA; at	at	’
qs = Db -Da = e0 (71,4• 103e~1101 -1,4- 103e"5650' - 7• 104) Кл/см2; 9se.„=P, -Pb=£o (60-103 - 57,2- 103e*11 °'—2,8- 103e"5eso') Кл/см2. Здесь e0 — в фарадах на сантиметр.
Энергия: W, = f ri2 dt = 108 мкДж; W = EayDaySa/2 = О
= ZraSoEaySa/2 = 310 мкДж; WK = J Ui dt = 620 мкДж. Энергия о
аз
потерь в реальном диэлектрике Wc = J aElSb dt = 202 мкДж; о
энергия суммарных потерь Wr + Wo = 310 мкДж = WJ2 = Ж 16.75. Плоский конденсатор с двумя слоями а и b реального диэлектрика подключается к источнику постоянного напряжения 100 В. Даны: параметры ега = 5,5; srb = 3,5; оа = = 10"14 См/см; оь=10"16 См/см и размеры 5 = 400 см2; а = 0,5 см; b = 0,5 см.
Определить зависимости от времени плотностей свободного и связанного зарядов на границе диэлектриков, плотностей токов проводимости и смещения, энергию, выделяющуюся в каждом диэлектрике за время переходного процесса, и мощность потерь в установившемся режиме.
16.76.	Для высокочастотного нагрева в плоский конденсатор помещены два слоя полупроводящего материала. Толщина слоев da = db = 1 см, параметры ега = 2; ггЬ = 4; па = 2 х х 10“6 См/см; = 10"6 См/см. Напряжение на конденсаторе 10 кВ, частота тока 1 МГц.
Определить зависимости от времени свободного и связанного зарядов на границе раздела диэлектриков. Сопоставить временное зависимости зарядов с временнбй зависимостью приложенного напряжения. Найти мощности потерь в полупроводящих слоях.
16.77.	Слой а плоского конденсатора — реальный диэлектрик (da = 1 см; £гв = 2; оа = 1,3 • 10"10 См/см), слой b -548
вязкий диэлектрик (db = 1 см; %г = 5; т — 5 мс). Конденсатор подключен к источнику синусоидального напряжения с амплитудой 1 кВ. Площадь пластины конденсатора S = 12,5 см2.
Определить частоты, при которых в слое b тангенс угла потерь равен единице. Для меньшей частоты найти комплекс-
ные амплитуды напряженности поля, смещения и поляризации в обоих слоях, комплексную проводимость конденсатора и мощность потерь в диэлектрике конденсатора. Определить, в какие моменты времени обращаются в нуль свободный и связанный заряды на поверхности раздела диэлектриков.
Рис. 16.78
16.78.	Между жилой радиусом = 3 мм и оболочкой коаксиального кабеля (рис. 16.78) для крепления жилы вставлены изоляционные кольца (в, = 2,2; ст = = 10"14 См/см). Толщина колец d = 5 мм. Расстояние между шайбами D = 50 мм, внутренний радиус оболочки г2 = 11 мм.
Определить усредненные емкость и проводимость кабеля на единицу длины. Найти зависимость усредненного по длине тангенса угла потерь от частоты. Рассчитать распределение заряда вдоль поверхности жилы при заданном напряжении U. Потерями в проводах пренебречь.
16.79(	Р). В неограниченном реальном диэлектрике (ег = 2; а = 10"6 См/см) находится сферический электрод радиусом а = 1 см, из которого растекается синусоидальный ток i = = 10 ]/2 sin (nt мА с частотой /= 1 МГц. Проводимость электрода много больше проводимости диэлектрика.
Определить потенциал электрода фэ (приняв <р = 0 при R -» оо), сопротивление растекания, мощность потерь в диэлектрике, плотность свободного заряда на поверхности
электрода и плотности тока проводимости и смещения в диэлектрике.
Решение. Вследствие сферической симметрии плотность тока имеет только радиальную составляющую. Полная плотность тока состоит из плотности тока проводимости и плотности тока смещения (16.34):
Уполн = оЁ + =ъЁ = //4лК2, следовательно,
.	. I 6,7-103	.О0
^^=4^ =^-^-48В/СМ’
где <2 = 1,49 • 10"6 z. 48° См/см.
По (16.35) <p, = f £</R = 6,7-103z-4874tw = 53,5z-48 В.
а
Сопротивление растекания Z — фэ// = 53 500 х. —48° Ом. Мощность потерь Р = Re (фэ/*) = Re (535 z. - 48° -0,01) = 3,58 Вт. Поверхностный заряд на сфере по (16.7)
<7$ = гг&оЁ (с?) = £гео//47соа2 = 0,095 • 10"3 zl —48° мкКл/см2.
Плотности тока проводимости и смещения на расстоянии R от центра электрода соответственно равны:
j = стЁ = 6,7 zl — 48°/4лЯ2 мА/см2;
Лм =	- 7,44 zl 42°/4itR2 мА/см2,
где R — в сантиметрах.
Из решения видно, что синфазно изменяющиеся напряженность поля и заряд отстают по фазе от тока.
16.80(F), Определить свободный заряд на поверхности сферы и напряженность поля в диэлектрике для электрода предыдущей задачи, если ток, растекающийся с электрода, изменится скачком от нуля до постоянного значения I.
Решение. Плотность тока и напряженность поля имеют только радиальные составляющие (сферическая симметрия). Плотность полного тока состоит из плотности тока смещения и плотности тока проводимости (16.28):
оЕ 4- £re0 dE/dt = 7ПОЛН = //4яЕ2.
Решение дифференциального уравнения представим в виде установившейся и свободной составляющих:
Е — Еу + Ecr = Еу + Aept,
где р = — о/£ге0 - корень характеристического уравнения, а Еу = = I/4nR2c.
Постоянную А определим из начальных условий. При t = 0 напряженность Е = 0, так как в первый момент заряд на электроде равен нулю (для его накопления нужно время), следовательно,
Е -
Поверхностный заряд на электроде
- дат’1 -
16.8	1(F)* Для прогрева земли в парниках применяют двух
проводную линию из неизолированного провода радиусом г0, проложенную в земле (рис. 16.81).
Определить емкость, проводимость и мощность потерь на единицу длины линии, если d = 60 мм; h = 20 мм; г0 = = 2 мм; ег1 = £г2 = 1;	=
- Ю”3 См/см; о2 = 0, напряжение питания и — 100 sin oat В, где о = 2,26 * 109 рад/с.
Решение. По методу зеркальных отражений для расчета поля в земле кроме растекающегося тока I вводим по (16.24) фиктивный ток Д = nJ (рис. 16.81Р,«), для расчета поля
Рис. 16.81
Рис. 16.81Р
в воздухе вводим фиктивный ток iz—thi (рис. 16.81Р, б), но с комплексными коэффициентами
«1 = (51 - 5г)/(51 + 51); п2 = ЗстзДод + о>),
и при Ст! =<?! +>e,1so=(10+2/) 10"4= 10,210"4 z. См/см и а2 =	+ Уо»ег2ео = j2 10-4 См/см получим nt =
= 0,935 z-21°50'; п2 = 0,375 z. 68° 10'.
Для вычисления комплексной проводимости линии на единицу длины Уо = Go + j<dC0 = i/U, приняв во внимание выражение (16.18) и заменив т на / и £0 на запишем связь между напряжением и током растекания на единицу длины линии (рис. 16.81Р, а):
U = —
г0
Л ln |/<*2 + 7KTi	2h
d
при этом Уо = Go + /соСо = (0,576 + /0,473) • 10 3 См/см, т. е. Go =0,576-10”3 См/см и Со = 0,209 • 10"12 Ф/см.
Мощность потерь Ро = G0U2 = 2,88 Вт/см.
Для расчета поля определим ток 7=У0[/ = 7,45х х 10“4 z. 39° 20' А/см.
Распределение потенциала в земле (рис. 16.81Р, а)
1 Г ]/(х - d/2)2 + (у + й)2
Ф1 = ----------- In -Ч --	 —
2*21 L ]/(х + d/2)2 4- Ср + h)2
+ "1 In
]/(х - d/2)2 + (y-h)2 -]/(х + d/2)2 + (у - ft)2 .
= [0,116 z. 28°  M (x, у) + 0,1085 z. 6° 10' • N (x, у)] B, в воздухе (рис. 16.8 IP, б)
in
ф2 = -^-M(x, у) = 0,223 л. 17° 20' • М (х, у) В.
2710*2
При t = Т/4, т. е. cot = 90°, получим:
ф! = [O,116sin(118°)-M(x, у)+ 0,1085 sin (96° 10')-N(x, у)] В; ф2 = 0,223 sin (107° 20х) • М (х, у) В.
16.8	2. Однопроводная линия подвешена над землей на высоте 4 м, диаметр провода 2 см. Задано напряжение между проводом и землей и = 6000 sin 314t В.
Определить плотность тока смещения в точке у нижней поверхности провода и у поверхности земли в точке под проводом. Землю считать идеальным проводником.
16.8	3(Р). Двухпроводная линия (рис. 16.83), протянутая в воздухе над реальным диэлектриком (сг2 = 10; о2 = = 10"8 См/см), находится под синусоидальным напряжением с Um — 500 В. Дано: радиус проводов г0 = 0,5 мм; d = 20 мм; h = 10 мм.
Определить емкость, проводимость и мощность потерь на единицу длины линии. Задачу решить для следующих частот: а) 50 Гц; б) 5 кГц; в) 50 кГц; г) 50 МГц. Потерями в проводах пренебречь.
Решение. Применяя метод зеркальных отображений (см. решение задачи 16.81), получаем:
io _____________________________
и In (d/r0) + nj In (]/d2 + 4й2/2й)
= ^0 +
См/см.
где Од ^jco8ri£o «ДО п//18 См/см; = q2 + >£r2e0 =
-i-10“2 18
Значения Go (См/см) и Со (пФ/см) при заданных частотах соответственно равны: а) 1,5-10“12; 0,835; б) 150-10"12; 0,085;
в)	15-10“12; 0,085; г) «0; 0,085. Мощность потерь на единицу длины вычислим по известной проводимости Р == G0U2: а) 0,188-10"6 Вт/см; б) 18,8-10"6 Вт/см; в) 1,88• 10“б Вт/см;
г)	«0.
16.84. Линия задачи 16.83 подключается к источнику постоянного напряжения U = 50 В. Определить заряд на положительно заряженном проводе и поверхностные свободный и связанный заряды на границе раздела сред.
77777777777777777777777,	f
; в г	о------------------
Рис. 16.83	Рис. 16.85
16.85(Р). Плоский конденсатор, заполненный реальным
неоднородным диэлектриком, подключается к источнику постоянного напряжения 17 = 1 кВ (рис. 16.85).
Определить напряженность поля, а также свободный и связанный заряды в диэлектрике: а) в начале процесса и б) в установившемся режиме. Задачу решить при параметрах: 1) ег — 2d/(d 4- х); ст = 10“10 См/см; 2) ег = 2,2; о = ст0/(1 4- кх); о0 = 10“14 См/см; к = 0,5 см-1; 3) ст = ае**; £r = be", где а, b и а - постоянные; 4) ст = а 4- Ьх; гг — а + Ьху где а и b — постоянные. Расстояние между пластинами конденсатора d = = 1 см.
Решение. 1а) При t = 0 свободный заряд в диэлектрике отсутствует, так как для его накопления необходимо время: р = div D = 0, т. е. D = Dx = const; Е = Ех — D/&r&0. Напряжение
на конденсаторе d	d
„	Г.,	fDW + x),..
V = £ dx = —х—з— dx —
J	J 2&od
0	0
л 4 s0(J _	2 17	.
откуда D = ~ —j—; E = — ~^(d 4- x)
3Dd
4s0
и
Рсвяз = — div P — — div D 4- e0 div £ = s0 dE/dx — 2&0U/3d2.
16)	При t -> оо (в установившемся режиме) ток смещения отсутствует, т. е. J = стЕ =.const; Е = U/d — const; D = e^qE = = 2&QU/(d 4- x) и P = e0 (Sr “ 1) E = (soW<0 [2d/(d 4- x) — 1]. По (16.2a) и (16.206) p = div D = ~2s0U/(d 4- x)2; рсвяз = -divP = = ~dP/dx = 2e0U/(J 4- x)2 = -p.
16.86.	Плоский конденсатор, заполненный неоднородным реальным диэлектриком, подключается к источнику постоянного напряжения U (рис. 16.85).	---
Указать, какое соотношение должно быть между зависимостями sr(x) и о(х), чтобы внутри реального диэлектрика: 1) образовался только свободный объемный заряд; 2) образовался только связанный объемный заряд; 3) образовались оба заряда одновременно; 4) не образовалось ни свободного, ни связанного заряда; 5) общий объемный заряд был бы равен нулю при неравенствах нулю свободного и связанного зарядов.
Задачу решить для: начала процесса (А) и установившегося режима (Б).
16.87.	Конденсатор задачи 16.67 подключается к источнику постоянного напряжения 17.
Определить напряженность поля, а также свободный и связанный заряды в диэлектрике: а) в начале процесса и б) в установившемся режиме.
16.5. Уравнения Лапласа и Пуассона
16.88.	Незаряженная проводящая сфера радиусом а внесена в однородное поле Ео, направленное по оси z. Для такой сферы известно, что в сферической системе координат с началом в центре сферы ср = — £0(R - a3/R2)cos&.
1)	Проверить, удовлетворяет ли это решение уравнению Лапласа и граничным условиям.
2)	Определить поверхностный заряд на сфере.
3)	Составить решение для потенциала в случае заряженной сферы (заряд q).
16.89	, Незаряженный проводящий цилиндр радиусом а внесен в однородное поле £0, перпендикулярное его оси (рис. 16.89). Для такого цилиндра известно, что (р = = -Ео (г - а2/г) cos а.
1)	Проверить, удовлетворяет ли это решение уравнению Лапласа и граничным условиям. 2) Определить поверхностный заряд на цилиндре. 3) Составить решение для потенциала в случае заряженного цилиндра (линейный заряд т).
16.90	(Р). Шар радиусом а из диэлектрика с относительной диэлектрической проницаемостью £н находится во внешнем поле (рис. 16.90) в среде с относительной диэлектрической проницаемостью £ге.
Найти распределение потенциала, напряженности поля внутри и вне шара и поверхностный связанный заряд на шаре. При решении пользоваться известным решением уравнения Лапласа в сферической системе координат: <р — CrR cosO + 4- (C2/K2)cos0 + К, где Сь С2 и К — постоянные.
Решение. Запишем выражение потенциала для внутренней Фг и внешней сре областей:
Фг “ CtR cos 6 + cos 9 + Ki;
К
фе = C3R cos 0 4- cos 0 + К2. R
При R -> 0 должно быть Ef = | — grad ф,-1 / оо, следовательно, С2 = 0. Положим ф£ = 0 при R = 0, тогда = 0. При R -> оо поле становится однородным и фе = — Eoz = — EoRcos0. Сле
Рис. 16.89
Рис. 16.90
довательно, — E0Rcos0 — C3R cos0 4- K2 при любом 0, т.е. С3 — — Ео; К2=0- Итак, ф£ = CXR cos0; фе =-E0R cos0 4-С4
4- -=vcos0.
Rz
При R »а и любом 0 должно быть (16.6) ф; = фе, т.е. Cta — -Еоа + С4/а2, и по (16.8а) Din = Den или £ritty>i/dR = = Ere ^Фе/^R, Т. е. e„Ci = - Еге (Ео + 2С4/а3), откуда Ci = ^O^Cre/fEri “Ь 2бге), С4 e Еоа (ер{ £re)/(Er[ 4- 2£Ре).
Окончательно
ч>< = ~£° ; к cos 6= -£0 - gr;
4- 2sre	£r( 4“ 2Sfg
t
фе — - E0R COS 0 4- Eq -----------C0S
Так как ф, = ф,(Д то внутри шара по (16.3)
Е£ = EIZ = -d^/dz = E03£re/(£rf 4- 2ere), вне шара
Ее^ —	~	— Eq cos 0 4“ 2Е0 io cos 0;
дК	К £Pj 4- 2&?е
1 ^фе	. л —	0^ £н — £Ге • л
£е9= “И~8(Г= -£oSin9 + £o к^^ТчГ81"9'
По определению (16.86) з$связ - Pin - Реп = £о (E?r - Eir) при R = G, Т. е. г/^связ ^CqEq COS 0 (£(’Р	ЕеР)/(£г/ 4" 2sre).
16.91,	Цилиндр радиусом а из диэлектрика с относительной диэлектрической проницаемостью eri находится в однород. ном поле Ео, перпендикулярном его оси (см. рис. 16.89) в среде с проницаемостью еге.
Найти распределение потенциала внутри и вне цилиндра, напряженность поля внутри и поверхностный связанный заряд на цилиндре.
При решении пользоваться известным решением уравнения Лапласа в цилиндрических координатах:
ср = С1Г cos а + (C2/r) cos а + К,
где Ci, С2 и К - постоянные.
16.92.	Построить качественно линии векторов напряженности поля, смещения и поляризации для цилиндра предыдущей задачи при Ео = 1 кВ/см, если: 1) sri = 5; гге = 1; 2) £„• = ~ 1» &ге ~
Определить в обоих случаях плотность связанного поверхностного заряда в точке на поверхности цилиндра при а = 60° (см. рис. 16.89).
16.93.	В диэлектрике плоского конденсатора (ег = 7) имеется нитевидное воздушное включение диаметром 0,02 мм, параллельное пластинам.
Найти пробивное напряжение конденсатора, если толщина диэлектрика 2 мм, пробивная напряженность воздуха 30 кВ/см.
16.94.	Для увеличения пробивной прочности масляных конденсаторов масло перед заливкой подвергается сушке, очистке и обезгаживанию (наличие примесей ухудшает изоляционные свойства масла).
В плоский конденсатор, заполненный маслом (г, — 2,2), с расстоянием между пластинами 10 мм попала капля воды диаметром 0,2 мм.
1)	Определить, при каком напряжении произойдет пробой масла у поверхности воды. Пробивная прочность масла 60 кВ/см. Воду считать проводником.
2)	Как изменится ответ, если вместо капли воды в масле образовался пузырек воздуха тех же размеров. Пробивная прочность воздуха 30 кВ/см.
3)	При каком напряжении произойдет пробой масла, если нет включений.
16.95	(Р). В электростатической машине для усиления поля в области 2 (рис. 16.95, а) в воздушное пространство внесен диэлектрик в форме шара с большим 8Г1. Через достаточно длительное время картина поля изменилась (рис. 16.95,6). Удельная проводимость воздуха сг2 больше, чем диэлектрика 556
(5i, вследствие ионизации воздуха. Дать объяснение изменению картины поля.
Решение. В первый момент после включения электрического поля свободный заряд на поверхности шара отсутствует и на его границе справедливы условия (pj = (р2 и Dln = = D2„, совпадающие с граничными условиями для идеального диэлектрика (16.6) и (16.8а). Соответ-
ственно картина поля получается такой, как для шара из диэлектрика с £ri > 1, находящегося в воздухе, т.е. линии поля втягиваются в диэлектрик у его полюсов (см. решение задачи 16.90).
Со временем изменения поля прекращаются, ток смещения становится равным нулю и остается только ток проводимости, линии поля совпадают с линиями плотности тока, соответственно они в основном огибают сферу, проводимость которой меньше проводимости окружающего
Рис. 16.95
пространства.
16.96	. Шар с параметрами материала eri = 10, of = = 10"16 См/см, радиусом а=1 мм (рис. 16.90) находится в вакууме в однородном внешнем электрическом поле, напряженность которого в момент t — 0 скачком изменяется от нуля до значения Ео — 1000 В/см.
Найти зависимости от времени составляющих напряженности поля в соседних точках А и В, лежащих по обе стороны поверхности шара при угле 0 = 45°. Рассчитать закон изменения поляризации шара во времени и удельную энергию, которая выделилась в шаре в виде тепла за время переходного процесса. Определить геометрические места вектора напряженности поля в тех же точках А и В.
16.97	. В кварцевой сфере радиусом а = 1 мм, находящейся в реальном диэлектрике (е, = 2; о =10"14 См/см), скачком возникла поляризация Ро = 5 мкКл/см2, которая в дальнейшем остается постоянной.
Определить свободный и связанный поверхностные заряды на сфере: 1) в начале процесса (Г = 0) и 2) в установившемся режиме.
16.98	(Р). Цилиндр радиусом а = 1 см из вязкого диэлектрика (sri =10; т = 1 мкс) находится во внешнем однородном поле (рис. 16.89), напряженность которого в момент t = 0
скачком изменяется от нуля до значения Ео = 1000 В/см. Внеш, няя среда — воздух.
Определить поверхностный заряд цилиндра при а = 45° в начальный момент (Г = 0) и в установившемся режиме (t -> оо).
Решение. Свободный заряд образоваться не может, так как обе среды не обладают проводимостью. Связанный заряд в начальный момент также не образуется, так как внешняя среда не поляризуется (сге — 1), а поляризация сферы из вяз
кого диэлектрика в течение переходного процесса нарастает
с нуля.
В установившемся режиме qs связ (оо) = Pin, где Pin = Pir =
= е0 (eri — 1) Eir == s0Eq-cos а, так как Eir = Eix cos а и
Sri “Ь 1
Eix = Ei = E0 —2-*- 
Sri "Ь &ге
При а = 45° имеем <?$связ = 1,12 мкКл/см2.
16.99	(Р). Диэлектрический цилиндр (ен = 3; о2- = 10“9 См/см) радиусом а — 1 см находится в однородном синусоидально изменяющемся поле (Ёо = 2 кВ/см, / =1 кГц, рис. 16.89). Внеш
няя среда — воздух.
Определить поляризацию цилиндра и мощность потерь на единицу его длины.
Решение. Решение уравнения Лапласа в цилиндрических координатах приведено в задаче 16.91. Приняв ф£ = 0 на оси цилиндра и учтя, что фе = — Ёох при х -* оо, напишем выражения для потенциала во внутренней <pf и внешней фе областях в комплексной форме:
ф( =в Ar cos а = Ах; фе = - Ёог cos а Н-cos а,
г
где А и В - постоянные.
Напряженность поля по (16.3)
Ё. = -
СХ
-А;
В
ег =----z— = Ео cos а + -5-C0S а;
дг	г2
г	1 дфе и	В .
Ее* =------;—= -Eosina+ -5-sin а.
г да	г2
При г = а должны выполняться граничные условия (16.40) и (16.41): ф{ = фе, т. е. Аа = —Еоа + В/а, и	т.е.
—Л о, = (£0 + Ё/а2) ое, где о,- =	отсюда
Eix = -А = £(,2^/(0* + О/).
Подставив числовые значения, получим: А — ___0,91 г. 24° 10' кВ/см = -Ёг, Pi = s0 - 1) Ё< = 2е0  0,91 х х 103 24° 10' = 1,82'103ео 24° 10' Кл/см2, т. е. Л = 1,82 х х 103бо ]/2 sin (cot + 24° 10') Кл/см2, где s0 - в фарадах на сантиметр.
Мощность потерь на единицу длины цилиндра Ро в -= CiEiKa2 = 2,6 мВт/см.
16.100	(Р). Диэлектрический цилиндр предыдущей задачи находится во вращающемся поле (Ео = 2 ]/2 кВ/см, со = = 2т • Ю3 рад/с), которое можно разложить на два синусоидально изменяющихся взаимно перпендикулярных в пространстве поля, сдвинутых по фазе на 90°.
Пользуясь решением предыдущей задачи, определить поляризацию цилиндра и действующий на него вращающий момент.
Решение. Разложим вращающееся поле на два взаимно перпендикулярных в пространстве синусоидальных поля, сдвинутых по фазе на 90°:
т. е.
Е = 121/2 sin cot + j2|/2 sin (cot — 90°).
Поляризация цилиндра в синусоидальном поле найдена в задаче 16.99. Пользуясь методом наложения, запишем поляризацию во вращающемся поле:
Р = 11,821/2 • Ю’е0 sin (<W 4- 24° 10') +
+ jl,82 ]/2  1О3ео sin (“1 + 24° 10' — 90°) Кл/см2, где 80 - в фарадах на сантиметр.
Вектор поляризации цилиндра вращается в пространстве со скоростью со, опережая внешнее вращающееся поле на угол 24° 10'. На единицу длины цилиндра мощность потерь pQ = « аЕ2ка2 = 5,2 мВт/см, т. е. вдвое больше, чем в синусоидальном поле задачи 16.99. Вращающий момент
Lo = Ро/и> = 0,83 мкДж/см.
16.101	(Р). Во вращающемся поле (Ёо = 2 кВ/см, со = = 2т • Ю6 рад^с) находится цилиндр радиусом а = 1 см (рис. 16.89) из вязкого диэлектрика (sri = 10, т = 1 мкс).
Определить поляризацию цилиндра, действующий на него вращающий момент и мощность потерь в цилиндре.
Решение. Разложим вращающееся поле на два взаимно перпендикулярных в пространстве синусоидальных поля, сдви-
нутых по фазе на 90°:
Ё = iEQ
Решим сначала задачу для цилиндра, находящегося в поле Ёх = Eq. Для диэлектрического цилиндра, находящегося в однородном гармоническом поле, приняв во внимание приведенное в задаче (16.91) решение уравнения Лапласа в цилиндрической системе координат, граничные условия (16.42) и (16.43), а также связь между потенциалом и напряженностью поля, получим аналогично решению задачи (16.99):
“Ё° = So(ён - 1)Ё1х = ЕоЕо -frj.1'  £ri + 1	§г» + 1
где по (16.39)	= 1,85	-48° 50' = 1,22 - >1,4 и
Eix = 1,525 zl 32° 20' кВ/см; Pix = £0 * 2,16-103 z. -49° 35' Кл/см2, где £0 — в фарадах на сантиметр.
Для цилиндра, находящегося в поле, Ёу = Ёо z. —90', комплексы напряженности поля и поляризация будут сдвинуты на -90°.
Для цилиндра, помещенного во вращающееся поле, получим:
Et « [й,525 z. 32°20' + >1,525 z (32°20' - 90°)] кВ/см;
Pi = [fe0 • 2,16• 103 z —49°35' +
+ >£0 • 2,16  103	(-49° 35' - 90°)] Кл/см2.
Вектор поляризации цилиндра вращается со скоростью со, отставая по фазе от внутреннего поля на угол 81 ° 55', а от внешнего однородного поля - на угол 49° 35'.
Цилиндр испытывает вращающий момент на единицу длины
= na2PiEQ sin (49° 35') = 9,1  10“7 Дж/см.
Мощность потерь на единицу длины по (16.45)
Ро = LqO = Сое'г/СоЕ = 5,72 Вт/см.
16.102	(Р). Между двумя плоскими электродами, подсоединенными к источнику постоянного напряжения U (рис. 16.49), распределен объемный заряд р - р0 (а2 - х2)/а2.
Определить закон изменения напряженности электрического поля и потенциала.
Решение. Уравнение Пуассона (16.4) в декартовой системе координат имеет вид:
у2фг=£ф_== _ _Р_ =	Ро Д2 - *2
dx2	£0	Ео Д2
откуда
rfcp _ _ ррх + рох3 dx s0 3a2s0
и
p0x2 Ф = “ ^тг—
Po*4 12a2s0
+ CjX + Cj.
При x = 0 (рис. 16.49) ф = U, т. е. С2 - U; при x-d задано ф = 0, т. е. О = -pod2/2so 4- p0d4/12a2s0 4- Ctd 4- L7, откуда С! « = pod/2so - Pod3/12а2£о - У/d.
Окончательно
_ роХ2 PqX4 _ p0d3x ро dx _ Ux
2s0	12a2s0	12а280	2s0 d
Е = -	= Рох _ Ро*3 + Pod3 _ Pod У
дх So За2е0 12a2s0	2s0 d'
16.103	. Два плоских электрода расположены на расстоянии d друг от друга и присоединены к источнику постоянного напряжения U (рис. 16.49). Между электродами распределен объемный заряд плотностью р = ро^вэс.
Найти распределение потенциала и напряженности поля между электродами.
16.104	. А. В условиях предыдущей задачи, но при р = == ЗООсох Кл/см3, d = 40 мм, U = 500 В найти распределение потенциала и напряженности поля и их значения при х — 20 мм.
Б. Определить, как изменится распределение потенциала, если при х = 20 мм параллельно пластинам расположена металлическая сетка: 1) не соединенная с электродами, 2) имеющая потенциал -100 В.
16.105	. Определить, может ли потенциал в области поля, где р = 0, выражаться функциями:
1)	ф = Зх2у — у3 4- 5х в декартовой системе координат;
2)	ф = Зг2 cos а - cos3 а 4- 5г в цилиндрической системе координат.
16.106	. Найти закон распределения объемного заряда, если в сферической системе координат потенциал ф = К cos а/Я.
16.107	(Р). Среда с sr = 1, ограниченная двумя цилиндрическими поверхностями, заполнена зарядом с объемной плотностью р (рис. 16.107). Радиус внешнего цилиндра ах, радиус внутреннего а2. Расстояние между осями цилиндров h. Длина цилиндрических поверхностей весьма велика по сравнению с их радиусами.
Найти напряженность поля внутри малого цилиндра.
Решение. Будем искать поле в любой точке М отверстия, не заполненного объемным зарядом, как результат наложения поля Ei в большом цилиндре, равномерно заряженном по
Рис. 16.107
Рис. 16.107Р
объему зарядом + р, и поля Е2 в малом цилиндре, равномерно заряженном по объему зарядом — р (рис. 16.107Р):
£-£‘+£‘-^-г"'-^
(см. задачу 15.13).
Иначе: ф = (pi + ф2 = ~-(-rf + г2), где r2 = **? 4- h2 -
— 2hrt cos a, t. e. ф =	(h2 — 2hx) и E = Ex = — dtp/dx — p/i/2e0.
4cq
16.6	. Энергия и силы в электрическом поле
16.108	(Р). Во сколько раз изменится энергия электрического поля уединенного металлического шара радиусом а = = 2 мм, который находится в воздухе и потенциал которого фш = 500 В (полагая ф = 0 на бесконечно большом расстоянии К), если шар покрылся слоем воды (ег = 80) толщиной Д = = 0,2 мм. Определить, как изменится решение задачи, если учесть проводимость росы. Выяснить, куда делась энергия и с какой силой (на единицу поверхности) электрическое поле стремится растянуть шар до его покрытия росой.
Решение. Шар не присоединен к источнику. Поэтому его заряд q = const, потенциал ф = ^/4яе0Я. Следовательно, заряд шара q = 4я€0фшд. Напряженность поля Е = ER = = 4/4тс£0Я2, смещение D = DR = q/bnR2.
Энергию электрического поля заряженного шара определим по (16.48). Для шара в воздухе энергия
_ 1 q2 f 4яЯ2 dR _ q2
(4л)2 £0 J R* “ 8яеоа *
Для шара, покрытого росой, энергия
|— в + Д	00
lq2 if 4jtR2dR f 4nR24R "T (4л)2 e0 [e, J R4 + J R4
a	a + A
= q2 Л + A
8яе0(а + Д)\ м /
При учете проводимости воды поле в ней отсутствует и энергия
= 1 q2 ? 4nR2dR q2
W*~ 2 (4л)2 e0 J R*	~ 8ле0 (a + A) ’
o+ A
_ a (
Wi a + A \
= 0,9102 и
И'з
———— — 0,9091. a + A
Отношение показывает, что после появления слоя росы энергия поля вокруг шара уменьшилась на величину, которая израсходована на нагрев этого слоя.
Сила, растягивающая шар, FR = — dW^/ca = q2/8n&oa2 = = 2ясоф2. Сила, действующая на единицу поверхности шара, Л = FR/4na2 = 0,276 Н/м2.
16.109	КР). Определить энергию электрического поля заряженного шара радиусом а = 0,1 м при объемной плотности заряда р = 10’6 Кл/м3. Относительная диэлектрическая проницаемость окружающей среды и материала шара ег = 1.
Решение. Напряженность поля внутри шара Е, == рЯ/Зе0; смещение D, = pR/З; напряженность поля вне шара Ее « == ра3/3£0#2; смещение De = pa3/37?2.
Энергия шара по (16.48)
pR
Зе0
4лR2 dR +
Р«3 3e0R2
pa3
3R2
4nR2 dR
2лр2 9eq
= 94,8-10" 8
Дж.
16.110	(Р). Определить работу, которую нужно произвести против сил поля, чтобы расстояние между пластинами плоского конденсатора: А) увеличить или Б) уменьшить вдвое. Работу подсчитать в двух случаях: а) конденсатор подключен к источнику постоянного напряжения V = 10 кВ; б) конденсатор заряжен и отключен от источника постоянного напряжения.
Первоначальная емкость конденсатора С = 10“9 Ф.
Решение. Работа в электростатическом поле равна разности энергий начального (1) и конечного (2) состояний. Если конденсатор подключен к источнику, то U = const и энергия W = CU2/2 ® e,£0S[72/2x, где х — расстояние между пластинами.
Работа против сил поля
SrEoSU2 /1	1 \ сиг( xt \
2 yxx x2 /	2 \ x2 J
Если конденсатор заряжен и отключен от источника, то заряд Q = const и энергия W = Q2/2C = б2х/2егг05. Работа
А = Ж —	= —  fl —
1	2 2С V *1 /
A) U = const: а) хх/х2 = 1/2; А = 2,5 • 10’2 Дж; б) хх/х2 в 2; 4= - 5-Ю’2 Дж.
Б) Q = const: а) хх/х2 = 1/2; А = -5 • 10“2 Дж; б) хх/х2 = = 2; А = 2,5- 10’2 Дж.
16.111.	Найти зависимость силы взаимодействия двух пластин воздушного плоского конденсатора от расстояния х между ними.
Дано: площадь пластины S = 20 см2, напряжение V = = 5000 В = const.
16.112.	Найти зависимость силы взаимодействия двух пластин плоского конденсатора площадью S = 20 см2 от расстояния х между пластинами при условии, что пластины были подсоединены к источнику постоянного напряжения 17 = 5 кВ при расстоянии между пластинами d == 3 мм, а затем источник был отключен. Диэлектрик — масло с = 2,2.
16.113.	Конденсатор переменной емкости состоит из семи подвижных полудисков и восьми неподвижных. Радиус каждого полудиска 10 см. Расстояние между соседними подвижным и неподвижным полу дисками 1 мм. Диэлектрик — воздух.
Найти зависимость момента, действующего на подвижные диски, от угла а перекрытия пластин, если постоянное напряжение между дисками V = 10 В при а = 30°. При этом угле поворота подвижные диски отсоединили от источника.
Предполагается, что угол перекрытия остается в таких пределах, при которых можно полагать емкость прямо пропорциональной углу.
16.114.	Решить задачу 16.113 при условии, что конденсатор не отсоединяется от источника постоянного напряжения U = = 10 В.
16.115.	У конденсатора задачи 16.113 емкость С = 40 + + 100а пФ, где а — угол перекрытия в радианах.
Определить вращающий момент, действующий на подвижные пластины, если к конденсатору приложено постоянное напряжение U — 1 кВ.
16.116.	У конденсатора задачи 16.113 емкость С = 20 + + 50а2 пФ, где а — угол перекрытия в радианах.
Определить вращающий момент, действующий на подвижные пластины, при а « я/6, если постоянное напряжение на конденсаторе U — 1 кВ.
16.117.	Найти значение и направление силы, испытываемой средней пластиной конденсатора задачи 16.23, если задано (pt = 50 В; (р2 = “Ю В; (р3 = —100 В.
16.118.	Найти потенциал средней пластины задачи 16.23, при Котором действующая на нее сила равна нулю, если дано q>! = 100 В; (рз = — 50 В.
16.119.	Определить, изменится ли сила, действующая на среднюю пластину конденсатора задачи 16.23, при изменении знака потенциала пластины 3, если потенциалы: а) ф! = 50 В; ф2 s -62,5 В; фз = -100 В; б) ф! = 100 В; ф2 = 0; ф3 = -50 В.
16.120(	Р). Вертикально расположенные пластины плоского
конденсатора (рис. 16.120) погружаются в жидкий диэлектрик
(ег2 = 4). Ширина пластин b = 30 см, высота h = 20 см, расстояние между пластинами d = 5 мм. Напряжение на конденсаторе постоянно: U = = 10 кВ.
Найти зависимости силы f притяжения между пластинами и вертикальной силы F от глубины погружения х.
Решение. Энергия конденсато
ра И7 = CU2/2, где С — [cr2x + Си (h - х)]/у и у = d.
Если конденсатор подключен к источнику напряжения, то
работа по перемещению диэлектрика на расстояние 6х равна
увеличению энергии поля:
£o^(^r2 £ri) 2
Fxbx = t.Wx =	_____
’	2 Sx	2d
и F, = 79,6  10" 3 H.
Аналогично
/,5у = 5И; =
и2 2
Оу и
= - е°^^и2 (1 + ег?....£и 2?| = _ 1(06(1 + 15х) Н.
2«	\ £r 1 П )
16.121.	Решить задачу (16.120) при условии, что конденсатор был заряжен до напряжения 'U — 10 кВ при х = h/2, после чего конденсатор был отключен от источника.
Глава семнадцатая
МАГНИТНОЕ ПОЛЕ
Введение к гл. 17
Основные уравнения rot H=J;	(17.1а)
$Hdl = $ JdS = I;	(17.16)
divB = 0;	(17.2a)
fBdS-O,	(17.26)
где I — контур интегрирования; S — поверхность интегрирования; J - плотность тока проводимости.
Векторный потенциал А вводится соотношением rot А = В.	(17.3)
Магнитный поток
ф = $BdS = $Adl.	(17.4)
В плоскопараллельном поле магнитный поток между точками 1 и 2 на единицу длины системы
Ф0 = Л1-Л2,	(17.5)
уравнение семейства линий магнитной индукции
А = const	(17.6)
В плоскомеридианном поле уравнение семейства линий магнитной индукции
г А = const.	(17.7)
В однородной среде уравнение Пуассона для векторного потенциала
72Л -	(17-8)
Граничные условия:
H2t - ни = Js,	(17.9)
где Ht — составляющая вектора напряженности поля, касательная к границе раздела сред; Js — поверхностная плотность тока;
В1„ = В2и,	(17.10)
где Вп — составляющая вектора индукции, нормальная к границе раздела.
Вместо (17.10) можно пользоваться граничным условием для векторного потенциала
Лк = Л2г	(17.11)
Для линейной среды по методу наложения
В=В1+В2 + ...=£Вк;	(17.12)
к
Л=Л,+Л2 + ...»£ЛЬ	(17.13)
к
где Вк и Ак — слагаемые, соответствующие возбуждающим их токам.
Связь между магнитными потоками и возбуждающими их токами
Ф1 =	+	7И12^2	+	т13^3	+	•	• • >	'
Ф1	+	^22^2	+	т23^3	+	•	• • I	(17.14)
Фз = Ш31Л +	^32^2	+ w33^3	+	•	• • >
..............................,
где ткк — собственные индуктивности контуров; mik — взаимные индуктивности контуров.
При расчетах магнитного поля в линейных средах часто применяется метод изображений. Особенно эффективно применение этого метода при плоской или цилиндрической поверхности раздела между двумя средами с различными магнитными проницаемостями.
Если граница плоская, то магнитное поле каждого проводника с током I в той среде, в которой он расположен,
определяется током I и фиктивным током расположенным по другую сторону границы на таком же расстоянии от нее, как и ток I, при этом магнитная проницаемость всего пространства должна быть принята равной магнитной проницаемости ц1г той области, в которой расположен проводник с током I и в которой по этой расчетной схеме определяется поле. Ток
11 = I (thr - Ш,)/(Ц2, + И1г) = mJ,	(17.15)
где ц2г - магнитная проницаемость другой среды.
Во второй среде поле определяется фиктивным током /2, расположенным там же, где и ток Z, магнитная проницаемость всего пространства равна Ток
Ь = I  2Ц1,/(Ц1, + g2,) = т2/.	(17.16)
В области, где отсутствуют токи, для описания магнитного поля может быть введен скалярный потенциал фм, определяемый соотношением
H=-gradcpM.	(17.17)
В неоднородной среде скалярный потенциал удовлетворяет уравнению
V2cpM = divM,	(17.18)
где М — вектор намагниченности.
В однородной среде скалярный потенциал удовлетворяет уравнению Лапласа:
V2(pM = 0.	(17.19)
Существует формальная аналогия между постоянным магнитным полем и электростатическим, в котором отсутствуют заряды. Аналогичными параметрами являются:
Магнитное поле	Н <рм В ргц0 Ф
Электростатическое поле Е <р D £,£0 Фр Здесь Фр - поток вектора электрического смещения.
В непроводящей магнитной среде при отсутствии магнитной вязкости можно применять при переменном поле те же решения, что и для постоянного поля.
Магнитная вязкость в первом приближении учитывается по уравнению
т dM/dt = (^ - 1) Н - М,	(17.20)
где т — постоянная времени магнитной вязкости.
В синусоидальном поле уравнение вязкости
= (цг - 1) Н -	(17.21)
Комплексная магнитная проницаемость, учитывающая вязкость,
Н, = ц; -	= (Hr + >?)/(! +>т).	(17.22)
Энергию магнитного поля можно определить:
1)	через векторы поля при помощи интеграла
объему^ V поля:
W =
f 1
-r-BHdV;
+4
по всему
(17.23)
2)	через токи и магнитные потоки контуров с токами:
(17.24)
3)	через векторы плотности тока и пртенциала по объему V, в котором протекают токи:
W = i-j-AJdV.	(17.25)
Потокосцепление катушки, обусловленное намагниченным телом (теорема о потокосцеплении),
Ч» = -J- Н,М dV,	(17.26)
где интегрирование проводится по объему намагниченного тела с намагниченностью М; Я/ — напряженность поля в случае, когда намагниченное тело удалено, а по катушке протекает ток I.
17.1. Постоянное магнитное поле в однородной неограниченной среде
17.1.	Определить закон изменения магнитной индукции вдоль оси витка радиусом а с током I (рис. 17.1).
17.2.	Пользуясь решением предыдущей задачи, определить закон изменения индукции вдоль оси соленоида радиусом а и длиной / (рис. 17.2) с числом витков на единицу длины w0.
Каково должно быть отношение диаметра соленоида к его длине, чтобы индукция в центре соленоида отличалась от
индукции в бесконечно длинном соленоиде не более чем на-а) 10%; б) 5%; в) 2 %?
17.3	(Р). Тонкое диэлектрическое немагнитное кольцо, заряженное с объемной плотностью заряда р, вращается вокруг оси, проходящей через центр кольца перпендикулярно его
Рис. 17,1
плоскости (рис. 17.3). Частота вращения кольца в секунду равна п. Радиусы кольца равны rj и г2, толщина его Ду. Относительная магнитная проницаемость окружающей кольцо среды равна единице.
Определить магнитную индукцию в точке М, лежащей на оси вращения на расстоянии у от плоскости кольца.
Решение. Плотность тока движущихся зарядов
j = ри = рог = р2лг(г,
где со - угловая скорость вращения.
Ток, приходящийся на элемент длины радиуса dr, di = J dr (Ду) = (Ду) p2nnr dr.
По закону Био — Савара напряженность поля на оси, обусловленная элементарным кольцевым током di,
dH = dHy — di ^^2 5*п P =	~— (Ду) рли sin3 p dr.
Искомая напряженность поля кольца на его оси Н = Ну = J (Ду) рли sin3 Р dr.
Так как г — у tg р (рис. 17.3) и dr = у jp/cos2 р, то
С	sin3 р
Н=	(Ayjpwiy—ГГ<*₽ =
UUd Р
V	г
Р1
= 2л (Ду) ри r2 tg — sin2 -7г- - rv tg — sin
В = ц0Я.
Если rj - 0, т. е. кольцо превращается в диск радиусом
г2, ™
Я = 2л (Ду) pnr2 tg -% sin2
Рис. 17.5
Рис. 17.3
Рис. 17.6
17.4.	Длинный диэлектрический цилиндр, заряженный с объемной плотностью р = 4 -10"6 Кл/м3, вращается вокруг оси z, совпадающей с осью цилиндра, с частотой п — 100 об/с. Радиус цилиндра г0 = 0,05 м. Относительные магнитные проницаемости материала цилиндра и окружающей среды равны 1.
Определить магнитную индукцию внутри цилиндра в средней его части в зависимости от расстояния г от оси.
17.5.	На коническую поверхность по окружности плотно намотана изолированная проволока (рис. 17.5). Число витков, приходящихся на единицу длины образующей конуса, равно w0. Высота конуса h. Радиус окружности основания конуса а. Относительные магнитные проницаемости материала конуса и окружающей среды одинаковы и равны 1.
Определить магнитную индукцию в центре окружности основания (точка М) при токе в обмотке, равном I.
17.6.	Обмотка катушки расположена на боковой поверхности усеченного конуса (рис. 17.6). Высота конуса h. Радиусы оснований г2 и гх. Число витков на единицу длины образующей конуса w0. Ток в обмотке I. Относительные магнитные проницаемости материала конуса и окружающей среды одинаковы и равны 1.
1) Определить магнитную индукцию на оси конуса.
2) На основании полученного решения определить магнитную индукцию на оси цилиндрической катушки длиной h и радиусом г0.
ПЛ, В плоской однослойной катушке (рис. 17.7) протекает постоянный ток I. Число витков на единицу радиуса катушки w0. Относительные магнитные проницаемости провода и окру, жающей среды равны 1.
Определить магнитную индукцию на оси кольца: а) непосредственно; б) считая известным решение задачи 17.6.
17.8. На сферический каркас радиусом а = 0,1 м виток к витку намотана изолированная проволока (плоскости витков параллельны друг другу). Число витков на всей поверхности сферы w = 200. Относительные магнитные проницаемости каркаса и окружающей среды равны 1.
Определить магнитную индукцию в центре сферы при постоянном токе в обмотке I = 5 А.
17.9(Р). Проводящая сферическая оболочка радиусом b — = 10 см вращается вокруг оси z, проходящей через ее центр, с частотой п = 100 об/с (рис. 17.9). Заряд оболочки q = 10"8 Кл. Относительная магнитная проницаемость оболочки равна 1.
Найти непосредственным интегрированием напряженность магнитного поля на оси вращения z внутри (1) и вне (2) сферы, считая известной напряженность поля на оси кругового витка (задача 17.1).
Решение. Поверхностная плотность заряда на оболочке qs = q/4nb\ Элементарный поверхностный заряд элемента b d$ сферы dq = qs2nrb dQ. Элементарный ток движущегося заряда dq
di = ndq = dQ.
2b
Напряженность магнитного поля на оси вращения в точке М, обусловленная током di (см. ответ к задаче 17.1),
dH = dH, = di
2 2r
Из рис. 17.9 следуют соотношения z3 = bcosG; sin р = г/р; - b2 - z2; р2 = z2 4- b2 - 2z3z, откуда d® - —dzjr и z dz3 =
-pdp, поэтому
,Л , ,	2	— р4 + 2р2 (z2 + Ь2) — (Ь2 — z2)2
dQ = Р dp/zr и г2 ----------------4Z2--------------
Подставив эти значения в выражение для dH, получим: , —nq р4 - 2р2 (z2 + Ь2) + (Ь2 - z2)2 , dH =	Р-------------dp
и после интегрирования по р
-ng
16bz3
Напряженность поля внутри оболочки ( — b < z < b) найдем, выбрав пределы интегрирования от рх = b — z до p2 = b + z:
Hi = nq/3b,
т.е. напряженность поля внутри оболочки на оси не зависит от координаты z точки наблюдения.
Напряженность поля вне оболочки (координата z изменяется от — оо до — b и от + b до + оо) найдем, подставив пределы интегрирования от р3 = (| z | + Ь) до р4 = (| z | - Ь) при отрицательных z и от р4 до р3 при положительных z:
Н2 = nqb2/3 | z |3,
оболочки.
Рис. 17.10
т. е. напряженность поля вне оболочки на оси убывает обратно пропорционально кубу расстояния от центра
17.10. Вдоль длинной тонкой ленты, ширина которой а = 0,2 м, протекает постоянный ток Г= 40 А (рис. 17.10).
Определить магнитную индукцию в воздухе в точке М, отстоящей от средней линии ленты на расстояние h = 0,05 м.
17.11(Р). Найти напряженность магнитного поля в точке М, создаваемого током длинной тонкой ленты (рис. 17.11).
Определить, на каком расстоянии от оси ленты поле можно считать практически таким же, как и поле тока /, сосредоточенного на оси ленты.
Решение. Ток, протекающий в элементе ленты dyr (параллельно оси z), а
Напряженность поля, создаваемая этим током,
2кг а 2кг
а составляющая напряженности в направлении оси у dHv = dH cos р = — 4^-cos р.
у	а 2кг
Рис. 17.12
‘>У
Из рис. 17.11 следует, что
г = x/cos р; tg Р = (у - уО/х и — ~х dP/cos2 Р,
при этом
и
dHy = -~df, у 2ка
Pi
Н,= I 2ка 2ка
02
Составляющая
напряженности в направлении оси х
____1 sin р R
dHX — _ П “Р 2ла cos Р
и
 = 1 In COSP2 = 1 In + ~ а^2 х 2ка cos pt 4яа х2 4- (у + а/2)2 ’
На оси у при а/2у с 1
2лу
1 а2
12/
Если у 2а, то с погрешностью не более 2 % напряженность Нх = -1/2пу, т.е. поле тока ленты на оси у такое же, как и поле тока, сосредоточенного на оси ленты.
На оси х при х а/2
т. е. практически на таком же расстоянии, как и по оси у, поле тока ленты можно считать как поле тока, сосредоточенного на оси ленты.
17.12.	Найти напряженность магнитного поля двухпроводной линии с постоянным током I, если проводами линии являются длинные тонкие немагнитные ленты шириной а. Расстояние между лентами равно d (рис. 17.12).
17.13.	Провод с постоянным током I = 360 А находится на оси стальной трубы. Радиус провода г0 — 0,4 см. Внутренний радиус трубы гi — 4 см, внешний радиус г2 = 5 см. Относительная магнитная проницаемость стали трубы при заданном токе = 200.
Определить напряженности магнитного поля в точках г = = 2 см; 4,5 см и 6 см. Изменятся ли найденные значения напряженности поля, если убрать стальную трубу?
17.14.	Для системы задачи 17.13 определить значения магнитной индукции В и намагниченности М в тех же точках: а) при наличии и б) при отсутствии стальной трубы.
17.15(	Р). Определить индуктивность коаксиального медного кабеля с радиусом жилы rj и радиусами оболочки г2 и г3, считая, что плотность тока постоянна как в жиле, так и в оболочке.
Решение. Индуктивность L кабеля можно и целесообразно определить из выражения W = Ы2/2, вычислив предварительно энергию магнитного поля на единицу длины кабеля:
Wo

Н22т1г dr,
где V — объем на единицу длины.
Определим напряженность поля Н, применив закон полного тока. При 0 < г < rj получим = 1г/2нг2; при < г < г2 находим И2 = 1/2кг; при г2 < г < г3 напряженность Н3 — / (rf — — г2)/2пг (ri — г2), поэтому
Ио |72(d-r2)2
/I-	/«2	„2\2 „
4?С J (г| - Г%)2 Г
Индуктивность кабеля на единицу длины
Первое слагаемое обусловлено магнитным полем внутри жилы, второе — полем между жилой и оболочкой, два последних — полем внутри оболочки. Обратим внимание на то, что индуктивность определяется отношениями радиусов, а не их абсолютными значениями.
В случае, когда оболочка достаточно тонкая, т. е. (г3 -
17.16.	Определить длину соленоида радиусом а ® 2 см с МДС, равной 10 А/см, если в точке, расположенной на оси внутри соленоида и отстоящей на 10 см от одного из его концов, напряженность поля равна 8 А/см.
Чему равна напряженность поля внутри такого же бесконечно длинного соленоида?
17.17(	Р). Определить напряженность магнитного поля постоянного тока I в плоском кольце шириной r2 —	= а
и малой толщины 8 (рис. 17.3) в произвольной точке М оси у кольца. Плотность тока: а) обратно пропорциональна радиусу J = К/r; б) во всех точках кольца одинакова.
Решение, а) Ток в элементе 8 dr кольца di — J (8 dr) = = &(K/r)dr. Ток в кольце г2 * , / = К8 — = К81п(г2/гД
т. е. Напряженность витка с током di) dH = dHy =	г * Jr _	1	dr In (г2/Г1) Г ' поля тока di на оси в точке М (поле sin3 р _	I	г dr 2г	2 In (г2/н) (у2 + г2)3/2 ‘
Напряженность поля на оси я = 7 f rdr = - 2 In (r2/ri) J (у2 + r2)3/2	:	I /	1 - in (rl/ri)\ ]/y2 4- r2
1	\ _ I COS Pi - COS p2
” j/7772/ “ 2 In (rjrj у
в плоскости кольца (у = 0)
' Р	И
21n(r2Ai) Vi	г2 /
б) В этом случае di = (I/a) dr и
I л sin3 Р I г2 dr 7 ~1Г~~ 2а (у2 + г2)3/2.
Напряженность поля на оси
If Г2 dr I / Г2 + j// + rj J {уг + г2)312 -2Д1П Г1 + 1/77Т? Г1
в плоскости кольца
17.18.	Два круговых контура, оси которых совпадают, отстоят один от другого на расстоянии 2h = 1 м. Радиусы контуров а = 50 см. Постоянный ток в каждом контуре I = 200 А. Направления токов одинаковы.
Найти зависимость магнитной индукции на оси контуров от расстояния х до середины между ними.
17.19.	Круговые контуры задачи 17.18 расположены под углом друг к другу так, что их оси пересекаются в точке М, образуя угол в 60°. Расстояние от точки М до центра первого контура 0,25 м, до центра второго контура 0,75 м. Для наблюдателя в точке М ток первого контура направлен по направлению движения часовой стрелки, ток второго контура — против направления движения часовой стрелки.
Определить значение и направление вектора индукции в точке М.
17.20.	Два тонких круговых контура лежат в параллельных плоскостях и имеют общую ось.
Найти взаимную индуктивность между контурами, если расстояние между их плоскостями h = 0,25 м, радиус первого контура ri =0,4 м, радиус второго контура г2 = 0,3 м.
17.21.	Двухпроводная линия длиной /»d (рис. 17.21) замкнута тонким проводником. По линии и проводнику протекает постоянный ток I.
Показать, что при указанных условиях продольная составляющая силы (направленная вдоль линии), действующей на проводник, не зависит от его формы.
17.2. Дифференциальные уравнения магнитного поля. Векторный и скалярный потенциалы
17.22(Р). Провод с постоянным током I спускается верти-
кально вниз и оканчивается в земле полусферическим заземли-
телем (удельная проводимость о3), радиус которого равен а
(рис. 17.22).
Считая удельную проводимость земли Oj с а3 постоянной
и второй электрод находящимся на расстоянии, много большем а, определить напряженность магнитного поля в земле и в воздухе.
Решение. Магнитное поле в земле удовлетворяет уравнению (17.1а). В силу симметрии плотность тока в земле имеет только радиальную составляющую (в сферической системе координат) J = — JR — I/2nR2, а магнитное поле не зависит от координаты а и Н — Нй, при этом для радиальной составляющей уравнение (17.1а) будет иметь вид (см. приложение 4):
—(RsmOH) = 2^r2 .
После интегрирования получим:
* лтт	COS 0	« . —.	__
R sin ОН » - —-----ч- /(К) + с.
На оси симметрии z, т. е. при 0 = 0,
R sin 9Н = 0 = —//2тг + f(R) + С.
Следовательно, f (R) не зависит от R, т. е. эта функция отсутствует, и постоянная С = 7/2тг. Подставив постоянную в (а), получим:
Н = JА (1 - cos 9) =	(1 - cos 0),
2яЯ sin 9	7 2тгг
так как R sin 0 = г.
В воздухе напряженность магнитного поля находим по закону полного тока: Н' - 1/2пг. Нетрудно видеть, что на границе (при 9 = я/2) получим Н = I/2nr = Н', т. е., как и должно быть, удовлетворяются граничные условия (17.9) и (17.10).
Рис. 17.23
Рис. 17.23Р
17.23(Р). На глубине h под поверхностью земли (рис. 17.23) находится сферический электрод (удельная проводимость ст3) радиусом а с h, к которому подводится постоянный ток I по изолированному вертикальному кабелю. Второй электрод расположен далеко от первого — на расстоянии, намного большем h.
Найти напряженность магнитного поля в земле и воздухе, считая удельную проводимость земли с?! « а3 и постоянной.
Решение. Для определения плотности тока в земле можно пользоваться методом зеркальных изображений: влияние границы раздела сред (поверхности земли) заменим током Г — I фиктивного электрода (рис. 17.2ЗР). Применив принцип наложения, определим напряженность магнитного поля в земле. Напряженность поля истинного тока, как найдено в задаче 17.22,
с заменой 2я на 4л (так как теперь заземлитель сферический)
Н1=Н1а =
-л—(1 - cos ОД 4яг
для изображения тока
«2 = Н2а = ~ (1 - cos 02)
и напряженность поля в земле
И = Н, = Н1 + Я2 =-т—(2 - cos01 - COS02). а 1	2
В воздухе, как и в задаче 17.22,
Н' = Hfa = 1/2пг.
На границе, т. е. при 02 = я — получим, как и должно быть, Н = l/2itr — И'.
17.24. По проводнику, выполненному в виде трубы с радиусом г2 = Згх — 1,5 см, протекает постоянный ток I. Для
охлаждения проводник помещен в жидкость, при этом темпе
ратура различных точек сечения проводника различна и вследствие этого не одинакова плотность тока J — Jz. Известна
напряженность магнитного поля внутри проводника: Н = На = — 25 (4г2 4- 9 — 5/г) А/см, где г — в сантиметрах.
Найти распределение плотности тока по сечению провод
ника и зависимость удельной проводимости от радиуса, если
напряженность электрического поля в проводнике Е = Ez = = 1,2-10”3 В/см.
17.25(F). Плотность тока в плазме газового разряда J = = Jz~ + М в цилиндрической системе координат (см. приложение 4). Здесь г — текущий радиус, Jq и а — постоянные.
Определить напряженность магнитного поля. Построить на одном графике зависимости J (г) и Н(г).
Решение. Напряженность поля найдем из уравнения
закона полного тока в дифференциальной форме (17.1а), кото-
рое в условиях задачи перепишем в виде
где Ня = Н.
После интегрирования получим:
rH = aJ0 [г — a In (г 4- «) С].
Постоянную С определим из условия Н = 0 при г = 0, т. е. О = — In. аС = 1п(1/аС), следовательно,
Зависимости J/Jo = /1 (г/а) и H/clJq — f2(rld) построены на рис. 17.25Р.
17,26(Р). Решить задачу 17.4, интегрируя дифференциальное уравнение магнитного поля.
Решение. Плотность тока
J = Ja = рг = р2яги.
Напряженность магнитного поля внутри цилиндра найдем из закона полного тока в дифференциальной форме (17.1а). Так как поле не зависит от координаты z (цилиндр длинный), то в цилиндрической системе координат (см. приложение 4) rota Н = - дНх/дг и - dHJdr - 2пгпр, откуда после интегрирования получим:
Hz ~ —ппрг2 + С.
Постоянную интегрирования легко определить из условия, что при г = г0 должно быть Hz = 0, т. е. С = яирго-
Магнитная индукция внутри цилиндра
В = ц0Яг = |10яир (г? - г2).
17.27,(Р). Считая известным, что магнитный потенциал фм = ф. = (CtR + C2/R2) cos 9 удовлетворяет уравнению Лапласа (К и 8 - сферические координаты), найти магнитную индукцию в любой точке внутри и вне сферической оболочки задачи 17.9.
Решение. Внутри оболочки, т. е. при R < b (рие. 17.9), токи отсутствуют и, следовательно, rot Hi = 0, т. е. магнитное поле потенциальное и напряженность поля можно представить в виде Hi = — grad9b где Ф1 — скалярный потенциал магнитного поля внутри оболочки. Аналогично при R > Ь, т. е. вне оболочки, Н2 = — gra<Up2.
Решение задачи ищем в виде
Ф1 = (CiR + C2/R2) cos 9; ф2 = (C3R + C4/R2) cos 0.
Постоянные найдем из условий: 1) в центре оболочки (R » 0), 2) в бесконечности (R = оо) и 3) на поверхности (R = Ь).
1)	Так как напряженность поля не может быть бесконечно большой, то С2 = 0.
2)	Так как в бесконечности поле отсутствует, то С3 = 0.
3)	Из граничного условия (17.10), т. е. HiR = H2R (так как Нм — Нг2 = 0» или ^Ф1/5Я = 5(p2/5R при R = b получим = = — 2С4//Л Из граничного условия (17.9) или — 5ф2/Я£0 + + dtyi/R дВ = Js при R = Ь,где Js = dl/b 50 = nqr/lb2 = nq sin 0/2Ь, получим C±/b3 -	= nq/2b. Из двух уравнений для Ci и С4
находим: Ct = -nq/3b‘, С4 = nqb2/6.
Потенциалы:
nq п л nq	nq b2
ф1 = -— Rcos0= — — z; Ф2= — ^cosO.
По известным потенциалам сразу находим напряженность поля:
Hi = Hlz = -dt^/dz « nq/ЗЬ; rr	5ф2 nq b2 _
н™-----5fT=~lems(>'
rr	дф2 «4 b2 . _
H2e= ~wT 7Fs'“0,
Рис. 17.28
в) х — d; у = 0; г) х = d + г0;
Это решение определяет напряженность поля внутри и вне оболочки в любой точке, а не только на оси. Нетрудно видеть, что для напряженности поля на оси решения задач 17.9 и 17.27 совпадают.
17	.28 (Р). В цилиндрическом медном проводе радиусом а есть цилиндрическое отверстие радиусом г0, расположенное на расстоянии d от оси провода (рис. 17.28). По проводу течет ток постоянной плотности J.
Определить векторный потенциал и магнитную индукцию, составить уравнения линий магнитной индукции: 1) внутри отверстия, 2) в проводе и 3) вне провода. Построить линии, проходящие через точки: а) х = 0; у = 0; б) x = d-r0; у = 0; у — 0; д) х = а; у = 0 при а =
= 2d = 4г0 и график зависимости Ву (х), при у = 0.
Решение. Применим принцип наложения следующим образом. Будем считать, что поле создано двумя токами —
током плотностью 7, протекающим по сплошному цилиндру радиусом а, и встречным током той же плотности, протекающим по цилиндру радиусом г0 (по отверстию). Поле двух токов равно сумме полей, созданных каждым из этих токов. Кроме того, каждое из рассматриваемых полей симметрично относительно своей оси.
Сначала определим поле первого тока. Для этого решим уравнение Пуассона для векторного потенциала (17.8).
Так как плотность тока имеет только z-ю составляющую, т. е. J — Jz, то и А = Az. В силу симметрии поле не зависит от координат а и z (краевой эффект не учитывается). Поэтому уравнение Пуассона в цилиндрической системе коор-
2By/}i0J(L
Рис. 17.28Р
динат принимает вид (см. приложение 4):
ЗА \
дг ) " ИоЛ
Проинтегрировав это уравнение, получим выражение для векторного потенциала внутри цилиндра
Л = - p0Jr2 + Ci In r + C2.
Вне цилиндра J = 0 и
Ae = C3 ln(r/C4).
Постоянные определим из условий на оси и на поверхности цилиндра. Так как напряженность поля на оси цилиндра конечна, то Ci ~ 0.
При r = a At = Ae (17.11) и (1/ц0Ц;г) dAi/dr = = (1/НоЦег) dAJdr (Нlt = H2t) или - p0J«2/4 + С2 = С3 In (а/С4) и -ц0/а/2 = С3/а, откуда
С3 = -^-ИоЛ; С2 = — ц07а2(1 \	С-4 J
Таким образом, векторный потенциал внутри и вне цилиндра определим по выражениям
1	(	CI2	г2 \
А = ~г Цо^а2 ( 1 — In ----г при г а;
4	у	С4	ст J
1	2 I ^4
Ае = — р0Лг In при г > а.
Постоянную С4 оставим неопределенной. Ее можно легко определить после выбора точки, где векторный потенциал равен нулю.
Поле второго тока определим по аналогичным выражениям. Их легко получить из предыдущих, заменив а на г0, г на rt, С4 на С5 и J на — J:
1	(	Y^	Г* \
goJi-g 1приг^го;
4	\	С5	Г0 /
1	,2, Cl
ае= - — In —5- при > г0.
4	Г1
Поле двух токов определим наложением полей первого и второго токов.
1) Точки внутри отверстия (т^ < г0) являются внутренними для обоих цилиндров, поэтому
1	/	/7 2	\
Л1 = 4i + at = -Т- n0J (а2 - г2 - rl + rj - a2 In + rl In
4	\	С4	С5 J
Выберем точку, где Ai = 0 — центр отверстия (п = 0 и г = d), при этом
0 = а2 - d2 - rl - a2 In In
С4	С5
и
A =	+ d - г2).
2) Точки в проводе (rt > г0; г а) являются внутренними для первого цилиндра и внешними для второго, поэтому
3) Точки вне провода (г > а) являются внешними и для большого цилиндра, и для малого, поэтому
А3 = Ле 4- ае - -j- Ь In + Н? + d2“
Уравнения линий магнитной индукции плоскопараллельного поля (17.6) легко определяются при известной функции векторного потенциала.
а)	Внутри отверстия это уравнение приводит к выражению d2 4- г2 — г2 = С. Имея в виду, что г2 — г2 = (х2 4- у2) — [(х — - d)2 4- у2] = 2dx — й?2, получим:
2d2 — 2dx = С или х = d — C/2d.
’ Таким образом, линии магнитной индукции в отверстии — прямые, параллельные оси у.
б)	В проводе
в)	Вне провода
,	a2 In — г? 1»	4- Гд 4- d2 — а2 = С.
В обоих выражениях г2 = х2 4- у2 и г2 = (х - J)2 + у2.
Если требуется определить уравнение линии магнитной индукции, проходящей через заданную точку М с координатами г и г' и гг — г\, то следует найти значение постоянной С, соответствующей этой точке, и подставить его в уравнение линии, при этом уравнения линий индукции примут следующий вид: 1) х = х0 при < г0; 2) [г2 - (rz)2]/r§ = In [r2/(r't)2] при ri > г о ri, г а г'; 3) (а2/го\ In [r2/(r')2] = In [г2 /(г i )2] при г а < г'.
Все линии индукции, проходящие внутри отверстия, входят в провод. Уравнение линии в проводе, проходящей через точку х0 (в отверстии),
In (г?До) = (Г2 - rj 4- d2 - 2dx0)/r$.
Часть линий из провода выходит в окружающее пространство.
Точка а расположена в проводе (г' = 0; ri = d). Уравнение линии индукции, проходящей через эту точку, г2/г§ = In (г2/<72). Для точки б (г' — d — r0; ri = г0) уравнение линии индукции [г2 - (d - r0)2]/r§ ~ In (rf/rj) или r2/rg = 1 + In (rf/rg). Точка в находится в отверстии (х = а); соответствующая линия индукции пересекается с поверхностью отверстия в точке ri = г0 и (г')2 = d2 +* Гд. Уравнение этой линии в проводе (г2 — d2 -— *о)Ло = In (г2/г§) или r2/rg = 5 4- In (r2/rg). Для точки г (г' « == d + r0; ri = г0) уравнение линии индукции [г2 — (d 4- г0)2]/гд = = 1п(г2/гд) или г2/гд = 9 4- 1п(г2/гд). Для точки д (г' — а; г\ = — а — d) уравнение линии индукции (она проходит вне провода) (a2/rg) In (r2/a2) = In [r2/(a - d)2] или 16 In (r2/a2) = In (4г|/д2).
По этим уравнениям линии индукции построены на рис. 17.28Р, а.
Вектор магнитной индукции определим при известной функции векторного потенциала по (17.3). Так как векторный потенциал имеет только одну составляющую А = Л2, то Вх = = дА/ду и Ву= — дА/дх. Внутри отверстия
= jp0J(d2 4- d2 — 2dx),
так как г2 - г2 = 2dx — d2 и В1Х — 0; Biy = ^Jd/Z.
В проводе
Г2 In (Х ""	+ З’2 , 2 , J2 2	2
Гд Ш	2-------Г Гд + Д — Л — у
Г0
Вне провода
и
1
В3у = — ц0/ а2
х
х2 4-у2
Зависимость Ву (х) при у = 0 показана на рис. 17.28Р, б.
17.29. Определить векторный потенциал коаксиальной линии, по которой протекает постоянный ток I — 1000 А. Внутренний проводник диаметром 2г х = 2 см выполнен из ферромагнитного материала (цг1 = 100), а оболочка с внутренним радиусом г2 = 2 см и внешним радиусом г3 = 2,24 см — из неферромагнитного материала.
17.30(Р). Определить векторный потенциал двухпроводной линии (рис. 17.30) с током Z, провода которой сделаны из неферромагнитного материала. Найти максимальный магнит-
ный поток на единицу длины линии, у которой отношение расстояния между осями проводов 2d к их радиусу а равно 4. Выяснить, как надо расположить контур, чтобы он охватывал максимальный поток.
Построить несколько линий поля, которые проходят: а) только ,вне проводов, б) только внутри провода, в) частично внутри, частично вне провода.
Решение. Выражение векторного потенциала для цилиндрического провода с током плотностью J = Jz было получено в задаче 17.28:
при < а;
при rt а,
где — расстояние от оси этого провода до точки наблюдения М.
Для второго провода с таким же током обратного направления
Ai = - -г Цо^П 1 - In "F5--г при r2 C a;
4	\ c6 fl /
1	c2
Лё = — — Цо^А2 1П —у- ПрИ Г2 > fl, 4	?2
где r2 — расстояние от оси второго провода до той же точки наблюдения.
Вне проводов
1	..2 г-2
4С = 4' + A:=-p0Ja2ln 4^-.
За точку нулевого векторного потенциала примем начало координат (гА = г2), тогда Cj/Cj = 1 и
.	1 Т 9 1 Г2
Ае = — HoJa In — при Г1 > а и г2 > а.
Z	Г1
Внутри первого провода
1	( Г2	О2 \
41=4; + 4>Tn0Ja211 - ‘ -In-p-j
при а и 2d — a^r2^2d + a.
Внутри второго провода
А 2 ~ Ае 4- Ai 5» — Цо J а I — 1 4- -^у 4- In -^у I
при г2 а и 2d — а < Tj 2d 4- а.
Уравнения линий магнитной индукции вне проводов определяются из уравнения (17.6): Ае = const, т.е. r2/i/\=K. Это уравнение такое же, как и уравнение для семейства эквипотенциален электрического поля двух заряженных осей, совпадающих с осями рассматриваемых проводов. Таким образом, линии магнитного поля вне проводов двухпроводной линии совпадают с эквипотенциалами электрического поля той же линии, если можно считать, что эквивалентные электрические оси совпадают с осями проводов.
Уравнение линий магнитной индукции внутри первого провода определяется из уравнения Xj = const, т.е. 1 — (г2/а2) 4-4- In (г2/а2) = С. Если задана точка координатами ri = г\ и г2 = г2, через которую должна пройти искомая линия, то это уравнение примет вид: [г? - (r'i)2]/a2 = In [r2/(r2)2].
Некоторые линии магнитной индукции построены на рис. 17.30Р.
Магнитный поток на единицу длины линии, пронизывающий контур, продольные стороны которого проходят через точки бив, Фбв = Аб - Лв, что следует из соотношения (17.4). 588
Максимальный поток будет в том случае, когда точки бив лежат на оси х симметрично относительно начала координат внутри проводов (рис. 17.ЗОР), при этом (г2 - 2d}2 а2
а2
'бв - 24i - 2я
где учтено, что на оси х имеем г2 = (г2 — 2d)2.
Максимальное значение потока определяется из условия d®6e/dr2 = 0 или r2 — 2dr2 — а2 = 0, откуда r2 = d + ]/d2 + а2. В точке б максимальное значение имеет векторный потенциал, а магнитная индукция равна нулю. Таким образом, максимальный магнитный поток
ц01 ( l/d2 + a2-d ]/d2 + a2 + d\
Ф^=— V-------------а---+,П------а-----}
При указанном в условии задачи соотношении 2d/а = 4 получим: Фтеях = 1,9|10//я.
17.31 (Р). Определить магнитную индукцию вне проводов двухпроводной линии задачи 17.30 и внутри первого провода. Построить зависимость Ву (х) при у — 0.
Решение. В решении задачи 17.30 получено для магнитного поля вне проводов
1	2 (х + d}2 + у2
Ае = — go’J" in ;-----г,
е 4 ™ (х - d)2 + у2
и
где учтено, что г2 = (х + d)2 + у2 и г2 = (х — d)2 + у2, следовательно,
Внутри первого провода
В частности, при у = О
Зависимость Ву(х) при у=0 показана на рис. 17.31Р.
<- Рис. 17.31Р
17.32.	Пользуясь выражениями для векторного потенциала, найденными в задаче 17.30 (см. решение), определить магнитный поток на единицу длины, который пронизывает соседнюю
двухпроводную линию, расположенную параллельно рассматриваемой (рис. 17.32). Соотношение размеров: Aa = 2d = b —
= 4di — 2h. Провода второй линии тонкие — их радиус намного меньше расстояния dt.
17.33.	Рассчитать индуктивности эквивалентной схемы
(рис. 17.33) трехпроводной трехфазной линии на единицу ее
длины без учета влияния земли. Расстояния между проводами
А о
В о
С о
равны соответственно dAB, dBC и dCA. Радиусы тонких проводов одинаковы и равны г0.
Указание. Магнитные потоки определяются после записи выражений для
рис	векторного потенциала, которые полу-
чаются аналогично тому, как это сделано в решении задачи 17.28 (для поля вне проводов).
17.34.	а) По тонкой немагнитной цилиндрической оболочке
радиусом а вдрлъ ее оси протекает постоянный ток I, Определить векторный потенциал внутри At и вне Ае
>болочки.
б)	Некоаксиальный кабель состоит из сплошного внутреннего медного провода радиусом г0 и тонкой цилиндрической медной оболочки радиусом а. Оси внутреннего провода и оболочки находятся на расстоянии b друг от друга (рис. 17.34). По кабелю протекает постоянный ток I.
Определить векторный потенциал в проводе Лх, между проводом и оболочкой Л2 и вне оболочки А3, приняв векторный потенциал в бесконечности равным нулю. Найти уравнения линий магнитной индукции в каждой области.
Рис. 17.34	Рис. 17.35
17.35.	а) По немагнитной трубе (радиусы и а2) вдоль ее. оси протекает постоянный ток I.
Определить векторный потенциал внутри трубы Ао, в теле трубы Ai и вне трубы Ае.
б) По некоаксиальному кабелю (рис. 17.35) протекает постоянный ток I.
Определить векторный потенциал во внутреннем медном проводе Ль между проводом и медной оболочкой Л2, вне оболочки Л3 и в оболочке Л4, считая векторный потенциал в бесконечности равным нулю. Показать, что из решения этой задачи предельным переходом при толщине стенки оболочки, стремящейся к нулю, т. е. при а2 получается решение задачи 17.34,6.
17.36(Р). Многослойная обмотка бесконечно длинной катушки с током плотностью J = const имеет внутренний радиус гь внешний — г2.
Считая обмотку равномерной и пренебрегая толщиной изоляции между витками, определить векторный потенциал Л и магнитную индукцию В: 1) внутри катушки; 2) в обмотке и 3) вне катушки.
Показать, как изменится решение задачи, если плотность тока J = К(г2.
Р е ш е н и е. В цилиндрической систетие координат с осью г, совпадающей с осью катушки, отсутствует зависимость поля от координаты z, так как катушка бесконечно длинная. Кроме того, поле симметрично относительно оси катушки, т.е. не зависит от координаты а. При этих условиях векторный потенциал удовлетворяет уравнению Пуассона (17.8):
где J = Ja и А « Аа.
Решение этого уравнения запишем отдельно для каждой из областей:
г С
1)	при г < Ti задано Л = 0 и At == Ci~ Н-—;
2 г
г2
2)	при ri < г < г2 задано J2 = J = const и А2 = ~Ho*J -у +
+ ^2 “у + С3/г, л*
г Сб
3)	при г2 < г задано J3 = 0 и А3 = С4— И---•
Вектор магнитной индукции найдем по (17.3). Он имеет
только одну составляющую В2 - В = -у — (гЛ), т.е. 1)	=
= Ci; 2) В2 = — Цо/г + С2; 3) В3 == С4.
Постоянные находятся из условий (17.11) и (17.9), т.е. равенства векторных потенциалов и напряженностей магнитного поля при г = и г = г2, а также из условий, что вне катушки поле отсутствует, а на оси оно конечно
Cl — 1W (г2 ~~ г1)> б?2 —	; Сз ~-------rli
при этом
A =	- n)г; Bi = ц07 (r2 - rt);
Если плотность тока J = К/г2, то изменится решение в области rj < г < г2:
,	г,
Л2 = ЦоК +
Вид решения внутри и вне катушки останется прежний. Постоянные определяются из тех же условий, что и выше. В этом случае
Ai —
А* Цо-K^l 2г^	2г);
17.3	. Мапштное поле в присутствии магнитных тел
В этом параграфе помещены задачи, в которых имеются границы раздела между магнитными средами с различными значениями магнитной проницаемости. Такие задачи рекомендуется решать либо интегрированием уравнения Лапласа для скалярного магнитного потенциала фм, связанного с напряженностью магнитного поля выражением (17.16), либо методом отображений от плоских и цилиндрических поверхностей. В этом же параграфе есть задачи по определению медленно изменяющегося магнитного поля в средах с магнитными потерями.
17.37	. Пользуясь известными выражениями для поля диэлектрических цилиндра и шара, помещенных в однородное электрическое поле, вычислить размагничивающий фактор N и магнитную проницаемость тела для шара и цилиндра.
Составить зависимости проницаемости тела цгт = В/Во от 1^, где В — нядуктщя внутри тела, Во — индукция внешнего однородного поля до внесения в него тела, рт — относительная магнитная проницаемость материала тела.
17.38	(Р). На оси х длинной катушки находится образец, однородно намагниченный параллельно оси с М — Мх == = 8000 А/см.
Определить потокосцепление магнитного потока, обусловленного образцом, с витками катушки. Известно, что в отсутствие образца напряженность поля, создаваемого током, который проходит по обмотке катушки, Н = Нх — kwol во всех
точках области, занятой образцом (kw0 = 100 см"1, если ток I — в амперах и напряженность поля — в амперах на сантиметр).
Образец: А) цилиндр с сечением S = 1 мм2 и длиной I = 2 см; Б) тонкостенная трубка, толщина стенок 100 нм, диаметр трубки d — 2 мм, длина 1 = 2 см; В) вытянутый эллипсоид с полуосями а = 1 см (ось вращения, параллельная оси катушки) и Ь = 1 мм; Г) диск толщиной 5 = 200 нм, диаметром d = 2 см (диаметр диска совпадает с осью катушки); Д) сплюснутый эллипсоид вращения с полуосями: а = 200 нм (ось вращения перпендикулярна оси катушки), b = 1 см.
Решение. В интеграле (17.26) по условию HjM = HjM = = const, при этом
Ч< =	= ц0 (Ц)МК
Численные значения даны в ответах.
17.39	(Р). Рассчитать магнитное поле внутри, вне и в стенке феррохмагнитной трубы, находящейся во внешнем однородном
нитного потенциала (17.16),
поле с индукцией Во (рис. 17.39). Относительная магнитная проницаемость материала трубы ц2г = = цг. Определить коэффициент экранирования К = BJBq, где -индукция внутри трубы.
Решение. Так как в рассматриваемой области поля отсутствуют токи, то rot Я = 0 и магнитное поле потенциально. Введя функцию скалярного маг-применив цилиндрические коорди
наты (см. приложение 4) и выбрав фм = ф = 0 ПРИ г = 0, реше-
ние уравнения Лапласа (17.19) можно представить в виде
1)	фх = (С\г + C2r) cos а при г < гг ;
2)	Фг = (C3r + С4/О cos а при < г < г2;
3)	фз = (С5г + Сб/г) cos а при г > г2.
При г = 0 поле должно оставаться конечным, поэтому С2 = 0. Труба заметно искажает внешнее однородное поле в точках, находящихся вблизи трубы. Вдали от трубы (г -> оо) ее искажающее действие мало и поле остается однородным, т.е. И = Нх = Но и фз = — HqX = —H0rcosa, отсюда следует, что С5 = -Яо.
Остальные четыре постоянные определим из граничных условий при а) г = г{ и б) г = г2:
а)	Фх = Фг и по (17.10) ц1г ckpj/Sr = ц2г дф2/дг, т. е.
Ciri = С3Г1 + CJrY и Cl = MG ~~ C4A1);	(1)
б)	аналогично
С3Г2 + C4/r2 = ~#0г2 + Сб/Г2 и
Hr (Сз - Q/r2) = (- Но - Сб/г1).	(2)
Совместное решение четырех уравнений (1) и (2) дает: Ci = 4ц,р; С4 = 2 (цг - 1) г?р; С3 = 2 (pr + 1) р; Сб = (ц2 - 1)(г? -- rj) р, где р = Hori/[rJ (цг - I)2 - ri (цг + I)2].
Таким образом, скалярные магнитные потенциалы найдены:
<Pi = 4цгрг cos а = 4цгрх;
<р2 = 2р [(р, + 1) г + (цг - 1) r?/r] cos а;
<Рз = [ —Ног + (р2 - 1) р (г? - r^)/r] cos а.
Напряженность магнитного поля в каждой области определим по (17.16):
1)	внутри трубы
Hi = Hlx = -д^/дх = — 4цгр, т.е. внутри трубы поле однородно (при однородном внешнем поле И 0);
2)	в стенке трубы
Я2г = -d^/Sr = —2р [(ц, + 1) - (ц, - 1) r?/r2] cos а;
Н2а = - Scp2/r За = 2р [(цг + 1) + (ц, - 1) гЦг2] sin а;
3)	вне трубы
Н3г = -Зсрз/йг = [Но + (и2 - 1) Р (г21 - rj)/r2] cos а;
Н3а = -Scps/rda = [-Но + (р,2 - 1) р (rf - r$)/r2] sin а.
Коэффициент экранирования
„ Bl = Н1 = -4р,р =_______________W;____________
Во Но Но г2 (Р. + I)2 - ri (р, - I)2 ’
Если ц, » 1, то К = 4г2/ц, (г2 — г2).
17.4	0. Параллельно поверхности толстого листа с относительной магнитной проницаемостью, намного большей единицы, на расстоянии h = 10 см протянут провод с постоянным током I= 100 А (рис. 17.40).
Определить зависимости индукции от координаты х при у = 0 и от координаты у при х = 0. Вычислить силу притяжения провода к листу на единицу его длины.
17.4	1 (Р). Параллельно оси бесконечно длинного цилиндра радиусом г0 на расстоянии b от оси расположен провод с постоянным током I (рис. 17.41). Относительная магнитная проницаемость цилиндра ц1г, окружающей среды — ц2/-
Определить векторный потенциал магнитного поля внутри и вне цилиндра.
Решение. Задачу решим методом изображений. Магнитное поле внутри цилиндра представим как поле истинного тока I и фиктивного тока расположенного на расстоянии а от оси цилиндра (рис. 17.41Р, а) в среде с такой же магнитной проницаемостью, как и у цилиндра. Фиктивный ток Ц должен создать внутри цилиндра такое же магнитное поле, как и связанные поверхностные токи на границе раздела обеих сред.
Поле вне цилиндра представим как поле двух фиктивных токов: тока 12, расположенного там же, где и истинный ток I (ряс. 17.41Р, 6), и тока /3, расположенного на оси цилиндра. При этом магнитная проницаемость во всем пространстве такая же, как и вне цилиндра, суммарное действие токов 12 и 13 вне цилиндра должно быть таким же, как и суммарное
действие истинного тока I и связанных поверхностных токов на границе раздела. Токи Zb Z2 и 13 и расстояние а нужно выбрать такими, чтобы были удовлетворены граничные условия.
Векторный потенциал магнитного поля в точке М внутри цилиндра (см. решение задачи 17.28)
Л1= - (Ип Г! + Л h Г2) + Сх	(1)
и вне цилиндра
Л2 = - ^2-(/3 In г +In rO+Q.	(2)
Естественно, что векторный потенциал имеет только осевую составляющую (А == Az), так как поле плоскопараллельное.
На границе при г — г0 по (17.11) и (17.9)
Ai = А2 и (1/y.oMi,) BAi/Br = (l/HoUzJ ВА2/8г
или, как следует из второго условия,
1 б/г, 1 dr2 _	1	1 drt
dr 1 r2 dr 3 r 2 rt dr
(3)
Из рис. (17.41P, а) следует, что г2 = г2 + b2 — 2rfecos a; r2 = r2 + a2 2ra cos a, следовательно, dr^/dr = (r — b cos а)/^; dr2/dr — (r — a cos a)/r2, при этом уравнение (3) при г = г0 приводится к виду
/т т ч r0 - cos a _ rQ - a cos a _ 1 Л ...
V-h) -2—-2--------+ Л -^—2----------h — = o. (4)
rl	r2	r0
Кроме того, h + Л = Д	(5)
что следует непосредственно из закона полного тока для контура, охватывающего цилиндр на рис. 17.41 и соответственно на рис. 17.41Р, б.
Подставив (5) в (4), получим:
/ r0 - b cos a 1 \ r0 - a cos a
2з I “2	/ + Zi----------= 0.	(6)
\ ri	ro)	r2
Это уравнение после замены и г2 приводится к виду 2roab (Z3 — ZJ cos2 a + [Zt (2r%b + r$a + ab2) -
- Z3 (2ab2 + br% — a2b)] cos a +
+ “(ro + о2) ” I So (rg + b2) = 0.	(7)
^0
Так как уравнение (7) должно удовлетворяться при любых а, то должны быть равны коэффициенты при каждой степени
cosot, следовательно, Л =	(3)
Ц (2?оЬ + r2a + ab2) - I3 (2ab2 + Ьг% + а2Ь) - 0;	(9)
Л —0*0 + а2) - Цг0 (г§ + Ь2) = 0.	(10)
го
Из (10) и (8) получим:
а = То/Ь.	(И)
Уравнение (9) удовлетворяется при (8) и (И) и дает тот же результат, что и в (5).
Первое условие теперь можно записать в виде
-plrJlnri - plr/i In г2 + 2лС1/цо =
= -ц2Дз In г о - ц2Д2 In rt + 2яС2/р0
или при г — г0 с учетом (5), (8), (11) и равенства rj/ri — Ь2/г1 получим:
[(И2г “ Hlr) I ~ (Н2г + И 1г) /3] 1П Г1 +
+ (И2, - Hir) Ц In Го + щДз In ь =	2п.	(12)
Но
Так как это соотношение не должно зависеть от то
1з = 1 (И2г - Ц1г)/(Ц2г + И1Д	(13)
Приняв на оси цилиндра (ri = Ь, г2 == а) векторный потенциал равным нулю, найдем из (1) постоянную
Сь =	(In Ь +	^-1п а)
2д \ ц2г + ц1г /
и из (12) постоянную
р _ МоМ1гМ2г I /1 , MlrV i ( M2r _L
с2-------------— I 1 4---in------1-1------Ь 1 1 in r0 .
Mir + M2r L\ M2r / r0 \Mlr /
По (1) и (2) векторный потенциал
MoMirM2r / ГЛ . Mir V b  Л	MirV a
Mir + M2r 2л L\	M2r J	\	p2r J r2
MoMlrMlr I (\^2r	A1„ ro ,
Hl, + ц2, 2n L\ Ulr / г
+ 2 in Zk + (+ Л ln A'.
Г1 \ М2Г J r0 _
17.42. Определить вектор магнитной индукции (в цилиндрических координатах) внутри и вне цилиндра предыдущей
задачи.
17.43(Р). Считая известным
решение задачи 17.41, полу-
чить уравнения линий вектора магнитной индукции внутри и вне цилиндра. При ц1г/ц2г = 1/2 и
fc/r0 = 1/2 построить линии, проходящие через точки: 1) г/г0 = 5/4;	-
- 7/4; 2) r/r0 « 1; rjro = 1/2; 3) r/r0 -= 0; rifro = 1/2; 4) r/r0 = 1/4; r,/r0 = = 1/4.
Решение. Уравнения линий вектора магнитной индукции внутри цилиндра определяются уравнением = const или в соответствии с выражением (14) из решения задачи (17.41);
(1)
(ц2г + Цц,) in — + (ц2, - Hir) In — = к Г1	г2
Для линии, которая должна проходить через точку = г\; г2 = г2, постоянная определяется по выражению
<Нг, + Н1г) In -у- + (ц2г - ц1г)1п-^- = К1.
Г1	г2
После подстановки значения в уравнение (1) получим уравнение линий магнитной индукции внутри цилиндра
ln£L=!^+±lLln2x.	(2)
Г2 Н2г - Mir 'I
Уравнение линий вектора магнитной индукции вне цилиндра определяется уравнением Л2 — const или с учетом выражения (15) из решения задачи (17.41):
— - 1)1п — + 2 In — = К2.
Ц1г / г П
Уравнение линии вектора магнитной индукции вне цилиндра, проходящей через точку г = г';	— ri,
Для заданного отношения ц1г/ц2г = 1/2 уравнения (2) и (3) упрощаются:
Г 2 = rZ2ri3/ri И Г — г'г^/г2.
Линии вектора магнитной индукции, проходящие через заданные точки, показаны на рис. 17.43Р.
17.44.	В ферромагнетике (ц2г 1) просверлено цилиндрическое отверстие радиусолМ г0 (рис. 17.41). Параллельно оси отверстия на расстоянии b от нее проходит провод с постоянным током I.
Введя фиктивные токи Ц, /2, 13 (см. решение задачи 17.41), определить векторный потенциал магнитного поля внутри отверстия и найти уравнение линий магнитной индукции. При Ь/г0 = V2 построить линии, проходящие через точки: 1)	—
= 5/4; r2/r0==ll/4; 2) ^ = 1; г2/г0 = 10/4; 3) rJrQ = 3/4; гг/го = 9/4; 4) rjro = 2/4; r2/r0 = 8/4; 5) rjro = 1/4; r2/r0 = 7/4.
Рис. 17.45P
17.45.	Проводник с постоянным током I проходит параллельно оси бесконечно длинного цилиндра (рис. 17.45) на расстоянии а от нее. Относительная магнитная проницаемость цилиндра ц1г, окружающей среды ц2г.
Определить векторный потенциал магнитного поля внутри Ai и вне Л2 цилиндра, принимая =0 на оси цилиндра.
Указание. Задачу можно решить аналогично тому, как была решена задача 17.41, вводя фиктивные токи Ц, 12 и (рис. 17.45Р, а, б). Токи /2, 73 и расстояние b определяются из граничных условий.
17.46.	Определить вектор магнитной индукции внутри и вне цилиндра задачи 17.45.
17.47.	Считая известным решение задачи 17.45, определить уравнения линий магнитной индукции: 1) внутри и 2) вне цилиндра. При ц1г/р,2г = 5 и а/г0 = 2 построить несколько линий.
17.48(	F). Между проводами двухпроводной линии, находящимися в среде с относительной магнитной проницаемостью ц2г, симметрично расположен ферритовый цилиндр радиусом г0 с относительной магнитной проницаемостью ц1г (рис. 17.48). Расстояние между проводами 2а, радиус проводов р0 с г0.
1)	Пренебрегая магнитным потоком внутри проводов, определить: а) индуктивность линии Lo на единицу ее длины; б) насколько индуктивность этой линии больше индуктивности такой же линии без ферритового цилиндра.
2)	Повторить расчет при условии, что ц1г » g2r.
Решение. 1а) Для решения этой задачи можно воспользоваться результатами решения задачи 17.45.
Рис. 17.48
Рис. 17.48Р
Векторный потенциал магнитного поля вне цилиндра обусловлен действием истинных токов I и фиктивных токов 12 (рис. 17.48Р). Фиктивные токи 13 (рис. 17.45Р, б) в рассматриваемой задаче компенсируют друг друга, поэтому (см. ответ к задаче 17.45 и рис. 17.48Р и 17.45Р, б)
^2 ~ Р-оИзг -у- I ш — + — — ш — 1.
271 \ Г2 Ц1г + Ц2г /
На поверхности правого провода г4 2а\ г2 = р0; г3 = = а + b = а + г%/а;	~ а — b = а — г%/а, так как b = r^/а (см.
решение задачи 17.41), и векторный потенциал
Л2 + ~ РоР-2г
z.71
М1г ~ р3г
Р1г + Ц2г
а2 + Гр а2 - rl
На поверхности левого провода Л2_ == — Л2 + . Поток на единицу длины линии по (17.5) Ф0 = Л2 + - Л2- =2Л2 + . Ин-дукгивность на единицу длины линии
, Фо Н0И2, Л 2л щ, - ц2г а2 + г% \
/	V Ро Plr + g2r а2 - Го J
16) При отсутствии цилиндра (Ц1Г = ц2г)
т > _ HoHir 1	.
Ьо —-------In —,
Я Ро
AL0 = Lo - Ь'о =
Я
Ц1Г - а2 + rj
1П 2 л •
Н1г + Н2г Я - >o
2) Если ц1г » у2г, то
L =	in
я \ Po
a2 + r8 \
2	2~ Ь
a2
№r ln
fl2 4- Гр a2 - Го *
&L0 —
я
17.49(P). Провода линии расположены параллельно оси цилиндра (рис. 17.49). Относительная магнитная проницаемость цилиндра ц1г, окружающей среды p2r. Радиус провода р0 намного меньше радиуса цилиндра г0 и расстояния между проводами 2Ь.
Рис. 17.49
Рис. 17.49Р
Пренебрегая магнитным потоком внутри проводов, определить: а) индуктивность линии Lo на единицу ее длины; 6) индуктивность Lq при ц2г = Ц1г.
Решение, а) Расчет векторного потенциала выполним аналогично расчету в задаче 17.41. Векторный потенциал магнитного поля внутри цилиндра обусловлен действием истинных токов I и фиктивных Ц (рис. 17.49Р). Поэтому аналогично выражению (14) в решении задачи 17.41
л	/ ГЛ +nuWlnA_ln±V
Н1г + ц2г 2тт ц2г / К г 1 г3 J
На поверхности правого провода ri = р0; r2 = а — b -— г2/Ь — Ь, так как а = г$/Ь (см. решение задачи 17.41); г3 == — 2d; г4 = а + b =	+ b и
На поверхности левого провода = — А1 + . Поток на единицу длины линии по (17.5) Ф0=Л1+ —	= 2Л1 + . Ин-
дуктивность на единицу длины линии
Фо ИоШгМгг 1 ГЛ ,	,
Lq — —— =--------------114------I In----h
1 Plr 4“ |12r 71 \	M-2r /	Po
Hi A. $ + ь2 н / n r2 h2 P2r / r0 ~~ &
б) При |i2r = Hir получим: LQ = —— In 7C
2b
Po’
17.50(P). На ферритовое кольцо (рис. 17.50) с относительной комплексной магнитной проницаемостью ^ = 400—J20 нанесена обмотка с числом витков w = 100. Размеры кольца: — 15 мм; г2 — 20 мм; h = 5 мм. Обмотка подключена к источнику синусоидального напряжения с Um = 10 В; f — = 1000 Гц.
Определить активную мощность, выделяемую в единице объема кольца, в зависимости от расстояния г (от оси).
Сопротивлением обмотки и рассеянием пренебречь.
Решение. Определим вначале мощность, выделяющуюся в цилиндрическом слое высотой Л, радиусом г и толщиной dr.
Магнитный поток в слое
= hB dr == dr,
где Н — iw/2nr‘, ц, = р' — /ц".
Напряжение на зажимах обмотки, соответствующее этому потоку,
•	•	Iw
dU = Jcow d& = /a)wpi0|j.r -z—h dr.
— Znr
Комплексная мощность
dS = /* dU = <оцоН2 (ц? 4- jW) dV = So dV,
где So = Pq + jQo — мощность, приходящаяся на единицу объема; dV — объем слоя.
Удельная активная и реактивная мощности: Ро =соМоИг/Н2-б0 = соцоРгН2. Эти выражения для удельных мощностей зависят от формы магнитопровода.
Для рассматриваемого кольца
U = dU =
откуда
1 = 2яС'7./сон’2ЦоР'Л In — и Н = | Н | =--------^7—7—т-r -Ц
“ ГХ	ор0wprh In (r2/ri) г
где pr = | pr |.
Удельная активная мощность p___________________^U2	1 _ 0,38 R , 3
°	C0W2po|Ll?/l2 In2 (r2/ri) r2 r2 T'CM ’
где r — в сантиметрах.
17.51	(P). Определить мгновенное значение силы, действующей на 1 м провода с током i = 20 • 104 sin 1000f А, который находится на высоте h = 20 см над непроводящим магнетиком (ферритом) с относительной комплексной проницаемостью цг = 1оо — до.
Решение. Применив метод изображений для определения поля в среде, где расположен провод с током, найдем фиктивный ток: ilm = 1т (цг — 1)/(цг + 1) = 1т • 0,98 z. — 0° 6,8'. Индукция магнитного поля на оси провода, обусловленная фиктивным током /1от, и ее мгновенное значение
Bt =	-r-г-sin(1000г - 0’6,8').
4тс/1
Мгновенное значение силы, действующей на провод, f = В til = 0,98 • 104 (1 - cos 20000 Н.
17.52.	Определить, в какой момент времени tt магнитная индукция поля, создаваемого синусоидальным током G == = 100 sin (104t 4- 30°) А двухпроводной воздушной линии, которая проходит параллельно плоской поверхности магнетика с относительной комплексной магнитной проницаемостью |ir = 10 — J4, совпадает с полем другого тока i2 в той же линии при отсутствии магнетика. Найти значения тока i2 и намагниченности магнетика М в этот момент времени.
17.53.	Определить потери на 1 м в непроводящем магнетике с относительной комплексной магнитной проницаемостью 604
= 4 — j’5, если над его плоской поверхностью на расстоянии J = 0,5 см находится двухпроводная воздушная линия. Ток в линии i = 2 sin 106t А. Расстояние между проводами линии = 10 см. Потерями в проводах линии пренебречь.
Определить, насколько комплексное сопротивление этой линии больше комплексного сопротивления такой же линии при отсутствии магнетика.
17.54.	Длинный ферритовый цилиндр радиусом г0 = 0,25 мм с относительной комплексной магнитной проницаемостью р1г = 400 - /4 помещен в однородное магнитное поле Но = 0,1 sin 2л х х 10бГ А/см, перпендикулярное оси цилиндра (рис. 17.54).
Определить индукцию Вг внутри цилиндра и мощность, поглощаемую в цилиндре на единицу его длины. Найти мгновенное значение вектора В в точке Л, лежащей у поверхности цилиндра в окружающей среде.
17.55(	Р). Внутри ферритового магнитопровода с относительной комплексной магнитной проницаемостью р2г = 3,5 — /3 находится сферическое включение из диэлектрика (ц1г = 1). Диаметр включения 2Я0 намного меньше размеров магнитопровода. Вдали от включения поле однородное: HQ = = 1 sin 2тс • 10бt А/см.
Построить геометрические места концов векторов В и Н за период в точке А, находящейся в феррите у поверхности сферы (рис. 17.55). На построенных кривых обозначить точки, соответствующие одним и тем же моментам времени.
Решение. Применив известное решение для шара в однородном поле к скалярному магнитному потенциалу в комплексной форме, получим для поля вне шара
 / Р1г - Й2г ЯП
Ф2м = - н0 я - -И1Г -J- cos е, \ Р1г “Ь 2ц2г В. J
откуда по (17.16) в сферической системе координат (см. приложение 4)
. / ulr — Р2г Ко \ . л
H2fl=-Ho 1-	° sin0
и
#2R = М^гР-О^г/?; #20 = Р2гИо^2О-
Для рассматриваемой точки (# = Ro; 0 = 45°)
H2R = Но---------------U = 0,15 г. 36° 50' А/см;
Р1г + 2ц2г J/2
3ll2r 1
Н20 = -Но-----------------0,69 л -3е46' А/см.
Pir + 2ц2р 1/2
Но
Рис. 17.55Р
Рис. 17.55
Мгновенные значения
H2R = 0,212 sin (сот + 36° 50') А/см;
Н29 = -0,975 sin (сот - 3°46') А/см;
#2л — Но • 0,975 sin (cat — 3°46') Вб/см2;
#2о = ~Но • 4,5 sin (cot — 44° 22х) Вб/см2,
где ц0 = 4л 10“9 Гн/см.
При соответствующем выборе масштабов геометрическое место для обоих векторов одно и то же (рис. 17.55Р, где указаны в градусах значения cot).
17.4.	Энергия и силы в магнитном поле
17.56.	Индуктивность однослойной короткой катушки на низкой частоте приближенно определяется выражением L = = 0,04r2w2/(9r + 10Z) мГн, где г — радиус витков, м; I — длина катушки, м; w — число витков катушки.
Определить силу, стремящуюся растянуть катушку, и силу, стремящуюся разорвать витки катушки, при токе I = 2,45 А, если г = 0,05 м; I = 0,2 м; w = 100 витков.
17.57.	Две катушки вариометра соединены последовательно. Индуктивности катушек Lx — 90 мкГн и Ь2 = 160 мкГн.
Коэффициент связи между катушками к = 0,4 cos а, где а - угол между осями катушек.
Определить вращающий момент, действующий на каждую из катушек, при к = 0,24 и токе в катушках 1 = 10 А.
17.58.	На стальное кольцо нанесена обмотка, содержащая w ₽ 600 витков. В кольце сделан поперечный зазор длиной ц = 0,4 мм. Средняя длина магнитной линии в кольце 12 = = 0,4 м. Поперечное сечение кольца S — 10"3 м2. Относительная магнитная проницаемость стали цг = 800.
Определить энергию магнитного поля в стали Wc и в воздушном зазоре 1УВ при токе в обмотке / = 1 А. Вычислив полную энергию магнитного поля, определить индуктивность катушки и силу, стремящуюся уменьшить зазор.
17.59(	Р). При поражении молнией трубчатого молниеотвода труба оказалась сплющенной.
Определить давление, действовавшее на трубу при токе молнии I == 200 кА в предположении, что ток протекал лишь в тонком поверхностном слое трубы (поверхностный эффект). Наружный радиус трубы г0 = 1,25 см.
Решение. Силу, с которой магнитное поле действует на поверхность трубы, определим из выражения Fn = dW/di], где W — энергия магнитного поля, т| — обобщенная координата, Fn — составляющая силы по этой координате.
Применим это выражение к силе, действующей на элемент поверхности dS — lr0 da.
Так как ток сосредоточен на поверхности трубы, то магнитное поле отлично от нуля лишь вне трубы. Если элемент поверхности под воздействием силы переместится на dr, то приращение энергии магнитного поля по (17.23)
dW = - Wo dV = - у ВН dS dr
и сила, действующая на элемент поверхности dS, dF, = cW/Sr = -±-BHdS.
&
Давление
р = dFr/dS = -~ВН=--^ р0Н2 = - 4 Ио (Wo)
2
= -407 Н/см2.
Знак минус указывает на то, что сила стремится уменьшить радиус, т.е. сжимает трубу.
17.60(	Р). Выяснить, можно ли силу в предыдущей задаче вычислить так: индукция В = цо7/2яго> на единицу периметра приходится ток IQ = 1/2пго и сила ? = ^о-
Решение. Таким путем силу определить нельзя. Это можно объяснить следующим образом. Хотя практически ток протекает по поверхности трубы, толщина слоя тока не равна нулю. Если на внешней поверхности токового слоя индукция равна указанному в условии значению В =	то на
внутренней поверхности токового слоя она равна нулю. Следовательно, не все элементы тока находятся в одном и том же магнитном поле. Указанное значение индукции является максимальным. Можно взять среднее значение индукции — максимальной и минимальной (равной нулю), при этом получаются правильные значения силы и давления, найденные в предыдущей задаче. Интересно обратить внимание на то, что решение не зависит от распределения плотности тока по толщине Д тока слоя, если она достаточно мала.
Действительно, сила, действующая на элемент тока, d2Fr = = —BJdV= —BJdSdr, trq J = JZ — плотность тока. В качестве dS выберем элемент цилиндрической поверхности dS = lr da. По (17.1а) при Н = На
т . „	1 6 , ггч Я дН
Jz = rotz Н = — — (гН) = — +
г дг г дг
Сила, действующая на элемент dS,
[г0Н20 + (Н2)ср Д].
Здесь применена теорема о среднем и учтено, что на глубине, большей Д, вектор Н = 0.
Если толщина Д->0, то
dF, = ~^darQH2Q = - 4 HoHo dS
и давление
_ dFr     Но гт2    Но / А dS “	2	0 “	2 \2тгг0 J ’
17.61.	Электромагнит (рис. 17.61, а) имеет обмотку, содержащую 1000 витков, по которой проходит ток 10 А. Зависимость между магнитным потоком и МДС, приходящейся на сталь, т. е. Ф — f представлена на рис. 17.61,6. Сечение воздушного зазора и стали S = 16 см2. Якорь, притягиваясь к сердечнику, совершает механическую работу против внешних сил.
Перемещение якоря из начального положения (зазор /в равен 2 мм) в конечное (зазор равен нулю) происходит настолько быстро, что магнитный поток в течение всего перемещения остается неизменным, при этом происходит уменьшение тока (вследствие наведения ЭДС). После прекращения движения ток возрастает до прежнего значения.
Рис. 17.61
Определить: а) совершенную механическую работу; б) силу притяжения якоря в начальном Fr и конечном F2 положениях; в) количество энергии, поступившей от источника, И’и; г) изменение энергии магнитного поля в стали AHZC и в воздушном зазоре AWB.
17.62.	Решить задачу 17.61 в предположении настолько медленного перемещения якоря (при тех же начальном и конечном положениях), что можно полагать неизменным ток в обмотке в течение всего процесса перемещения.
17.63.	Равномерное магнитное поле в воздушном зазоре магнитоэлектрического гальванометра фис. 17.63) направлено радиально. Индукция поля В = 0,15 Тл. Рамка гальванометра состоит из w = 200 витков, длина активной стороны рамки I = 2,5 см, ширина рамки b — 2 см. Момент сопротивления, развиваемый нитью подвеса при повороте подвижной системы на 1 деление шкалы, равен 61,2-10"6 г  см/деление.
Определить постоянную гальванометра по току, т.е. ток, вызывающий отклонение системы на одно деление шкалы.
17.64(	Р). На рис. 17.64 схематически показан якорь электрической машины, имеющий всего один виток. Продольная
длина якоря * I = 50 см, наружный диаметр якоря D = 20 см, диаметр окружности, на которой расположены провода, d = = 16 см. Относительная магнитная проницаемость стали = = 500. Ток в витке I = 50 А.
Считая поле под полюсами однородным с индукцией В = 1 Тл (при токе в витке, равном нулю), определить значение вращающего момента М, действующего на якорь; оценить силу Г, .действующую на провода, и момент Мо, обусловленный давлением проводов.
Решение. Обозначим индукцию в зазоре слева от проводника Вл, а справа Вп. Так как магнитная проницаемость стали намного больше проницаемости воздуха, то в соответствии с законом полного тока (17.16) можно считать, что (Вл — Вп) 5 = ц07, где 5 — зазор между статором и якорем.
Пусть при отсутствии тока в якоре индукция в зазоре Во, тогда Вл + Вп = 2В0. Энергия магнитного поля в зазоре (в единице объема) слева от проводника = В5/2ц0, справа И^п = = В^/2ц0. Приращение энергии при повороте якоря по направлению движения часовой стрелки на угол Аа
(п2 т>2 X	rj	/ j	\
2/8 — Аа = — Во /3D Аа = IBOID Аа. 2ц0	2ц0 J	2	\ 8	/
Изменением энергии в стали при повороте якоря на угол Аа можно пренебречь, так как цг» 1.
Вращающий момент, действующий на якорь, М = А РУ/А а = = IBqID = 5 Нм.
Силу, действующую на провод в пазу, можно оценить, исходя из следующих соображений. Если паз глубокий, то можно считать, что напряженность магнитного поля в нем приблизительно равна напряженности поля в стали, а индукция в раз меньше, чем в стали. Следовательно, сила, действующая на провод в пазу,
F = — II = 0,05 Н,
Мт
а момент этой силы
M0 = Fd = ^-d = M-^—=8-W~3 Нм. Hr	ОЦг
Таким образом, момент, действующий на провода в пазу, примерно в раз меньше момента, действующего на якорь.
Глава восемнадцатая
СПЕЦИАЛЬНЫЕ МЕТОДЫ РАСЧЕТА ПОТЕНЦИАЛЬНЫХ ПОЛЕЙ
Введение к гл. 18
Метод функций комплексного переменного
Действительная и мнимая части аналитической функции комплексного переменного w (z) = ср (х, у) + jty (х, у), где z = — х + jy, удовлетворяют двухмерному уравнению Лапласа g2(P , 82У	» „	п
дх2 Sy2	дх2 8у2
Естественно, что при этом и функция w удовлетворяет уравнению Лапласа. Поэтому каждая из функций ср и ф может представлять потенциал плоскопараллельного поля, тогда другая представляет функцию потока, при этом w — функция комплексного потенциала.
Уравнение семейства эквипотенциальных линий в плоскости х, у
ср = const (или ф = const).
Уравнение семейства линий поля (силовых) в плоскости х, У ф = const (или ср = const).
Составляющие напряженности поля _ dtp _ дф	дер	дф
дх ду'	у~ ду~ дх'
Комплексная напряженность поля Е = Ех + jEy может быть определена и непосредственно по функции комплексного потенциала w:	*
(18.1)
(18.2)
Поток вектора Е между линиями ф! и ф2 на единицу длины системы (в направлении, перпендикулярном плоскости х, у) определяется как разность функций потока:
Ф = ф1 -ф2.
Например, поле заряженной с линейной плотностью т оси в вакууме, проходящей через начало координат, описывается функцией комплексного потенциала
т .
w — — --------In z + С,
27TEq
где С — Ci 4- jC2 — комплексная постоянная; z = х + jy — re111
при этом
Т 1 С1 .	т
ф --------In—;	----а 4-С2.
2ле0 г	2тсе0
Метод интегральных уравнений
Пусть на некоторой поверхности S распределен заряд с плотностью qs. Потенциал электрического поля элементарного заряда qsdS, рассматриваемого как точечный, г7(р = qs б/5/4тгЕ0£гЯ.
Потенциал поля заряженной поверхности _ q$ dS 4л£0Ег2? ’
(18.4)
(18.5)
здесь R — расстояние между точечным зарядом или элементом dS и точкой наблюдения, в которой определяется потенциал. Если разность потенциалов каких-либо точек известна и равна U, то, совмещая точки наблюдения с этими точками,
получим уравнение
4л£ге0(7 =
'qSdS R
(18.6)
в котором неизвестная функция qs стоит под знаком интеграла — интегральное уравнение Фредгольма первого рода. Аналитические методы решения таких уравнений неизвестны. Для их решения применяются приближенные методы. Один из них — метод алгебраизации.
13.1. Применение функций комплексного переменного
Этот параграф содержит задачи на расчет плоскопараллельных электрических полей, для решения которых целесообразно применение понятия комплексного потенциала, при этом рекомендуется решать более сложные задачи, применяя полученные ранее решения для более простых задач. Построение картин поля помогает лучше понять суть метода и анализировать структуру полей при заданном расположении электродов.
18.1. Определить, поля каких электродов описываются комплексными потенциалами вида: a) w—J41nz+C; б) w = = A In z 4- С, где С — комплексная постоянная.
Получить выражения для функций потенциала (р и потока ф. Найти постоянные А.
18.2(Р). Считая известным выражение для комплексного потенциала заряженной с линейной плотностью т оси, распо-
ложенной в начале координат, w == — —— In z 4- С, найти 2 тс 8 о
1) комплексный потенциал, описывающий поле двухпроводной линии (рис. 18.2);
2) функцию потенциала и функцию потока; 3) уравнения эквипотенциалей и линий поля; 4) часть полного потока вектора напряженности, проходящую через отрезок оси у (на единицу длины двухпроводной линии) от
Рис. 18.2
у = О до у = а.
Решение. 1) Комплексный потенциал положительно заряженной оси, проходящей через точку z = х 4- jy — а, равен
w+ = — ------In fz — я) 4- С19 а отрицательно заряженной оси,
2TC£q
проходящей через точку z = — а, соответственно w_ =
=	---In (z 4- а) 4- С2. Комплексный потенциал поля двух осей
2tc£q
т 1 z 4- а
w — vv+ 4- w_ = -----In-------F C3.
—	— 2jte0 z - a ~
. 2) Положив при | z | = г -> оо комплексный потенциал равным нулю, получим С3 = 0 и
.. т . z 4- а т	z2
w = (р 4- уф = -т,-In------= ------In —,
~	2л£0 z — а	2ле0	Zj
где z2 - r2eja2 и zx —г^1 (рис. 18.2).
Следовательно, функция потенциала <р = Re w = ;~~In—' 2Л£о Г £
т	т
и функция потока ф = Im w = --------(а2 — aj = - ------а0.
2Л£о	2ТГ£о
3) Уравнение семейства эквипотенциалей
Г2/Г1 — const = К.
Это семейство окружностей с центрами на оси х.
Уравнение семейства линий поля
ф = const или ai — a2 = a0 == const.
Это семейство окружностей, проходящих через точки % = а и z = — а, с центрами на оси jy.
4) Значение функции потока для линии поля, проходящей через точку М (рис. 18.2),
 т	2ау
V ~ ШГarCtg а2 — х2 — у2 
Поток вектора напряженности через отрезок оси у (на единицу длины двухпроводной линии) от у = 0 до у = а
. ,	\	< /	т (	2а2	0 \ т
ф(у = а) - ф(у = 0) = —— arctg ,	, -arctg-;- = -т—.
ZTCbg \	G — Q	и j Ч’Со
Это составляет 1/4 часть полного потока.
18.3(Р). Найти выражение для комплексного потенциала поля, создаваемого п параллельными заряженными осями (нити сетки электронной лампы) с зарядами т на единицу длины (рис. 18.3). Оси проходят через точки окружности радиусом а,
лежащей в нормальной к ним плоскости, и расположены на равных расстояниях одна от другой и центра окружности. Подобрать постоянную так, чтобы потенциал в центре окружности равнялся нулю. Получить уравнения эквипотенциалей и линий напряженности поля. Построить несколько эквипотенциалей и линий поля при п = 6.
Решение. Комплексный потенциал оси, расположенной в начале координат (см. задачу 18.1),
W1 = -
т 2rcs0
In z 4- Cj.
Комплексный потенциал оси, расположенной в точке Zi = — a z_ 2тст/п,
(	. 2п \
Т |	J —т I
vv2 = - й-lnlz-яе " / + С2,
2Я£о х	s
где п — общее число осей; т — порядковый номер оси.
Комплексный потенциал всех осей
т= 1
In (z” - а") + С. 2тге0	“
Так как при z = 0 должно быть w = 0, то
С = ^-1п(-Я”), — 2яе0
при этом —И ЛИ	-	/	-Л \
х 1 г - а	т	/	— \
w = — —-----in------— = —• —---In I 1---3- I.
— 2пе0 —а 2л£0 у а у
Записав z для произвольной точки поля в виде z = rz. а, получим:
W = - Т-5—In [1 - (г/йУ.е"”].
2тС£о
Функция потенциала
Г /	\ 2п
X	/ I \
ф = Re w = - -л------In 1 + —	- 2 (r/а)" cos па
—	4тс80 \а)
Функция потока
, т х	sin па
ф = Im w = -----arctg  —----------
~ 2ле0 (ary — cos па
Уравнение семейства эквипотенциалей (<р = const)
1	- К + (r/a)2" v - ^2-Ф cos па = —, ------------при К = е т = const.
2	(г/а)п к
Уравнение семейства силовых линий (ф = const)
f_r_\n____________1___________
\а ] (sin па)/С + cos па
Ha рис. 18.3Р, где ф' = еоф/х, показаны некоторые экви-потенциали и линии поля (пунктир) при п = 6.
18.4.	На цилиндрической поверхности радиусом а на равных расстояниях друг от друга расположены п положительно и п отрицательно заряженных проводов (рис. 18.4). Радиус провода г0 намного меньше расстояния между проводами.
Найти: 1) комплексный потенциал электрического поля, функцию потока и функцию потенциала; 2) емкость системы на единицу длины; 3) уравнения семейства эквипотенциалей и семейства линий поля.
18.5.	На цилиндрической поверхности радиусом а на равных расстояниях друг от друга расположено п положительно заряженных проводов (рис. 18.5). Отрицательно заряженные провода (их тоже и) расположены на цилиндрической поверхности радиусом Ь и смещены относительно положительных на угол [3. Радиус провода г0 намного меньше расстояния между проводами.
Найти: 1) комплексный потенциал электрического поля, функцию потенциала и функцию потока; 2) емкость системы на единицу длины.
Рис. 18.4
18.6(	Р). 1) Найти комплексный потенциал электрического поля, создаваемого центральным положительно заряженным + проводом и параллельными отрицательно заряженными — т проводами, которые расположены на равных расстояниях
друг от друга и симметрично относительно центрального провода (рис. 18.6). Напряжение между центральным проводом и остальными (имеющими одинаковые потенциалы) равно U. Радиус каждого провода г0 намного меньше расстояния между проводами.
2) Определить емкость системы на единицу длины и сравнить ее с емкостью цилиндрического конденсатора, образованного тем же центральным проводом и оболочкой радиусом а при г0/а = 1/40 и и = 6,
3) Найти уравнения эквипотенциалей и линий поля; построить их при г0/а — 1/40 и п = 6.
Решение. 1) Комплексный потенциал можно представить как сумму потенциала обусловленного зарядом +пт на центральном проводе, и потенциала w2> обусловленного зарядами -т на остальных проводах (см. решение задачи 18.3):
w = wi + w2 = ~ --------------In z ----------In (zn - а”) + Ci =
2tcEq 2tceq
Постоянную С легко определить, если задаться потенциалом, например, периферийных проводов, равным нулю. Тогда . 2л j — т этих проводов, т. е. при z = ае " считать:

на поверхности
и г0 п, можно
. Л 2я
а
и
т
Ф = Re и1 = _
~	In 2п
Гл J 3--т
Rein пС-^еУ п -“ а
т . /	rQ \
= —— In I пС — = 0. 2яе0	\	a j
Следовательно, С = а/пг0 и
т . ( zn - ап а w = —-----In ------------
— 2тге0 V £ nrQ
а (<	й” _ ;яя
----- 1 е J nrQ \	гп
Комплексную переменную z для точки М поля (рис. представим в виде z = rejv, тогда
w =	—In
2tceq
18.6)

\2п Й \
откуда определим функцию потенциала: Т , ( а2

\ и а \ — cos па
г /
и функцию потока:
, т	sin па
ф = ------arctg	.
2тге0 (r/a)n — cos па
2) Потенциал центрального проводника (г = г0) при г0 а
тп
2jC£q
а
nrQ
Емкость системы на единицу длины при г0/а — 1/40 и п = 6
пт пт	2яе0 _ 2я£0
U (р+ .а 1 . а 3,37 '
In — + — In--------
r0 п пг0
Емкость цилиндрического конденсатора 2tL£q 21Т£о с = In (п/г’о) = W
с = .	1 In (д/игр) =	_1_
S0 п In (а/г0) п
In п
In (а/г0)
1,086.
Отметим, что при п — а/г0 емкость рассматриваемой системы равна емкости цилиндрического конденсатора с радиусами г0 и а.
3) Уравнение семейства эквипотенциалей (ср = const)
1 + (1 — К2)(г/п)2” г . . Г(п+!)^-1]
cos па =------------------при К =(a/r0)L	у Jn1-. UJ.
2 {ria}
Уравнения семейства линий поля (\|/ = const)
(г/п)" = cos па + (sin na)/N при N = tg-— ф.
т
На рис. 18.6Р, где <р' = 14<р/С7 и ф' = 12еоф/т, представлено семейство эквипотенциалей и линий поля (пунктир).
18	.7(Р). На оси проводящей трубки радиусом b расположен провод радиусом гх (рис. 18.7). Симметрично на расстоянии а от оси расположены п проводов радиусом г0- Радиусы проводов намного меньше расстояний между проводами. Линейная плотность заряда центрального провода каждого из периферийных проводов т.
Определить: 1) комплексный потенциал электрического поля внутри трубки, считая потенциал трубки равным нулю; 2) потенциал центрального провода и потенциалы периферий-
пых* проводов; 3) потенциальные коэффициенты и частичные емкости системы при п = 6; Ь/а — е\ а/гх =20; г0 = г1; 4) как изменится решение задачи, если центральный провод с зарядом
Ti отсутствует.
Решение. 1) Для решения задачи можно применить метод зеркальных изображений, тогда поле внутри трубки будет определяться всеми реальными проводами, расположенными внутри нее, и фиктивными проводами (изображениями проводов), расположенными вне трубки на расстоянии Ь2/а от оси на продолжении радиусов, проведенных из начала координат через эти провода. Суммарный комплексный потенциал (см. решение задачи 18.3)
Uy
Рис. 18.7
In
2К£()
- (W" д z’x/' [(z/а)" - 1] “J
Постоянную С определим из условия, что при z = Ьел потенциал равен нулю:
„ = _r_R 1 f -(fe/a)"^“[(We~J,,,-l]C] =
2пе0 1	[(Ь/а)" е» - 1] J
т 1ПГРТ
2л£0	Ьч/т_’
откуда
апЬ
Аргумент постоянной С определяет только начало отсчета функции потока и не имеет значения в рассматриваемой задаче, при этом
т , (z]b)n - (b/a)n w — -----in---------------------
2rcs0 [(z/а)" — 1] (z/Ь) 1
2)	На поверхности центрального провода, т. е. при z =
wt =	— In
ZTCEq
b\n(ri i* __ I I __ pja a / \ b
откуда потенциал центрального провода ф1= 2^1П
ьу (AY1'’’
а / V1 /
На поверхности периферийного провода z - aej2ianln + + roeJ₽, где т — порядковый номер провода.
Так как г0 д, то
zn = an
Г° ^j(3-2nm/n) a
и
W2 =
~ 2ле0
(а/ЬУ-(Ь/аТс>(v“ "р_ Vm "Т,
Потенциал периферийного провода Г (Ь/а)п - (а/Ь)п
фг=2^1п
п —	4 '
L а	-»
3)	Представив выражение для (pi в виде
Т1 1 ( b \ тг . / Ф1 = ~----In ---- +-7Z----In — ,
2яе0	\г1/	2ле0 \а /
найдем потенциальные коэффициенты:
an =^Д- 1п(Ь/Г1) и а12 = -=2—In (Ь/а).
ZHEq	ZTCEq
Аналогично из выражения для ср2
a21 = ln(b/a) = а12;
2тт£ о
a22 == ~-----ln
2леои
(Ь/аУ - (а/ЬУ nrQ/a
По известным потенциальным коэффициентам легко определяются частичные емкости:
г а22 ~ а12 .
an - ai2
а12 .
Т"’ С22
A где A = <Хца22 - ah-При указанных в условии параметрах
0611 = 0-0	а22 =	а12 — Э-е
2ке0	2я£0	27ГЁО
1	-	-	15 . п -О е 5
С12 — 2ЯЕо 19 •
4)	При отсутствии центрального провода во всех формулах следует положить гг = 0 и тх = О, при этом емкость между остальными проводами и трубой С = С22 — 1/«22-
18	.8 (Р). Найти напряженность электрического поля задачи 18.7. Построить зависимости напряженности электрического поля: 1) от радиуса г при а = 2пт/п (рис. 18.7, в плоскости,
проходящей через оси центрального и периферийного проводов);
_	2Л 7	1
2) от радиуса при а — — I т + — 7*2 \
(рис. 18.7, в меридианной плоскости, делящей пополам угол между соседними периферийными проводами); 3) от угла а при г = b (на поверхности проводящей трубки).
Расчет выполнить для двух случаев: А) пх = 2т i и Б) т = — 2тг Решение. Комплексное вы
Рис. 18.8Р
ражение напряженности поля по (18.2)
dw ти j п dz ~ 2itsoz I ™
1)	При z = r zl 2nm/n
_ tn f Tj (b2n — a2n)rn 1	.
~ 2кеог I tn [b2n — (ar)"] (rn — an) \	r ’
t. e. вектор напряженности электрического поля направлен по
радиусу. Для данных задачи
2тС£рГ
2
1 - (a/r)6 ’
1 +
где знак « + » соответствует случаю А, а знак «-» — случаю Б. Эти зависимости представлены на рис. 18.8Р, а, где N = 2ле0/ти.
„	;^(ш+1/2)
2)	При z = ге "
ти I тх 2тгеог 1 ти
(Ь2" - а2п) rn 1 J ~ (т + 1/2)
[Ь2п + (ar)"] (rn -I- ап) j е
j ^L[fn+ i/2)
= Ere п
Вектор напряженности направлен по радиусу. Для данных
задачи
Смысл знаков такой же, как и в первом случае. Эти зависимости представлены на рис. 18?8Р, б, где N = 2яе0/тн.
3)	При z = beja
тп 2пе0Ь
Ь2п — а2п
b2n + а2п — 2bnan cos на
eJa = Erej\
Для данных задачи
Е,	=» v-Ц? + И = -А-П ± 2), 2ле0Ь	2яе0о
т. е. напряженность поля практически не зависит от угла а.
18.9.	Комплексный потенциал электрического поля w = = jA arccos (zja) + С, где z = х + jy; С = C i + jC2 — комплексная постоянная; А и а — вещественные постоянные.
Найти уравнения линий поля и эквипотенциалей. Принять потенциал точки х = 5п, у = 0 равным нулю и нулевой линией поля - линию, проходящую через точку х = 0, у — 0. Определить постоянные Ct и С2.
18.10.	Внутри проводящей трубки диаметром 2R симметрично расположена лента шириной 2а и малой толщины. Ширина ленты намного меньше диаметра трубки.
Пользуясь ответом к задаче 18.9, определить постоянную А и емкость системы на единицу длины. Найти распределение поверхностной плотности заряда на ленте. Определить, цилиндром какого радиуса следует заменить ленту, чтобы емкость осталась такой же.
18.11.	Пользуясь ответом к задаче 18.9, определить емкость конденсатора на единицу длины, образованного двумя конфокальными эллиптическими цилиндрами при фокусном расстоянии 2а, большем диаметре внутреннего цилиндра 2а и .большем диаметре внешнего цилиндра 2а2.
18.12(	Р). Считая известным выражение для комплексного потенциала заряженной оси [см. задачу 18.2(Р)], найти комплексный потенциал, описывающий электрическое поле бесконечного ряда одноименно заряженных осей, которые расположены на оси х на равных расстояниях b друг от друга (рис. 18.12). Определить функцию потенциала и функцию потока. Найти уравнения семейств эквипотенциалей и линий поля. Построить несколько эквипотенциалей и линий поля.
Решение. Комплексный потенциал заряженной оси, проходящей через точку z = ± mb,
т 27U£q
In (z + mb) + С.
Комплексная напряженность поля оси по (18.2) Ei = т/2я£0 (z + mb).
Рис. 18.12
В
Рис. 18.12Р ->
Комплексная напряженность поля бесконечного ряда осей
т____L + 2£ V 1
2яе0 _ |	”	|2 _ т2^2
т= 1
Обозначив Zi = nz/b, получим: —	со	—
г :	±-2? У 1	.
2яе0 b	Z_j m2it2 — zi _
m= 1
«	* 'Т
Выражение в скобках есть разложенный в ряд ctgzp Таким образом, „ тя ♦ ттг^тс* Е = ----------------rCtgZi =-T——г-ctg—Z.
2яе0 b	2л£0 о b
Комплексный потенциал бесконечного ряда осей по (18.2)
Постоянная интегрирования здесь отброшена, что соответствует выбору точек нулевого потенциала: z = Ь/2 + mb.
Представим sin2 [ z ) в виде \ b
при этом функции потенциала и потока
х
Ф = - — 4яе0
, _ яу . тех \ сп 2 —----cos 2 -г-	;
b	b J
т thpry/b) 2ле0 % tg (ях/b) ’
Уравнение семейства эквипотенциален (ф = const) ch-^bL = cos -^““+ 2К при К = е"4псоф/т =
Уравнение семейства линий поля (\|/ = const) , лу ИХ ~ 2Л8ОФ  , th-£-= Ctg— при С = -tg-------------= - tgф'.
b	Ь	X
На рис. 18.12Р построены линии поля (пунктир) и экви-потенциали. Отметим, что вдоль оси у уже на расстоянии, меньшем, чем шаг ряда Ь, поле практически однородно.
18ЛЗ(Р). Поле бесконечного ряда одноименно заряженных осей, лежащих в одной плоскости (см. задачу 18.12), можно рассматривать как предельный случай поля осей, расположенных на поверхности цилиндра (см. задачу 18.3), если радиус цилиндра г стремится к бесконечности.
1) Что нужно изменить в задаче 18.3, чтобы предельным переходом г -► оо непосредственно получить решение задачи 18.12? Осуществить предельный переход.
2) Решение какой задачи получится, если предельный переход применить к задаче 18.3? Осуществить предельный переход.
Решение. 1) Поле задачи 18.12 симметрично относительно оси х: одна половина всего потока идет в сгорону положительной полуоси у, другая половина - в сторону отрицательной полуоси у. В задаче 18.3 аналогичной симметрии относительно окружности радиусом а нет: через окружность радиусом, большим а, проходит весь поток, а через окружность радиусом, меньшим п, общий поток равен нулю. Эта асимметрия, естественно, останется и при предельном переходе. Чтобы после предельного перехода получилось решение задачи 18.12, в задаче 18.3 следует половину общего потока направить внутрь окружности радиусом п, т. е. в центре окружности поместить ось, несущую заряд противоположного знака, численно равный половине общего заряда всех остальных осей, при этом комплексный потенциал, обусловленный всеми зарядами (и — число осей, т — номер оси), т , . „	пт
w = - -----In (z” — ап) + -А-
- 2яе0	4тсе0
т . zn - ап 2тге0 zn'2

_	J (т + V2)
Пусть потенциал равен нулю в точках z ~ ае п , т. е. на окружности радиусом а посередине между осями. В этих точках zn — —ап и получается С = ( — а”)1/2/( —2а”),
Комплексный потенциал т (z/а)" - 1	т
-- 2яе0 ln — 2j{z]a)nl2 ~ " 2к£0 Ш
Введем новые переменные zr = z — а и z2 — jzt, при этом
-и/2
Если расстояния по окружности радиусом а между соседними зарядами одинаковы и равны Ь, то 2тса - nb и (zja)nl2 = = (1 - j2nz2/nb)n[2 = (1 + 2z3/n)n/2, где z3 = -jz2n/b.
При неограниченном возрастании п выражение ^14-
„ \«/2
,	^3 )	*3
+ п/г)
Окончательное выражение для комплексного потенциала
w = — -----In sin -г- z2
- 2Я£О \ b
не отличается от полученного другим путем в задаче 18.12.
2) В задаче 18.3 было получено выражение для комплексного потенциала п заряженных осей, расположенных на окружности радиусом а:
т t Г, МП
2it£o \ a J
Аналогично тому, как было получено выше, / - \ л
lim ( —) -+е~'2*--г/ь при z2 = х2 +jy2 п х \ а /
-^ln(l - e-^6) = -
ZTTEq	ZTCEq
In е jKZ-2/b2j sin-£- z2 о
< ~ . п к ln2-J
Первое слагаемое соответствует полю, рассмотренному выше. Второе слагаемое — это однородное поле, комплексная напряженность которого по (18.2)
г Т . Я . Т
^2 — n J 1 J -Л к jEy, 2я£о b 2е0о
т.е. поле направлено вдоль оси у2 (рис. 18.13Р). Таким образом, общее поле создается заряженными осями +т, расположен ними на оси х2 на расстоянии b друг от друга, и заряженной плоскостью, параллельной оси х2 и несущей заряд — т/b на единицу длины вдоль оси х2. Плоскость находится на некотором расстоянии h от оси х2, большем, чем Ь, на котором поле осей практически однородно (см. решение задачи 18.12).
Если у2 < —Ь, то | e~i2n-i/b | — elny2‘h < e-2n << 1 и можно считать w = 0, т. е. потенциал всех точек этого пространства (у2 < — Ь) равен нулю — поле отсутствует.
Если у2 = h > b, то | е~&п-2/ь | = e2jly2?b > е2п » 1, при этом
W = -	= Л_[_й + j(x2 + Й/2)]
Z7v8q	l/Eq
и потенциал заряженной плоскости
ф_ — —zh/b&Q.
Если оси заменить тонкими проводами радиусом г0 (г0 Ъ\ то при z2 = mb + потенциал
Ф+ = - ~Re In (1 -	= ^-ln
2tt£q	2k£q 2яг о
Напряжение между проводами и плоскостью т / 1 b	h\
U = (р+ - <р_ = — —In ------+ -г .
£0 у 2л	2лг0	b J
Емкость системы, приходящаяся на единицу длины вдоль проводов и на ширину b вррль оси х2,
С° и _!_1	b	Jl’
2л П 2яг0	b
Это выражение для емкости можно получить и предельным переходом из формулы (п. 4) решения задачи 18.7.

Рис. 18.13Р
Рис. 18.14
18.14(Р). Считая известным выражение для комплексного потенциала бесконечного ряда одноименно заряженных осей, расположенных на оси х на равных расстояниях b друг от друга (см’, задачу 18.12), найти комплексный потенциал знакопеременного ряда заряженных тонких проводов радиусом г0 (г0	Ь), расположенных на оси х на равных расстояниях Ь/2
друг от друга (рис. 18.14).
Определить: 1) функцию потенциала и функцию потока; 2) емкость, приходящуюся на шаг b системы; 3) составить уравнения эквипотенциалей и линий поля.
Рекомендуется дополнительно получить комплексный потенциал рассматриваемой задачи предельным переходом в задаче 18.4.
Решение. Комплексный потенциал ряда положительно заряженных осей
т I тс \ w+ = — -т---In sin -г z .
- 2я£о \ ь -J
Ряд отрицательно заряженных осей сдвинут относительно ряда положительно заряженных осей на Ь/2, поэтому комплексный потенциал этого ряда
. Г • я ( Ь\ in sin \ Z + — b \~	2 /
т
W- = -Г--
2Я£о
Комплексный потенциал всех осей
T	/	IT	\
------In ( COS-j—и ). 2tc£q-\	b J
w — w+ + w_ =
т , / я \ -----In tg — z . 2тгЕ() у Ь J
1)	Отделив действительную часть w от мнимой, получим функции потенциала и потока:
, _ я * я ch 2 — у — cos 2 — х т . b	b
Ф = ~ ~л-----In---------------------;
4яе0
, Я	71
ch 2 — у + cos 2 — x b	b
sh 2^4“
t	b
-----arctg 2t18q
sin 2я
заряженных проводов полуповерхности тонких поло-т. е. положив z = mb +
на
2)	Потенциал положительно чим, поместив точку наблюдения жительно заряженных проводов, + гое^ (г0	Ь). при этом
ф + = v~~ln 2я£0 яг0
Аналогично получим для отрицательно заряженных про-7 ь т
водов при z = mb + — + потенциал ф_ = -ср+.
Напряжение между противоположно заряженными проводами
т , b ----In-----
ЯЕр яко
Емкость, приходящаяся на шаг системы,
Со = т/U = яс0/1п---.
яг0
3)	Уравнение эквипотенциалей (ср = const)
, у ~ х	. 2я£0Ф
ch 2я -у- — К cos 2я — при К = cth-----
b	b	т
F
Уравнение линий поля (ф = const)
1 У ~ х	2я£0\1/
§h 2л “ = С sin 2л — при С = — tg----------------—
b	b	т
18	.15(Р). Для прогрева плохо проводящего материала (£2р, о2 0) в нем уложены две системы проводов (+ и —), изображенных на рис. 18.15.
1) Определить комплексный потенциал и напряженность электрического поля в проводящем материале.
Рис. 18.15Р
2)	Определить проводимость системы на единицу длины вдоль осей проводов и на расстояние b вдоль оси х.
3)	Найти среднюю активную мощность, приходящуюся на квадратный метр граничной поверхности.
4)	Построить зависимости потенциала и напряжен-
ности поля: а) от х при у = U; б) от у при х = 0 и в) от у при х = ± Ь/4.
Напряжение между положительными и отрицательными проводами w = 100 sin 314г В. Радиус проводов г0=4 мм; Ь/2 — 60 см; h = 20 см;. е2г — 10; ст2 = 10"3 См/см.
Решение. Для решения задачи можно применить метод зеркальных изображений. Поле в проводящем материале (е2„ ст2) определяется при этом истинными токами +7 (на единицу длины вдоль осей проводов) и их изображениями +Л, причем
g2 -gl
Н2 +
±Л
. ст2 + >£0£2, ->gp ст2 + 7'(ве0£2г + >е0
При указанных в условии параметрах практически ±Л — = ±/.
1)	Комплексный потенциал ряда истинных- токов определяется так же, как и потенциал зарядов + т в задаче 18.14. Учитывая, что проводники расположены не на оси х, а сдвинуты на расстояние —h вдоль оси у, и применяя аналогию расчета полей токов и электростатических полей, запишем комплексный потенциал в виде
VV1 = -
tgy(z + jh)
Аналогично для изображений
w2 = -
------In
it . ч tg у (Z - jh)
Комплексный потенциал во второй среде
W == W1 + W2 —
i
2лст2
In
Л ,	... Л .
tgy + jh)-tg-y(z — jh)
Напряженность электрического поля по (18.2)
* dw I Г 1	1
~	_.. ------ у. —. —— — ——-----
dz о2Ь [_ sin 2л (z + jh)/b sin 2л (z — jhj/Ъ
__ 47 ch (2лА/Ь) sin (2лг/Ь) о2Ь ch (4л/1/Ь) — cos 4л (z/b) *
2)	Потенциал положительно заряженных проводов (z = — mb — jh + г0е7₽) при rQ h и r0 b
ф+ = Re w =
Для отрицательно заряженных проводов I z = mb + -z—
— Jh + потенциал ф_ = — ф+. Напряжение между положительно и отрицательно заряженными проводами
...	.	„. I - ( b , 2л/1 \
С/ = ф+ — ф_ = 2ср+ = ----In-----cth —:— 1.
ло2 \лг0 b J
Проводимость системы на единицу длины вдоль осей проводов и на ширину b вдоль оси х
Yo = 4~= —----------------r- 0,0654 См/см = Go.
U , / b , 2nh \
In -----cth —-—
у TD'o b J
3)	Ток, стекающий с 1 м провода, 100
I = UYv « UGq = —=^0,0654 = 4,61 A/m.
1/2
Средняя активная мощность, приходящаяся на 1 м2 поверхности, PQ = UI/b = 27 \ Вт/м2.
и
Рис. 18.16
&2г > <Э2
—о--о---о—
— — +
4а) При у=0 (рис. 18.15Р,а)
• _ 4/ ch (2nh/b) • sin (2nx/b)	_ •
- " <з2Ь ch (4яй/Ь) - cos 4л (x/b) “ д
_ t i ch (2ith/b) + cos (2jtx/b) 2ло2 П ch (2nh/b) - cos (2nx/b)'
46) При x = 0 (рис. 18.15P, 6)
Ф=2^’П
cth it
4в) При x= ±b/4 (рис. 18.15P,6)
= Ёх; ф =0.
На рис. 18.15P обозначено: А =1/2тт2\ B = I/n2b.
18.16	. Решить задачу 18.15 для системы проводов, изображенных на рис. 18.16.
18о2. Метод интегральных уравнений
18.17	(Р). Определить линейную плотность заряда т вдоль уединенного провода длиной I = 50 мм и диаметром 2а — 1 мм. Потенциал провода относительно бесконечно удаленной точки равен U. Рассчитать емкость провода.
Решение. Поле вокруг проводника аксиально-симметричное и зависит от координат г и z, поэтому можно считать, что весь заряд находится на оси провода с линейной плотностью t(z).
Рис. 18.17Р
Выделим на оси провода — на расстоянии от начала координат элемент dzx (рис. 18.17Р,а). Элементарный заряд этого элемента x(zi)dzi. По (18.4) потенциал элементарного заряда в произвольной точке М
^Ф = т (zj dZi/^TtGoR,
(1)
где R = j/r1 2 + (z - Zi)2.
Потенциал поля заряженного провода по (18.5)
1 ^(^1)^1 4яв0 . R о
Для точки
Ф — U и
(2)
М на поверхности провода (г = а) потенциал
i
т (zi)dzi
= Т9
(3)
•где Т = 4я£01Л
Это интегральное неоднородное уравнение Фредгольма первого рода относительно неизвестной плотности т (z), аналогичное (18.6).
Решим это уравнение методом приведения к системе линейных алгебраических уравнений (методом алгебраизации). Разобьем провод на и одинаковых участков с зарядами т,-и будем считать, что внутри каждого участка т, постоянно. Точку наблюдения у, потенциал которой U, возьмем посередине участка провода. В этом случае интеграл (3) заменится суммой
л h'n
Таких уравнений можно написать и (1 < j л).
Таким образом, получается система уравнений вида
II а || -1| т || = || 1 || • 7,	(5)
где || а || — квадратная матрица коэффициентов; || т || — матрица-столбец искомых линейных плотностей зарядов на участках;
|| 1 || — единичная матрица-столбец.
Если i ,	-Л то , 12j - 2i | + 1 о^ = 1п	0..	;	(6) J	| 2j - 2i | - 1
если i =;, то
аи = In [1 + (//ла)2]	2 In (//ла).	(7)
В (6) и (7) учтено, что а <§: /. Вычисления по (6) и (7) дают при л = 5 следующую матрицу коэффициентов:
5,994	1,099	0,511	0,336	0,251	
1,099	5,994	1,099	0,511	0,336	
0,511	1,099	5,994	1,099	0,511	(8)
0,336	0,511	1,099	5,994	1,099	
0,251	0,336	0,511	1,099	5,994	
Вследствие симметрии расположения зарядов Ti = т5 и т2 = = т4, поэтому вместо (8) можно записать матрицу
6,245 1,435 0,511
1,435 6,505 1,099
1,022 2,198 5,994
Решив систему уравнений (5) с матрицей коэффициентов (9), найдем заряды = 0,1267; т2 — 0,1087; т3 = 0,1057.
Заряд провода
q = 2xil/n + 2т2//и + т3//л = 0,5597 = 0,64 • 10’ 12U Кл,
т. е. емкость провода 0,64 пФ.
Для проверки точности решения повторим его, разбив провод на п — 10 частей. Вследствие симметрии расположения зарядов Tj = Tjo j ^2 =	^3 = ^8»	= ^7 5 ^5 ~
Матрица коэффициентов системы (5)
4,726	1,224	0,654	0,503	0,452
1,224	4,758	1,266	0,712	0,587
0,654	1,266	4,816	1,350	0,847
0,503	0,712	1,350	4,951	1,610
0,452	0,587	0,847	1,610	5,714
Решение уравнений (5): Tj = 0,146Т; т2 = 0,115Т; г3 = 0,1097; т4 = 0,1067; т5 =0,1057
На рис. 18.17Р, б приведены результаты расчета при и = 5 (залитые точки) и п = 10 (незалитые точки).
18Л8(Р). Определить распределение заряда вдоль провода задачи 18.17, который находится на расстоянии h = 25 мм над бесконечной проводящей плоскостью (рис. 18.18). Потенциал провода относительно проводящей плоскости равен U.
Рассчитать емкость между проводом и плоскостью.
Р е ш е н и е. По методу зеркальных изображений потенциал поля в верхней полуплоскости определяется зарядами на проводе и их зеркальными изображениями (рис. 18.18Р).
Потенциал поля элементарного заряда x(zx)dz\ и его зеркального изображения в произвольной точке М (см. решение задачи 18.17)
Т (Z1)	t(Zi)dZi
ф 4ite0K+	4ns0R_ ’
где R± = |/(j + h)2 + (z - zt)2.
Потенциал точки M
t(zi)dzt.
Поместив точку наблюдения на поверхность провода, получим:
1
]/4/i2 + (z - zj2
r(z1)dz1 = T,
(Ю)
где Т = 4л£0^-
Перейдем, как и при решении задачи 18.17, к системе алгебраических уравнений
здесь первый интеграл аналогичен интегралу (4) задачи 18.17.
Матрица коэффициентов || а || полученной системы уравнений состоит из двух подматриц:
II а II = 11 а' II -II а" II,	(И)
причем подматрица || а' || такая же, как и в задаче 18.17. Коэффициенты подматрицы || а" || вычисляются по формуле
„	12/ - 2) | + 3 + J/(| 2j - 2i | + З)2 + L2
oti'. = In-----------‘---------
12j - 2i | + 1 + /(| 2j - 2i | + I)2 + L2
где L — 4nh/l.
При и = 5
IIII =
II а II
0,196 0,186 0,171 0,156 0,090
0,186 0,196 0,186 0,171 0,156 0,171 0,186 0,196 0,186 0,171 0,156 0,171 0,186 0,196 0,186 0,090 0,156 0,171 0,186 0,196
5,798 0,913 0,340 0,180 0,161 0,913 5,798 0,913 0,340 0,180 0,340 0,913 5,798 0,913 0,340 0,180 0,340 0,913 5,798 0,913 0,161 0,180 0,340 0,913 5,798
Вследствие симметрии расположения зарядов = т5 и т2 = = т4, поэтому матрица коэффициентов
5,959 1,093 0,340
1,093 6,138 0,913
0,680 1,825 5,798
Решение системы алгебраических уравнений: Ti=O,138T; т2 = 0,121 Т; т3 ®0,118Т. Заряд провода q = (2?! + 2т2 + т3) 1/nZ = 0,636T = 0,707-10“12t7, Кл; емкость С =0,707 пФ.
Результаты расчета представлены на рис. 18.17Р, б (крестики).
18.19(Р). Определить распределение заряда вдоль провода задачи 18.17, если пр,овод расположен перпендикулярно бесконечной проводящей плоскости. Нижний конец провода находится на расстоянии h = 5 мм от плоскости (рис. 18.19). Потенциал прсзода относительно проводящей плоскости равен U. Рассчитать емкость между проводом и плоскостью.
Решение. По методу зеркальных изображений приходим к расчетной схеме, показанной на рис. 18.19Р. Последовательность расчетов такая же, как в задачах 18.18 и 18.17, но вместо (10) получим уравнение
и систему алгебраических уравнений (5) с матрицей (11). Под матрица || а' || остается без изменений. Коэффициенты под матрицы || а" || вычисляются по формуле
. 2; + 2i — 1 4- N
aii “ П 2Н72Г^Т+?/’
где N = 2nh/l.
При п = 5
II<*" II =
0,693 0,405 0,288 0,223 0,182 0,405 0,288 0,223 0,182 0,154 0,28.8 0,223 0,182 0,154 0,134 0,223 0,182 0,154 0,134 0,118
0,182 0,154 0,134 0,118 0,053
и по (И)
5,301 0,694 0,223 0,113 0.069 0,694 5,706 0,876 0,329 0,182 0,223 0,917 5,840 0,945 0.377 0,113 0,329 0,945 5,860 0,981 0,069 0,182 0,377 0,981 5,941
Решив систему (5) с полученной матрицей коэффициентов, находим заряды: Ti=0,162T; т2=0Д26Т; т3=О,117Т; т4 = = 0,1197; т5 = 0,1357. Заряд провода q = (?! 4- т2 + т3 + т4 + + т5) 1/п = 0,6597 = 0,732 • 10" 12Г, Кл; емкость С = 0,732 пФ.
18.20(Р). Заземлителем служит металлическая труба, забитая вертикально в землю (рис. 18.20). Длина трубы I = 5 м, диаметр 2а = 200 мм. Удельная проводимость земли о = = 5 • 10"1 См/м.
Рис. 18.20
Рис. 18.20Р
Пренебрегая падением напряжения вдоль заземлителя, найти сопротивление растекания заземлителя. При. токе I — — 100 А определить распределение потенциала по поверхности земли.
Решение. Применив метод зеркальных изображений, получим расчетную схему по рис. 18.2ОР. Потенциал произвольной точки М поля заземлителя — цилиндра длиной 21 и диаметром 2а, который находится в однородной неограни-
ченной среде с проводимостью о (см. решение задачи 18.17),
1 f Il(zl)dzl
4710 J |/r2 + (z - Z1)2 ’	( '
-I
где Ц (zi)dzL — ток, стекающий с элемента.^ трубы.
Для точки М на поверхности заземлителя
А	= /о,	(2)
J у a2 +(z - Zi)2
-i
где /О=4ло17 и 17 — потенциал заземлителя относительно бесконечно удаленной точки.
Решим это уравнение методом алгебраизации. Запишем систему линейных уравнений, эквивалентную уравнению (2):
II all-Hi II = 11 И1-/о,	(3)
где || а || — квадратная матрица коэффициентов; || It || — матрица-столбец неизвестных токов; || 1 || — единичная матрица-столбец.
Коэффициенты afj вычисляются по формулам
= In
I 2/ — 2i | + 1
I 2j — 2i | — 1
]/l + (na/l)2 + 1 j/1 + (na/l)2 - 1
(при i
a,7 = In
При n = 5
II a II
5,993	1,098	0,511	0,336	0,251
1,098	5,993	1,098	0,511	0,336
0,511	1,098	5,993	1,098	0,511
0,336	0,511	1,098	5,993	1,098
0,251	0,336	0,511	1,098	5,993
Вследствие симметрии частичных токов 1ц =Il5 и /12 = = /14, поэтому задача сводится к решению системы трех уравнений с тремя неизвестными, для которой
II a II =
6,244 1,434 0,511
1,434 6,504 1,098
1,022 2,196 5,993
Решив систему (3) с полученной матрицей коэффициентов, получим значения токов: 1ц =0,126/о; /12=0,108/o; Лз = 638
= 0,1O5ZO. Ток заземлителя I = (21ц + 2/12 + /i3) 1/п = (0,252 + + 0,216 + 0,105) 4naU = 0,36017. Сопротивление растекания заземлителя R3 — U/I = 1/0,360 — 2,78 Ом. При I = 100 А потенциал заземлителя U = 278 В.
Таблица 18.20
Г/1	0,02	0,5	1,0	2,0	5,0	10
(р(г), В	278	69,8	55,7	30,6	12,8	6,4
Распределение потенциала по поверхности земли (z = 0)
21ц In

1 + /1 + (г/Q2 3/5 + ]/(3/5)2 + (г/02
3/5 + ]/<3/5)2 + (г//)2	1/5 + |/(1/5)2 + (г//)2 I
+ 2Z12 In	—- + /1з In -------------- . _ —-
1/5 + [/(1/5)2 + (г/l)2	-1/5 + |/(1/5)2 + (г//)2 J
Результаты расчета сведены в табл. 18.20.
Глава девятнадцатая
ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
Введение к гл. 19
Распределение электромагнитного поля в пространстве находится как решение системы уравнений
rotH = J + dD/dt;	(19.1а)
rot Е =	(19.2а)
divD = p;	(19.3а)
divB=0	(19.4а)
и уравнений связи между векторами J = &Е; D = ег£0Е; В = ргЦоН,	(19.5) (19.6) (19-7)
где J — плотность тока проводимости; р — объемная плотность
свободного заряда; о — удельная проводимость среды; ц0 = = 4я • 10”7 Гн/м; цосо — 1/coJ с0 = 3-108 м/с — скорость света в вакууме.
При расчете гармонических полей, как и при расчете цепей синусоидального тока, целесообразно применять комплексный
метод. В комплексной форме
rot Н — j + jcoD = о£ + /08Г£0Ё;	(19.16)
rot Ё =	-j(£t6 = -jcoprgotf;	(19.26)
divD = p;	(19.36)
div$ —0.	(19.46)
Векторы поля в неподвижной среде можно выразить через электродинамические потенциалы — векторный магнитный А и электрический скалярный ф:
В = rot А;	(19.8а)
£ = -grad (р - dA/dt.	(19.9а)
Электродинамические потенциалы удовлетворяют соответственно векторному и скалярному уравнениям
72Л -	(19.10а)
V2<p —t-52<p/5t2 = -p/ere0	(19.11а)
С
и связаны зависимостью
div Л = — -^-dtp/dt,
где с = с0/|/ErHr
В комплексной форме
Й = го1Л;	(19.86)
£ = —grad ф — /соА;	(19.96)
• св	.
72Л + -j-Л =	(19.106)
с (7)2
\72ф + — ф = - р/е^о.	(19.116)
Из системы (19.1)—(19.7) можно получить одно уравнение для любого вектора поля, например для вектора Н:
V2H - |1гц0о SH/dt - Х-г1Н1Э? = 0.	(19.12а)
В комплексной форме
V2H - ;соцгцосуН 4—5- Н = О с или
V2H-y2H=0,	(19.126)
где у = а + Jp = ]//а)цгцоа - fc§srpr	(19.13)
— коэффициент распространения; а — коэффициент ослабления; Р - коэффициент фазы; к0 = со/со — волновое число для вакуума.
Если векторы поля зависят только от одной пространственной координаты, например z, то решение уравнения (19.126) в декартовой системе координат следующее:
Ъ = Сие^ 4- C2^z, i = х; у; z. (19.14)
Постоянные интегрирования Ci,2 определяются из граничных условий
Ёи-Ё21‘, Hlt = H2t.	(19.15)
Для поля в проводящей среде можно пренебречь плотностью токов смещения job по сравнению с плотностью токов проводимости J. В этом случае первое уравнение Максвелла
rotH = j	(19.1в)
и коэффициент распространения
У = а 4- jp = |//cd^oct.	(19.16)
Для поля в диэлектрике без потерь можно пренебречь плотностью токов проводимости по сравнению с плотностью токов смещения. В этом случае первое уравнение Максвелла rot Н =jti)D	(19.1г)
и коэффициент распространения
X =;Р = Ло |/ё^	(19.17)
Для диэлектрика с потерями
I = « + JP =jk0 ]/s^.	(19.18)
У плоской электромагнитной волны векторы Ё и Н орто-гональны и находятся в плоскости, перпендикулярной направлению распространения волны.
Для волны в проводящей среде, распространяющейся вдоль оси z при напряженности электрического поля
Ё = 1ЁХ, Ёх = Ёое^г,	(19.19а)
напряженность магнитного поля
H=jHy; Hy = HQe~^	(19.196)
где Eq и Но — напряженности поля при z = 0, а у рассчитывается по (19.16).
Отношение Ё/Н = Ёо/Hq = ZB — волновое, сопротивление
Z, = |/юц,ц„/а	(19.20)
Глубина проникновения плоской волны
?о = 1/а;	(19.21)
длина волны
X = 2л/р.	(19.22)
Для плоской волны в диэлектрике без потерь
Ёх - Ёое’Лг; Й, = Нае-*г,	(19.23)
где к = ко ]/егц, = <о/с — волновое число.
Волновое сопротивление
ZB = zB = ]/цгц0/ег£0 - 120тт |/цгДг Ом. (19.24)
Длина волны
X = 2тг/р = 2пс/со.	(19.25)
Движение энергии в электромагнитном поле характеризуется вектором Пойнтипга
П = [ЕЛ].	(19.26а)
В комплексной форме
П = [ЕЛ*].
По теореме Умова — Пойнтинга С ->	Г
-ОП</$ = Р+ ct
(19.266)
(19.27)
^LdK
St ’
где S — замкнутая поверхность интегрирования; Р — мощность преобразования энергии электромагнитного поля в другие виды энергии в объеме И, ограниченном поверхностью S; и Неплотности энергии электрического и магнитного полей в том же объеме.
В комплексной форме
-fSdS = P+)e,	(19.28)
где Р и Q — активная и реактивная мощности в объеме, ограниченном поверхностью S.
19.1. Теорема Умова — Пойнтинга
В этом параграфе приведены задачи на вычисление пото
ков мощности и энергии стационарных и квазистационарных полей в реальных средах.
19.1. По уединенному алюминиевому проводу радиусом 1 см протекает постоянный ток 1000 А. Удельная проводимость алюминия а = 32-104 См/см.
Пользуясь теоремой Умова - Пойнтинга, найти поток мощности, входящий внутрь провода длиной 1 м. Сравнить эту мощность с мощностью, определяемой по известной из теории цепей формуле Р = I2R. Показать, что известная формула сопротивления провода R == 1/cS получится, если применить теорему Умова - Пойнтинга.
19.2(Р). По двухпроводной линии постоянного тока передается мощность Р при напряжении U и токе I.
Пренебрегая сопротивлением проводов, радиус которых г0, найти зависимость вектора Пойнтинга от координаты х вдоль линии, соединяющей оси проводов (рис. 19.2).
Р е ш е н и е. На линии, соединяющей оси проводов (ось х), составляющие векторов как Е, так и Я, обуслов
ленные каждым проводом в отдельности, или совпадают по
направлению, или направлены противоположно.
На основании теоремы Гаусса (15.15) вне проводов получим для вектора Е, имеющего на оси х только составляющую Е
т / 1	1 \
£ = _____ I _________j
* 2тгв0 \ х х — d
где т = CqU и Сп = т - ,т- ч — емкость линии на единицу In (d/rQ)
длины.
По закону полного тока (15.19) вне проводов получим для вектора Я, имеющего на оси х только составляющую Ну,
у 2я \ х
х — d /’
Вектор Пойнтинга (19.26) вне проводов на оси х имеет только составляющую
п =
г х у 4л1п(б?/г0) x2(x-d)2’
Внутри проводов П = О, так как Е = 0.
19.3	. По двухпроводной линии, радиус проводов которой 2 мм (рис. 193, где расстояния указаны в миллиметрах), передается мощность 10 кВт при постоянном напряжении 220 кВ.
Пренебрегая сопротивлением проводов, найти значение и направление вектора Пойнтинга в точках Мь М2, М3. Выяснить, как изменится решение задачи, если задано не напряжение, а сопротивление нагрузки (при той же мощности).
19.4	(Р). По двухпроводной линии (рис. 19.2), радиус проводов которой 1,5 мм и расстояние между осями d == 300 мм, протекает постоянный ток 100 А при напряжении в начале линии ПО В. Удельная проводимость материала проводов а = 57 • 104 См/см (медь).
Определить значение и направление вектора Пойнтинга в воздухе у поверхности левого провода в точке М на расстоянии / - .10 м от начала линии. Нарисовать качественную картину распределения векторов Пойнтинга (по направлению) вдоль прямой, соединяющей провода (вдоль оси х).
Решение. Напряжение между проводами UM в сечении, где находится точка М, меньше напряжения U в начале линии из-за падения напряжения в проводах: UM = U - IR, где R = = 21/aS — сопротивление проводов линии.
Вектор Пойнтинга (19.26а) в точке М имеет две составляющие. Составляющая П2 (рис. 19.4Р), определяющая плотность потока мощности, передаваемого вдоль линии, находится по формуле, полученной в решении задачи 19.2, после замены U на и х на радиус провода г0:
4тс In (<//п>) r?(d-»o)2 Т-Г77ГТ -Г = 7200 Вт/см2. 4тг In (d/r0)
Вторая составляющая показывает плотность потока мощности потерь в самом проводе. Она определяется тангенциальной составляющей вектора Е на поверхности провода, которая, как следует из граничного условия для напряженности электрического поля, равна напряженности электрического поля в проводе:
Es = J /а = 7/атсго, и напряженностью магнитного поля тг	1 ( 1	1 \ i
у	2п \ r о	rQ — d J	2лг0
Эта составляющая вектора Пойнтинга направлена по радиусу внутрь провода:
Пг = EzHy - 72/2л2ого = 0,264 Вт/см2.
Рис. 19.5
100 м от начала кабеля
Г
Рис. 19.6
19.5	(Р). Пренебрегая сопротивлением проводников коаксиального кабеля (рис. 19.5), найти зависимость мощности, передаваемой внутри цилиндрической поверхности радиусом г, от значения этого радиуса.
Решение. В изоляции коаксиального кабеля без потерь вектор Е имеет только радиальную составляющую
Е =—^—
(см. задачу 16.32), вектор Н по (15.19) - азимутальную На = //2та*
и по (19.26а) вектор Пойнтинга имеет только продольную составляющую
VI
П = Пг = ErHa — —JI—7—ГТ* г “ 2тгг2 In (r2/>*i)
В жиле и оболочке вектор Пойнтинга равен нулю, так как Е - 0.
Мощность, передаваемая внутри цилиндрической поверхности радиусом г (?*! < г < г2),
П • 2тсг dr = -j—5^--: 7 In (r/fi).
ri
19.6.	По коаксиальному кабелю без потерь (рис. 19.6) с радиусами гг = 2 мм, г2 = 10 мм передается при постоянном токе мощность Р = 100 кВт.
Определить вектор Пойнтинга в точках М2, Л13 (точки и М2 в изоляции у поверхностей жилы и оболочки; г3 — 6 мм).
19.7.	Коаксиальный кабель с воздушной изоляцией (рис. 19.6) состоит из медной трубки (г2 — 10 мм, толщина стенки равна 1 мм) и расположенной на ее оси медной жилы (гх = 2 мм). Удельная проводимость меди 57 • 104 См/см. По кабелю течет постоянный ток 50 А при напряжении в начале кабеля 100 В.
Найти значение и направление вектора Пойнтинга в точках Mi, М2, М3 на расстоянии 100 м от начала кабеля (точки Mt и М2 в воздухе у поверхностей жилы и трубки, г3 = 6 мм).
19.8.	Коаксиальный кабель длиной 100 м, заполненный изоляцией с относительной диэлектрической проницаемостью, равной 4, и удельной проводимостью -10"11 См/см питает приемник с сопротивлением 50 Ом. Радиус жилы 3 мм, радиусы оболочки 10 и И мм.
Пренебрегая потерями в жиле и оболочке, • определить мощность, выделяемую в изоляции, токи в начале и в конце кабеля, мощность на входе кабеля и КПД линии передачи, если: 1) кабель подключен к источнику постоянного напряжения 10 кВ; 2) кабель подключен к источнику синусоидального напряжения 10 кВ с частотой 100 кГц.
19.9(	Р). Определить вектор Пойнтинга на поверхности тороида с равномерно распределенной обмоткой (без потерь) в переходном процессе при подключении обмотки к источнику постоянного напряжения U = 300 В через резистор с сопротивлением R = 300 Ом.
Средняя длина магнитной линии в тороиде I = 30 см, сечение тороида 5 =	= 0,8 см2, относительная магнитная
проницаемость материала тороида цг = 100, число витков w = 316.
Пользуясь полученным выражением, определить энергию, запасенную в магнитном поле, и сравнить ее с энергией, определенной по формуле WM = L/2/2, где L — индуктивность
тороида.
Влиянием токов в тороиде на ток в цепи пренебречь. Решение. При включении цепи пойдет ток
где I = U/R — ток установившегося режима; т = L/R — постоян-
ная времени цепи; L = grjLL0w2S//.
Рассматривая тороид как бесконечно длинный цилиндр, выберем систему координат так, чтобы ось z была направлена параллельно вектору индукции В (рис. 19.9Р), т.е. В = Вг.
По закону электромагнитной индукции (15.21)
jEdl — -d®/dt.
Рис. 19.9Р
Выбрав в качестве контура ин
тегрирования окружность радиусом г0, получим:
Еа • 2ти*0 = — 5 dB/dt,
поэтому по (19.26а) вектор Пойнтинга в любой точке на поверхности тороида имеет только составляющую, направленную по радиусу Пг = ЕЛН„ где по закону полного тока (15.19)
H2 = ^=Zr(1-e-n
следовательно,
Bz = цгИоНг = — ц,Мо (1 ~ e~tlx) = Во (1 - е’^);
dt т
- S #0 c-t/r. 2яг0 т
I X
Знак « —» показывает, что мощность во время переходного процесса поступает внутрь тороида.
Поток вектора Пойнтинга через боковую поверхность тороида
П, • 2лг01 = -	е-</.(! _	=
/т
Г I2
=	-е',/’)= -3,15(1 _e-8«’oo>)e-89soor Вт/см2.
Энергия, запасенная в магнитном поле тороида за время переходного процесса, 00
*	LI2
WM = (П, • 2wol) dt----Z---- 1,657 • 10” 3 Дж.
Лл V О
а,~1см
Рис. 19.11
19.10. У катушки с магнитопроводом — тороидом из ферромагнитного материала комплексное сопротивление Z = = 20 + /100 Ом, число витков w = 400, средняя длина магнитной линии в тороиде 30 см, его сечение 0,8 см2, активное сопротивление проводов обмотки 10 Ом.
Определить мгновенное значение вектора Пойнтинга на поверхности тороида, если к обмотке приложено напряжение и — 50 sin (10000г 4- 30°) В, и поток комплексного вектора Пойнтинга через поверхность тороида.
19.11. Определить значение вектора Пойнтинга на поверхности диэлектрика, помещенного в плоский конденсатор, во время переходного процесса (рис. 19.11). Емкость конденсатора, заполненного диэлектриком, С = 4 мкФ, сопротивление резистора г = 333 Ом, постоянное напряжение 17 = 100 В.
Пользуясь полученным выражением, вычислить энергию, запасенную в диэлектрике конденсатора.
линии (рис. 19.2) передается
энергия от генератора к приемнику. Расстояние между осями проводов d = 1 м; радиус провода г0 — 5 мм; напряжение между проводами линии u = 104sincot В; ток в линии i = = 100 sin (cor - п/3) A.
Найти среднее значение вектора Пойнтинга в двух точках, лежащих на линии, соединяющей оси проводов (на оси х). Первая точка М находится у поверхности одного из проводов, вторая — посередине между проводами. Влиянием земли и сопротивлением проводов можно пренебречь.
Решение. В решении задачи 19.2 получено выражение для вектора Пойнтинга вдоль линии, соединяющей оси проводов. Подставив вместо U и I мгновенные значения и = — sin сог и i = Im sin(ci)Z — (р) и вычислив среднее значение
19.12(Р). По двухпроводной
произведения, получим:
„ UmImcos<? d2	3,75	_ . ,
И = ” f	кВт/м2.
8л In (d/r0) x2 (x — d)2 x2 (x — I)2
В частности, при x = r0 = 5 мм и x = d/1 = 0,5 м получим соответственно 152  103 и 60,1 кВт/м2.
19.2	. Напряженность электрического поля в неподвижных и движущихся средах. Движение заряженных частиц
Задачи данного параграфа делятся на три группы: 1) расчет в неподвижной среде напряженности переменного электрического поля Е = -grad ср — dA/dt по известным значениям скалярного ср и векторного А потенциалов; 2) расчет напряженности переменного электрического поля в движущейся среде при скорости движения, намного меньшей скорости света; 3) вычисление траекторий движения заряженных частиц в электромагнитном поле и силы F — qE + qv х В, действующей на частицу с зарядом q, движущуюся со скоростью v.
19.13	, В линии длиной 20 км, состоящей из двух медных параллельных проводов (удельное сопротивление 17,6 Ом  мм2/км) радиусом 0,5 см при расстоянии между их осями 2 м, проходит ток 40 А, возрастающий со скоростью 30 кА/с. В конце линия замкнута накоротко.
Найти напряжение в начале линии.
19.14	(Р). Металлический диск, насаженный на вал, вращается с постоянной частотой вращения п — 3000 об/мин в однородном магнитном поле, индукция которого В = 1 Тл и перпендикулярна плоскости диска. Радиус диска R = 10 см.
Определить ЭДС, возникающую между валом и внешней окружностью диска.
Решение. Напряженность электрического поля определяется векторным произведением Е = v х В. В системе координат, изображенной на рис. 19.14Р, получим Е = Er — vaBz = = аагВ,
Электродвижущая сила я
* mR2B
е — E,dr = —— = TtnR2B/60 = 1,57 В,
о
поскольку со = 2 л/ = ли/30.
19.15. Металлический диск радиусом R, насаженный на вал эксцентрично (рис. 19.15), вращается в однородном магнитном
поле с индукцией В. Линии поля перпендикулярны плоскости диска. Число оборотов диска в секунду равно п. Расстояние между осью вала и осью диска равно d.
Найти ЭДС, возникающую между щетками, одна из которых скользит по окружности диска, а другая — по валу. Получить приближенное выражение для ЭДС в случае d/R «с 1.
В диске есть множество радиальных тонких щелей, и поэтому токами в диске можно пренебречь.
Рис. 19.14Р
Рис. 19.15
19.16. Индукционный виброграф состоит из неподвижного постоянного магнита (рис. 19.16), вставленного в массивный стальной стакан, и из подвижного соленоида, механически связанного с той системой, вибрацию которой надлежит измерить. Магнитный поток постоянного магнита Ф = 1,2 • 10“4 Вб замыкается через стальной стакан так, что и нижний, и верхний концы соленоида оказываются вне зоны магнитного поля. Соленоид намотан равномерно и имеет 50 витков на 1 см длины. Вибрация соленоида происходит в продольном направлении по закону х = 0,2 sin cot мм и в поперечном направлении - по закону у - 1 sin cot мм, где со = 2я • 200 с“ \
Найти ЭДС, индуктируемую в соленоиде.
Указание. Задача может быть решена двумя способами:
1)	Сторонняя напряженность электрического поля в витке Е = v х В, где v — скорость соленоида. Электродвижущая сила равна интегралу от напряженности электрического поля по всем виткам.
2)	Электродвижущая сила определяется как скорость изменения потокосцепления. Потокосцепление непостоянно из-за изменения числа витков, сцепленных с магнитным потоком.
19Л7(Р). Стержень AD движется в магнитном поле (рис. 19.17) со скоростью v = 0,25 м/с. Магнитная индукция между полюсами электромагнита (т.е. на площади 500мм х х 200 мм) изменяется во времени по закону В=В0(1 — kt), где BQ = 1 Тл, к = 5 с"х, t — время, отсчитываемое от момента,
когда стержень AD расположен, как показано на рисунке. В остальной части контура из провода, замкнутого вольтметром, магнитным полем можно пренебречь.
Определить ЭДС, наводимую в контуре (показание вольтметра К).
Решение. Электродвижущую силу, наводимую в контуре, определим по закону электромагнитной индукции:
dt dt	\ dt dt J
В условиях задачи S — a(l~ t?r); dB/dt= —BGk', dS/dt = = -av, где a = 500 мм; I = 50 мм и e — aBG (Ik + v — 2vkt) = = 0,25 - l,25t B.
Заметим, что часть ЭДС, обусловленная движением контура (В dS/dt), может быть определена иначе - по напряженности электрического поля aBG (1 — kt) и, возникающей в проводнике, который движется в магнитном поле.
19.18*	(Р). Медная цилиндрическая труба малой толщины 8 при среднем радиусе г коаксиально надета на провод с током и движется со скоростью v в направлении, совпадающем с осью проводника z (рис. 19.18).
Определить показания вольтметра, присоединенного к внутренней и внешней поверхностям трубы при помощи щеток. Ответить на вопрос: зависят ли показания вольтметра от магнитных и электрических свойств трубы.
Решение. Выберем цилиндрическую систему координат с центром на оси провода.
Вокруг провода с током существует магнитное поле, индукция которого в трубе малой толщины В — Ва = /цгц0/2яг. При движении трубы со скоростью v = vz в магнитном поле с индукцией Ва возникает радиальная составляющая напря
женности электрического поля Ест = — vB, которую назовем сторонней. В проводящей трубе под действием электрического поля должен протекать ток плотностью J — о (Е + Е^). Так как цепь разомкнута (считаем, что сопротивление вольтметра бесконечно велико) и, следовательно, 7 = 0, то Е~ —Е^ и в трубе есть радиальная составляющая напряженности поля, численно равная Ест, т. е. Er — vB.
Из общего выражения для напряженности поля Е = = — V<p — dA/dt следует, что в условиях задачи Ег — — (Vcp)r = = vB = f/prp0/27tr, так как магнитное поле не изменяется в точках, где определяется Е (в стенке трубы) и dA/dt = 0. Вне трубы электрическое поле равно нулю.
Показания вольтметра вычислим, применив закон электромагнитной индукции: §Edl = — d<$/dt. Отметим, что вольтметр показывает разность потенциалов между его электродами, поэтому под интегралом стоит Е = — Уф (не включающее Ест).
Выберем контур, проходящий через вольтметр, по соединительным проводам и вдоль радиуса трубы между щетками, связанный с направлением магнитного потока правилом правоходового винта. Для такого контура Его 4- V = — dQ/dt^ или V = -d<b/dt - vBd.
При движении немагнитной трубы поток, сцепленный с контуром, не изменяется, т. е. d®/dt =0 и U = — vBS = = —
При движении магнитной трубы с относительной проницаемостью материала конец трубы вытягивается из контура со скоростью v, что приводит к уменьшению магнитного потока dQ/dt = — р0(Цг ~ l)/i?8/2rcr и U = — 1>87ц0/2яг.
Как видно из приведенного решения, показания вольтметра не зависят от магнитных и электрических свойств трубы.
19.19,	Определяется ли полностью сила, действующая на движущийся заряд, заданными значениями скорости V, В, grad (р и их производными во времени (токами смешения и излучением пренебречь). Иллюстрировать на примере соленоида с переменным током.
19.20.	В зазоре магнитопровода соленоида при (х2 + у2) < < г $ (рис. 19.20) индукция В = Вг = 1 Тл и изменяется во времени (в рассматриваемый момент) со скоростью dB/dt — 10Тл/с; при (х2 + у2) > г? индукция В = 0 и dB/dt = 0.
Определить в зависимости от координаты х при у = 0 составляющие fx и fy силы, которые действуют на электрон с зарядом q < 0, движущийся со скоростью v = vx.
19.21.	То же, что и в задаче 19.20, но для скорости электрона v = vy.
19.22.	Электрон с зарядом q < 0 и массой т движется в магнитном поле с индукцией В = 8-10“4 Тл по окружности радиусом г = 1 см. Вектор магнитной индукции нормален к плоскости, в которой лежит окружность.
Определить скорость электрона.
Рис. 19.18	Рис. 19.20
19.23.	Известны три проекции траектории электрона в камере Вильсона с магнитным полем В = Вх=10“3 Тл: а) в плоскости ху траектория y = 2sinfcx; б) в плоскости yz траектория у2 4- z2 — 4z = 0; в) - в плоскости xz траектория z = 2(l— cos кх). Все размеры даны в сантиметрах, к — 6,28 см “
Найти составляющие начальной скорости электрона.
19.24.	Электроны с энергией 8000 эВ вылетают из точки п, лежащей на оси х, под углом а = 0 4- 8° к ней и движутся в однородном постоянном магнитном поле В = Вх = 10“2 Тл.
Определить, на каком расстоянии от точки а электроны вновь пересекут ось х.
19.25.	Частица с зарядом q > 0 и массой т движется в области, где существуют постоянные электрическое и магнитное поля, причем Eli?.
Найти траекторию движения заряженной частицы, пользуясь системой координат, движущейся со скоростью t?, при которой v х В = —Е.
19.26.	У плоского конденсатора расстояние между пластинами h и разность потенциалов между ними U. Электроны с зарядом q < 0 и массой т каждый движутся от отрицательной пластины к положительной, причем скорость равна нулю у отрицательной пластины.
Найти значение индукции В поперечного магнитного поля, при котором электроны не смогут достичь положительной пластины.
19.27(	Р). Электрон с энергией 100 эВ, зарядом q < 0 и массой т влетает со скоростью г0 в поле между пластинами
плоского конденсатора у края положительного электрода (рис. 19.27), причем вектор скорости образует угол а — 45° с нормалью к пластине. Расстояние между пластинами d = = 1 см, их ширина Ь = 3 см.
Найти, при каких значениях напряжения между пластинами V: а) электрон попадает на отрицательную пластину конденсатора; б) электрон попадает на положительную пластину конденсатора; в) электрон пролетает через конденсатор.
Рис. 19.27
Рис. 19.28
Решение. В системе координат, показанной на рис. 19.27, напишем уравнения движения электрона:
md2x/dt2 = qU/d; md2y/dt2 = 0.
Дважды их интегрируя, получаем:
х = qUt2/2md 4- С it 4- С2; у = С3Г 4- С4.
Начальные условия при t — 0 и выбранной системе коор
динат:
х (0) = 0; у (0) = 0, поэтому С2 = С4 = 0,
dx dt
= рх(О) = »о/1/2; -§ dt
Сз = Ю/jA
Окончательно
= vy (0) = г0/]/2,
откуда
Ci — Vo/j/2;
: = 0
х = vot/]/2 4- qUt2/2md; у = tV/|/2.
Исключив из этих уравнений время, получим траекторию электрона
х = у 4- qUу2/mdvQ.
а)	Электрон попадает на отрицательную пластину, если хтах > d, Определим Хмдх обычным методом. Производная dx/dy = 14- 2qUy/mdvQ = 0, откуда находим у, при котором х == 654
— % max И Хтах.
у = mdv$/2U I q I; хтах = mdv%/4U | q |.
Чтобы получить хтах > d, должно быть U С тг’о/41 q |.
б)	Электрон попадает на положительную пластину, если при х = 0 получим у Ь. Из уравнения траектории при х = О находим: yt =0; у2 — mdvo/U | q |, т. е. U > rndve/b | q [.
в)	Электрон пролетает через конденсатор, если
wi?o/4 | q | < U < mdvo/b | q |.
19.28. На рис. 19.28 показан униполярный генератор, диск которого имеет радиусы г t = 10 см, г2 = 50 см и вращается в однородном магнитном поле, направленном перпендикулярно диску.
Дано: и = 1000 об/мин; В = 2/п Тл; сопротивление цепи тока в диске Ro = 1 Ом; сопротивление нагрузки R = 7 Ом; момент трения М = 0,12/л Н • м.
Определить ЭДС мощность на валу двигателя, вращающего генератор, и КПД генератора, считая полезной мощность, выделяемую в сопротивлении нагрузки (при вычислениях не следует заменять я числовым значением).
19.3. Электромагнитное поле в проводящей среде.
Поверхностный эффект
19.29(Р). Для защиты от воздействия электромагнитного поля низкой частоты прибор помещен в ферромагнитный экран. Наименьший радиус кривизны поверхности экрана намного больше толщины стенки экрана, при этом в стенке экрана электромагнитные волны можно считать плоскими. Толщина экрана d — 6 мм, удельная проводимость стали О’ — 5 • 104 См/см, относительная магнитная проницаемость = 300. Частота волны f = 400 Гц.
1)	Найти мгновенное значение вектора Пойнтинга на глубине, равной глубине проникновения, если на внешней поверхности векторы Е и Н плоской волны параллельны поверхности стенки и напряженность магнитного поля Но = = 10 sin (cot + 20°) А/см.
2)	Вычислить отношение длины волны в стенке экрана к длине волны в воздухе.
3)	Определить, во сколько раз значения векторов поля на внешней поверхности стенки больше, чем в середине стенки.
Решение. Коэффициент распространения (поверхностного эффекта) по (19.16)
у = а + ;Р = 21,8 z. 45° = 15,35(1 4- J1) см-1.	,,,
Глубина проникновения по (19.21) z0 = 1/а = 0,065 с.м = = 0,65 мм намного меньше толщины стенки экрана, и, следовательно, в стенке распространяются только прямые волны от внешней поверхности к внутренней.
Если ось z направить от внешней поверхности внутрь стенки, то
Н (z\ = Home~*z sin (cot + 20° — pz).
На глубине, равной глубине проникновения,
Н (z0) = 10е"1 sin (co? + 20° - 57° 20') =
— 3,68 sin (cot — 37° 20') А/см.
Так как встречные волны отсутствуют, то Ё — HZ^, где по (19.20) волновое сопротивление ZR = 4,36 • 10“4 z. 45° Ом Мгновенное значение Е (z0) = 4,36 • 10“4 • 3,68 sin (со? — 37е 20' + + 45°) = 1,6 • 10" 3 sin (tor + 7°40') В/см.
1)	Мгновенное значение вектора Пойнтинга по (19.26а)
П = П2 (z0) = Е (z0) Н (z0) = 2,08 — 2,95 cos (2cot - 29° 40') мВт/см2.
2)	Длина волны в стенке экрана по (19.22) X = 2к/15,35 = = 0,41 см = 4,1 мм; длина волны в воздухе к0 = с0// = = 75 • 106 см; их отношение Х/Хо = 0,546 • 10“8.
3)	Отношение напряженностей поля на внешней поверхности и в середине стенки экрана
Н (0)/Н (с//2) = Е (0)/Е (d/2) = ead/2 = е416 « 100.
19.30.	В задаче (19.29) условия изменены следующим образом: экран медный с удельной проводимостью 5,8 х х 105 См/см, толщина стенки 3 мм, частота поля 50 кГц.
Определить, при каком поле (Ео, Но) на внешней поверхности экрана напряженность электрического поля на глубине, равной глубине проникновения, Е (t) = 1,84 • 10"5 sin (cot — — 27° 18') В/см. Найти, во сколько раз при этом напряженность электрического поля прямой волны на внутренней поверхности экрана меньше Ео.
19.31.	По плоскому угольному пласту с удельной проводимостью с = 500 См/см протекает ток промышленной частоты (50 Гц). На поверхности пласта среднее значение вектора Пойнтинга 0,2 Вт/см2.
Найти мгновенные значения напряженностей электрического и магнитного полей плоской волны на глубине 1,5 м, считая начальную фазу напряженности электрического поля на поверхности равной нулю. Сопоставить количества выделяющегося тепла в 1 см3 у поверхности пласта и на глубине 0,5 м. 656
19.32.	В проводящей среде в направлении оси z распространяется плоская волна. Относительная магнитная проницаемость среды ц, = 200, удельная проводимость о = 0,5 • 105 См/см, частота волны 50 Гц. В точке, координата z которой выбрана равной нулю, напряженность магнитного поля Н — HQnt sin cor = = 201/2 sin cor А/см.
Определить мгновенное значение дивергенции вектора Пойнтинга, мгновенное значение мощности, преобразуемой в теплоту, и мгновенное значение мощности, с которой изменяется энергия магнитного поля в каждой точке.
19.33(	Р). Тороид изготовлен из стальной ленты толщиной 2а = 0,35 мм и шириной b = 50 мм. Число витков ленты и — 50. Относительная магнитная проницаемость материала ленты цР — 1000, удельная проводимость о = 105 См/см. Средняя длина магнитной линии / = 80 см. На тороид нанесена обмотка w = 400 витков с сопротивлением г = 2 Ом. По обмотке протекает ток 7 = 0,4 А частотой / = 400 Гц.
1) Найти эффективную комплексную магнитную проницаемость (среднюю проницаемость) ленты цгср, среднюю по сечению индукцию в ленте Вср и напряжение на зажимах обмотки 17. Потоком рассеяния и магнитными потерями пренебречь.
2) Определить, при какой толщине ленты из того же материала поверхностный эффект практически не сказывается; вычислить напряжение на зажимах обмотки (общее сечение тороида остается тем же). Считать, что поверхностный эффект практически не сказывается, если мнимая часть средней проницаемости (обусловленная вихревыми токами) составляет не более 3 % проницаемости материала, при этом действительная часть средней проницаемости не отличается от проницаемости материала.
Решение. 1) По определению средняя проницаемость
Цг ср = Вср/цоНо = Mr th уа/уа,
где Йо — напряженность поля на поверхности и по (19.16) у = 39,7 (1 + J1) см’1.
Вычислим гиперболический тангенс комплексного аргумента по формуле
th у а = th(aa 4- jfia) = Те;<р,
где	у а = 0,98 z 45°;
ch 2аа — cos 2ра _ ch 2аа + cos 2ра
x sin 28л
= arctg ——-—= 27'40, при этом цсо = 940 z. -17° 20'. sh 2otn	-ср
Таким образом, средняя проницаемость существенно отличается от проницаемости материала, т.е. поверхностный эффект заметно влияет на процессы в тороиде.
Напряженность магнитного поля на поверхности ленты (по закону полного тока) Но = tw/l = 2 А/см и по определению Вср == ц, срц0Н0 = 0,236 z. - 17°20' Тл.
•Напряжение на зажимах обмотки
и = Ir 4- jawSBср = 0,8 4- 208 z. 72° 40' = 0,8 + (62 4- Д98) В.
2) Поверхностный эффект совсем не сказывается, если средняя проницаемость практически не отличается от проницаемости материала, при этом th у а % у а и цгср % цг. Учитывая в разложении гиперболического тангенса второй член, получаем:
ц,ср thya	уа-(уа)3/3	.	(уа)2	,	. IУ а |2
уа	уа	3	3
По условию | уа |2/3 = 0,03, откуда 2а = 2  0,3/1 Y I = 0,0107 см. В этом случае напряжение на зажимах обмотки
U = Ir 4- ;cdvvS|_i0Ср bv/7 = 0,8 4- (6,6 4- /220) В.
19.34(	Р). Определить комплексное сопротивление катушки задачи 19.33. Считая, что магнитная проницаемость материала ленты не зависит от частоты, построить частотные характеристики индуктивности, активного и реактивного сопротивлений катушки, действительной и мнимой частей средней комплексной проницаемости ленты. Определить, при какой частоте мнимая часть средней комплексной проницаемости достигает максимума. Построить зависимости тех же величин от толщины ленты при частоте 12,8 кГц и при неизменном общем сечении тороида.
Решение. Комплексное сопротивление катушки Z = U/1 = r+jtoL^^ = r + R 4- jx,
ОМ /Lrtp
2048 -
1024 -	, l _x(d)
51Z - Prep-Lq~<oLo^ 256 -1000 128 -
64 -800 -
32 -
16 -600-
8 -
4 -400-
2 -
1 -200 -0,5 -
Offl- 0 —l
Рис. 19.34P
// _ R(a)
*cp<tiLp
*(f)
где Lo = w2S|i0// = 0,22 мГн — индуктивность катушки с тороидом из материала с цг = 1; о = 0;
Рт ср Рт ср JPr ср Рт	=
_ цг (sh 2ад + sin 2аа) — j (sh 2сш — sin 2ая) 2ос<з	ch 2аа 4- cos 2ал
Следовательно, R = соЛоЦгсР и х = a>L0Prcp-
Индуктивность катушки с тороидом из стальной ленты
Г — х/(£) — Г'оРт Ср.
Из этих соотношений следует, что ЦуСр, ц/ср и L зависят от толщины ленты а так же, как и от квадрата частоты, так как по (19.16) а = {/соцгЦо^/2.
Рассчитанные по этим формулам зависимости представлены на рис. 19.34Р.
Мнимая часть средней проницаемости достигает максимального значения при частоте, определяемой из условия г/ц/ср/Жв = 0. Решение этого уравнения приводит к значениям: 2сад = 2,25 и f — 1050 Гц, при этом ц"сртвх = 415.
19.35.	Комплексная относительная магнитная проницаемость материала стальной ленты, учитывающая гистерезисные потери, у, = 1000 z. — 4° = 1000 — /70 при частоте 12,8 кГц; удельная проводимость о = 105 См/см.
Рассчитать и построить зависимости действительной и мнимой частей средней комплексной проницаемости ленты от ее толщины 2а для указанной частоты. Сравнить эти зависимости с соответствующими из задачи 19.34, построенными для этой же ленты, но без учета потерь на гистерезис.
19.36.	Магнитопровод трансформатора массой G — 1,5 кг изготовлен из ферромагнитной ленты толщиной 2а = 0,016 мм. Относительная магнитная проницаемость материала = 400, удельная проводимость ст = 105 См/см, плотность стали у = = 7,2 г/см3. Трансформатор работает на частоте 10 кГц.
Определить среднюю комплексную проницаемость ленты и мощность потерь на вихревые токи при действующем значении напряженности магнитного поля токов обмоток 2 А/см.
Вычислить, как изменятся эти величины, если магнитопровод изготовить из ленты толщиной 0,06 мм или из листов того же материала толщиной 0,2 или 0,5 мм.
19.37.	Магнитопровод трансформатора набран из листов трансформаторной стали толщиной аг = 0,5 мм. Удельная про-
водимость стали 105 См/см, относительная магнитная проницаемость — 400. Трансформатор работает на частоте /1—50 Гц.
Определить среднюю комплексную проницаемость листа на заданной частоте и при частоте /2 = 10 кГц. Выяснить, как надо изменить толщину листа, чтобы средняя проницаемость при частоте /2 осталась равной проницаемости при частоте Д.
19.38(	F). К первичной обмотке трансформатора приложено напряжение щ = 100 sin 12 000г -I- 50sin60 000f В. Магнитопровод набран из листов трансформаторной стали толщиной 2а = 0,2 мм; удельная проводимость стали о = 104 См/см, относительная проницаемость ц, = 800, сечение стали 5 = 2 см2, средняя длина магнитной линии I = 10 см. Первичная и вторичная обмотки имеют по = w2 = 100 витков. Можно считать, что сопротивление г = 2 Ом и индуктивность рассеяния Ld = 0,5 мГн каждой обмотки не зависят от частоты.
Определить напряжение на вторичной обмотке и ток в первичной обмотке при сопротивлении нагрузки: a) Z н = оо и б) Zh = rH = 100 Ом.
Решение. Расчет можно выполнить отдельно для каждой гармоники. Уравнения для первичного и вторичного контуров
Л (П + /©Lid) +Jco4>ow1 = t?i;
“Л (Zh + г2 + J®^2d) 4- ;C0O0W2 = 0,
где основной магнитный почок Фо = НоНоИгсР^ и Йо/ = liWL — ~~ Avv2.
Совместное решение этих уравнений приводит к выражению
й2/й1 = iiZJUx = z2iZH/(z11z22 - zh),
где Zi j = n + jcoLld +	сР$Д; Z2 x	cp^//;
Z22 = Z„ 4- r2 +j(i)L2d +	cpS/l.
Среднее значение магнитной проницаемости Иг ср = И, th уа/уа.
При а»! = 12000 рад/с получим: = 34,8 z. 45° см-1; У1Д = = 0,348 z. 45° = 0,246 (1 +/1); th у2а = 0,348 z. 42°40'; Ц1,ср = = 800 z. — 2°20'; Z2= 11,6 + /246 Ом; Z22=Za + ll,6 + + /246 Ом; Zl2 = 9,6 + /240 Ом = 240 z. 87°42' Ом; Й2/1Л = = 0,975 z. 0° 28'^„/(3,9 + /12 + ZJ.
Аналогично при <в5 = 60 000 рад/с получим: ц5гср = = 760 z. -110 20'; V2IUi = 0,97 z. 0° 14'Z,/(4 + /60 + ZJ
а)	Й2/1\ = 0,975 z. 0°28' при ш = coi и U2/Vi = 0,97 z. 0° 14' при w = со5. Кривая «2 практически не отличается от кривой 660
W1. При Zh = оо для каждой гармоники /t = C/2/Z21 и мгновенное значение первичного тока
= 406 sin (12 OOOt - 87° 14') 4- 42,5 sin (60 OOOt - 78°26') мА.
б)	йг/й^ = 0,932 z. — 6°О7' при со = coj и U2/ijl = = 0,808 z. — 30° при со — со5 и и2 - 93,2 sin (12 000г - 6°07') + + 40,4 sin (60 000t - 30°) В. При такой нагрузке кривая и2 заметно отличается от кривой
Для каждой гармоники тока
A=(Z22/Z21) и2/^.
Мгновенное значение первичного тока
= Ю45 sin (12 000t - 22°05') + 423 sin (60 000t - 34° 30') мА.
19	.39(P), В прямоугольном пазу машины, открытом сверху, заложена медная шина (рис. 19.39). Высота шины h = 1,5 см, ширина Ъ = 0,5 см. Толщина изоляции между шиной и пазом мала и можно считать, что ширина паза практически равна ширине шины. Проницаемость стали велика: ее можно считать бесконечно большой. Поверхностный эффект в стальных листах отсутствует, так как они достаточно тонкие. Удельная проводимость меди о = 5,7 • 105 См/см. Ток в шине 1 — 100 А, его частота f = 50 Гц.
Определить: а) распределение плотности тока в шине; б) координату точек, где ‘плотность тока совпадает по фазе с током в шине, и значение этой плотности
тока; в) активное и внутреннее реактивное сопротивление шины на 1 м длины; г) мощность потерь в шине на 1 м длины.
Решение, а) Плотность тока в шине распределена по закону j = jx = jochYz, где Jo = -iyjb sh yh -= —118 z.—46° 7' А/см2 — плотность тока на нижней грани шины, т. е. при z = 0 (знак минус получен потому, что положительное направление тока выбрано навстречу направлению оси х); по (19.16) у = 1,5 z 45° = 1,06(1 4- J1) см-1 (см/ также более подробное решение задачи 19.41).
При z = h получается максимальное по модулю значение плотности тока:	— j0 ch y/i = —276 z. 45° 10' А/см2.
б)	Запишем ch yzj = ch az^ cos (3zi + j sh az^ sin pzi в виде A z cpp Из полученного значения Jo видно, что плотность тока в точке zt будет совпадать по фазе с общим током
Рис. 19.39
в шине, если ср1=46'7/, при этом tg (pj = th otZi tg pzx = = tg46°7' = 1,04 (a = p = 1,06 см-1). Из таблиц тригонометрических и гиперболических функций определяем azx = 0,95 и Zj = 0,895 см. В этих точках j = -147,5 zi 0° А/см2.
в)	Комплексное сопротивление шины длиной I = 1 м
/у
Z = г + Двт = cth yh = 3,41 • 10"4 + Д43 • 10"4 Ом, до _ где хвт — реактивное сопротивление, определяемое потоком внутри шины.
Сопротивление этой же шины постоянному току R — = l/bha = 2,34-10"4 Ом.
г)	Мощность потерь в шине (длиной 1 м) Р = г!2 — = 3,41 Вт.
19.40	. Для шины задачи 19.39 определить, при какой высоте ее активное сопротивление минимально и чему при этом равно комплексное сопротивление шины.
19.41	(Р). В прямоугольном пазу машины находятся две последовательно соединенные медные шины (рис. 19.41). Размеры шин и допущения те же, что и в задаче 19.39. Ток в каждой шине / = 100 A; f = 50 Гц.
Определить: а) распределение плотности тока в каждой шине; б) активное и внутреннее реактивное сопротивления шин на 1 м длины; в) мощность потерь в шинах на 1 м длиУгы. Сопоставить значения этих величин со значениями, получаемыми при одной шине двойной высоты, по которой протекает двойной ток.
Решить дополнительно задачу для случаев: А) высота шин уменьшена в 2 раза; Б) высота шин увеличена в 2 раза.
Решение, а) На распределение электромагнитного поля в нижней шине наличие верхней шины не оказывает влияния. Действительно, граничные условия для нижней шины остаются теми же, что и в задаче 19.39: И = 0 при z = 0 и Н = I/Ь при z = /1, поэтому в нижней шине
Й" =	Sh^z;	~ hash2h Ch 1Z'
Для верхней шины граничные условия другие: Йв = 1/Ь при z — h и Нъ = 2l/b при z = 2h.
Решение целесообразно искать в виде
Нв = Нву = At sh у (2/1 - z) + Л2 sh у (z - /i), где Ai и А2 — постоянные.
При z = h получим i/b — A^shyh и при z = 2h получим 21/Ь = А2 sh yh. Из этих выражений определим постоянные 662
At — 1/b sh yh = A2/2, t. e.
HB =
-—;—- [sh у (2/i - z) + 2 sh у (z - /1)]. bshy/i
Напряженность электрического поля теперь находим по первому уравнению Максвелла (19.16) для проводящей среды: р = 6	1 d^y _ Ь
‘ вх	ст dz vbshyh
[ch у (2/i - z) — 2 ch у (z — /i)].
Рис. 19.41
При указанных в условии параметрах yh = 1,59(1 + jl); jH = аЁн = (- 1Т8 z. - 46° 7). х х chyz А/см2; jB = оЁв = = (-118	- 46° 7') [2 ch у (z -
— h) — ch у (2/i — z)] А/см2?
На границах шин jH (0) = == -118,/ -46°7'А/см2; jH(/i) = = - 276 z. 45° 10' А/см2; jB (/i) = = 368 ^85° А/см2; jB (2/z) -- 570,/ -122° 5Г А/см2.
Годограф вектора плотности тока в шинах показан на
z=h
Рис. 1Q.41P
z~2h
рис. 19.41Р.
6) По (19.266) вектор Пойнтинга П = Пг — ЁХН$, т. е. Д'= 0 при z = 0; П'н = — 72у chy/i/сг/)2 shy/z при z = h; Пв ==
12у	212у
= ~ l2~T ' Hch - 2) ПРИ 2 = /i; Пв =  2	(1 - 2 ch yh)
сг/r sh yh	ob sh yh	-
при Z = 2/1.
Комплексное сопротивление нижней шины
Z = - П" — -_______—___ch
-н /2 сгЬ sh yh СП ±
Комплексное сопротивление верхней шины lb ly
Zn = (IL - ПЭ -zy = — " , (5 ch yh
/	abshyh
Сопротивление двух последовательно соединенных шин
z2 = ZB + Z, = ,4 , (6 ch - 4).
сто sh yh x
При указанных в условии параметрах Z^ = 3,41 • 10 4 4-+ 73,43 -10"4 Ом; Zb = 11,4-10"4 + 723,3-10"4 Ом; Z2 = 14,8 x x 10~4 + J26,7 • 10"4 Ом.
b) P2 = r2I2 = 14,8 Вт.
В случае одной шины двойной высоты, по которой протекает двойной ток (см. решение задачи 19.39),
2/у
b sh 2yh
ch yz = (50 z_ 43°) ch yz А/см2.
На границах шины j (0) = 50 z. 43° А/см2; j (2h) = = 600 z. 225° А/см2.
Комплексное сопротивление шины ly
Zi = , - , ch2y/i = 3,72- 10“4 4- 73,72-10“4 Ом. ab sh 2yh
Мощность потерь (в 1 м шины) Pi = ц (2I)2 = 14,9 Вт.
Таким образом, мощность потерь в шине в этом случае практически равна мощности потерь в обеих шинах в предыдущем случае.
А) При уменьшении высоты шины в 2 раза yh = = 0,795(1 4-'jl); JH = ( — 266 z - 12°)chyz А/см2; jB = = (— 266 z — 12°) [2 ch у (z — h) — ch у (2h — z)] А/см2;	= 4,31 x
x 10“ 4 4-/1,74-10-4 Ом; Zb = 5,95 • 10’4 4- 713,6- 10-4 Ом; Z2 = = 10,26-10"4 4-715,34-10"4 Ом; P2 = 10,26 Вт.
При одной шине двойной высоты Zx = 3,41 • 10"4 4-4-73,43- 10"4 Ом; Pt = 13,64 Вт.
В этом случае мощность потерь в одной шине больше, чем в двух шинах половинной высоты, т. е. разделение шины на две половинной высоты приводит к уменьшению потерь.
Б) При увеличении высоты шины в 2 раза yh = 3,18 х х (14-71); jH=(25z43o)chyz А/см2; jB=(25 z 43°) [2 ch у (z-h)~ 664
_chx(2/i-z)J А/см2; £, = 3,72 • IO’4+/3,72  10“4 Ом; Z„= 19,9-10“4+/19,8-IO’4 Ом; Z, = 23,62 • 10“4 +/23,52 x x 10‘4 Ом; P2 = 23,6 Вт.
При одной шине двойной высоты Z[ = 3,72 • 10“4 + + /3,72-10~4 Ом; Pj = 14,9 Вт.
В этом случае разделение шины на две половинной высоты приводит к увеличению потерь.
19.42(Р). Построить зависимость сопротивления г2 двух последовательно соединенных шин задачи 19.41 от их высоты. На том же графике показать зависимость от высоты сопротивления Tj шины двойной высоты, а также отношение мощности потерь Р2 в двух шинах к мощности потерь в одной шине двойной высоты (при двойном токе). Определить, при какой высоте шин сопротивление г2 минимально.
Решение. Сопротивление двух последовательно соединенных шин найдено в задаче 19.41:
О 12 3 4	5
Рис. 19.42Р
у/
Z2 = ", -Т".' (6chyh - 4) = г2 + jx2. obshyh
Экстремальные значения г2 определяются из условия dr2/dh == 0.	(а)
Проще сначала дифференцировать Z2:
dZ2/dh =
/у2 (4 ch yh — 6) ab sh2 yh
После отделения действительной части от мнимой уравнение (а) принимает вид:
sh ah sin ah (ch2 ah + cos2 ah — 3 ch ah cos ah) = 0,
решения которого ch ah = 2,62 cos ah и sin ah = 0.
Первое удовлетворяется значением ah == 0,96, при этом r2 минимально. Второе удовлетворяется при ah = кя. Из всех последних экстремумов заметен лишь максимум при ah = я. Уже при ah = 2я сопротивление г2 практически достигает предельного значения: г2 = 6гю = €l/GbzQ.
На рис. 19.42Р представлены требуемые по условию задачи зависимости (r0 = l/obh — сопротивление постоянному току).
19.43(Р). Для шин задачи 19.41 сравнить комплексную мощность, выходящую из нижней грани верхней шины (длиной /), с комплексной мощностью, входящей в верхнюю грань нижней шины. Объяснить причину неравенства этих мощностей.
Определить, при какой высоте шин активная мощность, выходящая из нижней грани верхней шины, равна нулю и каковы при этом мощности, проходящие через другие горизонтальные грани шин, и комплексные сопротивления каждой шины.
Решение. Комплексный вектор Пойнтинга был определен в решении задачи (19.41). Комплексная мощность, выходящая из нижней грани верхней шины,
I2yl
& = -Hi/b = - ,	(2 - ch уй),
ooshyn J-
а комплексная мощность, входящая в верхнюю грань нижней шины,
I2yl
-пда = —4—Chy^.
abshyh
Мощности равны только при постоянном токе, когда v = 0 и chy/i= 1, при переменном токе мощности различны. Это объясняется тем, что существует еще мощность, проходящая через торцевые зазоры между шинами при любой малости этих зазоров. Действительно, мощность, входящая между шинами через задний зазор 5 (рис. 19.41), S'r = = -E'zH*b&, а мощность, входящая между шинами через передний зазор, S? = E"ZH*№!).
Через оба торцевых зазора входит мощность sT = s" + s; = (£; - £'z) н*ьь.
Разность напряженностей электрического поля определим, применив закон электромагнитной индукции к контуру, проходящему по нижней грани верхней шины, переднему торцу зазора, верхней грани нижней шины и заднему торцу зазора:
Ё'в1 - Ё''д - Ё”1 +	= 0.
В правой части уравнения — нуль, так как считаем, что зазор очень мал, и магнитным потоком через него пренебрегаем. Искомая разность напряженностей электрического поля
F' _ р"
и МОЩНОСТЬ
ST = 2Н2у (ch yh — l)/o& sh yh.
Ясно, что теперь баланс мощностей выполняется: S" = = £ + ST-
Активная мощность, выходящая из нижней грани верхней шины, равна нулю, если
Re S'n = Re
I2yl (2 — ch yh) ob sh yh
После преобразований получим уравнение
sh 2ah 4- sin 2ah = 4 (sh a/i cos a/i + ch ай sin ай).
Это уравнение можно решить построением левой и правой его частей. В точке пересечения ah = 1,49, при этом комплексная мощность, входящая через верхнюю грань верхней шины, 5" =/2г0 (4,12 +/6,51), комплексная мощность, выходящая через нижнюю грань верхней шины, = 72г0 (—/2,53), комплексная мощность, входящая через верхнюю грань нижней шины, 5" = I2rQ (1,36 4- /1,32), где r0 = l/cbh — сопротивление шины постоянному току.
Комплексное сопротивление верхней шины ZR = г0 (4,12 4-4- /9,04). Комплексное сопротивление нижней шины — = г0 (1,36 4-/1,32).
19.44.	Определить активное и внутреннее индуктивное сопротивления 1 м медного провода диаметром 2 мм при частотах: 1) 50 Гц; 2) 5 кГц; 3) 50 МГц. Удельная проводимость меди 57 • 104 См/см.
Найти отношение комплексной плотности тока на поверхности проводника к комплексной плотности тока на оси проводника при частоте 5 кГц.
19.45.	Найти, при каком диаметре алюминиевого провода плотность тока на его оси в любой момент времени противоположна по направлению плотности тока на поверхности, если частота тока 500 Гц. Удельная проводимость алюминия равна 35 • 104 См/см.
Определить отношение амплитуд плотности тока на поверхности и на оси.
19.46.	Для .провода задачи 19.45 определить отношение радиуса провода к глубине проникновения и разность фаз напряженностей электрического и магнитного полей на поверхности провода.
19.47.	Сравнить активное R и внутреннее реактивное х сопротивления стальной проволоки, определенные по точной
и по приближенной формулам для случая резко выраженного поверхностного эффекта, если радиус проволоки 1 мм, относительная магнитная проницаемость материала 100, удельная проводимость 105 См/см, частота тока 4550 Гц.
19.48(	Р). Определить, при каком отношении радиуса г0 к глубине проникновения z0: 1) активное сопротивление и 2) реактивное сопротивление цилиндрического провода можно считать по формуле для резко выраженного поверхностного эффекта, если погрешность должна быть меньше: а) 10%; б) 5%; в) 2%.
Решение. Комплексное (активное и внутреннее реактивное) сопротивление цилиндрического провода определяется по формуле
Z/Rq = (R + jX)/Rv = (£г0/2) Jo (£ro)/L (qr0),	(а)
где Rq = IIkyqG — сопротивление постоянному току; g = = ]/ — Jcoopr|i0; Jo и Ji — цилиндрические функции первого рода нулевого и первого порядков.
При резко выраженном поверхностном эффекте (со -> оо)
ZlxJRq — ^оэ/^0 + JXxJRq — JQr о/2 =
= jtq/'I = (аг о + jar0)/2.
Формулу (а) можно представить в виде
Z/Kw = (1 - /1) Jo fer0)/Ji (qr0).
Для больших аргументов справедливы асимптотические представления цилиндрических функций первого рода
/ I2 12-32-52
(	1!8х + З!(8х)3
cos
1-3	12-32 -5-7	\ . ( Зя\
------------------Ь • • • Sin X----—
1 !8х	З!(8х)3 J \	4 J
Если мнимая часть аргумента х намного больше единицы (более 2,5 - 3), то tg(x - я/4)	-J1, при этом
Z _ . х 1	.3	3	.63
Ro ~} 2 + 4 7 16х	16Р +j 256х3 +
где х = а - ja = qr0; а = ar0 = rQ/z0.
Разделив ряд на действительную и мнимую части, полу-
Следовательно,
R 1	3	63
~ + 2а + 16а2	512а4
X _	3_______3 _ 63
16а2	16а3	512а4
1) Активное сопротивление можно считать по приближенной формуле для резко выраженного поверхностного эффекта с погрешностью не более 10%, если
К < < <	1	3
—— = 1,1 = 1 + -----1- ~ 2---•  •
Roc	2а 16а
Решение этого уравнения дает: r0/z0 — а = 5,35; при погрешности 5% получим а = 10,35; при погрешности 2% получим а — 25,35.
2) Реактивное сопротивление можно считать по приближенной формуле для резко выраженного поверхностного эффекта с погрешностью до 5 %, если X/R^ = 0,95 = 1 — 3/16а2 — — 3/16а3 — 63/512а4..., т. е. при r0/z0 =а = 2,4. При погрешности 2 % получим а = 3,53.
19.49(Р). Определить, при каком отношении радиуса г0 к глубине проникновения z0 активное сопротивление цилиндрического провода можно считать по формуле для постоянного тока, если погрешность должна быть меньше: а) 10%; б) 5%; в) 2%.
Вычислить внутреннее реактивное сопротивление (по отношению к сопротивлению постоянному току).
Решение. При небольших значениях аргументов цилиндрические функции первого рода представляются в виде рядов:
/	\2	1	/	\4	1	/	\6
Т .	I Х \ I I х \	I х\
+(2ljr\Tj “ piFVV + '"’
1 ( х — ( Х\ 1 / X Y 1 ( X\S
-1 ” V/ ТЕГГ ^Т/ + 2!ЗТ\Т) “ ’   ’
при этом комплексное сопротивление цилиндрического провода, отнесенное к его сопротивлению постоянному току Ro, z X J0(x) I /ху 1 /ху 1 /х\6 Ro 2 IiW 1	2\2/	2!3!у2у	2!4! 2J
где х = дт0 = г0 \	= a - ja = (l - jl) r0/z0, т. е.
Z R . X	I (а\*	4 ( а V ,	,
Ro ~ Ro +J Ro “ L + 3 \ 2y 45 2 J + ' ‘ J,+
./аУГ,	1 /a\4	13 /a\8	1
\2/ L	6 \ 2J	270 \2/
а)	Активное сопротивление можно считать по формуле для постоянного тока с погрешностью не более 10%, если
= 1,1, откуда r0/z0 = а = 1,51.
б)	При погрешности 5 % получим а — 1,26.
в)	При погрешности 2 % имеем а = 1,0.
Внутреннее реактивное сопротивление при этих значениях
. ч X /а \2Г	1 (а V	13 (а \8 "I Л с„
г0/г0--	a)	6 (2/ + 270 V2j'‘j- ,536;
б) X/Ro = 0,387; в) X/Ro = 0,248.
19.50(F). Бесконечно длинный ферромагнитный цилиндр радиусом rQ, относительная магнитная проницаемость материала которого и удельная проводимость о, находится в однородном переменном магнитном поле напряженностью HQi параллельном оси цилиндра.
Определить электромагнитное поле внутри цилиндра, магнитный поток в цилиндре и среднее значение относительной комплексной проницаемости цилиндра р.ср = Вср/ц0Н0. Построить график цср | qr0 |, где q - ]/ -jcocrp,rp.o.
Задачу решить: а) непосредственным интегрированием уравнений поля; б) считая известным распределение электромагнитного поля в цилиндрическом проводнике с током /:
Iq	. I
е = о-------W =  -------------------——г- Ji (5г).
2^00/! (qrQ) -	2лг011 (фо) "
Решение, а) Направим ось z цилиндрической системы координат по оси цилиндра. Из симметрии следует, что вектор напряженности магнитного поля имеет только z-ю составляющую, а вектор напряженности электрического поля — 670
упрощается:
d ( dH\ 2 rj л
r —— — у H — 0 или dr I
1 dH
только а-ю составляющую. Кроме того, векторы поля зависят только от координаты г. Поэтому уравнение поля в проводящей среде (19.126) при у по (19.16) в рассматриваемом случае
1
г dr у dr ] 1 и dr2 т г dr - 11 v‘
Вводя q2 = — у2 и деля полученное уравнение на д2, приходим к уравнению Бесселя:
d2H 1 dH . Л
d (qr)2	(qr) d (qr)
решение которого будем искать в виде
где Jo (qr) и No (qr) - соответственно цилиндрические функции первого и второго рода нулевого порядка.
Функция No (qr) стремится к бесконечности, когда аргумент стремится к нулю. Вместе с тем напряженность магнитного поля на оси цилиндра конечна, поэтому = О и Н = Hz = ~ Л1 Jo (5Г)- На оси цилиндра (г = 0) имеем Н (0) = А1} так как Jo (0) = 1. Отсюда ясен смысл постоянной Ai — это напряженность магнитного поля на оси цилиндра.
Следовательно, Н = Н (0) Jo (qr). На поверхности цилиндра (г = г0) напряженность магнитного поля задана (Н0), поэтому Но = Н(0) IoQKo), и выражение для напряженности магнитного поля можно представить в виде
Н = Но Jo (gr)/J0 (qrQ).
Напряженность электрического поля определим из первого уравнения Максвелла (19.16) для проводника:
£• г 1	♦ й 1	НоЗ , , .
гг	еч Аг	гЛ tn* \ 1 (<£*)•
(У	су dr	crJo (qrо)
Магнитный поток в цилиндре определим при помощи закона электромагнитной индукции:
Ф = £ (г0) 2лг0/( -jw) = ZwoAoMioh (gr0)/qJ0 (gr0).
Среднее значение магнитной индукции в цилиндре
Вср = Ф/яго = 2Н0МгИо!1 (qro)/qrolo (^о)-
Среднее значение комплексной проницаемости цилиндра р, ср = Вср/Но#о =	Ji (qro)/qrolo (qr0\
Зависимости действительной ц'гср и мнимой составляющих средней комплексной проницаемости цилиндра от qrQ построены на рис. 19.50Р.
б) Из симметрии уравнений Максвелла следует, что при
одинаковых граничных поверхностях и аналогичных внешних
Рис. 19.50Р
полях решения «электрической» и «магнитной» задач’ будут аналогичными. Сопоставляя уравнения Максвелла для проводящей среды (19.16) и (19.26): гоГЯ = стЁ и rot Ё — — у®цгц0Я, легко устанавливаем взаимно аналогичные величины для «электрической» и «магнитной» задач:
Ё^Н; -;юцгц0;
М -усоФ (Z = f (7Ё
- рсоЦгРоЯ dS = ->Ф).
Поэтому, заменяя в решении «электрической» задачи все величины аналогичными, получаем ре
шение «магнитной» задачи, данное в п. «а».
19.51.	Насколько изменятся активное и реактивное сопротивления цилиндрической катушки длиной I = 20 см, если в катушку поместить медный цилиндр диаметром 2г0 = 2 см. Частота тока f = 5 кГц. Удельная проводимость меди ст = = 57 • 104 См/см. Число витков катушки w = 1000. Комплексное сопротивление катушки до помещения цилиндра Zo = 4 + + у 100 Ом.
Считать, что длина катушки и цилиндра намного больше
диаметра катушки.
19.52.	Решить задачу 19.51 в случае цилиндра из: а) свинца (ст = 4,9 • 104 См/см); б) нихрома (ст = 9,1 • 103 См/см); в) сверхпроводника. На основе решения для случая приведенного в п. «в», определить отношение сечения цилиндра к сечению катушки.
19.53.	Тороидальный магнитопровод катушки изготовлен из стальной проволоки диаметром 2г0 = 0,4 мм *с относительной проницаемостью — 2000 и удельной проводимостью ст = 105 См/см. Число витков проволоки п = 2000. Отношение сечения стали к общему сечению магнитопровода £i/S = 0,6. Число витков обмотки w = 1000. Средняя длина магнитной линии I — 30 см.
Определить комплексное сопротивление катушки, пренебрегая сопротивлением обмотки, при частоте: а) 50 Гц; б) 500 Гц. 672
19.54.	В переменном магнитном поле катушки параллельно ее оси расположены изолированные друг от друга проволоки.
Определить, при каком значении радиуса проволок и неизменных проводимости и магнитной проницаемости материала, частоте и амплитуде тока средняя по объему удельная мощность потерь в проволоках будет максимальной. Найти эту максимальную мощность.
Считать, что длины катушки и проволок намного больше диаметра катушки.
19.55.	В катушку с числом витков w = 1000 вставляется ферромагнитный цилиндр диаметром 2г0 = 1 см. Относительная магнитная проницаемость материала = 5, удельная проводимость о = 5 • 104 См/см; длины катушки I = 20 см и цилиндра намного больше диаметра катушки.
Определить, при какой частоте тока в катушке ее индуктивное сопротивление не изменится в результате введения цилиндра и насколько при этом изменится ее активное сопротивление.
19.56.	Решить задачу 19.55 при относительной магнитной проницаемости цг = 500.
19.57.	Определить сопротивление Zo на единицу длины двухпроводной воздушной линии при частоте тока 16 кГп. Выделить составляющие Zo, обусловленные: а) полем в воздухе между проводами и б) полем в проводах.
Расстояние между осями проводов 2а = 50 см настолько велико, что влиянием магнитного поля одного провода на другой (эффект близости) можно пренебречь. Радиус провода r0 = 1 мм. Материал проводов — бронза, для которой о = = 3,6-105 См/см; цг = 1.
19.58.	По медной трубе в направлении ее оси проходит ток.
Определить активное и внутреннее реактивное сопротивления трубы длиной I = 1 м, радиусами = 2,5 см и г2 = 3,5 см при частотах: а) 0; б) 50 Гц; в) 5 кГц.
Удельная проводимость меди о = 57 • 104 См/см.
19.59.	Найти распределение электромагнитного поля: а) в жиле; б) в оболочке; в) между жилой и оболочкой в медном коаксиальном кабеле с радиусами жилы г0 и оболочек гь г2. Заданы: ток кабеля 1 и напряжение U между жилой и оболочкой.
19.60.	Для коаксиального кабеля задачи 19.59 найти общее выражение комплексного сопротивления. Рассмотреть частные случаи: а) низкой частоты (глубина проникновения z0 »
22 п/р Ионкина П. А.
» r2 — отсутствует поверхностный эффект как в жиле, так и в оболочке); б) высокой частоты (z0	г0); в) настолько
высокой частоты, что и z0 « и :0 «: (г2 — гД
19.4.	Волны в диэлектрике, волноводы, резонаторы, излучение
В этом параграфе помещены задачи на следующие темы: 1) распространение волн в неограниченном диэлектрике; 2) отражение волн от плоской границы раздела сред при нормальном падении; 3) возбуждение волн ТЕ и ТМ в волноводах, критическая длина волны, приближенный учет потерь: 4) возбуждение полей ТЕ и ТМ в резонаторе, резонансные частоты, добротность; 5) мощность излучения диполя.
19.61	(Р). Приемная антенна выполнена в виде прямоугольной рамки (рис. 19.61) с размерами а = 20 см, b = 10 см.
Рассчитать ЭДС, наводимую в рамке при частоте 5 МГц в поле с напряженностью Н = 150 мкА/м. Найти самую низ
кую частоту, при которой можно применить эту рамку, если максимальная чувствительность приемника 10 мкВ. Ответить на вопросы: почему размер рамки в направлении распространения волны не может быть равен целому числу длин волн; какое значение имеет размер рамки в направлении, перпендикулярном направлению распространения волны.
Решение. Выберем систему координат, как показано на рис. 19.61Р. Примем Ё = Ёх — Ео при z = 0, тогда по (19.23) при z = а напряженность Ё — EQe~jka, где к = к0 = со/со = = 2n/Z0 — волновое число, Хо — длина волны в вакууме.
По закону электромагнитной индукции ЭДС, наводимая в рамке,
е = £ dl = - дФ/dt.
Поэтому задачу можно решить двумя путями: либо интегрированием напряженности электрического поля по контуру 674
рамки, либо путем определения производной по времени от магнитного потока, пронизывающего рамку.
Решим задачу первым путем. Обходя контур, как показано на рисунке, получим:
1= f Edl = Eoe~ik<,ab - Eob = £0Ь(е’Л°“ - 1).
Если размер рамки а намного меньше длины волны Хо, то в разложении показательной функции в степенной ряд можно оставить первые два слагаемых: е jk°a » 1 — jkoa, при этом
^== -jkQabEQ = ~j eq = -JI 19 мкВ, Ло
где Ео = zBH0 и по (19.24) zB = 376,7 Ом.
19.62.	Круглый виток диаметром 20 см находится в электромагнитном поле частотой 1 МГц. Напряженность электрического поля в месте расположения витка 100 мкВ/м.
Расположить виток так, чтобы ЭДС, наводимая в нем, была максимальной, и определить действующее значение этой ЭДС.
Указание. Электродвижущая сила, наводимая в витке (рамочной антенне), пропорциональна скорости изменения магнитного потока, пронизывающего рамку. При неизменной частоте поля ЭДС максимальна при максимальном потоке. Поэтому плоскость рамки должна быть перпендикулярной направлению вектора напряженности магнитного поля. При расчете ЭДС учесть, что размеры рамки намного меньше длины волны, и поэтому можно пренебречь различием фаз напряженности магнитного поля в разных точках внутри витка.
19.63.	Антенна сделана из ферритового стержня сечением 0,25 см2 и имеет в средней части катушку из пятидесяти витков. Средняя магнитная проницаемость стержня (с учетом формы тела — отношение средней индукции внутри стержня к напряженности внешнего магнитного поля, деленное на ц0) равна 16. Напряженность электрического поля в месте расположения антенны 30 мВ/м.
Определить значение ЭДС, наводимой в катушке приемной антенны, если передающая станция работает на частоте 600 кГц. Считать, что ось катушки совпадает с направлением вектора напряженности магнитного поля.
19.64.	Энергия плоской волны, падающей в воздухе на нормальную к ней абсолютно поглощающую площадку в 1 см2, составляет 2,2 кал в 1 мин.
Найти амплитуды напряженностей электромагнитного поля волны.
19.65.	Плоская электромагнитная волна падает на поверхность воды (е, = 80; о = 0,1 См/см) нормально к ней. Напряженность электрического поля в воздухе у поверхности воды 1 мВ/м.
Определить длину волны в воде и напряженность магнитного поля на глубине, равной длине этой волны. Расчет провести для двух частот: 1) 10 МГц; 2) 50 ГГц.
19.66.	Решить задачу 19.65 для случая, когда задано значение напряженности электрического поля падающей волны в воздухе у поверхности воды 1 мВ/м.
Рис. 19.69
19.67.	Для уменьшения отражения света от поверхности линз оптических приборов их покрывают слоем лака («просветленная оптика»). Действие этого слоя можно уподобить четвертьволновому трансформатору, согласующему входное сопротивление стекла (равное его волновому сопротивлению при отсутствии отраженной волны) и волновое сопротивление воздуха.
Найти толщину слоя лака и его относительную диэлектрическую проницаемость, если относительная диэлектрическая проницаемость стекла равна 7.
Расчет провести для средней длины волны видимой части спектра 0,6 мкм.
19.68.	Для уменьшения отражения от идеально проводящей поверхности применили двухслойное покрытие. Первый слой, прилегающий к проводящей поверхности,—диэлектрик с ег = 2,25, второй слой — проводник с о = 103 См/см.
Определить толщины диэлектрика и проводника, если нужно получить неотражающее покрытие при частоте 3 ГГц.
19.69.	На рис. 19.69, п — е изображены различные способы возбуждения прямоугольного волновода. Зная, что штырь по-676
мешается в область концентрации электрического поля, а рам ка — в область концентрации магнитного поля, определить, какие типы волн могут при этом возбуждаться. Написать уравнения для электрического и магнитного полей. Указать необходимые фазы токов в штырях на рис. 19.69,6 и е.
19.70(	Р). Какие типы волн могут возникнуть в прямоугольном волноводе с поперечными размерами 34x72 мм при частотах: 1) 3000 МГц; 2) 9000 МГц, если возбуждение производится: а) электрической антенной (штырем), располо женной в середине широкой стенки волновода (рис. 19.69, а); б) рамкой с током, которая находится в середине узкой стенки и плоскость которой параллельна широкой стенке волновода (рис. 19.69, г). Найти длину волны в волноводе.
Решение. В волноводе могут возникнуть те типы волн, у которых критическая длина волны Хкр больше длины волны в свободном пространстве Хо. Критическая длина волны опре деляется поперечными размерами волновода а и b (рис. 19.69)*.
|/(w/2a)2 + (п/2Ь)2
где тип — целые числа.
В табл. 19.70 приведены значения Хкр для разных значений тип при а = 34 мм и b = 72 мм.
Таблица 19.70
т	0	0	1	1	1	0	1
п	1 »	2	0	1	2	3	3
^•кр	14,4	7,2	6,8	6,5	5,1	4,7	4,0
т	0	2	2	2	1	0	3
п	4	0	1	2	4	5	0
^•кр	3,6	3,4	3,28	3,25	3,23	2,88	2,3
Из таблицы видно, что при f = 3 ГГц (Хо = 10 см) в волноводе может распространяться только волна ТЕтп при т = 0 и п = 1. При частоте f — 9 ГГц (Хо — 3,3 см) в том же волно
воде могут распространяться волны, типы которых имеют индексы 01, 02, 10, 11, 12, 03, 13, 04, 20.
а)	При возбуждении волновода штырем в середине широкой стенки могут возбуждаться волны ТЕтп с любым индексом т и нечетным индексом и, т.е. TEOi при Хо = 10 см, и с индексами 01, И, 03, 13, 21 при Хо = 3,3 см.
б)	При возбуждении рамкой могут возникнуть волны с нечетным индексом т. Следовательно, при Хо = 10 см волны распространяться не будут, а при Хо = 3,3 см могут быть волны ТМИ, ТЛ112, ТМ13.
19.71.	Определить потери в стенках медного (о = = 56-104 См/см) прямоугольного волновода с поперечными размерами 34x72 мм, длиной 50 см при частоте 3 ГГц, если по волноводу бегущей волной типа Т£01 переносится мощность 1 кВт. Вычислить коэффициент ослабления для волны этого типа в волноводе и уменьшение (в процентах) амплитуды бегущей волны на расстоянии 50 см.
19.72.	Решить предыдущую задачу для волны ТМП при частоте 6 ГГц.
19.73(	Р). Часть прямоугольного волновода с поперечными размерами 34 х 72 мм заполнена диэлектриком (е, — 2,5 — у'0,02).
Определить мощность, проходящую в волновод за диэлектриком, если мощность падающей волны до диэлектрика
Рис. 19.73Р

Ро = 1 кВт, частота 3 109 Гц, тип колебаний T£Oi Е0 зссх трех частях волновода, длина заполненной диэлектриком части волновода 0,2 м.
Решение. Мощность, передаваемую по волноводу, выразим при помощи потока вектора Пойнтинга через поперечное сечение волновода. В системе координат, изображенной на рис. 19.73Р, а, для волны ТЕ01 по (19.28) и (19.266)
Р = Re
(£xH*)riS = Re^-,
(1)
где Ео — напряженность электрического поля в волноводе при у = Ь/2 (действующее значение); Zr = 120тг/|/е, — (/о//)2 — характеристическое сопротивление волновода; /0 = Го/2Л> — критическая частота волновода при е, = 1; с0 — скорость света в вакууме.
В рассматриваемой задаче волновод состоит из трех частей (рис. 19.73Р, б). Отношение мощностей падающих волн в областях 1 и 3, как следует из формулы (1),
Р?/Р; = (Е0\/Е0+з)2,
где знаком плюс отмечены волны, движущиеся вдоль оси z. Отношение Eoi/Еоз зависит от условий на границах раздела частей 1-2, 2-3 и расстояния I между ними.
На границе 1-2 по (19.15)
Et (0) + ЕГ (0) = Ё2 (0) + ЁГ (0);
Ht (0) - нг (0) = Н2+ (0) - Нг (0) или
ЁГ (0) - ЁГ (0) = Ё2 (0) - Ё2~ (0) Zcl	Zc2
Аналогично на границе 2-3
Et (1) + Ё2“ (!) = Ё3+ (/);
Я? (О - (/) = Йз+ (0 или (0 ~ Ё1 ® = Ц®-.
^с2	“jc3
Далее,
(0 = £Г (0) Ё; (/) = £г (0) g',
где у вычисляется по (19.18).
Замечая, что в условиях данной задачи Z^ = 2ci, и обозначая (Zct — Zp7)/(ZH + Z^) = N, из написанных уравнений находим:
l-Nl ’ -" 1 + п ’
здесь п =
1 - (/о//)2 S, - (folf?
0,5 при/0//= 3  1010/2  7,2
3109 =
= 0,695;
N = (1 - 0,5)/(1 + 0,5) = 1/3;
*4 J
yl = -Г-/& - (/о//)2 = 2л • 2,84 (1 -/4,96  10-3)
— Ло
и
Ё0+1/Ё0+з = 1,3 z. -62° 30'.
Отношение мощностей равно отношению квадратов модулей напряженностей полей. Таким образом,
Pt = 1,3	= 592 Вт.
19.74.	Определить потери в диэлектрике, заполняющем волновод с поперечными размерами 23 х 10 мм, при частоте 1010 Гц для волны Т£01. Длина волновода, заполненного диэлектриком с е, = 1,5 — j0,015, равна 50 см. Мощность на входе волновода 1 кВт. Потерями в стенках волновода пренебречь.
19.75.	Решить предыдущую задачу для волны ТМП при частоте 2 • 1010 Гц.
19.76.	Определить резонансные частоты прямоугольного резонатора с размерами 10 х 23 х 30 мм при возбуждении колебаний типа: a) TE01i; б) Т£012; в) TEQ2i-
19.77(	Р). Прямоугольный резонатор имеет размеры а = = 10 мм, Ъ 23 мм (рис. 19.77). В резонаторе возбуждаются колебания типа Т£012.
Определить составляющие векторов £ и Я, а также размер с резонатора вдоль оси z, если резонансная частота должна быть равна 1О10 Гц.
Решение. Если поперечное сечение волновода или резонатора совпадает с плоскостью ху, то электрическое поле волны типа ТЕ может иметь только составляющие по осям х и у. Для волны типа Т£012, как и для других волн типа Т£ОиЬ составляющая поля Ех не зависит от координаты х. Из условия div £ = 0 следует, что в этом случае составляющая Еу = 0. Кроме того, составляющая Ех должна обращаться в нуль на тех стенках (четыре боковых) резонатора, где она будет тангенциальной. Поэтому для волны Т£012 имеем:
.	 . пу . 2itz
Ех — Л sin -j^-sin-,
be
где А — константа, определяемая мощностью возбуждения.
Напряженность поля Н найдем из второго уравнения Максвелла (19.26) при = 1, откуда
2яЛ4 . яу 2nz
Hv = —-—sin ——cos ------;
y Gj^qC b c
niA	ny . 2rcz
Hz =------——cos —-sin-----.
(Ogob P C
Размер с резонатора для волны TE012 должен равняться длине волны ТЕ01 в волноводе:
с = Хо/|/1 - (Х.0/2Л>)2 « 39,6 мм, где Хо — длина волны в вакууме при частоте 1О10 Гц.
Рис. 19.77
Рис. 19.81
19.78.	Найти размер с резонатора предыдущей задачи для колебаний типа ШП1 при частоте 2 • 1О10 Гц.
19.79.	У радиостанции мощностью 500 кВт, работающей на волне 1744 м, передающая антенна расположена вертикально и имеет высоту 150 м.
‘Считая, что антенна со своим зеркальным изображением может рассматриваться как электрический диполь, определить ток в антенне.
19.80.	В круглом витке диаметром 20 см ток равен 10 А при частоте 1 МГц.
Определить мощность и сопротивление излучения.
19.81.	Вдоль короткого прямолинейного проводника (диполь Герца), длина которого равна /, протекает синусоидальный ток i = /msincot (рис. 19.81).
Предполагая, что длина волны намного больше длины проводника и что ток по всей длине проводника один и тот же, определить векторный потенциал электромагнитного поля в точке наблюдения М при R » I. Задачу решить, применив декартову систему координат.
19.82.	Пользуясь уравнением связи между векторным и скалярным потенциалами электромагнитного поля, найти скалярный потенциал в точке М задачи 19.81 (см. также ответ к задаче 19.81).
19.83.	Пользуясь ответами к задачам 19.81 и 19.82, найти составляющие напряженности электрического и магнитного полей диполя Герца задачи 19.81 в декартовой системе координат.
19.84.	Пользуясь ответом к задаче 19.83, найти напряженности электрического и магнитного полей диполя Герца задачи 19.81 в ближней зоне. Ближней зоной считать область (рис. 19.81), для точек которой R Хо, где Хо - длина волны в вакууме при частоте тока со. Доказать справедливость формулы Био —Савара в этой области.
19.85.	Пользуясь ответом к задаче 19.83, найти напряженности электрического и магнитного полей диполя Герца задачи 19.81 в дальней зоне. Дальней зоной считать область (рис. 19.81), для точек которой R »Х0, где — длина волны в вакууме при частоте тока со. Найти среднее значение вектора Пойнтинга в дальней зоне.
19.86.	При решении задачи 19.85 выяснилось, что вектор Пойнтинга в дальней зоне направлен вдоль радиуса-вектора R (рис. 19.81), и было найдено его среднее значение за период (см. ответ к задаче 19.85).
Определить среднюю за период мощность, излучаемую диполем Герца.
ОТВЕТЫ К ЗАДАЧАМ ГЛ. 1
1.1.	1 = 6 А; Л =4 А; 12 = 1 А.
1.2.	л = /г2/(г, + r2); I2 = Iril(ri + г2).
1-3. пМп + г2).
1.4.	(г2г + г2г + г^2)1(г 1 + г2).
1.7.	См. решение.
1.8.	См. решение.
1.9.	i’i = i2 = 1'3 = 0; «с = 100 В; uL — 100 В.
1.10.	G = 0; i2 = -2 A; i3 = 2 А; ис = 100 В.
1.11.	ii = 0,5 A; i2 = — 3 A; i3 — -3,5 А; ис = 30 В; uL = 35 В.
1.12.	1) 1,6 В; 2) 2,4 В.
1.13.	1) 20 А; 2) -180 А.
1.14.	1) 21 А; 13 А; 16 А; 8 А; 8 А; 2) 1 А; 3 А; 2 А; 3 А; 5 А.
1.15.	1) 3112 Вт = 3112 Вт; 2) 230 Вт = 230 Вт.
1.16.	1) 22 А; 2) 3 А; 2 А; 3 А; 5 А.
1.17.	Л = 3 А; /3 = 1 А; 74 = 3 А; 15 = 1,5 А; 16 = -1,5 А; 37 Вт = 37 Вт.
1.18.	См. решение.
1.19.	(ра=6 В; (рс = 5 В; (р3 = 7 В; (pd=3 В; (рь = 3 В.
1.20.	21 А; 13 А; 16 А; 8 А.
1.21.	1а) г5 и г6; 16) нет; 2а) г5 и + г7; 26) и r7.
1.22.	1) 2,22 Ом; 2) 1,2 Ом; 3) 0,8 Ом; 4) 1,2 Ом.
1.23.	1) 4,4 Ом; 2) 10 Ом.
1.24.	3,25 Ом; 468 Вт.
1.25.	1А) 3 Ом; 1Б) 19 Ом; 2) 19 Ом; 40 Ом; 40 Ом.
1.26.	1) га = гс = 2 Ом; rb — 1 Ом; 2) 7 Ом; 4 Ом.
1.27.	1) rad = rcd = 10 Ом; = 13,33 Ом; 2) гЬс = 15,2 Ом; rbd = 19 Ом; rcd = 38 Ом.
1.28.	-8 А; 22 А.
1.29.	-8 А; 22 А.
1.30.	1) 440 Вт; 2) -240 Вт.
1.31.	1) -2,8 А; 3,6 А; 0,8 А; 2а) 360 Вт = (78,4 + 259,2 + + 6,4 + 16) Вт; 26) (140 + 56) Вт = (78,4 + 39,2 + 78,4) Вт.
1.32.	1 А; 3 А; 2 А; 3 А; 5 А.
1.33.	1) 230 Вт = 230 Вт; 2) 158 Вт - 158 Вт.
1.34.	См. решение.
1.35.	1,38 мс; 6 В.
1.36.	(2 + e’15f) A.
1.37.	(1 +e"80t) A; -8<?’80f B.
1.38.	2 —O,5e"750' A; 125e"750f B.
1.39.
1.40.
1.41.
1.42.
1.43.
1.44.
1.45.
1.46.
1.47.
— 0,5 A.
1.48.
См. решение.
10(1 -e-“>00‘) B; le"1000' A; 6,3 B; 0,37 A.
1 A; 1 A.
10(1 — e~75C") B; -O,75e’750' A.
2-103(l — e*2500') B; lOe*2500' A.
0,66e"'/15'10"6 A; 30+ Юе’"15'10~6 B.
См. решение.
0,5 A; -0,2 A; 0,5 A; 0,25 A; 0,75 A; 1,0 A; 0,25 A.
0,3 A; 0,15 A; 0,25 A; 0,5 A; 0,4 A; 0,25 A; 0,25 A;
1 -1 0 0 -1	0 0 0
0 011	0	100
0 0 0 0 -1 -1 1 0
0	1 1 0 0 0 0 1
1.49.
1.50.
1.52.
1.53.
0 0 0 1
0 0 0 0
0 110
10 10
1 о 0
0 1 0 0 0 1
0 0 0
1	0
1 1
0 -1
о 0
-1 1
о 0
1	0
0 -1
-10 1	0
110-1
-101	1 •
-10 1	1
-10-1	1-1	0
10	10 0 0
1 0 0	0	1	-1
01	1-1	0	1
-1	0 0
0	1	0
0	0-1’
I -1	1
0 0	0 0 1 0
1 1	0 0 0 0
0 0	1 0 0 1
-10-1100
1001	0-1
0 10 1	1	0
0010-1 -1
1000-1-1	0 -1 0
0 10 0	1	1	0	11
0 0 10	1	0-1 11 ;
0 0 0 1 -1	0	1	0 0
3)
1	-1 -1	110	0	0	0
1	-1 0	0	0 1 0	0 0
0	0 1	-1	0 0 1	0 0
1	-1 -1	0	0 0 0	1 0
0-1 -1	000001
1.54.	См. решение.
1.55.	0,075 А; 0,025 А; 0,1 А; 0,125 А; 0,075 А; 0,3 А; 0,125 А; 0,1 А; 0,1 А; -0,2 А.
1.56.	См. решение.
1.57.	2 А; 1 А; 0,25 А; 0,75 А; 0,25 А; 1,75 А; 1 А.
1.58.	См. решение.
1.59.	0,1 А; 0,1 А; 0,2 А; 0,3 А; 0,4 А.
1.60.	0,25 А; 0,14 А; 2,1 А; 0,11 А; 0,89 А.
1.61.	0,02 А; 0,02 А; 0,01 А.
1.62.	0,1 А.
1.63.	40 В.
1.64.	36,4 В.
1.65.	180 В; 120 В.
1.66.	56 В.
1.67.	См. решение.
1.68.	0,025 А; 0,05 А; 0,1 А; 0,125 А; 0,05 А; 0,1 А.
1.69.
1.70.
См. решение.
(01 + (7г + 0з)	~9з	0	~91 ~ 02
-9з	(0з + 04>	-04	О
О	—04	(04 + 05)	—05
—01—02	0	(01+02 + 05)
1.71.	См. решение.
1.72.	2	А;	5	А;	10 А;	-3	А; 4	А; 2	А.
1.73.	0,05	А;	0,1	А; 0,2	А;	0,1 А; 0,2	А; 0,05 А.
1.74.	См. решение.
1.75.	4	А;	2	А;	1 А; 3	А;	1 А;	4 А.
1.76.	5	А;	1	А;	6 А; 2	А;	3 А.
1.77.	1	А;	2	А;	3 А; 1	А;	4 А.
1.78.	См. решение.
Л Ъ h
1.80.
1.81.
(г 1 + r4 + Гз)
-Гз
-гз
(г2 + г5 + г3)
Л
12
Et +
Е2 - r5J
1.82. См. решение.
1.83. — 4 А; -8 А;
4 А.
1.84.	0,2 А.
1.85.	0,8 А.
1.86.	-6,4 А.
1.87.	2 А.
1.88.	-12 В.
1.89.	gi5 = 051 = 0,022 См.
1.90.	1) 8/15; 1/9; 4/9; 2) 10,7 Ом; 77,1 В.
1.91.	5,53 А; 7,03 А.
1.92.	См. решение.
1.93.	U5 = 11,33 - 8,34/3.
1.94.	3 А.
1.95.	Ц = 1,25 — 1,5/4 (токи - в амперах).
1.96.	t/i2= — 9 + 3(/34 (напряжения — в вольтах).
1.97.	3 мА; 1,25 мА; 1,75 мА; 0,75 мА; 1 мА; 0,5 мА; 0,5 мА.
1.98.	40 А; 10 А; 30 А; 20 А; 10 А; 4,8 А; 9,6 А; 14,4 А.
1.99.	8 мА; 8 мА; 2 мА; 6 мА; 4 мА; 2 мА.
1.100.	См. решение.
1.101.	3 А; 1 А; 2 А; 0; 1 А.
1.102.	0,2 А; 3,2 А; 30,8 Вт = 30,8 Вт.
1.103.	127 В; 0,111 Ом; 3,6 кВт; 4,8 кВт.
1.104.	См. решение.
1.105.	0,8 А.
1.106.	-30 мА.
1.107.	См. решение.
1.108.	5,08 А.
1.109.	2 А.
1.110.	0,9 А.
1.111.	1,71 А.
1.112.	3,2 кОм; 125 мВт.
1.113.	1 А.
1.114.	12,2 А.
1.115.	2,625.
1.116.	44.
1.117.	2,625: 44.
1.118.	См. решение.
1.119.	См. решение.
1.120.	50 В.
1.121.	0,321; 0,157; 0,066 В.
1.122.	0,0788 А.
1.123.	См. решение.
1.124.	0,5 Ом.
1.125.	-7,72 мА.
1.126.	См. решение.
1 128	= ah + cdh + св
х0 1 — eh — bd — ebd
1129 X1 -	+	• хз _ ah + cdh + eg
x0 1 — eh — bd — ebg x0 1 — eh — bd — ebg '
1.130.	Xi = ax0 4- dx2 4- ex3; x2 = cx0 4- bxL; x3 = hxx 4-
9X2 + fx3.
1.131.	См. решение.
1.132.	-18; -52; -14.
1.133.	Рис. 1.1330.
1.134.	См. решение.
1.135.	1,1 А.
ОТВЕТЫ К ЗАДАЧАМ ГЛ. 2
2.1.	См. решение.
2.2.	120 sin (cor - 66,8°) 4- 147е’8000г В.
2,3.	51/2 sin (314t + 135°) + 5е“314' А; рис. 2.30.
2.4.	0,45 sin (<ot - 26,6е) + 0,2<?“25‘ А.
2.5.	15,4cos (104t — 31,4°) + 13,le”16,3 io3' B? 8,6cos(104t -- 31,4°) + 7,3e”16,3' l°3' A.
2.6.	17,9 cos (2500t - 60,3°) + 8,87e”5'‘°3' B.
2.7.	1,64 sin (cot + 48°) — 0,977e”11,1'lo3' A.
2.8.	1) lOOsin co(t + 778) B; 2) lOOsin co (t + 774) B; 3) lOOsin to(t + 3T/8) B; 4) lOOsin cd(r + T/2) B; 5) lOOsin co(t + 4-3T/4) = 100 sin co (t — T/4) B.
2.9.	a) 7,07 sin cot A; 311 sin (cot + 90°) = 311 cos cot B; 6) 7,07 sin (cot 4-45°) A; 311 sin (cot 4-135°) В; в) 7,07 sin (cot--30°) A; 311 sin (cot 4-60°) B.
2.10.	100 sin (157t — 45°) B.
2.11.	См. рис. 2.110.
2.13.	-150° = 210°; 50 Гц; 10 210° A; 7,07 z. 210° A; -6,12-Д53 A.
2.14.	1) 60°; 120°; 2) -60°; -120°; 3) (10/|/2) z 60°; (10Д/2) z 120°; (10/J/2) z -60°; (10/J/2) z -120°.
2.15.	1) 220 z 20° = 205 +775; 2) 15 z 40° = 11,5 + 79,64; 3) 380 z -80° = 66 -;374; 4) 100 z -120° = -50 -786,6.
2.16.	1) 4,33 + 72,5 ; 2) 3,42 + 79,4 ; 3) -0,0347 + 70,197; 4) -0,0345+70,00607; 5) -2,41 -764,7 ; 6) -11,2-727,8; 7) 0,174 — -71,99; 8) -7190+ 329; 9) 0,297 • 10” 3 — 70,017; 10) -1000--734,9; 11) 15 +70,175.
2.17.	1) 100z53°10'; 2) 100z36°50'; 3) 316 z 198°26'; 4)72,8 z 106°; 5)9 z -3° 10'; 6) 100 z 181°43'; 7) 3-10”3 z 176,19°.
2.18.	A. 1) 5z36°50'; 2) 1,12 z 63°25'; 3) 7 z90°; 4) 5 z 53° 10'; 5) 7,28 z 74°4'; 6) 15 z 180°; 7) 3,46+72; 8) 22,8z66°50'; 9) 4,5 z-90°; 10) 0,9+71,07; 11) 61z4°42'; 12) 5 z 143’10'; 13) 1,12 z 26’35'; 14) 5z0°; 15) 5 z-36°50'; 16) 5 z 216°50' = 5 z -143° 10'; 17) 16,4 z 148’45'.
Б. 1,8885 z 5,1° = 1,88 4-JO,168;
В. 1,71 z 6,8° = 1,7 + JO,2.
2.19.	103 cos (1O4Z 4-76°) B; 66 cos (104z 4-63°27') B.
2.20.	ur — 20 sin (coz 4- 30°) B; uL = 25 sin (coz 4- 120°) B; uc = = 20 sin (of — 60°) В; и — 20,6 sin (coz 4- 44°) B; p = 17,67 — - 18 cos (2coZ 4- 74°) Вт.
2.21.	180 В; 0,0477 Гн.
2.22.	(0’=4^Y + W-r)4+-L 2 \Lj ~ у 4 \L J (LC)
2.23.	200 B; 1,73 A; 1 A; 300 Вт.
2.24.	63° 30'.
co = 3400 рад/с.
2.25.	72,4 sin (cot - 33°40') B; 72,4 sin (cot + 33°40') В; 1 A;
51 B; 51 B.
2.26.	1) 100 В; см. рис. 2.260; 2) 0.
2.27.	43,3 Ом; 25 Ом; /2/2.
2.28.	/2-2,5 sin cot В. Топографическая диаграмма: / = = 0,05 A; (pi = 0; (p2 = 7,5z-90° В; ф3 = 2,5-;2,5 В; ф4 = = 10 - j2,5 В; ф5 = 10 В.
2.29.	Токи: 2/2 А; -/2 А; -|/2 А; 2 /2 А; /2 А. Топографическая диаграмма: ф, = 0; ф2 = -/60/2 В; ф3 = = 5о/2-;6О/2 В; ф4 = 50/2 -/80/2 В; ф5 = 50/2 В.
2.30.	1) /1 А; -/1 А; 0; 1 А; 1 А; /1 А; 1 + /1 А; -/1 А; 1 А; 1 А; 2 А; 2) /2 А; -/0,5 А; /1,5 А: 1 А: 1 + /1.5 А; /2 А; 1 + /3,5 А; -/0,5 А: 1 +/3 А; 1 А; 2 + /3 А.
2.31.	xL/r, = xc/r2 = 1//3.
2.32.	См. решение.
2.33.	Л = -1 +/1 А; /2 = 1 -/1 А; /3 = 1 А; /4 = -/2 А; /5 = 1 -J2 А; фг/=;1 В; фс = 1 4-Д В; фь = 1 В; фу= -1 В; ф0 = 3—;4 В; E = 4-j4 В.
2.34.	i! = i3 — 5 sin (cor + 45°) A; i2 = 15 sin (cot — 135°) A; i4 = 15 sin (cot + 45°) A; uab = 150 sin (cot — 45°) В; uac = 300 sin (cot -— 45°) B; uad = 900 sin (cot — 45°) В. Топографическая диаграмма: ф„=150 В; ф„ = 75|/2zi -45° В; фс = 75/2	135° В; ф4 =
= 375 |/2 г- 135° В.
2.35.	10 А.
2.36.	6,5 А; 2,07 А; 7,55 А.
2.37.	См. решение.
2.38.	-ji мА.
2.39.	7,07 мА; 6,4z-6°20' мА; 5,01 z. 129° 20' мА; 4,5 г. 45° мА.
2.40.	18,3 z. 177° 19' мА.
2.41.	1) 0,708 z -135° А; 1,58 z 18°25' А; 0,946 z 45° А; 0,746 г. -63°25' А; 7,19 z 54° 35' В; 2) (pj - 7,92 z. 18°25' В; фз = 10 В; ф4 = 4,7 л. -45° В.
2.42.	(910 - уЗОЗ) В • А; (151 + >455) В • А.
2.43.	а) 0,52 А; ;0,52 А; 0,733 z 45° А; б) 0,364 -45° 10' А; l,04z89°50' А; 0,815	71°30' А; в) 0,867	123°40' А;
0,433 z 33°40' А; 0,685 z 142° А; 0,685 z 52° А; 0,97 z 97° А; г) l,22z78°50' А; -0,306 z - 101° 10' А; 0,915 z 78° 50' А; 0,966 z 186,5° А; 0,914 z -11° 10' А; 1,52 z 41°50' А.
2.44.	Рис. 2.440; rj = хй = г3 — 10 Ом; хс = 20 Ом.
2.45.	Показания не зависят от положения ключа: 2,5 А; 125 Вт-
2.46.	S] = EJ* (отдается); S2 = Ё21* (потребляется); £4 = = UAI* (потребляется); Ss= U£i* (потребляется).
$	а	б	в
S1	Р > 0; Q <0	Р < 0; Q < 0	Р > 0; Q > 0
5г	Р > 0; Q < 0	Р < 0; Q = 0	Р > 0; Q >0
	Р>0; б>0	Р<0; Q < 0	Р < 0; Q > 0
5б	Р = 0; Q < 0	Р < 0; Q > 0	Р > 0; Q >0
2.47.	10 А; 721 z 33,7° В.
2.48.	3,14 Вт; 7,08 Ом.
2.49.	а) 10 А; 7,07 + 135° А; 7,07	135° А; 7,07 z 45° А;
800 Вт; б) 3,51 z—34° 50' А; 5,5 z 18,5° A; 3,5z52°10' А; 1,37 z 71,5° А; 4,96 z 7° 10 А; 337 Вт.
2.50.	20 + >20 Ом; 7,4 z -19° А.
2.51.	2,23z_26°35' A; 2,23 z. 63° 2 5' A; 3,6 Z -123*40' A, 5,82 z. - 121° A.
2.52.	См. решение.
2.53.	См. решение.
2.54.	1) R = xc = 200 Ом; 2) R = 500 Ом; xc = 250 Ом.
2.55.	См. решение.
2.56.	a) xL — 43,8 Ом; r = 4,4 Ом; 6) x'L = 44,4 Ом; R = - 440 Ом.
2.57.	x'c = 6,33 кОм; r = 2 кОм.
П	Q -JXC 9
Рис. 2.440
2.58.	3,24 кОм.
2.59.	5,3 Ом; 3,86 Ом; 5,2 Ом; 4,34 кВ А; 4,06 кВт; 1,5 квар.
2.60.	2,4 кОм; 1,8 кОм.
2.61.	0,025; 577 В-А; 14,5 Вт; 577 вар.
2.62.	500 пФ; 200; 0,01 В.
2.63.	10б рад/с; 10" 6 Гн.
2.64.	J2 А.
2.65‘	. 50 А; 10"3 Ф; 5 Ом.
2.66.	Л = 13 — 10 A; xL = 10 Ом; г = хс = 5 Ом.
2.67.	15,75 Ом и 31,5 Ом или 0,25 Ом и 0,5 Ом.
2.68.	11,35 А; 11,35 А; 0; И А; 440 В.
2.69.	1) 20 А; 2) 176 мкФ; 3) 10 А.
2.70.	30 Ом; 20 А; 16 А; 12 А.
2.71.	0,9 - 1,11 рад/с; 4,77; 10 Ом; 4,77 • 10"3 Гн; 2,1 • 10’6Ф;
500 — J500 В • А; 500 + J500 В • А.
2.72.	При = 250 рад/с токи 2 А; 2/3 А; 8/3 А; при со2 = 500 рад/с токи 0; 0,1 А; 0,1 А.
2.73.	См. решение.
2.74.	1000 пФ; действующее значение тока не изменится, но его фаза изменится на 180°.
2.75.	50 Ом; 100 Ом.
2.76.	Рис. 2.760; ah = 811,5 • 103 рад/с (резонанс токов); со2 = 813 -103 рад/с (резонанс напряжений).
2.77.	Рис. 2.770; с»! = 3,67 • 107 рад/с (резонанс напряжений при (OiLj = 1/cOiCJ; со2 — 3,71 • 107 рад/с [резонанс токов при ®2^0 ~ 1/((02^1 — 1/оъС\)].
2.73.	См. решение.
/ю0Ь1Ь2 (/с12 — Q )
2.80.	500 + /500 Ом; 0,9 Вт.
2.81.	| хг | — 30 Ом; |х2| = 33,3 Ом; XjX2 < 0; 40 Вт; в 3,02 раза.
2.82.	|xt | = 33,3 Ом; [ х2 | = 30 Ом; XtX2 < 0; 0,331 от максимальной.
2.83. Рис. 2.830.
М23>0	Мгч<0;Мзч>0
Рис. 2.830
2.84.	144 В.
2.85.	Рис. 2.850; 8 В; 14 В.
2.86.	1) 97 В; 100 В; О В; 2) 0; 0; 62,5 В.
2.87.	6,8 мГн.
2.88.	/0,72 кОм; /2,16 кОм; не может.
2.89.	192 Вт; 59,4 В.
2.90.	4 А.
2.91.	а) 30 + /10 Ом; б) 1,2 + /8,4 Ом.
Рис. 2.850
2.92.	1) Рис. 2.920, а; Ц = 2,83 z 45° А; /2 = 2,24 z 63° 25' А; £ = 50 В; фй = 44,8 z 63° 26' В; фе = 72,5 z 106° В. 2) Рис. 2.920, б; Л = 2,83 z 98°8' А; I, = 3,13 z 116°34' В; £ = 73,36 z 78°55' В: фб = 62,6 z 116°34' В; ф« = 101 z 145°40' В.
Рис. 2.920
2.93.	1) 2 кОм; 2) 2 - /0,8 кОм.
2.94.	0,1 мкФ.
2.95.	1) При параллельном резонансе: 3,33 мА; 3,33 мА; 20 мА; 20 мА; при последовательном резонансе: 13,3 мА; 6,67 мА; 20 мА; 40 мА; 2) при параллельном резонансе: 10 мА; 10 мА; 20 мА; 20 мА; при последовательном резонансе: 40 мА; 20 мА; 20 мА; 40 мА.
2.96.	50/3 Ом; 1000 Вт.
2.97.	а) О A; 6 A; -6 A; 120 В; 0 Вт; 6) 32,5 z 33°45' A-27 A; ;18 A; 4850 Вт; в) (6 + ;6) A; 30 (j - 1) A; -3(1 + j) A; 8,5 A; 42,5 В; О В; 0 Вт; г) -10 + /15 A; 10 A; 150 B; 3000 Вт
2.98.	Рис. 2.980; 5,79 z -66° A; 5,33z96°23' A; 1,76 A; фб = 52,8 В; фв = 88 z 53° 10' В; фг = 118 z 63°20' В; фе = = 179 z 152° 40' В.
Рис. 2.980
2.99.	10 Ом; 100 Вт; 20 Ом.
2.100.	См. решение.
2.101.	100 В; 0.
2.102.	6,67 мкФ; 10 |/2 sin (cot + 34°) А; не изменится.
2.103.	0,129 -;0,3 кОм; 0,329 + ;0,7 кОм.
2.104.	25 В; 25 В; 12,5 В; 50 В.
2.105.	См. решение.
2.106.	7,23 + J432 Ом; (0,376 + /22,5)-10" 3 Ом.
2.107.	Рис. 2.1070.
2.108.	Значение напряжения не изменяется; фаза изменяется в пределах от 0 до 180°; это справедливо и при других значениях сопротивления
2.109.	Ua6 = 50 В = const (изменяется лишь фаза напряжения иа6).
2.110.	1) 14,7 А; 5,5 Ом или 6,32 А; 29 Ом; 2) 16,5 А: 4,1 Ом.
2.111.	1) 17,5 Ом; 2) 10 Ом; 3) Ц = 9,7 А; 12 = 5 А; / = 14.5 А.
2.112.	1) 35 Ом; 420 Вт; 2а) 12,7 Ом; 26) 95 Ом.
2.113.	1) 37 Ом; 254 Вт; 254 вар; 2,12 А; 85 В; 2) 2,92 А;
32 В; 85 Вт; 344 вар; 354 В-А.
2.114.	1) 0,79 А; 98 Ом; 2) 2,2 А; 33 Ом; 48°.
2.115.	1) 0,8 Ом; потребляет 965 Вт; 22,5°; 2) 2 Ом; 800 Вт.
2.116.	0,55 A; 17,6 Вт; 51,6 вар; 55 BA.
2.117.	См. решение.
2.118.	См. решение.
2.119.	10 z -45° А; 7,96 В.
2.120.	3,55 z -56°20' Ом; 23,6 В.
Рис. 2.1070
2.121.	0,372 z -68° 10';	9,65 z -79° 28'	Ом;
0,187 z -68°10' См; 2,89 z -49°7'; 53,6z68°10' В.
2.122.	См. решение.
2.123.	11,2 z 79° 32' В.
2.124.	0,227 z 20° 30'; 91 В.
ОТВЕТЫ К ЗАДАЧАМ ГЛ. 3
3.1.	См. решение.
3.2.	См. решение.
3.3.	1) X, У, Z или А, В, С; 2) X и В; Y и С; Z и А или А и У; В и Z; С и X.
3.4.	1) 220 В; 220 В; 380 В; 2) 220 В; 220 В; 220 В.
3.5.	а) 254 В; б) 254 В; в) 0.
3.6.	380 В; 760 В.
3.7.	127 В; 127 В.
3.8.	Н - 3 и 5; К-4 и 6.
3.9.	1) 4; 2; 6 или /; 5; 3; 2) 1 и 6; 2 и 3; 4 и 5 или 1 и 2; 3 и 4; 5 и 6.
3.10.	См. решение.
3.11.	И А.
3.12.	22 А.
3.13.	10 А; 17,3 А.
3.14.	34,6 А; 20 А.
3.15.	11 А; 19 А.
3.16.	207,5 В; 4 А; 2,3 А; 625 Вт; 950 Вт; г = 3 |/2 sin юг А.
3.17.	5 А; 8,65 А; 1900 Вт; i = 8,65 ]/2 sin (сог - 120°) А.
3.18.	538 В; 36,3 кВт; 36,3 кВт; 0; 72,6 кВт; 0. При UA = 220 В потенциал фа = 310 zl — 45 ’ В.
3.19.	140 кВт; 280 кВт. При UAB = 6600 z. 30е В потенциал фа = 3030 z. -37° В.
3.20.	4,8 А; 4,75 А; 6,7 А; 3,9 А. При йА = 220 В потенциал ф0 = 192 z. —30° В.
3.21.	1) 22 А; 22 А; 31,1 А; 12,7 А; 17,96 А; 539 В; 427 В; 14,5 кВт; 2) 9,82 А; 9,82 А; 0; 5,67 А; 0; 239 В; 190,5 В; 2,9 кВт.
3.22.	1,85 + ;1,39 Ом.
3.23.	164 А; 95 А.
3.24.	15 Ом; 20 Ом.
3.25.	3,22 мкФ; 1350 и 660 Вт.
3.26.	278 Вт; 109 Вт.
3.27.	834 Вт; 327 Вт.
3.28.	См. решение.
3.29.	7,07 А.
3.30.	5 А.
3.31.	3 А.
3.32.	1,1 кВт; уменьшить до значения 5,78 Ом.
3.33.	40 А; 54,6 А.
3.34.	5,45 А; 96,4 В; 132 В; 160 В.
3.35.	13,66 А; 8,67 А; 8,67 А; 3,65 А.
3.36.	195 В; 212 В; 259 В.
3.37.	175 В; 212 В; 298 В.
3.38.	170 В; 50 В; 190 В. При йА = 127 В потенциал ф„ = 80,5 z. - 108° В.
3.39.	2,6 А; 5 А; 5 А.
3.40.	220 В; 114 В; 114 В; 93 В.
3.41.	1646 Вт; 254 Вт.
3.42.	207 В.
3.43.	17,3 А.
3.44.	1) 24,5 А; 15,7 А; 15,7 А; 2) 7,3 А; 19,4 А; 19,4 А.
3.45.	1а) 197 В; 196 В; 196 В; 16) 381 В; 330 В; 330 В; 2а) 197 В; 573 В; 573 В; 26) 381 В; 526 В; 526 В.
3.46.	60 А; 34,6 А; 34,6 А.
3.47.	1) 10 А; 10 А; 10 А; 0; 2) 30 А; 17,3 А; 17,3 А; 0;
3)	0; 8,65 А; 8,65 А; 0.
3.48.	1) 0,35 A; 2) 156 В; 0; 156 В.
3.49.	0; 95 А; 95 А; 0; 33 А; 33 А.
3.50.	330	А;	190	А;	190	А;	330	А;	165 А;	165	А.
3.51.	НО	А;	110	А;	110	А;	ПО	А;	55 А;	55	А.
3.52.	380	В;	190	В.
3.53.	127	В;	63,5	В.
3.54.	10	А;	10	А;	10	А;	17,3 А;	19,3	А;	5,2	А.
3.55.	22	А;	15,6 А; 44 А; 58 А;	23,2	А;	59	А.
3.56.	10	А;	10	А;	10	А;	220 В.
3.57.	10	А;	10	А;	10	А;	110 В.
3.58.	110 В; 2360 Вт; 169 Вт; ]/з (2360 + 169) = 4400 вар.
3.59.	220 z. 30° В; 220 z -90° В; 220 z 150° В.
3.60.	2,54 А; 1,12 А; 2,61 А; 2,54 А; 1,55 А; 2,54 А.
3.61.	45,5 А; 19 А; 26,9 В; 26,9 А; 36,7 А; 55,3 А.
3.62.	а) 38 А; 19,7 А; 38 А; 73,4 А; 47,1 А; 47,1 А; б) 22 А; 38 А; 22 А; 22 А; 58,1 А; 58,1 А.
3.63.	а) 38 А; 19,7 А; 38 А; 19,6 А; 19,6 А; 19,6 А; б) 22 А; 38 А; 22 А; 38,1 А; 33,1 А; 33,1 А.
3.64.	1) 10 А; 0; 10 А; 17,3 А; 10 А; 10 А; 2) 5 А; 5 А; 10 А; 15 А; 0; 15 А..
3.65.	120 В; 108 В; 12 В.
3.66.	а) 220 В; 155,6 В; б) 155,6 В; 220 В; в) 220 В; 0.
3.67.	0; 95 А; 95 А; 33 А; 0; 33 А.
3.6$.	330 А; 190 А; 190 А; 165 А; 0; 165 А.
3.69.	158,6 А; 116,4 А: 44 А; 44 А; 88 А; 152,4 А.
3.70.	См. решение.
3.71.	а) 0,268; б) 0,366; в) 0,378; г) 0,5.
3.72.	а) 29,1 А; 5,18 А; 5,18 А; б) 25 А; 5 А; 5 А; в) 10 А; 10 А; 10 А; г) 17,3 А; 0; 17,3 А; д) 10 А; 10 А; 10 А.
3.73.	См. решение.
3.74.	’ Zt = Z2 — Z - j(aM; Zo = Z + 1>Z^ 4- j2d)M — j6d)MN.
3.75.	Zj — Z 4~ ciZm 4“ a2Zm; Z2 — Z 4- gi^Zm 4" flZ^; Zq — = Z 4- Zw 4- Zjn.
3.76.	См. решение.
3.77.	a) 44,4 A; 44,4 A; 19,1 A; 6) 57,6 A; 31,2 A; 31,2 A; в) 53,9 A; 36,1 A; 22,4 A; r) 5,1 A; 46,4 A: 46,4 A.
3.78.	См. решение.
3.79.	30 A; 62 B; 62 B; 121,2 B.
3.80.	40 B; 60 B; 20 B; 17,3 A.
3.81.	1) HO B; 155 B; 60 A; 0; 60 A; 0; 183 B; 2) 95 B; 59 B; 0; 45,8 A; 30 A; 120 B; 0; 3) 112 B; 74 B; 0; 48,5 A; 0; 112 B; 56 B; 4) 160 B; 131 B; 0; 34,6 A; 0; 160 B; 106 B.
3.82.	30 A; 8,66 A; 8,66 A; 0; 8,66 A; 8,66 A.
3.83.	22 A; 1,65 A; 1,65 A; 1,58 A; 1,65 A; 1,65 A.
3.84.	180 В; 151 В; 0; 69,2 А; 120 В.
I,	IZI .	.	3Z.Z2
h \Z+3Z2r A“ Z(Z! +Z2) + 3T.lZ1 
3.86.	90 В; 36 A.
3.87.	См. решение.
3.88.	1) и 2) Круговое вращающееся магнитное поле с индукцией В = klm, где к — коэффициент пропорциональности, и угловой скоростью со; направление вращения в случае 1 — по направлению движения часовой стрелки, в случае 2 — обратное. 3) Эллиптическое вращающееся магнитное поле с индукцией В — klm]/5/2 4- (3/2)cos2rof и угловой скоростью 4го/(5 + + 3cos2cot); направление вращения — по направлению движения часовой стрелки; В2х/В^ах + B2/B2in = 1. 4) Эллиптическое вращающееся магнитное поле с индукцией В = klm х х j/5/8 — (3/8)cos 2гог и угловой скоростью 4го/(5 — 3 cos 2rof); направление вращения — против направления движения часовой стрелки; Bi/B*in +	= 1.
3.89.	1) и 2) Эллиптическое вращающееся магнитное поле с индукцией соответственно В = klm |/1 + (1/2) sin 2соГ, где к — коэффициент пропорциональности, с угловой скоростью |/з го/(2 q: sin 2гог) и направлением вращения — соответственно по против направления движения часовой стрелки. Для системы координатных осей х' и у', повернутой относительно осей х и у на 30° по направлению движения часовой стрелки: B2x./B2in +	= i.
3.90.	1) и 2) Круговое вращающееся магнитное поле с индукцией В = klm, где к — коэффициент пропорциональности, и угловой скоростью, равной со; направление вращения — соответственно по и против направления движения часовой стрелки.
3.91.	1) Эллиптическое вращающееся магнитное поле с индукцией В = klm^2 + cos2rot, где к — коэффициент пропорциональности, и угловой скоростью ]/з го/(2 + cos 2гог); направление вращения — против направления движения часовой стрелки В2/В2ах + By/Bmin =	2) Круговое вращающееся магнитное
поле с индукцией В — klm и угловой скоростью го; направление вращения — по направлению движения часовой стрелки.
ОТВЕТЫ К ЗАДАЧАМ ГЛ. 4
4.1.	См. решение.
4.2.	См. решение.
4.3.	А11 — 4_22 ~ 2; A12 = 15 Ом; А_21 = 0,2 См; Zj । =
= — Z22 = 10 Ом; Z12 = -Z21 = -5 Ом; Ун = -У22=2/15См; У12= -bi = -1/15 См; Нп = 7,5 Ом; Н12 = Н21 = 0,5; Н22 = = —0,1 См.
4.4.	а) 4П = А22 = 1; Л12 = Z; Л21 = 0; матрицы Z не существует; Уп = — У22 = 1/Z; У12 = -У21 = -1/Z; б) Лп = — А22 = 1; Л12 = 0; Л21 = 1/Z; Z} i = —Z22 = — Z12 = Z2l = Z; матрицы Y не существует.
4.5.	Уи — — У22 = 0,06 См; Y\2 — — У21 ~ —0,05 См; = = 16,7 Ом; Hl2 = H_2i = 0,83; Н22 = -0,018 См.
4.6.	1 = Z]; Z12 = Z21 = 0; Z22 = — Z2; 1) Zxl — Zi2 =
— Z2i = 0; Z22 = — Z2; 2).	= Zj; Z12 = Z21 = Z22 = 0.
4.7.	Лл1 Wi/w2; Л12 = Л21 = 0; A22 = w2/wi-
4.8.	См. решение.	____________
4.9.	Zn = Zlx; Z12 — — Z21 = ]/Z2X (Zlx — Z1K); Z22 = — Z2x.
4.10.	a) 1; Z; 1/Z; 2; 20 B; 6) 0,5+./0,5; 20 + J20 Ом; (-1,25+>3,75)-10'2 См; 0,5+;0,5; 28,3 В; в) ]/2\ г. 45°; 0,1 z 90° Ом; 22,4 л. 63c3O' См; 1 z 90°; 14,2 B.
4.11.	См. решение.
4.12.	1) 6 мА; 24 B; 2) 7 мА; 12 В; 3) 8 мА; 0.
4.13.	См. решение.
4.14.	1) 1; 10 + J20 Ом; 0,02-;0,04 См; 2; 2) 56,6 В; 3) 4,5 мА; 4) 64,2 Вт.
4.15.	См. решение.
4.17.	5,54; 545 Ом; 0,0545 См; 5,54.
4.18.	1) Нельзя, так как у обоих четырехполюсников соответственно одинаковы сопротивления холостого хода и короткого замыкания, например Zlx — j5 Ом. 2) Можно, сопротивления холостого хода и короткого замыкания различны, например у 1-го четырехполюсника Zlx = J6,65 Ом, у 2-го четырехполюсника Zlx = 5,69 Ом.
4.20.	0,22 мкФ; 100 Ом; 35,6 мГн.
4.21.	16,5 пФ; 20 МГц; 3,4 кВт.
4.22.	См. решение.
4.23.	600 Ом; 1 Нп.
4.24.	См. решение.
4.25.	ZT = 0 и Zn = оо; А = 0; В = 180°.
4.26.	Zc = ]/l/C = const; А = 0; cos В = (1 — co2LC)/(l + + со2 LC).
4.27.	10 Ом; 20 Ом.
4.28.	Z/]/2; Z]/2.
4.29.	26,7 z -31°40' Ом.
4.30.	1) См. решение; 2) 44,7 Ом; 0,96 Нп.
4.31.	3,66 мВт; Zi/2 = 76,2 Ом; Z2 = 27,6 Ом.
4.32.	100 Ом; 2,4 Нп.
4.33.	См. решение.
4.34.	1.
4.35.	205 z. 38°20' Ом.
4.36.	1) Z1/2 = 8-j3 Ом; Z2 =-3+7'3 Ом; 2) Zt = = 8—7*3 Ом; Z2 = 2 + ;*3 Ом.
4.37.	1) Zi/2 = 10 + j5 Ом; Z2 = j5 Ом; 14,6 z. 40°40' Ом; 28,4 В; 2) Zr — 10 Ом; Z2 = 40 + уЗО Ом; Z3 = /10 Ом; 14,4 л 38°30' Ом; 20 В.
4.38.	См. решение.
4.39.	Zx = (Ли - 1)/421; Z2 = (422 - 1)/421; Z3 = 1/421.
4.40.	См. решение; 3,73.
4.41.	6 Ом; 5,5 Ом; 2 Ом.
4.42.	См. решение.
4.43.	См. решение.
4.44.	10 Ом; А = 0; В = -я/2.
4.45.	4ц=0,5; 412 = j‘3,75 Ом; А2х = 0,005 + /0,2 См; А22 = 0,5 4- j0,0375.
4.46.	1; 10 Ом; 0,01 См; 1,1.
4.47.	См. решение.
4.48.	4; 17,7 zi -45° Ом; 0,85	45° См; 4.
4.49.	1) 4„=2; Л12 = Зг; 421 = З/r; А22 = 5; 2) 411 = 1; 412 = г/2; 421 = 2/г; А22 — 2; 3) 4n — 1; 412 = 2г; А21 = 1/2г; Л22 = 2.
4.50.	Уи = - У22 = 5/300 См; У21 = - У12 = 4/300 См.
4.51.	См. решение.
4.52.	Уц = 0; У12 = 0; У21 = -0,01 См; У22 = -2-10"4 См.
4.53.	См. решение.
4.54.	0,5 — /0,5.
4.55.	4ц = 290  10“6; 412 = 79 Ом; 421 = 0,527-10"6 См; 422 = 1,05; Ал = 260-10’6.
4.56.	75 Ом; 2,5 • 10-4; 0,95; -5-Ю'7 См.
4,57.	См. решение.
4.58.	См. решение.
4.59.	См. решение.
4.60.	Сигнальный граф показан на рис. 4.600;
4.61.	425 Ом; —25 Ом; —2,5 МОм; —50 кОм.
4.62.	375 Ом; 49 975 Ом; 25 Ом; 40.
4.63.	1399 Ом; 0,9995; 40,98; -1,999 • 10-5 См.
4.64.	См. решение.
4.65.	-1; -1.
4.66.	1/(1 + jk), где к = rCco.
4.67.	Hv = 1/2 |/1 + (k/2)2; tg\|/ = -k/2, где к = rC®.
4.68.	a) J/c/(l -I- jk\ где к = rCco; 6) 1/(1 4- jk), где к = coL/r.
Рис. 4.600
4.69.	См. решение.
4.70.	8 • 10“3а [(9 - 0,8 • Ю'бсо2)2 + 0,059ф2]'1/2.
4.71.	См. решение.
4.72.	/(®) = 1(1 + 1/усот).
4.73.	(0,049 + j'1,65 • 10'6ф)/(0,00056 + у 1,6 5  10~6со).
4.74.	См. решение.
4.75.	1389 Ом; -22,22.
4.16,	См. решение.
* 4.77. -0,9834 г. -115,5°.
4.78. См. решение.
ОТВЕТЫ К ЗАДАЧАМ ГЛ. 5
5.1.	См. решение.
5.2.	2,84 Ом/км; 1,94 мГн/км; 0,70 мкСм/км; 6250 пФ/км.
5.3.	1) 11,7 мГн; 2) 15,1 мГн; 3) 65,6 • 103 км/с; 4) 818 км.
5.4.	г0 = 0,51 Ом/км; хо = ОД2 Ом/км; д0 = 0; bQ -= 54,3 мкСм/км; = 98,4 z. -38°30' Ом; у = (3,34 + ;4,16) х х 10"3 км-1.
5.5.	См. решение.
5.6.	1,33 мГн/км; 8,3 нФ/км; 400 Ом; 12 град/м.
5.7.	См. решение.
5.8.	См. решение.
5,9.	См. решение.
5.10.	См. решение.
5.11.	См. решение.
5.12.	См. решение.
5.13.	См. решение.
5.14.	См. решение.
5.15.	См. решение.
5.16.	См. решение.
5.17.	229 кВ; 700 А; 355 МВт.
5.18.	295 • 103 км/с; 5900 км; 84,5%.
5.19.	683 кВ; 820 А.
5.20.	272 МВт; 362 кВ; 527 А.
5.21.	См. решение.
5.22.	1) 416 кВ; 2) 229 кВ.
5.23.	82,2 кВт; 94,3 кВт; 82,7 кВт; 91,0 кВт; 87,3 и 91,0%.
5.24.	4,0 кВт.
5.25.	См. решение.
5.26.	См. решение.
5.27.	12 В; 0; 12 В; 0; 12 В; 0.
5.28.	См. решение.
5.29.	1) иХ/2, где п — целое число; 2) кХ/4, где /с - целое нечетное число; Umax = 120 В в конце линии; Umin = 60 В; 1тах - 0,4 А в конце линии; Imin = 0,2 А.
5.31.	20 мВ и 31,8 мВ; 20 мВ; 129 см (0).
5.32.	иХ/2, где п — целое число.
5.33.	Х/4; /г^з/со;	где Cq — скорость света
в вакууме.
5.34.	См. решение.
5.35.	0,29 А.
5.36.	2,72 м; 4,12 м.
5.37.	58,9 и 66,7 Вт; в 7 раз; 5 м.
5.38.	1) 9,12 м; 2) 693 Ом.
5.39.	218 и 232 В.
5.40.	См. решение.
5.41.	1,36 м; 850 Ом.
5.42.	См. решение.
5.43.	/0,5 zB sin 2|3х.
5.44.	См. решение.
5.45.	0,75 м.
5.46.	0,3 пФ.
5.47.	См. решение.
5.48.	503 г. 10° Ом.
5.49.	680 z. - 24° Ом.
5.50.	См. решение.
5.51.	1,06 МОм.
5.52.	См. решение.
5.53.	Zi/2 = 547 z. -14°30' Ом; Z2 = 307 zi 39° 30' Ом; 40,4 и 80 В.
5.54.	1) 6,6%; 2) 10%; 3) 99,8%.
5.55.	1,5 мкГн; 1,5 мкГн; 8,4 пФ.
5.56.	45 Ом; 45 Ом; 40 Ом.
5.57.	1)/795 Ом; ;795 Ом; —/795 Ом; 2) J795 Ом; —/795 Ом; —/795 Ом; 3) J795 Ом; -J795 Ом.
5.58.	200 Ом; 2,44 рад/м; /543 Ом; /543 Ом; -;309 Ом.
5.59.	60,7 км; 52,7 Ом; при частотах, меньших, чем граничная.
5.60.	См. решение.
5.61.	100 мВ; 0,224 мВт; 1,1 %.
ОТВЕТЫ К ЗАДАЧАМ ГЛ. 6
6.1.	См. решение.
6.2.	См. решение.
6.3.	50 — 40,5 cos cot - 4,50 cos 3ort - 1,62 cos 5ort В.
6.4.	а) 5,09 — 2,0 sin art — 3,42 cos 2cor — 0,67 cos 4cot В;
6) — 0,91 — 2,0 sin art — 3,42 cos 2cot — 0,67 cos 4art B.
6.5.	100 4- 191 sin (art — 60°) + 95,5 sin (2art + 60°) 4-
4-	63,7 sin (3cot + 180°) B.
6.6.	См. решение.
6.7.	5,0 sin (tot + 30°) + 3,0 sin (2cot — 60е), А; см. рис. 6.70.
6.8.	См. решение.
6.9.	а) 34,0 sin (озг + 45°) 4- 37,9 sin (Заз/ + 71° 35х) В; б) 34,0 sin (cot - 45°) + 12,6 sin (3cot - 18° 30х) В.
6.10.	170 sin (cot + 45°) 4- 42,4 sin (2cot + 135°) mA.
6.11.	См. решение.
6.12.	49,6 В.
6.13.	1 4- 0,707 sin (cot + 45°) 4- 0,408 sin (3cot 4- 45° 50х) A.
6.13.	1 4- 0,707 sin (cot 4- 45°) 4- 0,408 sin (3cot + 45° 50х) A.
6.14.	35,1 Вт.
6.15.	10 sin (cot 4- 90°) + 5 sin (3cor + 37°) + 3 sin (5cof + 22е 40') В.
6.16.	1)	20 sin (cot + 90°) + 20 sin (2cot + 53s 10') B;
2) 18,2 sin (cot + 95° 13') + 19,1 sin (2<ot 4- 58°O') B.
6.17.	1) uBX = 28,6 sin (cot 4-44° 30') + 31,0 sin (3cot 4-70° 40') B; «вых = 9,06 sin (cot 4- 84°50') 4- 13,5 sin (3cot 4- 82е20') В; 2) uBX — = 238 sin (cot 4- 5°47') + 120 sin (3cot 4- Г55') B; wBb[X — 200 sin (cot 4-4-6° 18') 4- 100 sin (3cot 4- 2е 6') В.
6.18.	См. решение.
6.19.	21,0 В; 20,0 В; 6,5 В.
6.20.	122 В; 3,48 А; 423 Вт.
6.21.	226 Вт; 1,97 А; 1,64 А; 0,71 А.
6.22.	1) 7,31 В; 2) 3,50 В; 0,272 А.
6.23.	0,172 В.
6.25.	9,82 А; 1,65 А; 10,69 А; 6,0 А; 96,2 В; 36 Вт.
6.26.	См. решение.
6.27.	0,9936; 0,9463.
6.28.	См. решение.
6.29.
	1	2	3	4	5	6
а	0	10,0	6,37	-6,37	3,18	-3,18
б	7,07	12,2	7,07	7,07	5,00	5,00
в	7,07	7,07	3,07	3,07	3,86	3,86
г	7,07	7,07	2,97	2,97	2,13	2,13
д	7,07	7,07	4,50	3,63	2,25	4,82
Все напряжения в вольтах.
6.30.	Для обоих напряжений: а) 0; б) 8,86 В; в) 8,86 В; г) 7,07 В; д) 7,00 В.
6.31.
	1	2	3	4		1	2	3	4
а	0	7,07	5,0	0	в	11,1	7,85	4,82	9,62
б	10,0	7,07	5,0	10,0	г	7,07	5,00	6,12	12,3
Все напряжения в вольтах.
6.32.	а) 4 Вт; б) 3 Вт; в) 3,2 Вт; г) 3,67 Вт; д) 2 Вт; е) 3 Вт.
6.33.	1,33 Вт.
6.34.	/сф=1; 1,154; 1,089; ка = 1; 1,73; 1,22; кНСК = 0,900; 0,993; 0,993.
6.35.	См. решение.
6.36.	39,2 sin (cor + 71°) + 60 sin Зсог, В.
6.37.	0,100 мкФ; 0,0185 мкФ; 6,00 мГн.
6.38.	0,451 мкФ; 3,62 мкФ.
6.39.	9,6 sin cor + 5,0 cos cor + 2,5 sin (Зои — 45°) A.
6.40.	Мгновенные значения: 1) 97,8 sin at — 3,79 sin (3co£ — - 69° 30')+ 0,80 sin (5cor-78° 10') мА; 2) 12,1 sin (cor + 82° 50') -- 37,9 sin 3cor +1,16 sin (5cor - 70° 50') mA; 3) 4,05 sin (cor + + 87° 35') — 1,99 sin (3<or + 79° 20') + 3,9 sin 5cor мА. Действующие значения: 1) 68,9 мА; 2) 28,1 мА; 3) 4,2 мА.
6.41.	Напряжение иг повторяет форму кривой напряжения и, но максимальное значение импульсов 8 В; токи: iL — = 2,75 sin (cor - 32° 10') — 0,17 sin (Зсо/ — 62° 20') + 0,039 sin (5cor — - 72° 10') A; ic = 1,72 sin (cor + 57°50') - 0,32 sin (3cot + 28°00') + + 0,123 sin (5cor + 17°40') A.
6.42.	См. решение.
6.43.	22,1 В.
6.44.	1) 130 В и 0; 2) 141 В, 165 В.
6.45.	3,38 А.
6.46.	См. решение.
6.47.	12,6 sin (cor + 48°) + 26,6 sin (Зсог — 45°) + 8,57 sin (5cor — - 179°) A; 80,2 sin (Зсог - 45°) A; 120 sin (cor + 120°) + + 113 sin (Зсог - 90°) + 30 sin (5cor - 90°) B; 104,2 B; 151,5 B; 118,5 B; 21,8 A; 56,7 A.
6.48.	20,8 sin (cor + 30°) + 5,2 sin (5cor - 30°) A; 15,2 A.
6.49.	3,69 A; 2,13 A; 179 B.
6.50.	7,58 B; 0,111 A.
ОТВЕТЫ К ЗАДАЧАМ ГЛ. 7
7.1.	См. решение.
7.2.	См. решение.
7.3.	Схема фильтра приведена в табл. 7.1, где L = 9,6 Гн и С/2 = 13,3 мкФ; 4,6 Нп; к рад; 4,6 + J3,14; 100, 0 и 20 Гц.
7.4.	10,2 мГн, 15,9/2 нФ; 2,62 Нп.
7.5.	1; 0,68; 0,28; 1; 1,88; 24 Гц.
7.6.	См. решение.
7.7.	220/]/з В; 1; -60°.
7.8.	0,35 г. -23°30' В; 89,6 z. 116°35' В.
7.9.	0-192 кГц и 96 - оо кГц; 1) 0; 0; 2) 1,4 Нп; 0.
7.10.	140 кГц.
7.11.	0,34 мГн; нет; три звена.
7.12.	См. решение.
7.13.	7,2 мГн; 0,1 мкФ; 6,62 кГц.
7.14.	См. решение.
7.15.	Увеличится в ]/2 раз (1250 ]/2 Гц).
7.16.	]/2/2; 1,76 Нп; 1,67/2.
7.17.	3,6 кГц; 8,94 Нп; 72 мВ.
7.18.	См. решение.
7.19.	См. решение.
7.20.	1) 0 и 4 МГц; 2) 4,62 МГц; 3) 0 и 3,77 МГц.
7.21.	1,71 Нп; в 5,5 раза.
7.22.	Нет, так как полузвенья не будут соединены по принципу согласования (Zn / Znjn).
7.23.	Рис. 7.230, где С2т/2 = 0,025 мкФ; Llw/2 = 50 мГн;
2С1т — 0,075 мкФ.
Рис. 7.240
7.24.	Рис. 7.240, где 2L2m = 0,17 мГн; Llm/2 = 0,095 мГн; 2С1т = 0,106 мкФ.
7.25.	0—3,98 кГц; 5,34 кГц; не изменится.
7.26.	1) 612 Ом; 2) ;707 Ом.
7.27.	О-оо.
7.28.	См. решение.
7.29.	0,6.
7.30.	См. решение.
7.31.	См. решение.
7.32.	1,53 Нп.
7.33.	159 кГц.
7.34.	См. решение.
7	35 II 1/ ЯМК2
/.». Л - I (1 _ иу2)2 +	(2n + j _ к)2 ,
НдБ = 201g nv2K — 101g [(1 - nv2)2 + v2 (2и + 1 — К-)2].
Результаты расчета амплитудно-частотной характеристики приведены в таблице:
График амплитудно-частотной характеристики показан на рис. 7.350.
ОТВЕТЫ К ЗАДАЧАМ ГЛ. 8
8.1.	См. решение.
8.2.	См. решение.
8.3.	2г"1501 А.
8.4.	О,5е"60' А.
8.5.	бе"40' А.
8.6.	О,4е" 1200' А.
8.7.	-2995 В.
8.8.	См. решение.
8.9.	См. решение.
8.10.	См. решение.
8.11.	0,2 —O,2e"7S0' А; 6Ое"750' В.
8.12.	8 —0,бе"500' А.
8.13.	6 —бе"600' А; 0,676 мс; 5,99 мс.
8.14.	2- 1,5е"250' А.
8.15.	1,33 —0,53е" 3001 А.
8.16.	3 —2е"400' А; е"400' А; З-Зе"400' А.
8.17.	2,5 - 1,5е" 120?‘ А; 2,5-2,5г"1200' А.
8.18.	2-l,2«f 1600' А; 1,5- 1,5е"1600' А.
8.19.	Г75-б,4е~445' А.
8.20.	1,5г"125' А; 3-0,5е"125' А; 6- 1е"1251 А; 9 —Зе"125'А; 3 — 2е"125' А.
8.21.	См. решение.
8.22.	См. решение.
8.23.	1) 1,572 sin (314г- 50,95°) + 1,220г"50' A; 2) 80,95° + + к  180°, где к = 0, 1, 2,...; 1,572 sin 314г A; 3) 170,95° + к  180°, где fc = 0, 1, 2, ...; 2,766 A.
8.24.	0,707 sin (1000г - 75°) + O,683e*1000' A; -141 sin (1000г + + 15°)+ 136,бе’1 °00' B.
8.25.	0,314sin(2500г- 63,69°)+ М81г’500' A.
8.26.	1,517 sin (314г + 47,67°) — O,413e“100’ A.
8.27.	0,447sin(1000г + 3,44°) + O,O64e’2000' A;
0,632 sin (1000г + 48,44°) - O,O64e’2000' A.
8.28.	См. решение.
8.29.	См. решение.
8.30.	lOOe’500' B; О,О5г’500' A.
8 31 SOe-400* B* 0 2e~4’OG' A
8.32.	60 + 6Oe"2’500' B; 60 - 240г~2500' В; O,8e’2500' A.
8.33.	-61,2e’1000' B.
8.34.	62e’125' B; 0,0775г’125' A.
8.35.	См. решение.
8.36.	См. решение.
8.37.	См. решение.
8.38.	1) 100 - lOOe’400' B; O,O4e’400' A; 2) 100 - 5Oe’400' В: 0,02e’4OOt A; 3) 100 - 15Oe’400' B; O,O6e’400' A.
8.39.	200 — 2OOe’500' B; 0,2e"500' A.
8.40.	80- 18Oe’4000' B; O,72e’4000' A.
8.41.	100- lOOe’200' B; 0,5 - O,2e’200' A; О,2г’200' A.
8.42.	60 + 120г’500' B; 0,5 - O,5e’500' A; 0,5 + l,Oe'5001 A.
8.43.	96 —96e’490' B; 1,200 - 0,166e'490' A.
8.44.	100+ 150e’625' B; 1,0 + 1,5г’625' A.
8.45.	60 — 60г’625' B; 1,0+ 1,5г’625' A.
8.46.	120 — 75e’ 10001 B; 1,0 + 1,25г’1 °00' A; 1,000-- O,625e"1000' A.
8.47.	80 —4Oe’800' B; O,4e’800' A.
8.48.	1,2г’400' A; 2 - 1,2г'400' A; 120 - 120г'400’ B; 160 - 72e’400' B.
8.49.	См. решение.
8.50.	См. решение.
8.51.	1) 39,4 sin (314г — 52,74°) + 31,3г’40' В; 1,238 sin (314г + + 37,26°) - O,126e’40' A; 2) 82,74° + к  180°, где к = 0, 1, 2 ...; 39,4 sin 314г В; 3) -7,26° + к • 180°, где fc = 0, 1, 2 ...; 65,8 В.
8.52.	54,6 sin (314г - 42,34°) + 66,8е’1001 В; 1,37 sin (314г + + 47,66°) — 0,53г’1 °0' А.
8.53.	169,4sin (314г - 2,13°) - 43,4г’500' В.
8.54.	24,4 sin(314г - 57°) + 20,5г’133' В; 73,2 sin (314г - 57°) -- 18,6г’133' В.
8.55.	См. решение.
8.56.	См. решение.
8.57.	См. решение.
8.58.	42,16г-501 sin (150t + 71,56°) В; 1,33г-50'sin 150t А.
8.59.	— 72,95е“100> sin (2001 - 43,26°) В; 1 ,ЗО5<?' ’°0' sin (2001 + + 73,3°) А.
8.60.	—20’ 1О31е- 1000' В; О,2г-1000'+ 2ОО1г-1000' А.
8.61.	26,56е-460' + 73.44г-1740' В; -0,144г-460' +
+ 0,544г-17401 А.
8.62.	О,734г-230' + 0,266г-870’ А; 0,544г-230' - 0,144г-870'А.
8.63.	См. решение.
8.64.	См. решение.
8.65.	См. решение.
8.66.	-0,5 А; -0,5 А; 0; -50 В; 100 В; 1000 А/с; О
1000 А/с; 0; -105 В/с.
8.67.	0; 0; -2 А; -2 А; 0; 0; 104 А/с; -104 А/с; 0;
2 -104 А/с; -0,4 Ю6 В/с; 0,4-Ю6 В/с.
8.68.	0,750 - 0,333г-200'- 0,417г-2000' А; 0,333г-200' -- 0,333г-20001 А.
8.69.	2,83 - г-30' + г-200’ А; Юг-30' + 75е-200' В.
8.70.	1,9г-400'+ 0,1г-2500’ А; 80 - 95г-400'+ 15г-25001 В.
8.71.	0,57г-200' + 4,43г-952’ А; 50 - 13,Зг-200' + 13,3г-952'В.
8.72.	0,6г-100'sin 20001 А; 120 — 120,1г -1 °0’sin (2000г + + 87,1°) В; 0,555 А; 222,5 В.
. 8.73. 0,125 - 0,150г-200<sin 2001 А; 37,5 + 53г-200'sin (2001-- 135°) В.
8.74.	2 + 3,33г-800' sin(600t - 144°) А; 2 + 2,11г-800'х х sin(6001 - 71°) А; 60 + 66,7г-800' sin(6001 + 37°) В.
8.75.	3 + 3,35г-2501 sin (2501 - 63,3°) А; 212г- 2501 sin (2501 + + 45°) В.
8.76.	0,1 -0,144г-"51 + 0,088г-435' А; 10 - 15,63г-115'+ + 15,63г-435’ В.
8.77.	-0,0023г-1151 + 0,0523г-435'	А; 10+1,8г-"5'-
- 6,8г-435' В.
8.78.	г-100’ + 201г-1 °0' А; 120 - 120г-1 °0' - 24001г-100' В
8.79.	12,5 - 0,48г-85' + 7,98г-945’ А; 3,71г-85' - 41,2г-945'В.
8.80.	12,5 - 13,73г-85'+ 1,23г-945' А; 62,5 + 41,21г-85'-- 3,69г-945' В.
8.81.	4,5 +7,78г-100'sin (100t+ 45°) А; 55 + 55 ]/2 е“ 100t х х sin (100t - 45°) В.
8.82.	1 + 2г-100' + 4Огг-100' А; 2 — 2г-100'- 401г-1001 А.
8.83.	0,5 +0,25г-277'+ 0,25г-723' А; 0,362г-277'+ + 0,138г-723' А; 100 + 50г-277'+ 50г-723' В.
8.84.	1) 0,5 sin 104t - 0,5г -1 °0' sin 1041 А; 250 sin (104t - 90°) + + 250г-100'cos 104t + 2,5г-100'sin 104t В; 2) 5 • 10-4 sin 104t-
— 5'10 Зе 2501 sin 105f A; 5sin(104r-90°)+5e"25°'cosl05t + + 0,0125e"2501 sin 105r B; 10.56; 3) -cos 105r + <?"100’cos 104t -- 0,01г"1 °0'sin 104r mA; -50sin 105t + 500г"I00' sin 104/ мВ; 10,71.
8.85.	3 sin (105г — 53°) + (4,4 — 2,16 • 106£) e-2'‘°5' A;
80 sin (105l + 37c) + ( —88 + 43,2 • 106t)e"2'io5' B.
8.86.	0,403 sin (104r — 45°) + O,218e'1<)3'+ 0,066e"15 ’ ,o3‘ A; 1,28 sin (104r + 26,7°) - 0,109e"lo3' + 0,034c" 15'io3' A.
8.87.	См. решение.
8.88.	10 —6,17г-69,4'- 3,83г-671' А; 2.96г-69,4'- 2,96г-671' A.
8.89.	20 -1,575г-56' — 18,425г-670' A; 10 - 6.48г-56'--3,52г-670' A.
8.90.	1,83 sin (lOOt-45,5°)+ 1,22г-30' + 0,07г- 1270' A;
0,782 sin (100t + 13,5°) - О,238г-30' + 0,065г" 1270' A.
8.91.	2,08 sin (lOOt - 32°) - 0,176г- 28' - 0,264г- 712' A;
1,30 sin (lOOt + 8°) + 0,0717г-28' - 0,2517г-712' A.
8.92.	См. решение.
8.93.	См. решение.
8.94.	См. решение.
8.95.	См. решение.
8.96.	См. решение.
8.97.	См. решение.
8.98.	См. решение.
8.99.	См. решение.
8.156.	См. решение.
8.157.	См. решение.
8.158.	,	—~[dl - гр') + p (1 - г-°')], где p = -r/L.
r (a + p)
8.159.	Рис. 8.1590. В интервалах времени 0 С t Т} с С t < Т2 и t Т2 ток ц соответственно равен: 0; 10"3 [15е-г-103«-10"3> _ 5] А и 10"3 [15е"2' ‘°3<*" '°3> -— 5г-210 ('-210 3>] А; напряжение и2 соответственно равно: 0;	15 [1 — г"2' 1о3(,“10 3)] - 104(t — 10-3) В и
- i5e-2-io3(t-io-3) + $е-2 - io3a-io“3) в
8.160.	- . -—~(рг₽' + ae~at\ где р = - 1/гС. г (а + р)
8.161.	В интервалах времени t < 0; 0 < t С Т/2; Т/2 Ct С С Т и t > Т ток i соответственно равен: 0; 0,4t - 1,2 х х 10-4 (1 - г- 1250') А; 0,4 (10-3 - t) + 1,2- 10-4 [1 4- 1г- 1250'-_ 2г- 12500-5 ’ 10~4)] А и 1,2-Ю-4[г- 1250'+ 1г- 1250 ('- 10‘3)-— 2г" 1250 ('- 5 ‘10 4)] А; напряжение и2 соответственно равно: 0; 0,6(1 -г" 1250') В; 0,6 [2г- 1250 <’-5 ‘ 10'4> - 1г- 1250' - 1] В и 710
0,6[2е- 1250 "~5• 10’4) - 1е- 12501 - 1е~ 1250	10’3>] В; i(fl) =
= 6,779- IO’5 A; i(t2) = 9,141 • 10*5 A; i(t3) = 1,896 КГ5 А; м2(г,) = 0,161 В; и2 (t2) = 4,298 • 10'2 В; и2 (t3) = -0,09481 В.
8.162.	В интервалах времени	ток i2
соответственно равен: 0; 0,4639е-4' l°3' + l,536cos 103rrf — - 0,3643 sin 103« - 8,3 - 10~6 мА; -2,228е*4 ’ ‘°3' мА; 0,9992 мА; -0,1109 мА.
8.163.	В интервалах времени t < 0; 0 t
ток соответственно равен 0; —— (р — 1)(1 — < РР L
Ur2
РР
t
и
Рис. 8.1640
8.164.	Рис. 8.1640. В интервалах времени t < 0; 0 < t Т/2; Т/2 t Т и Т напряжение wH соответственно равно: 0; 11,47 [5 sin 1027tr + 7c(e-5OOf — cos 102тсг)] В; —11,47 {5 sin 102Ttt — — л [(1 + 2e250T)е-500* + cos 102тгГ]} В; 36.04е“500' (1 + 2е25ОТ + + 1е5007) В.
8.165.	В интервалах времени г <0;	T^t^lT
Ut
ъ 2Т напряжение мн соответственно равно: 0; ----В----х
х
Ur„
+ г„
рТ
-L ]еР(Г-Т) _
рт)
рт
^(1-
Ur„ —— х + г„
где
Р = -(г + гп)/ггаС.
8.166.	Рис. 8.1660. При i = 5(l,5e"0’51°6' — le-1°6f) мА; uL= 5(2e"lo6f- le-°’5,1°6r) В.
Рис. 8.1660
8.167.	Рис. 8.1670. В интервалах времени t < 0; 0 < г
Tq‘, То t 2Т0 и t 2Т0 ток соответственно равен: 0; 100(1 - е’100') мА; 100(3 - 102f - 3,718е"100t) мА и 367,1г"100‘ мА.
8.168.	Рис. 8.1680. В интервалах времени t < 0; 0 < г Т и Г^Тток соответственно равен: 0; 2- 103г — 120(1 — е~100') мА и 1,762- 106с" 1001 мА.
8.169. См. решение.
8.171.	См. решение.
8.172.	См. решение.
8.173.	См. решение.
8.174.	0,7276 sin (103t + 44,04°) - 0,0965с"250' А.
8.175.	0,21/2 sin(104t — 45°) — 0,2е~1<>4' А.
8.176.	См. решение.
8.177.	6,07е"293г — 206с"17О7г А.
8.178.	0,784 sin (104t + 71,31°) + 0,2233с"	А.
8.179.	0,2397 sin (103г - 38,5°) + О,ОЗО8с"200t А.
1 8.180. См. решение.
8.181. См. решение.
>8.182. См. решение.
ОТВЕТЫ К ЗАДАЧАМ ГЛ. 9
9.1.	См. решение.
9.2.	Рис. 9.20 (см. стр. 714).
9.3.	Рис. 9.30. При 0 < х < 75 км ток i = 500 А; при
75 < х < 300 км ток
i = 106 (tj — х/с) + 106
, (	-2-Ю3 (11 -	\
— 103 yl — с \ с / \ А (см. стр. 714).
9.4.	Рис. 9.40. При 0 < t 0,3 мс иА = О, 0,3 < t С 0,7 мс иА = 300 кВ, iA = 600 А; при 0,7
iA = о; ПРИ t 1,4 мс
Ил =400(1 — е-з • 1°3 (r-0.7 ‘0 3) кВ	i4 = (400 + 800 x
X g-3-103 «-0,7-10-3)) д
9.5.	При 0 < х 1/2 и 1/2 < х I соответственно 20,2 кВ;
50,5 А и 8,1(1 + 4е-510’е) кВ; 81 (1 - e’s'1о30) А, где 0 =
Рис. 9.60, где при
О
9.6.
= 100 sin 2л х
х 107
X \ л сД'М'б
В; при
10
= 100 sin 2л х
х \ л 7/2) + Т
9.7. См. решение.
9.8. Напряжение и ток согласующей линии после третьего отражения: 199,6 В; 3,99 А.
х 107 (
+ 50 sin 2л • 107
21 — х\ л ? 1------7— ) + "7
м и
м и
. i	-2,2-104
9.9. и' = 127-113е
кВ;

= 282/2’2	А; и"= 14,1г'2'2 ’’°41,1 1"/с’ кВ; Г
А.
= 282e
9.10. Рис. 9.100,
60 км и = 0; i = 0; при
и' =
-5- 103 (г, - -* ~ *
-77,77 + 177,77с V
-5 • Ю3 (ti - —-
194,44 _ 444,44с	\
кВ;
при 72
120 км
-5- 103( - Z1-- Х I -5• 103 ( G - 40-Ю-6-\	/ - е X
- х' с
кВ;
,	-S-IO3/?,--^—-5  103 ( h — 40-(О-6
Г = -444,44 е V с )-е V
lj - *' с
при 120 х 138 км
и" = - 22,22 е
-5-10»Ь1-/1/г- 2-
\ f/2 ,
-5-Ю3 (li -40-10"6 -li/c- ~
- е х	с 12 
кВ;
I"
-5- 10s (г, - G/c- ~
-444,44 е V
-5-103 Н, -40- 10”6 - 4г — £	\	V *,
при 138 < x < 150 км
„	1	-5-Ю3 G
u = 22,22 1 — e '
кВ;
-5 Ю3 h
c/2
i" = 444,44 1 - e
A.
9.11.	Рис. 9.110, где при 0 < х' 30 км и' = 127 кВ; f — 317,5 А; при 30 < х' 150 км
-4,17 lO’fh - ll
i/= 152 1 —е V
с
кВ;
i' = 254 + 382e
-«.it-io> (r, -
при 0 < x" < 120 km
u" = 103 [1 -	- «'/О] kB;
i" = 254 [1 _e-4.i7 io’«,-x-/c)j A;
при 120 x" ^150 km u" = 0; i" — 0.
Здесь ti = 40-10-3 с — время после подхода прямой волны в первой линии к точке А (рис. 9.11); х' и х” — соответственно расстояния, отсчитываемые от начала первой и начала второй линий.
9.12.	Рис. 9.120, где при 0 < х' < 15,5 км и' = 5,8 кВ; Г = 116 А; при 15,5 < х' С 20 км
и
л	-2,6-10* ft, - L-
7,14 +4,46е V <72
кВ;
-2,6 • IO4 h - -—-
Г = 89,2 1-е V ‘/2
при 0 < х" < 9 км
и" = 7,14 [1 - е-2’6'10*<г‘ -кВ;
Г = 17,84 [1 -	- x/rtj А
где = 30-10’6 с - время после подхода прямой волны в первой линии к точке А (рис. 9.12); х' и х" — соответственно расстояния, отсчитываемые от начала первой и второй линий.
9.13.	При 0 С х' С 7,5 км и' = 10 кВ; f = 200 А; при 7,5 С х С 30 км и'=17,5 кВ; /'=50 А; при 0Сх"С15 км и'1 = 15 кВ; Г = 50 А; при 15 С х" < 30 км
о,зз ю5 (f2- ——
и" = 30 1 - е к
кВ;
100с
-0,33  10s
f.
А,
где х’ и х" — соответственно расстояния, отсчитываемые от начала первой и второй линий.
9.14.	См. решение.
9.15.	См. решение.
9.16.	Рис. 9.160, где при 0 С х С Ю км и = 63,5 кВ; i — 0; при 10 С х С 70 км
21,1 + 42,4е
кВ;
-6- 10s м -
106 1 - е V
А,
где G = 200 -10 6 с — время движения обратной волны от конца линии.
и —
9.17.	Рис. 9.170, где при 0 С х'С 60 км и' = 3 кВ; /' = = 620 А; при 60 < х'< 120 км и' = 27,3 кВ; /' = 681,8 А; при 0 С х" < 30 км м" = 27,3 кВ; /" = 545,4 А; при 30 С х" С 60 км 718
и” = 40,84 1
- 5.33  10“ (f, - --2 *-
- e V
кВ;
где x' и x" — соответственно расстояния, отсчитываемые от начала первой и второй линий.
Рис. 9.180
9.18.	Рис. 9.180, где при 0 < х' 6 км и' = 100 кВ; = 166,66 А; при 6 х' < 48 км и’ = 166,64 кВ; f = 0; О х" < 6 км и" — 33,36 кВ; Г = 0;
i' =
при
при 6 х" 18 км
и"
——
33,36 + 66,64е	\
кВ;
i"=-166,66e V < ) А;
при 0 < х'"	18 км
и'" = 33,36 + 66,64е
кВ;
-IO4 6, - 'j f" = 166,66e V ‘ J A;
при 18 < x"’ 24 km u'" = 100 кВ; f" = 166,66 A.
Здесь rt = 140 • 10"6 с — время, отсчитываемое с момента коммутации; х', х" и х"' — расстояния, отсчитываемые соответственно от начала первой, второй и третьей линий.
9.19.	См. решение.
9.20.	Рис. 9.200, где = Е [/ (? - т) - / (г — Зт) 4- / (t -- 5т) - 1 (г - 7т) + 1 (г - 9т) - ..
Рис. 9.200
9.21.	i2 = J/4 [1 (г - 2т) - 1 (t - 4т) + 1 (t - 6т) - 1 (t - 8т) + + ...], где т = 1/с.
9.22.	См. решение.
9.23. U х
г2 ch а (т — тх) + zB sh а (т — тх) t г2 ch ат 4- zB sh ат
U! г2 sh а (т — тх) 4- zB ch а (т - тх)
zB r2 ch ат 4- zB sh ат
9.24. u= СУ1е"а,*./(г-тх);
171 -CtTv , .	,
i = е x'l(t - тх), где а — коэффициент ослабления; т = //с; тх = х/с.
9.25.
и = Ut {С* • l(t - tJ - е~“	• 1 [t - (2т - тх)] +
+ г’<2’+т>,.;[Т-(2т+тх)]- ...};
i = —{е °Тх • 1 (г — т*) — е *<2’ ’х> • 1 [г — (2т — тх)] +
+	. 1 [t - (2т + tj]
где а — коэффициент ослабления; т = l/с, тх = х/с.
ОТВЕТЫ К ЗАДАЧАМ ГЛ. 10
10.1.	См. решение.
10.2.	См. решение.
10.3.	Схема начинается с продольной емкости С\ =0,13 мкФ и содержит еще поперечную индуктивность L2 — 6,62 мГн, про
дольную емкость С'3 = 0,028 мкФ и поперечную индуктивность Ь'4 = 4,92 мГн.
10.4.	Схема представляет собой параллельный контур с индуктивностью L2=0,13 Гн и емкостью С2=0,15 мкФ, последовательно с которым включена емкость Со = 0,30 мкФ.
10.5.	Схема представляет собой параллельный контур с индуктивностью Lj = 11,9 мГн и емкостью С: = 8,47 пФ, последовательно с которым включена =0,79 мГн.
10.6.	1) См. рис. 10.60,а; 2) качественно такая же, как и на рис. 10.1Р; 3) качественно такая же, как и на рис. 10.60,я; 4) См. рис. 10.60,6.
10.7.	Первая каноническая схема имеет два параллельных контура: 5,31 мкГн, 1460 мкФ и 12,05 мкГн, 84,8 мкФ; вторая каноническая схема с последовательным контуром 57,8 мкГн, 98,8 мкФ, параллельно которому включены индуктивность 17,5 мкГн и емкость 80,0 мкФ; первая цепная схема с продольными индуктивностями 13,4 мкГн, 4,1 мкГн и поперечными емкостями 80,0 мкФ, 1820 мкФ (начинается с емкости); вторая цепная схема с продольными емкостями 179 мкФ, 144 мкФ и поперечными индуктивностями 17,5 мкГн, 17,7 мкГн (начинается с индуктивности).
10.8.	1) Два последовательно соединенных параллельных контура 90,0 мГн, 11,1 мкФ и 11,1 мГн, 10,0 мкФ и последовательно с ними присоединенная индуктивность 10,0 мГн; 2) два параллельно соединенных последовательных контура 56,0 мГн, 4,5 мкФ и 220,0 мГн, 0,18 мкФ и параллельно с ними присоединенная индуктивность 111,1 мГн.
10.9.	Да.
10.10.	См. решение.
10.11.	Продольная индуктивность 0,294 Гн и поперечные емкости 0,10 мкФ, 0,204 мкФ (начинается с поперечной емкости).
10.12.	Продольные индуктивности 5,0 мГн, 32,8 мГн;
поперечные емкости около ОД мкФ, около 0,03 мкФ (схема начинается с продольной индуктивности).
10.13.	См. решение.
10.14.	Два параллельно соединенных последовательных контура 4,77 Ом, 0,75 Ф и 1,27 Ом, 0,21 Ф.
10.15.	Продольные емкости 1 Ф и 2/9 Ф; поперечные сопротивления 3 Ом и 1,5 Ом (схема начинается с продольной емкости).
10.16.	При разложении входного сопротивления на простейшие дроби — два параллельных контура: 6 Ом, 1/6 Ф и 2/3 Ом, 0,5 Ф и последовательно с ними 4 Ом. При разложении входной проводимости на простейшие дроби — два последовательных контура: 16 Ом, 1/32 Ф и 32/3 Ом, 3/128 Ф и параллельно с ними 32/3 Ом. Цепная схема с продольными сопротивлениями 4 Ом, 16/3 Ом, 4/3 Ом и поперечными емкостями 1/8 Ф, 3/8 Ф (схема начинается с продольного сопротивления). Цепная схема с продольными емкостями 7/128 Ф, 21/3872 Ф и поперечными сопротивлениями 32/3 Ом, 352/49 Ом, 176/3 Ом (начинается с поперечного сопротивления).
10.17.	Да.
10.18.	Да.
10.19.	См. решение.
10.20.	Параллельно соединенные три ветви: последовательный контур 0,1 мГн, 0,01 мкФ; активное сопротивление 100 Ом; емкость 0,01 мкФ.
10.21.	Рис. 10.210.
Рис. 10.210	Рис. 10.220
10.22.	Рис. 10.220.
10.23.	См. решение.
10.24.	Сопротивления Zx = jwLi; Z2 = — Л/®С2, где = = 10/3 мкГн; С2 = 10/3 пФ.
10.25.	Сопротивление Z_x — параллельно соединенные Li = = 10 мГн и гх — 100 Ом; сопротивление Z2 — последовательно соединенные С2 = 1 мкФ и г2 = 100 Ом.
10.26.	См. решение.
10.27.	Сопротивления Z{ = Z2 = JcoL2 — Jl/coC^, где Li = L2 = 4 мГн; C2 - 500 пФ.
ОТВЕТЫ К ЗАДАЧАМ ГЛ. 11
ПЛ. См. решение.
11.2.	Рис. 11.20.
11.3.	Рис. 11.30; от 14 до 16 В.
11.4.	0,2 А; 10 В; 25 В; 7 Вт; рис. 11.40,а и б.
11.5.	0,25 А; 0,1 А; 7 Вт; рис. 11.50.
Рис. 11.40	Рис. 11.50
lf.6. а) См. решение; б —е) рис. 11.60 (см. стр. 724).
11.7.	Для рис. 11.6, а: 1) 0,06 А; 18 В; 2) 0,17 А; 6 В; для рис. 11.6, д: 1) 0,04 А; 16 В; 2) 0,15 А; 4 В.
11.8.	См. решение.
11.9.	Рис. 11.90, а и б (соответственно для Е = О, Е = = 20 В) (см. стр. 724).
11.10.	См. решение.
11.11.	Рис. 11.110 (см. стр. 725).
11.12.	См. решение.
11.13.	0,1 А; 0,2 А; 0,1 А; рис. 11.130 (см. стр. 725).
•11.14. См. решение.
11.15.	0,2 А; 0,4 А; 0,6 А; 25 В.
11.16.	0,2 А; 184 Вт.
11.17.	40 В; 0,3 А.

11.18.	См. решение.
11.19.	0,28 А; 0,06 А; 0,22 А; 36 В; 14 В; 14 В; 14 Вт.
11.20.	0,04 А; 0,21 А; 0,25 А; 11 В; 21 В; 19 В.
I1tA U,B
Рис. 11.130
11.21.	8,6 Вт.
11.22.	См. решение.
11.23.	0,25 А; 0,08 А; 0,37 А; 22 В; 18 В; 48 В.
11.24.	а) См. решение; б) —ЗВ; —0,1 А; в) 2,5 В; 0,07 А.
11.25.	а) 21 В; 0,11 А; б) 27 В; 0,26 А.
11.26.	См. решение.
11.27.	а) 12,5 В; б) 17 В.
11.28.	Рис. 11.280.
0 0,1 0,2 0,3 0,4 0,5 В
Рис. 11.280
Рис. 11.290
11.29.	10 мА; 50 В; рис. 11.290.
11.30.	а) См. решение; б) 0,8 А.
11.31.	а, б) 0,50 А; 1,25 А; 0,75 А; 1 В.
11.32.	а) См. решение: б) 10 В; 0,05 А.
11.33.	а, б) 2 Вт.
11.34.	а, б) 0,67 В.
11.35.	См. решение.
11.36.	160 В; 2 A; 1 A; 1 A.
11.37.	1 A; 0,4 A; 0,6 A; 20 B; 10 B; 10 B.
11.38.	См. решение.
11.39.	30 Вт.
11.40.	См. решение.
11.41.	6,32 мА; 1,44 В; 1,56 В.
11.42.	1,53 А.
11.43.	20 В; 0,1 А; 16,8 Вт.
11.44.	См. решение.
11.45.	0,35 А; 0,30 А; 0,65 А; 4,4 В; 5,4 В.
11.46.	а, б) 4,1 В; 3,1 В; 3,9 В; 0,345 А; 0,250 А; 0,595 А.
11.47.	0,31 А; 0,34 А; 0,65 А; 3 В; 8 В; 4 В.
11.48.	2,7 В; 1,6 В; 3,7 В; 0,3 А; 0,2 А; 0,5 А.
11.49.	См. решение.
11.50.	8 В; 0,2 А; 8 Вт.
11.51.	10 В; 0,2 А; 0,3 А; 0,1 А.
11.52.	46 В; 0,2 А; 0,5 А.
11.53.	8 В; 0,2 А.
11.54.	См. решение.
11.55.	0,3 А; 0,2 А; 0,1 А; 28,5 В; 18 В.
ОТВЕТЫ К ЗАДАЧАМ ГЛ. 12
12.1.	См. решение.
12.2.	3,82-107 Гн"1; на ±33%; Ф = 2,62 • 10"8Zw Вб, где ток — в амперах.
12.3.	1аЬ = 40 мА.
12.4.	а) -60-10"8 Вб; 120-10“8 Вб; -60-10"8 Вб; в) 71-Ю’8 Вб; —90-10"8 Вб; 19-Ю’8 Вб.
12.5.	а) 0,75 мкВб.
12.6.	1,09 мВб.
12.7.	В случае рис. 12.7,6 в 2 раза меньше, чем в случае рис. 12.7, а.
12.8.
В, Тл . . . . 0 0,4 0,8 1,0 1,2 1,3 1,4 1,48 1,56 1,59 1,6 Н, А/см ... 0 2,87 5,73 7,67 10,60 13,07 16,53 22,11 31,68 41.52 51,47
12.9.	8,88 • 10"4 Вб.
12.10.	1080 А.
12.11.	2,4 мВб.
12.12.	См. решение.
12.13.	Fi = -858 А; Г3 = 1374 А.
12.14.	1,3 мм.
12.15.	См. решение.
12.16.	1,7 Тл; 1,1 Тл (поток Ф2 направлен навстречу МДС Г2).
12.17.	10 А.
12.18.	0,65 мм; 140.
12.19.	950 А; 2,4 мВб (вверх); 1,1 мВб (вниз).
12.20.	950 А; 2,4 мВб (вверх); 1,3 мВб (вниз).
12.21.
В, Тл .	0	0,5	1,0	1,5	1,0	0,5	0
ДА	...	19,25	23,10	32,75	98,25	4,0	-13,40	- 19,25
12.22.	a) +BS у тороидов х^; х2у3; *зУь хзУз; б) +BS у тороидов х2у!; х2у2; х3у3; у остальных -Bs.
12.23.	0,25 Тл.
12.24.	0,18 Тл.
ОТВЕТЫ К ЗАДАЧАМ ГЛ. 13
13.1.	См. решение.
13.2.	0,0638 А; 0,1 А; 10 Вт.
13.3.	2 А; 0,44 А; 36 В.
13.4.	0,127 А; 20 Вт; 400 В.
13.5.	2,11 А; 1,9 А; 800 Вт; 538 В; 0,95 А.
13.6.	0,25 мс; 0,52 мс.
13.7.	0,25 см.
13.8.	Рис. 13.80.
13.9.	См. решение.
13.10.	12,9 А; 13,05 А; 3400 Вт; 4,3 А; 540 В.
13.11.	0,524 мс.
13.12.	а) 20 В; б) 25,5 В; в) 38,2 В.
13.13.	См. решение.
13.14.	Рис. 13.140.
13.15.	Рис. 13.150.
13.16,	См. решение.
13.17.	Рис. 13.170, где i — 0,133 sin 1000? А при О С со? < 0,27л; 0,73л со? < 1,27л; i = -1,4 + 2 sin 1000? А при 0,27л < о)? С 0,73л; i =1,4 + 2 sin 1 000? А при 1,27л < сог < 1,73л.
13.18.	См. рис. 13.180, где	= 0,08 sin со? А, и2 = 0 при
2л/3 со? л; 5л/3	со? 2л; ?\ = 0; и2 = 20 sin со? В при 0 <
со? С 2л/3; л С со? 5л/3.
13.19.	а) 0,2455 sin со? — 0,0488 sin Зсо?, А; 0,177 А;
б) 0,0678 sin со? - 0,0061 sin Зсо? А; 0,048 А.
13.20.	См. решение.
13.21.	1 A; 53 В; 103 В; 88 В.
13.22.	См. решение.
13.23.	10,6 sin (4 • 104t - 90°) - 8 sin 6 • 104t мА.
13.24.	См. решение.
13.25.	lOOsin tot В.
13.26.	0,21 sin <ot A.
13.27.	10'3 Вб; 32°; 0,08 sin (104t - n) - 0,01 sin 3 (104r - r|) A.
13.28.	0,2 A; 15°40'.
13.29.	Рис. 13.290.
13.30.	См. рис. 13.300.
13.31.	См. рис. 13.300.
13.32.	См. решение.
13.33.	0,184 sin (104f — 45’40') + 0,004 sin (3 • 104t + 124’30') A.
13.34.	0,0181 sin(105t + 48°40')+0,0012sin(3-105Z —86’30') A; 173 sin (105t - 36°) - 9 sin (3 • 105t - 86’ 30') B.
13.35.	0,109 sin (104t + 27°) + 0,003 sin (3 • 104t — 101°) A;
45,6 sin (104t + 27°) + 1,2 sin (3 • 104t + 97°30') B; 0,157 sin (104t -- 19°) + 0,003 sin (3  104t - 82’30') A.
13.36.	0,3447 sin (104t - 14’30') + 0,0095 sin (3  104t + 124°) A; 60 sin (104t - 20°) + 3,6 sin (3 • 104t — 37’ 30') B.
13.37.	См. решение.
13.38.	Рис. 13.380.
13.39.	1900 витков; 0,17 A.
13.40.	1 A; 220 В.
13.41.	3 A.
ОТВЕТЫ К ЗАДАЧАМ ГЛ. 14
14.1.	См. решение.
14.2.	См. решение.
14.3.	а) г = 1/12,5 (0,2 +t)2 А; £д (?) = 0,5 + 2,5? Гн; б) i = = 2е-7’5' А; Ьл = 0,666 Гн при 0,5 A^i‘^2 A; i = = 0,5е~2,5 A; La — 2 Гн при 0 < i < 0,5 А, где t — в секундах.
14.4.	и2 = 12е'5г В при 0 < i 0,5 А; и2 = 8е-40('~81 ’10 > В при 0,5 А < i < 1,5 А. В отсутствие насыщения и2 = 12е"5' В.
14.5.	1,20 мс; 1,11 мс.
14.6.	а) 10-3[(1 - е’41°3')/(1 + е’41°3')] А; б) 10’2(1-— е’21°3') А; 0,65 мс.
14.7.	а) 1-Ю’3 с; б) 0,9-10’3 с; в) 1,04-10’3 с.
14.8.	и = 1,5(1 - е"5' 1о3‘) В при 0 «5 и 0,5 В; и = 0,75 -— 0,25с’104*'-81,1 10 6) В при 0,5 В С и 1,0 В, где t — в се-кундах.
14.9.	8,625 мс.
14.10.	1,0 мс; 0,7 мс.
14.11.	а) 10 + 140е’1,78' 1о5,В; 10 + 4Ое’0,715 ’1о5(1’7' 10'6>В; б) 10+ 140<?’1,3' loS‘ В.
14.12.	5,62 А.
14.13.	См. решение.
14.14.	См. решение.
14.15.	а01 = 0, устойчиво при е < 0; aQ2 — 2, устойчиво при е > 0.
14.16.	х0 = 0, устойчиво при £ < 0.
14.17.	(#д + 1/г) > 0, где да = di/du; рис. 14.170 (область, в которой возможны неустойчивые состояния равновесия, заштрихована).
14.18.	С < Ь/(г | гд |).
14.19.	(rrfC + L— цМ) < 0; рис. 14.190 (область возбуждения заштрихована).
14.20.	к > 3; а), б) область в первом квадранте, расположенная выше прямой, к = 3.
14.21.	к > 1 + а; -оо < к < 1; [/с2 (12 — а) - /с(24 + 13а) + + 12 + 14а + За2] > 0, где а = r/R.
14.22.	См. решение.
14.23.	Рис. 14.230.
14.24.	Рис. 14.240.
14.25.	di/dt = — (i/C)/[r + 1/(2
n da
dt
Рис. 14.240
(5- 10“2)2
14.26.	d^/dt = 250 - 62,б^2.
14.27.	Фазовый портрет дан на рис. 14.24,а: зависимость uc(t) приведена на рис. 14.240, п; состояние равновесия /0 = = 5 мА, Uo — 20 В — неустойчиво; Т = 0,561 мс.
..2	/,0ч 1Л~2\2
14.28.	а)
У2 (2,43 • 102)2 “ б) 28,344- Ю"4
У
14.29.	-гЛ
(2,24-102)2 х2
(23,1-10"2)2 = 1
с; в) 59,8• 10~4 с.
2 (х —
TF'+ ~—72— = l;x = J, у = 0 — состояние рав-
рис. 14.24,6:
новесия.
14.30.
a) 0 < к < 1 — устойчивый узел; 1 < к < 3 — устойчивый фокус; к — 3 — центр; 3 < к < 5 — неустойчивый фокус; 5 к < оо — неустойчивый узел; б) 0 < | к | < оо — устойчивый
узел.
14.31.	8>Ои82>у — устойчивый узел; 6 > 0 и 82 < у — неустойчивый узел; 8 = 0 — центр; 8 < 0 и 82 > у — устойчивый фокус; 8<0 и 82 < у - неустойчивый фокус, где 8 = rrtC +
14.32.	См. решение.
14.33.
Ч'ое_'/2рС cos \/kJCt +
3fc3^
-r/гС
14.34.	Q0e*'p''2Z-cos coof + -2
О
0)0
-tr.
14.35.	2,76-IO"5 с.
14.36.	22-IO'4 с.
, л . da 8 Р . dtp Зх 2 Р
14.37.	а) = - у а + - s.n <р;= у - -g-й2 cos <р;
где а — uc/UCm; т = cof; v = оэ/соо; % = 1/]/Ь0С; b = сооС; 6 = = o)0rC; d = Um/UCm- h = (LW/o)2.
14.40.
14.41.
14.42.
14.43.
См. решение.
См. решение. ________________________
цМ > rrfC + L; со = ]/(1 4- r/r^/LC.
а)	[2 |/(V - l)/3fc2r]
)/{[4(/С1Г — l)/3fc2rl/o] — 1} ^~k^’/rC + 1
б)	1/]/Ес; 2 ]/(к,г - 1)/Зк2г.
14.45.	Ulm = 2 ]/(fc, - 3)/3fe3; ю = 1/гС.
14.46.	1/J/LC; 2]/(Я1 - г}/3а2; а2 > г.
14.47.
2а - 9 + /81 + 12а
15 + /81 + 12а
где а = r/R.
14.48.	См. решение.
14.49.	См. решение.
14.50.	См. решение.
14.51.	4*). + ! =	+/5  0,06 sin (800л1к + а); ik+1 = 1,5Т£+1;
— 1,04 Вб; —1,84 А при а = 3,25.
14.52.	11,5 В при t = 0,25 с.
14.53.	а) иСтах = 23,303 В; imax = 7,321 мА; б) иСтах = = 320,851 В; imax = 1,527 А.
14.54.	4,75 мс.
14.55.	72,5 мВ.
ОТВЕТЫ К ЗАДАЧАМ ГЛ. 15
15.1.	См. решение.
15.2.	4.
15.3.	8,5 см/с.
15.4.	62° 40'.
15.5.	См. решение.
15.6.	См. решение.
15.7.	См. решение.
15.8.	См. решение.
15.9.	36,5а/18О° пФ, где а — в градусах.
15.10.	а) См. решение; б) 1) — 2,82 • 103 [1 — 0,4/R + + (0,08/R2) In (1 + 5R)] В/см; - ИЗО [0,25 - 2,5R + (1/5R + 1) х х In (1 + 5R)] В; 2) -424/R2 В/см; -424/R В, где R - в сантиметрах; <р = 0 при R = оо.
15.11.	См. решение.
15.12.	См. решение.
15.13.	См. решение. 1) — 11,3г мВ/см; 0,565-10“2г2 В;
2) — 0,113/г мВ/см; 0,565-10"4(1 + 21п Юг) В, где г — в санти
метрах.
15.14.	1) 0; 0; 2) 3,6/г В/м; 3,6 In (г0/г) В, где г — в метрах и ср = 0 при г = г0. Не изменится.
15.15.	a) Di = т/2яг = D2; x/lnr^; — т/2яг2; т/2лг3; б) — = т/2яг; D2 = 0; т/2лг!; — т/2яг2; 0; в) Di=O; D2 = т/2яг; 0; 0; т/2ш'3.
r U 910	U t . ..
15.16.	Е =	. — =------- В/см; (р = - - -- In (r2/r) =
rln^/rj г	ln(r2/rt)
= 910In(г2/г) В; С = ]п~'^д.') = 50 пФ/м; (р = 0 при г = г2.
15.17.	е к 2,7.
15.18.	См. решение.
15.19.	64 мкДж. Вращающий момент пропорционален току,
так как индукция магнитного поля постоянна.
15.20.	Если угол закручивания пружины пропорционален вращающему моменту, то у амперметра и вольтметра — шкалы квадратичные, а у ваттметра — равномерная шкала.
15.21.	3,46-10"4 Тл; 1,98 • 10’4 Тл; нет.
15.22.	См. решение.
15.23.	0,116 мГн; 11,6 мГн; 1,16 мГн; 1.
15.24. 150 Н; 0; 150 Н;/в = -173
— cos (2cot + 30°) Н;
2
2
15.25.	См. решение.
d12'd
1'2 А С I—	J
15.26.	——In ——--------= 4,5 мкГн, где атп — расстояния меж-
271 Wi2Ui'2'
ду соответствующими проводами.
15.27.	—0,874 cos 314? мВ.
15.28.	Для первого расположения проводов: а) 31,2 мВ/км; б) 31,2 мВ/км. Для второго расположения проводов: а) 0,628 мВ/км; б) 0.
15.29.	Нормальная к плоскости катушки индукция Вп = = 0,055 Тл. Нужно измерить другие составляющие вектора индукции.
15.30.	0,6 Тл.
15.31.	Изменится, так как уменьшится число витков катушки.
15.32.	Не изменится.
15.33.	См. решение.
15.34.	0,01 В; 0.
15.35.	См. решение.
15.36.	0,015 В; -0,005 В; 0,005 В.
15.37.	0,02 В; 0; 0,01 В.
15.38.	См. решение.
15.39.	0,02 В; -0,01 В; 0,005 В.
15.40.	0,03 В; 0; 0,015 В.
15.41.	Сдвинуть на 1/8 окружности по направлению движения часовой стрелки.
15.42.	См. решение.
15.43.	а) См. решение, б) См. решение, в) Потенциальное поле без истоков, например магнитное поле вне провода с током; 0; 0; г) потенциальное поле без истоков, например электрическое поле вне заряженного цилиндра; 0; 0.
15.44.	а) Потенциальное поле с истоками, например электрическое поле объемных зарядов; р = — с/х2; 0; — с/х2\ б) потенциальное поле с истоками, например электрическое поле равномерно распределенного объемного заряда; 0; с; в) потенциальное поле без истоков, например электрическое поле заряженного цилиндра радиусом а; 0; 0.
15.45.	1) р — -erEo^ofl/x2; 2) р=0, поле заряженного цилиндра радиуса а.
15.46.	1) rot Е = 2сег; div Е = 0; 2) rot Е — 0; div Е = 0; х2 — у2 — К, где К определяется электрическим потоком, проходящим в заданной силовой трубке. <р = Ci — сху, где = 0, если <р = 0 при х = у = 0.
15.47.	См. решение.
15.48.	— z^Eox/d2; 5</Е0/6; добавится слагаемое Е = (U — -
15.49.	1ООео/г Кл/см3, где г — в сантиметрах.
‘15.50. Вихревое поле без истоков; такое поле создается в прямоугольном волноводе (полой металлической трубе прямоугольного сечения), если возбуждающая антенна — штырь — расположена в середине большой стороны трубы или возбуждающая рамка расположена так, что ее плоскость параллельна торцу волновода.
15.51. 1) div Е = р/е0 = — 2,5 • 10-9/ео В/см2 при R < Ео; div Е = 0 при R > Ro. Поле всюду потенциальное (rotE = 0); 2) div Е = p/s0 = — 2,5 • 10"9л/(я + R) В/см2 при R < Ro; div Е = 0 при R > Ro. Поле всюду потенциальное (rot Е = 0).
15.52. div Е = р/в0 = -2 • 10” 15/е0 В/см2 при г < r0; div Е = = 0 при г > г0. Поле всюду потенциальное (rot Е = 0).
ОТВЕТЫ К ЗАДАЧАМ ГЛ. 16
16.1.	См. решение.
16.2.	См. решение.
16.3.	—0,0348 мкКл/м2; 0,0038 мкКл/м2; 0,0038 мКл/м2; 0,0178 мкКл/м2; 900 В.
16.4.	а) 19,5 мкН; б) 1,5 мкН.
16.5.	См. решение.
16.6.
т 1 z: 1 л4 COS 0 г» /	г ло 1 л4 Sin 0
= 2,16 • 10 —-у- B/см; £fl — 1,08 • 10  —3-
R	R
<р = 1,08• 104 В. При 6 = 0 Er = -б/- В/см:
R	R
„	_	_ _	1,08-Ю4 о/
при 0 = я/2 Er = 0; Ев — ----ч---В/см; для точечного
R
1 08 104
q = 12 • 10'9 Кл Ер =	— В/см; £е = 0.
R2
£о — 0;
заряда
16.7.	См. решение.
16.8.	См. решение.
16.9.	620 В/см; 700 В/см: 350 В/см; 435 В/см; 0; 0,98 кВ;
1,95 кВ; 0; 7,80 пФ/м; Е (х, 0)/£ (0, 0) = 20,4/(20,4 - х2);
U/2	3,58 1П
где х — в сантиметрах.
16.10.	Эквипотенциаль: 5,05 см: 0; радиус 2,28 см; силовая линия: 0;
16.11.
16.12.
16.13.
16.14.
16.15.
16.16.
16.17.
1,49 см; радиус 4,78 см.
См. решение.
26,6 пФ/м.
0,524 пФ/см; 21,8 кВ.
См. решение.
См. решение.
82,5 мкКл/км; —152 мкКл/км; 104,5 мкКл/км.
а)	См. решение.
6)	ф = 7500 In
— 2000у В;
qs= 3750
32
20
х2 + 25
+ 2000 80 Кл/м2,
е0 — в фарадах на метр.
где х и у — в метрах, 16.18. См. решение.
т
Рис. 16.190.
Рис. 16.190
16.20.	См. решение.
16.21.	а) Си = С22 = 15,2 пФ/м; С12 = 1,11 пФ/м; 6) Сп = ' С22 = 16,2 пФ/м; С12 = 0,940 пФ/м; в) = 17,5 пФ/м: 12 = 0,945 пФ/м; С22 = 14,5 пФ/м.
16.22.	-333 В; 97 мкКл/км; 682 мкКл/км; —779 мкКл/км.
16.23.	С12 = 5,9 пФ; С13 = 35,4 пФ; С23 = 17,7 пФ.
16.24.	-62.5 В.
16.25.	2.95 нКл.
16.26.	55,8 пКл; 28 мкН.
16.27.	Любое значение (q); qE.
16.28Р	. См. решение.
16.29.	Без зазора 100 кВ;- с зазором 4,05 кВ.
16.30.	1) 775 мкКл/см2; 775 мкКл/см2; 1250 В/см; 8750В/см: 664 мкКл/см2; 0; (10 — 8,75х) кВ при 0 < х < 0,5 см; (6,25 — — 1,25х) кВ при 0,5 см < х < 1,5 см; (17,50 — 8,75х) кВ при 1,5 см < х < 2 см; 2) 332 мкКл/см2; 332 мкКл/см2; —3750 В/см; 3750 В/см; — 3,75х кВ при 0 < х < 0,5 см; ( — 3,75 + 3,75х) кВ при 0,5 см < х < 1,5 см; (7,5 — 3,75х) кВ при' 1,5 см < х < 2 см.
16.31.	1) Eri < £г3 < ег2; 2) ф = Ux/d^ 3) диэлектрик слоя 3 имеет остаточную поляризацию; напряженности поля на данном участке.
16.32.	См. решение.
16.33.	См. решение.
16.34.	100 В/см; 150 В/см; 600ео Кл/см2; 300со Кл/см2; 200ко Кл/см2; 300ео Кл/см2; 100е0 Кл/см2, где 80 = = 8,86-10"14 Ф/см.
16.35.	См. решение.
16.36.	См. решение.
16.37.	См. решение.
16.38.	45 кВ см.
16.39.	См. решение.
16.40.	—12,7 кВ-см.
16.41.	12 нКл.
16.42.	12 нКл.
16.43.	0.
16.44.	20,3 кВ • см.
16.45.	10,1 кВ • см.
15.46.	См. решение.
16.47.	— 350 (1/г + 0,15г) пКл/см3, где г-в сантиметрах.
16.48.	-35х пКл/см3, где х —в сантиметрах.
16.49.	16,7 (0,2 + х) кВ/см; 147 (0,6 — х) пКл/см2; 147 пКл/см3; 4,72 пФ, где х — в сантиметрах.
16.50.	См. решение.
16.51.	133г В/см; 1890/г пКл/см2; (1890/г - 11,8) пКл/см2, где г — в сантиметрах; 23,6 пКл/см3.
16.52.	А/Г' где А — const.
16.53.	См. решение.
16.54.	9,1 • 10“9 См/м; 5,46 мкА/м; 216 мкА/м2; 108 мкА/м2; 46,5 мкВт/м3; 11,6 мкВт/м3; 3250 мкВт/м.
16.55.	6,06 мкА/см.
16.56.	См. решение.
16.57.	4,9-10'10 А.
16.58.	См. решение.
16.59.	220 В.
16.60.	См. решение.
16.61.	5,39' IO'10 См/см.
16.62.	См. решение.
16.63.	См. решение.
16.64.	См. решение.
16,65.	—256 пКл/см3; 256 пКл/см3.
16.66.	- 355-10-17(0,2+ х)2 Кл/см3; 2 мВт.
16.67.	1) 725/г В/см; 256-10"% Кл/см2; 0; 0; 455 • 10“12 См/см; 45,5 мкА/см; 2) 333 В/см; 118-10"12 Кл/см2; 89,5 • 10-12/г Кл/см3; 118-10-% Кл/см3; 209-Ю-12 См/см; 20,9 мкА/см; 3) 133г В/см; 47,2 • 10“ 12г Кл/см2; 71 • 10“12 Кл/см3; 94,4 -10-12 Кл/см3; 83,5 • 10"12 См/см;8,35мА/см;4) 1330/г2 В/см; 472 «10“12/г2 Кл/см2; — 355 • 10-12/г3 Кл/см3; —472 х х 10-12/г3 Кл/см3; 840-10"12 См/см; 84 мкА/см.
16.68.	См. решение.
16.69.	(1 - le-1I31°3') 103 В/см; [441 - 353е’2001 -
— 88с-113 ’ 1о3‘] пКл/см2; (352 — 353е“ 2001 + 1е~113' 1о3‘) пКл/см2; (О,7О8е-200' + 100е_113' ‘°3') мкА; W„ = W + Wr + W„ где W„ = - 442 нДж — энергия источника; W = 221 нДж — энергия, накопленная в электрическом поле; Wr = 46,7 нДж — энергия потерь в резисторе; Wx = 174 нДж — энергия потерь в вязком диэлектрике.
16.70.	См. решение.
16.71.	225 МГц.
16.72.	a) cf = 10-9 См/см; ст" = 4,86 • 10" 13со См/см; &'г = = 5,5*; s'' = 11,3 • 103/со, где со — в радианах на секунду; б) при всех частотах Е = 100 В/см; D = 550ео Кл/см2; Р = 45Оео Кл/см2; где Eq — в фарадах на сантиметр; плотности тока: 1) 0,10 мкА/см и 0,1 мкА/см при = 328 Гц; 2) 0,10 мкА/см и 0; 3) 0,10 мкА/см и -> сс.
16.73.	См. решение.
16.74.	См. решение.
16.75.	605(1 - 1е-,/79) пКл/см2; (-431 +417е"г/79) пКл/см2; 10"14(19,8 + 758е“'/79) А/см2; 10“16 (1980 - 758е",/79) А/см2; (—468 • 10" 14e-t/79) А/см2; 298  10" 14e-t/79 А/см2; 11,6 пДж; 1160 пДж; 790 пВт; 79 пВт.
16.76.	1,67 sin (cot + 132°) нКл/см2;	1,45 sin (cot —
— 35° 35') нКл/см2, если начальная фаза напряжения равна нулю; 58,6 Вт/см3; 25,8 Вт/см3.
16.77.	600 рад/с и 400 рад/с. При со = 400 рад/с 0,41 z. 9° 30' кВ/см; 73 z. 9°30' пКл/см2; 36,5 z. 9° 30' пКл/см2; 0,6 z. —6° 30' кВ/см; 150 z. —51°30' пКл/см2; 119z.-69°55' пКл/см2; (5,88 + ;4,68) 10"10 См; 0,294 мВт; при cott == 80° 40', при cot2 = 68° 20'.
16.78.	0,48 пФ/см; 0,483 • 10-14 См/см; tg 8 = ст^/со (8//+
+ £>)е0 — 1/100м; в воздухе —
П In r2Ai ’
в диэлектрике д5 =
80(1 -8Г)П
Г\ ln(r2/rj) ’ 9sCB5n ц In (г2/гх) *
16.79.	См. решение.
16.80.	См. решение.
16.81.	См. решение.
16.82.	2,49-10"8 cos 314г А/см2; 1,24 • 10"10 cos 314г А/см2.
16.83.	См. решение.
16.84.	4160 — 76,бе*’°4'	пКл/м; 13,2 (1 - 1е“1о4') х
0.012 + (0,02 — х)2	0,012+ х2 пКл/м2; 10,62г 10 ' х
1
0,012 + (0,02 - х)2
1
0,012 + х2
пКл/м2, где х — в метрах.
отсчитывается от точки, лежащей на поверхности земли под положительно заряженным проводом.
16.85.	1) См. решение; 2а) 5 кВ/см; 0; 0; 26) 3,3(1 + + 0,5х) кВ/см; 0,321 нКл/см3; —0,177 нКл/см3; За) L7ae"ax/(1 ~ - с“^); 0; J7eoa2ea (d-x); 36) совпадает с данными в п. За;
дя\ -	П-	сов-
b (а + bx) In [(a + bd)/a] ' ’ (а + bx)2 In [(л + bd)/a] падает с данными в п. 4а.
16.86.	А. 1) Всегда равен 0; 2) 8Г +const; 3) sr # const, но свободный заряд равен 0; 4) er = const; 5) невозможно. Б. 1) (ег — 1)/с = const; 2) a + const; er/n = const; 3) sr/o + Ф const; 4) 8r/o = const; (er — l)/cr — const, t. e. sr = const и у = const; 5) a = const; er/o + const.
16.87.	а) Во всех случаях E = 725/r В/см; p = 0; рсвяз = 0; 5) см. ответ к задаче 16.67.
16.88.	1) Удовлетворяет; 2) 3e0EocosQ; 3) ф = Ео (R — a3/R2)cos 0 + д/4яе0Я.
16.89.	1) Удовлетворяет; 2) 28oEoc°sa; 3) ф =
/р (	а2\	, т . а
- Ео г------cos a + -----In —.
\ г J 2я80 г
16.90.	См. решение.
16.91.	(р/ = —Eq -----—cos ос; Фе == - Eor cos а 4- Ео — х
Erj 4- Еге	Г
х	cosot; Е, = Ео 2Sfc ; <?ScMB = 2е0Е0 £fi-~ £" cos а.
16.92.	1) Линии векторов D и Е втягиваются в цилиндр, число линий Е внутри цилиндра уменьшается. Линии вектора Р существуют только внутри цилиндра. Поле внутри цилиндра однородно; 59 пКл/см2; 2) линии векторов D и Е выталкиваются цилиндром. Число линий Е внутри больше. Линии вектора Р существуют только в окружающем цилиндр диэлектрике. Поле внутри цилиндра однородно; —59 пКл/см2.
16.93.	3,42 кВ.
1)	20 кВ; 2) 24,5 кВ; 3) 60 кВ.
См. решение.
16.94.
16.95.
>1/2	1/2 t
~—ept В/см; Ef0 = EeQ = -250 ^~ept В/см;
,	|/2
EeR = 3000 —---- 500 ~~ept В/см, где p = - o/so (sn- 4- 2sPe) =
= -0,943 • 10“4 c’1; Pi = Pi2= 196soe^£ Кл/см2; 3,3-IO’8 Дж/см3. Геометрическое место вектора напряженности в точке А — прямая — получается из выражений EiR и EiQ; вектор напряженности в точке А во время переходного процесса не изменяется по направлению. Геометрическое место вектора напряженности в точке В — кривая — получается из выражений EeR и Ее0; вектор напряженности в точке В во процесса изменяется по направлению и режиме направлен по радиусу.
16.97. 1) 0; 3cos0 мкКл/см2; 2)
5 cos 0 мкКл/см2.
1^.98. См. решение.
16.99.	См. решение.
16.100.
16.101.
16.102.
16.96.
время переходного в установившемся
5 cos 0 мкКл/см2;
См. решение.
См. решение.
См. решение.
Ро " а2с0
ead- 1 d р / ах е^а — 1\ 4- -^4аеах---------—.
Еои \	d J
16.104. А. ( —50х3 4- 675х + 500) В; (150х2 - 675) В/см, где х-в см; 1450 В; —75 В/см; Б. 1) Ничего не изменится; 2) ( —50х3 + 500) В при х rf/2; (-50х3 + 1350х - 2200) В при
16.103.
х
1
d
16.105.	1) Да; 2) нет.
16.106.	Кг0 cos а/(7?3 sin2 9).
16.107.	См. решение.
16.108.	См. решение.
16.109.	См. решение.
16.110.	См. решение.
16.111.	2,21 • 10-7х~2 Н.
16.112.	5,4-10“2 Н.
16.113.	8,48-10~9а"2 Нм, где а —в радианах.
16.114.	-3,1 • 10"8 Н м.
16.115.	5-10“5 Н м.
16.116.	-26,2 -10’6 Нм.
16.117.	68,1 • 10’6 Н; сила направлена к пластине 1.
16.118.	-12,5 В; -125 В.
16.119.	а) Да; б) нет.
16.120.	См. решение.
16.121.	6,63/(1 + 15х)-Н; 0,497/(1 + 15х)2 Н.
ОТВЕТЫ К ЗАДАЧАМ ГЛ. 17
17.1.	р	-2 а-
2а	2	(х2 + i
х 4- 1/2
1 / »<£•
2
2
= (cos р! - cos р2); а) 0,485; б) 0,329; в) 0,204.
См. решение.
2
17.3
17.5.
2
cos у — sin у 4- sin2 у х
х ln .tg(Y/2 + n/4) tg (Y/2)
/и’о
2
х In - -	-,2-- ;
tg (Y/2 + Рг/2)_
2) В = Вг = ц0 ^2-(с<
17.7. В = Вг = Цо Ц°
sin р2 ~ sin Pi + In
17.8.	n0/w/4a = 3,14-10"3 Тл.
17.9.	См. решение.
17.10.	?^-arctg 8.9-10"5 Тл. ла 2п
17.11.	См. решение.
„_______I , Г *2 + О' - а^2 (х - У2 + (У + а/2)2
х 4ла _ х2 + (у + а/2)2 (х —.J)2 + (у - а/2)2
. /Г х у + а/2	. У ~ а/^	< У + <я/2
у = -— arctg ------------arctg ----------arctg 2.----— 4
у 2ла	х	х	х — d
+ arctg
17.13.	28,6 А/см; 12,7 А/см; 9,55 А/см; не изменятся.
17.14.	а) 36- 10"4 Тл; 0,32 Тл; 12 • 10“4 Тл; 0; 0; 2530 А/см; б) 36 • 10"4 Тл; 16  10’4 Тл; 12  10~4 Тл; 0; 0; 0.
17.15.	См. решение.
17.16.	11,6 см; 10 А/см.
17.17.	См. решение.
ц0^2 J 1	1	1 _
17.18.	-у-| |-а2 + (х _ й)2]3/2 + |-а2 +	+ Л)2]3/2 j -
-2,51 10	|	+ (2х _ 1)2р/2 + [-J + (2х + 1)2у/21 Тл.
17.19.	Вх = —46,5 • 10-6 Тл; Ву = 155 • 10-6 Тл, если ось х — ось второй катушки; ось у лежит в плоскости осей катушек и направлена от точки М в сторону первой катушки.
17.20.	ц0 l/'-i'-z [(2/С - С)к - (2/C) Е] = 2,4 • 10"7 Гн, где С2 = 4r1r2/[/i2 + 0*1 + г2)2] & — эллиптический интеграл первого рода; Е — эллиптический интеграл второго рода.
17.22.	См. решение.
17.23.	См. решение.
17.24.	75 (4г + З/r) А/см2; 25 • 104(г + 3/4г) См/см.
17.25.	См. решение.
17.26.	См. решение.
17.27.	См. решение.
17.28.	См. решение.
17.29.	Ах = (—100г2/г2 4- 101,5)- 10“6 Вб/см при г<гх-Л2 = [ — 2 In (r/rj + 1,5] • 10"6 Вб/см при rt<r<r2; 43 = = |/2A’i - Ю In (r/rj) + 3,05] 10“6 Вб/см при г2 < г < г3; Л4 = 0 при г > г3.
17.30.	См. решение.
17.31.	См. решение.
17.32. ^1п
4я
= ^-0,388.
4л
17.33. La = -H^ln d-^-Bdp ; J 4л rodBC
X]n^£..
r 0“АВ
17.34. a) Ai = C; Ae = -2л
6) A> =	’ln £)’ 42 “ 77!n 7F
r2
X In -At
П
Во внутреннем проводнике ri = Q; между ry = C2; вне оболочки r2/ri ~ С3, где Cj., С2 и ные, соответствующие линиям магнитной индукции. Все линии — окружности.
Mo 1 <^BC<^AB . rQdCA ’
г
— 4- С, где а
Мо/ < а2
4л
Мо/ Г a2 - г2
4я
а2
«2 “ «1
4я а2
а22 - а2 - ajl
Mo 4л
Л3 = ^х
4я
проводниками С3 — постоян-
2	2 ~1
4	at
2	2	2
a2 — at r
1	1 **2	Z-Ч	х-т
in — — in — + С, где С — постоян-
(Я
г
A ц0/ / a2 ная; 6) At = ~— -h-----------7
4ti \ a22 - a2
1 ai 1
In —4-4- In
<12
v2 r0
al
d \ A _ Mo/
Я? A2~
а2
<12 ” <11
«1
<12- <11
17.36.
17.37.
1	1
In “V — In
«2
<12
al \
v2 I’
4л
г2
In ZP
Но-/ (а22-г2 4ти \ а2 - а2
1п
3--1п
al
v2
См. решение.
Цилиндр: N = щ. —
Mr
1 + (И, - 1)/2 ’
Мт max ,
шар. N	__l)/3 y max
17.38.	См. решение.' A) 2-10"4 Вб; Б) 12,5 AO"8 Вб; B) 4,2 IO'4 Вб; Г) 6,28-IO"7 Вб; Д) 8,37-10"7 Вб.
17.39.	См. решение.
17.40.	В = By = Polx/it (h2 + x2) при v = 0: = |Л0/у/л: (&2 — У2) при x = 0; F = ц0/2/4к/1 == 10"2 H.
X
17.42. В
17.41. См. решение.
_Lsin а
.1^7 kUi 2л
Prl \ в Рг2/ Г2 I
9
РоЦг1Рг2
1а ..........
Prl V2 - £2
Рг2/ Л
Иг Л г2 - а2 ~
Цг2
2
_ М’0Рг1Рг2
2 г —	~	Г~~
„ РоРг1Цг2
#2а — ~	..
« ь .
2 -5-sm а;
Л
2 - Ь21
Нг2 , Г
17.43.	См. решение.
17.44.	А — (ц0//2я)1п (гоА1^г); rir2 = С; линии вектора магнитной индукции построены на рис. 17.440.
Рис. 17.440
17.45. А! = 2ЦоЦ1гМг
Рис. 17.470
А-2 — РоР-2г
1 а
In —;
' 2/ 31 Чf 5^~"
I t t 1 V ®-
Ц1 г Р2г
17.46.
_ 2цор1гЦ2г а sin а >
2
2цоц1гц2г	r-acosa
ТС	Z2 ’
п	1 . а
в2,= -Ц0Н2, 2^sina(-рт
Р1Г - Н2г Ь \
2
I 1 / г2 - п2 - ц2г г2 - Ь2 В2« = ^ЪГ2Г “И
,2 J . „2
/\2 „2п
/\2 ’
где п = (ц1г + |12г)/(Ц1г ~ Pir); г', г\ и г'2 — значения соответственно г, Г! и г2 вне цилиндра для точки, через которую должна пройти линия магнитной индукции. На рис. 17.470 показано несколько линий индукции.
17.48.	См. решение.
17.49.	См. решение.
17.50.	См. решение.
17.51.	См. решение.
17.52.	coti = -26°; 6,98 А; М = 0.
17.53.	0,74 Вт/м; AZ = j<o U° /r ~	In 1/1 4-	=
л (pr + 1)	|/ у 2h J
= 0,185(1 +J4) —. м
17.54.	В1т = 2,51  10"5 Тл; 0,775 • 10"10 Вт/см. В заданной точке В2г = ц0 • 0,173 sin cor Вб/см2; В2а = - ц0 • 0,25 • 10 "3 sin (cor + + 0°34'30") Вб/см2, где ц0 = 4л • 10"9 Гн/см.
17.55.	См. решение.
17.56.	Г, = dW/dl = — 2r2w2I2 • 10"4/(9r + 10/)2 = -0,005 H, где знак минус указывает направление силы: она стремится уменьшить размер /, т.е. сжимает витки катушки; Fa = = dW/d (2лг) = 2w2I2r(9r + 20/) 10" 5/(9r + 10/)2 2л = 0,0071 Н.
17.57.	—/2 |/LjL2 • 0,4 sin а = — 3,84-10"3 Дж. Знак минус показывает, что сила стремится уменьшить угол а.
17.58.	Iw | =0,14 Дж;	/w|xr-) =
2 2 V2 + M1/	2 1 у2 + М1/
/ т \ 2
= 0,112 Дж; 0,504 Гн; ~^5(цг - 1) ---------!Ц-| = 279,5 Н.
2	\ '2 + Рт 1 /
17.59.	См. решение.
17.60.	См. решение.
17.61.	а) В§Я/Но = 22,1 Дж; б) = BgS/p0 = 11 050 Н; F2 = B2S/n0 = 25 900 Н, где Во и Вк — индукция соответственно в начальном и конечном положениях якоря; в) Или = |/с/Ч/ = = 8 Дж; г) AWC = 8 Дж; А1УВ - —22,1 Дж.
17.62.	а) 39,1 Дж; б) 11 050 Н; 25 900 Н; в) 25 Дж; г) 8 Дж; — 22,1 Дж.
17.63.	4- 10"7 zA/деление.
17.64.	См. решение.
ОТВЕТЫ К ЗАДАЧАМ ГЛ. 18
18.1. а) Поле двух электродов-полуплоскостей разного потенциала, сходящихся в начале координат (рис. 18.10): ср, — ф2 . ср, — ф2 1 г л Ф1 — Фг
(р = epi — —----—а; ф = --------—In А = -------------; б) по-
а0	а0 ^2	Ко
ле х заряженной с линейной плотностью т оси, проходящей
т 1 Ci ।	т	_
через начало координат; <р = ------In—; ф = — --------а + С2;
2Л£0	Г	271£q
Рис. 18.10
18.2. См.
18.3.
См.
решение, решение.
т . ап + z” . т w -  ----In ——=-; ф =  -------arctg
~	2гс£0 а — z 2тг£0
+ (г/а)2п + 2 (r/a)n cos па _ ------------—----------•	2) ИЯ£оу
л
2 (r/a)n sin па
1 — (r/d)2n
Ф = ------in- —; 2) ия£0/1п----------------------------------; 3) се-
4тг£0	1 + (г/а)2п — 2 (r/п) cos	пго
К
мей’ство эквипотенциалей: cos па = — [(г/а)п + (а/г)п], где К = а\ (L^n г /	\ а
18.4.
т
In -
, 2л£оф
= th---—; семейство линии поля: sin па = С
wc=‘ltg^t. 2 т
Т-1П о 1	1
In —
9
18Л ^=2Л£ ф_ 4тге0
1-W ’
rjb)2n — 2 (r/b)n cos п (а + р).
/ г \2и	’
*(“) ~ 2 (r/a)n cos па
sin'np - (a/r)n sin п (а + Р) + (b/r)n sin па
т	_____________________
2я£0 arct° cos иР — (a/r)n cos п (а + Р) — (b/г)" cos па + (яЬ/г2)" ’
2) п2тссо/1п
(а2п + b2n) — 2anbn cos «Р (ab)n~1 м2Го
18.6. См. решение.
18.7. См. решение.
18.8. См. решение. х2	у2
1 о 9---------------------________
a2 sin2 (ф/п) a2 cos2 (ф/а) х2	у2
a2 ch2 (ф/4 — 2,3) + a2 sh2 (ф/4 - 2,3)
— линии поля;
— эквипотенииали.
18.11. -------------
1п [(«1 -]/<
2Л£д
2ле0 . )
In (2R/a) ’ V
2л£0
а
aj - п2)]
18.13.	См.
18.14.	См.
18.15.	См.
решение, решение, решение, решение.
18.16. 1) уу = -
2/ ch^-й ь
Ьс2
п sin —z
b ~
, 2л , 2л сп -т— h — cos -т— z b	b
n cos — z
b 
2л	2л
-т-h + cos -r-z b	b ~
« 0,045 Cm/m ;
3) 187 Bt/m2.
18.17.	См. решение.
18.18.	См. решение.
18.19.	См. решение.
18.20.	См. решение.
ОТВЕТЫ К ЗАДАЧАМ ГЛ. 19
19.1.	100 Вт.
19.2.	См. решение.
19.3.	9,8 Вт/см2; 7,5 Вт/см2; 1,72 Вт/см2.
19.4.	См. решение.
19.5.	См. решение.
19.6.	247 кВт/см2; 9,9 кВт/см2; 27,5 кВт/см2.
19.7.	1) П, = 11 400 Вт/см2; П„ = 28 • 10’3 Вт/см2; 2) П, = = 456 Вт/см2; Пй = 5 • 10’4 Вт/см2; 3) Пг = 2850 Вт/см2; П„ = = 8- 10“3 Вт/см2.
19.8.	1) 52,4 Вт; 200 + 5,24 • 10"3 А; 200 А; 2000 кВт; 1/(1 + 2,62-10"5); 2) 52,4 Вт; 231	29°50' А; 200 А; 2000 кВт;
1/(1 + 2,63-10"5).
19.9.	См. решение.
19.10.	12,65  10"3 — 0,1265 cos (2cot — 13°) Вт/см2; 1,2 + + J12 В • А.
19.11.	О,12е" 750'(1 -е"750') Вт/см2; 0,2 Дж.
19.12.	См. решение.
19.13.	1800 В.
19.14.	См. решение.
19.15.	илВ (К2 - 2d cos cor ]/R2 — d2 sin2 cor + d2 cos 2cof) »
/ d
nnBR21 1 — 2 — cos (at
при d R, где co = 2rcn.
19.16.	151 cos cof мВ
19.17.	См. решение.
19.18.	См. решение.
19.19.	Нет.
f х дВ\	_ . , г2 дВ
19.20.	0; |g|l fxB + y^-1 при г < г0 и 0; \q\
при
г0-
19.21.
II D I I Х № \Q\VyB;	при
г2 дВ -
г <г0 и g Ьг-’-йг; 0 при 2х dt
г > Го-
19.22.	v = | q | Вг/т = 1,41 -106 м/с.
19.23.	vx = 2,8 • 105 м/с; оу = 3,52 • 10б м/с; vz — 0.
19.24.	Xj = 19 см при а = 0; х2 = 18,7 см при а = 8°
19.25.	Окружность радиусом г = mv/qB.
19.26.	В = |/2mt>/| q |.
19.27.	См. решение.
19.28,	—r|) = 8 В; $1 4- юМ = 12 В; где co =
= 120ли • 58,2 %.
19.29.	См. решение.
19.30.	5 • 10"5 sin (cot 4- 30°) В/см; 0,584 sin (cot - 15°) А/см; e10-15.
19.31.	65 • IO"6 sin (coi — 270°) В/см; 0,73 sin (cot — 315°) А/см; 1,26 • 10~2 Вт/см3; 5,5-10"4 Вт/см3.
19.32.	— (cr£2 + dWJdt) = — #om&Wloe”2az [1/2 4- sin (2cot-— 2pz)] = - 0,315e“ 8,882 [1 4- 2 sin (2cof — 8,88z)]	Вт/см3;
O,315e"8,882 [1 + sin(2cot - 8,88z)J Вт/см3; dWJdt = O,315e" 8,882 x x sin (2cot — 8,88z) Вт/см3, где z - в сантиметрах.
19.33.	См. решение.
19.34.	См. решение.
io 15 ' = Р sh 2afl + а sin 2Ра = ^гср 17 |2 a,(ch 2ая 4- cos 2fa) _ 2,15 sh 2аа 4- 2,3 sin 2рд
a (ch 2аа 4- cos 2ря)
„ _ I В-1 а sh 2аа — р sin 2ря _ 2,3 sh 2аа — 2,15 sin 2p<z
ср | 7 |2 a (ch 2аа 4- cos 2pn) a (ch 2aa 4- cos 2pct)	* ГДС
7 = а 4-/р = \//сосу^Цо = 232 4- /217 см"
15,4 Зф 61,8 123,5 ihl'
21,3 43,3 87,5 175 350
2а,мкм
Рис. 19.350
Эти зависимости представлены на рис. 19.350, где пунктирные кривые соответствуют проницаемостям без учета потерь на гистерезис.
19.36. Р = а>цоц"срН2С/у;
2а, мм ....	0,016	0,06	0,2	0,5
Мт ср	•	400 - /2.7	397 - /38,2	198 -;163	63.6 - у’63.6
Р, Вт ....	0,071	1,6	4,3	1,67
19.37.	400 -JI3,4; 63,6 (1 -/1); 2а2 = 2^ ]/fl/f2 = 0,0353 мм.
19.38.	См. решение.
19.39.	См. решение.
19.40.	При hlzb = nl2 или h = 1,48 см; Z = ROT(1 + 4-jl) th (л/2) = 0,9177?(1 +/1), где Яда = //стЬго = 37,2-10“5 Ом/м-сопротивление при резко выраженном поверхностном эффекте; z0 - глубина проникновения. При других экстремальных значениях h сопротивление практически не отличается от R^.
19.41.	См. решение.
19.42.	См. решение.
19.43.	См. решение.
19.44.	1) Ro (1 + /0,0028); 2) Ro (1,025 + 7*0,28); 3) Ro (53 + /53), где Ro = 56-10“4 Ом; 1,077 zl 31° 11'.
19.45.	2,7 см; 6,33.
19.46.	3,55; 41°.
19.47.	По точной формуле R = 76-10“3 Ом/м; X = = 66,5-10"3 Ом/м. По приближенной формуле R = X = = 67,5-10"3 Ом/м.
19.48.	См. решение.
19.49.	См. решение.
19.50.	См. решение.
19.51.	AZ =/сои’2лго-у-(ус-р - 1) = 5,86 -/56,1 Ом, где цср
см. в решении задачи 19.50.
19.52.	а) 16,8-/42 Ом; б) 20,5-/12,1 Ом; в) -/62 Ом; 62/100.
19.53.	Z = Zo (цг^/S - SJS + 1), где Zo =/<mv2p.0S//, цгср = 2цг Ji (qrq)
= — а) 26,4 + /660 Ом; б) 2060 + /5510 Ом.
qr0 J0(qrQ)
Д9.54. При r0 = l,8z0, где z0 — глубина проникновения, Ртах — О,38со|лгцоНо, где Но — напряженность внешнего магнитного поля тока в катушке.
19.55.	10 200 Гц; 28,4 Ом.
19.56.	1,016 МГц; 3140 Ом.
19.57.	(19,3 + /257) 10“3 Ом/м; а)/248 • 10“3 Ом/м; б) (19,3 + + /8,9) 10“ 3 Ом/м.
io «Я 7 = N1 J° ^2) ~ Ji (^1) No (qr2)	=
2пг2ст Ji farJNi (grj - Ji (grJNi (qr2) ’
= ]/ — /(DCTprpo; J0(x), Ji (x) — цилиндрические функции первого рода соответственно нулевого и первого порядка; N0(x), Ni(x) — цилиндрические функции второго рода соответственно нулевого и первого порядка; a) Z = 0,935 10“5 Ом; б) Z = = (1,4 +/0,525) 10“5 Ом; в) Z = 8,5 (1+/1) • 10“5 Ом.

19.59. a) £ = £..=	 н = Н, = --
_________	zra-ocU! (gr0)	2Ttr0JI(jr0)
= ]/-;<вац0;
б) £ = £г =	~ [Jo (qr) Nt (qr2) - No (qr) Jt (£)-2)];
ZTir 1 СУ 1
, 1де
H =
=	= 2л:'г'т [Ji (Sr)N1(^2) - Nt (qr) Jt (qr2), где T =	(qr{) x
x NifarJ- Ji^rJNi (£n);
b) £, = —~; £. - Ёг (r0) - [£, (r0) - £2 (г,)]	где
r°
„ , . hh iq.ro)
Ez v о)	т / к 5
2дгоа11 (qr0)
E (r _h__^^lr2)h(qrl)~ Jl(qr2)^0(qrl) .	.	/
2nr^	Jl~(^2)NJ(£r1)’ a~2nr‘
lq 19.60. Z = ,	~riJ0(g/’o)
~ 2тгг1а	_ r0J 1 (qr0)
Ni (?r2) Jo (qr}) - Jt (gr2)N0 (qr{)	.	2j_
Ji (^i)Ni (qr2) - Jj (^JNi (qr i) ~ 1 ° rQ
где Jfc (z) и Nk (z) — цилиндрические функции соответственно первою и второго рода порядка к.
71 CT
2
ТТ г0
2	„2
2лГ1<5 [_ r0
Г0 J ~ г
\	. / ГI	ГI	ГI
+ j — + 1 + 2 -2-1п —
'	\ Го	?о	г0
19.61.	См. решение.
19.62.	0,0657 мкВ.
2TtrtOz0 r0
19.63.	7,5 мкВ.
19.64.	10,75 В/см; 0,0284 А/см.
19.65.	1) 31,4 см; 0,665 мкА/м; 2) 0,67 мм; 20,7 мкА/м.
19.66.	1) 31,4 см; 0,00985 мкА/м; 2) 0,67 мм; 4,16 мкА/м.
19.67.	92,5 нм; 2,64.
19.68.	1,67 см; 2,65 -	10"3 см.
19.69.	а) ТЕтп, т — любое; п — 2р 4-	1;	б)	TEW„,	т	—	любое,
п = 2р; в) TEwn, т = 2р,	п — любое;	г)	ТМ,„„,	пг =	2р	+	1,	п —
любое; д) ТМтя, т = 2р + 1, п — 2q + 1; е) ТМЖИ, пг = 2р + 1, n = 2q; в случаях б и е токи в штырьках в противофазе.
19.70.	См. решение.
19.71.	4,64 Вт; 4,46-Ю’6 Нп/см; на 0,082%.
19.72.	4,85 Вт; 4,85-10-5 Нп/см; на 0,24%.
19.73.	См. решение.
19.74.	772 Вт.
19.75.	936,4 Вт.
19.76.	а) 8,2; б) 11,9; в) 13,96 ГГц.
19.77.	См. решение.
19.78.	13 мм.
19.79.	207 А.
19.80.	3,8 10’7 Вт; 3,8-10"9 Ом.
19.81.	А — Az = |iol/e jkoR/4nR, где к0 = со/со; с0 — скорость света в вакууме; R = ]/х2 + у2 + z2.
19.82.
2 19.84. Ё, = -4jCO7l8oR	4j(D1T£0R
Р___________llz Л _ ЗгП. и = _ пУ . и = !!х
4jamz0R3 \ R2)' х 4nR3 ’ у 4itR3
Нг = 0.
19.85.	ех =	e~'k°R:	е-^-,
4nR3	у 4nR3
-	(z2	Лр
4tiR \R2	J
x e“^; Hz = 0; Пср
19.86. 80я2/2 ((До)2-
-ik^R. Л _	„-jkoR.
x~ 4njR2 '
_ co2|io/2Z2 (x2 + j?2)
1б7Г2С0К4	’
Ilkox 4njR2
Приложение 1
LZi	1
u

Приложение 2
Таблица оригиналов и их изображений по Лапласу
Оригинал	Изображение
Е * const	E P
6(0	1
t	J_ P2 ‘
e~al	1 p + a
I — e~at	a p(P + a)
te~al	1 (p + a)2
(1 — at}e~ai	P (p + a)2
a — h у	J	1 (p + a} (p + b)
r~— (be"bt — b — ay	j	P (p + a) (p + b)
I	1 (e~^‘ _ ab b ~ ay b	a J t	1 , e~at a a- a2 1 -e-a,(l +al)		[	 p(p + a) {p + b) p2(p + a) 1 p(p + a)2 e* (p ->w)
COS 0)/	p (p2 + 0)2)
sin co?	to (P2 + 0)2)
COS (CD/ + \(0	pcos^ — cosinij/ p2 + 0)2
sin (cor + ф)	p sin ф + cocos^ p2 + (J)2
е~а1со$ы	p + a (p + a)2 + 0)2
tj-arsinu)/		0)	 (p + a)2 + 0)2
r”"zcos(co/ + l|0	(p + a)cos\|/ — cosing (p + a)2 + 0)2
£>“a/sin(ti)/ + ф)	(p + g) sin ф + tocosvj/ (p + a)2 + 0)2
Кривые намагничивания сталей 1211, 1411, 1512, 1561
Марка стали, индукция	Н А/см												
	0	0,2	0,4	1	1,4	1,8	2,4	4	6	8	10	12	14
I2H, В Тл	0	0,03	о, и	0,53	0,73	0,90	1,10	1,23	1,32	1,38	1,42	1,45	1,48
141I. В, Тл	0	0,04	0,18	0,67	0,81	0,92	1,05	1,14	1,23	1,30	1.38	1,42	1,46
1512, В, Тл	0	0 ,1 I	0.35	0,73	0,87	0,96	1,06	1,16	1,25	1,32	1,37	1,40	1,44
I56I, В, Тл	0	0,20	0,44	0,75	0,88	0,98	1,11	1,20	1,27	1,32	1,37	1,40	1,42
Я. А/см
Марка
стали, индукция	18	22	24	40	80	120
1211, В, Тл	1,54	1,57	1,59	1,64	1,75	1,83
1411, В, Тл	1,50	1,53	1,55	1,59	1,69	1,78
1512, В, Тл	1,48	1,50	1,51	1,57	1,68	1,76
1561, В, Тл	1,44	1,46	1,47	1,54	1,65	1,74
Тл
1,75
1,5
1,25
1,0
0,75
0,5
0,25
В			1	2 К “	
			3		2
			у		S4
		2			
					
nil В-jl лг	-2 -1				
ill1 li SI					
Iff! iff/ Л					
О	20	40	60	80	Н,А/см
।-----1----1-----1-----1____।-----1
Л	2	Ч-	6	8	Н,А/см
1-1211; г-mu; з-1512;ц-15б1
Декартовы, цилиндрические и сферические координаты. Операции векторного анализа
Декартовы
Цилиндрические
Сферические
х = R sin 0 cos а; у = R sin 0 sin а; z — R cos 0
Элемент длины
dl — idx 4- jdy 4- kdz	dl — erdr 4- earda 4- ezdz	dl — e%dR 4- e^RdQ 4- eaR sin Qda
1	1	в
grad ф = V<p — idty/dx + jd<p/dy + kd<y/dz = e, dtp/dr + еа—Эф/да 4- ezdq/dz = e^dy/dR 4- e0—- Эф/<Э9 4- ——Эф/За; r	R	R sin 0
divF- VF = 4L.+ dF- I ... 1 d<rfJ I 1	• I = 1	.	1 «Marine) 1 №..
dx dy dz r dr r da. dz R2 dR RsinQ dQ Rsin0 da’
rot F = V x F =
i	i	b		er	ez		CR	ea
! J k.		ea ~		R
		r	r		R2 sin 0 R sin 0
d d d		d d d		д	д	d
—1	"	  .«1 1	1	 				
dx dy dz		dr da dz		dR	30	da
F. Fy Fz		Fr rFa Fz		Fr	RFq R sin 0 Fa
div grad ф = У2ф = Дф =
dx dv2 dz2
д2ф = 1 d2 (Кф) dz2 R dR2
1 d ( дф \ 1 д2ф r dr \ fir ) r2 doc2
1 d (sin 9 *рЛ .	1	d2(? •
R2 sin 0 d0 \ dQ J R2 sin2 0 da2
div rotF = V(V x F) — 0; rot gradф = V x \7ф = 0;
div (A x В) = V (A x В) ~ В rot A — A rot B;
rot rot F — V x (V x. F) — grad div F — V2F;
<f FdS = f div F dV; Fdl == f rot F dS. SV	IS
о о
ЕДИНИЦЫ ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ВЕЛИЧИН Единицы Международной системы СИ
Наименование величины	Наименование единицы	Выражение через единицы СИ	Обозначение единицы	
			русское	международное
Электрические Сила электрического тока	ампер	А	А	А
Количество электричества, заряд	кулон	А • с = Кл	Кл	С
Электрический потенциал, напряжение, ЭДС	вольт	кг - м2/( А • с3) = В	В	V
Напряженность электрического поля	вольт на мегр	кг  м/(А • с3) = В/м	В/м	V/m
Абсолютная диэлектрическая проницаемость	фарад на метр	А2  с4/(кг  м3)	Ф/м	F/m
Электрический момент диполя	кулон-метр	А • с • м = Кл • м	Кл - м	Cm
Электрическое смещение (индукция)	кулон на кв. метр	А • с/м2 = Кл/м2	Кл/м2	C/m2
Поляризованность	кулон на кв. метр	А • с/м2 = Кл/м2	Кл/м2	C/m2
Электрическая емкость	фарад	А2 - с4/(кг • м2) = с/Ом	Ф	F
Плотность тока	ампер на кв. мегр	А/м2	А/м2	A/m2
Электрическое сопротивление	ом	кг • м2/( А2 • с3) = В/А	Ом	Q
Электрическая проводимость	сименс	А2  с3/(кг • м2) = 1/Ом	См	S
Удельное электрическое сопротивление*	ом-мегр	кг • м3/(А2 • с3) — Ом • м	Ом • м	Q-m
Удельная электрическая проводимость**	сименс на метр	А2 • с3/(кгс  м3) = 1/Ом  м	См/м	S/m
Подвижность электронов	мегр в секунду, деленный	А - с2/кг = м2/(В- с)	м/с	m/s
	на вольт на метр		В/м	V/m
Полная мощность Реактивная мощность *	1 вольт-ампер вар	кг • м2/с3 КГ • м2/С3	В А вар	V А var
Магнитные				
Магнитный поток	вебер	кг • м2/(А - с2) = В - с	Вб	Wb
Магнитная индукция	тесла	кг/(А • с2) — В ♦ с/м2	Тл	Т
Абсолютная магнитная проницаемость	генри на метр	кг  м/(А2 • с2)	Гн/м	H/m
Магнит ный момент электрического тока, магнитный момент диполя	ампер-кв. метр	А  м2	А - м2	А • m2
Намагниченность	ампер на метр	А/м	А/м	A/m
Напряженность магнитного поля	ампер на метр	А/м	А/м	A/m
Индуктивность, взаимная индуктивность	генри	кг-м2/(А2с2) = В-с/А — = Вб/А = Оме	Гн	H
Магнитодвижущая сила, разность скалярных магнитных потенциалов	ампер	Л	А	A
Магнитное сопротивление	ампер на вебер	с2- А2/(м2- кг) = = А/Вб = 1/Гн	А/Вб	A/Wb
Магнитная проводимость	вебер на ампер	м2- кг/(с2- А2) — Гн	Вб/А	Wb/A
Векторный магнитный потенциал	вебер на метр	кг  м/( А • с2) = В • с/м	Вб/м	Wb/m
* 1 Ом • см = 10'2 Ом  м; 1 Ом • мм2/м = 10 6 Ом • м = 1 мкОм - м. ** 1 Ом-1-см-1 = 100-См/м; 1 м/Ом • мм2 = 10б • См/м = 1 МС/м,
СПИСОК ЛИТЕРАТУРЫ
1.	Бессонов Л. А. Теоретические основы электротехники. Электрические цепи.-М.: Высшая школа, 1978.- 528 с.
2.	Бессонов Л. А. Теоретические основы электротехники. Электромагнитное поле. — М.: Высшая школа, 1978.— 231 с.
3.	Нейман Л. Р., Демирчян К. С. Теоретические основы электротехники. Т. 1.—Л.: Энсргоиздат, 1981.- 536 с.
4.	Нейман Л. Р., Демирчян К. С. Теоретические основы электротехники. Т. 2.-Л.: Энергоиздат, 1981,—416 с.
5.	Задачник по теоретическим основам электротехники. Теория цепей/Под ред. К. М. Поливанова. — М.: Энергия, 1973.— 304 с.
6.	Колли Я. Н., Соболева Л. П., Фрадкин Б. М. Задачник по теоретическим основам электротехники. Теория поля. — М.: Энергия, 1972.- 168 с.
7.	Основы теории цепей/Г. В. Зевеке, П. А. Нонкин, А. В. Нету-шил, С. В. Страхов. — М.: Энергия, 1975.— 752 с.
8.	Поливанов К. М. Теоретические основы электротехники. Т. 1.—М.: Энергия, 1972.— 239 с.
9.	Жуховицкий Б. Я., Негневицкий И. Б. Теоретические основы электротехники. Т. 2. — М.: Энергия, 1972.— 200 с.
10.	Поливанов К. М. Теоретические основы электротехники. Т. 3. — М.: Энергия, 1975.- 208 с.
11.	Теоретические основы электротехники. Т. 1. Основы теории линейных цепей/Под ред. П. А. Ионкина. — М.: Высшая школа, 1976.- 544 с.
12.	Теореэ ические основы электротехники. Т. 2. Нелинейные цепи и основы теории электромагнитного поля/Под ред. П. А. Ионкина.—М.: Высшая школа, 1976.— 383 с.
13.	Атабеков Г. И, Теоретические основы электротехники. Ч. 1. Линейные электрические цепи.-М.: Энергия, 1978.— 592 с.
14.	Теоретические основы электротехники. Ч. 2 и 3. Нелинейные электрические цепи. Электромагнитное поле/Г. И. Атабеков, С. Д. Ку-палян, А. Б. Тимофеев, С. С. Хухриков. — М.: Энергия, 1979.— 432 с.
15.	Толстов Ю. Г. Теория линейных электрических цепей. — М.: Высшая школа, 1978.— 279 с.
ОГЛАВЛЕНИЕ
Предисловие	3
Глава первая. Линейные цепи с источниками постоянных ЭДС и токов (А. И. Донской, П. А. Ионкин, В. А. Кузовкин, В. Г. Миронов, М. Д. Пирогова) . - .	............. 5
Введение к гл. 1........................................... 5
1.1.	Простейшие электрические	цепи .......	15
1.2.	Переходные и установившиеся процессы в простейших цепях...................................................   23
1.3.	Применение уравнений Кирхгофа .....	28
1.4.	Применение узловых уравнений и уравнений с напряжениями ветвей дерева.............................. ....	33
1.5.	Применение контурных уравнений................... 41
1.6.	Метод наложения. Свойство взаимности............. 44
1.7.	Линейные соотношения между напряжениями и токами 47
1.8.	Преобразования электрических схем................ 49
1.9.	Эквивалентные источники (активные двухполюсники) 52
1.10.	Топологические методы расчета передаточных функций 55
1.11.	Применение сигнальных графов . .	...	59
Глава вторая. Линейные цепи с источниками гармонических ЭДС и токов (И. И. Баранов, С. И. Ващенко, Ф. П. Жарков, В. М. Юркевич)..................... ....	...	63
Введение к гл. 2....................................... 63
2.1.	Переходные и установившиеся процессы в простейших цепях ................................................  70
2.2.	Мгновенные значения синусоидальных величин. Простейшие операции с комплексными числами. Последовательное и параллельное соединения элементов цепи 73
2.3.	Разветвленные электрические цепи. Векторные и топографические диаграммы. Энергетические соотношения	77
2.4.	Эквивалентные схемы двухполюсников ....	89
2.5.	Резонанс. Режим согласованной нагрузки........... 92
2.6.	Электрические цепи с взаимной индукцией ....	99
2.7.	Диаграммы для цепей с изменяющимися параметрами	108
2.8.	Топологические методы анализа. Расчет схемных функций .................................................  113
2.9.	Применение сигнальных	графов.................... 115
Глава третья. Трехфазные цепи (Н. К. Круг, В. А. Майбога) 117
Введение к гл. 3.......................................117
3.1.	Соединение обмоток и разметка выводов трехфазных источников ...	. ..........................123
3.2.	Симметричная нагрузка............................ 126
3.3.	Несимметричная нагрузка.................. ....	131
3.4.	Симметричные составляющие. ......	141
3.5.	Вращающееся магнитное поле	....	150
Глава четвертая. Четырехполюсники (Б. Я. Жуховицкий, В. И. Па-ротькин) ...	....	153
Введение к гл. 4 ... .	....	. .	153
4.1.	Уравнения и коэффициенты пассивных	четырехполюсников 	 162
4.2.	Характеристические (вторичные)	параметры	.	.	170
4.3.	Схемы замещения.......................... ....	172
4.4.	Соединения четырехполюсников	.	............ 175
4.5.	Активные четырехполюсники.......... 179
4.6.	Передаточные функции	......	184
* Глава пятая. Цепи с распределенными параметрами (Б. Я. Жуховицкий)	.................... . .	192
Введение к гл. 5.....................................   192
5.1.	Параметры линии ........	. ,	196
5.2.	Линия с потерями...............................   199
5.3.	Линия без потерь.	.....	....	204
5.4.	Схемы замещения линии . .	....	212
Глава шестая. Л шейные цепи с негармоническими периодическими
источниками (В. А Киселева, В. Н. Кудин) ....	216
Введение к гл. 6 . .	........... ....	216
6.1.	Разложение периодических функций в ряд Фурье	.	.	.	220
6.2.	Периодические процессы в линейных цепях	.	.	.	224
6.3.	Мощность. Коэффициенты, характеризующие формы периодических кривых. Измерения в цепях несинусоидального тока.................................. . .	228
6.4.	Резонанс в цепях несинусоидального тока.......... 235
6.5.	Несинусоидальные режимы симметричных трехфазных цепей	......... . .	238
Глава седьмая. Фильтры (Б. Я. Жуховицкий, В. И. Паротъкин) 242
Введение к гл. 7.......... ....	.	242
7.1. Фильтры типа к .....	............. 246
7.2. Другие типы фильтров ...	. .	253
Глава восьмая. Переходные процессы в линейных цепях с сосре-
доточенными параметрами (Б. А. Болдов, В. И. Паротькин) 260
Введение к гл. 8	...	.......................... 260
8.1.	Переходные процессы в цепях rL (классический метод расчета).	........................ 267
8.2.	Переходные процессы в цепях гС (классический метод расчета).............................................   281
8.3.	Переходные процессы в цепях с несколькими реактивными элементами (классический метод расчета) 295
8.4.	Операторный метод расчета переходных процессов 315
8.5.	Переходные процессы при действии источников напряжения или тока произвольной формы....................... 324
8.6.	Переходные процессы при скачкообразных изменениях токов в индуктивностях и напряжений на емкостях 333
8.7.	Расчет переходных процессов методом переменных состояния .................... ...	.....	339
Глава девятая. Переходные процессы в цепях с распределенными параметрами (Е. С. Кухаркин, С. А. Левитан)............. 349
Введение к гл. 9........................................ 349
9.1.	Формирование прямой и обратной волн в линии без потерь.............................................. 352
9.2.	Переход волны с одной линии на другую............. 355
9.3.	Волны в линиях при подключении и отключении ветвей.................................................. 359
9.4.	Формирование импульсов ....	............ 362
9.5.	Волны в линии без искажений .	....	.	364
Глава десятая. Элементы синтеза линейных цепей (Б. Я. Жуховицкий) .............................................  366
Введение к гл.	10......................................  366
10.1. Двухполюсники без потерь.......................... 370
10.2. Двухполюсники с потерями. Мостовые четырехполюсники	................................   376
Глава одиннадцатая. Нелинейные цепи постоянного тока
(П. А. Ионкин, В. В. Каратаев, Ф. Н. Шакирзянов) .	.	380
Введение к гл. 11....................................... 380
11.1.	Графический метод расчета......................... 382
11.2.	Аналитический метод расчета....................... 395
11.3.	Численные методы расчета.......................... 399
Глава двенадцатая. Магнитные цепи при постоянных потоках (Г. П. Андреев) ..................................... 406
Введение к гл. 12 . .	............................. 406
12.1.	Линейная магнитная цепь........................... 407
12.2.	Нелинейная магнитная цепь без гистерезиса ....	409
12.3.	Расчет магнитной цепи с учетом гистерезиса. Постоянные магниты ....	......................... 416
Глава тринадцатая. Нелинейные цепи переменного тока (Б. А. Болдов, Г. Г. Гусев, В. В. Каратаев)....................... 418
Введение к гл. 13................................. ....	418
13.1.	Графические и графо-аналитические методы расчета 420
13.2.	Аналитические методы расчета .	428
13.3.	Расчет по действующим значениям токов и напряжений 437
Глава четырнадцатая. Переходные процессы в нелинейных цепях.
Автоколебания (Б. А. Болдов, Г. Г. Гусев, В. В. Каратаев) 439
Введение к гл. 14	...	....	439
14.1.	Аналитические и графические методы расчета .	447
14.2.	Устойчивость состояния равновесия................. 456
14.3.	Изображение переходных процессов на фазовой плоскости . .	...................... . .	462
14.4.	Метод усреднения........... .	...	.	467
14.5.	Автоколебания...................................   471
14.6.	Численные методы интегрирования................... 476
Глава пятнадцатая. Вводные задачи теории поля (Л. П. Соболева) 419
Введение к гл. 15 .....	. . . \.............. 479
15.1. Симметричные поля .	................. . .	483
15.2. Анализ полей...................................... 499
Глава шестнадцатая. Электрическое поле (Я. И. Колли, Л. Л. Соболева ).................. ....................... . .	503
Введение к гл. 16.................................... .	503
16.1.	Электростатическое поле в вакууме................. 509
16.2.	Электростатическое поле в диэлектрике............. 524
16.3.	Стационарное электрическое поле в проводящей среде 535
16.4.	Квазистатическое электрическое поле в реальной среде 543
16.5.	Уравнения Лапласа и Пуассона .	.....	554
16.6.	Энергия и силы в электрическом поле .............. 563
Глава семнадцатая. Магнитное поле (Б.	М. Фрадкин) 566
Введение к гл. 17................ .	......... 566
17.1.	Постоянное магнитное поле в однородной неограниченной среде ....	...	...	569
17.2.	Дифференциальные уравнения магнитного поля. Векторный и скалярный потенциалы ............................. 578
17.3.	Магнитное поле в присутствии магнитных тел . . .	593
17.4.	Энергия и силы в магнитном поле ......	606
Глава восемнадцатая. Специальные методы расчета потенциальных
полей (Я. Н. Колли, Б. М. Фрадкин) . ................... 611
Введение к гл. 18.............  .	............. 611
18.1. Применение функций комплексного переменного , .	612
18.2. Метод интегральных уравнений ..................... 632
Глава девятнадцатая. Электромагнитное поле (Я. Н. Колли, Б. М. Фрадкин).........................................  .	639
Введение к гл. 19.................................- .	639
19.1.	Теорема Умова — Пойнтинга......................... 643
19.2.	Напряженность электрического поля в неподвижных и движущихся средах. Движение заряженных частиц 649
19.3.	Электромагнитное поле в проводящей среде. Поверхностный эффект.......................................... 655
19.4.	Волны в диэлектрике, волноводы, резонаторы, излучение 674
Ответы к	задачам	гл.	I..................................  683
Ответы к	задачам	гл.	2..................................  687
Ответы к	задачам	гл.	3....................................695
Ответы к	задачам	гл.	4................................... 698
Ответы к задачам гл. 5................................... 701
Ответы к задачам гл. 6...............................  .	703
Ответы к	задачам	гл.	7.................................. 705
Ответы к	задачам	гл.	8.................................. 707
Ответы к	задачам	гл.	9 . . ............................. 713
Ответы к задачам гл. 10	................. ...	720
Ответы к	задачам	гл.	11..................................723
Ответы к	задачам	гл.	12................................  726
Ответы к задачам гл. 13.................................. 727
Ответы к	задачам	гл.	14.................... ....	730
Ответы к	задачам	гл.	15	. . ............... ....	733
Ответы к	задачам	1л.	16.................... ...	736
Ответы к	задачам	гл.	17................................  742
Ответы к	задачам	гл.	18..................................747
Ответы к	задачам	гл.	19	 749
Приложение 1. Разложение в ряд Фурье ......	754
Приложение 2. Таблица оригиналов и их изображений по
Лапласу ...	.............. 756
Приложение 3. Кривые намагничивания сталей 1211, 1411, 1512, 1561 ........................................ 757
Приложение 4. Декартовы, цилиндрические и сферические координаты. Операции векторного анализа 758
Единицы электрических и магнитных величин.................760
Список литературы.......................................  762
Георгий Павлович Андреев	 Сергей Николаевич
Андреев, Игорь Иванович Баранов, Борис Алексеевич Болдов, Светлана Ивановна Ващенко, Геннадий Григорьевич Гусев, Алексей Ивандвич Донской, Феликс Петрович Жарков, Борис Яковлевич Жуховицкий,	
Петр Афанасьевич Ионкин	, Евгений Иванович
Калугин, Владимир Васильевич Каратаев, Валерия Александровна Киселева, Яков Николаевич Колли, Наталья Карловна Круг, Всеволод Николаевич Кудин, Владимир Александрович Кузовкин, Евгений Степанович Кухаркин, Семен Аркадьевич Левитан, Виктор Алексеевич Майбога, Владимир Георгиевич Миронов, Владимир Иванович Паротькин, Мальвина Дмитриевна Пирогова, Лидия Петровна Соболева, Борис Михайлович Фрадкин, Феликс Нитматзянович Шакир зянов, Владимир Михайлович Юркевич
СБОРНИК ЗАДАЧ И УПРАЖНЕНИЙ ПО ТЕОРЕТИЧЕСКИМ ОСНОВАМ ЭЛЕКТРОТЕХНИКИ
Редакюр Б. Я. Жуховицкий
Редакторы издательства Л. А. Решмина, Н. Б. Фомичева Переплет художника В. Д. Козлова
Технический редактор О. Н. Адаскина
Корректоры 3. Б. Драновская, Л. С. Тимохова
И Б № 2795
Сдано в набор 13.07.81. Подписано к печати 24.03.82. Формат 84х 108/32. Бумага типографская № 2. Гарн. шрифта тайме. Печать высокая. Усл. печ. л. 40,32. Уч.-изд. л. 42,1, Тираж 50 000 экз. Заказ 18. Цена I р. 50 к.
Энергоиздат, 113114, Москва, М-114, Шлюзовая наб., 10
Ордена Октябрьской Революции, ордена Трудового Красного Знамени Ленинградское производственно-техническое объединение «Печатный Двор» имени А. М. Горькою Союзполиграфпрома при Г осу дарственном комитете СССР по делам издательств, полиграфии и книжной торговли 197136, Ленинград, П-136, Чкаловский пр., 15.