Автор: Швецкий М.В. Демидов М.В. Голанова А.В. Кудрявцева И.А.
Теги: языки программирования основы математики математическая логика программирование учебное пособие для вузов
ISBN: 978-5-534-11009-8
Год: 2022
М. В. Швецкий, М. В. Демидов, А. В. Голанова, И. А. Кудрявцева
ПРОГРАММИРОВАНИЕ
МАТЕМАТИЧЕСКАЯ ЛОГИКА
УЧЕБНОЕ ПОСОБИЕ ДЛЯ ВУЗОВ
2-е издание, переработанное и дополненное
Рекомендовано Учебно-методическим отделом высшего образования
в качестве учебного пособия для студентов высших учебных заведений,
обучающихся по ИТ-направлениям
Книга доступна на образовательной платформе «Юрайт» urait.ru,
а также в мобильном приложении «Юрайт.Библиотека»
Москва Юрайт 2022
https:it.ru
УДК 004.43(075.8)
ББК 22.12я73
Ш35
Авторы:
Швецкий Михаил Владимирович — доктор педагогических наук, про-
фессор кафедры информационных систем института информационных тех-
нологий и технологического образования Российского государственного
педагогического университета имени А. И. Герцена (г. Санкт-Петербург);
Демидов Михаил Владимирович — кандидат педагогических наук, веду-
щий программист отдела информатизации образования Российского госу-
дарственного педагогического университета имени А. И. Герцена (г. Санкт-
Петербург);
Галанова Анна Викторовна—кандидат педагогических наук, доцент кафе-
дры информатики и информационных систем факультета математики и инфор-
матики Ленинградского государственного университета имени А. С. Пушкина
(г. Пушкин);
Кудрявцева Ирина Андреевна—доцент, кандидат педагогических наук,
доцент кафедры информационных систем института информационных тех-
нологий и технологического образования Российского государственного
педагогического университета имени А. И. Герцена (г. Санкт-Петербург).
Рецензенты:
Пиотровская К. Р. — доктор педагогических наук, доцент, профессор
кафедры методики обучения математике и информатике факультета мате-
матики Российского государственного педагогического университета имени
А. И. Герцена (г. Санкт-Петербург);
Матюшичев И. Ю. — кандидат технических наук, доцент.
Швецкий, М. В.
Ш35 Программирование: математическая логика : учебное пособие для
вузов / М. В. Швецкий, М. В. Демидов, А. В. Голанова, И. А. Кудрявцева. —
2-е изд., перераб. и доп. — Москва : Издательство Юрайт, 2022. — 675 с. —
(Высшее образование). — Текст: непосредственный.
ISBN 978-5-534-11009-8
Учебное пособие представляет собой систему упражнений и лаборатор-
ных работ по курсу «Математическая логика и теория алгоритмов», содер-
жащих теоретические сведения по общей теории исчислений, исчислениям
математической логики, элементам интуиционистской логики, аксиомати-
ческой семантике языков императивного программирования.
В пособие включено значительное количество задач и упражнений для
самостоятельного решения.
Соответствует актуальным требованиям федерального государственного
образовательного стандарта высшего образования.
Книга предназначена для преподавателей, аспирантов и студентов педа-
гогических вузов для направлений, связанных с информационными техноло-
гиями.
УДК 004.43(075.8)
ББК22.12я73
Все права защищены. Никакая часть данной книги не может быть воспроизведена
в какой бы то ни было форме без письменного разрешения владельцев авторских прав.
© Швецкий М. В., Демидов М. В.,
Голанова А. В., Кудрявцева И. А., 2016
© Швецкий М. В., Демидов М. В.,
Голанова А. В., Кудрявцева И. А., 2019,
с изменениями
ISBN 978-5-534-11009-8 © ООО «Издательство Юрайт», 2022
https:/Л: rait.ru
Оглавление
Введение...................................................13
Часть 1
ОБЩАЯ ТЕОРИЯ ИСЧИСЛЕНИЙ
Упражнение 1. Слова в алфавите.............................25
Теоретические сведения..................................26
Предварительные наблюдения...........................26
Исходные понятия и представления.....................27
Синтаксическая переменная............................29
Предметный язык и метаязык...........................29
Алфавит. Буква.......................................29
Слово в алфавите.....................................30
Соглашения об обозначениях...........................35
Основные операции над словами в алфавите.............35
Предикат «равенство слов в алфавите».................37
Алгебраическая операция приписывания слов............38
Подслова и их вхождения в слово......................42
Операция замены подслов..............................45
Операция подстановки слова вместо буквы..............47
Варианты операции подстановки........................48
Числовые функции, определённые на множестве слов.....50
Функции, частично определённые на множестве слов.....51
Комментарий для любителей алгебры. Полугруппа. Моноид слов.52
Метод математической индукции как распознающая процедура...53
Контрольные вопросы.....................................57
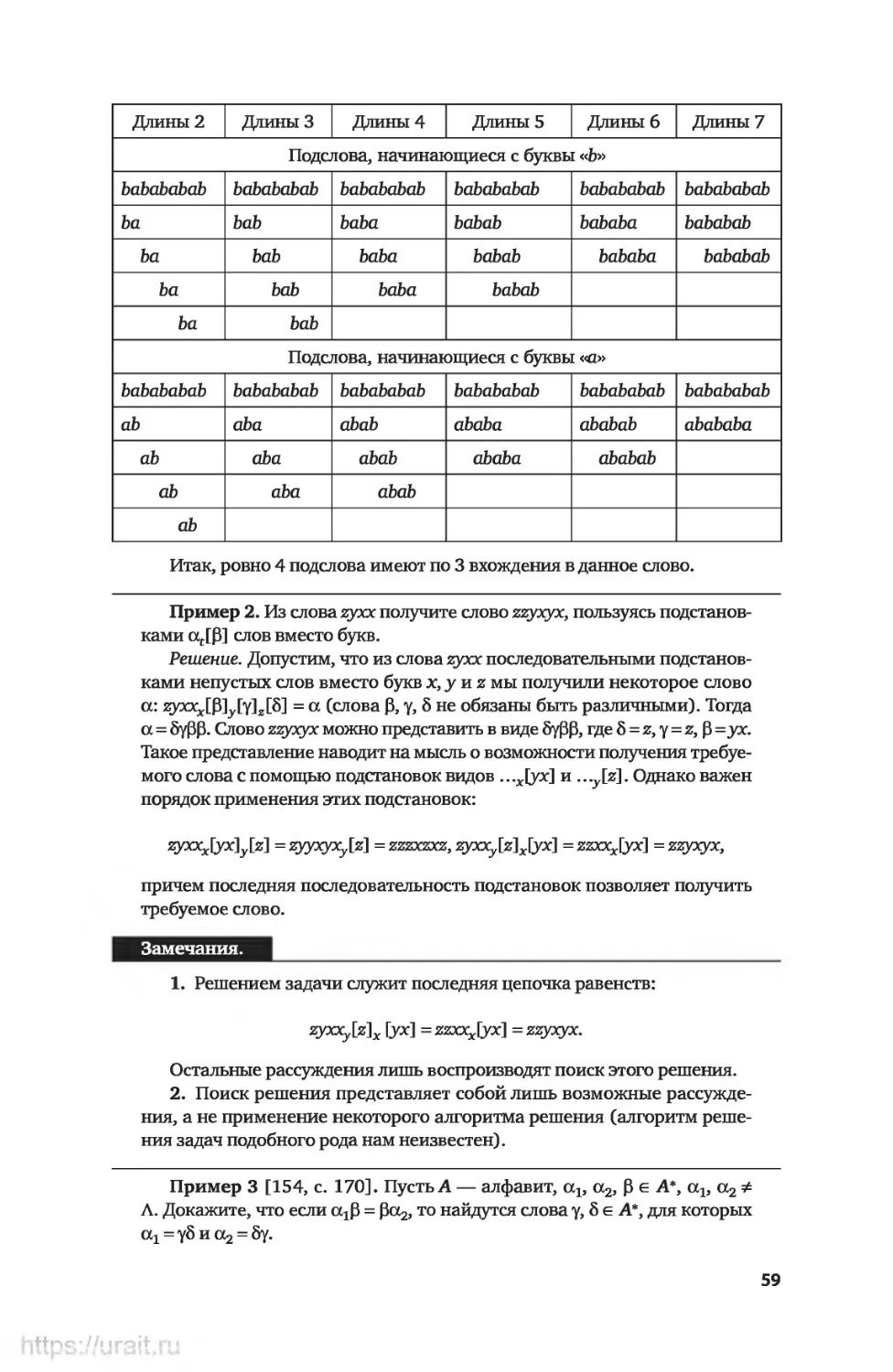
Примеры решения некоторых типов упражнений..............58
Упражнения для самостоятельного решения.................60
Упражнение 2. Индуктивное определение множества
слов в алфавите. Исчисления на словах в алфавите.
Формальные доказательства в исчислениях на словах
в алфавите.................................................63
Теоретические сведения..................................64
Индуктивное определение множества слов в алфавите....64
Пример индуктивного определения множества слов.......64
Индукция по построению множества объектов............65
Исчисление математических объектов...................66
3
Определение множества слов в алфавите с помощью
исчисления на словах.................................68
Доказательство в исчислении на словах................72
Вывод из посылок в исчислении на словах..............75
Допустимые правила в исчислении на словах............76
Определение функции индукцией по построению множества
слов.................................................77
Из истории создания буквенного исчисления............78
Контрольные вопросы.....................................80
Примеры решения некоторых типов упражнений..............80
Упражнения для самостоятельного решения.................82
Часть 2
ИСЧИСЛЕНИЯ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
Упражнение 3. Язык первого порядка: синтаксис..............89
Теоретические сведения..................................90
Алфавит. Сигнатура...................................91
Термы сигнатуры о....................................92
Индукция по построению множества термов..............93
Формулы сигнатуры о..................................94
Индукция по построению множества формул..............95
Язык формальных систем нулевого и первого порядка....96
Запись формул в метаязыке............................96
Синтаксическая однозначность представления выражений.....97
Синтаксическая однозначность представления вхождений
термов и формул.....................................102
Синтаксическое сохранение выражений при замене
вхождений подвыражений..............................103
Свободные и связанные вхождения переменных..........103
Свободные и связанные переменные....................104
Операция «подстановка терма вместо свободной переменной
в выражение»........................................106
Термы, допустимые для подстановки вместо переменных
в формулу...........................................107
Операция «подстановка предметной переменной вместо
свободной переменной в выражение»...................108
Операция «одновременная подстановка термов вместо
свободных переменных в выражение»...................109
Операция «переименование связанных переменных в формуле».111
Примеры решения некоторых типов упражнений.............113
Упражнения для самостоятельного решения................117
Упражнение 4. Гильбертовское исчисление первого
порядка: построение доказательств и выводов
с использованием основных правил вывода...................127
4
https:it.ru
Теоретические сведения...................................128
Аксиомные схемы и правила вывода гильбертовского
исчисления первого порядка...........................128
Линейное доказательство и линейный вывод из множества
гипотез..............................................130
Древесное доказательство и древесный вывод из множества
гипотез..............................................132
Индукция по построению доказательства................133
Соглашения об обозначениях при построении доказательств
и выводов............................................134
Гёделева нумерация языка формальной системы первого
порядка..............................................135
Контрольные вопросы.....................................140
Примеры решения некоторых типов упражнений..............140
Упражнения для самостоятельного решения.................142
Упражнение 5. Гильбертовское исчисление первого
порядка: установление существования доказательств
и выводов с помощью допустимых правил вывода...............151
Теоретические сведения..................................151
Прямые допустимые правила вывода.....................152
Непрямые допустимые правила вывода...................155
Примеры решения некоторых типов упражнений..............162
Упражнения для самостоятельного решения.................164
Упражнение 6. Исчисление дедуктивных
эквивалентностей. Предварённая и сколемовская
нормальная форма...........................................170
Теоретические сведения..................................170
Исчисление дедуктивных эквивалентностей..............170
Предварённая нормальная форма........................172
Сколемовская нормальная форма........................173
Примеры решения некоторых типов упражнений..............175
Упражнения для самостоятельного решения.................177
Упражнение 7. Моносукцедентное секвенциальное
исчисление первого порядка.................................179
Теоретические сведения..................................180
Секвенции. Секвенциальные схемы......................181
Смысл понятия «секвенция»............................182
Аксиомная схема. Основные правила вывода.............183
Содержательный смысл основных правил вывода..........185
Доказуемые (выводимые) секвенции. Доказуемые формулы..186
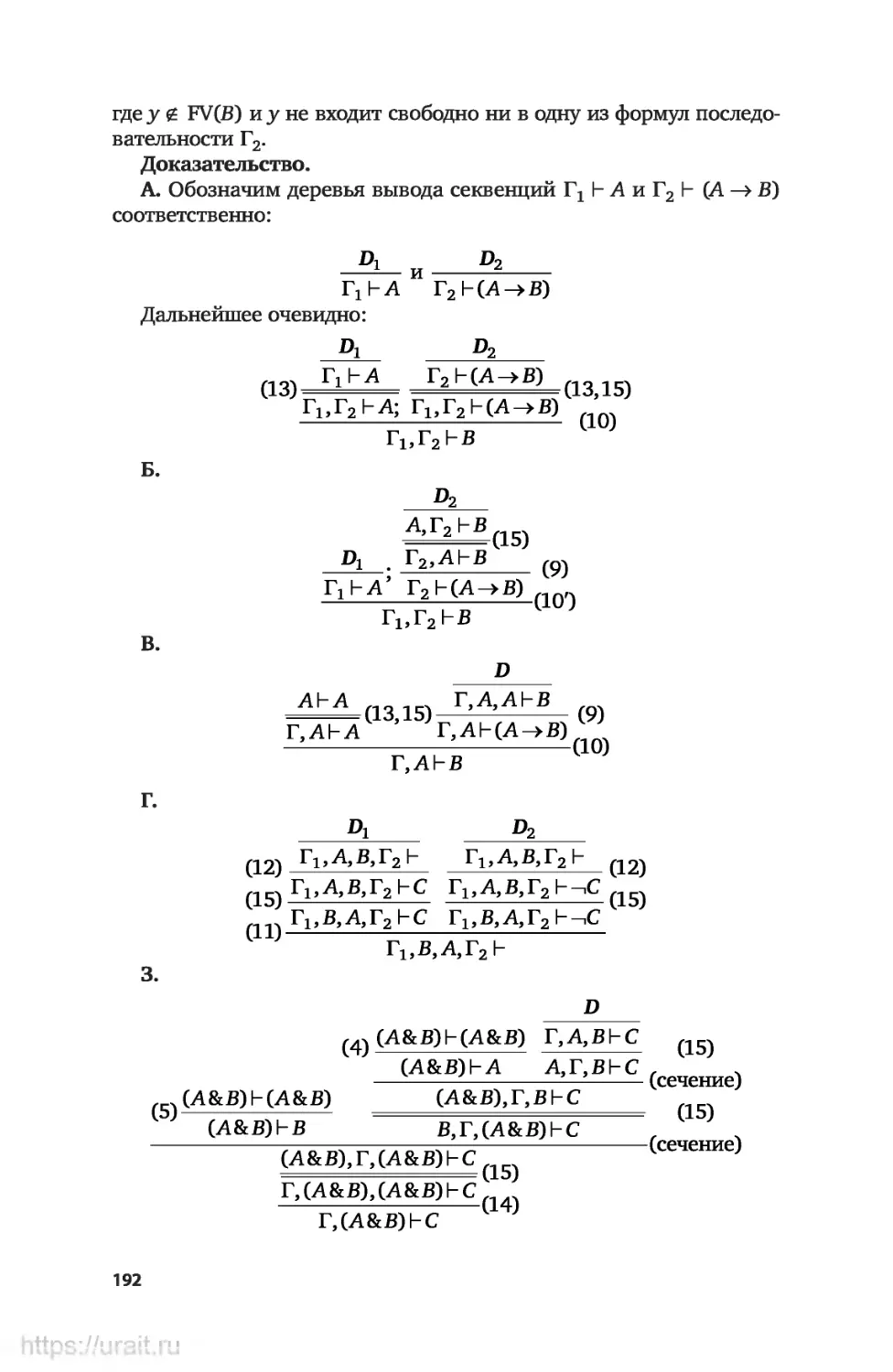
Допустимые правила вывода............................189
Доказательство допустимых правил вывода методом подъёма.... 194
Теорема Генцена об устранении сечения................196
Отношение дедуктивной эквивалентности. Дедуктивно
эквивалентные формулы................................197
Связь секвенциального и гильбертовского исчислений...203
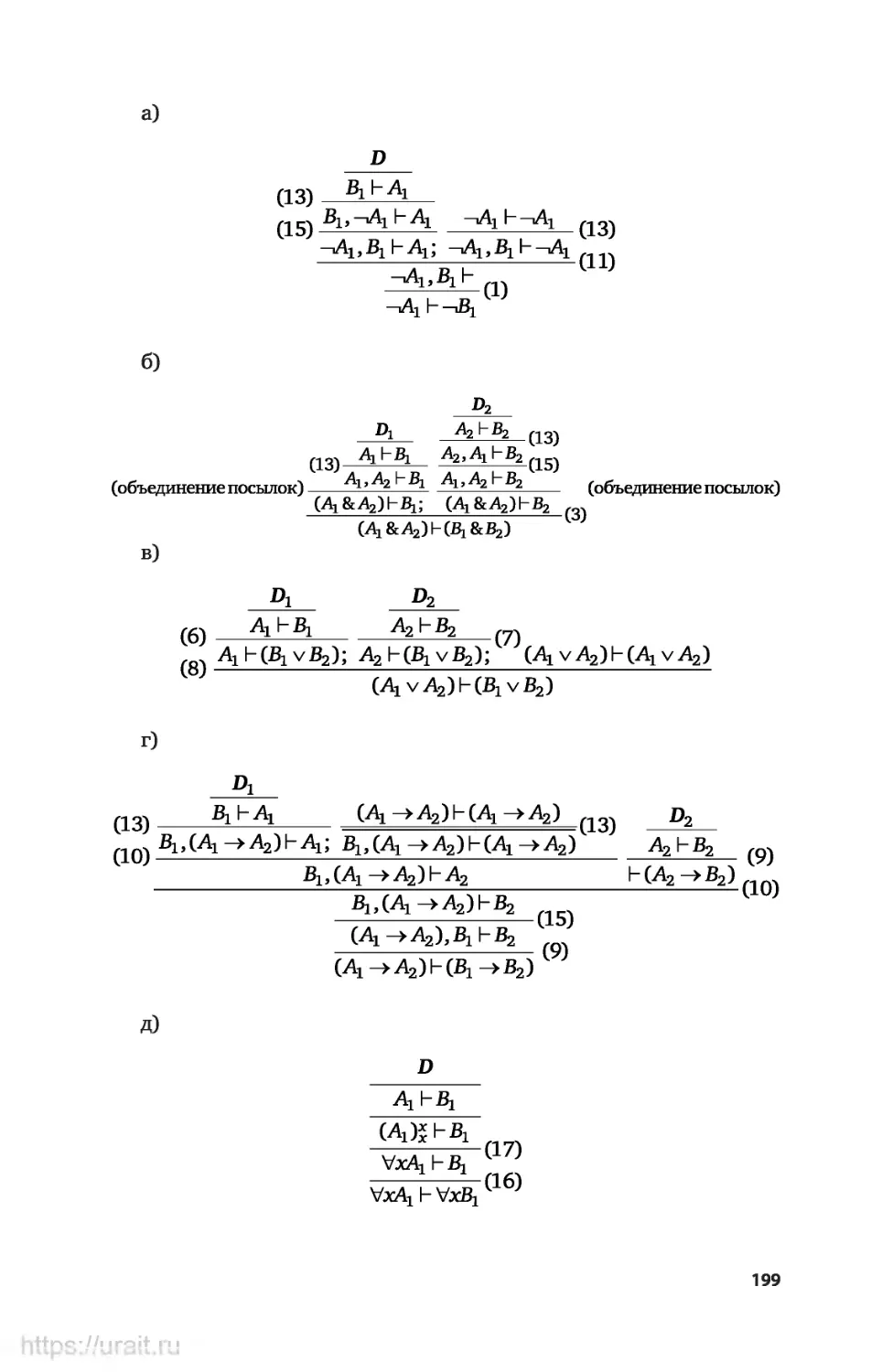
Примеры решения некоторых типов упражнений..............205
Упражнения для самостоятельного решения.................210
Упражнение 8. Многосукцедентное секвенциальное
исчисление первого порядка.................................215
Теоретические сведения..................................215
Секвенции. Аксиома. Основные правила вывода..........215
Вывод. Выводимые секвенции. Выводимые формулы........218
Допустимые правила вывода............................219
Обратные допустимые правила вывода...................220
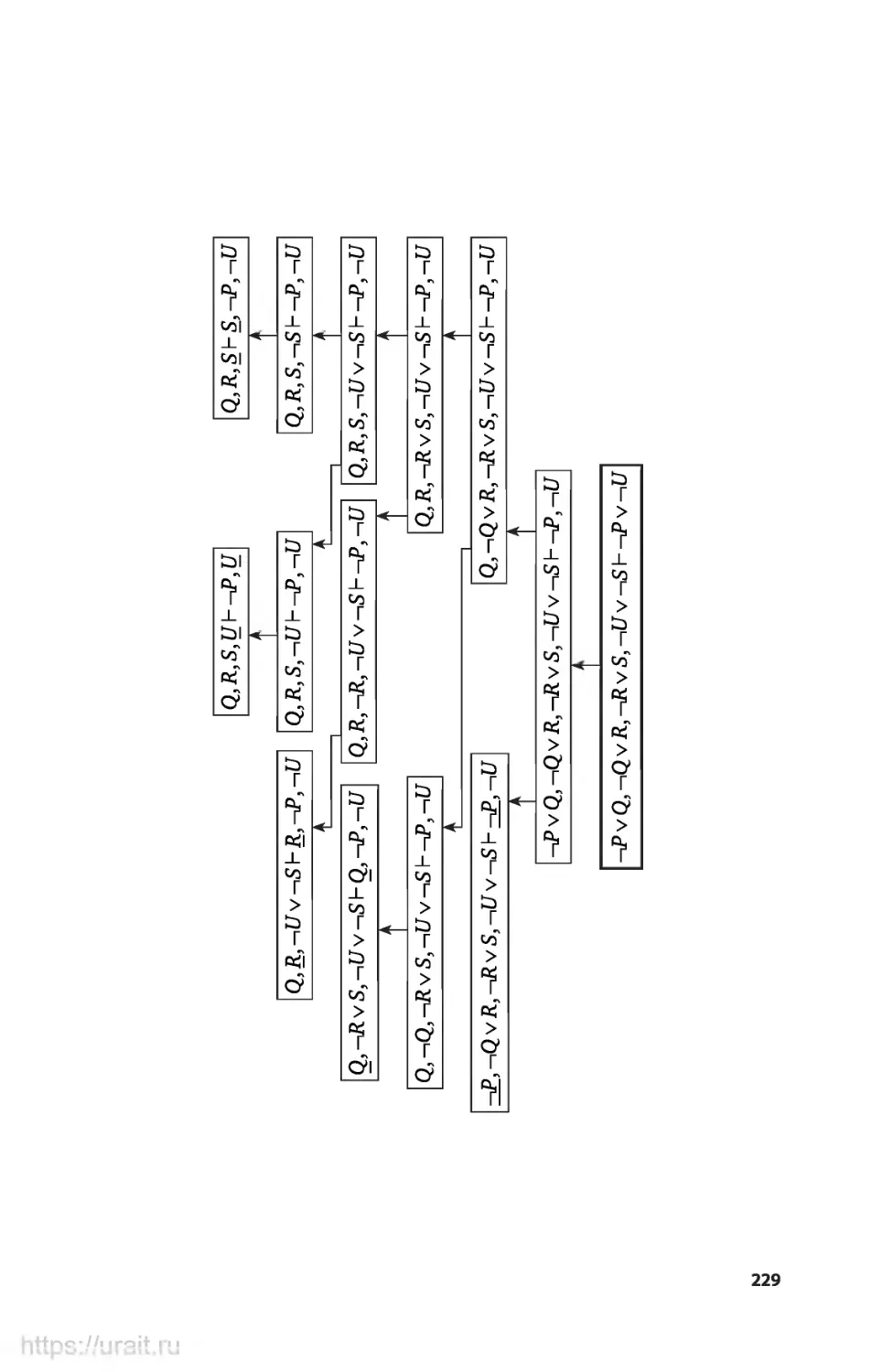
Алгоритм Хао Вонга для поиска вывода в пространстве
состояний логической системы.........................225
Примеры решения некоторых типов упражнений..............230
Упражнения для самостоятельного решения.................231
Упражнение 9. Генценовское исчисление натурального
вывода.....................................................234
Теоретические сведения..................................234
Фигуры заключения для интуиционистского исчисления
натурального вывода..................................235
Фигуры заключения для классического исчисления
натурального вывода..................................237
Фигуры прямого и косвенного заключения...............238
Правила заключения. Правила вывода...................238
Неформальное описание понятия «вывод»................239
Неформальное описание процесса построения вывода.....239
Биографические сведения..............................240
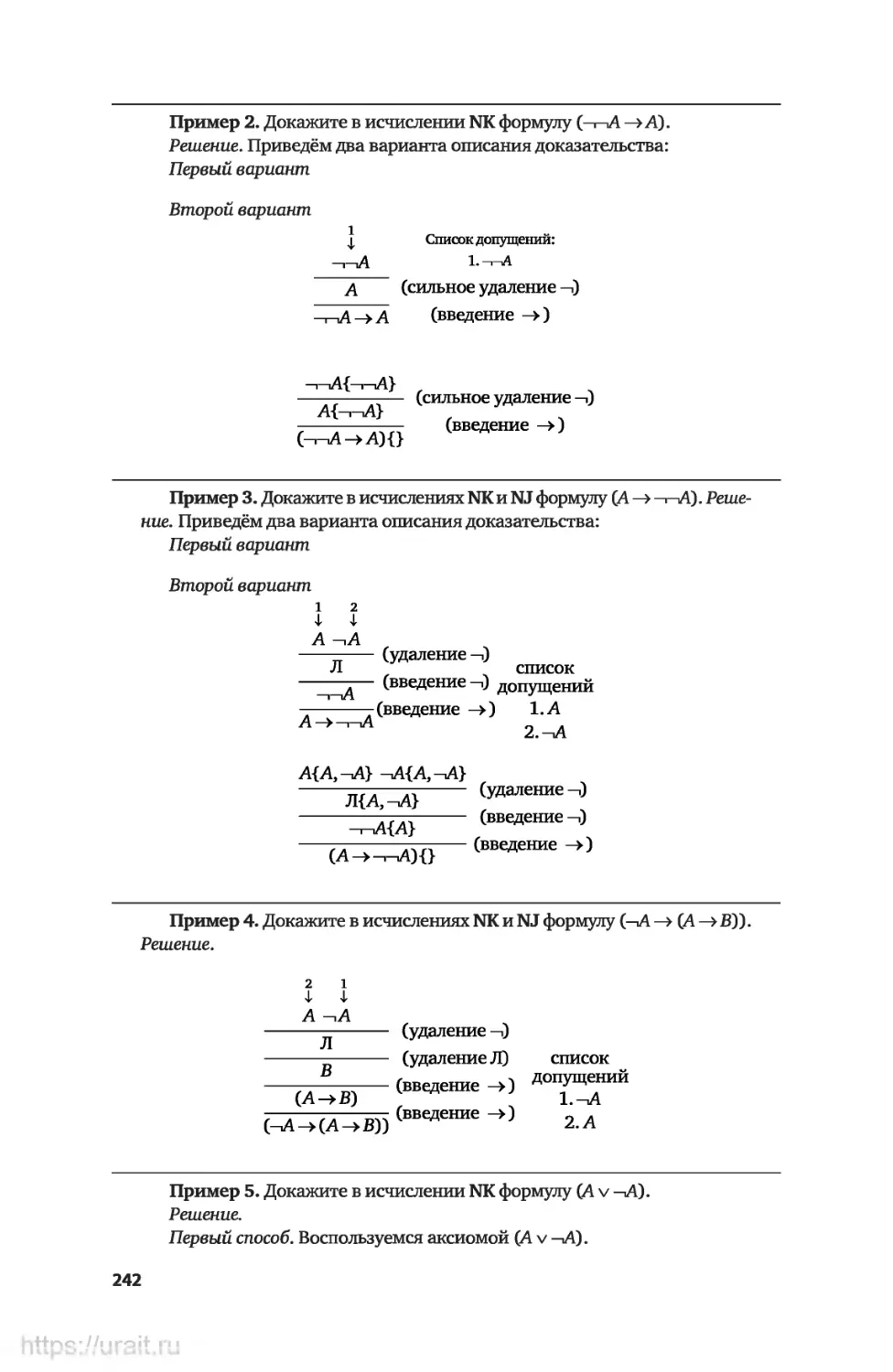
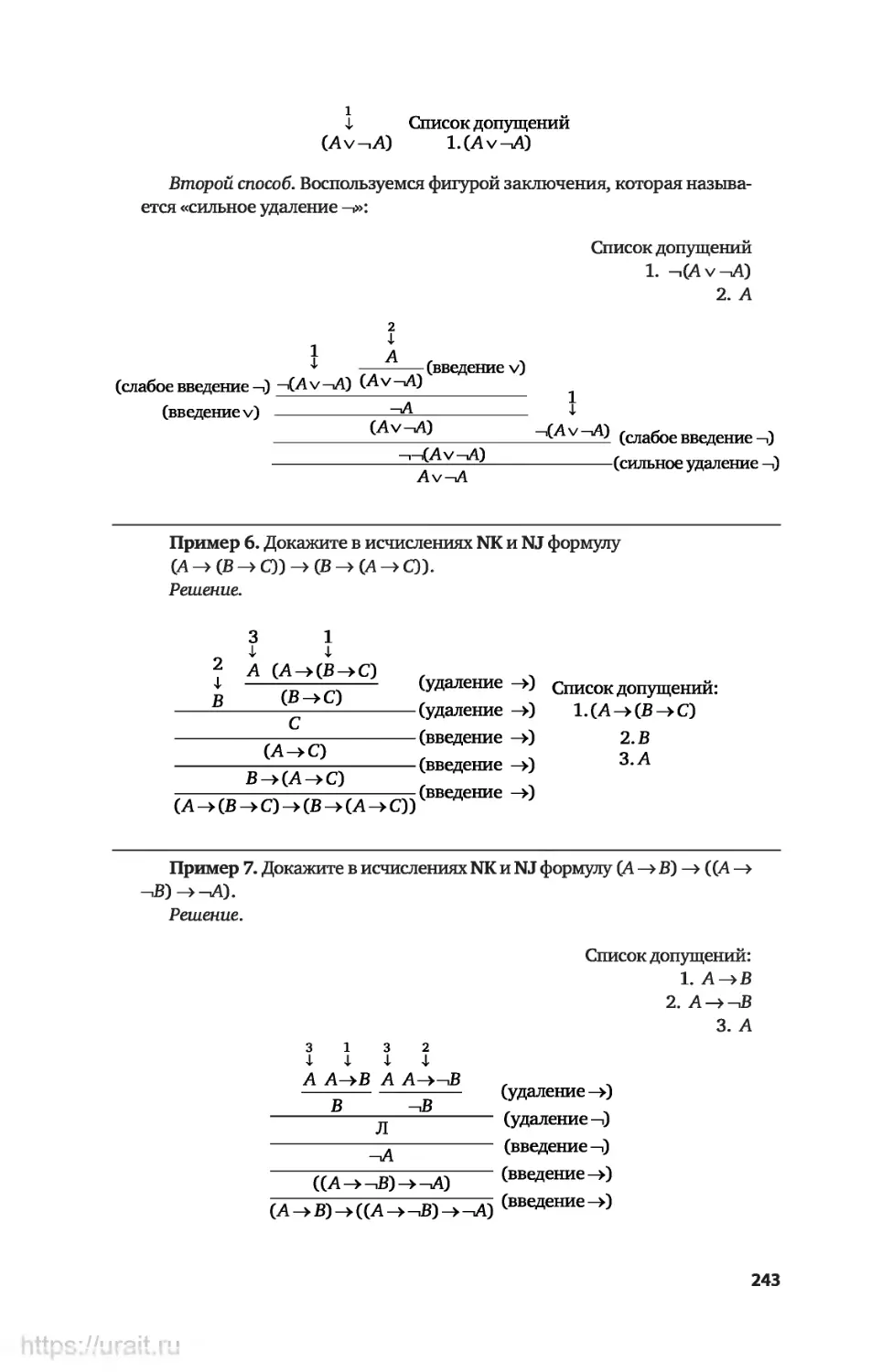
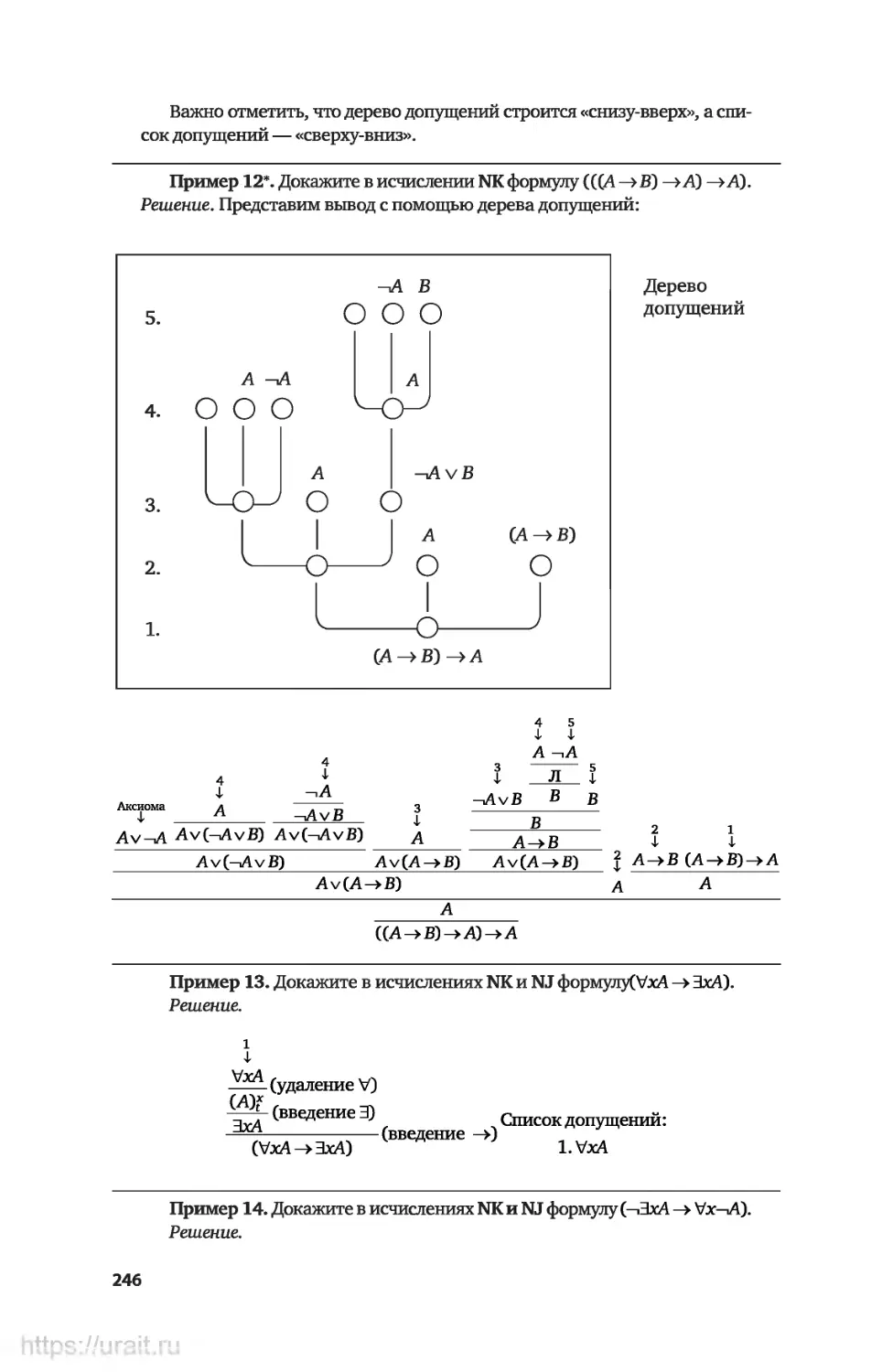
Примеры решения некоторых типов упражнений..............241
Упражнения для самостоятельного решения.................247
Упражнение 10. Метод аналитических таблиц для формул
языка первого порядка......................................251
Теоретические сведения..................................252
Представление об аналитических таблицах..............252
Критерии общезначимости формул.......................253
Определение необщезначимости формул..................255
Аналитические таблицы для отмеченных формул..........256
Примеры решения некоторых типов упражнений..............258
Упражнения для самостоятельного решения.................261
Упражнение 11. Понятие о математических теориях.
Теория равенства...........................................263
Теоретические сведения..................................263
Понятие о математической теории......................263
Гильбертовское исчисление первого порядка с равенством.264
6
https://и га it.ru
Практическое правило составления аксиомных схем
равенства............................................266
Квантор «существует единственное х, такое, что...»...269
Теории частичного, линейного и плотного порядка......271
Примеры решения некоторых типов упражнений..............272
Упражнения для самостоятельного решения.................273
Упражнение 12. Язык термов сигнатуры о.....................275
Теоретические сведения..................................275
Алфавит языка термов.................................275
Термы сигнатуры о...................................2177
Определение дополнительных связок....................278
Подтермы терма сигнатуры о...........................278
Индукция по построению множества термов..............279
Язык термов..........................................280
Упражнения для самостоятельного решения.................280
Часть 3
АВТОМАТИЗАЦИЯ ПОИСКА ЛОГИЧЕСКОГО ВЫВОДА
Лабораторная работа 13. Поиск логических выводов
в режиме диалога «Человек-Компьютер»: система
Deductio, гильбертовское исчисление.......................285
Теоретические сведения.................................286
Редакторы доказательств и автоматические генераторы
доказательств.......................................286
Краткие сведения по использованию системы Deductio..289
Примеры решения некоторых типов упражнений.............291
Задачи для самостоятельного решения....................299
Лабораторная работа 14. Поиск логических выводов
в режиме диалога «Человек-Компьютер»: система
Deductio, генценовское исчисление натурального вывода.....302
Теоретические сведения.................................302
Примеры решения некоторых типов упражнений.............304
Задачи для самостоятельного решения....................321
Часть 4
ИНТУИЦИОНИСТСКИЕ ЛОГИЧЕСКИЕ ИСЧИСЛЕНИЯ
Упражнение 15. Интуиционистские пропозициональные
логики....................................................327
Теоретические сведения.................................328
Содержательные определения понятия «доказательство».329
О разновидностях интуиции...........................333
Доказательство vs Интуиция..........................333
Интуиционизм. Интуиционистская логика...............337
7
https:it.ru
Формализация интуиционистской пропозициональной логики ....339
Биографические сведения...........................347
Примеры решения некоторых типов упражнений............348
Задачи для самостоятельного решения...................349
Упражнение 16. Интуиционистские пропозициональные
логики: минимальное позитивное исчисление Prop..........354
Теоретические сведения................................355
Импликативное позитивное исчисление Prop..........355
Модель гильбертовского пропозиционального исчисления.358
Метод моделей для исследования «населённости» типа
в системе ........................................363
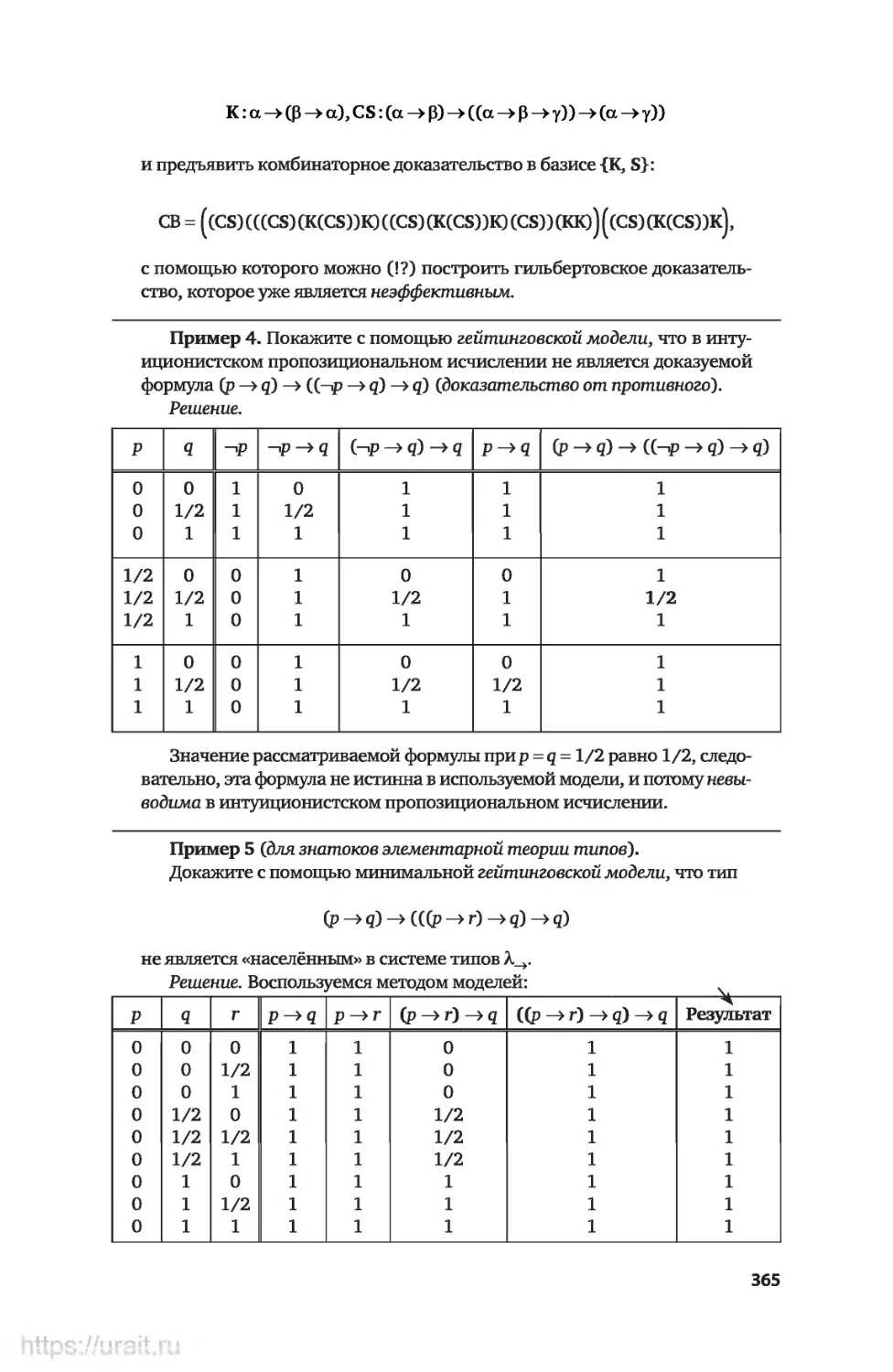
Примеры решения некоторых типов упражнений............363
Задачи для самостоятельного решения...................366
Упражнение 17. Интуиционистские пропозициональные
логики: секвенциальное исчисление Н. Н. Воробьёва —
Дж. Худельмайера без правила сокращения.................373
Теоретические сведения................................374
Исчисление Н. Н. Воробьёва — Дж. Худельмайера
без правила сокращения............................374
Разрешающая процедура для G4ip....................377
Решение задачи TIP в системе типов с помощью
исчисления G4ip...................................381
Биографические сведения...........................382
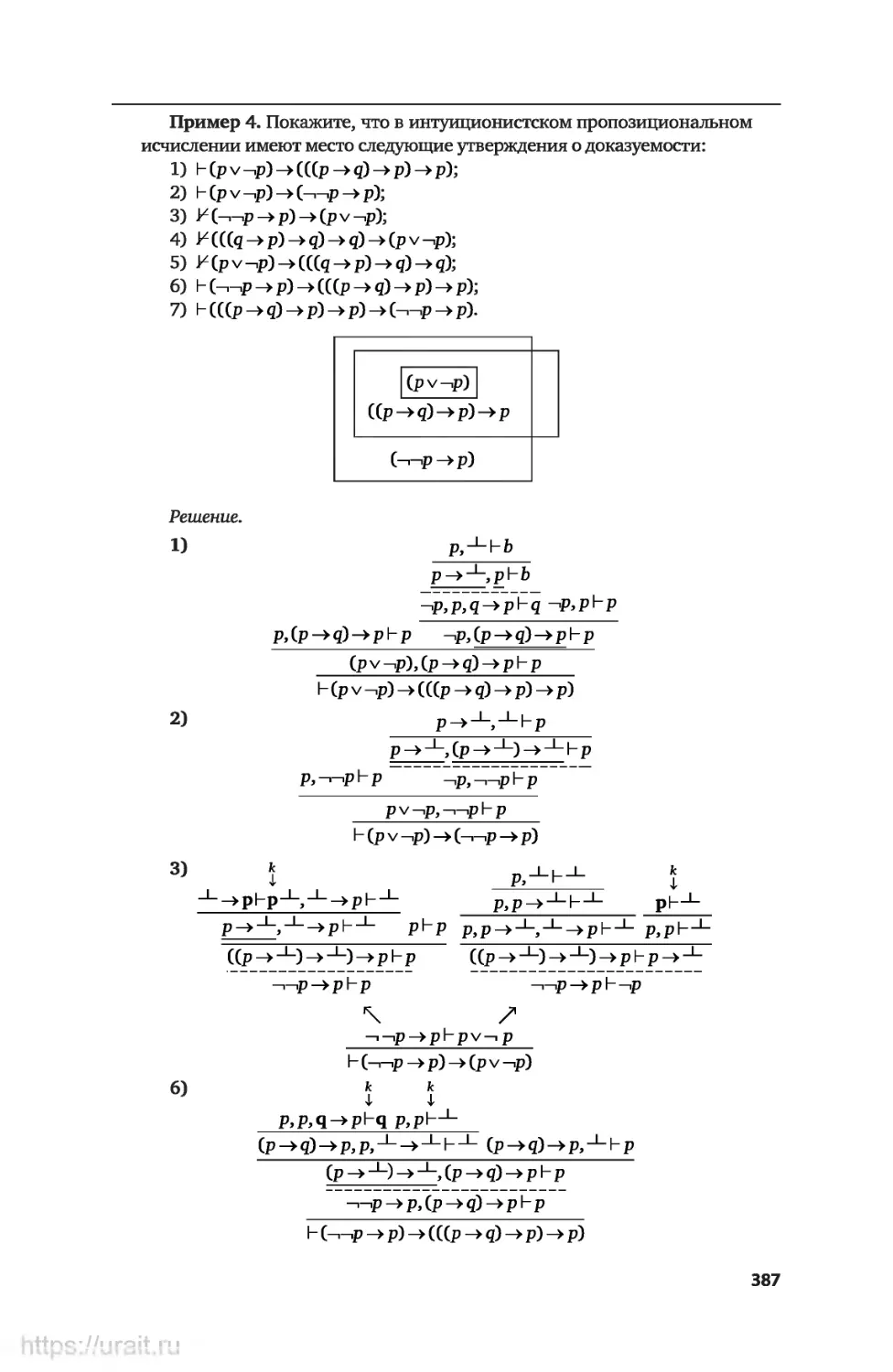
Примеры решения некоторых типов упражнений............383
Упражнения для самостоятельного решения...............391
Упражнение 18. Аналитические таблицы для
интуиционистской логики.................................398
Теоретические сведения................................399
Модель Крипке интуиционистской пропозициональной логики....399
Аналитические таблицы для интуиционистской логики.402
Биографические сведения...........................408
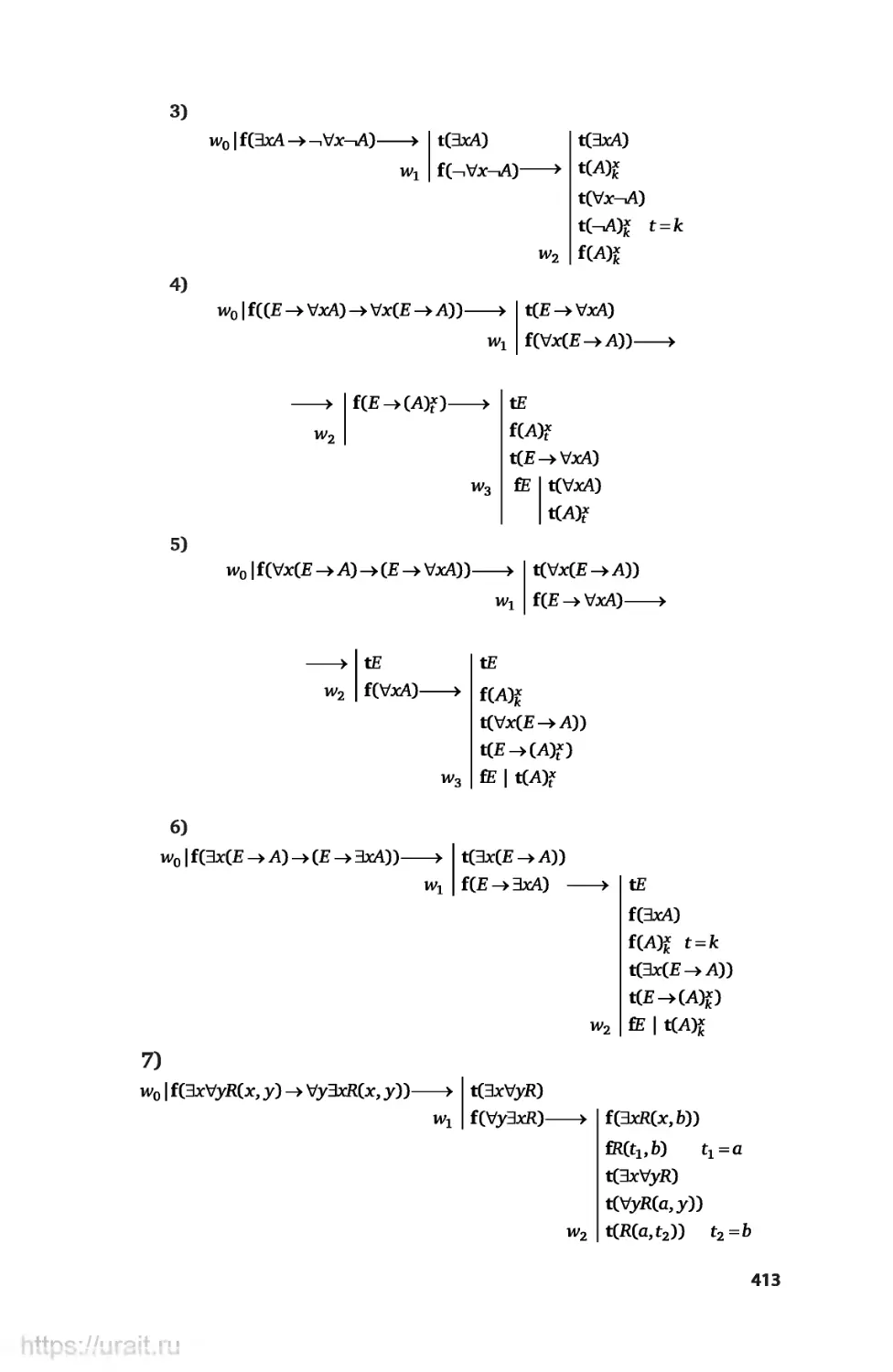
Примеры решения некоторых типов упражнений............409
Задачи для самостоятельного решения...................414
Часть 5. АКСИОМАТИЧЕСКАЯ СЕМАНТИКА ЯЗЫКОВ
ИМПЕРАТИВНОГО ПРОГРАММИРОВАНИЯ
Упражнение 19. Расширение языка первого порядка.........419
Теоретические сведения................................419
Вспомогательные понятия...........................420
Новые бинарные логические связки..................421
Новые функциональные символы......................422
Новые предикатные символы.........................423
Ограниченные кванторы для числовых множеств.......425
https://и га it.ru
Ограниченный квантор количества......................426
Упражнения для самостоятельного решения.................426
Упражнение 20. Формальный синтаксис модельных
языков программирования: грамматические модели............430
Теоретические сведения.................................431
Понятие о порождающих грамматиках...................432
Форма Бэкуса — Наура (БНФ)..........................434
Расширенная Бэкуса — Наура форма (РБНФ).............436
Формальный синтаксис языка программирования Н.......441
Формальный синтаксис языка программирования D.......445
Формальный синтаксис языка программирования М.......447
Упражнения для самостоятельного решения................450
Упражнение 21. Содержательная операционная
семантика модельных языков................................456
Теоретические сведения.................................456
Понятие «недетерминированность».....................456
Содержательная операционная семантика
детерминированного языка Н..........................457
Содержательная операционная семантика
недетерминированного языка D........................460
Содержательная семантика детерминированного языка М
с условными выражениями.............................463
Упражнения для самостоятельного решения................468
Упражнение 22. Аксиоматическая система Хоара
для модельных языков Н и D................................472
Теоретические сведения.................................473
Концепция доказательного программирования...........475
Из истории доказательного программирования..........476
Понятие «спецификация программы»....................477
Понятие «верификация программы».....................479
Подходы к формальной верификации....................480
Понятие «тройка Хоара»..............................481
Дедуктивная семантика языка программирования........483
Аксиоматическая система Хоара.......................484
Понятие «инвариант цикла»...........................486
Понятие «завершение программы»......................487
Понятие «частично правильная программа».............488
Технология доказательства частичной правильности
программы в системе Хоара...........................489
Технология доказательства полной правильности программы
в системе Хоара.....................................491
О неполноте системы Хоара...........................492
Недетерминированные программы в системе Хоара.......493
Примеры решения некоторых типов упражнений.............495
9
https:it.ru
Упражнения для самостоятельного решения...................498
Упражнение 23. Аксиоматическая система Дейкстры. Wp-
преобразователь предикатов...................................506
Теоретические сведения....................................506
Wp-преобразователь предикатов..........................507
Sp-преобразователь предикатов..........................508
Дедуктивная семантика команды..........................508
Доказуемая программа в системе Дейкстры................509
Аксиоматическая система Дейкстры.......................510
Структурные допустимые правила вывода..................510
Wp-семантика простейших команд.........................513
Wp-семантика команды ввода.............................514
Wp-семантика команды вывода............................514
Допустимые правила о подпрограммах.....................515
Контрольные вопросы.......................................516
Упражнения для самостоятельного решения...................517
Упражнение 24. Wp-семантика команды присваивания
и композиции команд..........................................521
Теоретические сведения....................................522
Аксиома и wp-семантика композиции команд...............522
Аксиома и wp-семантика команды присваивания............523
Sp-семантика команды присваивания и композиции команд..525
Аксиома обновления элемента массива....................526
Wp-семантика команды присваивания элементу массива.....527
Синтез команд присваивания.............................528
Понятие «уравнение в отношениях выводимости» в языке Н.529
Контрольные вопросы.......................................530
Примеры решения некоторых типов упражнений................531
Упражнения для самостоятельного решения...................533
Упражнение 25. Wp-семантика команды выбора Дейкстры... 537
Теоретические сведения....................................537
Аксиома и wp-семантика команды выбора Дейкстры.........537
Основная теорема о команде выбора Дейкстры.............538
Wp-семантика частных случаев команды выбора IFn........539
Допустимые правила вывода для команды выбора...........542
Синтез команды выбора..................................544
Контрольные вопросы.......................................544
Примеры решения некоторых типов упражнений................545
Упражнения для самостоятельного решения...................546
Упражнение 26. Wp-семантика команды цикла Дейкстры...........550
Теоретические сведения....................................551
Wp-семантика команды цикла DOn.........................551
Основные теоремы о команде цикла DOn...................552
10
https: "и га it.ru
Инвариант и ограничивающая функция цикла DOn..........554
Технология установления правильности цикла DOn......555
Допустимые правила вывода для команды цикла.........558
Денотационная семантика команды цикла While.........561
Синтез команд цикла Дейкстры........................563
Контрольные вопросы....................................564
Примеры решения некоторых типов упражнений.............564
Упражнения для самостоятельного решения................569
Упражнение 27. Эвристические методы синтеза
инвариантов цикла Дейкстры................................578
Теоретические сведения.................................578
Метод «воздушного шарика»...........................579
Метод устранения конъюнктивного члена постусловия...580
Метод замены константы переменной...................582
Метод введения новой переменной.....................583
Метод добавления дизъюнктивного члена...............585
О поиске инварианта для рекурсивных программ........585
Примеры решения некоторых типов упражнений.............586
Упражнения для самостоятельного решения................588
Упражнение 28. Синтетический подход к формальной
верификации программ......................................592
Теоретические сведения.................................592
Доказательство правильности как этап программирования.592
Когда доказывать правильность программы: после
ее написания или в процессе написания?..............594
Фундаментальные принципы Д. Гриса...................595
Структуры языка программирования....................596
Примеры решения некоторых типов упражнений.............600
Упражнения для самостоятельного решения................606
Часть 6
ЭЛЕМЕНТЫ МОДАЛЬНОЙ ЛОГИКИ
Упражнение 29. Модальные логики: аналитические
таблицы для модальной логики, нормальные модальные
исчисления К, Т, В, S4, S5.............................611
Теоретические сведения ..............................612
Математические сведения...........................612
Модальности. Модальная логика.....................612
Синтаксис пропозициональной модальной логики......615
Модель Крипке для формул модальной пропозициональной
логики............................................617
Аналитические таблицы для пропозициональной модальной
логики............................................621
Нормальные модальные исчисления...................625
https:it.ru
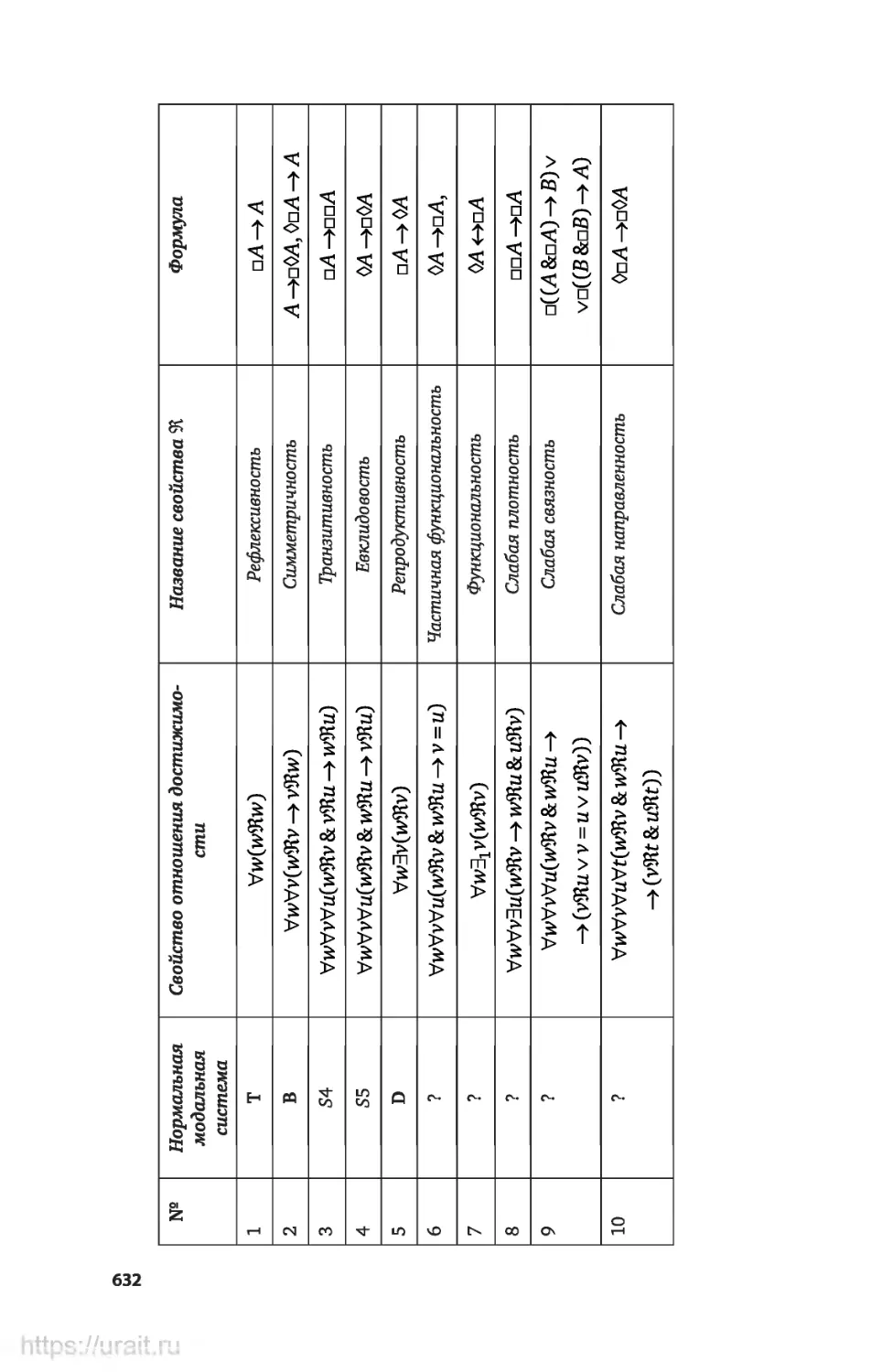
Характеризация отношений достижимости с помощью
модальных формул....................................631
Связи интуиционистской и модальной логики...........635
Корректность и полнота нормальных модальных исчислений.... 637
Биографические сведения.............................638
Примеры решения некоторых типов упражнений.............638
Задачи для самостоятельного решения....................644
Упражнение 30. Конструирование свойств шкал Крипке........652
Теоретические сведения.................................652
Конструирование свойств шкал Крипке................652
Примеры решения некоторых типов упражнений.............655
Задачи для самостоятельного решения....................659
Литература................................................663
Новые издания по дисциплине «Программирование»
и смежным дисциплинам.....................................673
https: //цга it.ru
Введение
В настоящее время интерес к математической логике значи-
тельно возрос ввиду широкого распространения вычислительной
техники, развития информатики и исследований по проблеме ис-
кусственного интеллекта, ведь в основе программирования и мно-
гих работ по искусственному интеллекту лежат базисные понятия
математической логики — формализованные языки, исчисления,
семантические модели и т. п.
Кроме того, развитие учебного процесса в вузе привело к необ-
ходимости расширения самостоятельной работы студентов, однако
недостаточность разнообразных учебных пособий по многим учеб-
ным дисциплинам сдерживает развитие активных форм самостоя-
тельной работы.
В настоящее время имеется значительное разнообразие учебных
книг по математической логике, изданных на русском языке, многие
из которых написаны выдающимися учеными или крупными специ-
алистами (Д. Гильбертом, В. Аккерманом, П. Бернайсом, П. С. Но-
виковым, А. Чёрчем, С. К. Клини, Э. Мендельсоном, Дж. Шёнфил-
дом, Ю. Л. Ершовым, Е. А. Палютиным, А. Н. Колмогоровым и др.).
Однако одни из этих книг трудны для первоначального изучения
предмета, другие не соответствуют программе и целям изучения
математической логики в педагогических вузах, третьи давно из-
даны и устарели в методическом отношении.
Налицо недостаток учебной литературы по этой дисциплине для
педагогических вузов. Предлагаемое вашему вниманию учебное по-
собие предназначено немного «сгладить» эту ситуацию.
Рассмотрим вопросы, неизбежно возникающие у начинающих
при изучении дисциплины «Математическая логика».
Что такое математическая логика?
Как всякая развитая наука, математика изучает, помимо других
своих объектов, также и саму себя для того, чтобы выработать кри-
терии научности своих результатов и методов.
Математику как науку изучают история математики и филосо-
фия математики (разумеется, своими методами). Математическая
логика изучает математику математическими методами: с одной
стороны — это математическая наука по методу, с другой — объ-
ектом ее изучения является сама математика.
13
https:it.ru
Более точно, математическая логика — это раздел математики,
который посвящён изучению математических теорий и, в частно-
сти, основного для математики понятия — «математическое до-
казательство».
Отметим, что в настоящее время логика всё более становится
не наукой о правильности рассуждений (и в этом проявился кризис
в моделировании истинно «человеческой» логики), а наукой о кон-
струкциях, логическая природа которых в высшей степени абстра-
гирована.
В этом смысле логика превращается именно в металогику
в ее совершенном новом назначении. Термин «металогика» пони-
мается (см. [151]) не в его традиционном понимании как исследо-
вание металогических свойств (непротиворечивость, полнота, раз-
решимость, независимость и т. д.) конкретной логической системы
или даже класса однотипных систем, а как:
а) глобальный подход в исследовании различных совокупно-
стей логик, выявлении структуры не отдельных логических систем,
а их целого класса;
б) взаимоотношения между различными логиками, множества-
ми логик и структурами этих множеств;
в) переводу и погружению одних логических систем в другие;
г) построению некоторой богатой конструкции, объединяющей
как можно больше логических систем, и изучению уже ее свойств.
Наконец, насущная необходимость формализации всего богат-
ства человеческих рассуждений (которые не исчерпываются мате-
матической логикой) привела к появлению научного направления,
называемого компьютерной логикой. Выделим некоторые задачи
компьютерной логики (которые в большей или меньшей степени
входят в сферу искусственного интеллекта), сформулированных
В. К. Финном1.
1. Методы автоматического доказательства теорем (в автома-
тическом и диалоговом режиме) будут применяться как в матема-
тике, так и в компьютерных системах для обработки информации.
Весьма перспективным направлением является комбинирование
дедукции и индукции в базах данных с неполной информацией или
для слабо формализованных дисциплин с хорошо структурирован-
ными данными. Также перспективными работами будут исследова-
ния по распространению на неклассические логики метода резолю-
ций.
2. Логика программ. Основными задачами здесь будут: доказа-
тельство правильности программ, доказательство эквивалентности
1 Финн В. К. Интеллектуальные системы: проблемы их развития и социальные
последствия // Будущее искусственного интеллекта. Москва : Наука, 1991. С. 157—
177.
14
https:/Л: rait.ru
программ, автоматический синтез программ, охватывающий как
извлечение программ из дедуктивного доказательства, так и ин-
дуктивный синтез программ по примерам. Заметим, что логика
программ входит в такое направление исследований, как описание
алгоритмов средствами языков логики. Развитие логик программ
связано с разработками динамических логик и логик процессов, яв-
ляющихся вариантами динамических логик.
По-видимому, можно ожидать соединение аппарата логик про-
грамм и теорий баз данных, что приведёт к построению эффектив-
ных моделей обработки данных.
3. Логическое программирование. К этому направлению относит-
ся применение процедур доказательства и языка логики в качестве
языка программирования. Важным примером для логического про-
граммирования является язык PROLOG.
4. Логические проблемы в базах данных. В ближайшие годы уси-
лия специалистов будут сосредоточены вокруг решения следующих
задач:
1) построение логических языков, содержащих в качестве тер-
мов представления структурированных объектов (например, мно-
жества, кортежи, слова, графы, пространственные графы);
2) применение неклассических логик для формализации не-
полноты информации, алгоритмических процессов переработки
информации, ответов на вопросы и т. п. (модальные логики, кон-
структивные логики, многозначные логики);
3) применение конструктивных логик в теории решения задач;
4) разработка теории немонотонных рассуждений, применяе-
мых в условиях неполноты информации с использованием процедур
распознавания невыводимости и непротиворечивости; применение
немонотонных рассуждений (основанных на соответствующих ло-
гиках) в компьютерных системах, реагирующих на пополнение зна-
ний;
5) разработка теории баз знаний на логической основе.
Как изучает свой объект математическая логика?
Элементы математической теории (аксиома, теоремы, доказа-
тельства) могут рассматриваться с двух точек зрения.
Мы можем интересоваться их смыслом или воспринимать их как
нечто, написанное на бумаге. Математик, создающий содержатель-
ную теорию, интересуется прежде всего смыслом. Однако имеется
важный довод и в пользу того, чтобы изучать аксиомы, теоремы
и доказательства именно как символьные объекты. Понятия со-
временной математики, о которых говорится в аксиомах, теоремах
и сами доказательства, часто бывают очень абстрактны, в то же вре-
мя, фигуры из символов, написанные на бумаге, являются объекта-
ми конкретными, их изучать легче.
15
https:it.ru
Если при этом удачно выбрать способ выражения аксиом, теорем
и доказательств, то их записи будут до некоторой степени отражать
их смысл. Основной подход математической логики к изучению ма-
тематической теории состоит в отображении ее в виде формальных
образов, символьных конструкций и изучении последних.
В качестве основной модели, посредством которой математиче-
ская логика исследует математические теории, выступает понятие
«формальная система» (которую называют также дедуктивной си-
стемой).
Первой частью формальной системы является ее язык. Для фор-
мальных систем используются искусственные языки — выражения
такого языка представляют собою точно описанные цепочки сим-
волов. Язык считается полностью определённым, когда определены
его символы и формулы (некоторые выражения языка).
Следующей частью формальной системы являются ее аксиомы;
единственное требование состоит в том, чтобы каждая аксиома
была формулой языка. Встречаются формальные системы, не име-
ющие аксиом, но в общем случае аксиомы должны быть.
Третьей частью формальной системы является совокупность
чисто формальных правил вывода и определение понятия «доказа-
тельство», позволяющие выводить новые формулы языка из акси-
ом и уже выведенных формул. Иногда в формальную систему вклю-
чают совокупность ее теорем (выводимых формул).
Заметим, что во всех учебных математических дисциплинах ос-
новное понятие — это «доказательство», но только математиче-
ская логика может ответить на вопрос: «Что же такое формальное
математическое доказательство?»
Наиболее важным классом формальных систем являются фор-
мальные теории первого порядка, формализующие какую-либо
область содержательной математики. Этот класс возник в связи
с программой Д. Гильберта обоснования математики и послужил
оправданием изучения формальных систем первого и второго по-
рядков.
Математическая логика изучает два аспекта формальных систем:
синтаксический аспект (когда изучают символьные конструкции
как таковые, безотносительно их содержания) и семантический
аспект (когда интересуются связями между синтаксическими свой-
ствами формальной системы и их смыслом).
Что даст студенту изучение математической логики?
Целью этой дисциплины мы считаем:
1) формирование у студентов, изучающих компьютерные на-
уки и информационные технологии, осознанных представлений
о дедуктивном характере математической науки, специфике мате-
матического языка, сущности аксиоматического построения дедук-
16
https:/Л: rait.ru
тивных теорий, понимания смысла и структуры математического
доказательства;
2) овладение в полной мере понятиями «алгоритм» и «исчисле-
ние»;
3) получение фундаментальных знаний для более глубокого по-
следующего изучения компьютерных наук.
Назначение, содержание и структура пособия
Структура пособия соответствует плану изучения его студентами
третьего курса, используемому в институте информационных техно-
логий и технологического образования РГПУ им. А. И. Герцена. При
этом акцент делается на элементах компьютерной логики, поэтому
содержание некоторых разделов пособия не является традиционным
для институтов компьютерных наук в силу следующих причин:
1) представлены элементы общей теории исчислений: рассма-
триваются слова в алфавите, а также исчисления на словах в алфа-
вите;
2) представлены различные первопорядковые исчисления (гиль-
бертовское, генценовское и секвенциальное), которые способству-
ют формированию общего понятия «исчисление» в полном его
объёме, а также быстрому приобретению навыка формальных до-
казательств в конкретных исчислениях;
3) представлена интуиционистская пропозициональная логика
(минимальная позитивная логика Prop), а также пропозициональ-
ное секвенциальное исчисление Н. Н. Воробьёва — Дж. Худельмай-
ера без правила сокращения;
4) представлены нормальные исчисления модальной пропози-
циональной логики (К, Т, В, S4, S5);
5) представлены аналитические таблицы для первопорядковой
логики, для интуиционистской предикатной логики и для модаль-
ной логики;
6) представлена система Deductio, предназначенная для поиска
логических выводов в режиме диалога «человек-компьютер», а так-
же система Coq — «доказыватель» теорем и язык функционального
программирования с зависимыми типами;
7) представлена аксиоматическая семантика языков императив-
ного программирования (системы Ч. Хоара и Э. Дейкстры).
Структурные единицы материала, на которые разделено посо-
бие, называются «Упражнения», поскольку формой организации
работы студента над этим пособием являются упражнения. На одну
структурную единицу (на одно упражнение) отводится от одного
до трёх аудиторных занятий (объемом два академических часа), од-
нако значительную часть работы студент выполняет как домашнее
задание после такого занятия.
17
https:it.ru
Упражнения системы строятся по единой схеме: вспомогатель-
ные понятия, основные понятия, краткие теоретические сведения
по теме (раскрытие смысла основных понятий и используемых ут-
верждений), примеры решения основных типов упражнений, а так-
же задачи, предназначенные для самостоятельного решения.
Некоторые задачи снабжены ответами или указаниями к реше-
нию, а трудные задачи отмечены звёздочкой.
В пособии также имеются лабораторные работы, которые стро-
ятся по следующей схеме:
1) обязательные результаты обучения, выраженные в терминах
«знания» и «умения»;
2) теоретические сведения, которые содержат основные поня-
тия, теоремы, леммы и алгоритмы;
3) примеры решения некоторых типов упражнений и (или) де-
монстрационные примеры, которые фактически являются образца-
ми оформления решения задач;
4) задачи для самостоятельного решения (некоторые снабжены
ответами, указаниями или решениями); часть задач при попытках
их решения не должны вызывать проблемы, однако «мастерский»
уровень овладения материалом требует решения большинства за-
дач.
Предварительная подготовка студентов
Как и при изучении многих других областей математики, при
изучении математической логики формально не требуется почти
никаких предварительных знаний, кроме первоначальных понятий
наивной теории множеств и алгебры, поскольку никакие другие
понятия в построении формально-математической теории не будут
использоваться без предварительных их определений. Однако для
понимания предмета требуется все-таки определенная степень ма-
тематической зрелости.
Предполагается, что студент, приступающий к изучению матема-
тической логики, знаком с различными математическими теориями
(в том числе и с аксиоматическими) и умеет проводить доказатель-
ства.
Предполагается также, что студент, начинающий использовать
настоящее пособие, уже свободно владеет языком содержательной
математики. Заметим, что студенты третьего курса факультетов ин-
формационных технологий имеют необходимую предварительную
подготовку и достаточный математический опыт.
Рекомендации для студентов по использованию пособия
Пособие дополняет лекционную часть курса и направлено на ак-
тивное ее усвоение, однако может использоваться и для первона-
чального изучения материала без обращения к другим источникам.
18
https: "и rait.ru
Оно может служить средством изучения материала не только
при наличии аудиторных занятий, но и при полностью самостоя-
тельном изучении материала всех или некоторых его тем.
При использовании пособия на аудиторных занятиях считаем це-
лесообразным, чтобы раздел «Теоретические сведения» по соответ-
ствующей теме или содержание соответствующей лекции изучались
студентом предварительно (до занятия по теме), а на самом заня-
тии проводилось краткое повторение или контроль подготовлен-
ности студентов и разбирались решения нескольких заданий для
самостоятельной работы.
Остальная часть заданий может быть предназначена для домаш-
ней работы.
В случае полностью самостоятельного изучения студентом той
или иной темы с помощью пособия (как единственного источни-
ка) рекомендуем прочесть сначала «Теоретические сведения», затем
«Примеры решения некоторых типов упражнений», а только затем
приступать к выполнению заданий для самостоятельной работы.
Пособие может использоваться и как справочник, так как в нем
приведен обширный список учебной и научной литературы.
Мы хотели бы, чтобы читатель эту книгу, как и всякую другую,
воспринимал в качестве собеседника. Однако только очень нелю-
бознательный человек может удовлетворится лишь одним собесед-
ником!
Авторы пособия не считают себя теми, кто имеет монополию
на толкование и преподавание математической логики. Именно по-
этому мы не только приводим ссылки на источники, из которых взя-
ли то или иное задание, то или иное необщепринятое определение,
тот или иной факт, но также приводим в конце пособия большой
список литературы, включающей в себя учебные, научно-популяр-
ные и научные издания.
Рекомендации для преподавателей по использованию пособия
Используя учебный материал пособия, можно построить содер-
жание фрагмента различных учебных дисциплин (например, «Ма-
тематическая логика и теория алгоритмов», «Теоретические осно-
вы программирования», «Представление знаний в информационных
системах») для студентов институтов компьютерных наук и факуль-
тетов информационных технологий.
Так, часть представленного выше содержания обучения включено
авторами в годовой курс «Прикладное программирование на язы-
ках высокого уровня» и семестровый курс «Представление знаний
в информационных системах» (бакалавры информационных систем
и технологий, 5 и 6 семестры 2015—2016 учебного года), а именно
рассматривались:
19
https:it.ru
1) язык первого порядка, элементы теории доказательств на базе
гильбертовского и генценовского исчисления;
2) интуиционистские пропозициональные логики: минималь-
ное позитивное исчисление Prop, метод моделей для выделения ча-
сти пропозициональных импликативных формул, не являющихся
доказуемыми в интуиционизме;
3) интуиционистская пропозициональная логика второго поряд-
ка Ргор2 и интуиционистская предикатная логика Pred.
В процессе обучения нами использовались следующие отече-
ственные и зарубежные средства обучения, а именно:
1) Deductio — система интерактивного поиска доказательства
теорем (А. В. Смирнов, А. Е. Новодворский, 1991—1996);
2) Coq — интерактивное программное средство для доказатель-
ства теорем, использующее собственный язык функционального
программирования с зависимыми типами;
3) Djinn (L. Augustsson, 2005—2014) — автоматический «дока-
зыватель» теорем интуиционистской логики, который позволяет
установить интуиционистскую доказуемость пропозициональной
формулы в Prop;
4) Agsy — подсистема языка программирования Agda для авто-
матического поиска термов по заданному типу в системах Х_^, Х2,
А.ш, ХР, которое также позволяет установить интуиционистскую до-
казуемость формулы в исчислениях Prop, Ргор2 и Pred.
Работа между авторами распределилась следующим образом
(создание упражнения или лабораторной работы означает разра-
ботку содержания обучения, построение типологии задач для само-
стоятельного решения и их подбор):
1) доц. А. Б. Михайлов и доц. И. А. Кудрявцева написали «Введе-
ние», содержащее концепцию построения пособия;
2) упр. № 9 и лабораторные работы № 13, 14 написаны доц.
А. В. Ролановой;
3) упр. № 21, 22, 23, 24, 27, 28 написаны канд. пед. наукМ. В. Де-
мидовым;
4) упр. № 12,19,20, 24,25,26,29,30 написаны проф. М. В. Швец-
ким;
5) упр. № 2 написано доц. А. Б. Михайловым;
6) упр. № 1, 15, 16, 17, 18 написаны доц. И. А. Кудрявцевой
и проф. М. В. Швецким совместно;
7) упр. № 3, 4, 5, 6, 7, 8,10,11 написаны авторами совместно.
Авторы выражают благодарность канд. физ.-мат. наук, доц. Ми-
хайлову Александру Борисовичу (РГПУ им. А. И. Герцена) за логиче-
ское мировоззрение, которое сформировало наш взгляд на процесс
обучения математической логике в университете, а также д-ру. пед.
наук Рыжовой Наталье Ивановне за предоставленные методические
материалы.
20
https:it.ru
Авторы выражают благодарность и признательность д-ру. физ.-
мат. наук, проф. Флегонтову Александру Владимировичу за внима-
ние и моральную поддержку, благодаря которым работа над посо-
бием была закончена в самый короткий срок.
2002—2016 (октябрь) гг. Голанова А. В., Демидов М. В.,
Санкт-Петербург Кудрявцева И. А., Швецкий М. В.
https:it.ru
Часть 1
ОБЩАЯ ТЕОРИЯ
ИСЧИСЛЕНИЙ
https:it.ru
Упражнение 1
СЛОВА В АЛФАВИТЕ
Эфэф обожал слова. Он шел
в Лес Словес, ставил там словушки,
а пойманные слова держал в словарях
и словниках. И радовался, когда на свет
появлялось новое словцо. «Славные
мои словечки...» — приговаривал он,
поглаживая их по буковкам. Эфэф
не сразу заметил, как сам стал
словом. А когда заметил, только
порадовался. И побежал в Лес Словес
со своими словами и словечками.
Виктор Кротов. Поезд наизнанку.
Сказки-крошки
Обязательные результаты обучения:
• знать вспомогательные понятия
—знак, символ, синтаксические переменные, слово;
—предметный (объектный) язык, язык исследователя (метаязык);
• знать основные понятия
— алфавит, подалфавит, расширение алфавита, буква алфавита, слово
в алфавите, однобуквенное слово, пустое слово, длина слова;
— элементарные операции построения слов: «правого присоединения
буквы к слову», «левого присоединения буквы к слову»;
— основные операции над словами: «равенство букв алфавита», «провер-
ка слова в алфавите на пустоту», «голова слова», «хвост слова», «последнее
в слове», «без последнего в слове», «длина слова»; предикат «равенство слов
в алфавите»; операции: «приписывания слова к слову», «обращение слова»,
«k-я степень слова», «примитивный корень из слова»; свойства операции
приписывания слова к слову;
— подслово слова, вхождение слова в слово, вхождение буквы в слово,
степень слова относительно заданной буквы;
— операцию замены подслов, операцию подстановки слова вместо буквы,
операцию одновременной подстановки слов вместо букв, операцию после-
довательного применения подстановки слова вместо буквы;
— типы числовых функций, определённых на множестве слов (аддитив-
ная, мультипликативная, аддитивно-мультипликативная функция, марков-
ская функция);
— функции, частично определённые на множестве слов;
25
https: "и га it.ru
—метод математической индукции как распознающая процедура, на-
туральная индукция, принцип математической индукции, модификации
натуральной индукции, полная (возвратная) индукция;
• знать дополнительные понятия
—полугруппа, моноид;
• уметь
— конструировать слова с требуемыми свойствами;
— выполнять элементарные операции построения слов и основные опе-
рации над словами, представленные выше;
— выполнять замену подслое в слове, подстановку слов вместо букв;
— конструировать доказательства утверждении о словах по индукции;
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
Теоретические сведения
Предварительные наблюдения
Что требует самых основательных,
самых упорных доказательств, так
это очевидность. Ибо слишком многим
недостаёт глаз, чтобы видеть ее.
Ф. Ницше
Всюду ниже мы будем говорить не о естественных, а об искус-
ственных языках.
Естественные языки (русский, английский, латинский и проч.)
возникали и развивались стихийно в процессе их практического
использования. Искусственный же язык с самого начала нам пред-
стоит строить как математический объект, соблюдая традиции ма-
тематики (мы должны будем давать определения, формулировать
и доказывать теоремы).
Исходным соображением при построении искусственных языков
может служить простая мысль о том, что он может строиться из тех
элементов, того «строительного материала», с помощью которого
построены естественные письменные европейские языки.
Самым мелким «кирпичиком» такого языка является языковый
знак. Из знаков составляются слова, предложения и тексты.
Еще одно (и очень важное!) соображение состоит в следующем:
если знак «пробел» считать самостоятельным знаком (т. е. признать
существование «нулевого» знака), то любой текст (и любая его
часть) может рассматриваться просто как последовательность зна-
ков. «Языковые сообщения в письменной форме строят обычно, за-
писывая знаки письма (графемы) друг за другом... По существу та-
кие сообщения являются последовательностями знаков» [83, с. 40].
26
https:/Л: rait.ru
Таким образом, знаки являются «кирпичиками», из которых
строится письменный язык, а универсальной конструкцией при по-
строении языка служат последовательности знаков, которые и бу-
дут являться первым объектом нашего тщательного изучения.
В математике сложилась традиция, при которой любая последо-
вательность знаков называется словом (даже если она и не является
словом какого-либо естественного языка и поэтому не имеет смысла).
Этой традиции мы и будем придерживаться.
Хотели бы, однако, при этом попросить читателя не связы-
вать математический термин «слово» только с представлениями
об «обычном» слове языка (русского, английского или искусствен-
ного). Ведь математический термин «слово» может быть отне-
сен не только к слову языка, но и к предложению языка или даже
к целому тексту, также являющемуся последовательностью знаков.
Вполне естественно, что слово может являться частью другого слова
(подсловом'), а также иметь несколько вхождений в него (например,
слово «он» имеет два вхождения в слово «понтон»). Слово может
быть началом или концом другого слова. В дальнейшем нам пред-
стоит дать точные определения, соответствующие этим наглядным
представлениям, а также рассмотреть простейшие операции над
словами (некоторые из них будут алгебраическими).
Исходные понятия и представления
Усомнись во всём хотя бы однажды,
пусть это даже будет утверждение, что
2-2 = 4.
Г. К. Лихтенберг
Математика... имеет свои границы, заданные
непреодолимыми границами материального
существования, и говорить о нашей математике
в мире с иными законами, нежели законы нашего
мира, значит говорить бессмыслицу.
С. Лем. История бит-литературы
Понятие «знак» будем считать исходным и неопределяемым, т. е.
оно известно заранее, еще до построения математических теорий.
Это понятие является абстрактным образом тех материальных зна-
ков, которые мы изображаем, например, на песке, грифельной до-
ске, листе бумаги и т. п. Можно привести лишь описание понятия
«знак».
Определение (по [173, с. 244]).
Знаки — «это предметы, относительно которых предполагается
только то, что мы умеем отличать одинаковые (тождественные)
знаки от различных».
27
https: "и га it.ru
Предполагается, что:
1) существует некоторая идеальная (т. е. мыслимая нами) пло-
скость;
2) существуют различные:
а) знаки, причем, рассматривая любые два из них, можно с уве-
ренностью установить, одинаковы ли они или различны;
б) экземпляры одного и того же знака;
3) знаки можно записывать в пределах идеальной плоскости;
4) при написании знаков можно:
а) написать сколько угодно экземпляров одного знака (разли-
чение «образца» знака и «экземпляров» этого образца является
одним из краеугольных положений семиотики — науки о знаках
и знаковых системах);
б) использовать линейный способ записи знаков слева направо
на идеальной плоскости. По мнению В. Ф. Турчина [173, с. 244]
«линейность естественных языков является результатом того, что
звуковой язык развёртывается во времени, а отношение следова-
ния во времени легко моделируется отношением порядка располо-
жения на пространственной прямой. Специализация естественного
языка привела к созданию математического линейного знакового
языка, который в настоящее время образует основу математики»;
в) использовать для удобства записи и другие способы упоря-
доченного расположения знаков на этой плоскости. Например,
Г. Генцен (цит. по [7, с. 11] называет упорядоченные наборы зна-
ков «фигурами»: фигуры — это «каким-либо образом упорядочен-
ные конечные множества знаков»;
5) знаки можно удалять (стирать) или вычёркивать с идеальной
плоскости.
Слова «знак» и «символ» считаются синонимами.
В дальнейшем мы познакомимся:
1) с простейшими символьными конструкциями, с помощью ко-
торых строятся символьные объекты;
2) с общими приемами конструирования символьных объектов,
т. е. приёмами их определений (построений);
3) с общими приёмами доказательства математических утверж-
дений о символьных объектах.
На самом деле простейшие символьные конструкции представ-
ляют собой широкое обобщение всех символьных моделей, с которы-
ми Вам предстоит встретиться в математике позднее.
Замечание [150, с. 245—246].
Символы — это тоже физические объекты, — скажем, чернильные
пятна на бумаге, — которые обозначают абстрактные объекты. И опять
мы полностью полагаемся на гипотезу, что физическое поведение симво-
лов соответствует поведению обозначаемых ими абстракций.
28
https:/Л: rait.ru
Следовательно, надёжность того, что мы узнаём, манипулируя этими
символами, полностью зависит от точности наших теорий об их физиче-
ском поведении и о поведении наших рук, глаз и т. д., с помощью кото-
рых мы манипулируем этими символами и наблюдаем за ними. Обман-
чивые чернила, из-за которых случайный символ изменил свой внешний
вид, когда мы не видели этого,... вскоре введут нас в заблуждение отно-
сительно того, что мы «определённо» знаем.
Синтаксическая переменная
Мы будем изучать слова точно так же, как изучаются числа
в алгебре или математическом анализе. Исследование проводится
на русском языке с добавлением специальных символов. Некоторые
из таких символов являются переменными (например, в математи-
ческом анализе переменная может означать любое действительное
число). При изучении же знаковых объектов значениями перемен-
ных могут быть слова в некотором алфавите или его буквы. Эти
переменные называют синтаксическими переменными, в качестве
которых будем использовать греческие буквы а, 0, у, 8, е, (возмож-
но с индексами), значениями которых являются слова в указанном
алфавите.
К использованию синтаксических переменных приводят пробле-
мы, возникающие при построении и исследовании языка, предна-
значенного для описания другого языка.
Предметный язык и метаязык
Определение.
1. Предметным языком (языком-объектом, объектным языком)
называется исследуемый язык.
2. Языком исследователя (метаязыком) называется язык, с по-
мощью которого изучается предметный язык.
В качестве метаязыка будем использовать тщательно и точно
сформулированные предложения разговорного языка.
Алфавит. Буква
Определение (содержательное).
1. [141] Алфавит — это совокупность букв, слоговых знаков
и других графем данной системы письма, расположенных в опре-
делённом порядке. Буква — это графический знак, который сам
по себе или в сочетании с другими знаками используется для
обозначения на письме звуков, фонем, их основных вариантов
и их типичных последовательностей.
29
https:/Л: га it.ru
2. [49, с. 7] Под алфавитом понимается конечный список элемен-
тарных (т. е. считающихся не членимыми далее) знаков, называ-
емых буквами этого алфавита.
Далее мы будем рассматривать термины «алфавит», «буква»
в смысле, отличном от традиционного.
Определение.
1. Алфавитом называется произвольное непустое множество знаков.
2. Подалфавитом алфавита В называется множество А сВ.
3. Расширением алфавита А называется такое множество В, что
АсВ.
4. Буквами алфавита называются элементы алфавита.
Следует иметь в виду, что элемент алфавита — это «буква-обра-
зец», с которой можно изготовить сколько угодно копий. Это согла-
суется и с обычным «нематематическим» употреблением термина
«алфавит» (алфавит содержит именно образцы букв).
Определение [138, с. 27; 169, с. 23].
1. Латинским алфавитом называется множество, содержащее
26 прописных и 26 строчных латинских букв.
2. Двоичным (бинарным) алфавитом называется множество {0,1}.
3. Тернарным алфавитом называется алфавит, количество букв
которого равно 3.
4. Кватернарным алфавитом называется алфавит, количество
букв которого равно 4.
Слова на основе кватернарного алфавита находят применение
при анализе последовательностей ДНК.
Слово в алфавите
— Видите ли, я никак не могу понять,
как из таких букв можно составить слово.
— Это вас интересует?
— Ужасно.
— Так вот, смотрите, сейчас я покажу
вам эту штуку. Погодите минуту...
Теперь смотрите внимательно.
А. Дюма. Виконт де Бражелон,
или Десять лет спустя
Определение (содержательное).
1. Слово (В. Даль) — а) исключительная способность человека выра-
жать гласно мысли и чувства свои; дар говорить, сообщаться разумно
30
https:/Л: rait.ru
сочетаемыми звуками; словесная речь; б) сочетание звуков, состав-
ляющее одно целое, которое по себе означает предмет или понятие.
2. [141] Слово — одна из основных единиц языка, служащая для
именования предметов, лиц, процессов, свойств.
Далее мы будем рассматривать термин «слово» в смысле, отлич-
ном от традиционного.
Пусть А — алфавит, п е N\{0}. Обозначим а1г а2, --;CLn — буквы
алфавита А (не обязательно различные).
Определение (содержательное).
1. [159] Слово — это горизонтальный ряд букв некоторого ал-
фавита.
2. Словом в алфавите А (или просто словом} называется конеч-
ная последовательность, состоящая из букв а1г а2, ап алфави-
та А. Слово записывают слева направо без разделительных зна-
ков в виде
^1^2* ”^п"
3. Однобуквенным словом в алфавите А назовём слово, состоя-
щее из одной буквы алфавита А.
4. Пустым словом (обозначается символом Л лишь для того, чтобы
его «увидеть») назовём слово, не содержащее ни одной буквы.
def
5. Длиной слова а = а1а2...ап (обозначается 1еп(а) или | а |) назы-
вается число п. Длина пустого слова считается равной 0.
Из приведённого определения следует, что: 1) все слова, с ко-
торыми будем встречаться, будут иметь конечную длину; 2) знак
Л не является буквой, т. е. Л g А для любого алфавита А.
Приведём индуктивное определение термина «слово в алфавите А».
Предварительно неформально опишем конструктивный процесс
порождения слов в алфавите в направлении слева-направо, отвеча-
ющем европейской традиции письма. Первый шаг построения сло-
ва всегда состоит в написании пустого слова Л (берётся чистый лист
бумаги, и рука заносится над некоторым его местом), затем к нему
справа (или слева) присоединяется (приписывается) первая буква
слова (собственно говоря, пишется сама эта буква), затем к полу-
ченному слову присоединяется справа (или слева) очередная буква
и т. д. до конца процесса.
Поэтому будем считать, что в нашем распоряжении находятся
следующие исходные элементарные операции, наличие которых
позволяет осуществлять процессы построения слов (А* обозначает
множество всех слов в алфавите А, включая Л) [34, с. 41]:
1) операция правого присоединения буквы из А к слову в А, кото-
рую обозначим
31
http
о- Hi ।rnit ri i
•:А*хА—>А*;
2) операция левого присоединения буквы из А к слову в А, кото-
рую также (для удобства) обозначим
•:А*хА—>А*.
В дальнейшем будем пользоваться обеими операциями совмест-
но, чередуя их применение нужным нам образом.
Определение.
1. Аксиомой операции правого присоединения буквы к слову назо-
вём утверждение:
(Va е А) Л • а = а.
2. Аксиомой операции левого присоединения буквы к слову назо-
вём утверждение:
(Va е А) а • Л = а.
3. Аксиомой ассоциативности операций правого и левого присое-
динения буквы к слову назовем утверждение:
(Va е A) (Vb е A) (Vc е А) ((а • Ь) • с = а • (Ь • с)).
Определение (индуктивное).
1. Знак Л g А (называется пустое слово) — это слово в алфави-
те А.
2. Если а является словом в алфавите А и а е А, то a • а также яв-
ляется словом в алфавите А (результат операции правого присо-
единения к слову а буквы а практически всегда обозначают оса).
3. Других слов, кроме полученных по пунктам 1 и 2, нет.
Примеры (слов в алфавите).
def
1. В алфавите А = {|}, содержащем единственную букву |, приме-
рами слов являются: |, 11, 111, | | 11, 1111 | I. Подобные последователь-
ности служили, по-видимому, первыми древними изображениями нату-
ральных чисел (в виде зарубок на дереве или кости [171, с. 23]). Одна
из книг древнегреческого математика Диофанта Александрийского начи-
нается фразой: «Ты, конечно, знаешь, что каждое целое есть просто неко-
торое количество единиц». Далее, древние греки обозначали цифры бук-
вами. Таким образом, они могли досчитать до 100 миллионов, дальше уже
не считали, так как букв не хватало.
2. Слово 01011 является словом в бинарном алфавите.
32
https: //ц га it. ги
3. Слова Л, b, а, аа, ababbab являются словами в алфавите {а, Ь}.
def
4. Слово алкоксиланил — это слово в алфавите А = {а, и, к, л, н, о, с},
а также в любом расширении алфавита А.
5. Натуральные числа мы привыкли записывать в виде слов в алфа-
вите {0,1, 2, 3, 4, 5, 6, 7, 8, 9}.
6. Следующие три последовательности знаков:
воробей
Слова «многочлен» и «полином» — синонимы
ва_рбБ,штл
являются примерами слов в алфавите, состоящем из всех строчных
и заглавных букв русского алфавита, знаков «“« и «”« (кавычки),«,» (запя-
тая) и «_«(пробел).
7. Текст, напечатанный на пишущей машинке, является словом
в алфавите, определяемом клавиатурой данной машинки (включая знаки
препинания и пробел).
8. Роман JI. Н. Толстого «Война и мир» является словом в подходящем
алфавите (каком?).
Замечания.
1. При определении терминов «алфавит» и «буква» А. А. Марков
избегает использование термина «множество». Так, буквами называ-
ются знаки, которые в данном их применении рассматриваются как
целые. (Буквы [25, с. 16] — это элементарные неделимые знаки.) По сло-
вам К. К. Жоля, «философский вопрос о том, что такое буква, хладно-
кровно опускается».
«Используя буквы, мы, как правило, имеем дело с конечным (и даже
не очень большим) их набором. Этот набор может быть задан в виде неко-
торого, специальным образом устроенного списка, который мы будем
называть алфавитом. Можно, например, условиться писать буквы алфа-
вита “в строку”, отделяя их друг от друга запятой и заключая всю запись
в целом в какие-нибудь специально отведенные для этого скобки, напри-
мер, фигурные» [34, с. 2—3].
2. Алфавит, его буквы и слова в этом алфавите можно с равным успе-
хом назвать «словарём», «словами» и «предложениями» соответственно
(подобная терминология применяется при формальном анализе есте-
ственных языков).
3. Слово в алфавите представляет собой достаточно общий тип кон-
структивного объекта, поэтому понятие «слово в алфавите» играет важ-
ную роль в конструктивной математике.
4. Мы рассматриваем слова в алфавите как знаковые комплексы, взя-
тые сами по себе, безотносительно к тому, что эти комплексы означают
(как правило, в математике знаки что-нибудь да означают), так, по сло-
вам Д. Дойча [150, с. 131], символы — это «физические объекты, создан-
ные из вещества в узнаваемых конфигурациях».
5. Индуктивное определение термина «слово в алфавите» делает
оправданным применение принципа математической индукции для дока-
зательства утверждений (типа всеобщности) о словах в данном алфавите.
33
6. При определении термина «слово в алфавите» можно опираться
на понятие «кортеж». Это можно сделать так. Словом в алфавите назо-
вем кортеж над данным алфавитом; пустым словом назовем пустой кор-
теж. Теперь равенство слов в алфавите можно определить как равенство
двух кортежей, длину слова — как длину кортежа и т. п. Остается (в отли-
чие от общепринятого способа записи кортежей) писать слова в алфа-
вите без скобок и запятых: так, если А — алфавит, а1г ..., ап — буквы этого
алфавита, то вместо <а13 а2,..., ап> будем писать ага2...ап. Иногда слова
в алфавите заключают в одинарные кавычки (пишут: ta1a2...aT^) для отли-
чия от слов естественного языка.
7. (С. С. Лавров [97, с. 127]) Понятие «список» (в программировании)
является обобщением понятия «слово». Списки, составленные только
из букв, полностью аналогичны словам. Возможность включать списки
в некоторый список в качестве его элементов придает ему структуриро-
ванность, иерархичность, не присущие слову согласно его определению.
В то же время интуитивно понятно, что любой список можно считать сло-
вом в некотором алфавите.
8. (М. В. Демидов) Пустое слово (пустой символ) — это абстракция
более высокого уровня, чем просто слово (символ): слово — это последо-
вательность символов, а пустое слово — это отсутствие символов.
Например, в математике 0 (отсутствие всякого количества) — это
абстракция более высокого уровня, чем любое натуральное число (отра-
жающая количество). Аналогом является, разумеется, и пустое множе-
ство в теории множеств.
Приведем также несколько примеров «из жизни».
а) Пустой символ иногда используется в программировании для ука-
зания конца строки (в диалекте TURBO Pascal существует тип данных
«ASCIIZ-строки», от ASCII&Zero). Этот символ имеет код 0 (т. е. ссылка
на него будет выглядеть в программе как #0). Строка, начинающаяся
с пустого символа, считается пустой строкой.
б) Пустой символ можно найти в довольно неожиданном источ-
нике: в средневековой (если верить вполне современным литературным
источникам) норманской системе гадания на рунах (набор пластинок
с рунами) была специальная «пустая» руна, не изображавшаяся никак
(чистая пластинка), которая означала Бога или судьбу.
в) Символ «пробел» как отсутствие буквы (в своем роде «пустой сим-
вол») тоже ведь появился много позднее, чем прочие буквы, достаточно
рассмотреть знаменитые новгородские берестяные грамоты или старин-
ные монеты, на которых отдельные слова друг от друга отделялись не спе-
циальным знаком, а концом строки или даже просто по смыслу. Возникает
интересный вопрос: когда был изобретен пробел (столь же интересный, как
вопрос «когда был придуман нуль?»). Видимо, необходимость как-то отде-
лять слова друг от друга появляется лишь тогда, когда отсутствие пробе-
лов приводит к существенным разночтениям, а это — следствие развитого
языка с большим количеством слов, которые различать по смыслу уже
сложно. Во всяком случае, знаки препинания появились ранее, чем пробел.
Таким образом, обобщая сказанное, можно утверждать, что сама идея
использовать обозначение для того, чего нет, т. е. вводить знак без дено-
тата — это показатель высокого уровня развития общества.
34
https:/Л: rait.ru
9. Слова на основе кватернарного алфавита находят применение при
анализе последовательностей ДНК.
Соглашения об обозначениях
Введем важные обозначения. Пусть А — произвольный алфавит.
Соглашение об обозначениях (по [166, с. 9]).
Будем обозначать:
А+ — множество всех непустых слов в алфавите А,
А* — множество всех слов в алфавите А, включая Л.
Пример,
Математики часто обозначают множество, содержащее один элемент,
самим этим элементом (разумеется, лишь в тех случаях, когда это не при-
водит к путанице), т. е. считают, что а = {а}. Поэтому можно писать а+
вместо множества {а}+ и а* — вместо {а}*, а тогда
def def def
А = {а} => А+ = {а}+ = а+ = {а, аа, ааа,...},
def def
А* = {а}* = а = {А, а, аа, ааа,...}.
Пусть п е N\{0}. Обозначим Ап— множество слов в А длины п.
Лемма.
1. А+=А1оА2о ...;А*=А+о{Л}.
2. Для любого А множество А* является бесконечным множе-
ством.
Доказательство. Упражняйтесь.
Замечание [34 ,с. 3]. «Мы специально подчеркиваем, что слова в алфа-
витах, вводимые нами как конструктивные объекты, т. е. как результаты
некоторых построений, только так и будут трактоваться в дальнейшем.
Мы не будем позволять себе — считая их слишком сильными — таких
актов воображения, когда процесс построения всех слов в данном алфавите
(принципиально, разумеется, незавершаемый!) считается, тем не менее,
протекшим “до конца” и завершившимся, в результате чего возникает
новый объект рассмотрения — множество всех слов в данном алфавите,
так что слова в данном алфавите суть элементы этого множества».
Основные операции над словами в алфавите
Соглашение.
1. Будем считать, что уже определён предикат
=:АхА—>{0,1},
который называется «равенство букв алфавита А».
//ijroit i-i
2. Будем считать, что уже определён предикат
=:А*—>{0,1},
который называется «проверка слова в алфавите А на пустоту».
Пусть ае А, а е А*.
Определение.
1. Головой слова изА+ назовём отображение Head: А+ —> А, если
def
Head(a-a) = а.
2. Хвостом слова из А+ назовём отображение Tail: А+ —» А*, если
def
Tail(a-a) = a.
3. Последним в слове изА+ назовём отображение Last: А+ -> А, ре-
зультат которого индуктивно определяется следующим образом:
def Head(a), если Tail(a) = A,
Last(a) = s
Last(Tail(a)), если Tail(a)^A.
4. Без последнего в слове изА+ будем называть отображение Body:
А+ А*, результат которого индуктивно определяется так:
def Гл если Tail (а) = Л,
Body(a) =
|Head(a)Body(Tail(a)), если Tail(a)^A.
Приведём индуктивное определение операции «длина слова в ал-
фавите А». Пусть a е А*.
Определение.
Длиной слова в алфавите А называется отображение len: А*—> N,
индуктивно определяемое следующим образом:
. r def 0, если а = Л,
1еп(а) — <
len(Tail(a))+l, если а^Л.
Пример (применения индутсшиеного определения).
def def
Пусть А = {а, Ь, с}, а = Ьса. Тогда
def def
len(a) = len(bca) = len(ca)+l = (len(a)+l) + l = (Qen(A)+l)-i-l)-i-l = 3.
https: "u rait.ru
36
Предикат «равенство слов в алфавите»
Интуитивно ясно, что графически равными (или просто равны-
ми) естественно назвать слова а и Р, записи которых одинаковы.
Пусть А — алфавит, п, k е N\{0}.
Определение (содержательное) (по [13, с. 18—19]).
1. Все пустые слова будем считать равными словами в алфавите А.
2. Будем считать два непустых слова а^.а^ и Ьг...Ьк в алфавите
А равными словами в алфавите А (и обозначать: a-^..Оц =
если п = к и аг = Ъ1} ..., ап = Ьк.
Приведём соответствующее индуктивное определение.
Пусть а, Р е А*.
Определение (индуктивное).
Назовём равенством слов в алфавите А предикат =: А* хА*—>В2,
индуктивно определяемый следующим образом:
И, еслиа = Л&0 = Л,
а = р = Head(a) = Head(P) & Tail(a) = Tail(P), если а Л & p Л,
Л, если (a^A&p = A)v(a = A&P^A).
Определение.
Неравными словами а и Р (обозначение: а ± Р) будем называть
слова
def
а и Р, для которых a = р = Л.
Пример (применения индуктивного определения).
def def def
Пусть А = {a, b, с}, a = abc, Р = abed. Установим, верно ли, что
а = 0:
def def def
a = p = abc = abed = (a = a)&(b = b)&(c = cd) =
def def def
= (a = a)&(b = b)&(c = c)&(A = d) = H&(A = d) = И&Л = Л=>а*р.
37
Алгебраическая операция приписывания слов
Действие надо начинать с того, чего
ещё нет... Ибо большое дерево вырастает
из маленького, девятиэтажная башня
начинает строиться из горстки земли,
путешествие в тысячу ли начинается
с одного шага.
Дао дэ Цзин, § 64
Основной двухместной алгебраической операцией на множестве
А* является операция приписывания слова 0 к слову а.
Пусть а, Р е А*.
Определение (содержательное).
Результатом операции приписывания слова 0 к слову а назовём
слово, обозначаемое а0 и получаемое записью слова 0 непосред-
ственно после слова а.
В другой терминологии слово а0 называют «соединением», «кон-
катенацией», «сцеплением», «катенацией» [166, с. 9], «умножени-
ем», «произведением» слов а и 0.
Операцию приписывания называют при этом соответственно
«операцией соединения слов», «конкатенацией слов», «сцеплением
слов», «катенацией», «умножением слов», «произведением слов».
Определение (индуктивное).
Операцией приписывания слова 0 к слову а назовём бинарную ал-
гебраическую операцию
о:А*хА*—>А*,
результат которой (обозначается: а° 0 или просто а0) индуктив-
но определяется так (а • а обозначает результат операции левого
присоединения буквы а е А к слову а):
def [0, если а = Л,
а°0 = <
Head(a)-(Tail(a)o0), если а^Л.
Пример (применения индуктивного определения).
def def def
Пусть А = {а, b, с}, а = ab, 0 = dcd. Тогда, если — знак операции
левого присоединения буквы к слову, то получим:
def def def
a°0 = a (boded) = a(b(Aodcd)) = a (b dcd) = abdcd.
38
https: "lira it.ru
Для определения операции приписывания слова 0 к слову а с по-
мощью операции правого присоединения буквы к слову воспользу-
емся алгебраической операцией «обращение слова».
Определение.
1. Обращением слова а (обозначается: Reverse (а) или aR) назы-
вается отображение
Reverse: А* А*,
результат которого определяется следующим индуктивным об-
разом:
def Л, если а = Л,
Reverse (а) =
Reverse(Tail(a))Head(a), если а Л.
2. Симметричным словом (палиндромом) в алфавите А будем на-
зывать такое слово а в алфавите А, для которого Reverse (а) = а.
Примеры.
def
1. Пусть а = 123 — слово в алфавите {1,2, 3}. Тогда:
def def def
Reverse(123) = Reverse(23)l = (Reverse (3)-2)-1 =
def def def
= ((Reverse(A)-3)-2)l = ((A-3)-2)l = 321.
Итак, a не является симметричным словом в {1, 2, 3}.
2. Reverse (рое) - вор; Reverse (ток) - кот; Reverse (телекс) - скелет.
Определение (индуктивное).
Операцией приписывания слова 0 к слову а назовём бинарную ал-
гебраическую операцию
о:А*хА*->А*,
результат которой (обозначается: a ° 0 или просто а0) индуктив-
но определяется следующим образом (а • а обозначает результат
операции правого присоединения буквы а е А к слову а):
def а, если 0 = Л,
а°0 = < (aoReverse(Tail(Reverse(0))))-Head(Reverse(0)), если 0^Л.
Слово р без последней буквы Последняя буква р
39
https:it.ru
Пример (применения индуктивного определения).
def def def
Пусть А = {а, b, с}, а = ab, 0 = dcd. Тогда, если — знак операции
правого присоединения буквы к слову, то получим:
def def def def def
a°0 = abodcd = (abodc)d = ((ab°d)-c)-d = (((aboA)d)c)-d =
def
= ((ab • d) • c) • d = abdcd.
Теорема (свойства операции приписывания слова к слову).
1. Ассоциативность. Для любых а, 0, у е А* выполняется
(а о р) о у= а о (0 о у) = а о р о у.
2. Сократимость (закон сокращения). Для всяких слов а, 0, у е А*:
а) если а ° 0 = ос ° у, то 0 = у;
б) если а ° 0 = Y ° 0, то а = у.
3. Существование в А* нейтрального элемента относительно
операции приписывания. Для любого слова а е А* выполнено
Л о а = а о Л = а.
Доказательство.
1. Зафиксируем слова 0 и у. Воспользуемся индуктивным опре-
делением слова в алфавите.
Вначале пусть a = Л, тогда, используя индуктивное определение
операции приписывания слова к слову, получим:
def
(а О Р) о у= (Л О Р) О у = Р о у}
def
а о (Р о у) = Л О (Р о у) = Р о у
и
(а ° Р) ° у=а ° (Р ° у).
Пусть теперь а Л, тогда а = а аг.
Предположим, что выполнено (аг о 0) о у = аг о (0 ° у), тогда
def def
(a°0)oy = ((a-ajjopjoy = Head((aa1)op)(Tail((aa1)op)oy) =
= а((а1 о0)о у) = а-а1 о(роу) = ао(0оу).
Итак, из предположения о том, что (cq о 0) о у = 04 о (0 о у)
удалось получить, что (а ° 0) ° у = а ° (0 ° у). Поэтому можно ут-
верждать, что доказательство пункта 1 завершено.
40
ittpS'/Z'JCSit !'!
2. Рассмотрим только доказательство пункта а. Воспользуемся
определением равенства слов в алфавите. Пусть а = Л. Тогда Л °
° Р = Л ° у, остаётся воспользоваться индуктивным определением
операции приписывания слова к слову и получить, что Р = у. Пусть
теперь а Ф Л, тогда а = а • аг. Предположим, что если cq ° Р = cq ° у,
то Р = у. Воспользуемся индуктивным определением равенства слов
в алфавите:
def
(аор) = (аоу) = (аа1)ор) =
def
= (а-(Xi) ° у = (а = а&аг °Р = а1 °у) = а1 °Р = а1 оу,
а тогда Р = у.
3. Доказательство следует из индуктивного определения опера-
ции приписывания слова к слову. Во-первых, очевидно, что Л ° а =
а; во-вторых, докажем, что а ° Л = а. Если а = Л, то Л о Д = Д. Пусть
теперь а Л, тогда а = а • Пусть аг ° Л = аг. Тогда
def def
аоД = (а-а1)оД = а-(аА оД) = а-а1 =а.
Теорема доказана.
Пусть k е N.
Определение.
к-й степенью слова а (относительно операции приписывания)
в алфавите А будем называть отображение к: А* —» А*, результат
которого индуктивно определяется следующим образом:
def
ак =
Л, если к = 0,
ак~г ° а, если к 0.
Теорема (по [166, с. 9]).
Для всех слов а, Р и неотрицательных целых к имеют место ра-
венства:
1) 1еп(аР) = 1еп(а)+1еп(Р);
2) len(afc) = klen(a).
Доказательство. Упражняйтесь.
Итак, функция «длина слова» обладает некоторыми формальны-
ми свойствами элементарной функции «логарифм».
Определение (содержательное) (по [166, с. 21]).
Примитивным корнем из слова а называется (и обозначается р(а))
слово Р наименьшей длины такое, что a = Pfc для подходящего на-
турального к > 1.
41
https:it.ru
Замечания.
1. Приведём несколько примеров палиндромов в естественном языке:
казак, шалаш, ротатор и т. д. Существует даже довольно распространён-
ная литературная игра, суть которой сводится к построению предложе-
ний, обладающих следующим свойством: если из него удалить все про-
белы и знаки препинания, а все заглавные буквы заменить строчными,
то получится слово-палиндром. Этой игрой увлекались многие писатели.
Приведём примеры:
а) «Я иду смечем, судия» (Г. Р. Державин);
здесь следует отметить не соответствующее нормам современной
грамматики склонение слова «меч» — в наши дни в творительном падеже
следует писать не «мечём», а «мечом»;
б) «А роза упала налапуАзора» (А. Фет).
2. Операцию приписывания слова Р к слову а можно определить
с помощью отображений Last и Body следующим образом:
а°Р
def [а, еслиР = Л,
(a°Body(P)) Last(P), если р^ Л.
Подслова и их вхождения в слово
Пусть а, Р, у, 8, Pi, Yi, 8j g А*, х g А, * g А.
Определение.
1. Подсловом слова а называется такое слово Р, для которого су-
ществуют такие слова у и 8, для которых а = уР8. При этом:
а) вхождением слова Р в слово а называется тройка (у, Р, 8);
б) ^-вхождением слова Р в слово а называется слово у*Р*8; левым
крылом *-вхождения у*Р*8 называется слово у; правым крылом
*-вхождения у*Р*8 называется слово 8; основой *-вхождения
у*Р*8 называется слово р.
Другими словами, вхождением слова Р в слово а можно назвать
слово Р вместе с местом его расположения в слове а.
2. Вхождением буквы b в слово а называется вхождение (у, Ь, 8)
в слово а однобуквенного слова Ь. Будем говорить, что буква b вхо-
дит в слово а, если существует вхождение буквы b в слово а.
3. «Различными вхождениями слова Р в слово а будем называть
такие два *-вхождения у*Р*8 и у1*Р*81, для которых у ± уг или 8 ± 81.
Определение.
Декатенацией называется операция представления слова в виде
конкатенации двух или более подслов.
Определение (индуктивное).
Индуктивное определение двухместного предиката «вхождение
буквы х в слово а« (обозначается Int(x, а)) выглядит так:
42
//i iroit pi ।
def Г Л, если а = Л,
= <
х = Head (а) vlnt(x, Tail(a)), если а^Л.
Пусть х е А.
Определение (содержательное) (по [154, с. 24]).
Степенью слова а относительно х (обозначается dx(a)) называ-
ется количество вхождений буквы х в слово а.
Определение (индуктивное).
Индуктивное определение двухместной функции «степень слова
а относительно х» (обозначается St (х, а)) выглядит так:
def
St(x, a) =
О, если а-А,
St(x,Tail(a)), если x^Head(a),
l+St(x,Tail(a)), если x = Head(a).
Теорема (по [154 ,c. 127]).
len(a)= X dx(a).
xeA
Доказательство. Упражняйтесь.
Определение.
1. Первым вхождением слова 0 в слово а будем называть такое
♦-вхождение У1*0*813 для которого слово Yi имеет наименьшую
длину среди всех слов у, для которых a = у08.
2. Последним вхождением слова 0 в слово а будем называть такое
♦-вхождение у1*0*81, Для которого слово 83 имеет наименьшую
длину среди всех слов 8, для которых a = у08.
Для некоторых подслов используется специальная терминология.
Определение.
1. Началом (префиксом) слова а называется такое слово 0, для
которого a = 08 для некоторого слова 8.
Другими словами, началом слова а называется любое *-вхожде-
ние Л*0*8 с пустым левым крылом.
2. Концом (суффиксом) слова а называется такое слово 0 для ко-
торого a = у0 для некоторого слова у.
Другими словами, концом слова а называется любое *-вхождение
у*0*Л с пустым правым крылом.
3. Собственным префиксом слова 0 назовём такое слово а Ф 0, ко-
торое является префиксом слова 0.
43
https:it.ru
4. Собственным суффиксом слова 0 назовём такое слово а Ф 0, ко-
торое является суффиксом слова 0.
Пример.
Для слова Ьа префиксами являются A, b, Ьа, суффиксами — Л, а, Ьа,
собственными префиксами — Л, Ь, собственными суффиксами — Л, а.
Лемма.
1. Л является подсловом, началом и концом любого слова.
2. Всякое начало и всякий конец любого слова являются его под-
словами.
3. В любом непустом слове существуют различные начала и раз-
личные концы.
Доказательство. Упражняйтесь.
Определение.
1. Будем говорить, что вхождение слова 0г в слово 0 является од-
новременно и вхождением его в слово а, если а = у0г8, 0 = у10181 и
а) либо у является концом слова у15 а 8г — началом слова 8;
б) либо Yi является концом слова у, а 8 — началом слова 8г;
в) либо Yi является концом слова у, а 8г — началом слова 8;
г) либо у является концом слова Yi, а 8 — началом слова 8Г
2. Будем говорить, что вхождение подслова 0г начинает вхожде-
ние (или является началом вхождения') подслова 0 в слово а, если
а = у08, a 0 = 0Д.
3. Будем говорить, что вхождения (у15 015 8г) и (у2, 02, 82) слов
01 и 02 соответственно в слово а не имеют общих вхождений букв
алфавита, если а = Yi0i830282 или а = у202830181 для некоторого
слова 83 (возможно пустого).
Замечание.
Использование в содержательных математических доказательствах
определения понятия «вхождение» с помощью понятия «кортеж» ока-
зывается не совсем удобным. Например, смысл фразы «вхождение слова
Yi в слово у2 является также и вхождением в слово а« совершенно поня-
тен, однако такое использование термина «вхождение» не соответствует
«языку троек». Поэтому на «языке троек» это утверждение выражается
менее удобным способом, и мы всюду стараемся пользоваться термино-
логией, которая основывается в значительной мере на зрительных пред-
ставлениях о понятии «вхождение». Приведём несколько примеров.
Пусть а — слово в некотором алфавите, a Yj и у2— его подслова.
1. Будем говорить, что вхождение ц = (015 у1} Si) слова Yi в слово а начи-
нает вхождение 0 = (02, $г) слова у2 в слово а, если = 02, а слово
б2 является концом слова 8V
Естественность такого определения иллюстрируется рисунком:
44
https: "и га-t.ru
^q^^^ZqZZqZZo^o——о—о—о——о——о
e -p2—--------y2------^s2—
------------a---------------
2. Будем говорить, что вхождение ц = (Р15 Yi, 8]) слова Yi целиком содер-
жится во вхождении 0 = ф2, у2, б2) слова у2 в слово а, если слово Р2 явля-
ется началом слова pv а слово б2 — концом слова 8Р
Естественность такого определения иллюстрируется рисунком:
6 -р2^------Y2-----^82—'
-----------a------------
3. Будем говорить, что вхождения ц = (Р15 Yi, 8J и 0 = СР2, Y2, §2)
содержат общее вхождение слова у3, если существует вхождение слова
Y3 в слово Yi,которое целиком содержится как во вхождении (Р1} Yi> 8Д
так и во вхождении СР2, Уг, б2).
Естественность такого определения иллюстрируется рисунком:
^Y3—'
6;---Р2--Y2--------—82-
Операция замены подслов
Определение (содержательное}.
Результатом трёхместной операции замены в слове а вхождения
у*Р*8 слова Р на слово Рг будем называть
def
Replace (а, у*р*8*р1) = уРД
(от англ, to replace — заменять}.
Пример.
def def
Пусть a = bababa, a Pi = ba. Тогда:
def def
1) если y*P*8 = b*aba*ba, to Replace (bababa, b*aba*ba, ba} = bbaba-,
def def
2} если y*P*8 = bab*aba*, to Replace (bababa, bab*aba*, ba} = babba.
Определение (индуктивное}.
Результат трёхместной операции замены в слове а *-вхождения
у*Р*8 слова Р на слово Рг определяется индуктивно так:
45
//| iroit
def
Replace(a,y,p,5,p1) =
Head (у) о Replace(a, Tail (у), p, 5, Pj) ,
если у Л,
HeadCPi) о Replace(a, у, p, 5, Tail^)),
если у = Л и рг Л,
Head(6) о Replace(a, у, р, Tail(5), Pi),
если Pi = Л и 5 Л, Л, если 5 = Л.
Пример (применения индуктивного определения).
def
Replace (abcdef, ab, cd, ef, gh) =
def def
= a о Replace (abcdef, b, cd, ef, gh) =
def def
= а о b о Replace (abcdef, A, cd, ef, gh) =
def def
= a о b ° g о Replace (abcdef, A, cd, ef, h) =
def def
= aobogoho Replace (abcdef, A, cd, ef, A) =
def def
= Gobogoftoeo Replace (abcdef, A, cd,f, A) =
def def
= a°bogohoe°f° Replace (abcdef, A, cd, A, A) =
def
= а о b о g о h о e ° f о A = abghef.
Замечание.
Часто используемое обозначение а (Р/Р]) для результата опера-
ции замены в слове а вхождения слова Р на слово Р] следует признать
не очень удачным, так как по данному обозначению (в котором исполь-
зованы лишь слова а, Р, Р]) непонятно, какое же вхождение слова 3 рас-
сматривается, а тогда является неопределённым и результат операции
замены. Отметим, что иногда применяется более удачное обозначение
а(у*Р*б, Р]). (Воистину, по Лао-цзы (Дао дэ цзин, § 1): «Имя, которое
может быть названо, не есть постоянное имя».)
46
Операция подстановки слова вместо буквы
Не осуждай ближнего своего, пока
не будешь на его месте.
Талмуд
Определение (содержательное).
Результатом трёхместной алгебраической операции подстанов-
ки в слово а вместо буквы х слова 0 будем называть (и обозначать
ссх [0] или ар, или (а)р ) результат операции замены в слове а всех
(!) вхождений буквы х на слово 0.
Примеры.
def def
1. (yxyxzx)* * * * * * * * * xX2X3 = yxyxzxx[x2x3] = yx2x3yx2x3zx2x3.
def
2. yxyxzxx[xyz] = yxyzyxyzzxyz.
Теперь приступим к построению индуктивных определений.
Определение (индуктивное).
Индуктивное определение двухместного предиката, который на-
зовём отсутствие вхождения буквы х в слово а (обозначается:
Nolnt(x, а)) выглядит так:
def [И, если а = Л,
Nolnt(x, а) = <{ ,, ч
х ф Head(a) & Nolnt(x, Tail(a)), если а Л.
Определение (индуктивное).
Трёхместной операцией подстановки в слово а вместо буквы
х слова 0 будем называть отображение
Subst: А* х А х А* -> А*
(от англ, substitution — подстановка), результат которого опреде-
ляется следующим индуктивным способом:
def
Subst(a, х, 0) =
а, если Nolnt(x, а) = И,
Л, если а = Л & Nolnt(x, а) * И,
Head(a) о Subst(Tail(a), х, 0),
если а ф Л & Head (а) ф х & Nolnt(x, а) * И,
0 о Subst(Tail(a), х, 0),
если а ф Л & Head (а) = х & Nolnt(x, а) ф И.
47
j [Hnc; Ih iroit 14
Примеры (применения индуктивного определения).
def def
1. Subst(abab, b, cd) = a о Subst(bab, b, cd) =
def def
a о cd о Subst(ab, b, cd) = a о cd о a о Subst(b, b, cd) =
def def def
= aocdoaocdoSubst(A,b,cd) = aocdoaocdoA = acdacd.
2. def def
Subst(bb, b, cd) = cd о Subst(b, b, cd) =
def def def
= cd ° cd ° Subst(A, b, cd) = cd°cd°A = cdcd.
def def
3. Subst(yxyxzx, x,x2x3) = у oSubst(xyxzx,x,x2x3) =
def def
= у о x2x3 ° Subst(yxzx, X, X2X3) =
def def
= у о X2X3 ° у ° Subst(X2X, X, Х2Х3) =
def def
= У о Х2Х3 оу о Х2Х3 о Subst(2X, X, х2х3) =
def def
= У ° Х2Х3 оу о Х2Х3 ozo Subst(X5 X, Х2Х3) =
def def
= У °х2х3 оу ох2х3 ozo х2х3 о Subst(A, X, Х2Х3) =
def
= У ° Х2Х3 ° у ° Х2Х3 ° 2 ° Х2Х3 о Л = УХ2Х3УХ2Х32Х2Х3.
Варианты операции подстановки
Пусть k е N\{0}, х15 хк е А, а, Ръ ..., Pfc е А*.
Определение (содержательное).
Результатом операции (одновременной) подстановки в слово
а вместо букв х1г ...,хк слов Р15 Pfc соответственно назовём
слово, полученное следующим образом: «просматривая» слово
а слева направо, заменим каждое встретившееся вхождение буквы
xm, me {1, ..., к}, на слово Рт. Результат операции (одновремен-
ной) подстановки обозначим:
tPli •••} РкК
Пример.
def
ааЬааЪ[х,ух] = ххухх.
48
Определение (индуктивное).
Операцией (одновременной) подстановки в слово а вместо букв х1г
х2, ...,хк слов Р1з 02> •••> Рк соответственно назовём отображение
Subst: А* х Ак х (А*)к -> А*,
результат которого определяется следующим индуктивным об-
разом:
def
Subst(a,x1J...Jxfcjp1J...Jpfc) =
а, если NoIntCXi, a) & Nolnt(x2, a) &... & NoIntCx*., a) = И,
Л, если a = A,
Head(a)oSubst(Tail(a), x15..., xfc,p15..., pfc),
def если Head(a) ф хг & Head(a) x2 &... & Head(a) ф xk,
P2 oSubst(Tail(a),x1,...,Xfc,P1,...,Pk), если Head(a) = x13
P2оSubst(Tail(a),х15...,хд.,Pk), если Head(a) = x2,
pfcoSubst(Tail(a),x1,...,Xfc,P1,...,Pk), если Head(a) = xfc.
Пример (применения индуктивного определения).
def
Subst(aabca, a, b, x, yx) =
def def def
= x о Subst(abca, a, b, x, ух) = x о x о Subst(bca, a, b, x, yx) =
def def def
= x ° x ° yx о Subst(ca, a, b, x, yx) = х°х°ухосо Subst(a, a, b, x, yx) =
def def def
= хохоухосохо8иЬ51(Л,а,Ь,х,ух) = x ° x° yx °c° x ° A. - xxyxcx.
Определение (содержательное).
Результат последовательного применения к раз операции под-
становки слова вместо буквы определим следующим образом:
аХ1[Р1]х2[р21-хДРк] = (-((«^[Pi]) Х2[р2])-) xJPkL
Пример.
def def def
abcaa[xy]x[a]a[b] = ((abcaa[xy])x[a])a[b] = (xybcxyx[a])a[b] =
def def
= aybcaya[b] = bybcby.
49
!!\ iroit 11
Определение (индуктивное).
Результат последовательного применения к раз операции подста-
новки слова вместо буквы определим индуктивно следующим об-
разом:
def
Subst(a,x1,...,xbp1,.--A) =
def fSubst(a, x13 рг), еслик=1,
= <
Subst(Subst(a,хг,...,xk,рг,...,pfc,k-T),xk,pfc), еслиk*l.
Пример (применения индуктивного определения).
def
Subst(abca, a, x, a, xy, a, b, 3) =
def def
= Subst(Subst(abca, a, x, a, xy, a, b, 2), a, b) =
def def
= Subst(Subst(Subst(abca, a, x, a, xy, a, b, 1), x, a), a, b) =
def def
= Subst(Subst(Subst(abca, a, xy), x, a), a, b) =
def def def
= SubstCSubstCxybcry, x, a), a, b) = Subst(aybcay, a, b) = bybcby.
Числовые функции, определённые на множестве слов
Определение (по [165, с. 101]).
1. Аддитивной числовой функцией, определённой на множестве
слов А*, будем называть отображение/: А* N, индуктивно опре-
деляемое для некоторой функции <р: А —> N следующим образом:
def о, если a = А,
/(а) = <
cp(Head(a)) + /(Tail(a)), если а А.
2. Мультипликативной числовой функцией, определённой на мно-
жестве слов А*, будем называть отображение/: А* N, индук-
тивно определяемое для некоторой функции <р: А —> N следую-
щим образом:
def 1 если a = А,
/(а) = <
cp(Head(a)) • /(Tail(a)), если а А.
3. Аддитивно-мультипликативной числовой функцией, опреде-
лённой на множестве слов А* (илиАМ-функцией), будем называть
пр //i iroi! ri
p’vJ.' i vjl UU.I v
50
отображение/: А* N, индуктивно определяемое для некоторых
функций ф, у: АN следующим образом (me N):
def т если а = Л,
/(а) = <
9(Head(a))+v(Head(a)) -/(Tail(a)), если а Л.
4. Марковской числовой функцией, определённой на множестве
слов А*, будем называть отображение/: А* —> N, которое индук-
тивно определяется для некоторой функции 6: А х N —> N следую-
щим образом (те N):
def т если а = Л,
/(а) = <
6(Head(a)), /(Tail(a))), если а Л.
Функции, частично определённые на множестве слов
Рассмотрим теперь две частичные алгебраические операции,
в определённом смысле «обратные» операции приписывания слова
к слову.
Определение (по [148, с. 20]).
1. Левым частным от деления слова а на слово 0 (обозначается
0\а и читается: «0 под а«) называется слово 8 такое, что a = 08.
2. Правым частным от деления слова а на слово 0 (обозначает-
ся а/0 и читается: «а над 0«) называется слово у такое, что a = у0.
Примеры [148, с. 21].
def def
1. око\окорок = рок, рокХрококо = око;
def def
2. рококо/око = рок; окорок/рок = око;
3. Не определен результат следующих операций:
рокХокорок, окоХрококо, окорок/око, рококо/рок.
Теперь определим индуктивно функции «левое» и «правое част-
ное от деления слова а на слово 0».
Определение (индуктивное).
1. Левым частным от деления слова а на слово 0 назовём ото-
бражение End: А* х А* А*, результат которого определяется так:
Не определено, если len(a)<len(0),
def
End (a, 0) = <
a, если 0 = Л,
End(Tail(a), Tail(0)), если 0 A&(Head(a) = Head(0)),
He определено, если 0 ф Л & (Head(a) ф Head(0)).
51
чНию-//i iroit ri .
2. Правым частным от деления слова а на слово 0 назовём ото-
бражение Rht: А* х А* А, результат которого определяется так:
def
Rht(a,0) = Reverse(End(Reverse(a),Reverse(P))).
Примеры.
def def def
1. End (окорок, око) = End (корок, ко) = End (орок, о) =
def def
= End (рок, Л) = рок.
def
2. End ((окорок, рок) = Не определено.
def
3. End (око, окорок) = Не определено.
def def
4. Rht (рококо, око) = Reverse (End (ококор, око)) =
def def
= Reverse (кор) = рок.
def def
5. Rht (окорок, око) = Reverse (End (короко, око)) = He определено.
Комментарий для любителей алгебры.
Полугруппа. Моноид слов
Как уже отмечалось, алгебраическая операция приписывания
слов в множестве А* всех слов в произвольном алфавите А ассоциа-
тивна, обладает свойством сократимости, а в множестве А* имеется
нейтральный относительно этой алгебраической операции элемент
(им является Л).
В алгебре множество с ассоциативной алгебраической операци-
ей принято называть полугруппой, а полугруппу с нейтральным эле-
ментом — моноидом. Таким образом, множество А* относительно
операции приписывания слов является моноидом. Моноидами так-
же являются: 1) множество натуральных чисел N (с нулём!), рассма-
триваемое относительно операции сложения натуральных чисел; 2)
множество натуральных чисел N, рассматриваемое относительно
операции умножения натуральных чисел.
Если использовать более точную алгебраическую терминологию,
то А* и А+ представляют собой свободный моноид и свободную полу-
группу с множеством образующих А.
Определение (по [159, кол. 1083-4]).
Свободными образующими называются буквы из А.
Свободная полугруппа над алфавитом А — это полугруппа, эле-
ментами которой являются всевозможные конечные последова-
тельности букв из А, а операция состоит в приписывании одной
последовательности к другой.
Свободный моноид — это свободная полугруппа с нулевым словом.
52
Метод математической индукции как распознающая процедура
Как стрелок выпрямляет стрелу, так
выпрямляет мудрец свою неустойчивую
и колеблющуюся мысль, строптивую
и непокорную.
Буддийская мудрость
Одним из способов описания характеристического свойства
элементов некоторого множества является задание распознающей
(в математике говорят разрешающей) процедуры, которая для лю-
бого объекта устанавливает, обладает ли он данным характеристи-
ческим свойством и, следовательно, является ли элементом данного
множества или нет. Одним из способов представления распознаю-
щей процедуры является метод математической индукции.
Метод математической индукции (от лат. inductio — наведе-
ние) — это основной метод доказательства в математике, применя-
емый для исследования характеристических свойств множеств слов
в алфавите.
Разновидности метода математической индукции укажем в сле-
дующей классификационной схеме:
Замечание (О. А. Иванов).
С формальной точки зрения суть метода математической индукции
состоит в том, чтобы избавиться от слов «и так далее до бесконечности»;
другими словами, избавиться в рассуждениях от многоточий.
1. Натуральная индукция
Кладите себе в уши мои слова.
И. Бабель
Натуральная индукция — это разновидность метода математи-
ческой индукции; более точно, натуральной индукцией называет-
ся метод доказательства утверждений в математике, основанный
на использовании принципа (аксиомы) математической индукции.
Пусть Р — некоторое свойство натуральных чисел.
53
https: //ц га it.ru
Определение (принцип математической индукции).
Допустим, что доказаны следующие утверждения:
1) натуральное число 0 обладает свойством Р;
2) если какое-нибудь натуральное число п обладает свойством
Р, то и следующее за ним число п' = п + 1 также обладает свой-
ством Р.
Тогда каждое натуральное число обладает свойством Р.
В доказательствах, использующих принцип математической ин-
дукции, мы будем пользоваться следующей терминологией. Пусть
требуется доказать предложение Р(п), состоящее в том, что нату-
ральное число п обладает свойством Р.
Определение (по [19, с. 27; 16, с. 155—156]).
1. Индукционным предложением (предложением индукции) назо-
вём предложение Р(п).
2. Индукционной переменной (переменной индукции, параметром
индукции) назовём переменную п.
3. Базисом индукции назовём доказательство предложения Р(0).
4. Индукционным шагом (шагом индукции, индукционным перехо-
дом) назовём доказательство предложения «если Р(п), то Р(п')».
5. Индуктивным предположением (предположением индукции)
назовём допущение Р(п), из которого в индукционном шаге вы-
водится Р(п').
Терминологию принципа математической индукции (для знато-
ков математической логики!) можно иллюстрировать следующим
образом:
Базис Индукционный Индукционное
индукции шаг предложение
Ф Ф Ф
Р(0) & Vn( Р(п) ->P(n')j ~>Vn Р(п)
I____________________I
?
Индуктивное
предположение
В математике используются различные типы индукционных
переменных: длина слова, сумма длин каких-либо слов, количество
вхождений в слово какой-либо буквы и т. п.
Математической индукцией можно пользоваться и при доказа-
тельстве предложения, зависящего не от натурального, а от целого
положительного числа; в этом случае базисом индукции является
доказательство предложения Р(1).
54
https:/Л: rait.ru
2. Модификации натуральной индукции
Определение (по [176, с. 343—344]).
1. Индукцией по отрезку [а, Ь] называется следующая схема до-
казательства. Пусть доказано, что:
а) Р(а);
б) Vn (а < п < b (Р(п) —» Р(п + 1))).
Тогда утверждение Р(п) для всех натуральных п из [а, Ь] доказано.
2. Индукцией спуска на отрезке [а, Ь] называется следующая схема
доказательства. Пусть доказано, что:
а) Р(Ъ);
б) Vn (а < и < b —> (Р(п + 1) —> Р(п))).
Тогда утверждение Р(п) для всех натуральных п из [а, Ь] доказано.
3. Индукцией с двойным базисом называется следующая схема до-
казательства. Пусть доказано, что:
а) Р(0) &Р(1);
б) Vn (Р(п) & Р(п + 1) Р(п 4- 2)).
Тогда утверждение Р(п) для всех натуральных п доказано.
(Подобным образом можно определить индукцию с тройным ба-
зисом, индукцию с четырёхкратным базисом и т. п.)
Пусть требуется доказать предложение Р(т, п), для всех нату-
ральных тип.
Определение (по [153 ,с. 57]).
Принципом двойной индукции называется следующая схема дока-
зательства. Пусть доказано, что:
а) Р(т, 0) для всех т;
б) Р(0, п) для всех п;
в) X/kX/l (P(k-1, Z) & P(k, Z—1) —> P(k, I) или (что эквивалентно):
в') VkVZ ((Vk' < k) (X/l' <l) (k' + 1' < k + l^ P(k', Z')) -> P(k, Z)).
Тогда утверждение P(m, ri) для всех натуральных тип доказано.
Определение (по [137]).
Методом мультипликативной индукции будем называть следу-
ющую схему доказательства. Пусть требуется доказать, что Р(п)
выполняется для каждого натурального числа п > 1, и пусть до-
казано, что:
а) Р(р) для всех простых чисел р;
б) (Vm > 1) P(m) Р(т • р)).
Тогда утверждение Р(п) для всех натуральных чисел п > 1 дока-
зано.
55
https: "и га it.ru
Замечания.
1. Метод математической индукции в неявном виде использовался
уже в «Началах» Евклида. Слово «индукция» было введено в математику
Валлисом («Всеобщая Арифметика», 1656), который заимствовал термин
из философии (у Бэкона), где он означал переход от частного к общему;
в отчётливой же форме он впервые встречается в работе Б. Паскаля о ком-
бинаторике (около 1665). После этого в течение долгого времени тер-
мин употребляли случайно как для обозначения метода математики, так
и в общефилософском смысле. Термин «математическая индукция» впер-
вые появился в Британской Энциклопедии (1838) в статье де Моргана
«Индукция (математическая)»; далее его многократно употреблял Тодген-
тер в учебнике алгебры, после чего термин стал общепринятым.
2. Метод мультипликативной индукции обосновывается теоремой
об однозначности разложения натуральных чисел, больших единицы,
на простые сомножители.
3. Полная (возвратная) индукция
Примем без доказательства (оно опирается на аксиому матема-
тической индукции) следующую важную теорему.
Теорема (полная индукция, возвратная индукция).
Пусть свойство Р таково, что для любого натурального числа
п из того, что этим свойством обладают все натуральные числа,
меньшие п, следует, что им обладает и число п. Тогда свойством
Р обладают все натуральные числа.
Сказанное можно записать формально следующими способами:
a) Vn (Vm (т < п Р(т)) Р(п)) Х/пР(п) (без базы индук-
ции);
б) Р(0) & (Х/п > 1) (Vm (т < п Р(т)) Р(п)) Х/пР(п) (с ба-
зой индукции).
Итак, для проведения индукционного шага можно допустить
в качестве индуктивного предположения не просто Р(п), а то, что
«выполняется Р(т) для всех т < п». Эта форма принципа математи-
ческой индукции называется полной (возвратной) индукцией.
Терминологию принципа полной индукции можно иллюстриро-
вать (для знатоков математической логики) следующим образом:
Базис Индукционный Индукционное
индукции шаг предложение
Ф Ф Ф
Р(0) & (Vn>l)(Vm(т<п—>Р(т)) —>Р(п)) —>Х/п Р(п)
।_________________________________।
Т
Индуктивное
предположение
56
ttps://ura it.ru
Контрольные вопросы
Конструктор Трурль создал однажды
машину, которая умела делать всё
на букву «Н». Закончив эту машину,
он на пробу заставил ее сделать Нитки,
потом намотать их на Напёрстки,
которые она также сделала, затем
бросить всё это в специально вырытую
Нору, окружённую Незабудками,
Наличниками и Настойками.
С. Лем.
Как уцелела вселенная
1. Имеет ли смысл словосочетание «множество слов русского языка»?
2. Укажите место в тексте «Теоретических сведений», в котором буква
х использовалась в качестве синтаксической переменной, и то место, где
буква х использовалась в качестве имени буквы алфавита?
def def def def
3. Пусть A = {0,1,2}, x = 01, у = 2, z = 011. Определите длины сле-
дующих слов в алфавите A: xy,yz, xyz, х4, х3у2, (ху)2, (ухх)3.
4.
А. Какие из слов ab, a, abb, ас являются подсловами слова baba?
Б. Сколько начал имеет слово хуху?
В. Сколько непустых начал имеет слово хрс-рсрс^ в алфавите {х1} х2}?
Г. Может ли начало слова также быть его концом?
Д. Выпишите все префиксы, все суффиксы и все подслова слов abc и adb.
Е. Выпишите все подслова слова ababa. Сколько различных вхождений
в это слово имеет каждое из его подслов?
5.
А. Сколько вхождений в слово ababab имеет слово bab?
Б. Каково последнее вхождение слова хух в слово ухухухуху?
В. Сколько различных подслов слова х1х2х1х2х1х2х1 в алфавите {х1} х2}
имеют в него ровно два вхождения?
Г. Сколько различных вхождений имеет пустое слово в слово abaca?
Д. [13] Сколько различных вхождений имеет пустое слово в слово длины п?
6.
А. Замените второе вхождение слова хух в слово хухухух на слово хх.
Б. Может ли в результате замены вхождения подслова в слово на новое
слово получиться слово длины меньшей, чем исходное слово?
В. Найдите подслова слова хрс-рсрс^хрс-р^ в алфавите {х1} х2}, имеющие
в него ровно два вхождения. Замените в найденных подсловах первое из этих
вхождений на слово XjX^.
7. Найдите результат применения к слову а следующих подстановок:
а) а[ЬаЬ],аъ[ЬаЬ];
def def
б) а.а[Р], если а = aababb, Р = bab;
в) хуххухх[я]у[х]2[у];
г) (а + b)ab([A]j[A];
д) хуххухху2![я,х,у].
57
https: //цга it.ru
8.
А. В каких случаях результат подстановки в слово а вместо буквы х слова
Р совпадает с исходным словом а, т. е. ос^ЕР] = а?
Б. Может ли после замены вхождения подслова в слово получиться
тот же результат, что и после подстановки в это же слово вместо буквы не-
которого подслова?
9. Определите термин «корень п-ой степени из слова» (п — натуральное
число) по аналогии с термином «корень п-ой степени из натурального чис-
ла». Например, корень четвертой степени из аЪаЪаЪаЪ — это аЪ, а корень
второй степени — abab.
10. Покажите, что встречающиеся в тексте раздела «Теоретические све-
дения» определения термина «длина слова» эквивалентны.
11. Покажите, что функция 1еп(а) является аддитивной числовой функ-
цией.
12.
А. Относительно какой операции множество слов является моноидом?
Б. Верно ли, что всякая группа является моноидом?
В. Может ли моноид всех слов в каком-либо алфавите быть группой?
Примеры решения некоторых
типов упражнений
— Дорогой мой, — сказала машина, —
если бяумела делать все на «Н» на всевозможных
языках, то я была бы Машина, Которая Может
Делать Все В Пределах Всего Алфавита, потому
что любая вещь на каком-либо из языков
наверняка начинается на «Н». Дело обстоит
не так хорошо. Я не могу сделать больше, чем
ты придумал. Азота не будет.
С. Лем. Как уцелела вселенная
def
Пример 1. Выясните, сколько различных подслов слова а = babababab
имеет в него ровно 3 вхождения.
Решение. Будем рассматривать подслова в порядке возрастания
и порядке убывания их длин поочередно.
1) Л имеет 10 различных вхождений в а:
A*babababab, b*A*abababab,..., babababab*A;
2) слово а имеет лишь одно вхождение в а;
3) однобуквенные слова а и b имеют соответственно 4 и 5 вхождений
в слово а;
4) слово а имеет длину 9; его подслово длины 8 должно быть либо
началом, либо концом слова а, поэтому не может иметь более двух вхож-
дений в слово а;
5) для подслов длин 2,3,4, 5,6, 7 удобно построить таблицу, из кото-
рой легко определить число их вхождений в слово а:
58
https:/Л: rait.ru
Длины 2 Длины 3 Длины 4 Длины 5 Длины 6 Длины 7
Подслова, начинающиеся с буквы «Ь»
babababab babababab babababab babababab babababab babababab
ba bab baba babab bababa bababab
ba bab baba babab bababa bababab
ba bab baba babab
ba bab
Подслова, начинающиеся с буквы «а»
babababab babababab babababab babababab babababab babababab
ab aba abab ababa ababab abababa
ab aba abab ababa ababab
ab aba abab
ab
Итак, ровно 4 подслова имеют по 3 вхождения в данное слово.
Пример 2. Из слова zyxx получите слово zzyxyx, пользуясь подстанов-
ками at[₽] слов вместо букв.
Решение. Допустим, что из слова zyxx последовательными подстанов-
ками непустых слов вместо букв х, у и z мы получили некоторое слово
a: zyxxr[P]y|y]z[5] = а (слова Р, у, 5 не обязаны быть различными). Тогда
а = буРР. Слово zzyxyx можно представить в виде буРР, где б=z, у=z, Р =ух.
Такое представление наводит на мысль о возможности получения требуе-
мого слова с помощью подстановок видов ...Х[ух] и ...y[z]. Однако важен
порядок применения этих подстановок:
syxx±[yx]y[z] = zyyxyxy[z] = zzzxzxz, zyxx^[z]x[yx] = zzxx^.[yx] = zzyxyx,
причем последняя последовательность подстановок позволяет получить
требуемое слово.
Замечания.
1. Решением задачи служит последняя цепочка равенств:
zyxx^[z]x [ух] = zzxx^fyx] = zzyxyx.
Остальные рассуждения лишь воспроизводят поиск этого решения.
2. Поиск решения представляет собой лишь возможные рассужде-
ния, а не применение некоторого алгоритма решения (алгоритм реше-
ния задач подобного рода нам неизвестен).
Пример 3 [154, с. 170]. Пусть А — алфавит, а15 а2, 3 е а1> а2 *
Л. Докажите, что если о^Р = Рсс2, то найдутся слова у, б е А*, для которых
«2 = уб и а2 = Sy-
59
Решение. Доказательство проведём с помощью полной (возвратной)
индукции по длине слова р.
База индукции.
Если 1еп(Р) = 0, то Р = Л, а тогда оцЛ = Ла2 и ocj = а2. Теперь остаётся
def def
положить у = а1} а 5 = Л.
Шаг индукции.
Пусть теперь:
1) 1еп(Р) > 0;
2) для всех Р' е А*, для которых len(P') < len(P), выполняется утверж-
дение: «если ocj Ф Л, а2 Ф Л, QjP' = Р'а2, то найдутся такие слова у, 8 е А*,
для которых ocj = уб и а2 = 8у«;
3) Р = Рсс2. Требуется доказать, что найдутся слова у, 8 е А*, для кото-
рых = у8 и а2 = 8у.
Для продолжения доказательства воспользуемся следующей теоре-
мой: если для слов а, Р, у, 8 в алфавите А выполнено ay = Р8, то истинно
хотя бы одно из двух утверждений: а) а есть начало Р, а 8 есть конец у;
б) Р есть начало а, а у есть конец 8.
Теперь можно утверждать, что выполнено хотя бы одно из условий:
а) есть начало слова Р, а сс2 есть конец Р;
б) Р есть начало слова Ор Р есть конец а2.
В случае пункта а имеем Р = оцР' для некоторого слова Р' е А* (тот
факт, что «сс2 есть конец Р« нам здесь не понадобится). Теперь с помощью
QjP = Ра2 получаем, что о^о^Р' = о^Р'о^, а благодаря сократимости опера-
ции приписывания слов и о^Р' = Р'сс2. Очевидно, что выполняется len (Р') <
< len (Р) и остается воспользоваться пунктом (2).
В случае б имеем: ocj = РР' и а2 = еР для некоторых слов Р', е е А*.
Теперь с помощью оцР = Ра2 получаем, что РР'Р = РеР, а благодаря
сократимости операции приписывания слов и Р' = е.
Поэтому ocj = РР', а2 = Р'Р
Упражнения для самостоятельного решения
Многие (...) предпочитают задачи,
которые можно без труда объяснить даже
полному профану в соответствующей
области, таким задачам, в которых
основная трудность заключается в том,
чтобы разобраться во введённых понятиях.
А. Саломаа
Конструирование слов с требуемыми свойствами
1. Найдите все слова в алфавите {а, Ъ}, имеющие: а) три различных не-
пустых подслова; б) четыре различных непустых подслова.
2. Приведите пример слова в алфавите {а, Ъ}, которое имеет вхождения
каждой из букв алфавита и ровно 5 непустых подслов.
3. Найдите все слова наибольшей длины в алфавите {а, Ь}, обладающие
тем свойством, что в каждое из этих слов всякое подслово, длина которого
больше единицы, входит не более одного раза.
60
https://urait.ru
4. Какое наибольшее количество различных подслов длины 2 может
иметь слово, содержащее вхождения ровно двух различных букв алфавита?
Приведите пример такого слова наименьшей длины.
5. Приведите пример слова а, содержащего все буквы алфавита, и такого,
что после удаления из него любого вхождения любой буквы получается сло-
во, имеющее то же множество подслов длины 2, что и слово а. Рассмотрите
два алфавита: {а, Ъ} и {а, Ь, с}.
6. Докажите, что в алфавите {а, Ь} для всякого п > 6 существует слово
ос длины и, имеющее вхождения различных букв и такое, что после вычерки-
вания из него любого вхождения любой буквы, получается слово, имеющее
то же множество подслов длины 2, что и слово а.
Операция подстановки в словах
7. А. С помощью подстановки вида oct[P] слова вместо буквы получите
из слова ху слово zxyzxy.
Б. Из слова ху получите слово zyxzyx, пользуясь подстановками слов
вместо букв oct[P].
В. Получите слово ЪаЪЪЪаЪЪ из слова abc, пользуясь подстановками вида
оЦР], где ос, Р g {a, b, с}*, х g {а, Ь, с}.
8. Приведите пример такого слова а в алфавитах {а, Ъ} и {а, Ъ, с}, что
aa[ab] = ось [Ьа]. Какова наименьшая длина такого слова?
9. Как подстановками вида осДр] из слова ab в алфавите {а, Ь, с} полу-
чить слово Ьа? Возможно ли это сделать в алфавите {а, Ь}?
10. С помощью подстановки слов вместо букв вида ol.v[P, у] получите
def def
из слова а = хууху слово 8 = уххухуухху. Как получить слово 8 в алфавите
{а, Ъ, х, у} из слова а подстановками слов вместо вхождений одной буквы
(т.е подстановками вида Pt[y]? Возможно ли это сделать в алфавите {х,у}?
11. Можно ли из слова х^зХзХ^Хз получить подстановками букв вместо
букв следующие слова: а) х-рсрс-рс-рсрс^, б) х-рсрс-рс-рсрс^
Свойства операции приписывания слов
12. (По [108, с. 20, № 28].) Обозначим Join (a, Р) результат операции
приписывания слова Р к слову а. Какое из следующих утверждений является
верным, если а * Л?
A. Join(Head(oc), Tail(a)) = a;
В. Head(Tail(a)) = Tail(Head(a));
C. Join(Head(a), a) = Join(a,Tail(a));
D. Head(Tail(a)) = a;
E. Tail(Head(oc)) = a.
13. Пусть a, P g А*. Докажите, что:
A. (aP)R = PRaR;
Б. (aR)R = a.
Рекомендация. А. Доказательство проведите индукцией по сумме длин
слов а и р. Б. Доказательство проведите индукцией по длине слова а.
14. (По [108, с. 20, № 29].) Результат какой из перечисленных ниже
операций совпадает с обращением непустого слова а?
A. Join(Reverse(Tail(oc)), Head(a));
В. Join(Tail(Reverse(oc)), Head(a));
С. Join(Tail(a), Head(a));
D. Reverse(Join (Head(o), Tail(oc)));
61
https:it.ru
E. Join(Head(a), Reverse (Tail (a))).
15. Докажите, что:
а) если для слов а, Р, у, 5 в алфавите А выполнено ay=Р8, и len(a) = 1еп(Р),
то а = Р;
6) [97, с. 15, № 1.1.4] если вхождения у = oqtpPj и у = а2фР2 различны,
то lenten) ф lenCo^).
Рекомендация. Доказательство пункта а проведите индукцией по сумме
длин слов а и у.
16*. (По [30, с. 19].) Докажите, что если для слов а, р, у, 8 в алфавите
А выполнено ay=Р8, то истинно хотя бы одно из двух утверждений: а) а есть
начало Р, а 8 есть конец у; б) Р есть начало а, а у есть конец 3.
Могут ли одновременно выполняться условия а и б?
Рекомендация. Доказательство проведите индукцией по сумме длин слов
а и у.
17. Пусть а, Р — слова в некотором алфавите А. Докажите следующие
утверждения:
а)* [157, с. 497; 30, с. 19; 154, с. 390; 143, с. 192—194] равенство
аР = Ра выполняется тогда и только тогда, когда существует слово у g А*
такое, что а = ут и р = уп для подходящих неотрицательных целых тип;
б)* (по [143, с. 192—194]) если аР ф Ра, то при всех т, п g N\{0} вы-
полнено ат ф Рп;
в) [143, с. 192—194] если аР Ф Ра, то равенство amPn = afcPfc при к, т,
п е N выполняется тогда и только тогда, когда к = т = п.
Рекомендация. Доказательство пункта а проведите индукцией по сумме
длин слов а и Р, начиная с суммы, равной 0, и воспользуйтесь результатом
задачи № 16.
18*. Пусть А—некоторый алфавит. Докажите, что существует единствен-
ный примитивный корень р(а) из любого непустого слова а из А*.
Рекомендация. Используйте тот факт, что: а) каждое слово из А* есть
натуральная степень некоторого слова из А*; б) в любом множестве нату-
ральных чисел существует наименьшее число.
19*. (По [30, с. 19].) Пусть А — произвольный алфавит, a, Р, у G А*. До-
кажите, что из равенства а2Р2 = у2 следует, что аР = Ра.
https: //ц га it.ru
Упражнение 2
ИНДУКТИВНОЕ ОПРЕДЕЛЕНИЕ МНОЖЕСТВА
СЛОВ В АЛФАВИТЕ. ИСЧИСЛЕНИЯ
НА СЛОВАХ В АЛФАВИТЕ. ФОРМАЛЬНЫЕ
ДОКАЗАТЕЛЬСТВА В ИСЧИСЛЕНИЯХ
НА СЛОВАХ В АЛФАВИТЕ
Эти правила, язык знаков и грамматика
Игры представляют собой некую разновидность
высокоразвитого тайного языка, в котором
участвуют самые разные науки и искусства,
но прежде всего математика и музыка
(или музыковедение), и который способен
выразить и соотнести содержание и выводы
чуть ли не всех наук.
Г. Гессе. Игра в бисер
Обязательные результаты обучения:
• знать основные понятия
— индуктивное определение множества слов в алфавите;
— индукция по построению объектов, индукция по построению слов
в алфавите;
— исчисление математических объектов;
— определение множества слов в алфавите с помощью исчисления на сло-
вах, аксиомы и правила исчисления;
— линейное и древесное доказательства в исчислении на словах;
— вывод из посылок в исчислении на словах;
— допустимые правила в исчислении на словах; линейное и древесное
квазидоказательства в исчислении на словах;
— определение функции индукцией по построению множества слов;
— элементы истории создания буквенного исчисления;
• уметь
— применять правила построения слов в исчислении на словах;
— формализовать правила построения (порождения) слов в исчислении
на словах, представленных на естественном языке;
— доказывать характеристические свойства множеств слов, определён-
ных (порождаемых) заданными исчислениями на словах;
— предъявлять множество слов, определяемое заданным исчислением
на словах;
63
https:/Л: rait.ru
— устанавливать соотношения между множествами слов, порождаемых
разными исчислениями на словах, и конструировать их доказательства;
— конструировать индуктивные определения множества слов в алфавите,
описанных на естественном языке;
— определять множества слов в алфавите (описанных на естественном
языке) с помощью исчисления на словах;
— конструировать линейные и древесные доказательства в исчислении
на словах;
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
Теоретические сведения
Индуктивное определение множества слов в алфавите
Сейчас нам понадобится умение математически определять
(описывать, задавать) различные множества слов, которые могут
быть бесконечными. Воспользуемся заданием множества с помо-
щью конструктивного способа (напомним, что он состоит в зада-
нии порождающей процедуры, описывающей способ получения эле-
ментов множества из уже полученных элементов, либо из других
объектов).
Этот способ описания множества слов осуществляется с помо-
щью индуктивного определения (описания') множества слов.
МетаОпределение 1.
Индуктивное определение (описание) множества слов М в некото-
ром алфавите содержит три пункта:
а) указываются некоторые слова из множества М;
Ь) указываются правила построения (порождения) слов из М, ко-
торые позволяют из слов М получать новые слова этого множе-
ства;
с) словами из множества М являются слова, получаемые соглас-
но пунктам а и Ь, и только они.
Пример индуктивного определения
множества слов
Verba volant, scripta manent
(слова улетают, написанное остаётся).
Определим индуктивно понятие «правильная скобочная система».
Определение (по [161, с. 104]).
А. Слово ab является правильной скобочной системой.
64
https:/Л: rait.ru
Вг Если а и P — правильные скобочные системы, то слово аР яв-
ляется правильной скобочной системой.
В2. Если а — правильная скобочная система, то слово ааЪ явля-
ется правильной скобочной системой.
С. Других правильных скобочных систем нет.
Определение (по [154, с. 32]).
Ограниченным языком Дика над алфавитом {а, Ь} (или правиль-
ным скобочным языком) назовём множество всех слов из {а, Ь}*,
являющихся правильными скобочными системами.
Оказывается, что очень удобным способом формализации ин-
дуктивного определения множеств слов является определение мно-
жества слов в алфавите с помощью исчисления на словах. Поэтому
ниже мы остановимся на понятии «исчисление».
Индукция по построению множества объектов
Индукция по построению математических объектов использует-
ся для доказательства утверждений об объектах, которые определе-
ны ранее с помощью индуктивного определения.
Пусть множество М объектов некоторого типа определено с по-
мощью индуктивного определения, а свойство Р является характе-
ристическим свойством множества М.
МетаОпределение 2.
Индукцией по построению множества объектов назовём следу-
ющий метод доказательства утверждения: «всякий элемент мно-
жества М обладает свойством Р» (или «свойство Р является ха-
рактеристическим свойством множества М»).
Пусть доказаны следующие утверждения: 1) всякий объект, опи-
санный в базисных пунктах индуктивного определения множества
М, обладает свойством Р; 2) всякий объект, полученный из эле-
ментов множества М по правилам, указанным в индуктивных пун-
ктах определения множества М, также обладает свойством Р.
Тогда всякий элемент множества М обладает свойством Р.
В конкретных случаях вместо слова «объектов» употребляют на-
звания типов изучаемых объектов, например: «слов», «формул», «до-
казательств» и т. п.
Определим, например, индукцию по построению множества слов
в алфавите. Пусть множество М слов в алфавите определено с по-
мощью индуктивного определения, а Р — характеристическое свой-
ство М.
65
https:it.ru
Определение.
Индукцией по построению множества слов в алфавите (индук-
цией по построению слов, индукцией по словам') назовём следу-
ющий метод доказательства утверждения: «каждое слово множе-
ства М обладает свойством Р» (или «Р является характеристи-
ческим свойством М»).
Пусть доказаны утверждения: 1) каждое слово, описанное в ба-
зисных пунктах индуктивного определения множества М, обла-
дает свойством Р; 2) всякое слово, полученное из слов множества
М по правилам, указанным в индуктивных пунктах определения
множества М, также обладает свойством Р.
Тогда всякий элемент множества М обладает свойством Р.
Исчисление математических объектов
В современной математике понятие «исчисление» является одним
из важнейших, оно используется для моделирования имеющегося
у нас расплывчатого представления о понятии «разрешение произ-
водить определённые действия».
Определение [35, с. 7].
В науке и практике часто встречаются системы, которые можно
описать следующим образом: имеется некоторое количество ис-
ходных объектов и некоторое количество правил построения
новых объектов из исходных и уже построенных. Такие системы
и называются дедуктивными или исчислениями.
Примеры (исчислений, не относящихся к математике).
1. Математические истоки понятия «исчисление» восходят к древно-
сти. Так игры с четкими правилами (шахматы, домино, маджонг, различ-
ные карточные игры) были, вероятно, первыми реальными примерами
исчислений. В этих играх имеется исходное состояние игры (позиция
вместе с очередностью хода) и правила перехода от одного допустимого
состояния к другому. Разумеется, что, рассматривая игру как исчисление,
мы полностью отвлекаемся от ее «игровых» аспектов — состязательно-
сти и прочего, — а интересуемся исключительно ее «юридической сто-
роной» — возможностью совершать действия, выполняемые по опреде-
лённым правилам.
2. Известная игра «15» является «физической» моделью некоторого
исчисления: начальная позиция костей (начальная конфигурация) явля-
ется аксиомой исчисления, а правила передвижения костей (разумеется,
известные всем) — правилами построения нового объекта (новой кон-
фигурации) из ранее полученных. Рассмотрим, например, следующие
начальные конфигурации:
66
https:it.ru
5 1 2 3
9 6 7 4
13 10 11 8
14 15 12
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15
5 1 2 3
9 7 6 4
13 10 11 8
14 15 12
(1) (2) (3)
Очевидно, что конфигурация (1) легко (подумайте, как?) преобразу-
ется к конфигурации (2), причём не единственным способом. Интере-
сен тот факт (доказанный в [93, § 18]), что к такому виду преобразуются
не все начальные конфигурации, т. е. существуют такие начальные кон-
фигурации, которые не приводятся к виду (2), например, конфигурация
вида (3).
В дальнейшем, в курсе «Математическая логика и теория алго-
ритмов» мы будем изучать различные исчисления с использовани-
ем понятий «аксиомы», «правила вывода», «линейное и древесное до-
казательства».
В связи с этим приведём обобщение этих понятий, которое по-
зволяет абстрагироваться от конкретных исчислений математиче-
ской логики и, тем самым, выразить общие черты исчислений, по-
нимание которых должно облегчить процесс овладения ими.
МетаОпределение 3 (по [34, с. 6]).
Исчисление (математических) объектов — это способ описания
индуктивного определения математических объектов, в котором:
1) указываются некоторые конструктивные объекты, которые
называются аксиомами исчисления;
2) указываются некоторые конструктивные объекты, которые
позволяют по уже полученным объектам строить новые; они на-
зываются правилами вывода исчисления;
3) указано, как с помощью аксиом и правил вывода исчисления
осуществлять конструктивные процессы, называемые выводами,
при этом:
а) выводом в исчислении называется конечная последовательность
объектов, каждый элемент которой является либо одной из ак-
сиом исчисления, либо получается из какого-либо числа предше-
ствующих элементов последовательности по одному из правил
вывода исчисления;
б) выводом объекта в исчислении называется вывод в исчислении,
последним элементом которого является данный объект;
в) объектом, выводимым в исчислении, называется объект, для
которого может быть предъявлен его вывод в этом исчислении;
г) построением объекта в исчислении называется его вывод в дан-
ном исчислении.
67
https: "и га it.ru
Замечания.
1. Поскольку любой «начальный отрезок» вывода в некотором исчис-
лении также является выводом, то всякий вывод в исчислении наряду
с построением своего «основного» объекта (последнего элемента вывода)
содержит в себе построения всех использовавшихся в нем по ходу дела
«вспомогательных» объектов.
2. [34, с. 6] Понятие «алгоритм (алгорифм)» используется для фор-
мирования нашего представления о понятии «предписание». Суще-
ственное различие между алгоритмом и исчислением состоит в том, что
в то время, как всякий алгоритм является некоторым предписанием дей-
ствовать в точности так-то и так-то и в такой-то последовательности,
исчисление является не предписанием, а лишь разрешением производить
такие-то действия. При этом таких разрешенных действий бывает обычно
несколько и на выбор того или иного из них, вообще говоря, не наклады-
вается никаких ограничений.
Определение множества слов в алфавите с помощью
исчисления на словах
Исчисление на словах в алфавите представляет собой частный
вид общего понятия «исчисление математических объектов». В ма-
тематике встречаются исчисления, заданные и на других матема-
тических объектах: натуральных, целых или рациональных числах,
целочисленных матрицах, конечных графах.
Определение.
Определение (описание) множества слов с помощью исчисления
на словах в алфавите содержит следующие пункты:
а) задаются некоторые слова описываемого множества слов, ко-
торые называются исходными словами исчисления (или его акси-
омами);
Ь) указываются правила исчисления, которые позволяют из слов
описываемого множества получать новые слова этого множества;
с) с помощью понятий «исходные слова» и «правила исчисления»
определены понятия «вывод в исчислении», «вывод слова в исчисле-
нии», «слово, выводимое в исчислении», т. е. описано, как именно
с помощью исходных слов и правил исчисления получать новые
слова;
d) словами определяемого множества являются слова, получае-
мые согласно пунктам а, Ь, с, и только они.
Пункт d определения формулируется одинаково, какое бы мно-
жество мы ни определяли, причём пункт d определения часто толь-
ко подразумевают, но (ввиду его стандартности) явно не выписы-
вают.
68
га it.!
Пусть п е N\{0}. Правила пункта b определения множества слов
с помощью исчисления на словах построены по единой схеме: «Если
слова ш1г w2, wn являются словами определяемого множества,
то слово v также принадлежит определяемому множеству».
При этом посылками правила исчисления называются слова ш1г
w2, wn, а заключением правила исчисления называется слово v.
Слова wl} w2, ...,wnnv — это выражения языка исследователя
(метаязыка): они могут содержать вхождения букв алфавита опре-
деляемого множества слов и вхождения синтаксических перемен-
ных (в примерах, рассмотренных ниже, — это буквы а и Р).
В метаязыке правила исчисления записывают так (буквы «;»
и «горизонтальная черта» не принадлежат основному алфавиту):
м^м^;...;^
v
Правило можно записывать также в виде слова w2; ...; wn/v,
если использовать вместо буквы «горизонтальная черта» букву «/»
или какой-либо другой разделительный знак.
Пусть {Р15 Р2> •••> Рк) — множество синтаксических переменных,
имеющих вхождения во все правила рассматриваемого исчисления.
Определение.
1. Результатом применения правила исчисления wf, w2; ...;
wn/v к кортежу слов {а1г..., ап) назовём слово у в алфавите опре-
деляемого множества слов, получаемое следующим образом:
а) вначале ищется решение системы уравнений в словах
ai=Wi,
an=wn
относительно синтаксических переменных Р15 Р2, •••> PkJ
б) если система уравнений имеет решение р°,Р2,...,Р°, то будем
говорить, что правило исчисления w^, w2;...; wn/v применимо к кор-
тежу слов {а1гап), а
def
Y = vPljP2j„.jPfc[p?,po,...,pO];
в) если система уравнений не имеет решения, то будем говорить,
что правило исчисления му; w2; ...; wn/v не применимо к кортежу
слов ..., an).
69
https: Цц га it.ru
2. Применением правила исчисления Wy, w2‘, •••; wn/v к кортежу
слов {а1гап) назовём следующий частный случай правила ис-
числения:
>,.*№1°...Р?]
Примеры.
1. Пусть множество слов М в алфавите {а} определено с помощью сле-
дующего исчисления на словах в алфавите {а}:
а) а е М;
Ь) если слово а е М, то ааа е М.
Попробуем понять, из каких слов состоит множество М (описать его
характеристическое свойство). По пункту а а е М, поэтому, взяв в каче-
стве а слово а, по пункту b получим, что ааа е М. Для применения пра-
вила из b мы можем взять а = ааа, следовательно, ааааа е М, ааааааа
g М и т. д. Итак, выдвинем следующую гипотезу о характеристическом
свойстве множества М: множество М состоит из всех слов в алфавите {а},
имеющих нечётную длину.
2. Определим множество D всех непустых слов в алфавите {а, Ъ},
не содержащих вхождений слов аа и ЪЬ (такие слова состоят из чередую-
щихся букв «а» и «Ь», они могут начинаться с любой из этих букв и обры-
ваться на любой из них). Каждое такое слово можно получить, выполняя
следующие действия:
1) выпишем однобуквенное начало этого слова (букву «а» или «Ь»);
2) припишем к полученному слову букву, противоположную его одно-
буквенному концу;
3) повторим операцию 2.
Таким образом, можно выдвинуть следующую гипотезу об аксиомах
и правилах вывода исчисления: определение множества D с помощью
исчисления на словах в алфавите {а, Ъ} имеет вид:
a) a, be D;
b) если оса g В, то ocab g D; если ab g D, то aba е D (а е {а, Ь}*).
3. Приведём ещё один вариант гипотезы об аксиомах и правилах
вывода исчисления:
a) a, be D;
b) если аа, bp е D, то осаЬр е D; если ab, а₽ е D, то аЬа₽е D (а, Р е {а, Ь}*).
Правила из примеров в принятых обозначениях запишутся так:
Пример 1 Пример 2 Пример 3
а ааа аа ab aab’ aba аа; bp ab; ар ааЬр ’ аЬар
а/ааа aa/aab ab/aba аа; ЬР/ааЬР ab; аР/аЬаР
70
Правила исчисления из примеров 1 и 2 называются однопосылоч-
ными правилами (каждое из них имеет одну посылку), а правила
из примера 3 — двухпосылочными правилами.
Важнейшее замечание.
Пусть дано индуктивное определение некоторого множества слов
в алфавите. Тогда слова, которые задаются в пункте а индуктивного опре-
деления, можно интерпретировать как исходные слова исчисления, а пра-
вила, излагаемые в пункте b индуктивного определения, — как правила
исчисления. Итак, имеет смысл следующая таблица, указывающая соот-
ветствие терминов:
Индуктивное определение множества слов Исчисление на словах (терминология С. Ю. Маслова)
Слова, задаваемые в пункте а Исходные объекты (аксиомы ис- числения)
Правила построения слов из пункта b Правила вывода исчисления
Слово из множества, определяемого индуктивным определением Объект, выводимый в исчислении
Поэтому часто говорят, что исчисление, заданное на словах в алфавите
(.исчисление на словах), является способом формализации индуктивного
определения множества слов, а индуктивное определение множества слов
называют также определением множества слов с помощью исчисления
на словах.
Важно отметить, что в приведённых выше примерах мы не до-
казали, что описанные в них исчисления на словах определяют
множества слов с указанными характеристическими свойствами.
Для этого необходим определенный метод доказательства, к опи-
санию которого мы сейчас и приступим. Переформулируем метод
доказательства, который ранее назван «индукцией по построению
слов в алфавите», для случая, когда множество М слов в алфавите
определено с помощью исчисления на словах, а Р является характе-
ристическим свойством множества М.
Определение.
Индукцией по построению слов в алфавите будем называть сле-
дующий метод доказательства утверждения: «каждое слово мно-
жества М обладает свойством Р» (или «Р является характери-
стическим свойством М»).
Пусть доказаны утверждения:
1) всякая аксиома исчисления обладает свойством Р;
2) всякое слово, полученное по правилам исчисления из слов мно-
жества М, обладающих свойством Р, также обладает свойством
Р (другими словами, для каждого правила исчисления доказано,
71
что если все посылки правила исчисления обладают свойством Р,
то заключение правила также обладает свойством Р).
Тогда всякий элемент множества М обладает свойством Р.
Теорема.
Индукция по построению слов в алфавите является обобщением
натуральной индукции.
Доказательство. Рассмотрим исчисление, определяющее не-
которое множество М слов в алфавите {|}. Пусть оно имеет одну
аксиому | и единственное правило исчисления: «из слова а можно
получить слово а |», где а е {| }*.
Это исчисление, очевидно, определяет (порождает) множество
М всех непустых слов в алфавите {|}. Каждому элементу множества
М можно поставить во взаимно однозначное соответствие натураль-
ное число, записанное в виде слова в алфавите {|}. (Подумайте, ка-
кому натуральному числу в этом случае соответствует слово | g М?)
Теперь для того, чтобы доказать индукцией по построению слов,
что каждый элемент М обладает некоторым свойством Р, достаточ-
но доказать два утверждения:
1) | обладает свойством Р;
2) если слово аеМ обладает свойством Р, то слово а | также
обладает свойством Р.
Однако описанный метод доказательства является натуральной
индукцией, сформулированной для натуральных чисел, записанных
в виде слов в алфавите {|}.
Теорема доказана.
Замечание [166, с. 149—150].
«Уравнения в словах можно считать источником современной теории
формальных языков и комбинаторики слов...».
Доказательство в исчислении на словах
Определим понятие «доказательство в исчислении на словах».
Будем исходить из следующих представлений о понятии «мате-
матическое доказательство» (Д. Гильберт, 1923):
1) доказательство (если говорить только о его форме) есть по-
следовательность выражений языка математической теории;
2) каждое выражение из этой последовательности является либо
аксиомой, либо ранее доказанной теоремой;
3) порядок следования выражений в доказательстве таков, что
каждое выражение, не являющееся аксиомой, получается из одно-
го или нескольких предыдущих выражений из этого доказательства
по правилам логики.
72
https: "и rait.ru
В разных вариантах, с теми или иными отклонениями и преоб-
разованиями гильбертовское понимание доказательства дожило
до наших дней.
Мы приведём два различных определения понятия «доказатель-
ство в исчислении на словах», а затем покажем, что они эквивалент-
ны в том смысле, что задают одно и то же множество теорем.
Пусть определено исчисление на словах в алфавите А, и а е А*.
Определение.
1. Линейным доказательством в исчислении на словах в алфави-
те А называется конечная последовательность слов в алфавите
А, каждый элемент которой есть либо аксиома исчисления, либо
заключение некоторого правила исчисления, все посылки кото-
рого предшествуют этому элементу последовательности.
2. Линейным доказательством слова а в исчислении на словах
в алфавите А называется линейное доказательство, последним
элементом которого является слово а.
3. Длиной линейного доказательства слова а в исчислении на сло-
вах называется количество слов, которые оно содержит.
Пусть п е N\{0}.
Определение (индуктивное).
Древесное доказательство (доказательство в виде дерева) слова
а в исчислении на словах в алфавите А определяется индуктивно:
1) если а — аксиома исчисления на словах в А, то слово а явля-
ется древесным доказательством слова а;
2) если D1} ..., Dn — древесные доказательства соответствен-
но слов а15 ..., ап в исчислении на словах, а слово а получается
из слов otp ..., ап применением правила исчисления, то
^1г^2г'“‘г^П
а
является древесным доказательством слова а в исчислении на сло-
вах.
Предложение.
Следующие утверждения выполняются или не выполняются од-
новременно:
1) слово а принадлежит множеству слов, определённому с помо-
щью исчисления на словах в алфавите А;
2) существует линейное доказательство слова а в данном исчис-
лении;
73
3) существует древесное доказательство слова а в данном исчис-
лении.
Доказательство.
1. Докажем, что если 1), то 2). Пусть М—множество слов, опре-
деленное данным исчислением, а а — произвольное слово из М. Ин-
дукцией по построению слов докажем, что существует линейное до-
казательство слова а:
а) если а — аксиома исчисления, то а является линейным до-
казательством слова а;
б) пусть слово а получается по правилу исчисления из слов
а15 ..., ап, а каждое из слов а15 ..., ап имеет линейное доказатель-
ство. Составим последовательность слов, записав друг за другом
линейные доказательства слов а15..., ап соответственно, и добавим
к ней в качестве последнего члена последовательности слово а. По-
лучим линейное доказательство слова а в данном исчислении.
2. Докажем, что если 2), то 3), т. е. что всякое слово а, имеющее
линейное доказательство, имеет также и древесное доказательство.
Рассуждения проведем индукцией по длине линейного доказатель-
ства. Если слово а имеет линейное доказательство длины 1, то а —
аксиома и является своим древесным доказательством.
Пусть теперь а имеет хотя бы одно линейное доказательство
длины п (п > 1), а всякое слово в алфавите А, имеющее линейное
доказательство меньшей длины, имеет и древесное доказатель-
ство. Пусть otp ..., а — линейное доказательство. Очевидно,
что а не является аксиомой и получается по правилу исчисления
из некоторых о^(1),..., as(fc) (sQ), ..., s(k) < п). Заметим, что каждая
из последовательностей аг,..., (т = 1, ..., к) сама является ли-
нейным доказательством. По индуктивному предположению слова
as(1),..., as(fc) имеют древесные доказательства. Пусть этими доказа-
тельствами являются Ds(1),..., соответственно. Тогда
а
является древесным доказательством слова а.
3. Докажем, что если 3), то 1). Пусть слово а имеет древесное
доказательство. Покажем, что а е М. Доказательство проведем
индукцией по числу вхождений знака «черта» в древесное доказа-
тельство. Если «черта» не входит в древесное доказательство слова
а, то а — аксиома, поэтому а е М. Пусть теперь знак «черта» имеет
п вхождений (и > 0) в древесное доказательство слова а, и пусть
любое слово, имеющее древесное доказательство с меньшим чис-
лом вхождений знака «черта», принадлежит М. Тогда древесное до-
казательство слова а есть
74
https:/Л: rait.ru
Di‘,D2‘, —>Dn
a
где Dlf ..., Dn — древесные доказательства некоторых слов alf
ап соответственно, а а получается из а15 ап по правилу исчисле-
ния. По индуктивному предположению Ор ..., ап е М, поэтому a е М.
Предложение доказано.
Теперь имеет смысл следующее
Определение.
Словом, доказуемым в исчислении на словах в алфавите А, назы-
вается слово, для которого существует или линейное, или древес-
ное доказательство в этом исчислении.
Доказанное Предложение позволяет использовать любую (из опи-
санных двух) модель понятия «доказательство». В математической
практике доказательства обычно записывают линейно, поэтому по-
нятие «линейное доказательство» лучше моделирует традиционное
понятие «математическое доказательство». Однако при анализе
доказательств удобнее древесное представление, так как оно лучше
фиксирует зависимость одних утверждений от других. В дальней-
шем мы будем использовать обе модели понятия «доказательство».
Замечание (по [34, с .6]).
Приведённое ранее индуктивное определение понятия «слово в алфа-
вите» можно легко оформить «в виде исчисления».
Доказательства в этом исчислении имеют следующий вид: аксиома
(пустое слово) встречается только один раз вначале, а все остальные
члены доказательства получаются применением правила вывода (пере-
ход от а к оса) к непосредственно предшествующим. Доказательства, обла-
дающие этим свойством, как раз и описывают процесс построения слов
в алфавите, развёртывающийся согласно индуктивному определению.
Вывод из посылок в исчислении на словах
В математических рассуждениях иногда используют такой прием:
предполагают, что некоторые утверждения истинны, и из них выводят
те или иные новые утверждения. Приведём определение понятия «вы-
вод из посылок» — понятия, моделирующего этот приём рассуждений.
Пусть определено исчисление на словах в алфавите А, п е N\{0},
а а15 ..., ап, а е А*.
Определение.
1. Линейным выводом слова а из посылок аг, а2, ..., ап в исчисле-
нии на словах называется линейное доказательство слова а в ис-
75
числении, полученном из данного исчисления добавлением в ка-
честве аксиом исчисления слов а1э а2, •••> ап-
2. Древесным выводом слова а из посылок а1г а2, • ••, с(п в исчисле-
нии на словах называется древесное доказательство слова а в ис-
числении, полученном из данного исчисления добавлением в ка-
честве аксиом исчисления слов а15 а2, ..., ап.
3. Словом, выводимым из посылок а1г а2, ..., ап в исчислении
на словах, будем называть слово, для которого существует вывод
(древесный или линейный) из посылок а15 а2, ..., ап в этом ис-
числении.
Пример.
Рассмотрим исчисление на словах в алфавите {а, Ь} с аксиомами
а, Ъ и правилами (а, Р е {а, Ь}*):
аа;Ьр аЬ;ар
ааЬр ’ аЬар
Вначале заметим, что слово ЪЪаЬ не является доказуемым в данном
исчислении. Этот факт можно установить простым перебором (редкий
случай!) применений правил исчисления (знак «?» обозначает тот факт,
что к слову ЪЪ правила исчисления не применимы):
(2)
? Аксиома
4, 4, Аксиома
bb; a t
—------------ Ъ
ЪЬа;__________
bbab
(1) или
Аксиома Аксиома
J, ф
I а; ь
ЬЪ; аЪ
bbab
(2)
Однако слово bbab выводимо из посылки bb:
a) a, b, ab, bb, bbab (линейный вывод слова bbab из посылки bb);
б) древесные выводы слова bbab из посылки bb приведены выше.
Допустимые правила в исчислении на словах
Получение слов, доказуемых в исчислении, и слов, выводимых
в исчислении из посылок, часто упрощается, если к правилам ис-
числения добавить некоторые новые правила. Эти новые правила,
однако, должны быть такими, чтобы их применение не приводило
к получению слов, не принадлежащих множеству, определённо-
му с помощью исчисления на словах (математики часто говорят:
«...к словам, которые данным исчислением не порождаются»).
76
g-//ijroit i-i ।
Определение.
Допустимым правилом в исчислении будем называть такое пра-
вило, добавление которого к правилам исчисления не расширяет
множество доказуемых слов в исходном исчислении.
Определение.
1. Линейным квазидоказателъством в исчислении будем называть
такую конечную последовательность слов, каждый член которой
является: а) либо аксиомой исчисления; б) либо заключением не-
которого правила исчисления, все посылки которого предшеству-
ют этому члену в последовательности; в) либо заключением не-
которого допустимого правила в данном исчислении, все посыл-
ки которого предшествуют этому члену в последовательности.
2. Линейным квазидоказателъством слова а в исчислении будем
называть такое линейное квазидоказательство, для которого слово
а является его последним членом.
Определение.
Древесным квазидоказателъством в исчислении будем называть
древесное доказательство в исчислении, полученном из данного
исчисления добавлением к нему допустимых правил.
Определение функции индукцией
по построению множества слов
Рассмотрим, как можно определить функцию, область определения
которой представляет собой множество слов М, заданное индуктивно.
Определение.
Будем говорить, что функция/определена индукцией (рекурсией)
по построению множества слов М, если:
а) задано значение функции/на каждом исходном слове а ис-
числения (т. е. заданы значения/(а) для всех исходных слов а);
Ь) для каждого правила исчисления
v
указано правило нахождения/(v) по набору значений/(wj, ...,
Л^п);
с) доказано, что при вычислении значения f(y) всегда получается
одно и то же значение (ведь может оказаться, что получить слово
v по правилам индуктивного определения можно двумя различ-
ными способами, а при этом, используя эти два разных способа
77
https: / Л it.ru
получения v для вычисления значения функции с помощью ее ин-
дуктивного определения, мы получим два разных значения/(v)).
Пример.
Пусть множество слов М в алфавите {а, Ь} определено с помощью сле-
дующего индуктивного определения (а е {а, Ь}*):
a) а е М, ba е М;
b) — (1); (2); (3).
ааЬ baba abab
Ha множестве М определим отношение g также с помощью следую-
щего индуктивного определения:
def def
a') g(a) = 0, g(ba) = 1;
def def def
b') g(aab) = g(aa)-l, gfbaba) - g(aba)+l, g(abab) = g(aba)+5.
Легко увидеть с помощью построения древесного доказательства
в заданном исчислении, что слово bob е М (приведем два способа):
— (1) к
-^- (2) или —— (3)
bob 1 J bab
def def
Следовательно, g(bab) = g(ab)+1 = (g(a) -1)+1=0, а с другой стороны,
g(bab) =g(ba) + 5 = 6.
Итак, индуктивное определение отношения g не определяет функцию
индукцией по построению множества слов.
Из истории создания буквенного исчисления
Еще в школе мы знакомимся с элементами символического язы-
ка математики. Основоположником этого языка можно считать
французского математика Ф. Виета (1540—1603), стремившегося
создать новую науку, — он назвал ее «аналитическое искусство» —
Ars analytica, которая обладала бы строгостью геометрии древних,
и вместе с тем, оперативностью алгебры. Это аналитическое искус-
ство должно было обладать такой силой, чтобы не оставалось не-
решенных задач: nullum non problema solvere (по [139, с. 190—192]).
Основы этой новой науки Ф. Виет изложил в трактате «In artem
analyticam isagoge» («Введение в искусство анализа»), в котором по-
строил буквенное исчисление, иными словами, описал язык, близ-
кий к языку современной алгебры. До этого буквенные обозначения
применялись только для неизвестного и его степеней. Такие обо-
значения ввел еще Диофант в труде «Арифметика и книга о мно-
гоугольных числах», а европейские ученые XV—XVI вв. несколько
их усовершенствовали. Следующий после Диофанта принципиаль-
78
https://urait.ru
но новый шаг сделал Ф. Виет — он ввел обозначения не только для
неизвестного, но и для параметров и, таким образом, впервые мог
записать в общем виде уравнения и тождества. Преимущество сим-
волического языка алгебры состоит не только в сокращенной запи-
си предложений, которые можно выразить и на естественном языке
(сокращенную запись даёт, например, стенография).
Главное в том, что с помощью буквенного исчисления мы за-
меняем часть рассуждений выкладками, т. е. чисто механически-
ми операциями. Как говорил Г. В. Лейбниц, буквенное исчисление
«разгружает воображение». Ф. Виет воспринял основной принцип
греческой геометрии, согласно которому складывать и вычитать
можно только однородные величины, и только однородные вели-
чины могут иметь отношение друг к другу. Поэтому все величины
он делит «по родам»: к первому роду относятся «длины», т. е. вели-
чины одного измерения. Произведение двух величин первого рода
относится ко второму роду, к которому принадлежат «плоские вели-
чины» или «квадраты» и т. д.
Буквенное исчисление Ф. Виета было усовершенствовано Р. Де-
картом (1596—1650), который придал ему современную форму.
В конце XVII в. исчисление было построено для анализа бесконеч-
но малых (который долгое время называли «алгеброй бесконеч-
ного») — это были метод флюксий и бесконечных рядов Ньютона,
а также дифференциальное и интегральное исчисление Лейбница.
В XVIII в. были построены вариационное исчисление и исчисление
для частных дифференциалов и производных. В XIX в. исчисление
было перенесено и в логику.
В настоящее время почти в каждой математической теории су-
ществует свое исчисление (векторное, тензорное и т. д.), более того,
специальные исчисления строятся для отдельных задач, теоретиче-
ских и практических. Приведём цитаты [35, с. 16], поясняющие зна-
чение понятия «исчисление»:
1. «Теория исчислений дает хороший, а в ряде отношений не-
заменимый аппарат количественного моделирования недетерми-
нированных процессов, допускающих достаточно адекватное дис-
кретное представление».
2. «Наиболее известные примеры связаны с применением фор-
мальных грамматик и составляют основное содержание математи-
ческой лингвистики. Аппарат грамматик используется при построе-
нии моделей роста биологических систем, при некоторых подходах
к фольклористике и исследовании поэтических систем».
79
Контрольные вопросы
Гарри поднялся с пола.
— Сэр... Профессор Дамблдор, —
нерешительно начал он. —Могу я задать
вам один вопрос?
— Кажется ты уже задал один
вопрос. — Дамблдор улыбнулся. — Тем
не менее, можешь задать ещё один.
Дж. К. Ролинг.
Гарри Поттер и философский камень
1. Могут ли два разных индуктивных определения (у которых различны
множества слов, описываемых в пункте а, и (или) различны правила пункта
Ъ), задавать одно и то же множество слов?
2. Обязательно ли бесконечно множество, заданное индуктивно?
3. Как может измениться порождаемое исчислением множество, если
к правилам исчисления добавить новое правило?
4*. Укажите какое-либо правило (алгоритм) построения линейного
доказательства в исчислении из древесного доказательства того же слова
и докажите, что получаемая по вашему правилу последовательность слов
действительно является линейным доказательством.
5*. Проблемный вопрос. Всякое ли множество слов в конечном алфавите
может быть задано индуктивно?
Примеры решения
некоторых типов упражнений
Пример 1. Пусть множество слов М в алфавите {а} задано с помощью
индуктивного определения: а) а е М; Ь) если слово а е М, то ааа е М.
Докажите, что М—это множество всех слов из {а}*, имеющих нечёт-
ную длину.
Решение.
1. Сначала докажем, что все слова из множества М имеют нечетную
длину. Доказательство проведем индукцией по построению слов.
База индукции. Слово а имеет длину 1.
Индуктивный переход. Пусть слово 0 е М и имеет нечетную длину.
Докажем, что слово, которое получается из 0 по правилу Ь, также имеет
нечётную длину. Действительно, по правилу b из слова 0 можно получить
только слово 0аа, которое имеет нечётную длину.
2. Остается доказать, что каждое слово из {а}* нечётной длины при-
надлежит множеству М. Доказательство проведем индукцией по длине
слова. В {а}* есть лишь одно слово длины 1 — слово а; а е М согласно пун-
кту а из определения множествам. Предположим, что для любого слова
из {а}* нечётной длины, меньшей п, утверждение выполняется. Пусть 0 —
слово из {а}* нечётной длины п, большей 1. Тогда 0 можно представить
80
https:/Л: rait.ru
в виде Р = ааа (а е {а}+). Слово а имеет нечетную длину, меныпую, чем
длина слова Р (так как его длина на 2 меньше длины слова Р). По индук-
тивному предположению а е М. Отсюда, применяя правило из пункта
b определения множествам, получаем, что Р е М.
Итак, множество М, заданное индуктивно, совпадает с множеством
всех слов из {а}*, имеющих нечетную длину.
Пример 2. Рассмотрим множество Мелов в алфавите {х,у}, заданное
следующим индуктивным определением (а, Р е {х,у}*):
а) ху, уу, хуух е М; Ь) если qyP е М, тоуахРу е М.
Докажем, что каждое слово из множества М имеет четную длину.
Решение. Воспользуемся индукцией по построению слова: 1) длина каж-
дого из слов ху,уу, хуух четна; 2) согласно индуктивному предположению,
длина слова ауР четна, поэтому и слово уахРу имеет чётную длину, так
как легко понять, что len (уахРу) = 1еп (ауР) + 2.
Пример 3. Рассмотрим исчисление на словах в алфавите {а, Ъ} с акси-
омами а, Ъ и правилами (а, Р е {а, Ь}*):
аа;Ьр аЬ;аР
ааЬр ’ аЬар
Приведем: а) древесное доказательство слова ababa; б) линейное дока-
зательство слова ababa.
Решение.
А. Приведем два варианта древесного доказательства:
(Правило!)
(Правило 2)
(Правило 1)
(Правило 2)
(2) ^-^12)
aba; b Ьа; Ьа
abab; a a; baba
ababa ababa
Б. Приведем несколько линейных доказательств слова ababa:
a, b, ab, a, aba, b, abab, a, ababa;
a, b, ba, ba, baba, ababa;
a, b, ab, aba, abab, ababa.
Для более короткой записи линейного доказательства повторяющи-
еся слова можно опускать.
81
https:it.ru
Упражнения для самостоятельного решения
Люди, обладающие некоторым талантом,
слишком склонны думать, что работа
должна быть для них лёгкой. Напрягай свои
силы постоянно, человек, если ты хочешь
создать нечто великое.
Г. К. Лихтенберг
Правила построения (порождения') слов
1. Пусть для слов в алфавите {х, у} задано правило (а, 0 е {х, у}*):
«Из слова ссф можно получить слово «Ру».
А. Выпишите все слова, которые можно получить из слова хухуу одно-
кратным применением этого правила.
Б. Перечислите все слова длины 3, к которым применимо заданное
правило.
В. Из каких слов можно получить слово уху однократным применением
рассматриваемого правила?
Г. Приведите пример слова, которое можно получить с помощью одно-
кратного применения рассматриваемого правила по крайней мере из шести
различных слов в алфавите {х,у}.
2. Пусть для слов в алфавите {а, Ь, с} задано правило Сф е {а, Ь, с}*):
«из слова ФП[Ь] можно получить слово а(р«.
А.. Покажите, что из слова Ьс однократным применением этого правила
можно получить как слово аас, так и слово аЬс.
Б. Сколько слов можно получить из слова bcbb однократным примене-
нием этого правила?
В. Какие слова могут служить результатами применения рассматрива-
емого правила?
Г. Существует ли слово в алфавите {а, Ь, с}, которое можно получить
однократным применением рассматриваемого правила из нескольких раз-
личных слов?
3. Пусть для слов в алфавите {х, у} задано правило (ф, у е {х, у}*):
«из слов фхф и фуф можно получить слово у(р\рх».
А. Какое слово можно получить однократным применением этого правила
к словам, взятым из множества слов {х,у}? Какое слово можно получить одно-
кратным применением этого правила к упорядоченной паре слов (хух,уух)?
Б. Из каких пар слов можно получить однократным применением этого
правила слово yxyyxl
4. Формализуйте следующие правила построения слов (т. е. задайте
их одной или несколькими словами метаязыка вида
Р
где 04, а2> •••> <*n> Р — слова, имеющие вхождения основных символов, ме-
тапеременных и, если необходимо, обозначений операций подстановки):
а) «из слова вычеркнуть одно любое вхождение подслова хух»;
б) «из слова вычеркнуть любые два вхождения буквы х и приписать слева
к полученному слову букву у»;
82
о Hi iroi! ri ।
в) «вычеркнуть первое вхождение первой буквы в слово и приписать
справа к слову слово уу»;
г) «из слова вычеркнуть все вхождения буквы х»;
д)* «из слова вычеркнуть все вхождения слова хх».
Характеристические свойства множеств слов, определённых
(порождаемых) исчислениями на словах
5. Пусть множество М слов в алфавите {а, Ь, *} определено с помощью
следующего исчисления на словах (ф, V G {и, Ь, *}*):
a) a*b*ba, ba*aa, ab*ba, aa*a*b, ab g М;
Ь) если ф*у, ф g М, то v е М.
Докажите, что: a) a*b g М; б) каждое слово из М содержит не более двух
вхождений символа *; в) каждое слово из М имеет длину не более шести;
г) множество М конечно.
6. Пусть множество М слов в алфавите {х, у} определено с помощью
следующего исчисления на словах (а, Р, у g {х,у}*): а) хуу g М; Ь) если ссфу
g М, то аРху g М; если a g М, то хауу g М.
А.. Докажите, что уху g М, хуухуу g М.
Б. Докажите, что всякое слово из Мимеет чётное число вхождений буквыу.
В. Выясните, верно ли, что длина любого слова из М кратна трём.
Г. Докажите, что имеет место хухуху е М.
Д. Докажите, что ххууууу е М.
7. Докажите, что любая правильная скобочная система t в алфавите {а,
Ь} обладает следующими свойствами:
a) len(t) является чётным числом;
б) da(t)=db(t);
в) (по [154, с. 32]) для любого разложения t = uv, и, v g {а, Ь}*, имеют
место da(u) > db(u) и da(v) < db(y).
8. Укажите, какое множество М слов в алфавите {□, х} определяет ис-
числение с единственной аксиомой сх и правилом (ф g {□, х}*); если фХ g
g М, то Сф g М?
9. Пусть М — множество слов в алфавите {а, Ъ}> определенное индук-
тивно так (ф g {а, Ъ}*):
a) a, b g М;
Ь) если ф g М, то фа g М, аф g М.
Докажите, что М является множеством всех непустых слов в алфавите
{а, Ь}, имеющих не более одного вхождения буквы «Ь».
10. Какое множество М слов в алфавите {х, у, z} определяет следующее
исчисление (а, Р g {х,у, z)*):
a) xyz, ххуу g М;
Ь) если слово ах?Р g М, то слово аР g М; если слово ауР g М, то слово
Ра g М?
11. Какое множество слов в алфавите {а, Ъ} определяет исчисление
с аксиомами a, b, ab, ba, aba, bab и правилами (а, Р g {а, Ь}*):
aabp m аЬар Q)?
aababp ’ ababap
12. Какое множество слов в алфавите {|, /, -} определяет исчисление
с аксиомой | и следующими правилами (ф, у g {| }*):
83
https:/Л: rait.ru
]ф_. Нф . 1ф;11 у . 1<р/Ну ,
Нф’ -Нф’ 1ф/|1у ’ -1ф/|1у ’
Соотношения между множествами слов,
порождаемых различными исчислениями
13. Пусть множество МТ слов в алфавите {а, Ь} определено с помощью
следующего исчисления:
al) ab;
bl) (<pe{a,b}*),
atpb
а множество М2 слов в этом же алфавите определено исчислением:
а2) ba;
Ъ2)—, A, A (<pe{a,b}’).
a<p cpa <pb
А. Докажите, что Мг cz М2.
Б. Докажите, что М2 не является подмножеством множества Мг.
В. Приведите пример исчисления, задающего множество слов М3 в ал-
фавите {а, Ь} и такое, то М3 с М2, Мг п М3 = 0.
Индуктивное определение множества слов. Определение множества
слов в алфавите с помощью исчисления на словах
14. Приведите индуктивное определение множества двоичных записей
целых чисел в алфавите {0,1,
15. Приведите индуктивное определение множества всех десятичных
записей четных натуральных чисел.
16. Приведите индуктивное определение множества записей целочис-
ленных одночленов в алфавите {х, |, -} (одночлены kxn и -кхп записывайте
в следующем виде
||...||х||...||и-||...||х||...||
I___I I___I I_____I I___I
к п к п
соответственно).
17. Определите исчисление, порождающее множество правильных ско-
бочных систем в алфавите {(,)}.
18. Определите исчисление, порождающее множество всех непустых
слов в алфавите {х, у, z}, содержащих ровно одно вхождение буквы х.
19. Определите исчисление, порождающее множество всех истинных
неравенств натуральных чисел в алфавите {|, <}, если натуральное число
представлено словом в алфавите {|}.
Доказательство в исчислениях на словах
20. Сформулируйте индуктивное определение понятия «линейное до-
казательство».
21. Рассмотрим исчисление на словах в алфавите {а, Ь} с исходными
словами a, b и правилами исчисления (а, Р е {а, Ь}*):
аа; bp ab; ар
aabp’ abap
84
https: "ига it.ru
А. Постройте древесное доказательство слов ababa, baba, abab в алфавите
{а, Ь}.
Б. Постройте линейное доказательство слов ababa, baba, abab в алфавите
{а, Ь}.
В. Доказуемо ли слово bbab в алфавите {а, Ь}?
Г. Приведите пример линейного доказательства слова ababa в данном
исчислении, длина которого равна 6.
22. Рассмотрим исчисление на словах в алфавите {а, Ь} с исходными
словами а, b и правилами исчисления (а, Р е {а, Ь}*):
аа; bp ab; ар
ааЬр’ аЬаР
Постройте линейный вывод слова bbab из посылки bb в исчислении.
23. (По [39, с. 235, 9.5.4].) Пусть определено исчисление на словах в ал-
фавите {а, Ь, с} с аксиомой «а» и правилами исчисления (а, Р е {а, Ь, с}*):
1) ааР 2) aQP 3)асЬЬР
ааЬр’ аср’ аЬЬар
А. Постройте древесное доказательство слова bbcb в данном исчислении.
Б. Перечислите все слова длины не более 5, которые доказуемы в данном
исчислении.
В. Приведите пример слова, имеющего два различных линейных дока-
зательства в данном исчислении.
Г. Приведите пример слова, не доказуемого в данном исчислении.
24. (По [39, с. 236,9.5.5].) Пусть определено исчисление в алфавите {а,
Ь} с аксиомой b и правилами (а е {а, Ь}*):
— (1), —(2).
ааа аа
А. Опишите множество слов, задаваемых исчислением.
Б. Покажите, что правило (3) является допустимым правилом в данном
исчислении (а, Р, Y е {а, Ь}*):
аЬр;рЬу
аЬу
Мф фШф
ФФ
25. (По [156, с. 84].) Пусть определено исчисление на словах в алфавите
{М, I, U}
a) MI;
Ф1
Ь) ---, -----,------,
<?IU Мфф ф(Л|/
А. Постройте древесное доказательство слов MIUIU, MUI, MUIIU в алфа-
вите {М, I, U}.
Б. Доказуемо ли слово MU в алфавите {М, I, U}?
26. В условиях Предложения докажите, что: а) если (1), то (3); б) если
(3), то (2); в) если (2), то (1).
http
о- Hi ।rnit ri ,
85
Определение функции индукцией по построению множества слов
27. Определим в алфавите {а, Ь} множество D всех непустых слов, не со-
держащих вхождений слов аа и вхождений слов bb, с помощью следующего
исчисления (а, 0 е {а, Ь}*):
a) a, b, ab, ba, aba, bab',
b) aabp аЬаР (2);
aababp abdbafi
или с помощью исчисления (а е {а, Ь}*):
а) а, Ь;
Ь) -^-(1), -^-(2).
ааЬ аоа
На множестве слов D индуктивно определим/следующим образом:
def def def def
/(a) = l,/(b) =-l,/(aab) = /(aa)-l,/(aba) = /(ab)+l,ae{a,b}\
А. Почему можно утверждать, что заданное индуктивное определение
действительно задает функцию?
Б. Вычислите/(bab).
В. Докажите индукцией по построению слов, что /(у) равно разности
количества вхождений буквы а и количества вхождений буквы b в у.
о- Hi ।rnit ri ।
kJ J O1 UU.I 14
Часть 2
ИСЧИСЛЕНИЯ
МАТЕМАТИЧЕСКОЙ
ЛОГИКИ
https:it.ru
Упражнение 3
ЯЗЫК ПЕРВОГО ПОРЯДКА: СИНТАКСИС
Есть предание о том, как один
известный математик начинал читать
логику второкурсникам. «Логика — это
наука о законах мышления, — сообщал
он. — Теперь я должен объяснить вам,
что такое наука, что такое закон
и что такое мышление. Что такое ’о’,
я объяснять не буду».
Ю. И. Манин [158, с. 137]
Обязательные результаты обучения:
• знать основные понятия
— алфавит языка первого порядка, сигнатура;
— терм, подтерм, индукция по построению термов;
— атомная формула сигнатуры о, формула сигнатуры о, выражение, под-
формула, индукция по построению множества формул;
— язык формальных систем нулевого и первого порядка;
— соглашение о записи формул в метаязыке;
— синтаксическая однозначность представления термов и формул;
— ранг терма, множество подтермов данного терма, ранг формулы, мно-
жество подформул данной формулы;
— синтаксическая однозначность представления вхождений термов
и формул;
— синтаксическое сохранение выражений при замене вхождений подвы-
ражений;
— область действия квантора, связанное и свободное вхождение пере-
менной в формулу, связанная и свободная переменная, множество свободных
переменных формулы и терма;
— замкнутый терм, замкнутая формула, открытая формула, бесквантор-
ная формула;
— операция «подстановка терма вместо свободной переменной в выра-
жение»;
— терм, допустимый для подстановки в формулу вместо предметной
переменной;
— операция «подстановка предметной переменной вместо свободной
переменной в выражение»;
— операция «одновременная подстановка термов вместо свободных пере-
менных в выражение»;
— операция «переименование связанных переменных в формуле», кон-
груэнтность формул, вариант формулы.
89
https:it.ru
• уметь
— распознавать терм, формулу и выражение языка первого порядка с по-
мощью соответствующих индуктивных определений;
— определять; подтермы терма, подформулы формулы;
— опускать и восстанавливать скобки в записях формул;
— определять; свободные и связанные вхождения переменных в формулы,
множество свободных и связанных переменных формулы;
— выполнять операции; «подстановка терма вместо свободной перемен-
ной в выражение», «одновременная подстановка терма вместо свободной
переменной в выражение»;
— определять допустимость заданного терма для подстановки в формулу
вместо предметной переменной;
— определять варианты формулы и конструировать доказательство кон-
груэнтности формул;
— конструировать доказательство свойств термов сигнатуры о, используя
индукцию по построению термов;
— конструировать доказательство свойств формулы сигнатуры s, исполь-
зуя индукцию по построению формул;
— конструировать доказательство синтаксической однозначности вы-
ражения;
— конструировать программы на любом языке программирования для
реализации индуктивных определений и операций, представленных в Упраж-
нении.
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
Теоретические сведения
В математической литературе используются как синонимы сле-
дующие термины: «язык формальной системы первого порядка»,
«язык первого порядка», «логический язык первого порядка», «логи-
ческий язык первой ступени», «язык функционального исчисления
первого порядка», «язык исчисления предикатов первого порядка»
90
https: //и га it.ru
Алфавит. Сигнатура
Я часто думаю, насколько легче
была бы моя жизнь и сколько времени
я смог бы сэкономить, если бы твердо
знал алфавит. Я не могу сказать,
как далеко в словаре I стоит от J,
не произнеся сначала про себя СиН.Я так
и не знаю, стоит ли Р до R или после,
а метарасположение Т для меня остается
чем-то, что я так, по-видимому, твердо
и не уясню.
С. Моэм
Пусть I, J, К обозначают произвольные множества.
Определение [27, с. 74—75].
Алфавит стандартного языка первого порядка — это множество
def
G = Gj LJ G2 О G3 LJ G4 LJ G5 LJ Gg,
где:
def
1) Gi = {х0,х1гх2,...} — множество предметных переменных;
def
2) G2 = {Pfn/} (i g I, rii gN) — множество предикатных символов;
при этом символ Pfn/ называется поместным предикатным сим-
волом (или предикатным символом арности nJ;
def п-
3) G3 (jg J,nj eN\{0}) —множество функциональных
символов; при этом символ называется поместным функцио-
нальным символом (или функциональным символом арности nJ;
def
4) G4 ={ak} (keK)—множество предметных констант;
def
5) G5 = {-1, &, v, <->, V, 3} — множество логических символов;
символы из множества G5 подразделяются на:
а) логические связки (или логические операторы):
-1 (отрицание),
& (конъюнкция),
v (дизъюнкция),
(импликация),
<-> (эквиваленция),
юнкторы (от лат. junctor — соединитель);
б) кванторы:
V (квантор (все)общности) — перевернутая буква «А» немецко-
го слова «Alte» — «все»,
91
https:it.ru
3 (квантор существования) — перевернутая буква «Е» немецко-
го слова «Existieren» — «существовать»;
6) G6 = {„ (, )} —множество вспомогательных символов; сим-
волы из множества G6 называются:, — (формальная) запятая,
( — (формальная) левая (открывающая) скобка, ) — (формаль-
ная) правая (закрывающая) скобка.
Предикатные и функциональные символы арности 2 называют
также бинарными, а символы арности 1 —унарными.
Формальную запятую мы печатаем жирным шрифтом, чтобы
не смешивать ее с «неформальной» запятой. В дальнейшем, если
опасность такого смешения возникать не будет, то (формальная)
запятая будет печататься обычным шрифтом.
Определение.
Сигнатурой (от средневек. лат. signatura — знак, подпись, лат.
signo —указываю, обозначаю) назовём множество
def
СУ = G2 О G3 LJ G4
Важность понятия «сигнатура» определяется тем, что различные
стандартные языки формальных систем первого порядка отличают-
ся друг от друга лишь сигнатурами.
Замечание (важное).
Для задания сигнатуры необходимо и достаточно выбрать множества
I,J, К и отображения множеств I и J в N. Меняя эти множества и отобра-
жения, мы можем изменить сигнатуру, а следовательно, и алфавит стан-
дартного языка.
Термы сигнатуры о
Выделим из множества всех слов в алфавите G «правильные» сло-
ва, для чего зафиксируем сигнатуру, обозначим ее о и приведём ин-
дуктивное определение понятия «терм сигнатуры о«. Для обозначе-
ния термов воспользуемся символами языка исследователя t1}..., tn.
Определение.
1. Предметные переменные и предметные константы являются
термами сигнатуры о.
2. Если/* 1 — n-местный функциональный символ из о, a tp ..., tn —
термы сигнатуры о, To/1(t1, ..., tn) — терм сигнатуры с.
о Hi iroi! ri 1
Ou i di OU.I va
Сказанное в пункте 2 определения можно записать в виде следу-
ющего правила построения терма:
3. Никаких других термов сигнатуры о, кроме построенных в пун-
ктах 1 и 2, нет.
Если J = 0 (сигнатура не содержит функциональных символов),
то правило построения термов 2 неприменимо, поэтому термами
являются только предметные переменные и предметные константы.
Индуктивное определение множества «правильных» слов некоторо-
го языка можно начинать словами [33, с. 12]: «... — это наименьшее
подмножество выражений языка, удовлетворяющее условиям...».
Определение.
Подтермом терма t сигнатуры о называется подслово терма t,
само являющееся термом сигнатуры о.
Определение.
1. Скобочным балансом слова в алфавите, содержащем буквы «(»
и «)», будем называть разность между числом открывающих и чис-
лом закрывающих скобок, имеющих вхождение в данное слово.
2. Словом, сбалансированным по скобкам, будем называть слово
(в алфавите, содержащем буквы «(« и «)»), скобочный баланс ко-
торого равен 0.
Индукция по построению множества термов
Обозначим Т — множество всех термов сигнатуры о.
Индуктивный характер определения множества Т предполагает
возможность использования способа доказательства, который назы-
вается индукцией по построению множества термов сигнатуры о.
Определение (индукции по построению множества 7) [22, с. 54—
55].
Для доказательства того, что некоторое свойство Р выполняется
для всех элементов множества Т, достаточно доказать, что:
1) каждая предметная переменная обладает свойством Р;
2) каждая предметная константа обладает свойством Р;
3) если t15 ..., tn являются термами сигнатуры о, обладающими
свойством Р, a/^i» •••> tn) — терм сигнатуры о, то/1^, ..., tn)
также обладает свойством Р.
93
https: //деа it.ru
Формулы сигнатуры о
Приведём индуктивное определение понятия «формула сигнату-
ры о» (или просто «формула»), для чего воспользуемся символами
языка исследователя: А, В, ... — для обозначения формул, х — для
обозначения предметной переменной.
Определение [27, с. 75].
Атомной (элементарной) формулой сигнатуры о назовём:
1) слово Р°, где Р° — О-местный предикатный символ;
2) слово Р4^, tn), где п е N\{0}, Рп — n-местный предикат-
ный символ из о, a tp ..., tn — термы сигнатуры о.
Определение.
1. Атомная формула сигнатуры о является формулой сигнатуры о.
2. Если А и В — формулы сигнатуры о, то —А, (А & В), (Av В),
(А В), (А В) являются формулами сигнатуры о.
Сказанное в пункте 2 определения можно записать в виде следу-
ющих правил построения формул —А, (А & В), (Av В), (А В),
(А^В):
А А В А В А В А В
^А’ (A&B)’(AvB)’ (А->В)’ (А<->В)’
3. Если А—формула сигнатуры о, а х—предметная переменная,
то VxA и ЗлА являются формулами сигнатуры о.
Сказанное в пункте 3 определения можно записать в виде следу-
ющих правил построения формул VxA и ЗлА:
х А х А
VxA’ ЗлА'
4. Никаких других формул сигнатуры о, кроме построенных
в пунктах 1—3, нет.
Определение.
1. Формулой, обратной к формуле (А В), назовём формулу (В —> А).
2. Формулой, противоположной к формуле (А В), назовём фор-
мулу (-А —В).
3. Контрапозицией формулы (А—> В) назовём формулу (-В —> -А).
Определение.
Подформулой формулы А сигнатуры с будем называть подслово
формулы А сигнатуры о, само являющееся формулой сигнатуры о.
94
https:/Л: rait.ru
Определение (по [22, с. 58]).
Выражением (сигнатуры о) будем называть слово в алфавите G,
являющееся термом или формулой (сигнатуры о).
Открывающие скобки в определениях понятий «терм», «атом-
ная формула» и «формула сигнатуры о« одинаковы по написанию,
но различны в том смысле, что вслед за открывающей скобкой
в определении понятий «терм» и «атомная формула» обязательно
располагается терм сигнатуры о, а вслед за открывающей скобкой
в определении понятия «формула» обязательно располагается фор-
мула сигнатуры о. Поэтому в случае необходимости мы будем ис-
пользовать термины «термальная скобка» и «формульная скобка».
Пусть А и В — формулы сигнатуры о.
Определение.
1. Строгой дизъюнкцией называется логическая связка v~, ис-
пользуемая в обозначении
def
(Av ~ В) = ((А & -iB) v (-А & В)).
2. [16, с. 417] Штрих Шеффера — это логическая связка | (введе-
на М. X. Шеффером, 1913), используемая в обозначении
def
(А|В) = —{А&В).
3. [16, с. 417] Стрелка Пирса — это логическая связка Ф (введе-
на Ч. С. Пирсом, 1880), используемая в обозначении
def
(АФВ) =-,(AvB).
Индукция по построению множества формул
Обозначим F — множество формул сигнатуры о.
Индуктивный характер определения множества F предполагает
возможность использовать следующий способ доказательства.
Определение (индукции по построению множества F) [22, с. 58].
Для того, чтобы доказать, что некоторое свойство Р выполняется
для всех элементов множества F, достаточно доказать, что:
1) каждая атомная формула сигнатуры о обладает свойством Р;
2) если формулы А и В сигнатуры о обладают свойством Р, то фор-
мулы (А & В), (A v В), (А В"), -А также обладают свойством Р;
3) если формула А сигнатуры о обладает свойством Р, то форму-
лы Х/хА и ЗлА обладают свойством Р.
95
https:it.ru
Язык формальных систем нулевого и первого порядка
Определение [42, с. 184].
Языком формальной системы первого порядка (или просто языком
def
первого порядка) будем называть кортеж Ц = (G,T,F).
Пусть I — некоторое множество.
Определение.
1. Языком формальной системы нулевого порядка (или просто языком
нулевого порядка) будем называть язык формальной системы перво-
def def def
го порядка - (G,0,F^,rfleG - Gx uG2 oG3 о G4 uG5 о G6,Gi = 0,
def def def def def
G2 ={PP} (iel), G3 = 0, G4 = 0, G5 = b,&,v,->,<->}, G6 ={(,)}.
def
Язык формальной системы нулевого порядка обозначим Lq = {G,F).
2. Пропозициональными переменными (атомами) называются
нульместные предикатные символы.
Итак, алфавит языка нулевого порядка содержит нульместные
предикатные символы (называемые атомами [21, с. 13], первичны-
ми формулами [46, с. 31], пропозициональными буквами [38, с. 22;
22, с. 45], пропозициональными переменными [13, с. 22]), логиче-
ские связки и круглые скобки.
Важно отметить, что любую формулу языка нулевого порядка
можно рассматривать как формулу некоторой «вырожденной» сиг-
натуры.
Язык формальной системы нулевого порядка во многих от-
ношениях проще языка формальной системы первого порядка.
Он не играет самостоятельной роли при формализации математи-
ческих теорий, а используется лишь как вспомогательное средство;
это «игрушечный» язык.
Запись формул в метаязыке
Напомним, что язык первого порядка мы изучаем с помощью
языка исследователя (метаязыка), в котором могут использовать-
ся знаки, не входящие в алфавит изучаемого языка (метасимволы).
Мы будем использовать различные метасимволы, в том числе:
1) А, В, Е, А1г Д2,... (прописные буквы начала латинского ал-
фавита с индексами или без них) — для обозначения формул;
2) х, у, z, ... — для обозначения предметных переменных;
3) t, ti, t2, ... —для обозначения термов.
В метаязыке для упрощения записи формул используют те или
иные договоренности (соглашения). Мы будем пользоваться таким
соглашением.
96
https://urait.ru
Соглашение (о записи формул в метаязыке).
Можно опустить все те скобки, которые будут восстановлены
при выполнении следующей процедуры: запись просматриваем сле-
ва направо и вокруг каждого очередного вхождения знака & рас-
ставляем пару скобок так, чтобы подслово, в котором эти скобки
служат началом и концом соответственно, являлось формулой, при-
чем возможно более длинной; затем ту же операцию повторяем для
связок v, —<-> (именно в этом порядке!). Таким образом, после-
довательность бинарных логических символов в порядке убывания
их «силы» в образовании кратчайших подформул такова: &, v, —
<->; из двух вхождений одной связки «более сильным» является то,
которое расположено левее.
Сокращенные записи формул (с удаленными скобками) опасно
использовать при выделении подформул — это может приводить
к ошибкам.
При нахождении подформул необходимо использовать записи
формул со всеми их скобками.
Синтаксическая однозначность представления выражений
Человеку, который владеет чудесами,
не стоит тратить всё время на то,
чтобы доказывать это.
Уильям Блейк
Во всех доказательствах данного пункта существенным образом
будет использован тот факт, что обозначения для предметных пере-
менных и констант, функциональных и предикатных символов чёт-
ко отличаются друг от друга.
Лемма 1 [54, с. 33].
1. Пусть и — термы сигнатуры о. Если хотя бы один из них
является началом другого, то = t{.
2. Пусть п е N\{0}, a t15 ..., tn, — термы сигнатуры о.
Если хотя бы одно из двух слов tlf ...,tn или является на-
чалом другого, то =t- для всех i = 1,..., п.
Доказательство. Обозначим а — слово в алфавите G.
1. Воспользуемся полной индукцией по длине слова tT.
А. Пусть lenCtJ = 1. Тогда (по определению понятия «терм»)
является либо предметной переменной, либо предметной констан-
def
той. Пусть для определенности = х, где х обозначает предметную
переменную, а терм является началом терма t{, т. е. =ха. Тог-
да (по определению понятия «терм») а = А и = х, поэтому tT =
Аналогично рассуждаем и в том случае, если является предметной
константой.
База индукции доказана.
Б. Пусть lenCtJ = к > 1. Предположим, что для всех термов и
длина которых меньше к, утверждение Леммы 1 справедливо, т. е.
если хотя бы один из них является началом другого, то Г, = t{.
Пусть для определённости терм длины к является началом тер-
ма т. е. t{ = tTa, тогда len(t{) > 1еп(^) > 1. Поэтому (по определению
понятия «терм»)
tl =yAm(tiA>_,tA), ti
где tf,..., t£, tf,..., — термы, fлт, f~s — функциональные симво-
лы, и можно написать:
f ~s(tr,..., t~) = f t£)a.
По определению предиката равенства слов функциональные
символы f~s и /лт совпадают, поэтому s = т. Далее, пользуясь свой-
ством сократимости операции приписывания слов, получим
ti > •••> = »•••»
Так как слова tf и tf являются началами одного и того же слова,
то хотя бы один из термов tf и tf является началом другого и по ин-
дуктивному предположению (ведь len(tf ) < к и len(tf ) < к) получаем,
что tf = tf.
Аналогичными рассуждениями последовательно получаем, что
поэтому a = Л и для термов, длина которых равна к.
Пункт 1 Леммы 1 доказан.
2. Воспользуемся полной индукцией по длине слова tlt..., tn.
А. Пусть len (tls ..., tn) = 1. Тогда (по определению понятия
«терм») tlt ...,tn = tlf т. е. и = 1, а терм является либо предметной
переменной, либо предметной константой. Пусть для определённо-
def
сти = х, и терм tj является началом терма t{,..., t'n, т. е. (ведь п = 1)
t{ = tja или t{ = ха. По определению понятия «терм» a = Л, поэто-
му = t{. Аналогично рассуждаем и в том случае, когда является
предметной константой. База индукции доказана.
Б. Пусть теперь len^,..., tn) = к > 1. Предположим, что для всех
слов tlf ...,tnw длины которых меньше к, утверждение Лем-
мы 1 справедливо. Пусть также слово tlt длины к является на-
чалом слова t{,...,t„. Так как случай п = 1 уже рассмотрен в пункте
1 Леммы 1, то предположим, что п > 1. Итак,
ti,..., tn =ti,...,tn(X
98
https://игаit.ru
Так как термы и tT являются началом одного и того же слова,
то один из них является началом другого, но
1еп(0 < 1еп(^,...,tn) = к, len(t{) <len(t{,..., tJJ
поэтому по индуктивному предположению = t{. Сократив, полу-
чим:
=^2>-->^па
Аналогичными рассуждениями получим, что t2 = t2,...,tn = t'n.
Пункт 2 Леммы 1 доказан.
Лемма 1 доказана.
Пусть n g N\{0}.
Предложение 1 (об однозначности представления терма)
(по [54, с. 33]).
1. Всякий терм сигнатуры о, являющийся предметной пере-
менной или предметной константой, представим соответственно
в виде: х(- или ак, где х(- — однозначно определенная предметная
переменная, ак — однозначно определенная предметная константа.
2. Всякий терм сигнатуры о, не являющийся предметной пере-
менной или предметной константой, представим в виде
fn(t1}...,tn),
где f1 — однозначно определённый для этого терма п-местный
функциональный символ, a ..., tn — однозначно определённые
для него термы сигнатуры о.
Это важное Предложение позволяет индукцией по построению тер-
мов задавать функции, определенные на множестве термов, поскольку
оно гарантирует однозначность определяемой функции (каждому тер-
му будет сопоставлено единственное значение функции).
В качестве первого примера приведём рекурсивное определение
функции rank: Т —> N, которую будем называть рангом терма (дли-
ной терма, функциональной сложностью терма [22, с. 56], синтак-
сической сложностью терма).
Определение.
def
1. rank(t) = 0, если t является предметной переменной или пред-
метной константой.
def
2. rank(fп (tj,..., tn )) = 1+rankfti)+... + rank(tn ).
Следствие (о семантике rank(t)) [22, с. 56].
Если t — терм сигнатуры о, то значение rank(t) равно количеству
вхождений функциональных символов в терм t.
99
https://ur2it.ru
В качестве ещё одного примера приведём рекурсивное опреде-
ление функции SubTerm: Т —> 2Т, которую будем называть множе-
ством подтермов терма сигнатуры о.
Определение.
def
1) SubTerm(x) = {х}, где х — предметная переменная;
def
2) SubTerm(a) = {а}, где а — предметная константа;
def
3) SubTerm(/n(t1,..., tn)) =
def
= {tntn, f n(t15..., tn)} o SubTermCtJ о... o SubTerm (tn),
где/1 — функциональный символ арности п, t1} tn — термы
сигнатуры о.
Лемма 2.
1. [13, с. 23] Пусть А и В — формулы сигнатуры о. Если одна
из них является началом другой, то А = В.
2. [33, с. 27] Собственная подформула формулы А сигнату-
ры о не может являться началом формулы А.
Доказательство.
Равносильность формулировок 1 и 2 Леммы 2 очевидна.
Докажем 1. Обозначим а, 0 — слова в алфавите G. Доказатель-
ство проведём индукцией по построению формулы А.
А. Если А — атомная формула, то А = Р1^, ..., tn), где Рп—
n-местный предикатный символ, atlftn — термы сигнатуры о.
Поскольку для некоторого слова а В = Р1^, ..., tn)a или для не-
которого слова 0 Pn(t1, ..., tn) = В0, то первым символом формулы
В является предикатный символ. Это возможно (по определению
понятия «формула») лишь в том случае, если В — атомная формула
с п-местным предикатным символом Р1. Поэтому В = Pn(t{,th) для
некоторых термов t’1}сигнатуры о. Отсюда либо
либо
Pn(ti,...,tn)a = Pn(t{,...,t;),
P4t1,..,tn)=Pn(t],...,t;)p.
Следовательно, благодаря свойству сократимости операции при-
писывания слов, t13...,tn)a = ,..., t„) или tj,..., tn) = ,..., t„)p.
В любом случае слова tL,...,tn и служат началами одного
слова, поэтому хотя бы одно из них (имеющее меньшую длину) яв-
ляется началом другого. По Лемме 1 получаем, что = th-
Следовательно А = В.
Б. Пусть теперь А = -А', где А' — формула, для которой утвержде-
ние Леммы 2 справедливо. Поскольку В = -А'а или -А' = В0, то фор-
мула В начинается с логической связки -i. Это (по определению по-
100
https:it.ru
нятия «формула») может выполняться только в том случае, если
В = —В' для некоторой формулы В'.
Итак, -А'а = —В' или —А' = —В'Р, откуда А'а = В' или А' = В'р.
В любом случае формулы А' и В' являются началом одного
и того же слова, поэтому хотя бы одно из них является началом
другого. В силу индуктивного предположения, имеем А' = В', откуда
—А' = —В'иА = В.
В. Аналогично случаю Б рассматриваются случаи: А = \/хА'
и А = НхА', где А' — формула сигнатуры о, х — предметная пере-
менная.
Г. Пусть А = (АотА1), где Ао и Ах — формулы, для которых выпол-
няется утверждение Леммы 2, ате {&, v, <->}.
Тогда либо В = (AgTAJa, либо (AqTAJ = вр.
В любом случае первым символом формулы В является (, поэто-
му В = (BqtBJ для некоторых формул Во, Вг, а т е {&, v, —
Имеем (АотА1)а = (BqTjBJ или (AgTAj) = (Вот1В1)Р.
Отсюда АотА1)а = Bo^BJ или AqtAJ = Вот1В1)р. Поскольку
хотя бы одно из слов Ао или Во является началом другого, то по ин-
дуктивному предположению Ад = Во. Отсюда тА1)а = i^Bj или tAJ =
= т1В1)Р.
Следовательно т = т1У откуда Aja = Вт) или AJ = Bjp. По индук-
тивному предположению получаем, что Ах = В1г а это влечёт А = В.
Лемма 2 доказана.
Предложение 2 (об однозначности представления формулы).
1. Всякая атомная формула сигнатуры о представима в одном
из следующих видов:
а) Р°, где Р° — однозначно определённый О-местный предикат-
ный символ;
б) Р1^, tn), где п е N\{0} — однозначно определённое на-
туральное число, Р1 — однозначно определённый n-местный пре-
дикатный символ, a tp ..., tn — однозначно определённые термы
сигнатуры о.
2. [13, с. 23—24; с. 106] Всякая формула сигнатуры о, не явля-
ющаяся атомной формулой, представима в одном и только одном
из следующих видов: -А, (А & В), (A v В), (А —> В), (А <-> В), VxA,
ЗлА для однозначно определённых формулА и В сигнатуры о и пред-
метной переменной х.
Предложение 2 обосновывает алгоритм, распознающий форму-
лы среди слов в алфавите G. Он состоит в том, что сначала читают
первый символ проверяемого слова и выясняют, может ли он быть
первым символом формулы, описанной в п. 1—2 (возможен лишь
один из них!).
Затем проверку повторяют для необходимых частей формулы.
Теперь мы имеем право задавать (с помощью индукции по по-
строению формулы) функции, определённые на множестве формул.
101
https:/Л: rait.ru
Определим индуктивно функцию rank: F —> N, которую будем
называть рангом формулы А. В литературе используются термины:
«длина формулы» [26, с. 104], «степень формулы» [47, с. 113], «логи-
ческая сложность формулы» [22, с. 59].
Пусть х — предметная переменная, А, Аь А2 — формулы сигна-
туры о.
Определение.
def
1) rank(A) = 0, если А — атомная формула;
def
2) rank(-A) = l + rank(A);
def
3) rankCCAjTAo)) = 1 + rankCAJ + rank(A2), где т g {&, v,
def def
4) rank(VxA) = 1 + rank(A), rank(SxA) = l + rank(A).
Следствие (о семантике rank (A)) [22, c. 59].
Если A — формула сигнатуры о, то значение rank (А) равно коли-
честву вхождений логических символов в формулу А.
В качестве еще одного примера приведём рекурсивное опреде-
ление функции SubForm: F —> 2F, которую будем называть множе-
ством подформул терма сигнатуры о.
Определение.
def
1) SubForm(РЧ^, •••> Q) = •••> Q},
где P11— n-арный предикатный символ, t1} — термы сигна-
туры о;
def
2) SubForm(-А) = {-A} о SubForm(A), где A — формула сигна-
туры о;
def
3) SubForm((AzB)) = {(АтВ)} о SubForm (А) о SubForm (В), где
А и В — формулы сигнатуры о, т g {&, v,
def
4) SubForm(AxA) = {ЛхА) о SubForm(A), где X g {X/, 3},А — фор-
мула сигнатуры о.
Синтаксическая однозначность
представления вхождений термов и формул
Предложение 3 (однозначность представления вхождений вы-
ражений).
1. (По [54, с. 34]) Пусть t — терм сигнатуры о.
Тогда каждое вхождение в t предметной переменной, предмет-
ной константы или функционального символа является началом
вхождения в терм t однозначно определенного терма сигнатуры о. 102
102
https:/Л: rait.ru
2. Пусть А — формула сигнатуры о. Тогда каждое вхождение
в А любой предметной переменной, предметной константы или
функционального символа является началом вхождения в формулу
А однозначно определенного терма сигнатуры о.
3. Пусть А — формула сигнатуры о. Тогда каждое вхождение
в формулу А предикатного символа и любой из букв (, 1—i, V, Я, где
( — формульная скобка, является началом вхождения в формулу
А однозначно определенной ее подформулы.
Следствие.
1. Каждое вхождение в терм сигнатуры о открывающей скобки
не начинает вхождения никакого терма.
2. Каждое вхождение в формулу сигнатуры о открывающей
скобки, не являющейся формульной, не начинает вхождения ника-
кого терма и никакой формулы.
Синтаксическое сохранение выражений
при замене вхождений подвыражений
Лемма 3.
1. Пусть t — терм сигнатуры о, a 0Х и 02 — вхождения в t термов
и t2 соответственно. Тогда либо 0Х и 02 не имеют общих вхождений
символов алфавита, либо одно из них целиком содержится в другом.
2. [13, с. 24; с. 106] Если А — формула сигнатуры о, а 0в и 0с —
вхождения в А подформул В и С соответственно, то либо
0в и 0С не имеют общих вхождений символов алфавита, либо одно
из них целиком содержится в другом.
Предложение 4 (о сохранении выражении при замене вхождении).
1. Пусть и t2 — термы сигнатуры о, a t — терм сигнатуры о,
содержащий хотя бы одно вхождение терма tp
Если слово t' получено из терма t заменой произвольного вхож-
дения на t2, то t7 является термом сигнатуры о.
2. Пусть А и В — формулы сигнатуры о, а СА — формула сигнату-
ры о, содержащая хотя бы одно вхождение формулы А.
Если слово Св получено из формулы СА заменой произвольного
вхождения А на В, то Св является формулой сигнатуры о.
Следствие.
Если все вхождения подформулы В в формулу А сигнатуры о за-
менить на формулу С, то получится формула сигнатуры о.
Свободные и связанные вхождения переменных
Определение (по [13, с. 106]).
1. Подформула формулы А сигнатуры о, начинающаяся с вхож-
дения квантора V, называется областью действия этого вхож-
дения квантора V в формулу А (или областью действия кванто-
рах/ в формуле А). 103
103
https:it.ru
2. Подформула формулы А сигнатуры о, начинающаяся с вхож-
дения квантора Я, называется областью действия этого вхожде-
ния квантора Я в формулу А (или областью действия квантора
Я в формуле А).
Определение (по [27, с. 75]).
1. Связанным вхождением предметной переменной х в формулу
А будем называть вхождение предметной переменной х, находя-
щееся в области действия квантора V или Я в формуле А, за кото-
рым сразу же расположена буква х.
2. Свободным вхождением предметной переменной х в формулу
А будем называть вхождение предметной переменной х, не нахо-
дящееся в области действия квантора V или Я в формуле А, за ко-
торым сразу же расположена буква х.
Таким образом, свободные и связанные вхождения переменных
играют в формуле различную синтаксическую роль.
Свободные и связанные переменные
Определение (по [27, с. 75]).
1. Свободной переменной формулы А будем называть предметную
переменную, имеющую хотя бы одно свободное вхождение в фор-
мулу А.
2. Связанной переменной формулы А будем называть предметную
переменную, имеющую хотя бы одно связанное вхождение в фор-
мулу А.
Итак, некоторая предметная переменная в одной и той же фор-
муле может быть одновременно и свободной, и связанной.
Пример.
Рассмотрим формулу VxjP2^, х2) —> Р1(х1), для которой укажем сво-
бодные и связанные вхождения предметных переменных ххи х2:
Свободные вхождения
г г
VXi Р2(Х!,Х2)
Т Т
Связаные вхождения
Предметная переменная х1 является в данной формуле одновременно
и свободной, и связанной.
Для дальнейшего удобно иметь индуктивное определение понятия
«множество свободных переменных формулы». Определим функцию
FV:F->2f.
104
https://urajt.rt!
Определение [46, с. 27—28].
def
1) FVCP^ti, ...» Q) = FVCtJ о FV(t2) о ... о FV(Q, где
..., tn) — атомная формула сигнатуры о, a FV(t() — мно-
жество предметных переменных, имеющих вхождение в терм tf,
i = l,..., п;
def
2) FV(-iA) = FV(A), где A — формула сигнатуры о;
def
3) FV((AtB)) = FV(A) о FV(B), где т g {&, v, <->}, А и В — фор-
мулы сигнатуры о;
def def
4) FV(VxA) - FV(A)\{x}, FV(SxA) - FV(A)\{x}.
Предложение.
1. Для любой формулы А сигнатуры о можно с помощью конеч-
ного числа применений пунктов определения найти все элементы
множества FV(A).
2. Для любой формулы А сигнатуры о множество FV(A) опреде-
ляется однозначно.
3. [13, с. 107] Пусть х—предметная переменная, х g FV(A) тогда
и только тогда, когда существует свободное вхождение этой пере-
менной в формулу А.
Таким образом, множество FV(A) можно назвать множеством
всех свободных переменных формулы А сигнатуры о.
В метаязыке будем использовать также следующие обозначения:
1) FV(t) — множество предметных переменных, входящих
в терм t сигнатуры о;
2) CV(A) — множество связанных переменных, входящих в фор-
мулу А сигнатуры о;
3) А(хъ ..., хп) обозначает, что FV(A) с {хъ ..., хп};
4) Г(хг,..., хп) обозначает, что FV(t) с {х15 ..., хп};
5) А[х] иногда обозначает [52, с. 44], что предметная перемен-
ная х имеет свободное вхождение в формулу А.
Определение.
1. [46, с.26] Замкнутым (константным') термом сигнату-
ры о будем называть терм t, для которого FV(t) = 0 (иначе гово-
ря, замкнутый терм не содержит предметных переменных).
2. Замкнутой формулой (или предложением) сигнатуры с будем
называть формулу А, для которой FV(A) = 0.
3. Открытой формулой сигнатуры о будем называть формулу,
каждая предметная переменная которой является свободной.
4. Бескванторной формулой сигнатуры о назовём формулу, не со-
держащую вхождения кванторов.
105
https:it.ru
Операция «подстановка терма вместо
свободной переменной в выражение»
Рассмотрим фундаментальную операцию, которая позволяет
по выражению языка формальной системы первого порядка найти
новое выражение и которая сокращённо называется подстановкой
терма вместо свободной переменной в выражение. Операция под-
становки заключается в том, что каждое свободное вхождение в вы-
ражение указанной предметной переменной заменяется на вхож-
дение указанного терма (одного и того же для всех вхождений
предметной переменной).
Следует заметить, что в очень ясном на первый взгляд понятии
«подстановка терма вместо свободной переменной в выражение»
таится «подводный камень»: если некоторый терм t подставляется
без предосторожностей вместо свободных вхождений переменной
х в формулу А, то некоторые предметные переменные, входящие
в терм t, могут оказаться связанными в формуле А.
Определим теперь формально трёхместную операцию
(o^FuTjx^xT-^uT,
которую будем называть подстановкой терма t вместо всех свобод-
ных вхождений предметной переменной х в терм или формулу.
Пустьх,у, z — предметные переменные, t, t15 ..., tn е Т, А, В е F.
Определение [16, с. 450—451; 39, с. 195].
Результат операции подстановки терма t вместо всех свободных
вхождений предметной переменной х в терм или формулу опреде-
ляется индуктивно следующим образом:
def
1)(а)? = а, если а — предметная константа;
def ft, если у = х,
у, если у ф х (у графически не совпадает с х);
2) (у)?
def
3) (fn(ti,...,tn))f = (ил, еслиуь-п-местный функ-
циональный символ;
def
4) (Р”^,...,^))? = Pn((t1)^,...,(tn)t^ если Рп— n-местный пре-
дикатный символ;
def
5) (-пА)? = -{А)?;
def
6) ((АтВ))? = (А)?т(В)?, где т G {&, v, <->};
def def
7) (VyA)? = VyA, если хе FV(VyA); (ЗуА)? = ЗуА, если хе FV(3yA);
8) подстановка без коллизии:
def
(VyA)? = Vy(A)?, если хе FV (А), у е FV (t);
106
https:it.ru
def
(ЗуА)* = Зу(А)*, если хе FV (А),у g FV (t);
9) устранение коллизии переменных при подстановке:
(\fyA~)? = Vz((A)£ j , еслих g FV (А),у g FV (t),z £ FV (t) о FV (A);
(3yA)* d=f 3z((A)^ , если x g FV (A),у g FV (t), z g FV (t) о FV (A).
Данное определение корректно в том смысле, что всякий раз
мы ссылаемся на подстановку для выражений уменьшающейся дли-
ны.
Термы, допустимые для подстановки
вместо переменных в формулу
Итак, к термам, участвующим в подстановке, предъявляются
определенные синтаксические требования. Опишем их содержа-
тельно (неконструктивно), для чего переформулируем пункт 8 опре-
деления результата операции подстановки терма t вместо всех сво-
бодных вхождений предметной переменной х в терм или формулу.
Определение.
1. [54, с. 35] Терм t называется термом, допустимым для подста-
новки вместо предметной переменной х в формулу А, если никакое
свободное вхождение х в А не находится в области действия ника-
кого из вхождений квантора V или 3, вслед за которым стоит пере-
менная, имеющая вхождение в t. В этом случае также говорят, что
терм t свободен для переменной х в формуле А [38, с. 55; 27, с. 75].
2. Терм t называется недопустимым для подстановки вместо
предметной переменной х в формулу А, если существует свободное
вхождение х в А, находящееся в области действия квантора V или
3, вслед за которым стоит переменная, имеющая вхождение в t.
Примеры определения допустимости терма t для подстановки
вместо предметной переменной х в формулу А оформим в виде сле-
дующей таблицы [38, с. 55]:
X А t FV(t) CV (A) Допустим?
хк W) {Xj} 0 Да
xi VxjP/Cxj) *k {Xj} Да
хг Vx^2 (Xi, х2 ) -> Pj1 (Xi) ^(х^Хз) {Xi, x3} {x2} Да
*1 Зх3 Vx2Pi2 (Xi, x2 ) Pf (Xj) ^(xbx3) {*1, x3} {x2, x3} Нет
107
https:/Л: rait.ru
Замечание.
Следует обратить внимание на нечёткость часто используемого обо-
значения A(t) для результата операции «подстановка терма t в формулу
А». При таком способе обозначения подразумевается, что фиксирована
некоторая предметная переменная х и производится подстановка допусти-
мого для подстановки терма t вместо всех свободных вхождений х в фор-
мулу А, но сама предметная переменная х при этом не указывается.
Операция «подстановка предметной переменной вместо
свободной переменной в выражение»
Определим формально трёхместную операцию
которую назовём подстановкой предметной переменной у вместо
всех свободных вхождений предметной переменной х в терм или фор-
мулу.
Пусть t и А — соответственно терм и формула сигнатуры о.
Определение.
Результат операции подстановки предметной переменной у вме-
сто всех свободных вхождений предметной переменной х в терм
или формулу определяется следующим образом:
(О*,еслиу £FV(t);
def
Му =
не определено, если у £ FV(t).
def
[А]* =
(А)*, если у £ FV(A);
не определено, если у £ FV(А).
Примеры.
(8)
def def
1. [VyA]* = (VyA)J = Vy(A)*.
zgFV(A) xeFV(A)
ygFV(Z)
Итак, преобразования имеют место, если хе FV(A), z g FV(A) и {у}.
2. Существенное различие между результатами операций (А)*
def J
и [А]* иллюстрирует следующий пример. Пусть А = Р2(х, у), тогда
def def def
(А)* = (Р2(х,у))* = Р2(у,у), в то время, как [А]£ = [Р2(х,у)]*
не определено, так каку е FV(P2(x,y)).
Возможна следующая характеризация подстановок вида [А]*.
108
https: "и rait.ru
Определение (по [32, с. 74]).
Будем говорить, что в формуле А возможна замена свободной
предметной переменной х на предметную переменную у, если
в результате замены каждого свободного вхождения х в форму-
лу А на у и последующей замены в полученной формуле каждо-
го свободного вхождения у на х получается исходная формула А.
Пусть х иу обозначают различные предметные переменные.
Предложение (по [32, с. 75]).
Если в результате замены каждого свободного вхождения пред-
метной переменной х в формулу А на предметную переменную
у и последующей замены в полученной формуле каждого свободно-
го вхождения у на х мы приходим к исходной формуле А, то
[А]*=(А)*.
Доказательство. Упражняйтесь.
Операция «одновременная подстановка термов вместо
свободных переменных в выражение»
Определим формально следующую операцию:
(o):-J : (F о Т) х Gf х Тп-> F и Т,
которую будем называть одновременной подстановкой термов вме-
сто свободных переменных в терм или формулу.
Будем обозначать
результат операции «одновременная подстановка термов tlf ...,
tn вместо всех свободных вхождений переменных х1г ...,хп соответ-
ственно в формулу А».
Пусть хг, ..., хп — попарно различные предметные переменные
(х( Ф Ху для i Ф j), у и z — предметные переменные, t15 ..., tn, slf
sn — термы сигнатуры о, А и В — формулы сигнатуры о.
Определение (А. В. Голанова, по [22, с. 69—70]).
Результат операции одновременной подстановки термов t1}
tn вместо всех свободных вхождений предметных переменных
х1г ..., хп в терм или формулу определяется индуктивно следую-
щим образом:
def
1) (а)^1’" = а, если а — предметная константа;
109
https:it.ru
t,, если у = x,
def для некоторого i g {l,...,n},
2) = ’у,еслиу*х£
(переменная у графически не совпадает с х()
для всех i g {1,...,п};
def , .
3) (/n(^,-,sn))J;Xn если fn —
n-местный функциональный символ, п е N\{0};
def
4) (рО)ХЪ-:ХП = ро.
Г1»—Лп
def z ч
С1,...,СП у А H,...,Ln Ll,...,Ln J
если Рп— n-местный предикатный символ, п е N\{0};
def
5) = -<АК1-'^;
Чэ—Лп
def
6) (АтВ)*1’"’*" = (А)?1’"’*" т(В)*1’"’*", где те {&, v,
Ч>—»Ln Ч>—>Ln Ll>—>Ln
def
7) (VyA)^;^n = VyA, если x1}...,xn gFV(VyA);
def
(ЗуА)*1’”’*'1 = ЗуА, если xb...,xn gFV(3yA);
ui f’>Ln
def
8) (VyA)*1”"’*^1’*/’*^1’-’*" = (VyA)*l’’‘^-VX£+17’Xn,
ti>—A-iAA+i.—>tn J fi>—Л-1Л+1>—>tn
если xf GFV(VyA) для некоторого i e {1,..., n};
def
(ЗуА)^1’";^-1;^’^1”"’^ = (ЗуА)^1”";^-1;^1’";’^,
tl>—Лп J tl>—/i-i/i+i,... ,tn
если xf GFV(VyA) для некоторого i e {1,..., n};
9) подстановка без коллизии:
def
(VyA)^’"’^n = Vy(A)^;^n,еслихь...,xn GFV(A),y gFV(t1)o...oFV(tn);
def
(ЗуА)*1’" ’*" = 3y(A)*1’" ’*n, если x1}...,xn g FV(A), у g FVfo) о... о FV(tn);
10) устранение коллизии переменных при подстановке:
если X!,...,xn g FV(A), у g FVfo) w... wFV(tn),
zGFV(t1)o...oFV(tn)oFV(A);
http
- // iroif ri i
al 4 Ml oiu.l VI
110
=3z(w)?CX">
еслих1г...,хп gFV(A),у gFV^)u...oFV(tn),
z^FV(t1)o...oFV(tn)oFV(A).
Предложение.
Результат операции «одновременная подстановка термов tlf ...,
tn вместо всех свободных вхождений переменных х1} ...,хп соответ-
ственно в формулу А» является формулой сигнатуры о.
Доказательство. Упражняйтесь.
Определение (по [13, с. 119]).
Будем говорить, что термы tlf..., tnявляются допустимыми для
одновременной подстановки вместо предметных переменных
х1г ...,хп соответственно, если для каждого i = 1,..., п терм яв-
ляется допустимым для подстановки вместо предметной перемен-
ной хг- в формулу А.
Операция «переименование связанных переменных в формуле»
Интуитивно понятно, что переименовывая связанные перемен-
ные в формуле А, мы можем избежать коллизии переменных при
выполнении операции «подстановка терма вместо свободной пере-
менной».
С этой целью применяют важную операцию, которая называет-
ся переименованием связанных переменных в формуле (или нахож-
дением варианта формулы) и позволяет по заданной формуле язы-
ка формальной системы первого порядка найти некоторую новую
формулу.
Операция переименования связанных переменных состоит
в том, что в некотором вхождении подформулы в данную формулу
каждое связанное вхождение некоторой предметной переменной
заменяется на другую предметную переменную (одну и ту же для
всех вхождений). Однако при переименовании связанной перемен-
ной семантика (смысл) формулы не изменится, если при этом со-
блкщать одну существенную предосторожность: никакая свободная
переменная в любой подформуле данной формулы не должна после
переименования оказаться связанной переменной.
Указанное недопустимое явление назовём коллизией переменных
при переименовании связанных переменных.
Например, если мы решим в формуле ЗуР3(х,у, z) заменить пред-
метную переменную у на предметную переменную х, то получит-
ся формула ЭхуР3(х, х, z), которая имеет иной смысл, чем исходная
формула.
Причина состоит в том, что после неудачного переименования
связанной переменной у первое вхождение переменной х, которое
раньше было свободным, стало связанным.
Для организации «борьбы» с коллизией переменных при переи-
меновании связанных переменных вначале определим индуктивно
на множестве формул языка формальной системы первого поряд-
ка бинарное отношение, которое назовем конгруэнтность формул
и обозначим символом «~а».
Пусть Рп— n-местный предикатный символ, t15 ..., tn — термы
сигнатуры о, а В, С, В1 Сг— формулы сигнатуры о.
Определение.
1) Q;
2) (ВтС) «а (В^СД если В «а Вг, С «а Q, т е {&, v,
3) -В ~а-1В15 если В ~а Вх;
4) VxB«a Vy[B]x; ЭхВ«аНу[В]*.
Приведём вариант определения понятия «конгруэнтность фор-
мул».
Определение (по [19, с. 139]).
Формулы А и В будем называть конгруэнтными формулами,
если А и В имеют одно и то же число к символов и для каждого
i (i = 1, к):
1) если i-й символ в формуле А не является предметной перемен-
ной, то он же является i-м символом в формуле В;
2) если i-й символ в формуле А — это свободное вхождение пред-
метной переменной, то i-й символ в формуле В — это свободное
вхождение той же предметной переменной;
3) если i-й символ в формуле А — это вхождение предметной пе-
ременной, связанное j-м квантором в А, то и i-й символ в форму-
ле В тоже является вхождением предметной переменной (не обя-
зательно той же самой), связанной j-м квантором в формуле В.
Другими словами, две формулы называются конгруэнтными
формулами, если они отличаются только связанными переменны-
ми, и соответствующие связанные переменные связаны соответ-
ствующими кванторами.
Определение.
1. Вариантом формулы А назовём формулу Ар для которой А ~а Ар
2. [54, с. 59] Будем говорить, что формула Ах является вариан-
том формулы А, если формула Ах может быть получена из фор-
мулы А с помощью последовательных замен следующего типа:
112
,о- // iroi! ri ।
A(VxB/Vy[B]*) , т. e. замены подформулы VxB формулы А на
Vy[B]* ;
А (ЗхВ / Зу[В]*), т. е. замены подформулы ЗхВ формулы А на Яу[В]*.
Приведём ещё один способ индуктивного определения функции
«вариант формулы А», которую обозначим Var:F F.
Определение.
def
1) Var(Pn(t15 ..., tn),y) = Pn(t1, ..., tn);
def
2) Уаг((ВтС),у) = Var(B,y)TVar(C,y), где т g {&, v, <->};
def
3) Var(-iB,y) = -iVar(B,y);
def def
4) Var(QxB,y) = Qy[B]*, где Q = {V, 3}.
Замечание.
Забегая вперёд, отметим, что с точки зрения семантики формул языка
первого порядка конгруэнтные формулы можно считать «несущественно
отличающимися друг от друга», т. е. математическая логика изучает
не отдельные формулы, а классы конгруэнтных формул.
Примеры решения некоторых типов упражнений
Пример 1. Покажите с помощью применения правил построения тер-
мов и формул, что слово Vx,1(P1Cxr1) —> Bx2Q2(fl(x2), *2)) является формулой
def
сигнатуры о = {PhQ2,/1}.
Решение. Построим древесное доказательство заданного слова:
f1 *2
Q2 /Чх2) х2
Р1 Хг х2 Q2(f1(x2),x2)
Р1 (X! ) 3x2Q2 (f1 (х2 ), Х2 )
X! P1(x1)^3x2Q2(f1(x2),x2)
VXi(Р1 (Xi) -> 3x2Q2(f1 (х2), х2))
Итак, применяя правила построения термов и формул, удалось постро-
ить древесное доказательство данного слова, поэтому данное слово явля-
ется формулой сигнатуры о.
Вывод. Для того, чтобы доказать, что некоторое слово в алфавите
языка первого порядка является формулой сигнатуры о, достаточно
предъявить доказательство построения этого слова по правилам постро-
ения формул сигнатуры о.
113
https:it.ru
Пример 2. Докажите, что не является формулой слово
Vx13ab(pi(x1)v-1(pi(x0)).
Решение. Воспользуемся тем, что в любую формулу сигнатуры о левая
скобка имеет ровно столько же вхождений, сколько и правая.
В данное нам слово левая скобка имеет 4 вхождения, а правая — 3.
Вывод. Для того, чтобы доказать, что данное слово не является фор-
мулой сигнатуры о, достаточно установить, что такого доказательства
не существует. Пока мы располагаем лишь одним способом для этого: ука-
зываем некоторое характеристическое свойство, которым обладает вся-
кая формула сигнатуры о (построенная по правилам) и не обладает дан-
ное нам слово. Естественно, что всякий раз подходящее для данного слова
свойство приходится подбирать (так, в качестве такого свойства высту-
пало свойство равенства количеств вхождений в формулу левой и пра-
вой скобки).
Пример 3. Восстановите опущенные скобки в записи следующей фор-
мулы в метаязыке: Vx2——> Р^(х15 х2, х3) v VxxP3(х1).
Решение. Воспользуемся соглашением об опускании скобок в записи
формул:
(VX2-J?(X!) -> (Р23(хъ х2, х3) V Vx^CxJ)).
Пример 4. Перечислите свободные и связанные вхождения каждой
из переменных в формулу Vx(3yP2(x,y) —> Q3(x,y, z)).
Решение. Область действия вхождения квантора V есть вся формула,
поэтому все вхождения предметной переменной х в данную формулу явля-
ются связанными. Предметная переменная z в этой формуле непосред-
ственно после квантора не встречается, следовательно, любое ее вхожде-
ние в эту формулу (а имеется лишь одно) является свободным.
Наконец, предметная переменная у имеет вхождение в рассматривае-
мую формулу, непосредственно следующее за 3; следовательно, у связана
в данной формуле. Однако, последнее вхождение предметной перемен-
нойу в эту формулу (попадающее в Q3(x,y, z)) свободно, поэтомуу также
и свободна в данной формуле.
Пример 5. Определите результаты следующих операций подстановки:
а) СРЧх!»^,;
г) (Vx2ff(x1,x2)->P11(x1))^(jfi^);
б) (VyA)*, если у;
д) Ox3Vx2^3(x1,x2,x4))^(xijX3).
в) (VXiPKxJ)^;
114
о Hi iroi! ri ।
Решение.
(4) (2)
def , . def
A. = P1 =
Б. (VyA)^, если x=y,
так какх g FV (VyA) = -x e FV (VyA) = -<(x e FV (A)\{y}) = -i(x e FV (A) &
x£ {y}) =x£ FV(A) vxe {y} =xg FV(A) vx=y.
B. (VXiPKXi))^ = Vx^Cxi).
(6)
def
Г. (Vx2P12(x1,x2)^P11(x1))^2 =
(6) (8),(4)
def def
= (,УХ2Р^Х1,Х2Щ^31 =
(4)
def def
= Vx2Uf -» W(*i. *з» =
(4)
def
= Vx2P12f12(x1, x3), x2) P}(ff(x1,x3)).
Д. (3x3Vx2P13(x1,x2,x4))^(xi хз) =
(9) (7)
def def
= M(Vx2P13(x1,x2,x4^3)^(xijX3) =
(8)
def def
= 3z(Vx2P3(x1,x2,x4))^(xijX3) =
(8) (4)
def def
= azVx2(P3(x1,x2,x4)n =
def
= 3zVx2P13(f12(x1,x3),x2,x4).
Пример 6. Укажите, допустим ли терм (Xj, Х3 ) для подстановки вме-
сто предметной переменной хх в формулу (Зх3 Vx2f^ (х1, х2 ) —> (х1).
Решение. Первое свободное вхождение предметной переменной хх
в заданную формулу находится в области действия квантора 3, вслед
за которым расположена предметная переменная х3, имеющая вхожде-
ние и в терм (Xj, Х3). Поэтому терм (хх, х3) не является допусти-
мым для подстановки вместо хх в заданную формулу.
115
https:/Л: га it.ru
Пример 7. Покажите, что Fj ~а F2 если
def def
Fi = Vx(A(x,c)v3xB(x)->3yG(x,y)),F2 =
def
= Vy(A(y, c) v 3zB(z) -> 3uG(y, u)).
Решение. Нетрудно увидеть, чтоxe FV (FJ ихе CV (FJ. Заметим,
что у g FV (А(х, с) v ЗхВ(х) 3yG(x,y)) и приступим к преобразованиям:
def (4)
Fj = Vx(A(x,c)v3xB(x)->3yG(x,y))»a
(4) def
»a Vy[A(x, с) V 3xB(x) -> 3yG(x, y)]* =
def def
= Vy(A(x, c) v3xB(x) —>3yG(x, y))* =
def def
= Vy((A(x,c)v3xB(x))* —>(3yG(x,y))*) =
def def
= Vy(A(y,c)v3xB(x))* —>(3yG(x,y))*) =
def
= Vy(A(y, с) V 3zB(z) -> 3uG(y, u)) = F2.
Поэтому FA ~a F2. Более того, легко видеть, что в результате получена
формула F2, для которой FV(F2) = {с}, а CV(F2) = {и,у, z}.
Пример 8. Установите, являются ли конгруэнтными формулы:
def
F] = Vz(P(z)&3zQ(x,z)—>3yR(z,y))vQ(z,x),
def
F2 = Vr(P(r)&3uQ(x,u)->3vP(r, v))vQ(z,x).
Решение. Воспользуемся определением С. Клини: вначале перенуме-
руем в каждой формуле кванторы в направлении слева направо, а затем
введем индексы, указывающие, какие вхождения предметных перемен-
ных связаны каждым квантором:
V ^(РО) & 3z2Q(x, z2) -> ЗузРС^!, уз)) v Q(z, х),
V ri(P(ri) & 3u2Q(x, u2) -> 3 v3P(/i, v3)) v Q(z, x).
Если теперь «стереть» сами связанные переменные, оставляя пустые
места, занумерованные индексами, то получим равные слова:
2Q(x, 3))vQ(z,x),
ViCPCJ&^QCx, 3))vQ(z,x).
Поэтому F± ==aF2.
116
o Hi iroit ri i
Упражнения для самостоятельного решения
Термы и формулы
1. Докажите, что слово /13(х3,У/(х0,а0),У13(а0,а1,а2)) является термом
стандартного языка первого порядка, имеющего сигнатуру
{а0,а1,а2,./?,./?,Р13}.
2. (По [27, с. 77, № 1]) Пусть/1 — одноместный, g2—двухместный, h3 —
трехместный функциональные символы некоторого стандартного языка
первого порядка.
Являются ли термами этого языка слова:
a) /^(x^xj);
г) g2(f1(x2, h3(x0,x1,x2)));
б) ^^(Xo^CxJ);
Д) f(g2(x0), h3(x0, хг, х2));
в) f(g2(x0), Яз^ХрХг));
е) g2(f1Cx2), h3(x0, g2(x3, х2), х15 х2))?
3. [27, с. 77, № 5] Опишите множество термов, в которые имеют вхожде-
ния кроме вспомогательных букв, только следующие буквы: а) предметная
переменная х0 и функциональный символ /*; б) предметная переменная
х0 и функциональный символ g2.
4. Докажите, что слово -(P/Cxq) & Зх1—,Vx0P22(x1, является формулой
некоторого стандартного языка первого порядка.
5. [27, с. 77, № 3] Покажите, что не является формулой слово
ЭХоУХ!...УхХо (Р1 (Хт ) &... & Р1(Ххъ )).
6. [27, с. 77, № 2] Пусть/1, g2, h3 обозначают соответственно одноместный,
двухместный, трёхместный функциональные символы стандартного языка
первого порядка, а Р1 — одноместный, Q3 — трехместный предикатные
символы. Являются ли формулами следующие слова:
a) Q3(x0,/1(x1), h3(x13 х2, х2));
б) Q3(P1(x0),/1(x1),/1(x2));
в) (РЧхд) VXjCQ^Xq, х1} xJ&P4g2(x0, Xi))));
г) fi(h3(x1,x2,x2')')?
7. Рассматривается стандартный язык первого порядка, сигнатура ко-
торого содержит символы Pf,P£,P3, fy,f2 ,f3, а1г а2, а3. Определите, явля-
ются ли следующие слова выражениями языка или нет:
a) //(ai);
б) /22(Р1(Х1,х2),а2);
в) Хр
г) Pi2C/i (х1}х2,х3));
д) /з(а1>а2,рз(а1У)'>
е) JfCxjJ&PfCxJ;
ж) /iv/2->/3;
з) (aXiP^CZ/Cxj)) Р23(х15 х2, а2));
HjaCx^CXi, х2) V Р23(хъ х2, х3)) Р/С/зСхь х2, х3));
к) (Р^Схх, /33(ai, а2, а3)) v Р23(хъ а2, х3) & Ух^Сх^).
117
https: "и га it.ru
8. [27, с. 77, № 4] Выпишите все подформулы формулы:
a) Q2(/1(x0),g2(x0,x1));
б) (3x0Q2(x0, Xj) ->(.Pl(g2(pc0, Xj)) & Vx2P1(x2))).
Записи формул в метаязыке
9. (По [38, с. 54])
Восстановите скобки в следующих записях формул:
a) VxjP/CxJ -> Рг2(хъ х2);
б) Vx1P11(x1)vP12(x1,x2);
в) Ух2-Р/(Х]) -> Р/(хь х2, х3)v VxjPJ(xj);
г) iVxjP/CxJ -> 3x2Pj(x2) -> P?(xlt х2) v Р^х2У,
д) Vx1Vx3Vx4P11(x1) Pj(x3) & -J^Cxj);
е) Зх^ХгЗхзР/(xj v Зх2-1Х/х3Р2(Хз, х2).
10. Опустите скобки в следующих формулах:
а) ((ро v -Р2°) -> (ро -> (Р2° & РО)));
б) ((З^РДхт) v 3x2-,Vx3P22(x3, х2)) v -n-.VXgPj1 (х3));
в) (Vx3((PRx3) Vxj-P/CxJ) pi(x3)) Sxj-P^Cxj));
г) Vxx(Vx3(X/x3(P2(x3) &-P/CxJ) (P2] (x3) &-Р/(xi))));
Д) ((((Зх^1 (x3) & Vx3-J^1(x1)) v P2i(x3)) & -iVxgP/(x3)) v Pi(x4)).
11. Придумайте формулу, в которую имеют вхождения все логические
символы и никакие скобки в записи которой (кроме самых внешних) нельзя
удалить.
Свободные и связанные вхождения переменных
12. [38, с. 55] Укажите свободные и связанные вхождения переменных
в формулы:
a) Vx3(Vx1P12(x1, х2) -> Рг2(х3, xj);
б) Х/х2Р12(х3,х2)—> Х7х3Р12(х3,х2));
в) Vx23x1P13(x1,х2, ff(xltх2))v -iVx1P12(x2, ^(Xj)).
13. Перечислите свободные и связанные вхождения каждой из пере-
менных в каждой из формул (внешние скобки опущены):
а) УхР(х);
д) 3xVy(P(x) & Q(y)) VyR(x,y);
б) УхР(х) —>Р(у);
е) ЗхЗу(Р(х,у) &Q(z));
в) Р(х) 3xQ(x);
ж) 3uVvB(u, v) v);
г) Зх(А(х)&В(х));
з) Vx(3yP(x,y) Q(x,y, z)).
Свободные и связанные переменные
14. Для каждой из следующих формул найдите множество ее связанных
переменных (внешние скобки опущены):
a) Vx23x1(P13(x0, хь х2) Р22(х2,xj);
б) Х7х2Р22(х3,х2)&Зх3Р^(х3,х2);
в) УхгЗх^Чх!, х2, $(х1г х2)) ->Vx1P22(x2, //(xj).
15. Для каждой из следующих формул найдите множество ее свободных
переменных:
a) 3x2Vx1(P12(x1, х2) Рг2(х2, хг));
б) (Х7х2Р12(х3,х2)->Зх3Р12(х3,х2);
в) Ух2Зх1Р23(х1, х2, /г2(х1} х2)) v —iVx1P12(x2, //(xj).
118
https: "ига it.ru
16. Для каждой из следующих формул найдите множество ее свободных
переменных, являющихся одновременно и связанными:
a) 3x0(P22(x0,x1)^Vx1P11(x1));
б) ЧЗх2Р22(х2, Xj) & P/Cf (хъ х2)));
в) ((Vx0P22(x0, xj VxjP32(x0, X])) v -nVx1P32(x2, ^(хх))).
17. Для каждой из следующих формул найдите множество ее связанных
переменных, не являющихся одновременно и свободными:
а) (Зх2Р2(х3, х2) &Зх3Ух2Р22(х3, х2));
б) (Vx2Vx1J^3(x0, х1} х2) Р2 (х2, xj);
в) (Ухг-ах^/Сх!,х2, х2)) VxjP^(x2, ^(xj)).
18. Приведите пример формулы А, содержащей вхождения двухместных
предикатных символов, и такой, что: а) никакая свободная переменная
формулы А не является связанной: б) всякая свободная переменная формулы
А является связанной: в) всякая свободная переменная формулы А явля-
ется связанной, но не всякая связанная переменная является свободной:
г) CV (А) с FV (А), т. е. всякая связанная переменная формулы А является
свободной, но не всякая свободная переменная является связанной.
Операция подстановки терма вместо свободной
переменной в выражение
19. Укажите смыслы следующих записей (хх,..., хп — предметные пере-
менные, t13 — термы, А — формула):
в) СА)^;"^П;
б) At1[ti]x2b-2]""XnlAi];
Г)
Можете ли Вы привести пример формулы А, для которой в результате
применения указанных подстановок получатся разные результаты?
20. (По [22, с. 67—68; с. 70].) Вычислите результаты следующих опе-
раций подстановки:
1) (3yP(x,y,z))^xy);
2) (3yP(x,y,z))J(xy);
3) (3yP(x,y,z))^xz);
4) (3zVyP(x, у) Q(x))^(x z);
5) (3yP(z,y,x))™;
6) (VyP(x,y)->Q(x))^(xz);
7) (P(x,y)^VyQ(y))^y)z;
8) (VyP(y,z)v3yR(x,y))J^y)z;
9) (Vx3yP(x, y, z) Bz\fyQ(x, у, «))^(хд);
10) (Vx2A(x3, x2)&Зх3А(х3,х2))^Хз y2);
11) (Ухг-Зх^Х!, x2, x3) v Vx3P(x3))J3xi хз);
12) (3x3Vx2P]3(x1, x2, x4) & -i3x3Qi (xx, x2, х3))/(Х2,Хз);
119
https://urait.ru
13) (ЭхзУхгР^Чхь X2, x4) & -.SxgQfCxj, x2, х3))дХ1,Х2);
14) (Vx2A(x3, x2) & Зх3А(х3, x2))J(Jy2)jf(X2A);
15) (3x3Vx2P13(x1, x2, x4) & -.ЗхзО^Сх!, x2, ^з))/(;2^дХ1>/(Х1>Х2);
16) (ЭхзУхгР/Схь x2, x4) &-,3x3Qf (x1} x2, *3))/(^Дх3 j(X1PC4);
17) (3x1Vx2P13(x0, x3, x4))/°iX*A0.g(x0r4)’
18) (VyP(x,y)->Q(x))* ;
(f3(x,y,z)y
C/2O,z))*
19) (BxgVXiP^CXi, x2, x3)&3x2Q^(xbx2, x4))J2Xi X3).
21. Найдите ошибку в приведённом ниже вычислении результа-
та операции подстановки и исправьте ее:
(6)
def
a) (Bx33x2P13(x1,x2,x4)&-iVx3Qf(x1,x2,x3))^X2 Хз) =
(5)
def
def
= (Зх3Зх2Р3(х1,х2,х4))^Х2 Хз) &(-.Vx3Qf (хьх2,х3))$Х2 Хз)
(9) (4)
def def
= 35(Эх2Р3(х1,х2,х4))^Х2 X3))&-iVx3(Q13(x1,x2,x3))^(X2 Хз)) =
(4) (8)
def def
= 3s3x2 (P{ (хг, x2, x4))^ Хз) & -iVx3Q3 (f(x2, x3), x2 x3) =
(8) (4)
def def
= 3s3x2P13(f(x2,x3),x2 x4)*}X2Лз) &-iVx3Qf (J(x2,x3),x2 x3) =
(4)
def
= 3s3x2P13(f(x2,x3),x2 x4)&-,Vx3Qf(f(x2,x3),x2 x3);
(6)
def
6) (Vx2A(x3,x2)&Vx3A(x3,x2))J3X3 y2) =
(6)
def
= (Vx2A(x3j х2))^Хзу2) &(Vx3A(x3, х2))^Хзу2)
(8),(4) (7)
def def
= Vx2A(f(x3, y2), x2) &(Vx3A(x3, х2))^Хз y2) =
(7)
def
= Vx2A(f (x3, y2)} x2) & Vf (x3, y2)A(f (x3, y2), x2);
(6), (7), (8)
def
B) (Vx2A(x35x2)&3x3A(x33x2))^2y2)/(X2jSi) =
def
= Vf (x2, St )A(f Cx3, y2), f (x2, St)) & 3f (x3, y2)A(f (x3, y2), f (x2, Sj)).
(8),(4)
def
120
22. Восстановите пропущенный фрагмент вычисления результа-
та операции подстановки:
(6)
def
а) (ЭХзУх2Р13(х1,Х2,Х4)&-1ЭХзС13(х1,Х2,Хз))^1 хз) =
(6) (5)
def def
= (ЭхзУхгР^Сх!, х2, х4ОДХ] хз) & (...^ хз) =
(5) (7)
def def
= (ЭхзУхгР^Схь х2, х4))^Х1 хз) & Ч...)^ьХз) =
(7) (9) (4)
def def def
= ...&43x3Q3(x],X2,x3))^X] хз) = ...&^3U(...)J2X1 X3) =
(4) (4)
def def
= 3x3Vx2Pl3(x1,X2,x4)&-i3u(...)^X1jX3) =
(9) (7)
def def
6) =...
(8) (4)
def def
... = 3zVx2P^(.x1,x2,x^bi^ = ...
23. (По [16, c. 451].) Докажите, что операция подстановки об-
ладает следующими свойствами:
1) если t и — термы сигнатуры о, то результат подстановки
терма t вместо предметной переменной х в терм является термом
сигнатуры о;
2) если t — терм сигнатуры о, а А — формула сигнатуры о,
то результат подстановки терма t вместо предметной переменной
х в А является формулой сигнатуры о;
3) а) (А)* = А ; б) (А)^ = А , если хе FV (А).
4) ((А)Л? =((АУ У , если у *х иуё FV (t2).
1 2 2
23г Вычислите результаты следующих операций подстановки:
1) ((Vx2P12(x1,x2)&P11(x2))5)^;
2) ССЗх2Р12(х1,Х2,Хз))^)^.
Термы, допустимые для подстановки вместо переменной в формулу
24. [27, с. 78, № 8] Докажите, что: а) терм, не содержащий предметных
переменных, допустим для подстановки вместо любой предметной перемен-
ной в любой формуле; б) любая предметная переменная х является термом,
допустимым для подстановки вместо х в любой формуле; в) если формула
А не содержит свободных вхождений предметной переменной х, то любой
терм допустим для подстановки вместо х в формулу А.
25. [38, с. 55] Допустим ли терм:
а) для подстановки вместо х; в формулу Д1 (х;);
б) Xj для подстановки вместо х{ в формулу Vx^P/Cxi);
121
https:it.ru
http
в) x3) для подстановки вместо хх в формулу
Vx2P12(x] , х2) P^Qxi);
г) ^(xj, х3) для подстановки вместо х1 в формулу
Зх3Ух2Р2(х1 , х2) Р/(Х1) ?
26. [27, с. 78, № 7] Является ли терм t допустимым для подстановки
вместо предметной переменной х1 в формулу А:
a) t =/2(хорс3), А = VxqP^Xq, xj;
б) t =/2(х1, х2), А = (Р2^, х2) Эх^Чх^);
в) t = f (xj, А = VxjP1 (xj ?
27. [38, с. 55] Допустим ли терм ^(Xj, х2) для подстановки вместо пред-
метной переменной хх в следующие формулы:
а) Р?(хъ х2) Х/х2Р^х2У, б) (\/x2Pf(x2, aj) v 3x2Jf (хъ x2).
28. Для подстановки в какие из формул
а) Зх1Р12(х1,У12(х1,х3));
в) 3x1P12(f12(x1,x3),f12(x2,x4))
б) Vx4P22(x3,f12(x2,x4));
вместо переменной х3 допустим терм ^(Xj, х2) ?
29. Для подстановки вместо каких из переменных в формулу
Vx^Cf^CXj, Х2), Х2) -> SXgP^CXj, х3)
допустим терм fi(x1} х2)?
30. Приведите пример терма с двумя предметными переменными, до-
пустимого для подстановки вместо переменной х1 в формулу
Зх2Р2(х2, Xj) Vx3(P2(x2, х3) v -^2(х2, х^)
и пример терма с двумя предметными переменными, не являющегося до-
пустимым для подстановки вместо Xj в ту же формулу.
31. Приведите пример формулы А, в которой единственными свободными
переменными являются х1 и х2 и такой, что:
а) терм /2(х3, х4) допустим для подстановки в формулу А вместо пере-
менной X] и не является допустимым для подстановки в формулу А вместо
переменной х2;
б) терм У1(х1г х2) не является допустимым для подстановки в формулу
А ни вместо переменной хр ни вместо переменной х2, ни вместо перемен-
ной х3 одновременно.
Варианты формулы. Отношение конгруэнтности формул
32. Докажите, что формула В является вариантом формулы А:
def def
а) А = Vx0P2(x0, X]), В = Vx2P2(x2, xj;
def def
б) А = VxqP^Cxo, xj & 3x2Jf(хь x2), В = \/x2PA2Qx2, xj & 3x2Jf(xj, x2);
def
A = 3x2(Vx0P2(x0, X]) -> Зх^Сху, x2)),
B) def
В = 3x0(Vx2Pj2(x2, Xi) -> Зх3Р2(х3, x0))
33. Является ли формула В вариантом формулы А:
def def
а) А = 3x0(P11(x0)vP11(x1)),B = SxjCP/CxJvP/Cxj));
def def
б) A = (ЗхоР/(x0) v P/CxJ), В = (SxjP/Cxj) v Р/(Xi));
122
Hi I roit !"i i
def def
в) A = ЭХоСР/(x2) P22(x0,*i))>b = ЭХзСР/Схг) P22(x3, xj);
def def
г) A = (Р/(x2) 3x0P22(x0, xj), В = (P,1 (x2) 3x2P22(x2, xj) ?
34. Установите, какие из формул являются вариантами формулы
Vx^P/tx^xJ:
a) Vx23x1P22(x2,x1);
в) Х/х1Зх0Р2(х1, х0);
б) VxjSxjP^txj, хх);
г) Vx23x]P22(x],x2) ?
35. Приведите пример формулы, являющейся вариантом формулы
А и такой, что никакая ее свободная переменная не является связанной:
def
а) А = Vx2(3x1P22(x2,x1)&P11(x1));
def
б) А = VXiPjKxj) -> Bx^CXi, х0);
def
в) А = (VxjP^Cxj, х2) v Зх2Р^х1г х2)).
36. Найдите вариант В формулы А такой, что терм t допустим для под-
становки в формулу В вместо переменной х0:
def def
a) t = ffrx^A = Vx2(P11(x1)v3x1P22(x0,x1));
def def
6) t = /22(хъ x2), A = (VX]P22(x0, xj -> 3x2P22(x0, x2)).
37. [22, c. 65] Укажите несколько вариантов формулы
Vz(P(z) & 3zQ(x, z) —> 3yR(z, y)) v Q(z, x).
Подумайте, какие переименования связанных переменных ведут к кол-
лизии при переименовании связанных переменных?
38. Докажите, что:
1) отношение конгруэнтности С=и) является отношением эквивалент-
ности на множестве формул сигнатуры о;
2) [22, с. 65] докажите, что если А ^А^ то: a) rank(A) = rankCAJ;
б) FV(A) = FVCAJ; в) А иА} имеют один и тот же главный логический сим-
вол (т. е. символ, который последним используется в процессе построения
формулы).
Индукция по построению термов
39. [22, с. 55] Докажите, что всякий терм сигнатуры о содержит одина-
ковое количество вхождений левых и правых скобок.
40. [22, с. 55] Докажите, что количество вхождений (формальных)
запятых в терм сигнатуры о равно (п - к), где п — сумма арностей всех
вхождений в терм функциональных символов, а к — количество вхождений
в терм функциональных символов.
41. [39, с. 185] Докажите, что в любом начале терма сигнатуры о от-
крывающих скобок не меньше, чем закрывающих.
42. [39, с. 185] Докажите, что начало терма сигнатуры о, содержащее
скобку и сбалансированное по скобкам, совпадает с самим термом.
Индукция по построению формул
43. Пусть del—функция, определённая на множестве всех слов G* и такая,
что del(a) для всякого а е G* получается из а удалением всех логических
123
https:/Л: rait.ru
связок 1. Докажите, что del (А) для каждой формулы А сигнатуры о также
является формулой сигнатуры о.
Рекомендация. Примените индукцию по числу вхождений в формулу
логических связок.
44. [22, с. 58] Докажите, что всякая формула языка первого порядка
содержит одинаковое количество вхождений левых и правых скобок.
45. [39, с. 185] Докажите, что в любом начале формулы открывающих
скобок не меньше, чем закрывающих.
46. [39, с. 185] Докажите, что начало формулы, содержащее скобку
и сбалансированное по скобкам, совпадает с самой формулой.
Синтаксическая однозначность выражений
Первый шаг мудрости — нападать
на всё, последний — переносить всё.
Г. К. Лихтенберг
47. Докажите, что всякий терм сигнатуры о, являющийся предметной
переменной или предметной константой, представим соответственно в виде:
х1 или ак, где хг — однозначно определённая предметная переменная, ак —
однозначно определённая предметная константа.
48. Пусть п g N\{0}. Докажите, что всякий терм сигнатуры о не явля-
ющийся предметной переменной или предметной константой, представим
в виде/^С^, ..., tn), где fn— однозначно определенный для этого терма
n-местный функциональный символ, a tp...»tn—однозначно определённые
для него термы сигнатуры о.
49. Докажите, что всякая атомная формула сигнатуры о представима
в одном из следующих видов: а) Р°, где Р° — однозначно определенный
О-местный предикатный символ; б) Р*^, ..., tn), где п е N\{0} — одно-
значно определённое натуральное число, Рп — однозначно определённый
n-местный предикатный символ, a tlt ..., tn — однозначно определённые
термы сигнатуры о.
50. [13, с. 23—24; с. 106] Докажите, что всякая формула сигнатуры о,
не являющаяся атомной формулой, представима в одном и только одном
из следующих видов: —А, (А & В), (A v В), (А В), (А <-» В), УхА, ЗхА для
однозначно определенных формул А и В сигнатуры о и предметной пере-
менной х.
51. (По [54, с. 34]) Пусть t — терм сигнатуры о. Докажите, что каждое
вхождение в t предметной переменной, предметной константы или функ-
ционального символа является началом вхождения в терм t однозначно
определённого терма сигнатуры о.
Рекомендация. Воспользуйтесь индукцией по длине терма t.
52. Пусть А — формула сигнатуры о. Докажите, что каждое вхождение
в А любой предметной переменной, предметной константы или функцио-
нального символа является началом вхождения в формулу А однозначно
определённого терма сигнатуры о.
Рекомендация. Однозначность следует из Леммы 1. Доказательство суще-
ствования проведите индукцией по построению формулы А.
53. Пусть А — формула сигнатуры о. Докажите, что каждое вхождение
в формулу А предикатного символа является началом вхождения в формулу
А ее однозначно определённой подформулы.
Рекомендация. Воспользуйтесь индукцией по построению формулы.
124
https:/Л: rait.ru
54. Пусть А — формула сигнатуры о. Докажите, что каждое вхождение
в формулу А любой из логических связок -i, V, 3 является началом вхождения
в формулу А однозначно определённой ее подформулы.
Рекомендация. Воспользуйтесь индукцией по построению формулы.
55. Пусть А — формула сигнатуры о. Докажите, что каждое вхождение
в формулу А формульной скобки является началом вхождения в формулу
А однозначно определённой ее подформулы.
Рекомендация. Воспользуйтесь индукцией по построению формулы.
56. Докажите, что каждое вхождение в терм сигнатуры о открывающей
скобки не начинает вхождения никакого терма.
Рекомендация. Выясните, какой вид имеет выражение, начинающееся с (,
и убедитесь, что вторым вхождением буквы в него должно быть вхождение
либо предикатной константы, либо одной из букв (, —i, &, v, —>, V, 3.
57. Докажите, что каждое вхождение в формулу сигнатуры о открываю-
щей скобки, не являющейся формульной, не начинает вхождения никакого
терма и никакой формулы.
Рекомендация. Выясните, какой вид имеет выражение, начинающееся с (,
и убедитесь, что вторым вхождением буквы в него должно быть вхождение
либо предикатной константы, либо одной из букв (, -i, &, v, —V, 3.
58* . Пусть t—терм сигнатуры о, а 61 и 62—вхождения в t термов tr и t2 со-
ответственно. Докажите, что тогда либо и 02 не имеют общих вхождений
символов алфавита, либо одно из них целиком содержится в другом.
59* . [13, с. 24; с. 106] Докажите, что если А — формула сигнатуры о,
а 0в и 0с — вхождения в А подформул В и С соответственно, то либо
0в и 0с не имеют общих вхождений символов алфавита, либо одно из них
целиком содержится в другом.
60. Пусть t1 и t2 — термы сигнатуры о, a t — терм сигнатуры о, содер-
жащий хотя бы одно вхождение терма ег. Докажите, что если слово t' полу-
чено из терма t заменой произвольного вхождения tr на t2, то t' является
термом сигнатуры о.
Рекомендация. Воспользуйтесь индукцией по построению терма, в кото-
ром совершается замена.
61. Пусть А и В — формулы сигнатуры о, а СА— формула сигнатуры о,
содержащая хотя бы одно вхождение формулы А. Докажите, что если
слово Св получено из формулы СА заменой произвольного вхождения
А на В, то Св является формулой сигнатуры о.
62. Если все вхождения подформулы В в формулу А сигнатуры о заменить
на формулу С, то получится формула сигнатуры о. Докажите.
63. Пусть А—формула сигнатуры о. Докажите, что если заменить любое
свободное вхождение предметной переменной в формулу А на произвольный
терм сигнатуры о, то результатом замены является формула сигнатуры о.
64. Докажите, что если заменить в формуле сигнатуры о все связан-
ные вхождения некоторой предметной переменной х на терм t, отличный
от предметной переменной, то полученное слово уже не будет формулой
сигнатуры о.
65. Докажите, что результат операции «одновременная подстановка
термов вместо всех свободных вхождений переменныхх1} ...,хп со-
ответственно в формулу А сигнатуры о» является формулой сигнатуры о.
Задачи на программирование
1. (По [97, с. 26].)
А. Постройте порождающую грамматику термов заданной сигнатуры—
исчисление, теоремами которого являются любые термы и только они.
125
https:/Л: rait.ru
Б.* Опишите распознающую грамматику термов заданной сигнатуры —
способ проверки, является ли слово термом в бесскобочной записи.
2. А. Постройте порождающую грамматику формул заданной сигнату-
ры — исчисление, теоремами которого являются любые формулы и только
они. Б.* Опишите распознающую грамматику формул заданной сигнатуры—
способ проверки, является ли заданное слово формулой в бесскобочной
записи.
3. Напишите программы на любом языке программирования:
1) для распознавания терма;
2) для выделения всех предметных переменных данного терма;
3) для выделения всех функциональных символов данного терма;
4) для определения сложности данного терма;
5) для нахождения всех подтермов данного терма;
6) для нахождения постфиксной формы записи данного терма;
7) для нахождения инфиксной формы записи данного терма.
4. Напишите программы на любом языке программирования:
1) для распознавания формул;
2) для выделения всех предметных переменных данной формулы;
3) для выделения всех функциональных символов данной формулы;
4) для выделения всех предикатных символов данной формулы;
5) для определения сложности данной формулы;
6) для нахождения главной связки формулы;
7) для нахождения всех подформул данной формулы;
8) для нахождения постфиксной формы записи данной формулы;
9) для нахождения инфиксной формы записи данной формулы.
5. Напишите программу на любом языке программирования для ре-
ализации операции подстановки терма сигнатуры о вместо предметной
переменной в заданной терм сигнатуры о.
6. Напишите программу на любом языке программирования для реализа-
ции операции подстановки терма сигнатуры о вместо свободной предметной
переменной в заданную формулу сигнатуры о.
7. * Напишите программу на любом языке программирования, выполня-
ющую семантическое сколемовское преобразование формулы в языке первого
порядка.
https: //цга it.ru
Упражнение 4
ГИЛЬБЕРТОВСКОЕ ИСЧИСЛЕНИЕ ПЕРВОГО
ПОРЯДКА: ПОСТРОЕНИЕ ДОКАЗАТЕЛЬСТВ
И ВЫВОДОВ С ИСПОЛЬЗОВАНИЕМ
ОСНОВНЫХ ПРАВИЛ ВЫВОДА
Природа — это храм, где камни говорят,
Хоть часто их язык бывает непонятен.
Вокруг —лес символов, тревожен, необъятен,
И символы на нас с усмешкою глядят.
Шарль Бодлер
Обязательные результаты обучения:
• знать основные понятия
— аксиомные схемы, аксиомы, основные правила вывода гильбертовского
исчисления первого порядка;
— линейное доказательство формулы, доказуемая формула;
— линейный вывод формулы из множества формул, выводимая формула
из множества формул, анализ (линейного) вывода (доказательства);
— общие свойства отношения выводимости (рефлексивность, монотон-
ность, транзитивность);
— древесное доказательство формулы;
— древесный вывод формулы из множества формул, высота древесного
вывода;
— соглашения об обозначениях при построении доказательств и выводов;
— арифметизация теории;
— гёделева нумерация языка формальной системы, первого порядка:
гёделев номер символа, гёделев номер выражения, гёделев номер последо-
вательности выражений (доказательств);
• уметь
— конструировать аксиомы по заданным аксиомным схемам;
— распознавать аксиомы в заданных формулах;
— конструировать доказательства формул в гильбертовском исчислении
первого порядка;
— определять, является ли последовательность формул выводом;
— по заданной последовательности формул извлекать гипотезы и выво-
димую формулу;
— конструировать выводы формул в гильбертовском исчислении первого
порядка;
127
https:it.ru
— конструировать доказательства и выводы формул в различных задан-
ных вариантах гильбертовского исчисления;
— определять гёделевы номера символов, выражений, вывода формулы
из указанных гипотез;
— конструировать объекты с заданными гёделевыми номерами;
— конструировать программы на любом языке программирования для
нахождения гёделевого номера формулы языка первого порядка и восста-
новления формулы языка первого порядка по ее гёделеву номеру;
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
Теоретические сведения
Аксиомные схемы и правила вывода гильбертовского
исчисления первого порядка
Истинные слова не могут быть
красивыми: красивые слова не могут
быть истинными.
Лао-цзы
В гильбертовском исчислении первого порядка (ИГ\) доказывают-
ся (выводятся) формулы. Поэтому зафиксируем произвольную сигна-
туру су, и все зависящие от сигнатуры понятия будут относиться к су.
Определение.
Формульной схемой (схемой формул) будем называть такое слово
метаязыка, что при любых подстановках в это слово вместо ме-
табукв для предметных переменных (например, х) конкретных
предметных переменных, вместо метабукв для термов (например,
t) — конкретных термов, вместо метабукв для формул (например,
А, В, С) — конкретных формул, а вместо метабукв для множеств
формул (например, Н, Н1} Н2) — конкретных множеств формул,
получается формула.
Частным случаем формульной схемы будем называть результат
подобной подстановки. Иногда формулой мы будем называть саму
формульную схему.
Определение [13, с. 142—143].
Аксиомы гильбертовского исчисления первого порядка — это фор-
мулы, которые получаются из приведённых ниже 15 формульных
схем (которые будем называть аксиомными схемами гилъбертов-
ского исчисления первого порядка) подстановкой вместо метаз-
наков А, В, С конкретных формул сигнатуры о, вместо метазна-
128
https:it.ru
ка о — конкретных предметных переменных, а вместо метазна-
ка t — конкретных термов сигнатуры о.
Аксиомные схемы для импликации (—>):
1) А —> (В —> А) (законупрощения);
2) (А —> В) —> ((А —> (В —> С)) —> (А —> С)) (силлогизм Фреге);
Аксиомные схемы для конъюнкции (&):
3) А^ (В^А&В);
4) А&В—>А;
5) А&В—>В;
Аксиомные схемы для дизъюнкции (v):
6) A^AvB;
7) B^AvB;
8) (А^ С) (A vB С));
Аксиомные схемы для отрицания (-<):
9) (Л >В) >((Л
10) -.-Л >А;
Аксиомные схемы для эквиваленции (<->)
11) (А В) -> ((В А) (А ++В));
12) (А <->В) —> (А —>В);
13) (А<-^В)->(В->А);
Кванторные аксиомные схемы:
14) \/хА—>(А)? (законуниверсальной конкретизации);
15) (А)^ —>ЗлА (закон экзистенциального обобщения).
В списке аксиомных схем имеются схемы для каждого логическо-
го символа (-1, &, v, <->, V, 3):
1) схемы 1 и 2 представляют собой аксиомные схемы для буквы
в частности, 1 выражает следующий логический закон: «Если выска-
зывание А истинно, то оно следует из любого высказывания В» (или
короче: «Истина следует из чего угодно»);
2) схема 3 вводит символ &, а схемы 4 и 5 его удаляют;
3) схемы 6 и 7 вводят символ v, схема 8 его удаляет;
4) схема 9 вводит символ схема 10 его удаляет;
5) схема 11 вводит символ <н>, схемы 12 и 13 его удаляют.
Определение.
Основными правилами вывода гильбертовского исчисления пер-
вого порядка будем называть следующие слова:
1) правило modus ponens (синонимы: правило МР, правило отде-
ления, правило удаления импликации, правило 1) (лат. «модус ут-
верждающий», произносится «модус поненс»)
А (А^В)
В~
http
о- Hi ।rnit i-i ।
129
причём формулы А и (А —> В) называются посылками основного
правила вывода МР, а формула В называется непосредственным
следствием формул Аи(А—>В) по основному правилу вывода МР’,
2) правило введения V (синонимы: правило Бернайса [120, с.29],
правило 2)
(А^В)
(A^-VxB)
xgFV(A),
причем формула (А В) называется посылкой основного правила
вывода 2, а формула (А VxB) является непосредственным след-
ствием формулы (А В) по основному правилу вывода 2;
3) правило удаления 3 (синонимы: правило Бернайса [120 ,с. 29],
правило 3)
(А—>В)
(ЗхА^В)
xgFV(B),
причём формула (А В) называется посылкой основного правила
вывода 3, а формула (ЗхВ В) является непосредственным след-
ствием формулы (А В) по основному правилу вывода 3.
Линейное доказательство и линейный
вывод из множества гипотез
Пусть п е N\{0}.
Определение [13, с. 143].
1) Линейным доказательством формулы А называется такая по-
следовательность А1} ...,Ап формул сигнатуры о, что Ап = А, и для
каждого 1 < i < п формула Аг- удовлетворяет одному из следую-
щих условий:
a) А- — аксиома;
б) Aj является непосредственным следствием некоторых формул
Aj иАк (j, к < i) по основному правилу вывода 1;
в) А^ является непосредственным следствием формулы Ат (т < i)
по одному из основных правил вывода 2 или 3.
2) Формулой, доказуемой в гильбертовском исчислении первого по-
рядка (доказуемой формулой или теоремой) (обозначается: НА или
hclA («classic» или «S. Cleene»)), будем называть формулу, для ко-
торой существует ее линейное доказательство.
Символ «Н» был введён Г. Фреге (1879), который дал отдельные
интерпретации его горизонтальной и вертикальной частям; данное
его употребление принадлежит Дж. Россеру (1935) и С. Клини (1934).
130
https:/Л: rait.ru
Условимся опускать до появления других исчислений «индекс»
С1 у буквы «И».
Обозначим Н — множество формул (которое может быть беско-
нечным).
Определение [13, с. 143].
1) Линейным выводом формулы А из множества формул Н назы-
вается такая последовательность А1}..., Ап формул сигнатуры о,
что Ап = А, и для каждого I < п формула Аг- удовлетворяет одно-
му из условий:
a) А{ — аксиома;
б) Д g Н;
в) А- является непосредственным следствием некоторых формул
Aj (j < i) по одному из основных правил вывода 1,2,3, причём при
применении основных правил вывода 2 и 3 предметная переменная
х не должна входить свободно ни в одну формулу из множества Н.
2) Формулой, выводимой из множества формул Н (обозначается:
Н I- А или Н hcl А), будем называть формулу, для которой суще-
ствует линейный вывод из множества формул Н. В этом случае
множество формул Н называется множеством гипотез.
Недоказуемость формул не следует смешивать с их недоказанно-
стью.
Если некоторая формула в тот или иной момент времени ещё
не доказана (является недоказанной формулой) в гильбертовском
исчислении, то это ещё не означает, что эта формула недоказуема
(т. е. не является теоремой) в этом исчислении.
Недоказанную формулу впоследствии, возможно, удастся дока-
зать, в то время как недоказуемая формула не может быть доказана
принципиально (если, конечно, гильбертовское исчисление являет-
ся непротиворечивым исчислением). Иначе говоря, не все недока-
занные формулы являются недоказуемыми формулами.
Определение.
1) Отношением выводимости назовём (и обозначим «И») бинар-
ное отношение между множествами 2F и F, которое определим так:
И, если А — формула, выводимая из множества Н;
def Л, если неверно, что А — формула, выводимая из Н;
ННА
не определено, если не установлен ни один
из предыдущих случаев;
2) Отношением доказуемости назовем (и обозначим «И») бинар-
ное отношение между множествами 0 и F, которое определим так:
131
https:it.ru
И, если А — формула, выводимая из множества аксиом;
def Л, если неверно, что А — формула, выводимая из аксиом;
НА = "
не определено, если не установлен
ни один из предыдущих случаев;
Очевидно, что доказуемость формулы эквивалентна ее выводи-
мости из пустого множества гипотез.
Итак, отношение выводимости Н Н А является частично опреде-
лённым отношением, так как выводимость А из множества Н либо
имеет место, либо не установлено ни то, ни другое, т. е. имеет место
«неопределённость» или «неизвестность» в смысле С. К. Клини [19,
§64].
Сформулируем на языке исследователя несколько лёгких нефор-
мальных утверждений, которые будем называть общими свойства-
ми отношения «И», ибо формулировка свойств не зависит от экон-
омных схем и правил вывода.
Предложение (общие свойства отношения выводимости) [19,
с. 83—84].
1) НI- А, если A g Н (рефлексивность);
2) если Нг I- А, то Нг и Н2 h А для любого множества формул
Н2 (в частности, можно рассматривать любую доказуемую формулу
как выводимую из любого множества гипотез) (монотонность)’
3) если Нг I- А, то Н21- А, где множество Н2 получается из множе-
ства Нг удалением любых формул, которые являются доказуемыми
или выводимыми из остающихся формул множества Н3 (транзи-
тивность).
Утверждение 3 данного Предложения может быть сформулиро-
вано следующим образом: если А1} ...,Ап, В, С — формулы,
{Д13Д2, ...,АП} НВ, {А1гА2, ...,Ап, В} Н С,
то {АъА2, ...,An} h С.
Древесное доказательство и древесный
вывод из множества гипотез
До сих пор мы имели дело с выводами в виде последовательности
формул, но часто вместо этого «полезно рассматривать (вхождения)
формул в некотором частичном упорядочении, которое прямо пред-
ставляет логическую структуру вывода» [19, с. 98—99].
В таком упорядочении посылки каждого вывода пишутся «непо-
средственно над» заключением и никакое (вхождение) формулы
не служит посылкой более чем для одного вывода.
132
https:/Л: rait.ru
Определение.
Понятие «древесное доказательство формулы А в гилъбертовском
исчислении» определим индуктивно:
1) древесным доказательством аксиомы гилъбертовского исчис-
ления является она сама;
2) если D1} Dn — древесные доказательства формул А1}
Ап соответственно, а формула А является непосредственным след-
ствием формул А1}..., Ап, по одному из основных правил вывода
1, 2, 3, то слово вида
А
является древесным доказательством формулы А.
Определение.
Понятие «древесный вывод формулы А из множества формул
Н в гилъбертовском исчислении» определим индуктивно:
1) древесным выводом аксиомы А из множества Н является А;
2) древесным выводом формулы Ае Низ множества Н является А;
3) еслиD1} ...,Dn — древесные выводы формул А1}Ап из мно-
жества Н соответственно, а формула А является непосредствен-
ным следствием формул А1}..., Ап по одному из основных правил
вывода 1,2,3, причём при применении правил вывода 2 и 3 пред-
метная переменная х не входит ни в одну формулу из множества
Н свободно, то слово вида
Р^—Ри
А
является древесным выводом формулы А из множества формул Н.
Теперь можно сокращённо обозначать древесный вывод форму-
def
лы А из множества формул Н = {Aj,..., А^ следующим образом:
Н {Aj,...^}
— ИЛИ ---i.
А А
Индукция по построению доказательства
Индуктивные определения оправдывают соответствующие виды
доказательств «с помощью математической индукции». Примером
является следующий способ доказательства, называемый индукцией
по построению доказательства формулы.
133
https:it.ru
Определение.
Индукцией по построению доказательства будем называть сле-
дующий способ доказательства утверждения от том, что каждая
доказуемая формула обладает некоторым свойством.
Пусть доказано, что:
1) каждая аксиома обладает некоторым свойством;
2) если посылки какого-либо основного правила вывода облада-
ют этим свойством, то и непосредственное следствие обладает
этим свойством.
Тогда каждая доказуемая формула обладает указанным свойством.
Определение.
1. (По [44, с. 52].) Анализом (линейного) вывода (доказатель-
ства), имеющего вид А1} ..., Ап, будем называть явное указание
на то, на каком основании каждая формула Д, i = 1,..., п, входит
в линейный вывод (доказательство): как аксиома, в качестве ги-
потезы или как формула, непосредственно выводимая из предше-
ствующих формул по определенному основному правилу вывода.
2. (По [120, с. 29].) Определение понятия «вывод» («доказатель-
ство») в логистическом исчислении будем называть эффективным
определением, если относительно любой последовательности фор-
мул мы, проведя анализ вывода (доказательства), можно однознач-
но установить, является она выводом (доказательством) или нет.
Определение.
Определим индуктивно функцию h, которую назовем высотой
древесного вывода и которая отображает множество всевозмож-
ных древесных выводов в множество N:
def
1) h(D) = 0, если D — древесный вывод аксиомы или формулы,
принадлежащей Н;
( П П Л def
2) h=l+max(h(D1),...,h(D1)),
I A J
если D1} ...,Dn — древесные выводы формул А1г ..., Ап из множе-
ства Н соответственно, формула А является непосредственным
следствием формул А1} ..., Ап по одному из основных правил вы-
вода, a max (а1л..., ап) — функция, значением которой является
наибольшее из oq,..., осп g N.
Соглашения об обозначениях
при построении доказательств и выводов
1. При построении доказательств и выводов применяемую
k-ю аксиомную схему будем обозначать через Axk (1 < к < 15).
134
https:/Л: rait.ru
2. Подстановки, применяемые к аксиомным схемам, будем ука-
зывать в квадратных скобках, например:
г А В] Г А В
Av, или (А (В —> А))Лг1
1|^(С->А) Aj ^[(С^А) А
Эта запись означает, что в первой аксиомной схеме (А (В
А)) выполнена замена А на формулу (С—> А) и В на формулу А, после
чего будет получена аксиома ((С —> А) —> (А (С —> А))).
3. Правило вывода МР будем записывать двумя способами:
А,А—>В
В
или
4. Для обозначения формул-гипотез в выводах будем использо-
вать символы 1ц (i = 1, 2,...) в качестве нижних индексов.
Гёделева нумерация языка формальной
системы первого порядка
Гёдель видел в своих первых успехах
реализацию следующей, часто забываемой,
но плодотворной общей схемы. Внимательно
рассматривая подходящие традиционные
философские концепции и вопросы,
анализируя их и, возможно, добавляя чуть-
чуть точности, мы безболезненно приходим
к нужным понятиям, правильным гипотезам
и достаточно простым доказательствам.
Г. Крайзелъ
Понятие «арифметизация»
Определение (по [160, с. 76]).
Арифметизация — это метод, применяемый в математической
логике и теории алгоритмов для замены рассуждений о выраже-
ниях какого-либо логико-математического языка рассуждениями
о натуральных числах.
С целью такой замены устанавливается какое-либо достаточно
простое взаимно однозначное отображение множества всех слов
(в алфавите рассматриваемого языка) в натуральный ряд; образ
слова называется его номером. Отношения и операции, опреде-
лённые на словах, переходят при этом отображении в отношения
и операции, определённые на номерах.
135
https: "и га it.ru
Требование «достаточной простоты биективного отображе-
ния» сводится к тому, чтобы основные отношения и операции пере-
ходили в отношения и операции, имеющие простую алгоритмиче-
скую природу.
Определение (по [38, с. 151—152]).
Арифметизацией языка формальной системы первого порядка
будем называть всякую функцию g, отображающую взаимно од-
нозначно множество всех символов, выражений и конечных по-
следовательностей выражений языка в множество целых поло-
жительных чисел.
При этом требуется, чтобы:
а) функция g была эффективно вычислимой функцией (данный
термин понимается интуитивно, как «практически вычислимая
функция»)'
б) существовала эффективная (практически реализуемая) про-
цедура, позволяющая для каждого натурального т определить,
является ли т значением функции g, и в случае, если является,
то построить тот объект х, для которого т = g(x).
Итак, «программистские» критерии для осуществления эффек-
тивной нумерации объектов любого типа таковы [172, с. 303]:
1) никакие два объекта не имеют одинаковый номер;
2) для любого объекта мы можем «эффективно» найти его но-
мер;
3) для любого натурального числа мы можем «эффективно»
определить, является ли оно номером какого-либо объекта и, если
это так, найти этот объект.
Понятие «гёделева нумерация»
Рассмотрим алфавит А.
Определение [168, с. 29].
Гёделевой нумерацией множества слов А* назовём любую взаимно
однозначную функцию g из А в (не обязательно на) множество N.
Итак, g является взаимно однозначным отображением, приписы-
вающим каждому слову ХвА* единственное положительное число
g(X).
Гёделева нумерация языка первого порядка
Нумерация символов, выражений и последовательностей выра-
жений языка первого порядка была предпринята К. Гёделем (1931)
с целью арифметизации теории доказательств, т. е. с целью заме-
ны утверждений о формальной системе эквивалентными высказы-
136
https:/Л: rait.ru
ваниями о натуральных числах с последующим выражением этих
высказываний в формальной системе (с тех пор термин «гёделев
номер» стал общепризнанным). Идея арифметизации стала ключом
к решению многих важных проблем математической логики.
В отличие от нумераций Кантора и Клини множество номеров Ге-
деля n-ок натуральных чисел имеет «дырки», которые частично за-
полняются при увеличении п. Этот «недостаток» оборачивается пре-
имуществами, когда возникает необходимость нумерации не только
кортежей натуральных чисел, но и любых текстов в любом алфавите.
Делается это примерно так [142, с. 63].
В алфавите {0, 1, а, Ь, с, ..., +, -, (, ), /, V, 3, ...} фиксируется по-
рядок символов, после чего алфавит отображается в N с помощью
некоторой инъективной функции ф(-).
Тогда тексту Т = -.sn, где Sj — символы алфавита, присваива-
ется номер
def
ф(Т) = 2^1) ...prtw.
При необходимости говорить о последовательности текстов
def
D = ВД...^
(например, о доказательствах) трюк повторяется.
Последовательности D сопоставляется номер
P(D) = 2а^ -З0^) -...-p“(Tfc).
Для простоты рассмотрим язык формальной системы первого по-
рядка лишь с двумя логическими связками (—, —») и одним кванто-
ром V, без предметной переменной х0 и предметной константы а0.
Определение.
def def
(AvB) = (-iA^B), (A&B) = -(A->-B),
def def
(A<->B) = (A—>B)&(B—> А), BxA = —iVx—A.
Пусть Pi есть i-e простое число, т. e.
Po = 2,pi = 3,p2 = 5, ...
Пусть k g N\{0}, n e N.
Определение [38, c. 150—151; 19, c. 228].
Гёделевой нумерацией языка формальной системы первого поряд-
ка называется следующая нумерация символов, выражений и по-
следовательностей выражений языка:
137
https:it.ru
1) каждому символу s алфавита языка поставим в соответствие
целое положительное число g(s), называемое гёделевым номером $:
def def def def def
g(O = 3;g()) = 5;gG) = 7;g(->) = 9;gH = 11;
def def
g(xfc) = 5 + 8-k; g(afc) = 7 + 8-k;
def def
) = 9 + 8-2"-3fc;g(Pfc") = 11 + 8-2"-3fc;
2) гёделев номер выражения s^..^ определим так:
def
g(Vxfc) = g((xfc));
def
g(s0Si-sr) = 2g(So) -3^1) •...•prg(sJ;
3) гёделев номер последовательности выражений е0, е1г ...,ег опре-
делим следующим образом:
g(eoe1...er) = -З^-...-р^.
Замечание (повторение).
Пусть п > 1 и п - р^р2-• -Рг является разложением п на простые сомно-
жители, причем среди чисел р1?р2, ";РГ могут быть и одинаковые. Пусть
Pi,p2, • • Рк— различные из этих чисел, a cij, а2,..., ак — кратности, с кото-
рыми они входят в разложение п = р^р2- • -Рг-
Каноническим разложением натурального числа п > 1 называется
представление (рг < р2 < ... < pfc)
п=рГ-р22---рГ-
Примеры.
1) g(xj = 13; g(x2) = 21; g(a4) = 39; g(f2) = 105; g(P2x) = 155;
2) g(P12(x1,x2)) = 2g(p2) -3S(0 .5g(xi) .7gC) .ng(x2) .13g0) =
= 2107-33-513-77-ll21-135 =
=121013211485025509887655072000911958003850
1539009810944860618752 -IO13 (77 значащих цифр);
138
https: /Л: гз jt.ru
def _ def
3) g(3x2P10) = g(-1Vx2^P1()) = 2Sb) .3g(Vx2) ,5gb) .ygGf) =
def _
= .3g«x2)) -5g(-0 .ygUf) =
= 2g(-') .328(O.3g(x2).5gO) _5g( 1) .ygC^i’) -29 . з23-321-55 .59 .y35.
4) число 12 не является геделевым номером.
Предложение.
Функция g взаимно однозначно отображает множество всех сим-
волов, выражений и конечных последовательностей выражений
языка первого порядка в множество целых положительных чисел,
причём множество значений функции g не совпадает с множеством
всех целых положительных чисел.
Докажите самостоятельно. При этом воспользуйтесь тем, что:
а) различным символам алфавита поставлены в соответствие
различные гёделевы номера; различные выражения языка получают
разные гёделевы номера; различные последовательности выраже-
ний языка имеют также различные гёделевы номера;
б) так как гёделевы номера последовательностей выражений
четны и, кроме того, имеют чётный показатель степени при 2,
то они отличны и от гёделевых номеров символов, и от гёделевых
номеров выражений (конечно, всякий символ языка можно рассма-
тривать как выражение, и тогда он снабжается гёделевым номером,
отличным от того, который ставится ему в соответствие как симво-
лу; однако, это не должно приводить к недоразумению);
в) для доказательства единственности гёделевской нумерации
определяющую роль играет основная теорема арифметики (К. Гаусс,
1801): любое натуральное число п > 1 представляется в виде произ-
ведения простых чисел, причём единственным образом, если не учи-
тывать порядок следования сомножителей (по [147, с. 15]).
Метаматематика (теория доказательств) становится ча-
стью арифметики натуральных чисел, если выбрать какую-нибудь
нумерацию формальных объектов, т. е. сопоставить различные
натуральные числа различным формальным объектам (используя
не обязательно все числа), а затем вместо формальных объектов
говорить о соотнесенных им числах (т. е. считать, что наши метама-
тематические утверждения относятся к индексам в этом пересчете,
а не к самим пересчитываемым объектам).
Замечание.
Рассмотренный способ построения геделевой нумерации не явля-
ется единственным: другие способы можно найти у С. Клини [19, с. 228]
и Р. Смальяна [168, с. 29; с. 59].
139
https:it.ru
Биографические сведения
НикодЖ. (1893—1924).
Контрольные вопросы
1. Приведите индуктивное определение понятий «линейное доказатель-
ство формулы А» и «линейный вывод формулы А из множества Н».
2. Приведите индуктивное определение понятия «анализ древесного
вывода (доказательства)».
3. (По [97, с. 20, № 1.1.10]) Пусть {С13 ..., Ck} I- А в исчислении 1г. По-
строим исчисление 12 с тем же множеством аксиом, что и у исчисления 1г,
и отличающееся от него лишь тем, что к совокупности правил вывода ис-
числения b добавлено правило
А
Докажите, что если НВ в исчислении 12, то НВ в исчислении 1г.
Примеры решения некоторых типов упражнений
Пример 1. Установите, является ли формула
\/хР3(у, х, z) Bw\/xP3(w, х, z)
аксиомой гильбертовского исчисления первого порядка. При этом в фор-
муле Р3(ю, х, z) предметные переменные w, х, z являются свободными
переменными, буквы w, х, z, у обозначают различные предметные пере-
менные.
Решение. Вначале выдвинем гипотезу: данная формула является част-
def
ным случаем аксиомной схемы 15. Обозначим А = P3(w, х, z) и с учетом
того, что по определению операции подстановки терма вместо свободных
вхождений переменной в формулу имеет место
def def
(\/xP3(w,x,z)y = Vx(P3(w,x,z))y = VxP3(y,x,z),
перепишем исходную формулу следующим образом:
(VxP3(w,x,z)y -^3w\/xP3(w,x,z) или (VxA)™ —>3wA
Следовательно, данная формула является аксиомой.
Пример 2 (по [27, с. 94, № 15]). Каким требованиям должна удовлет-
ворять формула А, содержащая свободную предметную переменную х,
чтобы последовательность формул
А(у) -> ЗхА(х), ЗуА(у) -> ЗхА(х)
140
https: "и rait.ru
являлась доказательством формулы ЗуА(у) ЕхА(х) в ИГ1.
Решение. Предположим, что хиу обозначают различные предметные
переменные. Тогда, исходя из содержательного смысла записи А (у), пере-
пишем последовательность формул следующим образом:
[А]£ ->ЭхА, Зу[А]* ->ЭхА.
Вначале заметим, что первая формула последовательности является
аксиомной схемой 15, так как
def
[А]* = (А)*.
Вторую формулу последовательности можно получить из первой путем
применения основного правила вывода 3, но при этому g FV (ЕхА) или
у g FV (А)\{х}, или у g FV (A) vy е {х}, а так какх иу обозначают различ-
ные предметные переменные, то у g FV (А). Таким образом, требования,
которым должна удовлетворять А, таковы: 1)у g FV (А); 2) терм у допу-
стим для предметной переменной х в формуле А.
Пример 2. Постройте в ИГ! следующий вывод:
{(Я->Р), (P->Q),P}bP&Q.
Решение. Обозначим гипотезы (Я —> P)hl, (R —> Q)h2, R^ и построим
древесный вывод:
(МР) W*->0)h2 Р,((P-HQ-HP&Q))))^ (мр)
Q,
(Q^(P&Q))
P&Q
(МР)
Построенный древесный вывод можно сокращенно записать так:
{(Я->Р),(Я->О),Я}
P&Q
Приведем также линейный вывод:
Rh3, (R -> Р), Р, (Р -> (Q ->(Р & Q))),
(Q ->(Р & Q)), Rh3, (R -> Q)h2, Q, Р & Q.
Пример 3. Постройте в ИГ1 вывод {(А —>В), (В —> С)} |- (А —> Q.
Решение. Обозначим гипотезы (А —> B)hl и (В —> C]h2 и построим древес
ный вывод
(A->B)hl,
(B->C)h2, А В ((А->В)->«А->(В->С))
((В^О-^А-^В^ОВд^в^с aJ —>(А—> C)))Ay2
А->(В->С), (А->(В->С))->(А->С)
(А—>С)
141
https: "и rait.ru
Пример 4. Постройте в И1\ вывод
{СА} I- (ЭуВ -> (СА)),у g FV (А) и FV (Q.
Решение. Обозначим гипотезу (С —> A)hl и построим древесный вывод:
Важно заметить, что мы применили правило 3 по предметной пере-
менной у, которая не входит свободно в гипотезу (С—>А).
Упражнения для самостоятельного решения
Аксиомные схемы
1. [29, с. 193, № 1.50] Запишите аксиомы, которые получаются в резуль-
тате указанных подстановок в следующие аксиомные схемы ИГ!:
2. Установите, являются ли следующие формулы аксиомами ИГ1:
a) VxP3(y, х, z) BwVxP3(w, х, z);
в) VyP3(y,у, х) 3z\/yP\z,у, х).
б) VyP3(x,y, z) 3ivVyP3(iv,y, z);
Доказательство формул
3. [29, с.194, № 1.57] Постройте доказательства в ИГ1 следующих формул:
a) A v В В vA; б) А —> А & А; в) А & В —> A v В; г) А & А <-» А;
д) A v (А<-^А).
Зд. Постройте доказательства в ИГ1 следующих формул:
а) (В —> (А &В —> А));
б) (А (СА v В) А)) (А -> А);
в) ((—1—А —> —А) —> —1—1—А);
http
о Hi iroit i'i ।
142
г) ((В -> В) ((СА & В) V В) ВУ);
д) (В —> ((В —>А vB)&В));
е) («А^В)^(А^В))^(А^В)^(А^В)));
ж) (((AvB)^C)^((AoB)^(B^A))).
32. Придумайте формулу, в древесном доказательстве которой в качестве
листьев будут:
а) аксиомы 11 и 4;
д) аксиомы 6 и 7;
б) аксиомы 3 и 1;
е) аксиомы 9 и 12;
в) аксиомы 8 и 10;
ж) аксиомы 13 и 6;
г) аксиомы 2 и 5;
з) аксиомы 12 и 2.
4. Постройте доказательства в ИГ1 следующих формул:
а) (Р->Р);
б) (PvP^P);
В)* (р
r)*^P^(P^Q);
д)* (Р Q) & (R-^ S) &(PvR) &-,((}&S)->(Q-> Р) &(S->R) (теорема
Гаубера).
5. (По [27, с.94, № 17]) Постройте доказательства в ИГ1 следующих
формул:
а) ЗхР (VxQ ЯхР);
б) (VxP УхР);
в) (ЯхА —> А); х g FV (А);
г) (VxA ЯхА);
д) VxA—>Vy[A]*;
е) (VxVyA УуУхА);
ж) (ЯхЯуА ЯуЯхА);
з) (3xVyA УуЯхА);
и) Vy[A]* —> VxA;
к) ЯхА->Яу[А]*;
л) (ЯхА -> (A v В)), х g FV (A v В);
м) (А&В^ VxA),xg FV(A&B).
Указания. Е. Воспользуйтесь дважды основным правилом вывода 2 и дваж-
ды аксиомой 14.3. Воспользуйтесь основными правилами 2,3 и аксиомами
14 и 15.
Вывод формул
6. [29, с. 193—194, № 1.51] Дан вывод формулы R из множества формул
{Р, Q, (Р —> (Q —>В))}
Р, Q, (Р -> (Q -> R), (Q -> Ю, R.
Проанализируйте его и запишите результат в виде {А1;..., Ап) I- В.
7. Проанализируйте вывода, (А —> В), В, (В —> О, С и запишите результат
в виде {Ап ...,АП) НВ.
8. [29, с. 194, № 1.53] Укажите, выводом какой из формул и из каких
гипотез является следующая последовательность формул:
143
https:/Л: rait.ru
a) A —> С, (A —> О —> ((В —> С) —> (A v В —> О), (В —> С) —> (A v В —> О,
В —> С, A v В —> С, A v В, С‘>
б) (А —> В) —> ((А —> —iB) —> —А), А —> В, (А^-.В)^^А,А^-1В,^А;
в) (А—>В) ЦР^А) -> (А В)), А —> В, (В—>А) (А <-> В), В —> А,
А<-^В;
г) ) (А^В) (^В^^А),А^В,-В^-А,-В,-А.
9. Установите, верно ли, что:
(а) если х g FV (А), то { А —> В} I- (А —> VxB);
(б) если х g FV (В), то { А —> В} I- (ЗхА -> В)?
10. [27, с. 94, № 14]
Являются ли выводами в ИГг следующие последовательности формул:
a) (Vx3yA(x,y) ЗуА(у,у));
б) (VxP(x) Р(уУ), (VxP(x) VyP(y));
в) (А(х) -> ЗхА(х)), ((А(х) -> ЗхА(х)) -> (\fxA(x) -> (А(х) -> ЗхА(х)))),
((VxA(x) -> (А(х) ЗхА(х)))?
11. [27, с. 94, №15].
Каким требованиям должна удовлетворять формула А (х), чтобы следую-
щая последовательность формул была доказательством в ИГг:
а) (А(у) -> ЗхА(х)), (ЗуА(у) -> ЗхА(х));
б) (VxA(x) —> А(у)), ((VxA(x) VyA(y))?
12. [27, с.94, № 18]
def
Является ли выводом из И = {(С —> А(х))} последовательность формул:
я Л (Г—(Г —МуДГ/П’
б) ((С—>А(х)) -> (В(у) -> (С—>А(х)))), (С—>А(х)), (ВО) (С->А(х))),
(ЗуВ(у) —> (С—>А(х))),
еслихё FV(O,y£ FV(O,y£ FV(A).
13. [21, с. 138] Являются ли выводами приведённые ниже деревья вывода?
Если нет, то найдите и объясните допущенную ошибку:
a) {3zVxP(y, х, z)} Ь 3wVxP(w, х, z)
Гипотеза VxP(y, x, z) -> BwVxP(w, x, z)
3zVxP(y, x, z); 3zVxP(y, x, z) 3wVxP(w, x, z)
3wVxP(w, х, z)
6)
в)
{3xVyP(x,y, z)} I- 3u/VyP(iv,y, z)
Гипотеза VyP(x, y, z) 3wVyP(w, y, z)
3xVyP(x, у, z); 3xVyP(x, y, z) 3wVyP(w, y, z)
3wVyP(w, y, z)
[{3yVyP(y,y, x)} I- 3zVyP(z,y, x)
Гипотеза VyP(y, y, x) 3zVyP(z, y, x)
3yVyP(y, y, x); 3yVyP(y, y, x) BzXfyPQz, y, x)
3zVyP(z, y, x)
i it^sVAjrsit.r
144
14. Постройте выводы в И1\:
а) {А, В}\~А&В;
б) {P&Q}HP;
в) {P}HPvQ;
г) {А —> В, А —>-iB} Н —А;
д) [А В, В —> А} I- А <-» В;
е) {Р <-» Q} Н Р —> Q.
15. (По [29, с. 194, № 1.55]) Постройте выводы в И1\:
а) {С^А, СВ, С} А &В;
б) {А&В,А—> (В->С)} НС;
в) {А В, В С} Н (А О;
г) {(А->О->С,А->В,В->С}НС;
д) {А —> В,-В} Н-А;
е) {А^В, С Е,—£&—£} Н -А &-.С;
ж) {А <->В, В —> С} Н А —> С;
з) {А —>С), —В —>А} Н (-В—>О;
и) {В—> —А, А} Н-В;
к) {А —> В, А —> —iB} I- —A v В;
л) {А <-> В, —iB} I- —А;
м) {А <-> В, В С} НА С;
н) {А}Н(В—>В);
о) {А} Н —i(B &-В);
п) {-А—>В, С&-В } НА;
р) {А,-А} НВ.
15v Постройте следующие выводы:
а)* {В С} Н (А В) -> (А О;
в)* Н(А—>В) -> ((В -> О -> (А -> О).
б)* {А ->В} Н (В О (А О;
16. (По [27, с. 94, № 19])
Постройте выводы в ИГг (у и z не входят в А(х) и В(х)):
a) {Vx(A —> В)} Н ЯхА —> ЯхВ; б) {Vx(A(x) В(х))} Н VyA(y) \/zB(z).
16j. (По [19], сохранена нумерация первоисточника) Докажите в гиль-
бертовском исчислении следующие теоремы:
22. {А —> (В —> О,-г-А,-i-B} Н-i-iC;
23. {-i—i(A —>В)} Н —А —> —i-B;
24. {—i-i( А —> В), -г-,(В О} Н —i(A О;
25. Н —.—.(А & В) <-4 —г-А & -1-В;
25а. Н -1-i(A нВ) е —.(А В) & -,-,(В А~);
49а. НА^^пА;
49b. Н -1-гпА<-> -А;
49с. НАv-А(-r-АА);
49d. Н (A v-А) (-i-A<-^A);
50а.Н-.(А<->-А);
51а. Н —г-1(А v —А);
51b.H-m(-mA->A);
56а. НА vB^-i(—А&—В);
56b. Н -A vB —.(А & -пВ);
57а. HA&B^^Hv^B);
57b. Н А & -В —> ->(-А v В);
58а. Н (А -> В) -> -.(А & -В);
58b. Н (А -> -В) <-> -.(А & В);
145
https:it.ru
58c I- —i(A & В) <-> (—i—А -В);
58d. I- С—-.В) <-> -1-.(-nA v -В);
58е. {-r-В —> В} Н (-.-А -> В) о (А ВУ
58f. {-г-В -> В} I- (А -> В) <-> -i(A & -В);
58g. Н (-mA -> В) -> -.(А & -В);
59а. Н-A vB —> (А —>В);
59ь. Н (А —>В) —> -m (-Av В);
59с. Н (-А —> В) —> -m (A v В);
60а. Н (А & В) —> -i(A -В);
6ОЬ. НА&-В—>—i(A—>В);
60с. Н —mA & В —> —.(А —>-В);
60d. I- -mA & -В о -.(А -+ВУ
60е. Н —.(А -> В) <-> —.(—.A v В);
60f. Н -.(-A vB) н —1—.СА & -В);
60g. I- —г-.СА -> В) <-> —,(А & -В);
60h. Н -.(А & -В) о (А ^ВУ
60р Н (А —> -,-В) <-> (-mA ^ВУ,
61а. НА vB—> (-А—> В);
61b. Н —,(А vB) н -.(-А -> В);
62а. Н (-А v -В) -> —.СА & В).
Варианты гильбертовского исчисления
17. (Д. Гильберт, В. Аккерман, 1947) В исчислении используются:
а) базовые логические связки: -i, v;
def
б) обозначение: (А —> В) = -A v В;
в) схемы аксиом: 1) A v А —> А; 2) А —> A v В; 3) A v В —> В v А; 4) (В —>
-^С) (Av В -4Av О;
г) правило вывода: modus ponens (MP).
1. Докажите в исчислении
а) Н (А^В)^((С^А)^(С^В));
б) Н (А^А);
в) Н A v -А;
г) Н(А—>—гпА);
д) Н^В^(В^С);
е) НА v (В v О ((В v (A v О) vА);
ж) Н (В v (A v О) v А —> В v (A v С);
з) Н A v (В v С) —> (В v (A v О;
п) {В А, —В —> А} Н А.
и) Н(А^(В^О)^(В^(А^О);
к) Н(С->А)->((А->В)->(С->В));
л) {А —> В} Н С v А —> С v В;
м) {С^>А,А^>В} Н (С^ВУ
н) {А^ (В^ОМ^В} НА^ (А^О;
о) {а^(в^о,а^в}Н(а^О;
2. Докажите, что все выводимые в исчислении формулы выводимы
также в классическом гильбертовском исчислении (и наоборот).
18. [38, с. 49] В исчислении Ь2, изученном Дж. Россером (1953), употре-
бляются:
а) базовые логические связки: &;
def
б) обозначение: (А^В) = -i(A&-iB);
146
С*" //< ! ио it i-i
в) схемы аксиом: 1) А —> (А & А); 2) (А & В) —> А; 3) (А —> В) —> (-i(B &
& С) —> —i(C &А));
г) правило вывода: modus ponens (МР).
1. Докажите в исчислении Ь2:
а) Н —(—А&А);
б) Ь^4^А;
в) Н —i(A & В) —> (В —> —А);
г) I- (А—>-г-А);
д) Н (А —> В) —> (-В —> —А);
е) Н(А—>А);
ж) Н(А&В—>В&А);
3) н (а-> (в->о)-> ((А&в)->О;
и) н ((А & в)-> о-> (А-> (в-> о);
к) НА (В -> (А & В);
л) НА—> (В А) ;
м) Н (-А —> А) —> А;
н) {А —>В, В —> С} Ь-i(-iC &А);
о) {А->В,В->С} Н (А->О;
п) {АВ, СD} (А & СВ & D~);
р) {В С} Н (А &В —>А & О;
с) {(А->В), (А->(В->О)}Н(А->О;
т) {—А —> —В} Н (В —> А);
у) {А->В} Н (С&А->В&О;
ф) {A—>B,B—>C,C—>D}\- (Д-^D);
х) {А->В,-А->В} НВ.
2. [27, с.73, № 41]
Докажите, что все выводимые в исчислении Ь2 формулы выводимы также
в классическом гильбертовском исчислении (и наоборот).
19. [53, с. 113; 26, с. 45]
В исчислении Р2 (исчисление Ч, система Чёрча) употребляются:
а) базовые логические связки: —i, —>;
def def
б) обозначения: (A v В) = (—А В), (А&В) = -i(A -В);
в) схемы аксиом: 1) А —> (В —> А); 2) (А —> (В —> О) —> ((А —> В) —> (А —>
->С)); 3) (—А—>-В) —>В—>А);
г) правило вывода: modus ponens (МР);
1. Докажите в исчислении Р2:
а) Н (А—>А);
б) Н—А—>(А—>В);
в) Н(^АчА);
г) Н(А—>->-А);
д) Н (А —>В) —> (-В —> —А);
е) Н-i—А —> (-i-А —> А);
ж) {(А->В), (В->О}Н(А->О;
з) {(А &В) v С} Н (A v О & (В v О;
и) {—i(A & В)} Н-A v-В;
к) {—A v-В} Н —i(A &В);
л) {А & В} Н A v В.
2. Докажите, что все выводимые в исчислении Р2 формулы выводимы
также в классическом гильбертовском исчислении (и наоборот).
20. [19; 38, с. 49]
147
https:/Л; rait.ru
В исчислении L4 (система Клини) употребляются:
а) базовые логические связки: &, v, -1;
def
б) обозначение: (А В) = (А -» В)&(В А);
в) схемы аксиом: 1) А (В —> А); 2) (А —> В) —> ((А —> (В —> О) (А
->О);3)А->(В->А&В);4)А&В->А; 5)А&В->В; 6)A^AvB; 7)В->
4AvB; 8) (А —> С) —> ((В —> С) —> (A v В —> С)); 9) (А—> В)—> ((А—>—В)—>
—>-А); 10) -mA А;
г) правило вывода: modus ponens (МР).
1. Докажите в исчислении L4:
а) I- (А—>А);
б) I- (А В) (-В -> -А);
в) Н(В->-тВ);
г) Н-В-> (В-> О;
д) hB->(mC->m(B->O)j
е) H-B-H-.C-^CBvO);
ж) Ь (тВ -> А) -> ((В А)) —>А);
з) {( а —> в), (в —> с)} I-(а —> с);
и) {В, -В} Н С.
2. Докажите, что все выводимые в исчислении L4 формулы выводимы
также в классическом гилъбертовском исчислении (и наоборот).
21. [38, с. 38—42]
В исчислении L (система Мендельсона) употребляются:
а) базовые логические связки: -i, -»
def def
б) обозначения: (A vВ) = (—А—>В), (А&В) = —i(A^—B);
в) схемы аксиом: 1) (А (В —> А)); 2) ((А —> (В —> О) ((А —> В) —> (А —>
О)); 3) ((mB -> mA) -> ((—В —> А) —> В));
г) правило вывода: modus ponens (МР).
1. Докажите в исчислении L:
а) Н(А—>А);
б) Ь (-А—>А)—>А;
в) Н (-В —>-А) —> (А —> В);
г) I- (—г-А—>А);
д) Ь (А —> —1—А);
е) Н —А —> (А —>В);
ж) НА—> (В—>А&В);
з) Н (А —>В) —> (-В —А);
и) НА —> (-В —>-i(A —>В);
к) Н (А —>В) —> ((—А —>В) —>В);
л) Н ((А —> В) —> А) —> А;
м) {(а—>в), (в—>О) н (А—>О;
н) {(А->(В->О)НВ->(А->С).
2. Докажите, что все выводимые в исчислении L формулы выводимы
также в классическом гилъбертовском исчислении (и наоборот).
22. [38, с. 51]
В исчислении Нико Рп (1917) употребляются:
а) базовая логическая связка: |;
б) схема аксиом: (А | (В | О) | ((Р | (D | D)) | ((Е | В) | ((А | Е) | (А | £)));
в) правило вывода:
А А|(В|О
С
148
Докажите следующие теоремы в исчислении Рп (В. Сергеева):
а) Н (G | (D | (D | D))) | СССА | (В | О | G) | «А| (В I Q) I G));
б) {(£ | (D | (D | D)))} I- (СА | (В | О) | Е);
в) Ь (G | ССА | (В | О) | Е)) | (ССЕ | С СЕ | (D | Е))) | G | ((£ | (Е | (D |
Е))) | G));
г) {(G | ССА | (В | Q) | Е))} I- ((£ | (Е | (Е | £>))) | G);
д) {(А | (В | О)} I- (Е | В) | ССА | Е) | (А | Е));
е) {(А | (В | О), (Е | В)} I- (А | £);
ж) {ССА | Е) | СЕ | СЕ | А))), СЕ | В), (А | (В | О)} Ь СЕ | А);
з) {СА | СВ | О), СВ | В), (А | Е) | (А | СВ | О)} Н СВ | О.
23. [38, с. 51]
В исчислении Мередита Рт С1953) употребляются:
а) базовые логические связки: -i,
б) схема аксиом: ССССА —> В) —> С~>С -£>)) —> С) —> Е) —> ССЕ —> А) —>
^СО^А));
в) правило вывода: modus ponens CMP).
Докажите следующие теоремы в исчислении Рт (И. Большакова'):
а) {ССССА ->В) -> C-<G—>—iD)) -> О ->Е)} Ь ССЕА) -> (Р —>А));
б) {ССССА В) С-С -> -iE)) —> С) —> Е), СЕ —> А)} Н (Р -> А);
в) {ССССА В) С-С -> -1Е)) О Е), СЕ А), Е} I- А;
г) {СССССА^В) -> C-C^^D)) ->О —>Е) -> СЕ^А) -> (Р^А))) ->
ССССА -> В) -> С-С -> -nD)) -> О -> Е)} Н ССССА -> В) -> С-С -> -1Е)) -> О -> Е);
д) {СССССА -> В) -> С-С -> -nD)) -> О -> Е) -> СЕ -> А) -> СЕ А))) ->
ССССА в) C-с -> -л)) о, СССА -> в) -> с->с -> -л)) -> С)} н Е;
е) {СССССЕ -> А) -> СЕ А)) В) C-С -> -Л)) С) CCCCG -> Н) ->
C-nl->-J)) ->1) ->К)} I- ССЕ^А) СЕ^А));
ж) {СССССЕ А) СЕ А)) В) C-С ^D)) О CCCCG Н)
С—J—> —J)) —>1) —>К),Е} Н ССЕ —>А) —> СЕА));
3) {СССССЕ А) СЕ А)) В) С-С -nD)) О CCCCG Н)
C-nl->-J)) ->1) ^К)} \-Р^> «Е^А) СЕ->А));
и) {СССССЕ А) СЕ А)) В) С-С -nD)) О CCCCG Н)
C-nl->-J)) ->1) ->К), СЕ^А)} Ь СЕ^А);
к) {СССССЕ А) СЕ А)) В) C-С -nD)) О CCCCG Н)
C-nl->-J)) ->1) ->К), (E—>A),F} I- А.
Гёделева нумерация языка первого порядка
1. [38, с. 151]
Найдите гёделевы номера символов: х2, аф /г2, Р£.
2. Найдите гёделевы номера выражений:
а) АЧаз);
б) -1P13Cai,x3,x5)^P11Cx2);
в) ЭхзР/Схз);
г) P11Cxi)vP21Cx3).
3. Постройте объекты с гёделевыми номерами 1944 и 47.
4. [38, с. 151]
Покажите, что если п нечётно, то 4п не является гёделевым номером
Снапример, число 12 не является гёделевым номером).
5. Как изменится определение гёделевой нумерации языка первого по-
рядка, если добавить в алфавит языка символы &, v, 3?
6. Определите гёделев номер вывода формулы А & В из гипотез А и В.
149
https:"!!
Задачи на программирование
1* . Напишите программы на любом языке программирования для на-
хождения гёделевого номера заданной формулы языка первого порядка.
2* . Напишите программы на любом языке программирования для вос-
становления формулы языка первого порядка по ее гёделевому номеру.
https:it.ru
Упражнение 5
ГИЛЬБЕРТОВСКОЕ ИСЧИСЛЕНИЕ ПЕРВОГО
ПОРЯДКА: УСТАНОВЛЕНИЕ СУЩЕСТВОВАНИЯ
ДОКАЗАТЕЛЬСТВ И ВЫВОДОВ С ПОМОЩЬЮ
ДОПУСТИМЫХ ПРАВИЛ ВЫВОДА
Говорят, лишившись зубов, человек
обретает большую свободу языка.
Е. Лец. Непричёсанные мысли
Обязательные результаты обучения:
• знать основные понятия
— методы установления существования доказательства формулы и суще-
ствования вывода формулы из множества формул;
— прямые допустимые правила вывода;
— непрямые допустимые правила вывода;
— линейный и древесный (прямой и непрямой) квазивывод формулы
из множества формулы в гильбертовском исчислении первого порядка;
• уметь
— конструировать доказательства допустимости прямых и непрямых
правил вывода в гильбертовском исчислении первого порядка (ИГ^;
— устанавливать существование доказательств формул в ИГг;
— устанавливать существование выводов формул из гипотез в ИГг;
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
Теоретические сведения
Существуют следующие основные методы установления доказуе-
мости формулы (выводимости формулы из множества формул}'.
а) построение (предъявление) доказательства формулы (вывода
формулы из множества формул);
б) установление существования доказательства формулы (выво-
да формулы из множества формул).
Приступим к изучению методов установления существования до-
казательства формулы (вывода формулы из множества формул).
151
https:it.ru
Прямые допустимые правила вывода
Используйте мягкие слова и твёрдые
аргументы.
Аноним
Пусть А1г..., Ап, В — формулы, Н, Нг,...,Нп — множества формул.
Определение.
Слово одного из следующих видов:
В
будем называть прямым допустимым правилом вывода в гилъбер-
товском исчислении первого порядка (допустимым правилом вы-
вода прямого типа или просто прямым допустимым правилом),
если при условии доказуемости формул А1г ..., Ап в гильбертов-
ском исчислении первого порядка доказуема формула В.
При этом формула В называется непосредственным следствием
формул Аг, ...,Аппо данному прямому допустимому правилу вы-
вода, а формулы А1} ...,Ап называются посылками прямого допу-
стимого правила вывода.
Предложение (по [13, с. 144]).
Добавление прямых допустимых правил вывода к гильбертов-
скому исчислению первого порядка не изменяет множество дока-
зуемых формул.
Определение [13, с. 143].
Линейным квазивыводом формулы А из множества Н называется
такая последовательность формул А1}..., Ап, что А1=Апи для каж-
дого i < п выполняется одно из следующих условий:
а) формула Af является доказуемой формулой;
б) Д g Н;
в) формула Af получается из «предыдущих» формул последова-
тельности с помощью основных правил вывода 1, 2, 3, причём
при применении правил вывода 2 и 3 предметная переменная
х не входит ни в одну формулу из множества Н свободно;
(г ) формула Aj получается из «предыдущих» формул последова-
тельности с помощью прямых допустимых правил вывода.
Определение.
Понятие «(прямой) древесный квазивывод формулы А из множе-
ства Н» определим индуктивно:
1) доказуемая формула А является (прямым) древесным квазивы-
водом формулы А из множества Н;
2) формула A g Н является (прямым) древесным квазивыводом
формулы А из множества Н;
152
https:/Л: rait.ru
3) еслиDlt ...,Dnявляются (прямыми) древесными квазивывода-
ми формул А1} ..., Ап из множества Н соответственно, а формула
А является непосредственным следствием формул А1} ...,Ап по ос-
новным правилам вывода 1,2,3, причем при применении правил
вывода 2 и 3 предметная переменная х не входит ни в одну фор-
мулу из множества Н свободно, то
РрР2- -Рп
А
является (прямым) древесным квазивыводом формулы А из мно-
жества Н;
4) еслиDlt ...,Dnявляются (прямыми) древесными квазивывода-
ми формул А1} ..., Ап из множества Н соответственно, а формула
А является непосредственным следствием формул А1}..., Ап по пря-
мому допустимому правилу вывода, то
А
является (прямым) древесным квазивыводом формулы А из мно-
жества Н.
Пусть А, В, С, D — формулы.
Предложение (бескванторные прямые правила вывода).
Следующие слова являются прямыми допустимыми правилами
вывода гильбертовского исчисления первого порядка:
def
а) (общелогическии принцип замены равного на равное);
б)----------------(введение &);
(А & В)
ч (А&В) ,
в) ——— (удаление &);
ч (А&В) ,
г)--------(удаление &);
Д) 7~л—™ (введение v);
(Av В)
« В г , ч
е) -------(введение v);
(Av В)
ж)
з)
-----(сильное удаление -i);
А
А —А
-----(слабое удаление -i);
В
и)
(упранзитивностъ);
153
httpaJ/uraiLft
к)
СА^СВ >СВ
(А&В^С)
(соединение посылок);
л)
(А&В—>С)
(А—>(В—>С))
(разъединение посылок);
. (А—>(В—>С)) , .
м) ————(перестановка посылок);
н)
AvB -Л
(единичная резолюция);
о)
AvB —BvC
AvC
(резолюция);
(А^В) ^В
п) ---------------(modus tollens);
P)
(modus ponendo tollens);
c)
(modus tollendo ponens);
t)
(modus ponendo ponens);
У)
(modus tollendo tollens);
_ (A^B) (A—>—B) . . . , , , .
ф) ---------------(yeductio ad absurdum).
Пусть x — предметная переменная, t — терм сигнатуры о. Пред-
ложение (кванторные прямые правила вывода) [13, с. 144].
Следующие слова являются прямыми допустимыми правилами
вывода в гильбертовском исчислении первого порядка;
д
а) (прямое правило универсального обобщения);
VxA
- VxA v
б) ----(прямое правило универсальной конкретизации);
(А)*
в) -—— (прямое правило экзистенциального обобщения);
ЗхА
(А)?->В. В—>(А)£ .
(VxA->B) (В->ЭхА)’
ЗхА ([А]*->В)
е) ---*--------у gFV(B) (прямоеудаление Я);
[А]х
ж) —— (вариант прямого правила универсального обобщения).
VxA
154
https: //ц га it.ru
Непрямые допустимые правила вывода
Определение [27, с. 65].
Слово вида
Н\-А
будем называть непрямым допустимым правилом вывода в гилъ-
бертовском исчислении первого порядка (или просто непрямым до-
пустимым правилом), если при выводимости формулы А- из мно-
жества для всех i = 1, п соответственно (т. е. при выпол-
нении Нг Н А1} Нп\- Ап) формула А выводима из множества
формул Н (т. е. НI- А).
Определение.
Определим индуктивно понятие «(непрямой) древесный квазивы-
вод формулы А из множества Н»:
1) (непрямым) древесным квазивыводом формулы А из множества
Н является слово НI- А, если существует выводА из множества Н;
2) если DT является (непрямым) древесным квазивыводом форму-
лы Аг из множества Н1г D2 является (непрямым) древесным ква-
зивыводом формулы А2 из множества Н2, ...,Dn является (непря-
мым) древесным квазивыводом формулы Ап из множества Нп, а
HjhA^H^An
Н\-А
является непрямым допустимым правилом вывода, то
Р1Р2...РП
Н\~А
является (непрямым) древесным квазивыводом А из множества Н.
1. Структурные непрямые допустимые правила вывода
Предложение (по Г. Генцену, 1934—35) [19, с. 84; 21, с. 52].
Следующие слова являются непрямыми допустимыми правила-
ми вывода, называемые структурными непрямыми допустимыми
правилами вывода гилъбертовского исчисления:
а) правило добавления гипотез (расширение)
Н\-А
Ни{В}\-А’
155
https:it.ru
б) правило удаления повторяющейся гипотезы (сокращение)
Ни{В}и{В}\~А
Ни{В}\-А ’
в) правило перестановки гипотез (перестановка)
Ни{А,В}\-С
Ни{В,А}К’
г) сечение (по Г. Генцену, 1934—35)
Н1\-А1;{А}иН2\~В
Н1иН2\~В ’
д) если п g N\{0}, то
Н1\-В1;...;Нп\-Вп;Нп+1и{В1}...,Вп}\-С ( .
— ----±----------——-----±---------(п-кратное сечение);
Н1иН2и...иН1Н,11-С
е) общее свойство отношения выводимости (транзитивность)
НгЬА
Н2ЬА’
где множество Н2 получается из множества Нг удалением любых
формул из Hlt которые являются доказуемыми или выводимыми
из остающихся формул множества Нг.
2. Предложение о дедукции
Предложение о дедукции (Ж. Эрбран, 1930) [26, с. 51—53;
с. 87—89; 13, с. 154—155].
1. Н\- (А—> В) тогда и только тогда, когда Н u {А} I- В.
2. Следующие слова:
, ч HF(A->B) Ни{А}\-В
(а )---------; (б)---------
Ни{А}\-В Н\-(А^В)
являются непрямыми допустимыми правилами вывода в гильбер-
товском исчислении первого порядка.
Следствие.
Непрямыми допустимыми правилами вывода являются следую-
щие слова:
х _________{А1,А2,...,Ап} 1~В_______
0 h Аг ->(А2 (... (Ап_1 Ап В))...))
(п-кратное введение —>);
б) 0 h (Д2 ->(...->(А„! ~^Ап^В))...))
{А1}А2,...,Ап}^В
(п-кратное удаление ^>).
156
С*" iroif ri ।
3. Правила введения и удаления логических связок
Предложение (правила удаления логических связок -i, &, v, —>).
Для любого конечного множества формул Н и для любых формул
А, В, С следующие слова являются непрямыми допустимыми пра-
вилами вывода, называемые правилами удаления логических связок
&, v,
а) удаление v (по Г. Генцену)
Н I- (A v В); Н о {А} I- С; Н и{В} h С
НУС ’
б) удаление &
Hj-(A&B) Hj-(A&B)
НУА ’ Н\-В ’
в) сильное удаление -i
Hh-i-iA.
НУА ’
г) слабое удаление -i
HI-В; Hh-B
HI-А ’
г*) удаление -i (доказательство от противного)
Н^>{—А}УВ; Ни{-^А}У^В
НУА ’
д) удаление
НУА; НУ(А—>В)
НУВ ’
е) п-кратное удаление &
Hu{A1&A2&...&A„}hB .
Hu{A1,A2,...,An}hB ’
ж) удаление <->
НУ(А++Ву НУ(А^В)
Ни{А}УВ’ Ни{В}УА
Предложение (правила введения логических связок &, v,
<н>). Для любого конечного множества формул Н и для любых фор-
157
https:it.ru
мул А, В, С следующие слова являются непрямыми допустимыми
правилами вывода, называемые правилами введения логических
связок -1, &, v, <->:
а) удаление v (по С. Клини) (разбор случаев)
Но {AR С; Ho{B}hC
HhfAvB—>С) ’
б) введение v
H\-A H\-B
H\-(AvB)’ H\-(AvB)’
в) введение &
HFA; HFB
HF(A&B) ’
г) введение —> (дедукция)
НЦА^В)’
д) слабое введение -i (приведение к абсурду)
Hu{A}FB; Ни{А}Ь-В
е) сильное введение -i
HI-А
ж) введение -i и (контрапозиция)
Ни{А}\-В
Ни{-пВ}\-^А’
з) п-кратное введение &
Ни{А1}А2,...,Ап}ЬВ
Hu{A1&A2&...&A„}I-B’
и) введение <-> в «сукцедент»
Н1-(А->В)&(В->А).
Н\-(А++В)
158
https://и гз it.ru
к) введение в «антецедент»
Ни{(В->С),(С->В)}1~А
Ни{В<^С}\-А
Замечания.
1. С помощью непрямого допустимого правила вывода «приведение
к абсурду» легко доказывается непрямое допустимое правило вывода
«доказательство от противного». В самом деле:
Но-ЬА}|-С; НиЫ}Ь^В
НН-г-А
ННА
(сильное удаление ->)
(приведение к абсурду)
2. [21, с. 59—60] Правило (удаление дизъюнкции (по С. Клини)» отве-
чает содержательному приёму доказательства, который называется разбо-
ром частных случаев: для того, чтобы вывести формулу С из (A v В), «уда-
ляют» дизъюнкцию и строят два различных вывода, один — выводя фор-
мулу С из А, другой — формулу С из В. Именно в этом смысле мы и будем
считать разбираемое правило правилом удаления.
Конечно, более естественно вписывается в схему «правил удале-
ния» формулировка Г. Генцена, приведённая в предыдущем Пред-
ложении, в которой буква v действительно удаляется из первой по-
сылки.
Следствие.
Следующие слова являются непрямыми допустимыми правила-
ми вывода:
_________{A1&A2&...&A„}hB_________
aJ 0\-А1—>(А2—>(...—>(Ап_1—>Ап—> В))...))
ние & и п-кратное введение —
б) 0ЬА1->(А2-> (... ->(An! -> А„ ->В))...))
{А1&А2&...&Ап}|-В
(п-кратное удале-
(п-кратное введе-
ние & и п-кратное удаление
Предложение (по [176, с.141]).
Следующие слова являются непрямыми допустимыми правила-
ми вывода, которые будем называть правилами доказательства
от противного:
ч Ни{-пА}ЬС&^С Ни{ЧА->В)}Ь^А
а) -------------; о)--------------;
Н\-А Ни{А}\-В
Ни{—{A—>В)}1~В
В Ни{А}\-В
Определение (важное).
Следующие непрямые правила вывода будем называть косвенны-
ми (непрямыми) способами доказательства:
159
https: "и га it.ru
Hu{A}HB „ _ .
1} hi-(a->b)
Hu{A}hC; Ни{В}И f *
2) -------------(разбор случаев)',
Hu{AvB}kC
_ Hu{A}HB; Hu{A}h^B . _
3) -------------------(приведение к абсурду);
H Н —А
.. Hu{-A}hB; HuH}h^B
4) н\~А--------------(доказательство от противного).
4. Кванторные правила введения и удаления кванторов
Пусть А обозначает формулу, Н — множество формул (возможно
пустое), t — терм, х — предметную переменную.
Предложение (кванторные правила введения и удаления)
[21, с. 143—148].
Следующие слова являются непрямыми допустимыми правила-
ми вывода, которые называются кванторными правилами введения
и удаления:
16Secv) введение V в «сукцедент», правило универсального обобще-
ния
Н\-А
Н\-\/хА’
где х не входит свободно в множество формул Н;
l^secv) введение V в «антецедент»
Hu{(A)f}\-B
Ни{УхА}\-В ’
l®Secv) введение 3 в «сукцедент», правило экзистенциального
обобщения
Н\-(А)?
Н\-ЗхА ’
19Secv) введение 3 в «антецедент»
Ни{А}\-В
Ни{ЭхА}\-В’
где х не входит свободно в множество Н и формулу В;
20Secv) удаление V из «сукцедента», правило универсальной кон-
кретизации
160
https:/Л: rait.ru
H\-VxA
H\-(A)f’
21Nat) удаление 3 из «сукцедента»
H1\-3xA;H2u{[A]^}\-B
где у g FV(B) и у не входит свободно ни в одну из формул множе-
ства Н2
Замечание.
Забегая вперёд, укажем, что:
1) допустимые правила вывода 16Secv, 17Secv, 18Secv и 19Secv синтаксиче-
ски «совпадают» соответственно с основными правилами вывода 16,17,
18,19 моносукцедентного секвенциального исчисления первого порядка;
2) правило вывода 20Secv является допустимым правилом этого исчис-
ления;
3) допустимое правило вывода (21Nat) весьма «напоминает» фигуру
заключения «удаление 3« исчисления натурального вывода.
5. Правила замены и подстановки
Предложение (правило замены) [21, с. 149—150].
Пусть СА — формула, в которой выделено вхождение формулы
А, а Св — формула, получаемая из СА заменой этого вхождения
на формулу В. Тогда имеет место следующее непрямое допустимое
правило вывода, которое называется правилом замены:
\-(А<^В)
\-(сА++св)'
Следствие (по [19, с.140]).
01- (AoVar (А)).
Докажите Следствие самостоятельно. При этом воспользуйтесь
существованием доказательства формул
(73) VxA<-> Vy[A]*; (74) ЭхА<->Зу[А]£.
Пусть терм t допустим для переменной х в формулах А1}Ап, В.
Предложение (правило подстановки) [27, с. 92].
Следующее слово является непрямым допустимым правилом вы-
вода, которое называется правилом подстановки:
______в_______________________
{(Аг)? ,(А2)?,...,(Аг)?}1-(В)? ’
https/'с г? и. ш
161
Примеры решения некоторых
типов упражнений
Пример 1. Докажите, что прямым допустимым правилом вывода в ИГХ
является слово
Ау—В CvB
АуС
(однолитерное правило Девиса и Патнема).
Решение. Воспользуемся следующими прямыми допустимыми прави-
лами вывода: правилом вывода (tr) и правилом вывода
Av-В
(В->А)’
к доказательству которого мы и приступим:
Аксиома 1 Аксиома 8
J. 1
(А->(В->А)) (А->(В->А))->((-В->(В->А))->САу-В->(В->А)))
-В—>(В—>А)(-В->(В->А))->(Ау-В->(В->А))
1 J Av-B—>(В—>А)
Доказательство формулы —В —> (В —>А) постройте самостоятельно.
Остаётся построить прямой древесный квазивывод:
Аксиомы
(В—>А) (A—>AvC) (С—>АуС) (С-»АуС)->((В-»АуС)->(СуВ-»АуС)) (мр)
& (В—>AvC)_____________(В—> AvC)—>(CvB—> АуС)________
CvB__________________(СуВ^АуС)______________________________
AvC
Замечание.
На доказанном правиле вывода основан принцип резолюции —
известный метод логического вывода, в основе которого лежит приведе-
ние доказываемого утверждения к множеству дизъюнктов и поиску в этом
множестве дизъюнкта, содержащего некоторый атом, и другого, содер-
жащего отрицание этого атома, для их последовательного устранения
из исходного множества. Если этот процесс через конечное число шагов
приводит к некоторому дизъюнкту (пустому дизъюнкту), то вывод успе-
шен. В противном случае формула недоказуема.
Пример 2. Покажите, что имеет место следующее прямое допусти-
мое правило вывода:
(А^В&С)
(А—>В)&.(А—>С)
162
https: //ц га it.ru
Решение.
Доказуемо Акс 4
АксЗ
Доказуемо Акс5 । А. —>В&С В&С —>В
, . А-»В&С В&С-»С (А-»В)-»((А-»С)->(А-»В)&(А-»С)) А-»В
(тр)-----------------------------------------------------------------------
_______А—>С_____________________(А -> С) -> (А -> В)&(А -> С)___________
(А—>В)&(А—>С)
(тр)
(МР)
(МР)
Пример 3. Покажите, что следующее правило является непрямым
допустимым правилом вывода в ИГХ:
НЬА->В _
---------: (дедукция)
Но{А}НВ
Решение. Пусть последовательность формул С15Сп_1; (А —>В) явля-
ется выводом формулы (А —> В) из множества Н.
Последовательность формул С1?Сп-1, (А —>В), А, В, очевидно, явля-
ется выводом В из Н о {А}.
Пример 4. Докажите, что следующее правило является непрямым
допустимым правилом вывода в ИГ1:
Но {А} НС; Но{В}НС , *
------------------; (удаление v).
Ho{AvB}HC
Решение. Пусть А, В, С — произвольные формулы. Построим непря-
мой древесный квазивывод формулы С из множества формул Н и {A vB};
Hh{A}l-C
(дедукция)
Но{В}НС НН(А^-С) Hh(A^C)^((B^C)^(AvB^C))AcS
Hh(B->C)
НН(В—>С)—>(AvB—>С)
HH(AvB—>С) .
—————— (дедукция)
Ho{AvB}hC
(удаление-»)
Пример 5. Докажите, что следующее кванторное непрямое правило
вывода (введение V в «сукцедент») является допустимым в ИГХ:
ННА
-------, где х не входит свободно в множество Н.
HhVxA
Решение. Воспользуемся «виртуальной» гипотезой: пусть Т —доказу-
емая формула, для которой xg FV (Т). Тогда
___________(расширение)
Ни{Т}ЬА (дедукция)
Н Н (Ч7 —> А)(докажите самостоятельно!)
НН(Т^УхА) 01-Т; Но{Т}НУхА HhVxA (дедукция) (сечение)
Пример 6. Установите существование доказательства в ИГ1 формулы
A->-i-A.
Решение. Воспользуемся непрямыми допустимыми правилами вывода
в ИГ1 и построим следующий непрямой древесный квазивывод:
163
https:/Л: га it.ru
{A} I-A {-A} I -A
{A,—A} HA {A, —A}b—A
{A}l~-i-A
0hA->^l
(расширение)
(введение —)
(дедукция)
Пример 7. Докажите существование вывода {A v —В, CvB}\- (AvC).
Решение. Воспользуемся непрямыми допустимыми правилами вывода:
{В}НВ
H(A->AvC) Ь(А—>AvC) H(C->AvC) {B,4AvC)}l~B
{A} I-(AvC) {A} I-(AvC) {C}|-(AvC) {-В,В}1--.ЧАуС)
{A, С} I-(AvC) {А, В} I-(AvC) {-B,C}l-(AvC) {-B,B}|-(AvC)
{A,CvB}H(AvQ_______________{-iB,CvB}|-(AvC)_______
{Av-£,CvB}h(AvC)
Анализ вывода проведите самостоятельно.
Упражнения для самостоятельного решения
Когда вы убедитесь, что теорема
верна, вы начинаете ее доказывать.
Традиционный профессор математики
(персонаж анекдотов о математиках)
1. Прямые допустимые правила вывода
1. (По [27, с. 70, № 24])
Докажите для гильбертовского исчисления первого порядка допустимость
следующих прямых правил вывода:
def
АВ = С., „
А(В / С) ^°^елогическии пРинЧип замены равного на равное);
А В . А . (А & В) . А . (А & В) . А .
------(введение &); в) (удаление &); г) (удаление &);
(А & В)-А-------------------В
——— (введение v); е) ——— (введение v);
AvB AvB
а)
б)
д)
—i—А А
ж) (сильное удаление -i); ж')---(сильное введение -i);
А -i-А
з) (слабое удаление -i);
В
. (А—>В) (В->С) , . . (А->(В->С)) , ,
и) ———-------(транзитивность); к) (соединение
посылок);
(А&В^С)
(А^(В^С))
. (А->(В->С))
М) ----------
(В—>(А—>С))
(разъединение посылок);
(перестановка посылок);
164
о //i iroi! ri ।
и)* ——— (преобразование v в —>);
. (В—>А) { . .
о) -------(преобразование —> в v);
-iBv А
х (А —> В) —lB - J 11 t
n) ----------(modus tollens);
\ (A ——'Ю /-j j t
p) ——(modus ponendo tollens);
t (—A —B) / j и j t
c) -------(modus tollendo ponens);
(—iB—> A)
t) (modus ponendo ponens);
. (B —A) r 1 11 J 11 t
y) ----------(modus tollendo tollens);
(—A —> —iB)
,. (A —GA —гл • ji. j \
ф) -------——-------(reductio ad absurdum);
,(A —> В & —iB) f . ii j ч
ф )----——-------(reductio ad absurdum);
. A<->B f , 4
x) -------(удаление <->);
A^B
. A<r>B , , .
ц) -------(удаление <-»);
В—> A
. A—>B В—>А _ » .
ч) -------------(введение <->).
А++В
1г. Докажите, что следующие слова являются прямыми допустимыми
правилами вывода гильбертовского исчисления первого порядка:
a) (единичнаярезолюция); б) CvB (резолюция).
В AvC
2. Докажите, что следующие слова являются прямыми допустимыми
правилами вывода в гильбертовском исчислении первого порядка:
д
а) (прямое правило универсального обобщения);
VxA
_ VxA .
б) ---(прямое правило универсальной конкретизации);
(А)^
(А)*
в) -—С (прямое правило экзистенциального обобщения);
ЭхА
г) (А)* ^В . В^>(А)* .
(VxA->B)’ (В->ЗхА)’
' ЗхА([А]*->В)
е) ---*— ------у g FV(B) (прямое удаление 3);
В
[А]х
ж) -—(вариант прямого правила универсального обобщения).
VxA
2. Непрямые допустимые правила вывода
3. Докажите, что следующие слова являются непрямыми допустимыми
правилами вывода в ИГг:
165
https:/Л: it.ru
ч Ни{А}НВ Ни{А}\~В . Н \~(\/хА^>В)
а) -----------(дедукция); б)-------------; в)-------------
Н\-(А—>В) H\~(XfxA—>B) Н^>{А}\-В
4. (По [27, с. 70, № 22])
Докажите, что следующие слова являются непрямыми допустимыми
правилами вывода в ИГр
а)
д)
--------(расширение);
Hv{B}hA
Ни{А}\-С; Ни{В}\-С , а
------------------(удаление v);
Hu{AvB}HC
_ Hu{B}u{B}U
б) -------------(сокращение);
Ни{В}\-А
. Ни{А}\-В; H\j{A}\-—iB . , .
е) --------------------(введение —
в)
Но {А, В} НС (
------------(перестановка);
Ни{В,А}\-С
Ни{-^В}\~А; Ни{-^В}\~^А
ж) ------------------------(доказательство от противного).
Н В
, . Hi НА ;Н2и{А}НВ .
(г) —----—-——------(сечение);
Нт оН2 ЬВ
5. [27, с. 94—95, № 20; с. 95, № 24] Докажите, что следующие правила
являются кванторными непрямыми допустимыми правилами вывода в ИГг:
а) введение V в «антецедент»
Hv{(A^Bt
Hv{XfxA}\-B’
б) введение 3 в «антецедент»
Ни{А}\-В .
Но{ЗлА}НВ’
где х не входит свободно ни в формулы Н, ни в В.
6. Докажите, что формула А выводима в ИТ^ тогда и только тогда, когда
выводима формула VxA.
7. (По [21, с. 149].) Пусть х — предметная переменная, А и В — фор-
мулы, и, кроме того, множество формул Н (возможно, пустое) таково, что
х не входит свободно в формулы из множества Н. Докажите, что тогда имеют
место следующие непрямые допустимые правила вывода:
а)
б)
в)
г)
НН(А—>В)
Н\-(УхА- Н\~(А- ->VxB)’ >В)
Н\-(ЗхА- >ЗхВ)’
Н\~(А< -+В)
HH(VxA< ->VxB)’
НН(А<- »В)
Н\-(ЗхА<- >ЗхВ)
3. Установление существования доказательства формул
8. [27, с. 70, № 28]
166
https:/Л: rait.ru
Установите существование доказательства в ИГг следующих формул:
а) (А&(В&О)<->((А&В)&О;
б) (Av(BvC))e((AvB)vC);
в) (А&В) (В &А);
г) (AvB)e(BvA);
д) (А & (В v О) <-> ((А&В) v (А & О);
е) (A v (В & О) <r+ ((AvB) & (A v О);
ж) (А & А) А;
з) (A v А) <-> А;
и) (A v (А & В)) <-» А;
к) (А & (A v В)) <-» А;
л) (—।—А А);
м) —i(A & -А);
н) (A v —А);
о) (А &В) -i(-iA v-В);
п) (A v В) -i(-iA &-В);
р) (А —>В) <-> —i(A &-В);
с) (А В) <-> (—A v В);
т) (А&В) <->-,(А->-В);
у) (AvB)<->(-nA->B);
ф) -.(А &В) н М v -В);
х) -.(A vB) н (-А& -В);
Ц) (—1—i—iA —А).
9. Установите существование доказательства в ИГ! формул:
14) (АеВ)н(А^В)&(ВчА);
23) (АеВ)н(ВнА);
26)* (А (В О) ((А о В) о О;
29) A v (В О <-> (A v В) (A v О;
30) A v (В <-> О <-> (Av В Av О;
31) (А^В&С) (А^В)&(А^С);
32) (А—>В vC) о (А—>В) v (А—>О;
33) А —> (В <-» О <-» (А —>В <-» А —> С);
33г) (А —> (В —> О) —> (А —> В) —> (А —> О) (самодистрибутивностъ
импликации);
44) —i(A—>В) ОА&-В;
45) -.(А нВ) е (A vB) & -.(А & В);
50) (А —>В) —> ((В —> О —> (А —> О) (закон гипотетического силлогизма);
51) (А —> (В —> О) <-> (В —> (А —> О) (закон коммутации);
52) А—>(В—>О<->(А&В—>О (закон экспортации-импортации);
53) -А —> (А —> В) (закон Дунса Скота);
54) (А —> В) (—В -Л) (закон простой контрапозиции);
54г) (А & В —> О (А & —iC —В) (закон сложной контрапозиции).
10. (По [19, с. 148; 21, с. 155—156; 29, с. 96]) Установите существование
доказательства приведённых ниже формул в гильбертовском исчислении
первого порядка.
Законы переименования связанных переменных:
1) VxB ++ Xfy[B]xy; 2) ЗхВ <-> 3y[B]J.
Законы перестановки одноименных кванторов:
3) VxVyA VyVxA; 4) ЗхЗуА НуЗхА.
Законы отрицания кванторов:
5) -.VxC Нх-.С; 6) -.НхС Vx-.C,
167
https:it.ru
Законы введения отрицания в формулы с кванторами:
7) VxC <->-,Ях-,С; 8) ЯхС -Л/х-,С.
Законы пронесения квантора общности через конъюнкцию:
9) VxB & VxC <-» Vx(B & О (дистрибутивность квантора общности
относительно конъюнкции)',
10) Е & VxC <-> Vx(£ & С), х £ FV(£).
Законы пронесения квантора существования через дизъюнкцию:
11) ЯхВ v ЯхС Ях(В v С) (дистрибутивность квантора существования
относительно дизъюнкции);
12) Е v ЗхС о Ях(£ vQ,xg FV(£).
Закон пронесения квантора существования через конъюнкцию:
13) Е & ЯхС о Ях(£ & О, х g FV(£).
Закон пронесения квантора общности через дизъюнкцию:
14) £ v VxC <-> Vx(£ v О, х g FV(£).
Изменение квантора общности на квантор существования:
15) VxB—> ЯхВ.
Перестановка разноименных кванторов:
16) НхХ/уА Х/уНхА.
Пронесение квантора существования через конъюнкцию:
17) Зх(В & О ЯхВ & ВхС.
Пронесение квантора общности через дизъюнкцию:
18) VxAv VxB-> Vx(AvB).
Дополнительные формулы:
19) VxA <-» А, х g FV(A); 20) ЯхА <-> А, х g FV(A);
21) VxVyA Х/х(А)У ; 22) Ях(А)£ -> ЯхЯуА;
23) (А—> VxB) > Vx(A —i >В), xg FV(A);
24) (А^ ЯхВ)<-> Ях(А^ В), xg FV(A);
25) (VxA —>В)<ч Ях(А^ В), xg FV(B);
26) (ЯхА ^В)^ Vx(A B),xg FV(B)
27) (VxA —>ЯхВ) <->Ях(А -+B);
28) (ЯхА -> VxB) -> Vx(A -^B).
4. Установление существования вывода формул из гипотез
11. [29, с. 200, № 1.70] Установите существование следующих выводов
вИГр
a) {A, -В} Н (А —> -В);
б) {—А&—В, А} НВ;
в) {-,(AvB),B}h(AvB);
г) {A->BvC,D->A,D&£->-B}HD&£->C;
д) {А & —В, А —> В} Н С;
е) {В, А & —iC, А —> (В ->О} И (А В);
ж) {А В, —iB} Н -А:
з) {А о В, В о С} Н (А О;
и) {А &^В, А -^В} Н С;
к) {A v В v С, D & —В, D —> -iC} Н А;
л) {А->В, А & С} НВ&С;
м) {А —> В v С, А & —В} Н С;
н) {A&B->C,-.C}H-Av-B;
о) {A v В-> С,-iC} Н-А &-В;
п) {-А &-В,-В —> А} Н С;
р) {В, А —>-В } Н —i(-B v А);
168
https:/Л: rait.ru
с) {-А->В, C&-BJ-I-A;
т) {A->B,C->D,-B&^D}l-^A&-iC;
у) {—А —>В, —iC—>D, —В & —J)} Н (A v С);
ф) {А & В —> С, А & —iC} Н-В;
х) {А —>В, С—>D, A v С,-В v —J)} Н (В —> А).
12. (По [27, с. 70, № 26])
Установите существование следующих выводов в ИГг:
а) {(АоВ)}Н(ВоА);
б) {(Ан6НВнО}Ь(АнС);
в) {(А<->В)} Н (—A<-»-iB);
г) {(А<-»В)} Н ((А&О <-» (В&О);
д) {(А <-> В)} I- ((С & А) <-> (С & В));
е) {(А<->В)} Н ((A vO <-> (В vO);
ж) {(А <-» В)} I- ((С v А) н (С v В));
з) {(А<-»В)} Н ((А->О <-» (В->О);
и) {(А <-> В)} I- ((С -> А) <-> (С -> В)).
13. Установите существование выводов данных формул из указанных
гипотез:
a) {Vx(P-> Q), VxP} Н VxQ;
б) {Vx(A v В)} I- —А \fxB, х е FV(A)'
в) {VxVyA} I- (А)ц’^ где и, v — предметные переменные, и £ FV(A);
г) [37, с. 191] (задача Э. В. Бетпа):
{Vx(P^->M),3y[S&M]*}l-az[S&-1P]* гдеуё FV(P).
о- Hi iroit i-i ।
Упражнение б
ИСЧИСЛЕНИЕ ДЕДУКТИВНЫХ
ЭКВИВАЛЕНТНОСТЕЙ. ПРЕДВАРЁННАЯ
И СКОЛЕМОВСКАЯ НОРМАЛЬНАЯ ФОРМА
Ты даёшь многое, если даже не дашь
ничего, кроме примера.
Сенека
Обязательные результаты обучения:
• знать основные понятия
— дедуктивная эквивалентность на множестве формул языка первого
порядка;
— исчисление дедуктивных эквивалентностей;
— предварённая (пренексная) нормальная форма, универсальная фор-
мула (V-формула), экзистенциальная формула (3-формул а);
— чистый язык (формальной системы) первого порядка;
— сколемовская нормальная форма (ЗУ-формула);
• уметь
— конструировать доказательства дедуктивных эквивалентностей формул
в классическом гильбертовском исчислении первого порядка;
— приводить формулы к предварённой нормальной форме;
— приводить формулы к сколемовской нормальной форме;
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
Теоретические сведения
Исчисление дедуктивных эквивалентностей
Пусть АиВ — формулы языка первого порядка.
Определение (по [13, с. 129].
1. Дедуктивной эквивалентностью на множестве формул перво-
го порядка будем называть бинарное отношение
FxF,
для которого (Д, В) g =d (записывается: A =d В) тогда и только
тогда, когда {А} I- В и {В} I- А в гильбертовском исчислении пер-
вого порядка.
170
https:/Л: rait.ru
2. Дедуктивно эквивалентными формулами будем называть фор-
мулы А и В, для которых {А, В) е 3d.
Лемма 1.
A =d В тогда и только тогда, когда формула (А <-> В) доказуема
в гильбертовском исчислении первого порядка.
Лемма 2 [38, с. 95—96].
В классическом гильбертовском исчислении первого порядка до-
казуемы следующие формулы:
Выражение логических связок &, v, <-> через связки -^и—,
Г) (А&В) -.(А -пВ); 2°) (A v В) <-> (-АВ);
3) (А^В)^((А^В)&(В^А));
Замена связанной переменной
4) VxA(x) ++ Vy [ А]*; 5) ЗхА(х) ++ Зу [ А]*;
Пронесение кванторов через -.
6°) -.VxA <-> Зх—А; 7) -.ЗхА <-> Vx-nA;
Пронесение кванторов через
8°) (VxA—>B)<->3y([A]* ->B),xgFV(B),y gFV(AuB);
9) (ЗхА ->В) <-> Vy([A]£ ->В), х g FV(B), у g FV(A uB);
10) (В -> VxA) <-> Vy(B [A]p, x g FV(B), у g FV(A u B);
11°) (В ЗхА) <-> 3y(B [A]p,x gFV(B),у gFV(A uB).
Следствие.
В классическом гильбертовском исчислении имеют место следу-
ющие дедуктивные эквивалентности:
1°) (А & В) =d -.(А -В); 2°) (A v В) =d (^А В);
3) (А^В)^((А^В)&(В^А));
4) VxA(x)=d Vy[A]*; 5) 3xA(x)=d Зу[А]*;
6°) -.VxA =d Зх—А; 7) -.ЗхА =d Vx-nA;
8°) (VxA—>B)=d Зу([А]* —>B),xgFV(B),y gFV(AuB);
9) (ЗхА—>B)=d Vy([A]* —>B),xgFV(B),y gFV(AuB);
10) (B VxA) =d Vy(B ->[A]p,x g FV(B),у gFV(A uB);
11°) (В 3xA) =d 3y(B [A]p,x gFV(B),у gFV(AuB).
Пусть CA — формула, в которой выделено вхождение формулы
А, а Св — формула, получаемая из СА заменой этого вхождения на В.
Определение.
Исчислением дедуктивных эквивалентностей является исчисле-
ние, аксиомными схемами которого являются дедуктивные экви-
валентности 1—11, а правилами вывода следующие слова:
A =d В
1) —-— (симметричность);
A=d В' B=d С
2) -----}—----(транзитивность);
А — С
(J- /[=d В
3) —— ----(замена равного на равное).
С А =
171
https:it.ru
Предварённая нормальная форма
В языке формальной системы нулевого порядка были введены
нормальные формы: конъюнктивная, дизъюнктивная и имплика-
тивная.
Приведение формулы к одной из этих нормальных форм позво-
лило упростить доказательство общезначимости формулы.
По аналогичным причинам введены нормальные формы и в язык
формальной системы первого порядка. Более того, проблемы, возни-
кающие при оперировании с областями действия кванторов, иногда
бывают достаточно сложными: в частности, к трудностям может при-
вести одновременное наличие в некоторой формуле свободных и свя-
занных вхождений одной и той же переменной. Положение заведомо
проще для случая записи формулы в предварённой нормальной форме.
Пусть п g N, х1л х2,..., хп — предметные переменные, причём xf
Xj для i А — бескванторная формула, a Q, е {V, 3} для всех i = 1,
2,..., п.
Определение (по [27, с. 81]).
1. Предварённой (пренексной) нормальной формой называется:
а) любая бескванторная формула в языке первого порядка;
б) любая формула вида при п > 0 (слово Q1x1...Qpql
назовём кванторной приставкой).
2. Универсальной формулой {У-формулой) называется предварён-
ная нормальная форма, у которой = V для всех i = 1, 2,..., п.
3. Экзистенциальной формулой (В-формулой) называется предва-
рённая нормальная форма, у которой Q{ = 3 для всех i = 1, 2,..., п.
Предложение [38, с. 97].
Существует эффективная (практически реализуемая) процедура,
преобразующая всякую формулу А к такой формуле В в предварён-
ной нормальной форме, что I- (А <-> В) в классическом гильбертов-
ском исчислении первого порядка.
Замечание (к доказательству).
Лемма 2 позволяет в преобразуемой формуле «постепенно передви-
гать влево» все кванторы; этот процесс и является существенной частью
доказательства.
Процедура построения приведена в [38, с. 97—98] и проводится
индукцией по рангу формулы А с использованием Предложения о замене
(см. [21, с. 160; 13, с. 132—134])
Одна и та же формула может допускать много эквивалентных
предварённых форм, так как вид результата зависит от порядка при-
менения аксиомных схем 1—11, а также от произвола при переиме-
новании предметных переменных в правилах вывода 1—3.
172
https:it.ru
Сколемовская нормальная форма
Определение (ср. [38, с. 98]).
Чистым языком (.формальной системы) первого порядка будем
называть язык формальной системы первого порядка, в котором
отсутствуют функциональные символы и предметные константы
и в котором для каждого целого положительного п имеется бес-
конечно много n-местных предикатных символов.
Пусть Xj х2,.... хп — предметные переменные, причём xf Ф Xj для
i ±j, А — бескванторная формула, a Q, е {V, 3} для всех i = 1, 2,..., п.
Определение (по [27, с. 81]).
Сколемовской нормальной формой (3V-формулой, нормальной фор-
мой Сколема) называется формула вида Q^.-.Q^x^A (п > 0), если
существует такое i, 0 < i < п, что Qp ..., Q, есть 3, a Q,+1,..., Qn есть V.
def
Пусть А = Зух.. .. .,уп, и), а Рр+1 — первый (п + ^-мест-
ный предикатный символ, не встречающийся в формуле А.
Определение.
(Дедуктивным) преобразованием Сколема назовём следующий
процесс:
1) построим формулу Ар
def
A = 3y1...3yn(Vu(B(y1,...,yn,u)->PJ1+1(y1,...,yn,u))->
-э>УиР/г+1(у1,...,уп,и))
2) приведём формулу Аг к предварённой нормальной форме.
Если в результате мы получим формулу в нормальной форме
Сколема, то процесс заканчивается; если — нет, то строим форму-
лу А2 описанным в пункте 1 способом, и повторяем процесс вновь.
Лемма.
Следующие слова являются прямыми правилами вывода гиль-
бертовского исчисления первого порядка:
х А Aj
а) ЗГ’ б)
Аг А
Доказательство.
def д
А. Обозначим уп = у1}...,уп и докажем, что слово — является
А.
прямым допустимым правилом вывода путем построения следую-
щего (непрямого) древесного квазивывода:
173
https: "и га it.ru
VuB, Vu(b -> Pf+1)} h Vuiy+1
{VuB} H Vu (В -> Pn'11 VuPf+1
По условию \ J J ’
h3y1...V„VuB; {3ri..3y„VuB}hЭУ1...Эу„ (vu(b->VuP^ )
01- 3y2 ...3yn (vu(B(yn, u) Р?+1(уп, u)j -> VuPp+1(yn, u)j
0FAT
r? IT Al
Б. Докажем, что слово —L является прямым допустимым прави-
А
лом вывода путём построения (непрямого) древесного квазивыво-
да. Однако вначале покажем, что доказуемой является формула
01- З/i ...3yn (Vu (В(уп, и) -> В(у п, и)) -> VuB(yn, и))
По условию
01- Эуг..3уп [\/и[в(уп, и) -> Р"+1(уп, и)) -> Х/иРр+1(уп, и))
0l-(3y1...ayn(vu(B(yn,u)^Pf+1(yn,u))^VuPf+1(yn,u))) 1 [В(уп,и)]
01- Эу1..3уп (\fu(B(yn, и) -> В(уп, и)) -> VuB(yn ,и)^
Дальнейшее очевидно:
01-(В->В) {VuB}l-VuB
01- Vu(B -> В); {Vu(B -> В), \/и(В -> В) -> VuB} h VuB
{Vu(B -> В) -> VuB} I- VuB
{Vu(B^B)->VuB}H3yi..3y„VuB
01- (Vu(B -> B) -> VuB); {3xi..3y„ (Vu(B ->B) -> VuB)) h 3yi...3y„V4B
0H3y1...3ynVuB(yn,u)
0HA
Лемма доказана.
Предложение [38, с. 99].
По всякой формуле А чистого языка первого порядка можно эф-
фективно построить такую формулу В в нормальной форме Сколе-
ма, что НА тогда и только тогда, когда НВ в классическом гильбер-
товском исчислении первого порядка.
Доказательство. См. [53, с. 214—218; 38, с. 99—100; 40, с. 244—
253].
Мы отметим лишь, что Предложение, доказывается по индукции
с помощью преобразования Сколема.
174
https:/Л: rait.ru
Примеры решения некоторых типов упражнений
Он был всё ещё заворожён тонкой игрой
двигавшихся, как марионетки, пальцев
и палочек, за которой так долго следил
и которая, хотя смысла ее нельзя было
угадать, казалась такой убедительно
осмысленной, а результат ее взял уже над
ним власть.
Г. Гессе. Игра в бисер
Пример 1 [38, с. 98]. Применяя исчисление дедуктивных эквивалент-
ностей, приведите к предварённой нормальной форме формулы
а) ЭхА(х) VxB(x);
б) Vx(P](х) -> Vy(P|(х, у) -> —iVzP2(у, z)));
в) Р2(х,у) -> Эу(р1(у) -> (ЗхР}(х) -> Р^(У)))-
Решение.
(9) (10)
А. ЗхА 3xB=d Vy ([А]у VxB) =d VyVz([A]£ [B]* ).
(6)
Б. Vxtpi (x) -> Vy(P22 (x, y) -> VzP32 (y, z))) =d
(11)
=d VxfPj1 (x) -> Vy(P22 (x, y) -> 3z-P32 (y, z))) =d
(10)
=d VxfPj1 (x) -> Vy3u(P22(x, y) -> -P32(y, u))) =d
(ii)
=d VxVv(P/(x) 3u(P22(x, v) -P32(v, u)))=d
(4)
=d VxVvBwfPj1 (x) —> (P22 (x, v) -P32 (v, w))) =d
(5)
=d VxVy3w(P-f (x) -> (P22(x, y) -> -P32 (y, w))) =d
=d VxVyMP-!1 (x) -> (P22(x, y) -> ->P32(y, z)));
(9)
B. Pfrx, y) -> 3y(pi(y) -> (3xf*(x) -> P24y)))^d
(10)
=d P?(x,y) ->3y(pi(y) -> VufP/fu) ->P2i(y))) =d
(11)
-d P?(x,y)->3yVv(pi(y) ->(pi(v)->pi(y)))^d
(10)
=d 3iv(P2(x,y)-> Vv(pi(w)->(pi(v)->P^(w)))) =d
^d 3wVz(P2(x,y)->(pi(M/)->(pi(z) ->P24w)))).
Пример 2 (no [38, c. 101]). Найдите нормальную форму Сколема для
def
формулы А = Vx3yM(x, у), где формула М(х, у) не содержит кванторов,
Решение. Выполним преобразование Сколема и получим формулу
175
https: га it.ru
def
Aj = Vx(3yM(x,y)^P11(x))^>VxP11(x).
Построим предварённую форму для Ар
def
Аг = Ух(ЗуМ (х, у) —> (х) ) —> VxP/ (х) =d
=d Bz((ByM(z, у) -> РДг)) -> УхРДх)) =d
=d Bz(\/u(M(z, и) Р^&У) УхРДх)) =d
=d 3z3v((M(z, v) P11(z)) VxP^(x)) =d
=d 3z3v\fw((M(z, v) РДя)) РДи/)) =d
=d 3x3yVz((M(x, y) -> Pj1 (x)) -> Pj10)3-
def
Формула S = 3x3yVz((M(x, y) —>P11(x)) —>P11(z)) является нор-
мальной формой Сколема.
Пример 3 [38, с. 100—101]. Найдите нормальную форму Сколема для
формулы VxVy3zC(x, у, z), где формула С(х,у, z) не содержит кванторов,
def
Решение. Пусть А = VxVy3zC(x, у, z). Выполним преобразование
Сколема и получим формулу
def
Аа = Vx(Vy3zC(x, у, z) -> pi (x)) -> VxPj1 (x).
Теперь построим предваренную форму для формулы Ар
def
Ai = Vx(Vy3zC Pi1 (х)) VxPi(х) =d 3x((Vy3zC -> Р}(х)) VxPi(х)) =d
=d Bx(By(BzC Р/(х)) VxPi(х)) =d 3x(3yVz(C Р}(х)) VxP/(х)) =d
=d 3xVy(Vz(C Р/(х)) VxPi (х)) =d ЭхЧуЗзЩС Р^(х)) VxP/(х)) =d
=d 3xVy3zVv((C Pi(х)) Р/(у)).
Повторим этот процесс вновь, теперь уже применительно к формуле
(С —> Р1(х)) —> Pi(v), которую обозначим черезП(х,у, z, v).
Пусть предикатный символ Р± не встречается в. Последовательно
строим формулы:
3x(Vy(3zVvD(x, у, z, v) -> Р? (х, у)) -> УуРг2 (х, у)) =d
=d 3xBy((3zVvD(x, у, z, v) -> Pf (x, y)) -> VyP2(x, y)) =d
=d 3x3y3zVv((D(x, y, z, v) -> P?(x, y)) -> VyP2(x, y)) =d
=d 3x3y3zVvVw((D(x, y, z, v) -> P?(x, y)) -> VyP^(x, w)).
Итак, нормальной формой Сколема формулы А будет:
3x3y3zVWw((D(x, у, z, v) -> Р? (х, у)) -> VyPT2 (х, и/)).
176
https://urait.rL!
Упражнения для самостоятельного решения
Вечная загадка — не та, у которой
вообще нет ответа, а та, у которой эти
ответы каждый день иные.
Е. Лец. Непричёсанные мысли
Исчисление дедуктивных эквивалентностей
1. Установите следующие дедуктивные эквивалентности в классическом
гильбертовском исчислении первого порядка:
1°) (А & В) =d -.(А -В); 2°) (A v В) =d (-А В);
3) (A<^B)=d((A^B)&(B^A));
4) VxA(x) =d Vy[A]J; 5) ЭхА(х) =d 3y[A]J;
6°) -.VxA =d 3x-iA; 7) -.ЯхА Vx-nA;
8°) (XfxA B) =d 3y([A]* -> B), x g FV(B), у £ FV(A uB);
9) (ЯхА B) =d Vy([A]J ->B),xg FV(B), у g FV(A uB);
10) (B -> XfxA)Xfy(B -> [A]p,x gFV(B),у gFV(AoB);
11°) (В 3xA) =d 3y(B [A]y), x g FV(B), у g FV(A uB).
2. Пусть А и В — формулы, x g FV (В). Докажите в классическом гиль-
бертовском исчислении первого порядка дедуктивные эквивалентности:
а) А (A v А);
б) А^(А&А);
в) -г-А^А;
г) (А&В)^(В&А);
д) (A vB) (В vA);
е) ((А&В) & О (А & (В & О);
ж) ((AvB) vO (A v (В vO);
з) (А & (В v О) ((А &В) v (А & О);
и) (A v (В & О) ((A vB) & (A v О);
к) —.(А & В) (-А v -В);
л) —.(A v В) (-А & -В);
м) (А —> В) (-А v В);
н) (VxA&B)^Vx(A&B);
о) (ЗхА v В) Нх(А v В);
п) (ЯхА & В) Эх(А & В);
р) (VxAvB)^Vx(AvB).
Предварённая нормальная форма
3. [27, с. 85, № 19; с. 93, № 10]
Приведите следующие формулы к предварённой нормальной форме
(формулы А и В являются бескванторными):
a) -.HxVySzVuA;
б) (3xVyA(x,y) &3xVyB(x,y));
в) (3xVyA(x,y) v 3xVyB(x,y));
г) (3xVyA(x, у) -> SxVyB (х, у));
д) Vx3y(A(x) В(у, z)) -> 3xVz(B(x, z) &А(у)));
е) VxP(x) Xjy{XfzQ{x, z) VuP(u))).
177
https:it.ru
4. (По [38, с. 98])
Приведите следующие формулы к предварённой нормальной форме:
a) \/х(Р](х) -> Vy(P|(x, у) -> ->VzP|(y, z)));
б) Р?(х,у) -> Ну(Р1(у) -> Vx(Pl(x) Р1(у)));
в) Vx(P] (х) -> Pf (х, у)) -> (ЗуР}(у) -> 3zPf (у, z));
г) 3xPf(x,y)—>(Р}(х)—>-13пР^(х, и)).
5. (По [15, с. 118—119, № 7.58])
Приведите следующие формулы к предваренной нормальной форме:
a) VxP(x) VxQ(x);
б) VyQ(x, у) Я(х, х);
в) VyQ(y, z)-> 3xR(x, t, z));
г) Р(у) ->(VxQ(x,y) Р(уУ);
д) 3xR(x,y, z) -iVxQ(x,y));
е) (Р(у) & Q(x)) -iVyR(y, z);
ж) Vx3yP(x,y) 3zVxQ(x, z);
з) Зу(Р(х) QiyY) -> Vy(P(y) v VzQ(z));
и) Зх(Р(х) v VxQ(x)) & (S(y) VxR(x));
к) Vx(P(x) Q(x)) (ЗхР(х) 3yQ(y));
л) VxP(x,y) v (ЗхР(х, х) Vz-i(Q(y, z) ЗхР(х, z));
м) VxQ(x,y) v (3xQ(x, х) z) 3xQ(x, х))).
Сколемовская нормальная форма
6. [38, с. 101]
Найдите нормальную форму Сколема для формул:
а) —.ЗхР] (х) Vu3yVxPf(и, х,у); б) Vx3yVu3vP14(x,y, и, v).
7. [27, с. 86, № 28]
Приведите следующие формулы к сколемовской нормальной форме:
a) (3xVyQ(x,y) —> Vx3j<Q(x,y));
б) 3xVy3zVvP(x,y,z, v);
в) Vx3yVv3zR(x,y, z, v).
8*. [38, c. 101]
def
Для формулы A = Vx3yM(x, у) найдите нормальную форму Сколема (обо-
значим ее В) и докажите, что Й (В <-» А).
о- Hi iroit i-i ।
Упражнение 7
МОНОСУКЦЕДЕНТНОЕ СЕКВЕНЦИАЛЬНОЕ
ИСЧИСЛЕНИЕ ПЕРВОГО ПОРЯДКА
Иль чума меня подцепит,
Иль мороз окостенит,
Иль мне в лоб шлагбаум влепит
Непроворный инвалид.
А. С. Пушкин. Дорожные жалобы
Обязательные результаты обучения:
• знать основные понятия
— секвенция;
— алфавит моносукцедентного секвенциального исчисления первого
порядка (ИС!), формула языка секвенций;
— (моносукцедентная) секвенция, схема секвенций;
— экономная схема и основные правила вывода секвенциального исчис-
ления первого порядка;
— линейное доказательство (вывод), доказуемая секвенция, доказуемая
формула, доказательство секвенции в виде дерева;
— секвенциальное исчисление первого порядка;
— допустимые правила вывода, линейный и древесный квазивывод сек-
венции;
— дедуктивно эквивалентные формулы;
— связь между секвенциальным и гильбертовским исчислением;
• уметь
— конструировать доказательства допустимости правил вывода в ИСг;
— устанавливать существование доказательств формульных схем и сек-
венций в ИСг;
— устанавливать существование выводов секвенций в ИС^
—конструироватьдоказательствадедуктивныхэквивалентностей формул
вИС^
—конструировать доказательства допустимости правил вывода в ИС1
в классическом гильбертовском исчислении первого порядка;
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
179
https:it.ru
Теоретические сведения
Формулы часто деформируют нас.
Е. Лец. Непричёсанные мысли
Приступим к изучению формальных систем, которые основыва-
ются не на формулах, а на более сложных объектах — секвенциях.
Если формулы можно интерпретировать с помощью высказыва-
ний естественного языка, то секвенции являются формами утверж-
дений (математических теорем), в которых можно отчетливо вы-
делить условия (посылки) и заключение.
Другими словами, основные правила вывода исчисления секвен-
ций отражают (формализуют) некоторые простейшие стандартные
логические способы рассуждения, позволяющие переходить от од-
них «истинных» утверждений (теорем) к другим «истинным» ут-
верждениям (теоремам).
Приведём иерархическую классификацию секвенциальных исчис-
лений:
Определение.
1. Секвенция (от лат. sequentia — последовательность) — это:
а) проведение мелодического оборота или многоголосного музы-
кального построения на определённый интервал выше или ниже
первоначального или (в последующих звеньях) предыдущего;
б) средневековые секвенции — церковные песнопения, возник-
шие из юбиляций на слове «аллилуйя» в григорианском пении.
2. [152, с. 318] Секвенция — это:
а) последовательность, следование каких-либо знаков;
б) повторение одной и той же музыкальной фразы теми же са-
мыми голосами по ступеням гаммы вверх или вниз.
180
https:/Л: rait.ru
Моносукцедентное секвенциальное исчисление
...понимание заключается в сведении
одного типа реальности к другому.
К. Леви-Стросс
Рассмотрим алфавит языка первого порядка G и зафиксируем не-
которую конечную или счётную сигнатуру о. Определим логисти-
ческое исчисление, которое будем называть (моносукцедентным)
секвенциальным исчислением первого порядка (или просто ИСД
Определение [27, с. 89].
1. Алфавитом (моносукцедентного) секвенциального исчисления
первого порядка будем называть множество
def
Gs = (Gu{h})\{<->}.
2. Формулами языка секвенций будем называть все формулы стан-
дартного языка первого порядка, не содержащие знака «<->«.
Соглашение об обозначениях,
def
(А <-> В) = ((А -> В) & (В -> А)), А и В — формулы в Gs.
Секвенции. Секвенциальные схемы
Пусть п g N\{0}, А, А1} А2, ..., Ап, В, С — формулы сигнатуры о,
а Г, Гр Г2, ... — последовательности (возможно, пустые) формул
сигнатуры о.
Определение [13, с. 119].
Секвенциями называются слова в алфавите Gs следующих типов:
1) Ар А2, ..., Ап I- В
(читается: «изАп А2, ...,Ап логически следует формула В»)', после-
довательность формулАр А2,..., Ап называется антецедентом сек-
венции, а формула В — сукцедентом секвенции;
2) НВ
(читается: «формула В доказуема» или «формула В логически сле-
дует из пустого антецедента»);
3) Ар А2, ..., Ап h
(читается: «система формул А1}А2, ...,Ап противоречива»);
4) h
(читается: «противоречие»).
Пример (секвенции).
Vx2 pl (хх ) & Эх2Р1 (х2 ), 3Xi Vx2P| (х2, Х2 ) h ЗххР^ (X! ).
ttps'/Zursit
181
Замечание (по [9, с. 454—455]).
Секвенции вида А1? А2, ...,Ап\~ В впервые были введены П. Герцем
(1923) в его логических исследованиях.
Соглашение об обозначениях.
Для задания секвенций в общем виде используют метаперемен-
ные — переменные для формул и переменные для конечных после-
довательностей формул (возможно, пустых):
а) в качестве формульных переменных будем использовать знаки
А, В, С,F, А1г А2, -А3, • • • >
б) в качестве переменных для последовательностей формул,
в том числе и пустых (не содержащих ни одной формулы) — знаки
Г, А, Г], А1л Г2, Л2,...
Определение [13, с. 26].
1. Схемой секвенций {секвенциальной схемой) будем называть
такое слово метаязыка, что при любых подстановках в это слово
вместо переменных для формул (А, В,...) и последовательностей
формул (Гг, Г2, ...) соответственно конкретных формул и после-
довательностей конкретных формул получаются секвенции.
2. Частными случаями данной схемы секвенций будем называть
результаты описанных выше подстановок.
Например, слово Гг, X, Г2 I- А метаязыка является схемой секвен-
ций, а если мы обозначим
def def
Г! = VjqPi (хх ), Эх2Р\ (x2 ); X = Vx2P| (x2, x2 );
def def
г2 = 0;A = ЭхЛСхД
то слово Vx^] (Xi ), 3x2P2 (x2 ), 3xj Vx2P| (Xi, x2 ) I- ЗххР| (Xi ) в алфави-
те Gs превратится в частный случай этой схемы.
Соглашение об обозначениях.
Секвенциальные схемы будем обозначать Е, Е1л..., Efc.
Если значения переменных для формул и последовательностей
формул в схеме секвенций Е зафиксированы, то схема Е превраща-
ется в имя конкретной секвенции и поэтому ее называют просто
секвенцией.
Смысл понятия «секвенция»
Можно считать, что понятие «секвенция» моделирует в формальном
языке утверждения о выводимости (доказуемости) утверждений.
182
https:it.ru
В частности, секвенция 1 есть модель утверждения о том, что
из формул А1} ...,Ап (точнее, утверждений ими моделируемых) мож-
но вывести формулу В (точнее, утверждение, им моделируемое).
Секвенция 2 моделирует утверждение о том, что утверждение,
выражаемое формулой В доказуемо.
Секвенция 3 есть модель утверждения, выражающего тот факт,
что из утверждений, выражаемых формулами А1} ...,Ап можно вы-
вести противоречие.
По словам Р. Тудстейна [149, с. 15—16], списки секвенций — это
«по существу списки утверждений, в которых под иным названием
фигурирует (вообще говоря) логическая связка “если... то”».
Аксиомная схема. Основные правила вывода
Введём в метаязык буквы: «;» (точка с запятой); «—» (черта);
«=» (двойная черта) (этой буквой в дальнейшем будем обозначать
сокращение количества указываемых шагов при выводе секвен-
ции).
Определение.
1. Схемой аксиом (аксиомной схемой) назовём схему секвенций
ДНА.
2. Аксиомой будем называть частный случай данной схемы ак-
сиом.
Пусть х обозначает предметную переменную, a t произвольный
терм сигнатуры о.
Определение (по [27, с. 89—90; 13, с. 120]).
Основными правилами вывода секвенциального исчисления перво-
го порядка назовем перечисленные ниже слова метаязыка (для
того, чтобы узнать название правила, прочтите заголовки соот-
ветствующего столбца и строки; в скобках указаны альтернатив-
ные названия правил):
Правила введения и удаления логических связок
Связка Введение... Удаление...
—1 1 Г’АН ' ГН-А о ГНА
(приведение к абсурду) (доказательство от противного)
& 3 Г1-А; ГЬВ ГН(А&В) 4 Г1-(А&В) Г1-(А&В) ГНА * ГНВ
V 6. ГНА 7. Г1~В fl-(AvB) FI-(AvB) 8 Г2,А1~С; Г3, ВИС; 1\|-(АуВ) Г^^.ГзНС (разбор случаев)
https-"ига it.
183
Окончание таблицы
Связка Введение... Удаление...
—> п Г,А\-В Л 9. (дедукция) ГН(А->В) ' J J 10 ГНА; ГН(А->В) ГЬВ (modus ponens)
Правила введения и удаления формульной схемы» & —»
Введение... Удаление...
противоречия ГНА;ГН-А гь ГН 12. (утончение)
Структурные правила вывода
Введение формулы в антецедент Удаление формулы из антецедента
ГНА , 13. (расширение) _ . Г,А,АНВ . . 14. д|_д (сокращение)
__ г1}а,в,г2нс. . 15. —1 (перестановка) ГъВ,А,Г2НС
Правила введения кванторов
Квантор ...(в) сукцедент(е) ...(в) антецедент(е)
V 16. ГНА , ГНУхА где предметная переменная х не входит свободно в Г (правило универсального обобщения) 17 Г,(А)? НВ Г,УхАНВ’
а ГН (А)? 1о. ГННхА 19. Г-АНВ , Г, ЗхА НВ где предметная перемен- ная х не входит свободно в Г, В (правило экзистен- циального обобщения)
Правила 1—12 и 16—19 называются (по Г. Такеути) логическими
(пропозициональными) правилами.
Если в основных правилах вывода в качестве Г, Г2 Г2, Г3 исполь-
зуются конкретные последовательности формул, в качестве А, В,
С — конкретные формулы, а в качестве х — конкретная предметная
переменная, то полученные слова называются частными случаями
(или применениями) основных правил вывода.
184
https:/Л: rait.ru
Пусть 0 обозначает применение основного правила вывода с но-
мером к. Верхней секвенцией (посылкой) 0 будем называть секвен-
цию, расположенную над буквой «черта». Нижней секвенцией (не-
посредственным следствием верхних секвенций) 0 будем называть
секвенцию, расположенную в 0 под буквой «черта».
Будем говорить, что нижняя секвенция 0 получается из верхних
секвенций 0 при помощи правила к.
Содержательный смысл основных правил вывода
Основные правила вывода, с одной стороны, определяют смысл
логических связок -i, &, v, —> и пустого сукцедента секвенции,
а с другой стороны, формализуют некоторые стандартные логиче-
ские способы рассуждений. Поэтому прокомментируем на содержа-
тельном уровне с этой точки зрения основные правила вывода.
Основные правила вывода 1 и 2 — это правила, поясняющие
(определяющие!) смысл буквы -i. Более того, правило 1 формализу-
ет способ рассуждения, который называется приведением к абсурду.
Предположим, что условия Г и А могут одновременно выполнять-
ся, приходим к противоречию и заключаем, что из выполнимости
условий Г следует выполнимость -А. Далее, допустимое правило
вывода 2 формализует способ рассуждения, называемый доказа-
тельством от противного. Предположим, что условия Г и —А мо-
гут одновременно выполняться, приходим к противоречию и заклю-
чаем, что из выполнимости условий Г следует А.
Правила 3, 4 и 5 — это правила, поясняющие (определяющие!)
смысл буквы &.
Правила 6 и 7 относятся к пояснению (определению!) смысла
буквы V.
Правило 8 формализует способ рассуждения, который называет-
ся разбором (возможных) случаев.
Правила 9 и 10 — это правила, поясняющие (определяющие!)
смысл буквы С другой стороны, правило 9 формализует прием
эквивалентной переформулировки математической теоремы (де-
дукция), позволяющий одно из условий теоремы помещать в ее за-
ключение, а правило 10 — это классическое логическое правило
рассуждения modus ponens", оно указывает, как можно «освободить-
ся» от посылки.
Правила 11 и 12 — это правила, поясняющие (определяющие!)
смысл термина «противоречие» (в классическом гильбертовском
исчислении этот термин описывается формульной схемой А & -А).
Содержательный смысл правила 12 Г. Генцен описал так: «Если име-
ет место нечто ложное, то имеет место любое высказывание».
Правило 13, называемое иногда правилом лишней посылки, отра-
жает тот тривиальный факт, что, добавляя к условиям содержатель-
ной математической теоремы лишнее условие, мы не нарушаем ис-
тинности заключения.
185
https:it.ru
Правила 14 и 15 носят технический характер: перестановка или
повторение посылок не влияют на истинность заключения.
Доказуемые (выводимые) секвенции. Доказуемые формулы
Пусть п е N\{0}.
Определение (по [13, с. 27—28]).
1. Линейным доказательством (линейным выводом) называется
конечная последовательность секвенций Еп, удовлетворя-
ющая следующему условию: каждая секвенция Ег- (i < п) либо яв-
ляется аксиомой, либо получается из некоторых «предыдущих»
секвенций (j < i) при помощи одного из основных правил вы-
вода 1—19.
2. Доказуемой (выводимой) секвенцией (или теоремой) называ-
ется секвенция Е, для которой существует линейное доказатель-
ство вида ..., Е.
3. Доказуемой формулой (или теоремой) называется формула
А сигнатуры о такая, что доказуема секвенция I- А.
Пример (линейного доказательства и доказуемой секвенции).
Секвенция -г-Л НА является доказуемой секвенцией (теоремой).
Определим индуктивно понятие «дерево секвенций».
Определение [13, с. 28].
1. Деревом секвенций является всякая секвенция.
2. Если Dlt ...,Dn — деревья секвенций, а Е — секвенция, то
также является деревом секвенций.
Определение [13, с. 28].
1. Вхождением секвенции в дерево секвенций D будем называть сек-
венцию вместе с ее местом расположения в дереве D.
2. Начальным вхождением секвенции в дерево секвенций D будем
называть такое вхождение секвенции в дерево секвенций D, «над»
которым отсутствует буква «черта».
186
Заключительным вхождением секвенции в дерево секвенций
D будем называть такое вхождение секвенции в дерево секвен-
ций D, «под» которым отсутствует буква «черта».
3. Переходом будем называть «часть» дерева секвенций, состоя-
щую из секвенций, расположенных непосредственно «над» некото-
рой буквой «черта», непосредственно «под» той же буквой «черта»
и самой буквы «черта».
Ясно, что дерево секвенций может иметь несколько начальных
секвенций, но заключительная секвенция в дереве секвенций толь-
ко одна.
Определение [13, с. 121].
1. Доказательством в виде дерева секвенций (деревом доказатель-
ства) называется дерево секвенций, все начальные секвенции ко-
торого являются аксиомами, а переходы — частными случаями
(применениями) основных правил вывода 1—19.
2. Доказательством секвенции Z в виде дерева (или деревом выво-
да секвенции Z) будем называть доказательство в виде дерева сек-
венций, заключительной секвенцией которого является Z.
Предложение [13, с. 29].
Секвенция Z имеет доказательство в виде дерева секвенций тог-
да и только тогда, когда в является теоремой.
Предложение доказывается индукцией по длине линейного дока-
зательства секвенции Z и индукцией по количеству вхождений зна-
ка «черта» в доказательство секвенции Z в виде дерева секвенций.
Определение.
1. Секвенциальным исчислением (формальной системы) первого
порядка будем называть логистическое исчисление секвенций,
характеризуемое:
а) аксиомной схемой;
б) основными правилами вывода 1—19;
в) определением понятия «линейное доказательство (вывод) сек-
венции».
2. (По [45, с. 94]) Секвенциальной системой генценовского типа
называется логистическая система, являющаяся формализацией
класса верных записей о выводимости. В качестве записей о вы-
водимости рассматриваются утверждения метаязыка вида ГI- А,
где Г обозначает множество (или последовательности) формул,
А — формулу.
187
https: "и га it.ru
Относительно записей о выводимости строится логистическая
система с понятием «формальное доказательство» обычного типа
(в виде дерева), в качестве ее аксиом принимаются записи о выво-
димости, соответствующие прямым правилам введения и удаления
логических символов и рефлексивности «И», в качестве правил вы-
вода — правила перехода от одних записей о выводимости к другим.
Примеры.
Построим в секвенциальном исчислении деревья вывода следующих
секвенций:
1) А,ВI- (А&В);
2) Г,A,-Ah;
3) H(Av-iA);
4) PGq) I- Hx-0Vx:(Pfr0) vPGq)).
Аксиома
г
Аксиома B\~B
; -------(13)
1) А\~В В,А\-В
-------- —-----(15)
А,В\~А А,В\-В
-_________-____О)
A,BH(A&B)
Аксиома
1
ДНА
2)
(13) А,Г,^А|-А
(15) =
Г,А,-АЬА;
(13)
(15)
(И)
3)
Аксиома
г
лчл —«(Av—iA)l- —(Av-A)
Аксиома
г
(2)
(6)
(И)
-АЫАуа/ j (15)j(13)
-(Av-A),-AI-(Av-A)
-(Av-A)l-A
-( A v -A) h (A v -A);
Аксиома
г
-.(Av-A)b-,(Av-A)
(2) v 7
I-(Av-A)
4)
PCqjl-PCqjvPfr)
P(x1)hVz(P(x1)vP(z))
P(X!)|-Vz(P(Xo)vP(z))^
P(x1)I-Vz(P(xq)vP(x1)^)^
P(x1)HVx1(P(x0)vP(x1))^ 1 У 1
P(*i) I- 3x0Vx1(P(x0) V P(Xi))
def
= Vz((A)£)*, ecnHxeFV(A),yeFV(t),zgFV(t)oFV(A)
188
Допустимые правила вывода
Для того, чтобы упростить процесс получения доказуемых секвен-
ций с помощью ранее установленных доказуемых секвенций и новых
(дополнительных) правил вывода, используются понятия «доказуе-
мая схема секвенций», «допустимое правило вывода» и «квазивывод».
Определение [13, с. 29].
Доказуемой схемой секвенций будем называть схему секвенций Z,
добавление которой в качестве схемы аксиом секвенциального ис-
числения не расширяет множество доказуемых секвенций (дру-
гими словами, если все частные случаи схемы секвенций Z дока-
зуемы).
Приведём несколько вариантов определения понятия «допусти-
мое правило вывода».
Определение.
1. (По [13, с. 29]) Допустимым правилом вывода называется слово
метаязыка
добавление которого в секвенциальное исчисление не расширя-
ет множество доказуемых секвенций.
2. (По [24, с. 24]) Допустимым правилом вывода назовём слово
метаязыка
такое, что по всякому выводу, содержащему применения этого
правила, можно построить вывод, не содержащий применения
этого правила, и такой, что у обоих выводов последние секвен-
ции совпадают.
3. (По [27, с. 65]) Допустимым правилом вывода назовём слово
метаязыка
такое, что из доказуемости секвенций Zls ..., следует доказуе-
мость секвенции Z.
189
https:it.ru
Очевидно, что по определениям 1 и 2 все основные правила
вывода 1—19 являются допустимыми правилами вывода в ИС15
а по определению 3 — нет.
Определение [13, с. 31].
1. Линейным квазивыводом секвенции называется конечная по-
следовательность секвенций Zls ..., обладающая следующим
свойством: каждая входящая в нее секвенция является доказуе-
мой секвенцией или получается из «предыдущих» по допустимо-
му правилу вывода.
2. Древесным квазивыводом секвенции Z (квазивыводом секвенции
Z в виде дерева D) называется дерево секвенций D, всякая началь-
ная секвенция которого является доказуемой секвенцией, заклю-
чительной секвенцией является секвенция Z, а переходы являют-
ся применениями допустимых правил вывода.
С учётом сказанного (а также определения понятия «непрямое
правило вывода») можно построить следующую классификацию
правил вывода секвенциального исчисления первого порядка:
Установим некоторые допустимые правила вывода ИСХ (заме-
тим, что большая часть из них отлична от основных правил вывода).
Предложение [13, с. 30; 27, с. 66—67].
Следующие слова метаязыка являются допустимыми правилами
вывода:
. НА;Г2 Н(А->В)
а) пГгТкв
(10') или (вариант modus ponens);
ai)
Г1~(А—>В)
Г,А1-В
(вариант (10'));
структурные допустимые правила вывода
б)
Гг I-А; А,Г2 НВ
ГЬГ2 НВ
(сечение),
формула А называется высекаемой формулой правила «сечение»;
190
https:it.ru
г,а,лив .
в) -F^hF(cc
rnA,B,r2l-.
r^A^h’
допустимые правила введения и удаления логических связок
л Г»АЬВ
д) --------(контрапозиция);
— (обратная контрапозиция);
ж)
(вариант контрапозиции);
ж*)
(вариант контрапозиции);
з)
и)
Г А ВИС
—-— -------(объединение посылок);
Г,(А&В)\-С
Г,(А&В)\-С . .
----------(расщепление посылок);
Г, А, ВИС
к)
Г (A В) НС каление v по Клини> разбор случаев);
л)
р——-— (удаление из сукцедента);
м)
(удаление <-> из сукцедента);
н)
Гь А,Г2,Ь В;1\,В, Г2,!-А
------------------------(введение <-> в сукцедент);
допустимые правила вывода для «противоречия»
ч ГЬА
°) ~——*>
чГ1-А&-А
п) ———;
кванторные допустимые правила вывода
ГI— X/jcA
р) -------(удаление V из сукцедента, правило универсальной
Г |- (А)*
конкретизации);
^1-ЯхА; Г2,[А]*1-В
р*)------------------(удаление Я из сукцедента),
ГЪГ21-В
191
где у g FV(B) и у не входит свободно ни в одну из формул последо-
вательности Г2.
Доказательство.
А. Обозначим деревья вывода секвенций Гг I- А и Г2 h (А —> В)
соответственно:
Pi
Гт Н А
Дальнейшее очевидно:
Д2
Г2|-(А—>В)
03} ПН А Г2 Н(А^В)
ГЬГ21-А; ГЬГ2 Н(А->В)
Г1,Г2ЬВ
(13,15)
(Ю)
Д2
ДЩ15)
г2, ai—в
ПЬА’ Г2 Н(А^В)
ГЪГ21-В
АНА п Г,А,АЬВ
Г,А1-АЦ ’ Jr,Ah(A^B)
Г,А1-В
(9)
(Ю)
(12)
(15)
(И)
Г1, А,В,Г2 I- г1? А,В,Г2 I- Ц2)
Г1; А, В, Г2 НС Г1? А,В,Г2 I- —1С ~
г1?в,а,г2 нс г1?в,а,г2
ГъВ,А,Г2|-
(A&B)h(A&B) Г,A,BI-C
(A&B)hA А,Г,BI-C
. (A&B)h(A&B) (А&В),Г,В1-С
(А & В) I- В В,Г,(А&В)|-С
(А&В),Г,(А&В)ЬС
Г,(А&В),(А&В)ЬС(
Г,(А&В)|-С 1 J
(15)
(сечение)
(15)
(сечение)
192
https:/7!.!
н.
(15)
(9)
(3)
&2
Г1,В,Г2,НA
Г1>Г2>В,1~ А
ГЪГ2Н(В->А)
Di
Г1, А, Г2, Н В;
гх,г2, а,нв
Г!,Г21-(А-»В)
Г!,Г2 Н((А->В)&(В->А)) (А++В)*= ((А—>В)&(В—> А))
ГЬГ2 Н(А<^В)
п.
Д1 Д1
(4) гНА&^А ГНА&-А (5)
ГНА Г Н —A rj j-j
ГН
Р. Пусть выводима секвенция ГНVxA. Приведём квазивывод
и вывод (так как использовано правило «сечение») секвенции
Г Н (А)^ в виде дерева:
D (А)* Н(А)? (17)
ГНУхА; VxAH(A)? f
----------------—ь- (сечение)
ГН (А)?
(луклу (17)
Р УхАКАУ (9)
ГНУхА; |-(УхА-»(АУ)
ГЬ(АУ
AI-A, А—([А]у)у ^заменаравногонаравн
АН([А]*Й р2
д'! АНЗУ[А]? rUA]^B (15,19)
Р2 ЗхАНЗу[А]*; Зу[А]*,Г2 НВ
^НЗхА; ЗхА,Г2 НВ
Г1,Г2 НВ
(сечение)
(сечение)
Предложение доказано.
Пример.
Приведём древесный квазивывод в ИСг секвенции
Р v Q, Р v R, -iQ v —iR, —iP Н
с помощью многократного применения допустимого правила вывода
«разбор случаев» и доказуемой секвенции Р, —Р Н:
Q,-.QH K,-iRH
Р,^РН Q,P,-.Qv^R,^PH Q,K,-.Qv^R,^PH
P,PvQ,-iQv-iK,-iPH Q,PvK,-iQv-iR,-iPH
PvQ,PvB,-iQv-iK,-iPH
193
https: "и rait.ru
Доказательство допустимых правил вывода методом подъёма
Суть метода подъёма, применяемого для доказательства некото-
рых допустимых правил вывода, изложена в процессе доказатель-
ства следующего Предложения.
Предложение (допустимые правила с пустым сукцедентом
в верхней секвенции).
Следующие слова метаязыка являются допустимыми правилами
вывода:
Г, А, А И ГН Н
С Г, АН ’Т) Г,А1-’У) НА&-1А*
р|_ ГАН
ф) -----(утончение); х) —----(приведение к абсурду);
Г И А ГН —А
ч Г1 НА;А,Г2 Н _ _
ч) —----------— (сечение для пустого сукцедента).
Г1>Г2 Ь
Доказательство.
С. Секвенцию Г, А, А Н можно получить лишь по основному
правилу вывода 11. Поэтому, если секвенция Г, А, А Н доказуема,
то для некоторой формулы В доказуемы секвенции Г, А, А Н В и Г,
А,АН^В.
Поэтому для доказательства «допустимости» слова
до-
статочно построить дерево секвенций, начальными секвенциями
которого будут либо доказуемые схемы секвенций, либо Г, А, А Н
В и Г, A, A h -В:
D1 ^2
. Г,A,AHA Г,А, АН—А
_^^АКВ__САН^В_
Г,АН 1 J
У. Данное допустимое правило докажем без использования ме-
тода подъёма:
D1 ^2
(12) <12)
НА&-А (3)
D1 ^2
НА&—А НА&—А
НА И—А
Н
Ф. Секвенцию Г И можно получить лишь по основному правилу
вывода 11. Поэтому, если секвенция Г Ндоказуема, то для некото-
рой формулы В доказуемы секвенции Г И В и Г И -В. Поэтому для
ГН
доказательства «допустимости» слова достаточно построить
дерево секвенций, начальными секвенциями которого будут либо
доказуемые схемы секвенций, либо Г И В и Г И —В:
194
https:it.ru
Di D2
(13)
l^-AH-J?;
(13)
(11)
X. Данное правило является основным правилом вывода.
Ч. Воспользуемся методом подъёма; тогда имеем следующие до-
казуемые секвенции: Га I- А; А, Г2 Ь В; А, Г2 h —В.
Дальнейшее очевидно:
И1^2
ПН А; А,Г21-А
ГьГ21-А;
Из П4
Г2,АЬВ; Г2,АН—>В
Предложение доказано.
Следствие.
Секвенция НА & -А выводима тогда и только тогда, когда выво-
дима «пустая» секвенция Н.
Предложение.
Множество доказуемых секвенций не изменится, если из списка
основных правил вывода исключить правила 1,12,14.
Доказательство. Нетрудно увидеть, что:
а) допустимость правила вывода «приведение к абсурду» (прави-
ла 1) доказано с помощью основных правил вывода с помощью под-
множества основных правил вывода
def
Aj = {2, 9, 10, 11, 13, 15};
б) допустимость правила вывода «утончение» (правила 12), до-
казано с помощью основных правил вывода из подмножества ос-
новных правил вывода
def
А2 = {2, И, 13};
в) допустимость правила вывода «сокращение» (правила 14) до-
казано с помощью основных правил вывода из подмножества ос-
def
новных правил вывода А3 = {9,10,13}.
Для завершения доказательства заметим, что
{1, 12,14} n Аа и А2 и А3 = 0.
Предложение доказано.
Тем не менее, включение в ИСа допустимых правил вывода об-
легчает построение многих формальных выводов и доказательств.
195
https:it.ru
Замечания.
1. В секвенциальных исчислениях получает формальное выражение
эвристическая процедура, применяемая в так называемых аналитических
(или регрессивных) доказательствах
Эту эвристическую процедуру Д. Пойа образно называет «работой
от конца к началу», приписывает Паппу (около 300 г. н. э.) и приводит
описание данного метода: «То, что называют эвристикой, можно кратко
определить как особое собрание принципов, предназначенное для тех, кто
после изучения обычных «Начал» имеет желание научиться решать мате-
матические задачи (...) Она обучает приемам анализа и синтеза. Исход-
ным пунктом анализа является то, что требуется доказать, ибо допуска-
ется, что задача уже решена. Мы определяем, из какого предшествующего
вывода можно получить интересующий нас вывод, затем вновь определяем,
из какого вывода можно получить этот предшествующий, и т. д., переходя
от одного вывода к предшествующему, вызвавшему его, пока не придём
к такому выводу, который был получен раньше или принимается за истину.
Этот приём мы называем анализом, или решением задач от конца
к началу, или регрессивным рассуждением.
При синтезе, меняя порядок этого процесса, мы начинаем с послед-
него вывода анализа, с того, что уже известно или принимается за истину.
Беря известное за исходный пункт, мы делаем тот вывод, который предше-
ствовал при анализе и продолжаем, таким образом, делать выводы, пока,
идя обратно по пройденному при анализе пути, мы, наконец, не прихо-
дим к тому, что требуется доказать.
Этот приём мы называем синтезом, или конструктивным решением
или прогрессивным рассуждением».
2. Секвенциальные исчисления (хотя они первоначально и не были
предназначены для этого) составили основу направления логических
исследований, называемого поиском логических доказательств.
Теорема Генцена об устранении сечения
Предположим теперь, что мы имеем дело с секвенциальным ис-
числением первого порядка, одним из основных правил вывода ко-
торого является слово
П НА;А,Г, НВ
--------------(сечение).
ГЪГ21-В
Основой большинства методов поиска вывода секвенций в сек-
венциальном исчислении подобного типа является знаменитая те-
орема Г. Генцена об устранении сечения (1934).
Определение (по [47, с. 18]).
Выводом без сечений в секвенциальном исчислении называется
вывод в секвенциальном исчислении, не содержащий примене-
ний правила вывода «сечение».
196
Примем без доказательства следующее
Предложение (теорема Генцена об устранении сечений) [47,
с. 29].
Если некоторая секвенция выводима, то она выводима и без се-
чений.
Таким образом, если в выводах секвенциального исчисления ис-
пользовать наряду с другими и основное правило вывода «сечение»,
то теорема Генцена утверждает, что все применения этого прави-
ла можно затем устранить (элиминировать) и получить вывод без
сечений (другими словами, всякую теорему можно вывести «пря-
мым» путем).
Замечания (важные).
1. Теорема Генцена об устранимости (допустимости) сечения является
фундаментальным результатом и имеет исключительно важное значение
в первую очередь для обоснования математической логики.
2. Эта теорема является нетривиальной лишь в том случае, если сече-
ние является основным правилом вывода рассматриваемого секвенци-
ального исчисления.
Отношение дедуктивной эквивалентности.
Дедуктивно эквивалентные формулы
У меня ровно столько логики, сколько
необходимо, чтобы понять простую
истину: два утверждения «Я слишком
хороша для вас» и «Вы слишком хороши
для меня» не могут быть истинными
одновременно в обе стороны.
Элизабет Барретт.
Из письма к Р. Броунингу
Пусть АиВ — формулы языка первого порядка (в которых, есте-
ственно, отсутствует логическая связка «<->«), а буква «=d» (читается:
«дедуктивная эквивалентность») принадлежит языку исследовате-
ля (заметим, что буква «=« была впервые употреблена Б. Риманом
(1857) в других целях).
Определение (по [13, с. 129].
1. Дедуктивной эквивалентностью на множестве формул перво-
го порядка будем называть бинарное отношение
FxF,
для которого (А, В) е 3d тогда и только тогда, когда секвенциаль-
ные схемы А I- В и В I- А выводимы в ИСа
197
ll\ ['[J
2. Формулы А и В, для которых {А, В} е =d (записывается:
А В и читается: «формула А дедуктивно эквивалентна форму-
ле В»), будем называть дедуктивно эквивалентными формулами.
Лемма 1 [13, с. 129].
Отношение =d является отношением эквивалентности на множе-
стве формул сигнатуры о, т. е. для любых формул А, В, С справедли-
вы следующие утверждения:
a) A=dA;
б) если А =d В, то В =d А;
в) если A =d В и В =d С, то A =d С.
Доказательство. Упражняйтесь.
Лемма 2 [13, с. 34—35].
1. Если A =d В, то формула А доказуема тогда и только тогда, ког-
да доказуема формула В.
2. Если A1=dB1nA2=d В2, то
б) (А11&А2)Й(В1&В2);
в) (Ат v А2) =d (Вг v В2);
г) (Ах —>А2) =<* (Вх —>В2);
д) VxA1 =d VxBj;
е) ЗлА2 =d НхВр
Доказательство.
1. Пусть A =d В и НА. Тогда дерево секвенций
НА; КА^В)
НВ
будет древесным квазивыводом формулы В. Аналогично из A =d
=d В и НВ получаем НА. Утверждение а доказано.
2. В силу симметричности вхождения формул Af и Bt (i = 1, 2)
в рассматриваемые отношения дедуктивной эквивалентности, до-
статочно построить выводы следующих секвенций:
а) —А] |- —1Вг;
б) (А1&А2)Н(В1&В2);
в) (Aj v А2) h (Bj v В2);
г) (А1^А2)Н(В1^В2);
д) VxAi h VxBj
е) ЗлА2 I- НхВр
Следующие шесть выводов (квазивыводов) завершают доказа-
тельство пункта 2:
198
https://urait.rL!
a)
D
(13) A
(15)
—Ab^i l~ A-i'}
"A1,B1I~ (1)
Li
4 (13)
—(11)
6)
d2
Pj Al Q3)
(13) A1 HB1 Az,A1 (15)
A A HBi A A \~B
(объединение посылок)-1^—?—— 1^—?----?---- (объединение посылок)
(A^A^I-fr; (А!&А2)1~В2
(А1&А2)Н(В1&В2)
в)
Dl В2
(6) __A1I~B1 A2^B2(7)
A1h(B1vB2); A2h(B1VB2); (Аг v A^HAj v A2)
(A1vA2)h(B1vB2)
r)
Di
Q3)_____Bi l~ A.___ (Ai —> A2) I- (Aj —> A2) p2
qq) Bi,(Ai ^2)b~ Ai> B1?(Аг A2) I-(Ai A2)_______A2 l~B2
____________Bj, (Aj A2) h A2______________l~(A2 ^B2)
B1?(A1^A2)HB2
(A1^A2),B1I-B2
(A1^A2)H(B1^B2) 1 j
D
Ai^-B.
(Ai)J hBi
---—----— (17)
VxA! I-Bi }
VxAjI-Vxb/16)
http
o- Hi iroit ri 1
»j.i i vlt tuli.i VJ
199
D
Ail-Bi
Al I- BxBi
ЗхАг H3xBi
(18)
(19)
Лемма 2 доказана.
Из Леммы 2(a) понятно, что понятие «дедуктивно эквивалент-
ные формулы» имеет большое значение, так как изучаемые нами
дедуктивные свойства формул сохраняются при переходе от неко-
торой формулы к формуле, ей дедуктивно эквивалентной. Поэтому
важно уметь находить для каждой формулы дедуктивно эквивалент-
ную ей формулу, но «устроенную по возможности более просто».
Приступим к решению этого вопроса.
Предложение (бескванторные дедуктивно эквивалентные фор-
мулы) [13, с. 36—37; 27, с. 68, № 9].
Пусть А, В, С — формулы. Тогда имеют место следующие дедук-
тивные эквивалентности:
а) (А—>В) (-А vB);
б) —1—А =d А;
в) -.(А & В) =d (^А v -В);
г) -.(AvB) =d (—А & —В);
д) A=d (AvА);
е) A=d (А&А);
ж) (А&В) =d(B&A);
з) (A v В (В v А);
и) ((А&В) & О (А & (В & Q);
к) ((Ах/В) v С) (Av (В vO);
л) (А & (В v Q) ((А&В) v (А & Q);
м) (A v (В & Q) ((AvB) & (A v Q).
Доказательство. Упражняйтесь.
Предложение (кванторные дедуктивно эквивалентные форму-
лы) [13, с. 129].
Пусть А и В — формулы, а х g FV(B). Тогда имеют место дедук-
тивные эквивалентности:
а) -13лА =d Vx-A;
б) -iVxA =d Зх-А;
в) ЗхА &B=d3x(A&B);
г) \/xA&B=d Х/х(А&В);
д) ЗхА v В =d Зх(А v В);
е) VxA v В =d Vx(A v В);
ж) VxA =d Vy[A]*;
з) 3xA=d3y[A]^.
200
https: "и га it.ru
Доказательство.
А.
AHA ЬА)£1--А
АН (А)? Л R1 Vx—АН—А
АНЭхА А Н —1 Vx—А
— (контрапозиция) —
—izIjcA Н —iA Л 61 ЭхА Н -1 Vx—А
—13хА И Vx—А Vx—А Н —13хА
(свойства операции подстановки)
(17)
(вариант контрапозиции)
(19)
(вариант контрапозиции)
В.
АЬА В\-В
В,А\-А; В,А\-В
В,АН(А&В)
В,АН(А&В)*
В,АНЗх(А&В)
В,ЗлАНЗх(А&В)
ЗхА,ВНЗх(А&В)
ЗлА&ВНЗх(А&В)
(13)
(3)
(свойства операции подстановки)
(18)
(19)
(15)
(объединение посылок)
(13)
А,В\-В
(объединение посылок) —д
(18) А&ВНЗлА;
А&ВНЗхА&В
Зх(А&В)НЗлА&В
А,В\~В (объединение посылок)
А & ВI- В (2^
(19), xgFV(b)
Д.
л o') 711~ А
(6)С18)анзла BhB
AvBHAvB; АНЗлАуВ; ВНЗлАуВ<оЛ
(8)
Зх(АуВ)НЗлАуВ
(6) А1~А
(18) Ah(AvB)
(19) Ah3x(AvB)
ЗхАуВНЗхАуВ; ЗхАНЗх(АуВ)
ЗлА у ВI- Зх(А у В)
ВНВ (7)
В И (А у В) ng)
Bh3x(AvB)
--------- (оJ
201
https: //цга it.ru
ж.
AhA
([A]p^hA
V^HA (16)
Vy[A]*hVxA
A I-A
(A)* I-[A]*
VxAh[A]*
VxAHVyEA]*
(свойства операции подстановки)
(17),xgFV(A)
(16)
Предложение доказано.
Предложение (о замене).
1. [13, с. 130—131] Если формула В сигнатуры о получается
из формулы А сигнатуры о заменой некоторого вхождения подфор-
мулы А' на формулу В' сигнатуры о и A' =d В', то A =d В.
2. [27, с. 68, № 8] Если формула В сигнатуры о получается
из формулы А сигнатуры о заменой некоторого вхождения подфор-
мулы А' на формулу В' сигнатуры о и А' V В', тогда выводима сек-
венция (В <-> В') I- (А <-> А').
Доказательство. Докажем утверждение в формулировке 1, для
чего воспользуемся натуральной индукцией по рангу формулы
А. Если ранг формулы А равен 0, то А' = А, и утверждение тривиаль-
но, так как А = A' =dB' = В. Выберем п е N\{0}.
Индуктивное предположение. Пусть для всех формул А, ранг ко-
торых меньше п, утверждение имеет место.
Индукционное предложение. Предложение о замене справедливо
для формулы, ранг которой равен п.
Доказательство индукционного шага распадается на шесть слу-
чаев:
А = -А1з А = (Ах & А2), А = (Ах v А2), А = (Ах —> А2), А = Х/хА1} А = ЭхАХз
после чего остается воспользоваться результатами Леммы 2(6).
Рассмотрим, например, случай А = -тА1. Отметим, что в силу ин-
дуктивного предположения, Ах 3d В15 где формула Вг получена заме-
ной в формуле Aj подформулы А{ на подформулу В{, причём А{ =d В{.
В силу Леммы 2(6), легко получаем -Аг =d —В^
Предложение о замене в формулировке 1 доказано.
Пример.
1. Воспользуемся Предложением о замене для доказательства
А (В -> О В (А С).
По Предложению о бескванторных дедуктивно эквивалентных фор-
мулах
(А —» В) (-1А v В), (A v В) (В v А) и A v (В v С) (A v В) v С,
202
http
о- Hi iroit i-i ।
поэтому легко построить следующую цепочку дедуктивно эквивалент-
ных формул:
А —> (В —> Q =dА (—В vQ —A v (—В vQ^ (—A v —В) vC^
=d (—В v —A) v С =d —В v (—A vC) —В v(A—>С)^В—>(А—>С).
2. Воспользуемся Предложением о замене для установления того, что
еслих g FV(B) и у g FV(B), то
(VxA->B>d3y([A]*->B).
С помощью Предложений о бескванторных и кванторных дедуктивно
эквивалентных формулах построим следующую цепочку дедуктивно экви-
валентных формул:
(VxA -> В) =d —.VxA vB=d Ях-nA v В =d Зх(^А v В) =d Зх(А -> В) =d Зу[(А -> В)]* =d
Зу([А]* ->[B]*)=d Эу([А]* ->В).
Связь секвенциального и гильбертовского исчислений
Я открыл, что Китай и Испания
совершенно одна и та же земля, и только
по невежеству считают их за разные
государства. Я советую вам нарочно
написать на бумаге Испания, то и выйдет
Китай.
Н. В. Гоголь. Записки сумасшедшего
Определение (по [13, с. 55]).
Будем говорить, что правило вывода моносукцедентного секвенци-
ального исчисления сохраняет выводимость в классическом гиль-
бертовском исчислении, если после замены в нём секвенциаль-
ной схемы
Ар..., Ап \-В на {Аъ..., Ап} НС1В,
а секвенциальной схемы
Ар А„ I- на {Ар ..., An) hcl (В & -В),
из существования выводов, расположенных «над» буквой «черта»,
будет следовать существование вывода, расположенного «под»
буквой «черта».
Предложение [13, с. 56].
Основные правила вывода 1—19 моносукцедентного секвен-
циального исчисления первого порядка сохраняют выводимость
в классическом гильбертовском исчислении первого порядка.
203
https/'u^'t.ru
Доказательство. Достаточно рассмотреть следующую таблицу:
Основные правила вывода секвенциального исчисле- ния первого порядка Соответствующие непрямые допусти- мые правила вывода в ГИг Название допусти- мых правил вывода в ГИг
1 Г»А|~ * ГН—А (приведение к абсурду) Но{А}Н(В&-В) НН—А слабое введение -i (приведение к аб- сурду)
2.1^АН ГНА (доказательство от противного) Но{—А} Н(В&—.В) ННА удаление -i (доказательство от противного)
ГНА; ГНВ ГН(А&В) ННА; ННВ НН(А&В) введение &
ГН(А&В) ГНА НН(А&В) ННА удаление &
ГН(А&В) ГНВ НН(А&В) ННВ удаление &
6 Г|~А ’ TI-(AvB) ННА HH(AvB) введение v
7 Г|~В ГН (Av В) ННВ НН (Av В) введение v
rjH(AvB); „ Г,, АНС; Г3, ВНС ГЬГ2,Г3 НС HH(AvB); Но{А}НС; Но {В} НС ннс удаление v по Г. Ген- цену (разбор случаев)
9 Г,АНВ ‘ ГН(А—>В) Но {А} НВ НН(А—>В) введение (дедукция)
10 ГНА; ГН(А—>В) ГНВ ННА; НН(А—>В) ННВ удаление (modus ponens)
ГНА;ГН—А ГН ННА; НН—А НН(В&-В) слабое удаление -i
12. ГНА ННВ; HH-iB ННА слабое удаление -i
13. Г|~А Г,ВНА ННА {В}оННА расширение
Г.АМ1-С 14. Г, А НС {А}о{А}оННС {А}оННС сокращение
о Hi iroi! ri ।
204
Окончание таблицы
Основные правила вывода секвенциального исчисле- ния первого порядка Соответствующие непрямые допусти- мые правила вывода в ГИг Название допусти- мых правил вывода вГИ:
15 Гъ А,В,Г2 НС ' ГьВ, А,Г2 НС Н1 о{А}о{В}оН2 НС Hj о{В}о{А}оН2НС перестановка
16.-T12L ГНХ/лА ННА HHVxA правило универсаль- ного обобщения
17 ГЛАСИВ T,VxAHB Но{(А)*}НВ Но{Х/лА}НВ введение V в «анте- цедент»
ГН (А)? J.O* ГНЭхА НН(А# ННЭхА правило экзистенци- ального обобщения
19. Г-АНВ Г,ЗхАНВ Но {А} НВ Но{ЗхА}НВ введение 3 в «анте- цедент»
Предложение доказано.
Равносильность в определённом смысле моносукцедентного сек-
венциального исчисления и классического гильбертовского исчис-
ления устанавливается следующим Предложением.
Предложение [13, с. 53].
1. Секвенция А1г Ап I- В тогда и только тогда доказуема в мо-
носукцедентном секвенциальном исчислении, когда формула В вы-
водима из {Als ..., Ап} в классическом гильбертовском исчислении.
В частности, множества доказуемых формул в моносукцедент-
ном исчислении секвенций и классическом гильбертовском исчис-
лении совпадают.
2. А1} ...,АпЬ тогда и только тогда доказуема в моносукцедент-
ном исчислении секвенций, когда формула (В & -iB) выводима
из множества {Als ..., Ап} в классическом гильбертовском исчисле-
нии.
Доказательство. См. в [13, с. 53—56].
Примеры решения некоторых типов упражнений
Замечание.
При отыскании доказательства записи удобно производить снизу
вверх: сначала записать секвенцию, доказательство которой нужно
построить, затем провести черту и около нее записать номер правила,
по которому эта секвенция получается, над чертой написать секвенции,
из которых она получается и т. д.
205
https:it.ru
Пример 1. Покажите, что формула (Р -пР) доказуема в ИСГ
Решение. Необходимо показать, что доказуема секвенция
I- (Р->->-Р).
Просматривая правила вывода, убеждаемся, эта секвенция может
быть получена по правилу «введение -»« (правилу 9) из секвенции
Р Н -I-1P, которая, к тому же, имеет меньше вхождений логических связок,
чем секвенция I— (Р —» -пР). В свою очередь, секвенция РI- —г-Р получа-
ется по правилу «введение -i« (правилу 1) из секвенции РI- -пР.
Единственное правило, по которому можно получить эту секвен-
цию, — правило (11), причем получить Р, —РI- по этому правилу можно
из секвенций Р Н Р и —Р I- —Р, которые являются аксиомами.
Теперь записываем древесное доказательство секвенции Н (Р —> -г-Р):
РНР
(13)—„
Р,-РН
Р^^-Р
Н(Р->-.-Р)
(13)
(15)
(И)
(1)
----(9)
Пример 2. Покажите, что формула (-i-Л —> А) доказуема в ИС-,.
Решение.
Пример 3. Постройте древесное и линейное доказательства секвен-
ции Р, Q I- (Р & Q).
Решение. Построим древесное доказательство данной секвенции:
QhQ (13)
Р1~Р (13) Q,PI~Q (15)
P,QI-P P,QI~Q
P,QH(P&Q)
Линейное доказательство можно получить из древесного, выписав,
например, вначале секвенции левой «ветви» дерева сверху вниз до сое-
динения ее с другой ветвью, затем — вторую ветвь, а затем — их соеди-
нение. В результате получим:,
Р I- Р; Р, Q Н Р; Q Н Q; Q, Р Н Q; Р, Q Н Q; Р, Q Н (Р & Q).
206
https:/Л: rait.ru
Пример 4. Покажите, что доказуема в ИС1 схема секвенций
-АН(А—>В).
Решение. Зафиксируем произвольные конкретные значения формуль-
ных переменных А, В. Построим доказательство секвенции -А Н (А —>В).
~пА1~^А (13)
(13) А1~А -А, А И-А-----
А,-АНА А,—АН—А
А,—А НВ
-A, Al-В
(12)
(15)
(9)
—АН(А—>В)
В силу произвольности значений переменных А и В, секвенциальная
схема -А Н (А —> В) доказуема в ИС-,.
Пример 5. Докажите, что допустимым правилом вывода в ИС1 явля-
ется следующее слово
Г,АНС;Г,ВНС , е
-------------(разбор случаев).
Г,(АуВ)НС
Решение. Предположим, что секвенциальные схемы Г, А Н С и Г, В С
доказуемы и покажем, что доказуема схема секвенций Г, (A v В) Н С.
Зафиксируем значения метапеременных Г, А, В, С. Тогда схемы
Г, А Н С; Г, В Н С и Г, (A v В) Н С станут именами конкретных секвенций.
Пусть
------ И ------
Г,АНС Г,ВНС
являются древесными доказательствами секвенций Г, А Н С и Г, В Н С.
Продолжим их до доказательства секвенции Г, (A v В) Н С:
^1^2
(AvB)H(AvB) Г,АНС Г,ВНС
(АуВ),Г,ГНС (14^~С
(АуВ),ГНС
Г,(АуВ)НС 1 J
В силу произвольности значений метапеременных, допустимость пра-
вила вывода доказана.
Пример 6. Докажите, что допустимым правилом вывода в ИС! явля-
ется следующее слово
Г,ВН-А .
———— (вариант контрапозиции).
207
https:it.ru
Решение. Предположим, что секвенциальная схема Г, В Н -Л доказу-
ема и покажем, что доказуема схема секвенций Г, А Н —В. Зафиксируем
значения метапеременных Г, А, В. Тогда схемы Г, В I- -А и Г, A I- -iB ста-
нут именами конкретных секвенций. Пусть является древесным
доказательством секвенции Г, В Н -А. Продолжим ее до доказательства
секвенции Г, А Н —В:
D
Г,ВН-А
Доказана г
А,гн-.в
Г, АН—.В
(15)
(контрапозиция)
(15)
(сечение)
В силу произвольности значений метапеременных, допустимость пра-
вила вывода доказана.
Пример 7. Докажите, что в ИС1 доказуема секвенция (Р v Q) I- (Q v Р).
Решение. Построим квазидоказательство в ИС1 используя уже доказанное
РНР (7) (6)
PKQvP) QKQvP)^
(PvQ)H(QvP)
Пример 8. Докажите, что в ИС-, выводима секвенция Vx(A <-> В) Н
(VxA<-> VxB).
Решение.
(10) АНА;(А—>В)Н(А—>В) BHB;(B->A)H(B->A)(1(n
В, (B—>A)HA (13)
(13) А,(А—>В)НВ B,(B—>A),(A—>B)H A (13)
(объединение А,(А—>В),(В—> А)НВ B,(A—>B),(B—>A)H A (объединение посылок)
посылок) А,(А—>В)&(В—> А)НВ B,(A—>B)&(B—> A)H A
А,А<->ВНВ B,A++B\-A
(17) (15) А,(А<->В)*НВ B,(A<h>B)*HA (17) (15)
A, Vx(A<->B)HB B, Vx(A<->B)HA
Vx(A<->B), АНВ Vx(A<->B),BH A
(17) (16) Vx(A<->B),(A)*HB Vx(A<->B),(B)*HA (17) (16) (введение о в сукцедент
Vx(A <-> B), VxA I- В Vx(A <-> B), VxB H A
Vx(A<->B), VxAH VxB; Vx(A<->B),VxBHVxA
Vx(A <-> В) H (VxA VxB)
Пример 9. Докажите дедуктивную эквивалентность (А -» В) =d
(-А v В). Решение. Приведём древесные квазивыводы (заметим, что
ранее уже была доказана секвенция Н (A v -А)):
208
https:/Л: rait.ru
fl3) A I-A (A->B)H(A->B)
J(A^B);AHA (A->B),AI~(A->B)
Доказуемая секвенция (д A H В '
H(Av-A); (A—>B),AH(-AvB);
-AH(-AvB) (6)
-----------(8)
(A —>B) H(—A vB)
AHA —A H —A
(11) —A, AHA —A, AH —A
(12)
(—A vB) H(A —>B)
(13)
(разбор случаев)
(9)
Пример 10. Докажите дедуктивную эквивалентность
(A v (В &Q) ((A vB) & (A vQ).
Решение.
(В&С)Н(В&С) (4) (В&С)Н(В&С) (5)
(6) АНА (В&С)НВ (7) (6) AHA (B&QHC
АН(АуВ); (В&С)Н(АуВ) АН(АуС); (В&С)Н(АуС) 1 J
(Ау(В&СЫ-(АуВУ,___________(Av(B&C))H(AvC)
(Av(B&C))H((AvB)&(AvC))
АНА (В&С)Н(В&С)
^А,СНА В,СН(В&С)
AHA (13) l J С, АН А С,ВН(В&С)
(13) 1 JAH(Av(B&C)) С,АН(Ау(В&С)); С,ВН(Ау(В&С))
(15) A,(AvB)H(Av(B&C)) ______C,(AvB)H(Av(B&C))________
(AvB),AH(Av(B&C));________(AvB),CH(Av(B&C))________
(AvB),(AvC)H(Av(B&C))
((АуВ)&(АуС))Н(Ау(В&С))
(15)
(7)
(15)
(разбор случаев)
(объединение
посылок)
Пример 11. Докажите дедуктивную эквивалентность -i(A v В)
=d (—А & —В).
Решение.
(6) А1~А----------В1~В (7)
(контрапозиция)______AH(AvB) BH(AvB)___________(контрапозиция)
ЧАуВ)Н^А; ЧАуВ)Н-.В ( .
ЧАуВ)Н(^А&^В)
(контрапозиция) (-iA&-iB)l~-iA (-iA&-iB)l~-iB
АН—1(—iA & —iB)j Bl- —^-A&—iB) (разбор случаев)
(AvB)|--i(-A&-iB)
(-A&-B)K-A&-B) (AvB),(-A&-B)l—<-A&-B)
1 (-A&-iB),(AvB)l-(-A&-iB); (-A&-B),(AvB)l--<-A&-B)
(^A&^B),(AvB)|-
(-A&-B)I--<AvB)
209
https: "и rait.ru
Пример 12. Докажите дедуктивную эквивалентность -iBxA =d \fx—A.
Решение.
АНА (^A)JH^A
А1~СА)£ (18) Л |_ qv-д Vx-A Н-А AH-iVx-A
(16) -13лА Н Vx-A ЗхАН—.Vx-А Vx^AH-dxA
(17)
(вариант контрапозиции)
(19)
(вариант контрапозиции)
Упражнения для самостоятельного решения
Пусть это оскорбительно: поймите
Есть блуд труда иону нас в крови.
О. Мандельштам (1931)
а)
б)
Допустимые правила вывода
1. [27, с.66—67, № 3] Докажите, что следующие правила вывода являются
допустимыми в исчислении секвенций ИСХ:
Гх Н А; А,Г2 НВ f
-------------(сечение);
Гъг2 НВ
Г,А,вне . .
----------(объединение посылок)'
Г,(А&В)НС
Г, (А&В)НС, .
----------(расщепление посылок);
Г, А, ВНС
Г,АНС;Г,ВНС, . .
-------------(разбор случаев);
T,(AvB)HC
Г,АНВ .
---------(контрапозиция);
в)
Д)
е)
Г (обратная контрапозиция);
ж) ---А»—Мп 1~В-----(введение & и ->);
H((Ax&...&An)->B)
. Н((А1&...&АП)^В)
з) ---±-------------(удаление & и —>);
А1}...,АПНВ
2*. [27, с. 67, № 6] Докажите, что следующие правила вывода допустимы
в исчислении секвенций ИСХ:
. Г,АНВ;Г,ВНА . , , .
а) (введение <-» в сукцедент);
б) k ; в) v
Г,АНВ Г,ВНА
(удаление <-> из сукцедента)
210
3*. (По [13, с. 30]) Докажите допустимость правил с пустым сукцедентом:
МДГг!-.
Г1,В,А,Г2(-’
Г,А,АН.
г)----------;
Г1~(А&—А)
ч ГН(А&—А)
а ГН
I- А; А,Г2 I-
г1?г2н
4*. Докажите, что в исчислении, полученном из ИС^ удалением правил
вывода 1,12,14, правила вывода 1,12 и 14 являются допустимыми.
Указание. Решение см. в [13, с. 31].
5*. Укажите все допустимые правила, используемые в приведённом ниже
доказательстве секвенции А & (В v Q Ь (А & В) v (А & Q:
(А&В)1~(А&В) (А&С)1~(А&С)
А, ВI-(А&В)А, СИ (А&В)
A,BI-(A&B)v(A&C); A,CI-(A&B)v(A&C)
________A,(BvC)l-(A&B)v(A&C)___________
A&(BvC)l-(A&B)v(A&C)
Доказательство формул в ИСг
6. [27, с. 68, № 9] Покажите, что в ИСХ доказуемы следующие формуль-
ные схемы:
а) (А &В) (В &А);
б) (A v В) <-> (В v А);
в) А & (В & О <-» (А & В) & С;
г) A v (В v С) е (A v В) v С;
д) А & (В v О (А & В) v (А & Q;
е) A v (В & О (A v В) & (A v Q;
ж) ->(А & В) <-> (-А v -iB);
з) —i(A v В) <-> (—А & —iB)j
и) (А—>В) (r-AvB);
к) (-AvА);
л) (А->В) v (В—>А).
Доказательство секвенций в ИСг
7. (А. Б. Михайлов) Покажите, что в ИС-, доказуемы секвенции:
а) (ро&Р°)1-Р§;
б) (VxjP^xJ & х2У) Ь VxjP^xJ;
в) Зх2Р](х2) h(3x2P{(x2) vP2);
г) Р2 Н (Р® —> Р2);
211
https:/7!.'га it.ru
д) I- (Valeri) (3x2pi (x2) -> VxjPKxj)));
e) (P0&^P?)h;
ж) 3x1Pl(x1),-3x1Pl(x1)h;
3) Pjh-i-Pj;
и) ^-.VxiPKxJ I- Vx^fxJ;
к) VxjP^Xi), Зх2Р|(х2) I- (VXiPjCxj) & 3x2P|(x2)).
8. [13, c. 34] Установите доказуемость схем секвенций:
а) Гх, А, Г2 h А; б) (А &В) Н (В&А~); в) (A v В) Н (В v А).
9*. [27, с. 66, № 1]
Постройте доказательства секвенций в исчислении секвенций ИСр
а) Н(Р—>Р);
б) (P^Q), (Q^r)h (Р^Ю;
в) h(^PeP);
г) (P^(Q^P)), (P^Q),PhR;
Д) (P->Q),-.QI--P;
е) Р,-.QH->(P->Q).
10. [27, с. 67, №5]
Покажите, что следующие схемы секвенций доказуемы в ИСХ:
а) (А—>В), (В^С)Н(А^С);
б) (A->(B->Q)|-(B->(A->C));
в) (А -> (В -> О) Н ((А&В) -> О;
г) ((A&B)->QI-(A->(B->C));
Д) (А В) Н ((В —> С) —> (А С));
е) (А —>В) Н ((С —>А) —> (С—>В));
ж) (А —> В) Н ((С & А) -> (С & В));
з) (А^В) Ь ((А & О (В & О);
и) (А —> В) Н ((С v А) -4 (Cv В));
к) (А —> В) Н ((С v А) (С v В));
л) -АН (А^В);
м) А Н (-А —> В);
н) В I- (А В);
о) (А —> В) Н (—В —> —А);
п) (А -> -.В) I- (В -> -А);
р) ЬА->В)|-(-1В->А);
с) (—А —>-iB) Н (В —> А).
11. [27, с. 67—68, № 7]
Покажите, что в ИСХ доказуемы следующие схемы секвенций:
a) (А^ В),(В^А) h(A<- ^В);
6) (А<н ,В)1-(А^В);
в) (А<н ► В) 1- (В^А);
г) (А^ В), А 1- В;
д) Н(А <^А);
е) (А<н ► В), (В<^С)|-(А< 40;
ж) (А<->В) 1~ (В<->А);
з) (А<->В) Н (-А <->-£);
и) (А В) Н ((А & О <-» (В & О);
к) (А <->В) I- ((С & А) (С & В));
л) (А <->В) I- ((A v Q ++ (В v С));
м) (А В) Н ((С v A) h(Cv В));
н) (A<^B)I- ((А-> Q <г+ (В Q);
о) (А В) h ((С А) (С В)).
http
о - Hi iroit i-i ।
212
12. [27, с. 92, № 4]
Постройте выводы следующих секвенций в ИС\:
а) НхА I- Зу[А]* ; 6)VxA Н Vy[A]*.
13. [27, с. 92—93, № 6]
Пусть х е FV(A). Докажите выводимость следующих секвенций в ИС^
a) I- VxA <-> А;
б) I- НхА <-> А;
в) Н VxVyB <-> VyVxB;
г) I- НхНуВ <-> НуНхВ;
Д) h (VxVyB—>Vx(B)J);
е) Н(Нх(В)£—> НхНуВ);
ж) I- НхВ <-> -iVx-iB;
з) I- VxB о —i3x-iB;
и) I—i\fxB <-> Hx-iB;
к) I—Их-iB Х/х—В;
л) Н (VxB & VxC) Х/х(В & О;
м) I- (НхВ v HxQ <-> Нх(В v Q;
н) Н (А & VxB) Xfx(A & В);
о) Н (A v НхВ) <-> Нх(А v В);
п) Н (А & НхВ) <-> Нх(А & В);
р) Н (A v VxB) <-> Vx(A v В);
с) Н Зх(В & С) (НхВ & ЗхС);
т) Н (VxB v VxC) -> Х/х(В v О;
у) Н (А -> VxB) <-> Vx(A В);
ф) Н (А —> НхВ) <-> Нх(А В) ;
х) I- (VxB -> А) Нх(В АУ,
ц) I- (НхВ —> А) Vx(B -^А);
ч) I- Нх(В —> С) <-> (VxB НхС).
14. [27, с. 93, № 7, (з), (и)]
Докажите, что в ИС^ выводимы секвенции:
a) Vx(A <-> В) I- (VxA <-> VxB); б) Vx(A <-> В) Н (ЗхА <-> НхВ).
Дедуктивно эквивалентные формулы
15*. Восстановите пропущенные фрагменты доказательства дедуктивной
эквивалентности —.(А & В) =d (-А v -iB):
—AI-(—Av—iB)
-(-Av-^)I-A; -.(-Ау-Д)НВ
-,(^Ау-Д)|-(А&В)
(A&B)|-(A&B) (A&B)|-(A&B)
(A&B)I~A (A&B)|-B
-АНЧА&В); -Д1-ЧА&В)
-,(A&B)(-(^Av-.B)
(—A v —iB) H —i(A & B)
16. [27, c. 68, № 9; 13, c. 36] Докажите, что имеют место дедуктивные
эквивалентности:
а) (А &В) =d (В&А); ж) (А ->В) =d ЬЛуВ);
б) (A v В) =d (В v А); з) —i-A =d А;
в) ((А & В) & О =d (А & (В & О); и) —i(A & В) (-А v -ВУ
г) ((A v В) v Q (A v (В v Q); к) -.(A vB) (^А & -iB);
д) (А & (В v Q) ((А & В) v (А & Q); л) А (A v А);
е) (А у (В & Q) ((А у В) & (A v Q); м) A (А & А).
213
https:/7!.! га it.ru
17. [13, с. 129]
Пусть А, В — формулы, хе FV(B). Докажите в ИС^ следующие дедуктив-
ные эквивалентности:
а) —>3xA Vx—1А;
б) —> VxA Зх—А;
в) (ЗхА & В) =d Зх(А &В);
г) (VxA & В) =d Vx(A & В);
д) (ЗхА v В) =d Зх(А v В);
е) (VxA v В) Vx(A v В);
ж) VxA =d Vy[A]*;
з) ЗхА =d Зу[А]*.
Связь между секвенциальным и гилъбертовским исчислением
18. Докажите, что основные правила вывода 1—19 моносукцедентного
секвенциального исчисления первого порядка сохраняют выводимость
в классическом гильбертовском исчислении.
Указание. Обратите внимание на основные правила вывода моносукце-
дентного секвенциального исчисления 1, 2,11,12.
о- Hi iroit i-i ।
vJ.M Ul (Ull.l VU
Упражнение 8
МНОГОСУКЦЕДЕНТНОЕ СЕКВЕНЦИАЛЬНОЕ
ИСЧИСЛЕНИЕ ПЕРВОГО ПОРЯДКА
Да, если Муза не может бежать, когда
с нее сняли путы, значит, ей просто
не хватает резвости.
Дж. Драйден (1697)
Обязательные результаты обучения:
• знать основные понятия:
— многосукцедентная секвенция, схема секвенций;
— аксиома, правила вывода многосукцедентного секвенциального исчис-
ления (HCnj, вывод секвенции, выводимая секвенция, выводимая формула;
—допустимые правила вывода, обратные правила вывода, квазивывод,
квазивыводимая секвенция;
— алгоритм Хао Вонга для поиска вывода в пространстве состояний ло-
гической системы;
• уметь:
— устанавливать существование доказательств формул в ИСГ^;
— устанавливать существование выводов секвенций в ИСП13
— конструировать доказательства допустимости правил вывода в ИСЩ
и схем секвенций;
— применять алгоритм Хао Вонга для поиска вывода в пространстве со-
стояний логической системы;
• владеть:
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
Теоретические сведения
Секвенции. Аксиома.
Основные правила вывода
Пусть Г, Гр Г2, Г3, Г4, А, Др Д2, П — конечные последовательно-
сти формул, которые могут быть пустыми (т. е. не содержать ни од-
ной формулы), Р и Q — формулы, х, у — предметные переменные,
t — терм.
Будем также предполагать, что для всех используемых формул
выполнено условие несмешанности переменных.
215
https:it.ru
Определение (по [24, с. 23]).
Секвенцией многосукцедентного секвенциального исчисления будем
называть слово вида
ГНА
(читается: «при допущении последовательности формул Г имеет
место одна из возможностей последовательности формул А»),
в котором последовательность формул Г называется антецеден-
том, а последовательность А — сукцедентом секвенции.
Определение (по [24, с. 23]).
Аксиомой будем называть любую секвенцию вида
Из определения следует, что секвенция является аксиомой тогда
и только тогда, когда в антецедент и в сукцедент имеет вхождение
одна и та же формула (как элемент последовательностей).
Определение (по [21, с. 346; 24, с. 24—27]).
Основные правила вывода многосукцедентного секвенциального
исчисления — это слова, перечисленные ниже (для наглядности
формулы Р и Q выделены «жирным» шрифтом).
Пропозициональные основные правила вывода
1. Введение -i в сукцедент
Г1,Р,Г2 и г3,г4
ГЪГ2|-Г3,^Р,Г4
2. Введение -i в антецедент
Г1,Г2 1~ Г3,Р,Г4
гь^р,г21-г3,г4
3. Введение & в сукцедент
riHl^P^ni-r^Q,^
---------------------- (г<х)
rxl-r2,(P&Q),r3
4. Введение & в антецедент
ri,P,Q,r2 ьг3
TMP&Q),Г2 НГ3
216
https: //u га it.ru
5. Введение v в сукцедент
г.нг2,р,о,г3
Hr2,(PvQ),r3
6. Введение v в антецедент
Г1?ЛГ2НГ3; Гьд,Г2|-Гз
Гь(РмО),Г2 ЬГ3
7. Введение —> в сукцедент
Г1,Р,Г2 1~ A1?Q, А2
ГЪГ2 ЬД^Р-^Дз
8. Введение —> в антецедент
Г1»Г2 l~A1,P,A2;r1,Q,r2 1-А1,А2
r1,(P^Q),r2l-A1,A2
9. Введение в сукцедент
ri,Q,r2 I- А1?Р, А2;Г1?Р,Г2 I- A1?Q, А2
Г1,Г21-А1,(Р^0),А2
10. Введение <-> в антецедент
ГХ,Г2 Н A1;Q,P, А2;ГъР,0,Г2 Н Аъ А2
r1,(P^Q),r2hA1,A2
Структурные основные правила вывода
11. Сокращение повторения в сукцеденте
АНГьР,Р,Г2
ангьр,г2
12. Сокращение повторения в антецеденте
ГъР,Р,Г21-А
ГьР,Г2|-А
Кванторные основные правила вывода
13. Введение 3 в сукцедент
Гг НГ2,(А)?,Г3
Гх НГ2,ЗхА,Г3
217
https:it.ru
14. Введение V в антецедент
Гь(А)?,Г2|-Гз
ГьУхА,Г21-Гз
15. Введение V в сукцедент
111-Г2,[А]*,Гз
Г!1-Г2,УхА,Г3
при этом у не должна входить свободно в формулы последова-
тельностей Г12 Г2, Г3.
16. Введение Я в антецедент
Гь[А]х,Г21-Гз
ГъЗхА,Г2|-Гз
при этом у не должна входить свободно в формулы последова-
тельностей Г12 Г2, Г3.
Вывод. Выводимые секвенции. Выводимые формулы
Определение [24, с. 24].
1. Линейным доказательством (выводом) в многосукцедентном
секвенциальном исчислении называется последовательность сек-
венций, каждая из которых является или аксиомой, или получа-
ется из «предшествующих» элементов последовательности по од-
ному из основных правил вывода.
2. Выводом секвенции Z в многосукцедентном секвенциальном ис-
числении называется вывод, последняя секвенция которого со-
впадает с Z.
3. Выводимой секвенцией называется секвенция, являющаяся по-
следней секвенцией некоторого вывода.
4. Выводимой формулой называется такая формула Р, для кото-
рой секвенция I- Р является выводимой.
Выводы в многосукцедентном исчислении секвенций имеют
замечательную особенность: посылки любого основного прави-
ла вывода состоят лишь из подформул формул в секвенции, рас-
положенной в заключении правила вывода. Таким образом, при
рассмотрении правил вывода «снизу вверх» формулы в секвенциях
лишь как бы «дробятся», при этом никакие «посторонние» формулы
не появляются.
218
https: "и га it.ru
В этом состоит так называемое свойство подформулъности сек-
венциального исчисления, которое во многих случаях облегчает по-
иск вывода секвенции.
Примеры [24, с. 35].
А. Докажем выводимость формулы VxA ЯхА
jawL(vh
УлАЬ(А)*
VxA Н ЯхА
Н(УхА->ЯхА)
Б. Докажем выводимость секвенции Ях(А v В) Н ЯхА v ЯхВ
[А]* Н [А]*, (В)*; [В]- I- (А)*, [В]*
[A]*v[B]*H(A)*,(B)* tV J
(НЯ)
[A v В]* Н ЯхА, ЯхВ
—-----2-----------(Hv)
[AvВ]* Н (ЯхА v ЯхВ) < J
------------------(ЯН
Яx(AvB)HЯxAvЯxB <
Допустимые правила вывода
Пусть Г, Гр ..., Гп — секвенции.
Определение (по [24, с. 24]).
Допустимым правилом вывода назовём слово метаязыка
Г
такое, что из выводимости каждой его посылки Гр Г2,..., Гп сле-
дует выводимость заключения Г.
Предложение (по [21, с. 397; 24, с. 51—53; с. 55—57]).
Следующие слова являются допустимыми правилами вывода,
которые будем называть структурными допустимыми правилами
вывода многосукцедентного секвенциального исчисления:
(DT) одновременное добавление в антецеденте и сукцеденте
ГНА
Г1,Г,Г2 h Als А, А2
(НУ; УН
(D2) перестановка в антецеденте
Т\,Р,Г2,О,Г3\-Ь
1 2 3--(П Н, Н)
Г^Г^ЛГзНА
//i iroit
219
(D3) перестановка в сукцеденте
АЬГ^ЛГг^Гз
---1 2 3 (н п, н ^>)
АНГ^Г^ЛГз
Предложение (теорема Генцена об устранении сечений) (по [23,
с. 109—110]).
Следующее слово является допустимым правилом вывода
П-АьЛА^ГьЛГгНАз
Г,ГЬГ2 Ь Als А2, А3
(сечение, #),
где формула Р называется высекаемой формулой.
Отметим, что по секвенции, являющейся заключением допусти-
мого правила вывода «сечение», трудно предсказать высекаемую
формулу.
Возможно уменьшение количества основных правил вывода
многосукцедентного секвенциального исчисления за счет исключе-
ния правил, относящихся к логическим связкам &, v, —>, <->, путём
использования определённых обозначений.
Лемма,
def def
Если (Р —> Q) = (-1Р v Q), (Р <-> Q) = (Р —> Q) & (Q —> Р), то основные
правила вывода многосукцедентного секвенциального исчисления
«введение в сукцедент и в антецедент», а также основные прави-
ла вывода «введение <-> в сукцедент и в антецедент» превращаются
в допустимые правила вывода.
Доказательство. Рассмотрим доказательство «допустимости» ос-
новного правила вывода «введение —> в антецедент». Предположим,
что существуют выводы DT и В2 секвенций Г15 Г2 I- Als Р, А2 и Г15 Q,
Г2 I- Ат, А2 соответственно. Дальнейшее очевидно:
ГЬГ2 1~ А1?Р, А2___Р2______
( } Гп^ГгНАьАг; Г1?д,Г2 НА1,А2
(vH) ГкС-пРуО.ГгНДкД,; (p^QW^PvQ)
(замена равного----------------------------------------
на равное) Гт, (Р -> Q), Г2 h Aj, А2
Остальные пункты Леммы докажите самостоятельно.
Лемма доказана.
Обратные допустимые правила вывода
В многосукцедентном секвенциальном исчислении каждому
из основных правил вывода, относящихся к введению логической
связки, можно поставить в соответствие некоторое допустимое пра-
вило вывода, которое называется обратным правилом вывода.
220
https: "и га it.ru
При этом однопосылочным основным правилам вывода, к кото-
рым относятся (-1 h), (I- -1), (I- v), (& h), (I- ->), ставится в соответ-
ствие одно обратное правило вывода, а двухпосылочным основным
правилам вывода, к которым относятся (I- &), (v I-), (—> h), (I- <->),
(<-> I-) — два обратных правила вывода.
Логистические исчисления с «обратимыми» правилами вывода
облегчают установление выводимости формул по сравнению с ис-
числениями, содержащими необратимые правила.
Предложение (по [24, с. 53—55]).
Следующие слова являются допустимыми правилами вывода
в многосукцедентном секвенциальном исчислении первого поряд-
ка, которые называются обратными (пропозициональными) прави-
лами вывода (правиламиудаления логических связок):
(DT) удаление v из сукцедента
HhAUPvQXA,
r1HA1,P,Q,A2
(D2) удаление v из антецедента
nXPvQ),^ l-Ai
--------------1У1 i- J
Г^ЛГгЬА!
(D3) удаление v из антецедента
FbCPvQ^hAi
-------------- Iv 2 । J
ГьОЛгЬА!
(D4) удаление & из сукцедента
r1hA1,(P&Q),A2
-------------- (I-Rij
Г1НА1,Р,А2
(D5) удаление & из сукцедента
Г11-Д1,(Р&<»,Д2
-------------- (h &2)
HI-A^Q^
(D6) удаление & из антецедента
Гъ(Р&О),Г21-Гз
--------------I-]
ГьР,С,Г21-Гз
(D7) удаление -i из антецедента
Г1,~Р,Г2 hГ3,Г4
ГьГ21-Гз,Р,Г4
221
https:it.ru
(D8) удаление - i из сукцедента ГЬГ21~ Г3,-|Р,Г4 Г!,Р,Г2|-Г3,Г4
(D9) удаление - > из сукцедента ri,r2hAi,(P->Q),A2 ГЬР,Г2 h Ai,Q,A2
(D10) удаление -> из антецедента ri,(P->Q),r2hAi,A2 Г1,Г2ЬА1,Р,А2 1
(Dn) удаление -> из антецедента ПЛР-^ГгЬА^ Fi,Q, Г2 h Ai, А2
(Di2) удаление <-> из сукцедента ri,r2hAi,(P^Q),A2 Fi,Q,r2hAi,P,A2 1
(Di3) удаление < (-> из сукцедента Fi,P,r2hAi,Q,A2 2
(Di4) удаление <-> из антецедента Fi,(P<->Q),r2hA!,A2 Fi,r2hAi,Q,P,A2 1
(Di5) удаление < из антецедента ^(P^Q),^ hA^A, Fi,P,Q,r2hAi,A2 2
Доказательство. Доказательство допустимости первых восьми
правил вывода аналогичны друг другу. Последние семь правил вы-
вода получаются с помощью первых восьми, поскольку основные
правила вывода, названные «введение —> и <->«, могут быть выведе-
ны на основе основных правил вывода, которые называются «введе-
ние v, -i« (см. последнюю Лемму).
222
.£*"// iroif Г1 1
vj .1 i U4
(DT) Рассмотрим слово, которое названо «удаление v из сукцеден-
та», и докажем, что оно является допустимым правилом вывода:
Аксиома
Аксиома
D PI~A1,P,Q,A2; QhA!,P,Q,A2
I^I-AnCPvQLAa; (PvQ)h AbP,Q, А2
Г*1 Ь Ai, А2, P,Q
(vh)
(сечение)
(D2) Рассмотрим слово, которое названо «удаление v из антеце-
дента», и докажем, что оно является допустимым правилом вывода:
Аксиома
г
(|- v) PhP,Q--------------
Ph(PvQ); TbCPvQ^rahA!
р,Г!,г21-а1(пн)
ГьЛГгНА!
(сечение)
(D7) Рассмотрим слово, которое названо «удаление -i из антеце-
дента», и докажем, что оно является допустимым правилом вывода:
Доказуемая
секвенция
г
0_j Г1?-1Р,Г2 I-г3,г4
Г1,Г2 hГ3,—1—iP,r4;
Р\-Р
ГЪГ2|-Г3,Р,Г4
(Н-)
Ы-)
(сечение)
(D9) Рассмотрим слово, которое названо «удаление из сукце-
дента», и докажем, что оно является допустимым правилом вывода:
_______D________
НА^Р—>Q), А2;
def
(Р—>Q) = (~PvQ)
ГьГгНА^ЬРуОХАг
ГЬГ2 h Ат,—iP, Q, А2
Г1,Р,Г2 h AlsQ,A2
(замена равного на равное)
(Hv)
(Н-)
Предложение доказано.
Определение (повторение).
Символом Шеффера называется символ «|», определяемый так:
def
P|Q - (-Pv-.Q).
223
https:it.ru
Предложение (по [45, с. 134]).
Следующие слова являются допустимыми правилами вывода
в многосукцедентном секвенциальном исчислении первого поряд-
ка:
Допустимые правила вывода для символа Шеффера
1. Введение | в сукцедент
ri,P,Q,r2 ь Ai, а2 .
ГЬГ2 h AbP|Q, А2
2. Введение | в антецедент
ГЬГ2 h АЪР, А2; ГьГ2 h A1?Q, А2
r1,P|Q,r2hA1,A2
Обратные допустимые правила вывода для символа Шеффе-
ра
3. Удаление | из сукцедента
Г1,Г21-Д1,Р|О,Д2
г1,р,<2,г21-д1,Д2
4. Удаление | из антецедента
Г1,Г2НД1,Р,Д2 11 г1,г2нд1,о,Д2
Доказательство.
1.
__________D_________
Г1> J\Q>r2 h А1? А2 (|-_|)
Г1,Р,Г21~ А1?—1Q, А2
Г1,Г2 I- A1,-iP,-iQ, А2
°’v)rI,r2l-Ai,(-nPv^Q),A2; P|Q='(^Pv^Q)
----------------------------!------------(замена равного
П, Г2 h Ат, Р | Q, А2 на равное)
D
rbP|Q,F2 НА^А^ p|Q=(^pv^Q)
Гь~»Ру-Ф,Г2 i~a1,a2 (v_
Г1,-Р,Г21-А1,А2 _
Г1,Г21-А1,Р,А2
(замена равного
на равное)
Предложение доказано.
224
Предложение.
Следующее слово является допустимым правилом вывода в мно-
госукцедентном секвенциальном исчислении первого порядка, на-
зываемым обратным (кванторным) правилом вывода (правилом
удаления V):
Г1НГ2,УлА,Г3
Г1НГ2,(А)?,г3
где t — терм.
Доказательство. Упражняйтесь.
Определение.
1. (Линейным) квазивыводом из секвенций Х2,..., Zfc называет-
ся последовательность секвенций, каждый элемент которой явля-
ется либо аксиомой, либо совпадает с Хг- при 1 < i <k, либо получа-
ется из предыдущих секвенций по допустимым правилам вывода.
2. Секвенцией, квазивыводимой из секвенций Zls Z2,..., Zfc, назы-
вается секвенция, которая является последней секвенцией неко-
торого квазивывода из секвенций Z2, ..., Zfc.
Замечание [45, с. 160; 37].
Известны построения секвенциальных исчислений без структурных
правил; такого рода системы называют кангеровскими системами.
Например, правила введения V и 3 сформулированы таким образом,
чтобы в них явно производилось сокращение:
Гь(А)?,УлА,Г21-А . , _ Гх 1-Г2,ЭхА,(А)^,А . ,
—----------------(введение V); —------------— (введение 3).
Гх^хА,Г21-А Гх1-Г2,ЗхА,А
Системы кангеровского типа удобны для осуществления поиска дока-
зательства.
Алгоритм Хао Вонга для поиска вывода в пространстве
состояний логической системы
Вы должны взглянуть на практику
языка и тогда вы увидите логику.
Л. Витгенштейн.
О достоверности, 501
Пусть D — дедуктивная система. Это означает, что заданы язык
для описания предложений системы, исходные «правильные» пред-
ложения (аксиомы) и правила получения новых «правильных»
предложений из уже построенных предложений (правила вывода).
225
https://urait.ru
Обычно дедуктивные системы строятся на базе формальной си-
стемы первого порядка.
Определение (В. П. Оревков).
Алгоритмом поиска доказательства в дедуктивной системе D на-
зывается любой алгоритм, который заканчивает работу над пред-
ложением системы D и выдаёт его доказательство, если оно вы-
водимо, а в противном случае выдаёт слово «Нет» или не закан-
чивает работу.
Определение (В. П. Оревков).
Разрешающим алгоритмом в дедуктивной системе D называется
любой алгоритм, который заканчивает работу над любым пред-
ложением системы D и выдаёт слово «Да», если предложение вы-
водимо, и «Нет» — в противном случае.
Построение разрешающего алгоритма для той или иной дедук-
тивной системы является важной задачей. К сожалению, для наи-
более интересных систем разрешающий алгоритм невозможен (на-
пример, для формальной системы первого порядка).
В этом случае задачу построения разрешающего алгоритма мож-
но заменить следующими задачами:
1) поиск разрешающего алгоритма не для всего класса предло-
жений системы, а только для некоторого подкласса;
2) построение алгоритма поиска доказательства, который над
не выводимыми в системе предложениями может работать беско-
нечно долго.
Для любой дедуктивной системы существует тривиальный алго-
ритм поиска доказательств в этой системе.
Работает этот алгоритм следующим образом: перебираем, начи-
ная с аксиом и правил вывода, все доказуемые в рассматриваемой
системе предложения и ждём, когда получим заданное предложение.
Очевидно, что тривиальный алгоритм не может учитывать осо-
бенности заданного для поиска доказательства предложения и пе-
ребирает излишне много доказательств, которые никак не связаны
с заданным предложением.
Тривиальный алгоритм поиска доказательств иногда называют
алгоритмом Британского музея. Неэффективность тривиального
алгоритма очевидна. Однако можно привести примеры [52, с. 314—
332], когда алгоритм Британского музея оказывается эффективнее
метода резолюций.
Хао Вонг (Гарвардский университет, США, 1960) разработал эф-
фективный алгоритм для (вывода) доказательства формул в клас-
сическом гильбертовском исчислении нулевого порядка, который
226
https:/Л: rait.ru
заключается в преобразовании слов в некотором алфавите, которые
будем называть секвенциями. Процедура продолжается до тех пор,
пока не будет получен вывод или опровержение выводимости.
Каждая секвенция включает произвольное количество формул
языка нулевого порядка (разделяемых между собой запятыми), рас-
полагающихся по обеим сторонам знака «И».
Определение.
Антецедентом (каквмногосукцедентном секвенциальном исчисле-
ний) будем называть слово, расположенное «слева» от знака «Н>.
Сукцедентом будем называть слово, расположенное «справа»
от знака «И».
Алгоритм Хао Вонга.
1. В первой секвенции гипотезы запишите в антецеденте, а вы-
водимую формулу — в сукцеденте:
Гипотеза 1,..., Гипотеза п I- Теорема.
2г. Если логической связкой формулы, находящейся в антеце-
денте, является отрицание, то опустите связку и перенесите форму-
лу из антецедента в сукцедент.
22. Если логической связкой формулы, находящейся в сукцеден-
те, является отрицание, то опустите связку и перенесите формулу
из сукцедента в антецедент.
23. Если главной связкой формулы, находящейся или в анте-
цеденте, или в сукцеденте, является —то замените эту формулу
на дизъюнкцию, т. е. воспользуйтесь тем, что (А —> В) (-А v В).
Зг. Если в качестве главной связки в формуле антецедента встре-
чается логическая связка &, то замените эту связку знаком «,».
32. Если в качестве главной связки в формуле сукцедента встре-
чается логическая связка v, то замените эту связку знаком «,».
4г. Если главной связкой формулы, расположенной в антецеден-
те, является v, то образуйте две новые строки, каждая из которых
содержит одну из двух подформул, заменяющих исходную формулу.
Все полученные таким образом строки должны быть выведены,
чтобы получить доказательство исходной теоремы.
42. Если главной связкой формулы, расположенной в сукцеден-
те, является &, то образуйте две новые строки, каждая из которых
содержит одну из двух подформул, заменяющих исходную формулу.
Все полученные таким образом строки должны быть выведены,
чтобы получить доказательство исходной теоремы.
5. Если одна и та же формула имеет вхождения и в антецедент,
и в сукцедент, то секвенция доказана.
6. Если в секвенции не осталось ни одной логической связки,
и если ни одна формула не присутствует одновременно ни в анте-
цеденте, ни в сукцеденте, то секвенция недоказуема.
227
https:/Л: rait.ru
Всякий раз при использовании правил 4j и 42, задача «расщепля-
ется» на две подзадачи, поэтому алгоритм порождает бинарное де-
рево, содержащее секвенции в своих вершинах.
Если число логических связок в гипотезах и выводимой (доказу-
емой) формуле равно т, то алгоритм Хао Вонга потребует в конеч-
ном итоге использования количества секвенций из [т, 2т].
Поскольку далеко не всегда все связки нуждаются в применении
правил 4г и 42, то потребуется меньше секвенций, чем 2т.
Замечание.
Очевидным способом реализации алгоритма Хао Вонга на компьютере
является: а) систематическое (скажем, в направлении слева направо) устра-
нение логических связок при рассмотрении последовательности секвен-
ций; б) построение бинарного дерева и его обход, например, в глубину.
Алгоритм всегда приводит к достижению цели, так как каждая ветвь
дерева не приводит к увеличению длины секвенции и посещается ровно
один раз. Однако, если мы постоянно будем проверять выполнимость пра-
вила 5, то доказательство обычно находится быстрее.
Примеры (использования алгоритма Хао Вонга).
1. Установим выводимость формулы
(А Q -> ((В -> О -> (A vB -> О).
Проведём вначале равносильные преобразования:
(A->Q->((B->C)->(.AvB->C))^-,(A->C) v-,(B->C) v-,(AvB) vC.
Дальнейшее очевидно:
2. Установим выводимость —Р v Q, -iQ v R, —R v S, —>U v —iS H —P v —>U.
Построим следующее дерево:
lh iroit
228
229
https:it.ru
Замечание (важное) [5, с. 25].
Сейчас принято считать, что автоматические рассуждения на основе
формальной логики относятся к слабым (weak) методам доказательства
теорем, и чисто синтаксические методыуправления поиском не способны
обрабатывать огромное пространство поиска при решении задач практи-
ческой сложности.
Поэтому альтернативой являются неформальные методы поиска,
ad hoc стратегии, эвристики и рассуждения здравого смысла, которые
человек использует при решении проблем.
Примеры решения некоторых типов упражнений
Пример 1. Докажите выводимость формулы ->(Р & -Р).
Решение. Построим доказательство секвенции I- ->(Р & -Р):
р|~р (-.1-)
(&Ю
(Р&^Р)\- ([ '
Н—<Р&—J>)
Показано, что секвенция Н -i(P & -iP) является выводимой, т. е. дока-
зали выводимость формулы -i(P & -iP).
Пример 2. Покажите допустимость следующего правила вывода:
Г11-Г2,Л,Г3;Г11-Г2,В,Гз
Г11-Г2,—.(—Л v —В), Г3
Решение.
Пусть
------±-----и-------------
Г!1-Г2,А,Гз Г!1-Г2,В,Гз
— древесные доказательства секвенций I- Г2, А, Г3 и I- Г2, В, Г3
соответственно. Дальнейшее очевидно:
А А
Г!1-Г2,А,Г3 ПНГ2,В,Г3
Г1д—1А1~Г2,Г3 ГЬ^В1-Г2,Г3
Гь(-пАу^В)|-Г2,Г3
А 1-Г2,-{-1Ау-1В),Гз'‘ "
Пример 3. Запишите правило вывода (Н v) и докажите его допусти-
мость.
230
https:/Л: rait.ru
Решение. Требуемое правило имеет вид:
Пусть--------------доказательство схемы секвенций Г: НАЪ
(AvB), А2Лг HAi’(AvBbA2
Построим доказательство нижней секвенциальной схемы правила
(hv):
______ДНА________________ВИВ_______
D А1,А,А2 HA1,A,B,A2; А1зВ, А2 Н Аъ А, В, Д2 (v|_)
Гг НАъ(АуВ), А2; Аь(АуВ), А2 НАъА,В,Д2
Пример 4. Рассматривается сокращённое исчисление И, полученное
из ИСЩ удалением из алфавита символа «—*<, из множества формул —
всех формул, содержащих «—х<, а из множества правил — правил (-» Н)
и (I- —>). Запись (А В) считается обозначением формулы (—A v В).
Докажите, что в исчислении И допустимо правило введения импли-
кации в сукцедент:
Г1, А,Г2 1-А^В, А2
ГьГгЬАьСА-^А/
Решение. Построим вывод нижней секвенциальной схемы правила
(I- —>), при условии, что имеется доказательство верхней:
Г1,Л,Г21~ Aj,B, А2
Г1,Г2 I- Аъ—А, В, Д2 л .
TbGI-A^C-nAvBLAa
Г^ГгНА^СА^ВХАг
Упражнения для самостоятельного решения
1. Многосукцедентное секвенциальное исчисление
1. Докажите выводимость следующих формул в ИСЩ (многосукцедент-
ном исчислении секвенций первого порядка):
a) Р—>(Q—>Р);
б) (P->Q)->((P->(Q->C))->(P->C));
в) Р-> (Q->P&Q);
г) Р & Q -> Р;
д) P->PvQ;
е) -tPvP;
231
https: "и rait.ru
Ж) (P->Q)->(-,Q.->^P);
з) (P^Q) v(Q^P);
и) ССР —> Q) —> P) —> P (.закон Пирса);
к) (P^C) ^((Q^C) ^(PvQ^C));
л) ((P Q) ((P -,Q) -P);
m) —i—iP—>P;
h) ((P^Q)^(CQ^P^(P^Q));
o) P->-i^P;
п) (-P v Q) v C—-Q v РУ
p) -.(P&^P).
2. Выведите в ИСП1 схемы секвенций (запись (А <-> В) есть обозначение
формулы (А В) & (В —> А)):
а) А В, -А С, В v С D Н D;
б) А -> В, С -В, (£)—>—А)—» С H-£v А -> (Е-> Dy
в) А —> С, В —> D, -iC v -J) Н -A v -В (гибельная дилемма);
г) I- (А <-> В) <-> (А & В) v (—А & -В);
д) I- —-СА В) (А & -пВ) v (—А&В).
3. Покажите допустимость в ИСП1 следующего правила вывода:
Г1; А, В, Г21~Г3
r!,-i(-Av-iB),r2 НГ3
4. Докажите в ИСП1 допустимость правил введения эквиваленции в ан-
тецедент (<-> К) ивсукцедент (Н <->):
Г1,Г2(-А1,В,А,А2 ГъВ,Г2 НА1;А,А2
Гъ А, В,Г2 1~ Аь А2 г<>|_у Г'1,А,Г2|-А1,В,А2 /|_<>^
ПХА^ВХГгЬАьАг Гъ Г2 h Аъ (А о В), А2
5. Рассматривается сокращённое исчисление И, полученное из ИСЩ
удалением из алфавита ИСТ^ символа «—>«, из множества формул — всех
формул, содержащих «—>«, а из множества правил — правил (—> Н) и (Н —>).
Запись (А —> В) считается обозначением формулы (—A v В).
Докажите, что в исчислении И допустимы правила введения импликации
в сукцедент (Н -») и в антецедент (—> Н):
Г1, Г2 Н Аг, А, А2
ГъА,Г2 НА^В^ ГьВ^НАьАа
Г1,Г2ЬА1,(А^В),А2 Л ГьСА-^ГгЬАьАг
6. Докажите допустимость в HCHj следующих правил вывода:
TjXAvBL^I-A! nXAvBL^HAj
------------(V1 г) , -----------(V о г).
ГьАГгЬА! ГьВ.ГгЬА!
7. Докажите допустимость в ИСЩ правил удаления конъюнкции в сук-
цеденте (H&f) и (Н&2).
8. Запишите правила вывода (Н (&_ Н) и докажите их допустимость
в ИСПГ
232
https:it.ru
9. Докажите, что секвенция выводима в ИСП1 тогда и только тогда, когда
выводим формульный образ этой секвенции.
10. Докажите следующие схемы секвенций в ИСПр
а) Н (VxA ЗхА);
б) (A v В) Н ЗхА, ЗхВ;
в) Зх(А v В) Н (ЗхА v ЗхВ);
г) (ЗхА v ЗхВ) Н Зх(А v В);
д) —iVxA, Vx(A & В) Н VxB;
е) -i3xA, —i3xB Н-i3x(A & В);
ж) -i3xA I- Vx-iA;
з) I- VxA, Зх-iA;
и) I—iVx-i3yA ЗуЗхА;
к) I- Зх(А —> В) —> (VxA ЗхВ).
2. Автоматизация доказательства теорем
в языке нулевого порядка
1*. Восстановите пропущенные секвенции в следующем выводе, постро-
енном в результате применения алгоритма X. Вонга:
AhC,A,B; ВН...,А,В
...И С, А, В
-iA,-iB, AvBhC;
..., —iB v С, A v В Н С
—Av С,..., AvB С
...,B-»C,AvBhC
H..,-,(B->C),4AvB),...
I- —(А —> С) v... v —(A v В) v С
2*. Напишите программу на любом языке программирования, реализу-
ющую алгоритм X. Вонга для установления выводимости в языке нулевого
порядка.
о- Hi ।rnit ri ।
О., i v41 UU.I VU
Упражнение 9
ГЕНЦЕНОВСКОЕ ИСЧИСЛЕНИЕ
НАТУРАЛЬНОГО ВЫВОДА
Тот, кто записывает свои секреты
таким способом, который не позволяет
скрывать их от посторонних —
сумасшедший.
Роджер Бэкон, ок. 1250
Обязательные результаты обучения:
• знать основные понятия
— генценовская система натурального вывода: аксиомы, фигуры заклю-
чения, правила заключения, правила вывода;
— интуиционистское исчисление натурального вывода (NJ);
— классическое исчисление натурального вывода (NK);
— неформальное описание понятия «вывод»;
• уметь
—конструировать доказательства формул в исчислениях NJ и NK;
—проводить анализ вывода в исчислениях NJ и NK;
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
Теоретические сведения
Обычно в математических работах доказываемое предложение
представимо в виде импликации: «если X, то У». Доказываемые
предложения обычно называют теоремами; причём в теоремах,
выразимых в указанном виде, X называют условием (предпосылкой,
допущением), а У — заключением (утверждением). Что же касается
непосредственно самого доказательства, то оно представляет со-
бой цепочку (последовательность) предложений, связанных отно-
шением логического следования.
Далее, можно заметить, что математические доказательства ча-
сто разворачиваются по следующей схеме: 1) доказательство начи-
нается введением в рассмотрение условия доказываемого предло-
жения в качестве допущения; 2) в дальнейшем из уже имеющихся
предложений, к которым всегда можно присоединить ранее уста-
234
https:it.ru
новленные результаты (аксиомы, доказанные теоремы и т. п.), вы-
водятся следствия; 3) доказательство заканчивается получением за-
ключения доказываемого предложения.
Генценовская система натурального вывода является достаточно
удобной и эффективной формализацией отношения выводимости
(доказуемости), приближённой к обычным математическим рас-
суждениям.
Г. Генцен [7, с. 9—10] пишет: «Моя исходная точка зрения за-
ключалась в следующем: формализация логических выводов, про-
ведённая, в частности, Фреге, Расселом и Гильбертом, очень далека
от тех способов рассуждений, которые применяются в действитель-
ности при математических доказательствах. Этим достигаются
значительные формальные преимущества. Я хотел бы прежде все-
го построить такой формализм, который был бы как можно ближе
к применяющимся в действительности рассуждениям. Так возник-
ло «исчисление натуральных выводов» («NJ» для интуиционистской
логики предикатов, «NK» — для классической)».
Вначале отметим, что важнейшее внешнее отличие NJ-выводов
от выводов в системах Б. Рассела и Д. Гильберта следующее: в по-
следних истинные формулы выводятся из некоторого множества
«логических основных формул» посредством применения немногих
правил вывода; «натуральные же выводы исходят вообще не из ло-
гических аксиом, а из допущений, из которых делаются логические
заключения. А затем посредством некоторых дальнейших заключе-
ний результат делается уже независимым от допущений. Мы будем
называть исчисления первого вида логистическими» [7, с. 18].
Определение (по [41, с. 12]).
Генценовская система натурального вывода определяется:
1) выделенным множеством формул (оно может быть пустым),
которое будем называть множеством аксиом;
2) множеством фигур заключения (которое не может быть пу-
стым);
3) множеством правил заключения (которое не может быть пу-
стым);
4) множеством правил вывода (которое не может быть пустым);
5) определением понятия «вывод» («доказательство»).
Приступим к последовательному определению понятий «правило
заключения», «аксиома», «правило вывода», «вывод», «доказательство».
Фигуры заключения для интуиционистского исчисления
натурального вывода
Пусть п g N\{0}, Alt ...,Ап, В — формулы.
Определение [7, с. 11; с. 15; 41, с. XVII].
Фигуры — это «каким-либо образом упорядоченные конечные
множества знаков».
235
https:it.ru
Фигурой заключения будем называть слова вида
АА,..Л , A1A2...AfcAffi]...A&,]
, £еЖ{0},или^-^--------------^-, neN\{0},
В В
причём Аъ А2,..., Ак+п будем называть верхними формулами, В —
нижней формулой, В1г..., Вп — допущениями фигуры заключения.
Определение.
Главной (логической) связкой формулы А будем называть:
а) логическую связку т е {&, v, <->}, если А = (ВтС) для некоторых
формул В и С;
б) логическую связку если А = —В для некоторой формулы В.
Определение.
Логической константой Л (читается: «противоречие», «ложь») на-
зовем некоторый предикатный символ 0-й арности.
Фигуры заключения систем натурального вывода подразделяют-
ся на фигуры введения логической связки, которые позволяют дока-
зывать формулы, в которых эта логическая связка является главной
связкой, и фигуры удаления логической связки, которые позволяют
использовать уже доказанную формулу, в которой данная логиче-
ская связка является главной связкой.
Определение [7, с. 19—24].
Список фигур заключения интуиционистского исчисления натураль-
ного вывода первого порядка (исчисления NJ) содержит фигуры вида:
Фигуры введения и удаления логических связок
Связка Введение... Удаление...
—1 [А] Л , — (приведение к абсурду) А -А Л
& А В А&В А&В А&В А ’ В
V А В АуВ’ АуВ [А] [В] АуВ С С , ,, (разбор случаев) С
—> [А] в (А^В) А(А^В) , , — (modus ponens)
<-> (А—>В) (В—>А) (А++В) (А<->В) (А<->В) (А—>В)’ (В^А)
С* //i iroif ri ।
236
Фигура удаления логической константы
Константа Введение... Удаление...
Л Л А
Фигуры введения и удаления кванторов
Квантор Введение... Удаление...
V [А# XfxA где переменная у не должна входить ни в одно из допущений, от которых зависит формула А VxA (А)?
Я (А)? ЯхА [[A1J] ЯхА В В где переменная у не долж- на входить ни в формулу В, ни в одно из допущений, от которых В зависит, ис- ключая допущение данной фигуры заключения
Фигура заключения «удаление Л» занимает особое место, так как
она описывает свойства логической константы Л (а не логической
связки).
Фигуры заключения для классического исчисления
натурального вывода
Пусть А — формула.
Определение [7, с. 24].
Список фигур заключения классического исчисления натурального
вывода первого порядка (исчисления NK) содержит перечислен-
ные выше фигуры заключения интуиционистского исчисления
натурального вывода.
Кроме того, к списку фигур заключения:
1) либо добавляется аксиомная схема (A v -А) в качестве «уни-
версального» допущения, в результате чего получается классиче-
ское исчисление натурального вывода со схемой аксиом;
2) либо добавляется схема фигур заключения:
(сильное удаление -i);
3) либо удаляется схема фигур заключения «удаление Л» и добав-
ляются следующие схемы:
(сильное удаление -i);
237
https: "и га it.ru
[A] [A]
В -nB
(слабое введение -i, вариант приведения к абсурду).
Фигуры прямого и косвенного заключения
Определение (по [41, с. 11]).
1. Фигурами косвенного заключения исчислений натурального вы-
вода (NJ и NK) будем называть следующие фигуры заключения;
[А]
g
——— (введение -ь, дедукция);
[А] [В]
AvB С С
С~
(удаление v, разбор случаев);
[А]
— (введение приведение к абсурду);
[А] [А]
В —В
(слабое введение вариант приведения к абсурду);
[[А]*]
ЗлА С . _
----—-----(удаление 3).
2. Фигурами прямого заключения исчислений натурального вывода
(NJ и NK) будем называть все фигуры заключения NK, не являю-
щиеся фигурами косвенного заключения.
Правила заключения. Правила вывода
Определение (содержательное).
1. Правилом заключения будем называть правило, описывающее
семантику (смысл) одной из фигур прямого заключения.
2. Правилом вывода будем называть правило, описывающее се-
мантику (смысл) одной из фигур косвенного заключения.
3. (По [41, с. 11]) Правилом вывода будем называть правило, по-
зволяющее получать формулу из целого вывода, взятого в каче-
стве «посылки», и определять, от какого множества формул зави-
сит полученная формула.
238
Формальное определение понятий «правило заключения» и «пра-
вило вывода» тесно связано с определением понятия «вывод».
Неформальное описание понятия «вывод»
Определение (содержательное) [7, с. 15—16].
«Фигура доказательства (или вывод) состоит из конечного числа
формул (по меньшей мере из одной формулы), которые образу-
ют между собой фигуры заключения...
Вывод называется древовидным, если все его формулы являются
нижними формулами не более, чем одной фигуры заключения...
Исходными формулами вывода называются формулы, которые
не являются нижними формулами никаких фигур заключения...
Исходные формулы некоторого вывода называются допущениями...
Конечной формулой вывода называется формула, которая не яв-
ляется верхней формулой никакой фигуры заключения... Вывод
с конечной формулой А называется выводом формулы А».
Неформальное описание процесса построения вывода
Приведём теперь неформальное описание процесса построения вы-
вода. Построение вывода начинается с получения заключения из при-
нятых математиком, производящим вывод, формул, называемых до-
пущениями, с помощью одного из правил заключения или правил
вывода. При этом допущения записываются над горизонтальной чер-
той, а выводимая из них формула — непосредственно под этой чертой.
Затем из полученной формулы и, возможно, других, полученных
таким же способом формул или новых допущений, принятых мате-
матиком, выводится новое заключение с помощью одного из правил
заключения или правил вывода. На этом шаге вывод записывается
так же, как и на первом: все посылки пишутся над горизонтальной
чертой, а заключение — непосредственно под ней.
Продолжая действовать таким способом, мы получаем конструк-
цию в виде «дерева вывода». На каждом шаге построения конструк-
ция является выводом самой нижней своей формулы из множества
формул, входящих в нее в качестве допущений.
Допущения являются самыми верхними вхождениями формул,
при этом будем говорить, что самая нижняя формула зависит
от этих допущений.
Однако в результате определенных шагов вывода полученная
в качестве заключения формула становится независимой от неко-
торых или от всех допущений, и тогда говорят [41, с. 6], что дан-
ные допущения закрываются (отбрасываются). Закрытие (отбра-
сывание) допущений связано с фигурами косвенного заключения,
239
https:it.ru
при этом закрываются только те допущения, которые фигурируют
в квадратных скобках в фигурах косвенного заключения.
Пусть Н — некоторое множество формул.
Определение [41, с. 6].
Правилами вывода (для каждой фигуры косвенного заключения)
будем называть следующие способы закрытия допущений:
1) если существует вывод формулы В из Н о{А}, то можно выве-
сти формулу (А —> В) и закрыть (отбросить) допущение А;
2) если существует вывод формулы Л из Н о{А}, то можно выве-
сти -А и закрыть (отбросить) допущение А;
3) если существует вывод формулы (A v В) из Нг о {А}, вывод
формулы С из Н2 о {А} и вывод формулы С из Н3 о {А}, то можно
вывести формулу С и закрыть (отбросить) допущения А и В, вхо-
дящие во второй и третий выводы соответственно (итак, можно
получить вывод формулы С из Н1 и Н2 и Н3, т. е. формула С не за-
висит от допущений А и В);
4) при наличии выводов формулы НхА из И и формулы В из И о {[А]*},
то можно вывести формулу В и закрыть (отбросить) допущение
[А]* при условии, что предметная переменная у не входит свобод-
но в В и в любое допущение (отличающееся от [А]*), от которого
в данном выводе зависит формула В.
Замечание (по [41, с. 9]).
Различия между классической логикой, интуиционистской логикой
и минимальной логикой просто и ясно выражаются в системах натураль-
ного вывода:
1) для выводов в минимальном исчислении натурального вывода
можно использовать только фигуры введения и удаления для логических
связок и кванторов;
2) для выводов в интуиционистском исчислении натурального вывода
можно использовать эти же фигуры вместе с фигурой «удаление Л»;
3) для выводов в классической логике можно использовать все фигуры
интуиционистского исчисления вместе с аксиомной схемой (A v -А), либо
с фигурой «сильное удаление —>».
Биографические сведения
Генцен Герхард (1909 — 04.08.1945) — немецкий математик.
Основные труды по основаниям математики и математической
логике (формальная система Генцена). Получил докторскую сте-
пень в 1933 г. в Гёттингене под руководством Г. Вейля.
Судьба Г. Генцена была трагичной. Он стал членом нацистской
партии и ректором Пражского университета во время нацистской
оккупации: в 1944—1945 гг. работал в Пражском университете.
За это он был расстрелян (по другим источникам умер в тюрьме).
240
https:/Л: rait.ru
Примеры решения некоторых типов упражнений
Указание (важное).
Введем для непрямых допустимых правил вывода гильбертовско-
го исчисления терминологию, относящуюся к натуральному выводу.
Поясним ее на примере правила «дедукция»:
j----допущение
Но {А} НВ (дедукция)
Н \~(А^В)
f
1--------закрытие (отбрасывание) допущения А
Назовем формулу А допущением, появление буквы А в некотором
множестве гипотез назовем введением допущения А, удаление буквы
А из множества гипотез (т. е. в слове Н Н (А —> В)) назовём закры-
тием допущения А.
Приведём ряд примеров построения натуральных выводов в ис-
числениях NK и NJ с указанием списка допущений и без него. Важно
отметить, что вначале список допущений является пустым, а затем
он постоянно пополняется в процессе построения вывода, который
обычно происходит в направлении «снизу вверх».
Пример 1. Докажите, что формула (А (В —> А)) выводима из пустого
множества {}.
Решение. Приведём два варианта доказательства существования
вывода:
а) в гильбертовском исчислении
{А,В)\-А;{А,В}\~А
{А,В}\~А&В
{А, В} НА
{А}Н(В—>А)
{}Н(А—>(В—> А))
(введение допущений А и В)
(закрытие допущения В)
(закрытие допущения А)
б) е исчислении NJ (приведём два варианта оформления)
А{А,В} В{А,В}
А&В{А,В}
А{А,В}
(В—>А){А)
(А^(В^А)){>
(введение допущений А и В)
(закрытие допущения В)
(закрытие допущения А)
А В
А&В
А
(В->А)
(А—>(В—>А))
(введение &)
(удаление &)
(введение ->)
(введение ->)
Итак, при построении вывода в исчислении NJ все введённые
допущения оказались закрытыми, поэтому построен вывод формулы
(А -> (В -> А)) из пустого множества гипотез.
241
https://urait.ru
Пример 2. Докажите в исчислении NK формулу (-i-A —> А).
Решение. Приведём два варианта описания доказательства:
Первый вариант
Второй вариант
1 j. Список допущении: --А 1. д (сильное удаление -) -а А (введение ) -^А{-.^А} — _— (сильное удаление —0 (введение ) (->-А—>А){} Д
Пример 3. Докажите в исчислениях NK и NJ формулу (А —> -i-A). Реше-
ние. Приведём два варианта описания доказательства:
Первый вариант
Второй вариант
1 2 А -1А (удаление Л список (введение—i) допущений - (введение -» ) 1. А А^-’-А „ . ЛА» U1 А{А, —А} —А{А, —А} ЛМ.^4} (удаление-0 (введение—.) (аТХ> —’
Пример 4. Докажите в исчислениях NK и NJ формулу (-А —> (А —> В)).
Решение.
2 1 г i А -1А (удаление - (удаление Л) список (А->В) Д°Т7И (^А^(А^В)) (вВедеНИе -° 2.А
Пример 5. Докажите в исчислении NK формулу (A v -А).
Решение.
Первый способ. Воспользуемся аксиомой (A v -А).
242
С*" //i iroit i-i ।
1
4 Список допущении
(Av-.A) l.(Av-A)
Второй способ. Воспользуемся фигурой заключения, которая называ-
ется «сильное удаление -»:
Список допущений
1. -i(Av-A)
2. А
2
1 А
-----------------------------(введение v)
(слабое введение -(Av-A) (Av-А)
(введение v) ----------------=А-- 1
____________________________-(Av-А) (слабое введение
-------------^AvA)------------------(сильное удаление -J
Av—А
Пример 6. Докажите в исчислениях NK и NJ формулу
(A^(B^Q)^(B^(A^Q).
Решение.
2 А (А->(В->С)
В (В->С)
с
(А—>С)
В—>(А—>С)
(А^(В^С)^(В^(А^СВ
(удаление ->)
(удаление ->)
(введение ->)
(введение ->)
(введение ->)
Список допущений:
1.(А—>(В—>С)
2.В
З.А
Пример 7. Докажите в исчислениях NK и NJ формулу (А —> В) —> ((А —>
—iB)—>—А).
Решение.
Список допущений:
1. А—>В
2. А—>—В
3. А
(А^В)^((А^В)^^А)
(удаление ->)
(удаление
(введение -О
(введение
(введение
243
https:/Л!га it.ru
Пример 8. Докажите в исчислении NK формулу (-.В -А) <-> (А В).
Решение. Приведём два варианта доказательства.
Первый вариант.
з 1
2 —.В (-1В—>-А)
А-------------- (удаление-»)
---------- (удаление-)
------------------- (введение -)
------—---(сильное удаление
------------------- (введение-»)
------ (введение ->)
(-1В—>-А)<-»(А—>В)
Список допущений:
1.(—В—>—А)
2. А
3.-.В
з 1
г г
А А->В I
В -,В
Список допущений:
1.А—>В
2.—iB
З.А
(А—>В)<->(—iB—>—А)
Второй вариант.
—iB{—В —> —A, А, —iB} (—В —> —A) {—В —> —A, A, —iB} f
A{—iB —> —A, A, —iB} —A{—iB —> —A, A, —iB}
Л-ЬВ->-А,А,->В} (удаление —i)
--£{-£ -> -A, A} (введение —i)
B{-B^-A,A} (сильное удаление —>)
(A-»B){(^B-»^A)} (введение —>)
((-B^^A^A^BM} (введение
Пример 9. Докажите в исчислении NK формулу
(^В^А)^С(В^А)^А).
Решение. В список допущений сразу включим формулу (В v -iB):
4 3 4 2
J. X X 4-
1 В В—>А -,В -Л->А
и _------7-------7-----(удаление-,)
В v —В 71 71
-----------------------(удаление v)
-----------------------(введение ->)
(В-»А)-»А
-----------------------(введение ->)
(^В^А)^((В^А)^А) Д
Список допущений
l.Bv-iB
2.-.В—>А
З.В-»А
4.B|-iB
Пример 10. Докажите в исчислениях NK и NJ формулу ((—Av—В)
->ЧА&В)).
https: "и га it.ru
244
Решение. Воспользуемся новым способом записи списка допущений:
A&B{-Av-£,-A,A&B} A&B{-Av-B,-B,A&B}
А{-А v-B, -Л, А&В} —А{—Av—В,—Л, А&В} B{-Av-B,-B, А&В} -B{-Av-B,-B, А&В}
B{-Av-B,-A,A&B} Л{—Av—В,—В, А&В}
—Av—iB{—Av—В} -t(A&B){—Av—В,—A} -,(A&B){-A v-B,-B}
—i(A&B){—Av—В}
((-Ау-Д)-»-4А&В))
Пример 11. Докажите в исчислениях NK и NJ формулу
((A^C)^((B->C)->(AvB->C))).
Решение. В приведённых выше примерах мы оформляли допущения
в виде списка допущений. Такое оформление допущений более удобно,
когда список допущений не имеет «ветвлений». Однако, если они есть,
то могут возникнуть трудности.
В этих случаях удобнее использовать дерево допущений, которым
является способ записи допущений в исчислениях NK и NJ, при котором
каждой формуле, являющейся допущением, кроме одной, предшествует
только одна формула, также являющаяся допущением.
Допущение, которому не предшествует ни одна формула, будем назы-
вать корнем дерева допущений.
Формулы, входящие в дерево допущений, будем называть вершинами
дерева допущений.
Приведём два варианта оформления допущений:
4 14 2
ф ф ф ф
? А (А->С) В (В->С) Список допущений:
AvB ~ ~ 1.(А^С)
------------------------ (удаление^
-------------------------(введение ->)
(AvB-»C)-----------------3.AvB
------------------------(введение ->)
((B^C)^(AvB^C))---------, Д J 4.АВ
------------------------(введение —>)
(А—>С)—>((В—>С)—>CAvB—>C)j
Дерево допущений.
245
Важно отметить, что дерево допущений строится «снизу-вверх», а спи-
сок допущений — «сверху-вниз».
Пример 12*. Докажите в исчислении NK формулу (((А —>В) —>А) —>А).
Решение. Представим вывод с помощью дерева допущений:
Av(A—>В) д
Дерево
допущений
А—>В (А->В)->А
А
_____А_____
((А^В)^А)^А
Пример 13. Докажите в исчислениях NK и NJ формулу(Х/лА ЯхА).
Решение.
tyX'A (удаление V)
1 (введение Я)
ЯхА_____________
(VxA ЯхА)
Список допущений:
(введение ^)
l.VxA
Пример 14. Докажите в исчислениях NK и NJ формулу (-1ЯхА \fx-A).
Решение.
С*" //< ! ио it i-i I
246
2
1
L Jy (выбор терма t = у) 1 (АН Т 4 (введение 3) -ЯхА ЗхА г , (удаление ->) Л (введение-1) —if Д Iх L свойство операции [-А]у подстановки Список допущений: 1,—.ЗхА 2. [А]*
Vx-A (введение V)
(-ЗхА-> Vx-A) (введение ->)
Пример 15. Докажите в исчислениях NK и NJ формулу
(3xVyA ->Vy3xA).
Решение.
Vy[A]* {Vy[A]* } (введение V)
[ГАТ* H{Vy[A]x } свойства операции
J2<1 * ~ J2>1
---------------- подстановки
[[A£]*{Vy[A]*}
3xVyA{3xVyA} 3x[A]J {Vy[A]* } (удаление 3)
3x[A]£{HxVyA} свойства операции
[МЯЭхУуА} подстановки
VyzLxA{ELxVyA} (введение V)
(zLxVyA VyELxA) (введение —>)
Упражнения для самостоятельного решения
Восстановление пропущенных фрагментов доказательства формул
1. Восстановите пропущенный фрагмент доказательства. В каком ис-
числении (NK или NJ) справедливо восстановленное доказательство?
а)
3 1 3 2
II II Список допущений:
А А^в ...... l.A^B
_______-______ 2....
((А > Л) 3 А
б)
4 3 4 2 Список допущений
Illi 1 В v В
1 В В^А ^В —В—>А
----------------(удаление ->) 2.-В->А
В v —В л л
----------------------(удаление v) 3. В —> А
- 4.В | -В
247
https://u га it.
Доказательство формул в исчислении NK и (или) NJ
2. Докажите следующие формулы в исчислении NK и (или) NJ (х и у—
предметные переменные, А, В, С — произвольные формулы, Е — формула,
в которую х не входит свободно).
Символом ° помечены формулы, которые доказуемы только в NK.
1) А^(В^А);
2) (А^В)^ ((А^(В^О)^(А^С));
3) А^ (В->А&В);
4) (А&В^А);
5) (А&В—>В);
6) (A—>AvB);
7) (B->AvB);
8) (А^С) ^((В^С) ^(А vB^C));
9) (А —> В) —> ((А —>-В) —>-,А);
10) ° (—г-А —> А);
11) (А В) ((В А) (А В));
12) (А^В)^(А^В);
13) (А <-> В) —> (В —> А);
14) (А В) (А В) & (В -> А);
15)0 (д в) v в);
16)0 (А —> В) <-> —.СА & -В);
17)0 (А & В) <-> -.(-A v -В);
18)0 (А & В) —.СА -В);
19)0 (A vB) н -.(-А & -В);
20)0 (A vB) н Мч В);
21) (А & В) <-> (В & А);
22) (AvB)h(BvA);
23) (А <-> В) <-> (В <-> А);
24) А & (В & О (А & В) & С;
25) A v (В v Q н (A v В) v С;
26) * (А (В О (А В) О;
27) А& (BvQhA&BvA&C;
28) A v (В & О (A v В) & (A v О;
29)0 A v (В С) (A v В) (A v О;
30)0 A v (в <-> О <-» (A v В) <-» (A v О;
31) (А —> В & С) <-> (А —> В) &(А^С);
32) ° (А В v С) (А В) v (А С);
33) А (В С) ((А -> В) ы (А О);
33J А —> (В —> С) <-> ((А —> В) —> (А —> С));
34) (А&А)<->А;
35) (A v А) <-> А;
36) A&(AvB)HA;
37) (Av А&В) <->А;
38)0 А & (В v-В) <_^д;
39) A v (В&-В) <->А;
40) (А & В & -В) (В & -В);
41)0 (A v В v -В) (В v -В);
42)0 _,(д & В) (-nA v -В);
43) -.(A v В) (-А &-В);
44)0 _,(д в) (А & -В);
248
https:/Л: rait.ru
45)° —i(A нВ) н (A vB) & -,(A & В);
46)°-i-A <-> A;
47) AeA;
48)°A v—A;
49) —i(A&—A);
50) (A —>B) —> ((В —> C) —> (A —> C));
51) (A —> (В —> C)) <-> (В —> (A —> C));
52) (A—> (B->O) <-> (A&B—>C);
53) -A—>(A—>B);
54)° (A -> B) <-> (-B -> -A);
54J (A & В —> C) —> (A &-iC —>-iB);
542)°(А- + В)<Г ->(-i(A- ->В)- 1 С & -.С);
543)°(А- + В)<Г -»(-i(A- ->В)- ^-А);
544)°(А- + В)<Г -»(-i(A- ->В)- ->в);
55) VxA<-> Vy[A]*;
56) 3xA<->3y[A]*;
57) VxVyA VyVxA;
58) ЗхЗуА <-> ЗуЗхА;
59)° -iVxA <-> 3x—A;
60) -i3xA <-> Vx—A;
61)° VxA <-> ->3x-A;
62)° ЗхА <-> -iVx-A;
63) Vx(A & B) <-> VxA & VxB;
64) Vx(E&A) <->£& VxA;
65)° Vx(E v А) н E v VxA;
66) 3x(A v В) н 3x4 v ЗхВ;
67) 3x(EvA) HEv3x4;
68) 3x(E&A) <->E&3xA;
69) VxE <-> E;
70) HxE^E;
71)° Зх(Е - >А)н >(E^> ЗхА);
72)0 _ >E)<^ > (VxA
73)0 Зх(д _ > (VxA ^3xB);
74) Vx(A — >E)<^. > (ЗхА
75) Vx(E- >A)<- >(E^ VxA);
76) VxA^ ЗхА;
77) 3xVyA —> Vy3xA;
78) 3x(A & В) —>3xA & ЗхВ;
79) (VxA v VxB)-> Vx(A v B);
80) (3xA —> VxB) —> Vx(A —> B);
81) VxVyA->Vx(A)£;
82) 3x(A)£ —>3x3yA.
3. Докажите следующие формулы в исчислении NK и NJ:
а)* (((АА —>В) —>А) —>А);
б) Vx3yP(x, у) & VxVy(P(x, у) Р(у, х)) Vx3y(P(x, у) & Р(у, х)).
Формализация вывода в виде дерева
4. Пусть А, В—произвольные формулы, х и z—предметные переменные.
Покажите, что следующие фигуры являются доказательствами соответству-
ющих формул в исчислении NJ (проведите анализ вывода):
249
https:it.ru
a)
б)
о- Hi iroit i-i ।
vJ.M Ul (Ull.l V4
Л
AvB В В
В
—А—>В
AvB—>(—A—>B)
Х/хА
(А)*
(А)* (А)*
Зх-пА Л
Л
-1Эх-1А
VxA —> -1Эх-1А
Упражнение 10
МЕТОД АНАЛИТИЧЕСКИХ ТАБЛИЦ ДЛЯ
ФОРМУЛ ЯЗЫКА ПЕРВОГО ПОРЯДКА
Истина есть бесценное сокровище,
приобретение которого не сопровождается
угрызениями совести и отнюдь не нарушает
покоя человека. Созерцание ее небесных чар,
ее божественной красоты в полной мере
может оправдать те усилия, которые
мы затрачиваем для ее открытия,
и небесное счастье есть не что иное, как
полное овладение бессмертной истиной.
О. Коши
Обязательные результаты обучения:
• знать основные понятия
— метод доказательства общезначимости и логического следования
формул языка первого порядка с помощью аналитических таблиц;
— правила редукции, применение правила редукции, посылки и заклю-
чение применения правила редукции, аналитическая таблица, замкнутый
список формул, замкнутая аналитическая таблица;
— критерий общезначимости и критерий правильности логического
следования в методе аналитических таблиц;
— аналитические таблицы для отмеченных формул;
• уметь
—конструировать доказательство общезначимости формул в языке перво-
го порядка с помощью аналитических таблиц;
—определять общезначимость формул языка первого порядка с помощью
аналитических таблиц;
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
251
https: //цга it.ru
Теоретические сведения
Единственное средство усовершенствовать
наши умозаключения состоит в том,
чтобы сделать их столь же наглядными,
как у математиков, — такими, что
их ошибочность можно было бы попросту
увидеть, увидеть глазами, а в случае
возникновения разногласий достаточно
было бы только сказать: «Посчитаем,
милостивый государь!», чтобы без дальнейших
околичностей стало ясно, кто прав.
Г. В. Лейбниц
Представление об аналитических таблицах
Известно, что для установления общезначимости формулы
А, в соответствии с определением, необходимо рассмотреть все мо-
дели и все возможные оценки предметных переменных и убедиться,
что в каждом случае формула А принимает значение 1. Однако по-
добный перебор всех моделей и оценок невозможен в силу того, что
их число бесконечно.
Более того, А. Чёрч показал, что не существует алгоритм рас-
познавания общезначимости формул языка первого порядка, в силу
чего решение указанного вопроса представляет собой творческую
задачу.
Однако в математической логике разработан ряд методов, по-
зволяющих упростить, сделать стандартной (и насколько возмож-
но, эффективной) процедуру обоснования общезначимости формул.
Рассмотрим (по [4, с. 112—125]) один из них, который называет-
ся методом аналитических таблиц (см. также всесторонний анализ
этого метода [1]).
Идея метода состоит в том, что утверждение о истинности (об-
щезначимости) формулы А обосновывается посредством доказа-
тельства от противного, т. е. предположение о ложности форму-
лы А должно привести к противоречию. Описанное рассуждение
оформляется в виде последовательности шагов, называемая ана-
литической таблицей, причём каждому шагу рассуждения соот-
ветствует некоторая строка этой таблицы, содержащая один или
несколько списков формул (различные списки разделяются буквой
«|», (вертикальная черта). Присутствие формулы С в некотором
списке соответствует утверждению о ее истинности, а наличие
в списке —iC — утверждению о ее ложности.
Первая строка таблицы, соответствующая первому шагу, содер-
жит один список формул, выражающий исходное допущение данно-
го рассуждения. Если мы собираемся доказать, что 1=А, то этот спи-
252
https:it.ru
сок содержит единственную формулу -А, выражающую допущение
о ложности А.
Переход от строки аналитической таблицы с номером п к строке
с номером (п + 1) осуществляется с помощью формальных правил,
называемых правилами редукции. Эти правила выражают условия
истинности и ложности формул вида (А & В), (A v В), (А —> В), -А,
Х/хА, ЗхА, указывая на следствия, которые могут быть получены
из факта истинности или ложности формул приведённых типов.
Каждое правило редукции позволяет заменять на (и + 1)-м шаге ка-
кой-либо из списков формул в строке с номером п на один или два
новых формульных списка.
Так как целью доказательства от противного является демон-
страция того, что исходное допущение с необходимостью приво-
дит к противоречию, то задача состоит в получении такой строки
аналитической таблицы, каждый формульный список которой со-
держит некоторую формулу С вместе с ее отрицанием —,С. При по-
лучении данного результата утверждение относительно общезначи-
мости А считается обоснованным.
Критерии общезначимости формул
Пусть буквы метаязыка А, В, С обозначают формулы, буквы Г и А
обозначают последовательности формул (возможно, пустые), t —
терм.
Определение (по [4, с. 115—119]).
1. Правилом редукции будем называть слова, перечисленные
в следующей таблице. В некоторых правилах используется сим-
вол «|», обозначающий тот факт, что в случае применения дан-
ного правила возникают два новых списка формул.
Для того, чтобы узнать вербальное название правила, необходи-
мо прочесть заголовки соответствующих столбца и строки (в ква-
дратных скобках указаны графические названия правил).
Правила редукции для логических связок
Буква Логическая связка Отрицание логической связки
& Г,(А&В),А L&J Г, А, В, А г,ча&в),а . L—i&J Г,-А, АI Г,-В, А
V Г, (А у В), А Г,А,А|Г,В,А LV Г,—i(AvB),A . _ г,-л,-в,д Hv]
—> Г,(А^В),Л Г,-А,А|Г,В,А Г,ЧА->В),А Г,А,-В,А
253
https:/Л; rait.ru
Окончание таблицы
Буква Логическая связка Отрицание логической связки
<-> Г,(А^В),Д Г,-А,-В, А | Г, А, В, А Г.ЧА^В).Д Г, А,-В, АI Г,-А, В, А
—1 Г,^А,А Г, А, А Г,-.^А,А Г, А, А
Правила редукции для кванторов
Буква Квантор Отрицание квантора
V г-УхА-А , [V] Г, VxA, (А)*, А где t — замкнутый терм Г,-1Ух4,Д Г, ЧА)*, А где а — предметная константа, не содержащаяся в верхнем спи- ске формул
а Г^А,В] г, САМ, А’ где а — предметная константа, не содержащаяся в верхнем списке формул Г»~,ЭхА»А [_,3] Г,-,ЭхА,ЧА)?,А где t — замкнутый терм
2. Частным случаем (применением) правила редукции называется
выражение, получающееся из правила заменой переменных для
формул и последовательностей формул формулами и последова-
тельностями формул соответственно.
3. Посылками (или данным списком формул) правиларедукции будем
называть последовательности формул, расположенные над чертой.
4. Заключением применения правила редукции, (новым списком
формул) назовём последовательности формул, расположенные
под чертой.
5. Будем говорить, что новый список формул, стоящий в & под
чертой, получается из данного списка формул, стоящего над чер-
той, по данному правили, если 0 — применение некоторого пра-
вила вывода.
Определение [4, с. 119].
1. Аналитической таблицей будем называть конечную или беско-
нечную последовательность строк 11} 12,..., каждая строка которой
1п содержит конечное число списков формул языка первого порядка.
Каждая последующая строка/п+1 получается из предшествующей
1п заменой какого-нибудь списка формул на один или два новых
списка формул на основании некоторого правила редукции.
2. Замкнутым списком формул назовём список формул, который
содержит некоторую формулу С и ее отрицание —,С.
254
https:/Л: rait.ru
3. Замкнутая аналитическая таблица — это аналитическая табли-
ца, содержащая конечное число строк, причем каждый список формул
в последней строке таблицы, является замкнутым списком формул.
Критерий общезначимости первопорядковых формул [4,
с.119].
Формула А является общезначимой формулой, если и только если
существует замкнутая аналитическая таблица, первая строка кото-
рой содержит единственный список формул, состоящий из един-
ственной формулы -А.
Критерий истинности логического следования [4, с. 119].
Из множества формул {А1з А2, Ап} логически следует формула
В, если и только если существует замкнутая аналитическая таблица,
первая строка которой содержит единственный список формул, со-
стоящий из формул А1г А2,..., Ап, -В.
Приведем (по [4, с. 119—120]) рекомендации, облегчающие про-
цесс установления общезначимости формул. Термин «рекоменда-
ции» используется, так как процедура построения аналитической
таблицы не является алгоритмической (в частности, процесс вы-
бора термов в кванторных правилах является творческим).
1. Правила редукции разделим на две группы:
а) правила, применение которых не увеличивает числа фор-
мальных списков в следующей строке таблицы ([&], [-iv], [-i —>],
[-.-.], [V], [-.V], [3], [-.3]);
б) правила, применение которых увеличивает количество фор-
мульных списков ([-1&], [v], [—>]).
Построение аналитической таблицы упростится, если правила
второй группы применять только после того, как применены все
возможные правила первой группы.
2. Среди правил первой группы в первую очередь следует при-
менять правила редукции (([&], [-iv], [-i —>], [—i—i],), а только после
этого применяются правила для кванторов ([V], [—1V], [3], [—13]).
3. Среди правил редукции для кванторов следует вначале при-
менять правила [—1V] и [3], которые требуют введения новых пред-
метных констант, а лишь затем правила [V] и [-13], не содержащие
ограничений на терм t. Причём в качестве t при применении пра-
вил [V], [—13] к некоторому формульному списку следует выбирать
какой-то из термов, уже содержащихся в формулах этого списка,
если таковые термы имеются.
В противном случае в качестве t выбирается любой замкнутый
терм.
Определение необщезначимости формул
Укажем случаи, когда построенная аналитическая таблица свиде-
тельствует о необщезначимости формулы А (или о том, что из фор-
мул А1} А2, ...,Ап логически не следует формула В).
255
https:it.ru
1. Первая строка таблицы включает единственный список, со-
стоящий из формулы -А (или из формул Ab А2, •••» Ап> а сама
таблица незамкнута, но содержит конечное число строк, и к фор-
мульным спискам последней строки невозможно применить ника-
кое правило редукции.
2. Аналитическая таблица, начинающаяся с формулы -А (или
с формул Аь А2, ..., An, -В), на каждом шаге своего построения яв-
ляется незамкнутой таблицей, но при этом остаётся возможность
дальнейшего применения правил редукции.
Указанная ситуация может возникнуть только в силу специфи-
ки правил редукции [V] и [—13], применение которых не устраня-
ет из соответствующих списков формулы VxA и -пЗхА и поэтому
может быть осуществлено многократно по отношению к одним
и тем же формулам.
Подобная аналитическая таблица может получиться в двух слу-
чаях:
а) если она в принципе не может замкнуться, сколь дол-
го бы мы ее не строили, т. е. когда А не является общезначимой
формулой (или из А1г А2, ,Ап логически не следует В);
б) если таблица не замыкается по причине того, что неудачно
используются правила [V] и [—13], а именно, в процессе их приме-
нения не удаётся найти нужную подстановку термов.
Поэтому в описанной ситуации нельзя делать однозначный вы-
вод о необщезначимости формулы А (или отсутствии следования
формулы В из формул А1г А2, ..., Ап).
В целях простоты изложения применение метода аналитических
таблиц будем ограничивать замкнутыми формулами (формулами,
не содержащими свободных переменных), т. е. аналитические та-
блицы будут строиться для обоснования того, что 1= А лишь в слу-
чае, когда А является замкнутой формулой.
Аналитические таблицы для отмеченных формул
Я в львиный ров и в крепость погружён
И опускаюсь ниже, ниже, ниже...
О. Мандельштам
Существуют различные варианты метода аналитических таблиц
(см. [1]). Кратко опишем один из них.
Определение (по [3, с. 190]).
Отмеченной формулой называется формула, префиксом которой
является или символ/, или символ t; при этом tA означает, что фор-
мула А оценивается как истинная, /А означает, что формула А оце-
нивается как ложная.
Аналитическая таблица строится в направлении сверху вниз, со-
стоит из отмеченных формул и представляет собой дерево отмечен-
256
https:/Л: rait.ru
ных формул, в котором выделятся цепи отмеченных формул, являю-
щиеся путями в дереве. При этом корнем дерева является:
1) fA, если доказывается утверждение 1= А;
2) tAlf tA2,..., tAn,fB, если доказывается утверждение А1г А2, ...,
AnkB.
Определение (по [3, с. 190]).
Цепью аналитической таблицы называется последовательность
формул (без пропусков вхождений отмеченных формул), начинаю-
щуюся с самой верхней формулы таблицы до одной из самых ниж-
них формул.
Дальнейшие шаги по построению аналитической таблицы осу-
ществляются с помощью правил редукции, которые применяются
к отмеченным формулам, находящимся в некоторой цепи таблицы,
и могут привести либо к продолжению построения данной цепи,
либо к ее расщеплению на две самостоятельные цепи.
Определение.
Замкнутым термом называется терм, не содержащий предмет-
ных переменных.
Определение (по [3, с. 191—194]).
Правилами редукции называются приведённые ниже слова.
Пропозициональные правила
tA tB t(AvB) tA|tB [‘V] £4|tB ^[4 fA
£4|fB fA fB KA-B) [f^l tA fB tA
Кванторные правила
t(VxA) г ,,, , -
-----[tV], где (А)^ результат подстановки вместо всех свобод-
tf-A)?
ных вхождений переменной х замкнутого терма t;
f(VxA)
------ [fV], где (А)£—результат подстановки вместо всех свобод-
f(A)k
ных вхождений переменной х предметной константы к, которая
не содержится в данной цепи таблицы;
-----[t3], где (A)£ — результат подстановки вместо всех свобод-
1(А)£
ных вхождений переменной х предметной константы к, которая
не содержится в данной цепи таблицы;
f(ELxA) [.эд где — результат подстановки вместо всех свобод-
f(A)?
ных вхождений переменной х замкнутого терма t.
257
Правила редукции всегда применяются к тем логическим связкам,
содержащимся в формуле А, следующей за префиксами tnf, ко-
торые являются в ней главными связками.
Определение [3, с. 194].
Аналитической таблицей называется конечное или бесконечное
древесно упорядоченное множество отмеченных формул (дерево
отмеченных формул'), получаемое из начальной цепи применени-
ем правил редукции.
Задача, решаемая построением аналитической таблицы, состо-
ит в получении аналитической таблицы, каждая цепь которой со-
держит и отмеченную формулу tC, и отмеченную формулу/С (такая
таблица называется замкнутой таблицей).
При получении этого результата утверждение об общезначимо-
сти формулы А считается обоснованным.
Критерий общезначимости формул и логического следования
(по [3, с. 195]).
1. Формула А является общезначимой (обозначается 1= А), если
и только если существует замкнутая аналитическая таблица, на-
чальная цепь которой начинается с отмеченной формулы fA.
2. Из формул А1г А2, ..., Ап логически следует В (обозначается А1г
А2, ..., Ап 1= В), если и только если существует замкнутая аналити-
ческая таблица, начальная цепь которой начинается с отмеченных
формул tA1} tA2, ..., tAn,fB.
Примеры решения некоторых типов упражнений
...объяснение — необычная пища:
большую порцию не обязательно труднее
проглотить.
Д.Дойч
Пример 1. Используя метод аналитических таблиц, докажите обще-
значимость формул: 1) A v -А; 2) (((А —> В) —> А) —> А);
3) (НхУуА—> УуЭхА).
Решение.
1)
—ща—>в)—>а)—>а)
(А—>В)—>А,-А
ЧА->В),-А|А,-А
А,-В,-А
258
3)
43xVyA -> Vy3xA)
3xVyA, -. Vy3xA -'
Vy(A)?,^Vy3xA ~ [3]
Vy(A)*,^3x(A)? bV]
Vy(A)?,(A)ff,^3x(AX [V]
Vy(A)?, (A)?£, -n3x(A)?, 4A)?£ [^3]
Пример 2. Исследуйте с помощью аналитических таблиц общезначи-
мость формул: 1) ЗхА XfxA; 2) ЗхА.
Решение.
1)
-(ЗхА VxA) [
ЗхА, -1 VxA р]
(А)?,-Л/хА
(А)?, ЧА)?
(А)?, (А)?
2)
-ЗхА |-^э1
-.ЗхА, ЧА)? [—.Я]
-пЗхА,ЧА)*,ЧА)?
В случае 1 формульный список последней строки не содержит формул
вида С и —iC. При этом дальнейшее применение правил редукции невоз-
можно, поэтому формула (ЗхА VxA) не является общезначимой.
В случае 2 сделать вывод о необщезначимости формулы нельзя.
Пример 3. Докажите с помощью аналитических таблиц логические
следования: 1) А & В1= А; 2) А, В1= А & В.
Решение. В первой строке каждой аналитической таблицы поместим
последовательность формул, содержащую формулы из посылок и формулу,
являющуюся отрицанием заключения:
А&В,—А _ п А,В,ЧА&В) _
------[——>] 2)--f-------— [
А,В,—А А, В,-А А, В,-В
Построенные таблицы получились замкнутыми, следовательно, логи-
ческие следования истинны.
Пример 4. Используя метод аналитических таблиц для отмеченных
формул, докажите общезначимость важных (!?) формул:
1) (А В) ((А -В) -А); 2) (-А В) ((-А -В) А).
Решение.
1)
f ((А В) -> с С а -> ^В) -> -А))
f((A—>-В)—>-А)
t(A->-В)
259
https://
t.!
2)
fA
t(-B)
fB
fbA)
tA
t(A->B)
£4 | tB
f ((-Л B) ((-A -nB) -> A))
t(-A—>B)
f(-A) tB
tA
f((-A->-B)->A)
£4
t(-A->-B)
f(-A) t(—B)
Пример 5. Используя метод аналитических таблиц для отмеченных
формул, постройте контрпример для формулы (А —> В) & В —> А.
Решение. Немного изменим обозначения и построим незамкнутую
аналитическую таблицу:
f((A—>В)&В—>А
£4
t((A—>В)&В)
tB
t(A^B)
£4 | tB
Теперь, используя только незамкнутую часть таблицы,
выпишем контрпример: (fA, tB).
Для полученных значений формула (А —> В) & В —> А при-
нимает значение «ложь».
Пример 6. Используя метод аналитических таблиц для отмеченных
формул, постройте контрпример для формулы (A v В) А & В.
Решение. Немного изменим обозначения и построим незамкнутую
аналитическую таблицу:
f((AvB)->A&B
t(AvB)
f(A&B)
tA tB
£4 | fB £4 | fB
Теперь, используя только незамкнутую часть таблицы,
выпишем контрпример: (tA,fB), (fA, tB).
Для полученных значений формула (A v В) А & В при-
нимает значение «ложь».
260
https://и га it.ru
Упражнения для самостоятельного решения
... неразрешимых проблем нет, есть
неприятные решения.
А. Маринина. Закон трёх отрицаний
1. Методом аналитических таблиц докажите общезначимость следующих
формул в языке первого порядка (х и у — индивидные переменные, А, В,
С—произвольные формулы, Е—формула, в которую х не входит свободно):
1) А^(В^А);
2) (А^В)^ ((A^(B^Q)^(A^C));
3) А^(В^А&В);
4) (А&В—>А);
5) (А&В^В);
6) (A—>AvB);
7) (В—>AvB);
8) (A->Q->((B->C)->(AvB->C));
9) (А ->В) -> ((А -> ^В) -> -.А);
10) (—i—А—>А);
11) (А^В)^ ((В^А)^(А^В));
12) (А^В)^(А^В);
13) (А^В)^(В^А);
14) (А«В)н(АчВ)&(В^А);
15) (A^B)hHvB);
16) (А->В) <->-,(А&-.В);
17) (А&В) h-i(^Av-iB);
18) (А & В) <-> -.(А -В);
19) (АуВ) <->-i(-A &-iB);
20) (АуВ) ++ (—А^В);
21) (А&В)^(В&А);
22) (АуВ) ++(В у А);
23) (А<->В)<->(В<->А);
24) А & (В & С) <-> (А &В) & С;
25) A v (В v Ц о (A v В) v С;
26) (Ао(ВнОн(ЛнВ)нО;
27) А& (В у С) ^А&В уА&С;
28) A v (В & С) <-> (A vB) & (A v С);
29) A v (В->О <-> (АуВ) -> (AvC);
30) A v (В <-> С) <-> (А у В) <-> (A v С);
31) (А—>В&С)<-> (А—>В) &(А—>О',
32) (А^ВуО<^(А^В)у(А^С);
33) А -> (В <-> С) <-> ((А ->В) о (А С))-
33j) А^ (В ->С) <-> ((А—>В) (А^ОУ
34) (А&А)<->А;
35) (AvA)hA;
36) А& (АуВ) <^А;
37) (AvA&B)<^A;
38) А & (В у —В) А;
39) A v (В & -В) А;
40) (А&В &^В) о (В &^В);
41) (А у В у—В) (В у-В);
42) -.(А &В) н R v -iB);
261
https:it.ru
43) -i(A v В) <-> (-Л &-В);
44) -i(A —> В) <-> (А & -В);
45) -i(A нВ) н (A vB) & -.(А & В);
46) -i-iA<hA;
47) А^А;
48) A v -Л;
49) ->(A&-iA);
50) (А~>В) ((В С) (А^ Q);
51) (А —> (В —> С)) <-> (В —> (А —> С));
52) (А—> (В->С)) <-> (А&В—»С);
53) -пА-»(А-»В);
54) (А —>В) <-> (—В —>-Л);
54J (А & В —> С) —» (А &-iC —>-В);
542)° (А -> В) <-> (-.(А В) С & -О;
543)° (А -> В) <-> (-.(А В) -А);
544) (А В) (-.(А В) В);
55) VxA <-> Vy[A]*;
56) 3xA<-»3y[A]*;
57) VxVyA XfyXfxA;
58) ЗхЗуА <-> ЗуЗхА;
59) -.VxA <-> Зх-Л;
60) -ЗхА <-> Vx-iA;
61) VxA <->-1Эх-1А;
62) ЗхА <-> -iVx-iA;
63) Vx(A & В) <-> VxA & VxB;
64) Vx(E&A) <->Е& VxA;
65) Vx(E v A) <-> E v VxA;
66) 3x(A v B) <-> ЗхА v ЗхВ;
67) 3x(EvA) ^EvHxA;
68) 3x(E & A) <-> E & ЗхА;
69) VxE <-> E;
70) 3xE<^E;
71) 3x(E -> A) ++ (E -> ЗхА);
72) 3x(A E) ++ (XfxA E);
73) Зх(А В) (VxA ЗхВ);
74) Vx(A E) (ЗхА E);
75) Vx(E A) (E VxA);
76) VxA—>3xA;
77) HxVyA —> VySxA;
78) Эх(А&В) ^ЗхА&ЗхВ;
79) (VxA v VxB) —> Xfx(A v B);
80) (HxA VxB) —> Vx(A —> B);
81) VxVyA-»Vx(A)£;
82) 3x(A)^3x3yA.
2. Методом аналитических таблиц определите, являются ли общезна-
чимыми следующие формулы языка первого порядка (х, у — предметные
переменные, А, В, С — формулы):
а) ЗхВ & ЗхС -> Зх(В & С);
б) Vx(A v В) (VxA v VxB);
в) Vx(A —> В) —> (ЗхА —> XfxB);
г) (ЗхВ —> XfxB);
д) (Vy3xA 3xVyA).
262
https:it.ru
Упражнение 11
ПОНЯТИЕ О МАТЕМАТИЧЕСКИХ ТЕОРИЯХ.
ТЕОРИЯ РАВЕНСТВА
Наши формализации исправляют
наши интуиции, в то время как
наши интуиции формируют наши
формализации.
Дж. Маихилл
Обязательные результаты обучения:
• знать основные понятия
— теория, формализация, формальная аксиоматическая теория;
— математическая теория первого порядка;
— гильбертовское исчисление первого порядка с равенством;
— теория равенства;
— теории частичного, линейного и плотного порядка;
• уметь
—конструировать доказательство формул и допустимости правил вывода
в гильбертовском исчислении первого порядка с равенством;
—устанавливать существование выводов формул из гипотез в гильбер-
товском исчислении первого порядка с равенством;
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
Теоретические сведения
Понятие о математической теории
Напомним, что основными объектами логики как раздела фило-
софии являются «понятие», «суждение», «умозаключение», «теория».
Определение.
Теория — это целостная система абстрактных объектов, отража-
ющая основные закономерности исследуемого явления.
Для построения теории используется метод, который называется
формализацией.
263
https:it.ru
Определение.
Формализация — это отображение результатов мышления в не-
который язык. Выделяют три уровня формализации в зависимо-
сти от используемого языка:
1) естественноязыковая (естественный язык);
2) научная (частично искусственный язык);
3) формальная теория (искусственный язык).
Остановимся на разновидности формальной теории, которая на-
зывается аксиоматической теорией.
Выделяют три этапа аксиоматической теории:
1) содержательная аксиоматическая теория;
2) полуформальная аксиоматическая теория;
3) формальная аксиоматическая теория.
Определение.
Формальная аксиоматическая теория содержит следующие ком-
поненты:
1) искусственный язык для записи понятий, содержащий: а) ал-
фавит; б) термы; в) формулы;
2) формализованную логику, которая содержит: а) логические
аксиомы; б) правила вывода; в) определение понятия «вывод»;
3) нелогические аксиомы теории.
Определение.
Математическая теория первого порядка — это формальная ак-
сиоматическая теория, искусственным языком которой являет-
ся язык первого порядка, формализованная логика представляет
собой логическое исчисление первого порядка, а нелогические
аксиомы «формулирует» содержательная математика.
Гильбертовское исчисление первого порядка с равенством
Мы пользуемся обычной интуитивной теорией
равенства, основанной на представлении, что
знаком = можно соединять лишь символы,
обозначающие один и тот же объект.
В. И. Нечаев. Числовые системы, 1975
Вначале напомним, что отношение равенства — это бинарное
отношение, состоящее из пар равных элементов некоторого множе-
ства и только из них.
В множество предикатных символов языка формальной системы
первого порядка включим двухместный предикатный символ, кото-
рый обозначается «=» и называется знаком равенства.
264
https:/Л: rait.ru
Замечание.
Знак «=» в 1557 г. предложил английский врач и математик Ре-
корд: «...ибо, — писал он, — нет ничего более равного, чем две
параллельные прямые» (цит. по [136]). Знак равенства, который
он писал, по крайней мере, в пять раз «длиннее» современного
и действительно подобен отрезкам параллельных прямых.
Знак равенства играет особую роль, состоящую в том, что при
последующей интерпретации этот символ в качестве своего значе-
ния имеет отношение настолько близкое к отношению равенства,
насколько это возможно. С этой целью к множеству аксиомных
схем классического гильбертовского исчисления первого порядка
добавляют новые формульные схемы, которые называются аксиом-
ными схемами равенства.
Существует несколько способов определения аксиомных схем
равенства. Все они основываются на философском принципе за-
мещения {взаимозаменяемости), принадлежащем Г. В. Лейбницу
и Г. Фреге.
Определение.
1. [175] Равенство (по Г. В. Лейбницу) — это отношение взаим-
ной заменимости (подстановочности) объектов, которые именно
в силу их взаимной заменимости считают равными.
2. [2, с. 520] Принцип замещения (взаимозаменяемости) на равно-
значное имя (по Г. Фреге) состоит в следующем: «Если одно из со-
ставляющих имён, входящих в данное сложное имя, заменить име-
нем, имеющим то же, что и у заменяемого, значение, то сложное
имя, получившееся в результате такой замены, будет иметь зна-
чение, совпадающее со значением исходного сложного имени».
3. [162] «И совмещающиеся друг с другом равны между собой»
(седьмая аксиома Евклида).
4. [6, с. 80] Принцип взаимозаменимости может быть сформули-
рован в виде следующего правила вывода:
Ф(а);а = Ь
Ф(Ь) ’
где а=Ъ обозначает, что а и Ъ являются именами одного и того же пред-
мета; Ф(а) — высказывание, в составе которого встречается имя «а»
(имеющее, возможно, несколько вхождений); Ф(Ъ) — результат за-
мены в этом высказывании каких-либо вхождений «а» на «Ь».
Принцип взаимозаменимости в математической логике выражен
в следующем способе определения аксиомных схем равенства, явля-
ющемся одним из наиболее распространённых.
Пусть х, у, z — метасимволы для обозначения предметных пере-
менных, t — метасимвол для обозначения терма, А — метасимвол для
обозначения формулы языка формальной системы первого порядка.
265
Определение.
1. (По [19, с. 353; 13, с. 143]) Гилъбертовским исчислением (ис-
числением предикатов) с равенством будем называть гильбертов-
ское исчисление первого порядка такое, что:
а) в алфавите языка первого порядка выделен двухместный пре-
дикатный символ «=» (читается: «равно»);
б) схемами аксиом являются схемы аксиом 1—15 классического
гильбертовского исчисления первого порядка, дополненные следу-
ющими аксиомными схемами (аксиомными схемами равенства):
\/х(х = х) (рефлексивность равенства);
\/х\/у(х = у -^((А)* ^(А)р) (подстановочностъ равенства).
Аксиомная схема «подстановочностъ равенства» часто (см. [53,
с. 271; 38, с. 86; 10, с. 231]) формулируется следующим «осла-
бленным» образом:
VxVy(x = у (А А*)),
где А — произвольная формула, а А* обозначает формулу, которая
получается из формулы А заменой каких-нибудь (не обязательно
всех) свободных вхождений предметной переменной х вхождения-
ми у, с соблюдением условия, чтобы переменная у была свобод-
ной для тех вхождений х, которые заменяются;
в) основные правила вывода совпадают с основными правилами
вывода классического гильбертовского исчисления первого по-
рядка.
2. [22, с. 111] Будем говорить, что гильбертовское исчисление
является исчислением предикатов с равенством, если аксиомные
схемы равенства имеют следующий вид:
а) х = х; б) x = y^(t = (t)y); в) х = у^(А++(А)*).
Практическое правило составления
аксиомных схем равенства
Все животные равны. Но некоторые
животные более равны, чем другие.
Дж.Оруэлл. Скотный двор
1. В число аксиомных схем включаются формульные схемы:
a) Vx(x = x) (рефлексивность равенства);
(б) VxVyVz(x =у (x = z^y = z)) (первая аксиома Евклида).
2. Для всякого п-местного функционального символа f1 2 в число
аксиомных схем включаются формульные схемы
Vx1...VxnVy1...Vyn(x1 =уг&...&хп = уп->
—>(fn(x1,...,xn) = fn(y1,...,yn))).
266
https://и гз it.ru
3. Для всякого п-местного предикатного символа Р (отличного
от предикатного символа «=») в число аксиомных схем включаются
формульные схемы
X/x1...X/xnXty1...Xtyn(x1 =уг&...&хп = уп->
-> (Рп(хг,хп) Рп(у1}..., уп))).
1. Правило существенно опирается на результаты, изложенные в [54,
с. 41; 27, с. 98].
2. Благодаря включению аксиомной схемы 1М, значение знака «=»
в любой интерпретации обязано содержать отношение равенства.
3. [162] Первая аксиома Евклида формулируется так: «Равные одному
и тому же равны между собой».
Иногда в качестве аксиомных схем равенства используются фор-
мульные схемы, отличные от получаемых с помощью описанного
Практического правила составления аксиомных схем равенства.
Это связано с тем, что новая система аксиом может более кратким
способом описывать множество доказуемых формул, а «неисполь-
зованные» аксиомные схемы равенства можно вывести из новых
аксиомных схем равенства и исходных аксиомных схем.
Приведём обоснование сказанного.
Пусть t — произвольный терм языка первого порядка.
Предложение (по [38, с. 86; 8, с. 214]).
В гильбертовском исчислении с равенством имеют место следу-
ющие утверждения:
a) I— t = t (рефлексивность равенства');
б) I-VxVy(x=y —>у = х) (симметричность равенства);
в) I- VxVyVz(x = у (у = z х = z)) (транзитивность равен-
ства);
г) I- VxVyVz(x = у (х = z —^у = z)) (первая аксиома Евклида);
д) \-х = у^((А)*++(А)*);
Симметричность
е) h Vx(x = x)&VxVy(x = y ^у = х)&
Транзитивность
& VxVyVz(x = у —> (у = Z —> X = z)) <->
<-> Vx(x = х) & VxVy Vz(x = у —>(х = z у = z)).
\_____________.,____________S
Первая аксиома Евклида
Теоремы а, б, в называются характеристическими свойствами
отношения равенства.
267
Доказательство.
А. Упражняйтесь.
Б.
Рефлексивность
равенства
Подстановочность
def
равенства (А = z=x)
——^2(перестановкапосылок)
(х = х); (х = х)->(х = у->у = х) умр)
х = у^у = х
(б) Подстановочность равенства
i г
X = y^y = X‘y = X^(y = Z^X = Z),
-------------------------------(транзитивность).
x = y^(y = z^x = z)
Г. Приведём доказательство, опирающееся только на характери-
стические свойства отношения равенства:
(б)
I
(в)
г
х = у —>у = х;у = х—>(x = z—>у = z),
--------------------------------(транзитивность).
x = y-»(x = z-»y = z)
Итак, формула VxVyVz(x = у —> (х = z —>у = z)) выводима из ха-
рактеристических свойств отношения равенства.
Д. Анализ приведённого ниже вывода выполните самостоятель-
но:
{x = y}hy = х;{у = х}Н(А)* -^(А)£
{х=у}Н(А)*->(А)*
Нх=у->((А)*<->(А)р
Е. Доказуемость формулы
(х = х) & (х = у —> у = х) & (х = у —> (у = Z —> X = Z)) —> (х = х) &
(х = у —> (х = z —>у = z)) установлена в теоремах а — г. Остается до-
казать формулу
(х = х) & (х = у —> (х = z —> у = z)) (х = х) & (х = у —> у = х) &
(х=у-> (y = z->x = z)J.
Упражняйтесь.
Предложение доказано.
268
https://иrsit.ru
Квантор «существует единственноех, такое, что...»
Иногда мы часами сидели в кафе.
Па клочке бумаги или мраморной
поверхности стола он писал один символ
или строчку вида у - f(x), и, подавая
или обсуждая различные идеи, мы оба
таращились на эту надпись. Словно
хрустальный шар, эти символы, которые
стояли у нас перед глазами, должны были
помочь нам сконцентрироваться.
С. Улам. Приключения математика
С предикатным символом «=» тесно связано широко распро-
странённое в математике утверждение: «существует единственное
х такое, что А».
Пусть А — формула, х иу — предметные переменные.
Определение.
1. [19, с. 180; 21, с. 184] Введём обозначение Е1!хА (читается: «су-
ществует единственное х, такое, что А») так:
def
а) 3!хА = 3x(A&Vy([A]* -^х = у));
def
б) 3!хА = 3x(A&Vy(^x = y-> ЧА]*)).
2. [38, с. 89] Введём обозначение З-рсА (читается: «существует
единственное х, такое, что А») следующим образом:
def
^хА = ЗхА & VxVy(A &[А]* -> х = у).
3. (По [43, с. 96]) Введём обозначение 3!хА (читается: «существу-
ет единственное х, такое, что А») следующим образом:
def
а) 3!хА = ЗхА&Vx(A&Vy([A]* -^х = у));
def
б) 3!хА = 3xVy((A)* <-> х = у).
Предложение.
В классическом гильбертовском исчислении первого порядка
с равенством справедливы следующие утверждения:
1) I-Зх(А&Vy([A]* ->х = у))<н>Зх(А&Vy(-iX = у ЧА]*));
2) I- 3iXA Зх(А & Vy([А]* -> х = у));
3) H3x(A&Vy([A]* ->x = y))<-^3xVy((A)* <^х = у);
4) [19, с. 180] {3!хА} Н (А)* -> ((A)* -> г = s),
где г и s — термы, х g FV(r) kJ FV(s).
Доказательство.
1. Упражняйтесь.
2. Построим следующее древесное доказательство:
269
httpaJ/yrai
{A, [ A]p h A & [ A]*; {A & [ A]xy,
A&[A]£ -^x = y}\-x = y
{A,[A]£,A&[A]£ -y-x = y}\~x = y
{A, VxVy(A & [A]* -> x = у) } h
(сечение)
(введение V, дедукция)
------~^x—22-----------------(введение V, у FV(A))
{A, VxVy(A & [A]* -> x = у) } h
bVy([A]* ->x = y)
{A, VxVy (A & [A]* -> x = у)} h
|-A&Vy([A]* —>x = y)
{A, VxVy(A & [A]* -> x = y) } h
I- 3x(A & Vy( [A]* -> x = y))
{ЗхА, VxVy(A & [A]* —> x = у) } h-
(введение &)
(введение 3)
(введение 3)
I- Зх(А & Vy( [A]* -> x = y))
0|-3xA&VxVy(A&[A]* ->x = y)->
(дедукция, введение
&)
3x(A & Vy( [A]* -> x = y))
3. Упражняйтесь.
4. Построим следующее древесное доказательство:
VxVyVz(x = у (х = z у = z))
{х = г, х = s} I- г = s
{А,(А)?,(А)*,(А)? ->х = г}и{(A)* ^x = s}hr = s
{(А)*,(А)*, A, Vy([A]*->х =
(расширение)
(введение V)
= y)}^{Vy([A]* ->x = y)}hr = s
{ (А)*, (A)J, A, Vy ([А]* -> х = у) } h г = s
{ (AV, (А V, Зх( А & Уу ([ А]^ х = у) ) } h г = s
{(AV,(AV,3!xA}hr = s
{3!хА} I- (AV ((А)? г = s)
(сокращение)
(введение 3)
(по определению 3!
итж.у gFV(A))
Предложение доказано.
Замечание (важное).
У логиков существует разногласие по вопросу о том, является ли пре-
дикатный символ «=» нелогическим знаком.
Так, по Е. Расёвой нР. Сикорскому [42, с. 222], «формализованные теории
первого порядка содержат в своем языке некоторый бинарный предикат,
который соответствует отношению равенства и называется знаком равен-
270
С*" //< ! ио it i-i I
ства». С другой стороны, в [54, с. 42] находим следующую формулировку:
«Функциональный символ или предикатный символ, отличный от =, называ-
ется нелогическим символом; остальные символы называются логическими».
Остается заметить, что выше мы фактически говорим о построении
теории равенства.
Теории частичного, линейного и плотного порядка
Равенство, которое мы требуем,
является наиболее прочным воплощением
неравенства.
Г. Лихтенберг
Определение (по [17, с. 53]).
Пусть о = (=2, <2).
Теория частичного порядка задаётся следующими аксиомами:
1) Vx(x<x);
2) VxVy(x<y&у<х —>х=у);
3) VxVyVz (х <у &у < z -ь х < z).
Определение (по [17, с. 53]).
Пусть о = (=2, <2).
Теория линейного порядка задаётся следующими аксиомами:
1) Vx(x<x);
2) VxVy(x<y &у <х—>х=у);
3) VxVyVz(x <у &у < z х < z);
4) VxVy(x<y vy <х).
Определение (по [17, с. 53]).
Пусть о = (=2, <2).
Теория плотного порядка задаётся следующими аксиомами:
1) Vx(x<x);
2) VxVy(x<y &у <х—>х=у);
3) VxVyVz(x <у &у < z х < z);
4) VxVy(x<y vy <х);
5) VxVy(x <у & —х =у 3z(x < z & -iZ = х & z <у & -iz =у));
6) ЗхЗу—х=у.
Определение (по [17, с. 54]).
Пусть о = (=2, <2).
Теория плотного порядка без концевых точек задаётся следующи-
ми аксиомами:
1) Vx(x<x);
2) VxVy(x <у &у <х —>х =у);
3) VxVyVz(x <у &у < z —>х < z);
271
https:/Л: га it.ru
4) VxVy(x<y vy<x);
5) VxVyfx <y & -ix =y —> Bz(x < z & -iz = x & z <y & —iz =y));
6) 3x3y(-ix=y);
7) Vx3y(x <y &-ix =y);
8) Vx3y(y <x & —oc =y).
Примеры решения некоторых типов упражнений
Пример 1. Покажем, что в классическом гилъбертовском исчислении
с равенством существует доказательство формулы
ЗхУу ([А]* <-> х - у) ЗхА.
Решение. Построим следующее древесное доказательство:
D
{ЗхУу([А]* <-> х = у)} I ЗхА
01- ЗхУу([А]* <-> X = у) ЗхА
введение Зв "антецедент"
дедукция
_____________\~У = У____________
{4A)J}l-y = y
{-(У = У)}Ь(А)*
{-(y = y)v[A]*}l-(A)*
{у = у->[А]£}Н(А)*
{([А]* ->х=у)*,(х=у->[А]ррI-(А)*
{([А]*->х = у)*}1-(А)*
{Уу([А]^->х = у)}1-(А)*
{Уу([А]* х = у)} I- ЗхА
D
расширение
контрапозиция
расширение
введение У в "антецедент"
введение Зв "сукцедент"
введение 3 в "антецедент"
Пример 2 [19, с. 180].
Пусть х — предметная переменная, А — формула, г и $ — термы,
х g FV(r) и FV(s). Докажите, что в гилъбертовском исчислении с равен-
ством существует вывод формулы (г = 5) из множества гипотез
{(А)*,(А)*,3!хА}
Решение.
______________________________________ введение 3
{(А)?, (А)* Зх(А& Уу([А]* -> х = у))} I- г = 5
r jy______________по определению3!
{(A)*,(A)*,3!xA}l-r = s ит. K.ygFV(A)
272
Докажите самостоятельно
4-
{X = Г, X = 5} Ь Г = 5
{А,(А)?,(А)?,(А)? -> х = r}o{(A)* -> х = s} Н г = s
{(A)*, (A)*, A, Vy([A]* -> х = у)}o{Vy[A]* -> х = у} h г = s
{(A)?, (A)*, A, Vy([A]* -> х = у)} I- г = 5
D
расширение
введение V
сокращение
введение Я
Упражнения для самостоятельного решения
Гилъбертовское исчисление первого порядка с равенством
1. (По [38, с. 86]) Докажите, что в гильбертовском исчислении с ра-
венством для любых предметных переменных х, у, z и для любого терма t:
a) I— t = t (рефлексивность равенства');
б) I- (х=у—>у = х) (симметричностьравенства);
в) Н (х = у —> (у = z —> х = z)) (транзитивность равенства);
г) Н (х = у —> (х = z —>у = z)) (первая аксиома Евклида);
д) Нх = у->((А)з<->(А)р;
е) I- Vx(x = х)& VxVy(x = у у = х)& VxVyVz(x = у (у = z х = z))
<-> Vx(x = х) & VxVyVz(x = у ^(х = z у = z)).
Указание. Для установления характеристических свойств отношения
равенства достаточно доказать две формулы: x = xnx=y^>(x = z^>y = z).
Отметим [8, с. 214], что вторая из этих формул может быть получена с по-
мощью характеристических свойств, так что система, содержащая формулы
х = х, х=у—>у = х, х=у—>(y = z—>x = z) равносильна системе, состоящей
из формул х - х, х-у —> (х - z ~^у - z).
2. [38, с. 86] Установите существование доказательства следующих фор-
мул в гильбертовском исчислении первого порядка с равенством:
a) Vx(B<->3y(x = y&[B]p);
б) Vx(B<-> Vy(x = y —>[В]р);
в) Vx3y(x = у).
3. Пусть х, у, z — различные предметные переменные, Н — множество
формул, не содержащих предметную переменную х свободно, А — формула,
г, s, t — термы, предметные переменные у, г, s, t свободны для х в формуле
А, а у g FV(A). Докажите, что в классическом гильбертовском исчислении
с равенством справедливы следующие утверждения:
1) свойства Я! [19, с. 180]:
Hu{(A)f,[A^}Ft=y>
а Ни{(А)^} НЭ!хА ’
б) H3!x(t = x);
в) {(A)*,(A)*,3!xA}|-r = s;
г) {3xVy(x = y <->(А)р} 1-ЭхА;
2) свойства [38, с. 90]:
a) HVx31y(x = y);
273
https://и га it.ru
6) H31xA^-3xVy(x = y
в) FVx(AoB)^(31xAo3lxB);
г) l-3xVy(x = y ч-КА^^ЗрсА;
3) свойства Вг и Вк
I- (^xA-^ixA).
Указание. В 2а воспользуйтесь рефлексивностью и транзитивностью
равенства.
Теории частичного, линейного и плотного порядка
1*. Сформулируйте и докажите несколько теорем теории: а) частичного
порядка; б) линейного порядка; в)* плотного порядка; г) плотного порядка
без концевых точек.
о- Hi iroit i-i ।
kJ J O1 UU.I 14
Упражнение 12
ЯЗЫК ТЕРМОВ СИГНАТУРЫ о
Сказать по правде, она понятия
не имела о том, что такое «широта»
и «долгота», но ей очень нравились
эти слова. Они звучали так важно
и внушительно!
Л. Кэррол
Обязательные результаты обучения:
• знать основные понятия
— алфавит языка термов, термы сигнатуры о;
— строгая дизъюнкция, штрих Шеффера, стрелка Пирса;
— подтермы терма сигнатуры о;
— индукция по построению множества термов;
— язык термов;
• уметь
— распознавать терм заданной сигнатуры;
— конструировать термы с заданными свойствами;
— конструировать доказательства утверждений о термах, используя
индукцию по построению множества термов сигнатуры о;
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленных в упражнении.
Теоретические сведения
Алфавит языка термов
Пусть JnKобозначают произвольные множества.
Определение [27, с. 74—75].
def
Алфавитом языка термов назовём множество G = Gz u G2 и G3 и
G4 о G., где
def
1) Gj = {х0, х1г х2, ...}—множество предметных переменных;
def п.
2) G2 = {fj}}, j g J, nj g N \ {0} —множество функциональных сим-
волов; при этом символ называется поместным функциональ-
ным символом (или функциональным символом арности п^;
275
https:/Л: га it.ru
def
3) G3 = {-i, &, v, ©, |,4-} — множество связок: при этом
связки имеют следующие названия: -i (отрицание), & (конъюнк-
ция), v (дизъюнкция), —> (импликация), <-> (эквиваленция), ©
(строгая дизъюнкция, сложение по модулю 2), | (штрихШеффера),
4 (стрелка Пирса);
def
4) G4 = {ak},ke К — множество предметных констант;
def
5) G5 = {„ (, )} —множество вспомогательных символов; сим-
волы из множества G5 называются: , — (формальная) запятая,
( — (формальная) левая (открывающая) скобка, ) — (формаль-
ная) правая (закрывающая) скобка.
Формальная запятая печатается «жирным» шрифтом для того,
чтобы не смешивать ее с «неформальной» запятой. В дальнейшем,
если опасность такого смешения возникать не будет, то (формаль-
ная) запятая будет печататься обычным шрифтом.
Определение [27, с. 74].
Сигнатурой (от средневек. лат. signature — знак, подпись, от лат.
def
signo —указываю, обозначаю) назовём множество о = G2 и G3 и G4.
Важность понятия «сигнатура» определяется тем, что различные
языки термов отличаются друг от друга лишь сигнатурами.
Заметим, что для задания сигнатуры необходимо и достаточ-
но выбрать множества J и К, а также отображения множества
J в N. Меняя эти множества и отображения, можно изменить сиг-
натуру, а следовательно, и алфавит языка термов.
Замечания.
1. Функциональные символы арности 2 называют также бинарными,
а символы арности 1 — унарными.
2. [10, с. 273] Символ «V» для дизъюнкции введён А. Уайтхедом
и Б. Расселом; Д. Гильберт и В. Аккерман обозначали импликацию зна-
ком «—>»; символ «&» как обозначение конъюнкции впервые использо-
ван, вероятно, Д. Гильбертом и В. Аккерманом; символ «-1» для отрица-
ния предложен А. Гейтингом (у Д. Гильберта и В. Аккермана этот символ
обозначается чертой над отрицаемым выражением).
3. В содержательной математике для функциональных символов часто
используют индивидуальные, специально придуманные для этого знаки,
например, «2»,«+», «•» случается, функциональный символ заменяют осо-
бым расположением переменных, например, ху.
Кроме того, бинарные функциональные символы обычно располагают
между переменными: так, пишут + х2 вместо + frj, х2) и т. п. Унарные
функциональные символы иногда пишут после переменной (х2), а ино-
гда—до переменной (самостоятельно придумайте пример).
Для удобства анализа «правильных» слов используется унифи-
цированный способ образования функциональных символов и уни-
фицированный способ их взаимного расположения с предметными
переменными.
Термы сигнатуры о
Для описания языка термов потребуется синтаксическая катего-
рия, «термы» (от ср.-век. лат. terminus — выражение, слово, термин).
Определение [160, с. 581].
Терм — это выражение формального языка, являющееся анало-
гом имени объекта или именной формы.
Данное понятие полностью соответствует школьному понятию
«выражение», оно позволяет строить «схемы вычислений» для полу-
чения одних элементов из других посредством заданных операций
(другими словами, получать «более длинные» выражения из «более
коротких»).
Выделим из множества всех слов в алфавите G «правильные»
слова, для чего зафиксируем сигнатуру о и приведём индуктивное
определение понятия «терм сигнатуры о». Для обозначения термов
воспользуемся символами языка исследователя tlf ..., tn.
Определение.
1. Предметные переменные и предметные константы являются
термами сигнатуры о.
2. Если/1 является n-местным функциональным символом из G2,
a tp ..., tn — термы сигнатуры о, то/01, ..., tn) является термом
сигнатуры о.
Сказанное в пункте (2) определения можно записать в виде сле-
дующего правила построения терма сигнатуры о:
fnh-tn
3. Если tT и t2 — термы сигнатуры о, то слова
~'^1» 01 & ^), 01v ^2)’ 01 ^г), 01 t2), 01 ® t2), 01112), (tj 4- t2)
являются термами сигнатуры о.
Сказанное в пункте 3 определения можно записать в виде следу-
ющих правил построения термов:
h h h *1 f2 0 *2 *1 *2 0 *2 h f2
—itj (ti&t2) Oivt2) 0i —>t2) (ti<->t2) 0i ©t2) O1O2) 01
277
https: Ou rait.ru
(4) Никаких других термов сигнатуры о, кроме построенных
в пунктах 1, 2 и 3, нет.
Приведённое определение не запрещает случая J = 0 (т. е. сиг-
натура о может не содержать функциональных символов из множе-
ства G2).
Замечание (по [33, с. 12]).
Индуктивное определение множества «правильных» слов некоторого
формального языка можно начинать словами:«... — это наименьшее под-
множество выражений языка, удовлетворяющее условиям...».
Определение дополнительных связок
Связки строгая дизъюнкция, стрелка Пирса и штрих Шеффера
синтаксически определяются с помощью отрицания, конъюнкции,
дизъюнкции.
Пусть А и В — формулы сигнатуры о.
Определение (синтаксическое).
1. Строгой дизъюнкцией называется связка ©, причём
def
(А ©В) = ((А & —iB) v (—А & В)).
2. [16, с. 417] Штрихом Шеффера {антиконъюнкцией) называет-
ся связка | (М. X. Шеффер, 1913), причём
def
(А | В) = -i(A&B).
3. [16, с. 417] Стрелкой Пирса (антидизъюнкцией) называется
связка Ф (Ч. С. Пирс, 1880), причём
def
(А 4, В) = —i(AvB).
Подтермы терма сигнатуры о
Определение (содержательное).
Подтермом терма t сигнатуры а называется подслово терма t,
само являющееся термом сигнатуры о.
Определение (индуктивное).
1. Если х — предметная переменная, то х является подтермом
терма х сигнатуры о.
278
https: "и га it.ru
2. Если а — предметная константа, то а является подтермом
терма а сигнатуры о.
3. Если/4*1, •••> tn) — терм сигнатуры о, то подтермами этого
терма сигнатуры о являются/"(tj, tn), t1} ..., 1пи все подтер-
мы термов tj, tn.
4. Если —itj, (tj & t2), (tj v t2), (tj —> t2), (tj <-> t2), (tj @ t2), (tj | t2),
(с2 t2) являются термами сигнатуры а, то подтермами этих
термов сигнатуры о являются:
“>^1> (^1 & 01 v 01 —> ^2^> 01 ^2)’ 01 ® ^2^» 01 | ^2)> 01 'I' ^2)
и все подтермы термов и t2.
5. Никаких других подтермов заданного терма сигнатуры о,
кроме построенных в пунктах 1, 2, 3, 4 нет.
Индукция по построению множества термов
Обозначим Т — множество всех термов сигнатуры о.
Для доказательства утверждений, относящихся к индуктивно
определённому множеству Т, используется следующий способ до-
казательства.
Определение (индукции по построению множества Т) [22, с. 54—
55].
Для доказательства того, что некоторое свойство Р выполняется
для всех элементов множества Т, достаточно доказать, что:
1) каждая предметная переменная обладает свойством Р;
2) каждая предметная константа обладает свойством Р;
3) если t1} являются термами сигнатуры о, обладающими
свойством Р, а...» tn) — терм сигнатуры о, то/ЧСи ...» tn)
также обладает свойством Р;
4) если t1} ...,tn являются термами сигнатуры о, обладающими
свойством Р, a -itp (t2 & t2), (ti v t2), (t2 -> t2), (г2 <-> t2), (t2 © t2),
(ti I t2), (t2 Ф t2) являются термами сигнатуры о, то —it2, (tx & t2),
Ui v t2), (ti -> t2), (ti <-> t2), (tj © t2), (ti I t2), (ti Ф t2) также обла-
дают свойством P.
Определение.
1. Скобочным, балансом слова в алфавите, содержащем буквы «(»
п «)», будем называть разность между числом открывающих и чис-
лом закрывающих скобок, имеющих вхождение в данное слово.
2. Словом, сбалансированным по скобкам, будем называть слово
(в алфавите, содержащем буквы «(« и «)»), скобочный баланс ко-
торого равен 0.
279
https:it.ru
Теорема.
1. [22, с. 55] Всякий терм сигнатуры о содержит одинаковое ко-
личество вхождений левых и правых скобок.
2. [22, с. 55] Количество вхождений (формальных) запятых
в терм сигнатуры о равно п - к, где п — сумма арностей всех вхож-
дений в терм функциональных символов, а к — количество вхожде-
ний в терм функциональных символов.
3. [39, с. 185] В любом начале терма сигнатуры о открывающих
скобок не меньше, чем закрывающих.
4. [39, с. 185] Начало терма сигнатуры о, содержащее скобку
и сбалансированное по скобкам, совпадает с самим термом.
Доказательство. Упражняйтесь. Воспользуйтесь индукцией
по построению множества термов сигнатуры о.
Язык термов
Язык есть машина и не следует
допускать, чтобы пружины его скрипели.
Автор неизвестен
Определение.
Языком формальной системы термов (или просто языком тер-
def
мое) будем называть кортеж Lt = (G, Т).
Язык формальной системы термов значительно проще языка
формальной системы нулевого и первого порядка. Поэтому из-
учение языка термов («игрушечного» языка) часто является лишь
подготовкой к изучению важнейшего класса формальных систем
математической логики — формальных систем нулевого и первого
порядка.
Замечание.
Каждая формула языка нулевого порядка, содержащая п атомов
А1г Д2, •••А определяет некоторую функцию от п аргументов, сопостав-
ляющую любому набору длиной п, составленному из элементов множе-
ства {0,1}, единственный элемент того же множества.
Возможно ли решение обратной задачи? Заметим, что для решения
этой проблемы приходится расширить алфавит языка нулевого порядка.
Упражнения для самостоятельного решения
Термы сигнатуры а
1. Докажите, что слово fi(x3, Oq), /^(oq, щ, a2)) является термом
сигнатуры {Oq, щ, а2, f22}.
280
https://urait.ru
2. (По [27, с. 77, № 1])
Пусть J1 — одноместный, g2 — двухместный, h3 — трехместный функ-
циональные символы. Являются ли термами сигнатуры {f1, g2, h3} слова:
a) ,f(g2(Xo,*i));
б) /Kg2^,/1^)));
в) /1(g2(x0),k3(x0,x1,x2));
г) g2(f1(^2,^3(^0,^l,^2)));
д) f1(g2(x0),h3(x0,x1,x2));
е) g2(f1(x2), h3(x0, g2(*i> x2), *i, x2))?
3. [27, c. 77, №5]
Опишите множество термов, в которые имеют вхождения кроме вспо-
могательных букв только следующие буквы: а) предметная переменная
х0 и функциональный символ/1; б) предметная переменная х0 и функцио-
нальный символ g2.
Индукция по построению термов сигнатуры о
4. [22, с. 55]
Докажите, что всякий терм сигнатуры о содержит одинаковое количество
вхождений левых и правых скобок.
5. [22, с. 55]
Докажите, что количество вхождений (формальных) запятых в терм
сигнатуры о равно и - к, где п — сумма арностей всех вхождений в терм
функциональных символов, а к — количество вхождений в терм функцио-
нальных символов.
6. [39, с. 185]
Докажите, что в любом начале терма сигнатуры о открывающих скобок
не меньше, чем закрывающих.
7. [39, с.185]
Докажите, что начало терма сигнатуры о, содержащее скобку и сбалан-
сированное по скобкам, совпадает с самим термом.
http
о- Hi iroit i-i ।
kJ J O1 UU.I 14
Часть 3
АВТОМАТИЗАЦИЯ ПОИСКА
ЛОГИЧЕСКОГО ВЫВОДА
https:it.ru
Лабораторная работа 13
ПОИСК ЛОГИЧЕСКИХ ВЫВОДОВ В РЕЖИМЕ
ДИАЛОГА «ЧЕЛОВЕК-КОМПЬЮТЕР»: СИСТЕМА
DEDUCTIO, ГИЛЬБЕРТОВСКОЕ ИСЧИСЛЕНИЕ
Распространение ЭВМ и программирования
делают математическую логику прикладной
наукой. Каста математических логиков —
жрецов-хранителей священного огня оснований
математики — к своему изумлению оказалась
перед лйцом нашествия орд программистов, чья
математическая культура близка к варварству,
но которые, тем не менее, вдохновляемые своими
пророками структурного программирования,
стремятся зажечь факел от животворного
огня и утащить его к себе, чтобы осветить углы
своих подразделений... Тем не менее, для того,
чтобы установить союз столь разных культур,
каждой стороне —логикам и программистам —
необходимо преодолеть свои комплексы
неполноценности, выработать способность
к взаимопониманию, а главное — увериться
в своей интересности для другой стороны.
А. П. Ершов
Обязательные результаты обучения:
• знать
— системы доказательства теорем;
— возможности системы интерактивного поиска доказательства теорем
Deductio;
— компоненты, интерфейс и опции системы Deductio.
• уметь
— описывать логические системы в системе Deductio;
— вводить данные, строить доказательство и вывод формул в гильбер-
товском исчислении в системе Deductio;
— осуществлять замену временного терма на предметную переменную.
• владеть
— знаниями, представленными выше;
—методами решения задач, представленных в Лабораторной работе.
285
https: "и га it.ru
Теоретические сведения
Редакторы доказательств и автоматические генераторы
доказательств
Логика, оторванная от своего
естественного носителя—человеческого
мозга, заморожена в микросхемах
современного компьютера.
Ю. И. Манин
В современном информационном обществе возникла задача
передачи части мыслительных действий человека компьютеру, что
отразилось в возникновении новой области исследований — ис-
кусственном интеллекте, в одном из своих направлений исследу-
ющей возможности автоматизации доказательства математи-
ческих теорем (деятельность такого рода обычно рассматривается
как «интеллектуальная», если ее осуществляют люди). Более того,
доказательство теорем является, в некотором смысле, естественным
направлением, в котором следует вести работы по расширению воз-
можностей компьютера.
Считается, что история современной математической логики бе-
рет начало в трудах Г. В. Лейбница (XVII в.), который предложил
создать формальный универсальный язык «linua characteristica»,
в котором можно было бы сформулировать любое утверждение,
а также построить для него исчисление — «calculus ratiocinator».
Если бы удалось создать такое исчисление, то оно автоматически
решало бы вопрос об истинности того или иного утверждения.
В появлением компьютеров были созданы две компьютерные про-
граммы, которые определили два основных направления в области
автоматического поиска доказательств. Первая программа была соз-
дана М. Дэвисом на ламповом компьютере Johniac (США, Institute for
Advanced Studies, 1954). Программа реализовала технику разреши-
мости для арифметики и «умела» доказывать, что сумма двух чётных
чисел является чётным числом (это первое в истории доказательство
математического утверждения, генерированное компьютером).
Вторая программа, умеющая доказывать ряд предложений
из классической книги «Principia Mathematica» Б. Рассела и Н. Уайт-
хеда, была создана А. Невелом, Дж. К. Шоу и Г. Саймоном.
Хао Ван (1958) разработал первую программу по автоматиче-
скому доказательству, которая доказала 350 теорем из «Principia
Mathematica» для чистого исчисления предикатов с равенством.
Независимо от этого над доказательством математических ут-
верждений работала группа учёных в национальной лаборатории
Аргонны (Argonne National Laboratory) под руководством Дж. Ф. Ро-
бинсона, которая обнаружила (1965) алгоритм доказательства тео-
рем, основанный на методе резолюций.
286
https: "и rait.ru
Современные системы доказательства теорем подразделяются
на две большие группы.
1. Системы интерактивного поиска доказательства тео-
рем (Proof Checker), называемые также редакторами доказательств
и представляющие собой системы, которые под своим контролем
дают возможность пользователю конструировать доказательство.
Более точно, для уменьшения объёма поиска при доказательстве
теорем система осуществляет взаимодействие с пользователем,
который может быть хорошо осведомлён о наилучшей стратегии
построения доказательства. Обычно такие системы помогают в по-
иске доказательства за счет сохранения списка действий, которые
должны быть проделаны, и предоставления подсказок о возможных
путях доказательства.
Как правило, для доказательства должно быть выполнено много
мелких шагов, и требуется «тесное» взаимодействия с пользовате-
лем. Обычно люди пропускают небольшие части доказательств (ис-
пользуя слова «тривиально» или «аналогично»), тогда как програм-
ма требует явного присутствия этих частей. Процесс верификации
с использованием программ автоматического доказательства тео-
рем является медленным и трудоёмким. Кроме того, используемые
инструменты обычно требуют достаточно высокой квалификации
пользователей для того, чтобы направлять и сопровождать процесс
доказательства.
Наконец, проблема доказательства теорем экспоненциально
сложна, т. е. формула длины п может иметь доказательство экспо-
ненциального размера от п, а поиск доказательства требует вре-
мени экспоненциального от его длины (другими словами, доказа-
тельство теорем дважды экспоненциально по отношению к длине
доказываемой формулы).
Для интерактивных программ доказательства теорем эта слож-
ность значительно уменьшается.
В большинстве своём системы интерактивного поиска доказа-
тельств основываются на теории типов.
Примером редакторов доказательств является программа
Deductio (А. В. Смирнов, А. Е. Новодворский, 1991—1996), с помо-
щью которой можно работать со следующими логическими систе-
мами:
1) алгебра логики;
2) аксиоматическое исчисление предикатов по Клини;
3) интуиционистская логика высказываний;
4) натуральный вывод с равенством;
5) натуральный вывод с равенством и эквиваленцией;
6) натуральный вывод с эпсилон-термом;
7) аналитические таблицы в форме натурального вывода;
8) система Пеано;
287
https: "и га it.ru
9) теория абелевых групп;
10) натуральный вывод с аксиомами родства, а также позволяет
конструировать собственные логические системы.
2. Автоматические генераторы доказательств (Automated
Prover), в которых роль пользователя сводится только к постанов-
ке задания системе («требуется доказать теорему»). Далее авто-
матический генератор работает до тех пор, пока не будет найдено
доказательство или не выполнится некоторое условие окончания
работы генератора, в качестве которого обычно используется кон-
струирование контрмодели для доказываемого утверждения.
Приведём примеры автоматических генераторов доказательств
теорем в натуральном выводе в логике первого порядка: Thinker
(Д. Пеллетье, 1998), Symlog (Ф. Портораро, 1998), Prover (В. А. Бо-
чаров, А. Е. Горчаков, В. О. Шангин, 1996—2000).
Задача проверки истинности формулы сводится к задаче провер-
ки ее выполнимости (напомним, что формула является истинной
в данной интерпретации, если ее отрицание не выполнимо).
Задача выполнимости для формул по-английски называется
«Satisfiability Modulo Theories» (SMT). В 1960 и 1962 гг. М. Дэвис,
X. Патнэм, Д. Лонгеман и Д. Лавленд показали, как решение задачи
SMT может быть реализовано в контексте доказательства формул
в языке первого порядка, а именно: авторы разработали алгоритм
DPLL (аббревиатура, составленная из первых букв фамилий авторов:
Davis — Putnam — Longeman — Loveland), который использует общую
процедуру проверки выполнимости формул в логике первого порядка
и является основой при построении алгоритмов решения задачи SMT.
На основе упомянутых результатов было разработано множество
алгоритмов проверки выполнимости в логиках, производных от ло-
гики первого порядка. Реализации таких алгоритмов используются,
в частности, в дедуктивной верификации программ и называются
SMT-системами проверки выполнимости (англ. SMT-solvers).
Из разработанных на текущий момент (2014) SMT-систем про-
верки выполнимости отметим такие (см. [104, с. 10]): Barcelogic,
Simplify, Theorema, Z3.
Алгоритм DPLL использует в своей работе алгоритм проверки
пропозициональных формул. Поскольку на данный момент извест-
ны только экспоненциальные по времени алгоритмы решения задачи
выполнимости пропозициональных формул, алгоритм DPLL имеет
экспоненциальное время работы, и в современных SMT-системах
проверки выполнимости используются различные эвристики для
снижения трудоемкости.
Замечание.
Современные системы формальной верификации программ, осно-
ванные на формальных спецификациях, используют в качестве основ-
ной составной части одну из SMT-систем проверки выполнимости.
288
https: //ц га it.ru
Краткие сведения по использованию системы Deductio
Рассмотрим более подробно программу Deductio, предназначен-
ную для интерактивного поиска доказательств и выводов теорем
языков нулевого и первого порядков при помощи аксиом, правил
вывода и алгоритмов автоматизации поиска вывода в следующих
исчислениях:
1) гилъбертовское исчисление с основными правилами вывода;
2) генценовское исчисление натурального вывода.
В системе Deductio экран разбит на два окна и строку между
ними.
Верхнее большое окно далее будем называть главным, нижнее
окно — окном ввода, строку между ними — рабочей строкой.
Верхняя строка экрана называется строкой состояния системы.
1. Выбор логической системы
Для выбора логической системы, войдите в главное меню клави-
шей <Esc> и выберите в нём позицию File\Logic. В появившемся
меню выберите логическую систему и нажмите клавишу < Enter >.
2. Ввод посылок и заключения
Для ввода доказываемой теоремы войдите в главное меню и вы-
берите режим File\New.
В главном окне появится знак И, который называется «штопор»
(в терминологии авторов — «дырка») и расположенный на месте
вывода, который предстоит построить. Ниже «штопора» может рас-
полагаться только одно заключение, выше — посылки.
После завершения вывода «штопор» исчезает.
Для ввода посылки необходимо:
1) нажать клавишу < Insert > ;
2) ввести посылку в окно ввода (внизу экрана есть подсказка,
с помощью которой можно ввести логические знаки, используя
функциональные клавиши);
3) нажать клавишу < Enter >.
В главном окне появится посылка.
Аналогичным образом вводятся и другие посылки.
Для ввода заключения необходимо:
1) переместить курсор под знак I- и нажать клавишу < Пробел >;
2) ввести заключение в окно ввода и нажать клавишу < Enter>.
В главном окне появится заключение.
Если необходимо внести исправления в уже введённую строку,
то поместите на нее курсор и нажмите клавишу < Пробел >; таким
образом можно откорректировать и посылки, и заключение.
Если требуется полностью удалить введённую строку, то поме-
стите на нее курсор и нажмите клавишу < Delete >.
289
https:/Л: rait.ru
Закончив ввод посылок и заключения, нажмите клавишу <Esc>
и выйдите из режима New.
3. Бескванторные правила вывода
Вспомним основное бескванторное правило вывода:
А (А—>В)
В
(modus ponens).
Основные правила вывода применяются сверху вниз, т. е. для
применения правила необходимо иметь посылку или аксиому, рас-
положенную выше знака К Нажав пробел (или <Esc> и Construct\
Apply Rule), мы входим в меню правил вывода.
Для применения аксиомы необходимо выбрать аксиомную схему
(установить на нее курсор и нажать <Enter>), а в окне ввода ука-
зать формулы для подстановки их вместо метабукв Fi3 следуя под-
сказкам программы. Применяя правило, необходимо установить
курсор в рабочем окне на нужную формулу, выбрать ее клавишей
«Пробел» и нажать < Enter >
Пример.
2 А
2 А
3 А —> В —> Modus Ponens —> 3 А —> В
4 В
4 В
В меню правил вывода выбираем Modus Ponens:
Fl; Fl—>F2I~F2.
В качестве Fl выбираем формулу в строке 2, Fl —> F2 — в строке 3.
В результате применения правила вывода получим В и построение
дерева вывода закончится.
4. Кванторные правила вывода
Вспомним основные кванторные правила вывода:
А^В
А^Х/хВ
,xgFV(A);
А^В
ВхА^В
,xgFV(B).
Будем писать А (х) и говорить «А — формула, в которую предмет-
ная переменная х входит свободно». Итак, в формуле VxA(x, у) пере-
менная х связана, а у — свободна.
290
j )Ни»о-//i iroit 1-1
Замечание.
Система Deductio контролирует свободные и связанные вхождения
переменных не во всех случаях, т. е. за этим приходится следить самому
пользователю.
При применении аксиом 14 и 15 языка первого порядка (в кото-
рых присутствует операция «подстановка» ) система Deductio
«просит» ввести переменную х и терм t.
Пример.
Применение аксиомы 14 для формулы А(х), свободной переменной
def
хи терма t = у даст следующий результат:
3 VxAQc) —>А(у)
1 I-
2 ... (заключение')
Опишем с помощью примеров процессы построения выводов
в гильбертовской системе.
Работа с примерами решения упражнений
См. Пример 1, Пример 2, Пример 3, Пример 4, Пример 5.
Вывод.
Система Deductio может быть использована в качестве средства
проверки выводов, построенных «вручную», однако она малоэффек-
тивна для поиска доказательств в гильбертовском исчислении.
Примеры решения некоторых типов упражнений
Мудрые не говорят пустых слов,
боясь того, чтобы дела их не были
несоответственны их словам.
Китайская мудрость
Пример 1. Постройте вывод в гильбертовском исчислении:
СоА,СоВ,С1-А&В.
Решение. После ввода посылок и заключения на экране появится:
2 С z) A premise
3 С Z) В premise
4 С premise
1 Ь
5 А&В
291
Условия задачи введены. Применим правило вывода: нажать клавишу
<Пробел>, выбрать правило из меню правил вывода и нажать <Enter>.
В рабочей строке находится выбранное правило вывода.
Применим правило «ModPon» к 4 и 2. В рабочей строке появится:
Fl;FloF2=>F2
где будет выделена абстрактная формула F1. Это означает, что система
Deductio просит указать формулу, соответствующую F1.
Для этого нужно: переместить курсор на формулу, соответствующую
F1, и нажать клавишу < Пробел >. В результате формула изменит цвет.
Далее выделится F1 о F2 и проделываются те же операции.
После нажатия клавишу < Enter > получим:
2 С о A premise
3 С э В premise
4 С premise
6
1
5
А
I-
А&В
МР; 4, 2
Применим правило «ModPon» к 4 и 3:
2
3
4
6
7
СоА
CdB
С
А
В
premise
premise
premise
МР; 4, 2
МР; 4, 3
1 I-
5 А&В
Воспользуемся аксиомой «&3». В рабочей строке появится:
=>Flo(F2o(Fl&F2)).
В окно ввода нужно ввести формулы, соответствующие абстрактным
формулам F1 и F2. В нашем случае А соответствует F1, а В соответствует
F2. После ввода каждой формулы нажмите клавишу < Enter>.
После проделанных операций на экране появится:
2
3
4
6
7
8
1
5
С^>А
С=)В
С
А
В
Ad(Bd(A&B))
h
А&В
premise
premise
premise
MP; 4, 2
MP; 4, 3
&3
Применим правило «ModPon» к 6 и 8:
2 СоА
3 CoB
4 С
6 А
7 В
8 Ао(Во(А&В))
9 Во (А&В)
premise
premise
premise
МР; 4, 2
МР; 4, 3
&3
МР; 6, 8
292
https:/Л: rait.ru
1 5 h А&В
Применим правило «ModPon» к 7 и 9:
2 3 4 6 7 8 9 5 С о A premise С о В premise С premise А МР; 4, 2 В МР; 4, 3 А о (В о (А & В)) &3 В о (А & В) МР; 6, 8 А&В МР; 7, 9
Вывод завершён.
Вывод можно перенумеровать. Для этого войдите в главное меню
и выберите в нём режим Construct\Renumber.
В результате перенумерации вывода произойдёт и соответствующее
перенумерование в анализе вывода. Тогда на экране появится:
1 2 3 4 5 6 7 8 С о A premise С о В premise С premise А МР; 3,1 В МР; 3, 2 А о (В о (А & В)) &3 В о (А & В) МР; 4, 6 А&В МР; 5, 7
Пример 2. Постройте вывод в гилъбертовском исчислении:
{С—>А,С—>В, С}\-А&В.
Решение. Вначале построим вывод «вручную»:
Гипотезы 1 г Гипотезы (J С—>А Аксиома3 J, | 1 С С^В А А—>(_В—>А&В) В В^А&В А&В
Введём данные:
2 3 4 1 5 С—>А premise С В premise С premise h А&В
Применим аксиому «Ах 3», заменив F1 на A, a F2 на В:
2 3 4 6 1 5 С—>А premise С В premise С premise А^(В^А&В) АхЗ& h А&В 293
httpaJ/yfaO
Применим правило «Modus Ponens» к строкам 4 и 2:
2 С- + А premise
3 С- + В premise
4 с premise
6 А- + (В- ->А&В) АхЗ &
7 А ModusPonen; 4, 2
1 h
5 А&В
Применим правило «Modus Ponens» к строкам 7 и 6:
2 С- + А premise
3 С- ->В premise
4 с premise
6 А- + (В->А&В) АхЗ &
7 А ModusPonen; 4, 2
8 В- + А&В ModusPonen; 7, 6
1 5 h А&В
Применим правило «Modus Ponens» к строкам 4 и 3, а также 9 и 8.
Вывод построен, и знак «1-« исчезает:
2 C- ->A premise
3 C- + B premise
4 C premise
6 A- ->(B—>A&B) АхЗ &
7 A ModusPonen; 4, 2
8 B- ->A&B ModusPonen; 7, 6
9 B ModusPonen; 4, 3
5 A&B ModusPonen; 9, 8
Пример 3. Докажите формулу (А —>А).
Решение. Вначале построим доказательство «вручную»:
Аксиома 1 Аксиома 2
1 г
ма 1 А->(А->А)) (А->(А->А))->((А->((А->А)->А))->(А->А))
А—>((А—> А)—> А) (А —> ((А —> А) —> А)) —> (А —> А)
А->А
Единственной логической связкой в формуле (А —> А) является импли-
кация, поэтому стоит предположить, что пользоваться придётся первыми
двумя аксиомами. Наша формула является достаточно «удобной» подфор-
мулой аксиомы 2. Введём данные:
1 I-
2 А->А
Применим аксиому «Ах 2 —>«
3 (А^> (А^А)) ((А—> ((А^А) —>А) (А^А)) Ах 2->
1 Н
2 А—>А
Применяя аксиому «Ах 1 —>« и правило «ModusPonen», получим:
3 (А —> (А —>А)) —> ((А —> ((А —>А) —>А) —> (А —>А)) Ах 2->
http^
//i । го it ri ।
294
4 А- »(А— ► А) Ах1 ->
5 (А ->«А —> А) —>А) —> (А —>А) ModusPonen; 4, 3
1 h
2 А- *А
Повторим знакомое действие:
3 СА- + (А- » А)) -> ((А -> ((А —> А) -> А) -> (А - ->А)) Ах2—>
4 Ан ► (А—> А) Ах 1 —>
5 (А- ССА- -> А) —> А) —> (А —> А) ModusPonen; 4, 3
6 h Ах 1 —>
2 Ан ► А ModusPonen; 6, 5
Пример 4. Выведите формулу (А \fxA).
Решение. Начало очевидно:
1 I-
2 А^> VxA
Теперь возможно применение правила 2, так какх £ FV(A):
3 А->А А->А
1 I-
2 А-> VxA
Остается показать, что (А —> А) — это теорема: воспользуемся эконом-
ной схемой (А —> А) из меню:
3 А->А А->А
2 А VxA Введ V
Теорема доказана.
Замечание (очень важное!).
Программа не может корректно проконтролировать применение пра-
вила к формуле А(х) -> VxA(x).
Пример 5. Постройте вывод в гильбертовском исчислении: Vx(A(x) о
z>В(х)) Н ЗхА(х) z> ЗхВ(х).
Решение. После ввода посылки и заключения на экране появится:
2 Vx(A(x) z>B(x)) premise
1 I-
3 ЗхА(х) z> ЗхВ(х)
Воспользуемся аксиомой «V14»; в рабочей строке появится:
=>VvFz)Sv, ТЕ
В окно ввода нужно ввести:
1) предметную переменную, соответствующую v;
2) формулу, соответствующую абстрактной формуле F;
3) терм, соответствующий абстрактному терму Т.
В нашем случае х соответствует v, А(х) z> В(х) соответствует F, х соот-
ветствует Т. После проделанных операций на экране появится:
2 4 1 3 Vx(A(x) z> В(х)) premise Vx(A(x) z) B(x)) z) (A(x) z) B(x)) V14 h 3xA(x) z> 3xB(x)
295
https:it.ru
Применим правило «ModPon» к 2 и 4:
2 Ух(А(х) зВМ) premise
4 Vx(A(x) z> В(х)) z> (А(х) z> В(х)) V14
5 А(х) Z) В(х) МР; 2, 4
1 I-
3 ЗхА(х) z> ЗхВ(х)
Воспользуемся аксиомой «315»; в рабочей строке появится:
=>Fz>3vST,vF.
В окно ввода нужно ввести:
1) формулу, соответствующую абстрактной формуле F;
2) предметную переменную, соответствующую v;
3) терм, соответствующий абстрактному терму Т, вместо которого
будет подставлена индивидная переменная, соответствующая v.
В нашем случае В(х) соответствует F, х соответствует v, х соответ-
ствует Т. Далее в окне ввода появится формула В(х), в которой перемен-
ная х будет выделена голубым цветом.
Чтобы произошла замена Т на v (в нашем случае х на х), необходимо
нажать клавишу < Пробел >, тогда выделенная переменная изменит цвет
выделения на красный, и нажать <Enter>.
После проделанных операций на экране появится:
2 Vx(A(x) z) В(х)) premise
4 Vx(A(x) z) В(х)) z) (А(х) z> В(х)) V14
5 A(x)z>B(x) МР; 2, 4
6 В(х) Z) ЗхВ(х) 315
1 I-
3 ЗхА(х) z> ЗхВ(х)
Воспользуемся аксиомой «z>2». В рабочей строке появится:
=> (Fl z> F2) z> CCF1 z> (F2 z> F3)) z> (Fl z> F3)).
В окно ввода нужно ввести формулы, соответствующие абстрактным
формулам Fl, F2, F3; в нашем случае А(х) соответствует F1, В(х) соответ-
ствует F2, ЗхВ(х) соответствует F3.
После проделанных операций на экране появится:
2 Vx(A(x) z> В(х)) 4 Vx(A(x) z> В(х)) z> (А(х) z) В(х)) 5 A(x)z>B(x) 6 В(х) z> ЗхВ(х) 7 ((А(х) z) В(х))) Z) (((А(х)) Z) ((В(х)) э (ЗхВ(х)))) э => ((А(х)) о (ЗхВ(х)))) 1 1- 3 ЗхА(х) z> ЗхВ(х) premise V14 МР; 2, 4 315 z>2
Применим правило «ModPon» к 5 и 7:
2 Vx(A(x) z) В(х)) 4 Vx(A(x) z) B(x)) z) (A(x) z) B(x)) 5 A(x)z>B(x) 6 B(x) z> 3xB(x) premise V14 MP; 2, 4 315
296
https:/Л: rait.ru
7 ((A(x) э B(x))) z (((A(x)) э ((B(x)) э (ЗхВ(х)))) z z2
о ((A(x)) => (ЗхВСс))))
8 (A(x)) z ((B(x)) z (ЗхВ(х)))) z ((A(x)) z> (3xB(x))) MP; 5, 7
1 I-
з 3xAG0 BxBGO
Воспользуемся аксиомой <ol»; в рабочей строке появится:
=> F1 z (F2 z F1).
В окно ввода нужно ввести формулы, соответствующие абстрактным
формулам F1 и F2; в нашем случае В(х) z ЗхВ(х) соответствует F1, А(х)
соответствует F2. После проделанных операций на экране появится:
2 Vx(A(x) zB(x)) premise
4 Vx(A(x) z B(x)) z (А(х) => B(x)) V14
5 A(x) z B(x) MP; 2, 4
6 B(x) z 3xB(x) 315
7 ((A(x) z B(x))) z (((A(x)) z ((B(x)) z (ЗхВ(х)))) z => ((A(x)) z (3xB(x)))) z2
8 (A(x)) z ((B(x)) z (3xB(x)))) z ((A(x)) z (3xB(x))) MP; 5, 7
9 (B(x) z 3xB(x)) z ((A(x)) z (B(x) z 3xB(x))) zl
1 1-
3 3xA(x) z 3xB(x) Применим правило «ModPon» к 6 и 9:
2 Vx(A(x) z B(x)) premise
4 Vx(A(x) z B(x)) z (A(x) z B(x)) V14
5 A(x) z B(x) MP; 2, 4
6 B(x) z 3xB(x) 315
7 ((A(x) z B(x))) z (((A(x)) z ((B(x)) z (3xB(x)))) z z ((A(x)) z (3xB(x)))) z2
8 (A(x)) z ((B(x)) z (3xB(x)))) z ((A(x)) z (3xB(x))) MP; 5, 7
9 (B(x) z 3xB(x)) z ((A(x)) z (B(x) z 3xB(x))) zl
10 (A(x)) z (B(x) z 3xB(x)) MP; 6, 9
1 h
3 ЭхА(х) z 3xB(x) Применим правило «ModPon» к 10 и 8:
2 Vx(A(x) z B(x)) premise
4 Vx(A(x) z B(x)) z (A(x) z B(x)) V14
5 A(x) z B(x) MP; 2, 4
6 B(x) z 3xB(x) 315
7 ((A(x) z B(x))) z (((A(x)) z ((B(x)) z (3xB(x)))) z z ((A(x)) z (3xB(x)))) z2
8 (A(x)) z ((B(x)) z (3xB(x)))) z ((A(x)) z (3xB(x))) MP; 5, 7
9 (B(x) z 3xB(x)) z ((A(x)) z (B(x) z 3xB(x))) zl
10 (A(x)) z (B(x) z 3xB(x)) MP; 6, 9
11 (A(x)) z (3xB(x)) MP; 10, 8
1 h
3 ЗхА(х) z BxBGO
Применим правило «Gener» к 11; в рабочей строке появится:
F=>VvSvl,vF,
297
https://
UF8it.ru
где будет выделена абстрактная формула F. Это означает, что система
Deductio просит указать формулу, соответствующую F.
Для этого нужно переместить курсор на формулу, соответствующую
F, и нажать клавишу <Пробел> (в результате формула изменит цвет).
После нажатия <Enter> в окно ввода нужно ввести предметные пере-
менные, соответствующие v и vl; в нашем случае х соответствует v, х соот-
ветствует vl. В результате на экране появится:
4 5 6 7 Vx(A(x) z> В(х)) z) (А(х) z) В(х)) V14 А(х) Z) В(х) МР; 2, 4 В(х) Z) ЗхВ(х) 315 ((А(х) о В(х))) о (((А(х)) о ((В(х)) о (ЗхВ(х)))) о о2 => ((А(х)) Z) (ЗхВ(х))))
8 9 10 11 12 1 3 (А(х)) z) ((В(х)) Z) (ЗхВ(х)))) Z) ((А(х)) э (ЗхВ(х))) МР; 5, 7 (В(х) Z) ЗхВ(х)) z) ((А(х)) z) (В(х) z> ЗхВ(х))) z>l (А(х)) z> (В(х) z> ЗхВ(х)) МР; 6, 9 (А(х)) Z) (ЗхВ(х)) МР; 10, 8 Vx((A(x)) о (ЗхВ(х))) g; 11 h ЗхА(х) z> ЗхВ(х)
Применим правило «Эе» к 12; в рабочей строке появится:
V v (Fl z> F2) => 3 v Fl z> F2,
где будет выделена V v (Fl z> F2). Это означает, что система Deductio про-
сит указать формулу, соответствующую V v (Fl z> F2).
Для этого нужно переместить курсор на формулу, соответствующую
V v (Fl z) F2), и нажать клавишу < Пробел >; в результате формула изме-
нит цвет. После нажатия < Enter> на экране появится:
4 Vx(A(x) z> В(х)) z) (А(х) Z) В(х)) V14
5 А(х) Z) В(х) МР; 2, 4
6 В(х) z> ЗхВ(х) 315
7 ((А(х) о В(х))) о (((А(х)) о ((В(х)) о (ЗхВ(х)))) о z>2
о ((А(х)) о (ЭхВ(х))))
8 (А(х)) z> ((В(х)) о (ЭхВ(х)))) z> ((А(х)) о (ЭхВ(х))) МР; 5, 7
9 (В(х) Z) ЭхВ(х)) z) ((А(х)) z) (В(х) Z) ЭхВ(х))) Z)1
10 (А(х)) z> (В(х) z> ЭхВ(х)) МР; 6, 9
11 (А(х)) о (ЭхВ(х)) МР; 10, 8
12 Vx((A(x)) Z) (ЭхВ(х))) g; и
3 ЗхА(х) z> ЭхВ(х) Зе; 12
Вывод завершён.
298
https://и гз it.ru
Задачи для самостоятельного решения
У Дефо нет ничего такого, чего
не знал бы любой лавочник.
В. Скотт
1. Доказательство бескванторных формул
1. Постройте древесные доказательства (выводы) следующих формул
в классическом гильбертовском исчислении, а затем проведите данные
доказательства в системе Deductio:
a) R & (Р v Q) -> R; б) {А, В, (А (В С)), (Q R)} Н С.
2. По данным фрагментам постройте древесное доказательство:
а) 3 (Р- ->Р)- >((Р- ->р)-> (PvP^ Р)) Ах 8 v
4 (Р- Р))~ Н(Р-> ((Р->Р) ->Р))- ЯР->Р)) Ах2->
5 Р- >(Р^ Р) Ах 1 —>
6 (Р- ->((Р- -+Р)- ->Р))- >(Р^Р) ModusPonen; 5, 4
7 Р- >((Р- >Р)- >Р) Ах 1 ->
8 Р- >Р ModusPonen; 7, 6
9 (Р- ->Р)- > (Pv Р->Р) ModusPonen; 8, 3
2 Pv Р->Р ModusPonen; 8, 9
б) 3 (А —>А) —> A v (А —>А)
4 (А—>А)
2 Av(A4A)
Ах 7 v
А^А
ModusPonen; 4, 3
3. По данным фрагментам постройте древесный вывод:
а) 1 —А -+В premise
2 А^ ► В premise
3 A v — premise
4 (А- ^В) —Н(-А—> В) ->(А v -А l —> В)) Ax 8 v
5 (—А ^В)^ (A v- А—>В) ModusPonen; 2, 4
6 A v —А - ->В ModusPonen; 1, 5
7 В ModusPonen; 3, 6
б) 1 В-> С premise
2 А-> В premise
3 (А- >В) —И(А ->(В->С))- HA -> Q) Ax 2
4 (А- Ив ->£)) ->(А->С) ModusPonen; 2, 4
5 (в- НЭ ->(А- (В О) Axl^>
6 А^> (в- ->С) ModusPonen; 1, 5
7 А—> с ModusPonen; 6, 4
4. Вставьте пропущенные строки в доказательстве (выводе) некоторой
формулы в системе Deductio:
2 С A premise
3 С В premise
4 ... premise
6 A^(B^A&B) Ax3&
7 ... ModusPonen; 4,2
8 В —> A & В ModusPonen; 7, 6
9 В ModusPonen; 4,3
5 A & В ModusPonen; 9, 8
299
https:it.ru
5. Докажите следующие формулы:
а) А (А В v С) А;
б) (P->QvP)->((Q&(QvP)->QvP)->(PvQ&(QvP)->QvP));
в) (В -> (В & -В)) ((В -> -i(B & -В) —> -В);
г) —1—1—iD —> —iD.
6. Постройте выводы следующих формул:
а) {С—>А, С^В, С}НА&В;
б) {А->В,А-> (В->А)} НА->А;
в) {-i-Л} Н А -i-Л;
г) {А—>В,В—>С} НА—>С;
д)*{А^(В^О}НВ^ (A^Q;
е) {А —> В, А —> —iB} I—А;
ж) {А —> (В->С)} \-А&В^С.
7. Постройте древесные доказательства:
а) А^А;
б) А —> -i-A;
в) -i(A&—А);
г) A v А <-> А;
д) А & А <-> А;
е) А^А v (А&В);
ж) -i( A v -А) —> А;
з) -i( A v -А) —А;
и) A v -А.
2. Доказательство кванторных формул
1. Докажите следующие формулы в гильбертовском исчислении (х иу—
предметные переменные, А, В, С — произвольные формулы, а В — формула
в которую х не входит свободно). Символом «°» помечены формулы, дока-
зуемые только в классическом исчислении.
55) VxA<->Vy[A]*;
56) ЗхА<->Зу[А]*;
57) VxVyA^VyVxA;
58) ЗхЗуАоЗуЗхА;
59)° —>VxA <-> Зх-А;
60) -13хА <-> Vx-A;
61)° VxA <-> -i3x—А;
62)° ЗхА <-> -iVx-A;
63) Vx(A & В) VxA & VxB;
64) Vx(E&A) <->Е& VxA;
65)° Vx(E v A) <-> E v VxA;
66) 3x(A v B) <-> ЗхА v 3xB;
67) 3x(E v A) <-> E v ЗхА;
68) 3x(E&A) <->E& ЗхА;
69) VxE^E;
70) 3xE<->E;
71)° 3x(E —> A) <-> (E —> ЗхА);
72)° 3x(A E) (VxA E);
73)° 3x(A B) (VxA 3xB);
74) Vx(A E) (ЗхА E);
75) Vx(E —>A) (E—> VxA);
76) VxA ЗхА;
https:/Л: rait.ru
77) HxVyA VyBxA;
78) 3x(A&B) ->3aA&3xB;
79) (VxA v VxB) -> Xfx(A v B);
80) (3xA —> VxB) —> Vx(A —> B);
81) VxVyA-> Vx(A)£
82) 3x(A)£->3x3yA.
o- Hi iroit ri i
vJ.M (Ull.l V4
Лабораторная работа 14
ПОИСК ЛОГИЧЕСКИХ ВЫВОДОВ В РЕЖИМЕ
ДИАЛОГА «ЧЕЛОВЕК-КОМПЬЮТЕР»: СИСТЕМА
DEDUCTIO, ГЕНЦЕНОВСКОЕ ИСЧИСЛЕНИЕ
НАТУРАЛЬНОГО ВЫВОДА
Наука, (дающая одновременно и (знание
того, что (что-нибудь) есть, и (знание) того,
почему (что-нибудь) есть, а не отдельно
знание того, что (что-нибудь) есть,
является более точной и высшей, чем наука,
(дающая знание только того), почему (что-
нибудь) есть.
Аристотель. Вторая аналитика.
Книга первая, гл.
Обязательные результаты обучения:
• знать
—режимы системы Deductio для автоматизации поиска доказательства
в генценовской системе натурального вывода;
—компоненты, интерфейс и опции системы Deductio;
• уметь
—вводить данные, строить доказательство и вывод формул в интуици-
онистском (NJ) и классическом (NK) исчислениях натурального вывода
в системе Deductio;
• владеть
—знаниями, представленными выше;
—методами решения задач, представленных в Лабораторной работе.
Теоретические сведения
В гильбертовском исчислении использовался способ доказатель-
ства «сверху вниз», т. е. от аксиом и посылок приходилось, применяя
основные правила вывода, «спускаться» к заключению, что могло
вызывать некоторые затруднения, связанные с отсутствием опыта
(малым запасом доказанных теорем). Доказательство же «от руки»
шло, зачастую, в другую сторону — снизу вверх. При этом практи-
302
https:it.ru
чески исключалась возможность использования дополнительного
инструментария.
Для генценовской системы натурального вывода Deductio является
достаточно удобной и эффективной: программа позволяет автомати-
зировать поиск доказательства с помощью использования следующих
режимов: фильтрации правил вывода, автоматической генерализа-
ции, автоматической унификации, а также минимизации вывода.
1. Фигуры заключения.
В список фигур заключения генценовской системы натурального
вывода включены:
1) восемнадцать основных фигур введения и удаления логи-
ческих связок, кванторов и логической константы Л (в сигнатуре
Deductio L), применяемых в направлении снизу вверх (с помощью
«нижней» формулы, получаем «верхние» формулы и допущения), об-
щих для интуиционистского (NJ) и классического (NK) исчислений;
2) пять фигур, применяемых сверху вниз (от допущений к за-
ключению, в меню они помечены апострофом «’»);
3) две фигуры и аксиому из NK;
4) две подстановки.
2. Применение правил вывода.
Для применения правила вывода нужно установить курсор
на нужное заключение (формулу ниже «штопора»), выбрать пра-
вило из меню правил вывода (нажать < Space > или <Esc>\File\
ConstructXApply Rule).
После первого применения правила вывод разделится на два
поддерева, каждое из которых будет отмечено —>?. Это сделано
не случайно, так как список допущений у каждой ветки может быть
различен.
Для работы с отдельным подвыводом нужно войти в него, устано-
вив курсор на соответствующий ему знак —>? и нажать <Insert>.
3. Фильтрация правил вывода.
В меню Tools находится опция Filter, предназначенная для филь-
трации правил вывода (это упрощает выбор применяемого правила).
Если фильтр включён, то при вызове меню правил вывода будут
доступны только те правила, в качестве первого параметра которых
может подойти формула, на которой в настоящий момент стоит
курсор.
Однако это не всегда означает применимость правила вывода,
так как можно не найти второго подходящего параметра.
4. Минимизация.
Минимизация находится в меню ConstructXMinimize и позволя-
ет удалять лишние элементы вывода, появляющиеся при построе-
нии вывода:
1) ими могут быть формулы, от которых не зависит заключение,
т. е. формулы, которые фактически не используются и могут быть
303
https:it.ru
удалены из вывода. В этом случае минимизация осуществляет толь-
ко удаление этих формул;
2) ими могут быть подвыводы без допущений, которые явля-
ются важным элементом дерева поиска вывода. Но необходимость
в подвыводе без допущений отпадает, как только такой подвывод
замкнут или сведён к другим подвыводам. В этих случаях можно
удалить подвывод, вставив принадлежащие ему формулы с анали-
зом в вышестоящий вывод.
Правильность вывода при этом не нарушается.
5. Унификация.
Напомним, что унифицируемыми выражениями называются два
выражения, которые могут быть приведены к одному и тому же син-
таксическому представлению подстановкой значений вместо сво-
бодных переменных.
При выполнении глобальной подстановки может потребоваться
указание системы подстановок вместо временных термов, такой,
что при ее выполнении замкнулись все или текущие подвыводы.
При включённом режиме унификации поиск такой системы под-
становок осуществляется автоматически.
Если найденная система позволяет замкнуть все ветви дерева
поиска вывода, подстановка выполняется и вывод оказывается по-
строенным.
Приведём примеры построения натуральных выводов в Deductio.
Работа с примерами решения упражнений
См. Пример 1, Пример 2, Пример 3, Пример 4, Пример 5.
Вывод.
Система Deductio может быть использована в качестве средства
проверки выводов, построенных «вручную» в генценовском исчис-
лении; более того, система позволяет автоматизировать поиск до-
казательства в генценовском исчислении с помощью следующих
режимов: фильтрации правил вывода, автоматической генерали-
зации, автоматической унификации, минимизации вывода.
Примеры решения некоторых типов упражнений
Гипотезы имеют огромное значение, так
как позволяют наметить продуктивные
направления исследований.
А. Тьюринг (1950)
Пример 1. Постройте вывод формулы ((А —В) -А).
Решение.
1. Введём условие:
1 Ь
2 (А->В)-> ((А->-В)->-Л)
304
https: "и rait.ru
2. Применим дедукцию (Введ 6):
1 —; >?
5 А- 3 Н 4 (А- 2 (А- >В ->-iB)—>-А э-В)->((А->-В)->^А)
3. Зайдём в подвывод со строки 1; для этого нажмём <Insert> :
1 —>?
5 А—>В
3 ь
4 | (A->-B)->-i
2 (А^В)^ ((А^-В)^^А)
4. Снова применим правило «Введ
1 5 3 8 6 7 4 2 | А—>В А^^В 1 ь || А-»-#)-»-, (А В) -> ((А -дВ) ^А)
5. Зайдём в подвывод со строки 3, применим правило «Введ -1»:
3
8
6
11
9
10
7
4
А->-В
£ —>?
£ А
Ь
Л
(А—>-В)—>-1А
2 (А->В)-> ((А^>-В)->^А)
6. В подвыводе строки 7 используем правило «Удал -1», в качестве
F введём В:
|В
h
305
https:it.ru
7. Войдём в подвывод со строки 12 и применим правило «Удал ->»;
левое поддерево замкнётся:
5
3
8
6
11
12
17
19
13
21
14
9
15
16
10
7
4
A
И
В
h
8. Чтобы замкнуть правое поддерево, войдём в него со строки 9 и при-
меним правило «Modus Ponens», введя формулу А:
5
3
8
6
11
12
17
19
13
21
14
9
22
24
15
26
16
10
7
4
А
И
В
И
306
https://urajt.ru
Пример 2. Постройте вывод формулы (А&.В) -1(-Л v -iB).
Решение.
1. Введём условие:
1 I-
2 (А & В) —> —1(—Л v —iB)
2. Применим правило «Введ —>» к строке 2:
1 —>?
5 А&В
3 Н
4 -.(-Av-^)
2 А&В^—(-Л v—iB)
3. Зайдём в подвывод со строки 1, нажав клавишу <Insert> :
1 —>?
5 ^А&В
3 ь
4 g —1(—Л v—В)
2 А&В —> —i(—Л v —В)
4. К строке 4 применим правило «Введ -1»:
5
3
8
6
7
4
2
А&В
—1(—A v —iB)
А & В —> —1(—A v —iB)
5. Зайдя со строки 3, применяем правило вывода «Удал -т», указав фор-
мулу В в окне ввода на запрос программы:
5 А&В
3
8
9
10
11
6
12
13
7
4
h
В
2 А&В—>-i(-A V-J3)
http
о - Hi I roif ri i
O.M Ul UU.I
307
6. Заходим в подвывод со строки 9 и применяем «Удал & 2»; это под-
дерево замкнётся:
5 А&В
3
8
9
10
15
11
6
12
13
7
4
2 A&B-^bAv-B)
7. В подвыводе строки 6 к строке 13 применим правило «Удал V»;
строка 18 замкнётся допущением в строке 8:
5
3
8
9
10
15
11
6
16
18
19
22
20
21
12
25
13
7
4
2 А&В —> —i(—Л v —В)
8. К строке 21 применим правило «Введ -1», зайдя перед этим в под-
вывод со строки 19:
308
https://и гз it.ru
5 А&В
3
8
9
10
15
11
6
16
18
19
22
20
28
26
27
21
12
25
13
7
4
2 А & В —> —i(—A v —iB)
9. К строке 27 применяем правило «Удал -1»:
309
https:it.ru
10. К строке 31 применяем правило «Удал &»:
5
3
8
9
10
15
11
6
16
18
19
22
20
28
29
30
35
31
26
33
27
21
12
25
13
7
4
А&В
2 А&В —i(-A v-B)
Пример 3. Построим вывод формулы (АэВ) d -A vВ.
Решение. После ввода заключения на экране появится:
1 I-
2 (Az>B)z>-AvB
Применим правило <o_ai» к 2. Для этого нужно:
1) указать курсором ту формулу, к которой будет применяться дан-
ное правило;
2) нажав клавишу < Пробел >, вызвать меню правил вывода;
3) выбрать правило <o_ai» (в рабочей строке появится текст
h Fl z> F2 => Fl I- F2)
и нажать клавишу <Enter>.
Так применяются все аналитические правила.
На экране появится:
310
1 —>?
5
3
4
AzB
Н
-AvB
assumption
2 (AzB)z-iAvB => J;5-4
Войдём в подвывод со строки 1. Для этого нужно указать курсором
строку, содержащую —>?, что символизирует «незамкнутый» подвывод
(в нашем случае строку 1) и нажать клавишу <Insert>.
На экране появится:
1 —>?
5 |iAz>B
з i i-
4 |1 -AvB
2 (A Z) В) Z) -A v В
assumption
z>_i; 5^1
Применим правило «v_ae» к 4. Для этого нужно:
1) указать курсором ту формулу, к которой будет применяться дан-
ное правило;
2) нажав клавишу < Пробел >, вызвать меню правил вывода;
3) выбрать правило «v_ae» (в рабочей строке появится текст
I- F3 => HF1 vF2 /Fl I- F3 /F2 Н F3)
и нажать клавишу < Enter >.
Далее ввести в окно ввода формулы, соответствующие абстрактным
формулам F1 и F2. На экране появится:
1 —>?
5 § 1 Az>B assumption
6 i ? —>?
7 i i h
e i 1 Av(-A)
9 1 :: >?
12? 1 A assumption
10? 1 h
11 i 1 AvB
3 1 1 — >?
15? —A assumption
131 1 h
141 1 -nAvB
4 1 1 -nAvB v_e; 7-8,12-11,15-14
2 (Az>B)z)-A vB —AvB z>_i; 5—4
http
о- Hi iroit i-i i
>j< v4i uii.l vj
311
Войдём в подвывод со строки 9:
5
6
7
8
9
12
10
11
3
15
13
14
4
2 (АзВ) d-А vB -Ах/В
assumption
assumption
assumption
v_e; 7-8,12-11,15-14
D_i; 5-4
Применим правило «v_ai_2» к 11. Напомним, что в рабочей строке оно
имеет вид: I- Fl v F2 => I- F2.
После применения правила на экране появится:
5
6
7
8
9
12
10
16
17
11
3
15
13
14
4
А=)В
2 (A z> В) z> —A v В
assumption
assumption
v_i_2; 16-17
assumption
v_e; 7-8,12-11,15-14
z>J; 5^1
Войдем в подвывод co строки 10:
312
https ://u rait.ru
5
6
7
8
9
12
10
16
17
11
3
15
13
14
4
Az>B
—>?
I-
Av(-iA)
—>?
A
—>?
g; h
g В
^AvB
—>?
h
AvB
—iAvB
2 (Az>B)z>-iAvB
assumption
assumption
v_i_2; 16-17
assumption
v_e; 7-8,12-11,15-14
zdJ; 5-4
Применим правило <o_se» к 12 и 5; для этого нужно:
1) нажав клавишу <Пробел>, вызвать меню правил вывода;
2) выбрать правило <o_se»;
3) нажать клавишу < Enter>.
В рабочей строке появится текст Fl; Fl F2 => F2, где будет выделена
абстрактная формула F1. Это означает, что система Deductio просит ука-
зать формулу, соответствующую F1.
Для этого нужно переместить курсор на формулу, соответствующую
F1, и нажать клавишу < Пробел >; в результате формула изменит цвет.
Далее выделится Fl z> F2.
После этого проделываются те же операции. В результате (после нажа-
тия клавиши <Enter>) на экране появится:
5
6
7
8
9
12
10
17
11
3
15
13
14
4
2 (AdB)dMvB
assumption
assumption
z>_e; 12,5
v_i_2; 17
assumption
v_e; 7-8,12-11,15-14
zd J; 5—4
Таким образом применяются все синтетические правила.
313
https: //цга it.ru
Знак —>+ в строках 9 и 10 означает, что подвыводы со строк
9 и 10 замкнуты.
Войдем в подвывод со строки 3:
1 —>?
5 А=)В
6 —>?
7 1-
8 Av(-iA)
9 —>+
12 А
10 —>+
17 1 в
11 —AvB
3 —>?
15
13 i ь-
14
4 -iAvB
2 А о В) о -Л v В
assumption
assumption
z>_e; 12, 5
v_i_2; 17
assumption
v_e; 7-8,12-11,15-14
z>_i; 5-4
Применим правило «v_ai_l» к 14. В рабочей строке указанное правило
имеет вид: I- Fl v F2 => I- Fl.
После применения правила на экране появится:
1 - >?
5 Az>B assumption
6 ->?
7 h
8 Av(-nA)
9 —>+
12 А assumption
10 —>+
17 1 в z>_e; 12,5
11 -AvB v_i_2; 17
3 —>+
15 : —iA assumption
13 : > +
19 ;:| —iA equ; 15
14 I -AvB v_i_l; 19
4 v_e; 7-8,12-11,15-14
2 (A Z) В) Z) —Л v В z>_i; 5^J
314
https://ura5t.ru
Войдём в подвывод со строки 6:
1
5 AdB assumption
6 —>?
7 1-
8 A v (—A)
9 —>+
12 A assumption
10 —>+
17 1 в z>_e; 12,5
11 —AvB v_i_2; 17
3 —>+
15 —iA assumption
13 —>+
19 1 - equ; 15
14 -AvB v_i_l; 19
4 -AvB v_e; 7-8,12-11,15-14
2 Az>B) Z)-iA vB z>_i; 5—4
Применим правило «Axiom» к 8. Для этого нужно:
1) указать курсором ту формулу, к которой будет применяться дан-
ное правило;
2) нажав клавишу < Пробел >, вызвать меню правил вывода;
3) выбрать правило «Axiom» (в рабочей строке появится: I- Fl v F2 =>);
4) нажать клавишу < Enter >.
После применения указанного правила «замкнётся» текущий подвывод
(подвывод со строки 7), а также и весь вывод, так как подвывод со строки
7 был последним из незамкнутых подвыводов.
На экране появится:
1 —> +
5 A^B
6 —>+
8 |j Av(^A)
9 —>+
12 A
10 —>+
17 1®
11 -nAvB
3 —>+
15 —A
13 —>+
19 1 ~
14 -nAvB
4 -AvB
2 (AdB)d^AvB
assumption
axiom
assumption
z>_e; 12,5
v_i_2; 17
assumption
equ; 15
v_i_l; 19
v_e; 8,12-11,15-14
z>_i; 5^
Вывод завершён.
315
https :/,игз-t.ru
Пример 4. Постройте вывод формулы Зх(А(х) & В(х)) ЗхА(х) &
&ЗхВ(х).
Решение.
1. Введём условие:
1 Ь
2 Зх(А(х) & В(х)) ЗхА(х) & ЗхВ(х)
2. Применим правило «Введ —>«, формула Зх(А(х) &В(х)) превратится
в гипотезу; останется доказать формулу ЗхА(х) & ЗхВ(х):
5 Ех(А(х)&В(х))
3 Н
4 3xA(x)&VxB(x)
2 Эх(А(х)&В(х)) ->3xA(x)&VxB(x)
3. Войдём в подвывод со строки 1, нажав клавишу <Insert>:
5
3
4
2
| Зх(А(х)&В(х))
|| Н
|| ЗхА(х) &ЗхВ(х)
Зх(А(х) &В(х)) ЗхА(х) & ЗхВ(х)
4. Применим правило «Введ &» и получим два поддерева:
1 —>?
5 || Зх(А(х) &В(х))
6 || —>?
7 i I-
8 || ЗхА(х)
3 |: _>?
9 1 н
10II ЗхВ(х)
8 || ЗхА(х) & ЗхВ(х)
2 Зх(А(х) & В(х)) ЗхА(х) & ЗхВ(х)
5. Заходим в подвывод в строчке 6 и применяем правило «Введ 3»:
5 Зх(А(х) &В(х))
6 —>?
7
11
12
8
3
I-
A(tl)
ЗхА(х)
9
10
4
Ь
ЗхВ(х)
ЗхА(х) &ЗхВ(х)
2 Зх(А(х) & В(х)) ЭхА(х) & ЗхВ(х)
316
https:/Л: rait.ru
6. В строке 12 появился абстрактный терм tl, на его место в фор-
муле можно поставить конкретный терм. Зайдя в подвывод со строки 7,
к строке 12 применим правило «Удал & 1», вместо метабуквы F2 укажем
формулу B(tl). Напомним, что
def
B(tl) = (B(x))*j
Ях(А(х) &В(х))
h
A(tl)&B(tl)
I A(ti)
3xA(x)
Н
ЗхВ(х)
ЗхА(х) & ЗхВ(х)
5
6
7
11
14
13
12
8
3
9
10
4
2 3x(A(x) &B(x)) BxA(x) & 3xB(x)
7. К поддереву в строке 11 применим правило «Удал Я»:
5
6
7
11
15
17
13
20
18
19
14
12
8
3
9
10
4
2 3x(A(x) & B(x)) 3xA(x) & 3xB(x)
Зх(А(х) &В(х))
Зх(А(х) &В(х))
|| A(wl)&B(wl)
II и
11 (A(tl)&B(tl))
II (A(tl)&B(tl))
| A(tl)
3xA(x)
Ь
ЗхВ(х)
ЭхА(х) & НхВ(х)
8. Применим подстановку к строке 19: вместо всех вхождений
абстрактного терма tl подставим временную (сколемову) функцию wl:
317
https:
5
6
7
11
15
17
13
20
19
14
12
8
3
9
10
8
2 3x(A(x) &B(x)) 3xA(x) & 3xB(x)
Ях(А(х) &B(x))
Ях(А(х) &В(х))
Ц A(wl) &B(wl)
| (A(wl) &B(wl))
(A(wl) &B(wl))
A(tl)
3xA(x)
b
3xB(x)
3xA(x) & 3xB(x)
Вывод замкнулся. Правый подвывод замыкается аналогично.
Замечание (для знатоков унификации).
Последнее выполненное действие можно было осуществить с помо-
щью унификации так (используется итеративный алгоритм унификации):
1. ® = {} stack = {A(wl)&B(wl) = A(tl)&B(tl)}
2. ® = {} stack = {A(wl) = A(tl), B(wl)=B(tl)}
3. © = {} stack = {wl = tl, B(wl)=B(tl)}
4. 0={tl = wl} stack - {B(wl) - B(wl)}
5. 0={tl = wl} stack = {wl=wl}
6. 0={tl = wl} stack = {}
Подстановка 0={tl=wl} является наиболее общим унификатором
данных формул.
Пример 5. Построим вывод в генценовском исчислении:
I- Х/хА(х) о —i3x—1А(х).
Решение. После ввода заключения на экране появится:
1 I-
2 I- VxA(x) z> —i3x—iA(x)
Применим правило <o_ai» к 2; в рабочей строке оно имеет вид:
1—Н Fl z> F2 => Fl h F2.
5 VxA(x) assumption
После np3i Мнения правила на экране появится:
4 -1Ях-1А(х)
2 Х/хА(х) о -1Ях-iA(x) z>J; 5-4
318
Войдём в подвывод со строки 1:
5
3
4
Х/хА(х)
I-
-Ях-1А(х)
2 VxA(x) Z) -1Ях-1А(х)
assumption
=)_i; 5^1
Применим правило «-i_ai» к 4; в рабочей строке оно имеет вид:
F-,F^FF-L.
После применения правила на экране появится:
1 —>?
5 || VxA(x) assumption
3 i —>?
8 3x-iA(x) assumption
6 i н
7
4 || -iHx-iA(x) --J; 8-7
2 VxA(x) z) -1Ях-1А(х) z>_i; 5^1
Войдём в подвывод со строки 3:
5
3
8
6
7
4
Х/хА(х)
—>?
|| Ях-1А(х)
iн
-i3x-iA(x)
2 VxA(x) z> -iHx-iA(x)
assumption
assumption
-i_i; 8-7
z>J; 5^1
Применим правило «Х/ se» к 5; в рабочей строке оно имеет вид:
V v F => S v, t F.
После применения правила на экране появится:
5
3
8
9
6
7
4
Х/хА(х)
—>?
Hx-iA(x)
II A(tl)
iн
-i3x-iA(x)
assumption
assumption
V_e;5
2 VxA(x) z> -i3x-iA(x)
-.J; 8-7
z>J; 5—4
В данном случае система Deductio автоматически выберет временный
терм (в нашем случае — это tl), который будет подставлен вместо пред-
метной переменной.
Применим правило «З ае» к 7; в рабочей строке оно имеет вид:
319
https: "и rait.ru
I- F2 => I- 3 V Fl / S V, w Fl I- F2.
После применения правила на экране появится:
1 - >?
5 Х/хА(х) assumption
3 ->?
8 ЯХ-1А(Х) assumption
9 A(tl) V_e; 5
10 : —> +
12 Й ЯхЬА(х)) equ; 8
6 :: >?
15 ;; -1A(W1) assumption
13 h
14 1
7 : | 3_e; 12,15-14
4 -i3x-iA(x) -.J; 8-7
2 VxA(x) z> -1Ях-1А(х) z>J; 5^1
В данном случае система Deductio автоматически выберет временную
функцию (в нашем случае — это wl), которая будет подставлена вместо
предметной переменной.
Войдём в подвывод со строки 6:
1 —>?
5 VxA(x)
3 — 8 9 10 >? 3x-iA(x) A(tl) —>+
12 | 6 3x(-iA(x)) —>?
15 -iA(wl)
13 I-
14 1 7 1
4 - i3x-iA(x)
2 VxA(x) z> -iHx-iA(x)
assumption
assumption
V_e;5
equ; 8
assumption
3_e; 12,15-14
-.J; 8-7
z>J; 5^1
Применим правило GlobSubst, которое является применимым как
только в выводе появляется хотя бы один временный терм.
В рабочей строке оно имеет вид: => G.
После выбора правила в меню правил вывода и нажатия < Enter>
на экране возникнет таблица, в которой строка соответствует времен-
ному терму, имеющемуся в выводе (в нашем случае — это tl).
Выбрать строку можно, нажав клавишу <Пробел>. В окне ввода необ-
ходимо определить значение временного терма — временную функцию,
т. е. в нашем случае нужно ввести wl и нажать клавишу <Enter>.
Для выполнения подстановки необходимо нажать <Esc>.
После применения правила на экране появится:
320
https:/Л: rait.ru
1 - >?
5 VxA(x) assumption
3 ->?
8 : ЯХ-1А(Х) assumption
9 i А(Н) V_e; 5
10 : > +
12 0 ЯхЬА(х)) equ; 8
6 i —>?
15 ; -A(wl) assumption
13 i h
14 1
7 1 3_e; 12,15-14
4 -i3x-iA(x) -.J; 8-7
2 VxA(x) о -1Ях-А(х) z>_i; 5^1
Применим правило «-i_se» к 9 и 15. В рабочей строке оно имеет вид:
После применения правила на экране появится:
1 —>?
5 VxA(x) assumption
3 ->?
8 3x-A(x) assumption
9 A(tl) V_e; 5
10 —>+
12 | 3x(-A(x)) equ; 8
6 —>?
15 -A(wl) assumption
13
14 1
7 1 3_e; 12,15-14
4 -i3x-iA(x) -.J; 8-7
2 VxA(x) z> -dx-iA(x) =>_i; 5^
Вывод завершён.
Задачи для самостоятельного решения
У Дефо нет ничего такого, чего
не знал бы любой лавочник.
В. Скотт
1. Докажите следующие формулы в исчислении NK и (или) NJ (х иу —
предметные переменные, А, В, С—произвольные формулы, а Е—формула,
в которую х не входит свободно).
Символом 0 помечены формулы, которые доказуемы только в NK.
1) А—> (В—>А);
2) (А—>В')—> ((А-> (В^С))^
321
https:it.ru
3) A—> (В—>А&В);
4) (А&В—>А);
5) (А&В—>В);
6) (A->AvB);
7) (В—>AvB);
8) (А —» С) —» ((В —» С) —» (A v В —» С));
9) (А->В)->((А->^В)->-А);
10)0 (_,^а^а);
11) СА^В)^ ((В^А)^СА^В));
12) (АоВ)ч(А^В);
13) (АоВН(В^А);
14) (А В) <г^ (А В) & (В-> АУ,
15)0 (А -> В) о (-nA v В);
16)0 (Д В) -,(А & —В);
17)0 (А & В) <-> ->(-пА v -В);
18)0 (А & В) <-> -.(А -> -В);
19)0 (A vB) о —.(—.А & -В);
20)0 (AvВ) о (-А—>В);
21) (А&В)^(В&А);
22) (AvB)o(BvA);
23) (АоВ)о(ВоА);
24) А & (В & О о (А &В) & С;
25) A v (В v Q о (A v В) v С;
26) * (А <-> (В <-> О <-> (А <-> В) <-> О;
27) А & (В v О о А & В v А & С;
28) A v (В & Q о (A vB) & (A v Q;
29)0 A v (В -> С) о (A v В) -> (A v О;
30)0 A v (в о О о (A vB) о (A v О;
31) (АчВ&С)о(АчВ)&(А^С);
32)0 (А->В vO <-> (А—>В) v (А-> О;
33) Ач(В«С)оВчВ)«(АчС));
33!) А -> (В -> О <-> ((А -> В) -> (А -> Q);
34) (А&А)<^А;
35) (Av А) о А;
36) А& (AvB) «А;
37) (AvA&B)oA;
38)0 А & (В v-В) ОА;
39) Av (В&-В) <^А;
40) (А&В&-В) о (В&-В);
41)0 (a v В v -В) (В v -В);
42)0 _,(а & В) о (-А v -В);
43) -.(A v В) о (-пА & -В);
44)0 _,(а —> В) о (А & -В);
45)-i(A В) (A v В) & -1(А & В);
4б)°-1—А А;
47) А<^А;
48) oav-A;
49) -i(A&—А);
50) (А-> В)-> ((В-> С)-> (А-> Q);
51) (A^(B^Q)o(B^(A^C));
52) (А^ (В^С)) о (А&В->О;
322
https: "и га it.ru
53) -A—> (A—>В);
54)° СА -> В) <-> С-пВ -> -пА);
54х) (А&В->О-> (А&-.С->-В);
542) (А -> В) <-» (-.(А —> В) —> С & -.С);
543) (А -> В) <-» С--СА —> В) —> -А);
544) (А -> В) <-> (-,СА В) В);
55) VxA <-> Vy[A]*;
56) ЗхА <-> Зу[А]*;
57) VxVyA о VyVxA;
58) ЗхЗуА <-» ЗуЗхА;
59) ° -.VxA о Зх—А;
60) -.ЗхА <-> Vx—А;
61)° VxA о —.Зх—А;
62)° ЗхА <-> —.Vx—А;
63) Vx(A&B)<-> VxA&VxB;
64) Vx(E & А) о Е & VxA;
65)° Vx(E v А) <-> Е v VxA;
66) Зх(А v В) <-> ЗхА v ЗхВ;
67) 3x(EvA) oEv3xA;
68) Зх(Е & А) <-> Е & ЗхА;
69) VxE о Е;
70) ЗхЕоЕ;
71)° Зх(Е -> А) <-> (Е ЗхА);
72)0 яХА -> Е) (VxA Е);
73)0 в) о (VxA ЗхВ);
74) Vx(A Е) (ЗхА Е);
75) Vx(E А) о (Е VxA);
76) VxA—>ЗхА;
77) 3xVyA —> Vy3xA;
78) Зх(А & В)->3xA & ЗхВ;
79) (VxA v VxB) Vx(A v В);
80) (ЗхА VxB) Vx(A В);
81) VxVyA Vx(A)^;
82) Зх(А)£->ЗхЗуА.
о- Hi rnit г. ।
О., i Ul (uit.l
Часть 4
ИНТУИЦИОНИСТСКИЕ
ЛОГИЧЕСКИЕ ИСЧИСЛЕНИЯ
https:it.ru
Упражнение 15
ИНТУИЦИОНИСТСКИЕ
ПРОПОЗИЦИОНАЛЬНЫЕ ЛОГИКИ
И тут-то котёнок подбежал к нему —
бегом промчался через весь бар — и стал
тереться о его руку и выпрашивать
креветку.
— Они слишком большие для тебя,
котёныш, — сказал Томас Хадсон.
Но всё же отщипнул пальцами кусочек
и подал котёнку, и тот, ухватив его,
побежал обратно на витрину табачного
прилавка и стал есть быстро и жадно.
Э. Хемингуэй. Острова в океане
Обязательные результаты обучения:
• знать вспомогательные понятия
— прямой вывод в гильбертовском исчислении;
— непрямой вывод в гильбертовском исчислении;
— генценовское исчисление (натуральный вывод);
— аналитические таблицы для пропозициональной логики;
• знать основные понятия
— содержательные определения понятия «доказательство»;
— интуиционизм, интуиционистская логика;
— формализация интуиционистской пропозициональной логики;
— интуиционистское понимание логических связок;
— гильбертовская формализация;
— минимальное пропозициональное исчисление;
— позитивное пропозициональное исчисление, положительные логики;
• уметь
— устанавливать доказуемость формул в классическом пропозициональ-
ном исчислении;
— устанавливать доказуемость формул в интуиционистском пропозици-
ональном исчислении;
— доказывать отсутствие существования доказательства формул в инту-
иционистском пропозициональном исчислении.
• владеть:
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
327
https:it.ru
Теоретические сведения
Исследования последней четверти XX века в области теоретиче-
ского программирования выявили особую роль интуиционистской
логики в вопросах синтеза программ, поскольку использование
этой логики в математических построениях позволяет выделить
их алгоритмические, вычислительные аспекты. Поэтому интуицио-
нистская логика является одним из актуальных разделов современ-
ной математической логики.
В частности, интенсивно изучается вопрос систематического из-
влечения программы из конструктивного доказательства теоремы
о существовании решения задачи. Постановка этой проблемы уже
делает формулы исчисления предикатов и программы однопорядко-
выми объектами.
Далее обнаруживается, что извлечение эффективной программы
из теоремы существования требует добавления к исчислению не-
которых нетривиальных посылок, составляющих специальную те-
орию задачи.
В основе методов решения задачи автоматического синтеза про-
грамм лежит следующий план действий:
Постановка задачи Теорема существования
—> Доказательство теоремы существования -^Программа.
Итак, необходимо уметь реализовывать:
1) трансляцию постановки задачи в формулу специально подо-
бранного логического исчисления, которая в этом исчислении явля-
ется теоремой, подлежащей доказательству;
2) поиск вывода в этом исчислении;
3) извлечение искомой программы из построенного вывода.
Второй этап является более или менее традиционным.
Первый и третий этапы требуют разработки специальных средств
и методов. Первый этап связан со спецификой проблемной области,
в которой решается задача, третий — с характером используемо-
го логического исчисления и применяемых в нём методов доказа-
тельства теорем.
Последнее утверждение требует пояснений.
Проблема извлечения программы из доказательства теоремы и во-
прос о том, какие доказательства позволяют это, а какие нет, привле-
кали внимание математиков задолго до появления компьютеров.
Дедуктивные средства, обеспечивающие такое извлечение, ста-
ли называться конструктивными дедуктивными средствами, а ло-
гики, использующие эти средства, — конструктивными логиками.
Общепринятое «конструктивное» ядро составляют интуицио-
нистские формальные системы, основной характеристикой кото-
328
https:it.ru
рых является согласованность с конструктивным пониманием ут-
верждений.
Например, это означает, что:
1) по формальному доказательству утверждения (Нх е N) А(х)
можно построить натуральное число Ъ, для которого верно А(Ь);
2) по формальному доказательству утверждения Vx3yA(x,y) мож-
но построить вычислимую функцию/, для которой верно VxA(x,/(x)),
т. е. программу, которая по данному х строит искомое числоу =/(х).
Построение программы по доказательству в интуиционистской
системе может быть «поручено» компьютеру. При этом размер про-
граммы, извлекаемой из доказательства, не намного больше разме-
ра самого доказательства.
Подчеркнем тот факт, что извлечение программ из доказательств
теорем связано с особенностями конструктивных систем: если ис-
пользовать классические исчисления, то можно столкнуться с тем,
что программа не может быть извлечена из доказательства.
Содержательные определения понятия «доказательство»
Математические доказательства, как
алмазы, тверды и прозрачны и поддаются
лишь самой строгой логике.
Джон Локк.
Второй ответ епископу Вустерскому
Хотя термин «доказательство» является едва ли не самым основ-
ным в математике (например, Г. Такеути [47, с. 8] утверждает, что
«математика представляет собой совокупность доказательств»),
у математиков отсутствует ясность в понимании его смысла.
По выражению В. А. Успенского [49, с. 9], термин «доказатель-
ство» «не имеет точного определения».
По словам Гегеля (цит. по [140, с. 65]), «различные виды бытия
требуют свойственных именно им видов опосредствования или до-
казательства или содержат их в себе. Поэтому и природа доказа-
тельства относительно каждого из них различна».
Попытки найти однозначную дефиницию понятия «доказатель-
ство», выделить некий абсолютный смысл «доказуемости», не яв-
ляющийся ни синтаксическим, ни семантическим, ни психологиче-
ским, являются безнадёжными. Однако это не мешает математикам
доказывать теоремы.
Тем не менее, работа математиков состояла, состоит и будет со-
стоять большей частью в нахождении и усовершенствовании дока-
зательств, оправдывающих идеи, соображения, аналогии, модели,
конструкции, которые возникают в повседневных размышлениях,
а основным содержанием математической литературы является
и будет являться изложение доказательств.
Вначале заметим, что понятие «доказательство» (по [48, с. 7])
не есть математическое понятие; по отношению к математике оно
329
https:/Л: rait.ru
не внутреннее, а внешнее и принадлежит не математике, а психоло-
гии (и отчасти лингвистике).
Поэтому вначале приведём несколько содержательных определе-
ний.
Определения.
1. (Словарь Вебстера, цит. по [88, с. 167]) Доказательство — это
«убедительное свидетельство, которое заставляет сознание верить
в истинность или действительность».
2. [164, с. 91] «Доказательством суждения называется всякий
честный приём, благодаря которому это суждение становится не-
оспоримым» (А. С. Есенин-Вольпин).
3. [174, с. 74—75; 48, с. 6]: «И сейчас, как во времена Евклида, ма-
тематическое доказательство продолжает оставаться не более,
чем убедительным рассуждением, которое в состоянии убедить
нас настолько, что мы становимся готовы убеждать с его помо-
щью других».
Далее, В. А. Успенский [48, с. 452] отметил, что сейчас каждый
специалист вынужден так или иначе использовать знания других.
Аналогично обстоит дело и с доказательствами: деятельность
в сфере производства и потребления доказательств стала в та-
кой же степени объектом разделения и кооперации, как и деятель-
ность в сфере производства и потребления знаний.
Итак, само понятие «убедительность» начинает терять индиви-
дуализированный оттенок и всё более приобретает коллективный
характер, поэтому следует постепенно приучаться говорить об убе-
дительности не для отдельного индивидуума, а для некоторого на-
учного коллектива.
При этом коллективная убедительность отнюдь не означает
равную «непосредственную убедительность» для каждого в отдель-
ности члена коллектива. Коллектив выступает не как простая сумма
членов, а как единое целое. Смысл коллективной убедительности
в том, что для каждой составной части доказательства найдётся
свой «отвечающий за нее» член коллектива, для которого непосред-
ственно убедительна именно эта часть (а другие члены коллектива
полагаются в данном вопросе на этого члена).
С учётом сказанного сформулируем следующее
Определение (содержательное).
Доказательство — это рассуждение, которое убеждает:
1) либо автора доказательства;
2) либо сообщество математиков (программистов и т. п.);
3) либо автомат (в частности, компьютер).
330
https: "и rait.ru
При этом важно отметить, что Н. Н. Непейвода [39, с. 97—98]
определил «математическое доказательство» как конструкцию,
синтаксическая правильность которой гарантирует семантическую.
Эта формулировка показывает, насколько различаются компьютер-
ные программы и математические доказательства (синтаксическая
правильность программы не гарантирует ее семантической пра-
вильности).
Итак, «убеждение» автомата требует дополнения проверки син-
таксической правильности программы средствами проверки ее се-
мантической правильности.
Поясним необходимость включения в определение п. 2, который
утверждает, что доказательство (в математике) — это обществен-
ный процесс, изменяющийся со временем.
Уверенность в правильности доказательства тем больше, чем
больше математиков (или специалистов по теоретическому про-
граммированию) соглашается с ним (оно принимается некоторым
сообществом).
Далее, стандартное определение знания в современной эписте-
мологии таково: субъект А знает р, если и только если справедливы
три условия (по [67, р. 23]):
а) имеет место р;
б) субъект А верит, чтор; причём его вера обоснована (т. е. субъ-
ект убеждён в том, чтор).
Другими словами, знание есть обоснованная истинная вера.
Рассмотрим (следуя [51, с. 49]) ситуацию, когда в ролир высту-
пает доказательство. Естественно, что решающим обстоятельством
в признании истинности доказательства выступает п. б, а именно,
обоснованность веры математика в истинность доказательства.
Такого рода обоснованность приобретается с помощью:
— эпистемологических аргументов: понимание доказательства,
его простоту и т. п.);
— эстетических аргументов: красота, изящество, элегантность.
Отметим, что многие математики полагают, что, например, ком-
пьютерные доказательства не дают понимания, не являются про-
стыми и элегантными.
Однако в случае математического знания обоснованность не яв-
ляется чисто эпистемологическим понятием, поскольку речь идёт
не о субъекте, а о сообществе. Другими словами, принятие опре-
делённых практик есть вопрос социологический, и широкое рас-
пространение компьютерных доказательств, возможно, является
поводом для утверждения об обоснованности знания, полученного
таким путём.
Эпистемология не может диктовать математической практике,
какие именно методы доказательства могут считаться допустимы-
ми: это дело математического сообщества, которое устанавливает
331
https:it.ru
стандарты строгости доказательства и разрешает концептуальные
споры относительно допустимости доказательства.
Наконец, необходимость включения в определение п. 3 обосно-
вывают результаты Е. Сварта (Swart Е. Л.) (см. [51, с. 87]), кото-
рый выделяет четыре типа теорем в зависимости от используемых
средств доказательства и от способов взаимодействия автора до-
казательства с этими средствами:
1) теоремы, доказательство которых можно выполнить устно
(«устное» доказательство). Вспомним, например, определение Ари-
стотеля: «доказательство — речь, в которой из положенного с не-
обходимостью вытекает нечто, отличное от положенного»;
2) теоремы, доказательство которых требует карандаша и бума-
ги («письменное» доказательство).
Доказательство (по [150, с. 249; с. 251]) — «это физический про-
цесс». Традиционно доказательство определяют как последователь-
ность утверждений, удовлетворяющих самоочевидным правилам вы-
вода, но чему физически эквивалентен процесс доказательства?..
«Надлежащие обстоятельства», которые придают выводу статус
доказательства, заключаются, говоря языком физики, в том, что
символы появляются на странице под другими символами, и по-
рядок появления символов соответствует определённым правилам,
а именно, правилам вывода.
Вспомним индийскую математическую традицию, которая пони-
мала доказательство так: приводя чертёж, поясняющий геометриче-
скую теорему, индийские математики обращали к читателю слово:
«Смотри»;
3) теоремы, которые требуют не только карандаша и бумаги,
но и значительного времени и усилий («письменное» доказатель-
ство, требующее значительных энергозатрат).
У Л. Витгенштейна [146, с. 70] имеются конкретные замеча-
ния по поводу обозримости математического доказательства; так
вторая часть «Замечаний по основаниям математики» начинает-
ся с утверждения: «Математическое доказательство должно быть
обозримым (ubersehbar). “Доказательством” мы называем только
ту структуру, которую несложно воспроизвести. Должно быть воз-
можным чётко определять, действительно ли мы дважды имеем
дело с одним доказательством или нет. Доказательство должно быть
конфигурацией, наверняка поддающейся точному воспроизведе-
нию <...> Должно быть возможным вновь легко и точно записать
это доказательство»;
4) теоремы, которые можно доказать только с помощью компьюте-
ра, причём выделяются два способа доказательства подобных теорем:
а) интерактивный способ, которым является взаимодействие
математика-пользователя с компьютерной системой с целью управ-
ления процессом компьютерного доказательства;
332
https:/Л: rait.ru
б) автоматический способ, которым является взаимодействие
с компьютерной системой, полностью исключающее вмешательство
математика (кроме формулирования теоремы или утверждения).
Итак [150, с. 261], «обоснованность конкретной формы до-
казательства зависит от истинности наших теорий о поведении
объектов, с помощью которых мы осуществляем доказательство.
Следовательно, математическое знание наследственно производно
и полностью зависит от нашего знания физики».
Замечание (шутливое) [177, с. 66].
Дж. Фон Нейман при доказательстве теорем исписывал всю доску фор-
мулами и потом настолько быстро их стирал, что коллеги в шутку назы-
вали его манеру «доказательством методом стирания».
О разновидностях интуиции
Интуиция (В. Ф. Асмус) — это непосредственное знание, в отли-
чие от опосредованного, дискурсивного знания, основанного на до-
казательстве. Это особое знание, рождаемое интуицией, происхо-
дит внезапно; это значит — без логики и причин.
Выделим следующие разновидности интуиции:
1) глобальная (по [50, с. 319]) — это минимальная интуиция, не-
обходимая для работы с формальной системой. Она нужна для того,
чтобы решить, «совпадают ли два рассматриваемых символа или нет»;
2) теоретико-множественная используется при оперировании
с первичными понятиями канторовской (наивной) теории множеств;
3) «брауэровская» интуиция следующим образом описывается
С. Клини [19, с. 52]: «...для математики не остаётся никакого дру-
гого источника, кроме интуиции, которая с непосредственной яс-
ностью помещает перед нашими глазами математические понятия
и выводы <...>
Анализируя идею натурального ряда чисел, мы видим, что она
может быть основана на возможности, во-первых, рассматривать
какой-либо предмет или опыт как данный нам независимо от все-
го остального мира, во-вторых, отличать одно такое рассмотрение
от другого и, в-третьих, представить себе неограниченное повторе-
ние процесса».
Доказательство vs Интуиция
Пока мяч в воздухе, коротко о составах
играющих команд.
Котэ Махарадзе
К тридцатым годам XX в. сложились несколько противоборству-
ющих подходов к математике, поэтому о математике в целом пра-
333
https:/Л: rait.ru
вильнее говорить во множественном числе, оставив единственное
число для обозначения любого из подходов. Никто не мог более
утверждать, что такая-то и такая-то теорема доказана правильно:
в это время непременно следовало пояснить, каким стандартам
правильности удовлетворяет данное доказательство.
По мнению М. Клайна [18, с. 361], математика — это «серия
интуитивных прозрений, тщательно отсеянных, очищенных и орга-
низованных с помощью той логики, которую занимавшиеся ее от-
бором люди хотели и могли применять, когда им заблагорассудит-
ся».
Чем больше усилий прилагалось к уточнению понятий и си-
стематизации дедуктивной системы математики, тем более изо-
щрёнными становились интуитивные представления. Дело в том,
что ни одно доказательство не является окончательным: новые
контрпримеры подрывают старые доказательства. Доказательства
пересматриваются, и новые варианты ошибочно считаются оконча-
тельными, но это означает лишь, что для критического пересмотра
доказательства еще не настало время.
В действительности математик не полагается на строгое дока-
зательство до такой степени, как обычно считают. Его результаты
обретают для него смысл до всякой формализации, и именно этот
смысл сам по себе придает реальность. Попытки установить точные
границы результата путем вывода его из системы аксиом могут ока-
заться в известной степени полезными, но, по существу, они доволь-
но слабо влияют на значение результата.
Интуиция может вселять большую уверенность, чем логика.
Когда математик спрашивает себя, почему верен тот или иной
результат, он ищет ответа в интуитивном понимании. Строгое до-
казательство ничего не значит для математика, если результат ему
непонятен интуитивно. Обнаружив непонимание, математик под-
вергает доказательство тщательному критическому пересмотру.
Если доказательство покажется ему правильным, то он приложит
все силы, чтобы понять, почему интуиция подвела его. Математик
жаждет понять внутреннюю причину, по которой успешно срабаты-
вает цепочка силлогизмов.
Прогрессу математики, несомненно, способствовали главным
образом люди, наделенные не столько способностью проводить
строгие доказательства, сколько необычайно сильной интуицией.
Великие математики заранее, ещё до того, как им удавалось най-
ти логическое доказательство, знали, что теорема верна, и иногда
ограничивались лишь беглым наброском доказательства.
А. Шопенгауэр объяснил это так: «Чтобы усовершенствовать ме-
тод в математике, необходимо прежде всего решительно отказаться
от предрассудка — веры в то, будто доказанная истина превыше ин-
334
https:/Л: rait.ru
туитивного знания». Р. Декарт, например, полагался на врожденные
интуитивные представления, а по поводу логики он заметил: «Я об-
наружил, что силлогизмы и большинство посылок логики более
пригодны, когда речь идет о вещах уже известных <...> или о ве-
щах, в которых говорящий несведущ». Более того, П. Ферма в клас-
сической работе по теории чисел и И. Ньютон в работе по кривым
третьего порядка не привели даже набросков доказательств.
Итак, понятие «доказательство» не играло той роли, которая
ему обычно отводилась. Возникновение противоборствующих фи-
лософий математики, каждая из которых отстаивала свои мерки
строгости доказательства, вызывало переоценку важности доказа-
тельства.
Критические нападки на понятие «доказательство» начались
еще до того, как успели сформироваться различные течения в осно-
ваниях математики.
Г. Г. Харди (1928) утверждал: «Строго говоря, того, что принято
называть математическим доказательством, не существует... Любое
доказательство представляет собой то, что мы с Литтлвудом назы-
ваем газом, — риторические завитушки, предназначенные для пси-
хологического воздействия, картинки, рисуемые на доске во время
лекции, средство для стимуляции воображения учащихся».
А. Уайтхед подверг критике ценность доказательства в своей
лекции под названием «Бессмертие»: «Резюмируя, можно сказать,
что логика, понимаемая как адекватный анализ процесса человече-
ского мышления, есть не более чем обман. Логика — превосходный
инструмент, но ей необходим в качестве основы здравый смысл».
А. Лебег (1928 г.), стоявший на позициях интуиционизма, заявил:
«Логика может заставить нас отвергнуть некоторые доказательства,
но она не в силах заставить нас поверить ни в одно доказательство».
Замечание (по [12, с. 368]).
Любой вывод в существующей логической аксиоматике является
в определенном смысле линейным умозрительным предсказанием экс-
траполяционного типа и поэтому ограниченным в своей познавательной
силе. Поэтому для добычи поистине нового знания необходим нелиней-
ный синергетический процесс, происходящий либо в мозгу человека, либо
в памяти компьютера».
Однако нельзя не признать важного значения логики для мате-
матики. Если интуиция — господин, а логика — ее слуга, то слуга
обладает определенной властью над господином. Логика сдержи-
вает необузданную интуицию. Хотя интуиция играет в математике
основную роль, сама по себе она может приводить к чрезмерно об-
щим утверждениям.
335
https:/Л: rait.ru
Правда, приверженность логике приводит к утверждениям
со множеством оговорок и допущений и обычно требует множества
теорем и доказательств, мелкими шагами преодолевая то расстоя-
ние, которое интуиция «перемахивает одним прыжком».
Более того, Д. Пойа (цит. по [28, с. 43]) указывает, что доказа-
тельства, даже если они неполны, устанавливают связи между мате-
матическими фактами и это помогает нам удерживать их в нашей
памяти, т. е. доказательства дают мнемотехническую систему.
Далее, интуиция может и обмануть нас: так, на протяжении
большей части XIX в. математики считали, что любая непрерывная
функция имеет производную. Но К. Вейерштрасс продемонстриро-
вал непрерывную функцию, ни в одной точке не имеющую произво-
дной. Такая функция оказалась недоступной интуиции.
Математическое доказательство не только дополняет интуицию,
но и подтверждает, исправляет, а в иных случаях и превосходит ее.
По словам Р. Уайлдера, доказательство — это проверка идей, под-
сказанных интуицией.
Ж. Адамар (начало XX в.) высказал следующую мысль: «Цель
математической строгости состоит в том, чтобы санкционировать
и узаконить завоевания интуиции».
Г. Вейль писал: «Логика — это своего рода гигиена, позволяющая
математику сохранять свои идеи здоровыми и сильными».
Итак, доказательство сводит к минимуму риск противоречий.
Замечание (важное).
А. Рейтинг [57, с. 28; 123] сформулировал вербальный критерий, при
помощи которого можно распознавать математические утверждения:
а) каждое математическое утверждение можно выразить так:
«Я выполнил в уме построение А». Если это построение выполнено,
то будем говорить, что построение доказывает высказывание А, и назы-
ваем его доказательством А;
б) математическое отрицание утверждения А можно выразить как
«Я выполнил в уме построение В, которое приводит к противоречию пред-
положение, что можно довести до конца построение в уме А».
Теперь и утверждение, и отрицание выражены в одинаковой форме.
С другой стороны, фактически отрицанием первого утверждения явля-
ется: «Я не выполнил в уме построение А»; это констатирование не имеет
формы математического утверждения.
336
https://ura5t.ru
Интуиционизм. Интуиционистская логика
Гений не совершает ошибок. Его
блуждания намеренны, они — врата
открытия.
Дж. Джойс. Улисс
В начале XX века математики заметили, что понятия «существо-
вать» и «быть построенным» стали заметно, различаться. В ре-
зультате возникло научное течение «интуиционизм», которое по-
пыталось решить проблемы, возникшие в основаниях математики
с помощью уточнения понятия «доказательство».
Определение (по [175]).
Интуиционизм — это направление в основаниях математики и ло-
гики, признающее главным и единственным критерием право-
мерности методов и результатов этих наук их наглядно-содержа-
тельную убедительность (интуицию).
Интуиционизм отвергает:
1) использование в математике и логике идеи актуальной бес-
конечности;
2) взгляд на логику как на науку, «предшествующую» матема-
тике.
Главную причину парадоксов классической математики и логики
интуиционизм усматривает в представлении, что математику мож-
но «обосновать» какими бы то ни было логическими средствами.
С точки зрения интуиционизма математику следует строить ис-
ключительно посредством тех средств, интуитивная убедитель-
ность (в случае доказательств) или интуитивная ясность (в случае
конструкций, построений) которых не вызывает сомнений.
Для интуиционизма понятия «доказательство» и «построение»
не могут быть охвачены одним «точным» определением. Поэтому
никакая система интуиционистски приемлемых правил рассужде-
ний, умозаключений и доказательств не может и не должна коди-
фицироваться в качестве раз и навсегда закреплённой и принятой
логики.
Замечание.
Идеи интуиционизма оказали большое влияние на конструктивное
направление в математике. Основное отличие конструктивизма от инту-
иционизма состоит в том, что неопределяемое и субъективное понятие
«интуиция» заменяется в конструктивизме какой-либо разновидностью
точно определяемого понятия «алгоритм» («вычислимая функция»).
337
https:it.ru
Вот, что пишут известные специалисты в области оснований ма-
тематики А. Френкель и И. Бар-Хиллел [50, с. 244]: «Число ученых,
придерживающихся интуиционистских принципов <...> было всег-
да невелико и заметной тенденции к росту не проявляет. Но весьма
замечательно, что в это число входили такие выдающиеся матема-
тики <...> как Кронекер, Пуанкаре, Борель, Лебег, Брауэр, Вейль,
Сколем».
Определение (по [160, с. 243]).
Интуиционистская логика — совокупность логических законов,
приемлемых с точки зрения интуиционизма, т. е. удовлетворяющих
интуиционистским требованиям к математическим рассуждениям.
В интуиционистской математике используются те же логические
связки, что и в классической математике, но некоторым из них
придается несколько иной смысл.
Для интуиционизма характерно представление о процессе уста-
новления истинности того или иного высказывания как о неко-
тором становящемся процессе. Наряду с суждениями, истинность
или ложность которых установлена к данному моменту, интуицио-
нист допускает непроверенные суждения. Такие суждения, не буду-
чи истинными в данный момент, не являются и ложными, однако
их истинность или ложность со временем может быть установлена.
Не останавливаясь на главных воззрениях интуиционистов, отме-
тим лишь их отношение к закону исключённого третьего (лат. tertium
non datur — третьего не дано; англ, law of the excluded middle), вы-
раженного формульной схемой (A v -А). Применимость закона к ко-
нечным множествам у интуиционистов сомнений не вызывала, од-
нако применимость его к бесконечным множествам они отвергали.
Для пояснения рассмотрим утверждение: «Для всякого простого
числа 2п + 1 найдётся большее простое число вида 2т + 1» (до сих
пор неизвестна истинность или ложность этого суждения). Неиз-
вестно, узнаем ли мы когда-нибудь, истинно оно или ложно. По-
этому не стоит утверждать, говорят интуиционисты, что всякое
утверждение либо истинно, либо ложно — возможен ещё вариант
«неопределённость».
Возникшую коллизию не удаётся устранить введением трёхзнач-
ной логики со значениями «истинно», «ложно» и «неопределённо».
Действительно, если установлено, что некоторое математическое
утверждение истинно (и при этом не совершено ошибок), то оно
и в будущем останется истинным; если установлено, что некоторое
утверждение ложно, то оно и в будущем останется ложным. Но если
установлено, что утверждение является неопределённым, то неиз-
вестно, останется ли оно в будущем неопределённым или же пре-
вратится в истинное или ложное.
338
https:/Л: rait.ru
Другими словами, третья возможность («неопределённо») не ана-
логична первым двум («истинно» и «ложно»).
Замечание.
Представители конструктивного направления (конструктиви-
сты), среди ведущих представителей которых отметим А. А. Маркова
и Н. А. Шанина, придерживаются аналогичных взглядов на закон исклю-
чённого третьего.
Формализация интуиционистской пропозициональной логики
Чистая математика — это такой
предмет, где мы не знаем, о чем мы говорим,
и не знаем, истинно ли то, что мы говорим.
Б. Рассел
1. Классическое исчисление Гильберта
Д. Гильберт [58, с. 418—430] предложил систему классической
пропозициональной логики, состоящую из следующих схем аксиом:
Г1. А —> (В —>А);
Г2. (А -> (А -> В)) —> (А —> В);
ГЗ. (А -> (В -> Q -> (В -> (А -> Q)
Г4. (В -> О -> ((А -^В) (А О);
Г5. А —> (-А —>В);
Гб. (А^В)^(-А^В)^В.
К
W
С
в
Ах: о. А/: о Va.a._/xr: о
—> (о —> Х/а.а) т
Недоказуема в интуиционизме...
Определение (по [65, с. 65]).
Исчислением Гильберта называется исчисление, задаваемое схе-
мами аксиом Г1 — Гб вместе с правилом modus ponens (МР).
Замечание (для знатоков интуиционистской логики).
Покажем недоказуемость аксиомы Гб в интуиционистской логике:
def
положим в аксиоме В = А v -А и построим доказательство формулы A v -А:
A—>Av-A (А—> Ау-А)—>((-А—> Ау-А)—> Ау-А)
(—А —A v —А) —A v —А А —A v А
--------------~л-----------------------№)
Av—А
2. Интуиционистское исчисление А. Н. Колмогорова
Первая попытка построения системы аксиом интуиционистской
логики была предпринята А. Н. Колмогоровым [61; 62, с. 45—69],
который исходил из исчисления Гильберта.
339
A. H. Колмогоров, подвергнув эту систему критическому анализу
с интуиционистской точки зрения, пришёл к системе аксиом инту-
иционистской логики, состоящей из схем аксиом Г1 — Г4 с добав-
ленной к ним новой схемы аксиом К5.
Определение.
Исчисление Колмогорова называется исчисление, задаваемое сле-
дующими схемами аксиом:
Г1. А^ (В^А);
Г2. (А —> (А —> В)) —> (А ^В);
ГЗ. (А^(В^С)^(В^(А^СУ)
Г4. (В -> О (СА ->В) -> (А ->
О);
К5. (А ->В) (А -В) -> -А.
К
W
С
в
X/: о —> т. Ag: о —> т —> Va.cc. Ах: о.
gx(fx): (о —> т) —> (о —> т Va. а) о—>
Va.a
Правилом вывода является modus ponens (МР).
Замечание (важное).
А. Н. Колмогоров выбрал в качестве аксиом формулы, являющиеся
типами комбинаторов М. И. Шейнфинкеля (К, С, В, S) и типом комбина-
тора W, вычисленных в системах типов А , и А2.
Исчисление Колмогорова явилось первой аксиоматизацией ин-
туиционистской пропозициональной логики. Другие системы акси-
ом были предложены В. И. Гливенко [69], А. Рейтингом [70], Г. Ген-
ценом [7], И. С. Новиковым [64]. Они эквивалентны между собой
в том смысле, что из них выводимы одни и те же формулы.
Например, приведем:
а) систему аксиом А. Рейтинга [57, с. 127]:
(1Неу)Р->Р&Р;
(2Неу) р & q q &р;
(3Неу) (р -> q) -> (р & г -> q & г);
(4Неу) (р -> q) & (q -> г) -> (р -> г);
(5неу) q -> (р q);
С6Неу) р & (р -> q) -> qj
(7Неу)р->р vq;
(8Неу) Р vq^q vp;
(9Неу) (Р -> г) & (q -> г) -> ((р v q -> г);
(ЮНеу) -пр -> (р -> q);
(11Неу) (р -> q) & (р -> -,q) -> -р;
б) систему аксиом П. С. Новикова [64, с. 54]:
(lNov) А —> (В —>В);
(2Nov) (А (В С)) ((А В) (А Q);
(3Nov) 0 А;
340
https:it.ru
(4nov) А&В —> A',
(5Nov) A&B^B;
(6Nov) (A^B)^((A^C)^(A^B&C));
(7nov) А ч A vB;
(8Nov) В ->AvB;
(9Nov) (A^C)^((B^Q^((AvB)^C);
(10’Nov)-A —> (A —>B).
3. Интуиционистское понимание логических связок
Эпитет «интуиционистская» (см. [21, с. 269]) связан не толь-
ко с выбором формальной системы, сколько с особенностями
ее интерпретации — как общелогической, так и математической
(то же относится к термину «конструктивная»'). Поэтому замена
одной аксиомной схемы ещё не превращает автоматически класси-
ческое исчисление в интуиционистское: для этого необходима ещё
интуиционистская интерпретация логических связок и всех акси-
омных схем, утверждение о которой может быть лишь результатом
специального исследования.
Главная особенность интуиционистского понимания суждений
заключается в том, что всякое утверждение А истолковывается
в смысле «А установимо», «А конструктивно доказано». Из сказан-
ного ясно, что в интуиционизме смысл логических связок понима-
ется иначе, чем в классической логике.
Приведём (по [63, с. 126—127]) постулаты установимости для
интуиционистской пропозициональной логики:
1) конъюнкция (А & В) установима тогда и только тогда, когда
установимо А и установимо В;
2) дизъюнкция (A v В) установима тогда и только тогда, когда
хотя бы один из ее членов можно установить, т. е. или А, или В.
Очевидно отличие от классической дизъюнкции, так как в по-
следнем случае мы всегда имеем право утверждать (A v -А) — даже
тогда, когда нам не известно, имеет ли место А или имеет место —А;
3) импликация (А —> В) установима тогда и только тогда, когда
установимость В может быть сведена к установимости А, т. е. если
всякий раз, когда будет установлено А, из этого факта можно из-
влечь установимость В.
Другими словами, импликация (А —> В) установима в том и толь-
ко в том случае, когда у нас имеется регулярный способ (алгоритм),
позволяющий по любому конструктивному доказательству А, по-
строить конструктивное доказательство В;
4) константа (читается: «ложь») понимается как некоторое
высказывание, которое заведомо не является установимым;
5) высказывание (-*—> В) считается установимым ввиду того,
что установимость антецедента невозможна, и потому можно го-
ворить о некотором тривиальном сведении установимости В к уста-
новимости всего высказывания;
341
https:/Л: rait.ru
6) отрицание -А установим© тогда и только тогда, когда А не-
установимо. Установимость -А равносильно установимости А —>
7) универсальное высказывание VxA считается установимым
(конструктивно доказанным), если и только если имеется общий
метод, позволяющий относительно произвольного конструктивно-
го объекта Ъ из предметной области установить (конструктивно до-
казать) А(Ь);
8) экзистенциальное высказывание ЗхА считается установимым
(конструктивно доказанным), если и только если указан конкретный
конструктивный объект Ъ из предметной области, относительно ко-
торого установима (конструктивно доказана) справедливость А(Ь).
Приведённое описание постулатов установимости нельзя счи-
тать математически строгим, т. е. у нас есть лишь интуитивное по-
нимание интуиционистской семантики логических связок.
Однако таких представлений достаточно, чтобы начать разработку
формальных систем интуиционистской пропозициональной логики.
4. Гильбертовская формализация интуиционистской
пропозициональной логики
Проведём доказательство от противного.
Допустим, что условие асимптотической
полноты не справедливо. Но это же абсурд!
Что и требовалось доказать.
Метод Голдбергера
Рассмотрим один из вариантов системы А. Рейтинга.
Определение (по [19, с. 65]).
Интуиционистским пропозициональным исчислением Lj называ-
ется формальная система, в которой используются:
а) базовые логические связки: —&, v, -ij
def
б) вспомогательная логическая связка: (А В) = (А—>В)&(В—>А);
в) схемы аксиом:
1) А^(В^А);
2) (А —> В) —> ((А —> (В —> С)) —> (А —> С));
3) А^ (В^А&В);
4) А&В—>А;
5) А&В—>В;
6) A->AvB;
7) B^AvB;
8) (A^C)^((B^C)^(AvB^C));
9) (А->В)->((А->^В)->^А);
10’)-А —> (А —>В);
. , АА^В А
г) правило вывода:---(modus ponens, МР).
342
https:it.ru
В интуиционистском гильбертовском исчислении отсутствует ак-
сиомная схема (10) (-г-А —> А), а потому неприменим один из кос-
венных способов доказательства — доказательство от противного,
состоящий в выведении противоречия из отрицания доказываемой
формулы.
Формульная схема (10’) содержательно выражает логический
принцип: «Из противоречия следует всё, что угодно».
Замечание (по [57, с. 27]).
Замена экономной схемы (10) (-nA -» А) аксиомной схемой 10’ свя-
зано с тем, что «доказательство невозможности невозможности какого-
нибудь свойства не всегда есть доказательства этого свойства».
Теорема 1 (важные формулы, доказуемые в интуиционизме').
1) -i(A & -А) (закон непротиворечия);
2) А —> -i-A (сильное введение -i);
3) —1—1(—1—«А -> А); (интуиционистский закон исключённого
третьего);
4) А (-А В) (закон Дунса Скота);
5) (А В) (—В -А) (контрапозиция);
6) (А В) (А —В) -А (приведение к абсурду);
7) (А В & —В) -А(приведение к абсурду);
8) (-А В & —В) -i-A (приведение к абсурду);
9) -i(A vB) <4 (-А & —В) (закон де Моргана);
10) (-А v —В) —> —i(A & В) (закон де Моргана).
Доказательство. Упражняйтесь.
Теорема 2 (важные формулы, недоказуемые в интуиционизме).
Если р и q — пропозициональные переменные, то недоказуемы
следующие формулы (не схемы'.):
1) р v —р (закон исключённого третьего);
2) -i-р -^р; (закон двойного отрицания);
3) (—р —> q & —<q) -^р (доказательство от противного);
4) (—р —> q) —> (—р —iq) -^р (доказательство от противного);
5) (-i(p q) —р) (р q) (доказательство от противного);
6) (-i(p q) q) (р q) (доказательство от противного);
7) (—р -iq) <-» (q ~^р) (контрапозиция);
8) -i(p & q) —> (—р v -iq) (закон де Моргана);
9) (р -> q) р р (закон Пирса).
Доказательство. Упражняйтесь.
Замечание (важное).
Если недоказуемую в интуиционизме формулу -r-р —>р записать в виде
формульной схемы как -nA —» А, где А — произвольная пропозициональ-
343
https:/^!^ it.ru
ная формула, то в результате подстановки вместо А формулы —р получается
формула -i-т-р —р, которая уже доказуема в интуиционизме.
Итак, приведение к абсурду и доказательство от противного
имеют различный логический статус:
1) приведение к абсурду является своеобразным определением
логической связки -i (в частности, в классическом пропозицио-
нальном исчислении с помощью приведения к абсурду доказывают-
ся правила «доказательство от противного» и «контрапозиция»');
2) доказательство от противного и контрапозиция являются
использованием нетривиальных свойств этой логической связки,
т. е. оба правила можно считать свойствами связки -i.
Работа с примерами решения некоторых типов упражнений
См. Пример 1, Пример 2, Пример 3.
Замечание.
Контрапозиция—это, выражаясь шахматным языком, рокировка фор-
мул. Редкая шахматная партия обходится без рокировки, и редкое доказа-
тельство проходит без использования контрапозиции.
5. Минимальное пропозициональное исчисление
Говорить мы учимся у людей,
молчать —у богов.
Плутарх
Разновидностью интуиционистской логики является минималь-
ное пропозициональное исчисление (или просто минимальное исчис-
ление), которое введено И. Юхансоном [73].
Определение 1 (по [57, с. 127]).
Минимальным исчислением (исчислением Юхансона) называется
исчисление, которое задаётся схемами аксиом 1—9:
1) А^(В^А);
2) (А—>В) ((А^ (B^Q) (A->Q);
3) А^ (В —>А&В);
4) А&В—>А;
5) А & В^> В;
6) A^AvB;
7) ВчАуВ;
8) (A->C)->((B->C)->(AvB->C));
9) (А —> В) —> ((А —> —В) —>-А).
Итак, минимальное исчисление не содержит формулы (10’) -А —>
—> (А —> В) в качестве аксиомы.
344
https:/Л: rait.ru
Определение 2 (по [Гудстейн, 1961, с. 44]).
Минимальной логикой (логикой Юхансона) называется исчисле-
ние, отличающееся от интуиционистской логики тем, что исчис-
ление содержит аксиомную схему -А —> (А —> -i-iB) вместо акси-
омной схемы 10’.
Формульная схема -iA (А -> -i-iB) содержательно выражает ло-
гический принцип: «Из противоречия следует двойное отрицание
“всего, что угодно” (а не “всё, что угодно”)».
6. Позитивное пропозициональное исчисление
Простота — это крайняя степень
изощрённости.
Леонардо да Винчи
Позитивное исчисление является вариантом формализации по-
ложительной логики.
Определение (по [116, с. 386]).
Положительные логики — это логики, построенные без исполь-
зования логической связки -i. Их можно разделить на два вида:
1) положительные логики в широком смысле слова (или просто
квазипозитивные логики), построенные без использования логи-
ческой связки -I, но эта логическая связка может быть выражена
средствами их логических, систем. Примерами квазипозитивных
логик являются логики, построенные только на логической связке
«штрих Шеффера» и только на логической связке «стрелка Пирса»;
2) положительные логики в узком смысле слова, построенные
без использования логической связки -i, и эта логическая связ-
ка не может быть выражена средствами их логических систем.
Важным отличием положительных логик в широком и узком
смыслах является следующее:
1) квазипозитивные логики являются моделями пропозицио-
нальной логики;
2) положительные логики в узком смысле являются ее подсисте-
мами, т. е. они «слабее» пропозициональной логики.
Рассмотрим позитивное исчисление, предложенное Д. Гильбер-
том и П. Бернайсом.
Определение (по [8, с. 99]).
Позитивная логика представляет собой формализацию тех спо-
собов логических умозаключений, которые не зависят от предпо-
ложения о том, что для каждого высказывания имеется ему про-
тивоположное.
345
https:it.ru
Определение.
Позитивным исчислением называется исчисление, которое зада-
ётся схемами аксиом 1—8:
1) А->(В->А);
2) (A^B)^((A^(B^C))^(A^Q);
3) А^ (В^А&В);
4) А&В^А;
5) А&В^В;
6) A->AvB;
7) ВчАуВ;
8) (Д—>С) ((В^С) -> (A v В-> Ol-
Итак, позитивное исчисление — это исчисление, полученное ис-
ключением схемы аксиом (9) из минимального исчисления.
Теперь рассмотрим соотношение между минимальным и пози-
тивным исчислением.
Пусть А — пропозициональная формула, -I-пропозициональ-
ная переменная, не входящая в А. Через Ар обозначим результат по-
следовательной замены в А подформул вида —В на В —> -Ц
Формулу Ар назовём -^-образом формулы А.
Теорема [65, с. 68]).
Формула А выводима в минимальном исчислении тогда и толь-
ко тогда, когда ее образ Ар выводим в позитивном исчислении.
Доказательство. Тот факт, что если формула А выводима в ми-
нимальном исчислении, то ее образ Ар выводим в позитивном ис-
числении, доказывается индукцией по длине вывода формулы А в ми-
нимальном исчислении с учётом следующих замечаний.
1. образ всякой аксиомы минимального исчисления является
аксиомой позитивного исчисления.
Действительно, -L-образ любой из аксиом 1—8 имеет ту же логи-
ческую форму и является аксиомой позитивного исчисления.
-L-образ аксиомы 9 имеет вид
(Ар Вр) -> ((Ар (Вр -> -L)) -> (Ар -L)),
т. е. получается по схеме аксиом (2).
2. Если формула В получена по правилу МР из формулА и (А —> В),
то Вр получается по правилу МР из формул Ар и (А В)р = (Ар Вр).
Отсюда следует, что если в выводе формулы А в минимальном
исчислении каждую формулу заменить на ее -L-образ, то получится
вывод формулы Ар в позитивном исчислении.
Докажем теперь, что если формула Ар выводима в позитивном
исчислении, то формула А выводима в минимальном исчислении.
Для этого заметим, что если формула Ар выводима в позитив-
ном исчислении, то она выводима и в минимальном исчислении.
Поскольку для рассматриваемых исчислений имеет место правило
346
https:/Л: rait.ru
подстановки, то в минимальном исчислении выводима и формула
Ар1, полученная подстановкой в Ар формулы -(-!—> -*-) вместо про-
позициональной переменной
Оказывается (докажите!), что какова бы ни была формула
В, формулы В —> -i(-l—> -•-) и -В дедуктивно эквивалентны в мини-
мальном исчислении.
Следовательно, в силу Теоремы об эквивалентной замене фор-
мулы Apj дедуктивно эквивалентны в минимальном исчислении,
поэтому, если в минимальном исчислении выводима формула Ар1г
то выводима и А.
Теорема доказана.
Теорема [65, с. 69]).
Формула Р —> (-iP —> Q) невыводима в минимальном исчислении.
Доказательство. образ рассматриваемой формулы есть фор-
мула
P->((P->-L)->Q),
очевидно, не являющаяся доказуемой в классическом пропозицио-
нальном исчислении. Но в позитивном исчислении выводятся толь-
ко классически доказуемые формулы. Следовательно, образ фор-
мулы Р —> (-Р —> Q) невыводим в позитивном исчислении, и в силу
предыдущей Теоремы сама эта формула невыводима в минималь-
ном исчислении.
Теорема доказана.
Биографические сведения
Рейтинг Аренд (9 мая 1898, Амстердам — 9 июля 1980, Луга-
но) — голландский математик и логик, студент и последователь
Л. Э. Я. Брауэра, член Нидерландской королевской АН.
Окончил Амстердамский университет (1922); работал там же
(с 1948 — профессор). Исследования посвящены основаниям мате-
матики. Один из виднейших представителей интуиционизма после
Брауэра, опубликовал работу с изложением формальных правил ин-
туиционистской логики высказываний. Интуиционистская логика
стала частью математической логики.
347
https:it.ru
Примеры решения некоторых типов упражнений
Язык ещё не выдает нам своей сути:
того, что он — дом истины бытия.
М. Хайдеггер
Пример 1. Постройте доказательство формулы -i(A & -А) (закон
непротиворечия) в интуиционистском гильбертовском исчислении.
Решение.
Аксиома (3) Аксиома (9)
1 г
Аксиома(4) (А&^А)^>А ((А&^А)->А)->((А&^А)->А)->ЧА&^А))
ф ----------------------------------------------------(МР")
(А&^А->^А)->ЧА&^А) 'мр'
-i(A&-A)
Пример 2. Постройте доказательство формулы (А —> А & —А)
—А в интуиционистском генценовском исчислении:
Решение.
J.2 |1
(modusponens)
|2 А&—iA
А —А
-------- (слабое удаление отрицания)
Л (приведение к абсурду)
—--- ------------ (дедукция)
(А->А&-А)->-А
Список допущений:
1.А—>А&-А
2. А
Пример 3. Постройте в интуиционистском гильбертовском исчисле-
нии следующие выводы: а) {А —> В, А —> -В} I—A v В; (б) {A, -A} I- -i-B.
Решение.
а)
Гипотеза Аксиома (9)
J, 1
Гипотеза А->В (ДВ)->((АВ)В)
А^^В (А—>-В)—>-В Аксиома (6)
(1) ------------------ 4-
m ——А—>(—AvB)
—AvB
б)
Гипотеза Аксиома (1)
Л Л ('—R —> А1 Аксиома (9) Гипотеза Аксиома (1)
—----- 1 J J. I (1)
((—В—>—A)—>—i—В) (—В—>—A)
348
https ://и rait.ru
Задачи для самостоятельного решения
Они не могли выбраться из просёлков
раньше полудня. Без девчонки было бы
трудно сделать и это, потому что
дороги расползлись во все стороны, как
пойманные раки, когда их высыплют
из мешка.
Н. В. Гоголь. Мёртвые души, т. 1
1. Классическое пропозициональное исчисление (повторение)
1. (По [53, с. 105])
Установите в классическом пропозициональном исчислении доказуемость
следующих формул:
1) ((р -> q) -> г) -> ((г —> р) —> (s —> р));
2) ((р г) (s р)) (((г —> q) —> р) —> (s —> р));
3) ((г -> q) -> (s -> р)) ((г -^p)^(s^ р));
4) (((г —> р) —> р) —> (s —> р)) (((р —> q) —> г) —> (s —> р));
5) С((р -> г) -> q) -> q) -> ((q -> г) -> (р -> г));
6) (р —> q) —> (((р —> г) —> q) —> q);
7) ((p^s) ^р) ^((с^р) ^Ъ) ^р.
Решение. Докажем формулы 1—7 в классическом пропозициональном ген-
ценовском исчислении. Воспользуемся методом построения доказательств,
основанном на применении дедуктивной эквивалентности (А -> В) =d -A v В
к одному или нескольким допущениям, а затем фигуры заключения, назы-
ваемой «разбором случаев».
4 2 4
4* <L*L
| р&-.д г^>р г
p&-,qx/r Р Р
Список допущений:
1. (р -> q) -> г =d р&-iq v г
2.г—>р
3.S
4.p&-iq|r
2) 4
ф
r&-.q I
г г—^р
1 I р
r8i—<qv(s—>p) s^p s—>p з
______________________________ ф
s^>p s
__________________p__________________
((r -> q) -> (s -> p)) ->((r ->p) ->(s -> p))
Список допущений:
l.(r —>q)—>(s—>p)=d
=d r&—iq\/(s—>p)
2.r^p
3.s
4.s->p|r&-iq
https: "ura it. ri!
349
3)
4 3 4
*L 'L 'L
J Р&-.Г s s^p
p &.—>г \/(sp) p p
______________________p______________________
(Cp -> r) -> (s -> p)) (CO q) p) -> (s -> p))
Список допущений:
1. (p —> г) —> (s —>p) =d
=d (-pvrH(s^>p) =d
=d p&—,rx/Cs^p)
2.(r—>q)—>p
3.s
4.p&-ir |(s—>p)
4)
5 4 5
2 4' *L *L
I p&—.q r^p r J 4
I rvp&-iq P P s -is
(r —> p) V —iS P P
_________________________p_________________________
C((r p) p) -> (s -> p)) (CCp -> q) -> r) (s -> p))
Список допущений:
l.((r->p)->p)->
—> (s —> p) ^d
=d -1Г & -p V —iS v p =d
=d -1Г & -p V p V —iS =d
=d -1Г V p V -1S =d
=d (r^p)x/ -1S
2.(p^q)^-r=d
=d r x/p&—,q
3.s
4. r p | -is
5.r|p&-iq
Приведём доказательство формулы, дедуктивно эквивалентной (в клас-
сическом смысле) доказанной формуле (4):
((г ->р) v ^s) -> ((г vp & -.q) ->($->р)),
в программном средстве Coq, которое является «доказывателем» теорем
и языком функционального программирования с зависимыми типами:
Theorem 4:
forall Р Q R S: Prop, ((R-> P)\/~S) -> ((R\/PA~Q) -> (S -> P)).
Proof.
intros.
elim H; [intro; elim HO; [assumption | intro; apply H3] |
apply absurd; assumption].
Qed.
5) Список допущений:
l.((p^r)^q)^-q=d
=d(4p^r)vq)^-q=d
=d (p^r)&-iqvq=d
4 2 3 4 Я r
г I I I I =dQp^r)\/q
I q q^r p p^»r 2.q^r
(p^>r)vq r r 3 p
-------------------------------- 4.p->r\q
C((p^r)^q)^q)^((q^r)^(d^r))
350
6) 3
I P&^r
I Ip^q p
p&-,rvq q 4
____________q___________
(p—>q)—>(((p—>r)—>q)—>q)
Список допущений:
l.p^q
2. (p —> r) —> q =d p&—,rx/q
3. q | p & -ir
Приведём также доказательство формулы, дедуктивно эквивалентной
(в классическом смысле) доказанной формуле (6):
(р -> q) -> ((р & ~>г v q) q),
в программном средстве Coq:
Theorem 6: forall Р Q R: Prop, (P -> Q) -> ((PA~R\/Q) -> Q).
Proof.
intros; elim HO;
[intro; apply H; apply Hl | intro; assumption].
Qed.
7) з
1 Список допущений:
। p&-iS । l.(p—>$)—>p=d p&-iS vp
P p 2, (c—>p)->b
----------------------------- 3. p & I p
((p -> s) p) ((c p) b) p
2*. Исследуйте классическую доказуемость формулы
C(r р) (s р)) ^ (((г q) р) (s р)).
3. Установите в классическом пропозициональном исчислении доказуе-
мость следующих формул:
1) ((А —> В) —> А) —> А (закон Пирса);
2) (((А -> В) Q (А В)) (А В) (35-закон Пирса);
3) ((((А —> В) —> А) —> А) —> А) —> А (обобщённый закон Пирса);
4) ((А —> В) —> В) —> ((В —> А) —> А) (коммутативность дизъюнкции).
5) (A v -А)^ (((А —> В) —> А) —> А);
6) (((А -> В) -> А) -> А) -> (^-.А -> А).
Решение.
1), 4) Докажем в классическом генценовском исчислении NK:
з
I А&—В I
A&-BvA А д
А
((А^В)^А)^А
3 2 3
4, J,
| А&—В В—>А В
А&—BvB А А
Список допущений:
1. (АВ) -> A) =d А&-В v А
2.А&—.В | А
А
______(В^А)^А_______
цА^В)^В)^((В^>А)^А)
Список допущений:
l.(A^B)^B)=d A&-BvB
2.В^А
З.А&—В|В
351
https:/.^гз-t.ru
2) Доказательство формулы 2 получается из доказательства 1.
3) Убедимся в общезначимости формул 3 и 4 с помощью построения
аналитических таблиц (!):
-Ч((((А->В)->А)->А)->А)->А)
(((А->В)->А)->А)->А,^А
-Ч((А->В)->А)->А),^А I А,-А
(А^>В)^>А,^А,^А
—(А—>В),—А I А,^А
А,-В,^А
Теперь, воспользовавшись полнотой гильбертовского пропозициональ-
ного исчисления, получаем, что 3 и 4 доказуемы.
4. (По [57, с. 83]) Установите в классическом пропозициональном ис-
числении доказуемость следующих формул:
1) ((—р->р)->(—pv^p))->(^p v-ip) (формула Янкова);
2) ~(Р1 &р2) & bpi -> Qi v q2) & Ьр2 91 v q2) ->
(--Р1 -> 91) V (—-Р1 92) V (—Рг -> 91) V (—Р2 -> 9г) (формулаЦейтина).
Решение.
н^р^р{^р^р(
{ (——.р -> р) -> (-.-.р V -.р) } I- —.р V -р
I- (Х->-р -^р}^ V -.р)) (->-р V -.р)
2. Интуиционистское гилъбертовское
пропозициональное исчисление
1*. [20, с. 109—110]
Установите в интуиционистском пропозициональном исчислении Lj до-
казуемость следующих формул:
1) А->^А;
2) —А —> —А;
3) (A v-А) —> (—I—А —> А);
4) (Av^)4(^oA);
5) —i(A<->—А);
6) —I—i(Av—А);
7) (A vB) ->-,(-пА&-В);
8) -^(^А->А);
9) (—A vB) —>-i(A &—В);
10) А &В —> —1(—A v -В);
11) (А -> В) —i(A & -В);
12) А & —В —> —1(—A v В);
13) (А -> -В) <-> —i(A & В) о (->^А -> -В) <-> —,—.(—A v -В);
14) (-^А -> В) о (А -> В) о —i(A & -В);
15) (-,^В^В)^(-,^А^В)
16) (-1—А —> В) —> —i(A & —В);
17) (-nAvB)
18) А & В -> -.(А -В);
19) (A^B)^-,-,(-nAvB);
20) А & -В —> —i(A В);
21) (-пА^В) (AvB);
22) -i-А & В -,(А -В);
23) AvB^ (,-пА^ВУ,
352
https:/Л: rait.ru
24) (i^A & -В) <-> -i(A -> В) <-» ->(-nA v В) о —,СА & -В);
25) —.—.(А -> В) <-> -.(А & -В) <-> (А -> ->-В) <-> (-i-A -.-В);
26) (—A v —В) —>-i(A&B).
27) -.(A v В) о -п(-А В);
28) (А —> В) —> (—В —> —А);
29) -i(A & В) о (-.-А & -i-B);
30) (-.^А v-i-B)->-i-.(AvB);
31) -i(A v В) о -А & -В.
2*. (По [21, с. 26—27; с. 45; 20, с. 105])
Докажите, что в интуиционистском гильбертовском пропозициональном
исчислении не существует доказательство следующих формул:
1) A v —А;
2) —i—А—>А;
3) (А—>В) о (-В—>-А);
4) -,(А & В) о (—A v -В);
5) -i(A—>В) о (А&-В);
6) (A vB) <-»-i(-A &-В);
7) (А&В) о-,(-пА v-B);
8) (А -> В) о —i(A & -В);
9) (А —> В) <-» (—A v В);
10) (А&В) о-i(A->-B);
11) (AvB) о (-^А^В);
12) (А & (В v —В)) <->А;
13) (AvB v—В) <-> (В v —В);
14) (-пА->В)<->ЬВ->А);
15) (-А -> -В) <-> (В А).
3. Докажите, что для интуиционистского гильбертовского пропозицио-
нального исчисления не существует доказательство формул:
1) (A->B)->(-nAvB);
2) —i(A & -В) —> (А —> В);
3) —i(—А & —В) (AvB);
4) (-nA->B)->(AvB);
5) ((А —> В) —> В) —> (A v В);
6) —1(—A v —В) —> А & В;
7) —i(A—>—В) ->А&В;
8) (-пА- ^^В)- ^(В- ->А);
9) 1 ((-А -^В)- >(-пВ ->А);
Ю) А^ (Bv^B);
И) (—А ^А)- >А;
12) ((А- -+В)^> •А)-) А;
13) (— 4->А) -+(А v —А);
14) (А — >В) v (В^А);
15) —.—.(A v В) - тА v —।—В)
16) -i(A&B) -> (—А' ^-В);
17) -.-.(A v В) - tAv—1—В)
4*. Найдите ошибку в утверждении: «Все формулы, выводимые в интуи-
ционистском исчислении Lj выводимы также в классическом гильбертовском
пропозициональном исчислении (и наоборот)».
353
https:/Л: rait.ru
Упражнение 16
ИНТУИЦИОНИСТСКИЕ
ПРОПОЗИЦИОНАЛЬНЫЕ ЛОГИКИ:
МИНИМАЛЬНОЕ ПОЗИТИВНОЕ
ИСЧИСЛЕНИЕ PROP
Как будто мы жители разных планет.
На вашей планете я не проживаю.
Я вас уважаю, я вас уважаю,
но я на другой проживаю. Привет!
Александр Володин
Обязательные результаты обучения:
• Знать вспомогательные понятия
— прямой вывод в гильбертовском исчислении;
— непрямой вывод в гильбертовском исчислении;
— генценовское исчисление (натуральный вывод);
— формализация интуиционистской пропозициональной логики;
• знать основные понятия
— минимальное позитивное исчисление Prop;
— логическая матрица, выделенные истинностные значения, оценка
в логической матрице;
— формула, истинная в логической матрице; формула, опровержимая
в логической матрице;
— модель гильбертовского пропозиционального исчисления;
— точная модель гильбертовского пропозиционального исчисления;
— гейтинговская модель, минимальная гейтинговская модель;
— метод моделей для доказательства несуществования решения задачи
TIP в системе типов А_^;
• уметь
— конструировать доказательства формул в исчислении Prop;
— конструировать выводы формул в исчислении Prop;
— устанавливать недоказуемость формул в исчислении Prop с помощью
гейтинговской модели;
— проверять правильность утверждений в соответствии с заданной ло-
гической матрицей;
— устанавливать несуществование решения задачи TIP в системе
методом моделей;
354
https: "и rait.ru
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
Теоретические сведения
Импликативное позитивное исчисление Prop
В науке ты можешь сравнить то, что
ты делаешь, скажем, с постройкой дома.
Сначала ты должен заложить твердый
фундамент. Заложив его однажды, ты больше
не можешь его трогать или сдвигать с места.
В философии мы не закладываем фундамент,
а приводим в порядок комнату, в процессе
чего мы должны всё трогать по многу раз.
Л. Витгенштейн. Из лекций 1930 г.
Определение (по [8, с. 99]).
Импликативной формулой называется пропозициональная формула,
в которой единственной логической связкой является импликация.
Л. Гильберт и И. Бернайс [8, с. 101] отметили, что для представ-
ления всех импликативных формул достаточно использовать только
две импликативные формулы:
А (В ->А), (А (В С)) (А ->В) (А Q.
Определение.
Импликативным позитивным исчислением называется позитив-
ное исчисление, содержащее только аксиомные схемы 1 и 2.
В теории типов оно называется минимальной логикой Prop.
Пусть I — непустое множество.
Определение.
1. Алфавитом минимальной логики Prop называется множество
def
Gprop = о G2 u G3 и G4 и G5 и G6,
def def def def def def
rfleGi = 0,G2 ={P?},ieI,G3 = 0,G4 = 0, G5 = M}, G6 = {(,)}.
2. Пропозициональными переменными называются нульместные
предикатные символы Р®, i е I, которые будем обозначать строч-
ными греческими буквами (возможно с нижними индексами), т. е.
def
G2 = {а, ₽, у, 8, е, £, т], &, i, к, X, ц, v, £, о, л, р, о, т, и, ср, %, у, со}.
355
https: "и га it.ru
Определение (повторение).
1. Пропозициональная переменная является формулой.
2. Если А и В — формулы сигнатуры о, то (А -> В) — формула.
3. Никаких других формул, кроме построенных в пп. 1—2, нет.
Иногда индуктивное определение понятия «формула» записывается
в виде BNF-нотации так QF— синтаксическая категория «Формулы»):
•F:: = G2| CF^F).
Замечание (повторение).
Аббревиатура BNF означает «Backus-Nauer Form» (форма Бэкуса-
Наура): этот способ представления синтаксиса формальных языков явля-
ется в настоящее время широко распространённым как в логике, так
и в других областях, связанных с формальными языками — например,
в теории языков программирования.
Обозначим .FprOp — множество формул Prop.
Определение.
1. Языком минимальной логики Prop называется язык формаль-
ной системы первого порядка
def
Li = (GProp, 0, Fprop),
def
который будем обозначать и так: Prop = (G, FProp).
Определение (гилъбертовский вариант, прямые правила вывода).
Исчисление минимальной логики Prop содержит (а, Р, е FProp):
1) аксиомные схемы для связки —
ос —> (Р —> ос) (законупрощения);
(а —> Р) ((а —> (Р —> у)) —> (ос —> у)) (силлогизм Фреге);
а ос (а—>Р) г , ,
2) основное правило вывода:-----— (modus ponens, МР);
Р
3) допустимые правила вывода:
(а->р) (Р->у) , .
-------------(транзитивность);
(а->у)
(а^(Р^у))
----------— (перестановка посылок).
(Р—>(а—>у))
Соглашение об обозначениях (повторение).
Выводимость формулы А из множества гипотез Н обозначается
Н hProp А или ННА.
356
https:/Л: rait.ru
Определение (гильбертовский вариант, непрямые правила вывода).
Исчисление минимальной логики Prop содержит (а, Р, g FProp):
1) структурные непрямые правила вывода:
Н\-а
H<u{p}ha
(расширение);
Ни{р}и{р}Ьа
Н<и{р}|-а
(сокращение);
Ни{а,р}И
Ни{р,а}ЬС
(перестановка);
f^l-а ;{а}иН2Ьр
нГЦНгТр
(сечение);
2) правила введения и удаления связки
НН а; Hl-а—>р
Н1-р
(удаление
Ни{а}Ьр. _ .
--------- (введение -^).
Н1-а->р
Определение (генценовский вариант).
Исчисление минимальной логики Prop содержит:
1) фигуры заключения (а, Р, g FProp):
[а]
а (modus ponens); -—(дедукция);
2) правило закрытия допущения: если существует вывод форму-
лы Р из Н о {а}, то можно вывести формулу (а —> Р) и закрыть
допущение а.
Работа с примерами решения некоторых типов упражнений
См. Пример 1, Пример 2.
Для построения доказательств иногда удаётся воспользоваться
существованием изоморфизма Карри — Говарда между системой ти-
пов и логической системой Prop, т. е. доказуемые формулы в Prop
являются типами системы а доказательства в Prop представи-
мы в виде Х-термов системы
В качестве примера рассмотрим следующее утверждение о типи-
зации в системе в стиле Чёрча:
X/:a^p.Xg:p^-y.Xx:a.gC/x) : (a^p)^(p->y)^(a^y)
' 1-терм (доказательство) ' Тип ^TePMa (доказуемая фоРмула)
Итак, Х-терм может являться способом представления доказа-
тельства формулы в Prop.
357
https:it.ru
Работа с примерами решения некоторых типов упражнений
См. Пример 3.
Замечания (важные).
1. Записывать и читать формальные доказательства, как и любые дру-
гие строгие рассуждения — тяжёлая работа. Но, в конце концов, она оку-
пается. Формальное доказательство доступно любому человеку, облада-
ющему определённой подготовкой, и оно будет читаться во всех странах,
во всех культурах и во все времена.
2. «Ручное» доказательство, выполняемое человеком, часто не ока-
зывается «полезным» для компьютера. Однако человек может шагнуть
за рамки логической системы и воспользоваться любыми средствами для
построения доказательства.
Модель гильбертовского пропозиционального исчисления
Тем не менее многие весьма
ученые и мудрые люди пользуются
этим новым способом выражения
своих мыслей при помощи вещей.
Единственным его неудобством является
то обстоятельство, что, в случае
необходимости вести пространный
разговор на разнообразные темы,
собеседникам приходится таскать
на плечах большие узлы с вещами... При
встрече на улице они снимали с плеч
мешки, открывали их и, достав оттуда
необходимые вещи, вели таким образом
беседу в продолжение часа; затем
складывали свою утварь, помогали
друг другу взваливать груз на плечи,
прощались и расходились.
Дж. Свифт.
Путешествие Гулливера в Лапуту
Вначале построим некоторую алгебраическую систему, для чего:
1) явно укажем фиксированное множество истинностных значе-
ний, принимаемые пропозициональными переменными;
2) опишем интерпретацию логических связок в виде функций,
определённых на этом множестве истинностных значений.
Пусть М — непустое множество, D с М.
Определение.
1) Логической матрицей называется алгебраическая система
def
M = (M;D,*,+,
358
https: "и га it.ru
где
*:МхМ->М,+:МхМчМ,„>:МхМ->
^М, <
2) Выделенными истинностными значениями называются эле-
менты множества D с М.
Определение.
Оценкой (интерпретацией) в логической матрице М называется
функция f: G2 —> М, которая индуктивно определяется так:
1) f(P)eM,Pe G2;
def
2) f(-A) = _f(A);
def
3) f(A&B) = f(A) *f(B);
def
4) f(AvB) = f(A)+f(B);
def
5) f(A—>B) = f(A) ~> f(B);
def
6) f(A^B) = f(A) <_> f(B).
Пусть A — формула, построенная из пропозициональных пере-
менных Р1г ...,Рпс помощью логических связок &, v, <-», -i.
При каждой оценке в логической матрице М формула А получает
некоторое значение из множества М.
Определение.
Формулой, истинной (общезначимой) в логической матрице М на-
зывается формула А, для которой f(A) g D при любых значениях
пропозициональных переменных в множестве М, т. е. если фор-
мула А принимает выделенное значение.
Определение.
Формулой, опровержимой в логической матрице М, называется
формула А, для которой существует оценка, при которой f(A) £ D.
В этом случае логическая матрица называется контрмоделью для А.
Теперь рассмотрим интуиционистское гильбертовское пропози-
циональное исчисление.
Определение.
1. Моделью пропозиционального исчисления называется такая ло-
гическая матрица, для которой любая формула, доказуемая в ис-
числении, является истинной в этой логической матрице, т. е.
НА =>НМА.
359
2. Точной моделью пропозиционального исчисления называет-
ся логическая матрица, для которой в исчислении доказуемы
те и только те формулы, которые истинны в этой матрице.
Определение.
Гейтинговской моделью называется следующая логическая ма-
трица:
def def def
М = (M;D,*,+, _>,<_>, _),М = {0,1/2,1},D = {1};
def
х*у = min(x,y),
def
x + y = max(x,y),
def если X < у,
x~ > у = < ’ ’ (трёхзначная импликация Рейтинга);
[у, если х > у
def def ft если х - 0,
~Х = Х->0 = 5 .
0, если х = 1/2, х=1;
def
х <~> у = min(x -> у, у -> х).
В таблицах значения х ~> у их < ~ > у находятся на пересечении
строки, соответствующей х, и столбца, соответствующего у.
х~>У 0 1/2 1
0 1 1 1
1/2 0 1 1
1 0 1/2 1
х<~>У 0 1/2 1
0 1 0 0
1/2 0 1 1/2
1 0 1/2 1
Теорема (важная).
Пусть классическое (или интуиционистское) пропозициональ-
ное исчисление имеет единственное правило вывода modus ponens.
Тогда логическая матрица М является моделью исчисления, если
и только если все аксиомы истинны в матрице М.
Теорема (важная) (по [64, с. 73—75]).
1. Моделью минимального позитивного исчисления является сле-
дующая логическая матрица (минимальная гейтинговская модель):
360
https: "и га it.ru
def def def
M = {M;D, _>},M = {0,1/2,1}, D = {1};
def если X < у,
x~>y = < ’ ’ (трёхзначная импликация Рейтинга);
у, если х > у
В таблице значение х ~> у находится на пересечении строки, со-
ответствующей х, и столбца, соответствующего у.
х~>У 0 1/2 1
0 1 1 1
1/2 0 1 1
1 0 1/2 1
2. Минимальная гейтинговская модель не является точной моде-
лью минимального позитивного исчисления.
Доказательство.
1. Покажем, что общезначимыми в используемой логической ма-
трице являются аксиомы Prop и правило вывода:
а —> (Р —> а), ((а —> (Р —> у)) —> (а —> Р) —> (а —> у)) (аксиомы),
p&(p—>q) <r+p&q,p & (р —>q) ~>q (modusponens),
для чего построим таблицы:
а Р Р —> а а —> (Р —> а)
0 0 0 0 1/2 1 1 0 0 1 1 1
1/2 1/2 1/2 0 1/2 1 1 1 1/2 1 1 1
1 1 1 0 1/2 1 1 1 1 1 1 1
Р q р & (р -> q) p&q р & (р -> q) q
0 0 1 0 0 1
0 1/2 1 0 0 1
0 1 1 0 0 1
1/2 0 0 0 0 1
1/2 1/2 1 1/2 1/2 1
1/2 1 1 1/2 1/2 1
1 0 0 0 0 1
1 1/2 1/2 1/2 1/2 1
1 1 1 1 1 1
https-"и гз it.
361
а Р Y ₽->Y а ->(₽-> у) а—> Р а—> у (а —> Р) —> (а —> у) Результат
0 0 0 1 1 1 1 1 1
0 0 1/2 1 1 1 1 1 1
0 0 1 1 1 1 1 1 1
0 1/2 0 0 1 1 1 1 1
0 1/2 1/2 1 1 1 1 1 1
0 1/2 1 1 1 1 1 1 1
0 1 0 0 1 1 1 1 1
0 1 1/2 1/2 1 1 1 1 1
0 1 1 1 1 1 1 1 1
а Р Y P->Y г та ® Р у (а -> Р) -> —> (а —> у) Резуль- тат
1/2 0 0 1 1 0 0 1 1
1/2 0 1/2 1 1 0 1 1 1
1/2 0 1 1 1 0 1 1 1
1/2 1/2 0 0 0 1 0 0 1
1/2 1/2 1/2 1 1 1 1 1 1
1/2 1/2 1 1 1 1 1 1 1
1/2 1 0 0 0 1 0 0 1
1/2 1 1/2 1/2 1 1 1 1 1
1/2 1 1 1 1 1 1 1 1
а Р Y P->Y а (Р Y) а—> Р а—> у (а Р) (а у) Результат
1 0 0 1 1 0 0 1 1
1 0 1/2 1 1 0 1/2 1 1
1 0 1 1 1 0 1 1 1
1 1/2 0 0 0 1/2 0 0 1
1 1/2 1/2 1 1 1/2 1/2 1 1
1 1/2 1 1 1 1/2 1 1 1
1 1 0 0 0 1 0 0 1
1 1 1/2 1/2 1/2 1 1/2 1/2 1
1 1 1 1 1 1 1 1 1
Кроме того, доказано, что логическая матрица М является нор-
мальной матрицей (по Лукасевичу — Тарскому).
2. Импликативная формула ((р г) (s р)) (((г q)
р) —> (s —> р)) является общезначимой в гейтинговской модели (до-
кажите!'), однако она является недоказуемой в минимальном по-
зитивном исчислении.
Теорема доказана.
Работа с примерами решения упражнений
См. Пример 4.
Теорема (К. Гёдель, 1932) (по [59, с. 102]).
Не существует конечной логической матрицы М такой, что мно-
жество всех формул, выводимых в интуиционистской пропозицио-
362
https: "и га it.ru
нальной логике, было бы в точности равно множеству всех формул,
принимающих в М выделенное значение при любой оценке.
Другими словами, интуиционистское пропозициональное исчис-
ление не имеет точной конечной модели; однако существует точная
счётная модель интуиционистского пропозиционального исчисления.
Например, рассмотрим формулу -i-ip v —р, недоказуемую в ин-
туиционистском пропозициональном исчислении, и воспользуемся
гейтинговской моделью:
р -Р -.-.р ч -,-р v -р
0 1 0 1
1/2 0 1 1
1 0 1 1
Формула является общезначимой, поэтому необходимо искать
другую модель, а ответ на вопрос о доказуемости формулы остаётся
открытым.
Метод моделей для исследования
«населённости» типа в системе
Приведём метод исследования невозможности построения кода
(к-терма) в системе к^ по заданному типу (формуле).
Тип очевидным образом записывается в виде формулы в Prop
и выбирается некоторая модель этого исчисления (мы будем ис-
пользовать гейтинговскую модель).
Теперь для доказательства того, что для заданной формулы
(типа) невозможно построить код (k-терм) в системе к^, доста-
точно проверить на общезначимость заданный тип (формулу).
Если формула не является общезначимой, то код (к-терм) невоз-
можно построить в системе к^> т. е. тип «не населён».
Работа с примерами решения упражнений
См. Пример 5.
Однако метод моделей применим не всегда.
Если формула является общезначимой в рассматриваемой логи-
ческой матрице, то необходимо искать другую модель.
Примеры решения некоторых типов упражнений
Пример 1. Пользуясь гилъбертовским и генценовским исчислениями,
установите доказуемость формулы (а -> Р) -> (Р -> у) -> (а -> у) в Prop.
363
https: "и rait.ru
Решение.
{P->y}l~P->y
{g—>P,g}l~P {p,p~>y}l-y
{g—>Р,Р—>y,g}Hy
{g—>Р,Р—>y}Hg—>у
{g—>Р}Н(Р—>у)—>(g—>у)
I-(g —> P) —> (P —> у) —> (g —> у)
3 1
i г
gg~»P J
у
(g->y)
(P —> y) —> (g —> y)
(g —> P) —> (P —> y) —> (g —> y)
Список
допущений:
l.g—>P
2.p->y
3.g
Пример 2. Пользуясь генценовским исчислением, установите доказу-
емость в Prop формул, «похожих» на аксиомные схемы.
Решение.
2 „
4, Список допущении:
g i.p
—а^а 2. g
Р —> (а —> а)
Комбинаторныепредсгавления
3 1 3 2
X 'L 'L
g g—>(P-»y) g a—>p
У
a—>y_____
_______(a —> P) —> (a —> У)__
(a —>(P~>y))—>((a—>P)—>(a—>y))
Список
допущений:
l.g—>(P—>у)
2.g—>p
3. g
доказательств:
СК: р —> (а —> а)
S:(a—>(Р—>у))-»((а—>Р)-»(а—>у))
Пример 3 (для знатоков элементарной теории типов).
Постройте доказательство формулы (А->В)->((В->С)->(А->С))
в интуиционистском гильбертовском исчислении.
Решение. Воспользуемся изоморфизмом Карри—Говарда, для чего вна-
чале решим задачу TIP для типа (д Р) -> ((Р -> у) -> (д -> у)):
х:а f:a—>$
fa:P g:P~>y
g(fa):y
M3:y
M2:g—>y ,
М] :(P^y)^(a^y)
М:(д->Р)->((Р->у)->(д->у))
M3=g(fx)
М2 - Ах: д. М3
Итак, тип обитаем и доказательством является Х-терм
M^f.'kg.kx.gifx)
Остаётся построить короткое комбинаторное доказательство:
я я
Xf. Xg. Ах. g(fa) = If. Xg. Ах. Bgfx^kf. Xg. Bgf = kf. Xg. CBfg^CB,
Можно также вспомнить типы комбинаторов
364
К:а—>(₽—>a),CS:(a—>р)—>((а—>р—>у))—>(а—>у))
и предъявить комбинаторное доказательство в базисе {К, S}:
СВ = ^(CS)(((CS)(K(CS))K)((CS)(K(CS))K)(CS))(KK)^(CS)(K(CS))K^,
с помощью которого можно (!?) построить гильбертовское доказатель-
ство, которое уже является неэффективным.
Пример 4. Покажите с помощью гейтинговской модели, что в инту-
иционистском пропозициональном исчислении не является доказуемой
формула (р q) ((-р —>q)—>q) (доказательство от противного).
Решение.
р q -Р -.p->q Ьр -> q) -> q p^q (р -> q) -> ((-р -» q) q)
0 0 0 0 1/2 1 1 1 1 0 1/2 1 i i i i i i 1 1 1
1/2 1/2 1/2 0 1/2 1 0 0 0 1 1 1 0 1/2 i 0 i i 1 1/2 1
1 1 1 0 1/2 1 0 0 0 1 1 1 0 1/2 1 0 1/2 1 1 1 1
Значение рассматриваемой формулы прир = q = 1/2 равно 1/2, следо-
вательно, эта формула не истинна в используемой модели, и потому невы-
водима в интуиционистском пропозициональном исчислении.
Пример 5 (для знатоков элементарной теории типов).
Докажите с помощью минимальной гейтинговской модели, что тип
(р Ф) (((р -> г) -> q) -> q)
не является «населённым» в системе типов
Решение. Воспользуемся методом моделей:
Р q г p^q p^r (р Г) q ((р г) q) q Результат
0 0 0 1 1 0 1 1
0 0 1/2 1 1 0 1 1
0 0 1 1 1 0 1 1
0 1/2 0 1 1 1/2 1 1
0 1/2 1/2 1 1 1/2 1 1
0 1/2 1 1 1 1/2 1 1
0 1 0 1 1 1 1 1
0 1 1/2 1 1 1 1 1
0 1 1 1 1 1 1 1
365
https:it.ru
р q г p^q p^r (p r) q ((p r) q) q Результат
1/2 0 0 0 0 1 0 1
1/2 0 1/2 0 1 0 1 1
1/2 0 1 0 1 0 1 1
1/2 1/2 0 1 0 1 1/2 1/2/
1/2 1/2 1/2 1 1 1/2 1 1
1/2 1/2 1 1 1 1/2 1 1
1/2 1 0 1 0 1 1 1
1/2 1 1/2 1 1 1 1 1
1/2 1 1 1 1 1 1 1
1 0 0 0 0 1 0 1
1 0 1/2 0 1/2 0 1 1
1 0 1 0 1 0 1 1
1 1/2 0 1/2 0 1 1/2/ 1
1 1/2 1/2 1/2 1/2 1 1/2 1
1 1/2 1 1/2 1 1/2 1 1
1 1 0 1 0 1 1 1
1 1 1/2 1 1/2 1 1 1
1 1 1 1 1 1 1 1
Р q г p->q p^r (p r) -> q C(p r) -> q) -> q Результат
Значение формулы прир = q = 1/2, г = 0 равно 1/2, следовательно, эта
формула не истинна в используемой модели, и потому недоказуема в инту-
иционистском пропозициональном исчислении.
Задачи для самостоятельного решения
Если теорему так и не смогли
доказать, она становится аксиомой.
Евклид
1. Минимальное исчисление Prop
1. Докажите следующие формулы в исчислении Prop (а, 0, у — пропо-
зициональные переменные):
1)* a-> (P-> а) (закон Фреге);
2)* (a - >P)- ► ((а н (P н у)) h (a h у)) (закон Фреге);
3)* (a - >(P- ►7))->((анР)н(ану));
4)*((a - ->P)- -> (а н у)) н (а н (Р н у));
5)* (a - >P)H ► ((Р н у)) н (а н у)) (сильная транзитивность);
6)*(0H ► y)-> ((а н р) н (а н у)) (слабая транзитивность);
7)* (a - >(Ph ► у))->(Рн(ану));
8)* (ан ► (a — >Р))н(анР);
9)*(a н (ан >Р))н((анР)на)нр.
Ю)* (CP на) нр)н((рна)на).
11) (a- ->(P- ->а)нр)н(((ан0)н0)н0)
С*" //< ! ио it i-i I
366
Решение.
4) 3 Аксиома
1 1
Р Р~>Р) j, Список допущений
а^Р (a->P)->(a->Y) х . (a _> р) _> (a _> у)
“______________2. a
---------------¥--------------- 3.₽
((a —> Р) —> (a —> у)) —> (a —> (Р —> у))
Комбинаторное представление доказательства: 2/. С(В/К) = ВС(СВК)
9) Первый способ.
з 1
1 г
II । a a->(a->p)
J a a—>(a—>P) a a—>P
a a —>P । P Список допущений:
P (a—>P)—>a а~>Р i. a _> (a _> p)
a~>P___________________« 2.(a—>P)—>a
_______________P_______________ 3 a
(a->(a->P))->((a->P)->a)->p
Представление доказательства в виде Х-терма таково:
Xf. A#.f(g(Ax. Дх))(£(Лх.Дх))
Второй способ. Воспользуемся меньшим количеством допущений, так
как будем считать уже доказанными формулы a —> а и (a —> (a —> Р)) —>
—> (а —> а) —> (а —> Р):
о- Hi iroit i-i ।
vJ.M (Ull.l V4
367
СО
//i I г о it
Список допущений:
1.а->(а->Р)
2. (а —> Р) —> а
Представление доказательства в виде Х-терма таково:
¥-W(g(S/I))(g(S/I)).
Ю)
Теорема Аксиома
1 I
(Р^а)^(₽^а) ((Р^а)^(Р^а))->((Р->а)->Р)->((Р->а)->а)
(СР а) Р) (СР а) а)
Комбинаторное представление доказательства: S(SKK).
11) Самостоятельно установите, что доказательством является
V. А(Кх)) : (а (Р а) Р) (((а Р) Р) ₽).
2. (По [53, с. 105])
Установите доказуемость следующих формул в исчислении Prop:
1)* (г q) (((г q) р) (s р));
2)* (((г^р)^($^р))^((((р^д)^г)^Р1)^(д1^(((р->д)->г)->
->Р1)))).
Решение.
1 2
1 1
(1) г->д (г->д)->р
р Список допущений:
((г —> q) —> р) —> (s —> р) l.r->q
(г —> q) —> (((г —> q) —> р) —> (s —> р)) 2.(r^q)^p
3.s
3. (По [8, с. 101]) Постройте вывод импликативной формулы
(а —> (Р —>у)) —> (а —> Р) —> (а —> у), используя только формулы
(Р^у)^((а^Р)^(а->у)),(а->(Р->у))->
(₽ (а у)), (а (а ₽)) (а ₽) •
Может ли помочь следующее равенство: S = B(BW)(BC(BB))?
2. Метод моделей для исследования
«населённости» типа вХ^>
1. Докажите с помощью гейтинговской модели, что не являются дока-
зуемыми в интуиционистском пропозициональном исчислении формулы:
1) --^р->р;
2) pv-p;
3) (-р —> р) —> р (закон Клавия);
4) (-р —> —<q) —> (q —> р);
5) р v СР Ч) (обобщённый закон исключённого третьего);
6) Cp^q)^-(->pvq);
7) -<p&--q)^(p^q);
8) (-.p^q&-.q)^p;
9)* Чр & q) -> (-пр v -iq).
369
https: "и ra;t.ru
Решение.
12 3
р ~Р -.-.р ч р v-p -р^р (-р->р)->р
0 1 0 1 1 0 1
1/2 0 1 1/2 1/2 1 1/2
1 0 1 1 1 1 1
4 5
Р q -Р -p^q q^p (-p->-,q)->(q->p) p v (p q)
0 0 1 1 1 1 1 1
0 1/2 1 0 0 0 1 1
0 1 1 0 0 0 1 1
1/2 0 0 1 1 1 1 1/2
1/2 1/2 0 0 1 1 1 z i 4
1/2 1 0 0 1 1/2 1/2 1
1 0 0 1 1 1 1 1
1 1/2 0 0 1 1 1 1
1 1 0 0 1 1 1 1
6 7 к 8
p q —p -.p V q ж— (p—>q)—> (-p v q) -i(p&-iq?-^ (~p~>q &\q)
0 0 1 i 1 1 1
0 1/2 1 i 1 1 1
0 1 1 i 1 1 1
1/2 0 0 0 1 1 1/2.
1/2 1/2 0 1/2 1/2 1 \i/2e
1/2 1 0 1 i 4 1 4l/2^
1 0 0 0 i 1 i
1 1/2 0 1/2 i 1/2 i
1 1 0 1 i 1 i
9
p q -P ->q p&q -i(p &q) -P v-iq Результат
0 0 1 1 0 1 1 1
0 1/2 1 0 0 1 1 1
0 1 1 0 0 1 1 1
1/2 0 0 1 0 1 1 1
1/2 1/2 0 0 1/2 0 0 1
1/2 1 0 0 1/2 0 0 1
1 0 0 1 0 1 1 1
1 1/2 0 0 1/2 0 0 1
1 1 0 0 1 0 0 1
370
https:/Л: rait.ru
Заметим, что формула 9 оказалась общезначимой в гейтинговской модели,
поэтому следует искать другую модель.
2*. Пусть пропозициональные переменные рассматриваются как перемен-
ные, принимающие значения из множества {0,1,2}, а пропозициональные
связки интерпретируются с помощью функций:
def
О, если х > О,
2, если х = О,
def 2, если х> О, def def
х—>у = х&у = min(x,y), xvy = max(x,y).
у, если х > у,
Проверьте правильность утверждения: «формула —i(p & q) —> (—р v -iq)
является общезначимой в заданной интерпретации».
3. (По [53, с. 105])
Докажите с помощью метода моделей, что не являются «населёнными»
следующие типы в системе типов А^:
1) ((р -> q) -> г) -> ((г —> р) —> (s —> р));
2)* ((р —> г) —> (s —> р)) -> (((г —> q) —> р) —> (s —> р));
3) С(г -> q) -> ($ -> р)) ((г ->р) ->($-> р));
4) (((г ->р} -^р) (s ->р)) -> (((р -> q) -> г) -> (s ->р));
5) СССР -> г) -> q) -> q) -> ((q—> г) -> (р -> г));
6) (р q} (((р г} q) q};
7) ((рs}р}((с -> р) -> Ь) -> р.
Решение. Все формулы не являются доказуемыми в интуиционистском
исчислении, что устанавливается с помощью метода моделей:
1) для формул 1, 3, 4, 5, 6, 7 используется гейтингова модель;
2) для формулы 2 можно воспользоваться моделями, найденными В. Каль-
ницким (1 курс, РГПУ им. А. И. Герцена, 30.06.2016), в которых:
2ч
х~>У 0 1 2 3
0 3 1 3 3
1 0 3 3 3
2 0 1 3 3
3 0 1 2 3
А х~>У 0 1 2 3
0 3 3 3 3
1 0 3 3 3
2 0 1 3 3
3 0 1 2 3
4*. Докажите с помощью гейтинговской модели, что не являются «на-
селёнными» следующие типы в системе типов А_^:
1) (р q) ->р) -+р (закон Пирса}-, 2) ((р -> q) -> q) -> (Cq ->р) ->р).
371
https:/Л; га it.ru
Решение.
1 2
p q Результат P q P-><? (p -> q) -> q q->p (q->p) ->p Результат
0 0 1 0 0 1 0 1 0 1
0 1/2 1 0 1/2 1 1/2 0 1 1
0 1 1 0 1 1 1 0 1 1
1/2 0 1/2 1/2 0 0 1 1 1/2 1/2
1/2 1/2 1 1/2 1/2 1 1/2 1 1/2 1 4
1/2 1 1 1/2 1 1 1 1/2 1 1
1 0 1 1 0 0 1 1 1 1
1 1/2 1 1/2 1/2 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1
Упражнение 17
ИНТУИЦИОНИСТСКИЕ
ПРОПОЗИЦИОНАЛЬНЫЕ ЛОГИКИ:
СЕКВЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Н. Н. ВОРОБЬЁВА — ДЖ. ХУДЕЛЬМАЙЕРА
БЕЗ ПРАВИЛА СОКРАЩЕНИЯ
Пусть не корят меня за то, что
я не сказал ничего нового: ново уже само
расположение материала; игроки в мяч
бьют по одному и тому же мячу, но не
с одинаковой меткостью. С тем же успехом
меня могут корить и за то, что
я употребляю давным-давно придуманные
слова. Стоит расположить уже известные
мысли в ином порядке — и получится новое
сочинение, равно как одни и те же, но по-
другому расположенные слова образуют
новые мысли.
Б. Паскаль. Мысли, 22
Обязательные результаты обучения:
• знать вспомогательные понятия
— секвенциальное пропозициональное исчисление;
• знать основные понятия
— исчисление Н. Н. Воробьёва — Дж. Худельмайера (G4ip) без правила
сокращения;
— разрешающая процедура для исчисления G4ip;
— импликативное интуиционистское секвенциальное исчисление
S. Abramsky и R. Dyckhoff со встроенными Х-термами (минимальное исчис-
ление G4ip);
• уметь
— конструировать доказательства формул и правил вывода в исчислении
G4ip;
— конструировать опровержение доказуемости формул в исчислении
G4ip;
— решать задачу TIP в системе X > с помощью минимального исчисления
G4ip;
373
https:/Л: rait.ru
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
Теоретические сведения
Исчисление Н. Н. Воробьёва — Дж. Худельмайера без правила
сокращения
Пожалуйста, тогда ещё одно определение,
очень возвышенное и благородное.
А. и Б. Стругацкие. Пикник на обочине
Н. Н. Воробьёв [55; 56] построил важное интуиционистское сек-
венциальное пропозициональное исчисление. J. Hudelmaier [72]
и R. Dyckhoff [68] повторно открыли исчисление Н. Н. Воробьёва
и исследовали его свойства.
В настоящее время оно называется:
1) G4ip (англ. Vorob’ev’s Calculus) (Dyckhoff, 2013);
2) Urf[74];
Основной целью рассматриваемого исчисления является ограни-
чение применения структурных правил вывода секвенциального
пропозиционального исчисления. Напомним эти правила:
ГНА , . Г,А,АЬВ .
------ (расширение); ------------------ (сокращение);
Г, В Н А Г, А Н В
V1,A,B,V2\-C f . П I- А; Д,Г2 \~В .
—------------ (перестановка); —------------ (сечение).
r1}B,A,r2l-C F ГЬГ2|-В
В силу основной теоремы Генцена, правило «сечение» можно
не использовать для интуиционистской логики.
От правила «перестановка» частично можно отказаться, если
ввести шкалу последовательности применения логических правил
вывода, основываясь на статье С. Клини [60].
Правило «сокращение» можно устранить, если:
1) в качестве аксиомы выбрать слово Г15 Д,Г2 I- А;
2) существенно перестроить логические правила вывода.
Одним из вариантов такой перестройки является секвенциальное
исчисление, свободное от сокращений (англ, constraction-free), пред-
ложенное Р. Дикхофом [68] и Дж. Худелъмайером [72].
При этом освобождение от правила «сокращение» достигается пу-
тём введения различных правил для правила «импликация слева»,
применение которых зависит от структуры формулы А.
Соглашения об обозначениях.
1. Обозначим -L (читается: «противоречие, ложь») выделенную
пропозициональную переменную, которую назовём логической кон-
стантой.
374
https:it.ru
def
2. -A = A (P. Дикхоф).
Итак, можно вообще не использовать связку «-i« (это не очень
привычно, но удобно с технической точки зрения).
Определение (исчисление G4ip) [63, с. 132—134].
Правилами вывода и аксиомами (интуиционистского секвенциаль-
ного пропозиционального исчисления) назовём следующие слова
метаязыка.
Аксиомы:
Гг,А, Г2 h А (1); Г„ А Г2 h В (2).
Основные правила вывода:
r,A\~D Г,ВЫ)
r,AvBI-D
Г’ДВНР (&Ь);
Г,А&ВЫ)
ГНА Г,ВЫ) . ,
ГНА
D-AvB
(hv);
Г1-В
D-AvB
(Hv);
ГНА D-В
Г1-А&В
(h&);
Г,А1-В
ГНА—>B
(I- дедукция).
Допустимые правила вывода:
Г д |_ * Г В \~ D
—I-) (правило У. Москато);
Г,р,ВЫ) f , Л
-----------(р—> I-), р — пропозициональная переменная (пра-
Г,р,р—>ВЫ)
вило У. Москато);
Г,А1}А2—>В\-А2 Г,ВЫ)
Г,(А1^А2)^ВНГ
г,А!^в,а2^вы>
r,(A1VA2)->BhD
Г, Ат —>(А2 —>B)I~D
Г,(А!&А2)^ВЫ)
Определение понятия «вывод» является стандартным для секвен-
циального исчисления.
Лемма (обоснование допустимых правил вывода).
Г д|—L г ВЫ)
1) г —b\-D (-1 (пРавшю У- Москато);
375
http^
/ /i icfiit ri ।
2)
3)
r,p,B\-D f ч| .
-----------(p ->b),
Г,р,р—>BhD
p — пропозициональная переменная
(правило У. Москато);
Г,А1}А2^В\-А2 Г,ВЫ)
Г,(А! —> А2)—>ВЫ)
(v-> h);
(&-> h).
Г,А1^В,А2^В\-Р
Г,(А^А2)->ВЫ)
Г,А1Н>(А2н>В)НР
} Г,(А1&А2)^В1-В
Доказательство.
г,А1—*-
Г}А^В^ Г,ВНР
Г, (А->-*-)-> ВЫ) 1 }
Г,—А—>В\-Р
2.
г,р\-р Г,р,в\-Р
Г,р,р—>В\-Р
р\-р г,р|-р Г,р,В1~В
Г,р,р^В\-р Г,р,р^В\-В
Г, p,p->Bhp&B
Г,р&(р->В)1-р&В
(н&)
Г,р&в\-Р
Г,р&(р^В)\-Р
Отметим, что второй способ доказательства состоит в использо-
вании на первом шаге (снизу) правила «сечения».
3. Выведем вначале вспомогательное правило, которое является
конструктивным, так как вывод осуществляется в «оригинальном»
генценовском исчислении:
Г, Л2, А11~ А2
Т,А2,УА^А2 Г,В,А2ЬВ
Г,(Аг-> А2)->В, А2 НВ Г,АьА2->ВНА2
Г,(Д ->a2)->bi-a2 ->в 1 J г,а2^в\-а1^а2 1 \
r,(A->A2)->BhA->A2
(*) АМ2 ~^в\- а2
г,(а1^а2)^в\-а1^а2
Теперь воспользуемся этим правилом:
Г,А1,А2^ВЬА2 Г,ВЫ)
T/A^A^^BI-A^Az Г,(А!^А2)^В,В1-Р
Г,(At ^A2)^B,(A! -+А2)^>В\-Р
Г,(А1^А2)^ВЬВ
(утончение)
(->Н)
(сокращение)
376
https: "и га it.ru
4. Для построения правила (v—» h) применим правило «сечение»:
Г,А1ЬА1
Г, Ai Н Ал v А2 Г, Ал, В Н В . .
Г, Aj, (Ai V А2) -> В I- В Аналогично
r.CAi vA2)^BHA1 ->В Г,(А^А2)->В|-А2->В Г,Aj ->В,А2 -+B\-D
Г, (Ах v Л2) —>В h(Ax —>В)&(А2 —>В) Г,(АХ->В)&(Л2->В) hD
Г,(АХ vA2)->BHZ)
5. Для построения правила (&—> I-) применим правило «сечение»:
Г, А1? А2 h At Г, А1? А2 Ь А2
Г, А1? А2 h Aj & А2_Г, В, А1? А2 Н В
Г,(А1&А2)-»В,А1,А2 1~В~
Г, (Ai & А2 ) -> В I- Ai -> (А2 -> В)
Г, (Ai & А2 ) —> В Н D
(сечение)
Лемма доказана.
В работах [68; 75] доказаны семантическая корректность, пол-
нота и разрешимость исчисления G4ip.
Замечание (важное).
Идея построения исчисления G4ip состоит в использовании следую-
щих эквивалентностей:
р&(р->В)<->р&В (для построения (р —> Н));
((Ах v А2) -> В) <-> (Aj -> В)&(А2 -> В)
((Ai & А2) —> В) <-> (Ai —> (А2 —> В))
Ах & ((Ai -> А2) -> В) <-> Ai & (Аг -> В)
(для построения (v —> Н));
(для построения (& Н));
(для построения (—> Н).
В качестве иллюстрации приведём доказательство правила (—> Н):
Г, Ал, А2 —В Н А2 г
----’ 1? 2----------- (<^)
Г,(Аг -> А2)->В, Ai I-А2 Г,ВНР
r,(Aq ^Azj^BhAx ^А2 Г,(Ах->А2)->В,ВНР
Г,(А! ^A^^B/A^Azj^BI-D
Г,(АХ-> A2)->BhD
(утончение)
(->Н)
(сокращение)
Работа с примерами решения упражнений
См. Пример 1, Пример 2.
Разрешающая процедура для G4ip
Где слабый ненавидит — сильный
уничтожает.
А. Грин
Определение (повторение).
Разрешимым исчислением называется исчисление U, для которо-
го существует алгоритм, который по любой формуле U позволя-
ет установить выводимость этой формулы в данном исчислении.
377
https:it.ru
Теорема (по [65, с. 124]).
Интуиционистское пропозициональное исчисление разрешимо.
В работе [76] предложены две разрешающие процедуры для ис-
числения G4ip:
1) первая объединяет результаты более ранних работ (см. [71]);
2) вторая является альтернативой первой для импликативного
фрагмента интуиционистской пропозициональной логики.
Рассмотрим только первую процедуру, которая является алгорит-
мом, строящим доказательство или контрмодель для секвенции Г НА.
Алгоритм состоит из трёх действий, которые будем называть
«Поиск 1», «Поиск 2» и «Поиск 3».
Вначале выполняются действия «Поиск 1».
Последовательно применяется (если, конечно, это возможно)
правило (I- —>), которое позволяет привести доказываемую секвен-
цию к одному из следующих видов:
Г I- р, р — пропозициональная переменная; D-A&B;D-AvB.
Далее применяются в направлении снизу вверх основные и до-
полнительные правила:
(Н &), (& h),(v h), (v-> h), (&->h), (p->h),
\_____V______/ \________v________/
Основные Допустимые
обладающие свойством сохранения контрмодели при переходе
от посылок к заключению.
Отметим, что в приведённом списке отсутствуют правила
Основные Допустимые
Если доказательство ещё не построено, то выполняется последо-
вательность действий «Поиск 2»:
1) если «верхние» секвенции имеют вид Г15 (Вх —> В2) —> С, Г2 h D,
то по правилу (—>—> F-) происходит переход к доказательству секвенций
Г1,ВиВ2 —>С,Г2 hB2, ГЬС,Г21-Р,
которое далее происходит в режиме выполнения действий «Поиск 1»;
2) если «верхние» секвенции имеют вид Г, -А —> В I- D, то по пра-
вилу (—1—>1-) происходит переход к доказательству секвенций
г, Ah-1-, г, b\-d,
которое далее происходит в режиме выполнения действий «По-
иск 1»;
378
https:/Л: rait.ru
3) в противном случае применяется (если, конечно, это возмож-
но) правило (I- v).
Если доказательство ещё не построено, то применяется оставше-
еся правило (—> I-).
Это правило относится к числу необратимых правил вывода, так
как именно здесь происходит «потеря» существенного для построе-
ния вывода вхождения формулы в сукцедент секвенции.
Поэтому приходится включить в алгоритм поиска доказатель-
ства полный перебор (!) последовательностей применения правила
вывода (—» h) к различным импликативным формулам, находящим-
ся в антецеденте секвенции. Число таких последовательностей име-
ет порядок и! по каждой секвенции вывода, где п — число таких
импликативных формул.
Другими словами, исчисление G4ip требует использование пра-
вила «перестановка», т. е. поиск доказательства в исчислении со-
пряжён с применением этого правила.
Пример (важный) (по [63, с. 138—139]).
Построим интуиционистское доказательство импликативной фор-
мулы
((((a->b)->a)->a)->b)->((c->d)->r)->b.
Для решения потребуется перебор вариантов применения правил, поэ-
тому приведём несколько попыток доказательства.
При этом:
а) знаком «подчёркивание» выделены формулы, к которым применяется
используемое правило вывода;
б) знаком «>|Л» помечены секвенции, из которых выделяется контрмодель.
a,b\-b £ J
c,d->r,a->b,a,b->a\-b c,bHd c,b,rHd
с, d —> г,(а -> b) ->a,a->bha c,d->r,bbd
(((а -> b) -> а) -> а) -> b, c,d->rl-d ((а b) -> а) -> а) -> b,r Ь b
(((а ->b) а) a) ->b, (c->d)->r I- b
Конечно, рассмотрение конкретного доказательства ещё не обосно-
вывает неприемлемость данной формулы в интуиционистской логике,
но отсутствие прямого доказательства уже делает ее подозрительной.
Однако продолжим попытки:
a,b\-b
(а —> b) —> а, а b, с, d —> г Hd
a->b,r,a,b->a\-b a->b,r,a\-a
(a—>b)—> a, a->b,r\-a
к
г
r, (a —> b) —> a, a b I- a
(((а a) a) ^>b, (c^>d)^>r\-b
(c-*d)-*r,b\-b
379
//i iroit rii
a,b\-b
(c->d)->r, a->b, a, b -> a I- b (c^>d)^>r,a^>b,a\-a
(c^> d) a,a^>b\- a (c^>d)^>r,b\~b
(( (a ->b)->d)->d)->b, (c->d)->r\-b
Итак, «несущественное» добавление формулы (с —> d) —> г в антецедент
доказуемой секвенции (((а —> Ь) —> а) —> а) —> b I- b приводит к необходи-
мости организации перебора применяемых правил вывода.
Наконец, если исходная секвенция по-прежнему ещё не дока-
зана, то выполняются действия «Поиск 3», предназначенные для
построения контрмодели и основанные на использовании правил
опровержения:
ГИВ!,ГИВП->СП ГИАр ГИДг
ГИД^А!
da)
(1б)
(2)
Здесь используются обозначения:
а) Г = Го, (В^ Cj) —> Bp ..., (Вп Сп) —> Dn, Гр
при этом (Bj —> Q) —>Dp..., (Вп —> Сп) —>Вп, — это все формулы по-
добного вида, входящие в Г;
б) ГИВп->Сп, п>0, ГИр, ГИ
означают недоказуемость соответствующих секвенций;
в) к секвенциям Г I- Г I- р, Г I- Др v АТ уже неприменимы пра-
вила из «Поиска 1».
Контрмоделъю для секвенции ГИД (представляющей собой за-
ключение правил (1а), (1б), (2)) является дерево К с корнем со, в ко-
тором истинны все формулы из множества
{р | р — атомарная формула, являющаяся элементом списка Г},
и из которого достижимы вершины, опровергающие посылки пра-
вил (1а), (Ip), (2).
Пример [63, с. 135].
380
https
//i jroit rii
HAv-iA
def
Миром, опровергающим I- А, является кг -0(0—пустое множество),
def
а миром, опровергающим I—А, является к2 = {А}.
Таким образом, контрмоделъю для заданной секвенции является
def
дерево с корнем к3 = 0, из которого достижимы кг и к2, т. е.
к3=0
кг=0
к2={Л}
Работа с примерами решения упражнений
См. Пример 3, Пример 4.
Решение задачи ИР в системе
типов X , с помощью исчисления G4ip
... даром получили, даром давайте.
Мф. 10.8
Рассмотрим импликативное интуиционистское секвенциальное
исчисление, которое построено S. Abramsky [66, § 2.2] и R. Dyckhoff
[68, р. 802—803]), и в которое встроены Х-термы, интерпретирую-
щие доказательства в смысле Карри-Говарда:
ГН:АгВ,АН(х):С
Г, f :А—>В,А\-и\х:= ft]:C’
Г,а:А,х:В\- g(x): G
Г, р: А^В, а: A I- g[x := pa]: G ’
Г, z: D В I- q(z) :С -^D Г, х: В I- g(x): G
Г, р: (С —> D) —> В I-g[x := p(q(BpK))]: G ’
Теперь с помощью указанных правил можно решать задачу TIP
в системе типов Х_^: вначале строится «чистое» доказательство фор-
мулы, представляющей заданный тип, а затем это доказательство
последовательно в направлении сверху вниз аннотируется нужными
Х-термами.
Примеры (решения задачи TIP).
1. Рассмотрим тип а->((₽-> а)-> у)-> у.
Вначале построим «чистый» интуиционистский вывод соответствую-
щей секвенции (расположен слева), а затем аннотируем его соответству-
ющими Х-термами в направлении сверху вниз:
381
https:/Л: rait.ru
a, P, a —> у I- a a, у Ь у
a, ф -> a) -> у I- у
I-a-> (ф-> a)-> y)-> Y
q(z)=Xiz. у => q=Xz.lu.y
у :a.,z‘.a.-^y\-'ku..y ф->а g(J2 ~x
y.a.,w.^>,Z'.a.^y\-y.a. y:ct,x‘.y\-x‘.y
y:a,p:(p->a)->yH Р&и-У)
a, a —> у I- P —> a
I- Xy. Xp. р&и. у): a -> CCP -> a) -> y) -> Y
Превратим полученное доказательство в комбинаторное доказатель-
ство с помощью очевидных преобразований:
п
Ху. Хр. p(Xu.y) = Ху. Хр. р(Ку)=Ху. Хр. CI(Ky)p ->Ху. С1(Ку) = В(С1)К
2. Рассмотрим тип ((a —> Р —> а) —> у) -> у.
Вначале построим «чистый» интуиционистский вывод соответствую-
щей секвенции, а затем аннотируем его соответствующими Х-термами:
СР —> а) —> у I- а -> Р -> а
а, (Р —> а) —> у Ь Р -> а
а, Р, ф -> а) -> у Н а
а,(Р —>а) —>уЬР->a у Ь у
1~((а—>Р—>а)—> у)—> у
q(z)=K => q=Xz. К
z: ф —> а)—> у 1~ К: а —> Р —> а
z: СР -> а) -> у I- и: а -> Р -> а
и: a, z: СР -> а) -> у Н Xw. и: р —> а
и: a, w:p, г:ф—>а)—> у И и: a Х
u:a,z:CP->a)->yl-Ku:P->a х: у Ь х: у
(а —> Р —> а) —> у И у
р:(а->Р->а)->уН х[х := p((Xz. К) СВрК))]: у
р: (а —> Р —> а) —> у I- рК: ((а ~> Р ~> а) —> у) —> у
1-Хр.рК:((а->Р->а)-> у)-> у
Работа с примерами решения упражнений
См. Пример 5, Пример 6, Пример 7, Пример 8, Пример 9.
Биографические сведения
Воробьёв Николай Николаевич (18.09.1925, Ленинград —
14.07.1995, Санкт-Петербург) — советский и российский матема-
тик, специалист в области алгебры, математической логики и те-
ории вероятностей, основатель советской школы в области теории
игр.
Закончил математико-механический факультет Ленинградско-
го государственного университета (1948, специальность алгебра).
В 1952 защитил кандидатскую диссертацию (логические правила
дедукции в системах с сильным отрицанием), в 1961 — доктор-
скую диссертацию (в области физико-математических наук). С 1965
года — профессор.
Работал в Ленинградском отделении Математического института
АН СССР (1951—1965), Ленинградском отделении экономико-мате-
матического института АН СССР (1965—1975), Институте социаль-
382
https:it.ru
но-экономических проблем АН СССР (1975—1990). Активно препо-
давал в ЛГУ и РГПУ им. А. И. Герцена.
Разрабатывал аппарат коалиционной теории игр, что в процессе
изучения рандомизированного поведения агентов потребовало на-
хождения решений нестандартных проблем из области теории ве-
роятностей и комбинаторной топологии.
Примеры решения некоторых типов упражнений
Странности... Нет никаких странностей.
Есть просто неровности...
А. и Б. Стругацкие. Попытка к бегству
Пример 1. Постройте интуиционистские доказательства следующих
импликативных формул:
1) ((Р-> а)-> Р)-> ((Р-> а)-> а);
2) а —> Р —> ((у —> Р) —> а —> 8) —> 8;
3) ((а-> Р)-> Р)-> (Р-> а)-> ((Р-> (а-> Р))-> (Р-> а));
4) (8 —>(8 —> а))—>((у —>а)~>((а —>Р) —>(8—>(у —>Р))));
5) (а^Р)^(у^а)^(у^Р);
6) (r^q)^(((r^q)^p)^(s^p));
7) (8 —> 8 —> а) —> (у —> а) —> (а —> Р) —> 8 —> у —> Р;
8) ((((а->Р)->а)->а)->Р)->Р;
9) ((((a^P)^a)^a)->P)->((c->d)->r)->P;
10) (а—>Р—>у)—>((а—>г)—>г)—>((Р—>г)—>г)—>(у —>г)—>г.
Решение. Знаком «подчёркивание» выделены формулы, к которым при-
меняется некоторое правило вывода;
1.
Р, aha р,аНа
Р,а—>Р,Р—>а1~а Р~>а,pi-а
(Р —> а) —> Р, (Р —> а) I- а
1~((Р-> а)->Р)->((Ра)
2.
а, 81-8
а, Р, у, Р -> (а -> 8) Н Р а, Р, а -> 8 Н 8
а, р, (у —> Р) —> (а -> 8) I- 8
1~ а —> Р —> ((у —> Р) —> а —> 8) —> 8
3.
а,рНа
Р -> а, Р Н а
(а -> Р) -> Р, Р -> а, Р -> (а -> Р), Р Н а
Н(а^Р)^Р)^(Р^а)^((Р->(а->Р))->(Р->а))
htfnc*"Hi i-i ।
upuj j dl UU.I vi
383
4.
а, рнр
8, а, у —> а, а —> Р, у I- Р
8,8—>а, у -> а, а —> Р, yl-p
8 -> (8 -> а), у —> а, а —> Р, 8, у 1~ Р
Ь(8-»(8-»а))-»((у-»а)-»((а-»Р)-»(8-»(у-»Р))))
5.
а, Р, у Н Р
а -> Р, у, а Н Р
а—> р, у —> а., у Н р
Н (а-> Р)-> (у-> а)-> (у-> Р)
6.
г,д>-д
г-> q, г Fq
г->q,s,r,q->p\-q г^>q,s,p\~p
г—>q,(r—>q)—>p,sF р
H(r->q)->(((r->q)->p)->(s->p))
7.
8, у —> а, у, а, Р Н р
8, а, у —> а, а —> Р, у Н Р
8,8—>а, у —> а, а —> Р, yl-p
8—>8—>а, у ->а, а ->Р, 8,у I-Р
I- (8 -> 8 -> а) -> (у -> а) -> (а -> Р) -> 8 -> у -> Р
а -> Р, а I- а
(а —>Р)~>а,а—>рНа рнр
(((а->Р)->а)->а)->р|-р
у, а -> Р, а Н а
у,(а->Р)->а,а->р1-а у,рнр
(((а^Р)^а)^а)^Р,уНр
Ь((((а^Р)^а)^а)^Р)^у^р
10.
гЬг
у,а,р,у->гНг
а—>р—>у,у—>г,а, г—>г,р,г—>г|-га—>р—>у, у—>г, а,г—>r, г|-г
а->р->у>(Р~*г)->г,у->г,а,г->г Hr а->р->у,(р->г)->г, у->г,г Hr
а->р->у/а~>г)~>г/Р~> г)->r,y->r Hr
Н(а->р->у)^(Ха->Г)^г)->((р->г)->г)->(у->г)->г
Пример 2. Постройте интуиционистские доказательства формул,
содержащих логические связки &, v, -i:
1)(р v -р) (-.-р -> р); 2) р -,-р; 3)(р v q) & (р v г) -> (р v (q & г)).
384
Решение.
1)
P^-L,-Ll-P
p,—pbp -p,-i-pl-p
р v —р, —i—»р Н р
Н (р v ^р) -> (-.^р -> р)
2)
_______p^^-L^-L_______
(р —> -*“) —> р —> I—L р —> I—L
(((p-^-^-^^-hp-^i—L
(((р“Ч-»* -1- 2 3Нр
I- —1—1—1—ip -> —1—p
3)
к q&r\-q&r
q,rtp (l>rpl&r
p,p\-p p,r\~p q,p\-p .
---—-— ---------------------*-*-— - q, r I- p v (q & r)
p,pbpv(q&r) p,rHpv(q&r) q,pHpv(q&r)
p,pvrHpv(q&r)-----------------------q,pvrHpv(q&r)
pvq,pvr \-pv(q8tf)
H(pvq)&(pvr)^(pv(q&r))
Пример 3. Постройте опровержение доказуемости импликативных
формул в интуиционистском исчислении:
1) ((p^q)^p)^p;
2) ((((а^Р)^а)^а)^а)^а;
3) ((p^q)^q)^((q^p)^p).
Решение.
1. Вначале попытаемся построить интуиционистский вывод (при этом
знаком «4Л> будем обозначать недоказуемые секвенции):
JA JA
pl-q p,pl~q
p,q->pl~q р1~р
(p^q)^pl~p(*)
b((p^q)^p)^p
=> Теперь необходимо построить контрмоделъ; вначале с помощью
секвенции (*) введём обозначения:
def def def
r=(p^q)^p,Bi =p,Ci =q.
385
https:it.ru
Установим двумя способами (р —> q) —> р У р —> q (р = -1- —> -1-, q = -*-):
(1) lfc lfc
P,pbq p,p,pl~q
p,q->p,pi-<i pi-q
(p->q)->p,phq
((p->q)->p)i-p->q
(2) w0
| f (((p->q)->p)->(p->q))
w1
Kp^q)
tp
fq
W2
t((p->q)->p)
tp | f(p->q)
tp
>w3 fq
t((p->q)->p)
Теперь с помощью правила опровержения (la) получаем:
Г/Bj ->CX (p->q)->p/p->q
ГИр (p-»q)-»p/p
(p->q)->p/p.
Контрмоделью для секвенции (р —> q) —> р Ь р является следующее
дерево К с корнем со, в котором истинны все формулы из множества
{р | р — атомарная формула, являющаяся элементом списка Г} = 0
и из которого достижимы вершины, опровергающие посылки использу-
емого правила (1а):
К = 0 —> = {р = -* L—>-L, q = -L},
где импликация -*—> -*- обозначает истинную формулу.
В дальнейшем не будем явно выписывать контрмодель, подразумевая,
что это можно выполнить при необходимости.
2.
к к
I 1
g,g|-p q,g,al-p {a = _i_ _i_ р = _i_}
g,g,P->g,l-p gl-g
g,P—>g,g—>ghP g->g,g|-g
(g —> P) —> g, g —> g l~ g gHg
(((g —> P) —> g) —> g) —> g I- g
Ь ((C Ca -> P) -> g) -> g) -> g) -> g
3.
к к
I I
pl-q p,ql~q p\~q p,q\~q =>{p = _i_^_i_ g = _i_}
p,q->qhq p,q->q,phq p,qhp
p,q^q,q^p|-q q^p,ql-p
(p^q)^q,q^pl-p
bf(p^q)^q)^ttq^p)^p)
386
http
o- Hi iroit i'i ।
Пример 4. Покажите, что в интуиционистском пропозициональном
исчислении имеют место следующие утверждения о доказуемости:
1) b(pv^p)->(((p->q)->p)->p);
2) h(pv^p)->(-,^p->p);
3) Hf-i-p^pJ-^pv-p);
4) >р)—>q)—>q)—>(pv—р);
5) /(pv^p)->(((q->p)->q)->q);
6) Ь (—i—p —> p) —> (((p —> q) —> p) —> p);
7) Ь (((p —> q) —> p) —> p) —> (—i—p —> p).
(pv—p)
Решение.
1) p, 1- b
р^-^,р\-Ь
-p,p,q^>p\-q -p,p\-p
p, (p —> q) —> p h p -np,(p->q)->pl-p
(pv^p),(p->q)->php
H(p v-p) -> CCCp q) p) -^p)
2) p—> -1-, H p
p,-.^pl-p ^ZZphp
pv—Р,—i—pl—p
k (p v ^p) -> (-.^p -> p)
3) i p,-1-!--1- $
-L->pl~p-L,-L->pl—L p, p -> 1—L pl—L
р^~*~,-1-pЬp\~P pjp-»-*-,-*--^!--1- p,pl—L
((p^-L)^-L)->pi-p ((р^-Ч^-Ч^рЬр^-1-
—p^pi-p -.^р^рй^р
-,^p->p|-pv-.p
I- (-1-ip p) (p V -ip)
6) I 5
p,p,q->pl~q p,pl—L
(p^q)^p,p,-L^-L|--L (p^qj^p^hp
(p-»-1-)-»-1-, (p -> q) -> p H p
-^р->р,(р->д)->рйр
I- (-,-p p) -> ((Cp -> q) -> p) -> p)
387
https:it.ru
к к
I I
p,4^p,p\—L- р,д-»р,~^д
(p->-L)->-L,p,g->pi-g pi~p
(р^-*-)^-*-,(р^д)^р1-р
-.-.p->p,(p->q)->pl-p
Н Q->-.p -> р) -> (((р -> q) -> р) -> р)
Пример 5. Решите задачу TIP в системе типов Х_^ для типа
(а->(Р-> у))-> (а-> Р)-> а-> у.
Решение. Вначале построим «чистое» доказательство секвенции
I-(а-> (Р-> у))-> (а-> Р)-> а-> у,
а затем аннотируем его соответствующими Х-термами:
к к
I 1
р,д->р,р>—*- р,д^р,-*-ьд
(р—>-1-)р> д—> р ь д pi-p
Ср -> -*-) -> (р->д)->р и р
-.^р->р,(р->д)->рНр
н(-,^р -> р) -> (ССр -> д) -> р) -> р)
а:а,Ь:Р,с:уНс:у
а:аНа:а а: а, Ь:р, рф—>у l~c[c:=pb]:y
g:а —>Р,а:аhа:а g: а -> Р,а:а,р: Р —> у hpb[b:= ga]:у
f :a->(P->y),g:a->P,a:al-p(ga)[p:=fa]:y
h(a->(P->y))->(a->P)->a->y
=>pb:y
=>p(ga):y
=>/a(ga)
=>X/.Xg.Xa./a(ga)
Построенное доказательство: Xf: a —> (P —> y). kg: a —> p. Xa: a. /a(ga).
Пример 6. Решите задачу TIP в системе для типа ((а -> а) -> а) -> а.
Решение. Вначале построим «чистый» вывод соответствующей секвенции,
а затем «навесим» на него соответствующие Х-термы:
q(z) -z^q-'kz.z
I
z:a^aHz:a^a
x:a,z:a->al-x:a
g(x)=x
x:al-x:a
a,a->aba a Ha
(a —> a) —> a Н a
I- ((a —> a) —> a) —> a
p: (a -> a) -> a I- x[x := p((Xz. z)(BpK))]: a
p: (a -> a) -> a I- p(BpK): a
I- Xp: (a -> a) -> a. p(B pK): ((a -> a) -> a) -> a
Построенное доказательство: Хр: (a a) a. p(BpK).
Проверка (в Hugs-98):
> :t \p -> p ((.) p const)
\p -> p (p . const) :: ((a -> a) -> a) -> a
Ранее эта задача решалась так:
388
https:it.ru
p:(a—>a)—>a I:a—>а
pl: а
Мра
М: ((а —> а) —> а) —> а
, М1=р1
М = Хр: (а —> а) —> а. Мх = Хр: (а—> а) —> а. р1=СП
Пример 7. Решите задачу TIP в системе Х_^ для типа ((а —> а) —> Р) —> р.
Решение. Вначале построим «чистый» вывод соответствующей секвен-
ции, а затем аннотируем его соответствующими Х-термами:
a->pi-a->a
a,a —>Рha P H P
(a->a)->pi-p
H((a->a)->P)->p
q(z) = I => q = Xz. I
J-
z: a —>pi~J:a —>a
------------------------- g(x) = x
z: a —>P l~Xy. у: a —> a-\
y:a, z:a—>pi~y:a x: p I- x: P
p: (a -> a) -> P Hx[x := p((Xz. I) (BpK))]: p
I- Xp: (a -> a) -> p. pl: ((a —> a) —> P) —> P
Построенное доказательство: Xp: (a —> a) —> p. pl.
Проверка (в Hugs-98):
> :t \p -> p id
\p -> p id :: ((a-> a) -> b) -> b
Пример 8. Решите задачу TIP в системе типов Х_> для типа
((P^a)^p)^((p^a)^a).
Решение. Вначале построим «чистый» вывод соответствующей секвен
ции, а затем аннотируем его соответствующими Х-термами.
Первый способ.
a,pHa
Р -> а, Р Н а
(Р —> а) —> Р, Р —> а I- а
Н((Р->а)->Р)->((Р->а)->а)
х: а, у: РI- х: а
g:p^a,y:pl-x[x:=gy]:a
g:p->a,y:pHgy:a
/:(p^a)^p,g:p^aHg(fg):a
H((P->a)->P)->((P->a)->a)
=>X/:(P-> a)->p. Xg:p~> a. g(fg)
Второй способ. a, p 1- a a, p 1- a
x:a,y:pi-x:a P—>a,p,a—>pHa p,p->al-a
g:P~>a,y :P,h:a—>pi~x[x:=gy]:a (p—>a)—>p,p—>aba
g:P->a,y:P,h:a->pi-gy:a g:P—>a,h:a—>pi- Ay.gy: p —> a g:p->a,h:a->p|-g:p—>a g:P—>a,h:a->pi- Mi. g: p -> a H((P^a)^p)^((p^a)^a) x: а, у: p I- x: a g:P~>a,y:pi-gy:a
p:(P~>a)—>pi-g(pg):a
|-((P—>a)—>p)—>((P~>a)~>a)
=> Xp:(P->a)->p.^g:p->a.g(pg)
389
https: "и rsit.ru
Ранее эта задача решалась так:
f :(P->g)->P g:P->g
g:P~>g_________fg:p
g(fg):g => M=Xf:(p->g)->p.Xg:p->g.g(fg)
((P->g)->P)->((P->g)->g)
Пример 9. Решите задачу TIP в системе типов X , для типа
((((а —> Ь) —> а) —> а) —>b) —>b (.формула Крипке).
Решение. Вначале построим «чистый» вывод соответствующей секвен-
ции, а затем аннотируем его соответствующими Х-термами:
x:a,y:b\-y:b
g:b->a,f:a->b,x:a\-y[y:=jx]:b
g:b^>a, f :a^>b,x:a\- fic:b
g:b->a~f:a->b\~k.fx:a->b
~f:a->b,g:b->a\-~f:a->b
f:a->b,g: b-> a\-Xg7f: a->b
a,b\-b
a,b^a,a^bhba,a^b: a
(a^b)^a,a^>b\-a b\-b
(.(.(a->b)->a)->a)->b\-b
\-((((a->b)->a)->a)->b)->b
x:a\-x:a
f :a^>b,x:a\~ x:a
f :a^>b,p:(a^>b)^>a\-pf :a
f:a->b\-kp.pf:((a->b)->a)->a
f: a -> b hXf. kp. pf: ((a -> bj -> a) -> a
y:b\-y:b
y:bHXy.y:b
Pi: (((a -> b) -> a) -> a)^> b h p1(}p. p(Bp^)): b
Построенное доказательство:
Xpi. Pi(Xp. p(Bp1K)): ((((a -> b) -> a) a) b) b.
Выполним рефакторинг полученного результата двумя способами:
1) с помощью ^-редукции:
п
Xpi. Р! (Хр. pfBpjK)) = Xpi. Pi(Xp. CI(Bp1K)p) ^Xpi. PitCKBpiK));
2) в виде комбинатора:
Xpi.piCkp. pfBpjK)) = X/. /(Xg. g(B/K)) = X/. /(CI(B/K)) =
= X/. /(CI(CBl^)) = X/. /(B(CIXCBK)/) = X/. B/(B(CIXCBK))/ =
= X/. CB(B(CI)(CBK))ff = W(CB(B(CI)(CBK)))
Проверка (в Hugs-98):
> :t \pl -> pl (\p -> p ((.) pl const))
\pl -> pl (\p -> p (pl. const))
:: ((((a -> b) -> a) -> a) -> b) -> b
wxy=xyy
f=w (flip (.) ((.) (flipid) (flip (.) const)))
> -tf
f:: ((((a -> b) -> a) -> a) -> b) -> b
390
https:
I/I iroif ri I
Упражнения для самостоятельного решения
Это
Почти неподвижности мука —
Мчаться куда-то со скоростью звука,
Зная прекрасно, что есть уже где-то
Некто,
Летящий
Со скоростью
Света!
Л. Мартынов
1. Исчисление Н. Н. Воробьёва —Дж. Худельмайера
без правила сокращения
1. Постройте доказательства формул в интуиционистском секвенциаль-
ном пропозициональном исчислении:
1) A—>-i-A;
2) —i—i(—i-A —> А);
3) ii-A—>-А;
4) —i(A &-А);
5) (-А v В) —> (А —> В);
6) -А & -В —> (A v В);
7) (А —>-В) —> (В—>-А);
8) -i(A v В) —> —А & —В;
9) -i-i(A —> (В v-В) &А);
10) (A v —А) —> (В —> —1—В);
11) (А ->В) & (С—>В) & (A v С) & -i(B &В) -> (В —> А) & (В С)
(теорема Гаубера).
Решение.
2)
А1--L-
(А->-ЧА->-*-1—*- -LH-L
(((А->-ЧA)->-Ll—1-
ь (СССА -> -Ч -> -Ч -> А) -> -Ч -> -L-
I—.Ч-1-А->А)
3)
a,-li—l
А^-L,-LАI--1- АЬ
((A^-L)^-L-)^-L,AI—*-
((А-> ~Ч-> ~ЧЬ А
____________
2*. Определите, какими должны быть формулы а и 0, чтобы формула
(ос —> Р) —> Р являлась доказуемой: а) в классическом исчислении; б) в ин-
туиционистском исчислении.
Ответ; a) -ice I- Р; б) I- а
3*. (Важная.) Для указанных ниже формул-эквиваленций, доказуемых
в классическом секвенциальном исчислении установите их импликативные
части, доказуемые в интуиционистском секвенциальном исчислении:
http
о- Hi ।rnit i-i i
391
1) (А->В)<->(^В->^А);
2) ^а^а-,
3) A&Bv-B)<->A;
4) A v В v —iB (В v —iB);
5) AvB<->—1(—A&—iB)j
6) A&B++—1(—Av—iB)j
7)
8) (A^B)o^AvB;
9) A&B<-»4A->->B);
10) AvB<H>(-A-»B);
(->)
(<-)
(<-)
(<-)
(->)
(->)
11) —i(A&B)<-> —A v—iBj (<—)
12) -4AvB)<->(-A&-B);
(o)
13) (A->C)&(B->C)<->(AvB->C); (<^)
14) Av(B&Go(AvB)&(AvC). (<->)
Постройте контрмоделъ Крипке для импликации в обратную сторону.
Решение.
1)
А-^В-^НВ-»-1-
-""а’^в^^вн^а---
А^ВН—iB^—iA
Н (А —> В) —> (—В —> —А)
10)
А,-*-|-В
J A,-Ll--L
А, ВН-1- ЛВМ^-*-!--1- А,-1-НВ
_А, В,-*--> (А->-*-) Н-*- А,А->-*-1-В
А, (В(А->-*-)!-В
X,—В—>—АЫВ
Н (—iB —А) (А В)
АН-1- А,ВН-*-
A,-l^BH-l- BHAvB
А,А^-*-!-В B,A^-*-l-B
(A^-*-)^BHAvB
А1--А->В ВН-А^В
AvBI—А^В
H(AvB)<^(-A^B)
-A^BHAvB
H(-A^B)^(AvB)
ID
k
I
AHB A.-LH-1-
B.A^fB^^H-1-
А,А->(В->-ЧЬ-L
д-'-н-1-
A^A-»-*-!--1-
a^Aa&bh^-
A^-i-hA&B^-1- Аналогично
A&B —H—A v—i В
-АНЧА&В) -iBH-i(A&B)
A,B->^k^
—i(A&B)H—Av—iB
-Av—iBH-.(A&B)
H—i(A&B)^(—Av—В)
H(—Av—iB)^—i(A&B)
392
https
12)
ab->-*-i-(a—>-*-)&(в—>-*-)
A v В -> -*-(A -> -*-)&(B -> -*-)
4AvB)V^A&^B
H—i(A vB)—>(—A&—iB)
-A^BMvBh-1-
-Aj-iBHAvB-»-1-
—A & —iB H —1( A v B)
H —A & —iB —> —(A v B)
14} BHAvB CHAvC
AH(AvB);AI-(AvC) B&CHAvB; B&CI-AvC
AI~(AvB)&(AvC) B&CI~(AvB)&(AvC)
Av(B&C)H(AvB)&(AvC)
HAv(B&C)->(AvB)&(AvC)
B,CI~B&C B,AHA {A} I-A
B,CI-Av(B&C) B,AbAv(B&O A,AvCbA
B,AvCI~Av(B&C)A,AvCI~Av(B&C)
AvB,AvCI-Av(B&C)
(AvB)&(AvC)l-Av(B&O
H(AvB)&(AvC)->Av(B&C)
def def
4. Пусть - -,(p -> p), ~г - p->p. Докажите, что в интуиционистском
пропозициональном исчислении выводимы формулы:
1) -*-vp=dp;
2) -r&-L=d-1-;
з) ->-*-=а-г;
4) -гй-^-Ч
5)p-»-r=d~r;
6) p^p=d-r;
7) -j-v=d-j-.
Решение. Вспомним, что — дедуктивная эквивалентность
4) р1~Р
£PztP2zlZLJz?zz>_?
—L -Чр->р)Нр->р -,(р~>р)Ыр->р)
t5Pzzt?l&ztzz>_z*z Zt Z? f?
I—I—L—
5. Постройте опровержение доказуемости (если это возможно) формул
в интуиционистском секвенциальном пропозициональном исчислении:
1) -i^p^p;
2) (p^q)^(C^p^q)^q);
3) Чр&^р);
4) 4pvq)^^p&-.q;
5) pv^p;
6) 4p&q)^(--pv-.q).
Решение.
1)
k
I
pH-1- p,-*-!--1-
p, -*- —> -*- н -*- -*-i-p
^zhl^ Jz_p
—-P bp
H-,-.p^-p
393
https:it.ru
2)
к к
I I
p->q,pl—*- p->q,p,ql—*~
p—>g, p,^—>g p-»q,q^q
p—>q,—ip—>ql~q
Hp ~> q) ~> ((^p ~> q) ~> q)
3)
P^l—L
P,P^-LI—*-
P&^pb-1-
hp&^p^-L
H4p&-p)
4)
p —> -*-, q —> -*-1- p —> -*- p-> -*-, q —> -*-1- q —> -*-
______________________
-.(pvq)|-^p&-,q
H—i(pvq)—>—ip&—q
6. Постройте опровержение доказуемости следующих формул в интуи-
ционистском исчислении:
1) ((p^q)^r)^((r^p)^(s^p));
2) ((p^r)->(s->p))->(((r->q)->p)->(s->p));
3) ((г -> q) -> (s -> рУ) -> ((г -> р) -> ($ -> р));
4) (((г -> р) -> р) -> ($ -> р)) -> СССр q) г) ($ -> р));
5) (((p^r)^q)^q)^((q^r)^(p^r));
6) (p^q)^(((p^r)^q)^q);
7) ((p^s)^p)^((c^p)^b)^p.
Решение.
1)
к к к
4- 4, 4-
s,pl-r s,p,p\-q r,p,s,r\-q
r->p,s,p\-q r->p,s,p,r\-q GpHp
r —> p, s, p, q -> r I- q r —> p, s, r I- p
(p^q)^r,r^p,shp
b((p->q)->r)->(fr->p)->(s->p))
2) i
s, p, p, r, q->pHq
Sj p, r, s -> p, q -> p I- q
s, p, r -> (s —> p), r, q —> p I- q s, p, r (s —> p), p I- r
______s,p\~p_____
(r^q)^p,s,s^p\-p
(r p,s,p,r (s p) I- r
(p^r)^(s^p),(r^q)^p,sl-p
b((p->r)->(s->p))->(((r->q)->p)->(s->p))
394
https: "и rait.ru
3) *
Ф
I к
P,s,r\-q /
rp,s,rI-q r->p,s,r,s->p\-q s,p\-p
r -> p, s, r, q -> ts -> p) Ь q r -> p, s, s -> p Ь p
(r->q)->(s->p),r->p,sl-p
b((r->q)->(s->p))->((r->p)->(s->p))
Дальнейший перебор вариантов выполните самостоятельно.
4) к
I
s, p,r->p, р, q—>rhq
s, г -> р, р, s р, q -> г I- q г, р I- р
s,r->p,p->(s->p),p,q->rhq s,r -> р, р -> (s -> р), г Ь р (р -> q) -> г, s, р Ь р
(p->q)->r,s,r->p,p->(s->p)l-p(p->q)->r,s,s->pl-p
(Xr->p)->p)->(s->p),(p->q)->r,sl-p
b(((r^p)^p)^(s^p))^(((p^q)^r)^(s^p))
Дальнейший перебор вариантов выполните самостоятельно.
5) i 5
p,rHq p,r,qhq p,rhq p,r,q\-q
p,r,q->q\-q p,r,q->q,r\-q
q—>r,p,r,q—>q\-q q,r,p\-r
q^r,p,p^r,q^q\-q q->r,p,qbr
(Xp->r)->q)->q,q->r,pl-r
^CCCp—>q)—>q)—>C(.q—>r^—>(p—
Дальнейший перебор вариантов выполните самостоятельно.
6)
к к
I 1
p,qHr p,q,q\-r
p—>q,p,r—>q\-r p—>q,q\~q
p->q,(p->r)->qhq
к к
I 1
pl-r p,ql~r J
p,r->qhr qHp
(p->r)->ql~p (p->r)->q,qhq
p—>q,(p—>r)—>ql~q
b(p^q)^(((p^r)^q)^q)
7. Для каких n, me N, n > m, формула
n m
доказуема в интуиционистском секвенциальном пропозициональном ис-
числении. Примеры доказуемых формул:
р -i-ip, -i-i-ip —> -р, -i-i-i-ip —> —i-ip.
8. Постройте доказательства формул и правила вывода в интуицио-
def
нистском секвенциальном пропозициональном исчислении (-,ЕА = А ->Е):
395
tfnc*" II* Ifoit i-i ।
1) А-ъ —'е—<еА;
2) —^А <->i£A;
3) —1£—1£ (AvB) <-^—1£—1£ (-!£—!£ Av—1£-1£В);
4) —1£—1£ (А&В) <-^—1£—1£ (-!£-!£ А &—1£—1£В);
________Ai,...A„ 1~В_____
~,е~,еА1,--;—<е—,еАп Ь-i£-ieB
2. Решение задачи TIP в системе типов Х^ с помощью исчисления G4ip
1. Решите задачу TIP для следующих типов:
1) ((а->Р)->у)->((Р->у)->а->Р)->у;
2) ((a->P)->(P->a))->(P->a);
3)* ((((a^P)^P)^a)^y)^(((((P^a)^a)^P)^y)^y).
Решение.
1) Построим «чистый» интуиционистский вывод секвенции, а затем
аннотируем его соответствующими Х-термами:
Р,уНу a,pi-p
a,p —>y,P,у->(a->P)Hу a.,P —>y, a —>pi~p
a, p —> у, (P —> y) —> a —> P I- P у, (P -> y) -> a -> P I- у
(a->P)->y, (P -> у) -> a -> P I- у
H((a->p)->y)->((p->y)->a->p)->y
b: p, с: у I- с: у
a:a,/:P->y,b:P,g:y->(a->P)l-yb:y a:a,b:pi-b:p
a:a,7:P->y,g:y—>(a->P)T-7b:P->Y a:a,/:p^y,g:a^pl-ga:p
a: a, /: P -> у, p: (P -> y) -> (a -> P) I- pfa: P с: у I- с: у
/:р—>y,p:(p—>y)—>(a—>p)hXa.p/a:a—>p c:y,p:(p—>y)—>a—>pl~c:y
Pi: (a -> P) -> у, p: (P -> y) -> a -> p I- c[c := Pi((X/. la. pfa) (ВрДО)]: у
px: (a -> p) -> у, p: (p -> у) -> a -> p H pi(p(BpiK j): у
I- Zpv Xp. p1(p(Bp1K)): ((a -> P) -> у) -> ((P -> y) -> a -> P) -> у
Построенное доказательство: X/. Xg. J(g(B/K)).
Выполним его рефакторинг:
n
х/. Xg. /(g(B/K))=X/. Xg. B/(CI(B/K))g->X/. B/(CI(B/K)).
2) Самостоятельно установите, что
X/. Xx. /(Kx)x: ((a ->₽)->(₽-> у)) ->-> (p -> у).
2*. Решите задачу TCP для следующих утверждений о типах; вначале
решите задачу TIP:
1) Xf. f(BfK): ((a -> a) —> a) -> a;
2) Xf. f(CI(BfK)): ((((a -> P) -> a) -> a) -> P) -> P;
> :t \f-> f (flip id ((.) f const))
\f->f (flip id (f. const))
:: ((((a -> b) -> a) -> a) -> b) -> b
3) Xf. f(CI(CI(BfK))) : ((((((a -> p) -> y) -> y) -> a) -> a) -> p) -> p;
> :t \f_> f (Аф id (flip id ((•) f const)))
396
o- Hi iroi! ri i
\f->f (flip id (flip id (f. const)))
:: ((((((a -> b) -> c) -> c) -> a) -> a) -> b) -> b
(4 ) Xf. f(CI(CI(CI(BfK)))) :
((((((((a -> P) -> y) -> y) -> 5) -> 5) -> a) -> a) -> P) -> 0.
> :t V_> f (flip id (flip id (flip id ((.)f const))))
\f-> f (flip id (flip id (flip id (f. const))))
:: ((((((((a -> b) -> c) -> c) -> d) -> d) -> a) -> a) -> b) -> b
3. (Для знатоков теории типов.)
Докажите, что в системе X , не существуют Х-термы с типами:
1) (Р ~^р) ->р; 2) ((р ->s) ->р) -> (((С ->р) -> Ь) ->р).
Решение. Достаточно обосновать опровержимость секвенций в G4ip:
2)
к к
I |
p,bHs p,b,p\~s
p,s р,с,р —>Ы~ р p,s->p,b\-s
p,s->p,(c->p)->b\-s р,(с^> p)^>b\- р
(p^s)^p,(c^p)^bHp
H((p->$)->p)->(((C->p)->b)->p)
Рассмотрим ещё один вариант попытки построения доказательства:
p,s->p,c,p->b\-s c,p->b,p\-p b,p,s->p\-s b,p\-p
c,p->b,(p->s)->p\-p
b,(p^>s)^>p\-p
(p^s)^p,(c^p)^bHp
b((p^s)^p)^(((c^p)^b)^p)
4. (J. Kiviniemi, Sh. Ben-Kiki)
Докажите дедуктивную эквивалентность в интуиционистском пропо-
зициональном исчислении:
1) закона Пирса (англ. Peirce’s law);
2) закона исключённого третьего (англ, law of excluded middle);
3) закона двойного отрицания (англ, double negation elimination).
Все законы представлены в виде типов языка Haskell, остаётся лишь за-
менить пропуски термами-доказательствами.
{-# LANGUAGE Rank2Types #-}
type Not a = a -> forall a.a
type Peirce = forall a b. ((a -> b) -> a) -> a
type LEM = forall a. Either (Not a) a
type DNE = forall a. Not (Not a) -> a
---LEM = > DNE, LEM = > Peirce
call_Lem_Dne :: LEM -> DNE
call_Lem_Dne - undefined
call_Lem_Peirce :: LEM -> Peirce
call_Lem_Peirce = undefined
397
https:it.ru
Упражнение 18
АНАЛИТИЧЕСКИЕ ТАБЛИЦЫ ДЛЯ
ИНТУИЦИОНИСТСКОЙ ЛОГИКИ
Сегодня я буду кутить. Весело, добродушно,
со всякими безобидными выходками.
Из фильма М. Захарова
«Обыкновенное чудо»
Обязательные результаты обучения:
• знать вспомогательные понятия
—метод аналитических таблиц для формул языка первого порядка;
• знать основные понятия
— множество возможных миров, действительный мир;
— отношение достижимости мира из другого мира;
— интерпретирующая функция;
— модельная структура интуиционистской пропозициональной логики
(модель Крипке);
— функция оценки формул в возможном мире;
— модель Крипке формулы в интуиционистской пропозициональной
логике;
— корректность, полнота и разрешимость интуиционистского пропо-
зиционального исчисления;
— метод аналитических таблиц в интуиционистской логике;
• уметь
— конструировать доказательство общезначимости интуиционистских
пропозициональных формул методом аналитических таблиц;
— опровергать общезначимость интуиционистских пропозициональных
формул методом аналитических таблиц;
— устанавливать «населённость» типа в системе типов методом ана-
литических таблиц;
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
398
https://ur3it.ru
Теоретические сведения
Модель Крипке интуиционистской пропозициональной логики
Однажды на дворцовой лестнице
Григорий Орлов встретил очередного
фаворита императрицы Г. Потёмкина
и на его вопрос: «Что нового?» —
ответил: «Ничего, кроме того, что
вы поднимаетесь, а я опускаюсь».
Анекдот
1. Основные понятия
Для интуиционизма характерно представление о процессе уста-
новления истинности высказывания как о становящемся процессе,
т. е. наряду с суждениями, истинность или ложность которых уста-
новлена к данному моменту, допускаются непроверенные суждения,
которые, не являются ни истинными, ни ложными в данный мо-
мент, однако их истинность или ложность со временем может быть
установлена.
Этот характер интуиционистской истинности нашел отражение
в модели Крипке, к определению которой мы приступим (по [3,
с. 318—319; с. 352—353]).
1. Непустое множество W называется множеством возможных
миров.
2. Один из элементов м/0 е W наделяется особым статусом —
объявляется действительным миром. При этом С. Крипке прямо
следует за Г. Лейбницем: действительный мир — это всего лишь
один из возможных миров (понятие «возможный мир» оказывается
более фундаментальным, нежели понятие «действительный мир»}.
3. Бинарное отношение 91 связывает возможные миры между со-
бой и называется (по С. Крипке) отношением достижимости одно-
го мира из другого; для его обозначения используется также термин
«отношение альтернативности».
Теперь метаязыковое выражение 91 (w, и/') означает, что «из мира
w достижим мир w'«, или что «мир w' является альтернативой
миру и/».
Бинарное отношение 91 для интуиционистской логики является:
1) рефлексивным, т. е. каждый возможный мир достижим сам
из себя;
2) транзитивным, т. е.
Vu/iVw2Ww3 (91(14/!, М/2 )9l(w2, w3) => 91(14/!, w3)).
Определение.
Шкалой Крипке называется пара (W, 91).
399
https: "и га it.ru
4. Возможными значениями пропозициональных переменных
являются И («истина») и Л («ложь»). Однако оценка переменных
в семантике интуиционистской логики релятивизируется относи-
тельно возможных миров: пропозициональные переменные оцени-
ваются как истинные или ложные не сами по себе, а в каком-то воз-
можном мире, причём в различных мирах одна и та же переменная
может принять разные значения.
Техническое оформление этой идеи осуществляется следующим
способом: интерпретирующая функция I определяется как двух-
местная, она сопоставляет значения из множества {И, Л} парам,
состоящим из пропозициональной переменной и возможного мира.
Например, 1(р, и/) = И означает, что переменная р в возможном
мире w принимает значение И.
5. Множество возможных миров W, выделенный действитель-
ный мир w0, отношение достижимости 91 и интерпретирующая
функция I составляют модельную структуру.
Приведём формальную запись семантики для интуиционистско-
го пропозиционального исчисления Рейтинга.
Определение (по [3, с. 352]).
Модельной структурой интуиционистской пропозициональной
логики (моделью Крипке) называется кортеж
(W, w0, 91, Г), W # 0, w0 е W, в котором:
1) 91 с W х W — рефлексивное и транзитивное бинарное отно-
шение, заданное на множестве W;
2) /: G х W —> {И, Л},
где G — множество пропозициональных переменных, И и Л —
истинностные значения.
При этом функция I обладает свойством монотонности (сохран-
ности) для пропозициональных переменных:
I(A, wx) = И & SlCwp w2) => I(A, w2) = И.
Определение (по [3, с. 352—353]).
Функция оценки формул в возможном мире w е W модельной
структуры (W, и/0,91, Г) определяется так:
1) |A|w = И <=> Z(A, w) = И, |A|W = Л фф/(А, w) = Л;
2) |А&В|„ = И« |А|„ = Ии |В|„ = И;
|А&В|„ = Л« |А|„ = Лили |В|„ - Л;
3) |АуВ|„ = И<=>|А|„ = Иили |В|„ = И;
|AvBL = B« |А|„ = Ли |В|„ = Л;
4) |А^В|,„ = И» Ур(9?(и',у)=>(|А|г = Лили |В|„ = И));
|A^B|w = B«3v(9i(w, v) и |А|„ = Ии |В|„ = Л)
5) |-AL = H«Vv(9?(w,v)=> |А|У = Л);
|-Л|„ = Л «3v(9i(w, v) u |A|V = И).
400
https:"ur3!t.iu
Из приведённого определения следует, что для конъюнктивных
и дизъюнктивных формул сохраняется их классическая трактовка.
Замечание (важное для знатоков модальной логики).
Условия истинности и ложности формул - А и (А —» В) в интуиционист-
ской семантике совпадают с условиями истинности и ложности формул
□-1А и □ (А —> В) в модальной логике.
Определение (по [3, с. 353]).
1) Будем говорить, что формула А истинна в модельной структу-
ре (W, w0,% 7), если А принимает значение И в мире w0.
2) Будем говорить, что формула А интуиционистски общезначи-
ма, если А истинна в каждой модельной структуре (W, w0,9i, 7).
3) Будем говорить, что из множества формул логически следу-
ет формула А в интуиционистской логике, если во всех модель-
ных структурах, где истинна формула из Г, формула А также яв-
ляется истинной.
Определение.
1) (По [3, с. 353]) Модель (Крипке) К формулы А (обозначается
К1= А) — это модельная структура этой логики, в которой форму-
ла А принимает значение И.
2) Контрмоделью К для формулы А (обозначается К ¥ А) называ-
ется модельная структура этой логики, в которой А не принима-
ет значение И.
Отметим, что свойство монотонности действует в данной се-
мантике не только для пропозициональных переменных, но и для
любой формулы: если формула А истинна в некотором мире wlt
и из этого мира достижим мир w2, то формула А обязательно ока-
жется истинной и в мире w2.
Указанная особенность семантики Крипке позволяет трактовать
интуиционистскую логику как логику роста и накопления знаний
(в русле кумулятивной модели развития научного знания). Воз-
можные миры здесь уместно трактовать как совокупность знаний
на разных этапах истории. Причём (в полном соответствии с куму-
лятивной моделью) знание принципиально не исчезает, оно может
только прирасти, расшириться.
2. Корректность, полнота и разрешимость
интуиционистского исчисления
Теорема (о корректности) [65, с. 115].
Если пропозициональная формула А выводима в интуиционист-
ском пропозициональном исчислении, то А истинна в любой моде-
ли Крипке.
401
https:it.ru
Определение (по [65, с. 71; с. 118]).
1) Простая конъюнкция — это конъюнкция пропозициональных
формул
р,—р,р—>q,p—>q\/r,p &q—>r, (р—>q}—>г,
где p,q,r — пропозициональные переменные.
2) Простая импликация — это формула вида К р, где К—про-
стая конъюнкция, р — пропозициональная переменная.
3) Рангом простой импликации назовём количество конъюнктив-
ных членов вида (р q} г в простой конъюнкции.
Теорема (по [65, с. 71]) (без доказательства}.
Всякая пропозициональная формула дедуктивно эквивалентна
в интуиционистском пропозициональном исчислении некоторой
простой импликации.
Определение (по [65, с. 118]).
Будем называть строгой контрмоделъю для простой импликации
К—>р модель Крипке К, для которой К1= К, К ¥ р.
Замечание.
См. понятие «шкала Крипке» в [65, с. 117].
Теорема (о полноте} (по [65, с. 118]).
Пусть F — простая импликация, d — ее ранг. Тогда:
1) либо формула F выводима в интуиционистском пропозицио-
нальном исчислении;
2) либо существует строгая контрмоделъ для F на шкале Крипке
Kd
Другими словами, интуиционистское пропозициональное исчис-
ление полно относительно моделей Крипке.
Теорема (о разрешимости} (по [65, с. 124]).
Интуиционистское пропозициональное исчисление разрешимо.
Аналитические таблицы для интуиционистской логики
Джек вскочил.
— У нас будут правила, — крикнул
он вдохновенно.
— Много всяких правил. А кто
их будет нарушать...
У. Голдинг. Повелитель мух
Ранее был рассмотрен метод аналитических таблиц для язы-
ка первого порядка. Этот метод позволял в определённых случаях
402
https:/Л: rait.ru
устанавливать общезначимость формул языка первого порядка или
наличие логического следования некоторой формулы В из посылок
^1, AfT
Метод аналитических таблиц может быть исполь зован в интуи-
ционистской логике. Правда, в этом случае он несколько усложня-
ется.
Усложнение метода будет состоять в том, что при проверке обще-
значимости формул мы будем в общем случае иметь дело не с од-
ной аналитической таблицей, а с некоторым упорядоченным мно-
жеством аналитических таблиц, а именно, деревом таблиц (иначе
говоря, мы будем иметь дело с дважды упорядоченным деревом).
С одной стороны, каждая аналитическая таблица, входящая
в данную структуру аналитических таблиц, будет древесно упоря-
дочиваться посредством правил редукции для пропозициональных
переменных:
[t&], [/&], [tv], [/vL
С другой стороны, само многообразие аналитических таблиц, ко-
торое возникает при проверке на общезначимость некоторой фор-
мулы, также будет древесно упорядочиваться посредством правил
редукции для логических связок —> и -ь
[t->], [t-n], [f-J.
Из описания аналитических таблиц для первопорядковой логики
известно, что для каждой аналитической таблицы всегда имеются
линейно упорядоченные множества отмеченных формул.
Как и ранее, будем называть цепями линейно упорядоченные
множества отмеченных формул для конкретных аналитических та-
блиц.
С другой стороны, в древесной структуре совокупности самих
аналитических таблиц также будут находиться линейно упорядо-
ченные множества этих таблиц.
Будем называть эти линейно упорядоченные множества ана-
литических таблиц, входящих в систему аналитических таблиц,
их ветвями.
Рассматривая метод аналитических таблиц, будем полагать, что
аналитические таблицы — это синтаксические аналоги некоторых
миров.
1. Пропозициональные правила редукции
Отметим, что так как интуиционистские системы строятся
на базе пропозициональной логики, то мы без каких либо измене-
ний принимаем все правила редукции, относящиеся к связкам &
и V.
403
https: "и rait.ru
Определение (по [3, с. 194]).
Пропозициональными правилами редукции называются приве-
денные ниже слова:
[t&] t(A&B) в цепи таблицы w [/&] f(A&B) в цепи таблицы w
tA tB в цепи таблицы w £4|fB в цепи таблицы w
[tv] t(AvB) tA|tB в цепи таблицы w в цепи таблицы w [/v] f(AvB) fA fB в цепи таблицы w в цепи таблицы w
Правила редукции для логических связок —> и -i формулируются
следующим образом [3, с. 354—355].
1. Правило [t-^].
Допустим, что в некоторой цепи таблицы w содержится формула
t(A В), утверждающая истинность формулы (А —> В) в этой цепи.
Согласно условию истинности импликации в интуиционистской
логике (см. «функцию оценки формулы в возможном мире»)
|А^В|„ = И«фУу(Я(м,,у)=>(|А|у=Лшш |B|v = M));
это означает, что в любой таблице у, достижимой из данной цепи
таблицы w (эти таблицы уже обязательно должны быть к этому
моменту построены), имеет место ложность утверждения А или ис-
тинность утверждения В.
Поэтому в таблицу v можно поместить отмеченные форму-
лы/А и tB, расщепив таблицу на две цепи. Итак:
t(A—>В)
£4|tB
в цепи таблицы w
в каждой таблице у, достижимой из цепи таблицы w.
Замечание (важное).
В силу рефлексивности отношения достижимости в интуиционистской
логике, каждая таблица достижима сама из себя, а потому по отношению
к любой построенной таблице w всегда существует таблица, которая уже
заранее построена (таковой является сама таблица w).
2. Правило [Д->].
Пусть в некоторой цепи таблицы w содержится формулаДА В),
утверждающая ложность в этой цепи таблицы w формулы (А —> В).
Согласно условию ложности импликации в интуиционистской
логике (см. «функцию оценки формулы в возможном мире»)
|A->BL = B^3v(W,v) и |A|v = Hu |B|V = Л);
это означает, что существует таблица у, в которой антецедент А импли-
кации является истинным утверждением, а консеквент В — ложным.
404
https:
Поэтому необходимо обязательно построить новую таблицу v,
с которой начинается новая ветвь аналитических таблиц, объявить
ее достижимой из цепи таблицы w, и поместить в нее утверждения
об истинности антецедента и ложности консеквента, т. е.
f(A —> В) в цепи таблицы w->
fB в новой таблице v.
3. Правило [t-1].
Предположим, что в некоторой цепи таблицы w содержится фор-
мула t(—А), утверждающая истинность в этой цепи формулы -А.
Согласно условиям истинности отрицания в интуиционистской
логике (см. «функцию оценки формулы в возможном мире»)
|-А L = И <=> Vv(<R(w, v) => |А | v = Л);
это означает, что в каждой таблице v, достижимой из данной цепи
таблицы w (эта таблица обязательно уже должна быть к этому мо-
менту построена), имеет место ложность утверждения А.
Поэтому в такую таблицу можно поместить отмеченную форму-
лу fA:
t(—А) в цепи таблицы w
£4 в каждой таблице v, достижимой из цепи таблицы w.
4. Правило [f-1].
Предположим, что в некоторой цепи таблицы w содержится фор-
мула f(-A), утверждающая ложность формулы -А в этой цепи.
Тогда, согласно условию ложности отрицания (см. «функцию
оценки формулы в возможном мире»)
|-1А|и, = Л<^>3v(9i(w,v) и |A|V = H);
это означает, что существует таблица v, достижимая из данной цепи
таблицы w, в которой формула А является истинной.
Поэтому необходимо обязательно построить новую таблицу,
с которой начинается новая ветвь аналитических таблиц, которая
объявляется достижимой из цепи таблицы w и в нее помещается
утверждение об истинности А, т. е.
f(-A) в цепи таблицы w-> | tA в новой таблице v.
Другими словами, если установлено, что формула -А в мире w яв-
ляется ложной, то необходимо построить новый мир v и положить,
что этот мир достижим из мира w и в новом мире формула А истинна.
Новые правила редукции подразделяются на локальные и гло-
бальные.
Определение.
1. Локальными правилами называются правила |f->] и [f-J, т. е.
те правила, которые в обязательном порядке требуют конструи-
рования новых таблиц.
405
https:it.ru
2. Глобальными правилами называются правила [t—>] и [t-i], т. е.
те правила, по которым работают с уже построенными таблицами
и которые можно применять повторно по мере появления новых
достижимых таблиц.
При применении метода аналитических таблиц рекомендуется
вначале всегда применять локальные правила.
Замечание (для знатоков модальной логики).
При применении глобальных правил необходимо помнить, что отно-
шение достижимости обладает различными свойствами в различных
логических системах:
а) в интуиционистской логике отношение достижимости обладает
свойствами рефлексивности и транзитивности;
б) в модальной логике отношение достижимости может обладать сле-
дующими свойствами:
— рефлексивности (система Т);
— рефлексивности и симметричности (система Брауэра);
— рефлексивности и транзитивности (система S4);
— рефлексивности, симметричности и транзитивности (система S5).
Определение.
1. Принцип монотонности. Если tp в мире а и 91(а, 0), то tp имеет
место в мире 0, где р — произвольная пропозициональная пере-
менная.
2. Обобщённый принцип монотонности. Если tA в мире
а и 91(а, 0), то tA имеет место в мире 0, где А — произвольная
пропозициональная формула.
Введем ряд понятий, связанных с применением метода аналити-
ческих таблиц для интуиционистской логики.
Определение [3, с. 324].
1. Аналитической таблицей назовём:
а) аналитическую таблицу, которая начинается с отмеченной фор-
мулы/?! (при обосновании общезначимости формулы А);
б) аналитическую таблицу, начинающуюся с отмеченных формул
tAlt tA2,..., tA^fB (при обосновании следованияА15 А2» •••, Ап 1=В).
2. Системой аналитических таблиц называется множество ана-
литических таблиц, древесно упорядоченное с помощью отноше-
ния достижимости 91.
Определение (по [Бочаров, Маркин,2008, с. 325]).
Будем говорить, что цепь аналитической таблицы w является
замкнутой, если:
406
https:/Л: rait.ru
а) в ее составе встречаются две отмеченные формулы вида С и —iC;
б) в ветви среди таблиц, достижимых из данной цепи таблицы
w, найдётся хотя бы одна замкнутая таблица.
Определение (по [3, с. 325]).
1. Будем говорить, что аналитическая таблица w является зам-
кнутой, если все ее цепи замкнуты.
2. Будем говорить, что система аналитических таблиц является
замкнутой, если замкнута аналитическая таблица w0.
Построение замкнутой системы аналитических таблиц для не-
которой формулы А, с учётом специальных свойств достижимости
для интуиционистской логики, означает, что эта формула является
общезначимой в этой логике.
Аналогично построение замкнутой системы аналитических та-
блиц, используемой для проверки наличия логического следования
формулы В из посылок А1} А2, ---j Ап> с учётом специальных свойств
достижимости для интуиционистской логики, означает, что нали-
чие данного следования в этой логике имеет место.
Работа с примерами решения некоторых типов упражнений
См. Пример 1, Пример 2.
2. Кванторные правила редукции
Вначале напомним, что замкнутым термом называется терм,
не содержащий предметных переменных.
1. Правило [tV].
Пусть в некоторой цепи таблицы w содержится формула t(VxA),
утверждающая истинность формулы VxA в этой цепи таблицы w.
Тогда в любой таблице v, достижимой из данной цепи таблицы
w (эти таблицы уже обязательно должны быть построены), имеет
место истинность утверждения (A)f, являющегося результатом под-
становки замкнутого терма t вместо всех свободных вхождений
переменной х:
tVxA в цепи таблицы w
t(A)* в каждой таблице v, достижимой из цепи таблицы w.
2. Правило [/V].
Пусть в некоторой цепи таблицы w содержится формула /(VxA),
утверждающая ложность формулы VxA в этой цепи таблицы w.
Тогда необходимо в обязательном порядке построить новую та-
блицу v, с которой начинается новая ветвь аналитических таблиц,
объявить ее достижимой из цепи таблицы w, и поместить в нее ут-
верждения о ложности (А)£, являющегося результатом подстановки
вместо всех свободных вхождений переменной х предметной кон-
станты к, не содержащейся в данной цепи таблицы:
407
httnC'//1 Н
upoj i Ul Uil.l
/(VxA) в цепи таблицы w--> I f(-A)£ в новой таблице v.
3. Правило [S].
Пусть в некоторой цепи таблицы w содержится формула t(SxA),
утверждающая истинность формулы ЯхА в этой цепи.
Тогда в каждой таблице v, достижимой из данной цепи таблицы
w (эта таблица обязательно уже должна быть построена'), имеет
место истинность утверждения (А)£, являющегося результатом под-
становки вместо всех свободных вхождений переменной х предмет-
ной константы к, не содержащейся в данной цепи таблицы:
tBxA в цепи таблицы w
tCA)j£ в цепи таблицы w--------> ^^k в новой таблице v.
4. Правило [/3].
Пусть в некоторой цепи таблицы w содержится формула/(ЯхА),
утверждающая ложность формулы ЯхА в этой цепи.
Тогда в каждой таблице v, достижимой из данной цепи таблицы
w (эта таблица обязательно уже должна быть построена), имеет место
истинность утверждения (A)f, являющегося результатом подстановки
замкнутого терма t вместо всех свободных вхождений переменной х:
f(3xA) в цепи таблицы w
f(A)* в каждой таблице v, достижимой из цепи таблицы w.
Замечание (важное).
Процедура построения аналитической таблицы не является алгорит-
мической (в частности, процесс выбора термов в правилах для кванторов
носит творческий характер).
Работа с примерами решения некоторых типов упражнений
См. Пример 3, Пример 4.
Биографические сведения
Крипке Сол (Kripke Saul Aaron) (род. 13 ноября 1940) — американ-
ский философ и логик языка. Учился в Гарвардском и Оксфордском
университетах. С 1976 — профессор Принстонского университета.
Основные работы — по математической логике, философии язы-
ка, философии математики, метафизике, эпистемологии, теории
множеств. Большая часть работ остаётся неопубликованной, суще-
ствует лишь в виде аудиозаписей или в виде рукописей, распростра-
няемых лично.
В возрасте 19 лет опубликовал первую статью «Теорема полноты
в модальной логике». Начиная с этого времени, его работы по ло-
гике активно стимулировали развитие семантики «возможных ми-
ров». Этот подход, который нашел широкое применение в филосо-
фии и ведёт своё происхождение от идеи Лейбница о необходимой
истине как об истине во всех возможных мирах.
408
https: "и га it.ru
Последующие работы оказали глубокое влияние на аналитиче-
скую философию, наиболее значительным вкладом считается мета-
физическое описание модальности, включающее идею возможных
миров (семантика Крипке). Внёс вклад в изучение философии Вит-
генштейна, оригинальная интерпретация получила известность под
названием «Крипкенштейн».
Наиболее известной работой Крипке является монография «Име-
нование и необходимость» (1980).
Является почётным профессором Гарвардского университета.
Лауреат премии Р. Шока по философии и логике (2001); согласно
одному из опросов, входит в десятку наиболее важных философов
последних двухсот лет.
Примеры решения некоторых типов упражнений
...в книгах нет ни людей, ни вещей.
А есть одни чёрные крючочки и закорючки,
собранные на странице в длинные рваные
цепочки. Их просто надо перебирать
глазами — и всё... Труд это небольшой,
но уважаемый.
А. Аствацатуров. Осень в карманах
Пример 1. Используя метод аналитических таблиц, докажите обще-
значимость пропозициональных формул:
1) (А—»А);
2) А—>(В—>А);
3) A v^A4 (-i-А -> А);
4) -А^(А^В);
5) bAv-B)->-i(A&B);
6) -i-i(Av-A);
7) (А —> В) —> (А —>-В) —>-А;
8) (А —> В & —iB) —> —А.
Решение. Будем обозначать знаками «=>» и «<=» переносы отмечен-
ных формул из одного мира в другой.
1) w01 f(А —> А)-> tA
Таблица w1 замыкается (в ней содержатся отмеченные формулы
tA ufA), а так как эта таблица по транзитивности достижима из началь-
ной таблицы w0, то начальная таблица тоже замыкается и потому вся
система аналитических таблиц замкнута, и формула (А —> А) общезна-
чима в интуиционистской логике.
2)
w0 | f(A -> (В -> А)) —> tA ~>
Wi f(B—>А)—> tB
fA
w2 tA<~
409
https:it.ru
3) Построим систему аналитических таблиц:
w0 | f(A v -А (-.-Л А)) —>
t( A v —А) ~>
f(-i-A->A)
w2
t(—А) *>
f(-A) <«
fA
t(A v —А)
tA |t(-A)
Таблица w2 замыкается (в ней содержатся отмеченные формулы
tA,fA и t(-A),/(-A)), а так как эта таблица по транзитивности дости-
жима из начальной таблицы w0, то начальная таблица тоже замыкается
и потому вся система аналитических таблиц замкнута, т. е. формула обще-
значима в интуиционистской логике.
4)
wo I fi-A (А В)) —>
t(—А) ->
f(A->B)—>
w2
Таблица w2 замыкается (она содержит отмеченные формулы tA nfA).
5)
w0 I 'A v —iB) —> —i(A & B)) —>
t(-Av-iB)
f(-,(A&B)) —> t(A&B)
w2
tB
t(—A v —iB)
t(—A) t(—iB)
fA fB
Таблица w2 замыкается (см. формулы tA,fA и t(B),/(B)).
6)
wo I f C-'(A v ~tA)) —>
t(—i(Av—A)) ~>
f(Av-A)
fA
f(-A)—> tA
t(-i(Av-A)) <~
f(Av-A)
w2 f(—A)
Таблица w2 замыкается (см. отмеченные формулы tA nfA).
410
https:/Л: га it.ru
7)
w2
f(-A)
tA
w3
tB
KnB)
fB
Таблица w3 замыкается (см. формулы tA,fA, а также tB,fB).
8)
w0 |f ((А->В&-,В)->-А)-----> t(A-»B&->B)
w1 f(—iA)
»
tA
t(A—>B&—iB) <
fA
t(B&->B)
tB
tbB)
w2
Таблица w2 замыкается.
Пример 2. Используя метод аналитических таблиц, опровергните
общезначимость пропозициональных формул:
1) Av-A;2)-,-A->A;3)(((A->B)->A)->A);
4) (-Л-> В)-> (-ЛА.
Решение.
1)
w0
f(Av-iA)
fA
f(-nA)—>
tA
Таблица не замыкается, так как отмеченная формула tA находится
в мире wlt а отмеченная формула^! — в мире w0.
2)
w0 | f (-i-A —> А)—>
t(—А) *>
f(-A)
fA ----->
w2
tA
t(—A) <«
f(-A)--------> tA
vv3 ...
Ни одна из таблиц w0,w1,w2, ... не является замкнутой, поэтому вся
система аналитических таблиц не замкнута.
411
3)
w0|f(((A^B)^A)^A)^
t((A—>B)—>A) *>
fA
tA I f(A—>B)
tA
fB
w2
t((A—>B)—>A) <«
Таблица w2 не замыкается, так как отмеченная формула tA находится
в мире w2, а отмеченная формула^! — в мире w1.
4)
w0 | f СС^А -> В) -> ((-А -> -iB) -> А))
f(bA->^B)->A)—>
w2
Wi
t(—А—>—В) ~>
fс—-В) I f(-A)
M tA
w3
t(->B) f^A)
® w4|tA...
Пример 3. Используя метод аналитических таблиц, докажите обще-
значимость первопорядковых формул:
1) (А)*->ЗхА;
2) VxA-> ЗхА;
3) ЗхА—>-Vx-A;
4) (Е —> VxA) —> Vx(E —> A), xgFV(E);
5) Vx(E —> А) —> (Е —> VxA), xgFV(E);
6) Зх(Е -> А) -> (Е -> ЗхА), х FV(E);
7) 3xVyR(x,y)^ Vy3xR(x,y);
8) (A->3xB)->3x(A->B), xgFV(A).
Решение.
1)
w0|f((A)?- ->3xA)— —> t(A)? f(HxA) f(A)?
2)
w01 f(VxA —> ЗхА)__>
t(VxA)
t(A)?
f(HxA)
f(A)?
412
http
rait.ru
3)
w01 f(3xA —> -iVx-iA)-> t(3xA)
шг f(—Vx—A)----->
t(3xA)
t(A)^
t(Vx-A)
t(-A)£ t = k
w2
4)
w01 f(CE —> VxA) —> Vx(E —> A))-> t(E —> VxA)
w1 f(Vx(E —> A))---->
-> f(E->(A)*)
w2
w3
fU)?
t(E —> VxA)
fE t(VxA)
t(A)?
5)
w0 | f (Vx(E —> A) —> GE —> VxA))-> t(Vx(E —> A))
w1 f(E —> VxA)—
w2 f(VxA)------>
w3
f(A)£
t(Vx(E —> A))
t(E->(A)*)
fE | t(A)*
6)
w01 f(3x(E -> A) -> (E -> ЗлА))
-> t(3x(E->A))
ivq f(E —> BxA)
w2
f(BxA)
f(A)^ t = k
t(3x(E->A))
t(E^(A)^)
fE | t(A)^
7)
w01 f(3xVyR(x, y) -> Vy3xR(x, y))-> t(3xVyR)
wi f(Vy3xR)
w2
f(3xR(x, b))
fR(t1}b) ^-a
t&xVyK)
t(VyR(a,y))
t(R(a,t2)) t2=b
https: "lira it.ru
413
8)
w0 | f((A -> ЗхВ) -> Зх(А -> B))->
wx
t(A->3xB)
f(3x(A—>B))--->
> f(A- 4(В)-)_ —> tA
W2 f(B)£ t = k
fA t(3xB)
w3
Пример 4. Используя метод аналитических таблиц, опровергните
общезначимость формулы -№х—А НхА.
Решение.
w0 | f (-iVx-A - >HxA)- —> t(-iVx-A)
f(Vx-A) - —> f(—>(А)£) >
f(HxA) w2 w3
f(A)?
Таблица w3 не замыкается, так как отмеченная формула t(A)£ нахо-
дится в мире w3, а отмеченная формула f(A)^ — в мире w1 (кроме того,
предметная константа к является новой в мире w3).
Задачи для самостоятельного решения
— Учиться? Д-da! А чему они-то научат?
Чему? — горячо возразил Чапаев.
— Вы думаете, скажут, что делать
надо?.. Поди-ка, сказали!..
Д. А. Фурманов. Чапаев
1. Методом аналитических таблиц докажите общезначимость следую-
щих интуиционистских пропозициональных формул (А, В, С — формулы):
1) А->(В->А);
2) А^С(А^В)^В);
3) (А —> (В —> С)) —> (СА —> В) —> (А —> С));
4) (А^В)^(В^С)^(А^С);
5) ((((А-> В)-> А)-> А)-> В)-> В;
6) -ЧА&^А);
7) А->-,-А;
8MAv^A);
9) —А —> —A j
10) —।—।—।—А —> —।—А;
11) -i-i(-i-A —> А);
12) —А—>(А—>В);
13) (А->В)->ЬВ->^А);
о - //i iroif i-i ।
414
14) (А^ВЫ(А^М^);
15) (-nA->B)->(-A->-B)->-,-A;
16) bAvB)->(A->B);
17) —i(A v В) —> —A & —В;
18) -A&-B->-MvB);
19) (Av(B^O)^(AvB^AvC);
20) (Av^)->(^A^A).
Решение.
5)
A, A -> В H A
(A —> В) —> A, A —> В l~ A BHB
(((A —> В) —> A) —> A) —> В I-В
H ((((A —> В) —> A)-> A)-> В)-> В
w0 | f CCCCCA -> В) -> A) A) В) B)-------->
Wj
t((((A —> В) —> A) —> A) —> B) «>
fB
tB | f(((A^B)^A)^A)
w2
ЩА^Е)^А)
fA
tA | f(A—>B)
tA
fB
w3 tB
f(((A->B)-> A)—> A)
w4
t((A^B)^A)
fA
tA
94 | fC-1-.^A -> —A)----->
Wj
t(-,-,-A) «>
f(—A) ---->
w2
tA
t(-i-i-A) <«
f(-i-A) ----> t(^A)
fA
w3 tA
10)
w0 I f(—।—।—।—A ——।—A)-----t(—।—।—।—A)
wr f(-i—A) ------>
w2
tbA)
tb^^A)
f (-.^A) ->
t(—A)
f(-A)
w3 t(—A)
415
https:,
/uraitju
2. Методом аналитических таблиц опровергните общезначимость инту-
иционистских пропозициональных формул (А, В, С — формулы):
1) Av—А;
2) -^А->А;
3) -Av-.-А;
4) ((А->В)->А)->А;
5) -4A&B)->^Av-B;
6) bAvB)->(A->B);
7) (—iB —> —А) —> (А В);
8) —iAv-i—А.
3. Исследуйте опровержимость в интуиционистской логике следующих
первопорядковых формул:
1) Зх(А(х) —> VyA(y)), 3xVy(A(x) —> А(у)) {«принцип пьяницы»);
2) Зх(ЗуА(у) -> А(х)) {«принцип горького пьяницы»).
Комментарии {шутливые).
Название формул 1 объясняется одной из их интерпретаций: «суще-
ствует такой человек, что если он пьёт, то все люди пьют».
Эта интерпретация комментируется анекдотом отР. Смаллиана [167,
с.205]): «Заходит ковбой в бар и говорит бармену: “Мне налей и всем
налей. Такой уж я человек: когда я пью, все пьют”. Через некоторое время:
“Мне повтори и всем повтори. Такой уж я человек: когда я пью, все пьют”.
Затем кладёт на стойку деньги: “С меня возьми и со всех возьми. Такой
уж я человек: когда я плачу, и все платят”».
Название формулы 2 объясняется одной из их интерпретаций: «суще-
ствует такой человек, что если кто-нибудь пьёт, то и он пьёт».
Доказательство формул 1 и 2 в классическом гильбертовском исчислении
получается с помощью следующих общезначимостей:
Зх(А(х) -> VyA(y)) о (VxA(x) -> VyA(y)),
Зх(ЗуА(х) А(х)) <-> (VyA(y) VxA(x)).
4. Установите методом аналитических таблиц «населённость» типа
{{а а) b) —> b и решите для этого типа задачу TIP {если это возможно).
Решение.
w011 f ({{а ->a)->b)-> Ь)->
t((a -> а) -> b)
tb | f(a—>а)
fb \
w2
I:аa f:{a->a)->b
Mx:b =>Mx=fI
M:((a->a)->b)-> b => M =
о - Hi I roif ri
o.r < Ul UU.I v
Часть 5
АКСИОМАТИЧЕСКАЯ
СЕМАНТИКА ЯЗЫКОВ
ИМПЕРАТИВНОГО
ПРОГРАММИРОВАНИЯ
https:it.ru
Упражнение 19
РАСШИРЕНИЕ ЯЗЫКА ПЕРВОГО ПОРЯДКА
Прошу, забудь все, чему ты учился
в школе, потому что ты этому не научился.
Прошу, однако, всюду вызывать в своем
представлении соответствующие разделы
школьного курса; потому что тебе
всё же не следует его забывать.
Э. Ландау
Обязательные результаты обучения:
• знать основные понятия:
— состояние (для математических логиков), состояние памяти, массив,
элемент массива;
— новые функциональные символы: целочисленное деление, остаток
от деления, обновление массива В;
— новые предикатные символы;
— новые бинарные логические связки: условная дизъюнкция, условная
конъюнкция;
— ограниченные кванторы для числовых множеств, ограниченный кван-
тор количества;
• уметь:
— конструировать доказательства утверждений о равносильности
формул, содержащих новые предикатные символы и бинарные логические
связки;
— осуществлять перевод содержательных математических утверждений
в расширенный язык первого порядка;
— описывать содержательную семантику формул расширенного языка
первого порядка;
— выполнять операцию подстановки терма вместо свободной переменной
в выражение с ограниченными кванторами;
• владеть:
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
Теоретические сведения
Будем предполагать, что читателю известен смысл терминов:
1) «язык формальной системы первого порядка»;
2) «гильбертовское исчисление первого порядка»;
419
https:it.ru
3) «теория моделей для языка первого порядка»;
4) «формальная арифметика (теория S)»;
5) «формальная теория множеств (М+)».
В дальнейшем будем считать синонимами термины: «предмет-
ная переменная языка первого порядка», «индивидная переменная»,
«переменная», «идентификатор».
Напомним, что Gj обозначает множество предметных перемен-
ных, Т — множество термов, F — множество формул языка первого
порядка.
Вспомогательные понятия
Пока ограничимся простым русским
языком, стараясь не прибегать
к смысловым и лингвистическим изыскам
и вывертам.
С. С. Лавров
Пусть п е N\{0}, М — непустое множество.
Определение (повторение').
1. О-местными предикатами (на множестве М) называются
1 («истина») и 0 («ложь»); 1 — это предикат, истинный на всех
элементах множества М, 0 — предикат, ложный на всех элемен-
тах множества М.
2. п-местным предикатом Р называется отображение
Р:Мп—>{1,0}.
Пусть Z — множество целых чисел.
Определение (для программистов) (по [80, с. 137]).
Состоянием памяти называется означивание переменных, рас-
сматриваемых в данной задаче или в данном контексте, т. е. функ-
ция, отображающая переменные в их значения.
Вообще говоря, это отображение является частичным отобра-
жением, так как значения некоторых переменных могут быть
не определены.
Определение (для математических логиков) [88, с. 19].
Состоянием s будем называть отображение s: GT М.
Определение (для программистов) [96, с. 37].
Состояние w — это частичная функция ZU{d?}, где IV —
множество переменных некоторой программы, сопоставляющая
каждой переменной v, объявленной в программе, ее текущее значе-
ние w(v), возможно неопределённое (обозначаемое символом d?).
420
https: //ц га it.ru
Пусть;, к е Z, j < к, В: Z М.
Определение.
def
1. Массивом назовём кортеж В [jк] = {В [у],..., В [к]), содержащий
некоторые значения отображения В.
2. Элементами массива В назовём компоненты В [j], ..., В [к].
т, п е Z.
Определение.
def {т,т+1,т+2,...,к-1},еслмт<к-1,
[т, к} = <
0 в противном случае.
Приступим к расширению языка первого порядка.
Новые бинарные логические связки
Из-за нашего невежества мы потратили
очень много времени на то, чтобы бить
по воде вместо того, чтобы плавать.
Задним числом я могу сказать, что лучше
всего для меня было бы пройти хороший
курс логики 10 лет назад. Я убедил в этом
многих студентов, но сам такого курса
никогда не слушал.
Д. Грис [88, с. 302]
Введём две новые бинарные логические связки:
1) &CAND (читается: «условная конъюнкция»};
2) vCOR (читается: «условная дизъюнкция»}.
Эти логические связки будем интерпретировать алгебраическими
операциями, которые будем обозначать также &CAND и vCOR, а значе-
ниями операндов которых являются:
1 (читается: «истина»},
0 (читается: «ложь»},
Н (читается: «неопределённость»}.
Пусть В и С — формулы.
Определение (таблицы истинности для операций &CAND и vCOR)
[88, с. 77].
в с В &CAND С В VCOR С
1 1 1 1
1 0 0 1
421
https:it.ru
Окончание таблицы
в с В &CAND С В VCOR С
1 н н 1
0 1 0 1
0 0 0 0
0 н 0 н
н 1 н н
н 0 н н
н н н н
Пусть (М, а)— модель, а 0 — оценка языка L± в этой модели.
Из приведённых таблиц истинности следует, что о результатах
операций &CAND и vC0R можно судить по значению первого операн-
да.
В самом деле:
ValMj(Xjp (В &CAND
def
С) =
ValM а р(С),если ValM>a>p(B) = 1,
О, если ValM a p (В) = О;
ValMjCtjp
ММсли Уа1м,а.р(В) = 1,
vcor ’-|уа1ад(С),еслиУа1м,а,р(В)=О.
Новые функциональные символы
Пусть В — массив, i и t — термы расширенного языка.
Добавим к сигнатуре языка первого порядка новые функциональ-
ные символы:
ч-(2) (читается: «целочисленное деление»},
MOD® (читается: «остаток от деления»),
(B;i:t)^ (читается «обновление массива В»)
Определим интерпретацию этих функциональных символов так:
1) функциональный символ +&> интерпретируем функцией двух
целочисленных аргументов
«-=-(2) =х-=-у,
значением которой является наибольшее целое число, не превосхо-
дящее х/у;
2) функциональный символ MOD® интерпретируем функцией
двух целочисленных аргументов
«MOD® = MOD(x,y),
422
https://urait.ru
значением которой является остаток от деления целого числа х > О
на целое число у > 0;
3) функциональный символ (B;i:t) интерпретируем функцией/3,
которую будем называть обновлением массива В и значением кото-
рой является массив, полученный из массива В заменой значения
i-ro элемента массива В значением терма t.
Новые предикатные символы
Расширим смысл понятия «формула языка первого порядка».
Добавим к сигнатуре языка первого порядка новые предикатные
символы нулевой арности, которые обозначим И, Л и назовём логи-
ческими константами.
Определение.
1. И и Л есть формулы языка первого порядка.
2. Атомная формула есть формула языка первого порядка.
3. Если А и В есть формулы языка первого порядка, то (АтВ), где т е
е {&, v, <->, vC0R, &САГЛ)} и -А есть формулы языка первого порядка.
4. Если А — формула языка первого порядка, ах — предметная
переменная, то ЗхА и VxA есть формулы языка первого порядка.
5. Никаких других формул, кроме построенных по пп. 1—4, нет.
Определение (семантика логических констант),
def def
1) ValMa р(И) = 1; 2) Уа1м>а>р(Л) = 0.
Предложение (лёгкое).
1) И = (A v -А); 2) Л = (А & —А).
Доказательство. Упражняйтесь.
Включим в сигнатуру языка формальной системы первого поряд-
ка новый двухместный предикатный символ -s.
Для его интерпретации определим бинарное отношение на мно-
жестве FUT, которое будем обозначать также и называть отноше-
нием графического равенства (или графическим равенством).
Пусть А и В — выражения языка первого порядка, т. е. А, В е FUT.
Определение (семантика предикатного символа =s).
Будем говорить, что слова А и В находятся в отношении гра-
фического равенства (обозначается: А В и читается: «слово
А такое же, как слово В») тогда и только тогда, когда выражения
А и В побуквенно совпадают (т. е. слова А и В идентичны).
Также включим в сигнатуру языка первого порядка новые пре-
дикатные символы | С2), Integer^1), Event1), OdcF1), Primed), Ordered^1),
Inranget2),G (2) и определим их интерпретацию:
423
https://urait.ru
1) символу | & поставим в соответствие двухместный предикат
def
а|(2) = у|х,
который означает, что х делится на у без остатка (или у делит х);
2) символу Integer^1) поставим в соответствие одноместный пре-
дикат
def def 1, если f е Z,
Integer® = ieZ = <!
О, в противном случае;
3) символу Event1) поставим в соответствие одноместный пре-
дикат
def def Г1, если х - чётное число,
Even(x) = MOD(x, 2) = 0 =
О, в противном случае,
а символу Odd^1) — одноместный предикат
def
Odd(x) = M0D(x,2)=l
def [ 1, если x - нечётное число,
= <
О в противном случае.
Другими словами, предикат Even(x) истинен, если х — чётное
число, а предикат Odd(x) истинен, если х — нечётное число;
4) символу Primed) поставим в соответствие следующий одно-
местный предикат:
def def
Prime(n) = п > 1 & (Vk g [1, n)) (MOD(n, k) 0) =
def
= n > 1 & Vk(k g [1, n) MOD(n, k) * 0);
5) символу Inranget2) поставим в соответствие следующий двух-
местный предикат:
def
Inrange(B,i) = i g Domain(B),
где Domain(B) (от англ, domain — область определения} обозначает
множество значений индексов массива В;
6) символу g (2) поставим в соответствие двухместный предикат
def
х g В =d (3k g Domain(B)) (x = B[k]) = 3k(k g Domain(B) & (x = B[k])),
где В — массив;
7) символу Ordered^1) поставим в соответствие следующий одно-
местный предикат:
def
Ordered (В[0: j -1]) = (Vk g [0, j -1) ) (B[ k] < B[k+1]).
424
https:"!.! rait.ru
Замечание (методическое).
В пунктах (4), (6), (7) намеренно допущена синтаксическая ошибка
при записи формулы, а именно: заключена в скобки атомная формула.
Подумайте, с какой целью это сделано?
Ограниченные кванторы для числовых множеств
Пусть т, к g N, a AmfAm+1, ...,Ак— формулы языка первого по-
рядка.
Определение (индуктивное) (по [88, с. 80]).
def ГЛ, если m = к+1,
(3iG[m,k+l))Ai = s
|Д. v(3iG[m,k))Ai, если т< к+1.
Определение (по [88, с. 81]).
def
(ViG[m,k+l))A/ = -i(3ie[m, k+l))-iA;.
Предложение (лёгкое).
1. Формула (3i е [т, к+1))Аг истинна на любой модели и при лю-
бой оценке, для которой истинна по меньшей мере одна из формул
Ai} где i = т, т + 1, ..., к.
2. Формула (ViG[m,k+l))Ai истинна на любой модели и при
любой оценке, для которой истинны все формулы Ai} где i = т,
т + 1, ..., к.
Доказатель с тво. Упражняйтесь.
Следствие (по [88, с. 81]).
a) Am v Am+1 v...v Ak =(3ie[m,к+1))Аг-;
б) Ат & Ат+1 &... & Ак = (X/i g [m, к+1))Д;
в) (Vi g [т, m))Ai = И.
Доказательство.
А. Опираясь на содержательную семантику символа Ат v Am+1 v...
vA*., можно ввести следующее определение:
Ат
т
v Am+1 v...v А^.
def [Л, если т = к+1,
= <
Ак v Um v Am+i v...v4-i), если m< k+1.
Дальнейшее очевидно.
Б. Am &Am+1 &...&Ak =—l—l(Am &Am+1 & ...&Ak) =
=—'(—An & —An+i & ••• & ~Ac) =
= -1(3 i g [m, к+1))-Ai = (Vi g [m, к+1))Аг.
def
B. (Vi g [m, m))Ai = -i(3i e [m, m))-Aj ~ -JI “ И.
425
https: "ura-t.ru
Следствие доказано.
Ограниченный квантор количества
Определение [88, с. 82].
Ограниченным квантором количества (счёта) будем называть
слово
(NiG[m,k+l))Ai,
обозначающее количество различных натуральных значений
i g [т, k+1), при которых формула истинна.
Предложение.
1) (3i е [т, к+1))Аг = (Ni g [т, к+1))Аг > 1;;
2) (ViG[m,k+l))Ai = (NiG[m,k+l))Ai = k+l-m.
Доказательство. Упражняйтесь.
Упражнения для самостоятельного решения
Свойства новых логических операций
1. Докажите, что операции &CAND и vCOR являются некоммутативными
операциями. Опишите все интерпретации, в которых не выполнены законы
коммутативности
41 &CAND = А2 &CAND А1} Ах vCOR Л2 = Л2 vCOR Aj.
2. [88, с. 77—78] Докажите следующие равносильности:
а) законы ассоциативности:
Al &CAND (А2 &CAND A3) = (Ах &CAND А2) &CAND A3;
Ai vC0R (А2 vcor А3) = (Al vcor А2) vcor А3;
б) законы дистрибутивности:
Ai &cand (А2 vcor А3) = (Ах &cand А2) vcor (Al &cand A3);
Ai vcoR (A2 &cand A3) s (Al vcor A2) &СДГ4О (Al vcor A3);
в) законы де Моргана:
-CAl &cand A2) = -Ai vCOR —A2;
-ЧА1 vcor A2) = —Al &оше) “Аг5
г) закон исключенного третьего:
Ai vCOR -Al =И
(при условии, что значениями Аг могут быть 1 или О);
426
С*" iroif 1-1 1
д) закон противоречия:
A &CAND “А = Л
(при условии, что значениями А1 могут быть 1 или О);
е) законы упрощения vCOR:
A vcor А = A j
vCOR И = И (если значениями Ах являются 1 или О);
Л vcor Л = Al
A VCOR (A &CAND A) s А;
ж) законы упрощения &CAND:
A &CAND А = А,
A &cand И =
A &cand Л = Л (если значениями Aq являются 1 или О);
A &CAND (A VCOR A) = Ai
з) прочие законы:
И vCOR Ai=H; Л &cand А Л.
Перевод содержательных математических утверждений
в расширенный язык первого порядка
3. Пусть Aq, А1г Ап— формулы. Запишите утверждение о том, что:
а) к является третьим по величине из всех чисел, таких, что формула
Ак принимает значение 1;
б) к является наименьшим числом таким, что формула Ак принимает
значение 1.
4. [88, с. 82] Напишите предикат, утверждающий, что значение х встре-
чается в массивах В[О:п - 1] и C[O:m - 1] одинаковое число раз.
5. (По [88, с. 82]) Напишите предикат Perm(B,C), утверждающий, что
массив В[О:п - 1] является перестановкой элементов массива С[О:п - 1].
Указание. Будем говорить, что массив В является перестановкой масси-
ва С, если каждое значение встречается одинаковое число раз и в массиве
В, и в массиве С.
6. [88, с.82—83] Рассмотрим массив В[О:п - 1], и > 0. Пусть) и к — два
числа, таких, что 0 < j < k +1 < и. Переведите следующие предложения на язык
первого порядка (некоторые из предложений могут быть двусмысленны;
в этом случае попытайтесь перевести обе возможности):
427
https:/А га it.ru
а) все элементы массива В |/:к] нулевые;
Ь) ни один элемент массива В |/:к] не нулевой;
с) некоторые значения массива В |/:к] нулевые;
d) все нули массива В[О:п - 1] находятся в массиве В[j:k];
е) некоторые нули массива В[О:п - 1] находятся в массиве В|/:к];
f) некоторые значения массива В[О:п - 1] содержатся в массиве В|/:к];
g) неверно, что все нули массива В[О:п - 1] находятся в ВЦ:к];
h) если в массиве В[О:п - 1] есть нуль, то он есть и в В|/:к];
i) если в массиве Bfj:k] есть два нуля, то / = 1;
j) либо B[l; /], либо ВЦ:к] (либо оба) содержат 0;
к) значения массива В |/:к] расположены в возрастающем порядке;
1) если х находится в В[j:k], то х + 1 находится в В[к + 1: п - 1];
т) массив Bfjtk] содержит по меньшей мере два нуля;
п) каждое значение массива В [j:k] встречается ивВ[к+1:п-1];
ог) j является степенью двойки, если/ встречается в массиве В|/:к];
о2) укажите ошибку в приведённом ниже решении задачи 6(0^:
3iG[/,k + l))/ = B[i]^(3k>0)/ = 2fc;
р) любой элемент В[0:/] меньше х, а любой элемент Bfj + 1:п - 1] пре-
восходит х;
q) если значениями В[1], В [2], В[3] являются соответственно 3, 4, 5,
то значением переменной / является 3.
7. Выразите в виде предиката Prime (i) утверждение, состоящее в том,
что натуральное число i > 2 является простым.
8. Запишите в виде формулы утверждение о существовании таких i nj,
расположенных между 1 и 99, что i — простое число, a i • j - 1079.
9. [88, с. 89—90] Выразите в виде формулы языка первого порядка вы-
сказывание о существовании сколь угодно больших простых чисел.
10. П. Л. Чебышёв (1850) доказал, что между каждым числом и числом,
превышающим его вдвое, найдется простое число. Выразите данное выска-
зывание в виде формулы языка первого порядка.
def
11. [88, с. 92] ПустьРоо1(р,Г) = «Можно обманывать человека ре течение
времени t». Переведите следующие предложения на язык первого порядка:
а) можно обманывать некоторых людей некоторое время;
б) можно обманывать всех людей некоторое время;
в) нельзя обманывать всех людей всё время.
Замечание.
Вспомните откровение А. Линкольна: «Вы можете дурачить
какое-то время какую-то часть людей, вы можете дурачить каких-то людей
все время, но вам не удастся дурачить все время всех людей. Но, может
быть, мне это удалось».
12. (По [88, с. 92]) Запишите следующие предложения на языке перво-
го порядка:
а) квадрат целого числа неотрицателен;
Ь) три числа являются длинами сторон треугольника, если сумма любых
двух из них не меньше третьего (обозначим Стороны (а, Ь, с) предикат, возвра-
щающий И, если а, Ь, с являются длинами сторон некоторого треугольника);
428
С*" //i ! ио it i-i I
с) для любого положительного целого числа и существует решение урав-
нения wn + хп +уп - zn, где w, x,y,z — положительные целые числа;
d) число и является совершенным числом, т. е. сумма всех делителей
числа и, кроме самого п, есть и.
Описание содержательной семантики формул расширенного языка
первого порядка
13. (По [99, с. 85]) Пусть Х(М) — количество элементов массива М, а
def
Pnat(M, k) = Z(M) = k & (Vi g [1, k] )3j( j g [1, k] & M[ j] = 1).
Приведите содержательную семантику формулы Pnat(M, k).
14. Верно ли, что х = (х -5-у) • у + MOD(x, у)?
Операция подстановки терма вместо свободной переменной
в выражение с ограниченными кванторами
15. Выполните операцию подстановки:
1) ((Vi g [j, k + DKj = B[i] (3k > 0) (j = 2fc)))/+y;
2) ((Vi g [j, k +1)) (j = B[i] (3k > 0) (j = 2fc)))f+1;
3) ((3f e [1, j +1)) (B[i] = 0) v (3i g [j, k +1)) (B[i] = 0))* k+j;
4) ((Vi G[j,k + l))(j = B[i] —>(3k>0)(J = 2к)))р’^-11/с1 j.
def
16. (По [88,c.88]) Пусть A =(Vi g[0, n))(B[i]<B[i + l]). Выполните опе-
рацию подстановки:
а) (А)‘; в) (А$; д) (A)f+1;
б) (А);+1; г) (Afe е) (А)Й-
17. (По [88, с. 88])
def
Пусть А = (и > i) & ((Nj g [1, и)) (и -г- j = 0) > 1).
Выполните операцию подстановки:
а) (А)$; в) (А)}+1; д) ((A%+i)j;
б) (А)”+/; г) (А)‘; е) (А)"<г
def
18. Пусть А = (Vi g [0, n)) (B[i] = 0 —> i g [j, k)).
Выполните операцию подстановки:
а) (А)}; в) (A)j+1; д) ((А)"+/)|;
б) (А)^+/; г) (А& е) (А)^.
о - Hi I roif ri ।
О.М U1 Oll.l
Упражнение 20
ФОРМАЛЬНЫЙ СИНТАКСИС МОДЕЛЬНЫХ
ЯЗЫКОВ ПРОГРАММИРОВАНИЯ:
ГРАММАТИЧЕСКИЕ МОДЕЛИ
...профессор объяснил мне, что
он работает над изготовлением особых
механических приборов, предназначенных
для открытия отвлечённых истин...
Между тем благодаря его изобретению
самый невежественный и бездарный
человек при небольшой затрате средств
и физических усилий может писать книги
по философии, поэзии, политике, праву,
математике и богословию. Тут он подвёл
меня к раме, по бокам которой рядами
стояли все его ученики. Рама эта имела
двадцать квадратных футов и помещалась
посередине комнаты. Поверхность
ее состояла из множества деревянных
дощечек, каждая величиной с игральную
кость — одни побольше, другие поменьше.
Все они были сцеплены между собой
тонкими проволоками. Дощечки были
обклеены кусочками бумаги, и на этих
бумажках были написаны все слова языка
Валънибарби в различных наклонениях,
временах и падежах, но без всякого порядка.
Дж. Свифт.
Путешествия Лемюэля Гулливера
Обязательные результаты обучения:
• знать основные понятия
— понятие «формальный язык» (повторение);
— понятия «порождающая грамматика» и «форма Бэкуса—Наура (БНФ)»,
«расширенная форма Бэкуса — Наура (РБНФ)»;
— терминальный алфавит языка Н (языка D, языка М), нетерминальный
алфавит языка Н (языка D, языка М), формальный синтаксис языка програм-
мирования Н (языка D, языка М);
430
https:/Л: rait.ru
— языки императивного программирования Н, D и М;
— допустимая программа на языке Н (языке D, языке М);
• уметь
— определять множество цепочек, получаемых по заданным правилам
БНФ и РБНФ;
— конструировать правила БНФ и РБНФ по множествам цепочек, опи-
санным на естественном языке;
— описывать формальный синтаксис «игрушечных» языков, заданных
правилами БНФ (РБНФ), и распознавать синтаксическую правильность
представленных предложений на соответствующих языках;
— находить и исправлять ошибки в заданные фрагментах РБНФ для язы-
ков программирования Н, D, М;
— определять допустимость заданных слов в языке D;
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
Теоретические сведения
Профессор попросил внимания, так как
собирался пустить в ход свою машину.
По его команде ученики взялись за железные
рукоятки, вставленные по краям рамы,
и быстро повернули их. Все дощечки
перевернулись, и расположение слов
совершенно изменилось. Тогда профессор
приказал тридцати шести ученикам
медленно читать образовавшиеся строки
в том порядке, в каком они разместились
в раме. Если случалось, что три или четыре
слова составляли часть осмысленной
фразы, ее диктовали остальным четырём
ученикам, исполнявшим роль писцов.
Это упражнение было повторено три
или четыре раза. Машина была устроена
таким образом, что после каждого оборота
дощечки поворачивались и передвигались,
и слова размещались по-новому.
Дж. Свифт.
Путешествия Лемюэля Гулливера
Известны два способа построения формального языка:
1) вначале построить формальный синтаксис, а затем — семантику
(другими словами, от формальной системы — к ее интерпретации);
2) вначале построить формальную семантику, а лишь затем —
формальный синтаксис (другими словами, от интерпретации —
к формальной системе).
431
https:/Л: rait.ru
Ниже мы будем опираться на один из основных принципов по-
строения формального языка (следующий непосредственно
из определения понятия «формальный язык»): синтаксис формаль-
ного языка строится независимо от его семантики. Другими слова-
ми, в формулировках синтаксических понятий формального языка
не разрешается использовать семантические понятия (проще гово-
ря, все синтаксические определения должны быть понятны челове-
ку, незнакомому с семантикой языка).
Указанный принцип приводит к существенным отличиям есте-
ственных языков от формальных (например, возможны формаль-
ные языки с одинаковым синтаксисом, но различными семантика-
ми).
Итак, вначале мы определим формальный синтаксис, для чего
воспользуемся метасинтаксическими языками: порождающими
грамматиками и формами Бэкуса — Наура.
Понятие о порождающих грамматиках
Мир беспорядочно усеян
упорядоченными формами.
П. Валери
Любой язык программирования (как и вообще любой язык
в формальном смысле этого слова) может быть определен, как не-
которое множество цепочек из некоторого непустого конечного
множества символов, называемого алфавитом языка. При задании
языка программирования необходимо задать: 1) множество симво-
лов, которые можно использовать для записи программ; 2) множе-
ство синтаксически правильных программ; 3) множество смыслов
для синтаксически правильных программ (семантику языка).
Здесь мы обсудим только первые два пункта.
При формальном определении любого языка неизбежно возни-
кает проблема выбора формального способа его описания. Если
язык состоит из конечного числа цепочек, то самый легкий и оче-
видный способ — перечислить все возможные допустимые цепоч-
ки этого языка. Но описываемый язык может быть и бесконечным,
и потенциально бесконечным (в случае языков программирования
обычно так и случается), и необходимо для такого языка также оты-
скать конечные способы его описания (ясно, что перечисление бес-
конечного числа цепочек не будет конечным описанием). Сделать
это можно, если для описания языка использовать грамматику,
описывающую правила, по которым образуются предложения опи-
сываемого языка. Грамматика языка может быть реализована как
порождающая или распознающая.
Порождающая грамматика — это система, используя которую
можно получить (породить) все предложения описываемого языка
432
https:it.ru
и только их, описав при этом их синтаксическую структуру. Распоз-
нающая грамматика — это система, которая для любой цепочки
выдает ответ на вопрос: «Принадлежит ли эта цепочка языку?». Для
описания синтаксиса любого языка программирования удобнее
всего использовать порождающие грамматики, так как этот способ
более ориентирован на человека, который создает программу на ка-
ком-либо языке программирования.
Определение (неформальное).
Формальная грамматика называется порождающей, если она
«умеет построить» любую правильную цепочку, давая при этом
указания о ее строении, и «не умеет строить» неправильные це-
почки.
Определение (формальное).
Грамматикой называется четверка
def
G = (N,X,P,S)
1) N — конечное множество нетерминальных символов, или не-
терминалов (иногда называемых вспомогательными символами,
металингвистическими или синтаксическими переменными);
2) Z — не пересекающееся с N конечное множество терминаль-
ных символов (терминалов);
3) Р — конечное подмножество множества (N и h)*N(N и Z)*x
(N u Z)*, элемент (а, 0) множества Р называется правилом (про-
дукцией) и записывается в виде ос —> 0;
4) S — выделенный символ из N, называемый начальным (исход-
ным) символом или аксиомой грамматики.
Словарём грамматики G называется множество символов N и S.
Для обозначения п правил грамматики с одинаковыми левыми
частями: ос —» 015 ос —» 02, ..., ос —> 0П — удобно пользоваться сокра-
щённой записью следующего вида:
ос->011 02 |... | 0П
Примеры.
1. Пусть S — единственный нетерминальный символ, а
def
G = <S, {0,1, 2, 3, 4, 5, 6, 7, 8, 9}, {S —> О |1|2|3|4|5|6|7|8| 9},S>.
Порождаемый данной грамматикой языкL(G) — это, очевидно, множе-
ство, состоящее лишь из десяти цифр. Заметим, что L(G) — конечное мно-
жество, которое может быть задано простым перечислением его элементов
{0,1,..., 9}, но применение грамматики возможно и в этом частном случае.
//i iroit 1ч
433
def
2. G = ({E,T,F),{a,+,*, (,)}, {E->E+T | T,T^T*F \ F,F^(E) | a},£).
Язык L(G) — бесконечное множество арифметических выражений,
построенных из единственного символа «а» с использованием знаков «+»
и «*« и скобок, например: (а), а + а * а, а * (а + а),...
Рассмотрим подробнее наиболее часто используемые на практи-
ке различные формы записи порождающих грамматик.
Форма Бэкуса — Наура (БНФ)
Я довольно быстро понял, что лучше всего
обратиться к языку знаков. После этого
понадобилось придумать нотацию, которая
должна была быть по возможности простой
и достаточно выразительной, легко
понимаемой непосвящёнными и удобной для
запоминания.
Charles Babbage (1826)
Начнём с нотации, введённой Дж. Бэкусом (J. W. Backus), кото-
рая называется формой Бэкуса—Наура, сокращённо БНФ (в англий-
ском оригинале — Backus Naur Form или BNF; как отметил Д. Кнут
[110], эту аббревиатуру многие неправильно расшифровывают как
«Backus Normal Form» — «нормальная форма Бонуса». Впрочем, из-
начально аббревиатура расшифровывалась именно так). БНФ была
разработана Дж. Бэкусом для описания языка Алгол в сообщении
о языке Алгол-60. Редактором этого сообщения был П. Наур [113].
БНФ представляет собой разновидность порождающей фор-
мальной КС-грамматики. В этой форме записи грамматики вместо
символа «используется (читается «по определению есть»), а нетер-
минальные символы представляют собой произвольные последова-
тельности букв (слова), заключенные в угловые скобки ( ). Для БНФ
также справедливо соглашение о том, что вертикальная черта «|»
обозначает выбор одного из возможных правил.
Правила грамматики, записанные в БНФ, называются металинг-
вистическими формулами, а символы «|»,«(» и «)»—метасимволами.
Пример.
Пусть
def
G= <{Е, T,F), {а, +,*,(,)}, {Е->Е + Т| Т,Т^>Т*F \ F,F^> (Е) | а},£>.
Запишем синтаксис языка с помощью БНФ:
<£>:: = (£> + <!) | <Т)
(7):: = {Т) * (F) | (F)
<F):: = «E)) |а
434
https: //цга it.ru
Пример (по [105, р. 27—32]).
Рассмотрим БНФ, которая генерирует арифметические выражения,
состоящие из однозначных чисел, скобок и знаков четырёх арифметиче-
ских операций.
(Выражение) :: = (Число) | (Выражение) (Знакоперации) (Выражение) |
((Выражение))
(Знак операции) :: = + | - | * | /
(Число) :: = 0|1|2|3|4|5|6| 71 8 | 9
У этого варианта имеется одно неоспоримое преимущество: его про-
стота. Но эта простота может обернуться неприятными последствиями.
Действительно, рассмотрим процесс порождения строки 5*3-2 (стрелки
здесь будут означать последовательные шаги):
а) (Выражение)
— > (Выражение) (Знак операции) (Выражение)
— > (Выражение) * (Выражение)
— > (Выражение) * (Выражение) (Знак операции) (Выражение)
— > (Выражение) * (Выражение) + (Выражение)
- >...5*3 + 2
(многоточие означает, что нам безразлична последовательность порож-
дения цифр).
б) (Выражение)
— > (Выражение) (Знак операции) (Выражение)
— > (Выражение) + (Выражение)
— > (Выражение) (Знак операции) (Выражениё)+ (Выражение)
— > (Выражение) (Выражение) + (Выражение)
- >...->5*3 + 2
Обе эти последовательности приводят к одному результату. Но первая
из них сначала генерирует произведение, а вторая — сумму.
Если представить эти две последовательности в виде деревьев вывода,
то получим:
[—► (Выражение) 5
(а)
(Выражение) (Знак операции) *
—> (Выражение)
(Выражение) —> 3
—> (Знак операции) ~^+
—> (Выражение) 2
[—► (Выражение)
(б)
> (Выражение) —>5
—> (Знак операции) —> *
—> (Выражение) ^>3
(Выражение) - —> (Знак операции) —> +
—> (Выражение) —> 2
Допустим теперь, что эти деревья используются программой-трансля-
тором не только для описания синтаксиса языка, но и для других целей,
например, для перевода в постфиксную форму или для вычисления зна-
чения выражения.
435
ll\ |'{J
Механизм вычисления выражения может быть таким: в процессе
левого обхода дерева (операции выполняются слева направо) вычис-
ляются промежуточные результаты для каждого поддерева, состоящего
из трёх ветвей: двух операндов и знака операции. Тогда первое дерево
будет соответствовать выражению: 5 * (3 + 2) = 25, а второе — выражению
(5 * 3) + 2 = 17. Так как только второй путь приводит к верному резуль-
тату, необходимо это учесть в БНФ: ввести в рассмотрение старшинство
операций.
Исправленная БНФ выглядит следующим образом:
(Выражение):: = (Выражение) + (Терм) | (Выражение) - (Терм) | (Терм)
(Терм) :: = (Терм) * (Множитель) | (Терм)/(Множитель) | (Множитель)
(Множитель) :: = (Число) | ((Выражение))
(Число) :: = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
Этот вариант БНФ уже позволяет порождать выражения, применяя
правильный порядок применения правил, и тем самым однозначно вычис-
лить значение любого порождённого ею выражения.
При всех своих достоинствах, БНФ имеет и недостатки.
Рассмотрим в качестве примера диалект TURBO Pascal, в кото-
ром запрещается использовать идентификаторы (имена перемен-
ных, типов и т. п.) длиной более 63 символов (вообще говоря, ис-
пользовать их можно, но компилятор распознаёт идентификаторы
по первым 63 символам, так что их использование бессмысленно).
Мы хотим зафиксировать это в БНФ.
Пример.
Идентификатор должен начинаться с буквы, остальные символы могут
быть любые (многоточие в БНФ здесь означает, что некоторые элементы
пропущены, но их легко восстановить из контекста):
(Идентификатору) ::= (Буква) |
(Буква) (Символ) |
(Буква) (Символ) (Символ) |
(Буква) (Символ) (Символ) (Символ) |
(Буква):: =А | В | ... | Z | а | Ъ | ... | z |_
(Цифра) :: = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
(Символ) :: = (Буква) | (Цифра)
Эта запись, разумеется, конечна (определение идентификатора содер-
жит в точности 63 альтернативы), но обозримой ее назвать сложно.
Именно это заставило Н. Вирта предложить усовершенствование БНФ,
которое получило название
Расширенная Бэкуса — Наура форма (РБНФ)
Существуют различные модификации БНФ. Они обладают та-
кой же как и она мощностью, т. е. то, что может быть описано ка-
ким-либо из этих способов, может быть также описано и в БНФ,
436
https'//uFd' t !'U
но во многих отношениях они обладают большей, чем БНФ нагляд-
ностью.
Такие виды БНФ будем называть расширенной или модифици-
рованной формой Бэкуса — Наура (РБНФ или МБНФ). Расширение
БНФ происходит за счёт увеличения множества метасимволов.
Определение (содержательное) [98, с. 24].
РБНФ — это язык для записи правил грамматики с использова-
нием метасимволов.
Отличия РБНФ от БНФ (если БНФ — метаязык, то РБНФ — это
фактически «метаметаязык») заключаются в следующем (применя-
емая нами модификация БНФ соответствует предложениям Н. Вир-
та и принята в качестве английского национального стандарта):
а) выделяются с помощью одинарных кавычек (символ «апо-
строф») символы терминального алфавита языка (нетерминальные
символы по-прежнему заключаются в угловые скобки);
б) применяются: круглые скобки — для факторизации, т. е. груп-
пировки нескольких вариантов конкретизации понятия (нескольких
альтернатив), квадратные скобки — для указания на возможность
опускать их содержимое, фигурные скобки — для указания на воз-
можность выписывания их содержимого нуль и более раз подряд.
Рассмотрим эти нововведения подробнее.
1. Кавычки.
Использование кавычек удобно в тех случаях, когда:
а) необходимо использовать метасимволы БНФ в роли терми-
нальных символов или
б) терминальные символы (также как и нетерминальные) могут
содержать несколько букв.
Если второй из этих вариантов кажется несколько экзотическим,
то первый встречается повсеместно. Кроме того, иногда одинарные
кавычки употребляются только в том случае, когда в качестве тер-
минальных символов употребляются метасимволы БНФ, но этот ва-
риант мы здесь рассматривать не будем.
Пример (упрощенный).
Предположим, что мы желаем описать оператор условного перехода
языка Pascal. В рамках БНФ это можно сделать так:
(Условный оператор):: = if (Условие) then (Блок) |
if (Условие) then (Блок) else (Блок)
(Условие) :: = true | false | ((Условие)) | not (Условие)
| (Условие) (Логическая операция) (Условие)
| (Выражение) (Сравнение) (Выражение)
(Логическая операция) :: = and | or | хог
(Сравнение) :: = < | <= | = | >= | >
437
Допустим теперь, что эту БНФ должен читать не человек, а компью-
тер. Тогда строка
«< I <= I = I >= I >»
может быть принята за нетерминал, что неизбежно приведёт к ошибке.
Мы будем далее использовать следующую форму записи: если
несколько терминалов следуют подряд в правой части правила,
то в кавычки будет заключаться вся эта группа, т. е. не
(Условный оператору) :: = ’i’ Т (Условие) ’f ’h’ ’е’ ’п’ (Блок) |
Т ’f (Условие) ’t’ Ъ’ ’е’ ’п’ (Блок)
’е’ Т ’s’ ’е’ (Блок)
а (Условный оператору):: = ’if (Условие) ’then’ (Блок) |
’if (Условие) ’then’ (Блок) ’else’ (Блок).
Это сокращает запись, но приводит к одному явлению: в такой записи
ключевые слова if, then и else могут считаться как терминальными цепоч-
ками, так и терминальными символами грамматики, описанной с помо-
щью РБНФ.
Иногда возникает необходимость использовать в качестве тер-
минального символа символ, являющийся одновременно и мета-
символом, например, ::=, |, {, [, (. Тогда нам и помогают кавычки.
Например, правила БНФ на языке РБНФ можно описать так:
{Правило) :: = {Девая часть) =’ {Правая часть).
Апостроф, если он является терминалом, будем представлять
двумя апострофами, заключая их в кавычки.
Например, в языке Pascal апострофами выделяются строковые
константы. В этом случае каждый апостроф, попавший внутрь ка-
вычек, удваивается, т. е.
{Строковая константа) :: = ”” {{Символ)}””,
здесь четыре апострофа подряд означают один терминал-апостроф
(два — метасимволы и один — удвоенный апостроф в роли терми-
нала).
Замечание.
Возникает естественный вопрос: зачем удваивать апострофы?
Допустим, мы этого не будем делать. Тогда приведённое правило РБНФ
приняло бы вид:
{Строковая константа) :: = ’’’{{Символ)}”’.
Читаем правую часть слева направо: первые два апострофа — пустая
цепочка, затем — терминальная цепочка ’{{Символ)}’, потом опять пустая
цепочка, т. е. с точки зрения читающего (особенно если это компьютер)
эта запись получается эквивалентной записи
{Строковая константа) :: = ’{{Символ)}’
(посОкольку приписывание или отбрасывание пустых цепочек ничего
не изменяет), то есть любая строковая константа состоит в точности
из этих 10 букв (’{’, ’<’, ’с’, ’и’, ’м’ и т. д.) и ни из каких других.
Удваивание апострофов призвано избежать подобных ситуаций:
мы принимаем за аксиому, что в правой части два подряд идущих апо-
438
https:/Л: rait.ru
строфа считаются метасимволами, если перед ними было чётное число
апострофов и одним терминальным символом «’», если нечётное.
2. Фигурные скобки.
В БНФ список произвольного числа элементов задаётся только
с помощью рекурсии.
Пример.
Определить в БНФ целое положительное число, являющееся последо-
вательностью цифр произвольной длины, можно следующим образом:
(Целое):: = (Цифра) | (Целое) (Цифра)
(Цифра) :: = 0|1|2|3|4|5|6|7|8|9.
Расширим БНФ, предположив, что метасимволами являются также
фигурные скобки { и }, которые используются для указания на тот факт,
что цепочка, в них заключенная, может либо отсутствовать, либо повто-
ряться любое число раз. Применяя фигурные скобки, можно определить
целое положительное число в РБНФ (обращаем Ваше внимание на апо-
строфы вокруг терминалов):
(Целое):: = (Цифра) {(Цифра)}.
(Цифра):: = ’0’ | ’1’ | ’2’ | ’3’ | ’4’ | ’5’ | ’6’ | ’7’ | ’8’ | ’9’.
Этот способ, так же, как и приведённая выше БНФ, задаёт не-
ограниченное число повторений цепочки.
Для того, чтобы указать минимальное или максимальное их число
могут быть применены после фигурных скобок соответственно над-
строчные или подстрочные индексы. Подстрочный индекс указывает
минимальное количество повторений, надстрочный — максимальное.
Иначе говоря, запись вида:
(Нетерминал) :: = {а}” ,
где а — произвольная допустимая последовательность терминалов,
нетерминалов и метасимволов, а т < п, означает то же, что и
(Нетерминал) :: = сс-.лх | сс-.лх |... | а...ос.
траз т+1раз праз
Пример.
Вооружившись РБНФ, попробуем ещё раз описать синтаксис иденти-
фикатора для Turbo Pascal:
(Идентификатор):: = (Буква) {(Символ)} q2
(Буква):: = ’А’ | ’В’ | ... | ’Z | ’а’ | ’Ь’ | ... | У |
(Цифра):: = ’0’ | ’1’ | ’2’ | ’3 ’ | ’4’ | ’5’ | ’6’ | ’7’ | ’8’ | ’9’
(Символ) :: = (Буква) | (Цифра)
При введении данных в компьютер желательно сохранить линейную
запись (без индексов). Для этого примем соглашение о том, что мини-
мальное число вхождений цепочки, заключённой в фигурные скобки,
равно 0, а максимальное число будет записываться сразу вслед за закры-
вающей фигурной скобкой без пробела между ними. С помощью послед-
него соглашения идентификатор Turbo Pascal можно описать так:
439
https: //и га it.ru
(Идентификатор):: = (Буква) {(Символ)} 62
Фигурные скобки позволяют использовать внутри них метасимвол «|»
для указания на возможный выбор, т. е. запись {а | 0 | у} означает, что
каждая из цепочек а, 0 или у может входить в последовательность 0 или
более раз.
Воспользуемся этой возможностью и перепишем синтаксис иденти-
фикаторов без лишнего нетерминала (Символ) так:
(Идентификатор):: = (Буква) {(Буква) | (Цифра)} 62
3. Квадратные скобки.
Квадратные скобки [ и ] используют для того, чтобы указать цепоч-
ку, которая может входить в последовательность лишь один раз или
не входить совсем (такие цепочки называют факультативными).
Итак, запись [а] эквивалентна записи {а}1.
Пример.
Перепишем, используя квадратные скобки, БНФ для условного опе-
ратора языка Pascal. Как известно, этот оператор имеет необязательную
часть, которая начинается с ключевого слова «else», что можно записать
в БНФ так:
(Условный оператор) :: = if (Условие) then (Блок) |
if (Условие) then (Блок) else (Блок),
а в РБНФ:
(Условный оператор) :: = ’if (Условие) ’then’ (Блок) [’else’ (Блок)].
4. Круглые скобки.
Используя в качестве метасимволов круглые скобки ( и ), мы по-
лучаем возможность переписать правила вида (U) :: = «0 | ау | аЗ,
как (U) :: = а (Р | у | 3), где общая для всех альтернатив голова це-
почек а вынесена за скобки (этот приём часто называют фактори-
зацией по аналогии с вынесением в арифметике общего множителя
за скобки).
Круглые скобки могут быть любой степени вложенности,
def def
Пусть в рассмотренном выше примере у = pv, 3 = рк. Тогда при-
ведённое правило можно переписать так:
(U):: = a(0 | р (v | к)).
440
https://urait.ru
Формальный синтаксис языка программирования Н
Самым надёжным способом правильно
расставить знаки препинания является
старый испытанный метод наборщиков:
«Печатайте до тех пор, пока способны
сдерживать дыхание без того, чтобы
лицо стало синим; при выдохе ставьте
запятую; когда вам хочется зевнуть,
отметьте это точкой с запятой; а когда
вы чихаете, наступило самое время для
параграфа».
Р. Хендриксон.
Литературная жизнь
и другие забавные вещи
Со времени опубликования знаменитого «Сообщения об алго-
ритмическом языке АЛГОЛ-60» (1960) никакой уважающий себя
ученый, занимающийся теоретическим программированием, не по-
зволит себе обойтись без формального определения синтаксиса
языка программирования с помощью нормальной формы Бэкуса —
Наура (БНФ) или ее модификаций.
Так же поступим и мы: опишем формальный синтаксис всех ис-
пользуемых модельных языков с помощью метаязыка, называемого
расширенной нормальной формой Бэкуса — Наура (РБНФ).
Определение.
Буквами метаязыка будем называть элементы множества
|,{, },С), [,]}•
Рассмотрим язык программирования, который назовем языком
программирования Н (или просто языком Н) в честь Ч. Э. Хоара.
Язык программирования Н — очень простой, однако он является
моделью многих практически важных языков программирования.
В шутливом смысле его можно назвать праязыком языков импера-
тивного программирования.
Определение [145].
Праязык — это языковая система, рассматриваемая в качестве
предка (языка-источника) некоторой группы (семьи) языков
и устанавливаемая путём сравнительно-исторической рекон-
струкции.
Определим базовые объекты предметного языка Н, с помощью
которых будут строиться «правильные» слова (программы) языка Н.
441
https:/Л: rait.ru
Определение.
1. Терминальным алфавитом языка Н будем называть множество
Ан = {а, Ъ, с, х,у, z} о {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} о
и {=, А <,>,<,>} о {„ (,),[,]} о {var, arr, begin, end} о
о {;, :=, skip, trap, if, then, else, fi, while, do, od, repeat, until}.
2. Терминальными символами языка H будем называть элемен-
ты множества Ан.
Определение.
1. Нетерминальным алфавитом языка Н будем называть мно-
жество
def
= {программа, объявление, команда, присваивание, перемен-
ная, индекс, выражение, функция, развилка, цикл while, цикл repeat,
условие, имя, число, буква, цифра}.
2. Нетерминальными символами {синтаксическими понятиями, син-
таксическими категориями) языка NH будем называть элементы NH.
3. Начальным синтаксическим понятием назовём нетерминаль-
ный символ программа.
Определение (по [95, с. 287]).
Правилами РБНФ для языка Н являются следующие слова:
1Н) {программа) :: = ’begin’ {{объявление) ’;’} {{команда) ’;’} ’end’
2Н) {объявление) :: = (’var’ | ’arr’) {имя) {’;’ {имя)}
Зн) {команда) :: = {присваивание) | {развилка) | {цикл while) |
{цикл repeat) | ’skip’ | ’trap’
4Н) {присваивание):: = {переменная) ’:=’ {выражение)
5Н) {переменная) :: = {имя) [{индекс)]
6Н) {индекс) {выражение) ’]’
7Н) {выражение) :: = {переменная) | {число) | {функция)
8Н) {функция) :: = {имя) ’(’ {выражение) {’,’ {выражение)} ’)’
9Н) {развилка) :: = ’if’ {условие) ’then’
[(команда) {’;’ {команда)}]
[’else’ {команда) {’;’ (команда)}] ’fi’
10н) {цикл while) :: = ’while’ (условие) ’do’
[{команда) {’;’ (команда)}] ’od’
11н) {цикл repeat) :: = ’repeat’ [{команда) {’;’ (команда)}]
’until’ (условие)
12н) (условие) :: = (выражение) (’<’ | ’<* | ’=’ | ’=#’ | ’>’ | ’>’)
(выражение)
13н) (имя) :: = (буква) {{буква) | (цифра)}
14н) (число) :: = (цифра) {{цифра)}
15н) (буква) :: = 'а' | ’b’ | V |’d’ | ’е’ | ’/ | ’g’ | 7Г | Т | ’/ | ’к’ | Т |
442
https: "и га it.ru
’m’ | ’n’ | ’o’ | ’p’ | ’r’ | ’s’ | ’f | ’u’ | V | W | У |
У | У
16н) {цифра) :: = ’0’ | ’1’ | ’2’ | ’3’ | ’4’ | ’5’ | ’6’ | ’7’ | ’8’ | ’9’
Левая часть правила (т. е. слово, расположенное слева от симво-
ла «:: =») является нетерминальным символом, а правая часть пра-
вила (т. е. слово, расположенное справа от символа «:: =») — непу-
стой цепочкой, состоящей из нетерминальных (заключённых в «(»
и «)») и терминальных (заключённых в «’» символов, а также букв
метаязыка
G), [,],Ь Ъ I-
Определение.
Формальным синтаксисом языка программирования Н назовём
кортеж
{NH, Ан, Рн, {программа)),
где Рн—множество, содержащее правила (1н),..., (16н) для языка
Н.
Пусть а, у, 6 е (NH о Ан)*, 0 е NH.
Определение.
1. Будем говорить, что цепочка у непосредственно выводима из це-
def def
почки (р (и писать: (р =>ну), если <р = a0y, V = а 0 :: = 5 е Рн.
2. Будем говорить, что цепочка у выводима из цепочки а (и писать:
а =>*н у), если существует вывод цепочки у из цепочки а, т. е. су-
ществует последовательность
«1» •••»
где а0, ..., ak е (NH и Ан)*, а = а0, =>н а,-, ак = у, i = 1, 2
к, к > 0.
3. Допустимой программой языка Н (или просто программой
языка Н) будем называть такую цепочку w е А*н, для которой
{программа) =>*н w.
Другими словами, допустимой программой языка Н назовём слово
в терминальном алфавите Ан, которое можно получить последо-
вательным порождением по правилам Рн из начального синтак-
сического понятия {программа).
def
4. Языком Н назовем кортеж LH = {Ан, Ргн), где Ргн—множество
допустимых программ языка Н.
го it i-i ।
1 ull.l ku
443
https:"!.!
Итак, порождение допустимой программы языка Н происходит
так:
1) начинаем порождение с цепочки, состоящей лишь из началь-
ного синтаксического понятия {программа);
2) далее выполняем замену одного из нетерминальных симво-
лов правой части правила (1Н) на соответствующую правую часть
одного из правил (2Н), ..., (16н);
3) повторяем описанную операцию замены до тех пор, пока
не получится цепочка, состоящая лишь из терминальных символов,
т. е. допустимая программа языка Н.
Определение.
Командой языка Н будем называть цепочку w е А*н, для которой
{команда) =>*н w.
Другими словами, командой языка Н назовём слово в терминаль-
ном алфавите Ан, которое можно получить последовательным по-
рождением по правилам Рн из нетерминального символа {команда).
Замечание (о контекстных условиях) (М. В. Демидов).
Рассмотрим фрагмент программы на языке программирования Н:
begin* := plus(y, 3); if* > 5 then* := 5 fi; end
В этой программе как*, такиу—целочисленные переменные, причём
полагаем, что значение переменной у было присвоено заранее.
В нашем примере единственным, пожалуй, контекстным условием
должно быть то, что переменные х и у объявлены заранее. Если бы язык
Н поддерживал концепцию типов, то нужно было бы потребовать от них
также совместимости по присваиванию друг с другом и с целочислен-
ными константами.
В связи с этим рассмотрим ещё один пример. Если Вы внимательно
посмотрите на РБНФ языка Н, то обнаружите, что она не запрещает напи-
сать такую «программу»:
begin var if; then; else; while;
else := 3;
if else < 2 then while := 8 else while := else fi;
if := else;
then := while;
if then > 3 then else := plus (if, then) fi;
end.
Эта программа корректна как с точки зрения синтаксиса языка, так
и с точки зрения его операционной семантики: здесь слова «if», «then»,
«else» и «while» используются в качестве имён переменных.
Но как человек, читающий текст этой программы, так и программа-
транслятор с языка при попытке транслировать данную программу неиз-
бежно «запутаются», так как в тексте программы нигде не отмечено, какое
444
https:/Л: rait.ru
из этих слов является именем переменной, а какое — служебным словом.
Если бы в тексте служебные слова как-то выделялись (например, шриф-
том), то такая проблема бы не возникла. Но так как в большинстве систем
программирования такого способа выделить служебное слово в тексте
не существует, то приходится вводить следующее контекстное условие:
в качестве имени переменной не может фигурировать служебное слово.
В РБНФ это правило зафиксировать довольно сложно (предлагается
читателю в качестве упражнения), поэтому контекстные условия фикси-
руются отдельно, в виде описаний на естественном языке (для людей) или
специальных видов грамматик (для компьютеров).
Формальный синтаксис языка программирования D
Теперь рассмотрим язык программирования, который назовём
языком программирования D в честь Э. Дейкстры (по [95, с. 287]).
Определение.
1. Терминальным алфавитом языка D назовём следующее множе-
def
ство: Ad = {а, Ь, с, ..., х,у, z} о {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} о
и {=, А <,>,<>} о {„ (,),[,]} о {var, arr, begin, end} о
о {;, :=, skip, trap, if, fi, □, =>, do, od}.
2. Терминальными символами языка D будем называть элемен-
ты множества AD.
Определение.
1. Нетерминальным алфавитом языка D будем называть мно-
жество
def
= {программа, объявление, команда, присваивание, перемен-
ная, индекс, выражение, функция, выбор, цикл, вариант, условие,
имя, число, буква, цифра}.
2. Нетерминальными символами {синтаксическими понятиями,
синтаксическими категориями) будем называть элементы мно-
жества Nd.
3. Начальным синтаксическим понятием назовём нетерминаль-
ный символ программа.
Определение (по [95, с. 287]).
Правилами РБНФ для языка D называются следующие слова:
1р) {программа) :: = Ъegin’ {{объявление) {{команда) ’;’} ’end’
2d) {объявление) :: = (’var’ | ’arr’) {имя) {’,’ {имя)}
Зр) {команда) :: = {присваивание) | {выбор) | {цикл) | ’skip’ | ’trap’
4р) {присваивание) :: = {переменная) ’:=’ {выражение)
5р) {переменная) :: = {имя) [(индекс)]
6р) {индекс) :: = ’[’ {выражение) ’]’
445
https:it.ru
7D) {выражение) :: = (переменная) | (число) | (функция)
8р) (функция) :: = (имя) ’(’ (выражение) {’,’ (выражение)} ’)’
9р) (выбор) :: = ’if {(вариант)} ’fi’
Юр) (цикл) :: = ’do’ {(вариант)} ’od’
lip) (вариант) :: = (условие) ’=>’ (команда) {’;’ (команда)}
{’□’ (условие) ’=>’ (команда) {’;’ (команда)}}
12р) (условие) :: = (выражение) (’<’ | ’< | ’=’ | V’ | ’>’ | ’>’)
(выражение)
13р) (имя) :: = (буква) {(буква) | (цифра)}
14р) (число) :: = (цифра) {(цифра)}
15р) (буква) :: = ’а’ | ’b’ | V |’d’ | ’е’ | ’/ | ’g’ | ’h’ | Y | | ’к’ | Т |
’т’ | ’п’ | ’о’ | ’р’ | ’г’ | ’s’ | ’f | ’и’ | V | V | У |
У | У
16p) (цифра) :: = ’0’ | ’1’ | ’2’ | ’3’ | ’4’ | ’5’ | ’6’ | 7’ | ’8’ | ’9’
Определение.
Формальным синтаксисом языка программирования D назовём
кортеж
(Nd, Ad, PD,(программа)),
rp,ePD—множество, содержащее правила (1р),(16р) для языка
D.
Пусть а, у, 6 g (ND о Ар)*, 0 е ND.
Определение.
1) Будем говорить, что цепочка у непосредственно выводима
из цепочки (р (и писать: (р =>D у), если
def def
<р = a0y, V = afy, а 0 :: = 5 g PD.
2. Будем говорить, что цепочка у выводима из цепочки а (и писать:
а =>р у), если существует вывод цепочки у из цепочки а, т. е. суще-
ствует последовательность а0, а1}..., afc, где а0,..., ak е (ND о UD)*,
а = а0, =>D ai} ак = у, i = 1, 2 к, к > 0.
3. Допустимой программой языка D (или просто программой
языка D) будем называть такую цепочку w е Ар, для которой
(программа) =>р w.
Другими словами, допустимой программой языка D назовём слово
в терминальном алфавите Ар, которое можно получить последо-
вательным порождением по правилам PD из начального синтак-
сического понятия (программа).
def
4. Языком D назовем кортеж LD = (AD, PrD), где PrD — множество
допустимых программ языка D.
446
Определение.
Командой языка D будем называть цепочку w е Ар, для которой
{команда) =>р w
Другими словами, командой языка D назовем слово в терминаль-
ном алфавите AD, которое можно получить последовательным по-
рождением по правилам PD из нетерминального символа {команда).
Замечания.
1. (По [89, с. 56—57]) Формальный синтаксис команды выбора
и команды цикла в языке программирования D определим так:
1) {команда) :: = {выбор) | {цикл)
2) {охраняющийзаголовок):: = {логическое выражение) => {команда)
3) {охраняемая команда) :: = {охраняющий заголовок) {; {команда)}
4) {набор охраняемых команд) :: = {охраняемая команда) {□ {охраняе-
мая команда)}
5) {выбор):: = if {набор охраняемых команд) fi
6) {цикл) :: = do {набор охраняемых команд) od,
где символ «□» выступает в роли разделителя вариантов.
2. Язык программирования (с точки зрения синтаксиса) представ-
ляет собой бесконечное множество синтаксически правильных текстов.
Множество текстов, обладающих смыслом (например, вычисляющих
значения какой-либо функции), редко удается определить конструктивно.
Такое множество для языков программирования является подмножеством
всех синтаксически правильных текстов, поскольку некоторые синтакси-
чески правильные тексты бессмысленны (например, вычисления не могут
быть выполнены за конечное число шагов).
Формальный синтаксис языка программирования М
Рассуждай токмо о том, о чём понятия
твоитебесиедозволяют. Так: незнаязаконов
языка ирокезского, можешь ли ты делать
такое суждение по сему предмету, которое
не было бы неосновательно и глупо?
Козьма Прутков
Рассмотрим некоторый модельный язык императивного програм-
мирования М, для которого в дальнейшем построим денотационную
семантику. Ясно, что его синтаксис должен быть по возможности
простым (мы вводим его лишь в иллюстративных целях), однако,
с другой стороны, он должен быть «похож» на распространенные
языки императивного программирования высокого уровня (чтобы
быть достаточно близким к практике программирования и привыч-
ным читателю).
447
https:it.ru
Опишем его формальный синтаксис. Вначале определим базовые
объекты модельного языка, с помощью которых будут строиться
программы.
Определение.
1. Терминальным алфавитом языка М будем называть множество
def
= {а, Ь, с, ..., х,у, z} и {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} о
О {=, Ф, <, > } VJ {,, (, ) } VJ {+, —, *, /, \} VJ {—I, Л, V, >, ~} VJ
о {true, false} о {var, begin, end} о
о {;, :=, abort, skip, if, then, else, fi, while, do, od, read, write}.
2. Терминальными символами языка M будем называть элемен-
ты множества Ем.
Естественно, что знаки «abort», «begin» и т. п. — это не слова,
а буквы, т. е. они рассматриваются как неделимые единицы языка.
Определение.
1. Нетерминальным алфавитом языка М будем называть мно-
жество
def
= {программа, объявление, оператор, присваивание, перемен-
ная, выражение, арифметическая операция, условие, логи-
ческая операция, развилка, цикл, имя, число, буква, цифра).
2. Нетерминальными символами {синтаксическими понятиями, син-
таксическими категориями) языка М будем называть элементы NM.
3. Начальным синтаксическим понятием назовём нетерминаль-
ный символ программа.
Далее иногда мы будем записывать элементы множества NM за-
ключёнными в угловые скобки «( )» для того, чтобы отличать
их от слов «обычного» языка.
Определение.
Правилами РБНФ для языка М являются следующие слова:
1М) {программа) :: = ’begin’ {{объявление) ’;’} {команда) ’end’
2М) {объявление) :: = ’var’ (имя)
Зм) {оператор) :: = {программа) | ’skip’ | ’abort’ | {присваивание)
{развилка) | {цикл) | {оператор) ’;’ {оператор)
’read’ ’(’ {переменная), {{переменная)} ’)’ |
’write’ ’(’ {выражение), {{выражение)}’)’
4М) {присваивание) :: = {переменная) ’:=’ {выражение)
5М) {переменная) :: = (имя)
6М) {выражение) :: = {переменная) | {число) ’-’ {выражение) |
’(’ {выражение) ’)’ |
{выражение) {арифметическая операция) {выражение) |
448
https://urait.ru
’if (условие) "then' (выражение) ’else’ (выражение) ’fi’
7M) (арифметическая операция) | ’-’ | ’*’ | 7’ | ’\’
8М) (условие) :: = ’true’ | ’false’ | ’—i’ (условие) | ’(’ (условие) ’)’ |
(условие) (логическая операция) (условие) |
(выражение) (’<’ | ’<’ | ’=’ | ’*’ | ’>’ | ’>’) (выражение) |
’if’ (условие) ’then’ (условие) ’else’ (условие) ’fi’
9М) (логическая операция) :: =’л’ | V | |
10м) (развилка) :: = ’if’ (условие) ’then’ [(оператор)]
’else’ (оператор) {’;’ (оператор)}] ’fi’
11м) (цикл) :: = ’while’ (условие) ’do’ [(оператор)] ’od’
12м) (имя) :: = (буква) {(буква) | (цифра)}
13м) (число) :: = [’-’] (цифра) {(цифра)}
14м) (буква) :: = ’а’ | ’b’ | V |’d’ | ’е’ | ’/ | ’g’ | ’h’ | Т | ’;’ | ’к’ | Т
’т’ | ’и’ | ’о’ | ’р’ | ’г’ | ’s’ | ’f | ’и’ | V | V | У
У | У
15м) (цифра) :: = ’0’ | ’1’ | ’2’ | ’3’ | ’4’ | ’5’ | ’6’ | ’7’ | ’8’ | ’9’
Левая часть правила является нетерминальным символом (за-
ключённым в скобки «( )»), а правая часть правила — непустой це-
почкой, состоящей из нетерминальных и терминальных символов,
а также метасимволов (,),[,],{,}, !,(,)•
Определение.
Формальным синтаксисом языка программирования М назовём
кортеж
Рм, (программа)),
где Рм— множество, содержащее правила (1М) — (15м) для языка
М.
Пусть а, у, 6 е (NM о Ем)*, 0 е NM.
Определение.
1. Будем говорить, что цепочка ц/ непосредственно выводима из це-
почки (р (и писать: <р =>м у), если
def def
Ф = а0у, У = ос8у, а 0 :: = 5 е Рм.
2. Будем говорить, что цепочка у выводима из цепочки а (и писать:
а =>м у), если существует вывод цепочки у из цепочки а, т. е. су-
ществует последовательность
a0, а15..., ак, где а0,..., ак е (NM о Ем)*, а = a0, =>м ai} ак = у,
i = 1, 2 к, к > 0.
3. Допустимой программой языка М (или просто программой
языка М) будем называть такую цепочку w е ^*м, для которой
(программа) =>*м w.
449
https: "и га it.ru
Другими словами, допустимой программой языкам назовём слово
в терминальном алфавите Ем, которое можно получить последо-
вательным порождением по правилам Рм из начального синтак-
сического понятия {программа).
def
4. Языком М назовем кортеж LM = {Ъм, Ргм), где Ргм — множе-
ство допустимых программ языка М.
Итак, порождение допустимой программы языкам происходит так:
1) начинаем с цепочки, состоящей лишь из начального синтак-
сического понятия {программа),
2) далее выполняем замену одного из нетерминальных симво-
лов правой части правила (1М) на соответствующую правую часть
одного из правил (2М), ..., (15м);
(3 ) повторяем описанную операцию замены до тех пор, пока
не получится цепочка, состоящая лишь из терминальных символов.
Определение.
1. Множеством {синтаксическим классом) целочисленных выра-
жений языка М (обозначим его IE) назовем множество слов языка
М, выводимых в его РБНФ из нетерминала {выражение).
2. Множеством {синтаксическим классом) логических выраже-
ний языка М (обозначим его BE) назовем множество слов языка
М, выводимых в его РБНФ из нетерминала (условие).
3. Множеством {синтаксическим классом) операторов програм-
мы на языке М (обозначим его St) назовем множество слов языка
М, выводимых в его РБНФ из нетерминала {оператор).
Упражнения для самостоятельного решения
Целью синтаксического исследования данного
языка является построение грамматики,
которую можно рассматривать как механизм
некоторого рода, порождающий предложения
этого языка.
Н. Хомский
1. Формы Бэкуса — Ноура. Расширенные формы Бэкуса — Наура
1. Определите множества цепочек, которые могут быть получены по сле-
дующим правилам БНФ:
a) (S) :: = а(Д), (А> :: = Ъ{В), (В) :: = с;
б) (S) :: = (А)Ьс | Ьс, (А) :: = аа(А) | аа;
в) (S>:: = a(S> | а{В), (В) :: = Ъ;
г) (S) :: = a{S) \ а{В), (В) :: = Ъ{В) \ Ъ;
д) (S) :: = а(А), (А) :: = Ь{В), <В> :: = с | c{S).
450
https:/Л: rait.ru
Ответы: a) {abs}; б) {a2nbc | п > 0}; в) {anb | п > 1};
г) {атЬп | п,т > 1}; д) {(abc)n | п > 1}.
2. [114, р. 28, № 43]
Пусть нетерминальный символ (S) определяется следующим описанием
в форме Бэкуса — Наура: (S) ::-rl | r(S) | (S) (S).
Какие из следующих цепочек:
1) rrlrrl, 2) rllrrrll, 3) rrlrlrllrlrrl
могут быть получены из (S) по этому определению?
Варианты ответов: А) только 1; В) только 2; С) только 3; D) 1 и 3; Е) 2 и 3.
Решение. Построим несколько выводов терминальных цепочек в данной
грамматике:
a) S => SS => rSS => rSrS => rrlrrl;
б) S => rl, S => rS => rrl, S => SS => rlS => rlrS => rlrrl,
S => rS => rSS => rSSS => rrlrlrl,
S => rS => rSS => rSSS => rSSSS => rrlrlrlrl, ...
Исходя из приведённых в пункте б выводов цепочек и описания символа
(S) в форме Бэкуса — Наура, можно высказать гипотезу, заключающуюся
в том, что пользуясь данными правилами вывода мы никогда не получим
в данной грамматике такую цепочку, которая в качестве своей подцепочки
содержала бы цепочку И. Итак, цепочки 2 и 3 оказываются невыводимыми
из (S) . Поэтому, ответ: А.
3. [114, р. 59, № 33]
Дана грамматика с множеством правил {S —> aSb | bSa | SS | е}.
Какие из следующих предложений:
А) все цепочки, имеющие вид a*b/afc, где i + j = к;
В) все цепочки w в алфавите {а, Ь}, для которых w =
С) все цепочки с равным числом символов а и Ъ;
D) все цепочки вида wwR, где w g {а, b}*;
Е) все цепочки в алфавите {а, Ь} с четной длиной,
наилучшим образом характеризуют язык, порождаемый грамматикой?
Ответ: С
4. Опишите с помощью РБНФ:
а) множество всех неотрицательных констант целого типа (будем назы-
вать неотрицательной константой целого типа конечную последователь-
ность арабских цифр, содержащую не менее чем одну цифру);
б) язык арифметических выражений в алфавите
{0,1, 2, 3, 4, 5, 6, 7, 8, 9, (, ), +, -, *}.
Ответ: а) (Константа) :: = (Цифра) (Константа) (Цифра)
(Цифра) :: = 0|1|2|3|4|5|6|7|8|9
б) (Выражение) :: = (Слагаемое) {(+ (Слагаемое) | - (Слагаемое))}
(Слагаемое) :: = (Множитель) {* (Множитель)}
(Множитель) :: = (Константа) | ((Выражение))
(Константа) :: = (Цифра) {(Цифра)}
(Цифра) :: = 0|1|2|3|4|5|6|7|8|9
5*. Опишите с помощью стандартной БНФ синтаксис набора продукций
самой БНФ и расширенной БНФ.
Решение.
БНФ, порождающая «сама себя»:
(Продукция):: = (Продукция) :: = (Выражение) |
451
https:it.ru
{Выражение} :: = {Выражение}
{Выражение} :: = {Продукция} :: = {Выражение} |
{Выражение} :: = {Выражение}
Мы смогли написать БНФ, порождающую саму себя (да еще такую ко-
роткую), благодаря тому, что в стандартной БНФ терминальные символы
никак не выделяются, и поэтому, например, терминальный символ «:: =»
по написанию не отличается от метасимвола, а терминальный символ
«{Выражение}» по написанию не отличается от нетерминального символа
«Выражение», заключённого в метасимвол «{}».
Но это сходство терминальных символов с метасимволами и комбина-
циями метасимволов и нетерминальных символов, которое очень помогло
нам написать порождающую саму себя БНФ, может очень навредить при
попытке ею воспользоваться. Сами-то мы понимаем, где у нас терминальные
символы, где — метасимволы, где — нетерминальные символы, можем для
себя выделить терминальные символы с помощью каких-нибудь метамета-
символов, например апострофов, как в РБНФ:
{Продукция}:: = ’{Продукция}’ {Выражение} |
’{Выражение}’ =’ {Выражение}
{Выражение} :: = ’{Продукция}’ = ’{Выражение}” | ’
’{Выражение}’ ’{Выражение}’
Но если мы предъявим нашу БНФ некоторому интерпретатору БНФ,
не понимающему наших объяснений и наших метаметасимволов, то ин-
терпретатор может неправильно определить, где — терминальный символ,
а где — метасимвол или комбинация метасимволов и нетерминальных
символов и построить с помощью нашей БНФ совсем не то, для чего она
предназначена.
Замечание.
Казалось бы, аналогичная задача — написать РБНФ, порождающую
саму себя, на самом деле гораздо сложнее и, возможно, вообще не имеет
решения. Сложность здесь в том, что в РБНФ принято терминальные сим-
волы заключать в апострофы. При написании порождающей саму себя
РБНФ нам придётся порождать апострофы, а чтобы порождать апостроф,
его придётся включить в множество терминальных символов, а включить
апостроф в множество терминальных символов — это значит «сдвоить»
его и заключить в апострофы и таким образом, чтобы породить в записи
РБНФ один апостроф, нам нужно иметь (т. е. породить) в ней 4 апострофа,
а чтобы породить 4 апострофа, нужно породить 6 апострофов и т. д. Итак,
для того, чтобы написать порождающую саму себя РБНФ, нам нужно
«победить стремление апострофов к бесконечному увеличению их коли-
чества», а это сложно.
452
https: //u rait.ru
2. Формальный синтаксис «игрушечных» языков
Не оскорбляй другого на языке,
которого тот не знает\ Это садизм.
Е. Лец. Непричёсанные мысли
1. (По [90, с. 92—93, № 5.2])
Правила РБНФ для «игрушечного» языка Лепет таковы:
1) {предложение} :: = {подлежащее} {предикат}
2) {предикат} :: = {переходный глагол} {дополнение} |
{непереходный глагол}{{наречие}}
3) {подлежащее} :: = ’МАМА’ | ’БУБА’
4) {переходный глагол} :: = ’КОРМИТ’ | ’КУПАЕТ’
5) {дополнение} :: = ’ПАПУ5 | ’БУБУ5
6) {наречие} ::=’МЕДЛЕННО’ | ’БЫСТРО’
7) {непереходный глагол} :: = ’ШАЛИТ’
Приведите формальный синтаксис языка Лепет. Определите, какие из сле-
дующих предложений являются синтаксически правильными в языке Лепет:
а) МАМА КОРМИТ БУБУ МЕДЛЕННО.
б) БЫСТРО МАМА КУПАЕТ БУБУ.
в) БУБА ШАЛИТ МЕДЛЕННО БЫСТРО.
г) МАМА МЕДЛЕННО КОРМИТ ПАПУ.
д) МАМА ШАЛИТ БУБУ.
Решение.
а) Нет, так как в этом предложении присутствует переходный глагол
и значит оно не может оканчиваться наречием;
б) нет, так как оно начинается с наречия, а не с подлежащего;
в) да;
г) нет, так как после подлежащего идет наречие, а должен быть пере-
ходный или непереходный глагол;
д) нет, так как после непереходного глагола может идти только наречие.
2. (По [90, с.92—93, № 5.1])
Правила РБНФ для «игрушечного» языка Показушка таковы:
1) {предложение} :: = {подлежащее} {предикат}
2) {подлежащее} ::= {именная группа}
3) {предикат} :: = {глагол} {{именная группа} | {наречие}}
4) {именная группа}:: = [(список прилагательных}}
{существительное}
5) {список прилагательных}:: = {прилагательное}
{’,’ {прилагательное}}
6) {существительное} :: = ’КОШКА’ | ’МЫШКА’
7) {прилагательное} ::=’ЧЕРНАЯ’ | ’БЕЛАЯ’ | ’ТОЩАЯ’ | ’УПИТАННАЯ’
8) {глагол} :: = ’БЕЖИТ’ | ’ЕСТ’
9) {наречие} ::=’БЫСТРО’ | ’МЕДЛЕННО’
Приведите формальный синтаксис языка Показушна. Являются ли следу-
ющие фрагменты текста синтаксически правильными в этом языке:
а) МЫШКА БЕЖИТ БЫСТРО.
б) БЕЛАЯ КОШКА ЕСТ ЧЕРНУЮ КОШКУ.
в) УПИТАННАЯ, ТОЩАЯ, ЧЕРНАЯ, БЕЛАЯ МЫШКА ЕСТ МЕДЛЕННО.
453
https:it.ru
г) КОШКА БЕЖИТ ЗА ОЧЕНЬ ТОЩЕЙ МЫШКОЙ.
Ответ: а) да; б) нет; в) да; г) нет.
3. [100, с. 139—140, № 6]
Синтаксис обезъяннего языка очень прост, но только обезьяны умеют
говорить на нём, не делая ошибок. Алфавит состоит из {а, Ъ, d, #}, причём
# используется в качестве пробела. Грамматика задана следующим образом:
(остановка) ::—Ъ | d
(звук) :: = (остановка) а
(слог) :: = (звук) | (звук) (остановка) | а (звук) | а (остановка)
(слово):: = (слог) | (слог) (слово) (слог)
(предложение) :: =(слово) | (предложение) # (слово).
Кто из перечисленных ниже ораторов — секретный агент, замаскиро-
ванный под обезьяну?
Горилла: ba#ababadada#bad#dabbada
Шимпанзе: abdabaadab#ada
Бабуин: dad#ad#abaadad#badadbaad
Ответ: бабуин
3. Формальный синтаксис языков H,DuM
1. Укажите и исправьте ошибку в следующем фрагменте РБНФ для языка
программирования Н:
14d) (число) :: = (цифра) {(цифра)}
16D) (цифра) :: =’0’ | ’1’ | ’2’ | ’3’ | ’4’ | ’5’ | ’6’ | Т | ’8’ | ’9’
Решение. При таком определении формального синтаксиса языка Н «чис-
лами» будут являться слова, которые с точки зрения «обычного» определения
числами не являются, например: 00000, 00001234,
00000007658. Приведём вариант исправления:
14н) (число) :: = ’0’ | (Цифра) {’О’ | (цифра)}
16н) (цифра):: = Т | ’2’ | ’3’ | ’4’ | ’5’ | ’6’ | ’7’ | ’8’ | ’9’.
2. Укажите и исправьте ошибку в следующем фрагменте РБНФ для языка
программирования D:
9d) (выбор) :: = ’if {(вариант) ’□’} ’fi’
10D) (цикл) :: = ’do’ {(вариант)} ’od’
11D) (вариант) :: = {условие) ’=>’ (команда) {’;’ (команда)}
12d) {условие) :: = (выражение) (’<’ | | ’=’ | ’** | | ’>’) (выражение)
Решение. Хотелось, чтобы значок ’□’ разделял варианты в командах выбора
и цикла. А при данном определении формального синтаксиса языка D этот
значок в команде выбора стоит не только между вариантами, но и перед
словом ’fi’, а в команде цикла вовсе отсутствует.
Вариант исправления приведён в теоретической части упражнения:
9d) (выбор) :: = ’if {(вариант)} ’fi’
10D) (цикл) :: = ’do’ {(вариант)} ’od’
11D) (вариант) :: = (условие) ’=>’ (команда) {’;’ (команда)}
{’□’ (условие) ’=>’ (команда) {’;’ (команда)}}
454
https:/Л: rait.ru
12d) (условие) :: = (выражение) (’<’ I I ’=’ I ’** I I ’>’)
(выражение).
3. (По [95, с. 288—289]) Допустимы ли следующие слова в языке про-
граммирования D:
a) begin var х, i, п; arr m; х := m[l]; i := 1; do i < n => i := plus(i, 1);
if m[i] > x => x := m[i] □ m[i] <x => skip fi; od; end
6) begin var x, i, n; arr m; x := m[l]; i := 1; do i < n => i := i + 1;
if m[i] > x => x := m[i] □ m[i] <x => skip fi; od; end
в) begin var x, i, n; x := m[l]; i := 1; do i < n => i := plus(i, 1);
if m[i] > x => x := m[i] □ m[i] <x => skip fi; od; end
r) begin varx, i, n; x :=M[1]; i1; do i < n -> iplus(i, 1);
if M[i] > x => x M[i] □ M[i] < x => skip fi; od; end?
Ответы: А. Да. Б. Нет, так как не определена буква «+». В. Да. Г. Нет.
4. Укажите и исправьте ошибку в следующем фрагменте РБНФ для языка
программирования М:
(13м) (число) :: = (цифра) {(цифра)}
(15м) (цифра) :: = ’0’ | ’1’ | ’2’ | ’3’ | ’4’ | ’5’ | ’6’ | 7’ | ’8’ | ’9’
Решение. Приведем один из вариантов:
(14м) (число) ". = Cl’ | ’2’ | ’3’ | ’4’ | ’5’ | ’6’ | 7’ | ’8’ | ’9’)
{(цифра)}
(16м) (цифра):: = ’0’ | Т | ’2’ | ’3’ | ’4’ | ’5’ | ’6’ | 7’ | ’8’ | ’9’
https: //цга it.ru
Упражнение 21
СОДЕРЖАТЕЛЬНАЯ
ОПЕРАЦИОННАЯ СЕМАНТИКА
МОДЕЛЬНЫХ ЯЗЫКОВ
Сегодня одно лишь действие без
первоначального истолкования мира
не изменит положения в этом мире.
М. Хайдеггер
Обязательные результаты обучения:
• знать основные понятия
— недетерминированность (в языках программирования);
— аварийное завершение программы;
— содержательная операционная семантика команд языка Н: пустая ко-
манда, команда аварийного завершения, команда присваивания, команда
условного перехода (развилка), команда цикла while, команда цикла repeat;
• содержательная операционная семантика команд языка D: команда
выбора, команда цикла;
—охраны, охраняемые команды;
—содержательная операционная семантика команд языка М;
• уметь
—конструировать программы на языках Н, D и Pascal (или С, C++, Ассем-
блер) по заданной постановке задачи;
—описывать содержательную операционную семантику программ, на-
писанных на языках Pascal и М;
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
Теоретические сведения
Понятие «недетерминированность»
Когда двое делают одно и то же, это
уже не одно и то же.
Теренций
Вначале остановимся на трактовке термина «недетерминирован-
ность» в языках программирования.
456
https:it.ru
Определение [163].
1. Детерминированность — это свойство алгоритма, означающее
определенность, однозначность результата описываемого им про-
цесса при заданных исходных данных.
2. Недетерминированность — это свойство режима вычисле-
ний, при котором в определенных точках процесса осуществля-
ется выбор варианта его продолжения.
Итак, при выполнении детерминированной программы для фик-
сированных значений входных переменных возникает единствен-
ный путь вычислений, который может быть как конечным, так
и бесконечным; если же выполняется недетерминированная про-
грамма, то возникает множество независимых путей вычислений.
Элементы недетерминированных вычислений встречаются уже
в простейших программах на языках императивного программиро-
вания:
1) при выполнении оператора присваивания два различных под-
выражения в правой части оператора могут быть вычислены в про-
извольном порядке;
2) порядок перебора значений параметра цикла в циклах по эле-
ментам множества может быть произвольным;
3) теоретико-множественные операции типа «выбрать х из А»,
«найти х такой, что Р(х)» также являются недетерминированны-
ми.
Превращение подобных недетерминированных операций в де-
терминированные происходит с помощью выбора определённого
компьютерного способа представления множеств, состоящем, как
правило, в полном или частичном упорядочении элементов.
Содержательная операционная семантика
детерминированного языка Н
Это недостойно философа —
произносить слова, которые ничего
не означают.
Дж. Беркли. О движении
Определение.
Аварийным завершением (аварийным остановом, авостом) про-
граммы будем называть прекращение ее выполнения без выда-
чи результата.
Опишем содержательную операционную семантику команд язы-
ка Я.
1. Пустая команда skip (англ, skip — игнорировать) не вызывает
действий.
457
https:/Л: rait.ru
2. Команда аварийного завершения trap (англ, trap — капкан, ло-
вушка') производит аварийное завершение программы.
3. Команда присваивания предписывает вычислить значение це-
лочисленного выражения в ее правой части (если завершить это вы-
числение не удалось, то команда присваивания приводит к аварий-
ному завершению программы) и присвоить результат переменной,
имя которой указано в левой ее части. Затем управление передаётся
следующей команде программы.
4. Приведём неформальный синтаксис композиции команд
Si и S2:
S^’, S2.
До введения композиции команд мы могли создавать только од-
нокомандные программы; теперь можно писать программы в виде
последовательности команд S2; S2;...; Sn, п > 1.
Определение (содержательная операционная семантика ком-
позиции).
Для выполнения композиции команд Sp S2 необходимо вначале
выполнить команду Sp а затем — команду S2.
5. Команда условного перехода позволяет выбрать для исполне-
ния одну из нескольких команд в зависимости от условия.
Вначале приведём неформальный синтаксис команды условного
перехода (команды «развилка»):
а) полная форма:
def
IF = if В then else S2 fi,
где В — предикат, и S2 — команды;
б) краткая форма:
def
IF = ifBthenSfi,
где В — предикат, S — команда.
Определение (содержательная операционная семантика коман-
ды условного перехода).
Полная форма. Если значением предиката В является 1, то выпол-
няется команда Sp Если значением предиката В является О, то вы-
полняется команда S2. Затем (в обоих случаях) управление пере-
даётся следующей команде программы.
Краткая форма. Если значением предиката В является 1, то вы-
полняется команда S, а затем управление передаётся следующей
458
команде программы. Если же значением В является О, то управ-
ление передается команде, следующей за командой IF.
6. Команда цикла предназначена для выполнения входящих
в ее состав команд (которые называются командами тела цикла)
несколько раз (возможно, ни разу).
Вначале приведём неформальный синтаксис команды цикла
while (которую иногда называют командой цикла с предусловием):
while В do S od,
где В — предикат, S — команда.
Определение (содержательная операционная семантика коман-
ды цикла while).
Значение предиката В вычисляется перед каждым выполнением
команды S. Если первоначальным значением предиката В явля-
ется О, то команда S не будет выполнена ни разу.
Если значением В является 1, то команда S выполняется, и управ-
ление передается на вычисление значения предиката В. Если зна-
чением предиката В является О, то команда S не выполняется,
и происходит выход из цикла.
Если же значением В первоначально является 1, а В ни при каких
обстоятельствах не принимает значение О, то команда S выпол-
няется бесконечное число раз (в этом случае говорят, что «проис-
ходит зацикливание команды цикла while»).
7. Опишем неформальный синтаксис команды цикла repeat (ко-
торую иногда называют командой цикла с постусловием):
repeat S until В,
где S — команда, В — предикат.
Определение (содержательная операционная семантика коман-
ды цикла repeat).
Выполняется команда S, затем вычисляется значение предиката
В; если его значением является О, то вновь выполняется команда
S; если же значением предиката В является 1, то цикл заканчи-
вается, и выполняется следующая команда программы. Если зна-
чением предиката В сразу является 1, то команда S выполнится
лишь один раз.
Если предикат В никогда не принимает значение 1, то команда
S выполняется бесконечное число раз (говорят, что «происходит
зацикливание команды цикла repeat»).
459
https:it.ru
Содержательная операционная семантика
недетерминированного языка D
История программирования для цифровых
вычислительных машин характеризуется
широким разнообразием операций,
частично обусловленным необузданной
изобретательностью разработчиков
оборудования, которые получив возможность
довольно свободно и без особых затрат
комбинировать различные триггеры, поистине
наслаждались, предлагая экзотические
операции, зачастую применимые только
в самых специальных случаях; с другой стороны,
очень многие программисты чувствовали себя
просто обязанными использовать любое мало-
мальски привлекательное средство, доступное
в наборе машинных команд.
В. Турский
Рассмотрим содержательную операционную семантику недетер-
минированных команд выбора и цикла.
1. Пусть n g N\{0}, В1г В2, Вп — формулы расширенного язы-
ка первого порядка, S15 S2, ..., Sn— команды языка D.
Определение (неформальный синтаксис команды выбора IFn)
[88, с. 136—137].
Команда выбора IFn имеет следующий неформальный синтаксис:
def
IFn = ifBn => пВ2=> 52п...оВп=> Sn fi,
где формулы Bt называются охранами (предохранителями), S{ —
охраняемыми командами, i е {1, 2, ..., п}.
Замечание.
Команду выбора IFn называют также:
1) недетерминированной командой выбора;
2) командой выбора Дейкстры, так как идея охраняемого разбора слу-
чаев принадлежит Э. Дейкстре (1975);
3) n-членной охраняемой командой [84, ч. 2, с. 571].
Определим содержательную операционную семантику команды
выбора:
def
IF„ = ifB,=> S, nB9 => S2 => S„ fi
ft L А лл лл IL IL
460
о -1li iroif ri i
Определение (содержательная операционная семантика коман-
ды выбора).
1. (По [88, с. 136—137]) Команда IFn выполняется следующим об-
разом. Вначале вычисляются значения охран В1г Въ Вп. По край-
ней мере одно из вычисленных значений должно быть равно 1,
в противном случае происходит аварийное завершение программы.
Если по крайней мере одна из охран имеет значение 1, то произ-
вольным образом выбирается и выполняется одна из охраняемых
команд Si} у которой значение охраны В( равно 1.
2. (По [95, с. 289]) Пусть команда IFn начинает выполняться в не-
котором состоянии о. Сначала в состоянии о асинхронно (неза-
висимо, а возможно, и параллельно) вычисляются все условия Bt.
Каждое из них либо нормально завершается и возвращает 1 или
О, либо завершается отказом (в частности, зацикливанием).
Если хотя бы одно В{ даёт отказ, то выполнение команды IFn за-
вершается отказом.
Если все условия В( нормально завершаются (состояние о при
этом не меняется!), то случайным образом выбирается команда
Si0 — одна из тех и только тех команд Si} для которых значение
В( равно 1.
Результат выполнения этой команды Si0 в состоянии о является
результатом выполнения команды выбора IFn.
Если же значения всех В( равны О, то IFn завершается отказом.
Пример (по [99, с. 39—40]).
Рассмотрим недетерминированную команду выбора
def
IF2 = if 2 | x—> x:-x+2 □ 3 | x-> x :=x + 3 fi.
Если x не делится на 2 и на 3, то при выполнении команды возникнет
аварийное завершение программы.
Если х не делится на 6, но делится на 2 или 3, то при выполнении
команды будет получен единственный результат.
Если х делится на 6, то при выполнении будет случайным образом
выбран один из двух результатов (х+2 или х + 3).
2. Пусть пе N.
Определение (неформальный синтаксис команды цикла DOn)
[88, с. 141].
1. Командой цикла DOn называется следующее слово:
def
DOn = do Вг => Sj □ В2 => S2 □...□ Вп => Sn od
461
> и
2. Охранами называются формулы В(.
3. Охраняемыми командами называются команды S, (i = 1,2,..ri).
Замечание.
Команду цикла часто называют недетерминированной командой цикла
или командой повторения Дейкстры.
Определение.
def def
BB = Вт vB2 v...vBn; ie[1,n] = ie{l,2,...,n}.
Определение (операционная семантика команды цикла DOn).
1. (По [88, с. 141]) Повторяется следующее действие (пока это
возможно): выбирается охранаВ(, значение которой равно 1, и вы-
полняется соответствующая команда St.
Если же значения всех охран равны О (значение предиката
ВВ равно О), то выполнение цикла завершается.
Недетерминизм команды цикла заключается в том, что если две
или больше охран принимают значение 1, то выбирается любая
из них (но только одна), и выполняется соответствующая охра-
няемая команда.
2. (По [95]) Пусть команда DOn начинает выполняться в некото-
ром состоянии о. Если значения всех условий В( равны О, то ко-
манда DOn нормально завершается с состоянием о (его действие
равносильно пустой команде). Когда же выбирается S/o, то после
его нормального завершения в некотором состоянии о/0 цикл DOn
снова выполняется в состоянии о/0.
Другими словами, цикл выполняется до тех пор, пока значения
всех условий В( не будут равны О или не возникнет отказ (в по-
следнем случае выполнение команды DOn завершится отказом).
3. (По [99, с. 39—40]) При выполнении команды DOn вначале вы-
бирается произвольное условие Вп, значение которого равно 1,
и выполняется команда S(1, затем выбирается истинное условие
В/2 (возможно, что ц = i2) и выполняется команда S/2, и так до тех
пор, пока значения всех условий В15 ..., Вп окажутся равными 0,
и тогда выполнение команды DOn завершится.
Предложение.
1. Содержательная операционная семантика команды цикла
doB=> S od
эквивалентна содержательной операционной семантике команды
цикла
462
https: "и га it.ru
while В do S od.
2. Содержательная операционная семантика команды цикла
def
DOn - doBj => Sj nB2=> S2 □...□Bn=> Sn od
эквивалентна содержательной операционной семантике команды
цикла
do (В^В2 v...vBn) => if Вг => Sj пВ2=> S2 □...□Bn=> Sn od
или в сокращенном виде
doBB => IFn od
Доказательство. Упражняйтесь.
Замечания.
1. Операционная семантика языка D является «однородной» в том
смысле, что она симметрична относительно различных вариантов
составных конструктов. «Радующая глаз симметричность операторов»
(см. [88, с. 178]) — это одно из следствий того, что мы допускаем неде-
терминизм. Более того, недетерминированность является важным преи-
муществом (даже если окончательный текст программы окажется детер-
минированным), поскольку она позволяет с помощью операционной
семантики построить аксиоматическую семантику языка D, а тем самым
разработать методику доказательного программирования.
2. [100, с. 499] Ни в одном из распространённых языков программи-
рования не реализованы охраняемые команды в виде, предложенном
Э. Дейкстрой. Тем не менее концепция недетерминированного выполне-
ния действительно возникает при разработке программного обеспечения
операционных систем.
Содержательная семантика детерминированного языка М
с условными выражениями
Вначале опишем содержательную операционную семантику вы-
ражений.
Определение.
1. Операция (в языках программирования) — это действие, выра-
батывающее некоторое значение, называемое ее результатом.
Операндами называются исходные данные для операции.
2. Выражения языка программирования — это синтаксические
конструкции, описывающие правила вычисления значений пе-
ременных и порождения новых значений посредством примене-
ния операций.
463
Другими словами (по [96, с. 91]), выражение — это программная
единица, обладающая значением.
3. Выражение — это допустимое слово языка программирования,
денотатом которого может являться некоторое значение: число-
вое для целочисленных выражений и логическое — для логиче-
ских выражений.
Семантикой выражения будем называть смысл такого имени.
Замечание.
С формальной синтаксической точки зрения можно назвать выра-
жением любую цепочку терминальных символов, которая может быть
порождена в РБНФ модельного языка из нетерминалов (Выражение)
и (Условие): в первом случае мы будем иметь дело с целочисленными выра-
жениями, во втором — с логическими выражениями.
Пусть b — логическое выражение, а ЕТ и Е2 — выражения (цело-
численные или логические).
Определение (по [144, ч. 1, с. 112; 96, с. 29]).
Условным выражением называется следующее слово:
if b then Ej else Е2 fi
Определение (содержательная операционная семантика услов-
ного выражения).
Если значение b не определено, то значение условного выраже-
ния также не определено. Если логическое выражение b принима-
ет значение true, то значение условного выражения равно значе-
нию выражения Е1г а если выражение b принимает значение false,
то значение условного выражения равно значению выражения Е2.
Семантика целых чисел (констант) может считаться очевидной:
записи числа в десятичной системе счисления соответствует само
это число. Аналогично обстоит дело с семантикой логических кон-
стант: true соответствует 1, семантика false есть О.
Семантика переменной — это ее значение в текущий момент
времени.
Очевидной является содержательная семантика следующих вы-
ражений:
1) ц a i2, где a: Zх Z при этом арифметические операции
имеют следующий смысл: «+» — сложение, «-» — вычитание, «*» —
умножение, «/» — деление нацело, «\» — остаток при делении на-
цело;
2) —ib, где -ь В —> В — логическое отрицание;
464
https:/Л: rait.ru
3) Ьг X b2, где X: В х В —> В — двухместные логические операции
со стандартными именами л, v, <->;
4) ij р i2, где р: Z х Z В — операции отношения.
Опишем содержательную операционную семантику операторов.
Определение.
(1) (По [96, с. 91]) Оператор — это программная единица без
значения.
(2) (М. В. Демидов) Оператор — это имя, денотатом которого яв-
ляется не значение (как в случае выражения), а некоторое дей-
ствие.
1. Пустой оператор skip (от англ, skip — игнорировать) не вы-
зывает никаких действий.
2. Оператор аварийного завершения программы abort произво-
дит аварийное завершение программы.
3. Оператор присваивания v := е предписывает вычислить зна-
чение целочисленного выражения в ее правой части (если завер-
шить это вычисление не удалось, то команда присваивания приво-
дит к аварийному завершению программы) и присвоить результат
переменной v, имя которой указано в левой ее части. Затем управ-
ление передаётся следующему оператору программы.
4. Последовательность операторов S2; S2; ...; Sn означает, что
операторы S, выполняются в том порядке, в котором они перечис-
лены.
5. Оператор условного перехода (развилка) позволяет выбрать
для исполнения один из нескольких операторов в зависимости
от условия.
Вначале приведём неформальный синтаксис оператора условно-
го перехода (оператор «развилка»):
а) полная форма:
def
IF = if A then else S2 fi
где A — предикат, называемый условием, ST и S2— операторы;
б) краткая форма:
if A thenSfi,
где А — предикат, S — оператор.
Определение (содержательная операционная семантика опера-
тора условного перехода).
Полная форма. Если значение А равно 1, то выполняется опера-
тор Sp Если значение А есть О, то выполняется оператор S2. Затем
465
https:/Л: га it.ru
(в обоих случаях) управление передается следующему за развил-
кой оператору программы.
Краткая форма. Если значением предиката А является 1, то вы-
полняется оператор S, а затем управление передаётся следующему
оператору программы. Если же значением А является О, то управ-
ление передается оператору, следующему за оператором IF.
Итак, можно утверждать, что содержательная операционная се-
мантика краткой формы оператора условного перехода
if A then S fi
совпадает с содержательной операционной семантикой оператора
условного перехода
if A then S else skip fi.
6. Оператор цикла служит для того, чтобы выполнять входящие
в его состав операторы (операторы тела цикла) несколько раз (воз-
можно, ни разу).
Вначале приведем неформальный синтаксис оператора цикла
while:
while A do Sod,
где А — предикат, aS — оператор.
Определение (содержательная операционная семантика опера-
тора цикла while).
Значение предиката А вычисляется перед каждым выполнением
оператора S. Если первоначальное значение предиката А есть О,
то оператор S не будет выполнен ни разу.
Если значение логического выражения А есть 1, то оператор S вы-
полняется, и управление повторно передается на вычисление зна-
чения А; если значение А есть О, то оператор S не выполняется,
и происходит выход из цикла (переход к следующей за ним ко-
манде).
Если же значение А первоначально истинно и ни при каких об-
стоятельствах не становится ложным, то выполнение оператора
цикла никогда не завершится (в этом случае говорят, что «проис-
ходит зацикливание команды цикла while»).
7. Оператор ввода имеет следующий содержательный синтаксис:
read(v1,v2,...,vn),
где vlf v2,..., vn— имена переменных.
466
https:it.ru
Определение (содержательная операционная семантика опера-
тора ввода read).
Выполнение оператора ввода read(v15 v2,..., vn) приводит к изме-
нению значений переменных v15 v2,..., vn. Новые значения «бе-
рутся извне» программы — вводятся с клавиатуры, считываются
из памяти, генерируются другой программой и т. п. — эти новые
значения никак не зависят от прежнего значения этих или каких-
либо других переменных.
8. Оператор вывода имеет следующий содержательный синтаксис:
write(е1з е2,..., еп),
где е1г е2, еп— имена переменных.
Определение (содержательная операционная семантика опера-
тора вывода write).
Оператор вывода write (е1зе2,..., еп)передает значения выражений
«вовне» программы, например, на дисплей или в файл. Он не из-
меняет значений переменных — с этой точки зрения его семан-
тика совпадает с семантикой оператора skip.
9. Объявление переменной имеет такой содержательный синтаксис:
varv,
где v — имя переменной.
Объявление переменной имеет целью указать, что заданное имя
переменной резервируется для хранения данных (числа, в случае
модельного языка) и не может быть более использовано в других
целях в рамках данного блока begin — end. Отметим, что если вло-
женный блок (подпрограмма) содержит переменные с именами,
идентичными именам переменных объемлющего его блока, то зна-
чения последних должны восстанавливаться после завершения вы-
полнения вложенного блока.
Приведем типичный пример такой ситуации:
begin var х; — объявили переменную х
— произвели некоторые действия
begin var х; — открыли новый блок и объявили
другую переменную, но с тем же име-
end нем х
— в этом месте переменной х возвра-
щается ее значение до входа во вло-
женный блок
end
467
https:га it.ru
Замечание.
Любая программа на модельном языке жестко детерминирована: зная
только ее текст, можно однозначно сказать, что эта программа делает, т. е.
ее результат работы (а значит — и семантика) однозначно определен. Это
свойство модельного языка нарушилось, если бы мы ввели в него недетер-
минированные операторы (например, обращения к генератору случай-
ных чисел или оператор выбора, который случайно выбирал бы очеред-
ную команду) или операторы для обмена данными с «внешней средой»,
например, чтения входных данных с клавиатуры. Любой такой оператор
способен привести программу к непредсказуемым последствиям, так как
часто не позволяет однозначно определить, какая команда будет выпол-
нена следующей после него.
Упражнения для самостоятельного решения
Это была первая программа, которую
составил Фёдор Симеонович без всяких
советов, подсказок и указаний с моей
стороны. Я внимательно просмотрел
программу и с удовольствием убедился,
что составлена она грамотно, экономно
и не без остроумия.
А и Б. Стругацкие.
Понедельник начинается в субботу
Замечание.
Программы напишите: а) на языке Н; б) на языке D; в) на языке Pascal
(С, C++, Ассемблер).
1. [88, с. 188]
Напишите программу, которая для заданного массива В[0: п -1], п > О,
присваивает х наименьшее значение из В. В случае, если наименьшее зна-
чение встречается в В более одного раза, программа может быть недетер-
минированной .
Ответ'.
i := 1; х := В[0];
doi#и => ifB[i] >x=> i :-i+ 1 nB[i] <x=> x :=B[i]; i := i + 1 fi od
2. [88, c. 188]
Напишите программу, которая для заданного п > 0 присваивает i наи-
большую степень двойки, не превосходящую п.
Ответ:
i := 1; do 2 • i < п => i := 2 i
468
https://и га it.ru
3. [88, с. 188]
Напишите программу, которая для данного целого числа и > 0 и массива
целых чисел В [0: п -1] помещает в переменную S сумму элементов массиваВ.
Ответ:
i:- п; do i Ф 0 => i:- i - 1; S := S + B[i] od
4. [88, с. 198—199]
Напишите программу, которая по данному целому числу п > 0 определяет
наибольшее целое число А, не превосходящее п1/2.
Ответ:
а := 0; do а2 < п => а := а +1 od
5. [88, с. 200—201]
Дан массив В[0: т -1], т > 0, причём известно, что заданное значение
х находится в В [0: т -1]. Напишите программу, которая определяет первое
вхождение х в массив В, т. е. помещает в переменную i значение наимень-
шего натурального числа, для которого B[i] = х.
Ответ:
i :=0; doi < п &x^B[i] => i :=i + 1 od
6. [88, с. 202]
Напишите программу, которая по данным двум целым числам х иу, х > 0,
у > 0, находит частное q и остаток г от делениях на у, причём в программе
запрещается использовать операции умножение и деление.
Ответ:
r:=x;q := 0; do г >у => г := г -у; q := q + 1 od
7*. [88, с. 261—265]
Максимальная восходящая последовательность. Напишите программу,
которая по данной последовательности В [0: п], где п > 0, вычисляет длину
ее максимальной (самой длинной) восходящей подпоследовательности
(ее значения не убывают).
Решение. Приведём программу на языке D:
i:=l;k := 1; m[l] :=В[0];
do i # п => if
B[i] >m[k] => k :=k + l; m[k] :=B[i] □
B[i] <m[l] => m[l] :=B[i]n
m[l] <B[i] < m[k] => h := l;j :=k;
do h *j -1 => e := (h +j) -s- 2;
if m[e] <B[i] => h :-e □
m[e] > B[i] => j :-e
fi
od;
m[j] :=B[i]
469
https: //цга it.ru
fi;
i: = i + 1
od
Приведём программу на языке Pascal, решающую похожую задачу:
PROGRAM P_r_i_m_e_r;
{Найти одну из самых длинных возрастающих подпоследовательностей
данной последовательности чисел}
van
k, i, j, n, d: Integer;
a, q, b: Array [1..100] of Integer;
BEGIN
Randomize;
к := 0; j := 0; d := 0;
Write ('Укажите количество элементов: '); Read(n);
Write ('Исходная последовательность: ');
For i := 1 to n do
begin a[i] := Random(100) + 1; Write(a[i], ' ') end;
For i := 1 to n do q[i] := n - 1;
For i := 1 to n - 1 do
For j := i + 1 to n do
If a[i] < a[j] then If q[i] < q[j] + 1 then q[j] := q[i]
- i;
k := q[l];
For i := 2 to n do If k > q[i] then k := q[i];
d := k;
WriteLn; WriteLn ('Нужно удалить ', k, ' элементов.');
i := n;
Repeat
If q[i] = k then begin b[k + 1] := a[i]; k := k + 1 end;
i := i - 1
until i = 0;
Write('Одна из самых длинных возрастающих ');
WriteLn('подпоследовательностей: ');
j := n;
Repeat Write (' ', b[j], ' '); j := j - 1 until j = d;
WriteLn;
END.
8. Опишите содержательную операционную семантику следующей про-
граммы, написанной на языке программирования TURBO Pascal:
PROGRAM Primer_9;
var
a, x, z: Real;
b, n: Integer;
BEGIN
Read(a); Read(b); x := a; n := b; z := 1;
While n <> 0 do
If not Odd(n)
then begin n := n div 2; x := x * x end
470
https:it.ru
else begin z:= z*x;n:=n-l end;
WriteLn(z)
END.
Ответ: программа возводит число а в степень Ъ g N следующим спосо-
бом: если Ъ = 2к • т, то программа сначала возводит а в степень 2, а затем
полученное число возводит в степень т.
9. (М. В. Демидов) Опишите содержательную операционную семанти-
ку следующих двух программ на языке М, написанных: а) в стиле Pascal;
б) с одним оператором write:
begin var a; var b; var c;
read(a, b, c);
if a < b then
if a < c then write (a)
else write (c) fi
else
if b < c then write (b)
else write (c) fi
fi
end
begin var a; var b; var c;
readfa, b, c);
write (if a < b then
if a < c then a
else c fi
else
if b < c then b
else c fi
fi)
end
Ответ: программы предназначены для вывода наименьшего из трёх
чисел.
https:it.ru
Упражнение 22
АКСИОМАТИЧЕСКАЯ СИСТЕМА ХОАРА ДЛЯ
МОДЕЛЬНЫХ ЯЗЫКОВ НИ D
...логику приходится, конечно,
первоначально изучать как нечто такое,
что мы, правда, понимаем и постигаем,
но в чём мы не находим сначала широты,
глубины и более значительного смысла.
Лишь на основе более глубокого знания
других наук логическое возвышается
для субъективного духа не только как
абстрактно всеобщее, но и как всеобщее,
охватывающее собой также богатство
особенного... Таким образом, логическое
получает свою истинную оценку, когда оно
становится результатом опыта наук.
Гегель. Наука логики
Обязательные результаты обучения:
• знать основные понятия
— концепция доказательного программирования;
— спецификация программы, формальная спецификация программы,
предусловие программы, постусловие программы;
— утверждение, аннотированная программа;
— верификация программы, формальная верификация программы;
— тройка Хоара, дедуктивная семантика языка программирования (по Хо-
еру), аксиоматическая система Хоара;
— нелогические аксиомы системы Хоара;
— инвариант цикла;
— частично правильная программа, тотально правильная программа;
— недетерминированные программы в системе Хоара, частичная пра-
вильность недетерминированной программы, тотальная правильность не-
детерминированной программы;
• уметь
— записывать формальную спецификацию для поставленных задач;
— восстанавливать пропущенные фрагменты: в записи аксиом системы
Хоара, в доказательстве прямого допустимого правила вывода;
— распознавать в заданных словах теоремы системы Хоара;
— конструировать доказательства допустимости прямых правил вывода
в системе Хоара;
472
https: "и га it.ru
— восстанавливать пропущенные фрагменты в доказательстве частичной
правильности программ;
— конструировать частичную правильность программ в системе Хоара;
— конструировать полную правильность программ в системе Хоара;
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
Теоретические сведения
Актуальность исследования свойства
«правильность программы»
Аксиоматический подход рассеивает
таинственность, не уменьшая очарование
самой идеи.
Г. С. М. Коксетер
Напомним, что аксиоматическая семантика языка программиро-
вания предназначена для описания абстрактных свойств программ.
Постараемся ответить на важный вопрос: почему нас особенно
интересует такое свойство написанной программы, как «быть пра-
вильной»?
1. Сущность деятельности программиста заключается в предо-
ставлении некоторому исполнителю (отличному от него самого)
набора правил, руководствуясь которым исполнитель может ре-
шить проблему или выполнить задание. Предполагается, что испол-
нитель не изучал проблему или задание, что он слепо повинуется
командам программы и не имеет возможности обратиться за сове-
том, что бы ни произошло. Именно эта законченность программы,
ее замкнутость, невозможность вмешаться, если что-то идёт не-
верно, и заставляет программиста искать гарантии того, что в про-
грамме предусмотрены все случайности.
Итак, задачей программиста является не просто создание про-
граммы, но и доказательство того, что написанная программа об-
ладает свойством «быть правильной (надёжной)».
2. Существующая практика программирования такова, что
точное знание, воплощённое в условии задачи и описании метода
ее решения, не находит своего закономерного и неискаженного во-
площения в программном тексте, а служит лишь справочной инфор-
мацией, «сырьём» для программиста. Эта утрата исходного знания,
постоянно происходящая в практическом программировании, явля-
ется главной причиной его неэффективности и одновременно сти-
мулирует создание научных основ программирования. Становится
ясным, что имеет смысл таким образом изменить процесс програм-
473
https:it.ru
мирования, чтобы любая попытка написать в программе команду,
не вызванную условием задачи и применяемым методам ее реше-
ния, приводила бы к формально обнаруживаемому противоречию.
Другими словами, процесс программирования должен приобре-
сти черты доказательности.
3. Современному программированию свойственен эмпириче-
ский подход. Компьютер — это автомат, который, полностью под-
чиняясь командам программы, демонстрирует определённое по-
ведение. Эмпирический характер программирования означает,
что правильность программы определяется путём апостериорного
(последующего за программированием) наблюдения за поведением
компьютера, исполняющего данную программу.
Этот процесс испытания получил название «отладка програм-
мы» и повсюду признается не только неотъемлемым, но и самым
трудоёмким этапом на пути ее создания.
Процесс отладки проходит, как правило, в два этапа: на первом
этапе предпринимаются попытки «заставить» программу рабо-
тать, на втором — проверить, что работающая программа ведет
себя так, как предполагалось. Однако очевидно, что отладка — это
очень неадекватное средство решения проблемы правильности
(по Э. Дейкстре [155, с. 41]: отладка (тестирование) «программы
может быть очень эффективным способом демонстрации наличия
ошибок, но оно безнадёжно неадекватно для доказательства их от-
сутствия»), она является необходимой составляющей любого про-
цесса установления правильности; по крайней мере, — это способ
избавиться от «орфографических ошибок».
Если использовать аналогию с математикой, то отладка подобна
читке корректуры («ни одна теорема не верна, если она неверно
записана» [103, с. 37]).
4. Потребность в доказательстве правильности программы но-
сит (по А. П. Ершову) главным образом эстетический характер,
так что она присуща только лучшим программистам. Лишним под-
тверждением этого служит и тот факт, что стандарты доказатель-
ства существенно зависят от уровня эстетического развития про-
граммиста (нечто аналогичное справедливо и для математики).
Под «правильностью программ» понимают:
1) отсутствие ошибок в программе; так, под корректностью
программы понимается [39, с. 164] правильная работа программы:
«она не зацикливается и не зависает, на приличных данных требу-
ет приличное количество ресурсов и времени и не делает то, чего
мы от нее не хотели»;
2) соответствие программы ее спецификации;
3) возможность формального вывода программы из формально-
го набора предпосылок.
474
https:/Л: rait.ru
Концепция доказательного программирования
Доказательство — это «убедительное
свидетельство, которое заставляет
сознание верить в истинность или
действительность».
Из словаря Вебстера
Если мы согласимся с тем, что математические методы явля-
ются наиболее эффективным средством преодоления сложности
возникающих задач, то не останется другого выбора, как только
перестроить таким образом деятельность, относящуюся к програм-
мированию, чтобы стало возможным применять математические
методы. Поэтому как только программирование вышло за пределы
допустимой сложности пришлось обратиться к математической
логике, главной целью которой в течение веков было применение
эффективного структурирования с целью преодоления сложности
возникающих лингвистических задач.
Если согласиться, что правильность — это важнейшее качество
программы, то понятен интерес исследователей к таким методам
создания программ, которые бы в максимальной степени способ-
ствовали устранению ошибок в программах. Среди них особое ме-
сто принадлежит классу методов, в основе которых лежит концеп-
ция математического доказательства правильности программы
(или, короче, концепция доказательного программирования).
Определение (по [95, с. 281]).
Концепция доказательного программирования — это совокупность
методов программирования, в которых строится:
1) математическая модель программы;
2) математическая модель внешнего мира (программной среды),
в котором выразимо понятие «правильная программа».
Итак, данная концепция подразумевает представление как самой
программы, так и требований к ней с помощью определённых ма-
тематических объектов.
Подход к доказательному программированию связан со свой-
ствами языка программирования, к которому этот метод приме-
няется. Методы, которые мы рассмотрим ниже, ориентированы
на класс языков императивного программирования. Характерное
ограничение состоит в том, что динамическая структура програм-
мы в них хорошо согласована с ее статической структурой (другими
словами, составить представление о процессе выполнения програм-
мы относительно легко по ее тексту).
Однако платой за использование доказательного программиро-
вания является необходимость манипулирования с объёмами тек-
стовой информации, превышающими на порядок объём текста са-
475
https:it.ru
мой программы. Поэтому доказательное программирование может
стать практически применяемым только при компьютерной под-
держке.
Из истории доказательного программирования
Доказательство—это идол, которому
математики приносят себя в жертву.
А. Эддингтон
Ч. Э. Хоар [155, с. 187] писал: «...одним из первых, кто отстаивал
метод проверки программы с помощью утверждений, был не кто
иной, как сам Алан Тьюринг. В июне 1950 г. на конференции в Кэм-
бридже Тьюринг прочёл короткое сообщение, озаглавленное “Про-
верка большой программы”, в которой эта идея очень ясно объясня-
лась. “Как можно проверить большую программу, чтобы убедиться,
что она верна? Чтобы облегчить задачу проверяющего, програм-
мист должен сделать некоторое число определённых утверждений,
которые можно было бы проверить по отдельности и из правильно-
сти которых следовала бы правильность всей программы”».
Повторно эта же идея построения доказательства правильности
программы была высказана Дне. Маккарти [111]: «...вместо того,
чтобы испытывать программы на тестовых примерах до тех пор,
пока они не окажутся отлаженными, нужно доказывать, что они
имеют желаемые свойства».
Итак, к началу 70-х годов возникла необходимость в точном опи-
сании семантики языков программирования. Первый известный
метод формальной верификации программ, названный методом
индуктивных утверждений, был предложен Р. Флойдом [107] для
применения к операторным схемам. Формальный метод верифика-
ции программ, написанных на языках императивного программи-
рования, принадлежит Ч. Э. Хоару [109] и развивает идеи более ран-
них работ П. Наура [112], Р. Флойда и ученых польской логической
школы (А. Сельвицкий, 1970).
В 1975 г. Э. Дейкстра [106] опубликовал статью, явившуюся
предшественницей его же книги [89], в которой введено для языка
D понятие «слабейшее предусловие» и показано, как его можно ис-
пользовать для построения исчисления для вывода программ.
По словам Д. Гриса [88, с. 304] стало понятно, что «акцент на те-
орию и формализм, смягчённый здравым смыслом, на самом деле
может привести к построению программ более надёжным спосо-
бом».
Понятие «правильность» рассматривалось также в работах по те-
ории схем программ, начатых Ю. И. Яновым (1957) (см. [91]).
Кстати, заметим, что В. М. Глушков (1965) предложил алгорит-
мические алгебры (впоследствии послужившие прообразом динами-
476
https:it.ru
ческих логик), а Ф. Энгелер (1967) — языки с бесконечно длинными
формулами для выражения бесконечного множества возможностей,
возникающих при различных исполнениях программы.
Понятие «спецификация программы»
Определение.
1. [88, с. 103] Спецификация программы — это средство для точ-
ного описания того, что должно быть совершено в результате вы-
полнения программы.
2. [102, с. 287—288] Спецификацией назовем достаточно точное
и достаточно полное описание задачи, которое человеку, участву-
ющему в решении, легче написать, понять, прочесть, чем про-
грамму решения этой задачи на доступном ему языке програм-
мирования.
Средства спецификации — это любые средства получения и по-
строения таких описаний. Язык спецификаций — это рациональ-
но организованный и синтаксически оформленный набор таких
средств.
3. [163] Спецификация программы — это точная и полная форму-
лировка задачи, содержащая информацию, необходимую для по-
строения алгоритма (программы) решения этой задачи.
4. Команда-комментарий — это спецификация программы, выра-
женная с помощью помещённого в программу утверждения (или
приказа) на псевдокоде.
Мы часто вынуждены обращаться к формальным спецификаци-
ям, так как естественный язык (используемый в псевдокоде) обла-
дает таким свойством, как полисемия.
Определение [141].
Полисемия — это наличие различных (но в какой-то мере свя-
занных) смыслов и (или) значений у одного и того же слова
(словосочетания, фразы), различных интерпретаций у одного
и того же знака или знакосочетания.
Пусть PL — некоторый язык программирования (в частности,
им может являться один из модельных языков Н, D, М), APL— его
алфавит, G — алфавит языка первого порядка.
Определение (синтаксическое).
1. Формальной спецификацией программы S будем называть слово
{Q}S{R}
477
в алфавите G и APL и {{,}}, где Q, и R — формулы языка первого
порядка, S — программа на языке PL.
Предусловием программы S называется формула Q.
Пустым предусловием программы S называется предусловие
Q=SH.
Постусловием программы S называется формула R.
2. Языком спецификаций назовём язык для записи предусловий
и постусловий.
Примеры.
1. [88, с. 107] Для задачи о суммировании элементов массиваВ[0: п -1]
и помещении результата в переменную S предусловие и постусловие
имеют следующий вид:
def def
Q = п>1, R = S = B[0]+B[l] + ...+B[n-l].
2. Для вычисления целой части квадратного корня из натурального
числа п и помещения результата в целочисленную переменную S предус-
ловие и постусловие имеют следующий вид:
Q = п>0, R = S2<n&n < (S + 1)2.
3. Для задачи сортировки массиваВ[0: п -1] предусловие и постусло-
вие имеют следующий вид:
def def
Q = п>1, R = (Vie [0, n-l))(B[i] <B[i + l]).
Определение (no [88, c. 106]) (семантическое).
Интерпретация формальной спецификации {Q} S {Я} такова: если
выполнение программы S началось в состоянии, удовлетворяю-
щем Q, то имеется гарантия, что оно завершится через конечное
время в состоянии, удовлетворяющем R.
Определение.
1. Утверждением будем называть содержательную или формаль-
ную спецификацию, включённую в текст программы.
2. Аннотированной программой будем называть программу, со-
держащую утверждения между каждой парой соседних команд.
Итак, аннотированная программа является «формулой» в языке
вида:
Язык программирования + Язык спецификаций.
478
Использование аннотированных программ открывает широкие
возможности для формальных преобразований программ и фор-
мальных доказательств их свойств, что является основой для вери-
фикации и оптимизации программ.
Понятие «верификация программы»
Определение.
1. [14] Верификация — это понятие, используемое в логике и ме-
тодологии научного познания для обозначения процесса уста-
новления истинности научных утверждений посредством их эм-
пирической проверки. Проверка заключается в соотнесении ут-
верждения с реальным положением дел с помощью наблюдения,
измерения или эксперимента.
Верифицируемость научных утверждений и теорий считается
одним из важных признаков научности. Утверждения и теории,
которые в принципе не могут быть верифицированы, обычно
не считаются научными.
2. [170] Верификация (в философии неопозитивизма) — это прин-
цип опытной проверки, согласно которому истинность каждого
утверждения о мире должна быть в конечном счёте установлена
путём его сопоставления с чувственными данными, «непосред-
ственным опытом».
3. [99, с. 89—90] Верификация (программы) — это установление
соответствия между программой и ее спецификацией, описыва-
ющей цели разработки.
Будем говорить, что соответствие между программой и ее спец-
ификацией отсутствует, если либо программа, либо специфи-
кация, либо оба этих объекта содержат ошибки.
4. Верификация (с точки зрения математической логики) — это
вычисление истинности предиката, зависящего от двух перемен-
ных: программы (на языке программирования) и спецификации
(на языке спецификаций). Истинность этого предиката устанав-
ливает свойство правильности программы (если, конечно, специ-
фикация не содержит ошибок); однако его ложность, вообще го-
воря, ещё не означает наличие ошибок в программе, а требует
более тонкой проверки.
5. (По [163]) Верификация (в программировании) —это доказа-
тельство правильности программ.
Определение (по [163]).
Формальная верификация программы — это приведение доказа-
тельства правильности программы к доказательству некоторой
теоремы в исчислении первого порядка.
479
https: "и га it.ru
Замечание.
Перефразируя известное изречение Э. Дейкстры о тестировании,
можно утверждать, что «верификация способна доказать отсутствие оши-
бок в программе, но не всегда доказывает их присутствие».
Подходы к формальной верификации
Различают следующие подходы к формальной верификации
[99, с. 6; 94]:
1) аналитический подход, при котором проводится верификация
готовой программы или ее фрагмента; программирование (как соз-
дание текста программы) здесь «опережает» доказательство свойств
полученной программы;
2) синтетический (конструктивный) подход, при котором про-
грамма конструируется по шагам параллельно с доказательством
ее правильности; спецификация отдельных фрагментов разраба-
тываемой программы здесь «идёт впереди» соответствующих про-
граммных текстов;
3) верификация динамических свойств вычислений, при которой
обнаруживаются аномалии, такие, как незавершение циклов, не-
корректность операций (например, деление на нуль), выход за гра-
ницы массива, тупики в параллельных программах и т. п. Отличи-
тельной особенностью верификации этих свойств является то, что
она может производиться при частичном или даже полном отсут-
ствии спецификаций.
Итак, программирование в синтетическом подходе (называемое
синтезирующим программированием) — это программирование
в наиболее чистом виде, т. е. процесс получения программы «из ни-
чего», исходя из спецификации задачи и метода ее решения. В по-
следующем конструировании программы по спецификациям разли-
чают два направления: логическое и трансформационное (по [88]).
Спецификация в логическом направлении трактуется как форму-
лировка теоремы, утверждающей существования решения задачи.
Синтез программы состоит в поиске доказательства этой теоремы
существования в некотором логическом исчислении. Если такое
доказательство удаётся построить, то существуют формальные пра-
вила, позволяющие преобразовать доказательство в программу,
находящую решение задачи. Существенно, что существует универ-
сальная контролирующая процедура, которая проверяет правиль-
ность доказательства и применения правил перехода от доказатель-
ства к программе.
Спецификация в трансформационном направлении трактуется
как уравнение относительно программы, которое можно подвер-
гать символическим преобразованиям, при которых символ неиз-
480
https:/Л: rait.ru
вестной программы «рассыпается» на систему вспомогательных
неизвестных, а они, в свою очередь, заменяются либо другими не-
известными, либо конкретными программными конструкциями.
По мере преобразования синтезируемая программа постепенно
«прорастает» в тексте спецификации, в конце концов превращая
ее в законченный программный текст.
Правильность выполнения символических преобразований мо-
жет формально проверяться на каждом шаге.
Ниже мы будем пользоваться аналитическим подходом и логи-
ческим направлением в синтетическом подходе к формальной ве-
рификации.
Замечания.
1. Несмотря на то, что современные теоретические исследования
по проблемам верификации все больше перемещаются в область синте-
тического подхода, аналитический подход сохраняет свое фундаменталь-
ное значение для прикладных методов верификации.
2. Синтез программы — это некоторый способ манипулирования зна-
ниями: специальным, знанием, воплощенным в условии задачи, предмет-
ным знанием, характеризующим область, в которой возникла задача,
и универсальным знанием, отражающим общематематические законо-
мерности и правила доказательного рассуждения. (Слово «манипулиро-
вать» здесь не случайно, оно подчеркивает некоторое осязаемое и точ-
ное представление знания, позволяющее проследить и проконтролиро-
вать последствия его использования.)
В целом такое словоупотребление оказалось методологически весьма
плодотворным, поскольку позволило объединить универсальную стро-
гость математической логики с разнообразием предметных областей, про-
ницательность человеческой интуиции с пунктуальностью компьютер-
ной обработки.
Понятие «тройка Хоара»
Языки для нас нечто большее, чем
системы передачи мыслей. Они —
невидимые покровы, облекающие наш
дух и придающие предопределённую
форму всяческому его символическому
выражению. Когда выражение
приобретает необычную степень
многозначительности, мы называем
его литературой.
Э. Сепир. Язык и литература
Первоначально мы рассмотрим систему Ч. Э. Хоара, которую бу-
дем называть аксиоматической системой Хоара (или просто систе-
мой Хоара).
481
https:it.ru
Математической моделью программы (в системе Хоара) являет-
ся аннотированная программа, а математической моделью внешне-
го мира — определённые правила преобразования, которые могут
быть применены к аннотированной программе.
Более точно, язык системы Хоара является расширением языка
первого порядка с помощью формул вида {Q} S {Я}, где Q и R —
формулы языка первого порядка, S — программа на используемом
языке программирования. Поэтому можно утверждать, что в ак-
сиоматической системе Хоара средства декларативного (непро-
цедурного) описания (формулы языка первого порядка) языка про-
граммирования сочетаются со средствами процедурного описания
(командами).
Отмеченная «тройка» в данной аксиоматической системе явля-
ется элементарной единицей рассуждений о свойствах программ
и является основным элементом утверждений о свойствах команд
языка программирования.
Определение [95, с. 291] (синтаксическое).
Тройкой Хоара будем называть слово вида {Q} S {R}, где Q, R —
формулы языка первого порядка, S — программа на языке LH.
Все свободные переменные формул R и Q в Q} S {Я} неявно свя-
заны внешним квантором V.
Предусловием программы S называется формула Q.
Постусловием программы S называется формула R.
Определение (семантическое).
1. (По [95, с. 291]) Содержательный (неформальный) смысл трой-
ки Хоара {Q} S {Л}состоит в следующем: если формула Q прини-
мает значение 1 непосредственно перед выполнением програм-
мы S, а выполнение программы S завершается, то формула R при-
нимает значение 1 для значений переменных, соответствующих
завершению программы S.
При этом (см. [84, ч. 2, с. 567]) если в формулах Q и R встреча-
ется предметная переменная, то предполагается, что она иници-
ализирована.
2. (По [85, с. 34]) Говорят, что Q есть предусловие для постус-
ловия R по отношению к программе S (и пишут {Q} S {R}), если
из истинности Q непосредственно перед выполнением програм-
мы S следует истинность R после выполнения этой программы.
Указанная интерпретация тройки Хоара позволяет рассматривать
ее как математический объект, принимающий значение 1 или О.
482
https://иrsit.ru
Дедуктивная семантика языка программирования
Определение.
Дедуктивной семантикой языка программирования (по Ч. Э. Хоару)
будем называть множество правил, сопоставляющих каждой про-
грамме, написанной на данном языке, множество ее троек Хоара.
Семантика каждой команды S описывается с помощью отображе-
ния, называемого преобразователем предикатов: каждая команда
S выступает преобразователем предусловия Q (свойства состояния
памяти перед выполнением команды S) в постусловие R (свойство
состояния памяти после выполнения команды S).
Опишем инструменты, которые понадобятся для построения дедук-
тивной семантики языка программирования (на примере языке Н).
1. Необходимо уметь от свойств одних фрагментов программы
переходить к свойствам других фрагментов программы (в частно-
сти, соседних или вложенных). Ясно, что это удобно делать далеко
не для каждого языка программирования. Интуитивно понятно, что
следить за свойствами программы относительно легко, если дина-
мика ее исполнения согласована со структурой ее текста; другими
словами, если об исполнении программы удобно рассуждать, «чи-
тая» ее текст последовательно, без скачков и разрывов (этот прин-
цип согласования положен в основу структурного программирова-
ния). Отметим, что язык программирования Н удовлетворяет этому
требованию.
2. Для каждой команды необходимо сформулировать правила
вывода соответствующих троек Хоара, т. е. ее дедуктивную семан-
тику.
Если теперь дедуктивная семантика согласована с содержатель-
ной операционной семантикой языка программирования так, что
выводимость тройки гарантирует ее истинность, то в распоряже-
нии программиста оказывается аппарат формального доказатель-
ства разнообразных свойств программ, например, доказательства
их правильности.
Замечание (по [95, с. 294]).
Верить доказательству правильности программ нужно «по модулю»
доверия к правильности связи между дедуктивной и операционной семан-
тиками программных конструкций. Обычно предполагается, что эта связь
тщательно проверена. Впрочем, польза от доказательства правильности
программы не столько в гарантии правильности, сколько в системати-
ческом исследовании программы с нетривиальной точки зрения, несо-
мненно, способствующей нахождению ошибок в программе.
483
https: "и га it.ru
Аксиоматическая система Хоара
Исходные аксиомы бессмысленны, если
они только формальны, если в них нет
того, что вне их, если они не «о...»
В. С. Библер
Определение.
Аксиоматической системой Хоара (исчислением троек Хоара, или
просто системой Хоара) для данного языка программирования
будем называть исчисление, содержащее:
1) аксиомы гильбертовского исчисления первого порядка;
2) основные правила вывода гильбертовского исчисления пер-
вого порядка;
3) нелогические аксиомы, описывающие свойства троек Хоара для
данного языка программирования;
4) определение понятия «вывод тройки Хоара».
Пусть Sb S2—программы языка Н; Q, R, Q15 R1} В,Р — формулы
расширенного языка первого порядка, t, — термы расширенного
языка первого порядка.
Определение (по [99, с. 68; с. 115; с. 117; с. 127]).
Нелогическими аксиомами системы Хоара назовем следующие
слова:
(H-J {Q} skip {Q} (аксиома пустой команды);
(Н2) {(Q)*}x := t{Q} (аксиома простого присваивания или аксио-
ма присваивания Хоара);
(Н3) {Q}x := t{3y([Q]* & х - [t]* ) } (аксиома присваивания Флойда);
(Н4) {(Q)^. z. t)}B[i] := t{Q} (аксиома присваивания элементу мас-
сива);
(Н5) (В; i: t) [/] = <-> i = j & t = t1vi¥=j&B[j] = t1 (аксиома обнов-
ления элемента массива);
(Н6) {Q} S {R v -В} (аксиома тавтологии);
(Н7) {Q & —iQ} S {R} (аксиома тавтологии);
(Н8) (Q C{Qj} S {В} {Q} S {В}) (закон консеквенции:
усиление предусловия);
(Н9) {Q} S {В1} ((Rx —> R) —> {Q} S {В}) (закон консеквенции:
ослабление постусловия);
(Hlo) {Q} {R1} ({Bj} S2 {В} {Q} Sj; S2 {В}) (последователь-
ность команд);
(Hn) {Q & B} Sj {B} & {Q & -.В} S2 {B} <r+ {Q} if В then Sj else
S2 fi {В} (командаусловного перехода);
(H12) {P & В} S {P} <-> {P} while В do S od {P & -iB} (команда цикла
while);
484
(H13) {Q} S {P} & (P & -1B Q) <r+ {Q} repeat S until В {P & В} (ко-
манда цикла repeat).
Замечание.
Законы консеквенции (Н8) и (Н9) содержательно утверждают, что для
любой команды S можно произвольным образом «ослаблять» постусло-
вие и произвольным образом «усиливать» предусловие (не изменяя истин-
ного значения тройки Хоара).
Предложение (по [99, с. 115—116]).
Следующие слова являются прямыми допустимыми правилами
вывода:
n (Q->Qi); {Qi}S{K}.
{Q}S{R}
{QySIRJ; (Pi-»В).
{Q}S{R}
3) {Q}Si{^}; {PJSJP}.
{Q}Si;S2{P}
4) {Q&BIS^P}; {Q&—B}S2{R}.
} {Q}ifBthenS1e\seS2fi{R} ’
{Q} if В then else S2 fi {Я}
J {Q&BlSjfPl&fQ&^BlSafP}’
6) {P&B}S{P}
{P} while В do S od {P & -B} ’
{P} while В do S od {P & -В}
{P&B}S{P} ’
{Q}S{P}; (P&-B^Q)
{Q} repeat S until В {P & B} ’
{Q} repeat S until В {P & B}
3 {Q}S{P}&(P&^B^Q) ’
Доказательство.
1)
Доказуемая формула
i Г
Доказуемая тройка Q-yQ^ (Q-Х^)->({Q! }S{R}->{Q}S{R})
{QJSU};_________________{Qi}S{R}^{Q}S{R}_____________
{Q}S{R}
2)
Доказуемая тройка (Н9)
До"зу«ма« формула {Q}S{R1}; {Q}S{Rt} ^ (( Rt -> R)-> {Q}S{R})
(R^R);<
{Q}S{R}
Остальные утверждения докажите самостоятельно.
Предложение доказано.
Понятие «инвариант цикла»
Мы понимаем, что происходит изменение
только потому, что что-то остается
неизменным, а неизменность определяется
только на фоне преобразования.
Джеральд Уейнберг
Определение.
1. [170] Инвариант (в математике) — это выражение, остаю-
щееся неизменным при определённом преобразовании перемен-
ных, связанных с этим выражением.
2. [163] Инвариант — это математический или программный
объект, который остаётся неизменным при каких-либо преобра-
зованиях или при выполнении каких-либо действий.
Остановимся на одном из важнейших понятий программирова-
ния — понятии «инвариант цикла». В правильном подборе инвари-
антов циклов состоит суть доказательства свойств программ, а по-
скольку явно или неявно этот инвариант должен иметься в виду при
написании программы, то в этом же заключается само искусство
программирования (хотя некоторые весьма искусные программи-
сты могут и не согласиться с этим тезисом [96, с. 16]).
Определение.
1. [101, с. 50] Инвариант цикла — это свойство ситуации или
объекта, с которыми имеет дело алгоритм, такое, которое не ме-
няется при исполнении тела цикла.
2. Инвариант цикла — это соотношение между значениями пе-
ременных, которое остается справедливым при любом прохож-
дении цикла.
Более точно, инвариантом цикла называется предикат, истин-
ный перед выполнением и после выполнения каждого шага цикла.
3. Инвариантом цикла называется формула Р в аксиоме (Н12).
486
Замечание.
Пункт 16.10 из пособия для школьного учителя информатики [79]
посвящен понятию «инвариант цикла». При этом утверждается, что хоро-
ший программист отличается от плохого, в частности, тем, что он пони-
мает, что такое «инвариант», и может применять это понятие на практике.
Понятие «завершение программы»
Определим понятие «правильность (корректность) программы»
с помощью двух вспомогательных понятий: «частичная правиль-
ность» и «завершение программы».
Выделение этих вспомогательных понятий следует рассматри-
вать как методический приём, направленный на уменьшение слож-
ности доказательства правильности программ.
Определение.
1. (По [85, с.35]) Будем говорить, что программа завершается,
если ее выполнение доходит до конца за конечное время и при
этом отсутствуют ошибки во время выполнения.
2. Завершение программы — это достижение выхода программы
в процессе выполнения программы, начатой в допустимом (для
входной спецификации) состоянии.
Свойство завершения программы не является очевидным для та-
кого объекта, как программа, ввиду наличия частично-определён-
ных операций и циклических вычислений. Ситуации, когда свой-
ство завершения не выполнено, обычны для программ, содержащих
ошибки. Особенность свойства завершения вычислений в программе
состоит в том, что оно не зависит от постусловия программы и для
фиксированной программы полностью определяется предусловием.
Имеется по меньшей мере две причины, по которым программа
с предусловием Р может не обладать свойством завершения:
1) обращение к частично определённой функции со значением
аргумента вне области определения. Эта причина может приводить
к аварийному завершению даже нециклических программ (напри-
мер, при выполнении деления на 0);
2) выполнение бесконечной последовательности операторов
в цикле (зацикливание). Эта причина присуща программам, содер-
жащими циклы. Её анализ представляет большой интерес для по-
следовательных программ, поскольку зацикливание возможно даже
для программ, не использующих частично определённых функций.
В общем случае формальный анализ свойства завершения пред-
ставляет сложную проблему.
487
https: Цц га it.ru
Понятие «частично правильная программа»
Определение.
1. (По [163]) Частичная верификация — это доказательство пра-
вильности программ, учитывающее основные, но не все возмож-
ные факторы.
2. (По [85, с. 35]) Говорят, что программа является частично
правильной (корректной), если выполнение программы приво-
дит к получению правильного результата (когда бы она ни завер-
шилась).
3. (По [159, стб. 652]) Будем говорить, что программа S частич-
но правильна относительно предусловия Р и постусловия Q (что
обозначается {Р} S {Q}), если в случае, когда предикат Р истинен
для входных значений переменных и программа S завершает ра-
боту, то предикат Q истинен для выходных значений переменных.
Итак, частичная правильность программы — это удовлетворение
спецификациям при условии завершения выполнения программы.
Определение.
1. (По [85, с. 35]) Говорят, что программа является полностью
правильной (корректной), если программа является частично пра-
вильной и, кроме того, доказывается, что выполнение програм-
мы действительно заканчивается.
2. [159, с. 652] Будем говорить, что программа S является то-
тально правильной (что иногда обозначается (Р) S (Q)), если про-
грамма S частично правильна относительно Р и Q, а также про-
грамма S завершает работу для входных значений переменных,
удовлетворяющих условию Р.
Каждое из двух отмеченных свойств правильности программы,
может выполняться или не выполняться. Поэтому выделим следую-
щие основные задачи анализа правильности, связанные с исследова-
нием (по [99, с. 90—91]):
1) частичной правильности программы;
2) завершения программы;
4) тотальной правильности программы;
3) незавершения программы;
5) частичной некорректности программы (это исследование не-
корректности программы при условии ее завершения);
6) некорректности программы (исследованием незавершения
программы или ее частичной некорректности).
488
https:it.ru
Замечание (важное).
В общей постановке (для произвольных программ) каждое из этих
свойств (завершение и частичная правильность) является алгоритмиче-
ски неразрешимым. Однако для некоторых классов программ могут быть
развиты достаточно эффективные методы анализа свойств правильно-
сти, позволяющие вручную или в автоматизированном режиме прово-
дить соответствующие доказательства.
Технология доказательства частичной правильности
программы в системе Хоара
Мы будем предполагать некоторое
умение выводить формулы в исчислении
предикатов и иногда будем опускать
доказательства того, что та или иная
формула выводима. Начинающему при
этом полезно по крайнеймереубеждатъся,
что рассматриваемая формула является
логическим законом.
А. Н. Колмогоров, А. Г. Драгалин
Для доказательства частичной правильности программы S в си-
стеме Хоара задача записывается в виде утверждения о том, что
h{Q}S{R},
где Q — заданное предусловие, R — заданное постусловие.
Далее применяем некоторое допустимое правило вывода для S.
Это правило применяется для того, чтобы «разбить» доказываемое
исходное утверждение о правильности на последовательность бо-
лее простых утверждений о правильности. Процесс продолжается
до тех пор, пока не остаются лишь утверждения о правильности ко-
манд присваивания, которые проверяются непосредственно с помо-
щью аксиом присваивания.
Процесс вывода тройки Хоара, выражающей свойство частич-
ной правильности программы, можно представлять как вывод бо-
лее «мелких» троек Хоара, начиная с «крайних» пред- и постусловий
(удобнее начинать с постусловий, так как постусловие выражает
цель работы фрагмента программы). Поэтому фактически завер-
шающий фрагмент программы автоматически формулирует цель
для предшествующего фрагмента и т. д., пока не удается получить
условие, выполненное в исходном состоянии.
Другими словами, доказательство частичной правильности про-
граммы можно отождествить с доказательством правильности пре-
образования постусловия в предусловие.
489
https:/Л: rait.ru
Пример [109].
Докажем частичную правильность программы, вычисляющей част-
ное q и остаток г от деления х на у (х, у—целые неотрицательные числа):
{х >у &у > 0 & г > 0}
г :=х; q := 0; while г >у do г := г -у; q := q + 1 od
{г <y&x = q-y + r}
Предположим, что цикл заканчивается. Обозначим:
def def
Р = x>y&y>0&r>0;Q = г <y&x=q-y + r;
def
While = while r > у do rr -y; q q +1 od.
Пусть Qj и Q2 — пока неизвестные предикаты. Первый шаг вывода
очевиден:
{Pk-xjQJ; {Q1}q:=0{Q2}; {Q2}While{Q}
{P}rx; q0; While{Q}
Предикат Q2 легко определяется из следующего вывода (R—пока про-
извольный предикат):
Теорематеории S
r>y&x=q-y+r—>x=q-y+r
r>y&x = q y+r->x = (q+l) y+r-y OJ)
{x = (q+l)y+r-y}r:=r-y{x = (q+l)y+r} (Пр (1))
{r>y&x = qy+r}r:=r-y{x = (q+1) y+r} {x=(q+l>y+r}q:=q+l{x =q-y+r}
{r>y&x = qy+r}r:=r-y{K};{K}q:=q+l{x = qy+r}
fr*У&x = q y + r}r:= r-y;q:=q+l{x = qy + г} (Пр
{Q2}while r>y do r:=r-y;q:=q+lod{-ir> у&x=qy+r}
{Q2}whiler>y dor :=r-y;q:=q+lod{r <y&x = qy+r}
{Q2}While{Q}
Итак, Q2 =?x = q • у + г. Далее рассмотрим тройку Хоара
{QJq :=0{x = q y + r),
которая превращается в аксиому команды присваивания (Н2), если
мы положим Qi -sx=0 • у + г.
Наконец:
Аксиома гильбертовского исчисления Т еорематеории S
Х=Х->(Х>У &у > 0 & Г>0^>Х = Х); Х = Х Теорема теории®
х>у &у > 0& г>0->х=х х=х^х=0у+х ("2)
х>у &у > 0 & г>0->х=0-у+х; {х=0-,у+х}г:=х{х=0 у+г}
--------- --------------------------------------------(Пред. (1))
{х>у & у> 0 & r>O}r:=x{jc = O-y+r}
490
Проделанные построения представляются чудовищно громозд-
кими для доказательства «очевидного» свойства очень простой
программы. Но не будем забывать, что аппарат гильбертовского
исчисления первого порядка (по словам С. С. Лаврова [96, с. 36]) —
это своего рода машинный язык для математиков. Доказывая свои
теоремы, «работающие математики» пользуются языками гораздо
более высокого уровня, а главное — значительно менее формализо-
ванными (что не всегда хорошо, так как ошибки в доказательствах
становятся менее заметными).
«Работающие программисты» также должны развивать интуи-
цию, позволяющую им убеждаться в правильности своих программ
ещё до начала их отладки и тестирования (как известно, дале-
ко не гарантирующих желаемого) и быстро находить и устранять
ошибки в ходе отладки.
Замечания.
1. Этот пример наглядно показывает, что формальный вывод про-
грамм с помощью формального исчисления требует немалой изобрета-
тельности (вспомните, например, что тщательно разработанные правила
интегрального исчисления сами по себе не могут заменить человеческой
изобретательности в задачах вычисления определённых интегралов).
2. Формальные правила помогают в решении задачи, «подсказывая»
нужные преобразования.
3. Логический анализ семантических свойств программ в аксиома-
тике Хоара не является однозначным процессом, поскольку на каждом
шаге применимо, вообще говоря, не единственное правило вывода или
аксиома. Причина неоднозначности заключается в том, что система Хоара
сконструирована для отдельных команд независимо от контекста (среды,
в которую команда помещена).
Технология доказательства полной
правильности программы в системе Хоара
Во всех делах твоих помни о конце твоём.
Книга премудростей Иисуса
сына Сирахова, 7, 36
Для того, чтобы доказать полную правильность программы в си-
стеме Хоара, необходимо показать, что каждое циклическое вычис-
ление в программе будет выполняться лишь конечное число раз.
Рассмотрим методы анализа завершения программ в системе Хо-
ара. Мы ограничимся рассмотрением методов анализа завершения
циклических вычислений без учета других возможных причин не-
завершения (т. е. предполагая, что любая нециклическая команда
завершается). Для логического анализа завершения циклических
491
https: "и га it.ru
вычислений применяются два метода: метод Флойда и метод счёт-
чиков.
Рассмотрим метод счётчиков, идея которого состоит во введе-
нии в исследуемую программу новых переменных-счётчиков, добав-
ляемых по одной в каждый цикл программы. Переменная-счётчик
должна инициализироваться перед входом в цикл и увеличивать
свое значение при каждом прохождении по циклу. В преобразо-
ванной таким образом программе измененные инварианты циклов
представляются в виде, содержащем условие ограниченности зна-
чений счётчиков функциями, зависящими только от входных пере-
менных. Это указывает на существование верхней грани значений
счетчиков.
Для преобразованной программы с указанными инварианта-
ми циклов доказывается частичная правильность, которая одно-
временно характеризует и завершение программы, т. е. ограни-
ченность значений счётчиков. Успех доказательства завершения
в методе счётчиков определяется тем, удастся ли подобрать соот-
ветствующее (доказуемое) условие ограниченности счётчика в ин-
варианте цикла. Этот важнейший момент требует творческого уча-
стия программиста.
Итак, метод введения счетчиков позволяет сводить для про-
грамм, расширенных посредством счётчиков, проблему полной пра-
вильности к проблеме частичной правильности.
Чаще всего метод счётчиков реализуется с помощью понятия
«ограничивающая функция». Рассмотрим, например, способ доказа-
тельства полной правильности цикла определённого вида.
Предложение.
Пусть Р — инвариант цикла while В do S od, at — терм (ограни-
чивающая функция), принимающий целые значения и такой, что
в системе Хоара доказуема «формула»
(P&B->t>O)&Vx{P&B&t = x}S{t<x}.
Итак, доказательство завершимости программы заключается
в подборе ограничивающих функций для каждого выполняемого
цикла.
О неполноте системы Хоара
Если лицам разных профессий поручить
одинаковую работу, то математик
сделает ее лучше.
Г. Штейнгауз
Пусть рассматривается система Хоара, у которой в качестве язы-
ка для записи условий выбран язык арифметики первого порядка.
492
https:it.ru
Определение (по [159, стб. 654]).
1. Истинным утверждением называется утверждение о частичной
правильности программы, которое является истинным по отноше-
нию к операционной (или денотационной) семантике программы.
2. Выводимым утверждением называется утверждение о частич-
ной правильности программы, которое является выводимым в рас-
ширении системы Хоара посредством добавления истинных фор-
мул арифметики.
3. Состоятельной логикой Хоара называется система Хоара, в ко-
торой каждое выводимое в ней утверждение истинно.
4. Полной логикой Хоара (относительно арифметики) называет-
ся система Хоара, в которой каждое истинное утверждение вы-
водимо.
Аксиоматическая система Хоара для программ, состоящих из ко-
манд присваивания, команд условного перехода, команд цикла
и составных команд, является неполной, если языком специфика-
ций (языком для записи предусловий и постусловий) выбран язык,
устроенный «по образцу» языка первого порядка [77, с. 78—83]. Та-
кой язык использует, в частности, обозначения всех констант, пре-
дикатов и функций, допустимых в самих программах.
Недетерминированные программы в системе Хоара
Определение.
1. Частичная правильность (корректность) недетерминирован-
ной программы S относительно входного условия Q и выходного
условия R (обозначение {Q} S {Я}) определяется следующим об-
разом: если программа S начинает выполняться, когда истинно
условие Q, то для каждого пути выполнения, который достигает
выхода программы, на выходе истинно условие R.
2. Тотальная правильность (корректность) недетерминирован-
ной программы S относительно входного условия Q и выходного
условия R (обозначение [Q] S [Я]) определяется так: если програм-
ма S начинает выполняться, когда истинно условие Q, то каждый
путь выполнения достигает выхода программы, причем на выхо-
де истинно условие R.
Итак, бесконечные пути, а также пути, которые завершаются
аварийным завершением, не влияют на частичную правильность
программы.
В случае тотальной правильности бесконечные пути отсутству-
ют; отсутствуют также пути, начинающиеся с истинного входного
условия и оканчивающиеся аварийным завершением.
493
https:/Л: rait.ru
Систему правил вывода условий частичной правильности детер-
минированных программ удается обобщить на недетерминирован-
ные программы без привлечения новых понятий. Причиной этого
является независимость различных путей вычислений недетерми-
нированной программы для фиксированных значений входных
переменных.
Определение (по [99, с. 234—235]).
Нелогическими аксиомами системы Хоара для недетерминирован-
ных команд выбора и цикла будем называть следующие слова:
1) {Q&B1}S1{R}&...&{Q&Bn}Sn{R}->{Q}if В, =>Si=>Sn fi{R};
2) {P&B1}S1{P}&...&{P&B„}S„{P}^
^{P}doB2 =>S1n...nBn =>Sn od{P&—iBj &...&—iBn};
3) {P&B1}S1{P}&...&{P&B„}S„{P}&(P&-B1&...&-Bn
{P} do Br =>S1n...ciBn =>Sn od{P};
4) (P&(B1v...vBn)->t>O)&(P&-B1&...&^Bh->B)&
&[P&B!]tb :=t;S1[P&t<to]&...&[P&Bn]to := t;Sn[P&t<t0]->
^[PJdoBj =>51п..х|Д1 =>Sn odfR].
Предложение (no [99, c. 234—235]).
Следующие слова являются прямыми допустимыми правилами
вывода.
1. Частичная правильность для недетерминированной команды
выбора:
{Q&B1}S1{R};...;{Q&Bn}Sn{R}
{Q} if Bj => Si □...□Bn => S„ fi {R} ’
Если все условия B( являются ложными, то для команды выбора
возникает аварийное завершение, но при аварийном завершении
программа считается частично правильной. В этом случае все по-
сылки правила истинны и, следовательно, заключение правила так-
же истинно.
2. Частичная правильность для недетерминированной команды
цикла
{P&B1}S1{P};{P&B2}S2{P};...;{P&Bn}Sn{P}
{Р}боВг =>S1n...nBn =>Sn od{P&—iBi &...&-iBn}
Если все условия В( являются ложными, то выполнение команды
цикла завершается. В этом случае посылка правила истинна неза-
висимо от вида Р, поэтому заключение этого правила истинно, что
соответствует семантике недетерминированной команды цикла.
494
https: "и га it.ru
3. Частичная правильность для недетерминированной команды
цикла
{P&B1}S1{P};...;{P&Bn}Sn{P}; (P&^&...&-nBn -+R)
{Р} doВ2 =>S1n...nBn => Sn od {Я}
4. Тотальная правильность для недетерминированной команды
цикла
Р&(_Вг \/...\/Bn)—>t>O;P&—iB1&...&—Bn —>R;
[P&BJt0 := t;S^P&t<tp];[P&Bn]t0 := t;Sn[P&t<t0]
[P] doB2 =>S1n...nBn => Sn od [Я]
Доказательство. Упражняйтесь.
Примеры решения некоторых
типов упражнений
Логические методы требуют
абсолютной сосредоточенности.
А. и Б. Стругацкие. Далёкая Радуга
Пример 1 [36, с. 336].
Докажем частичную правильность следующей программы вычисле-
ния значения функции «факториал»:
{И} fact := 1; i := Ojwhile i * n do i := i +1; fact := fact • i od {fact = n!}.
Решение. Введём следующие обозначения:
def def def
While - while i ± n do i := i +1; fact := fact • i od, Q - fact = nl, R - И.
Предположим, что цикл заканчивается. Первый шаг вывода очевиден:
{R}fact := 1{QJ; {QJi := 0{Q2}; {Q2} While{Q}
{R}fact:=l;i:=O;While{Q} P‘ ’
где Qq и Q2— пока неизвестный предикат.
Предикат Q2 определяется из следующего вывода:
(Н2)
4-
D {fact -i = i! &i < n} fact:=fact-i {fact=i!&i < n}
{i n&i < n&fact=i! }i:=i+ 1{P}: {P}fact:=fact -i {fact=i! &i < n}
{i Ф n&i < n&fact=i! }i:=i+1; fact:=fact • i {fact=i! &i < n}
{Q2}while i Ф n do i:=i+1; fact:=fact -i od{i=n&i < n&fact=i!}; i=n&i < n&fact=i! -> fact=n!
{Q2}while i n do i:=i+1;fact:=fact iod{fact=n!}
{Q2}while i n do i:=i+1; fact:=fact -i od{R}
495
https://urast.rL!
Теорема теории S Определение функции "факториал"
i*n&i<n->i+l<n; fact = i!-> fact-(i+1) = (i+1)!
i^n&i<n&fact = i!->fact-(i+l) = (i+l)!&i+l<n
{i *n&i< n&fact = i!}t := i+1 {fact-i -i\&i <n}
D
def
Следовательно, Q2 = fact = i! & i < n. Далее:
0*2)
{fact = 0!&0 < n}i := 0{fact = i!& i < n}
{Qi }* := 0{fact = i! & i < n}
{Qi}i:=0{Q2}
def
Следовательно Qi = fact=O!. Далее:
Определение функции факториал
1 = 0!
И->1 = 0!
{И} fact := l{fact := 0!}
{RHact^HQJ
Докажем тот факт, что цикл завершается:
Теорема теории S
a) i = n&i<n&fact = i!->n-i>0
g) Теорематеории S
n-i = x->n-(i+l)<x
i = n&i<n&fact = il&n-i=x^n-(i+T)<x (/^2)
{i=n&i<n&fact=i!&n-i=x}i:=i+l{n-i<x} {n-i <x}fact:= fact-i{n-i<x}
{i=n&i <n&fact=i\&n-i=x}i :=i+l; fact := fact- i{n-i<x}
Пример 2. Докажем частичную правильность программы, написан-
ной на языке TURBO Pascal:
PROGRAM M_i_n;
const a=10;
varx,y: Integer;
BEGIN
y:=a;x:=y + 3;
Ifx>5 then x :=5;
WriteLn('min{'у+З, ',5}=',х)
END.
Решение. Запишем программу на языке Н:
{а = 10}у := а; х :=у + 3; if х > 5 then х := 5 else skip fl{x = min{y + 3,5}}.
496
https:/Л: га it.ru
Заметим, что в теории S
def
x=min{y+3,5} = y+3>5&x=5vy+3<5&x=y+3.
Введём следующие обозначения:
def def
Р = а=10; Q = x = min{y+3,5}.
Первый шаг вывода очевиден:
{P}x:=a{Qi}; {QJx^y+3{Q2};{Q2}if х>5thenx:=5fi{Q}
----------------------------------------------------(1 Ip. (3J )
{P}y := a; x := у+3; if x > 5 then x := 5 else skip fi{Q}
где Q1 и Q2— пока неизвестные предикаты.
Предикат Q1 можно определить из следующего вывода, воспользовав-
шись аксиомой присваивания Флойда (Н3):
(н3)
{a=10}у := a{3z([a=10]^ &у=[а]*)}
{a=10}x:=a{Q1}
{P}x:=a{Q!}
Итак,
def
Qi = {3z([a=10]* & у=[<)} s 3z(a=10& у=a) = a=10& у=a.
Предикат Q2 определим из следующего вывода:
(н3)
{a=10&y = a}x:=y+3{3z(Ia=10&y = a];£&x = [y+3]*)}
{a=10& у = a}x := у+3{Q2}
{Qi}*:=y+3{Q2}
Следовательно,
def
Q2 = 3z([a=10&y = a]*&x = [y+3]*)} =
= 3z(a=10&y = a&x = y+3) = a=10&y = a&x = y+3.
Далее получим:
______________________Di_______________________
{a=10&y = a& x = y+3&x>5}x:= 5{x = min{y+3,5}}; D2
{a=10&y = a& x = y+3}ifx>5 then x := 5 else skip fi{x = min{y+3,5}}
{Q2 } if x > 5 then x := 5 else skip fi{Q}
Теорематеории S
y+3>5->5 = min{y+3,5}
x=y+3&x>5->5=min{y+3,5}
a=10&y = a&x = y+3&x>5->5=min{y+3,5}; {5=min{y+3,5}}x:=5{x=min{y+3,5}}
a=10&y = a&x=y+3->x>5;-i(x>5)->x<5(Ч7)
-------------------—-------(общ. 31)
а=10&у = а&х=у+3&-1(х>5)->х>5&х<5;{x>5&x<5}skip{x=min{y+3,5}}
{а = 10&у = а&х=у+3&-i(x >5)} skip{x=min{y+3,5}}
02
Упражнения для самостоятельного решения
Главное педагогическое значение
математики состоит в том, что
в математике, преимущественно
перед другими предметами, ученику
предоставляется самостоятельная
умственная работа.
Д. Д. Мордухай-Болтовский
Формальная спецификация задач
О. [88, с. 109] Запишите формальную спецификацию для следующих
задач:
1) найдите место максимального значения в массиве В[0: п - 1];
2) найдите место первого максимального значения в массиве В [0: п -1];
3) определите, является ли данное целое число х > 1 простым;
4) определите, упорядочен ли массив целых чисел В[0: п - 1] в порядке
возрастания;
5) присвойте каждому элементу массива В [0: п -1] сумму всех значений
массива В.
Аксиомы системы Хоара
1. Восстановите пропущенные фрагменты в записи аксиом:
а) (Н2) {...}t := t + 1{5 = с +1 & t < у};
б) (Н5) ((В; v. е); j: ej [к] =е2
в) (Н8) (Q&B^K)^ ({...} S {...});
г) (Н9) {...} S {...} -> ((Р & —их ^...) {Q} S {Я};
Д) (Hn) {...^{х = 1}& {-}S2{x = 1} <-> {у = 5} if у = О then else S2 fi{...};
е) (Н12) while2i<ndoi:=2iod{0<i&i<n<2i&3p
(2₽=i)};
ж) (Н13){а = 0}а := а + За {а = к} & {а = к & а -> а = 0} <-> {...} repeat... until...
{...}.
2. (По [99, с. 68]) Докажите, что следующие слова являются теоремами
системы Хоара:
а) (В; к: t) [к] = t;
б) ((В; i: t); i: tj) [i] = tf,
в) ((B; j: t);j + 1: t + 2) Ц] = t.
3. Восстановите пропущенные фрагменты в доказательстве следующего
прямого допустимого правила вывода:
{H}S{x = a&p>
{H}S{x = а}
498
https:га it.ru
Доказуемая тройка (Н9 )
Доказуемая формула {И}5{х = fl & ft}; {H}S{...} «... -> X = fl) ->
(...—>х = а); х = а)->{H}S{...}
{И}5{х = а}
Прямые допустимые правила вывода
4*. Докажите, что следующие слова являются прямыми допустимыми
правилами вывода:
n (Q->Qi); {QJSW.
{Q}S{K}
{QISW; R^R,
{Q}S{R}
3) {Q}S]{^}; {RJS^R}.
{Q}Si;S2{K}
4) {Q&B}S2{R}; {Q&-.B}S2{R}.
{Q} if В then else S2 fi {R} ’
i-ч {Q> if В then Sj else S2 fi {R}
J {Q & B}Si {R} & {Q & -iB}S2 {R} ’
6) {P&B}S{P}
{P} while В do S od {P & —iB} ’
{P} while В do S od {P & —iB} .
{P&B}S{P} ’
8) {Q}S{P>; (p&^b->Q) .
{Q} repeat S until В {P & B}’
о-» {Q> repeat S until В {P & B}
{Q}S{P}&(P&^B^Q) ’
5. Докажите, что следующие слова являются прямыми допустимыми
правилами вывода:
а) У-»Ц; {У11ЗД1}; Ri^R.
{V}S{R}
б) . {V^}S{R} ;
{Vj&VJSfR}’
в) {V}S{R1}; {V}S{R2}.
{V}S{Rx&R2} ’
r)« {V}S{RJ ;
{V}S{R1VR2}’
4 {V1>S{R}; {V2}S{R}.
{V1VV2}S{R} ’
e) {V1}S{R1>; {V2}S{R2}.
* {Vi&VjSfRj&Ra} ’
ж) {Vi}S{Ri>; {V2}S{R2}
* {V^V2}S{R^R2} ’
499
https:it.ru
з) {Ц
6. Докажите, что следующие слова являются прямыми допустимыми
правилами вывода:
а) .
{Q}skip{R}’
в) _______________________{v2}s2{K}
BJ { (Vi & В) v (V2 & -1В) } if В then % else S2 fi {R} ’
r) {VJS^K}; {V2}S2{R}
rJ {Vi & V2} if В then S1 else S2 fi {R} ’
•J {Vr&Bys^R}; {V2&^b}s2{R}
M {Vi & V2} if В then else S2 fi {R} *
7*. Докажите в системе Хоара следующие прямые правила вывода:
а) {Q}S{Q>
* {Q} repeat S until В {Q & В} ’
6) {Q}S{Q&—В}
* {Q} repeat S until —B {Q} ’
* {Q} repeat S until В {P & B}
8. (По [81, c. 38])
Докажите, что следующие слова являются прямыми допустимыми пра-
вилами вывода:
. {V}Init{P}; {P&B}S{R}; P&^B^R
* {V}Init; while В do S od {R}
6) {Q}S{P>; (P&^B^R) .
{Q}S; while -B do S od {P & B}’
{Q} repeat S until B{P & B}
BJ* {Q}S; while -B do S od {P & BY
9. (По [92, c. 122])
Пусть n g N\{0}, a Sx, ..., Sn— последовательность команд. Докажите
индукцией по и, что прямое допустимое правило вывода для программы Sx;
Sn имеет следующий вид:
{Qo>sb •••> Sn{Qn}
10. (По [92, с. 115])
Докажите в системе Хоара следующие прямые допустимые правила вы-
вода, которые называются правилами замены:
500
https:/Л: га it.ru
ay Qi^{Q}S{K}. б) {Q!&Q}S{K}
{Qi&Q}S{R}’ Q!^{Q}S{K}
Восстановление пропущенных фрагментов в доказательстве частичной
правильности программ
11. Восстановите пропущенный фрагмент доказательства частичной
правильности следующих программ:
а) {х = 5} у :=х + 1 (у = 6}
Теорема теории S
def
... —>х+1 = 6; х+1 = 6 =Су=6)^+1
{х=5}у:=х+1{у=6}
(замена равного на равное)
(...)
б) {к = а}к:=к + 1; m:=kk{m = (a + l).(a + l)}
(н2)
D {...}m:=kk{m = (a + l).(a + l)}
{k = a}k:=k + l{R}; {R}m:=k-k{m = (a+l)-(a+l)}
{k = а} к := к +1; m := к • к {т = (а +1) • (а +1)}
def
Следовательно, R = .... Далее,
Теорема теории S
ф
—к=а->-—(...)
{k = a}k:=k + l{...}
12. Восстановите пропущенный фрагмент доказательства частичной
правильности программы:
{H}ifb < Othenx :=-b elsex :=b fi;x := 1 +x{x= 1 + |b|}
(H2)
D {...l+x = l+|b|}x:=l+x{x=l+|b|}
{И} if b<0 thenx := -b else x :=b fi{R}; {R}x := 1+x{x=1+1 b |}
{H}ifb<Othenx:=-b elsex:=b fi;x:=l+x{x=l+|b|}
def
Следовательно, R = .... Далее,
Определение модуля Теорема теории S
J, J,
Определение модуля Теорема теории S
4, 4,
b<O->-b=|b|; -Ь=|Ь|->... ...^-НЫ; (сечение)
(сечение)__________Ь<0^>..._________f6 » __________________ (6б)
{Ь < 0}х {...}х-.= Ь{...} (4 }
{И}if Ь<0 thenx:= -b elsex:= b 4
501
http
s://u rait.ru
13. Восстановите пропущенный фрагмент доказательства частичной
правильности следующей программы:
{и > 0} i := 1; while 3 • i < п do i := 3 - i od {0 < i & i < n < 3 • i & Bp (3p = i)}.
Введём следующие обозначения:
def
While = while 3 • i < n do i := 3 • i od,
def def
Q = 0 <i &i<n < 3 • i &Bp (3p = i), P = n > 0.
Предположим, что цикл заканчивается. Первый шаг вывода очевиден:
{QJ While {Q}
{P}i:=l; While {Q} 3
где Qi — пока неизвестный предикат, который определяется из следующего
вывода:
Теорема теории S
ф
{Q1&..£}i:=3i{Q1}
В |Qi&—।
{Qx} While 3i < п do i :=3i od{0 <i&i<n&n<3i&Bp(3P = i)}
_ (46)
т Таким образом
def
Qi = -
{QJ While {Q}
Теорема теории S
г
{п >0}г:=1{...}(6б)
{P}i:=l{Qi}
Доказательство частичной правильности программ
14. Докажите частичную правильность программы в системе Хоара:
а) {а = а0 & b = Ьо} t := а; а := Ъ; Ъ := t {а = b0 & b = а0};
б) {а = а0 & b = Ьо} а := а + b; b := а - b; а := а - b {а = Ьо & Ъ = а0}.
15. (По [78, с. 94, № 2])
Используя систему Хоара, установите, для каких исходных значений
а и b переменные а и b будут иметь равные значения после выполнения
следующих программ:
а) а := а - b; b := а - Ь;
б) а := (т + а) • b; b := а + т • Ъ;
в) a t= а + b; b а - Ь; а а - Ь.
16. (По [99, с. 118])
Найдите предусловие, для которого программа
{?}В[В[2Ц := 1 {В[В[2Ц = 1}.
является частично правильной в системе Хоара.
17. Докажите, что следующие слова являются теоремами системы Хоара:
502
https:/Л: rait.ru
a) {z>6&x=l + z& x<5}S {Q};
6) {Even(x) &Odd(y)}x e + 2 {MOD(x,y) = 0 vx = q j+r & 0 < r <y};
в) {Q & -iB} if В then S else skip fi {Q & -B}.
18. Докажите частичную правильность следующих программ:
a) {M>0}i:=lV;y :=M;z:=0; whiley > Odoy :=y-l;z:=z+xod{z=lV-lW};
б) {И} while -iOdd(n) do n := n + 2 od {Odd(n)};
в) {s = c +1 & t < y} repeat s := s + 1; t := t + 1 until t=y {s = c +y};
r) {s = c +1 & t <y} while t Фу do s := s + 1; t := t + 1 od {s = c +y};
д) {n > 0} i := 1; while 2i<ndoi:=2iod{0<i&i<n<2i & 3p(2P = i)};
e) {n > 0} a := 0; while (a + l)2 < n do a := a + 1 od {a > 0 & a2 < n &
&n < (a + l)2};
ж) {И} S :=B[n]; i := n;
while i Ф 0 do i := i - 1; S := S +B[i] od {S = B[0] +B[1] + ... +B[n]};
з) {i = n} while i > n do i := i + 1 od {i = n};
и) {i = n + 1} while i > n do i := i + 1 od {i > n}.
Указание. Воспользуйтесь следующими инвариантами цикла:
a) z + x -у = N • М;
б) И;
в) s = c + t&t <у;
г) s = с + t;
Д) п > 0;
е) п>0;
ж) 0 < i < n & S = B[i]+B[i + 1] + ...+В[п];
з) i = n;
и) i > п.
19. Докажите частичную правильность следующей программы, напи-
санной на языке программирования TURBO Pascal:
{Демонстрация фундаментальных свойств инварианта цикла на }
{примере цикла While языка программирования TURBO Pascal, }
{предназначенного для «быстрого» возведения вещественного }
{числа в натуральную степень. }
{Инвариант цикла Р известен из косвенных соображений: }
{ n b }
{ Р = (п >= 0) & (z * х = а) }
{ }
{ }
PROGRAM Stepen;
Uses CRT;
var а, {Основание степени }
x: Real; {Вспомогательная переменная}
b, {Показатель степени }
n: Integer; {Параметр цикла }
z: Real; {Результат }
BEGIN
Write('Введите основание степени: '); Read(a);
Write('Введите показатель степени: '); Read(b);
х := a; n := b;
z := 1;
WriteLn('Значение инварианта до выполнения цикла : ',
(п >= 0) AND (z*Exp(n*Ln(x)) = Exp(b*Ln(a))));
503
https:it.ru
While n < > 0 do
begin
If NOT Odd(n)
then begin n := n DIV 2; x : = x*x end
else begin z := z*x; n := n - 1 end;
WriteLn(JЗначение инварианта во время выполнения цикла
(п >= 0) AND (Trunc(z*Exp(n*Ln(x))) =
Trunc(Exp(b*Ln(a)))))
end;
WriteLn(JЗначение инварианта после выполнения цикла : J,
(п >= 0) AND (Trunc(z*Exp(n*Ln(x))) =
Trunc(Exp(b*Ln(a)))));
WriteLn(JРезультат возведения в степень: z);
ReadKey
END.
19p С помощью программирования на языке TURBO Pascal покажите
для приведённых ниже аннотированных программ, что инвариант цикла
истинен до выполнения цикла, в теле цикла и после окончания цикла:
а) {М > 0} х := N; у М; z 0; while у > 0 do у := у - 1; z := z + х od
{z = N-M};
б) {И} while -iOdd(n) do n := n + 2 od {Odd(n)};
в) {s = c +1 & t < y} repeat s := s + 1; t := t + 1 until t =y {s = c +y};
r) {s = c +1 & t <y} while t*y do s := s + 1; t := t + 1 od {s = c +y};
д) {n > 0} i1; while 2i<ndoi:=2iod{0<i&i<n<2i& 3p(2p = i)};
e) {n > 0} a := 0; while (a + I)2 < n do a := a + 1 od
{a>0&a2<n&n< (a + l)2};
ж) {И} S :=B[n]; i := n;
while i 0 do i := i - 1; S := S + B[i] od {S = B[0] +B[1] + ... +B[n]};
з) {i = n} while i > n do ii + 1 od {i = n};
и) {i = n + 1} while i > n do i := i + 1 od {i > n}.
Указание. Воспользуйтесь следующими инвариантами цикла:
a) z + х • у = N • М;
б) И;
в) s = c + t&t <у;
г) s = c + t;
Д) п > 0;
е) п > 0;
ж) 0 < i < n & S = B[i]+B[i + 1] + ...+В[п];
з) i = n;
и) i > п.
Доказательство полной правильности программ
20. Докажите полную правильность следующих программ:
а) {М > 0} х := N; у := М; z := 0; while у > 0 do у := у - 1; z := z + х od
{z = N-M};
б) {и > 0} а 0; while (а + I)2 < п do а а + 1 od
{a>0&a2<n&n< (а + I)2};
в) {И} S := В[п]; i := и;
while i * 0 do i := i - 1; S := S + В[i] od {S = B[0] + B[l] + ... + B[n]};
504
https:/Л: rait.ru
Указание. Воспользуйтесь следующими инвариантами цикла и ограни
чивающими функциями:
def def
а) Р = z + x-y = N-M,t = у;
def def
б) Р = a2<n,t = п-а;
def def
в) Р = 0<i<n & S = B[i] +B[i + 1] + ... + B[n], t = i.
21. Докажите полную правильность следующих программ на языке Н:
а) {г = 0 & i = Ъ} while i > 0 do г := г + a; i := i - 1 od {г = а • Ъ},
def def
Р = r = a(b-i),t = v,
б) {И} s := a; i 0; while i < b do s := s + 1; i i + 1 od {s = a + b}, P
def def
= s = a + i&i<b, t = b-i;
в) {И} fact := 1; i := 0;
while i n do i := i + 1; fact := fact • i od {fact = n!},
def def
P = fact = i! & i < n, t = n-i;
r) {i = n} while i > n do i := i + 1 od {i = n},
def def
P = i = n, t = n-i.
Команды цикла for-to-do ufor-downto-do
22. Добавим к языку H две команды с «привычным» синтаксисом:
1) for i := a to b do S od;
2) for i := b downto a do S od.
Согласны ли вы с включением приведённых ниже формул в число не ло-
гических аксиом системы Хоара?
(Н14) {a < i < Ъ & Vj (a < j < i -> PG))} S {Vj (a < j < i -> PG))} ->
-> {Vj (a <j < a^> PG))} for i := a to b do S od {Vj (a < j < b —> PG))} (ко-
манда цикла for-to-do);
(H15) ~ {a < i < b & Vj (i < j < b -> PQ))} S {Vj (i < j < b -> PG)) W
-> {Vj (b <j <b—> PG))}for i := b downto a do S od {Vj (a <j<b—> P(j))}
(команда цикла for-downto-do).
При анализе учтите, что к этим формулам необходимо добавить следу-
ющее фундаментальное словесное ограничение (без него не представляется
возможным формализовать семантику цикла в приемлемой форме): команда
тела цикла for не может изменить значение параметра цикла (i) и границ
цикла (а и Ь).
23. Докажите, что инвариантом цикла for в точке входа является
Vj (a<j <i^P(j)).
24. Докажите, что следующие слова являются прямыми допустимыми
правилами вывода:
{а < i < b & Vj(g < j < t -> P(j))}S{Vj(a < j < i P(j))}
{Vj(a < j < i -> P( j)) } for i: =a to b do S od {Vj(a < j < b —> P( j))} ’
~ ________{a < i < b & Vj(i < j < b -> P(j))}S{Vj(i < j < b -> PCj))}_
{Vj(b < j < b -> P( j))} for i:=b downto a do S od {Vj(a < j < b -> P(j))}
https/'и rsit.ru
Упражнение 23
АКСИОМАТИЧЕСКАЯ СИСТЕМА ДЕЙКСТРЫ.
^-ПРЕОБРАЗОВАТЕЛЬ ПРЕДИКАТОВ
Герой получает волшебное
средство и с его помощью сражается
с Антагонистом.
В. Я. Пропп. Морфология сказки
Обязательные результаты обучения:
• знать основные понятия
— гур-преобразователь предикатов (слабейшее предусловие), аксиомы
слабейшего предусловия;
— sp-преобразователь предикатов (сильнейшее постусловие), аксиомы
сильнейшего постусловия;
— дедуктивная wp-семантика команды языка программирования;
— дедуктивная sp-семантика команды языка программирования;
— эквивалентные программы в ivp-семантике;
— доказуемая программа (в системе Дейкстры);
— аксиоматическая система Дейкстры;
— гур-семантика простейших команд skip и trap;
— гур-семантика команды ввода и команды вывода;
— структурные допустимые правила вывода;
— допустимые правила о подпрограммах;
• уметь
— восстанавливать пропущенные фрагменты: в записи аксиом
гур-преобразователя предикатов;
— упрощать слабейшие предусловия;
— устанавливать слабейшие предусловия;
— конструировать доказательства допустимости прямых правил вывода
в системе Дейкстры;
— конструировать доказательства свойств wp-преобразователя предикатов;
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленньх в Упражнении.
Теоретические сведения
Дедуктивная семантика Хоара для языка Н сопоставляет каждой
отдельной конструкции языка некоторое преобразование преди-
506
https: "и rait.ru
катов на множестве состояний памяти. В дедуктивной семантике
Дейкстры для языка D основным инструментом, исполняющим роль
преобразователя предикатов, является предикат, называемый сла-
бейшим предусловием.
Wp-преобразователь предикатов
Пусть St — множество команд языка программирования D, a F—
множество формул в расширенном языке первого порядка.
Определение.
1. Обозначим wp<2> (от «Weakest Precondition», читается: «wp-
преобразователъ формул» или «слабейшее предусловие») — выде-
ленный предикатный символ в расширенном языке первого по-
рядка.
2. Wp-преобразователем предикатов (или слабейшим предусло-
вием) назовём отображение
wp: StxF^F,
являющееся интерпретацией символа wp&X
В дальнейшем будем обозначать wp-преобразователь формул и wp-
преобразователь предикатов одинаковым образом, так как из кон-
текста обычно понятно, о каком математическом объекте идёт речь.
Определим предикатный символ wpW с помощью нелогических
аксиом. Пусть S — программа языка D, a Q и R — формулы расши-
ренного языка первого порядка.
Определение (по [88, с. 115—116]).
Аксиомами слабейшего предусловия называются следующие фор-
мулы:
(Dj) {Q} S {R} (Q wp(S, R)) (аксиома связи тройки Хоара и
слабейшего предусловия);
(D2) wp(S, Л) о Л (аксиома исключённого чуда);
(D3) (R—>Q)—> (wp(S, R) wp(S, Q)) (аксиомамонотонности);
(D4) wp(S, R) & wp(S, Q) о wp(S, R & Q) (аксиома дистрибутив-
ности &);
(D5) wp(S, R) v wp(S, Q) wp(S, R v Q) (аксиома дистрибутив-
ности v для детерминированной команды S);
(D6) wp(S, R) v wp(S, Q) —> wp(S, R v Q) (аксиома дистрибутив-
ности v для недетерминированной команды S).
Замечание.
Э. Дейкстра [89] приводит следующее разъяснение: «Условие, характе-
ризующее множество всех начальных состояний, при которых запуск обя-
507
зательно приведёт к событию правильного завершения, причём система
(машина, конструкция) останется в конечном состоянии, удовлетворяю-
щем заданному постусловию, называется слабейшим предусловием, соот-
ветствующим этому постусловию».
Sp-преобразователь предикатов
Определение.
1. Обозначим sp№ (от «Strongest Postcondition», читается: «sp-
преобразователъ формул» или «сильнейшее постусловие») — вы-
деленный предикатный символ в расширенном языке первого по-
рядка.
2. Sp-преобразователем предикатов (или сильнейшим постусло-
вием) назовём отображение
sp'.FxSt—>F,
которое является интерпретацией символа
В дальнейшем будем обозначать sp-преобразователь формул и sp-
преобразователь предикатов одинаковым образом, так как из кон-
текста обычно понятно, о каком математическом объекте идёт речь.
Приведём некоторые (не все!) аксиомы сильнейшего постусловия.
Определение.
Аксиомами сильнейшего постусловия называются следующие фор-
мулы:
1) {Q} S {К} (sp(Q, S) —>R) (аксиома связи тройкиХоара и силь-
нейшего постусловия);
2) sp(H, S) <-> И (аксиома исключённого чуда).
Дедуктивная семантика команды
Определение.
1. (По [89, с. 36—37]) Дедуктивная wp-семантика команды
S языка программирования (или просто wp-семантика) — это пра-
вило, описывающее, как для заданного постусловия R можно вы-
вести соответствующее слабейшее предусловие wp(S, R).
2. Дедуктивная sp-семантика команды S языка программирова-
ния (или просто sp-семантика) — это правило, описывающее, как
для заданного предусловия Q можно вывести соответствующее
сильнейшее постусловие sp(S, R).
508
https://urajt.rL!
Определение (по [82, с. 90]).
Эквивалентными программами (в wp-семантикё) будем называть
программы S] и S2 такие, что для любого постусловия Q существу-
ет в системе Дейкстры доказательство формулы
wp(S1} Q) wp(S2, Q).
Доказуемая программа в системе Дейкстры
...Н —логический символ, означающий
«доказуемо, что...».
В. Турский [103, с. 45]
Пусть S — программа языка D, Q — предусловие, R — постусло-
вие программы S.
Определение.
Доказуемой программой будем называть программу S, для кото-
рой существует доказательство в системе Дейкстры тройки Хоара
{Q} S {К}.
Предложение (лёгкое).
Для любой программы S и любых формул Q и R в системе Дейк-
стры справедливы следующие прямые допустимые правила вывода:
Q^>wp(S,R) sp(Q,S)^>R
{Q}S{R} ’ {Q}S{R}
Доказательство.
1.
Аксиома (1)
Доказуема {Q}S{R} <^(Q^Wp(S,R))
Q -> iyp(S, R) (Q -> wp(S, R)) -> {Q}S{R} <3^™e
{Q}S{R}
На первый взгляд выполнение прохода «назад по программе»
может показаться странным. Однако преимущество такого способа
заключается в том, что по достижении начала программы мы по-
лучим самое слабое предусловие, выполнения которого достаточно
для подтверждения истинности постусловия.
Термин «самое слабое предусловие» означает, что его «включает
в себя» любое другое предусловие. Более точно, если h (Q —> R), то спе-
циалисты, не занимающиеся математической логикой, говорят, что
«формула Q сильнее формулы R» или «формула R слабее формулы Q>>.
509
Теперь мы завершим доказательство правильности программы,
если покажем, что исходное предусловие включает в себя полученное
самое слабое предусловие, т. е. формула ( Q -> wp(S, R) ) доказуема.
2. Упражняйтесь.
Если мы будем двигаться «вперед» по программе, то при дости-
жении конца программы будем иметь самое сильное постусловие,
вытекающее из известного нам предусловия. Термин «самое сильное
постусловие» означает, что оно предполагает выполнение любых
других постусловий.
Теперь мы завершим доказательство, если покажем, что это
самое сильное постусловие включает в себя исходное постусловие.
Возникающая при таком подходе проблема заключается в том, что
просмотр программы «вперед» приводит к накоплению множества
истинных утверждений, не имеющих отношения к доказательству.
Предложение доказано.
Аксиоматическая система Дейкстры
Определение.
Аксиоматической системой Дейкстры (или просто системой
Дейкстры) для данного языка программирования будем называть
формальную систему, состоящую из:
1) аксиом гильбертовского исчисления первого порядка;
2) основных правил вывода гильбертовского исчисления перво-
го порядка;
3) нелогических аксиом, которыми являются аксиомы слабейше-
го предусловия;
4) нелогических аксиом, которыми являются аксиомы, описыва-
ющие wp-семантику каждой команды рассматриваемого языка
программирования;
5) определения понятия «доказательство тройки Хоара».
https:
Структурные допустимые правила вывода
...определение точного смысла некой
программы требует объяснения того,
что является объектами вычисления
(в некотором смысле статику проблемы)
и каким образом они трансформируются
{динамику проблемы).
Д. Скотт
Теорема (Р^ (усиление предусловия и ослабление постусловия)
[85, с. 37—38].
(V -> Vi), {VJStKi},№ ->К) h {V}S{R}.
510
Ih iroit ri i
Доказательство (содержательное). Если условие V истинно пе-
ред выполнением оператора S, и если (V—> VJ, то V] истинно перед
выполнением S. Если является предусловием для по отноше-
нию к S, то Kj будет истинным после выполнения оператора S. Если,
наконец, CR3 —> R), то и R будет истинным после выполнения опе-
ратора S.
Итак, из истинности V перед выполнением S следует истинность
R после его выполнения. Следовательно, V является предусловием
для R по отношению к S.
Доказательство (формальное). Воспользуемся аксиомами
{V} S {R} <-> (V—>wp(S, R)), (R± -> R) (wp(S, RJ -> wp(S, R)).
Построим непрямой вывод в классическом гильбертовском ис-
числении первого порядка:
______________________D_______________________
wp(S, R^ARi^R)^^ wp(S, R);V^ wp(S, R) I- {V}S{R}
-+R)\-{V}S{R}
wp(S, R) I- wp(S, R)
wp(S, Rj) wp(S, R), wp(S, Rj) I- wp(S, R)
(Ri -^R^^wp^S.RQ^wpQS.R^.wptS.RQARi -+RV-wp(S,R)
wpO^RjMR! ->R)Hwp(S,R); Vi.Vi ->wp(S,R1)l-ivp(S>R1)
V,(V-> Vj)I-Ц; Vi, Vj -> wp(S,Rj),(Rj -> R) I- wp(S,R)
V, (V -> Ц), Ц -> wp(S, RJ, (Rj -» R) I- wpjS, R)
D
Итак, продвигаясь по программе «в обратном направлении»,
можно «усилить предусловие». Усиление может быть достигнуто
путём добавления произвольной формулы с помощью логической
связки & или удаления формулы, «участвующей» в логической связ-
ке V.
В то же время, двигаясь по программе «в прямом направлении»,
можно, как говорят, «ослабить постусловие» путём добавления про-
извольной формулы с помощью логической связки & или удаления
формулы, «участвующей» в логической связке v.
Теорема (Р^ доказана.
Замечание.
Разумное усиление предусловий или ослабление постусловий (что
встречается реже) может привести к сокращению количества преобра-
зований в процессе доказательства. Вместе с тем, здесь следует соблю-
дать известную осторожность, чтобы не усилить предусловие или не осла-
бить постусловие настолько сильно, что нельзя будет завершить доказа-
тельство.
511
https: //ц it.ru
Теорема (DC!) («разделяй и властвуй-1») (по [85, с. 49]).
{ч }S{Ki}, {v2 }S{r2 } h {Vi & v2 & R2 }.
Доказательство.
Аксиома (4)
(упражняйтесь)
l~ wp(S, R,) & wp(S, R2 ) —> wp(S, Rl&R2)
wp(S,R1)&wp(S,R2)Fwp(S,R1&R2)
x x (упражняйтесь)
Ц & V2, Ц -> wp(S, Rj), V2 -> wp(S, R2) I- wp(S, Ri &R2)
V! -nypCS^), V2 -nypteR^I-^&Va &R2) (Дедукция)
{Vi }S{RT}, {V2}S{R2} I- {Ц & V2}S{R! &R2}
Теорема (ВСг) доказана.
Теорема (DC2) («разделяй и властвуй-2») (по [85, с. 50]).
{V1}S{R1},{V2}S{R2} h{Vi v V2}S{R1 vR2}.
Доказательство.
Аксиома (3)
г
Ях ->Ях vR2 Ь wp(S,Ях) -> wp(S,Ях vЯ2)
V2 -> wp(S, R2 ) I- wp(S, Kx ) -> wp(S, Kx v R2 )
ivp(S, Kx), V2 -> wp(S, R2) I- wp(S, Rx vJ?2)
Аксиома (3)
J,
R2 ->Kx vR2 bu'p(S,K2)->U'p(S,Kx vJ?2)
->ivp(S,Kx)l-ivp(S,K2)->ivp(S,Kx vJ?2)
wp(S, Я2), Ц -> wp(S, .Rx) H wp(S, Kx v K2)
V1,V1 -^ivp(S,Kx), V2 ->wp(S,K2)l-wp(S,Kx vR2); V2,Vi ->vip(S,Kx),V2 ->ivp(S,K2)l-ivp(S,Kx vK2)
Vl v V2, Vi -> wp(S,Kx), V2 up(S,Я2) H wp(S,Kx vK2)
Vx -> wp(S,Kx), V2 -> wp(S,Я2) I- Vi v V2 -> wp(S,Kx vK2)
{Vi}S{Kx},{V2}S{K2}HVi v V2}S{KX vR2}
Теорема (DC2) доказана.
Теорема (DC3) («разделяй и властвуй-З») (по [85, с. 51]).
{V}S{Ri}, {V}S{R2} h {V}S{Ri &R2}.
Доказательство.
Аксиома (4)
I
wp(S, Ri ) & wp(S, R2 ) h wp(S, R] & R2 )
V,V^wp(S,Ri),V^wp(S,R2)l-wp(S,Ri&R2)
V wp(S} R^, V -> wp(S, R2) h V wp(S, R! &R2)
{V}S{R1},{V}S{R2}h{V}S{R1 &R2}
Теорема (DC3) доказана.
512
https: 'k: rait.ru
Теорема (DC4) («разделяй и властвуй-4») (по [85, с. 51—52]).
{V}S{RT}, {V}S{R2} h {V}S{KT vR2}.
Доказательство.
Аксиома (4) Аксиома (3)
J, J,
wp(S,Ry)& wp(S,R2) I- wp(S,Ry &R2); Ry&R2—>RyVR2,wp(S,Ry&R2)h wp(S,R1vR2)
wp(S,Ry)&wp(S,R2) hwp(S,Ry vR2)
V, V -> wp(S,Rj), V -> wp(S, R2) I- wp(S, Rj vR2)
V -> wp(S, Ry),V -> wpQS, R2) I- V -> wp(S, Ry v R2)
{V}S{R1},{V}S{R2}I-{V}S{R1 vR2}
Теорема (DC4) доказана.
Предложение (структурные прямые допустимые правила выво-
да).
Следующие слова являются прямыми допустимыми правилами
вывода, которые называются структурными допустимыми прави-
лами вывода:
n (V->Vi) {V1}S{K1} (Hl ->R)
{V}S{R}
(Pi);
2) {V1}S{K1} {V2}S{R2}
(DCj);
3) {Vi}S{Ri} {V2}S{R2}
J {V1vV2}S{R1vR2}
(DC2);
.. ms{Ry} ms{R2y
J
{V}S{Ri&R2}
5) mS{Ry} {V}S{R2}
{V}S{R1VR2}
(DC4).
Доказательство. Упражняйтесь.
Wp-семантика простейших команд
Определение.
Простейшими командами назовём команды skip и trap.
Пусть R — формула.
Определение.
1) up (skip, R) <r^R (аксиома команды skip);
2) up (trap, R) Л (аксиома команды trap).
513
https^^u^'t.ru
Определение (wp-семантика команд skip и trap) [88, с. 117].
def def
1) iyp(skip, R) = R; 2) ivp(trap, R) = JI.
Wp-семантика команды ввода
Помимо команд Дейкстры IFn и DOn, недетерминированность
возникает при использовании команды input(x) — команды ввода
значения переменной х (переменная х принимает значения в мно-
жестве X, содержащее элементы того же типа, что и переменная х).
Определение (по [77, с. 98]).
wp (input (х), R) х g X &CAND VxR (аксиома команды input).
Определение (wp-семантика команды input) (по [77, с. 98]).
def
wp(input(x), R) = xg X&CANDVxR.
Пример.
def
wp(input(k), y = k-x + 3) = Vk(y = k-x + 3).
Выполнение команды ввода input(x) вносит значительную нео-
пределённость в состояние программы, так как значение перемен-
ной х меняется, а вместе с ним могут измениться значения любых
выражений или предикатов, зависящих от этих переменных.
Wp-семантика команды вывода
Определение.
wp(output(х), R) R (аксиома команды output).
Определение (wp-семантики для команды output).
def
wp (output (x), R) = R.
Итак, дедуктивная семантика команды вывода совпадает с де-
дуктивной семантикой команды skip.
514
https:it.ru
Допустимые правила о подпрограммах
Теорема (8Рг) (подпрограмма-!) [85, с. 52].
Если значения всех переменных предиката В остаются неизмен-
ными при выполнении программы S, то доказуема тройка Хоара
{B}S{B}.
Доказательство (содержательное). Если в предикате В исполь-
зуются лишь такие переменные, значения которых одинаковы
до и после выполнения S, очевидно, что значение В до исполнения
S равно значению В после исполнения. Следовательно, В является
предусловием для самого себя по отношению к программе S.
Доказательство (формальное). Нетрудно видеть, что операцион-
ная семантика команды S (по отношению к переменным предика-
та В) совпадает с операционной семантикой команды skip, а тогда
Аксиома команды skip
{B}skip{B}
{B}S{B}
Теорема (8Рг) доказана.
Теорема (SP2) (подпрограмма-2) (по [85, с. 52—53]).
Если значения всех переменных предиката В остаются неизмен-
ными при выполнении программы S, то следующие слова являются
прямыми допустимыми правилами вывода:
ms{R} ms{R}
{V&B}S{R&B}’ {VvB}S{KvB}’
Доказательство (формальное). Теорема (SP2) непосредственно
следует из (8РД (DCj) и (DC2):
(sp)
{V}S{R} {B}S{B}
{V&B}S{R&B} 1 1
(s₽i)
{V}S{R} {B}S{B}mr
{VvB}S{KvB} 1 2)
Теорема (SP2) доказана.
Чтобы применить допустимые правила (SP2), необходимо разде-
лить постусловие на две части: в одной части должны быть ссылки
лишь на те переменные, чьи значения не изменяются в результате
выполнения S (эта часть постусловия является его собственным пред-
условием); во второй части постусловия содержатся все те перемен-
ные, значения которых изменяются в результате выполнения S. Тем
самым будет получено предусловие для этой части постусловия.
И наконец, эти два частных предусловия нужно «объединить»,
образовав требуемое предусловие.
Теорема (SP3) (подпрограмма-3) [85, с. 53—54].
515
https:it.ru
Если значения всех переменных предиката В остаются неизмен-
ными при выполнении программы S, то следующие слова являются
прямыми допустимыми правилами вывода:
(У->У1) {V1}S{K1} (Rj—tR) (V->V1) {V1}S{K1} (Rj—tR)
{V&B}S{R&B} ’ {yvB}S{RvB}
Доказательство (формальное).
(У ->У1) {У1}5{В1} (Bi -+R)
________ms{Ry_________
{V&B}S{R&B}
(Pi)
(SP2)
(У ->4) {У1ЖВ1} (Rj^R) (p)
----------------------(SP2)
{yvB}S{RvB}
Теорема (SP3) доказана.
Итак, часть постусловия, которая зависит от результата выполне-
ния S, может быть более слабой по сравнению с тем постусловием,
которое в действительности устанавливается при выполнении S;
аналогично, соответствующая часть предусловия, которая в дей-
ствительности удовлетворяет до выполнения S, может оказаться
сильнее того предусловия, которое требуется для выполнения S.
Замечание (важное).
Языки императивного программирования обладают богатыми сред-
ствами для описания алгоритмических процессов, но именно из-за этого
возникают трудности с доказательствами свойств программ средствами
содержательной операционной семантики.
Логико-математические языки (т. е. логические языки, формально
описывающие содержательные математические теории) обладают боль-
шой выразительной силой при крайне бедном наборе выразительных
средств. Эти языки придуманы не для того, чтобы на них было легко
и удобно «программировать», а для того, чтобы было удобно доказывать
свойства описываемых объектов.
Семантика типа wp-семантики играет связующую роль между языками
этих двух типов.
Контрольные вопросы
1. Определите понятие «вывод тройки Хоара в системе Дейкстры».
2. Определите понятие «эквивалентные программы» (в семантике Хо-
ара) по аналогии с понятием «эквивалентные программы» (в семантике
Дейкстры).
3*. Расширьте (с обоснованием) список аксиом сильнейшего постусловия.
516
https://urait.ru
Упражнения для самостоятельного решения
Аксиомы wp-преобразователя предикатов
1. Восстановите пропущенные фрагменты в записи аксиом преобразо-
вателя предикатов:
a) (DJ {х = а & у = b}S{x = b&y = a}++ (... -> wp(...,...));
б) (Оз) (... ->...) -> (mtCSA) Ю);
в) (D4) wp(S, х Ф у) & wp(S, х < у) <-> wp(S,...));
г) (D5) wp(Ini,Even(n)&a = n)v wp(Ini,Odd(n)&a = n-l)<-> wp(...,...);
д) (D6) wpQS,...) v wpG..,...) wp(S, BB v -ia).
def def def
2. Пусть wp(S, R) = Odd(x), wp(S, Q) = x = y + 1& Odd(y), wp(S, P) =
def
= Even(x).
Найдите и упростите следующие слабейшие предусловия:
a) wp(S, Q & R); в) wp(S, —R Р);
б) wp(S, R&Pv Q); г) wp(S, -iQ v -iP R).
3. Найдите слабейшие предусловия, если известно, что значения всех
переменных предиката В остаются неизменными при выполнении детер-
минированной программы S:
a) wp(S, Odd(n) & Odd(2 • и) v В); б) wp(S, а> 1 & В & Prime(2 • a)).
4. Верно ли, чтоу > х & a > 0 является слабейшим предусловием для про-
граммы S и постусловия у = q • а + г, если у > х & а > 0 является слабейшим
предусловием для программы S и постусловия у = q- a + r& r<x?
5. Упростите следующие формулы:
а) wp(input(x), х < 0) & ivp(input(y), х > 0);
б) wp(output(m), п э* 2 • m) v wp(input(и), 3 m (n = 2 • m));
в) wp(output(n), Odd(n));
r) wp(output(n), n = k +1) v wp(input(k), 3n(n k + 1).
6. Упростите следующие формулы, если известно, что значения всех
переменных предиката В остаются неизменными при выполнении детер-
минированной программы S:
а) wp(S, Odd(x)) & wp(S, 3n(n > 0 & x = 2n)) & wp(S, Bi);
6) wp(S,d > 1) & wp(S, Prime(c)) & wp(S, c = d • d) -> wp(S, B);
в) wp(S, x < у v B) v wp(S, x = y) v wp(S, x > y).
7. (По [88, c. 121, № 3])
Определим «команду» Сделатъ_истинным для всех формул R так:
def
уур(Сделать_истинным, R) = И.
Почему «команда» Сделать_истинным не является правильной командой?
Прямые допустимые правила вывода
8. (По [88, с. 118])
Установите, являются ли следующие слова прямыми допустимыми пра-
вилами вывода в системе Дейкстры:
Q^>wp(S,R)
} {VxQ}S{VxR}’
Q^>wp(S,R).
J {3xQ}S{3xR}’
517
3xQ->wp(S,R)
{Q}S{R} ;
3xQ -> wp(S, R)
Г) {VxQ}S{3yR} ’
9. (По [88, c. 165, № 1])
Рассмотрим тройки Хоара {Q} S {R}, {VxQ} S {R}, {3xQ} S {R}, где
идентификатор x не используется в команде S и не входит свободно в пре-
дикат R. Предположим, что первая тройка доказуема в системе Дейкстры.
Являются ли доказуемыми вторая и третья тройки?
10*. (По [89, с. 105])
Свойство непрерывности. Установите доказуемость в системе Дейкстры
формулы
wp(S, (Зг > 0)Сг) <-> (3s > 0) wp(S, Cs)
для любой программы S языка D и любой бесконечной последователь-
ности формул Со, Q, С2, ..., таких, что в системе Дейкстры: 1) доказуема
формула Со; 2) доказуемы формулы (Сг Сг+У) для г > 0.
11. Докажите, что следующие слова являются прямыми допустимыми
правилами вывода в системе Дейкстры:
(A&B^C)^wp(S,R) (А -> В) & (А -> С) -> wp(S, R)
3 {A^>(B^>C)}S{R} ’ {A—>B&C}S{R}
12. (По [92, с. 115])
Докажите в системе Дейкстры следующие прямые допустимые правила
вывода, которые будем называть правилами замены:
а) Qi^{Q}S{R}. б) {Qi&Q}S{R}
{Qi&Q}S{R}’ Qi->{Q}S{R}‘
13. Восстановите пропущенные фрагменты доказательства того, что
следующие слова являются прямыми допустимыми правилами вывода
в системе Дейкстры:
ЗхВ(х) -> wp(S, R)
aJ {VxA(x) & (А(х) -> B(x))}S{R} ’
Теорема
—М(х)1~— (введение 3)
—— (введение V)
А(х)—>B(x),VxA(x)H3xB(x) г Теорема
---------------------------(введение &) *
VxA(x) & (А(х) -> В(х)) I- ЗхВ(х);
-----------------------------------------——(сечение)
ЗхВ(х)-> wp(S, R), VxA(x) & (А(х)-> В(х)) I-wp(S, R)
ЗхВ(х) -> wp(S, R) I- {VxA(x) & (А(х) -> B(x))}S{R}
б) ________(D & £ —> С) —> iyp(S, R)__.
J {(A^BvC)&(P^A)&(P&£^-1B)}S{R}’
518
https ://и rait.ru
с:
Теорема D—>A,D\-... f ч (перестановка, расширение) j) у д D & £ у —£ —iC h А Докажите самостоятельно (сечение) ’ (расширение) * — (введение -,) А BvС,DA,D&E —В,D&E h... (сильное удаление -Л A—>BvC,D—>A,D&.E—>—B,...\-... Т* (дедукция) А—>BvC,D—A,D&Е——iBНD&Е—^С', (Р&£->С)->1Ур(5,Л),(А->ВуС)&(Р-> А)&(Р&£->^В)Ьгур(5,Ю (D & Е -> С) -> wp(S, R) h { (А -> В v С) & (D -> А) & (D & Е -> ^В) }S{R}
U1
—1
VO
Свойства wp-преобразователя предикатов
14. (По [88, с. 121, № 1])
Докажите, что определение wp (skip, R) удовлетворяет аксиомам:
a) wp(S, Л) <-> Л;
б) (R->Q)->(wp(S,R)->M/p(S,Q));
в) M/p(S,Q)&ivp(S,R)<^M/p(S,Q&R);
г) ivp(S, Q) v wpQS, R) <-> wpQS, Q v R) (для детерминированных S).
15. (По [88, с. 121, № 2])
Докажите, что определение wp (trap, R) удовлетворяет аксиомам:
a) wp(S, Л) <-> Л;
б) (R^Q)^(wp(S,R)^ivp(S,Q));
в) M/p(S,Q)&ivp(S,R)<^M/p(S,Q&R);
г) ivp(S, Q) v wpQS, R) <-> wp(S, Q v R) (для детерминированных S).
о- Hi iroit ri i
Упражнение 24
WP-СЕМАНТИКА КОМАНДЫ ПРИСВАИВАНИЯ
И КОМПОЗИЦИИ КОМАНД
Пусть У—университет, Г — греческий,
п — профессор, тогда ГП — профессор
греческого.
Л. Кэрролл
Обязательные результаты обучения:
• знать вспомогательные понятия
—уравнения с отношением выводимости;
• знать основные понятия
— аксиома и wp-семантика композиции команд;
— включение утверждения;
— аксиома и wp-семантика команды присваивания;
— sp-аксиома команды присваивания и композиции команд;
— sp-семантика команды присваивания и композиции команд;
— аксиома обновления элемента массива;
— wp-семантика команды присваивания элемешу массива;
— стратегия синтеза команд присваивания;
• уметь
— восстанавливать пропущенные фрагменты в записи аксиом и прямых
допустимых правил вывода системы Дейкстры;
— конструировать доказательства свойств wp-преобразователя предика-
тов;
— вычислять значения wp-преобразователя предикатов;
— устанавливать доказуемость троек Хоара в системе Дейкстры;
— конструировать доказательства допустимости правил вывода в системе
Дейкстры;
— восстанавливать правую часть команд присваивания в тройках Хоара
для их доказуемости в системе Дейкстры;
— решать уравнения в отношениях выводимости;
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
521
https:it.ru
Теоретические сведения
Аксиома и wp-семантика композиции команд
Чтобы добраться до истоков, надо
плыть против течения.
Е. Лец. Непричёсанные мысли
Пусть S] и S2 — команды языка программирования D.
Определение.
wpCSj; S2, R) <-> wp(Sj, wp(S2, R)) (аксиома композиции команд).
Определение (wp-семантика композиции команд) [88, с. 120].
def
wpCSj; S2, R) = wp(Si, wp(S2, Ю)
Примеры.
Вычислим значения следующих wp-преобразователей предикатов:
def def def
1) wp(skip; skip, R) - wp(skip, wp(skip, R)) - wp(skip, R) - R;
def def def
2) wp(trap; trap, R) = wp(trap, wp(trap, R)) = wp(trap, Л) = Л;
def def
3) wp(S; trap, Ю = wp(S, wp (trap, R)) = ivp(S, Л)=Л.
Итак, программа S; trap семантически эквивалентна программе,
содержащей только команду trap, поэтому команда trap приводит
к состоянию — «ловушке», из которого нет выхода.
Теорема (ST) (композиция команд) (по [85, с. 45].
{V}^} {RJS^R}
{V}S1;S2{R}
Доказательство (формальное).
{RJS^R}
Аксиома (3)
4.
Rl^wp(S2,R) (R^ -^wp(S2,R))^(wp(S1,Rl)^wp(S1;wp(S2,R)))
(wp(S1,R1) wp{S1;wp(S2,R)))
V мфС^; wp(S2,R))
V—>wp(S1;S2,P)
{V}Si;$2{R}
Теорема (Sj) доказана.
Важный вывод.
Для того, чтобы отыскать слабейшее предусловие для заданного
постусловия R для композиции команд, вначале отыскивается слабей-
522
http
о Hi iroit г' ।
шее предусловие для R по отношению к последней команде композиции.
Затем его используют в качестве постусловия по отношению к предыду-
щей команде композиции и т. д. Полученное таким образом слабейшее
предусловие для первой команды композиции является также слабейшим
предусловием для R и всей композиции.
Пусть S1 и S2 — программы, Q, R, U — формулы.
Определение (по [99, с. 127]).
Включением утверждения назовём следующее слово:
def def
{Q}Si; {R}S2{U} = {Q}Sa{{R}S2{U}} = Q -> wpCSb R -> wpfS,, LT)).
Аксиома и wp-семантика команды присваивания
Мир познанный есть искаженье мира.
М. Волошин
Пусть Domain^ — предикатный символ арности 1, е — терм
в расширенном языке первого порядка.
Определение.
wp(x := е, R) <-> (Domain(x))* &саж) (R)% {аксиома команды присваи-
вания)
Часто будем записывать аксиому команды присваивания так:
wp(x:=e,R)++(R)*.
Предикатный символ Domain^ будем интерпретировать одно-
местным предикатом (с тем же именем), описывающим множество
всех состояний, в которых значение терма е определено.
Определение (wp-семантика команды присваивания) [88, с. 122].
def
wp(x := е, R) = (Domain(x))* ^cand (R)*
Итак, в описании wp-семантики команды присваивания предикат
Domain «исключает» все состояния, в которых вычисление значения
в не приводит к получению результата (например, деление на 0).
Часто будем записывать wp-семантику команды присваивания так:
def
wp(x:=e,R) = (R)*.
523
https:it.ru
Примеры [88, с. 123].
Вычислим значение следующих wp-преобразователей предикатов
и «упростим» полученные формулы (С. Клини [21, с. 46] о смысле тер-
мина «упрощение формулы» пишет следующее: «Говоря, что некоторая
формула F „проще”, чем другая формула Е, мы будем иметь в виду практи-
ческую точку зрения: с F легче оперировать, ее легче понять, независимо
от того, короче она или нет. Простота — это вопрос привычки и зависит
от облика часто встречаемых формул»):
def def
1. wp(x := х, R) = (R)* = R,
t. e. wp-семантика команды присваивания x := x совпадает c wp-семантикой
команды skip;
def
2. wp(x:= e, x = c) = (x = c)f = e = (c)f =e-c, еслиc — константа;
def
3. wp(x := e, у = c) = (y = c)f = у = с, если c — константа.
Этот важный пример показывает, что выполнение команды присва-
ивания для одной переменной (х) не может изменить значение другой
переменной (у); в этом случае говорят, что «при выполнении команды при-
сваивания не допускаются побочные эффекты»',
def
4. wp(x := 5, х = 5) = (5 = 5) = И; ясно, что ValM a p(wp(x := 5, х = 5)) = 1;
5. wp(i:=i+l,i<l) = i+l<l = i<0;
def
6. up(x:=a-5-b,P(1)(x)) = b^0&CAND Р(1)(ач-Ь);
7. если [0,10] — область значений индексов массива В, то
def
wp(x := B[i], х = B[i]) = 0 < i < IO&cand (B[i]=B[i]) - 0 < i < 10.
Теорема (Aj) (проверка предусловия команды присваивания)
(по [85, с. 40]).
у->(Юе*
{V}x:=e{R}
(Ат)
Доказательство (содержательное) [85, с. 40].
Если V —> (R)* и {(R)*}x := e{R}, то из правила вывода (Р2) следует,
что V является предусловием для R по отношению к команде присва-
ивания. Из аксиомы следует, что {(R)£}x := e{R}. Поэтому достаточ-
но показать, что V (R)%, если требуется доказать, что {V}x := e{R}.
Доказательство (формальное).
V^>(R)* wp(x:=e,R)++(R)*
V wp(x := е, R)
{V}x:=e{R}
Теорема (Аг) доказана.
524
Замечание.
1. Модели языков программирования, рассмотренные Ч. Хоаром
и Э. Дейкстрой, содержат команду присваивания, аксиома Хоара (Н2)
которой описывает получение слабейшего предусловия по задан-
ному постусловию. Этим и обосновывается связь тройки Хоара
с wp-преобразователем предикатов.
2. Уже для программ, содержащих только команды присваивания,
видно, как различаются логическое толкование программ (аксиомати-
ческая семантика) и их операционное толкование (операционная семан-
тика) : если для операционного толкования легко объяснить, что изме-
нится в состоянии памяти после исполнения той или иной конструкции
языка программирования, но редко можно восстановить то, что было
до исполнения, то при логическом толковании — наоборот.
3. [96, с. 32] В реальных языках программирования описание семан-
тики оператора присваивания содержит достаточно много подробностей
и оговорок.
Sp-семантика команды присваивания
и композиции команд
Великой истиной может
называться лишь та истина, чья
противоположность — также
великая истина.
Н. Бор
Пусть Q — формула, S — программа.
Определение.
1) sp(Q, х := е) <-> Эу( [Q]* & х[е]* ) (sp-аксиома команды присваива-
ния или аксиомаР. Флойда);
2) sp(Q, Sj; S2 ) о sp(sp(Q, Sj), S2 ) (sp-аксиома композиции команд)
Определение (sp-семантика команды присваивания и компози-
ции команд) (по [88, с. 125]).
def
1) sp(Q,x:=e) = 3y([Q]* &х[е]*);
def
2) sp(Q,S1;S2) = sp(sp(Q,S1),S2).
По меткому замечанию С. С. Лаврова [96, с. 33], «квантор суще-
ствования приносит мало радости (если, вернувшись домой, Вы об-
наружили, что квартира ограблена, то Вы знаете, что кто-то сделал
это, но ещё неизвестно, будет ли он пойман?)».
525
https: it.ru
Примеры.
Вычислим значение следующих sp-преобразователей предикатов:
def
1) sp(x = 2, х:=5) = Ну(у = 2&х = 5);
def
2) sp(a = a0&b = b0,z:=a;a:=b;b:=z') =
def def
= sp(sp(a = a0&b=b0,z:=a),a:=b;b:=z') =
def def
dff spGyi([a = do & b=b0]^ & z = [a]^ )flg:= b; b := z) =
= sp(a = a0&b=b0&z = a;a:=b;b:=z) =
def def
= sp(sp(a = a0&b=b0&z = a,a:=b)Jb:=z) =
def def
= spCByiCta = do & b=b0 & z = a]^ & a = [b]^ ), b := z) =
def def
= $pGy1(y1=d0&b = b0&z = y1&d = b),b:=z) =
def def
= Эу2([Зу1(У1 =a0&b=b0&z = y1&d = b)]b2&b = [z]y =
def
= By2 Gyi (У! = do & y2 = b0 & z = У! & a = y2 ) & b = z).
Теперь легко получить, что
sp(d = Oq & b=b0, z := a; a := b; b := z) -
= b = z&By2(y2 =b0&d = y2&Ey1(y1=d{)&z = y1)) = b = z&b0 =d&do=z =
= d=bo&b = cio.
Аксиома обновления элемента массива
Есть множество способов для того,
чтобы понять, уточнить, а значит,
испортить поэзию вещи.
А. Арто
Определение [88, с. 96].
(В; i: е) [j] = ег <-> i = j & е = ег v i j & B[j] = ег (аксиома обновления
элемента массива В)
Примеры [88, с. 98].
Опираясь на аксиому обновления элемента массива, упростим следу-
ющие формулы с помощью устранения обновления массива В:
def
1) (B;i:5)[j] = 5 = i = j&5 = 5x/i*j&B[j] = 5 = i = jvB[j] = 5;
526
iroif ri I
def
2) (В;i:5)[i] = (В;i:5)[j] = i = i&(B;i:5)[j] = 5vi^i&B[i] = (B;i:5)[j] =
def
= (B;i:5)[j] = 5 = i = j&5 = 5 vi^ j&B[j] = 5 = i = j vB[j] = 5;
def
3) (B; i: B[i]) [i] - i - i - i& i - B[i] = B[i] - i;
def
4) (B; i: B[i]) [j] = (B; j: B[j]) [j] =
def
= i = j & (B; j: B[ j] ) [ j] = B[i] vi*j&(B;j: B[ j] ) [ j] = B[ j] ) =
= i = j&B[j] = B[i] v i Ф j&B[j] = B[j] = i = j v i * j = И.
Wp-семантика команды присваивания элементу массива
Определение.
wp(B[i] := t, R) о Inrange(B, i) &CAND Domain(t) &cand (K)^B;i:t)
(аксиома команды присваивания элементу массива)
Определение (wp-семантика команды присваивания элементу
массива) [88, с. 129].
def
wp(B[i\:=t,R) = Inrange(B,i)&CAND Domain(t)&CAND (К)(в;ад-
Часто будем записывать wp-семантику команды присваивания
элементу массива так:
def
wp(B[i] := t, R) = Inrange(B, i) &CAND (K)®B.i:t).
Замечание (no [88, c. 131]).
Обозначение (В; i: t) мы будем использовать при определении присва-
ивания элементам массива и при доказательстве правильности программ,
но не в программах на языке D.
Из традиционных соображений команда присваивания элементу мас-
сива в программах записывается в виде В [i] := t.
Примеры [88, с. 130—131].
Пусть массив В описан как В [О: п -1], а все индексы находятся в необ-
ходимых границах. Определим и упростим слабейшие предусловия:
def def def
1. wp(B[i] := 5, B[i] := 5) = (B[i] := 5)fB;i:5) = (B; i: 5) [i] = 5 = 5 = 5.
Легко получить, что ValM a p(wp(B[i] := 5, B[i] := 5)) = 1.
527
https: "lira it.ru
def def def
2. wpCB[i] := 5, B[i] = B[j]) = (B[i] = B[j])fB;i:5) = (B; i: 5) [i] = (B; i: 5) [j] =
def def
= (B;i:5)[j] = 5 = i = j&5 = 5vi^j&B[j] = 5 = i = jvB[j] = 5.
Руководствуясь только интуитивными соображениями, можно «поте-
рять» формулу i =j, однако wp-семантика превосходит интуицию.
def
3 wpCB[B[i] ] := i, B[i] = о = (B[i] = i)fB;B[i]:i) = (В; B[i]: i) [i] = i =
= B[i] / i& B[i ] - i v B[i ] - i & i - i = B[i] - i.
Выполните данный пример, используя только содержательную опера-
ционную семантику команды присваивания В [В [i] ] := i.
def def
4 M/p(B[i] := i, B[B[i]] = i) = (B[B[i]] = i)fB;i:i) = CB; i: i) [(B; i: i) [i]] = i =
= i=(B;i:i) [i]&i = i vi * (B;i: i) [i]&B[(B; i: i) [i]] = i=И,
def
так как (В; i: i) [i] = i = i = i&i = ivi^i&B[i] = i = H.
def def
5. wp(B[i] := 5, (3j g [i, n)) (B[i] < B[j])) = ((Bj g [i, n)) (B[i] < B[j]))fB;i:5) =
def
= (3j G [i, n)) ((B; i: 5) [i] < (B; i: 5) [ j]) = (3j g [i, n)) (5 < (B; i: 5) [ j]) =
= (3jG[i,n))(i = j&5>5vi^ j&B[j]>5) = (BjG[i,n))(i = jvB[j]>5).
Замечание [85, c. 55].
Приведём сводную таблицу, предназначенную для выбора одной
из рассмотренных выше теорем в зависимости от вида команды про-
граммы и от того, задано ли предусловие или же его следует получить.
Вид команды Предусловие... Теорема
Последовательность команд ...задано ...требуется получить или (SJ + (PJ (SJ
Команда присваивания ...задано ...требуется получить (Ai)
Синтез команд присваивания
Доказательство должно появляться
как приятный сюрприз.
Критерий Г. Харди
Wp-семантика может использоваться для построения команд
присваивания. Пусть {Q}x := t{R} — тройка Хоара, где t — неизвест-
ный терм (разумеется, его местность также неизвестна!).
528
https:it.ru
Поставим задачу о нахождении терма t такого, что тройка
{Q} := t{R} является доказуемой в системе Дейкстры (называемую
также задачей о синтезе команды присваивания).
Легко видеть, что
{Q}x := t{R} = Q -> wp(x -.= t,R) = Q^> (К)?.
Отсюда следует следующая стратегия синтеза команды присва-
ивания.
Решите уравнение с отношением выводимости
HQ->(P)?
относительно неизвестного терма t (при этом рассмотрите различ-
ные значения местности терма).
Понятие «уравнение в отношениях
выводимости» в языке Н
Добавим к терминальному алфавиту языка Н букву «?», которая
обозначает неизвестную формулу языка первого порядка.
def
В результате получим алфавит AHs = Ан и{?}.
Определение.
Уравнением в отношениях выводимости для языка Н будем назы-
вать слово одного из следующих видов:
1) h{P}S{?}
2) h{?}S{Q};
3) {?}S{Q},A1,A2,...,AnhB;
4){P}S{?},A1,A2,...,AnhB,
где В — тройка Хоара, Д- — либо формула языка первого поряд-
ка, либо тройка Хоара.
Пусть дано уравнение в отношениях выводимости для языка Н.
Определение.
1) Будем говорить, что формула F является решением уравнения
в отношениях выводимости 1, если
h{P}S{F},
т. е. F — постусловие, показывает, в каком состоянии завершит-
ся программа S при предусловии Р;
2) Будем говорить, что формула F является решением уравнения
в отношениях выводимости 2, если
h{F}S{Q},
529
т. е. F — предусловие, показывает, каким должно быть предусло-
вие, чтобы данная программа завершилась в состоянии, удовлет-
воряющим Q;
3) Будем говорить, что формула F является решением уравнения
в отношениях выводимости 3, если
{F}S{Q},А1,А2,...,АП НВ,
т. е. ищем предусловие тройки Хоара таким образом, чтобы из ис-
тинности А1г А2, • ••, Ап и соответствующей тройки Хоара {F}S{Q}
следовала истинность тройки Хоара В;
4) Будем говорить, что формула F является решением уравнения
в отношениях выводимости 4, если
{P}S{F},A1,A2,...,AnhB,
т. е. ищем постусловие тройки Хоара таким образом, чтобы из ис-
тинности А1г Д2, ..., Ап и соответствующей тройки Хоара {P}S{F}
следовала истинность тройки Хоара В.
Определение.
Будем говорить, что формула F является тривиальным решени-
ем уравнения в отношениях выводимости, если:
1) F — общезначимая формула (для уравнений типа 1 и 4);
2) F — невыполнимая формула (для уравнений типа 2 и 3).
Все остальные решения уравнений в отношениях выводимости
будем называть нетривиальными решениями.
Определение.
Решить уравнение в отношениях выводимости — это означает
найти хотя бы одно из его нетривиальных решений.
Для решения уравнений в отношениях выводимости использует-
ся классическое гильбертовское исчисление первого порядка с до-
пустимыми правилами вывода.
Работа с примерами решения некоторых упражнений
См. Пример 5, Пример 6.
Контрольные вопросы
1. Сформулируйте и докажите обобщение теоремы CSX) на композицию
п команд, п > 2.
2. Вычислите и упростите результаты операции wp:
а) шр(х := х - у, х-у = с);
б) wp(B[i] := 3; В[2] := 4, В[i] = 3);
530
в) wp(B[i] := 4; B[2] := 4, В[i] = 3).
3. [97, с. 169]
Пусть перед присваиванием а[а[2]] := 1 переменные а[1] и а[2] имеют
значение 2. Каким значением будут обладать переменные а [1], а [2] и а [а [2] ]
после исполнения присваивания?
4. [82, с. 90]
Установите, что формула Q —> wp(x := х2, х > 0) доказуема в системе
Дейкстры для любой формулы Q.
5. (По [88, с. 121, № 6])
Докажите, что ivp(x := е; trap, R) = Л для любого предиката R безотноси-
тельно к определению wp(x := е, R).
Примеры решения некоторых типов упражнений
Пример 1. [81, с. 53] Установите, что тройка Хоара
{а - Oq&b - b0} zа; аb; bz{b= aQ&a = b0}
является доказуемой в системе Дейкстры.
Решение. Вычислим значение wp-преобразователя предикатов:
def
wp(z:-a;a:-b'b :=z,b = aG&a =b0) = wp (za; a b, wp(b :=z,b = aG&
def def
a = b0)) - wp(z :=a;a:=b,z = a0&a = b0) - wp(z := a, wp(a :=b,z = a0&a = b0))
def def
= wp(z :=a,z = a0&b = b0) = a = aG&b = bG.
Следующее дерево прямого вывода завершает доказательство:
a = a0&b = b0^a = a0&b = b0 , л
-------------У------у------У----у----------(замена равного на равное)
а-а^&Ь-Ьо^ wp(z :-a;a:-b;b:-z,b-aG&a-b0)
{a = a0&b = b0}z:=a;a:=b;b:=z{b = a0&a=b0}
Пример 2. Установите, что является доказуемой в системе Дейкстры
тройка Хоара {S = х • у & -iOdd(x) }у := 2 • у; х := х -s-2{S = х • у}.
Решение. Вычислим значение wp-преобразователя предикатов:
def def
wp(y :=2y;x:=X4-2,S=xy) = wp(y :=2y;wp(x:=X4-2,S=xy)) =
def def
= ivp(y:=2y;S = (xH-2)y) = $=(х^2)-2-у.
Следующее дерево прямого вывода завершает доказательство:
Докажите самостоятельно в теории S (для знатоков!)
S=xy&-iOdd(x)—>S = (x+2)2y f
-------------------—-------------—---------(замена равного на равное)
S = x-y&-iOdd(x)—>wp(y:=2-y;x:=X4-2,S = x-y)
{S = х • у & -iOdd(x) }у := 2 • у; х := х ч- 2{S=х • у}
531
https: "и rait.ru
Пример 3 [88, с. 128—129]. В каждой из следующих троек х — это
неизвестный терм, который необходимо определить:
1) {И}Ь:=х;а:=а+1{Ь = а+1};
2) {И}а:=а+1;Ь:=х{Ь = а+1}.
Решение.
def def
1) wp(b:=x;а:= а+1,b = a+l) = wp(b:=x,(b = a+l)“+1) =
def def def
= wp(b:=x,b = a+2) = (b = a+2')b = x = a + 2;
def def
2) wp(a:= a+l;b:=xb = a+1) = ivp(a:=a+l,(b = a+l)^) =
def def def
= wp(a:=a+l, x = a+l) = (x = a+l)“+1 = (x)“+1 = a+2.
Потребуем доказуемость формулы И —> (х)“+1 = a+2.
Пусть арность терма х равна 1, т. е. х=х(а), тогда доказуемой должна
быть формула (х)“+1 = a+2 или х = a +1.
Пример 4. Восстановите правую часть команды присваивания (обо-
значенную знаком «?») в следующем программном фрагменте:
{x = X&y = Y}x:=x-y;y:=x+y;x:=?{x = Y&y = X}.
Решение. Обозначим искомый терм t (с неизвестной арностью).
Тогда
def
wp(x:=x-y;y:=x+y‘,x:=t,x = Y&y = X) =
def def
= wp(x:=x-y;y:=x+y,t = Y&y = X) =
def def def
= wp(x:=x-y,(t = y&x+y=X)J+y) = wp(x:=x-y,(t)x+y = У&х+у = Х) =
def def
= «0?+у = У & x + у = ХУх-у = ((tg+y)J_y = у & X = X.
Теперь потребуем, чтобы формула
(х=X & у = У) -> (((t)£+yМ-у = У & х=X) или ((t)?+y )J_y = У
была доказуема в системе Дейкстры.
Пусть, например, арность терма t равна 2, т. е. t = t(x,y), тогда
def def
C(t)£+y)£-y = (t(x,x + y))*_y = t(x-y,x).
Остается решить уравнение t(x-y, х) =у. Переобозначив переменные
Xj =х-у,у1 =х, получим tCx^yJ =yj -Xj или t(x,y) =у—х.
Итак, искомый фрагмент программы имеет следующий вид:
х :=х-у;у: =х+у;х: =у-х.
Пример 5. Решите уравнение в отношениях выводимости вида:
{?}S{Q} Н {А ->(В C)}S{Q}.
532
https: //u rait.ru
Решение. Для его решения требуется найти формулу F:
{F}S{Q} \-{А^>(В^> C)}S{Q}
(2)
4.
\-(A—>(B—>C))—>F; (A^(B^C))^F,{F}S{Q}^{A^(B^C)}S{Q}
(сечение)
{F}S{Q} Н{А (B—>C)}S{Q}
Итак, необходимо найти формулу F такую, что (А -> (В —> С)) Н В. Пред-
положим, что искомой формулой является (А & В) —> С.
Для проверки покажем, что I- (А -> (В -> С)) I- ((А & В) -> С) :
Ах5
г
НА&В—>В
{В->С,В}НВ->С; {А&В}НВ
НА&В—>А {А->(В->С),А}НВ->С;{В-> С, А&В} НС
{А&В} НА; {А -> (В -> С), А, А&В} Н С
{А->(В->С),А&В}НС
{А->(В->С)}Н(А&В)->С
(сечение)
(сечение)
(сечение)
(дедукция)
Итак, (А & В) —> С—искомое решение.
Пример 6. Проверим, является ли формула (А & -А) решением урав-
нения в отношениях выводимости вида Н {?} S {Q}.
Решение. Известно, что имеет место Н {Л} S {Q}, поэтому для проверки
достаточно показать, что Н -i(A & -А):
Ах4
г
Ах5
1
НА&-А->А НА&-А->А
(дедукция)
(введение —)
{А&-А}НА; {А&—А}Н—А
Н—(А&—А)
Итак, (А & -А) — решение данного уравнения.
Упражнения для самостоятельного решения
Аксиомы wp-преобразователя предикатов
1. Восстановите пропущенные фрагменты в записи формул и прямых
допустимых правил вывода системы Дейкстры:
a) wp (skip; S1} а = Ь) <->... (wp-аксиома композиции команд);
def
б) wp(x :=..., х > 2) = (Domain (х))^ &CAND (...)?
(wp-аксиома команды присваивания);
def
в) wp(x := s,...) = (Domain(х))* &CAND (Q & D)x
(wp-аксиома команды присваивания);
г) ((В;j + l:t);i:t)[k] = t++...
(аксиома обновления элемента массива);
533
https/'u^'t.ru
д) wp(B[...] :=t,R) <-> Intrange(..., j) &cand Domain(...) &CAND (R)(B;...;t)
(аксиома команды присваивания элементу массива);
...->(...)?
{V}... := ...{R}
ж) sp(R,... :=...) Зу([...]* & х = Q]*)
(sp-аксиома команды присваивания или аксиома Р. Флойда);
з) sp(..., S1; S2) sp(sp(s = а + Ь,...), S2)
(sp-аксиома композиции команд);
def def
и) {Q}S];{...}S2{...} ={...}S2 {{₽}...{...}} = Q^M/p(S1,P^M/p(...,W))
(включение утверждения).
Свойства wp-преобразователя предикатов
2. (По [88, с. 121, № 4; № 5; 89, с. 53])
Пусть для программ и S2 выполняются аксиомы слабейшего пред-
условия. Докажите, что определение wp(Sx, S2; R) удовлетворяет аксиомам
слабейшего предусловия:
a) wp(S, Л) <-> Л;
б) (R Q) (wp(S, R) -> wp(S, Q));
в) wp(S, Q) & wp(S, R) <-> wp(S, Q & R);
г) ivp(S, Q) v ivp(S, R) <-> wp(S, Q v R),
т. e. композиция команд «не вносит недетерминизма».
3. (По [88, с. 125, № 2])
Докажите, что определение ир(х := t, R) удовлетворяет аксиомам сла-
бейшего предусловия:
a) wp(S, Л) <-> Л;
б) (R -> Q) -> (wp(S, R) wp(S, Q));
в) wp(S, Q) & wp(S, R) <-> wp(S, Q & R);
r) ivp(S, Q) v wp(S, R) wp(S, Q v R),
т. e. команда присваивания является детерминированной командой.
Вычисление значений wp-преобразователя предикатов
4. [88, с. 131]
Упростите следующие слабейшие предусловия (массив В описан
какВ[О: п - 1], причем все индексы находятся в необходимых границах):
a) ivp(B[i] := 5, (3j g [i, n)) (B[i] < BQ]));
6) n/p(B[i] := 5, B[0: n - 1] = C[0: n - 1]);
в) wp(B[i] := B[i - 1] + B[i], BQ] = B[l] + B[2] + ... + BQ - 1]);
r) wp(t := B[i]; B[i] := BQ]; BQ] := t, B[i] = x & BQ] =y);
д) wp(tB[i]; B[i] := BQ]; BQ] := t, k * i & k * j & B[k] - C).
5. [88, c. 98]
Упростите следующие формулы, устранив обновление массива В:
а)
б)
в)
6.
Найдите предусловие тройки Хоара {?} В [В [2]] := 1 {В [В [2]] = 1} такое,
чтобы тройка стала доказуемой в системе Дейкстры.
7. (По [84, ч. 2, с. 569; 88, с. 125, № 5])
Доказуема ли в системе Дейкстры формула
(CB; i: B[i]); j: BQ])Q] = ((B; j: BQ]); i: B[i])Q];
((B; i: BQ]); j: BQ])Q] = ((B; j: BQ]); i: BQ])Q];
CCB; i: BQ]); j: BQ])[i] = ((B; i: BQ]); j: BQ])Q].
(По [99, c. 118])
Q <-> wp(x1, sp(Q, x1))?
534
https ://игз it.ru
8. (По [85, с. 59—60])
Определите слабейшие предусловия для следующих троек Хоара:
а) {?}х :=z-y{x-y> 0};
б) {?}х := z-у(у-х > 0};
в) {?}i := i + 1 {i > 1};
г) {?}s :=s + z{s=x+y + z};
Д) {?}* := 5 - z{w • у - 2 • iv2 < z}.
Доказуемость троек Хоара в системе Дейкстры
9. Доказуемы ли следующие тройки Хоара в системе Дейкстры:
а) {10 <у<х&0<х< 13} х := х - 5 {10 < у & х < 8};
б) {п<т}п:=п + т{п<2т};
в) {z = аъ & -iOdd(b)} Ъ := Ъ 4-2; а := а • a {z = аь};
г) {х = Y & у = X} х := х + у; у := х - у; х := х - у {х = X & у = У};
д) {И} V] := х • х; v2 := v1 • v1; v3 := v2 • x; у := v3 • v3 {y = x10};
e) {x = X & у = Y & z = Z} w := x + у; x := у + z; у := z + w; z := w + x;
w := у - z; x = z - w; у := w - x; z := x - у
{w = -Y&x = X + 3Y + Z&y = -X-4Y-Z&z = 2X + 7Y + 2Z}.
10. (По [88, c. 125, № 4])
Покажите, что выполнение x := t при истинном Q обязательно завершится
при истинном sp(Q, х := t), т. е. тройка Хоара
{Q}x:= t{sp(Q,x:=t)},
доказуема в системе Дейкстры (говорят, что «определение sp(Q, х := t)
согласовано с моделью выполнения присваивания»).
11. (По [82, с. 90])
Покажите, что программы х :=у; х :=у и х :=у эквивалентны в семантике
Хоара и в семантике Дейкстры.
12. Установите, что формула {Q}skip{K} <->(Q—>R) доказуема в системе
Дейкстры.
Прямые допустимые правила вывода в системе Дейкстры
13. (По [99, с. 110; с. 127])
Докажите, что:
а) ШВД} .
{Q}S;x:=t{K}’
б) {Q}S{(^:t)} .
{Q}S; B[i] := t£R}’
{Q}S{Q}
в)
д)
{включение команды);
{Q}S1{K}<^{Q}S;S1{K}
---------------(правило включения утверждения);
{QlS-ARys^W}
{Q}S {Rys^W} . «. .
------------(правило исключения утверждения).
{Oys-^w}
535
https:it.ru
Синтез команд присваивания
14. Восстановить правую часть команды присваивания (обозначенную
знаком «?») таким образом, чтобы перечисленные ниже тройки Хоара были
доказуемыми в системе Дейкстры:
а) {z-2-у >0}х:=?{х-у >0};
б) {2-y-z>0}x:=?{y-x>0};
в) {i >0}i :=?{i>l};
г) {sum+ z = x + у + z}sum := ?{sum = x + у + z};
Д) {w-y-2-w2 <z}x :=?{w-y-2-w2 < z};
e) {10<y&x<13}x:=?{10<y&x<8}.
15. [88, c. 128—129]
Определите неизвестные термы (обозначенные t и U) таким образом,
чтобы тройки Хоара были доказуемыми в системе Дейкстры:
a) = + =
б) {i = j}j:=t;i:=i + l{i = j};
в) {z + a • b = c}z := z + b; a := t{z + a • b = c};
r) {H}i := 0; s := t{s = B[0] + B[l] +... + B[i -1]};
д) {i > 0 & s = B[0] + B[l] +... + B[i -1]}i := i +1; s := t{s = B[0] + B[l] +... + B[i]};
e) {x = X&y = Y}x:=x-y,y:=U;x:=y-x{x = Y&y = X}.
16. Проверьте, каким из следующих термов может быть заменен неиз-
вестный терм t в тройке Хоара
{z + a-b = c}z:=z + b;a:=t{z + a-b = c} так, чтобы она стала доказуемой
в системе Дейкстры:
a) t - а - Ъ; б) t - а - 1; в) t - а • а.
Решение уравнений в отношениях выводимости
17. Решите следующие уравнения в отношениях выводимости:
1) {?}S{Q},{CvB}S{Q}l-{AvC}S{Q};
2) {?}S{Q}H{V1&V2}S{Q};
3) {?}S{Q} Н Р —> {K}S{Q};
4) {P}S{?}H{P}S{Vx(EvC(x))};
5) {P}S{—A—>B},{Pi}S{?}\-{P1&P2}S{A};
6) {P}S{A -> B}, {P}S{C -> D}, {P}S{-^B & -,D} I- {P}S{?};
7) {A}S{Vi}, {?}S{V2} b{A v(B С)}£{Ц & V2};
8) {A & В C^PJ, {A & -.C}S{P2} I- {?}S{^ & P2}.
Ответы: 1) A v —B; 2) или V^, или V2; 3) P & R; 4) E v VxC(x); 5) C & —B;
6) -A & -iC; 7) В —> С или -B v C; 8) —B.
18. Проверьте, является хотя бы одна из формул -i(-B v А), В, -А & В,
В v —А решением уравнения в отношениях выводимости вида:
{B}S{Q1},{?}S{Q2} I- {?}S{Q1 & Q2}.
19. Проверьте, является хотя бы одна из формул A v —А, (А —> В) & С,
—А & —В решением уравнения в отношениях выводимости вида:
А В, {Pr}S{A & —В}, {P2}S{?} I- {Pi v P2}S{?}.
https:it.ru
Упражнение 25
ИФ-СЕМАНТИКА КОМАНДЫ ВЫБОРА
ДЕЙКСТРЫ
Выражение «tertium non datur» есть,
собственно, бессмыслица. (Ибо в р v —р
ни о каком третьем нет и речи.')
Л. Витгенштейн
Обязательные результаты обучения:
• знать вспомогательные понятия
—уравнения с отношением выводимости;
• знать основные понятия
— аксиома команды выбора IFn;
— wp-семантика команды выбора IFn;
— основная теорема о команде выбора Дейкстры;
— теорема о команде ветвления языка Н;
— wp-семантика частных случаев команды выбора;
— допустимые правила вывода для команды выбора;
— стратегия синтеза команд выбора;
• уметь
— определять wp-семантику команд выбора;
— вычислять значения wp-преобразователя предикатов;
— устанавливать доказуемость троек Хоара в системе Дейкстры;
—синтезировать команды выбора в соответствии с поставленной задачей;
• владеть
— основными понятиями, представленными выше;
— методами решения задач, представленньх в Упражнении.
Теоретические сведения
Аксиома и wp-семантика команды выбора Дейкстры
Напомним следующие обозначения:
def
1) IFn = if Bi =>S!OB2 =>S2a...aBn =>Sn fi;
def
2) BB = Bj vB2 v...vBn;
def
3) I6[l,n] = i6{l,2,...,n}.
537
https://игаit.ru
Определение.
wp(IFn,R)<^Domain(BB)&(3iG[l,n])BI-&(Viе[1,п])(Вг ~^wp(Si}R))
(аксиома команды выбора IFn).
Определение (wp-семантика команды выбора IFn) [88, с. 137].
def
wp(IFn,R) = Domain(BB)&BB(V16[l,n])Bi ~^wp(Si}R)).
Первый конъюнктивный член в определении wp-семантики ко-
манды выбора IFn указывает на то, что все охраны должны быть
определены, второй — на то, что по крайней мере одна охрана
должна быть истинной, а остальные — на то, что выполнение лю-
бой команды Sf, для которой охрана Bf истинна, заканчивается при
истинном значении R.
Используем следующие формы записи аксиомы команды выбора:
1) wp(IFn,R)<^(3iG[l,n]^&(У1с[1,п])(Д ->wp(SifR')');
2) wp(IFn,B)^BB&(ViG[l,n])(Bi ->wp(Sf,R));
3) wp(IFn, R) <-> (Д vB2 v... vBn)&(Bi -> wp(S1,R))&...&(Bn ->
^>wp(Sn,R)).
Основная теорема о команде выбора Дейкстры
Предложение (теорема о команде выбора Дейкстры)
(по [88, с. 140—141]).
В системе Дейкстры доказуема следующая формула:
(Q -> wp(IFn, R)) <-> (Q -> ВВ) & (Vi g [1, и]) (Q & Д -> wp(Sf, R)).
Доказательство.
1. Установим доказуемость следующей формулы, важной для
практического использования:
(Q -> ВВ) & (Vi g [1, n])(Q & Д -> wp(Sf,R)) ->(Q -> wp(IFn, R)).
Построим непрямой древесный вывод:
(Q -> ВВ), (Vi е [1, и])(Q&Bf -> wp(S,, R)) h (Q -> ВВ) & (Vi е [1, и]) (Q&Bf -> wp(S,, R))
(Q ВВ), (Vi е [1, n]) (Q & В,-> wp(Si,R)) h (Q -> ВВ) & (Vi е [1, и]) (Q -> (В, wp(Si}R)))
(Q -> ВВ), (Vi е [1, п]) (Q & В,-> wp(Si,R)) h (Q -> ВВ) & (Q (Vi е [I, и]) (В, -> wp(S,; R)))
(Q^BB),(Vie[l,n])(Q&Bi ->wp(S;,R))HQ->BB&(Vie[l,n])(Bi -+wp(Si,R))
(Q -> BB) & (Vi e [I, n]) (Q & Bf -> wp(St, R)) H (Q -> up(IFn, R))
h (Q -> BB) & (Vi g [1, n]) (Q & B; -> wp(St, R)) -> (Q -> wp(IFn, R))
2. Доказуемость формулы
(Q wp(IFn, R)) (Q BB) & (Vi G [1, n]) (Q & Д wp(Sf, R))
538
https: "'j rait.ru
установите самостоятельно.
Предложение доказано.
Следствие 1.
В системе Дейкстры доказуема следующая формула:
(R & ВВ wp(IFn ,R))++(\/ic [1, n]) (R & Bi wp(S,, R)).
Доказательство. Установим лишь доказуемость формулы
(Vi g [1, n]) (R & Bi wp(St ,R))^>(R&BB^> wp(TFn, R)):
Аксиома i G и] -> (R & В; -> Wp(Si, R)) R&BB&Bj^R&Bj R&Bf->(ig[1, и]->wp(Sf,R)) R&BB&B; ->(ig[1,и]->ivp(Sf,R)) i e [1, n] -> (R & BB & B, -> wp(S,, R)) Аксиома Vi(ig[1,n]->(R&BB&Bi-> wp(Si,R))) R&BB^BB (ViG[l,nB(R&BB&Bi ->wp(Si,R)) (удаление V) (перестановка посылок) (транзитивность —>) (перестановка посылок) (введение V) (по определению Vi е...)
------------------------------ (теорема о команде выбора)
R&BB->wp(IFn,R)
Следствие 1 доказано.
Следствие 2 (теорема о команде ветвления языка Н).
В системе Дейкстры доказуема следующая формула:
(Q -> wp(if В then Sj else S2 fi, R)) <->
<-> (Q & В wpQ, R)) & (Q & -B -> wp(S2, R)).
Доказательство (содержательное). Сопоставив содержательную
операционную семантику команды выбора
def
IF2 = if Вт = > Si □ = > S2 fi
языка D и содержательную операционную семантику команды
«развилка»
if В then else S2 fi
языка H, можно утверждать, что эти команды обязаны обладать
одинаковой wp-семантикой, что формализуется утверждением о до-
казуемости формулы
(Q wp(IF2, R)) ++ (Q & В wp(S1, R)) & (Q & -В -> wp(S2, R)).
Следствие 2 доказано.
Wp-семантика частных случаев команды выбора IFn
Предложение.
1) wp(IF0, R) = Л;
539
https:it.ru
2) wp(IF1} R) = В & wp(S1} R);
3) wp(IF2, R) = (Br v B2) & (Bi —> wp(S1} R)) & (B2 —> wp(S2, R));
4) wp(if В then S] fi, R) = (B v R) & wp(S1} R) v -B & R;
5) wp(if В then S] else S2 fi, R) = (-B v wp(S1} R)) & (B v wp(S2, R)).
6) iyp(ifB1
then S2
else if B2
then S2
else S3 fi, R) =
= (Bj v —iBj & B2 v—iBj & —iB2) &
& (Вг —> wp(S1} R)) & (B2 —> wp(S2, R)) &
& (-.Bi & -B2 wp(S3, R))
Доказательство.
1) Упражняйтесь.
Итак, wp-семантика команды IF0 совпадает с wp-семантикой ко-
манды trap, останавливающей выполнение любой программы.
def def
2) wpU^, R) = wp(if В => Sj fi, R) = В & (В -> wp(S! ,R)) =
В & (-В v wp(S!, R) ) = В & -В v В & wp(S!, R) =
= Л vB&wp(S1,R) = B&wp(S1,R).
aef def
3) wp(IF2,R) = BB&CViG^nDCBi —>wp(S1,R)) =
def
= (Bi vB2)&(Bj ->wp(S],R))&(B2 ->wp(S2,R)>
= (Bj v B2) & (-Bj v wp(Sl , R)) & (~B2 v wp(S2, R)).
4) В случае «однорукой» команды
if В then Sj fi
языка H (команды условного перехода без альтернативы) имеем:
wp(if В then Sj fi, R) = wp(if В then Sj else skip fi, R) =
def
= wp(if В => Sj a-B => skip fi, R) =
def
= (B v -В) & (B -> wp(Sj, R)) & (-B -> wpfskip, R)) =
^CB^wp^R^&^^R)^
^(-By/wp^^'i'i&QBv R) =
= -B&Bv-B&RvB&wp(S1,R)vR&wp(S1,R) =
= -B&Rv(BvR)&wp(S1,R).
Итак, wp-семантика «однорукой» команды языка Н и охраняемой
команды IF] языка D является различной.
5) Ясно, что содержательная операционная семантика «обыч-
ной» команды условного перехода
if В then S-, else S2 fi
540
https://urait.ru
языка Н эквивалентна содержательной операционной семантике
двучленной охраняемой команды
if В => ST а-iB => S2 fi языка D.
Поэтому
def
wp(if В then Sj else S2 fi, R) = wp(if В => п-В => S2 fi, R) =
def
= (В V -B) & (B -> wpCSi, Rf) & (-B -> wp(S2, R)) =
= (B^> wp(_S1 ,R))& (-B -> wp(S2, R)) =
= (-B v wpCSj ,K))&(B v wp(S2, R)).
6) wp(if BT then Sj else if B2 then S2 else S3 fi, R) =
= wp(if => Sj □—& B2 => S2 □—& —B2 => S3 ).
Дальнейшее очевидно.
Предложение доказано.
Замечание [92, с. 130].
Команда выбора Дейкстры с точки зрения надёжности, наглядности
и простоты существенно лучше детерминированной команды условного
перехода по следующим причинам:
1) порядок охраняемых команд в команде выбора Дейкстры не суще-
ственен;
2) выбор определяется явно сформулированными условиями, разме-
щёнными «рядом» с охраняемыми командами;
3) недетерминированная природа этой команды позволяет избегать
анализа и учета излишних деталей реализации (так, в команде условного
перехода
ifx1 > х2 then у :=хг elsey :=х2 fi
языка Н для определения значения функции у = max(xn х2) необхо-
димо задуматься над тем, какую из двух команд присваивания выполнять,
если сравниваемые величины равны, хотя это совершенно безразлично).
о- Hi 1 rnit i-i 1
O.f 4 vJl Oil.I VI
541
Допустимые правила вывода для команды выбора
Не так уж трудно построить серию
выводов, в которой каждый последующий
простейшим образом вытекает
из предыдущего. Если после этого удалить
все средние звенья и сообщить слушателю
только первое звено и последнее, они
произведут ошеломляющее, хотя и ложное
впечатление.
А. Конан Дойл. Пляшущие человечки
Определение.
def
IF = If В then Sj else S2 fi-
Теорема (If-j) (проверка предусловия команды IF) (по [85, с. 41]).
{v&Bys^R} {V&^B}S2{K}
------------------------ (1Li)
{V}IF{K}
Доказательство (содержательное) [85, с. 41].
Если условие V истинно перед выполнением оператора IF, то и V,
и В истинны непосредственно перед выполнением (если этот
оператор выполняется). Поскольку V&B является предусловием для
R по отношению к S1} то R будет истинным после выполнения
Поступая аналогичным образом, получаем, что R будет истин-
ным после выполнения S2. Таким образом, из истинности V перед
выполнением условного оператора в обоих случаях следует истин-
ность R после его выполнения. Поэтому V является предусловием
для R по отношению ко всему оператору IF.
Доказательство (формальное). Предъявим прямой древесный
вывод:
{У&ВУВДЛ} {V&-,B}S2{R}
(V ->wp(S],R)) (V&-iB->iyp(S2,R))
(V & В -> ivpCSi, R) ) & (V & -В -> up(S2, R) ) Доказано ранее
v -> (В -> wp(Si,R)) &(-£-> wp(S2, R)) wp(lF, R) = (В wp^, R)) & (-iB -> wp(S2, R))
V->wp(IF,R)
{V}IF{R}
Теорема (If-j) доказана.
Теорема (If2) (получение предусловия команды IF) (по [85, с. 42]).
{VJSiW {V2}S2{K}
{V1&BvV2&-B}IF{K} 1 2
542
Доказательство (формальное). Воспользуемся теоремой (IfJ
сУ=5У1&ВуУ2& —В для построения следующего прямого древес-
ного вывода:
Ц&В-^ {yjsjK}
{V^ByS^R}
{Ц &ВуУ2 &-B&B}S!{K}
У2&^В->У2 {У2}52{В} лр }
{V2&^B}S2{R} 1
{Ц &В&-ВуУ2 &-B}S2{K}
{(^&B^V2&^B)&B}S1{R} {(У!&BvV2&^B)&^B}S2{R}
{V1&B\/V2&^B}TF{R}
(Ifl)
Итак, теорема (If2) следует из теорем (If2) и (Рх).
Теорема (If2) доказана.
Теорема (If3) (команда If-З) (по [85, с. 44]).
{yjSjW {V2}S2{R}
------------------UXoj
{У!&У2}1Р{К}
Доказательство (формальное). Воспользуемся теоремами (IfT)
и (Р]) для построения следующего прямого древесного вывода:
У&Уз&В-»^ {yjSJK} Уг & У2 & —В —> У2 {V2}S2{R}
1 {У^Уа&В^да__________{Уг&У2&-B}S2{B} 1
{у^УзЯРШ 1
Теорема (If3) доказана.
Теорема (If4) (команда If-4) (по [85, с. 44).
{Vy&ByS^R} {V2&—B}S2{R}
{Vj&VjHHK} 4
Доказательство (формальное). Воспользуемся теоремами (If^)
и (Pj) для построения прямого древесного вывода:
Vi&У2&В-> Ц&В {Vi&B1SJR} У1 &V2&-B->V2&-В {У2&-B}S2{B}
{Ц & V2 & —iB}IF{B} 1
{Ц &V2&B}IF{B}
{V!&V2}IF{R}
Теорема (If4) доказана.
Замечание [85, с. 55].
Приведём сводную таблицу, предназначенную для выбора одной
из рассмотренных выше теорем в зависимости от вида команды
программы и от того, задано ли предусловие или же его следует по-
лучить:
543
https:/Л: rait.ru
Вид команды Предусловие... Теорема
Команда условного перехода ...задано ...требуется получить (И^) (в некоторых случаях (If3) или (If4) (If2)
Подпрограмма ...задано ...требуется получить (SP2) (иди (SP3)) (SP2) (иди (SP3))
Синтез команды выбора
Пусть Q и R — известные формулы, IFn — неизвестная команда
выбора Дейкстры.
Поставим задачу о синтезе команды выбора; другими словами,
определим команды IFn такую, что {Q} IFn {R} превратится в дока-
зуемую тройку Хоара.
Основная теорема о команде выбора позволяет сформулировать
следующую стратегию синтеза команды выбора (по [88, с. 1783).
Решите следующую системууравнений с отношением выводимости:
h(ViG[l,n])(Q&Bf ^wpCS^R)),
vB2 v...vB„)
относительно неизвестных формул Blt В2, Вп, п е N\{0}, и про-
грамм S1? S2, ..., Sn.
Технология решения системы уравнений такова:
1) положите i = 1;
2) угадайте программу Si} рассматривая подформулы формулы R;
3) определите формулу Bf так, чтобы в системе Дейкстры была
доказуема формула Q & Bf —> wp(Si} R);
4) проверьте, доказуема ли в системе Дейкстры формула Q —> Bf:
— если «да», то система уравнений решена и п = i;
— если «нет», то положите i := i + 1 и повторите процесс реше-
ния, начиная с пункта (2).
Контрольные вопросы
1. (По [78, с. 94, № 3])
Выведите необходимые и достаточные условия доказуемости в системе
Дейкстры тройки Хоара {AJ if В then Р fi {А2}.
2*. Определите sp-семантику команды выбора IFn.
544
https: //u га it.ru
Примеры решения некоторых типов упражнений
Пример 1 [88, с. 141].
Вычислите и упростите ivp(IF2, q-w + r=x&r>0) для команды выбора:
if w < г => г := г - w; q := q +1 □ w > г => skip fi.
Решение.
def
wp(IF2,q-w+r=x&r >0) =
def
= (w<rvw>r)&(w<r->wp(r :=r-w;q:=q+l,q-w+r = x&r>0))&(w>r —>wp(skip,qw+r = x&r>0)) =
= (w<r—>q-w + r = x&r-w>0)&:(w>r—>q-w + r = x&r>0) =
= (w<r —>w<r&qw+r = x)&(w>r —>qw+r = x&r >0) =
= (iv<r->q-w+r =x)&(w>r->q-w+r=x&r>0).
Пример 2 [88, c. 176—177].
Напишите программу, которая присваивает z значение, равное наи-
большему из заданных целых чисел хиу.
Решение. Требуется определить команду S так, чтобы в системе Дейк-
стры была доказуема тройка Хоара {И} S {z = max (х, у) }.
Нетрудно получить
def
R = z = max (х,у) =z>x&z>y & (z=xvz=y).
Возникает естественный вопрос: какую команду можно было выпол-
нить, чтобы предикат R был истинным? Попробуем z :=х. Тогда
def def
wp(z:=x, К) = wp(z:=x,z>x&z>y&(z=xvz=yy) = х>у.
Это даёт требуемое условие, и первая попытка написать программу
может быть следующей: if х >у => z := х fi.
Напомним, что по основной теореме о команде выбора необходимо,
чтобы предусловие Q влекло за собой дизъюнкцию охран.
Следовательно, необходима по крайней мере ещё одна охраняемая
команда, которая получается аналогичным образом из анализа команды
присваивания z :=у.
После добавления этой охраняемой команды получим программу:
{И} ifx>y=> z :=хпу>х=> z :=yfi{J?}.
Пример 3 [88, с. 179—180].
Напишите программу перестановки значений целочисленных пере-
менных х иу таким образом, чтобы имело место х <у.
Решение. Вначале построим формулы:
def def
Q = x-X&y-Y, R = х<у&(х = Х&у = У vx = Y&y = X).
Предусловие Q является подформулой формулы R, так что имеется воз-
можность того, что команда skip «обеспечит» предикат R при некоторых
условиях (это и есть использование предусловия для получения дополни-
тельной информации). Другой возможностью может быть перестановка
t := х; х :=у; у := t, поскольку она также «обеспечивает» второй конъюн-
ктивный член R.
Должны быть доказуемы формулы Q & —> wp(Si} R), i = 1,2.
545
https:/Л; га it.ru
def def
1) Пусть S1 =s skip. Тогда wp (S1}R) = wp (skip, R) - R.
Пусть формула Вг пока неизвестна, поэтому решим уравнение с отно-
шением выводимости
|-х = Х&у = У&В1 ->х<у&(х = Х&у = У vx = Y&y = Х)
относительно неизвестной формулы В1
___________В1Нх<У____________
______x = X,y = Y, B1\-x<y&x = X&y = Y___
x = X,y = Y, B1\-x<y&(x = X&y = Yvx = Y&y = X')
|-х = Х&у = У&В1->х<у&(х = Х&у = Уух = У&у = Х)
I-Q&Bj wpfSjjR)
Выберем B1 =s x <y.
2) Пусть теперь S2 t := x; x :=y; у := t. Тогда
def def
wp(S2,R) = wp(t :=x;x:=y;y :=t,x<y&(х=Х&у = Уух = У&у=Х)) =
def
= x<y&(у=Х&х = У уу = У&х=Х).
Аналогично решим следующее уравнение с отношением выводимости:
l-Q&B2 ->wp(S2,R) или l~ х = Х&у = У & В2 —> х < у&(у = Х&х = У v у = Y&x = X)
относительно формулы В2, из которого легко получить, что B2=sx<y.
В результате команда выбора Дейкстры имеет следующий вид:
{Q}ifx<y=> skipnx>y=> t:=x;x:=y;y :=tfi{R}.
Упражнения для самостоятельного решения
Определение wp-семантики команд выбора
1. Определите wp (if fi, R) для произвольного предиката R. Извест-
на ли Вам уже команда с таким определением?
2. Установите доказуемость следующих формул в системе Дейкстры:
a) (Q -> wp(IFn, R)) (Q -> ВВ) & (Vi е [1, и]) (Q &Bf -> wp(Sh R));
б) (R & ВВ -> wp(IFn, R)) <-> (Vi e [1, n]) (R & Bf -> wp(S{,R)).
3. (По [92, c. 126—127])
Определите wp-семантику общей формы команды условного перехода.
Указание. Общая форма команды условного перехода имеет следующий
неформальный синтаксис (опишем его с помощью определённого располо-
жения команды «на плоскости»):
if Вг then Si
elsif В2 then S2
elslf B3 then
elsif Bn-1 then else Sn
fi.
546
o Hi iroi! ri i
Содержательная операционная семантика команды такова: вычисляется
значение выражения Вх; если оно истинно, то выполняется Sx; в противном
случае вычисляется В2; если его значение истинно, то выполняется S2 и т. д.;
если не выполняется ни одно из условий Bb i = 1,2,..., п -1, то выполняется Sn.
Вычисление значения wp-преобразоватпеля предикатов
4. [85, с. 71]
Определите слабейшие предусловия:
а) {?} if х < 0 theny := -х else у := х {у > 0};
б) {?} if х < 0 theny := -х else у := х {у > 0};
в) {?} if х < 0 theny := -х else у := х (у < 0};
г) {?} if х < 0 theny := -х else у := х (у < 0}.
5. (По [84, ч. 2, с. 572])
Докажите, что
И = wp(x := п; if х < т then х := т else skip fi, х = max (т, n)).
6. [88, с. 141; с. 142]
а) Вычислите и упростите wp (IF2, а > 0 & b > 0) для команды выбора
IF2 = if а > b => а := а - Ъ □ Ъ > а => Ъ := Ъ - a fi.
б) Пусть swap(x,y) обозначает «команду», содержательная операционная
семантика которой такова: переменные х и у обмениваются значениями.
Вычислите и упростите wp(IF2, х < у) для команды
ifх > у => swap(x, у) □ х <у => skip fi.
7. [88, с. 142]
Массивы F[0: и] и G[0: m] являются списками людей, упорядоченными
в алфавитном порядке. Известно, что по крайней мере одно имя содержится
в обоих списках. Пусть X — первое (в алфавитном порядке) такое имя. Вы-
числите и упростите слабейшее предусловие для следующей команды выбора
по отношению к предикату R, записанному после нее (предполагается, что
i и j лежат в границах массива):
ifF[i] < GQ] => i: = i + 1 □
F[i] - GQ] => skip □
F[i] > G[j] => j :=j + 1
fi{K},
где R = Ordered(F[0: n]) & Ordered(G[0: m]) & F[i] <X & GQ] <X.
Доказуемость троек Хоара в системе Дейкстры
8. Установите доказуемость следующих троек Хоара в системе Дейкстры
(другими словами, установите правильность приведённых программных
фрагментов):
а) [81, с. 53, №5]
{а > b & Ь > 0} if a>b=>a:=a-bna<b=>bt=b-afi{a>b&b>O};
б) [81, с. 53, №6]
547
https:it.ru
{c = p-xn&x*0&n>0}
if Odd(n) then p := p • x; n := n 4- 2; x := x • x fi
{c = p • xn & x ф 0};
в) (no [99, c. 235])
{И} if Odd(x) => x := 2 • x fi {Even(x)};
r) [85, c. 71]
{3 < I x I < 4} if x < 0 then у := -x else у := x fi {2 < у < 4};
д) [88, с. 142]
{y>0&z + yx = ab}
if Odd(x) -> zz + у; xx -1 □ Even(x) -> skip fi; у 2 - у; x := x 4-2
{y>0&z + yx = ab};
e) [88, c. 142]
{0<i<n&m = max (B[0: i -1]}
if B[i] > m => m := B[i] □ B[i] < m => skip fi
{0<i<n&m = max(B[0:i]};
(эта тройка Хоара может быть использована в программе, которая опре-
деляет максимальное значение т в массиве В[0: п - 1]);
ж) {И}
if х < 2 => f :=5-2-хп2<х<3=> f := 1 □ х > 3 => f := 2 • х - 5 fi
{/ - mod(x - 2) + mod(x - 3);
з) {И}ifx<3=>v:=2 x-3nx>3=>v:=9-2 xfi{v = 3-mod(6-2• x)};
и) {И} if у >0->z:-x-yuy <0=> z:=x + у fi {z = max(y-x, x + y)};
к) {И}if 2• x > 1 then f := 2• x-1 else f := 1 - 2 • xfi{/ = mod(2• x-1)};
л) {И} if 3 > 2• x then m := 3 else m := 2• xfi{m = min (3,2• x)};
м)* {И}
if и > 2 • v
then if и > 1 + v
then к := и
else к := 1 + v
fi
else if 2 • v > 1 + v
then к := 2 • v
else к := 1 + v
fi
fi
{k = max {u, 2 • v, 1 + v}}.
9. Установите, для каких формул Q доказуема в системе Дейкстры сле-
дующая тройка Хоара:
548
https:it.ru
{Q}
if a>b & a> c -> y:-an
—i(a >b &a>c) & b>c => у := b □
b < с => у :=c
fi
(y>a&y>b&y>c&(y = avy = bvy = c)}.
Синтез команд выбора
10. (По [81, с. 53, № 8])
Напишите команду выбора, проверяющую, являются ли х, у и z длинами
сторон треугольника.
Указание. Будем говорить, что величиных,у, z являются длинами сторон
треугольника, если х > 0, у > 0, z > 0 и справедливы соотношения:
х +у >z,x + z>y,y + z>x.
11. (По [88, с. 181])
Постройте программу для установления z равным abs (х).
12. [88, с. 181]
Пусть х обозначает количество нечётных целых чисел в массиве В[0:
к -1], к > 0. Напишите программу увеличения к на единицу с сохранением
этого соотношения. Это означает, что после ее завершения к должно быть
больше на 1, чем первоначально, ах должно по-прежнему обозначать число
нечётных элементов массива В[0: к -1].
13. [81, с. 53, №7]
Постройте команду выбора, изменяющую значения переменных х,
у, z таким образом, что переменная х содержит наибольшее значение,
а переменная z — наименьшее.
14. (По [84, ч. 2, с. 577])
Постройте команду выбора IFn, если в системе Дейкстры является до-
казуемой тройка Хоара {И} IFn{x2 - a v х2 - -а}.
https: //цга it.ru
Упражнение 26
WP-СЕМАНТИКА КОМАНДЫ ЦИКЛА
ДЕЙКСТРЫ
Мы будем лучше справляться с нашей
работой программистов, если только
мы будем подходить к этой работе
с полным сознанием ее ужасающей
сложности, если только мы будем
верны скромным и элегантным языкам
программирования, если мы будем
учитывать природную ограниченность
человеческого ума и приниматься
за эту работу как Очень Смиренные
Программисты.
Э. Дейкстра
Обязательные результаты обучения:
• знать вспомогательные понятия
—уравнения с отношением выводимости;
• знать основные понятия
— wp-семантика команды цикла DOn;
— инвариант цикла DOn, ограничивающая функция цикла DOn;
— основная теорема о команде цикла DOn;
— условия правильности цикла DOn (While);
— допустимые правила для команд цикла While и Repeat;
— денотационная семантика команды цикла While;
— стратегия синтеза команд цикла;
• уметь
— конструировать доказательства свойств инвариантов и охран циклов;
— конструировать доказательство совпадения wp-семантики циклов DOn
и While;
— конструировать доказательства частичной правильности программ;
— конструировать доказательства полной правильности программ;
— конструировать доказательства допустимости правил вывода в системе
Дейкстры;
— описывать семантику программ, содержащих команды цикла;
— конструировать программы в соответствии с поставленной задачей,
используя команды цикла Дейкстры;
— конструировать доказательство или опровержение свойства заверша-
емое™ заданной программы;
550
https:/Л: rait.ru
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленньх в Упражнении.
Теоретические сведения
Циклы — это важнейшее средство для описания потенциально
неограниченной последовательности действий ограниченными
по длине предписаниями. Этим средством удается пользоваться
только за счёт того, что у всех повторений цикла обнаруживает-
ся некоторое общее свойство (называемое инвариантом цикла),
не меняющееся от повторения к повторению.
Wp-семантика команды цикла DOn
По моему убеждению, законы
мышления произошли от того, что связи
между внутренним представлением,
которое мы составляем о предметах, все
более приспосабливались к связи между
самими предметами. Все условия связи,
ведущие к противоречию с опытом,
отбрасывались и, напротив, те, которые
всегда вели к правильным результатам,
утверждались с такой энергией и они
передавались столь последовательно
потомкам, что мы наконец усмотрели
в этихусловиях аксиомы, или врожденные
непременные методы мышления.
Л. Больцман
Пусть п, k е N. Будем обозначать (как и ранее):
def
BB = Вт vBa v — vBn,
def
IFn = if BT => SiqB2 => S2a...aBn => Sn fi,
def
DOn = doBT =>S1aB2 =>^a...aBn =>Sn od.
Определение (wp-аксиома команды цикла DOn).
def
wp(DOn,R)^(3k>0)Hk(R), Hk(R) =
-BB & R, если k = 0,
wp(IFn, Hk_r (R), если k g N \ {0}.
551
https: "u rait.ru
Определение (wp-семантика команды цикла DOn) [88, с. 144
145].
def def
wp(DOn,R) = (Bk>O)Hk(R'), Hk(R) =
-BB&R, если к = 0,
wp(IFn, Hfc_T (К), если k g N \ {0}.
Определение (содержательная операционная семантика Hfc(R))
(по [88, с. 144—145]).
1) Предикат H0(R) определяет множество состояний, в которых
выполнение команды DOn завершается за 0 шагов в силу того,
что значения всех охран Bf равны 0 в начале выполнения цикла.
2) Предикат Hk(R) при k е N\{0} определяет множество состоя-
ний, в которых выполнение команды DOn заканчивается не более,
чем за к шагов при значении предиката R, равном 1.
Важное замечание.
Индуктивно определённое слово wp(DOn, К) является формулой языка
первого порядка лишь для фиксированных значений к, так как слово
wp(DOn, R) определяется с помощью бесконечно длинной «формулы» (воз-
никает язык бесконечно длинных формул, рассмотренный К. Энгелером).
Более того, доказано, что проблема «Имеется ли конечное выражение
для wp(DOn, R)?» неразрешима для языка формальной системы первого
порядка, а тем более для языка натуральной арифметики.
Вся история алгоритмической логики—это интеллектуальная борьба
с возникающей бесконечностью: а) можно игнорировать бесконечность,
но тогда она «мстит» неполнотой построенных систем; б) можно увели-
чивать, либо уменьшать выразительную силу логического языка, чтобы
сформулировать условия, наложенные на цикл в конечном виде.
Основные теоремы о команде цикла DOn
И тут же, с глухим стуком,
прямо с неба на бумагу валятся
доказательства — каждое в самый
подходящий момент'
А. Гротендик. Урожаи и посевы
Предложение 1.
Если цикл DOn завершается за конечное число шагов, то для
любой формулы Р справедливо следующее утверждение в системе
Дейкстры:
(Vi g [1, n])(Р&Bf -> wp(Si, Р)) I- {P}DOn(P&-ВВ}.
Доказательство. Построим следующий прямой древесный вы-
вод:
552
https:/Л: rait.ru
h(Vte[l,n])(P&Bj ->ivp(%P))
h (Vi e [1, n]) (B, -> (P -> wpQSj, P)))
h(Vie[l,n])(Bi^{P}Si{P})
Пусть цикл завершается после к итераций (по условию). Тогда его
содержательная операционная семантика совпадает с содержатель-
ной операционной семантикой композиции, содержащей к команд St.
Но для такой композиции
{P}Sai;Sa2;...:Safc {Р&-ВВ},
так как после выполнения последней команды Sak условие Вак будет
нарушено.
Предложение 1 доказано.
Рассмотрим следующий цикл DOn:
{Р} do Bj => S1 □ В2 => S2 □ ... □ Вп => Sn od {P & —BB}.
Пусть t — терм, x <t FV(t).
Предложение 2.
Если в системе Дейкстры для любой формулы Р выводимы фор-
мулы
(ViG[l,n])(P&Bf ->wp($,P)),
(3k>0)(t<k),P&BB^t>0,(ViG[l,n])(P&Bi^ivp(x:=t;Si,t<x)),
то цикл завершается за конечное число шагов.
Построение формального доказательства данного предложения
невозможно из-за невыразимости на языке системы Дейкстры свой-
ства завершения выполнения программы.
Замечание [39, с. 472—473].
Г. С. Цейтин (1970) заметил, что для обоснования правильности про-
граммы недостаточно тех значений, которые присутствуют в ее тексте
и при ее вычислении. Нужны также величины, лишние и даже порой вред-
ные для вычислений, но необходимые, чтобы обосновать их корректность.
Например, если мы пишем цикл While Р do S, то мы не заинтересованы
(как правило) в том, чтобы он работал бесконечно долго. Но вычисление
числа шагов цикла может быть не менее трудной задачей, чем вычисле-
ние самого цикла, и, чтобы не делать двойную работу, нужно ввести зна-
чение-призрак со (мы специально здесь применили обозначение, вызыва-
ющее аналогии и с нестандартными числами и с ординалами; действи-
тельно, данный призрак не обязан быть натуральным числом, он может
быть любым идеальным объектом, гарантирующим конечность реаль-
ного процесса), ограничивающее сверху число шагов цикла, и доказать,
что оно действительно обладает таким свойством.
Этот пример показывает еще одну сторону значений-призраков.
553
https:it.ru
Если мы можем построить со как обычное натуральное число и доста-
точно быстро вычислить его, то в цикле можно поставить аварийный
завершитель, если число его повторений превзошло известную верхнюю
границу со. Таким образом, призраки зачастую вновь обретают «плоть»,
если мы интересуемся диагностикой ошибок.
Интересно отметить, что призраки появляются и в выводах математи-
ческой логики. Построим, например, непрямой древесный вывод:
{A(t, и) & В(и, г) -> C(t, г) } I- A(t, и) & В(и, г) -> C(t, г)
{A(t, и), В(и, г), A(t, и) & В(и, г) -> C(t, г) } Н C(t, г)~
{A(t, и), В(и, г), Vz(A(t, и) & В(и, z) C(t, z)) } I- C(t, r)
{A(t, u), B(u, r), Vy Vz(A(t, y) & B(y, z) -> C(t, z))} I— C(t, r)
{A(t, u), B(u, r), VxVyVz(A(x, y) & B(y, z) -> C(x, z)) } I- C(t, r)
{VxVyA(x, y), VxVyBfx, y), VxVyVz(A(x, y) & B(y, z) C(x, z) ) } I— C(t, r)
Тогда все построения, проделанные для нахождения и, нужны для обо-
снования, но и не фигурирует в доказываемом утверждении.
Итак, практически любая нетривиальная импликация порождает при-
зраки. Очевидными случаями порождения значений-призраков являются
случаи, когда призраками становятся значения, построенные в отброшен-
ных альтернативах разбора случаев, либо при приведении к абсурду.
Инвариант и ограничивающая функция цикла DOn
Не забыть бы мне вернуться.
А. и Б. Стругацкие. Гадкие лебеди
Практически любому циклу предшествует инициализация цикла,
т. е. выполнение некоторого фрагмента программы (назовём его
Init), единственным назначением которого является установка ис-
тинности некоторого предиката (часто неявно выраженного), кото-
рый называется инвариантом цикла. По словами. Вирта [86, с. 38],
«явное указание инварианта для каждого цикла представляет наи-
большую ценность в любой программной документации».
Рассмотрим тройку Хоара {Q} Init; DOn {К}.
Определение (синтаксическое).
Инвариантом цикла DOn будем называть формулу Р, для которой
доказуемыми в системе Дейкстры являются следующие формулы:
1) Q wp (Init, Р);
2) (Vi g [1, и]) (Р & -> wp(Si} Р)).
Определение (семантическое).
Инвариантом цикла DOn будем называть предикат Р, удовлетво-
ряющий следующим условиям:
554
https:/Л: rait.ru
1) выполнение инициализации цикла завершается при истин-
ном предикате Р;
2) выполнение каждой охраняемой команды Sf завершается при
истинном предикате Р.
Определение (синтаксическое).
Ограничивающей функцией (или вариантом цикла) называется
терм t, фигурирующий в Предложении 2 о команде цикла DOn.
Определение (семантическое).
Ограничивающей функцией будем называть интерпретацию
терма t.
Замечание.
Понятие «ограничивающая функция» встречался в старых школьных
учебниках по информатике (см. [101, с. 50]): «Лимитирующей функцией
называется функция, ограничивающая количество исполнений тела
цикла числом своих значений».
Технология установления правильности цикла DOn
Рассмотрим цикл DOn:
{Q}do => SiqB2 => S2a...aBn => Sn od {К}.
При этом известны инвариант цикла Р и ограничивающая функ-
ция t.
Из Предложений 1 и 2 о команде цикле DOn получим, что для
установления правильности команды цикла достаточно проверить
выполнимость следующих условий, которые назовём условиями
полной (тотальной) правильности цикла DOn:
1) формула
Q —> wp(Init, Р)
является доказуемой в системе Дейкстры (другими словами, пре-
дикат Р является истинным перед выполнением цикла);
2) формула
(Vie [l,n]) {Р& В,} S,{P}
является доказуемой в системе Дейкстры (другими словами, вы-
полнение каждой охраняемой команды завершается при истинном
предикате Р);
3) формула
P&—BB—>R
555
https:it.ru
является доказуемой в системе Дейкстры (другими словами, в мо-
мент завершения цикла истинен искомый результат — предикат R);
4) формула
P&BB^>t> о
является доказуемой в системе Дейкстры (другими словами, функ-
ция t ограничена снизу до тех пор, пока цикл не завершился);
5) формула
(Vi е [1, n]) (Р & Bi —> wp(x := t; Sit t < x))
является доказуемой в системе Дейкстры (другими словами, каж-
дый шаг цикла приводит к уменьшению значения функции t).
Пример (по [88, с. 151]).
Докажем полную правильность следующей программы, которая запи-
сывает в переменную s сумму элементов массива А [1:10]:
{И} i := 10; s := 0; {Р} do i * 0 => s := s+A[i]; ii -1 od {Л},
def 10 def def 10
P = 0<i<10&s= £ A[k],t = i,R = s=£A[k].
k=i+l fc=l
10 def
(1) wp(i: = 10; s: = 0,0 < i < 10&s - £ =
def 10 k=i+l
= 0 < 10 < 10&0 = £ A[k] =И.
k=n
Итак. P истинен перед началом выполнения цикла.
(2) Покажем, что тройка
(P&BJ s: = s+A[i]; i: = i -1 {P}
доказуема в системе Дейкстры:
def
wp(s: = s + A[i];i: = i-l,p] -
def 10 10
= 0<i-i< lO&s + A[i] = A[k] = 1 <i< ll&s = £ A[k],
k=i k=i+l
def 10 10
P&Bi =i^0&0<i<10&s= £ A[/c] = l<i <10&s = £ A[k],
k=i+l k=i+l
10 10
P&Bj —> wp(s :=$ +A[i]; i :=i-l, P) = l<i <10&s = A[k]->l<i<ll&s = A[k] =
k=i+l k=i+l
=l<i<10->l<i<ll=l<i<10->l<i<10vi=ll.
def
3) Покажем, что формула P & —iBB —> R, где BB = i / 0, доказуема
в системе Дейкстры:
def/ 10 Л / 10 Л
Р&-ВВ= 0<i<10&s = X A[k]&i = o s s=£A[k] ,
\ k=i+l J \ k=l J
10 10
P&—BB^>R = s='£A[k]^>s = £Д[к>И.
k=l k=l
556
4) Покажем, что формула Р & ВВ —> t >0 доказуема в системе Дейк-
стры:
def / 10 Л
P&BB->t>0 = I i^0&0<i<10&$ = £ A[k]—>i>0 .
\ k=i+l >
Дальнейшее очевидно:
0<i,i*0\-i>0
0<i<10,i^0l-i>0
io
0<i<10&s= £ A[k]&i^0H>0
____________fc=t+i___________
_____________________________p&BBht>o_
HP&BB->t>0
(5) Покажем, что тройка Хоара
{P&i*0}x:= t;s:=s+A[i];i:=i-l{t<x}
доказуема в системе Дейкстры:
def
vvpCx:=t;s:=s +A[i];i:=i—1, t<x) -
def def
- wp(x:=i;s:=s+A[i];i:=i-1,i<x) = wp(x:=i,i-l<x) = i-l<i,
далее, P&i^0->i-l<i = PL
Доказательство полной правильности программы закончено.
Подобные доказательства для программ обладают всеми свой-
ствами элегантных математических построений, в том числе и эф-
фектом разрезных картинок-загадок (по [103, с. 50]): «... кажущи-
еся бессмысленными кусочки, оказываясь на нужном месте, вдруг
неожиданно приобретают значение».
Объём работы, необходимый для доказательства правильности
программы, по меньшей мере на порядок величины больше, чем
объём работы, затраченной на написание самой программы. За-
дним числом оценить объём работы достаточно трудно, в качестве
грубого приближения можно измерять количество строк получен-
ного текста. И если можно не особенно тревожиться из-за того, что
требуется несколько страниц для записи маленькой, на полстрани-
цы, программы, то уже никак не приемлемо то, что доказательство
программы в 5000 строк потребует 50 000 строк текста доказатель-
ства (к сожалению, текст такой длины с большой вероятностью со-
держит хотя бы несколько ошибок).
В этом заключается главная причина непопулярности идеи до-
казательства правильности программ у программистов-практиков,
больше полагающихся на интуицию и отладку. Ради справедливо-
557
сти следует упомянуть об ожидаемом сокращении длины доказа-
тельства благодаря дальнейшему совершенствованию его формаль-
ных методов.
Замечание.
1. Интуитивно понятно, что удобнее определять инварианты ещё
в процессе написания программы, так как «вылавливать» идеи циклов
(для построения инвариантов) из написанных программ — непростая
работа.
2. (По [99, с. 119—120]) С точки зрения (как аксиоматической, так
и операционной) семантики команды цикла — это качественно новые
формы композиции по сравнению с последовательной композицией
и командой условного выбора.
Причина различия в том, что цикл задает последовательную цепочку
команд, длина которой может зависеть от исходных данных. Правила
вывода для композиции команд и команд выбора обладают важным для
практического анализа качеством: они позволяют автоматически опре-
делять (вычислять) свойство целого по известным свойствам частей или,
наоборот, переходить от свойств целого к свойствам частей.
К сожалению, для более сложных композиций команд, таких как
циклы, указанное качество уже не имеет места: некоторые свойства про-
грамм оказываются невыводимыми из свойств составных частей. Опреде-
ление таких свойств требует дополнительной информации о композиции.
Эта информация в общем случае не может быть определена (вычислена)
автоматически, а должна быть задана как исходная (наряду с предусло-
вием и постусловием). Такой дополнительной информацией является,
в частности, инвариант цикла, играющий ключевую роль в аксиомати-
ческой семантике циклов.
Таким образом, семантические свойства команды цикла в общем слу-
чае не могут быть определены дедуктивно только из свойств конструк-
ций, составляющих цикл (условия и тела цикла). Для определения свойств
цикла должен использоваться принцип индукции, что приводит к необхо-
димости задания дополнительной информации о свойствах вычислений.
Допустимые правила вывода для команды цикла
Математика даёт самый блестящий
пример чистого разума,удачно расширяющегося
самопроизвольно, без помощи опыта.
И. Кант
Определение.
def
1. While = while В do S od.
def
2. Repeat = repeat S until B.
Теорема (Wj) (цикл While без инициализации).
558
о Hi iroi! ri i
Если цикл While завершается, то справедливо следующее прямое
допустимое правило вывода в системе Дейкстры:
{P}While{P&-,B} 1
Доказательство (содержательное) [85, с. 46].
Если предикат Р истинен перед началом выполнения цикла While,
то и Р, и В будут истинными до первого выполнения команд тела
цикла S. Поскольку Р & В является предусловием для Р по отноше-
нию к S, то Р будет истинным после первого выполнения S. Поэтому
и Р, и В будут истинными до второго выполнения тела цикла S и т. д.
Предикат Р будет истинным после каждого выполнения команды S.
Если когда-то выполнение цикла закончится, то предикат Р будет
истинным, а предикат В ложным, т. е. предикат Р & -В будет истин-
ным при завершении цикла.
Доказательство (формальное) (по [84, ч. 2, с. 573—574]).
Вначале построим следующий прямой древесный вывод:
{P&B}S{P}
B&P—>wp(S,P))
B—>(P—>wp(S,P))
В—>{P}S{P}
Пусть цикл завершается после к итераций (по условию). Тогда
его содержательная операционная семантика совпадает с содержа-
тельной операционной семантикой композиции, содержащей к ко-
манд S.
Но для такой композиции {P}S; S;...; S{P&-B}, так как после вы-
полнения последней команды S условие В будет нарушено.
Предикат Р истинен и до, и после каждого выполнения S, поэто-
му предикат Р является инвариантом цикла.
Теорема (И^) доказана.
Теорема (W2) (цикл While с инициализацией) [85, с. 47].
Пусть цикл While завершается, а формула Р — инвариант цикла.
Тогда справедливо следующее прямое допустимое правило вывода:
{V}Init{P} {P&B}S{P} {P&—B—>R}
-------------------------------(W7)
{V}Init; While{P}
Доказательство (формальное).
Теорема (W2) следует из теорем (SJ, (PJ и (WJ:
{P&B}S{P}
(Р->Р) {P}While{P&-iB} 1 {Р&-В->Я} ( .
{V}Init{P}______________{P}While{P}______________ 1
{V}Init; While{P} 1
559
https://'d ra it.ru
Теорема (W2) доказана.
Теорема (J^) (цикл Repeat без инициализации) (по [81, с. 38]).
{0}5{РНР&^В^0)
{Q}Repeat{P&B} 1 1аЛ
(Q Р & —В) {Р & —B}S{P}
{Q}Repeat{P&B} 16 ’
{Q}S{P} {P&^B}S{P}
{Q}Repeat{P&B} 1в *
a)
б)
в)
Доказательство. В результате сопоставления содержательной се-
мантики команд While и Repeat получим, что
{Q} repeat S until В {Р & В} = {Q} S; while —В do S od {Р & В}.
Теперь построим следующие прямые древесные выводы;
(Р&—В—>Q) {Q}S{P} (Р->Р)
{Р&—iB}S{P} *
{Q}S{P} {P}while-BdoSod{P&B}
{Q}S; while —B do S od {P & B} 1
{Q} repeat S until B{P & B}
6)
(Q^P&^B) {P&^B}S{P} (P^P)fp. {P&-B}S{P}
___________{Q}S{P}___________1 1J {P}while-Bdo Sod{P&B} 1
{Q}S; while-B do Sod{P&B} 1
{Q} repeat S until B{P & B}
{Q}S{P} {P&^B}S{P} (P&B P&B)
{Q}S; while -B do S od {P & B} 2
{Q} repeat S until B{P & B}
Теорема (RT) доказана.
Теорема (R2) (цикл Repeat с инициализацией) (no [99, c. 127]).
{Q}Init;S{P} {P&^B}S{P} (P&B^R)
{Q}Init;Repeat{R} 2
Доказательство.
{Q}Init;S{P} {P&-B}S{P} (P&B—>R)
Q}Init; S; while -B do S od {P & B}
{Q}Init; Repeat{R}
(W2)
(совпадение содержательных
операционных семантик циклов)
Теорема (R2) доказана.
560
https://t!ra:t.ru
Замечание [85, с. 55].
Приведём сводную таблицу, предназначенную для выбора одной
из рассмотренных выше теорем в зависимости от вида команды и от того,
задано ли предусловие или же его следует получить.
Вид команды Предусловие... Теорема
Цикл While с инициализацией ...задано ...требуется полу- чить ТО ТО
Цикл While без инициализации ...задано ...требуется полу- чить (IVJ или (IVJ + (PJ То
Цикл Repeat без инициализа- ции ... задано ... требуется полу- чить (Rj) или (RJ + (PJ (Bj)
Для всех команд ...задано ...требуется полу- чить (DCJ — (DC4) (DCJ — (DC4)
Денотационная семантика команды цикла While
Находящееся в бесконечном движении
не достигает предела. Не достигая
предела, оно возвращается к своему
истоку.
Лао Цзы. Дао Дэ Цзин
Интуитивно понятно, что команда цикла описывает некоторый
алгоритмический процесс, который по своей природе является
рекурсивным (можно утверждать, что команда цикла «скрывает»
рекурсию). Сказанное подтверждается, например, тем, что wp-
аксиома для команды цикла имеет рекурсивное представление.
Рассмотрим частный случай команды цикла DOn:
def def
DOj = do => IF2 od = do Bj => if Bj => Sj fi od.
Нетрудно видеть, что содержательная операционная семантика
команды DOT совпадает с содержательной операционной семан-
тикой команды цикла while Bj do Sj od в языке H, а следовательно,
и с содержательной операционной семантикой команды
if then Sj; while Bj do Sj od else skip fi
в языке Н.
561
https:/Л: it.ru
Определение.
def
WP = wpfwhile Bj do od, R).
Предложение.
В системе Дейкстры является доказуемой формула
WP о (Bi v Л) & wpC^, WP) v & R.
Доказательство. Опираясь на сказанное выше, можно утверж-
дать, что доказуемыми в системе Дейкстры являются следующие
формулы:
WP о wp(if В2 then S]; while B1 do od else skip fi, R),
wp(if Bj then ; while B1 do od else skip fi, R) о (B1 v R) & tvp(Sj, WP) v -Д & R.
Предложение доказано.
Определение.
wp-аксиомой команды цикла while Bj do od назовём формулу
WP о (Bj v R) & wpCSj, WP) v & R.
Теорема (о денотационной семантике команды цикла While)
(по [84, ч. 2, с. 585]).
Формула
WP<->(3k>0)Wfc, Wk
defJ-iBj&R, еслик = О,
wp(if Bj then Sj else skip fi, ), если k e N \ {0},
является решением следующего уравнения с отношением выводи-
мости относительно WP:
|-WP<o(B1vR)&wp(S1,WP)v^B1&R.
Доказательство. Упражняйтесь.
562
ttps://urait.r
Синтез команд цикла Дейкстры
Я хочу узнать, как Бог создал этот мир.
Меня не интересует то или иное явление,
спектр того или другого элемента. Я хочу
узнать, о чём Он думал, всё остальное —
детали.
А. Эйнштейн
Пусть необходимо построить цикл Дейкстры при известных
предусловии Q, постусловии R, инварианте Р и ограничивающей
функции t.
Рассмотрим цикл с одной охраняемой командой
do В => S od.
Приведём неформальное описание стратегии синтеза команд
цикла Дейкстры с одной охраняемой командой [88, с. 185]:
1) вначале постройте такую охрану В, чтобы формула (Р & —В —» R)
была доказуемой в системе Дейкстры (другими словами, «ищите ох-
рану ещё до поиска команды»);
2) постройте тело цикла таким образом, чтобы оно уменьшало
ограничивающую функцию при сохранении инварианта цикла.
Итак, каждый цикл с одной охраняемой командой имеет следую-
щую интерпретацию в более содержательных терминах:
{Р} do В => Уменьшить t, сохраняя истинность Р od {Р & —В}
Приняв во внимание неформальную стратегию синтеза цикла
и воспользовавшись основными теоремами о команде цикла, по-
строим формальную стратегию синтеза тела цикла с одной охра-
няемой командой:
1) решите следующую систему уравнений в отношениях выво-
димости относительно неизвестной охраны В:
|-(Р&-В->Я),
h(P&B^t>0)
(на самом деле для нахождения неизвестной охраны достаточно
лишь первого уравнения, второе уравнение необходимо лишь для
проверки);
2) покажите, что тройка Хоара {Р & В} х := t; S {t < х} является
доказуемой в системе Дейкстры;
3) покажите, что тройка {Р & В} S {Р} (или формула Р & В —>
wp(S, Р)) является доказуемой в системе Дейкстры.
Теперь рассмотрим стратегию синтеза Цикла Дейкстры с не-
сколькими охраняемыми командами (по [88, с. 190])
563
def
DOn = dol^ =>S1aB2 =>S2a...aBn =>Sn od.
1. Напишите команды инициализации, делающие инвариант до-
казуемым в системе Дейкстры перед выполнением цикла.
2. Стройте охраняемые команды, создавая каждую команду та-
ким образом, чтобы она приближала цикл к завершению, а соответ-
ствующую охрану так, чтобы обеспечить сохранение инварианта.
Процесс создания охраняемых команд завершается, если их создано
достаточно, чтобы можно было доказать формулу (Р & —,ВВ R)
в системе Дейкстры.
Итак, знание инварианта цикла помогает создавать программы.
Контрольные вопросы
1. Вычислите: а) HX(R); б) H2(R); в) H3(R).
2. (По [78, с. 94, № 4])
Докажите, что в системе Дейкстры для любой формулы А доказуема
тройка {A} while В do S od {-В}.
3*. Определите wp-семантику команды цикла Repeat.
4*. Определите sp-семантику команды цикла DOn.
Примеры решения некоторых
типов упражнений
https:
Пример 1 (по [99, с. 97—98]).
Докажите полную правильность программы (написанной на языке
Pascal) нахождения приближённого значения корня монотонно возрас-
тающей функции Func на отрезке [а, Ь] с заданной точностью Eps:
{Q} с := a; h := Ъ - а;
while h > Eps & Func(c) * 0 do
begin h := h/2; if Func(c) > 0 then с := c - h else с := c + h end
{R}>
где
def
Q = a <b &1 > Eps > 0 & Mon(Func, a, b) & Nil(Func, a, b),
def
R = Nil(Func, c - Eps, c + Eps),
def
Mon (Func, a, b) = VxVy(a <x <у < b -» Func(x) <Func(y)) —
предикатный символ, интерпретируемый трёхместным предикатом, при-
нимающим значение 1 тогда и только тогда, когда функция Func моно-
тонно возрастает на отрезке [а, Ь],
564
//i । го it i-i ।
def
Nil(Func, a, b) = Sz(a < z < b & Func(z) = 0) —
предикатный символ, интерпретируемый трехместным предикатом, при-
нимающим значение 1 тогда и только тогда, когда существует корень
функции Func на [а, Ь].
Введённые предикатные символы удовлетворяют следующим свой-
ствам (приведённые ниже теоремы докажите самостоятельно):
1) Mon(Func, х,у) & (х <у) -» Func(x) < Func(y);
2) Mon(Func,х,у) &(x<z<у) —> Mon(Func,х, z) &Mon(Func, z,y);
3) Func(z) = 0 —> Nil(Func, z, z);
4) Nil (Func, x,y) & (m<x<y<n) —>Nil(Func, m, ri);
5) Mon(Func, x,y) Nil(Func, x,y) <-> Func(x) < 0 & Func(y) > 0.
Решение. Напишем программу на языке D:
{Q} с := a; h := Ъ - а;
do h > Eps & Func(c) * 0 => h := h/2;
ifFunc(c) > 0 => c :=c-hn
Func(c) < 0 => с := c + h
fi
od
{R}.
Покажем, что выполняются все условия для проверки правильности
def
цикла для инварианта Р = Nil (Func, с - h, с + h) & Eps > 0 & h > 0 и огра-
def
ничивающей функции t = h - Eps.
def
1) wp(c :=a;h:=b- a, Nil(Func, c - h, c + h) & Eps > 0 & h > 0 =
def
= Nil(Func, 2 • a - b, b) & Eps > 0 &b-a > 0;
Теорема Теорема (4)
a<bl-2-a-b<a<b<b;2'a-b<a<b<b,Nil(Func,a,b)l-Nil(Func,2'a-b,b)
a < b, 1 > Eps > 0, Mon(Func, a, b), Nil(Func, a, b) I- Nil(Func, 2 a - b, b)
a < b & 1 > Eps > 0 & Mon(Func, a, b) & Nil (Func, a, b) I- Nil (Func, 2 • a - b, b) & Eps >0&b-a>0
2) wp(h := h/2; if Func(c) > 0 => c :=c-hn Func(c) < 0 => с := c + h fi,
def
Nil(Func, c - h, c + h) & > Eps > 0 & h 0) =
def
= wp(h h/2, (Func(c) > 0 —> wp(c :-c-h, Nil(Func, c-h, c + h) & Eps >
def
> 0 & h > 0)) & (wp(c :-c + h, Nil(Func, c - h, c + h) & Eps > 0 & h > 0)) =
def
= wp(h h/2, (Func(c) > 0 —> Nil(Func, c - 2 • h, c) & Eps > 0 & h >
def
> 0) & Nil(Func, с, c + 2 • h) & Eps > 0 & h > 0) =
def
= (Func(c) > 0 —> Nil(Func, c - h, c) & Eps > 0 & h/2 >
> 0) & (Func(c) < 0 —> Nil(Func, с, c + h) & Eps > 0 & h/2 > 0)
565
httpsit.ru
Теорема
Eps>ОНEps>O;h>O\-h>O; Nil(Func,c-h,c+h),h>0,Func(c)>01-
I- Nil (Func, c - h, c)
Nil(Func,c-h,c+h), Eps > 0, h > 0, Func(c) >01-
I- Func(c) > 0 -> Nil(Func,c - h, c) & Eps >0&h/2>0;
Nil (Func,c-h,c+h), Eps > 0, h > 0, h > Eps, Func(c) >01-
l-Func(c)>0-> Nil (Func,c-h,c)&Eps>0&h/2>0&
&Func(c) < 0 -> Nil (Func, с, c+h) & Eps >0&h/2>0
Nil (Func, c - h, c+h) & Eps >0&h>0&h> Eps & Func (с) > О I- wp(h :-h/ 2;
if Func(c) > 0 => с := c -hnFunc(c) <0=>c:=c+hfi
Nil(Func, c - h, c+h) & Eps > 0 & h > 0
Теорема
Func(c) > 0, Func(c) < 0 H Nil (Func, с, c+h) & Eps >0&h/2>0
Nil (Func,c-h,c+h), Eps > 0, h > 0, Func(c) <0h
I-Nil (Func,c,c+h)&Eps>0&h/2>0
Nil(Func,c- h,c+h), Eps > 0, h > 0, h > Eps, Func(c) >01-
I- Func(c) < 0 -> Nil(Func, с, c+h) & Eps >0&h/2>0
D
Теорема Теорема
Nil (Func, c - h, c+h) & < Eps I- Eps > 0 & Func(c) = 01-
l-Nil(Func,c-Eps,c+ Eps); l-Nil(Func,c-Eps,c+ Eps)
Nil (Func, c - h, c+h) & Eps > 0 & h > 0 & (h < Eps v Func (с) = О I—
|-Nil(Func,c-Eps,c+ Eps)
Теорема
h>Epsl-h-Eps>0
Nil (Func, c - h, c+h) & Eps >0&h>0&h> Eps & Func(c) О I- h - Eps > 0
5) wp(x :=h- Eps; h := h/2;if Func(c) > 0 => c :=
def
= c - h □ Func(c) < 0 => с := c + h fi, h - Eps < x) =
def
= wp(x :=h- Eps; h := h/2, wp(if Func(c) > 0 => c :=
def
= c - h □ Func(c) < 0 => с := c + h fi, h - Eps < x)) =
def
= wp(x :=h- Eps;h := h/2, (Func(c) > 0 —> wp(c :=
def
= c-h,h- Eps < x)) & (Func(c) < 0 —> wp(c :=c + h,h- Eps < x))) =
def
= wp(x :-h- Eps; h h/2, (Func(c) > 0 —> h - Eps <
def
< x) & (Func(c) < 0 —> h - Eps < x)) =
def
= (Func(c) > 0 —> h/2 - Eps < h - Eps) & (Func(c) < 0 —> h/2 - Eps <
< h - Eps)) s (Func(c) > 0 —> h/2 < h) & (Func(c) < 0 —> h/2 < h));
566
https ://ига it.ru
h>0\-h/2<h h>0\-h/2<h
h>0;Func(c)>0l-h/2<h h>0;Func(c)<0l-h/2<h
h>0l-(Func(c)>0->h/2<h) h>0l-(Func(c)<0->h/2<h)
Nil (Func, c - h, c+h) & Eps >0&h>0&h> Eps & Func (c)^Oh
h(Func(c)>0->h/2<h)&(Func(c)<0->h/2<h)
I- Nil (Func, c - h, c+h) & Eps >0&h>0&h> Eps & Func (c) * 0 ->
-^(Func(c) >0^h/2<h)&(Func(c)<0^h/2<h)
Проверены условия 1—5 для проверки правильности цикла и тем
самым доказана правильность фрагмента программы.
Пример 2 (по [87]).
Постройте программу возведения целого числа т в степень п е N.
def
Решение. Формализуем постусловие: R - р-тп и будем стремиться
к цели посредством цикла Дейкстры.
def
Угадаем (!) инвариант цикла: Р = р-ш"1 = тп.
Инициализация цикла записывается очевидным образом: р := 1;
т1 := т; nx := п.
Выберем формулу В как решение уравнения с отношением выводи-
мости
I-P&-1B—>Р:
р-ш"1 = тп,п1=О\-р = тп
р-т"1 -тп,—В\-р-тп
l-p-m"1 = тп&-В^>р = тп
\-P&—B—>R
Итак, В =s пг Ф 0, получено условие выхода из цикла и следующий
набросок программы:
р := 1; mi := m; := п; do пг 0 =>? od.
В теле цикла необходимо уменьшать. При этом множитель т"1
mF1 будет уменьшаться. Чтобы инвариант не менялся, р необходимо
во столько же раз увеличивать. В результате получаем программу
р := 1; т1 := т; щ := п; do + 0 => пг := пг -1;р :=р • т1 od {р = тп}
Остается формально доказать, что:
а) Р является инвариантом цикла:
p-m"1 =тп l-p-m"1 =тп
р-ш"1 =шп,П!^01-p-ni! m"1-1 = тп
1-Р&П! ^0—>ир(п! ^Hi-ljp^pniijP)
567
https://?.! га it.ru
б) работа программы завершится после конечного числа повторений
цикла. Во-первых, легко показать, что \-Р&п1 = О^>р = тп, а во-вторых,
def
угадаем t = пг и покажем, что I- Р &В -> wpCjq := t; S, t < Xi) :
p-m"* 1 =mn,n! ^Ol-n1-l<n1
I- P&B->wp(.x1 :=t;n! :=n1-l;p:=p-m1,t<x1)
\-P&B^wp(.x1 :=t;S,t<x1)
Итак, построенный цикл завершается.
Пример 3 [88, с. 188]. Напишите программу, которая при данном мас-
сиве А[0: п -1], где п > 0, придаёт* наименьшее значение из А. В случае,
если наименьшее значение встречается в А более одного раза, программа
может быть недетерминированной. Предусловие Q, постусловие R, инва-
риант цикла Р и ограничивающая функция t следующие:
def def
Q = 0<n,R = x<A[0:n-l]&(3jG[0,n))(x = A[J]),
def def
P - l<i<n&x<A[0:n-l]&(3jG[0,i))(x = A[j]),t = n-i.
Будем считать, что смысл словах <А[0: и -1] понятен.
Решение. Решим уравнение с отношением выводимости I- (Р & -В —> Ю
относительно неизвестной формулы В:
1 — i — и, Oj е [О, 0) О = А[ j]), i = и Н (Я/ g [0, n)) (х = А[ j])
1 < i < и, (3j g [0,0) (х = А[ j]), -пВ I- (3j g [0, и)) (х=А[ j])
1 < i < п, х < А[0: п -1], (3J g [0,0) (х=А[Л ), -В И
I- х < А[0: и -1] & (3j е [0, п)) (х = А[ Л )
|-1 <i <n&x < А[0 g[0, i))(x = А[Л)&-В
____________-4- х < А[0: n-l]&Oj g [0, п)) (х=А[Л )
нр&-в->я
Итак, В =« i Ф п.
Для уменьшения ограничивающей функции необходимо увеличивать
i, например, в теле цикла может присутствовать команда i := i +1.
Угадаем инициализацию цикла i := 1рс :=А [0] и докажем допустимость
такой инициализации:
п>01-п>1
n>0hl<l&l<n&A[0] = A[0]&(3jG[0,0))(A[0] = A[j])
l-n>0^1<l&l<n&A[0]<A[0:n-l]&(3jG[0,l))(A[0] = A[j])
I- и > 0 -> wp(i :=1; х :=А[0], Р)
Теперь приведём первоначальный вариант программы:
i := 1; х :=А[0]; do i + п =>?; i := i +1 od
Выдвигаем гипотезу о доказуемости в системе Дейкстры формулы
Р& (i*ri) &A[i] <х—>ир(х :=A[i]; i :=i + l,P).
Превратите гипотезу в теорему самостоятельно с учетом того, что:
568
P&iVn&A[i]<x=s l<i<n&x<A[0:n-l]&(3/G[0,i))(.x: = A[j]&i^n&A[i]<x;
def
vvpCjc := A[f]; i := i+1, P) = 1 <i+l <n&A[i]<A[0:i]&(3jG[0, i+l))(x = A[j]) =
^0<i<n-l&A[i]<A[0:i]&(3jG[0,i+l))(A- = A[J]).
Остаётся ещё показать, что
l~P &i и&x<Ari] —$wp (i: = i + 1,P).
Приведём лишь окончательный вариант программы:
i :=1;х:=А[0];
doi^n => ifA[i] >x=> i :=i +1 nA[i] <x=>x :=i[i]; i :=i +1 fi od
Упражнения для самостоятельного решения
Создается впечатление, что
по мере того, как расширяются наши
возможности в решении задач, круг
задач расширяется с той же скоростью.
В результате за горизонтом всегда
оказываются новые категории задач,
требующие еще больших усилий.
Дейвид Химмелъблау
Свойства инвариантов и охран циклов
1*. Рассмотрим цикл while В do S od. Докажите, что инвариант тела цикла
S является инвариантом Р этого цикла, т. е. имеет место следующее прямое
допустимое правило вывода
________{P}S{P}_______
{Р} while В do S od {Р & -В}
Вывод (важный).
«Кандидаты» в инварианты цикла могут отбираться среди инвариантов
тела этого цикла.
2*. Докажите, что тройка Хоара {Р} while В do S od {Р} доказуема в системе
Дейкстры при условии доказуемости тройки {P}S{P}.
3. (По [88, с. 242])
Пусть в цикле Дейкстры имеются (по меньшей мере) две охраняемые
команды с охранами Вг и В2. Докажите, что усиление В2 до В2 & —>В1 не из-
менит ВВ, а следовательно, и доказуемости формулы (Р & —ВВ —> R).
4. [95, с. 301]
Докажите, что конъюнкция инвариантов некоторого цикла Дейкстры
остается инвариантом этого цикла. Верно ли обратное?
Определение wp-семантики циклов
5. (По [92, с. 137])
Докажите, что wp-семантика цикла Дейкстры DOn совпадает с wp-
семантикой цикла
569
https:/Л: rait.ru
while Bx v ... v Bn do if Вг => ST и...пВп => Sn fi od
Доказательство частичной правильности программ
6. Докажите частичную правильность следующей программы, которая
оптимальным способом вычисляет произведение целых чисел:
{Q} z := 0; {Р} while у > 0 do
if Even(y) thenx := x+x;у :=y/2 else у :=y-1; z := z+x
fi
od
{R}>
def def def
где Q = x-a&y-b&b>0, R = z-a -b,P = y>0&x-y + z = a-b.
7. (По [99 ,c. 160])
Докажите частичную правильность следующей программы, которая
проверяет, является ли заданное число а простым числом (число а является
простым числом тогда и только тогда, когда j = 0):
{Q} i := 2; {Р} while i < а & rest(a, i) Ф 0 do
i := i + 1; if i > a then j := 0 else
j :=1 fi
od
{R}>
def
где rest(a, i) — остаток от деления а на i, Q = a > 2,
def
R = (j - 0 —> Vk(2 < k < a) —> rest(a, k) Ф 0)) v (/=]—> 1 < i < a &
& rest(a, i) = 0),
def
P = 1 < i < a & \fk(2 <k < a) rest(a, k) Ф 0).
8. (По [99, c. 158—159])
Докажите частичную правильность следующей программы, которая
по упорядоченному массиву М[1: п] и числу х (М[1] < х < М[п]) находит
такое i, что М[1] < х < M[i + 1] :
{Q} i := 1; j := п; {Р} while i + 1 Ф j do
fc:=[(i+j)/2];
if M[k] < x then i := k else j := k fi
od
{R}>
def def
где Q = M[l] < x < M[n] & Ordered (M[l: n]) & n > 1, R = 1 < i < n & M[i]
<x < M[i + 1],
def
Ordered(M[l: n]) = Vm(l < m < n) —>M[m] <M[m +1]),
def
[x/r] — целая часть числа x/r, P = 1 < i < j < n & M[i] < x < MQ].
9. [81, c. 43]
Приведите доказательство частичной правильности программы:
{х > 0 &у > 0} z := 0; и :=х;
{z + u- y=x-y&u>0} repeat z :=z+y,u:=u-l until и = 0 {z=x • y}.
570
https:/Л: rait.ru
10. Докажите частичную правильность следующей программы:
п := М; s := 0; while п > 0 do
s :=s + п п;п:=п-
1
od,
def
где Р = n>0&n<M&s = (n + I)2 + (п + 2)2 + ... + М2.
Доказательство полной правильности программ
11. (По [88, с. 151])
Докажите полную правильность следующей программы, которая запи-
сывает в s сумму элементов массива А[1:10]:
{И} i := 1; s :=А[0]; {Р} do i < 11 => s :=s + A[i]; i := i + 1 od {R}>
def i-1 def def 10
гдеР = l<i<ll&s= £ A[k],t = ll-i,R = s= £ A[k].
k=0 k=l
12. Докажите полную правильность следующей программы, которая
записывает в z значение а Ъ при Ъ > 0, но без использования операции
умножения:
{Q} х := а; у := b; z := 0;
{Р} do у > 0 & Even(y) = > у := у + 2;
х := х + хп
Odd(y) —> у :=у-1; z :-z + x
od
{R},
def def def def
где Q = b > 0, P = y>0&z + x-y = a-b, t = y,R = z = a b
13. Докажите полную правильность фрагмента программы
{Q} {Р} do у Ф х => у :=у +1 od {Я},
def def def def
где Q = x > 0 &y = 0, P = x >y, t = x-y, R = у = x.
14. (По [88, c. 152])
Докажите полную правильность следующей программы, вычисляющей
и - е число Фибоначчи:
{Q} i := 1; а := 1; Ъ := 0; {Р} do i < п => i := i +1; z := a; a := a + b; b := z od {R},
def def def def
где Q = n>0, P=l<i<n&a=Fj&b = Ft_1} t = n - i, R = a = Fn.
Указание. Числа Фибоначчи Fn определяются рекуррентными соотноше-
ниями Fo - 0, Fj - 1, Fn - + Fn_2, n > 1.
15. [88, c. 152]
Докажите полную правильность следующей программы, вычисляющей
частное q и остаток г от деления х на у:
{Q} q := 0; г := х; {Р} do г >у => г := г -у; q := q + 1 od {R},
def def def
где Q - x>0&y>0, P - 0<r&0<y&qy + r = x, t - r,
def
R = 0<r<y&qy + r = x.
16. Докажите полную правильность следующей программы:
571
https:it.ru
{Q} г := 0; x := b; {P} while x Ф 0 do r := r + a; x := x - 1 od £R},
def def def def
где Q = b > 0, P = r = a • (b - x~), t = x, R = r = a -b.
17. [88, c. 152]
Докажите полную правильность следующей программы, ищущей та-
кое целое число к, что В [к] является максимальным значением в массиве
В[0: п -1] (заметим, что если максимальное значение встречается в массиве
более одного раза, то программа становится недетерминированной):
(Q) i := 1; к := 0; {Р}
do i < п => ifB[i] <B[k] => skip
□
B[i] >B[k] => k:=i
fi;
i := i + 1
od
{R}>
def def def def
где Q = n > 0,P = 0< i<n &B[k] >B[0: i-1], t = n-i,R = B[k] >B[0: n-1].
18*. (По [99, c. 97—98])
Пусть
def
Mon(Func, a, b) = VxVy(a<x <y<b->Func(x) <Func(y))
— предикатный символ, интерпретируемый трехместным предикатом,
принимающим значение 1 тогда и только тогда, когда функция Func моно-
тонно возрастает на отрезке [а, Ь];
def
Nil(Func, a, b) = Ez(a < z < b & Func(z) = 0)
— предикатный символ, интерпретируемый трёхместным предикатом,
принимающим значение 1 тогда и только тогда, когда существует корень
функции Func на [а, Ь].
А. Докажите следующие теоремы для введённых предикатных символов:
1) Mon(Func, х,у) & (х < у) Func(x) < Func(y);
2) Mon(Func, х, у) & (х < z <у) —> Mon(Func, х, z) & Mon(Func, z, у);
3) Func(z) = 0 Nil(Func, z, z);
4) Nil(Func, x, у) & (m < x < у < n) Nil(Func, m, n);
5)* (Mon(Func, x,y) Nil(Func, x,y)) Func(x) < 0 & Func(y) > 0.
Б. Докажите полную правильность программы на языке Pascal нахож-
дения приближённого значения корня монотонно возрастающей функции
Func на отрезке [а, Ь] с заданной точностью Eps:
{Q} c:-a;h:-b-a;
while h > Eps & Func(c) 0 do
begin h := h/2; if Func(c) > 0 then с := c - h else c :=
c + h end
{K},
def
где Q = a < b &1 > Eps > 0 & Mon(Func, a, b) & Nil(Func, a, b),
it i-i i
572
def
R = Nil(Func, c-Eps, c + Eps).
Прямые допустимые правила вывода в системе Дейкстры
19. (По [99, с. 127])
Докажите, что следующие слова являются прямыми допустимыми пра-
вилами вывода в системе Дейкстры:
{Q}S{P} {P&alS^P}
{Q}S; {P} while a do od {R}
6) {Q}S;Si(P} {Р&^аЩР} P&a^R
{Q}S; repeat S2{P} until a {R}
20. (По [99,с.11О])
Докажите, что следующие слова являются прямыми допустимыми пра-
вилами вывода в системе Дейкстры:
ч P<->P'vP Q->P' {P'&a}S{P}
а) {упрощение
{Q}{P} while a do S od {R} <-> {Q}{P'} while a do S od {R}
инварианта цикла);
~ = {Q}x:=t{R} . 4
6) --------------{изменение присваивания);
в) {преобразование ко-
{P} if a then S fi {P} <-> {Р}{1} while a do S od {P}
манды условного перехода в цикл);
. _ {Q}{P} while ou do if a2 then S, else & fi od {R} .
r)* --------i-------------------------— {преобразование цикла
{Q}{P} while a1 do {P} while (сц & a2) do Sx;
{P} while (ai & -ia2) do S2 od od od {R}
с командой условного перехода);
{Q}{P} while cq do {P} while (cq &a2) do Sx;
. {P} while (ou & -ia2) do & od od od {R} ,
A)*-------------------------------------------{преобразование цикла
{Q}{P} while ax do if a2 then Sx else S2 fi od {R}
с командой условного перехода)
Описание семантики программ
21. (По [99, с. 40—41])
Опишите семантику следующих программ:
а) i :=0;j :=0; к :=0;
doMJi] < M2fj] => i := i +1 □ M2[j] < M3[k] => j :=j +1 □
M3[k] < Mx[i] => к := к +1 od,
где МД0: m], M2[0: m], M3[0: m] — массивы, строго упорядоченные по воз-
растанию:
б) i :=0;j :=0;
do 2|x v 3 |x=> if 2|x=> х :=х/2; i :=i + 1 □ 3|x=> х :=x/3;j :=j+ 1 fi od.
22. Опишите семантику следующей программы (TURBO Pascal):
№р$
Ih iroif ri i
i i ui ou.i vi
573
PROGRAM Primer_22;
var a, b, c, h, Eps, Epsl: Real;
{ }
FUNCTION Func (x: Real): Real;
BEGIN
Func := sin (x)/cos (x) - 200
END;
{--}
BEGIN
a := 0; b := PI/2 - 0.0000000001;
Write (’Введите исходную информацию: ’); Read(Eps, Epsl);
c a; h b - a;
While (h > Eps) AND NOT (ABS(Func(c)) < Epsl) do
begin h := h/2; If Func(c) > 0 then с := c - h else с := c + h end;
WriteLn; Write (’Результат: Func(c), c); WriteLn
END.
Синтез команд цикла
23. [88, с. 188]
Напишите программу, которая при данном массиве В[0: п -1], где п > 0,
придает х наименьшее значение из В. В случае, если наименьшее значение
встречается в В более одного раза, программа может быть недетерминирован-
ной. Предусловие Q, постусловие R, инвариант цикла Р и ограничивающая
функция t заданы так:
def def
Q = 0<n,R = x<B[0:n-l]&(3je[0,n))(x = B[j]),
def def
P = 0<i<n&x<B[0:n-l]&(3/e[i,n))(x=B[j]),t = i.
24. (По [88, c. 188])
Напишите программу, которая присваивает i наибольшую степень
двойки, не превосходящую заданного п > 0. Предусловие Q, постусловие R,
инвариант цикла Р и ограничивающая функция t заданы так:
def def def def
Q = 0<n,R = 0<i<n<2i&3p(i = 2₽),P = 0<i<n&3p(i = 2₽),t = n-i.
25. [88, c. 188]
Напишите программу, которая для данного целого числа п > 0 и массива
целых чисел В [0: п-1] записывает в переменную S сумму элементов массива
В. Воспользуйтесь инвариантом и ограничивающей функцией:
def п-1 def
Р = 0<i<n&S= ^B[j],t = i.
j=i
II I
574
Доказательство свойств завершаемости программ
26. Докажите завершаемость программ на языке Pascal:
a) PROGRAM Test_l;
var х, у, z: Integer;
BEGIN
Write (’Введите положительное целое число: Read(x);
Write (’Введите целое число: Read (у);
z:= 0;
While х< > do
begin
if Odd(x) then begin z := z + у; x := x - 1 end;
у :=y * 2; x := x DIV 2
end;
WriteLn(’Pe3ynbTaT: ’, z)
END.
6)
PROGRAM Test_2;
varx,y,z,f: Integer;
BEGIN
Write (’Введите натуральное число n > 2: ’); Read (n);
x:=l;y:=l;/:= 0; i := 2;
While i < n do
begin/ :=x+y;x :=y; у :=f; i := i + 1 end;
WriteLn (’Результат вычислений : ’, z)
END.
Замечание.
При доказательстве завершаемости программ разумно поменять син-
таксис языка Pascal на синтаксис языка Н по двум причинам:
а) второстепенная; с формальной точки зрения для конструкций,
написанных на языках Н и D, мы умеем находить слабейшие предусло-
вия, а для конструкций, написанных на языке Pascal — нет;
б) главная; конструкция, написанная на языке Н, как правило, короче
аналогичной (т. е. имеющей сходный синтаксис и такую же операцион-
ную семантику) конструкции, написанной на языке Pascal. Это происходит
из-за того, что в языке Н внутри операторов ветвления и цикла не исполь-
зуются операторные скобки begin—end. Их вполне заменяют слова fi и od.
27*. (По [78, с. 93])
Докажите завершаемость следующей программы:
п := п0;
while п > 1 do
if Even(n) then n := n/2 else n := n + 1 fi
od.
Указание. Ограничивающая функция имеет вид:
0, если п = 1;
п + (-1)п, если п > 1.
28*. (По [81, с. 50—51])
575
def
t(n) = <
https: "и га it.ru
Пусть функция z = Нод(х, у) обладает следующими аксиомами:
Нод(а, а) = а, Нод(а, Ь) = Нод(Ь, а), а > b —> Нод(а, Ь) = Нод(а - Ъ, Ь).
Установите условия незавершения следующих программ, вычисляющих
наибольший общий делитель натуральных чисел х и у:
а) {х > 0 &у > 0] а х; Ъ :-у; {а > 0 & Ъ > 0 & Нод(а, Ъ) - Нод(х, у)}
repeat
while a>b do a := a-b od;
while b > a do Ъ b - a od
until a = b
{а = Нод(х, у) & b = Нод(х, у)};
б) {х > 0 &у > 0] а :=х; b :=у; {а>0&Ь>0 & Нод(а, Ъ) = Нод(х,у)}
repeat
while а > Ъ do а := a-b od;
while b > a do b := b - a od
until a = b
{а = Нод(х, у) & b = Нод(х, у)};
29*. [78, с. 94, № 5]
Докажите, что выполнение циклической конструкции
while п > 1 do
if Even(n) then n := n/2 + 1 else n := n + 1 fi
od
не завершается ни для какого натурального п > 1.
Указание. Решение см. в [77, с. 26].
30**. Докажите (или опровергните) завершаемость следующей про-
граммы:
п := п0;
while п > 1 do
if Even (n) then n := n/2 else n := 3 • n + 1 fi
od.
31**. Докажите (или опровергните) завершаемость следующей про-
граммы на языке С:
/* Демонстрация неожиданного поведения рекурсивной функции. */
/* Тестовые примеры: */
/* (1) п = 5: 5,16, 8, 4, 2, 1; */
/* (2) п = 172: 172, 86, 43,130, 65,196, 98,49,148, 74, 37, */
/* 112, 56, 28, 14, 7, 22, И, 34, 17, 52, 26, 13, */
/* 40,20,10,5,16,8,4,2,1: */
/* (3) п = 123456789: для достижения 1 требуется 177 итераций */
/* _________________________________________________ * /
576
https://и гз it.ru
#include<stdio. h>
#include<conio. h>
int Paradox_l (int);
int Paradox_2 (int);
int mainQ
{
int n;
printf(“Введите n: ”); scanf(“%d”, &n);
Paradox_l(n), printf(“\n”), Paradox_2(n), printf(“\n”);
getchQ;
return 0;
}
/
int Paradox_l (int n)
{
printf (“%d n);
if(n = =l)
return 1;
else return (n %2 = = 0)?Paradox_l(n/2): Paradox_l(3 * n + 1);
}
_________________* /
int Paradox_2 (int n)
{
printf(“%d “ n);
while (n! = 1)
if (n %2 = = 0)
printf (“%d n/ = 2);
else printf(“%d n = 3 * n + 1);
return n;
}
https:/Л; it.ru
Упражнение 27
ЭВРИСТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА
ИНВАРИАНТОВ ЦИКЛА ДЕЙКСТРЫ
За нашими мыслями, истинными или
ложными, всегда расположено тёмное
основание, котороемы только позднее можем
вывести на свет и выразить как мысль.
Л. Витгенштейн
Обязательные результаты обучения:
• знать основные понятия
— метод устранения конъюнктивного члена, стратегия построения охра-
ны цикла;
— метод замены константы переменной;
— метод введения новой переменной;
— метод добавления дизъюнктивного члена;
— метод извлечения инварианта цикла из рекурсивных программ;
• уметь
—конструировать программы по постановке задачи, используя синтети-
ческий подход к формальной верификации программы (метод устранения
конъюнктивного члена постусловия, метод замены константы переменной,
метод введения новой переменной);
—конструировать программы по постановке задачи, используя аналити-
ческий подход к формальной верификации программы (метод устранения
конъюнктивного члена постусловия, метод замены константы переменной,
метод введения новой переменной, метод добавления дизъюнктивного члена,
метод использования рекурсивных определений);
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
Теоретические сведения
Пусть необходимо построить программу S, удовлетворяющую ус-
ловию
Ь {Q}S{K}
при данных Q и R, и уже решено использовать цикл Дейкстры (вме-
сте с командами инициализации).
578
https:/Л: rait.ru
Возникает естественный вопрос: «Как перед написанием тела
Цикла найти для него инвариант и ограничивающую функцию?».
Вначале приведём два важных замечания:
1) инвариант цикла заключает в себе знания, закладываемые
человеком в проектируемый алгоритм решения задачи (програм-
му). Поэтому в общем случае нахождение инварианта цикла требу-
ет участия программиста, проектирующего цикл;
2) инвариант цикла не является единственным.
«Слабейшим» инвариантом цикла является предикат Р = И, не не-
сущий полезной информации о семантике цикла. «Более сильные»
инварианты цикла описывают отношения между глобальными пе-
ременными цикла (переменными, значения которых используются
вне цикла), и характеризуют функцию, вычислимую циклом.
Метод «воздушного шарика»
— Вот это ты очень хорошо придумал,
Пятачок! Ведь Иа нужно развеселить.
А с воздушным шариком кто хочешь
развеселится! Никто не может грустить,
когда у него есть воздушный шарик!
А. А. Милн
В последующем изложении будем следовать Д. Грису [88, гл. 16].
Изобразим множество всех состояний, в котором выделим под-
множество состояний, для которых истинно постусловие R, и мно-
жество возможных начальных состояний IS (оно образовано с помо-
щью команд присваивания), а так как инвариант Р — это предикат,
который истинен перед каждым выполнением тела цикла и после
его выполнения, то множество состояний, для которых истинен
предикат Р, должно содержать как IS, так и R:
IS
р
R
Будем интерпретировать R состоянием некоторого «полунадуто-
го» воздушного шарика, а Р — состоянием полностью надутого воз-
душного шарика перед началом выполнения цикла.
Каждое выполнение шага цикла будем интерпретировать про-
цессом выпускания из шарика некоторого количества воздуха, при-
чем таким образом, чтобы при выполнении последнего шага цикла
шарик вернулся в спущенное состояние R. Изобразим сказанное
на рисунке:
IS
Р0 = Р
579
I it*ps://L,ra!t.r
где Ро = Р — это воздушный шарик перед первым шагом цикла, Рг —
после выполнения первого шага, Р2 — после выполнения второго
шага и т. д.
Теперь необходимо узнать, как первоначально «надуть воздуш-
ный шарик» (ослабить постусловие R) так, чтобы выполнение тела
цикла могло опустошить его полностью (другими словами, как най-
ти инвариант Р и ограничивающую функцию t).
Напомним, что вначале нам известны только предикат R и мно-
жество исходных состояний IS.
Ниже мы опишем три способа ослабления R [88, с. 198].
При этом общая стратегия построения цикла такова: сначала
создается охрана, а лишь затем — тело цикла.
Метод устранения конъюнктивного члена постусловия
О ужас! Эта тряпочка — это и был,
именно был! — его воздушный шар
А. А. Милн
Метод устранения конъюнктивного члена постусловия таков:
1) угадайте, какой конъюнктивный член постусловия R можно
удалить, чтобы получить инвариант цикла;
2) попытайтесь использовать отрицание устраненного члена
постусловия в качестве охраны В цикла (этот пункт называется
стратегией построения охраны цикла [88, с. 199]).
Обоснование метода опирается на следующие факты:
1) формула (А1 & Д2 & ... & Ап —» А2 & ... & Ап) является теоремой,
поэтому формула Aj &А2 & ... & Ап может быть «ослаблена» до фор-
мулы А2& ... &Ап;
2) описанный способ выбора формулы В автоматически обеспе-
чивает доказуемость формулы (Р & -В —> Я).
Метод устранения конъюнктивного члена постусловия рассмо-
трим на примере.
Пример (по [88, с. 198—199]).
Напишем программу, которая по данному целому числу п > 0 опреде-
лит наибольшее целое число а, такое, что а < п1/2.
def def
Известно, что Q = {п > 0}, R - а2 < и & п < (а +1)2.
Решение. Для нахождения инварианта воспользуемся методом устра-
нения конъюнктивного члена постусловия.
Предположим, что инвариантом является формула Р = а2 < п. Опреде-
лим охрану цикла В как решение уравнения с отношением выводимости
I- (Р&-В->Я):
-iBI-n<(a+l)2
а2 <п,-В\-а2 <п8гп<(а+1)2
На2 <п&-В->а2<п&п<(а+1)2
\-(P&—B^>R)
580
https://urajt.ru
Откуда —iB =s n < (a+1)2, В =s n > (a+1)2, что приводит к «почти» закон-
ченной программе:
а := 0; do п > (a +1)2 =>? od
(отметим, что инициализация цикла сохраняет истинность инварианта
цикла). Назначение команд тела цикла—приближать его к завершению.
Ясно, что если охрана цикла истинна, то можно приблизиться
к завершению, увеличив а. Выберем самый простой способ увеличения
а (a := a +1) и приходим к программе:
а := 0; do п > (a +1)2 => а := а +1 od
Покажем, что Р действительно является инвариантом цикла.
1. проверим доказуемость тройки {п > 0}а := 0{Р}:
п>0Н0<п
I- п > 0 -> wp(a :=0, а2 < п)
|-{п> 0}а :=0{Р}
2. Установим доказуемость формулы Р & В —> wp(S, Р). Вычислим:
wp(a := a +1; Р) = (a +1)2 < п.
Далее построим дерево непрямого вывода:
n>(a+l)2 H(a+1)2 <п
a2 <n,n>(a+l)2 H(a+1)2 <п
l-a2 <n&n>(a+l)2 ->(a+l)2 <п
\-P&B—>wp(S,P)
def
3) Предположим, что t - n - а и покажем, что I- Р & ВВ —> t > 0:
(a+1)2 <п\-а<п
а2 <n,(a+l)2 <п\-а<п
На2 <п&(а+1)2 <п->п-а>0
\-P&BB^>t>0
4) Покажем, что I- Р & В —> wp(x := t;S,t <х).
Вначале преобразуем:
def def
wp(x := t; S, t < х) = wp(x :=n-a;a:=a + l,n-a <x) =
def def
= wp(x:=n-a, n-a-1 < x) = n-a-1 < n-a.
Тогда имеем:
Н0<1
l-n-a- 1 <n-a
Р&ВЬп-а-1 <n-a
FP&B-> wp(x :=t; S,t<x)
581
https:/Л: it.ru
Итак, искомой программой является следующая:
{Q} а := 0; do п > (а + I)2 => а := а +1 od {R}
Метод замены константы переменной
Метод замены константы переменной состоит в следующем:
1) в постусловии происходит замена интуитивно выбранной
константы новой переменной (полученную формулу обозначим RJ;
2) формально описывается множество возможных значений но-
вой переменной (полученную формулу обозначим Я2);
3) формула & R2 может являться инвариантом цикла.
Пример.
def
Пусть R = х < В[1: 10]. Для построения формулы, подозрительной
def
на инвариант, введём новую переменную i и построим формулу RT =х <
B[l: i].
def
Нетрудно увидеть, что R2 - 1 < i < 10.
Остаётся проверить, будет ли являться инвариантом формула
x<B[l:i] &l<i<10
Метод замены константы переменной рассмотрим на примере.
Пример (по [88, с. 202—203]).
Напишем программу, которая по данному целому числу и > 0 и мас-
сиву целых чисел В[0: и - 1] находит сумму элементов В и записывает
ее в переменную S.
Решение. Вначале формализуем предусловие и постусловие:
def def
Q = n>0,R = S = B[0]+B[l] + ...+B[n-l].
При построении инварианта цикла воспользуемся методом замены
константы переменной: попытаемся ослабить постусловие R до подходя-
щего инварианта Р путём замены и на новую переменную i:
def
Р = 0<i<n&S=B[0] +В[1] + ...+B[i-l].
Инициализация i := 0; S := 0 устанавливает инвариант (докажите).
Установим охрану цикла; для этого решим уравнение с отношением
выводимости I- (Р&-В —>R):
582
-^Bhi = n S=B[O]+ ...+B[n-l]l-S = B[O]+...+B[n-l]
0<i<n-l,-BH = n; i = n,S=B[O]+ ...+B[i-l],-BI-S = B[O]+...+B[n-l]
O<i<n-lvi = n,S=B[O]+B[l]+...+B[i-l],-BI-S = B[O]+B[l]+...+B[n-l]
O<i<n,S=B[O]+B[l]+...+B[i-l],-BI-S = B[O]+B[l]+...+B[n-l]
H0<i<n&S=B[01+B ll+...+B[i- 1]&-В->5 = ВГ01+вГ11+...+В[п- 1]
H(P&-B->K):
Откуда получаем, что-В =?1 = пиВ=Н*п.
Дальнейшее построение программы очевидно (выполните формаль-
ное доказательство самостоятельно):
i := 0; S := 0;
doi *п=> S :=S+В[i]; i := i +1 od
Из рассмотренного примера следует, что может представиться выбор,
какую из нескольких констант заменить переменной: для получения инва-
рианта можно было бы заменить в К и две другие константы.
Например, при замене константы 0 получается
def
Р = 0<i<n&S = B[i]+B[l] + ...+B[n-l].
В общем случае константа выбирается так, чтобы можно было легко
установить получившийся инвариант, чтобы охраны цикла были проще
и, конечно, чтобы можно было легко написать команды цикла.
Важно отметить, что это — процесс проб и ошибок.
Метод введения новой переменной
Метод введения новой переменной рассмотрим на примере.
Пример.
Напишем программу, которая по данному х и упорядоченному по воз-
растанию массиву В [1: п], удовлетворяющему В[1] <х < В[п], находит
место, в которое х можно поместить в массив, т. е. устанавливает для
новой переменной i значение, для которого
def
R = 1 <i < и&B[i] <х < В [i +1].
Решение. Вначале построим пред- и постусловия:
def def
Q - п > 1 &В[1] <х < В[п],К = 1 <i < п &B[i] <х < В [i+ 1].
Далее построим инвариант методом введения новой переменной (вме-
сто выражения i +1 используем переменную;):
def
Р = l<i<j<n&B[i]<x<B\j]-
583
https: "u it.ru
Определим охрану цикла, решив уравнение P&—B\-R:
__________-Bl-j = i+l__________
l<i< j<n,-iBI-l< j-l<n&j = i+l;
1< j-l<n, j = i+l, B[i] < x < B[ j] Ь
l-l<i<n&B[i]<x<B[i+l]
1 < i < j < n & B[i] < x < B[ j], —B I-1 < i < n & B[i] < x < B[i+1]
l<i< j<n&B[i]<x<B[j]&-BI-l<i<n&B[i]<x<B[i+l]
Отсюда получим, что -В =s (j = i +1), В =s (j i +1).
Угадаем инициализацию цикла i1; jn и покажем справедливость
такой инициализации:
Теорема Теорема
n>l,l-l<l<n<n В[1]<х<В[п]1-В[1]<х<В[п]
n>l,B[l]<x<B[n]l-l<l<n<n; n>l,B[l]<x<B[n]l-B[l]<x<B[n]
n>l,B[l]<x<B[n]l-l<l<n<n&B[l]<x<B[n]
п >1 &В[1] < х < В[п] I- wp(i :=1; j :=n,l<i < j < n&B[i] < x < B[j]J
Теперь построим первоначальный вариант программы:
i := l;j := и; do i +1 *j =>? od
Назначение команд тела цикла — приближать его к завершению.
Ясно, что если охрана цикла истинна, то приблизиться к завершению
можно, увеличив i, если искомое i не найдено, или уменьшив j — в про-
тивном случае. Тело цикла можно построить командой выбора
ifB[l] <х=> i :=i + 1 nB[i] > х=> j :=j- 1 fi.
Докажем оставшиеся пункты для установления правильности постро-
енного фрагмента программы:
1) установим доказуемость тройки Хоара {Р & В} S {Р}:
________________________________D,______________________________
l<i< j<n&B[i]<x<B[j]&i+l?t jH(B[i+l]<x->l<i+l< j<n&B[i+l]<x<B[j]; D2
l<i< j<n&B[i]<x<B[j]&i+l?t jl-B[i+l]<x->l<i+l<j<n&B[i+l]<x<B[j])&
_________________&B[i]>x—>l<i< j-l<n&B[i]<x<B[j-l])_________________
1 < i < j < n&B[i] < x < B[j]&i+1 * j h wp(if B[i+1] < x -> ii+ln
□B[i+l]>x=> j:= j-lfi,l<i< j<n&B[t]<x<B[j])
{P&B}S{P}
Теорема
l<i< j<n&B[i]<x<B[j]&i+l^ j,B[i+l]<xl-l<i+l< j<n&B[i+l]<x<B[j];
Теорема
l<i< j<n&B[i]<x<B[j]&i+l^ j, B[i+1] > x I—1 < i < j-l<n&B[i]<x<B[j-l]
l<i< j<n&B[i]<x<B[j]&i+l^ jl-B[i+l]>x->l<i< j-l<n&B[i]<x<B[j-l]
~ D2
584
https://urajt.ru
def
2) установим выводимость Р & BB I-1 > 0, где t = j - i:
i< j\- j-i>0
1 < i < j < n, B[i] < x < B[ j] ,i+l*j\-j-i>0
l<i<j<n&B[i]<x<B[j]&i+l*j\-j-i>O
3) установим доказуемость (P & B}y :=j - i, S{j - i <y}:
def
wp(y := j - i; if B[i] < x -> ii+laB[i] > x -> jj -1 fi, j - i < y) -
def def
= wp(y:=j-i,(B[i]<x-> j-(i+l)<y)8t(B[i]>x->(j-l)-i<y) =
def
=(B[i] < x j -a+i) < j -i) &(B[i] > x a -i)-i < j -i) s
= (B[i]<x->l>O)&(B[i]>x->l>O = H.
Итак, построенная программа имеет вид:
i := l;j :=п
doi +1 *}=> ifB[i] <x=> i :=i +1 □
B[i] >x=>j:=j-lfi
od.
Метод добавления дизъюнктивного члена
Метод основан на том факте, что формула (А —> A v В) является до-
казуемой в классической гильбертовском исчислении, поэтому форму-
лу А можно ослабить до формулы (A v В), где В — некоторая формула.
Частным случаем этого метода является метод расширения об-
ласти значений переменной.
Например, формулу 5 < i < 10 можно ослабить до формулы 1 <
i < 10, так как доказуемой является формула 5 <i < 10 —> 1 < i < 4 v
5 < i < 10.
Однако этот способ ослабления формул редко используется
в программировании, несмотря на свою общность.
О поиске инварианта для рекурсивных программ
Если спецификация задачи задана в рекурсивном виде, то из со-
ответствующего рекурсивного часто можно извлечь «естественный»
инвариант.
Пример [84, ч. 2, с. 579].
Из рекурсивного определения функции
Mult(x,y)
def [О, если у = 0,
х+Mult(x, у -1) в противном случае
htt^S IFdit
585
«естественным» образом извлекается инвариант цикла
def
z + MultQc, у) = z+x + Mult(x, у -1).
Примеры решения некоторых типов упражнений
Пример 1 [88, с. 202]. Напишите программу, которая по данному
целому числу и > 0 находит наибольшее целое число i не большее и, явля-
ющееся степенью двойки,
def def
Известно, что Q = n > 0,R - 0 <i&i<n <2-i&Зр(2Р = i).
Решение. Для нахождения инварианта цикла воспользуемся методом
устранения конъюнктивного члена постусловия. Построим:
def
Р = 0 < i<n&3p(2P = i).
Охрану цикла выберем из решения уравнения с отношением выводи-
мости Н(Р&-В Я):-В =s n<2-i,B=s n>2-i.
Угадаем инициализацию: i := 1.
Построим цикл: i := 1; do п > 2 • i =>? od.
Выбираем тело цикла: i := 2 • i.
1) Установим, что перед выполнением цикла доказуема формула
Q—>wp(i := 1,Р):
п>0\-п>1 п>01~20=1
п>01-0<1<п п>0НЗр(2Р =1)
п>01-0<1<п&ар(2Р=1)
\-n>0^wp(i:-l,0<i<n&Bp(2P =i))
- HQ->wp(i:=l,P)
2) Установим доказуемость формулы (P&B—>wp(S, Р)):
def
P&B->wp(S,P) - 0<i<n&3p(2P = i)&n > 2i ^wp(i :=2-i, 0< i <n&3p(2?-i)} =
= 0<i<n&3p(2P =i)&n>2-i->0<2-i<n&3p(2P =2-i).
Далее:
___________________D____________________
0<i<n,3p(2P =i),n>2-i->0<2-i<n&3p(2P =2-i)
\-0<i<n&3p(2P =i)&n>2-i->0<2-i<n&3p(2P =2-i)
l~P&B—>wp(S,P)
_________2P=ih2P=i_________
0<i<n,2P =i,n>2i\-(2P =2i)P+1
0<i<n,3p(2P =i),n>2-i\-Bp(2P =2-i)
D
586
psr/Zu rait.ru
def
3) Выберем t - n-i. Докажем, что формула Р & BB —> t > 0 является
доказуемой:
0<i,i = n,n>2-i\-n>i; i<n\-n>i
0<i,i = nvi<n,3p(2₽ =i),n>2i\-n>i
0<i<n,3p(2P =i),n>2-i\-n-i>0
\-P&BB^>t> 0
4) Покажем, что формула P & В wp(x := t; S, t < x) доказуема.
Вначале выполним следующие преобразования:
def def
wp(x:=n-i;i:=2-i,n-i<x) = wp(x:=n-i,n-2-i<x) = n-2-i<n-i.
Далее:
0<i<n\-n-2-i<n-i
0<i<n,3p(2₽ =i),n>2-i\-n-2-i<n-i
_______\-P&B^n-2i<n-i________
\-P&B^> wp(x1; S,t<x)
def
Следовательно, t = n - i является убывающей функцией и доказано,
что
{Q} i := 1; do п > 2 • i => i := 2 • i od {К}
является искомой программой.
Пример 2. Докажем полную правильность следующей тройки Хоара:
{H}x:=N;y:=M;z:= 0;
whiley > 0 doy :-у -1; zz+х od
{z = N-M}.
Решение. Из рекурсивного определения функции
Mult(x,y)
def [О, если у = 0,
х+Mult(x, у -1) в противном случае
извлечём инвариант цикла z+х • у = N • М.
Проверим выполнение всех условий полной правильности:
def
1) wp(x:=N',y :=M',z:=0,x-y + z = a-b) = N-M=N-M = H;
2) докажем, что I- {P &B}S{P} :
Теорема
x-y + z = N-M\~z + x-y = N-M
y>0&x-y + z-N-M\-z+x-y-N-M
y>O&x-y + z = N-M\-z+x + x-(,y-l) = N-M
y>O&x-y+z = N-M\~wp(y:=y-l;z:=z+x,z+x-y = N-M)
587
3) докажем, что I-P&-B^>z = N-M :
Теорема Теорема
у<ОНу = О; y = O,z + x-y-N-MFz-N-M
z+x-y = N-M&y<OFz = N-M
\-P&y<O->z = N-M
Итак, проверены условия 1—3 и доказана частичная правильность
фрагмента программы;
def
4) докажем,чтоI-P&B—>t>0,t = у:
Теорема
_______у>01-у>0______
z + x-y = N-M&y>0\-y>0
HP&y>O->t>O
5) докажем, что I- {Р & B}w := у; S{y < w} :
def def
wp(w:=y;y:=y-l;z:=z+x,y<w) = wp(w:=y;y :=y-l,y <w) =
def def
= wp(w:=y;y-l<w) = y-l<y
Теорема
_______y>oi-y-l<y_______
z+x-y = N-M&y >Q|-y-l<y
I- {P & B}wy; S{y < w}
Итак, проверены условия 4—5 и доказана полная правильность фраг-
мента программы.
Упражнения для самостоятельного решения
Мои результаты мне давно известны;
я только не знаю, как я к ним приду.
К. Ф. Гаусс
Синтетический подход к формальной верификации программы
1. Метод устранения конъюнктивного члена постусловия
1. [88, с. 202]
Напишите программу, которая по данному целому числу и > 0 определяет
наибольшее целое число а, не превосходящее п1/2.
def def
Известно, что Q = и > 0, R = а > 0 & а2 < и & и < (а +1)2.
2. [88, с. 202]
Напишите программу, которая по двум целым числам х и у, удовлетво-
ряющим условиям х > 0 и у > 0, находит частное q и остаток г от деления
х на у (в программе нельзя использовать умножение и деление).
588
https:/Л: га it.ru
3. [88, с. 200—201]
Дан массив В[0: т - 1], т > 0, а заданное значение х находится в мас-
сиве В[0: т - 1]. Напишем программу (линейный поиск в массиве), которая
определяет первое вхождение х в В, т. е. записывает в переменную i значение
наименьшего натурального числа, для которого В [г] = х.
2. Метод замены константы переменной
4. (По [88, с. 208])
Напишите программу для суммирования элементов массива В[0: п -1],
def
если К = S = B[0]+B[l] + ...+B[n-l].
а) Замените константу, обозначенную (и - 1);
б) замените константу 0.
5. Напишите программу, вычисляющую n-й член ряда Фибоначчи.
6. Напишите программу для вычисления факториала натурального п.
3. Метод введения новой переменной
7. Напишите программы, которые по данному массиву В [1: и] устанав-
ливают переменной i значение, для которого:
def
a) R = 1 < i < п & B[i - 1] < В[i] < B[i + 1] или 0 в противном случае;
def
б) R = 1 < i < и & B[i -1] < B[i] < 2 • B[i +1] или 0 в противном случае;
def
в) R = 1 < i < п & В [i] < В [i - 1] + В [i + 1] или 0 в противном случае.
Аналитический подход к формальной верификации программы
1. Метод устранения конъюнктивного члена постусловия
8. Докажите выводимость тройки
{Si е [1, и - 1](В[1: и - 1]) & и > 1}
j 1; while BQ] > 0 do j :-j + 1 od
{1 < j < n & BQ] = 0}.
9. Докажите частичную правильность следующей тройки Хоара:
{а > 0}х :=а; whilex > 1 dox :=х-2 od {Sq > 0 (а = 2 • q+x&0<x< 1)}.
2. Метод замены константы переменной
10. Докажите полную правильности следующей тройки Хоара:
{а > 0 & п > 0} i := 0; z := 1; while i Ф n do z := z • a; i := i +1 od {z=x"}.
11. (По [77, c. 75])
def
Пусть Q = while a>Odob: = b + l;a:=a-lod — программа, после
выполнения которой значение переменной Ъ равно сумме исходных значе-
ний переменных а и Ь.
А. Определите инвариант цикла Р. Б. Докажите, что цикл завершается.
12. [81, с. 53, № 10]
Установите полную правильность следующей тройки Хоара:
{s = с +t & t <у} while t фу do s := s + 1; t := t +1 od {s = c +y}.
589
https: "ига it.ru
13. [81, с. 53, № 11]
Установите доказуемость следующей тройки Хоара:
{s = c +1 & t <y}repeats :=s +1; t := t +1 until t=y{s = c+y}.
14. Докажите полную правильность следующих программ, предназна-
ченных для вычисления биноминального коэффициента
. def n-(n-l)-...-(n-k + l)
=--------------------, п,к — натуральные числа, 0 < к < п.
к\
а) х := 0; у := 1; do х ф п => у := у • (п - х) / (х +1); х := х +1 od;
б) У1 := п; у2 := 0; уз := 1;
do уг ф п - к => у2 := у2 +1; Уз > Уз У15 У1 •= У1 ~ 1; Уз •= Уз / У2 об.
3. Метод введения новой переменной
15. (По [77, с. 75])
Установите доказуемость тройки
{а > с} while а > 0 do b := b +1; а := а -1 od {Ъ > с}.
16. Пусть функция z = НОД(х, у) обладает следующими аксиомами:
НОД(а, а) = а; НОД(а, Ь) = НОД(Ь, а); а > b -> НОД(а, Ь) = НОД(а - Ь, Ь).
Докажите полную корректность программы, предназначенной для вы-
числения наибольшего общего делителя натуральных чисел х и у:
{х > 0 & у > 0} |
а :-х; b '.-у,
while а Ф b do
if а > b then а := а - b fi;
if Ъ > a then Ъ := Ъ - a fi;
od
{а = НОД(х,у)}.
4. Метод добавления дизъюнктивного члена постусловия
17. (По [81, с. 53, № 9])
Установите доказуемость следующей тройки Хоара:
{И} while -iOdd(n) do п := п -г- 2 od {Odd(n)}.
18. Докажите частичную правильность тройки Хоара:
{i = n} while i > п do i := i +1 {i = n}.
5. Метод использования рекурсивных определений
19. (По [81, с. 55, № 18])
Докажите правильность следующей тройки Хоара:
{х0 > 0}
х:=х0;у :=y0;z:= 0;
while х Ф 0 do
if Odd(x) then z := z +y; x := x - 1 fi;
590
http
0-//1 iroit i-i i
у :=у-2;х:=х + 2
od
{z = x0-y0}.
20. Докажите правильность следующей программы:
x:=A-0;n:= п0;у:=1;
while и > 0 do
while Even(n) do n := n/2; x := x od;
n := n-1; у :=y-x
od
{z = xn}.
6. Различные методы определения инварианта
21. (По [77, с.84])
Установите доказуемость следующей тройки Хоара:
{а =А & b = 1} while а > 1 do b := 2 • Ь; а := [а/2] od {А < 2 • а • Ь}.
22*. (По [77, с. 34])
Исследуйте доказуемость следующей тройки Хоара:
{т = и} while к > 0 do k := к -1; и := и + (-1)п od {| п - т | < 1}.
23. (По [81, с. 46])
Пусть функция z = НОД(х, у) обладает следующими аксиомами:
НОД(а, а) = а; НОД(а, Ь) = НОД(Ь, а); а > b -> НОД(а, Ь) = НОД(а - Ь, Ь).
Докажите полную корректность программы, предназначенной для вы-
числения НОД натуральных чисел х и у:
{х > 0 & у > 0}
а := х; Ъ := у;
{а > 0 & В > 0 & НОД (а, Ь) = НОД(х, у)}
repeat
while а > Ъ do а :=а-Ъ od;
while Ъ > a do Ъ Ъ - a od
until а = Ъ
{а = НОД(х,у) & Ъ = НОД(х,у)}.
https: "u it.ru
Упражнение 28
СИНТЕТИЧЕСКИЙ ПОДХОД К ФОРМАЛЬНОЙ
ВЕРИФИКАЦИИ ПРОГРАММ
Знаки и символы управляют миром,
а не слово и не закон.
Конфуций
Обязательные результаты обучения:
• знать основные понятия
—фундаментальные принципы Д. Гриса;
—структуры языка программирования;
• уметь
—конструировать программы по заданной постановке задачи, учитывая
фундаментальные принципы Д. Гриса и используя информационные и управ-
ляющие структуры (данные и вычисления) языка программирования;
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленньх в Упражнении.
Теоретические сведения
Доказательство правильности как этап программирования
Доказательство правильности программы должно стать обя-
зательным этапом процесса программирования, т. е. каждая про-
грамма должна сопровождаться доказательством ее правильности.
По мере того, как программист становится более искушённым в во-
просах доказательства, он может опускать часть деталей доказа-
тельства.
Однако существует минимум деталей, которые необходимо явно
выписывать, а не просто формулировать. По-видимому, любой хо-
роший программист так и проверяет свою программу за столом.
Мы пытаемся сделать такую проверку более систематичной и по-
этому настаиваем, чтобы программист сознательно сформулировал
и выписал основные утверждения, описывающие работу програм-
мы, и основные допущения, связанные с данными для программы.
Если программист хорошо понимает свою программу, то при со-
ответствующей практике он может сформулировать необходимые
592
https:/Л: rait.ru
утверждения и провести доказательство. Если же такого понима-
ния нет, то процесс формулирования и записи утверждений будет
полезен уже потому, что заставит его хорошо продумать свою про-
грамму.
Ясно, что доказательное программирование в принципе не в со-
стоянии полностью избавить от содержательных ошибок в програм-
ме по следующим причинам:
1) используемые математические модели понятия «программа»
являются лишь приближением к реальному миру программ;
2) формальное по виду «доказательство» может содержать и не-
точности, и ошибки.
Тем не менее, если доказательное программирование и не избав-
ляет от ошибок, то по крайней мере может способствовать весьма
тщательному, хорошо структурированному проектированию и ана-
лизу программы.
Более того, поскольку при этом происходит оперирование точ-
ными математическими объектами, то существенная ее часть
может быть автоматизирована. Нельзя забывать слова Дж. Бэку-
са [36, с. 48]; «Я думаю, что из-за сложности традиционных фон-
неймановских языков программисты едва ли смогут когда-либо
пользоваться доказательствами и методами преобразований про-
грамм, написанными на этих языках, без помощи автоматических
систем».
Важность дедуктивного анализа широко признана специалиста-
ми в области вычислений. Этот метод оказал значительное влияние
на подходы к разработке программного обеспечения (например,
понятие «инвариант» заимствовано из исследований по дедуктив-
ному анализу).
Тем не менее, процесс дедуктивного анализа требует чересчур
много времени и может быть осуществлён только экспертами, об-
ладающими знаниями в области логического вывода и имеющими
немалый практический опыт. Доказательство правильности от-
дельного фрагмента программы может занять целые дни или даже
месяцы. Поэтому дедуктивный анализ применяется нечасто. Он ис-
пользуется главным образом для проверки систем, наиболее чув-
ствительных к ошибкам и сбоям.
Важно осознавать также, что некоторые математические задачи
не могут быть решены алгоритмическим способом. Теория вычис-
лимости устанавливает пределы того, что может быть решено алго-
ритмически.
В частности, доказано, что не существует алгоритма, способного
распознавать, завершается ли работа произвольной вычислитель-
ной программы (записанной на одном из языков программирова-
ния). Это, конечно, ограничивает и возможности автоматической
верификации.
593
https:it.ru
Далее, правильность завершения работы программы в общем
случае нельзя проверить автоматически. По этой причине большин-
стве систем построения доказательств не могут быть полностью ав-
томатизированы.
Преимущество методов дедуктивного анализа состоит в том, что
они могут быть применены к системам с бесконечным числом со-
стояний. Эту задачу можно до определенных пределов автоматизи-
ровать. Однако даже в том случае, когда проверяемое свойство дей-
ствительно выполняется, нельзя наложить никаких ограничений
на промежуток времени и объём памяти, необходимый для поиска
доказательства.
Когда доказывать правильность программы: после
ее написания или в процессе написания?
На первый взгляд кажется, что проще доказывать правильность
уже написанных программ. Однако на практике оказывается, что
доказывать правильность программы, «упавшей с неба», относи-
тельно заданных предусловия и постусловия непросто в силу сле-
дующих причин:
1) при применении системы Дейкстры часто приходится уси-
ливать слабейшее предусловие (добавляя конъюнктивный член)
или ослаблять сильнейшее постусловие (добавляя дизъюнктивный
член). Большая свобода этого правила усиления посылки или осла-
бления заключения сопряжена с муками выбора;
2) найти подходящие инварианты цикла и ограничивающие
функции даже в простых случаях бывает нелегко;
3) ошибочная (не удовлетворяющая спецификации) программа
вообще не верифицируема, а возможность обнаружения ошибки
в программе при бесплодных попытках верификации весьма со-
мнительна.
Поэтому целесообразнее использовать идеи доказательства пра-
вильности ещё при разработке программы для осознания ее струк-
туры.
В этом случае программы получатся яснее, изящнее и зачастую
эффективнее, чем программы, написанные бессистемно.
Итак, на практике доказательство правильности должно прово-
диться программистом во время самого процесса написания про-
граммы. Не следует ожидать, что кто-нибудь возьмет большую
законченную программу и начнет доказывать ее правильность. Ин-
теллектуальные затраты на такую работу будут очень велики. Не-
обходимо доказывать правильность небольших фрагментов по мере
того, как они составляются. В процессе доказательства правильно-
сти больших частей программы многие из подчастей, которой уже
доказаны, можно трактовать как отдельные абстрактные операторы.
594
https:it.ru
Дело в том, что проектирование и реализация программ часто
подразделяются на программирование в большом и программирова-
ние в малом (программирование в миниатюре). Именно в послед-
нем в процессе поэтапного составления программы для правильно
поставленной задачи наиболее часто используются математические
методы, поэтому можно утверждать, что технология программиро-
вания в малом уже получила научную базу. Более того, способность
строить правильные маленькие программы является необходимым
условием для построения правильных больших программ. Легко
убедиться в справедливости этого утверждения на следующем при-
мере [88, с. 172—173].
Предположим, что программа состоит из п небольших компо-
нентов (процедур или модулей), каждый из которых правилен с ве-
роятностью р. Тогда вероятность Р правильности всей программы
удовлетворяет неравенству Р < рп. Так как п велико для любой до-
статочно большой программы, то надеяться на правильность про-
граммы можно лишь при значениях р близких к 1.
Замечание.
Доказательное программирование в целом получило столь серьезное
развитие, что некоторые специалисты склонны считать владение им обя-
зательным атрибутом квалифицированного программиста.
Фундаментальные принципы Д. Гриса
...другая практическая проблема,
которая начинает сейчас принимать
угрожающие размеры, и для которой
трудно будет найти удовлетворительное
решение, это проверка правильности
больших программ.
С. Гилл, 1965
Метапринцип [88, с. 174].
Никогда не отвергайте как очевидный никакой фундаменталь-
ный принцип, так как только осознанное применение таких прин-
ципов может принести успех.
Мы преследуем сугубо практическую цель — научиться писать
несложные программы быстро и без ошибок, а более сложные с ми-
нимальным количеством ошибок. Поэтому с точки зрения методики
построение программы и ее верификацию лучше проводить парал-
лельно шаг за шагом. Но следует помнить, что при применении этой
методики на практике не следует впадать в крайности и доказывать
очевидные вещи: если промежуточные утверждения, инварианты
циклов и прочее помогают писать программу быстро и без ошибок,
595
https:/Л: rait.ru
их следует применять; если же они только загромождают текст про-
граммы и ничего не проясняют, необходимо обходиться без них.
По мере накопления опыта многие вещи начинают делаться
в уме. Вместе с тем даже в самых простых задачах часто обнаружи-
вается масса «подводных камней». Поэтому при малейших сомне-
ниях в правильности программы следует пытаться взглянуть на нее
с формальных позиций.
Принцип 1 [88, с. 168—169].
А. Программа и ее доказательство должны строиться одновре-
менно с тенденцией опережающей разработки доказательства.
Б. Пользуйтесь теорией для проникновения в суть дела; приме-
няйте здравый смысл и интуицию там, где это возможно, но сра-
зу же возвращайтесь к формальной теории за поддержкой, когда
возникают трудности.
Принцип 2 [88, с. 177].
Программирование — это целенаправленная деятельность.
Это означает, что ожидаемый результат (или цель) постусловие
R играет при построении программы более важную роль, чем пред-
условие Q. Целенаправленность программирования — одна из при-
чин, по которой программные конструкции определялись через сла-
бейшие предусловия (а не через сильнейшие постусловия).
Принцип 3 [88, с. 178].
Прежде чем строить программу, уточните и разъясните себе
пред- и постусловия.
Принцип 4 [88, с. 181].
При прочих равных условиях делайте охраны в командах выбора
настолько сильными, насколько возможно, с тем, чтобы некоторые
ошибки приводили к аварийному завершению программы.
Например, никогда не меняйте более сильную охрану; = 9 на ме-
нее сильную; < 9 (j > 9), так как «сбой» при работе компьютера или
ошибка в программе может привести к тому, что; = 10, выполнится
другая охраняемая команда, а ошибку будет найти не просто.
Принцип 5 [88, с. 185].
При прочих равных условиях делайте охраны в команде цикла воз-
можно слабее, чтобы ошибка могла вызвать зацикливание.
Принцип 6 [88, с. 203—204].
А. Вводите новую переменную лишь в том случае, если для этого
есть серьёзные основания.
Б. Определяйте для каждой новой переменной подходящий диа-
пазон изменения.
Структуры языка программирования
Как известно, основные объекты языка программирования раз-
деляются на две категории: связанные с представлением данных
(информационные структуры) и связанные с представлением вы-
596
https:/Л: rait.ru
числений (управляющие структуры). В дополнении к ним была
выделена (см. [99, с. 12—13]) ещё одна категория, называемая кон-
тролирующими структурами. Данная категория составляет избы-
точную информацию о фрагментах программы или данных, пред-
назначенную для контроля в процессе разработки, отладки и (или)
при выполнении программы.
Контролирующие структуры играют важную роль при верифи-
кации программы и во многих других процессах (таких как тести-
рование).
Приведём классификационную схему структур языка програм-
мирования
Информационные структуры, представляющие обрабатывае-
мые данные, определяют используемые константы, переменные
и их свойства, существенные для выполнения операций над данны-
ми. В программах, как правило, используются разнородные данные,
поэтому одним из центральных является понятие «тип данных».
Тип данных — это множество значений и набор операций, вы-
полняемых над этими значениями. Понятие «тип данных» позволя-
ет провести чёткое различие между разнородными данными (мно-
жествами), достичь логической ясности для используемых данных
и операций, предотвращая «бессмысленные» операции (например,
такие, как сложение чисел со строками символов).
Управляющие структуры объединяют операции и данные в про-
грамму или совокупность программ. Управляющие структуры мож-
но разделить на два класса:
1) операционные структуры, используемые для управления вы-
числениями внутри выражений;
597
https:/Л: rait.ru
2) операторные структуры, определяющие последовательность
выполнения операторов программы (для языков программирова-
ния, ориентированных на модель вычислений Дж. фон Неймана,
операторная структура является необходимым элементом компози-
ции программ из операций и данных).
Операционные управляющие структуры определяют состав и по-
рядок выполнения операций в выражениях языка. Основной меха-
низм управления последовательностью операций в выражениях —
это функциональная композиция. Порядок выполнения операций
задается порядком записи операций, системой приоритетов (фик-
сированной для языка программирования) и скобками.
Операторные управляющие структуры — более сложные и специ-
фичные конструкции языка программирования. Они определяют
правила композиции операторов и выражений в конструкцию, явля-
ющуюся оператором. Оператор есть более общая конструкция, чем
операция (функция). Основное различие состоит в том, что в обычном
понятии функции предполагается неизменность аргумента при вы-
числении значения функции, в то время как оператор не имеет таких
ограничений. Он в общем случае выступает как функция с побочным
эффектом, которая может воздействовать на свои аргументы (изме-
нить их значение). Введение столь мощного понятия, каким является
«оператор», направлено на повышение эффективности вычислитель-
ных процессов (например, перестановку элементов массива эффектив-
нее реализовать как оператор, а не операцию над массивом).
Контролирующие структуры — это специальный класс струк-
тур языка программирования, характеризующий свойства данных
и вычислений по программе, т. е. создающих метаинформацию
о программе — избыточность, необходимую для контроля ошибок
на стадиях разработки, отладки или использования программы
по назначению.
Введение контролирующих структур в язык программирования
есть свидетельство повышения уровня языка с целью обеспечения
качества программ. Такое развитие закономерно и приближает в не-
котором смысле язык программирования к естественному языку.
В современных языках программирования контролирующие
структуры имеют разнообразную форму. Выделяются две группы
этих структур:
1) используемые для характеризации данных;
2) используемые для характеризации вычислений.
Первая группа включает структуры, дающие избыточную инфор-
мацию, используемую для контроля ошибок в данных (структуры
для объявления данных и комментарии данных, являющиеся не-
формальными спецификациями свойств данных).
Объявления данных — это широко распространенные средства
для указания используемых переменных совместно с их основны-
598
https:/Л: rait.ru
ми свойствами. Важнейшим таким свойством является тип данных.
Типы используемых данных содержат информацию о схемах опе-
раций, на основе которой может осуществляться контроль типов
во время компиляции программы.
Структуры данных с избыточностью, вводимой для контроля, —
это общий подход к контролю имён или значений данных, возник-
ший в задачах передачи и хранения данных. Его распространение
на сложные структуры данных языка программирования приводит
к понятию синтаксически защищенных структур, т. е. такой орга-
низации избыточных структур, когда наиболее вероятные искаже-
ния вызывают переход в класс синтаксически некорректных кон-
струкций языка, обнаруживаемых синтаксическим анализатором
языка (например, запрещённые имена или недопустимые символы
в кодах значений).
Вторая группа контролируемых структур, используемая для ха-
рактеризации вычислений, содержит три разновидности структур:
1) контрольные утверждения;
2) контрольные мониторы;
3) неформальные спецификации (комментарии вычислений).
Наиболее важную разновидность образуют контролирующие
структуры для логической спецификации вычислений, описываю-
щие отношения между переменными программы для соответствую-
щих фрагментов (региональные утверждения) или отдельных точек
(локальные утверждения).
Программа, снабжённая такими логическими спецификациями,
называемая аннотированной программой, — необходимый эле-
мент для доказательства корректности или анализа семантических
свойств программных текстов. Логические спецификации могут
рассматриваться и как выполнимая часть текста программы в за-
дачах тестирования или при построении структур программ с само-
защитой от ошибок.
Контрольные мониторы в отличие от логических спецификаций
в своей основе — процедурные средства. Они порождают контроль-
ную информацию только о ходе конкретного вычислительного про-
цесса. Этот вид структур широко используется на стадии отладки
программ.
Комментарии вычислений выполняют функцию неформальных
спецификаций, представляемых на естественном языке и служащих
пояснениями для программиста.
599
httpsr/Ajr^'tj'L!
Примеры решения некоторых типов упражнений
Пример 1 (максимальная восходящая последовательность}
[88, с. 261—265].
Напишите программу, которая по данной последовательности
В [0: и -1], где п > 0, вычисляет длину ее максимальной (т. е. самой длин-
ной) восходящей последовательности.
Решение. Обозначим lup(s) длину самой длинной максимальной вос-
ходящей последовательности из s. Тогда:
def def
Q - n>0,R - k = lup(B[0:n-l]).
Заметим, что1ир(В[0:п-1])=1.
Построим первоначальную версию инварианта цикла:
def
Р = l<i<n&k = lup(B[0:n-l]).
Набросок цикла:.
i := 1; к := 1; do i Ф п => Увеличить i, сохраняя Р od
Пересмотрим инвариант:
def
Р = l<i<n&k = lup(B[0:n-1]) & (тявляется наименьшим значением
в В[0: i -1], завершающим восходящую последовательность длины к).
С учётом этого факта:
i := 1; k := 1; ш:=В[0];{Р}
doi^n=> ifB[i] >т=> к :=к +1; т :=B[i] □ B[i] < m=>? fi; i :=i+1 od
Ещё раз пересмотрим инвариант:
def
Р - l<i<n&k = lup(B[0:n-l]) & (V/ e [1, к]) (m|j] является наи-
меньшим значением, заканчивающим восходящую последовательность
длины; в массивеВ[0: п -1]).
Изменим программу:
i := 1; к := 1; ш[1] :=В[0];{Р}
doi*n=> ifB[i] >m[k] => к :=k +1; m[k] :=B[i] □ВШ < m[k] =>? fi;
ii +1 od
Массив m упорядочен, поэтому окончательный вариант программы
имеет следующий вид:
i := 1; к := 1; ш[1] :=В[0];
do i п => if
B[i] > m[k] => к := к +1; m[k] :=B[i] □
B[i] < m[l] => m[l] B[i] □
m[l] <B[i] <m[k] => h := l;j :=k;
600
https rait.ru
do h Ф j -1 -> e (h + j) -г- 2;
if m[e] < B[i] => h := e □
m[e] > B[i] => j :=e
fi
od;
m[j] :=B[i]
fi;
i :=i +1
od
Пример 2 (no [88, c. 191]).
Напишите программу для решения следующей задачи. Дана перемен-
ная* и двухмерный массив В[0: т -1, 0: п -1], где т, п > 0.
Найдите, пользуясь двумя переменными i nj, значение C[i, j], равное*;
если хе В, то присвойте i значение т.
Решение. Вначале выпишем постусловие:
def
R = (0<i<m&0< j<n&*=B[i, ;])v(i = m&*gB[0: т-1,0: n-1]).
В инварианте Р, построенном с помощью следующей диаграммы
0 j п -1
°1------------
Здесь с-----
P:0<i<m&0<j<n& i нет*
m-ll --------------------------
утверждается, что * не находится в уже проверенных строках В[0: i - 1]
и в уже проверенных столбцах В [i, 0:; -1] текущей строки;:
Теперь формализуем инвариант:
def
Р = 0<i<m&0< ;<n&*gB[0:i-l,0:n-l]&*gB[i,0: ;-1].
Ограничивающая функция является суммой числа значений в непро-
веренной части массива и числа строк в непроверенной части:
def
t - (m-i) • n-j + m-i.
Требуется дополнительное значение m-i, поскольку возможно, что
j = п = 0.
В качестве первого шага построения определим команду задания
начальных значений для создаваемого цикла. Очевидный выбор — это
i := 0; j := 0, так как тогда «кусок» массива, в котором нет *, пуст.
Далее должны быть построены охраняемые команды цикла.
Какова простейшая возможная команда и какова подходящая для
нее охрана? Очевидно, можно попробовать применить команду; :=; +1,
поскольку она уменьшает t. Подходящая охрана должна обеспечить сохра-
нение истинности Р. Можно убедиться в том, что может быть использо-
вано условие i Ф т &J + п &CAND* Ф B[i,;], и охраняемой командой будет
601
https:/Л: it.ru
i*m&j*n &CANDxB[i,j] -> j :-j +1.
Цикл с такой охраняемой командой может завершиться при i < т &
& j = п, а этого даже вместе с инвариантом недостаточно для доказатель-
ства R. Конечно, если в первой строке В не содержится х, то цикл закон-
чится после просмотра только первой строки. Нам нужны охраняемые
команды, которые увеличивают i.
Команду i := i + 1 можно выполнить лишь при i < т. Более того, она
может сохранить истинность Р только тогда, когда в строке i не содер-
жится х, так что рассмотрим ее выполнение лишь при добавочном усло-
вии j = и. Но это означает, что заодно с присваиванием i надо сделать;
нулём, чтобы сохранилось условие на текущую строку i.
Это приводит к программе:
i:= 0;;:= 0;
do i + m & j + n &CAND x => j :=j + 1 □ i * m & j = n => i := i + 1;
j := 0 od.
Проверим требуемые условия:
def
wp(i:=0; j :=0,0<i<m&0< ;<n&xgB[0:i-l,0:n-l]&xgB[i,0: ;-l]) =
def
= 0<0<m&0<0<n&xgB[0:-l,0:n-l]&xgB[0,0:-l]) = Q;
2) Докажем, что H P &Вг -> wp(Si}P):
a)
Теорема Теорема
x«B[i,0:;-l],x*B[i,;']bx«B[i,0:;']; i*m, ;*п,0<;<пН0< ;+l<n
0< j<n,x£B[i,0: j+l<n&x£B[i,0: j]
0<j<n,xgB[0:i-l,0:n-l],xgB[i,0:j-l],iVm,j7tn,x?tB[i,j]l-
l-0< j+l<n&xgB[0:i-l,0:n-l]&xgB[i,0:j]
0<i<m,0<;<n,xgB[0:i-l,0:n-l],xgB[i,0:;-l],i^m&;^n&CANDx^B[i,;]l-
H0<i<m&0<;+l<n&xgB[0:i-l,0:n-l]&xgB[i,0:;]
0<i<zn&0<j<n&xgB[0:i-l,0:n-l]&xgB[i,0:j-l]&i7tzn&j?tn&CANDX7tB[i,j]l-
H0<i<m&0<;+l<n&xgB[0:i-l,0:n-l]&xgB[i,0:;]
g; Теорема
x gB[0:i-1,0:n-1],xйB[i,0: j-1], j = nI-x <£B[0:i,0:n-1]; D
0 < i < m, 0 < j < n, x <£ B[0: i-1,0: n-1], x й B[i, 0:j-l],i*m,j = n\-
H0<i+l<m&xgB[0:i,0:n-l]
0<i<m,0<;<n,xgB[0:i-l,0:n-l],xgB[i,0:;-l],i^m&;VnH
H0<i+l<m&0<0<n&xgB[0:i,0:n-l]&xgB[i+l,0:-l]
0<i<m&0<;<n&xgB[0:i-l,0:n-l]&xgB[i,0:;-l]&i^m&; = nH
H0<i+l<m&0<0<n&xgB[0:i,0:n-l]&xgB[i+l,0:-l]
Теорема
0<i<m,i*m\-0<i+l<m
D
3) докажем, чтоP&-BBНЯ.
602
https://urait.ru
Приведём неформальное доказательство. Предположим, что охраны
ложны. Тогда возникают два случая:
а) может быть i = т;
б) если i Ф т, то из ложности второй охраны следует; + п; поэтому из лож-
ности первой охраны следует х = В [i, j].
Итак, охраны ложны при условии, что истинно следующее предложе-
ние, которое вместе с инвариантом Р влечёт результат R:
i=mvCOR(i*m&j*n&x=B[i,;].
Формальное доказательство постройте самостоятельно.
4) Покажем, что HP&BB->t>0:
0<i<m&0< j <n\-(m-i)-n-j+m-i>0
0<i<m&0< ;<n&xgB[O:i-l,O:n-l]&xgB[i,O: j-l]&
j*n&QwDx*B[iJ]\/i*Tn&j = ri)\-(Tiri-i)n-j+nri-i>O
l-P&BB->t> 0
Это выполнено так как (m - i) • n -j — число элементов в непроверен-
ной части массива.
5) Покажем, что Н Р & Bt wp (х := t; S{, t < х).
Выполним следующие преобразования:
def def
wp(x:=t;S1,t<x) = wp(x:=(m-i)-n-j+m-i;j:=j+l,(m-i)-n-j+m-i<x) =
def
= (m-i)n-j-l<(m-i)n-j = H;
def def
wp(x:=t;S2,t<x) = ivp(x :=(m-i)n-j+m-i;i:=i+l; j=O,(m-i)n-j+m-i<x) =
def
-(m-i-T)n+m-i-l<(m-i)n-j+m-i = -n-l<-j = n+l> j = M.
Итак, проверены условия 1—5, и доказана правильность построен-
ной программы.
Пример 3 (двоичный поиск в массиве) [88, с. 208, № 4].
Напишем программу, которая по данному х и упорядоченному (по <)
массивуВ[1: и], удовлетворяющему В [1] <х<В[п], находит, гдехможно
вставить в массив, т. е. устанавливает для новой переменной i
def
R = l<i<n&B[i]<x<B[i+l].
Время выполнения этой программы должно быть пропорционально
log п. Написав эту программу, включим ее в программу для решения более
общей задачи поиска: определить i, удовлетворяющее
(i = 0 &х < B[l]) v (1 <i < п &B[i] <х < B[i +1]) v (i = n &B[n] <x),
где значения x не ограничены.
Решение. Вначале построим пред- и постусловия:
def def
Q = п > 1 &В[1] <х < В[п],К = 1 <i < п &B[i] <х < B[i + 1].
603
https:/Л: it.ru
Далее построим инвариант методом введения новой переменной (вме-
сто выражения i +1 используем переменную;):
def
Р = l<i<n&B[i]<x<B[;].
Определим охрану цикла, решив уравнение Р & -В I- R:
_________-В I- j = i+l____
l<i< j<n,-BI-l< j-l<n&j-i+1;
1 < j -1 < n, j = i+1, B[i] < x < B[ j] I-
hl<i<n&B[i]<x<B[i+l]
l<i< j<n,B[i]<x<B[;],-BI-l<i<n&B[i]<x<B[i+l]
l<i< ;<n&B[i]<x<B[;]&-BI-l<i<n&B[i]<x<B[i+l]
Отсюда получим, что -В =s(j = i +1) и В =?(j * i +1).
Угадаем инициализацию цикла i := 1; j := п и покажем справедливость
такой инициализации:
Теорема Теорема
п>11-1<1<п<п В[1] < х < B[n] I- В[1] < х < В[п]
n>l,B[l]<x<B[n]l-l<l<n<n; n>l,B[i]<x<B[n]l-B[l]<x<B[n]
п > 1, В[1] < х < В[п] 1-1<1<п<п & В[1] < х < В[п])
п > 1 & В[1] < х < В[п] I- wp(i := 1; j;=n,l<i< j <п& B[i] < х < В[ j])
Теперь построим первоначальный вариант программы:
i := 1; j :=п
doi +1 *;=> е := (i+j) + 2; if В [е] <х=> i :=е пВ[е] > х=> j :=е fiod
1) установим доказуемость тройки Хоара {Р & В} S {Р}:
Теорема Теорема
l<i< j<n,i+l*jhl<(i + j)+2< j<n; B[i]<x<B|j],B[(i +;)н-2]<х l~
_________________________________________l-B[(i + j)-5-2]<x<B[j]
l<i<;<n&B[i]<x<B[j]&i+l?tj,B[(i+j)-5-2]<xl-
I-1 < (i+;)-5-2 < ; < n&B[(i+;)-i-2] < x < B[j]
l<i<j<n&B[i]<x<B[j]&i+l*jhB[(i+j)-5-2]<x->
->l<(i+j)-:-2< ;<n&B[(i + ;)-5-2]<x<B[j];
_____________________________________________________________Pi
1 < i < ; < n & B[i] < x < B[j] & i+1 * ; I-iyp(e := (i+;) ^-2; if B[e] < x => i := en
oB[e] > x => j := efi, 1 < i < j < n&B[i] < x < B[ j])
Теорема Теорема
l<i<j<n,i+l*j\-l<i<(i+j)+2<n; B[i]<x<B[;],B[(i+;)ч-2]>х1-
I- B[i] < x < B[(i + ;) -s-2]
l<i<j<n&B[i]<x<B[j]&i+l?tj&B[(i+j)-5-2]>xl-
I-1 < i < (i+j)-5-2 < n & B[i] < x < B[ (i+;)-5-2]
l<i< j<n&B[i]<x<B[;]&i+l^ ;l-B[(i+j)-^2]>x->
->l<i<(i+;)-5-2<n&B[i]<x<B[(i+;)-5-2]
Di
604
https ://,j raH.ru
def
2) установим выводимость Р & ВВ I-1 > 0, где t = log( j - i) > 0 :
Теорема Теорема
j—i > 11— log(j—i) > О
1 < i < j < n, i+1 j I- log( j - i) > 0
1 < i < j < n, B[i] < x < B[j], 14-1 * j Hlog(j -i) > 0
l<i< j<n&B[i]<x<B[j]&i+l* j I— logCj—0 > 0
3) установим доказуемость {P & B}y := log(j - i); S{log(j - i) < y} :
def
wp(y := log(j -1); e(i+j) 4- 2; if B[e] < x -> ieoBfe] > x -> je fi, log(j -i)<y) =
def def
= wp(y := log(j - 0; e := (i+j) 4- 2, B[e] < x log( j - e) < y) & B[e] > x logfe - i) < y) ) =
def
= (B[ (i 4- j) 4- 2] < x log(j - (i+j) 4- 2) < log(j - 0) & B[e] > x log( (i 4- j) 4- 2 - i) < log( j - i)).
Теорема Теорема
l<i<j,t4-l^jl-j-(i4-j)4-2< j-i; j-(i4-j)4-2<j-il-log(j-(i4-j)4-2)<log(j-i))
_______________1 < i < j < n, i 4-1j I- log( j - (i 4- j) 4- 2) < log( j - i))_
l<i<j<n&B[i]<x<B[j]&i4-l* j, (B[(i 4-j) 4-2] < x I-logfj-(i 4-j) 4-2) <log( j-i))
l<i< j<n&B[i]<x<B[j]&i4-l* jl-(B[(i4-j)4-2]<x->log(j-(i4-j)4-2)<log(j-i)); P2
l<i< j<n&B[i]<x<B[j]&i4-l?t jh(B[(i4-jH2]<x->log(j-(i4-jH2)<log(j-i))&
& (B[ (i 4- j) 4- 2] > x -> log( (i 4- j) 4- 2 - i) < log( j - i)
Теорема Теорема
l<i< j<n,i+l* j\-(i+j)+2-i< j-i; (i+j)+2-i<j-H-log((i+j)+2-i)<log(j-i)
l<i< j<n&B[i]<x<B[j]&i+l* j,B[(i+j)+2]>xl-log((i+j)4-2-i)<log(j-i))
1 <i< j<n&B[i]<x<B[j]&i4-l j|-(B[(i +j)4-2]>x^log((i+j)4-2-i)<log(j-i))
^2
Итак, построенная программа имеет вид:
i := 1; j :=п
do i +1 *j => e := (i +j) 4- 2; ifB[e] <x => i := e
□ B[e] > x=> j :=e
fi
od
Вариантом решения второй части задачи является помещение про-
граммы для решения первой ее части в качестве одной из альтернатив
команды выбора:
ifx < Ь[1] =>i:=0
□В[1] <х < В[п] => i := l;j :=п
do i ч-1 # j => e := (i 4- j) 4- 2;
ifB[e] <x=> i :=e
□B[e] > x-> j :-e
fi
od
□B[n] < x=> i :=n 4-1
fi
http
о - Hi iroit i’i
o»/ i di I v
605
Упражнения для самостоятельного решения
Я недурно проводил время, даже во время
уроков, решая математические задачки.
Скоро те, что я находил в учебнике,
перестали меня удовлетворять. Может
быть, потому, что чем дальше в лес,
тем ясней проявлялась в них тенденция
как-то уж чересчур смахивать друг
на друга — но ещё более потому, что они
словно бы падали с неба одна за другой,
длинной вереницей, не извещая, откуда они
взялись и куда направляются. Трудности
в задачах были книжные, а не мои.
А. Гротендик. Урожаи и посевы
1. (По [88, с. 181—182, № 1])
Постройте программы для решения следующих задач.
а) Установите х равным Abs(x).
б) Пусть целочисленные переменные а и Ъ удовлетворяют 0 < а + 1 < Ъ,
а множество {а, а + 1,..., Ъ} содержит по меньшей мере три элемента.
Допустим, что выполняется условие Р = а2 < п & Ъ2 > п.
Возможно ли поделить [а, Ь] пополам, установив а (либо b) (а + b) -г- 2 та-
ким образом, чтобы Р сохранилось истинным?
2. (По [84, ч. 2, с. 577—588])
Постройте программу, которая для целочисленных т > 0 и п вычисляет
z = п • т (используйте только операции сложения, вычитания и предикат
сравнения).
3. [88, с. 209, № 6]
Напишите программу, которая по данному фиксированному массиву
В[0: п - 1], где и > 0, находит в В место некоторого максимального значе-
ния, т. е. устанавливает
def
R = 0<k < и&B[k] >В[0: и-1].
Если максимальное значение встречается в В более одного раза, то про-
грамма может быть недетерминированной.
4. Напишите программу, которая для данного массива В[0: п - 1],
и > 0, помещает в d:
а) количество чисел, кратных 3;
б) [88, с. 209, № 7] количество нечетных чисел в В[0: п - 1];
в) абсолютную величину разности между наибольшим и наименьшим
числами в В[0: и - 1].
5*. [88, с. 194, № 1]
Напишите программу для решения следующей задачи. Дан трёхмерный
массив С[0: т - 1, 0: п - 1, 0: р - 1], т, п, р > 0. Дана переменная х.
Найдите, пользуясь тремя переменными i,j, к, значение C[i, j, к], равное
х; еслих g С, то присвойте i значение т.
6. [88, с. 202, № 4]
Напишите программу, которая по данному массиву В[0: т - 1, 0: п - 1]
и по значению х в массиве В определяет первое вхождение х в В.
606
https:/Л: rait.ru
Указание. Под первым вхождением понимается то вхождение х, при кото-
ром х нет в предыдущих строках или в предыдущих столбцах той же строки,
т. е. программа должна, используя переменные i nj, установить предикат:
def
R = 0<i<m&0<j< п &x=B[i,j] B[0: i-1,0: n-1] B[i, 0:j-l].
7. [88, c. 209, № 8]
Даны два упорядоченных массива F[0: т - 1] и G[0: п - 1], т, п > 0.
Известно, что никакие два элемента массива F не равны, и никакие два
элемента массива G не равны. Напишите программу для определения числа
значений, встречающихся как в массиве F, так и в массиве G.
8. [88, с.209, № 9]
Напишите программу, которая по данному массиву В[0: п - 1], где
и > 0, определяет, состоит ли В из одних нулей, т. е. устанавливает, используя
def
новую переменную s, что R = s = (Vj е [0, и)) (ВQ] = 0).
9. Напишите программу, которая находит наибольший общий делитель
всех членов данной последовательности В[0: и], где п > 0.
10*. [88, с. 261—265]
Максимальная восходящая последовательность. Напишите программу,
которая по данной последовательности В[0: и], где п > 0, вычисляет длину
ее максимальной восходящей подпоследовательности.
11**. [88, с. 266]
Период десятичного разложения. При и > 1 десятичное разложение
1/п является периодическим, т. е. оно состоит из начальной последователь-
ности цифр dlt ..., di, за которой следует последовательность di+1, ..., di+j,
которая повторяется вновь и вновь.
Например, 1/4 = 0,2500..., так что повторяется последовательность
0 (i = 2 и j = 1), в то время как 1/7 = 0,142857142857..., так что повторяет-
ся последовательность 142857 (i = 0 и j = 6, хотя можно было бы принять
в качестве i и любое другое положительное число).
Напишите программу для нахождения длины повторяющегося периода;
(пользуйтесь только простыми переменными, а не массивами).
о-Hi ।rnit i-i ।
O.f i Ul UU.I VI
Часть б
ЭЛЕМЕНТЫ МОДАЛЬНОЙ
ЛОГИКИ
https: "и it.ru
Упражнение 29
МОДАЛЬНЫЕ ЛОГИКИ: АНАЛИТИЧЕСКИЕ
ТАБЛИЦЫ ДЛЯ МОДАЛЬНОЙ ЛОГИКИ,
НОРМАЛЬНЫЕ МОДАЛЬНЫЕ ИСЧИСЛЕНИЯ
К, Т, В, $4, S5
Человеческие существа не общаются
непосредственно с объективным миром
и с обществом в том смысле, как это
обычно понимается. Они в значительной
мере зависят от того конкретного
языка, который стал их средой общения.
Это совершенная иллюзия — полагать,
что кто-то может согласовать
себя с сущностью реальности без
использования языка и что язык —
всего лишь случайное средство решения
конкретных задач общения и мышления.
Э. Сапир
Обязательные результаты обучения:
• знать вспомогательные понятия:
— классическое пропозициональное исчисление;
—метод аналитических таблиц для формул языка первого порядка;
• знать основные понятия:
— модальность, элегические модальности, модальная логика;
— синтаксис пропозициональной модальной логики;
— множество возможных миров, действительный мир;
— отношение достижимости одного мира из другого, интерпретирующая
функция, шкала Крипке;
— модельная структура модальной пропозициональной логики;
— функция оценки формул в возможном мире;
— модель Крипке в модальной пропозициональной логике;
— аналитические таблицы для пропозициональной модальной логики;
— нормальные модальные исчисления; К, Т, В, гёделевские расширения
систем S4 и S5;
— характеризация отношений достижимости модальными формулами;
— связи интуиционистской и модальной логики;
— корректность и полнота нормальных модальных исчислений;
611
https: "и it.ru
• уметь:
— определять модальности высказываний: необходимые, возможные
и невозможные;
— записывать заданные утверждения в виде модальных формул;
— определять условия истинности и ложности модальных формул;
— конструировать доказательство универсальной общезначимости фор-
мул в системах К, Т, В, S4 и S5;
— определять нормальные модальные системы, в которых: заданные
формулы общезначимы; имеют место заданные отношения логического
следования;
— проверять истинность заданных утверждений, используя шкалу Крипке
и интерпретирующую функцию;
• владеть:
—основными понятиями, представленными выше;
—методами решения задач, представленньх в Упражнении.
Теоретические сведения
Математические сведения
Пусть ЗрсА обозначает высказывание «существует единственное
х, такое, что А».
Определение (по [126, с. 41]).
Говорят, что бинарное отношение р на множестве А обладает:
1) репродуктивностъю, если (Vxg А)(3у g А)(хру);
2) евклидовостъю (симметричностью и транзитивностью), если
(Xfx,y,ze A)(xpy&xpz^ypz);
3) слабой плотностью, если
(Vx,y, z g А)(х ру (3z g А)(х р z & z ру));
4) слабой связностью, если
(Vx, у, 2G А)(хру&хргч (ypz vy = z vzpy));
5) слабой направленностью, если
(Vx,у, z g А)(х ру & х р z 3v(y р v & z р v));
6) функциональностью, если
def
(Vx G А) (Зу G А) (х р у) = (Vx G А) (Зу G А) ((х р у) & \/z(x р 2 —>
~^У = г));
7) частичной функциональностью, если
(VxG A)(Vy G A)(V2G A)(xpy &xp2—>y = 2).
Модальности. Модальная логика
В современных логических исследованиях сформировалась ло-
гическая теория модальностей (модальных операторов) [128; 125;
121, § 8.7; 118, (а), гл. 8].
Модальность — это категория, выражающая отношение гово-
рящего к содержанию суждения. Для анализа модальных суждений
612
https:/Л: rait.ru
играет роль характер самого акта утверждения, так как в нем со-
держится оценка действительности. Модальность может иметь зна-
чение утверждения, приказания, пожелания и др.
В естественном языке модальности выражаются специальными
формами наклонений, интонацией, модальными словами, а в логи-
ке — модальными операторами. Свойства модальных операторов
задаются с помощью специальных схем аксиом, дополняющих схе-
мы аксиом классического исчисления нулевого порядка.
В логике термин «модальность» употребляется в двух смыслах.
Определение.
1. Модальностями (в широком смысле) называются самые раз-
личные свойства суждений; например, «известно, что А», «дока-
зуемо, что В», «сомнительно, что С».
2. Модальностями (в узком смысле) называются такие свойства
суждений, как необходимость, действительность, возможность,
случайность. Например:
а) модальность необходимости суждения А констатируется нами,
когда мы утверждаем: «необходимо, что А»;
б) модальность возможности суждения В констатируется, когда
мы говорим: «возможно, что В»;
в) модальность действительности суждения С — когда мы про-
сто говорим: «С».
Для обозначения модальностей в узком смысле слова употребля-
ют термин «алетические модальности» (греч. осХцОеш, алетейя —
«истина»), который вводится для того, чтобы отличить эти мо-
дальности от модальностей других разновидностей.
Разнообразие модальностей разделено на классы: существу-
ют классы нормативных, оценочных, эпистемических, временных
и т. п. модальностей, причём каждый класс модальностей служит
предметом изучения соответствующего раздела логики.
В логике принято считать основными алетическими модальностя-
ми модальности необходимости, действительности и возможности.
Причём в связи с алетическими модальностями используется
следующая терминология:
1) ассерторическими называют суждения, выражающие дей-
ствительность; другими словами, ассерторическими считаются суж-
дения, выражающие суждения, выражающие те или иные фактиче-
ски существующие обстоятельства или положения вещей;
2) аподиктичесними называют суждения, выражающие необ-
ходимость; другими словами, необходимость присуща логическим
правилам вывода, законам логики и других наук, а также положени-
ям, которые выводятся из этих законов по этим правилам;
613
https:it.ru
3) проблематическими называют суждения, выражающие воз-
можность; другими словами, возможность приписывается таким
положениям вещей, которые фактически, быть может, и не суще-
ствуют, но существование которых не противоречит законам логи-
ки и других наук.
Определение.
1. [125, с. 119] Модальная логика (логика модальностей) — это
специальный класс пропозициональных исчислений и исчисле-
ний предикатов, в которых помимо обычных пропозициональных
связок фигурируют модальные операторы. Формулы, включаю-
щие такие операторы, называют модальными формулами. Те или
иные модальные формулы добавляются в качестве новых аксиом
к системе аксиом какого-либо немодального исчисления, назы-
ваемого в этом случае базисным исчислением, задавая таким об-
разом различные модальные исчисления.
2. [160] Модальная логика — это область логики, в которой на-
ряду с обычными высказываниями рассматриваются модальные
высказывания, т. е. высказывания типа «необходимо, что...», «воз-
можно, что...» и т. п. В математической логике рассматривают-
ся различные формальные системы модальной логики, выявля-
ется взаимосвязь между этими системами, изучаются их интер-
претации.
Большое разнообразие систем математической логики объясня-
ется тем, что понятия «возможно» и «необходимо» можно уточнять
различными способами и, кроме того, по-разному трактовать слож-
ные модальности типа «необходимо возможно» и «взаимоотноше-
ния» модальностей с логическими связками.
В настоящее время можно говорить о семействе родственных
логических систем со сходной формальной структурой, которое со-
держит следующие «виды» логик:
1) алетическая логика исследует понятия «необходимость»,
«возможность», «случайность», «невозможность»;
2) временная логика (или логика времени) исследует временные
контексты с помощью следующих понятий: «в прошлом», «раньше»,
«вчера», «завтра», «в будущем» [120, с. 136—157];
3) динамическая логика исследует возможности синтеза и вери-
фикации программ [117, с. 233—247];
4) деонтическая логика исследует понятия «разрешено», «запре-
щено», «обязательно», «безразлично» (другими словами, это общее
название для логики норм, характеризующей нормативное поведе-
ние, и логики оценок);
5) эпистемическая логика исследует понятия знания и веры: «ве-
рифицировано», «неразрешимо», «фальсифицировано», «нефалъсифи-
цировано» [120, с.183—209];
614
https:/Л: rait.ru
6) экзистенциальная логика исследует понятия «универсаль-
ный», «существующий», «частичный», «пустой»;
7) аксиологическая логика.
Этот перечень отдельных видов модальных логик не является
завершённым и будет пополняться по мере дальнейшего развития
модальной логики (частично под влиянием философии).
Существует возможность объединения различных видов модаль-
ных логик в рамках одного логического исчисления: например, ло-
гика предвидения может быть получена комбинированием логики
знания, изучающей выражения вида «а знает А», и логики времени,
изучающей выражения вида «будет А». В свою очередь логика зна-
ния может быть получена объединением нескольких модальных
логик.
Синтаксис пропозициональной модальной логики
Следует озаботиться тем, чтобы
математические знаки были удобными
для открытий...
Г. В. Лейбниц
Определение.
Алфавитом модальной пропозициональной логики назовём мно-
жество знаков
def
Ам = {Р, Q, ...,Z,PltP2, ....Z^, ...}и{р, q, ...,z,pbP2r'’>№2> ...}и
u {-1, &, v, —>, <->} u {□, 0} u {(, )},
элементы которого будем называть буквами.
Буквы подразделяются на следующие категории:
1) прописные и строчные буквы латинского алфавита (возмож-
но с индексами) называются пропозициональными переменными
(или атомами);
2) буквы -I (читается: «отрицание»), & («конъюнкция»), v («дизъ-
юнкция»), —> («материальная импликация»), <-> («материальная
эквиваленция») называются логическими связками (оператора-
ми, символами);
3) буквы □ (читается: «знак необходимости»), 0 (читается: «знак
возможности») называются модальными связками;
4) буквы ( (читается: «открывающая (левая) скобка») и ) («закры-
вающая (правая) скобка») называются вспомогательными знака-
ми (буквами).
Модальные формулы строятся из счётного числа пропозициональ-
ных переменных, логических связок, одноместных модальных связок
и круглых скобок по следующему индуктивному определению.
615
https:it.ru
Определение.
1. Атомы являются модальными формулами.
2. Если А — модальная формула, то -А — модальная формула.
3. Если А и В — модальные формулы, то слова (А & В), (A v В),
(А В), (А В) являются модальными формулами.
4. Если А — модальная формула, то слова пА и ОА являются мо-
дальными формулами.
5. Других формул, кроме перечисленных в пункте (1) и постро-
енных по правилам пунктов 2—4, нет.
Приоритеты логических связок располагаются в порядке убыва-
ния следующим образом: -i, □, 0, &, v, <->.
Замечание [122, с. 242—243].
Связки -1, &, v, —<-> классической логики относятся к экстенсиональ-
ным логическим операторам, для которых логическое значение образо-
ванного с их помощью сложного высказывания однозначно определяется
логическими значениями его компонентов.
Однако существуют и не экстенсиональные операторы к которым,
в частности, относятся модальные операторы □ и 0.
Определение.
def
Языком модальной логики назовём кортеж 1М = (АМ,ЕМ), гдеАм—
алфавит, a FM — множество модальных формул.
Отметим, что логические связки &, v, <-», а также модальные
связки □ и 0 можно ввести в модальную логику как сокращения.
Определение.
def def
1) Р v q = & —-q), p q = -i(p & -^q),
def
p<^q = (p—>q)& (q—>p);
def
2) Op = -in-ip (если модальная связка □ уже определена);
def
□р = —10—ip (если модальная связка 0 уже определена).
Определение.
def
1) р => q - -10 (р & -iq) (=> — «строгая импликация»);
def
2) р <=> q = (р => q) & (q =>р) (<=> — «строгая эквиваленция»);
def def
3) VA = 0А & О-A; VA = -inA & -in-А (V — «знак случайности»).
616
https: //u
Модель Крипке для формул модальной
пропозициональной логики
Я провожу чёткое различие между
реальным, действительным миром
и несколькими модельными мирами,
созданными человеческим умом.
Следовало бы воздать хвалу тому, кто
додумался до различия этих миров.
Дж. Синг.
Беседы о теории относительности
В современной логике распространена интерпретация алетиче-
ских модальностей с помощью системы «возможных миров» — аб-
страктной интерпретации, которая может быть конкретизирована
различным образом.
Предположим, что имеется некоторое количество п предметных
моделей, которые логики называют «мирами». Ситуация в каждом
из «миров» описывается при помощи некоторого класса т простых
суждений. Разница между мирами заключается в следующем: то, что
истинно в одном из них, может оказаться ложным в другом. Для каж-
дого суждения из списка т существует совокупность «миров», в ко-
торых оно истинно, и совокупность «миров», в которых оно ложно.
Один из «миров» выделяют особо и считают моделью действи-
тельности: то, что истинно в этом «мире», истинно в действитель-
ности.
По отношению к «действительному миру» остальные оказыва-
ются только «возможными»; в них являются ложными некоторые
из тех суждений, которые истинны в «действительном мире». Раз-
умеется, что в каждом «возможном мире» имеются такие истинные
суждения, которые истинны и в «действительном мире».
Модальности при помощи системы «возможных миров» интер-
претируются следующим образом:
1) ассерторические суждения являются суждениями, истинны-
ми в «действительном мире»;
2) аподиктические суждения являются истинными во всех «ми-
рах»;
3) проблематические суждения являются истинными хотя бы
в одном из «возможных миров».
Этот характер истинности нашёл отражение в модели Крипке,
к определению которой приступим, следуя учебнику [3, с. 318—
319; с. 322—328].
1. Множество W называется множеством возможных миров. Воз-
можные миры понимаются предельно абстрактно, как некие «точки
соотнесения» формул языка с внеязыковой сферой, благодаря которым
(точкам соотнесения) формулы приобретают истинностные значения.
617
https:it.ru
Единственное требование, предъявляемое к множеству возмож-
ных миров, — непустота последнего.
2. Один из элементов W (обозначим его w0) наделяется особым
статусом — объявляется действительным миром. При этом С. Крип-
ке прямо следует за Г. Лейбницем: действительный мир — это всего
лишь какой-то из возможных миров; теперь понятие «возможный
мир» оказывается более фундаментальным, нежели понятие «дей-
ствительный мир».
Тупиковым миром называется мир, из которого не достижим
ни один мир (в том числе он сам).
3. Бинарное отношение связывает возможные миры между со-
бой и называется (по С. Крипке) отношением достижимости одно-
го мира из другого (для его обозначения используется также термин
«отношение альтернативности»).
Метаязыковое выражение SR(w, и/) означает, что из мира w до-
стижим мир и/, или что мир w' является альтернативой миру w.
Определение.
Шкалой Крипке называется упорядоченная пара (W, SR), WV 0.
Шкалу Крипке можно моделировать ориентированным графом,
вершинами которого являются элементы W, а дуги определяются
парами из SR.
Например,
wx w2 w3
(-О-->О----->О
\.п
w5 О-------->О<-9
def ^4
W = {1, 2, 3, 4, 5},
def
9t = {(1,1), (1, 2), (2, 3), (1, 5), (5, 4), (4, 4), (4, 3)}.
Замечания (для знатоков).
1. Бинарное отношение 91 для интуиционистской логики является:
а) рефлексивным: каждый возможный мир достижим сам из себя;
б) транзитивным: ViVp w2, м'3(Э1(14/1, w2) & 9i(w2, w3) => w3)).
2. Бинарное отношение 91 для модальной системы Т является рефлек-
сивным: 91 (и/, w) для любого мира w.
4. Возможными значениями пропозициональных переменных
являются И («истина») и Л («ложь»). Однако оценка переменных
в семантике модальной логики релятивизируется относительно
возможных миров: пропозициональные переменные оцениваются
618
https/^jr^t.ru
как истинные или ложные не сами по себе, а в каком-то возможном
мире, причём в различных мирах одна и та же переменная может
принять разные значения.
Техническое оформление этой идеи осуществляется следующим
способом: интерпретирующая функция I определяется как двух-
местная, она сопоставляет значения из множества {И, Л} парам,
состоящим из пропозициональной переменной и возможного мира.
Например, l(p,w) = И означает, что пропозициональная перемен-
ная р в возможном мире w принимает значение И.
5. Множество возможных миров W, выделенный действитель-
ный мир w0, отношение достижимости SR и интерпретирующая
функция 1 составляют модельную структуру.
Теперь приведем формальную запись семантики для модальной
пропозициональной логики.
Определение (по [3, с. 319]).
Модельной структурой модальной пропозициональной логики на-
зывается кортеж (IV, SR, I, w0), W Ф 0, woe IV, в котором:
1) SR с IV xlV — это бинарное отношение, заданное на множе-
стве IV;
2) 1:СхИМ{И,Л},
где G — множество пропозициональных переменных, И и Л —
истинностные значения.
Определение (по [3, с. 319—320]).
Функция оценки формул в возможном мире w eW модельной струк-
туры (W, SR, I, w0) определяется так (ре G; А, В — модальные фор-
мулы):
1)
2)
3)
4)
5)
6)
p|w = H^l(A,iy)=H; |р|и, = Л<=>ДА,и/)=Л;
-A|w
А&В
А&В
AvB
AvB
= И<^ |А „ = Л; |-A|W = Л<=> |A|W = И;
W = H^ А|„ = Ии |В|„ = И;
w ~ Л A w Л или | В | w Яд — Л,
W = A w = Miuiu |B|W = H;
„ = Л <=> А „ = Л и |В|w = Л;
А—»В
А^В
= И<=> |А|и, = Лплп |В|„ = И;
= Л<=> |А|„ = Ии |B|W = Л;
□ A w = И <=> Vv(SR(w, у) => |A|V = И);
□ А w = И <=> | А | w = И (для тупикового мира);
□ A w = Л <=> 3v(SR(w, v) u |A|V = Л).
Другими словами, формула пА истинна в возможном мире w в том
и только в том случае, когда в каждом мире, достижимом из w,
оказывается истинной формула А; формула пА ложна в возмож-
ном мире w в том и только в том случае, когда А ложна, по край-
ней мере, в одном возможном мире, достижимом из мира w.
619
https:it.ru
7) OA w = И Ж*. v) и |А | v = И);
ОА w = Л <=> VvCiR(w, v) => |A|V =Л);
ОА W = JI<^ | A w = Л (Эля тупикового мира).
Другими словами, формула ОА истинна в возможном мире w в том
и только в том случае, когда существует мир, достижимый
из данного, в котором формула А оказывается истинной; форму-
ла ОА ложна в возможном мире w в том и только в том случае,
когда А ложна в каждом мире, достижимом из мира w.
Итак, можно сказать, что необходимое высказывание — это вы-
сказывание, истинное в каждом из возможных миров; возможное
высказывание — это высказывание, истинное в каком-то из воз-
можных миров; невозможное высказывание — это высказывание,
ложное в каждом из возможных миров.
Из приведённого определения следует, что для формул, содержа-
щих только -1, —>, &, v, сохраняется их классическая трактовка.
Замечание {для знатоков интуиционистской логики).
Условия истинности и ложности формул -А и (А —> В) в интуицио-
нистской семантике совпадают с условиями истинности и ложности фор-
мул □—А и п(А —> В) в семантике модальной логики.
Определение (по [3, с. 320]).
1) Будем говорить, что формула А истинна в модельной струк-
туре (IV, SR, I, w0), если А принимает значение И в действитель-
ном мире данной структуры, т. е. мире w0.
2) Будем говорить, что формула А является общезначимой форму-
лой, если А истинна в каждой модельной структуре (W, SR, I, w0).
3) Будем говорить, что из множества формул Г в модальной логи-
ке Т логически следует формула А, если во всех модельных струк-
турах, где истинна каждая формула из Г, формула А также явля-
ется истинной.
Определение (по [3, с. 353]).
Моделью Крипке формулы А в модальной логике М называется мо-
дельная структура логики М, в которой формула А принимает зна-
чение И.
Модель Крипке формулы А в М будем обозначать М1= А.
Замечание.
В современной логике используются кроме рассмотренных выше реля-
ционной семантики модальных систем используются алгебраическая
и окрестностная семантика.
620
https: "и rait.ru
Работа с примерами решённых упражнений
См. Пример 1.
Аналитические таблицы для пропозициональной
модальной логики
Доехав до речки Рубикон, Юлий долго
юлил (51—50 до Р. X.) перед нею, наконец
сказал: «Жребий брошен» — и полез в воду.
Всеобщая история, обработанная
«Сатириконом» (1910)
Ранее был рассмотрен метод аналитических таблиц для языка
первого порядка, который позволял в определённых случаях устанав-
ливать общезначимость формул языка первого порядка или наличие
логического следования некоторой формулы В из посылок А1,А2,...,Ап.
Метод аналитических таблиц может быть использован в модаль-
ной логике, но теперь он усложняется, так как теперь аналитические
таблицы являются синтаксическими аналогами возможных миров.
Усложнение состоит в том, что при проверке общезначимости
модальных формул мы будем в общем случае иметь дело не с од-
ной аналитической таблицей, а с некоторым упорядоченным мно-
жеством аналитических таблиц, а именно, деревом таких таблиц:
1) с одной стороны, каждая аналитическая таблица, входящая
в структуру аналитических таблиц, будет древесно упорядочиваться
посредством правил редукции для пропозициональных перемен-
ных: [£&], [/&], [tv], [fv], [t->L [ML [t-'L [f-] (см. ниже);
2) с другой стороны, многообразие аналитических таблиц, кото-
рое возникает при проверке на общезначимость некоторой модаль-
ной формулы, также будет древесно упорядочиваться посредством
правил редукции для модальных связок □ и 0: [tn], [/□], [tO], [f>].
Из описания аналитических таблиц для первопорядковой логики
известно, что в ней для каждой конкретной аналитической табли-
цы всегда имеются линейно упорядоченные множества отмеченных
формул.
Цепями будем называть линейно упорядоченные множества от-
меченных формул для конкретных аналитических таблиц.
С другой стороны, в древесной структуре совокупности самих
аналитических таблиц будут находиться линейно упорядоченные
множества этих таблиц.
Ветвями будем называть линейно упорядоченные множества
аналитических таблиц, входящих в систему аналитических таблиц.
1. Пропозициональные правила редукции
В силу того, что модальные системы строятся на базе пропозици-
ональной логики, то без каких либо изменений мы принимаем все
правила редукции для пропозициональных связок -i, &, v, —».
621
https:it.ru
Определение (по [3, с. 191—194]).
Пропозициональные правила редукции — это приведённые ниже
слова:
[t&] t(A&B) tA tB в цепи таблицы w в цепи таблицы w [/&] f(A&B) £4|fB в цепи таблицы w в цепи таблицы w
[tv] t(AvB) tA|tB в цепи таблицы w в цепи таблицы w [fv] f(AvB) fA fB в цепи таблицы w в цепи таблицы w
[t->] t(A->B) £4| tB в цепи таблицы w в цепи таблицы w [f->] f(A^B) tA fB в цепи таблицы w в цепи таблицы w
[t-.] t(-A) в цепи таблицы w УЧ f(~A) в цепи таблицы w
fA в цепи таблицы w tA в цепи таблицы w
2. Правила редукции для модальных связок
Придумать зеленое солнце легко',
трудно создать мир, в котором оно
было бы естественным...
Дж. Р. Р. Толкиен. Из письма.
Правила редукции для модальных связок с и 0 формулируются
следующим образом [3, с. 323—324].
1. Правило [tn].
Допустим, что в некоторой цепи таблицы w содержится формула
t(oA), утверждающая истинность формулы оА в этой цепи.
Согласно условию истинности модальной связки □ (см. «функцию
оценки формулы в возможном мире»)
|nA|w = ИVv(<R(w,v) => |A|V = И),
это означает, что в любой таблице v, достижимой из данной цепи
таблицы w (эти таблицы уже обязательно должны быть к этому
моменту построены), имеет место истинность утверждения А, т. е.
tA.
Поэтому в таблицу v помещаем отмеченную формулу tA. Итак:
t(aA) в цепи таблицы w
в каждой таблице v, достижимой из цепи таблицы w.
Замечание (для знатоков нормальных модальных систем).
В нормальных модальных системах Т, В, S4, S5 отношение достижимо-
сти рефлексивно, т. е. каждая таблица достижима сама из себя, а потому
по отношению к любой таблице w всегда имеется таблица, которая уже
заранее построена (такой таблицей является w).
622
2. Правило [/о].
Пусть в некоторой цепи таблицы w содержится формула/(оА),
говорящая о ложности в этой цепи таблицы w формулы оА.
Согласно условию ложности модальной связки □ (см. «функцию
оценки формулы в возможном мире»)
|пА^Л <=>3v(9i(w, v) и |A|V = Л),
это означает, что существует таблица v, достижимая из данной цепи
таблицы w, такая, что формула А оценивается в ней как ложная. Эта
таблица должна отличаться от таблиц, которые уже были построены.
Поэтому необходимо обязательно построить новую таблицу v,
с которой начинается новая ветвь аналитических таблиц, объявить
ее достижимой из цепи таблицы w, и поместить в нее утверждение
о ложности формулы А. Итак:
/(□А) в цепи таблицы w--->v |JA в новой таблице v.
3. Правило [tO].
Предположим, что в некоторой цепи таблицы w содержится фор-
мула t(OA), говорящая об истинности в этой цепи формулы ОА.
Согласно условию истинности для модальной связки 0 (см.
«функцию оценки формулы в возможном мире»)
|0A|w = H<=>3v(W,v)u |А|У = И),
это означает, что существует таблица v, достижимая из данной цепи
таблицы w, в которой формула А является истинной. Поэтому обя-
зательно строится новая таблица v, с которой начинается новая
ветвь аналитических таблиц, она объявляется достижимой из цепи
таблицы w и в нее помещается утверждение об истинности А, т. е.
t(OA) в цепи таблицы w--->v | tA в новой таблице v.
4. Правило [/0].
Допустим, что в некоторой цепи таблицы w содержится формула
/(ОА), утверждающая ложность формулы ОА в этой цепи.
Тогда, согласно условию ложности для модальной связки 0 (см.
«функцию оценки формулы в возможном мире»)
|OA|W = A<=> VvCR(w, v) => |А|„=Л),
это означает, что в каждой таблице v, достижимой из данной цепи
таблицы w (эти таблицы обязательно уже должны быть к этому
моменту построены), имеет место ложность утверждения А.
Поэтому в такую таблицу помещаем отмеченную формулу JA:
f(0A) в цепи таблицы w
в каждой таблице v, достижимой из цепи таблицы w.
Новые правила редукции подразделяются на локальные и гло-
бальные.
623
https:/Л: rait.ru
Определение.
1) Локальными правилами называются правила [/□] и [tO], т. е.
правила, которые обязательно требуют конструирования новых
таблиц.
2) Глобальными правилами называются правила [tn] и [f>], т. е.
правила, по которым работают с уже построенными таблицами
и которые можно применять повторно по мере появления новых
достижимых таблиц.
При применении метода аналитических таблиц рекомендуется
вначале всегда применять локальные правила.
Замечание (для знатоков модальной логики).
В процессе применения глобальных правил необходимо помнить, что
отношение достижимости обладает различными свойствами в различ-
ных логических системах:
а) в интуиционистской логике отношение достижимости обладает
свойствами рефлексивности и транзитивности;
б) в модальной логике отношение достижимости может обладать сле-
дующими свойствами:
— рефлексивностью (Т);
— рефлексивностью и симметричностью (В);
— рефлексивностью н транзитивностью (S4);
— рефлексивностью, симметричностью, транзитивностью (S5).
Введём ряд понятий, связанных с применением метода аналити-
ческих таблиц для модальной логики.
Определение [3, с. 324].
1. Аналитической таблицей назовём:
а) аналитическую таблицу, которая начинается с отмеченной фор-
мулы/^ (при обосновании общезначимости формулы А);
б) аналитическую таблицу, начинающуюся с отмеченных формул
tA1} tA2,..., tAn,fB (при обосновании следованияА13А2, ...,АП 1=В).
2. Система аналитических таблиц — это множество аналити-
ческих таблиц, древесно упорядоченное с помощью отношения
достижимости.
Определение (по [3, с. 325]).
Будем говорить, что цепь аналитической таблицы w является
замкнутой, если:
а) в ее составе встречаются две отмеченные формулы вида С и -iC;
б) в ветви среди таблиц, достижимых из данной цепи таблицы w,
найдётся хотя бы одна замкнутая таблица.
624
https:/Л: rait.ru
Определение (по [3, с. 325]).
1. Будем говорить, что аналитическая таблица w является зам-
кнутой, если все ее цепи замкнуты.
2. Будем говорить, что система аналитических таблиц является
замкнутой, если замкнута аналитическая таблица w0.
Построение замкнутой системы аналитических таблиц для не-
которой формулы А, с учётом специальных свойств достижимости
для используемой модальной системы, означает, что эта формула
является общезначимой в этой логике.
Аналогично построение замкнутой системы аналитических та-
блиц, используемой для проверки выполнения А1г А2,..., Ап 1= В с учё-
том специальных свойств достижимости для используемой модаль-
ной системы, означает, что наличие данного следования имеет место.
Нормальные модальные исчисления
— Из того, что вы сказали, я не понял
ни слова. Но мне отчего-то кажется, что
вы правы.
Е. Водолазкин. Авиатор
Каким бы расширениям или модификациям ни подвергалась
классическая логика, она всегда останется орудием обоснования
простых, но важных в практической и теоретической деятельности
человека видов рассуждений; так классическая пропозициональная
логика составляет неотъемлемую часть модальной логики, поэтому
модальную логику трудно изучать без знания классической.
К. Гёдель (1933) предложил новый принцип аксиоматизации не-
которых модальных исчислений, а именно: берётся любая система
аксиом и правил вывода классического пропозиционального исчисле-
ния и к нему добавляются:
1) некоторые модальные схемы аксиом;
2) модальное правило вывода (правило Теделя): если Р—формула,
выводимая в этом исчислении, то пР — также выводимая формула.
Определение.
Принципом аксиоматизации Теделя называется способ построения
модальной системы, состоящий в следующем: в качестве исход-
ных положений аксиоматизируемой модальной системы берутся
аксиомы и правила некоторого классического пропозициональ-
ного исчисления (называемого базисным'), и к нему добавляются
некоторые модальные схемы аксиом и модальные правила вывода.
Итак, язык пропозициональной модальной логики оказывается
языком классической логики высказываний с дополнительными
связками.
625
https:it.ru
А. Прайер и Э. Дж. Леммон (см. [124, с. 22]) с помощью прин-
ципа аксиоматизации Гёделя аксиоматизировали канонические мо-
дальные системы Льюиса S1 — S5, т. е. сформулировали гёделев-
ским способом некоторые модальные системы и доказали затем
их эквивалентность системам S1 — S5 соответственно (для систем
S1 — S3 вместо правила Гёделя были взяты более слабые модальные
правила).
Современные системы логики элегических модальностей, назы-
ваемые нормальными модальными исчислениями, конструируются
именно как расширения классических логических теорий.
Определение.
Модальная логика называется квазинормалъной, если она не удов-
летворяет правилу Гёделя.
1. Минимальная нормальная модальная логика (исчисление К)
Определение (Д. Макинсон, 1966).
Модальное исчисление К содержит:
а) аксиомные схемы классического пропозиционального исчис-
ления;
Ь) модальную аксиомную схему
п(А—>В) —> (оА —> аВ) (аксиома нормальности, аксиома (К));
с) правила вывода:
А А^>В г , А . .
--------(modus ponens);----(правило Геделя).
В пА
С содержательной точки зрения правило Геделя означает, что
любой логический закон является необходимым утверждением.
Определение (логических символов 0, =>, <=>).
def
1) ОА = -о-А;
def
2) А=>В = п(А—>В);
def
3) А^В - (А=>В) & (В=>А).
Работа с примерами решённых упражнений
См. Пример 2.
Замечание.
Исчисление D получается с помощью добавления к системе К акси-
омы сА —> ОД (аксиома (D)).
626
2. Система Фейса-Райта (исчисление Т)
Определение (системы Т).
Система Т содержит:
а) аксиомные схемы классического пропозиционального исчис-
ления;
Ь) модальные аксиомные схемы:
1) п(А —> В) —> (пА —> аВ); 2) оА —> А (аксиома (Т));
с) правила вывода: modus ponens, правило Гёделя.
Теорема.
Для системы Фейса-Райта имеет место следующая фигура:
Г,А1-В
ГНА—>В
(дедукция).
Исчисление Фейса-Райта включает все теоремы классической
пропозициональной логики, а также дополнительные теоремы, ис-
пользующие модальности.
Теорема [3, с. 313].
Следующие формулы являются теоремами системы Т:
1) □(А&В)<-»(пА&пВ);
2) (nAvnB) —>п(Аv В);
3) п(А—>В)—>(0А—>0В);
4) 0(А—>В)<->(пА—> ОВ);
5) 0(А vB) <->(0А vOB);
6) 0(А&В)^(0А&0В);
7) (ОА —> ОВ) —> 0(А —> В).
Доказательство. Напомним, что отношение достижимости для
системы Т является рефлексивным и построим системы аналитиче-
ских таблиц:
1)
М70
f(n(A&B)^(nA&nB)) м/0
f((nA&nB)->n(A&B))
t(n(A&B))
t(A&B)
tA
tB
ffciA&nB)
f(nA) f(nB)
M fB
t(nA&nB)
t(nA) ~>
t(nB) ~>
f(n(A&B))--------> f(A&B)
M | fB
tA <«
w1 tB <«
627
4)
w0 f(0(A^B)^(nA^0B)) w0 f((nA^0B)^0(A^B))
t(O(A—>В)) «> t(nA-»0B)
t(A->B) <« f(nA) t(OB)
£4 | tB £4 tB <«
— ——
f(nA—>0В)
t(nA) f(A-»B)
tA tA
f(OB) fB
fB
5) 7)
w0 f(0(AvB)^(0Av0B)) u/0 f((0A^0B)^0(A^B))
t(0(AvB)) ~> f(O(A—>B)) «>
t(AvB) <« f(A->B) <«
tA | tB tA
f(OAvOB) fB
f(OA) «> t(OA^OB)
£4 <« f(OA) «> t(OB) «>
f(OB) «> £4 <« tB <«
fB <«
Теорема доказана.
Работа с примерами решённых упражнений
См. Пример 3.
3. Система Брауэра (исчисление В)
Определение (системы В).
Система Брауэра получается из системы Т присоединением до-
полнительной схемы аксиом (два варианта):
3) А —> пОА (аксиома Брауэра или (В))
(«всё действительное с необходимостью
является возможным»};
3') А —> c-iC-A
(«всё действительное с необходимостью
является возможным»).
1) п(А —>В) —> (пА —> сВ);
2) пА—>А;
3) А —> пОА
1) п(А —> В) —> (пА —> пВ);
2) пА—>А;
3) А —> □—in—А
628
Теорема [3, с. 314].
Следующие формулы являются теоремами системы Брауэра:
1) ОоА->А;
2) ОоА —> пОА (закон перестановки модальностей).
Доказательство. Упражняйтесь.
Напомним, что отношение достижимости для системы В являет-
ся рефлексивным, и симметричным.
4. Гёделева аксиоматизация системы S4
Определение.
Гёделева аксиоматизация системы S4 получается из исчисления
Т присоединением дополнительной схемы аксиом
3) пр —> ипр (аксиома (4),
«всё необходимое с необходимостью является
необходимым.»).
1) n(A —>В) —> (пА —> сВ);
2) пА->А;
3) пр —> пор
Теорема [3, с. 314].
Теоремами гёделевой аксиоматизации системы S4 являются фор-
мулы:
1) 00А—»0А;
2) оА <-> оА;
3) 00...0А<^0А.
Доказательство. Упражняйтесь.
Работа с примерами решённых упражнений
См. Пример 4.
Определение (по [125, с. 124]).
1. Парадоксами материальной импликации называются формулы:
р —> (q —>р) («ложное суждение влечёт любое суждение»);
-p—>(p—>q) («истинное суждение следует из любого суждения»).
2. Парадоксами строгой импликации называются формулы:
□ р => (q => р) («если р необходимо, то оно следует из любого q»);
—iOp => (р => q) («если р невозможно, из него следует любое q»).
Теорема.
Парадоксы строгой импликации являются теоремами систе-
мы S4.
Доказательство. Вначале применим определение связки «=>»
629
https: "и га it.ru
def
□ P => (q =} p) = n(np -> n(q ->p));
def
- iOp=>(p=>q) = n(-iOp —> n(p —> q)).
Воспользуемся методом аналитических таблиц (напомним, что
отношение достижимости для S4 является рефлексивным и транзи-
тивным'):
f(n(np —>n(q р)))--->
----> f(np^n(q^p))
t(np) ~>
w1 fn(q -> р)---> f(q -> р)
tq
w2 tp <«
f(n(-iOp q)))---------->
----> f(-iOp—>n(p—>q))
tbOp)
wT fn(p—>q)----->
w2
f(p^q)
tP
fq
f(Op)
Теорема доказана.
5. Гёделева аксиоматизация системы S5
Определение.
Гёделева аксиоматизация системы S5 получается одним из сле-
дующих способов:
1) из системы Т присоединением схемы аксиом
ОА —> пОА (аксиома (5),
«всё возможное с необходимостью возможно»);
2) из системы Т присоединением схемы аксиом
—1СА —> □-1пА;
1) п(А —>В) —> (пА —> пВ);
2) пА—>А;
3) ОА—>пОА
1) с(А —> В) —> (пА —> пВ);
2) пА—>А;
3) —idA □—idA
3) из системы В присоединением схемы аксиом
□А —> опА («всё необходимое с необходимостью
является необходимым»).
1) с(А —> В) —> (пА —> пВ);
2) пА->А;
3) А пОА;
4) пА —> спА
Теорема [3, с. 314].
Теоремами гёделевой аксиоматизации системы S5 являются фор-
мулы:
1) ОпА^оА;
2) МпВ <-> аВ;
3) МЪВ<г+ 6В.
Здесь М—любая конечная последовательность операторов □ и О,
расположенных в ней в произвольном порядке.
630
https:it.ru
Доказательство. Упражняйтесь.
Напомним, что отношение достижимости для системы S5 явля-
ется отношением эквивалентности.
Работа с примерами решённых упражнений
См. Пример 5.
Соотношения в которых находятся рассмотренные пять модаль-
ных системы изобразим графически [129, с. 349]. При этом мно-
жество теорем системы, обозначение которой стоит у основания
стрелки, включено в множество теорем системы, обозначение ко-
торой расположено у острия той же стрелки.
ВО
D т/ \
>О Гёделева
f аксиоматизация S5
О Гёделева аксиоматизация S4
KcDcTcBcS5;
KcDcTcS4cS5
Итак, самой «слабой» системой является система К, а самой
«сильной» — геделева аксиоматизация системы S5.
Характеризация отношений достижимости с помощью
модальных формул
Мудрость обитает во взаимосвязях.
Ю. И. Манин
Произвольная модельная структура (W, 91,I, w0) определена дву-
мя элементами, а именно: непустым множеством возможных миров
W и отношением достижимости 91, определяемым на W.
Когда мы некоторым образом уточняем свойства одного из этих
параметров, то тем самым определяем класс структур миров. Далее,
относительно некоторых классов структур оказываются общезначи-
мыми некоторые формулы, специфичные для структур с указанны-
ми свойствами.
Рассмотрим ряд свойств, которыми может обладать бинарное от-
ношение 91, и некоторые формулы, которые являются общезначи-
мыми в структурах с соответствующим 91.
Теорема (по [123, с. 356—357]).
Пусть (W, 91) — шкала Крипке. Отношение достижимости 91 обла-
дает каким-либо из свойств 1—10 тогда и только тогда, когда соот-
ветствующие формулы 1—10 общезначимы в шкале Крипке (W, 91).
Другими словами, модальная формула общезначима на шкале
Крипке тогда и только тогда, когда эта шкала (точнее, отношение
достижимости 91) обладает указанным свойством.
631
https:/Л: rait.ru
632
№ Нормальная модальная система Свойство отношения достижимо- сти Название свойства SR Формула
1 Т Рефлексивность □А-> А
2 В VwVvfwSRv -> vSRw) Симметричность А —>пОА, ОпА —> А
3 S4 VwVvVufwSHv & vSRu -> w4Ru) Транзитивность □А -юаА
4 S5 X/wX/vX/uty/iRv & wVIil -> vKii) Евклидовостъ ОА ->пОА
5 D Vw3v(wSHv) Репродуктивностъ □А—>0А
6 ? VwVvVu(w9?v & w9?u ~^v = u) Частичная функциональность ОА —>□ А,
7 7 VwBjVfwSHv) Функциональность 0А<->пА
8 7 VwVv3u(wSRv -> w4Ru & uSRv) Слабая плотность □□А —>пА
9 7 VwVvVufwSRv & wSRu -> -> (уЧЯи v v = и v uSRv)) Слабая связность □((А &пА)—>B)v vn((B&nB)—> А)
10 7 VwVvVuVt(wSKv & wVIil -> ->(vSRt&u9lt)) Слабая направленность On А ->пОА
Иногда «слабую связность» называют «детерминированностью»,
а «слабую направленность» — «конфлюентностъю».
Доказательство. Рассмотрим только доказательства «в направ-
лении слева направо», т. е. предположим, что 91 обладает каким-ли-
бо из свойств 1—10 и докажем общезначимость соответствующей
формулы.
1. М70
f(nA—>А)
t(nA) «>
tA <«
£4
2. w0 f(A—>пОА) tA
f(nOA) > f(OA) £4 <~ w1
В силу рефлексивности отношения
достижимости выполняется w091w0,
поэтому отмеченные формулы
tA и fA оказались в одном мире; си-
стема аналитических таблиц зам-
кнута.
В силу симметричности отношения
достижимости выполняется
WoSlu/j —> WjSIwq, поэтому отмечен-
ная формула/4 появилась в мире
w0; система аналитических таблиц
оказалась замкнутой.
3. w0 f(nA —>nnA)
t(nA) «> f(nnA) > f(nA)
14?! £4
w2 tA
4. м/0
w1
f(OA—>пОА)
t(OA)
f(nOA) \
г
w2
f(OA) «>
tA
£4 <«
В силу транзитивности отношения
достижимости выполняется
m/oSIm/j & m^SIu^ —» w091w2; отмечен-
ная формула t(oA) порождает отме-
ченную формулу tA, которая перено-
сится в мир w2 (уже построенный),
отмеченные формулы tA и fA оказа-
лись в одном мире; система анали-
тических таблиц замкнута.
В силу евклидовости отноше-
ния достижимости выполняется
WoSlwj & w091w2 —> м/191м/2; отмечен-
ная формула/(ОА) порождает отме-
ченную формулу fA в мире w2 (уже
построенном), отмеченные форму-
лы tA и fA оказались в одном мире;
система аналитических таблиц зам-
кнута.
5. Напомним, что репродуктивность 91 означает, что «из каждо-
го мира достижим некоторый мир».
633
https:/Л: rait.ru
iv0
f(nA—>0A)
t(nA) ~>
f(OA) \
В силу репродуктивности отно-
шения достижимости существует
мир w13 для которого выполняет-
ся отмеченные формулы
tA и fA переместятся в мир wf, си-
стема аналитических таблиц зам-
кнётся.
6. Напомним, что частичная функциональность 91 означает, что
«из каждого мира достижим не более, чем один мир».
М70
w2
f(OA—>пА)
t(0A)
f(nA) \
w1
М
В силу частичной функционально-
сти отношения достижимости вы-
полняется
WoSlwj & w091w2 —>14/! = w2;
отмеченные формулы tAnfA оказа-
лись в одном мире; система анали-
тических таблиц замкнута.
7. м/0
f(OA—>пА)
t(0A)---->
f(nA)---->
w1
В силу функциональности отноше-
ния достижимости для мира w0 су-
ществует единственный достижи-
мый мир wf, отмеченные формулы
tAnfA оказались в одном мире; си-
стема аналитических таблиц зам-
кнута.
М70
f(nA-»0A)
t(nA) ~>
f(OA) «>
В силу функциональности отноше-
ния достижимости для мира w0 су-
ществует единственный достижи-
мый мир wf, отмеченные формулы
tAnfA оказались в одном мире; си-
стема аналитических таблиц зам-
кнута.
8. w0
f(nnA ->пА)
t(nnA)
f(nA)----> £4
t(nA)
w1 £4
В силу слабой плотности отноше-
ния достижимости выполняется
WqSIwj —» iVoSlu/j & WjSlu/p отме-
ченная формула t(oA) переносится
в мир w1 п порождает в этом мире
отмеченную формулу tA; в результа-
те отмеченные формулы tA nfA ока-
зались в одном мире; система ана-
литических таблиц замкнута.
634
9. Пусть (в силу слабой связности отношения достижимости)
выполняется M/gSlM/j & w091w2 —>14/! = м/2; отмеченные формулы
tAnfA оказались в одном мире; система аналитических таблиц зам-
кнута:
14/q f(n(A&iziA—>B)vd(B&qB—> А))
f (п(А &пА —> В))---------->
f(n(B&LiB—> А))
f((B&nB)->A)
t(B &пВ) w1
f((A&nA)—>В)
t(A&nA)
tA
t(cA)
fB
/X
14/0O OM/j = W2
X/
° w2
Случаи m/o^Rm/j & w091w2 —> m/191m/2 и m/q^Rm/j & w091w2 —> w23iw1 рас-
смотрите самостоятельно.
10. м/0
f(OnA^-nOA)
t(OnA)
f(nOA)
t(nA)
tA
M <«
OM/j
/ X
14/0 О OWj
X /
OM/2
f(OA) «>
14/2
В силу слабой направленности отношения достижимости вы-
полняется m/q^Rm/j & w091w2 —> m/j^Rm/j & w^w^, отмеченная формула
/(ОА) порождает отмеченную формулу fA в достижимом мире мг; от-
меченные формулы tAnfA оказались в одном мире; система анали-
тических таблиц замкнута.
Теорема доказана.
Связи интуиционистской и модальной логики
К. Гёдель (1933) (см. [130, с. 301—303]) показал, что все теоремы
интуиционистской логики имеют эквивалентные теоремы в класси-
ческой модальной логике S4. Целью исследований К. Гёделя явля-
лось построение неинтуиционистской интерпретации гейтингов-
ской интуиционистской системы.
Дж. Мак-Кинси и А. Тарский [131] построили функции «перево-
да» выводимых формул интуиционистского пропозиционального
исчисления в выводимые формулы системы Льюиса S4.
Приведём «погружающие» функции (поМ. Медейрос [132; 133]).
Определение.
Определим функцию g: Lj —> LS4 индуктивным образом:
def
1) g(A) = nA, где А — пропозициональная формула;
635
2) gGA—>В) = c(g(A) —»g(B)),g£A&B) = g(A)&g(B),
def
g(AvB) = qg(A)vqg(B);
def
3) gA =
def def def def
g(~A) = g(A ->-*-)= D(g(A) -> = a(g(A) ->-*-)= a^g(A).
Лемма [133].
ri-M=>g(r)i-S4gU).
Определение.
Определим функцию/: LS4 -^Lj индуктивным образом:
def
1) f(A) = А, где A — пропозициональная формула;
def def
2) f(A -> В), = ДА) ^ДВ), ДА & В) = ДА) &ДВ),
f(A v В) “да) v/(B);
I def I
3) Дх) =
def def
4)/(oA) = /(A);/(0A) = /(A).
Пример (вычислений с использованием функции/).
/(-nA) = /(A^-L) = /(А)->/(-*-) = /(А)^-* 1- = -/(А).
Лемма [133].
1) g(DHS4g(A)^/(g(r))h/(g(A));
2) bAo/(g(A)).
Работа с примерами решения упражнений
См. Пример 6, Пример 7, Пример 8.
Замечание (важное).
Интерес к изучению интуиционистских модальных логик вызван
рядом причин:
1) многие логики-интуиционисты по философским соображениям
склонны считать интуиционистскую, а не классическую логику, логикой,
которую необходимо использовать для проверки корректности рассужде-
ний. Ясно, что при формализации рассуждений о «возможности» и «необ-
ходимости» интуиционисты хотят использовать именно интуиционист-
скую логику, в качестве базиса для построения модальных логик;
htt
636
2) интуиционистские модальные логики стали применяться для фор-
мального моделирования задач, возникающих в различных приложениях
логики, главным образом, в теоретическом программировании.
Например, Е. Moggi [134] расширил формальную семантику функ-
циональных языков программирования, основанную на Х-исчислении
с типами, новой конструкцией — монадой, используемой для функцио-
нального моделирования побочных эффектов языков функционального
программирования. Оказалось, что монады имеют типы, соответствую-
щие модальностям типа S4 (вспомним изоморфизм Карри-Говарда между
Х-исчислением с простыми типами и интуиционистской пропозициональ-
ной логикой).
Корректность и полнота нормальных
модальных исчислений
Вы должны взглянуть на практику
языка и тогда вы увидите логику.
Л. Витгенштейн.
О достоверности, 501
Сформулированные исчисления К, Т, В, S4, S5 являются адек-
ватными формализациями понятия «общезначимость» («истин-
ность»).
Теорема (по [123, с. 370]).
Для любой модальной формулы А
1) hKA^kKA;
2) hT А <=> 1=т А;
3) НВА<=>1=ВА;
4) hS4 А 1=54 А;
5) l“S5 А <=> l=S5 А.
Импликация в направлении слева направо соответствует свой-
ству корректности, которое состоит в том что всякая доказуемая
в исчислении формула является общезначимой на соответствую-
щем классе структур.
Импликация в направлении справа налево соответствует свой-
ству полноты, которое состоит в том, что всякая формула, обще-
значимая на соответствующем классе структур, является теоремой
в данном исчислении.
Другими словами,
1) если свойства отношения 91 неизвестны, то шкала Крипке (W, 91)
является адекватной интерпретацией исчисления К;
2) если 91 —рефлексивно, то шкала Крипке (W, 91) является адек-
ватной интерпретацией исчисления Т;
3) если 91 —рефлексивно и симметрично, то шкала Крипке (W, 91)
является адекватной интерпретацией исчисления В;
637
https:/Л: rait.ru
4) если 91 —рефлексивно и транзитивно, то шкала Крипке (W, 91)
является адекватной интерпретацией исчисления S4;
5) если 91 — отношение эквивалентности, то шкала Крипке (W, 91)
является адекватной интерпретацией исчисления S5.
Биографические сведения
Гёдель Курт Фридрих (28.04.1906, Брюнн, ныне Брно —
14.01.1978, Принстон, США) — выдающийся логик и математик.
К. Гёдель получил докторскую степень в Венском университете
(1930), где работал приват-доцентом математического факультета
(1933—1938). С 1940 работал в Принстонском институте перспек-
тивных исследований (США) (с 1953 — профессор Принстонского
университета).
Основные направления исследований — математическая логи-
ка и теория множеств. Занимался философией математики. Им до-
казана теорема о невозможности полной формализации процесса
логического вывода. В теории множеств известна его работа о не-
противоречивости гипотезы континуума. В классическом исчисле-
нии предикатов сформулировал и доказал теорему о полноте (1930)
и теорему о неполноте (1931).
К. Гёделю принадлежат крупные результаты в области интуи-
ционистской логики и математики (например, разработка приема
погружения интуиционистской арифметики в классическую). К. Гё-
дель (1939) доказал относительную непротиворечивость обобщен-
ной континуум-гипотезы и аксиомы выбора, для чего ввёл понятие
«конструктивное множество».
Льюис Кларенс Ирвинг (12.04.1883 — 03.02.1964) — американ-
ский логик и философ. Родился в Стонеме (Калифорния). Профес-
сор философии Гарвардского университета.
Основоположник современной модальной логики. Логические
работы посвящены в основном разработке модальной логики
и ее приложениям к формализации логического следования, а так-
же вопросам логической семантики. Разработал ряд исчислений
строгой импликации.
Примеры решения некоторых типов упражнений
Пример 1. Определите в рамках семантики возможных миров условия
истинности для следующих формул:
1) п(0р -> q); 2) р -юр; 3) -Х>р -> -р.
Решение. Задача решается с помощью построения (незсинкнутьос) ана-
литических таблиц.
638
https://и гз it.ru
1) Wo t(n(Op - t(Op-> f(Op) fp ->q)) q) tq Формула a(0p -> q) истинна, если в мире w0 или fp, или tq.
2) w0 t(p -юр) t(np) tP Формула р —>пр истинна, если пропозициональ- ная переменная р или ложна, или истинна в мире w0.
3) w0 t(—iOp- t(-p) fp ->-P) fbOp) t(Op) |tp Формула -10р -> —р истинна, если: 1) winfp в мире w0; 2) или если существует мир wlt достижимый из w0, в котором tp.
Пример 2. Докажите, что следующие формулы обладают универсаль-
ной общезначимостью, не зависящей от свойств отношения достижимости:
1) п(А —>В) —>(пА —>пВ);
2) 0(А —> В) —> (□ А —> ОВ);
3) (□ А —> ОВ) —> 0( А —> В);
4) п(А&В) —>(сА&пВ);
5) (□А&пВ)->о(А&В);
6) 0(А vB) —>(0А vOB);
7) (OAvOB) —>0(А vB).
Решение.
1) f(n(A—>В) — f (dA —>qB) > (nA —>nB))
t(nA) f(cB) t(n(A-
> & tA <«
t(A -^B) tB
2) w0 f(O(A- >B)- ► (□A->0B))
t(O(A- > t(A
f(cA-> OB) fA tB
t(aA) «> tA fB
f(OB) «>
639
https:/Л: jt.ru
3)
W0
f((nA -> OB) -> 0(A -> B))
f(O(A—>B)) «>
t(nA—>0B)
f(nA) | t(OB)
w1
4)
fA
f(A->B) <®
tA
fB w2
tB
f(A->B) <®
tA
fB
f (□( A & B) —> (□ A &cB))
t(c(A&B)) «>
f(□A&nB)
f(nA) | t(nB)
W]
fA
t(A&B)
tA
tB w2
fB
t(A&B)
tA
tB
5)
w0
f((nA&nB)->n(A&B))
t(cA&QB)
t(nA) ~>
t(cB) ->
f(b(A&B))
w1
f(A&B)
fA fB
tA tB <«
iv0 f(0(AvB)^(0Av0B))
f(OAvOB)
f(OA) ->
f(OB) ->
t(0(AvB))
И»!
t(AvB)
tA tB
fA fB <«
640
w1
w0
f((OAvOB)->O(AvB))
f(O(AvB)) «>
t(OAvOB)
t(OA) | t(OB)
tA
f(AvB) <®
1A
fB w2
tB
f(AvB) <»
fA
Пример 3. Докажите в системе Т общезначимость следующих формул:
1) пр=>0р; 2) пр^-п-р; 3) (p=>q)&-iq=>-p.
Решение. Выполним преобразования и построим искомые таблицы:
def
1) пр => Op = п(ар -> Ор)
w0 | f >0р))----------
def
2) op => —p = d(dP -> —iQ—p)
w0 I f(□(□p —> —O—p))----
f(np->0p)
t(ap)
*Р
f(Op)
f (mp —> —p)
t(ap)
f(^n^p)
t(EMp)
t(-p)
Ф
def
3) (p=>q)&—.q=>—p = □(□(p—>q)&—iq—>—p)
iv0 | f(n(n(p^q)&^q^^p))
f (n(p -> q) & ^q -> ^p)
fbp)
t(n(p->q)&^q)
t(--q)
%
t(n(p->q))
t(p^q)
fy | tq
o- Hi iroil ri i
O.f i Ui (uit.I VI
641
Пример 4. Докажите в системе S4 общезначимость следующих фор-
мул:
1) (□AvnB)->n(nAvDB); 2) O(OAvn-iA).
Решение.
1)
w0
f((nA vnB) ->п(пА vdB))
f(n(nAvnB))---------->
t(cAvaB)
t(cA) ~>
t(aB) «>
И»!
f(cA vnB)
f(nA)---->
f(oB) iv2
\ fB
w3 tB <«
fA
tA <®
В силу транзитивности отношения достижимости выполняется
iVqSRwj & W]%v2 —> w0%v2 и w0%V] & w-]%v3 —> iv0SRiv3; отмеченная фор-
мула t(nA) порождает отмеченную формулу tA, которая переносится в мир
w2 (уже построенный!), отмеченная формула t(cB) порождает отмечен-
ную формулу tB, которая переносится в мир w3 (уже построенный!); отме-
ченные формулы tAnfA оказались в мире w2, а отмеченные формулы
tB nfB оказались в мире w3, система аналитических таблиц замкнута.
2)
w0
f(0(0Avn-iA))
f(OAvn-iA)
f(0A) «о
f(c-iA)-----> w1
f(-A)
tA
fA <®
В силу транзитивности отношения достижимости выполняется
w0%V] & iV]%V] —> w0%V]; отмеченная формула /(ОА) порождает отме-
ченную формулу fA, которая переносится в мир (уже построенный!),
отмеченные формулы tAnfA оказались в мире w1} система аналитиче-
ских таблиц замкнута.
Пример 5. Воспользовавшись определением строгой импликации
def
р => q = и(р -> q), установите общезначимость формулы ООр => Ор в систе-
ме S5.
def
Решение. Вначале установим, что ООр => Ор = с(00р —> Ор).
Остается построить систему аналитических таблиц (напомним, что
отношение достижимости для системы S5 является рефлексивным., сим-
метричным и транзитивным'):
iv01 f(n(00p -> Op))-->
f(OOp->Op)
t(OOp)----->
f(Op) ~> w2
t(Op)---->
w3
tp
642
https ://игз it.ru
Пример 6. Установите общезначимость формулы (А —> -г-А) в интуи-
ционистской логике с помощью ее «погружения» в систему S4.
Решение. Займёмся вычислениями в системе S4 (ниже двойной линии
приведена система аналитических таблиц, устанавливающая общезначи-
мость формулы в интуиционистской системе):
def def def
g(A -> -.-A) - d(g(A) -> g(-i-A)) - d(dA ->□-g(-A)) - п(пА -w-d-dA);
w01 f(a(aA ->□-D-dA)) ->
w1
f (elA .nA)
t(cA) ~>
f (□—!□—!□ A)--->
w01 f (A —> -i-A)
tA ~>
w1 f(-i-A)
t(-A)
fA
iv2
f(-iQ—oA)
t(n-iCiA)
t(nA)
f(oA)-
fA
w3
w2
Заданная формула доказуема в интуиционизме.
Пример 7. Установите общезначимость формулы —.(А & -А) в интуици-
онистской логике с помощью ее «погружения» в систему S4.
Решение. Займёмся вычислениями в системе S4 (справа от двойной
вертикальной черты приведены аналитические таблицы, устанавливаю-
щие общезначимость формулы в интуиционистской системе):
def def def
g(-i(A&-A)) = □-g(A&-A) = □—i(g(A)&g(—A)) = □-.(□A&d-dA);
w01 f(c—i(cA&o—.nA))— —> f(—i(cA &□—.nA)) w0 |f(-i(A&-A))— —> t(A&^A)
t(nA&D-oA) tA
t(nA) t(—A)
t(c-ciA) И?! fA
t(—.nA)
И»! f(nA)
Пример 8. Установите доказуемость в системе S4 формулы
□(□((□А&пВ) —>dC) —>q(qA —>□(□£} —>qC)))
с помощью ее «погружения» в интуиционистскую систему.
Решение. Займёмся вычислениями в интуиционистской системе:
def
/(□(□((□А &пВ) —>пС) ->п(пА —>и(пВ —>пС)))) = (А & В С) -> (А -> (В -> С));
643
f(A^(B^C))^
w2
tA
f(B->c)Z
U>3
tB
fC
t(A&B->C} <
f(A&B) | tC
fB
t(A&B->C) ~>
Формула доказуема в системе S4.
Задачи для самостоятельного решения
И теперь мы можем решить задачу
вообще без всякой математики с помощью
одной лишь теории групп.
Профессор из Кембриджа
1. Истинность модальных формул
1. (По [118, (а), с. 55—57, № 1.8])
Какие из приведённых высказываний являются необходимыми, возмож-
ными, невозможными:
1) если все многоклеточные существа смертны, то все они со временем
умирают;
2) если все люди — поэты, то некоторые из людей — поэты;
3) всякое домашнее животное или послушно, или не является послушным;
4) если криптон — инертный газ, он не способствует горению;
5) снег является не белым, а голубоватым;
6) если металлический стержень нагреть, длина его не изменится;
7) если бы Аристотель не открыл закон противоречия, это сделал бы кто-то
другой;
8) свинец применяется в аккумуляторах, и вместе с тем он не исполь-
зуется в них;
9) в метре иногда бывает больше чем 100 сантиметров;
10) не у всех отцов были или есть дети.
2. (По [118, (а), с. 55—57, № 2.8, 3.8])
Запишите в виде модальных формул следующие утверждения:
1) если высказывание возможно, то неверно, что его отрицание является
необходимым;
2) если высказывание необходимо, то неверно, что его отрицание воз-
можно;
3) если отрицание высказывания не является необходимым, само вы-
сказывание возможно;
4) если отрицание высказывания не является возможным, само выска-
зывание — необходимо;
5) если высказывание случайно, то возможно как оно само, так и его
отрицание;
644
https:it.ru
6) если возможно и высказывание, и его отрицание, то такое высказы-
вание является случайным;
7) противоречивое высказывание не является возможным;
8) отрицание противоречия необходимо;
9) если необходимо, что если собака лает, то она лает, то возможно, что
когда собака лает, она лает;
10) если муха — животное, то возможно, что она животное.
Ответы: 1) ОА ——о—А; 2) пА ——i0—А; 3) —о—А —ОА; 4) —<0—А —миА;
5) VA -> ОА & 0—А; 6) ОА & О^А -> VA; 7) -,0(А & -А); 8) ем(А & -А);
9) п(А —> А) —> 0(А А) ;10) А ОА.
3. [3, с. 328]
Определите в рамках семантики возможных миров условия истинности
и ложности следующих формул:
1) пр -> 0q; 2) 0q -> Ор; 3)п0пр; 4) 0(пр &nq).
4. [127, с. 156]
Определите в рамках семантики возможных миров условия истинности
следующих формул:
1) n(Op^q);
2) Опр;
3) р-мзр;
4) -,Ор->^р;
5) р—>п0р;
6) □(—р&0—>q);
7) -10(-1Пр v 0q);
8) п-iOp <-> 00-iq;
9) п(0р —>nq) —> 0(пр —> 0q);
10) ->п(0р&п0р);
11) 0-i(n—10р —>0-inq);
12) 0(0р&п-р).
2. Нормальная модальная система К
5*. Докажите, что следующие формулы обладают универсальной обще-
значимостью (не зависящей от свойств отношения достижимости), для
мира w0, являющегося тупиковым миром:
1) п(А -> В) -> (А -> В); 2) (0А ->пВ) -> (А -> В).
Решение.
1) w0 f (п(А —> В) —> (А —> В)) 2) w0 f((OA—>nB)—>(A—>B))
f(A—>В) f(A^B)
tA tA
fB fB
t(n(A—>В)) t(OA ->nB)
t(A->B) f(OA) t(nB)
£4 | tB £4 tB
6*. (По 123, с. 361; с. 369)
645
https: "и rait.ru
Докажите, что формулы обладают универсальной общезначимостью
(не зависящей от свойств отношения достижимости) (система К):
1) —iOA <-—А;
2) —сА 0—Aj
3) п(А —> В) —> (оА —>пВ);
4) 0(А—>В)—>(иА—>0В);
5) (пА^ОВ)^О(А^В);
6) п(А&В) <-> (пА&пВ);
7) (пА&пВ) —>п(А&В);
8) 0(А v В) <-> (ОА v ОВ);
9) (ОА v ОВ) —> 0(А v В);
10) (nA—>0(В—>С))—>(пВ—>(пА—>0С));
11) (□А&0(В->С))->(о(А->В)->0(А&С)).
Решение.
10) w0
f((nA -> 0(В С)) (пВ -> (пА ОС)))
f(nB—>(оА—>0С))
t(oB)
f(oA—>0С)
t(nA) ~>
f(OC) ->
t(nA—> 0(B—>C))
f(oA) | t(O(B->C))
и»! £4
tA <
t(B^C)
fB tC
tB fC
11) w0 f((nA&0(B->C))->(n(A^>B)->0(A&C)))
f(n(A->B)->O(A&C))
t(n(A^B)) *>
f(O(A&C)) *>
t(nA&O(B->C))
t(nA) ~>
t(O(B^C))
t(B^C)
fB
t(A^B)
fA | tB
tA
tC
tA
f(A&C)
fA | fC
7*. [127, c. 157]
Докажите в системе К универсальную общезначимость формул:
1) (ОА v ОВ) —> 0(А v В);
2) ОА —о—A j
3) —iOA —А;
4) 0(А—>В)<—(nA—>0В);
5) п(0(А&В) —>0А);
6) □(□A—>n(AvB));
7) □((□А&пВ)—>п(А<-»В));
8) п(А —>В) —>(0А —>0В);
9) □((□(А&В—>С)) <->(п(А&—1С —В))).
Решение.
8)
м/0
f(n(A —> В) —> (ОА ОВ))
t(n(A—>В)) *>
f(OA—>0В)
f(OB) *>
t(OA)----------------->14?!
tA
fB
t(A->B)
fA | tB
3. Нормальная модальная система T
8. (По [127, с. 158; 123, с. 369]) Докажите общезначимость следующих
формул на структурах, в которых отношение 91 обладает свойством рефлек-
сивности (система Т):
1) А -> ОА;
2) 0(А—>пА);
3) п(0А v О-A);
4) □(□А^А&пА);
5) п(А н (A v пА)).
9. (По [3, с. 313])
Докажите в системе Т общезначимость следующих формул:
1) □(А->В)->(0А->0В);2)0(А->В)<->(пА->0В);3) (0А->0В)->0(А->В).
10. [115, с. 139]
Докажите в системе Т общезначимость следующих формул:
1) пр=>р;
2) р=>Ор;
3) пр=>Ор;
4) п(р & q) опр &nq;
5) 0(pvq)o0pv0q;
6) пр vnq =>п(р v q);
7) 0(р & q) => Op & Oq;
8) пр =>n(-p q);
9) (p=>q)&p=>q;
10) (p=>q)&np=>nq;
11) (p => q) & 0-iq => 0-p;
647
https://'draft.!
12) (p=>q)&->q=>-p;
13) (p&-p)=>q.
4. Нормальная модальная система В
11. [127, с. 158; 123, с. 369]
Докажите общезначимость формул на структурах, в которых отношение
91 обладает рефлексивностью и симметричностью (система В):
1) (ОпА&ОоА) —>пО(А&В);
2) ОпА —>пОА ;
3) ОпА^А;
4) Оп А & ОпВ —>пО(А & В);
5) Оп(А—>пОА);
6) п(0пА -> ОА);
7) пОА —>00А.
5. Нормальная модальная система S4
12. (По [127, с. 158])
Докажите общезначимость формул на структурах, в которых отношение
91 обладает рефлексивностью и транзитивностью (система S4):
1) 00А—>0А;
2) □(□А—юОоА);
3) п(А —>п(В —>оА));
4) □(□(A v—А) <->(А v—А));
5) ОпОА—>0А.
13. (По [123, с. 369])
Докажите в системе S4 общезначимость следующих формул:
1) 00А<-»0А;
2) (nA vnB) —>п(пА vnB);
3) пОА <->пОпОА ;
4) ОпАО’ОпОпА;
5) ЕХаВ—>п(А—>пВ));
6) □(□А—>пОпА);
7) □(ОпОА—>0А);
8) □(□((□ А &пВ) —>пС) —>□(□ А —>п(пВ —>пС) ) ).
6. Нормальная модальная система S5
14. [127, с. 158]
Докажите общезначимость формул на структурах, в которых отношение
91 обладает рефлексивностью, симметричностью и транзитивностью:
1) пОА^-ОА;
2) пОпА^-юА;
3) ОпОА<-»ОА;
4) 0(п А & ОВ) ->п(пВ ->пА);
5) п(0(А&0В) <->(0А&0В));
6) □(□A v В) Оп(А vqB);
7) ОпА —> (ОВ —>п(А & ОВ));
8) □((0А&п(А->0В))->0В.
15. [123, с.369]
Докажите в системе S5 общезначимость следующих формул:
1) ОпА—>пА;
2) ОА опОА ;
http
о- /Л iroit
648
3) пАоОпА;
4) п(А voB) о (nA voB);
5) п(А v ОВ) <-> (nA v ОВ);
6) 0(А&0В)<->(0А&0В);
7) 0(А &пВ) о (ОА &оВ);
8) ОпА—>(0В—>п(А&0В)).
7. Дополнительные задачи
16. (По [3, с. 328—329])
Определите нормальные модальные системы, в которых являются обще-
значимыми следующие формулы:
a) -р—ю-пр;
б)п(р -> q) -> (пр -> (q v г));
в) -.пр—>□-ар;
г) Опр-юОр;
д) 0p->->0-i0p;
е) п(р & q) —>-{-ср v-cq).
17*. [3, с. 328—329]
Определите, в каких нормальных модальных системах имеют место
следующие отношения логического следования:
а) п(р & q) 1= On-i(p & -iq);
б) пр,-.(q vr) l=-in(p—>q);
в) п(р —>q), Oq, 0—iq 1= q —>р.
18. Определите, в каких нормальных модальных системах общезначимы
следующие формулы (известные еще античным логикам):
1) пР^Р
(«всё необходимое действительно») ;
2) Р->ОР
(«всё действительное (истинное) возможно»);
3) оР—>0Р
(«всё необходимое возможно»);
4) nP^-iO-iP
(«утверждение необходимо тогда и только тогда, когда невозможно его
отрицание»);
5) ОРо—Р
(«утверждение возможно в том и только в том случае, когда его от-
рицание не является необходимым»),
19. Установите общезначимость следующих формул:
1)
2) ппА о -100—А;
3) —nA 0—Aj
4) On-iA <-> —iDqA;
5) □—А —iOAj
6) iA <-> —100А;
7) nO—iA о -iOelA;
8) On—A о —idOA.
Замечание (no [119, c. 41]).
Полученные в процессе решения задачи результаты позволяют сфор-
мулировать правило □ — 0 замены: в любой последовательности рядом
стоящих модальных знаков каждое вхождение 0 можно заменить на □
649
https:it.ru
и каждое вхождение □ — на 0, если отрицание -i вставить непосред-
ственно до и после этой последовательности; в результате будет получена
формула, эквивалентная исходной.
20. [119, с. 59,60]
Докажите общезначимость следующих модальных формул (формулы
5 и 6 читаются: «каждое утверждение или необходимо, или невозможно,
или случайно»):
1) V(A&B)^VA&VB;
2) V(AvB)->VA&VB;
3) V(A->B)->VA&VB;
4)
5) nAvVAvn-A;
6) oAv—iOAvVA.
Решение.
1)
V( A & B) —VA & VB = —o( A & B) & —□—1( A & B) ——о A & —о—A & —oB & —□—iB
w0
f (—d(A & B) & —о—(A & B) ——oA & —о—A & —cB & —□—iB)
t(-in(A & B) & -£i-i(A & В))
t(—,□( A & B) )
f(n(A&B))---------------> w1
t(—□—(A & B) )
f (□—{А & B))-----------> w2
f (—oA & —о—A & —cB & —□—iB)
f (—.nA & —A)
f(—idA) f( o—A)
t(aA) »> t(n—A) »>
21. Докажите, что:
1) | A vB|w= И«-|^A&-.B|W=H;
2) |-oA|w=H<^|0-A|w=H;
3) |-iOA|w=H<=>|izi—A|W=H.
f(A&B)
fA fB
tA ~> tB
f(4A&B))
t(A&B)
tA
tB
t(-A)
fA
f(—idB&—В)
f(—nB) f(—п—B)
f(nB) t(n-iB)
22. Рассмотрим шкалу Крипке и интерпретирующую функцию:
def def
W = {1, 2, 3, 4, 5}, 91 = {(1,1), (1, 2), (2, 3), (1, 5), (5, 4), (4, 4), (4, 3)},
1(р, wj - I(p, w2) = I(p, w5) = И, l(q, м/г) - I(q, vv3) - l(q, w4) - И.
Проверьте истинность следующих утверждений:
650
1) bP Li= Ьр кз= И, |np |w4= Л;
2) |izMp|w3=H,|iziq|w3=H;
3) |Oq&O-iq|wl=H,|nq|wl= Л;
4) |0q|w2=|nq|w2=H;
5) | Op —> Oq |w= И во всех мирах W.
Решение. Построим ориентированный граф по заданной шкале Крипке
и построим аналитические таблицы, соответствующие условиям (выводы
сделайте самостоятельно!):
tp, tq tp tq
w1 w2 W3
tp W4
1) w11 t(np) -> w2 I tp
IViltp
2) w3
o - Hi iroit i-i i
J O1 LHl.l V4
w3
t(np)
tp
w4|f(np)->w3|fp
w4|fp
t(Oq & 0-iq)
t(Oq)
t(O-.q)
tq
fq
t(np)
tp
w1|f(nq)^w2|fq
ivi|fq
3) Wi
Упражнение 30
КОНСТРУИРОВАНИЕ СВОЙСТВ ШКАЛ КРИПКЕ
А ведь часто правильно поставленный
вопрос означает больше чем наполовину
решение проблемы.
В. Гейзенберг. Физика и философия
Обязательные результаты обучения:
• знать основные понятия
—теорема Салквиста, алгоритм Салквиста;
• уметь
—описывать множество миров, обладающих отношениями достижимо-
сти с указанными свойствами;
—определять свойства шкал Крипке, относительно которых заданные
формулы являются общезначимыми;
• владеть
—основными понятиями, представленными выше;
—методами решения задач, представленных в Упражнении.
Теоретические сведения
Конструирование свойств шкал Крипке
1. Теорема Салквиста
Когда вы убедитесь, что теорема
верна, вы начинаете ее доказывать.
Традиционный профессор математики
(персонаж анекдотов о математиках)
Исследуем свойства шкал, задаваемые модальными формулами.
Ранее мы доказали, что формула (оА —» А) является общезначи-
мой относительно шкалы (W, 91) тогда и только тогда, когда 91 явля-
ется рефлексивным бинарным отношением, а формула (оА ппА)
является общезначимой относительно (W, 91), тогда и только тогда,
когда 91 является транзитивным бинарным отношением.
Возникает вопрос о способе нахождения свойств шкал Крипке,
относительно которых заданная формула является общезначимой.
Один из способов решения этой проблемы принадлежит X. Салк-
висту (Н. Sahlqyist).
652
https:/Л: rait.ru
Добавим к алфавиту языка пропозициональной логики пропози-
циональную переменную И, а также воспользуемся общезначимо-
стью (А В) —1 (А & —1В) и определениями:
def def
□А = —10—iA, ОА = —о—iA.
Пусть p — пропозициональная переменная модальной логики.
Определение.
1. Строго позитивными формулами называются формулы:
р, пр, ппр,...
2. Позитивной формулой называется формула, в которую не вхо-
дит связка -1.
3 Негативной формулой называется отрицание позитивной фор-
мулы.
4. Несвязной формулой называется формула, полученная из стро-
го позитивных и негативных формул с помощью связок & и 0.
5. Формулой Салквиста называется отрицание несвязной форму-
лы.
Примеры (модальных формул и эквивалентных им формул Салкви-
ста). Формулы Салквиста подчёркнуты.
1. (пр -> р) <-> -.(ар & -р).
2. (пр ->ппр) <-> -(пр & -.ппр) <-> —(ар & —с-10—р) <-> —{пр & 00-р).
3. (Ор —>п0р) <-> -(0р & -сОр) <-> -<0р & -i-iO-iOp) <-> -(Op & 0-i0p).
4. (Опр —>п0р) <-> —(Опр & -пОр).
Примеры.
Приведем формулы, не являющиеся «салквистовыми», т. е. не эквива-
лентные никакой формуле Салквиста:
1. п(пр->р).
2. п(пр —> р) —>пр.
3. п0р->0пр (формулаМак-Кинси).
4. (а0р^>0пр)&(00р^>0р).
X. Салквист [135] установил, что каждой формуле Салквиста со-
ответствует некоторое свойство шкалы Крипке.
Теорема (Салквиста, о соответствии).
1. Каждой формуле Салквиста А соответствует некоторое свой-
ство шкал Крипке, выраженное с помощью языка первого порядка.
Шкала Крипке обладает этим свойством тогда и только тогда,
когда формула А является общезначимой относительно этой шкалы.
653
2. Существует алгоритм получения этого свойства шкал Крипке
по заданной формуле Салквиста А.
2. Алгоритм Салквиста
О Господи, если Ты существуешь, спаси
мою душу, если она существует.
Э. Ренан. Молитва скептика
Вначале научимся переводить модальные формулы в формулы
языка первого порядка.
Пусть х—предметная переменная, Ж — отношение достижимости.
Определение.
Переводом формулы А называется формула А*(х) языка первого
порядка, имеющая не более одной свободной переменной и опре-
делённая по индукции следующим образом:
1) р = р*(х), гдер— пропозициональная переменная,
р* — унарное отношение;
def def def def
2) И* = И; (-А)* = -А*; (А&В)* = А*&В*; (AvB)* = A*vB*;
def def
3) (oA)*(x) = Vy(x9ly ^A*(y)); (0A)*(x) = 3y(x9ly &A*(y)).
Примеры.
Пусть x, ye W.
def def
1. (ap—>p)*(x)<-> (-.(np&-p))‘(x) = 4np*(x)&-p*(x)) =
= -(Vy(x9?y->p*(y))&-ip*(x)).
def def
2(n(pv0q))*(x) = Vy(x9?y->(pv0q)*(y)) =
def def
= Vy(x9?y->(p*(y)v(0q)*(y))) = Vy(x9iy ->(p*(y)v3z(y9iz&q‘(z)))).
Опишем алгоритм, сопоставляющий формуле -А формулу
-iBta(t) для шкалы (W, 91), относительно которой формула -А будет
общезначимой.
Например, в случае -А =пр->р на входе алгоритма будет фор-
мула -i(np & -р), а на выходе — формула языка первого порядка
Vw(w91w).
Пусть -А — формула Салквиста.
Алгоритм Салквиста.
Вход: Формула -А, где А — несвязная формула.
Выход: Свойство шкал Крипке, соответствующее формуле -А.
1. Выделите негативные и строго позитивные части формулы А.
2. Нарисуйте схему, показывающую, что означает выполнение
формулы А в начальном мире t; включите в нее имена построенных
654
https:/Л: rait.ru
при этом миров (t13t2, ...), проведите между ними дуги отношения
достижимости 91 и отметьте миры, в которых истинны строго по-
зитивные формулыр, пр, пор, ....
Отметим, что количество возможных миров совпадает с количе-
ством символов 0 в заданной модальной формуле.
3. Определите ленивую оценку, делающую строго позитивные
оценки истинными в их мирах.
Ленивая оценка определяет формулы р*(х) следующим образом:
рассматриваем подформулыр, пр, пар, ..., для которых существуют
миры среди t, t13t2, ... и определим пути к соответствующим мирам
формулой
P*(x) = (t = x)vt91xv3x1(t9ix1 &x19lx)v...v3x13x2...3xrn(t9ix1 &Xj
ях2&...&хтад.
4. Для перевода формулы А в A* (t):
а) расположите перед формулой А* (0 кванторы 3s, где s «пробе-
гает» по именам миров, соответствующих «ромбикам» 0;
б) найдите строго позитивные подформулы и замените их на И;
в) замените все оставшиеся предикаты р*(х), q*(y), ..., соответ-
ствующие пропозициональным переменным;
г) произведите упрощения, если это возможно.
В результате работы алгоритма получаем формулу a(t), истин-
ность которой означает, что формула А верна на шкале (W, 91) в не-
котором мире t относительно некоторой оценки.
Значит, формула -А будет общезначимой тогда и только тог-
да, когда (W, 91) удовлетворяет формуле -i3ta(t) (как модель языка
первого порядка, состоящего из единственного предикатного сим-
вола 91).
Работа с примерами решения упражнений
См. Пример 1, Пример 2, Пример 3, Пример 4, Пример 5.
Примеры решения некоторых типов упражнений
Мудрые не говорят пустых слов,
боясь того, чтобы дела их не были
несоответственны их словам.
Китайская мудрость
def
Пример 1. По формуле —А = пр ->р найдите свойство шкал Крипке
(IV, 91), относительно которых формула является общезначимой.
Решение. Найдём формулу -ioc(t) языка первого порядка для заданной
формулы. Выполним первый шаг перевода:
655
httpaJ/yrai
—A = (np->p)<->-inpvp<->-i(np&-ip)=>A=np&-ip=>A*(t) - p*(t)&-p*(t).
Заменяем строго позитивную формулу p*(t) на И, ибо ленивая оценка
делает ее истинной. Поскольку р* (О имеет ленивое определение р*(х) =
def
= ТО
А* (О = И &-ip*(t)== -А* (О = t$Rt.
Если A — общезначимая формула, то
(W, 91) 1= -ata(t) => (W, 91) 1= Vt(dRt),
и отношение достижимости 91 должно быть рефлексивным..
Аналитическая таблица, устанавливающая общезначимость формулы
□р —>р, такова (91 —рефлексивное отношение):
t f (пр —> р)
t(np) ж
tp <
Ф
Пример 2. По формуле -А = (пр ->ппр) найдите свойство шкал Крипке
(IV, 91), относительно которых формула является общезначимой.
Решение. Вначале выполним очевидные преобразования:
def def
-А - (пр ->ппр) => А = (пр & -ппр) => A* (t) - пр* (t) & -ппр* (t).
Оценка р* (О = И даёт ленивое определение р*(х) = t9Ix.
Ленивая оценка превращает формулу-innp*(t) в следующую:
-nnp*(t) = -iVx(t9lx —>пр*(х)) = -iVx(t9?x-> Vy(x9ly->p*(y))) =
=-iVxVyftfRx -> (x9ty -> p*(y))) = -iVxVy(t9?x & x9ty -> p*(y)).
Следовательно, a(t) - - VxVy(t9?x & x9ty —> t9ly).
Утверждение (IV, 91) 1= -i3ta(t) превращается в утверждение
(IV, 1= -i3ta(t) = -i3t-iVxVy(t9lx & x9ty -> t^Ry) =
- VtVxVy(t9?x & x9iy —> t9iy),
и отношение достижимости 91 должно быть транзитивным.
Аналитическая таблица, устанавливающая общезначимость исходной
модальной формулы (91 — транзитивное отношение), такова:
656
С*" //< ! ио it i-i I
f(np —>пор)
t(np) ~>
f(nop)-----> f(op)---------> fp
fl t2 tp <»
Пример 3. По формуле —p —> oO-p найдите свойство шкал Крипке (IV,
91), относительно которых формула является общезначимой.
Решение. Преобразуем формулу в формулу Салквиста так:
—р ->пО-р = (—1—ip vnO—р) = —(—р & -.ПО—р) = —i(—р & —(—<>—QO—p) =
= -i(—р & O-iO-p) = —i(—ip & Опр).
Положим А - —р&<)пр и выполним стандартный перевод:
&np*(ti)>3t1bp*(t)&t9it1 &np*(ti)).
Так как □p*(t]) = H, то получаем ленивое определение p*(x)=t19lx,
с помощью которого
A*(t)=
Формула -А будет являться общезначимой формулой относительно
шкалы Крипке (IV, 91) тогда и только тогда, когда
(IV, 91) 1= —i3ta(t)=-313 ti (-<ti9it) & tVtt]) =
Итак, отношение достижимости 91 должно быть симметричным.
Аналитическая таблица, устанавливающая общезначимость исходной
модальной формулы (91 — симметричное отношение), такова:
fC-р—>о0—р)
t(-p)
f«Hp) ->
f(nO-p)---->
ti
f(-₽) <«
tp
Пример 4. Найдите свойство шкал Крипке (IV, 91), относительно кото-
рых является общезначимой формула
def
А = 0(0q & 0(-i(cp v q) & Опор) ) & ООпр.
о- //i iroif i-i ।
657
Решение. Тогда
A* to = mti & t?Jit2 & ti9Tt3 & t39Tt4 & t$Rt5 & t59Tt6 &
&q*(t2) & -4op‘(t3) v q*(t3)) &nop‘(t4)& P‘&) •
Ленивое определение получаем из условия: p*(t4)&p*(t6) = И.
Мы установили, что
Р* W = 3y(t49ty &y9ix) v W(t6, х), q*M = О = t2).
Поставив найденные результаты в формулу для A*(t), получим:
A* to = tSitj & tn lKt2 & tj9it3 & t39it4 & tSR t5 & t5*Rt6 & ~.(ap* (t3) v q* (t3));
ato = 3t]3t23t33t43t53t6(t9k] & t/Jit2 & & t39?t4 & t9Tt5 & t5*Rt6 &
&4Vx(t39?x -> p* (x)) v (t3 = t2))) =
= 3 t^EI t23133143 Р5Е1(tSRti & ti9it2 & ti$Kt3 & t39?t4 & t9Tt5 & tflltf, &
&4Vx(t39?x -> 3y(t49iy & yWx) v 9l(t6, x)) v (t3 = t2))).
Аналитическая таблица (незамкнутая!), построенная для анализа вза-
имосвязи миров для 0(0q & 0(—.(пр v q) & Оппр)) & ООпр, такова:
t t(O(Oq&0(—(пр v q)&Оппр)) & ООпр)
t(O(Oq & 0(—.(пр v q) & Опор)))
t(00np)) \
t(Oq & 0(-1(пр v q) & On пр))
t(Onp) ->
t(ap)
t(—(пр v q) & Опар)
t(-.(npvq))
f(npvq)
f(np)
fq
t(Ocnp)
t4|t(nnp)
Пример 5. Найдите свойство шкал Крипке (W, относительно кото-
рых является общезначимой формула
-{ООпр & Опр & -i(np v q)).
Решение. Положим:
658
с*" //| iroH 1'1 >
def
A - 00пр&0пр&—.(пр vq);
a(t) = Bt^t^CMt, ti) & Mtb t2) &ap*(t2) & Mt, t3) &nq*(t3) &ЧорЧО v q*(t))).
Из условий истинности:
□p‘(t2) = Vx(Mt2, x) -> p‘(x)), Пд‘а3) = Vx(Mt3, x) -> q‘(x)),
найдём ленивые определения:
p*(x) = Mt2,x), q*(x) = Mt3,x).
Подставляя в a(t) и учитывая, что p*(t2) = И и q*(t3) = И, получим:
a(t) = q) & 9i(ti, t2) & Mt, t3) & -4Vx(Mt, x) -> Mt2, x)) v Mt3, x))).
Утверждение (W, 9t) 1= —приводит к формуле первого порядка:
VtV^ Vt2Vt3(^9i(t, tj v -iMti, t2) v -,Mt, t3) v Vx(Mt, x) -> Mt2, x)) v Mt3, t)).
Задачи для самостоятельного решения
Не существует ничего более
поэтического и страшного, чем
битва небоскребов с небесами.
Г. Лорка
1*. Опишите словами множество миров, обладающих отношениями до-
стижимости со следующими свойствами:
1) Vw(w%v);
2) \/w\/v(w9iv —> v9iw);
3) VwVvVu(w91v & —> w9iu);
4) VwVvVu(wW & wJiu —> v9ta);
5) Vvv3v(w5Rv);
6) VwVv\/u(w9tv & wJiu —>v = u)-,
7) VwBjvCwSRv);
8) VwVv3k(ivSRv wSiu & u9tv);
9) VwVvVu(wW & w9iu —> (VRu v v = и v u9lv));
10) Vu'VvVuVt(u'91v & wSRu (v91t & u91t))-
2. Найдите свойства шкал Крипке, относительно которых следующие
формулы являются общезначимыми (р—пропозициональная переменная):
1) пр^Ор;
2) Ор—>ибр;
3) Ор->пр;
4) ппр^пр;
5) Опр—>п0р.
659
https: "ига it.ru
Ответы:
1) Vw3v(w9lv);
2) VwVvVk(wSRv & w%-i —> vShu);
3) VwVv\/u(mARv &v/Ru —>v = u);
4) VwVvSk(wW —> w9lu & u9iv);
5) VwVvVuVt(w9lv & wSRu —> (v9U & uSRt)).
3. Найдите свойства шкал Крипке, относительно которых следующие фор-
мулы являются общезначимыми (р, q — пропозициональные переменные):
1) р->ар;
2) п(р v q) —> (пр vnq);
3) пр—юпр.
Ответы:
1) VxVy(x9?y —> х = у);
2) VxVy(x9?y-> Vz(x9lz->z = y));
3) VxVy(x9?y -> Vz(y9?z -> x9te)).
4. Найдите свойства шкал Крипке, относительно которых следующие
формулы являются общезначимыми:
1) (А —> В) —> (ОА —>пВ);
2) —d((A&0—iA)v(—А&ОА));
3) -i(00nA&0nB&(-i(nAvB))).
Указание. Рассмотрите следующие аналитические таблицы:
w0
f((A—>B) —>(0A—>nB))
f (OA —>пВ)
1)
W0
t(OA)
f(nB)---->
t(A^B) w2
£4|tB
>
tA
2)
f C^n((A & 0—iA) v (—iA & OA)))
t(a((A & O^A) v (^A & OA)))
t((A & O^A) v (—iA & OA))
t(A & 0—A)
tA
t(O^A)
t(—iA&OA)
t(-iA)
fA
t(OA)
t(-A)
и»! fA
w2 I tA
660
https ://игз it.ru
3)
w0
f (ЧООпА & OoB & (ЧпА vB))))
t(OOn A & OnB & (—.(□ A v B)))
t(OOn A)------>
t(-i(nAvB)) w-.
t(OnA)---->
w2
t(nA)
f(oAvB)
f(nA)—
> fA
fB
t(OnB) —>
w3
t(oB)
w4
Ответы: 2) рефлексивность; 3) симметричность.
5. [123, с. 361]
Докажите, что формула □(□А -> 0(В —> С)) —> 0(пВ —> (пА -> ОС)) является
общезначимой только на шкале Крипке, в которых для каждого мира име-
ется хотя бы один мир, достижимый из него.
Решение. По условию для мира w0 найдётся мир для которого построим
следующую систему аналитических таблиц:
w0
f(n(nA -> 0(В -> С)) -> 0(пВ -> (пА -> ОС)))
Ц0(пВ—>(аА—>0С)))
t(n(aA—>0(В—>С)))
w2
f((nB -> (nA —> ОС))
t(nB)
f (nA -> ОС)
t(nA) ~>
f(OC) *>
t(nA—>0(B—>C))
f(nA) | t(0(B^C))
£A
tA <~
w3
t(B->C)
fB tc
tB <~ fc <~
6*. Докажите, что формула □(□A -> А) —>nA (аксиома Леба) является
общезначимой на тех и только тех шкалах Крипке, которые транзитивны
и обратно фундированы.
Указание. Бинарное отношение 91 на множестве W называется обратно
фундированным (нётеровым), если не существует бесконечной цепи
XpRXjjSbCg...
Другими словами, бинарное отношение 91 на множестве W называ-
ется обратно фундированным, если во всяком непустом подмножестве
X с W существует максимальный элемент, т. е. такой элемент х g X, что
не существует такиху е X, что х91у.
66i
https:
f/ufaittu
Подумайте, будет ли полезным рассмотрение следующей незамкнутой
аналитической таблицы, построенной для аксиомы Лёба?
w0
f(n(aA -> А) —>оА)
t(n(EiA —> A)) ~>
f(nA)
£А
t(nA—>А) <»
tA | f(nA)
w2
£4
t(nA^A) <»
tA | f(oA)
t(n(n A —> A) ) t(nA A)
Wo M/j
О--->O
W3O<—OlV2
t(nA -> A) t(oA -> A)
w3
Справа изображено семейство миров vv0, w13 w2, w3, ... и «движение
по мирам» отмеченной формулы t(n(nA —> А)).
Замечание [151, с. 242—243].
Известно, что аксиома Лёба определяет модальную систему W, с помо-
щью которой конструируется модальная система K4W, называемая логи-
кой Гёделя-Лёба GL и представляющая собой логику доказуемости, в кото-
рой модальный оператор □ понимается как формальная доказуемость
в некоторой аксиоматической теории подобной арифметике Пеано.
Логика GL полна относительно арифметической интерпретации:
модальная формула А доказуема в GL, тогда и только тогда, когда А есть
общезначимость в арифметике Пеано.
7*. Язык логики доказуемости, наряду с обычными связками логики вы-
сказываний, содержит одноместные связки, обозначаемые □ и 0: пА выражает
доказуемость высказывания А, ОА — его непротиворечивость.
1) Являются ли общезначимыми следующие формулы:
□А&пВ—>п(А&В), п(АvВ) —>пАveiB, оА—>паА, ОА—>пОА, пА—>А?
2) Какие принципы логики доказуемости следует считать общезначимы-
ми формулами, т. е. верными (истинными или доказуемыми?') независимо
от смысла элементарных высказываний, из которых они построены?
3) Описать множество всех общезначимостей логики доказуемости.
4) Существует ли алгоритм, распознающий общезначимость?
Литература
I. Исчисления математической логики
1. Антонова, О. А. Табличные методы в логике / О. А. Антоно-
ва. — Санкт-Петербург : Издательство СПб. ун-та, 2003.
2. Бирюков, Б. В. Теория смысла Готлоба Фреге / Б. В. Бирю-
ков // Применение логики в науке и технике. — Москва, 1960.
3. Бочаров, В. А. Введение в логику : учебник / В. А. Бочаров,
В. И. Маркин. — Москва : Форум; ИНФРА-М, 2008.
4. Бочаров, В. А. Основы логики / В. А. Бочаров, В. И. Маркин. —
Москва : ИНФРА-М, 1997.
5. Вагин, В. Н. Достоверный и правдоподобный вывод в интел-
лектуальных системах / В. Н. Вагин [и др.]. — Москва : Физматлит,
2004.
6. Войшвилло, Е. К. Логика / Е. К. Войшвилло, М. Г. Дегтярев. —
Москва : ВЛАДОС, 1998.
7. Генцен, Г. Исследования логических выводов / Г. Генцен // Ма-
тематическая теория логического вывода. — Москва : Наука, 1967.
8. Гильберт, Д. Основания математики. Логические исчисления
и формализация арифметики / Д. Гильберт, П. Бернайс. — Москва :
Наука, 1979.
9. Гильберт, Д. Основания математики. Теория доказательств /
Д. Гильберт, П. Бернайс. — Москва : Наука, 1982.
10. Гладкий, А. В. Математическая логика / А. В. Гладкий. — Мо-
сква : Российск. гос. гуманит. университет, 1998.
11. Гудстейн, Р. Л. Математическая логика / Р. Л. Гудстейн. —
Москва : ИЛ, 1961.
12. Ершов, А. П. Избранные труды / А. П. Ершов. — Новоси-
бирск : ВО «Наука». Сибирская издательская фирма, 1994.
13. Ершов, Ю. Л. Математическая логика / Ю. Л. Ершов, Е. А. Па-
лютин. — Москва : Наука, 1979; 1987.
14. Ивин, А. А. Словарь по логике / А. А. Ивин, А. Л. Никифо-
ров. — Москва : ВЛАДОС, 1997.
15. Игошин, В. И. Задачник-практикум по математической логи-
ке / В. И. Игошин. — Москва : Просвещение, 1986.
16. Карри, X. Основания математической логики / X. Карри. —
Москва : Мир, 1969.
17. Кейслер, Г Теория моделей / Г. Кейслер, Ч. Ч. Чэн. — Мо-
сква : Мир, 1977.
663
https:it.ru
18. Клайн, М. Математика. Утрата определённости / М. Клайн. —
Москва : Мир, 1984.
19. Клини, С. К. Введение в метаматематику / С. К. Клини. —
Москва : ИЛ, 1957.
20. Клини, С. К. Введение в метаматематику / С. К. Клини. —
Москва : URSS, 2009.
21. Клини, С. К. Математическая логика / С. К. Клини. — Мо-
сква : Мир, 1973.
22. Колмогоров, А. Н. Введение в математическую логику /
А. Н. Колмогоров, А. Г. Драгалин. — Москва : Изд-во МГУ, 1982.
23. Колмогоров, А. Н. Математическая логика. Дополнительные
главы / А. Н. Колмогоров, А. Г. Драгалин. — Москва : Изд-во МГУ,
1984.
24. Косовский, Н. К. Элементы математической логики и ее при-
ложения к теории субрекурсивных алгоритмов / Н. К. Косовский. —
Ленинград : ЛГУ, 1981.
25. Косовский, Н. К. Логики конечнозначных предикатов на осно-
ве неравенств / Н. К. Косовский, А. В. Тишков. — Санкт-Петербург :
Изд-во СПбГУ, 2000.
26. Лавров, И. А. Логика и алгоритмы / И. А. Лавров. — Ново-
сибирск : Изд-во НГУ, 1970.
27. Лавров, И. А. Задачи по теории множеств, математической
логике и теории алгоритмов / И. А. Лавров, Л. Л. Максимова. — Мо-
сква : Физматлит, 1995.
28. Лакатос, И. Доказательства и опровержения / И. Лакатос. —
Москва : Наука, 1967.
29. Латотин, Л. А. Математическая логика / Л. А. Латотин
[и др.]. — Минск : Высшая школа, 1991.
30. Линдон, Р. Заметки по логике / Р. Линдон. — Москва : Мир,
1968.
31. Логика и компьютер. Моделирование рассуждений и про-
верка правильности программ / Н. А. Алешина [и др.]. — Москва :
Наука, 1990.
32. Макаридина, В.А. Элементы математической логики /
В. А. Макаридина. — Санкт-Петербург : ЛГОУ, 1996.
33. Манин, Ю. И. Доказуемое и недоказуемое / Ю. И. Манин. —
Москва : Сов. радио, 1979.
34. Марков, А. А. Теория алгорифмов / А. А. Марков, Н. М. На-
горный. — Москва : ФАЗИС, 1996.
35. Маслов, С. Ю. Теория дедуктивных систем и ее применения /
С. Ю. Маслов. — Москва : Радио и связь, 1986.
36. Математическая логика в программировании: сборник ста-
тей 1980—1988 гг. — Москва : Мир, 1991.
37. Математическая теория логического вывода. — Москва : На-
ука, 1967.
664
https:/Л: rait.ru
38. Мендельсон, Э. Введение в математическую логику / Э. Мен-
дельсон. — Москва : Наука, 1976; 1984.
39. Непейвода, Н. Н. Прикладная логика / Н. Н. Непейвода. —
Ижевск : Изд-во Удмуртского ун-та, 1997; Новосибирск : Изд-во Но-
восибирского ун-та, 2000.
40. Новиков, П. С. Элементы математической логики / П. С. Но-
виков. — Москва : Наука, 1973.
41. Правиц, Д. Натуральный вывод / Д. Правиц. — Москва :
ЛОРИ, 1997.
42. Расёва, Е. Математика метаматематики / Е. Расёва, Р. Сикор-
ский. — Москва : Наука, 1972.
43. Смирнов, В. А. Логические методы анализа научного зна-
ния / В. А. Смирнов. — Москва : Эдиториал УРСС, 2002.
44. Смирнов, В. А. Теория логического вывода / В. А. Смир-
нов. — Москва : «Российская политическая энциклопедия» (РОС-
СПЭН), 1999.
45. Смирнов, В. А. Формальный вывод и логические исчисле-
ния / В. А. Смирнов. — Москва : Наука, 1972.
46. Справочная книга по математической логике. Ч. 1. Теория
моделей / под редакцией Дж. Барвайса. — Москва : Наука, 1982.
47. Такеути, Г. Теория доказательств / Г. Такеути. — Москва :
Мир, 1978.
48. Успенский, В. А. Простейшие примеры математических дока-
зательств / В. А. Успенский. — Москва : МЦНМО, 2009.
49. Успенский, В. А. Теорема Гёделя о неполноте / В. А. Успен-
ский. — Москва : Наука, 1982.
50. Френкель, А. Основания теории множеств / А. Френкель,
И. Бар-Хиллел. — Москва : Мир, 1966.
51. Целищев, В. В. Эпистемология математического доказатель-
ства / В. В. Целищев. — Новосибирск : Параллель, 2006.
52. Чень, Ч. Математическая логика и автоматическое доказа-
тельство теорем / Ч. Чень, Р. Ли. — Москва : Наука, 1983.
53. Чёрч, А. Введение в математическую логику. Т. 1 / А. Чёрч. —
Москва : ИЛ, 1960.
54. Шёнфилд, Дж. Математическая логика / Дж. Шёнфилд. —
Москва : Наука, 1975.
II. Интуиционистские логические исчисления
55. Воробьёв, Н. Н. Новый алгоритм выводимости в конструк-
тивном исчислении высказываний / Н. Н. Воробьёв // Труды
МИ АН СССР им. В. А. Стеклова. — 1958. — Т. 52. — С. 193—225.
56. Vorob’ev, N. N. (1970). A new algorithm for derivability In the
constructive propositional calculus. Amer. Math. Soc. Transl. Vol. 94 (2).
P. 37—71.
57. Гейтинг, А. Интуиционизм / А. Гейтинг. — Москва : Мир,
1965.
665
https: //ц гз jt.ru
58. Гильберт, Д. Избранные труды. Т. 1. Теория инвариантов. Те-
ория чисел. Алгебра. Геометрия. Основания математики / Д. Гиль-
берт. — Москва : Факториал, 1998.
59. Драгалин, А. Г. Конструктивная теория доказательств и не-
стандартный анализ / А. Г. Драгалин. — Москва : Едиториал УРСС,
2003.
60. Клини, С. К. Перестановочность применений правил в ген-
ценовских исчислениях LK и LJ / С. К. Клини // Математические
теории логического вывода. — Москва : Наука, 1967.
61. Колмогоров^. Н. О принципе tertium non datur / А. Н. Колмо-
горов // Математический сборник. —1925. — № 32. — С. 646—667.
62. Колмогоров, А. Н. Избранные труды. Математика и механи-
ка / А. Н. Колмогоров. — Москва : Наука, 1985.
63. Логика и компьютер. Вып. 5. Пусть докажет компьютер /
А. Е. Болотов [и др.], РАН. — Москва : Наука, 2004.
64. Новиков, П. С. Конструктивная математическая логика с точ-
ки зрения классической / П. С. Новиков. — Москва : Наука, 1977.
65. Плиско, В. Е., Хаханян В. X. Интуиционистская логика /
В. Е. Плиско, В. X. Хаханян. — Москва : Изд-во МГУ, 2009.
66. Abramsky, S. (1990, October). Computational Interpretations
of Linear Logic. Technical Report DOC 90/20. Imperial College,
Department of Computing.
67. Dancy, J. (1996). Introduction to Contemporary Epistemology.
Blackwell.
68. Dyckhoff, R. (1992). Contraction-free Sequent Calculi for
Intuitionistic Logic. The Journal of Symbolic Logic. Vol. 57 (3). P. 795—
807.
69. Glivenko, V. I. (1929). Sur quelques points de la logique de M.
Brouwer. Bulletin Classe des Sciences Academic Royal Belgique. Serie 5,
15. P. 183—188.
70. Heiting, A. (1930): Die formalen Regeln der intuitionistischen
Logik. Sitzungsberichte der Preussischen Akademie der Wissenschaften.
Physikalisch-mathematische Klasse. P. 42—52.
71. Hudelmaier, J. (1993). An O(n-log n)-space decision procedure
for intuitionistic propositional logic and Kuroda logic. Rapporto intemo
99—93. Dipartimento di Scienze dell’Informazione. — Universitd degli
Studi di Milano.
72. Hudelmaier, J. (1988). A PROLOG Program for Intuitionistic
Logic. SNS-Bericht. Universitat Tubingen.
73. Johansson, I. (1937): Der Minimalkalkul, ein reduzierte
intuitionistischer Formalismus. Compositio Mathematica. № 4. P. 119—
136.
74. Korn, D. (1999): Konstruktiv adaquate Beweisautomatisierung
fur intuitionistische Logik. Sankt Augustin: Infix. Dissertationen zur
kunstlichen Intelligenz. Bd. 198.
666
https: //ц rait.ru
75. Miglioli, P., Moskato, U., Ornaghi, M. (1994). An Improved
Refutation System for Intuitionistic Predicate Logic. Journal of Automated
Reasoning. Vol. 13. P. 361—373.
76. Weich, K. (1998). Decision Procedures for Intuinistic Propositional
Logic by Program Extraction. Proceedings of the TABLEAUX 98 Conference.
LNCS 1397. Springer-Verlag. P. 292—308.
III. Аксиоматическая семантика языков императивного про-
граммирования
77. Абрамов, С. А. Элементы анализа программ. Частичные
функции на множестве состояний / С. А. Абрамов. — Москва : На-
ука, 1986.
78. Абрамов, С. А. Элементы программирования / С. А. Абра-
мов. — Москва : Наука, 1982. — 96 с.
79. Авербух, А. В. Изучение основ информатики и вычислитель-
ной техники : пособие для учителя / А. В. Авербух [и др.]. — Мо-
сква : Просвещение, 1992.
80. Агафонов, В. Н. Спецификация программ: понятийные сред-
ства и их организация / В. Н. Агафонов. — Новосибирск : Наука,
1987.
81. Алагич, С. Проектирование корректных структурированных
программ / С. Алагич, М. Арбиб. — Москва : Радио и связь, 1984.
82. Бауэр, Ф. Л. Информатика: задачи и решения / Ф. Л. Бауэр,
Р. Гнац, У. Хилл. — Москва : Мир, 1978.
83. Бауэр, Ф. Л. Информатика. Вводный курс. Ч. 1 / Ф. Л. Бауэр,
Г. Гооз. — Москва : Мир, 1990.
84. Бауэр, Ф. Л. Информатика. Вводный курс. Ч. 2 / Ф. Л. Бауэр,
Г. Гооз. — Москва : Мир, 1990.
85. Бейбер, Р. Л. Программное обеспечение без ошибок /
Р. Л. Бейбер. — Москва : Радио и связь, 1996.
86. Вирт, Н. Систематическое программирование. Введение /
Н. Вирт. — Москва : Мир, 1977.
87. Въюкова, Н. И. Систематический подход к программирова-
нию / Н. И. Вьюкова, В. А. Галатенко, А. Б. Ходулев. — Москва :
Наука, 1988.
88. Грис, Д. Наука программирования / Д. Грис. — Москва : Мир,
1984.
89. Дейкстра, Э. Дисциплина программирования / Э. Дейк-
стра. — Москва : Мир, 1978.
90. Джонстон, Г. Учитесь программировать / Г. Джонстон. —
Москва : Финансы и статистика, 1989.
91. Ершов, А. П. Введение в теоретическое программирование
(беседы о методе) / А. П. Ершов. — Москва : Наука, 1977.
92. Калинин, А. Г. Универсальные языки программирования. Се-
мантический подход / А. Г. Калинин, И. В. Мацкевич. — Москва :
Радио и связь, 1991.
667
https:/Л: rait.ru
93. Калужнин, Л. А. Преобразования и перестановки / Л. А. Ка-
лужнин, В. И. Сущанский. — Москва : Наука, 1985.
94. Камкин, А. С. Введение в формальные методы верификации
программ / А. С. Камкин. — Москва : МАКС Пресс, 2018.
95. Кауфман, В. Ш. Языки программирования. Концепции
и принципы / В. Ш. Кауфман. — Москва : Радио и связь, 1993.
96. Лавров, С. С. Лекции по теории программирования /
С. С. Лавров. — Санкт-Петербург : НЕСТОР, 1999.
97. Лавров, С. С. Программирование. Математические основы,
средства, теория / С. С. Лавров. — Санкт-Петербург: БХВ-Петербург,
2001.
98. Молчанов, А. Ю. Системное программное обеспечение /
А. Ю. Молчанов. — Санкт-Петербург : Питер, 2003.
99. Непомнящий, В. А. Прикладные методы верификации про-
грамм / В. А. Непомнящий, О. М. Рякин. — Москва : Радио и связь,
1988.
100. Пратт, Т. Языки программирования: разработка и реали-
зация / Т. Пратт, М. Зелковиц. — Санкт-Петербург : Питер, 2002.
101. Сенокосов, А. И. Информатика : учебник для 8—9 классов
школ с углубленным изучением информатики / А. И. Сенокосов,
А. Г. Гейн. — Москва : Просвещение, 1995.
102. Требования и спецификации в разработке программ. — Мо-
сква : Мир, 1984.
103. Турский, В. Методология программирования / В. Тур-
ский. — Москва : Мир, 1981.
104. Яхонтов, С. В. Современные методы и инструменты фор-
мальных спецификаций и дедуктивной верификации императив-
ных программ / С. В. Яхонтов. — Санкт-Петербург : Изд-во СПб.
ун-та, 2014.
105. Aho, А. V., Sethi, R., Ullman, J. D. (1988). Compilers: Principles,
Techniques, and Tools. Addison-Wesley.
106. Dijkstra, E. W. (1975, August). Guarded commands,
nondeterminacy and the formal derivation of programs. Comm. ACM.
Vol. 18. P. 453—457.
107. Floyd, R. (1967). Assigning meaning to programs.
In Mathematical Aspects of Computer Science, Providence. P. 19—32.
108. Graduate Record Examinations Computer Science Tests.
Descriptive Booklet, 1993—1995. (1993). Educational Testing Service.
109. Hoare, C. A. R. (1969, October). An Axiomatic Basis of Computer
Programming. Comm. ACM. Vol. 12. P. 576—580, 583.
110. Knuth, D. E. (1964). Backus Normal Form vs. Backus Naur.
Comm. ACM. № 7:12. P. 735—736.
111. McCarthy, J. A. (1961). Basic for a Mathematical Theory
of Computation. Proc. Western Joint Comp. Conf. — Los Angeles, may.
P. 225—238.
668
https: //ц rait.ru
112. Naur, P. (1966). Proofs of Algorithms by general snapshots. BIT.
№ 6. P. 310—316.
113. Naur, P. (1963). Revised report on the algorithmic language
Algol 60. Comm. ACM. № 6:1. P. 1—17.
114. Practing to take the Graduate Record Examinations Computer
Science Tests. (1992). — Warner Books.
IV. Элемент модальной логики
115. Герман, О. В. Введение в теорию экспертных систем и обра-
ботку знаний / О. В. Герман. — Минск : Дизайн ПРО, 1995.
116. Гетманова, А. Д. Логика / А. Д. Гетманова. — Москва : Но-
вая школа, 1995.
117. Ершов, Ю. Л. Определимость и вычислимость / Ю. Л. Ер-
шов. — Новосибирск : Научная книга, 1996.
118. (а) Ивин, А. А. Логика / А. А. Ивин. — М. : Просвещение,
1996; (б) Ивин, А. А. Практическая логика: Задачи и упражнения /
А. А. Ивин. — М. : Просвещение, 1996.
119. Костюк, В. Н. Элементы модальной логики / В. Н. Ко-
стюк. — Киев : Наук, думка, 1978.
120. Логика и компьютер. Моделирование рассуждений и про-
верка правильности программ / Н. А. Алешина [и др.]. — Москва :
Наука, 1990.
121. Переверзев, В. Н. Логистика: Справочная книга по логике /
В. Н. Переверзев. — Москва : Мысль, 1995.
122. Серебрянников, О. Ф. Эвристические принципы и логиче-
ские исчисления / О. Ф. Серебрянников. — Москва : Наука, 1970.
123. Символическая логика / под редакцией Я. А. Слинина,
Э. Ф. Караваева, А. И. Мигунова. — Санкт-Петербург : Изд-во СПб.
ун-та, 2005.
124. Слинин, Я. А. Современная модальная логика: Развитие тео-
рии алетических модальностей (1920—1960 гг. ) / Я. А. Слинин. —
Ленинград : ЛГУ, 1976.
125. Слинин, Я. А. Теория модальностей в современной логике /
Я. А. Слинин // Логическая семантика и модальная логика. — Мо-
сква : Наука, 1967. — С. 119—147.
126. Логический подход к искусственному интеллекту: От мо-
дальной логики к логике баз данных / А. Тейз [и др.]. — Москва :
Мир, 1998.
127. Упражнения по логике. Сборник / Э. Ф. Караваев [и др.];
под редакцией Л. Г. Тоноян. — Москва : Проспект, 2016.
128. Фейс, Р. Модальная логика / Р. Фейс. — Москва : Наука,
1974.
129. Формальная логика. — Ленинград : Изд-во ЛГУ, 1977.
130. Godel, К. (1986). An Interpretation of the Intuitionistic
proposicional calculus. Vol. I. / Feferman S. [et al.]; eds. collected
works. — N. Y. : Claredon.
669
https: //ц rait.ru
131. McKinsey, J. С. C., Tarski, A. (1948). Some theorems about the
sentential calculi of Lewis and Heyting. The Journal of Symbolic Logic.
№ 13. P. 1—15.
132. Medeiros, M. P. N. (2006). A New S4 Classical Modal Logic
in Natural Deduction. Journal of Symbolic Logic. Vol. 71. № 3.
133. Medeiros, M. P. N. (2009). A reviewed syntactic proof of Godel
interpretation of intuitionistic logic into S4. Logic Colloquium. Sofia,
Bulgaria, July 31 — August 5.
134. Moggi, E. (1991). Notions of computation and monads.
Information and Computation. № 93 (1). P. 55—92.
135. Sahlqyist, H., ed. S. Kanger (1975). Completeness and
correspondence in the first and second order semantics for modal logic.
Proceedings of the Third Scandinavian Logic symposium. Amsterdam :
North-Holland,. P. 110—143.
V. Дополнительная литература
136. Александрова, H. В. Математические термины. Справоч-
ник / Н. В. Александрова. — Москва : Высшая школа, 1978.
137. Архипов, Г. И. Лекции по математическому анализу /
Г. И Архипов, В. А. Садовничий, В. Н. Чубариков. — Москва : Выс-
шая школа, 1999.
138. Ахо, А. Теория синтаксического анализа, перевода и компи-
ляции. Т. 1. Синтаксический анализ / А. Ахо, Дж. Ульман. — Мо-
сква : Мир, 1978.
139. Башмакова, И. Г. История диофантова анализа от Диофан-
та до Ферма / И. Г. Башмакова, Е. И. Славутин. — Москва : Наука,
1984.
140. Блехман, И. И. Механика и прикладная математика: Логика
и особенности приложений математики / И. И. Блехман, А. Д. Мыш-
кис, Я. Г. Панковко. — Москва : Наука, 1990.
141. Большой энциклопедический словарь. — Москва : Большая
Российская энциклопедия; Санкт-Петербург : Норинт, 1998.
142. Босс, В. Лекции по математике. Т. 6: От Диофанта до Тью-
ринга / В. Босс. — Москва : КомКнига, 2006.
143. Брауэр, В. Введение в теорию конечных автоматов / В. Бра-
уэр. — Москва : Радио и связь, 1987.
144. Брой, М. Информатика. Основополагающее введение. Ч. 1 /
М. Брой. — Москва : Диалог-МИФИ, 1996.
145. Васильева, Н. В. Краткий словарь лингвистических терми-
нов / Н. В. Васильева, В. А. Виноградова, А. М. Шахранович. — Мо-
сква : Русский язык, 1995.
146. Витгенштейн, Л. Философские работы. Ч. I / Л. Витген-
штейн. — Москва : Гнозис, 1994.
147. Галочкин, А. И. Введение в теорию чисел / А. И. Галочкин,
Ю. В. Нестеренко, А. Б. Шидловский. — Москва : Изд-во МГУ, 1995.
670
https:/Л: rait.ru
148. Гладкий, А. В. Формальные грамматики и языки / А. В. Глад-
кий. — Москва : Наука, 1973.
149. Гудстейн, Р. Д. Рекурсивный математический анализ /
Р. Д. Гудстейн. — Москва : Наука, 1970.
150. Дойч, Д. Структура реальности / Д. Дойч. — Москва;
Ижевск : НИЦ «Регулярная и хаотическая динамика», 2001.
151. Карпенко, А. С. Развитие многозначной логики / А. С. Кар-
пенко. — Москва : Издательство ЛКИ, 2010.
152. Комлев, Н. Г Словарь иностранных слов / Н. Г. Комлев. —
Москва : Эксмо, 2006.
153. Кострикин, А. И. Введение в алгебру / А. И. Кострикин. —
Москва : Наука, 1977.
154. Лаллеман, Ж. Полугруппы и комбинаторные приложения /
Ж. Лаллеман. — Москва.: Мир, 1985.
155. Лекции лауреатов премии Тьюринга. — Москва : Мир, 1993.
156. Лоръер, Ж.-Л. Системы искусственного интеллекта / Ж.-Л.
Лорьер. — Москва : Мир, 1991.
157. Ляпин, Е. С. Полугруппы / Е. С. Ляпин. — Москва : ГИФ-
ФМЛ, 1960.
158. Манин, Ю. И. Математика как метафора / Ю. И. Манин. —
Москва : МЦНМО, 2008.
159. Математическая энциклопедия. Т. 4. — Москва : Советская
энциклопедия, 1984.
160. Математический энциклопедический словарь. — Москва :
Советская энциклопедия, 1995.
161. Минский, М. Вычисления и автоматы / М. Минский. — Мо-
сква : Мир, 1971.
162. Мордухай-Болтовский, Д. Д. Начала Евклида. Книги I—VI /
Д. Д. Мордухай-Болтовский. — Москва; Ленинград : Гостехиздат,
1948.
163. Першиков, В. И. Толковый словарь по информатике /
В. И. Першиков, В. И. Савинков. — Москва : Финансы и статистика,
1991; 1995.
164. Проблемы Гильберта. — Москва : Наука, 1969.
165. Романовский, И. В. Дискретный анализ / И. В. Романов-
ский. — Санкт-Петербург : Невский диалект, 1999; 2004.
166. Саломаа, А. Жемчужины теории формальных языков /
А, Саломаа. — Москва : Мир, 1986.
167. Смаллиан, Р. Как же называется эта книга? / Р. Смалли-
ан. — Москва : Мир, 1981.
168. Смалъян, Р. Теория формальных систем / Р. Смальян. — Мо-
сква : Наука, 1981.
169. Смит, Б. Методы и алгоритмы вычислений на строках /
Б. Смит. — Москва : ООО «И. Д. Вильямс», 2006.
671
https:it.ru
170. Современный словарь иностранных слов. — Москва : Рус-
ский язык, 1999. — 742 с.
171. Стройк, Д. Я. Краткий очерк истории математики /
Д. Я. Стройк. — Москва : Наука, 1978.
172. Тан, К. Ш. Символьный C++: Введение в компьютерную ал-
гебру с использованием объектно-ориентированного программиро-
вания / К. Ш. Тан, В.-Х. Стиб, И. Харди. — Москва : Мир, 2001.
173. Турчин, В. Ф. Феномен науки: Кибернетический подход
к эволюции / В. Ф. Турчин. — Москва : ЭТС, 2000.
174. Успенский, В. А. Машина Поста / В. А. Успенский. — Мо-
сква : Наука, 1979.
175. Философский энциклопедический словарь. — Москва : Со-
ветская энциклопедия, 1983; 1989.
176. Шиханович, Ю. А. Введение в современную математику /
Ю. А. Шиханович. — Москва : Наука, 1965.
177. Энциклопедия для детей. Т. 22. Информатика. — Москва :
Аванта, 2003.
https: //цга it.ru
Новые издания по дисциплине
«Программирование» и смежным дисциплинам
1. Бессмертный, И. А. Системы искусственного интеллекта :
учебное пособие для академического бакалавриата / И. А. Бес-
смертный. — 2-е изд., испр. и доп. — Москва : Издательство Юрайт,
2019.
2. Васюков, В. Л. Категорная логика : учебное пособие для ака-
демического бакалавриата / В. Л. Васюков. — 2-е изд., перераб.
и доп. — Москва : Издательство Юрайт, 2019.
3. Васюков, В. Л. Формальная феноменология : учебное пособие
для вузов / В. Л. Васюков. — 2-е изд., перераб. и доп. — Москва :
Издательство Юрайт, 2019.
4. Вечтомов, Е. М. Математика: логика, множества, комби-
наторика : учебное пособие для бакалавриата и специалитета /
Е. М. Вечтомов, Д. В. Широков. — 2-е изд. — Москва : Издательство
Юрайт, 2019.
5. Демин, А. Ю. Информатика. Лабораторный практикум : учеб-
ное пособие для прикладного бакалавриата / А. Ю. Демин, В. А. До-
рофеев. — Москва : Издательство Юрайт, 2019.
6. Дубров, Д. В. Система построения проектов СМаке : учебник
для магистратуры / Д. В. Дубров. — Москва : Издательство Юрайт,
2019.
7. Жмудь, В. А. Моделирование замкнутых систем автоматиче-
ского управления : учебное пособие для академического бакалаври-
ата / В. А. Жмудь. — 2-е изд., испр. и доп. — Москва : Издательство
Юрайт, 2019.
8. Зимин, В. П. Информатика. Лабораторный практикум. В 2 ча-
стях. Ч. 1 : учебное пособие для вузов / В. П. Зимин. — Москва :
Издательство Юрайт, 2019.
9. Зимин, В. П. Информатика. Лабораторный практикум. В 2 ча-
стях. Ч. 2 : учебное пособие для вузов / В. П. Зимин. — Москва :
Издательство Юрайт, 2019.
10. Зыков, С. В. Программирование : учебник и практикум для
академического бакалавриата / С. В. Зыков. — Москва : Издатель-
ство Юрайт, 2019.
11. Зыков, С. В. Программирование. Объектно-ориентирован-
ный подход : учебник и практикум для академического бакалаври-
ата / С. В. Зыков. — Москва : Издательство Юрайт, 2019.
673
https:it.ru
12. Зыков, С. В. Программирование. Функциональный подход :
учебник и практикум для академического бакалавриата / С. В. Зы-
ков. — Москва : Издательство Юрайт, 2019.
13. Казанский, А. А. Объектно-ориентированный анализ и про-
граммирование на Visual Basic 2013 : учебник для прикладного
бакалавриата / А. А. Казанский. — Москва : Издательство Юрайт,
2019.
14. Казанский, А. А. Прикладное программирование на Excel
2013 : учебное пособие для прикладного бакалавриата / А. А. Ка-
занский. — Москва : Издательство Юрайт, 2019.
15. Казанский, А. А. Программирование на Visual C# 2013 : учеб-
ное пособие для прикладного бакалавриата / А. А. Казанский. —
Москва : Издательство Юрайт, 2019.
16. Крупский, В. Н. Теория алгоритмов. Введение в сложность
вычислений : учебное пособие для бакалавриата и магистратуры /
В. Н. Крупский. — 2-е изд., испр. и доп. — Москва : Издательство
Юрайт, 2019.
17. Кувшинов, Д. Р. Основы программирования : учебное посо-
бие для вузов / Д. Р. Кувшинов. — Москва : Издательство Юрайт,
2019.
18. Лебедев, В. М. Программирование на VBA в MS Excel: учеб-
ное пособие для академического бакалавриата / В. М. Лебедев. —
Москва : Издательство Юрайт, 2019.
19. Малявко, А. А. Формальные языки и компиляторы : учебное
пособие для вузов / А. А. Малявко. — Москва: Издательство Юрайт,
2019.
20. Мамонова, Т. Е. Информационные технологии. Лаборатор-
ный практикум : учебное пособие для прикладного бакалавриата /
Т. Е. Мамонова. — Москва : Издательство Юрайт, 2019.
21. Маркин, А. В. Программирование на SQL. В 2 частях. Ч. 2 :
учебник и практикум для бакалавриата и магистратуры / А. В. Мар-
кин. — Москва : Издательство Юрайт, 2019.
22. Методы оптимизации: теория и алгоритмы : учебное посо-
бие для академического бакалавриата / А. А. Черняк, Ж. А. Черняк,
Ю. М. Метельский, С. А. Богданович. — 2-е изд., испр. и доп. — Мо-
сква : Издательство Юрайт, 2019.
23. Нагаева, И. А. Программирование: Delphi: учебное пособие
для академического бакалавриата / И. А. Нагаева, И. А. Кузнецов;
под редакцией И. А. Нагаевой. — Москва : Издательство Юрайт,
2019.
24. Огнева, М. В. Программирование на языке C++: практиче-
ский курс : учебное пособие для бакалавриата и специалитета /
М. В. Огнева, Е. В. Кудрина. — Москва : Издательство Юрайт, 2019.
25. Скорубский, В. И. Математическая логика : учебник и практи-
кум для бакалавриата и специалитета / В. И. Скорубский, В. И. По-
ляков, А. Г. Зыков. — Москва : Издательство Юрайт, 2019.
674
https:/Л: rait.ru
26. Судоплатов, С. В. Математическая логика и теория алго-
ритмов : учебник и практикум для академического бакалавриата /
С. В. Судоплатов, Е. В. Овчинникова. — 5-е изд., стер. — Москва :
Издательство Юрайт, 2019.
27. Тузовский, А. Ф. Объектно-ориентированное программирова-
ние : учебное пособие для прикладного бакалавриата / А. Ф. Тузов-
ский. — Москва : Издательство Юрайт, 2019.
28. Федоров, Д. Ю. Программирование на языке высокого уровня
Python: учебное пособие для прикладного бакалавриата / Д. Ю. Фе-
доров. — 2-е изд., перераб. и доп. — Москва : Издательство Юрайт,
2019.
29. Федоров, Д. Ю. Программирование на языке высокого уровня
Python : учебное пособие для прикладного бакалавриата / Д. Ю. Фе-
доров. — Москва : Издательство Юрайт, 2019.
https: //цга it.ru